БИОИНФОРМАТИКА
И МОЛЕКУЛЯРНАЯ БИОЛОГИЯ
I ! -■'.„. f
I ! М. Бородовский, С. Екишев. ^ ^*,
! . '-, ^У
J | ЗАДАЧИ И РЕШЕНИЯ^1Г"
\ ПО АНАЛИЗУ .-?>>^%
1 ! БИОЛОГИЧЕСКй'хСК
ПОСЛЕДЬг * •Б^НО'сТ.ЕЙ
i > A'VV у **

R&C
T><fHA*dC4

PROBLEMS AND SOLUTIONS IN
BIOLOGICAL SEQUENCE ANALYSIS
MARK BORODOVSKY AND SVETLANA EKISHEVA
CAMBRIDGE
UNIVERSITY PRESS

МАРК БОРОДОВСКИЙ
СВЕТЛАНА ЕКИШЕВА
ЗАДАЧИ И РЕШЕНИЯ
ПО АНАЛИЗУ БИОЛОГИЧЕСКИХ
ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Перевод с английского А. А. Чумичкина
Под редакцией д. б. н., проф. А. А. Миронова
Москва ♦ Ижевск
2008

УДК 57:007
ББК 28.071.3
Б 833
Издание выполнено при частичной финансовой поддержке
Научно-исследовательского института физико-химической биологии им.
А.Н.Белозерского.
Бородовский М., Екишева С.
Задачи и решения по анализу биологических последовательностей. —
М.Ижевск: НИЦ «Регулярная и хаотическая динамика», Институт
компьютерных исследований, 2008. — 440 с.
Данное издание является первым и единственным в своем роде задачником по
биоинформатике, в котором богатая подборка задач сопровождается подробными
решениями. Следуя структуре книги «Анализ биологических последовательностей»
Дурбина Р., Эдди III., Крог А., Митчисон Г. (НИЦ «РХД», 2006), авторы значительно
расширяют набор поддающихся решению задач. Таким образом, обе эти книги
представляют собой полноценный учебный комплект, который был опробован и одобрен
в зарубежных университетах, и может успешно использоваться в российских вузах
на соответствующих специальностях. Предлагаемый задачник способствует более
глубокому пониманию теоретического материала, изложенного в книге Р.
Дурбина и др., а также позволяет освоить практические навыки рационального решения
биологических задач, что является залогом успешных исследований в таких
стремительно развивающихся областях науки, как биоинформатика и системная биология.
ISBN 978-5-93972-644-3 ББК 28.071.3
© М. Бородовский, С. Екишева, 2006
© Перевод на русский язык:
НИЦ «Регулярная и хаотическая динамика», 2008
This publication is in copyright. Subject to statutory exception and to the provisions of relevant
collective licensing agreements, no reproduction of any part may take place without the written
permission of Cambridge University Press.
Все права на данное издание защищены, за исключением случаев, установленных
законом и условий, предусмотренных соответствующими лицензионными соглашениями,
заключенными на коллективной основе. Никакая его часть не может быть воспроизведена, если на
то нет письменного разрешения издательства Cambridge University Press.
http ://shop.rcd.ru
http://ics.org.ru

Посвящается:
М.Б.:
Ричарду и Джуди Линкофф
С. Е.:
Сергею и Наташе

Оглавление
Предисловие 10
Введение 12
Глава 1. ЗНАКОМСТВО С ПРЕДМЕТОМ 17
1.1. Оригинальные задачи 18
1.2. Дополнительные задачи 22
1.3. Дополнительная литература 45
ГЛАВА 2. ПОПАРНОЕ ВЫРАВНИВАНИЕ 46
2.1. Оригинальные задачи 47
2.2. Дополнительные задачи и теория 69
2.2.1. Получение матриц замен аминокислот (ряд ПТМ) . . . 73
2.2.2. Распределения счетов подобия 86
2.2.2.1. Теоретическое введение в задачи 2.19 и 2.20 . 86
2.2.3. Распределение длины длиннейшего общего слова для
нескольких несвязанных последовательностей 93
2.3. Дополнительная литература 97
Глава 3. МАРКОВСКИЕ ЦЕПИ И СКРЫТЫЕ МАРКОВСКИЕ
МОДЕЛИ 99
3.1. Оригинальные задачи 100
3.2. Дополнительные задачи и теория 112
3.2.1. Вероятностные модели последовательностей
символов: выбор модели и оценка параметров 122
3.2.2. Байесов подход к анализу состава
последовательностей: модель сегментации Лю и Лоренса 133
3.3. Дополнительная литература 141
Глава 4. ПОПАРНОЕ ВЫРАВНИВАНИЕ С ПОМОЩЬЮ СММ 143
4.1. Оригинальные задачи 144
4.2. Дополнительные задачи 156
4.3. Дополнительная литература 170

8 Оглавление
Глава 5. ПРОФИЛЬНЫЕ СММ ДЛЯ СЕМЕЙСТВ
ПОСЛЕДОВАТЕЛЬНОСТЕЙ 171
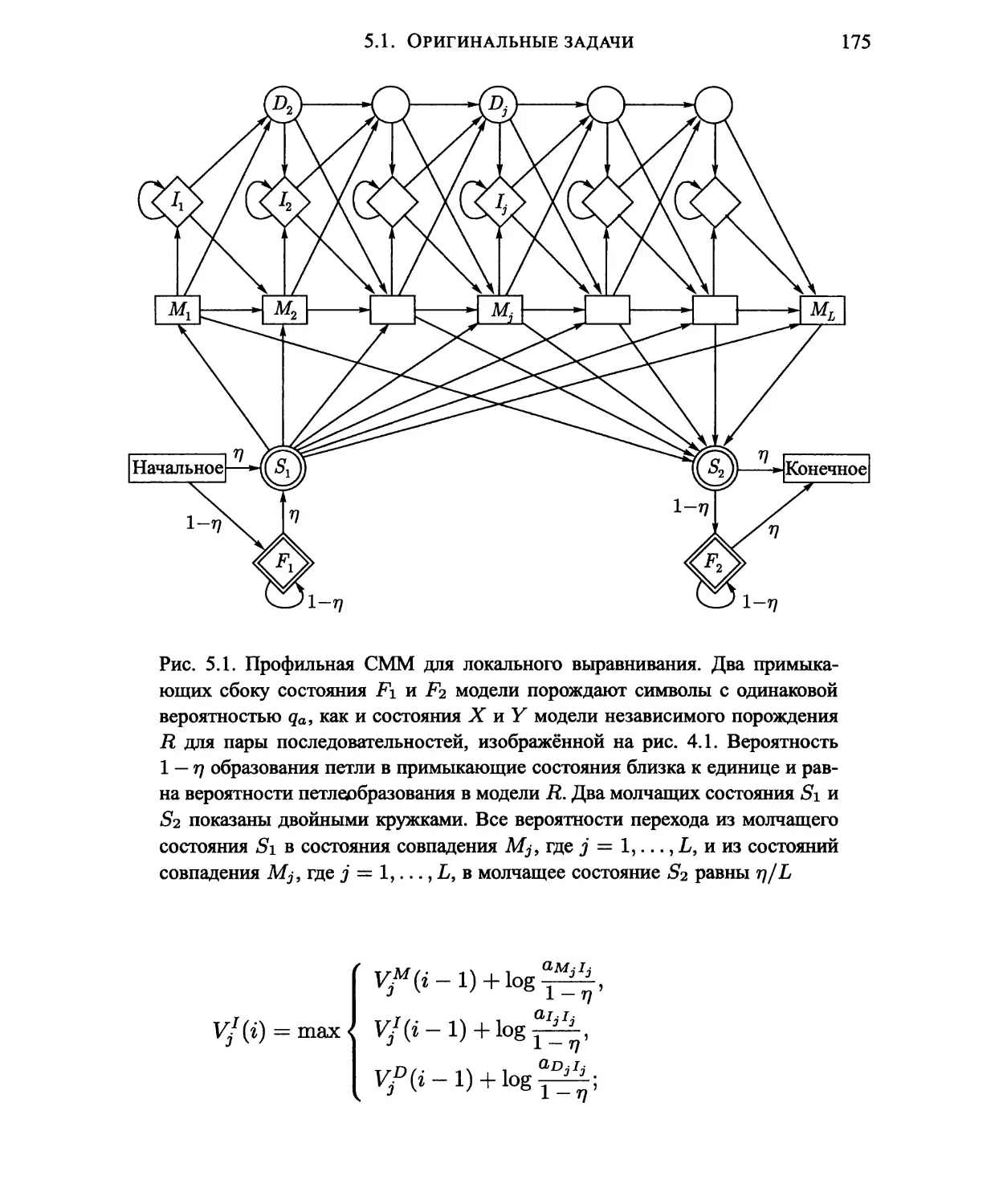
5.1. Оригинальные задачи 173
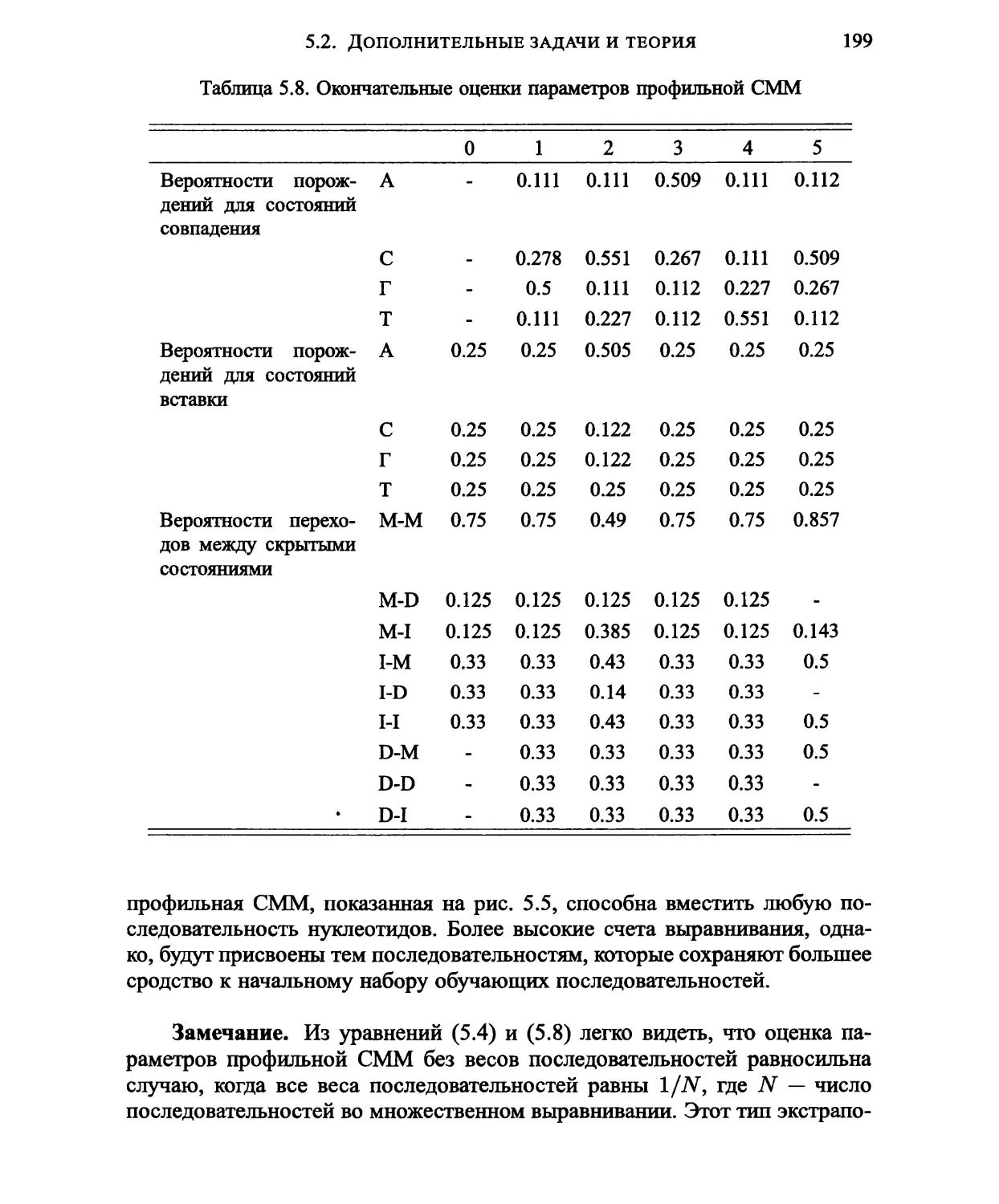
5.2. Дополнительные задачи и теория 184
5.2.1. Различающая функция и максимальные
различительные веса 200
5.2.1.1. Теоретическое введение в задачу 5.11 .... 200
5.3. Дополнительная литература 214
Глава 6. МЕТОДЫ МНОЖЕСТВЕННОГО ВЫРАВНИВАНИЯ
ПОСЛЕДОВАТЕЛЬНОСТЕЙ 215
6.1. Оригинальная задача 216
6.2. Дополнительные задачи и теория 217
6.2.1. Алгоритм множественного выравнивания Каррилло-
Липмена 217
6.2.2. Прогрессивные выравнивания: алгоритм Фэна-Ду-
литтла 227
6.2.3. Алгоритм выборки Гиббса для локального
множественного выравнивания 235
6.3. Дополнительная литература 237
Глава 7. ПОСТРОЕНИЕ ФИЛОГЕНЕТИЧЕСКИХ ДЕРЕВЬЕВ 240
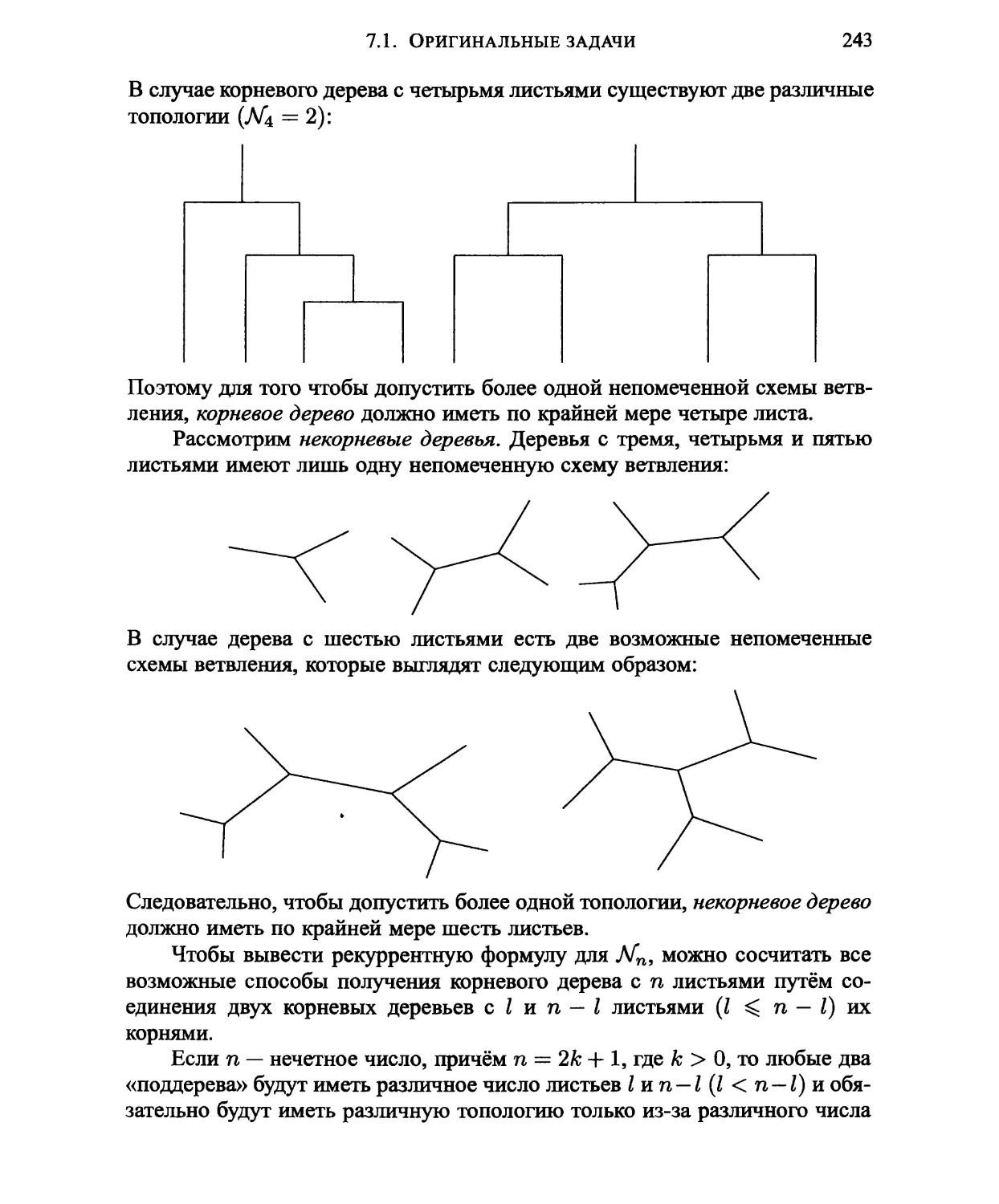
7.1. Оригинальные задачи 241
7.2. Дополнительные задачи 273
7.3. Дополнительная литература 279
Глава 8. ВЕРОЯТНОСТНЫЕ ПОДХОДЫ К ФИЛОГЕНИИ .281
8.1. Оригинальные задачи 282
8.1.1. Байесов подход к отысканию оптимального дерева и
алгоритм Мау-Ньютона-Ларге 301
8.2. Дополнительные задачи и теория 330
8.2.1. Связь между моделями эволюции
последовательностей, описываемыми марковским и пуассоновским
процессами 337
8.2.2. Модель эволюции последовательностей Торна-Кисино-
Фельзенштейна с заменами, вставками и удалениями . 345
8.2.3. Дополнительные сведения об интенсивностях замен . 350
8.3. Дополнительная литература 351

Оглавление 9
Глава 9. ТРАНСФОРМАЦИОННЫЕ ГРАММАТИКИ 354
9.1. Оригинальные задачи 355
9.2. Дополнительная литература 367
ГЛАВА 10. АНАЛИЗ СТРУКТУРЫ РНК 368
10.1. Оригинальные задачи 369
10.2. Дополнительная литература 389
Глава 11. ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
ВЕРОЯТНОСТЕЙ 392
11.1. Оригинальные задачи 392
11.2. Дополнительная задача 412
11.3. Дополнительная литература 413
Литература 414
Предметный указатель 433

Предисловие
ЗАДАЧИ И РЕШЕНИЯ ПО АНАЛИЗУ БИОЛОГИЧЕСКИХ
ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Эта книга первая из разряда задачников по биоинформатике, в которой
довольно обширный подбор задач сопровождается решениями.
Примечательно, что представленный в ней набор задач включает в себя все задачи,
предлагаемые в книге «Анализ биологических последовательностей» [67],
принятой многими ведущими университетами мира в качестве
рекомендуемого источника материала для чтения курсов биоинформатики. Хотя
многие из задач, приведённых в «АБП» в качестве упражнений, неоднократно
использовались для домашних и контрольных работ, подробные решения
к этим задачам отсутствовали. В связи с этим преподаватели
биоинформатики часто выражали желание иметь полностью проработанные решения
и располагать более широком набором задач для своих курсов.
Данная книга даёт именно это: следуя структуре, принятой в «АБП»,
и значительно расширяя набор поддающихся решению задач, она облегчит
более глубокое понимание содержания глав «АБП» и поможет её
читателям развить навыки решения задач, чрезвычайно важные для проведения
успешных исследований в расширяющемся поле биоинформатики. Весь
материал книги был опробован её авторами на учебных занятиях в
Технологическом институте Джорджии, где была проведена самая первая программа
подготовки выпускников со степенью магистра наук по биоинформатике.
Марк Бородовский — регент-профессор1 биологии и
биомедицинских технологий, а также Директор Центра биоинформатики и
вычислительной биологии в Технологическом институте Джорджии в Атланте. Он
является основателем программ подготовки и выпуска специалистов по
биоинформатике со степенью магистра наук и доктора философии в
Технологическом институте Джорджии. Направления его исследований
пролегают в областях биоинформатики и системной биологии. Он преподаёт курсы
биоинформатики с 1994 года.
Регент — член правления в некоторых американских университетах. — Прим. перев.

Предисловие
11
Светлана Екишева — учёный-исследователь «Школы биологии»
при Технологическом институте Джорджии в Атланте. Её
исследовательские интересы направлены на решение вопросов биоинформатики,
прикладной статистики и стохастических процессов. В сферу её компетенции
входит преподавание теории вероятностей и математической статистики
в университетах России и США.

Введение
Биоинформатика, будучи неотъемлемой частью постгеномной
биологии, закладывает принципы и рождает идеи, применяемые в области
вычислительного анализа биологических последовательностей. Эти идеи
облегчают преобразование волны данных секвенирования последовательностей,
порождённой недавним информационным всплеском в биологии, в
непрерывный поток открытий. Не удивительно, что новая биология двадцать
первого века привлекла интерес многих талантливых выпускников
университетов различного профиля. Преподавание биоинформатики столь разноликой
аудитории представляет собой известный вызов педагогическому
мастерству учёных. Во многих университетах, в том числе и в Технологическом
институте Джорджии в Атланте, США, принят подход, согласно которому
студентам надлежит сначала усовершенствовать свои знания в области
программирования на компьютере и математической статистики и лишь затем
приступать к изучению всестороннего основного курса биоинформатики.
В 1998 году, в начале осуществления разработанной нами программы
выпуска магистрантов и докторантов, мы выбрали на то время недавно
выпущенную книгу Ричарда Дурбина, Андерса Крога, СейнаР. Эдди и Грэми
Митчисона «Анализ биологических последовательностей» («АБП») в
качестве учебного пособия для основного курса биоинформатики. С
течением времени «АБП», в которой идеи главных алгоритмов биоинформатики
описаны в замечательно краткой и последовательной манере, стала
популярным источником материала для преподавания курсов биоинформатики
в ведущих университетах по всему Земному шару. Многие задачи,
включенные в «АБП» в качестве упражнений, неоднократно использовались для
домашних и контрольных работ. Однако подробных решений этих задач не
имелось. Проблема отсутствия подобного познавательного ресурса
неоднократно отмечалась как студентами, так и преподавателями.
Цель этой книги, «Задачи и решения по анализу биологических
последовательностей», состоит в том, чтобы восполнить этот пробел, расширить
набор поддающихся решению задач и помочь читателям развить навыки их
решения, весьма важные для проведения удачных изысканий на
расширяющейся ниве биоинформатики. Мы надеемся, что эта книга облегчит
понимание содержания глав «АБП» и, кроме того, предоставит дополнительную

Введение
13
точку опоры (необходимую читателям, у которых не было возможности
изучить базовый курс биоинформатики) для углублённого чтения «АБП».
Мы расширили набор оригинальных задач «АБП», добавив много новых
задач, прежде всего тех, которые предлагались магистрантам и докторантам
Технологического института Джорджии.
В исследовательском аппарате биоинформатики часто применяется
вероятностное моделирование и статистический анализ. Основные
алгоритмы биоинформатики, предназначенные для попарного и множественного
выравнивания последовательностей, поиска генов, обнаружения ортологов
и построения филогенетических деревьев, не могли бы работать без
рационального выбора модели, без оценки параметров, без должным образом
обоснованных систем очков и без оценки статистической значимости. Эти
и многие другие элементы эффективных инструментов биоинформатики
требуют, чтобы специалист принимал во внимание случайный
(вероятностный) характер последовательностей белка и ДНК.
Как было показано авторами «АБП», вероятностное моделирование
заложило основу для развития мощных методов и алгоритмов интерпретации
биологических последовательностей и открытия их функционального
значения и эволюционных связей. Примечательно, что вероятностное
моделирование представляет собой обобщение строго детерминированного
моделирования, которое имеет поразительно глубокую традицию в
естествознании. Эту традицию можно проследить в объяснении астрономических
наблюдений движения планет Солнечной системы Исааком Ньютоном,
который предложил краткую компактную модель, сочетающую в себе недавно
открытый им закон всемирного тяготения с законами динамики.
Принцип наибольшего правдоподобия, известный в математической
статистике, вопреки моде его традиционного применения также уходит
своими корнями в «детерминированную» науку, согласно которой выбранная
структура и параметры теоретической модели обеспечивают наилучшее
соответствие между предсказаниями и экспериментальными наблюдениями.
Например, метод наибольшего правдоподобия можно узнать в принятии
Фрэнсисом Криком и Джеймсом Уотсоном модели двойной спирали ДНК,
выбранной из комбинаторного числа биохимически жизнеспособных
альтернатив как дающую наилучшее соответствие с данными рентгенострук-
«урного анализа трёхмерной структуры ДНК, а также с другими
экспериментальными данными, имевшимися в их распоряжении.
В изучении процессов наследования и молекулярной эволюции, где
случайные факторы играют важные роли, на сцену выходят совсем уже
оперившиеся вероятностные модели. Классический цикл, в который
входит проведение экспериментов, анализ данных и моделирование с поиском

14
Введение
наилучшего соответствия моделей данным, был разработан и осуществлён
Грегором Менделем. Его замечательная многолетняя исследовательская
деятельность обеспечила доказательство существования дискретных единиц
наследственности — генов.
Когда мы имеем дело с данными, исходящими из менее
управляемой среды, например, с данными о естественной биологической эволюции,
охватьгоающими периоды времени, измеряемые миллионами лет, задача
построения моделей требует ещё большего напряжения. И всё же ситуация не
совсем безнадёжна. Модели молекулярной эволюции, предложенные
Маргарет Дейхофф с сотрудниками, Джуксом и Кантором, а также Кимурой,
являются классическими примерами фундаментальных достижений в
моделировании сложных процессов эволюции ДНК и белка. Эти модели
главным образом сосредоточиваются лишь на отдельно взятом участке
молекулярной последовательности и требуют дальнейшего упрощающего
допущения о том, что отдельные участки последовательности эволюционируют
независимо друг от друга. Тем не менее такие модели представляют собой
полезные отправные точки для понимания функций и эволюции
биологических последовательностей, а также для разработки алгоритмов,
проливающих свет на такого рода функциональные и эволюционные связи.
Например, счета замен аминокислот являются критически
важными параметрами алгоритмов оптимального глобального (Нидлмена-Вунша)
и локального (Смита-Уотермена) выравнивания последовательностей.
Получение счетов замен, имеющих биологический смысл, невозможно без
построения моделей эволюции белка.
В середине 1990-х гг. понятие скрытой марковской модели (СММ),
имевшей широкое практическое применение в распознавании речи, было
введено в поле биоинформатики и быстро вошло в основную колею
методов моделирования, используемых в анализе биологических
последовательностей.
Достижения теории за период с середины 1990-х гг. и до наших дней
показали, что задача выравнивания последовательностей имеет
естественную вероятностную интерпретацию на основе скрытых марковских
моделей. В частности, алгоритм динамического программирования (ДП) для
попарного и множественного выравнивания последовательностей имеет
эквивалент, основанный на СММ, — алгоритм Витерби. Если тип вероятностной
модели для биологической последовательности выбран, то параметры
модели могут быть выведены статистическими методами (обучающейся
машины). Может быть проведено сравнение двух конкурирующих моделей, с
тем чтобы определить в их числе ту модель, которая даёт наилучшее
соответствие.

Введение
15
События и отборочные силы, имевшие место в далёком прошлом и
двигавшие эволюцию биологических видов вперёд, приходится
восстанавливать по текущим данным расшифровки биологических
последовательностей, содержащим существенные помехи, обусловленные всеми
изменениями, произошедшими за всё время жизни исчезнувших поколений. Эту
трудность можно преодолеть до некоторой степени при помощи общей
концепции самосогласованных моделей, где параметры многократно
корректируются, с тем чтобы соответствовать растущему собранию данных секвени-
рования последовательностей. Вследствие этого, для осуществления такой
концепции необходимы алгоритмы с максимизацией математического
ожидания, способные оценивать параметры модели одновременно с
перегруппировкой данных и в результате производить структуру данных (такую как
множественное выравнивание), которая в большей степени соответствует
модели. В «АБП» описано несколько алгоритмов с максимизацией
математического ожидания, в том числе самообучающийся алгоритм для
профильной СММ и самообучающийся алгоритм для филогенетической СММ.
Учитывая, что практика работы со многими алгоритмами, описанными в
«АБП», требует программирования на компьютере в большом объёме,
можно ожидать, что описание решений могло бы ввести нас в сложные
компьютерные программы и таким образом увести далеко от начальных концепций
и идей. Однако большая часть приведённых в «АБП» упражнений имеет
аналитические решения. В некоторых случаях мы иллюстрировали
реализацию алгоритмов упрощёнными «модельными» примерами.
Компьютерные программы для таких примеров, написанные на языках C++ и Perl,
имеются на веб-сайте opal.biology.gatech.edu/PSBSA. Обратите внимание,
что в разделах «Дополнительная литература» мы упоминаем главным
образом те источники, которые были изданы после 1998 г. — года публикации
«АБП». Наконец, мы должны упомянуть, что встречающиеся в тексте
данной книги ссылки на страницы в «АБП» относятся к изданию 2006 года.
Благодарности
Мы благодарим Сергея Латкина, мужа Светланы, за замечательную
помощь в подготовке рисунков и таблиц для вёрстки в пакете Latex. Мы
крайне признательны Александру Ломсадзе, Райану Миллсу, Юаню Тяню,
Ьуржу Бакир, Джиттиме Пирияпонгсе, Вардгесу Тер-Хованисяну, Вэньха-
и к) Чжу, Джеффри Юнсу и Мэтью Бергински за неоценимую техническую
помощь в подготовке материалов книги; Сооцзиню И и Галине Глазко за
ссылки на полезные источники по молекулярной эволюции; Михаилу Ройт-

16
Введение
бергу за продуктивные беседы на предмет трансформационных грамматик
и конечных автоматов. Мы сердечно благодарим нашего редактора Катри-
ну Холлидей за огромное терпение и неустанную поддержку, без которой
эта книга никогда не вышла бы в свет. В особенности хочется
поблагодарить Ричарда Дурбина, Андерса Крога, СейнаР.Эдди и Грэми Митчи-
сона за поддержку, действенную критику и дельные предложения. Далее,
с удовольствием выражаем нашу признательность за сильную поддержку
«Школе биологии» при Технологическом институте Джорджии и
Факультету биомедицинских технологий имени Уоллеса X. Каултера в
Технологическом институте Джорджии и Университете Эмори. Наконец, мы желаем
вьфазить нашу индивидуальную, особую благодарность своим семействам
за большое терпение и неизменное участие.
М.Б. иС.Е.

Глава 1
ЗНАКОМСТВО С ПРЕДМЕТОМ
Читатель быстро обнаружит, что организация этой книги была выбрана
аналогичной организации книги «Анализ биологических
последовательностей» [67]. Первая глава «АБП» знакомит читателя с фундаментальными
понятиями анализа биологических последовательностей: подобием
последовательностей, гомологией, выравниванием последовательностей, а также
с основными концепциями вероятностного моделирования.
Тот факт, что столь разные концепции описаны в книге бок о бок, на
первый взгляд кажется удивительным. Однако давайте вспомним
несколько важных вопросов биоинформатики. Как следует строить попарное
выравнивание последовательностей? Как необходимо строить множественное
выравнивание последовательностей? Каким образом можно восстановить
филогенетическое дерево нескольких биологических последовательностей?
Как мы можем предсказать вторичную структуру РНК? Ни к одному из этих
вопросов нельзя обратиться надлежащим образом без применения
вероятностных методов. Математическая сложность этих методов колеблется от
основных теорем и формул до сложной архитектуры скрытых марковских
моделей и стохастических грамматик, способных уловить едва различимые
особенности состава эмпирических биологических последовательностей.
Подобный взрыву, неудержимый рост количества данных
расшифровки биологических последовательностей создал превосходную возможность
для имеющего практический смысл применения дискретных
вероятностных моделей. Возможно, не будет большого преувеличения, если мы
скажем, что значение, результаты, последствия этого нового подхода можно
сравнить со значением революционного для восемнадцатого века
применения исчисления и дифференциальных уравнений для решения задач
классической механики.
Рассматриваемые в этой вводной главе задачи связаны с
фундаментальными концепциями, которые играют важную роль в анализе
биологических последовательностей: наибольшее правдоподобие и максимальная
апостериорная (Байесова) оценка параметров модели. Эти концепции
являются важнейшими для понимания статистического вывода из эксперимен-

18
Глава 1
тальных данных и не могут быть введены без понятий условной и
безусловной вероятности, а также вероятности совместного наступления событий.
Часто возникающая задача параметризации модели по природе своей
трудна, если под рукой имеется лишь короткая обучающая
последовательность. Можно по-прежнему пытаться использовать методы, подходящие
для больших обучающих последовательностей. Но этот шаг может
привести к чрезмерной подгонке и порождению смещённых оценок параметров.
К счастью, такое смещение может быть до некоторой степени устранено;
модель может обобщаться по мере того, как обучающая последовательность
приращается искусственно вводимыми наблюдениями, или
псевдоотсчётами.
Включённые в эту главу задачи предназначены для того, чтобы
предоставить читателю практику применения понятий безусловной и условной
вероятностей, теоремы Байеса, наибольшего правдоподобия и Байесовой
оценки параметров. Необходимые определения этих понятий и концепций,
часто встречающихся в «АБП», могут быть найдены в учебниках по теории
вероятностей и математической статистике для студентов (например, [195],
[175], [120], [44] и [121]).
1.1. Оригинальные задачи
Задача 1.1. Рассмотрите принцип работы эпизодически нечестного
казино, в котором используют два вида игральных костей. Из всех
костей 99 % правильные, но 1 % смещён так, чтобы в 50 % бросаний
выпадала шестёрка. Мы берём игральную кость со стола наугад.
Чему равны Р(шестёрка | Дмещ.) и Р(шестёрка \Ощт)1 Каковы вероятности
Р(шестёрка, Дмещ.) и Р(шестёрка, Д^ав.)? Какова вероятность выпадения
шестёрки на взятой нами наугад кости?
Решение. Все возможные исходы бросания правильной игральной кости
равновероятны, то есть Р(шестёрка lA^an.) = 1/6. С другой стороны,
вероятность выпадения шестёрки на смещённой кости, Р(шестёрка |Дмещ.),
равна 1/2. Для того чтобы вычислить вероятность совместного наступления
событий (шестёрка, Дмещ.) — выпадения шестёрки и выбора смещённой
кости, — мы воспользуемся определением условной вероятности:
Р(шестёрка, £>смещ.) = Р(Лсмещ.)Р(шестёрка | £>смещ.). (1.1)

1.1. Оригинальные задачи 19
Поскольку вероятность выбора смещённой кости равна 1/100, равен-
i'tho (1.1) даёт:
Р(шесгёрка,Ясмещ.) = i5o • | = абб-
Исходя из подобных рассуждений, имеем
/'(шестерка, Дфав.) = Р(шестёрка|ЛПрав.)Р(Лправ.) = - • — = —.
I вероятность выпадения шестёрки на взятой наугад игральной кости вычис-
имстся как полная вероятность события «шестёрка», произошедшего
совместно либо с событием Dcuem., либо с событием Дправ.:
/'(шестёрка) = Р(шестёрка, £>смещ.) + ^(шестёрка, Дфав.) = tjqq = щ)"
П
Задача 1.2. Сколько шестёрок подряд должно выпасть в игре по условию
in дачи 1.1, прежде чем станет более вероятным то, что мы выбрали (и
бросаем) именно смещённую кость?
Решение. Для того чтобы определить условную вероятность выбора
смещённой кости при условии, что подряд выпало п шестёрок —
^(Ошещ]п шестёрок), — достаточно воспользоваться теоремой Байеса:
ryfrk , .. v Р(П ШеСТёрОК |Дшещ.)^(А>мещ.)
P(Dcuan.\n шестерок) = — - =
Р(п шестерок)
_ Р(п ШеСТёрОК | Д;мещ.)^(А;мещ.)
Р(п ШеСТёрОК |^смещ.)^(^смещ.) + Р(пшеСТёрОК |AipaB.)^(AipaB.)
Ьросания как правильных, так и смещённых костей независимы, поэтому
(1/100)•(1/2)п
P(DCUGBl]n шестёрок) =
(99/100)•(1/6)п +(1/100)•(1/2)п
1
11 • (1/3)п~2 + 1
' )гот результат заказывает на то, что вероятность Р (ДшещJ n шестёрок)
приближается к единице по мере того, как п (длина наблюдаемой
последовательности шестёрок) возрастает. Неравенство
Р{Р>с^щ\п шестёрок) > 1/2

20 Глава 1
показывает, что более вероятно то, что нами была выбрана именно
смещённая кость. Это неравенство верно, когда
п-2
п ^ 5.
/ \ TI — Z
Поэтому появление пяти и более шестёрок подряд указывает на то, что
более вероятным является выбор смещённой кости. □
Задача 1.3. С помощью определения условной вероятности докажите
следующую теорему Байеса:
P{X)P{Y\X)
P{X\Y)
P(Y)
Решение. Для любых двух событий X и У, таких что P(Y) > 0, условная
вероятность наступления события X при наступлении события Y
определяется выражением вида
Р(Х П Y)
P(X\Y) =
P(Y)
Применяя это определение еще раз, чтобы подставить P(X)P(Y\X) на
место Р(Х П У), мы получаем уравнение
которое эквивалентно теореме Байеса. □
Задача 1.4. Обнаружена редкая генетическая болезнь. Хотя известно, что
её носителем является лишь один человек из миллиона, вы раздумываете о
том, стоит ли пройти проверку. Вам сказали, что генетический анализ
чрезвычайно надёжен: он обладает 100 %-й чувствительностью (всегда верен,
если вы больны) и 99,99 %-й специфичностью (даёт ложный
положительный результат только в 0,01 % случаев). С помощью теоремы Байеса
объясните причину, по которой вы можете отказаться от такого исследования.
Решение. До прохождения проверки вероятность P(D) того, что вы
являетесь носителем этой генетической болезни, равна 10_6, а вероятность Р(Н)
того, что вы здоровы, составляет 1 — 10~6. Насколько такая проверка
изменит сию неопределённость? Рассмотрим два возможных исхода.

1.1. Оригинальные задачи
21
Если проверка дала положительный результат, то Баиесовы
апостериорные вероятности наличия и отсутствия болезни, соответственно,
следующие:
P(non.\D)P(D)
Р(£>|пол.)
Р(пол.)
P{non.\D)P{D)
P(uoji.\D)P(D) + Р(пол.|Я)Р(Я)
10"6
10-6 + 0,999999-10-4
= 0,0099,
Р(Я|пол.) = Р<^;'Н>^Я> =0,9901.
v ' ' Р(пол.)
Если же результат проверки отрицательный, то Баиесовы апостериорные
вероятности принимают значения
P{oTp.\D)P{D)
Р(Б\отр.) =
Р(отр.)
Р(отр.|£>)Р(£>)
P(<yrp.\D)P(D) + Р(отр.|Я)Р(Я)
= 0 = 0
0 + 0,9999-(1-Ю-6)
Таким образом, значения априорных вероятностей P(D) и Р(Н) измени-
иись весьма незначительно:
\P(D) - P(D\non.)\ = 0,0099, \P(D) - P(D\vrp.)\ = Ю"6,
\Р(Н) - Р(#|пол.)| = 0,0099, \Р(Н) - Р(#|отр.)| = 10"6.
Мы видим, что даже при положительном результате исследования
вероятность наличия болезни изменяется с 10_6 до Ю-2. Таким образом,
проходить эту проверку не стоит ввиду её нецелесообразности. □
1идача 1.5. Нам нужно проверить игральную кость, которая, предположи-
к'ш.ио, смещена некоторым образом. Мы бросаем эту кость десять раз
подряд и наблюдаем исходы: 1, 3, 4, 2, 4, 6, 2, 1, 2 и 2. Какова полученная

22
Глава 1
нами методом наибольшего правдоподобия оценка вероятности выпадения
двух очков р2? Какова будет Байесова оценка, если мы добавим по
одному псевдоотсчёту на категорию? Что изменится, если мы добавим по пять
псевдоотсчётов на категорию?
Решение. Полученная методом наибольшего правдоподобия оценка
вероятности р2 есть (относительная) частота исхода «два», таким образом, р2 =
= 4/10 = 2/5. Если добавлено по одному псевдоотсчёту на категорию, то
Байесова оценка равна р2 = 5/16. Если мы добавляем по пять
псевдоотсчётов на категорию, то р2 = 9/40. В последнем случае Байесова
оценка р2 лучше приближается к вероятности события «два» после бросания
правильной игральной кости — р2 = 1/6.1
В любом случае обоснованность этих альтернативных подходов трудно
оценить без дополнительной информации. Наилучший способ улучшить
оценку — собрать больше данных. □
1.2. Дополнительные задачи
Следующие задачи, написанию которых послужила причиной
необходимость разобрать некоторые вопросы, возникающие при анализе
биологических последовательностей, требуют умения применять формулы из
комбинаторики (задачи 1.6, 1.7, 1.9 и 1.10), элементарного вычисления
вероятностей (задачи 1.8 и 1.16), а также знания свойств случайных величин
(задачи 1.13 и 1.18). Наша цель здесь состоит в том, чтобы помочь
читателю распознавать вероятностный характер этих (и подобных им) задач с
биологическими последовательностями.
В этом разделе для описания свойств последовательностей ДНК
применяются основные распределения вероятностей: геометрическое
распределение — для описания распределения длин фрагментов рестрикции
(задача 1.12) и открытых рамок считывания (задача 1.14); распределение
Пуассона — как хорошее приближение для числа появлений олигонуклеотидов
в последовательностях ДНК (задачи 1.11, 1.17, 1.19 и 1.22). Мы будем
использовать понятие «модели независимого порождения», представляющей
собой последовательность независимых одинаково распределённых (н. о. р)
случайных величин со значениями, взятыми из такого конечного
алфавита Л (то есть, алфавита нуклеотидов или аминокислот), что вероятность
Нетрудно догадаться, [что] если мы добавим по 1000 псевдоотсчетов, то получим значение
совсем близкое к 1/6. Надо (важно!) понимать, что добавляя равномерные псевдоотсчеты, мы
используем наше априорное представление о правильности кости. Добавив очень большое
количество псевдоотсчетов, мы тем самым игнорируем результаты опыта. — Прим. ред.

1.2. Дополнительные задачи
23
появления символа а в любом участке последовательности равна qa и при
этом J2 Qa = 1. Таким образом, фрагмент последовательности ДНК или
а€А
белка, #1,..., #п, порождённый моделью независимого порождения, имеет
п
вероятность Yl Qxi- Следует иметь в виду, что в тексте «АБП» [67] та же
г=1
модель названа моделью случайной последовательности. Модель
независимого порождения используется для описания последовательностей ДНК
в задачах 1.12, 1.14, 1.16 и 1.17.2
Вводный уровень главы 1 всё же позволяет нам оперировать с
понятием проверки гипотез. В задаче 1.20 такая проверка помогает опознать
CpG-островки в последовательности ДНК, тогда как в задаче 1.21 мы
рассматриваем критерий для проведения различия между областями
последовательности ДНК с более и менее высоким содержанием G + C.
Наконец, в задачах 1.16, 1.18 и 1.19 рассматриваются вопросы
сравнения вероятностных моделей.
Задача 1.6. В геноме вируса герпеса нуклеотиды С, G, А и Т встречаются
с частотами, соответственно, 35/100, 35/100, 15/100 и 15/100. При
допущении о модели независимого порождения для этого генома определите, чему
равна вероятность того, что случайно выбранный фрагмент ДНК длины 15
и. н. содержит восемь нуклеотидов С или G и семь нуклеотидов А или Т?
Решение. При заданных частотах появления нуклеотидов из группы С и G
и АиТ, равных, соответственно, 0,7 и 0,3, вероятность того, что во
фрагменте длины 15 п. н. находится восемь нуклеотидов С или G и семь
нуклеотидов А или Т, равна 0,78 • 0,37 = 0,0000126. Это число должно быть
умножено на (х85) = 15!/8!7! — число возможных взаимных расположений
представителей этих групп нуклеотидов среди пятнадцати нуклеотидных
позиций. Таким образом, мы получаем вероятность, равную 0,08. □
1идача 1.7. Затравка ДНК, используемая в полимеразной цепной реакции,
представляет собой фрагмент однонитевой ДНК, предназначенный для
связывания (гибридизации) с одной из нитей молекулы целевой ДНК. Бы-
||о замечено, что затравки могут гибридизироваться не только со своими
; Такие случайные последовательности называются в математической литературе
последом"» ельностями независимых одинаково распределенных случайных величин. Бернуллиевы
последовательности — это их частный случай (когда каждая случайная величина принима-
II ронно два значения). Очевидно, Бернуллиева последовательность не может быть моделью
пиоиогических последовательностей, изучаемых в этой книге, поскольку число значений слу-
•И1Й111.1Х величин равно либо 4, либо 20. — Прим. ред.

24
Глава 1
абсолютными комплементами, но также и с фрагментами ДНК такой же
длины, имеющими один или два нуклеотида, не дающих совпадение. Если
геномная ДНК будет «достаточно длинной», то сколько различных
последовательностей ДНК могут связаться с затравкой длины восемь нуклеотидов?
Понятие «достаточной длины» подразумевает, что в целевой геномной ДНК
присутствуют все возможные олигонуклеотиды длины 8 н.
Решение. Мы рассматриваем более общую ситуацию, где длина
затравки равна п. Есть три возможных случая гибридизации между затравкой
и ДНК: без несовпадения, с одним несовпадением и с двумя
несовпадениями. Очевидно, что в первом случае опознаётся только одна
последовательность ДНК, в точности комплементарная затравке. Второй случай
(одно несовпадение) со свободой выбора одного из трёх типов
несовпадающих нуклеотидов в одной позиции комплементарной
последовательности даёт Зп возможных последовательностей. Наконец, число сочетаний
двух позиций, содержащих несовпадающие с затравкой нуклеотиды,
равно п(п — 1)/2. Каждое сочетание этих двух позиций даёт девять
возможностей выбора двух нуклеотидов, не дающих совпадения. Таким образом,
общее число возможных последовательностей с двумя несовпадениями
составляет 9п(п — 1)/2. Следовательно, при п = 8 существует
1 + 3 • 8 + ^|^ = 277
различных последовательностей, способных гибридизироваться с данной
затравкой. □
Задача 1.8. Реакция секвенирования ДНК выполнена с коэффициентом
ошибок 10 %; таким образом, вероятность неправильного опознавания
данного нуклеотида равна 0,1. Для того чтобы минимизировать частоту
появления ошибок, ДНК секвенируют п = 3 независимыми реакциями, затем
расшифрованные фрагменты выравнивают, после чего нуклеотиды
опознают в соответствии со следующим правилом большинства. Тип нуклеотида
в конкретной позиции опознаётся как а, где a G {Т, С, A, G}, если в этой
позиции выровнено больше нуклеотидов типа а, чем всех остальных типов
вместе взятых. Если в позиции выравнивания никакой тип нуклеотида не
появляется более п/2 раз, то тип нуклеотида не опознаётся (тип N).
Каков ожидаемый процент а) правильно и б) неправильно опознанных
нуклеотидов? в) Какова вероятность того, что в конкретном участке
опознание невозможно? г) Как изменится результат а при п = 5 и при п = 7?

1.2. Дополнительные задачи
25
Сделайте допущение о том, что присутствуют только ошибки типа
замены (нет вставок или удалений) и все замены равновероятны (нет смещения
к какому-либо определённому типу нуклеотида).
Решение, а) В каждой выбранной позиции мы рассматриваем результаты
трёх реакций секвенирования как исходы трех Бернуллиевых испытаний,
где «успех» имеет место в том случае, если нуклеотид опознан правильно
(с вероятностью р = О,9), а «неудача» — в противном случае (с
вероятностью q = О,1). Тогда вероятности следующих событий описываются
биномиальным распределением и могут быть определены непосредственно:
Р3 = Р(«Успех» набл. три раза) = р3 = 0,93 = 0,729 (72,9 %),
Рг = Р(«успех» набл. дважды) = ( )p2q =
= 3-0,92- 0,1 = 0,243 (24,3%).
Согласно правилу большинства, ожидаемый процент Е правильно
опознанных нуклеотидов определяется как
Е£=3 = Р(«успех» набл. по кр. мере дважды) • 100 % =
= (Рз + Р2)' Ю0% = 97,2%.
б) Для того чтобы определить вероятность неправильного
опознания нуклеотида на данном участке, мы должны уметь классифицировать
«неудачи»; таким образом, мы должны обобщить биномиальное
распределение к мультиномиальному. А именно — в каждом независимом
испытании (выполненном на данном участке последовательности) мы можем
иметь «удачу» (с вероятностью р = 0,9) и три других исхода: «неудача 1»,
«неудача 2» и «неудача 3» (с равными вероятностями qi = q2 = Яз = 1/30).
Опознать нуклеотид неправильно означало бы наблюдать по крайней мере
дне «неудачи г», где г = 1,2,3, среди п = 3 испытаний. Поэтому:
Рз = («неудача г» набл. трижды) =
= q* = (1/30)3 = 0,000037 (0,0037 %),
Р£ = Р(«неудача г» набл. дважды) =
= 6 • (1/30)3 + 3 • (1/30)2 • 0,9 = 0,00356 (0,356 %).

26
Глава 1
Наконец, ожидаемый процент неправильно опознанных нуклеотидов
находим из
Е-=3=( ]Г (^ + ^))-100% =
\г=1,2,3 /
= 3(Р^ + Р2')-Ю0% = 1,1%.
в) На всяком отдельно взятом участке обращение к основаниям
дает в результате три взаимно исключающих события: «правильное
опознание», «неправильное опознание» или «опознание невозможно». Тогда
вероятность последнего исхода определяется как
Р (ГбТопознГ) - 1 - (рз + Рг) - т + Н) = 0,0172 (1,72 %).
г) Для того чтобы вычислить ожидаемый процент Е£ правильно
опознанных нуклеотидов при п = 5 и п = 7, мы применяем те же самые
соображения, что и в пункте а, разве только вместо трёх мы рассматриваем,
соответственно, пять и семь Бернуллиевых испытаний. Мы находим:
Е£=5 = Р(по кр. мере 3 «успехов» среди пяти исп.) • 100 % =
= рь + 5 • 0,94 ■ 0,1 + 10 • 0,93 - 0,12 = 99,14 %.
Точно так же
Е£=7 = Р(по кр. мере 4 «успеха» среди семи исп.) • 100 % =
= 99,73 %.
Как и следовало ожидать, увеличение числа независимых реакций
улучшает качество секвенирования. □
Задача 1.9. В силу избыточности генетического кода, последовательность
аминокислот может быть кодируема несколькими последовательностями
ДНК. Каковы нижний и верхний пределы числа возможных
последовательностей ДНК, которые могли бы содержать код для заданного белкового
фрагмента длины десять аминокислот?
Решение. Если все десять аминокислот были бы представлены метиони-
ном или триптофаном (аминокислотами, кодируемыми единственными ко-
донами), то мог бы быть достигнут нижний предел, равный единице. В этом

1.2. Дополнительные задачи
27
случае последовательность аминокислот уникально определяет
кодирующую её последовательность нуклеотидов. Верхний предел был бы
достигнут, если последовательность аминокислот состояла бы из лейцина,
аргинина или серина — аминокислот, кодируемых шестью колонами каждая.
11оследовательность длины десять аминокислот, состоящая из Ьещ Ser или
Arg (в любом взаимном расположении) может быть закодирована б10 =
60 466176 различными последовательностями нуклеотидов. □
Задача 1.10. Было обнаружено, что формы жизни с планеты XYZ имеют
и основе своей ДНК и белки, причём белки состоят из двадцати
аминокислот. В ходе анализа состава белка было определено, что средние частоты
появления всех аминокислот, исключая Met и Тгр, равны 1/19, тогда как
частоты Met и Тгр равны 1/38. Принимая во внимание высокую темпера-
iypy на поверхности планеты XYZ, было высказано предположение, что
ДНК имеет чрезвычайно высокое содержание G + С. Каково наиболее
высокое возможное среднее содержание G + С в кодирующих белок областях
(при соответствии указанному выше среднему аминокислотному составу),
если для кодирования белков форм жизни с планеты XYZ используется
стандартный (такой же, что и на планете Земля) генетический код?
Таблица 1.1. Максимальное число 1а нуклеотидов С и G, которые
появляются (присутствуют) в одном из синонимичных кодонов, кодирующих
аминокислоту а
1а
1
2
3
Asn,
Asp, Cys, Gin,
Аминокислота а
lie, Lys, Met, Phe,
Glu, His, Leu, Ser,
Ala, Arg, Gly, Pro
Tyr
Thr, TYp,
Val
Решение. Для того чтобы обеспечить возможно большее содержание
нуклеотидов G + Св кодирующей белок области, которое удовлетворяло бы
ограничениям на аминокислотный состав, во всех случаях должны быть
использованы синонимичные кодоны с самым высоким содержанием G + C.
Согласное со стандартным генетическим кодом распределение кодонов с
имсоким содержанием G + С приведено в таблице 1.1 (где 1а обозначает

28
Глава 1
наибольшее число нуклеотидов С и G в кодоне, кодирующем
аминокислоту а).
Поэтому среднее арифметическое содержания G -\- С в кодирующей
белок области определяется как
(G
Здесь /а — частота появления аминокислоты а.
Замечание. Исходя из подобных соображений можно получить
оценки верхнего и нижнего пределов содержания G + С в геномах прокариотов
(планета Земля), где кодирующие белок области, как правило, занимают
приблизительно 90 % от всей длины ДНК. □
Задача 1.11. Фермент рестрикции разрезает ДНК на палиндромном3
участке длины 6 п. н. Определите вероятность того, что кольцевая хромосома —
двунитевая молекула ДНК длины L = 84 000 п. н. — будет разрезана
ферментом рестрикции ровно на двадцать фрагментов. Сделайте допущение
о том, что последовательность ДНК описывается моделью независимого
порождения с равными вероятностями появления нуклеотидов Т, С, А и G.
Подсказка: используйте распределение Пуассона.
Решение. Вероятность того, что участок рестрикции начинается в той
или иной выбранной позиции последовательности ДНК, составляет р =
= (1/4)6 = 0,0002441. Если мы не принимаем во внимание взаимную
зависимость появлений участков рестрикции в позициях г и j, где \i — j\ ^ 6,
то число X участков рестрикции в последовательности ДНК можно
рассматривать как число успехов (с вероятностью р) в последовательности L
Бернуллиевых испытаний; поэтому число X имеет биномиальное
распределение с параметрами р и L. Поскольку L велико, а р мало, мы можем
использовать распределение Пуассона с параметром А = pL = 20,5 в
качестве приближения биномиального распределения. Тогда
Р(Х = 20) = е"А^ = 0,088.
Примечательно, что вероятность разрезания этой же последовательности
ДНК на любое другое заданное число фрагментов будет ниже, чем Р(Х =
= 20). Действительно, отношение Rk вероятностей двух последовательных
3Палиндромом в ДНК называется самокоплиментарная последовательность, например
GAGCTC. - Прим. ред.

1.2. Дополнительные задачи 29
значений величины X,
Р(Х = к + 1) х
Rk =
Р(Х = к) к + 1'
показывает, что Р(Х = к) возрастает по мере того, как к растёт от 0 до Л,
и убывает по мере того, как к растёт от Л до L, и, таким образом, достигает
своего максимального значения в точке к = А. Другими словами, если А
не целое число, то наиболее вероятное значение случайной переменной с
распределением Пуассона равно [А], где [А] обозначает наибольшее целое
число, не превышающее А. В противном случае наиболее вероятные
значения равны А — 1 и А. □
Задача 1.12. Определите среднюю длину фрагментов рестрикции,
получаемых при действии 6-рестриктазы Smal с участком рестрикции CCCGGG.
Рассмотрите а) геном с содержанием G + С, равным 70 %, и 6) геном с
содержанием G + С 30 %. Сделано допущение, что геномная
последовательность может быть представлена моделью независимого порождения со
следующими вероятностями нуклеотидов: qc = qc и qA = Qt- Учтите, что
фермент Smal разрезает двойную нить ДНК в середине участка CCCGGG.
Решение. Обозначим вероятность того, что участок рестрикции
начинается в конкретной позиции последовательности буквой Р, а длину фрагмента
рестрикции — буквой £. Если в некоторой позиции последовательности
начинается участок рестрикции, мы соотносим с ней число 1, в противном
случае — число 0. Тогда в полученной последовательности единиц и нулей
длины отрезков из нулей (равные длинам фрагментов рестрикции) можно
рассматривать как значения случайной переменной L. Если мы не
принимаем во внимание взаимную зависимость появлений участков рестрикции
в позициях г и j, где \г — j\ ^ 6, то случайная переменная L имеет
геометрическое распределение: P(L = п) = (1 — Р)п~1Р. Ожидаемое значение L
определяется как
71=1 П=1

30 Глава 1
d(J:(i-p)n)
dP Р2 р'
Для случая а мы имеем
Ра = P{CCCGGG) = (0,35)6 = 1,8- НГ3,
и средняя длина фрагмента рестрикции составляет ELa = 1/Pa = 544 п. н.
Точно так же, в случае б
Рь = P(CCCGGG) = (0,15)6 = 1,14 • 1СГ5,
и средняя длина фрагмента рестрикции составляет EL& = 87788 п. н. В
случае б вполне могла ожидаться большая средняя длина фрагментов
рестрикции, поскольку богатый G + С участок рестрикции CCCGGG появлялся
бы менее часто в богатой А + Т геномной ДНК. □
Задача 1.13. Рассмотрите последовательность ДНК длины п,
описываемую моделью независимого порождения с равными вероятностями
появления нуклеотидов. Пусть X — число появлений динуклеотида АА, &Y —
число появлений динуклеотида AT в этой последовательности. Каковы
значения математического ожидания и дисперсии случайных переменных X и
У? Для простоты рассмотрите кольцевую ДНК длины п.
Решение. Определим случайные переменные Xiuyi, где г = 1,..., п,
следующим образом:
_ J , если динуклеотид АА нач-ся в г-й позиции посл-ти,
иначе;
С:
-и
если динуклеотид AT нач-ся в г-й позиции посл-ти,
иначе.
п п
Очевидно, что X = ^ жь а ^ = *52Уг- Согласно однородной моде-
г=1 г=1
ли независимого порождения, математические ожидания Xi и у*, где г =
= 1,..., п, определяются как
EXi = Ejfc = P(Xi = 1) = Р(Уг = 1)
W 16-

1.2. Дополнительные задачи 31
Таким образом, среднее арифметическое величин X и Y равно ЕХ =
= ЕУ = п/16. Точно так же мы можем утверждать, что ожидаемое число
появлений любого другого динуклеотида в последовательности также
равно п/16.
Мы обозначаем кратчайшее расстояние между позициями г и j в
кольцевой ДНК через r(i,j) и находим второй момент величины X:
ex2 = e(J>J =
п
= 5^ Ear? + $3 E*iSj+ $3 Ея*^- О-2)
г=1 i,j:r(i,j)^2 itj:r(i,j)=l
п
Поскольку х\ — хи постольку первая сумма в уравнении (1.2) равна ^2 =
i=i
= Еж? = nExi = п/16.
Если расстояние r(i,j) ^ 2, то случайные переменные Xi и а^
независимы и
53 Ея*с,-= 53 ^^^ = П 256
Если г (г, j) = 1, то позиции г и j смежные и, для определённости, мы
делаем допущение о том, что позиция г предшествует позиции j. Тогда
произведение x%Xj принимает следующие значения:
X<lXj —
1, если триплет AAA начинается в позиции г,
О, иначе
и "ExiXj = P(x{Xj = 1) = (1/4)3 = 1/64. Поэтому второй момент
величины X принимает вид
FY2 = !L + n(n ~ 3) . 2n n(n +21)
16 + 256 ^ 64 256 '
и дисперсия величины X определяется из

32
Глава 1
Точно так же второй момент величины Y мы находим из:
ЕУ2 = Е(£>) =Х>уг2+ £ Eyiyj+ £ Еад. (1.3)
\г=1 / г=1 i,j:r(i,j)^2 ij'-r(i,j)=l
Первые две суммы в уравнении (1.3) те же, что и в уравнении (1.2).
Однако, если г (г, j) — 1, то произведение yiyj всегда равно нулю, потому что
динуклеотид AT не может начинаться в двух смежных позициях г и j этой
последовательности. Поэтому
т^2 П , П(П-З) П(П+ 13)
16 ' 256 256
^у-ЕГ.-даТ-!^-^.
13п
256
Мы видим, что дисперсия числа появлений всякого динуклеотида зависит
от его структуры: если он состоит из разных букв (и, таким образом, не
может перекрываться с соседом того же самого вида), то дисперсия равна
13п/256; если же динуклеотид состоит из одинаковых букв (и, значит,
может перекрываться с соседом того же самого вида), то дисперсия возрастает
до 21п/256.
Замечание. Более подробное рассмотрение первого и второго
моментов частот слов в биологических последовательностях может быть найдено
в [216]. □
Задача 1.14. Кодирующий белок ген прокариота обычно состоит из
непрерывной последовательности нуклеотидных триплетов, или кодонов. Такая
последовательность начинается с определённого старт-кодона (чаще всего,
ATG) и заканчивается одним из трёх стоп-кодонов: ТАЛ, TAG или TGA.
Последовательность с такой структурой называют «открытой рамкой
считывания» (ОРС). Однако не каждая ОРС, встречающаяся в геномной ДНК
прокариотов, является функциональным геном. При допущении о том, что
триплет ATG является единственным возможным старт-кодоном,
определите, каково распределение длин случайно наблюдаемых ОРС?
Рассмотрите модель независимого порождения с равными вероятностями появления
нуклеотидов четырёх типов.

1.2. Дополнительные задачи 33
Решение. Существует 43 = 64 триплета (кодона), которые появляются в
последовательности с равными вероятностями. Три из этих шестидесяти
четырех суть стоп-кодоны. Поэтому вероятность встретить стоп-кодон при
просмотре последовательности триплет за триплетом равна 3/64 = 0,047.
Вероятность появления ОРС длины L (в кодонах) определяется из
Р(ОРС длины L начинается в данной позиции) =
= P(ATG) • Р(не CTon-KOflOH)L~2 • Р(стоп-кодон) =
= J_ Л aV"2 3 = 3 /61
64 V 64 у 64 4096 V64
Чтобы вывести функцию распределения длин ОРС, мы используем
определение условной вероятности:
Р(длина ОРС равна L) =
_ Р(ОРС длины L начинается в данной позиции) _
Р(любая ОРС начинается в данной позиции)
Р(ОРС длины L начинается в данной позиции)
~~ +оо ""
Y^, Р(ОРС длины L начинается в данной позиции)
L=2
= (3/4096)(61/64)L-2 = _3_ /61
1/64 64 \64
Таким образом, мы получили геометрическое распределение длин
случайных ОРС наряду с параметрами этого распределения. □
Задача 1.15. При допущении о том, что некодирующая ДНК описана
моделью независимого порождения с вероятностями нуклеотидов, равными 1/4,
покажите, что в 75 % случаев можно ожидать, что начало гена (допуская,
что единственный старт-кодон представлен кодоном ATG) совпадёт с
началом «длиннейшей ОРС».
Решение. Примем допущение о том, что определённый кодон ATG есть
действительное начало гена, не перекрываемое смежным геном. Тогда
последовательность ДНК, расположенная выше данного кодона ATG,
представляет собой некодирующую ДНК, описываемую моделью независимого
\ LJ — A

34
Глава 1
порождения. Каждый возможный триплет появляется в описываемой этой
моделью последовательности с вероятностью 1/64. Для того чтобы
найти вероятность того, что данный кодон ATG, расположенный в
действительном начале гена, является ближайшим к 5'-концу ATG в ОРС, мы
рассмотрим дополняющее событие, состоящее в том, что выше
действительного начала существует ещё один кодон ATG, в котором начиналась
бы ещё более длинная ОРС. Путём изучения неперекрывающихся
триплетов, расположенных выше от данного кодона ATG, по одному за раз, и
начиная с непосредственно примыкающего к ATG, мы наблюдаем один из
следующих возможных исходов. 1) Выбранный триплет — один из
шестидесяти кодонов, в число которых не входят триплеты ATG, TAA, TGA и
TAG. В этом случае мы продолжаем процесс изучения триплетов. 2) Этот
триплет — один из трёх стоп-кодонов (ТАА, TGA и TAG). Мы
останавливаемся и делаем вывод, что первоначально рассмотренный кодон ATG
является крайним левым триплетом ATG в ОРС. 3) Изучаемый триплет —
ATG. Мы останавливаемся и заключаем, что первоначально
рассматриваемое действительное начало гена не является крайним левым триплетом
ATG в ОРС. Вполне очевидно, что завершение процедуры просмотра при
достижении одного из стоп-кодонов будет происходить в три раза чаще,
чем завершение по достижении кодона ATG. Поэтому в 75 % случаев
начало действительного гена в кодоне ATG совпадает с крайним левым ATG
в ОРС, что указывает на длиннейшую ОРС при заданном стоп-кодоне на
3'-конце. □
Задача 1.16. Предположим, что мы рассматриваем две модели
независимого порождения, описывающие последовательности нуклеотидов. Первая
модель, М\, имеет те же самые вероятности появления нуклеотидов, что
и в задаче 1.6. Вторая модель, Мч, приписывает каждому типу нуклеоти-
да вероятность появления в любой позиции, равную 1/4. При наблюдении
последовательности х = ACTGACGACTGAC сравните правдоподобия
этих моделей.
Решение. Правдоподобие некоторой модели определяется как условная
вероятность данных (последовательность х) для заданной модели ([67],
стр. 6). Таким образом, мы должны сравнить вероятности
последовательности х в каждой модели. Правдоподобие модели М\ определяется как

1.2. Дополнительные задачи
35
Точно так же правдоподобие модели М% описывается выражением
Р{х\М<2) = (1/4)13. Отношение правдоподобия определяется как
Р(х\М2) _ 2013 2 озээ, !
Р{х\М,) -413-36-77" '
11оэтому для наблюдаемой последовательности х модель М^ имеет
большее правдоподобие, чем модель М\. □
Задача 1.17. Кольцевая двунитевая ДНК длины L = 3400 п. н. была разре-
чана ферментом рестрикции. Последующее разделение посредством гель-
электрофореза указало на присутствие пяти фрагментов ДНК. Оказалось,
что рассеянный исследователь не мог вспомнить точный тип фермента
рестрикции, который был использован. Однако он знал, что химикат был взят
из коробки, содержащей равное число 4-рестриктаз 6-рестриктаз
(ферменты рестрикции, которые узнают (и разрезают в них), соответственно,
определённые участки длины 4 п.н. и определённые участки длины 6 п.н.).
Какова апостериорная вероятность того, то была использована именно 4-
рестриктаза, если последовательность ДНК может быть представлена
моделью независимого порождения с равными вероятностями появления нук-
леотидов Т,С, А и G.
Решение. Вероятность появления участка рестрикции в некоторой
рассматриваемой позиции последовательности ДНК равна р\ = (1/4)4 =
= 0,003906 для 4-рестриктазы и р2 = (1/4)6 = 0,000244 для
6-рестриктазы.
Мы делаем допущение о том, что в обоих случаях число X участков
рестрикции в последовательности может быть приближено распределением
Пуассона с параметром Ai = piL = 13,28 для 4-рестриктазы и А2 = P2L =
= 0,83 для 6-рестриктазы (см. решение задачи 1.11). Тогда мы получаем
(Хл)5
Р(Х = 5|4-рестриктазы) = e"Al^- = 0,00588,
5!
Р(Х = 516-рестриктазы) = е-*2^—f- = 0,00143.
о!
Для вычисления апостериорной вероятности того, что фрагменты
рестрикции были получены 4-рестриктазой, мы используем теорему Байеса:
Р(4-рестриктазы|Л' = 5) =

36
Глава 1
Р(Х = 5|4-рестриктазы)Р(4-рестриктазы)
Р(Х = 5|4-рест-зы)Р(4-рест-зы) + Р(Х = 5|6-рест-зы)Р(6-рест-зы)
0,00588-0,5
0,00588-0,5 4-0,00143-0,5
0,804.
Поскольку шанс того, что была использована 4-рестриктаза, составляет
80,4 %, первоначальная неопределённость, кажется, устранена. □
Задача 1.18. Приверженцы одной теории заявляют, что последний общий
предок птиц и крокодилов жил 120 миллионов лет назад (млнл.н.), тогда
как последователи другой теории полагают, что это время вдвое больше.
Сравнение гомологичных генов х1 и х2 двух видов, нильского крокодила и
средиземноморской чайки, показало в среднем 365 различий во фрагменте
длины 1000 п. н. Принято допущение о том, что мутации на различных
участках ДНК происходят независимо и в каждом участке число мутаций,
закрепившихся в ходе эволюции, приближается пуассоновским процессом.
Частота р закрепления мутаций на нуклеотидный участок в год равна Ю-9.
Для заданного наблюдаемого числа различий а) сравните правдоподобия
этих двух теорий и б) методом наибольшего правдоподобия определите
оценку времени расхождения. Для простоты сделайте допущение о том,
что за всю последовательность поколений на любом данном нуклеотидном
участке могло произойти не более одной мутации.
Ai(0)=JVi(0)=0
W)
N2(t)
Рис. 1.1. Простейшее филогенетическое дерево Т с парой гомологичных
генов х1 их2 в качестве его листьев (см. задачу 1.18)

1.2. Дополнительные задачи
37
Решение, а) Допуская, что расхождение двух видов произошло t лет назад,
мы рассматриваем простейшее филогенетическое дерево Т с листьями х1
и х2. Появление замен по ветвям этого дерева может быть описано двумя
независимыми пуассоновскими процессами Ni(r) и N2(7-) с параметром р.
Момент расхождения соответствует т = 0, а настоящее время — т = t (см.
рис. 1.1).
Мы будем сравнивать правдоподобия дерева Т при двух значениях
прошедшего времени, t = t\ = 120 млнл.н. и t = t2 = 240 млнл.н.,
связанных с конкурирующими теориями. Правдоподобие двулистного дерева
со свойством молекулярных часов зависит только от t. Тогда (условное)
правдоподобие на участке и, содержащем совпадающие нуклеотиды в
последовательностях ДНК, определяется как
Lu(t) = Р{х„ = х\|£, не более одной мутации на участке г) =
= P(N!(t) = 0,N2(t) = 0|ВД + N2(t) < 1) =
= Р(Мг(1) = 0,N2(t) = 0,iVi(*) + N2(t) < 1) =
P(tfi(t) + l\r2(t)<l)
= P(N1(t)=0,N2(t) = 0)
P(N1(t) + N2(t)^l) '
Числитель последнего выражения в уравнении (1.4) равен
P(iVi(t) = 0)P(N2(t) = 0) = e"2pt
«виду независимости процессов N±(г) и N2(r), тогда как величина JVi(£) +
Ь ЛГгС*) — опять же пуассоновская случайная величина (скажем, iV3(£))
с параметром 2р в силу известного свойства распределения Пуассона.
Таким образом, мы имеем
P(N!(t) + N2(t) < 1) = P(tf3(t) О) = P(N3(t) = 0) + P(W3(t) = 1) =
= e"2pt + 2^e-2pt,
и правдоподобие Lu(£) из уравнения (1.4) принимает вид
(1.4)

38 ГЛАВА 1
Точно так же на участке и с несовпадающими нуклеотидами правдоподобие
определяется как
Lu(t) = Р(х\ ф x^\t, не более одной мутации на участке г) =
= Р(ЗД) = О, N2(t) = l|iVi(t) + N2(t) ^ 1)+
+P(tfi(t) = hN2(t) = 0\N!(t) + N2(t) < 1) =
= 2P(Ni(t)=0)P(N2(t) = l) =
P(^i(*) + JV2(t)<l)
- 2е"Р^е"Р* - 2pt(l + 2P*)-1. (1.6)
-2p* i Oritp-lpt
e-?pt + 2p£e
Из уравнений (1.5) и (1.6) мы выводим правдоподобие дерева Т с двумя
листьями, которые представляют геномные последовательности длины N,
выровненные между собой с М несовпадениями:
N
L(t) = Д Lu{t) = (1 + 2pt)-N(2pt)M. (1.7)
Для проверки этих двух теорий мы вычисляем логарифмическое отношение
шансов при t\ = 120 млн л. н. и t2 = 240 млн л. н.:
In ^р( = Nln(l + 2P*2) - iVln(l + 2ph) + Mln(2p*i) - Af ln(2p*2) =
L(t2)
= -252,99<0.
Поэтому имеющиеся данные поддерживают теорию, что птицы и
крокодилы разошлись 240 млнл.н., так как эта теория имеет большее (условное)
правдоподобие, чем конкурирующая с ней.
6) Мы определяем методом наибольшего правдоподобия оценку t*
времени расхождения этих двух видов как точку максимума логарифма
правдоподобия L(t), формула (1.7):
dlnLjt) _ 2Np 2pM
It ~ ~l + 2pt* + 2^*~ ~ '
** = „ ,^ wx = 2>874 *1о8-
2p(N - М)

1.2. Дополнительные задачи 39
Таким образом, t* = 287,4 млнл.н. — время расхождения с наибольшим
правдоподобием, тогда как значение наибольшего правдоподобия per se
определяется как
Lmax = L(t*) = (1 + 2pt*)~N(2pt*)M = Ю-285. п
Задача 1.19. Известно, что у высших эукариотов CpG-островки
относительно богаты динуклеотидами CpG,4 тогда как в остальной части
хромосомы эти динуклеотиды встречаются довольно редко. Принято допущение,
что частота появлений динуклеотидов CpG в GpG-острове может быть
приближена распределением Пуассона с двадцатью пятью
динуклеотидами CpG на фрагмент длины 250 п.н. в среднем, тогда как в остальной
части ДНК это среднее число — десять CpG на 250 п. н. Предложите ал-
тритм типа Байесова для опознавания CpG-островка. Как этот алгоритм
охарактеризует фрагмент ДНК длины 250 п. н., содержащий девятнадцать
динуклеотидов CpG?
Решение. Мы делаем допущение о том, что числа появлений
динуклеотидов CpG и в CpG-островках и в не-СрС-островках описываются
распределением Пуассона (с параметрами, соответственно, Ai = 25 и Аг = 10).
Если данный фрагмент ДНК длины 250 п. н. содержит п
динуклеотидов CpG, то насколько правдоподобна гипотеза о том, что этот фрагмент
ДНК принадлежит к CpG-острову? Мы должны сравнить две
апостериорные вероятности: Pi = Р(является GpG-островком при п наблюдаемых
динуклеотидах CpG) и P<i = Р(является He-CpG-островком при п
наблюдаемых динуклеотидах CpG). Допуская, что обе альтернативные гипотезы
(о том, что данный фрагмент является GpG-островком, и о том, что он
является He-GpG-островком) a priori одинаково правдоподобны, мы используем
теорему Байеса, чтобы вычислить Р\ и Рз-
Рх = Р(фр-т ДНК с п CpG имеет распр-е Пуассона с Ai = 25) =
P{nCpG\\1=2b)\
Р(п CpG\X1= 25) \ + Р{п CpG|A2 = 10)i
= 25ne"25
10ne-io + 25ne-25'
4CpG — это CG диноклеотид на одной цепи. Буква р в этом обозначении появилась для
того, чтобы не путать с Уотсон-Криковскими CG-парами, когда нуклеотиды С и G живут на
разных цепях. CpG-островки — это скопление CpG-nap, играющее биологическую (регуля-
торную) роль. — Прим. ред.

40 Глава 1
Выше мы применяли формулу для распределения Пуассона и сокращали
общий множитель п\. Точно так же
Pi = Р(фр-т ДНК с п CpG имеет распр-е Пуассона с \2 = 10) =
P(nCpG\X2 = Ю) i
Р(п CpG\Xi = 26)| + Р(п CpG\X2 = 10)|
_ 10ne~10
10ne-io _|_ 25ne"25
или P2 = 1 — Pi. Простой алгоритм опознавания в случае CpG-островка
работает следующим образом. Для данного фрагмента ДНК длины 250 п. н.
с и наблюдаемыми динуклеотидами CpG вычисляется значение Pi. Если
Pi > 0,5 (Pi > P2), то данный фрагмент ДНК опознаётся как часть CpG-
островка. В противном случае этот фрагмент опознаётся как часть не-GpG-
островка.
При п = 19 мы имеем
(25)19е~25
р. = v ; = и Q2
1 (25)19е"25 + (10)19е"10 ' '
Р2 = 1-Р1 = 0,08,
и мы заключаем, что данный фрагмент ДНК принадлежит к GpG-острову.
П
Задача 1.20. При условиях, оговорённых в задаче 1.19, принято
следующее правило принятия решения: если во фрагменте ДНК длины 250 п. н.
наблюдается более восемнадцати динукеотидов CpG, то он опознаётся как
GpG-островок. Определите частоты ложного положительного и ложного
отрицательного результатов этого метода5.
Решение. Коэффициент ложных положительных результатов (КИПР)
определяется как вероятность того, что правило опознало He-GpG-островок в
качестве GpG-островка. Поскольку число X динуклеотидов CpG в любом
5 Вообще говоря, задача не корректна, поскольку биологический объект CpG-островок
не определен и не показана выборка биологических CpG-островов. Здесь же ложно-
положительно и ложно-отрицательно определяются относительно другого метода
предсказания. — Прим. ред.

1.2. Дополнительные задачи 41
uc-CpG-ocrpoBQ описывается распределением Пуассона с параметром Л =
10, мы имеем
КЛПР = Р(более восемнадцати CpG из 250|не-СрС-островок) =
+оо 18
= Р(Х > 18|А = 10) = ^ Р(Х = п) = 1 - ^Р{Х = п) =
п=19 п=0
= 1_уе-ю!0^ о,007.
71=0
Коэффициент ложных отрицательных результатов (КЛОР)
определяется как вероятность того, что CpG-островок будет опознан как KQ-CpG-
островок. Поскольку число У динуклеотидов CpG в области CpG-островка
имеет распределение Пуассона с параметром А = 25, коэффициент ложных
отрицательных результатов определяется как
КЛОР = Р(не более восемнадцати CpG из 250|Ср6?-островок) =
18
= P(Y ^ 18|А = 25) = ^2 P(Y = *) =
18 П=°
71=0
Обратите внимание, что КИПР < КЛОР. Это означает, что более
правдоподобным будет тот исход, при котором правило классификации решит, что
ДНК Ср(7-островка является не-СрС-островком ДНК, чем
противоположный. □
Задача 1.21. Неоднородная последовательность ДНК, как известно,
содержит как области, богатые по составу С + G, так и области с
несмещённым (однородным) составом нуклеотидов. Мы делаем допущение о том,
что области с высоким содержанием С + G описывает модель
независимого порождения (модель Р) с параметрами рт = 1/8, рс = 3/8, рл = 1/8
и ра = 3/8. Области с однородным составом нуклеотидов описываются
моделью независимого порождения (модель Q) с параметрами qr = 1/4,
qc = 1/4, qa = 1/4 и qo = 1/4. Для заданного фрагмента ДНК X
определяется логарифмическое отношение шансов L = log2[P(X\P)/P(X\Q)],
и если L ^ 0, то фрагмент X классифицируется как фрагмент с высоким
содержанием С + G; если L < 0, то фрагмент X классифицируется как
несмещённый по составу. Определите вероятности ошибки первого рода

42
Глава 1
(коэффициент ложных отрицательных результатов) и ошибки второго рода
(коэффициент ложных положительных результатов) классификации
фрагмента ДНК длины п. Рассмотрите п = 10, 20 и 100.
Решение. Для последовательности ДНК X длины га, мы проверяем
нулевую гипотезу,
Но = {X принадлежит к области, богатой С + G} = {X е Р},
против альтернативной гипотезы,
На = {X принадлежит к области с однородным составом} = {X е Q}.
Логарифмическое отношение шансов определяется как
L = log2[P(X\P)/P(X\Q)\ =
1 „ ((РА\П1 /РС\П2 (РТ\ПЗ (PG\ni\
=1о(ЦЫ (w) Ы Ы ) =
13 13
= щ log2 - + п2 log2 2 + пз log2 2 + n4 log2 2 ~
« 0,585(п2 + гс4) - (ni + п3),
где щ, гс2, гс3 и П4 — соответственно, числа нуклеотидов Л, С, Г и (7,
наблюдаемые во фрагменте X. Мы принимаем гипотезу Щ (и отвергаем #а),
если L ^ 0, то есть если Р(Х|Р) ^ P(X|Q); и мы отвергаем Щ (и
принимаем На) в противном случае. Ошибка первого рода а (уровень значимости
теста) определяется из выражения
а = Р(ошибка первого рода) = Р(Н0 отвергнута|Я0 верна) =
= P(L < 0\Х еР) = Р(0,585(п2 + п4) - (ni + п3) < 0|Х е Р).
Затем мы определяем исходы бернуллиевого испытания, интерпретируя
появление А или Т в данном участке последовательности X как «успех»,
а появление С или G как «неудача». Если р — вероятность «успеха», то
число «неудач» в п бернуллиевых испытаниях, S = п\ + пз, имеет
биномиальное распределение с параметрами пир. Ошибка первого рода, а,
принимает вид
а = Р(0,585(п2 + га4) - (гц + п3) < 0|Х е Р) =
= Р(0,585(п - S) - S < 0|5 е В(п,р = 1/4)) =

1.2. Дополнительные задачи 43
P(S > 0,369n|S G B(n,p = 1/4)) =
fc /~\ п—к
- Е ©(!)(!) -(1) Е С)--
fc:0,369n<fc^n V / \ / \ / V / fe:0,369n<fe<n Ч 7
Из центральной предельной теоремы следует, что, по мере того как п —* ос,
последовательность случайных переменных (S - Е£)/VVarS слабо
сходится к стандартному нормальному распределению. Поэтому при
больших п
a = P(S> 0,369п|5 6 В(п,р = 1/4)) =
= р (s-ES > 0,369п-Е5^\
= Р
Vv™s VSferS J
S~°'^n > 0,2748Vn I « 1 - Ф(0,2748V^).
0,25V3^ J
Чдесь
*<x)-^/
e 2dt
является функцией распределения стандартного нормального
распределения.
Точно так же, вероятность ошибки второго рода мы находим как
/3 = р(ошибка второго рода) = Р(Щ принята|Яо ложная) =
= P(L ^ о\х eQ) = Р(0,585(п2 + п4) - (т + п3) ^ 0\Х е Q) =
= Р(0,585(п - S) - S ^ 0\S е В{п,р = 1/2)) =
= P(S ^ 0,369njS € В(п,р = 1/2)) =
= е o(j)'ar-a)" s о-
fc:0^fc^0,369n \/\/\/ \ / fc:0^fc^0,369n Ч 7
И снова, при больших п применение центральной предельной теоремы
ведет к равенству:
ft = P(S < 0,369n|S е B(n,p = 1/2)) = P (^Jj| < 0.369n-Eg\ =
yvVarS vVarS у
= P I S ~ °?ДП < -0,262^ | « Ф(-0,262Vn).
У 0,5v/n /

44
Глава 1
При п = 10, 20, 100 мы вычисляем:
а10 = P(S ^ 4|5 € В(10,р = 1/4)) =
= 0,1460 4- 0,0584 + 0,0162 + 0,0031 4- 0,0004 = 0,2241,
/?ю = P(S < 3|5 € В(Ю,р = 1/2)) =
= 0,001 4 0,0098 + 0,0439 + 0,1172 = 0,171;
азо = P(S > 8|5 G В(20,р = 1/4)) =
= 0,069 + 0,0271 + 0,0099 + 0,003 + 0,0008 + 0,0002 = 0,1019,
/320 = P(S < 7\S G В(20,р = 1/2)) =
= 0,0002 4 О, ООН 4 0,0046 4 0,0148 4 0,037 4- 0,0739 = 0,1316;
аюо = 1 - Ф(2,748) « 0,0028,
/?юо = Ф(-2,62)«0,0044.
Как и следовало ожидать, а и /3 убывают при возрастании длины
последовательности нуклеотидов и увеличении количества статистических данных.
□
Задача 1.22. Олигонуклеотид ТТТТАААА наблюдался в кодирующих
белок областях частично секвенированного генома бактерии с частотой 0,008.
Такой же олигонуклеотид наблюдался в некодирующих областях этого же
генома с частотой 0,003. Во вновь секвенированном фрагменте ДНК
длины 400 п. н. олигонуклеотид ТТТТАААА встретился четыре раза.
Найдите апостериорную вероятность того, что этот фрагмент является частью
кодирующего белок гена. Априорную вероятность того, что произвольно
отобранный фрагмент ДНК длины 400 п. н. находится в кодирующей белок
области, принято считать равной 0,8.
Решение. Мы определяем следующие события:
В\ = {фрагмент 400 п. н. расположен в кодирующей белок области},
Дг = {фрагмент 400 п. н. расположен в некодирующей области},
С = {ТТТТАААА встретился четыре раза во фрагменте 400 п. н.}.
По условию P(Bi) = 0,8 и Р(В2) = 1 - P(Bi) = 0,2. Апостериорная
вероятность Р(В\\С) может быть рассчитана с помощью теоремы Байеса:
P(Bl\C) Р(С\В1)Р(В1)
P(C|Bi)P(Bx) + Р(С\В2)Р(В2)

1.3. Дополнительная литература
45
Так как вероятность р «успеха» мала, а число испытаний N велико, в
качестве приближения биномиального распределения числа появлений олиго-
нуклеотида ТТТТАААА («успехов») мы используем распределение
Пуассона с параметром А = pN. Таким образом, для кодирующей и некодирую-
щей последовательностей мы имеем, соответственно, Ai = 3,2 и Х2 = 1,2.
Вероятности наблюдения четырёх олигонуклеотидов ТТТТАААА
определяются как
Р(С\Вг) = Р(четыре ТТТТАААА\Вг) = е~3'2^- = 0,1781,
Р(С\В2) = Р(четыре ТТТТАААА\В2) = е"1'2^- = 0,0260.
Тогда апостериорная вероятность того, что рассматриваемый фрагмент
ДНК длины 400 п. н. является частью кодирующего белок гена, принимает
вид
( . . _ 0,1781-0,7 _
П*1\Ч- 0,1781.0,7 + 0,026-0,3 -°>94- П
1.3. Дополнительная литература
С середины 1990-х гг. было издано много учебников по
биоинформатике и вычислительной геномике. См., например, [275], [18], [76], [161],
[132], [62]. Они отличаются подбором охваченных тем, что отражает
поразительное разнообразие задач и направлений исследований в
биоинформатике сегодняшнего дня. Также мы хотели бы упомянуть монографию по
молекулярной биологии [36], в которой содержится всестороннее и краткое
описание геномики с позиции молекулярного биолога.

Глава 2
ПОПАРНОЕ ВЫРАВНИВАНИЕ
Понятие подобия последовательностей, возможно, является самым
фундаментальным понятием анализа биологических последовательностей.
Точно так же, как подобие морфологических признаков служило
свидетельством генетических и функциональных отношений между видами в
классической генетике и биологии, подобие биологических последовательностей
могло бы во многих случаях указывать на структурную и
функциональную консервативность среди эволюционно связанных последовательностей
ДНК и белков. Введение биологически значимой количественной меры
подобия последовательностей — счёта1 подобия — представляет собой
далеко не тривиальную задачу. Ничуть не проще другая задача — разработка
алгоритмов, которые могли бы при заданной системе очков найти
выравнивание двух последовательностей с возможно лучшим счётом. Наконец,
третий необходимый компонент вычислительного анализа подобия
последовательностей — метод оценки статистической значимости выравнивания.
Такой метод, устанавливающий предельные значения, в пределах которых
наблюдаемые счета являются статистически значимыми, работает должным
образом, как только статистическое распределение счетов подобия
определено аналитически или же вычислительными методами.
Глава 2 «АБП» включает двенадцать задач, которые требуют знания
концепций и свойств алгоритмов попарного выравнивания. Традиционно
эта тема известна биологам лучше всего ввиду её огромного практического
значения. И в самом деле, исследование любой последовательности
начинается с поиска гомологичных последовательностей в базах данных с
помощью программы BLAST. Эта программа основана на очень эффективном
эвристическом алгоритме попарного выравнивания.
1В некоторых источниках для обозначения понятия счёта употребляется термин «вес»,
однако это не совсем корректно. Во-первых, для поиска подобия или выравнивания
последовательностей нередко применяются методы теории графов, и тогда понятия счетов
последовательностей и весов рёбер соотносятся друг с другом, поэтому не следует их путать. Во-
вторых, система «очков» и «штрафов» предполагает скорее накопление определённого счёта,
чем набор веса. В третьих, отрицательная величина счёта менее абстрактна, чем
отрицательное значение веса. — Прим. перев.

2.1. Оригинальные задачи
47
Дополнительные девять задач дают вспомогательную информацию,
необходимую для лучшего понимания теории эволюции белка (после
ознакомления с логарифмическими счетами шансов замен аминокислот), а
также моделей, используемых при оценке статистической значимости
наблюдаемых счетов подобия последовательностей.
2.1. Оригинальные задачи
'Задача 2.1. Аминокислоты D, Е и К являются заряженными; V, I и L —
гидрофобными. Каков средний счёт BLOSUM50 в пределах группы из трёх
заряженных аминокислот? Каков он в пределах гидрофобной группы?
Чему равен счёт между двумя группами? Дайте обоснование наблюдаемой
структуры распределения2.
Решение. Счета замен BLOSUM50 в пределах группы заряженных
аминокислот и в пределах группы гидрофобных аминокислот были взяты из
таблицы 2.1 и показаны в таблице 2.2.
Средний счёт замен в пределах заряженной группы Sch = 2,66, а
таковой в пределах гидрофобной группы — Sh = 3,22.
Счета замен между аминокислотами из различных Ypynn приведены
в таблице 2.2, в (со средним значением S = —3,44).
Как и следовало ожидать, счета замен между аминокислотами с
подобными физико-химическими свойствами (в пределах группы заряженных
или гидрофобных аминокислот) выше, чем счета замен между
аминокислотами с различными свойствами (между группами). Алгоритмы
выравнивания последовательностей, максимизирующие полный счет, стремятся
максимизировать число выровненных пар аминокислот с подобными физико-
химическими свойствами. □
Задача 2.2. Покажите, что распределения вероятности f(g) длины
пропуска д, которые соответствуют пропорциональной и линейной схемам
штрафов за пропуски, являются геометрическими распределениями формы
f(g) = fce-Ч3
2 Строго говоря, задача не корректна, поскольку усреднение должно проводиться с учетом
частот встречаемости остатков! — Прим. ред.
3В соответствующей модели генерации пропусков — например, если пропусков устроена
так, что пропуски бывают только длины 10, то распределение вероятностей будет
дискретным. — Прим. ред.

Глава 2
II ' I I I I I I I I I III II
"^' I I I I I I I I III III I
11^11 I I I I I I I I I I I I I I lH
III I I I I I I I I I I I I I II
||73|rHH^OHOHOHCOMO<NCCHl/)N^CM(N
I I I III III III
|1рц|1-1сосч|т^^^т^с<1с<1со^гне0'^01-нтнт^сосо
I I I I I I I I I I I I I H I I I I
I II II I II I I III
11^ I I I I I III I I I I I
IMh nOHC0(SH(NOWW^(N^HOHCC(NW
1,Л| ' M I II III I I I I
||^|CSlCO^^CSI<^CO^COr4lf)COfnr-H^COi-ICSi-l^-H
I I I I I I I I I I I I I I I
I I I I I I I I I I I I I I I
|И"" I II lHl I I I I I I I I
||С5|ОС0ОтН(^С^С000<^^т}<<^С0^С^ОС<1С0С0^
11 ' I I I I I I I I I I I I I I I I
||Щ |т—I OOMWfS«WO^WrH(NCOHHHCO(NM
I I II I I I I I I I I
11 ' ' I II II II I I I I
1,11 I I lHl I I I I I I I I I I I I I I
||n|NW(N»^O(NHH^r}(H^L0HOHWC0^
11 ' II I I I I I I I I I I I I I
ll^1 'I I I I I I I III
11 ' I III I II I I I I I I I I
|ГЧ I I I I I I I I I I I I I II

2.1. Оригинальные задачи
49
Таблица 2.2. Счета замен для трёх групп аминокислот
а) б) в)
РЕК V I L V I L
D 8 2 -1 V 5 4 1 D -4 -4 -4
Е 2 б 1 I 4 5. 2 Е -3 -4 -3
К -1 1 6 L 1 2 5 К -3 -3 -3
Решение. Штраф за пропуск j(g) определяется как логарифмическая
вероятность появления пропуска заданной длины д: ^у(д) = log(/(^)).
Таким образом, если штраф за пропуск ^у(д) налагается пропорционально как
j(g) = —gd со штрафом за введение пропуска d, то
етЫ = e-gd = /(ff).
г)то равенство соответствует формуле f(g) = ке~Хд при к = 1 и А = d.
Если штраф за пропуск определен линейным счётом j(g) = — d —
- (д — 1)е со штрафом за введение пропуска d и штрафом за продолжение
пропуска е, то
е7Ы = f^ = ee-de-9e
Теперь снова f(g) = ке~Хд при к = ee~d и А = е.
Замечание. Обратите внимание, что в обоих вышеописанных
случаях функция штрафов за пропуски f(g) не определяет собственно
нормализованное распределение вероятностей длин пропусков. Действительно,
в случае пропорциональной схемы с любым положительным штрафом за
введение пропуска d мы имеем
оо оо
Точно так же, при линейной схеме
оо оо
£/(<?) = Eee-de-9e =
9=0 д=0

50 Глава 2
Однако ситуация может быть исправлена введением постоянных
нормализации: С = 1 — e~d для пропорционального счёта; С = 1 — e~e/ee~d
для линейного счёта. Тогда может быть определено собственно
распределение вероятностей длин пропусков:
Р(длина пропуска равна д) = Р(д) = Cf(g).
Обратите внимание, что в своей конечной форме вероятность отдельно
взятой длины пропуска при линейной схеме не зависит от штрафа за введение
пропуска d. □
Задача 2.3. Типичные параметры штрафа за пропуски, применяемые на
практике, следующие: d = 8 при пропорциональной системе очков и в
случае линейной -й=12ие = 2 (счета выражены в полубитах). Бит —
единица, получаемая, если взять логарифм по основанию 2 от вероятности,
так что в единицах натуральных логарифмов эти штрафы за пропуски
имеют вид, соответственно: d' = 8 In 2/2 и d' = 12 In 2/2, е' = 2 In 2/2. Каковы
соответствующие вероятности того, что в некоторой позиции начинается
пропуск (любой длины), и распределения длины пропуска при условии,
что в данной позиции есть пропуск?
Решение. Учтите, что если величина х измеряется в полубитах (у =
= 2 log2 x) и в единицах натуральных логарифмов (z = In ж), то величины
у и z связаны между собой следующей формулой:
0i „ „. 21пх 2z
Таким образом, если в полубитах штраф за введение пропуска d = 8, то
в единицах натуральных логарифмов d' = 8 In 2/2. Точно так же, если в
полубитах штраф за введение пропуска d = 12 и штраф за продолжение
пропуска е = 2, то в единицах натуральных логарифмов d! = 12 In 2/2,
e' = 21n2/2.
В случае пропорциональной системы очков (см. задачу 2.2),
распределение вероятности длины пропуска определяется следующей формулой:
Р(д) = Р(длина пропуска равна д) = (1 — e~d )e~gd .
Если d' = 4In2, то Р(д) = (15/16)(1/16)у. Вероятность того, что в
некоторой позиции начинается пропуск (любой длины), мы определяем из:
Р(пропуск присутствует) = 1 — Р(нет пропуска) =
= 1 - Р(0) = 1 - 15/16 = 1/16.

2.1. Оригинальные задачи
51
11ри существовании пропуска (д > 0) распределение длины пропуска
определяется условными вероятностями
Р(длина пропуска равна ^|пропуск существует) =
И случае линейной системы очков (задача 2.2) распределение вероятности
дпины пропуска определяется следующей формулой:
РЫ = (1-е-е')е-<
Ото распределение не зависит от штрафа за введение пропуска d!.) Ec-
ии с/ = In 2, то распределение вероятностей Р{д) принимает вид Р(д) =
(1/2)р+1. Подобно случаю пропорциональных штрафов, сначала мы
вычисляем вероятность существования пропуска в данной позиции:
Р(пропуск существует) = 1 — Р(д = 0) = 1— т* = «•
Наконец, вероятность пропуска некоторой длины д, при существовании
пропуска (любой длины), определяется как
Р(д) /г\9
Р(д\щ>опуск существует) = —— = 2Р(д) = ( - I . Q
1ндача 2.4. С помощью матрицы BLOSUM50 (таблица 2.1) и линейного
ш графа за пропуски d = 12, е = 2 вычислите счета двух
нижеприведённых выравниваний: а) альфа-глобина человека и леггемоглобина жёлтого
шопина:
IIBA_HUMAN GSAQVKGHGKKVADALTNAVAHV D-DMPNALSALSDLHAHK
++ ++++H+ KV + +А ++ +L+L+++H+ К
I,C,B2_LUPLU NNPELQAHAGKVFKLVYEAAIQLQVTGWVTDATLKNLGSVHVSK
б) та же самая область белковой последовательности альфа-глобина
человека и её гомолога — глутатион-8-трансферазы нематоды, называемой
l'llGll.2:
I IBA_HUMAN GSAQVKGHGKKVADALTNAVAHVDDMPNALSALSD LHAHK
GS+ + G + +D L ++ H+ D+ A +AL D ++AH+
V11G11.2 GSGYLVGDSLTFVDLL—VAQHTADLLAANAALLDEFPQFKAHQ

52 Глава 2
Решение. Полный счёт всякого выравнивания представляет собой сумму
счетов замен выровненных аминокислот и штрафов за пропуски,
определяемых формулой j(g) = —12 — 2(0 — 1), где д — длина пропуска. Для первого
вьфавнивания мы вычисляем
Si = a(G,N) + e(S, N) + • • • + s(#,S) + з(К9К) =
= 0 + 1-1 + 2 + 1 + 2 + 0 + 10 + 0-2 + 6 + 5-3-1-2 + 1-2+
+0 + 5 + 0-1 + 1 + 1- Щпропуск) - 1 - Щпропуск) -4-1-1-1+
+0 + 5 + 0-1 + 5 + 0 + 0 + 1 + 10 + 0-1 + 6= 10.
Для второго вьфавнивания
52 = s(G,G) + s(G,G) + • • • + з(Н,Н) + s(K,Q) =
= 8 + 5 + 0-1 + 1-3 + 8-1+0-3-1-1 + 0 + 8-2+
+5 - Щпропуск) +0 + 0-1 + 10 + 0-2 + 8 + 3-4-1 + 5-4+
+1 + 5 + 5-3 + 8- Щпропуск) + 1+0 + 5 +10+ 2 = 39.
Удивительно, что структурно и эволюционно правдоподобное
выравнивание альфа-глобина человека с леггемоглобином (первое выравнивание)
получает более низкий счёт, чем выравнивание альфа-глобина человека с
никак не относящейся к нему последовательностью белка нематоды (второе
выравнивание). Этот пример подчеркивает важность экспертной оценки
при заключении о гомологии на основании компьютерного анализа. □
Задача 2.5. Покажите, что число способов взаимной вставки двух
последовательностей длин п и га, с тем чтобы получить единую
последовательность длины 71 + га, при сохранении порядка символов в каждой,
равно (n+m).
Решение. Процесс вставки последовательности з/1,...,г/т в другую
последовательность #i,..., хп может быть описан как заполнение строки из
п + га пустых ячеек п + га символами sci,..., хп, yi,..., ут (один символ
на ячейку) при сохранении исходного порядка символов в обеих
последовательностях. Каждый вариант выбора п ячеек для символов х\,..., хп
определяет только один способ размещения этих символов, которые нельзя

2.1. Оригинальные задачи
53
переставлять между собой. Как скоро х-сы размещены, позиции для
символов 2/i,..., угп также определяются однозначно, так как они заполняют
оставшиеся пустые ячейки без перестановок. Следовательно, общее число
различных взаимовставленных последовательностей равно числу способов
выбора п ячеек из п + т ячеек:
\ п )~\ т )~
(п + т)\
\п\ ' □
mini
Задача 2.6. Верно ли утверждение, что, выбирая символы поочерёдно из
верхней и нижней последовательности всякого выравнивания, а затем
выбрасывая знаки пропусков, можно определить взаимно однозначное
соответствие между содержащими пропуски выравниваниями этих двух
последовательностей и взаимовставленными последовательностями, подобными
описанным в задаче 2.5?
Решение. Учтите, что рассмотрение этой задачи весьма громоздко.
Сначала мы покажем, что предложенная процедура не устанавливает взаимно
однозначное соответствие между содержащими пропуски выравниваниями
>1их двух последовательностей и взаимно вставленными
последовательностями, представленными в задаче 2.5.
В качестве примера мы рассмотрим содержащее пропуски
выравнивание А последовательностей х = х\,..., х± и у = yi,..., у&:
^ _ | ~ Xi - Х2 Х3 Х4 \
\ 2/1 2/2 2/з -2/4 2/5/
Чатем, развёртывая столбцы символов, мы переписываем выравнивание А
в виде одной последовательности (с символами пропусков): —, yi, х\, уъ, —,
/Aii #2, — )Яз> 2/4 >Я4) 2/5- Исключение знаков пропусков даёт
последовательность 2/ъжъ 2/2> 2/3) #2> #3)2/4* #4* 2/5 — взаимовставленную
последовательность, описанную в задаче 2.5. Таким образом, для заданного
выравнивания А последовательностей х и у мы строим точно одну
взаимовставленную последовательность. Очевидно, то же самое верно для
любого другого содержащего пропуски попарного выравнивания. Однако
можно показать, что любая взаимовставленная последовательность (кроме
/Л > ?У2) • • •) 2/ш) яъ #2) • • •) хп) соответствует более чем одному
выравниванию с пропусками. Например, одна и та же взаимовставленная последо-
вптельность 2/ъ#ъ 2/2)2/3) #2) £з>2/4> #4) 2/5 могла быть получена из восьми

54
Глава 2
различных содержащих пропуски выравниваний А\-А8 (и только из них):
Аг =
А2 =
А3 =
А* =
Аъ =
А6 =
А7 =
А8 =
U1
" \У1
\2/i
" \У1
\У1
\У1
' \2/1
" \2/1
XI
2/2
Xi
Х\
2/2
Х\
2/2
XI
Х\
Х\
2/2
Х\
2/з
2/2
2/з
2/з
2/2
2/2
2/з
2/2
#2
2/з
#2
Х2
2/з
2/з
я2
2/3
хз
2/4
#2
^3
#з
2/4
я2
#2
#3
Ж2
хЛ
Уь)"
хз
2/4
2/4
Х4
хз
хз
2/4
2/4
хз
хЛ
Уъ)"
хЛ
Уь)>
V*)'
- хЛ
2/4 2/5/ '
Х4 ~\
- Уь)л
Х4 -\
- Уь)'
— Хд —
2/4 - 2/5
Вообще, любая взаимовставленная последовательность, содержащая к
пар смежных символов Xi,yj, соответствует 2к различным содержащим
пропуски выравниваниям последовательностей х и у. Это подразумевает не
только то, что не существует никакого взаимно однозначного соответствия
между попарными выравниваниями с пропусками и взаимовставленными
последовательностями, но также и что число ЛГп,т возможных
выравниваний последовательностей х±,..., хп и yi,..., уш строго больше (n^m) —
числа взаимовставленных последовательностей, которые могут быть
получены из последовательностей х и у (см. задачу 2.5).
Число Мп,гп возможных попарных выравниваний с пропусками
Для того чтобы найти ЛГп,т, мы обращаемся к двумерной решётке L
порядка (п + 1) х (га + 1) (см. рис. 2.1).
Столбцы решётки L соответствуют элементам последовательности
xi,... ,хп (слева добавлен столбец с индексом 0); строки соответствуют
элементам последовательности г/ъ • • •, 2/т (сверху добавлена строка с
индексом 0). Диагональная стрелка, ведущая к ячейке (г, j)9 где г = 1,..., п

2.1. Оригинальные задачи 55
Х\ Х2 Хз Хп
Рис. 2.1. Двумерная решётка L порядка (га + 1) х (т + 1)
и j = 1,..., га, соответствует выровненным символам (**); горизонтальная
стрелка, ведущая к ячейке (г, •), где г = 1,..., п, соответствует символу х^
выровненному с пропуском (^); вертикальная стрелка, ведущая к ячейке
(•,j), где j = 1,..., га, соответствует символу 2/j, выровненному с
пропуском (~). Пусть ячейка (0,0) — начальный угол, а ячейка (п, га) — конечный
у.юл решётки L. Легко видеть, что любой непрерывный путь (ломаная
линия из стрелок) от начального угла до конечного угла уникально определяет
отдельное содержащее пропуски выравнивание последовательностей х и у.
И наоборот, любое выравнивание х и у соответствует только одному
непрерывному пути через решётку L, соединяющему её начальный и конечный
углы. Таким образом, существует взаимно однозначное соответствие
между содержащими пропуски выравниваниями последовательностей х и у и
непрерывными путями через решётку L, ведущими от её начального угла
до конечного. Следовательно, отыскание числа таких полных путей
позволит в то же самое время определить число Nn,m-
Мы приписываем горизонтальные, вертикальные и диагональные
стрелки, соответственно, к векторам (1,0), (0,1) и (1,1). Каждый
допустимый путь через решётку L соответствует последовательности
векторов (ii,ji),..., (iqjq), где каждый вектор (ii,ji) представляет собой вектор
(1,0), или (0,1), или (1,1), и
я
J2(UJi) = (n,m). (2.1)
/=i
С другой стороны, каждая такая последовательность определяет один
допустимый путь, то есть одно выравнивание. Теперь мы должны определить,
сколько таких последовательностей существует. Если число векторов (1,1)

56
Глава 2
в сумме в уравнении (2.1) равно к, где к = 0,..., min(n, га), то число
векторов (1,0) и (0,1) должно быть равно, соответственно, п — к и га —
— к, а общее число q членов в сумме в уравнении (2.1) при этом равно
п + т — к. Число способов расположить эти векторы в
последовательности (ii,ji),..., (in+m-k,jn+m-k) равно мультиномиальному
коэффициенту (fc ]^L™~^_fe). Следовательно, число разрешённых путей через решётку L
(и число содержащих пропуски выравниваний последовательностей длин п
и га) равно
min(n,m) / , v
л/* — V^ ( п + т — к \
n'm i^ \к,т — к*п — к)
fc=o х ' ' 7
Формула (2.2) ведёт к нескольким следствиям.
Следствие 1. Рекуррентная формула для Л/*п,т
Согласно редукционистскому подходу сложную задачу надлежит
сводить к комбинации более простых. Сейчас мы обсудим пути
осуществления этого общего принципа. Весь набор возможных выравниваний может
быть разделён на три класса: 1) выравнивания, заканчивающиеся
выровненной парой (*п); 2) выравнивания, заканчивающиеся пропуском в
последовательности х: (~); 3) выравнивания, заканчивающиеся пропуском
в последовательности у: (х"). Поэтому содержащее пропуски
выравнивание последовательностей х\,..., хп и yi,..., ym может быть получено из
более коротких выравниваний одним из трёх возможных способов, в
зависимости от пары символов в последнем столбце выравнивания: из
выравнивания последовательностей х\,..., хп-\ и ух,..., ym-x путём добавления
выровненной пары (*п); из выравнивания последовательностей х\,..., хп
и 2/1, • • • ,2/m-i посредством добавления пары ( ~ ) или из выравнивания
последовательностей х\,..., хп-\ и ух,•••, ym, добавляя пару (^). Это
виртуальное построение даёт следующую рекуррентную формулу
нахождения числа содержащих пропуски выравниваний двух последовательностей
с длинами пит:
Nn,m = Л/*п-1,т-1 + Л/"п,т_1 + Л/"п_1,т. (2.3)
Начальные значения величины Мп^ш СЛ/"п,о и Л/"о,т) определяются путём
непосредственного применения формулы (2.2):
КГ _ / п \ _ п\ _ -I
yVn'° to,o,fJ o!0!n! ' /24)
кг _ ( гп \ _ т\ _ л
лоУт - to>mi0; - 0!шЮ! - i.

2.1. Оригинальные задачи 57
Таблица 2.3. Результаты вычисления Мп trn при малых значениях ть и тгь
О 1
0 1
1 ]
2 1
3 ]
4 1
1 1
1 3
1 5
1 7
L 9
1
5
13
25
41
1
7
25
63
129
1
9
41
129
321
С помощью уравнений (2.4) и (2.3) значения Ып,*т могут быть
вычислены при любых целых числах пит. Например, в таблице 2.3 приведены
значения величины Nn,m при п, га < 4.
Следствие 2. Число содержащих пропуски выравниваний без
выровненных пар символов
Член, соответствующий к = 0 в уравнении (2.2), даёт число выравни-
наний, не содержащих выровненные пары символов. Хотя случай к = О не
имеет особого практического значения, легко видеть, что
_ fn + m\ _ (n + ra)! _ /n + ra\
а°= \0,m,n) = 0!m!n! = ^ m у
что означает, что а$ равно числу вставленных последовательностей длин
и и га (задача 2.5). Взаимно однозначное соответствие между этими двумя
множествами может быть установлено в соответствии с процедурой,
предложенной в утверждении задачи 2.5.
Обратите внимание, что при п, га > 1 член, соответствующий к = 1
II формуле (2.2), строго больше а^:
_/ §п + 171 —1 \_ (n + m-1)! _
ai= \l,m-l,n-l) = l!(m-l)!(n-l)! "
пт (п + гп\ пт л . п
П + т\^ 772 ) 71 + 771
Следствие 3. Асимптотическое поведение Л/*п,п, нижний и верхний
пределы
В случае последовательностей х иу с равными длинами, п = га,
формула (2.2) принимает вид
^\к,п-к,п-к)

58
Глава 2
По мере того как п возрастает до бесконечности, асимптотическое
поведение членов на правой стороне уравнения (2.5) можно было бы прояснить.
Итак, мы замечаем, что член, соответствующий к = 0 (см. задачу 2.7),
определяется в виде
\0, 71, П/ \П ) 0П
7ГП
В случае к = 1 член (см. следствие 2) определяется как
п2 4nv^
а1 = —а0^——г.
2п 20г
При к = п, случае не содержащего пропуски выравнивания с п
выровненными парами символов, мы имеем
п -( п \ -гА-л
В общем случае, при а^ = (к п-кп-к)9 анализ отношения
Qfc+i _ (п - fc)2
°>к ~ (2n-fc)(fc + l)
показывает, что члены суммы (2.5) возрастают по мере того, как к растёт
от нуля до
к* =
1 \/8n2 + 8п + 1
П"4 4
и убывают, когда к растет от к* до п. При больших п мы делаем
допущение, что к* « (1 — (1/у/2))п, и находим, применяя формулу Стерлинга,
что максимальный член в сумме (2.5) может быть приближен следующим
выражением:
(3 + 2v/2)n
ак* ^
27ГП
При больших значениях п мы имеем
maxafc = a*.* < Л/*п,п < (п + 1)ак*;
А:

2.1. Оригинальные задачи
59
м мотгому нижний и верхний пределы числа Afn,n содержащих пропуски
имравниваний двух последовательностей длины п, следующие:
(3 + 2^2)п кг (3 + 2^2)п
Замечание 1. Асимптотическое выражение для Л/"п,п при больших п,
, ! (3 + 2^)("+1/2)
П,П _ 2V40F 0J
(>ыло выведено Лакэром [174].
Замечание 2. Некоторые алгоритмы попарного выравнивания,
например, алгоритм Витерби для парной скрытой марковской модели (СММ),
обсуждаемой в главе 4 (см. рис. 4.3 и рекуррентные уравнения (4.5)-(4.7)),
допускают к соревнованию за оптимальность только те выравнивания
последовательностей х и у, где пара ж-пропуск не следует за парой г/-пропуск
и наоборот. Пусть Ап,т — множество таких попарных выравниваний
последовательностей х = xi,..., хп и у = ух,..., ут. Должно быть определено
ЧИСЛО |Ai,m|.
Сначала примем во внимание, что описанная в задаче 2.6 процедура не
устанавливает взаимно однозначного соответствия между множеством вза-
имовставленных последовательностей длины п + га и множеством Лп,т.
При том что всякое выравнивание из Лп,т соответствует некоторой вза-
имовставленной последовательности, существуют такие взаимовставлен-
ные последовательности, которые не соответствуют никакому
выравниванию в Ащт- (Например, никакое выравнивание из Лз,з не соответствует
вставленной последовательности sci, j/i, г/2> х2, жз, Уз-)
Для того чтобы найти |Дп,т|, схема, использованная выше для
вычисления числа Afn,m всех возможных выравниваний х и у, должна быть
изменена. Теперь в сумме (2.1) порядок векторов (1,1), (1,0) и (0,1),
соотносимых, соответственно, с парой выровненных символов, парой у-пропуск
и парой х-пропуск, должен удовлетворять следующему ограничению:
векторы (1,0) и (0,1) не могут быть смежными друг с другом. Число
последовательностей векторов (1,1), (1,0) и (0,1), удовлетворяющих этому
ограничению, равно |Ai,m|- Если число векторов (1,1) в сумме (2.1)
равно к, где 1 < к < min(n,ra), то они присутствуют в сумме в форме г
подсчётов, 1 ^ г ^ к, которые соответствуют блокам последовательных

60
Глава 2
совпадений в выравнивании. Число способов разбить множество из к
элементов на г непустых подмножеств равно N(k, г) = (*I*) ~ числу способов
разместить к неразличимых предметов в г ящиков (см. задачу 11.14). Для
каждого значения г, числа блоков векторов (1,1) в пределах суммы (2.1),
есть три возможности: а) сумма в (2.1) начинается и кончается блоками
векторов (1,1); б) сумма в (2.1) либо начинается, либо заканчивается
блоком векторов (1,1); в) сумма в (2.1) ни начинается, ни кончается блоком
векторов (1,1). В случае ai — 1 блоков векторов (0,1) или блоков векторов
(1,0) должно быть расположено между г блоками векторов (1,1). Если п —
— А: векторов (1,0), соответствующих ^-пропускам, разбиты на I блоков, где
I < г — 1 (существует N(n — fc, /) способов сделать это), тот — к векторов
(0,1), соответствующих ж-пропускам, должны быть разбиты на г — 1 — I
оставшихся блоков (существует N(m — k,i — 1 — I) способов сделать это).
Число способов поместить I блоков векторов (1,0) в г — 1 возможных
местоположений при сохранении порядка блоков равно (*71)- Теперь позиции
для i — 1 — l блоков векторов (0,1) определяются однозначно. Когда порядок
всех блоков (и их длины) в сумме (2.1) закреплён, цепь векторов является
однозначно определенной. Поэтому число iVi последовательностей,
соответствующих случаю а, принимает вид
min(n,m) к г-1 ,. -ч
Nx= Y1 Е^МЕРТ )Щп-к,1)Щт-Ы-1-1).
к=1 г=1 1=0 ^ '
Подобные же доводы ведут к формулам чисел N2 и iV3 возможных
последовательностей векторов в сумме (2.1), соответственно, для случаев бив:
min(n,m) fe г / .ч
^ = 2 £ ^N(k,i)^r)N(n-kJ)N(m-k,i-l)-
к=1 г=1 1=0 ^ '
min(n,m) к г+1 / • , * \
^з= X) Х>(М)£Д* j" )N(n-k,l)N(m-k,i + l-l).
fe=l «==1 (=0 ^ '
Объединяя числа последовательностей для случаев а, б ив, мы получаем
min(n,m) к , ч Гг—1 • . ..ч
К—X Ъ—л. L*—U

2.1. Оригинальные задачи
61
+ £ (Z t X ) N(n ~ k> l>>N(m - М + 1 - 0
Здесь ЛГ(0,0) = 1; 7V(<z,0) = ЛГ(0,д) = 0 при q > I; JNT(g,i) = (qqZ)) при
j ^ 1, О j; N(q,j) = О при j^ 1, 1 ^ q < j.
Например, в случае двух коротких последовательностей х = х\,х2
и У — 2/1)2/2,Уз формула (2.2) даёт следующее значение числа всех
возможных содержащих пропуски выравниваний последовательностей х и у:
А/2,3 = 25; при этом |Л2,з| — 5. Эти пять выравниваний в А2,з следующие:
(х\ х2 —\ I- х\ х2\ (xi х2 - — \
г/1 У2 уз) \yi У2 уз) \- г/1 уг уз/'
(- - xi х2\ ( xi - х2\
г/i уг уз -/ \г/1 уг уз /
Следуя той же логике, что и в следствии 1, можно вывести для |Дп,т|
аналог формулы (2.3), полученной для А/^,т. Мы оставляем читателю
возможность проверить справедливость утверждения, что следующее
рекуррентное уравнение верно:
771 П
|^П,77l| — |«^Цг—1,771— 1 ,771— 1 •
г=2 г=2
На правой стороне уравнения первый член отражает число вьфавниваний
т
в Лп7т с выровненными символами хп и ут; сумма ]Г] — число выравни-
г=2
п
наний в Ап,т9 где ут выровнен с пропуском; и сумма J] — число вырав-
г=2
ниваний в Лп,тп) где хп выровнен с пропуском.
Принимая допущение о том, что |Лп,о| = |А),тп| = 1? мы вычисляем
значения Ап,т при п,ш<4и приводим их в таблице 2.4.

62
Глава 2
Таблица 2.4. Результаты вычислений Лп,т при малых числах пит
0 12 3 4
0 ]
1 ]
2 ]
3 ]
4 1
L 1
L 1
L 2
1 3
1 4
1
2
3
5
8
1
3
5
9
15
1
4
8
15
27
Замечание (предложено Андерсом Крогом).
Рассмотрим подвыравнивания между выровненными парами символов
в содержащем пропуски попарном выравнивании (с выровненными парами
на концах выравнивания). В примере
*-хХ--Х*
*y-YyyY*
мы помещаем заглавные буквы для выровненных пар и выровненные *-ки
на концах. Будем называть сечение выравнивания между выровненными
парами «невыравниванием». Две подпоследовательности могут быть «не
выровнены» многими различными способами; например, хх и уу могут
дать эти «невыравнивания»:
/— — х х\ (— х — х\ (х — — х
\у у - -)\у - у -)\- у у -
{— х х —\ f х — х —\ f х х — —
\У ~ ~ У)\- У ~ У)\- ~ У У
Можно утверждать, что бессмысленно считать их как отдельные
выравнивания, потому что нет никакого разумного способа различить их
между собой (разве что вы фактически отмечали эволюцию шаг за шагом). При
линейной системе штрафов за пропуски только первое и последнее имели
бы шанс выжить в процедуре построения оптимального выравнивания; и во
многих программах ни одному из них это не удалось бы, потому что
пропускам не дозволяется следовать за пропусками. Однако если мы считаем
все эти невыравнивания только единожды и позволяем им быть
представленными выравниванием, в котором все у-вставки стоят до я-вставок
(первая форма в вышеприведённом примере), то легко видеть, что число 7Vn,m
•
•

2.1. Оригинальные задачи
63
таких выравниваний равно (n^m), поскольку есть точно одно
выравнивание для любой вставки и наоборот.
Мы покажем, что есть взаимно однозначное отображение между
взаимными вставками и выравниваниями последовательностей, в которых мы
допускаем вставки в нижней (у) последовательности перед вставками в
верхней (х) последовательности, но не наоборот. Чтобы показать это, мы
должны показать, что любое выравнивание отображается на одну, и только
па одну взаимную вставку, что любые два выравнивания отображаются на
различные взаимные вставки и что существует такое выравнивание,
которое отображается на любую взаимную вставку. Первая часть легка, потому
что существует точно одна взаимная вставка для данного выравнивания,
что следует из метода построения взаимной вставки из выравнивания,
описанного в задаче 2.5.
Взаимная вставка интерпретируется следующим образом.
1) Любая пара ху соответствует выровненной паре в выравнивании.
Добавляем виртуальные выровненные пары к концам взаимной вставки.
2) Между двумя выровненными парами мы можем иметь некоторые
у-ш, сопровождаемые некоторыми х-ми во взаимной вставке. Если числа
у-в и х-в равны, соответственно, к и /, то это означает, что мы имеем к
у-вставок, сопровождаемых / ж-вставками в выравнивании. И к и I могут
быть равны нулю. При этом у-ки не могут следовать за ж-ми, потому что
это означало бы, что мы забыли отметить выровненную пару.
Это показывает, что для любой взаимной вставки существует
дозволенное выравнивание.
Наконец, ясно, что на данную взаимную вставку отображается только
одно дозволенное выравнивание. Допустим, что два выравнивания дают
одну и ту же взаимную вставку. Тогда они должны были бы иметь одно
и то же множество вьяювненных пар и то же самое число у-вставок и х-
вставок между всеми выровненными парами, так что эти два выравнивания
были бы идентичны.
На этом доказательство взаимно однозначного соответствия
завершено; следовательно, АГп,т = (n*m). □
Задача 2.7. С помощью формулы Стерлинга (х\ ~ л/27гя 2 е х)
докажите следующее уравнение:
22п
с;)
\ркп

64
Глава 2
Решение. Чтобы доказать вышеупомянутое равенство, мы применяем
формулу Стирлинга для (2п)! и п\:
/2п\ _ (2г0! _ у/2^(2п)(2п+2)е~2п _
\п)" Jri)2 " 2тгп2п+1е-2п
22nV2n{2n+*)e-2n 22n
л/27гп2п+1е~2п у/тгп'
D
Задача 2.8. Найдите два оптимальных выравнивания с равным счётом в
матрице динамического программирования, представленной в таблице 2.5.
Решение. Существование нескольких оптимальных выравниваний с
одинаковым счётом передаётся «развилками» в графе обратного
прослеживания, охватывающем матрицу динамического программирования (ДП)
(таблица 2.5). Развилка появляется в том случае, если процедура обратного
прослеживания, восстанавливающая оптимальный путь, достигает в
матрице ДП ячейки (i,j), оптимальное значение которой F(i,j) было выведено
из более чем одной «родительской» ячейки. Альтернативное использование
родительских ячеек процедурой обратного прослеживания порождает
различные пути через матрицу ДП и, следовательно, различные оптимальные
выравнивания.
В матрице ДП для последовательностей HEAGAWGHEE
и PAWHEAE (таблица 2.2) значение F(3,1) н^ обратном пути может
быть получено как из ячейки (2,0), так и из ячейки (2,1):
F(3,1) = F(2,0) + з(А, Р) = -16 - 1 = -17,
F(3,1) = F(2, l) - d = -9 - 8 = -17.
Эти возможности соответствуют двум оптимальным выравниваниям со
счётом 1:
HEAGAWGHE-E
--P-AW-HEAE
и
HEAGAWGHE-E
-P--AW-HEAE п

о
К
Таблица 2.5. Матрица выравнивания последовательностей HEAGAWGHEE и PAWHEAE,
полученная методом динамического программирования
п
Н Е А G А W G НЕЕ
О < 8 < 16 <- -24 <- -32 <- -40 <- -48 <- -56 4- -64 4- -72 4- -80
\ ч X \ \ \
Р -8 -2 -9 < 17 < 25 -33 4- -42 4- -49 4- -57 -65 -73
т т \ \ ч
А -16 -10 -3 -4 4- -12 -20 4- -28 <- -36 f- -44 ^- -52 <- -60 3
т т т ч \ \ ч |
W -24 -18 -11 -6 -7 -15 -5 4- -13 4- -21 <- -29 <- -37 £
т \ \ ч ч ч тчч §
Н -32 -14 -18 -13 -8 -9 -13 -7 -3 4- -11 «- -19 |
т т ч тчч т ч ч ч |
Е -40 -22 -8 <- -16 -16 -9 -12 -15 -7 3 -5
т т т ч ч ч ч т т ч
А -48 -30 -16 -3 4- -П -11 -12 -12 -15 -5 2
т т т т ч ч ч ч ч ч ч
Е -56 -38 -24 -11 -6 -12 -14 -15 -12 -9 1

66
Глава 2
Задача 2.9. Рассчитайте матрицу ДП и оптимальное выравнивание для
последовательностей ДНК GAATTC и GATTA, назначая +2 очка за
совпадение, —1 за несовпадение и линейный штраф за пропуски d = 2.
Решение. Вычисление матрицы ДП и последующее определение
указателей обратного прослеживания даёт результат, представленный в
таблице 2.6.
Таблица 2.6. Матрица выравнивания последовательностей GATTC и
GATTA, полученная методом динамического программирования
G
А
Т
Т
А •
0
-2
-4
-6
-8
-10
ч
G
-2
2 4-
т ч
0
т
-2
т
-4
т
-6
А
-4
0 <-
Ч
4 4-
2
0
2
А
-6
-2 <-
2 <-
ч
3
1
т
2
т
-8
-4 <-
0 <-
Ч
4 4-
ч
5
т ч
3
т
-10
-6 <-
-2 <-
2 4-
6 4-
тч
4
с
-12
-8
-4
0
4
5
Алгоритм обратного прослеживания восстанавливает два оптимальных
выравнивания с одинаковым счётом (равным 5):
GAATTC
G - А Т Т А
и GAATTC
G А - Т Т А п
Задача 2.10. Вычислите счёт приведённого в качестве примера выравнива-
ШШ VLSPAD-K
HL--AESK
при d = 12 и е = 2.

2.1. Оригинальные задачи
67
Решение. Использование счетов замен, определяемых матрицей BLOSUM50
(таблица 2.1), позволяет нам вычислить
S = s(V,H) + 8(L,L)-d-e + 8(A,A) + 8(D,E)-d + 8(K,K) = -12. п
Задача 2.11. Заполните точные значения с(г, j) для глобального
выравнивания приведённой в примере пары последовательностей HEAGAWGHEE
и PAWHEAE, полученные в первом проходе алгоритма с линейным
пространством памяти (и = 5).
Замечание. Алгоритм с линейным пространством ([204]) строит
оптимальное выравнивание двух последовательностей длин пит, используя
пространство памяти 0(п + га) вместо 0(п х га), необходимого для
стандартного алгоритма ДП. Такое сокращение важно при выравнивании
последовательностей большой длины. Главная проблема в изобретении
алгоритма с линейным пространством — преодолеть требование сохранять матрицу
ДП счетов, имеющую размер п х га. Вполне осуществимо найти счёт
глобального (или локального) попарного выравнивания, используя
пространство хранения 0(п + га), так как стандартный алгоритм ДП может
выполняться столбец за столбцом (или строка за строкой) при сохранении только
данных, необходимых для вычисления очередного столбца (строки). Точно
так же «расширенные указатели обратного прослеживания» c(i,j) могут
вычисляться столбец за столбцом и сохраняться при вычислении счетов в
каждом столбце г, где г ^ и+1. Таким образом, пространство, необходимое
для хранения расширенных указателей, также равно 0(п + га). Результат
первого прохода алгоритма — отыскание ячейки (и, с(п, га)), пересечения
столбца и с оптимальным путём через матрицу ДП. Эта информация
позволяет делить начальную задачу динамического программирования на две
части, работая с двумя отдельными подматрицами (с диагоналями,
соответственно, от (0,0) до (и,с(п, га)) и от (и,с(п, га)) до (п,га)). Каждая из
таких подматриц может быть разбита тем же самым способом, и данная
процедура продолжается до тех пор, пока подматрицы, полученные в
последнем шаге, не будут содержать только один столбец (или одну строку).
Теперь полное оптимальное выравнивание может быть уникально
определено через совокупность ячеек (u',i/), где оптимальный путь пересекает
все га столбцов матрицы ДП.
Решение. В первом проходе алгоритм должен определить значения c(i,j),
начиная с пятого столбца (и = п/2 = 5). Когда мы вычисляем c(i,j) по

68
Глава 2
значениям F(i,j) матрицы ДП, мы должны помнить, что в реальном
алгоритме после вычисления нового столбца значений F(i,j) и c(i,j) данные в
предыдущем столбце будут стёрты.
Мы заполняем ячейки матрицы С значениями c(i,j): c(5,j) = j при
любых j; при г > 5 c(i,j) = c(i\f), если значение F(i,j) в ячейке (i,j)
матрицы ДП (таблица 2.5) получено из значения F(if,jf) в ячейке (г',/).
Вычисления дают результат, показанный в таблице 2.7.
Таблица 2.7. Матрица значений c(i,j), полученных алгоритмом с линейным
пространством
ФьЭ)
0
1
2
3
4
5
6
7
5
0
1
2
3
4
5
6
7
6
0
1
2
2
2
4
5
6
7
0
1
2
2
2
2
4
5
8
0
1
2
2
2
2
2
4
9
0
0
2
2
2
2
2
2
10
0
0
2
2
2
2
2
2
Значение с(10,7) = 2 определяет расширенный указатель обратного
прослеживания к ячейке (и, v) = (5,2), которая принадлежит к
оптимальному пути. Ячейка (5,2) является точкой разбиения матрицы ДП на две
подматрицы размера 5 х 2 и 5 х 5, которые должны будут использоваться
во втором проходе алгоритма с линейным пространством. □
Задача 2.12. Алгоритм с линейным пространством позволяет нам
сократить память, необходимую для нахождения оптимального выравнивания
двух последовательностей длины п и га, с 0(пт) (как в стандартном
алгоритме ДП) до 0(п + га). Покажите, что время, необходимое алгоритму
с линейным пространством, только примерно вдвое больше времени счёта
стандартного алгоритма с пространством 0{пт).
Решение. Сначала мы оценим время, необходимое для прогона
стандартного алгоритма глобального выравнивания с назначением
пропорциональных штрафов за пропуски. (Налагание линейных штрафов за пропуски мо-

2.2. Дополнительные задачи и теория
69
жет работать подобным же образом.) Алгоритм заполняет n x га ячеек
матрицы счетов F(i,j)9 выполняя четыре операции для каждой ячейки:
вычисления значений F(i — l,j — 1) 4- s(i,j), F(i — l,j) — d, F(i,j — 1) — d
и их максимума. Следовательно, полное время счёта (измеряемое в числе
операций) алгоритма глобального выравнивания определяется выражением
Tst ~ 4пга.
У алгоритма с линейным пространством полное время счёта равно
сумме периодов времени, требуемой для N прогонов:
В первом прогоне он вычисляет тхп счетов F(i,j)9 заполняет (га х п)/2
значений c(i,j) и в конечном счёте находит значение v = с(п,т). Таким
образом, Т\ « 4пга. Во втором прогоне он вычисляет элементы двух
подматриц Fi(i,j) и F2(i,j) приблизительного размера (n/2) x (m/2)
(фактические порядки зависят от v), заполняет значениями ci(i,j) и C2(i,j) и
находит v\ ИУ2- Тогда Т2 ~ (п/2) х (га/2) х 4 х 2 = 2пга. По мере работы
алгоритма, в k-м прогоне, он вычисляет элементы 2к~1 подматриц
размера (п/2к~1) х (тп/2к~1), таким образом, Т*. ~ птп/2к~3. Поэтому время,
необходимое алгоритму с линейным пространством, оценивается как
N N / ч г оо • \ г
^£Р = 8™£(|) <8-ЕШ =8птп-
г=1 Z г=1 Ч ' г=1 Ч '
Замечание. Максимальное число N прогонов алгоритма с линейным
пространством может быть оценено следующим образом. Размеры
подматриц (п' х га') сокращаются по крайней мере вдвое за каждый
прогон алгоритма. Процесс «разделяй и властвуй» продолжается до тех пор,
пока последняя оставшаяся подматрица не будет уменьшена до одной-
единственной ячейки {или до матрицы из одной лишь строки или из одного
лишь столбца). Для самой длинной ветви процесса разбиения матриц мы
имеем max(n,ra)
Таким образом, N « [log2 max(n, га)]. □
2.2. Дополнительные задачи и теория
Несколько задач, включённых в этот раздел, касаются вывода
матрицы счетов замен — краеугольного камня системы очков для попарного
выравнивания последовательностей (задачи 2.15-2.17), а также
распределения счёта дающих высокий счёт локальных выравниваний двух случайных

70
Глава 2
последовательностей, необходимых для оценки статистической значимости
локального попарного выравнивания (задачи 2.18-2.21).
Так как найти оригинальный труд [57] о получении семейства ПТМ
матриц замен довольно трудно, мы приводим в разделе 2.2.1 развёрнутое
описание представленного в нём метода. Также мы иллюстрируем
«модельным» примером (задача 2.17) идеи, которые ведут к получению семейства
BLOSUM матриц замен ([116]).
Краткий обзор теоретических результатов касательно распределения
статистики счетов пар с высоким счётом в выравнивании случайных
последовательностей (случаи с пропусками и без них) дан в теоретических
введениях в задачи 2.18 и 2.19. В теоретическом введении в задачу 2.20
мы обсуждаем результаты относительно распределения длины
длиннейшего общего слова среди нескольких не связанных друг с другом случайных
последовательностей. Ожидаемое число установленной длины слов, общих
для двух фрагментов ДНК, рассчитывается в задаче 2.21.
Задача 2.13. Докажите, что время счёта алгоритма ДП для оптимального
попарного выравнивания двух последовательностей длины п с функцией
штрафов за пропуски общей формы равно 0(ns).
Решение. В случае функции штрафов за пропуски ^(д) общей формы
уравнение ДП оптимального счёта F(i,j) описывается следующей
формулой:
[ F(i-l,j -l)-\-s(xi,yj),
F(iJ) = max I F(fc,j)+7(i-fc), fc = 0,...,t-l; (2.6)
[ F{i,k) + j(j-k), fc = 0,...,j-l.
Здесь s(xi,yj) — счёт замены для пары остатков (а^, yj). Чтобы определить
F(i,j) по уравнению (2.6), требуется выполнить 2(г + j) + 2 операций.
Тогда число операций, необходимых для вычисления целой матрицы размера
пх п, определяется как
г=0 j=0 \ г=0 j=0
4(п + 1)п(П0+1) + «2 = 2п3 + 5п2 + 2п - 0{nz).
п2,=
□

2.2. Дополнительные задачи и теория 71
1н;щма 2.14. Найдите оптимальное попарное глобальное выравнивание по-
« исдоиательностей TACGAGTACGA и ACTGACGACTGAC с услови-
|'м, что нуклеотиды G, показанные полужирным шрифтом, должны быть
it i.i pom юны друг относительно друга. Параметры системы очков
следующие: |-2 за совпадение, —1 за несовпадение и пропорциональный штраф за
пропуски d = —2.
Гаисние. Легко видеть, что средние нуклеотиды G делят каждую
поедено интельность на две идентичные подпоследовательности.
Следовательно, если мы найдём оптимальное выравнивание подпоследовательностей
ГЛ( 1(мА и ACTGAC, то оптимальное глобальное выравнивание, удовле-
шоряющее определенному выше условию, будет сцепкой этих двух «под-
имршшиваний» с парой выровненных нуклеотидов G между ними. Мы
иычисляем матрицу ДП (см. таблицу 2.8), определяем счёт оптимально-
!о «подвыравнивания» и впоследствии строим само «подвыравнивание»,
Таблица 2.8. Матрица выравнивания последовательностей TACGA
и ACTGAC, полученная методом динамического программирования
О -2 -4 -6 -8 -10
\ ч \
А -2 -1 о «- -2 «- -4 «- -6
ч т ч т ч
С -4 -3 -2 2 «- 0 «- -2
\ \ т т \ \
Т -6 * -2 «- -4 О 1 «- -1
т \ т ч \
G -8 -4 -3 -2 2 <- 0
т ч ч т т ч
А -10 -6 -2 <- -4 0 4
т т ч т т
С -12 -8 -4 0 <- -2 2
применяя процедуру обратного прослеживания. Счёт оптимального подвы-
рпнпинания S = F(5,6) = 2. Полный счёт условного глобального выравни-

72
Глава 2
вания равен сумме счетов, S = S + s(G, G)+ 5 = 2 + 2 + 2 = 6, а само
выравнивание выглядит следующим образом:
TAC-GA-GTAC-GA-
-ACTGACG-ACTGAC
Замечание. Оказывается, что показанное выше условное оптимальное
выравнивание совпадает с одним из двух «безусловных» оптимальных
глобальных выравниваний заданных последовательностей. Второе
оптимальное глобальное выравнивание (с тем же самым счётом, равным 6) имеет
следующий вид:
TAC-GAGTAC-GA-
-ACTGACGACTGAC
В этом выравнивании два нуклеотида G не выровнены друг
относительно друга. Однако потеря положительного счёта за совпадение
компенсирована уменьшением числа пропусков. □
Задача 2.15. Матрица счетов замен для выравнивания
последовательностей нуклеотидов задана в следующем виде (где логарифмические счета
шансов определены в битах):
т
1
0
1
-1
с
0
1
-1
-1
А
-1
-1
1
0
G
-1
-1
0
1
а) Определите средний счёт на пару нуклеотидов для
последовательностей ДНК, описываемых моделью независимого порождения с равными
вероятностями нуклеотидов (A J.
б) Найдите «целевые частоты» пар нуклеотидов (частоты замен в
выравниваниях), для отыскания которых в выравниваниях эволюционно
связанных последовательностей эта матрица и предназначена.

2.2. Дополнительные задачи и теория
73
Решение, а) В не содержащем пропуски выравнивании двух случайных
последовательностей нуклеотидов средний счёт Н на выровненную пару
определяется как
Чдссь Sij — элементы матрицы счетов замен, сумма берётся по всем шест-
мпдцати возможным парам нуклеотидов, а qi и qj — вероятности появления
нуклеотидов вида г и j при однородной модели независимого порождения.
I In >тому
н= Тб1^ = -1б = "0'25-
в) По определению счёта замены как логарифмического счёта шансов:
Pij
^' = log2M?
•де pij — «целевые частоты» выровненной пары (г, j) нуклеотидов. Тогда
ишчение целевой частоты щ$ — 0-/QiQj)2Sij• Например, ртт = 1/16 • 2 =
1/8. Все «целевые частоты» р^ показаны в нижеследующей таблице:
Т 1/8 1/16 1/32 1/32
С 1/16 1/8 1/32 1/32
А 1/32 1/32 1/8 1/16
G 1/32 1/32 1/16 1/8
□
2.2.1. Получение матриц замен аминокислот (ряд ПТМ)
Описание этого метода требует знания ключевых понятий построения
филогенетического дерева ([67], глава 7).
Матрица замен — важный компонент системы очков для попарного
ммривнивания последовательностей. В [57] предложен основательный тео-
|к' i ический подход к определению элементов матриц замен, масшабирован-
Ш.1Ч эволюционным расстоянием, на основании подсчётов замен аминокис-
ипг. ')ти подсчёты были рассчитаны как частоты выровненных пар остатков

74
Глава 2
в тщательно построенных выравниваниях тесно связанных
последовательностей белков из семидесяти одного семейства. Множественные
выравнивания этих последовательностей были сокращены до семидесяти одного не
содержащего пропусков блока выравнивания (каждая последовательность в
блоке должна была быть по крайней мере на 85 % идентична любой другой
последовательности в блоке). Наиболее экономичное (с минимальным
числом замен по рёбрам) филогенетическое дерево или несколько деревьев,
если экономичность не была уникальна, были построены для
последовательностей из каждого блока. Чтобы иллюстрировать метод, мы используем
искусственный блок без пропусков, который рассматривается в [57]:
А С G Н
D В G Н
A D I J
С В I J
Четыре наиболее экономичных дерева, 7\, Тг, Тз, Т4, для
последовательностей из блока (2.7) показаны на рис. 2.2. Для каждой пары различных
аминокислот (г, j) было рассчитано общее число ац замен с аминокислоты г
на аминокислоту j по нисходящим ориентированным рёбрам деревьев Т^,
где к = 1,..., 4, и была получена матрица А принятых точечных мутаций
с элементами Aij = Aji = а^ + ciji, где i ф j (см. таблицу 2.9).
Таблица 2.9. Матрица А подсчётов принятых точечных мутаций
А
В
С
D
G
Н
I
J
А
0
4
4
0
0
0
0
В
0
4
4
0
0
0
0
С
4
4
0
0
0
0
0
D
4
4
0
0
0
0
0
G
0
0
0
0
0
4
0^
Н
0
0
0
0
0
0
4
I
0
0
0
0
4
0
0
J
0
0
0
0
0
4
0
Обратите внимание, что мы сохраняем термин «принятая точечная
мутация» и два других, каковые появятся ниже («относительная мутабиль-

2.2. Дополнительные задачи и теория
75
ABGH
ABGH
H-J\G-I
ABIJ
B-D
В-С\ \A-D
ACGH DBGH ADIJ CBIJ
I
ABU
А-С
3-Е I-G
ABGH
ABIJ
В-С
B-D
A-D
ACGH DBGH ADIJ CBIJ
I
ABIE
A-C
\I-G
ABGH
H-J\
ABIJ
B-C
B-D
A-D
ACGH DBGH ADIJ CBIJ
I
ABGJ
A-C
\J-H
ABGH
G-I\
ABIJ
B-C
A-D
B-D
A-C
ACGH DBGH
ADIJ CBIJ
Рис. 2.2. Наиболее экономичные деревья Ti, T2, Тз и Т± (в порядке сверху
вниз) с «наблюдаемыми» в блоке (2.7) последовательностями аминокислот
в листьях; каждое дерево несёт в общей сложности шесть замен. Предковые
последовательности (ненаблюдаемые, но выведенные) помещены в корень и
внутренние узлы; по рёбрам обозначены замены аминокислот

76
Глава 2
ность» и «вероятностная матрица мутаций»), которые были употреблены
в [57], хотя в современной литературе термин «мутация» в данном
контексте был заменён термином «замена».
Затем для каждой аминокислоты j была определена относительная му-
табильность rrij следующим образом. Ребро дерева Тк, где к = 1,... ,4,
связывается с не содержащим пропуски попарным выравниванием двух
последовательностей, соединённых этим ребром. Таким образом, любое
дерево Тк на рис. 2.2 порождает шесть выравниваний; например, для Т\ они
следующие:
А
А
А
D
В
В
В
В
G
G
G
G
Н
Н
Н
Н
А
А
А
А
В
В
В
D
G
I
I
I
Н
J
J
J
А
А
А
С
В
С
В
В
G
G
I
I
Н
Н
J
J
Относительная мутабильность rrij определяется как отношение общего
числа раз, которое аминокислота j изменялась во всех двадцати четырёх
попарных выравниваниях, к количеству раз, которое аминокислота j
появлялась в этих выравниваниях. Значения rrij сведены в таблицу 2.10.
Таблица 2.10. Значения относительной мутабильности rrij аминокислот,
полученные из блока выравнивания последовательностей (2.7)
Аминокислота
Изменения (замены)
Частота появления
А
8
40
В
8
40
I
4
24
Н
4
24
G
4
24
J
4
24
С
8
8
D
8
8
Относит-я мутаб-ть m 0,2 0,2 0,167 0,167 0,167 0,167 1 1
Теперь мы вводим действительную частоту fj аминокислоты j. Это
понятие принимает во внимание разницу в изменчивости
консервативности первичной структуры в белках с различными функциональными
ролями (таким образом, два блока выравнивания, соответствующие двум
различным семействам, могут по-разному влиять на величину fj, даже если
число появлений аминокислоты j в этих блоках одинаковое).
Действительная частота fj определяется как
л = *£<^>

2.2. Дополнительные задачи и теория
77
где сумма берётся по всем блокам выравнивания Bf, q-l — наблюдаемая
частота аминокислоты j в блоке B&Ni— число замен в дереве, построенном
для Bi\ коэффициент к выбирается таким образом, чтобы сумма частот fj
обязательно была равна 1. В нашем примере только с одним блоком (2.7),
значения действительных частот равны значениям композиционных частот
(fj = qj) и показаны в таблице 2.11. Действительные частоты двадцати
аминокислот, полученные из семидесяти одного оригинального блока
выравнивания ([57]), приведены в таблице 2.12.
Таблица 2.11. Действительные частоты аминокислот fj, полученные из
блока выравнивания последовательностей (2.7)
Аминок-та ABIHGJCD
Частоты / 0,125 0,125 0,125 0,125 0,125 0,125 0,125 0,125
Таблица 2.12. Действительные частоты аминокислот /г, определённые по
данным оригинального выравнивания ([57], таблица 22)
Gly(G) Ala (A) Leu (L) Lys (К) Ser (S) Val (V) Thr (T)
0,089 0,087 0,085 0,081 0,070 0,065 0,058
Pro(P) Glu(E) Asp(D) Arg(R) Asn (N) Phe (F) Gin (Q)
0,051 0,050 0,047 0,041 0,040 0,040 0,038
lie (I) His(H) Cys(C) Tyr(Y) Met (M) Trp (W)
0,037 0,034 - 0,033 0,030 0,015 0,010
Следующий шаг — найти элементы вероятностной матрицы мутаций
М = (М^). Элемент Мц определяет вероятность того, что аминокислота
в столбце j была заменена аминокислотой в строке i за данный
эволюционный период. Недиагональные элементы матрицы М определяются по
следующей формуле:
Щ - ^, (2-8)
к
где Л — постоянная, определение которой будет дано ниже; rrij — отно-

78
Глава 2
сительная мутабильность аминокислоты j (таблица 2.10); Aij — элемент
матрицы принятых точечных мутаций А (таблица 2.9). Диагональные
элементы матрицы М мы определяем из выражения
Mjj = l-\mj. (2.9)
Следует иметь в виду, что если mi ф Щ при некоторых г ф j, то
матрица М является несимметричной.
Коэффициент Л отражает степень свободы, которую можно
использовать, с тем чтобы связать матрицу М с масштабом времени эволюции.
Например, коэффициент Л может быть подобран таким образом, чтобы
в среднем на сотню остатков происходило заданное (малое) число замен.
Такой подбор коэффициента Л был осуществлён в [57] следующим
образом. Ожидаемое число аминокислот, которые останутся неизменными в
последовательности белка длины сто аминокислот, определяется формулой
lOO^T/jMjj = 100^/j(l — \rrij). Если на сотню остатков допускается
3 3
только одна замена, то Л рассчитывается из уравнения
100]Г/,(1 - Am,-) = 99. (2.10)
з
Впоследствии уравнения (2.8) и (2.9) использовались для вычисления всех
элементов матрицы М. Такая вероятностная матрица мутаций связана
с эволюционным периодом 1 ПТМ (одна принятая точечная мутация на
сотню аминокислот) и называется матрицей 1 ПТМ. Из данных расшифровки
последовательности в блоке выравнивания (2.7) мы получаем Л = 0,0261 и
приведённую в качестве примера матрицу М (таблица 2.13). Фактическая
матрица М 1 ПТМ, полученная из оригинальных данных в [57],
представлена в таблице 2.14.
Далее делается допущение о том, что вероятностная матрица
мутаций М служит матрицей вероятностей переходов для стационарной
(однородной) марковской цепи хп, где п € N, представляющей собой модель
эволюционного изменения на каждом участке последовательности белка.
Поэтому стохастическая матрица М 1 ПТМ, соотносимая с одной
единицей (1 ПТМ) эволюционного расстояния, может быть использована для
получения матриц, соотносимых с более продолжительными
эволюционными расстояниями (множителями 1 ПТМ). Тогда вероятностная матрица
мутаций для эволюционного расстояния п ПТМ будет совпадать с
матрицей Мп вероятностей переходов марковской цепи хп за п единиц
времени, которым соответствует n-я степень матрицы М. (О том, как получить

2.2. Дополнительные задачи и теория
79
Таблица 2.13. Пример вероятностной матрицы мутаций для эволюционного
расстояния 1 ПТМ, рассчитанной по блоку выравнивания (2.7).
Элемент Mij отражает вероятность того, что аминокислота в столбце j была
заменена аминокислотой в строке г за эволюционный период 1 ПТМ
А
В
С
D
G
Н
I
J
А
0,9948
0
0,0026
0,0026
0
0
0
0
В
0
0,9948
0,0026
0,0026
0
0
0
0
С
0,0131
0,0131
0,9740
0
0
0
0
0
D
0,0131
0,0131
0
0,9740
0
0
0
0
G
0
0
0
0
0,9957
0
0,0043
0
Н
0
0
0
0
0
0,9957
0
0,0043
I
0
0
0
0
0,0043
0
0,9957
0
J
0
0
0
0
0
0,0043
0
0,9957
марковский процесс, который представляет собой вариант с непрерывным
временем марковской цепи хп, см. задачу 8.18.) Легко проверить прямым
вычислением, что М3, вероятностная матрица мутаций для единиц
времени 3 ПТМ, строго положительная; поэтому марковская цепь с матрицей М
вероятностей переходов есть регулярная марковская цепь. Из теории
стохастических матриц ([21]; [192]) известно, что для регулярной марковской
цепи существует уникальное строго положительное инвариантное
(стационарное) распределение 7г: Мтт = 7г и для любого начального распределения
вероятностей состояний (в нашем случае — аминокислот) яо,
Мпщ
(2.11)
по мере того как п —> +оо. Оказывается, что вектор / действительных
частот (Д, Д,..., До) (таблица 2.12), в котором порядок компонентов
соответствует порядку строк (столбцов) матрицы М, удовлетворяет
уравнению Mf = f для стационарного распределения. Тогда сходимость в
уравнении (2.11) подразумевает, что / есть вектор равновесных частот
матрицы М:
( /а /а "• 1а\
J rt J rt J si
Mn
(2.12)
\fv fv
fv/

Таблица 2.14. Вероятностная матрица мутаций М для эволюционного расстояния 1 ПТМ (то есть одна
принятая точечная мутация на сотню аминокислот).
Элемент этой матрицы, Mij, отражает вероятность того, что аминокислота в столбце j была заменена
аминокислотой в строке г за эволюционный период 1 ПТМ. Фактические вероятности переходов умножены на
10000, чтобы упростить вид матрицы ([57], рис. 82)
Ala Arg Asn Asp Cys Gin Glu Gly His He Leu Lis Met Phe Pro Ser Thr Trp Tyr Val
Ala 9867 2
Argl
Asn 4
Asp 6
Cys 1
Gln3
Glu 10
Gly 21
His 1
He 2
Leu 3
Lis 2
Met 1
Phe 1
Pro 13
Ser 28
Thr 22
Trp 0
Тут 1
Val 13
9
9913 1
1
0
1
9
0
1
8
2
1
37
1
1
5
11
2
2
0
2
10
0
9822 36
42
0
4
7
12
18
3
3
25
0
1
2
34
13
0
3
1
3
1
0
9859 0
0
5
56
11
3
1
0
6
0
0
1
7
4
0
0
1
8
10
4
6
9973 0
0
0
1
1
2
0
0
0
0
1
11
1
0
3
3
17
0
6
53
0
9876 27
35
3
20
1
6
12
2
0
8
4
3
0
0
2
21
0
6
6
0
1
9865 4
7
1
2
1
7
0
0
3
6
2
0
1
2
2
10
21
4
1
23
2
9935 1
0
0
1
2
0
1
2
16
2
0
0
3
6
3
3
1
1
1
3
0
9912 0
0
4
2
0
2
5
2
1
0
4
3
4
1
1
0
0
3
1
1
1
9872 9
22
4
5
8
1
2
11
0
1
57
2
19
13
3
0
6
4
2
1
2
9947 2
1
8
6
2
1
2
0
1
11
6
4
0
0
0
4
1
1
0
12
45
9926 20
4
0
2
7
8
0
0
1
2
1
1
0
0
0
0
1
2
7
13
0
9874 1
4
1
4
6
0
0
17
22
4
2
1
1
6
3
3
3
0
3
3
0
9946 0
1
3
1
1
21
1
35
6
20
5
5
2
4
21
1
1
1
8
1
2
9926 12
17
5
0
0
3
32
1
9
3
1
2
2
3
1
7
3
11
2
1
4
9840 38
32
1
1
2
0
8
1
0
0
0
0
0
1
0
4
0
0
3
0
5
9871 0
0
1
10
2
0
4
0
3
0
1
0
4
1
2
1
0
28
0
2
2
9976 1
2
0
18
1
1
1
2
1
2
5
1
33
15
1
4
0
2
2
9
0
9945 1
2
99<

2.2. Дополнительные задачи и теория
81
по мере того как п —> +оо. Схождение (2.12) было подтверждено в [57]
прямым вычислением: было показано, что М2034 хорошо приближает матрицу
равновесных частот.
Далее описанная выше теория была использована для получения
матрицы логарифмических шансов замен аминокислот. Эти матрицы
чрезвычайно важны для алгоритмов выравнивания белковых
последовательностей. Так как мы имеем семейство вероятностных матриц мутаций Мп,
где п = 1,2,..., мы можем получить семейство матриц замен Sn, где п =
= 1,2,..., с элементами sn(i,j) логарифмических счетов шансов
следующим образом. Для пары аминокислот (г, j), где г, j = 1,..., 20,
логарифмический счёт шансов sn(i,j) определяется следующей формулой:
щ
sn(ij) = log-г,
h
где M'ji = Р(хп = j\xq = i) — элемент матрицы Мп. Интерпретация
счёта замены sn(i,j) с точки зрения эволюции белковой последовательности
начинается с применения свойств марковской цепи {#&}, где feeN:
,. л , Щ , Р(хп = j\x0 = i) fiP(xn = j\x0 = i)
*п(м) = log -т- = log = log — =
Jj Jj JiJj
E hP(xn = j\xn/2 = a)P(xn/2 = a\x0 = i)
= bg T-f . (2.13)
JiJj
Обратите внимание, что при больших п мы имеем Мг™ ~ /г и MJJ « fj,
так как / — вектор равновесных частот для матрицы М в силу
уравнения (2.12). Поэтому даже при том, что марковская цепь {xk} не обладает
свойством обратимости (fjMij ^ f%Mji при некоторых г ^ j), при
достаточно больших п мы можем принять допущение о том, что /jM^ « fiM?*-
при любых i,j. Тогда уравнение (2.13) принимает вид
YjhP{xn = j\xn/2 = а)Р(хп/2 = а\х0 = г)
sn(ij) = log — y~ «
JiJj
«log
fifj

82
Глава 2
T,faP(xn/2 = зЫ = а)Р(хп/2 = i\x0 = a)
= log~ М =
Р(хп/2 = h х'п/2 = З\хъ = хо)
= log j-f , (2.14)
JiJj
где {х'к} — независимая копия марковской цепи {#&}. Последнее
выражение в уравнении (2.14) — отношение логарифмических шансов, которое
вовлекает марковскую эволюционную модель со свойством молекулярных
часов, и модель независимого порождения R для пары
последовательностей с вероятностями порождения, определёнными как действительные
частоты fa, где г = 1,..., 20. Числитель в (2.14) — вероятность того, что две
выровненные последовательности белка, разошедшиеся от общего предка
п/2 ПТМ единиц времени назад, имеют в данном участке аминокислоты г
и j, при допущении о том, что замены в белках описываются марковским
процессом {хк}.
Член fifj в знаменателе выражения (2.14) — вероятность наблюдения
аминокислот г, j на данном участке двух выровненных
последовательностей белка при модели независимого порождения для пары
последовательностей R. Поскольку те же доводы, что и в уравнениях (2.13) и (2.14),
верны для счёта замены sn(j,i) = logM-fi/fi, мы имеем sn{i^j) « sn(j,i).
Таким образом, в отличие от вероятностной матрицы мутаций Мп,
матрица замен Sn является симметричной. Для практического удобства
значения логарифмических шансов sn(i,j) перемасштабированы (умножением
на десять или на другой масштабный коэффициент) и затем округлены до
ближайшего целого.
Среди матриц замен ПТМ наиболее часто используют матрицу 250
ПТМ, показанную в таблице 6.1.
В связи с быстрым ростом количества данных о белковых
последовательностях, в [132] было предпринято обновление матриц ряда ПТМ.
Авторы использовали тот же приём для подсчёта замен аминокислот, что
и в [57]. Другая эмпирическая модель эволюции белка, которая сочетает
в себе подсчёт на основе экономичности и подход наибольшего
правдоподобия, была построена в [279]. Пространные описания модели Маргарет
Дейхофф могут быть найдены в [281] и [93].
Важный практический вопрос состоит в том, как выбрать
оптимальную матрицу замен для выравнивания двух заданных (гомологичных)
последовательностей белка х и у. Точный ответ включил бы оценку
эволюционного расстояния (периода) п между последовательностями хиу, которая

2.2. Дополнительные задачи и теория
83
требует построения выравнивания последовательностей х и у, чтобы
определить степень различия d (процент несовпадений в выровненных
участках). Соответствие между степенью различия d и эволюционным
расстоянием п (в ПТМ) может быть определено из следующего уравнения:
100^/,M£ = 100-d,
з
где M?j — элементы вероятностной матрицы мутаций Мп для
эволюционного периода п ПТМ. При заданной степени различия d это уравнение
позволяет нам выбрать подходящую вероятностную матрицу мутаций Мп
и матрицу замен Sn (в таблице 2.15, полученной М. Дейхофф [57],
приведены некоторые пары соответствующих значений п и d). Однако построение
выравнивания последовательностей х и у, с тем чтобы найти d, требует
матрицы замен в первую очередь! Возможный, но трудоёмкий способ
нарушить эту замкнутую цепь логических построений состоит в том, чтобы
использовать итеративный метод. Однако при поиске в базе данных
дополнительные итерации требуют непомерных затрат.
Таблица 2.15. Соответствие между наблюдаемой степенью различий
аминокислот d между двумя выровненными гомологичными
последовательностями и эволюционным расстоянием п (в ПТМ) между ними.
При увеличении эволюционного расстояния вероятность многократных
замен на одном и том же участке, обращающих первоначальные изменения,
становится больше и обусловливает более медленный рост наблюдаемой
степени различия ([57], таблица 23)
d
п
d
п
1
1
50
80
5
5
55
94
10
11
60
112
15
17
65
133
20
23
70
159
25
30
75
195
30
38
80
246
34
47
85
328
40
56
45
67
Задача выбора подходящей матрицы замен для локального
выравнивания последовательностей была изучена в [2] в ракурсе теории
информации. Автором было показано, что если должна быть выбрана какая-либо
одна матрица, то для поиска в базе данных наиболее уместной является
матрица 120 ПТМ, тогда как для сравнения двух специфических белков с
предполагаемой гомологией наилучшим выбором будет матрица 200 ПТМ.

K4
Глава 2
Наконец, чтобы строить выравнивания с пропусками, система очков
должна быть пополнена схемой штрафов за пропуски. К этому вопросу
обращались, например, в [273], [214], [199] и [220].
Задача 2.16. Оригинальная матрица замен 250 ПТМ ([57]) назначает за
замену аминокислоты Gly аминокислотой Arg отрицательный счёт — 3
(использованы десятичные логарифмы и масштабный коэффициент 10 с
округлением до ближайшего целого). Средняя частота Arg в базе данных
последовательностей белка равна 0,041. На основании этих данных при
помощи описанного в разделе 2.2.1 метода оцените вероятность того, что Gly
будет заменён Arg за период времени 250 ПТМ.
Решение. Элемент Sij матрицы замен 250 ПТМ и частота аминокислоты qj
в базе данных белковых последовательностей (набор данных, из которого
получены параметры фоновой модели независимого порождения) связаны
следующей формулой:
"mi ^^j за 250 ПТМ)
10 lg щ
Поэтому вероятность замены Gly на Arg мы определяем из
P(Gly^Arg за 250 ПТМ) = 0,041 • Ю-0'3 = 0,0205. Q
Задача 2.17. В алгоритмах выравнивания белковых последовательностей
часто используются матрицы ряда BLOSUM. Метод нахождения счетов
замен аминокислот, используемых в матрицах BLOSUM, был представлен
супругами Хеникофф в [116]. Из следующего блока множественного
выравнивания, сгруппированного на три сечения с 75 %-м порогом:
A D A D
A D С D
А С С D
D С А А ,
D С А А
А А С С
D А С С

2.2. Дополнительные задачи и теория 85
определите матрицу счетов замен типа BLOSUM размера (3x3), используя
в качестве единиц полубиты.
Решение. Мы определяем матрицу F подсчётов с элементами /^ = fji,
равными числу (взвешенных) пар аминокислот г и j по всем столбцам
блока. Принцип вычисления /^ мы объясняем на примере нахождения
взвешенного подсчёта /аа- Прежде всего обратите внимание на то, что каждый
остаток из первой группы (последовательности 1-3) имеет вес 1/3, и также
на то, что каждый остаток из второй группы (последовательности 4, 5) и
третьей группы (последовательности 6, 7) имеет вес 1/2, поскольку полный
вес остатков из последовательностей одной и той же группы (на столбец)
должен быть равен 1 (каждая группа учитывается в выравнивании как
отдельная последовательность). В первом столбце есть три остатка А из
первой группы (каждый с весом 1/3) и один остаток А из третьей группы (с
весом 1/3). Таким образом, общий взвешенный подсчёт (на столбец 1) замен
А на А между различными группами определяется как f\A = 1/3-1/24-
+ 1/3 • 1/2 + 1/3 • 1/2 = 1/2. Нет никаких замен А на А между группами
в столбцах 2 и 4. Полный подсчёт замен А на А в столбце 3 составляет
f\A = 1/3 • 1/2 = 1/3. Наконец, fAA = f\A + f\A + fAA + f\A = 1/3 +
+ 0 4-1/2 + 0 = 5/6. Повторяя эту схему подсчёта для каждой пары г и j,
мы заполняем следующую симметричную матрицу F подсчётов для пар:
А
С
D
А
5/6
13/3
11/3
С
13/3
1
5/3
D
11/3
5/3
1/2
Наблюдаемая частота появления пары (г, j) определяется следующей
формулой: j.
_ Jij
4ij — : ,
Z-/ Z-/ Jij
г j=l
которая даёт следующие значения qij:
А С D
А 5/72 13/36 11/36
С 1/12 5/36
D 1/24

86
Глава 2
Затем ожидаемая частота е# появления пары аминокислот (г, j)
определяется выражениями ец — р% и е^ = 2piPj, где г ф j (здесь р^ — вероятность
появления аминокислоты г). Наблюдаемые частоты pi определяются
следующей формулой:
Рг = ди + оУ^Уч-
Таким образом, мы имеем рл = 29/72, рс = 19/72, р& = 1/3, и ожидаемые
частоты пар е^ выглядят следующим образом:
А 0,1622 0,2683 0,2125
С 0,1108 0,1757
D 0,0696
Наконец, вычисляя логарифмические отношения шансов в единицах
полубитов Sij = 2\og2qij/eij и округляя их до ближайшего целого числа,
получаем матрицу счетов замен (3 х 3):
А -2 1 1
С 1 -1 -1
D 1 -1 -1
□
2.2.2. Распределения счетов подобия
2.2.2.1. Теоретическое введение в задачи 2.19 и 2.20
Развитие сравнительной и эволюционной геномики было бы
невозможно без эффективных алгоритмов поиска подобия. Однако как только
подобие, характеризуемое высоким счётом, найдено в ходе поиска в базе
данных, возникает необходимость убедиться в том, что этот высокий счёт
не появился случайно. Чтобы установить доверительный уровень при
опознавании подобий, естественно изучить выравнивания случайных
последовательностей и определить пороги статистической значимости для счетов
подобия. Для углублённого обсуждения вопроса необходимо дать
несколько определений.

2.2. Дополнительные задачи и теория
87
Пусть биологическая (белковая) последовательность описывается
моделью независимого порождения с вероятностью qa появления
аминокислоты а в любой позиции, ^ qa = 1. Счёт не содержащего пропуски
попарного выравнивания определяется как сумма счетов для пар аминокислот,
тогда как счёт для пары аминокислот (а, Ь) определяется элементом s(a, b)
матрицы замен S (матрицы типа BLOSUM или ПТМ). Локальные попарные
выравнивания без пропусков, счета которых не могут быть улучшены
путём их продолжения или усечения, называют парами сегментов с высоким
счётом (ПСВС).
Элементы матрицы замен и параметры модели независимого
порождения должны удовлетворять условию отрицательной определенности
Y2qaqbs(a,b) <0,
а,Ь
что означает, что средний счёт на позицию выравнивания отрицателен.
Это условие предотвращает увеличение полного счёта локального
выравнивания из-за простого увеличения длины выравнивания. С другой
стороны, некоторые элементы матрицы S должны быть положительными,
иначе все ПСВС будут иметь нулевую длину. Обратите внимание, что
условие отрицательной определенности подразумевает, что функция /(A) =
— ^2 QaQb^Xs^a,b^ — 1 имеет только один положительный корень А (см.
задать
чи 5.3-5.5).
Распределения статистики счетов ПСВС были изучены в
многочисленных работах, например, в [129]; [179]; [221]; [251]; [138], [139]; [146]; [59],
[60]; [3].
В [60] было доказано, что для (генетически) независимых
последовательностей X и Y с достаточно большими длинами пит распределение
числа Ns ПСВС со счетами, превышающими S, может быть хорошо
приближено распределением Пуассона с параметром Л = Knme~xs. Здесь
А — положительный корень /(А), а постоянная К зависит только от {qa} и
матрицы счетов замен S. Поэтому математическое ожидание числа ПСВС
со счетами, превышающими S, определяется из уравнения
ENS и Л = Knme~xs,
а вероятность наблюдения некоторого числа z таких ПСВС — из уравнения
P(Ns = z)*e-^.

88 Глава 2
Распределение Ns может быть использовано для отыскания
распределения вероятностей максимального счёта 5тах (счёт оптимального не
содержащего пропуски локального выравнивания последовательностей X и У)
следующим образом:
P(Sm^ >S) = P(NS > 0) = 1 - P(NS = 0) « 1 - e"Ei4 (2.15)
Величину EiVs называют Е-значением (e-value) счёта S; значение
вероятности Р(5гтах ^ S) = 1 — e~EJVs называют Р-значением (p-value) счёта 5.
Е-значение часто используется для характеризации статистической
значимости числа ПСВС, наблюдаемого при поиске в базах данных.
Нормализованная сумма Тг счетов 5i,..., SV для г пар сегментов с
наивысшим весом,
Tr = \ (X^fc) -lnlT-ln(mn)r,
также может представлять интерес. В [139] было показано, что при
достаточно больших пит функция плотности вероятности ТТ приближается
выражением ж
^ = «0w.f»'-2°-'""'"*-
r\(r - 2)
и
Моменты этого распределения могут быть рассчитаны с помощью
преобразования Лапласа. В частности,
ЕТГ « г ( 1 + 7 - Y, 1/к ) ~ г(1 - Ь г) - 1/2,
VarTr «г2 (тг2/6-]Г1//с2) +г»2г-1/2,
где 7^0) 577 — постоянная Эйлера.
Вместо выравниваний без пропусков и ПСВС (пар сегментов с
высоким счётом), Нейгаузер [207] рассматривает локальные выравнивания со
вставками и удалениями, но без несовпадений (так что в паре выровненных
остатков (xi,yj) выполняется равенство Xi = yj). Нейгаузер предложила
алгоритм, ищущий локальные выравнивания последовательностей X и Y
с t парами, дающими совпадения, к пропусками и длиной каждого
пропуска не более I (так называемые (£, к, Z)-выравнивания). Было доказано, что
в случае независимых последовательностей X и Y (причём обе описаны

2.2. Дополнительные задачи и теория
89
моделью независимого порождения), имеющих достаточно большие
длины п и т, число W (£, к, Z)-выравниваний, найденных этим алгоритмом,
приближённо имеет распределение Пуассона с параметром
Л = Сктп(1 -Р)(*~к *)IV~fc,
где вероятность совпадения р и постоянная С зависят только от параметров
модели независимого порождения. Тогда при достаточно больших пит
наибольшее число S* пар совпавших символов в любом локальном
выравнивании с к пропусками (длина которых не превышает I) имеет следующее
распределение:
P(S* < t) и е"Л.
Наконец, формула Р-значения счёта выравнивания была выведена для
общего случая содержащего пропуски локального выравнивания (с
разрешёнными несовпадениями в выровненных парах) двух независимых
последовательностей и системой очков, основанной на матрице
логарифмических шансов замен S. Результаты были получены эвристически [199], [200]
и [201], а также аналитически [247], [248]. Ниже мы вкратце приводим
главные результаты по статистике счетов выравниваний с пропусками [247].
Мы делаем допущение, как это было сделано для ПСВС, что условие
отрицательной определенности сохраняется для элементов матрицы S и
параметров модели независимого порождения и что Л является единственным
положительным корнем функции /. В случае пропорциональной функции
штрафов за пропуски j(g) = —6д9 при достаточно больших пит, хвост
распределения максимального счёта S^ax локального выравнивания с не
более j пропусками может быть приближено следующей формулой:
Здесь постоянные К', Ь и сц зависят только от {qa} и матрицы счетов S,
а верхний предел сц равен 1/(еЛ<5 — 1).
В случае функции счёта j(g) = —d — Sg (линейный счёт за
пропуски) и достаточно больших пит счёт Smax оптимального локального
выравнивания (с любым числом пропусков) приближённо имеет следующее
распределение:
P(.Smax 2 S) « K'nme-xs £ ^Ше~^У £ ooa*e-A*!. (2.16)

90
Глава 2
В уравнении (2.16) К', Ь и а\ — те же постоянные, как и в случае
пропорциональной функции штрафов за пропуски, и принимается допущение о том,
что Ad = In S + С при некоторой постоянной С. Если, кроме того,
скорости роста п, т и S удовлетворяют условию nme~s —> v при некотором
конечном положительном v, то формула для Р-значения принимает вид
P(Sm*x>S)*l-eA, (2.17)
где Л определяется выражением в правой части уравнения (2.16). Если
в выражении для Л мы устанавливаем j = 0 и поэтому рассматриваем
только локальные выравнивания без пропусков, то уравнение (2.17) для Р-
значения сводится к уравнению (2.15), выведенному в [60]. Р-значения,
используемые в оригинальной программе BLAST ([6]) для поиска счетов
подобия не содержащих пропуски локальных выравниваний, были
рассчитаны по формуле (2.15). Примечательно, что в версии программы BLAST
с допущением пропусков [7] использовали приближённую формулу (2.17)
для Р-значений, при этом значения постоянных, входящих в выражение
для Л, оценивались численно для каждого отдельно взятого поиска. В [239]
был использован аналог распределения, определяемого уравнением (2.15),
для оценки статистической значимости суммы парных счетов не
содержащего пропусков блока нескольких аминокислотных последовательностей.
Дальнейшие разработки и обсуждения задач, относящихся к
распределениям счёта, могут быть найдены в [276], [8], [278], [15] и [109]. Обзор
статистических методов анализа последовательностей приведён в [137].
Распределения статистики счетов попарного выравнивания Ns, Smax,
S* или Smax обеспечивают строгий критерий для проверки гипотез
об эволюционной связи последовательностей X и У. Могут быть
рассмотрены следующие два теста для нулевой гипотезы,
Но = {X и У — несвязанные (независимые) последоват-ти},
против альтернативной гипотезы,
На = {X и У — (эволюционно) связанные последоват-ти}.
В тесте 1, основанном на статистике Smax, Но принимается (На
отвергается), если Smax < S°; в противном случае Но отвергается (На принимается).
В тесте 2, основанном на статистике Tr, Hо принимается (На отвергается),
если \ТГ - ЕГГ| < б*; в противном случае Н0 отвергается (На
принимается). Обратите внимание, что предельные значения 5° и е* должны быть
определены а priori (до рассмотрения собственно последовательностей X
и У).

2.2. Дополнительные задачи и теория
91
Задача 2.18. С целью установления эволюционной связанности локально
выровненных последовательностей белка X и Y длины, соответственно,
п = 100 и т = 300 применены тест 1 и тест 2. Принято допущение о том,
что К = 0,1 и А = 0,7.
а) Определите критическое значение 5°, соответствующее уровню
значимости ai (коэффициент ложных отрицательных результатов) теста 1,
равному 0,05.
б) Оцените уровень значимости oli теста 2 при критическом значении
£* = 13,8иг = 5.
в) Для следующих наблюдаемых счетов Si = 15, S2 = S3 = 12, 54 =
= 11, S5 = 10 пар сегментов с наивысшим счётом используйте тесты 1 и 2
с критическими значениями, аналогичными оговорённым в пунктах а и б,
чтобы проверить гипотезу if о в сравнении с гипотезой На.
Решение, а) Из определения уровня значимости теста а± и
уравнения (2.15) мы имеем
ai = Р(ошибка 1-го рода) = Р(Щ отвергнута|Яо верна) =
= ^(Smax ^ S°\X и У — несвязанные (случайные) посл-ти) «
Таким образом, уровень значимости теста 1 для любого критического
значения 5° равен Р-значению величины 5°. Для данного ai значение 5°
должно удовлетворять уравнению —Kmne~xs = ln(l — а±). Решая это
уравнение, мы устанавливаем, что для проверки гипотезы Но
относительно На с уровнем значимости а\ = 0,05 должно быть выбрано критическое
значение 5° = 16.
б) Для того чтобы оценить уровень значимости теста 2 для данного
критического значения е*9 мы применяем неравенство Чебышева в
форме (11.10):
а2 = Р(ошибка 1-го рода) = Р(Щ отвергнута|Я0 верна) =
= Р(\ТГ — ЕТГ| ^ €*\Х и У — несвязанные (случайные) посл-ти) =
= Р(\ТГ - ЕТГ\ ^ е*\Тг имеет ф.п.в. /(*)) < ^ г.

92
Глава 2
При г = 5 дисперсия нормализованной суммы Var T5 ~ 2 • 5 — 1/2 = 9,5;
таким образом, при критическом значении е* = 13,8 уровень значимости
теста а2 < 0,05.
в) Чтобы проверить гипотезу Но в сравнении с гипотезой На, мы
вычисляем статистику Smax (чтобы использовать в тесте 1) и Т$ (чтобы
использовать в тесте 2) для наблюдаемых счетов выравнивания:
^max = Si = 15,
T5 = \(j2Sk) - ЫКГ - ln(mn)r = 42 - 51n3 - 15 In 10 = 1,968.
Поскольку Smax = 15<16 = 5°, мы принимаем Но (отвергаем На) в
тесте 1 с уровнем значимости ai = 0,05. Чтобы выполнить тест 2, мы
должны вычислить математическое ожидание нормализованной суммы: ЕТ5 =
= 5(1 - In5) - 1/2 = -3,547. Поскольку \ТЪ - ЕТ5| = 5,515 < 13,8 = е\
нулевая гипотеза принимается (а альтернативная гипотеза отвергается) в
тесте 2 с уровнем значимости а2 < 0,05. Поэтому наблюдаемые счета пяти
пар сегментов с наивысшим счётом не поддерживают гипотезу о
существовании эволюционной связи между последовательностями белка X и Y при
уровне значимости теста не более 0,05. □
Задача 2.19. Белковая последовательность X длины m аминокислот
используется в качестве запроса для поиска подобия в базе данных белковых
последовательностей, содержащей к последовательностей белка Yi,..., У&
длины, соответственно, ni,... ,п&. Найдите соотношения а) между Е-
значениями попарного сравнения последовательностей X и У* — Ег, где
г = 1,..., к, и i^-значением полного поиска в базе данных; б) между Р-
значениями попарных сравнений — Р\ где г = l,...,fe, и Р-значением
полного поиска в базе данных.
Решение. При поиске подобия между последовательностью X и базой
данных ожидаемое число ПСВС со счётом, превышающим S, равно сумме
значений ЕЛГ£ для оптимальных локальных выравниваний пар
последовательностей X и Yi, где г = 1,..., к. Если мы примем допущение о том,
что все последовательности в базе данных, а также последовательность X

2.2. Дополнительные задачи и теория
93
произведены моделью независимого порождения, то ^-значение поиска в
базе данных определяется из
Е = ENS = ^'ЕЩ = Y,El = ^Kmme~xs =
г=1 г=1 г=1
к
= Kme-xsY^n>i = Kmne~xs, (2.18)
г=1
где п — общая длина последовательностей в базе данных. Таким образом,
при вычислении ^-значения поиска в базе данных, базу данных можно
рассматривать как единую последовательность длины п.
Р-значение поиска в базе данных может быть определено как функция
Pi, P2,..., Рк из уравнения (2.18) следующим образом:
Р - -P(5max > S) « 1 - e~ENs = 1 - eSiE% =
г=1 г=1
2.2.3. Распределение длины длиннейшего общего слова для нескольких
несвязанных последовательностей
Теоретическое введение в задачу 2.21. Последовательности геномной
ДНК различных видов могут обладать виртуально идентичными
непрерывными подпоследовательностями, которые являются поразительно
длинными. Идентификация и интерпретация таких общих подпоследовательностей
представляет значительный биологический интерес. Могут быть
исследованы связанные с этим вопросом статистические задачи: каковы свойства
распределения длины длиннейшего общего слова, наблюдаемого в двух (или
более) случайных последовательностях, при заданном типе модели
последовательности? Как изменится распределение, если разрешить не более к
несовпадений в общем слове?
Математическое исследование подобных задач проводилось Эрдо-
шем [74], который определил (почти наверное) верхний и нижний
пределы для длиннейшей последовательности орлов в серии п подбрасываний
правильной монеты, а также для последовательностей орлов, прерываемых
не более чем к решками. В [11] было доказано, что при известной длине
длиннейшего общего слова М(п,т) двух последовательностей с длинами

94
Глава 2
п и га, согласно допущению о том, что последовательности (независимо)
порождены (не обязательно одинаковыми) моделями независимого
порождения, справедливо выражение
М{п,т) =к\=1
bgi/p (mn)
Здесь р — вероятность совпадения, р = Р(х{ = yj), а К — постоянная,
зависимая от отношения скоростей роста пит, а, также от параметров модели
последовательности. Этот результат был обобщен для случая нескольких
последовательностей, описываемых либо моделями независимого
порождения, либо марковскими цепями. Для распределения длиннейшей
непрерывной последовательности Мь{п, т) совпадений между двумя независимыми
последовательностями при разрешении не более к несовпадений в [12]
были определены математическое ожидание, дисперсия и предельное
распределение величины Мк(п, т) при п, га —► +оо. Если к = 0, рассматривается
непрерывная последовательность и как п, так и т растут с одинаковой
скоростью, то Мо(п,т) = М{п,т) имеет приблизительно то же
распределение, что и максимум (1 — р)пт независимых геометрически
распределённых (с параметром р) случайных переменных. Математическое ожидание и
дисперсия величины Мк(п,т) описываются следующими формулами:
EMfe(n, га) « log1/p((l - р)тп) + к log1/p log1/p((l - р)тп)+
)g
VarMk(n,m) « ^ + ^
+fclog1/p i^ - log1/p(fc!) + 7bg1/p(e) - |, (2.19)
12'
Здесь 7 и 0,577 — постоянная Эйлера. Далее, в [144] и [145] было
получено асимптотическое распределение длины длиннейшего общего слова
среди г или более из s независимых последовательностей, порождённых
стационарными процессами с равномерным перемешиванием.
Задача 2.20. Последовательности X и Y длин 1000 и 10000 порождены
(независимо друг от друга) моделью независимого порождения с равной
вероятностью порождения символов. Какова ожидаемая длина
длиннейшего общего слова между X и Y, если несовпадения запрещены (к = 0) и
если разрешено не более двух несовпадений (к = 2)? Рассмотрите
алфавиты а) нуклеотидов и б) аминокислот.

2.2. Дополнительные задачи и теория
95
Решение, а) Поскольку нуклеотиды всех четырёх типов имеют равные
вероятности qa = 1/4 появления в данной позиции последовательностей X
и Y, постольку вероятность р = P(xi = t/j) наблюдения совпадающих
символов в позициях г в X и j в Y для любой пары г и j определяется как
P = ]Cfcrfa = 4-^=0,25
Уравнение (2.19) математического ожидания величины Mk(n, га) даёт
ЕМ0(1000; 10000) = log4(0,75 • 1000 • 10000) - °^77 - \ = 11,335;
ЕМ2(1000; 10 000) = ЕМ0(1000; 10 000) + 2 log4 log4(7 500 000)+
+21og43-log42 = 15,934.
Поэтому математическое ожидание длины длиннейшего общего слова
между последовательностями X и Y равна 11 п. н., тогда как средняя
длина длиннейшего общего слова с не более чем двумя несовпадениями
равна 15 п. н.
б) Так как аминокислоты двадцати типов имеют равные вероятности
qa = 1/20 появления в данной позиции последовательностей X и Y, мы
определяем, что р = Y^QaQa = 20 • 1/400 = 0,05. Мы находим ожидае-
a
мую длину длиннейшего общего слова в последовательностях X и Y при
помощи уравнения (2.19):
П ^77 1
ЕМ0(1000; 10000) = log20(0,95 • 1000 • 10000) - -—jrz - ^ = 5,056;
in и, Uo л
ЕМ2(1000; 10 000) = ЕМ0(1000; 10 000) + 2 log20 log20(9 500 000)+
+21og2019-log202 = 7,912.
Естественно, что ожидаемая длина длиннейшего общего слова
возрастает по мере того, как разрешается всё большее число несовпадений. Также
вполне можно было ожидать, что длиннейшее общее слово в
последовательностях аминокислот в среднем короче, чем длиннейшее общее слово
в последовательностях нуклеотидов той же длины — из-за меньшей
вероятности р совпадения в данной паре позиций рассматриваемых
последовательностей. □

96
Глава 2
Задача 2.21. Алгоритм сравнения последовательностей по точечной
диаграмме опознаёт подобия в последовательностях ДНК по следующему
правилу. Пара фрагментов ДНК длины /, начинающихся, соответственно, в
позициях г и j двух последовательностей X и Y, рассматриваются как
«совпадающая пара», если по крайней мере к нуклеотидов из / образуют пары
идентичных символов (вставки или удаления не допускаются) с
несовпадениями, разрешёнными только во внутренних парах. Определите
математическое ожидание числа «совпадающих пар» для последовательностей ДНК
X и Y длины 1000 п.н. при / = 8 и к = 6. Последовательности описаны
моделью независимого порождения с вероятностями Т, С, А и G равными,
соответственно, 0,3, 0,2, 0,3 и 0,2.
Решение. Нуклеотиды, занимающие позиции г в последовательности X
и j в последовательности Y, идентичны с вероятностью
Р(*г = У,)=Р{(*г,Уз) = (Т,Т), или (а*,у,) = (С,С)
Km(xi,yj) = (A,A)9 или (а*, од) = (б?, б?)} =
= 0,32 + 0,22 + 0,32 4- 0,22 = 0,26.
Выравнивание двух сегментов ДНК производит последовательность пар
нуклеотидов, соотносимую с последовательностью Бернуллиевых
испытаний, где «благоприятный» исход («нуклеотиды в паре идентичны»)
наступает с вероятностью 0,26. Тогда пара фрагментов, начинающаяся в
позициях (i,j), будет «совпадающей парой» с вероятностью
Р(совпадающая пара, начинающаяся в (i,j)) =
= Р(8 «благоприятных» исходов в 8-ми исп-х)+
+Р{1 «благопр-х» исходов в 8-ми исп-х, включая нач-е и конечное)+
+Р(6 «благопр-х» исходов в 8-ми исп-х, включая нач-е и конечное) =
= 0,268 4- 0,267 • 0,74 • 6 + 0,266 • 0,742 • Г J = 0,0029.
В двух последовательностях ДНК длины 1000 п. н. существует
N = (1000 - 7)(1000 - 7) = 9932 = 986049

2.3. Дополнительная литература
97
пар фрагментов длины 8. Здесь снова используется схема Бернуллиевых
испытаний. Мы рассматриваем N Бернуллиевых испытаний с «успехом», под
которым понимается «пара фрагментов, начинающаяся в позициях (i,j) —
совпадающая пара», имеющих место с вероятностью р = 0,0029. Тогда
математическое ожидание числа «совпадающих пар фрагментов»
определяется из выражения
Е = Np = 986049 • 0,0029 и 2860.
2.3. Дополнительная литература
Характеристики алгоритмов попарного выравнивания
последовательностей оценивались и системы очков рассматривались многими авторами,
в том числе [213], [214] и [31]. В [245] представлен разработанный
алгоритм с комбинаторным продолжением (КП) для попарного выравнивания
двух белковых последовательностей. Выравнивание в алгоритме с КП
было определено по выровненным парам белковых фрагментов, отражающим
структурное подобие. Алгоритмы попарного выравнивания, основанные на
Байесовском подходе, были предложены в [290] и [277].
В [136] развит новый метод получения матрицы замен, который
максимизирует средний доверительный уровень идентификации гомологии,
проверяемый по набору пар гомологичных и негомологичных белков из базы
данных COG ([261]). Ещё один метод оптимизации матрицы замен, который
улучшает точность поисков гомологии, был предложен в [125]. В [228]
приводится анализ качества выравниваний белковых последовательностей в
сумеречной зоне (для пар последовательностей с идентичностью на 20-35 %).
Алгоритмы для сравнения целых геномов были разработаны Делхе-
ром [58] и Шварцем [240]. Брудно [37] разработал алгоритм LAGAN для
быстрого попарного выравнивания гомологичных геномных
последовательностей: сначала выбирается оптимальный набор неперекрывающихся
локальных выравниваний, после чего промежуточные фрагменты
последовательностей выравниваются алгоритмом Нидлмена-Вунша. Алгоритмы для
выравнивания последовательностей кДНК с геномными
последовательностями ДНК были предложены в [87] (SIM4) и [151] (BLAT).
Алгоритмы выравнивания последовательностей были включены в
предсказание трёхмерной структуры белка ([188]) и в идентификацию событий
слияния генов в полных геномах ([73]).

98 Глава 2
Алгоритмы выравнивания последовательностей часто использовались
в проектах сравнительной геномики. Один из наиболее важных
источников информации о геномах человека и других видов, база данных Ensembl
([126]; [50]), использует автоматическую поточную линию аннотирования
генов, в которую входят инструменты для поиска гомологии. В базе
данных KEGG [135] применяется всесторонний поиск подобий с помощью
алгоритма Смита-Уотермена, чтобы передавать функциональную
аннотацию белков и устанавливать отношения типа ортолог-паралог кодирующих
белки генов в полных геномах, хранящихся в секции SSDB базы данных
KEGG.

Глава 3
МАРКОВСКИЕ ЦЕПИ И СКРЫТЫЕ
МАРКОВСКИЕ МОДЕЛИ
Краеугольным камнем этой книги является глава из «АБП», в которой
описываются марковские цепи и скрытые марковские модели. Алгоритмы
сравнения последовательностей, описанные в главе 2, не могли быть
разработаны без введения теоретически обоснованных счетов подобия и
статистической теории распределений счёта подобия. Эти достижения в свою
очередь были бы неосуществимы без рационального выбора вероятностных
моделей последовательностей ДНК и белка. Как марковские цепи, так и
скрытые марковские модели часто оказываются исключительно хорошими
вариантами при выборе моделей последовательностей. Более того, скрытые
марковские модели (СММ) представляют собой потенциально более
гибкие средства для анализа биологических последовательностей, потому что
они позволяют осуществлять одновременное моделирование наблюдаемых
и ненаблюдаемых (скрытых) состояний. Наличие состояний двух типов
наилучшим образом соответствует потребности моделировать некоторую
важную дополнительную информацию, существующую помимо
последовательностей/^ se, такую как функциональное значение элементов
последовательности, совпадения и несовпадения символов в парах выровненных
последовательностей, эволюционно консервативные области во множестве
выравниваемых последовательностей, филогенетические отношения и т. д.
В главе 3 «АБП» представлены фундаментальные алгоритмы теории
СММ: алгоритм Витерби, прямой и обратный алгоритмы, а также
алгоритм Баума-Велша. Все эти алгоритмы находят разнообразные
применения в анализе биологических последовательностей. Конечно, некоторые из
таких построений на СММ существуют параллельно с их
невероятностными аналогами; например, сравните алгоритм Витерби для парных СММ
и классический алгоритм динамического программирования для попарного
выравнивания. Так, для поиска консервативных доменов, построения
филогенетических деревьев и т. д. известны подходы, основанные как на СММ,
так и не на СММ.

100
Глава 3
Приведённые в этой главе задачи из «АБП» сосредоточены на выводе
формул, которые образуют основание для вероятностного моделирования
и построения опирающихся на СММ алгоритмов. Дополнительные
задачи сфокусированы на применениях основных алгоритмов на СММ,
сравнении конкурирующих моделей и оценке параметров моделей. Мы обсуждаем
также альтернативный, основанный не на СММ, подход к задаче
сегментации последовательности на однородные по составу сегменты.
3.1. Оригинальные задачи
Задача 3.1. Выражение суммы вероятностей всех возможных
последовательностей состояний длины L может быть записано следующим образом:
х х\ Х2 xl г=2
Покажите, что эта сумма равна 1.
Решение. Путём изменения порядка суммирования и применения
определения вероятности перехода мы переписываем выражение суммы
следующим образом:
£*»(*) = ЕЕ •••£*>(*1)Па**-1«.=
х х\ Х2 хь г=2
L
= Е " Е П а*г-1*г Е P(Xl)a*l*2 =
Х2 XL i=3 Х\
L
= £"-£Па*«-1**£р(*1)*,(*2|*1). (з-1)
Х2 xl г=3 xi
Очевидно, что внутренняя сумма (по х{) даёт вероятность х^ потому что
суммирование выполняется по всем возможным состояниям в позиции г =
= 1. Поэтому последнее выражение в уравнении (3.1) принимает вид
L L
Е Е П ***-!*л**) = Е Е П ^-i** E р(х2)ры*2)-
Х2 xl г=3 хз xl i=4 хг

3.1. Оригинальные задачи
101
Теперь мы можем применить тот же довод к внутренней сумме по х^ и так
далее. После L — 1 шага мы получаем
£Р(х) = £Р(*ь) = 1.
Последнее равенство верно, так как сумма включает вероятности всех
возможных состояний марковской цепи в позиции L. □
Задача 3.2. Допустим, что некоторая модель имеет конечное состояние
и что переход из любого состояния в конечное состояние имеет
вероятность т. Покажите, что сумма вероятностей по всем последовательностям
длины L (собственно заканчивающимся переходом в конечное состояние)
равна т(1 — t)l_1.
Решение. Принимая допущение, что вероятности перехода из любого
состояния в конечное состояние е равны т, мы имеем аХ1£ = т для любого
состояния xi, что подразумевает следующее:
{х2:х2фе}
Точно так же для любого состояния xi, такого что х ф е, мы имеем
У ; 0>XiXi+l = 1 ~ Г>
{xi+i:xi+i^e}
где г = 1,..., L — 1. Тогда сумма вероятностей всех последовательностей
длины L, заканчивающихся в конечном состоянии е, описывается
выражением вида
^ = / _, / ^ ' ' ' / J *\х1)а'х1Х2аХ2Хз ' ' ' ахь-1Хьахье =
xi {х-2'.х-2фе} {хь'-хьфе}
= TJ2 5Z "" J2 p{xi)aXlX2 ■ ■ ■
xi {x2:x2#e} {xb_i:xr,_i^e}
( V
' ' ' 0'XL-2XL-1 I / у &XL-1XL
\{хьхьфе}

102 Глава 3
Xl {XL-2'XL-2^e}
*XL-3XL-2 | / j ^XL-2XL-1 J ' (3-2)
Лхь-1-XL-i^e}
После повторения подобной перегруппировки членов и разложения на
множители (L — 1) раз сумма Е в уравнении (3.2) принимает вид
E = r(l-r)^-1X;P(x1) = r(l-r)^-1.
□
Задача 3.3. Покажите, что сумма вероятностей по всем возможным
последовательностям любой длины равна 1. Это доказывает, что марковская цепь
действительно описывает собственное распределение вероятностей по
всему пространству последовательностей.
Решение. Наша цель состоит в проверке следующего равенства:
оо / \
l=i vxi -г#. xl )
где е — конечное состояние марковской цепи. В задаче 3.2 было доказано,
что сумма Sl вероятностей по всем последовательностям длины L
(собственно заканчивающимся конечным состоянием е) равна т(1 — r)L_1, где
г — вероятность перехода в конечное состояние. Тогда
AX2#3 * ' ' aXL-lXLaXL£
S I S S '"^2Р(х^)ах1х2а,
Xl XL
оо оо
L=l L=l
п

3.1. Оригинальные задачи
103
Задача 3.4. Пусть Р(х,7г) — вероятность совместного наступления
событий наблюдения последовательности х и последовательности состояний 7Г.
Мы определяем наиболее вероятный путь 7Г* как 7Г* = argmax^ Р(х,тг).
Покажите, что это определение эквивалентно 7Г* = argmax^ Р(тг|х).
Решение. Согласно определению условной вероятности, Р(тт\х) =
= Р(х,7г)/Р(х). Поскольку Р(х) не зависит от 7Г, постольку одна и та
же последовательность состояний 7г* даст максимальное значение и для
Р(х,7г) и для Р(х,7г)/Р(х):
argmax^ Р(х, 7г) = argmax^ Р(7г|х) = 7Г*. г-.
Задача 3.5. Выведите формулу
P(7Ti = /С, 7Гг+1 = *|Ж, в) = , (3.3)
где прямая переменная Д (г) = P(#i,..., ж$, 7Г» = fc) есть вероятность
совместного наблюдения подпоследовательности ал,...,а:» и определённого
скрытого состояния TTi = fc; аы и ег(жг), суть, соответственно, вероятности
перехода и порождения; обратная переменная bk(i) = Р(ж»+1,..., xl, Щ =
= к) — вероятность совместного наблюдения подпоследовательности
Xi+i,..., ££ и определённого скрытого состояния П{ = к.
Решение. Теорема умножения вероятностей,
Р(АГ)ВПС) = Р(А)Р(В\А)Р(С\А ПВ),
позволяет нам представить левую часть уравнения (3.3) следующим
образом:
Р(7Гг = «, 7Гг+1 = 1|Ж, 0) = —^— —
Р(*|6)
hi = ^|«1
хР(ж£+2,...,жь|ж1,...,я:.,а:»+1,7Г. = к,щ+! = 1,6). (3.4)
= р/ |гчч 'P(Xi,...,Xi,1Ti = *;|в)Р(ж<+1,7Гг+1 =1|Ж1,...,Я:»,7Г» = fc,6)x
Р(ж|В)

104
Глава 3
Поскольку состояние щ+х в позиции г + 1 марковской цепи первого
порядка зависит только от состояния щ в предыдущей позиции г,
уравнение (3.4) принимает вид
Р{Щ = fc, 7Ti+i = 1\х, в) =
= P(de)'[р(хь''''**'** = fc'e)x
ХР(ж.+ 1,7Г<+1 =/|7Гг = Й,в)Р(ж»+2,...,Я:ь|7Г»+1 =*,6)].
Наконец, прибегнув к определениям переменных Д(г) и &г(г), а также
aw и ej(xt+i), мы получаем
Р(тГ; = fc,7Ti+1 = 1\Х, 6) = ^^ . Q
Задача 3.6. Выведите следующее уравнение:
i П J {г:^=6}
для ожидаемого числа 2?&(Ь) раз, при котором наблюдаемое состояние
(символ) Ъ порождается из скрытого состояния к. Здесь внутренняя сумма
берётся по всем позициям г, порождающим символ Ь, а внешняя сумма берётся
по всем обучающим последовательностям хК
Решение. Рассматриваемая формула является частью алгоритма Баума-
Велша ([20]) и используется для оценки параметров скрытой марковской
модели, включая вероятности порождения е^(6) из набора реализаций,
который служит набором обучающих последовательностей. Этот алгоритм
работает на итерациях. Для определения текущих оценок е'к{Ь) и а'к1
прямые переменные f3k{i) и обратные переменные &£(г) рассчитываются для
каждой обучающей последовательности х* при помощи, соответственно,
прямого и обратного алгоритмов. Новая оценка ек(Ь) определяется как
оценка методом наибольшего правдоподобия:
ек(Р) =
ЕЗДУ
V

3.1. Оригинальные задачи
105
где Ekib) — математическое ожидание числа порождений символа Ь из
скрытого состояния к и сумма ]С £*(&') даёт математическое ожидание
v
числа появлений состояния к для данного набора обучающих
последовательностей. Чтобы вывести уравнения математических ожиданий Ek(b), мы
вводим счётную случайную величину 5\:
d _ J 1» если состояние к появляется в позиции г посл-ти х*,
у 0, иначе.
Тогда N(k) = ^2^26j — число появлений состояния к в путях скры-
3 i
тых состояний, и математическое ожидание величины N(k) определяется
как
ЕЩк) = Е Е Е<5* = Е Е pW = fc> И.е) =
3 г 3 i
Здесь в обозначает вероятностную модель, связанную с набором текущих
оценок параметров. Точно так же мы выводим уравнение математического
ожидания Ek(b) числа раз, при котором символ Ъ порождается из
скрытого состояния к при заданном наборе обучающих последовательностей.
Единственное отличие заключается в том, что в величинах 8{(Ъ) должны
теперь отсчитываться появления состояния к только в том случае, если оно
порождает символ Ь. Итак, мы завершаем вывод следующим образом:
вд = Е Е шцъ) = ^ Е pw' = *,i^,e) =
** {г:х{=Ъ} хо {{:Х{=Ъ}
3 {ъ:х\=Ь}
Обратите внимание, что в итеративной процедуре обновлённая оценка
вероятности порождения е£(6) принимает вид
е mm
„,_, Ек{Ь) Ек(Ь) i р(^1е) {i:xj=b}
efcW = _
j Г\Х \КУ) i

106 Глава 3
Задача 3.7. Вычислите общее число переходов, необходимое в
представленной на рис. 3.1 прямой связной модели с длиной L. Вычислите то же
самое для модели с молчащими состояниями, изображённой на рис. 3.2.
Рис. 3.1. Прямая связная цепь состояний
Решение. В прямой связной цепи из L состояний (см. рис. 3.1) общее
число переходов определяется по формуле
*1 *1 н *"1
Рис. 3.2. Модель с молчащими состояниями, изображёнными в виде кружков
В модели с молчащими состояниями (см. рис. 3.2) есть два
перехода из каждого «регулярного» состояния, кроме последних двух состояний.
Есть два перехода из каждого молчащего состояния (их число равно L — 2)
за исключением последнего. Так, общее число состояний определяется из
выражения
N2 = (L - 2)2 + 1 + (L - 3)2 + 1 = AL - 8.
Предпочтительны модели с меньшим числом возможных переходов между

3.1. Оригинальные задачи
107
состояниями1. В коротких цепях (L < 6) число N± меньше, чем АГ2. По
мере увеличения L величина N± возрастает быстрее, чем iV2, и при L ^ 7
величина N становится больше, чем No.. D
i.TAVLS^/ J W^lIA 1VXUA/A -■-* А*^*АЖЛ. АЯЛ~М.Л.ЩЛ> ■*• ' J_ **XS** Ъ*\Л>'%* Л. %A*
величина Ni становится больше, чем iNfe.
Задача 3.8. Покажите, что число путей через ряд из п состояний
(подобный представленному на рис. 3.3) равно (^V) при длине I.
Г>
1 ГьУ
р]
ГТ^Г
г>
__h^
г>
_J~b
►
Рис. 3.3. Ряд состояний с петлями
Решение. Любой путь длины I через ряд из п состояний (I > п) состоит из
п— 1 перехода в следующее состояние (с вероятностью 1 — р каждый) и1—п
перехода в то же самое состояние (с вероятностью р каждый). Последний
переход в пути должен быть «выходом» из n-го состояния. Поэтому число
различных путей равно числу способов выбора I — п переходов,
возвращающихся к тому же самому состоянию из I — 1 внутренних переходов в этом
пути. Это число равно биномиальному коэффициенту:
(1-1)!
(1-Л = (1-Л= (|
\1 -п) \n-lj (п-
1)!(/-п)!
Обратите внимание, что распределение вероятностей длины L путей
через эту модель представляет собой отрицательное биномиальное
распределение: // _ 1 \
J?(L = 0=(;_^-n(l-p)n, (3.5)
где 1^ п. □
Задача 3.9. (В новой формулировке, представленной Андерсом Крогом.)
Рассмотрите модель п состояний с петлями (рис. 3.3), на основании которой
было выведено уравнение (3.5). а) Какова вероятность наиболее
правдоподобного пути через модель, которую найдет алгоритм Витерби? б)
Пригоден ли при работе с алгоритмом Витерби такой тип моделирования длины?
^адо понимать, что меньшее число переходов накладывает определенные ограничения
на распределение длин порожденных последовательностей. В частности, модель 3.1.
позволяет генерировать, например, последовательности четной длины (как?), а модель 3.2. этого не
может в принципе (почему?). — Прим. ред.

108
Глава 3
Решение. (Андерса Крога). а) Любой пролегающий через модель путь
длины I, где I ^ п, имеет вероятность р1~п{1 — р)п. Таким образом, наиболее
правдоподобный путь также будет иметь эту вероятность, так что алгоритм
Витерби «не видит» отрицательное биномиальное распределение. Тогда
ответ на вопрос б — «нет». □
Задача 3.10. Ген всякого прокариота представляет собой непрерывную
последовательность нуклеотидных триплетов, или кодонов. Ген начинается
старт-кодоном ATG и заканчивается одним из трёх стоп-кодонов: ТА А,
TAG или TGA. Вычислите число параметров в такой модели кодонов.
Набор данных содержит порядка 300 000 кодонов. Возможно ли на основании
такого набора данных получить оценку марковской цепи второго порядка?
Решение. Сначала мы сделаем допущение о том, что последовательность
кодонов смоделирована марковской цепью первого порядка с состояниями,
определяемыми как шестьдесят один смысловой кодон. Три стоп-кодона
сгруппированы вместе в конечное состояние марковской цепи. Так как ген
начинается кодоном ATG, начальные вероятности состояний определяются
следующим образом: P(ATG) = 1 и ноль для всех остальных состояний.
Чтобы описать такую марковскую цепь, необходимо определить 61 -61 =
= 3721 вероятностей переходов между смысловыми кодонами и 61 -3 = 183
вероятностей переходов из смысловых кодонов в конечное состояние.
Поэтому общее число параметров модели первого порядка определяется как
iVi = 3721 + 183 = 3904.
Если последовательность кодонов смоделирована марковской цепью
второго порядка, то число параметров значительно увеличивается.
Действительно, есть шестьдесят одна начальная вероятность для всех возможных
пар (ATG,XYZ) начальных кодонов, 613 = 226981 вероятность
переходов между смысловыми кодонами и 612 • 3 = 11532 вероятность переходов
из пар смысловых кодонов (XiYiZi,X2Y2Z2) в конечное состояние.
Таким образом, общее число параметров, необходимых для марковской цепи
кодонов второго порядка, определяется как
N2 = 61 + 226981 + 11532 = 238205.
Можем ли мы получить надежные оценки этих N2 параметров на
основании набора данных, включающего 300000 кодонов?
Производимая методом наибольшего правдоподобия оценка вероятности перехода

3.1. Оригинальные задачи
109
P(XsYsZs\XiYiZiy X2Y2Z2) этой марковской цепи второго порядка есть
отношение N1/N2, где iVi — подсчёт триплетов кодонов {X{Y\Z\, X2Y2Z2,
ХзУз^з), а АГ2 — подсчёт пар кодонов {X{Y\Z\, X2Y2Z2) в наборе данных.
Вероятно, что многие из 613 = 226 981 различных триплетов кодонов могут
никогда не появиться в выборке, содержащей приблизительно 300000
триплетов кодонов. Наблюдаемые нулевые подсчёты триплетов кодонов (если
мы не используем псевдоотсчёты) дают нулевые вероятности переходов и
таким образом ведут к сверхсоответствию модели. Ясно, что набор данных,
содержащий порядка 300 000 кодонов, недостаточен для оценки параметров
марковской модели второго порядка. □
Задача 3.11. Какое усовершенствование может быть сделано для
построенной на марковской цепи первого порядка модели кодирующей белок ОРС
с состояниями кодонов?
Решение. Вместо марковской цепи кодонов мы можем рассматривать
неоднородную марковскую цепь (НМЦ) или скрытую марковскую модель
(СММ), в которых состояния определяются как отдельные нуклеотиды, а не
как триплеты нуклеотидов. Такие НМЦ и СММ имеют существенно
меньшее число параметров (см. задачу 3.12). Можно показать ([28]; [24]; [165];
[39]), что подобные модели описывают регулярные комбинации нуклеотид-
ного состава в кодирующих белок и некодирующих областях с точностью,
достаточной для проектирования точных алгоритмов поиска генов. □
Задача 3.12. Хорошо известно, что в кодирующих белок генах три
позиции кодонов имеют различную статистику частот нуклеотидов, и поэтому
для моделирования кодирующих белок областей естественно использовать
неоднородную трёхпериодическую марковскую цепь ([27]). Три периода
модели нумерованы от 1 до 3 согласно позиции в кодоне. При допущении
о том, что х\ находится в 1-й позиции кодона, вероятность Ж1,Ж2,#з> • • •
будет равна
12 3 12
Х1Х2 X2X^ X3X4 Х^Х^ Х^Хб * * ' '
где ак — элементы вероятностной матрицы переходов периода к. Опишите
СММ, которая соответствует этой неоднородной марковской цепи первого
порядка.

по
Глава 3
Решение. Набор скрытых состояний такой СММ может быть определен
как
{А\, А2, As, Ci, C2, С3, G\, G2, G3, Ti, Г2, Г3},
где индекс г при Х^ обозначает позицию нуклеотида X в кодоне.
Наблюдаемые состояния, символы нуклеотидов А, С, G, Т, порождаются скрытыми
состояниями с вероятностями ex. (X) = 1 и ех% (У) = 0 при Y ф X, где
X,Ye{A,C,G,T}.
Для определения этой СММ требуется семьдесят два параметра:
двенадцать начальных вероятностей aoxi, aox2> а°хз> сорок восемь
вероятностей переходов между скрытыми состояниями, axxY2, a>x2Y3, ах3У1» и Две~
надцать вероятностей переходов в конечное состояние, аххо, ах2о, о>х3о-
Обратите внимание, что некоторые переходы между скрытыми
состояниями невозможны:
axiYi = ax2Y2 = a>x3Y3 = axiY3 = ах2уг = &x3y2 = 0.
Такие параметры с нулевым значением не включены в вышеупомянутые
подсчёты. □
ь
Задача 3.13. Докажите, что Р(х) = Ц Sj9 если масштабные перемен-
3=1
ные Sj определяются следующими уравнениями2:
П 8j <
Решение. Если масштабные переменные s^, где г = 1,...,L, выбраны
так, чтобы удовлетворять уравнениям ]Г] fi (г) = 1 при любых г, уравнение
i
прямого алгоритма для определения вероятности Р(х) последовательности
х = (х\,..., хь) принимает вид
Р<Р) = ^fk(L)ak0 = [£ A(L)aw ) f[sj = f[Sj.
k \ k J j=l j=l
2Речь идет об использовании масштабирования вероятностей при работе с СММ (см.
параграф 3.6 «АБП»). — Прим. ред.

3.1. Оригинальные задачи 111
Здесь вероятности перехода из любого состояния к в конечное состояние,
afco, равны 1 в позиции L, и, таким образом, все последовательности имеют
неизменную длину L.
При таком выборе Si справедливы следующие рекуррентные
уравнения:
Л(* + !) = ^ei{xi+i)Y;h{i)a>ki,
к
В случае обратных переменных, перемасштабируемых тем же самым
множеством Sj, рекуррентное уравнение принимает вид
Ьк{г) = Ji^akibiii + l)ei(xi+1).
Использование перемасштабированных переменных fi (г) (или &&(г))
позволяет нам избегать ошибки из-за потери значимости при работе прямого
(обратного) алгоритма с длинными последовательностями. □
Задача 3.14. С помощью результата, полученного в задаче 3.13, покажите,
что следующие уравнения:
А" = Е р^у E/fcWewei^iW(< + 1),
ЗД)=Е^ Е тш
3 V ' {i:xJ.=b}
используемые в алгоритме Баума-Велша для оценки параметров СММ,
упрощаются при использовании масштабированных переменных / и Ь.
Решение. Если масштабные переменные Si, где г = 1,..., L, выбраны так,
как оговорено в задаче 3.13, то ожидаемое число переходов из скрытого
состояния к в скрытое состояние I определяется следующей формулой:
^ = E^E^'«n^o4i)^+i) П 4 =
j \ ' г д=1 д=г+1

112 Глава 3
L
= Е J7^ Е /*{i)akleM+Mi + 1) = £$(0<*«e««i)bfr + 1).
j ^ ' i j,i
Здесь сумма берётся по всем обучающим последовательностям х^ и всем
позициям г. Ожидаемое число порождений символа Ь в состоянии к
принимает вид
i ^ ^ {i:x{=b} Q=1 {j,i:x{=b}
где сумма берётся по всем обучающим последовательностям х? и
позициям г, занятым состоянием к, порождающим символ Ь. □
3.2. Дополнительные задачи и теория
Практика работы с классическими алгоритмами для простой СММ
была нашей целью в задачах 3.15-3.18: алгоритм Витерби (задачи 3.15 и 3.16),
прямой алгоритм (прямого просмотра) (задача 3.17), обратный алгоритм
(обратного просмотра) (задача 3.17), прямой алгоритм с
масштабированными прямыми переменными (задача 3.17) и алгоритм апостериорного
декодирования (задача 3.18).
Остальные задачи из этого раздела относятся к общему вопросу
отбора моделей для биологических последовательностей (конечно, СММ — одна
из таких моделей). В задаче 3.19 сравниваются две стохастические модели
(модель независимого порождения и СММ); сравнение основано на
правдоподобиях моделей, вычисленных сначала как полные вероятности (по всем
путям), а затем как вероятности путей Витерби.
В теоретическом введении в задачи 3.20 и 3.21 описаны основные
представления, связанные с отбором моделей для описания биологической
последовательности, проверкой моделей, подходом наибольшего
правдоподобия к оценке параметров и с основными свойствами полученных методом
наибольшего правдоподобия оценок параметров модели независимого
порождения и стационарной марковской цепи первого порядка. В задаче 3.21
выполняется проверка отбора соответственной модели для фрагмента ДНК,
в задачах 3.20 и 3.21 — оценка вероятностей перехода марковской цепи.
В задаче 3.22 описана процедура осуществления выборки путей скрытых

3.2. Дополнительные задачи и теория
113
состояний из апостериорного распределения. Ещё одна модель
эмпирической последовательности — основная модель сегментации — описана в
теоретическом введении в задачу 3.23 наряду с Байесовым подходом к оценке
параметров модели. Используя эти представления, мы находим
апостериорные распределения неизвестных параметров и отсутствующие данные для
заданной последовательности, порождённой моделью сегментации
(задача 3.23).
Задача 3.15. Скрытые марковские модели могут быть использованы в
алгоритмах предсказания вторичной структуры белков. В одном довольно
прямом подходе конформации вторичной структуры а-спиралъ, (3-нитъ и
изгиб представлены в виде скрытых состояний, порождающих наблюдаемые
аминокислоты. Принято допущение о том, что частоты появления каждой
из двадцати аминокислот в любой из перечисленных конформации были
определены посредством анализа белков с трёхмерными структурами,
известными из эксперимента. Начертите состояние СММ и опишите
алгоритмы Витерби и апостериорного декодирования, которые можно было бы
применять для предсказания вторичной структуры белков3.
Решение. Диаграмма состояния СММ показана на рис. 3.4. Есть три
скрытых «структурных» состояния Н, Е и Т, соотносимых, соответственно,
с а-спиралъю9 (3-нитъю и изгибом. Эти состояния порождают символы
аминокислотных остатков с вероятностями е# (j), e#(j) и er(j),
оцениваемыми по частотам появления аминокислоты j, где j = 1,..., 20, в
соответствующих конформациях. Начальное состояние В и конечное
состояние £ не порождают никаких символов. Прочие параметры СММ
следующие: начальные вероятности а^Е, о>вт* а>вн, a>BS* вероятности переходов
о>ее, cleh, clet, &TE, &ТН, <*>тт-> о>не-> а>нн, а>нт\ вероятности окончания
а>Е£* ат£, а>Н£- Общее число параметров такой СММ составляет семьдесят
шесть.
Для заданной последовательности белка х = (xi,X2,... ,жп)
алгоритм Витерби определяет наиболее вероятную последовательность 7г =
= (тп, тг2, • • •, тгп) скрытых структурных состояний. Для каждой позиции г
в последовательности, где г = 1,2,..., п, он максимизирует вероятность
vt(i) = ei(xi)max(vk(i - 1)аы)
3Надо иметь в виду, что описанная модель не учитывает важнейшие свойства структурных
элементов: а-спираль должна иметь периодичность ~ 3,6 остатков, /3-нить имеет период 2.
Кроме того есть известные распределения длин элементов. — Прим. ред.

114
Глава 3
Рис. 3.4. Диаграмма состояния СММ, которая может быть использована в
алгоритмах предсказания вторичной структуры белка. Скрытые состояния
Н (а-спиралъ), Е (/З-нить) и Т (изгиб) порождают символы аминокислот
(наблюдаемые состояния СММ)
и существенно определяет подпоследовательность скрытых состояний
вплоть до позиции г в последовательности, которая, вместе с
наблюдаемой подпоследовательностью аминокислот (a?i,..., Xi)9 имеет наибольшую
вероятность совместного появления. В последнем шаге алгоритм Витерби
вычисляет вероятность совместного наступления событий — наблюдения
полной последовательности х и оптимального пути 7г:
Р(х,7г) = max(vk(n)ake).
к
После этого процедура обратного прослеживания восстанавливает
собственно ПуТЬ 7Г.
Алгоритм апостериорного декодирования определяет для заданной
белковой последовательности х апостериорные позиционные
распределения скрытых структурных состояний. Для позиции г в последовательности
он находит скрытое состояние fc, в котором, для заданной
последовательности х, апостериорная вероятность Pfa = к\х) является максимальной.
Как алгоритм Витерби, так и алгоритм апостериорного
декодирования подходят для отыскания последовательности структурных состояний
{Ну Е,Т}:в виде оптимального пути или пути Витерби (с помощью алго-

3.2. Дополнительные задачи и теория
115
ритма Витерби) и как последовательность скрытых состояний, отбираемых
по их наибольшим апостериорным вероятностям в последовательных
позициях белковой последовательности (алгоритмом декодирования). Такие
последовательности структурных состояний могут не совпадать, так как в
данной позиции скрытое состояние с наибольшей апостериорной
вероятностью может и не принадлежать к оптимальному пути. Однако обе
последовательности могут быть интерпретированы как предсказанная вторичная
структура белка. □
Замечание. Мы не располагаем сведениями о прямом использовании
описанной СММ для предсказания вторичной структуры белков. Однако
более общая СММ с такой же диаграммой состояния действительно была
использована для предсказания вторичной структуры белка [236].
Задача 3.16. Действительные последовательности ДНК неоднородны и
могут быть описаны скрытой марковской моделью со скрытыми
состояниями, представляющими различные типы состава нуклеотидов. Рассмотрите
СММ, которая включает два скрытых состояния Н и L, соответственно, для
более высокого и более низкого содержания C + G. Начальные вероятности
и для Н и для L равны 0,5, тогда как вероятности переходов следующие:
а>нн = 0,5, ань = 0,5, аьь = 0, б, аьн = 0,4. Нуклеотиды Т, С, A, G
порождаются из состояний Н и L с вероятностями, соответственно, 0,2, 0,3,
0,2, 0,3 и 0,3, 0,2, 0,3, 0,2. С помощью алгоритма Витерби определите
наиболее вероятную последовательность скрытых состояний для «модельной»
последовательности х = GGCACTGAA.
Решение. Вычисления алгоритма Витерби выполнены здесь в
логарифмическом режиме (по основанию 2), что, как правило, рекомендуется во
избежание ошибки из-за потери значимости. Для обозначения новых значений
параметров мы используем тильду, так что dki = log2 аы и т. д. В качестве
рекурсивных уравнений мы имеем
Щг + 1) = ei(xi+i) + max(Vfc(i) + aw),
к
где V — логарифм v. Алгоритм Витерби инициализируется в начальном
состоянии, обозначаемом как 0, и поочерёдно рассчитываются счета V#(i)
г = 0, У0(0) = 0, VH(0) = -оо, VL(0) = -оо;
i = 1, VH(1) = eH(G) + a0tf = -2,736966,
Vb(l) = eL(G) + clol = -3,321981;

116
Глава 3
i = 2,VH(2
VL(2
i = 3, VH(3
VL{S
i = 4, VH{A
Vl(4
• = 5, VH(5
VL(5
i = 6, VH(6.
VL(6
i = 7, VH(7
Vl(7.
i = 8, VH(8.
Vl($
i = 9, Vff (9
VL(9
= eH(G) + VH(l) + aHH = -5,473931,
= eL(G) + Vff(l) + aHL = -6,058893;
= ён(С) + VH(2) + аНн = -8,210897,
- ёь(С) + VH(2) + aHL = -8,795859;
= ён(А) + VH(3) + aHH = -И, 532825,
= eL(A) + VH(3) + aHL = -Ю, 947862;
= ён(С) + Vl(4) + aLH = -14,006756,
= ёь(С) + Vl(4) + aLL = -14,006756;
= ён(Т) + VH (5) + анн = -17,328684,
= ёь(Т) + VL(5) + aLL = -16,480673;
= eH(G) + VL(6) + aHH = -19,539581,
= iL(G) + Vl(6) + aLL = -19,539581;
= ён(А) + У* (7) + aHH = -22,861509,
= eL(A) + VL(7) + aLL = -22,013512;
= ён(А) + VL(8) + aLH = -25,657368,
= iL(A) + VL(8) + aLL = -24,487443.
Наиболее вероятный путь п* определяется процедурой обратного
прослеживания: ir*=HHHLLLLLL, тогда как Р(я,тг*)=2^(9)=4,251528 • ИГ8.
Для последовательности х путь Витерби ж* уникален, потому что в
каждом шаге г алгоритма максимальный счёт V,(i) был получен однозначно из
только одного из двух предыдущих значений V9(i — 1). □
Задача 3.17. Для скрытой марковской модели, определённой в задаче 3.16,
и фрагмента последовательности ДНК х = GGCA найдите Р(х) и
прямым и обратным алгоритмом. Повторите вычисление прямым алгоритмом
с использованием масштабных переменных (задача 3.13).
Решение. Прямой алгоритм работает следующим образом.
Инициализация:
i = 0, /о(0) = 1, /я(0) = 0, Д(0) = 0;
i = 1, /я(1) - ен(х1)о0я = 0,3 • 0,5 - 0,15,
/l(1) - eL(xi)o0L = 0,2 • 0,5 = 0,1;
* = 2, /я(2) = eH{G){fH(l)aHH + fL(l)aLH) =

3.2. Дополнительные задачи и теория
117
= 0,3(0,15-0,5+ 0,1-0,4) = 0,0345,
Д(2) = eL(G)(fH{l)aHL + /ь(1)аЬь) =
= 0,2(0,150,5 + 0,1-0,6) = 0,027;
г = 3, /я(3) = ен(С7)(/я(2)аяя + /ь(2)аья) =
= 0,3(0,0345 -0,5 + 0,027 • 0,4) = 0,008415,
FL(3) = eL(C)(fH(2)aHL + /ь(2)оьь) =
= 0,2(0,0345 • 0,5 + О,027 • 0,6) = 0,00669;
* - 4, /я(4) = ен(Л)(/я(3)аНя + /ь(3)оья) =
= 0,2(0,008415 • 0,5 + 0,00669 • 0,4) = 0,0013767,
/ь(4) = еь(Л)(/н(3)ояь + /ь(3)оЬь) =
= 0,3(0,008415 • 0,5 + 0,00669 • 0,6) = 0,00246645.
В шаге окончания мы имеем
Р(х) = P(GGCA) = /H(4) + /L(4) = 0,00384315.
Здесь мы предполагаем, что вероятности переходов в конечное состояние
ано и аьо равны 1 в позиции L = 4, так как мы имеем дело с
последовательностями длины 4.
Обратный алгоритм, начинающийся с позиции 4, работает следующим
образом:
г = 4,Ья(4) = 1,М4) = 1;
г = 3, Ья(3) = аннен{А)Ън{4) + aHLeL(A)bL(4:) =
= 0,5-0,2 + 0,5-0,3 = 0,25,
ЫЗ) = вьявя(^)Ья(4) + аььеь(Л)Ьь(4) =
= 0,40,2 + 0,60,3 = 0,26;
г = 2, 6Я(2) = аяяея(С)6н(3) + аНьеь(С)Ьь(3) =
= 0,5-0,3-0,25+ 0,5-0,2-0,26 = 0,0635,
М2) = оьяея(С)Ья(3) + oLLeL(C)6b(3) =
= 0,4-0,3-0,25+ 0,6-0,2-0,26 = 0,0612;
г = 1, Ья(1) = аяяея(<3)6н(2) + aHLeL(G)bL(2) =
= 0,5 0,3-0,0635+ 0,5 0,2-0,0612 = 0,015645,
Ml) = aLHeH(G)bH(2)+aLLeL(G)bL(2) =
= 0,4-0,3-0,0635+ 0,6-0,2-0,0612 = 0,014964.

118 Глава 3
В шаге окончания мы имеем
Р(х) = P(GGCA) = eH(G)bH(l)a0H + eL(G)bL(l)a0L =
= 0,3-0,015645 • 0,5 + 0,2 • 0,014964 • 0,5 = 0,00384315.
Как и следовало ожидать, значения вероятности Р(х), определённые
прямым и обратным алгоритмом, равны.
Теперь мы снова вычисляем вероятность Р(х), используя прямой
алгоритм с перемасштабированными переменными / и масштабными
переменными s^ определёнными в задаче 3.13. Поскольку переменные si9 где
г = 1,...,4, были определены так, чтобы Y^fi(^) — 1 иРи любых г, по-
i
4
СТОЛЬКУ Р(х) = Л Sj.
i=i
Рекуррентные уравнения следующие:
I к
/*(* + !) = 5^TeK«i+i)S/fcWaw'
к
4
с окончанием Р{х) = YL sj- Итерации осуществляются следующим обра-
i=i
зом (программы на языках PERL и C++ доступны на веб-сайте
«Дополнительные материалы сети», расположенном по адресу:
opal.biology.gatech.edu/PSBSA). В шаге инициализации мы имеем
i = 0, /o(0) = 1>/h(0)=0,/l(0) = 0;
* = 1, в1 = 0,25,/я(1) = 0,6,Л(1)=0,4;
х = 2, s2 = 0,246, /н(2) = 0,560976, Д(2) = 0,439024;
г = 3, s3 = 0,245610, /я (3) = 0,557100, Д(3) = 0,442810;
г = 4, s4 = 0,254429, /я(4) = 0,358222, /L(3) = 0,641778.
Шаг окончания даёт
Р(х) = P(GGCA) = 5i • 52 • s3 • 54 = 0,00384315.
Преимущество использования перемасштабированных переменных /
заключается в уходе от ошибок, возникающих из-за потери значимости, кото-

3.2. Дополнительные задачи и теория
119
рые могут появиться при вычислениях исчезающе малых /-значений у
последовательностей с большими длинами. Даже в случае короткой
последовательности GGCA можно видеть быстрое уменьшение значений прямых
переменных / и относительно устойчивое поведение
перемасштабированных переменных /. □
Замечание. Так как последовательность х = GGCA является
префиксом последовательности GGCACTGAA, рассмотренной в задаче 3.16,
путь Витерби 7г* для х может быть непосредственно определён как префикс
пути Витерби, найденного в задаче 3.16. Таким образом, 7г* = HHHL.
Значение вероятности совместного наступления событий Р(хутг*) = v(4) =
— 0,154 = 0,00050625. Обратите внимание, что вклад пути Витерби в
полную вероятность последовательности х составляет около 13 %.
Задача 3.18. Найдите апостериорную вероятность состояний Н и L в
позиции 4 последовательности ДНК х = GGCA. Используйте скрытую
марковскую модель, описанную в задаче 3.16.
Решение. Апостериорные вероятности могут быть найдены по следующей
формуле:
Прямая и обратная переменные /(4) и 6(4) были определены в ходе
решения задачи 3.17. Поэтому мы имеем
р(7Г _ „\ГГГА\ - /*(4)М*) - °.°0137671 _ п «R22
Р(тг4 - H\GGCA) - p{GGCA) - о,00384315 " °'35822-
Подобным же образом
PU Т\ГГГЛ\ ^(4)fe^4) 0,002466457-1
Р(тг4 = L\GGCA) = p{GGCA) = о,00384315 =
= 0,64178 = 1 - Р(тг4 = H\GGCA).
Мы видим, что вероятность появления в позиции 4 состояния L больше,
чем вероятность появления в этой позиции состояния Н. Между прочим,
состояние L в данном случае появляется в позиции 4 наиболее вероятного
(Витерби) пути 7г* = HHHL (см. замечание к задаче 3.17). Однако мы

120
Глава 3
должны помнить, что состояния пути Витерби и наиболее вероятные
состояния, полученные алгоритмом апостериорного декодирования, не
обязательно совпадают. □
Задача 3.19. В особый день в некотором казино либо используют
правильную игральную кость всё время (режим F), либо используют правильную
кость большую часть времени, но иногда переходят к смещённой кости
(режим L). В режиме L вероятность перехода от правильной к смещённой
кости перед каждым бросанием равна £, а вероятность обратного
перехода — ф. Для заданной последовательности х из 300 бросаний, наблюдаемой
в особый день,
315116246446644245311321631164152133625144543631656626566666
651166453132651245636664631636663162326455236266666625151631
222555441666566563564324364131513465146353411126414626253356
366163666466232534413661661163252562462255265252266435353336
233121625364414432335163243633665562466662632666612355245242
опишите процедуру статистического вывода, различающего два режима F
и L работы казино. Примите допущение о том, что параметры режима L
равны ф = 0,1 и £ = 0,05 и что смещённая кость имеет вероятность 0,5
выпадения шестёрки и вероятность 0,1 вьшадения любого из остальных
чисел.
Решение. Для проведения различия между режимами F и L предлагается
следующее статистическое правило: если отношение S= log P(L\x)/P(F\x)
положительно, то более правдоподобно, что казино работает в режиме L;
если S отрицательно, то более правдоподобно, что казино работает в
режиме F; наконец, если S = 0, никакое решение не принимается.
При допущении о том, что априорные вероятности режимов F и L
равны, отношение S становится логарифмическим отношением шансов:
_ / P(x\L)P(L) P{x\L)P{L) + P(x\F)P(F) \ _
g\P(x\L)P(L) + P(x\F)P(F) P(x\F)P(F) )
]nrP(*\L)

3.2. Дополнительные задачи и теория
121
Для режима F (используя основание логарифма 10)
logP(x|F) = log (фЛ = -234 + log3,586.
Вычисление правдоподобия P(x\L) более сложно. Использование
правильной или смещённой кости определяет скрытое состояние (1 или 2).
Переходы между состояниями и события порождения наблюдаемых чисел зависят
от вероятностей переходов ац = 1 — £ = 0,95, а\2 = £ = 0,05, a2i = ф =
= 0,1, а,22 = 1 — Ф = 0,9иот вероятностей порождения е\{г) = 1/6, при
г = 1,..., б, е2(1) = е2(2) = е2(3) = ei(4) = ei(5) = 1/10, е2(6) = 1/2.
Теперь Р(ж|Ь) определяется как сумма вероятностей того, что
последовательность бросаний х порождена всеми возможными последовательностями 7Г
скрытых состояний: ^-^
P(z|L) = $>(*, tt|L).
7Г
Полная вероятность P(x\L) определяется прямым (обратным) алгоритмом.
Прямой алгоритм начинается с инициализации: /о(0) = 1, Л(0) = 0
при к > 0; продолжается рекурсией при г = 1,..., L: //(г) = ei(xi) Y^ fk(i—
к
— 1)аы и заканчивается вычислением полной вероятности
последовательности х:
P(x) = Y^fk(L)ak0 = P(x\L).
к
Общий прямой алгоритм был реализован и на языке PERL и на С++
(см. веб-сайт «Дополнительные материалы сети», доступный по адресу
opal.biology.gatech.edu/PSBSA). С помощью вычислительных методов
было установлено, что
\ogP{x\L) = -225 +log 3,294.
Поэтому логарифмическое отношение шансов принимает вид
5 = 8 + log 9,186 = 8,963145 > 0.
Таким образом, согласно статистическому выводу данная
последовательность бросаний игральной кости х наблюдалась, когда казино работало в
режиме L.
Замечание. Мог быть предложен ещё один подход к различению
между режимами F и L — с использованием статистического вывода. Вместо
полных вероятностей последовательности х при заданных режимах F и L
мы могли бы сравнить вероятности Витерби, то есть вероятности Р(ж, 7г^)
и Р(ж, -ттр) наиболее правдоподобных путей для последовательности х при

122
Глава 3
заданных режимах L и F. Тогда логарифмическое отношение шансов S*
определяется следующей формулой:
5* = log
P(x,irFy
В режиме F (использование только правильной игральной кости)
существует только один возможный путь скрытых состояний (состоящий из
состояний правильной кости) для любой наблюдаемой последовательности
бросаний, таким образом, вероятность Р(ж, ttf) та же, что и полная
вероятность P(x\F):
logP(x,irF) = log P(x\F) = -234 +log 3,586.
В режиме L вероятность Р(х,тгь) наиболее правдоподобного пути
вычисляется алгоритмом Витерби (см. задачу 3.16 и компьютерные программы
на языках PERL и C++, представленные на веб-сайте «Дополнительные
материалы сети» по адресу: opal.biology.gatech.edu/PSBSA). Для наблюдаемой
последовательности х мы получаем
Р(ж, ttl) = argmax^ Р(ж, тг) = 1,585 • 10"236,
5*=log^^4=log0,004<0.
Интересно, что статистический вывод на основании путей Витерби привёл
к заключению, что казино работало в режиме F. Это заключение
противоречит тому, что было выведено моделью на полной вероятности!
Причина изменения исхода принятия решения на противоположный
состоит в том, что путь Витерби даёт только долю полной вероятности
наблюдаемой последовательности. Поэтому есть риск принятия неверных
решений, когда для осуществления вывода используется путь Витерби. Этот
вопрос будет рассмотрен подробнее в задачах 4.4-4.6. □
3.2.1. Вероятностные модели последовательностей символов: выбор
модели и оценка параметров
Теоретическое введение в задачи 3.20 и 3.21
Чтобы описать подходы к отбору моделей, мы будем следовать [222].
Биологическую последовательность х = х\,..., xn можно рассматривать

3.2. Дополнительные задачи и теория
123
как реализацию случайной последовательности символов из конечного
алфавита Л, где |Л\ = 4 в случае ДНК и \Л\ = 20 в случае белков.
Последовательность х может быть описана множеством различных вероятностных
моделей.
Простейшая модель — однородная модель независимого порождения
М — основана на допущении о том, что появления символов в различных
участках последовательности суть независимые события и вероятность
появления некоторого символа а, где а € Л, в любом участке
последовательности равна ра, J2 Ра = 1- Если мы допустим, что наблюдаемая последо-
аеЛ
вательность х порождена моделью М с неизвестными параметрами {ра},
то оценки величины ра методом наибольшего правдоподобия определяются
отношениями вида
Voc = —др, (3.6)
где N(a) — число символов а, наблюдаемых в последовательности х.
Более общая модель, а именно модель М(т), представляет собой
стационарную марковскую цепь т-го порядка с вероятностями переходов
Pai,...,a:m,am+i — ±\%1 = &т+1 \%i—1 = С^т) • • • > xi—m = ^lj)
где ctk € Л, г = т + 1,..., N. Очевидно, что модель независимого
порождения М — это марковская цепь порядка т = 0, М = М(0). Известно,
что для заданной последовательности х, порождённой марковской моделью
первого порядка М(1) с неизвестными параметрами, оценки вероятностей
переходов ра,р, где а, /3 е А, полученные методом наибольшего
правдоподобия, определяются отношениями подсчётов:
Здесь N(a(3) — число появлений пары смежных символов (а, 0) в
последовательности х, а N(cf) = ]Г) N(a/y). Обратите внимание, что N(cf) =
= N(a), если xn ф ос, и iV(a*) = N{a) — 1 в противном случае. Точно так
же для последовательности ж, порождённой моделью М(га) с
неизвестными параметрами, оценки методом наибольшего правдоподобия, полученные
для вероятностей переходовpai,...,am,am+i> определяются отношениями
вида
_ N(ai ■■■amam+i)
N(a± • • • am#)

124
Глава 3
Здесь N(ai • • • од) обозначает число появлений слова из к букв (c*i,..., од)
в последовательности х, a N(a\ • • • ат%) = Yl N(ai • • • amj).
-уел
Отбор наиболее соответствующей модели для последовательности х
среди моделей М(га), где т ^ О, может быть проведён на основе проверки
по критерию х2- Сначала мы проверяем, является ли модель независимого
порождения М(0) соответствующей моделью для последовательности х.
Нулевая гипотеза о независимости,
Н0 : Р(хг = а,Жг+i = /3) = рарр, г = 1,..., JV - 1, а,/5еЛ,
должна быть проверена в сравнении с альтернативной гипотезой На,
согласно которой единственное ограничение на вероятности совместного
наступления событий P(xi = а, Хг+i = Р) заключается в том, что они не
зависят от г. Если гипотеза Но верна, то оценка методом наибольшего
правдоподобия, полученная для P(xi = a,xi+\ = (3), где г = 1,...,ЛГ — 1,
определяется как
Рно(«,0)= N_1N_r
Здесь N(*0) = Y1 N(7/?). Обратите внимание, что
N(a»)N(»0) . .
где ра — оценка методом наибольшего правдоподобия для ра, основанная
на последовательности х\,..., х^-ъ &Рр — оценка методом наибольшего
правдоподобия для рр, основанная на последовательности ^2,..., хц. Если
верна альтернативная гипотеза, то оценка методом наибольшего
правдоподобия для P(xi = a, Xi+i = /3), где г = 1,..., N — 1, определяется как
Тогда
х2 = у у W - 1)РнЛ<*,0) -(N- 1)Рн0(а,(3))2 _
£а%£а (N-l)PHo(a,0)
l)N(a0) - N(a»)I
(N - l)N(am)N(»0)
ST ST «N ~ WW) ~ N(a»)N(*/3))2
a£AP€A

3.2. Дополнительные задачи и теория
125
определяет пирсоновскую статистику х2, которая, согласно нулевой
гипотезе, асимптотически имеет распределение х2 с (|Л| —I)2 степенями свободы.
Таким образом, мы отвергаем гипотезу Но, когда выборочное значение
статистики х2 (3.8) превышает критическое значение распределения х2>
соответствующее заданному уровню значимости; в противном случае мы
принимаем гипотезу Но. Мы должны использовать распределение х2 с
девятью степенями свободы для последовательностей ДНК и распределение х2
с 361 степенью свободы для последовательностей белка.
Если гипотеза Но отвергнута, то должна быть проведена проверка на
зависимость более высокого порядка. В следующем шаге нулевая гипотеза,
согласно которой марковская цепь первого порядка М(1) является
подходящей моделью для последовательности х, может быть сформулирована
следующим образом:
Н0 : P(xi = a, xi+i = (3, xi+2 = 7) =
= P(xi = a)P(xi+! = P\xi = a)P{xi+2 = 7 Iя* = a> xi+i = P) =
= P(Xi = a)pa^Pf3yJ = 22 ^(^Pxuxa ' •••' Рх^иаРа,0Р0л =
Xl,X2,..-,Xi-l
при i=l,...,JV-2HQ!,i3,7GA Здесь 7Г — стационарное распределение
марковской цепи М(1). Нулевая гипотеза должна быть проверена в
сравнении с альтернативной гипотезой На, основанной на допущении о том, что
единственное ограничение на вероятности P(xi = a, xi+\ = (3, Хг+2 = 7)
состоит в том, что они не зависят от г.
Согласно нулевой гипотезе, оценка методом наибольшего
правдоподобия для P(xi = a, Xi+i = /3, Xi+2 = 7)5 гДе * = 1) • • • > N — 2, определяется
как
N(a ♦ •) iV(a/3») Щш0ч) _ Ща/Зш) Щшру)
N-2 АГ(а • •) 7V(#/?#) ~ N-2 N (•&•)'
Здесь N{af5*) — число появлений триплетов, начинающихся с символов
(а,/3); N(a • •) = J] JV(a/?«); N{%^) — число появлений триплетов,
(Зел
заканчивающихся символами (/?, 7); iV(*/3*) = Y1 ^(9Pl)-
чел

126
Глава 3
Согласно гипотезе На, оценка методом наибольшего правдоподобия
для Р(х{ = а, Жг+i = /?, #г+2 = 7)> где г = 1,..., N — 2, определяется как
Ряа (<*,/?, 7) = N •
Тогда согласно гипотезе Но пирсоновская статистика х2,
((N - 2)РНа (а, /3, <y)-(N- 2)РНо (а, /3,7))2
х2 = Е££
аел /Зед7еД (^ " 2)Р#о (<*> А 7)
*y)N(m0m) - N(a(3m)N
= W V (N(afr)N№) - N{aj3.)N(*fa))*
асимптотически имеет распределение х2 с (|Л|2 — 1)(|Л| — 1) — Z
степенями свободы, где Z — число триплетов (а,/3,7)> причём а,/3,7 € *4 такие,
что число ожидаемых подсчётов (ЛГ — 2)Р#0(а,/?,7) равно нулю (таким
образом, соответствующие Z члены
((ЛГ - 2)РЯо (а, /3,7) - (JV - 2)РЯ„ (а, /?,7))2
(ЛГ-2)РНо (<*,/?> 7)
не могут быть должным образом определены, и они будут отсутствовать в
сумме для статистики х2)- Применение такой проверки к
последовательностям ДНК при заданном уровне значимости требует, чтобы мы сравнили
наблюдаемое значение статистики х2 с критическим значением
распределения х2 с 45 — I степенями свободы, тогда как для последовательностей
белка нам нужно распределение х2 с 7581 — I степенью свободы. Если
нулевая гипотеза отвергнута, то аналогичным образом должна быть выполнена
проверка марковской цепи на принадлежность к цепям второго порядка.
Подробные описания статистических тестов на независимость,
однородность, марковость и порядок марковской цепи могут быть найдены в
классических публикациях [100], [22], [23] и [167].
Возвратимся к модели независимого порождения М(0) и сделаем
допущение о том, что х2 тест установил, что последовательность х =
= a?i,..., хм порождена моделью М(0) с неизвестными параметрами ра,
где a G Л. Тогда мы имеем оценки методом наибольшего правдоподобия в
уравнении (3.6) для параметров модели и мы сталкиваемся с естественно

3.2. Дополнительные задачи и теория 127
возникающим вопросом: насколько близки эти оценки к истинным
значениям параметров? Оценки методом наибольшего правдоподобия ра являются
несмещёнными:
Состоятельность (ра —> ра) и сильная состоятельность (ра —> ра с
вероятностью 1) оценок ра следуют, соответственно, из закона больших чисел
и из усиленного закона больших чисел. Эти свойства подразумевают, что
оценка ра, где a Е А, становится ближе к истинному значению ра по мере
того, как размер выборки N (длина последовательности х) возрастает.
Обозначим Pi = Ра.9 где г = 1,..., fc, для алфавита размера fc, где
Л = {ai,..., ak}. Свойство асимптотической нормальности многомерной
оценки метода наибольшего правдоподобия ([56], раздел 9.2)
подразумевает, что случайный вектор У = (Р — T?)VN с компонентами Yt = (pi —
— pi)VN, где г = 1,..., fc, является асимптотически центрированным
Гауссовым вектором с ковариационной матрицей R = (r^) = (cov(Yi,Yj)), где
г, j = 1,..., fc, с элементами
гц =Pi—Pi, Гц = -piPj, г ^ j.
В частности, это означает, что каждая компонента Yi = (pi —pi)\/N вектора
Y — асимптотически центрированная нормальная случайная величина.
Затем для эргодической стационарной марковской цепи первого
порядка с неизвестными вероятностями переходов, оцениваемыми по
формуле (3.7), и стационарного распределения 7г, оцениваемого по выражению
7г(а) = N(a)/N, также легко показать, что оценки метода наибольшего
правдоподобия 7г(а) являются несмещёнными:
N
Етг(а) = ±EN(a) = ^ £ P(Xi = а) =
г=1
N
= ~k^2 H Ф1)Рхих2 ' • • • -Pxt-ua = ^(а) = *"(<*)•
г=1 xi>X2,.'.,Xi-i
Оценки п(а) являются состоятельными, и вектор £ с компонентами & =
= (7г(скг) — 7Г(ai))VN, где г = 1,..., fc, — центрированным асимптотически
Гауссовым вектором ([23], лемма 3.2, теорема 3.3).

128
Глава 3
В случае алфавита размера к, Л = {ai,..., од}, мы обозначим рц =
= Pcticxj, где г, j = 1,..., к. Также известно, что полученные методом
наибольшего правдоподобия оценки вероятностей переходов являются
состоятельными: pij —> р^, где г,j = 1,...,& ([23], теорема 4.1). &2-мерный
вектор 7] = (г/и,..., 771*,..., rfki,..., Щк) с компонентами
N(aiaj) - N(ai)pij
Vij =
^ы
где г, j = 1,..., fc, является асимптотически центрированным нормальным
вектором ([23] с ковариационной матрицей R = (rij^i) = (Ещт}31), где
ij, 5,1 = 1,..., fc: rij>z = 0, при г ^ 5, и j, / = 1,..., к; rijtij = py - p^-
при t, j = 1,..., fc; Tij^i = -Pij№ при г, j, Z = 1,..., к и j'ф I.
Эти теоретические результаты касательно асимптотических свойств
оценок метода наибольшего правдоподобия могут быть полезны для оценки
возможных ошибок оценок параметров статистических моделей,
используемых в алгоритмах биоинформатики.
Дальнейшее обсуждение стохастических моделей
последовательностей ДНК может быть найдено в: [92]; [1]; [84]; [142]; [26], [27]; [49]; [262];
[55]; [143]; [140]; [141]; [147]; [156]; [235]; [226]; [72].
Задача 3.20. Последовательность ДНК длины 4200 п. н. используется в
качестве обучающей последовательности для оценки параметров
статистической модели ДНК. Наблюдаемые подсчёты шестнадцати динуклеотидов,
Nxy> следующие:
G
Т 510 380 210 190
С 240 170 360 230
А 370 200 220 210
G 190 170 220 220
Методом наибольшего правдоподобия найдите оценки а) вероятностей
переходов Ртт, Pag марковской модели первого порядка для
последовательности ДНК; б) вероятностей переходов Ртт> Pag марковской модели
первого порядка для последовательности ДНК, комплементарной заданной
обучающей последовательности.

3.2. Дополнительные задачи и теория
129
Решение, а) В случае марковской модели первого порядка полученные
методом наибольшего правдоподобия оценки вероятностей переходов
определяются по формуле (3.7):
Ртт= zTTNTX = m = °>395->
X=A,G,C,T
Ь _ Nag 21 _ n 91
Pag~ £ ivAxi66-°'2L
X=A,G,C,T
б) Динуклеотид ТТ в комплементарной нити соответствует динуклео-
тиду АА в прямой нити. Поэтому мы используем подсчёты динуклеотидов,
известные для прямой нити:
X=A,G,C,T
Подобным же образом для динуклеотида AG (направление 5' —► 3'),
расположенного в комплементарной нити, мы используем подсчёт
динуклеотида СТ (направление 3' —► 5'), расположенного в прямой нити. Поэтому мы
имеем
a NCT 24 п 17л
AG = —£—n^ 136 = °'176' п
X=A,G,C,T
Задача 3.21. В некодирующей области генома человека наблюдалась
представленная ниже последовательность х длины 100 п. н.:
TGACTTCAGTCTGTTCTGCAGAAGTGATTCTGATGTCATGAAACTGCCTG
CACTTGGCTGAGAGGATGATAGGGGCAGAGAAGGGTTGTTTAAGCCATAT
Определите простейшую вероятностную модель последовательности х
среди моделей М(ш), где га ^ 0, которая прошла бы описанную выше
проверку на соответствие при уровне значимости 0,05. Приведите найденные
методом наибольшего правдоподобия оценки параметров полученной вами
модели.

130
Глава 3
Решение. Сначала мы проверяем, соответствует ли модель независимого
порождения последовательности х9 путём использования описанной выше
проверки на независимость. Мы находим подсчёты нуклеотидов и динук-
леотидов в последовательности х следующим образом:
N(Am) = 25, N(Cm) = 15, iV(G#) = 31, N(T%) = 28,
N(mA) = 25, N(mC) = 15, N(mG) = 31, N(mT) = 28;
N(AA) = 6, N(CA) = 5, N(GA) = 12, N(TA) = 2,
N(AC) = 3, N(CC) = 2, AT(GG) = 5, N(TC) = 5,
N(AG) = 9, N(CG) = 0, N(GG) = 8, N(TG) = 14,
N(AT) = 7, N(CT) = 8, N(GT) = 6, N(TT) = 7.
Затем по уравнению (3.8) рассчитывается значение статистики х2:
v2= V ((АГ - l)N(a/3) - N(a.)N(.[3))2
Так как все ожидаемые подсчёты (N—1)Ph0 (a, /3)=N(cf)N(m/3)/(N—
— 1), где а,(3е {А, С, G, Т}, являются положительными, нулевая гипотеза
проверяется путём сравнения значения статистики х2 с критическим
значением распределения х2 с девятью степенями свободы, соответствующим
уровню значимости 0,05. Мы имеем х2 = 19,22 > 16,92 = Хообэ» по~
этому гипотеза Но должна быть отвергнута с 5 %-м уровнем значимости.
Другими словами, согласно процедуре проверки модель независимого
порождения М не соответствует последовательности х, при этом вероятность
отклонения модели М при том, что она верна, составляет 0,05.
Затем мы проверяем нулевую гипотезу, согласно которой
последовательность х порождена марковской моделью первого порядка М(1). Чтобы
применить проверку, основанную на статистике х2 (3.9), нам нужны
подсчёты триплетов из алфавита {А, С, G, Т}, которые выглядят следующим
образом:
N(AAT)=N(ACA)=N(ACC)=N(ACG)=N(ATC)=N(CAA)
=N(CAC)=N(CCC)=N(CCG)=N(CGA)=N{CGC)=N(CGG)
=N(CGT)=N(CTA)=N(CTC)=N(GCG)=N(GTA)=N{TAC)
=N(TAG)=N(TCC)=N(TCG)=0;
N(AAA)=N(AAC)=N(AGC)=N(ATT)=N(CCA)=N(CCT)

3.2. Дополнительные задачи и теория
131
=N(GCT)=N(GGT)=N(GTG)=N(TAA)=N(TAT)=N(TTA)
=N(TTT)=1]
N(AGG)=N(AGT)=N(ATA)=N(CAT)=N(CTT)=N(GAC)
=N(GAG)=N(GCA)=N(GCC)=N(GGA)=N(GGC)=N(GTC)
=N(TCA)=N(TGC)=N(TTG)=2;
N(ACT)=N(ATG)=N(CAG)=N(GGG)=N(GTT)=N(TCT)
=N(TGG)=N(TGT)=N(TTC)=3;
N(AAG)=N(AGA)=N(GAA)=N{GAT)=4;
N(CTG)=N{TGA)=6.
Мы вычисляем значение статистики х2 (3.9) следующим образом:
?7)iV(«/?«) - N(a/3^N(i
N(a(3m)N(^)N№)
2 = v {N{af31)N{.f3.)-N{ap.)N{.f31)f =
a,/3,7€{A,C,G,T}
и сравниваем его с критическим значением распределения х2 с 45 — 7 =
= 38 степенями свободы (потому что семь из ожидаемых подсчётов равны
нулю). Поскольку х2 = 45,32 < 58,38 = Хо,05,38> гипотеза Щ должна
быть принята с 5 %-м уровнем значимости. Поэтому марковская модель
первого порядка прошла проверку на соответствие последовательности х.
Оценки вероятностей переходов марковской цепи, определённые методом
наибольшего правдоподобия (3.7), следующие:
Рл,л = 0,24, рс,л = 0,33, рс,л = 0,39, рт,л = 0,07,
рл,с = 0,12, pCjC = 0,13, pGjC = 0,16, рт,с = 0,18,
Pa,g = 0,36, >c,g = 0,00, pG,G = 0,26, pT,G = 0,50,
рл,т = 0,28, рс,т = 0,54, pG|T = 0,19, рт,т = 0,25.
Учтите, что для последовательности довольно малой длины (100 п. н.)
оценки р^ не являются очень надёжными — в том смысле, что вероятность
того, что истинные значения параметров р^ лежат в близкой окрестности
оценок р^ при всех г и j, является маленькой. Увеличение длины
обучающей последовательности гарантирует лучшее приближение к истинным
значениям вероятностей переходов.
Тем не менее, мы должны помнить, что реальные биологические
последовательности нельзя вполне обоснованно рассматривать как
реализации некоторой теоретической случайной модели. Такое моделирование все-

132
Глава 3
гда является приближением, с большей или меньшей степенью точности,
которая зависит от размера и природы реальной последовательности. □
Задача 3.22. Для осуществления выборки из апостериорного
распределения путей {7г} скрытых состояний СММ, при заданной реализации х =
= xi,..., xl, предложен следующий алгоритм. Сначала прямым
алгоритмом определяется матрица прямых переменных F = (fj(i)) для
последовательности х. Во вторую очередь строится путь 7Г из скрытых состояний щ,
рекурсивно выбираемых стохастическим алгоритмом обратного
прослеживания. Рекурсия проходит следующим образом:
• при текущем конечном состоянии выбирается состояние 7гь с
вероятностью
Р(Х) '
• при текущем состоянии 7гь выбирается состояние тть-\ с вероятностью
"-7T.L -17Г£, JTZL — 1
(L-1)
U{L)
• при текущем состоянии ttl-i выбирается состояние тть-2 с вероятностью
(L-2)
/„_,(£-1)
• при текущем состоянии 7Г2 выбирается состояние тт\ с вероятностью
(х2)а
7Г17Г2
Л2(2)
• при текущем состоянии 7Ti выбирается начальное состояние с
вероятностью
/irx(l) '
Покажите, что такой алгоритм действительно выполняет выборку из
апостериорного распределения путей, состоящих из скрытых состояний.

3.2. Дополнительные задачи и теория 133
Решение. Апостериорная вероятность пути 7г = 7Ti,... ,7Tl при
наблюдении последовательности х определяется следующей формулой:
. Р(х,-7г) а07г1е7П(х1)а7Г17Г2е7Г2(х2)"-а7ГЬ_17Гье^ь(хь)а7Гьо
Р(тг\х) = п, ч = —г-т .
Описанный вьппе алгоритм стохастического осуществления выборки
выберет путь 7г с вероятностью Р, равной произведению вероятностей Pi
выбора его последовательных состояний тсс
i=L
(L-l)
P(x) UAL) *
7Г17Г2 /tti(1) e7ri(xi)a07ri
Мы видим, что в последнем отношении и в числителе и в
знаменателе находятся одни и те же прямые переменные fm(i)- После сокращения
всех /7Fi (г) мы получаем
ы.. (хь)а>тгьо „, , ч
р= W) =Р(ф).
Таким образом, предлагаемый стохастический алгоритм обратного
прослеживания представляет собой рекуррентное выполнение выборки из
апостериорного распределения траекторий скрытых состояний, при
наблюдении последовательности х. □
3.2.2. Байесов подход к анализу состава последовательностей: модель
сегментации Лю и Лоренса
Теоретическое введение в задачу 3.23
При анализе биологических последовательностей нам часто
приходится отбирать определённую вероятностную модель (такую как модель
независимого порождения, марковская цепь, СММ) со статистическими
свойствами как можно ближе к наблюдаемым в реальной последовательности.

134
Глава 3
После выбора типа модели традиционный статистический вывод
полагается на точечные оценки неизвестных параметров модели, которые обычным
образом определяются методом наибольшего правдоподобия (см.
теоретическое введение в задачи 3.20 и 3.21).
Байесов подход к анализу состава последовательностей также
начинается с отбора типа модели. После отбора вероятностной модели Байесова
статистика рассматривает все неизвестные параметры модели, наряду с
наблюдаемыми данными и недостающими данными, как случайные
величины и приписывает ко всем им соответствующие априорные распределения.
Цель этого подхода состоит в том, чтобы использовать данные для
получения апостериорных распределений всех неизвестных параметров, а не их
точечных оценок, как в традиционном частотном подходе. Поэтому Байесов
вывод полагается на апостериорные распределения параметров.
Лю и Лоренс [181] разработали Байесов метод для анализа состава
последовательностей, опирающийся на основную модель сегментации (см.
также [30]), которая может быть описана следующим образом. Мы
рассматриваем набор из М моделей независимого порождения для алфавита
размера D; г-я модель имеет неизвестные параметры (#1,г, #2,г, • • • > #D,i) =
= вг (вг ф 6г+ъ г = 1,..., М — 1). Основная модель сегментации может
служить моделью неоднородности в составе последовательностей ДНК или
белка, соответственно, с D = 4 или D = 20. Последовательность х =
= х\,..., xn символов из алфавита порождается основной моделью
сегментации следующим образом: первые С\ символов производятся первой
моделью, следующие Съ символов порождаются второй моделью и так
далее. Наконец, последние C^+i символов последовательности х
производятся моделью /i + 1, где \i < т — 1. Вектор точек перехода Аш, где т =
т
= 1,..., /i, состоит из целых чисел Ат = ]Г) С» -I-1. Число точек перехода
г=1
/i и вектор точек перехода А = (А\, Ач,..., А^) неизвестны. Мы делаем
допущение о том, что данные наблюдений (последовательность ж),
недостающие данные (число точек перехода /л и случайный вектор точек
перехода А = (Ai, A2l..., Ар)) и параметры моделей независимого порождения
суть случайные величины, а также о том, что a priori 0(Oi,...,Om) =
= 0 и /i являются независимыми. При известных априорных
вероятностях P(/i), P(A\fi), P(&i) применяется теорема Байеса для определения
апостериорной вероятности случайной величины ф (ф = /i, Am (где т =
= 1,..., /х), параметры модели независимого порождения Q(j) в позиции j9
где.7 = 1,...,АГ):

3.2. Дополнительные задачи и теория
135
Вероятности Р(х) и P{x,ij}) могут быть рассчитаны из совместного
распределения всех переменных Р(ж, A, 0,/i) посредством
интегрирования (или суммирования). Так как совместное распределение может быть
записано в виде
Р(х, Л, 0, ц) = Р(х\А, в)Р(А\»)Р(р)Р(в),
мы имеем следующее выражение для Р(х)
м г
Р(х) = ^ P(/i = m) J2 Р(Л\^ = т) Р(Х\А> &)d& (ЗЛ°)
т=1 А:||А||=т 0
Здесь внутренняя сумма берётся по всем возможным наборам из га
точек перехода. Естественный выбор априорного распределения для
параметра 9г = (01,г,#2,г>-- • > #D,i) модели независимого порождения г —
сопряжённое априорное V{ai) распределение Дирихле с параметром oti =
= («1,2,^2,2, • • • ,«D,i)» такое что среднее по O^i равно а&,г/2аМ- Тогда
i
из уравнения (3.10) мы выводим
Р(х\/а = га) = ]Г Р0% = т) f Р(х\А, 0)d0 =
А:\\А\\=т I
Здесь Г(у) — гамма-функция; n^i — подсчёт (количество)
символов типа d в г-м сегменте x[At_i:Ai)=(a;Ai_i, • • • , #Аг_ 1) ДОЯ набора
(Ль Л2,... ,Лп, Лп+i), Лт+1 = N + 1; и X>d,i = Q. Для завершения
суммирования в уравнении (3.11) используется динамическое
программирование. Если Р(х[г : j]\m) обозначает вероятность наблюдения
подпоследовательности х[г : j] = (ж,... ,Xj) при условии, что она состоит из га
сегментов, то рекурсивное уравнение выглядит следующим образом:
Р(х[1 : j]\m) = J2P(x[l : l]\m - l)P(x[l : j]\l). (3.12)
Кз
Апостериорное распределение компонент Am может быть определено
из следующего уравнения:
Р(для некоторых mAm = l\x) =
= lh\Y,Y, Р№ ■■ П\т)Р(х(1: j]|/i - m). (3.13)

136
Глава 3
Поскольку точки перехода Ai, А2,..., А^ — взаимно зависимые
случайные величины, постольку апостериорное распределение случайного
вектора А не может быть определено как произведение
распределений (3.13) компонент Ат. Однако приближённое распределение вектора А
может быть получено при помощи выборки методом Монте-Карло: мы
производим выборку из апостериорного распределения величины /л = га,
устанавливаем Am и находим точки перехода Ai, A2,..., -Ат-ъ рекурсивно
осуществляя выборку из распределения в обратном направлении:
ПАг-1-3\х,А-к)- P(x[l:k]\i)
Усреднение выборок даёт распределение, которое сходится к
апостериорному распределению случайного вектора точек перехода по мере
того, как число выборок возрастает. Наконец, апостериорное распределение
вероятностей символа в каждой позиции может быть получено также из
частот символов (при известной сегментации) путём усреднения по всем
возможным сегментациям.
Задача 3.23. Чтобы иллюстрировать Байесов подход к анализу
последовательностей ДНК, мы рассмотрим «модельную» нуклеотидную
последовательность х = GGCA (такую же, как в задаче 3.17, где было сделано
допущение о том, что последовательность х порождена СММ с двумя скрытыми
состояниями). В данном случае мы рассматриваем последовательность х
в контексте основной модели сегментации с М = 4. Априорные
вероятности следующие: Р(ц = га) = 1/4, где га = 0,1,2,3; Р(А : \\А\\ = га|/х =
= га) = (^) = (^) (таким образом, все возможные сегментации с га
точками перехода одинаково правдоподобны при условии /х = га); для всех
моделей независимого порождения 6*, где г = 1,..., 4, априорное
распределение параметров (частоты появления нуклеотидов) есть Х>(1,1,1,1) —
распределение Дирихле с параметрами (ал,и осс,%, <*Gyu ^т,г) = (1? 1,1> !)•
Вычислите апостериорные распределения числа \л точек перехода J\.m*
где га = 1,..., //, и вероятностей нуклеотидов Q(j) = (Oa(J), 6c(j), OgU),
Ot(J)) во всех позициях j в последовательности.
Замечание. Мы понимаем, что последовательность х слишком
коротка, чтобы демонстрировать что-либо кроме самого алгоритма. Кроме того,
поскольку х — короткая последовательность, для вычисления
апостериорных распределений мы не используем рекурсии динамического
программирования, определяемые уравнениями (3.12) и (3.13); вместо этого мы

3.2. Дополнительные задачи и теория 137
выполняем непосредственные вычисления, учитывая все возможные
варианты сегментации.
Решение. Для того чтобы вычислить Р(х\ц = га), где га = О,1,2,3, мы
применяем уравнение (3.11). Если ц = О, то последовательность х
описывается единственной моделью независимого порождения с параметрами 9i
и мы имеем
Р(ф = 0)Р(М = 0) = ^ • \ = 0,0006. (3.14)
При \х = 1 возможны три варианта сегментации: с А = 2, А = 3 или
А = 4. Используя свойство независимости распределений, мы вычисляем
Р(х\А = 2) = P((G) £ в!)Р((ССЛ) £ 92) = ^|- = 0,0021,
Р(*И = 3) = P((GG) & вг)Р((СА) 4, 62) = ^1 = 0,005,
Р(Х|Л = 4) = P((GGC) & е1)Р((А) А 62) - ^У^ = 0,0042;
Р(х\ц = 1)Р(р = 1) = Р(х|Л = 2, ^ = l)P(i4 = 2|а» = 1)Р((л = 1)+
+Р(х|Л = 3,/х = 1)Р(А = 3|/х = l)P(/i = 1)+
+Р(х| А = 4,ц = 1)Р(А = 4|/г = l)P(/i = 1) =
= ^(Р(х|Л = 2) + Р(х\А = 3) + Р(ж|Л = 4) = 0,0009. (3.15)
Точно так же при /х = 2 и /х = 3 мы получаем
Р(х|М = 2)Р(а* = 2) = ^(Р(а;|Л=(2,3),/х=2) + Р(хИ=(2,4),/.=2)+
+Р(х\ А = (3,4), ц = 2)) = 0,001,
Р(х\/л = 3)Р(р = 3) = ±Р(*|Л = (2,3,4), м = 3) =
1 (З!)4
= W=0-001- (316)

138 Глава 3
Уравнения (3.10) и (3.14)—(3.16) дают полную вероятность
последовательности х при выбранной модели сегментации:
з
Р(х) = J2 Р(х\р = т)Р{/л = т) = 0,0036.
тп=0
Апостериорное распределение числа точек перехода /л может быть
найдено непосредственно из теоремы Байеса следующим образом:
РО,-о|.)-^-у^-,8-о,ш»,
Р(х)
РЬ-ВД-^-^-') =0,264,
Р(х)
Р(х)
РЬ-ЗМ- P(l1" ^- 3> =0,275.
Для апостериорного распределения точки перехода Лт теорема Байеса
даёт
з
Р{АШ = j для некот-го т\х) = Y^ P(Am=j для некот-го m,fjb = i\x) =
г=0
з
= У^ Р(ж| Ат = j для некоторого т, /х = г) х
PW г=0
хР(А + т = j для некоторого ra|/i = г)Р(/х = г);
Р(Ат = 2 для некоторогот|ж) =
= щ (з^(*и = (2)-к=1) + hp{x\A = (2'3)) м = 2)+
+ ^Р(х|Л = (2,4),/х = 2) + 1р(х|Л = (2,3,4),/х= 3) J = 0,470578;

3.2. Дополнительные задачи и теория 139
Р(АШ = 3 для некоторого т\х) =
= Щ (hP^A = (3). /* = 1) + ^ПМ = (2,3), /i = 2)+
+Д Р(х|Л = (3,4), М = 2) + |р(х|А = (2,3,4), /i = 3) J = 0.612363;
Р(Ат = 4 для некоторого т\х) =
^Р(я|Л = (4), /i = 1) + ±Р{х\А = (2,4), м = 2)+
Рф^г v~'" ^'"" ~' " 12
+ ^Р(ж|Л = (3,4),/х = 2) + |р(ж|Л = (2,3,4),М = 3) J = 0,592806;
Р(нет точек перехода|ж) = Р(ц = 0|ж) = 0,167627.
Наконец, функция плотности распределения апостериорных
вероятностей /](9а,9с,9с,9т\х) вероятностей нуклеотидов в участке j, где j =
= 1,2,3,4, имеет вид
Ъ(вА,вс,9о,вТ\х) = Y^ Р(сегмет\в,)Р(е,)Р(сегмет). (3.17)
сегмент,
покрывающ. j
Формула (3.17) позволяет нам вычислить функции плотности
распределения апостериорных вероятностей:
fi(9A, во во, 9т\х) = \v(2, 2,3,1) + ±2>(1,1,2,1) + lD(l, 1,3,1)+
+^D(1,2,3,1);
f2(0A, 6c, во, 0т\х) = \V{2,2,3,1) + ^2>(2,2,2,1) + i©(l, 1,3,1)+
+ ^2?(1,2,3,1) + \V{\, 1,2,1) + iD(l, 2,2,1);
h{9A, 9C, 9G, 9t\x) = \V{2,2,3,1) + ±V(2,2,2,1) + ±2>(2,2,1,1)+
+ ^P(1,2,3,1) + ^£>(1,2,2,1) + ±D(1,2,1,1);

140
Глава 3
h(0A, Be, ва, вт\х) = \V(2,2,3,1) + ±V(2,2,2,1) + ±2>(2,2,1,1)+
+±©(2,1,1,1). (3.18)
Обратите внимание, что каждая функция плотности апостериорных
вероятностей нуклеотидов представляет собой смесь распределений Дирихле.
Из (3.18) мы определяем оценку апостериорного среднего (ОАС)
вероятности появления каждого нуклеотида на участке j, где j = 1,2,3,4,
следующим образом:
ЕгвА = 0,2022, Е2вА = 0,2065,
Ei0c = 0,2141, Е20с = 0,2323,
Ei0G = 0,4128, Е2в0 = 0,429,
Ег0т = 0,1709; Е2вт = 0,1634;
Е3вА = 0,2343, Е40А = 0,3487,
Е30с = 0,3268, Е40с = 0,2419,
E30G = 0,2755, E40g = 0,2453,
Е30т = 0,1634; Е40т = 0,1709.
Замечание. Применение СММ, описанной в задаче 3.16, к модельной
последовательности х = GGCA позволяет нам вычислить апостериорное
распределение «точек перехода» посредством прямых и обратных
переменных, определённых в задаче 3.17. Фактически мы должны вычислить
апостериорные вероятности событий Aj = (скрытые состояния на участках
j — 1 и j разные), где j = 2,3,4. Обратите внимание, что вероятность Р(х)
была определена в задаче 3.17 и равна 0,0038. Мы получаем
Р(А2\Х) = Р(7Г1 = #,7Г2 = L\X) +Р(7Г1 = L,7T2 = Н\Х) =
_ Р(7Г1 = Я, 7Г2 = I/, X) P(7Ti = L, 7Г2 = Я, х) _
= рй + W) =
Р{х)
-\-Р(хих2,х3,х^тг1 = £,тг2 = Я)) =
= -—--[Р(Х1,Х2,1Г1 =#,7Г2 = L)P(X3, Ж4|Ж1,Ж2,7Г1 =Я,7Г2 = L) +
Р(ж)

3.3. Дополнительная литература 141
+Р(Ж1,Ж2,7Г1 = Ь,7Г2 = #)Р(Ж3,Ж4|Ж1,Ж2,7Г1 = L, 7Г2 = Я)] =
= ^К(аояея(С)аяьеь(С)6я(2) + aQLeL{G)aLHeH{G)bL(2)) =
Р[х)
= О,2389 + 0,1983 = 0,4372.
Точно так же мы вычисляем другие апостериорные вероятности:
Р(А3\х) = ——-(Р(Ж1,Ж2,Жз,Ж4,7Г2 =#,7Г3 = Ь) +
Р(ж)
+Р(Ж1,Ж2,Ж3,Ж4,7Г2 = £,7Г3 = #)) =
= 0,2334 + 0,2108 = 0,4442;
Р(А4\х) = —7-г-(Р(Ж1,Ж2,Жз,Ж4,7Гз = #, 7Г4 =1/) +
Р(ж)
+Р(ж1,Ж2,Жз,Ж4,7Гз = Ь,7Г4 = Я)) =
= 0,3279 + 0,1392 = 0,4671.
□
3.3. Дополнительная литература
Со времени издания «АБП» появилось поразительно большое число
публикаций по предмету применений марковских цепей и СММ для
моделирования биологических последовательностей. Мы можем привести лишь
ссылки на несколько часто цитируемых работ, изданных позже 1997 года.
Марковские цепи и скрытые марковские модели обеспечивают
полезный формализм для моделирования геномных последовательностей и часто
используются в методах и алгоритмах предсказания генов. Бурге и Карлин
[39] в своей компьютерной программе обнаружения (предсказания) генов
GENSCAN использовали трёхпериодическую (неоднородную) марковскую
цепь пятого порядка, чтобы моделировать кодирующие области
последовательностей ДНК. Алгоритм GeneMark.hmm ([184]) использует структуру
СММ с границами генов, моделируемыми в виде переходов между
скрытыми состояниями; GLIMMER — алгоритм для обнаружения генов в геномах
микробов ([232]) — использует интерполированные марковские модели.

142
Глава 3
В [148] описан метод SAM-T98 для отыскания отдаленных
гомологов белковых последовательностей; в [272] предложен новый метод
поиска трансмембранной топологии с наибольшим правдоподобием среди всех
возможных топологий данного белка; в [40] предлагается HMMSTR,
скрытая марковская модель для предсказания трёхмерной структуры белка,
основанного на 1-участках, мотивах структуры последовательности; в [103]
предложен метод приписывания гомологов к белковым продуктам,
закодированным в геномах, с помощью библиотеки СММ, представляющих все
белки с известной структурой; в [89] описан новый метод обнаружения
регулятивных областей в последовательностях ДНК посредством поиска
групп c/s-элементов; в [164] представлен разработанный ТМНММ метод
для предсказания топологии мембранных белков; в [183] предложен новый
алгоритм множественного выравнивания последовательностей, который
сочетает в себе подход СММ, алгоритм прогрессивного выравнивания и
вероятностную модель эволюции, описывающую замены нуклеотидов или
аминокислот.

Глава 4
ПОПАРНОЕ ВЫРАВНИВАНИЕ
С ПОМОЩЬЮ СММ
Из главы 3 «АБП» мы узнали, что алгоритм ДП для попарного
выравнивания последовательностей допускает вероятностную интерпретацию.
Действительно, в логарифмической форме алгоритма Витерби для
скрытой марковской модели содержащего пропуски выравнивания
последовательностей, присутствуют эквивалентные уравнения. Скрытые состояния
такой модели, называемой парной СММ, соответствуют парам в
выравнивании: совпадению, паре я-пропуск и паре у-пропуск. Диаграмма
состояния парной СММ топологически подобна диаграмме конечного автомата
([67], рис. 4.1), хотя параметры парной СММ имеют чёткие
вероятностные значения. Оптимальное выравнивание конечного автомата, найденное
стандартным алгоритмом ДП, эквивалентно наиболее вероятному пути
через парную СММ, определённому алгоритмом Витерби. Алгоритмы ДП как
для оптимального глобального, так и для оптимального локального
выравнивания имеют аналоги Витерби для соответственно определённых СММ.
Интересно, что СММ имеет преимущество перед конечным автоматом,
потому что СММ может вычислить полную вероятность того, что
последовательности X и Y могаи быть порождены данной парной СММ; таким
образом, может быть введена вероятностная мера, помогающая установить
эволюционные отношения. Такая полная вероятностная модель определяет
также 1) апостериорное распределение по всем возможным
выравниваниям для заданных последовательностей X и Y и 2) апостериорную
вероятность того, что отдельный символ х последовательности X выровнен с
отдельным символом у последовательности Y. Однако реальные
биологические последовательности нельзя рассматривать как точные реализации
вероятностных моделей. Это объясняет трудности, с которыми
сталкиваются основанные на СММ методы выравнивания для поиска подобия ([67],
раздел 4.5), при том что более простые методы на конечных автоматах
работают достаточно хорошо.

144
Глава 4
Приведённые в главе 4 задачи из «АБП» иллюстрируют свойства
парных СММ и более подробно рассматривают сравнение СММ и модели
независимого порождения, порождающих символы из заданного алфавита.
Дополнительные задачи посвящены практическому применению
парных СММ для выравнивания последовательностей, вычисления полной
вероятности двух выровненных последовательностей и вычисления или
апостериорной вероятности оптимального пути или апостериорной
вероятности данной пары выравниваемых символов. В конце рассматриваются
отношения между параметрами основанной на логарифмических счетах шансов
версии алгоритма Витерби для парной СММ и параметрами классического
алгоритма ДП выравнивания с линейными счетами за пропуски.
4.1. Оригинальные задачи
Задача 4.1. На рис. 4.1 представлена модель независимого порождения R
для пары последовательностей. Главные состояния X и Y порождают две
полные последовательности х и у по очереди и независимо друг от друга.
Молчащее состояние S между X и Y, а также начальное и конечное
состояния не порождают никаких символов. Каждое главное состояние имеет
петлю, выходящую из них и в них входящую же с вероятностью 1 — rj, и
вероятности переходов из У в конечное состояние и из S в конечное
состояние равны rj. Какова вероятность того, что последовательность х имеет
длину t согласно модели независимого порождения R для пары
последовательностей?
Рис. 4.1. Случайная модель независимого порождения R, порождающая пару
последовательностей
Решение. Пусть Lx и Ly — длины последовательностей х и у. Сначала мы
найдём вероятность того, что Lx = t при условиях Lx < n, Ly < m для

4.1. Оригинальные задачи 145
некоторых целых чисел пит. Так как мы интересуемся только
распределениями длины, мы можем не учитывать вероятности порождения. Для
целого числа t, такого что t > п,
P(LX — t\Lx ^n,Ly < га) = 0.
Если t ^ n, мы получаем
P(LX = t,Lx < n, Ly < m)
P(LX = t\Lx ^n,Ly ^ ra) =
P(La; ^n,Ly ^ m)
__ P(La; = t,Ly < m)
P(LX <:П,ЬУ < m)
z=o
71 771
fe=0 J=0
E^(l-7,)^
z=o (1 - f?)
n m
EE#-i)w £(i-»?)fc
fc=0 J=0 fc-0
"С-"' (4.1,
(1-(1-,)»)•
Обратите внимание, что в силу независимости последовательностей х
и у условная вероятность P(LX = t\Lx ^ n, Ly ^ га) не зависит от т. Если
ограничение на длину последовательности х снято (так что п = +оо), то
уравнение (4.1) принимает вид
P{Lx = t) = r1{l-ri)t. п
Задача 4.2. Чему равно математическое ожидание длины
последовательностей, порождаемых моделью независимого порождения R для пары
последовательностей, представленной в задаче 4.1? Каким следует установить
параметр г/?

146
Глава 4
Решение. Формула математического ожидания длины
последовательностей х и у при условиях Lx < n и Ly < m для некоторых целых чисел
пит выведена как прямое продолжение задачи 4.1. Из уравнения (4.1) мы
находим условное математическое ожидание длины Lx следующим
образом:
п
ЩЬХ\ЬХ ^n,Ly ^m) = ^2kP(Lx = k\Lx ^n,Ly < га) =
fc=0
S"(i-(i-.n-(i-(i-.nS"(1-77)
Ф -v) = v_
-77)") (1-(1-
7? (1-Т7)(1-(п+1)(1-7))п + тг(1-Г7)п+1)
~(1 -(!-„)«) r?
_ (1 - 7/)(l - (П + 1)(1 - 77)" + n(l - T?)"+1)
77(1 -(1-77)")
Подобным же образом мы определяем условное математическое
ожидание длины Ly\
(1 - ч)(1 - (ш + 1)(1 - v)m + т(1 - rj)m+1)
ЩЬУ\ЬХ ^n,Lv < га) =
77(1 - (1 - г;)-)
Наконец, если длины последовательностей, порождённых моделью R,
не ограничены, то математические ожидания длины определяются из
ELX = BLy = .
Поэтому если характеристическая длина L последовательностей х и у
известна, то параметр rj в модели независимого порождения R для пары
последовательностей разумно установить равным 1/(L + 1). □
Задача 4.3. Пример неопределённости в расположении пропуска показан
ниже (три существенно различных варианта размещения пропуска в
выравниваниях глобина 7Г1,7г2,7Гз с весьма близкими счетами):
HBA_HUMAN KVADALTNAVAHVD DMPNALSALSDLH
KV + +А ++ +L+ L+++H
LGB2_LUPLU KVFKLVYEAAIQLQVTGVWTDATLKNLGSVH

4.1. Оригинальные задачи
147
HBA_HUMAN KVADALTNAVAHVDDM PNALS ALS DLH
KV + +A ++ +L+ L+++H
LGB2_LUPLU KVFKLVYEAAIQLQVTGVWTDATLKNLGSVH
HBA_HUMAN KVADALTNA VAHVDDMPNAL SALS DLH
KV + +A V V +L+ L+++H
LGB2_LUPLU KVFKLVYEAAIQLQVTGVWTDATLKNLGSVH
Счета выравниваний щ, 7Г2, и 7Гз, рассчитанные с помощью матрицы
BLOSUM50 (см. табл. 2.1) со штрафом за введение пропуска —12 и
штрафом за продолжение пропуска —2, равны, соответственно, 3, 3 и 6.
Относительные счета для вариантов размещения пропуска зависят только от
счетов замен, и не зависят от счетов за пропуски. Почему это так, и как это
скажется на точности выравнивания при использовании алгоритмов ДП?
Решение. Каждое из трёх заданных выравниваний имеет один пропуск
длины 5. Так как штраф за пропуск зависит только от его длины, эти три
пропуска вносят равные вклады в счета выравниваний. Следовательно,
разница между полными счетами выравниваний обусловлена лишь
различиями в счетах замен, назначенных каждому выравниванию.
Первые два выравнивания имеют равные полные счета и,
следовательно, равные суммы счетов за замены, тогда как сумма счетов замен для
последнего выравнивания больше на 3, чем для первых двух выравниваний.
Такой исход естественней для функции штрафов за пропуски,
независимой от позиции пропуска в выравнивании. Счёт пропуска с
зависимостью от позиции мог быть введён для выравнивания белковой
последовательности посредством налагания более высоких штрафов за введение
пропуска и за продолжение пропуска в областях полипептида с регулярной
вторичной структурой (а-спиралъ или /3-нить). Эта возможность, однако,
имеет свою цену, поскольку на шаге предварительной обработки
необходимо определить вторичные структуры белка для обеих вьфавниваемых
последовательностей.
Итак, алгоритм ДП для выравнивания последовательностей с
независимыми от позиции штрафами за пропуски производит столько
оптимальных выравниваний, сколько есть возможностей смещения пропусков
относительно наилучшего выравнивания (без изменения при этом суммы
счетов замен). Такой набор выравниваний с равными счетами должен быть
просмотрен экспертами, с тем чтобы выбрать вариант, адекватный с точки
зрения структурных, функциональных и эволюционных характеристик. □

148 Глава 4
Задача 4.4. На рис. 4.2 представлен пример простой СММ: состояние А
порождает символы с вероятностями qa, а последовательный блок В из
четырёх состояний порождает постоянную строку abac с вероятностью 1.
Покажите, что сравнение полной вероятностной модели независимого
порождения с такой показательной СММ позволяет отличать случайные
данные от данных, порожденных моделью1.
Рис. 4.2. Пример СММ
Решение. Эта задача непростая. Мы рассматриваем две стохастические
модели, порождающие последовательности символов из одного и того же
алфавита: СММ, представленную на рис. 4.2 (модель М), и модель
независимого порождения (модель Я), которые производят символы с
одинаковыми вероятностями порождения qa, как определено для состояния А
модели М. Имея наблюдаемую последовательность х = хг,..., хп, мы должны
опознать наиболее правдоподобную модель, М или R, которая её
порождает. Чтобы принять решение, мы сравниваем апостериорные вероятности
моделей, Р(М\х) и P(R\x). При допущении о равенстве априорных
вероятностей моделей отношение апостериорных вероятностей преобразуется к
отношению шансов следующим образом:
Р(М\х) _ Р(х\М) Р(х\М) + P(x\R) _ P{x\M)
P{R\x) " Р(х\М) + P(x\R) P(x\R) " P(x\R) '
^а самом деле эта СММ не содержит начального и конечного состояния. Для более
аккуратной модели с начальными и конечными состояниями на ответ будут влиять также
вероятности переходов из начала и в конец. — Прим. ред.

4.1. Оригинальные задачи 149
Таким образом, всё, что нам нужно, — это сравнить правдоподобия
моделей, Р(х\М) и P(x\R). Чтобы решить эту задачу шаг за шагом, мы
начнём с двух особых типов последовательности х.
1) Если последовательность х = Xi,...,xn не содержит строк abac,
то P(x\R) = f[qXi9 P(x\M) = ап П fe и P(x\R) > Р(х\М) при лю-
г=1 г=1
бом значении вероятности перехода а. Поэтому более правдоподобно, что
последовательность х без строк abac порождена моделью независимого
порождения R.
2) Если х = abac, то P(x\R) = q2qbqc> тогда как Р(х\М) определяется
формулой полной вероятности
Р(х\М) = Р(х, А\М) + Р(х, В\М).
Здесь Р(х, А\М) — вероятность того, что строка abac порождается
состоянием А (за четыре шага), а Р(х, В\М) — вероятность того, что строка
abac порождается блоком В. Поэтому
P(x\M) = a4q2aqbqc + (l-a).
Чтобы сравнить условные вероятности, удобно анализировать
значение А:
Д = Р(х\М) - P(x\R) = a4q + (1 - а) - ?/ = (а - l)(rj(a + 1)(а2 +1) -1),
где rj обозначает q2qbqc- Поскольку а — 1 всегда отрицательна, знак
величины Д определяется знаком второго множителя. Функцию трёх переменных
г) (т] = rj(x, у, z) = x2yz, где х, у и z принадлежат к интервалу [0,1] и
выполняется равенство x + y + z = a^l), мы получаем в виде
г}(х, у, z) = г)(х, у) = х2у(а -х-у)= ах2у - х3у - х2у2.
Чтобы определить максимальное значение г) при х,у € [О,1], мы
решаем следующую систему уравнений:
р- = 2аху - Зх2у - 2ху2 = ху(2а - Зх - 2у) = О,
tj^ = ах2 - х3 — 2х2у = х2(а — х - 2у) = 0.
Значения переменных, которые максимизируют rj, составляют х*= а/2,
у* = а/4, z* = а/4, а само максимальное значение — rj(x*, у*, z*) = a4/64.
Таким образом, параметр rj удовлетворяет неравенству 0 ^rj ^ 1/64 при

150 Глава 4
любом выборе вероятностей порождения q, а член г)(а + 1)(ск2 + 1) — 1
отрицателен. Поэтому А положительно, Р(х\М) > P(x\R) и отношение
шансов г принимает вид
_ Р(х\М) _ а*д2адьдс + (1 - а) _ a*V + (1 - а)
~ P(x\R) ~ qlqbqc ~ r, > *> №
где логарифмическое отношение шансов S(x) = logP(x\M)/P(x\R) > 0.
Таким образом, наблюдение последовательности abac позволяет нам
опознать модель М как источник последовательности независимо от значений
вероятностей порождений и переходов.
3) Наконец, мы рассматриваем общий случай последовательности х =
= ал,..., хп, содержащей fc строк abac (где 0 < fc ^ п/4). В этом случае
правдоподобие модели независимого порождения R определяется из
P(x\R) = {q2aqbqc)k Ц qXi = rf Ц qXi,
где X — подпоследовательность последовательности х, которая состоит из
к строк abac из последовательности х (не следует забывать, что строки
abac не могут перекрываться). Правдоподобие модели М рассчитывается
как Р(х\М) = ^2 Р(ж, 7г|М), где сумма берётся по всем путям 7Г, порожда-
7Г
ющим наблюдаемую последовательность х. Если путь 7Г порождает I строк
abac из состояния А (каждая строка за четыре последовательных шага)
и к — I строк abac из блока В9 то вероятность совместного появления х и 7г
определяется из
P(x,n\M) = (a4q2aqbqc)l(l-a)k-lan-4k Д «*•
Число таких путей ж равно (*), а правдоподобие модели М принимает
вид:
Р(х\М)
= (£1(к1)(<х4Я2аЯьЯс?(1-*)к-1а»-А П &.=
= fE(t)«4V(l-ar'a"-4fc>) П *ц =

4.1. Оригинальные задачи
151
Тогда отношение шансов принимает вид
РШ) _ (а4т,+ (1-а)\к _ 4к (а*т, + (1-а)\к _ 4кк
P(x\R)-a { а^п ) ~а { Ч ) ~а "'
где г определяется из уравнения (4.2), а г > 1. Поэтому логарифмическое
отношение шансов предстаёт перед нами как
Р(х\М)
S{x) = log = (n - 4fc) log a + к log r.
Вполне очевидно, что значение P(x\M)/P(x\R) зависит от
параметров пик. Если к = 0, то более правдоподобно, что последовательность х
без строк abac порождена моделью независимого порождения R (см.
случай 1 выше).
Если к = п/4, то
P(x\R)
и более правдоподобно, что последовательность х порождена моделью М.
По мере того как к возрастает от нуля до п/4, отношение шансов
P{x\M)/P{x\R) увеличивается от ап < 1 до гп/4 > 1, где Р(х\М) =
= P(x\R) при к = к*, причём
* п log a n log a
4 log a - log r log(a4qlqbqc) - iog(a4qlqbqc + 1 - а)
Поэтому мы заключаем, что при А: < fc* последовательность х
опознаётся как порождённая моделью R; при к > к* — как порождённая
моделью М; при к = к* никакая модель не отбирается. Как и следовало
ожидать, последовательность х с высокой «плотностью» строк abac опознаётся
как порождённая моделью М. □

152
Глава 4
Задача 4.5. Сравните применение полной вероятностной модели в
задаче 4.4 с употреблением пути Витерби в модели М, в которой
вероятность переходов к блоку В была увеличена до такого значения т, что
г > РА{аЪас).
Решение. Мы должны возвратиться к решению задачи 4.4 и использовать
вероятность пути Витерби вместо полной вероятности наблюдаемой
последовательности.
1) Если последовательность х = х±,..., хп не содержит строк abac,
то обе модели, М и R, имеют только по одному пути скрытых
состояний, посредством которого можно произвести эту последовательность, где
P(x\R) = П Ях<, Р(х\М) =anf[ qXi. Тогда P{x\R) > Р(х\М) независи-
г=1 г=1
мо от значения вероятности переходов а, а последовательность х опознана
как порождённая моделью независимого порождения R.
2) Если х = abac, то правдоподобие модели R равно P(x\R) =
— QaQbQc — V- При заданной модели М и условии г > РА(сьЬас) наиболее
вероятный путь 7г* проходит через блок В. Таким образом,
Р(ж, тг* \М) = Р(ж, В\М) = 1-а.
Тогда отношение шансов определяется из
Р(ж,тг*1М) 1-д 1-а
Следовательно, если а < 1 — ту, то г > 1 и модель М опознаётся
как источник последовательности х\ если а > 1 — г), то г < 1 и более
правдоподобный источник последовательности ж — модель независимого
порождения R.
3) Теперь, если последовательность х = х\,..., хп содержит к строк
abac, где 0 ^ к ^ п/4, то правдоподобие модели R (где только один путь
соответствует последовательности х) то же, что и в задаче 4.4:
P(x\R) = (q2aqbqc)k Ц qXi = V* Ц &«•
XiiXigX XiiXigX
Для того чтобы породить последовательность х на пути Витерби 7г*
через модель М, все к строк абас должны порождаться из блока В.
Поэтому вероятность совместного появления х и 7г* имеет вид
P(x,7r*|M) = (l-a)fcan-4fc П «*•

4.1. Оригинальные задачи
153
Тогда мы находим
P(x\R) a { V ) а
г
где г определено в уравнении (4.3). Тогда логарифмическое отношение
шансов принимает вид
Р(х 1г*\М)
S(x) = log у ' ; = (п - 4fc) log a + fclogr.
Если а < 1 — 77 = 1 — ЯаЯъЯс, то г > 1 и значение отношения шансов
P(x)tt*\M)/P(x\R) зависит от параметров п и к. Из уравнения (4.3) мы
находим, что Р(ж, 7г*|М) = Р(ж, Д) при
/. _ Tilogo: _ nloga _ „
4 log a - log r log(a4qlqbqc) - log(l - a)
Поэтому если строка абас появляется в последовательности х к раз
и к < к*, то модель Д опознаётся как источник последовательности х; при
к > к* модель М опознаётся как источник последовательности х.
Если а> 1-г) = 1 — q%qbqc, то г < 1 и
^ . , ^ч = О! Г < 1.
Р(ж|Д)
В этом случае, независимо от числа к появлений строки abac в
последовательности х, в качестве источника последовательности х опознаётся модель
независимого порождения Д.
Замечание. Здесь мы снова видим, что, в случае, когда сравнение
проводится с использованием полных правдоподобий моделей (рассмотренных
в задаче 4.4), использование вероятностей пути Витерби для сравнения
моделей может привести к различным заключениям. Так как основанный на
полной вероятности подход более точен и позволяет получить более
надёжное опознание модели при одних и тех же данных, здесь мы снова видим
предупреждение, что сведение критерия до пути Витерби может привести
к ошибочным решениям при отборе модели. □

154
Глава 4
Задача 4.6. Мы можем далее видоизменить модель, установив все
вероятности порождения в состоянии А в одно и то же значение, 1/А, где А —
размер алфавита. Различие между этой моделью и моделью независимого
порождения в точности определяется числом строк abac в данных.
Одинаковым ли качеством различения обладают видоизменённая модель и модель
на полной вероятности?
Решение. Мы должны следовать решению задачи 4.5 и вносить поправки
там, где это необходимо.
1) Случай последовательности х = xi,..., хп без строк abac не
затрагиваем. Логарифмическое отношение шансов, как и прежде, имеет вид
п
Р(х\М) аП 0 9х<
S(-x1 = log 1*Ш\ = 1о8 Г1 =п\оёа<0.
[х1Щ п &,
г=1
Следовательно, последовательность х всегда опознаётся как
порождённая моделью независимого порождения R.
2) Если х = abac, то, как доказано в задаче 4.5, для пути Витерби 7г*
отношение шансов г определяется из
Р(ж,7г*|М)= 1-д
РЫЛ) Ч2аЧьЧс
Если вероятность переходов а удовлетворяет условию
то г > 1 и последовательность ж опознаётся как порождённая моделью М;
если а > 1 — (1/А4), то г < 1 и х опознаётся как последовательность,
порождённая моделью независимого порождения R.
3) В общем случае последовательности х = х±,..., хп, содержащей к
строк abac, где 0 ^ к ^ п/4, отношение шансов, вовлекающее путь
Витерби 7г* через модель М, которое было вьгаедено в задаче 4.5, принимает
вид
P(x\R)
1-оЛ = ап-4к А-оЛ*

4.1. Оригинальные задачи
155
Если а < 1 — (1/А4), то отношение шансов зависит от параметров п
и к. При
nlogQ!
к = к* =
4 log Act — log(l — а)
никакое решение не может быть принято, так как Р(ж,7г*|М) = P(x\R).
Если к < А;*, то в качестве источника последовательности х опознаётся
модель R; если к > А;*, то в качестве источника последовательности х
опознаётся модель М.
Если а > 1 — (1/А4), то отношение шансов P(x,tt*\M)/P(x\R) < 1
при любом к, и х опознаётся как последовательность, порождённая
моделью независимого порождения R.
Ниже приведён свод правил принятия решения, выведенных из
основанного на полной вероятности подхода (задача 4.4) и подхода,
использующего путь Витерби. Мы делаем допущение, что все вероятности
порождения q равны 1/А Критические значения к$ и к% определяются из
k* = nloga
41og(aA) — log((aA)4 + 1 — а)
для проверки на основе полной вероятности, Т\ и
k* = nloga
2 A\og{aA) — log(l — а)
для проверки Тг, основанной на пути Витерби. Обратите внимание, что
Источник последовательности х длины п с к строками abac опознаётся
следующим образом. Если а < 1 — (1/А4), то есть три возможных случая.
1) При к < к^ обе проверки опознают модель независимого
порождения R.
2) При к{ < к < Щ проверки дают различные результаты: проверка Т\
опознаёт модель М, тогда как проверка Тъ опознаёт модель R.
3) При к > &2 обе проверки опознают модель М.
Если а > 1 — (1/А4), то проверка Тг всегда опознаёт модель R; однако
проверка 2\ опознаёт модель R при к < к$ и модель М в противном
случае. □

156
Глава 4
4.2. Дополнительные задачи
Четыре задачи, включённые в этот раздел, представляют собой
практические упражнения по использованию парных СММ: построение
оптимального вьфавнивания двух последовательностей с помощью алгоритма
Витерби (задача 4.7); вычисление посредством прямого алгоритма
вероятности того, что эти последовательности связаны согласно парной СММ
(задача 4.8); определение апостериорных вероятностей выравнивания,
выровненной пары символов, а также математического ожидания точности
заданного вьфавнивания (задачи 4.9 и 4.10).
Вывод уравнений алгоритма Витерби в единицах логарифмических
шансов — цель задачи 4.11. Логарифмические счета шансов, которые
заменяют вероятностные функции, естественно происходят из отношений
правдоподобия парной СММ и модели независимого порождения для пары
последовательностей.
Задача 4.7. Парная СММ, представленная на рис. 4.3, порождает две
выровненные последовательности ДНК х и у. Состояние М порождает
выровненные пары нуклеотидов с вероятностями порождения PXiyj,
определяемыми следующим образом:
Ртт = Рсс = Раа = Pgg = 0,5, Рст = Pag = 0,05,
Pat = Pgc = 0,3, РСт = Рас = 0,15.
Состояния вставки X и Y порождают (выровненные с пропусками)
символы, соответственно, из последовательности х и у. Вероятности
порождения для обоих состояний вставки одни и те же:
ЯА = Яс = Qg = Чт = 0,25.
Никакие символы не порождаются начальным и конечным
состояниями. Значения вероятностей переходов следующие:
пвх = kby = пых = яму = 5 = 0,2,
7ГВЯ = 7ГМЯ = ЪХН = KYO = Т = 0, 1,
тгхх = 7гуу = е = 0,1, тгхм = ъум = 1 — е-т = 0,8,
7ГВМ = 7ГММ = 1 - 25 - Г = 0, 5.

4.2. Дополнительные задачи
157
С помощью алгоритма Витерби для парной СММ найдите
оптимальное выравнивание последовательностей ДНК х = TTACG и у = TAG.
Начальное
Конечное
Рис. 4.3. Полная вероятностная версия парной СММ, порождающей
выровненные последовательности х иу
Решение. Оптимальное выравнивание сопоставлено с наиболее вероятным
путём через парную СММ, порождающую выровненные
последовательности х иу. Алгоритм Витерби начинается со следующей инициализации:
VM(0,0) = 1,все остальные v*(i,0), г>*(0, j) = 0. (4.4)
Пусть vm(i,j) — вероятность порождения выровненных
подпоследовательностей х\,..., Xi и 2/i, • • •, yj парной СММ с подвыравниванием,
заканчивающимся а) выровненной парой Хг и yj (vm(i,j) = vM(i,j))9 б)
остатком Xi> выровненным с пропуском (v*(i,j) = vx(i,j)), и в) остатком yj,
выровненным с пропуском (vm(i,j) = vY(i) j)). Тогда рекуррентные
уравнения, необходимые для вычисления значения вероятности v*(i,j)9
следующие:
„м
(ij) = PXuyjmax<
ttmmv
{ nYMVY{i- l,j- 1);
(4.5)

158 Глава 4
v*{i,j) = qXir*J*MxvMx<fr^ (4.6)
[ пххул{1- l,j);
vr(iJ) = qyiraJWV^-V> (4.7)
Мы начинаем вычисления следующим образом:
vM (1,1) = Ртттгммум (0,0) = 0,25, VX(1,1) = 0, <;у(1,1) = 0
и продолжаем, используя уравнения (4.5)-(4.7), заполняя вычисленные
значения вероятности vm(i,j) в ячейки матрицы ДП (таблица 4.1). На
завершающем шаге мы имеем:
v = г max(vM(5,3), vx(5,3), vY (5,3)) = 1(Г5.
Обратное прослеживание через матрицу ДП определяет оптимальный путь:
Vм(5,3) -+ Vх(4,2) -+ Vм(3,2) -+ Vх(2,1) -+ <;м(1, 1).
Выравнивание с наивысшим счётом, соотносимое с наиболее вероятным
путём 7г* через состояния парной СММ, имеет следующий вид:
Т Т А С G
Т - А - G
Вероятность оптимального пути 7г* (и оптимального выравнивания)
определяется на заключительном шаге алгоритма Витерби: Р(х,у,тг*) =
= v = 10"5.
Реализации алгоритма Витерби для выравнивания посредством парной
СММ, написанные на языках программирования PERL и C++, доступны на
веб-сайте «Дополнительные материалы сети» по адресу:
opal.biology.gatech.edu/PSBSA.
Замечание. При условиях инициализации алгоритма Витерби для
парной СММ, описанных в уравнениях (4.4) ([67], стр. 84), получающееся
выравнивание двух последовательностей будет всегда начинаться с пары
совпавших символов xi,yi для любых двух последовательностей х и у.
Следовательно, выравнивание, произведённое парной СММ с таким
ограничением на шаг инициализации, может не быть оптимальным.

Таблица 4.1. Матрица значений вероятности гЛ(г, j), определённых алгоритмом Витерби для
последовательностей TTACG и TAG. Каждая ячейка (i,j) содержит три значения, vM(i,j), vx(i,j) и vY(i,j),
записанные в порядке сверху вниз. Записи на оптимальном пути выделены полужирным шрифтом
3=0
3 = 1
3 = 2
j = 3
г = 0
1
0
0
0
0
0
0
0
0
0
0
0
t = l
0
0
0
0,25
0
0
0
0
0,0125
0
0
3,125 • Ю-4
г = 2
0
0
0
0
0,0125
0
0,0375
0
0
0,0015
0
0,001875
г = 3
0
0
0
0
3,125 • 10~4
0
0,005
0,001875
0
9,375-Ю-4
7,5 • 10~5
2,5-Ю-4
г = 4
0
0
0
0
7,813 • Ю-6
0
3,75 • 10~5
2,5 Ю-4
0
7,5-Ю-4
4,688 • 10~5
1,875-Ю-6
г = 5
0
0
0
0
1,953 • Ю-7
0
3,125 • Ю-7
6,25 • Ю-6
0
10~4
3,75 • 10~5
1,563-Ю-8
О
Я
о
X
К
и
X
IE3;
fa
>
X

160
Глава 4
Чтобы допустить отыскание оптимального пути, который начинается с
пропуска, достаточно видоизменить уравнения инициализации (4.4) в
алгоритме следующим образом:
vM(0,0) = l, vx(0,0) = 0, vy(0,l) = 0;
им(г,0) = 0, иу(г,0) = 0, г > 1; п
vM(0J) = 0, vx(0J) = 0, j>l.
Задача 4.8. С помощью прямого алгоритма определите вероятность того,
что пара последовательностей ДНК х = TTACG и у = TAG может быть
порождена парной СММ, описанной в задаче 4.7.
Решение. Полная вероятность определяется формулой
Р(х,у) = ^2р(х>У>7Г)>
7Г
где сумма берётся по всем возможным путям 7г через парную СММ,
порождающую пару последовательностей х и у. Значение полной
вероятности может быть определено прямым алгоритмом для парной СММ. Для
каждой пары (i,j) алгоритм вычисляет полную вероятность /fe(i,j) всех
выровненных подпоследовательностей (a?i,..., Xi) и (уъ .. •, %), гДе по~
следняя пара символов порождается скрытым состоянием к (М, X или Y).
Прямой алгоритм начинается с инициализации:
/м(0,0) = 1, /х(0)0) = /у(0,0) = 0, все /(г,-1),/(-1, j) = 0.
Значения fk(i,j) при i = 0, ...,5 и j = 0, ...,3 определяются по
следующим формулам:
fM(i,j) = PXiVi{nMMfM{i - l,j ~ l) + *XMfX(i - 1,3 ~ 1)+
+nYMfY(i-l,j-l));
fX(iJ) = qXi(*MxfM(i - l,j) + *xxfx(i - l,j));
fY(iJ) = qyj(*MYfM(i,j - 1) + тгуу/у(г, j - 1)).
Значения прямых переменных помещены в ячейках матрицы F,
представленной в таблице 4.2.

4.2. Дополнительные задачи
i-OT
953-
о
,-ОТ
375-
,-ОТ
258-
о
,-ОТ
944-
Г-0Т
268-
;-0Т
688-
,-ОТ
639-
г-ОТ
919-
,-ОТ
730-
гН Oi I—t
CN Oi Oi
I
О
I
О
гЧ
° Ю °
CN
- О
о
I
о
I
о
ю
CN
о ^
о
о
I
о
I
о
со
о
о
I
о
со
. . о °
Я> сГ
2 S
о .
о
о
' о
00125
сГ
о
CN
0,0
CN
1—«
О
сГ
ю со . ^
t- о Д с*
со о 2 о
о о ^ о
сГ о4 ° о4
CN
CN
о о
I
о
т-( О О О О
о о о
о
1—i
II
г->
CN
II
•^
со
II
•^
00 CN
.. О О
О СО О
I
О
CN ^
О О
— о
I
О

162
Глава 4
В заключительном шаге мы имеем:
/я(5, з) = т(/м(5,3) + /х(5,3) + fY(5,3)) = 3,632 • ИГ5.
Следовательно, вероятность того, что последовательности х и у
порождены парной СММ со всеми вариантами выравнивания, определяется
из
Р(х, у) = /Я(5,3) = 3,632 • Ю-5.
Замечание. Реализации прямого алгоритма в виде компьютерных
программ на языках PERL и C++ включены в «Дополнительные материалы
сети», доступные по адресу: opal.biology.gatech.edu/PSBSA. □
Задача 4.9. Для последовательностей х = TTACG и у = TAG найдите
апостериорную вероятность Р(тг*\х,у) оптимального выравнивания,
полученного алгоритмом Витерби с парной СММ, описанной в задаче 4.7.
Решение. Апостериорная вероятность пути 7г* описывается формулой
Р(*,2/,тг*)
р(1г|х^)=-р^г-
Оптимальное выравнивание
TTACG
Т - А - G
было построено в задаче 4.7. Это выравнивание соотнесено с наиболее
вероятным путём 7Г* через парную СММ. Было установлено, что его
вероятность равна Р(х, у, 7г*) = Ю-5. Вероятность того, что выровненные
последовательности х и у порождены СММ, составляет Р(х, у) = 3,632 • 10~5
(задача 4.8). Таким образом,
Р(тг*\х,у) = 10~5 _ = 0,275.
V ' J 3,632- ИГ5
Учтите, что существует ещё одно оптимальное выравнивание 7Г**:
TTACG
- Т А - G

4.2. Дополнительные задачи
163
с такой же вероятностью Р(х,у,тг**) = Р(х,у,тг*). (В замечании к
задаче 4.7 объяснено, почему это второе оптимальное выравнивание не было
восстановлено процедурой обратного прослеживания алгоритма Витерби.)
Совместный вклад этих двух выравниваний в значение полной вероятности
превышает 55 %. Такая относительно большая доля может быть объяснена
следующим образом. Прежде всего, число возможных выравниваний
(вносящих вклад в сумму вероятностей) коротких последовательностей хиу
является довольно маленьким. Действительно, парная СММ (рис. 4.3)
порождает только такие содержащие пропуски выравнивания
последовательностей х и у, в которых пара ж-пропуск не следует за парой у-пропуск и
наоборот. Во втором замечании к задаче 2.6 мы подсчитали число |Лп,ш|
таких выравниваний для последовательностей длин п и га. В случае
последовательностей длин 5 и 3 число |Лб,з| = 24. Некоторые из этих
двадцати четырех выравниваний с пропусками имеют весьма малые вероятности.
Например, выравнивание ж1
Т Т А С G -
- - Т - A G
имеет вероятность 3 • Ю-9, что в 333 раза меньше, чем вероятность
оптимального выравнивания, и вносит менее 1 % в полную вероятность Р(х,у).
При этом 7г' — не «худшее» выравнивание в данном примере! □
Задача 4.10. Для последовательностей хиу, описанных в задаче 4.7,
определите а) апостериорные вероятности всех выровненных пар в
оптимальном выравнивании ж* и б) ожидаемую точность 7Г*.
Решение, а) Выровненную пару символов в выравнивании
последовательностей хиу мы обозначим вьфажением XiOyj. Апостериорная вероятность
выровненной пары определяется из
Вероятность совместного наступления событий, расположенная в
правой части уравнения (4.8), может быть вычислена с помощью прямых и
обратных переменных f(i,j) и b(i,j), определяемых для прямого и
обратного алгоритмов с парной СММ следующим образом:
P(x,y,Xioyj) = fM(i,j)bM(i,j).

164 Глава 4
Переменные /(г, j) были уже рассчитаны (задача 4.8), и всё, что нам
нужно, — это вычислить значения переменных Ь(г, j) при помощи
обратного алгоритма. Условия инициализации следующие:
Ьм (5,3) = Ьх (5,3) = Ьу(5,3) = т,все b(t,4),b(6,j) = 0.
Рекуррентные уравнения имеют след? ^.
Ьм(г, j) = {l-26- r)PXi+m+1bM(i + 1J + 1)+
+S(qXi+1bx(i + l,j) + qyj+1bY(i,j + 1));
Ьх(г, j) = (1 - е - т)Рх<+1ад+1Ьм(г + 1, j + 1) + eqXi+1bx(i + 1, j);
6у(г, j) = (1 - е - т)РХ4+т+1Ьм(г + 1, j + 1) + e<bi+1bY(i,j + 1).
Мы вычисляем переменные b(i,j)9 где г = 5,..., 1 и j = 3,2,1, шаг за
шагом и заполняем ячейки матрицы обратных переменных (таблица 4.3).
Таблица 4.3. Обратные переменные b*(i,j), определённые обратным
алгоритмом.
Каждая ячейка (i,j) содержит три значения, 6м(г, j), bx(i,j) и bY(i,j),
написанные в порядке сверху вниз
i = 3
i = 2
j = i
г = 5
0,1
0,1
0,1
0,005
0
0,0025
1,25 Ю-4
0
6,25 Ю-5
г = 4
0,005
0,0025
0
0,25
0,04
0,04
0,00213
0,0002
_0,0012.
г = 3
1,25-Ю-4
6,25-Ю-5
0
0,0275
0,0022
0,0012
0,00195
0,00301
0,00303
г = 2
3,125 • 10~6
1,563-Ю-6
0
1,131 • Ю-4
6•10~5
5 • Ю-6
8,38-Ю-4
0,001175
0,0011
г = 1
7,813-Ю-8
3,91 -Ю-8
0
3,234-Ю-6
1,875-Ю-6
3,75 • Ю-7
7,574-Ю-5
5,653 Ю-5
2,716-Ю-5
Замечание. Реализации обратного алгоритма на языках PERL и C++
доступны на веб-сайте «Дополнительные материалы сети» по адресу:
opal.biology.gatech.edu/PSBSA.

4.2. Дополнительный задачи юз
Оптимальное выравнивание 7г* последовательностей х и у
(определённое в задаче 4.7) выглядит следующим образом:
Т Т А С G
Т - А - G.
Для того чтобы вычислить апостериорные вероятности всех
выровненных пар оптимального вьфавнивания 7Г*, необходимо иметь значение
полной вероятности Р(х, у) (вычисленное прямым алгоритмом в задаче 4.8).
Таким образом, мы имеем
Р(Х1оуих,у) /М(1,1)ЬМ(1,1)
P{x1oyi\x,y)= -
Р(ХзОУ2\х,у)
Р(х,у)
0,25-7,574-НГ
3,632-КГ5
Р(хз<>У2,х,у)
Р{х,у)
0,01 • 0,00275 _
3,632-10~5
Р{хьоуъ,х,у) _
Р{х,у)
-5
— П >л91 •
— U, u^rl,
/М(3,2)ЬМ(3,2)
Р{х,у)
■■ 0,757;
_/м(5,3)Ьм(5,3)
Р(хъоу3\х,у) =
9 fiSQ . 10"4 . П 1
= 0,727.
P(x,y) P(x,y)
2,639-10"4-0,1
3,632 КГ5
б) Ожидаемая точность вьфавнивания 7г* определяется следующей
формулой ([67], стр. 96):
А**) = Yl p(xi<>yj\x,y),
(i,j)€n*
где сумма берётся по всем выровненным парам в 7г*. Тогда
Д(тг*) = Р(хг о 2/i\х, у) + Р(х3 о у2\х, у) + Р(х5 о у3\х, у) = 2,005,
что даёт в среднем 0,668 на выровненную пару. Сравним этот результат
с таковым, полученным для далекого от оптимального вьфавнивания 7г',
рассмотренного в задаче 4.9:

166 Глава 4
Т Т А С G -
- - Т - A G
Ожидаемая точность п' определяется из
,, ,л /М(3,1)&М(3,1) + /М(5,2)ЬМ(5,2)
л{ж) = рм) = °'016
со средним значением 0,008 на выровненную пару. □
Задача 4.11. В случае парной СММ (модель М), представленной на
рис. 4.3, вероятностные функции vM, vx, vY алгоритма Витерби
определяются рекуррентными уравнениями (4.5)-(4.7). Присовокупите модель
независимого порождения для пары последовательностей R, изображённую на
рис. 4.1, выведите аналоги этих уравнений в единицах логарифмических
шансов. Покажите соотношения между параметрами вероятностных
уравнений алгоритма Витерби и аналогичных уравнений в единицах
логарифмических шансов.
Решение. Мы делаем допущение, что состояния X и Y моделей М и R
порождают символ а с одинаковой вероятностью qa. Полная модель
независимого порождения R для пары последовательностей порождает пару
последовательностей х = х\,..., хп и у = ух,... ,ут с вероятностью
п m
Р(х, y\R) = г,2(1 - пГ+т Д qXi Д qyi.
г=1 j=l
Логарифмические счета шансов Vm(i,j), где г = 1,...,п и j =
= 1,..., га, определяется следующими уравнениями:
где vm(i,j) — вероятность выровненных подпоследовательностей xi,... Х{
и 2/15 • • • > Ujy или из уравнения (4.5), уравнения (4.6) или из уравнения (4.7),
a w(i,j) — вероятность того, что эти подпоследовательности были
порождены моделью R. Мы переписываем уравнения алгоритма Витерби в
единицах логарифмических счетов шансов Vm(i,j) следующим образом. Шаг

4.2. Дополнительные задачи
инициализации принимает форму:
167
Vм(О,0) = log -±г = -21og77, все остальные V(i, 0), V(0J) = -оо
V
и рекурсия г = 1,..., п и j = 1,..., га:
fM^') = los«5§ + max<
log
(1-„)2
1-е-т
+ log
tog1/rg"aT+log
w(i-l,j-l) '
«*(i-l,j-l) =
w(i-l,j'-l) '
vY(i-l,j-l),
, "n* , , 1 — 26 — т , ,
= log^7 + log (1-^ + ma*<
(1-7/)2 ' ~& W(t-l,j-l)'
VM(i - 1, j - 1),
log
log
log:
* fM(<-U)
max <
V (г,,)-max g ^^
I 6 1-/7 w(i-l,j) '
log^+^-u),
logT^ + Vx(i-l,j);
8i-»? t»(t,i-i) '
g t;y(j,j-l).
1-7? w(i,j-l) '
Ml
VY(i,j) = max<
log
= max
loglf^ + ^y(t,i-l).
Заключительный шаг выглядит следующим образом:
V = max(VM(n, m), Vх (п, та), VY(n, та)).

168 Глава 4
Приведённые выше уравнения могут быть преобразованы в более
обычную форму ДП, если мы определим новый набор логарифмических
счетов шансов V(i,j) согласно следующим формулам:
Затем мы определяем счета замен, штрафы за введение и продолжение
пропусков следующим образом:
s(a'b)=los^+i°g1(7!^2r»
(4.5)
6(1-е-т) е
d = -l0e(l-r))(l-2S-rye = -l°eT^n-
Тогда рекуррентные уравнения алгоритма Витерби в форме
логарифмических шансов принимают вид
Vм(г- 1,J - 1),
VM(i,j) = s(xi,yi) + max { Vx(i -1,3 - 1),
VY(i-l,j-l);
( Vx(i-l,j)-e;
лгу с -\ I VM(i,j-l)-d,
{ VY(i,j-l)-e.
Заключительный шаг имеет вид:
V = max( Vм (п, го), Vх (п, го) + с, VY (n, го) + с),

4.2. Дополнительные задачи
169
где с = log(l — 28 — т)/(1 — е — г). Значение V — логарифмический счёт
шансов для оптимального выравнивания последовательностей х и у,
соотнесённого с путём Витерби. Путь Витерби и оптимальное выравнивание
могут быть найдены процедурой обратного прослеживания.
Замечание. Легко дать вероятностную интерпретацию параметров
системы очков попарного выравнивания в уравнении (4.9), если в парной
СММ (рис. 4.3) вероятности переходов в состояние совпадения М равны
друг другу (1-26-г = 1-е-т).
Член log Раь/ЯаЯь в счёте замены s(a,b) — логарифмическое
отношение правдоподобия порождения пары (а, Ь) при парной СММ к
порождению этой пары при модели независимого порождения R для пары
последовательностей. Член log(l — 26 — т)/(1 — г})2 — логарифмическое
отношение правдоподобия перехода в состояние М в парной СММ к таким двум
переходам в модели независимого порождения R для пары
последовательностей, которые увеличивают длины обеих последовательностей х и у на
один символ.
При штрафе за введение пропуска d и штрафе за продолжение
пропуска е логарифмическое отношение правдоподобия порождения равно нулю,
так как вероятности порождения из состояний X и Y СММ и модели
независимого порождения R для пары последовательностей равны. Поэтому
штраф за введение пропуска d = —log6/(1 — rj) равняется
отрицательному логарифмическому отношению шансов перехода из состояния
совпадения М в состояние X или состояние Y в парной СММ (что соответствует
началу пропуска), к переходу в модели независимого порождения R для
пары последовательностей, который увеличивает длину одной из
последовательностей х или у на один символ. Точно так же штраф за продолжение
пропуска е = — loge/(l — rj) становится отрицательным логарифмическим
отношением шансов петли или из X, или из Y, входящей в себя же, в
парной СММ, соответствующей продолжению пропуска, к переходу в R,
который увеличивает длину одной из последовательностей х или у на один
символ. Обратите внимание, что в этом случае параметр с = 0 и
оптимальный счёт выровненных последовательностей х и у, порождённых парной
СММ, принимает вид
V = max(VM(n,m),Vx(n,m),VY(n,m)).
Примечательно, что система очков (4.9) с параметрами s(a, b), d и е,
подходящими для выравнивания последовательностей с пропусками,
представляет собой обобщение системы очков для выравниваний без пропусков,

170
Глава 4
которая определяется исключительно матрицей счетов с элементами s(a, b).
В том случае каждый счёт замены s(a, b) является логарифмическим
отношением правдоподобий: наблюдения пары (а, Ь) при некоторой модели
замен М к наблюдению пары (а, Ь) при модели независимого порождения
для пары последовательностей R (см. раздел 2.2.1). □
4.3. Дополнительная литература
Традиционно попарные выравнивания последовательностей были
выстраиваемы алгоритмами ДП (Нидлмена-Вунша, Смита-Уотермена и т. д.)
без прямой ссылки к парным СММ. Однако недавние наработки в
области применения парных СММ для предсказания генов, в котором
используется выравнивание синтенных областей ДНК, были описаны в ([193],
[194]), а также в [210]. Программа DOUBLESCAN ([193]) предсказывает
гены в двух синтенных последовательностях ДНК близкородственных
видов, обнаруживая консервативные подпоследовательности в пределах
кодирующих и некодарующих белок областей. Программа Projector ([194])
предсказывает гены в последовательности ДНК с неизвестным
содержанием генов, строя выравнивание этой последовательности с аннотированной
последовательностью ДНК эволюционно связанных видов.
Новый статистический метод попарного выравнивания, использующий
парную СММ и модель эволюции последовательности со вставками и
удалениями, был предложен в [160].

Глава 5
ПРОФИЛЬНЫЕ СММ
ДЛЯ СЕМЕЙСТВ
ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Классификация биологических последовательностей на семейства —
один из главных вызовов биоинформатики. Действительно, обеспечить
точное определение семейства (например, семейства белков) трудно. Даже
с введением понятия консервативного в ходе эволюции белкового домена
в качестве структурного определителя семейства белков, с тем чтобы
классифицировать многодоменные белки обоснованно, эта задача не становится
проще. Тем не менее для практических целей важно разработать
эффективные вычислительные средства, способные приписывать белок,
транслированный с недавно предсказанного гена, к одному из уже установленных
семейств, таким образом, характеризуя белок лишь на основании его
аминокислотной последовательности.
Вычислительные средства характеризации белков должны
распознавать в последовательности нового белка специфические для семейств
признаки. Часто такие обнаружимые общие признаки проявляются в виде
статистически значимых консервативных участков структуры.
Вычислительные средства, которые необходимы для решения задачи классификации,
должны быть способны 1) учитывать известные структурные регулярные
комбинации, специфические для данного семейства, 2) обнаруживать
регулярные комбинации семейств в новой последовательности белка путём
выравнивания нового белка с моделью семейства и 3) оценивать
статистическую значимость обнаруженного подобия, с тем чтобы помочь правильно
опознать истинных членов семейства.
Эти три свойства алгоритма характеризации белков подобны
свойствам алгоритма попарного выравнивания последовательностей, но есть
существенные различия. Во-первых, наличие нескольких
последовательностей обусловливает необходимость применения дифференциальной
системы очков за совпадения аминокислот, где совпадения (несовпадения)

172
Глава 5
в консервативных позициях получают более высокие (более низкие)
счета, чем счета подобных событий в неконсервативных позициях. Во-вторых,
алгоритм выравнивания последовательности с моделью семейства должен
отражать естественное различие партнёров выравнивания, в
противоположность попарному выравниванию, где две выравниваемые
последовательности имеют равный статус. В-третьих, метод оценки статистической
значимости должен принимать во внимание детали вычисления счёта
выравнивания. Поскольку такая система вычисления счёта становится более сложной
по сравнению с вычислением счетов попарного выравнивания,
необходимыми становятся вычислительные, а не аналитические приближения к
распределениям счетов.
Позиционные матрицы счетов (ПМС, [PWM, PSSM]) и
невероятностные профили были первыми моделями белковых доменов, сигнатур
белковых семейств. Первое средство было далее развито и применено в PSI-
BLAST ([7]), который в течение прогона итеративно извлекает наборы
подобных последовательностей и обновляет текущую ПМС в
полуавтоматическом режиме. Основные идеи последнего средства могут быть
прослежены в часто используемом эвристическом алгоритме
множественного выравнивания последовательностей CLUSTAL. И вновь, поскольку
действительные биологические последовательности не могут рассматриваться
как точные реализации определённой вероятностной модели, нет
теоретически установленного преимущества определённого подхода к
моделированию ДНК и выравниванию белковых последовательностей. Параметры
любой начальной теоретической модели могут требовать дополнительных
исправлений, обусловленных реалиями жизни, которые не были
приняты во внимание. Например, оценка параметров профильной СММ по
заданному обучающему набору (множественному выравниванию нескольких
последовательностей) часто нуждается в исправлении, чтобы
компенсировать эффекты от малой выборки (введение псевдоотсчётов) и от
возможного смещения обучающего набора к поднабору семейства (введение весов
последовательностей).
Задачи, включенные в главу 5 «АБП», иллюстрируют взаимосвязь
(сравнение) между алгоритмом локального попарного выравнивания и
алгоритмом локального выравнивания последовательности с профильной
СММ. Так как анализ частот замен аминокислот в выравниваемых
последовательностях белков естественно ведет к анализу свойств логарифмических
счетов шансов замен, в нескольких задачах затронуты аналитические
свойства матрицы счетов замен аминокислот и её масштабного коэффициента А.
Также охвачена важная тема приписывания весов к последовательностям из
обучающего набора.

5.1. Оригинальные задачи 173
Дополнительные задачи обеспечивают практику построения
выравнивания последовательности с профильной СММ и оценки параметров
профильной СММ и ПМС с и без использования псевдоотсчётов. Подходы к
приписыванию весов к последовательностям, как видно, весьма
разнообразны; дополнительные задачи расширяют обзор существующих методов
приписывания весов.
5.1. Оригинальные задачи
Задача 5.1. На рис. 5.1 представлена профильная СММ для локального
выравнивания. Покажите, что такая профильная СММ даёт видоизмененные
уравнения, подобные таковым для локального попарного выравнивания
последовательностей (введённым в [250]).
Решение. Сначала мы должны вспомнить уравнения алгоритма,
строящего оптимальное локальное выравнивание двух последовательностей х =
= Xi,...,xn и у = yi,..., ут с линейными штрафами за пропуски.
Алгоритм находит три матрицы динамического программирования Vм,
Vх и VY с элементом, определённым как наилучшие счета локального
выравнивания до символов Х{ и yi, учитывая, что a) Xi выровнен с yj
(VM(i,j)), 6) Xi выровнен с пропуском (Vх (г, j)), в) yj выровнен с
пропуском (VY(i, j)). Уравнения обновления для счетов следующие:
о,
^ Vх {г-1 J-l) + s(xi>yj),
VY(г - l,j - 1) + s(xi,yj);
0,
Vх(i,j) = max I vM(i-l,j)-d,
( Vx(i-l,j)-e;
0,
VM(i,j-l)-d,
{ VY(i,j-l)-e.
(5.1)
VY(iifl — max \
Здесь s(xi,yj) — счёт замены, d — штраф за введение пропуска и е —
штраф за продолжение пропуска. Как только все элементы матриц Vм, Vх

174
Глава 5
и VY определены, алгоритм даёт
VM{i\f)=maxVM(i,j),
счёт, связанный с оптимальными локальными выравниваниями
последовательностей х и у. Обратное прослеживание от ячейки (i*,j*) до ячейки
(i',f) с Vм(i',f) = 0 определяет выравнивание последовательностей Хг,
г = г1... г*, и yj, j = jf ...j*9 — наилучшее локальное выравнивание
последовательностей х и у.
Чтобы провести аналогию между уравнениями (5.1) и уравнениями
алгоритма построения оптимального локального выравнивания
последовательности Хг, где г = 1,..., N, с профильной СММ (рис. 5.1), мы должны
показать в явном виде уравнения, которые определяют для
последовательности х путь Витерби через профильную СММ. Для
подпоследовательности xi,..., Xi пусть VjM(i) обозначают логарифмический счёт шансов
наиболее вероятного пути через профильную СММ, заканчивающегося
символом Xi, порождаемым состоянием Mj. Точно так же Vj(i) обозначает счёт
наиболее вероятного пути, заканчивающегося символом х^ порождаемым
состоянием Ij, VP(i) — счёт наиболее вероятного пути, заканчивающегося
в состоянии Dj, и VF(i) — счёт наиболее вероятного пути,
заканчивающегося элементом Хг, порождаемым состоянием F^ Условия инициализации
следующие:
v/(i)
-ОО,
VP(1) = -оо,
VF(1) = -оо,
гМ(л\ _ i_ P(xi\M) _ ,_ {rf/L)eMi{xi) _ ,_ eMj(xi)ri
VV(1) = log V; "' = bg ,'Г Т = lQg •
Р(ая|Д) 6 (1-ч)в.! g,4L(l-«j)'
при любых j: j = 1,..., L. Уравнения обновления следующие:
rM/-\ i^ _ eMj{Xi)
VjM(i) = log ^'4m8x{
^-i(^-l)+log^:
%«-D +log 5^.
log "2 •
(1-ftfL'

5.1. Оригинальные задачи
175
Конечное
Рис. 5.1. Профильная СММ для локального выравнивания. Два
примыкающих сбоку состояния F\ и Fi модели порождают символы с одинаковой
вероятностью qa, как и состояния X и Y модели независимого порождения
R для пары последовательностей, изображённой на рис. 4.1. Вероятность
1 — т] образования петли в примыкающие состояния близка к единице и
равна вероятности петлеобразования в модели R. Два молчащих состояния S\ и
#2 показаны двойными кружками. Все вероятности перехода из молчащего
состояния Si в состояния совпадения Mj, где j = 1,..., L, и из состояний
совпадения Mj, где j — 1,..., L, в молчащее состояние £г равны rj/L
v/(i)
max <
ам;1~
V/(i-l) + \og^,
[^(i-D + log^j;

176
Глава 5
aMj-iDj
^iW + bg^
Vf(i) = max^ V/_1(i) + ]og^=^..
^(0 + bg^f;
/ max,- Vf(i - 1) + log I,
V (г) = max < L (5.2)
I VF(i - 1).
Обратите внимание, что член logr/2/(l — r/)L в уравнении для VjM(i)
соответствует прямому переходу из молчащего состояния Si в состояния
совпадения Mj — случай, когда первые г — 1 остатков
последовательности х порождаются примыкающим состоянием F\. Тогда логарифмическое
отношение шансов принимает вид
log
г-1
р, IЛ/Гч (1 " VY'1 П qxtV2eMj (xi)/L
Р(ап,...,а*|Д) " *
(! ~ */) П fe
= 1°g—я" +1°g
qXi *(1-V)L'
В заключительном шаге мы имеем
V = max(max(^M(AT) - logL), VF(N) - log г/).
з J
Значение V — полный счёт пути Витерби для последовательности х,
идущего через профильную СММ локального выравнивания. Сам путь
может быть восстановлен путём применения процедуры обратного
прослеживания. Подпоследовательность последовательности х, порождаемая на пути
между появлениями первого состояния совпадения My и последнего
состояния совпадения Mj*, которое предшествует молчащему состоянию #2,
участвует в наилучшем локальном выравнивании последовательности х с
профильной СММ. Это оптимальное локальное выравнивание описывается
частью пути между состояниями совпадения My и Mj*, где f < j*.
Сравнение уравнений обновления (5.1) и (5.2) показывает, что эти два
алгоритма имеют много общего. Порождение символа Xi из состояния
совпадения Mj профильной СММ соответствует выровненной паре (xi,yj)
в попарном выравнивании; порождение символа xi из состояния вставки

5.1. Оригинальные задачи
177
соответствует выравниванию символа Xi с пропуском в попарном
выравнивании; и появление состояния удаления Dj соответствует выравниванию
символа yj с пропуском в попарном выравнивании. Обратите внимание, что
в предельном случае, когда набор выровненных последовательностей,
служа набором обучающих последовательностей для профильной СММ,
сжимается до одной-единственной последовательности, обозначаемой как у,
отыскание оптимального пути через профильную СММ, порождающего
последовательность х, становится эквивалентным задаче обнаружения
оптимального попарного локального выравнивания последовательностей х и у.
Формально оптимальный текущий счёт Vj^(i) в уравнениях (5.2)
соответствует VM(iyj) в уравнениях (5.1), Vj(i) соответствует Vх (г, j), a VP(i) —
VY(i,j). Интерпретация счёта замены s(xi,yj) в уравнениях (5.1)
представляет определённую трудность, так как в уравнениях (5.2) он
разлагается на три члена: logeMj(xi)/qXi + ^ам^гм5/{1 - г/), logeM.(xi)/qXi +
+logaIj_lMJ(l-v)nlogeMj(xi)/qXi+logaDj_1Mj/(l-v)- Если все
вероятности переходов в состояние совпадения Mj одинаковые, значения этих
трёх членов также будут равны. Подобным же образом штраф за введение
пропуска d в уравнениях (5.1) соответствует следующим членам в
уравнении (5.2): -logCLMjiJil-v), где j = l,...,L-l9n-\ogaMj-1Di/0'-v)y
где j = 2,...,L— 1. Эти члены равны, если все разрешённые переходы из
состояний совпадения в состояния вставки и удаления имеют равные
вероятности. Наконец, штраф за продолжение пропуска е в уравнениях (5.1)
соответствует следующим членам в уравнениях (5.3): — log 0^/(1 — rj),
где j = 1,..., L - 1, и - logaDj_lDj/(l - rj), где j = 3,..., L - 1, которые
снова сходятся к одному-единственному значению, если значения
вероятностей перехода aijij и aDk^Dk равны.
Замечание. Взаимосвязь между вероятностными параметрами парной
СММ и параметрами Алгоритма попарного выравнивания была
рассмотрена в замечании к задаче 4.11. □
Задача 5.2. Объясните причины (обращаясь к задаче 5.1) каких бы то ни
было различий между алгоритмом оптимального локального попарного
выравнивания (5.1) и алгоритмом (5.2) для оптимального локального
выравнивания последовательности с профильной СММ.
Решение. Для того чтобы определить либо наилучшее локальное попарное
выравнивание двух последовательностей х и у, либо наилучшее
выравнивание последовательности х с профильной СММ с примыкающими
состояниями, мы должны вычислить элементы трёх матриц динамического про-

178
Глава 5
граммирования, соответственно, с помощью уравнений (5.1) или
уравнений (5.2). Чтобы построить наилучшее локальное попарное выравнивание,
мы используем уравнения (5.1) метода динамического программирования
и находим значения величин VM(i,j), Vx(i,j) и VY(i,j) при допущении
о том, что счета замен s(xi,yj), штраф за введение пропуска d и штраф
за продолжение пропуска е не зависят от позиций i,j. Параметры
уравнений (5.2), применяемых для отыскания наилучшего выравнивания
последовательности х с профильной СММ (рис. 5.1), вероятности порождения
емД^г) и вероятности перехода (ам^м^ aij^Mj, clDj_iMj,- • •) явно
зависят от j. Таким образом, использование большего числа параметров в
алгоритме на основе профильной СММ позволяет нам включить
информацию о позиционных консервативных регулярных комбинациях в
биологической последовательности. Например, алгоритм (5.1) для
последовательностей белка требует 212 параметров: 210 счетов замен s(а, 6), штраф за
введение пропуска d и штраф за продолжение пропуска е. Обратите внимание,
что общее число параметров, 212, не зависит от длин последовательностей
х и у. С другой стороны, алгоритм (5.2) использует профильную СММ с
L состояниями совпадения Mj и двумя примьпсающими состояниями. Для
такой модели нужно 3(3(L—2)+2) = 9L—12 вероятностей перехода между
скрытыми состояниями, параметр rj, 20L вероятностей порождения ем, (xi)
для состояний совпадения, двадцать вероятностей порождения qXi для
состояний вставки (принято допущение, что набор qXi, где г = 1,..., 20, один
и тот же для всех L — 1 состояний вставки профильной СММ и совпадает
с набором вероятностей порождения фоновой модели независимого
порождения, используемой для определения логарифмических счетов шансов в
уравнениях (5.2)). Таким образом, общее число параметров профильной
СММ, 29L + 9, зависит от числа L его состояний совпадения и при L > 1
превышает число 212.
Еще одно отличие между этими двумя алгоритмами заключается в том,
что переходы Ij-\ —► Dj и Dj —► Ij обычно допускаются в профильной
СММ (см. рис. 5.1), тогда как в попарном выравнивании, как видно из
уравнений (5.1), пара ж-пропуск не может непосредственно следовать за
парой ^/-пропуск и наоборот. □
Задача 5.3. С помощью условия отрицательной определенности
J2QaQbs(a>i Ь) < 0 покажите, что функция
ДА) = $><*,e^«» - 1
а,Ь
является отрицательной при достаточно малых Л > 0.

5.1. Оригинальные задачи 179
Решение. При А = 0 мы имеем
/(о) = 5>«ь -1 = (Х>) (j>) -1 = о-
а,Ь \ а / \ 6 /
Первая производная от / определяется следующим выражением:
/,(А) = Ев»»еА*(в,Ь)«(о.Ь),
а,6
и, в силу условия отрицательной определенности, /'(О) = Yl <7а<7ьз(а, b) < 0.
a,b
В окрестности точки нуль дифференцируемая функция /(А) может быть
разложена в ряд
ДА) = /(0) + /'(0)А + о(А2).
Поэтому при достаточно малых А > 0 функция /(А) отрицательна. □
Задача 5.4. С помощью условия, что есть по крайней мере один
положительный s(a, Ь), покажите, что /(А) становится положительной при
достаточно больших А.
Решение. В выражении
/(А) = $>Ф>еА^6>-1
a,6
сумма может быть разбита на две суммы Ei и Ег, где Ei соответствует
s(a, b) с положительными значениями (существует по крайней мере один
такой член), а Ег соответствует s(a, b) с неположительными значениями.
По мере того как А > 0 растёт, Ei возрастает по экспоненте за счёт
множителя (-лей) eXs(a,b\ Вторая сумма Е2 положительна и ограничена снизу.
Таким образом, при достаточно больших А, таких что Ei > 1, функция
/(А) становится положительной и чётной:
lim /(А) = +оо. п
Задача 5.5. Покажите, что вторая производная функции /(А) является
положительной, и что этот и результаты предьщущих двух задач показывают,
что есть одно и только одно положительное значение А, удовлетворяющее
равенству /(А) = 0.

180
Глава 5
Решение. Было показано, что функция /(А) обладает следующими
свойствами:
«)/(0)=0,
б) /(А) является отрицательной при достаточно малых А > 0,
в) f становится положительной при достаточно больших А и стремится
к +оо по мере увеличения А.
Поскольку / — непрерывная функция, существует по крайней мере
одно положительное А*, такое что /(А*) = 0. Для того чтобы доказать, что
существует только одно положительное А* : /(А*) = 0, мы находим вторую
производную функции /:
ЛА) = £<?аФ>еМа'Ь)КМ))2.
а,Ь
Легко видеть, что /"(А) > 0; поэтому первая производная /'
монотонно возрастает в интервале [0; +оо), начиная с некоторого отрицательного
значения в точке 0. Очевидно, что в этом интервале /' имеет только один
корень А', причём знак производной /' изменяется в точке А' с
отрицательного на положительный. Таким образом, в этой стационарной точке А'
функция / имеет локальный минимум с отрицательным значением. В
интервале [А', +оо) функция / монотонно возрастает по мере увеличения А и
граф функции / пересекает ось х только в одной точке А*: А* > А' > 0,
/(А*) =0. □
Задача 5.6. Вычислите веса для набора последовательностей х\ = AGAA,
Х2 = CCTG, хз = AGTC при помощи методов взвешивания,
предложенных в следующих источниках: а) [264]; б) [94]; в) [5]; г) [117]; д) [166].
Решение. Для применения некоторых из методов взвешивания,
упомянутых выше, требуется дерево, соотносящее рассматриваемые
последовательности. Поэтому мы начнём с построения дерева посредством классической
процедуры группировки, UPGMA, предложенной в [254]. Мы определяем
расстояние d^ между последовательностями Xi и Xj, выровненными без
пропусков, как долю выровненных нуклеотидных пар с несовпадениями.
Таким образом, мы получаем di2 = 4/4 = 1, dis = 2/4 = 0,5 и d23 = 2/4 =
= 0,5. В первом шаге алгоритма UPGMA каждая последовательность х%
приписывается к своей собственной группе d и лист г для каждой
последовательности Xi помещается на нулевую высоту (дерево будет начерчено с

5.1. Оригинальные задачи
181
листьями на уровне основания и корнем наверху). На следующем шаге мы
должны выбрать две группы, отделённые минимальным расстоянием.
Поскольку dis = с^2з = 0,5, мы можем выбрать или пару Ci-Сз, или Су-Съ-
Скажем, мы выбрали группы С% и Сз и объединяем их в новую группу
С4 = {Сг, Сз} = {х2, #з}. Расстояние di± = 0,75 определяется из
следующей формулы:
1
dij —
\ЪЩ
ds
pq.
После этого узел 4 помещается на высоту t2 = t$ = с^з/2 = 0,25
над дочерними узлами 2 и 3. В результате остаётся две группы С\ и С±
и корень, узел 5 помещается на высоту t\ = ^14/2 = 0,375. В итоге мы
построили следующее дерево:
1 2 3
а) Вычисление весов последовательностей методом «напряжения»,
предложенным в [264].
Принято допущение о том, что каркас изображённого выше дерева
сделан из провода постоянной толщины и что напряжение V приложено
к точке корня. Сопротивление принято равным длинам рёбер, а все
листья установлены на нулевой потенциал, и мы должны найти токи в рёбрах
непосредственно выше листьев. Значения токов будут искомыми весами
последовательностей. Если ток и напряжение в узле п равны, соответственно,
1п и Vn, то из следующей диаграммы:
4+4'
№
к

182
Глава 5
и закона Ома следует, что 14 = 0,25^2 = 0,25/з, V5 = 0,375ii =
= 0,125(^2 + ^з) + 0,25/2- Следовательно, отношения токов (и весов)
выглядят следующим образом:
h : h- h = wi :W2'.W3 = 4:3:3.
б) Вычисление весов последовательностей методом, описанным в [94].
Принято допущение, что начальные веса листьев дерева определяются
как длины рёбер с листьями: w\ = 0,375, W2 = W3 = 0,25. Тогда узел 4
с длиной ребра 0,125 выше него, являющийся предком по отношению к
листьям 2 и 3, вносит равный вклад 0,125/2 = 0,0625 в каждый из весов
W2 и ws. Таким образом, W2 = ws = 0,25 + 0,0625 = 0,3125. При w\ =
= 0,375 мы имеем
W\ : W2 : ws = 6 : 5 : 5.
в) Вычисление весов последовательностей методом Альтшуля-Кэррол-
ла-Липмена ([5]).
Принято допущение, что непрерывная переменная £ с Гауссовым
распределением соотнесена с деревом следующим образом. Вероятность
замены одного значения, х, величины £ другим значением, у, по ребру дерева
длины t равна е(—(х — y)2/2t). Можно показать, что среднее значение \х
переменной £ в корне дерева зависит линейно от ^-значений Xi в листьях,
так что \i = Y^ wixi- Согласно допущению, коэффициент Wi является весом
последовательности при листе яг», где г = 1,2,3. В случае
представленного выше дерева веса последовательностей рассчитываются по следующим
формулам:
*2*3 + *4(*2+*з)
*2*3 + (*1+«4)(*2
ht3
*2*3 + («1 + *4)(*2
«1*2
+ «з)
+ *з)
*2*3 + (*1+*4)(*2+*3)
Следующие два метода не требуют дерева для вычисления весов
последовательностей.
г) Вычисление весов последовательностей методом блочного
выравнивания [117].

5.1. Оригинальные задачи
183
Для заданного «блочного» выравнивания последовательностей х\9 х2
их3,
A G А Л
С С Т С
A G Т С
мы берём подсчёты kia буквы а в каждом столбце (позиции) г. Первый
столбец (kiA = 2 и к\с = 1) имеет два различных типа символов (mi =
= 2). Вес Wu последовательности xi9 соотносимый с весом wu первого
столбца в последовательности х», определяется формулой wu = l/miklxk.
Мы получаем
^11 = ^2=0,25, ti;i2 = 27i = 0,5, ^13 = ^2=0,25.
Здесь к двум последовательностям хх и х3, с общим символом А,
приписаны меньшие веса, чем к последовательности х2, потому что вместе
они вносят во множественное выравнивание то же количество информации
о возможных типах символов в первом столбце, как последовательность #2
в отдельности. Подобная обработка оставшихся столбцов даёт следующие
зависимые от столбцов веса последовательностей х\, ж2 и х$\
ги21 = 0,25, w22 = 0,5, w23=0,25;
ги31=0,5, гиз2 = 0,25, ги33 = 0,25;
w4i=0,5, wi2 = 0,25, гУ43 = 0,25.
Наконец, зависимые от столбцов веса для каждой
последовательности суммируются по всем столбцам и нормализуются. Мы получаем w\ =
= 0,375, w2 = 0,375 и ws = 0,25.
д) Вычисление весов последовательностей методом максимальной
энтропии, предложенным в [166].
Веса последовательностей выбираются таким образом, чтобы
максимизировать сумму энтропии Hk(wi,w2, ги3) = - £>fca log2pfca, определён-
а
ных для каждого участка выравнивания к = 1,2,3,4, при заданном
ограничении Y^Wi = 1. Здесь рка, взвешенная частота появления символа а на
г
fc-м участке, определяется следующим образом:
Рка = /2 1(символ а появляется на участке к последовательности i)wi,
г=1,2,3

184 Глава 5
где 1(A) — индикатор события А и сумма берётся по всем
последовательностям во множественном выравнивании. Таким образом, мы имеем
#i(wi, w2, w3) = -(wi + w3) log2(wi + ws) - w2 log2 w2;
H2(w1,W2,w3) = -(wi+ w3)log2(iui + w3) - w2 log2 w2;
H3(wi,w2, w3) = -(w2 + ws) log2(w2 + ws) - wi log2 wi\
H±(wi,w2,ws) = -{w2 + ws) log2(w2 + ws) - wi log2 w\.
Чтобы найти максимум функции Е = Y2Hi(w\,w2,ws) с ограниче-
г
нием Ylwi = 1> мы должны решить систему уравнений с множителем
г
Лагранжа А:
Ж + А = -21og2(wi + w3) - 21og2 «л - 4 + А = 0;
J^ + А = -21og2(w2 + w3) - 21og2 w2 - 4 + A = 0;
Ж + A = -2 log2(wi + w3) - 2log2(w2 4- w3) - 4 + A = 0.
Система может быть сведена к выражению
(wi + ws)wi = (w2 + ws)w2 = (wi + ws)(w2 + ws)
и, наконец, ws = 0, w\ = w2 = 0,5. Нулевое значение веса г^з
кажется неожиданным. Однако можно возразить, что последовательность х% не
привносит никакой новой информации в выравнивание, так как её префикс
AG присутствует в последовательности х±, а её суффикс ТС — в
последовательности х2. □
5.2. Дополнительные задачи и теория
В этом разделе теория профильных СММ иллюстрируется вариантами
их практического применения. Профильная СММ может быть построена из
множественного выравнивания фрагментов ДНК либо без псевдоотсчётов
(задача 5.7), или с псевдоотсчётами, определяемыми по правилу
Лапласа (задача 5.8). Подобные выводы могут быть сделаны для случая, когда
выровненные последовательности взвешены (задача 5.10). Для построения
выравнивания последовательности с профильной СММ с полной
диаграммой состояний можно использовать видоизменённый алгоритм Витерби для
профильных СММ (задача 5.9).

5.2. Дополнительные задачи и теория 185
В теоретическом введении в задачу 5.11 мы определяем различающую
функцию профильной СММ и максимальные различающие веса
последовательностей. Тот факт, что эти взвешенные оценки вероятностей порождения
и перехода максимизируют различающую функцию, а также взвешенную
сумму логарифмических отношений шансов, доказывается в задаче 5.11.
Байесов подход к оценке параметров профильной СММ иллюстрирован в
контексте задачи 5.12: принимая априорное распределение Дирихле для
вероятностей порождения, можно получить средние значения оценок
апостериорного распределения и максимума апостериорной вероятности (МАВ).
В задаче 5.13 мы находим элементы (вероятности порождения)
позиционной матрицы счетов (ПМС) для заданного не содержащего пропуски
выравнивания последовательностей аминокислот.
ПМС для последовательностей ДНК рассматриваются в задачах 5.14
и 5.15. В задаче 5.14 позиционная модель независимого порождения R\
используется для описания рибосомного участка связывания в геноме Е. coli.
В задаче 5.15 Куллбека-Лейблера расстояние между моделью R\ и фоновой
моделью независимого порождения Q сравнивается с Куллбека-Лейблера
расстоянием между моделью независимого порождения для кодирующей
белки области и моделью Q.
Задача 5.7. Оцените параметры профильной СММ для следующего
множественного выравнивания последовательностей ДНК:
G
G
G
G
А
G
G
А
С
-
—
С
-
—
-
—
А
—
А
Т
А
А
G
А
G
G
G
G
С
С
G
С
Начертите диаграмму состояний.
Решение. Согласно эвристическому правилу, столбец выравнивания с
долей символов пропуска ниже 0,5 соответствует состоянию совпадения
профильной СММ; в противном случае он соответствует состоянию вставки.
(5.3)

186
Глава 5
Поэтому мы приписываем столбцы (кроме второго) во множественном
выравнивании (5.3), соответственно, к состояниям совпадения М±, М2 и Мз.
Диаграмма состояния СММ включает начальное состояние В (то же, что
и Мо), конечное состояние £ наряду с состояниями вставки Iq, Ii, I2, h
и состояниями удаления D\9 D2, D$. Подсчёты Ek{x) порождений нук-
леотидов и подсчёты А\а переходов скрытых состояний, наблюдаемых в
выравнивании (5.3), показаны в таблице 5.1. Тогда полученные методом
наибольшего правдоподобия оценки параметров профильной СММ
определяются следующими формулами:
а>ы =
V
ek{x) =
Ek(x)
ЕМ*')'
(5.4)
Здесь индексы к и / обозначают скрытые состояния; аы и е^(х) —
соответственно, оценки вероятностей перехода и порождения. Уравнения (5.4)
дают оценки параметров профильной СММ, приведённые в таблице 5.2.
В
,
1
щ_
м2
Щ_
S
Рис. 5.2. Диаграмма состояний профильной СММ, полученной из
множественного выравнивания (5.3) и содержащей только те состояния и
переходы, которые разрешены данным выравниванием
Так как многие из вероятностей порождения и перехода равны нулю,
несколько состояний, определённых для порождающей профильной СММ,
недостижимы и не присутствуют в заключительной диаграмме состояний
(рис. 5.2), показывающей довольно разреженную профильную СММ. □
Задача 5.8. Оцените параметры профильной СММ, полученной из того
же множественного выравнивания (5.3), если к подсчётам порождений и
переходов добавлены псевдоотсчёты, определяемые по правилу Лапласа.
Начертите диаграмму состояний.

5.2. Дополнительные задачи и теория
187
Таблица 5.1. Подсчёты порождений нуклеотидов и переходов между
скрытыми состояниями, наблюдаемыми в блоке выравнивания (5.3)
Подсчёты порождений для состояний совпадения
Подсчёты порождений для состояний вставки
Подсчёты переходов между скрытыми состояниями
А
С
G
Т
А
С
G
Т
М-М
M-D
M-I
1-М
I-D
I-I
D-M
D-D
D-I
0
-
-
-
-
0
0
0
0
8
0
0
0
0
0
-
-
-
1
2
0
6
0
0
2
0
0
5
1
2
2
0
0
0
0
0
2
5
0
1
1
0
0
0
0
7
0
0
0
0
0
1
0
0
3
0
3
5
0
0
0
0
0
8
-
0
0
-
0
0
-
0
Решение. Для того чтобы применить правило Лапласа, каждый подсчёт,
приведённый в таблице 5.1, должен быть увеличен на единицу. Обратите
внимание, что ячейки, соответствующие порождением (или переходам),
которые являются невозможными для диаграммы состояний порождающей
профильной СММ, не затрагиваются этим действием. Обновлённые
подсчёты могут быть непосредственно использованы для оценки
вероятностей переходов и порождений, а\а и е^(х), профильной СММ по
уравнениям (5.4). Такие же оценки могут быть получены при помощи обновлённых
уравнений
Аы + 1 Ек(х) +1
afci=E^+mfc' ek{x)=ZEk(X>) + K> (5'5)
V х'
где значения Аы и Е^{х) выбираются из таблицы 5.1. В уравнениях (5.5)

188 Глава 5
Таблица 5.2. Значения оценённых параметров профильной СММ
А
С
G
Т
А
С
G
Т
м-м
M-D
M-I
1-М
I-D
I-I
D-M
D-D
D-I
0
-
-
-
-
0
0
0
0
1
0
0
0
0
0
-
-
-
1
0.25
0
0.75
0
0
1
0
0
0.625
0.125
0.25
1
0
0
0
0
0
2
0.72
0
0.14
0.14
0
0
0
0
1
0
0
0
0
0
1
0
0
3
0
0.375
0.625
0
0
0
0
0
1
0
0
-
0
0
-
0
снова к и / обозначают скрытые состояния, а Аы и Ek(x) —
соответственно, подсчёты наблюдаемых переходов и порождений. Также тпк обозначает
число переходов из состояния к, разрешённого диаграммой порождающих
состояний профильной СММ, тогда как К — размер алфавита. Полученные
параметры профильной СММ сведены в таблицу 5.3.
Диаграмма состояний определённой профильной СММ показана на
рис. 5.3. Применение правила Лапласа делает все регулярные переходы
между состояниями профильной СММ возможными, и граф связей
между скрытыми состояниями становится полным по сравнению с графом,
построенным ранее (рис. 5.2). □
Вероятности порождений для
состояний совпадения
Вероятности порождений для
состояний вставки
Вероятности переходов между
скрытыми состояниями

5.2. Дополнительные задачи и теория
189
Таблица 5.3. Параметры профильной СММ, оценённые при помощи
псевдоотсчётов, определённых по правилу Лапласа
А
С
G
Т
А
С
G
Т
М-М
M-D
M-I
1-М
I-D
I-I
D-M
D-D
D-I
0
-
-
-
-
0,25
0,25
0,25
0,25
0,82
0,09
0,09
0,33
0,33
0,33
-
-
-
1
0.25
0,08
0.58
0,08
0,17
0,5
0,17
0,17
0.55
0.18
0.27
0,6
0,2
0,2
0,33
0,33
0,33
2
0.55
0,09
0.18
0.18
0,25
0,25
0,25
0,25
0,8
0,1
0,1
0,33
0,33
0,33
0,5
0,25
0,25
3
0,08
0.33
0.5
0,08
0,25
0,25
0,25
0,25
0,9
-
од
0,5
-
0,5
0,5
-
0,5
Задача 5.9. С помощью версии алгоритма Витерби с логарифмическими
счетами шансов выровняйте последовательность GCCAG с профильной
СММ, построенной в задаче 5.8. Для того чтобы определить
логарифмические счета шансов, сделайте допущение о том, что фоновая модель —
это модель независимого порождения с параметрами Р(А) = Р(Т) = 0,3
Решение. Оптимальное (наиболее вероятное) выравнивание
последовательности с профильной СММ определяется путём скрытых состояний,
порождающих символы заданной последовательности, в соответствии с ал-
Вероятности порождений для
состояний совпадения
Вероятности порождений для
состояний вставки
Вероятности переходов между
скрытыми состояниями

190
Глава 5
в
ц_
м2
Щ_
£
Рис. 5.3. Диаграмма состояний профильной СММ, полученной из
выравнивания последовательностей (5.3), параметры которой были оценены с помо-
пдью псевдоотсчётов, определённых по правилу Лапласа
горитмом Витерби. Версия алгоритма с логарифмическими счетами
шансов работает следующим образом. Пусть VjM(i) — логарифмический счёт
шансов дающего наивысший счёт выравнивания подпоследовательности
x\...Xi с символом Xi, порождаемым состоянием Mj. Точно так же
Vj{i) — счёт дающего наивысший счёт выравнивания этой же
подпоследовательности с символом х^ порождаемой состоянием Ij, и VjD(i) — счёт
дающего наивысший счёт выравнивания подпоследовательности х\,..., Xi,
заканчивающейся в состоянии Dj. При обработке профильной СММ с N
состояниями совпадения и последовательности х длины L алгоритм
проходит следующие шаги.
Шаг инициализации: VQM(0) = 0, У07(0) = -со, V0D(0) = -со.
Уравнения обновления для логарифмических счетов шансов
следующие:
^(O-Iog^-Ь
max <
eijixi)
V- (г) = log —^ h max <
4.Xi I
[ УД(г - 1) + logaM^lMj,
V/_! (i - 1) + logai^Mj,
I VP.!(г - 1) + logaDi_lMi;
[ VV(i-\) + \ogaMiIi,
У/(г-1)+1оёа/./я
{ VP(i-I) + logaDjIj;
VjP(hJ) = ™ax-{
V^ii) + log aMj-lDi,
V/^ii)+ logaij_lDj,

5.2. Дополнительные задачи и теория 191
В заключительном шаге,
V = max{Vtf(L) + 1оёам„е; V&{L) + logo/jv£; Vfi(L) + logaDN£},
вычисляется логарифмический счёт шансов V оптимального пути. Теперь
мы применяем алгоритм Витерби, чтобы найти выравнивание заданной
профильной СММ (рис. 5.3) и последовательности GCCAG. Алгоритм
работает следующим образом (используются натуральные логарифмы):
V0M(0)=0,
V?(0) = V0M(0) + In aMoDi = 0 + In 0,09 = -2,408,
V2D (0) = V° (0) + In aDl D2 = -2,408 + to 0,33 = -3,5166,
V3D (0) = V2D (0) + to aD2D3 = -3,5166 + to 0,25 = -4,903;
vm{1) = ь ел^О + vm{q)+ lnaMoMi = to ^ + InO, 82 = 0,866,
V2M (1) = to "^'^ + V? (0)+ to aDl м2 = to ^ -2,408+ to 0,33 = -3,622,
V3M(1) = In CM^ + V2D(0)+lnaD2M3 = to ^|-3,5166+In0,5 = -3,293;
V0J(1) = In ^^- + V0M(0)+ InoMo/o = In ^ + InO, 09 = -2,185,
V/(l) = In ^^ + ^(Oj+lno^^ = to^ - 2,408+ ln0,33 = -3,679,
V2'(l) = to ^|j^ + V2D(0)+lnaD2/2 = to^ - 3,5166 + toO, 25 = -4,680,
Vi (1) = In *£*! + Vf (0)+ In aD3/3 = to ^ - 4,903 + to 0,5 = -5,373;
Чх\ ь U, z
ViD(l) = У07(1) + lnaJoDl = -2,185 + InO, 33 = -3,293,
V2D(1) = ViM(l) + In aMlD2 = 0,866 + InO, 18 = -0,849,
V3D(1) = V2D(1) +lnaD2D3 = -0,849 + In 0,25 = -2,235.
Вычисления продолжаются до тех пор, пока все значения VjM(i), У*{г)
и V?(i) при г = 1,..., 5, j — 1,2,3 не будут вычислены (таблица 5.4).
Мы находим счёт оптимального выравнивания V = V3M(5) = 0,569.
Процедура обратного прослеживания начинается от У^(Б) и показывает
последовательность логарифмических счетов шансов
V3M(5) - V2M(A) - V?(3) - t?(2) -> ^м(1) - V0M(0),

192
Глава 5
Таблица 5.4. Логарифмические счета шансов V*(i)9 определённый
алгоритмом Витерби.
Элементы, стоящие на наилучшем пути, выделены полужирным шрифтом
х\ = G #2 == С хз = С Х4 = А #5 = G
Mi
м2
М3
/о
/i
/2
h
Dt
D2
D3
0.866
-3.622
-3.293
-2.185
-3.679
-4.680
-5.373
-3.293
-0.849
-2.235
-4.210
-0.530
-1.041
-3.070
0.473
-2.012
-2.705
-4.179
-1.136
-2.523
-5.095
-0.836
-0.252
-3.956
-0.220
-2.299
-2,993
-5.065
-1.829
-3.139
-5.247
-0.125
-2.381
-5.247
-2.397
-3.321
-2.737
-6.355
-4.007
-2.427
-5.291
-3.014
0.569
-6.132
-4.169
-2.204
-2.897
-7.241
-5.779
-3.313
выделенных полужирным шрифтом в таблице 5.4. Оптимальный путь 7г,
соотносимый с этой последовательностью логарифмов отношения
правдоподобия, определяет оптимальное выравнивание последовательности
GCCAG с профильной СММ. Так как выбор способа поместить остатки,
порождаемые состоянием вставки, в выравнивание, построенное
профильной СММ, произвольный ([67], стр. 151), путь 7г также определяет два
выравнивания (с перестановкой столбцов 2 и 3) последовательности GCCAG
со множественным выравниванием (5.3), набором обучающих
последовательностей для профильной СММ:
G
G
G
G
А
G
G
А
G
С
—
—
С
—
—
—
—
с
-
—
—
—
—
—
—
—
с
А
—
А
Т
А
А
G
А
А
G
G
G
G
С
С
G
С
G
G
G
G
G
А
G
G
А
G
-
—
—
—
—
—
—
—
С
С
—
—
с
—
—
—
—
с
А
—
А
Т
А
А
G
А
А
G
G
G
G
С
С
G
С
G

5.2. Дополнительные задачи и теория 193
Замечание. Учтите, что диаграмма состояний профильной СММ,
полученной из множественного выравнивания (5.3), совершенно иная в
отсутствие псевдоотсчётов (рис. 5.2). Та профильная СММ могла вмещать
последовательности длин 2, 3 и 4, но не большей длины (включая GCCAG).
Даже некоторые короткие последовательности длины 2, 3 и 4 не будут
соответствовать модели (рис. 5.2) ввиду нулевых значений вероятностей
порождения некоторых нуклеотидов (см. табл. 5.2). Использование
псевдоотсчётов для оценки параметров СММ в уравнениях (5.5) в результате даёт
архитектуру СММ, способную вмещать (описывать) более широкий набор
последовательностей, потенциально связанных с набором обучающих
последовательностей. □
Задача 5.10. Множественное вьфавнивание набора последовательностей
ДНК задано в следующем виде:
с
G
G
G
С
С
С
т
с
с
-
А
А
-
—
-
А
Т
-
—
А
А
А
С
А
Т
G
Т
Т
т
с
с
с
G
С
Определите параметры и диаграмму состояний профильной СММ для
множественного выравнивания (5.6). Примите во внимание веса
последовательностей, определённые методом, предложенным в [117]. Рассмотрите
выборочную возможность использования псевдоотсчётов, определяемых по
правилу Лапласа.
Решение. В первую очередь множественное выравнивание (5.6) должно
быть сведено к блоку без пропусков следующего вида:
С С А Т С
G С A G С
G Т А Т С
G С С Т G
С С А Т С
Затем веса последовательностей в строках блока (5.7) получают в виде
линейной комбинации зависимых от столбцов весов. Вес Wji последова-
(5.6)
(5.7)

194
Глава 5
тельности г, приходящийся на столбец j, рассчитывается по формуле Wji =
= 1/rrijk.j, где rrtj — число типов букв в столбце j, x[ — буква на участке
(столбце) j последовательности г и к-э — число букв из х[ в столбце j.
Тогда веса в первом столбце wu следующие:
™11 = 1/4, Wi2 = 1/6, ^13 = 1/6, Wu = 1/6, Wi5 = 1/4.
Подобным же образом зависящие от столбцов веса в других четырёх
столбцах имеют следующие значения:
w2i = 1/8, w22 = 1/8, W2S = 1/2, W24 = 1/8, w25 = 1/8;
wsi = 1/8, wS2 = 1/8, w33 = 1/8, w34 = I/2) ™35 = 1/8;
W4i = 1/8, W42 = 1/2, W43 = 1/8, W44 = 1/8, W45 = 1/8;
W51 = 1/8, W52 = 1/8, W53 = 1/8, W54 = 1/2, W55 = 1/8.
Суммирование зависящих от столбцов весов w^ для каждой
последовательности г, и последующая нормализация дают веса
последовательностей Wi'.
W! = 3/20, w2 = 5/24, w3 = 5/24, w4 = 17/60, w5 = 3/20.
Теперь, чтобы определить число состояний совпадения профильной
СММ по выравниванию последовательностей, мы используем
эвристическое правило, сформулированное ранее: столбец с долей символов пропуска
ниже 0,5 отмечается как состояние совпадения; в противном случае он
отмечается как состояние вставки. Таким образом, существует пять состояний
совпадения Mi,..., М5, соответствующих, соответственно, столбцам 1, 2,
5, 6 и 7 множественного выравнивания (5.6). Диаграмма состояний
должна включать также начальное состояние В, конечное состояние £, состояния
вставки /о, Д,..., /5 и состояния удаления (молчащие) Di, Д2, • • •, Db- Для
оценки параметров профильной СММ мы используем взвешенные
подсчёты порождений и переходов, соответственно, Е™(х) и A™t. Для данного
состояния к взвешенный подсчёт порождения (перехода) равен сумме
весов обучающих последовательностей, где некоторый символ порождается
из состояния к (наблюдается переход). Например, для состояния
совпадения М2 взвешенный подсчёт порождения нуклеотида С равен сумме весов
последовательностей 1, 2, 4 и 5:
^(CH^ + ^ + t^ + t*-£ + £ + g + £ = §.

5.2. Дополнительные задачи и теория
195
Взвешенные подсчёты порождений и переходов приведены в
таблице 5.5. Чтобы найти оценки параметров профильной СММ, мы могли или
использовать видоизменённые подсчёты, представленные в таблице 5.5 и
уравнениях (5.4), или, что равносильно, подсчёты порождений и переходов,
определенные прямым способом (см. задачу 5.7), и обобщённые варианты
уравнений (5.4):
аы
V
ек(х)
Щ{х)
ЦЕ%{х')
N
Y, eki(i)wi
г=1
N '
Е Yjeki'(i)wi
V г=1
N
_ г=1
х' г=1
(5.8)
Здесь W{, где г — 1,..., N, — вес г-й последовательности; еы(г) —
число переходов из скрытого состояния к в скрытое состояние I,
произошедших в обучающей последовательности г; 5kx(i) — число порождений
символа х из состояния к последовательности г. Оценки вероятностей
порождений и переходов, рассчитанные по уравнениями (5.8), приведены в
таблице 5.6.
В
К
%
М0
м,
мА
м.
Рис. 5.4. Диаграмма состояний профильной СММ, полученной из
множественного выравнивания (5.6), где присутствуют только те состояния и
переходы, которые разрешены данными выравниваниями
Диаграмма состояний этой профильной СММ (рис. 5.4) показывает,
что все кроме одного состояния вставки и все состояния удаления
отсутствуют, поскольку вероятности перехода к этим отсутствующим
состояниям равны нулю. Обратите внимание, что эта «редуцированная» СММ
ограничена в своей способности описывать последовательности, — только не
в отношении ограничения на длину последовательности (см. замечание к

196
Глава 5
Таблица 5.5. Подсчёты наблюдаемых порождений нуклеотидов и переходов
между скрытыми состояниями, видоизменённые посредством весов
последовательностей
0 12 3 4 5
А - 0 0 43/60 0 0
С
G
Т
А
С
G
Т
м-м
-
-
-
0
0
0
0
1
3/10
7/10
0
0
0
0
0
1
19/24
0
5/24
5/8
0
0
5/24
7/12
17/60
0
0
0
0
0
0
1
0
5/24
19/24
0
0
0
0
1
43/60
17/60
0
0
0
0
0
1
M-D
M-I
1-М
I-D
I-I
D-M
D-D
D-I
0
0
0
0
0
-
-
-
0
0
0
0
0
0
0
0
0
5/12
5/12
0
5/12
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
-
0
0
-
0
0
0
задаче 5.9), но в плане их нуклеотидного состава. Это ещё один пример
того, как в отсутствие псевдоотсчётов оценка параметров по ограниченному
набору обучающих последовательностей может вести к сверхсоответствию
модели реальному объекту.
Чтобы применить правило Лапласа, один нормализованный
псевдоотсчёт 1/5 (в общем виде 1/N, если N — число последовательностей)
прибавляется ко всем взвешенным подсчётам (таблица 5.5) за исключением
подсчётов для таких состояний, из которых порождение (или переходы)
не возможны в архитектуре порождающей профильной СММ. Результаты
Подсчёты порождений
для состояний
совпадения
Подсчёты порождений
для состояний вставки
Подсчёты переходов
между скрытыми
состояниями

5.2. Дополнительные задачи и теория 197
Таблица 5.6. Параметры профильной СММ, оценённые по выравниванию
взвешенных последовательностей
Вероятности порождений
для состояний
совпадения
Вероятности порождений
для состояний вставки
Вероятности
переходов между скрытыми
состояниями
А
С
G
Т
А
С
G
Т
М-М
M-D
M-I
1-М
I-D
I-I
D-M
D-D
D-I
0
-
-
-
-
0
0
0
0
1
0
0
0
0
0
0
-
-
1
0
0.3
0.7
0
0
0
0
0
1
0
0
0
0
0
0
0
0
2
0
0.792
0
0.218
0.75
0
0
0.25
0.583
0
0.417
0.5
0
0.5
0
0
0
3
0,717
0.293
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
4
0
0
0.218
0.792
0
0
0
0
1
0
0
0
0
0
0
0
0
5
0
0.717
0.293
0
0
0
0
0
1
0
0
-
0
-
0
приведены в таблице 5.7. Наконец, чтобы оценить параметры профильной
СММ, мы можем или включить подсчёты, представленные в таблице 5.5,
в уравнения (5.8), видоизменённые добавлением нормализованных
псевдоотсчётов:
о>ы =
вк(х) =
(5.9)
E EXW) + k/n "
xf i=l

198
Глава 5
Таблица 5.7. Подсчёты наблюдаемых порождений нуклеотидов и переходов
между скрытыми состояниями, вычисленные по подсчётам из таблицы 5.5
при помощи псевдоотсчётов Лапласа
Подсчёты
порождений для
состояний совпадения
Подсчёты
порождений для
состоянии вставки
Подсчёты
переходов между
скрытыми состояниями
А
С
Г
Т
А
С
G
Т
м-м
M-D
M-I
1-М
I-D
I-I
D-M
D-D
D-I
0
-
-
-
-
1/5
1/5
1/5
1/5
6/5
1/5
1/5
1/5
1/5
1/5
-
-
-
1
1/5
1/2
9/10
1/5
1/5
1/5
1/5
1/5
6/5
1/5
1/5
1/5
1/5
1/5
1/5
1/5
1/5
2
1/5
119/120
1/5
49/120
33/40
1/5
1/5
49/120
47/60
1/5
37/60
37/60
1/5
37/60
1/5
1/5
1/5
3
11/12
29/60
1/5
1/5
1/5
1/5
1/5
1/5
6/5
1/5
1/5
1/5
1/5
1/5
1/5
1/5
1/5
4
1/5
1/5
49/120
119/120
1/5
1/5
1/5
1/5
6/5
1/5
1/5
1/5
1/5
1/5
1/5
1/5
1/5
5
1/5
11/12
29/60
1/5
1/5
1/5
1/5
1/5
6/5
-
1/5
1/5
1/5
1/5
1/5
или непосредственно использовать подсчёты, приведённые в таблице 5.7,
чтобы включить в уравнения (5.8). В обоих случаях результаты вычислений
вероятностей порождений и переходов одинаковые и сведены в таблицу 5.8.
Из таблицы 5.8 мы видим, что добавление псевдоотсчётов делает
вероятности всех порождающих переходов положительными и устанавливает
все возможные (разрешённые) связи между скрытыми состояниями. Теперь

5.2. Дополнительные задачи и теория 199
Таблица 5.8. Окончательные оценки параметров профильной СММ
Вероятности
порождений для состояний
совпадения
Вероятности
порождений для состояний
вставки
Вероятности
переходов между скрытыми
состояниями
•
А
С
Г
т
А
С
Г
Т
М-М
M-D
M-I
1-М
I-D
I-I
D-M
D-D
D-I
0
-
-
-
-
0.25
0.25
0.25
0.25
0.75
0.125
0.125
0.33
0.33
0.33
-
-
-
1
0.111
0.278
0.5
0.111
0.25
0.25
0.25
0.25
0.75
0.125
0.125
0.33
0.33
0.33
0.33
0.33
0.33
2
0.111
0.551
0.111
0.227
0.505
0.122
0.122
0.25
0.49
0.125
0.385
0.43
0.14
0.43
0.33
0.33
0.33
3
0.509
0.267
0.112
0.112
0.25
0.25
0.25
0.25
0.75
0.125
0.125
0.33
0.33
0.33
0.33
0.33
0.33
4
0.111
0.111
0.227
0.551
0.25
0.25
0.25
0.25
0.75
0.125
0.125
0.33
0.33
0.33
0.33
0.33
0.33
5
0.112
0.509
0.267
0.112
0.25
0.25
0.25
0.25
0.857
-
0.143
0.5
-
0.5
0.5
-
0.5
профильная СММ, показанная на рис. 5.5, способна вместить любую
последовательность нуклеотидов. Более высокие счета выравнивания,
однако, будут присвоены тем последовательностям, которые сохраняют большее
сродство к начальному набору обучающих последовательностей.
Замечание. Из уравнений (5.4) и (5.8) легко видеть, что оценка
параметров профильной СММ без весов последовательностей равносильна
случаю, когда все веса последовательностей равны 1/N, где N — число
последовательностей во множественном выравнивании. Этот тип экстрапо-

200
Глава 5
в
3.
М*_
Мг_
Щ_
Ц,
е
Рис. 5.5. Диаграмма состояний профильной СММ, полученной из
множественного выравнивания (5.6) взвешенных последовательностей, где
параметры оценены при помощи псевдоотсчётов, определённых по правилу
Лапласа
ляции также остаётся верным для взвешенных псевдоотсчётов, что следует
из сравнения уравнений (5.5) и (5.9).
□
Begin
1"*7
End
Рис. 5.6. Полная модель независимого порождения R, порождающая
одиночную последовательность
5.2.1. Различающая функция и максимальные различительные веса
5.2.1.1. Теоретическое введение в задачу 5.11
Оценка параметров профильной СММ может быть смещена, если
некоторые семейства последовательностей чрезмерно представлены
[перепредставлены] в наборе обучающих последовательностей. Несколько
методов, разработанных для устранения такого смещения путём
взвешивания обучающих последовательностей, уже были рассмотрены (задачи 5.6
и 5.10). Еще одна схема взвешивания бьша предложена в [70]. В этой схеме
веса последовательностей wi,W2,-.-,wn, предназначенные для использо-

5.2. Дополнительные задачи и теория
201
вания в уравнениях (5.8), определяются следующим образом:
Wi = А(1 - Р(М(в)\Хг)), 5^117* = 1. (5.10)
г
Здесь М(в) — вероятностная модель с набором параметров 9. В
случае когда М представлена профильной СММ, в представляет собой набор
вероятностей порождений е&(аг) и вероятностей переходов аы. Модель М
рассматривается наряду с фоновой моделью независимого порождения R
(полная вероятностная версия модели R показана на рис. 5.6).
Определение, данное в уравнениях (5.10), обусловлено следующим. Предположим,
что набор параметров 9 максимизирует различающую функцию D
модели М (в):
я = Пр(м(в)Ы-П ^|м(э))Р(м(е))
Различающая функция D есть произведение апостериорных
вероятностей модели М при заданных последовательностях xi,..., хп. Набор
параметров в, максимизирующий различающую функцию D, может быть
найден в алгоритме, который использует уравнения (5.8) и (5.10) для
итеративной переоценки параметров и весов последовательностей ([70]). Начиная
с начального набора весов, параметры в = {е&(а;),аы} определяются по
уравнениям (5.8). Затем значения весов обновляются по уравнениям (5.10).
Эти два шага повторяются до схождения функции D к максимуму
(возможно, локальному). В этой точке уравнения (5.10) для весов
последовательностей определяют максимальные различительные веса.
Уравнения обновления с псевдоотсчётами могут быть определены по
уравнениям (5.9) и (5.10), если нормализованные простые подсчёты 1/N
в уравнениях (5.9) заменены нормализованными псевдоотсчётами Дирихле
oti/N (см. также задачу 5.13).
Задача 5.11. а) Покажите, что оценки параметров, дающих максимум
различающей функции D, удовлетворяют уравнениям (5.8), если при этом веса
последовательностей «л,..., wn определены уравнениями (5.10).
6) Докажите, что если набор параметров в* максимизирует D, то
он также максимизирует взвешенную сумму логарифмических отношений
шансов Lw, где N р(Т.\м\
с весами Wi = А(1 - Р(М(6*)|ж»)), где г - 1,... ,N.

202
Глава 5
Решение, а) Мы рассматриваем две конкурирующие модели:
профильную СММ М(9) с диаграммой состояний и параметрами,
полученными из заданного множественного выравнивания последовательностей
#1, #2,..., xn\ и модель независимого порождения R.
Пусть К — набор всех скрытых состояний (в том числе молчащих)
и пусть К\ — набор состояний, порождающих наблюдаемые символы
(состояния совпадения и состояния вставки), причём К\ С К. Мы хотим
найти набор 9 параметров профильной СММ, 9 = (#i,02> • • • >#l) =
= {ek'(x),aki\kr € K\,k,l € К}, максимизирующих различающую
функцию D (и её логарифм) при следующих условиях:
1 (5.П)
£ ек(х) = 1, кеКг.
х€А
Мы делаем допущение, что отношение априорных вероятностей
P(R)/P(M) = га не зависит от 9, и обозначаем \Xi = P(xi\R), yi =
= P(xi\M) при г = 1,..., N. Тогда мы имеем
>ogZ> = £,ogP(Mk)=X> ГЫМ)НМ)
г=1 г=1
N
P(Xi\M)P(M) + P(Xi\R)P(R)
^(logyi - log(yi + m/Xi)).
г=1
Далее, мы получаем следующие выражения частных производных
функции logD:
dlogD = " Л % _ 1 дуЛ =
Э°3 i=l \ Vi Mi У г + m/Xi а0, /
а<97
(5.12)
= ТП'У Mi ayi =ту* /Xj a log l/j
г=1 Уг(Уг + ГПщ) d6j ^Уг + ГТЦЦ dOj
Аналитическое выражение для yi в единицах параметров модели М
выглядит следующим образом:
yi = P(Xi\M)= J] Y[(ek(x))'-W П (аыу»Ю.
к£Кг хеЛ k,l£K

5.2. Дополнительные задачи и теория
203
Здесь Ski(i) — число переходов из скрытого состояния к в скрытое
состояние I в последовательности х^ а 6kx(i) — число порождений символа
х из состояния к в последовательности Х{. Таким образом, частная
производная dlogyi/d9j принимает вид
——, если ej = ek(x);
ek{f[ (5.13)
-gjj-, если Оэ=ак1.
Задача условной оптимизации для log D при ограничениях, заданных
в уравнениях (5.11), может быть решена с использованием множителей
Лагранжа Aj, где j = 1,...,L. Тогда уравнения (5.12) и (5.13) ведут к
следующей системе уравнений:
-^+A,=m^ + m +А,=0, если в, = ек(х);
г=1 v
dlogD ^^ Mi £ki(i) , , n a
^ г=1
(5.14)
Обратите внимание, что уравнения для параметров Oj, которые
являются значениями вероятностей из одного и того же распределения
вероятностей, содержат одну и ту же величину А^. Из уравнений (5.14) мы находим
N
т J2 (Vi/Vi + mfii)6kx(i)
ей{х) = г ,
(5.15)
N
™> 2 (Vi/Vi + rnfXi)£kl(i)
i=l
Q>kl = x •
Значения всех Xj, X'- могут быть определены из уравнений (5.11)
следующим образом:
N
V J V г=1

204 Глава 5
х'еА J х'еЛг=1
Подстановка значений \j, Xj в уравнения (5.15) и использование
определений величин \ii и уi ведет к искомым уравнениям:
Е <Мг)(1 - Р(М|хО)
вк(х) =
ЕЕ^(0(1-^№))
х' г=1
£e«(i)(l-P(Af|xO)
г=1
OfcJ =
(5.16)
ЕЕ e«'W(i-*W*))
г' «=i
6) Чтобы решить задачу условной максимизации функции Lw, где
N „/ ,,,\ JV
P(a?i|M)
г=1 ч ' ' г=1
с ограничениями, заданными в уравнениях (5.11), нам нужны выражения
для частных производных функции Lw. Они вьшщцят следующим образом:
Г_Д(1 Л±_ % _ v «и aiogyi -
Х><%^, если 0, = ел(х); (5.17)
Е™*~а1й~' если вз=аы-
г=1
Из уравнений (5.17) мы получаем следующую систему уравнений со
множителями Лагранжа Aj, где j = 1,..., L:
|р »«^о 0) если
°^ г=1 e*W
dlogD , . * Wi£ki(i)
-fi— + XJ = £ оы + AJ = °» если *i = <***•

5.2. Дополнительные задачи и теория
205
Тогда
N
T,wiSkx(i)
/ ч г=1
ек(х) = г ,
лз
аы =
N
г=1
При том что значения А^ определяются из уравнений (5.11):
N
v i v г=1
N
^2 ек(х) = --у ]С YlWiSkx^ = lj
х€.А ^ хЕЛ г=1
мы, наконец, достигаем уравнений для параметров СММ, которые
максимизируют взвешенную сумму логарифмических отношений шансов Lw:
N
J2 Skx(i)wi
ек(х) = —^ ,
Е £ ukx'(i)wi
х' г=1 ,
5.18
N
^2 eki(i)wi
i=i
аы = •
ЕЕ£ы'(*М
V i=l
Можно видеть, что набор параметров, удовлетворяющих
уравнениям (5.16), будет удовлетворять также уравнениям (5.18), причём веса Wi,
где г = 1,..., N, определяются из уравнений (5.10). Поэтому набор
параметров О* профильной СММ, который максимизирует различающую
функцию D, максимизирует также взвешенную сумму логарифмических
отношений шансов Lw, если wi = А(1 — P(M(@*)\xi))9 где г = 1,..., N. □
Задача 5.12. Основной шаг в построении профильной СММ из
множественного выравнивания N белковых последовательностей — оценка
вероятностей порождений для состояния совпадения, соотносимого с данным

206
Глава 5
столбцом х = xij..., х^ множественного выравнивания. С помощью
априорных распределений Дирихле найдите оценки вероятностей порождений в
виде а) средних значений апостериорного распределения и б) оценок
максимальной a posteriori вероятности (МАВ).
Решение. Сначала мы вводим некоторые обозначения и формулы,
которые необходимы и для пункта а, и для пункта б. Мы обозначаем
вероятности порождения из скрытого состояния совпадения как e(a,i) = pi, где
г = 1,..., К, где К — размер алфавита. Затем мы делаем допущение о
том, что модель независимого порождения М с вероятностями pi
определяет распределение вероятностей порождения из скрытого состояния. Тогда
правдоподобие модели М для наблюдаемого столбца х = a?i,..., xn
определяется из
Р(х\М) = Цр?.
г=1
Здесь щ — число символов щ среди xi,..., xn. Мы допускаем, что
априорная вероятность параметров pi9 где г = 1,..., К, модели М определяется
распределением Дирихле с параметрами «i,..., ак, причём at > 0:
к
Р(М) = Р-о(ръ ... ,РК) = Z"1 Пр?4"1»
г=1
где Z = Y[F((*i)/F(%2ai) — постоянная нормализации распределения Ди-
г i
рихле. Поэтому апостериорная вероятность Р(М\х) модели М принимает
вид
Р(М\х) = Р(Х|^(М) = (ZP(z))-1 П^"1- (5-19)
^ ' г=1
а) Уравнение (5.19) подразумевает, что апостериорное распределение
параметров модели М есть распределение Дирихле с параметрами п\ +
+ «1,..., пк + olk- Таким образом, оценки средних значений вероятностей
порождений определяются из
л/ ч Щ + OLi Щ + OLi
e(ai) =Pi= -
к к
j=i j=i

5.2. Дополнительные задачи и теория
207
где г = 1,2,..., К. Легко видеть, что оценки средних значений совпадают с
оценками методом наибольшего правдоподобия с использованием
псевдоотсчётов ai9 где г = 1,..., К. Например, если а* = 1, где г = 1,..., К, то pi
совпадёт с оценками методом наибольшего правдоподобия, полученными с
использованием псевдоотсчётов Лапласа.
б) Чтобы определить оценки вероятностей порождения методом МАВ,
мы должны найти точку максимума апостериорного распределения Р(М\х).
В логарифмической форме (по основанию 2) искомое выражение выглядит
следующим образом:
к
log2 Р{М\х) = ^2(щ + oti - 1) log2pi - log2 Z - log2 P(x),
i=l
где только первая сумма К членов зависит от параметров pi. Для двух
дискретных распределений Р и Q относительная энтропия
ff(p|« = £p(».)ioS,£g
всегда неотрицательная и достигает своего минимального нулевого
значения тогда и только тогда, когда Р = Q. Поэтому
J2 Р(Уг) log2 Q(Vi) ^ Yl P(^) lQg2 Р^)'
г г
причём равенство имеет место тогда и только тогда, когда Р — Q. Если
распределение Q задаётся набором вероятностей pi,... ,рк, а распределение
Р — набором вероятностей
П1 + OL\ - 1 ПК + OLK - 1
г г
то сумма Y^P{yi)^°zQ(yi) наРялУ с log2Р(М\х) становится максималь-
г
ной, когда pj = (rij + cxj — l)/(N -f ^ oti — К) при j = 1,..., К. Тогда
г
оценки методом МАВ определяются следующими формулами:
щ + щ - 1
e*(ai)=pj

208
Глава 5
где г = 1,2,..., К. Если щ = 1, где г = 1,..., К, то оценки методом МАВ
совпадают с оценками методом наибольшего правдоподобия. □
Задача 5.13. Выравнивание фрагментов последовательности цитохрома-с
Rickettsia conorii, Rickettsia prowazekii, Bradyrhizobium japonicum
и Agrobacterium tumefaciens (в порядке сверху вниз) выглядит следующим
образом:
N1PELMKTANADNGREIAKK
NIQELMKTANANHGREIAKK
PIEKLLQTASVEKGAAAAKK
PIAKLLASADAAKGEAVFKK
Из этого блока выравнивания получена позиционная матрица счетов
(ПМС). Определите параметры сечения (3 х 3) ПМС, содержащей счета
аминокислот A, R и N в столбцах 4, 5 и 6. Используйте псевдоотсчёты,
определённые смесями матрицы замен с параметром Ai = bRi, где Щ —
число различных типов остатков, наблюдаемых в г-м столбце. Матрица
замен BLOSUM50 приведена в таблице 2.1. Для простоты фоновые частоты
этих двадцати аминокислот приняты равными 1/20.
Решение. Счёт Sa аминокислоты а в столбце г определяется из
следующей формулы:
где qa — фоновая частота аминокислоты а, а в{ (а) — вероятность
порождения аминокислоты а в позиции г. Оценки вероятностей порождений
задаются смесями матриц замен ([115]):
/ \ ^ia "г 9га /г ПГХ\
6i(a) = Г(П Мп V (5-20)
2^ (Ога' + 9iot>)
а'
где Сia — число появлений аминокислоты а в столбце г, и псевдоотсчёт рга
определяется из
а -Аа V^e5^)

5.2. Дополнительные задачи и теория
209
Здесь N — число выровненных последовательностей и S(a, /3) —
логарифмический счёт шансов замен а на /3, взятый из матрицы замен BLOSUM50.
Для заданного блока последовательностей N = 4 и А± = 5 х 2 = 10. Тогда,
например, псевдоотсчёт для аланина в столбце 4 рассчитывается
следующим образом:
** = £§ (!eS(A,E) + ieS{A,K)) = i(e-1+е_1) = °'184-
Для того чтобы определить оценки вероятностей порождения е^А),
е±(В) и e±(N), мы должны использовать подобные формулы, чтобы
получить псевдоотсчёты для всех двадцати аминокислот (сами вычисления не
показаны). Тогда мы находим из уравнения (5.20):
е4(А) = 0,00084, е4(Д) = 0,02394, e4(N) = 0,00227.
Далее, счета аминокислот A, R и N в столбце 4 ПМС следующие
(использованы натуральные логарифмы):
с4 1 е^А) 1 0> 00084 л по,
SA = Ь«-й- =1°g-0^5" = -4'086'
^4 1 е4(й) , 0,02394 „ тп
о4 1 е4(^) , 0,00227
^ = log^=log -^05" = -3,092.
Подобные вычисления дают параметры счетов ПМС в столбцах 5 и 6:
„5 , еь(А) 0,00068
об weeH) w Q. 00038 ,„sn
^л = bg -^- = log -pj- = -4,880,
^5 , е6(Д) . 0,00025
S& = log-^i= log ^- = -5,298,
5* = log -te~ = log -0705~ = _5'878'
<?s we*W 1n 0,00009 fi49n
5^ = 1°s-^r = log-o7o5_ = ~6,320,
-6 W^W 0,00012
S% = log "^ = log-Vn^ = "6,032.

210
Глава 5
Счета замен аминокислот A, R и N, округлённые до ближайшего
целого, показаны в подматрице ПМС порядка 3x3 следующего вида:
А
R
N
4
-4
-1
-3
5
-4
-5
-6
6
-5
-6
-6
Отрицательные счета не являются неожиданными, поскольку
аминокислоты A, R и N обладают различными физико-химическими свойствами
по сравнению с аминокислотами, находящимися в столбцах 4, 5 и 6
выравнивания, за исключением случая аминокислоты Д, которая, будучи
положительно заряженной, подобна К (расположенной в столбце 4). □
Задача 5.14. Параметры позиционной модели независимого порождения
для рибосомного участка связывания (РУС) Е. coli были оценены
экспериментальными позиционными частотами нуклеотидов, представленными в
таблице 5.9.
Определите параметры логограммы, представленной в [238].
Используйте единицы битов для представления значений энтропии и количества
информации.
Таблица 5.9
12 3 4 5 6
Т 0,16 0,05 0,01 0,07 0,12 0,24
С 0,08 0,04 0,01 0,03 0,05 0,11
А 0,68 0,11 0,02 0,86 0,16 0,41
G 0,08 0,80 0,96 0,04 0,67 0,24
Решение. Правила изображения логограммы предполагают, что в
позиции j сумма высот четырёх букв равна количеству информации Ij
позиции j, и высота Н& буквы а пропорциональна вероятности её появления в

5.2. Дополнительные задачи и теория 211
этой позиции:
lj = iimax ~~ -"j*
Таким образом, количество информации в позиции j равно
разности максимальной энтропии, соответствующей равномерному дискретному
распределению, и энтропии для частот нуклеотидов модели РУС в
позиции j. Сначала мы вычислим Ятах и Яь
Ятах = - XIIlog2 4 = 2'
■4~вд4
а
#1 = - (рт log2 р\, + р^ log2 ргс + р\ log2 р^ + р\} log2 р^) =
= -(-0,423 - 0,292 - 0,378 - 0,292) = 1,385.
Точно так же мы определяем энтропию Hj9 где j = 2,..., 6:
#2 = 1,01, Я3= 0,303, Я4 = 0,794, Я5 = 1,393, Я6 = 1,866.
Теперь мы можем найти количество информации lj и высоты букв Я£,
где j = 1,..., 6. Здесь мы приводим значение lj и максимальную высоту
буквы в позиции j, где j = 1,..., 6. Другие значения опущены (однако они
используются, чтобы изобразить логограмму):
h = Ятах - #1 = 2 - 1,385 = 0,615, h = Ятах - Я4 = 2 - 0,794 = 1,21,
Н\= Pa /i=0,68... 0,615 = 0,4182; Ял = pi = 0,86... 1,21 = 1,04;
/2 = Ятах - Я2 = 2 - 1,01 = 0,99, h = Ятах - Я5 = 2 - 1,393 = 0,607,
я£=р^/2 = 0,8... 0,99 = 0,792; Н% = р%15 = 0,67... 0,607 = 0,4067;
/з = Ятах - Я3 = 2 - 0,303 = 1,697, /6 = Ятах - Я6 = 2 - 1,866 = 0,134,
Н% = Pah = 0,96... 1, 697 = 1,63; Н\ = р6А16 = 0,41... 0,134 = 0,055.
Логограмма показана на рис. 5.7. □
Задача 5.15. Определите значение H(Pi | \Q) относительной энтропии
(расстояние Куллбека-Лейблера) для позиционной модели независимого
порождения для РУС, описанной в задаче 5.14 (модель Pi) при допущении
о том, что фоновая модель (модель Q) для некодирующей
последовательности ДНК Е. coli представляет собой модель независимого порождения

212
Глава 5
Рис. 5.7. Логограмма для позиционной модели независимого порождения
нуклеотидного состава рибосомного участка связывания в геноме Е. coli
(таблица 5.9). Вертикальная линия слева соответствует максимально
возможному количеству информации /, 2 битам, наблюдаемому в такой позиции,
где один из четырёх символов имеет вероятность один
с параметрами qr = О,26, qc = О,23, qA = О,26, qc = 0,25.
Определите длину Е. coli из кодирующей белок ДНК, которая была бы достаточна,
чтобы дать то же самое расстояние Куллбека-Лейблера с тем же самым
фоновым распределением Q. В качестве модели кодирующей белки области
Е. coli используйте модель независимого порождения (модель Р2) с
параметрами рт = О,23, рс = 0,25, рл = 0,25, ро = 0,27. Учтите, что модель
Рг отличается от модели Q.
Решение. Относительная энтропия двух распределений, Pi и Q
определяется как сумма энтропии по шести позициям (учтите, что распределение Pi
является зависимым от позиции, a Q независимым от позиции)
H(PiWQ)
j=\ a=A,T,C,G

5.2. Дополнительные задачи и теория 213
В качестве приближения вероятностей р^, где j = 1,... ,6, мы
выбираем их оценки методом наибольшего правдоподобия, приведённые в
позиционной матрице частот (таблица 5.9), чтобы найти
tf(ft||Q) = (o,161og2 £g+0,081og2 [g+0,681og2 jjg+0,081og2 jjg) +
+ (0,051og2 j^+0,041og2 j^+0,lllog2 ^4-0,81og2 £|) +
4- (0,011og2 5§4-0,011og2 ^+0,021og2 ^+0,961og2 g) +
+ (°'°71^ W6+°mog> Ш+°'861og2 5S+0'041og2 5§) +
+ (°'121^ m+0fi5log> m+0'161og2 6S+0'671og2 Si) +
+ (°'241°^ §i+0'llk* т+олио*> Ш+°>Шо*> Ш) =
= 5,125.
Так как оба распределения Р2 и Q независимы от позиции,
относительная энтропия Н(Р2\\Q) для п позиций только в праз больше относительной
энтропии в одной позиции:
H(P2\\Q) = n J2 P°log2ff =
a=A,T,C,G
(п ™, 0,23 ппгл 0,25 ппгл 0,25 п „„, 0,27\
= » (°«231о& Й61°'25log2 0723+°'25bg2 0726+°'2?bg* 0T23J ^
= 0,ООббп.
Следовательно, относительная энтропия (расстояние Куллбека-Лейб-
лера) между распределениями Р^ и Q для шести позиций будет равна
расстоянию Куллбека-Лейблера между распределениями Pi и Q для п
участков, когда
Н(Р2 \\Q) = 0, ООббп = 5,125 = tf(Pi||Q).
Итак, нам нужно п = 777 позиций, что намного больше, чем шесть
позиций РУС, так как значение H(P2\\Q) на позицию намного меньше,
чем среднее значение Н(Р\\\Q) на позицию. □

214
Глава 5
5.3. Дополнительная литература
Со времени своего создания база данных PROSITE была важным
ресурсом данных об эволюционно консервативных белковых доменах ([17];
[127]). PROSITE — производная банка данных о белковых
последовательностях SWISS-PROT ([16]), заслужившая уважение за высокие стандарты
функциональной аннотации. Регулярные комбинации в
последовательностях, обнаруженные в консервативных белковых доменах, были
смоделированы в PROSITE при помощи регулярных выражений.
PROSITE положил начало Pfam, собранию профильных СММ и
множественных выравниваний последовательностей белковых доменов ([255]).
Новая версия Pfam ([19]) использует структурные данные, чтобы улучшить
построенную на основе доменов аннотацию белков.
Дальнейшее развитие программы BLAST, PSI-BLAST (Position-Specific
Iterated BLAST) — позиционный итерационный BLAST ([7]) стал
подручным инструментом для обнаружения гомологичных белковых
последовательностей. Использование PSI-BLAST требует особого внимания во
избежание ложных положительных совпадений ([4]; [234]).
Развитие и усовершенствование методов (в том числе основанных на
профильных СММ) для обнаружения отдалённой гомологии — вопрос,
который продолжает привлекать большое внимание ([148]; [211], [212]).
В [185] предложено несколько мер подобия между профильными СММ,
а также алгоритм, который вычисляет эти меры. Этот подход позволяет
проводить сравнение семейств последовательностей путём сравнения
профилей семейств вместо отдельных членов этих семейств.
Основанный на профильной СММ метод использовался не только в
моделировании доменов белковых последовательностей. Новый
основанный на профильной СММ алгоритм отделения псевдогенов от
функциональных генов был представлен в [53] и применён в компьютерной
программе PSILC.
В [229] описано применение профилей последовательностей для
предсказания трёхмерной структуры белка. В [150] предложен метод
обнаружения белковых гомологов, 3-D-PSSM (трёхмерная позиционная матрица
счетов), который сочетает в себе множественные выравнивания
последовательностей, выстраиваемые PSI-BLAST, с основанными на структуре
профилями.
В [68] приведён обзор литературы по основанным на профильных
СММ алгоритмам и соответствующему программному обеспечению.

Глава 6
МЕТОДЫ МНОЖЕСТВЕННОГО
ВЫРАВНИВАНИЯ
ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Согласно теории, описанной в главе 5 «АБП», построение
множественного выравнивания нескольких биологических последовательностей
должно быть частью алгоритма обучения профильной СММ. Как
предполагается, такой итеративный метод максимизации математического ожидания
оценивает параметры профильной СММ по невыровненным
последовательностям посредством построения множественного выравнивания параллельно
с оценкой параметров СММ. Конечное выравнивание может быть
истребовано на последнем шаге алгоритма через оптимальное выравнивание
каждой отдельной последовательности с только что построенной профильной
СММ. Тем не менее, так как этот внушительный теоретический проект
сталкивается со многими практическими затруднениями, достаточно
подробно рассмотренными в «АБП», его еще не применяли в чистом виде в
качестве эффективного средства для множественного выравнивания
последовательностей.
Одна из главных трудностей на пути к универсальному и
эффективному алгоритму множественного выравнивания последовательностей состоит
в следующем. Очень сложно установить золотой стандарт для
множественного выравнивания последовательностей, который помог бы отличать
хорошее выравнивание от наилучшего. Поскольку эволюционируют и
последовательность и структура, а предковые последовательности и структуры
могут быть восстановлены только теоретическими средствами,
невозможно проверить экспериментально ни выравнивания, ни филогении1. Тем не
менее формальное приписывание счёта выравнивания непосредственно
ведет к понятию наилучшего выравнивания для данного набора
последовательностей; однако выводы из определённого таким образом оптимального
*На самом деле структуры эволюционируют достаточно медленно — значительно
медленнее, чем последовательности (за исключением петель). Поэтому в качестве золотого стандарта
используют структурные выравнивания. В настоящее время построено несколько выборок со
структурными выравниваниями. — Прим. ред.

216
Глава 6
выравнивания необходимо принимать с достаточной бдительностью. Есть
несколько обоснованных в биологическом отношении вариантов выбора
для приписывания счёта. Например, счёт парных сумм в вычислительном
отношении удобен и поэтому часто используется, однако он имеет
известные теоретические недостатки ([67], стр. 141).
Помимо важной темы определения счёта выравнивания, мы
интересуемся строгим алгоритмом, который выдаёт множественное выравнивание
с наилучшим счётом. Такой алгоритм — стандартный алгоритм
динамического программирования (Д11) — известен в теории, но он непрактичен,
поскольку требует время, сопоставимое с возрастом Земли, для того
чтобы выровнять лишь десять белковых последовательностей средней длины
(задача 6.1). Поэтому непростительно высокая вычислительная сложность
побуждает учёных к поиску эвристических алгоритмов, которые были бы
способны находить приближённое оптимальное выравнивание за разумное
время.
Бремя непомерных вычислительных усилий, связанных с решением
задач множественного выравнивания последовательностей, ограничивает
число теоретических задач, которые могли бы быть предложены для
упражнения без необходимости серьёзного и трудоёмкого программирования на
компьютере. Это соображение может объяснить причину, по которой в этой
главе «АБП» была предложена лишь одна задача.
В разделе «Дополнительные задачи» приведены «модельные
примеры», способствующие освоению азов применения сложного, но всё же
строгого алгоритма ДП, изобретённого Каррилло и Липменом [42], а также
приближённого метода множественного выравнивания — алгоритма
прогрессивного выравнивания.
6.1. Оригинальная задача
Задача 6.1. Допустим, что мы имеем некоторое число
последовательностей, которые имеют длину пятьдесят остатков, и что попарное сравнение
двух таких последовательностей занимает одну секунду времени
центрального процессора в нашем компьютере. Выравнивание четырёх
последовательностей (N = 4) занимает (2L)N~2 = io2JV~4 = 104 секунд (несколько
часов). Если бы наш компьютер имел неограниченную память и мы
желали бы ожидать ответа ровно до тех пор, пока Солнце не сгорит через пять
миллиардов лет, то сколько последовательностей он смог бы выровнять за
это время?

6.2. Дополнительные задачи и теория
217
Решение. Время Т, необходимое для выравнивания N
последовательностей длины пятьдесят остатков, составляет Т = (2L)N~2 = 102JV~4
секунд. При Т = 5 миллиардов лет мы имеем (в секундах): 102JV~4 =
= 5 • 109 • 365 • 24 • 60 • 60 = 1,57 • 1017 и, таким образом, N = 10,6.
Поэтому полный алгоритм динамического программирования,
применяемый на таком компьютере, будет иметь достаточно времени для построения
множественного выравнивания десяти последовательностей длины
пятьдесят остатков, прежде чем Солнце сгорит через пять миллиардов лет. □
6.2. Дополнительные задачи и теория
В этом разделе мы показываем, как применять алгоритм Каррилло-
Липмена для поиска оптимального (с минимальной стоимостью)
множественного выравнивания трёх последовательностей нуклеотидов
(задача 6.2). Также мы приводим наглядный пример применения эвристического
последовательного алгоритма множественного выравнивания Фэна и Ду-
литтла для построения множественного выравнивания четырёх коротких
последовательностей белка (задача 6.3). Построение множественного
выравнивания без пропусков параллельно с построением вероятностной
модели может быть выполнено при помощи метода наибольшего
правдоподобия. Мы показываем, что такое выравнивание с наибольшим
правдоподобием будет обладать минимальной энтропией (задача 6.4).
6.2.1. Алгоритм множественного выравнивания Каррилло-Липмена
Теоретическое введение в задачу 6.2
Полный счёт множественного выравнивания часто определяется как
сумма счетов всех попарных выравниваний, однозначно определённых
посредством множественного выравнивания. Счёт такого вида называют
счётом парных сумм (ПС). Максимальный счёт ПС (или минимальная
стоимость ПС) выравнивания N последовательностей длин к\,..., км
может быть определён алгоритмом ДП на TV-мерной решётке L размера
&i х • • -хкн. После этого оптимальное множественное выравнивание
(оптимальный путь через решётку L) определяется процедурой обратного
прослеживания. Время счёта такого алгоритма пропорционально
произведению к\ х • • • х км, что становится с практической точки зрения недопустимо
большим в случае выравнивания более десяти белковых
последовательностей средней длины (задача 6.1).

218
Глава 6
Каррилло и Липмен [42] предложили алгоритм, сокращающий
решётку L до меньшей iV-мерной области, которая также содержит
оптимальный путь с минимальной стоимостью. Таким образом, алгоритму ДП для
отыскания оптимального решения потребуется намного меньше времени
вычислений.
Алгоритм работает следующим образом. Для N последовательностей
х\,..., xjv мы определяем TV-мерную решётку L с начальным углом,
соответствующим первым символам и конечным углом, соответствующим
последним символам всех последовательностей. Решётка L состоит из
к\ х • • • х км АГ-мерных кубов. Разрешённый путь 7 определяется как
непрерывная состоящая из отрезков линия через решётку L, соединяющая
начальный угол и конечный угол, при этом каждый отрезок линии
соединяет вершины отдельного куба в решётке L. Конечная точка каждого отрезка
должна быть ближе к конечному углу, чем начальная точка отрезка.
Можно показать, что любой отдельно взятый путь у соответствует
уникальному множественному выравниванию х\,..., xn и наоборот. Проекция pij (7)
пути 7 на плоскость (г, j), связанную с последовательностями Хг и Xj,
определяет попарное выравнивание последовательностей Хг и Xj. Стоимость ПС
S(j) пути 7 определяется как сумма стоимостей проекций пути рц(п)'-
Sb)= £ S(py(7)).
Очевидно, что это определение подразумевает, что система очков
попарного вьфавнивания, вызванного множественным вьфавниванием, игнорирует
участки, в которых множественное выравнивание содержит два
выровненных знака пропуска в обеих последовательностях х\ и Xj. Это происходит
потому, что соответствующий отрезок пути 7 ортогонален к плоскости (г, j)
и поэтому отсутствует в проекции пути Pijij)-
Пусть S%i обозначает стоимость оптимального попарного
вьфавнивания последовательностей Хк и х\. В [42] было доказано, что если 7е —
разрешённый путь через решётку L, то для любых i,j, где 1 ^ г < j^ N,
значение Uij, определяемое из
(fe,0*(i,i)
даёт верхний предел стоимости Pij{j*) — проекции оптимального пути 7*
на плоскость (i,j).

6.2. Дополнительные задачи и теория
219
Пусть X — множество путей У через решётку L, удовлетворяющих
следующему условию: S(pij(/y')) < U^, где 1 < г < j < N. Нам
нужно конструктивное определение множества X, чтобы использовать его в
алгоритме оптимизации. В двумерной решётке L(i,j) мы рассматриваем
множество ячеек уц, которые пересекаются двумерными путями, причём
каждый путь имеет стоимость меньше Uij, и затем выбираем множество
кубов Yij iV-мерной решётки L, удовлетворяющих условию p%j{Yij) = yij.
Если множество Y определяется как
у= П Y&
то X С Y из уравнения (6.1). Поэтому для отыскания оптимального
пути среди всех путей в решётке L достаточно применить iV-мерный
алгоритм ДП только к подобласти Y решётки L. Учтите, что чем «ближе»
отобранный путь 7е к (всё же) ещё неизвестному оптимальному пути 7*> тем
меньше объём области Y и задача динамического программирования менее
дорогая в вычислительном отношении.
Задача 6.2. Постройте оптимальное множественное выравнивание
последовательностей х\ = ТС AC A, X2 = С АС ижз = GTAC при помощи
алгоритма Каррилло-Лштмена со стоимостью замен нуклеотидов
S(A, А) = S(C, С) = S(G, G) = S(T, T) = О,
S(C, Т) = 5(Г, С) = S(A, G) = S(G, A) = l,
S(A, T) = S(T, A) = S(A, С) = S(C, А) =
= S(G, С) = S(C, G) = S(G, Г) = S(T, G) = 2,
стоимостью введения пропуска d = 3 и стоимостью продолжения пропуска
е = 2.
Решение. Мы определяем путь 7е как путь через решётку L,
соответствующий следующему множественному выравниванию:
С Т С А С А
С - - А С -
G - Т А С -

220
Глава 6
Стоимость пути 7е определяется из
s(7e)= £ s(Pij(r)) = sl ° т с лл Z А ) +
l^i<j^N \ С — —
= S(C,C) + d + e + S(A,A) + S(C,C) + d + S(G,C) + d + S(C,T)+
+S(A, А) + S(C, С) + d + 5(С, G) + d + S(A, Л) + S(C, С) = 22.
Оптимальное (глобальное) попарное выравнивание последовательностей xi
и xJ? где г, j = 1,2,3, наряду с минимальной стоимостью S*j могут быть
найдены алгоритмом ДП. Для данной пары (г, j) мы рассматриваем три
типа вьфавниваний последовательностей ж» и Xj вплоть до элементов Xi(k)
и хА1): вьфавнивание, где Xi(k) совпадает с Xj(l) (минимальная стоимость
S™(k,l)); вьфавнивание, где Хг(к) выровнен с пропуском (минимальная
стоимость £7 (&,/)); и выравнивание, где Xj(l) выровнен с пропуском
(минимальная стоимость SJ(k, I)).
Рекуррентные уравнения выглядят следующим образом:
SM(k,l) = S{xi{k),Xj{l)) +min {
SM(к-1,1-1),
ST(k-1,1-1), (6.2)
I SJ(k-l,l-l)',
Qifu 7^ • / SM(k-l,l) + d, ,_
S{kJ) = mm\s4-l,lHe-, (6'3)
5^,/) = min{5;^/-1) + d' (6.4)
K J \ SJ{k,l-l) + e. V '
Для x\ = CTCACA и Х2 = С АС матрица стоимостей S'(k, l)
определяется уравнениями (6.2)-(6.4) и представлена на рис. 6.1. Запись с
минимальным значением в правой нижней ячейке на рис. 6.1 (к = 6, I = 3)
определяет минимальную стоимость Si2 = 8. Процедура обратного прослеживания
через матрицу ДП восстанавливает два пути с одинаковой стоимостью. Эти

6.2. Дополнительные задачи и теория
221
пути соответствуют двум наилучшим выравниваниям последовательностей
х\ и Х2, имеющим стоимость Si2 — 8:
(1) С Т С А С А (2) С Т С А С А
С - - А С - - - С А С -
Го1
!-Т
\
С
14
т
п
с
7
9
11
13
-
7
5
5
т
8
5
Т
7
8
Т
5
8
5^
7
12
\
То
*8
12
Рис. 6.1. Матрица значений стоимости S*(k,l) для последовательностей
xi и Ж2, вычисленная алгоритмом ДП по уравнениям (6.2)-(6.4). Записи
SM(k, I), S*(k, I) и SJ(k, I) каждой ячейки (&, /) приведены в порядке
сверху вниз. Два пути с минимальной стоимостью, идущие через матрицу,
показаны стрелками

222
Глава 6
Точно так же для последовательностей х\ = СТСАСА и хз =
= GTAC уравнения (6.2)-(6.4) дают оптимальное выравнивание со
стоимостью #13 = &
(3) С Т С А С А
G Т - А С -
Наконец, для последовательностей х^ и х$ алгоритм ДП выдаёт наилучшее
выравнивание со стоимостью 5^3 = 4:
(4) - С А С
G Т А С
Теперь мы можем найти, применяя уравнение (6.1), верхние пределы Uij
значений стоимости проекций все ещё неизвестного оптимального
множественного выравнивания 7* на плоскости (г,.;):
U12 = 5(7е) - (5Гз + 52*3) = 22 - 12 = 10,
U13 = 5(7е) - (S*12 + 52*3) = 22 - 12 = 10,
и2г = 5(7е) - (S*l2 + S*l3) = 22 - 16 = 6.
Следующая цель состоит в отыскании множеств у^9 где г < j. Для каждой
пары последовательностей Xi,Xj мы применяем алгоритм ДП в обратном
направлении. В результате для каждой ячейки (к,1) двумерной решётки
L(i,j) мы знаем и оптимальный путь от верхнего угла до этой ячейки (из
первоначального прямого прогона алгоритма) и оптимальный путь от
нижнего угла до этой ячейки (из обратного прогона алгоритма). Обратите
внимание, что последний путь совпадает с оптимальным путём от ячейки до
нижнего угла решётки L(i,j). Два значения оптимальной стоимости
связаны с этими двумя путями, которые встречаются в ячейке (к, I). Поэтому для
каждой ячейки (к, I) в решётке L(i,j) мы определяем оптимальный путь,
проходящий через эту ячейку, как сцепку этих двух оптимальных путей.
Стоимость S*otal(k, l) целого пути равна сумме значений стоимости его
частей. Если S*otal(k, I) ^ Uij, то ячейка (к, I) принадлежит ко множеству yij.
Множества у^, у\з, 2/23 показаны на рис. 6.2, 6.3 и 6.4 как множества
ячеек с непустыми записями S*otal(k, l), соответственно, на решётках L(l, 2),
L(1,3)hL(2,3).
Теперь из рис. 6.2 мы получаем множество попарных выравниваний
последовательностей х\ и Х2, соответствующих возможным проекциям pi2
оптимального пути 7*: вышеупомянутое оптимальное выравнивание (3)

6.2. Дополнительные задачи и теория
223
С
Но7"
т
То
8
С
Т
8
Л
С
А
-
9
-
8
10
-
СП ГГ
-
-
9
9
8
9
10
8
Рис. 6.2. Значения стоимости S™tai{k,l), S(otal(k,l), Siotai(h,l)
оптимальных путей, проходящих через ячейки (к, I) решётки L(l, 2) показаны внутри
(fc, I) ячеек, если их значения удовлетворяют условию S*(k, I) < U12 = 10.
Значения стоимости 5?otai(fc, l), превышающие 10, опущены
со стоимостью 8; выравнивание (5) со стоимостью 9 и выравнивания (6),
(7) и (8) со стоимостью 10:
(6)
(5) С Т С А
С А С -
С Т С А С А (7)
- С - А С -
(8) С Т С А
С - - А
С А
— —
С Т С А С А
- - С А - С
С А
- С
Точно так же рис. 6.3 позволяет нам отобрать попарные выравнивания
последовательностей х\ и х^, соответствующие возможным проекциям
Pi3 наилучшего пути 7*' вышеупомянутое оптимальное выравнивание (3)

224
Глава 6
G
С
т
Т
т
9
С
-
А
-
с
-
А
-
-
8
9
8
-
-
-
-
-
10
8
10
10
-
8
10
8
Рис. 6.3. Значения стоимости (как и на рис. 6.2) оптимальных путей,
проходящих через ячейки (fc, I) решётки L(l, 3)
со стоимостью 8; выравнивания (9) и (10) со стоимостью 9,
(9) С Т С А С А (10) С Т С А С А
- G Т А С - G - Т А - С
и выравнивания (11)и(12)со стоимостью 10,
(11) С Т С А С А (12) С Т С А С А
G Т А - С - G Т - А - С

6.2. ДОПОЛНИТЕЛЬНЫЕ ЗАДАЧИ И ТЕОРИЯ
225
5 4 - -
- 5 - -
- - 4 -
- - - 4
Рис. 6.4. Значения стоимости (как на рис. 6.2) оптимальных путей,
проходящих через ячейки (к, I) решётки L(2,3)
Наконец, из рис. 6.4 мы получаем два попарных выравнивания
последовательностей #2 и х$, соответствующие возможным проекциям Р23
оптимального пути 7*: вышеупомянутое выравнивание (4) со стоимостью 4
и выравнивание (13) со стоимостью 5,
(13)
G - А С
С Т А С
Можно показать, что выравнивания проекций (1)—(13) определяют
множество X семи трёхмерных путей 7» через решётку L:
1) путь 7i и множественное выравнивание А\ с проекциями (1), (3)
и (13) и со стоимостью 5(7i) = 5(1) + 5(3) + 5(13) = 21:
(Аг) С Т С А С А
С - - А С -
G Т - А С -

226 Глава 6
2) путь 72 и множественное выравнивание Ач с проекциями (2), (9)
и (4) и со стоимостью 5(72) = 5(2) + 5(9) + 5(4) = 21:
(А2) С Т С А С А
- - С А С -
- G Т А С -
3) путь 7з и множественное вьфавнивание Аз с проекциями (6), (3)
и (4) и со стоимостью 5(7з) = S(6) + 5(3) + 5(4) = 22:
(А3) С Т С А С А
- С - А С -
G Т - А С -
4) путь 74 и множественное вьфавнивание А* с проекциями (6), (9)
и (13) и со стоимостью 5(74) = 24:
(At) С Т С А С А
- С - А С -
- G Т А С -
5) путь 75 — 7е и множественное вьфавнивание А$ с проекциями (1),
(10) и (13) и со стоимостью 5(7s) = S(-ye) = 22:
(А5) С Т С А С А
С - - А С -
G - Т А С -
6) путь 7б и множественное вьфавнивание Ае с проекциями (2), (10)
и (4) и со стоимостью 5(7б) = S(2) + 5(10) + 5(4) = 21:
(Аз) С Т С А С А
С - - А С -
G - Т А С -
7) путь 77 и множественное вьфавнивание Ау с проекциями (8), (12)
и (13) и со стоимостью 5(77) = 5(8) + 5(12) + 5(13) = 25:
(А7) С Т С А С А
С - - А - С
G Т - А - С

6.2. Дополнительные задачи и теория
227
Три пути 7i j 72 и 7б имеют стоимость 21 — минимальную стоимость среди
путей из множества X; следовательно, А\, Ач и Ае — оптимальные
множественные выравнивания последовательностей х\, хч и х$. □
6.2.2. Прогрессивные выравнивания: алгоритм Фэна-Дулиттла
Теоретическое введение в задачу 6.3
Один из часто используемых методов множественного
выравнивания — прогрессивное выравнивание, основная идея которого заключается
в использовании серии попарных выравниваний, чтобы сначала выровнять
пары последовательностей, затем последовательности с группой и,
наконец, пары групп последовательностей.
Напомним себе основные шаги новаторского алгоритма
прогрессивного выравнивания Фэна и Дулиттла [80]. Мы делаем допущение о том, что
имеем дело с N последовательностями белка х\,..., xn-
1) По счёту Sij оптимального глобального попарного выравнивания
последовательностей Х{ и Xj, вычисленному алгоритмом Нидлмена-Вунша,
определяется расстояние Dij между последовательностями Х{ и Xj, где
iJ = l,...,N:
Dij = -ln„Sij-_Srqand . (6.5)
О max &rand
Здесь Smax = (Su + Sjj)/2 — среднее арифметическое счетов каждой
последовательности, выровненной с самой собой, a Srand — ожидаемый счёт
выравнивания двух случайных последовательностей одинаковой длины и
состава остатков:
Srand = (1/Ь)^^5(а,Ь)ЛГ,(а)ЛГ,(Ь)ЛГЫ^. (6.6)
aei bej
В уравнении (6.6) Ni(a)(Nj(b)) — число раз, которое остаток а(Ь)
появляется в последовательности Х{ (xj); S(a,b) — счёт замены аминокислот
а и 6; N(g) — число пропусков в оптимальном выравнивании
последовательностей XiUXjid — штраф за пропуск; L — полная длина выравнивания
последовательностей xi и Xj. Вычисляется матрица N(N — l)/2 расстояний
между всеми парами N последовательностей.
2) По матрице расстояний Dij с помощью алгоритма группировки
Фитча и Марголиаша [85] строится путеводное дерево.

228
Глава 6
3) Выстраивается множественное выравнивание — в порядке,
установленном путеводным деревом, начиная с попарного выравнивания двух
наиболее близких последовательностей. Добавление всякой
последовательности к уже построенному вьфавниванию производится согласно дающему
наивысший счёт попарному вьфавниванию этой «новой»
последовательности с некоторой последовательностью из выровненной группы. В ходе
работы алгоритма путеводное дерево может потребовать выравнивания двух
уже выровненных групп. Тогда выравнивание группа-с-группой
направляется дающим наивысший счёт выравниванием между парой
последовательностей — одной из первой группы и одной из второй группы. Обратите
внимание, что порядок шагов в построении выравнивания и само
окончательное множественное выравнивание не зависят от длины рёбер путеводного
дерева; значение имеет только помеченная история, соотносимая с деревом
(см. главу 7).
Более поздний и в настоящее время повсеместно применяемый
алгоритм множественного выравнивания CLUSTALW ([265]) использует схему
прогрессивного выравнивания с попарными расстояниями D^, предложен-
нуюв[154]: Aj = _ln(l-dy-4/5).
Здесь d^ — число несовпадений в оптимальном выравнивании
последовательностей Хг и Xj, поделённое на длину выравнивания без учёта
позиций с пропусками. Путеводное дерево в CLUSTALW строится из
матрицы расстояний D = (Dij) алгоритмом соединения соседей ([230]).
Чтобы построить выравнивание последовательность-с-группой или группа-с-
группой, CLUSTALW сначала вычисляет профиль группы — систему очков,
в которую входят позиционные штрафы за пропуски, а также веса
последовательностей в группе.
Задача 6.3. Ниже представлены (в порядке сверху вниз) четыре фрагмента
белков из надсемейства I-иммуноглобулина: х±, #2, #3 и х±:
ILDMDWEGSAARFDCKVEGYPDPEVMWFKDDNPVKESRHFQIDYDEEGN
RDPVKTHEGWGVMLPCNPPAHYPGLSYRWLLNEFPNFIPTDGRHFVSQTT
ISDTEADIGSNLRWGCAAAGKPRPMVRWLRNGEPLASQNRVEVLA
RRLIPAARGGEISILCQPRAAPKATILWSKGTEILGNSTRVTVTSD
С помощью метода Фэна-Дулиттла постройте множественное
выравнивание этих последовательностей. Рассмотрите следующие наборы
параметров:
а) 250 ПТМ (таблица 6.1) и пропорциональный штраф за пропуски
(2 = 8;

6.2. Дополнительные задачи и теория 229
б) BLOSUM62 (таблица 6.6) и пропорциональный штраф за пропуски
d = 6. Оба набора (а и б) были предложены в [81].
Решение, а) Для каждой пары последовательностей Xi,Xj, где i,j =
= 1,2,3,4, алгоритм Нидлмена-Вунша производит представленные ниже
оптимальные выравнивания Ац со счётом Sij.
Выравнивание А^ со счётом S\2 = 31:
ILDMDWEGSAARFDCKVEG-YPDPEVMWFKDDNPVKESRHFQIDYDEEGN
RDPVKTHEGWGVMLPCNPPAHYPGLSYRWLLNEFPNFIPTD-GRHFVSQTT
Выравнивание Ais со счётом Sis = 44:
ILDMDWEGSAARFDCKVEGYPDPEVMWFKDDNPVKESRHFQIDYDEEGN
ISDTEADIGSNLRWGCAAAGKPRPMVRWLRNGEPL-ASQN-RV-EVLA-
Выравнивание А\± со счётом Si4 = 13:
ILDMDWEGSAARFDCKVEGYPDPEVMWFKDDNPVKESRHFQIDYDEEGN
RRLIPAARGGEISILCQPRAAPKATILWSKGTE-ILGNST-RV-TVTSD
Выравнивание A2s со счётом #23 = 15:
RDPVKTHEGWGVMLPCNPPAHYPGLSYRWLLNEFPNFIPTDGRHFVSQTT
ISDTEADIGSNLRWGCAAAGKPRPMV-RWLRNGEP—LASQNR---VEVLA
Вьфавнивание А24 со счётом S24 = 16:
RDPVKTHEGWGVMLPCNPPAHYPGLSYRWLLNEFPNFIPTDGRHFVSQTT
RRLIPAARGGEISILCQPRAA-PKATILW-SKG-TEILGNSTRVTVT-SD
Вьфавнивание Asa со счётом S34 = 45:
ISDTEADIGSNLRWGCAAAGKPRPMVRWLRNGEPLASQNRVEVLA-
PRLIPAARGGEISILGQPRAAPKATILWSKGTEILGNSTRVTVTSD
Выравнивания этих четырёх последовательностей с самими собой дают
следующие счета: Sn = 262, 522 = 287, 533 = 222, 544 = 215. Затем
уравнения (6.6) и (6.5) дают значения величины Srand и попарные
расстояния Diji
Srand(l,2) = -66,94, D12 = l,25;
Snmd(l,3) =-80,28, Di3 = 0,95;
Smnd(l, 4) = -70,48, £>i4 = 1,31;
Srandfr3) = -82,86, D23 = 1,24;
Srond(2,4) = -72,52, D24 = 1,30;
Srand^A) = -37,85, D34 = 1,13.

230
Глава 6
Алгоритм Фитча-Марголиаша для построения дерева работает следующим
образом. В каждом шаге он отбирает и соединяет пару ближайших узлов
из множества свободных текущих узлов. Действительное расстояние между
двумя внутренними узлами к и I определяется как среднее расстояний Вц
между всеми возможными парами г и j, где г — лист-потомок узла к, a j —
лист-потомок узла L Шаг соединения узлов повторяется до тех пор, пока
последние два узла не будут соединены в корневой узел.
Здесь мы начинаем с листьев 1, 2, 3 и 4 для последовательностей,
соответственно, х\, Ж2, #з и х±. Ближайшие листья — листья 1 и 3,
разделённые расстоянием D\z = 0,95. Их соединение создаёт узел 5, и для
нового множества узлов 2, 4 и 5 действительные расстояния следующие:
#25 = (А21 + Агз)/2 = 1,245 и L>45 = (An + Ata/2 = 1,22. Расстояние
£>24 = 1,30 не изменяется. Затем мы соединяем узлы 4 и 5 и создаём
новый узел 6. В последнем шаге алгоритм соединяет оставшиеся узлы 2 и 6
и производит следующее путеводное дерево:
6J
4 13 2
Теперь мы должны добавлять последовательности к растущему
множественному выравниванию в том же порядке, в котором листья соединены в
путеводном дереве. Выравнивание Ахз последовательностей х\ и хз
выбирается из списка оптимальных выравниваний и служит начальной
затравкой. Чтобы выровнять последовательность х± с выравниванием А\3, мы
будем использовать в качестве руководства выравнивание А34, а не А^,
так как S34 > Su- Пропуски в последовательность #4 следует вставлять
в соответствии с выравниванием А34- Эта операция ведёт к следующему
выравниванию последовательностей х±, х$ и х± (в порядке сверху вниз):
ILDMDWEGS7VARFDCKVEGYPDPEVMWFKDDNPVKESRHFQIDYDEEGN
ISDTEADIGSNLRWGCAAAGKPRPMVRWLRNGEPL-ASQN-RV—EVLA-
RRLIPAARGGEISILCQPRAAPKATILWSKGTEIL-GNST-RV—TVTSD
Наконец, последовательность #2 добавляется к представленной выше
группе в соответствии с выравниванием А\2 — выравниванием с наивысшим
счётом среди выравниваний Ai2, где г = 1,3,4. Поэтому множественное
выравнивание четырёх последовательностей (в первоначальном порядке)
выглядит следующим образом:

6.2. Дополнительные задачи и теория
231
>
н
ел
Он
о
w
сх|
и
Q
<
о
ГО
1
-
-
-
СП
1
■
i—I
CN
1
1
i
-
О
о
CN
i
О
О
cn
1
CN
<
Ч
i
CN
I
О
о
1
о
СП
СП
1
<?
CN
СП
1—4
1
-
1
1—4
1
О
чо
CN
i
Рч"
i
CN
Т
О
i—I
О
СП
1
CN
-
СП
1
CN
CN
О
-
у—4
1
CN
CN
О
О
Ъ
Ч
*
■
о
о
-
1
СП
О
4f
CN
у—4
j—4
СП
CN
1
4t
CN
j—4
О
Q
<?
о
oo
CN
i
О
СП
1
1
1
«о
1
чо
1
<?
СП
1
СП
1
«о
1
«о
CN
1
1
■
CN
и
CN
Tt
«r>
i—1
-7
О
I
i
1—4
CN
i
CN
i
СП
т—1
1
CN
^t
1
CN
-
-
О
<?
T
■
о
о
1
i
CN
■
О
СП
1
г?
-
о
^t
CN
«о
i
СП
1—4
1
о
о w
1
•о
1
о
-
о
1
СП
1
<?
1
СП
CN
1
«о
о
1
СП
1
-
о
СП
1
-
о
CN
о
СП
1
1
1
о
CN
CN
о
CN
1
CN
i
ЧО
CN
i
*-ч
СП
СП
1
т—1
CN
CN
1
Я
4t
1
1
о
1
CN
i
*-н
CN
CN
i
CN
«О
CN
СП
CN
■
CN
i
CN
i
CN
CN
i
<?
•7
h-H
CN
V
<?
CN
СП
1
СП
i
CN
^t
СП
1
ЧО
CN
CN
■
t
СП
1
CN
чо
1
1
СП
i
СП
CN
1
J
<?
t
СП
о
о
1
1
О
*n
СП
1
CN
1
о
CN
1
о
*-н
1
О
-
СП
I
М
CN
CN
i
т1-
i
<*
CN
i
О
ЧО
о
*■
CN
CN
СП
1
CN
1
i
»о
СП
CN
о
1
5
1—1
1
г-
о
СП
1
СП
1
«г>
о\
о
V4
1
CN
-
CN
1
1
«о
т
чо
1
СП
1
СП
1
Рч
1—(
1
«о
1
ЧО
1
о
*-н
чо
i
CN
i
i
СП
1
CN
1
о
о
1
О
СП
1
1
о
О
т—1
Он
1
СП
1
CN
i
»—i
CN
*-н
СП
1
CN
i
О
СП
1
1
i
-
О
i
О
о
*-ч
О
-
ел
о
СП
1
СП
-
о
СП
1
»-Н
1
о
CN
О
*—<
i
О
о
1
CN
i
О
о
*-н
i
-
н
ЧО
О
с^
«о
1
CN
1
чо
1
о
т
СП
1
CN
1
«о
1
СП
1
Гр
1
«о
1
00
1
1
1
CN
чо
1
CN
1
о
1—1
о
СП
1
СП
1
«о
1
г-
CN
1
т
V
1
о
1
^t
1
о
1
CN
1
т
СП
1
^t
ч
ЧО
1
о
»-Н
1
1
CN
CN
1
CN
^
^
1
CN
CN
1
CN
CN
i
CN
CN
О
£ > >\\

232
Глава 6
>
Jh
£
Н
о
CN
СО
О
ГО
i
CN
1
ел
1
1
СЛ
CN
1
т
о
сл
1
СЛ
1
т
1
^ о
CN *—< CN СЛ
? ^
сл «7
CN О - -
о ^ о V
V о о см
V ^ о о
О СЛ СЛ СЛ
<? <? — VO
^ О VO i-h
V ^ О <N
^ V ^ ^
< * £ Q
*7 © ©
СЛ !-• 1-»
I I I
CN СЛ СЛ
I I I
- о <?
ел ^ ^
1-" cs сл
I I I
*—I СЛ СЛ
I I I
v ел о о
ГЛ -н <N ^
гч гч CN ^н
I I I I
CN CN ГЛ CN ГЛ уч
I I I I I I
CN CN *-ч *-ч *-ч у—i
i i i i i i
О —• <N <N о ^
(S (S n
ГЛ *—< о
(Л М н
I I I 1 w' I I I v—' I
ГЛ
1
о
CN
i
ГЛ
1
1—4
^
О
»o
t
v©
О
r^
T
cn
t N 1Л
<7 Ш CN
OS СЛ Tf
^ О CN
СЛ о О
с? - О
о v V
1-
1-
CN
i
v©
<?
CN
i
ГЛ
1
ГЛ
i
00
CN
i
О
О
CN
^
ГЛ
1
1
ГЛ
1
сл
1
^
CN
СЛ
1
т
СЛ
<?
CN
1
СЛ
1
1
CN
-
^н
CN
1—4
CN
СЛ
ч
о
о
о
1
сл
1
сл
СЛ
1
сл
1
сл
1
CN
CN
1
1—4
1
-
СЛ СЛ '-ч
г-1 г-1 СЛ ^t *-ч СЛ
О — сл
CN о гл
О CN
О К
^ CN
i i
О CN
о т
о ^
CN СЛ - -
о *7
m о <N f
ГЛ CN rsJ r-i СЛ CN
I I *• ^ I I I
I I I I I I
НН_1^;§ИНР1НСЛН
СЛ
1
CN
i—1
1—4
CN
i
ел
i
t
1—4
1
СЛ
CN
i
СЛ
1
CN
i
CN
i
СЛ
1
CN
i
CN
i
i
^
СЛ
1
СЛ
1
£
v
Г-
CN
CN
1
CN
i
СЛ
1
СЛ
1
CN
1
1—4
1
1
CN
ел
CN
i
i
CN
i
СЛ
1
CN
CN
i
CN
Jh
^t
1—4
1
ел
i
О
CN
i
CN
i
1—4
1
1—4
CN
i
-
СЛ
СЛ
c^
1
CN
1
CN
i
1—4
1
ел
i
ел
ел
i
О
>

6.2. Дополнительные задачи и теория
233
IIDMDWEGSAARFDCKVEG-YPDPEVMWFKDDNPVKESRHFQIDYDEEGN
HDPVKTHEGWGVMLPCNPPAHYPGLSYRWLLNEFPNFIPTD-GRHFVSQTT
ISDTEADIGSNLRWGCAAAG-KPRPMVRWLRNGEPL-ASQN-RV—EVLA-
PRLIPAARGGEISILCQPRA-APKATILWSKGTEIL-GNST-RV--TVTSD
6) При другом наборе параметров выравнивания — матрица замен
аминокислот BLOSUM62 и пропорциональный штраф за пропуски d = 6 — та
же процедура выполняется в виде серии следующих шагов. В качестве
исходных попарных выравниваний мы имеем следующее:
Выравнивание А^ со счётом 5i2 = 4:
ILDMDWEGSAARFDCKVEG-YPDPEVMWFKDDNP—V-KESRHFQIDYDEEGN
RDPVKTHEGWGVMLPCNPPAHYPGLSYRWLLNEFPNFIPTDGRHF-V—SQT-T
Выравнивание Ais со счётом Sis = 37:
ILDMDWEGSAARFDCKVEGYPDPEVMWFKDDNPVKESRHFQIDYDEEGN
ISDTEADIGSNLRWGCAAAGKPRPMVRWLRNGEPL-ASQN-RVEV—LA-
Выравнивание Ai± со счётом 514 = —4:
ILDMDWEGSAARFDCKVEGYPDPEVMWFKDDNPVKESRHFQIDYDEEGN
PPLIPAARGGEISILCQPRAAPKATILWSKGTEILGNSTRVTVTSD
Выравнивание А23 со счётом 523 = 3:
PDPVKTHEGWGVMLPCNPPAHYPGLSYRWLLNEFPNFIPTDGRHFVSQTT
ISDTEADIGSNLRWGC-AAAGKPRPMVRWLRNGEP—LASQNR—VEVLA
Выравнивание А24 со счётом 524 = 9:
SDPVKTHEGWGVMLPCNPPAHYPGLSYRWLLNEFPNFIPTDGRHFVSQTT
PJLIPAARGGEISILCQPRA-APKATILW—SKGTEILGNSTRVTVT-SD
Выравнивание A^ со счётом 534 = 24:
ISDTEADIGSNLRWGCAAAGKPRPMVRWLRNGEPLASQNRVEVLA-
RRLIPAARGGEISILCQPRAAPKATILWSKGTEILGNSTRVTVTSD
Счета выравниваний последовательностей с самими собой равны: 5ц =
= 277, 522 = 294, 53з = 238, 544 = 232. Теперь мы используем уравнения
(6.6) и (6.5), чтобы вычислить Srand и Dij для каждой пары
последовательностей:
5mnd(l,2) =-101,65, Dia = l,30;
Srandih 3) = -78,64, D13 = 1,07;

234
Глава 6
Srand{lA) = -75,04, £>14 = 1,53;
Standi 3) = -81,38, D23 = 1,42;
Srand% 4) = -75,12, D24 = 1,39;
Sw(3,4) = -45,83, Дм = 1,39.
Для того чтобы построить путеводное дерево, мы сначала соединяем
ближайшие листья 1 и 3 (£>1з = 1,07) в узел 5 и вычисляем новые попарные
расстояния: D25 = (D2i + D23)/2 = 1,36 и D45 = (D4i + £>4з)/2 = 1,46
(£)24 = 1,39 не изменяется). В последнем шаге соединение оставшихся
узлов 4 и 6 завершает построение путеводного дерева, имеющего следующий
вид:
6J
2 13 4
Помеченная история этого дерева отличается от помеченной истории
путеводного дерева, построенного в пункте а. Наконец, мы выравниваем
последовательности в порядке, определяемом путеводным деревом: мы
добавляем последовательность х2 к выравниванию А\$ (руководствуясь А\2)\
затем последовательность х± выравнивается с группой из трёх
последовательностей (руководствуясь А%±). В итоге получаем следующее
множественное выравнивание:
ILDMDWEGSAARFDCKVEG-YPDPEVMWFKDDNP--V-KESRHFQIDYDEEGN
RDPVKTHEGWGVMLPCNPPAHYPGLSYRWLLNEFPNFIPTDGRHF-V—SQT-T
ISDTEADIGSNLRWGCAAAG-KPRPMVRWLRNGEP-- L—ASQN-RVEV—LA-
RRLIPAARGGEISILCQPRA-APKATILWSKGTEI—L—GNST-RVTV— TSD
Замечание. Сравнение результатов работы алгоритма при выборе
наборов параметров а и б поучительно, поскольку оно показывает не только
то, что более низкий штраф за пропуски допускает дополнительные
пропуски в случае б, но также и что изменение в матрице счетов может
изменить помеченную историю путеводного дерева и привнести изменения в
конечное множественное выравнивание в целом. □

6.2. Дополнительные задачи и теория
235
6.2.3. Алгоритм выборки Гиббса для локального множественного
выравнивания
Алгоритм выборки Гиббса для множественного выравнивания,
представленный в [176], опознаёт регулярную комбинацию (не содержащий
пропусков мотив длины w), содержащуюся в каждой из белковых
последовательностей Si, #2, • • • > Sn- Принято допущение о том, что появления
символов в пределах мотива описаны позиционной моделью независимого
порождения с параметрами qia (вероятность появления символа а в
участке г мотива, где г = 1,..., w). Фоновая модель независимого порождения
с параметрами ра описывает появления символов вне мотива. Начальный
шаг алгоритма — приписывание начальных позиций мотива ai, аг,..., un
в каждой из последовательностей, соответственно, Si, S2, • • •, Sn-
Последовательности выравниваются с сопоставлением позиций ai,a2,. •. , ajv>
при этом мотивы выравниваются как единый блок без пропусков. Далее
алгоритм продолжает работу следующим образом:
1) Шаг оценки. Одна из последовательностей, скажем Sj=(xi,... ,xm),
выбранная или наугад, или в заданном порядке, удаляется из набора. Для
оставшихся N — 1 последовательностей параметры qia и ра
переоцениваются методом наибольшего правдоподобия по подсчётам символа а в
соответствующих участках, соответственно, в пределах или вне мотива. При
малых значениях N могут быть использованы псевдоотсчёты Ьа.
2) Шаг осуществления выборки. Новая начальная позиция a,j мотива
в последовательности Sj отбирается с вероятностью P(a,j), равной
нормализованному значению отношения шансов Raj:
QlxajQ2xaj+1 X • • • X g«;a5ei+w_1
3 PxajPxaj+l X • • • X Рх^+п-г
Таким образом, множество начальных позиций ai,..., ам мотива
переопределяется и алгоритм возвращается к шагу 1.
Поскольку правдоподобие L = П^=1 ^<ъ> как ожидается, должно
возрастать на каждом шаге итеративной процедуры, алгоритм сходится ко
множеству начальных позиций al,a2,...,a*N мотива (в каждой
последовательности), которое максимизирует правдоподобие L, хотя оно может быть
и локальным максимумом. Одновременно с этим по выравниванию
определяется не содержащее пропусков оптимальное локальное выравнивание,

236
Глава 6
связанное с числами а\, а\,..., a*N, которые отмечают начальные позиции
мотива в последовательностях Si, S2,..., Sn-
Алгоритм может быть видоизменён так, чтобы он мог работать со
множественными мотивами в пределах последовательностей и определять
оптимальную ширину мотива w в процессе итераций. Чтобы избежать
запирания в неоптимальном локальном максимуме, авторы предлагают вводить
после установленного числа итераций смещения во всех текущих
начальных позициях ai,..., ам. Эти смещения делаются наугад с вероятностью
отбора нового множества начальных позиций, пропорциональной
правдоподобию L выравнивания, связанного с этим множеством. Время счёта
алгоритма равно М х N х L х w, где L — средняя длина выравниваемых
последовательностей и М — число итераций (для единственного мотива
среднее число итераций до схождения, как ожидается, будет не более ста).
Подробное описание осуществления выборки Гиббса может быть
найдено в [180].
Задача 6.4. Покажите, что не содержащее пропусков локальное
множественное выравнивание с максимальным правдоподобием обладает
минимальным значением суммы позиционных энтропии. Сделайте допущение
о том, что в качестве статистической модели мотива, связанного с
локальным множественным выравниванием без пропусков, выбрана позиционная
модель независимого порождения.
Решение. Правдоподобие блока выравнивания последовательностей,
имеющего размер w (без пропусков), определяется как произведение значений
правдоподобия последовательностей х^, где к = 1,2,..., N, участвующих
в выравнивании:
N N
k=l fc=l
Здесь ргх — параметр позиционной модели независимого порождения —
отражает вероятность появления символа х из алфавита размера М в
позиции г. Мы преобразуем выражение для правдоподобия L от произведения
«по строкам» к произведению «по столбцам» следующим образом:
L = PlxlPl! ■ ~р%р№. ■ ■ -РЫА ■ • 'И» =

6.3. Дополнительная литература
N N N
= nrfiIR-IIrir =
г=1 г=1 г=1
ММ М
771=1 771=1 771=1
Здесь пгт обозначает число появлений символа т в позиции j, и nJm ~ р>шN
при достаточно больших N. Тогда
м
l0g2 L~N EPml0g2Pm +
771=1
м м
+АГ £ z£>g2*4 + • • • + N £ р£log2p- = (6.7)
m=l m=l
= -AT £ Я,.
г=1
Уравнение (6.7) подразумевает, что — log2 L/N = Н, где Н — сумма
значений позиционной энтропии Щ. Поэтому значение энтропии Н не
содержащего пропуски выравнивания с максимальным правдоподобием L
минимально.
Замечание. В [25] было получено решение задачи в приведённой
выше постановке для случая последовательностей, описываемых
неоднородной марковской цепью. □
6.3. Дополнительная литература
С середины 1990-х гг. было представлено несколько новых
алгоритмов множественного выравнивания последовательностей. В [32] предложен
симметрически-итеративный метод множественного выравнивания
белковых последовательностей. Этот метод сочетает в себе статистическую
процедуру поиска мотивов с локальным динамическим программированием.
В алгоритме DIALIGN, разработанном Моргенштерном [198],
множественное вьфавнивание основывается на множестве не содержащих пропуски
попарных локальных выравниваний (связанных с диагоналями матрицы).
Счёт целого выравнивания определяется как сумма весов затронутых
диагоналей (штрафы за пропуски не налагаются). Новая версия этой
программы, DIALIGN 2 ([197]), выбирая меньше, но более длинных диагоналей,

238
Глава 6
работает значительно быстрее, чем DIALIGN. Алгоритм T-Coffee
прогрессивного типа был предложен в [208]. Вместо матрицы замен,
используемой в традиционных методах прогрессивного выравнивания, этот
алгоритм использует для вьфавнивания последовательностей позиционную
систему очков. В [183] представлен алгоритм, сочетающий в себе алгоритм
прогрессивного выравнивания с профильной СММ и вероятностной
моделью эволюции ДНК или белка. В [223] предложен итеративный алгоритм
со взвешенными парными суммами, который использует стратегию типа
разделяй-и-властвуй (DCA; см. [271]) наряду с динамическим
программированием в сокращённом пространстве поиска. Авторы [37]
разработали Multi-LAGAN — алгоритм прогрессивного выравнивания для
гомологичных геномных последовательностей. Попарные выравнивания в Multi-
LAGAN выстраиваются программой LAGAN ([37]), которая отбирает
оптимальное множество неперекрывающихся локальных выравниваний с
последующим выравниванием промежуточных фрагментов последовательностей
посредством алгоритма Нидлмена-Вунша. В [157] предложен алгоритм
оптимального выравнивания по принципу максимальной экономичности с
линейной стоимостью пропуска для любого числа последовательностей,
связанных деревом (с целью сокращения требуемой памяти этот алгоритм
использует алгоритм с линейным пространством, представленный в [118]).
В [64] была представлена вероятностная непротиворечивость —
модификация системы счетов парных сумм, включающая в себя полученные
с помощью СММ апостериорные вероятности и непротиворечивость
трёхходового выравнивания. Та же группа разработчиков предложила алгоритм
прогрессивного множественного выравнивания белков ProbCons, в котором
функция счёта основана на вероятностной непротиворечивости.
Другая целевая функция для множественного выравнивания, norMD,
была представлена в [268]. В norMD — системе очков на основе столбцов —
используются счета средних расстояний (СР), применяемые в CLUSTALX.
Счета СР нормализуются по числу выравниваемых последовательностей и
по их длинам.
Модель распространения множественного выравнивания,
представленная в [182], объединяет подход, построенный на профильных СММ, с
опирающейся на блоки выборкой Гиббса.
В [266] приводится сравнительная оценка десяти часто применяемых
алгоритмов множественного выравнивания. В качестве эталонного теста
авторы использовали набор BAHBASE — множество структурно
проверенных выравниваний ([267]). Выравнивание, построенное каждым из
испытуемых алгоритмов, было оценено несколькими целевыми функциями,
определяющими близость вьфавнивания к соответствующему эталонному

6.3. Дополнительная литература
239
выравниванию. Данная сравнительная оценка алгоритмов множественного
выравнивания позволила произвести идентификацию стратегий
выравнивания, наиболее подходящих для данного набора последовательностей.
Характеристики программ множественного выравнивания, такие как
устойчивость, мобильность, удобство для пользователя, подвергаются
непрерывному усовершенствованию (см., например, [48], в котором
сообщается об относительно недавних обновлениях в серии программ
CLUSTAL).

Глава 7
ПОСТРОЕНИЕ
ФИЛОГЕНЕТИЧЕСКИХ ДЕРЕВЬЕВ
Обсуждение концепции попарного выравнивания последовательностей
и алгоритмов поиска оптимальных выравниваний было разделено в «АБП»
на две главы (главы 2 и 3). Глава 2 была посвящена обычным
детерминистическим (невероятностным) алгоритмам динамического программирования,
а глава 3 — полному вероятностному подходу к попарному выравниванию
последовательностей с помощью парной СММ.
Точно так же обсуждение концепций филогенетических деревьев
и алгоритмов построения филогенетических деревьев было распределено
в «АБП» между главами 7 и 8. В главе 7 были представлены
невероятностные методы и приведены основные определения, инвентарь
топологий деревьев, разъяснение свойств эволюционного расстояния и описание
обычных невероятностных алгоритмов, таких как алгоритмы группировки
(UPGMA) и соединения соседей, а также алгоритмов на принципе
экономичности. Этот всесторонний материал заканчивался описанием
невероятностных алгоритмов одновременного выравнивания и построения
филогении. Перевод теории построения филогенетических деревьев на
вероятностные рельсы был оставлен для главы 8.
Задачи, включенные в главу 7, требуют знания комбинаторики и теории
графов. Возможно, уровень трудности некоторых из этих задач один из
наиболее высоких в «АБП».
Дополнительные задачи предлагают практику работы с алгоритмом
UPGMA и методами построения дерева на принципе соединения соседей,
а также дают шанс вывести полезную комбинаторную формулу для
вычисления числа помеченных историй.

7.1. Оригинальные задачи 241
7.1 • Оригинальные задачи
Задача 7.1. Начертите корневые деревья, полученные путём добавления
корня (в семи возможных позициях) к представленному на следующем
рисунке некорневому дереву.
*й»!!Ш5аШШ!Щ*53»ЙКЗ&
Решение. Добавление корня по очереди к каждому из семи рёбер
позволяет получить семь деревьев с различными помеченными схемами,
представленных на рис. 7.1. □
Задача 7.2. Сколько листьев должно быть на корневом и на некорневом
дереве, чтобы было возможно получить более одной непомеченной схемы
ветвления? Найдите рекуррентное соотношение для числа корневых
деревьев.
Решение. Пусть Мп — число корневых деревьев с п листьями. Очевидно,
что М\ = N2 = Л/3 = 1, и эти типы непомеченных схем ветвления
(топологии) следующие:

242
Глава 7
Корень Корень
Корень Корень 4 Корень
Рис. 7.1. Семь деревьев, построенных по принципу, изложенному в задаче 7.1

7.1. Оригинальные задачи
243
В случае корневого дерева с четырьмя листьями существуют две различные
топологии (Л/4 = 2):
Поэтому для того чтобы допустить более одной непомеченной схемы
ветвления, корневое дерево должно иметь по крайней мере четыре листа.
Рассмотрим некорневые деревья. Деревья с тремя, четырьмя и пятью
листьями имеют лишь одну непомеченную схему ветвления:
В случае дерева с шестью листьями есть две возможные непомеченные
схемы ветвления, которые выглядят следующим образом:
Следовательно, чтобы допустить более одной топологии, некорневое дерево
должно иметь по крайней мере шесть листьев.
Чтобы вывести рекуррентную формулу для Afn, можно сосчитать все
возможные способы получения корневого дерева с п листьями путём
соединения двух корневых деревьев с I и п — I листьями (I < п — I) их
корнями.
Если п — нечетное число, причём п = 2к + 1, где А; > 0, то любые два
«поддерева» будут иметь различное число листьев 1ип — 1(1<п — 1)и
обязательно будут иметь различную топологию только из-за различного числа

244
Глава 7
листьев. Поэтому, соединяя дерево с I листьями и дерево с п — I листьями
корнями, можно получить MiMn-i различных топологий. Следовательно,
рекуррентная формула имеет вид
к
1=1
При п = 2к, где к > 1, в подобной формуле мы должны сделать
корректировку для члена М%, соответствующего соединению «поддеревьев» с к
листьями каждое, дабы избежать многократного подсчёта топологий,
связанных зеркальной симметрией. Член М% должен быть заменён на ( £) -Ь
-Ь М, где ( 2fc) — число возможных пар различных топологий среди Мк,
а Мк — число пар деревьев с топологиями одинакового типа. Таким
образом, искомое рекуррентное соотношение имеет вид
Мп=Мги = £-W„_, + Щ^1 +Мк =
1=1
1=1
При малых п рекуррентные формулы дают: Мъ = 3, Л/в = 6, Mr = 11,
Ms = 23, М9 = 46, Mo = 98. □
Задача 7.3. Все деревья, которые мы рассматривали до сих пор, были
бинарными, но легко представить троичные деревья, у которых в корневой
форме из внутренних узлов выходят по три ветви. Поэтому у некорневых
деревьев из каждого внутреннего узла исходит по четыре ребра. Если в
некорневом троичном дереве есть т внутренних узлов, то сколько на нём
листьев и сколько в нём рёбер?
Решение. Обозначим число листьев и рёбер некорневого троичного дерева
с т внутренними узлами, соответственно, как Lm и Ет. Минимальное
троичное дерево с т = 1 внутренним узлом имеет четыре листа и четыре
ребра, таким образом, L\ = Е\ = 4. Троичное дерево ст—1 узлом может
быть преобразовано в троичное дерево с т узлами путём замены одного

7.1. Оригинальные задачи
245
из листьев на новый узел с тремя листьями. Поэтому Lm = Lm_i + 2
и Еш = Ет-\ + 3 и мы имеем
Lm = Lm-i + 2 = (Lm_2 + 2) + 2 = • • • =
= Li + 2(m - 1) = 4 + 2m - 12 = 2m + 2,
^m = ^m-1 + 3 = (Em-2 + 3) + 3 = • • • =
= £?i + 3(m - 1) = 4 + 3m - 3 = 3m + 1.
□
Задача 7.4. Рассмотрите составное некорневое дерево с m троичными
внутренними узлами и п бинарными внутренними узлами. Сколько
листьев на нём и сколько рёбер? Пусть Nm,n обозначает число различных
помеченных схем ветвления этого дерева. Обобщите рассуждения,
использовавшиеся для бинарных деревьев, с тем чтобы показать, что
Nm,n = (3m + 2n - l)iVm,n_i + (n + l)iVm_i,n+1. (7.1)
Решение. В первую очередь, число листьев Ln и число рёбер Еп
двоичного дерева с п внутренними узлами определяется из выражений Ln = п + 2
и Еп = 2п + 1, которые непосредственно вытекают из рекуррентных
уравнений Ln = Ln-i + 1 и Еп = En-i -Ь 2 при L\ = 3 и Е\ = 3.
Далее, мы определяем число листьев и рёбер составного некорневого
дерева с m троичными внутренними узлами и п двоичными внутренними
узлами, соответственно, как Lm>n и i£m,n- Добавляя корневой узел к
определённому ребру, мы'получаем корневое дерево с m троичными узлами, п
двоичными узлами и корневым узлом (корневой узел не считается за
двоичный узел). Перечислением рёбер путём нисходящего обхода вершин дерева
(начиная с двух рёбер, выходящих из корня), мы пройдем через три ребра
дерева, выходящие из каждого троичного узла, с общим количеством Зт
рёбер, и два ребра, выходящих из каждого двоичного узла, с общим
количеством 2п рёбер. Наконец, добавляя ребро, соединённое своей вершиной
с корнем дерева, мы получаем
Етуп = Ет + Еп - 1 = Зт + 1 + 2п + 1 - 1 = Зт + 2п + 1-
Та же самая логика позволяет нам вывести формулу для числа
листьев Lm>n. Снова, совершая обход дерева в нисходящем порядке начиная

246
Глава 7
от корня, мы будем спускаться вдоль Зга -Ь 2п + 2 рёбер дерева (ребро с
корнем подсчитывается дважды). Спуск по ребру приведёт нас или к
внутреннему узлу, или к листу. Мы встретим внутренние узлы га + п раз и
листья (Зга + 2п + 2) — (га + п) раз. Поэтому
Ьт,п = (3™ + 2п + 2) - (га + п) = 2га + п + 2.
Теперь пусть Nm^n обозначает число различных помеченных схем
ветвления рассматриваемого составного дерева. Это дерево может быть
построено либо 1) из составного дерева с га троичными узлами и п — 1 двоичными
узлами путём добавления нового ребра к одному из i£m>n_i = Зга + 2п — 1
существующих рёбер и создания таким образом дополнительного
двоичного узла; либо 2) из составного дерева с га — 1 троичными узлами и п + 1
двоичными узлами посредством добавления ребра к одному из п+1
двоичных узлов и создания таким образом нового троичного узла. Поэтому мы
имеем рекуррентную формулу для Nm^n в следующем виде:
Nm,n = (Зга + 2n - l)JVmin_i + (n + l)iVm_i,n+1.
Здесь Зга + 2п — 1 — число способов добавления нового ребра к
существующему ребру дерева с га троичными узлами и п — 1 двоичными узлами, то
есть число рёбер дерева Sm,n-i = Зга + 2(п — 1) + 1 = Зга + 2п — 1; точно
так же п + 1 — число способов добавления нового ребра к двоичному узлу
дерева с га — 1 троичными узлами и п + 1 двоичнными узлами, которое,
как очевидно, равно п + 1.
Замечание. Учтите, что для двоичных деревьев с п внутренними
узлами (га = 0) мы имеем ЛГ0)П = (2п — 1)ЛГ0,п-1, причём ЛГ0)1 = 1. Тогда
No,n = (2n — 1)!! или, в единицах числа листьев, NEn = (2Еп — 5)!!. □
Задача 7.5. С помощью рекурсивного соотношения из задачи 7.4
вычислите для малых значений га число АГт0 различных чисто троичных деревьев
с га внутренними узлами. Проверьте, удовлетворяют ли вычисленные числа
выражению
AU,0 = n(l + ^). (7.2)
Докажите формулу (7.2).

7.1. Оригинальные задачи
247
Решение. В первую очередь мы используем рекуррентную формулу (7.1),
чтобы определить для нескольких малых значений т число различных
помеченных схем ветвления троичных деревьев с т внутренними узлами.
Поскольку Nmy-i = 0, мы имеем
Nlt0 = АГ0,1 = (2 - 1)!! = 1,
N2,o = Nltl = 4ATlj0 + 2iV0,2 = 4 + 2(3!!) = 10,
N3,0 = N2,i = 7iV2,0 + 2Nh2 = 70 + 2(6АГ1Д + 3iV0,3) =
= 70 + 2(60 + 3(5!!)) = 280,
iV4,o = N3A = 10AT3,o + 2AT2)2 = 2800 + 2(9AT2jl + WhS) =
= 2800 + 2[9(7iV2,0 + 2АГ1)2) + 3(8ЛГ1>2 + 4АГ0,4)] =
= 2800 + (9 • 280 + 3 • 1260) = 15 400.
Очевидно, что при увеличении т величина iVmjo очень быстро
возрастает. Можно легко убедиться в том, что расчётные значения величины Nmjo
удовлетворяют уравнению iVm)o = I"I£Li(l + 9*(« — 1)/2):
АГ1)0 = 1 = (1 + 9-1-0/2),
^2,0 = 10 = ^,0(1 + 9.2.1/2),
N3,o = 280 = ЛГ2)0(1 + 9 • 2 • 3/2),
АГ4,о = 15 400 = АГ3,о(1 + 9 • 3 • 4/2).
Во-вторых, мы представим доказательство уравнения (7.2). Мы убедимся в
том, что при п ^ 3 существует взаимно однозначное соответствие между
деревьями Тп с п помеченными (внутренними и листовыми) узлами и пп~2
последовательностями (ai, a2,..., an_2), которые могут быть образованы
из чисел 1,2, ...,га. Это утверждение представлено в виде теоремы 2.1
в [196] со ссылкой на гораздо раннюю работу [47]. Мы начинаем
доказательство взаимно однозначного соответствия, убеждаясь в том, что дерево
с п узлами определяет последовательность (ai,a2,... ,an_2). Процедура
порождения этой последовательности для дерева Тп с узлами,
помеченными целыми числами 1,2,..., п, названа построением Прюфера ([218]). Мы
опознаём лист с наименьшей меткой и удаляем этот узел и входящее в него
ребро из дерева Тп. Метка узла, с которым удалённый узел был соединён,
становится <ц. Мы повторяем этот процесс для приведённого дерева Tn_i,
чтобы определить а2, и продолжаем его до тех пор, пока не останутся
только два узла, соединённых ребром. Различные деревья Тп и Т'п определяют
различные последовательности (ai,a2,..., an_2) и (JE?i, JE?2,..., J5n_2).

248
Глава 7
Остаётся показать, что последовательность Ап-2 = (ai, a2, • • •, ап-2)
из п — 2 чисел, выбранных из чисел 1,2,..., п, уникально определяет
дерево Тп. Это можно показать постепенным восстановлением рёбер
дерева, которые мы ранее удаляли одно за другим при выполнении алгоритма
Прюфера. Мы определяем список целых чисел Ln-2 = (fti,...,bfc), где
1 < Ь\ < Ъ2 < • - - < bk < п, состоящий из чисел, отсутствующих в Ап-2 (в
Ln_2 есть по крайней мере два элемента). Очевидно, что в силу правил
построения Прюфера Ь\ — лист, соединённый с а\. В первом шаге мы удаляем
а\ из Ап-2, Ъ\ из Ln-2 и получаем Ans = (аг,..., ^п-г). Если а\
появляется в Ап-з, то мы определяем новый список как Ln_3 = (&2, • • • ,Ь*);
в противном случае Ьп-з = (&2> • • •, &fc, ai). После перестановки
элементов последовательности Ln_3 (если необходимо) в порядке возрастания мы
получаем Ln_3 = (Ъ'ъ ..., Ь'к) (или Ln_3 = (bi,..., bJb_i)) и приходим к
выводу, что Ь[ — узел, соединённый с а2. В следующем шаге мы
удаляем а2 из .Ап_з, Ь[ из Ln_3, повторяем процедуру, описанную выше, чтобы
определить узел Ь", прикреплённый к аз в дереве Тп, и так далее. Когда
этот алгоритм достигает шага п — 3, мы будем иметь одноэлементную
последовательность А\ = (an_2), и мы можем доказать, что список L\ будет
содержать ровно два элемента Ь\ и Ь^. Действительно,
|Li| = fc - (п - 3) + (п - к + 1) = 2,
где к — размер начального списка Ln-2> п — 3 — число принудительных
удалений наименьших членов списков, а п — fc + 1 — число вставок
элементов аш в списки Ln_3,..., L2, равное числу различных элементов среди
(ai, аг,..., ап-з)> не равному an_2. В этом (предзаключительном) шаге Ь\
соединяется с an_2. Затем an_2 повторно вставляется в А0, а &£
соединяется с an_2. В результате мы имеем последовательность из п — 1 рёбер
(bi, ai), (bi, a2), (Ь", аз), • • •, (bj, an-2), №2» an-2), которая уникально
определяет дерево Тп (все рёбра различны, потому что в каждом шаге после
соединения аш минимальный Ъщ удаляется из списка; каждое число от 1 до п —
конец по крайней мере одного ребра в наборе (bi, ai),..., (ft^, a>n-2))- Более
того, применяя алгоритм Прюфера к дереву ТП9 мы должны получить ту же
самую последовательность Ап-2 = (ai, аг> • • • j ^n-2)- Следовательно,
построение Прюфера определяет взаимно однозначное соответствие между
этими последовательностями и деревьями Тп.
Из доказанного утверждения мы можем вывести достаточно общее
следствие о числе помеченных деревьев в единицах степеней их узлов.
Степень узла определяется как число рёбер, входящих в этот узел. Мы
можем связать с деревом Тп последовательность степеней (di, cfo,..., dn),
где di — степень узла г, причём г = 1,...,га. В последовательности

7.1. Оригинальные задачи
249
(ai,a2,... ,ап-2)? построенной для дерева Тп посредством построения
Прюфера, каждое число г, где г = 1,..., п, будет появляться в точности
di — 1 раз. В случае дерева Тп с данной последовательностью степеней
узлов число способов выбора позиций для меток равно полиномиальному
коэффициенту
( п~2 )■
\di - l,d2 - l,...,dn - 1/
Поэтому благодаря взаимно однозначному соответствию между
деревьями и последовательностями, число Л/* деревьев с п помеченными
(внутренними и листовыми) узлами 1,2,... ,га и последовательность степеней
(di, с?2,..., dn) определяются одним и тем же полиномиальным
коэффициентом:
\di - 1, d2 - 1,..., dn - 1/
(7.3)
Рассмотрим троичное дерево Т с та внутренними узлами. Согласно
формуле, доказанной в задаче 7.3, это дерево имеет 2т + 2 листьев. Общее
число (внутренних и листовых) узлов дерева Т равно Зт 4- 2; пусть листья
будут помечены числами от 1 до 2га + 2, а внутренние узлы — числами
от 2га + 3 до Зга + 2. Тогда последовательность степеней,
соответствующая дереву Т, имеет вид (1,..., 1,4,..., 4) и содержит 2га + 2 единиц и га
четвёрок. Согласно уравнению (7.3) число деревьев с такой
последовательностью степеней определяется выражением
/ (Зга + 2) - 2 \ _ / Зга \
у>,..-,о,з,...,зу и...,о,з,...,з;
(Зга)! _ (Зга)!
(3!)m ~ 6т "
Чтобы определить число N^ троичных деревьев с помеченными
листьями (и непомеченными внутренними узлами), мы отмечаем, что среди всех
(Зга)!6_7П деревьев есть группы размера га! с закреплёнными листьями и
всеми возможными перестановками меток для внутренних узлов, которые
опознают одно и то же дерево с помеченными листьями и непомеченными
внутренними узлами. Следовательно, мы имеем
N* = ^1. (7.4)
m 6mro! *- '
Хотя это и не очевидно, но формулы (7.2) и (7.4) эквивалентны.
Действительно,
»-,-n(i+^)-

250
m
i=l
1-2
2 + 9г2 -
2
•4-5-7
Глава 7
Jti
•8-
(3m)!
i=l
... • (3m -
2m
- 2)(3i -
2
- 2) (3m
(3m)! _
ill:
-1)
= лг*
(2m)3 • 6 • 9 •... • (3m) 6mm!
Замечание З. Интересно, что формула (7.3) числа деревьев в
единицах степеней узлов дерева может быть использована для вывода формулы
(в явном виде) числа ЛГШ)П составных деревьев с га троичными, и п
двоичными внутренними узлами, и помеченными листьями (см. задачу 7.4).
Любое составное дерево с га троичными и п двоичными внутренними
узлами имеет ЬШуП = 2га + п + 2 листьев (это было доказано в задаче 7.3).
Общее число (внутренних и листовых) узлов дерева равно Зга + 2п + 2; мы
приписываем к листьям числа от 1 до 2га + п + 2 и ко внутренним узлам —
числа от 2га+п+3 до Зга+2п+2. Существует (7ПТ^П) последовательностей
степеней (di,d2,. •. ,йзт+2п+2), соответствующих составным деревьям с
такой разметкой узлов (так как есть (mr^n) возможностей выбрать га
позиций, чтобы разместить четвёрки среди d2m+n+3, • • •, d3m+2n+2; di = • • ■ =
= d2m+n+2 = 1)- По уравнению (7.3) каждая из этих последовательностей
степеней определяет
(Зга + 2п)! _ (Зга + 2п)!
(3!)m(2!)n ~ 6m2n
составных деревьев с помеченными внутренними и листовыми узлами.
Чтобы определить число Nmjn составных деревьев с помеченными
листьями (и непомеченными внутренними узлами), мы отмечаем, что (га+п)!
различных деревьев с закреплёнными метками листьев и всеми возможными
перестановками меток внутренних узлов (среди (7Пт^п)(Зга + 2n)!6~m2~n
деревьев с помеченными внутренними и листовыми узлами) опознают
одно и то же дерево с помеченными листьями и непомеченными внутренними
узлами. Таким образом, мы получаем
ГГ)(3™ + 2п)! (3m + 2n)!
m,n~ 6m2n(m + n)! -*»««»-•-•• ('-D}

7.1. Оригинальные задачи 251
Замечание 4. Уравнения (7.4) — частный случай уравнения (7.5) при
п = 0.
Замечание 5. Рекуррентное соотношение, представленное
уравнением (7.1), может быть выведено также и из уравнения (7.5):
(Зтп + 2n - l)iVm,n-i + (гг + l)ATm_lin+1 =
,ч (Зггг + 2гг-2)! . . (Зтп + 2гг -1)!
= (Зггг + 2п - 1)-1—-т——4т: + (гг + 1)-
e^^mKn-l)! y6m-12n+1(m-l)!(n + l)!
(3m + 2n-l)! (3m + 2n-l)! ,
6m2n-1m!(n - 1)! Ьт-12п+1{т - 1)!
(Зт + 2гг-1)!
\6т An J
(Зт + 2п-1)! Зт + 2п Зт + 2гс)!
6m-i2n-i(m _ 1)|(п _ Х)| 12тгг 6т2пт!гг!
= tfw
Дополнительные сведения по подсчёту полихотомических деревьев могут
быть найдены в [79]. □
Задача 7.6. Покажите, что если расстояния между группами Ci,Cj
определяются через среднее расстояние между элементами
и если Ck = CiU Cj,*To dki при любых Z определяется из
dulCil-^djilCjl
dki
ICil + IQI
Решение. Если Ck = CiU Cj aCi — любая другая группа, то из
определения расстояния между группами, приведённого выше, мы имеем
*РЯ
У у dpq — 2_^ dpq + 2^ dp
jgCj, pecf, ?eCj,
jGC^fc д€С* g€Cj
= d«|Ci||C,| + d„|Ci||C,|. (7.7)

252
Глава 7
Поскольку \Ск\ = \Ci\+\Cj\, уравнение (7.7) позволяет переписать формулу
для dki следующим образом:
, _ 1 v^ , _du\Ci\\Ci\ + djl\Cj\\Cl\ _
** ~ \Ci\\Cu\ jbl™ Ш|С,| + |С,|) "
eecfc
= du\Cj\ + dji\Cj\
Задача 7.7. Покажите, что в дереве, построенном алгоритмом UPGMA,
всякий узел всегда находится выше своих дочерних узлов.
Решение. При построении корневого дерева алгоритм UPGMA в каждом
шаге выбирает две группы г и j с минимальным расстоянием d^,
объединяет их в новую группу к и помещает новый узел на высоте Кц = dij/2.
Затем он удаляет минимальное значение dij из множества всех попарных
расстояний и замещает все расстояния du и dj\ (I — любая другая
группа) расстояниями dki между новой группой к и группой /, определяемой
уравнением (7.6). Мы покажем, что
di'ji ^ dij (7.8)
для любого расстояния dyj» во множестве попарных расстояний,
определённых для следующего шага алгоритма UPGMA. Если d^j» не включает
в себя новую группу к, то неравенство (7.8) верно, потому что d^
было отобрано как минимальное расстояние после сравнения всех d^j*, тогда
как di'j' остается одним и тем же для пар г', f, таких что if,jf^i,j. Теперь
dki ^ mm(du,dji)
для любой группы I, поскольку dki — взвешенное среднее расстояний du
и dji (см. задачу 7.6). С другой стороны, неравенства du ^ dij и dji ^ dij
верны при любых I, поскольку dij было выбрано как минимальное
расстояние, таким образом, dki ^ dij при любых I. Это доказывает
неравенство (7.8). Отыскание минимума среди расстояний dyj» (скажем, di*j*)
определит новую пару групп г* и j* для объединения в новый узел с
высотой hi*j* = di*j*/2. Мы имеем hi* j* ^ Кц и видим, что
последовательность высот узлов, последовательно выстраиваемая алгоритмом UPGMA,
неубывающая. Для любого дочернего узла родительский узел будет
найден в одном из более поздних шагов алгоритма и, следовательно, никакой
дочерний узел не может лежать выше своего родительского узла.

7.1. Оригинальные задачи
253
Замечание. Здесь представлен простой пример, когда высота
дочернего узла равна высоте родительского узла. Допустим, что три
последовательности х\9 Х2, хз удовлетворяют равенству d\2 = ^23 = ^13 = d. В первом
шаге процедуры группировки мы можем выбрать любую пару листьев для
объединения в новую группу 4. Мы выбираем листья 1 и 2 и помещаем
узел 4 на высоте d/2. Новое расстояние сЦз = dis = с^з = d\ таким
образом, после этого мы объединяем группу 4 и лист 3, после чего помещаем
узел 5 на высоте d/2. Так как дочерний узел 4 и родительский узел 5 имеют
равную высоту, они слияются и образуют троичный узел. Таким образом,
последовательности х\9 Х2, хз становятся дочерьми троичного узла, что
является наилучшим способом построить дерево для этих
последовательностей. □
Задача 7.8. Говорят, что расстояния между последовательностями
являются ультраметрическими, если для любой тройки последовательностей
xl,xj,xk расстояния dij,djk,dik или все равны, или два из них равны, а
третье меньше каждого из них. Можно показать, что если расстояния d+j
являются ультраметрическими и если дерево построено из этих расстояний
алгоритмом UPGMA, то расстояния, полученные из этого дерева путём
выбора вдвое большей высоты узлов на пути между г и j, идентичны dy.
Проверьте, верно ли это утверждение в примере, где алгоритм UPGMA
применён к пяти последовательностям и расстояния являются
ультраметрическими.
Решение. Чтобы проверить это свойство, мы рассмотрим три возможные
различные непомеченные схемы корневых деревьев с пятью листьями.
Принято допущение, что все деревья построены алгоритмом UPGMA из
расстояний, удовлетворяющих условию ультраметричности. В каждом случае
листья дерева помечены для удобства.
а) В следующей, представленной ниже, схеме ветвления (обозначаемой
как (((2 + 1) + 1) + 1)): .
9|
8
1\
6.
1
2 3 4 5

254
Глава 7
самые близкие группы в первом прогоне алгоритма UPGMA — листья 1 и 2.
Расстояние d\2 вдвое больше высоты узла 6. Затем листья 1 и 2
объединяются в новую группу 6, и все расстояния d^, где г = 3,4,5, удовлетворяют
выражению с^г = \{du + d2i) = dii = d>2i ввиду свойства ультраметрично-
сти. В ходе второго прогона алгоритм соединяет ближайшие группы 6 и 3,
тогда как расстояние с^з = ^13 = ^23 вдвое больше высоты узла 7. Теперь
мы объединяем группу 6 и лист 3 в новую группу 7 и для расстояний dji,
где г = 4,5, мы имеем d7i = i(dii + d2i + d3i) = du = d2i = d3i в силу
свойства ультраметричности. Следующая пара ближайших групп —
группа 7 и лист 4, и расстояние с?74 = du = d24 = с?34 такого же размера, как
высота узла 8. Группа 7 и лист 4 объединяются в новую группу 8, тогда
как dS5 = \{di5 + d25 + d35 + d4b) = d13 = d2b = d35 = d45
благодаря свойству ультраметричности. Последний узел, 9, помещается на высоте
2^85 = 2^15 = |^25 = |^35 = ^45- Таким образом, мы убедились в том,
что расстояние dij между листьями г и j вдвое больше, чем высота самого
высокого узла дерева между г и j.
б) Во второй схеме ветвления ((2 + 2) + 1):
I 9
|8
17
1б
1 2 3 4 5
самые близкие группы в первом прогоне алгоритма UPGMA — листья 1 и 2.
Расстояние d\2 вдвое больше, чем высота узла 6. Мы соединяем листья 1
и 2 в новую группу 6, и все расстояния й&, где г = 3,4,5, удовлетворяют
выражению d^ = ~ (di* + d2i) = du = d2i по свойству ультраметричности.
На втором прогоне ближайшие группы — листья 3 и 4 и расстояние d34
вдвое превышает высоту узла 7. Затем листья 3 и 4 объединяются в новую
группу 7 и тогда d76 = |(di3 + d23 + du + d24) = d13 = d23 = du =
= c?24 и ^75 ^(d35 + с?4б) = d35 = d^ из-за свойства ультраметричности.

7.1. Оригинальные задачи
255
Следующая пара ближайших групп — группы 6 и 7 и расстояние d67 =
= di3 = ^2з = du = ^24 вдвое больше высоты узла 8. Мы определяем
новую группу 8, соединяя группы 6 и 7, тогда как dg5 = \{di5 + g?25 +
+ dss + ^45) = di5 = c?25 = ^35 = ^45- Поэтому для последнего узла, 9,
помещённого на высоту ^с?85> мы имеем dss = ^15 = ^25 = fe = ^45, что
завершает доказательство для случая б.
в) В последней схеме ветвления ((2 + 1) + 2):
\9
18
[7
16
1 2 3 4 5
ближайшие группы в первом прогоне алгоритма UPGMA — листья 1 и 2.
Расстояние d\2 вдвое больше высоты узла 6. Мы соединяем листья 1 и 2 в
новую группу 6, и для всех расстояний dGi, где г = 3,4,5, равенство й6г =
= \{d\i + с?2г) = ^1г = с?2г верно из-за свойства ультраметричности. Во
втором прогоне ближайшие группы — 6 и 3, и расстояние d63 = d\z = с^з
вдвое больше, чем высота узла 7. Мы вводим новую группу, 7, соединяя
группу 6 и лист 3, и для обоих расстояний мы имеем d?i = ^(du + dii +
+ ^зг) = du = d2i =>dsi из-за свойства ультраметричности. Следующая
пара ближайших групп — листья 4 и 5, и расстояние d±b вдвое больше
высоты узла 8. Листья 4 и 5 объединяются в новую группу 8. Теперь для
расстояния d78 мы имеем d78 = h(di4 + di5 + б?24 + d2s + d34 + d35) =
= di4 = di5 = б?24 = ^25 = 6^34 = ^35- Поэтому для последнего узла, 9,
помещённого на высоту ^drs9 мы имеем d78 = ^14 = ^15 = ^24 = ^25 =
= 6^34 = ^35- На этом доказательство завершено. □
Задача 7.9. В дереве с аддитивными длинами рёбер d мы определяем
расстояние Dij между листьями г и j следующим образом:
Dij=dij-(ri + rj), (7.9)

256
Глава 7
где
и \L\ обозначает мощность множества листьев L. Покажите, что
наименьшие расстояния Dij в представленном ниже дереве соответствуют взаимно
соседним листьям.
0.1
Решение. Здесь \L\ = 4, и мы с помощью уравнения (7.9) получаем:
П = |(0,5 + 0,3 + 0,6) = 0,7,
г2 = ^(0,5 + 0,3 + 0,6) = 0,7,
гз = ±(0,5 + 0,6 + 0,9) = 1,
г4 = ±(0,5 + 0,6 + 0,9) = 1.
Поэтому
D12 = d12 - (n + r2) = 0,3- (0,7 + 0,7) = -1,1,
D13 = d13-(r1+r3) = 0,5 -(0,7 + 1) = -1,2,
D14 = dM - (ri +г4) = 0,6- (0,7+ 1) = -1,1,
D23 = d23 - (r2 + ra) = 0,6 - (0,7 + 1) = -1,1,
Aw = d24 - (ra + r4) = 0,5 - (0,7 + 1) = -1,2,
#34 = <*34 " (ГЗ + Г4) = 0,9 - (1 + 1) = -1, 1.
Мы можем видеть, что два равных минимальных значения D, D\3 =
= Дм = —1,2 действительно соответствуют парам соседних листьев: (1,3)
и (2,4).

7.1. Оригинальные задачи
257
Замечание. Обратите внимание, что D, определяемое
уравнением (7.9), не удовлетворяет свойствам обычного расстояния. Как мы
увидели, D^ может быть отрицательным и, что удивительно, Da = da — 2ri =
= -2п ф 0. □
Задача 7.10. Покажите, что в случае дерева с четырьмя листьями
значения D^ для пары соседей меньше, чем D для всех остальных пар на «длину
мостика», то есть длину ребра, соединяющего два внутренних узла в
дереве.
Решение. Следует обратить внимание на то, что в задаче 7.9 значения Dis
и £>24 Для пар соседей действительно меньше, чем Dij для остальных пар
листьев на «длину мостика» 0,1. Доказательство этого свойства для
общего дерева с четырьмя листьями, |L| = 4, не вызывает затруднений (см.
рис. 7.2).
Рис. 7.2. Обозначение рёбер, принятое в задаче 7.10
Для заданных равенств
r2 = ±(d2 + d1+d2 + d + d3 + d2 + d + d4) = d+dl+Sd2 + d3+d\
rs = kd3+d4+d3+d+d1+ds+d+d2)=d+di+d2tsd3+d\
u = ±(d4 + d3 + d4 + d + d1 + d4 + d + d2) = d+dl + d2\d3 + 3d4

258
Глава 7
мы находим
#12
#13 :
#14 :
= di2 -
= dis -
= du -
- (п. +r2) =
- (ri + r3) =
- (ri + r4) =
= di
= di
= di
+ d2 - r\
+ d + d3-
+ d + d4-
-r2
-ri -
-ri -
= —2d — d\ — d2 — ds — бЦ,
гз = — d — d\ — d2 — ds — c?4,
Г4 = — d — d\ — d2 — ds — сЦ,
#23 = d2s — (r2 -\- rs) = d2 -\- d -\- ds — r2 — rs = —d — di — d2 — ds — сЦ,
#24 = d24 — (r2 + Г4) = d2 + d + сЦ — r2 — Г4 = —d — di — d2 — ds — d±,
#34 = d34 - (гз + Г4) = ds + сЦ - r3 - r4 = -2d - di - d2 - ds - d4.
Таким образом, для этого дерева условие верно: если D' есть значение для
двух соседей (D\2 или #34), a D" — значение для несоседей, то D" — #' =
= d, где d — длина ребра, соединяющего два внутренних узла дерева. □
Задача 7.11. Покажите, что традиционный алгоритм на принципе
экономичности ([233]) даёт ту же стоимость, что и таковой на взвешенной
экономичности ([83]), использующей веса 5(а, а) = 0 для всех а, и 5(а, Ь) = 1
для всех а фЬ.
Решение. Мы будем использовать математическую индукцию по числу
листьев дерева. Для данного участка последовательности и мы сравним
значения стоимости дерева, определяемые по методам взвешенной
экономичности и традиционной экономичности.
Сначала мы рассмотрим дерево Т2 с двумя листьями. Если обе
последовательности х\ и х2 имеют остаток а на участке и, то традиционный
алгоритм на принципе экономичности приписывает список остатков Rc3 =
= аГ\а = {а} к корневому узлу 3, и определяемая традиционной
экономичностью стоимость дерева Т2, минимальное число замен на участке и,
равна нулю (Ст2 = Cs = 0) для предкового остатка а в корне. Алгоритм
на взвешенной экономичности работает с деревом Т2 следующим образом.
В каждом листе стоимость остатка а равна нулю, а стоимость любого
другого остатка —Ьоо. Тогда Ss(a) = 0 и Ss(b) = 2, где Ь ф а. Таким образом,
список обладающих минимальной стоимостью остатков в корне есть Rs3 =
= {а}, и определяемая взвешенной экономичностью стоимость Т2 равна
St2 = Ss(a) = 0. Следовательно, St2 = Ст2-
Если остатки а и Ъ на участке и различны, то для традиционной
экономичности список остатков в корневом узле 3 есть Rc3 = a U Ь = {а, Ь}

7.1. Оригинальные задачи
259
и традиционная стоимость Ст2 равна 1 — минимальному числу замен.
Взвешенная экономичность дает Ss(a) = 5з(Ь) = 1 и Ss(x) = 2 при х ф а, 6.
Тогда определённая взвешенной экономичностью стоимость дерева та же,
что и стоимость любого остатка из списка Rc3 в корне: St2 = Ss(a) =
= 53(Ь). И снова St2 = Ст2-
Точно так же равенство St3 = Ст3 может быть проверено для
дерева Тз с тремя листьями. Теперь мы рассмотрим дерево Tn с N
листьями. Предположим, что для двух дочерей корня г и j мы имеем Si = Ci
и Sj = Cj, и для каждого узла список минимальной стоимости и
список экономичных остатков, сохраняемые обоими алгоритмами, идентичны:
Rsi = Rd = Ri и Rsj = Rcj = Rj- Мы покажем, что в корне список
предковых остатков с минимальным числом замен и список остатков с
минимальной стоимостью Sk одинаковые, и докажем, что St = Ст-
Если RiClRj = Ф9 то список Rk остатков для традиционного алгоритма
экономичности есть Rk = i2tUi2j, а стоимость дерева Tn равна Ст = С к =
= Ci + Cj + 1. Мы предполагаем, что Ri = {ai,..., am}, Rj = {&i,..., bn}
и, следовательно, что
Sk(ai) = Si(ai) + Sj(h) + 1 = d + Cj + 1,
Sk(bq) = Si(ai) + 1 + Sj(bq) = d + Cj + 1,
Sk{x) = Si(ai) + 1 + Sj(bi) + 1 = Ci + C,- + 2
при всех х 0 i?fc, / = 1,..., m и q = 1,..., п. Таким образом, по принципу
взвешенной экономичности стоимость дерева Tn равна
ST = SkM = ••• = Sk(am) = Sk(h) = ••• = Sk(bn) = С* + С* + 1 = CT
и список остатков с минимальной стоимостью в корне имеет вид
Rsk = {ai,..., am, bi,...,bn} = RiU Rj = Rck -
Наконец, мы принимаем допущение, что списки Ri и Rj имеют непустое
пересечение: RiC\ Rj = {ci,... ,с$}. Тогда список Rk для традиционного
алгоритма экономичности есть Rk = {ci,..., с*}, и стоимость дерева Tn
равна Ст = Ск = Ci + Cj. В то же самое время взвешенная стоимость
остатков в корне определяется из
Sk(cp) = Si(cp) + Sj(cp) = Ci + Cj,
Sk(ai) = Si(ai) + Sjih) + 1 = ^ + ^ + 1,
Sfc(bg) = Si(ai) + 1 + Я,-(Ьд) = Q + Q + 1,
5*(ж) = Si(ai) + 1 + S^bi) + 1 = C* + Cj + 2

260
Глава 7
при всехр = 1,...,t, щ £ Rk, bq £ Rk, x £ RiURj. Таким образом, список
остатков с минимальной взвешенной стоимостью в корне имеет вид
Rsk ={ci,...,ct} = Rk
и по взвешенной экономичности стоимость дерева Т/у равна
St = Sk(a) = ... = Sk(ct) = d + Cj = Ст*
Поэтому мы доказали, что традиционный алгоритм экономичности дает ту
же самую стоимость, что и алгоритм взвешенной экономичности с весовой
функцией S, такой что 5(а, а) = 0 и S(a, b) = 1 при а ^ 6. □
Задача 7.12. Покажите, что определяемая по методу взвешенной
экономичности минимальная стоимость не зависит от позиции корня при условии,
что стоимость замены является метрикой, то есть что она удовлетворяет
равенству 5(а, а) = 0, условию симметрии 5(а, b) = S(b, а) и неравенству
треугольника
5(a,c)<5(o,b) + S(b,c)
при любых а, Ъ и с.
Решение. Сначала мы выведем формулу стоимости St корневого дерева Г
при допущении о том, что мы завершили процедуру прохождения в
обратном порядке алгоритма на взвешенной экономичности. Мы допускаем, что
г и j — дочерние узлы корня к, как показано на следующем рисунке:
Допустим также, что мы знаем стоимости Si(a) и Sj(b) поддеревьев,
нисходящих из г и j для любых остатков а и Ъ. Тогда
5*(с) = mm(Si{a) + S(c, a)) + шт(^(6) + S{by с))
a b

7.1. Оригинальные задачи
261
и
ST = mmSk(c) = Sk(c*) = 5*(а*) + S(c\a*) + Sj(b*) + S(b*,c*). (7.10)
с
Обратите внимание, что с* обязательно должен быть или а* или Ь*, чтобы
минимизировать правую сторону в (7.10). Действительно, если с* = а* (или
с* = Ь*), мы имеем, для любого другого с':
ST = ^(а*) + £(с*,а*) + 5^6*) + 5(6*, с*) <
< £(а*) + S(c', а*) + 5,-(Ь*) + S(b\ с')
в силу неравенства треугольника. Поэтому мы приходим к выводу, что
ST = imn{Si(a) + Sj(b) + S(a, Ь)).
Теперь мы хотим показать, что стоимость дерева не изменится, если мы
переместим корень на другое ребро. Без потери общности мы рассмотрим
перемещение корня к одному из рёбер, нисходящих из узла г с двумя
дочерними узлами I и т:
С новым корнем fc', расположенным на ребре (г, I), стоимость
дерева Т" принимает вид»
ST> = min($(a) + Si(d) + 5(a, d)).
a,d
Здесь d обозначает символ, прикреплённый к узлу I, a, S'(a) — стоимость
поддерева, исходящего из узла г (поддерево в дереве Т", отличное от
поддерева, нисходящего из г в дереве Т). Теперь мы будем работать с
выражениями для St и St', используя рекуррентные уравнения (е — символ,
расположенный в узле га) следующим образом:
ST = min ( тт(5т(е)Н-5(е,а))Н-тт(5/(бг)Н-5(бг,а))Н-5^(Ь)Н-5(а,Ь)) ,
(7.11)

262 Глава 7
ST> = min f min(5m(e)H-5(e,a))+min(5^b)+5(a,b))+5z(d)+5(a,d) ) .
a,d \ e b J
(7.12)
Оба выражения в правой части уравнений (7.11) и (7.12) эквивалентны
выражению
iin (т1п(Зш(е)+3(е,а))+т1п(31{^+3(^а))+1тп{Зу(Ь^ + S(a,b))] .
aye d b J
mm
Поэтому St = Sts а это означает, что минимальная стоимость дерева,
определяемого методом взвешенной экономичности, не зависит от позиции
корня, если стоимость замены есть метрика. □
Задача 7.13. Алгоритм Хейн ([112]) может быть расширен на общие
веса S(a, Ь) за счёт приложения к каждому ребру в графе последовательности
множества минимальной стоимости Si(a) (как в алгоритме на взвешенной
экономичности) вместо множества Ri. а) Покажите, что равенство
S(x,z) + S(z,y) = S(xiy)
может быть удовлетворено, когда последовательность z имеет общий
остаток с последовательностью х или у при условии, что S(a1 а) = 0 при всех а.
б) Оцените минимальную стоимость дерева Т (принимая алфавит
аминокислот или нуклеотидов)
ТАС
САС
СТСАСА
используя алгоритм Хейн для графов последовательности.
Решение, а) Предположим, что последовательности х и у соотнесены с
дочерними узлами узла I и с помощью уравнений динамического
программирования с весами £(а, Ь) найдено выравнивание последовательностей х

7.1. Оригинальные задачи
263
и у с минимальной стоимостью. В узле I мы определяем предковую
последовательность z с минимальной стоимостью, выровненную с обеими
последовательностями х и у следующим образом. На любом участке
последовательность z имеет общий символ с последовательностью х или у (или
с обеими). Предположим, что на данном участке оптимальное
выравнивание последовательностей х и у имеет совпадение, где остаток Хг выровнен
с остатком yj. Тогда, если Zk = хь мы получаем
S(xi, zk) + S(zk, yj) = Sfa, Xi) + S(xiy yj) = S(xi, yj);
если Zk = yj, мы имеем
Sfa, zk) + S(zk, yj) = S(xu yj) + S(yj,yj) = S(xu yj).
Если выравнивание последовательностей имеет пропуск на участке
(скажем, ^/-пропуск), мы выбираем или пропуск или остаток Х{ для предковой
последовательности z. Тогда на этом участке вклады в обе стороны
равенства £(х, z) + S{z, у) = S(x) у) тождественны и равны либо стоимости
введения пропуска d (если пропуск следует за совпадением), либо
стоимости продолжения пропуска е (если пропуск следует за парой у-ироиуск).
Ещё одно правило управляет выбором z-остатков. Если несколько
последовательных пропусков в одной последовательности появляются в
оптимальном выравнивании последовательностей х и у, то предковая
последовательность z должна или пропустить полный набор остатков, выровненных
с пропуском, или вобрать их все.
б) Теперь мы найдем минимальную стоимость S дерева Т с
листьями z = ТАС, у = С АС и х = СТСАСА с помощью алгоритма
динамического программирования для графов последовательностей,
представленного в [112]. Мы должны вычислить текущие стоимости, сравнить их
и выбрать минимальное значение, чтобы заполнить ячейки матриц
динамического программирования. Параметры алгоритма выбраны следующим
образом: стоимости замен 5(Л, Г) = 5(Г, А) = 5(Л, С) = S(C, A) =
= S(G,C) = S(C,G) = S{G,T) = S(T,G) = 2, S(C,T) = S(T,C) =
= S(A, G) = S(G, A) = 1; стоимость введения пропуска d = 3 и стоимость
продолжения пропуска е = 2.
Чтобы осуществить эту процедуру, мы соотносим последовательности
х, у и z, соответственно, с графами Gi, Gi и Gs9 определёнными
следующим образом. Каждый из этих графов — простой линейный граф с
числом рёбер, равным длине соответствующей последовательности. Кроме
того, мы прикрепляем к ребру г, где г = 1,..., 6, графа G\ вектор
стоимости замен [S(A,Xi),S(C,Xi),S(G,Xi),S(T,Xi)]; к ребру j, где j = 1,2,3,

264
Глава 7
графа Gi — вектор стоимости замен [S{A,yj),S(C,yj),S(G,yj),S(T,yj)\
и к ребру I, где I = 1,2,3, графа Gi — вектор стоимости замен
[S(AzO,S(C,zO,S(G,20,S(7>0]-
Тогда мы получаем следующие простые линейные графы:
[2,0,2,1] [2,1,2,0] [2,0,2,1] [0,2,1,2] [2,0,2,1] [0,2,1,2]
(jr • • • • • • •
_ [2,0,2,1] [0,2,1,2] [2,0,2,1]
G2 • • • •
G [2,1,2,0] ^ [0,2,1,2] [2,0,2,1]
Стоимость S(G, G*) между графами последовательностей G и G*
определяется как минимальная стоимость попарного выравнивания между
последовательностями s и s*, причём s G G и s* G G*. Для простых графов
(опознающих одну последовательность каждый), таких как G\ и G2,
стоимость S{G\, G2) представляет собой только стоимость оптимального
выравнивания этих двух последовательностей. Чтобы определить 5(Gi,G2)
и построить оптимальные выравнивания последовательностей х и у, мы
используем динамическое программирование для графов G\ и G2. Пусть
SM(г, j), 5х(г, j), SY(i,j) обозначают минимальную стоимость
описываемых графами выравниваний вплоть до элементов Хг и 2/j5 где SM{i,j)
соответствует совпадению (х*,^), 5х(г, j) — выравниванию символа ж*
с пропуском и SY{i,j) — выравниванию символа yj с пропуском.
Рекуррентные уравнения следующие:
S <*' Я = K=^G,TiS{K' X*)+S^K' W))+ т1П \
SM(i-l,j-l),
Sx(i-l,j-l),
SY(i-l,j-l);
(7.13)
^(U) = min{^-1-f) + * (7.14)
ey,. л . / SM(i,j-l) + d, ,_.„
5 (u)=mm \'-f ' (7.15)
I 5y(t,j-l) + e.
Мы применяем эти уравнения, чтобы заполнить матрицу текущих значений
стоимости S'(i,j), представленную на рис. 7.3. Мы находим минимальную
стоимость S(Gi, G2) = 8 как минимальную запись в правой нижней
ячейке матрицы на рис. 7.3 (г = 6,j = 3) и используем процедуру обратного

7.1. Оригинальные задачи
265
прослеживания, чтобы определить оптимальный путь через матрицу
стоимости. Есть два оптимальных пути, которые определяют следующие два
оптимальных выравнивания последовательностей хиу:
(1) С - - А С -
С Т С А С А
(2) - - С А С -
С Т С А С А
со стоимостью 5(1) = 5(2) = S(G\,G2) = 2d + е = 8. Чтобы
найти возможные предковые последовательности для последовательностей х
и у, мы получаем новый граф последовательности G± (показанный на
рис. 7.4) из выравниваний (1) и (2). Каждый путь через граф G± (рис. 7.4, б)
уникально определяет последовательность нуклеотидов векторами
стоимости замен, приписанными к рёбрам на этом пути. Есть четыре пути
через граф G±, опознающих четыре последовательности СТСАСА, С АС,
СТСАС и С АС А. Любая последовательность s £ G4 удовлетворяет
условию S(s,x) + S(s,y) = S(Gi1G2) = 8. Эти последовательности можно
рассматривать в качестве потенциальных предков последовательностей х и
у в дереве Т с минимальной стоимостью.
Теперь мы повторяем динамическое программирование для графов G^
и (?з с видоизменёнными рекуррентными уравнениями (7.13)—(7.15) при
г = 1,..., 6 и j = 1,2,3 следующим образом:
SM («, 3)
mm
KJ?%G,T(S(K>Xi')+S(K>yi'»
mm <
sM(i'JV
sx(i',f),
{ SY(i',f); ■
eX,- .4 • • f'SM(i',j) + d,
S Au,7) = mmmm< VK '
' «' {Sx(i',j) + e;
SY (hi) = minmin
i
SM(i>j') + d,
SY(i,j') + e.
Здесь минимум выбирается по всем предшествующим узлам г' узла г в
графе G± и по всем предшествующим узлам f узла j в графе G%.
Поскольку G3 — граф единственной последовательности, постольку j' = j — 1.
При вычислении текущих значений стоимости Sm(i,j) мы заполняем
ячейки матрицы, показанной на рис. 7.5. Минимальная стоимость 5(С?з> G*) —
= 1 — минимальная запись в правой нижней ячейке матрицы на рис. 7.5

266
Глава 7
i = О г = 1 г = 2 г = 3 г = 4 г = 5 г = 6
3=0
3=1
3 = 1
i=3
3
Го]
4
-N.,.
—
—
i—
5
N
-5
\
V
л
К\
9
7
9
9
—
13
11
—
_
-
7
5
-
5
т
8
5
Т
7
8
Т
5
8
~5^
7
12
\
~й)
*8
12
Рис. 7.3. Матрица текущих значений стоимости 5#(г, j) для графов G\ и 6?2.
Каждая ячейка (г, j) содержит три записи SM (г, j), 5х (г, j) и 5^ (г, j),
приведённые в порядке сверху вниз. Два оптимальных пути показаны стрелками
(г = 65<7 = 3). Процедура обратного прослеживания восстанавливает
только один оптимальный путь через матрицу текущей стоимости. Этот путь
соответствует оптимальному выравниванию последовательностей z e Gs
и у е G4:
(3) Т А С
С А С
со стоимостью 5(3) = S(Gs)G^) = S{T,C) = 1. Чтобы найти набор воз-

7.1. Оригинальные задачи
267
, ч [2,0,2,1] [2,1,2,0] [2,0,2,1] [0,2,1,2] [2,0,2,1] [0,2,1,2]
(а) -
(Ь)
6 6
[2,0,2,1] [2,1,2,0] [2,0,2,1] [0,2,1,2] [2,0,2,1] [0,2,1,2]
[2,0,2,1] Р'0'2'1!
Рис. 7.4. Граф последовательности GU, полученный из путей через
матрицу в таблице 7.1: а) Граф с фиктивными рёбрами (отмеченными буквой 6);
6) тот же самый граф, в котором фиктивные рёбра заменены рёбрами,
помеченными векторами стоимости замен
можных предковых последовательностей для корневого узла дерева Т, мы
получаем из выравнивания (3) новый граф последовательности G^'.
[2,0,2,1] [2,1,2,0] [2,0,2,1]
[2,1,2,0]
Два пути через граф Gs опознают две последовательности у = С АС и
z = ТАС как возможные предковые последовательности, соотносимые с
корневым узлом. Граф Gs, полученный из оптимального пути в графах Gs
и G4, обладает важным свойством, которое состоит в том, что существуют
последовательности s € G3 и s* € G4, такие что S(y1 s) + S(y, s ) =
= ^(Сз, G4) = 1. To же самое верно для последовательности z.
Теперь мы видим, что каждый набор предковых последовательностей
всегда включает последовательность у при внутреннем узле и у или z при
корневом узле. Эти два возможных варианта выбора предков
представлены на рис. 7.6. Каждый вариант выбора минимизирует стоимость дерева:
min ST = S(GUG2) + S(G3, G4) = 9.
Задача 7.14. Процедура соединения соседей для восстановления
некорневого двоичного дерева Т, предложенная в [230], при каждой итерации
находит минимум функции Dij и объединяет соответствующие листья г и j
в единственный родительский узел. Функция D определяется
уравнениями (7.9) для заданных расстояний dki, где к J = 1,..., N, обладающих
свойством аддитивности. Покажите, что эта процедура восстанавливает
истинных соседей, то есть что минимальное значение D^ опознаёт соседние

268
Глава 7
г = О г = 1 г = 2 г = 3 г = 4 г = 5 г = 6
3=0
3=1 П
i=2
-
—
5
5
—
4
т
8
6
т
6
4
1
8
12
\
6
4
у
1Г
4
13
i=3
-
-
7
т
-
6
т
8
6
т
8
6
т
6
4
т
8
9
Т
4
9
Рис. 7.5. Матрица текущих значений стоимости 5* (г, j) для графов G* и 6?з.
Каждая ячейка (г, j) содержит три записи SM(г, j), 5х (г, j) и Sr (г, j),
приведённые в порядке сверху вниз. Оптимальный путь, найденный процедурой
обратного прослеживания, показан стрелками
листья г и j в случае, когда родительский узел по отношению к j (или к г)
является родителем двух листьев.
Решение. Эта задача уже была решена непосредственно для дерева с
четырьмя листьями (задача 7.10). Теперь мы рассмотрим дерево Г с N ^ 5
листьями.

7.1. Оригинальные задачи
269
САС
1
ТАС
ТАС
САС
сас ТАС
8
СТСАСА
1
САС
САС
СТСАСА
Рис. 7.6. Два возможных варианта выбора предковых последовательностей,
при которых стоимость дерева St = 9 минимальна
Сделаем допущение, что значение Dij является минимальным, но узлы
г и j не являются соседями. Мы ищем противоречие.
Утверждается, что другая дочь родительского узла к листа j является
листом, скажем, листом га. Так как узлы г и j не являются соседними
листьями, есть по крайней мере два узла на пути между ними, скажем I и к,
как показано на следующей схеме:
Пусть L\ — множество N\ листьев (N\ > 0), полученное из третьего ребра,
исходящего из узла I (ни ребро (Z, г), ни путь (Z, к) рёбер). Мы определяем
множество Lk, содержащее только лист га, и множество Lx с Nx листьями
(Nx ^ 0), содержащее все листья х, полученное из пути (Z,fc). Очевидно,
что N = Ni + Nx + 3.
Мы покажем, что D^ > Djm. По определению (7.9) значения D мы
имеем D^ = di3
(п + г5) и Djrn = djm - (rj + rm), где
N-2
Е
все листья и
Мы рассматриваем разность между D^ и Djm и используем свойство ад-

270 Глава 7
дитивности расстояния d:
Dij — Djm = du + dik + dkj — djk — dkm — П — Tj + Tj + rm =
= du + dik + dkm — N _ 9 ( 2_^ diU — 2_^ d„
В сумме
N-2
\все листья и все листья и
£i = 2L^ diU
все листья it
член du равен нулю; то же самое верно для члена dmrn во второй сумме
Е2 = / ^ dmu.
все листья и
Суммы Ei и Е2 также имеют пару равных членов (dim и dmi)- Другие
члены в сумме Ei следующие:
dij = du -{-dik ~{-dkj,
diz = du +diz,
(J*ix == (^il i ^*Ze i ^*ex
при любых z e Li и x € Lx. Точно так же для членов суммы Е2:
dmj = dmk "Г flfcj 5
^mz = rfmfc + dkl + б?Ь,
Таким образом, разность Ei — E2 принимает вид
Ei - Е2 = (N - 2)du -(N- 2)dmk - (N1 - l)dik +Y^dle~Y^ dke
x£Lx xELx
(обратите внимание, что расстояния die и dke в последних двух суммах
зависят от последовательности х). Поэтому
Aj — Djm = du + dik + dkm — at _2 (^ ~~ ^2) =
\ x£Lx x£Lx /

7.1. Оригинальные задачи 271
= N _2 1 Nxdlk + 2dlk ~ ]С dle + ]C dke ) =
\ xeLx xeLx /
V xeLx J
Мы доказали, что Dij > Djm, а. это противоречит начальному допущению
о том, что, когда значение D%j минимально, листья г и j не являются
соседями. Следовательно, узлы г и j являются соседними листьями. □
Задача 7.15. Завершите доказательство теоремы, сформулированной в
задаче 7.14, для случая, когда множество листьев Lk содержит по крайней
мере два листа тип, как показано на следующей диаграмме:
Решение. Мы снова покажем, что D^ > Dmn. Мы сделаем допущение о
том, что Ni > Nk (см. обозначения в решении задачи 7.14); в противном
случае мы рассматривали бы двух соседей из множества L\ вместо листьев
тип из Nk.
Для любого листа у из Lk, такого что у ф т и у ф п, по свойству
аддитивности справедливо равенство diy + djy = d^ + 2dky. Точно так же
dmy + dny = dmn + 2dpy. Таким образом,
("iy i (*jy ("my tiny — ("ij i ^u>ky А&ру &тт1'
(7.16)

272
Глава 7
Если у = пиу = т, то мы имеем, соответственно, din + djn = dij +
4- 2dkn и dim 4- djm — d^ 4- 2dfcm, а также
^m ~r 6tjn umn = (Z^j 4" AUjcn и>тпты
dim ~r Gtjm ^mn = Ctij ~г ^кт dmn- ('•! ')
Для любого листа z во множестве L/ верны равенства diZ 4- dj2 = ^г? 4- 2d/^
и rfm2J 4- dnz = dmn 4- 2dPk 4- 2dfcj 4- 2d/^, и тогда
d»* 4- dj^ — dmZ — dn2 = d^ — 2dVk — 2d&/ — dmn. (7.18)
Наконец, для любого листа х из Lx мы имеем diX 4- dja; = d^ + 2dea;,
4x 4- dnx = dmn 4- 2dpfc 4- 2dfce 4- 2dex и, таким образом,
Q>ix "4 Cljx Q"mx dnx ~~~ d%j U"mn ^dpfa Z&ke- \'•■'■*'/
Из определения (7.9) величины Вц мы находим
Uij J-^mn = d%j Q"mn "77 о / ^ ^ и dju б&тгш dnu).
все листья и
Используя уравнения (7.16)—(7.19) для листьев w и тот факт, что при и— г
uu = j
Uij U"mi dni 4" dij djjij dnj = Qdpfc Zdfnnj
мы получаем следующее вьфажение:
-b'ij J-^mn = ^ij ^ran "Tr q I ^/ ^ \dij-\-Zdky G^ran ZdpyJ-rZdmfi
^3/6Lfc
-4dpfc - 2dmn 4- 2_j №i ~~ ^dpfe - 2dfc/ — dmn)4
zebi
4- 2^ (d^ - dmn — 2dpfc - 2dfce) J
xeLx /
Мы воспользовались тем фактом, что член 2dpy отсутствует в
уравнениях (7.17), а это подразумевает, что члены —2dpy при у = тиу = п могли

7.2. Дополнительные задачи
273
быть включены в сумму по всем листьям в Lk при условии, что мы
добавляем 2dpTn+2dpn = 2dmn к этой сумме. Кратности величин d^ и йшп после
суммирования по всем листьям, равны, соответственно, N — 2 и — (N — 2).
Таким образом,
\j/6Lfc
+ ^2 (2dpk + Мы) + X] (2dpfe + 2d*<=) ) •
zeLi xeLx /
(Обратите внимание, что расстояния dvy и dky зависят от у и что dke
зависит от х.) С учётом неравенства dpy — dky > —dvk мы имеем
n n 2dpfc(-JVfc + 2 + JVi + ЛГ.) п
Aj - Dmn > —" ^2 > °
при любом Nx ^ 0 в силу допущения Ni ^ ATfc. Поэтому неравенство
D^ > Ошп противоречит допущению о том, что значение Вц является
минимальным, когда г и j не являются соседями. Следовательно, листья г
и j должны быть соседями. П
7.2. Дополнительные задачи
В этом разделе мы имеем дело с построением филогенетического
дерева для заданного набора фрагментов белка: мы должны построить корневое
дерево со свойством молекулярных часов с помощью алгоритма UPGMA
(задача 7.16), или же мы должны найти некорневое дерево при помощи
алгоритма объединения соседей (задача 7.17). Также мы выводим формулу
числа помеченных историй с п листьями (задача 7.18).
Задача 7.16. Не содержащее пропусков множественное выравнивание
фрагментов цитохрома-с четырёх различных видов — Rickettsia conorii,
Rickettsia prowazekii, Bradyrhizobium japonicum и Agrobacterium tumefaciens —
представлено ниже (в порядке сверху вниз):

274
Глава 7
NIPELMKTANADNGREIAKK
NIQELMKTANANHGREIAKK
PIEKLLQTASVEKGAAAAKK
PIAKLLASADAAKGEAVFKK
Используя эволюционное расстояние, определяемое формулой d^ =
= — ln(l — pij), где pij — доля несовпадений в попарном выравнивании
последовательностей i и j, постройте корневое филогенетическое дерево
для заданных последовательностей с помощью алгоритма UPGMA.
Покажите, что расстояния d*j, определяемые деревом, построенным алгоритмом
UPGMA, не всегда совпадают с начальными расстояниями dij.
Решение. Пусть х^ где г = 1,2,3,4, обозначает г-ю последовательность
белка данного выравнивания в порядке сверху вниз. По подсчётам
несовпадений в попарном выравнивании последовательностей xi и Xj мы
определяем попарные расстояния dij, где i,j = 1,..., 4, следующим образом:
di2 = — In
dis = - In
du = — In i
^23 = — In i
C?24 = — In
ds4 = — In
1 - 3/20) = 0,1625,
1-12/20) = 0,9163,
1-13/20) = 1,0498,
1-12/20) = 0,9163,
1-13/20) = 1,0498,
1-9/20) = 0,5978.
Чтобы применить алгоритм UPGMA, мы приписываем каждую
последовательность Xi к её собственной группе С», где г = 1,..., 4, а также к листу г
дерева с четырьмя листьями. Минимальное расстояние среди d^ есть d\2 =
= 0,1625, таким образом, мы определяем новую группу Сь = С\ П Сг и
помещаем узел 5 на высоту /г5 = eta/2 = 0,0813. После этого мы удаляем
группы С\ и Сч из списка групп и вычисляем следующие новые
расстояния:
йбз = |(Й1з + *з) =0,9163,
d54 = |(di4 + d24) = 1,0498.
Минимальное расстояние среди расстояний d^, с^4 и ds4 — ^34 = 0,5978.
Так что мы вводим Се = Сз П С±, помещаем новый узел 7 на высоту

7.2. Дополнительные задачи
275
^6 = ^34/2 = 0,2989 и определяем расстояние между группами С*, и Cq
следующим образом:
^56 = т№з + di4 + ^23 + ^24) = 0,9831.
При том, что осталось только две группы С& и Cq, мы определяем С7 =
= Сь П Cq и помещаем корневой узел 7 на высоту h? = с?5б/2 = 0,4915. На
этом построение дерева завершено (см. рис. 7.7).
<к
5
<к
<к
7
*
6
4,
Рис. 7.7. Корневое дерево, построенное алгоритмом UPGMA для
последовательностей, заданных в задаче 7.16
Тогда длины рёбер дерева определяются следующим образом:
d1=d2 = h5 = О,0813,
d3 = d4 = h6 = 0,2989,
' d5 = h7-d1= 0,4102,
d6 = h7-d3 = 0,1926.
Теперь легко видеть, что попарные расстояния d\^ определяемые недавно
построенным деревом, не всегда совпадают с эволюционными
расстояниями diji
d\2 = d\ + d2 = 0,1625 = di2,
d*3 = di + d5 + d6 + d3 = 2Л7 = 0,9831 ф 0,9163 = d13,
dj4 = di + d5 + d6 + d4 = 2Л7 = 0,9831 ^ 1,0498 = d14,
dl3 = d2 + d5 + d6 + d3 = 2/i7 = 0,9831 ф 0,9163 = d23,

276
Глава 7
d*4 = d2 + d5 + d6 + d4 = 2h7 = 0,9831 ф 1,0498 = d24,
d*4 = d3 + d4 = 0,5978 = d34.
П
Задача 7.17. Для заданных последовательностей белка в задаче 7.16 с
эволюционными расстояниями dij а) постройте некорневое дерево Т методом
объединения соседей и покажите, что свойство аддитивности сохраняется;
б) покажите, что свойство молекулярных часов не сохраняется для любого
корневого дерева, полученного из дерева Т путём добавления корня.
Решение, а) Мы вычисляем значения г» и D^ для i,j = 1,..., 4 по
уравнению (7.9):
4
ri = \Yld4 = | (0,1625+ 0,9163+1,0498) = 1,0643,
i=i
4
г2 = ± ]Г d2j = 1(0,1625 + 0,9163 + 1,0498) = 1,0643,
i=i
4
г3 = | ]Г d3j = |(0,9163 + 0,9163 + 0,5978) = 1,2152,
4
r4 = |]Г^ = | (1,0498+1,0498 + 0,5978) = 1,3487;
3=1
D12 = d12-(n+r2) = -1,9661,
i?i3 = di3-(ri+r3) =-1,3632,
£>u = d14 - (ri + r4) = -1,3432,
Дю = d23 - (r2 + r3) = -1,3632,
£>24 = C?24 - (r2 + Г4) = -1, 3632,
£>34 = <fe4 - (r3 + Г4) = -1, 9661.
Чтобы начать построение дерева, мы выбираем пару листьев 1 и 2 с
минимальным расстоянием D±2 и объединяем их в новый узел 5. Новые рёбра
имеют длину d5i = \(di2 + r\-r2) = 0,08125 и db2 = di2-d$i = 0,08125.

7.2. Дополнительные задачи
277
Тогда мы находим расстояния от узла 5 до листьев 3 и 4:
*з = |(*з + d23 ~ d12) = О,83505,
d54 = |(dw + d24 - d12) = 0,96855.
Мы удаляем листья 1 и 2, добавляем узел 5 ко множеству листьев и
определяем Г5 и Dij для г, j = 3,4,5:
Г5 = |(Й63 + Й54) = 0,9018,
Aw = d34 - (г3 + r4) = -1,9661,
А*5 = 4зб - (гз + гб) = -1,28195,
£>45 = ^45 " (Г4 + Гб) = -1, 28195.
Затем мы выбираем листья 3 и 4, для которых минимальным является
расстояние £>34, и соединяем их в новый узел 6 рёбрами длины dse = ^(^34 +
+ гз — г4) = 0,23215 и с?4б = ^34 — ^36 = 0> 36565. Наконец, мы соединяем
два оставшихся узла 5 и 6 новым ребром длины d56 = ^(^53 + ^54 — ^34) =
= 0,6029 и получаем дерево Т (рис. 7.8).
4*
Рис. 7.8. Некорневое дерево, построенное методом соединения соседей для
тех же последовательностей, что и на рис. 7.7
Свойство аддитивности остаётся верным для дерева Т, поскольку
можно непосредственно удостовериться в том, что:
d\2 = di5 +^52,

278
Глава 7
^13 = C?i5 + С?5б + C?63 j
C?i4 = C?i5 + C?56 + C?64,
^23 = ^25 H~ ^56 + ^63 j
d>24: = dlb H- ^56 H~ ^64-
б) Очевидно, что если новый корень 7 добавляется к одному из рёбер
(1,5), (2,5) или (5,6), то ^73 < ^74- Если корень 7 добавляется к ребру
(3,6), то 6^73 < di4- Если корень 7 добавляется к ребру (4,6), то с?74 < ^71 =
= d56 + dei- Таким образом, любой вариант выбора позиции корня даёт
корневое дерево, которое не обладает свойством молекулярных часов. □
Задача 7.18. Эдварде (1970) [71] ввёл следующее понятие помеченной
истории. Множество деревьев со свойством молекулярных часов определяет
одну и ту же помеченную историю, если эти деревья имеют одну и ту же
топологию и тот же самый порядок внутренних узлов во времени. Покажите,
что число Ln помеченных историй для деревьев с га листьями определяется
следующей формулой:
_ nl(n-l)!
Решение. Помеченная история определяется, если выбран порядок
внутренних узлов во времени. Множество внутренних узлов мы рассматриваем
как множество общих предков, которых мы должны проследить обратно во
времени. Для га листьев число способов выбрать первые два из них, чтобы
соединить (в пути назад во времени), равно (£) = (га(га —1))/2. Следующие
два узла, которые нужно соединить, выбираются из числа оставшихся га — 2
листовых узлов и внутреннего узла (предка), полученного в первом шаге.
Число способов сделать это равно (п~ ) = ((га — 1)(га — 2))/2. Мы
продолжаем процесс соединения не имеющих родителей узлов и подсчёта числа
вариантов выбора в каждом шаге, до тех пор пока не останутся последние
два не имеющих родителей узла, и мы соединяем их одним единственно
возможным способом. Таким образом, общее число возможных порядков
соединения всех узлов дерева определяется выражением
_га(п-1) (га-1)(п-2) 2 • 1 _ пКп ~ 1У-
п ~ 2 2 " *' НГ ~ 2""1 " □

7.3. Дополнительная литература
279
7.3. Дополнительная литература
Алгоритм соединения соседей (СС) Сайту и Нея [230] часто
использовался для восстановления филогенетических деревьев. Было предложено
несколько модификаций СС: Гескьюл [91] предложил обобщённую
формулу эволюционного расстояния, уменьшающую дисперсию оценок новых
расстояний при каждой итерации. Бруно, Соччи и Хелперн (2000) [38]
представили версию алгоритма СС с весами расстояний, компенсирующими
ошибки в оценках более длинных расстояний и увеличивающими
правдоподобие восстановленного дерева.
«Мозаика квартетов» — основанный на методе наибольшего
правдоподобия алгоритм восстановления топологии филогенетического дерева —
была представлена Штриммером и фон Хеселером (1996) [257]. Этот
алгоритм, будучи трёхшаговой процедурой, сначала восстанавливает все
возможные квартетные деревья с наибольшим правдоподобием, затем
неоднократно включает квартетные деревья в полное дерево и, наконец, вычисляет
по правилу большинства голосов согласованное дерево для всех
промежуточных деревьев — мозаичное дерево квартетов. Шмидтом с сотрудниками
[237] была выполнена параллелизация алгоритма сборки мозаики
квартетов. Еще один алгоритм, IQPNNI, основанный на понятии квартета, был
представлен в [274]. В [111] предложен простой алгоритм, реализованный
в компьютерной программе PHYML. В каждом шаге PHYML
видоизменяет текущее дерево, построенное на исходных данных, так, чтобы увеличить
его правдоподобие; при этом достаточно лишь нескольких итераций, чтобы
достичь сходимости.
Алгоритмы, упомянутые выше ([257]; [111]; [274]), сходятся быстро;
однако пространство деревьев, исследуемое этими алгоритмами, все ещё
представляет собой лишь маленькое подмножество пространства всех
возможных деревьев. Например, алгоритм PHYML рассматривает самое
большее 3(га —3) некорневых топологий для га последовательностей листьев при
подборе длин рёбер, с тем чтобы увеличить правдоподобие, тогда как всего
существует (2п — 5)!! различных топологий (задача 7.4). Даже при малых га
(га > 4) алгоритм проходит менее половины топологий, тогда как при
больших га он останавливается на исследовании исчезающе малой доли всех
возможных топологий: при га = 20 мы имеем, соответственно, 3(га — 3) =
= 51 и (2га — 5)!! « 2,22 • 1020 ([79]). Поэтому успех таких алгоритмов в
построении дерева, близкого к оптимальному (с наибольшим
правдоподобием), коренным образом зависит от удачного выбора начального дерева.
Гришин ([105], [106]) предложил новые формулы для оценки
эволюционных расстояний между последовательностями гомологичных белков

280
Глава 7
(традиционно определяемых как среднее число замен на участок). При
допущении о независимости замен на различных участках автор обеспечил
строгую обработку многократных и обратных замен, а также изменчивость
частоты замен среди аминокислот и среди участков последовательности.
Используя эти «исправленные» эволюционные расстояния, Фэн, Чжо и Ду-
литтл [82] вычислили времена расхождения основных групп эукариотов и
восстановили основную филогению эукариотов. Гюйнен и Борк [128]
применили формулы Гришина, чтобы определить времена расхождения архей
и бактерий по полным последовательностям геномов девяти видов
организмов из каждой группы. Сравнение полных геномов привело к созданию
новых способов измерения эволюционного расстояния и построения
филогенетических деревьев ([86]; [252]; [263]; [34]; [178]; [ПО]; [219]).
Всесторонний обзор методов построения филогенетических деревьев на основе
полных геномов приведён в [253].
К проблемам оценки времени расхождения и восстановления деревьев
обращались следующие группы ученых: [168] (некоторые виды
позвоночных); [10] (виды приматов); [206] (некоторые виды млекопитающих); [95]
(главные роды видов приматов); [162] (вирусы из группы HIV-1 М); [282]
(растения, животные и виды грибов).
Во всестороннем обзоре [9] описаны недавние достижения в оценке
времени расхождения по молекулярным данным, а также в масштабах
времени филогенетики и популяционной генетики. Авторы подчеркнули
важность испытания модели для оценки времени расхождения.
Совместимость гипотезы о молекулярных часах с оценками времени
расхождения для видов многоклеточных организмов, полученными по
палеонтологическим данным, показана в [14]. Расширенное обсуждение
свойства молекулярных часов приведено в [33].
Методы построения дерева, как правило, применяются не только для
восстановления филогении, но также и для визуализации эволюционных
отношений среди биологических последовательностей. Новый подход к
такой визуализации был предложен в [108]. Этот метод обеспечивает
изометрическое преобразование набора белковых последовательностей с
эволюционными расстояниями между ними (определяемыми как среднее
число замен на участок) в точки многомерного Евклидова пространства.
После чего точки группируются согласно предложенной авторами
процедуре группировки, использующей смесь плотностей многомерных Гауссовых
распеределений.

Глава 8
ВЕРОЯТНОСТНЫЕ ПОДХОДЫ
К ФИЛОГЕНИИ
Установление филогенетических отношений между видами — одна из
центральных задач биологической науки. Тогда как в главе 7 читатель был
введён в невероятностные методы построения филогенетических деревьев
для последовательностей ДНК и белков, глава 8 продолжает
рассмотрение данного предмета с точки зрения обоснованной вероятностной
методологии. Эволюция биологических последовательностей рассматривалась по
большей части как случайный процесс, и было предложено несколько
вероятностных моделей с различными уровнями сложности. Поэтому
восстановление филогенетических отношений может быть сформулировано также
в вероятностных понятиях.
Несколько вводных задач «АБП» в главе 8 касаются свойств
простейших вероятностных моделей эволюции, таких как модели Джукса-Кантора
и Кимуры.
Имея набор последовательностей (соотнесённых с листьями дерева) и
модель процесса замен в последовательности ДНК или белка, важно знать,
каким образом можно вычислить правдоподобие дерева с данной
топологией. Алгоритм Фельзенштейна обращается к этой проблеме, используя
прохождение в обратном порядке. Фельзенштейн разработал также алгоритм
ЕМ-типа для поиска оптимальных (с наибольшим правдоподобием) длин
рёбер дерева. Однако по мере увеличения числа листьев число топологий
дерева растёт слишком быстро, чтобы быть обработанным за разумное
время.
Поэтому поиск оптимального дерева среди всех возможных деревьев
при довольно большом числе последовательностей (листьев) — одна из
главных проблем. Господствующий подход к преодолению такой
проблемы — выборка из апостериорного распределения в пространстве деревьев.
Для построения филогенетических деревьев может быть применена
описанная в «АБП» концепция СММ дерева при использовании наиболее

282
Глава 8
общих моделей эволюции последовательностей. Однако полное
воплощение этого внушительного теоретического подхода в эффективный
вычислительный метод все ещё представляет непреодолимую трудность ввиду
сложности алгоритма.
Большинство приведённых в этой главе задач из «АБП» касается
свойств простых вероятностных моделей эволюции биологических
последовательностей. Реалистические модели, которые допускают различные
частоты появления мономеров, а также их вставок и удалений на разных
участках последовательности, становятся слишком сложными на
практике без чрезмерного использования компьютера. Однако одна из моделей
этого вида, модель ТКФ (Торн, Кисино и Фельзенштейн [269]),
используется в одной из дополнительных задач. Наконец, ещё две теоретические
задачи сосредоточены на вероятностной интерпретации алгоритмов,
описанных в главе 7, на методах экономичности и расстояния, а также на
алгоритме одновременного восстановления дерева и построения
выравнивания ([233], [112]).
8.1. Оригинальные задачи
Задача 8.1. Покажите, что матрицы замен нуклеотидов Джукса-Кантора
и Кимуры, представленные, соответственно, в [134] и [153], являются муль-
типликативными: S(t)S(s) = S(t + s) при любых значениях s и t.
Решение, а) Матрица замен Джукса-Кантора для времени t имеет
следующий вид:
(\{1 + 3e~4at) i(l - e~4at) i(l - e~4at) ±(1 - e"4"') \
±(l-e-4*') i(l + 3e-4*<) i(l-e"4*<) \{l-e~^)
44 ' 4V ' ' 4V y 4
1
4
±(l-e-4"') i(l-e-4«') i(l + 3e-4*') \{l-e~^)
Ц(1-е-4"*) i(l-e-4«<) i(l-e-4"') \(1 + Зе-*«*))
Здесь Sij(t) = P(Aj\Ai,t) — вероятность того, что нуклеотид типа Ai был
заменён нуклеотидом типа Aj за время t. Чтобы доказать
мультипликативность, мы должны показать, что при всех г, j = 1,..., 4
(S(t)S(s))ij=Sij(t + s).

8.1. Оригинальные задачи 283
Это равенство остаётся верным для диагональных элементов следующим
образом:
4
(S(t)S(s))u = ^2sik(t)Ski(s) =
k=i
= ^(1 + Зе"4а*)(1 + 3e"4as) + ^(1 - е"4а<)(1 - е~4аз) =
= тб(1 + 3e"4at + 3e"4as + 9e-4a(t+e> + 3 - 3e~4a< - 3e"4ae+
lo
+3e-4a(t+S)) = 1 (1 + ge-4a(t+*)j = £..(£ + ^
Точно так же для недиагональных элементов,
4
= ^(1 + 3e"4at)(l - e"4as) + ^(1 + 3e"4as)(l - e~4at)+
+ ^(l-e-4^)(l-e-4as) =
= 4(1 - e"4at + 3e"4as - 3e-4a(s+*>+
lo
+1 _ e-4as +*3e_4at - 3e"4a(s+t) + 2 - 2e"4at - 2e~4as+
+2e-4a(,+t) = 1(1 _ e-4a(t+*)j = ^.(t + e).
Следовательно, семейство матриц Джукса-Кантора мультипликативно,
б) Матрица замен нуклеотидов Кимуры
(п qt Щ qt\
qt п qt щ
I Щ qt П qt J
\qt щ qt и)

284
Глава 8
имеет элементы
ft = i(l-e-«*),
ut = i(l + e-^-2e-2(e+«t),
rt = l-2qt- щ.
И вновь мы должны показать, что при всех г, j = 1,..., 4
(5(«)5(в))у=^(« + в).
Это равенство остаётся верным для диагональных элементов следующим
образом:
4
(5(t)5(e))« = 5^5ifc(t)5w(e) = rtrs + 2ад, + wtws =
fc=i
= ^(l-e-4^)(l-e-4^)+
+JL(1 + e-4f* - 2e-2(a+W)(l + e-^° - 2е~^а+^Л-
+^(1 + e-4^' + 2е-2<а+Я*)(1 + e"4* + ге"2^^ =
= I + Ie-4«t+.) + Ie-2(a+/3)(t+s)) = 5..(i + s)
Для недиагональных элементов Sij, таких что сумма г + j является
нечётным числом, мы имеем
512(« + в) = Su(t + в) = 52Х (« + «) = 5аз(* + я) = -Ы* + в) =
= 5з4(* + в) = Ah (* + в) = 54з(* + в) = а+. =
= l(l_e-W+s))
С другой стороны,
(S(t)S(s))12 = (S(t)S(s))u = (S(t)S(s))21 = (S(t)S(s))23 =

8.1. Оригинальные задачи 285
= (S(t)S(s)32 = (5(t)5(s))34 = (S(t)S(s))41 = (S(t)S(s))42 =
= т. + qtra + utqs + qtua = ^(1 + е~4^ + 2е-^а+^(1 - e~4^)+
+^(1 + e-W° + 2e-a(«+/»).)(i _ e-*f*)+
+ ^(1 + e-4^* - 2е-2(«+")*)(1 - е-4^)+
+^(1 + e~^a - 2е-2(а+П*)(1 - е-4?*) =
= I(l-e-^<t+')).
Наконец, для недиагональных элементов Sij, таких что сумма i+j является
чётным числом, мы имеем
Sl3(t + в) = 524 (t + S) = S3l(t + s) = S42(* + S) = Wt+S =
= 1(1 + e-4/3(t+e) _ 2e-2(a+i9)(t+s)^
и соответствующие элементы произведения матриц 5(£) и 5(s) выглядят
следующим образом:
(S(t)S(s))13 = (5(t)5(e))24 = (5(*)5(e)3i = (S(t)S(*))42 =
= г*ив + 2gtgs + u*rs =
= ^(1 + e~4^ + 2e-2(a+«*)(l + e~^s - 2e-2<a+«')+
+ A(i_e-^)(l-e-^)+
+ i(l + e-4/w - 2е-2(в+»*)(1 + e"4^ + 2e-2<a+«') =
16
= 1(1 + e-4/3(t+e) _ 2e-2(a+/3)(t+S)^
Мы непосредственно продемонстрировали, что произведение матриц
S(t)S{s) имеет те же элементы, что и матрица S(t + s); поэтому свойство
мультипликативности сохраняется для семейства матриц замен Кимуры.
□

286
Глава 8
Задача 8.2. Пусть выражение P(a(t2)\b(ti)) обозначает вероятность того,
что остаток 6, присутствующий во время tu был заменён остатком а ко
времени t2. Стационарность означает, что мы можем написать это
выражение в виде P(a\b,t2 — h). Марковость означает, что если to < h, то
P(a(t2)\b(ti), c(to)) = P(a(t2)\b(ti))9 то есть что вероятность замены
остатка b на остаток а не зависит от события, состоящего в том, что этот остаток
был с в более раннее время to. Покажите, что
5^P(a(e + *)|b(t)>c(0))P(b(t)|c(0)) = P(a(e + t)|c(0))> (8.1)
b(t)
и приведите доказательство, что мультипликативность сохраняется.
Решение. Марковость позволяет нам преобразовать каждый член на левой
стороне уравнения (8.1):
P(a(s + t)\b(t),c(0))P(b(t)\c(0)) = P(a(s + t)\b(t))P(b(tMO))-
Условие стационарности позволяет нам записать
P(a(s+t)\b(t))P(b(t)\c(0)) = P(a\b,s+t-t)P(b\c,t-0) = P(a\b,s)P{b\c,t).
Возвращаясь к сумме по всем возможным типам остатков b(t) в момент t,
мы получаем следующее выражение:
^2 p(a\hi s)P(b\c, t) = P(a|c, s + t),
b(t)
которое является вероятностью того, что остаток с будет заменён остатком
а за время s + t. И вновь обращение к условию стационарности позволяет
получить выражение
P(a|c, s +1) = Р(а|с, s +1 - 0) = P(a(s + *)|с(0)),
которое завершает доказательство равенства (8.1).
Свойство мультипликативности S(s)S(t) = S(s 4-1) непосредственно
следует из выражения
Y^ Р(а\Ъ, s)P(b\c, t) = P(a|c, s + t),
ь
которое показывает, что элемент матрицы замен S(s +1) может быть
получен из элементов матриц S(s) и S(t) по правилу умножения матриц. □

8.1. Оригинальные задачи 287
Задача 8.3. Пусть г* обозначает диагональный элемент матрицы замен
Джукса-Кантора, rt = ^(l+3e_4at), и пусть st обозначает недиагональный
элемент этой матрицы, st = j(l — e-4at). Покажите, что члены rtlrt2 +
+ Зв^з^ и 2sti«t2 + stirt2 + st2rti являются результатом произведения
матриц Джукса-Кантора для значений времени ti и £2, и покажите, что они
могут быть написаны, соответственно, в виде г^+ь2 и sti+t2-
Решение. Пусть матрица
/а Ъ Ь Ъ\
л \ b a b Ь \
А = \
\ЬЬаЬ\
\Ь Ь Ь а)
обозначает произведение матриц замен Джукса-Кантора S{t\) и S(tz),
соответственно, для значений времени ti и £2, то есть А = S(ti)S(t2).
Согласно правилу умножения матриц а = rtl + Sstlst2 иЬ = rtlst2 -f rt2stl +
4- 2stlst2. С другой стороны, S(ti)S(t2) = S(ti -f £2), поскольку матрицы
S(t) обладают свойством мультипликативности (см. задачу 8.1). Поэтому
rti+t2 =a = rtl+ 3stlst2,
s*i+t2 =b = rtlst2 + rt2stl 4- 2stlst2.
D
Задача 8.4. Пусть P(x1,x2,x3\T,ti,t2,tz) — правдоподобие
трихотомического дерева Т с длинами рёбер t\, t2, £3 и листьями ж1, ж2, ж3, где ж1, ж2,
х3 — три нуклеотидные последовательности, состоящие только из нуклео-
тидов С и G:

288
Глава 8
Покажите, что если не содержащее пропусков выравнивание
последовательностей ж1, х29 х3 содержит п\ участков с остатками одного и того же
типа, п2 участков с остатками типа CCG или GGC, п3 участков с
остатками типа CGC или GCG и п± участков с остатками типа GCC или CGG,
то
хЬ(*1,*з,*2)ПзЬ(*з,*2,*1)П4,
где a(ti, t2) £3) и 6(ti, t2, £3) определяются из
a(*i М М) = 1 + Зе"4а(*1+*2) + Зе"4а(*1+*з) + Зе"4а(*2+*3> + 6е-4а(*1+*2+*3>
и
b(ti,t2,t3) = l + 3e~4a(<1+t2) -e"4a(tl+t3) -3e"4a(t2+*3) -2е~4а(*1+*2+*3).
Решение. Предположим, что данные три последовательности нуклеотидов
имеют длину N; тогда, согласно допущению о независимости участков, мы
можем написать
N
P{x\x2,x*\T,h,t2M) = l[P(xlxlxl\T,tut2,t3).
и=1
Теперь мы рассмотрим возможные сочетания нуклеотидов на данном
участке и. Вероятность появления нуклеотида С на участке и во всех трёх
последовательностях листьев, выраженных в единицах вероятностей замен,
элементов матрицы Джукса-Кантора, и вероятности qa появления остатка
а в корне дерева определяется из
P(xlxlxl\T,tut2,t3) =
= P(CCC\T,hM,U) =
= qcP{C\C, ti)P(C|C, t2)P(C|C, t3)+qGP{C\G, h)P(C\G, t2)P(C|G, t3)+
+qAP(C\A, t!)P(C\A, t2)P(C\A, t3)+qTP{C\T, ti)P(C|T, t2)P(C\T, t3) =
= Qcrtlrt2rt3 + qGStlst2st3 + qA8t18t28t3 + Qcst1st2st3-

8.1. Оригинальные задачи 289
Согласно допущению о том, что частоты появления нуклеотидов в корне
являются равными равновесным частотам матрицы Джукса-Кантора, q& =
= Qc = Qg = Qt = 1/4, мы имеем
P(CCC\T,tut2,t3) = \(rtlrt2rt3 +3stlst2st3) =
= 4"4((1 + 3e~4a<1)(l + 3e"4a<2)x
x(l + 3e"4a*3) + 3(1 - e"4atl)x
x(l-e-4at2)(l-e"4a<3)) =
= 4~3(1 + 3e"4a(tl+<2) + 3e-4of(tl+t3)+
_|_ge-4a(i2+t3) _|_ ge-4a(ti+t2+t3)\
Ввиду симметрии процесса замены, выражение вероятности P(GGG\T, ti,
t2,t3) появления нуклеотида G на участке и будет точно таким же.
Правдоподобия для других сочетаний нуклеотидов на участке и будут
определяться из следующих выражений. Для триплетов GCC (и CGG):
P{GCC\T,ti,t2,t3) = qcs^r^rts+qGr^s^sts+qAS^s^Sts+qTS^s^s^ =
= ^(r^StzSta + Stirt2rt3 + 2stlSt2St3) =
= 4~3(1 _ e-4a(ti+t2) _ e-4o(ti+t3) +
+3e-4a(t2+t3) _ 2e-4a(*i+*2+t3)V
для триплетов GGC (и CCG):
P{GGC\T,ti,t2,t3) = qcs^s^rts+qGr^r^Sts+qAS^s^Sts+qTS^s^Sts =
= l(stiSt2rt3 +rtlrt2st3 + 2stlst2st3) =
= 4~3(1 - е~4а(*1+*2) _ e~4a(t2+t3) +
+3e-4a(ti+t2) _ 2е-М*1+*2+*зЬ.
для триплетов GCG (и CGC):
P(GCG\T,tut2,t3) = qcSt1rt2St3^rqGrt1st2rt3'\rqASt1st2St3+qTSt1st2st3 =
= ^(stin2st3 -\-rtlst2rt3 + 25tist25t3) =

290 Глава 8
= 4_3(1 - e-4a(*i+*2) _ e-4a(t2+t3) +
+3е-4«(*1+*з) _ 2e-4<*(*i+*2+t3h
Поэтому если вьфавнивание последовательностей ж1, ж2, х3 содержит п\
участков с остатками одного и того же типа (ССС или GGG), n2 участков
типа CCG или GGC, пз участков типов CGC или GCG и пд участков
типов GCC или CGG, то правдоподобие трихотомического дерева Т
принимает вид
Р(*\ х\ ж3|Г, 1Ъ t2> t3) = 4-3(П1+Пя+Пв+я*)а(*1, t2> *з)П1Ь(*ъ*2,*з)П2х
Здесь
a(*i, t2, t3) = 1 + 3e~4a(tl+t2) + 3e"4a(tl+*3) + Зе~4а^2+*3) + бе~4а(*1+*2+*з)
и
b(ti,t2,t3) = l + 3e"4a(tl+t2) -e"4a(tl+t3) -3e"4a(t2+t3) -2e~4a(tl+t2+t3^
П
Задача 8.5. Семейство матриц замен S(t) для алфавита с тремя остатками
{А, В, С} определяется как
Щ п st
st Щ rt/
с элементами
, = l(l + 2e-/2eos(^)),
8t = ±(l- С™'2 cos (^\ + л/Зе-3»*/8 sin (^
щ = 1 Л _ e-3«*/2cos fv|*A _ V3e-3«t/2sin /^

8.1. Оригинальные задачи
291
Покажите, что это семейство мультипликативно, имеет положительные
элементы и что интенсивности замен определяются следующей матрицей:
Найдите предельное распределение и покажите, что свойство
обратимости, то есть
P{b\a,t)qa = P{a\b,t)qb,
оказывается неверным при почти всех t > 0.
Решение. 1) Для того чтобы доказать мультипликативность, мы должны
показать, что при всех г, j = 1,2,3,
(5(t)5(e))y =^-(« + в).
В результате прямого умножения и сравнения диагональных элементов
£#(•), где г = 1,2,3, мы получаем на правой стороне:
Su(t + s) = r(t + ,) = I (l + 2e--^>/2 cos (^|±4) ) =
= I + |e--(«+.)/a«и (^) cos h&»\ +
+|e--3a(t+s)/2sin A/jfcA cos (VfoA
и на левой стороне:
(S(i)S(s))u = rtrs + stue + utss =
= I (l 4- 2e"3-/2 cos №?*\\(l + 2e"3-/2cos ^п) ) +
+ 1 Л _ e-3Q*/2cos Л/|*Л + V3e-3^2sin (^)) x

Глава 8
+
i (l - e-3-/2 cos (&A _ VSe-a-/* sin №?*\ \ x
V^OiS \ nz Sast/2 •
as
x 1 _ e-3aS/2 cog V0O£ + ^-3^/2 gin
= | + |в-з«(^)/2cos №f*\ cos (^) +
+|e-3a(t+s)/2sin Л/&Л sin ^V^^\ .
Подобную демонстрацию для недиагональных элементов двух типов, st
и ии мы оставляем читателю.
2) Чтобы показать, что элементы S(t) являются положительными, мы
вводим функции fi переменной х, где г = 1,2,3их = y/3at/2 ^ 0:
fi(x) = Srt = 1 + 2e_v^x cosx,
/2(ж) = Sst = 1 - e_v^x cosx + V^e"^ sinx,
/3(x) = 3t*t = 1 - e~^x cosx - \/Зе"^х sinx.
Для того чтобы доказать, что функции fi являются положительными,
достаточно показать, что они являются положительными в точке (точках) своего
глобального минимума. Для производной /{(х) мы имеем
/{(ж) = -2у/3е~^х cosx - 2е^х sinx =
_AeVsx I \/3 cogx + I sinx \ = _4eVsx sin
(i-)-
Мы находим, что /{(х) = 0 при х = — (7г/3) + 7rn, где п — положительное
целое число, тогда как /{(х) < 0 при х G (—(7г/3) + 27гп, (27г/3) + 2тгп).
Поэтому точки х = (27г/3)+27ГП (п — положительное целое число)
являются точками минимума функции /i(x), поскольку в этих точках функция /{

8.1. Оригинальные задачи 293
изменяет знак с отрицательного на положительный. Поскольку
/,(f + 2™)=1-е-^+2™>>0,
диагональный элемент rt = /i(x)/3 матрицы S(t) является положительным
при всех t > 0.
Точно так же для функции /г мы имеем
/2(х) = 1 - e_V5x cosx + VZe'^"sinx =
= 1 _ 2е-^х Ц cosx - ^ sinx ) =
f'2{x) = 2V3e-^x sin (| - a;) + 2е-^х cos f J - x\ =
= 4e-^x^Sin(|-x) + IcoS(|-x)) =
Функция /г достигает минимальных значений в точках х = (47г/3) + 27гп,
где п — положительное целое число, причём
h (** + 2-кЛ = 1 - e-V3((4-/3)+2-) > 0
Следовательно, st > 0 при всех £ > 0 (so = 0).
Наконец,
/з(х) = 1 - е_л/5х cosx - VSe-^xsinx =
2
4е-^х8ш|
= l-2e-^x(icosx+^
sinx =
= 1 - 2е-^х sin
in(|+x),

294
Глава 8
f3(x) = 2V3e~^xsin (| + x\ - 2e~^x cos (§+*) =
(t+*H4H) =
smx.
Функция /з достигает минимальных значений в точках х = 2тгп, где п —
положительное целое число, при этом
/з(2тгп) = 1-е-2-^7ГП>0.
Следовательно, щ > 0 при всех t > 0 (гго = 0). Таким образом, мы
показали, что все элементы матрицы замен S(t) являются положительными при
всех t> 0 (so = щ = 0).
3) Если R — матрица интенсивностей замен для семейства S(t), где
t ^ 0, то S'(t) = S(t)R. В момент t = 0, когда 5(0) = I (I — единичная
матрица порядка 3), это уравнение принимает вид 5'(0) = IR = R.
Чтобы вычислить производные элементов матрицы 5, мы вновь используем
производные функций fi(x)9 где г = 1,2,3 и х = (y/3/2)at. Мы имеем
П = Шх),
St = |/2(ж),
Поэтому
л/3 3
R = 5'(0)
-a: sn
^=<*sinf
л/3 3
wt = |/з(ж),
а; гхд = —=asin0 = 0.
л/3
r& ^ гх[)
\s0 гх0 т*0,
4) Когда £ стремится к бесконечности, строки матрицы замен S(t)
сходятся к стационарному распределению остатков. Из аналитических
выражений для элементов ru st и щ мы получаем
lim S(t)
/1 1 1\
3 3 3
III
3 3 3
. 1 1 1
\3 3 3/
r9A 9B qc"
4a яв qc
\$a qe qc/

8.1. Оригинальные задачи
295
где А, В и С обозначают типы остатков. Таким образом, все равновесные
частоты равны, то есть qA = Чв = Чс — \-
о
Пусть а и Ь — остатки двух различных типов. Свойство обратимости
остаётся верным тогда и только тогда, когда
P(b\a,t)qa = P(a\b1t)qb
при всех t > О, что ведёт к выполнению равенства P(b\a, t) = Р(а\Ъ, t) при
qa = qb. Для этого необходимо, чтобы Sij = Sji при всех г ф j, где i,j =
— 1,2,3, то есть чтобы матрица S(t) была симметричной. Однако в нашем
случае симметрия не имеет места. Например, Р(В\А, t) = ии а Р(А\В, i) =
= St, и значения этих двух матричных элементов являются различными
при t ф 2im/\/ba, где п — положительное целое число. Следовательно,
свойство обратимости отсутствует. □
Задача 8.6. Свойство обратимости вероятностной модели процесса
мутации означает, что
P(b\a,t)qa = P(a\b,t)qb
для любых остатков а, 6 и любого времени t. Можно показать, что
благодаря данному свойству и мультипликативности матрицы замен
правдоподобие дерева становится независимым от положения корня дерева. Что
произойдёт, если корень будет перемещён в один из его листьев?
Решение. Примем допущение о том, что п последовательностей длины N
соотнесены с листьями некорневого дерева Т. Допустим также, что
последовательность хг соотнесена с листом г, соединённым с внутренним
узлом j ребром (i,j) длины t (рис. 8.1, а).
Если корневой узел (2п — 1) добавлен к ребру (г,.?*) (рис. 8.1, б), таким
образом создавая два ребра с длинами U и tj, то на участке и правдоподобие
P(L2n-i|a) дерева Т, при том что остаток а помещён в корне, может быть
вычислено алгоритмом Фельзенштейна ([78]) следующим образом:
P(L2„_i|a) = '£p(b\a,ti)P(Li\b)P(c\a,ti)P(Lj\c).
Тогда правдоподобие дерева Т с длинами рёбер tm на участке и принимает
вид
Ц, = P(xmu\T,U) = Y,P(L2n-i\a)qa = ^Р«|а,^)Р(с|а,^)Р(^|с)да.
а а,с

296 Глава 8
(а) (б)
Рис. 8.1. а) Начальное некорневое дерево Т. б) Результат добавления
корневого узла (2га — 1) к ребру (г, j)
Здесь мы приняли во внимание, что, так как г — листовой узел, P(Li\b) = 1
при b = хги и P(Li\b) = О в противном случае. Свойства обратимости и
мультипликативности позволяют нам устранить зависимость
правдоподобия Щ* от типа находящегося при корне остатка а следующим образом:
Lt = ^2P{xi\aJti)P{a\citj)qcP(Lj\c) =
а,с
= Л fe^k^^Mi)) P(Lj\c)qc =
С С
Принимая допущение о независимости участков последовательности, мы
имеем, для правдоподобия дерева Г:
N N
LT = П LUT = П ^Р(х*и\с,г)Р(Ь\с)дс. (8.2)
it=l n=l с
Если корневой узел совпадает с листовым узлом г, то новое дерево Т*
имеет га — 1 лист, и последовательность при корневом узле г — хг:
г
3

8.1. Оригинальные задачи 297
Для участка и вероятность появления остатка хги в корне равна qx%^ и
правдоподобие дерева Т* с длинами рёбер t$ принимает вид:
2*. = P(L2n_!K)<H =^P{c\xlu,t)q±lP(Li\c).
С
Правдоподобие дерева Т* по всем участкам определяется из
N N
Ьт- = П Ьт- = П fei EP(cK,*)9xiP(^|c).
lt=l U=l С
Тогда, согласно уравнению (8.2) и свойству обратимости,
N N
ьт = П £р(с1<'*№;1с)<н = П <н Ер(с|4,*)р(^|с) = £*•..
и=1 с и=1 с
Поэтому ни у какого дерева правдоподобие не изменится, если его корень
будет перемещён в один из листовых узлов. □
Задача 8.7. В последовательностях х1 и х2 равной длины присутствует
только два типа нуклеотидов, С и G. Имея не содержащее пропусков
выравнивание последовательностей х1 и х2, вычислите правдоподобие
дерева, связывающего эти последовательности, опираясь на модель Джукса-
Кантора. Покажите, что рёбра оптимальной длины t\ и t2 (наиболее
правдоподобные) удовлетворяют следующему уравнению:
1 ^ 3(щ + п2)
Здесь п\ — число участков выравнивания с идентичными (совпадающими)
остатками, а п^ — число участков с несовпадениями.
Решение. Рассмотрим дерево Т с листьями ж1 и ж2 и значениями длины
рёбер t\ vLt2:

298 Глава 8
На участке и есть четыре возможных варианта выбора пар нуклеотидов на
листьях дерева: СС, CG9 GC и GG. Для пары СС мы имеем
Р(х1х2и\т,гъг2) = Р(СС|т,м2) =
= qcP{C\CM)P{C\CM) + qGP(C\GM)P(C\GM)+
+qAP{C\A, h)P(C\A9 t2) + qTP(C\T, h)P(C\T, t2) =
= ЯсП±П2 + QGStlst2 + qAStxSt2 + Qcstlst2-
Здесь rt и st - элементы матрицы замен Джукса-Кантора, г. qa —
вероятность пребывания нуклеотида а при корне дерева. При допущении о том,
что qa = 1/4 для всех типов нуклеотидов, правдоподобие на участке и
с парой СС на листьях принимает вид
P(CC\T,t1,t2) = \{rtlrt2 + Sstlst2) =
= 4"3((1 + 3e"4atl)(l + 3e~4at2) + 3(1 - e"4atl)(l - e"4at2)) =
= ^(l + 3e"4a(tl+t2)).
В силу симметрии процесса замены правдоподобие для пары GG будет
описано таким же выражением. Если участок и имеет пару CG на листьях,
то правдоподобие определяется из
P(CG\T,t1,t2) = qcrtlst2 + qGStln2 + qAStlst2 + qTStlst2 =
= 4(^1^2 + s*irt2 + 2stlst2) =
= JL(l_e-4a(t1+t2))
Точно такое же выражение можно вывести для P(GC\T,ti,t2). Наконец,
если rii участков имеют совпадения (СС или GG), а п2 участков имеют
несовпадения (CG или GC), то правдоподобие дерева Т выражается в виде
ni+n2
P(x\x2\T,t1M)= П Р(х1и,х1\ТММ) =
_ 1 (I _|_ 3e-4a(*i+*2)>\niQ _ e-4a(ti+t2)\n2
2gni+n2 ^ ' V '

8.1. Оригинальные задачи
299
Это правдоподобие — функция двух переменных t\ и t2: Р(хг, х2 |Г, ti, £2) =
= P{t\,t2). Формально отыскание максимума функции P(ti,t2) потребует
взятия частных производных dP/dti и dP/dt2, приравнивания их к нулю
и т.д. Однако легко видеть, что правдоподобие P{t\,t2) фактически
является функцией одной переменной t = t\ + t2.
Чтобы упростить дальнейшие вычисления, мы переходим от функции
P(t) к функции lnP(t). Натуральный логарифм — монотонно
возрастающая функция, и, следовательно, функции Р и In P достигают
максимального значения в одной и той же точке t*. Таким образом, мы находим
lnP(t) = -(щ + п2) In 16 + ты ln(l + 3e"4at) + n2 ln(l - e"4at),
Пт1 РМУ - l2<*nie4at , 4an2e-4at
[innt)) - 1 + 3e-4-t+ 1-е-4-*'
Решение уравнения (1пР(£*))' = 0 даёт
1 ^3(ni+n2)
Г = —In — •
4a 3ni — 7i2
Максимальное значение функции P(£), достигнутое в точке t*, имеет вид
Р(Г) = Р(х\а?\Т,ЬЬ)
П\П2
16n!+n2-l 3(П1 + П2)
Здесь значения длины рёбер t\ и t2 удовлетворяют уравнению t\-\-t2 = t*.
Интересно, что, хотя точка максимума t* = t\ +12 зависит от параметра а
модели Джукса-Кантора, значение наибольшего правдоподобия от него не
зависит.
В качестве примера рассмотрим две нуклеотидные
последовательности длины 11:
CCGGCCGCGCG
CGGGCCGGCCG'
где rii = 8 и П2 = 3. Опираясь на модель Джукса-Кантора с параметром
а = 10~9, мы следующим образом вычисляем значение наибольшего
правдоподобия:
Р(х\х2\ТММ) = —-4тТп = 6'61' 1()13'
11-16

300
Глава 8
которое достигается, когда эволюционное время £* = ti+^2 между
последовательностями равно 113 миллионов лет. Согласно свойству молекулярных
часов это означает, что время расхождения последовательностей х1 и х2
составляет t\=t2 = 56,5 млн л. н. □
Задача 8.8. Рассмотрите упрощённое филогенетическое пространство,
состоящее из двух деревьев ГиГс вероятностями Р(Т) и Р{Т), Если
процедура предложения всегда предлагает другое дерево, то есть то, которое
не является текущим деревом, покажите, что алгоритм Метрополиса
производит последовательность, где частоты ГиГ сходятся к их вероятностям.
Решение. Алгоритм Метрополиса представляет собой процедуру
осуществления выборки, которая производит последовательность деревьев,
в которой каждое новое дерево зависит от предыдущего. Пусть Pi =
= Р(Г, U\x9) = Р(Т) (или Р(Т)) — апостериорная вероятность текущего
дерева, тогда Р2 = P{T,im\xm) = Р{Т) (или Р(Т)) — вероятность
предложенного нового дерева. Если Р2 ^ Р\, то новое дерево принимается
в качестве следующего элемента последовательности деревьев безусловно;
если Р2 < Ръ то новое дерево принимается с вероятностью Р2/Р1.
Сначала рассмотрим случай, когда Р(Г) = Р(Г) = \. Процедура
предложения предлагает дерево Т в качестве нового дерева, когда Т —
текущее дерево. Тогда, поскольку Р{Т) = Р(Т)9 по правилу Метрополиса в
качестве следующего дерева принимается дерево Т. В следующем шаге
дерево Т предлагается и принимается как следующее дерево по той же самой
причине и так далее. Поэтому в результате мы получаем строго
чередующуюся последовательность: либо Г,Г,Т,Т,Т,Т,..., либо Г,Г,Г,Г,Т,Т,....
В обоих случаях частоты появления деревьев Т и Т сходятся к их
вероятностям:
Um^ = i=P(T), ]im£ = i = P(f).
В общем случае, когда Р(Т) ф Р(Г) (предположим, что Р(Г)>Р(Г)),
процедура Метрополиса работает следующим образом. Если текущее
дерево — Т, то процедура предложения предлагает дерево Т и следующим
деревом будет дерево Т (с вероятностью q = Р(Т)/Р(Т)) или дерево Т
(с вероятностью р = 1 — q). Однако в том случае, если текущее дерево — Т,
следующим деревом будет дерево Т с вероятностью 1. Последовательность

8.1. Оригинальные задачи
301
деревьев, полученная алгоритмом Метрополиса, может быть описана
марковской цепью с двумя состояниями 1 (Т) и 2 (Т), а также с вероятностями
переходов pn = р, pi2 = q, P21 = 1, Р22 = 0. Пусть rai (712) — число
деревьев Т (Т) в последовательности длины га (п = п\ + гаг). Согласно сла-
бсшу закону больших чисел, для эргодической марковской цепи с конечным
числом состояний ([88]) мы имеем
Пх Р 712 Р
где (7Г1, 7Г2) — стационарное распределение состояний марковской цепи. Эр-
годическая теорема для марковских цепей гласит, что стационарные
вероятности удовлетворяют следующей системе линейных уравнений:
7Г1 + 7Г2 = 1,
7Г1 = 7Г1Р+ 7Г2,
7Г2 = TTiq.
Решение этой системы — щ = Р(Т) и 7Г2 = -Р(Т) — показывает, что
частоты появления деревьев Т и Т в последовательности деревьев,
произведенной алгоритмом Метрополиса, сходятся по вероятности к вероятностям
этих деревьев:
8.1.1. Байесов подход к отысканию оптимального дерева и алгоритм
Мау-Ньютона-Ларге
Теоретическое введение в задачи 8.9 и 8.10
Отыскание дерева с наибольшим правдоподобием требует решения
задачи оптимизации для алгоритмически определённой функции многих
переменных. Такие задачи печально известны как дорогие в вычислительном
отношении, разве что может быть предложена эффективная стратегия
поиска максимума.
Другой альтернативой может послужить Байесов подход к отысканию
оптимального дерева. May, Ньютон и Ларге ([191]) приспособили
алгоритм Метрополиса, один из методов Монте-Карло с марковскими
цепями (МКМЦ), к осуществлению выборки из апостериорного распределения
7г в пространстве Т филогенетических деревьев со свойством
молекулярных часов. (Позже этот алгоритм был обобщён Ларге и Саймоном ([172])

302
Глава 8
с тем чтобы он мог обрабатывать также корневые деревья, не
обладающие свойством молекулярных часов.) Приближённое апостериорное
распределение деревьев может быть определено по имеющимся данным
расшифровки последовательности, стохастической модели этих данных и по
априорному распределению в пространстве Т. Для того чтобы определить
правило предложения Q алгоритма Метрополиса, дерево Теп листьями,
где Т G Т опознаётся его каноническим представлением (<r,t). Здесь а =
= (<т(1),..., <т(га)) — порядок листовых узлов дерева Т слева направо
(перестановка чисел 1,2,..., п), at = (ti,..., £n_i) — вектор соотносимых
моментов времени расхождения: U = -D<7(i),<7(i+i)/2, где г = 1,... ,га — 1,
a Dij определяется как расстояние между листьями г и j в дереве Т.
Например, для дерева Ть показанного на рис. 8.1, а, каноническое представление
имеет вид (cr,t) = ((1,2,3,4,5), (/i6, h9,hg, h7)).
Правило предложения Q применяется за два шага и работает с
текущим деревом Т следующим образом. Для дерева Теп листьями
существует 2n_1 деревьев (в том числе дерево Т), полученных всеми возможными
перестановками п — 1 пары рёбер, исходящих из каждого внутреннего узла
дерева Т. В первом шаге Q\ правило предложения Q выбирает с равной
вероятностью l/2n_1 одно из этих 2n_1 деревьев с переставленными
рёбрами. Таким образом, после шага Q\ новый порядок листьев а*
производится как порядок, соотносимый с вновь (последним) выбранным деревом.
Во втором шаге Q<i компоненты вектора t изменяются независимо друг
от друга. А именно значение £*, компонента нового вектора t*,
выбирается из равномерного распределения на интервале (U — S, U + S), где S —
постоянная подстройки. Чтобы восстановить предложенное дерево из
канонического представления (<r*,t*), нужно разместить листовые узлы по
горизонтальной оси в порядке, определяемом <т*. Затем из каждой точки на
середине расстояния между смежными листьями а* (г) и а* (г +1) провести
вертикальную линию и поместить узел на высоту, равную
соответствующему времени расхождения £j. Самый высокий построенный узел будет
корнем дерева. Затем в порядке сверху вниз от каждого внутреннего узла
проводятся ветви к самым высоким, не имеющим родителей узлам,
расположенным как по левую, так и по правую сторону от внутреннего узла.
Например, каноническое представление дерева Т\ на рис. 8.2, б может быть
преобразовано в соответствии с правилом предложения Q к каноническому
представлению (<т, t*) = ((1,2,3,4,5), (/ц, hg, /17, hg)) (где в шаге Q\
выбирается одна и та же ориентация для всех ветвей и шаг Qi сокращает время
расхождения £з = £>34/2 = hg на hg — hjn увеличивает время расхождения
£4 = £*45/2 = hr на hg — hr). Предложенное дерево Т2, восстановленное из
нового канонического представления, изображено на рис. 8.2, б.

8.1. Оригинальные задачи
303
Рис. 8.2. Дерево Т±: изменяется в дерево Тъ (а) в результате (б) взаимного
изменения высот узлов 7 и 8 (в шаге Qi правила предложения Q)
Обратите внимание, что в шаге Q\ правило не изменяет топологию
дерева, тогда как в шаге Q2 она может либо изменить её, либо оставить
неизменной: большее значение 5 предоставляет больше шансов перехода к
новой топологии. Правило предложения Q = Q2°Qi является
симметрическим в том смысле, что для любых двух деревьев Т\ и Т2 из пространства Т
вероятность предложения дерева Т2 при текущем дереве Т\ равна
вероятности предложения дерева Т\ при текущем дереве Т2.
Наконец, стандартное правило принятия в алгоритме Метрополиса
заменяет текущее дерево Т\ на новое предложенное дерево Т2 с
вероятностью
1
<Т2)
min I 1,
LT2P(T2)
Ьт,Р{Тх)

304
Глава 8
Здесь Lt» и P(Ti) — соответственно, правдоподобие и априорная
вероятность дерева Т*. Итоговая последовательность деревьев — марковская цепь,
которая имеет важное свойство ([180], раздел 5): почти во всех реализациях
такой марковской цепи (относительная) частота конкретного дерева Т,
наблюдаемого в последовательности деревьев, сходится к апостериорной
вероятности 7г(Т) этого дерева (см. задачу 8.8). (То же утверждение верно для
любой топологии дерева и вообще для любого семейства деревьев.)
Поэтому дерево с наиболее высокой апостериорной вероятностью будет иметь
наиболее высокую частоту в достаточно длинной реализации марковской
цепи и, следовательно, может быть обнаружено методом МКМЦ.
Задача 8.9. Преобразование некоторого дерева из пространства Т,
следующее из шага Q2 процедуры предложения, представленной в [191],
называется изменением профиля. Рассмотрите изменение профиля, преобразующее
дерево Т\ в дерево Т^ (рис. 8.2). Предположите, что узлы 8 и 7 дерева Т\
на рис. 8.2 расположены на высоте hg и h7 и их высота изменяется,
соответственно, на h7 и hg. Покажите, что по мере стремления к нулю разности
hg — h7 итоговое изменение правдоподобия тоже стремится к нулю.
Решение. Пусть hi обозначает высоту внутреннего узла i текущего
дерева Ti, где г = 1,2,3,4. В дереве Т2 узел 7' помещён на высоту hg, тогда
как узел 8' помещён на высоту h7. Пусть последовательности хг, где г =
= 1,..., 5, будут листьями деревьев Т\ и Т2. Для оценки изменения
значения правдоподобия дерева, происходящего в результате взаимного
изменения высоты узлов, мы используем алгоритм Фельзенштейна. Сначала мы
определим правдоподобие дерева Ti на участке и. Проходя его в порядке
снизу вверх, мы получаем
P(L6\b) = P(x1u\b,h6)P(xl\bih6),
P(L7\d) = P(xi\d,h7)P(xl\d,h7),
P(L8\c) = J2P(xl\c,hg)P(d\c,hg - h7)P{L7\d) =
d
= £P(a£|c>*e)P(rf|c>fte - h7)P{xi\d,h7)P{xl\d,h7),
d
P(L9\a) = ^P(b|a,h9 - he)P(L6\b)P(c\a,hg - hg)P(Ls\c) =
b,c

8.1. Оригинальные задачи 305
= ^2 Р(Ь\а, h9 - he)P(xi\b, h6)P(x2u\b, /i6)x
x P(c|a, h9-hs)P(x3u\c, hs)P(d\c, hs-h7)P{x4u\d, h7)P(x5u\d,h7).
Поэтому правдоподобие на участке и определяется из
P(xl\Tut.) = P(xl,a*,xl,xtxl\T1) =
= ^2<1аР(Ь9\а) =
а
= J2 qaP(b\a,hg - h6)P(x1Jb,h6)P(xl\b,h6)x
a,b,c>d
xP(c|a, h9-hs)P{x3u\c, hs)P(d\c, hs-h7)P(x4u\d, h7)P(x5u\d, h7).
Мы делаем допущение о том, что выравнивание последовательностей хг,
где г = 1,..., 5, содержит N независимых участков. Тогда для
правдоподобия дерева Т\ мы имеем
U = P^sV,*4,*6^) = f[ Р{х1\Тг) =
и=1
N
= П Е qaP(b\a,h9-h6)P(x1u\b1h6)P(x2u\b,h6)x
u=l a,b,c,d
xP(c\a,h9 - hs)P{xl\c,hs)P{d\cM ~ h7)P(x4u\d,h7)P(x5u\d,h7).
Точно так же правдоподобие дерева Т2 с тем же набором
последовательностей листьев определяется из
N
L2 = Р{х\х2,х\х\хъ\Т2) = JJ Р«|Т2) =
N
= П Е qaP(b\a,h9-h6)P(x1u\bih6)P(x2u\b,h6)x
u=l a,b,c,d
xP(c|a,/i9 - h8)P(xl\c,h8)P(d\c,hs - h7)P(xl\d,h7)P(x4u\d,h7).
Изменение правдоподобия AL может быть написано следующим образом:
AL = Li - L2 =

306 Глава 8
N
= ^2 ]JqaiP(bi\auh9 - h6)P(x1i\biih6)P(x2i\bilh6)x
CLi,bi,Ci)di 2=1
xP(a\au h9 - h8)P(di\cil h8 - h7)P{x$\du Л7)Д, (8.3)
где
Д = P(x?|c«, hs)P(xl\di, h7) - P{x\\du Ы)Р{х\\ъ, hs).
Теперь мы найдём предел величины AL при /i8 — h7 —> 0, принимая во
внимание, что вероятности переходов P(x\y,t), элементы матриц замен,
представляют собой непрерывные функции переменной t.
Сумма в уравнении (8.3) содержит члены двух типов. Для всех членов
с Ci ф dc
lim P{di\aM ~ h7) = P(di|ci,0) = 0,
h8 —hj—►O
так как при t = 0 матрица замен превращается в единичную матрицу. Со
всеми другими ограниченными сомножителями мы имеем
N
lim V T\qaiP(bi\ai,hg-h6)P(x}\bi,h6)P(^\bi,he)x
hs—hr—^O ' ■* л"л-
xP(a\au h9 - hs)P(di\ci, h8 - h7)P{xi\du h7)A = 0. (8.4)
Для всех членов с с\ — dc
lim Д= lim (P(xf|ci,M^fl^)M-^fki,M^(^5ki,M)=0.
hs—*h7 /l8—>ГЬт
Все другие сомножители ограничены; поэтому
N
lim V JJqaiP(bi\auhg - h6)P{x1i\bhh6)P(x2i\bhh6)x
xP(ci|oi, /i9 - h8)P(ci\ci, h8 - h7)P(xj\ci, h7)A = 0. (8.5)
Равенства (8.4) и (8.5) дают
lim AL = 0.
h8-h7^0
Следовательно, функция правдоподобия изменяется непрерывно от высоты
узла, даже если такие изменения высоты ведут к «молекулярным» скачкам
в топологии дерева. □

8.1. Оригинальные задачи
307
Задача 8.10. Покажите, что в результате изменения профиля несмежные
листья не могут стать эволюционными соседями.
Решение. Сначала обратите внимание, что в шаге Q\ правила
предложения Q любые два листа могут стать смежными, но шаг Qi не изменяет
топологию дерева, и, таким образом, все соседи остаются теми же
самыми. В шаге Q2, однако, смещение высоты внутренних узлов вверх и вниз
может произвести новую топологию дерева и, таким образом, новых
соседей. Пример того, как смежные листья стали соседями после шага Q^
представлен на рис. 8.2 (листья 3 и 4).
Покажем, что после изменения высоты узлов несмежные листья не
могут стать соседями. Из правил восстановления дерева из канонического
представления следует, что для смежных листьев г и j узел на
вертикальной линии, проведённой из точки, расположенной посередине между
ними, — последний общий предок узлов г и j. Тогда для любых двух листьев г
и j (как смежных, так и несмежных) последним общим предком будет
самый высокий узел, расположенный выше интервала (г, j). При допущении
о том, что между листьями in j есть листья /i,..., Ik, мы обозначаем
время расхождения между листьями г и 1\ как t\, время расхождения между
листьями 1\ и I2 — как t<i и так далее и, наконец, время расхождения между
листьями Ik и j — как tk+i. Тогда время расхождения между листьями г
и j будет t = max(£i,..., £fc+i)- Расстояние между листьями г и j в дереве
со свойством молекулярных часов д,ц = 2max(ti,..., £fc+i). Точно так же
dux = 2*i, du2 = 2 max(£i, t2),..., duk = 2 max(£i,..., tk); таким образом,
dux ^ du2 ^ • • • ^ duk ^ d*j.
Мы принимаем допущение о том, что листья г и j — соседи, и ищем
противоречие. Необходимое условие, которому должно удовлетворять
расстояние dij между двумя соседними листьями, — dij = minm^i dim. Минимум,
взятый по всему множеству листьев кроме г не превышает минимум,
взятый по его подмножеству {Zi, Z2) • • •, h, j}- Поэтому
dij = mindim ^ dnx < dij,
тфг
если t\ ф max{£i,..., tk+i}. Если t\ = max{ii,..., £fc+i}> то применение
той же логики, что и выше, к расстояниям djik, djik_1,..., dji, позволяет
получить
dij = min djm ^ djik < dji,
тфз

308
Глава 8
поскольку t\ ф £fc+i и tfe+i < max{£i,..., £fc+i}. Таким образом, мы
пришли к противоречию d^ < d^. Поэтому в шаге Q<i процедуры предложения
дерева два несмежных листа не могут стать эволюционными соседями. □
Задача 8.11. Плоское априорное распределение длин рёбер приписывает
априорную вероятность к любой топологии, которая получается
интегрированием по всем возможным длинам рёбер в этой топологии. Этот
интеграл будет определённым, если, согласно [191], мы устанавливаем предел
на полную длину ребра от корня до любого листа; назовём этот предел В.
Рассмотрите случай, где выполняется свойство молекулярных часов, и
покажите, что дерево с четырьмя листьями и топологией ((12) (34)) имеет
суммарную априорную вероятность В3/3; покажите, что этот интеграл
равен Вг/6 для топологии ((1(23))4). Это показывает, что различные
топологии могут иметь различные априорные вероятности. Покажите, однако, что
если определить помеченную историю как определенный порядок для
моментов времени внутренних узлов относительно настоящего времени (при
допущении о молекулярных часах), то все помеченные истории для
четырёх листьев будут иметь одну и ту же априорную вероятность. Расширьте
это свойство на дерево с п листьями.
Решение. В случае представленного ниже дерева с четырьмя листьями Т\
и топологией ((12)(34)):
12 3 4
переменные t±, £2, £3 — моменты времени молекулярных часов,
соотнесённые с внутренними узлами дерева Т\. Априорная вероятность дерева Т\
определяется тройным интегралом следующим образом:
*3 / «3
Р(Тг) = J IJ ПdtA dt2\ A3.

8.1. Оригинальные задачи
309
Здесь для времени £3 установлен верхний предел В. Интегрирование даёт
простую формулу:
в / t3
Р(Тг) = j ljtsdt2 Аз = У*!Аз = Xе
о \о / о
В дереве Т2 с четырьмя листьями и топологией ((1(23))4), представленном
ниже:
1
переменные t\, t2, £3 — моменты времени молекулярных часов,
соотносимые с внутренними узлами дерева Т2. Тогда априорная вероятность
дерева Т2 определяется из
Р№>=/(/(/ 7 7
*з =
в / t3
= I[It2dt2)dt3 = I(^dt3)=f-
Разность априорных вероятностей Р(Т±) и Р(Т2) — очевидный результат
разницы верхних пределов интегралов, определяемых топологиями
деревьев. Тогда как топология ((1(23))4 устанавливает зависимость между
высотами внутренних узлов 5 и 6, топология ((12)(34)) позволяет или узлу 5
или узлу 6 быть выше другого. Однако если порядок высот узлов или
помеченная история определена, то при допущении о свойстве молекулярных

310
Глава 8
часов оба интеграла будут иметь одно и то же множество интервалов
интегрирования и плоские априорные вероятности деревьев Т\ и Т2 будут
равны:
*3 / *2
PPU-1W)-/ / /
dt\ ) dt2 ) dts = -^-.
о \o \o
To же самое верно для любого дерева с четырьмя листьями Т4: при
известной помеченной истории плоская априорная вероятность дерева Т4
равна В3/6.
Последнее утверждение может быть расширено до дерева Тп с п
листьями и свойством молекулярных часов. Если порядок высот внутренних
узлов известен, то плоская априорная вероятность дерева Тп определяется
из
р(тп) = I I \ I " 11dtl I '"dtn-3 J dtn~21 dtn-x =
I
4.71-2
ln-\ ,, _ Bn~
-atn-\
(ra-2)! 74_i (n-1)! П
о
Замечание. Мы показали, что все помеченные истории с п листьями
имеют одну и ту же плоскую априорную вероятность Вп~1 /(п — 1)!, где
В — верхний предел полной длины рёбер от корня до любого листа дерева
со свойством молекулярных часов. Существует п\(п — 1)!/2п-1
помеченных историй с п листьями (см. задачу 7.18). Поэтому чтобы определить
собственное плоское априорное распределение множества помеченных
историй, мы должны использовать плоскую функцию плотности
распределения вероятностей с нормализующей постоянной Сп = (2/В)(п\)~1^п~1\
В таком случае мы получим следующее выражение суммы априорных
вероятностей по всем помеченным историям:
п\(п-1)\ , яч
on—1 v '
--^Hh-{H
•dtn-2 I dtn-i =
n!(n —1)! 2n_1
271-1 n!(n-1)! ~

8.1. Оригинальные задачи
311
Однако если плоское априорное распределение определяется, с тем
чтобы использоваться на шаге принятия в алгоритме Метрополиса,
нормализация не требуется. Действительно, если текущая помеченная история
произведенной последовательности — Ti, новая помеченная история Т2
принимается как следующий элемент последовательности с вероятностью
min(l, Lt2P(T2)/Lt1P(Ti)), где Li и Р(Т*) — соответственно,
правдоподобие и априорная вероятность дерева Т*. Тогда равные коэффициенты
нормализации для априорных вероятностей P(Ti) и Р(Т2) будут взаимно
уничтожены. Фактически, поскольку плоские априорные вероятности
помеченных историй равны друг другу, отношение в правиле принятия становится
отношением правдоподобия помеченных историй Т2 и Т\.
Задача 8.12. При процессе Юла плотность вероятности того, что ни одно
расщепление не произойдёт в течение интервала от 0 до t, определяется
пределом функции (1 - \6ty/5t при St —» 0, и поэтому равна е .
Выведите, что априорная вероятность Юла для дерева с п листьями
пропорциональна е_л^*% где ti — все длины рёбер. Следуя тем же рассуждениям,
что и в предыдущей задаче, покажите, что априорные вероятности для всех
помеченных историй на четырех листьях равны по априорной вероятности
Юла. Расширьте это утверждение на дерево с п листьями.
Решение. Ради иллюстрации мы интерпретируем процесс Юла Et, где t ^
О, как размер популяции во время t. Мы принимаем допущение о том, что
каждый член популяции может делиться и производить двух потомков в
случайный момент времени и независимо от других членов. Интенсивность
деления Л одна и та же для всех членов популяции. Вероятность того, что
никакое деление не происходит в отдельной линии родословной в течение
временного интервала [0,t), равна е~Л*.
Пусть Т — обладающее свойством молекулярных часов дерево с п
листьями (см. рис. 8.3), такое что сумма длин рёбер от корневого узла 2п — 1
к каждому из листьев 1,2,..., п равна Т. Мы можем рассматривать такое
дерево как реализацию процесса Юла Et, где 0 ^ t ^ T, с начальным
условием Eq = 2. В дереве Т каждый внутренний узел к, где к = п +
+ 1,..., 2п — 1, представляет событие деления и появления двух потомков;
п — 1 горизонтальная штриховая линия (кроме нижней) соответствует
моментам времени таких событий деления (воспроизводства). Число
пересечений рёбер дерева с горизонтальной линией, указывающей время t, где
О < t < Т (не совпадающей с любой из штриховых линий), равно размеру
популяции Et во время t. В частности, Ет = п.

312
Глава 8
2n-l
2n-3
2n-2 \
1
i
1
J
П "
n+2
Рис. 8.З. Дерево Ten листьями и свойством молекулярных часов
представляет реализацию процесса Юла в течение временнбго интервала [О, Т]:
каждый внутренний узел соответствует событию деления (воспроизводства),
а п листьев представляют популяцию во время Т
Мы найдем априорную вероятность дерева Т с длинами рёбер
*i j • • ■ j ^2n-i- Сначала мы обращаем внимание, что п горизонтальных
штриховых линий создают разбиение временнбго интервала [О, Т] на п — 1
временных отрезков t'i9 где г = 1,..., п — 1. В пределах временнбго отрезка г
размер популяции равен г + 1. Вероятность Pi слоя дерева Т в пределах
г-го временнбго отрезка равна вероятности того, что никакой потомок не
произведен в течение временнбго интервала t\ каким-нибудь членом
популяции и, поскольку история каждого члена независима от всех остальных,
равна произведению гI + 1 сомножителей:
Pi
t+i
IF
1
■а*;
= е
-A(t+i)t;

8.1. Оригинальные задачи
313
Вероятность деления в данный момент t для отдельного индивидуума равна
нулю (в отличие от временного интервала). Это подразумевает, что
вероятность деления в данный момент для любого конечного числа индивидуумов
также равна нулю. Следовательно, априорная вероятность дерева Т —
произведение вероятностей Р* по всем временным интервалам t[,..., ^п_х\
п-1
Р(Т) = П Pt = е
-aV(*+i)*;
г=1
г=1
Мы можем выразить Р(Т) в единицах длин рёбер t\,..., tin-\ дерева Т,
поскольку, ввиду выбора разбиения, существует простое соотношение
между ti,. • -,*п-1 И *Ь- • • 5*2п-1*
п-1 2п-1
г=1 j=l
Таким образом, априорная вероятность дерева Т с данными длинами рёбер
принимает вид
-л Е tj
P(T,ti,...,t2n-i) = e j=1 •
(8.6)
Теперь мы определим априорную вероятность Юла для дерева с п листьями
и заданной помеченной историей при допущении о том, что верхний предел
времени от корня до любого листа равен В (подобно задаче 8.11).
Мы начинаем со случая п = 4. Пусть Т4 — дерево с четырьмя
листьями, с помеченной историей ((1(23))4) и временными переменными t\, £2,
£3, соотносимыми с внутренними узлами следующим образом:
12 3 4

314 Глава 8
Уравнение (8.6) даёт априорную вероятность дерева Т4 с длинами рёбер t\,
P(T ,ti,ti,t2,t2 — *1>*3>*3 — *2) =
_ e-A(ti+ti+t2+(t2-ti)+ts+(*s-*2)) _
= е-Л(*1+*2+2*з).
Интегрирование функции плотности вероятности по значениям
переменных ti,t2,ts, разрешённых помеченной историей, даёт априорную
вероятность Юла для помеченной истории такую, как и в дереве Т4:
? (1 (1 \
Р(Т4) = / 2Ае-2А'3 / Ае-А'2 / Xe-Xtldh dt2)dt3 =
= ?2Хе-2Мз ( /Ae-At2(l-e-A'2)dt2) dt3 =
в
= /2Ae-2At3(1~e""At3)2^3 =
АВ\3
е~ха)
fair")
Эти доводы остаются верными и для дерева с четырьмя листьями,
соотносимого с любой другой помеченной историей.
Точно так же мы допускаем, что в дереве Тп с п листьями
временные переменные £i,£2>-•->£п-ь соотносимые с внутренними узлами
дерева, были перечислены в порядке, определённом помеченной
историей дерева Тп (U < £i+i)- Мы применяем уравнение (8.6), чтобы
определить априорную вероятность Юла дерева Тп с длинами рёбер £i, £i, *2> *2 —
— ti,...,tn-i,tn-i — tn-2 следующим образом:
P(Tn,ti,ti,t2,t2 —ti,...,tn-i,tn-i —tn-2) =

8.1. Оригинальные задачи
315
Интегрирование по всем разрешённым областям переменных t\, £2, • • •, tn-\
даёт априорную вероятность Юла для помеченной истории, связываемой с
деревом Тп:
Р(Тп)= f 2\e'2Xin-1l f Ae"At"-2.-- I f Xe-xtldtX • A-aU-i =
-/
ко \o
в
(Л _ *>-Atn-i\n-2
о
2
(1_е-АВГ-1( 1 +в-ЛвУ
(п-2)
И снова все доводы и, следовательно, формула априорной вероятности Юла
Р(Тп) остаются верными для дерева с п листьями с любой помеченной
историей при условии, что временные переменные *i, *25 ■ • • j tn-i выбраны
именно так, как описано выше.
Подобно случаю плоской априорной вероятности (задача 8.11), мы
показали, что помеченные истории всех деревьев с п листьями и полной
высотой не более В имеют равные априорные вероятности Юла. Легко
видеть, что утверждение остаётся верным даже без ограничения на «возраст»
дерева, поскольку интегралы экспоненциально убывающих функций
являются конечными и по ограниченным и по неограниченным областям
интегрирования. Именно в этом состоит отличие от случая плоской
априорной вероятности, где ограничение на полную высоту дерева обеспечивает
необходимое и достаточное условие конечности интегралов и поэтому
собственно определяет плоские априорные вероятности помеченных историй.
О нормализации априорных вероятностей и о том, почему нормализация
априорных вероятностей, используемых в алгоритме Метрополиса, не
требуется, повествуется в замечании к задаче 8.11. □
Замечание. В процессе Юла вероятность перехода Pkn(t) = P(Et =
= п\Ео = к), где п> к, определяется по следующей формуле ([77]):
/п-1\
\п-к)
—кХЬ/л „—\t\n-k
p-w=U-fcJe (1~е }
Интересно установить соотношение между вероятностью перехода Pkn(t)
и априорным распределением Юла для деревьев, рассмотренных выше.

316
Глава 8
Обратите внимание, что процесс Юла — частный (особый) случай
хорошо изученного процесса рождения и гибели с показателем
(интенсивностью) смертности, установленным в ноль. Как мы уже видели, любое
дерево со свойством молекулярных часов и плотностью вероятности Ае~л*
по его рёбрам представляет реализацию процесса Юла с уровнем
рождаемости (воспроизводства, деления) Л и начальным состоянием Е$ = 2.
Вероятность перехода P2n(t) может быть найдена из уравнения (8.7) путём
приравнивания высоты tn-\ корневого узла к t и интегрирования по
высотам всех внутренних узлов ti, £г> • • • > tn-2 (соответствующих дальнейшим
потомкам корневого узла) в одном и том же интервале [0,£). Таким
образом, если в качестве высоты корневого узла выбрана временная
переменная tn-i, мы получаем вероятность
e~2Xt ff f /Ae-^A* ] = е-2Л*(1 - е~м)п~\
Так как есть (п— 1) способ выбора высоты корневого узла среди временных
переменных £i, £г> • • • > *п-ь вероятность перехода принимает вид
P2n(t) = (п- 1)е"2Л*(1 - e~xt)n-2.
Поэтому мы вывели формулу вероятности перехода в процессе Юла при
к = 2. В теории стохастических процессов такие формулы выводятся путём
решения системы дифференциальных уравнений Колмогорова ([77]).
Задача 8.13. При допущении о свойстве молекулярных часов вычислите
математические ожидания длины всех ветвей корневых деревьев с двумя,
тремя или четырьмя листьями при априорной вероятности Юла с
интенсивностью деления А и коалесцентной априорной вероятностью с размером
популяции в.
Решение. Мы начинаем с дерева Т2 о двух листьях. В силу свойства
молекулярных часов, два ребра дерева Т2 имеют равную длину; она
определяется как случайная переменная L и принимает значения t, где 0 < t < +oo.
При априорной вероятности Юла (задача 8.12) вероятность дерева Т2 равна
Py(T2,t,t) = e~2Xt, а функция плотности вероятности — py(t) = 2Xe~2Xt.
Тогда математическое ожидание значения длины ребра определяется из
EyL = J tp(t)dt = J 2tXe~2Xtdt =

8.1. Оригинальные задачи
317
+оо
= Г td(-e-2Xt) = -te~2Xt
+00
/
-2А*
2Л
+оо
t=0
+ I e
t=o о
= _1_
2Л'
-2Xt
dt
При коалесцентной априорной вероятности с размером популяции в
вероятность дерева Т2 — Pc(T2,t,t\6) = (2/0)e~2t/e, а функция плотности
вероятности — pc(t) — (2/9)e~2t/e. Поэтому
+оо
+оо
2t
ECL= ftp(t)dt= f |e '*=§.
Теперь мы рассмотрим дерево Т3 с тремя листьями, расположенными
следующим образом:
Мы делаем допущение о том, что длины рёбер дерева определяются
случайными переменными L\ и 1,2, принимающими, соответственно, значения
t\ и t2, где 0 ^ ^ < +оо и 0 ^ t\ < t2. При априорной вероятности Юла
вероятность дерева Т8 имеет вид
/V(T3,ti,*i,*2,t2-ti) = e-2Atae-Atl,
а функция плотности вероятности — вид
Ру(НМ) = Ae-Atl2Ae"2At2.
Тогда
+оо t2 +оо / t2 \
ErLi =11 tip(tut2)dt1dt2 = J 2Ae~2At2 ( f ^Xe'^dh J <ft2 =
t2=0ti=0 0 \0 /

318 Глава 8
О
+ 00 *2 +00 / *2 \
EyL2 =[[ t2p(t1,t2)dt1dt2 = I 2t2Xe~2Xt2 I I Xe'^^dtx J dt2 =
t2=0*i=0 0
= / 2t2Ae"2A*2(l - e"At2)^2 =
t2=0*i=0 0 \0
2A 9A 18A
о
При коалесцентной априорной вероятности дерево Т3 имеет вероятность
Pc(T\tutut2,t2-t1\e)=(^j eV VeV V,
и функция плотности вероятности описывается вьфажением вида
/^ . \ 4 (""^/2 (""/)
Тогда математические ожидания значений Li и L2 определяются из
+оо t2
EcLi = / / tip(ti,t2)dtidt2 =
t2=oti=o
+00 / 2t2 \ / *2 / 4ti \
= /?,H f$eH,
+00 / 2t2 \ / *2
/KT,/:
0 \0
eV / cfti J d£2 =
+00 / 2fe\ / / 4*2 \ / 4*2
= _в__е_ , 0 е.
18 12^4 9'
ECL2 = / / t2p(ti,t2)dtidt2 =
t2=0*i=0

8.1. Оригинальные задачи
319
dt\ I dt2 =
0
+оо
/
0
в
2
в
в
18
2t2
~~ё~
40
9 '
1-е
Наконец, мы рассматриваем деревья с четырьмя листьями и двумя
возможными топологиями. Пусть Т* — дерево с топологией ((12)(34)) и длинами
рёбер t\, ^i,^2,*2,^3 -ti,h —t2'-
Мы делаем допущение о том, что случайные переменные L\, L2, L3
определяют высоты внутренних узлов дерева и принимают, соответственно,
значения ti, t2, ts, где 0 < £з < +о°, 0 ^ ti < t3, 0 ^ ^2 < *з- При априорной
вероятности Юла вероятность дерева Т4 имеет вид
Py(2?,tutiMM,ts-tuts- t2) = e-2A*3e-A*2e-Atl
и функция плотности вероятности — вид
Py{tiMM) = \e-xtl\e-xt22\e-2Xt3.
Тогда
+оо *з *з
EyLi = / / / t1pY(tut2,t3)dt1dt2dt3 =
£3=0*2=0*1=0
+00 / *3 \ / *з \
= / 2Ае"2А*3 I /tiAe-Atldti J I f \e~xt2dt2 J <Й3 =

320 Глава 8
+оо
= J 2Ае"2Л'з (_*3е-^ - ^ + ±) (1 - e~^)dt3 =
о
= -A + l_l + i,l = _5_.
9А 8А ЗА 2А А 72А'
+00 *3 *3
EyL2 = / / / t2PY(ti,h,ts)dtidt2dts =
t3=ot2=oti=o
= / 2Ae"2At3 [ J Xe-^dh J f f t2Xe~Xt4t2 J dt3 =
+00
= J 2Ае-2Л'з Ь3е-«з _ §-* + A (1 _ e-At,)Aa =
о
5 ,
72A'
+00 *з *з
EyL3 = III t3pY(t1,t2,t3)dt1dt2dt3 =
t3=0*2=0ti=0
+oo / *з \ / t3
= f 2t3\e~2Xt* I f \e-xtldh j I f \e~Xt*dt2 I <Й3 =
+oo
= / 2t3Ae"2A*3(l - e"At3)2^3 =
1 4 , 1 = 11
2Л 9Л 8Л 72Л"
При коалесцентной априорной вероятности дерево Т* имеет вероятность
Pc{Ti ,^1,^1,^2,^2,^3 —ti,t3 — t2\6) =
= (§)
3 / 2*з \ / 4t2\ / 6*i
ч в У V ^ / \ *
е v / е \ / е

8.1. Оригинальные задачи
и функция плотности вероятности вьфажается в виде
6*Л
Для того чтобы найти математические ожидания величин Li, L2
должны завершить следующее интегрирование:
+оо *з *з
EcLi = / / / t1p(ti,t2,t3)dt1dt2dt3 =
*3=0*2=0*i=0
+00 / 2*3 \ / *з ( 4*2 \ *3 / 6*! \ \
0 \0 0 /
+00 / 2*3\ /
4*з
0
6*з \ / 6t3
x |_*3eV V -|eV V+||^3
32 16^6^72^24 18 96'
+00 *з *з
ECL2 = / / / t2p(ti,t2,ts)dti,dt2,dts =
*3=0*2=0*i=0
*3=0*2=0*i=0
+ OO ( 2tZ\ / ( 6*3 \ \ / *3 / 4*2
0 \ / \0
+OO / / 6*3 \ / 6*3 \ / 2*3
-/ -*
"-1еГ»;+1е, -,+
12*з \ / 12*з\ / 8*3N
^el-0+iehJ-ieh/|A3 =

322
Глава 8
+оо *3 *з
ЕсЬз = / / / *зр(*1»*2,*з)*1,А2,Аз =
*3=0*2=0*i=0
+00 / 2*3\ / / 4*3\
= /^еЫ(1-еЫ
о \
+оо / / 2t3 \ / 8t3 \
21
в
6t3
в
12*з V
в-е\ / +-^-eV / |Л3 =
в_±_±±= 590
2 32 18^72 288*
Обратите внимание, что математические ожидания высот L\ и 1,2
внутренних узлов дерева Т* равны при априорной вероятности Юла, но имеют
различные значения (EcLi > ECZ,2) при коалесцентной априорной
вероятности. Симметрия функции плотности вероятности ру в противовес
отсутствию симметрии функции рс относительно переменных t\ и t<z объясняет
это различие.
Заключительный случай — дерево Т$ с топологией (((12)3)4) и
длинами рёбер £i,£i,£2j*2 — £ъ£з3£з — *2-
<2
Мы принимаем допущение о том, что случайные переменные L\, L2, L3
определяют неравные высоты внутренних узлов и принимают,
соответственно, значения ti, £2, *з, где 0 < £з < +оо, 0 < t\ < £2, 0 < *2 < *з- При
априорной вероятности Юла вероятность дерева Т$ определяется из
Py(T2 ,ti,ti,t2, £2 — £ъ£з,£з ~~ ^2) = е
-2Л*з„-Л*2„-Л*1

8.1. Оригинальные задачи 323
и функция плотности вероятности ру выражается в виде
PvitiMM) = Ae"AtlAe-At22Ae-2At3.
Тогда
+00 t3 *2
EyLi = / / / tiPY(ti,t2,ts)dtidt2dts =
t3=0t2=0ti=0
= I 2Ae"2At3 / (-Af2e-2At2 - е"2А'2 + е"л'2) <Й2 <Й3 -
+oo
= J (\tse-4Xi>£e-4Xt> + ie-2At* - 2е"ЗА'Л dt3 =
о
-I- + JL + J__JL = JL.
16A 8A 4A ЗА 48А'
+oo t3 t2
EyI/2 = / / / *2Py(tl,*2j*3)d*ld*2dt3 =
t3 =0t2 =0ti=0
= / 2Ae-2A*3 / (At2e~At2 - Ai2e-2A<2) <Й2 dt3 =
+oo
= /" ^3Ае-ЗА'3-2е-ЗА*3+|е-2А*3+А«зе-4А*3+|е-4А'Л dt3 =
о
= _2 2_ + _3_ + J_ + J^= 11
9A ЗА 4A 16A 8A 144A'
+ 00 t3 *2
EyL3 = / / / tspY(ti,t2,ts)dtidt2dts =
t3=0t2=0ti=0
= /* t3Ae"2At3 (1 - 2Ae"A<3 + e"2A<3) A3 =
о
1 2 + 1 _ 13
4A 9A 16A 144A*

324 Глава 8
При коалесцентной априорной вероятности вероятность дерева Т% та же,
что и вероятность дерева Tj4:
■Рс(Г2, tl,*l,*2j*2 ~ *Ъ*3?*3 — ^2|0) =
- (|)3е(--)е(--)е(--
Таким образом, функция плотности вероятности рс та же, что и для
дерева Т?:
6ti \ / 4t2 \ / 2t3
и * 4. \ 6 1~ в J 4 I 0 2 ^
Рс(*ь*2,*з) = ^е\ /^eV /-ev
Интегрирование даёт следующие математические ожидания значений Li,
EcLi = / / / tip(t1,t2,t3)dt1dt2dt3 =
i3=0t2=(Hi=0
+00 / 2t3 \ / *3 / 4t2 \
0 \0
x j f^e\ 9 )dt1\dt2\dU =
+00 / 2t3 \ / *з
*3 / 4t2
(9
6*2 \ / 6t2
x|-fceV e'-feV в/+||А2|Аз
+oo / / 12t3 \ / 12*з
-/ Э
6 75е
2t3 \ / 6t3
-^"•^ЬГ''|*-

8.1. Оригинальные задачи 325
+00 *з *2
ECL2 = / / / t2p(ti,t2,t3)dt1dt2dts =
+оо
-л-
О
*з / / 4*2\ / 10t2V
О \0
+оо / 2*зЧ
it
eV / - — eV / I dt2 I <&з =
/ -f
+oo / / 6t3 \ / 6*3
0
+ 50eV / + 50eV /+25eV /|d*3 =
= -1- 6> . 2ig (9 , в е.
18 12 + 100 + 45 ^ 150 10'
+ 00 *3 *2
ECL3 = / / / t3P(ti,t2,ts)dtidt2dts =
t3=0*2=0*\=0
+00 / 2*3 \ / *з / 4*2 \ / / 6*i
-/¥-ы(/^(""г)(1-(""г
0 \0 \
<f^2 I dta =
о
30 в в Ыв
10 18 + 15 45 '
П

326
Глава 8
Задача 8.14. При достаточно большом числе бросаний N апостериорное
распределение Р(р\тН1 пТ) вероятности выпадения орла р, описываемое
распределением Дирихле, имеет следующее нормальное приближение:
(m-Np)2
Р(р\гпН,пТ) с у1 е"^^>.
y/2irNp(l-p)
Точно так же оценка методом наибольшего правдоподобия P(pML = р)9
полученная из данных самонастройки, асимптотически следует за
нормальным приближением, то есть при достаточно больших N
(m-Np)2
p(pML =pj „ N+l fl" 2mn/N
y/27rmn/N
Покажите, что обе вероятности либо являются очень маленькими, либо,
в противном случае, принимают почти равные значения.
Решение. Мы рассматриваем подбрасывание монеты с вероятностью р
выпадения орла. Предположим, что в результате N подбрасываний выпало га
орлов (Я) и п решек (Т). При больших N мы имеем, что почти наверное
в силу усиленного закона больших чисел. Поэтому при больших N
rm^p(1_p)N
И
(m-Np)2 (m-Np)2
N+l e~ 2mn/N ^ N + l c~2Np(l-p)^
y/2irmn/N y/27rNp(l - p)
Таким образом, при больших N распределения P(pML =p)n P(p\mH, nT)
приближаются друг к другу. П
Задача 8.15. Покажите, что отыскание наиболее экономичного дерева с
опорой на взвешенную экономичность со стоимостью S(a,a) = —loga,

8.1. Оригинальные задачи
327
S(a,b) = — log/3 при а ^ b и условии /3 < а является эквивалентным
традиционной экономичности со стоимостью замены, равной 1.
Замечание. Параметры а и /3 интерпретируются как элементы
матрицы замен, в которой диагональные элементы равны а, а недиагональные
элементы равны /3.
Решение. Сначала мы замечаем, что неравенство /3 < а подразумевает, что
S(a1a) < S(a,b) при а фЬ. Предположим, что мы должны опознать
наиболее экономичное дерево для п последовательностей х1,..., хп, каждая
длины N. Для заданного дерева Т мы вычисляем минимальную стоимость
SU(T) на каждом участке и, где и = 1,..., N, и тогда минимальная
стоимость дерева Т определяется из
N
S(T) = J2Su(T).
Существует (2п — 3)!! корневых деревьев с п листьями, и наиболее
экономичное дерево среди них определяется из выражения
T*=argminS(T).
т
Мы покажем, что одно и то же дерево Т* минимизирует и стоимость
взвешенной экономичности SW(T), и стоимость традиционной
экономичности Str(T). Если ки — число замен на участке и в дереве Т, то стоимость
взвешенной экономичности на участке и равна — (log/3)ки — (log а)(п— 1 —
— ки), так как корневое дерево с п листьями содержит п — 1 внутренний
узел, и общее количество совпадений и замен по рёбрам дерева Т равно
п-1.
Для дерева Т стоимость традиционной экономичности Str равна сумме
минимальных чисел замен ки на каждом участке и и выражается
следующим образом: N
Str(T) = Y^ku,
u=l
тогда как стоимость взвешенной экономичности имеет вид
N
SW(T) = ]T(-log/3fcn - logc*(n - 1 - к*)) =
u=l
N
= (loga - log/3) ^ fcn - loga(n - 1),
u=l

328
Глава 8
с теми же самыми числами замен fci,..., kw. Множество fci,..., fc/v,
минимизирующее Str и Sw, одно и то же, так как log а — log /3 > 0.
Поэтому одно и то же дерево Т* минимизирует стоимость взвешенной
экономичности и традиционной экономичности:
Г* = argmin Sw (Г) = argmin Str (Г). Q
Задача 8.16. Получите расстояние Джукса-Кантора из принципа
минимальной относительной энтропии.
Замечание. Относительная энтропия H(P\Q) двух дискретных
распределений Р и Q, принимающих положительные значения на одном и том
же множестве {yj}, определяется следующей формулой:
Тот факт, что для любого распределения Р и Q относительная энтропия
Н(P\Q) всегда является неотрицательной и принимает нулевое значение
тогда и только тогда, когда Р = Q, следует из неравенства (х > 0):
logx < х — 1,
причём равенство имеет место только при х = 1. Если х = Q(yi)/P(yi), то
г г
причём равенство имеет место лишь при Р = Q. Поэтому
£ Р(ш) log Qivi) < Y. р(У^ lo§ p(^)' <8-8>
г г
при этом равенство возникает тогда и только тогда, когда Р — Q.

8.1. Оригинальные задачи 329
Решение. Мы делаем допущение о том, что не содержащее пропусков
выравнивание последовательностей ДНК х1 и х2 длины N содержит п\
совпадений и П2 несовпадений. Наиболее правдоподобное расстояние (НПР)
между последовательностями х1 и х2 определяется как
£gL = argmax (f[ P(x2u\xi,t) J .
При модели Джукса-Кантора НПР принимает вид
d%L=MgmaX(rt)nl(st)n*,
t
где rt = P(a\a,t) = i(l + Зе"4"') и st = P(a\b,t) = i(l - e~4oit) суть,
соответственно, диагональный и недиагональный элементы матрицы замен
Джукса-Кантора.
Максимизация функции P(i) = (rt)ni(st)n2 может быть достигнута
стандартными методами исчисления (задача 8.7), а точка максимума
функции P(t) определяется из выражения
r = d^ = fln3f1 + "2)=-f 1пЛ-|/У (8.9)
12 4а 3ni-n2 4а \ 3J J v '
Здесь / = nz/N — доля участков с несовпадениями (переменных участков).
Расстояние Джукса-Кантора d определяется как математическое
ожидание числа замен на участок за время dML. Поскольку в модели Джукса-
Кантора математическое ожидание числа замен на участок в единицу
времени равно Зек, мы имеем
d(*V) = 3ad^ = -|ln(l-f/).
Теперь мы покажем, что с помощью свойства неотрицательности (8.8)
относительной энтропии может быть получен тот же самый результат. Взятие
натурального логарифма функции P(t) = (rt)ni(st)n2 даёт следующее
выражение:
In P(t) = Til In Tt + 712 In St =
=w(^.»r,+^1„sl+^.»„+^,»s,)=

330
Глава 8
где Q и Р — дискретные распределения, определяемые на одном и том
же множестве четырёх точек с вероятностями, соответственно, rt,st,st, st
и rii/N, n2/3iV, П2/ЗАГ,?г2/ЗАГ. Согласно уравнению (8.8), функция
J]P(t/;)ln<2(t/j) достигает своего максимума при Р = Q. Решая относи-
г
тельно t систему двух уравнений
г, = !(1 + 8е-~) = £,
* 4^ е ' ЗАГ
мы находим точку максимума
«"--В*—^b(i-^)—ib(i-g/).
Мы видим, что £** = £* = df2L; поэтому расстояние Джукса-Кантора d
между последовательностями х1 их2,
d(x\x2) = 3ad%L = -|ln (l - §/) ,
было выведено из свойств относительной энтропии. Тогда как отыскание
U = d$L было осуществлено путём отыскания точки максимума функции
P(t) через стандартные необходимые условия стационарной точки,
отыскание £** было выполнено непосредственно из условия Р = Q посредством
решения алгебраических уравнений.
Замечание. Значение требования Р = Q следующее. Вероятности
rt = P(a\a,t) и st = P(b\a,t)9 где афЬ, определяют ожидаемые доли,
соответственно, «постоянных» и «переменных» участков, по мере протекания
времени t. Наибольшее правдоподобие наблюдаемых данных будет
достигнуто, когда rt = щ/N и st = пгДЗЛГ), так как ni/N — наблюдаемая доля
постоянных участков, и П2/(ЗАГ) — наблюдаемая средняя доля переменных
участков для одного из трёх типов несовпадений. D
8.2. Дополнительные задачи и теория
В этом разделе содержатся теоретические и вычислительные задачи
с вероятностными моделями молекулярной эволюции.

8.2. Дополнительные задачи и теория
331
Несколько задач посвящены модели Джукса-Кантора. Мы показываем,
что наиболее правдоподобное дерево для набора трёх заданных
последовательностей нуклеотидов отличается от дерева, составленного из попарных
наиболее правдоподобных расстояний (задача 8.17). При принятой
модели Джукса-Кантора мы сравниваем правдоподобия деревьев,
соответствующих конкурирующим гипотезам о моментах времени расхождения двух
видов, и вычисляем наиболее вероятное время расхождения (задача 8.18).
В теоретическом введении в задачу 8.18 мы доказываем, что
стохастический процесс, подсчитывающий число замен, управляемых стационарным
марковским процессом, является процессом Пуассона, если все
диагональные элементы матрицы частот замен равны между собой (этому условию
удовлетворяет и модель Джукса-Кантора и модель Кимуры).
Марковский процесс с непрерывным временем замен аминокислот,
подобный моделям Джукса-Кантора и Кимуры для эволюции ДНК
(задача 8.19), был получен (обобщён) из стационарной марковской цепи с
матрицей вероятностей переходов 1 ПТМ (раздел 2.2.1). Однако существует и
важное различие: семейство матриц замен ПТМ t, t ^ 0, и матрица
частот замен (также полученная в задаче 8.19), в отличие от матриц Джукса-
Кантора и Кимуры, не зависят от параметров.
Вероятностная модель эволюции последовательностей ДНК или белка,
допускающая замены, вставки и удаления (модель связей или ТКФ (Торна-
Кисино-Фельзенштейна) [269]) сочетает в себе описывающий замены
марковский процесс с непрерывным временем и процесс рождения и гибели с
иммиграцией, описывающий вставки и удаления (см. теоретическое
введение в задачу 8.20). Мы используем эту модель для вычисления вероятности
того, что последовательность х преобразовалась в последовательность у за
время £, а также для отыскания правдоподобия дерева с заданными узлами
и длинами рёбер (задача 8.20).
Наконец, в разделе 8.2.3 представлено краткое описание моделей,
учитывающих изменчивость частот замен среди участков последовательности.
Задача 8.17. Принято допущение о том, что нуклеотидные
последовательности х1, х2 и х3 (приведённые ниже в порядке сверху вниз)
CCGGCCGCGCG
CGGGCCGGCCG
GCCGCCGGGCC
эволюционировали от общего предка. Принимая модель Джукса-Кантора,

332
Глава 8
покажите, что наиболее правдоподобное дерево для этих
последовательностей не составлено из попарных наиболее правдоподобных расстояний
между ними.
Решение. Согласно модели Джукса-Кантора наиболее правдоподобное
расстояние dfjL между нуклеотидными последовательностями Xi и Xj
описывается уравнением (8.9) (два подхода к выводу уравнения (8.9)
рассмотрены в задачах 8.7 и 8.16). Поэтому попарные наиболее правдоподобные
расстояния между последовательностями хг,х2 и х3 определяются из
*1-ib.(i-iA.)-ib(i-J.^)-^b,^
*1-Eh(1-ib)-ib(i-|.A)-ih,g,
*t-ita(i-|Ai)-ib.(i-|.i)-i1.a.
Здесь fy9 где г, j = 1,2,3, — доли несовпадений в выровненных без
пропусков последовательностях хг и х?9 а а — параметр модели Джукса-Кантора.
Теперь мы принимаем допущение о том, что последовательности ж1,
х2 и х3 связаны представленным ниже некорневым деревом Т с тремя
листьями и длинами рёбер ii, i2, f3 -
-z3
Если ti, t2 и £з удовлетворяют следующим уравнениям:
h + £2 = d12 ,
*i + £3 = d13 ,
*2 + £3 = ^23 J

8.2. Дополнительные задачи и теория 333
то длины ветвей определяются из
- 1 ,„ 119 _ 0,0230
Ч~ 8а 143 ~ а '
- 1 91 0,0900
*2 = ~8а"1п187 = ~^Г->
7 _ 1,„ 221 _ 0Д429
*3-~8а"1п693-—о— •
Теперь мы можем показать, что дерево Т не является наиболее
правдоподобным деревом для последовательностей ж1, х2 и х3.
Правдоподобие дерева Т с длинами ветвей t\9 ti-> £3 и
последовательностями при листьях ж1, х2 и ж3 имеет следующий вид (задача 8.4):
b(r,ti,*2,t3)=P(a:1,x2,a;3|r,ti,t2,t3) =
= 4_3(П1+п2+пз+п4)а(^
Здесь rii — число участков с триплетами ССС или GGG; П2, пз и П4 -
соответственно, число участков с триплетами CCG или GGC9 триплетами
CGC или GGG и с триплетами GCC или GGG, тогда как
a(h, t2, *з) = 1 + 3e_4Q:(tl+t2) + 3e"4a(tl+t3) + Зе~4а(*2+*з) + бе_4а(*1+*2+*з)
b(*i»*2,t3) = 1 + Зе-^*1+*2> _e-4a(tl+t3) -3e~4a(t2+t3) -2e"4a(tl+t2+t3).
В наиболее правдоподобном дереве длины ветвей должны
максимизировать функцию правдоподобия L (и её логарифм InL). В точке максимума
функции In L необходимо, чтобы при г = 1,2,3
<91nL
%
= 0. (8.10)
Непосредственные вычисления левых частей уравнения (8.10) с помощью
пакета MATLAB с подстановкой 1\, ?25 *з дерева Т и п\ = 5, п2 = 3, пз = 2
и П4 = 1 дают
%^(*1,*2,*3) =

334
Глава 8
Ч*1»*2,*з; + ,/r ~ ~ ч ^i (*1,*2,*з;+
a(fi,t2,f3) a*i ' ' Ь(Мг,*з) ^i
+ wr г г ч /^ (*Ь*2,*3) + wr г г ч я7 (*Ь*2,*3) =
Ь(*Ь*3,*2) ^1 b(*3,*2,*l) ^1
= -206,44а ф 0. (8.11)
Точно так же мы вычисляем
^(*1,«2,?з) = 2363,7а^0,
^(£ь£2,?з) = 353,71а^0.
(8.12)
Уравнения (8.11) и (8.12) показывают, что необходимые условия в
уравнении (8.10) для стационарной точки не удовлетворены. Поэтому дерево Т,
построенное из попарных наиболее правдоподобных расстояний, не
является наиболее правдоподобным деревом для последовательностей ж1, х2
и х3. Было бы интересно распространить это утверждение на общий
случай с п последовательностями. □
Задача 8.18. (Пересмотр задачи 1.18.) Одна теория утверждает, что
последний общий предок птиц и крокодилов жил 120 миллионов лет назад,
тогда как другая теория полагает, что это время вдвое больше. Сравнение
фрагментов гомологичных генов двух видов (нильского крокодила и
средиземноморской чайки) показало в среднем 365 различий во фрагменте
длины 1000 п. н. Было принято допущение (задача 1.18), что замены на
различных участках ДНК происходят независимо и что на каждом участке число
замен описывается процессом Пуассона с параметром р, равным Ю-9
замен в год. Принимая допущение об адекватности модели Джукса-Кантора,
а) сравните правдоподобие этих двух теорий; б) определите наиболее
правдоподобное расстояние между этими двумя видами.
Решение. Матрица интенсивностей замен нуклеотидов Джукса-Кантора
должна иметь такой параметр а, чтобы За = р = 10~9, таким образом,
а = 3,33-10-10.
а) Мы делаем допущение о том, что последовательности ДНК х1 и х2
двух видов и последовательность у их последнего общего предка связаны
следующим деревом Т со свойством молекулярных часов:

8.2. Дополнительные задачи и теория
335
Правдоподобие каждой из этих теорий определяется как правдоподобие
дерева Т с длиной ветвей t, равной времени расхождения, предполагаемому
конкретной теорией (t = ti = 120 000 000 лет или t = t2 = 240 000 000 лет).
Учитывая, что замены по двум рёбрам дерева независимы, при том что
для модели Джукса-Кантора верны обратимость и марковость,
правдоподобие Lu на участке и определяется из
Lu(t) = P(xlx2u\T,t,t) = P(xlx2u\t) = J2*yM*l\Vu>t)P(*l\Vu,t) =
Уи
Уи
Следовательно, правдоподобие совпадения нуклеотидов (х^ = х£) на
участке и определяется из
Lu(t) = Р^(1 + Зе-4"«+0) = ^(1 + 3e-8at).
Точно так же в участие и с несовпадением (х^ ф х%) мы имеем
Lu(t) = ^(1 - е-4«(*+*)) = i(l - е-8"*).
Далее, принимая допущение о независимости замен на различных
участках, мы выводим выражение правдоподобия дерева Т с длинами рёбер t и
последовательностями при листьях х1 и х2:
N
L(t) = P(x\x2\T,t,t) = Y[ Lu(t) = 16"N(1 + 3e"8at)N-M(l - e"8at)M.
(8.13)

336
Глава 8
Здесь N — длина обеих последовательностей ДНК, М — число участков с
несовпадениями. При N = 1000, М = 365 и а = 3,33 • 10~10
логарифмическое отношение правдоподобия для деревьев с длинами рёбер t\ и ^
определяется из
L(*i) _ (1 + 3e"8atl)635(l " е"8"*1)365 _
R ~ 1П ~Щ) " Ь (1 + 3e"8at2)635(l - е-8"4*)365 "
= 635(1п(1 + Зе"0'32) - 1п(1 + Зе~°'64))+
+365(1п(1 - е"0'32) - 1п(1 - е"0'64)) =
= 132,00 - 199,23 = -67,23 < 0.
Поэтому модель Джукса-Кантора с параметром а = 3,33 • Ю-10
предполагает, что наблюдаемые данные поддерживают теорию, согласно которой
нильский крокодил и средиземноморская чайка разошлись от общего
предка 240 млн лет назад.
Здесь мы пришли к тому же заключению, что и в решении задачи 1.18,
где появление замен было описано процессом Пуассона с частотой р = За.
Преимущество модели Джукса-Кантора состоит в том, что она устраняет
довольно нереалистичное допущение о том, что за время расходящейся
эволюции на одном участке могло произойти не более одной замены. Более
подробное описание связи между эволюционной моделью замен (марковский
процесс) и процессом Пуассона, описывающим число замен, приведено в
разделе 8.2.1.
б) Эволюционное расстояние между двумя видами, связанными
некоторым путём в филогенетическом дереве, равно сумме всех ветвей на этом
пути. Мы вспоминаем формулу суммы длин рёбер дерева с двумя
листьями Т, максимизирующей правдоподобие L(T) дерева, связывающего
последовательности х1 и х2 (задачи 8.7 и 8.16):
Здесь п и Т2 — длины рёбер в таком дереве. Поэтому наиболее
правдоподобное (эволюционное) расстояние между последовательностями х1 и х2
двух видов равно т\ + т^ = 500 000 000 (500 миллионов лет). Свойство
молекулярных часов предполагает, что эти две филогенетические линии
разошлись от последнего общего предка 250 млн лет назад. □

8.2. Дополнительные задачи и теория
337
8.2.1. Связь между моделями эволюции последовательностей,
описываемыми марковским и пуассоновским процессами
Если в качестве модели эволюции ДНК применяется стационарный
марковский процесс X(t)9 где t ^ 0, с пространством состояний 5 =
= { Д С, G, Т}, мы принимаем допущение о том, что замены нуклеотидов
на данном участке последовательности ДНК рассматриваются как
переходы между состояниями процесса X(t)9 описываемого семейством матриц
вероятностей замен S(t) = (sij(t))9 где i,j £ S nt^ 09 и матрицей интен-
сивностей замен R = (г^), где i,j eS.
Мы определяем случайный процесс N(t), где t^ 0, как число
изменений состояний (нуклеотидов) процесса X(t) во временном интервале [0, t].
Мы покажем, что если все элементы главной диагонали матрицы R равны,
гм = —р при всех г £ 5, то стохастический процесс Nfo) представляет
собой процесс Пуассона с частотой р (обратите внимание, что все
диагональные элементы матрицы R отрицательны, так что р > 0).
Мы должны убедиться в том, что N(t), где t > 0, удовлетворяет
определению процесса Пуассона с интенсивностью р:
1) N(0) = 0;
2) процесс имеет стационарные приращения, то есть Nfo) — Nfo)
и Nfo + s) — Nfo + s) имеют одно и то же распределение при всех 0 ^
t\ ^ *2 и s > 0;
3) процесс имеет независимые приращения, то есть Nfo) — Nfo)
и Nfo) — Nfo) суть независимые случайные переменные при всех t\ <
£2 ^ ^з ^ U;
4) P(N(t) =n) = e-^(pt)n/n\ при п > 0.
Очевидно, что свойство 1 удовлетворено: во временном интервале
[0,0] не происходит ни одной замены. Стационарность приращений
процесса следует из стационарности марковского процесса X(t):
распределение числа изменений состояний процесса X(t) во временном интервале
зависит только от длины этого интервала. Поскольку (£2 + s) — fo + s) =
= t2 - tu Nfo) - Nfo) и Nfo + s) - Nfo + s) являются тождественно
распределёнными.
Чтобы доказать, что свойства 3 и 4 удовлетворены, мы определяем
случайную переменную Tj9 j > 1, как время между (j — 1)-м и j-м
изменениями состояний процесса X(t). Из теории стохастических процессов ([227])
известно, что если процесс X(t) находится в состоянии г, где г 6 5, после
(j — 1)-го изменения состояния, то переменная Tj экспоненциально
распределена с параметром — г^, а случайные переменные Tj, j ^ 1, независимы.

338 Глава 8
В нашем случае — г^ = р при всех г Е S и случайные переменные Tj
независимы и тождественно распределены с функцией плотности вероятности
f(t) = pe~pt. Теперь мы определяем функцию распределения Fn(t) случай-
п
ной переменной Тп = J2 Tj; — время, которое требуется, чтобы наблюдать
п изменений состояний процесса X(t). При п = 1,2,3 мы имеем
Fi(t) = Р(Тг ^t)= P(Ti < t) = 1 - е~р\
t
F2(t) = P(T2 < t) = P(Ti + T2^t) = j/(y)P(Ti + T2 ^ t|Ti = </)d</ =
о
t t
= У /Ы^№ < * - у|Ti = y)dy = j f(y)P(T2 < t - y)dy =
о о
t
= fpe-py(l - e-p<*-y>)dy = 1 - e"pt - pte~p\ (8.14)
о
t
F3(*) = P№ < *)=Р(Г1+Г2+Г3 < t)= J f(y)P(T2+T3 < t\T3=y)dy
о
= У /(y)F2(* ~ </)*/ = 1 " e"pt - pte~pt - М-*-*
2"e
Выражения для функций распределения Рп, n = 1,2,3, имеют
аналогичную форму, которая позволяет нам предложить общую формулу для Fn(t)
в следующем виде:
Fn(t) = Р(Тп < *) = 1 - в"* J2 ^Г" (8Л5>
г=0
Докажем равенство (8.15) математической индукцией. Основание этой
индукции было установлено в уравнениях (8.14). Теперь мы принимаем
допущение о том, что
Fn-1(t) = l-e-*Y:(pt)
j=0

8.2. Дополнительные задачи и теория 339
и находим Fn(t) следующим образом:
t
Fn(t) = Р(Гп-г +Tn^t)=f f(y)P(Tn-1 + Тп < t\Tn = y)dy =
о
t t f Г\ . V
= ff(y)Fn^(t-y)dy = [pe-™ (1 - е-^-У) £ ^ " V))% ) dy =
о о V i=o • /
= i _ e~vt _ V- yttl = ! _ e-Pt V-
2-*(i + l)! 4-j « •
г=0 ч ' г=0
Таким образом, мы убедились в том, что формула (8.15) правильная. Она
непосредственно ведёт к аналитическому выражению для функции
плотности вероятности fn переменной Тп:
fn(t) = K(t) = f^e-'*. (8.16)
{п - 1)!
Теперь мы покажем, что процесс N(t) удовлетворяет свойству 4.
Действительно, из уравнения (8.15) мы находим
P(N(t) = n) = P(N(t) < n) - P(N(t) < n - 1) =
= P(N(t) < п + 1) - P(N(t) <п) = Р(Тп+1 > t) - Р(Тп >t) =
= (l-Fn+1(t))-(l-Fn(t)) =
/ П-1
WL,-.-»fM -■*«!
- >--ЕТ - i--E
г=0 / \ г=0 /
Наконец, мы обращаемся к свойству 3. Так как приращения процесса N(t)
стационарны (по свойству 2), достаточно доказать свойство 3 для
приращений 7V(*i) - N(0) = N(ti) и N(t3) - N(t2), 0 < h < t2 < *3.
Фактически мы подтвердим независимость трёх приращений N{t\), N(t2) — N(t\)
и N(ts) - N(t2):
P(N(h) = n, AT(t2) - N(tx) = J, N(ts) - N(t2) = m) =
= P(AT(ti) = n)P(N(t2) - Nth) = l)P(N(t3) - N(t2) = m) (8.17)

340
Глава 8
для любых положительных целых чисел п, I и т. Очевидно, что если эти
три приращения взаимно независимы, то любые два из них также
независимы. Стационарность приращений и свойство 4 позволяют нам переписать
правую сторону уравнения (8.17) в виде
P(N(t!) = n)P(N(t2) - N(h) = l)P(N(t3) - N(t2) =m) =
n\ l\ ml
пп+1+т
С другой стороны, левая сторона уравнения (8.17) может быть
преобразована в то же самое выражение, что и приведённое выше, при помощи тех
же аргументов, как в уравнениях (8.14):
Р(ЩЬ) = п, N(t2) - N(h) = I, N(t3) - N(t2) = m) =
= P(%i^ti,%i+l>tl, ^+^2, %i+l+l>t2,Tn+i+m^t3,Tn+i+m>t3) =
ti t2-yi t2-3/i-2/2 t3 -2/1 -2/2 -2/3 *з-2/1-2/2-2/3-2/4
-III I I ('-ы*
2/i=0 2/2 =ti—2/i 2/3=0 2/4=*2—2/1—2/2—2/3 2/5=0
Х/Ы/*-1Ы/Ы/т-1Ых
x?(Tn+Hm+i > t3 — 2/i — 2/2 — 2/3 — У4 — yb))dyidy2dy3dy4dy5 =
Pny^~l Pl~lyl<T2
y yi p-P2/1 -„p-P2/2 ^ y3 -P2/3 r,P-P2/4 v
(n-l)!e Рв {l-2)\C Pe
pm-lym-2 \
x^ fL-e-^e-*-»1-^-^! dyidy2dy3dyAdyb =
(m-2)! /
nn+Z+ra
= е-Р*зР
nlllml
= «.-*»2—«ftfc - «O'ft, - «a)"
На этом мы завершаем доказательство уравнения (8.17). Итак, мы
показали, что процесс N(t), где t > 0, удовлетворяет определению процесса
Пуассона.
Одно из следствий этого утверждения — то, что в моделях эволюции
ДНК и Джукса-Кантора и Кимуры число N(t) изменений состояний (нук-
леотидов) во временнбм интервале [0,£] является процессом Пуассона с

8.2. Дополнительные задачи и теория
341
интенсивностью За (в модели Джукса-Кантора) и с интенсивностью 2/3 +
+ а (в модели Кимуры). Таким образом, пуассоновскую модель замен,
используемую в задаче 1.18, можно рассматривать как модель, соотносимую
с моделью Джукса-Кантора (задача 8.18). Такая соотносимая модель
Пуассона позволяет нам подсчитывать замены (как изменения состояний), но не
располагает информацией о текущем типе нуклеотида на данном участке,
потому что процесс Пуассона N(t) не может проводить различие между
нуклеотидами (состояниями) марковского процесса X(t). Другими
словами, процесс X(t) однозначно определяет процесс Пуассона N(t), но
обратное не верно; марковский процесс X(t) не может быть восстановлен из
процесса Пуассона N(t).
Разница значений правдоподобия дерева с двумя листьями и длиной
ветвей t, вычисленных по уравнениям (1.7) и (8.13) (соответственно,
задачи 1.18 и 8.18), проистекает из того факта, что в задаче 1.18 мы вычисляли
правдоподобие, основываясь на допущении о том, что за всю
последовательность поколений в одном участке могло произойти не более одной
замены. Если бы мы включили то же условие в утверждение задачи 8.18, то
(условное) правдоподобие было бы таким же, что и в уравнении (1.7), и
полученная методом наибольшего правдоподобия оценка времени
расхождения изменилась бы с 250 млн лет до 287,4 млн лет назад. (Если допускается
не более одной замены на участок, то для появления наблюдаемых
несовпадений М необходимо большее время расхождения.)
Задача 8.19. В разделе 2.2.1 было подробно показано, как получать
матрицы ПТМ при допущении о том, что замены аминокислот в белках
могут быть описаны стационарной марковской цепью. Этот метод производит
ряд матриц вероятностей мутаций п ПТМ, соответствующих дискретным
интервалам эволюционного времени, кратных единице времени 1 ПТМ.
Получите матрицу вероятностей мутаций t ПТМ, явно зависимую от
непрерывного времени t ^ 0, — аналог матрицы замен S(t),
определённой для моделей эволюции ДНК Джукса-Кантора и Кимуры. Помимо этого
необходимо получить матрицу R интенсивностей замен.
Решение. Мы будем использовать обозначение S(l) для матрицы 1 ПТМ
с элементами Мц (таблица 2.7).
Матрица 5(1) может быть интерпретирована как матрица линейного
оператора S в основании ei,..., его из R20. Все собственные значения А$,
г = 1,..., 20, оператора S различны (таблица 8.1). Поэтому в R20
существует базис собственных векторов е'1з..., е'20 линейного оператора S. То-

342
Глава 8
Таблица 8.1. Множество собственных значений Ai,..., А20 матрицы
вероятностей мутаций 1 ПТМ = S(l)
1(А1а) 2(Arg) 3(Asn) 4(Asp) 5(Cys) 6(Gln) 7(Glu)
0,978 0,981 1,000 0,983 0,984 0,985 0,987
8(Gly) 9(ffis) 10(Ile) ll(Leu) 12(Lys) 13(Met) 14(Phe)
0,987 0,998 0,997 0,997 0,989 0,990 0,996
15(Pro) 16(Ser) 17(Thr) 18(Trp) 19(Tyr) 20(Val)
0,995 0,991 0,993 0,993 0,992 0,992
Таблица 8.2. Значения параметров /х^, где \ii = — lnA* и г = 1, ...,20,
употребляемые в уравнении (8.20)
1 2
0,022 0,020
11 12
0,003 0,011
3
0,000
13
0,011
4
0,018
14
0,004
5
0,017
15
0,005
6
0,016
16
0,009
7 8
0,014 0,013
17 18
0,007 0,007
9
0,002
19
0,008
10
0,003
20
0,008
гда матрица 5(1) может бьпъ записана в виде 5(1) = VDV"1, где матрица
D — диагональная матрица со значениями А*, г = 1,..., 20, на диагонали
(D — матрица оператора S в базисе е'ъ ..., е'20)9 V — матрица
преобразования координат от базиса ei,..., е2о к базису е'1з..., е'20 и V-1 —
матрица, обратная матрице V. Матрицы V и V-1 представлены в таблицах 1
и 2 с веб-сайта «Дополнительные материалы сети», доступного по адресу:
opal.biology.gatech.edu/PSBSA.
Так как все собственные значения А^, где г = 1,..., 20, принадлежат
к интервалу (0,1] (таблица 8.1), мы можем записать их в виде А* = е~^г,
где [ii ^ 0. Для S(n) — матрицы вероятностей замен аминокислот за время,
равное п единицам ПТМ, мы имеем:
(S(l))n = S(n) = (VDV-1)71 = VDV^VDV-1... VDV"1 = VT>nV-1.
(8.18)
Поэтому из уравнения (8.18) мы находим элементы матрицы S(n)
Sid(n) = Х>*АХ/ = $>fce-^X7- (8Л9>
к к
Здесь Vik и v^1 — соответственно, элементы матриц V и V-1. Значения /ль,

8.2. Дополнительные задачи и теория
343
где к = 1,..., 20, приведены в таблице 8.2. Замена п в уравнении (8.19)
непрерывной переменной t, где t ^ 0, даёт формулу для элементов
матрицы S(t), где t ^ 0. Таким образом, вероятность того, что некоторая
аминокислота в столбце j будет заменена какой-либо аминокислотой в строке г
по прошествии времени £, равна
20
k=i
Обратите внимание, что подобием элементов матриц замен в моделях
Джукса-Кантора и Кимуры Sij(t) служит линейная комбинация
экспоненциальных функций.
Элементы матрицы R, являющиеся интенсивностями замен
аминокислот, могут быть получены из уравнения (8.20) и условия Sf(0) = R
следующим образом:
20 20
Rij = J2 -Wike'^Vkj1 = J2 "MfcVifcVfc/.
Матрица R представлена в таблице 8.3.
Другой подход к моделированию марковского процесса замены
аминокислот с непрерывным временем, связанный с моделью Дейхофф [57], был
предложен Уилбером [281].
Семейство матриц замен с непрерывным временем (8.20) хорошо
зарекомендовало себя при определении наиболее правдоподобного
эволюционного расстояния между двумя последовательностями белков, сравнении
правдоподобий конкурсных эволюционных деревьев для данного набора
последовательностей листьев, отыскания наиболее вероятных длин ветвей
для данной топологии дерева и т. п. Учтите, что решение таких задач для
реальных последовательностей обходится дорого в вычислительном
отношении.
Ради предоставления «модельного» примера мы определим наиболее
правдоподобное расстояние t* (в единицах ПТМ) между двумя
аминокислотными последовательностями х = KVAD и у = KVFK. Согласно
допущению о независимости участков, мы имеем следующее произведение
t ПТМ элементов, определенных уравнением (8.20):
P(t) = Р(х был заменен на у за время t) =
= Si2,l2(t)S20,2o(t)Si4,l(t)Si2,4(t) =

Таблица 8.3. Матрица R интенсивностей замен аминокислот для версии модели эволюции белка Маргарет
Дейхофф с непрерывным временем.
Элемент FUj — мгновенная интенсивность замены некоторой аминокислоты в столбце j на какую-либо
аминокислоту в строке г. Все элементы матрицы были умножены на 104 и округлены до ближайшего целого для
удобства представления. Обратите внимание, что концепция мгновенной замены аминокислоты а на
аминокислоту Ь, согласно которой в одном кодоне должно быть заменено более одного нуклеотида, не является в
полной мере реалистичной; поэтому при малых значениях t такая модель является непригодной
Ala
Arg
Asn
Asp
Cys
Gin
Glu
Gly
His
He
Leu
Lys
Met
Phe
Pro
Ser
Thr
Trp
Туг
Val
Ala
-134
1
4
6
1
3
10
21
1
2
3
2
1
1
13
28
22
0
1
13
Arg
2
-88
1
0
1
9
0
1
8
2
13
37
10
11
5
11
2
20
0
2
Asn
9
1
-180
43
0
4
7
12
18
3
0
25
0
0
2
35
13
0
3
1
Asp Cys
10
0
37
-142
0
5
57
11
3
1
0
6
0
0
1
7
4
0
0
1
3
1
0
0
-27
0
0
1
1
2
6
0
2
0
18
11
13
0
3
3
Gin
8
10
4
6
0
-125
35
3
20
1
1
12
0
0
3
4
2
0
0
2
Glu
17
0
6
54
0
27
-136
7
1
2
1
7
0
12
2
6
2
0
1
2
Gly
21
0
6
6
0
1
4
-65
0
0
4
2
0
8
5
16
1
0
0
3
His
2
10
21
4
1
23
2
1
-88
0
22
2
5
6
1
2
11
0
4
3
He
6
3
3
1
1
1
3
0
0
-129
-53
4
84
0
2
2
2
0
1
58
Leu
4
1
1
0
0
3
14
1
1
9
2
1
-127
4
2
1
8
0
10
11
Lys
2
19
13
3
0
6
1
2
1
2
45
-75
10
-54
1
7
6
0
0
1
Met
6
4
0
0
0
4
0
1
0
12
13
20
1
0
1
4
1
1
21
17
Phe
2
14
1
0
0
0
3
1
2
7
3
0
2
2
-75
3
5
0
0
1
Pro
22
6
2
1
1
6
4
3
3
0
1
3
0
1
12
17
32
1
1
3
Ser
35
1
20
5
5
2
2
21
1
1
3
8
0
3
4
-161
-130
0
1
2
Thr
32
8
9
3
1
2
0
3
1
7
4
11
4
28
0
38
0
-24
2
10
Trp Туг
0
0
14
0
0
0
1
0
14
0
2
0
0
0
5
2
1
-55
0
2
1
1
0
3
0
2
0
1
1
15
1
2
2
9
0
1
2
Val
18
1
2
1
5
33
1
2
-100
2
>
>

8.2. Дополнительные задачи и теория 345
20
fc,Z,ra,g=l
Пакет MATLAB позволяет нам найти точку максимума функции P(t), t* «
119,75ПТМ, с Р(х был заменен на у за время Г) = 0,00010279. Обратите
внимание, что t* — эволюционное расстояние между последовательностями
х и у. □
8.2.2. Модель эволюции последовательностей
Торна-Кисино-Фельзенштейна с заменами, вставками
и удалениями
Теоретическое введение в задачу 8.20
Вероятностная модель эволюции последовательностей ДНК или
белка как процесса замен, вставок и удалений (модель связей или ТКФ)
была предложена в [269] и позже обобщена таким образом, чтобы допускать
вставки и удаления нескольких оснований [270]. Модель ТКФ обеспечивает
основание для новых алгоритмов выравнивания, разработанных Хейн [113],
а также Холмсом и Бруно [123]. В дальнейшем мы будем использовать
терминологию последовательности ДНК: однако все доводы могут быть
отнесены и к последовательностям аминокислот.
Модель ТКФ сочетает в себе марковский процесс с непрерывным
временем (описывающий замены нуклеотидов) с процессом рождения и
гибели с иммиграцией (описывающим вставки и удаления). Подобно моделям
Джукса-Кантора и Кимуры, марковский процесс определяется семейством
матриц замен S(t) =.(st(a, 6)), где t ^ 0. Элемент s*(a, 6) матрицы S(t)
определяет вероятность того, что нуклеотид а был заменён нуклеотидом Ь
за время t. В любое время процесс рождения и гибели позволяет
отдельному нуклеотиду породить дочерний нуклеотид или умереть. Дочерний
нуклеотид вставляется смежным с родительским справа от него, мёртвый
нуклеотид удаляется из последовательности. Чтобы допустить вставки в левом
конце последовательности, где нуклеотиды не могут появиться в
результате событий рождения, события иммиграции регулируют появления новых
нуклеотидов (вставки) в левом конце последовательности. Интенсивность
таких вставок (иммиграция) принята равной уровню (интенсивности)
рождаемости для отдельно взятого нуклеотида. Поэтому вставки в начале
последовательности соответствуют событиям иммиграции процесса
рождения и гибели. Условие А < /х для уровня рождаемости и иммиграции А и

346
Глава 8
уровня смертности /х предотвращает1 как бесконечный рост, так и полное
исчезновение последовательности и необходимо для существования
равновесного распределения длин последовательностей. Модель ТКФ определяет
стационарное распределение на последовательностях ДНК:
р(в) = (1-м)00 V^«t.
где I (I ^ 0) — длина последовательности; тга, ^с> ^g и тгт — равновесные
частоты нуклеотидов, па — число появлений нуклеотида а в
последовательности s. Пусть pn(t) — вероятность того, что данный нуклеотид выжил
и породил п — 1 потомка за время t; пусть qn(t) — вероятность того, что
ко времени t нуклеотид умер, оставив п потомков; и пусть gn(f) —
вероятность того, что п иммигрировавших нуклеотидов было вставлено в левом
конце последовательности ко времени t. Эти функции вероятности должны
удовлетворять системе дифференциальных уравнений ([123]) с решением
в нижеследующей аналитической форме:
Ро = 0,
Pn(t) = а(г)(РЮ)п-г(1 - /3(t)), п>1,
tt(t) = (l-a(t))(l-7(*))i
qn(t) = (1 - a(t))(l - №ЫШ*))п-г> п>1>
gn(t) = (l-/3(t))(P(t)r, n^O.
Здесь
А(1 - е(А-">*)
№ =
7(«) = 1 "
ц - Ае<А-")* '
д(1 - е<А-^*)
(1 - е~1*)(р - Ае<А-">*)
При заданном семействе матриц замен S(t), где t ^ 0, и известных
параметрах А и (j, можно определить вероятности различных событий в эволюции
последовательности ДНК, такие как вероятность того, что
последовательность х эволюционировала в последовательность у за время t,
правдоподобие филогенетических деревьев с заданными листьями и длинами рёбер U
и т. д.

8.2. Дополнительные задачи и теория
347
Задача 8.20. При допущении о том, что замены нуклеотидов в модели ТКФ
происходят согласно модели Джукса-Кантора с параметром а' = 2 • 10~9,
тогда как интенсивности вставок и удалений равны, соответственно, А =
= Ю-9 и \i = 2 • 10~9, найдите а) вероятность Р(у\х, t = 108) того, что
последовательность х = С А эволюционировала в последовательность у =
= AAA за время t = 100 миллионов лет; б) вероятность Р(х, у, z\T, ti, £2)
того, что последовательности х, у и z = GA связаны представленным ниже
деревом Т с длинами рёбер t\ = £2 = Ю8.
Решение, а) Для того чтобы определить вероятность Р(у\х, t = 108)
последовательностей х = (xi,..., хп) и у = (yi,..., ут), мы применяем
рекуррентную процедуру ([113]), которая позволяет нам разложить
вероятность подпоследовательности P(yi,..., yj\x\,..., Xi, £), j ^ га, где i ^ n,
на вероятности независимых событий, включающие либо х\,..., ж$_ь
либо #i*
Р(Уи • • •,Уз\хи • • •>Xi,t) = qo(t)P(yu ...,у,\хи • • •,a?i-i, t)+
xCpjfe^s^i^j-fc+ijTr^-fc^,..-,%) + 9fc(*)7r(yj-fc+i,.. .,%•))> (8.21)
^(Уь • •, Vj\xo, t) = 9j(t)ir(yu • • •, Уз)] (8.22)
где ^(последовательность) обозначает \[аепоследовательность тг(а). Согласно
модели Джукса-Кантора с интенсивностью замен а' = 2 • Ю-9, мы имеем
следующие вероятности замен за время t = 100 миллионов лет:
s(a,a) = 1(1 + 3е-4в'*) = 0,5870,
5(a,b) = i(l-e~4at) = 0,1377,

348
Глава 8
с равновесной частотой 7га = 0,25 для любого нуклеотида а. При А =
= Ю-9, /х = 2 • Ю-9 и t = 108 вычисление нескольких начальных значений
вероятностных функций рп(Ю8) = рп, qn(Ws) = qnn ^п(Ю8) = дп даёт
ро = 0,0000, до = 0,1738, ^о = 0,9131,
рг = 0,7476, qx = 0,0068, дх = 0,0793,
р2 = 0,0650, q2 = 0,0006, #2 = 0,0069,
рз = 0,0056, q3 = 0,0001, дг = 0,0006.
Из уравнений (8.21) и (8.22) для последовательностей х = С А и у = AAA
(согласно принятому допущению все представленные ниже элементы
последовательностей с нулевым индексом х0, у о и zo рассматриваются в
качестве пустых множеств) мы имеем:
Р(уо|*о,* = Ю8) = <7o = 0,9131,
P(yi\x0,t = Ю8) = дтл = 0,0198,
Р(»ь 2/2^0, t = 108) = ^ = 0,0004,
Р(УьУй,Уз|*о,* = Ю8) = <7з^ = 0,00001.
(8.23)
После нескольких шагов рекурсии мы получаем
P(y\x,t= 10s) =P(yuy2,ys\xux2,t=W8) = qoP(y\xut= 108)+
+Р(уи 2/2^1, t = 108)(pi5(A, A) + gi7rA)+
+P(yi\xut = 10s)(p2s(A, А)тгА + q27TA)+
+P(yo|*i,t = 108)(p3s(A А)тг^ + g37ri) = 0,00299.
Теперь мы находим вероятность того, что последовательности х и у
взаимосвязаны в эволюционном отношении:
P(x,y\t = 108) = P(x)P(y\x,t = Ю8) =
= (* - д) (д) *с1гаР(у|М = 108) = 2,33 • Ю-5.
Вероятность Р(ж, у|£ = 108) — сумма вероятностей всех возможных
выравниваний последовательностей х и у. Для того чтобы найти выравнивание
с наибольшей вероятностью (оптимальное выравнивание
последовательностей х и у), необходимо изменить уравнение (8.21), заменяя суммирование

8.2. Дополнительные задачи и теория
349
операцией взятия максимума, и выполнить эту видоизменённую рекурсию
до последнего шага, в котором и будет определена вероятность
оптимального выравнивания. Само оптимальное выравнивание может быть опознано
процедурой обратного прослеживания.
б) Так как события эволюции по различным рёбрам дерева Т
независимы, правдоподобие дерева с длинами рёбер t\ = t2 = Ю8,
последовательностью х при корне и последовательностях при листьях у и z определяется
из
Р(х, у, z\T, h = t2 = 108) = Р(х)Р(у\х, t = 10s)P(z\x, t = 108).
Мы уже вычислили вероятность Р(х)Р(у\х, t = 108); для того чтобы найти
вероятность P(z\x,t — 108), мы применяем рекурсивные уравнения (8.21)
и (8.22). Первые три шага дают те же самые результаты, как и в
уравнениях (8.23). Мы продолжаем рекурсщо и получаем
P(z\x,t = 108) = P(zuz2\x1,x2lt = 108) = q0P(z\xut = 108)+
+P(*i|si, t = 108)(Pls(A, A) + giO, 25)+
+P(z0\xut= 108)(p2e(i4,G)0,25 + ft0,252) =0,0447.
Наконец, мы находим правдоподобие дерева Т:
Р(ж, у, z\T, h=t2 = Ю8) = 2,33 • 10"5 • 0,044701 = 1,05 ■ 1(Г6.
Замечание. Вообще говоря, модель ТКФ позволяет нам обобщить
результаты, полученные для задач построения деревьев, использующих не
содержащие пропусков выравнивания последовательностей, до задач,
затрагивающих построение деревьев, использующих выравнивания с
пропусками. К таким задачам относятся: отыскание оптимальных длин рёбер для
дерева с заданной топологией, листовыми и внутренними узлами;
определение оптимальных предковых последовательностей при внутренних узлах,
при заданных дереве и последовательностях при листьях; построение
наиболее правдоподобного дерева для заданного набора последовательностей
при листьях. Следует, однако, иметь в виду, что решение этих и связанных
с ними задач с помощью модели ТКФ как в вычислительном, так и в
аналитическом отношении намного труднее, чем решение таких задач с опорой
на модели Джукса-Кантора или Кимуры; это связано с тем, что
вероятностные функции модели ТКФ намного сложнее. □

350
Глава 8
8.2.3. Дополнительные сведения об интенсивностях замен
Описанные ранее модели эволюции ДНК и белка (Джукса-Кантора,
Кимуры и Дейхофф) требуют допущения о том, что интенсивности замен
на всех участках последовательности ДНК или белка равны. Несколько
попыток были сделаны, чтобы преодолеть это ограничение. Например, Голд-
мен, Торн и Джонс [97] использовали три различных обратимых
стационарных марковских процесса, описывающих замены аминокислот на участках
белка, которые, согласно предположению, были расположены в пределах
вторичной структуры трёх различных типов: а-спирали, /3-листе и
петле, интерпретируемых как скрытые состояния СММ (где каждое скрытое
состояние характеризуется своей собственной матрицей мгновенных ин-
тенсивностей замен, а не множеством вероятностей порождения). Авторы
оценили вероятности переходов между скрытыми состояниями, используя
последовательности белков с известными вторичными структурами.
Интенсивности замен аминокислот были получены из анализа тесно связанных в
эволюционном отношении пар белков при допущении о том, что
эволюционное время, отделяющее эти последовательности, достаточно мало и что
вероятность замены приблизительно равна произведению интенсивности
замен и прошедшего времени.
В [205] представлено распределение относительных интенсивностей
замен среди участков в форме плотности гамма-распределения (х ^ 0):
Р(х) = ^х°~1е~аХ- (8-24>
Здесь Г — гамма-функция, а а — параметр гамма-распределения.
Согласно допущению о том, что распределение относительных
интенсивностей замен среди участков не изменяется со временем (но при
этом абсолютные интенсивности для отдельных участков могут
изменяться), Гришин, Вольф и Кунин [107] определили приближённые внутрибелко-
вые и межбелковые распределения интенсивностей. Здесь внутрибелковое
распределение интенсивностей отражает изменчивость интенсивностей
замен участков в пределах белков из одного семейства, тогда как
межбелковое распределение интенсивностей отражает изменчивость интенсивностей
замен между белками из разных семейств. Для внутрибелкового
распределения интенсивностей в виде уравнения (8.24) авторы оценили параметр
а по множественным вьфавниваниям четырнадцати больших белковых
семейств. Эти выравнивания произвели долю неизменных участков и и
среднее число замен на участок d(u). Далее, было сделано допущение о том,

8.3. Дополнительная литература
351
что величины и, d и р связаны между собой следующей формулой:
u(d) = I p(x)e~xddx.
о
Тогда u(d) — производящая функция моментов внутрибелкового
распределения интенсивностей с математическим ожиданием и дисперсией,
равными, соответственно, 1 и 1/а. Первая оценка параметра а была получена из
\jol = ^-| (0) — 1. Вторая, независимая, оценка параметра а была получена
dd
как точка минимума статистики х2, составленной из разностей между
распределениями нормализованных эволюционных расстояний для всех пар
девятнадцати полных геномов. Примечательно, что оба метода привели к
одному и тому же результату: а « 0,31.
Эмпирическое межбелковое распределение интенсивностей было
получено из анализа пар ортологичных белков, найденных как взаимные
наилучшие совпадения программы «BLAST» ([7]) при поиске по принципу
«каждый с каждым» в девятнадцати полностью секвенированных геномах.
Функция плотности распределения вероятностей г], определённая как
наилучшее соответствие данным, была описана выражением вида
ф) = ЩА(1-е-Пе-ь*.
Здесь х ^ 0, Ь = 1,01 и с = 5,88. Авторы утверждают, что присутствие
экспоненциально затухающей части функции в межбелковом
распределении интенсивностей делает это распределение совместимым с постоянной
частотой мутаций. Поэтому изменение белка в течение больших
эволюционных периодов достаточно хорошо приближается гипотезой о
молекулярных часах.
8.3. Дополнительная литература
В [280] приведено описание и сравнительный анализ нескольких часто
используемых моделей замен нуклеотидов и аминокислот. Авторы привели
также обзор современных статистических методов, имеющихся в
молекулярной филогенетике: вывод методом наибольшего правдоподобия,
проверка эволюционных моделей, проверка топологий деревьев и т. д. Вопросы
относительно проверки моделей замены нуклеотидов и отбора наиболее

352
Глава 8
адекватной модели при имеющихся эмпирических данных были
обсуждены в [217].
В [279] была предложена эмпирическая модель эволюции белка,
объединяющая в себе подсчёт на основе экономичности (как в модели Дей-
хофф [57]) и метод наибольшего правдоподобия. Построенная на основе
кодонов модель замены нуклеотидов в кодирующих белок
последовательностях ДНК, представленная независимо в [96] и в [203], позже была
видоизменена ([284]), с тем чтобы учитывать так называемую интенсивность
принятия ш, определяемую как отношение d^/ds числа несинонимичных
замен к числу синонимичных замен на участок. При этой модели
методом наибольшего правдоподобия были получены оценки частоты и и был
определён положительный отбор (соответствующий значениям и > 1) для
некоторых генов ([288]). В дальнейшем были развиты статистические
методы оценки djv и ds9 а также измерения приспособления молекул ([285]
и [286]). Используя модификацию метода, описанного в [286], Кларк [51]
проверил гипотезы о наличии положительного отбора в генах человека.
В [177] представлен обзор моделей эволюции последовательностей — как
основанных на кодонах, так и основанных на вторичной структуре.
Были разработаны два метода восстановления филогении, основанные
на дискретном исчислении Фурье: метод инвариантов ([46];[171];[75];[259])
и метод сопряжения Адамара ([114]; [256]). Эти методы применимы к
последовательностям ДНК, при том что замены могут быть описаны моделью
Кимуры с тремя параметрами, моделью Кимуры с двумя параметрами
(модель Кимуры в «АБП») и моделью Джукса-Кантора.
В [287] предложен Байесов метод оценки филогенетических деревьев
на основании данных секвенирования последовательностей ДНК. В этом
методе используется процесс рождения и гибели, с тем чтобы определить
априорное распределение на пространстве деревьев, и метод Монте-Карло
с марковской цепью — для определения дерева с наибольшей
апостериорной вероятностью. Сравнительный анализ методов на основе наибольшего
правдоподобия с Байесовым подходом для оценки филогенетических
деревьев может быть найден в [258], [122] и [65]. Кисино и Хасегава [155]
предложили метод оценки стандартной ошибки и доверительных
интервалов разности значений логарифмического правдоподобия двух
различных топологий (проверка КХ). Проверка КХ часто использовалась на
практике — даже для сравнения нескольких топологий. В последнем случае
проверка могла привести к чрезмерной доверительности для
неправильного дерева. Поэтому Симодайра и Хасегава [243] разработали
модификацию проверки КХ, способную обрабатывать множественные сравнения.
В [98] были рассмотрены проверка КХ и другие основанные на методе

8.3. Дополнительная литература
353
наибольшего правдоподобия проверки топологии филогенетических
деревьев.
Симодайра и Хасегава [244] разработали программу CONSEL для
оценки доверительного уровня отбора дерева, которая выдаёт Р-значения
деревьев. В [242] представлена приближённо несмещённая (ПН)
проверка для проверки топологии деревьев. Проверка ПН обеспечивает ещё
одну процедуру для оценки доверительного уровня отбора дерева и вносит
поправки в смещение отбора, игнорируемое в самонастраивающемся
алгоритме и проверке КХ.
Программное обеспечение Molecular Evolutionary Genetics Analysys
(MEGA) — Анализ молекулярной эволюционной генетики (АМЭГ),
разработанное Кумаром, Тамурой и Неем [169], сфокусировано на анализе
эволюционных изменений в последовательностях белка и ДНК.
Последняя версия, MEGA3 ([170]), содержит программы для выравнивания
последовательностей, информационной проходки размещённых в сети баз
данных, вывода филогенетических деревьев, оценки эволюционных
расстояний и проверки эволюционных гипотез.

Глава 9
ТРАНСФОРМАЦИОННЫЕ
ГРАММАТИКИ
Одномерная строка — слишком простая модель, для того чтобы в
полной мере отражать свойства реальной биологической молекулы, которые
были в конечном итоге обусловлены её трёхмерной структурой, отобранной
в ходе эволюции. Физические взаимодействия аминокислот и нуклеотидов
в трёхмерных свёртках (структурах) должны быть описываемы моделями,
которые выходили бы за пределы учёта взаимосвязей ближнего порядка —
типичных объектов моделей на основе марковских цепей.
Взаимозависимости дальнего порядка более важны для белков, чем для ДНК, которая
имеет довольно равномерную структуру двойной спирали. Однако
структура другой нуклеиновой кислоты, РНК, как правило, в немалой степени
определяется особыми взаимодействиями дальнего порядка, которые
могли бы служить мишенью для вероятностных моделей иного класса.
В главе 9 представлена иерархия детерминированных
трансформационных грамматик Хомского — моделей, изначально разработанных для
естественных языков и затем применявшихся к компьютерным языкам. Эти
грамматики могут быть легко используемы для описания белка (регулярная
грамматика может порождать аминокислотные последовательности,
описанные как регулярные комбинации PROSITE) и РНК (контекстно
свободная грамматика может порождать последовательности РНК с заданной
вторичной структурой).
Дальнейшее обобщение этих классов детерминированной
грамматики до стохастических расширяет возможности моделирования
последовательностей. Можно показать, что стохастические регулярные грамматики
являются эквивалентными скрытым марковским моделям. Стохастические
контекстно свободные грамматики (СКСГ) хороши для моделирования
последовательностей РНК. Главные алгоритмы на СКСГ решают задачи,
поразительно подобные таковым для главных алгоритмов на скрытых
марковских моделях (глава 3 «АБП»): алгоритм выравнивания CYK находит

9.1. Оригинальные задачи
355
оптимальное выравнивание последовательности с уже параметризирован-
ной СКСГ; алгоритм на принципе «изнутри наружу» находит вероятность
последовательности при заданной параметризированной СКСГ; алгоритм с
максимизацией математического ожидания оценивает параметры СКСГ по
набору обучающих последовательностей, используя внутренние и внешние
переменные.
Глава 9 включает двенадцать задач, которые облегчают понимание
главных концепций, представленных в этой главе, а также их взаимосвязь.
Эти задачи предлагают практику использования правил выведения
грамматик для декодирования входных последовательностей, создания правил
грамматики для конкретных классов последовательностей и полных
языков, преобразования правил производства грамматик в нормальную форму
Хомского. Наконец, эти задачи объясняют взаимосвязь между 1) конечным
автоматом и автоматом Мура, 2) детерминированными и
недетерминированными автоматами, 3) магазинными автоматами и стохастическими
контекстно-свободными грамматиками и 4) СММ и стохастическими
регулярными грамматиками.
9.1. Оригинальные задачи
Задача 9.1. Преобразуйте автомат FMR-1, представленный на рис. 9.1,вав-
томат Мура, в котором каждому состоянию соответствует определённый
символ, вместо того, чтобы каждому переходу был сопоставлен
определённый символ.
5}^КбН1Ч7л *■
а
Рис. 9.1. Этот конечный автомат FMR-1 распознаёт повторные области
триплетов, содержащие любое число триплетов нуклеотидов CGG или AGG
Решение. Для того чтобы построить автомат Мура, каждая пара состояние-
переход, определяемая как (ж, п) в автомате FMR-1, преобразуется в
состояние автомата Мура, принимающее символ, соотносимый с переходом. Мы

356
Глава 9
используем S как начальный нетерминальный символ, G*, С$, Ai и Т* —
как нетерминальные символы, соответствующие состояниям автомата
Мура. При преобразовании автомата FMR-1 начальное состояние S остается
тем же самым. Пара состояние-переход (#,1) в автомате FMR-1 даёт новое
состояние Gi, пара (с,2) — состояние С^ и т.д., пока состояние 6 в
автомате FMR-1 не будет достигнуто. Выход из состояния 6 возможен через
одну из трёх пар состояние-переход. В продолжении процесса схождения
пара (с, 7) производит состояние CV автомата Мура, пара (с, 4) производит
состояние С± и пара (а, 4) создаёт дополнительное состояние А&.
Состояния CV, С*4 и А& принимают, соответственно, символы с, с и а. Прямое
добавление остальных состояний, Tg и Gq9 завершает построение автомата
Мура, представленного на рис. 9.2. □
Рис. 9.2. Автомат Мура, который распознаёт моделируемые автоматом
FMR-1 области повторения триплетов, содержащие любое число триплетов
CGG или AGG
Задача 9.2. Преобразуйте автомат FMR-1 в детерминированный автомат.
Решение. Автомат FMR-1 является недетерминированным, так как
состояние 6 имеет два возможных перехода для одного и того же символа с
входного языка. Недетерминированный конечный автомат (НДКА) может
быть преобразован в детерминированный посредством следующей общей
процедуры ([43]).
Если данный недетерминированный конечный автомат (НДКА),
названный N, со множеством состояний S, предполагается преобразовать в
детерминированный конечный автомат (ДКА) А, мы должны сохранять
последовательность всех состояний, которые могут быть достигнуты
некоторой строкой в НДКА. В качестве первого шага мы определяем пространство
состояний ДКА А как показательное множество множества S, то есть мно-

9.1. Оригинальные задачи
357
жество всех подмножеств множества S. Таким образом, каждое состояние
в новом автомате будет помечено некоторым подмножеством множества S.
Далее, мы обозначаем НДКА как N = (5, Е, S, g, F) со множеством
состояний S, алфавитом входного языка Е, множеством начальных
состояний q9 множеством поглощающих (конечных) состояний F и функцией
перехода 6, где J:.SxS-> p(S)- Здесь p(S) — показательное множество
множества S. Функция 6 такая, что при всех s е S и a е Е, S(s, a) =
= {$1, • • •, $п}> где Si G 5, и S(s, e) = {s} для пустой строки е.
Обозначение для соответствующего ДКА следующее: А = (S",E,£',
tf,F')9 где S' = p(S)9 q' = q и F' = {T e S'\T П F ф 0}. Чтобы
осуществить нашу общую стратегию «запоминания» всех состояний, которые
могут быть достигнуты посредством некоторой входной строки, мы
определяем функцию перехода S'9 такую что 8' : S' х Е —► S", следующим
образом: при любых Т € S' и а е Е
<J'(T, a) = (J J(t, а) и *'(Т, е) = Г.
В НДКА FMR-1 С S = {50,^1,^2,^3,^4,^5,^6,^7,^8,^9},
Е = {#, с, a, t}, множеством начальных состояний q = {So} и множеством
конечных состояний F = {Wg} функция переходов состояний S
определяется по таблице 9.1.
Таблица 9.1. Переходы состояний в НДКА FMR-1
9
So {Wi}
Wx 0
W% {W3}
W3 0
W4 {W5}
W5 {W6}
We 0
W, 0
W8 {W9}
W9 0
с
0
{W2}
0
{W4}
0
0
{W4,W7}
0
0
0
f
0
0
0
0
0
0
0
{W8}
0
0
a
0
0
0
0
0
0
{W4}
0
0
0
Соответствующий ДКА имеет состояний, но большинство из них
не достижимо переходами, разрешёнными функцией переходов 5'. В
таблице 9.2 приведены лишь только достижимые состояния ДКА. ДКА с состо-

358
Глава 9
яниями и переходами, представленными в таблице 9.2, показан на рис. 9.3.
Для ясности начальное состояние {So} показано буквой S, конечное
состояние {Wg} показано буквой е, промежуточные состояния {Wi,...,{Ws}
показаны пронумерованными кружками 1,..., 8, а состояние {W4, Wr}
показано кружком 7. □
Таблица 9.2. Переходы состояний в ДКА FMR-1
{So}
т
{W2}
{W3}
{W4
Ш
{w6}
{W4,W7}
{Ws}
{W9}
9
{Wx}
0
{W3}
0
№}
{We}
0
Ш
{W9}
0
с
0
{W2}
0
{W4}
0
0
{WA,W7}
0
0
0
t
0
0
0
0
0
0
0
{W8}
0
0
0
0
0
0
0
0
0
Ш
0
0
0
'^ э-^^ъ^^У^
Рис. 9.3. Детерминированный конечный автомат FMR-1
Задача 9.3. Содержащаяся в базе данных PROSITE ([17]) регулярная
комбинация для цинкового пальца С2Н2 — важного мотива связывающего ДНК
белка — выглядит следующим образом:
С - ж(2,4) - С - ж(3) - [LIVMFYWC] - ж(8) - Я - х(3,5) - Я.
Начертите конечный автомат, который принимает эту регулярную
комбинацию.

9.1. Оригинальные задачи
359
Решение. Легко видеть, что длина этого мотива изменяется от двадцати
одного до двадцати пяти остатков. В мотив входят четыре позиции с
сильно консервативными остатками С и if, а также отрезки
последовательности аминокислот со слабой консервативностью, где любая аминокислота х
может появиться. Было бы обременительно чертить конечный автомат с
двадцатью переходами аминокислот, показанными индивидуально,
следовательно, вместо этого мы используем один переход с символом х. Точно
так же мы обозначим через z символ из набора {L, J, V, М, F, У, W, С}.
Рис. 9.4. Автомат для распознавания регулярной комбинации цинкового
пальца С2Н2, помещённой в базу данных PROSITE
Диаграмма конечного автомата для распознавания размещённой в базе
данных PROSITE регулярной комбинации цинкового пальца С2Н2 показана
на рис. 9.4. Обратите внимание, что этот автомат — детерминированный.
D
Задача 9.4. Напишите последовательности вывода для представленных на
рис. 9.5 последовательностей пос.1 и пос.2, используя контекстно
свободную грамматику (КСГ), описанную ниже:
S -> aWiulcWxglgWxcluWxa,
W\ —► aW2u\cW2g\gW2c\uW2d,
W2 —► aWsu\cWsg\gWsc\uW3a,
W3 —► gaaa\gcaa.

360
Глава 9
seql
А А
G А
G* С
Am U
Cm G
sexfl
С А
G А
Um A
Cm G
Gm С
seq3
С А
G А
Ux С
Сх U
Gx G
С С с лЛЛ
CAGGAAACUG seql
GCUGCAAAGC secfl
GCUGCAACUG seq3
Рис. 9.5. Последовательности 1 и 2 образуют шпилечную структуру со
стеблем и петлёй
Решение. Последовательность вывода для пос.1 следующая:
S =$■ cSg => caSug => cagScug => caggaaacug;
тогда как таковая для пос.2 выглядит следующим образом:
S => gSc => gcSgc => gcuSagc => gcugcaaagc. p.
Задача 9.5. Запишите регулярную грамматику, которая порождает
последовательности пос.1 и пос.2, но при этом не порождает пос.З из примера,
представленного на рис. 9.5.
Решение. В условии задачи не оговорено, должна ли регулярная
грамматика порождать только последовательности пос.1 и пос.2, или же она
может порождать множество последовательностей наряду с пос.1 и пос.2 в их
числе и не порождать лишь пос.З. Мы покажем решения к обеим
интерпретациям условия.
Сначала мы запишем регулярную грамматику, которая порождает
только последовательности пос.1 и пос.2. Она разветвляется на первом символе
и затем просто продолжает работу с порождением либо пос.1 либо пос.2:
S-^cW1\gW2,
W1 -+ aWs, W2 -> cW4,
W3 -> gWb, WA -> uW6,
W5 -> gW7, W6 -> gWs,

9.1. Оригинальные задачи
361
W7^aW9, Ws-*cW10,
W9-*aWlu W10^W12,
Wn —> aWiz, W12 —► aWu,
W13-*eWlb, W14^aW16,
W15 -> uWn, Wis -> gWi%,
W17 -> #, Wis -► c.
Теперь мы запишем регулярную грамматику, которая порождает
последовательности пос.1 и пос.2, а также небольшое число других, набранных
из того же самого алфавита (таких как ссддааасдд), последовательностей,
но ни в коем случае не пос.З:
S-tcW^gWu
W1-+aW2\cW2, W7-*cWlu
W2-*gW3\uW3, W8^aW9,
W3 -> gW*, W9 -> aWio,
~W4-*aW5\cWs, W10-*aWlu
Wb -* aW6, Wn -* uW12\gW12,
W6 -> aW7, W12 -* g\c.
Развилка после состояния W\ ведёт к порождению фрагментов ааас и сааа,
соответственно, из последовательностей пос.1 и пос.2. Ни один из этих
фрагментов не присутствует в пос.З: таким образом, данная грамматика не
порождает фрагмент саас последовательности пос.З и поэтому не способна
породить саму последовательность пос.З. □
Задача 9.6. Рассмотрите полный язык, произведенный КСГ в задаче 9.4.
Опишите регулярную грамматику, которая порождает точно такой же язык.
Является ли хорошей идеей описание этого семейства последовательностей
посредством регулярной грамматики?
Решение. Язык, порождённый известной грамматикой, состоит из
последовательностей с десятью символами. В каждой последовательности
первые три символа дополняют последние три символа, как определено
правилами S, W\ и W2 КСГ (задача 9.4). Регулярная грамматика должна
«помнить» первые три символа последовательности, чтобы породить
правильное окончание. Поэтому регулярная грамматика будет состоять из:

362
Глава 9
• четырех правил для порождения первого символа;
• шестнадцати правил для порождения второго символа;
• шестидесяти четырёх правил для порождения третьего символа;
• шестидесяти четырёх правил для порождения четвертого символа,
который представлен знаком д во всех них;
• 128 правил для порождения пятого символа, которым может быть
символ а либо с;
• шестидесяти четырёх правил для порождения шестого символа,
который представлен символом а;
• шестидесяти четырёх правил для порождения седьмого символа,
которым является символ а;
• шестидесяти четырёх правил для порождения восьмого символа;
• шестнадцати правил для порождения девятого символа;
• четырёх правил для порождения десятого символа.
Таким образом, регулярная грамматика состоит из 488 правил порождения
вместо четырнадцати, как в КСГ. Так что, по всей вероятности, применение
регулярной грамматики для описания этого семейства последовательностей
не представляется хорошей идеей. □
Задача 9.7. Видоизмените алгоритм синтаксического анализа на
магазинном автомате таким образом, чтобы он произвольно порождал одну из
возможных действительных последовательностей на языке контекстно
свободной грамматики.
Решение. Видоизменённый магазинный автомат будет порождать
последовательность в порядке слева направо. Стек автомата инициализируется
путём «проталкивания» в него начального нетерминального символа.
Затем следующие шаги вьшолняются итерациями, до тех пор пока стек не
будет пуст.
Вытолкнуть символ из стека.
Если вытолкнутый символ нетерминальный, то:
• выбрать правило порождения наугад из набора разрешённых правил
порождения для этого нетерминального символа;
протолкнуть правую сторону выражения для выбранного правила
порождения в стек, в первую очередь крайние правые символы.
•

9.1. Оригинальные задачи
363
Если вытолкнутый символ — терминальный, то:
• породить этот терминальный символ как часть последовательности.
□
Задача 9.8. В образованных спаренными основаниями стеблях РНК
приняты пары G-U, но они появляются с более низкой частотой, чем пары
Уотсона-Крика G-C и A-U. Переделайте контекстно свободную
грамматику петли стебля РНК из задачи 9.4 в стохастическую контекстно свободную
грамматику, допускающую появление пар G-U в стебле с вдвое меньшей
вероятностью, чем у пар Уотсона-Крика.
Решение. Чтобы допустить пары G-U, оригинальная КСГ должна быть
снабжена правилами порождения, разрешающими переходы Wi —> gWi+\u,
Wi —> uWi+ig, где i = 0,1,2 и Wo = S. Чтобы преобразовать КСГ в
стохастическую, мы должны приписать вероятности к правилам порождения
оригинальной КСГ. Наконец, правила порождения СКСГ и их вероятности
должны быть определены следующим образом:
S -> aWm, S -> cWig, S -* gWic,
(0.2) (0.2) (0.2)
S -► uWia, S -► gWxu, S -► uW±g,
(0.2) (0.1) (0.1)
Wi -> aW2u, Wi -> cW2g, Wx -> gW2c,
(0.2) (0.2) (0.2)
W\ —> uW2a, W\ —> flfW^w, Wi —> uW2g,
(0.2) (0.1) (0.1)
W2 —> aWzu, W2 —► cWzg, W2 —> 0W3C,
(0.2) (0.2) (0.2)
Wi —► uW^a, И^2 —> ffWeu, И^2 —► uW33,
(0.2) (0.1) (0.1)
И^з —> #ааа, W3 —> дсаа.
(0.5) (0.5)
Задача 9.9. Расширьте алгоритм на магазинном автомате из задачи 9.7 так,
чтобы он мог порождать последовательности из стохастической контекст-

364
Глава 9
но-свободной грамматики согласно их вероятности. (Примечание: это
позволяет создать эффективный алгоритм осуществления выборки
последовательностей из любой СКСГ, включая более сложные СКСГ РНК в главе 10.)
Решение. Видоизменённый магазинный автомат порождает
последовательность в порядке слева направо. Стек автомата инициализируется
проталкиванием в него начального нетерминального символа. Затем
следующие шаги выполняются итерациями, до тех пор пока стек не опустеет.
Вытолкнуть символ из стека.
Если вытолкнутый символ нетерминальный, то:
• выбрать правило порождения для нетерминального символа согласно
его вероятности;
• протолкнуть правую сторону выражения для выбранного правила
порождения в стек, в первую очередь крайние правые символы.
Если вытолкнутый символ — терминальный, то:
• породить этот терминальный символ как часть последовательности.
□
Задача 9.10. Рассмотрите простую СММ, которая моделирует состав
оснований в ДНК двух видов. Модель имеет два состояния, полностью
взаимосвязанные четырьмя переходами состояний. Состояние 1 порождает
богатые С + G последовательности с вероятностями символов (pa,Pc,Pg,Pt) =
= (0,1, 0,4, 0,4, 0,1), а состояние 2 порождает богатые А + Т
последовательности С ВерОЯТНОСТЯМИ СИМВОЛОВ (PaiPoPgiPt) = (0, 3, 0, 2, 0, 2, 0, 3).
а) Начертите такую СММ.
б) Установите вероятности переходов такими, чтобы ожидаемая длина
серии состояний 1 была равна 1000 оснований, а ожидаемая длина серии
состояний 2—100 оснований.
в) Представьте ту же самую модель в виде стохастической
регулярной грамматики с терминальными и нетерминальными символами, а также
правилами порождения с приписанными к ним вероятностями.
Решение, а) Схема СММ выглядит следующим образом:
рГ^) 1-р

9.1. Оригинальные задачи
365
Вероятности переходов между состояниями, как предполагается,
являются такими, что рп = р, р12 = 1 - р, р22 = q, P21 = 1 - Ч, где р и q —
из интервала (0,1). Состояния 1 и 2 порождают четыре символа А, G, G, Т,
соответственно, с вероятностями ei(A) = О,1, е\(С) = 0,4, e\{G) = 0,4 и
ei(T) = 0,1, а также е2(А) = 0,3, е2(С) = 0,2, e2(G) = 0,2 и е2(Т) = 0,3.
б) Вероятности переходов определяются следующим образом. Если
случайная переменная L\ — длина последовательности символов,
порождаемых состоянием 1, то L\ имеет значения п = 1,2,... со следующими
вероятностями: P(Li = п) = gpn_1(l — р) (первый переход должен быть
из состояния 2 в состояние 1, за которым последует п — 1 переход из
состояния 1 в само себя, и последний переход должен быть из состояния 1
в состояние 2). Точно так же мы определяем случайную переменную L2
как длину серии состояния 2, со значениями к = 1,2,... и вероятностями
P(L2 = к) = p<7fc-1(l — я)- Ожидаемые значения величин L\ и L2
определяются из
+оо
EL1 = ^2nqpn~1(l
п=1
+оо
EL2 = ^kpqk-1{l
fc=i
Условия ELi = 1000 и EL2 = 100 ведут к двум уравнениям для
параметров ри q. Решение системы даёт р = 0,999 и q = 0,99.
в) Представление рассматриваемой модели в виде регулярной
грамматики состоит из нетерминальных символов W\ и W2, а также следующих
правил порождения:
Wi -* aWi\cW1\gW1\tW1\aW2\cW2\9W2\tW2J (9.1)
W2 -► aWi|cWi|^i|tWi|aW2|cW2|^2|tW2. (9.2)
Чтобы преобразовать регулярную грамматику в стохастическую
регулярную грамматику, мы должны приписать к восьми правилам
порождения (9.1) для W\ следующие вероятности переходов: ei(A)p, e\(C)p9
ei(G)p, ei(T)p, ei(A)(l-p), ei(C)(l-p), ei(G)(l-p), ei(T)(l-p) в
порядке, установленном уравнением (9.1); и к восьми правилам порождения (9.2)
для W2 — вероятности переходов е2(А)(1 — q), е2(С)(1 — q)9 e2(G)(l — q),
e2(T)(l-q), e2(A)q, e2(C)q, e2(G)q, e2(T)q в порядке, установленном (9.2).
Поэтому мы имеем следующий список правил порождения (стохастической
р)
ч)
9(1
(1-
р{У
-р)
-р?
zA-
ч
1-р
р
(1-Я)2 1-9

366
Глава 9
регулярной грамматики) и их вероятностей:
W1-^aW1, Wi-^cWi, Wi-±gWi, Wi-+tWu
(0,0999) (0,3996) (0,3996) (0,0999)
W1->aW2, W1^cW2, W1^gW2, Wi->tW2,
(0,0001) (0,0004) (0,0004) (0,0001)
W2-+aWu W2->cWu W2->gWu W2-+tWu
(0,003) (0,002) (0,002) (0,003)
W2->aW2, W2-*cW2, W2->gW2, W2->tW2.
(0,297) (0,198) (0,198) (0,297)
□
Задача 9.11. Преобразуйте правило порождения W —► aWbW к
нормальной форме Хомского. Если вероятность оригинального правила порождения
равна р, покажите вероятности правил порождения в вашей,
представленной в нормальной форме, версии.
Решение. Поскольку нормальная форма Хомского требует, чтобы все
правила порождения имели форму Wv —> WyWz или Wv —* а, правило
W —* aWbW заменяется следующей последовательностью правил:
W->WiW2, Wi-+WaW, W2^WbW, Wa^a, Wb -+ b.
Для каждого из нетерминальных символов W\, W2, Wa, Wb
существует только одно правило порождения; следовательно, к каждому правилу
порождения должна быть приписана вероятность 1. Правило W —> W\W2
унаследовало вероятность оригинального правила порождения. Поэтому
в нормальной форме Хомского мы имеем
W-+WiW2,
(Р)
Wi^WaW, W2^WbW, Wa^a, Wb^b. D
(1) (1) (1) (1)
Задача 9.12. Преобразуйте правила порождения Wz —► дааа\дсаа из
грамматики модели стебля РЕПС в задаче 9.4 к нормальной форме Хомского.

9.2. Дополнительная литература 367
При допущении о том, что Ws —> дааа имеет вероятность pi, a Ws —> gcaa
имеет вероятность рг = 1 — Рь припишите вероятности к вашим
правилам порождения в нормальной форме. Покажите, что ваша, представленная
в нормальной форме, версия правильно приписывает вероятности р\ и р2,
соответственно, для петель GAAA и GCAA.
Решение. Подобно предыдущей задаче, мы преобразуем правило
порождения контекстно свободной грамматики к следующей нормальной форме
Хомского:
W3-+WgWl9
(1)
Wi -> WaW2, Wi -+ WCW2,
(Pi) Ы
W2->WaWa, W9^g,
(1) (1)
Wa -> a, Wc -* a
(1) (1)
Для вероятностей петель GAAA и GCAA мы имеем
P(GAAA) = P(Ws -* WgWJPiW! -+ WaW2)P(W2 -* WaWa)x
xP(Wg - g)P(Wa -> a)P{Wa - a)P(Wa - a) = Pl>
P(GCAA) = P(W3 -> WpWi)P(Wi -> WCW2)P(W2 -> WaWa)x
xP(W9 -+>g)P(Wc -+ c)P(Wa -> a)P(Wa -♦ a) = p2.
Результаты подтверждают, что нормальная форма правильно приписывает
вероятности к петлям GAAA и GCAA. □
9.2. Дополнительная литература
В дополнение к работам, упомянутым в разделе 9.7 книги [67],
следующие учебники могут быть полезны для читателя, будучи
последовательными и подробными описаниями теории формальных языков,
трансформационных грамматик и теории автоматов: [43]; [163]; [249]; [152]; [202];
[101]. Недавние достижения в теории автоматов описаны в [231] и [130].

Глава 10
АНАЛИЗ СТРУКТУРЫ РНК
Стохастические трансформационные грамматики, а в особенности
стохастические контекстно-свободные грамматики, как оказалось, являются
эффективными инструментами моделирования для анализа
последовательностей РНК. Предсказание вторичной структуры РНК и построение
множественных выравниваний семейств РНК — задачи, интересные с
биологической точки зрения. Нестохастические алгоритмы для предсказания
вторичной структуры РНК были разработаны более двадцати лет назад (Нуссинов
[209], а также Дукером и Штиглером [292]). Примечательно, что алгоритм
Нуссинов мог быть непосредственно переписан в операторах СКСГ в виде
версии алгоритма Коке-Янгера-Касами (КЯК). Интерпретация СКСГ
обеспечивает понимание вероятностного значения параметров оригинального
алгоритма Нуссинов и, кроме того, предлагает статистические процедуры
для оценки параметров. Подобный перевод в операторы СКСГ возможен и
для алгоритма Цукера.
Интересно, что эквивалентность между невероятностным алгоритмом
выравнивания последовательностей, построенным на методе
динамического программирования, и алгоритмом Витерби для парной СММ аналогична
эквивалентности между невероятностным алгоритмом предсказания
структуры РНК и алгоритмом КЯК для СКСГ. Есть также аналогия между
использованием профильных СММ для выравнивания множества
последовательностей ДНК или белка и использованием основанных на СКСГ
профилях структуры РНК, называемых ковариационными моделями (КМ), для
построения структурно-устойчивых выравниваний множества
последовательностей РНК. Кроме того, параметры ковариационных моделей могут
быть получены работающим на принципе «изнутри наружу» алгоритмом
с максимизацией математического ожидания (сравните с одновременной
оценкой параметров профильных СММ и построением множественного
выравнивания последовательностей). Наконец, алгоритм КЯК для
локального выравнивания геномной ДНК с данной ковариационной моделью может
быть использован для поиска в базе данных последовательностей нуклеоти-
дов специфического типа генов РНК (сравните с поиском гомологов в базе

10.1. Оригинальные задачи
369
данных белков с помощью алгоритма локального выравнивания белковой
последовательности с профильной СММ, представляющей белковый
домен).
Предлагаемые в главе 10 задачи дают полезные иллюстрации
применения как детерминированных, так и вероятностных алгоритмов анализа
последовательностей РНК. Также они показывают взаимосвязи между
этими алгоритмами — например, взаимосвязь между детерминированным
алгоритмом предсказания вторичной структуры РНК и алгоритмом КЯК,
который находит наиболее вероятную вторичную структуру для заданной РНК.
Использование КЯК, алгоритмов типа «внутрь» и «наружу», их элементов
и модификаций составляет предмет нескольких задач.
ЮЛ. Оригинальные задачи
Задача 10.1. Для вычисления взаимной информации по следующей
формуле:
щ = 53 f***ilog2 ~гт~
Xi,Xj JXiJXj
необходимо произвести подсчёт частот всех шестнадцати различных пар
оснований. Этот способ имеет то преимущество, что в нём не
требуется никаких допущений об уотсон-криковском спаривании оснований, так
что взаимная информация может быть определена между коварьирующи-
ми неканоническими парами, такими как А-А и G-G. С другой стороны,
такое вычисление требует большого числа выровненных
последовательностей, для того чтобы получить достоверные частоты для шестнадцати
вероятностей. Запишите альтернативную, известную в теории информации,
меру корреляции спаривания оснований, которая рассматривает только два
класса тождеств г, j вместо всех шестнадцати: пары Уотсона-Крика и пары
G-U сгруппированы в первый класс, а все остальные пары сгруппированы
во второй. Сравните свойства такого вычисления с вычислением М^ как
при малом числе последовательностей, так и (в пределе) при бесконечном
наборе данных.
Решение. Для двух столбцов г и j в структурном отношении правильного
множественного выравнивания N последовательностей РНК х1, х2у..., xN
взаимная информация Мц определяется как сумма шестнадцати членов,

370
Глава 10
где каждый несёт информацию о частоте определённой пары рибонуклео-
тидов (в заданном порядке). Например, для пары (A, G) такой член имеет
вид
йМа)^Шк- (101)
Здесь fij(AG) — частота пары (A, G) в столбцах г и j, a fi(A)(fj(G)) —
частота основания A (G) в столбце г (j).
Теперь мы определяем два класса пар оснований. Первый класс СР
(комплементарные пары) состоит из пар Уотсона-Крика (G,C), (C,G),
(A,U), (U,A), наряду с парами (G,U) и (U,G). Второй класс NCP
состоит из других десяти пар оснований. Мы определяем распределения
fjiij и Vij в двухточечном пространстве {CP,NCP} следующим образом:
/Ху (СР) — частота пар СР, наблюдаемых в столбцах i и j, /x^-(NCP) —
частота пар NCP, наблюдаемых в столбцах i и j, z/y(CP) — вероятность
наблюдения пары СР в двух независимых столбцах с такими же частотами
появления оснований, как и в столбцах г и j, ^j(NCP) — вероятность
наблюдения пары NCP в двух независимых столбцах с такими же частотами
оснований, как и в столбцах in j. Очевидно, что
МСР)= X) ^i(ob),
(а,Ь)€СР
My(NCP)= J2 М<й)>
(а,6) GNCP
(а,Ь)€СР
i/«(NCP) - J] Л(а)/,-(Ь).
(a,b)GNCP
Мы определяем новую меру информации М.ц между столбцами i и j
следующим образом:
М, = ^(СР) log2 -^ + ^(NCP) log2 ^^CP) ■
Согласно этому определению, M%j есть фактически расстояние Куллбека-
Лейблера между распределениями jiij и уц .

10.1. Оригинальные задачи
371
Сравним свойства Мц и Mij. Прежде всего, в отличие от М^, мера
информации Mij чувствительна к комплементарным парам. Например, для
двух пар столбцов:
* 3
А С
А С
С G
С G
г к
A U
A U
С G
С G
М^ = Mik = 1, тогда как Mij < Mik {Mij = 1-1 log2 3, Mik = 1).
При небольшом числе последовательностей мы можем ожидать, что
многие из частот /^ (ab) будут равны нулю, вследствие чего
соответствующие члены в сумме для Мц также будут нулями. Касательно Mij, однако,
мы ожидаем, что даже при малом числе последовательностей N оба члена
вносят в сумму положительные значения. Когда число N растёт и частоты
сходятся к значениям вероятностей, мы имеем
EPij уО'Ь)
Pij(ab) bg2 ,
— ajb Pi{a)Pj{b)
(\ £ Pij(ab)
У^ Pijiab) logo ^ T-. 77T +
Mir- 7 (JLn(o)aW
(\ £ Pij(ab)
vp , , v \ , (a,b)£NCP
, £ Piii) g2 E ft(aW6)-
Здесь p^ (a&) — вероятность появления пары оснований (a, b) (в заданном
порядке) в столбцах i и j, Pi(a) — вероятность появления основания а в
столбце г и Pj(b) — вероятность появления основания b в столбце j. □
Задача 10.2. С помощью процедуры обратного прослеживания алгоритма
Нуссинов для свёртки РНК ([67], стр. 272) найдите ещё две оптимальные
структуры для последовательности GGGAAAUCC с тремя парами
оснований, помимо представленной на рис. 10.1. Видоизмените алгоритм об-

372
Глава 10
ратного прослеживания таким образом, чтобы он находил одну из новых
структур вместо представленной на рис. 10.1.
G
G
г G
1 А
А
и
С
С
G
0
0
G
0
0
0
G
0
0
0
0
з-
А
0
0
0
0
0
А
0
0
0
0
0
0
А
0
0
0
0
0
0
@
и
1
1
1
Ф
Ф
0
0
с
2
2
1
1
1
0
0
0
с
(з)
®
2
1
1
1
0
0
0
(1)
А • U
А
А
Gm С
Gm С
G
Рис. 10.1. Путь обратного прослеживания, произведенный алгоритмом
свёртки Нуссинов для последовательности GGGAAAUCC. Счета на
оптимальном пути обозначены кружками. Отправная точка пути расположена в
верхнем правом углу. Вторичная структура (1), соотносимая с оптимальным
путём, показана справа
Решение. Процедура обратного прослеживания алгоритма Нуссинов для
свёртки РНК ([209], 1978) выглядит следующим образом.
Инициализация: протолкнуть (1, L) в стек.
Рекурсия: повторять до тех пор, пока стек не будет пуст:
•рор(м);
• if г > j continue;
• else if 7(2 + 1,j) = ^(ij) push (г + 1, j);
• else if 7(г, j - 1) = 7(2, j") push (ij - 1);
• else if 7(2 + 1, j - 1) + S(i, j) = 7(2, j)
• record г, j base pair
• push (2 + 1,,? - 1);
• else for к = ii + 1 to j — 1: if 7(2, k) + 7(fc + 1, j) = 7(2, j):
• push (k + 1, j)
• push (2, k)
• break.

10.1. Оригинальные задачи
373
(2)
Am U
А
А
Gm С
Gm С
G
(3)
Am U
А
А
а
U G.C
Gm С
(7)
А^ >А
\4. U'
Gm С
Gm С
G
(4)
Am U
А
Gm С
Gm С
G
(8)
А^ ^4
\4. и'
Gm С
G
Gm С
(5)
iU
А
Gm С
G
Gm С
(9)
А^ >4
\4* U'
G
Gm С
Gm С
(6)
Qfi
А
G
Gm С
Gm С
Рис. 10.2. Восемь альтернативных вторичных структур (с тремя парами
оснований) последовательности GGGAAAUCC
Алгоритм обратного прослеживания возвращает путь через
полуматрицу, показанную на рис. 10.1, наряду с соответствующей вторичной
структурой РНК. Хотя представленная структура содержит три пары Уотсона-
Крика (максимально возможное число пар для этой последовательности),
она, что неправдоподобно в топологическом отношении, образует петлю
шпильки нулевой длины за счёт образования водородных связей между
смежными рибонуклеотидами. Восемь других структур могли бы иметь три
пары оснований (рис. 10.2). Каждая из таких восьми структур может быть
возвращена соответствующей модификацией алгоритма обратного
прослеживания. Например, структура (7) может быть найдена следующим
алгоритмом.
Инициализация: протолкнуть (1,L) в стек.
Рекурсия: повторять до тех пор, пока стек не будет пуст:
• pop (г,.?);
• if г > j continue;
• else if S(i, j) = 7(2, j) and S(iJ) = 1
• record i,j base pair
• push (i + l,j-1);
• else if 7(2 + 1J) = 7(1 J) push (2 + I J);
• else if 7(2, j - 1) = 7(2, j) push (ij - 1);
• else if 7(2 + 1, j - 1) + 8(i,j) = 7(2, j)

374
Глава 10
• record i,j base pair
• push (i + l,j- 1);
• else for к = i + 1 to j — 1: if 7(г, к) + 7(fc + 1, j) = 7(1, j):
• push (k + l,j)
• push (г, к)
• break.
Путь через полуматрицу для данной последовательности показан на
рис. 10.3. □
GGGAAAUCC
£00000012(3)
G 0 0 0 0 0 0
г G 0 0 0 0 0 1
А 0 0 0 0 (Г) 1 !
Л 0 0 ©1 1 1
А
U
С
С
Рис. 10.3. Та же самая матрица счетов пар оснований, как на рис. 10.2.
Кружки показывают путь обратного прослеживания, соответствующий вторичной
структуре (7), представленной на рис. 10.2
Задача 10.3. Алгоритм Нуссинов в том виде, в котором он был описан,
может произвести бессмысленные «пары оснований» между смежными
комплементарными остатками (например, несколько структур, допущенных в
предыдущей задаче, содержат такую пару оснований AU). Видоизмените
алгоритм свёртки Нуссинов таким образом, чтобы петли шпильки имели
минимальную длину h. Приведите новые рекуррентные уравнения для
процедур заполнения полуматрицы и обратного прослеживания.
Решение. Для того чтобы гарантировать, что алгоритм предсказания
вторичной структуры не производит петель шпильки с длиной ниже h, полу-

10.1. Оригинальные задачи
375
мач рица, порождаемая алгоритмом Нуссинов, должна иметь нули в h 4- 1
иоддиагоналях. Такой тип инициализации алгоритма устраняет спаривание
и образование петли шпильки в пределах по крайней мере h
последовательных оснований. Видоизменённый алгоритм Нуссинов для свёртки РНК
работает следующим образом. Для заданной последовательности РНК х =
(#1,..., хь) мы определяем S(i,j) = 1, если нуклеотиды х\ и Xj
образуют комплементарную пару оснований; в противном случае S(i,j) = 0. Для
каждой пары (г,,?') счёт ^(ijj) обозначает максимальное число пар, которые
могут быть образованы подпоследовательностью xi,...,Xj с длиной петли
шпильки по крайней мере h. Поэтому в шаге инициализации алгоритма мы
приписываем
7(г, г - 1) = 0 при г = 2 до L;
7(г, г + к) = 0 при г = 1 до L — к, к = 0 до h.
И шаге рекурсии при j — i + l = h+l,...,L мы вычисляем
j{ij) =max^
7(* + 1»Я>
7(t + l,j-l) + <J(t,j),
max (7(г, к) + 7(fc + l, j))-
k i<k<j
11равила обратного прослеживания те же самые, что и для алгоритма
Нуссинов с h = 0. □
Задача 10.4. Покажите, что алгоритм свёртки Нуссинов может быть
тривиально расширен, с тем чтобы он мог находить структуру с наивысшим
счётом, где пара оснований между остатками а и Ъ получает счёт s(a, b).
Решение. Единственная часть алгоритма, которая должна быть
изменена, — определение функции 5(i,j). Теперь мы определяем S(i,j) =
~ s(xi,Xj). В процедуре заполнения матрицы алгоритма не требуется
никаких изменений.
Инициализация:
7(г, г - 1) = 0 при г = 2 до L;
7(г, г) = 0 при г = 1 до L.

176
Глава 5
VP{i) = max I
f^W + log^f,
[^(O-Mog^f;
„, ч Г max,- V,M(i - 1) + log ^,
VF(i) = max{ J J v ' ^ (5.2)
l^(z-l).
Обратите внимание, что член \ogrj1 /(1 — rj)L в уравнении для VjM(i)
соответствует прямому переходу из молчащего состояния Si в состояния
совпадения Mj — случай, когда первые г — 1 остатков
последовательности х порождаются примыкающим состоянием Fi. Тогда логарифмическое
отношение шансов принимает вид
log
г-1
P(xi,...,Xi\M) i=i 3___
P(xi,...,Xi\R) " *
(1 - VY П fe
z=i
. емД^г) т/2
= loS —^ + loS ■
fe b(l-77)L*
В заключительном шаге мы имеем
V = тах(тах(Км(АГ) - logL), VF{N) - logr/).
з J
Значение V — полный счёт пути Витерби для последовательности х,
идущего через профильную СММ локального выравнивания. Сам путь
может быть восстановлен путём применения процедуры обратного
прослеживания. Подпоследовательность последовательности х, порождаемая на пути
между появлениями первого состояния совпадения Mj> и последнего
состояния совпадения Mj*, которое предшествует молчащему состоянию S2,
участвует в наилучшем локальном выравнивании последовательности х с
профильной СММ. Это оптимальное локальное выравнивание описывается
частью пути между состояниями совпадения My и Mj*, где j' ^ j*.
Сравнение уравнений обновления (5.1) и (5.2) показывает, что эти два
алгоритма имеют много общего. Порождение символа Х{ из состояния
совпадения Mj профильной СММ соответствует выровненной паре (#г,2Л?)
в попарном выравнивании; порождение символа xi из состояния вставки

5.1. Оригинальные задачи
177
соответствует выравниванию символа Xi с пропуском в попарном
выравнивании; и появление состояния удаления Dj соответствует выравниванию
символа yj с пропуском в попарном выравнивании. Обратите внимание, что
в предельном случае, когда набор выровненных последовательностей,
служа набором обучающих последовательностей для профильной СММ,
сжимается до одной-единственной последовательности, обозначаемой как у,
отыскание оптимального пути через профильную СММ, порождающего
последовательность х, становится эквивалентным задаче обнаружения
оптимального попарного локального выравнивания последовательностей х и у.
Формально оптимальный текущий счёт V^M(i) в уравнениях (5.2)
соответствует Vм(г, j) в уравнениях (5.1), V*(i) соответствует Vх (г, j), a VjD(i) —
VY(i,j). Интерпретация счёта замены s(xi,yj) в уравнениях (5.1)
представляет определённую трудность, так как в уравнениях (5.2) он
разлагается на три члена: logeMj(xi)/qXi + loga^-iA^VC1 ~ V)9 logeMj(xi)/qx. +
+logai^Mj /(1-v) и 1оёeMj (xi)/qXi +logaDj_lMj/(l-ff)- Если все
вероятности переходов в состояние совпадения Mj одинаковые, значения этих
трёх членов также будут равны. Подобным же образом штраф за введение
пропуска d в уравнениях (5.1) соответствует следующим членам в
уравнении (5.2): - bgojwr, 1^/(1 - rj), где j = 1,..., L - 1, и - logaMj_lDi/(l - rj),
где <7 = 2,...,L — 1. Эти члены равны, если все разрешённые переходы из
состояний совпадения в состояния вставки и удаления имеют равные
вероятности. Наконец, штраф за продолжение пропуска е в уравнениях (5.1)
соответствует следующим членам в уравнениях (5.3): — loga/././(l — ту),
где j = 1,..., L - 1, и - \ogaDj_lDj/(l - rj), где j = 3,..., L - 1, которые
снова сходятся к одному-единственному значению, если значения
вероятностей перехода ajjij и a>Dk_1Dk равны.
Замечание. Взаимосвязь между вероятностными параметрами парной
СММ и параметрами алгоритма попарного выравнивания была
рассмотрена в замечании к задаче 4.11. □
Задача 5.2. Объясните причины (обращаясь к задаче 5.1) каких бы то ни
было различий между алгоритмом оптимального локального попарного
выравнивания (5.1) и алгоритмом (5.2) для оптимального локального
выравнивания последовательности с профильной СММ.
Решение. Для того чтобы определить либо наилучшее локальное попарное
выравнивание двух последовательностей х и у, либо наилучшее
выравнивание последовательности х с профильной СММ с примыкающими
состояниями, мы должны вычислить элементы трёх матриц динамического про-

378
Глава 10
Как видно, наборы правил порождения (6), (8) и (9) оказываются
идентичными, а наборы (1) и (3) определяют, по сути, один и тот же язык. Однако
эти правила порождения различны в отношении семантического значения
и в плане фактических вероятностных параметров, к ним относящихся. □
Задача 10.7. Напишите уравнения переоценки для алгоритма типа «внутрь»,
алгоритма типа «наружу» и алгоритма типа «изнутри наружу» при СКСГ
свёртки РНК типа Нуссинов, представленного ниже:
(10.2)
S —► aS\cS\gS\uS (неспаренный г),
S —> Sa\Sc\Sg\Su (неспаренный j),
S —> aSu\cSg\gSc\uSa (пара г, j),
S —► SS раздвоение.
Решение. Уравнения переоценки алгоритма типа «внутрь», алгоритма
типа «наружу» и алгоритма типа «изнутри наружу» могут быть определены
для любой СКСГ в нормальной форме Хомского. Чтобы преобразовать
заданную СКСГ (10.2) к нормальной форме Хомского, мы используем
символ W\ в качестве начального нетерминального символа наряду с девятью
нетерминальными символами Wi,..., Wg:
Wx — W6W±\W7Wx|WsW±\W9W! (неспаренный г),
Wx — WiWelWiWrlWiWelWi^Q (неспаренный j),
Wi -> HW2|VM^3|WW4|WW5 (пара г, j),
W\ —» W\W\ раздвоение,
W2 — WxWg, W6 -► a,
Ws-^WxWs, W7^c,
WA -+ WlW7, Ws -> g,
W6->WiWe, W9-+u.
Мы делаем допущение о том, что вероятностные параметры СКСГ
обозначаются p(aS), p(aSu) и т. д. Тогда вероятности, соотносимые с принятыми

10.1. Оригинальные задачи
379
в СКСГ правилами порождения, следующие:
*, (6,1) = p{aS), ti(7,1) =p(cS), ti(8,1) =p{gS), ti(9,1) =p(uS),
*i (1,6) =p(Sa), *i(l,7) =p(Sc), *i(l,8)=p(5p), ti(l,9)=p(Su)>
*i(6,2)=p(aSu), ti(7,3)=p(cSp), t1(814)=p(gSc), *i(9,5)=p(iiSa),
*i(l,l)=p(SS),
t2(l, 9) = 1, *з(1,8) = 1, t4(l, 7) = 1, t5(l, 6) = 1,
e6(a) = l, e7(c) = l, e8(^) = l, e9(w) = l.
Все прочие значения величин tv(y, z), ev(a), ev(c), ev(g), ev(u) при v,y,z =
- 1,..., 9 равны нулю.
Для последовательности РНК х = (х\,...,xl), xi G {a, с,#,u},
алгоритм типа «внутрь» ([173]) определяет вероятность а (г, j, v) поддерева
синтаксического анализа, имеющего корень при нетерминальном символе Wv
для подпоследовательности Xi,...,Xj при всех возможных г, j и v.
Алгоритм состоит из следующих шагов.
Инициализация: при г = 1 до L и v = 1 до 9,
a(i,t,v) = е^(жг)-
Итерация: при г = 1 до L — 1, j = г +1 до L и v = 1 до 9,
9 9 J-1
3/=1 2=1 fc=i
Завершение: Р(ж]0) = a(l,L, l).
Таким образом, алгоритм типа «внутрь» определяет вероятность (счёт)
последовательности х, порождаемой СКСГ из уравнения (10.2), с набором
параметров, обозначаемых как 0.
Алгоритм типа «наружу» ([173]) находит вероятность /3(i,j,v) дерева
синтаксического анализа с корнем при начальном нетерминальном
символе W\ для полной последовательности ж, исключая поддерево
синтаксического анализа для подпоследовательности Xi,..., Xj с корнем при
нетерминальных символах Wv при всех возможных i,jnv. Алгоритм типа
«наружу» основан на допущении о том, что «внутренние» вероятности a(i,j,v)
известны. Алгоритм работает следующим образом.
Инициализация: /3(1, L, 1) = 1; при v = 2 до 9: /3(1, L, v) = 0.

380 Глава 10
Итерация: при г = 1 до L, j = L до г, v = 1 до 9,
г-1
0(i,j,v) = '£'52<x(k,i-l,z)l3(k,jiy)ty{ziv)+
L
+ ]>^ J2 <*U + 1>k,z)0(i,k,y)tv(v,z).
V,z k=j+l
Завершение:
9
P(x\0) = У^ /?(г, г, v)ev(a;i) при любых г.
v=l
Вероятности правил порождения для нетерминальных символов W»,
где г = 1,..., 9, могут быть оценены уравнениями переоценки с
максимизацией математического ожидания (ММО) ([61]). Для нетерминального
символа W\ мы имеем
L-l L j-1
Е Е Е /?(*> j\ i)a(*i&> з/)<*(* +1> j» *)*i(г/, *)
а , ч г=1 j=£+l fc=i
*i(y»*) = y~i >
г=1 j=i
где пары (у, z) принимают значения (1,1), (1,6), (1,7), (1,8), (1,9), (6,1),
(6,2), (7,1), (7,3), (8,1), (8,4), (9,1) и (9,5). Все остальные значения
величины ti(y, z) равны нулю.
Уравнение переоценки с ММО для вероятностей правил порождения
для нетерминальных символов ИЪ, • • •, Ws имеет следующий вид:
Е1 Е Z P(iJ,v)a(i,k,l)a(h + lJ,U-v)
tv(l, 11 - v) = — ,
E E<*(M>)/?(i,j,v)
i=l j=i
где v = 2,..., 5. Для всех остальных пар (y,z) величины ^(у^), • • • $ъ{У->г)
равны нулю.

10.1. Оригинальные задачи 381
Наконец, для нетерминальных символов Wq, ..., Wg мы имеем
£ /?(м,б)
ё6(а)
ЕЕ«(и',ВДи',б)
г= lj=i
JC/(m,7)
ё7(с) =
г=1 j=i
EEa(t,j,8)№i,8)
г=1 j=i
£ /?(М,9)
e9(u) = -J— •
££a(z,j,9)/?(i,.7,9)
г=1.7=г
Значения всех остальных величин ev(a), ev(c), ev(^) и ev(tt) равны нулю.
П
Задача 10.8. По аналогии с алгоритмом осуществления выборки условно-
оптимального выравнивания с помощью профильной СММ создайте
алгоритм для осуществления вероятностной выборки структур из вашей
внутренней матрицы.
Решение. Предположим, что мы закончили выполнение алгоритма типа
«внутрь» и заполнили ячейки трёхмерной матрицы динамического
программирования a(i,j,v) порядка L x L х М (где L — длина
последовательности х, а М — число нетерминальных символов в СКСГ).
Значение a(l,L, 1) полной вероятности последовательности х при заданной
СКСГ представляет собой сумму вероятностей всех возможных
синтаксических анализов последовательности х при заданной СКСГ (сумма
вероятностей всех возможных структур свёрток последовательности х). Мы
должны определить такое распределение вероятности по всем возможным

382
Глава 10
структурам, при котором вероятность каждой структуры является
пропорциональной вкладу этой структуры в значение а(1, L, 1). Чтобы произвести
типовую структуру, мы проходим назад через трёхмерную матрицу а (г, j, v)
и приписываем вероятности к поддеревьям синтаксического анализа
следующим образом. Предположим, что мы достигли ячейки (г, j, v),
соотносимой с поддеревом синтаксического анализа, имеющим корень при
нетерминальном символе Wv для подпоследовательности Xi,...,Xj. Вероятность
<*(м\ г>), где г = 1,..., L — 1, j = г + 1,..., L и v = 1,..., М, этого
поддерева синтаксического анализа определяется алгоритмом типа «внутрь»
следующим образом:
М М з-\
aih j, v) = ]Г) Yl Yl a(*' *' 2/)а(* + 1? Э> *)1*(У>z)-
у=\ z=l k=i
Для пары состояний у, z и индекса к, где к = г,..., j — 1, мы
рассматриваем поддерево синтаксического анализа TijtV(y, z, к) с корнем при
состоянии v, которое включает пару поддеревьев синтаксического анализа для у
и z и более коротких подпоследовательностей ж»,..., Хк и £fc+i, • • • > #j:
1 t fe fe+1 j L
К поддереву TijyV(y, z, к) мы приписываем следующую вероятность:
а(г, /с, 2/)а(/с + 1, j, z)tv(у, z)
P(TitjtV(y,z,k))
a(ij,v)
Тогда наименьшие деревья Т^+1,и(2Л -*, г), г = 1,..., L — 1, имеют
следующие вероятности:
а(г, г, у)а{г + 1, г + 1, z)tv(y, z)
P(TM+ijf,(y, *,<)) =
а(г,г + l,v)
gy(a?i)eg(a;t+i)^(y>^)
a(i,i + l,t;)

10.1. Оригинальные задачи
383
По завершении процедуры обратного прослеживания мы определяем
вероятность любой структуры свёртки последовательности х следующим
образом. Для каждой структуры мы находим аналогичную описанной выше
согласованную последовательность поддеревьев (начинающуюся с дерева
T\,L,i(y, z, к) для состояний у, z и индекса к и заканчивающуюся
наименьшими поддеревьями Т^+1>1;(р, q, i) для всех г, г = 1,..., L — 1и некоторых
состояний р и q). Тогда вероятность структуры равна произведению
вероятностей входящих в её состав поддеревьев. Следовательно, мы определили
распределение вероятности по набору всех возможных вторичных структур
последовательности х при заданной СКСГ. □
Задача 10.9. Покажите, как именно следует употреблять ваши внутренние
и внешние переменные, чтобы вычислить вероятность того, что позиции
i,j спарены основаниями и просуммированы по всем структурам.
Функциональная форма ответа будет аналогична выведенным вами уравнениям
переоценки для алгоритма типа «изнутри наружу».
Решение. СКСГ свёртки РНК в нормальной форме Хомского (задача 10.7)
подразумевает, что позиции i,j спарены основаниями, когда произведения
выполнены. Сделаем допущение о том, что отдельно взятое произведение,
скажем W\ —> W^W^ имеет вероятность перехода ti(6,2). Вероятность
события, что подпоследовательность ж»,..., Xj подверглась синтаксическому
анализу с помощью этого правила порождения, равна вероятности
синтаксического анализа целой последовательности за исключением
подпоследовательности Хг,..., Xj. Это значение определяется как произведение
значения /?(г, j, 1), найденного алгоритмом типа «наружу», и вероятности
поддеревьев синтаксического анализа с корнями при выбранном правиле
порождения и имеет следующий вид:
*i(6,2)X;a(<,fc,6)a(fc + l,j,2)
к=г
Е Е a(i'J',W,j',l)
г'=1 j'=i'

384
Глава 10
Тогда вероятность р(г, j) того, что позиции г, j спарены основаниями, равна
сумме таких вероятностей для всех четырёх правил порождения:
i-i
PihJA) Е tifaz) Е <x(i,k,y)a(k + l,j,z)
P(«,j) = £ £ >
Е Е афЛЛЩг'ЛА)
где П = {(6,2), (7,3), (8,4), (9,5)}. □
Задача 10.10. Перепишите список правил порождения с не содержащей
пропусков модели РНК так, чтобы символы порождались независимо от
предыдущего состояния, как это имеет место в СММ. Это — формальная
стохастическая трансформационная грамматика, которая соответствует
графическому представлению СКСГ на рис. 10.4.
Решение. Следуя логике, употреблявшейся в задаче 9.1, мы используем
нетерминальные символы Wb,..., И^з ДО* моделирования состояний
переходов. Нетерминальные символы, участвующие в порождении символов,
Pi, LiuRi, сохранят то же самое значение, как и в оригинальной
грамматике. Каждое из шестнадцати попарных правил порождения будет
соотнесено с одной из шестнадцати вероятностей порождения (для всех возможных
пар); порождение отдельного нуклеотида четырьмя правилами
порождения «влево» и четырьмя правилами порождения «вправо» будет
определено двумя группами по четыре вероятности. Другие правила порождения
(раздвоение, начало, конец) будут иметь вероятности, равные единице.
Тогда полная стохастическая трансформационная грамматика
описывается правилами порождения, представленными на рис. 10.5 (ради краткости
для каждого нетерминального символа показано только одно из возможных
правил порождения). □
Задача 10.11. Предположим, что нам задали длинную последовательность
нуклеотидов и наша задача состоит в том, чтобы найти одну или более
подпоследовательностей, которые соответствуют ковариационной модели РНК.
Путём применения преобразования системы координат матрицы
динамического программирования мы можем употребить эффективный алгоритм

10.1. Оригинальные задачи
385
{А ^U^
GmC GmC
Am U Gm С
А С
CmG Gm С
U G А А
и с с
®
А<
С<
и<
и<
и<
С<
Щ
щ
ш
щ
ц\
ц\
ц\
щ
А
А
>С
>и
>А
>G
и<
24
(а)
Рис. 10.4. а) Графическое представление примера не содержащей пропусков
СКСГ РНК. Квадратики, помеченные буквой Р, представляют шестнадцать
попарных правил порождения; квадратики с буквами L и R представляют,
соответственно, четыре правила порождения «влево» и четыре правила
порождения «вправо»; квадратики, помеченные буквами S9 В и Е9
представляют, соответственно, начальные символы, символы раздвоения и конечные
терминальные символы, б) Структура консенсуса РНК перечерчена так,
чтобы в большей степени соответствовать структуре дерева СКСГ. в) Дерево
синтаксического анализа для этой структуры РНК, в котором рибонуклеоти-
ды приписаны к состояниям в СКСГ
(алгоритм типа КЯК, «внутрь» или «наружу») для поиска локальной
подпоследовательности в базе данных.
По сравнению с КЯК, алгоритм типа «внутрь» имеет то преимущество,
что он суммирует вероятности всех возможных структур и выравниваний
подпоследовательностей, хотя в вычислительном отношении он не сложнее
алгоритма КЯК. Приведите пример алгоритма типа «внутрь» для поиска
совпадений локальных подпоследовательностей длины не более D.

386
Глава 10
Стебель 1 Стебель 2
Si -^W2 S5-^ W6 5i5 -> W16
W2 —► aL2\... И^б —> #Pec|... Wie —► uLiel • •.
L2 -> W3 Pe^ W7 Li6 -+ W17
W3-»aL3|... Wr -> аР7^|... Wi7 -> gPnc\...
L3 -► B4 *V -► Wg Pit -> Wis
B4 -+ 555i5 W8 -► Два|... Wi8 ^ 9Pi8c\...
Д8 -► Wg Pig -► Wig
Wg -> cP9g\... Wi9 -> cL19\...
Pq —» Wio £19 —» W20
W10 -> wLio|... W20 -► ^P2oc|...
Ью —► Wn P20 —► W21
W11 —> uLn\... W21 —» a^2i| • • •
Ln —» VF12 L21 —> W22
W12 —► CL12I... W22 —* CL22I. • •
L12 —> W13 £22 —► W23
W13 —► #Li3|... W23 —► аЬ2з| • • •
L13 —» £^14 L23 —* #24
-Ё/14 —► £ £*24 ~~>" £
Рис. 10.5. Правила порождения стохастической трансформационной
грамматики не содержащей пропусков модели РНК
Решение. Мы рассматриваем ковариационную модель (КМ) с М
состояниями (нетерминальными символами), обозначаемыми W\,..., Wm- Семь
типов состояний помечены как Р, L, R, D, S, В и Е, соответственно, для
попарного порождения, порождения «влево» (5'), порождения «вправо» (3'),
удаления, начала, раздвоения и конца; W\ — начальное (корневое)
состояние для всей КМ. Состояния семи типов соотнесены с вероятностями
порождения символа и перехода между состояниями (таблица 10.1). Матрица
динамического программирования индексируется значениями v,j,d
(вместо и, г, j в случае СКСГ), где d — длина подпоследовательности ж»,..., ж^
(d = j — i + 1) и d ^ D. Удобства ради мы будем употреблять
обозначение ev(xi,Xj) для всех вероятностей порождения. Для состояний L,
вероятность ev(xi,Xj) = ev(xi)9 для состояний R — ev(xi,Xj) = ev(xj), а для

10.1. Оригинальные задачи
387
непорождающих состояний — ev(xi,Xj) = 1. Числа Д£ и Д^ суть
числа символов, порождаемых состоянием v, соответственно, влево и вправо.
Пусть sv — тип состояния, s € {Р, L, R, D, 5, В, Е}, указывающий один
из семи возможных типов правила порождения. Пусть Cv — множество
возможных детей состояния v, представленное списком одного или более
индексов у состояний Wy, в которые состояние Wv может сделать переход.
Здесь преобразование нумерации состояний подразумевает, что у > v при
всех у е. Cv, за исключением состояний вставки, где у ^ v при всех у GCV.
Таблица 10.1. Семь типов состояний ковариационной модели
Состояние (sv)
Р
L
R
D
S
В
Е
Пр-ло порожд-я
Wу ' Xг ** yXj
Wv — xiWy
Wv — WyXj
Wv^Wy
WV^Wy
Wv — WyWz
JVV — e
L-xv
1
1
0
0
0
0
0
1
0
1
0
0
0
0^
Порождение
&V yXi 7 Xj J
Gv\Xi)
Cv \Xj )
1
1
1
1
Переход
tv(y)
tv(y)
tv(y)
tv(y)
*v(y)
1
1
Алгоритм типа «внутрь», ищущий совпадения локальных
подпоследовательностей, работает следующим образом.
Инициализация: при j = 0 до L и v = М до 1,
при sv = Е : 1;
при sv £ D,S : £ tv(y)ay(j,0);
при sv =B,CV = (y,z) : ay(j,0)az(j,0);
при sv e. P,L,R: 0.
Рекурсия: при j = 1 до L, d = 1 до min(D, j) и v = M до 1,
[ при sv = E : 0;
при sv = P, nd < 2 : 0;
<*v{j,d) = <
при sv = B,CV = (y,z) : £ ay(j -k,d-k)az(j,k);
k=0
иначе: ev(xj-d+i,Xj) J2 1у{у)<*у(з - A?,d - Aj - A*).
y€Cv

388
Глава 10
Когда рекурсия закончена, ячейки ai(j, d) должны содержать вероятности
совпадений для подпоследовательностей Xj-d+ъ • • •, Xj с длинами не
более D. П
Задача 10.12. Видоизмените алгоритм КЯК так, чтобы он сохранял
информацию обратного прослеживания в каждой ячейке, с тем чтобы
использовать её при восстановлении оптимального дерева синтаксического
анализа. Какова минимальная информация, которая должна быть сохранена
для обратного прослеживания, начиная от состояния раздвоения? Какова
минимальная информация, которая должна быть сохранена для обратного
прослеживания, начиная от любого другого состояния?
Решение. Мы видоизменим алгоритм КЯК посредством системы индексов,
описанной в задаче 10.11. Для каждого значения iv(j,d) мы будем
сохранять соответствующее значение обратного прослеживания r(j, d).
Видоизменённый алгоритм КЯК работает следующим образом.
Инициализация: for v = М,..., 1,
• ifsv = Е, then jv(0,0) = 0, rv(0,0) = 0,
• else if sv E D, S, then
7* (0,0) = тах(7з/(0,0) + log^(y)),
y£Cv
rv(0,0) = argmax(7y(0,0) + log £„(?/)),
yecv
• else if sv = B, with Cv = (y, z), then
7«(0,0) = 72/(0,0) + 7,(0,0),т„(0,0) = 0,
• else 7W(0,0) = -oo, t„(0,0) = 0;
• fiirj = l,...,L,7t,(j,0)=7t,(0,0),rt,0",0)=rt,(0,0).
Рекурсия: for j = 1,..., L, d = 1,..., min(j, D), v = M,..., 1,
• if sv = E, then jv(j, d) = -oo, rv(j, d) = 0,
• else if sv = P and d < 2, then 7v(j, d) = —oo, rv(j, d) = 0,
• else if sv = B, with Cv = (y, z), then
7«0\d) = , max hy{j -k,d-k)+ yz(j,fc)),
fc=0,...,a
t«0"> d) = argmax(72/(j - fc, d - fc) + 7*(j, fc)),
fc=0,...,d

10.2. Дополнительная литература
389
• else
7«0\ d) = max(7l,(j - Д?, d - Д£ - Д*) + log Ъ(у))+
+ logev(xj-d+i,Xj),
rv{j, d) = axgmax(7y(i - Д*, d - Д£ - Д*) + log t„(y)).
Здесь ev(o,b) = log(ev(a,b)/fafb) при sv = P; log(e„(a)//a) при sv = L
и log(ev(b)/fb) при 5V = i?; /a, Д — частоты отдельно взятых оснований.
Обратное прослеживание начинается с 71 (j, d) для
подпоследовательности длины d с наивысшим счётом, заканчивающейся в позиции j, и
проходит назад. Следует иметь в виду, что в случае глобального выравнивания,
в отличие от локального, обратное прослеживание начинается с *yi (L,L).
Алгоритм обратного прослеживания работает следующим образом:
Для счёта 7«Q",d)
• if rv(j, d) = 0, then stop;
• if sv = B, with Cv = (2/, z), then let к = rv(j, d), make bifurcation to
7y(j -k,d-k) and 7^, fc);
• else let у = r„(j, d), go to 7y(j - Д*, d - Д£ - Д*).
Минимальная информация, которая должна быть сохранена для того,
чтобы можно было проследить назад путь от состояния раздвоения, — точка
разветвления подпоследовательности к, которая даёт наивысший счёт.
Минимальная информация, которая должна быть сохранена для того, чтобы
проследить назад путь от любого другого состояния, — индекс
нетерминального состояния у, который дает максимальный счёт. □
10.2. Дополнительная литература
Стохастические контекстно-свободные грамматики продолжают
использоваться как эффективные инструменты моделирования для
алгоритмов предсказания вторичной структуры РНК. В [158] был предложен новый
алгоритм, использующий СКСГ и эволюционную историю для отыскания
вторичной структуры с наибольшей апостериорной вероятностью (НАВ)
для набора последовательностей РНК. Позже этот алгоритм был
применён в виде программы Pfold, способной строить выравнивание вплоть до
сорока последовательностей длины 500 оснований ([159]). В [124]
предложено несколько алгоритмов динамического программирования (алгоритм

390
Глава 10
типа «внутрь», алгоритм КЯК, алгоритм типа «изнутри наружу») для
парных СКСГ, обобщающих концепцию (единичных) СКСГ. Дуэл и Эдди [66]
оценили точность различных разработок СКСГ для предсказания
вторичной структуры РНК по одной последовательности на эталонном тесте
последовательностей РНК с проверенными структурами. Также приводится
сравнение с точностью предсказаний, полученных методами минимизации
энергии.
В [69] был предложен алгоритм динамического программирования для
выравнивания целевой последовательности РНК с неизвестной структурой
и последовательности запроса с известной структурой. Этот алгоритм
применяет ковариационную модель вторичной структуры РНК и использует
стратегию «разделяй и властвуй», которая значительно сокращает
требуемый объём памяти, по сравнению с основанными на СКСГ алгоритмами,
что делает возможным вычисление оптимальных структурных
выравниваний для больших молекул РНК.
Было разработано несколько алгоритмов предсказания вторичной
структуры РНК с псевдоузлами. В [260] предложен подход, в котором
применяется алгоритм взвешенного совпадения из [90], чтобы найти
оптимальный набор взаимодействий типа спаривания оснований, включая
псевдоузлы и другие троичные пары. Этот алгоритм работает в полиномиальном
времени и памяти. Риваш и Эдди [225] разработали алгоритм
динамического программирования, который производит структуру с минимальной
энергией для единственной последовательности РНК. Этот алгоритм
использует стандартные термодинамические параметры свёртывания РНК, в
том числе описывающие термодинамическую стабильность псевдоузлов.
Мэтьюс [189] пополнил обычный алгоритм динамического
программирования с минимизацией энергии для предсказания вторичной структуры
РНК новыми термодинамическими параметрами, которые определяют
стабильность мотивов вторичной структуры с расширенной зависимостью от
состава последовательности. Дальнейшее уточнение этих параметров
наряду с экспериментальным определением ограничений химической
модификации способствовало дополнительному усовершенствованию этого
алгоритма ([190]). В [291] представлен обзор алгоритмов с минимизацией
свободной энергии.
Хуан и Уилсон [133] разработали вычислительный метод
идентификации эволюционно консервативной вторичной структуры в наборе
выровненных гомологичных последовательностей РНК, основанный на
сочетании анализа свободной энергии и анализа ковариации. Динг и Лоренс [63]
предложили статистический алгоритм предсказания вторичной структуры
РНК, который работает путём осуществления выборки из равновесного рас-

10.2. Дополнительная литература
391
пределения вероятностей Больцмана, определённого на наборе возможных
вторичных структур для заданной РНК. Новые алгоритмы предсказания
вторичной структуры РНК были разработаны также Городкиным, Стрикли-
ным и Стормо [102], а также Перрике, Тузе и Доше [215].
В настоящее время имеется несколько баз данных
последовательностей РНК и серверов обработки РНК: база данных Ribonuclease P ([35])
— компиляция заимствованных из БД RNase P последовательностей,
выравниваний последовательностей РНК, вторичных структур и трёхмерных
моделей; проект базы данных рибосомной РНК ([187]) включает и данные
расшифровки последовательностей, и программное обеспечение для
выравнивания последовательностей рРНК, построения филогенетических
деревьев и предсказания вторичной структуры рРНК; база данных European
Large Subunit Ribosomal RNA ([283]) содержит полный список
последовательностей больших субъединиц рРНК, множественные выравнивания
РНК и вторичные структуры, предсказанные в ходе сравнительного
анализа последовательностей; база данных Pfam ([104]) включает собрание
множественных выравниваний последовательностей и ковариационных
моделей, отражающих семейства некодирующей РНК; база данных тмРНК
([293]) предоставляет регулярно обновляемый список тмРНК,
множественные выравнивания, вторичную и третичную структуру молекулы каждой
тмРНК. Кеннон [41] развил сравнительный веб-сайт РНК (CRW) —
базу данных сравнительной информации о последовательности и структуре
для рибосомной, интронной и других РНК. Сервер вторичной структуры
РНК Vienna ([119]) предлагает предсказание вторичной структуры РНК по
единственной последовательности, предсказание согласованной вторичной
структуры для набора выровненных последовательностей и проектирует
последовательности РНК, которые могут быть уложены в заданную
структуру.

Глава 11
ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ ИЗ
ТЕОРИИ ВЕРОЯТНОСТЕЙ
В последней главе «АБП» представлен краткий обзор некоторых
важных концепций теории вероятностей и аналитических результатов, в том
числе свойства часто используемых распределений вероятностей,
обсуждение понятий энтропии и взаимной энтропии, принципа наибольшего
правдоподобия и принципов рационального осуществления выборки и
оценки параметров. Глава заканчивается описанием общего алгоритма с
максимизацией математического ожидания (ММО), который лежит в
основе нескольких важных и, возможно, наиболее сложных алгоритмов,
рассмотренных в «АБП», таких как алгоритм оценки параметров профильной
СММ параллельно с построением множественного выравнивания
последовательностей, и алгоритм оценки параметров ковариационной модели
параллельно с построением множественного выравнивания
последовательностей РНК. Предлагаемые в этой главе задачи дополнительно иллюстрируют
главные математические концепции, используемые в анализе
биологических последовательностей.
11 Л. Оригинальные задачи
Задача 11.1. Вычислите среднее арифметическое и дисперсию
биномиального распределения.
Решение. Для случайной переменной X, биномиально распределённой с
параметрами р и N, так что Р(Х = к) — (%)рк(1 — p)N~k, к — О,1,..., N
и 0 < р < 1, формулы для среднего арифметического т и дисперсии Var X
могут быть выведены тремя различными способами.

11.1. Оригинальные задачи 393
1) По определению,
т = ЕХ = £> (^у (1 - р)""* = £ ^f^y^(l - р)""* =
JV
После замены индекса суммирования на I = к — 1 и использования
биномиального разложения мы имеем
m=pn Ё /i^-'i-'oi^^ " p)iv~1-'=piV(p+(1"p))iv_1=piV-
(ил)
Поскольку
VarX = EX2 - (EX)2 = EX2 - m2,
нам нужно лишь выражение для второго момента -ЕХ2. Мы вводим новые
индексы суммирования I = к — 1 и j = к — 2и выполняем следующие
действия (учтите, что 0! = 1):
N /, 1\ЛТ* N
= p*N(N-l)-£ ,,(^"21'yPH'-p)"-*-' +pN(p+(l-p))'"-1 ~
= p2N{N-l)(p + (l-p))N~2 + pN = p2N2-p2N + pN.
Таким образом, мы получаем
Var X = p27V2 - p2N + pN - p2N2 = Np(l - p). (11.2)

394 Глава 11
2) Случайную переменную X можно рассматривать как сумму N
независимых бернуллиевых переменных Yi,..., Yjy. Это представление может
быть использовано, чтобы вывести уравнения (11.1) и (11.2) довольно
легким способом. Каждая из переменных Yi, где г = 1,..., 7V, имеет
распределение вероятностей Р(1* = 1) = р, где Р(1* = 0) = 1 — р. Поэтому
Е15 = 1.р + 0-(1-р)=р,
VarYi = Elf - (EYi)2 = l2 -p + О2 • (1 -p) -p2 = p(l -p).
N
Для X = YL Yi мы имеем
г=1
m
г=1 / г=1
N \ N
VarX = Var ]Гу* = ]Г Var У* = iVp(l -p).
^г=1 / г=1
3) Наконец, мы покажем подход, в котором иллюстрировано
применение одного важного аналитического метода. Мы рассматриваем
биномиальное разложение для двух переменных р и q:
<P + 9)lr = Jb(I£)W-h <П-3>
fc=0
и дифференцируем обе части уравнения (11.3) по переменной р:
N
Nip + q)»-1 = S>(^y-V-*. (П.4)
Умножение обеих частей уравнения (11.4) на р даёт
N / \
Npfr+q)"-1 = I>mpVV-fc- (П-5)
fc=l ^ '
Тогда, если q = 1 — р, уравнение (11.5) принимает вид
fc=l ^ ' fe=0 ^ '
N-k
га.

11.1. Оригинальные задачи 395
Точно так же, дифференцируя биномиальное разложение в уравнении (11.3)
дважды по переменной р, мы имеем
N
N(N - 1)(р + q)N~2 = £ Цк - 1) (^)pfc-V"fe =
= Ek(k-i)fiV-v-* =
fc=i ^ '
=ivfiy-v-* -tk(Nk)pk~2qN~k=
k=i ^ ' fe=i ^ '
=£,k2(T)pk~2qN~k -tk(T)pk-2*N-k-
К—U К—U
Мы умножаем обе части последнего равенства на р2 и при условии q = 1 — р
получаем
N(N - 1)р2 = ЕХ2 - EX.
Поэтому
EX2 = N2p2 - Np2 + EX = N2p2 - Np2 + Np.
Наконец,
VarX = EX2-(EX)2 = N2p2-Np2+Np-N2p2 = Np-Np2 = Np(l-p).
□
Задача 11.2. Примите допущение о модели, в которой Pi(a) —
вероятность появления аминокислоты а в г-й позиции некоторой
последовательности длины /. Аминокислоты считаются независимыми. Какова
вероятность Р(х) какой-либо конкретной последовательности х = х\,..., х\1
Покажите, что среднее число логарифма вероятности — отрицательная
энтропия ^2P(x)logP(x), где сумма берётся по всем возможным
последовательностям х длины /.
Решение. При допущении о независимости аминокислот в различных
позициях последовательности вероятность последовательности х определяет-

396
Глава 11
ся из
i
Р(х) =P(xU...yXl) =Pl(x1)- ...-pi(xi) = Y[Pi(Xi)- (11-6)
г=1
Уравнение (11.6) описывает распределение вероятностей Р по всем
аминокислотным последовательностям длины I. Энтропия этого распределения
имеет вид
Я(Р) = -£>(х) log Р(х).
X
С другой стороны, среднее логарифма вероятности последовательности х
выражено в виде
E(logP(x)) = ^P(x)bgP(x) = -Н(Р).
□
Задача 11.3. Докажите эквивалентность количества информации и
относительной энтропии при равномерном распределении Q.
Решение. Относительная энтропия (или расстояние Куллбека-Лейблера)
двух дискретных распределений Р и Q, принимающих положительные
значения на одном и том же множестве {х}, определяется следующим
образом:
i Ч\хг)
Если распределение Q приписывает равные вероятности #i,..., xn, to
относительная энтропия принимает вид
H(P\\Q)= £ P{xi) log feL ]Г P(Xi) \ogP{Xi)- Y, P(xi) log(l/iV) =
г ' г i
= -H(P) - \og(l/N) = -H(P) - J2 l/Nlog(l/N) =
i
= -H(P) + H(Q).
Здесь Н(Р) и H(Q) — соответственно, энтропия распределения Р и Q.
Мы можем интерпретировать значение H(Q) = logiV как энтропию
определённого a priori распределения на х\,..., xn (априорное распределение,

11.1. Оригинальные задачи
397
предположительно, является равномерным), тогда как Н(Р) — энтропия
эмпирического распределения (с вероятностями исходов, наблюдаемыми в
эксперименте, определёнными как частоты исходов). Поэтому количество
информации I определяется в виде
I = Kbefore ~ Hafier = H(Q) ~ H(P) = H(P\\Q). n
Задача 11.4. Покажите, что M(X;Y) = M(Y;X).
Решение. Мы рассматриваем случайные переменные X и У, которые
принимают значения {х{} и {%}, соответственно, с вероятностями P(xi)
и P(yj). Случайный вектор (X, У) принимает значения (ж$, yj) с
вероятностями P(xi,yj). Взаимная информация M(X\Y) определяется следующей
формулой:
Эта формула является симметрической относительно X и Y; таким
образом, М{Х- Y) = M(Y\X). □
Задача 11.5. Покажите, что
M(X;Y) = Н(Х) + H(Y) - #(У,Х), (11.7)
где H(Y,X) — энтропия совместного распределения Р(Х, Y).
Решение. Определения взаимной информации и энтропии позволяют нам
вывести цепь равенств следующего вида:
= ^р(хиУэ)1°%р(х^Уэ) -^2p(xi^yj)^gP{xi)P(yj) =
= -H(Y;X) - £p(*,, i^togPfa) - Y,P(*i>Vi)b8P(Vi)-
ЬЗ M

398 ГЛАВА 11
Мы должны показать, что последние две суммы определяют энтропии
Н(Х) и H(Y). Действительно,
-^P{XiiVj)]QgP(xi) = -J2 I ^P(xijW)l0gP(Xi) j =
= -J2P(xi)logP(xi) = Н(Х),
г
-Х)Р(аи,»)Ь§Р(%) = -£ (£P(a*,%)logP(lfc)) =
= - £Р(%) bg P{Vi) = H{Y).
3
Таким образом, доказательство формулы (11.7) завершено. □
Задача 11.6. Слабый закон больших чисел гласит, что среднее
арифметическое выборки размера N отличается от истинного среднего на величину d
или более с вероятностью a2/(Nd?)9 где а2 — дисперсия этого
распределения. Покажите, что это означает, что rii/Y^nk стремится к P(wi) по мере
того, как ^ п/е —> оо, где щ — частота появления Wi.
Решение. Слабый закон больших чисел является следствием неравенства
Чебышева. Ниже мы докажем необходимые нам утверждения.
1) Если случайная переменная £ является неотрицательной почти
наверное, то при всех е > 0 верно следующее неравенство Чебышева:
Р« > е) < Щ. (11.8)
Мы отмечаем, что
где 1{ А} обозначает индикатор события А. Беря математические ожидания
обеих сторон уравнения (11.9), мы получаем неравенство Чебышева в виде
выражения (11.8). Точно так же для любого целого числа п,
Щп > Р(£ > е)еп.

11.1. Оригинальные задачи 399
2) Как следствие неравенства (11.8) мы можем утверждать, что для
случайной переменной £, положительного е и целого числа п следующие
неравенства верны:
Р{\Ц-Щ\>е)^Щ-£^\п_
Последнее неравенство в особенности широко известно при п = 2:
Var Р
Р(К-Е£|>е)< —j±. (11.10)
Теперь мы рассмотрим выборку х = (xi,... ,xn) из распределения
с математическим ожиданием Еж* = d и дисперсией Varxi = а2,
где г = 1,...,7V. Выборочная средняя ж = (l/N)Y2xi имеет мате-
г
матическое ожидание Еж = (l/N)^2"Exi = d и дисперсию Varж =
г
= (1/N2) ^2 Var#i = (a2/N). Для случайной переменной ж и положи-
i
тельного е неравенство Чебышева, уравнение (11.10), означает, что
P(\x-d\>e)^^.
Ne2
Если объём выборки N стремится к бесконечности и при этом дисперсия
а2 < +оо, то правая сторона неравенства Чебышева сходится к нулю и
Р(\х - d\ ^ е) -> 0.
Последнее утверждение эквивалентно определению схождения по
вероятности. Таким образом, когда N —» +оо,
х —> Еж = d.
Действительно, поскольку х\,..., хп независимы и а2 конечна,
выборочное среднее подчиняется усиленному закону больших чисел Колмогорова,
а именно
х —> Еж = d
почти неверное.
В частности, если элементарное событие w появилось п раз среди N
независимых повторений случайного эксперимента, то для ж*, где г =
= 1,..., N, определённого как индикатор появления события w в г-м экс-

400
Глава 11
перименте, мы имеем: х = (n/N), d = Fl(w) = P(w)9 а2 = P(w)(l —
— P(w)) < -f оо. Теперь из закона больших чисел следует, что для
элементарного события w
#-w
D
Задача 11.7. Пусть f(x) = 2(1 — х) — плотность в интервале [0,1].
Покажите, как она преобразуется к плотности на у при условии х = у2. Покажите,
что и максимум, и оценка апостериорного среднего (ОАС) плотности
смещаются при таком преобразовании.
Решение. Если случайная величина X характеризуется функцией
плотности вероятностей /, а случайная величина Y определена как X = У2, то
существует несколько методов определения функции плотности
вероятностей g величины Y. Здесь мы используем два основных метода.
1) Сначала мы используем определение интегральной функции
распределения (ИФР) и соотношение между ИФР и функцией плотности
вероятностей. ИФР величины X определяется из
х
F{x) = j f(r)dr =
о,
/(2-
0
/(2-
^ 0
- 2r)dr =
- 2r)dr =
= 2x-
= 1,
гЛ
x < 0,
0<x
x > 1.
O,
Тогда формула интегральной функции распределения G величины Y
выводится непосредственно из определения ИФР:
G(x) = P(Y < х) = Р(л/Х < х)
х < 0,
Р(Х < х2) = F(x2), z^0;
0, х < 0,
2х -я4, 0<ж<1,
{ 1, х>1.
Тогда функция плотности вероятностей g величины Y выражается в виде
4ж-4#3, 0 < х < 1,
вне интервала.
»(*)
■ffw-{?

11.1. Оригинальные задачи 401
2) Теперь мы используем правило преобразования: если X = <j>(Y), то
д(у) = Жу))\Ф'Ш-
В нашем случае ф(у) = у2 и
5(У) = 1(У2)2У = 2(1 - у2)2у = 4у- 4у3.
Так как случайная величина X принимает значения в интервале [0,1],
величина Y = X2 принимает значения также в интервале [0,1]. Следовательно,
д(у) = [4у-4у3> О^^1'
|^ 0, вне интервала.
Для того чтобы убедиться в том, что функция д является функцией
плотности вероятностей, мы проверяем условие нормализации:
+°° г ■ - ii
J g(x)dx = J(4x - 4x*)dx = (±f - *f)
= 2-1 = 1.
x=0
Функция плотности вероятностей f(x) имеет максимум в точке х = 0,
при этом тахх f(x) = /(0) = 2. Однако функция плотности вероятностей
д(х) достигает своего максимума в точке х = 1/л/З, причём тахх д(х) =
= д(1/у/3) = 8/3л/3. Преобразование от X к Y изменяет также
математическое ожидание:
/ xf(x)dx = / 2ж(1 — x)dx
-оо 0
+оо 1
ЕУ = / xg(x)dx = / х(Ах - Ax3)dx = j=.
D
Задача 11.8. Покажите, что функция
ах\ух~г
(аА 4- ухУ

402 Глава 11
является функцией плотности вероятностей в интервале 0 < у < оо.
Покажите, что равномерная выборка х из (0,1) и отображение х на у = а(ж/(1 —
— х))1/* равносильна выборке из д(у).
Решение. Функция д(у) является положительной при всех у > 0, и нам
необходимо проверить условие нормализации:
Ху =1.
i= ]яШу)= f ■£
А\2
(ах + ух)
— ии и
Действительно, использование новой переменной z = ах + ух, dz =
= \yx~1dy, где z принимает значения в интервале [аА, +оо), ведёт к
следующему равенству:
+ос
А
Оно означает, что функция д — функция плотности вероятностей.
Пусть X — равномерная случайная величина в интервале [0,1],
и Y = а(Х/(1 — Х)у/Х. Мы хотим доказать, что функция д является
функцией плотности вероятностей случайной величины У. ИФР случайной
величины X выражается в виде
F(x)
Тогда интегральная функция распределения G величины Y определяется
следующим образом:
= <
кх<&)-*Ш-'*"-

11.1. Оригинальные задачи
403
Значение ух/(ух + ах) принадлежит к интервалу [0,1] при всех
положительных у; поэтому мы видим, что
G(y) =
о,
ух + ах
У<0,
Наконец, функция плотности вероятностей случайной величины Y имеет
вид
ГО, у < 0,
G'(y)={ д^Ху^1 ^п
, л Лч2, У^О,
I (о:Л+ул)2
или С (у) = £(у). На этом доказательство завершено. □
Задача 11.9. Определите отображение ф переменных (ж, у) на (u,w)
посредством правил х = uw и у = (1 — гг)ги. Покажите, что J(0) = ги, где J —
якобиан.
Решение. Якобиан многовариантного отображения ф : у —► ж, где ж^ =
= Фг{у\1 • • • j 2/n) и г = 1,..., п, является определителем J(0) = |а#|
порядка п с элементами, определяемыми частными производными: а^ =
= дфг/dyj. Поэтому мы имеем
J =
дх/ди dx/dw
ду/ди dy/dw
w и
-w 1-й
= w(l — и) 4- uw = w.
П
Задача 11.10. Предположим, что мы выбираем две случайные переменные
Х\ и Хч в диапазоне [0,1] и отображаем (xi,x2) на выборочную точку
cos(27rxi)y/in(l7^|y. Докажите, что это равносильно точной выборке из
распределения Гаусса. Такой метод называют методом Бокса-Мюллера.
Решение. Метод Бокса-Мюллера ([29]) был разработан для генерации двух
независимых распределённых по стандартному Гауссову распределению

404 Глава И
случайных переменных из двух независимых равномерно
распределённых случайных переменных. Он работает следующим образом. Пусть Х\
и!2- независимые равномерно распределённые случайные переменные в
интервале [0,1]. Мы определяем переменные Yi и Y2 следующим образом:
yi = Vln(^cos(27rXl)'
F2=Vln(^sin(27rXl)'
Чтобы показать, что переменные Y\ и Y2 являются независимыми
стандартными Гауссовыми случайными переменными, мы начнём с отыскания ИФР
Fjt случайной переменной R = i/ln(l/(X2)2). Если х < 0, то Fr(x) =
= P(R < x) = 0. Если х неотрицательна, то
№)2 < х2
FR(x) = P(R ^x) = P(R2 < х2) = Р [ In / v 2
= Р ((Х2)2 > е-2) = Р (Х2 ^ е"*2/2) = 1 - FX2 (е-2/2) .
Здесь Fx2 — ИФР равномерного распределения в интервале [0,1].
Поскольку е~х /2 принадлежит к интервалу [0,1], ИФР Fr принимает вид
™-{1
F*(x) = < "' 2/2 X < °'
- е~х /2, х > 0.
Соответствующая функция плотности вероятностей имеет вид
bM-nw-f^:^
Для того чтобы вычислить функцию плотности совместного распределения
случайного вектора (Yi, Y2), мы должны определить отображение ф: Х\ =
= 0i (Yi, Y2), Д = 02 (Yi, Y2), которое, как это видно, выглядит следующим
образом:
1 Уо
Xi = -arctan-,
R=yjY2 + Y2.

11.1. Оригинальные задачи
Тогда якобиан отображения ф определяется как
2/2 Ух
405
АФ)
дф\ дфх
дух ду2
дф2 дф2
дух ду2
=
Ух 2/2
VVx + 2/2 л/2/i + 2/2
27Г^У12 + 2/2
Наконец, функция плотности совместного распределения вероятностей
случайного вектора (Yi, Уг) определяется многомерной версией формулы
преобразования:
#(2/1,2/2) = /х1{ф1{УиУ2))/н(ф2(УиУ2))\^Ф)\ =
е &* =
= 0l(2/l)02(2/2).
Здесь 0i и Q2 — функции плотности вероятностей стандартного
нормального распределения. Таким образом, мы установили, что переменные Y\ и Y^
суть независимые стандартные Гауссовы случайные переменные. □
Задача 11.11. Покажите, что формула
оо
f6(u + v- ^e'^iuw^^e^ivw^^wdw
D(u,v) =
r(ai)r(a2)
on
u<*i-iv<**-i5(u + v-l)
r(ai)r(o2)
/
e-V1^-1^ =
= исч-1ь*»-15(и + v - l)^+^> = V(u, v\ai,a2)
может быть расширена на случай К гамма-распределений, то есть что
выборка из g(x, cti, 1), где г = 1,..., К, с последующим усреднением
равносильна выборке из распределения Дирихле P(6i,..., вк|«1, • • •, «г).

406
Глава 11
Решение. Предположим, что мы выбираем значения х\,...,хк из К
гамма-распределений, соответственно, с параметрами а\,..., оск и
определяем К значений ui,...,uk как щ = XijYiiXi. Равносильно этому мы
можем принять Xi = фг{и\,..., uk-i, w) = щи), г = 1,..., К — 1, хк =
к-\
— Фк(^1, • • •, ик-\, гу) = (1 — Yl ui)wK интегрировать по переменной w.
г=1
Якобиан отображения ф : {и\
Щ) =
[txi,..
дфг
III
дфг
ди\
дфк
ди\
w
0
0
—w
• >ик.
Ill
дф2
ди2
дфг
ди2
дфк
ди2
0
w
0
—w -
-ь^) -
III
дф2
диз
дфг
диг
дфк
диг
0
0
w
-w • • •
-> (я?1,...,а
дфг 1
dw
дф2
dw
дфг
dw
дфк
dw |
Ui
и2
иг
к
1- Е иг
г=1
Чтобы вычислить якобиан 3(ф)9 мы добавляем к последней строке
определителя все остальные строки и получаем выражение J(<£) = юк~г.
Плотность совместного распределения D значений щ,..., ик принимает вид
D(ui,U2,...jUK) =
оо К /К \
/ *(£ tii - 1) ( П e'UiW(uiw)ai-1 wK~1dw
0 г=1 \г=1 /
П Г(оч)
г=1
\г=1 / г=1
П Г(оч)
г=1
оо
/
е "ги*

11.1. Оригинальные задачи 407
= 6
/к \ к Г ( Ё аг)
Vi=i ) i=i п г(а.)
г=1
Так как последнее выражение — плотность V{u\, и^,..., ик \ot\, ol<i,..., ак)
распределения Дирихле с параметрами а\,..., ак, задача решена. □
Задача 11.12. Докажите, что для функции плотности вероятностей д(х, а, 1)
гамма-распределения д(х, а, 1) = е~хха~1/Т(а)9 где х > 0, и функции
f (х\ = 4е-аал+ажл-1
Л } Г(а)(ал+ял)2
неравенство д(х, а, 1) ^ /(ж) остаётся верным при всех х > 0, а > 1
и 1 ^ А < \/2а — 1. Что произойдёт при А ^ \J2ol — 1?
Решение. Для того чтобы доказать, что д(х, а, 1) < /(ж) при всех
положительных ж и заданных значениях параметров а и Л, мы берем отношение
R(x) = f(x)/g(x) и удостоверяемся в том, что R{x) ^ 1 при всех
положительных х. Мы записываем R(x) в следующем виде:
R(x) = Щ= , 4 , 0ех-<*ах+ахх-<*.
\ 9(х) (ах+хх)2
Обратите внимание, что если Л — а > 0, то R{x) —► 0 при х —► 0. Таким
образом, условие А < а является необходимым для выполнения неравенства
R(x) ^ 1.
Чтобы изучить поведение функции R, мы рассматриваем
In R(x) = 1п4 - 21п(аЛ 4- хх) 4- (х - а) + (а 4- Л) In а 4- (Л - а) In ж.
Мы вычисляем производную функции In R(x) следующим образом:
dlnR(x) _ жЛ+1 4- {-а - Х)хх + ахх 4- (Л - а)ах
dx ~ х{ах+хх) '

408 Глава И
затем вводим новую переменную £, где х = at, и обозначаем
выражение (11.11) как Q(t)\ таким образом,
_ atX+1 + (-<* ~ л)*Л + at + (л ~ а)
Q{t) ~ atb+i+at *
Производная
dQ(t) (a + X)t2X + 2(a - X2)tx + (a - А)
dt at2(tx + l)2
(11.12)
является положительной при всех t > 0 тогда и только тогда, когда
числитель в выражении (11.12) положителен. Поэтому если 4(а — А2)2 — 4(а +
+ Л)(а — А) < 0 (что верно при условии Л < yj2a — 1), то dQ(t)/dt > 0.
Поскольку и Q(t) и t = х/а суть монотонно возрастающие функции (при
t > 0 и х > 0), их композиция d\nR{x)/dx также является монотонно
возрастающей функцией в интервале (0, +оо). Она растёт от больших
отрицательных значений (в окрестности х = 0) до 1 (когда х стремится к +оо) и
поэтому имеет только один корень х = а. Следовательно, и In R(x) и R(x)
имеют одну и ту же критическую точку, х = а, которая является общей
точкой минимума этих двух функций. Мы имеем
f(x)
R(x) = Ц-1 ^ min Д(ж) = R(a) = 1
д(х) х>о
и заключаем, что f(x) ^ д(х) при всех положительных х, а>1и1<Л<
>/2а - 1.
Если Л ^ \J2ol — 1, то dQ(t)/dt = 0 имеет либо одно либо два
положительных решения. Поэтому может существовать не один, но несколько
интервалов монотонности функции Q(t) и, следовательно, dinR(x)/dx = 0
может иметь более одного решения, a R(x) = f(x)/g(x) может иметь более
одной точки минимума. Например, если А = а = 1, то dlnR(x)/dx = (х —
— 1)/(х + 1) и R(x) имеет только одну точку минимума х = 1. Если А = 2
и а = 2,1, то
dlnRjx) _ а;3-4,1ж2 + 4,41ж-0,441
dx ~ х(х2 4-4,41)
и R(x) имеет три положительные критические точки: точку максимума
х\ = (2 + у/3,16)/2 и две точки минимума х<ь = (2 — \/3,16)/2 и д?з =
= 2,1. Поэтому доводы, рассмотренные выше для 1 < А < \J1ci — 1, не

11.1. Оригинальные задачи
409
могут быть применены в случае, если Л ^ у/2а — 1; существует множество
подслучаев, которые нужно рассматривать по отдельности. □
Задача 11.13. Случайный вектор (X, Y) характеризуется следующей
функцией плотности вероятностей:
f{x,y) = 0,5I[o,i]x[o,i](z,2/) + 0,5I[0,99,i,99]x[o,99,i,99](z,2/),
где 1а — индикатор множества А. При выборке Гиббса мы выбираем точки
из условных распределений P(X\Y), P(Y\X), P(X|F), P{Y\X),...
Каково ожидаемое число выборок в пределах одной области, которые можно
получить прежде, чем произойдёт переход в другую область?
Решение. Сначала мы найдём функции плотности вероятностей
переменных X и Y, а также функции плотности условных распределений f(x\y)
и f(y\x)- Пусть д{х) определяет ф. п. в. случайной переменной X:
9(х)= J f(x,y)dy =
—оо
+оо
= / (0?51[о,1]х[0,1](^?2/) + 0,51[о,99,1,99]х[0,99,1,99](^)2/))Ф =
/ш =
0, 51[0>1](ж) + 0, 51(0,99,1,99] (»)»
f(x,y) _ 1[0,1]х[0,1](Д?»У) + 110,99,1,99] х[0,99,1,99] (^ У)
9(х) 1[0,1] (х) + 1[0,99,1,99] 0*0
В силу симметрии функция плотности вероятностей переменной У
представлена функцией д{у) и плотность условного распределения имеет вид
f ( \ \ - ЛЖ>^) _ ^[О.ЦхрД]^»!/) + 110,99,1,99] X [0,99,1,99] (а?, У)
9{У) 1[0,1] (У) + 1[0,99,1,99] (У)
Мы определяем два сегмента — носителей плотности f(x,y) — как Si =
= [0,1] х [0,1] и 52 = [0,99,1,99] х [0,99,1,99]. Согласно [45], мы
генерируем «последовательность Гиббса» случайных переменных Yq,Xq,Y{,X[9

410 Глава 11
Y2, XI},... в соответствии со следующим правилом. Для начального
значения Yq = у'0 остальная часть последовательности получается итеративно —
путём генерирования значений из Xj с распределением f(x\Y-=yj)n
последующего генерирования Y- с распределением f(y\Xj = x'^). Теперь мы
определяем случайную последовательность Z = (Zi) следующим образом:
Зм+1 = 1, если 1? €[0,1],
Z2i+i=2, если У/ € [1,1,99],
Z2i = l, еслиХ^€ [0,1],
Z2i = 2, еслиХг'е [1,1,99].
Мы убеждаемся в том, что (Zi) — марковская цепь с двумя
состояниями {1,2}, и определяем её начальное распределение и вероятности
переходов. При любых г
P(Z2i+l = k2i+\\Z\ = fci, Z2 = к2, • • • , Z2i = &2г) =
= P(Y( € A(fc2i+1)|Y0' g А(Ы,*о € A(fc2),... ,X< e A(k2i)) =
= P(Y( e A(k2i+1)\x'i e A(k2i)) = P(Z2i+1 = k2i+1\z2i = k2i).
Здесь kj — или состояние 1, или состояние 2 при условии А(1) = [0,1]
и А(2) = [1,1,99]. Точно так же марковость сохраняется для всех
членов Z2i. Начальное распределение марковской цепи Z определяется как
1
Р1 = Р(гг = 1) = Р(У0' е [0,1]) = f g(y)dy =
1 о
Г(0,51[0,1]Ы 4-0,51[0,99,1,99]Ы)Ф = 0,5 4-0,5 х 0,01 = 0,505,
о
Р2 = P(Zl = 2) = P(Y£ e [1,1,99]) = 1 - pi = 0,495
1
/<
и вероятности переходов — как
Pii = Р(^2 = l\Zt = 1) = Р(Х0 € [0,1]|У0' € [0,1]) =
1 1 1
= JP(X'0 е [0,1]|У0' = уоМУо = j jf(x\y)dxdy
О 0 0

11.1. Оригинальные задачи 411
1 1
//
о о
1
■/
1[0,1]х[0,1](#> У) +1(0,99,1,99] х [0,99,1,99] (#, у) _
1[0,1](2/)+1[0,99,1,99]Ы
(1[0, 1](у) + 0, 01I[0|99|lf99] (y))dy =
I[0,l](2/)+![0,99,l,99](2/)
= 0,99 + ^0,01 = 0,99505,
Р12 = P{Z2 = 2|Zi = 1) = Р(Х'0 е [0,99,1,99]|1S € [0,1]) =
= 1 - pii = О,00495.
Пусть £ — число точек (X'j, Y'j) «последовательности Гиббса», таких что
(X'j,Y'j) € Si, прежде, чем первый переход к области S2/S1 происходит
(S2/S1 = S2 — ($2 П Si)). Чтобы найти распределение случайной
переменной £ со значениями 0,1,2,..., мы используем марковскую цепь Z:
Pit = *») =
= Р(ВД0,1],ВДо,1],... .ВД0,1],х;е[0, l], {Y^.1,X^l)eS2/S1) =
= P(Zi = 1, Z2 = 1, • . • , ^2n-l = 1> ^2n = 1) %2п+1 = 2) +
+ P(Zi = 1, Z2 = 1, . . . , ^2n-l = 1, ^2n = 1, ^2n+l = 1> ^2n+2 = 2) =
= PlPll_1Pl2 +P1P11P12 = PlPll_1Pl2(l + Pll).
Затем мы находим математическое ожидание величины £ следующим
образом:
+ 00 ► +00
Я£ = 5Z nPlPl?~Vl2(l + Pll) =PlPl2Pll(l +Pll) 5Zn(Pll)n_1 =
n=0 n=l
PiPi2Pn(l + Pii) pipn 0,505 • 0,99505
(1 - Pii)2 Pw(l + P11) 0,00495 • 1,99505
50,8835.
Ввиду симметрии ожидаемое число точек, выбранных в пределах
сегмента S2 прежде, чем произойдёт переход к сегменту Si, также равно
Е£ « 50,8835. Следовательно, в среднем пятьдесят одна выборочная точка
в ряде расположена в пределах одного из сегментов (Si или S2), перед тем
как первый переход в другой сегмент произойдёт. □

412
Глава 11
11.2. Дополнительная задача
Задача 11.14 представляет собой комбинаторное упражнение. Мы
хотим доказать вспомогательное утверждение, употреблённое в замечании 2
(задача 2.5), чтобы получить для последовательностей длины пит
число Ап,т попарных вьфавниваний, в которых пара ж-пропуск не следует за
парой у-пропуск и наоборот.
Задача 11.14. В ([246], раздел 1, упр. 6) было доказано, что число способов
поместить к неразличимых предметов в г ящиков равно биномиальному
коэффициенту (г+*-1)- Покажите, что при дополнительном ограничении,
согласно которому никакой ящик не должен оставаться пустым, это число
становится равным CjT_\)-
Решение. Пусть N(k,i) — число способов поместить к неразличимых
предметов в г ящиков при условии, что каждый ящик содержит по
крайней мере один предмет. Очевидно, что если к < г, то iV(fc, г) = 0.
При к ^ г мы докажем формулу N(k,i) = (%Z\) Щ>и помощи
математической индукции. Легко видеть, что N(m, 1) = 1 = (JJJlJ) и N(m, 2) =
= т — 1 = (™1з) ЯР11 всех т> где т ^ *• Д^1^» мы предполагаем, что
ЛГ(ш, г) = (™1*), где т ^ к, и проверяем выполнение равенства N(k, г +
+ 1)= (^Т*). Число N(k, г + 1) равно числу векторов х — (х\,... ,#i+i)
длины г + 1 с положительными целочисленными компонентами, таких что
#1 4- #2 Н 1- #г+1 = к (компонента х\ обозначает число предметов в 1-м
ящике, где I = 1,..., г + 1). Очевидно, что x^+i может принимать
целочисленные значения от 1 до к — (i — 1) = к — г + 1. Если xi+\ = 1, то сумма
первых г компонент вектора х должна быть равна к — 1; таким образом,
число возможных векторов х равно N(k — 1,г). Если x^+i = 2, то сумма
первых г компонент вектора х должна быть равна к — 2, а число
возможных векторов х — N(k — 2, г). Наконец, для максимально возможного числа
предметов х^\ = к — г + 1в(г + 1)-м ящике существует только один путь
N(i,i) = 1 выбора оставшихся компонент: х\ = 1,Х2 = 1,...,Жг = 1.
Следовательно, мы получили рекуррентную формулу
N(k, г + 1) = N(k - 1, г) + N(k - 2, г) + • • • + N(i + 1, г) + N(i, г). (11.13)
Далее, к каждому члену, кроме последнего на правой стороне
уравнения (11.13), мы применяем допущение об индукции. Используя свойство

11.3. Дополнительная литература 413
биномиальных коэффициентов (™) = (mJbl) — G™i)> мы получаем
= VVfc - 1 - г) ~ \к - 2 - г)) + \\к - 2 - i) ~ \к - 3 - i)) +
♦■■■♦(m-GHV)- <->
На правой стороне уравнения (11.14) суммы второго и третьего
биномиальных коэффициентов, четвертого и пятого и т. д., и двух последних, равны
нулю. Поэтому мы получаем равенство
которое равносильно искомому. Исходя из этого доказательство можно
считать завершённым. □
11.3. Дополнительная литература
Во введении в главу 1 уже было приведено несколько ссылок на
популярные учебники по теории вероятностей и математической статистике.
В дополнение к ним мы даём ссылки на учебники по теории информации:
[241], [13], [54], [224], [186] и [99].

Литература
[1] Almagor, H. (1983). A Markov analysis of DNA sequences. Journal of Theoretical
Biology 104, 633-645.
[2] Altschul, S. F. (1991). Amino acid substitution matrices from an information
theoretic perspective. Journal of Molecular Biology 219, 555-565.
[3] Altschul, S.F. and Gish,W. (1996). Local alignment statistics. Methods in
Enzymology 266, 460-480.
[4] Altschul, S. F. and Koonin, E. V. (1998). Iterated profile searches with PSI-BLAST
— a tool for discovery in protein databases. Trends in Biochemical Sciences 23,
444-447.
[5] Altschul, S. R, Carroll, R. J., and Lipman, D. J. (1989). Weights for data related by
a tree. Journal of Molecular Biology 207, 647-653.
[6] Altschul, S.F., Gish,W., Miller, W., Myers, E.W., and Lipman, D.J. (1990), Basic
local alignment search tool. Journal of Molecular Biology 215, 403-410.
[7] Altschul, S.F., Madden, T.L., Schaffer, A. A., Zhang, J., Zhang, Z., Miller, W., and
Lipman,D.J. (1997). Gapped BLAST and PSI-BLAST: A new generation of
protein database search programs. Nucleic Acids Research 25, 3389-3402.
[8] Altschul, S.F., Bundschuh, R., 01sen,R., and Hwa,T. (2001). The estimation
of statistical parameters for local alignment score distributions. Nucleic Acids
Research 29, 351-361.
[9] Arbogast,B.S., Edwards, S. V., Wakeley,J., Beerli,R, and Slowinski, J. B. (2002).
Estimating divergence times from molecular data on phylogenetic and population
genetic time scales. Annual Review of Ecology and Systematics 33, 707-740.
[10] Arnason,U., Gullberg,A., and Janke,A. (1998). Molecular timing of primate
divergences as estimated by two nonprimate calibration points. Journal of
Molecular Evolution 47, 718-727.
[11] Arratia, R. and Waterman, M. S. (1985). Critical phenomena in sequence matching.
The Annals of Probability 13, 1236-1249.
[12] Arratia, R., Gordon, L., and Waterman, M. (1986). An extreme value theory for
sequence matching. The Annals of Statistics 14, 971-993.
[13] Ash, R. B. (1990). Information Theory (New York: Dover Publications).
[14] Ayala,F.J., Rzhetsky,A., and Ayala,F.J. (1998). Origin of the metazoan phyla:
Molecular clocks confirm paleontological estimates. Proceedings of the National
Academy of Sciences of the USA 95, 606-611.

Литература
415
[15] Bailey,T.L. and Gribskov,M. (2002). Estimating and evaluating the statistics of
gapped local-alignment scores. Journal of Computational Biology 9, 575-593.
[16] Bairoch,A. and Apweiler,R. (1999). The SWISS-PROT protein sequence data
bank and its supplement TrEMBL in 1999. Nucleic Acids Research 27, 49-54.
[17] Bairoch, A., Bucher, P., and Hofmann, K. (1997). The PROSITE database, its status
in 1997. Nucleic Acids Research 25, 217-221.
[18] Baldi,P. and Brunak, S. (2001). Bioinformatics: The Machine Learning Approach,
2nd edn (Cambridge, MA: The MIT Press).
[19] Bateman, A., Birney,E., Cerruti,L. et al. (2002). The Pfam protein families
database. Nucleic Acids Research 30, 276-280.
[20] Baum, L. E. (1972). An equality and associated maximization technique in
statistical estimation for probabilistic functions of Markov processes. Inequalities
3, 1-8.
[21] Berman, A. and Plemmons, R. J. (1979). Nonnegative Matrices in the Mathematical
Sciences (New York: Academic Press).
[22] Billingsley, P. (1961a). Statistical Inference in Markov Processes (Chicago, IL: The
University of Chicago Press).
[23] Billingsley, P. (1961b). Statistical methods in Markov chains. The Annals of
Mathematical Statistics 32, 12-40.
[24] Borodovsky, M. and Mclninch, J. (1993). GeneMark: Parallel gene recognition for
both DNA strands. Computers & Chemistry 17, 123-133.
[25] Borodovsky, M. and Peresetsky, A. (1994). Deriving non-homogeneous DNA
Markov chain models by cluster analysis algorithm minimizing multiple alignment
entropy. Computers & Chemistry 18, 259-267.
[26] Borodovsky, M. Y., Sprizhitsky, Y. A., Golovanov, E. I., and Alexandrov, A. A.
(1986a). Statistical patterns in the primary structure of the functional regions of
the Escherichia coli genome. I. Frequency characteristics. Molecularnaya Biologia
20, 826-833 (English translation).
[27] Borodovsky, M. Y, Sprizhitsky, Y A., Golovanov, E. I., and Alexandrov, A. A.
(1986b). Statistical patterns in the primary structure of the functional regions of the
Escherichia coli genome. II. Nonuniform Markov models. Molecularnaya Biologia
20, 833-840 (English translation).
[28] Borodovsky, M. Y, Sprizhitsky, Y A., Golovanov, E. I., and Alexandrov, A. A.
(1986c). Statistical patterns in the primary structure of the functional regions
of the Escherichia coli genome. III. Computer recognition of coding regions.
Molecularnaya Biologia 20, 1144-1150 (English translation).
[29] Box, G. E. P. and Muller, M. E. (1958). A note on the generation of random normal
deviates. The Annals of Mathematical Statistics 29, 610-611.
[30] Braun,J.V. and Muller, H-G. (1998). Statistical methods for DNA sequence
segmentation. Statistical Science 13, 142-162.

416
Литература
[31] Brenner, S. E., Chothia,C. and Hubbard, Т. J. P. (1998). Assessing sequence
comparison methods with reliable structurally identified distant evolutionary
relationships. Proceedings of the National Academy of Sciences of the USA 95,
6073-6078.
[32] Brocchieri, L. and Karlin,S. (1998). A symmetric-iterated multiple alignment of
protein sequences. Journal of Molecular Biology 276, 249-264.
[33] Bromham, L. and Penny, D. (2003). The modern molecular clock. Nature Reviews
Genetics 4, 216-224.
[34] Brown, J. R., Douady,C.J., Italia, M. J., Marshall, W. E., and Stanhope, M. J.
(2001). Universal trees based on large combined protein sequence data sets. Nature
Genetics 28, 281-285.
[35] Brown, J. W. (1999a). The ribonuclease P database. Nucleic Acids Research 27,
314.
[36] Brown, T. A. (1999b). Genomes (New York: John Wiley & Sons, Inc.).
[37] Brudno,M., Do, С. В., Cooper, G.M. et al. (2003). LAGAN and Multi-LAGAN:
Efficient tools for large-scale multiple alignment of genomic DNA. Genome
Research 13, 721-731.
[38] Bruno, W. J., Socci,N.D., and Halpern,A.L. (2000). Weighted neighbor joining:
A likelihood-based approach to distance-based phylogeny reconstruction.
Molecular Biology and Evolution 17, 189-197.
[39] Burge,C. and Karlin, S. (1997). Prediction of complete gene structures in human
genomic DNA. Journal of Molecular Biology 268, 78-94.
[40] Bystro£f,C, Thorsson,V, and Baker, D. (2000). HMMSTR: A hidden Markov
model for local sequence-structure correlations in proteins. Journal of Molecular
Biology 301, 173-190.
[41] Cannone, J. J., Subramanian, S., Schnare,M.N. et al. (2002). The comparative
RNA web (CRW) site: An online database of comparative sequence and structure
information for ribosomal, intron, and other RNAs. BMC Bioinformatics 3, 2-33.
[42] CarrillOjH. and Lipman,D. (1988). The multiple sequence alignment problem in
biology. SIAM Journal of Applied Mathematics 48, 1073-1082.
[43] Carroll,! and Long,D. (1989). Theory of Finite Automata: With an Introduction
to Formal Languages (Englewood Cliffs, N.J.: Prentice Hall).
[44] Casella, G. and Berger, R. L. (2001). Statistical Inference, 2nd edn (Pacific Grove,
С A: Duxbury Press).
[45] Casella,G. and George,E.I. (1992). Explaining the Gibbs sampler. The American
Statistician 46, 167-174.
[46] Cavender, J. A. and Felsenstein, J. (1987). Invariants of phylogenies in a simple
case with discrete states. Journal of Classification 4, 57-71.
[47] Cayley, A. (1889). A theorem on trees. Quarterly Journal of Mathematics 23, 376-
378.

Литература
417
[48] Chenna,R., Sugawara,H., Koike, Т. et al. (2003). Multiple sequence alignment
with the Clustal series of programs. Nucleic Acids Research 31, 3497-3500.
[49] Churchill, G. A. (1989). Stochastic models for heterogeneous DNA sequences.
Bulletin of Mathematical Biology 51, 79-94.
[50] Clamp, M., Andrews, D., Barker, D. et al (2003). Ensembl 2002: Accommodating
comparative genomics. Nucleic Acids Research 31, 38-42.
[51] Clark, A. G., Glanowski, S., Nielson,R. et al. (2003). Inferring nonneutral
evolution from human-chimp-mouse orthologous gene trios. Science 302, 1960-
1963.
[52] Cocke, J. and Schwartz, J. T. (1970). Programming Languages and their
Compilers: Preliminary Notes. Technical report, Courant Institute of Mathematical
Sciences, New York University.
[53] Coin,L. and Durbin,R. (2004). Improved techniques for the identification of
pseudogenes. Bioinformatics 20 (suppl. 1), i94-il00.
[54] Cover, Т. М. and Thomas, J. A. (1991). Elements of Information Theory (New York:
Wiley).
[55] Cowan, R. (1991). Expected frequencies of DNA patterns using Whittle's formula.
Journal of Applied Probability 28, 886-892.
[56] Cox, D. R. and Hinkley, D. V. (1974). Theoretical Statistics (London: Chapman and
Hall).
[57] Dayhoff, M. O., Schwartz, R. M., and Orcutt, В. С (1978). A model of evolutionary
change in proteins. In Dayhoff, M. O., ed., Atlas of Protein Sequence and
Structure, vol. 5, supplement 3 (Washington, D.C.: National Biomedical Research
Foundation), pp. 345-352.
[58] Delcher,A.L., Kasif,S., Fleischmann,R.D., Peterson,!, White,O., and
Salzberg, S.L. (1999). Alignment of whole genomes. Nucleic Acids Research 27,
2369-2376.
[59] Dembo, A., Karlin,S., and Zeitouni,0. (1994a). Critical phenomena for sequence
matching with scoring. The Annals of Probability 22, 1993-2021.
[60] Dembo, A., Karlin, S., and Zeitouni, O. (1994b). Limit distribution of maximal
non-aligned two-sequence segmental score. The Annals of Probability 22, 2022-
2039.
[61] Dempster, A. R, Laird, N.M., and Rubin, D.B. (1977). Maximum likelihood from
incomplete data via the EM Algorithm. Journal of the Royal Statistical Society 39,
1-38.
[62] Deonier,R., Tavare,S., and Waterman, M. (2005). Computational Genome
Analysis: An Introduction (New York: Springer-Verlag).
[63] Ding,Y. and Lawrence, С. Е. (2003). A statistical sampling algorithm for RNA
secondary structure prediction. Nucleic Acids Research 31, 7280-7301.

418
Литература
[64] Do, С. В., Mahabhashyam, M. S. P., Bmdno,M., and Batzoglou,S. (2005).
ProbCons: Probabilistic consistency-based multiple sequence alignment. Genome
Research 15, 330-340.
[65] Douady,C.J., Delsuc,R, Boucher, Y., Doolittle, W. F, and Douzery, E. J. P. (2003).
Comparison of Bayesian and maximum likelihood bootstrap measures of
phylogenetic reliability. Molecular Biology and Evolution 20, 248-254.
[66] Dowell,R.D. and Eddy,S.R. (2004). Evaluation of several lightweight
stochastic context-free grammars for RNA secondary structure prediction. BMC
Bioinformatics 5, 71-85.
[67] Durbin,R., Eddy,S., Krogh,A., and Mitchison, G. (1998). Biological Sequence
Analysis: Probabilistic Models of Proteins and Nucleic Acids (Cambridge:
Cambridge University Press).
[68] Eddy, S. R. (1998). Profile hidden Markov models. Bioinformatics 14, 755-763.
[69] Eddy,S.R. (2002). A memory-efficient dynamic programming algorithm for
optimal alignment of a sequence to an RNA secondary structure. BMC
Bioinformatics 3, 18-34.
[70] Eddy, S. R., Mitchison, G., and Durbin, R. (1995). Maximum discrimination hidden
Markov models of sequence consensus. Journal of Computational Biology 2, 9-23.
[71] Edwards, A. W. F. (1970). Estimation of the branch points of a branching diffusion
process. Journal of the Royal Statistical Society В 32, 155-174.
[72] Ekisheva,S. and Borodovsky, M. (2006). Probabilistic models for biological
sequences: Selection and maximum likelihood estimation. International Journal
of Bioinformatics Research and Applications 2, 305-324.
[73] Enright,A.J., Iliopoulos, I., Kyrpides,N.C, and Ouzounis, С A. (1999). Protein
interaction maps for complete genomes based on gene fusion events. Nature 402,
86-90.
[74] Erdos,P. and Revesz,P. (1975). On the length of the longest head-run; Topics in
Information Theory. Colloqia Math. Soc. J. Bolyai 16, 219-228.
[75] Evans, S. N. and Speed, T. P. (1993). Invariants of some probability models used in
phylogenetic inference. The Annals of Statistics 21, 355-377.
[76] Ewens,W.J. and Grant, G.R. (2001). Statistical Methods in Bioinformatics: An
Introduction (New York: Springer-Verlag).
[77] Feller, W. (1971). An Introduction to Probability Theory and its Applications, 2nd
edn, Vols I, П (New York: John Wiley & Sons).
[78] Felsenstein, J. (1981). Evolutionary trees from DNA sequences: A maximum
likelihood approach. Journal of Molecular Evolution 17, 368-376.
[79] Felsenstein, J. (2004). Inferring Phylogenies (Sunderland, MA: Sinauer Associates,
Inc.).

Литература
419
[80] Feng,D-F. and Doolittle, R. F. (1987). Progressive sequence alignment as a
prerequisite to correct phylogenetic trees. Journal of Molecular Evolution 25, 351-
360.
[81] Feng,D-F. and Doolittle, R. F. (1996). Progressive alignment of amino acid
sequences and construction of phylogenetic trees from them. Methods in
Enzymology 266, 368-382.
[82] Feng, D-F., Cho, G., and Doolittle, R. F. (1997). Determining divergence times with
a protein clock: Update and reevaluation. Proceedings of the National Academy of
Sciences of the USA 94, 13 028-13 033.
[83] Fitch, W.M. (1971). Toward defining the course of evolution: Minimum change
for specific tree topology. Systematic Zoology 20, 406-416.
[84] Fitch, W.M. (1983). Calculating the expected frequencies of potential secondary
structure in nucleic acids as a function of stem length, loop size, base composition
and nearest-neighbor frequencies. Nucleic Acids Research 11, 4655-4663.
[85] Fitch, W. M. and Margoliash, E. (1967). Construction of phylogenetic trees. Science
155, 279-284.
[86] Fitz-Gibbon, S. T. and House, С. Н. (1999). Whole genome-based phylogenetic
analysis of free-living microorganisms. Nucleic Acids Research 27, 4218-4222.
[87] Florea, L., Hartzell, G., Zhang, Z., Rubin, G. M., and Miller, W. (1998). A computer
program for aligning a cDNA sequence with a genomic DNA sequence. Genome
Research 8, 967-974.
[88] Freedman,D. (1983). Markov Chains (New York: Springer-Verlag).
[89] Frith, M. C, Hansen, U., and Weng,Z. (2001). Detection of cw-element clusters in
higher eukaryotic DNA. Bioinformatics 17, 878-889.
[90] Gabow,H. W. (1973). Implementations of algorithms for maximum matching on
nonbipartite graphs. Ph.D. Dissertation, Department of Computer Science, Stanford
University.
[91] Gascuel, O. (1997). BIONJ: An improved version of the NJ algorithm based on a
simple model of Sequence data. Molecular Biology and Evolution 14, 685-695.
[92] Gatlin,L.L. (1972). Information Theory and the Living System (New York:
Columbia University Press).
[93] George, D. G., Barker, W C, and Hunt, L. T. (1990). Mutation data matrices and its
uses. Methods in Enzymology 183, 333-353.
[94] Gerstein,M., Sonnhammer, E. L. L., and Chothia,C. (1994). Volume changes in
protein evolution. Journal of Molecular Biology 236, 1067-1078.
[95] Glazko,G.V. and Nei,M. (2003). Estimation of divergence times for major
lineages of primate species. Journal of Molecular Evolution 20, 424-434.
[96] Goldman, N. and Yang,Z. (1994). A codon-based model of nucleotide substitution
for protein-coding DNA sequences. Molecular Biology and Evolution 11, 725-736.

420
Литература
[97] Goldman, N., Thome, J. L., and Jones, D.T. (1996). Using evolutionary trees in
protein secondary structure prediction and other comparative sequence analyses.
Journal of Molecular Biology 263, 196-208.
[98] Goldman, N., Anderson, J. P., and Rodrigo, A. G. (2000). Likelihood-based tests of
topologies in phylogenetics. Systematic Biology 49, 652-670.
[99] Goldman, S. (2005). Information Theory (New York: Dover Publications).
[100] Goodman, L. A. (1959). On some statistical tests for M-th order Markov chains.
The Annals of Mathematical Statistics 30, 154-164.
[101] Gopalakrishnan, G. (2006). Computational Engineering: Applied Automata Theory
and Logic (New York: Springer).
[102] Gorodkin, J., Stricklin, S. L., and Stormo, G. D. (2001). Discovering common stem-
loop motifs in unaligned RNA sequences. Nucleic Acids Research 29, 2135-2144.
[103] Gough,J., Karplus,K., Hughey,R., and Chothia,C. (2001). Assignment of
homology: to genome sequences using a library of hidden Markov models that
represent all proteins of known structure. Journal of Molecular Biology 313, 903-
919.
[104] Griffiths-Jones, S., Bateman, A., Marshall, M., Khanna, A., and Eddy, S. R. (2003).
Rfam: An RNA family database. Nucleic Acids Research 31, 439-441.
[105] Grishin, N. V. (1995). Estimation of the number of amino acid substitutions per site
when the substitution rate varies among sites. Journal of Molecular Evolution 41,
675-679.
[106] Grishin, N. V. (1999). A novel approach to phylogeny reconstruction from protein
sequences. Journal of Molecular Evolution 48, 264-273.
[107] Grishin, N. V., Wolf, Y I., and Koonin,E.V. (2000). From complete genomes to
measures of substitution rate variability within and between proteins. Genome
Research 10, 991-1000.
[108] Grishin, V. N. and Grishin, N. V. (2002). Euclidian space and grouping of biological
objects. Bioinformatics 18, 1523-1533.
[109] Grossman, S. and Yakir,B. (2004). Large deviations for global maxima of
independent superadditive processes with negative drift and an application to
optimal sequence alignments. Bernoulli 10, 829-845.
[110] Gubser,C, Hue,S., Kellam,R, and Smith, G.L. (2004). Poxvirus genomes:
A phylogenetic analysis. Journal of General Virology 85, 105-117.
[Ill] Guindon,S. and Gascuel,0. (2003). A simple, fast, and accurate algorithm to
estimate large phylogenies by maximum likelihood. Systematic Biology 52, 696-
704.
[112] Hein,J. (1989). A new method that simultaneously aligns and reconstructs
ancestral sequences for any number of homologous sequences, when the phylogeny
is given. Molecular Biology and Evolution 6, 649-668.

Литература
421
[113] HeinJ., Wiuf,C, Knudsen,B., M0ller,M.B., and Wibling,G. (2000). Statistical
alignment: Computational properties, homology testing and goodness-of-fit.
Journal of Molecular Biology 302, 265-279.
[114] Hendy,M.D., Penny, D., and Steel, M. A. (1994). A discrete Fourier analysis for
evolutionary trees. Proceedings of the National Academy of Sciences of the USA
91, 3339-3343.
[115] Henikoff, J. G. and Henikoff, S. (1996). Using substitution probabilities to improve
position-specific scoring matrices. Computer Applications in the Biosciences 12,
135-143.
[116] Henikoff, S. and Henikoff, J. G. (1992). Amino acid substitution matrices from
protein blocks. Proceedings of the National Academy of Sciences of the USA 89,
10915-10 919.
[117] Henikoff, S. and Henikoff, J. G. (1994). Position-based sequence weights. Journal
of Molecular Biology 243, 574-578.
[118] Hirschberg, D. S. (1975). A linear space algorithm for computing maximal common
subsequences. Communications of the ACM 18, 341-343.
[119] Hofacker, I. L. (2003). Vienna RNA secondary structure server. Nucleic Acids
Research 31, 3429-3431.
[120] Hogg,R.V. and Craig, A. T. (1994). Introduction to Mathematical Statistics, 5th
edn (Upper Saddle River, N.J.: Prentice Hall).
[121] Hogg,R. V. and Tanis,E. A. (2005). Probability and Statistical Inference, 7th edn
(Upper Saddle River, N.J.: Prentice Hall).
[122] Holder,M. and Lewis,P.O. (2003). Phylogeny estimation: Traditional and
Bayesian approaches. Nature Reviews Genetics 4, 275-284.
[123] Holmes, I. and Bruno, W. (2001). Evolutionary HMMs: A Bayesian approach to
multiple alignment. Bioinformatics 17, 803-820.
[124] Holmes,I. and Rubin,G.M. (2002). Pairwise RNA structure comparison with
stochastic context-free grammars. Pacific Symposium on Biocomputing 2002
(Singapore: World Scientific), pp. 163-174.
[125] Hourai,Y., Akutsu,T., and Akiyama,Y. (2004). Optimizing substitution matrices
by separating score distributions. Bioinformatics 20, 863-873.
[126] Hubbard, Т., Barker, D., Birney, E. et al, (2002). Ensembl genome database project.
Nucleic Acids Research 30, 38-41.
[127] Hulo,N., Sigrist,C.J.A., Le Saux,V. et al. (2004). Recent improvements to the
PROSITE database. Nucleic Acids Research 32 (Database issue), D134-D137.
[128] Huynen,M. A. and Bork,P. (1998). Measuring genome evolution. Proceedings of
the National Academy of Sciences of the USA 95, 5849-5856.
[129] Iglehart, D. L. (1972). Extreme values in the GI/G/1 queue. Annals of Mathematical
Statistics 43, 627-635.

422
Литература
[130] Ito,M. (2004). Algebraic Theory of Automata & Languages (Singapore: World
Scientific).
[131] Jones, D. Т., Taylor, W.R., and Thornton, J. M. (1992). The rapid generation
of mutation data matrices from protein sequences. Computer Applications in
Biosciences 8, 275-282.
[132] Jones, N. С and Pevzner,P.A. (2004). An Introduction to Bioinformatics
Algorithms (Cambridge, MA: The MIT Press).
[133] Juan, V. and Wilson, C. (1999). RNA secondary structure prediction based on free
energy and phylogenetic analysis. Journal of Molecular Biology 289, 935-947.
[134] Jukes, T. H. and Cantor, C. (1969). Evolution of protein molecules. In Munro, H. N.
and Allison, J. В., eds, Mammalian Protein Metabolism (New York: Academic
Press), pp. 21-132.
[135] Kanehisa,M., Goto,S., Kawashima, S., and Nakaya,A. (2002). The KEGG
databases at GenomeNet. Nucleic Acids Research 30, 42-46.
[136] Kann,M., Qian,B., and Goldstein, R. A. (2000). Optimization of a new score
function for the detection of remote homologs. Proteins: Structure, Function, and
Genetics 41, 498-503.
[137] Karlin, S. (2005). Statistical signals in bioinformatics. Proceedings of the National
Academy of Sciences of the USA 102, 13 355-13 362.
[138] Karlin, S. and Altschul, S. F. (1990). Methods for assessing the statistical
significance of molecular sequence features by using general scoring schemes.
Proceedings of the National Academy of Sciences of the USA 87, 2264-2268.
[139] Karlin, S. and Altschul, S.F. (1993). Applications and statistics for multiple high-
scoring segments in molecular sequences. Proceedings of the National Academy of
Sciences of the USA 90, 5873-5877.
[140] Karlin, S. and Brendel, V. (1992). Chance and statistical significance in protein and
DNA sequence analysis. Science 257, 39-49.
[141] Karlin, S. and Dembo,A. (1992). Limit distributions of maximal segmental score
among Markov-dependent partial sums. Advances in Applied Probability 24, 113-
140.
[142] Karlin, S. and Ghandour, G. (1985). Comparative statistics for DNA and protein
sequences: Single sequence analysis. Proceedings of the National Academy of
Sciences of the USA 82, 5800-5804.
[143] Karlin, S. and Macken,C. (1991). Assessment of inhomogeneities in an E. Coli
physical map. Nucleic Acids Research 19, 4241-4246.
[144] Karlin, S. and Ost, F. (1987). Counts of long aligned word matches among random
letter sequences. Advances in Applied Probability 19, 293-351.
[145] Karlin, S. and Ost,F. (1988). Maximal length of common words among random
letter sequences. The Annals of Probability 16, 535-563.

Литература
423
[146] Karlin,S., Dembo,A., and Kawabata,T. (1990). Statistical composition of high-
scoring segments from molecular sequences. The Annals of Statistics 18, 571-581.
[147] Karlin,S., Burge,C, and Campbell, A. M. (1992). Statistical analyses of counts
and distributions of restriction sites in DNA sequences. Nucleic Acids Research
20, 1363-1370.
[148] Karplus,K., Barrett, C, and Hughey,R. (1998). ffidden Markov models for
detecting remote protein homologies. Bioinformatics 14, 846-856.
[149] Kasami,T. (1965). An efficient recognition and syntax algorithm for context-
free algorithms. Technical Report AFCRL-65-758, Air Force Cambridge Research
Laboratory Bedford, MA.
[150] Kelley, L. A., MacCallum, R. M., and Steinberg, M. J. E. (2000). Enhanced genome
annotation using structural profiles in the program 3D-PSSM. Journal of Molecular
Biology 299, 499-520.
[151] Kent, W. J. (2002). BLAT - the BLAST-like alignment tool. Genome Research 12,
656-664.
[152] Khoussainov, B. and Nerode,A. (2001). Automata Theory and its Applications
(Boston, MA: Birkhauser).
[153] Kimura,M. (1980). A simple method for estimating evolutionary rates of base
substitutions through comparative studies of nucleotide sequences. Journal of
Molecular Evolution 16, 111-120.
[154] Kimura,M. (1983). The Neutral Theory of Molecular Evolution (Cambridge:
Cambridge University Press).
[155] Kishino,H. and Hasegawa,M. (1989). Evaluation of the maximum likelihood
estimate of the evolutionary tree topologies from DNA sequence data, and the
branching order in Hominoidea. Journal of Molecular Evolution 29, 170-179.
[156] Kleffe,J. and Borodovsky, M. (1992). First and second moment of counts of
words in random texts generated by Markov chains. Computer Applications in
Biosciences 8, 433-441.
[157] Knudsen,B. (2003). Optimal multiple parsimony alignment with affine gap cost
using a phylogenetic tree. In Benson, G. and Page,R., eds, Proceedings of
Algorithms in Bioinformatics, Third International Workshop, Lecture Notes in
Computer Science 2812 (Berlin: Springer), pp. 433-446.
[158] Knudsen,B. and Hein,J. (1999). RNA secondary structure prediction using
stochastic context-free grammars and evolutionary history. Bioinformatics 15, 446-
454.
[159] Knudsen,B. and Hein, J. (2003). Pfold: RNA secondary structure prediction using
stochastic context-free grammars. Nucleic Acids Research 31, 3423-3428.
[160] Knudsen,B. and Miyamoto, M. M. (2003). Sequence alignment and pair hidden
Markov models using evolutionary history. Journal of Molecular Biology 333,
453-460.

424
Литература
[161] Koonin,E.V. and Galperin, M. Y. (2003). Sequence-Evolution-Function:
Computational Approaches in Comparative Genomics (Norwell, MA: Kluwer
Academic Publishers).
[162] Korber, В., Muldoon, M., Theiler, J. et al (2000). Timing the ancestor of the HIV-1
pandemic strains. Science 288, 1789-1796.
[163] Kozen,D. С (1999). Automata and Computability (New York: Springer).
[164] Krogh, A., Larsson,B., Heijne,G. von, and Sonnhammer, E. L. L. (2001).
Predicting transmembrane protein topology with a hidden Markov model:
Application to complete genomes. Journal of Molecular Biology 305, 567-580.
[165] Krogh, A., Mian, I. S., and Haussler, D. (1994). A hidden Markov model that finds
genes in E. coli DNA. Nucleic Acids Research 22, 4768-4778.
[166] Krogh, A. and Mitchison,G. (1995). Maximum entropy weighting of aligned
sequences of proteins or DNA. In Rawlings, C, Clark, D., Airman, R., Hunter, L.,
Lengauer, Т., and Wodak, S., eds Proceedings of the Third International Conference
on Intelligent Systems for Molecular Biology (Menlo Park, CA: AAAI Press), pp.
215-221.
[167] Kullback,S., Kupperman, M., and Ku,H.H. (1962). Tests for contingency tables
and Markov chains. Technometrics 4, 573-608.
[168] Kumar, S. and Hedges, S.B. (1998). A molecular timescale for vertebrate
evolution. Nature 392, 917-920.
[169] Kumar, S., Tamura,K., and Nei,M. (1993). Manual for MEGA: Molecular
Evolutionary Genetics Analysis Software (Philadelphia, PA: Pennsylvania State
University).
[170] Kumar, S., Tamura,K., and Nei,M. (2004). MEGA3: Integrated software for
Molecular Evolutionary Genetics Analysis and sequence alignment. Briefings in
Bioinformatics 5, 150-163.
[171] Lake, J. A. (1987). A rate-independent technique for analysis of nucleic acid
sequences: Evolutionary parsimony. Molecular Biology and Evolution 4, 167-191.
[172] Larget,B. and Simon, D.L. (1999). Markov chain Monte Carlo algorithms for the
Bayesian analysis of phylogenetic trees. Molecular Biology and Evolution 16, 750-
759.
[173] Lari,K. and Young,S.J. (1990). The estimation of stochastic context-free
grammars using the inside-outside algorithm. Computer Speech and Language 4,
35-56.
[174] Laquer,H.T. (1981). Asymptotic limits for a two-dimensional recursion. Studies
in Applied Mathematics 64, 271-277.
[175] Larson, H.J. (1982). Introduction to Probability Theory and Statistical Inference,
3rd edn (New York: Wiley).

Литература
425
[176] Lawrence, С. Е., Altschul, S. F., Boguski, M. S., LiuJ.S., Neuwald,A.E, and
Wootton,J.C. (1993). Detecting subtle sequence signals: A Gibbs sampling
strategy for multiple alignment. Science 262, 208-214.
[177] Lewis,P.O. (2001). Phylogenetic systematics turns over a new leaf. Trends in
Ecology and Evolution 16, 30-37.
[178] Li,M., Badger, J. H., Chen,X., Kwong,S., Kearney, P., and Zhang, H. (2001). An
information-based sequence distance and its application to whole mitochondrial
genome phylogeny. Bioinformatics 17, 149-154.
[179] Lipman,D.J., Wilbur, W. J., Smith, T.F., and Waterman, M. S. (1984). On the
statistical significance of nucleic acid similarities. Nucleic Acids Research 12, 215-
226.
[180] Liu, J. S. (2001). Monte Carlo Strategies in Scientific Computing (New York:
Springer-Verlag).
[181] Liu, J. S. and Lawrence, С E. (1999). Bayesian inference on biopolymer models.
Bioinformatics 15, 38-52.
[182] Liu, J. S., Neuwald,A.R, and Lawrence, С E. (1999). Markovian structures in
biological sequence alignments. Journal of American Statistical Association 94,
1-15.
[183] L6ytynoja,A. and Milinkovitch, С (2003). A hidden Markov model for
progressive multiple alignment. Bioinformatics 19, 1505-1513.
[184] Lukashin, A. V. and Borodovsky, M. (1998). GeneMark.hmm: New solutions for
gene finding. Nucleic Acids Research 26, 1107-1115.
[185] Lyngs0,R.B., Pedersen,C.N.S., and Nielsen, H. (1999). Metrics and similarity
measures for hidden Markov models. Proceedings of International Conference in
Intelligent Systems for Molecular Biology (Menlo Park, CA: AAAI Press), pp.
178-186.
[186] MacKay, D. J. C. (2003). Information Theory, Inference, and Learning Algorithms
(Cambridge: Cambridge University Press).
[187] Maidak,B.L., Cole, J. R., Lilburn,T.G. et al. (2000). The RDP (Ribosomal
Database Project) continues. Nucleic Acids Research 28, 173-174.
[188] Marti-Renom,M.A., Stuart, A. C, Fiser,A., Sanchez, R., Melo,F., and Sali,A.
(2000). Comparative protein structure modeling of genes and genomes. Annual
Review of Biophysics and Biomolecular Structure 29, 291-325.
[189] Mathews, D.H., Sabina,J., Zuker,M., and Turner, D.H. (1999). Expanding
sequence dependence of thermodynamic parameters improves prediction of RNA
secondary structure. Journal of Molecular Biology 288, 911-940.
[190] Mathews, D. H., Disney, M.D., Childs,J.L., Schroeder, S. J., Zuker,M., and
Turner,D.H. (2004). Incorporating chemical modification constraints into a
dynamic programming algorithm for prediction of RNA secondary structure.
Proceedings of the National Academy of Sciences of the USA 101, 7287-7292.

426
Литература
[191] Май, В., Newton, M. A., and Larget,B. (1999). Bayesian phylogenetic inference
via Markov chain Monte Carlo methods. Biometrics 55, 1-12.
[192] Meyer,CD. (2000). Matrix Analysis and Applied Linear Algebra (Philadelphia,
PA: Society for Industrial and Applied Mathematics).
[193] Meyer, I. M. and Durbin,R. (2002). Comparative ab initio prediction of gene
structure using pair HMM. Bioinformatics 18, 1309-1318.
[194] Meyer, I. M. and Durbin,R. (2004). Gene structure conservation aids similarity
based gene prediction. Nucleic Acids Research 32, 776-783.
[195] Meyer, P. L. (1970). Introductory Probability and Statistical Applications, 2nd edn
(Reading, MA: Addison-Wesley).
[196] Moon, J. W. (1970). Counting Labelled Trees. Canadian Mathematical Monographs
(London and Beccles: William Clowes and Sons Ltd).
[197] Morgenstern, B. (1999). DIALIGN 2: Improvement of the segment-to-segment
approach to multiple sequence alignment. Bioinformatics 15, 211-218.
[198] Morgenstern,В., Frech,K., Dress,A., and Werner,T. (1998). DIALIGN: Finding
local similarities by multiple sequence alignment. Bioinformatics 14, 290-294.
[199] Mott,R. (1999). Local sequence alignments with monotonic gap penalties.
Bioinformatics 15, 455-462.
[200] Mott,R. (2000). Accurate formula for P-values of gapped local sequence and
profile alignments. Journal of Molecular Biology 300, 649-659.
[201] Mott,R. and Tribe, R. (1999). Approximate statistics of gapped alignments.
Journal of Computational Biology 6, 91-112.
[202] Motwani,R., UllmanJ.D., and Hopcroft, J. E. (2003). Introduction to Automata
Theory, Languages, and Computation, 2nd edn (Upper Saddle River, N.J.: Pearson
Education).
[203] Muse,S.V. and Gaut,B.S. (1994). A likelihood approach for comparing
synonymous and nonsynonymous nucleotide substitution rates, with application
to the chloroplast genome. Molecular Biology and Evolution 11, 715-724.
[204] Myers,E.W. and Miller, W (1988). Optimal alignments in linear space. Computer
Applications in the Biosciences 4, 11-17.
[205] Nei,M., Chakraborty, R., and Fuerst,P.A. (1976). Infinite allele model with
varying mutation rate. Proceedings of the National Academy of Sciences of the
USA 73, 4164^168.
[206] Nei,M., Xu,R, and Glazko,G. (2001). Estimation of divergence times from
multiprotein sequences for a few mammalian species and several distantly related
organisms. Proceedings of the National Academy of Sciences of the USA 98, 2497-
2502.
[207] Neuhauser, С (1994). A Poisson approximation for sequence comparisons with
insertions and deletions. The Annals of Statistics 22, 1603-1629.

Литература 427
[208] Notredame,C, Higgins, D. G., and HeringaJ. (2000). T-Coffee: A novel method
for fast and accurate multiple sequence alignment. Journal of Molecular Biology
302, 205-217.
[209] Nussinov,R., Pieczenik, G., Griggs, J. R., and Kleitman, D. J. (1978). Algorithms
for loop matchings. SLAM Journal of Applied Mathematics 35, 68-82.
[210] Pachter, L., Alexandersson, M., and Cawley, S. (2002). Applications of generalized
pair hidden Markov models to alignment and gene finding problems. Journal of
Computational Biology 9, 389-399.
[211] Park, J., Teichmann,S.A., Hubbard, Т., and Chothia,C. (1997). Intermediate
sequences increase the detection of homology between sequences. Journal of
Molecular Biology 273, 349-354.
[212] Park, J., Karplus, K., Barrett, С et al. (1998). Sequence comparisons using multiple
sequences detect three times as many remote homologues as pairwise methods.
Journal of Molecular Biology 284, 1201-1210.
[213] Pearson, W.R. (1995). Comparison of methods for searching protein sequence
databases. Protein Science 4, 1145-1160.
[214] Pearson,W.R. (1996). Effective protein sequence comparison. Methods in
Enzymology 266, 227-258.
[215] Perriquet, O., Touzet,H., and Dauchet,M. (2003). Finding the common structure
shared by two homologous RNAs. Bioinformatics 19, 108-116.
[216] Pevzner, P. A., Borodovsky, M. Yu., and Mironov,A.A. (1989). Linguistics of
nucleotide sequences I: The significance of deviations from mean statistical
characteristics and prediction of the frequencies of occurrence of words. Journal
of Biomolecular Structure and Dynamics 5, 1013-1026.
[217] Posada, D. and Crandall, K. A. (2001). Selecting the best-fit model of nucleotide
substitution. Systematic Biology 50, 580-601.
[218] Priifer,H. (1918). Neuer Beweis eines Satzes uber Pemutationen. Archiv fur
Mathematik und Physik 27, 142-144.
[219] Qi,J., Wang, В., and Hao,B.I. (2004). Whole proteome prokaryote phylogeny
without sequence alignment: K-string composition approach. Journal of Molecular
Evolution 58, 1-11.
[220] Reese, J. T. and Pearson, W. R. (2002). Empirical determination of effective gap
penalties for sequence comparison. Bioinformatics 18, 1500-1507.
[221] Reich, J. G., Drabsch,H., and Daumler,A. (1984). On the statistical assessment of
similarities in DNA sequences. Nucleic Acids Research 12, 5529-5543.
[222] Reinert,G., Schbath,S., and Waterman, M. S. (2000a). Probabilistic and statistical
properties of words: An overview. Journal of Computational Biology 7, 1-46.
[223] Reinert,K., Stoye,J., and Will,T. (2000). An iterative method for faster sum-of-
pairs multiple sequence alignment. Bioinformatics 16, 808-814.

428
Литература
[224] Reza,F.M. (1994). An Introduction to Information Theory (New York: Dover
Publications).
[225] Rivas,E. and Eddy,S.R. (1999). A dynamic programming algorithm for RNA
structure prediction including pseudoknots. Journal of Molecular Biology 285,
2053-2068.
[226] Robin, S. and Schbath, S. (2001). Numerical comparison of several approximations
of the word count distribution in random sequences. Journal of Computational
Biology 8, 349-359.
[227] Ross, S. M. (1996). Stochastic Processes, 2nd edn (New York: John Wiley & Sons,
Inc.).
[228] Rost, B. (1999). Twilight zone of protein sequence alignments. Protein Engineering
12, 85-94.
[229] Rychlewski,L., Jaroszewski,L., Li,W., and Godzik,A. (2000). Comparison of
sequence profiles. Strategies for structural predictions using sequence information.
Protein Science 9, 232-241.
[230] Saitou,N. and Nei,M. (1987). The neighbor-joining method: A new method for
reconstructing phylogenetic trees. Molecular Biology and Evolution 4, 406-425.
[231] Salomaa,A., Wood,D., and Yu,S., eds (2001). A Half-Century of Automata
Theory: Celebration and Inspiration (Singapore: World Scientific).
[232] Salzberg,S.L., Delcher, A. L., Kasif,S., and White, O. (1998). Microbial gene
identification using interpolated Markov models. Nucleic Acids Research 26, 544-
548.
[233] Sankoff,D. and Cedergren, R. J. (1983). Simultaneous comparison of three or
more sequences related by a tree. In Sankoff,D. and Kruskal,J. В., eds, Time
Warps, String Edits, and Macromolecules: The Theory and Practice of Sequence
Comparison (Reading, MA: Addison-Wesley), Chap. 9, pp. 253-264.
[234] Schaffer, A. A., Aravind, L., Madden, T. L. et al. (2001). Improving the accuracy of
PSI-BLAST protein database searches with composition-based statistics and other
refinements. Nucleic Acids Research 29, 2994-3005.
[235] Schbath, S. (2000). An overview on the distribution of word counts in Markov
chains. Journal of Computational Biology 7, 193-201.
[236] Schmidler, S. C, Liu,J.S., and Brutlag,D.L. (2000). Bayesian segmentation of
protein secondary structure. Journal of Computational Biology 7, 233-248.
[237] Schmidt, H. A., Strimmer,K., Vingron,M., and Haeseler,A. von (2002). TREE-
PUZZLE: Maximum-likelihood phylogenetic analysis using quartets and parallel
computing. Bioinformatics 18, 502-504.
[238] Schneider, T.D., Stormo,G.D., Gold,L., and Ehrenfeucht, A. (1986). Information
content of binding sites on nucleotide sequences. Journal of Molecular Biology
188,415-431.

Литература
429
[239] Schuler, G. D., Altschul, S. F., and Lipman, D. J. (1991). A workbench for multiple
alignment construction and analysis. Proteins: Structure, Function, and Genetics
9, 180-190.
[240] Schwartz, S., Zhang, Z., Frazer,K. A. et al (2000). PipMaker — a web server for
aligning two genomic DNA sequences. Genome Research 10, 577-586.
[241] Shannon, С E. and Weaver, W (1963). The Mathematical Theory of
Communication (Urbana-Champaign: University of Illinois Press).
[242] Shimodaira, H. (2002). An approximately unbiased test of phylogenetic tree
selection. Systematic Biology 51, 492-508.
[243] Shimodaira, H. and Hasegawa,M. (1999). Multiple comparisons of log-likelihoods
with applications to phylogenetic inference. Molecular Biology and Evolution 16,
1114-1116.
[244] Shimodaira, H. and Hasegawa, M. (2001). CONSEL: For assessing the confidence
of phylogenetic tree selection. Bioinformatics 17, 1246-1247.
[245] Shindyalov, I.N. and Bourne, P.E. (1998). Protein structure alignment by
incremental combinatorial extension (CE) of the optimal path. Protein Engineering
11, 739-747.
[246] Shiryaev, A.N. (1996). Probability, 2nd edn (New York: Springer-Verlag).
[247] Siegmund,D. and Yakar,B. (2000). Approximate P-values for local sequence
alignments. The Annals of Statistics 28, 657-680.
[248] Siegmund,D. and Yakar,B. (2003). Correction: Approximate P-values for local
sequence alignments. The Annals of Statistics 31, 1027-1031.
[249] Simon, M. (1999). Automata Theory (Singapore: World Scientific).
[250] Smith, T. F. and Waterman, M. S. (1981). Identification of common molecular
subsequences. Journal of Molecular Biology 147, 195-197.
[251] Smith, T.F., Waterman, M. S., and Burks, С (1985). The statistical distribution of
nucleic acid similarities. Nucleic Acids Research 13, 645-656.
[252] Snel,B., Bork,P., and Huynen,M.A. (1999). Genome phylogeny based on gene
content. Nature Genetics 21, 108-110.
[253] Snel,B., Huynen,M.A., and Dutilh,B.E. (2005). Genome trees and the nature of
genome evolution. Annual Reviews in Microbiology 59, 191-209.
[254] Sokal,R.R. and Michener, С D. (1958). A statistical method for evaluating
systematic relationships. University of Kansas Scientific Bulletin 28, 1409-1438.
[255] Sonnhammer, E. L. L., Eddy, S. R., Birney, E., Bateman, A., and Durbin, R. (1998).
Pfam: Multiple sequence alignments and HMM-profiles of protein domains.
Nucleic Acids Research 26, 320-322.
[256] Steel, M., Hendy,M.D., and Penny, D. (1998). Reconstructing phylogenies from
nucleotide pattern probabilities: A survey and some new results. Discrete Applied
Mathematics 88, 367-396

430
Литература
[257] Strimmer,K. and Haeseler, A. von (1996). Quartet puzzling: A quartet maximum-
likelihood method for reconstructing tree topologies. Molecular Biology and
Evolution 13, 964-969.
[258] Suzuki, Y., Glazko,G.V., and Nei,M. (2002). Overcredibility of molecular
phylogenies obtained by Bayesian phylogenetics. Proceedings of the National
Academy of Sciences of the USA 99, 16 138-16 143.
[259] Szekely,L.A., Steel, M. A., and Erdos,P.L. (1993). Fourier calculus on
evolutionary trees. Advances in Applied Mathematics 14, 200-216.
[260] Tabaska,J.E., Сагу, R. В., Gabow,H.N., and Stormo,G.D. (1998). An RNA
folding method capable of identifying pseudoknots and base triples. Bioinformatics
14, 691-^99.
[261] Tatusov,R.L., Galperin,M. Y, Natale,D.A., and Koonin,E.V. (2000). The COG
database: A tool for genome-scale analysis of protein functions and evolution.
Nucleic Acids Research 28, 33-36.
[262] Tavare, S. and Song,B. (1989). Codon preference and primary sequence structure
in protein coding regions. Bulletin of Mathematical Biology 51, 95-115.
[263] Tekaia,F., Lazcano, A., and Dujon,B. (1999). The genomic tree as revealed from
whole proteome comparisons. Genome Research 9, 550-557.
[264] Thompson, J. D., Higgins, D. G., and Gibson, T. J. (1994a). Improved sensitivity of
profile searches through the use of sequence weights and gap excision. Computer
Applications in the Biosciences 10, 19-29.
[265] Thompson,J.D., Higgins,D.G., and Gibson,T.J. (1994b). CLUSTAL W:
Improving the sensitivity of progressive multiple sequence alignment through
sequence weighting, position specific gap penalties and weight matrix choice.
Nucleic Acids Research 22, 4673-4680.
[266] Thompson, J. D., Plewniak, F., and Poch, O. (1999a). A comprehensive comparison
of multiple sequence alignment programs. Nucleic Acids Research 27, 2682-2690.
[267] Thompson, J. D., Plewniak, F., and Poch,0. (1999b). BAliBASE: A benchmark
alignment database for the evaluation of multiple alignment programs.
Bioinformatics 15, 87-88.
[268] Thompson, J. D., Plewniak, F., Ripp,R., Thierry, J-C, and Poch,0. (2001).
Towards a reliable objective function for multiple sequence alignments. Journal
of Molecular Biology 314, 937-951.
[269] Thorne,J.L., Kishino,H., and Felsenstein, J. (1991). An evolutionary model
for maximum likelihood alignment of DNA sequences. Journal of Molecular
Evolution 33, 114-124.
[270] Thorne,J.L., Kishino,H., and Felsenstein, J. (1992). Inching toward reality: An
improved likelihood model of sequence evolution. Journal of Molecular Evolution
34, 3-16.

Литература
431
[271] T6nges,U., Perrey,S. W, Stoye, J., and Dress, A. WM. (1996). A general method
for fast multiple sequence alignment. Gene 172, GC33-GC41.
[272] Tusnady, G.E. and Simon, I. (1998). Principles governing amino acid composition
of integral membrane proteins: Application to topology prediction. Journal of
Molecular Biology 283, 489-506.
[273] Vingron,M. and Waterman, M. S. (1994). Sequence alignment and penalty choice:
Review of concepts, case studies and implications. Journal of Molecular Biology
235, 1-12.
[274] Vinh,L. S. and Haeseler, A. von (2004). IQPNNI: Moving fast through tree space
and stopping in time. Molecular Biology and Evolution 21, 1565-1571.
[275] Waterman, M. S. (1995). Introduction to Computational Biology (New York:
Chapman and Hall).
[276] Waterman, M. S. and Vingron,M. (1994). Rapid and accurate estimates of
statistical significance for sequence data base searches. Proceedings of the National
Academy of Sciences of the USA 91, 4625-4628.
[277] Webb, B-J. M., Liu, J. S., and Lawrence, С. Е. (2002). BALSA: Bayesian algorithm
for local sequence alignment. Nucleic Acids Research 30, 1268-1277.
[278] Webber,С and Barton,G.J. (2001). Estimation of P-values for global alignments
of protein sequences. Bioinformatics 17, 1158-1167.
[279] Whelan, S. and Goldman, N. (2001). A general empirical model of protein
evolution derived from multiple protein families using a maximum-likelihood
approach. Molecular Biology and Evolution 18, 691-699.
[280] Whelan, S., Lio,R, and Goldman, N. (2001). Molecular phylogenetics: State-of-
the-art methods for looking into the past. Trends in Genetics 17, 262-272.
[281] Wilbur, W.J. (1985). On the РАМ matrix model of protein evolution. Molecular
Biology and Evolution 2, 434-447.
[282] Wolf, Y. I., Rogozin, I. В., and KooninE. V. (2004). Coelomata and not Ecdysozoa:
Evidence from genome-wide phylogenetic analysis. Genome Research 14, 29-36.
[283] Wuyts, J., De Rijk, P., Peer, Y. Van de, Winkelmans, Т., and De Wachter, R. (2001).
The European Large Subunit Ribosomal RNA database. Nucleic Acids Research
29, 175-177.
[284] Yang,Z. (1998). Likelihood ratio tests for detecting positive selection and
application to primate lysozyme evolution. Molecular Biology and Evolution 15,
568-573.
[285] Yang,Z. and Bielawski, J. P. (2000). Statistical methods for detecting molecular
adaptation. Tree 15, 496-503.
[286] Yang,Z. and Nielsen, R. (2000). Estimating synonymous and nonsynonymous
substitution rates under realistic evolutionary models. Molecular Biology and
Evolution 17, 32-43.

432
Литература
[287] Yang,Z. and Rannala,B. (1997). Bayesian phylogenetic inference using DNA
sequences: A Markov chain Monte Carlo method. Molecular Biology and
Evolution 14, 717-724.
[288] Yang,Z., Nielsen, R., Goldman, N., and Pedersen, A-M. K. (2000). Codon-
substitution models for heterogeneous selection pressure at amino acid sites.
Genetics 155, 431^49.
[289] Younger, D.H. (1967). Recognition and parsing of context-free languages in
time n3. Information and Control 10, 189-208.
[290] Zhu,J., Liu, J. S., and Lawrence, С. Е. (1998). Bayesian adaptive sequence
alignment algorithms. Bioinformatics 14, 25-39.
[291] Zuker,M. (2000). Calculating nucleic acid secondary structure. Current Opinion
in Structural Biology 10, 303-310.
[292] Zuker,M. and Stiegler,P. (1981). Optimal computer folding of large RNA
sequences using thermodynamic and auxiliary information. Nucleic Acids Research
9, 133-148.
[293] Zwieb,C, Gorodkin,J., Knudsen,B., Burks,!, and Wower,J. (2003). tmRDB
(tmRNA database). Nucleic Acids Research 31, 446-447.

Предметный указатель
£7-значение, 89, 94
Р-значение, 89, 94
250 ПТМ матрица логарифмических
шансов, 83, 84, 229
BLAST, 46, 91, 214, 351
BLOSUM50, 147, 207
BLOSUM62, 229
CLUSTAL W, 228
CpG-остров, 22, 38, 40
FMR-1 автомат, 355
PROSITE, 356
PSI-BLAST, 172, 214
UPGMA, 179, 251, 253, 272
Автомат
— детерминированный, 355, 359
— конечный, 355, 356
— магазинный, 361, 364
Алгоритм
— CLUSTAL W, 228
— UPGMA, 179, см. также UPGMA
— Байесова типа, 38
— Баума-Велша, 104, 111
— Витерби, 107, 112, 115, 157
— Витерби для парной СММ, 157, 166
— КЯК, 376, 385, 388
— Каррилло-Липмана, 217
— Метрополией 299-302
— Нидлмена-Вунша, 226, 229
— Нуссинов, 371, 374-376
— Прюфера, 247
— Сайту и Нея соединения соседей, 267,
275
— Смита-Уотермена для локального
выравнивания, 172
— Фельзенштейна, 295, 303
— Фитча-Марголиаша, 228
— Фэна-Дулиттла прогрессивного
выравнивания, 216, 226, 229
— апостериорного декодирования, 112
— выборки Гиббса для локального
множественного выравнивания, 235
— глобального выравнивания, 69
— динамического программирования,
70, 135, 217, 221, 262
— обратный, 116, 121
— обратный для парной СММ, 164
— прогрессивного выравнивания, 226
— прямой, ПО, 116, 121
— с линейной памятью, 67, 69
— с традиционной экономичностью, 257
— со взвешенной экономичностью, 257,
261
— сравнения последовательностей, 96
— типа «внутрь», 377, 381, 385
— типа «наружу», 377, 385
Апостериорная вероятность, 20, 36, 43,
114, 118, 160, 162
Апостериорного декодирования
алгоритм, 112
Байеса теорема, 19, 20, 36, 38, 45, 134
Байесова оценка, 22
Баума-Велша алгоритм, 104, 111
Бернуллиевы испытания, 24, 42, 98
Бинарное дерево, 244

434
Предметный указатель
Биномиальное разложение, 393
Биномиальное распределение, 24,42,45,
392
Биномиальный коэффициент, 106
Бокса-Мюллера метод, 403
Большинства правило, 24
Вероятностная матрица мутаций ПТМ,
74,80
Вероятность
- апостериорная, 20, 36, 43, 114, 118,
160, 162
- испускания, 102, 104, 109, 112, 115,
148, 156, 177, 185
- перехода, 100-102, 105, 107, ПО, 112,
115, 117, 123, 128, 144, 148, 156, 173,
185, 364
- совместного наступления событий,
152
- условная, 18, 19, 102
- эмиссии, 102, 104, 109, 112, 115, 148,
156, 177, 185
Веса
- последовательностей
Альтшуля, Кэрролла и Липмена,
182
Герштейна, Соннхаммера и Чотиа,
182
Хеникофф, 182, 194
максимальной энтропии, 183
максимальные различительные, 200
метода напряжения, 181
Взаимная информация, 369, 397
Взвешенная экономичность, 257, 259,
261, 327, 329
Витерби
- алгоритм, 107, 112, 115, 157, 188
для парной СММ, 157, 166
- путь, 116, 118, 151, 155
Внешняя переменная, 382
Внутренняя переменная, 382
Вставки состояние, 185, 194
Второго порядка марковская цепь, 107
Выборка подоптимального
выравнивания, 381
Выравнивание
— без пропусков, 236
— множественное, 236, 369
— оптимальное, 64, 65, 70, 157
локальное, 172
— прогрессивное, 141, 226, 228, 238
— с пропусками, 53
Выравнивание минимальной стоимости,
216-218
Выравнивание с пропусками, 53
Гамма-распределение, 351, 406
Гауссово (нормальное) распределение,
42, 43, 182, 403, 404
Геном, 23, 28, 43, 99, 129, 140, 279, 351
Геометрическое распределение, 29, 33,
47,95
Гиббса выборка, 235, 408
Глобального выравнивания алгоритм, 69
Гомология, 36, 46, 84, 98, 99, 140, 214,
238, 279, 335, 390
Граф последовательности, 262, 265
Групповой метод невзвешенных пар с
вычислением среднего
арифметического, 179, см. также UPGMA
Дейхофф, Шварца и Оркатта модель
эволюции белка, 74
Дерево минимальной стоимости, 257,
259, 261, 327
Детерминированный автомат, 355, 359
Джукса-Кантора
— модель, 282, 286, 288, 297, 330, 332,
335, 348
— расстояние, 329
Динамического программирования
алгоритм, 70, 135,217,221,262
Динамического программирования
матрица, 64, 72, 381, 386
Дирихле априорное распределение, 134,
184, 205

Предметный указатель
435
Дирихле распределение, 134, 205, 406
Длиннейшее общее слово, 95
Изменение профиля, 303
КСГ, 359, 361, 363
КЯК алгоритм, 376, 385, 388
Казино, 18, 120
Каноническое представление дерева,
301, 306
Каррилло-Липмена алгоритм, 217
Кимуры
- модель, 282, 341
— расстояние, 228
Коалесцентное априорное
распределение, 317
Ковариационная модель, 386
Кодон, 27, 32, 33, 107, 109
Коке-Янгера-Касами алгоритм, 376, см.
также КЯК алгоритм
Количество информации, 210, 395
Конечное состояние, 100, 101, 112, 144,
156
Конечный автомат, 355, 356
Корневое дерево, 240, 242
Куллбака-Лейблера расстояние, 211,
370, 395
Лапласа правило, 185
Линейный штраф за пропуск, 47, 65, 72,
229
Логарифмических шансов матрица, 84,
85
Логарифмическое отношение шансов,
38, 41, 42, 83, 88, 120, 121, 149, 166
Логограмма, 210
Локальное множественное
выравнивание, 235
MAP оценка, 205
Магазинный автомат, 361, 364
Максимальные веса энтропии, 183
Максимальные различительные веса,
200
Максимизация математического
ожидания, 380
Марковость, 81, 285, 336, 410
Марковская цепь, 79, 81, 99-101, 107,
140, 238, 299, 302, 342, 410
Марковский процесс, 337, 344
Матрица
— замен, 83, 88, 282, 286, 297, 330, 342
BLOSUM, 85
Методов напряжения, 181
Метрополиса алгоритм, 299-302
Множественное выравнивание, 185, 205,
217, 226, 236, 369
Модель
— Дейхофф, Шварца и Оркатта, 74
— Джукса-Кантора, 282, 286, 288, 297,
330, 332
— Кимуры, 282
— ковариационная, 386
— независимых порождений, 22, 23, 28,
29, 32-35, 41, 73, 88, 90, 94-96, 122,
129, 133, 134, 148, 152, 153, 184, 188,
200, 211, 235
для пары последовательностей, 83,
144, 145, 156, 166, 168, 169, 173
— основная сегментации, 134
— позиционная независимости, 210, 211,
235, 236
— прямая связная, 105
— с молчащими состояниями, 105
— связей, или ТКФ, 344
— случайной последовательности, 22
Молекулярные часы, 275, 278, 301, 306,
308, 311, 317, 336
Молчащее состояние, 105, 144, 173
Монте-Карло метод на марковских
цепях (МКМЦ), 301
Мотив, 235, 236, 356
Мультипликативность, 282, 285, 291
Мура автомат, 355
Набор обучающих последовательностей,
104, 128, 172, 176, 192, 196, 197, 200

436
Предметный указатель
Наиболее вероятный путь, 102, 116
Наиболее правдоподобное дерево, 301,
332
Наиболее правдоподобное расстояние,
329, 332, 335, 344
Наиболее экономичное дерево, 74, 327
Начальное состояние, 112, 115, 156
Некорневое дерево, 240, 242, 244
Неоднородная марковская цепь, 109
Неравенство Чебышева, 93, 398
Нетерминальные символы, 355, 361, 364,
366
Нидлмена-Вунша алгоритм, 226, 229
Нормальное распределение, 42, 43, 182,
403, 404
Нуссинов алгоритм сворачивания РНК,
371, 374-376
Обратимость, 81, 290, 295, 336
Обратная переменная, 104
Обратный
— алгоритм, 116, 121
для парной СММ, 164
Оптимальная структура, 371
Оптимальное выравнивание, 64, 65, 157,
217, 226
Оптимальное локальное выравнивание,
172
Оптимальное множественное
выравнивание, 217
Ортологи, 99, 351
Основная модель сегментации, 134
Открытая рамка считывания (ОРС), 32,
33
Относительная мутабильность, 76
Относительная энтропия, 211, 329, 330,
395
Отрицательное биномиальное
распределение, 106
Оценка
— Байесова, 22
— MAP, 205
— методом наибольшего правдоподобия,
22, 207, 297
ПМС см. позиционная матрица счетов,
207
Парная СММ, 156, 160
Пары сегментов с высоким счётом, 88
Первого порядка марковская модель, 128
Плоское априорное распределение, 308
Подобие, 88, 94
Позиционная матрица счетов, 207
Позиционная модель независимости,
210,211,235,236
Полиномиальное распределение, 24
Полиномиальный коэффициент, 55, 248
Помеченная история, 278, 308-311, 313,
314
Попарное выравнивание, 47, 70, 143
Правдоподобие модели, 33
Правила
— Лапласа, 185, 192
— большинства, 24
— преобразования, 400
Предсказание генов, 109, 140
Примыкающее состояние, 173
Прогрессивное выравнивание, 141, 228,
238
Пропорциональный штраф за пропуск,
47,50
Профильная СММ, 171, 177, 185, 188,
205, 381
Процедура обратного прослеживания,
65, 72, 174, 191, 217, 263, 376, 382
Процесс рождения и гибели, 315, 344
Прюфера алгоритм, 247
Прямая
— переменная, 104
— связная модель, 105
Прямой алгоритм, ПО, 116, 121
Псевдоподсчёт, 22, 185, 192, 207
Пуассона процесс, 36, 335, 338
Пуассона распределение, 28, 35, 38, 45,
89

Предметный указатель
4W
Путеводное дерево, 228
Равновесные частоты, 81, 295, 347
Равномерное распределение, 395, 402,
404
Различающая функция, 200
Распределение
— Гауссово (нормальное), 42, 43, 182,
403, 404
— Дирихле, 134, 205, 406
— Пуассона, 28, 35, 38, 45, 89
— биномиальное, 24, 42, 45
— гамма, 351, 406
— геометрическое, 29, 33, 47, 95
— отрицательное биномиальное, 106
— полиномиальное, 24
— равномерное, 395, 402, 404
— хи-квадрат, 126, 129
Регулярная грамматика, 360, 361, 365
С линейной памятью алгоритм, 67, 69
СКСГ, 364, 376, 377, 381, 384
СММ, 99, 109, 111, 112, 115, 118, 143,
148, 364
Саиту-Нея алгоритм, 267, 275
Скрытая марковская моделя, 99, см.
также СММ
Слабый закон больших чисел, 398
Случайной последовательности модель,
22
Смита-Уотермена алгоритм, 172
Совместное распределение, 397, 404
Совпадения состояние, 177, 185, 194
Соединения соседей алгоритм Сайту и
Нея, 228, 267, 275
Составное дерево, 244, 249
Состояние удаления, 185
Сравнения последовательностей
алгоритм, 96
Стационарность, 285
Стирлинга формула, 64
Стоимость замены, 259
Стохастическая контекстносвободная
грамматика, 363, см. также СКСГ
Стохастическая регулярная граммшикп,
364
Стохастическая трансформационнам
грамматика, 384
Счёта матрица, 69
Счет
— BLOSUM 50, 47
— выравнивания, 50
— замены, 70, 73, 81, 147, 174
— парных сумм, 217
Теорема
— Байеса, 19, 20, 36, 38, 45
— умножения, 102
— центральная предельная, 42
— эргодическая для марковской цепи,
301
Терминальные символы, 363, 364
Топология дерева, 243, 278, 279, 302,
306-309, 320, 344, 350
Торна, Кисино и Фельзенштейна модель,
344
Точность выравнивания, 162
Традиционная экономичность, 257, 327
Трихотомическое дерево, 244, 246
Ультраметрическое расстояние, 253
Уотсона-Крика пары, 363, 369, 372
Усиленные закон больших чисел, 326
Усиленный закон больших чисел, 399
Условная вероятность, 18, 19, 102
Фельзенштейна алгоритм, 295, 303
Функция штрафов за пропуски, 70
Фэна-Дулиттла прогрессивного
выравнивания алгоритм, 216, 226, 229
Хейн, 261
— алгоритм, 261
Хомского нормальная форма, 366, 379
Целевые частоты, 73
Центральная предельная теорема, 42
Частота

438
Предметный указатель
— ложных отрицательных результатов,
40, 41, 91
— ложных положительных результатов,
40,41
— с пропорциональным счётом, 47
Эволюционное расстояние, 80, 84, 272
Экономичность
— взвешенная, 257, 259, 329
— традиционная, 257, 327
Энтропия, 210, 395, 397
Юла
— априорное распределение, 311, 317
— процесс, 311
Штраф
— за открытие пропуска, 47, 147, 174,
218
— за открытик пропуска, 262
— за продолжение пропуска, 47, 147,
174, 218, 262
— с линейным счётом, 47, 229

Бородовский Марк
Екишева Светлана
Задачи и решения по анализу
биологических последовательностей
Дизайнер А. А. Гурьянова
Технический редактор А. В. Широбоков
Корректор Г. Г. Тетерина
Подписано в печать 19.09.2008. Формат 60 х 84У16.
Печать офсетная. Усл.печ.л. 25,58. Уч. изд. л. 25,12.
Гарнитура Тайме. Бумага офсетная №1. Заказ №48.
Научно-издательский центр «Регулярная и хаотическая динамика»
426034, г. Ижевск, ул. Университетская, 1.
http://shop.rcd.ru E-mail: mail@rcd.ru Тел./факс: (+73412) 500-295

Уважаемые читатели!
Интересующие Вас книги нашего издательства можно заказать через
наш Интернет-магазин http://shop.rcd.ru или по электронной почте
subscribe@rcd.ru
Книги можно приобрести в наших представительствах:
МОСКВА
Институт машиноведения им. А. А. Благонравова РАН
ул. Бардина, д. 4, корп. 3, к. 414, тел.: (499) 135-54-37
ИЖЕВСК
Удмуртский государственный университет
ул. Университетская, д. 1, корп. 4, 2 эт., к. 211, тел./факс: (3412) 500-295
Также книги можно приобрести:
МОСКВА
Московский государственный университет им. М. В. Ломоносова
ГЗ (1 эт.), Физический ф-т (1 эт.), Гуманитарный ф-т (0 и 1 эт.),
Биологический ф-т (1 эт.).
Российский государственный университет нефти и газа им. И. М. Губкина
ГЗ (3^4 эт.), книжные киоски фирмы «Аргумент».
Магазины:
МОСКВА: «Дом научно-технической книги»
Ленинский пр., 40, тел.: 137-06-33
«Московский дом книги»
ул. Новый Арбат, 8, тел.: 290-45-07
«Библиоглобус»
м. «Лубянка», ул. Мясницкая, 6, тел.: 928-87-44
ДОЛГОПРУДНЫЙ: Книжный магазин «Физматкнига»
новый корп. МФТИ, 1 эт., тел.: 409-93-28
САНКТ-ПЕТЕРБУРГ: «Санкт-Петербургский дом книги»
Невский проспект, 28
Издательство СПбГУ, Магазин №1
Университетская набережная, 7/9