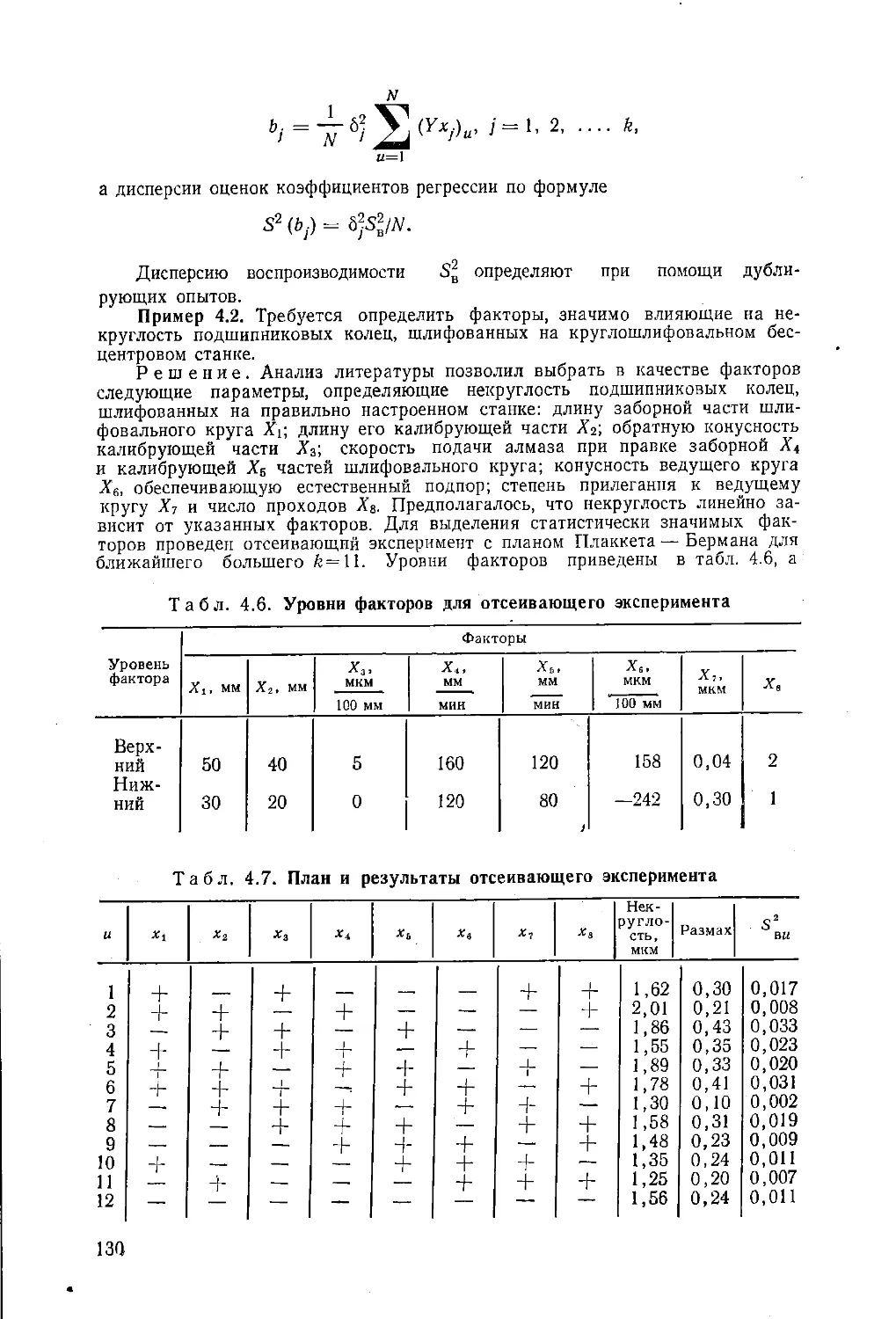
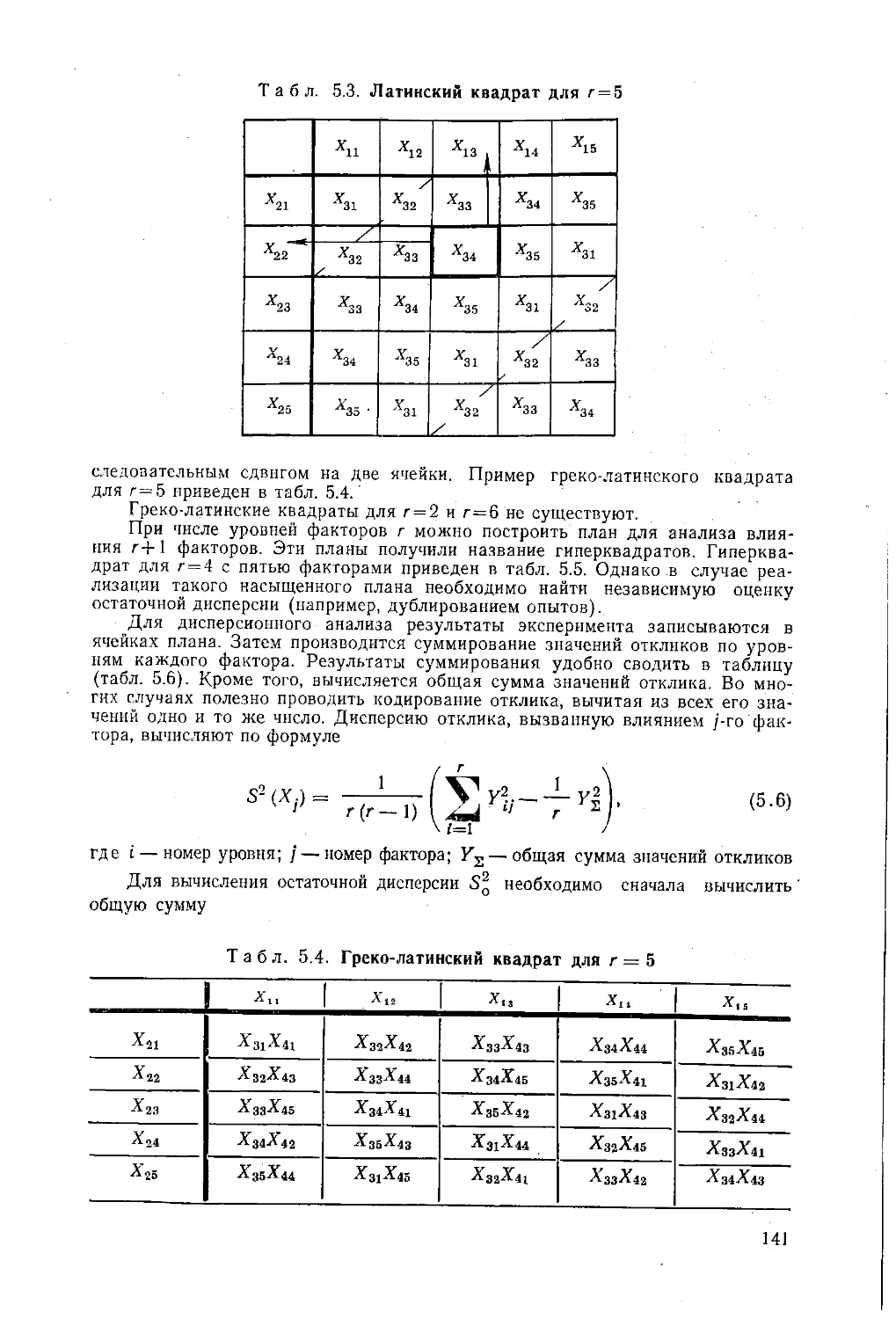
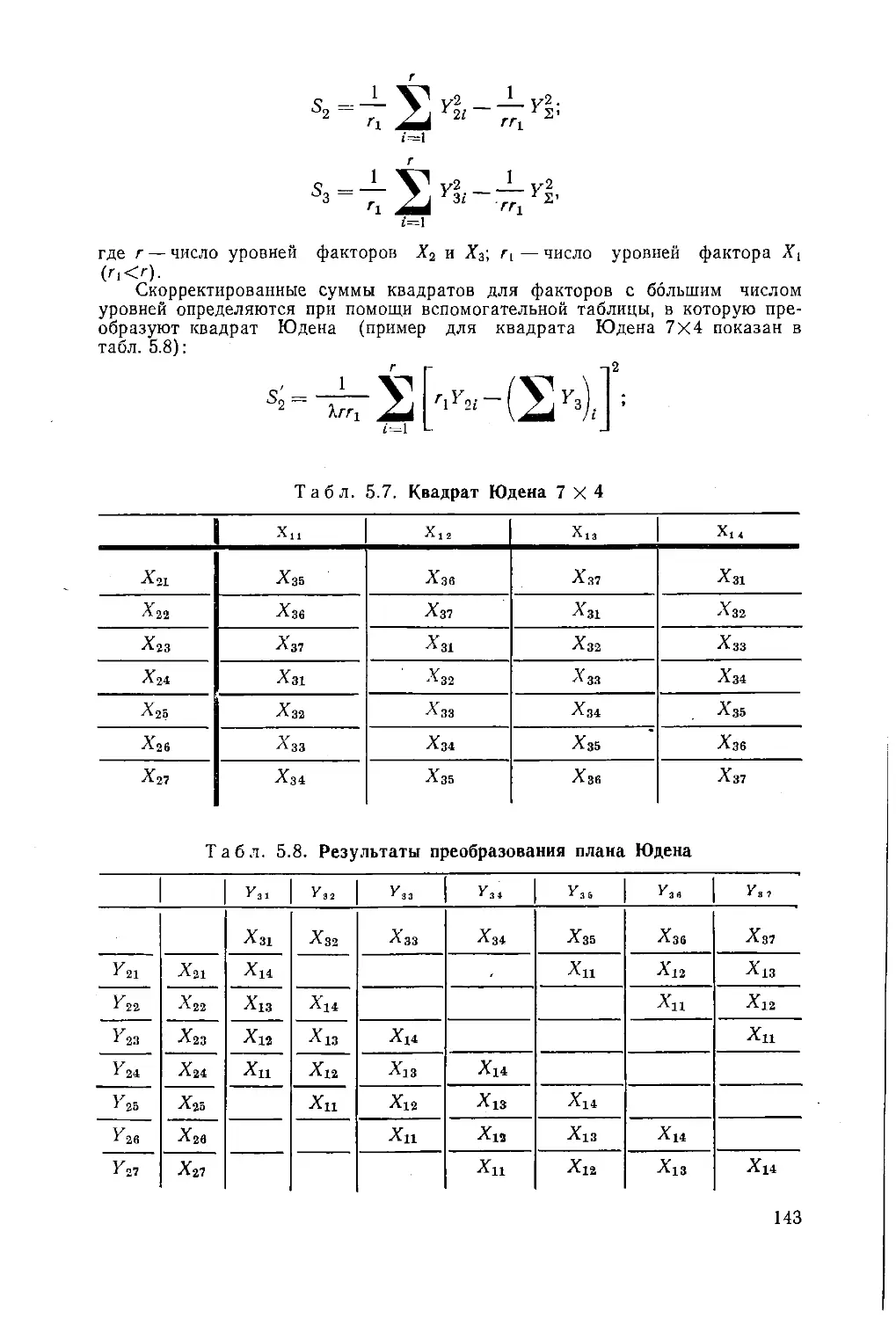
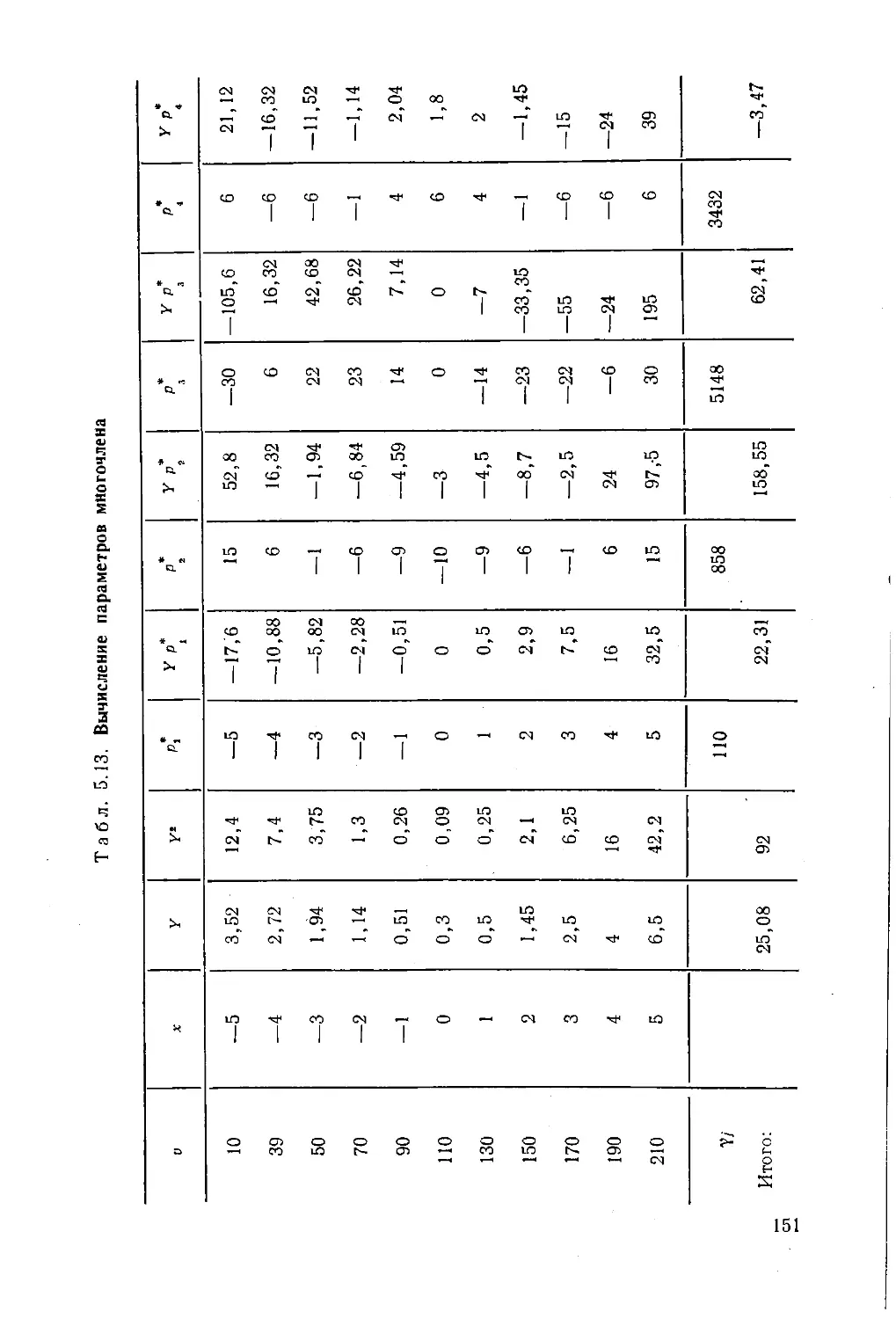
Автор: Ящерицын П.И. Махаринский Е.И.
Теги: общее машиностроение технология машиностроения машиноведение машиностроение
Год: 1985
Похожие
Текст
П. И. ЯЩЕРИЦЫН, Е. И. МАХАРИНСКИЙ
ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА В МАШИНОСТРОЕНИИ
МИНСК «ВЫШЭЙШАЯ ШКОЛА» 1985
ББК 34.4я2
Я97
УДК 621.002 : 658.512 : 519.242(035.5)
Рецензенты: В. Г. Митрофанов, доктор технических наук, профессор Московского станкоинструментального института; Ю. М. Иванов, доктор технических наук, профессор, зав. кафедрой «Технология машиностроения» Львовского политехнического института
2701010000—147
Я М 304(05)—85 109-85
© Издательство «Вышэйшая школа», 1985.
ПРЕДИСЛОВИЕ
Основой современного технического прогресса является опережающее развитие машиностроения, осуществляемое по следующим главным направлениям: существенное улучшение и разработка новых технологических процессов производства деталей и сборки машин; создание системы высокопроизводительного технологического оборудования, оснастки и инструмента; повышение уровня автоматизации на всех этапах производственного процесса.
Принятие проектных решений в машиностроении и оценка их качества в основном осуществляются на основании данных эксперимента. А усложнение объектов испытания вызвало резкое повышение стоимости их исследования. Поэтому задача извлечения наибольшего объема информации об изучаемых процессах или устройствах при ограничениях по затратам является в настоящее время достаточно актуальной. Решению указанной проблемы способствует широкое внедрение в практику прикладных исследований статистических методов планирования экспериментов, которые дают не только способ обработки экспериментальных данных, но позволяют также оптимально организовать эксперимент. Цели и критерии оценки качества исследования необходимо выявлять системно, анализируя затраты, важность ожидаемых результатов, последствия недостаточной точности и ошибочности решений.
Планирование эксперимента и математическая обработка его результатов все больше входят в круг вопросов, необходимых студентам старших курсов технических вузов, аспирантам и инженерам-исследователям. Усвоение и использование методов планирования эксперимента позволяют повысить его эффективность тем больше, чем больше контролируемых факторов, воздействующих на объект исследования, учитывается в данной задаче.
В математической статистике разработаны методы, позволяющие проводить обработку результатов наблюдений некоторыми наилучшими приемами, которые дают так называемые эффективные оценки. Так как при этом оценка параметров и установление их доверительных границ производятся одним из стандартных методов, то можно для сходных объектов в различных исследовательских организациях получать сопоставимые результаты.
Поскольку основой эксперимента являются измерения, то в первой главе справочного пособия излагаются сведения о методах и средствах измерения линейных и угловых величин, параметров движения, силовых и энергетических величин, температуры, а также о современных методах и средствах определения механических свойств и обрабатываемости машиностроительных материалов. Сведения о погрешностях измерений, об их числовых характеристиках и оценках, о расчете и компенсации погрешностей средств измерений приведены во второй главе. Эти материалы позволят исследователю обоснованно выбрать способ и средство измерения, в полной мере соответствующие поставленной задаче.
В третьей главе пособия последовательно и сжато излагаются вопросы математической обработки результатов эксперимента при решении различных задач (от простой оценки отклика до построения математической модели исследуемого объекта). Основные процедуры предпланирования эксперимента, целью которых является снижение его трудоемкости путем уменьшения
3
размерности факторного пространства, излагаются в четвертой главе. Методам планирования эксперимента при построении математических моделей исследуемого объекта и оптимизации его структуры или режима работы посвящены пятая и шестая главы книги. В седьмой главе справочного пособия излагаются вопросы автоматизации эксперимента на базе современных средств вычислительной и аналоговой техники.
Чтобы облегчить восприятие идей и методов теории планирования экспериментов непрофессионалами в этой области, большая часть теоретических положений и методов иллюстрируется примерами, имеющими отношение к технологии машиностроения.
Авторы
1. МЕТОДЫ И СРЕДСТВА ИЗМЕРЕНИЯ В МАШИНОСТРОЕНИИ
1.1. ИЗМЕРЕНИЯ И ИЗМЕРЯЕМЫЕ ВЕЛИЧИНЫ
Общие положения. Измерение является одним из важнейших путей познания. Его определяют как нахождение значения физической величины опытным путем с помощью специальных технических средств [10]. Измерение дает количественную оценку физической величины на основе измерительного преобразования, при котором устанавливается взаимно однозначное соответствие между размерами измеряемой (преобразуемой) и преобразованной величин, сохраняющее для некоторого множества размеров преобразуемой величины все определенные для нее отношения и операции [13].
Физическая величина (кратко — величина) — свойство, общее в качественном отношении для многих физических объектов (физических систем, их состояний и происходящих в них процессов), но индивидуальное в количественном отношении для каждого объекта. Размер физической величины отражает количественное содержание в данном объекте свойства, соответствующего понятию «физическая величина». Значение физической величины (значение величины) — ее оценка в виде некоторого числа принятых для нее единиц.
По отношению к изучаемой системе измеряемые величины можно разделить на первичные и вторичные [13]. Первичными являются те, которые можно выбрать в качестве обобщенных координат и их производных по времени при описании изучаемой системы (сила, координата, скорость, напряжение, давление и т. д.). Ко вторичным относятся величины, которые характеризуют свойства изучаемой системы и их проявление в первичных величинах. Значения вторичных величин находят в процессе обработки данных о первичных измеряемых величинах. К ним относятся, например, различные размерные и безразмерные частотные характеристики механической системы (динамическая жесткость, импеданс, частотные характеристики системы и т. д.).
Описание свойства, характеризуемого данной величиной, осуществляется через другие, ранее определенные величины. Эта возможность обусловливается наличием объективно существующих взаимосвязей между свойствами объектов, которые можно отразить системой уравнений связи между величинами. Но так как число уравнений всегда меньше числа входящих в них величин, принято выделять в отдельную группу некоторые физические величины, число которых k должно равняться разности между числом величин п и числом независимых уравнений т. Эти величины и соответствующие нм единицы называются основными величинами и основными единицами [10]. Все остальные величины и единицы определяются однозначно через основные и называются производными. Совокупность основных и производных величин образует систему величин. Так же создаются и системы единиц. В уравнение связи между величинами входят универсальные постоянные.
Размерность физической величины — это выражение, отражающее ее связь с основными величинами системы. Размерность величины представляет собой произведение основных величин, возведенных в соответствующие степени.
Эксперименты в машиностроении сопряжены с необходимостью измерения разнообразных физических величин: геометрических (линейных размеров
5
и углов, макро- и микроотклонений формы); кинематических (скоростей, ускорений, частот, параметров вибрационных процессов); силовых и энергетических (усилий, давлений, мощностей); тепловых (температур и теплофизических констант); технологических (параметров обрабатываемости резанием).
Кроме того, при исследовании технологических процессов и конструкций в машиностроении необходима экспериментальная оценка свойств машиностроительных материалов (прочности, твердости, износостойкости) и параметров их внутреннего строения (структуры, размеров зерна).
Виды измерений. В зависимости от характера изменения измеряемой величины во времени различают измерения статических величин и динамических величин.
По способу получения значения измеряемой величины измерения разделяют на прямые, косвенные, совокупные п совместные. При 'прямом измерении искомое значение величины находят непосредственно из опытных данных. Косвенным называют измерение, при котором значение величины определяют на основании известной зависимости между этой величиной и величинами, которые подвергаются прямым измерениям (например, определение плотности однородного тела по измеренной массе, когда известны его геометрические размеры). Измерения, при которых одновременно производится прямое измерение нескольких одноименных величин, а искомое значение физической величины находят решением системы уравнений (например, определение компонентов линейного ускорения полюса или углового ускорения твердого тела путем решения в реальном времени системы уравнений, аргументами которых являются сигналы прямолинейных акселерометров, установленных в различных точках этого тела), называются совокупными. Совместными называют одновременные измерения двух или нескольких неодноименных физических величин для нахождения зависимости между ними [10].
Средства измерений. Средство измерения — техническое устройство, используемое при измерениях и имеющее нормированные метрологические свойства [10].
Принцип измерения — совокупность физических явлений, на которых основаны измерения, а метод измерения — совокупность приемов использования принципов и средств измерения. В названиях методов обычно указываются только главные отличительные особенности метода, например принцип действия (электродинамический, оптический), либо прием использования (бесконтактный, уравновешивания), либо используемые средства измерения (электрические, пневматические).
Измерительные преобразователи — технические устройства, которые осуществляют преобразования величин и образуют канал передачи измерительной информации. При описании принципа действия измерительного устройства, включающего последовательный ряд измерительных преобразователей, часто представляют его в виде функциональной блок-схемы (измерительной цепи), на которой отражают функции отдельных его частей в виде символических блоков, связанных между собой.
Измерительные преобразователи можно условно разбить на три класса: пропорциональные, функциональные и операционные [13]. Первые предназначены для подобного воспроизведения входного сигнала в выходном сигнале; вторые —• для вычисления некоторой функции от входного сигнала; третьи — для получения выходного сигнала, являющегося решением некоторого дифференциального уравнения. Операционные преобразователи являются инерционными, так как у них значение выходного сигнала в любой момент времени зависит не только от значения входного в тот же момент времени, но и от его значений в предшествующие моменты времени.
По характеру изменения входных и выходных сигналов во времени преобразователи делятся на непрерывные (аналоговые), непрерывно-дискретные, дискретно-непрерывные и дискретные.
1.2. МЕТОДЫ И СРЕДСТВА ИЗМЕРЕНИЯ ЛИНЕЙНЫХ РАЗМЕРОВ И УГЛОВ
1.2.1. Шкальные средства для ручного измерения
Эти средства предназначены для измерения длины, диаметров и углов методом сравнения со штриховой мерой (шкалой) или эталоном. Первый принцип реализован в штангенинструментах, микрометрических инструментах и угломерах типа УМ и УН. Для повышения точности отсчета в этих устройствах применяются нониусы. Допускаемая погрешность штангенинструментов ±0,05 мм, микрометров — ±0,004 мм, угломеров—±2'...±5'[74].
Второй принцип реализуется в рычажно-механических приборах (индикаторах часового типа, измерительных головках с рычажно-зубчатой передачей, пружинных головках). Эти приборы показывают на стрелочных шкалах отклонения измеряемого размера от известного размера эталона. Для повышения точности в них используются механо-механические измерительные преобразователи. Технические характеристики индикаторов и измерительных головок приведены в [74]. Погрешность данных средств измерения находится в пределах от 0,01 до 0,0001 мм.
1.2.2. Пневматические измерительные приборы
Пневматические приборы применяются для линейных измерений методом сравнения с эталоном. Они обеспечивают высокую точность и относительно небольшие затраты времени на измерения и позволяют их осуществлять бесконтактным и контактным методами.
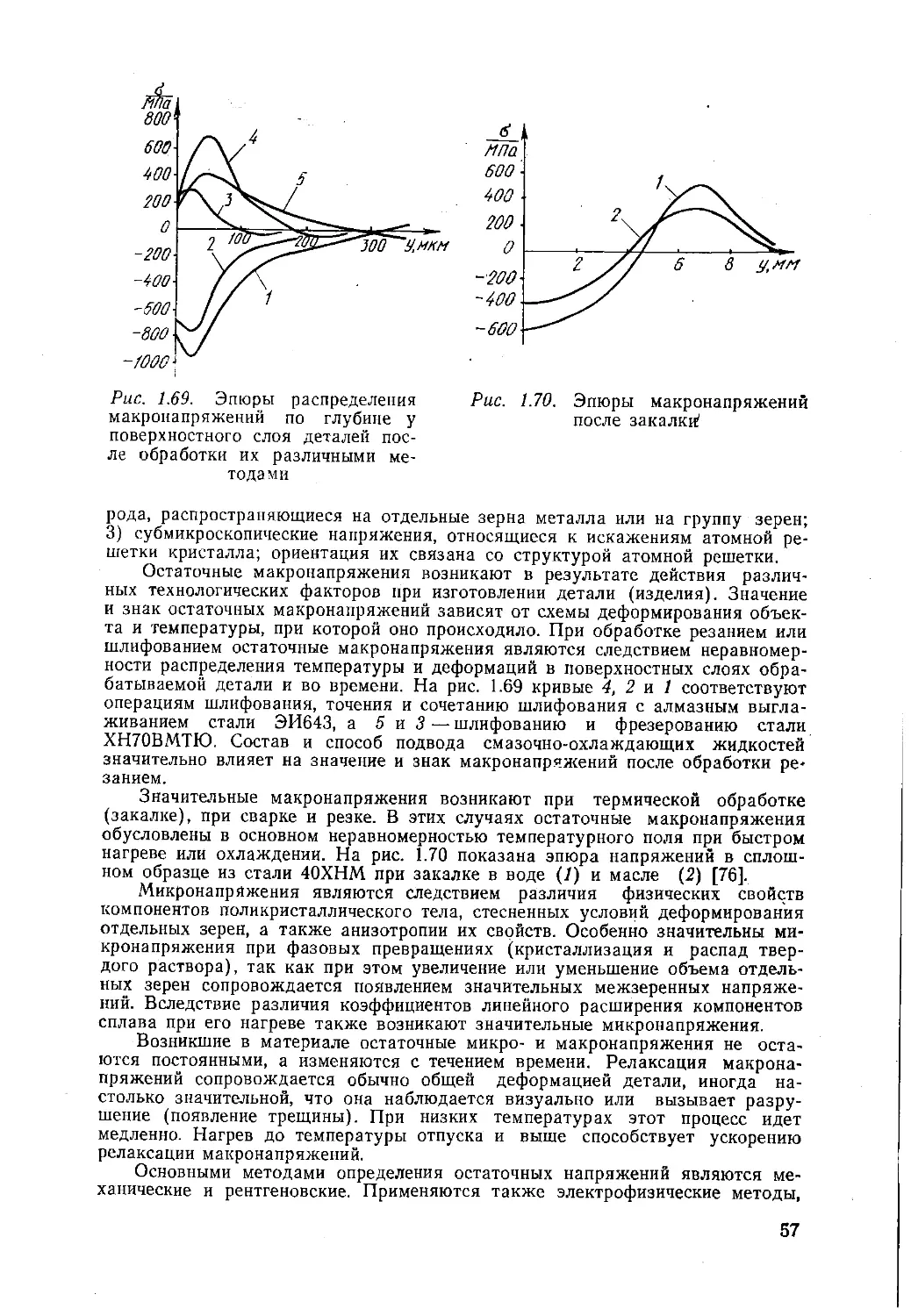
На рис. 1.1 показана блок-схема пневматического эжекторного прибора для бесконтактного измерения отклонения / размера измеряемого изделия 3 от эталона (обычно блока концевых мер). Сжатый воздух под постоянным избыточным давлением истекает из входного сопла 1 непосредственно в измерительное сопло 2 и далее через кольцевой зазор в атмосферу. Постоянство давления и чистота сжатого воздуха, подаваемого из источника 9, обеспечиваются стабилизатором давления 7 и фильтром очистки 8. Давление в измерительной камере 4 зависит от величины зазора I. Эта зависимость имеет значительный линейный участок (для сопла диаметром 1,75 мм при I от 0,190 до 0,600 мм). Давление при помощи измерительной схемы 5 преобразуется в сигнал, удобный для регистрации индикатором 6.
Наиболее совершенной является дифференциальная измерительная схема, в которой измерителем (жидкостным, сильфонным или мембранным манометром) определяется разность давлений в двух ветвях системы—рабочей
Рис. 1.2. Схема дифференциального пневматического эжекторного прибора для линейных измерений
Рис. 1.1. Блок-схема эжекторного прибора для измерения линейных размеров
7
и калибровочной (с регулируемым зазором /). Схема дифференциального пневматического эжекторного прибора для контактного измерения отклонения размера объекта показана на рис. 1.2. При изменении размера объекта 1 перемещением штока 2 с конической заслонкой изменяется величина кольцевого зазора в сопле рабочего пневматического преобразователя 3 и в его измерительной камере устанавливается давление pi, отличающееся от давления р2 в измерительной камере калибровочного пневматического преобразователя 4. Разность давлений (pi — р2) измеряется и преобразуется индикатором 6 в удобный для регистрации сигнал. Работа прибора обеспечивается стабилизированным источником сжатого воздуха 7. Для настройки на размер по эталону служит регулировочный винт 5. Цена деления шкалы пневматических длиномеров низкого давления составляет от 0,5 до 5 мкм. Разработаны пневматические приборы низкого и высокого давления с наименьшей ценой деления 0,1 мкм и широким диапазоном измерений [74]. Пневматические приборы позволяют осуществлять дистанционный контроль, а в сочетании с меха-ноэлектрическими измерительными преобразователями автоматизировать процесс регистрации результатов измерения.
1.2.3. Индуктивные приборы
Индуктивные приборы отличаются высокой точностью, пригодны для ведения дистанционных измерений, легко сочетаются с ЭВМ, что позволяет при необходимости автоматизировать процесс обработки результатов измерений.
В индуктивных преобразователях используется свойство катушки индуктивности изменять свое реактивное сопротивление при изменении некоторых ее параметров. Для этого один из элементов магнитной цепи (якорь) выполняется подвижным, и от его положения относительно неподвижной части зависит магнитное сопротивление цепи, а следовательно, и индуктивное сопротивление катушки. Перемещение якоря связывается с измеряемой линейной или угловой величиной, при этом изменяется или воздушный зазор, или площадь сечения воздушного зазора плоскостью, перпендикулярной к вектору магнитной индукции.
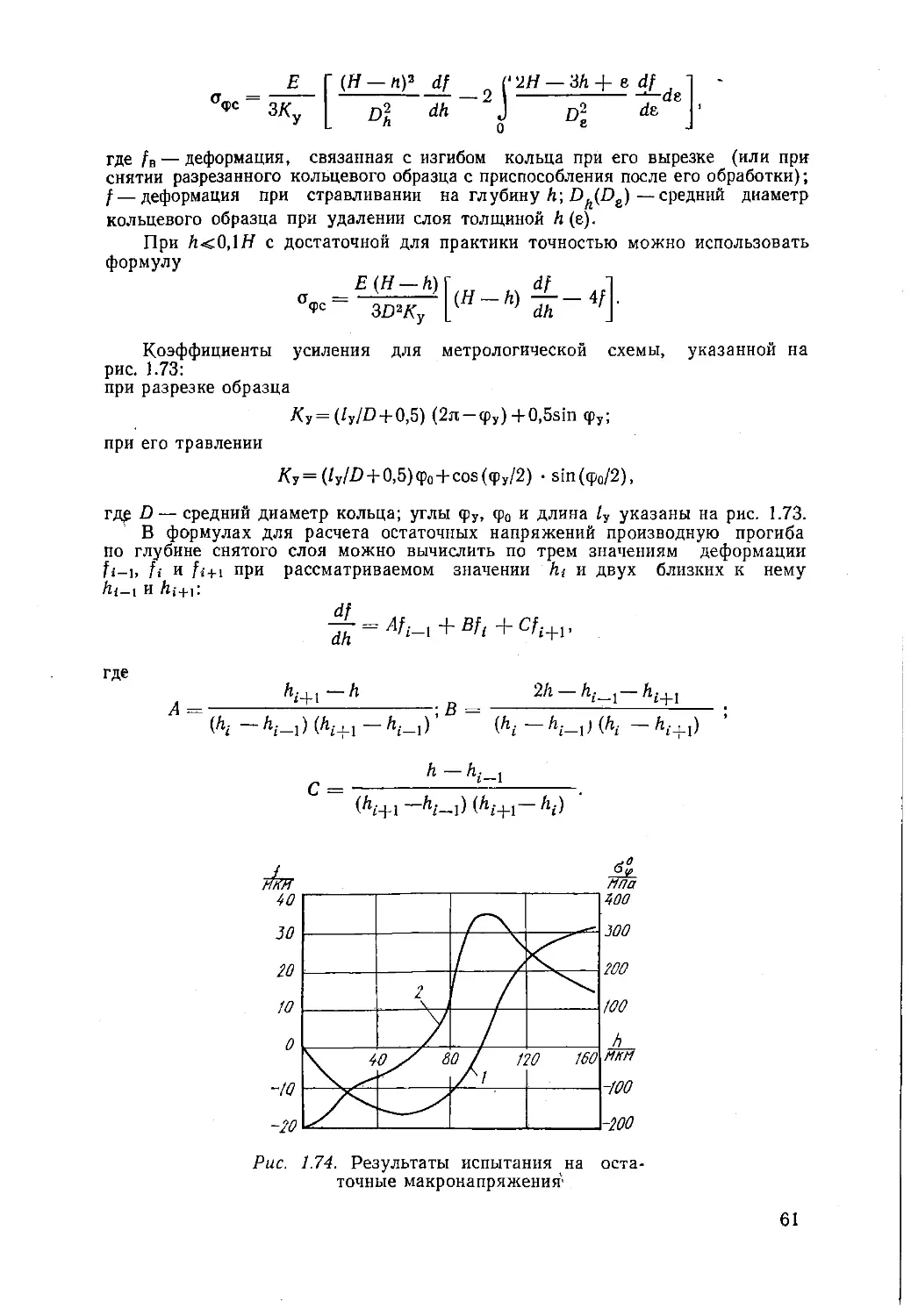
Для повышения чувствительности индуктивные преобразователи выполняются дифференциальными с подключением обеих катушек в измерительную (например, мостовую) схему. На рис. 1.3 показана схема индуктивного прибора с дифференциальным преобразователем. При воздействии объекта измерений 1 на шток 2 изменяются зазоры 6i и б2 между якорем 3 и магнитопроводами с катушками 4 и 5, которые подключены к мостовой измерительной схеме 6. Сигнал рассогласования через усилитель 7 подается на индикатор
Рис. 1.3. Схема индуктивного прибора с дифференциальным преобразователем
8
i-iLC. 1.4. Дифференциальные индуктивные преобразователи: а — соленоидного типа; б — трансформаторного типа!
(показывающее или записывающее устройство) 8. Для работы прибора необходим источник питания 9.
Индуктивные преобразователи с переменным зазором имеют нелинейную характеристику [16], поэтому диапазон измерения приборами с таким преобразователем невысок (0,1...0,3 мм). Индуктивные преобразователи с переменной площадью зазора имеют линейную характеристику, но относительно невысокую чувствительность. Их можно использовать для измерения больших отклонений линейных или угловых величин. Предпочтительно использование аналого-цифровых преобразователей в индикаторах.
Для измерения линейных или угловых величин со значительным диапазоном отклонений применяют индуктивные приборы с дифференциальным преобразователем соленоидного типа (рис. 1.4, а). Соленоидный преобразователь состоит из двух катушек 4 и 2, внутри которых помещен ферромагнитный сердечник (якорь) 3. При перемещении якоря вдоль оси катушек индуктивность последних изменяется. Характеристика соленоидного преобразователя линейна, а измерительные усилия незначительны. В существующих приборах с усилителями эти преобразователи позволяют получить цену деления от 0,05 до 1 мкм и пределы измерения от очень малых (±3 мкм) до относительно больших (±1,5 мм) [16].
В индуктивных трансформаторных преобразователях (рис. 1.4, б) используется зависимость индуктивной связи между катушками 5 и 7 от положения якоря 6. При симметричном расположении якоря ток в измерителе 8 равен нулю, так как первичные катушки 7 (и, аналогично, вторичные 5) одинаковы и включены последовательно. При перемещении якоря под действием объекта измерения 1 из среднего положения магнитные сопротивления, а следовательно, и магнитные потоки, пронизывающие вторичные катушки, будут неодинаковыми, и в измерителе появится сигнал, пропорциональный разности индуцированных во вторичных катушках э.д.с.
1.2.4. Механотроны
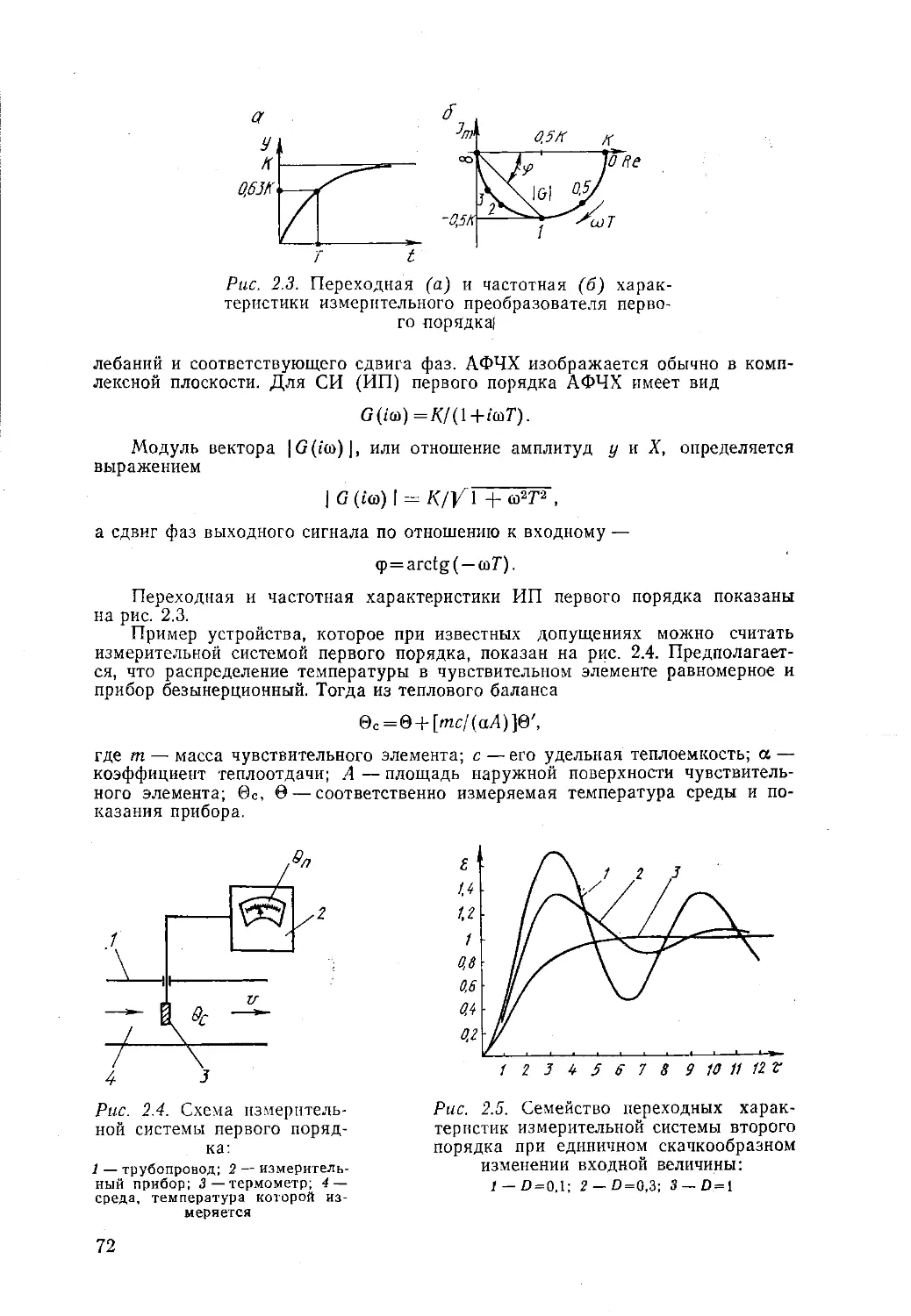
Механотрон (рис. 1.5) является измерительным преобразователем высокой чувствительности. Он представляет собой диод с подогреваемым катодом, причем расстояние 6 между катодом К и анодом А изменяется вследствие
9
Рис. 1.5. Схема механотрона
изменений измеряемого размера объекта 3 на величину бя. Перемещение аноду передается рычагом 2, закрепленным на мембране 1. Для повышения чувствительности применяют, как правило, двойные диоды. В этом случае уменьшается влияние колебаний питающего напряжения и температуры. Такие механотроны, включенные в мостовую измерительную схему, при относительно небольших габаритах (30X80 мм) имеют диапазон измерений ±0,1 мм, измерительное усилие ±100 мН и вариации показаний в пределах ±0,04 мкм [74].
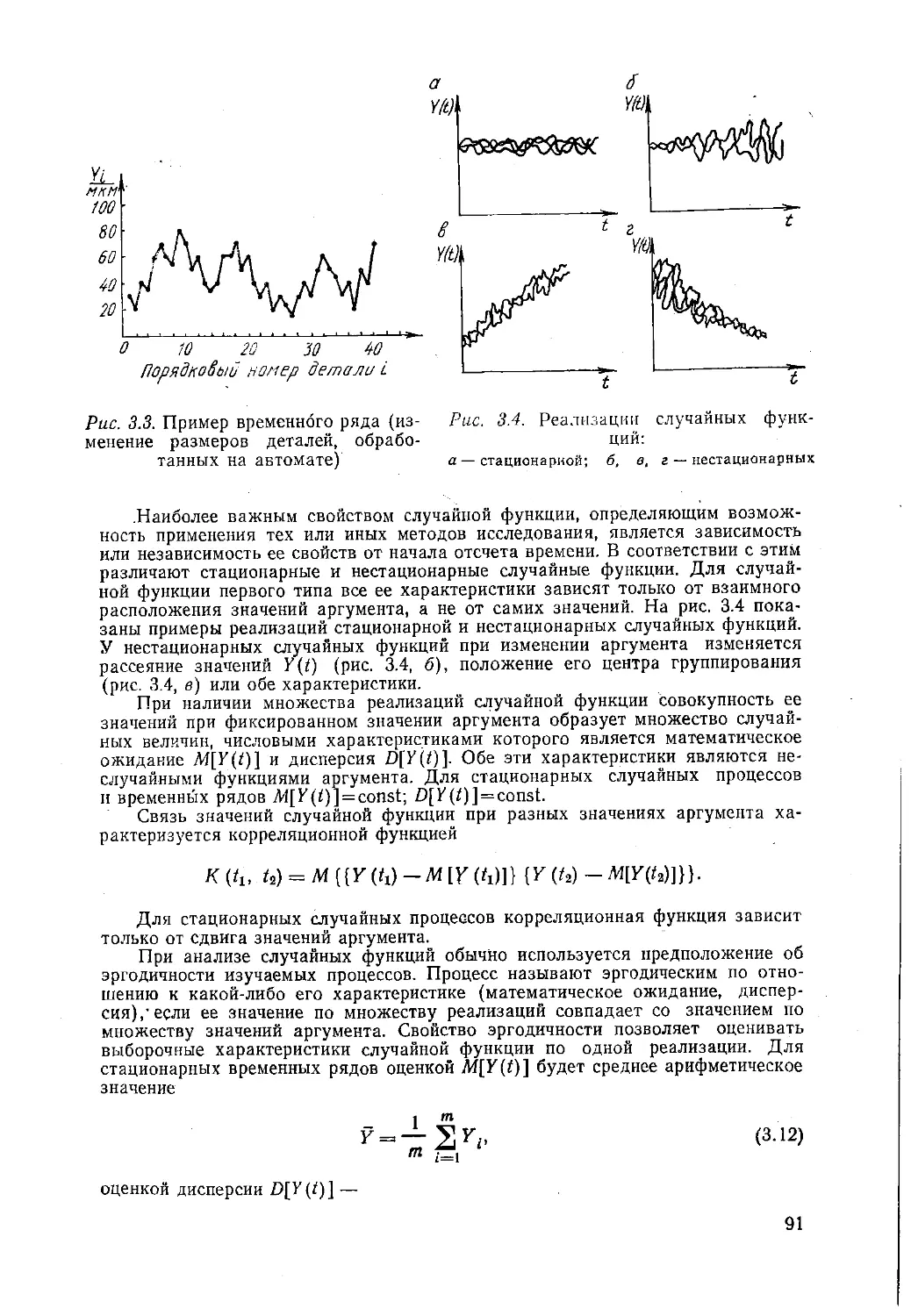
1.2.5. Оптико-механические и оптические приборы
Для контроля линейных и угловых величин применяются оптиметры, оптические длиномеры, измерительные микроскопы, катетометры, делительные головки и столы, интерферометры.
Оптиметры работают по принципу оптического рычага. При перемещении измерительного наконечника изображение шкалы с ценой деления 1 мкм, наблюдаемое в окуляр, смещается относительно неподвижного индекса. В оптических длиномерах для повышения точности отсчета применяется окулярный спиральный микрометр.
Измерительные микроскопы предназначены для измерения в прямоугольных и полярных координатах линейных и угловых размеров резьбовых изделий, режущего инструмента, профильных шаблонов и других изделий, а также расстояний между осями отверстий и т. п. В большинстве микроскопов используется проекционный метод измерения (в проходящем и отраженном свете), метод осевого сечения (с помощью измерительных ножей) или контактный способ. Измеряемая деталь может базироваться в центрах или на стекле стола. Цена деления шкал микроскопов: отсчетной системы измерения длины — от 0,005 до 0,001 мм, угломерной головки — 1', нониуса круглого стола — от 30" до 5' [74].
Катетометры применяются для измерения линейных размеров изделий, не доступных для непосредственного измерения. Визирная труба последовательно наводится на начало и конец измеряемого отрезка. Перемещение трубы, определяемое на шкале с помощью нониуса или микроскопа, равно длине измеряемого отрезка.
Для измерения центральных углов и длины в полярных координатах применяются оптические делительные головки. Цена деления у них от 2" до Г. Измеряемые объекты крепятся в шпинделе головки или в центрах. Для тех же целей, что и делительные головки, применяют оптические делительные столы. Цена деления отсчетной шкалы у делительных столов от 1' до 20". Роль фиксатора при измерениях углов выполняют индикаторы часового типа, измерительные головки или автоколлиматоры.
Из всех источников излучения оптического диапазона газовые лазеры характеризуются наибольшей степенью когерентности и монохроматичности генерируемого ими излучения. Кроме того, газовые лазеры могут длительное время работать при комнатной температуре без специальных устройств охла-
10
No original page
No original page
a
Рис. 1.8. Эхо-импульсный толщиномер: а — блок-схема; б — схема совмещенного пьезоэлектрического искателя
Из известных методов акустического контроля для измерений толщин применяют эхо-метод и реже резонансный метод. В первом случае измеряется время прохождения ультразвукового импульса через слой, толщийу которого измеряют, или амплитуда и фаза отраженных колебаний. Во втором измерение толщины основано на явлении резонанса в контролируемом изделии или других интерференционных явлениях при прохождении акустических волн.
Эхо-импульсные толщиномеры применяются для измерения изделий с чисто обработанными параллельными поверхностями (группа А) и грубо обработанными непараллельными поверхностями (группа Б). Минимальная толщина плоских изделий (или стенок), измеряемая приборами группы А, составляет 0,2...0,3 мм при абсолютной погрешности измерения не более 10 мкм. Толщина измеряемых стенок труб должна быть не менее 1 мм. Минимальная толщина, измеряемая приборами группы В, составляет 1,2...1,5 мм при абсолютной погрешности измерения 0,1...0,2 мм. Максимальная измеряемая толщина — 20...100 мм.
Блок-схема эхо-импульсного толщиномера показана на рис. 1.8, а [60]. Импульс ультразвукового излучения генератора зондирующих импульсов, пройдя от искателя 1 путь /, отражается противоположной стороной стенки изделия //и возвращается в искатель 1, откуда передается в приемник 2. Усилитель 3 передает отраженный сигнал в измерительный триггер 4, длительность импульса которого равна времени прохождения ультразвуковых волн в изделии. Для этого в триггер 4 поступает также сигнал от генератора развертки 7. Блок временной регулировки чувствительности 8 предназначен для уменьшения чувствительности приемника 2 в момент излучения зондирующего импульса и для восстановления ее. Блоки 7, 10 и 8 управляются синхронизатором 9. Он обеспечивает одновременный (или с задержкой на некоторое определенное время) запуск генераторов зондирующего импульса 10 и развертки 7. При измерении малых толщин длительность выходного импульса измерительного триггера слишком мала. Поэтому для повышения точности измерения используют блок умножения интервала 5. В блоке индикации 6 применяют стрелочные или цифровые индикаторы длительности импульса измерительного триггера, использующие преобразователь время — напряжение. Искатель 1 преобразовывает электромагнитные колебания в ультразвуковые, излучает ультразвуковые волны в изделие, принимает отраженные волны и преобразовывает их в электромагнитные.
Схема совмещенного пьезоэлектрического искателя приведена на рис. 1 8,6. Пьезопластина 16 приклеена или прижата к демпферу 15. Между пьезопластиной и изделием 11, в которое производится излучение, может располагаться несколько тонких промежуточных слоев — один или несколько протекторов 12 и прослойка смазочного материала 17. Искатель размещен в корпусе 14. Выводы 13 соединяют пьезопластину с генератором 10 и приемником 2.
13
Пьезопластина обычно имеет толщину, равную половине длины ультразвуковой волны в пьезоматериале. На противоположных поверхностях пластины располагаются металлические электроды для подвода переменных электрических зарядов. Демпфер служит для гашения свободных колебаний пьезопластины, т. е. для получения коротких импульсов, а также для предупреждения механических повреждений пластин.
Протектор представляет собой пластинку толщиной 0,1...0,5 мм из кварца, сапфира или смолы с наполнителем, приклеенную к пьезоэлементу. Он служит для улучшения акустического контакта с изделием и защиты пьезоэлемента от абразивного изнашивания. Корпус обеспечивает экранировку пьезоэлемента и выводов от магнитных полей.
1.3. МЕТОДЫ И СРЕДСТВА ИЗМЕРЕНИЯ ОТКЛОНЕНИЙ ФОРМЫ И ШЕРОХОВАТОСТИ ПОВЕРХНОСТИ
1.3.1. Измерение непрямолинейности и неплосностности
Измерения производятся при помощи поверочных линеек и плит, механических, индуктивных и оптических приборов.
Для проверки плоскостности «на краску» используют поверочные л и н е й к И’ и плиты. При этом линейку или плиту, покрытую тонким слоем краски (смесь берлинской лазури или турунбулевой сини с машинным маслом), перемещают по проверяемой поверхности. Отклонение от плоскостности определяют по числу пятен краски в квадрате со стороной 25 мм, оставшихся на выступах проверяемой поверхности (погрешность проверки — 3...5 мкм):
Число пятен в квадрате 25X25 мм Степень точности проверяемых поверхностей
Свыше 20 до 30 3...4
Свыше 12 до 20 5...6
Свыше 5 до 12 7...S*
До 5 9...10
К механическим приборам для измерения неплоскостности можно отнести уровни, карусельные плоскомеры и накладные плоскомеры.
Карусельный плоскомер завода «Калибр» (рис. 1.9) состоит из стойки 3, вокруг которой поворачивается кронштейн 2 с измерительной головкой 1. При помощи винтов 4 прибор устанавливается так, чтобы показания измерительной головки были одинаковы в трех точках проверяемой поверх-
Рис. 1.9. Схема карусельного плоскомера
14
5,
Рис. 1.10. Накладной плоскомер
ности, не лежащих на одной прямой. По этим точкам измерительная головка устанавливается на нуль, и затем определяются отклонения в других точках поверхности [74].
Накладной плоскомер (рис. 1.10) имеет двухступенчатые само-устанавливающиеся опоры 3, каждая из которых опирается на два качающихся балансира 2. Перемещая плоскомер по проверяемой плоскости 1 и замеряя отклонения в равноотстоящих точках при помощи измерительной головки 5, установленной в штанге 4, можно получить 25...50 результатов измерений для их гармонического анализа на ЭВМ, который позволит описать профиль поверхности рядом Фурье, начиная со второй гармоники до любой N-Й [18].
Схема измерения непрямолинейности и неплоскостности при помощи эталонной линейки и двух индуктивных преобразователей показана на рис. 1.11. Линейка 2 устанавливается на двух опорах 1. Индуктивные преобразователи 5 крепятся к каретке 7, которую перемещают по контролируемой поверхности, и подключаются к измерительной схеме 4. Определяется полусумма или разность измеренных отклонений. Результаты записываются самописцем 3. Устройство работает от источника питания 6.
Для измерения непрямолинейности применяют также линейки с одним индуктивным преобразователем [74].
Схема способа измерения непрямолинейности при помощи автоколлиматора приведена на рис. 1.12. Автоколлиматор 6 устанавливается рядом с проверяемой поверхностью 1 на подставке 8 и выверяется при помощи винтов 7 так, чтобы его ось была перпендикулярна к плоскости зеркала 3 и находилась на одной высоте с центром этого зеркала. Выверка производится при двух крайних положениях каретки 2. При этом разница в отсчетах не должна превышать 20". Для контроля каретка с зеркалом последовательно перемещается из одного крайнего положения в другое с шагом, равным h. Вследствие непрямолинейности поверхности наклон зеркала изменяется при каждом перемещении и отраженный луч смещается. Это смещение можно изме
Рис. 1.11. Схема измерения непрямолинейности с помощью эталонной линейки
Рис. 1.12. Схема измерения непрямолинейности с помощью автоколлиматора
15
рять при помощи окуляр-микрометра автоколлиматора или фотоэлектрического преобразователя. Полученный сигнал усиливается в измерительной схеме 5 и в аналоговой или цифровой форме выдается индикатором 4 [74].
Для измерения неплоскостности и непрямолинейности применяют также оптические линейки, принцип действия которых аналогичен описанному для прибора, показанного на рис. 1.11. Но в данном случае роль линейки играет луч света, и щуп с освещаемой маркой касается измеряемой поверхности. Отклонения изображения марки измеряют при помощи окуляр-микрометра или другого автоматически действующего преобразователя.
Непрямолинейность и неплоскостность небольших поверхностей высокой точности проверяются с помощью интерферометров [74].
1.3.2. Измерение некруглости
В современных приборах для измерения некруглости — кругломерах — используется принцип образцового вращения. Может вращаться как измерительный наконечник, так и измеряемая деталь. Биение шпинделей этих приборов не превышает 0,05...0,07 мкм. На рис. 1.13 показана схема прибора первого типа. Измеряемая деталь 1 закрепляется на призме 4 прихватом 2. При помощи крестового стола 3 ось детали совмещается с осью шпинделя 7, на котором закреплены направляющие 8 индукционного преобразователя 6. При вращении шпинделя деталь ощупывается по окружности наконечником 5. Увеличенные в 103...104 раз перемещения наконечника записываются в полярной системе координат на бумажном диске (круглограмме). Круглограмма позволяет определять отклонения формы детали от прилегающей окружности. На кругломерах можно также измерять непрямолинейность наружных или внутренних образующих цилиндрических деталей и неплоскостность торцов. Для этого используется прямолинейное движение бабки со шпинделем по направляющим 9.
Некруглость можно также измерять с помощью измерительных головок при установке проверяемой детали в центрах делительной головки или в призме (рис. 1.14, а). Однако при установке и вращении измеряемой детали в призме показания измерительной головки зависят не только от отклонения от круглости, но и от соотношения числа выступов и впадин на детали и угла призмы. Чтобы уменьшить возникающую при этом погрешность измерения, реко
Рис. 1.13. Схема измерения некруглости методом образцового вращения
Рис. 1.14. Схемы измерения некруглости:
а — в призме; б — в самоустанавливающей-ся многозвенной призме
16
мендуется применять самоустанавливающиеся многозвенные призмы (рис. 1.14, б). Отношения показаний (6) по шкале измерительной головки к двойной амплитуде (а) отклонения при угле призмы 90° в зависимости от номера гармоники п (если некруглую поверхность аппроксимировать рядом Фурье) следующие [74]:
л
Ь/а
2 3 4 5 67 8 9
1 2,06 0,04 2,08 1 0,06 2,41 0,06
1.3.3. Измерение параметров шероховатости
Методы измерения параметров шероховатости поверхности можно разделить на контактные и бесконтактные. Приборы, реализующие контактные методы (щуповые): профилометры, непосредственно показывающие среднее арифметическое отклонение профиля поверхности Ra-, профилографы, записывающие профиль поверхности; профилографы-профилометры.
Блок-схема прибора, использующего щуповой метод, показана на рис. 1.15. В процессе измерения поверхность детали 1 ощупывается алмазной иглой 3, закрепленной на рычаге 4, колебания которого при помощи индуктивного или механотронного преобразователя 5 превращаются в электрические. В измерительной схеме 7 эти сигналы усиливаются, интегрируются по перемещению и передаются на индикатор 8, градуированный в значениях 7?а, или (без интегрирования) на записывающее устройство 9. Необходимое для измерения перемещение сообщается протяжным механизмом 6. При этом корпус преобразователя, шарнирно связанный с узлом 6, опирается на поверхность детали дополнительной опорой 2, ширина которой достаточна, чтобы не реагировать на микронеровности детали.
Радиус ощупывающей иглы — от 2 до 12 мкм. Скользя по поверхности, она изнашивается и тупится. Кроме того, при сканировании возможны отскоки иглы и пластические деформации микронеровностей. Все это приводит к большим погрешностям при измерениях (в среднем ±10%). Чем меньше Ra, тем менее достоверна информация о реальном профиле, получаемая с помощью щупового прибора.
Наибольшее распространение из бесконтактных методов получили методы светового сечения, теневой проекции и интерференционные методы. Принципиальная схема метода светового сечения показана на рис, 1.16, а. Через осветительную диафрагму 3 контролируемая поверхность 1 освещается узкой полоской света от источника 2. В поле зрения микрометра 4 видна картина, показанная на рис. 1.16, б. Высота микронеровностей измеряется от визирной линии 5 микрометром 4. Разность отсчетов при совмещении этой линии с верхним и нижним краем неровности считывается с микрометрического барабанчика и позволяет определять значения hi, необходимые для расчета Ra и Rz [74].
Рис. 1.15. Схема измерения параметров шероховатости методом ощупывания
17'
й
Рис. 1.16. Схема измерения параметров шероховатости методом светового сечения
Метод теневой проекции отличается от описанного тем, что граница между светом и тенью создается острием ножа.
При интерференционном методе измерения параметров шероховатости поверхность рассматривается в микроскоп. На изображении поверхности возникают интерференционные полосы, по искривлению которых судят о шероховатости. Метод предназначен для оценки параметров шероховатости чисто обработанных поверхностей с диапазоном изменения Ra от 0,02 до 0,16 мкм [74].
Основной недостаток оптических приборов — относительно большая трудоемкость измерения. Этого недостатка лишены методы измерения параметров шероховатости при помощи лазера. Наиболее точным и удобным из лазерных методов измерения является метод сдвига частоты излучения [29].
Блок-схема лазерного профилографа с устройством сдвига частоты излучения, работа которого основана на изменении оптической длины измерительного плеча интерферометра с постоянной скоростью, показана на рис. 1.17. Выходное излучение лазера 5 после прохождения телескопической системы 4 направляется на сканирующее устройство, перемещающее сфокусированное излучение лазера вдоль измеряемой поверхности с постоянной скоростью По. Сканирующее устройство состоит из кубика 3 с отражающей поверхностью и микрообъектива 2, позволяющего сфокусировать на измеряемой поверхности 1 лазерный пучок до 6...8 мкм. Отраженное от поверхности излучение приобретает доплеровский сдвиг частоты, пропорциональный вертикальной составляющей относительной скорости движения поверхности, которая определяется углом подъема освещенного элемента микропрофиля. После вторичного прохождения через сканирующее устройство и резонатор лазера отраженное излучение принимается фотоприемником 6. С выхода фотоприемника электри-
Рис. 1.17. Блок-схема лазерного профилографа
18
ческий сигнал после прохождения через амплитудный ограничитель 7 и узкополосный усилитель 8 поступает на частотный детектор 9. Выходной сигнал частотного детектора подается на интегрирующий усилитель 10, формирующий напряжение, пропорциональное мгновенному значению высот микронеровностей поверхности [29].
В лазерных профилографах применяют также метод последовательного преобразования фазы (рис. 1.18). Излучение лазера расщепляется на две части (1 и 2), которые фокусируются объективом 3 на исследуемую поверхность 4. Отраженные составляющие излучения снова собираются объективом и после фотоэлектронной обработки преобразуются в сигнал, пропорциональный разности длин оптических путей первого и второго луча. При движении исследуемой поверхности по координате х (или лучей относительно поверхности) и постоянном расстоянии получаемый сигнал пропорционален скорости приращения координаты у. После интегрирования данного сигнала на выходе образуются сигналы, пропорциональные координате у профиля поверхности [30].
Рис. 1.18. Схема измерения параметров шероховатости методом последовательного преобразования фазы
1.4. МЕТОДЫ И СРЕДСТВА ИЗМЕРЕНИЯ ПАРАМЕТРОВ ДВИЖЕНИЯ
1.4.1. Измерение скоростей движения
Для измерения частоты вращения вала машины используются тахометры различных типов. Наиболее простой конструкцией отличаются механические тахометры. Характерным для них является то, что прибор потребляет энергию от самого объекта измерения, а показание получается непосредственно у места измерения или на небольшом расстоянии от него. По физическому принципу, положенному в основу измерения, различают центробежные тахометры и тахометры на вихревых токах.
В центробежных тахометрах вращающийся маятник отклоняется под действием центробежной силы и через рычажную передачу приводит в движение стрелочный механизм. Отклонение стрелки является мерой частоты вращения. Погрешность измерения составляет +0,5%.
Тахометр на вихревых токах имеет вращающийся постоянный магнит, поле которого возбуждает вихревые токи в алюминиевом диске, соединенном с указателем. Возникающий при этом вращающий момент пропорционален частоте вращения магнита, и указатель перемещается до тех пор,, пока момент, создаваемый вихревыми токами, не уравновесится моментом, созданным пружиной возврата. Тахометры данного типа измеряют частоту вращения только в одном направлении. Погрешность измерения составляет ±1% [31].
Механические тахометры на вихревых токах могут измерять частоту вращения в пределах до 5000 об/мин, центробежные — 30...50 000 об/мин.
Для соединения с объектом измерения на входной вал ручного тахометра в зависимости от конкретных условий насаживаются различные поводки, па-пример, с резиновым заостренным наконечником 1 (рис. 1.19, а) или с обрезиненным ролцком 2 (рис. 1.19,6), наружный диаметр которого должен быть согласован с диаметром вала так, чтобы передаточное отношение соответствовало шкале тахометра.
Кроме ручных тахометров, для измерения частоты вращения применяют-
2* 19
Рис. 1.19. Способы соединения тахометра с объектом:
а — при помощи резинового наконечника /; б — при помощи обрезиненного ролика 2
ся также счетчики оборотов, указывающие число оборотов вала в течение заданного промежутка времени (3 или 6 с).
Значительно удобнее для автоматизации обработки измерительных сигналов электрические тахометры. К ним относятся и тахометры с тахогенераторами, которые, как и механические тахометры, связываются с объектом измерения. Тахогенераторы вырабатывают непрерывный сигнал, пропорциональный измеряемой частоте вращения, который может приниматься дистанционно [4].
Выходной характеристикой тахогенератора постоянного тока с независимым электромагнитным возбуждением (рис. 1.20) является зависимость напряжения ия на зажимах 2 якоря 3 от частоты вращения якоря при постоянном магнитном потоке возбуждения Фв и постоянном сопротивлении нагрузки в показывающем индикаторе 1.
Чаще применяются тахогенераторы переменного тока. Их достоинством является отсутствие подвижных токосъемных деталей (щеток). Погрешность измерения тахогенераторов не превышает 1% [4, 31].
Наилучшими эксплуатационными характеристиками обладают бесконтактные тахометры. Связь такого тахометра с объектом измерения осуществляется индукционным, магнитным или фотоэлектрическим способом. При работе с бесконтактным фотоэлектрическим тахометром (рис. 1.21) на вращающийся объект 1 наносится светлая метка (М), отражающая способность которой значительно больше, чем остальной части поверхности объекта, освещаемого светом от источника 2. Отраженные импульсы воспринимаются фотоприемником 3. Частота импульсов, пропорциональная частоте вращения объекта, воспринимается частотным детектором 4, вырабатывающим сигнал, который преобразуется в индикаторе 5 в удобную для восприятия форму [31, 68].
Тахометры используются также для измерения скорости линейного движения, которое при помощи зубчато-реечного или фрикционного зацепления
Рис. 1.20. Схема тахогенератора
Рис. 1.21. Схема бесконтактного фото электрического тахометра
20
превращается во вращательное. Для этой цели часто применяется обрезиненный ролик (см. рис. 1.19,6) и тахометр, шкала которого проградуирована непосредственно в единицах скорости [31].
1.4.2. Измерение характеристик механических колебаний
Под механическими колебаниями в данном случае будем понимать только периодическое изменение во времени параметров движения (перемещение, скорость, ускорение). Различают детерминированные и стохастические колебания. В последнем случае процесс описывается случайной функцией и является следствием случайной совокупности различных причин. Цель измерения характеристик механических колебаний — получение информации об амплитуде, частоте и фазе параметров движения. В случае измерения характеристик стохастических колебаний определяются статистические оценки параметров движения (дисперсия, среднее значение максимальных и минимальных отклонений, вероятность выбросов, корреляционные и спектральные функции).
В настоящее время для измерения характеристик вибраций в основном применяют электрические и оптические измерительные приборы, однако находят применение и механические (особенно для измерения относительно низкочастотных вибраций). Принцип действия механических приборов следующий. Колебания объекта измерения 5 (рис. 1.22) воспринимаются механическим щупом 4 и передаются пишущему перу 2, которое записывает процесс колебаний на движущейся с заданной скоростью ленте 1. Предельная измеряемая частота колебаний зависит от жесткости пружины 3 и приведенной массы щупа 4 с пером 2. Устройство привода ленты находится в корпусе 6. Нижняя предельная измеряемая частота 3...5 Гц, а максимальная не превышает 250 Гц [13].
В электрических приборах измерительная цепь состоит из измерительного преобразователя, воспринимающего механические колебания и преобразующего их в электрические сигналы, усилителя электрических сигналов (измерительной схемы) и регистрирующего прибора. Для осуществления избирательного измерения какого-либо из параметров вибраций измерительный сигнал подается на соответствующий анализатор.
Корпусу 6 измерительного преобразователя абсолютных виброперемещений (рис. 1.23), который крепится к объекту измерения /, сообщается движение последнего. При этом инерционный элемент 5, подвешенный на пружине 4, под действием сил инерции стремится сохранить состояние покоя. Однако на
Рис. 1.22. Схема измерения вибраций механическими приборами)
Рис. 1.23. Схема измерительного преобразователя абсолютных виброперемещений
21
него через пружину действует сила, определяемая движением объекта. Перемещение груза 5 под действием этой силы зависит от соотношения собственной частоты колебаний системы груз — пружина и измеряемой частоты вибраций. Демпфер 7 расширяет диапазон измеряемых частот вибраций. В данном преобразователе отношение измеряемой частоты колебаний к собственной частоте колебаний инерционного элемента обычно больше 1,5...2. Относительные перемещения инерционного элемента и корпуса измеряются при помощи индуктивного (или другого) преобразователя 3, который при помощи гибких проводов 2 подключается к измерительной схеме [13].
Кроме индуктивных, применяются электродинамические, электромагнитные и трансформаторные преобразователи. Измерительные преобразователи (акселерометры), сигнал которых пропорционален виброускорению, являются основным средством измерения характеристик вибраций. Их широкое распространение обусловлено тем, что именно акселерометры обладают наиболее высокими эксплуатационными качествами. Знание же виброускорений позволяет сравнительно просто определить другие кинематические характеристики.
Принцип действия акселерометров аналогичен принципу действия преобразователя абсолютных виброперемещений. Однако их максимальная рабочая частота ниже частоты собственных колебаний инерционного элемента. В этом случае сила инерции груза слишком мала, чтобы удерживать его в неподвижном состоянии, как это имеет место в преобразователях виброперемещений. Сила инерции вызывает отклонения груза по отношению к корпусу, пропорциональные квадрату частоты, т. е. прямо пропорциональные ускорению. Эти отклонения можно измерять встроенным преобразователем перемещений. Для получения возможно более широкого диапазона рабочих частот акселерометра частота его собственных колебаний должна быть по возможности высокой (масса груза небольшой, а пружина очень жесткой). Диапазон рабочих частот оптимально демпфированных акселерометров находится в пределах от О до 60 % частоты их собственных колебаний [13].
Наибольшее распространение получили пьезоэлектрические акселерометры (рис. 1.24). Корпус 5 крепится к изучаемому объекту. Силы инерции, действующие на инерционный элемент (груз) 4, воспринимаются пьезоэлементом 1, который может работать как на сжатие (рис. 1.24, а), так и на сдвиг (рис 1.24, б). В первом случае груз прижимается к пьезоэлементам при помощи крышки 3 и тарельчатой пружины 2.
Современные акселерометры могут измерять виброускорения от 10-3 до 105 м/с2 в диапазоне частот от 0,5 Гц до 50 кГц. Однако наиболее широко применяют акселерометры, рассчитанные на измерение ускорений до 104 м/с2
Рис. 1.24. Пьезоэлектрические акселерометры
22
Рис. 1.25. Схема бесконтактного вихретокового измерительного преобразователя относительных виброперемещений
с частотами до 10... 15 кГц. Основная погрешность измерений 2...10%. Масса некоторых акселерометров составляет десятые доли грамма [13].
Для уменьшения погрешностей измерения виброускорений высокой частоты необходимо резьбовое крепление акселерометра уплотнять клеем. Кабель следует закреплять, особенно в непосредственной близости от акселерометра. Чрезмерно высокая чувствительность прибора обусловливает увеличение нелинейных искажений. После первичного преобразователя рекомендуется включать фильтр, ограничивающий с обеих сторон рабочий диапазон частот.
В тензорезисторных акселерометрах инерционный элемент изгибает плоскую пружину, а проволочные тензорезисторы, наклеенные на пружину, изменяют свое сопротивление пропорционально ее деформации [13].
Во многих случаях хорошо себя зарекомендовали бесконтактные измерительные преобразователи относительных виброперемещений. Действие такого преобразователя (рис. 1.25) основано на том, что в находящемся в магнитном поле рабочей катушки 2 токопроводящем колеблющемся теле 1 (объекте измерения) возникают короткозамкнутые (вихревые) токи, отсасывающие энергию поля. Поэтому амплитуда переменного тока в рабочей катушке зависит от расстояния х до колеблющегося тела, электропроводности и магнитных свойств его материала. Катушка 3 установлена для температурной компенсации. Обе катушки изолированы от корпуса 6 изоляционными втулками 4 и 5 [13].
К бесконтактным относятся также оптические методы измерения параметров вибрации. В лазерном измерительном преобразова-
ние. 1.26. Блок-схема лазерного измерительного преобразователя виброскорости
23
Рис. 1.27. Схема лазерного прибора для измерения виброперемещений
теле виброскорости (рис. 1.26) излучение лазера 1, направляемое зеркалом 2 на поверхность колеблющегося объекта 10, модулируется по частоте в результате эффекта Допплера и попадает в интерферометр (обведен штриховой линией), где делится призмой 3 на два пучка, проходящих из-за несимметрии плеч разный путь. Первый пучок прямо идет к соединительной призме 4, а второй проходит более длинный путь от призмы 3 через зеркала 9 и 8. Соединяемые в призме 4 пучки создают интерференционную картину, перемещающуюся в результате изменения частоты отраженного излучения в ту или другую сторону. Щелевая диафрагма 5 ограничивает поле зрения фотопреобразователя 6 участком, меньшим по сравнению с расстоянием, между. интерференционными полосами, что позволяет получать на выходе фототок, пропорциональный виброскорости объекта. Сигнал фотопреобразователя направляется в измерительную схему 7 для преобразования и индикации или регистрации.
Более совершенны интерферометры с преобразователями одночастотного излучения лазера в двухчастотное, так как в них легче осуществлять фильтрацию низкочастотных шумов фотоприемника и лазера [29].
Кроме описанных, для измерения параметров вибраций применяются также приборы с пространственным разделением и модуляцией излучения лазера. Работа таких систем (рис. 1.27) основана на пространственном смещении отраженного луча лазера 2, направленного под углом на колеблющийся объект 1. Это смещение, пропорциональное отклонению х объекта, обрабатывается позиционно-чувствительным фотоприемником 3 п измерительной схемой 4. В случае измерения медленных смещений к фотоприемнику подключается модулятор 5. Частота переменного напряжения модулятора в 5... 10 раз больше максимальной частоты колебаний объекта измерения. Исследования [29] показали, что минимальные значения вибросмещений, обнаруженные данным методом, составляют 0,5 мкм. Относительная погрешность измерений — 0,15...0,4%.
1.5. МЕТОДЫ И СРЕДСТВА ИЗМЕРЕНИЯ СИЛОВЫХ И ЭНЕРГЕТИЧЕСКИХ ВЕЛИЧИН
1.5.1. Измерение сил
Для измерения сил используют физические эффекты, в которых имеет место линейная зависимость между механической нагрузкой на чувствительный элемент преобразователя и другими величинами, например упругой деформацией, электрическим зарядом, магнитной проницаемостью и т. д. В большинстве методов используется линейная зависимость между силой и упругой деформацией пружинных элементов. Деформацию измеряют механическими или электрическими методами, описанными выше (см. § 1.2). Упругий элемент
24
вместе с приданными ему элементами (механическими, электрическими), выполняющими функции преобразования, образует преобразователь силы (динамометр).
Механические динамометры применяются преимущественно для единичных измерений постоянных сил в тех случаях, когда требования к точности сравнительно невелики. Пример простого механического динамометра показан на рис. 1.28. Под действием силы F скоба 1 деформируется. Упругая деформация измеряется индикатором часового типа 2. Установка прибора на нуль осуществляется при помощи винта 3 с контргайкой.
Среди электрических динамометров наибольшее распространение получили тензорезисторные, так как они пригодны для измерения сил в широком диапазоне значений (от 5 Н до 10 МН). Относительная погрешность измерения силы этими динамометрами зависит от качества измерительной схемы и может быть снижена до 0,03%.
На рис. 1.29, а показан тензорезисторный преобразователь больших сил электрического динамометра. Тензорезисторы 3 (рис. 1.29, б) наклеиваются на специально подготовленные места упругого элемента 1. Корпус 2 обеспечивает защиту тензорезисторов и закрепление выводных проводов. В данном случае упругий элемент работает на сжатие и его деформация передается проволочкам тензорезистора, активное сопротивление которых изменяется пропорционально этой деформации. Тензорезисторы включаются в измерительную (обычно мостовую или полумостовую) схему. Чтобы компенсировать влияние температуры на показания таких динамометров, применяют компенсирующие тензорезисторы, которые наклеиваются на ненагруженный элемент динамо-
Рис. 1.29. Тензорезисторный измерительный преобра зователь больших сил
25
Рис. 1.30. Тензорезистор-ный измерительный преобразователь небольших сил
Рис. 1.31. Мостовая схема включения тензорези-сторов
метра или перпендикулярно к направлению действия силы. Эти тензорезисто-ры позволяют также компенсировать сдвиг нуля, если они наклеиваются на деформируемую регулировочным винтом балочку.
Для измерения относительно небольших сил применяют чувствительные элементы, которые работают на изгиб (рис. 1.30). В этом случае тензорезисторы 1 и 4 работают на растяжение, а тензорезисторы 2 и 3 — на сжатие. При их включении в мостовую схему, как это показано на рис. 1.31, выходное напряжение
£/=0,25K(e2-ei + e3-e4)Hs = K7L/s,
где е,- — относительная деформация 1-го тензорезистора.
Как следует из этого выражения, данная мостовая схема при одинаковых тензорезисторах гарантирует сохранение стабильности показаний, поскольку при изменении температуры все изменения упругой деформации в тензорезисторах будут одного знака и поэтому компенсируются [5].
Тензорезисторные динамометры пригодны для измерения как постоянных, так и переменных сил. Вследствие большой жесткости эти динамометры отличаются достаточно высокой частотой собственных колебаний, которая может достигать нескольких килогерц. Для суммирования или вычитания отдельных сил можно включать в одно плечо моста несколько тензорезисторов, соединенных последовательно и (или) группами.
Достаточно широко применяются динамометры, где упругая деформация чувствительного элемента измеряется индуктивными измерительными преобразователями. Такие динамометры обладают высокой чувствительностью и обеспечивают погрешность измерения в пределах от 1 до 0,2%. С их помощью можно измерять силы от 10 мН до 20 кН. Однако температурная погрешность индуктивных динамометров несколько выше, чем тензорезисторных [5].
В настоящее время в промышленности широко используют магнитоупругие измерительные преобразователи силы, которые с успехом могут заменить тензорезисторы и индуктивные преобразователи. Магнитоупругие измерительные преобразователи при относительной простоте конструкции обладают высокой чувствительностью и надежностью. Они могут работать в самых тяжелых производственных условиях. Высокая жесткость магнитоупругих преобразователей соизмерима с жесткостью наиболее совершенных силоизмерительных преобразователей — пьезоэлектрических, но выходное сопротивление магнитоупругих преобразователей гораздо меньше, чем у пьезоэлектрических, что облегчает создание тракта передачи информации и согласование преобразователя с другими элементами измерительной системы [48].
26
Рис. 1.32. Магнитоупругие дроссельные измерительные преобразователи усилий-
У магнитоуиругих преобразователей возникающие в упругом элементе объемные напряжения, пропорциональные измеряемому усилию, обусловливают изменение магнитных свойств упругочувствительного элемента, воспринимаемое катушкой индуктивности. При этом можно использовать один из двух принципов: генераторный и параметрический [31].
В первом случае механическая нагрузка вызывает изменение остаточной индукции постоянного магнита (или индукции при неизменной напряженности поля в сердечнике), которое способствует появлению э.д.с. в измерительной обмотке. Во втором случае при механической нагрузке изменяется магнитное сопротивление в сердечнике, а следовательно, и индуктивное сопротивление обмотки, надетой на сердечник. Механическая нагрузка модулирует электрическую энергию постороннего источника сравнительно большой мощности, поэтому для магнйтоуиругих преобразователей типична большая мощность сигнала.
Генераторные магнитоупругие преобразователи применяются редко, а параметрические действуют с локализованным в пространстве или распределенным магнитным полем (анизотропные).
В магнитоуиругих дроссельных измерительных преобразователях сердечник чувствительного элемента I под действием усилия F сжимается (рис. 1.32, а). При этом изменяется его магнитная проницаемость (или индукция при данной напряженности магнитного поля), а следовательно, изменяется индуктивное сопротивление измерительной катушки 2. Магнитный поток замыкается через кожух 4, в котором смонтирован вывод 3 для проводов. В зависимости от конструкции преобразователя сердечник упругого элемента может иметь различную форму. Часто применяют сердечники из Ш-образных пластин, склеенных между собой. При этом уменьшаются потери на вихревые токи и существенно повышается рабочая частота преобразователя. Погрешность таких измерительных преобразователей не превышает 2,5% [31].
Основным недостатком магнитоупругих измерительных преобразователей является наличие начального выходного напряжения при отсутствии входного воздействия. Для компенсации начального сигнала применяют дифференциальные схемы. На рис. 1.32,6 показан дифференциальный дроссельный магнитоупругий преобразователь. Его чувствительный элемент 3 представляет собой два магнитопровода 2 и 1, соединенных последовательно. В среднем сечении элемента 3 имеется выступ, с помощью которого усилие передается на стакан 6. Упругие напряжения сжатия возникают только в верхнем магнитопроводе 2. Нижний магнитоировод 1 является элементом сравнения, в нем упругих напряжений не возникает. Преобразователь имеет две дроссельные обмотки 4 и 5, которые питаются от сети через регулировочные резисторы. Выпрямленное напряжение на выходе зависит от разности полных сопротивлений катушек 4 и 5 и представляет собой линейную функцию от силы F. Эта схема осуществляет также термокомпенсацию при изменении температуры
27
Рис. 1.33. Магнитоупругие трансформаторные измерительные преобразователи усилий: а — обычный; б — дифференциальный
окружающей среды. Суммарная погрешность преобразователя не превышает ±1 % [48, 31].
Если к дроссельному преобразователю добавить дополнительную обмотку, то он становится трансформаторным (рис. 1.33, а). Трансформаторный преобразователь позволяет легко согласовать его параметры с нагрузкой и разделить цепи питания. Для трансформаторных магнитоупругих измерительных преобразователей также применяют дифференциальную схему включения (рис. 1.33,6). Обмотки 5 являются намагничивающими, а 3 — измерительными. Стакан 4 воспринимает нагрузку, приложенную к элементу 1 и передаваемую втулкой 2, которая составляет часть нагруженного магнитопровода. При дифференциальной схеме существенно увеличивается протяженность линейной части характеристики. Такой преобразователь рассчитан на нагрузку до 5 • КУ* Н, основная погрешность измерений — ±2,5 % [5].
Особый класс составляют магнитоанизотропные трансформаторные преобразователи. Сердечник преобразователя (рис. 1.34, а) представляет собой пакет пластин из магнитоупругого материала, на диагоналях которых симметрично расположены четыре отверстия. В каждую пару отверстий укладывают обмотку. Плоскости обмоток располагают под углом 45° к направлению действия сил, сами обмотки взаимно перпендикулярны. Одна обмотка является намагничивающей, а вторая — измерительной. При возбуждении намагничи-
Рис. 1.34. Схема магнитоанизотропного трансформаторного преобразователя усилий
28
Рис. 1.35. Пьезоэлектрические измерительные преобразователи: а— для измерения переменных сил; 6 — постоянных
вающей обмотки в пакете пластин создается магнитное поле с индукцией В& (рис. 1.34,6), которое в центре пакета перпендикулярно к плоскости намагничивающей катушки и, следовательно, совпадает с плоскостью измерительной катушки. При этом э.д.с. в измерительной катушке не наводится. При сжатии пакета в направлении оси У условия намагничивания по осям X и У становятся различными, а составляющие индукции неодинаковыми. Поэтому результирующий вектор поворачивается на небольшой угол относительно своего первоначального положения. При этом появляется составляющая индукции Вя, перпендикулярная к плоскости измерительной обмотки и вызывающая в ней э.д.с., пропорциональную приложенной нагрузке. Такие преобразователи с успехом применяются для измерения больших усилий. При этом они- отличаются большей стабильностью и меньшей погрешностью (не более 1 %) по сравнению с дроссельными преобразователями. Однако в изготовлении магнитоанизотропные преобразователи сложнее дроссельных [5].
Для увеличения мощности выходного сигнала целесообразно применять многоэлементные преобразователи, в которых измерительные обмотки включены последовательно (напряжения в отдельных обмотках суммируются).
Пьезоэлектрические измерительные преобразователи применяют обычно для измерения динамических сил. На рис. 1.35, а приведена схема «измерительной шайбы». При ее нагружении силой вдоль оси на поверхностях кварцевых пластинок 1 и 4 появляется пропорциональный нагрузке электрический заряд. Элементы 3 и 6 шайбы создают предварительное нагружение пластинок за счет завальцовки, что необходимо для повышения жесткости преобразователя. Пластинки кварца прилегают друг к другу гранями противоположной полярности, т. е. они включены в электрическую цепь параллельно. Сигнал с электрода 2 снимается проводником через вывод 5 и при помощи усилителя с большим входным сопротивлением преобразуется в соответствующее электрическое напряжение [5]. Такой преобразователь позволяет измерять динамические силы высоких частот (до 100 кГц). Погрешность измерения не превышает 1%.
Для измерения статических и медленно, непериодически изменяющихся сил можно применять пьезоэлектрические резонаторы или пьезоэлектрические трансформаторы [78]. На рис. 1.35, б показана схема пьезоэлектрического трансформатора, который представляет собой пьезоэлемент 1 с тремя электродами 7, 3 и 6, образующими две системы. Часть пьезоэлектрического трансформатора, подключенную к источнику питания, называют возбудителем, а часть, подключенную к измерительной схеме 4,— генератором. В возбудителе переменный ток за счет обратного пьезоэффекта преобразуется в энергию акустических волн, которые, зарождаясь на границах электродов, распространяются по всему объему трансформатора.
29
В генераторе'механическое напряжение за счет прямого пьезоэффекта преобразуется в электрический сигнал. Пьезоэлемент с электродами помещен между демпфирующими прокладками 2 и 5. Под действием измеряемого усилия фактическая площадь упругого контакта между поверхностями пьезоэлемента и демпфирующих прокладок изменяется. Вследствие этого изменяются контактная жесткость системы и собственная частота преобразователя. Расчеты и эксперименты показывают, что входное напряжение генератора пропорционально фактической площади контакта пьезопластины с демпфирующими прокладками. Работа пьезоэлектрических трансформаторов может быть также основана на изменении резонансной частоты колебаний резонатора под действием измеряемого усилия.
1.5.2. Измерение крутящих моментов
Чаще всего крутящие моменты измеряют непосредственно на вращающихся объектах, что представляет определенные трудности. Кроме того, следует учитывать, что любая исследуемая установка представляет собой колебательную систему, и при измерении динамически изменяющегося крутящего момента измерительный преобразователь, действующий как торсионная пружина, может изменить колебательные характеристики всей установки [48, 31].
Простейшими измерительными преобразователями крутящего момента являются механические, действующие по принципу измерения реакций опор. Пример такого преобразователя показан на рис. 1.36. Под действием движущего момента М и момента сопротивления Мс в опорах шестерни 3 возникает реакция R, пропорциональная измеряемому моменту М«МС. Рычаг 1, в котором расположены опоры шестерни 3, опирается одним концом на динамометр 2, что позволяет измерить крутящий момент. Подобные преобразователи применяются главным образом в стендах, предназначенных специально для измерения крутящих моментов. ,
На рис. 1.37 показана принципиальная схема тензорезисторного преобразователя крутящего момента. Такие преобразователи имеют широкий диапазон измерения (от 10 Н-м до 50 кН-м). Важнейшей частью преобразователя является цилиндрический чувствительный элемент 7, который закручивается под действием приложенного к нему момента. Возникающие при этом деформации (или напряжение сдвига) служат мерой крутящего момента. Эти деформации воспринимаются тензорезисторами 3, которые приклеивают к чувствительному элементу под углом 45° к его продольной оси и включают в мостовую измерительную схему через контактные кольца 2 и съемные щетки б, поджимаемые к кольцам пружинами 5. Токосъемные
Рис. 1.36. Механический преобразователь крутящего момента
30
Рис. 1.37. Тензорезисторный измери- Рис. 1.38. Бесконтактный индуктивный тельный преобразователь крутящего измерительный преобразователь кру-момента тящего момента1
щетки монтируются в неподвижном корпусе 4, который иногда связывают с валом 1 подшипниками. Контактная схема питания тензорезисторов и съема сигнала дает значительные погрешности особенно при больших скоростях вращения. Тензорезисторные измерительные преобразователи крутящего момента с бесконтактным съемом сигнала имеют довольно сложную конструкцию. При этом на торсионе 7, кроме тензорезисторов, необходимо разместить элемент индуктивной передачи (катушки), блок выпрямления и стабилизации, преобразователь напряжения в частоту вращения и элемент емкостной связи [68].
Более простыми являются бесконтактные индуктивные измерительные преобразователи крутящего момента (рис. 1.38). Преобразователь состоит из ротора и статора. Ротор представляет собой торсионный вал 6, к которому при помощи трех дисков 7 из немагнитной стали крепятся три цилиндра 3, 1 и 5 из мягкой магнитной стали. Эти цилиндры являются частями магнитопроводов, разъединенными зазорами и б2 между косыми зубцами. При нагрузке крутящим моментом цилиндры 1 и 5 смещаются относительно цилиндра 3 и при этом один из зазоров увеличивается (б2), а другой уменьшается, за счет чего изменяется магнитное сопротивление магнитопровода (пропорционально приложенному крутящему моменту и соответственному изменению сопротивления цепи измерительных катушек 2 и 4). Эти катушки соединены между собой по дифференциальной схеме. Точность измерения момента зависит от точности изготовления, сборки преобразователя и составляет 1...2%.
Лучшими эксплуатационными характеристиками обладают магнитоупругие измерительные преобразователи момента. Они обеспечивают измерения в широком диапазоне частот вращения вала (до 6000 об/мин) с точностью ±0,25%. Диапазон измерений ограничивается в основном механическими свойствами чувствительного элемента, а не характеристиками преобразователя. В общем случае магнитоупругие измерительные преобразователи имеют две системы: возбуждения, создающую внешний поток энергии, и измерительную, регистрирующую изменение направления легкого намагничивания или соответствующее ему изменение магнитной проницаемости при определенной ориентации поля упругих напряжений.
При нагружении валов крутящим моментом наибольшие напряжения возникают на поверхности вала по направлениям, составляющим угол 45° с образующей, и по которым, следовательно, будет иметь место и наибольшее изменение магнитной проницаемости. Поскольку напряжения в двух взаимно перпендикулярных направлениях имеют различные знаки (растяжение и сжатие), то и наиболее эффективными будут дифференциальные измерительные схемы. Этот принцип использован в конструкции дифференциального магни-
31
Б~В
А -А
Рис. 1.39. Дифференциальный магнитоупругий измерительный преобразователь крутящего момента
тоупругого измерительного преобразователя (рис. 1.39), разработанного в Челябинском политехническом институте [48].
Внешнее магнитное поле создается катушками возбуждения 2, расположенными равномерно по окружности вала и соединенными встречно-последовательно так, что обеспечивается чередование магнитных полюсов. Вектор этого поля лежит в плоскости, перпендикулярной к оси вращения. При отсутствии нагрузки э.д.с., наводимые в обеих измерительных секциях 3, при изотропных магнитных свойствах материала чувствительного элемента будут равны. Если эти сигналы выпрямить и произвести их алгебраическое сложение, то выходной сигнал измерительного преобразователя будет равен нулю. После приложения крутящего момента происходит изменение сигнала в каждой из измерительных секций. При этом в секциях, расположенных над растянутыми волокнами, э.д.с. увеличивается, а в секциях над сжатыми волокнами — уменьшается. Выходной сигнал равен разности этих э.д.с. При изменении направления приложения нагрузки выходной сигнал изменяет знак. В схеме предусмот-
рим. 1.40. Схема фотоэлектрического измерительного преобразователя крутящего момента
32
рены потенциометры для установки нуля (для грубой и тонкой регулировки). Корпус 1 выполняется обычно из немагнитного материала.
На торсионном валу 1 фотоэлектрического измерительного преобразователя момента (рис. 1.40) закреплены диски 8 с радиальными прорезями. Эти диски вращаются вместе с валом. На статоре неподвижно укреплены: источник света 5, диафрагмы 3 и 6 с узкой щелью и фотоэлементы 2 и 7. Лампа помещена посередине между дисками. При отсутствии крутящего момента прорези правого и левого дисков могут одновременно открывать щели диафрагм, через которые освещаются оба фотоэлемента одновременно. И в данном случае фототоки обоих фотоэлементов будут совпадать по фазе. При приложении крутящего момента происходит сдвиг щелей и освещение обоих фотоэлементов будет неодновременным, вследствие чего их фототоки будут сдвинуты по фазе. При номинальном значении крутящего момента угол сдвига фаз между фототоками равен 180°. Измерительная схема 4 фотоэлектрического преобразователя осуществляет измерение времени между импульсами фототоков, пропорционального приложенному крутящему моменту [31, 39].
1.5.3. Измерение мощности
Между силой резания, температурой в зоне резания или другими показателями технологического процесса и мощностью на валу электродвигателя существует тесная функциональная связь. Поэтому по мощности, потребляемой электродвигателем, можно косвенно судить об уровне значений различных параметров технологического процесса. Например, между мощностью, потребляемой из сети двигателем АО2-52-4, и крутящим моментом на его валу существует зависимость
^=0,03^ + 0,93^ + 0,04,
где Ур = Р/Рн', М/М^, ? и ₽н— соответственно потребляемая и номинальная мощность; М и Л1Н — моменты на валу, соответствующие Р и Рн.
С погрешностью не более 0,4 % эту зависимость можно заменить линейной: ур = 0,036 + 0,96?^.
Мощность, потребляемая двигателем из сети, должна быть преобразована в сигнал, удобный для регистрации или индикации. Измерительный преобразователь мощности должен произвести перемножение мгновенных значений тока i и напряжения и, чтобы получить значение мгновенной мощности. Интегрированием находится средняя мощность:
т
Р = — = П/созф.
о
Наиболее часто используются измерительные преобразователи мощности (рис. 1.41), основанные на эффекте Холла [31]. Пластинка преобразователя 1 помещается в зазоре ферромагнитного сердечника 2, обмотка которого включена через добавочный резистор R1 на напряжение цепи. Магнитная индукция в зазоре является функцией мгновенного напряжения на зажимах электродвигателя. Одна пара электродов включена на напряжение, снимаемое с трансформатора тока 3, и поэтому через элемент Холла протекает ток, пропорциональный току статора двигателя. При этом напряжение, снимаемое со второй пары электродов, пропорционально произведению тока на напряжение, т. е. мощности. Блок 4 регулировки фазовых отношений в цепи преобразователя состоит из дросселя L и реостата R2. Такие преобразователи при простой конструкции имеют небольшие габариты и обладают хорошими динамическими характеристиками. Погрешность измерений не превышает 2,5%.
В станкостроении широко применяются преобразователи мощности, вклю-3. Зак. 1001 33
Рис. 1.41. Схема измерительного пре- Рис. 1.42. Схема измерительного преоб-образователя мощности, основанного разователя мощности на нелинейных на эффекте Холла" электрических элементах
чающие нелинейные электрические элементы с квадратичной вольт-амперной характеристикой (рис. 1.42). На вход преобразователя с помощью трансформатора тока 1 и трансформатора напряжения 4 подаются два напряжения, пропорциональные току и напряжению в цепи статора двигателя. Трансформатор напряжения имеет две вторичные обмотки, на которых образуются равные напряжения, сдвинутые по фазе на 180°. Благодаря этому на вход квадраторов 3 и 2 подаются сигналы, пропорциональные сумме и разности входных напряжений U] и и2. Выходные напряжения квадраторов вычитаются. Тогда, согласно тождеству (ui + u2)2—(ui~«2)2=4mi«2i выходной сигнал пропорционален произведению и на i, т. е. мгновенной мощности [48].
1.6. МЕТОДЫ И СРЕДСТВА ИЗМЕРЕНИЯ ТЕМПЕРАТУРЫ
1.6.1. Механические термометры
Механические термометры основаны на явлении теплового расширения тел. Эти тела могут быть твердыми, жидкими или газообразными. Механические термометры отличаются надежностью, точностью, низкой стоимостью и простотой обслуживания. Считывание показаний с них, как правило, осуществляется на месте измерения. Однако с помощью механоэлектрического или ме-ханогидравлического преобразователя можно передать сигнал на ограниченное расстояние.
В машиностроении применяют биметаллические, жидкостные п газовые термометры.
Чувствительный элемент биметаллических термометров изготавливается из пластины, состоящей из двух или более слоев разнородных металлов, сваренных между собой по всей плоскости соприкосновения. Пластина может быть предварительно деформирована. При нагреве биметаллической пластины из-за различия коэффициентов линейного расширения ее слоев возникает деформация изгиба, пропорциональная изменению температуры. На рис. 1.43 показаны наиболее распространенные конструктпвные исполнения чувствительных биметаллических элементов. Варианты а и б используются главным образом в качестве реле температуры, в к г — для непосредственного отсчета показаний термометров. Для этого один конец чувствительного элемента закрепляется, а второй соединяется с передаточным или непосредственно с показывающим устройством. Диапазон измерения биметаллических тер-
34
a 5
Рис. 1.43. Биметаллические измерительные преобразователи температуры
мометров лежит в интервале от —50 до 600 °C, причем от 500 до 660 °C термометр можно использовать только кратковременно. Погрешность измерения— от ±1 до ±3%.
В жидкостных термометрах измеряемой величиной, характеризующей температуру, является изменение объема термометрической жидкости. Термобаллон, в котором находится основная часть жидкости, изготавливается из стекла или стали. К термобаллону подключен капилляр диаметром 0,1... 0,2 мм. У стеклянного термометра капилляр находится рядом со шкалой непосредственного наблюдения. У жидкостных манометрических термометров капилляр подключен к манометру, показания которого пропорциональны температуре. Длина капилляра в таких термометрах может достигать 60 м. Чувствительный элемент, капилляр и указатель в них образуют замкнутую, неделимую, герметичную термосистему, которая монтируется и демонтируется только целиком. Диапазон измерения термометров зависит от свойств термометрической жидкости:
этиловый спирт ртуть в вакууме ртуть под давлением толуол
толуол под давлением
( — 110)...210 °C
(—30)...150 °C
(-30)...630 °C
( —90)...110°С
(-90) ...230 °C
Погрешности измерения температуры при помощи жидкостных механических термометров обусловлены различием температур жидкости в термобаллоне и в капилляре и зависят также от длины капилляра. Для повышения точности в жидкостных манометрических термометрах применяют компенсационный капилляр. Погрешность в таком случае уменьшается с ±2% до ±0,5% [31].
Основными недостатками механических термометров являются значительная инерционность и невозможность объединения с другими информационными сигналами для дальнейшей обработки. Поэтому в машиностроении температуру измеряют в основном термометрами, принцип действия которых основан на изменении электрических свойств веществ при изменении температуры.
з*
1.6.2. Электрические контактные термометры
Все виды электрических контактных термометров разделяются на две группы: термометры сопротивления, в которых с изменением температуры изменяется активное сопротивление чувствительного элемента, и термоэлектрические термометры (термопары), где при изменении температуры первичного преобразователя изменяется его термо-э.д.с.
У металлических проводников сопротивление обычно возрастает с повышением температуры, а у полупроводниковых — падает.
Чаще всего применяются платиновые или медные термометры сопротивления, каждый из которых обладает номинальным сопротивлением Ro при О °C в пределах от 1 до 500 Ом. При температурах выше 0 °C зависимость сопротивления платиновых термометров от температуры имеет вид
Rr=R0(l + АТ+ВТ*),
где /1 = 3,9685 • 10~3; В = — 5,847 • 10-7; Т — абсолютная температура, К.
Область применения технических платиновых термометров (—260)... 1100 °C.
Температурная зависимость сопротивления медных термометров
Rr =/?0 (1 + аТ), где a = 4,28 • 10-3.
Медные термометры могут работать в интервале температур от —50 до 200 °C.
В чувствительных элементах платиновых и медных термометров сопротивления тонкая проволока (0,05...0,1 мм) наматывается на каркас изоляционного материала, например кварца, либо проволочная спираль помещается в керамический каркас, а спираль заполняется изолирующим порошком и обеспечивается герметизация чувствительного элемента [31].
Полупроводниковые термометры сопротивления выпускаются для измерения температуры в диапазоне от —200 до 300 °C. Обычно каждый такой термометр требует индивидуальной градуировки. Зависимость сопротивления полупроводниковых термометров от температуры приближенно описывается выражением
Рис. 1.44. Схема измерительной цепи металлического термометра сопротивления
Rr = RoexpB(l/7’-l/T0), где RQ — сопротивление при эталонной температуре TQ; Ry — сопротивление при измеряемой температуре Т; В — параметр, зависящий от материала преобразователя (В = = 3000... 4000 К); Т — абсолютная температура объекта, К-
Хотя большая нелинейность характеристики преобразователя является нежелательной из-за усложнения измерительной схемы терморезисторов, тем не менее полупроводниковые термометры сопротивления получили распространение в лабораторной и производственной практике благодаря высокой чувствительности, простоте, прочности, транспортабельности и возможности использования без дополнительного усилителя. Поскольку сопротивление полупроводниковых термометров лежит в интервале от 1 кОм до 1 МОм, то можно пренебречь изменением сопротивления клемм и
36
соединительных проводов. Чувствительные элементы полупроводниковых термометров состоят главным образом из смесей окислов металлов, которые при высокой температуре сплавляются в форме маленьких пластинок, стерженьков или шариков. Благодаря малым размерам обеспечиваются хорошие динамические свойства таких термометров.
Для измерения сопротивления термометров используются автоматические мосты и логометры, питаемые постоянным, а иногда и переменным током. На рис. 1.44 показана схема измерительной цепи металлического термометра сопротивления с трехпроводной линией связи. Три плеча моста составляют манганиновые резисторы Rl, R2 и R3. Четвертое плечо состоит из преобразователя термометра RK и подгоночных резисторов (на схеме не показанных). Последовательное соединение каждого из подводящих проводов соответственно с резисторами R1 и R3 позволяет автоматически компенсировать влияние колебаний их температуры на результат измерения. Показания логометра, рамки которого 1 и 2 подключены к двум точкам моста непосредственно и к одной через резистор R4, пропорциональны изменению сопротивления первичного преобразователя температуры RK.
Погрешность металлических термометров сопротивления в зависимости от исполнения составляет от ±0,5% до ±3%, а у полупроводниковых 0,5%. За счет специального отбора и индивидуальной градуировки можно снизить погрешность полупроводниковых термометров сопротивления до ±0,01 °C [31].
Принцип действия термоэлектрического термометра (термопары) основан на термоэлектрическом явлении, в результате которого в цепи, состоящей из двух разнородных проводников, возникает термо-э.д.с., зависящая от температуры в местах соединений этих проводников. Для измерения температуры одно из соединений разнородных проводников (рабочие концы) помещают в среду, температуру которой измеряют, а температура другого соединения (свободных концов) известна. Термо-э.д.с. термоэлектрического термометра не изменится, если в его цепь будет включен третий проводник или измерительный прибор, и температура мест его соединения будет одинаковой.
Свободные концы термоэлектрического термометра нужно располагать в месте, удобном для стабилизации или измерения температуры. Для этого применяют удлиняющие (компенсационные) провода, которые присоединяют к термоэлектродам.
Зависимость между термо-э.д.с. и разностью температур рабочих и свободных концов в общем случае является нелинейной и может быть аппроксимирована уравнением третьей степени. Если сузить диапазон измеряемых температур, то характеристики многих термопар могут быть линеализированы без большого ущерба для точности измерений.
Зависимость термо-э.д.с. от измеряемой температуры для наиболее употребительных пар материалов, характеристики которых приведены в табл. 1.1, показана на рис. 1.45 (температура свободных концов 0°С).
Табл 1.1. Характеристики термоэлектрических преобразователей
Тип преобразователя Материал термоэлектродов Термоэлектроды Диапазон измеряемых температур (длительно), СС Предел кратковременного применения, ° С
положительные отрицательные
ТПП Платинородий — 10% Rh; 100% Pt 0...1300 1600
ТХА платина Хромель — алюмель 90% Pt Хромель Алюмель (—50).. .1000 1300
тхк Хромель — копель Хромель Копель (—50)... 600 800
37
Рис. 1.45. Характеристика наиболее употребительных термоэлектрических преобразователей:
1 — хомель — копель; 2 — железо — константан;
3 — хромель — алюмель; 4 — платинородий — платина
Рис. 46. Схема измерения температуры в зоне резания при помощи естественных термопар
Если контрольная температура свободных концов отличается от нуля и поддерживается равной, например 20 °C, то в замеренное значение термо-э.д.с. следует внести поправку, которая соответствует отклонению контрольной температуры t0 от 0 °C. Положительным считается тот электрод, от которого идет ток к спаю термопары при t>t0- При обозначении термопары на первом месте указывается материал положительного электрода. Кроме указанных в табл. 1.1, применяются также железоконстантановые (диапазон измерения ( — 250)... 700 °C) и медьконстантановые (от —250 до 400 °C) термоэлектрические преобразователи.
Погрешность измерения температуры составляет от 0,25 % для преобразователей типа ТПП и до 0,8 % для ТХА [31].
Кроме стандартных термоэлектрических термометров, в лабораторной практике и при исследованиях находят применение и нестандартные. Но все нестандартные средства измерения температур требуют индивидуальной градуировки.
На рис. 1.46 приведена схема измерения температуры в зоне резания при помощи так называемой однорезцовой и двухрезцовой естественной термопары. Переключение режимов работы производится трехпозиционным переключателем 5. Для однорезцовой термопары замыкаются контакты а — а или с — с. Тогда термо-э.д.с., образующаяся в месте контакта стружки из материала детали 1 и передней грани режущей пластинки резца 2 из стали Р18 (или резца 3 из твердого сплава Т15К6), измеряется, усиливается и регистрируется прибором 6. Для снятия термо-э.д.с. с вращающейся детали применяется ртутный токосъемник 7 с гибким вращающимся электродом. При замыкании контактов с — с образуется естественная двухрезцовая термопара Р18 — Т15К6. При замыкании контактов а — а необходима изоляция 4 резца и детали, а для двухрезцовой термопары достаточно изолировать только резцы. Но при двухрезцовой обработке трудно создать одинаковые температуры в зоне резания обоих резцов, поскольку их материалы обладают -разной теплопроводностью. Эксперименты показали [66], что различие в показаниях одно- и двухинструментных термопар составляет 7...9 % Правильное тарирование естественных термопар является важной проблемой, поскольку от его качества зависит достоверность результатов измерений. При тарировании желательно создать условия контакта, близкие к реальным, что особенно важно для инструмента, снабженного пластинками из твердых сплавов.
В ГДР предложен (патент 105662) способ комбинированного тарирования (рис. 1.47). Установка включает геометрически подобные резцы 1 (основ-38
Рис. 1.47. Схема комбинированного тарирования естественной термопары:
а — схема установки; б — тарировочный график
Рис. 1.48. Схема однорезцовой естественной термопары
ной) и 4 (вспомогательный), изготовленные из разных материалов. В схему входит токосъемник 3, переключатель 5 и измерительный прибор 6. Тарирование производят в несколько этапов. Вначале в патроне станка закрепляют образец 2 из сравнительно легкоплавкого материала, например алюминия, температура плавления £ которого известна. Переключатель 5 установлен в положение «К.2». Скорость резания плавно увеличивают до тех пор, пока в зоне резания материал обрабатываемого образца начинает плавиться. Э.д.с. термотока £i фиксируется измерительным прибором 6. Если предположить в первом приближении, что зависимость между Е и t линейна, а при /=0°С £=0, то можно построить тарировочный график 7 двухрезцовой термопары. Второй этап тарировки состоит в том, что в патрон станка устанавливают новый образец из испытываемого материала. При определенном режиме резания, используя двухрезцовую термопару, замеряют э.д.с. £2, по которой с помощью графика 7 определяют температуру в зоне резания tz- Затем вспомогательный резец отводится, а переключатель 5 ставится в положение «К1». Основной резец 1 продолжает резание в прежнем режиме, и на третьем этапе прибор фиксирует новое значение э.д.с. £3, измеренное новой однорезцовой естественной термопарой резец 1 — обрабатываемый материал. Это значение э.д.с. соответствует температуре tz, так как условия резания для резца 1 не изменились. Полученная таким образом точка С позволяет построить тарировочный график 8 для однорезцовой термопары.
На рис. 1.48 показана цепь однорезцовой естественной термопары, позволяющей снимать показания без специального токосъемника [66]. Для этого па заднюю грань резца 1 наносится изоляционный слой, а на него — токопроводящий слой 3. Э.д.с. естественной термопары, образующейся в процессе резания между инструментом 1 и деталью 2, регистрируется измерительным прибором постоянного тока 4.
Известен способ измерения температуры в зоне шлифования при помощи полуискусственной термопары (рис 1.49.), которая образована двумя частями 1 и 2 шлифуемого на плоскошлифовальном станке образца и тонкой копелевой проволочкой 3, изолированной от образца тонкими пластинками слюды 4 (0,02 мм). Расплющенный конец проволоки (рис. 1.49, б) защемляется между двумя половинками образца в верхней части клинового разъема. Спай образуется при шлифовании за счет пластического деформирования поверхностно-
39
Рис. 1.49. Схема измерения температуры в зоне шлифования при помощи полуискусственной термопары:
а — схема установки; б — схема заделки термоэлектрода; в — термоэлектрод
Рис. 1.50. Схема измерения температуры в зоне шлифования с термоэлектродом в круге
го слоя и выходящей на поверхность части проволоки. Сигнал через усилитель 6 попадает на регистрирующее устройство 5 (например, осциллограф).
Полуискусственная термопара может быть получена и при установке одного из проводников в шлифовальный инструмент (рис. 1.50). Между двумя плотно притертыми друг к другу половинками шлифовального круга 4 и 2 укладывается фольга 3 толщиной 0,01...0,05 мм, которая образует с деталью 1 полуискусственную термопару с тонким спаем, равным по длине ширине зоны шлифования (1.5...3 мм). Сигнал термопары, соответствующий средней температуре зоны контакта, через ртутный токосъемник 5 попадает в усилитель 6 и затем в регистрирующий прибор 7. Преимуществом такой термопары является непрерывность и устойчивость сигнала [66J.
1.6.3. Бесконтактные методы измерения температуры
Поверхность всякого нагретого тела испускает электромагнитное излучение. Приборы, которые могут по тепловому излучению определять температуру излучателя, называются пирометрами. При помощи оптики излучение на
40
гретого тела фокусируется и направляется на приемник. Различают следующие виды приемников теплового излучения: термопары, термометры сопротивления, фотоэлементы, фоторезисторы, фотодиоды и фототранзисторы. Чувствительность термопар и термометров сопротивления практически не зависит от длины волны, включая ультрафиолетовую и инфракрасную области излучения. Поэтому они пригодны для измерения сравнительно низких температур (до 1500°C). Остальные приемники излучения являются чувствительными только в узком спектральном интервале, их характеристики сильно зависят от длины волны. Но абсолютная чувствительность у них существенно больше, чем у термопар или термометров сопротивления.
Пирометрические оптические устройства создают изображение излучающей поверхности (или ее участка) на приемнике и тем самым делают измерение потока излучения в широком диапазоне независимым от расстояния до изучаемого объекта. Линзы ограничивают и неравномерно пропускают измеряемое излучение, коэффициент пропускания зависит от длины волны. Использование линз становится неприемлемым при измерении сравнительно низких температур, когда излучаются волны большой длины (инфракрасный диапазон). В этих случаях следует использовать вогнутые зеркала [31, 85].
Радиационные пирометры (пирометры полного излучения) — приборы, которые воспринимают излучение во всем спектральном диапазоне и преобразовывают его в соответствующий сигнал. Излучение (рис. 1.51) через защитную пленку 6, пропускающую инфракрасные лучи, попадает на сферическое зеркало 4, которое фокусирует его на теплоприемнике 5, представляющем собой звездообразную термобатарею из ряда последовательно соединенных V-образных хромель-копелевых или нихром-константановых термопар 2. Свободные концы термопар приварены к металлическим полоскам 1, которые приклеены к кольцу $ из слюды. Это кольцо закладывается между двумя такими же. Плоские рабочие концы термопар образуют венчик, зачерненный с одной стороны. На этот венчик фокусируется излучение.
С повышением измеряемой температуры растет погрешность измерения за счет влияния температуры кожуха. Для компенсации температурной погрешности термобатарея подключается к измерительному прибору 7 через ряд резисторов. Резисторы R2 и R1 выполняются из меди или никеля и располагаются возле концов термобатареи, остальные плечи моста выполнены
Рис. 1.51. Схема радиационного пирометра1
41
в виде резисторов из манганина. Мост компенсирует постоянную составляющую погрешности, а резистор R1, включенный параллельно термобатарее, компенсирует переменную составляющую, связанную с изменением температуры [85].
Для приборов с пределами измерений 400...1200 °C вместо сферического зеркала применяют линзы из кварцевого стекла, характеризующегося малым поглощением инфракрасных лучей.
Применение радиационных пирометров возможно лишь в тех случаях, когда полная мощность излучения объекта измерения мало отличается от полной мощности излучения абсолютно черного тела при той же температуре. Большинство закрытых печей и топок с небольшими отверстиями и окнами удовлетворяют этому условию.
В промышленности применяются также цветовые пирометры. В них определяется отношение интенсивностей излучения данного тела в лучах двух заранее выбранных длин волн. Это отношение для каждой температуры будет различным и вполне однозначным. Следовательно, оно может служить критерием абсолютной температуры тела. Цветовые пирометры применяются, как правило, с фотоэлементом, т. е. являются фотоэлектрическими пирометрами. Преимущества их перед радиационными: уменьшение погрешности, связанной с неполнотой излучения; независимость показаний от расстояния до излучающей поверхности и размеров последней.
Принцип действия фотоэлектрического цветового пирометра иллюстрируется на рис. 1.52. Излучение от объекта исследования 1 линзой 2 фокусируется на обтюраторе 3, который вращается синхронным электродвигателем 4, и затем воспринимается фотоэлементом 5. На диске обтюратора имеется ряд отверстий, половина которых закрыта красным светофильтром, а половина — синим. Таким образом, на фотоэлемент поочередно попадают то красные, то синие лучи. Кроме того, благодаря отверстиям фототок оказывается промодулированным с несущей частотой, определяемой числом отверстий в обтюраторе и частотой вращения последнего. Айодулирован-иый ток в нагрузке фотоэлемента через усилитель 6, который снабжен устройством 7 для автоматической регулировки чувствительности, поступает в фазочувствительный выпрямитель 8. После этого с помощью коммутатора 9 сигнал разделяется соответственно отношению интенсивностей красных и синих лучей и воспринимается измерителем отношения 10. Необходимость в регулировке чувствительности усилителя, т. е. в стабилизации выходного напряжения, обусловлена тем обстоятельством, что при повышении измеряемой температуры яркость излучения как в синей, так и в красной области спектра возрастает значительно сильнее, чем отношение этих яркостей. При надлежащем режиме работы фотоэлемента фотоэлектрические цветовые пирометры могут обеспечить измерение температуры с погрешностью, не превышающей 1 % [85].
Рис. 1.52. Схема фотоэлектрического цветового пирометра
42
1.6.4. Цветовые индикаторы температуры
Цветовые индикаторы температуры (термоиндикаторы) — это вещества, изменяющие свой цвет в зависимости от температуры. По принципу действия термоиндикаторы подразделяются на четыре основных типа: термохимические; плавления; жидкокристаллические; люминесцентные [1].
Термохимические индикаторы — сложные вещества, которые при достижении определенной температуры резко изменяют свой цвет за счет химического взаимодействия компонентов. Они обеспечивают точность измерения температуры в пределах от 5 до 10 °C.
Термоиндикаторы плавления изменяют цвет в результате плавления одного или нескольких их компонентов, имеющих строго определенную температуру плавления. Погрешность измерения температуры этими индикаторами составляет 0,5...1,5, реже 2,5%, что примерно соответствует точности измерения температуры наиболее распространенными измерительными приборами.
Жидкокристаллические термоиндикаторы — вещества, которые в определенном интервале температур переходят в жидкокристаллическое состояние, обладающие свойством при незначительном изменении температуры (иногда в пределах десятых долей градуса) так изменять свою структуру, что падающий на них луч света разлагается и отражается с изменением цвета.
Люминесцентные термоиндикаторы в зависимости от температуры изменяют либо яркость, либо цвет, либо цветовой тон излучения. Погрешность измерения температуры термоиндикаторами двух последних типов составляет 0,1...0,5%.
По способности к физико-химическим превращениям термоиндикаторы делятся на три группы: обратимые, необратимые и квазиобратимые. К обратимым относятся термоиндикаторы, которые, изменяя цвет после нагревания до или выше температуры перехода, восстанавливают первоначальный цвет при понижении температуры ниже критической. Такие термоиндикаторы можно использовать многократно. Необратимые индикаторы указанным свойством не обладают, и их первоначальный цвет после охлаждения не восстанавливается. Квазиобратимые термоиндикаторы восстанавливают первоначальный цвет при понижении температуры постепенно, под воздействием влаги, имеющейся в воздухе. Их также можно использовать многократно.
Термоиндикаторы плавления являются только необратимыми, а жидкокристаллические и люминесцентные — обратимыми. Термохимические индикаторы могут быть обратимыми, необратимыми и квазиобратимыми..
Ряд термоиндикаторов имеет один строго определенный температурный
Табл. 1.2. Характеристики необратимых термопигментов, однократно изменяющих цвет
Название и химическая формула Цвет до нагрева Температура перехода. °с Цвет после нагрева
Фторсиликат кобальта CoSiF6 Бледно-розовый 100 Ярко-розовый
Метаванадий аммония NH4VO3 Белый 150 Коричневый
Азотнокислый свинец Pb(NO3)2 Бесцветный 215 Красный
Кобальт щавелевокислый CoC2Oi Светло-красный 280 Черный
Карбонат кадмия CdCO3 Белый 360 Коричневый
Окись свинца РЬО Красный 489 Желтый
Сульфид кобальта CoS Серый 680 Красный
43
Табл. 1.3. Характеристики необратимых термопигментов, многократно изменяющих цвет
Название и химическая формула Цвет до нагрева Температура перехода, °C Цвет после нагрева
Кобальт-аммоний фосфорнокислый Пурпурный 140 Синий
NH4COPO4H2O 500 Серо-голубой
Тиосульфит натрия Na2S2O3 Бесцветный 300 Желтый
600 Темно-желтый
Пирофосфат марганца аммония Фиолетовый 320 Серый
NH4MnP2O7 480 Белый
Комплексное соединение Белый ПО Бледно-желтый
3(NH4)2OFe2O3- 12МоО3- 19Н2О 300 Черный
380 Темно-желтый
Смесь карбоната кадмия с серой Белый 275 Коричневый
2 части CdCO3 -|- 1 часть S 370 Черный
(по массе) 410 Кирпичный
переход, а другие-имеют их несколько. Термоиндикаторы плавления изменяют свой цвет однократно, остальные — многократно.
Серийно выпускаются термоиндикаторы трех типов: термохимические в виде краски и карандашей; термоиндикаторы плавления в виде краски; жидкокристаллические в виде порошка или его раствора в хлороформе.
Табл. 1.4. Характеристики термопигментов для индикаторов плавления
Название и химическая формула Цвет до нагрева Температура плавления, °C
Цинь; бромноватокислый Zn(BrO3)2 Бесцветный 100
Аммоний роданистый NH4SCN Бесцветный 149,6
Медь сернокислая CuSO4 Зеленовато-
белый 200
Натрий муравьинокислый NaHCOa Белый 283
Селен хлористый SeCl Бесцветный 305
Кадмий азотокйслый Cd(NO3)2 Бесцветный 350
Натрий сернокислый Na2S2O7 Белый 400,9
Перекись бария ВаО2 Бесцветный 450
Медь бромистая СиВг2 Черный 498
Калий рениевокислый KReO4 Белый 550
Железо иодистое FeJ2 Серый 592
Олово селенистое SnSe2 Белый 650
Литий молибденовокислый Ы2МоО2 Белый 705
Свинец кремнекислый PbSiO3 Бесцветный 766
Германий сернистый GeS2 Белый 800
Натрий углекислый Na2CO3 Белый 852
Кальций азотистый Ca2N2 Коричневый 900
Калий борнокислый К2ВгО4 Бесцветный 947
Железо мышьяковистое FeAs2 Серебряно-
серый 990
44
Табл. 1.5. Характеристики и состав многоступенчатых термокрасок
I Номер термо-1 краски 1 Цвет до нагрева Температура перехода, °C Цвет после нагрева Массовая доля компонентов, %
Термопигменты Наполнитель Связующее
хромпик ОКИСЬ железа углекислый кобальт свинцовый сурик гидрат окиси бария кварцевый песок углекис-. лый натрий жидкое стекло
1 Темно-оранжевый 500 Коричневый 3,5 1,5 1 — 36 25 11 22
600 Бежевый
700 Салатный
800 Зеленый
900 Темно-зеленый
2 Ярко-оранжевый 1000 300 Черный Оранжевый 6,5 — 1 6,5 33 23 10 20
400 Бежевый
500 Хаки
600 Салатный
700 Зеленый
800 Ярко-зеленый
В состав всех термоиндикаторов входят четыре компонента: термопигменты, связующие, растворители и наполнители. Термопигменты являются обязательной составной частью термоиндикаторов. Состав и характеристики некоторых термопигментов, входящих в состав термохимических необратимых индикаторов, приведены в табл. 1.2, 1.3, а термопигментов, входящих в состав термоиндикаторов плавления,— в табл. 1.4. Одни вещества из приведенных в табл. 1.4 при плавлении меняют лишь цветовой оттенок, другие резко изменяют цвет. В табл. 1.5 приведены характеристики нескольких многоступенчатых термокрасок.
Температура перехода термоиндикаторов зависит от условий нагрева. С увеличением скорости нагрева и давления она несколько увеличивается.
Термоиндикаторы наносятся на поверхность объекта исследования в виде тонкой пленки. В зависимости от способа подвода тепла к объекту температура индикатора несколько выше или ниже измеряемой. Но это различие незначительное.
1.7 МЕТОДЫ И СРЕДСТВА МЕХАНИЧЕСКИХ ИСПЫТАНИЙ
1.7.1. Испытания статическим нагружением
При статических испытаниях для определения характеристик прочности и пластичности исследуемый образец подвергается действию постоянной или медленно и плавно увеличивающейся нагрузки, что дает возможность измерять с достаточной точностью нагрузку, приложенную к образцу, и деформацию последнего в любой момент испытания. Наиболее распространенным является испытание на растяжение. При этом гладкий ненадрезанный образец растягивают в испытательной машине в направлении его оси до разрыва, а зависимость между растягивающей силой и изменением длины образца регистрируют в виде диаграммы «нагрузка — абсолютное удлинение». Если нагрузку F отнести к исходной площади поперечного сечения образца Ло, а удлинение Л/ — к начальной расчетной длине 1а, то получим диаграмму «напряжение — относительное удлинение» (рис 1.53).
На начальной стадии испытания относительное удлинение пропорцональ-но напряжению (до точки а). Этот участок диаграммы позволяет определить модуль упругости
т.2
Рис. 1.53. Диаграмма растяжения стали
где и, — масштаб напряжений, МПа/мм; т2 — масштаб относительных деформаций, мм-1; 0 — угол наклона прямолинейного участка диаграммы.
Предел упругости сгу является максимальным напряжением, при котором после разгрузки образца не наблюдаются остаточные пластические деформации. Точно определить этот параметр практически невозможно, поэтому техническим условным пределом упругости (cTo.oi) называют напряжение, при котором относительная остаточная деформация составляет 0,01 %.
При дальнейшем повышении нагрузки отмечается рост пластической деформации и для многих материалов на диаграмме можно выделить так называемую площадку текучести, когда деформация
46
увеличивается при постоянном напряжении. Соответствующее напряжение называют пределом текучести <гт. Для материалов без четко выраженной площадки текучести определяют условный предел текучести (а0,2), который соответствует относительной остаточной деформации 0,2 %.
При напряжениях, превышающих предел текучести, зависимость между деформациями и напряжениями нелинейна. Когда способность к деформированию образца исчерпана, наступает разрушение при нагрузке, соответствующей участку подъема кривой «напряжение — деформация», либо (у пластичных материалов) при деформации, соответствующей снижающемуся участку кривой на диаграмме растяжения. Максимальное условное напряжение — отношение максимальной растягивающей силы к начальной площади поперечного сечения образца — называют временным сопротивлением сп.
Испытания на растяжение позволяют также оценить пластические свойства материала, которые характеризуются обычно относительным удлинением после разрыва 6.
Аналогичные характеристики получают при испытании на сжатие, изгиб и кручение.
Для оценки поведения материала при повышенных температурах проводят испытания на длительную прочность — до тех пор, пока при данной температуре и нагрузке не будет достигнута максимальная остаточная деформация или произойдет разрушение образца.
При этих испытаниях определяют предел длительной прочности и предел ползучести. Пределом-длительной прочности называют максимальное (условное) напряжение, которое может выдержать образец без разрушения при данной температуре в течение неограниченно долгого времени. Предел ползучести при определенной температуре— максимальное (условное) напряжение, при котором скорость ползучести за определенное время испытания (25...35 ч) не превосходит 10-4 %/ч. При этом относительное остаточное удлинение не должно превышать 0,2% после 45 ч испытания под нагрузкой. Пределы прочности и ползучести определяют для сталей в интервале температур 350...700 °C.
1.7.2. Испытания ударной нагрузкой
Испытания на ударный изгиб позволяют оценить сопротивление хрупкому разрушению вязких материалов. Для этого стандартный образец (рис. 1.54,а), свободно установленный на опоры копра, разрушается за один удар тяжелого маятника по стороне, противоположной надрезу (рис. 1.54, б). Кроме U-образ-ного концентратора, показанного на рис. 1.54, применяются V-образные с углом раствора 45° и радиусом скругления 0,25 мм. Скорость маятникового копра в момент соударения зависит от угла падения а и обычно лежит в интервале 5...7 м/с.
Количественной характеристикой вязкости при ударном разрушении
Рис. 1.54. Испытание образца на ударную вязкость:
Д — образец; б — схема испытания1
Рис. 1.55. Зависимость ударной вязкости стали от температуры испытания
47
является отношение работы Ц7К, необходимой для разрушения образца, к площади его поперечного сечения, измеренной в плоскости симметрии надреза. Этот параметр aK = Wv/A0 (Дж/м2) округляют до целого числа и называют ударной вязкостью. Поглощенную при разрушении образца работу можно определить по формуле
W7h= mgl(cos р —cos а),
где т — масса маятника копра; I—его длина; 3 — угол подъема маятника после разрушения образца; g — ускорение свободного падения.
Зависимость ударной вязкости стали от температуры показана на рис. 1.55. В диапазоне температур, меньших происходит хрупкий излом, а больших /а — вязкий. Если то наблюдается смешанный излом. Значение
h—ti зависит от структуры стали, вида ее термической обработки, предварительной холодной пластической деформации образца и его старения.
Кроме испытания ударом на изгиб (но значительно реже), применяют испытание ударом на растяжение и скручивание.
1.7.3. Испытания циклической нагрузкой
При циклических нагрузках в исследуемом образце происходит постепенное накопление повреждений, приводящих к изменению свойств, образованию трещин, их развитию и разрушению. Этот процесс называют усталостью. Параметрами циклического нагружения являются: среднее напряжение цикла ат = = 0,5 (<Jmax + crmin), амплитуда напряжения <та, частота циклов f (или период Т цикла), коэффициент асимметрии = amin/crmax (рис. 1.56). Цикл, у которого максимальное и минимальное напряжения равны, но противоположны по знаку, называется симметричным.
Схема нагружения должна в той или иной мере воспроизвести в образцах напряженное состояние, характерное для эксплуатационных условий работы детали, так как от соотношения касательных и нормальных напряжений зависит сопротивление усталостному разрушению и характер разрушения.
Характеристиками сопротивления усталости материала являются; предел выносливости о^ — максимальное напряжение цикла с коэффициентом ассим-метрии R, соответствующее заданному (базовому) числу циклов напряжения; предел выносливости при симметричном цикле o_i; циклическая долговечность N — общее число циклов, выдержанных нагруженным объектом до образования усталостной трещины определенной протяженности или до усталостного разрушения.
Для определения предела выносливости испытывают 10...15 одинаковых образцов. Для первого образца максимальное напряжение обычно составля
Рис. 1.56. Схема измерения на- Рис. 1.57. Типовая схема резуль-
грузки на образец при испы- татов испытания на усталость
танин на усталость
48
ет 0,75<тв. Определяется число циклов нагружения, которое он выдерживает до разрушения Ni. Напряжения при испытании второго образца назначаются в зависимости от N’,. При jVi<2-105 02=01 — 20 МПа, при М!>2 - 105 02 = О! + + 20 МПа. Максимальное напряжение цикла для каждого последующего образца понижается на 8... 12 % до. тех пор, пока i-й образец не выдержит без разрушения базовое число циклов нагружения.
Уточнение предела выносливости производится при испытании нескольких других образцов, для которых Oi+1 = 0,5(oi + o1-1). На уровне предела выносливости должно быть испытано не менее трех образцов. По результатам испытаний строится кривая усталости (рис. 1.57). Критическое напряжение Ок, выше которого уже с первых циклов нагружения возникают субмикроскопические трещины и отсутствует инкубационный период, делит диапазон о_| — Ов на две области — малоцикловой и многоцикловой усталости.
Для сокращения трудоемкости испытаний на усталость разработано много прямых и косвенных ускоренных методов [84]. Наиболее распространенным является метод ступенчатого нагружения, который основан на гипотезе о линейном характере накопления усталостных повреждений. В данном случае на каждом уровне периодически повышаемой на Дог амплитуды напряжений осуществляется л,- циклов нагружения. Испытание продолжается до разрушения образца. Полученные результаты позволяют определить искомый предел выносливости.
В косвенных методах используется связь предела выносливости с другими характеристиками механических свойств материалов или резкое изменение некоторых параметров при достижении предела выносливости. В первом приближении значение о-i можно определить по формуле
ог-1 = 5+ 0,25 (ов + от).
Другой косвенный метод заключается в измерении температуры образца, который испытывается при непрерывном возрастании амплитуды напряжений. При достижении напряжения, равного пределу выносливости, нарушается линейная зависимость между амплитудой напряжений и температурой.
Однако косвенные методы не могут выявить влияние на предел выносливости шероховатости поверхности образца или коррозии. Прямые же методы показали, что предел выносливости полированного образца на 27% больше, чем у точеного. При коррозии предел выносливости может снизиться в 4...6 раз.
1.7.4. Измерение твердости
Измерение твердости относится к наиболее распространенным видам механических испытаний материалов. Это обусловлено относительной простотой методов измерения и возможностью по твердости приближенно оценить характеристики других механических свойств материала. Методы измерения твердости основаны на том, что в испытуемый материал вдавливают индентор, а пластическую деформацию при этом рассматривают как меру твердости. Наиболее распространенными инденторами являются: закаленный шарик, алмазный конус и четырехгранная алмазная пирамида с углом при вершине 136° (рис. 1.58).
При определении твердости по Бринеллю шарик в течение установленного времени вдавливается с определенной силой в испытуемый образец. В результате на его поверхности образуется отпечаток в виде части сферы диаметром d и глубиной h. Число твердости НВ рассчитывают как отношение приложенной нагрузки к площади отпечатка. Для определения последней при помощи специальной лупы замеряется диаметр отпечатка. Число твердости по Бри-
лП (D — /О2 — d2) '
где F — приложенная нагрузка, Н; D — диаметр шарика, мм.
4. Зак. 1001
Рис. 1.58. Инденторы, применяемые при измерении твердости:
а — шарик; б — конус; в —пирамида
Диаметр шарика и нагрузка выбираются в зависимости от механических свойств испытуемого материала и толщины образца. Число твердости по Бринеллю может определяться и по специальным таблицам.
Твердость по Виккерсу HV определяют аналогично. Различие заключается лишь в твердости и форме индентора. Для определения площади отпечатка измеряют при помощи микроскопа его диагональ d. При указанном выше угле пирамиды число твердости по Виккерсу вычисляется по формуле
HV=0,189F/d2.
Определение твердости по методу Роквелла является самым распространенным видом технологического конт-
роля металлических деталей. По сравнению с методом Бринелля у него следующие преимущества-, простота определения числа твердости путем отсчета по шкале индикатора без вычисления или пользования таблицами; малая повреждаемость поверхности; высокая производительность при измерениях. К недостаткам метода можно отнести отсутствие единой шкалы и произвольность ее выбора.
Твердость по Роквеллу HR, выражаемую в условных единицах, вычисляют как линейную функцию разности глубин, на которые вдавливается конический индентор под действием двух последовательно прикладываемых нагрузок — предварительной Fa и общей F, которая равна сумме предварительной и основной Fi нагрузок:
HR=A-(h-fi0)/C,
где А — некоторая постоянная, которая выбирается в зависимости от применяемой шкалы; /г0— глубина вдавливания при действии предварительной нагрузки; h — глубина вдавливания при действии общей нагрузки, измеренная после снятия основной; С — цена деления шкалы измерительного устройства в условных единицах твердости (С=0,002 мм); для шкал А и С принимают А = 100, а для шкалы В А = 130 мкм.
Нагрузки при измерении по методу Роквелла строго регламентированы: предварительная — 98 Н, общие — 589, 981 и 1471 Н.
Для определения твердости относительно мягких материалов по Роквеллу вместо алмазного конуса используется стальной закаленный шарик диаметром 1,588 мм. Чаще всего на практике применяется шкала С. Шкала А применяется для очень твердых материалов, например твердых сплавов, а шкала В — при использовании сферического индентора. Число твердости по Роквеллу обозначается через HR с добавлением обозначения соответствующей шкалы: HRA, HRC3, HRB.
1.7.5. Испытания на износостойкость
Целью испытания на износостойкость является изучение поведения контактных поверхностей двух деталей 1 и 2, находящихся в относительном движении и прижатых друг к другу с определенной силой (рис. 1.59). Между этими деталями обычно находится промежуточный слой 3 вещества, которое может замедлить или, наоборот, ускорить изнашивание. Испытания можно проводить на модели либо анализируя износ элементов реальной промышленной установки. Испытания на модели — обычно скоростные — проводят в более жестких, чем на практике, условиях. Хотя к результатам испытаний на модели следует относиться с осторожностью, последние распространены довольно широко.
50
Рис. 1.59. Схема испытания на износостойкость
Рис. 1.60. Схемы испытаний на износостойкость методом моделирования
Одной из основных причин изнашивания деталей машин и режущих инструментов является усталость материала в поверхностных слоях при упругом деформировании и охрупчивание при повторном пластическом деформировании. При наличии в структуре трущихся материалов твердых частиц (например, карбидов железа, хрома и т. д.) возможно микрорезание этими частицами, т. е. абразивное изнашивание. Оно может иметь место также при наличии абразивных частиц в промежуточном слое. При значительной удельной нагрузке и относительно малой скорости резания часто наблюдается адгезионное изнашивание. При достаточно высокой температуре поверхностей трения развивается изнашивание, связанное с диффузией атомов одного из тел в другое. При этом могут изменяться химический состав и структура, а следовательно, и механические свойства поверхностных слоев, что способствует увеличению скорости других видов изнашивания. В некоторых случаях изнашивание может быть связано с окислением трущихся поверхностей, эрозией и т. д.
На рис. 1.60 показаны различные схемы испытаний на износостойкость методом моделирования, которые проводятся на различных лабораторных установках. Испытуемый образец 1 с заданной силой F прижимается к периферии ролика 2 или торцу диска 3. Приведенные схемы испытаний обеспечивают разный коэффициент взаимного перекрытия (отношение площадей трения контактирующей пары): от близкого к нулю (рис. 1.60, а) до 1 (рис. 1.60, д').
Для оценки в лаборатории износостойкости пары трения применительно к заданным эксплуатационным условиям необходимо: 1) обеспечить коэффициент взаимного перекрытия, который имеет место при эксплуатации; 2) обеспечить скорость скольжения, максимально приближающуюся к эксплуатационной; 3) подобрать такую нагрузку, при которой контактная температура будет соответствовать эксплуатационной; 4) определить фактическую площадь касания; 5) вычислить удельный износ. Удельный износ будет совпадать с эксплуатационным при одинаковых параметрах шероховатости поверхностей в реальном узле и у испытуемых образцов.
Для определения износа материала и его распределения по поверхности трения применяют различные методы. Наиболее распространенным является метод измерения линейного износа, для чего измеряют размеры элементов пары трения до и после испытания. Для измерения размеров пользуются микрометром, контактными или бесконтактными электрическими или пневматическими приборами.
Часто применяется также весовой метод измерения износа, при котором образцы взвешиваются до и после испытания. Однако этот метод не дает возможности определить закон распределения износа по поверхности
4*
51
Рис. 1.61. Схемы искусственных баз для измерения износа
трения. В случае неравномерного износа образцов его измерение удобно проводить при помощи профилографа.
Для измерения износа элементов пар трения в действующей машине хорошо себя зарекомендовал метод искусственных баз. В основе этого метода лежит косвенное определение износа по изменению размеров суживающегося углубления заранее известного профиля (рис. 1.61). Такое углубление можно получить вдавливанием конического или пирамидального индентора, вырезанием остроугольной лунки вращающимся резцом или шлифовальным кругом.
Линейный износ Д6 определяется по следующим формулам. Если размер диагонали пирамидальной лунки изменился от dt до d2, то
d. — di а
Lb = —-------- ctg —.
2 8 2
Если длина лунки радиуса г в результате изнашивания наружной цилиндрической поверхности изменилась от di до d2, то
Д6 —0,125 (df —4) (1/г+1/Я), а в случае измерения износа внутренней цилиндрической поверхности
Д& = 0,125 (df — dty (1/г— 1/R).
Для плоской поверхности
Lb = 0,125 (d, — d|)/r.
Объем продуктов изнашивания можно также определить путем химического анализа смазочного материала. Этот метод обладает высокой точностью, но не дает возможности оценить износ каждой из трущихся деталей. Если в материал детали, износ которой требуется определить, внести радиоктивные изотопы, то по мере изнашивания в слой смазочного материала будет попадать пропорциональное износу количество атомов этого изотопа. По интенсивности излучения изотопа в пробе масла можно судить об объемном износе за определенное время. Изотопы чаще всего образуются в поверхностном слое испытуемой детали облучением ее потоком нейтронов.
52
1.7.6. Неразрушающие методы определения механических свойств и структуры конструкционных материалов
Данные методы основаны на корреляционной зависимости между структурой и механическими свойствами материалов, с одной стороны, и их магнитными и акустическими характеристиками, с другой. Такова, например, связь между твердостью углеродистых и низколегированных сталей и их коэрцитивной силой ас. Чем больше содержание углерода в сплаве, тем выше коэрцитивная сила. Но в различных структурных составляющих углерод в разной степени способствует увеличению коэрцитивной силы сплава: в меньшей степени, когда он находится в форме графита, сильнее — в перлите и мартенсите и наиболее сильно — в цементите. Зависимость между коэрцитивной силой и твердостью сталей 30X13 и 20Х17Н2 показана на рис. 1.62, а зависимость коэрцитивной силы и твердости стали ШХ15 от температуры отпуска—-на рис. 1.63 [59, 60].
При перемагничивании ферромагнитных тел магнитная индукция В зависит не только от напряженности магнитного поля о, но и от предшествующего магнитного состояния. Вид кривой цикла перемагничивания, называемой петлей гистерезиса, показан на рис. 1.64, где отрезок Od характеризует остаточный магнетизм, т. е. магнитную индукцию при а=0, Ое — коэрцитивную силу ос, т. е. напряженность магнитного поля, необходимую для полного размагничивания.
Блок-схема коэрцитиметра показана на рис. 1.65. Участок контролируемого объекта 1 намагничивается при помощи электромагнита 2 и катушек 8. Перемычкой электромагнита служит сердечник 7 феррозонда с питающей 5 и измерительными 4 катушками. Катушки 8 получают питание от силового трансформатора 11 через стабилизирующие выпрямители намагничивания 10 и размагничивания 12 и затем через коммутатор 14. Индикаторы 9 и 13 показывают соответственно ток намагничивания и размагничивания. Катушка 5 получает питание через блок 6, а напряжение на выходе измерительной катушки измеряется прибором 3.
После намагничивания при помощи коммутатора отключается ток намагничивания и плавно увеличивается ток размагничивания до тех пор, пока прибор 3 не покажет отсутствие магнитного потока на контролируемом участке. Показания индикатора 13 в этот момент пропорциональны измеряемой коэрцитивной силе. Прибор обеспечивает точность измерения ±3%.
В других приборах измеряется не коэрцитивная сила, а пропорциональная
между коэрцитивной силой и твердостью:
1 — сталь 30ХВ; 2 — сталь 20X17Н2
Семлеротура, °C
Рис. 1.63. Зависимость коэрцитивной силы и твердости от температуры отпуска стали ШХ15
53
Рис. 1.64. Кривая перемагничивания
Рис. 1.65. Блок-схема коэрцитиметра
ей остаточная индукция В (см. рис. 1.64) или магнитная проницаемость, равная согласно определению отношению В/о. Индукционный метод измерения магнитной (динамической) проницаемости основан на том, что если поддерживать постоянной амплитуду напряженности намагничивающего поля, то амплитудная или динамическая проницаемость будет пропорциональна амплитуде индукции в контролируемой детали. Обычно используют дифференциальную схему, с помощью которой определяют изменение магнитной проницаемости контролируемой детали по сравнению с эталонной. Погрешность измерения прибором ЭМТ-2, построенным на данном принципе, не превышает HRCa 1 для сталей 50ХФА и ЗОХГСА £59, 60].
Электромагнитный метод (метод вихревых токов) основан на регистрации изменении электромагнитного поля вихревых токов, наводимых возбуждающей катушкой в электропроводящем объекте контроля. Его можно применять для измерения параметров механических свойств материала, если существует корреляционная зависимость между ними и удельным электрическим сопротивлением или магнитной проницаемостью испытуемого материала. Экспериментально установлено, что удельная электрическая проницаемость стали тем меньше, чем выше в ней содержание углерода и чем больше углерода при закалке перейдет в твердый раствор. Выявлена связь между удельной проводимостью алюминиевых сплавов у и свойствами их после термической обработки. Так, например, если в состоянии поставки сплав АК6 имеет в среднем у = 27,4 МСм/м, то при нормальной закалке — у = 22,1 МСм/м. Если при закалке материал перегрет, то у = 21,1 МСм/м. В зависимости от времени старения значение у изменяется в пределах от 20 до 24 МСм/м, сначала уменьшаясь, а затем увеличиваясь.
Электромагнитными структуроскопами измеряют мгновенное значение несинусоидального напряжения измерительного вихретокового преобразователя ВТП или амплитуду и фазу одной из его гармоник при перемагничивании в высокочастотных полях малой напряженности, в низкочастотных полях большой напряженности, либо в двух- и многочастотных полях. Это позволяет контролировать вариации химического состава, структуру металлов и сплавов, а также механические напряжения в них. С помощью электромагнитных приборов с ВТП можно контролировать качество термической и химико-термической обработки, состояние поверхностных слоев деталей после механической обработки (шлифование, наклеп), обнаруживать усталостные трещины на ранних стадиях развития, наличие a-фазы и т. д. Таким образом, измеренный электромагнитным структуроскопом сигнал несет информацию о многих параметрах, что является, с одной стороны, преимуществом, а с другой — недо-54
Рис. 1.66. Схемы вихретоковых измерительных преобразователей:
а — накладного; б — накладного экранного; в — проходного вихретокового; 1 — испытуемый образец; 2 — возбуждающая обмотка; 3— измерительная обмотка; 4— сердечник
статком, так как требуются специальные приемы разделения информации об отдельных параметрах объекта.
По виду преобразования параметров объекта в выходную величину ВТП делят на трансформаторные и параметрические. В трансформаторных ВТП, имеющих минимум две обмотки (возбуждающую и измерительную), параметры объекта преобразуются в напряжение измерительной обмотки, а в параметрических, имеющих, как правило, одну обмотку,— в комплексное сопротивление. Схемы некоторых преобразователей показаны на рис. 1.66.
Акустические методы контроля физико-механических свойств материалов (размеров зерна, модулей упругости, твердости, текстуры, прочности и т. п.) основаны на связи этих свойств со скоростью распространения и коэффициентом затухания звуковых волн в испытуемом материале.
Одним из важнейших показателей качества кристаллических материалов, в частности металлов, является размер зерна, определяющий прочностные характеристики изделия. В первом приближении зависимость между номером шкалы (в баллах) N и размерной характеристикой зерна D (мкм) можно аппроксимировать уравнением
/7=352ехр(-0,35А).
Наибольшее влияние размера зерна на коэффициент затухания ультразвука наблюдается при 5<X/D<15 (X — длина ультразвуковых волн). Для измерения затухания наибольшее применение получил импульсный метод, основанный на сравнении амплитуд двух или нескольких ультразвуковых сигналов разной частоты. При этом опорную Частоту выбирают низкой, так что затухание ультразвуковых волн при ней практически не зависит от структуры материала. Рабочие частоты соответствуют приведенному выше неравенству. При рабочей частоте 0,65...10 МГц можно оценить размер зерна от 1 до 7 баллов. Для измерения размера зерна можно применять серийные импульсные дефектоскопы (ДСК-1, УС-ПИ, УС-10П и т. д.).
Измеряя скорость распространения ультразвуковых волн в материале, можно определить его модуль упругости и другие упругие постоянные. Кроме того, по относительному изменению скорости различных ультразвуковых волн можно определить напряженное состояние материала. На экспериментальной
55
Рис. 1.67. Схема измерения механических свойств материалов акустическим методом
Рис. 1.68. Блок-схема прибора «Звук-1М»
установке УЗМД [60] контролируют остаточные поверхностные напряжения в стальных или чугунных отливках с точностью ±0,2 МПа.
Предел прочности стеклопластиков можно определить по формуле
Ов=Е[А+В/ас) ],
где А и В — коэффициенты; а — коэффициент затухания; с — скорость распространения ультразвуковых волн в материале; Е — модуль упругости стеклопластика, который определяют по полученным значениям с и плотности материала.
Излучающий 2 и приемный 1 искатели (см. рис. 1.8, б) устанавливают на очищенную и смазанную маслом поверхность стеклопластика 3 (рис. 1.67). Расстояние между искателями 10 обычно составляет 200 мм. Скорость распространения звука определяют по времени t его прохождения в материале: с= = lolt. Для измерения коэффициента затухания один из искателей устанавливают на расстоянии Л = /0/2. По изменению амплитуды сигнала находят значение а.
Для измерения твердости абразивного инструмента используют корреляционную связь ее со скоростью распространения ультразвуковых волн в материале, которую определяют резонансным методом при помощи прибора «Звук-1М» (рис. 1.68) [33]. Генератор 1 создает электрические колебания, частота которых изменяется в пределах от 5 до 550 кГц. При помощи пьезоэлектрического излучателя 7 эти колебания преобразуются в механические, передаются образцу 6 и воспринимаются пьезоэлектрическим приемником 5, который осуществляет обратное преобразование. Электрические колебания с приемника проходят через усилитель 4 и поступают на амплитудный 3 и фазовый 2 индикаторы резонанса. Одновременно на фазовый индикатор подается опорное напряжение с генератора. При совпадении частоты генератора с частотой собственных колебаний образца наступает резонанс, который фиксируется в момент раскрытия сектора глазка амплитудного индикатора или (более точно) по минимальным показаниям стрелочного прибора фазового индикатора. Градуировочные таблицы позволяют оценивать твердость абразивного инструмента по замеренной резонансной частоте в зависимости от размеров инструмента.
1.7.7. Методы определения остаточных напряжений
Остаточные напряжения можно классифицировать по протяженности силового поля: 1) макронапряжения, или напряжения 1-го рода, охватывающие области, соизмеримые с размерами испытуемого объекта; они имеют ориентацию, зависящую от формы объекта; 2) микронапряжения, или напряжения 2-го
56
макронапряжений по глубине у поверхностного слоя деталей после обработки их различными методами
Рис. 1.70. Эпюры макронапряжений после закалки'
рода, распространяющиеся на отдельные зерна металла или на группу зерен; 3) субмикроскопические напряжения, относящиеся к искажениям атомной решетки кристалла; ориентация их связана со структурой атомной решетки.
Остаточные макронапряжения возникают в результате действия различных технологических факторов при изготовлении детали (изделия). Значение и знак остаточных макронапряжений зависят от схемы деформирования объекта и температуры, при которой оно происходило. При обработке резанием или шлифованием остаточные макронапряжения являются следствием неравномерности распределения температуры и деформаций в поверхностных слоях обрабатываемой детали и во времени. На рис. 1.69 кривые 4, 2 и 1 соответствуют операциям шлифования, точения и сочетанию шлифования с алмазным выглаживанием стали ЭИ643, а 5 и 3 — шлифованию и фрезерованию стали ХН70ВМТЮ. Состав и способ подвода смазочно-охлаждающих жидкостей значительно влияет на значение и знак макронапряжений после обработки ре-занием.
Значительные макронапряжения возникают при термической обработке (закалке), при сварке и резке. В этих случаях остаточные макронапряжения обусловлены в основном неравномерностью температурного поля при быстром нагреве или охлаждении. На рис. 1.70 показана эпюра напряжений в сплошном образце из стали 40ХНМ при закалке в воде (7) и масле (2) [76].
Микронапряжения являются следствием различия физических свойств компонентов поликристаллического тела, стесненных условий деформирования отдельных зерен, а также анизотропии их свойств. Особенно значительны микронапряжения при фазовых превращениях (кристаллизация и распад твердого раствора), так как при этом увеличение или уменьшение объема отдельных зерен сопровождается появлением значительных межзеренных напряжений. Вследствие различия коэффициентов линейного расширения компонентов сплава при его нагреве также возникают значительные микронапряжения.
Возникшие в материале остаточные микро- и макронапряжения не остаются постоянными, а изменяются с течением времени. Релаксация макронапряжений сопровождается обычно общей деформацией детали, иногда настолько значительной, что она наблюдается визуально или вызывает разрушение (появление трещины). При низких температурах этот процесс идет медленно. Нагрев до температуры отпуска и выше способствует ускорению релаксации макронапряжений.
Основными методами определения остаточных напряжений являются механические и рентгеновские. Применяются также электрофизические методы,
57
Табл. 1.6. Растворы для травления
Материал образца Состав электролита или травителя (в массовых долях) Метод травления
Углеродистые и 18...20% серной кислоты, осталь- Электрохимиче-
низколегированные ное — вода ский
стали Высоколегиро- 20 % азотной кислоты, остальное — вода 45% ортофосфорной кислоты, 45% То же
ванные стали Чугун серной кислоты, остальное — вода 60...65% ортофосфорной кислоты, 15...20% серной кислоты, 0,5% хромового ангидрида, 7% глицерина, 0,5% сернокислого железа, остальное — вода 15...20% азотной кислоты, 20... 25% щелочи натрия, остальное — вода 30% азотной кислоты, остальное — вода 35% бисульфата натрия, осталь- Химический Электрохимиче-
Сплавы алюми- ное — вода 8... 10% соляной кислоты, остальное — вода 10... 15% натриевой щелочи, ос- СКИЙ Химический
НИЯ Латуни, бронзы тальное — вода 91% ортофосфорной кислоты, 9% хромового ангидрида 100% ортофосфорнй кислоты Электрохимический То же
при которых остаточные напряжения находятся по изменению электромагнитных свойств материала поверхностного слоя детали.
Механические методы основаны на предположении, что разрезка или удаление части детали с остаточными напряжениями эквивалентны приложению к оставшейся детали на вновь появившихся поверхностях напряжений, равных остаточным, но с обратным знаком. Они вызывают деформирование детали или появление усилия в устройствах, препятствующих деформации. Измеряя возникшие деформации или силы, можно вычислить остаточные напряжения.
Различия механических методов заключаются: а) в форме образцов; б) в предположениях относительно закона распределения остаточных напряжений; в) в способе измерения деформаций образца или реакций опор, способных устранить эти деформации.
Наиболее широкое применение для вырезки образцов нашли методы элек-троэрозионной прошивки. Для деталей из жаропрочных и титановых сплавов весьма перспективны методы электрохимической прошивки. Они производительны и не вызывают дополнительных остаточных напряжений. После механической вырезки образцов рекомендуется стравливать с вновь образованных поверхностей слой толщиной до 0,2 мм для удаления напряжений, возникающих при вырезке.
Наиболее распространенными методами удаления напряженных слоев металла при исследовании остаточных напряжений являются электролитическое и химическое травления. Рекомендуемые составы травителей и электролитов для различных материалов приведены в табл. 1.6. Электрохимическое травление при прочих равных условиях предпочтительнее, так как изменяя плотность тока, можно изменять скорость снятия металла, а также о бес-
58
лечить ее стабильность, что важно для автоматизации записи кривой деформирования образца. Поверхности образца, не подлежащие травлению, и детали подвески защищаются покрытиями, стойкими при данной температуре. При температурах до 30 °C можно использовать парафин и воск. Лаки ХВЛ-21 и Э1 можно использовать и при более высоких температурах. Травление составами, указанными в табл. 1.6, проводится при температуре 20 °C [76].
Форма вырезаемых образцов
Рис. 1.71. Форма образцов для определения эпюры макронапряжений
показана на рис. 1.71. Напряженное
состояние в них считается одноосным. Напряжения изменяются только в зависимости от расстояния h от рассматриваемой точки А до обработанной поверхности С. Образцы в виде стержней прямоугольного сучения (рис. 1.71, а) широ-
ко используются для исследования влияния различных технологических факторов, в частности методов поверхностной обработки, на распределение остаточных напряжений. Кроме того, прямоугольные призматические образцы вырезаются из цилиндрических деталей для определения нормальных остаточных напряжений в поверхностном слое детали вдоль образующих. При этом рекомендуется соблюдать соотношение
3 < В <0,4/ЯК,
где И — высота образца; R — наружный радиус цилиндрической поверхности.
Однако не рекомендуется принимать ширину В образцов больше 15 мм. Их высота Н должна более чем в три раза превосходить максимальную глубину исследуемого поверхностного слоя. С увеличением высоты образца снижаются погрешности, связанные с внесением дополнительных остаточных напряжений при вырезке. Вместе с тем увеличение высоты образца ограничива-
Рис. 1.72. Метрологическая схема определения макронапряжений в призматическом образце:
1— пружина для компенсации измерительного усилия;
2 — индикатор; 3 — стержни усилителя; 4 — образец; 5 — ванна из кислотоупорного материала; 6 — пластина для подачи напряжения
59
Рис. 1.73. Метрологическая схема определения макронапряжений в кольцевом образце!
ется необходимостью получения достаточно больших прогибов при данной длине в процессе травления. Чтобы увеличить допустимую толщину образцов, рекомендуется применять метрологические схемы измерения деформаций с большими коэффициентами усиления Ку (рис. 1.72, 1.73).
Для определения окружных остаточных напряжений в цилиндрических деталях вырезают кольцевые образцы (см. рис. 1.71, б), удовлетворяющие неравенству Я<0,2£).
Остаточные напряжения о® в точке А, отстоящей от поверхности призматического образца на расстоянии h, представляют в виде суммы двух составляющих: o'XBi определяемой по^деформации образца при вырезке из детали или после снятия отдельно обрабатываемого образца с приспособления, и crtf, вычисляемой по кривой деформации образца при стравливании его на глубину h 176):
= <ДВ + ахс, где .
aIB = 8£(0,5//-/i)/s/£Е 2 *+£eJ:B;
4F Г df hC 1:
°- = [(Я - А)2 dh - 4 - Л) f + 2 J
и у о
Е — модуль упругости; /0 — длина участка, подлежащего травлению; Ку — коэффициент усиления метрологической схемы; — деформация при вырезке; f — деформация при стравливании; е1В — среднее относительное удлинение образца при вырезке.
Для метрологической схемы, указанной на рис. 1.72, Ку = 81у/1о-
Остаточные напряжения в кольцевых образцах определяются по формулам:
Gfp ' 0"<рв "Ь 0<рс*
2Ef
СТфв ~ D2Ky № ~ —
60
_ Е Г (fl — »)2 df — ЗА + е df ' -^С-ЗК £>2 dA~2J d2 d& ’
L n о г J
где fB— деформация, связанная с изгибом кольца при его вырезке (или при снятии разрезанного кольцевого образца с приспособления после его обработки); f — деформация при стравливании на глубину h; £>Л(£>г)—средний диаметр кольцевого образца при удалении слоя толщиной Л(е).
При й<0,1Я с достаточной для практики точностью можно использовать формулу
Е(Н — Л) Г df 1
Коэффициенты усиления для метрологической схемы, указанной на рис. 1.73:
при разрезке образца
Ку= (Zy/D + 0,5) (2л —фу) +0,5sin фу;
при его травлении
Ку=(/у/П + 0,5)фо+соз(фу/2) • 81п(ф0/2),
г др D— средний диаметр кольца; углы фу, ф0 и длина /у указаны на рис. 1.73.
В формулах для расчета остаточных напряжений производную прогиба по глубине снятого слоя можно вычислить по трем значениям деформации fi_b fi и f,+i при рассматриваемом значении ht и двух близких к нему hi-i и
df
-^ = Af^+Bfl+Cfi+l,
где
АН-1~Л 2/г —Л/+1
2П = ‘ D = 1
(hi (hi-hi_i)(.hi ~hi+i)
c_ h-hj-j
(^i+l (Ei+l~Ed
Puc. 1.74. Результаты испытания на остаточные макронапряжения'
61
Информация для вычислений берется по графикам изменения прогибов f в зависимости от Л. В качестве примера на рис. 1.74 показана такая кривая (/), полученная при травлении образца, вырезанного вокруг отверстия в шестерне из стали 12Х2НВФА [76]. Там же приведена полученная расчетом эпюра остаточных напряжений (кривая 2).
Наличие остаточных напряжений в поликристаллических телах, какими являются металлы, обусловливает различные интерференционные эффекты рентгеновских лучей, отраженных от поверхности образцов, в зависимости от размеров зоны, в которой эти напряжения уравновешиваются. Макронапряжения имеют постоянную ориентацию на исследуемом участке поверхности, и вследствие этого изменяются межатомные расстояния, что вызывает угловое отклонение лучей, отраженных от поверхности (от определенных кристаллографических плоскостей в поверхностном слое). В результате появляется смещение линий на рентгенограммах, по которому и вычисляются остаточные напряжения 1-го рода. В отражении участвуют только определенным образом ориентированные кристаллы поверхностного слоя толщиной от 3 до 50 мкм. Полученное при этом смещение пропорционально усредненному значению остаточных напряжений, распределенных по определенному закону в этом слое.
Микронапряжения, уравновешивающиеся в объемах отдельных кристаллов и блоков, нельзя определить механическими методами. Но они легко определяются по уширению интерференционных линий на рентгенограмме.
Описанные ранее электромагнитные методы контроля структуры можно применять и для измерения остаточных напряжений. Но точность этих методов пока относительно низкая, и для определения эпюры остаточных напряжений, так же как и при механических методах, требуется последовательное стравливание слоев металла.
1.8. МЕТОДЫ ОПРЕДЕЛЕНИЯ ОБРАБАТЫВАЕМОСТИ РЕЗАНИЕМ И ШЛИФОВАНИЕМ
1.8.1. Метод торцевой обточки
Общепринятой количественной характеристикой обрабатываемости материалов резанием является скорость резания vt, соответствующая определенному периоду стойкости инструмента Т и другим стандартным условиям испытания (глубина резания, подача, геометрия режущей части инструмента). Кроме того, часто анализируется возможность получения требуемых параметров шероховатости обработанной поверхности, характер образующейся стружки (степень ее дробимости) и сила резания. Для сравнения обрабатываемости различных материалов резанием один из самых распространенных материалов принимается за эталон. Тогда относительная обрабатываемость любого другого t-ro материала выражается отношением (щ/оэ)т.
Для определения показателя обрабатываемости резанием vT необходимо экспериментально определить пара-
Рис. 1.75. Типовая зависимость износа инструмента от продолжительности и скорости резания*.
метры математической модели, которая описывает семейство кривых износа h инструмента в зависимости от продолжительности t и скорости v резания (рис. 1.75):
h=Cvmt\ (Г.1)
где С, m, X — искомые параметры; h — накопленный за время t износ задней поверхности.
При заданных стандартных значениях допустимого износа Лд и выбранном t=T, где Т—принятый период стойкости,
62
vT = yhA/(СТ j у' .
Обычные методы стойкостных испытаний требуют значительных затрат времени, материала и инструментов. Поэтому для определения параметров С, и и X лучше пользоваться одним из приведенных ниже методов ускоренных испытаний [45].
При подрезании торца скорость резания изменяется по линейному закону. Если подрезание начинается от относительно малого диаметра и проводится по направлению от центра детали, то закон изменения скорости
2nn2st v =----------,
1000
где п — частота вращения шпинделя, об/мин; s — подача на 1 оборот, мм; t — продолжительность резания, мин.
Время, в течение которого будет подрезан торец, Zi=rf/(2rts), где d — максимальный диаметр заготовки.
Износ, накопленный за время одного подрезания,
h, С / 2itn2s / d \т+Л,
- т+ Х\ 1000 J \ 2ns )
Эксперимент включает три этапа, в каждом из которых с постоянной глубиной резания К. раз подрезается торец заготовки. На первом этапе обрабатывается заготовка диаметром d\ при частоте вращения иь на втором — диаметром di при той же частоте вращения. На третьем этапе обрабатывается заготовка диаметром dx при частоте вращения пг (d2=2dj и /z2=2«i). Максимальная частота вращения заготовки га2 выбирается в зависимости от заданной максимальной скорости резания
ил= ЮООо та х/(лс(1).
После каждого этапа замеряется накопленный износ резца по задней грани— Ль Л2 и й3 соответственно. Искомые параметры модели (1.1.) можно вычислить по формулам:
/п=0,5(1 +оф)/а; Х=0,5(1 — сф)/а;
1,443 Л“ —Л“
а = 0,91 1п (Ла/Лз); 0 =------1п —------— ;
а Л“
х
С = -упГ₽т)~1/а; В =
При абсолютной погрешности измерения накопленного износа ЛЛ средние погрешности оценки значений т и X: Am 8 АЛ; ДХ«6АЛ.
1.8.2. Метод ступенчатого изменения диаметра
При точении или растачивании цилиндрической поверхности скорость резания зависит от частоты вращения шпинделя и диаметра заготовки, который при выполнении ряда последовательных проходов будет изменяться ступенчато с дискретой, равной глубине резания а. После К проходов скорость реза-изменится от о । до
о2=И1[1±2а(К- l)/d,], где dt — начальный диаметр заготовки; минус соответствует наружному точению, а плюс — растачиванию.
63
Эксперимент проводится в три этапа, после каждого из которых замеряется накопленный износ Ль й2 и Л3. При обработке каждой заготовки постоянной длины L производится К проходов с постоянной глубиной резания а и постоянной подачей s. На первом этапе обрабатывается Kt заготовок при частоте вращения шпинделя П|, на втором — К2 заготовок при той же частоте вращения. На третьем этапе обрабатывается К3 заготовок при частоте вращения, равной п2- Если исследуемый диапазон скоростей резания заключен меж-Ду Vmin И Vmaii ТО
rt! > lOOOomin/(ла!,); п2<1000утах/{л[с/1 —2а(/(—1)]}.
Искомые параметры модели (1.1):
In(Л2/Л1) . Г 1пЛ I
X — , tTl —• At I 1 ' J
In [(K1 + K2)/Kl] 1. Чп(п2/П1)Г
P1 . Kt ht
p = -—; A = — ------------; C = --------------;
% Кз ft₽ (/СхП7)хи1т-А'
К
1=1
Если погрешность измерения накопленного износа равна Aft, то погрешность определения значений параметров X и т можно оценить по приближенным формулам: AX«2Aft; A/n«4Aft.
1.8.3. Метод ступенчатого изменения скорости резания
Данный метод удобно применять в производственных условиях при обработке партий одинаковых заготовок с постоянной длиной обработки L, глубиной резания а и подачей s. Скорость резания ступенчато изменяется от минимальной vt до максимальной при переключении коробки скоростей станка:
Vi = 01<pi-1,
где i — порядковый номер ступени; <р — характеристика коробки скоростей.
Износ инструмента за время обработки одной детали при условии, что после обработки каждой из предшествующих деталей скорость резания, начиная с наименьшей, повышалась на одну ступень:
ft₽-
где i—порядковый номер детали; р=1/Х; а=тГ/.-, —продолжительность
обработки первой детали.
Накопленный износ после обработки i деталей с последовательным повышением скорости
/(ot—1) _ । ft? = C₽o“f, -----;-----.
1 11 <р«-1 _ 1
Предположим, что исследуемый диапазон скоростей обеспечивается за счет 2k ступеней. Тогда партия из N обрабатываемых деталей, где N=k(6kt+k2), разбивается на три части: Nt = N2 = 3kkt и N2=kk2. После обработки каждой части партии деталей измеряется накопленный износ /гь /г2 и ft3. Изменение скорости резания при обработке первых Nt деталей производится в следующем порядке. Сначала обрабатывается k деталей с последовательным увеличением скорости от Vt до Vk, а затем 2k деталей с последовательным увеличением ско-64
роста после обработки каждой детали от vt до vu- Этот цикл повторяется kt раз. Аналогично обрабатывается вторая часть партии с числом деталей Nt. Число kt подбирается так, чтобы после обработки Л^+Мг деталей накопленный износ достиг 60...70% допустимого. При обработке третьей части партии обрабатывается k деталей с последовательным увеличением скорости от Oj до Vk', данный цикл повторяется раз.
Искомые параметры определяются по формулам:
X => 3,322 1g (Л2/Л1); т = X[lg A/(k lg <р) !]; а =
k2 h2 [ \QOOsU U
д _,-----------------2 • С =_____- I__________ *
2k, h£-h$ ’ \ ^ttdL / '
X v Z 1
и = (ф06-1 — 1)/(ф2й(а-1) + ф*(а-|) — 2),
где d — диаметр заготовки (или инструмента при определении обрабатываемости сверлением или зенкерованием).
1.8.4. Определение объективных показателей обрабатываемости
Общепринятая характеристика обрабатываемости определяется допустимым износом Ад и периодом стойкости инструмента Т, которые принимаются по экономическим соображениям, причем стойкость инструмента зависит не только от свойств режущего материала и стойкости инструмента, но и от стоимости станка. Допустимый износ не одинаков для черновой и чистовой обработки одним и тем же инструментом. Поэтому в работе [43] в качестве количественных показателей обрабатываемости предлагаются оптимальная скорость резания и относительный поверхностный износ Л0.п, соответствующий этой скорости.
Относительным поверхностным износом называется радиальный (в направлении, перпендикулярном к обработанной поверхности) износ инструмента (мкм), отнесенный к 1м2 обработанной поверхности:
Рис. 1.76. Типовая зависимость относительного поверхностного износа и температуры в зоне резания от скорости резания и подачи при точении:
/ — s=0.07 мм/об; 2 — 5=0,11 мм/об; 3 — 5 = =0,14 мм/об.
5. Зак. 1001
65
где hT — текущее значение радиального износа, мм; йн — начальный радиальный износ, мм; I — путь резания, м; /н — путь резания, на котором образовался начальный износ, м; s— подача, мм/об.
Отсюда следует, что для оценки Л0.п рассматривается только период нормального (установившегося) износа.
Экспериментально установлено [43], что зависимость ho n от скорости резания имеет минимум при некоторой скорости v0 (см. рис. 1.76). Причем для каждой пары материалов (инструмент — заготовка) этой скорости при разных подачах и глубинах резания соответствует одна и та же температура резания, о которой судят по значению э.д.с. термопары £0. Обработка со скоростью резания обеспечивает максимальную размерную стойкость инструмента.
Для определения v0 при данной подаче s и глубине резания а можно использовать один из методов однофакторного поиска (см. § 6.2), а при других условиях обработки для той же пары инструмент — заготовка можно вместо износа измерять температуру резания.
1.8.5. Определение обрабатываемости шлифованием
В зависимости от интенсивности процесса шлифования и свойств шлифовального круга последний работает в одном из трех режимов: полного самозатачивания, частичного самозатачивания и затупления. Основным показателем интенсивности процесса шлифования является радиальная сила Fy, так как в большинстве случаев производительность шлифования ей пропорциональна: Q = KPFV. Коэффициент ЛР называют коэффициентом режущей способности круга или удельной интенсивностью шлифования [58]. При работе в режиме самозатачивания Лр постоянен, а при работе в режиме затупления уменьшается при увеличении продолжительности работы круга:
Кр = КрОе-«,
где Лро — начальное значение коэффициента режущей способности после правки круга; X — коэффициент, зависящий от свойств инструмента и обрабатываемого материала, а также от Fy.
При работе круга в режиме полного самозатачивания интенсивность его изнашивания
где Ли, и Лиг — коэффициенты, характеризующие износостойкость круга.
При работе круга в режиме затупления W близка к нулю.
Качество шлифованной поверхности зависит также от радиального усилия шлифования [49]:
Хд = ^д(^-^о). = W-
где Лд— глубина дефектного слоя (прижогов); Fу0 — максимальная сила шлифования, при которой еще не образуется дефектный слой; Ra — среднее арифметическое отклонение профиля; Лд Л^ —коэффициенты качества.
Коэффициенты режущей способности и износостойкости шлифовального круга можно определять на специальном стенде, который обеспечивает возможность шлифования с заданным радиальным усилием, или на обычном оборудовании, где шлифование возможно только с заданной поперечной подачей. В первом случае эксперимент проводится при фиксированных значениях Fy. После каждого опыта измеряются размеры заготовки и круга, что позволяет определить расчетом значения параметров Лр, Ли, и Лиа-
При отсутствии стенда для сокращения трудоемкости эксперимента можно использовать один из следующих методов определения некоторых параметров обрабатываемости шлифованием [86].
Первый метод удобен для определения Лр при круглом врезном шлифова-
66
Рис. 1.77. Схема определения коэффициента режущей способности шлифовального круга при круглом врезном шлифовании
Рис. 1.78. Типовая осциллограмма изменения радиального усилия (1) и радиуса детали (2) в процессе врезного шлифования с постоянной подачей
Ту //77/~
нии в режиме затупления, когда износом круга можно пренебречь (рис. 1.77). Деталь 1, установленная на оправке 2, шлифуется следующим образом. Вручную, при помощи механизма поперечной подачи, осуществляется ускоренное врезание до тех пор, пока индикатор 3 не покажет натяг (деформацию заднего центра), на 0,01..Д,02 мм больший заданного. Подача прекращается, и фиксируется время /, в течение которого натяг у изменяется (за счет уменьшения диаметра шлифуемого образца) в пределах от yi до г/2. Значение Кр вычисляется по формуле
Kv=ndLI(jt) Ag(yily2),
где d и L — соответственно диаметр и длина шлифуемой поверхности; / — жесткость крепления детали (определяется предварительно путем нагружения детали заданной силой и измерения соответствующей упругой деформации).
Второй метод отличается тем, что во время круглого шлифования с постоянной поперечной подачей s (мм/мин) регистрируют изменение во времени радиальной силы шлифования Fv и радиуса шлифуемой детали г. Пример получаемой при этом осциллограммы показан на рис. 1.78. Сила Fv измеряется при помощи тензометрических преобразователей, наклеенных на центр задней бабки, а изменение радиуса детали оценивается с помощью индукционного или тензометрического преобразователя линейных перемещений. Коэффициент режущей способности в этом случае
Кр = ndLbrjAp
где Аг — изменение радиуса детали за время шлифования Ар— площадь, ограниченная осциллограммой радиальной силы, осью времени и вертикальной прямой, соответствующей моменту времени 1г.
Полученную в опыте (на осциллограмме) информацию можно использовать для определения жесткости системы СПИД, которую (если износом круга можно пренебречь) вычисляют из выражения
._______Ар
1 = 0,53/2 — аг ’
где Аг — площадь, ограниченная осциллограммой изменения радиуса шлифуемой детали.
В тех случаях, когда износом круга нельзя пренебречь, шлифование нужно проводить до стабилизации радиальной силы, а жесткость определять из выражения
5'
67
s(^p^c^i — л dLAr)
где Fvc — стабилизированное значение Fy.
Значения площадей AF и Аг определяются любым из методов численного интегрирования с учетом масштаба. Согласно формуле трапеций:
AF = т1таА1 | — °’5Рп р
\ i=l /
(п \
2 ht — 0,5hn j, 1=1 /
где hi и Pt — сигналы, пропорциональные соответственно текущим значениям Аг и Fy-, mi и т2 — масштабы, полученные при тарировке измерительных преобразователей усилия и размера; Л/ — шаг интегрирования по времени; т3 — масштаб времени, определяемый согласно сигналам отметчика времени.
Относительная погрешность оценки параметров:
6Кр = /(6F)2 + (6г)2; 6/ = /(6F)2 + 0,25№ (6г)2,
где К — постоянная времени переходного процесса при врезном шлифовании: K=jKv/(jidL); 6г — относительная погрешность измерения радиуса шлифуемой детали; 8F — относительная погрешность измерения максимальной силы шлифования.
2. ПОГРЕШНОСТИ ИЗМЕРЕНИЙ
2.1. ВИДЫ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЙ
Погрешности измерений в зависимости от источника возникновения разделяются на погрешности классификации, методические, алгоритмические, аппаратурные (инструментальные) и внешние.
Погрешность классификации обусловлена несоответствием реального (исследуемого) объекта или процесса приписанной ему модели. Например, измеряя диаметр детали, предполагаем, что она представляет собой идеальный цилиндр. Такая идеализация неизбежна при несоответствии между параметром модели (в данном случае диаметр) и реальным свойством объекта (поверхность реальной детали имеет отклонения от цилиндричности как в поперечном, так и в продольном сечении). Это несоответствие называют пороговым. Чтобы измерение было возможным, погрешность, обусловленная пороговым несоответствием, должна быть меньше полной погрешности измерения.
Погрешность метода возникает вследствие недостаточной разработанности теории тех явлений, которые положены в основу измерения, и тех соотношений, которые используются для оценки измеряемой величины.
Алгоритмическая погрешность зависит от степени соответствия алгоритма измерения математическому определению измеряемой характеристики (чаще всего это относится к измерению параметров случайных процессов).
Аппаратурная погрешность обусловлена несовершенством средств измерений, их схемного решения, недостаточной точностью реализации принятого алгоритма измерений.
Внешние погрешности возникают при действии различных факторов, внешних по отношению к средству измерения. К ним часто относят ошибки экспериментатора при настройке средства измерения и пои снятии показаний.
Различают систематические и случайные погрешности.
Систематическая погрешность — составляющая погрешности измерения, которая остается постоянной или закономерно изменяется при повторных измерениях одной и той же величины.
Обнаруженная и оцененная систематическая погрешность исключается из результата измерения путем введения поправки. Однако полностью устранить таким образом систематическую погрешность невозможно.
Случайная погрешность — индивидуально непредсказуемая составляющая погрешности измерения, характеристики и закономерности изменения которой проявляются лишь на значительном числе результатов измерения.
Качество измерений, отражающее близость к нулю систематической погрешности результатов измерений, называют правильностью измерений. Качество измерений, отражающее близость результатов измерений, выполненных в одних и тех же условиях, называется сходимостью. Хорошая сходимость измерения свидетельствует о малости случайных погрешностей. Качество измерений, отражающее близость результатов измерений, выполняемых в различных условиях (в различное время, в различных местах, различными средствами), называют воспроизводимостью измерений.
69
Возможны также грубые погрешности и промахи. Грубая погрешность — погрешность, существенно превышающая уровень, оправданный условиями намерения, свойствами применяемых средств измерений и квалификацией экспериментатора. Такне погрешности могут возникать, например, вследствие резкого кратковременного изменения напряжения в сети питания. Грубые погрешности измерения обнаруживают статистическими методами и исключают из рассмотрения.
Промахи — следствие неправильных действий экспериментатора, например, описка при записи результатов наблюдений, неправильно снятые показания прибора и т. д. Промахи обнаруживаются нестатистическими методами, и их следует всегда исключать из рассмотрения.
Различают абсолютные, относительные и приведенные погрешности.
Абсолютная погрешность — это разность результата измерения величины X и ее истинного значения Хи, выраженных в одинаковых единицах: ДХ=А—Х„. Однако, поскольку истинное значение измеряемой величины остается неизвестным, на практике можно дать лишь приближенную оценку погрешности измерения.
Относительная погрешность — отношение абсолютной погрешности измерения к истинному значению измеряемой величины: 6= (АХ/ХИ) 100.
Приведенная погрешность относится не к конкретному значению измеряемой величины, а к максимально возможному в данном исследовании или к максимальному значению шкалы прибора: бпр= (ДХ/Хтах) 100. Относительная и приведенная погрешности обычно выражаются в процентах.
2.2. ХАРАКТЕРИСТИКИ СРЕДСТВ ИЗМЕРЕНИЙ
Общие положения. Различают метрологические и эксплуатационные характеристики средств измерения (СИ) и (или) измерительных преобразователей (ИП). Первые определяют результаты и погрешности измерений, вторые — условия применения СИ и ИП [10].
Метрологические характеристики: функция преобразования; характеристики погрешности; вариация показаний; порог чувствительности и разрешающая способность СИ и ИП.
Порогом чувствительности СИ (ИП) называют значение измеряемой (преобразуемой) величины, для которой относительная погрешность составляет 100%. Понятие разрешающей способности употребляется в разных значениях. Если измеряемая величина медленно и непрерывно изменяется от любого, отличного от нуля значения, то под разрешающей способностью понимают изменение входной величины, необходимое для начала изменения показаний. Если показания изменяются дискретно, то разрешающей способностью называют шаг изменения показаний. Это определение совпадает с понятием разрешающей способности цифровых показывающих приборов.
Вариацией называется разность показаний, получаемая при одном и том же значении измеряемой величины при медленном непрерывном или шаговом подходе к метке шкалы один раз с меньшего, а другой раз с большего значения. Причины вариации могут быть различными: люфт в механических передающих элементах, сухое трение, гистерезисные явления в механических и электромагнитных системах.
Эксплуатационные характеристики: предел измерений (преобразования); полный диапазон измерений (преобразования)— интервал значений. измеряемой (преобразуемой) величины от порога чувствительности до верхнего предела измерений; рабочий диапазон измерений и частот.
Функция преобразования. Средства измерения и измерительные преобразователи характеризуют функцией преобразования — функциональной зависимостью между сигналом на входе X и сигналом на выходе у, задаваемой аналитическим выражением или графиком [63].
Если X изменяется медленно или остается в процессе измерения постоян-
70
Рис. 2.1. Типовые градуировочные ха- Рис. 2.2. Типовые входные контроль-рактеристики средств измерения ные сигналы:
а. — единичная импульсная функция; б — единичная функция; в — линейная функция; г — гармоническая функция
ным, то функцию преобразования называют градуировочной характеристикой. Идеальная градуировочная характеристика линейна:
У = КХ,
где К — коэффициент преобразования.
Реальные градуировочные характеристики могут быть нелинейными (рис. 2.1, а) или гистерезисными (рис. 2.1, б).
Статической чувствительностью S(x) ИП (СИ) называют отношение приращения у к приращению X. Для линейной градуировочной характеристики чувствительность равна коэффициенту преобразования. У некоторых ИП статическая чувствительность отсутствует (пьезоэлектрические и электродинамические ИП, фильтры и др.).
Если входной сигнал X быстро или периодически изменяется во времени, то функция преобразования СИ (ИП) задается в виде дифференциального уравнения, импульсной характеристики, переходной характеристики, передаточной функции или в виде амплитудно-частотной (АЧХ) и фазово-частотной (ФЧХ) характеристик. При этом СИ (ИП) рассматриваются как линейные стационарные системы непрерывного действия с сосредоточенными параметрами. Свойства линейной системы характеризуются ее реакцией (видом выходного сигнала) на определенный, типовой входной сигнал. Этот выходной сигнал можно определить расчетным путем в результате решения дифференциального уравнения или экспериментально [31].
Основными типовыми сигналами являются: единичная импульсная функция, единичная функция, линейно нарастающая функция и гармоническая функция (рис. 2.2).
Измерительная система первого порядка описывается дифференциальным уравнением первого порядка
КХ = у+Ту'.
Переходная характеристика, представляющая собой решение этого дифференциального уравнения для типового единичного сигнала:
у = К[1-ехр( —t/T)],
где Т — постоянная времени СИ; К— коэффициент передачи.
Если X является гармонической функцией времени, то после завершения переходного процесса у будет иметь ту же частоту, но другие амплитуду и фазу. Амплитудно-фазово-частотная характеристика (АФЧХ) представляет собой векторное изображение отношения амплитуд входных и выходных ко-
71
Рис. 2.3. Переходная (а) и частотная (б) характеристики измерительного преобразователя первого порядка!
лебаний и соответствующего сдвига фаз. АФЧХ изображается обычно в комплексной плоскости. Для СИ (ИП) первого порядка АФЧХ имеет вид
G(ta)=A/(H-icoT).
Модуль вектора |G(ia>)|, или отношение амплитуд у и X, определяется выражением
| G (to) I = K./V 1 + а2Т2 , а сдвиг фаз выходного сигнала по отношению к входному —
<р=arctg (— (йТ).
Переходная и частотная характеристики ИП первого порядка показаны на рис. 2.3.
Пример устройства, которое при известных допущениях можно считать измерительной системой первого порядка, показан на рис. 2.4. Предполагается, что распределение температуры в чувствительном элементе равномерное и прибор безынерционный. Тогда из теплового баланса
0с=0 + [шс/(аА)]0',
где m — масса чувствительного элемента; с — его удельная теплоемкость; а — коэффициент теплоотдачи; А — площадь наружной поверхности чувствительного элемента; 0с, 0 — соответственно измеряемая температура среды и показания прибора.
Рис. 2.4. Схема измерительной системы первого порядка:
1 — трубопровод; 2 — измерительный прибор; 3 —термометр; 4 — среда, температура которой измеряется
Рис. 2.5. Семейство переходных характеристик измерительной системы второго порядка при единичном скачкообразном изменении входной величины:
Г —Д = 0,1; 2 — 0 = 0,3; 3 — D = l
72
Рис. 2.6. Частотная характеристика измерительного преобразователя второго порядка:
1 — D=0,16; 2 — £> = 0,3; 3 — D=0,5
:, представляющих собой решение
Измерительный прибор, у которого масса подвижной части не является пренебрежимо малой, может быть описан дифференциальным уравнением [31].
-^=aof/+aiJ//+a2j///- (2.1)
Для установившегося состояния (у' = = у”=0) это уравнение упрощается: ^о = аоУо*
Если ввести безразмерные характеристики входного х — Х/Х» и выходного е = у/уа сигналов, а также времени т = iti>t (ш0 = Vav/a2) > то дифференциальное уравнение (2.1) будет иметь вид
X=e+2De' + e", (2.2)
где £>=а1/(2<о0) —демпфирование.
Семейство переходных характеристш
уравнения (2.2) при единичном скачкообразном изменении входной величины и при разных значениях параметра D, показано на рис. 2.5. Переходные характеристики при £)<1 отличаются от характеристик при £)>1 наличием колебательной составляющей.
Для рассматриваемой системы второго порядка АФЧХ имеет вид
G(iQ) = 1/[1 +2Р/Й+ (»Q)2], где й = ш/(Оо— безразмерная частота.
При Й«=1 имеет место резонанс.
Частотная характеристика (АФЧХ) для ИП второго порядка при разных значениях параметра D приведена на рис. 2.6.
Если ИП привести к системе, которая включает массу т, пружину жесткостью j и демпфер с характеристикой Л, то резонансная частота недемпфированной системы <00 = ]^ j/m , а безразмерный параметр D = Л/(2 У jm).
Погрешности средств измерения. В результате воздействия большого числа различных случайных и детерминированных факторов, возникающих в процессе изготовления, хранения и эксплуатации СИ (ИП), их показания неизбежно отличаются от истинных значений измеряемых величин. Эти отклонения характеризуют погрешности средств измерения.
Абсолютная погрешность равна алгебраической разности показания прибора Хп и истинного значения измеряемой величины X: ДХ=ХП—X. Однако на практике вместо X приходится пользоваться Хд (действительным значением X), полученным с такой точностью, что указанная замена допустима.
Относительная погрешность — 6= (ДХ/Хд) 100.
Если диапазон измерения прибора охватывает и нулевое значение измеряемой величины, то относительная погрешность вблизи нуля обращается в бесконечность. В этом случае оценивают приведенную погрешность у = = (ДХ/Хв)Ю0, где ХЕ — нормирующее значение измеряемой величины, в качестве которого может приниматься диапазон измерений или верхний предел измерений СИ.
Погрешности СИ принято подразделять на статические, имеющие место при измерении постоянных величин после завершения переходных процессов в элементах прибора, и динамические, появляющиеся при измерении переменных величин и обусловленные инерционными свойствами СИ.
Различают также основную и дополнительную погрешность СИ (ИП). Первая возникает при использовании ИП в нормальных условиях, а вторая при отклонении одной из влияющих величин от нормальных значений или ее выхо-
73
де за пределы нормальных значений. Для СИ вместо дополнительных погрешностей принято определять изменение показаний.
Погрешность средства измерений может иметь и систематическую, и случайную составляющие. Систематические погрешности вызываются неточностями шкал, изменением во времени упругих свойств пружины, температуры, влажности, напряжения питания и т. д. Выделение систематических погрешностей в отдельную группу обусловлено лишь тем, что при проверке СИ они могут быть определены для каждой точки шкалы и исключены из результатов последующих точных измерений.
Случайные погрешности СИ возникают при случайном изменении параметров составляющих его ИП и случайных погрешностях отсчета. В общем случае их следует рассматривать как случайную функцию времени, измеряемой величины и влияющих величин. В частном случае измерения постоянных величин в области нормальных значений влияющих величин случайную погрешность можно считать одномерной случайной величиной, если ее временной дрейф невелик.
Фактически любой ИП имеет несколько входов: основной для измеряемой величины и дополнительные для влияющих величин, которые не должны измеряться, но проявляются в выходном сигнале. Ввиду разного характера воздействия влияющих величин появляется два вида погрешностей: мультипликативные и аддитивные. Первые возникают вследствие влияния неизмеряемых величин на статическую чувствительность ИП, а вторые прибавляются к сигналу от измеряемой величины. По механизму воздействия различают аддитивные факторы 1-го и 2-го рода. Аддитивные факторы l-ro рода воздействуют на вход ИП, а 2-го рода — на выходные цепи ИП.
Обобщенной характеристикой СИ, определяемой пределами допускаемых основных и дополнительных погрешностей, а также другими свойствами СИ, влияющими на их точность, является класс точности. Класс точности СИ определяется по их основной погрешности и способу ее выражения.
2.3. УМЕНЬШЕНИЕ СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ СРЕДСТВ ИЗМЕРЕНИЙ
Различают постоянные и закономерно изменяющиеся систематические погрешности СИ. Последние в свою очередь подразделяются на прогрессирующие, периодические и изменяющиеся по сложному закону. Одной из главных составляющих систематической погрешности СИ является кинематическая погрешность, обусловленная нелинейностью функций преобразования (градуировочных характеристик) его ИП. Такие погрешности характерны для рычажных ИП (рис. 2.7). Так как отсчет У прямолинейного перемещения штока производится по дуговой шкале, то относительная кинематическая погрешность такого преобразователя 'пропорциональна фц/6 для синусного ИП и фц/Здля тангесно-го [16] (Фо — угол поворота стрелки, характеризующий крайние точки шкалы). Погрешность можно уменьшить, если скорректировать градуировку круговой шкалы так, чтобы при <р = О,86фо и ф => 0 кинематическая погрешность отсутствовала. Тогда максимальная относительная кинематическая погрешность составит фд/24 для синусного и фц/12 для тангенсного ИП.
Малыми кинематическими погрешностями при относительно больших пределах измерения обладают двухрычажные ИП (рис. 2.8). При а = 2г кинематические погрешности двухрычажнэго ИП пропорциональны —фд/180, что на два порядка меньше, чем у рычажного.
Нелинейностью обладают не только механические, но и пневматические, электрические, электромагнитные и акустические ИП.
Кинематические погрешности, органически присущие различным ИП, не следует смешивать с технологическими кинематическими погрешностями, связанными с погрешностями их изготовления, сборки и регулировки (погрешность шага и профиля элементов передачи, эксцентриситеты элементов передач и шкал, погрешности градуировки, непрямолинейность направляющих и т. д.). 74
Рис. 2.7. Рычажные измерительные преобразователи: а — синусный; б — тангенсный
Существует два способа уменьшения технологических погрешностей: путем назначения более жестких допусков на отдельные элементы цепи передачи сигналов и посредством введения в конструкцию приборов регулировочных элементов или подвижных компенсаторов.
В общем случае в конструкции измерительного прибора должны быть предусмотрены два регулировочных узла: регулировка нуля и регулировка чувствительности. Регулировкой нуля уменьшают влияние аддитивной погрешности, постоянной для каждой точки шкалы, а регулировкой чувствительности — мультипликативных погрешностей, изменяющихся линейно с изменением измеряемой величины. Одновременной регулировкой нуля и чувствительности можно свести систематическую погрешность к нулю в нескольких точках шкалы и уменьшить ее максимальное значение в несколько раз.
Систематические погрешности можно уменьшить посредством экранирования помех, компенсации погрешности или введения обратной связи.
Главными величинами, влияющими на измерения с помощью электрических ИП, являются температура окружающей среды и внешние электромагнитные поля. Температура окружающей среды оказывает влияние на точность измерений с использованием механических ИП. Экранирование от действия этих влия-
Рис. 2.8. Двухрычажный измерительный преобразователь
75
Рис. 2.9. Схема компенсации паразитных токов соединением нулевых проводов по схеме звезды
Рис. 2.10. Схема компенсации влияния температуры при измерении усилий или деформаций при помощи тензометров
ющих величин осуществляется помещением прибора в замкнутое пространство с постоянной температурой (термостатирование), заземлением металлических кожухов приборов и металлической экранирующей оплетки подводящих и отводящих приводов.
Многие из выпускаемых в настоящее время электронных измерительных приборов имеют измерительный вход, один полюс которого соединен с корпусом. Корпус измерительных приборов, питаемых от сети, должен быть заземлен по условиям безопасности, что обычно осуществляется через сетевой штепсельный разъем. На рис. 2.9 показана схема измерительной системы из трех приборов 1, 2 и 3. Провода защитного заземления 4 и 5, а также нулевой провод 7 образуют с проводом 6 измерительной линии петли, в которых внешние магнитные поля могут вызвать паразитные сигналы. Чтобы ислючить появление паразитных сигналов в проводах с измерительным током, следует систему заземления и нулевых проводов соединять по схеме звезды. На рис. 2.9 это достигается удалением проводов, показанных штриховой линией.
Образование замкнутой цепи возврата через защитное заземление можно предотвратить, применяя приборы с изолированным от прикосновения блоком питания или включая защитный трансформатор в цепь питания от сети для каждого прибора. Эффективным средством защиты от паразитных наводок является гальваническое разделение цепей при помощи оптоэлектронных эле
ментов связи.
Компенсация погрешности основана на том, что возмущающий сигнал от влияющих величин при помощи дополнительного ИП и измерительно-вычислительной схемы меняет свой знак и складывается с возмущающим сигналом на выходе основного ИП, компенсируя его. Наиболее характерным примером при-
Рис. 2.11. Схема компенсации мультипликативной помехи при помощи вычислителя:
1 — измерительное устройство; 2 — дополнительный измерительный преобразователь; 3 — вычислитель
менения этого принципа в случае аддитивной помехи является компенсация влияния температуры при измерении усилий или деформаций при помощи тензометров (рис. 2.10), когда температурное изменение сопротивления рабочего тензорезистора 2 компенсируется точно таким же изменением сопротивления в пассивном компенсационном тензорезисторе 1.
Для компенсации мультипликативной помехи необходима дополнительная обработка измерительного сигнала и сигнала помех в вычислителе (рис. 2.11).
Принцип обратной связи можно использовать для устранения как аддитивных, так и мультипликативных помех, особенно там, где
76
требуется сравнительно большая выходная мощность сигнала и имеются такие внутриприборные помехи, как сухое трение, люфт и т. д. Этот способ основан на том, что выходная величина сравнивается с сигналом чувствительного элемента и при несоответствии их значений усилитель или интегрирующее устройство должным образом изменяют выходные сигналы.
2.4. РАСЧЕТ ПОГРЕШНОСТЕЙ СРЕДСТВ ИЗМЕРЕНИЙ
Расчет результирующей погрешности СИ по погрешностям их ИП можно осуществить методом структурного анализа [8]. При этом задача может решаться применительно к отдельному прибору или к совокупности приборов определенного типа. В первом случае находят погрешности (и поправки) прибора на отдельных отметках шкалы либо оценивают границы, в которых лежат погрешности данного прибора. Эти задачи приходится решать при создании уникальных средств измерений и при поэлементной проверке. Во втором случае применительно к совокупности однородных СИ необходимо чаще всего определять долю приборов, погрешность которых находится в пределах заданных границ.
В общем случае информативный параметр сигнала на выходе прибора у связан с информативным параметром сигнала на входе X, параметрами блоков прибора помехами и другими причинами аддитивных погрешностей Zj зависимостью
y=f{X, Hr. 2j), (i=l, 2, .... n), (/=1, 2, tn). (2.3)
Абсолютная погрешность прибора при показании у
дп = +
где е* — относительное отклонение параметра от его номинального значения iiof: Ei = (T]i-Ло*)/Ло<; Уг—коэффициент влияния погрешности параметра T|i:
df т).
V, =------
У
В7; — коэффициент влияния аддитивной погрешности Zy.
Удобнее оценивать не абсолютную, а относительную погрешность прибора, отнесенную к конечному значению шкалы прибора yt:
Ч = 2^- + 2^//Ук-
Для решения задачи необходимо знать вид и параметры модели (2.3), а также характеристики е, и Zj. Обычно задаются предельными значениями С и Zj. Тогда доверительная граница систематической погрешности приборов
Динамическая погрешность средства измерения определяется как разность его погрешности в динамическом режиме и статической погрешности. Типичным случаем измерения, для которого существенна динамическая погрешность, является измерение с регистрацией сигнала, изменяющегося во времени. В этом случае абсолютная динамическая погрешность
77
&я= (B/K~l)X,
где В — оператор; К— коэффициент преобразования.
Оператор В зависит от формы сигнала на входе. Если на входе сигнал является единичной функцией (см. рис. 2.2), то для измерительной системы первого порядка
Дд=ехр(-//Т).
Для измерительной системы второго порядка при Д<1
Дд = ехр (—От)[cos (т /1 — О2) + [О sin (т /1 — О2)]//'1 — О2},
где D —демпфирование; т — безразмерное время.
Если входной сигнал является гармоническим, с единичной амплитудой и частотой © ,то [31]
Д* = [б (»©)- I]2.
2.5. ОПИСАНИЕ СЛУЧАЙНЫХ ПОГРЕШНОСТЕЙ
Конкретное значение случайной погрешности предсказать невозможно. Но совокупность случайных погрешностей измерения подчиняется статистическим закономерностям. Это обстоятельство позволяет применять к изучению и описанию случайных погрешностей измерения методы теории вероятностей и математической статистики.
В вероятностной модели случайные погрешности ДХ (значит, и сами результаты измерения) рассматриваются как непрерывные случайные величины, которые могут принимать любые действительные значения. Причем каждому интервалу (xi.-хг) соответствует вполне определенное число, называемое вероятностью попадания значения случайной величины X в этот интервал и обозначаемое P(xi<X<x2). Находить эти вероятности можно на основе закона распределения вероятностей случайной величины X. Чаще всего принимают Xi=— оо. Тогда, обозначив х2=х, имеем:
F(x) = P(X<x),
где F(x) —интегральная функция распределения:
F W = f Р W dx>
—со
р(х)—некоторая неотрицательная функция, называемая плотностью распределения и подчиняющаяся условию:
00
J р (х) dx = 1.
—оо
При решении большинства практических задач нет необходимости знать все возможные значения случайной величины и соответствующие им вероятности. Удобнее пользоваться некоторыми количественными показателями, которые дают в сжатой форме достаточную информацию о случайной величине. Такие показатели называют числовыми характеристиками случайной величины. Основными из них являются: математическое ожидание М(Х), мода, медиана, дисперсия.
Для непрерывной случайной величины X, возможные значения которой принадлежат интервалу (Х1...Х2), математическое ожидание
х2
М (X) = J хр (х) dx.
Х1
78
Модой Мо непрерывной случайной величины называют такое ее значение X, при котором плотность распределения р(х) имеет максимум.
Медиана Me непрерывной случайной величины — такое ее значение X, для которого справедливо равенство Р(Х<Ме)—Р(Х>Ме), т. е. равновероятно, что случайная величина окажется меньше или больше медианы. Если распределение одномодальное и симметричное, то математическое ожидание, мода и медиана совпадают.
Дисперсия является характеристикой рассеяния случайной величины относительно ее математического ожидания:
П(Х)=М[Х-М(Х)]2.
При оценке рассеивания удобнее пользоваться средним квадратическим отклонением
о = Yd (X) ,
которое называют также стандартным отклонением или стандартом. Дисперсию можно представить в виде
Р(Х)=М(Х2)-[М(Х)]2.
Случайные погрешности измерения чаще всего подчиняются закону нормального распределения (закону Гаусса). Функция плотности распределения в данном случае имеет вид
р(х)=_^"ЙгехрЬ
[Х-М(Х)Р
2<т2
где параметр а характеризует точность измерений. При расчетах широко применяется нормированное нормальное распределение, которое получается при переходе к случайной величине z=[X—М(Х)]/<т:
1 / z2 \
р (г) = Г------ехр —— ;
' ’ / 2л \ 2 )
2
Рис. 2.12. Графики плотности распределения погрешностей:
а — нормальный закон; б — закон Рэлея; в — равномерное распределение
79
Для нахождения F(z) применяют таблицы значений функции Лапласа Ф(а), определяемой выражением
о
При -г > 0 F(z) =0,5+Ф(а), а при z<0 F(z) =0,5 —Ф(з).
Распределение Максвелла (Рэлея) случайной величины R = X3 -|- У2, принимающей только неотрицательные значения (X и У — случайные координаты точки, распределенные независимо и нормально), характеризует такие погрешности, как эксцентриситет, несоосность, биение, разностенность, непарал-лельность или неперпендикулярность. Если в качестве нормированной переменной принять z = RI<s, vjifia — стандартное отклонение параметра R, то функция плотности распределения Максвелла
/ 0,6552га \
р (г) >= 0,6552zexp I —------).
Равномерное распределение свойственно погрешностям округления до ближайшего деления шкалы прибора, а также погрешностям, соизмеримым с отсчетом. В данном случае функция плотности распределения имеет вид
{0 при х < Ь;
1/(с — Ь) при О при х > с.
На рис. 2.12 показаны графики плотности распределений для рассмотренных законов.
2.6. ЧИСЛОВАЯ ОЦЕНКА СЛУЧАЙНЫХ ПОГРЕШНОСТЕЙ
Совокупность всех возможных значений исследуемой случайной погрешности называется генеральной совокупностью. Множество значений случайной погрешности, полученное в результате наблюдения над нею, называют случайной выборкой или просто выборкой. Число объектов в генеральной совокупности и в выборке характеризует их объем. Генеральная совокупность может иметь бесконечный объем.
Основной задачей является получение научно обоснованных выводов о числовых характеристиках генеральной совокупности случайных погрешностей по выборке. Выборочная оценка должна обладать следующими свойствами: несмещенностью, эффективностью и состоятельностью.
Оценку А'параметра А называют несмещенной, если ее математическое ожидание равно оцениваемому параметру. Требование несмещенности гарантирует отсутствие систематических ошибок при оценке параметров. Так как А — случайная величина, значение которой изменяется от^выборки к выборке, то меру ее рассеивания характеризуют дисперсией Д(Д). Из двух оценок А следует отдать предпочтение той, которая обладает меньшим рассеиванием (т. е. меньшей дисперсией).
Несмещенную оценку А, которая имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра А, вычисленных по выборкам одного и того же объема, называют эффективной оценкой.
Оценку А параметра А называют состоятельной, если при неограниченном увеличении объема выборки ее значение приближается сколь угодно близко к значению оцениваемого параметра.
На практике не всегда удается удовлетворить одновременно требованиям несмещенности, эффективности и состоятельности оценки параметра. Иногда для простоты расчетов целесообразно использовать незначительно смещенную оценку.
80
Оценку неизвестного параметра генеральной совокупности одним числом называют точечной оценкой. Точечной оценкой математического ожидания Л1(Х) случайной величины X является среднее арифметическое значение X, вычисленное по результатам т независимых наблюдений:
_ 1 т х=—2хг т
Эта оценка является несмещенной, состоятельной и эффективной. Она имеет дисперсию <Р/т, если дисперсия случайной величины X равна <т2.
Несмещенной оценкой дисперсии генеральной совокупности D(X) является исправленная выборочная дисперсия
1 т
s2=-42(^-^)2-
Эта оценка является состоятельной, но не эффективной.
При малом числе наблюдений необходимо использовать интервальное оценивание, так как в этом случае точечная оценка недостаточно надежна. Необходимо по данным выборки построить числовой интервал, в котором с заранее выбранной вероятностью находится значение оцениваемого параметра.
Доверительным интервалом (Л2—Л1) для параметра А называют такой интервал, для которого с заранее выбранной вероятностью Р=1 — а, близкой к единице, можно утверждать, что P(Xt<4<A2) = l —а.
Чем меньше для выбранной вероятности (Л2—Д]), тем точнее оценка параметра А. Доверительный интервал меняется от выборки к выборке.
Вероятность Р=1 — а называется доверительной вероятностью, а число а — уровнем значимости. Выбор доверительной вероятности зависит от конкретной решаемой задачи.
Если случайная величина распределена нормально, а дисперсия этого распределения неизвестна, то доверительный интервал для математического ожидания Л4(Х) определяется неравенством
: X — t (Р, т) • S/К т < М (X) < X + t (Р, т) S// т,'4
где i(P, т)—критерий Стьюдента (табл. П. 1) при доверительной вероятности Р и числе степеней свободы f=m—l.
Если случайная величина распределена нормально, доверительный интервал для дисперсии генеральной совокупности при доверительной вероятности Р=1 — а определяется неравенством
^J_s2<a2<^zls2>
X? 7.2
где у2 — критерий Пирсона (табл. П.4), который для у2 соответствует доверительной вероятности, равной 0,5а, для /|—О— 0,5а); определяется при f = m— 1 (в табл. П. 4 заданы отношения "х]/(иг— 0 и Хг/О71— 0 в зависимости от Р и т).
2.7. ОБЪЕДИНЕНИЕ РЕЗУЛЬТАТОВ НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ
Одну и ту же величину часто измеряют различными приборами, в разных лабораториях или разные операторы. Иногда возникает задача объединения полученных данных, с тем чтобы получить наиболее точную оценку измеряемой величины. Пусть имеется п групп измерений одной и той же величины А с со
81
ответствующими оценками измеряемой величины Хр Х2, Хп, причем М (Xj) = М (Х2) = ... = М (Хп) = А, Известны оценки дисперсии Sp S2, .... S2n и число наблюдений в каждой группе тр т^, .... тп. Оценка А по данным всех измерений
__ п
1=1 где
п 1/S?
Si-~---------;
. <=> gi — вес i-й серии наблюдений.
Дисперсия, характеризующая точность оценки величины А, определяется по формуле
п
S2(X) = l/Vm./S2.
1=1
Погрешность определения веса любой серии наблюдений практически не отражается на точности объединенной оценки параметра А:
АХ Kg | X — Х(. | ~8 % '
Второй сомножитель правой части этого неравенства — порядка 0,01. Поэтому погрешность оценки среднего взвешенного из-за погрешности определения весов будет не менее чем в 100 раз меньше последней.
В отдельных случаях можно пренебречь систематическими погрешностями измерения и предположить, что полученные оценки отличаются незначительно и обусловлены случайными погрешностями измерения.
Гипотеза о равенстве дисперсий в п группах измерений проверяется с помощью критерия Пирсона %2. Наблюдаемое значение критерия
/Г 1 /п 1 1 \
7.'2 = М/ 1 + ------------7Г 2 --------------
/ [ 3(п —1) mi —1 N I
где
1 п
М = Л/1П
-2(щ(.-1) InS2; г=1
п
N =2 (mt — *); mi > 4; п > 2. 1=1
Для выбранной доверительной вероятности Р и числа степеней свободы I/ = п—1 определяется (табл. П.2) критическое значение критерия Пирсона . Если Хн < Х2к > то гипотеза о равенстве дисперсий принимается. Тогда вес / п \
i-й серии наблюдений следует определять как = mi/N1 I = У, mi I, а дис-ч t=l /
Персию оценки параметра A — по формуле 82
s2(X) =
i
Ni (ATi — 1)
n n _
(*/-*)
_Z=1 Z=1
При измерении одной величины п приборами возможны ситуации, когда реальные погрешности измерения неизвестны, а известны только оценки границ погрешностей Д, (i=l, 2, .... п) объединяемых результатов измерений при заданном значении доверительной вероятности Р. Тогда доверительная погрешность оценки параметра А, если погрешности приборов имеют равномерное распределение и Д,=Д, будет
ДЕ = КД//Т,
где К зависит от доверительной вероятности (может колебаться от 1,1 при Р=0,95 до 1,4 при Р=0,99).
2.8. ПОГРЕШНОСТИ КОСВЕННЫХ ИЗМЕРЕНИЙ
Искомое значение величины У при косвенных измерениях находят путем согласованных измерений других величин Xi, связанных с измеряемой величиной известной зависимостью. Величина X, называется аргументом. Значения аргументов чаще всего определяют в результате прямых измерений.
Различают линейные и нелинейные косвенные измерения. В первом случае
п
1=1
где bi — постоянный коэффициент; п — число слагаемых.
Во втором случае
п
г= .пЛ(х0-
Оценка У при линейных косвенных измерениях определяется по формуле
п
У = V
1=1
где Xf — оценка математического ожидания t-ro аргумента.
Погрешность косвенного измерения У в данном случае
п ду = 5&г (ДХ,). 1=1
где ДХ; — погрешность измерения i-ro аргумента.
Дисперсия оценки величины У при косвенном линейном измерении
S2 (у) = 2Ш)-(=1
где S? (х/| — дисперсия оценки аргумента Хр
Это выражение верно в случае независимости погрешностей измерений аргументов.
При нелинейных косвенных измерениях значение У оценивается выражением п
1=1
83
Такая оценка является несмещенной и состоятельной, если оценки X, являются состоятельными. Погрешность косвенного измерения в данном случае
ду = 2^ (Л\),
/=1
где Wi —коэффициент влияния i-ro аргумента:
д Wi=-dx7(^-
При отсутствии корреляционной зависимости между погрешностями измерений аргументов дисперсия оценки У вычисляется по формуле
л
S2(r) = S«W*z)-
1=1
Если WlSi (xj <0,3S(y), то погрешность оценки i-ro аргумента несущественно влияет на погрешность косвенного измерения. Аналогичный вывод можно сделать относительно нескольких (/) аргументов, если
S ^2 (х,.) <0,35 (У).
Повышение точности косвенного измерения необходимо обеспечивать за счет повышения точности оценки тех аргументов, которые дают существенный вклад в дисперсию оценки У.
2.9. ОБНАРУЖЕНИЕ ГРУБЫХ ПОГРЕШНОСТЕЙ
Если в полученной группе результатов измерений одно-два резко отличаются от остальных, а описки, ошибки в снятии показаний и тому подобные промахи не установлены, следует проверить, не являются ли они грубыми погрешностями, подлежащими исключению. При решении данной задачи предполагается, что результаты наблюдений подчиняются нормальному закону распределения. Грубые погрешности возникают при случайном резком изменении условий измерения.
Для решения задачи имеющиеся результаты измерения располагают в вариационный ряд монотонно возрастающих значений Х< (i= 1, 2, ..., т). Проверке подлежит наименьший X] (или наибольший Хт) член ряда. Сначала вычисляются числовые характеристики результатов наблюдений:
*= —«2 = -Ц-2(*1-*)2. т ’ т — I '
затем наблюдаемое значение критерия vH= |Х—XJ/S.
Задавшись доверительной вероятностью Р, определяем по табл. П. 3 критическое значение критерия Vk, которое зависит также от числа измерений т. Если va<Vk, то принимается гипотеза И,—все наблюдения проводились в одинаковых условиях и значение Х[ (или Хт) составляет с остальными результатами однородную выборку. Если это неравенство нарушается, т. е. vH>Vk, то «подозрительный» результат X! следует исключить из дальнейшего рассмотрения.
Если в выборке несколько «подозрительных» результатов измерения, то данная процедура может применяться поочередно к каждому из них в отдельности.
.'84
Пример 2.1. Результаты измерения выборки деталей, обработанных на бесцентровошлифовальном станке, образуют следующий ряд отклонений от номинала (мкм): 26; 30; 25; 28; 40; 32; 26; 22; 28; 31. Требуется определить с доверительной вероятностью, равной 0,95, является ли отклонение в 40 мкм грубой погрешностью.
Решение.
X = —288 = 28,8; S2 = —219,6 = 24,4;
10 9
vH = | 28,8 — 40 |/ V24,4 = 2,267.
Согласно табл. П.З, vK = 2,294. Так как vH<vK, то отклонение в 40 мкм не является грубой ошибкой.
3. МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ЭКСПЕРИМЕНТА
3.1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
Эксперимент — система операций и (или) наблюдений, направленных на получение информации об объекте исследования. Составной частью эксперимента является опыт — воспроизведение исследуемого явления в определенных условиях при возможности регистрации и количественной оценки состояния или результатов функционирования исследуемого объекта. Эксперимент проводится на промышленном оборудовании, лабораторной установке или физической модели. При этом механизм изучаемого процесса обычно известен лишь частично или совсем неизвестен. В таких случаях объект исследования можно условно представить в виде «черного ящика» — системы внутренних связей, не доступных исследователю. Известны лишь переменные величины, воздействующие на объект исследования, и величины, характеризующие его состояние или результаты функционирования (рис. 3.1). Первые называют входными величинами или факторами, а вторые — выходными или откликом.
Все факторы делятся на три группы:
1) группа постоянных или случайно изменяющихся в ходе исследования факторов W, значения которых известны;
2) группа управляемых факторов U, значения которых выбираются и целенаправленно изменяются в ходе исследования (две первых группы часто объединяют в одну группу контролируемых факторов X);
3) группа неконтролируемых факторов Z, значения которых остаются по той или иной причине неизвестными в ходе исследования.
Изменение отклика Y под действием монотонно изменяющихся во времени неконтролируемых факторов называется временным дрейфом отклика, а зависимость математического ожидания отклика от контролируемых факторов — функцией отклика. Геометрическое представление функции отклика называется поверхностью отклика. Чтобы такое представление стало возможным, вводится понятие факторного пространства, у которого координатные оси соот
Рис. 3.1. Кибернетическая модель объекта исследования
Рис. 3.2. Геометрическая модель трехфакторного пространства
86
ветствуют отдельным факторам. Пример трехмерного факторного пространства показан на рис. 3.2.
Любая точка факторного пространства характеризуется набором значений факторов, при которых производится измерение отклика. Фиксированное значение фактора называют также уровнем фактора. При количестве факторов, большем трех, геометрическое моделирование факторного пространства становится невозможным. Поэтому чаще всего множество уровней факторов, при которых производится измерение отклика, задается матрицей условий эксперимента. Эта матрица для k факторов и N измерений имеет вид
X2i Х31 ^ki
Y — I ^12 ^22 ^32 • • •
Х2н X3N ... XkN
Значения отклика, полученные при данных измерениях, также представляются в матрице, которая имеет один столбец и называется матрицей наблюдений-.
Г1\
F = | 2 I. (3.1)
\yN'
По характеру организации и методам обработки результатов эксперимент может быть пассивным или активным.
При реализации пассивного эксперимента исследователь наблюдает за объектом, не вмешиваясь в процесс его функционирования. Поскольку в данном случае уровни факторов случайным или закономерным образом изменяются во времени, то появляется возможность, измеряя их значения и значения отклика, исследовать зависимость между факторами и откликом. Примером пассивного эксперимента является исследование точности обработки деталей на настроенном станке. Факторами в данном случае будут погрешности заготовок, их твердость, износ инструмента, жесткость станка, откликом — погрешность обработанных деталей.
При реализации активного эксперимента исследователь сам изменяет уровень факторов и поддерживает их на нужном уровне в течение данного этапа эксперимента.
К контролируемым факторам предъявляются следующие требования, которые должны учитываться при подготовке активного эксперимента.
1. Управляемость фактора — возможность поддерживать выбранный уровень фактора в течение необходимого для измерения отрезка времени.
2. Достаточно высокая точность, с которой поддерживается и измеряется уровень фактора.
3. Независимость фактора — возможность задать любой уровень данного фактора вне зависимости от уровней других факторов.
4. Совместимость факторов — безопасность функционирования объекта исследования и возможность измерения отклика в любой точке той части факторного пространства, которая является областью экспериментирования.
Кроме факторов, каждому уровню которых после измерения можно поставить в соответствие определенное число, могут быть и качественные факторы (например, рецепты связок шлифовальных кругов, материалы режущей части инструмента, химический состав обрабатываемого материала). В этом случае каждому уровню качественного фактора нужно поставить в соответствие число натурального ряда (код). Порядок уровней качественных факторов может быть произвольным, но после кодирования он фиксируется. Для упрощения расчетов при обработке результатов эксперимента рекомендуется проводить нормализацию факторов — преобразование их в безразмерные величины с (по возможности) целочисленными значениями. При симметричной нормализации расчетная формула имеет вид
87
хц=(Хц-Х1)/&Х], (3.2)
где хц — нормализованный i-й уровень у-го фактора; Хц — натуральный i-й уровень у-го фактора; ДХ; — постоянный шаг изменения натурального значения у-го фактора; Xj — средний уровень у-го фактора:
^/ = 7 2^/; (33)
' j=l
г — число уровней фактора.
Чтобы нормализованные факторы приняли целочисленные значения, число уровней их должно быть нечетным. Например, при г=5 коды факторов принимают значения —2; —1; 0; 1; 2.
При несимметричной нормализации
1 4" (X,j—Xi min)/AXj, (3.4)
где Xi min — минимальный уровень у-го фактора.
В данном случае нормализованные факторы принимают значения 1, 2, 3, .... г. В качестве факторов могут приниматься не только физические или геометрические величины, но и некоторые функции от них (например, логарифмы или показательные функции).
При выборе отклика из нескольких, обычно функционально связанных показателей результата функционирования исследуемого объекта должно учитываться следующее.
1. Необходимо, чтобы отклик был однозначным в статистическом смысле, т. е. заданному набору уровней факторов должно соответствовать одно (с точностью до погрешности измерения) значение отклика.
2. Отклик должен быть эффективным в статистическом смысле. Это значит, что из нескольких функционально связанных откликов выбранный можно измерить с наибольшей точностью.
3. Желательно, чтобы отклик можно было оценить количественно. Если нет способа количественного измерения результата, то следует пользоваться ранжированием. При этом отклику присваиваются оценки — ранги по заранее выбранной шкале.
План эксперимента — совокупность данных, определяющих число, условия и порядок реализации опытов. План эксперимента обычно записывается в виде матрицы плана — прямоугольной таблицы, строки которой отвечают отдельным опытам, а столбцы — факторам. Элементами матрицы плана обычно являются нормированные уровни факторов, т. е. (и, /)-й элемент равен нормированному уровню у-го фактора в и-м опыте. Матрица плана может иметь совпадающие строки. Чтобы сократить запись, используется матрица спектра плана, составленная из всех строк матрицы плана, отличающихся уровнем хотя бы одного фактора, и матрица дублирования — квадратная диагональная матрица, элементы которой равны числам параллельных (дублирующих) опытов в соответствующих точках спектра плана.
План, содержащий все возможные комбинации всех факторов на определенном числе уровней равное число раз, называется полным факторным планом. Если план содержит только часть комбинаций полного факторного плана, то его называют дробным факторным планом или дробной репликой полного факторного плана.
3.2. ОЦЕНКА ОТКЛИКА
Отклик оценивается по результатам прямых или косвенных измерений [67, 77]. Способ оценки зависит от природы отклика (случайная или неслучайная величина) и точности измерений. Основной задачей в данном случае является получение обоснованных выводов о действительном значении отклика с учетом погрешностей измерения при ограниченном числе измерений. Опре
88
деления понятий выборка, несмещенность оценки, эффективность и состоятельность оценки, а также точечная и интервальная оценка приведены в § 2.6.
Возможны следующие подходы к оценке отклика.
1. Отклик является неслучайной величиной и ошибки измерения малы по сравнению со значениями отклика. При i-м измерении получаем
Y=yi+bi,
где Y — истинное значение отклика; у, — измеренное значение отклика; Д,- — погрешность измерения.
Если Д;< (0,01...0,02) yit то погрешностью измерения можно пренебречь и полученное после первого измерения значение yi принять за истинное.
2. Отклик является неслучайной величиной, но погрешностями измерений нельзя пренебречь. Для уменьшения влияния погрешностей измерения на точность оценки производится многократное измерение отклика в одинаковых условиях (в одной и той же точке факторного пространства).
Точечной оценкой истинного значения отклика в данном случае будет среднее арифметическое значение результатов параллельных измерений
। т
У=—^У1, (3.5)
т i=i
где т — количество параллельных измерений.
Точность соответствия у истинному значению тем выше, чем больше т. При относительно небольшом числе измерений целесообразно применять интер-вальнчю оценку отклика
у — t (Р, т) S/1^ т < У < у Д-1 (Р, т) S/У т , (3.6)
где t(P, т) —критерий Стьюдента (табл. П.1); S — оценка стандартного отклонения погрешностей измерения; Р — доверительная вероятность.
Точечная оценка стандартного отклонения определяется из выражения
I т
<3.7)
3. Отклик является случайной величиной, а размах ошибки измерения пренебрежимо мал по сравнению с полем рассеяния значений отклика. В данном случае наиболее полной характеристикой отклика будет закон распределения его значений. Но в большинстве практических задач достаточными считаются числовые характеристики распределения случайной величины Y. Минимально необходимыми являются: а) математическое ожидание М(У), определяющее положение центра группирования значений отклика; б) дисперсия D (У) или стандартное отклонение ст (У) = D (У) , характеризующие рассеивание значений отклика.
В качестве точечной оценки математического ожидания М(У) принимается среднее арифметическое значение результатов параллельных измерений у, которое вычисляется по формуле (3.5). При т>30 удобнее группировать значения У по интервалам одинаковой длины h. Все поле рассеяния делится на нечетное число (7...15) интервалов длиной h и подсчитывается количество т,-значений отклика, попавших в каждый i-й интервал. Принимается, что все значения отклика, попавшие в i-й интервал, равны координате его середины. Тогда h * / k+ 1\
^ = Уо + -2^-— (3-8)
где г/о — координата середины среднего интервала; k—количество интервалов; к
m = S mi-
1==1
89
Точечной оценкой дисперсии является наблюдаемая дисперсия S2, значения которой при 10</п<30 можно определить по формуле (3.7). Если число параллельных измерений мало (nt<15), то оценку стандартного отклонения можно проводить по размаху
Rm —Утлх — l/mln-
В данном случае
•S — Rmfdm.
(3.9)
где dm — среднее значение относительного размаха, т. е. отношения размаха к стандартному отклонению (табл. П.5).
При zn>30 и группировании по интервалам одинаковой длины
(З.Ю)
т,, „„„ ____ _________________ ________ .
zinicpjsdJionaM ицспла магемгиическию ожидания находится с ПОМОЩЬЮ выражения (3.6), где S определяется по формуле (3.9).
Интервальная оценка стандартного отклонения:
а) при т< 15
Rm/dmt<C.G<Z.Rm/dm2,
где dmi, dm2 — критерии, определяемые по табл. П.5 в зависимости от доверительной вероятности Рит;
б) при т>15
S (1 — <?) < о < S (1 + q) или—------ S2 < а2 < ™ 1 S2, (3.11)
-/.I xi
где q — критерий, который определяется из табл. П.6 в зависимости от Р и т; значение %2/(т— 1) определяется из табл. П.4; S определяется из (3.7) или (3.10).
4. Отклик является случайной величиной, а ошибки измерения существенны, т. е. не пренебрежимо малы по сравнению с размахом значений отклика. Если исключена систематическая погрешность измерения, то оценка математического ожидания производится по формулам (3.5), (3.6) или (3.8). Поскольку погрешность измерения и отклик являются независимыми случайными величинами, то оценка стандартного отклонения отклика находится из выражения
S2(y) = S2-S2,
где — оценка стандартного отклонения, полученная путем обработки результатов, серии измерений; 5И — оценка стандартного отклонения погрешности измерения (для определения Зи проводится специальный эксперимент).
Если SH > <Ss, то считаем S (К) =0.
5. Отклик является случайной функцией У(0, где аргумент t может быть непрерывной (например, время) или дискретной величиной (например, порядковый номер обрабатываемой детали). В отличие от случайной выборки в данном случае порядок следования измерений является существенным для выявления причинных механизмов, обусловливающих свойства отклика. Если t может принимать любые значения в заданном интервале, то У(/) называют случайным процессом. Если t принимает только определенные дискретные значения, то Y (0 называется случайной последовательностью или временным рядом. На рис. 3.3 приведен пример временного ряда, образованного отклонениями Y размеров деталей, обработанных на токарно-револьверном автомате [54]. Полученная экспериментально последовательность значений У(/) называется реализацией случайного процесса (или временного ряда).
90
Рис. 3.4. Реализации случайных функций:
а — стационарной; б, в, г — нестационарных
Рис. 3.3. Пример временного ряда (изменение размеров деталей, обработанных на автомате)
.Наиболее важным свойством случайной функции, определяющим возможность применения тех или иных методов исследования, является зависимость или независимость ее свойств от начала отсчета времени. В соответствии с этим различают стационарные и нестационарные случайные функции. Для случайной функции первого типа все ее характеристики зависят только от взаимного расположения значений аргумента, а не от самих значений. На рис. 3.4 показаны примеры реализаций стационарной и нестационарных случайных функций. У нестационарных случайных функций при изменении аргумента изменяется рассеяние значений Y(t) (рис. 3.4, б), положение его центра группирования (рис. 3.4, в) или обе характеристики.
При наличии множества реализаций случайной функции совокупность ее значений при фиксированном значении аргумента образует множество случайных величин, числовыми характеристиками которого является математическое ожидание Л1[У(/)] и дисперсия £)[У(/)]. Обе эти характеристики являются неслучайными функциями аргумента. Для стационарных случайных процессов и временных рядов A4[K(Z)] = const; £)[У (£)] = const.
Связь значений случайной функции при разных значениях аргумента характеризуется корреляционной функцией
К(/ь /2) = Л1{{У(/1)-Л1[Г(М]} {У (/2) - Л1[У(/2)]}}.
Для стационарных случайных процессов корреляционная функция зависит только от сдвига значений аргумента.
При анализе случайных функций обычно используется предположение об эргодичности изучаемых процессов. Процесс называют эргодическим по отношению к какой-либо его характеристике (математическое ожидание, дисперсия),-если ее значение по множеству реализаций совпадает со значением по множеству значений аргумента. Свойство эргодичности позволяет оценивать выборочные характеристики случайной функции по одной реализации. Для стационарных временных рядов оценкой Л4[У(£)] будет среднее арифметическое значение
1 т
(3.12) т /=1
оценкой дисперсии D[Y(0J —
91
Рис. 3.5. Корреляционная функция отклонений размеров’
1 т «2=—[2 <313)
а оценкой корреляционной функции —
1 т _
т = 1, 2, .... п. (3.14)
Для сравнения свойств временных рядов с разными масштабами измерения используют нормированную корреляционную функцию
г(т) =7((t)/.S2.
Добавление к случайной функции Y(t) неслучайной величины Уо или неслучайной функции ф(/) не влияет на значение корреляционной функции. Типичная корреляционная функция отклонений размеров деталей показана на рис. 3.5.
Пример 3.1. Требуется оценить математическое ожидание и среднее квадратическое отклонение стойкости резцов с пластинками твердого сплава марки Т15К6 при обработке деталей из стали 18ХГТ с глубиной резания а=2 мм, подачей s=0,23 мм/об и скоростью резания ц = 80 м/мин. Испытывалась партия резцов из 791 шт.
Решение. Результаты испытания и вычислений приведены в табл. 3.1. Диапазон рассеивания отклика разбит на 9 интервалов с шагом АТ=2 мин. Во втором столбце табл. 3.1 приведена стойкость резцов Т, соответствующая середине интервала.
В данном случае середине среднего интервала соответствует отклик у0= = 7’о=56 мин. По формуле (3.8)
2
Г = 56 + 19 = 56,05 мин;
по формуле (3.10)
Табл 3.1. Распределение частот и результаты вычислений
i mi . 2 /. fe+iy 2 / /. w-iv (г- т)mi
1 48 3 —4 — 12 16 48
2 50 17 —3 —51 9 153
3 52 75 —2 — 150 4 300
4 54 194 —1 — 194 1 194
5 56 228 0 0 0 0
6 58 155 1 155 1 155
7 60 91 2 182 4 364
8 62 23 3 69 9 207
9 64 5 4 20 16 80
Итого: 791 0 19 1501
92
22
S2^ —-------Г (1501 — 791 • 0,052) = 7,6; 5 = 2,76 мин.
Пример 3.2. В результате испытания партии из 30 сверл получены следующие характеристики их стойкости Т: среднее значение Г= 18,76 мин, наблюдаемая дисперсия S=5,63. Требуется найти доверительные интервалы для математического ожидания М(Т) и среднего квадратического отклонения о с доверительной вероятностью Р=0,95.
Решение. По заданной Р при данном числе измерений из табл. П. 1 находим значение критерия Стьюдента t = 2,045, а из табл. П.6 и П.4, соответственно, значения критериев q = 0,28; '/^1(т— 1) = 1,577; 'fy(m—1) = = 0,533. По формуле (3.6) определяем ошибку в оценке математического ожидания е = +2,045 /5,63/30 = +0,885. Тогда М (Т) = 18,76 + 0,885 мин.
По формуле (3.11) доверительный интервал для ст, согласно критерию q:
/+63 (1 — 0,28) < ст </+63 (1 + 0,28) или 1,71 < ст < 3,04.
Доверительный интервал для ст, согласно критерию Пирсона (формула (З.Н)):
5,63/1,577<ст2<5,63/0,533 или 1,89<ст<3,25.
Критерий Пирсона дает такой же доверительный интервал для ст, что и критерий q, но незначительно смещенный вверх.
3.3. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ [28, 44]
3.3.1. Основные определения
Статистическая гипотеза — предположение относительно статистических параметров генеральной совокупности или закона распределения случайных величин, проверяемое на основе выборочных данных.
Основная проверяемая гипотеза (нулевая гипотеза) обычно обозначается Нй. Одновременно формулируется альтернативная или конкурирующая гипотеза Hi. Например, если проверяется равенство математического ожидания генеральной совокупности некоторому значению ц0, нулевая гипотеза На~ М (У) = go, альтернативная гипотеза л/ —Л1(У)+ц0.
Критерием статистической гипотезы называют правило, позволяющее принять или отвергнуть гипотезу на основании выборки из генеральной совокупности. Принимая или отклоняя гипотезу Но, можно допустить ошибки двух видов. Ошибка первого рода состоит в том, что гипотеза На отвергается, в то время как в действительности она верна, ошибка второго рода — гипотеза Но принимается, в то время как верна гипотеза Hi.
Вероятность ошибки первого рода обозначается а. Ее часто называют уровнем значимости критерия гипотезы. Вероятность ошибки второго рода обозначается р. Вероятность 1 —р принятия гипотезы Hi, когда она верна, называется мощностью критерия гипотезы Но относительно альтернативной гипотезы Hi. Очевидно, что при проверке гипотезы Но относительно альтернативной гипотезы Ht лучшим является тот критерий, который обеспечивает наибольшую мощность при том же самом уровне значимости а.
3.3.2. Проверка гипотезы о равенстве математического ожидания заданному значению
Пусть сформулирована нулевая гипотеза (На) Л4(У)=ц0 и альтернативная (Hi) М(У)+=р.о- Выборка наблюдений объемом т для проверки нулевой гипотезы осуществляется из генеральной совокупности значений случайной вели
93
чины У, распределенных по нормальному закону. Оценкой математического ожидания по выборке будет среднее арифметическое у (формула (3.5)), а оценкой дисперсии — S2 (формула (3.7)). Для проверки нулевой гипотезы вычисляется наблюдаемое значение критерия Стьюдента
/ _ Р - Но I
tH —-— — •
S т
Критическое значение критерия /к определяется для выбранной доверительной вероятности Р=1 — а и заданного объема выборки т из табл. П.1. При /н<^к можно считать, что данные выборки не противоречат нулевой гипотезе; если /н>/к, гипотеза отвергается.
3.3.3. Проверка гипотезы о равенстве средних значений
Пусть выборки наблюдений объемом mi и берутся из двух генеральных совокупностей с нормальным распределением, причем дисперсии генеральных совокупностей и Oj равны. Необходимо проверить гипотезу На о равенстве математических ожиданий М (Kj) = М (У2)-
По данным выборок определяются оценки математических ожиданий и дисперсий у2, S2 и S2. Объединенная оценка дисперсии генеральных совокупностей
S2 = [Sf (m, - 1) + Si («2 ~ *)]/("*1 + m2 - *) (3-15)
Для проверки нулевой гипотезы вычисляется наблюдаемое значение критерия Стьюдента
, 1/ -"О-. (зле»
S V «1 + т2
Критическое значение критерия определяется для данной доверительной вероятности Р и m = mi+m2. При ?H<fk гипотеза принимается; если она отвергается.
Пример 3.3. В одинаковых условиях было обработано по 25 втулок развертками диаметром 6 и 10 мм. Результаты измерений показали, что средняя величина разбивки отверстий (разность диаметра развертки и диаметра отверстия) для разверток диаметром 6 мм составляет 10,9 мкм, а диаметром 10 мм— 9,8 мкм. Оценки дисперсий в обоих случаях соответственно S2 = 3,8 мкм2; 8^ = = 4,76 мкм2. Необходимо установить, влияет ли диаметр развертки на разбивку отверстия.
Решение. Согласно (3.15),
3,8 24 + 4,76 • 24
S2 = -------—’-------- =4,19;
49
согласно (3.16), _ 10,9 — 9,8 /~ 25 - 25
tn~ /4Д9 V 25 + 25 = ’ •
По табл. П. 1 при Р=0,95 и т = 50 находим fn=2,01. Поскольку ta<tk (1,9<2,01), можно считать, что изменение диаметра развертки в пределах от 6 до 10 мм не оказывает существенного влияния на величину разбивки развернутого отверстия.
94
3.3.4. Проверка гипотезы о равенстве дисперсий
При обработке экспериментальных данных часто требуется выяснить вопрос об однородности выборочных дисперсии т. е. их равенстве дисперсии генеральной совокупности.
Пусть для двух независимых выборок из нормальной генеральной совокупности с объемами mi и т2 вычислены согласно (3.9) или (3.13) оценки S2 и S|. Требуется проверить нулевую гипотезу(//0) а2 _ относительно альтернативной гипотезы (Wj) о2 > а2. Проверка проводится при помощи критерия Фишера F.
Наблюдаемое значение критерия
Fn=^/Sl (3.17)
сравнивается с критическим Ek, которое определяется из табл. П.7 для выбранных доверительной вероятности и mi и т2. Если Ен<Ек, то выборочные данные не противоречат нулевой гипотезе.
При анализе выборочных данных могут выдвигаться гипотезы об однородности дисперсий в нескольких выборках. В этом случае можно использовать критерий Кохрена. Наблюдаемое значение критерия GH определяется по формуле
(3-18) 11=1
где S2imayi — максимальная оценка дисперсии среди п сравниваемых дисперсий (все п выборок имеют одинаковый объем т).
Критическое значение критерия определяется из табл. П.8 в зависимости от принятых доверительной вероятности Р, объема выборок т и их числа п.
Пример 3.4. Проверить гипотезу о равенстве дисперсий в примере 3.3.
Решение. По формуле (3.17) определяем наблюдаемое значение критерия Фишера Ен=4,76/3,8= 1,25. Из табл. П.7 для Р = 0,95, mi = m2=20 находим Ек = 2,16, а для mi = m2=30—Fk= 1,84. Искомое значение Ek для m! = m2=25 находим линейной интерполяцией: Ек = (1,84+2,16)/2 = 2.
Так как Ен<Ек (1,25<2), нулевая гипотеза о равенстве дисперсий принимается.
Пример 3.5. С четырех автоматов, настроенных на обработку одних и тех же деталей, взято по одной текущей выборке объемом т = 10. Оценки дисперсий их размеров имели следующие значения: Sf — 106 mkm2;S|=294; S2=216; S2 = = 410 мкм2. Требуется определить, одинакова ли точность автоматов, т. е. можно ли принять гипотезу об однородности дисперсий.
Решение. Согласно (3.18),
н 106 + 294 + 216 + 410
По табл. П.8 для Р=0,95, т=10 и п=4 находим Gk=0,502. Поскольку G„<Gk (0,3996<0,502), то можно считать точность автоматов практически одинаковой.
3.3.5. Проверка случайности и независимости результатов измерений в выборке
До статистической обработки результатов измерения отклика необходимо убедиться в том, что они являются стохастически независимыми. Альтернативной гипотезой может быть предположение о наличии монотонного или цикли
95
ческого смещения (дрейфа) значения отклика, вызванного неконтролируемым фактором. Подобный случай может иметь место при анализе размеров деталей, обрабатываемых на настроенном станке, когда вследствие изнашивания инструмента или нагрева станка центр группирования размеров постепенно смещается при неизменной стандартной погрешности. Наиболее мощным критерием проверки нулевой гипотезы будет критерий последовательных разностей т.
Наблюдаемое значение критерия
th=c2/S2, где т—1
С = 2(m — 1) ~ Г02’
г=1
т — объем выборки; i — порядковый номер измерения отклика в выборке; 52 — оценка дисперсии, вычисляемая по формулам (3.7), (3.9) или (3.10).
Критическое значение Ти определяется из табл. П.9 в зависимости от принятой доверительной вероятности Р и объема выборки т. Если тн<Тк, то гипотеза о независимости и случайности измерений в выборке отвергается.
Пример 3.6. По результатам измерения деталей, обработанных на токарноревольверном автомате (см. рис. 3.3), необходимо проверить наличие или отсутствие дрейфа размеров. Объем выборки /и=40.
Решение.
40 40
у = Yi =45 мкм- 6'2 = ’S(Yi _^)2= 267,95 м™2,
1=1 1=1
39
? = 2(40— !) (Г«-+1 - Г02 = 114’74 мкм2- тн = 114,74/267,95 = 0,428.
«=1
По табл. П.9 для т = 40 и Р=0,95 получаем тк = 0,742. Так как тн<тк (0,428<0,742), гипотезу об отсутствии дрейфа следует отклонить. Следовательно, размер обрабатываемых деталей зависит от неучтенного фактора, вызвавшего циклическое смещение центра группирования размеров.
3.4. ДИСПЕРСИОННЫЙ АНАЛИЗ [20, 44]
3.4.1. Однофакторный дисперсионный анализ
Дисперсионный анализ предназначен главным образом для выявления степени влияния контролируемых факторов на отклик. В зависимости от количества факторов, включенных в анализ, различают однофакторный, двухфакторный и многофакторный дисперсионный анализ.
Проведение дисперсионного анализа возможно, если результаты измерений являются независимыми случайными величинами, подчиняющимися нормальному закону распределения с одинаковыми дисперсиями.
При однофакторном дисперсионном анализе выявляется степень влияния одного фактора X на математическое ожидание отклика А4(У). Фактор может быть количественным (скорость резания, размер заготовки и т. д.) или качественным (модель станка, марка инструментального материала и т. д.). В процессе эксперимента фактор поддерживают на п уровнях. На каждом уровне фактора проводится т дублирующих опытов. Значение т может быть одинаковым или разным для каждого из уровней. Результаты всех измерений удобно представлять в виде таблицы, которую называют матрицей наблюдений (табл. 3.2). I
96
Табл. 3.2. Матрица наблюдений
Номер уровня фактора Уровень фактора Наблюдения Число дублирующих опытов
1 X! Yu, Уи, , Ylh •• -, У1Ш,
2 х2 ^21> Y22, Г2/, •, Y2m2 m2
i Xf У a, Yi2, Yif, , Y imi mi
п Хп Yni, Yni, •••, Ynh •• , Ynmn mn
Вначале для каждой серии дублирующих опытов вычисляют оценки M(Ytyt равные yt, и дисперсии воспроизводимости
т/ mi
!<ЗЛ9)
7=1 7=1
Затем проверяют однородность ряда дисперсий Sp ......S?, ..., S? для
каждой пары при помощи критерия Фишера, если mt- различны, или при помощи критерия Кохрена, если mt = const (см. § 3.3.4). После подтверждения гипотезы об однородности дисперсий можно приступать к анализу. При этом полагают, что результат любого измерения Y{j можно представить моделью
l,U=P+Y«+e<j, где ц — общая средняя; yi — отклонение, вызванное изменением контролируемого фактора; е,,—отклонение, вызванное неконтролируемыми факторами. Задача дисперсионного анализа состоит в оценке существенности влияния изменения уровня фактора.
Влияние неконтролируемых факторов, т. е. вклад е,можно оценить средней дисперсией воспроизводимости п
Общее рассеивание значений отклика, вызванное как контролируемым, так и неконтролируемыми факторами, оценивается полной (или общей) дисперсией
п т1
1=1 /=1 где п п
i=1 i—1
Рассеивание значений отклика, вызванное контролируемым фактором, оценивается дисперсией
7. Зак. 1001 97
Табл. 3.3. Матрица наблюдений
Номер уровня факто* ра (марки СОЖ) Уровень фактора . — Значения Ra в опытах
1 2 3 4 5 6
1 Хг 0,72 0,6 0,65 0,32 0,8 0,52
2 0,15 0,62 0,22 0,4 0,25 0,3
3 х3 0,45 0,3 0,5 0,58 0,48 0,32
4 х< 1,2 0,92 0,72 0,8 1 0,8
5 х6 0,58 0,9 0,7 1 0,48 0,6
S2 (X 1 ) “ п— 1 п 1=1 (3.22)
Для выявления степени влияния фактора X и сопоставления ее с разбросом, вызванным случайными, неконтролируемыми причинами, проверяют однородность дисперсий S2 (X) и S2 методами, изложенными в § 3.3.4. Если отношение FB = S2(X)/S2 окажется меньше критического FK, найденного для заданной доверительной вероятности Р и числа степеней свободы fx = п — 1 и / = N— п, то влияние фактора X несущественно и все полученные результаты измерений принадлежат одной генеральной совокупности, распределенной нормально с параметрами о2 и М (У), точечное оценки которых равны соответственно S2 и (1. Чтобы определить FK по табл. П.7, следует принять mi = = fх + 1 и т2 = fB + 1. При Fa > Ёк влияние фактора существенно. Считается, что в данном случае есть п нормально распределенных совокупностей, каждая из которых имеет одну и ту же дисперсию с2 и соответствующее математическое ожидание р... Точечной оценкой о2 в данном случае является S2, а математического ожидания— yt, Оценку дисперсии средних значений, вызванную влиянием исследуемого фактора X, производят по формуле
= [S2W-«b]- (3.23)
Пример 3.7. Требуется оценить качество пяти марок СОЖ, используемых для бесцентрового шлифования. Критерием качества выбрана шероховатость деталей, прошлифованных при одинаковых режимах.
Решение. Марки СОЖ ранжированы цифрами натурального ряда 1...5. Результаты опытов приведены в матрице наблюдений (табл. 3.3).
По формуле (3.19)'получены: у(. = 0,6; 0,32; 0,44; 0,91; 0,71; 62 = 0,028; 0,028; 0,012; 0,031; 0,04. Однородность дисперсий проверяем при помощи критерия Кохрена (3.18): GH = 0,04/ 2 S2 = 0,29.
i=l
Согласно табл. П.8, при т = 6, п = 5иР = 0,95 GK = 0,507. Поскольку Он < 0к, то разницу между дисперсиями можно считать незначимой и принять 5
нулевую гипотезу. По формуле (3.20) S2 = —S2 = 0,0278, а, согласно
zil
98
___ 5
(3.21) и (3.22), g = 'yi = °’596; s2U)=1~tS^_^2=0’212‘ z=i «=1
Наблюдаемое значение критерия Фишера FH=0,212/0,0278 = 7,63. Число степеней свободы /х = 5—1=4; /в = 30 — 5 = 25.
По табл. П.7 при Р = 0,95, гщ—5 и щ2=26 находим fk«2,74. Поскольку FK>FK (7,63>2,74), то изменение шероховатости детали при изменении марки СОЖ следует считать значимым. Согласно (3.23),
3^ = 4 (0,212 — 0,0278)/30 = 0,0246.
Для более глубокого анализа рекомендуется оценить значимость различия влияния СОЖ марок 1 и 3, которые обеспечивают минимальную высоту микронеровностей. Это делается при помощи критерия Стьюдента (см. § 3.3.3).
3.4.2. Двухфакторный дисперсионный анализ
В данном случае при оценке степени влияния двух одновременно действующих факторов Xi и Х2 предполагается, что каждый фактор изменяется независимо от другого. В процессе эксперимента первый фактор поддерживается на п уровнях, а второй — на г. Для каждого сочетания i-ro уровня фактора и j-го уровня фактора Х2 проводится mij дублирующих опытов. В частном случае тц=1 пли тц=т. Результаты опытов заносятся в матрицу наблюдений (табл. 3.4), где в (i, /)-й ячейке записывается в общем случае матрица наблюдений (3.1):
Результаты любого наблюдения можно представить моделью
>'ij,J = g+YiB+gi0+vii+eiJ-1J,
где g—общая средняя; — отклонение, вызванное влиянием первого фактора на i-м уровне в и-м дублирующем опыте; gj„ — отклонение, вызванное влиянием второго фактора на /-м уровне; vu — отклонение за счет взаимодействия факторов; ец„ — отклонение, вызванное влиянием неконтролируемых факторов.
На первом этапе для каждой ячейки вычисляются:
Табл. 3.4. Матрица наблюдений
X2t х1г x2i x2r
Хц y12 Г*/ Fir
Х12 Y12 У2/ Y2r
Хи Yn Yi2 Yii Yir
Х1П Ym Уn2 Ym У nr
т
99
Табл. 3.5. Таблица первичной обработки результатов наблюдений
АН х„ Х22 *2j Х2г Средние по строкам
—
Хц 1/11 У1, 1/1/ У\г 4 У1
Х12 У„ У 2 2 У2] У 2г У2
—
Хп У12 1/ij У 1г yi
_.
Х\п ут Уп2 Уп/ Упг Уп
Средние ' _ ! > _ >
по столбцам 1/1 Уг У! Уг р-
Затем проверяется однородность полученного ряда дисперсий. После подтверждения нулевой гипотезы приступают к вычислениям средних по строкам и столбцам матрицы наблюдений (табл. 3.5).
Средняя дисперсия воспроизводимости
дисперсия изменчивости отклика под влиянием фактора Xt
п
s!w = zrr
дисперсия изменчивости под влиянием фактора Х2
эд-тд-Ук-# (325>
дисперсия за счет взаимодействия факторов Х1 и Х2 100
п г
s <Х>’ S “"'+ '°2' <3-26) /=1 1=1
Формулами (3.24)...(3.26) можно пользоваться, если количество дублирующих опытов постоянно и равно т. Методика анализа при разном числе дублирующих опытов изложена в [62].
Значимость влияния факторов Xi и Х2, а также их взаимодействия проверяется при помощи критерия Фишера. Наблюдаемые значения критерия определяются по формулам:
МЛ1)= s2(*i)/Sb; /(/>)= S2(X2)/S2b; Fh(Xp X2) = S2(X1, X2)/S2,
а критические — по табл. П.7 согласно заданному значению доверительной вероятности Р, числу степеней свободы f{Xl)=n— 1; f(X2)=i — 1; f(Xb Х2) = = (n— 1) (г— 1); fB=nr(m— 1). В данном случае m2=fB + l; mi=f(X1) + 1; mi = =f(-^2) + l; nii=f(Xi, X2) + l.
Если m=l, т. e. при каждом сочетании уровней факторов проводится только один опыт, то анализ можно проводить, если эффект взаимодействия факторов X, и Х2 незначим. Тогда дисперсия воспроизводимости вычисляется по формуле (3.26).
3.5. КОРРЕЛЯЦИОННЫЙ АНАЛИЗ [44, 47]
3.5.1. Парная корреляция
Основная задача корреляционного анализа — выявление значимости связи между значениями различных случайных величин. Величины, значения которых не зависят от того, какие значения получили некоторые другие величины, называются независимыми от них.
Зависимость между величинами (в том числе и случайными), при которых каждому значению одной величины (аргумента) отвечает одно или несколько вполне определенных значений другой, называют соответственно однозначной или многозначной функциональной зависимостью.
Зависимость между величинами, при которой каждому значению одной величины отвечает с соответствующей вероятностью множество возможных значений другой, называют вероятностной (стохастической, статистической). В общем случае вероятностной связи при изменении значения одной величины изменяется условный закон распределения другой.
Если при наличии вероятностной зависимости между .двумя величинами с изменением значения одной величины изменяется только математическое ожидание второй (и наоборот), а дисперсия, области возможных значений и тип закона распределения остаются неизменными, то для таких величин характерна корреляционная зависимость.
Примерами корреляционной связи являются зависимости: между пределами прочности и текучести стали определенной марки, между погрешностью размера и погрешностью формы поверхности детали, обработанной определенным методом, между температурой испытания и ударной вязкостью стали, между усилием прижима ролика и шероховатостью накатанной детали. В первых двух примерах имеет место корреляционная связь между двумя откликами, а в третьем и четвертом — между фактором, который является случайной величиной в связи с погрешностью измерения, и откликом.
Пусть X и Y — случайные переменные, имеющие нормальное распределение. Силу линейной статистической связи между ними можно оценить коэффициентом корреляции
_ Г X —М(Х) 1 Г Y — M(Y) 1 р~ ЛЧ kW jL /щ*Т J’
101
который принимает значения в интервале (—1, +1) и не зависит от выбора начала отсчета и единиц величин X и У. Чем больше отличается от нуля коэффициент корреляции, тем сильнее зависимость между величинами X и У. Коэффициент корреляции независимых величин равен нулю. Однако обратное утверждение не всегда является верным, потому что на коэффициент корреляции оказывает влияние также отклонение от линейности связи.
Характеристикой нелинейной корреляционной связи является корреляционное отношение
= {М [М (У|Х = х) — М (У)]2}/М [У — М (У)]2,
где Л1(У|Х=х)—условное математическое ожидание случайной переменной У, рассматриваемое как функция х.
Оценкой коэффициента корреляции является значение коэффициента г. Для его вычисления необходимо знать оценки математических ожиданий Л((Х) и ЛГ(У), а также дисперсий D(X) и Д(У) (см. § 3.2). Если выполнено т наблюдений,
г =
т
2 (*z -X) (У4. - Y)]/[(m - 1) S (X) S(Y)].
J==l
(3.27)
При относительно небольшом т удобно пользоваться следующими формулами:
£(xt.-x)(y(._y)=£
1=1 t=l
(3.28)
Рис. 3.6. Поле корреляции совместных измерений предела прочности сп и предела текучести от стали ЗОХГСА
На практике при небольших значениях т для вычисления выборочного коэффициента корреляции г используют поле корреляции и корреляционную таблицу.
Пару случайных чисел Х{, У,-можно изобразить графически в виде точки с координатами (X;; У,). По осям координат откладываются интервалы изменения переменных и наносится координатная сетка. Каждую пару переменных из данной выборки изображают точкой в соответствующей клетке. Такое изображение называют полем корреляции. На рис. 3.6 показано поле корреляции для 106 совместных измерений предела прочности Ов и предела текучести ат стали ЗОХГСА.
102
Табл. 3.6. Корреляционная таблица для ов и <гт
925 (0) 975 (1) 1025 (2) 1075 (3) 1125 (4) 1175 (5) 1225 (6) 1275 (7) Итого
1025 (2) 1 1
1075 (3) 1 1 2
1125 (4) 2 4 2 8
1175 (5) 1 7 11 1 20
1225 (6) 1 13 13 27
1275 (7) 1 2 15 9 27
1325 (8) 4 10 1 15
1375 (9) 1 3 4
1425 (Ю) 1 1 2
Итого 2 5 13 28 33 20 5 1 106
Поле корреляции позволяет построить корреляционную таблицу (табл. 3.6). В ячейки, образованные пересечением строк и столбцов, заносятся частоты тху попадания пар значений (X, К) в соответствующие интервалы поля корреляции. В первом столбце и первой строке корреляционной таблицы указывают середины интервалов изменения случайных величин, а в последних — суммы частот тху по строкам и столбцам (тх и ту соответственно).
Формулы (3.28) можно преобразовать следующим образом:
т т m-j т2
2 - X) "S х‘у‘Пх¥ S х‘т* У
1=1 1=1 i=l 1=1
у/ту;
(3.29)
103
где л(- и у. — середины соответствующих интервалов изменения величин; — число столбцов, а т2 — число строк корреляционной таблицы; т =^тХу = “ 5 = S тУ
Если диапазоны изменения X и У разделены на равные интервалы (Дх и Ду), то вместо натуральных значений можно использовать целочисленные коды. Для этого нужно выполнить линейное преобразование х и у по формулам:
V ___ Х1 xmin . xmin /о ОЛ\
-----—х--------(3 30)
Тогда коды Xi примут значения Хк< = 0, 1, 2. i, а коды yi будут сдвину-
ты на целое число Д=ут1п/Ду—Xmin/Дх.
Проверка значимости коэффициента корреляции производится при помощи критерия Стьюдента. Наблюдаемое значение критерия
*н = г у (3-31)
Критическое значение критерия определяется из табл. П.1 по принятому значению доверительной вероятности Р и числу степеней свободы f=m—2. Поэтому при выборе /к следует принимать m=f + l. Если |/н|</к, то принимается нулевая гипотеза р = 0. В противном случае она отклоняется.
Выборочное корреляционное отношение вычисляется по формуле
П2=$2(У|х)/£2(У), (3.32)
где £2(У) вычисляется по (3.29); 52(У|х) —условная дисперсия:
S2(K|x) =— 5 [у (х) — у12тх'< (3.33)
т
У(Х) =
(3.34)
Корреляционное отношение ц2 связано с р2 следующим образом: 0 р2 <11]^ <1 1. В случае линейной зависимости между переменными р2 = »]?•
Разность Пт — Р2 может служить показателем нелинейной связи.
Пример 3.8. На основании данных корреляционной табл. 3.6 необходимо определить выборочный коэффициент корреляции г между огт и <тв.
Решение. Кодом для ав выбираем х, а для от—У- Тогда Д = 2. Коды записаны в корреляционной таблице под действительными значениями в скобках.
На основании (3.29) получим коды:
106
(Xz — X) (У4. — У) = 2569 — 667 384 = 152,698;
1=1
mS2 (X) = 4429 — — 6672= 231,934; S (х) = 1,479;
mS2 (У) = 1566 — 3842 = 174,906; S (у) = 1,285.
Согласно (3.27), г= 152,698/(105 • 1,479 • 1,285) =0,763.
Пример 3.9. Для условий примера 3.8 определить корреляционное отношение. Значения у(х), вычисленные по формуле (3.34), для соответствующих значений кодов <ув (первый столбец табл. 3.6):
104
__х 2 3 4 5 6 7 8 9 10
у(х) 0 0,5 2 2,6 3,44 4,19 4,8 5,75 6,5
Решение, у — — V'л).ту = 3,62; S2(E|x)= 1,317; п2= 1,317/1,2852 =. /71
= 0,798; г2 = 0,7632 = 0,582. Характеристика нелинейности в данном случае т]2 — г2 = 0,798 — 0,582 = 0,216.
Если соединить значения у(х), обозначенные на рис. 3.6 светлыми точками, штриховой линией, то будет видно, что полученная ломаная линия незначительно отклоняется от прямой.
3.5.2. Многомерный корреляционный анализ
Если имеется многомерная нормально распределенная совокупность с п признаками X,, Х2, .... Хп, то взаимозависимость между ними описывается корреляционной матрицей, под которой понимают матрицу, составленную из парных коэффициентов корреляции;
1 Р12 Р13 • • • Pife • Pin
Р21 1 Р23 • ’ ’ Р2* • • Р2л
<?„ = .................... ,
P/i Р/2 Р;з ••• Pjk Р/п
Р«1 Рп2 РлЗ • ' • РлА ' • • * , где — парные коэффициенты корреляции.
Оценку парного коэффициента корреляции находят по формулам (3.27)... (3.29), в которые вместо х,- подставляют xtj, а вместо у, — хм-
В случае многомерной корреляции нельзя ограничиться одной корреляционной матрицей, так как зависимости между признаками сложны. Для более детального анализа используются частные коэффициенты корреляций различных порядков, позволяющие оценивать связь между двумя признаками при фиксированном значении остальных.
Если исходная совокупность состоит из п признаков, то частный коэффициент корреляции 1-го порядка отражает зависимость между двумя из них при фиксированных значениях I признаков из (п — 2) оставшихся. Если имеется, например, система из трех признаков Хь Х2 и Х3, то можно определять частные коэффициенты корреляции только первого порядка, так как в данном случае нельзя фиксировать больше одного признака. Если фиксировать значение Х3, то
Р12,з= (Р12 Pi 3Р23) 1 Р?з)О Р23)’ (3.35)
где pi2,3'~ частный коэффициент корреляции между признаками Xi и Х2 при фиксированном значении Х3; р12, р]3, ри — парные коэффициенты корреляции.
Аналогично определяются р]3,2 и ргз,!-
Расчет частных коэффициентов позволяет оценить взаимное влияние признаков. Если, например, корреляция между X] и Х2 основана только иа общем влиянии Х3, то pi2;3=0. Если имеются четыре признака, то можно зафиксировать значения одного или двух признаков. В последнем случае
Р12.4 Р13,4Р23,4 Р12.3 Р14,зР24,3
~ Р?зл) 0 — Ргзл) 0 ~ Р?4,з) 0 ~ Р24.3)
Частные коэффициенты корреляции вычисляются на основании оценок парных коэффициентов корреляции. Так же, как и для парных, проверяется зна-
105
чимость частных коэффициентов корреляции, но при этом число степеней свободы при исключении каждого признака уменьшается на единицу. Если фиксируется значение одного признака, то в (3.31) вместо (т —2) следует подставить (т—3), а если фиксируется значение двух признаков,— (т—4).
Для оценки линейной связи одного из признаков со всеми остальными используется множественный, или совокупный, коэффициент корреляции. Для случая трех признаков коэффициент множественной корреляции оценивается по формуле
^123 = (Г12 + г?3 2/'12г13г2з)/(1 ~ Г2з):
при этом Х2 и Хз, зависимость признака Xi от которых оценивает считаются независимыми.
Для случая четырех признаков
^1234 == 1 — (1 — — ^З.гК1 — Г14,2з)-
Значимость коэффициента множественной корреляции определяется при помощи критерия Фишера. Наблюдаемое значение критерия
_ т—1 — 2
н “ 1 — /?2 I
где т — число наблюдений; l=n— 1; п — число признаков.
Критическое значение критерия Фишера определяется из табл. П.7 согласно принятым доверительной вероятности Р и числу степеней свободы ft=m— — 1—2; f2=l. Принимается m1=ft + l; m2=f2+l.
Пример 3.10. При изучении бесцентрового шлифования роликов методом на проход контролировались следующие показатели качества: погрешность формы X], погрешность размера Х3 и параметр шероховатости Х2. Всего было прошлифовано 50 образцов. При этом получена следующая матрица парных коэффициентов корреляции:
/1 0,85 0,62\
?з= 1 0,53 .
\ 1 /
Необходимо установить характер взаимовлияния признаков.
Решение. Согласно (3.35),
г12,з = (0-85 — 0,62 • 0,53)/]/'(! — 0.622) (1 — 0,532) =0,784;
г23 , = (0,53 — 0,85 0,62)/К(1 —0,852) (1 — 0.622) = 0,007;
г31>2 =. (0,62 — 0,85 • 0,53)/К(1 — 0,85а) (1 — 0,532) = 0,379.
Проверяем по (3.31) значимость частных коэффициентов корреляции:
/Н1 =0,784 /47/(1 — 0,7842) = 8,658;
/н2 = 0,007^47/(1 — 0.0072) = 0,048;
/н3 = 0,379 /47/(1 — 0,3792) = 2,808.
Согласно табл. П.1, при Р=0,95 ?к = 2. Поскольку и <нз>^к, то нулевая гипотеза о незначимости связи между Л) и Х2, а также Xi и Х3 отвергается. Но ts2<tw поэтому величины Х2 и Х2 являются независимыми. Следовательно, условия шлифования, обусловливающие изменение погрешностей формы влияют одновременно и на уровень значения параметра шероховатости и погрешности размера. Причем эти условия сильнее влияют на шероховатость, чем на погрешность размера, так как /'i2,3>r31,2.
106
3.5.3. Корреляционные уравнения [47]
Получение корреляционных уравнений — заключительный этап исследования связей между случайными величинами. Корреляционные уравнения позволяют вычислить вероятные значения одной случайной величины в зависимости от значений других случайных величин. Вероятным значением случайной величины У называется ее значение, вычисленное с помощью корреляционного уравнения и близкое к условному математическому ожиданию Л/(У |Х,=Х1).
Корреляционное уравнение удобнее всего записывать в виде разложения по ортогональным многочленам Чебышева, что позволяет последовательно уточнять математическую модель с вычислением ошибки аппроксимации корреляционного уравнения полиномом данной степени.
Вначале корреляционная модель предполагается линейной:
(У—Т)5(У)=ге, (3.36)
где
е=(Х-Х)/[ДХ -S(X)];
г — оценка коэффициента корреляции между У и X; S(X), 5(У) —оценки стандартного отклонения случайных величин X и У; X, У — оценки математического ожидания величин; АХ — шаг разбиения интервала изменения случайной величины X (см. формулу (3.30)).
Значения S(X) и5(У) определяются из (3.29), г — из (3.27), k 1
£=1 /=1
где k и I — соответственно количество строк и столбцов корреляционной таблицы; и ttij — суммы частот mXY соответственно по i-й строке и /-му столбцу; т — общее число наблюдений; х{ и у/—середины интервалов значений случайных величин.
Оценка ошибки определения У с помощью корреляционного уравнения осуществляется по остаточной дисперсии
S2 = S2 (У) • (1 — г2).
Проверка линейности связи между У и X производится при помощи критерия линейности
Ki = 'n5-^, который вычисляется с ошибкой
s (Ki) = /ТТ/т.
Значение т]2 вычисляется по формулам (3.32) и (3.33). Если незначимо отличается от S(Ki), то можно остановиться на линейной модели (3.36). Если Kt значимо отличается от нуля, то корреляционное уравнение предполагается в виде полинома второй степени , —. b-i
(Y - K)/S (У) = ге + (в2 + г30е - 1),
ai где
а\ =г40-г30- &1 = Г21 ~''зол
ЦЗО И 40____________|<21____
Гз° = S3 (X)’ Г4° = S4 (X) ’ Г21 “ S2 (X) • S (У) ’
107
Изо — ^зо — Зр20М10 — Л420; р20 — Л420 — Л420 = S2(X);
Ню = ‘^40 — 6р20Л420 Л4ц>;
Pai = Мах — 2|1цМю — AfaoMox;
Ни = — Л1юЛ^01> Л11о = X; Мщ = Y;
k k
м2о = -^^] ^тг> мзо=~ *X-;
I —1
k1™ i
M40 = V M02 = -^ У У2;"1,’
i k i k
Mn = У У х1У1тху\ M2i = У У х2У(тху-f—1 L—1 /=1 i=1
Погрешность определения Y с помощью корреляционного уравнения второго порядка оценивается остаточной дисперсией
S2 = S2(n (l-r2-&2/ai).
Проверка квадратичности связи между У и X производится при помощи критерия квадратичности
К2 = Ki 6[Мр
который вычисляется с ошибкой
S(Ka)=
Если Кг значимо отличается от нуля, то корреляционное уравнение можно представить в виде полинома второй степени [47] и т. п.
3.6. РЕГРЕССИОННЫЙ АНАЛИЗ [40]
Основная задача регрессионного анализа — установление вида и параметров зависимости математического ожидания отклика Л1(У) от уровней одного или нескольких факторов X, когда результаты эксперимента представлены в виде независимой выборки пар Х1, Уь Х2, Y2; Хп, Yn. Искомая функция называется моделью регрессионного анализа или регрессионной моделью У на X, а ее параметры — коэффициентами регрессии.
Не существует стандартных, формализованных методов, позволяющих только на основании результатов эксперимента установить теоретическую регрессию — истинную функциональную зависимость, отражающую действительную связь между откликом и контролируемыми факторами, не искаженную влиянием погрешностей измерения и неконтролируемых факторов. Если нет теоретических соображений о виде регрессионной модели, то ее обычно представляют в виде
rf
У=5Р//(х)+е, (3.37)
/=о
108
где Х= |Xi, Xi... Хл| —вектор значений факторов; 0,-—неизвестные коэф-
фициенты регрессии; fj(X)—базисные функции; е — аддитивная погрешность.
Система базисных функций f>(X) должна быть выбрана до проведения эксперимента. Наиболее часто в качестве базисных функций используются: а) полиномы; б) системы ортогональных полиномов того или иного класса; в) тригонометрические функции. Если Х=|Х], Х2, Х31, то в первом случае выражение (3.37) имеет вид
У = Ро + PjA'j + 02Х2 4- ₽3Х3 + p12XjX2 -|- 013XjX3 + 023X2X3 +
+ ₽пх* + ₽22х1 + р33х|.
Однофакторную регрессионную модель при помощи системы ортогональных полиномов Чебышева можно записать следующим образом (если число равноотстоящих уровней фактора равно 11):
У=Ро+Р1Х+р2(Х2-10) +Рз(Х3—17,8Х) +Р«(Х4-25Х2+72).
Тригонометрические регрессионные однофакторные модели обычно имеют вид
k
у “ ₽о + 2 [“/cos + V/ sin (/соХ)].
/=1
По известным измеренным значениям X всегда можно рассчитать и значения любой базисной функции fj(X).
Аппарат классического регрессионного анализа можно применять, если выполняются следующие'условия.
1. Ошибка измерения фактора X, который может быть как неслучайной величиной, принимающей заданные значения, так и случайной контролируемой величиной, пренебрежимо мала.
2. Погрешность е подчиняется нормальному распределению с математическим ожиданием, равным нулю, и с постоянной дисперсией, не зависящей от уровней фактора.
3. Значения погрешности е в различных наблюдениях не коррелированы, т. е. r(et, ej)=O,
Неизвестные коэффициенты регрессии определяются методом наименьших квадратов — путем минимизации суммы квадратов отклонений измеренных значений отклика от получаемых с помощью регрессионной модели, т. е. путем минимизации функции
Й=1 /=0
где Ь, — оценка коэффициента регрессии 0,-; п—число наблюдений (опытов).
Рассматривая как переменные величины, приравниваем нулю частные производные:
dS
dbi
109
После преобразования получаем систему линейных уравнений относительно искомых оценок by.
b0 2 /о + 2 V1 + ь2 2 М2 + • • • + bd 2 fofd = 2 YM
*о2 Mi + bi 2 fi + 62 2 M2 + • + Мл = 2 «Зв»
*o2Md + 6i2Md + ^2Md + ••• + ^2^ = 2УМ
где суммирование производится по всем и опытам; fi=fj(Xg); Y=Yg.
Решение системы (3.38), обычно называемой системой нормальных уравнений, можно проводить любым известным способом.
Полученные методом наименьших квадратов оценки коэффициентов регрессии bj являются несмещенными и эффективными. Для оценки доверительного интервала и значимости этих оценок необходимо определить дисперсию воспроизводимости и дисперсию оценок bj.
Дисперсию воспроизводимости определяют обычно постановкой дублирующих опытов. Ее оценка вычисляется по формулам (3.19) и (3.20).
Дисперсия оценок /-го коэффициента регрессии
S2 (bj) = S|C/;, (3.39)
где S2 — оценка дисперсии воспроизводимости; С;/. — элемент матрицы Ф-1, обратной информационной.
Информационная матрица Ф составляется из коэффициентов системы нормальных уравнений (3.38):
/2fo 2 Mi ••• 2МД
ф= 2Mi 2f? ••2МЛ.
\2Md 22^ /
Коэффициент корреляции между коэффициентами регрессии bj и Ьк определяется по формуле .
SB
г (b,, bh) =-----5-----Cih. (3.40)
h) S(bj) ,S(bh) *
Проверка значимости полученных коэффициентов регрессии сводится к последовательной проверке гипотез Но—Р? = 0, Нх — fJ^O, j=0, 1, 2, .... d. Для этого вычисляются наблюдаемые значения критерия Стьюдента
\bj\IS{bj). (3.41)
Эти значения критерия Стьюдента сравниваются с табличным tK (табл. П.1) в соответствии с числом степеней свободы f=m— 1, если опыты по определению остаточной дисперсии дублировались в одной из точек факторного пространства т раз, или f=n(m— 1), если в каждой из п точек факторного пространства дублирование проводилось одинаковое число раз. Если при выбранной доверительной вероятности Р tBj^tK, то нулевая гипотеза отвергается и коэффициент bj считается статистически значимым.
Так как коэффициенты регрессии бывают связаны между собой, то после отбрасывания незначимого коэффициента bq необходимо провести коррекцию оценок остальных коэффициентов и их дисперсий в соответствии с формулами:
C]k = Cjk-^; S*(b;.) = S^r (3.42)
110
Доверительные интервалы для значимых коэффициентов регрессии определяются неравенством
fr’-/KS(6*)<P/<6’ + ;KS(ft*)- (3-43)
Проверка адекватности полученной регрессионной модели и функции отклика позволяет оценить правильность выбора вида модели. Для этого сопоставляется дисперсия воспроизводимости, полученная путем реализации дублирующих опытов, и остаточная диспепсия
л
J] <з'441
g=l
где Yg — предсказанное по уравнению регрессии значение отклика в g-м опыте; — измеренное значение отклика в том же опыте.
Сопоставление производится путем проверки гипотезы о равенстве дисперсий (см. § 3.3.4). Наблюдаемое значение критерия Фишера FH = S^/S^ сравнивается с табличным FK (табл. П.7), которое определяется в соответствии с выбранным значением доверительной вероятности и числами степеней свободы /у = = п — d и f2 = m—1, где d — число параметров модели; т — число дублирующих опытов при определении S^. Условием адекватности модели и функции отклика являются FH < FK.
Для сокращения объема вычислений и получения при этом независимых оценок коэффициентов регрессии с минимальными дисперсиями необходимо, чтобы базисные функции были ортогональны на множестве точек факторного пространства, в которых ставились опыты. Аналитическое условие ортогональности имеет вид
2(/М = 0’ g=i
Тогда система нормальных уравнений значительно упрощается:
йо2^ = 2гА>;
^2^ = 2rA= .
а оценка каждого коэффициента регрессии вычисляется независимо от других:
6/=(2г4)/2^- (3-45)
Поскольку информационная матрица для ортогональных базисных функций
[2 % 0 0 . . 0
0 2/? 0 . . 0
ф = 0 0 2^1 • . 0
. 0 0 0 . •2^.
будет ортогональной, то, согласно (3.40), коэффициент корреляции r(bj, Ьц) = = 0 и оценки коэффициентов регрессии являются статистически независимыми.
111
Табл. 3.12. Полный факторный план 23
Номер опыта и Х1 Х2 xt
1 +1 +1 +1
2 —1 +1 4-1
3 +1 —1 +1
4 —1 —1 +1
5 +1 +1 —1
6 —1 +1 —1
7 +1 —1 —1
8 —1 —1 —1
Если в качестве базисных функций выбрать нормализованные полиномиальные переменные, то они будут ортогональны на множестве точек двухуровневого факторного плана. В данном случае х, может принимать значения либо — 1, либо +1. Полный факторный план для трех факторов приведен в табл. 3.12. Реализация этого плана позволяет оценить параметры регрессионной модели вида
3 3
У = 6о + ^blXj + £bjhXjxh, h^j. (3.46)
3
В данном случае J} — где N — общее число опытов, и, согласно (3.45), /=1
N
(3.47)
Произведение х,хь можно также рассматривать как фактор, и тогда bjh определяется по формуле (3.47), где fj=XjXh-
Если модель (3.46) линейна, т. е. 6ja = O, то число опытов плана, указанного в табл. 3.12, на 4 больше, чем число определяемых параметров. Свойство плана, задающееся разностью между числом точек спектра плана и числом оцениваемых параметров, называется насыщенностью плана. План, в котором число точек спектра плана совпадает с числом оцениваемых параметров, называется насыщенным планом. Если применять насыщенные планы, то для регрессионного анализа (оценка адекватности модели, дисперсии и доверительного интервала коэффициентов регрессии) необходимо проведение дублирующих опытов.
Пример 3.11. Определить вид и коэффициенты регрессионной модели, отражающей зависимость радиальной силы Fy (Н) от поперечной подачи s (мм/дв. ход) при плоском электрохимическом алмазном шлифовании. В результате реализации эксперимента получены следующие данные:
s-102 2,5 3 3,5 4 4,5 5 5,5 6 6,5 7 7,5 8 8,5 9 9,5
F у 50 60 67 75 85 86 93 95 100 98 104 103 106 107 108
При каждом значении s проводился один опыт. Пять дублириющих опытов для оценки дисперсии воспроизводимости проводились при s = 0,05 мм/дв. ход. Получено, что 5^ = 0,032.
Решение. По виду кривой на рис. 3.7 предполагаем, что регрессионная модель имеет вид
112
у=0о+М+М2.
где y=FB- IO-1; X=s- 102.
Базисные функции в данном случае имеют вид: f0=l; Л=Х; fo=X2. Тогда,согласно (3.38), можем записать систему нормальных уравнений
*0 2 *? + *1 3 + *2 S *1 = 2 </Л'2^
0,02 0,04 0,06. 0,08 O,t‘
Додача, мм/dS.xod
Рис. 3.7. Зависимость усилия резания от поперечной подачи при плоском электрохимическом шлифовании
После вычисления сумм получим 15йв + 90/>! + 610£>г = 133,7;
9O6o + 610&1 + 4500&2 = 856,35;
бЮ&о + 4500&J + 35144,562 = 6051,925.
Решение системы дает: 6о=О,О175; 61=2,4029; &а=—0,1358.
Информационная матрица в данном случае имеет вид
Ф =
• 15 90 610 '
90 610 4500
.610 4500 35144,5,
Обратная матрица определялась по формуле
(Doo Dm О20'
Doi Du D2i Doo D12 D22,
где Djk — алгебраическое дополнение элемента матрицы в /-й строке и k-tt столбце.
В результате вычислений получено
/4,389 1,544 0,122 ф-^1 1,544 0,573 0,047
\ 0,122 0,047 0,0039
Согласно (3.39),
32(&0) =0,032 • 4,389=0,14;
52(6,) =0,032-0,573=0,018;
S2 (62) = 0,032 • 0,0039=0,000125;
3(Ь0) =0,375;
3(6,) =0,135;
S(b2) =0,0112.
Значения Гц:
0,032 - 1,544
Гог = -----------= 0,976; г02 =
0,375-0,135
0,032 • 0,122
—'----------- =0,93;
0,375-0,0112
0,032 0,047
0,135 0,0112
= 0,995,
8. Зак. 1001
113-
вычисленные по формуле (3.40), показывают, что коэффициенты регрессии тесно связаны.
Согласно (3.41),
/н0=0,0175/0,375=0,047; /в1 = 2,4029/0,135= 17,8;
/н2=0,1358/0,0112= 12,13.
Для Р=0,95 и т = а по табл. П.7 /к=2,776.
Поскольку /но<<к, то коэффициент регрессии Ьо незначим и можно считать, что Зо = О. Остальные коэффициенты являются значимыми.
По формулам (3.42) получаем скорректированные значения коэффициентов регрессии:
. 1,544
В* = 2,4029 — —Н—- 0,0175 = 2,379;
и 4,389
* 0,122
В* = —0,1358 — —------0,0175 = —0,1363;
Г2 4,389
С2 1,5442
С*. = СИ — г—= 0,573 —-т-ооп =0,0298;
11 11 C/QQ 4,003
, 0,122а
С* = 0,0039 — -J-— = 0,0005;
22 4,389
S2 (&*) = 0,032 • 0,0298 = 0,00095; S (&*) =0,031;
S2(&‘) = 0,032 0,0005 = 1,6 10~5; $((,*) =0,004.
Согласно (3.43), 2,311 <(3, <2,483; -0,1474<02<-0,1252.
Остаточная дисперсия, определяемая по (3.44), составляет S2 = 0,043. Наблюдаемое значение критерия Фишера Гн = 0,043/0,032 = 1,344. Табличное значение критерия определялось при Р = 0,95; /1 = 15 — 2 = 13; f2 = 5 — 1 = — 4. В нашем случае тг = 14 и тг = 5. Поскольку значения ги, и т2 в табл. П.7 являются промежуточными (10 < nij < 15; 4<m2<6), то критическое значение FK = 6,67 было определено интерполяцией. Поскольку Fa < FK, то полученная модель Fy = 2379s— 1363s2 адекватно описывает зависимость радиально-составляющей силы от поперечной подачи.
4. ПРЕДПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА
4.1. ОСНОВНЫЕ ПОНЯТИЯ И ПРОЦЕДУРЫ
Предпланирование эксперимента — это решение ряда вопросов, позволяющих перейти от замысла к плану эксперимента [2]. Главным вопросом является четкая постановка задачи эксперимента, которая должна быть формализована. Для этого переходят от реального объекта исследования к его схеме, которая называется моделью «черного ящика» (см. § 3.1) или «серого ящика». В последнем случае на основе известного механизма функционирования объекта исследования можно теоретически получить функцию отклика, а экспериментальному определению подлежат только ее параметры.
Главным на первом этапе формализации является выявление всех факторов, определяющих характер функционирования объекта, и всех откликов. Требования к факторам и откликам сформулированы в § 3.1. На втором этапе формулируется цель исследования. Это может быть либо построение математической модели исследуемого объекта, либо его оптимизация.
Математическая модель — символическое выражение, с требуемой точностью отражающее те количественные связи, которые характеризуют исследуемый объект, и игнорирующее его второстепенные свойства и признаки. При построении экспериментальной математической модели нужно избегать как чрезмерного упрощения реальных объектов, так и излишней их детализации. Ниже рассматриваются методы построения только аналитических моделей, в которых зависимость между уровнями факторов и отклика выражается комбинацией функций известного вида (рациональных, дробно-рациональных, показательных, логарифмических и т. д.).
В зависимости от количества учитываемых факторов различают два класса моделей — однофакторные и многофакторные, а в зависимости от статистической природы факторов и отклика каждая из этих моделей может быть детерминированной, регрессионной или корреляционной.
Детерминированная модель может применяться для описания объекта, если факторы и отклик по своей природе являются неслучайными величинами, погрешностями измерения которых можно пренебречь. В данном случае каждому набору значений факторов соответствует одно или четко определенное множество значений отклика.
Если объект описывается регрессионной моделью, то данному набору уровней факторов однозначно соответствует определенный набор параметров закона распределения случайных значений отклика. В данном случае отклик является случайной по своей природе величиной или его делает таким процесс измерения, т. е. случайными погрешностями измерения нельзя пренебречь. Факторы являются неслучайными величинами, уровни которых можно во время измерения отклика зафиксировать с достаточной точностью.
Корреляционная модель отражает связь между случайными по своей природе величинами.
Если вид оператора f модели и значения ее параметров р, не изменяются во времени, то модель называют статической. Модели, не обладающие данным свойством, называются динамическими. Построить экспериментальную дпна-
8*
115
мическую модель значительно труднее, чем статическую. Некоторые методы построения динамических моделей освещены в § 5. 6.
Оптимизация — это процесс поиска такого сочетания уровней факторов \точки ограниченного факторного пространства), при которых отклик, называемый в данном случае параметром оптимизации, принимает экстремальное (максимальное или минимальное в зависимости от смысла задачи) значение. Однако чаще всего объект является многооткликовым. Например, откликами процесса обработки на токарном автомате являются: производительность, себестоимость продукции и такие параметры ее качества, как точность размеров и формы, а также шероховатость поверхности обработанных деталей.
В некоторых случаях в качестве параметра оптимизации можно выбрать один из откликов, в то время как остальные служат ограничениями. Тогда оптимизация процесса обработки на токарном автомате будет заключаться, например, в поиске такого сочетания режимов обработки, конструктивных параметров режущих инструментов, стратегии восстановления размерной настройки, параметров точности заготовок, при котором себестоимость обработки будет минимальной. Ограничениями при этом служат заданные значения параметров качества обработанных деталей и минимально допустимая производительность станка.
Однако во многих случаях такая постановка задачи неправомерна. Например, задачей оптимизации структуры объекта исследования может быть одновременное улучшение нескольких критериев его качества, причем каждому из критериев может соответствовать своя оптимальная точка факторного пространства. В таких случаях делаются попытки уменьшить число параметров оптимизации путем установления между ними корреляционной связи или априорного ранжирования по значимости. Если эти попытки не дают успеха, то рекомендуется переформулировать задачу или свести ее к последовательности задач, в каждой из которых улучшается один из критериев качества.
Эффективным методом уменьшения количества параметров оптимизации является использование так называемых функций желательности.
На следующем этапе предпланирования эксперимента определяется область экспериментирования, т. е. область факторного пространства, где могут размещаться точки, отвечающие условиям проведения опытов. Каждый фактор имеет свою область определения, которая задается либо принципиальными ограничениями, либо по технико-экономическим соображениям, либо исходя из конкретных условий (отсутствие подходящей аппаратуры, установок, инструмента или невозможность значительных отклонений от принятой технологии). После выбора области определения необходимо найти локальную область для проведения эксперимента — размах варьирования каждым фактором. Эта задача плохо поддается формализации и решается в каждом конкретном случае исходя из смысла общей задачи исследования.
В общем случае факторы — размерные величины, а числа, выражающие значения (уровни) факторов, могут иметь разные порядки. Поэтому с факторами в исходном (натуральном) масштабе обычно не работают, а проводят их предварительную нормализацию (см. § 3.1). При этом происходит центрирование, т. е. перенос начала координат факторного пространства в точку с координатами Хи Х2, Х3...Xi, ..., Хк, где Х.: определяется по формуле (3.3).
Однако выбранных на первом этапе предпланирования факторов может оказаться слишком много. И прежде чем перейти к решению основной задачи эксперимента, необходимо тем или иным способом уменьшить размерность факторного пространства. Эта подзадача решается либо на основании подробного анализа априорной информации (априорное ранжирование факторов), либо переходом от размерных факторов и откликов к безразмерным критериям подобия, определяемым на основании л-теоремы методом -нулевых размерностей, либо экспериментально путем реализации отсеивающего эксперимента.
4.2. МЕТОДЫ УМЕНЬШЕНИЯ ЧИСЛА ПАРАМЕТРОВ ОПТИМИЗАЦИИ
4.2.1. Использование корреляционного анализа
Суть способа заключается в определении коэффициентов парной корреляции между каждыми двумя параметрами на основании имеющихся экспериментальных данных. При наличии высокой корреляционной связи между параметрами любой из них можно исключить из рассмотрения, так как он не содержит какой-либо дополнительной информации об объекте исследования, кроме полученной при помощи другого. Исключаются, естественно, те параметры, которые методически труднее определять экспериментально. Методы парного корреляционного анализа приведены в § 3.5.1. Однако существуют и более простые способы расчета коэффициента корреляции. Один из них [55] при относительно небольшом объеме вычислений дает приемлемые по точности результаты.
Вначале определяются размахи откликов Y, и Уя, их разностей и сумм:
R(y, ) = ^max - J%in; R(Yh ) = ГАтах - rhmin;
R(Yj -yh) = (У,- - yh )max - (У,- - yh Jmin.
Wj +Ук) = (У,' + Ук U - (У, + У Jmin-
С учетом знаков получающихся величин формулы для расчета коэффициента парной корреляции имеют вид:
у ^(Г,) + ^(ГА) + ^(г,--гА)
h 2R (У{) R (yh)
R2(Yj + Yh)-R*(Y})-R*(Yh)
r(yRYh)~ 2R(Yj)-R(Yh)
r V/> yh> —
(4-1)
2R(Yf) R(YH)
Можно пользоваться любой из этих формул, но последняя (4.1) предпочтительнее, так как включает размахи всех типов.
После установления статистически значимых корреляционных связей между парой параметров оптимизации можно построить уравнение регрессии, позволяющее предсказать значение одного из параметров по значению другого (см. § 3. 6). Если коэффициент корреляции определялся согласно (4. 1), то формулы для расчета оценок коэффициентов регрессии линейной модели имеют вид:
t R2(yi + yh)-R2.(y,~yl,) Di ----------------------------
2R (Yh)
N N
U=1 U=I
Выявленные при помощи корреляционного анализа линейные связи между параметрами оптимизации удобно отразить в виде графа (рис. 4.1), где его вершинам (точкам) соответствуют отклики Yj, а каждое ребро (линия) указывает на наличие статистически значимой линейной связи между верши
Рис. 4.1. Граф линейных связей между откликами
117
нами. Вершина графа, из которой выходит наиоолыиее число ребер, считается наиболее влиятельной [55]. На рис. 4. 1 наиболее влиятельной вершиной является У3. Кроме того, «могущественность» вершины зависит от того, насколько влиятельны другие вершины, связанные ребрами с данной. Для выявления наиболее «могущественной» вершины составляют корреляционную матрицу (см. § 3.5.2). При этом все коэффициенты парной корреляции считаются положительными. Для примера, показанного на рис. 4. 1, корреляционная матрица имеет вид
(1 r12 r13 r14 rl5 г 16
Г 21 1 /"23 Гц Гц . Гц
Гц г32 1 Гц <35 <35
<41 <42 <43 1 <45 Гц
<51 <52 Л53 <54 1 <56
Г 61 <62 г63 <64 <65 1
где <jh = r(Yjt Yh).
Ранг «могущества» первого порядка любой вершины определяется суммой значимых коэффициентов корреляции по строкам матрицы
F11 — 1 + <12 + г13 + е14 + <15 + г1б! F 21 = ^21 + 1 + г23 + г24 + <25 + <261
F ц — Гц -|- <62 + f 63 + г64 + /-65 + 1 ,
где Fn — сила связи первого порядка для /-й вершины.
По значениям Рц распределяются места вершин по «могуществу». Вершина с наибольшим значением Fu получает первое место. Если значения Fjt и Fhi равны, то между этими вершинами делятся смежные места.
Распределение рангов «могущества» проверяется последующими итерациями. Силы связи второго порядка определяются по формулам:
Е„ = Ец + Г12Е 21 + <1зЕз1 + <1«Е 41 + <15^51 + <1бЕ 61!
F 22 = Г 21F11 + F 21 + г азЕ 31 + < 21F 41 + < 25Е 51 + < 2»F 61!
Ев2 — г61Fи + гезЕ21 + гвзЕ31 Д- гцР41 + гesE51 + гei-
На третьей итерации:
F 1з = Е12 + Г12Е зг+ПзЕ 32 + Гцр 42 + <15Е,52 + Г цР 62!
Е23 = Г21Е12 Е22 <23Е32~\~ Г24Е42 Н- r25Es2 <2бЕ62^
Е63 = ^61Е12 4- <62 Е22 + г6зЕз2 + ГцР ц + r65Е50 + Е62-
Если последующие 1—2 итерации подтверждают распределение мест, полученное на предыдущей, то процесс на этом заканчивается.
В качестве параметра оптимизации лучше всего выбирать отклик наиболее могущественный и обладающий к тому же наибольшей методической простотой экспериментального определения. Но так как такое совпадение является редким, решение о выборе какого-либо из конкурирующих откликов в качестве параметра оптимизации принимается на основе компромисса. Так, например, если могущество двух вершин графа различается незначительно, можно выбрать в качестве параметра оптимизации вершину с меньшим могуществом, но более влиятельную и методически легче определяемую.
4.2.2. Функции желательности
Под «желательностью» d понимают тот или иной желательный уровень параметра оптимизации. Значение d может меняться от 0 до 1. Шкала желательности выглядит следующим образом:
118
d = O...O,37 — недопустимо низкий уровень качества;
d=0,37...0,6— допустимый и достаточный уровень качества;
d = 0,6...0,8 — допустимый и хороший уровень качества;
d = 0,8... 1 — допустимый и превосходный уровень качества.
Значения d на шкале желательности можно смещать в зависимости от конкретных ситуаций.
Каждый из параметров оптимизации обычно ограничен с одной (Kjsgyj max; Y^YS min) или с двух сторон (Xjmin Kjsg:Yj miI). Если ограничения односторонние, то
dj = exp [-exp (— У))],
где Y'- — безразмерная величина, линейно связанная с Y j, например, Yj = = 4 (2Yj Yj mix)/Yj max или Yj = (Yj 4Y j min)/Kj min.
Если ограничения двусторонние, то
d/ = exp[-(|y;|)'1], где
Y'i =[2У/ - (Г/ max + Yi min) Wj max ~ Yj min) =
n — положительное число.
Показатель n можно вычислить, если задать некоторому отклику Ул значение dh (предпочтительно в интервале 0,6...0,9):
п = [Inin (l/dA)]/ln |ул|.
Выбирая разные значения п, можно задавать различную кривизну кривой желательности. Это обстоятельство позволяет учесть степень важности данного отклика. Для важного отклика п будет иметь большее значение, и малому изменению отклика вблизи ограничивающих пределов будет соответствовать резкое изменение желательности. Графики изменения функции желательности dj в зависимости от Yj показаны на рис. 4.2, 4.3.
Идея использования функции желательности в качестве параметра оптимизации заключается в том, что на основании полученных частных функций
Рис. 4.2. Функция желательности при односторонних ограничениях
Рис. 4.3. Функция желательности при двусторонних ограничениях
119
желательности dj формируется обобщенная функция желательности da, представляющая собой среднее геометрическое желательностей отдельных параметров оптимизации:
~ у/ ^1^2 * * * dg *
В результате обобщенная функция желательности становится единственным параметром оптимизации вместо многих.
Кроме указанных, в зависимости от постановки задачи можно использовать и другие формы функций желательности. Например, в работе [3] описан следующий обобщенный показатель при односторонних ограничениях:
д
d0 = 2 ((Г/ - К/0)/Г/0]2, (4.2)
;=1
где Yjo — желаемое (или заданное) значение параметра оптимизации Fj; а, — коэффициент веса параметра, устанавливаемый, например, в результате опроса специалистов.
В случае, когда все частные параметры совпадают со своими желаемыми значениями, do = 0. Поэтому чем меньше d0, вычисленный по формуле (4.2), тем лучше.
При двусторонних ограничениях предлагается использовать следующий обобщенный показатель:
4.3. МЕТОДЫ УМЕНЬШЕНИЯ РАЗМЕРНОСТИ ФАКТОРНОГО ПРОСТРАНСТВА
4.3.1. Априорное ранжирование факторов
Априорное ранжирование факторов представляет собой своеобразный психологический эксперимент, когда возможно более широкому кругу специалистов, работающих в данной области, предлагается расположить (ранжировать) факторы в порядке убывания степени их влияния на отклик. Априорное ранжирование обычно осуществляется в несколько этапов. !
Этап 1. Постановка задачи, организация и проведение опроса. iOnpoc можно проводить методом анкетирования или другим [55] способом. При ранжировании фактор, оказывающий с точки зрения специалистов наибольшее влияние на отклик, получает ранг 1, следующий за ним — ранг 2 и т. д. Если два или более факторов считаются равнозначными, им приписываются одинаковые ранги. Специалисту разрешается включать в анкету дополнительные факторы, если их список кажется ему неполным.
Установлено, что ранжирование факторов может зависеть от порядка, в котором они предъявлены специалисту. Поэтому в анкетах порядок расположения факторов целесообразно сделать случайным и сообщить об этом специалисту перед началом опроса.
Этап 2. Первичная обработка результатов опроса. Результаты опроса обычно представляют в форме табл. 4.1. Первичная обработка заключается в под-т
счете сумм рангов У а» по столбцам таблицы (/'— номер фактора; i — услов-1=1
ный номер специалиста; — ранг, присвоенный i-м специалистом /-му фактору; т — число опрошенных специалистов), которые являются показателем силы
120
Табл. 4.1. Первоначальные результаты опроса специалистов
Условный Факторы (/)
номер специалиста 1 X, Х3 х.
1 3 4 1 2
2 4 3 2 1
3 2 2 1 1
4 2 1 1 1
5 3 4 2 1
6 1 2 4 3
7 1 3 4 2
8 1 1 1 1
9 1 1 2 2
10 2 1 3 4 '
И 2 3 4 1
12 2 3 4 1
13 1 4 3 2
14 1 4 3 2
26 36 35 25
0/ (1) 2 4 3 1
влияния факторов на отклик. Это позволяет провести новую ранжировку. Ранг = 1 получает тот фактор, для которого сумма рангов, присвоенных всеми специалистами, будет минимальной.
Этап 3. Переформирование рангов. Установлено, что одни специалисты проводят ранжирование уверенно (например; 1-й, 2-й, 5-й, 6-й в табл. 4. 1), а другие, хотя и различали факторы, но менее уверенно (3-й, 4-й, 9-й). Так, 3-й специалист приписал двум факторам хз и х< ранг 1, а двум факторам Xi и Хз — ранг 2. В таких случаях вводятся так называемые «связанные ранги» и проводят переформирование рангов.
Если факторы х;, Xh и xi имеют одинаковые ранги и разделяют, например, n-е, (п+1)-е и (п+2)-е места, то их переформированный ранг будет равен [п+ (и+1) + (и+2)]/3. Переформированные результаты опроса специалистов указаны в табл. 4.2. Точно так же, как при первичной обработке результатов, определяются суммы рангов по столбцам и ранги 0,(2).
Этап 4. Проверка адекватности первоначальной и переформированной таблиц результатов опроса. В общем случае гипотезу об адекватности можно проверить по коэффициенту ранговой корреляции га Спирмена [36];
k
/=i где k — число факторов.
Если га=1, то ранжировки полностью совпадают, а если rs= —1, ранжировки полностью противоположны. В случае rs = 0 между ранжировками нет никакого соответствия. Статистическую значимость г8 (при fe>10) можно проверить по критерию Стьюдента, наблюдаемое значение которого определяется по формуле [55];
Коэффициент г3 считается статистически значимым (отличающимся от нуля), если tn<tK, где tK определяется по табл. П.1 при числе степеней свободы f=k-2(m=k-\).
121
Табл. 4.2. Переформированные результаты опроса специалистов
Условный номер специалиста 1 ’ Факторы Т{
дг2 ха *3
1 3 4 1 2 0
2 4 3 2 1 0
3 3,5 3,5 1.5 1.5 12
4 4 2 2 2 24
5 3 4 2 1 0
6 1 2 4 3 0
7 1 3 4 2 0
8 2,5 2,5 2,5 2,5 60
9 1,5 1,5 3,5 3,5 12
10 2 1 3 4 0
И 2 3 4 1 0
12 2 3 4 1 0
13 1 4 3 2 0
14 1 4 3 2 0
2 aii 31,5 40,5 39,5 28,5 2 Т{ = 108
0/ (2) 2 5 3 1
А/ 3,5 5,5 4,5 6,5
Д'/ 12,25 30,25 20,25 42,25 Sa’= 105
Если таблицы окажутся неадекватными, необходимо провести анкетирование снова. Причинами неадекватности может быть либо недостаточно высокая квалификация специалистов, либо неоднозначное понимание ими каждого фактора.
Этап. 5. Проверка наличия согласованности в мнениях специалистов. Гипотезу о наличии согласия в мнениях специалистов проверяют с помощью коэффициента Кендэла (коэффициента конкордации) [36]:
для несвязанных рангов
для связанных рангов
12
т2 (ft3 — k)
/=1
W = 122 А// m2 (ft3 —ft) — ? i
/=1 / L i=l
(4.3)
где Aj — отклонение суммы рангов для /-го фактора от общей средней суммы рангов:
т km
(4.4)
k
(4.5)
ij — число одинаковых рангов при i-ранжировании.
Например, если третий специалист приписал каждой паре факторов одинаковые ранги, то Т3=(23—2) + (23—2) = 12, а если четвертый специалист при писал одинаковые ранги трем факторам,— 7\=33 — 3=24.
122
Коэффициент конкордации меняется от 0 (согласие в мнениях отсутствует) до 1 (полное согласие). Статистическую значимость коэффициента W оценивают при помощи критерия Пирсона %2. Наблюдаемое значение критерия определяется по формуле
XH2 = m(A-l) W. , (4.6)
Гипотеза о наличии согласия между специалистами принимается, если x„
где Хк определяется из табл. П.2 для принятой доверительной вероятности Р и числа степеней свободы f = k~ 1. Если 'Z,2 < 7.2, то необходимо проводить повторное анкетирование, так как либо квалификация специалистов низка, либо изучаемый объект слишком сложен.
В табл. 4.2 приведены результаты расчетов по формулам (4.4) и (4.5). Тогда, согласно (4.3) и (4.6), W = 12 • 105/Ц42 (43 — 4) — 14 • 108] = 0,123;
= 14 • 3 • 0,123 = 5,17. При Р = 0,95 и f = 13 по табл. П.2 находим Хк = = 22,36. Так как у2 < у2, то согласия между специалистами нет.
Этап 6. Анализ и интерпретация результатов ранжирования. Степень влияния каждого фактора на отклик можно характеризовать:
т
суммой рангов 2 aij> приписанных данному фактору;
£=1 пг - 1 V средним рангом а. =— у d ац\
»=1
т I т k
коэффициентом весомости /И;- =
1 = 1 / 1 = 1 ;=1
Чем меньше каждая из этих характеристик, тем больше значимость фактора.
Для анализа результатов ранжирования строятся априорные диаграммы рангов (рис. 4.4). Если убывание силы влияния почти экспоненциальное (рис. 4.4, а) или параболическое, то есть возможность разделить факторы на группы и отсеять несущественные. Если же сила влияния изменяется почти линейно (рис. 4.4, б), следует включить в эксперимент все факторы. Почти равномерное распределение факторов по суммам рангов говорит о том, что либо специалисты не могли выбрать среди предложенных наиболее сильно влияющие факторы, либо все факторы действительно влияют сильно, либо
б
Рас. 4.4. Априорные диаграммы рангов: а — экспоненциальная; б — линейная
123
низок уровень априорной информации. И в данном случае в эксперимент включаются все факторы.
Проверку правильности разбиения факторов на группы можно проводить при помощи критерия Линка и Уоллеса. Наблюдаемое значение этого критерия определяется по формуле [28]:
/о
/=1
где v — число сравниваемых средних рангов; R(aj)— размах сравниваемых средних; Rj —_размахи выборок, средние значения которых сравниваются; /?(flj)=flmax— Amlni Rj — ^ti max — mln.
Если КнККк, где Кк—табличное значение критерия, то считается, что сравниваемые средние не различаются между собой. Значения приведены в табл. П.10 для Р=0,95.
4.3.2. Критериальные математические модели
Независимо от цели эксперимента при формулировании его задачи предполагается, что между факторами и откликом существует связь, которую можно отразить математической моделью вида
Y=f(Xlt Х2.... Х}, Х„). (4.7)
Размерность факторного пространства можно сократить, если такую модель с натуральными уровнями факторов, каждый из которых имеет определенную размерность, преобразовать в критериальную
Ло-г(р.( Л ], Л2, ••., Лj, ..., Л г ),
где я, —- безразмерный комплекс, или критерий подобия.
Критерием подобия называют произведение нескольких физических величин, возведенных в различные степени, составленное так, что оно приводится к произведению основных величин (масса, длина, время, температура) в нулевой степени.
Например, при анализе механических колебаний может иметь место следующий критерий:
Яу = тх/(Ра12),
где т — масса; х — отклонение от точки равновесия; Fo — амплитуда внешней силы; t — время.
Из л-теоремы (одной из главных теорем теории подобия) известно, что если отклик является функцией от k факторов, для описания которых используется I основных величин, то существует также функция от (k — l) линейно независимых критериев подобия, составленных из этих факторов. Откликом в новой модели также будет критерий подобия л0, содержащий в себе основной отклик У.
Линейная независимость критериев означает, что ни для одного из них невозможно образовать тождество л,-=/(ла, Л]..лг), где r=k—l.
В образовании критериев подобия могут участвовать не только переменные, но и фундаментальные константы (например, ускорение свободного падения).
При преобразовании исходной математической модели в критериальную форму необходимо учитывать все факторы, оказывающие существенное влияние на отклик. Одним из методов приведения модели к критериальной форме является метод нулевых размерностей. Сущность его заключается в следующем. Из исходной модели (4.7) выбираются / факторов Xj (Z—число основных физических величин в данной задаче). Эти факторы условно считаются новыми основными величинами, поэтому их нельзя выбирать произвольно. Предположим, в задаче используются четыре основные величины: масса, длина, время и температура. Тогда размерность каждого фактора имеет вид
124
[X/l = [Л*]»*/ [L]x/ [Г]т/
При выборе четырех факторов в качестве новых основных величин должно соблюдаться условие
Д =
|11 А.! Ра Ла На Ла Р4 Л.4
Т1 |1
Та Sa
Та 5з
Т4 ?4
0.
Новые основные величины позволяют преобразовать исходную модель к следующему виду:
Y f X. Хь '
10 к
----а--------- = Ф I -----------1 • • • , - У^Оу^Оу^О у”о-I у^5 у^5 yVg у^5-y^k y$k yVky^k
Л1 л2 л3 Л4 \Л1 Л2 Л3 Л4 Л1 Л2 Л3 Л4
Значения показателей степени находятся из условия, что каждый из входящих в (4.8) комплексов является безразмерной величиной:
---------> Я1=---------
Х^хР'ХрХр X?‘X^X^‘X7S
1X04 1 X О <
Величины, входящие в критерий Ло, имеют следующие размерности:
[К] = [M]^[L]X’[7’]'i<’[0]4
[%!]«<> =. [M]a«^1[L]a°K‘[7’]a»T1[0]a«£‘-,
[Х2]Ро = [Л4]р“Ц2[Л](1“Хг]7’]|3“Т2[0](1“^;
[X3]Vo = [JHjV°M.a[£,]Vo^3[7']Vo'T3[0]VeES;
[Xi]1!» = [Л1]11»И4[£]Т1о^[7’]Лот< [QjTloS* _
Чтобы величина л0 была безразмерной, необходимо соблюдение условий:
Piao + Р2Р0 + РзТо + Р4Т]о = Ра!
Л1«о + ЛаРо + ЛзУо + Л4Т]о = Ло; .Q-.
ТхИо + Т2В0 + Т3Уо + Т4Т]0 = То; 1 '
£1<Хо + ?аро + §з?о + В-а/По = Во-
Решением системы (4.10) находятся показатели степени а0, 0О, у0 и т]0. Аналогично определяются показатели степени при факторах в других критериях подобия.
Полученные (г+1) линейно независимых критериев подобия можно путем умножения друг на друга легко преобразовать в (г+1) других линейно независимых критериев.
Особенно просто критерии подобия находятся в том случае, когда имеется дифференциальное уравнение, описывающее поведение системы. Для получения критериев подобия в дифференциальном уравнении следует опустить знаки дифференцирования и поделить все члены уравнения на один из них. Получившиеся выражения, а также аргументы входящих в уравнение неоднородных функций являются критериями подобия. Например, поведение технологической системы токарного станка с фрикционным нелинейным виброгасителем описывается следующим дифференциальным уравнением:
mx++isign x+jx + cx3=f cos(<ol),
где т — приведенная масса технологической системы; — сила сухого трения в виброгасителе; signx=l или —1 в зависимости от направления относительного перемещения центра масс; / — жесткость технологической системы при малых деформациях, когда нелинейной частью можно пренебречь; х — откло
125
нения центра масс от положения равновесия; с — коэффициент нелинейности; F — амплитуда отклонения силы резания от среднего значения Fa\ <о — частота вынужденных колебаний; t — время.
Опустив знаки дифференцирования и функцию безразмерного комплекса <о/, получим условное равенство
т — + Fi + jx -|- сх3 = F,
поделив все члены которого на
его первый член, имеем следующие
критерии:
, Fit2 , jt2 , cx2t2 , Ft2
Л Г> , Л| — , Лл —— а Л О —— а
тх т т тх
Вместо текущих значений координат х и времени t можно подставить некоторые их характерные значения: вместо х — амплитуду колебаний А, вместо t— период колебаний Т (Т = 1/<о). Тогда, учитывая что j/m = (Oq (<о0—частота собственных колебаний), после несложных алгебраических преобразований получаем:
F, F <а F2c
По = ; Лз = ~
/А соо I3
Аналитическое исследование процесса работы нелинейного виброгасителя является сложной задачей. Экспериментальное исследование работы виброгасителя — определение оптимального сочетания его параметров, обеспечивающих наиболее эффективное гашение вибраций, легко провести, определив вид и параметры критериальной математической модели
i I F со
А — = ср —, —, Ft \ Ft соо
\ Fr ( F
--- или А = — ® —
/3 / / Ч/ч
(0
со/
с3 /
Вид функции ср и ее параметры будут зависеть от конструкции виброгасителя и ориентации его осей жесткости по отношению к направлению силы резания.
Пример 4.1. Необходимо получить эмпирическую формулу для расчета температуры в зоне круглого врезного шлифования.
Решение. Из теоретических и экспериментальных исследований выявлено, что процесс нагрева детали при шлифовании описывается математической моделью
T=HQ. V, Кг, а, К, s),
где Т — установившаяся температура в зоне шлифования, К; Q — объемная производительность процесса шлифования, м3/с; Кг — коэффициент режущей способности шлифовального круга, Н • с/м3; о — скорость вращения детали, м/с; « — коэффициент теплоотдачи, Вт/(м-К); К—коэффициент тепловой активности материала шлифуемой детали, Вт2-с/(м4-К); s— размерная характеристика шлифуемой детали, м8.
Коэффициент режущей способности Кг характеризует состояние рабочей поверхности, материал, структуру и скорость вращения шлифовального круга. Он зависит также от материала и диаметра шлифуемой детали. Коэффициент режущей способности является технологической характеристикой процесса и вычисляется по формуле
Kt-FJQ,
vjis Fz — касательная составляющая силы шлифования. Коэффициент тепловой активности
К=А.ср,
126
где Л — коэффициент теплопроводности, Вт/(м - К); с —удельная теплоемкость Дж/(кг - К); р — плотность материала шлифуемой детали, кг/м3.
Размерная характеристика детали вычисляется по формуле
s=/Z),
где I и D — соответственно длина и диаметр шлифуемой детали.
Так как для описания шести факторов и отклика применяются четыре основные величины, то в качестве новых основных величин выберем Четыре следующих фактора: о, Кг, а и К:
М=[£][Г]-1; [a]=[Af][T]-3[0]->;
[KJ=[JM] [1]-2[Т]-1; [К]==[Л1]2[Г]-5[в]-2.
Вычислим определитель
2 0—5—2
Значит, выбранные факторы могут служить новыми единицами. На основании (4.9) исходная модель может быть записана в виде Т I Q s \
v^K^a^K^ t>aiK₽*aT>KTii }
или Ло=ф(Л1, Лз).
Размерность критерия л0: . [1]а“-2Р“[Г]—а°_₽0_3'1’“~5г|о[Л1]|3о+т“+211о[0]“7"~2г10 откуда а0—2ро=О; —а0—Ро—Зуо—5т]о=О;
-Уо-2т]о=1; Ро + Уо + 2т]о = О.
Решив-эту систему, получаем: ао=2; р0= 1; Yo= — 1; t]o = O. Тогда
Та Qa4 ло — „ . — , o2Kz v3K2 sa4 Ло v2K2
Поделив л, на л2, получаем критерий л( = Q/(sv) и записываем исходную модель в критической форме
Та / Q sal
= Ф — , - o2A'z---------------\ sv v2K2
Таким образом, вместо шестифакторной модели получили двухфакторную, параметры которой определить сравнительно нетрудно.
4.3.3. Метод насыщенных планов
Этот метод можно применять, если верно предположение, что имеют место только линейные эффекты, т. е. объект можно описать моделью вида k
г=р0 + 2₽л- <4Л1)
127
Табл. 4.3. Комбинации знаков, используемые для построения насыщенных планов Плаккета—Бермана
Число опытов насыщенного двухуровневого плана Af=£+1. Такие планы можно строить методом Плаккета и Бермана. Чтобы получить новую строку плана, сдвигают все элементы предыдущей на одну позицию вправо (или влево), а на освободившуюся первую (или последнюю) позицию ставят последний (или первый) элемент. Этот процесс повторяется (IV—2) раз. Последняя строка плана состоит из элементов (— 1). Вместо чисел +1 и — 1 можно использовать только знаки ( + ) и ( —). Чередование знаков в первой строке планов Плаккета — Бермана приведено в табл. 4.3. Цифры в строке таблицы показывают число элементов в серии с одинаковыми знаками, указанными для каждого столбца таблицы.
В качестве примера в табл. 4.4 приведен насыщенный план Плаккета — Бермана для k= 11. Если число анализируемых факторов k\ отличается от чисел, указанных в табл. 4.3, то используют ближайший насыщенный план с k>k}.
Например, если анализируется степень влияния 9 факторов, то используется насыщенный план для fe=ll, в котором отбрасываются два лишних столбца. Получается ненасыщенный план с относительно небольшим избытком опытов (в общем случае не более 3).
Построенный насыщенный план является ортогональным, т. е. система базисных функций в виде нормализованных переменных (факторов) ортогональна на множестве точек плана. Поэтому коэффициенты регрессии модели (4.11) можно оценивать по формуле (3.47), полагая fj=Xj. Дисперсию оценок коэффициентов регрессии S2(b3) можно найти путем реализации дублирующих опытов. Если, как это чаще всего делается, дублирование проводилось в одной из точек плана (например, в центре), то дисперсия воспроизводимости опыта определяется по формуле (3.19), а если в нескольких, то необходимо дополнительно использовать формулу (3.20). Тогда
S2 (&;.) = S2/AT, (4.12)
где N — число опытов в плане.
Значимость коэффициентов регрессии можно проверить при помощи критерия Стьюдента (3.41). Другой способ оценки значимости заключается в сравнении доверительного интервала коэффициента регрессии ДЬ3 с его значением. Коэффициент регрессии считается значимым, если | b3 | »Д63, где
Д&3 = /(Р, f) -5(6,); (4.13)
f — число степеней свободы, равное (т— 1) при дублировании опытов в одной точке и п(т— 1) при дублировании в п точках.
Для отсеивающего эксперимента можно применять также насыщенные симплекс-планы первого порядка, точки которых размещаются в вершинах
128
Табл. 4.4. Насыщенный план Плаккета—Бермана для k= 11
k План Константы
4 « | 1 х* 1 *3 I Xt at= 0,666667 a2 = 0,707107 61=52=63= 1,290994 64= 1,224746
1 2 3 4 5 —1 1 0 —Ог аг 1 0 — 1 —аг аг ei d О — — Q « 1 1 1 1 1 — Й ft
и 1 ** 1 X3 1 x | Xs
5 ] 2 3 4 5 6 —1 — 1 1 —О! аз 1 1 1 » е» »— — »— Ы te —1 1 —Я] Cl‘ —1 a 1 1 1 1 —ai a2 —1 1 —1 1 1 <?3 ^3 ai= 0,181920 a2= 0,384324 o3 = 0,797596 6/ = 1,253767
и Х1 хг *5
6 1 2 3 4 5 6 7 —1 —1 01 —#2 1 вз а — 1 01 —«2 1 аз — 1 а ai —a2 1 аз —1 — 1 a —a2 1 a3 — 1 — 1 «1 a 1 аз — 1 —1 ai —a2 a a3 —1 — 1 01 —аг I a a1 = 0,654694 ae= 0,591235 o3 = 0,140923 a = 0,795618 6/= 1,256885
симплекса. Симплексом называется простейшая выпуклая геометрическая фигура, имеющая в ^-мерном факторном пространстве (й + 1) вершину. Для k=2 это треугольник, для k = 3 — треугольная пирамида и т. д.
Симплекс-планы для нормированных факторов при £ = 4, 5 и 6 приведены в табл. 4.5 [55]. При использовании указанных планов расчет коэффициентов регрессии производят по формуле
9. Зак. 1001
129
jv
b> = T^^(Yx^’k’ u=\
а дисперсии оценок коэффициентов регрессии по формуле
S2 (*,) = 62S>.
Дисперсию воспроизводимости S2 определяют при помощи дублирующих опытов.
Пример 4.2. Требуется определить факторы, значимо влияющие на некруглость подшипниковых колец, шлифованных на круглошлифовальном бесцентровом станке.
Решение. Анализ литературы позволил выбрать в качестве факторов следующие параметры, определяющие некруглость подшипниковых колец, шлифованных на правильно настроенном станке: длину заборной части шлифовального круга Х\; длину его калибрующей части Х2; обратную конусность калибрующей части Х3; скорость подачи алмаза при правке заборной Х4 и калибрующей Х5 частей шлифовального круга; конусность ведущего круга Х6, обеспечивающую естественный подпор; степень прилегания к ведущему кругу Х7 и число проходов Хе- Предполагалось, что некруглость линейно зависит от указанных факторов. Для выделения статистически значимых факторов проведен отсеивающий эксперимент с планом Плаккета—Бермана для ближайшего большего й=11. Уровни факторов приведены в табл. 4.6, а
Табл. 4.6. Уровни факторов для отсеивающего эксперимента
Факторы
Уровень фактора Xi, мм Х2, мм Хз. мкм х<, мм мин мм МИИ х6, мкм х7, мкм х,
100 мм 100 мм
Верхний 50 40 5 160 120 158 0,04 2
Нижний 30 20 0 120 80 / —242 0,30 1
Табл. 4.7. План и результаты отсеивающего эксперимента
и х2 X, х7 Х& Некруглость, мкм Размах s2 RU
1 + + __ + + 1,62 0,30 0,017
2 + + + — — — + 2,01 0,21 0,008
3 + + + — — — 1,86 0,43 0,033
4 4- + + — —- 1,55 0,35 0,023
5 + — + — 1,89 0,33 0,020
6 + + —. + + + 1,78 0,41 0,031
7 — + + -4- + + — 1,30 0,10 0,002
8 — + + + + + 1,58 0,31 0,019
9 — — + + + + 1,48 0,23 0,009
10 _L_ —. — + + + — 1,35 0,24 0,011
11 — — — + + + 1,25 0,20 0,007
12 — — —' — — — 1,56 0,24 0,011
130
план и результаты эксперимента в табл. 4.7. Указанная в последней таблице некруглость является средней для пяти деталей. Указан также размах отклика в каждой серии замеров.
В результате расчета по (3.47) получены следующие оценки bj-. Z>o=l,6; &i = 0,098; 62=0,079; 0,012; 0,034; 0,054; -0,151; -0,104; 0,018.
Дисперсия воспроизводимости в каждом опыте оценивалась по размаху со* гласно (3.9). Значение dm для т = 5, согласно табл. П.5, равно 2,326. Тогда S^i = (0,3/2,326)2 = 0,0166. Аналогично были получены остальные значения SbU , указанные в табл. 4.7.
Однородность дисперсий проверялась при помощи критерия Кохрена. Наблюдаемое значение критерия, согласно (3.18), GB = 0,033/0,191 = 0,173. Табличное значение критерия GK определялось по табл. П. 8 при Р = 0,95, т = 5 и N = 12: GK = 0,288.
Так как GH < GK, то разница между дисперсиями воспроизводимости является случайной и поэтому S2 = 0,191/12 = 0,016. По (4.12) S2 (&J =0,016/12= = 0,00133, а по (4.13) при Р = 0,95, т = 5 и N = 12 (t = 2) доверительный интервал &Ь. — 2 У 0,00133 = 0,073.
Сравнивая А&3- и bj, можно сделать заключение, что параметры Х3, Х4, Х5 и Хв являются статистически незначимыми и в дальнейших экспериментах их можно не учитывать. Остальные факторы по убыванию силы своего влияния образуют следующий ряд: Хе, Х7, Xlt Х2.
4.3.4. Метод случайного баланса
Предполагается, что число значимо влияющих факторов х> и их парных взаимодействий XjXn значительно меньше, чем число коэффициентов регрессии модели типа
k k
Y = bo +2 bixi + 2 bjhxjxh- h i-i=i 1=1
Планы отсеивающих экспериментов в данном случае являются сверхнасыщенными, где число опытов меньше числа факторов и их парных взаимодействий (т. е. числа рассматриваемых эффектов влияния). Число опытов N в сверхнасыщенном плане выбирается в зависимости от общего числа факторов k и количества эффектов влияния k3:
k 8 10 12 14
N 8 16 32 64
k3 36 55 78 105
План строится следующим образом. В зависимости от числа рассматриваемых факторов выбираются две одинаковые полуреплики от полного факторного плана, строки которых смешиваются случайным образом: из каждой реплики отбирается по одной строке случайным образом, и эти строки объединяются в одну с k элементами. Эта операция выполняется N раз. В табл. 4. 8 приведена для примера полуреплика для k = 8, а в табл. 4. 9 — полученный с помощью этой полуреплики сверхнасыщенный план.
Обработка результатов эксперимента, реализованного согласно сверхнасыщенному плану, проводится при помощи диаграммы рассеяния значений отклика для отдельных эффектов. В качестве примера на рис. 4.5 приведены диаграммы рассеяния значений отклика по уровням пяти факторов. На каждой диаграмме нанесены все точки по N результатам отсеивающего эксперимента. Эти точки разбиты на две группы: одна из них характеризует те опыты, где соответствующий фактор был на верхнем уровне, а вторая группа относится к опытам, в которых тот же фактор был на нижнем уровне.
9’
131
Рис. 4.5. Диаграммы рассеяний
Значимые факторы выделяются прежде всего визуально, при сравнении разностей медиан, нанесенных на диаграмме рассеяния.
Медианой называется значение отклика Ум, которое делит совокупность опытных точек, полученных при верхнем (или нижнем) уровне рассматриваемого фактора, на две равные по числу вариантов части. Значимыми будут те факторы, у которых разница между медианами достаточно велика. В случае, изображенном на рис. 4.5, это будут факторы Xi и х2.
Для приближенной количественной оценки влияния выделенных факторов строятся вспомогательные таблицы с п входами. Вспомогательная таблица представляет собой матрицу полного факторного эксперимента 2". В качестве условного отклика в этой таблице вычисляются
Ри
о=1
где Zu — условный отклик для u-й строки вспомогательной таблицы; ри — частота значений исходного отклика У,, приходящаяся на u-ю строку вспомогательной таблицы.
В качестве примера на основании данных рис. 4.5 построена вспомогательная таблица с двумя входами для хг (табл. 4. 10). Во вспомогательной таблице производятся также вычисления построчной дисперсии
Ри
0=1
Табл. 4.8. Полуреплика Табл. 4.9. Сверхнасыщенный план
для k = 8 для k = 8
132
Табл. 4.10. Вспомогательная таблица
и Xi Xi у z lit) Ри zu м X—ч С 1 S""w su
1 55; 69; 80; 91; 99; 5 78,8 1220,8 305,2
2 + — 105; 115; 125; 3 115 200 100
3 + 50; 60; 65; 3 58,3 116,7 58,4
4 + + 25; 84; 96; 110; 120; 5 97 1352 338
Коэффициенты регрессии приближенной модели для выделенных факторов определяются по формулам:
где q — количество строк вспомогательной таблицы.
Для проверки значимости полученных приближенных коэффициентов регрессии необходимо определить дисперсию их оценок:
2 (?«“’)
5Ъ) = 52Ы = 5оМ где Sq—остаточная дисперсия.
Наблюдамое значение критерия Стьюдента
I
5 (Ьу)
bih
s (М
Критические значения критерия tK определяются по табл. П. 1 при выбранной доверительной вероятности Р и условном числе опытов
Q
ти= 2 Ри~~я+ 1-ы=1
Если tB > tK, то коэффициент регрессии и соответсвующий ему эффект являются статистически значимыми.
Обработка данных табл. 4. 10 указанным методом дала следующие результаты: ii= 18,7; &2=~ 9,6; &12 = 0,63; 5(&j)=4,01; iHi = 4,68; /нг = 2,4; /hi2=0,12; Щи = 13.
Критическое значение критерия Стьюдента для Р = 0,95 и т=13, согласно табл. П.1, /к = 2,179. Следовательно, статистически значимыми будут эффекты Xi и Х2, а эффект взаимодействия xiXj статистически незначим.
Статистический анализ данных вспомогательной таблицы возможен только в тех случаях, когда ри>2. Если рц<2, то необходимо уменьшить число входов вспомогательной таблицы, исключив фактор с меньшим вкладом (с меньшей разностью медиан).
На следующем этапе анализа для оценки влияния эффектов, которые не
133
были выделены на первом этапе, корректируют отклик в матрице планирования отсеивающего эксперимента по формуле
y'u-Yu-'Zb, Kfe+D,
4=1
где п — количество выделенных факторов; k — индекс выделенного фактора; и — номер строки сверхнасыщенного плана.
На следующих этапах строятся диаграммы рассеяния и для факторов и для их парных взаимодействий.
4.3.5. Последовательное отсеивание
В данном случае предполагается, что значимых эффектов совсем мало и ошибкой опыта можно пренебречь.
Сущность метода легко понять из следующего примера. Допустим, в программу исследования включено девять независимых факторов Xi, х2, ..., Хд, которые варьируются на двух уровнях. Нужно выделить несколько эффектов среди 45 возможных (9 линейных и 36 парных взаимодействий).
Независимые факторы случайным образом группируются в блоки. В случае 9 факторов их следует разделить на 3 блока, по 3 фактора в каждом. Случайность выбора можно обеспечить с помощью таблицы случайных чисел. В результате получились следующие блоки: х8х6х2, XiX3Xs, x7xgxt. Затем составляется матрица отсеивания из 12 опытов, в каждом из которых только три фактора находятся на верхнем уровне, а остальные на нижнем (табл. 4. 11). Эту матрицу строят следующим образом. Вначале на верхнем уровне поочередно поддерживаются факторы, сгруппированные в блоки (первые три опыта). Затем поочередно объединяют на верхнем уровне каждый фактор первого блока с первым, вторым и третьим элементами второго и третьего блоков.
В матрице последовательного отсеивания каждый из факторов случайным образом четыре раза поддерживается на верхнем уровне и восемь раз на нижнем. Каждое из 36 парных взаимодействий типа XjXh один раз испытывается в комбинации (+ +), пять раз в комбинации (— —) и по три раза в комбинациях (+ —) и ( — +). Допустим, что после реализации матрицы планирования только значения У2, Т6, Ys, Уп, и У|2 существенно отличаются от остальных (больше или меньше). Эти значения вместе с определяющими их факторами, находящимися в экспериментах на верхнем уровне, выписываем в таблицу анализа (табл. 4. 12).
Так как в экспериментах 2, 6, 9 и 12 фактор х5 был на верхнем уровне,
Табл. 4.11. Матрица последовательного отсеивания
134
Табл. 4.12. Таблица анализа
У Выделяющий блок Возможная причина эффекта
У* *1*3*5 *5
У в *8*5*4 *5
У» *6*5*7 *5
Ун *2*3*7 *2*3 > *2*7, *3*7
У12 *2*5*9 *5
то линейный эффект от действия этого фактора можно считать значимым. Другие факторы не могут быть причиной выделения отклика в этих опытах, так как в экспериментах, где они также были на верхнем уровне, существенного различия в значениях отклика не наблюдалось.
Эксперимент 11 показывает, что значимым может быть одно из трех указанных в табл. 4.12 парных взаимодействий. Для проверки необходимо провести эксперимент, в котором все факторы, кроме, например х% и х?, будут на нижнем уровне. Если в этом эксперименте значение отклика отличается от среднего уровня, то именно *2*7 будет значимым эффектом. Если эксперимент даст значение отклика, близкое к среднему, то нужно аналогично проверить следующее из указанных в табл. 4.12 парное взаимодействие.
Эффекты всех парных взаимодействий, которые не образованы из выделяющего блока *2*з*7 (например, XtXa, х?ха и т. д.), не являются значимыми, так как в опытах, где уровень произведения этих факторов равен +1, так же, как и в опытах 2, 6, 9 и 12, не наблюдалось существенного изменения отклика.
Таким образом, на основании 13—14 опытов можно выделить значимые факторы (х$ и *3*7) из большого числа подозреваемых.
Если количество исследуемых факторов 4 < k < 9, то можно пользоваться той же матрицей, отбросив лишние столбцы.
5. ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА
5.1. ОСНОВНЫЕ ПРИНЦИПЫ и понятия
Основной принцип, положенный в основу теории планирования эксперимента,— получение максимума информации при минимальных затратах времени и средств на эксперимент.
Для получения исчерпывающей информации о свойстах функции отклика необходимо проведение опытов во всех точках области экспериментирования. В противном случае всегда существует возможность не выявить некоторую особенность поверхности отклика. Указанную разновидность эксперимента называют экспериментом с полным перебором всех входных состояний. Такой эксперимент в принципе нереализуем, так как число входных состояний бесконечно велико.
В теории планирования эксперимента сознательно отказываются от эксперимента, близкого по конструкции к эксперименту с полным перебором входных состояний. Выбор числа уровней варьирования по каждому фактору непосредственно связывается с выбором модели, аппроксимирующей функцию отклика. В частности, при наиболее распространенных полиномиальных регрессионных моделях выбор числа уровней варьирования факторов определяется степенью аппроксимирующего полинома.
При отсутствии априорной информации о свойствах функции отклика нет смысла сразу строить сложную математическую модель объекта, так как это потребует значительных затрат времени и средств, в то время как может оказаться, что в сложной модели нет необходимости, поскольку таковы свойства объекта. Поэтому теория планирования эксперимента рекомендует, как правило, начинать с простейшей модели, соответствующей имеющейся априорной информации, что требует проведения сравнительно небольшого числа опытов. Если проверка показывает, что полученная простейшая модель пригодна, то эксперимент заканчивается. Если же модель непригодна, реализуется следующий этап (цикл) эксперимента, позволяющий получить более сложную модель, которую также проверяют на адекватность. Если и в этом случае проверка указывает на неадекватность, то цикл эксперимента повторяют с целью получения еще более сложной модели.
Указанная логика экспериментирования составляет часть общей концепции последовательного эксперимента, согласно которой при проведении эксперимента необходимо использовать последовательную, шаговую стратегию. После каждого шага производится анализ результатов, на основании которого принимается решение о дальнейших опытах. Данная концепция находит свое воплощение в задачах построения математических моделей, в поисковых процедурах экспериментальной оптимизации, при проверке статистических гипотез и т. д.
Проверка адекватности построенной модели и другие проверки производятся с помощью статистических критериев, за счет чего формализуется процедура принятия решений после каждого этапа исследования, облегчается работа экспериментатора и уменьшается риск принятия необоснованных «волевых» решений при подгонке результатов эксперимента под теоретическую концепцию исследователя. При проверке адекватности проводится сопоставление систематической погрешности аппроксимизации с погрешностями, связанными с влиянием неконтролируемых факторов и случайными ошибками измерений.
136
При планировании эксперимента используется принцип рандомизации плана, позволяющей свести эффект некоторого неслучайного фактора, который не поддается учету и контролю, к случайной ошибке. Этот фактор можно рассматривать как случайную величину и учитывать или нейтрализовать его влияние статистически.
Рандомизация плана предполагает случайный порядок реализации опытов (строк матрицы плана), что позволяет устранить в математической модели смещения, вызванные действием неконтролируемых неслучайных фак-
торов.
При других статистических исследованиях рандомизация предусматривает случайный выбор анализируемых элементов из общей совокупности, подлежащей изучению. Тем самым обеспечивается представительность полученной выборки, т. е. гарантируется возможность с помощью измерения свойств конечного набора элементов высказать обоснованное суждение о всей совокупности в целом.
Центральным в теории планирования эксперимента является принцип оптимальности плана. В соответствии с ним план эксперимента должен обладать некоторыми оптимальными свойствами, с точки зрения определенного, заранее выбранного критерия или группы критериев [51].
Критерии оптимальности планов эксперимента, целью которого является построение математической модели объекта, можно разбить на три группы. К первой относят критерии, связанные с точностью оценок коэффициентов регрессии, ко второй — связанные с ошибкой в оценке самой модели, а к третьей — связанные с трудоемкостью обработки результатов эксперимента.
К первой группе относятся критерии A, D и Е- План называется Л-оп-тимальным, если сумма дисперсий оценок коэффициентов регрессии будет минимальной; .D-оптимальным, если определитель его информационной матрицы (см. параграф 3.6) будет минимальным, т. е. при этом минимизируется обобщенная оценка коэффициентов регрессии; Е-оптимальным, если он минимизирует максимальное значение дисперсии оценок коэффициентов регрессии. Связь между данными критериями иллюстрируется для двухмерной задачи на рис. 5. 1. На нем изображен эллипсоид рассеяния оценок коэффициентов регрессии. Согласно критерию А, минимизируется сумма квадратов сторон описанного прямоугольника, т. е. диагональ прямоугольньика, согласно критерию D,— площадь эллипса рассеяния, а согласно критерию Е,— его большая ось.
Ко второй группе относятся критерии G и Q. План называется G-оптимальным, если он минимизирует максимальную дисперсию предсказанных моделью значений отклика; Q-оптимальным, если он соответствует минимуму средней дисперсии значений отклика по отношению к предсказанным мо
делью.
К третьей группе относится критерий ортогональности плана, который требует такого выбора точек факторного пространства для измерений откли-
ка, чтобы процедура вычисления оценок параметров модели данного вида была самой простой. В таком случае значения каждого параметра модели вычисляются независимо от значений других параметров.
К планам могут предъявляться и другие требования, например, композиционности, униформности и ротатабель-ности.
Композиционность — это свойство плана, позволяющее разделить эксперимент на несколько этапов и постепенно переходить от простых моделей к более сложным, используя результаты предыдущих наблюдений. Например, сначала составляется и реализуется план для
Рис. 5.1. Эллипсоид рассеяния оценок коэффициентов регрессии
137
оценки коэффициентов регрессии полинома первого порядка. В случае необходимости на втором этапе к имеющемуся плану добавляется несколько измерений в определенных точках факторного пространства, так что все вместе они дают возможность оценить коэффициенты регрессии модели второго порядка и т. д.
Униформность — критерий, требующий, чтобы дисперсия предсказания отклика в некоторой области вокруг центра эксперимента была практически постоянной.
План называется ротатабельным, если дисперсия предсказания отклика может быть представлена как функция расстояния до центра плана. Выполнение этого условия делает любое направление от центра плана равнозначным в смысле точности оценки отклика.
5.2. ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА ПРИ ОЦЕНКЕ ОТКЛИКА [37]
Целью планирования в данном случае является определение минимально необходимого числа параллельных опытов т для оценки отклика с заданной точностью.
Если отклик является неслучайной величиной, а его оценкой — среднее арифметическое значение у, согласно (3. 5), то по (3. 6)
S \Y-y\^t(P, (5.1)
V т
Задавшись доверительным интервалом или допустимой ошибкой оценки До, из (5. 1) получаем
S2
щ>/2(Р, т)— . (5.2)
До
Если априори известна оценка погрешности измерения отклика S2, то т следует выбирать из табл. 5. 1 в зависимости от доверительной вероятности Р и отношения Ao/S или, пользуясь табл. П.1, подбирать такое значение т, чтобы для данной Р соблюдалось неравенство /п(Д0/5)2>ЦР, т).
Если значение S заранее неизвестно, то проводится последовательный эксперимент. Сначала производится серия параллельных опытов, позволяющих в первом приближении оценить S2. Затем, согласно (5. 2), вычисляется т-2. При этом критерий Стьюдента определяется в предположении, что т = — mi. При т2 tn-i после проведения (от2 — /«i) опытов уточняется значение S и, согласно (5. 2), вычисляется /и3. Если т3 < т2 или т3 незначительно больше т2, то испытание заканчивается. Когда отклик является случайной величиной, процедура планирования эксперимента для оценки его математического ожидания является такой же, как в случае неслучайного отклика.
Предположим, что задана также требуемая точность оценки стандартно-
Табл. 5.1. Количество параллельных опытов, необходимых при оценке Y
Ao/S Число опытов при доверительной вероятности
0,9 0,95 0,98 0,99
1 5 7 9 11
0,75 7 10 12 16
0,5 13 18 25 31
0,4 19 27 37 46
138
Табл. 5.2. Количество параллельных опытов, необходимых при оценке а(У)
Д(о)/а Число опытов при доверительной вероятности
0,9 0,95 0,98 0,99
1,5 4 5 6 7
1,25 5 6 8 9
1 6 8 10 12
0,75 10 14 18 22
0,5 28 40 50 60
го отклонения а(У). Параметр точности Л(о) в данном случае равен половине доверительного интервала для о (К). Тогда требуемое количество параллельных опытов можно определить по табл. 5. 2 в зависимости от доверительной вероятности Р и отношения Д(<г)/<т.
Можно также, выполняя процедуру последовательного планирования, пользоваться формулой
т^Р(Р, m)S2/[2A2(o)]. (5.3)
Если необходимо определить коэффициент корреляции с заданной точностью Д(г), то минимально необходимый объем выборки определяется по формуле
где Р,— доверительная вероятность:
А = 1-(1-Р)/2;
Р—заданная доверительная вероятность; U(Pi) — квантиль нормированного нормального распределения (табл. П.11).
Когда отклик является случайной функцией (см. § 3.2), целью планирования будет определение необходимой длины t реализации, по которой находятся Л1[У(£)] и Х(т). Любую реализацию можно представить в виде ряда Фурье
п
У (0 = У. + 2 ас sin + Фг)-
i=l
Если задана допустимая относительная погрешность оценки Л4[У(/)] — бтах=ДтахМтах (Дтах—допустимая абсолютная погрешность оценки, а атах — максимальный размах гармоники), то
Z(M)> 6max(0min + Mrnax)
(5.4)
где (Bmin и (Отах—минимальная и максимальная частоты разложения, определяемые на основании анализа задачи или по нижней и верхней границам частот, пропускаемых измерительным устройством.
Если задана допустимая относительная погрешность оценки корреляционной функции б(К) =А(К)/атах (А(К)—допустимая абсолютная погрешность оценки), то
4
Z(K)“ »m(<omIn+%x) ’
где /(7() — необходимая длина реализации для оценки /((т) с заданной точностью.
139
При анализе характеристик случайных процессов с применением ЭВМ непрерывную реализацию преобразовывают в дискретную с определенным шагом по времени и по амплитуде, т. е. квантуют. Если задана относительная допустимая погрешность аппроксимации бтах, то шаг квантования по времени
tк '' б m а x/й) max-
Пример 5.1. Определить количество параллельных опытов, необходимых для оценки с точностью до 5 мкм среднего квадратического отклонения размера шлифованных валиков, если после первой серии опытов получены следующие результаты: 19,95; 19,97; 19,94; 19,95; 19,96 мм.
Решение. Размах в данной выборке /?=30 мкм. Тогда, согласно (3.9) и табл. П.5, получаем первую оценку о: S=P/dm = 30/2,326= 12,9 мкм. Подставляя это значение 5 в формулу (5.3), при Р = 0,95 и т = 5 получим » 2,7762 • 12,92/ (2 • 52)) = 25,6.
Выбирая новое значение t при «г = 25 и повторяя вычисления, имеем ш>2,0642- 12,97(2 - 52))= 14.
При т= 14 получим т^2,162-12,92/(2 • 52) = 15,5.
Окончательно принимаем т= 16.
После реализации 11 дополнительных опытов получена новая оценка о: 5=10,4 мкм. Согласно неравенству (3.11), при Р = 0,95 7,7<о<16,1, т. е. доверительный интервал равен 8,4 мкм, а его половина А(а)=4,2<5.
5.3. ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА ПРИ ДИСПЕРСИОННОМ АНАЛИЗЕ
Если результат эксперимента зависит одновременно от нескольких факторов, то наилучший эффект дает одновременный дисперсионный анализ всех этих факторов [22]. При дисперсионном анализе можно использовать как полный, так и дробный факторный план. Последний применяется чаще, хотя при этом теряется часть информации. Особенно широко используются дробные планы, в которых теряется информация о взаимодействиях изучаемых факторов. В таких случаях модель результатов наблюдения, например, для четырех факторов можно представить в виде суммы
У{ jktv — (1 + Pi и +б/щ + 1) +Zijkl4. (5.5)
где [x — общая средняя; — отклонение, вызванное влиянием первого фактора на t-м уровне при ц-м дублировании; бй„ —отклонение, вызванное влиянием третьего фактора на /г-м уровне при v-м дублировании; ZijMv— отклонение, вызванное влиянием неконтролируемых факторов.
В данной модели отсутствуют эффекты произведений, например, (0£)п или (PYS)ijK. Для дисперсионного анализа объектов, соответствующих моделям типа (5.5), наиболее удобными являются планы в виде так называемых латинских и греко-латинских квадратов. Латинские квадраты применяются для трех факторов Х2 и Х3, каждый из которых может находиться на г уровнях. Число опытов в этом случае равно г2, т. е. числу ячеек квадрата.
Пример латинского квадрата для г = 5 приведен в табл. 5.3, где к каждому из сочетаний уровней факторов Xi и Х2 (сочетание строки и столбца) добавляется один из уровней фактора Х3 так, что в каждом столбце (строке) он встречается только один раз. Строится латинский квадрат следующим образом. В первой строке располагают фактор Х3 с упорядоченным расположением уровней. Во второй строке записывается первая строка, сдвинутая влево (или вправо) на одну ячейку, которая записывается в конце (начале) строки. Каждой ячейке соответствует определенное сочетание уровней трех факторов, которое встречается в плане только один раз. Так, восьмой (выделенной) ячейке табл. 5.3 соответствует сочетание уровней Х^, Х^, Хц.
Греко-латинский квадрат применяется для четырех факторов и строится аналогично путем записывания в ячейку уровней четвертого фактора Xt с по-140
Табл. 5.3. Латинский квадрат для г = 5
*11 *12 *13 *14 *15
*21 *31 *32 *33 *34 *35
*34 *35 *31
Х22 *32 *33
*23 Х33 *34 *35 *31 Х32^ /
*2 4 *34 *35 *31 *32 *33
*25 *зз- *31 *32Х *33 *34
следовательным сдвигом на две ячейки. Пример греко-латинского квадрата для г=5 приведен в табл. 5.4.
Греко-латинские квадраты для г = 2 и г=6 не существуют.
При числе уровней факторов г можно построить план для анализа влияния г+1 факторов. Эти планы получили название гиперквадратов. Гиперквадрат для г=4 с пятью факторами приведен в табл. 5.5. Однако в случае реализации такого насыщенного плана необходимо найти независимую оценку остаточной дисперсии (например, дублированием опытов).
Для дисперсионного анализа результаты эксперимента записываются в ячейках плана. Затем производится суммирование значений откликов по уровням каждого фактора. Результаты суммирования удобно сводить в таблицу (табл. 5.6). Кроме того, вычисляется общая сумма значений отклика. Во многих случаях полезно проводить кодирование отклика, вычитая из всех его значений одно и то же число. Дисперсию отклика, вызванную влиянием /-го фактора, вычисляют по формуле
(5-’>
\ /=1 1
где i — номер уровня; j — номер фактора; — общая сумма значений откликов
Для вычисления остаточной дисперсии необходимо сначала вычислить' общую сумму
Табл. 5.4. Греко-латинский квадрат для г=5
Х12 х., xIt Х„
X31X41 *32*42 Х33Х43 Х34Х44 Х35Х45
*22 Х32Х43 Х33Х44 Х34Х45 Х35Х41 Х31Х42
Х23 Х33Х45 Х34Х41 Х35Х42 Х31Х43 Х32Х44
*24 Х34Х42 Х35Х43 ХЭ1*44 Х32Х45 X33X41
Х25 Х35Х44 х31х45 Х32Х41 Х33Х42 Х34Х43
141
Табл. 5.5. Гиперквадрат для г = 4 и пяти факторов
*11
Xjj Х31Х41Х51 Х32Х42Х52 X33X43^53 Х34Х44Х54
Хаа Хз4%43^52 ^33^44^51 Хз2^41-Х54 Хз1Х4аХзз
Хаз X31X43X54 Х34Х41Х53 Х31Х44Х52 Х32Х43Х51
^24 Х32Х44Х53 X31Y 43-^54 Хз4^42^51 Х33Х41Х52
Табл. 5.6. Суммы значений откликов по уровням факторов
Фактор Уровень фактора
1 | 2 | . . . г—2 г-1 <
Xi У11 Г12 У1 (г—2) У1 (Г— 1) Лг
Ха У 21 /22 У2(г-2) Г2(г-1) У 2г
У.2 УА(г-2) (Г-1) ykr
/=1 /=1
(5.7)
Тогда
° (г — 1) (г — А + 1)
k
S—(г — 1) ^S2(Xy)
(5.8)
Остаточная дисперсия отражает влияние неконтролируемых факторов и отождествляется с дисперсией воспроизводимости.
Проверку значимости влияния фактора X, производят при помощи критерия Фишера, наблюдаемое значение которого
FH = S2 (Xy)/S2.
Критическое значение критерия определяется по табл. П.7, как указано в § 3.4.
Бывают ситуации, когда число уровней одного из трех исследуемых факторов меньше, чем у двух остальных. В таких случаях используются планы в виде квадратов Юдена [22], которые можно рассматривать как неполные латинские квадраты. Пример квадрата Юдена 7X4 приведен в табл. 5.7.
Обработка результатов эксперимента, реализованного согласно квадрату Юдена, производится следующим образом. Вначале суммируются отклики по уровням факторов и определяется их общая сумма. Затем результаты заносятся в таблицу типа табл. 5.6 и вычисляются суммы, которые для трех факторов имеют вид:
142
где г — число уровней факторов Х2 и Х3; rt—число уровней фактора X! ('•!<')
Скорректированные суммы квадратов для факторов с большим числом уровней определяются при помощи вспомогательной таблицы, в которую преобразуют квадрат Юдена (пример для квадрата Юдена 7X4 показан в табл. 5.8):
Табл. 5.7. Квадрат Юдена 7x4
Хц Х12 Х1э Х14
Х2х Х35 Азе Х37 Аз1
х22 Х36 А37 А.з1 Х32
Х23 Х37 А31 Х32 Хзз
Х24 ХзХ А32 Азз Х34
Х25 Х32 А33 Х34 А35
х26 А33 Х34 Х35 Хзз
Х27 Х34 Аза Хзб Х37
Табл. 5.8. Результаты преобразования плана Юдена
у31 У,2 Угз Г34 У3„ узв у3,
Хз1 ^32 Хзз Х34 Хзз Хзз Х37
Уп Х2х а14 Хц Х12 Xis
К22 х22 Xis Х14 Хц Х12
у23 Х23 Х12 Х1з Х14 Хц
Х24 ХП Х12 х13 Х14
У25 Г26 Х25 Хц ХХ2 Ххз х14
х2в Хц х13 Х13 х14
У27 Х27 Хц Х12 Ххз Х14
143
где Л=Г1(г1— 1)/(г— 1); (2У2);— сумма значений Уц, соответствующих тем строкам столбца У3, вспомогательной таблицы, в- которых размещены значения Хн; (2У3){—сумма значений Уз,-, соответствующих тем столбцам строки У2,, в которых размещены значения Ли-
Так, например, согласно табл. 5.8,
иУзз- (2У2)з=4Узз— (У23+У24+У25+ Узе).
Дисперсия, вызванная влиянием факторов Х2, Хз и Хь определяется по формулам:
S2(X1) = S1/(r-l); S2(X2) = S2/(r-l); S2(X3) = S3/(r-I).
Для определения остаточной дисперсии вычисляется общая сумма
Л л(г.)
J=1 1=1
Остаточная дисперсия определяется по формуле
5о = 5Л^-2^-^1+2)-где
Se = S — (s2 - s2 + ^) = s — (s3 — S3 + Sj).
Проверка значимости влияния факторов производится аналогично указанному выше, только число степеней свободы для остаточной дисперсии f2= = rrl — 2r — ri + 2.
Табл. 5.9. План и результаты эксперимента
Уровень фактора х2 Уровень фактора Хг
1 1 2 1 з 1 4 5
100 31 10 Х32 12 Хзз 20 Х34 6 Х35 0
120 Х32 9 Х33 10 Х34 24 Х35 0 Хз1 5
140 Х33 12 Х34 3 Х35 25 Хз1 7 Хз-1 2
170 Х34 16 Хзз 6 Хз1 18 Аз2 4 Х33 6
200 Х35 14 Хз1 8 Х32 23 Хзз 9 Хз1 3
Табл. 5.10. Суммы по уровням факторов
Фактор Уровень фактора
1 1 2 з 4 5
Xi 61 39 ПО 26 4
х2 48 48 49 38 57
Х3 56 51 52 46 35
144
Пример 5.2. Необходимо оценить значимость влияния марки СОЖ (X,), частоты вращения детали (Х2) и амплитуды продольной осцилляции круга (Хз) на производительность врезного шлифования.
Решение. Был составлен план эксперимента типа латинского квадрата 5X5 со следующими уровнями факторов: Х2= 100; 120; 140; 170; 200 об/мин; Х3=20; 40; 60; 80; 100 1/мин; Xi=l; 2; 3; 4; 5 (Xi— ранги, присвоенные СОЖ разного состава).
План и результаты эксперимента, где откликом была производительность шлифования при постоянном радиальном усилии У (мм3/мин), приведены в табл. 5.9. В этой таблице в качестве отклика представлены его коды y=Y— — 1300. Результаты суммирования по уровням факторов приведены в табл. 5.10, где первая строка представляет собой суммы значений кодов отклика по столбцам табл. 5.9, вторая — по строкам этой таблицы, а третья — по диагоналям, одна из которых отмечена в табл. 5.3 для второго уровня фактора Х3.
Сумма кодов откликов в любой строке табл. 5.10 = 240.
По формуле (5.6)
$2 (ХП =—!— Г(613 + 392 + ПО2 + 262 + 42) — 4- 2402| = 325,7;
4 • 5 [ 5 J
S2 (Х2) = 9,1; S2 (Х3) = 13,1.
Из формул (5.7) и (5.8) 5^ = 12,03. Наблюдаемые значения критерия Фишера FH (Xj) — 27,07; Fa (Х2) = 0,76 и FH (Х3) = 1,09. Число степеней свободы для факторов Л= 4, а для остаточной дисперсии /2= 4-3=12. Тогда при Р = 0,95 по табл. П.7. 3,34 < FK < 3,86. В результате интерполяции получено FK = 3,65.
Сопоставляя значения FK и FB, можно сделать вывод, что значимым является влияние только фактора Xi, т. е. состава СОЖ. Влияние же других факторов несущественно.
5.4. ПЛАНИРОВАНИЕ ПРИ ОДНОФАКТОРНОМ РЕГРЕССИОННОМ АНАЛИЗЕ
5.4.1. Определение вида линейной по параметрам однофакторной модели
Однофакторная, линейная по параметрам, модель имеет вид
(5-9>
1=0
где Ф»(Х) —известные функции; bi — параметры модели.
Часто применяются функции вида:
qpz (X) = sin (i<bX); <р(. (X) = cos (icoX);
k
<рДХ) = (Х)г; Ф/(Х)= ^a-X',
/=1
где и и а — известные параметры.
В данном пособии рассматриваются модели, использующие функции двух последних видов.
Нет алгоритма априорного выбора числа и расположения уровней фактора, и эта задача решается эвристически в зависимости от трудоемкости и требуемой точности эксперимента.
Рекомендуется расстояние между уровнями факторов, при которых будет производиться измерение отклика, брать постоянным. Число уровней лучше
10. Зак. 1001
145
выбирать нечетным. Нормализацию фактора следует проводить симметрично, •согласно формуле (3.2). Количество параллельных опытов на каждом уровне фактора должно быть одинаковым.
После реализации предварительного эксперимента строится график в координатах х— У. По виду графика высказывается гипотеза о виде модели. Методом наименьших квадратов определяются предварительные оценки параметров модели. Затем вычисляется остаточная дисперсия отклика
S° ~ N _ 1 IS
(5.10)
где N—число уровней фактора; Уи—среднее значение отклика, когда нормализованный фактор находится на уровне хи.
Если при каждом уровне фактора проведено т измерений, то дисперсия воспроизводимости отклика
в
I
N(m— 1)
(5.П)
Данным выражением можно пользоваться, если ряд полученных дисперсий (для всех уровней фактора) будет однородным, т. е. различие между дисперсиями носит случайный характер. Проверку однородности дисперсий следует проводить с помощью критерия Кохрена (см. § 3.3), а проверку адекватности модели — по критерию Фишера (см. § 3.5).
Если на каждом уровне фактора проведено однократное измерение отклика, то для определения дисперсии воспроизводимости отклика необходимо провести дополнительный эксперимент на одном-трех уровнях фактора. На каждом из IV] выбранных уровней проводится по т измерений. Тогда
N
(5-12)
/V — 1 а=1
Предварительно порядок полинома следует определять методом разностей. Формулы для вычисления разностей 1...4-ГО порядков:
Ь2Уи = - Л'Еи_1 = У_и - 2У U_1+ у„_2;
д3Уц = Л'У - Д2Уи_1 = У„ - ЗУи_1 + ЗУ„_2 - V 3;
^Уи = Д3Уи - Д3У„_1 = Уи - 4Уи_, + 6У„_2 - 4У„_3 + Уи_<;
где и — порядковый номер уровня фактора.
Порядок полинома соответствует тому порядку разностей, ряд которых образует величины, незначимо отличающиеся друг от друга.
Если на каждом уровне фактора проведено одинаковое число измерений (»г), то проверку гипотезы о том, что различие между значениями разностей является случайным, следует проводить при помощи критерия Стьюдента, наблюдаемое значение которого определяется по формуле
146
, A^max-Anrmln i Гtn-y V 2
где n — порядок разности;
S = V S2B ;
en—параметр, значение которого для разностей 1...4-го порядков составляет соответственно 2, 6, 20, 70.
Критическое значение критерия tK определяется по табл. П.1 для значений тп, зависящих от порядка разностей:
тп=пт— 1.
Если ts<iK, то различие между значениями Д’1 У одного порядка является случайным. При tB>tK это различие является существенным.
Для предварительной оценки параметров моделей, имеющих вид полиномов, применяются следующие формулы:
для полинома первого порядка
У = ав -|- aix\
(5-14)
где
для полинома второго порядка
У = а0 + + а2я3;
1 2 2 х1
йл = -
^2(^)« 2х«
2
2х«
(5.15)
2Г« /V2 (А/2 — 1) (АГ2 —4)
2(х2У)„; 180
для полинома третьего порядка
У = а0 + ахх + а2х2 + а3х3;
_l2f« 2-« fl22(^)u 2*«
2_у 2^
D^xl ^У)и
1
ОЗ~ D3
2 2 хи ;
2(^)и 2х“ 2-« 2(^)« 2^ 2№’
(5.16)
№ (№ — 1) (№ — 4) (Д2 — 9)
Оз =
33 600
10*
147
Табл. 5.11. Значения параметров D и стандартных сумм
D„ D,
5 10 34 130 70 144
7 28 196 1588 588 6048
9 60 708 9780 2772 85 539
11 НО 1958 41 030 9438 697 536
13 182 4550 134 342 26026 3747 744
15 280 9352 369 640 61 880 16 039 296
Поскольку нормализованный фактор Х; принимает целочисленные значения, то в зависимости от числа экспериментальных точек можно из табл. 5.11 определить некоторые из величин, подставляемых в формулы (5.14)...(5.16).
Определение параметров Ь; натуральной модели по найденным значениям параметров нормализованной модели производится по следующим формулам: для линейной модели
Х_ . at
Ь» — а0~ а± , = •
ДХ ДХ
для модели второго порядка
X / х \2
&о = До — — Ц- а2 —— ;
ДХ \ ДА]
1 / X \ я2
Ь\ 1 -- 2<2п I * Ь2 i
ДХ ДХ) (ДХ)«’
для модели третьего порядка
X / X \2 / X
Ьц = о-о — Я1 ~~Z + TZ I — аз Tv ) ’ ДХ \ДХ/ \чДХ/
. _ 1 Г 0 х . , / х V
ДХ [ ДХ ^ДХ у J
. 1 / 2 о X У \ а*
(ДХ)У дху (ДХ)3
Представление моделей в виде обычных многочленов имеет следующие недостатки: а) с повышением степени многочлена увеличивается погрешность оценки его параметров; б) при необходимости повысить степень многочлена (например, при уточнении модели) расчет значений всех параметров нового многочлена приходится начинать сначала.
Этих недостатков лишена модель в виде суммы ортогональных полиномов Чебышева [67]:
у=_£ 6/р.(х)> (5.17)
/=о
где Pj(.v)—ортогональные полиномы Чебышева; Ь,—параметры модели:
148
п
6/ = ^7 Г“Р/ (х“)’1’= °’1121 ''' ’"< N'’
п — степень многочлена.
Значения величин Hj и pj(xu) определяются по формулам:
ПО = N-, Из =--—----; Н2 = ------------
М(№—1) (№ —4) (№ —9) л» =-------------£------
2800 25 (№-25) п 5 = П 4 " ' 4-9-11
Не = Ht
Ро (х) = 1; рх (х) = х; рг (х) = хг
Рз (х) = х3 —
3№ — 13
р4 (х) = х4 —-------
р5 (х) = хр4 (х) —
Ре (х) = хр5 (х) —
180
4 (№—16)
7-9
9 (№ — 36) 11-13 ’
№— 1
12 '
3№ — 7
20 *’
„ , 3(№—1) (№ —9) х2 4-------------
4-140
4 (№—16) ---------Рз (х);
7 • 9
25 (№ — 25)
Для облегчения вычислений коэффициентов модели (5.17) разработаны таблицы значений ортогональных полиномов Чебышева. В них (см. табл. П.12) приведены значения скорректированных полимонов ру (х), которые отличаются от ру (х) только постоянными множителями
ру (х) = р. .р* (х).
Множители pij выбраны таким образом, чтобы значения скорректированных полиномов в точках хи = 0; ±1; ±2; ±3... были целыми числами, не имеющими общего множителя.
Значения р* (хы) даны для неотрицательных хи, а при отрицательных хи определяются из формул:
р* (— х) = Р* (х) ПРИ четном /;
р* (— х) = — р* (х) при нечетном /.
При пользовании таблицами N
bi = YuPj (хи)>
где у3- —параметр, приведенный в табл. П.12.
Остаточная дисперсия, указывающая на степень приближения моделью того или иного порядка результатов эксперимента,
149
s
2 on
1
N- (n + 1)
где n — порядок полинома; N — количество уровней варьирования факторов;
причем
Значения Ци можно найти из табл. 5.12.
Табл. 5.12. Значения рп
7 | 9 I 11 13 | > 15 | 17 | 19
1 2 1 1 1 3 1 1 1 1 1 3 1 1 1 1
3 1/6 5/6 5/6 1/6 5/6 1/6 5/6
4 7/12 7/12 1/12 7/12 35/12 1/12 7/12
5 7/20 3/20 1/40 7/120 21/20 1/20 1/40
Доверительный интервал оценок параметров модели (5.17) определяется по формуле
Л (»,)-+, (Л ]/
где А (&у)—доверительный интервал для параметра бу S?— дисперсия воспроизводимости; t (Р, т) — критерий Стьюдента.
Пример 5.3. Для оптимизации режимов чистового точения чугунных деталей по размерной стойкости инструмента определить зависимость удельной интенсивности изнашивания <sb=h[l резцов с режущей пластинкой из ВК8 от скорости резания v (Л (мкм) —радиальный износ задней грани; I (м) —путь резания; период приработки инструмента не учитывается).
• Решение. Опыты проводились при глубине резания а = 0,5 мм и подаче s=0,l мм/об. Предполагалось, что модель имеет вид полинома, степень и параметры которого следует определить. Для оценки погрешности определения параметров модели и проверки ее адекватности необходимо найти дисперсию воспроизводимости. С этой целью при скоростях 30, 90 и 170 м/мин было проведено по 5 испытаний. Ниже для указанных скоростей приведены средние значения <о:
и 1 2 3 4 56789 10 11
v 10 30 50 70 90 110 130 150 170 190 210
<о 3,52 2,72 1,94 1,14 0,51 0,3 0,5 1,45 2,5 4 6,5
Наблюдаемые дисперсии в каждой из этих серий имели соответственно значения; S2 = 0,02; S\ = 0,012; S2 = 0,025.
Наблюдаемое значение критерия Кохрена в данном случае 0,025
G =--------------------- =0,43.
н 0,02 + 0,012 + 0,025
150
Табл. 5.13. Вычисление параметров многочлена
V X У У2 р* Y р* 1 р* 2 У р* 2 р* 3 У г’ 3 р* 4 У р‘ 4
10 —5 3,52 12,4 —5 — 17,6 15 52,8 —30 — 105,6 6 21,12
39 —4 2,72 7,4 —4 —10,88 6 16,32 6 16,32 —6 — 16,32
50 —3 1,94 3,75 —3 —5,82 — 1 — 1,94 22 42,68 —6 —11,52
70 —2 1,14 1,3 —2 —2,28 —6 —6,84 23 26,22 —1 —1,14
90 — 1 0,51 0,26 —1 —0,51 —9 —4,59 14 7,14 4 2,04
ПО 0 0,3 0,09 0 0 —10 —3 0 0 6 1,8
130 1 0,5 0,25 1 0,5 —9 —4,5 — 14 —7 4 2
150 2 1,45 2,1 2 2,9 —6 —8,7 —23 —33,35 — 1 — 1,45
170 3 2,5 6,25 3 7,5 —1 —2,5 —22 —55 —6 — 15
190 4 4 16 4 16 6 24 —6 —24 —6 —24
210 5 6,5 42,2 5 32,5 15 97,-5 30 195 6 39
ТУ Итого: 25,08 92 ПО 22,31 858 158,55 5148 62,41 3432 —3,47
Критическое значение критерия при доверительной вероятности Р=0,95, согласно табл. П.8, равно 0,707. Так как GH<GK, то различие между дисперсиями незначимо и можно считать, что
„ 1
Si = — (0,02 + 0,012 + 0,025) = 0,019.
и
Анализ результатов эксперимента показывает, что моделью процесса изнашивания инструмента может быть полином не ниже второго порядка. Вычисления параметров ba, blt 62 удобно проводить в табличной форме (табл. 5.13); значения скорректированных полиномов р*, (чисел Чебышева) выбираются из табл. П.12:
&о = -77 V1, Y = -^-25,08 = 2,28; N л-Л 11
‘. = ^^^>^22,31. 0,2028;
Остаточная дисперсия для модели второго порядка
причем — -у yJ = 92 — -jy 25,082 = 34,82;
2i=2o — ifvi/H = 34,82 — 0,20282 • 110/1 =30,3;
У2 = —A‘72/ii.2 - 30,3 —0,18482 858/1 = 1.
Для проверки адекватности модели в виде полинома второго порядка определяем наблюдаемое значение критерия Фишера: Ан2 = 32о2/$1 = 0,125/0,019 = = 6,58. Табличное значение критерия Фишера для доверительной вероятности Р = 0,95 при т211 и -5= 15 выбираем из табл. П.7: FK = 2,23. Поскольку Ftt > FK (6,58 >2,23), то модель в виде полинома второго порядка неадекватна,
Предположим, что моделью процесса является полином третьего порядка. Тогда
1 • 1
6 =------Yp„ = -------62,41 = 0,0121;
3 у3 3 5148
2з = V2 — ^Т3/р3 = 1—0,01212 . 5148 • 6/5 = 0,094;
9 1 1
S2 =--------V, =---------- 0,094 = 0,0134.
Л7 _ А / Jo 11 ____ А
Наблюдаемое значение критерия Фишера в данном случае Ан3 = Sq3/S3 = = 0,0134/0,019 = 0,705. Поскольку < FK (0,705 < 2,23), то модель в виде полинома третьей степени приемлема. Следовательно, для отражения зависимости удельной скорости изнашивания резца от скорости резания можно остановиться на следующей.математической модели:
Т=&о+61р1 (х) +Ь%р2(х) +ЬзРз(х).
152
70 JO 50 70 90 f10 750 750 770М/Мин 790
V -----
Рис. 5.2. Зависимость удельной интенсивности изнашивания от скорости резания (результаты эксперимента и построение модели)'
Согласно (5.18) и табл. П.1, для доверительной вероятности /’=0,95 определяем доверительные интервалы оценки параметров модели:
/0,019 1
-4— — = ± 0,048; 5 11
, Л 0,019 1
Д (М = ± 2,571 1/ -V-— =±0,0151;
V о 11 и
Д (62) = + 2,571 1/ = ± 0,0055;
V О ООО
Г 0,019 5
ММ-±2,5711/ — -^^-±0,00195.
1'огда йо=2,28±О,О48; Ь1=0,2028±0,0151; й2= 0,1848 ±0,0055; й3=0,0121± ±0,00195. Округляя параметры, с учетом значений доверительных интервалов получаем по таблице ортогональных полиномов Чебышева (табл. П.12)
У=2,3+0,21х+0,185(х2- 10) +0,012 (х3—17,8х) = 0,45+0,185х2+0,012х3.
Для перехода к натуральной модели подставляем в полученную нормализованную модель значение нормализованного фактора х= (о—110)/20. Окончательно получаем
V / V \2
<0= 4,05 —4,7— —0,325 — 100 \100/
На рис. 5.2 показаны результаты эксперимента и математические модели в виде полиномов второго и третьего порядка.
5.4.2. Определение вида нелинейной по параметрам однофакторной модели
В нелинейной ио параметрам однофакторной модели могут быть использованы: дробнорациональные, иррациональные, показательные, логарифмические или тригонометрические функции, а также их комбинации (сумма или ироизведение) с полиномами разных степеней. Рекомендации по выбору чис
153
ла уровней фактора и числа параллельных измерений отклика на каждом уровне даны в § 5.4.1.
После реализации предварительного эксперимента строится график в координатах X— Y. Исходя из формы графика высказывается гипотеза о виде модели. Затем производится спрямление (выравнивание) экспериментального графика путем соответствующей замены координат. Например, если предполагается, что модель имеет вид
У=&0Хехр(-Ь1Х), то после деления правой и левой части на X и логарифмирования получаем
1п(У/Х) =1п Ь0-Ь,Х
или
Z—dQ-YdiU,
где Z=ln(Y/X); a0=lnb0; a^bj; U=X.
Способ выравнивания зависит от вида модели и числа ее параметров.
Предварительное заключение о пригодности выбранной модели принимается, если в системе координат Z—U можно провести такую прямую, к которой достаточно близко лежат экспериментальные точки. Определив параметры уравнения данной прямой (а0 и czi), можно вычислить оценки параметров предполагаемой модели. Однако вычисление параметров а0 и щ методом наименьших квадратов в данном случае приводит к систематической ошибке, так как минимизация суммы квадратов отклонений преобразованного отклика Z от его прямой регрессии на U не означает, что тем самым минимизирована сумма квадратов отклонений отклика У от модели, полученной обратным преобразованием координат.
Если 2=<р(У), U=X, то хорошие результаты дает введение весовых коэффициентов
Ма=[Ш(Уи)]2-
Тогда параметры а0 и aL можно вычислять по формулам метода наименьших квадратов:
ZX2 — XZ X N -XZ-XZ aQ =--------------; а, =-------------,
NX2 — (X)2 NX2 — (x)2
где
T 2ХЛ 7 2ZA
2“u 1 2“a 1
-r-2 2 Xuau — 2
A = —--------J AZ = ------------.
2 2
В других случаях можно получить неплохие результаты, если прямая проводится ближе к тем экспериментальным точкам, которые соответствуют максимуму (или минимуму) и участкам наиболее интенсивного изменения отклика [56]. Адекватность выбранной модели устанавливается по критерию Фишера.
Если данному виду графика соответствует модель с тремя параметрами, то для спрямления необходимо зафиксировать одну из точек графика. Фиксация точки графика означает, что кривая, координаты которой будут вычислены согласно полученной модели, обязательно пройдет через зафиксированную точку. В качестве фиксированного можно принимать любой уровень фактора Ха и соответствующий ему отклик Уо, однако оценка последнего должна быть значительно точнее, чем значений отклика, полученных при других уровнях фактора. Для этого рекомендуется на фиксированном уровне фактора провести несколько дополнительных опытов.
154
Например, если предполагаемая модель имеет вид
то ее легко можно преобразовать следующим образом:
X/y=&o+61t/+62(72) (5.20)
где U=X2. *
Подставив в (5.20) координаты фиксированной точки (Хо; Уо) и вычтя полученное равенство, получим
^-^^(и-и^+ь^-и^,
I I о откуда
X/r-X0/r0 ,, ,, = (bi -|- b,U0) + bsU
U — Uq
ИЛИ
Z = aQ-\-d\Ut
где G,q= Ь1 + Д| = ^2-
Таким образом, получена спрямляющая подстановка для модели (5.19), превращающая ее в линейную модель с двумя параметрами, где
2 = хд2^у01 и = х2
X2 — xl
Спрямляющие подстановки для моделей с двумя и с тремя параметрами приведены в табл. П. 13...П.19.
Для некоторых видов моделей с тремя параметрами возможно вычисление одного из них непосредственно, без спрямления. Таким образом, остаются неизвестными только два параметра, и можно проводить спрямление. Например, если модель имеет вид
У=60 + 61ехр(&2Х) ; (5~-'
и АХ является величиной постоянной, то
откуда
^»+1 ~ ьо Yu — b0
?и-Ьа ~ Yu_i-bb ’
Yl-Yu^Yu+l bn - — -----------
°‘ 2Уц-Гы_;-Г„+1 соответствует любым трем уровням фактора, расстояние между которыми одинаковое. Среднее значение Ьо:
b0i’
155
Табл. 5.14. Определение одного из параметров трехпараметрической модели
Вид модели Формула вычисления одного из параметров
y = i0 + —!— b2 X _ (^о+1 ~Ь ^-|) ^+1 1 Ьы о v v v 1 и 1и+1^“ги-1
Y = b0Xbl exp (й2 X) 1П уц+, + In Yu_, - 2 In Уц bal ~ In (Х2и — ДХ2) - 2 In Xu
К = ho exp (&1 X 4-&2 X2) 1пУц+1+1пГ»-1-21пГч 2; ~ 2 (ДХ)2
y-‘" + », + V X X < <1 7 + 1 . = as Ч х х | 1 3 „ i I _ 1 11 J е СЭ II
Y ь»+ьг + ь2х2 ь-- Т-ка Yu+i ~ Уи 2XU-SX “ 2Хи + ДХ
где п — число сочетаний равноотстоящих троек уровней фактора, по которым вычислялись значения boi. Следовательно, вместо исходной модели (5.21) спрямляется модель с двумя параметрами
№= У—&0 = 6! ехр (62Я).
Формулы для вычисления одного из параметров некоторых трехпараметрических моделей при ДХ=Хи+1—Xu =const приведены в табл. 5.14.
При сравнении двух адекватных моделей предпочтение следует отдавать
Рис. 5.3. Зависимость удельной интенсивности съема от рабочего зазора при магнитно-абразивном полировании (результаты эксперимента)
156
Рис. 5.4. Спрямление экспрнментальной зависимости (рис. 5.3)
той, в которой при одинаковом числе параметров меньше остаточная дисперсия. Если остаточные дисперсии сравниваемых моделей различаются незначительно, то предпочтение следует отдавать модели с меньшим числом параметров.
Пример 5.4. Для оптимизации процесса магнитно-абразивного полирования определить характер и модель зависимости удельной интенсивности съема металла q от рабочего зазора 6.
Решение. Остальные параметры процесса не изменяются. На каждом уровне фактора проводилось по 5 параллельных опытов. Результаты измерений (средние значения q и его стандартное отклонение 3) приведены ниже и на рис. 5.3.
«12 3 4 5 6 7 8 9
6и 0,5 0,75 1 1,25 1,5 1,75 2 2,25 2,5
qa 2,6 3,35 3,75 4 4,1 4,05 3,95 3,75 8,55
Sa 0,1 0,15 0,12 9,15 0,08 0,17 0,1 0,2 0,07
10 11
2,75 3
3,35 3,1
0,12 0,1
Согласно табл. ПЛЗ, П.15 и П.19, данному графику могут соответствовать модели 5, 16 и 40 (рис. 5.4). Спрямление конкурирующих моделей проводилось с помощью указанных в этих таблицах подстановок; Z,L соответствует модели 16, Z2— 5, a Z3 — 40. Анализ данных графиков показывает, что в первом приближении экспериментальным данным соответствуют все три модели, так как экспериментальные точки после спрямления достаточно близко располагаются около прямой линии..
Однако спрямленные графики не позволяют отдать предпочтение одной из этих моделей. Для выбора одной из трех конкурирующих моделей были определены их параметры, остаточная дисперсия и адекватность. Согласно рис. 5.4: для модели 16 а0=1,98; at = ~0,655;
для модели 5 «о=0,17; а( = 0,0875;
для модели 40 а0= 0,068; «1 = 0,0762.
Значения параметров 5, исходных моделей определялись по формулам, зависящим от их вида:
для модели 16
Y=baX exp(&iX);
157
bi=ai = — 0,655; 60=exp a0=exp 1,98=7,24;
<7=7,246 exp (— 0,6556);
для модели 40
У=-----------------;
b0 + b2X + &2X2
при Xo=0,5 и Уо=2,6 62=ai = 0,0762; b t = aa- b2Xa=0,068 - 0,0762 • 0,5 = 0,0299;
b0 = X0/y0 —&!%(, —= 0,5/2,6 — 0,0299 • 0,5 — 0,0762 • 0,25 = 0,1619;
__________________________________6______________ q ~ 0,1619 + 0,02996 + 0.076262’ для модели 5
Y = ---------;
b0 + M2
6o = ao = 0,17; &1 = aI = 0,0875;
__________6
<?-0,17 + 0.087562'
Расчеты остаточной дисперсии для данных моделей приведены в табл. 5.15. Проверка однородности дисперсий производилась с помощью критерия
Кохрена (см. § 3.5). Наблюдаемое значение критерия
0,22
G =-------------------------------•------------------------------= 0 222
в 3 • 0,12 + 2 0,152 + 2 • 0,122 + 0,072 + 0,052 + 0,172 + 0,22
При доверительной вероятности Р = 0,95 табличное значение критерия (см. табл. П.8) GK= (0,331+0,288)/2 = 0,31. Так как GH = GK, различие между наблюдаемыми дисперсиями незначимо. Тогда дисперсия воспроизводимости s| = (3 • 0,12 + 2 • 0,152-4-2 • 0,122 + 0,072 + 0,052 + 0,172 + 0,22)/11 = 0,0164.
Табл. 5.15. Расчет остаточной дисперсии
в Q Значения q для моделей Квадраты отклонений (X IO4) для моделей
16 40 5 16 40 5
0,5 2,6 2,61 2,55 2,61 1 25 1
0,75 3,35 3,32 3,3 3,42 9 25 49
1 3,75 3,76 3,73 3,88 1 4 169
1,25 4 3,99 3,93 4,08 1 49 64
1,5 4,1 4,07 3,97 4,09 9 169 1
1,75 4,05 4,03 3,91 4 4 196 25
2 3,95 3,90 3,8 3,85 25 225 100
2,25 3,75 3,73 3,66 3,67 4 144 144
2,5 3,55 3,52 3,51 3,49 9 16 36
2,75 3,35 3,29 3,35 3,31 36 0 16
3 3,1 3,05 3,2 3,13 25 100 9
Сумма 124 953 614
Остаточная дисперсия SqX Ю4 12,4 95,3 61,4
158
Адекватность сравниваемых моделей определялась по критерию Фишера. Наблюдаемое значение критерия:
для модели 16 12,4 • 10“4 Ен= -= 0,0756; 16,4 10~3
для модели 40 95,3 • 10“4 F = : = 0,581; 16,4 0~3
для модели 5 16,4 10~4 Ен- — 0,374. 16,4 • 10“3
Табличное значение критерия по доверительной вероятности Р = 0,95ит = = т1 — 55 (табл. П.7) FK = (1,69 + (,53)/2 = 1,61. Сравнение наблюдаемых и табличного значений критерия показывает, что все три модели адекватны. Поскольку значение для модели 16 является наименьшим, то она и принимается для описания процесса магнитно-абразивного полирования.
5.4.3. Уточнение параметров однофакторной модели
Если вид модели найден с помощью предварительного эксперимента, но точность определения ее параметров не удовлетворяет исследователя, то планируется и реализуется уточняющий эксперимент. Планы экспериментов данного типа отличаются от рассмотренных ранее следующими особенностями: 1) число уровней фактора в опытах выбирается минимально необходимым — равным числу параметров модели; 2) планы являются оптимальными или в смысле минимизации погрешности оценки параметров модели, или в смысле простоты обработки результатов эксперимента.
D-оптимальные планы для моделей, имеющих вид полинома степени п, представлены в табл. 5.16.
Областью планирования является отрезок (—1, +1), т. е.
-l<xs£l, где
2(Х— X) X — X
X = ~ --А--- ’
•^max '^min ^Х
X — среднее значение фактора.
Табл. 5.16. £>-оптимальные планы для полиномов
и Степень полинома п
1 1 2 3 4 5
1 — 1 — 1 —1 — 1 —1
2 1 0 —0,447 —0,655 —0,765
3 1 0,447 0 —0,285
4 1 0,655 0,285
5 1 0,765
6 1
159
Число параллельных опытов т в каждой точке плана должно быть одинаковым.
Параметры нормализованной модели определяются по формуле [32]:
ai=DilD,
(5.22)
где
1 X] X) ... х[ ... х”
1 х2 х2 • • • х2 • ' х2
1' хи Хи ' Хи • х и
1 Хл-Н Хп+1 Хп+1 *л+1
1 X, X2 . . . Yj ... х'/
1 х2 х2 ... У2 х2
1 х х2 У хп
1 хи хи 1 и * ’ ли
1 Хл + 1 Хл+1 ^л+1 Хл+1
(5.23)
(5.24)
Yu — среднее значение отклика в u-й серии опытов; п — порядок модели. Разложив определитель £>, по элементам (i+ 1)-го столбца, получим
Л-J-l
Di = 2 YU (- l)i+u+I^(/+D = 2 МжЖ)’ (5-25) u=l U=1
Табл. 5.17. Значения определителей и алгебраических дополнений для D-оптимальных планов
п £> и Лц для i
0 1 2 3 4 5
1 2 1 1 — I
2 1 1
2 2 1 0 1 1
2 1 0 —2
3 0 1 1
3 8 1 —1 1 5 -5
2 2,5 -11,18 —5 11,18
3 2,5 11,18 —5 —11,18
4 —1 — 1 5 5
4 3 1 0 1,125 —1,125 —2,625 2,625
2 0 —4 6,125 4 —6,125
3 3 0 —10 0 7
4 0 4 6,125 —4 —6,125
5 0 —1,125 — 1,125 2,625 2,625
5 60 1 3,74 —3,74 —52,5 52 ,5 78,71 —78 ,71
2 — 11,66 15,2 155,2 —202,83 -143,5 187,58
3 37,95 —133 —10,27 360,34 64,8 —227,31
4 37,95 133 —10,27 —360,34 64,8 227,31
5 —11,66 —15,2 155,2 202,83 —143,5 —187,58
6 3,74 3,74 —52,5 —52,5 78,71 78,71
160
Табл. 5.18. Планы для однофакторных полиномов
Степень полинома п
и 1 2 3 4 3
1 2 3 4 5 6 —1 1 —1 0 1 —2 —1 1 2 —2 — 1 0 1 2 —3 —2 —1 1 2 3
где /—номер столбца определителя (5.51); и — номер строки определителя; Afu(i+1)— минор n-го порядка для элемента Уи; Au(i+i) — алгебраическое дополнение элемента Yu.
В табл. 5.17 даны значения D и алгебраических дополнений элементов Yu для полиномов различных порядков. Если дисперсия воспроизводимости мала, т. е. рассеяние значений отклика мало по сравнению со средним его значением, можно применять неоптимальные планы (табл. 5.18). Значения определителя D и алгебраических дополнений, необходимые для вычисления параметров модели, приведены в табл. 5.19.
Дисперсия оценок параметров щ кодированной модели вычисляется по формуле
(5.26)
Табл. 5.19. Значения определителей и алгебраических дополнений для неоптимальных планов
п D и Аи для i
0 | 1 | 2 1 3 1 4 6
1 2 1 1 —1
2 1 1
2 2 1 0 1 1
2 1 0 —2
3 0 1 1
3 12 1 —2 1 2 — 1
2 8 —8 —2 2
3 8 8 —2 —2
4 —2 —1 2 1
4 24 1 0 2 —1 ' —2 1
2 0 —16 16 4 —4
3 24 0 —30 0 6
4 0 16 16 —4 —4
5 0 —2 —1 2 1
5 240 1 12 —4 —15 +5 3 —1
2 —72 18 80 —40 —8 4
3 90 —90 —65 +65 5 —5
4 90 90 -65 —65 5 5
5 —72 —18 80 +40 —8 —4
6 12 4 — 15 -5 3 1
11. Зак. 1001
161
где Sg — дисперсия воспроизводимости; fi — функция, по которой определялся i-й параметр; Yu — среднее значение отклика на u-м уровне фактора.
Для определения составляющих суммы (5.26) можно пользоваться табл. 5.17 или табл. 5.19, так как значение частной производной по У» равно частному от деления на D. Например, для полинома третьей степени, если его параметры определялись из эксперимента с планом согласно табл. 5.18, получаем
0,944;
(Д1)
2 В
S2 (а») S2 (аа)
—^ = 0,111; —^ = 0,069.
«2В
S
Доверительный интервал оценок параметров
S (fl/)
Д (at.) = +1 (Р, т) (5.27)
V т — 1
где t—критерий Стьюдента (табл. П.1); т. — число параллельных опытов.
Если задана средняя точность оценки параметров Да и из предварительного эксперимента известна оценка 'дисперсии воспроизводимости S%, то можно, используя формулы (5.27) и (5.2), определить потребное число параллельных опытов:
т > /2 (Р)
(« + 1)Да
(5.28)
где t(P) определяется из табл. П.1 для т=60.
Определение параметров натуральной модели й; по полученным параметрам нормализованной модели а; производится по формуле
п _
‘‘=Ё“-(и)'С- ' <5'29>
1=0
где п—порядок полинома; С; — коэффициенты, зависящие от п (табл. 5.20).
Оптимальное планирование эксперимента в случаях, когда модель является нелинейной по параметрам, проводится в соответствии со следующими рекомендациями: 1) соотношения между координатами точек плана выбираются такими, чтобы облегчалось вычисление параметров; 2) области, наиболее подходящие для опытов, находятся в окрестности максимумов, минимумов или точек перегиба графика, полученного по результатам предварительного эксперимента, а для монотонных кривых — в окрестностях значений X, соответствующих минимуму производной [56].
Вид формулы для вычисления параметров модели зависит от вида последней. Если известна спрямляющая подстановка, то параметры модели с двумя параметрами определяются по формулам:
162
Табл. 5.20. Значения коэффициентов для вычисления параметров натуральной модели
п bi C{ для i
0 I 1 2 3 4
1 bo 1 —1
bt о x—1
2 bo 1 —1 1
bi 0 X-1 —2X —1
0 о x-2
3 bo 1 -1 1 — 1
bt 0 X-1 —2X-1 3X-1
bo 0 0 x-2 —3X-2
Ьз 0 0 0 X-3
4 bo 1 -1 1 — 1 1
bl 0 x-1 —2X-1 3X-1 —4X-1
bo 0 0 x-2 —3X-2 6X-2
Ьз 0 0 0 X-3 —4X-3
&4 0 0 0 0 X-4
Zit/a - Z2Ui Zo- -Zi
Uo — Ui Uo- -Ui'
где а.— параметры спрямленной модели Z=a0+ai^; Z;— значение переменной, вычисленное по /(У,, Xi); Ui— значение переменной, вычисленное по <р(Х4); f(Y, X), <р(Х)—формулы преобразования координат; У,— среднее значение отклика при Xf.
Определение параметров Ьо и bt исходной модели производится по формулам, зависящим от способа преобразования координат. Для дробнорациональных и иррациональных моделей с двумя параметрами &о=Оо и &1=аь Для показательных моделей с двумя параметрами типа У=&оЛ(X)exp[&Jg(X)] Ьо=ао, 61 = вг, логарифмических типа У=&оЛ(Х)1п 6J2(X) bo=ao, Ьг = =exp(a0/“i).
После преобразования моделей с тремя параметрами во многих случаях (модели 36...40 в табл. П.19) получаются трехпараметрические модели, линейные по параметрам. В таких случаях параметры преобразованных моделей определяются по формулам (5.22)... (5.25). Если же указанное преобразование невозможно, то следует использовать план, позволяющий решить систему из трех уравнений. Так, например, если модель имеет вид.
Y=b0-f-b1Xbl,
то при выборе уровней фактора следует соблюдать отношение Хз1Х2=Хо1Х1. После реализации эксперимента параметры этой модели вычисляются по формулам;
ь и У2~Ь0 1п (К2 — &0) — 1п (У^ — *0)
2У2-Г,-Г3 Х2‘ 1пХ2-1пХ1
Пример 5.5. Определить параметры модели изнашивания резца при чистовом точении с погрешностью, не превышающей 0,8 X 10—2, если предварительный эксперимент показал, что зависимость между износом резца h и временем его н’ 163
работы Т (в пределах до 40 мин) можно выразить полиномом третьей степени, а дисперсия воспроизводимости = 1,95 х 10~4.
Решение. Выбран план эксперимента для п=3 (см. табл. 5.18). Необходимое число параллельных опытов определяется по формуле (5.28) с учетом данных табл. 5.19:
„ 1,95-10—4 (0,944 + 0,903 + 0,111 +0,069) = 5,9.
nt и, си 4 - 0,64 • 10-4
Принимаем т=6.
Результаты эксперимента:
Т, мин 0 10 30 40
X — -2 — 1 1 2
h, мм 0 0,25 0,5 0,75
S2 X 10* 1,8 1,6 2,1
Параметры нормализованной модели находятся по формулам (5.22) и (5.25) с учетом данных табл. 5.19:
а0 = — (8 • 0,25 + 8 • 0,5 —2 0,75) =0,375; Я1 = -!-(—8 • 0,25+8 0,5— 12 12
— 1 -0,75) =0,104; я2 = -^-(—2 • 0,25 — 2 0,5 + 2 • 0,75) = 0; а3 = -^Х
X (2 • 0,25 — 2 • 0,5 + 1 • 0,75) = 0,0208.
Дисперсия воспроизводимости эксперимента
п+1
S2 = —V S2Bt. = 4 (1,8 + 1,6 + 2,1) 10-4 = 1,83- 10-4.
П + 1 о
1=1
Дисперсия значений параметров нормализованной модели, согласно (5.26) и табл. 5.19:
S2(a0) = l,83 • 10-4-0,944= 1,73-10-4;
S3(ai) = 1,83 • 10-4 -0,903= 1,65-10-4;
S2(a3) = l,83 • 10~4 -0,069 = 0,13-10~4.
Доверительный интервал оценок параметров определяется по формуле (5.27). Критерий Стьюдента при Р = 0,95 и т=16 (табл. П.1) равен 2,132. Тогда
Д (о0) = ± 2,132 • 10-21^ 1,73/15 = + 0,724 • 10~2;
Д(Я1) = +2,132- 10~2 |/ 1,65/15 = + 0,707- 10~2;
Д (аз) = ± 2,132 • 10“2]/ 0,13/15 = +0,2 - 10~2.
Полученные доверительные интервалы значений параметров модели меньше допустимой погрешности. Параметры натуральной модели определяются по формуле (5.29) с учетом данных табл. 5.20. Окончательно получена следующая модель процесса изнашивания резца при чистовом точении:
Л=3,54 • 10"2Т-1,25 • 10~+2 +2,08 • 10-5Т3.
164
5.5. ПЛАНИРОВАНИЕ ПРИ МНОГОФАКТОРНОМ РЕГРЕССИОННОМ АНАЛИЗЕ
5.5.1. Определение вида линейной по параметрам многофакторной модели* (последовательное планирование)
Предполагается, что в общем случае модель может иметь вид
k k k
у = 6Q + 2 bLxi + 2 bnxixi + • + 2 buxl (5.30) 1=1 1=1 1=1
1V1
Порядок модели до опыта неизвестен. В данном случае применяют последовательное планирование эксперимента.
На первом этапе выдвигается гипотеза о линейности модели, т. е.
k
i=i
(k— число контролируемых факторов), и реализуется эксперимент, необходимый для определения ее параметров. Проверяется адекватность линейной модели (для этого число сочетаний уровней факторов должно быть больше их количества). Если линейная модель неадекватна, то выдвигается гипотеза о значимом влиянии взаимодействия факторов, сначала парных, затем тройных и т. д.:
k k
Y = b0 + S + 2 b^X.. (5.31)
i=i 1=1
Вычисляются параметры данной модели и производится проверка ее адекватности. Если модель типа (5.31) неадекватна, то выполненные ранее опыты дополняют новой серией, позволяющей вычислить коэффициенты Ьц квадратичной модели. Если неадекватной является и модель второго порядка, то следует переходить к планированию третьего порядка. Однако последнее делается чрезвычайно, редко и поэтому в данном пособии не рассматривается.
С целью облегчения обработки результатов эксперимента факторы нормализуют. Для определения параметров линейной модели достаточно в опыте каждый фактор фиксировать на одном из двух уровней: верхнем или нижнем. Верхним уровнем фактора называется его большее значение, а ннжним — меньшее. Верхний уровень нормализованного фактора равен ( + 1), а нижний ( — 1).
Эксперимент, в котором используются все возможные сочетания уровней факторов, называют полным факторным экспериментом (ПФЭ). Когда число уровней каждого фактора равно 2, то число опытов ПФЭ составляет N=2h, где N — число опытов (или серий параллельных опытов); k — число факторов.
План проведения эксперимента и его результаты записываются в виде таблицы, которая называется матрицей планирования (МП). Если результаты эксперимента в таблицу не записываются, то такая таблица, содержащая только уровни факторов, называется факторным планом (ФП).
Наиболее простым способом построения ФП при любом ч'исле факторов является метод последовательного достраивания полного факторного плана (ПФП). Он заключается в том, что для построения ПФП при k факторах повторяют дважды план для (k— 1) факторов, сначала при нижнем уровне й-го фактора, а затем при его верхнем уровне. Последовательное достраивание ПФЭ при увеличении k от 2 до 4 показано в табл. 5.21 (для простоты записи верхний уровень фактора можно обозначать знаком ( + ), а нижний — ( —) ).
Определение параметров нормализованной линейной модели производится по формулам:
165
w
"=7р<; ,5'32>
U=1
N
a‘= TF S X‘“Y“’ (5,33)
U=1
где a, — параметры нормализованной модели; i=l, 2, 3, .... k — номер фактора; u=l, 2, 3, N— номер опыта (или серии опытов); k — число факторов; N — число опытов; Хш — значение в u-м опыте.
Таким образом, способ расчета параметров модели очень прост; к столбцу Yu следует приписать знаки соответствующего столбца xt, алгебраически сложить значения отклика и результат разделить на число опытов матрицы планирования. Важно подчеркнуть, что для подсчета параметра а{ используется только столбец xt, т. е. все параметры определяются независимо друг от друга.
Все параметры линейной модели определяются с одинаковой дисперсией
S2(ai) = S>,
где S2 — дисперсия воспроизводимости.
Если в каждой серии проводилось по т параллельных опытов, то
N т
s-= (S'34’
U=1 i=l
где N — число серий опытов в плане; и — номер серии опытов; / — номер опыта в серии; Yu — среднее значение отклика в u-й серии опытов.
Табл. 5.21. Планы ПФЭ от 22 до 24
План Номер серии опытов и Х1 Х2 х. Хл,
1 t
1 —I —1 —1 —1
2 +1 —1 —1 —1
22 3 —1 +1 —1 —1
93 4 +1 4-1 —I —1
5 —1 —1 +1 —1
6 +1 —1 +1 —1
7 —1 4-1 +1 —1
8 +1 +1 +1 —1
9 —1 —1 —1 4-1
10 +1 —1 —1 4-1
11 —1 + 1 —1 4-1
12 +1 4-1 —1 4-1
13 —1 —1 +1 + 1
14 4-1 —1 4-1 4-1
15 —1 4-1 + 1 4-1
16 + 1 +1 4-1 4-1
166
Если каждому и соответствует один опыт, то для определения дисперсии воспроизводимости в центре плана проводится серия из т опытов. Тогда
т
<5-35)
Доверительный интервал для параметров линейной модели
SB
Дяг = + / (Р, mN)-----=. (5.36)
V mN
Параметр считается статистически значимым, если его абсолютная величина больше доверительного интервала: | at | > | |. Значение критерия Стьюдента
t(P, mN) определяется из табл. П.1. Статистически незначимые параметры считаем равными нулю. Остаточная дисперсия (или дисперсия адекватности) для линейной модели определяется по одной из следующих формул. Если каждый опыт плана проводился только по одному разу, то
где k — число факторов; N — число опытов в матрице планирования. Если каждый опыт в матрице планирования повторялся т раз,
S2 =
0 т (N — k— 1)
где j — номер опыта в серии.
Затем определяется наблюдаемое (значение критерия Фишера FH = S2/S2, Если S2 найдено по (5.37), то S2 следует определять по (5.35), а если по (5.38), то S2 определяется по (5.34).
Критическое значение критерия Фишера FK определяется по табл. П.7 в зависимости от доверительной вероятности Р, числа параллельных экспериментов в серии т(т^) и mr = N — k—1. В случае, если S2 определяется по'(5.37), то — это число параллельных опытов, проведенных при xi = 0 для определения дисперсии воспроизводимости.
Если Ев<Ек, то модель адекватна. При FH>Ftt следует переходить к следующему этапу планирования.
Так как число опытов при ПФЭ больше числа параметров линейной модели, можно определить эффекты взаимодействия факторов, которые характеризуют влияние данного фактора в зависимости от уровней других. Примеры математических моделей с эффектами парного п тройного взаимодействия:
Y=bg + bi X] +
У + +Z?2^2_h&3^3"F^ 12^1^2 4“ ^13^1^3 4" ^23^2^3 "Ь
+ b 123Х1Х ?Х з.
Для определения параметров таких моделей нужно построить расширенную матрицу планирования (для трехфакторного эксперимента приведена в табл. 5.22). Знаки в столбцах взаимодействий получаются путем перемножения единиц со знаками соответствующих сомножителей.
167
Табл. 5.22. Расширенная матрица ПФЭ 23
ао = лГS (JC°y,“: = Т 2(XiY)u’ U=1 U=1
N
a‘i = “V S (Х1Х/П“’ ‘
N
а‘>'1== 7г2(х<л'х'у,“’
И=1
Знаки произведений XiXj находятся в соответствующих столбцах расширенной матрицы планирования. Таким образом, метод вычисления параметров модели с учетом взаимодействия факторов принципиально аналогичен методу вычисления параметров линейной модели. Для проверки адекватности модели, так же как для линейной модели, определяем дисперсию воспроизводимости и доверительный интервал оценки параметров.
Дисперсия адекватности:
если каждый опыт
проводился один раз —
= (yu~fu^
если каждый опыт повторялся т раз —
• J7/-™
= F(^T) S (Уц/ ~ ,в/) ’ ‘ u=l j=l
где fu — значение отклика, вычисленное по модели при уровнях факторов, соответствующих опыту (или серии опытов) с номером u; j — номер опыта в серии и.
Адекватность линейной модели с взаимодействиями определяется с помощью критерия Фишера. Если данная модель неадекватна, то, чтобы получить модель второго порядка, к плану проведенных опытов, который называется «ядром» эксперимента, добавляется некоторое количество специальным образом расположенных точек. Такой план называется центральным (так как
168
Рис. 5.5. Центральный композиционный план для двух факторов
Рис. 5.6. Центральный композиционный план для трех факторов
центр плана является центром симметрии для всех его точек) и композиционным, т. е. последовательно строящимся.
На рис. 5.5 и 5.6 показано центральное композиционное планирование второго порядка для случаев, когда число факторов Л=2 и k=3. Около каждой из точек плана указаны ее координаты в нормализованном масштабе. Квадратные точки на рисунках—центр плана (основной уровень), зачерненные — ядро плана, а светлые — добавление, или «звездные» точки, на расстоянии «звездного» плеча а от центра плана. Общее число опытов при k факторах
М = ЛГ1+2/г+по,
где — число опытов ядра плана; 2k — число «звездных» точек; па — число опытов в центре плана.
Число уровней варьирования каждого фактора в данном случае равно 5: — а; —1; 0; 1; а. Для облегчения вычислений и, главное, для того, чтобы параметры модели определялись независимо, план должен быть ортогональным. Это достигается введением вместо х? нового нормализованного фактора
N
x'i = *1и =
Ы=1
где и — номер опыта; х?— среднее значение х?, которое при числе факторов k — 2, 3, 4, 5 равно соответственно 0,667; 0,73; 0,80; 0,776.
Кроме того, необходимо выбрать «звездное» плечо а по формуле
а2 = 0,5 [V (N1 + 2k + na) — Л\] или табл. 5.23.
При fe>4 применение полного факторного плана в качестве ядра является неэффективным. В данном случае применяются дробные реплики ПФЭ. которые получаются, если в расширенной матрице планирования ПФЭ для (k— 1) факторов заменить взаимодействия факторов (тройные или более высокого порядка) новым (й-м) фактором или разделить матрицу ПФЭ на две части. В табл. 5.24 приведена полуреплика ПФЭ для k = 5, которая служит ядром плана.
169
Табл. 5.23. Значения а
«0 Значение ОС при k/N
3/8 4/16 5/16
1 1 1,215 1,414 1,574
2 1,077 1,285 1,471 1,606
3 1,148 1,353 1,546 1,664
4 1,214 1,414 1,606 1,718
5 1,267 1,471 1,664 1,772
6 1,320 1,525 1,718 1,819
Табл. 5.24. Полуреплика ПФЭ 25 — \ х5 = х^ХзХ^
и *1 х2 х3 и *1 х2 *3 X,
1 9 — +
2 + — — — — 10 + — — + +
3 — + 1 — — — 11 — 4- — + +
4 + + -— — + 12 + — + —
5 + — — 13 — — 4- + +
6 + — — + 14 + —- + —
7 — + + — + 15 — + + + —
8 -j- + + — — 16 + + + + +
В табл. 5.25, 5.26 и 5.27 приведены матрицы центрального композиционного ортогонального планирования (МЦКОП) для задач соответственно с двумя, тремя и четырьмя факторами. При этом п0=1.
В силу ортогональности планирования все параметры нормализованной модели второго порядка определяются независимо друг от друга:
2 Х1и^и 2 ^Х1Х^иУи
U=1 и=1
—n ; ач =• n
2 2 (xtxPu
и=1 и=1
N
В числителях данных формул находятся суммы произведений значений отклика и значений нормализованного фактора в соответствующем столбце, а в знаменателе — сумма квадратов значений нормализованных факторов из соответствующих столбцов.
Дисперсия оценок параметров модели находится по формулам:
N N
S2 (О(.) = S2/2 (х,)2; S2 (аг/)= (х.х-)2;
u—i и=1
170
N
•ь'2(ап) = «2/2 (^)2;
u=l
f=l
Доверительные интервалы для параметров модели определяются при помощи критерия Стьюдента
Д(а) = ±ЦР, N)S(a), (5.39)
где Д(а)—доверительный интервал для параметра a; S(a)—стандартное отклонение параметра а.
Значение t(P, N) определяется из табл. П.1.
Для перехода к натуральной модели необходимо в полученную новую модель подставить значение нормализованного фактора х=(Л’—Х)/ДХ. Провер-
Табл. 5.25. МЦКОП второго порядка при 6=2
и *0 Л2 х±х2 Х1 Хг Уи Примечание
1 +1 —1 —1 +1 + 1/3 + 1/3 У1 ПФЭ
2 +1 —1 +1 —1 + 1/3 + 1/3 То же
3 +1 +1 +1 +1 + 1/3 + 1/3 Уз »
4 +1 +1 —1 —1 +1/3 + 1/3 Yi »
5 +1 +1 0 0 +1/3 —2/3 Уз «Звездные» точки
6 +1 —1 0 0 + 1/3 —2/3 уе То же
7 +1 0 +1 0 —2/3 -г 1/3 Y„ »
8 +1 0 —1 0 —2/3 -.-1/3 Уз »
9 +1 0 0 0 —2/3 —2/3 Уз Нулевая точка
Табл. 5.26. МЦКОП второго порядка при й=3
и Xi Х2 хз XtX2 ^1^3 Х2Х3 Х1 -Ч х'з уи
1 +1 —1 —1 —1 +1 +1 +1 +0,27 +0,27 +0,27 Уу
2 +1 +1 —1 +1 —1 +1 —1 +0,27 +0,27 +0,27 У?,
3 +1 —1 +1 +1 —1 —1 +1 +0,27 +0,27 +0,27 Уз
4 +1 +1 +1 -1 +1 —1 —1 +0,27 +0,27 +0,27 Yi
5 +1 —1 +1 —1 —1 +1 —1 +0,27 +0,27 +0,27- Уз
6 + 1 +1 +1 +1 +1 +1 +1 +0,27 +0,27 +0,27 YK
7 +1 +1 —1 —1 +1 +1 —1 —1 +0,27 +0,27 +0.27 У1
8 + 1 —1 —1 —1 —1 +1 +0,27 +0,27 +0,27 Уз
9 +1 + 1,215 0 0 0 0 0 +0,745 —0,73 —0,73 у9
10 +1 —1,215 0 0 0 0 0 +0,745 —0,73 —0,73 Ую
11 +1 0 + 1,215 0 0 0 0 —0,73 +0,745 —0,73 Уи
12 +1 0 — 1,215 0 0 0 0 —0,73 +0,745 —0,73 У13
13 +1 0 0 + 1,215 0 0 0 —0,73 —0,73 +0,745 У13
14 +1 0 0 -1,215 0 0 0 —0,73 —0,73 +0,745 Уи
15 +1 0 0 0 0 0 0 —0,73 —0,73 —0,73 Уи
171
Ш
tO tOtOtOtOtO^-й-ь-ь-^н-н-н-н- СП ^ООЮь-фСООО'ЧОСЛ^СОЬОь-фЮОО^ФСл^СоЮ*- R
Ч—1—1—1—1—1—1—1—1—1—!—1—1—1—1—1—1—1—1—1—1—1—1—1—Н >— h—» Н» н» ни Н— 1— Н— Н» НН Н-* И— 1—н И—‘ Н~1 НН И
____,_ + । ++ 1 + 1 1 + 1 + 1 Ч-Ч-1 1 + 1 ОООООСОн- — Н—— НН.—*—. — — — .—«н—н— *
__+1_+l++l + lI++I++I11 О О О О О Н— Н-. О О •—* — 1— —. Н— Н— н— Н-^-Н-М-М-Н-М-
+ 1 1 ++++ 1 1 1 Ч-Ч- 1 1 1 Ч-Ч- 1 ффф^-н—фОФФ^-f—— — .^-н->— 4* 4ь 4». 4* *
+ 1 Н—1—F Illi Н—Ь 1 + 1 Н—h 1 1 Он-^-ффффффн-—. Н-Н-Н-!— >— М-Н- — Н-Н-Н-Н- — — R й
+ 1 1 ++ 1 1 Н—И 1 1 + 1 + 1 + ФФФФФФФОФ^-И- — — н- н-и н- — н-м-^-н- И
1 Ч-1 + 1 + 1 ++ 1 1 1 -ь 1 Ч-+ ФООФФФФООи— Н-Н->— Н-^-Н-Н-И— Н- — н->— — н- Н-. H T:
-J—]_ 1 1 _|—1_ 1 1 _]_-|—1_ 1 1 1 1 J_ ФФФФФФФФФн— — — — Н- — >— Н-,— Н---—> — — — н- h
_____ 1 I++I I+++++I 111 + Ф Ф Ф О о О Ф ф ф •— н- М- М- н- м- >—> н- н- — н- н- ►— >— — k ib
_ __ +1 +1 +1 +1 +1 1 1 +1 ++ фффффффффн-— ^-н-н-н-н->—— h * *
1 ++ 1 1 Ч-Ч-1 Ч- 1 1 + 1 + 1 + ФФФФФФФФФ—.Н-н-^-н- — — Н-—И — н— — и- 4
1111111++ ффффффф»—•—фффффффффффффффф 00 00 00 00 00 00 00 to to to to to to to to to to to to to to to to to Ю
1 1 1 1 1+4-1 1 Ф О О О О Ф Ф Ф Ф Ф Ф Ф Ф ф Ф о Ф Ф Ф Ф Ф Ф Ф oooooooooototooooototototototototototototototototo *
11I++IIII ФФФ^-Н— ФФФФФФФФФФФФФФФФФФФФ cooooototoooooooootototototobototototototototototo C? H
I++I1II11 О^-м- ФФФФФФФФФФФФОСФФФФОФФФ 00 to to 00 00 00 00 00 00 to to to ko to to to to to to to to to to to io *
t4 w W tj ti w и н‘н-‘Н‘н^н‘нин‘н-нн te <xi ‘-г c> й w t5 h v*i&WfcOi-‘©«a>Hic>V’frwfcai-»o
Табл. 5.27. МЦКОП второго порядка при k=
ка адекватности модели второго порядка производится так же, как и модели первого порядка с взаимодействиями.
Недостатком центрального композиционного ортогонального планирования (ЦКОП) второго порядка является то, что параметры модели определяются с различной точностью (у них различны дисперсии). Поэтому информация о поверхности отклика, содержащаяся в модели, полученной после реализации ЦКОП второго порядка, различна в разных направлениях факторного пространства.
Существует другой способ ЦКП второго порядка, позволяющий при помощи полученной модели описывать поверхность отклика с одинаковой точностью по всем направлениям. При этом остаточные дисперсии на одинаковых расстояниях от центра плана являются равными и наименьшими из возможных. Такое планирование получило название ротатабельного (ЦКРП).
При ЦКРП значение звездного плеча определяется по формуле
а = ,
где — число опытов ядра плана.
В зависимости от выбора числа опытов в центре плана обеспечивается либо так называемая униформность, либо ортогональность плана. В первом случае дисперсия предсказания сравнительно мало изменяется (или совсем не меняется) в радиусе от центра плана до х<=±1. Для обеспечения униформ-ности плана должно соблюдаться равенство
n0 = X (^ + 4 + 4) — A/j — 2k, (5.40)
где X для числа факторов k=2, 3, 4, 5, 6, 7 равно соответственно 0,7844; 0,8385; 0,8705; 0,8918; 0,907; 0,9185.
Чтобы ротатабельный план был ортогональным, число опытов в центре плана должно соответствовать равенству
«о = 4 VnT — 2k + 4.
Эта формула получена из (5.40) при Х=1. Расчет по (5.40) в некоторых случаях дает дробные значения п0, поэтому их приходится округлять до бли-
Табл. 5.28. Характеристики ЦКРУП второго порядка
Число факторов k Число опытов ядра Ni Число «звездных» точек 2 k Число нулевых точек «Звездное» плечо а N
2 4 4 5 1,414 13
3 8 6 6 1 ,682 20
4 16 8 7 2 31
5 16 10 6 2 32
Табл. 5.29. Значения di для вычисления параметров модели
k N di d2 dt У di d,
2 13 0,2 0,1 0,1250 0,2500 0,1251 0,0187 0,1438
3 20 0,1663 0,0568 0,0732 0,1250 0,0625 0,0069 0,0695
4 31 0,1428 0,0357 0,0417 0,0625 0,0312 0,0037 0,0350
5 32 0,1591 0,0341 0,0417 0,0625 0,0312 0,0028 0,0341
173
жайшего целого числа, нарушая тем самым условия униформности. Однако эти отклонения оказываются настолько незначительными, что ими можно пренебречь [35]. Данные, необходимые для построения некоторых матриц центрального композиционного ротатабельного униформ-планирования (ЦКРУП) второго порядка, приведены в табл. 5.28.
Матрицы ротатабельного униформ-планирования не ортогональны, поэтому параметры модели рассчитываются более сложным способом, чем при ортогональном планировании:
ао ~ ^1 2 У и ^2 2 2 x1iXu '
и=1 »=1 и=1
W
= ^3 2 х1иХ и’
(5-41]
й(.у = ^4 (хixj)и* i)>
и—1
N kN N
aii = ^6 2 х1иУи + ^6 2 2 х1и^и ^2 2 Уи •
и=1 :=1 и=1 и=1 )
Соответствующие значения di для разных случаев указаны в табл. 5.29.
Дисперсии параметров модели:
52 * *(ао) = ^;52(а£) = ^ |
> (5.42)
S2 (al7) = d4s2; S2 (а„) = d,S2. |
Так как при униформ-планировании несколько опытов проводятся параллельно при основном уровне факторов, то результаты этих экспериментов позволяют оценить дисперсию воспроизводимости
«о
5"-»7Ь2(г‘“-5 * * В’")г' 's-43’
U=1
Проверка адекватности модели производится при помощи критерия Фишера. Дисперсия адекватности в данном случае определяется по формуле
2 (Yu расч - У и экеп)2 ~ 2
^2 гг—1___________________и=1_______
ад = W —й' — (ге0 — 1)
где k' — число статистически значимых параметров модели.
Наблюдаемое значение критерия Фишера FH = 52д/52 сравнивается с таб-
личным FK (табл. П.7). Однако в этом случае вместо т1 = N — k—1 принимается mx= N — k' — reQ+ 1, /и2= п0— 1, Если FH < FK, то модель адекватна.
В качестве примера в табл. 5.30 приведена матрица центрального композиционного ротатабельного униформ-планирования второго порядка для трех факторов.
При использовании ротатабельных планов исключать из модели без пересчета остальных можно только незначимые оценки а, и а,3-. Исключение любого из незначимых параметров аа и а.ц требует пересчета остальных в данной группе.
174
^о)2
(5.44)
Табл. 5.30. Матрица ЦКРУП второго порядка для k =3
и Хо Х1 х2 Х3 XiX £ х? уи Примечание
1 +1 +1 +1 ' +1 +1 +1 +1 +1 +1 +1 Yi ПФЭ 23
2 +1 +1 +1 — I +1 —1 —1 +1 +1 +1 у2 То же
3 +1 +1 —1 +1 —1 +1 —1 +1 +1 +1 Уз
4 +1 +1 —1 —1 —1 —1 +1 +1 +1 +1 Vi »
5 +1 —1 +1 +1 —1 —1 +1 +1 +1 +1 Уб »
6 +1 —1 +1 —1 -1 +1 —1 +1 +1 +1 Уб »
7 +1 —1 —1 +1 +1 —1 —1 +1 +1 +1 У? »
8 +1 —1 —1 —1 +1 +1 +1 +1 +1 +1 ув »
9 +1 -1,682 0 0 0 0 0 +2,83 0 0 У» «Звездные» точки
10 +1 4-1,682 0 0 0 0 0 +2,83 0 0 У10 То же
И +1 0 —1,682 0 0 0 0 0 +2,83 0 Уи »
12 +1 0 + 1,682 0 0 0 0 0 +2,83 0 У13 »
13 +1 0 0 —1,682 0 0 0 0 0 +2,83 У13
14 +1 0 0 + 1,682 0 0 0 0 0 +2,83 У14 »
15 +1 0 0 0 0 0 0 0 0 0 У15 Нулевые точки
16 +1 0 0 0 0 0 0 0 0 0 У10 То же
17 +1 0 0 0 0 0 0 0 0 0 У17
18 +1 0 0 0 0 0 0 0 0 0 У18
19 + 1 0 0 0 0 0 0 0 0 0 У19
20 +1 0 0 0 0 0 0 0 0 0 У2о
Табл. 5.31. Условия эксперимента
Пределы варьирования Факторы (обозначение)
Содержание (массовая доля) лития, % (Xt) Температура старения, °C (Х2) Время старе-ния, ч (Х3)
Основной уровень (0) 1 175 4
Шаг варьирования ДХ 0,5 25 2
Верхний уровень (+1) 1,5 200 6
Нижний уровень (—1) 0,5 150 2
Звездная точка (+а) 1,6 205 6,4
Звездная точка (—а) 0,4 145 1,6
Табл. 5.32. МППФЭ 2»
и xt *1 х3 *3 Xijff *1-4 JCSX3 Y (ав)
1 +1 +1 +1 +1 +1 +1 +1 25
2 +1 —1 +1 +1 —1 —1 +1 20
3 +1 +1 —1 +1 —1 +1 —1 38
4 +1 —1 —1 +1 +1 —1 —1 41
5 + 1 +1 +1 —1 +1 —1 —1 45
6 +1 —1 +1 —1 —1 +1 —1 26
7 +1 +1 —1 —1 —1 —1 +1 25
8 +1 —1 —1 —1 +1 +1 +1 28
Пример 5.6. Необходимо построить математическую модель зависимости предела прочности алюминиевого сплава от содержания в нем лития, температуры и времени старения.
Решение. Уровни факторов приведены в табл. 5.31. Прежде всего был реализован полный факторный эксперимент типа 23, состоящий из 8 опытов, как это вместе с результатами показано в табл. 5.32. По результатам эксперимента были рассчитаны параметры модели первого порядка с взаимодействиями:
аа =. — (25 + 20 + 38 + 41 + 45 + 26 + 25 4- 28) = 31; 8
а1 = — (25 — 20 + 38 — 41 + 45 —26 + 25 — 28) = 2,25; 8
аналогично получено а2= — 2; аз=0; <212=3,75; а2з=—6,5; ai3= —1,75; 0,23= = -1,75.
Из параллельных опытов в центре плана установлено, что = 4. Тогда
1
дисперсия определения параметров линейной модели будет S1 2 (а) = — 4 О
= 0,5;
S (а) = 0,71.
Доверительный интервал значений параметров Д(а) = ±2,365- 0,71 = ±1,67.
Следовательно, все параметры, кроме а3, будут статистически значимыми.
Для проверки адекватности полученной модели были использованы опыты в центре плана, когда все факторы поддерживались на основном уровне. При
176
Табл. 5.33. МЦКОП второго порядка
и х3 XiXa Х2Х3 Jlfj 3 Уи
1 +1 +1 +1 +1 +1 +1 +1 0,27 0,27 0,27 25
2 +1 —1 +1 +1 —1 —1 +1 0,27 0,27 0,27 20
3 +1 +1 —1 +1 —1 +1 =1 0,27 0,27 0,27 38
4 +1 —1 —1 +1 +1 —1 —1 0,27 0,27 0,27 41
5 +1 +1 + 1 —1 +1 —1 —1 0,27 0,27 0,27 45
6 +1 —1 +1 —1 —1 +1 —1 0,27 0,27 0,27 26
7 +1 +1 —1 —1 —1 —1 +1 0,27 0,27 0,27 25
8 +1 —1 —1 —1 +1 +1 +1 0,27 0,27 0,27 28
9 +1 0 0 0 0 0 0 —0,73 —0,73 —0,73 28-
10 +1 + 1,215 0 0 0 0 0 0,745 —0,73 —0,73 30
11 +1 —1,215 0 0 0 0 0 0,745 —0,73 —0,73 36
12 +1 0 + 1,215 0 0 0 0 —0,73 0,745 —0,73 25
13 +1 0 —1,215 0 0 0 0 —0,73 0,745 —0,73 30
14 +1 0 0 + 1,215 0 0 0 —0,73 —0,73 0,745 24
15 +1 0 0 — 1,215 0 0 0 —0,73 —0,73 0,745 32
2х2| 15 | 10,95 | 10,95 | 10,95 1 8 1 8 1 8 | 4,63 4,36 4,36
этом значение отклика У(0; 0; 0)=28. Вычисленное согласно модели значение отклика У=а0=31. Наблюдаемое значение критерия Стьюдента
|я,- У(0; 0; 0)|/V /31 — 28| КТ 5в 2 ~4,25'
По табл. П.1 критическое значение критерия при доверительной вероятности Р=0,95 и Р=0,99 составляет /к(8; 0,95) =2,365; /к(8; 0,99) =3,5. В обоих случаях значит полученная модель неадекватна, т. е. разницу между наблюдаемым значением отклика и расчетным нельзя считать статистически незначимой.
Поэтому реализованная матрица планирования была дополнена звездными точками с плечом 1,215. Всего дополнительно было проведено 6 опытов. Окончательная матрица ЦКП представлена в табл. 5.33, в которой вместо х? введены столбцы х; = х?— 0,73.
По результатам всех экспериментов рассчитаны параметры модели второго порядка:
в1 = (25 — 20 + 38 — 41 + 45 — 26 + 25— 28 + 1,215 30 — 1,215 . 36)=
= 0,98;
я2 = (26 + 20 — 38 — 41 +45 + 26 — 25—28+ 1,215 • 26 — 1,215 • 30)=
= — 1,9;
!—(25 + 20 + 38 + 41 —45 —26 —25—28+ 1,215 24—1,215 32) = 3 10,95
= — 0,89.
Аналогично, ai2 = 3,75; czia= —1,75; а^=— 6,5; Яц = 3,20; а^=— 0,19; Язз — = -0,19;
12. Зак. 1001
177
а0 = (25 + 20 4- 38 + 41 + 45 + 26 + 28 + 25 + 28 + 30 + 36 + 24 4- 26 +
4- 30 4- 32) —0,73 (3,2 — 0,19 — 0,19) = 28,2.
Дисперсии оценок параметров:
S2(a,) = S2(a2) =S2(a3) =4/10,95 = 0,365;
S2 (Л12) =S2(a13) =S2(a23) =4/8 = 0,5;
S2(ail) = S2(a22) = S2(a33) =4/4,36 = 0,918;
4
S2 (ae) = —+ 3 • 0,918 • 0,73 = 1,735.
Доверительные интервалы оценок параметров:
А (а,) = Д(а2) =Д (а3) = ±2,145 • 0,365= ±1,3;
Д(Я12) =Д(Я1з) =Д(а23) = ±2,145 • 0,5= ±1,5;
Д(ац) =Д(а22) =Д(а33) = ±2,145 • 0,918 = ±2,06;
Д(яо) = ±2,145-1,735= ±2,84.
Сравнивая их со значениями параметров, приходим к выводу, что параметры «3, <122, <1зз являются статистически незначимыми. Тогда получаем нормализованную модель
У = 28,2 — 1,9х2 3,75х,х2 — 1,75xjX3 — 6,5х2х3 4- 3,2xj.
Проверку адекватности модели производим при помощи критерия Стьюдента (формула (3.16)) в трех точках (0; 0; 0), ( + 1; +1; +1) и ( — 1; —1; — 1):
(28,2-281 УЙГ (25 -25|]/Л5
‘н0 — 2 “ 0,388, гн1 — 2 —0;
|28 —28,8/КТб"
^-11 = J---------г-------=1-54-
Критическое значение критерия для Х=15 и Р=0,95 tK = 2,145. Так как во всех случаях /н<7к, то модель адекватна.
Натуральная модель с использованием значений нормализованных факторов
7.21i!_,h,fe!5.+w±'«.-i”
25 0,5
,.75fcl*±
0,5 4
25
, . Х2-175 Х3—4 „/Xt- 1\2
— 6,5--------------4-3,2 ------- ,
25 2 V 0,5 J
откуда
У=8,8 — 7,ИХ.4-0,144%,4- 24Х-4- 0,ЗХ,Х,~ 1.75Х.Х,— 0,13Х,Х,4- 12,8Х?.
X а и L Л X О а О 1 I
5.5.2. Определение вида нелинейной по параметрам многофакторной модели
Двухфакторная модель. Для выяснения особенностей модели каждый фактор необходимо варьировать на достаточно большом количестве уровней. Так как вид модели заранее неизвестен, то расстояние между уровнями факторов берется постоянным, а число уровней принимается одинаковым для обоих фак-
178
Табл. 5.34. Полный план эксперимента для fe=2 и /=5
1 1 1 6 2 1 11 3 1 16 4 1 21 5 1
2 1 2 7 2 2 12 3 2 17 4 2 22 5 2
3 1 3 8 2 3 13 3 3 18 4 3 23 5 3
4 1 4 9 2 4 14 3 4 19 4 4 24 5 4
5 1 5 10 2 5 15 3 5 20 4 5 25 5 5
торов. Общее количество комбинаций уровней двух факторов, каждый из которых варьируется на I уровнях, равно I2. С увеличением I быстро растет трудоемкость эксперимента. Минимально необходимыми считаются 5 уровней. После реализации эксперимента с пятью уровнями факторов можно, в случае необходимости, увеличить число уровней за счет уменьшения ДХ; в 2 раза. Чтобы облегчить обработку результатов эксперимента, рекомендуется проводить несимметричную нормализацию факторов согласно формуле (3.4).
План, реализующий все возможные комбинации уровней факторов, называется полным (табл. 5.34). Результаты эксперимента следует заносить в таблицу с двумя входами, которую называют комбинационным квадратом, что облегчает обработку результатов эксперимента (табл. 5.35).
Обработка результатов эксперимента проводится следующим образом. Вначале строятся графики, определяются вид и параметры частных однофакторных моделей Yt=f i(xi) при постоянных значениях хг. Эти модели обычно принадлежат к одному классу, но отличаются значениями параметров, которые зависят от уровня хг. Методы определения вида таких однофакторных моделей и расчета их параметров рассмотрены в § 5.4.
В результате первого этапа обработки результатов эксперимента получают ряд моделей вида
Уг=[(аОг, ац, ..., atli, %i). (5.45)
Желательно выбирать модель с минимальным числом параметров.
На втором этапе обработки результатов эксперимента строятся графики и определяются вид и параметры частных моделей типа aj=<p3-(.X2). Окончательно, после подстановки этих моделей в (5.45),
У=Я<р0(х2), <pi(x2), ..., <рл(х2), Xj].
При анализе графиков частных однофакторных моделей типа (5.45) необходимо учитывать следующее: 1) если графики частных однофакторных моделей Л(Х|), f2(*i), fa(*i)--- параллельны, то полная двухфакторная модель имеет вид
У=/(*|)+<Р(*2);
2) если графики однофакторных частных моделей в исходной системе коор-
Табл. 5.35. Комбинационный квадрат при k—2 и 1=5 (N=25)
Уровень фактора х2 Уровень фактора xt
1 1 2 3 4 5
1 Уп У21 Г31 У и /51
2 /12 У22 у32 /42 /52
3 /13 /23 yS3 /43 /53
4 У14 /24 /84 /44 /б4
5 У15 У28 Ум /45 /55
12*
179
Табл. 5.36. Дробный план для 2<fe<6 и .1—5
Хз Xt
4
5 1
2
3
4
5
1
2
3 4
5
4 1
2 3
4 1
5 3
4 1
5 2
4 1
1
5
2 3
4
4
1
5 2
3
3
2
1
2
3
5
4
2
3
4
1
5
4
3
3
4
5
2
1
2
3
4 1
5
динат пересекаются, а в логарифмической системе координат (2=1пУ; И= = ln X) параллельны, то двухфакторная модель имеет вид
У=Нм)<р(х2).
Планирование эксперимента при fe>2. Применение полного плана при числе факторов, большем двух, обусловливает резкое повышение трудоемкости эксперимента. Так, при й = 3 и 1=5 полный план содержит 125, а при k=4— — 625 опытов. Поэтому при А >2 применяются дробные планы, которые должны удовлетворять следующим требованиям: 1) координаты опытов эксперимента должны быть равномерно распределены по факторному пространству; 2) в любой паре столбцов плана не должно быть одинаковых сочетаний уровней факторов, составляющих строку. Такие планы можно сформировать на базе латинских, греко-латинских квадратов или квадратов Юдена (см. § 5.3). Один из этих планов для k=5 приведен в табл. 5.37. Если fe<6, то лишние столбцы отбрасываются.
Математическая обработка результатов эксперимента состоит из трех этапов [61].
1. Полученные значения отклика Yu заносятся в комбинационные квадраты с двумя входами. Распределение значений откликов по клеткам квадратов производится в соответствии с уровнями факторов, при которых были получены отклики.
180
Табл. 5.39. Комбинационный квадрат
1 2 3 4 5 ^бср
1 ум У 8 У г у20 У12
2 У13 Г21 Гю у» УИ
3 г16 Угг У 8 Уз
4 У 3 У17 Уц у23 У в
5 У 7 У< У1» Гц У25
^ср
В качестве примера в табл. 5.37...5.39 распределены значения отклика, полученные в эксперименте с планом, соответствующим табл. 5.36. Индекс при У указывает номер строки плана. Складывая элементы столбцов и строк комбинационных квадратов, получаем осредненные значения отклика, зависящие только от одного из факторов. Например, согласно табл. 5.39:
Табл. 5.40. Вид графиков осредненных однофакторных моделей в зависимости от вида многофакторной модели
Номер модели Вид многофакторной модели Вид графика осредненной модели
1 k t==l Все графики в координатах У/ср xi гладкие
2 у = /i (xi)S h i=2 Один график (1) в координатах У/ср—х(- гладкий, остальные с изломами
3 k г = ад ад + зад 1=3 Два графика (1 и 2) в координатах У(. — xi гладкие, остальные с изломами
4 k г = пад <=i Все графики в координатах У(Ср — имеют изломы, а в координатах (In УЛ — х, гладкие
5 г k n y= n Ш) I ft (*.) Все графики в координатах У(ср — х£ имеют изломы, а в координатах (МУ(-)ср —ОДИН (!) гладкий
6 k Y = fi(x1)f'<x>'> П ад <=3 Все графики в координатах У/ср — xt имеют изломы, а в координатах (In У£)ср — xt два графика (1 и 2) гладкие
181
W1) = Т (У24 + Г13 + У16 + У5 + ^7);
1
^5 ср <2) = 5 (^8 + ^21 + ^15 + ^17 + ^4)‘>
У5 ср (3) = -у- + Гю + У22 + У14 + У18) и т. д.
2. Строятся графики осредненных однофакторных моделей
У;сР = <р(Х1). (5.46)
График может быть гладким или иметь резкие изломы. Если погрешность измерения отклика пренебрежимо мала и так же мало влияние неконтролируемых случайных факторов, решение о гладкости кривой графика принимается по виду графика. Если же при повторении опыта в одной и той же точке факторного пространства получается значимый разброс значений отклика, то необходимо сравнить дисперсию воспроизводимости с остаточной дисперсией модели (5.46). Дисперсия воспроизводимости определяется по формулам (5.11) или (5.13), а остаточная дисперсия — соответственно по (5.10) или (5.12). Вид и параметры осредненных однофакторных моделей определяются методами, указанными в § 5.4.1.
Гипотеза о виде многофакторной модели выдвигается в зависимости от сочетания гладких и «изломанных» кривых на графиках осредненных моделей (табл. 5.40). Условия, приведенные в табл. 5.40, являются необходимыми, но не достаточными: вид модели определяет вид графиков, а обратное утверждение может оказаться неверным. Формализованный алгоритм, позволяющий по виду осредненных графиков точно определить вид многофакторной модели, пока не разработан.
3. Вид и параметры частных однофакторных моделей ft(Xi) можно определить по виду и параметрам соответствующих осредненных однофакторных моделей срДх,). Способ., определения зависит от вида многофакторной модели.
Для модели 1 (табл. 5.40) зависимость между частными моделями имеет вид
fi(xt) = <P«(Xi)+6i, где bi — постоянная.
Тогда
k
y = ^Vi (*.) + С. (5.47)
i=l
где С — постоянная, которую можно вычислить из уравнения (5.47), подставив в него значения факторов и отклика, соответствующих u-й строке плана:
k
С = Уи-li <М*Д1-1=1
Для контроля правильности выбора вида модели следует значения С определять при разных значениях и. Если полученные значения будут различаться незначительно, то модель выбрана правильно.
Для модели 2 зависимость между частными моделями имеет вид:
Л(^1)=й1<Р1(Х1);
fi(xi)= <fi(.Xi)+bi, где l<i.^k.
Чтобы определить вид и параметры осредненных моделей <рДхг), в дан ном случае необходимо для всех значений и провести пересчет отклика по формуле
182
Y,
<₽1 (*i)u '
Затем с помощью комбинационных квадратов с двумя входами строятся гра фцки
2icp = (pi(Xi).
Тогда
Y = («J
й
У; Ф( (Х£) + С »=2
где постоянные 61 и С определяются из системы уравнений
с хл
_ т.ад.1 ь‘2и
1=2
С Yu2 h V Г Г
i-2 J
В этих уравнениях ul и u2— номера строк плана, которым соответствуют наборы уровней X, и отклики ¥и.
Для модели 3 зависимость между частными моделями
fi (xi)f2(x2) =&tpi (хОф2(х2) -ЬС[Ф1 (*1) +ф2(х2)]+ЬС2. (5.48)
Для определения параметров b и С необходимо провести минимум три дополнительных опыта согласно плану, приведенному в табл. 5.41. В этом плане варьируются только те факторы (xj и х2), графики осредненных моделей которых оказались гладкими. Согласно результатам дополнительных опытов, параметры Ь, ЬС и ЬС2 определяются из уравнений:
b = Dr/D; ЬС = D2/D; ЬС2 = Dl/fDDJ, (5.49)
где
D = Mi М2 ; £г = Yr ^12 ; r>2 = f-u Yr ; (5.50
Ml М2 Ya ^аа ^22 Y2
Yr— Узе — Ygi; Ya—K2s — Узе J
^11 — фг (3) фа (3)—фг (5) фа(1); ^га — фг (5) + фа (1)— фг (3)—фа (3); (5.51)
^21 — Фг (3) фа (3) — ф1 (1) фа (5); А,22 — фг (1) + фг (5) — Фх (3) — ф2 (3);
Ф1 (3) — значение осредненной одномерной модели при %i = 3 и т. д.
Табл. 5.41. План дополнительных опытов для 2<Л^6 и /—5
и Xi Х2 ХЯ Xi X,
26 1 5 3 3 3 3
27 5 1 3 3 3 3
28 3 3 3 3 3 3
183
Табл. 5.42. Комбинационный квадрат для k=2 и 1=5
Уровень Уровень фактора xt
фактора х2 1 2 3 4 5
1 1 1,43 1,67 1,82 1,92
2 1,25 2 2,5 2,86 3,12
3 1,36 2,3 3 3,53 3,94
4 1,43 2,5 3,33 4 4,55
5 1,47 2,62 3,56 4,35 5
Получив по (5.48) fi(xi)f2(x2), производят пересчет по формуле
2« = У«-[Л(Х1)/2(х2)]„. (5.52)
Затем при помощи комбинационных квадратов строятся графики осредненных моделей <p((xi), где 2<1^6. Вид и параметры соответствующих им моделей fi(Xj) определяются по методике, описанной выше (для модели 1).
Для модели 4 связь между частными моделями имеет вид
<₽i (Xi) = 1п bi +1П fi (х,).
Поэтому искомые однофакторные модели с точностью до постоянных сомножителей можно получить построением графиков в координатах ехр Z, — х,, где
Zi = (1П У;)ср = фг(Х/).
Если график Zi = <pi(xi) является выпуклым вниз, то лучше строить график в координатах ехр(—Z<) —х,, который позволит определить модель типа 1/[Ь</,(х;)]. Неизвестный постоянный сомножитель определяется при подстановке в полученную модель
У = Ь
где ф;(х;)=ехр Z«, значений У и х , соответствующих любой строке.
Определить вид и параметры моделей /<(х,), составляющих многофакторную модель 5, без дополнительных опытов можно только в том случае, когда хотя бы одна из моделей (i=#=l) имеет вид степенной функции с известным показателем степени, например,
/2 (х2) = а0х2’,
Рис. 5.7. Результаты двухфакторного эксперимента
Рис. 5.8. Спрямление экспериментальной зависимости (рис. 5.7)
184
Рис. 5.9. Зависимость параметра модели от уровня фактора
Рис. 5.10. Результаты спрямления экспериментальной зависимости (рис. 5.9)'
После логарифмирования модель 5 становится (в логарифмической системе координат) идентичной многофакторной модели 2.
Логарифмирование модели 6 приводит (в логарифмической системе координат) к модели 3.
Пример 5.7. Необходимо определить вид и параметры модели по результатам экспериментов, приведенных в комбинационном квадрате (табл. 5.42).
Решение. Графики fi(xi) показаны на рис. 5.7. Их вид соответствует модели 1 в табл. ПЛЗ: y=Xi/(a0+aiJCi).
Применяя выпрямляющую подстановку Z=Xi/Y и U=xh получаем графики, показанные на рис. 5.8. Поскольку все экспериментальные точки расположены близко к прямым, то модель выбрана правильно. Параметры частных моделей:
П =-------; Г,=---------------; у3 =---------------;
О.б + ОЛх/ 0,6 + 0,2х! 0,6 + 0,13x1
у = Х1 у = Х1
4 0,6 + 0, 1х/ 5 О.б + О.Овх/
Табл. 5.43. Дробная матрица планирования и результаты четырехфакторного эксперимента
и Xl *2 Х3 *4 и Х1 х2 *3
1 1 14 3 6 2 12 14 —0,062 3 1351 4,246 4 1425 0,806 5 1532 1,201 6 2 1 1 2 3,8 7 2 2 5 3 6,735 8 2 3 2 4 0,691 9 2431 0,212 10 2 5 4 5 4,002 11 3 155 13,7 12 3 2 2 2 0,812 13 3 3 3 3 1,839 14 3 4 4 4 3,819 15 3 5 11 —2,197 16 4 1 2 1 8,8 17 4 2 3 5 3,55 18 4 3 4 2 3,183 19 4 4 I 3 —0,675 20 4 5 5 4 6,003 21 5 1 3 4 14,5 22 5 2 4 1 3,69 23 5 3 1 5 0,028 24 5 4 5 2 5,231 25 5 5 2 3 0,304 Дополнительные опыты 26 1 5 3 3 1,703 27 5 1 3 3 -14,2 28 3 3 3 3 1,839
185
Табл. 5.44. Комбинационный квадрат
X1 Х2 1 2 3 4 5 SY фг (x2)
1 6 3,8 13,7 8,8 14,5 46,8 9,36
2 —0,062 6,735 0,812 3,55 3,69 14,839 2,96
3 4,246 0,691 1,839 3,183 0,028 9,987 1,99
4 0,806 0,212 3,819 —0,675 5,231 9,393 1,88
5 1,201 4,002 —2,197 6,003 0,304 9,311 1,86
SY <Р1 (Xi) 12,201 2,44 15,440 3,09 17,973 3,59 20,861 4,17 23,753 4,75
где индексы при У показывают, какому уровню х2 соответствует модель. Из анализа полученных моделей следует, что аа= const, а а, зависит от уровня х2 (рис. 5.9).
Эта зависимость ближе всего соответствует модели 14 в табл. П.14 «1 = ьох2 *•
Применяя соответствующую выпрямляющую подстановку, получим график, показанный на рис. 5.10. Согласно' этому графику, модель хорошо удовлетворяет экспериментальным точкам. Параметры модели: Z?o=O,4; b,= —1, т. е. ai = 0,4/x2. Окончательно получаем
5Х!Х2
2xi 4“ Зх2
Пример 5.8. Необходимо определить вид и параметры четырехфакторной модели по результатам эксперимента, приведенным в матрице планирования (табл. 5.43).
Решение. Параллельные опыты в центре плана показали, что погрешностью воспроизводимости можно пренебречь. Распределяем значения отклика в комбинационных квадратах (табл. 5.44 и 5.45) и строим графики осредненных однофакторных моделей (рис. 5.11, 5.12). Так как два графика из четырех являются гладкими, то предполагаем, что искомая модель относится к типу 3, т. е. имеет вид произведения двух однофакторных моделей с прибавлением суммы остальных однофакторных моделей.
Очевидно, что первая осредненная модель <р1 (xj является линейной. Методом наименьших квадратов находим q>)(X|) = l,89+ 0,573xI.
Рис. 5.11. Гра фикн осредненных однофакторных моделей
186
Рис. 5.12. Графики осредненных од-. кофакторных моделей
Табл. 5.45. Комбинационный квадрат
1 2 3 4 5 ф, (х4)
1 —2,197 8,8 * 0,212 3,69 4,246 14,751 2,94
2 3,8 0,812 1,201 3,183 5,235 13,231 2,64
3 —0,675 0,304 1,839 6 6,735 14,203 2,84
4 —0,062 0,691 14,5 3,819 6,003 24,961 4,99
5 0,028 0,806 3,55 4,002 13,7 22,076 4,42
SK фз (Хз) 0,904 0,182 11,413 2,28 21,302 4,26 20,694 4,14 35,919 7,18
Вторая осредненная модель ф2(х2), согласно графикам П.13...П.15, соответствует сдвинутой модели 15, т. е.
1Г=ф2(х2) =a0+at ехр(а2х2).
Подставляя уравнений
в данную модель значения х2, равные 1, 3, 5, получим систему
= ,ехр [аа (5 ~ 3)1 = ехр ’
(3) — й0 ._ .
——------------= ехр [а2 (3 — 1) = ехр (2л2) ,
W (1) — а0
откуда
[W (3)р — Г (1) П7 (5) _ 1,99^ — 9,36 1,86
°0 = 2«7(3)—Ц7(1)— «7(5) = 2 • 1,99 — 9,36— 1,86
= 1,85.
После спрямления модели (Ц7—1,85) а2 = —2; <2, = 55,49=7,51 ехр2. Тогда
ф2 (х2) = 1,85+7,51ехр[—2 (х2— 1) ].
Для определения постоянных Ь, ЬС и ЬС2 проводим три дополнительных эксперимента (табл. 5.43) и вычисляем по формулам (5.51): yi= 1,839—14,2= = -12,361; у2= 1,839-1,708=0,131; Z,i =3,59 • 1,99-4,75-9,36=-37,35; Х|2= = 4,75+9,36-3,59-1,99=8,53; Л2| =3,59 • 1,99-2,46-1,86=2,59; Х22=2,46+
+ 1,86—3,59—1,99= —1,26; по формулам (5.50)—/)= —37,35(—1,26)—2,59X Х8,53 = 25; £,= -12,361 (-1,26)-8,53 • 0,131 = 14,485; £>2= -37,35-0,131-
Табл. 5.46. Комбинационный квадрат
*3 *4 I 2 3 4 5 SZ Ф< (Х<)
1 —2,2 — 1,2 0,2 2 4,2 3 0,6
2 — 1,2 —0,2 1,2 3 5,2 8 1,6
3 —0,7 0,3 1,7 3,5 5,7 10,5 2,1
4 —0,4 0,6 2,0 3,8 6 12 2,4
5 —0,2 0,8 2,2 4 6,2 13 2,6
—4,7 0,3 7,3 16,3 27,3
фз (%з) —0,94 0,06 1,46 3,26 5,46
187
Рис. 5.13. Графики осредненных однофакторных моделей после пересчета значений отклика (рис. 5.12).
Рис. 5.14. Результаты спрямления осредненных графиков (рис. 5.13)!
—2,59(—12,361) =27,1; по формулам (5.49) — 6= 14,485/25=0,581; ЪС= =27,1/25=1,083; &С2=27,17(25 14,485) =2,03.
Подставляя вычисленные значения Ь, ЬС и &С2 в формулу (5.48), получим
/i(x()/2(x2) = (2,5x^0,07)ехр[-2(х2-1)]-0,01(9+2x0.
Отбрасывая статистически незначимые слагаемые, получаем окончательно
к(хМг(хг) =2,5xiexp[-2(х2- 1)].
Производим пересчет всех значений отклика из табл. 5.43 по формуле (5.52) и группируем значения Zu по одинаковым значениям факторов хз и х4 (табл. 5.46).
Графики осредненных однофакторных моделей ср3(хз) и <р4(х4) показаны на рис. 5.13. После пересчета ломаные графики (см. рис. 5.12) сгладились.
Согласно типовым графикам (табл. П.19), третья осредненная однофакторная модель имеет вид
23 = <Р3 (*з) = “о + ¥з + а2хз-
Выпрямляющая подстановка ir3=[Z3—Z3(l)]/(x3— 1) превратила график <р3(х3) в прямую (рис. 5.14), откуда
23=<рз(хз) = 1,74+ 0,2 (хз+1)2.
Аналогично, по типовым графикам определяются вид и параметры четвертой осредненной однофакторной модели. Выпрямляющая подстановка 1Г4= = (х4— 1)/[Z4—Z4(l)] превращает график <р4(х4) в прямую линию (см. рис. 5.14), откуда
6
<р4 (х4) = 3,5 — -—•—.
1 + xt
Истинные модели f3(x3) и f4(x4) определяем методом подстановки. При х3=3 и х4=3 имеем: Z3+Z4=6,94, Z=l,7 (см. табл. 5.46), 6 = 6,94—1,7=5,24. Значит,
/з(х3) +/4(х4) =<р3(хз) + <р4(х4) —5,24 или
„ 6
/з (Хз) + Л (х4) = 0,2 (х3 + I)2 - —-.
Г 'П %4
188
Окончательно искомая математическая модель
6
У = 2,5х!ехр [— 2 (Xj — 1)] + 0,2 (х3 + I)2 — —---
1 -г xi
5.5.3. Уточнение параметров линейной по параметрам многофакторной модели
В тех случаях, когда вид модели определен с помощью предварительного эксперимента или из теоретических соображений, для уточнения (или определения) параметров модели применяются D-оптимальные и близкие к D-опти-мальным планы с минимальным числом опытов.
Для линейной модели следует применять насыщенные планы Плаккета — Бермана, приведенные в табл. 4.4 и 4.6 или построенные с помощью табл. 4.5. Если k меньше указанного в таблице, то лишние столбцы отбрасываются.
Некоторые D-оптимальные планы для неполных двухфакторных полиномов приведены в табл. 5.47.
Знаки (+) в этой таблице указывают, в каких точках факторного пространства следует проводить опыты эксперимента. Расположение и координаты этих точек показаны на рис. 5.15.
Насыщенные планы, близкие к D-оптимальным, для двух-, трех- и четырехфакторных моделей типа k k k
У = а0 + 2 aixl + 2 aljxixi + aitxl (j ¥ i) 1=1 1=1 1=1
приведены в табл. 5.48...5.50.
Параметры моделей после реализации указанных планов вычисляются по формуле
а= (Х'Х')~1Х>'У, (5.53)
где X — матрица условий эксперимента, т. е. план, в который включают все эффекты, указанные в модели; X' — транспонированная матрица X; У— матрица откликов.
Табл. 5.47. D-оптимальные планы для неполных двухфакторных полиномов
Модель At A, A, л4 Аб л. Аа А.
Y = Go d~ ^2-^2 d- 012*1*2 + + 4-
Y = Gq d- #i*i d~ g%x% -j- + + + + + +
У Go d- #1*1 + g%x% d- G12X1X2 -J- вцХ^ + + d- + + +
Y = Gq d“ 01*1 + #2*2 d“ ^11^1 d“ #22*2 + + + + + + + + +
У = «0 d- #1*1 d" ^2X2 d- 012*1*2 + ®ll*f d“ d- #22*2 "b flH2*lX2 + ^122*1*2 + + + + + + + +
У — Gq d- Пц*| + ^22*2 + + + +
У « Gq d" 012*1*2 + +
189
Табл. 5.49. Насыщенный план для /г=3
Табл. 5.48. Насыщенный план для k=2
U х2 । и Ч х> и X 1 х2 Х2 | Л.1
1 —1 — 1 4 +1 +1 1 1 —1 1 6 —1 0 1
2 -4-1 — 1 5 —1 0 2 1 1 —1 7 —1 0 —1
3 — 1 +1 6 0 0 3 I —1 —1 8 —1 -1 0
4 1 1 1 9 0 -1 1
5 —1 1 0 10 0 0 0
Табл. 5.50. Насыщенный план для k=-4
и Х1 х2 Х3 Х4 и Х1 Xt X з Х<
1 —1 1 1 1 9 —1 0 1 —1
2 1 —1 1 1 10 —1 1 0 —1
3 1 1 -1 1 11 1 —1 —1 0
4 1 1 — 1 —1 12 —1 1 —1 0
5 1 —1 I —1 13 —1 —1 1 0
6 —1 —1 —1 1 14 1 1 1 0
7 8 —1 0 —1 1 —1 1 —1 —1 15 0 0 0 0
Например, для модели
2 2
Y = ао + S atxi + а12*1 *2 + 2 azz*?
z=i t=i
1 *11 *21 (*1*2)1 2 *11 х2 ' *21
1 *12 *22 (*1*2)2 JC2 *12 X2 *22
1 *13 *23 (*1*2)з 2 *13 X2 *23
X = 1 *14 *24 (*1*2)4 X2 *14 х2 *24
1 *15 *25 (*1*2)5 г2 *15 г2 *25
1 *16 *26 (*1*г)б X2 *16 JC2 *26J
11 1
—1 1 —1
—1 —1 1
1 —1 —1
1 1 1
.111
1 —1
1 1
1 —1
1 1
1 —1
1 0
1 1 1
1 —1 О
1 О о
1 о о
1 1 о
1 о о
—1 1 1
—1 —1 1
1 —1 1
1 1 1
О 0 1
О 0 0
1
1
1
1 о
0
Элемент ha матрицы Х'Х равен соответственно сумме произведений элементов i-й строки матрицы X' на соответствующие элементы /-го столбца матрицы X. Например, Л23= (—1) (—1) + 1 (—1)+ (—1) 1 +1 • 1+ (—1)0+0 • 0=0; й16=1-1 + 1 • 1 + 1 1 + 1 -1 + 1 -0+1 -0=4.
Все операции с матрицами, ранг которых больше 3, целесообразно производить при помощи ЭВМ с использованием стандартных программ.
190
Af 2 A? Aj ' 7-/+“^ W4 7/.Z?
A4 As___________As _____t
" 'h;o) (0;0) М)*1
4/ ^s, Z5', 1
Puc. 5.15. Расположение точек D-оптимальных планов для неполных двухфакторных полиномов
Рис. 5.16. Центральный ротата-бельный план для двухфакторной модели второго порядка
В определенных условиях, когда необходимо обеспечить независимость точности оценки отклика от направления оси, проведенной через центр плана, рекомендуется применять центральные ротатабельные планы. Такой план для двухфакторной модели второго порядка (рис. 5.16) приведен в табл. 5.51.
Расчет параметров модели второго порядка в данном случае производится по формулам:
.10 10
а\ = 0,333 2 х1цУц; а2 = 0,333 2 х2цУц;
и—\ 11—\
10
«12 = 1,333 2 (^х2)и¥и-,
Н=1
ai{ — 0,883
/ 10 10 \ 10
2 *?Л + 2 4Л« -°>52
\«=1 и—1 / а=1
(5.54)
ю ю ю
«22=i-5 2 4у« + °-1662 4ли-о>5 2 yU’
и=1 и~1 11=1
10 10 10
«0=0-4 2 ^-0,32 4Л-0.72 xhYu u=l и—1 U=1
Дисперсии оценки параметров модели можно определить из выражений:
S2 (а0) = 0,125S2;IS2 (aj = S2 (а2) = 0,333 S2;
S2 (а12) = 1,333 S2; S2(an) = S2 (a22) = 0,75 S2.
Для моделей с числом факторов более двух предлагаются некомпозиционные планы второго порядка, в которых каждый фактор варьируется на трех
Табл. 5.51. Ротатабельный план для k=2
и х2 и Х1 х2
1 2 3 4 5 . +1 —1 +0,5 +0,5 —0,5 0 0 +0,87 —0,87 +0,87 6 7 8 9 10 —0,5 0 0 0 0 —0,87 0 0 0 0
191
Табл. 5.52. Некомпозиционный план второго порядка для k=3
U Х1 Хг х3 и *1 Х2 хз и Xi Xt Х3
1 1 1 0 6 1 0 —1 и 0 —1 1
2 1 —1 0 7 —1 0 1 12 0 —1 —1
3 —1 1 0 8 —1 0 —г 13 0 0 0
4 —1 —1 0 9 0 1 1 14 0 0 0
5 1 0 1 10 0 1 —1 15 0 0 0
Табл. 5.53. Некомпозиционный план второго порядка для k=4
и Х1 Х2 Xi хл и Xi х2 Х3 Х4 и Xi Xi *3 Xi
1 —1 —1 0 0 10 —1 0 0 —1 19 0 —1 0 —1
2 1 —1 0 0 11 1 0 0 —1 20 0 1 0 —1
3 —1 1 0 0 12 —1 0 0 1 21 0 —1 0 1
4 1 1 0 0 13 1 0 0 1 22 0 1 0 1
5 0 0 —1 —1 14 0 —1 —1 0 23 —1 0 —1 0
6 0 0 1 —1 15 0 1 —1 0 24 1 0 —1 0
7 0 0 —1 1 16 0 —1 1 0 25 —1 0 1 0
8 0 0 1 1 17 0 1 1 0 26 1 0 1 0
9 0 0 0 0 18 0 0 0 0 27 0 0 0 0
Табл. 5.54. Некомпозиционный план второго порядка для k = 5
и Xi А'2 X, | Xi Xi и Xi Xt Xi Xi Xi
1 1 1 0 0 0 24 0 1 1 0 0
2 1 —1 0 0 0 25 0 1 —1 0 0
3 —1 1 0 0 0 26 —1 —1 1 0 0
4 —1 —1 0 0 0 27 0 —1 —1 0 0
5 0 0 1 1 0 28 1 0 0 1 0
6 0 0 1 —1 0 29 1 0 0 —1 0
7 0 0 —1 1 0 30 —1 0 0 1 0
8 0 0 —1 —1 0 31 —1 0 0 —1 0
9 0 1 0 0 1 32 0 0 1 0 1
10 0 1 0 0 —1 33 0 0 1 0 —1
11 0 —1 0 0 1 34 0 0 —1 0 1
12 0 —1 0 0 —1 35 0 0 —1 0 —1
13 1 0 1 0 0 36 1 0 0 0 1
14 1 0 —1 0 0 37 1 0 0 0 —1
15 —1 0 1 0 0 38 —1 0 0 0 1
16 —1 0 —1 0 0 39 —1 0 0 0 —1
17 0 0 0 1 1 40 0 1 0 1 0
18 0 0 0 1 —1 41 0 1 0 —1 0
19 0 0 0 —1 1 42 0 —1 0 1 0
20 0 0 0 —1 —1 43 0 —1 0 —1 0
21 0 0 0 0 0 44 0 0 0 0 0
22 0 0 0 0 0 45 0 0 0 0 0
23 0 0 0 0 0 46 0 0 0 0 0
192
Табл. 5.55. Значения коэффициентов к формулам (5.55) и (5.56)
k А В с D р
3 0,125 0,250 —0,0625 0,250 2 3
4 0,0835 0,125 —0,0208 0,250 2 3
5 0,0625 0,0835 —0,0104 0,250 2 6
уровнях ( — 1; 0; 1). Эти планы представляют собой определенные выборки строк из плана ПФЭ 3h. Их достоинством является меньшее число опытов по сравнению с ротатабельными планами и большая надежность по сравнению с насыщенными. Такие планы для трех, четырех и пяти факторов приведены в табл. 5.52...5.54. Параметры этих моделей определяются по следующим формулам:
«о W
w
(5.55)
ац = D S (xixi)uYu’ ‘ * /;
u=t N kN nt
Значения коэффициентов n0, А, В, C, D и p приведены в табл. 5.55 в зависимости от числа факторов k.
Дисперсии параметров модели:
S2 (а0) =S2; 32(О/) = ЛЗ|;
Пд
S2 (ач} = DS2; S2 (aLi) = (в + S2.
(5.56)
Одни из наиболее рациональных по числу опытов планы предложены Хартли [55]. Их достоинствами являются также близость к D-оптимальным планам и композиционный принцип построения. Как и все композиционные планы, они включают ядро, звездные точки и опыты в центре плана. Характеристики некоторых планов Хартли на сфере приведены в табл. 5.56.
Табл. 5.56. Характеристики планов Хартли
Номер плава Число факторов k Ядро плана Число опытов в ядре Ki Звездное плечо а Число звездных точек Число опытов в центре Общее число опыт о
1 3 23—1; 1 = Xi-чхз 4 1,732 6 1 11
2 4 24 —i; 1 = XtX2X3 8 2 8 1 17
3 5 26 —4; j = X1X2X3XtXi 16 2,236 10 1 27
13. Зак. 1001
193
Табл. 5.57. Вспомогательные константы для планов Хартли
Номер плана k 4, ^2 d, dt 4. 4. 4j 4.
1 3 1 0,3333 0,0556 0,1037 0,1 0,25 0,1667 0,4167
2 4 1 0,25 0,0313 0,0586 0,0625 0,125 0,125 0,25
3 5 1 0,2 0,02 0,0375 0,0385 0,0625 0,1 0,1125
Планы Хартли нельзя сделать ортогональными или ротатабельными путем подбора звездного плеча а (за исключением случая й=5). Коэффициенты нормализованной квадратичной модели определяются в данном случае по формулам:
N k N
а0 = 2 У и d2^j 2
ы=1 1=1 и=1
N kN N
ай- = ^з2 (*?Пн+^2 2 Yu>
u=l 1=1 u=l u=l
N N
ai (.xiYy)U’ “</=42 (xixjYy>u<
U=1 U=1
Г N N 1 1
= d7 £ (*Л)и-2 ;
Lu=l u=l JI
N N t
aH = d8 2 (XiXtY)u-d7 2 u=! u=l }
(5.57)
(5.58)
а,
(5.59)
Формулы (5.59) применяются для определения коэффициентов регрессии при факторах и парных взаимодействиях, индексы которых входят в трехбуквенный определяющий контраст l=x,XjXi. Например, при £=4 (табл. 5.56) коэффициенты ab а2, аи, His и а23 необходимо определять по формуле (5.59), а при й=5 все коэффициенты —по формулам (5.57) и (5.58).
Дисперсии коэффициентов регрессии:
S2(a0) = d,S2; 52(пг1.)= (d3 + d4)S2;
S2(a(.)=dsS2; S2 (alf) = d6S2B;
(5.60)
S2 (<*/) — S2 (ац) — d8S2.
Табл. 5.58. Способ построения насыщенных планов Рехтшафнера
Номер множества Точки множества Число опытов множества
1 (—1; —1; . . . —1) для всех k 1
2 (—1; 1; 1; . . .1) для всех k k
3 (—1; —1; 1) для k = 3; (й—1)Хг/2
(1; 1; —1; —1; . . . —1) для /г>3
4 (1; 0; 0; . . .0) для всех k k
194
Табл. 5.59. План Рехтшафнера для k = 3
и Х1 Xi *3 Примечания
1 Множество 1
2 — + + Множество 2; остальные строки — пе-
3 + — + рестановкой
4 + + То же
5 + Множество 3; остальные строки — пе-
6 — + рестановкой
7 + — То же
8 1 0 0 Множество 4; остальные строки — пе-
9 0 1 0 рестановкой
10 0 0 1 То же
Коэффициенты di для формул (5.57)...(5.60) приведены в табл. 5.57. Не-ортогональность планов Хартли обусловливает необходимость пересчета остальных коэффициентов при исключении статистически незначимых.
Рехтшафнер [55] предложил полностью насыщенные планы, представляющие собой выборки строк из плана ПФЭ 3й. Способ построения планов ясен из табл. 5.58. Пример плана Рехтшафнера для k=3 приведен в табл. 5.59. Квадратичная модель для k = 3 имеет 10 членов, столько же опытов содержит план Рехтшафнера, в то время как план Хартли при тех же условиях — 11 опытов.
На рис. 5.17 и 5.18 для сравнения показаны соответственно планы Хартли и Рехтшафнера при й=3. £)-оптимальность планов Рехтшафнера несколько выше, чем у планов Хартли.
Структура планов Рехтшафнера была использована Боксом и Дрейпером [20] для построения насыщенных D-оптимальных планов на кубе. Эти планы строят из множества точек, указанных в табл. 5.60. Значения X и ц для планов разных размерностей:
k X ц
2 -0,1315 0,3944
3 0,1925 -0,2912
4 0,4114 -0,6502
k X
5 0,5355 -0,8108
6 0,6183 -0,8854
7 0,6772 -0,4242
Рис. 5.17. План Хартли для трехфакторной модели второго порядка
Рис. 5.18. План Рехтшафнера для трехфакторной модели второго порядка
13*
195
Рис. 5.19. План Бокса и Дрейпера для трехфакторной модели второго порядка
Расчет коэффициентов моделей после реализации насыщенных D-оптимальных планов Бокса и Дрейпера проводится в общем случае по формуле (5.53). На рис. 5.19 показан план Бокса и Дрейпера для й=3.
В некоторых случаях удобно пользоваться многофакторными планами, систематизированными В. 3. Бродским [9]. Эти планы позволяют определить коэффициенты регрессии в некоторых полиномиальных моделях, степень которых выше второй. Они строятся при помощи вспомогательных матриц, откуда согласно таблице планов выбираются столбцы.
Вспомогательные матрицы (приложение 2) обозначены DN, где N — число опытов в плане. Элементами этих матриц являются нессиметрично нормированные факторы (х; = = 0; 1; 2; ...; S{).
Факторы могут иметь разное число уровней S,. В таблице планов (табл. П.20) приведены только планы главных эффектов, т. е. в моделях нет эффектов взаимодействия, так как в результате реализации предварительного эксперимента или из теоретических соображений можно считать их незначимыми.
Например, требуется построить модель главных эффектов до второго порядка для четырех факторов
4 4
у=ао +2 aixi+2 аих1 1=1 1=1
Число параметров этой модели равно 9, следовательно, и опытов должно быть не менее 9. В табл. П.20 подходящим оказывается план 4—34//9, в котором четыре фактора поддерживаются на трех уровнях. Этот план представляет собой все столбцы вспомогательной матрицы D3 (приложение 2). Предположим, что из пяти факторов четыре влияют на отклик линейно, а один нелинейно, т. е.
4
У = а0 +2 aiXl + а55х5 + а555*5’
1=1
Всего данная модель содержит 8 параметров, а пятый фактор нужно поддерживать на четырех уровнях. В данном случае подходит план 6—24х4//8. Его можно построить из 1, 2, 3, 7 и 8-го столбцов вспомогательной матрицы Ds.
Пример 5.9. Необходимо установить зависимость показателя стойкости центровочных сверл из Р6М5 диаметром 4 мм от трех факторов: угла в плане 2<р, заднего угла а и толщины сердцевины Е.
Табл. 5.60. Способ построения насыщенных D-оптимальных планов Бокса и Дрейпера
Номер множества Точки множества Число опытов множества
1 (-1; -1; ... -1) 1
2 (+1; -1; ... -1) k
3 (X; %; —1; ... —1) k (k—1)/2
4 (р; +1; ... +1) k
196
Табл. 5.61. Условия эксперимента
Уровень фактора Факторы (их обозначения)
2<р (Xj) | а (х2) Е (х3)
Верхний (+1) 151 36 1,4
Средний (0) 147 32 1,2
Нижний (—1) 143 28 1,0
Решение. Из литературных данных известно, что искомую зависимость можно выразить многомерным полиномом второго порядка. Поэтому для экспериментального определения параметров математической модели стойкости был принят некомпозиционный план второго порядка (см. табл. 5.52). Испытания проводились на сверлильном станке при обработке стали 45 со скоростью резания 20,7 м/мин и подачей 0,063 мм/об до момента поломки сверла. Количество отверстий, просверленных до поломки сверла, принято за показатель его стойкости. Уровни факторов и расширенная матрица планирования с результатами опытов приведены соответственно в табл. 5.61 и 5.62.
Расчет параметров модели производится по формулам (5.55) и табл. 5.62.
а0= (1214+1201+ 1185)/3= 1200;
fli = 0,125 (751 +827- 1298-1520+1287+974- 1844-1668) = -311,37;
а2=0,125 (751 - 827+1298 -1520+ 1042 + 544-961 -937) = -76,25;
а3=0,125(1287-974 +1844 +1042-544 + 961-937) = 126,37;
012=0,25(751 — 827—1298+1520) =36,5;
0,3=0,25(1287-974- 1844+1668) =34,25;
а2а=0,25 (1042 - 544 - 961 + 937) = 118,5;
Х|=(1214+1201 + 1185)/(3-2)=600;
12= -0,0625 -2(751 +827+1298 + 1520+1287+974+ 1844 +
+1668 +1042 + 544 + 961 + 937) = -1706,62;
%2-Xi= -1706,62-600= -2306,62;
в11=0,25(751 +827+1298+1520+1287+974+1844+ 1668)-2306,62 = 234,63;
Табл. 5.62. Расширенная матрица некомпозиционного плана
и х0 *1 *2 ХЭ Х1Х2 *1*3 х3хл 2 Х1 2 X» 2 X» У и
1 +1 +1 4-1 0 4-1 0 0 4-1 4-1 0 751
2 +1 +1 —1 0 —1 0 0 4-1 4-1 0 827
3 +1 4-1 + 1 0 —1 0 0 4-1 + 1 0 1298
4 +1 —1 —1 0 4-1 0 0 4-1 + 1 0 1520
5 +1 + 1 0 4-1 0 +1 0 4-1 0 +1 1287
6 +1 4-1 0 —1 0 —1 0 4-1 0 4-1 974
7 +1 —1 0 4-1 0 —1 0 4-1 0 4-1 1844
8 4-1 —1 0 —1 0 4-1 0 + 1 0 4-1 1668
9 4-1 0 4-1 + 1 0 0 4-1 0 4-1 4-1 1042
10 +1 0 +1 — 1 0 0 —1 0 4-1 4-1 544
11 4-1 0 —1 4-1 0 0 —1 0 —1 4-1 961
12 +1 0 —1 — 1 0 0 +1 0 + 1 +1 937
13 4-1 0 0 0 0 0 0 0 0 0 1214
14 4-1 0 0 0 0 0 0 0 0 0 1201
15 4-1 0 0 0 0 0 0 0 0 0 1185
197
а22=0,25(751 +827+1298+ 1520+1042+544+961 + 937) -
-2306,62=-334,12;
Дзз=0,25 (1287+974 +1844 +1668 +1042 + 544+961 + 937) -
-2306,62 = 7,63.
Дисперсия воспроизводимости определяется по размаху отклика при опытах в центре плана: /?(У) = 1214—1185=29; SB = 29/1,693= 17,13, где значение = 1,693 взято из табл. П.5.
Дисперсии параметров модели вычисляются по формулам (5.56): S2(a0) =0,333 • 17,132 = 97,8; 52(аД =0,125 • 17,132 = 36,68;
S2 (а..) = 0,250 17,132 = 73,36; S2 (а,,) = (0,250 + ——) 17,132 = 97,8.
Доверительные интервалы для параметров модели по формулам (5.36):
Л (а0) = ± 4,303 К97,8/3 = + 24,6; Д (а,) = + 2,201 V 36,68/12 = + 3,85;
Д (о0) = ± 2,201 V 73,36/12 = + 5,45; Д (а„) = + 2,1451^97,8/15 = + 5,5.
Значение критерия t определяется из табл. П.1 при доверительной вероятности Р=0,95.
Сравнив значения доверительных интервалов со значениями параметров модели, устанавливаем, что все параметры, кроме Щз, статистически значимы. Округляя их значения, согласно доверительным интервалам, получаем окончательно нормализованную модель
Y = 1200 — 310х( — 75х2 + 125х3 Ц- 35 + 120х2х3 Д-235х2 —335х2-
5.6. ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА ПРИ ИДЕНТИФИКАЦИИ
5.6.1. Основные понятия
Идентификация — построение математической модели (статической или динамической) объекта на основе экспериментальных данных. Это понятие в настоящее время преимущественно связывают с задачей построения динамических моделей (см. § 4.1).
Динамический объект можно представить в виде «черного ящика>, на входе которого действует случайная векторная функция времени X(t) с компонентами Xi(0, Х2(Д, ..., A„(t), а на выходе получается векторная случайная функция Y(t) с составляющими УДО, Уг(О> •••, Ут(0- Функции ХД<) и Yj(t) измеримы в процессе нормального функционирования объекта, т. е. можно получить их реализации в виде временных рядов (см. § 3.2). Задачей эксперимента является определение характеристики объекта исследования, приводящей в соответствие случайные функции Xt(t) и УДО- Такой динамической характеристикой объекта в общем случае является оператор — закон, в соответствии с которым по одной функции X(t) определяется другая Y(t).
Понятие оператора является более общим, чем понятие функции, которая ставит в соответствие значения двух переменных X и У, или функционала, ставящего в соответствие значения переменной величины и функции. Примерами операторов являются операторы дифференцирования или интегрирования. .
Конкретное представление динамической модели объекта может быть различным в зависимости от поставленных целей, свойств объекта и т. д. Так, например, динамической моделью линейного объекта может быть дифференциальное уравнение, импульсная переходная (весовая) функция, амплитудно-фазово-частотная характеристика или алгебраическая функция. Эти модели эквивалентны, так как имея один из видов описания объекта, можно в результате соответствующих преобразований перейти к другому.
198
Следовательно, под построением динамической модели объекта понимается нахождение оператора, ставящего в соответствие входную X(t) и выходную У(/) функции объекта. При этом существенно, что при идентификации оператор находится по результатам измерений X(t) и У(1), полученных в процессе нормального функционирования объекта. Результаты измерения фактора и отклика рассматривают как реализации случайных функций X(t) и Y(t). По этим реализациям необходимо найти не сам оператор А, а его оценку А*, которая и используется в качестве характеристики неизвестного истинного оператора А. При этом на Л* накладывается требование близости к А в определенном смысле. Чаще всего требуется, чтобы выход оператора У*(/) = =А*Х(/) был близок к выходу объекта Y(t), т. е. чтобы математическое ожидание квадрата разности между Y*(t) и У(<) было минимальным.
Наиболее широко применяется так называемая параметрическая идентификация, когда на основе априорной информации выдвигаются гипотезы о классе и структуре оператора Л, на основе измерений оцениваются только параметры оператора, а затем проверяется гипотеза об адекватности динамической модели.
5.6.2. Определение параметров динамических моделей с аддитивным дрейфом [56]
Этому случаю соответствует следующая модель объекта:
k
Y=bQ (t) +2 & Х /=1
(5.61)
где bj — неизвестные параметры модели;
т
Л=1
t — время; Ch — неизвестные параметры.
Исследователь имеет возможность поставить N опытов в моменты времени tlt t2, .... tN (N > k + m + 1), по результатам которых необходимо с помощью метода наименьших квадратов найти оценки коэффициентов Ь- и Ch. Задача планирования эксперимента в данном случае ставится следующим образом: найти план
*11 *12 •• *14
*21 *22 *2A
X = , (5.62)
*U1 *u2 • • xuk
V’jvi XN2 XNk)
исключающий влияние дрейфа на оценки 6/ (/=1, 2. k) и обеспечивающий
минимальные дисперсии этих оценок. В соответствии с теоремой Бокса при определении й+1 коэффициентов зависимости вида
k
У=^а1х1
199
с помощью плана X (матрица X ранга k +1), для которого имеют место усло-N N
ВИЯ 2 х/и — °* 2 x/u = N, необходимым и достаточным условием мини-U=l и=1
мума дисперсии оценок коэффициентов является ортогональность столбцов матрицы X, т. е.
N
У (XjXr)u = Q при /=1, 2, k; f^r. U=1
Для построения плана сначала строятся ортогональные степенные полиномы Чебышева <ри (/) для значений аргумента ti, .... tn с максимальной степенью N— 1. Вычисление ортогональных полиномов осуществляется с помощью следующей рекуррентной процедуры. Полином <ро(О принимается равным единице. Полином <Pi(Z) ищется в виде
<Pi(O=i-6io.
где
N
и=1
ф2(О=^-б21ф1(О-б20.
полином фа(О —в виде
где
N
и=1
N
2 1^Ф1 (01а ц=1
N
2 Ф1(*«) u=l
Аналогично
Фз(О =/3-6з2ф2(0 -M>t(0 -&зо, где
N
2^3Ф1 (01а
h _______________
31 ” N 2
2 Ф1 «и) и=1
2Рф2 (01а
h ц=1
32 ~ N 2
2 ф! (у
Ц=1
N
«=1
Когда опыты проводятся через равные интервалы времени, значения ортогональных полиномов Чебышева для разного числа опытов сведены в таблицы [22]. Аргумент tu в этих таблицах является несимметрично нормированным, т. е. принимает значения 1, 2, .... А, совпадающие с номером опыта и. Для плана необходимо использовать нормированные полиномы
Ч>а(0 =
Ф«(0
Матрицу значений нормированных ортогональных полиномов в X опытах обозначают ЧЛ Она имеет размерность МхА:
200
'Рю 'I’ll Ф12 ••• Ф1<ЛГ—1)
11’2о 'hi '’Ргг • • • 'Фгсм—1)
%0 %! ‘‘Риг •• 't’ufJV—1)
/Фа'о 'Фл'! Ч’д'2 ••• 'Рачат—I)
В качестве плана (5.62) используются столбцы значений ортогональных полиномов степени (т+1), (т+2), .... (М-1), т. е. матрица Ч'™ размера kxN. Чтобы исключить влияние дрейфа на оценку параметров, необходимо провести рандомизацию, полагая
X=4mQ, где X— матрица плана размера МХ^; £2 — случайная матрица размера (N—т— 1) Xk:
(“11 “12 ••• “1А
“21 “22 • • “2J l =
“/1 “/2 ••• “м/
Матрица й нормирована так, что
2 (“«/)’=!• и=1
В этом случае
I xuj ~ 2 ('+m}uarj’ r=l
т. е. нормированное значение /-го фактора в u-м опыте представляет собой линейную комбинацию значений I ортогональных полиномов в u-м опыте, взятых со случайными весами.
Для обеспечения ортогональности плана X необходимо и достаточно, чтобы матрица Q была также ортогональной, т. е.
V со со = /° ПРИ i * 2^ Ы“‘ (1 при j=i.
Для формирования матрицы й выбираем из таблиц случайных чисел (п. 21) k столбцов случайных чисел с I элементами в каждом:
Полученные столбцы ортогонализуются. Для этого полагается:
8] =8р = е2 С>21е1 > е3 = е3 ^32®2 ^31е1 и т- Д-
Коэффициенты С/7 определяются из условия ортогональности е.. всем ранее полученным векторам £; по формуле
201
2 eine*n
си = ?=г-------i = i’'2........(/—0-
2 (ein)J
Л=1
Затем полученные векторы е^- нормируются:
ш.. == .
/« I
2 <е/г>2 /=1
Для вычисления параметров нормализованной модели (5.61)
Y = ао + 2 аЛ + 2 aixi (5-63)
й=1 /=1
вводятся обозначения: f011 = l; fiu=xlu, .... fku=xgu; f(k+i}=^iu...A»+m)u =
=фти- Тогда модели (5.63) можно придать вид
где
N
-! “ Т 2(/'У)-
Остаточная дисперсия определяется выражением
( N М-m \
“/ )•
U=1 /«=1 /
Оценки дисперсий всех коэффициентов а.) одинаковы и вычисляются по формуле
S2(a/) = S>.
Доверительный интервал для оценок а, определяется при помощи критерия Стьюдента, значение которого выбирается при заданной доверительной вероятности Р и числе степеней свободы f=N— (m+fe+1) из табл. П.1. Оценка значимости коэффициентов а, и проверка адекватности модели проводятся как для статических моделей (см. § 5.5).
5.6.3. Построение динамической линейной модели [77]
Динамический объект называется линейным, если для него справедлив принцип суперпозиции, т. е. результат влияния на объект нескольких входных переменных равен сумме результатов влияния отдельных входных переменных. Если на объект действует входная переменная X(t), представляющая собой линейную комбинацию факторов
п х(0= 2 /=1
202
то выходная переменная линейного объекта У(/) является такой же линейной комбинацией
«—I
выходных переменных объекта, соответствующих результатам воздействия отдельных входных переменных Xi(t).
Динамический объект называется стационарным, если результат действия на него входной переменной X (t) зависит только от интервала времени между моментом начала действия t0 и фиксированным моментом t и не зависит от значения ta.
Если в качестве модели динамического линейного стационарного объекта использовать импульсную переходную (весовую) функцию g(T), причем
V (f) = j* g(T)X(i— т) dr,
• о
то при бесконечно большой длительности наблюдения ее можно определить путем решения интегрального уравнения
^Xy(0 = f Я(т)Кхх(/-т)ат, (5.64)
о
где Кхх — корреляционная функция стационарной входной случайной функции X (0; КХу — взаимная корреляционная функция стационарных и стационарно связанных случайных функций входа X (/) и выхода Y (t).
Решение уравнения (5.64) вызывает значительные трудности. Их преодоление возможно путем использования ЭВМ или специализированных вычислительных средств — коррелометров, спектроанализаторов и т. п. Ниже рассмотрен алгебраический метод решения интегрального уравнения (5.64), легко реализуемый на ЭВМ.
Интеграл аппроксимируется конечной суммой, что легко осуществляется, поскольку практически значения корреляционной и взаимной корреляционной функций входа и выхода по реализациям X (/) и У(/) также подсчитываются на ЭВМ. Если интервал записи случайных функций Т разбить на п равных частей длиной t и оперировать значениями в середине полученных интервалов Л = А ti=it, in=nt, то n—m
*хх 2 [Х (ti) ~ m*] [Х (G+m) ~ mx] ’
где m — количество интервалов сдвига; тх — математическое ожидание функции X (t); п п
n—m
*ху ('"О = [X W - «х] [Г (W - «у1-
i=i
Уравнение (5.64) можно представить в виде
^ух (т^ ~ У BiX.xx(mt—it)t, (5.65)
i=l
где gi = g(it).
203
Уравнение (5.65) можно записать для каждого значения т, которое можно изменять от 1 до п. Тогда получается система из п линейных уравнений с п неизвестными:
KYX(t) ^l^xx (°) + ^2^хх (0 + S^KXX (2/) 4- ... 4- gnKxx [(га — 1)/] = * ;
КУХ(2/)
Si^xx W + S2KXX (0) 4-g3Kxx (0 4- 4- [(rt — 2V1 = ] ;
KYX(3t) /(5.66)
(2/) + g2Kxx (/) + 8з%хх (0) 4~ ... + gnKxx [(га — 3)/]= j
Kxx (ra/)
gi Kxx [(n - 1)7] 4- g2Kxx [(« - 2) /] 4- • • + gnKxx (0) =--t-.
Для решения системы (5.66) в настоящее время имеются стандартные программы практически на всех ЭВМ. В результате решения получается ряд значений ординат весовой функи in для дискретных значений /, на основании которых можно построить ее математическую модель методами, описанными в §5.4.
В данном случае проводится пассивный эксперимент и планирование сводится к определению интервала Т (см. § 5.2).
5.6.4. Построение параметрических моделей временных рядов
В общем случае элементы временного ряда (см. § 3.2) можно представить в виде
Г(/)=Г(/)+Х(/)+£(/),
где К(/)—функция математического ожидания; X(t)—скоррелированная составляющая; Z(t) —случайная составляющая.
Совокупность X(/)+Z(/) представляет собой реализацию стационарного случайного процесса. Предполагается, что процесс является эргодическим (см. § 3.2). Тогда оценки среднего, дисперсии и корреляционной функции для временного ряда y(t) = У(/) — У(/) можно вычислять по формулам (3.12)...(3.14).
Параметрическая модель дискретного временного ряда г/(/) имеет вид
Н0 = 2 PTj/(i-T)4-2(i), (5.67)
т=1
где у (/) — значение отклика в момент I; у (/ — т) — сдвинутое в прошлое на величину т значение отклика; 0Т — весовые коэффициенты.]
Полагаем, что при т > I = 0. Модель (5.67) позволяет с точностью до Z (i) предсказывать значения y (i). Прогноз значений у (i) будет обладать наибольшей точностью, если оценки весовых коэффициентов находить методом наименьших квадратов, т. е. из условия минимума средней квадратической погрешности предсказания
* I
2 —т) — У
Л=1
Тогда получается система линейных алгебраических уравнений относительно весовых коэффициентов:
КуЮ = S bsKy(i-i), т=1, 2, 3, ...
/=1
в2 (у) = М
204
Полученная параметрическая модель
X(i)= 2 М(‘ —т)= М(‘ — 1) + b2y(i — 2» ... +bly(i — I) (5.68) т=1
может применяться для автоматического регулирования технологического процесса обработки деталей [54], если, например, y(i) являются отклонениями фактического размера детали от заданного. В таком случае на основании замеренных значений у (I—1), у (i — 2), ... для уже обработанных деталей автоматическая система вырабатывает корректирующий сигнал Л£ =—X (i). Но после коррекции Д£ повторное использование выражения (5.68) для предсказания X (i + 1) становится неправомерным, так как с введением поправок Д£ изменяются статистические характеристики исходного временного ряда, в частности его корреляционная функция. Поэтому значения коэффициентов &т в формуле (5.68) тоже изменяются. Если обозначить значения новых весовых коэффициентов ах, то их вычисление можно проводить при помощи рекуррентной формулы
<4 = bx ~ , (5.69)
/=1
Из формулы (5.69) следует тождество at=sbi.
6. ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА В ЗАДАЧАХ ОПТИМИЗАЦИИ
6.1. ОСНОВНЫЕ ПОНЯТИЯ И ПРОЦЕДУРЫ
Понятие оптимизации дано в § 4.1. Методы экспериментальной оптимизации можно разбить на два класса.
1. Методы определения оптимальной точки факторного пространства при помощи построенной предварительно математической модели объекта. В зависимости от сложности модели и вида ограничений оптимум определяется при помощи приравнивания нулю первых производных или методами математического программирования.
2. Методы прямого поиска. В данном случае математическая модель объекта исследования играет вспомогательную роль и описывает поведение объекта не во всем допустимом факторном пространстве, а только в некоторых его локальных областях.
Набор правил для определения последовательности сочетаний уровней факторов, при которых будут проводиться поисковые измерения (опыты), называется стратегией поиска. Среди всех возможных стратегий поиска исследователь стремится выбрать ту, которая приводит к цели при минимальных затратах времени и средств. В этом смысле стратегия поиска должна быть оптимальной.
Стратегии поиска разделяются на две группы: статические и последовательные.
При статическом поиске заранее, до начала эксперимента выбирается его план, т. е. весь набор сочетаний уровней факторов, при котором будут проводиться измерения. При увеличении количества факторов требуемое количество измерений резко возрастает, так как возможное число сочетаний значений k факторов, каждый из которых может поддерживаться на I уровнях, N=lh. >
При последовательном поиске выбор каждой точки факторного пространства для измерений отклика зависит от результатов предыдущих измерений. В данном случае требуемое число измерений значительно меньше, чем при прямом переборе возможных сочетаний уровней факторов.
Рис. 6.1. Примеры унимодальных за- Рис. 6.2. Примеры многоэкстремаль-висимостей! ных зависимостей
206
Эффективность последовательной стратегии поиска достаточно высока, если поверхность отклика является унимодальной, т. е. в исследуемой области факторного пространства имеется единственный максимум (или минимум). Примеры унимодальных поверхностей отклика для одно- и двухфакторного объекта показаны на рис. 6.1. Если поверхность отклика имеет несколько экстремумов (локальных максимальных или минимальных значений), то результаты поиска зависят от координат первого измерения. Примеры многоэкстремальных поверхностей отклика показаны на рис. 6.2. Если начинать поиск максимума из точки с координатой Xit то он приводит к локальному максимуму II, а не к глобальному I.
Критерием оптимальности стратегии поиска в однофакторном эксперименте является отношение оставшегося после п измерений интервала неопределенности к исходному. Если после серин из п измерений можно утверждать, что соответствующий максимальному (или минимальному) из измеренных значений отклика уровень фактора X* отвечает неравенству Xi-i<X*<Xi (i — порядковый номер уровня фактора), то интервал неопределенности определяется неравенством ln=Xi—Х,_,. Величина 1п характеризует эффективность проведенного эксперимента и как априорный критерий не годится, так как до проведения эксперимента ее нельзя определить. Поэтому в качестве априорного критерия эффективности стратегии поиска принимается величина
E=Ln[La, rpfi — начальный интервал неопределенности:
Eo = ^maz“Xmiai
Ln—максимально возможное для данной стратегии поиска значение 1п-
Для однофакторных задач используются следующие стратегии поиска различной эффективности: 1) метод дихотомии; 2) метод чисел Фибоначчи; 3) метод «золотого сечения»; 4) поиск по дискретным точкам. После проведения десяти опытов, спланированных по методу дихотомии, исходный интервал неопределенности уменьшается в 32 раза, по методу чисел Фибоначчи — в 89 раз, по методу «золотого сечения» — в 76 раз, а при поиске по дискретным точкам — в 143 раза.
Многофакторные стратегии поиска. являются значительно менее эффективными. Во-первых, пока не найдена априорная мера эффективности многофакторного поиска. Во-иторых, с увеличением числа факторов резко уменьшаются относительные размеры искомой области неопределенности, т. е. увеличивается потребная точность поиска. Например, если достаточно точным для любого i-ro фактора считается интервал неопределенности, равный О,1Во<, то при решении задачи поиска с тремя факторами искомая область неопределенности составит только 0,13=0,001 от исходной.
Для поиска экстремума в многофакторных задачах применяются методы: 1) крутого восхождения (или скорейшего спуска); 2) подъема по гребню; 3) симплекс-планирование эксперимента.
Поиск оптимума в многофакторных задачах включает следующие этапы.
1. Постановка задачи. Содержание данного этапа такое же, как и при построении математической модели.
2. Сбор априорной информации. Подробное знакомство с объектом исследования, сбор информации о решении подобных задач.
3. Предпланирование эксперимента. Выделяются все факторы, которые могут влиять на функционирование объекта исследования и параметр оптимизации. Разрабатывается способ измерения и статистической оценки параметра оптимизации. Составляется план предварительного эксперимента.
4. Реализация предварительного эксперимента. Отлаживается экспериментальная установка и устройства для измерения параметра оптимизации. Экспериментально выделяются факторы, значимо влияющие на параметр оптимизации.
5. Планирование эксперимента для исходной точки поиска. Выбирается исходная точка поиска. Чем ближе к оптимуму находится исходная точка,
207
тем быстрее он может быть определен. Составляется план эксперимента и при градиентном поиске выбирается вид модели для описания поведения отклика в локальной области, близкой к исходной точке. Для симплекс-поиска на данном этапе вид локальной модели не имеет значения.
6. Реализация эксперимента в исходной точке. По результатам измерений определяется направление движения в факторном пространстве к области оптимума.
7. Поиск области оптимума. Это повторяющаяся процедура, включающая вычисление координат новой точки последовательного плана согласно найденному направлению движения и выбранному шагу, а также измерения отклика в этой точке. Полученные результаты сравниваются с предыдущими, что позволяет принимать решение о продолжении или прекращении процедуры поиска. В некоторых случаях приходится для уточнения ситуации повторять этапы 5 и 6, в результате чего определяется новое направление поиска.
8. Планирование.эксперимента в области оптимума. Цель — определение плана для построения модели, описывающей поведение объекта исследования в локальной области, охватывающей точку оптимума. Обычно это модель второго порядка.
9. Реализация эксперимента. Согласно разработанному плану проводятся измерения отклика.
10. Анализ результатов. Вычисляются оценки параметров локальной квадратичной модели и по ней окончательно определяется точка оптимума.
6.2. ПЛАНИРОВАНИЕ ОДНОФАКТОРНОГО ПОИСКА [79]
6.2.1. Метод дихотомии (половинного деления)
Предположим, что в однофакторном процессе поведение отклика соответствует кривой, изображенной на рис. 6.3. Первые два опыта проведем вблизи середины интервала варьирования фактора на расстоянии е — наименьшем расстоянии между уровнями фактора, при котором становится возможным обнаруживать отличие между соответствующими значениями отклика. Сравнивая эти значения, обнаруживаем, что Это позволяет сделать вывод, что оптимум находится в интервале неопределенности между xi и Ь, равном £2. Затем делим этот интервал пополам и опять проводим два эксперимента в точках Хз и Xi на расстоянии 0,5е от середины интервала. Поскольку У3> >У4, можно сделать вывод, что оптимум находится в интервале от Xi до Х4, равном Повторяя предыдущую процедуру, находим новый интервал не-
Рис. 6.3. Схема поиска методом дихотомии
208
определенности L$ и т. д. После проведения п экспериментов (п должно быть, четным) оптимум окажется заключенным в интервале
Ln=io[2-O's" + (1—2-0'5п)е].
Таким образом, метод дихотомии (так же как другие методы однофакторного поиска) основан на сравнении двух значений отклика, полученных в смежных экспериментах, что позволяет выявить бесперспективную область и направить поиск в тот интервал неопределенности, где находится единственный экстремум.
6.2.2. Метод Фибоначчи
Этот метод более совершенный, чем метод дихотомии, и базируется на. последовательности чисел Фибоначчи:
л 1 2 3 4 5 6 7 8 9 10 11 12 13
Fn 1 2 3 5 8 13 21 34 55 89 144 233 377
В этой последовательности каждое число, начиная с третьего, равно сумме двух предыдущих. Вначале следует задаться требуемой точностью поиска,, т. е. интервалом неопределенности Ln после проведения п опытов.
Затем вычисляется ориентировочное значение числа Фибоначчи
п Ln — 0,38е ’
(6.1>
где в — интервал различимости отклика.
Естественно, что £п>е. Если предположить, что в пределе Ln = 2e, то из формулы (6.1) получаем
Е* = О,62£о/е. (6.2)
По полученному значению Fn подбирается из таблицы чисел Фибоначчи ближайшее число опытов п. Например, при Lo = 100 и е = 2 по (6.2) получаем Г* = 0,62 100/2 = 31. Ближайшим числом Фибоначчи будет 34, а соответствующее ему число опытов п = 8.
Затем вычисляются координаты точек первых двух экспериментов Xt = ^a+Lj и Xi=b—Li (рнс. 6.4), где
£1 = £2 = £оА^-- <6'3>
гп
Предположим, что после реализации первых двух опытов оказалось, что Уг>Уь Тогда интервалом неопределенности будет отрезок между Xt и а, равный Li. Вычисляем координату точки Х3 для третьего опыта: X3=Xi—£3, где
г г ?л—2 ... ..
^ = 47— = ( 1
‘ п—1 л
Если после реализации этого опыта оказалось, что Уа>Уз, то интервалом неопределенности будет отрезок £3 между Xt и Х3.
Аналогично определяется координата четвертого опыта Xi=X3+Li, те
£ —£ ^--£
4 8 Fn_, Fn •
14. Зак. 1001
209
Рис. 6.4. Схема поиска методом Фибо-
наччи и «золотого сечения»
Если У,>У2, то интервалом неопределенности будет отрезок £«между Х3 и Xt. Координата Х5 для пятого опыта будет X^Xj+Xs, где
L = L 5 4 р
ГП—3
”Л° F
‘ п
Аналогично определяются координаты остальных точек эксперимента.
В зависимости от расположения экстремума возможны и другие варианты движения к нему. Например, если после третьего опыта оказалось, что Уз<Уз, то интервалом неопределенности будет отрезок L3 между точками а и Х2, если же У2 = У3— отрезок между Х2 и Х3. В таком случае скорость сходимости поиска резко увеличивается. Однако для дальнейшего определения координат точек опытов следует использовать уравнение (6.3), в которое вместо подставляется расстояние между Х2 и Х3, а вместо Fn-t и Fn— Fn-з и Fn-t, т. е. Lt=LS’= (Х2—X3)Fn_tIFn_3. Затем применяются формулы типа (6.4).
6.2.3. Метод «золотого сечения»
Установить заранее значения Ln и е часто бывает невозможно, так как об отклике до начала опытов ничего неизвестно. Предельное же значение Ln зависит от соотношения погрешности эксперимента и скорости изменения отклика вблизи экстремума. Если погрешность опытов можно оценить в самом
210
начале эксперимента, то скорость изменения отклика вблизи оптимума — только после того, как найден оптимум. Поэтому лучше для однофакторного поиска применять метод «золотого сечения», который по своей эффективности близок к методу Фибоначчи, однако не требует предварительного задания Ln и числа предполагаемых опытов. Последовательные опыты размещают так, чтобы соблюдались условия
L{—\jLi —LijLt+\—т,
(6.5)
где т= 1,618.
По результатам Двух измерений устанавливают (как и при поиске экстремума методом Фибоначчи), какой из отрезков на оси исключается из исследования. В оставшемся интервале неопределенности будет находиться один из. предыдущих опытов, и чтобы продолжить поиск, необходимо в этом интервале выполнить опыт, симметричный предыдущему (см. рис. 6.4). Если известен исходный интервал неопределенности £0, то из (6.5) следует: L1=£2=L0/t; Xi=a+Li; Хз=Ь—Li- После первых двух опытов (Yt<Y2) определяются £з=£з/т; Х3=Х1—£3. Так как отклик в третьем опыте Y3<Y2, то Xi=X3+Li, и т. д.
После л опытов приходим к интервалу неопределенности
£„=£0/т"-1.
Этот интервал при большом числе измерений (л>5) составляет 1,17 интервала, найденного методом Фибоначчи.
6.2.4. Поиск по дискретным точкам
Этот метод применяется в тех случаях, когда фактор может принимать только диксретные значения или диапазон варьирования фактора искусственно делится фиксированными точками на уровни. Желательно, чтобы число дискретных точек в диапазоне варьирования фактора было близко к одному из чисел Фибоначчи. Пример поиска приведен на рис. 6.5. Если число дискретных точек Kn=Fn+i —1 (Fn+i — число Фибоначчи; Кп—число точек, которые можно методом Фибоначчи привести к единственному экстремуму максимум за п опытов), то первые два опыта следует проводить в точках с номерами, соответствующими числам Фибоначчи Fn-i и Fn. В примере на рис. 6.5 /(„ = 20, тогда F„+1=21, F„ = 13, Fn-i = 8, а максимальное число опытов, необходимое для отыскания экстремума, равно 6.
На рис. 6.6 показаны различные варианты поиска по двадцати дискретным точкам в зависимости от положения экстремума и соотношения между полученными в опытах значениями отклика. В квадратах записаны номера точек, в которых необходимо проводить эксперимент исходя из результатов предыдущих опы-
Yi
Y?
Опыт fu2
Y2>Yf Lz-13
№>2 M 16 18 20 X
Yi
z,- 8
Yz v ОпытЗ
3 y2>y3
2 6 5 8 10 12 X
у. У?!
Олытб Y^YZ
zp
Y
г 25 0пыт5'
y5>y^
/4 6 8 10 12 14 16 18 20 X
у. Опыт 6
YS<YS
2 4 6 8 /О /2 14 16 18 20 X
Puc. 6.5. Схема поиска по дискретным точкам
Lf5
14*
211
Рис. 6.6. Варианты поиска по двадцати дискретным точкам
тов (записаны на строках в виде неравенств). При «удачном» расположении экстремума он находится за меньшее число опытов (от 5 до 3).
Рассмотренные в данном параграфе методы однофакторного поиска являются достаточно эффективными в тех случаях, когда погрешностями опыта и измерения отклика можно пренебречь. Если же погрешности являются значительными, то для сопоставления двух откликов следует проводить при каждом значении фактора по т экспериментов и при помощи критерия Стьюдента оценивать значимость различия средних значений отклика. Если дисперсия воспроизводимости (ее можно определить в первой серии экспериментов по размаху) имеет тот же порядок, что и допустимая ошибка в оценке отклика, то, определив по (5.2) требуемое число экспериментов в серии т, можно использовать для поиска экстремума метод «золотого сечения» или метод поиска по дискретным точкам. В противном случае может оказаться более выгодным построить математическую модель процесса, аппроксимировав ее полиномом или другой кривой (см. § 5.4), и, пользуясь ее параметрами, вычислить координату экстремума. Затем в окрестности этой координаты необходимо провести уточняющие эксперименты.
Следует проявлять осторожность в принятии решения, если при поиске методами Фибоначчи или «золотого сечения» сравнение откликов в смежных опытах покажет, что они равны. Тогда, согласно стратегии поиска, нужно искать экстремум в промежутке между соответствующими факторами (рис. 6.7, а). Однако, если функция отклика имеет вид, показанный на рис. 6.7, б, то такое заключение может привести к ошибке. Если опыт, прове-
2212
a <f
Рис. 6.8. Зависимость некруглости шлифованной детали от скорости ведущего круга (результаты эксперимента)
денный в интервале Xi—Xt-i, не дает изменения отклика, то это значит, что оптимум может находиться вне этого интервала.
Пример 6.1. Необходимо оптимизировать процесс бесцентрового врезного шлифования на станке модели ЗМ-182 за счет изменения скорости вращения ведущего круга ов в пределах от 10 до 90 м/мин. Параметром оптимизации является некруглость (Н) шлифованных деталей. Поскольку замер некруглости является трудоемкой операцией, желательно определить оптимум за минимальное количество опытов.
Решение. Некруглость шлифованных деталей в первой серии из пяти опытов при пв = 20 м/мин составляла: 3; 3,5; 3,3; 4,2; 4,1 мкм. Тогда Н=(3 + + 3,5+3,3+4,2+4,1)/5 = 3,62 мкм; S = R!dm = (4,2—3)/2,326=0,515 мкм, где dm =2,326 взято из табл. П.5.
Требуемая точность оценки некруглости принимается равной 0,4 мкм. По формуле (5.2) и табл. 5.1 получаем при доверительной вероятности Р=0,95 т 3,85 0,515а/0,42=6,36. Принимаем т=7.
Из предыдущих экспериментов найдено, что наименьшее изменение скорости ов, при котором замечается изменение некруглости, равно 5 м/мин. Поэтому весь диапазон изменения скорости vs можно разбить на участки дискретными точками, число которых п— (90—10)/5= 16. Ближайшее большее число Фибоначчи равно 21, поэтому можно вести поиск по 20 дискретным точкам (4 лишние, где опыты не ставятся). Поиск по 20 дискретным точкам, как это видно из рис. 6.6, может быть закончен максимум за 6 и ми
213
нимум за 3 серии опытов. Наиболее вероятным будет завершение поиска за 5 серий. Тогда это потребует /V| = 5-7=35 замеров некруглости.
Если провести по одному эксперименту во всех 16 точках, то это потребует всего 20 замеров некруглости (5 уже было проведено при постоянном уровне 1>в), т. е. в данном случае статическое планирование оказалось более / выгодным. Результаты экспериментов приведены на рис. 6.8. Они ясно показывают, что оптимальное значение скорости ведущего круга равно 45...50 м/мин.
6.3. ГРАДИЕНТНЫЕ МЕТОДЫ МНОГОФАКТОРНОГО ПОИСКА [3, 53]
6.3.1. Планирование и анализ результатов эксперимента А исходной точке
Процесс многофакторного поиска оптимума градиентными методами начинается с выбора в факторном пространстве исходной точки поиска. Данная процедура не является формализованной. Поэтому решение о выборе координат исходной точки полностью зависит от информации об оптимизируемом процессе или объекте, которая имеется в распоряжении исследователя, а также от интуиции и опыта последнего. Чем ближе исходная точка к области оптимума, тем меньше затраты на поиск. Целью эксперимента на данном этапе является определение наиболее «перспективного» направления в факторном пространстве, двигаясь вдоль которого можно кратчайшим путем достигнуть области оптимума. Это направление определяется на основе анализа линейной модели, построенной по данным эксперимента, проведенного в окрестностях исходной точки поиска, с помощью полного или дробного (в зависимости от k) факторного плана с центром в исходной точке. Наиболее экономным будет насыщенный план, однако чем более дробной является реплика, тем с большей погрешностью оцениваются параметры модели.
Очень важно правильно выбрать интервалы варьирования факторов. Неудачное соотношение между их величинами обусловливает повышение трудоемкости поиска, так как выбор масштаба факторов оказывает влияние на вид нормализованной модели и соответствующую форму поверхности отклика. С другой стороны, чем уже интервалы варьирования факторов, тем выше точность линейной аппроксимации. Однако ни формализованного способа, ни общих рекомендаций по выбору интервалов варьирования факторов также нет.
После построения плана и его реализации определяются параметры линейной модели и оценивается их статистическая значимость, для чего вычисляются дисперсия воспроизводимости и доверительные интервалы для параметров (см. § 5.5.1). Затем проверяется гипотеза об адекватности линейной модели в данной локальной области факторного пространства.
Если модель адекватна и все ее параметры статистически значимы, то следует переходить к следующему этапу поиска — крутому восхождению (спуску) в найденном перспективном направлении (по градиенту). Если же при адекватности линейной модели часть ее параметров оказывается незначимой, то прежде чем приступить ко второму этапу поиска, следует рассмотреть ряд гипотез о причинах незначимости эффектов: 1) неудачный выбор интервалов варьирования; 2) включение' факторов, не влияющих на параметр оптимизации; 3) значительная погрешность оценки отклика; 4) очень высока дробность реплики и влияние фактора искажено влиянием парных взаимодействий.
Для проверки первой гипотезы следует расширить интервал варьирования для незначимых факторов и поставить новую серию опытов. При этом иногда выгодно перенести центр эксперимента в точку факторного пространства, соответствующую наилучшим результатам предыдущего эксперимента. Если и в этом случае проверяемые факторы останутся статистически незначимыми, то: а) принимается вторая гипотеза и они исключаются из дальнейших экспериментов; б) при более осторожной тактике производится достройка плана с целью проверки четвертой гипотезы. Достройку плана можно осуществлять несколькими методами: 1) методом «перевала» — у исходной реплики изменяют знаки на обратные (в этом случае основные эффекты не сме
214
шиваются с парными эффектами взаимодействия); 2) переходом к полному факторному эксперименту; 3) переходом к реплике меньшей дробности.
Для уменьшения погрешности оценки отклика (третья гипотеза) следует увеличить число параллельных опытов в каждой точке факторного пространства.
Реализация любого способа проверки причины незначимости влияния некоторых факторов в модели требует значительных затрат времени и средств на дополнительные эксперименты на первом этапе поиска. Поэтому можно и. не следовать строго правилу «двигайтесь по всем факторам», а пойти на некоторый риск и двигаться только по значимым факторам.
При анализе результатов первого этапа поиска возможны случаи, когда линейная модель будет неадекватной. Это значит, что могут оказаться значимыми эффекты взаимодействия факторов или сумма коэффициентов при квадратичных членах модели 2дн. Оценкой этой суммы служит разность аа и значения отклика в центре плана Ya. Если эта разность превосходит погрешность воспроизводимости, то гипотеза незначимости коэффициентов ац не может быть принята. Однако надо учитывать, что. если ац имеют разные знаки, то сумма их может оказаться незначимой и при значимых квадратичных эффектах.
Если линейная модель оказалась неадекватной, то может быть принято одно из следующих решений: 1) уменьшить интервал варьирования; 2) достроить план для получения квадратичной модели с эффектами взаимодействия (ПФЭ); 3) включить в модель эффекты взаимодействия и двигаться по градиенту, направление которого будет меняться после каждого шага.
Иногда отказываются от построения адекватной модели, чтобы на нескольких опытах проверить возможность движения по градиенту. Это решение часто принимается в тех случаях, когда опыты трудоемки.
Особый случай возникает при использовании насыщенных планов, так как при значимости всех параметров модели невозможно оценить ее адекватность. Только движение по градиенту в данном случае может подтвердить правильность предположения о том, что параметры модели являются оценками линейных эффектов.
Пример 6.2. Необходимо определить оптимальные условия суперфинишной обработки цилиндрической детали охватывающей головкой с брусками марки 24А М40 СМ1 К. В качестве параметра оптимизации выбрана производительность процесса, характеризуемая интенсивностью съема припуска Q (мкм/мин), в качестве влияющих факторов — частота колебаний брусков f (мин-1), частота вращения детали п (об/мин), давление в гидроцилиндре, прижимающем бруски к детали, р (МПа), амплитуда осцилляции А (мм).
Решение. Исходный уровень факторов и интервалы их варьирования приведены в табл. 6.1. Планом исходного эксперимента была выбрана полуреплика от ПФЭ 24 (см. табл. 6.2).
Расчеты по формулам (5.32) и (5.33) дали следующие результаты: аа= = 32; ai =-0,5; а2=6; а3=1,75; а«=3,25. Опыт в нулевой точке факторного пространства повторялся 10 раз.
Расчет по формуле (5.35) показал, что дисперсия воспроизводимости =1,37. Доверительный интервал для параметров модели определялся по
Табл. 6.1 Условия исходного эксперимента
Пределы варьирования Факторы (их обозначения)
f (*.) п (*,) р (*>) А (х«)
Верхний уровень (+1) 1020 31,5 2,5 4
Нижиий уровень (—1) 750 20 2,0 3
Основной уровень (0) 885 25,75 2,25 3,5
Интервал варьирования 135 5,75 0,25 0,5
215
Табл. 6.2. План и результаты исходного эксперимента
и ±2 х3 Х4 Y = Q
1 - 21
2 + — + — 26
3 — — + + 31
4 — + — + 42
5 + + — 32
6 + — — + 26
7 — + + 36
8 + + + + 42
формуле (5.36) при доверительной вероятности Р = 0,95: А (а.) = ± 2,365 х X 1,17/]/ 8 =±0,98. Поскольку laj < 0,98, то этот параметр считается статистически незначимым.
Остаточная дисперсия вычислялась по (5.37):
S2 = -----j [212 ± 2 • 262 ± 312 ± 2 • 422 ± 322 ± 362 — 8 (62 ± 1,752 ±
± 3,25а ± 322)] = 3,78.
Наблюдаемое значение критерия Фишера FB = 3,78/1,37=2,76. Согласно табл. П.7, при доверительной вероятности Р=0,95 Рк=3,86. Поскольку FH< <РК, линейная модель адекватна.
Для проверки причины незначимое™ ai нужно достроить план до полного факторного, т. е. провести еще 8 опытов. Принята гипотеза, что влияние фактора Л] действительно очень слабо и его можно из дальнейшего исследования исключить, зафиксировав на нижнем уровне (так как щ-СО). Решено двигаться в трехфакторном пространстве (п, р, А) по градиенту.
6.3.2. Поиск области оптимума
Градиентом функции называется вектор
k
dY -» дх, в‘’
dY
где —----— частные производные функции отклика по i-му фактору; е,—еди-
дх
ничный вектор, направленный по оси i-ro фактора.
Так как для линейной модели
dY
дх, ~а‘’
(6.6)
то в задачах поиска градиентными методами k
grad Y = ai е
Изменяя факторы пропорционально значениям а; (с учетом знака), можно
216
двигаться в направлении градиента. Этот путь к экстремуму является самым коротким и быстрым.
Для движения по градиенту необходимо рассчитать координаты проведения будущих опытов в факторном пространстве, задавшись параметром Л, который определяет величину шагов по осям факторов. Не существует формализованного способа выбора Л. При малом значении % замедляется движение к оптимуму, а при слишком большом увеличивается вероятность пропуска области оптимума. При выборе Л следует учитывать возможность фиксирования факторов в некоторых случаях на дискретных, вполне определенных уровнях. Например, при наличии в станке зубчатой коробки скоростей и подач последние можно фиксировать только на определенных уровнях и изменять по закону геометрической прогрессии. Тогда каждому шагу движения по градиенту будет соответствовать определенное изменение значения X.
В общем случае шаг изменения координат (факторов) для движения по градиенту
Д/ц;=]А,а(ДХ<1 (6.7)
где Д/iij—изменение уровня i-ro фактора (отсчет ведется от нулевого уровня) на j-м шаге; / — номер шага крутого восхождения (спуска); % — параметр (0,2...4); а,—параметр модели для i-ro фактора; &Х,—интервал варьирования i-ro фактора.
Если фактор изменяется дискретно, то его изменение при движении по градиенту происходит путем последовательного перехода от одного уровня к другому, или, при очень коротких шагах, можно переходить по четным уровням, пропуская нечетные. Тогда, обозначив номер этого фактора i=l, из (6.7) получим
Если крутое восхождение оказалось эффективным и в результате его достигнут оптимум, то экспериментатор может закончить исследование или продолжить его с целью подробного изучения области оптимума. Если же в результате эффективного крутого восхождения оптимум не достигнут, то исследование следует продолжать с целью дальнейшего поиска оптимума. Для оценки ситуации необходимо принять за центр линейного плана нового эксперимента точку факторного пространства, соответствующую нанлучшему результату крутого восхождения (движения по градиенту). Когда после реализации нового линейного плана выявилось, что линейная модель неадекватна, факт достижения оптимума является достаточно вероятным. Когда же новая модель (линейная) адекватна, следует повторить крутое восхождение по новому градиенту.
Если при реализации матрицы планирования на первом этапе получены достаточно высокие значения параметра оптимизации и при крутом восхождении улучшить их не удалось (движение по градиенту оказалось неэффективным), то может быть принято одно из решений: 1) закончить исследование (оптимумом считается точка факторного пространства, в которой получен наилучший в данном плане результат); 2) подробно изучить область первого плана.
Недостатком описанного выше простого градиентного метода поиска является зависимость направления градиента от соотношения интервалов варьирования (масштабов) факторов. При неудачном сочетании поиск требует большего числа крутых восхождений. Однако методов, позволяющих до отыскания оптимума найти наилучшее сочетание интервалов варьирования (масштабов) факторов, нет.
Если многомерная поверхность отклика имеет особенности типа «гребней» или «оврагов», то эффективность поиска экстремума методом градиента резко снижается. В качестве примера на рис. 6.9 показана при помощи линий уровня топография двухфакторной поверхности отклика «овражного» типа. Эллипсы постоянного уровня оказались сильно вытянутыми. Числа, относящиеся к линиям уровня, указывают значения параметра оптимизации. Опти-
217
Рис. 6.9. Схема градиентного поиска при двухфакторной поверхности отклика «овражного» типа'
*1
Рис. 6.10. Схема градиентного поиска при двухфакторной поверхности отклика «овражного» типа с искривлением
мум — точка О, где параметр оптимизации имеет минимальное значение. Исходной точкой поиска является Аь Движение по градиенту gi стало неэффективным после достижения точки А3. В этой точке опять ставится ПФЭ для определения градиента g%. Движение по нему становится неэффективным после достижения точки Аз, которая в свою очередь становится центром нового ПФЭ, и т. д.
Таким образом, движение к оптимуму идет очень медленно. Если «овраг» прямой, то к цели быстро приведет движение по вектору vit проведенному через точки Aj и А3. Проверить гипотезу об отсутствии искривления «оврага» или «гребня» можно, сравнив, направления градиентов gt и g3. Если они совпадают, то принимается гипотеза о прямолинейности «оврага». Условие параллельности градиентов gi и g3 для k факторов имеет вид
ф;= аи/а;3=const, (6.8)
где аи — параметры линейной модели, полученные реализацией ПФЭ в точке Aj; а,з — параметры линейной модели, полученные реализацией ПФЭ в точке Аз.
Поскольку параметры линейных моделей определялись с некоторыми одинаковыми дисперсиями и имеют одинаковые конечные доверительные интервалы, то условие (6.8) следует понимать как статистическую гипотезу, требующую проверки. Для этого сначала вычисляется среднее значение отношения параметров модели
1=1
и доверительный интервал Л(а<) по (5.36). Гипотеза о параллельности гради-—> —►
ентов gi и g3 принимается, если для всех i соблюдается неравенство
at
На рис. 6.10 показан пример «овражной» поверхности с искривлением. И в данном случае простой градиентный метод поиска из исходной точки Aj очень медленно приводит в точку оптимума, но ускоренное движение по век-218
тору t'i в данном случае невозможно, так как после каждого шага направление его изменяется неизвестным для исследователя образом. Для ускорения поиска в случае с искривленной «овражной» поверхностью предлагается следующий метод.
Из двух случайно выбранных исходных точек Ао и А^ методом простого градиентного поиска определяются точки А2 и А3, где движение по градиентам go и gi становится неэффективным. Затем, если в точке А3 значение параметра оптимизации лучше, чем в А2, делается из нее большой шаг (или 2—3 шага) по вектору v2, проведенному через точки А2 и А3, до точки Л<. Из А< выполняется простой градиентный поиск до точки А$ и затем из нее снова совершается большой шаг по вектору из, проведенному через точки А3 и Д5, и т. д. Параметрическое уравнение прямой, проходящей через две фиксированные точки А3 и А2 в й-факторном пространстве, имеет вид
Xi=xi2+(Xi3~ xi2)t, (6.9)
где I — номер фактора; хц, xt3 — координаты соответственно точек А2 и А3; t — параметр.
От значения параметра t зависит шаг поиска. При /=1, согласно формуле (6.9), xt =х>з, поэтому всегда />1. Формальных способов выбора t нет, и он основывается на имеющейся информации об исследуемом процессе и интуиции исследователя.
Пример 6.2 (продолжение). Станок для суперфинишной обработки имеет коробку скоростей, обеспечивающую следующий ряд частот вращения: 20, 25; 31; 5; 40; 50; 63; 80; 100; 125; 140; 160 об/мин. Так как из всех параметров а2 является наибольшим, принято решение двигаться по этому фактору от основного уровня по=25 об/мин по следующим дискретным значениям: «1 = = 63; /12=100; п3= 125; «4=160. Тогда
. 63 — 25 „ 100 — 25 , 125 — 25
1, = ------------= 1,1; 1» =------------= 1; к. =--------------= 0,9;
1-6-5,75 2-6-5,75 3-6-5,75
Координаты второго фактора вычислялись по формуле Xll = Xi0A-4-Дуа/ЛХр Р1 = 2,25Д- 1-1,1-1,75-0,25 = 2,7; р2 = 2,25 + 2-1 • 1,75-0,25 = = 3,1; рз = 2,25 + 3-0,97-1,75-0,25 = 3,5. Так как максимально допустимое давление, в гидроцилиндре составляет 3,5 МПа, то после третьего шага движение по этому фактору пришлось прекратить, зафиксировав его на самом высоком уровне.
Аналогично получаем At=3,5+1 • 1,1 -3,25-0,5=5,3. Так как амплитуда осцилляции на данном станке не может превышать 4 мм, то на этом уровне она поддерживалась на всех шагах движения по градиенту.
Координаты точек факторного пространства, в которых производился последовательный поиск, и результаты эксперимента:
i f п Р А У
1 750 63 2,7 4 76
2 750 100 3,1 4 125
3 750 125 3,5 4 120
4 750 160 3,5 4 57
Видно, что первый и второй шаги крутого восхождения были эффективны. Третий шаг был уже неэффективным, так как производительность станка уменьшилась. Для дополнительной проверки гипотезы о неэффективности дальнейшего продвижения в том же направлении был сделан четвертый шаг, который показал резкое уменьшение производительности. Таким образом, дальнейшее продвижение по градиенту после второго и третьего шагов не имеет смысла. Поэтому следует проанализировать создавшуюся ситуацию и принять решение о дальнейших опытах.
219
б.З.З. Планирование и анализ результатов эксперимента в области оптимума
Подробное изучение поведения параметра оптимизации в области факторного пространства, содержащей точку оптимума, производится при помощи моделей второго порядка. Для их построения применяются композиционные планы, что дает возможность использовать результаты опытов линейного плана, реализованных для выяснения ситуации после завершения крутого восхождения. Если поставлена задача при помощи модели описать с одинаковой точностью поведение параметра оптимизации во всех направлениях, можно-применять ротатабельные планы. Реализация композиционного плана позволяет получить модель в виде (5.30), адекватно описывающую поверхность-отклика в области оптимума. Однако анализировать уравнение второго порядка в такой форме сложно. Поэтому его иногда предварительно приводят к каноническому (стандартному) виду.
Каноническое преобразование многофакторной модели второго порядка заключается в выборе новой системы координат, в которой уравнение принимает вид
^-^ = М = М+--- + ^2, (6.10)
где Ув — значение параметра оптимизации в центре Н новой системы координат; Z], 7.1, ..., Z* — новые оси координат, повернутые в факторном пространстве на некоторый угол относительно осей xi, х2, .... хь; &ц, b22, .... bkh—параметры модели.
Уравнение (6.10) позволяет легко определить геометрические характеристики поверхности отклика и провести ее анализ. Для приведения исходной модели к каноническому виду переносят начало координат и поворачивают оси координат так, чтобы коэффициенты при линейных членах и парных взаимодействиях были равны нулю. Расчеты по каноническому преобразованию модели рекомендуется выполнять с помощью ЭВМ, так как они требуют значительных затрат времени. Вручную вычисления целесообразно вести только при числе факторов не более трех.
Для параллельного переноса координат исходное уравнение дифференцируют по каждому фактору и приравнивают частные производные нулю. Решая систему полученных (линейных) уравнений типа
k
д¥ VI
= ai + 2j a‘iXi + 2а“Х‘ = °’
/=1
можно найти координаты нового центра Н в старых осях координат (хщ, х2в, .... х^в). Подставляя эти новые координаты в исходную модель, можно определить значение параметра оптимизации в центре Н (Ув),
Для определения параметров Ьц необходимо решить характеристическое уравнение
(ап — Ь) 0,5а12 0, .. 0,5alfe
0,5а21 (а22 0,5а23
/(*) = 0,5а31 0,5а32 (азз — = 0. (6.11)
°-41 0,5аА2 °>4з
Корни этого уравнения й-го порядка являются искомыми параметрами. Если все параметры Ьц отличны от нуля и центр Н лежит в области эксперимента, то возможны следующие случаи: 1) все Ьы<0, тогда в центре Н параметр оптимизации принимает максимальное значение; 2) все Ьы>0, в центре Н зна-
220
Табл. 6.3. Условия контрольного эксперимента
Факторы (их обозначения)
Пределы варьирования Л (X.) Р (*а) Л (х.)
Верхний уровень (4-1) 125 3,3 3,8
Нижний уровень (—1) 80 2,7 3,2
Основной уровень (0) 102,5 3,0 3,5
Интервал варьирования 22,5 0,3 0,3
Табл. 6.4. План и результаты контрольного эксперимента
и 1 Хг 1 1 У и
1 — 76
2 + — 70
3 — 4- —- 110
4 4- 4- — 100
5 — — 4- 105
6 4- — 4- 86
7 — 4- 4- 100
8 + 4-_ + 80
Табл. 6.5. Расширенная матрица ЦКРУП второго порядка
и х2 *3 х4 *2*3 Х2Х4 *3*4 2 х2 2 *3 2 х4
1 —I —1 —1 + 1 +1 +1 +1 1+1 4-1 1 76
2 + 1 —1 —1 —1 —1 +1 +1 4-1 4-1 1 70
3 —1 + 1 —1 — 1 +1 —1 +1 4-1 4-1 НО
4 + 1 +1 —1 + 1 —1 —1 +1 4-1 4-1 100
5 —1 — 1 +1 + 1 —1 —1 +1 4-1 4-1 105
6 + 1 —1 + 1 — 1 +1 —1 +1 + 1 4-1 86
7 —1 + 1 + 1 — 1 —1 +1 +1 4-1 4-1 100
8 + 1 + 1 + 1 + 1 +1 +1 + 1 4-1 + 1 80
9 —1,682 0 0 0 0 0, 2,83 0 0 112
10 1,682 0 0 0 0 о| 2,83 0 0 72
11 0 —1,682 0 0 0 0 0 2,8с 0 52
12 0 1,682 0 0 0 0 0 2,83 0 95
13 0 0 —1,682 0 0 0 0 0 2,8с 93
14 0 0 1,682 0 0 0 0 0 2,83 102
15 0 0 0 0 0 0 0 0 0 124
16 0 0 0 0 0 0 0 0 0 120
17 0 0 0 0 0 0 0 0 0 120
18 0 0 0 0 0 0 0 0 0 123
19 0 0 0 0 0 0 0 0 0 122
20 0 0 0 0 0 0 0 0 0 126
чение параметра оптимизации минимально; 3) часть параметров Ьц меньше, а часть больше нуля, тогда движение из центра только по тем Zt, для которых Ьц>0, ведет к увеличению параметра оптимизации.
Пример 6.2 (окончание). Для выяснения ситуации, создавшейся после крутого восхождения, был поставлен полный факторный эксперимент 23 с цен
221
тром, соответствующим наилучшему результату, т. е. второму шагу движения по градиенту. В табл. 6.3 и 6.4 приведены условия, план и результаты контрольного эксперимента. Значение А, соответствующее центру плана, было решено принять равным 3,5 мм.
Расчет по формулам (5.32) и (5.33) дал следующие результаты: <го=9О,9; «а=—6,87; а3=6,65; а4=1,8. Остаточная дисперсия по формуле (5.67):
S2 = о---5----71762 + 7°2 + 1102 + ЮО2 + 1052 + 862 + 1002 + 802 — 8 (90,92+
о 3 — 1
+ 6,87s + 6,65s + 1,8s)] = 19.
Наблюдаемое значение критерия Фишера FB = 19/1,37= 13,8. Поскольку FB>FB (13,8>3,86), то линейная модель неадекватна. Поэтому принимается решение построить модель второго порядка при помощи центрального композиционного ротатабельного униформплана (ЦКРУП), Его расширенная матрица и результаты опытов приведены в табл. 6.5. К проведенным 8 опытам линейного плана были присоединены 6 опытов в звездных точках и 6 — в центре плана. Параметры модели найдены по формулам (5.41). Константы для этих формул определялись из табл. 5.29:
20 4 20
а0 = 0,1633 2 Yu — 0,0568 2 2 = 0,1633 - 1988 — 0,0568 (1256,21 +
и=1 1=2 и=1
+ 1161,01 + 1278,85) = 120,67;
20
а2 = 0,0732 2 х2иУи = 0,0732 (— 122,28) = — 8,95; ы=1
а3 = 0,0732 128,33 = 9,39; <u = 0,0732 • 30,14 = 2,21;
20
«23 = 0,125 2 (x2x3)aYu = 0,125 (— 5) = — 0,625;
U=1
ам = 0,125 (— 23) = — 2,88; «34 = 0,125 (— 75) = — 9,4;
20 4 20 20
в22= 0,0625 2 4К«+0,0069 2 2 *2Л-0-05682 У„=0,0625.1256,21+ «=! i=2 u=l и=1
+ 0,0069 • 3696,07 — 0,0568 • 1988 = — 8,91;
а33 = 0,0625 • 1161,01 +0,0069 • 3696,07 — 0,0568 - 1988 = —14,9;
а« = 0,0625 • 1278,85 + 0,0069 • 3696,07 — 0,0568 1988 = —7,49.
Дисперсия воспроизводимости по формуле (5.43):
6
Согласно (5.42), дисперсии параметров модели:
52(ло) =0,1663-5,5=0,92; S2(«,) =0,0732-5,5=0,403;
Ss(a<j) =0,125 • 5,5=0,69; S2(atl) =0,0695 • 5,5=0,382.
Доверительные интервалы для параметров (формула (5.39)) при доверительной вероятности 0,95:
Д (а0) = ± 1,729 У 0,92 =±1,66; Д (а,-) = ±1,729 V 0,403 = + 1,1;
222
л (а0) = ± 1.729]/ 0,69 = ± 1,43; А (ан) = ± 1,729 V0,382 = ± 1,07.
В соответствии с доверительными интервалами можно округлить значения параметров модели следующим образом: ао=120; а2=—9; а3=9,5; щ= =2; О2з=0; Oj^——3;.Оз4= 9,5; о22=—9; д33= 15; Щ4=—7,5.
По формуле (5.44) дисперсия адекватности
20 — 8 — 5 <гб1.2-а7,5) = 33.4.
Наблюдаемое значение критерия Фишера FB = 33,4/5,5=6,07. Критическое значение критерия (табл. П.7) FK=6,26. Поскольку FB<FK, квадратичная модель адекватна.
Затем при помощи модели процесса суперфиниширования
У = 120 — 9х2 + 9,5х3 + 2х4 — Зх2*3 — 9,5*3*4 — 9*^ — 1,5х3 — 7,5х4
уточнено положение оптимальной точки в факторном пространстве. Для этого приравнивались к нулю частные производные:
дУ „ дУ
—----= — 9— 3*4 — 18*2 = 0;
, =9,5 — 9,5*4—30*3 = 0;
дхз
дУ
—-----= 2 — 3*2 — 9,5*3 — 15*4 = 0.
<3*4
Главный определитель этой системы
18 О
D= 0 30
3 9,5
3
9,5 = 6205,5
15
не равен нулю, поэтому система имеет решение. Дополнительные определители системы:
-9 0 3
Аа = | 9,5 30 9,5 = — 3372;
2 9,5 15
18 —9 3
D3 = 0 9,5 9,5 = 1881;
3 2 15
18 0 —9
Dt = 0 30 9,5 = 265,5.
3 9,5 2
Координаты нового центра: х2я=—3372/6205,5=—0,543; хзя= 1881/6205,5= = 0,30; *4В = 265,5/6205,5 = 0,043. После подстановки этих значений в модель Ун = 120 + 9 0,543 + 9,50,30 + 20,043 + 3-0,54-0,043 — 9,5-0,30,043 — —9-0,54а — 15-0,30а — 7,5-0,0432 = 123,6.
Характеристическое уравнение для определения параметров канонической модели (6.10):
/(*) =
(-9-6) 0
0,5 (- 3)
0 0,5 (—3) I
(— 15 — 6) 0,5 (— 9,5) = (—9 — 6) (— 15 — 6) (—7,5 — 0,5(— 9,5) (—7,5 —6)|
—6) —(—15 —6) • 0,5 (—3) 0,5 (—3) —(— 9 — 6) • 0,5 (-9,5) • 0,5 (—9,5)=0; 6» + 31,56а + 340,16 + 1249,3 = 0.
223
Для определения знака корней характеристического уравнения используется критерий. Гурвица. Для уравнения 3-й степени условиями отрицательности всех его корней являются положительность всех его коэффициентов (это условие выполнено) и выполнение неравенства Аа=31,5 • 340,1 —1249,3>0. Поэтому все Ь;,<0. Следовательно, новый центр (начало координат) и является оптимумом.
В натуральном масштабе ган= 102,5—0,543 • 22,5»90 об/мин; рн=2,7+ + 0,3 0,3 — 2,8 МПа; Ан = 3+0,04 • 0,3«3 мм.
6.4. ПОСЛЕДОВАТЕЛЬНОЕ СИМПЛЕКС-ПЛАНИРОВАНИЕ
Последовательное симплекс-планирование, или просто симплекс-планирование, является одним из методов многофакторного поиска экстремума. Оно состоит в следующем.
Зная факторы, влияющие на процесс, выбирают их значения для исходной серии опытов. Если факторов k, то серия содержит (6+1) опыт, причем опыты ставятся в точках факторного пространства, образующих 6-мерный симплекс.
Симплекс — выпуклая геометрическая фигура (многогранник), образованная множеством (6+1) независимых вершин в 6-мерном пространстве. Так, например, на плоскости симплекс образуется любыми тремя точками, не лежащими на одной прямой, в трехмерном пространстве — любыми четырьмя точками, не лежащими в одной плоскости (т. е. любая треугольная пирамида), и т. д.
Симплекс называют регулярным, если все расстояния между его вершинами равны (равносторонний треугольник, тетраэдр и т. д.). При симплекс-планировании обычно используют регулярные симплексы. Но регулярность симплекса зависит также от масштаба координат факторного пространства. Соответствующим преобразованием системы координат можно нерегулярный симплекс сделать регулярным, и наоборот.
После проведения первой серии опытов результаты их сравнивают между собой и выбирается опыт (вершина симплекса), где результат наихудший. Затем вычисляются координаты точки, симметричной наихудшей вершине симплекса по отношению к оставшейся после ее отбрасывания грани. Эта новая точка совместно с оставшимися образует новый симплекс. Доказано, что если поверхность отклика в области, ограниченной симплексом, близка к гиперплоскости, то центр нового симплекса сдвигается к области оптимума в. направлении градиента (или антиградиента).
Затем в новой точке ставится опыт, вновь сопоставляются результаты опытов во всех вершинах симплекса (включающего эту новую точку), опять выявляется наихудшая точка, которая заменяется ее зеркальным отражением относительно центра противолежащей грани, и т. д. Процесс отбрасывания наихудших вершин и построения симплексов повторяется, в результате чего происходит последовательное перемещение к оптимуму по линии, близкой к линии градиента. В данном случае движение к оптимуму ведется не после серии опытов, как при использовании градиентных методов, а после каждого, начиная с (6+1)-го, опыта. Достигнув почти стационарной области, близкой к оптимуму, симплексы начинают вращаться вокруг своей наилучшей точки — «зацикливаются». Это служит сигналом, что крутое восхождение в область оптимума можно считать законченным.
В качестве примера на рис. 6.11 показана схема поиска оптимума методом симплекс-планирования для двух факторов. Вначале было поставлено три опыта в вершинах 1, 2 и 3 исходного симплекса. Опыт в точке 2 дал наихудшие результаты. Точка 4 является отражением худшей точки 2 относительно грани 1—3. В новом симплексе 1—3—4 (после реализации в точке 4) худшее значение отклика оказалось в точке 1. Ее зеркальным отражением относительно грани 3—4 является точка 5. Последовательное отбрасывание наихудших точек симплекса и зеркальное их отражение приводит на 16-м опыте в область оптимума, где происходит «зацикливание» симплексов вокруг точки 16.
224
Рис. 6.11. Схема двухфакторного поиска методом симплекс-планирование
Однако при движении к оптимуму бывают ситуации, когда на «гребне» поверхности отклика движение прекращается из-за «колебаний» симплекса вокруг своего ребра. Например, в симплексе 11—12—13 наихудшей оказалась точка 12, при ее отражении получаем точку 21, в которой параметр оптимизации также имеет наихудшее значение для вновь образованного симплекса. Отражение точки 21 опять приводит в точку 12. В таких случаях отражают ту вершину спмплекса, в которой параметр оптимизации лучше, чем в точке 12, но хуже, чем во всех остальных, т. е. точку 11.
Для симплекс-планирования при поиске оптимума необходимо: 1) строить матрицы исходного симплекса; 2) осуществлять движение к оптимуму, применяя определенные правила отражения точек с наихудшим значением параметра оптимизации; 3) определять момент достижения области экстремума. Важно также уметь перейти от симплекс-плана к планированию эксперимента, выполняемого для описания области оптимума.
На первом этапе матрица исходного симплекса строится для нормализованных факторов. При этом центр симплекса помещается в начало координат,
Рис. 6.12. Схемы исходных симплексов: а — двухфакторного; б — трехфакторногЦ
15. Зак. 1001
225
одна из вершин v^+i — на ось хь, а остальные вершины — симметрично относительно координатных осей. На рис. 6.12 показано такое расположение для двух- и трехфакторного симплекса. Тогда координаты вершин симплекса равны соответствующим радиусам вписанных (г,) и описанных (Л<) гиперсфер симплексов размерности от 1 до k. Так, координаты вершины а, двухфакторного симплекса—(7?!; -r2)t вершины v2 — (-Rf, г2), а вершины v3— (0; R2).
В общем случае координаты вершин исходного £-факторного симплекса определяются строками матрицы
-/•] -г2 -г3 ~г4 ... -гк\
R1 г2 + ~ г4 • • • — rk
О R2 — г3 — г4 ... —rk
С= 0 0 R3 -Г4 ... -rk.
О 0 0 R4 ... -rk
0 0 0 0 ... Rk
Если длина ребра симплекса равна 1, то радиусы вписанной и описанной сфер можно вычислить по формулам:
= J-----------; Ri = Jfj------ (6.12)
V2i(i + 2) V 2(1+1)
где 1=1, 2, 3, .... k.
В качестве примера в табл. 6.6 приведены нормализованные координаты исходного симплекса при £=10. Если £<10, то координаты его вершин можно получить из этой же таблицы, выделив в ней k первых столбцов и £+1 первых строк. В данной таблице N соответствует числу опытов в исходной серии.
При движении в область оптимума целесообразно пользоваться натуральным масштабом факторов. Поэтому координаты исходного симплекса пересчитываются из нормализованного масштаба в натуральный. Если для каждого 1-го фактора задан основной уровень XiCi и интервал варьирования AXi, то
Xiu ~ XiQ + AXiXi и, (6.13)
где xiu—нормализованное значение 1-го фактора в zz-м опыте; Х,„—значение 1-го фактора в u-м опыте в натуральном масштабе.
Кроме регулярных, в качестве исходных можно применять нерегулярные симплексы, которые являются более удобными в тех случаях, когда по резуль-
Табл. 6.6. Координаты вершин исходного симплекса при £=10
Нормализованные факторы
N Х1 1 х< I X, | X, | X. I Х9 | *10
1 -0,5 —0,289 —0,204 —0,158 —0,129 —0,109 —0,095 —0,083 -0,075 —0,067
2 0,5 —0,289 —0,204 —0,158 —0,129 —0,109 —0,095 —0,083 —0,075 —0,067
3 0 0.578* —0,204 —0,158 —0,129 —0,109 —0,095 —0,083 —0,075 —0,067
4 0 0 0,612 —0,158 —0,129 —0,109 —0,095 —0,08 —0,075 —0,067
5 0 0 0 0,632 —0,129 —0,109 —0,095 —0,083 —0,075 —0,067
6 0 0 0 0 0,645 —0,109 —0,095 -0,083 —0,075 —0,067
7 0 0 0 0 0 0,655 —0,095 —0,083 —0,075 —0,067
8 0 0 0 0 0 0 0,611 —0,083 —0,075 —0,067
9 0 0 0 0 0 0 0 0,666 —0,075 —0,067
10 0 0 0 0 0 0 0 0 0,671 —0,067
11 0 0 0 0 0 0 0 0 0 0,674
226
Tao л. 6.7. Исходный симплекс для k — 2
Табл. 6.8. Исходный симплекс для k = 3
N хг N Xi *2 Ха
1 2 3 —1 +1 +1 d 2 +i ° —1 +1 —1 +1 —1 —1 +1 +1 +1 —1 —1 +1
Табл. 6.9. Исходный симплекс для k = 4
N Х1 Х2 Х3 Xi
1 —1 +1 +1 +1
2 +1 —1 +1 +1
3 +1 +1 —1 +1
4 +1 + 1 + 1 —1
5 —0,618 —0,618 -0,618 —0,618
Табл. 6.10. Исходный симплекс для k = 5
N Xi хл Xi *6
1 —0,0488 +1 —1 —1 0,8139
2 0,8139 —0,0488 —1 —1 —1
3 —1 0,8139 —0,0488 + 1 —1
4 —1 —1 0,8139 —0,0488 + 1
5 + 1 —1 —1 0,8139 —0,0488
6 + 1 +1 + 1 + 1 + 1
тэтам их реализации необходимо рассчитать параметры линейной модели процесса (табл. 6.7...6.12).
Движение симплекса в область оптимума производится по правилу отражения, когда вершина симплекса с наихудшим значением параметра оптимизации заменяется новой, симметрично отраженной по отношению к противолежащей грани. Координаты новой вершины в натуральном масштабе определяются по формуле
k
и=1
где xft+2
— координата по оси X новой вершины fe-факторного симплекса; k — количество факторов; X* — координата вершины с наихудшим значением параметра оптимизации; Xiu — сумма координат (по оси Х;) остальных факторов за исключением X*.
После достижения области экстремума можно попытаться уточнить положение оптимальной точки, перейдя к описанию области при помощи компози-
15*
227
Табл. 6.11. Исходный симплекс для /г = 6
N Xi X2 XA X< xt X»
1 0 +1 +1 —1 —1 +1
2 +1 0 —1 +1 —1 +1
3 +1 —1 0 —1 +1 +1
4 —1 +1 —1 0 +1 +1
5 —1 —1 + 1 + 1 0 +1
6 —0,707 —0,707 —0,707 —0,707 —0,707 —1
7 0,707 0,707 0,707 0,707 0,707 —1
Табл. 6.12. Исходный симплекс для k = 7
N Xl X2 x3 Xi Xt, Xi Xt
1 —1 —1 —1 +1 + 1 +1 —1
2 +1 —1 —1 —1 —1 +1 +1
3 —1 +1 —1 —1 +1 —1 +1
4 +1 +1 —1 +1 —1 —1 —1
5 —1 —1 +1 +1 —1 —1 +1
6 +1 —1 +1 —1 +1 —1 —1
7 —1 +1 +1 —1 —1 + 1 —1
8 +1 +1 +1 +1 +1 +1 +1
циониых планов второго порядка, ядром которых служит симплекс-план. Для случая двух факторов проще всего получается план, состоящий из 6 точек, расположенных в вершинах правильного шестиугольника и включающий некоторое количество опытов в центре (центром в данном случае является точка, вокруг которой зацикливается семейство симплексов). План такого типа показан на рис. 5.16, а его матрица приведена в табл. 5.51.
Параметры нормализованной модели второго порядка определяются по формулам (5.54). Если анализ полученной модели показал, что оптимум находится в точке А с координатами х1Л и +гл, то натуральные координаты этой точки легко определяются по формуле (6.13).
В процессе поиска методом симплекс-планирования может возникнуть ситуация, когда необходимо ввести в экспериментирование еще один фактор. При этом ^-факторный симплекс достраивается до (&+1)-факторного.
У й-факторного симплекса /г + 1 вершина. Координаты (& + 2)-й вершины (&+1) -факторного симплекса определяются следующим образом. По «старым» k осям искомые координаты являются средним арифметическим координат k-факторного симплекса, а по новой (&+1)-й оси координата выбирается исходя из выбранного интервала варьирования нового фактора, размерности симплекса и уровня, на котором поддерживался этот фактор в серии экспериментов, предшествующей достраиванию.
Таким образом, если до достраивания было проделано N экспериментов, то
= х‘-“; (6Л4)
и=т
X(N+V) (4+1) = Xk+l + I+ Я)1*+1 ’ (6-15)
Л1> + 1; m = N — k— 1; i = 1, 2, ... k,
228
где X(W+i) (А+1) — координата новой вершины симплекса по оси (А+1)-го фактора; Х^+1 — уровень (k + 1)-го фактора, на котором он был зафиксирован в предыдущих опытах; ДХ^-р — выбранный интервал варьирования (k + 1)-го фактора; — коды
(k-\- 1)-го фактора, взятые из табл. 6.7 или вычисленные по формулам (6.12), если k + 1 > 10.
Для уменьшения количества опытов при движении к экстремуму можно воспользоваться ускоренным симп-лекс-планированием. Сущность метода ясна из следующего примера (рис. 6.13).
В исходном симплексе 1—2—3 лучшее значение параметра оптимизации было получено в точке 2. Тогда отбрасываются сразу две худшие точки 1 и 3, которые заменяются новыми точек определяются по формулам:
Рис. 6.13. Схема двухфакторного поиска методом ускоренного симплекс-планпрованпя
вершинами 4 и 5. Координаты новых
Хцп+2) — 2Xi0C X;iot ;
Xi(n + 3) = 2Xioc —Х^2от,
где Хцп+2), Хцп+з) — координаты по оси X,- (п+2)-й и (н + 3)-й вершин нового симплекса; X, 00 — координата оставшейся вершины исходного симплекса; XiioT, Х;2от — координаты отбрасываемых вершин.
В новом симплексе наилучшей оказалась вершина 5. На этом основании отбрасываются вершины 2 и 4, которые заменяются вершинами 6 и 7. И далее действуем аналогично. Анализ показывает, что при k = 2 выигрыша по существу нет, однако при /г>2 он может быть существенным. В й-факторном симплексе можно сразу заменять т вершин. Оставшиеся k+1—т вершин вместе с т новыми образуют симплекс с координатами вершин
fe-H—т
Хць+1+1) = k 1 _т ос — Xii от’
7=1
где /= 1, 2, 3, ..., т.
Симплекс-планирование хорошо приспособлено для непрерывного слежения за оптимумом, который по каким-либо причинам сдвигается во времени, так как решение о направлении движения симплекса принимается на основании самых свежих наблюдений (используются только последние fe-f-1 вершины). Процедура симплекс-планирования достаточно формализована и практически не усложняется при увеличении числа факторов. Вычисления просты и не требуют знания специальных разделов математики. Эффективность метода увеличивается с ростом числа факторов. При симплекс-планировании можно использовать и нерегулярные симплексы, что позволяет применять его при оптимизации дискретных параметров (например, параметров режимов резания при ступенчатой их регулировке, когда фактические значения ступеней частоты вращения и подач могут не совпадать со значениями, которые диктуются движением симплекса). Результаты, получаемые при симплекс-планировании, не зависят от формы поверхности отклика.
Недостатком симплексного метода является то, что с его помощью нельзя получить информацию о взаимодействии факторов. Кроме того, стандартной симплекс-процедурой не предусматривается возможность корректирования интервалов варьирования факторов в ходе поиска.
229
Табл. 6.13. Условия эксперимента
Пределы варьирования Факторы (нормализованные факторы)
Л (х,) о РМ S (х3) а (х4>
Основной уровень 7 30 0,5 0,05
Интервал варьирования 2 10 0,2 0,03
Табл. 6.14. Исходный симплекс
N л ’ V S б
1 6 27,1 0,46 0,045
2 8 27,1 0,46 0,045
3 7 35,8 0,46 0,045
4 7 30 0,62 0,045
5 7 30 0,5 0,069
Пример 6.3. Необходимо определить оптимальные условия врезного бесцентрового шлифования роликов диаметром 20 мм из стали ШХ15. Параметром оптимизации в данном случае была некруглость шлифованной детали Н (мкм), которая измерялась кругломером завода «Калибр». В качестве факторов выбраны: превышение оси заготовки h. (мм); скорость ее вращения v (м/мин); снимаемый за один цикл припуск б (мм); поперечная подача s (м/мин).
Табл. 6.15. Симплекс-плширование и результаты опытов при оптимизации бесцентрового врезного шлифования
Номер опыта Симплекс Отброшенная вершина л V S б н
1 1—2—3—4—5 6 22,1 0,46 0,045 4,8
2 1—2—3—4—5 — 8 27,1 0,46 0,045 4
3 1—2—3—4—5 — 7 35,8 0.46 0,045 4,2
4 1—2—3—4—5 — 7 30 0,62 0,045 4,5
5 1—2—3—4—5 — 7 30 0,5 0,069j 3,9
6 2—3—4—5—6 1 8,5 34,4 0,56 0,057 3,7
7 . 2-3—7—5—6 4 8,25 33,7 0,53 0,063 3,2
8 2—8—7—5—6 3 8,87 32,6 0,57 0,072 2,8
9 9—8—7—5—6 2 8,31 38,2 0,66 0,086 2,3
10 9—8—7—10—6 5 9,96 39,5 0,66 0,070 2,2
11 9-8—7—10-11 6 9,19 37,6 0,65 0,089 1,8
12 9—8—12—10—11 7 9,92 40,3 0,74 0,096 1,2
13 9—13—12—10—11 8 9,82 45,3 0,79 0,099 0,8
14 14—13—12—10—П 9 11,14 43 0,78 0,091 0,7
15 14—13—12—15—11 10 11,07 43,6 0,82 0,117 0,7
16 14—13—12—15—16 11 11,73 48,5 0,89 0,112 0,8
17 14—13—17—15—16 12 11,96 49,9 0,9 0,113 0,9
18 14—18—17—15—16 13 13,33 47,2 0,9 0,117 0,8
19 14—18—19—15—16 17 11,57 51,6 0,98 0,138 1,1
20 14—18—19—15—20 16 11,73 44,2 0,85 0,119 0,7
21 14—15—18—20—21 19 11,66 37,4 0,69 0,084 1,6
230
Решение. Для определения координат вершин исходного симплекса использован выделенный фрагмент табл. 6.7 из четырех столбцов и пяти строк. Основные уровни и интервалы варьирования факторов в натуральном масштабе указаны в табл. 6.13. Расчет производился ио формуле (6.13), где коды фактора брались из выделенного фрагмента таблицы. Результаты расчета приведены в табл. 6.14.
Результаты поиска оптимума методом симплекс-планирования приведены в табл. 6.15. Значение Н, которое заносилось в таблицу, является средним арифметическим некруглости пяти деталей, прошлифованных в одинаковых условиях. После 15 опытов симплекс «зациклило», и до 21-го опыта параметр оптимизации не был улучшен. Поэтому с известным приближением можно считать оптимальным следующее сочетание параметров: h=ll мм; о=43 м/мин; s = 0,8 мм/мин; 6 = 0,1 мм.
Пример 6.4. Оптимизировать условия бесцентрового шлифований роликов диаметром 30 мм из стали ШХ15 при постоянных уровнях скорости поперечной подачи s (0,1 мм/мин) и съема 6 (0,05 мм).
Решение. Параметром оптимизации выбрана некруглость шлифованных деталей Н (мкм), а в качестве факторов — превышение оси заготовки h (мм) и скорость ее вращения v (mIwhi). Основные уровни и интервалы варьирования факторов указаны в табл. 6.17. Они выбраны так, чтобы в вершинах исходного симплекса значения факторов в натуральном масштабе были целыми числами.
Табл. 6.16. Условия эксперимента
Пределы варьирования Фактор (нормализованный фактор)
г> (Jfi) | h (х2) в S (х4)
Основной уровень 25 8,67 0,045 0,1
Интервал варьирования 5 2,3 0,025 0
Табл. 6.17. Результаты поиска при оптимизации условий бесцентрового шлифования
Номер опыта Симплекс Отброшенная вершина V h б Н
1 1-2—3 30 8 0,05 4,3
2 1—2—3 —. 20 8 0,05 4,5
3 1—2—3 — 25 10 0,05 3,5
4 1—4—3 2 35 10 0,05 3,2
5 5—4—3 1 30 12 0,05 2,8
6 5—4—6 3 40 12 0,05 2,4
7 5—7—6 4 35 14 0,05 2
8 8—7—6 5 45 14 0,05 1,8
9 8—7—9 6 40 16 0,05 1,1
10 8—10—9 7 50 16 0,05 2,4
11 11-7—9 8 30 16 0,05 2,3
12 7—8—9—12 — 40 15,3 0,06 0,9
13 13—8—9—12 7 48,4 16,2 0,057 1
14 13—14—9—12 8 40,6 17,7 0,061 0,8
15 13-14—15-12 9 46 16,8 0,069 0,7
16 16—14—15—12 13 36 17 0,070 0,6
17 16—14—15—17 12 41,8 19 0,073 0,75
18 16-18—15—17 14 42 17,5 0,080 0,65
19 16—18—15—19 17 40,9 15,2 0,073 0,6
231
10 20 30 20 50 tl/минбО
Рис. 6.14. Результаты поиска оптимального сочетания значений параметров наладки бесцентрово-шлифовального станка (числа около номеров
Для получения исходного симплекса использовались нормализованные факторы из табл. 6.7. Так, для фактора х2 г2= — 0,289 и R2= — 0,578. Желательно, чтобы в натуральном масштабе расстояние между вершинами симплекса по оси х2 было 2 мм. Тогда
2
ДХ, =---------------
0,578 + 0,289
2,3 мм.
Задавшись минимальным значением /г = 8 мм, получим Х20=8 + 2,3-0,289 = = 8,67 мм.
Результаты поиска по факторам h и v приведены в табл. 6.17 и на рис. 6.14. Видно, что оптимизация по параметрам /г и v шла успешно до девятого опыта (номер опыта — вершина симплекса — обозначена цифрой внутри круга, число рядом с кругом — значение параметра оптимизации, полученное в данном опыте). Дальнейшее движение путем отбрасывания вершин 7 и 8 привело к
вершин характеризуют некруглость ухудшению результатов — параметр шлифованной детали в микрометрах) оптимизации начал увеличиваться.
Поэтому принято решение ввести в эксперимент еще один фактор — б, который в предыдущих опытах поддерживался на постоянном уровне. Для этого к симплексу 7—8—9 была добавлена еще одна вершина, координаты которой вычислялись по формулам (6.14) и (6.15): й12= (14+14+161/3= 15,3 мм; vl2= = (35+45+40)/3=40 м/мин; 6J2=0,05 + 0,025(—0,204 + 0,612)=0,06 мм.
. После 16-го опыта, как показали опыты 17, 18, 19, улучшения параметра оптимизации не наблюдалось и было принято решение прекратить поиск. Таким образом, ориентировочно оптимальными можно считать следующие значения параметров: Л=15,2 мм; и = 41 м/мин; 6 = 0,08 мм.
Пример 6.5. Уточнить положение оптимума, полученное в примере 6.4 пос-
ле зацикливания симплекса.
Табл. 6.18. Условия и результаты эксперимента
и Х1 xtx2 х2 1 2 X 2 Уа
11 —1 0 0 1 0 2,3
10 + 1 0 0 1 0 2,4
21 +0,5 +0,87 +0,43 0,25 0,75 2,3
8 +0,5 —0,87 —0,43 0,25 0,75 1,8
20 —0,5 4-0,87 —0,43 0,25 0,75 2,6
7 —0,5 —0,87 +0,43 0,25 0,75 2,0
9 0 0 0 0 0 1,1
9 0 0 0 0 0 1,2
9 0 0 0 0 0 1,0
9 0 0 0 0 0 1,3
232
Решение. Для уточнения положения оптимума был реализован план, матрица которого приведена в табл. 6.18.
Параметры нормализованной модели вычисляются по формулам (5.54):
ai = 0,333(-:2,34-2,4+0,5 • 1,8-0,5 -2,6-0,5-2)= -0,333 • 0,15= -0,05;
а2=0,333(2,3-1,8 + 2,6-2)0,87=0,312;
я12 = 1,333 • 0,43(2,3-1,8-2,6 + 2) = -0,057;
an=0,833[2,3+2,4+0,25(2,3+1,8+2,6+2)+0,75(2,3+1,8+2,6 + 2)] - 0,5(2,3+ +2,4+2,3 + 1,8+2,6+2 +1,1+ 1,2+1 + 1,3) =0,833-13,4-0,5- 18=2,16;
а22=1,5 • 0,75(2,3+1,8 + 2,6 + 2) +0,166(2,3+2,4 + 0,25(2,3+ 1,8 + 2,6+2)1-0,5-18 = =9,79+1,14-9=1,93;
ао = 0,4- 18-0,3(2,3+2,4 + 0,25(2,3+1,8 + 2,6+2)1 -0,7-0,75(2,3 +1,8 +2,6 + +2) =7,2-2,06-4,56 = 0,58.
Таким образом, модель имеет вид
Г = Н = 0,58 — 0,05^ -4- 0,312х2 — 0,057x^2 4- 2,16xf Н- 1,93х|.
Для определения координат оптимума вычислялись частные производные:
= — 0,05 — 0,057х2 + 4,32xj = 0;
дх2
= 0,312 — 0,057xj 4- 3,86х2 = 0.
Решением этой системы уравнений найдено: х2=—0,08; Х| = 0,011. Тогда, согласно формуле (6.13), /1=16-0,08-2,3=15,82 мм; и = 40 + 0,011 • 5 = = 40,06 м/мин. Полученное смещение оптимума по отношению к найденному прямым поиском незначительно.
6.5. МЕТОДЫ СЛУЧАЙНОГО ПОИСКА [56]
Алгоритм простого метода случайного поиска включает следующие процедуры.
1. Определение начальной точки поиска. Эта процедура не формализована. Координаты начальной точки выбираются возможно более близкими к области оптимума на основании априорной информации.
2. Выбор шага поиска X. Шаг также выбирается на основании интуиции исследователя. Если координаты и-й точки факторного пространства
х2и
\ xku /
то координаты (и + 1)-й точки определяются по формуле
Xu+i=Xu+Аеи+|,
е«+1 —
е1(ч+1)
е2(«+1)
еЛ(«+1)
233
Табл. 6.19. Выборка случайных чисел
и £1 е2 е3 es
1 —0,4765 2,0345 —1,5989 —0,5215 1,6215
2 —0,9294 —0,3344 —0,7525 0,4731 0,1250
3 —0,1525 0,1979 — 1,7877 0,8923 1,4526
4 —0,5120 —0,7500 —0,2285 —0,8517 0,3798
5 0,4107 — 1,7743 —0,6804 —1,4610 0,0164
6 —0,9660 0,5628 —0,1299 0,1336 -0,1762
7 — 1,5757 —1,4184 —0,3715 2,0166 —0,3041
8 1,0609 0,8875 0,5223 0,4415 0,8202
9 0,0439 —0,0446 1,9094 0,9074 0,5486
10 0,0016 0,4127 —1,5124 —1,5748 0,6182
И 1,8247 0,3322 —0,7284 —0,8422 0,1557
12 —0,1854 —1,4842 1,2537 -0,6061 1,5144
13 0,3146 0,2319 0,2969 0,1958 —0,8868
14 1,2570 —0,1053 —0,2110 1,0075 0,6359
15 0,1087 1,4527 0,5419 —1,5424 0,7148
16 0,9076 —0,5267 —0,2901 0,5797 —0,4548
17 —0,1082 0,1410 0,6059 —1,1592 —1,3564
18 0,2169 1,3089 —0,6326 0,9296 —0,5401
19 1,0575 —0,2703 2,1833 —1,3910 0,3011
20 1,5246 0,8726 0,1023 1,4343 —0,9312
матрица первого ранга, члены которой представляют собой выборку независимых, нормально распределенных случайных чисел с нулевым математическим ожиданием и единичной дисперсией (табл. 6.19). Каждая выборка представляет собой полную случайную строку (если k = 5) табл. 6.19. Номер строки выбирается с помощью таблицы равномерно распределенных случайных чисел (табл. П.21). Если й<5, то отбрасываются лишние столбцы, а если й>5, то выборка представляет собой набор чисел из двух последовательно выбранных случайным образом строк.
3. Движение к области оптимума. Выполняются опыты в исходной и первой случайной точках. Если первый шаг является успешным, т. е. при поиске максимума У]> Уо, то следующий шаг в случайном направлении делается из первой точки. Если же Yi<Y0, то второй случайный шаг делается опять из исходной точки. Аналогично осуществляется любой шаг в зависимости от того, был ли успешным предыдущий. Поиск прекращается, если определенное число (равное k) шагов не приводит к увеличению отклика.
Поиск будет идти быстрее, если в случае неуспешного п-го шага следующий шаг делать из Хи в противоположном направлении, т. е.
-Xu-f-2~Xu ^6и + 1.
Если и этот шаг окажется неуспешным, следует осуществлять новые из точки Хи или уменьшить %.
Усовершенствованный метод случайного поиска максимума — метод Нол-лау и Фюрста. В данном случае предполагается, что отклик ограничен сверху Ут, а поверхность отклика в области оптимума является гладкой. Координата на (н + 1)-м шаге определяется по формуле
Хи + 1 ~ Ци + 1 +Su + 16u + l, (6.16)
где [Хц-!-! — математическое ожидание величины ; S^j — дисперсия этой величины.
Значение Ци+i определяется координатами хи и х*, где х* — координата, которой соответствует наибольшее из найденных в и опытах значение отклика У*. Если У„>У* + Д (при поиске максимума), то
234
ни+1 = *и + 7^ (*« - (6-17)
1 и 1 о
а если Уи<У*+Л,
fPu+1 = x*+7- (ри-х‘). (6.18)
1 т
где Уо—значение отклика в исходной точке факторного пространства; Д— корректирующий фактор, зависящий от дисперсии воспроизводимости S^; принимается
A=4SB.
Дисперсия случайного вектора координат факторного пространства определяется на основании зависимостей:
•Vh — у -Л)-1 т
где
Sq—Rx/fy
(Xlmax •*Tmin
Л'2тах x2min
*femax ^femin
(6.19)
(6.20)
(6.21)
Пример 6.6. Необходимо определить оптимальное сочетание параметров наладки бесцентрово-шлифовального станка (скорости ведущего круга v, превышения оси заготовки Л, скорости подачи при правке шлифовального круга s и припуска на чистовое шлифование б), при котором обеспечивается минимальная некруглость роликов диаметром 18 мм и длиной 60 мм, шлифованных методом врезания на станке ЗМ182.
Решение. Для удобства анализа обозначаем: v=xlt h=x2, s=x3, 6 = =х<. Выбираем начальный вектор факторного пространства и начальный размах:
' 30 \ / 50 — 20 \
8 |- 0 = 1 16 —6 | 300 Г К I 600 — 200 I ,0,05/ \0,1—0,02/
' 30 \
10 I
400 I .0,08/
Предположительное значение Ут1п=0,6 мкм. Значение Д=0,2 мкм было определено предварительно из 5 параллельных опытов.
После опыта, реализованного в точке с координатой хо, получено Уо= = 4 мкм. При расчетах в данном случае удобнее пользоваться величиной, обратной отклику, Z=l/y. Тогда Zm=l,67, a Zo=O,25.
Первый шаг, согласно (6.19), (6.21) и (6.16): pi=x0;
So- 6
' 5 \ / 5 \ /4,25
1,7 1 . q 1,67 — 0,25 / 1>7 1,45
67 1 ’ 1 1,67 1 67 / 1 57
.0,013/ \0,013/ . \0,011
235
/ 30 \ /4,25\ /—0,9660\ /25,9\
х / 8 | / 1,45 \ 0,5626 |/ 8,8 |
1 I 300 /"г| 57 /1—0,1299 / I 293 Г \0,05/ \0,011/ \ 0,1336/ \0,05/
Реализация опыта в точке с координатой xt дала У1 = 3,2 мкм, т. е. Zi = 0,31.
Второй шаг: так как Yi<Y0—Д, то, согласно (6.17) и (6.16):
/25,9\ /25,9 — 30 \ / 22 \
8.8 | 1,67 — 0,31 / 8,8 — 8 |_19,6|.
I 293 /+ 1,67 — 0,25 I 293 — 300 /I 286 Г \0,05/ \0,05 — 0,05/ \0,05/
(22 \ / 5 \ / 1,2570\ / 27 \
9,6 ] , 1,67 — 0,31 / ij7 \ _ о,1053 1/ 9,6 )
286 / ~1- 1,67 I 67 /1—0,2110/ I 286 '
0,05/ \0,013/ \ 1,0080/ \0,05/
При реализации опыта в точке с координатой х2 получено 72=2,8 мкм (Z2= = 0,36).
Третий шаг: поскольку У2<У1~Д,
' 27 \ / 27 — 25,9\ / 28 \
9,5 1 274 1 1 1,67 1 1,67 — 0,36 — 0,25 । / 9,5 274 — 8,8 | — 293 1 1 10,1 1 256,5
.0,06/ \0,06 — 0,05/ \ 0,07 /
28 \ ' 5 ' \ /1,5246\ / 34
х =| 1011 1 I. 1’67~°’36 / 1,7 ]/ 0,8726 1/ 11,3 )
3 I 256,5 ) ' 1,67 I 67 И 0,1023 / I 262 Г
\0,07/ \0,013/ \1,4343/ \0,085/
Реализация опыта в точке с координатой х3 дает У3= 1,1 мкм (Z3=0,91).
Четвертый шаг: так как У3<У2—Д,
/ 34 ' / 34 — 27 \ /37,7 \
_/ и,з | 262 \ 1,67 — 0,91 + —: 1— \ 1,67 — 0,25 / н.з 1 262 — 9,5 )=, — 274 1 । / 12,3 |. 255,6 ’
\0,085. \0,085 — 0,06/ \0,098/
/37,7\ / 5 \ / 0,0439\ /37,8'
1213 ) 1,67 — 0,91 1 + ’ 1 1,7 ) / — 0,0446 i / 12,3
1 255,6 / 1,67 1 67 / 1 1,9094 1 1 1 314
\0,098/ 0,013/ \ 0,9074/ \0,1г
Реализация опыта в х4 дает У4=0,75 мкм (Z4=l,33). Пятый шаг: так как У4<У3—Д,
(37,8\ /37,8 — 34 \ /38,7\
12.3 | , 1,67— 1,33 / 12.3— 11.3 12,5 1.
314 1 + 1,67 — 0,25 I 314 — 262 / I 326 Г
0,1/ \ 0,1 —0,085/ \0,104/
'38,7\ / 5 \ / 1,8247\ /40,6\
12,5 | . 1,67— 1,33 / ii7 1/ 0,3322 1_/ 12,6 |
326 Г~ 1,67 I 67 /1 —0,7284 / I 316 Г .0,104/ \0,013/ \ 0,8422/ \0,104/
Реализация опыта в х5 дает У3=0,8 мкм (Z5=l,25).
236
Шестой шаг: так как У5>У4—А, то, согласно (6.40):
/37,8\ / 37,7 —37,8\ /37,7\
I 12,31. 1,33 | 12,3—12,3 I = / 12,3 I.
Ив I 314 Р~ 1,67 1 255,6 — 314 I I 267 ’
\0,1/ \0,098 —0,1 / \0,099/
/37,7\ / 5 \ /— 0,1525\ /37,5\
/ 12,3 1 1,67— 1,33 / 1>7 \( 0,1979 I = 1 12,4 ]
I 267 Г' 1,67 I 67 /1 — 1,7877 / I 243 / \0,099/ \0,013/ \ 0,8923/ \0,1/
Реализация опыта в хе дает У6=0,7 мкм. Поскольку это значение близко к Упнп и учитывая, что погрешность измерения некруглости А = 0,2 мкм, считаем оптимумом значение xs. Оптимальными приняты следующие значения параметров наладки станка: п = 37,5 м/мин; /г=12,4 мм; s = 240 мм/мин; 6 = = 0,1 мм. '
6.6. ОПТИМИЗАЦИЯ ПРИ НАЛИЧИИ ОГРАНИЧЕНИЙ
6.6.1. Основные понятия
При наличии ограничений усложняется задача экспериментальной оптимизации. Различают три типа ограничений. К первому относятся ограничения на значения отдельных факторов
Xi min^Ai^CAj шаг.
Ограничения этого типа фактически всегда присутствуют при решении любой задачи оптимизации, поскольку любой физический показатель изменяется только в определенных пределах, зависящих от свойств исследуемого объекта.
Ограничения второго и третьего типа — это так называемые функциональные ограничения
A j min (Aj, X%, ..., Xk) ^Aj max, (6.22)
причем вид функции ограничения второго типа и ее параметры известны до начала эксперимента, а для ограничений третьего типа определяются экспе-
риментально.
При оптимизации многооткликовых объектов часто требуется получить
экстремальное значение одной из наложенных на другие. Например, параметры наладки бесцентрово-шлифовального станка оказывают влияние не только на производительность процесса шлифования, но и на такие показатели качества шлифованных деталей, как точность размеров и формы, шероховатость. В данном случае необходимо найти такое сочетание значений параметров наладки станка, при котором обеспечиваются максимальная производительность и показатели качества, не превышающие заданных. Можно минимизировать, например, некруглость шлифованной детали, если задана минимальная производительность и максимальная шероховатость. В рассмотренных примерах до эксперимента неизвестны вид и коэффициенты математических моделей ограничений.
функций отклика при ограничениях,
Рис. 6.15. Схема области допустимых значений уровня двух факторов
237
В общем случае ограничения определяют в факторном пространстве область Q допустимых сочетаний уровней факторов. Пример образования такой области в двухмерном пространстве приведен на рис. 6.15. Штриховка указывает прилегающую к границе часть области недопустимых сочетаний значений факторов. Следовательно, задачу оптимизации при наличии ограничений можно математически сформулировать как задачу поиска экстремума У (X) на подмножестве значений X, принадлежащих области Q. Данную задачу можно решать одним из указанных в § 6.1, но несколько модифицированным методом.
6.6.2. Оптимизация на базе математических моделей [15, 73]
На первом этапе оптимизации строятся математические модели для параметра оптимизации и ограничений. Затем аналитически (или графически) определяется условный экстремум параметра оптимизации, в то 'время как математические модели ограничений служат уравнениями связи между уровнями факторов. В окрестности аналитически найденной оптимальной точки ставится ряд опытов и их результаты сопоставляются с результатами вычисления по модели параметра оптимизации.
Для аналитического определения условного экстремума можно использовать метод неопределенных множителей Лагранжа. Суть его заключается в следующем. Пусть требуется определить координаты оптимума для модели
У=/(Х1, xi, ..., Xk)
при условии, что k факторов связаны р (p<k) уравнениями (моделями):
= <Pj (хр' х2, ..., хк);
Z2 = ср2 (хр х2, ..., xk);
Zp = (Pp(x1, х2, .... xk).
Составляется функция
F=f(xi, х2, ..., х*)+%1[ф|(х1, х2, ..., Xh)-Zi] + +Х2[ф2(хь х2, .... Xfc)-Z2]+...+%p^p(xi, хг, ..., Xk)-Zp]
и приравниваются нулю ее частные производные по всем факторам и множи-
телям Х3 (7=1, 2, ..., р). Из системы k+p уравнений типа: dF df VI , d(Pj A ~ A + A <6'23) dxj 0Xf 1 dxt /=1 dF aX. - <Р/(xl’ x2> ••• ^)~z/-° (6-24)
определяются значения xoi и Х3-. Уравнения (6.23) и (6.24) определяют необходимые условия существования экстремума. Чтобы выяснить, соответствуют ли найденные координаты xai максимуму (или минимуму), необходимо определить знак полного дифференциала второго порядка функции F. Если при положительных значениях dxi d2F>0, то в точке с координатами x3i имеет место минимум, а если d2F<0,— максимум.
Во многих случаях вместо решения системы (6.23), (6.24) проще опре: делить на ЭВМ условный оптимум методом перебора. Суть метода в следующем. Предположим, необходимо оптимизировать процесс, описываемый моделью
238
k k k
Y = ao +2 aixi + 2 aiixi.xi + 2 aHxl, (I j), (6.25)
1=1 1=1 1=1
причем факторы процесса связаны зависимостью
k k k
Zo = 6o + S Mz + 2 bijxixi + ^i baA- <6-26)
z=i z=i i=i
Для выбранных из массива значений k—1 факторов и заданного значения Zo по (6.26) определяется значение 6-го фактора
= {-с+У~Г)/(2Ькк), где k
c=bk + "£i bikxi< l = <?~ 4mbkk-,
£ ] k I £ I
т = ьо + 2 bixi + 2 baxixi + 2 bu*i - Z0-i=l 1=1 1=1
Если оно находится в пределах от —1 до +1, то с использованием его и выбранных значений факторов вычисляется по (6.25) значение Y, которое сравнивается с полученными ранее. В случае поиска максимума (минимума) запоминаются большие (меньшие) значения. Данная процедура повторяется до перебора всех значений факторов.
Если шаг поиска будет h, то при k факторах необходимо просчитать п вариантов, причем
п=(й-1)(2+Ю/\ (6.27)
Сначала рекомендуется принимать достаточно большой шаг, чтобы сузить область поиска, а затем уменьшить его до значения, диктуемого точностью установки уровней факторов.
После окончания каждого цикла поиска его шаг уменьшается в два раза. При этом область поиска уменьшается в 2 й раз. Такое ступенчатое уменьшение шага дает значительный выигрыш в машинном времени. Так, например, при 6=4 и /г=0,125, согласно (6.27), м= 1,2914 • 108. Если же Ai = 0,5, Л2=0,25 и /1з=0,125, то п=729, что в 177 000 раз меньше, чем в первом случае.
Иногда факторы процесса связываются неравенством типа
k k k
zi > bo + 2 bixi + 2 btjxixi + 2 6iixz- * /)• i=i i=i i=i
Тогда необходимо вести поиск при нескольких значениях Шаг изменения и минимальное значение Zi определяются на основании опыта и интуиции исследователя.
Пример 6.7. Необходимо определить условия наплавки рабочей поверхности детали, которые обеспечивают заданную толщину наплавленного слоя /1 (ограничение) при минимальном припуске на последующую механическую обработку (параметр оптимизации). С увеличением параметра волнистости Z увеличивается требуемое значение припуска (рис. 6.16). Наплавке в среде
Рис. 6.16. Схема наплавленной поверхности
239
Табл. 6.20. Условия эксперимента
Пределы варьирования Фактор (нормализованный фактор)
»Э <*1) »н (х,) Нхэ)
Основной уровень 80 41,4 4
Верхний уровень 112 62,1 5
Нижний уровень 48 20,7 3
Интервал варьирования 32 20,7 1
углекислого газа с помощью головки ВГ-8М-УПИ подвергались образцы диаметром 110 мм из стали 45. Диаметр электродной проволоки 2,5 мм.
Решение. Для получения математических моделей в виде полиномов второго порядка был реализован некомпозиционный план (см. табл. 5.52). Уровни факторов приведены в табл. 6.20. В качестве факторов рассматриваются: скорость подачи электродной проволоки v3 (м/ч), скорость наплавки (м/ч), шаг наплавки t (мм).
На основании обработки результатов эксперимента по формулам (5.55), (5.56) и (5.36) получены следующие модели:
Z = 0,3 — 0, 178а:, + 0,126х, -4- 0,149х, — 0,148х,х9 — 0,163х,х, -4- 0,073х9хч +
+ 0, Их2 + 0,078х|;
h = 1,995 + 0,749х( — 1,208х2 — 0,661х3 + 0,273х2х3 + 0,423х2.
Предположим, что задано Л = 2 мм. Тогда, полагая, что значение х0; находится на поверхности сферы радиуса р, получим
F = 0,3 — 0,178х1 + 0, 126х2 + 0,149х3 — 0,148xfx2 — 0,163xjX3 + 0,073х2х3+
+ 0,11 х\ + 0,078х3 + Xj (1,995 + 0,749х, — 1,208х2 — 0,661 х3 + 0,273х2х3 +
+ 0,423х2 — 2) + Х2 (х2 + х2 + х3 — р2).
Дифференцируя F по х, и ?.3, получим:
— 0,178 — 0, 148х2 — 0,163х3 + 0,22х! + 0,749^ + 2х^2 = 0;
0,126 — 0,148xj + 0,073х3 + ^ (— 1,208 + 0,273х3 + 0,846х2) + 2х2Х2 = 0;
0,149 — 0,163хх + 0,073х2 + 0,156х3 + (0,273х2 — 0,661) + 2х3Х2 = 0;
— 0,005 + 0,749Х] — 1,208х2 — 0,661х3 + 0,273х2х3 + 0,423х2 = 0;
xi + х2 + х| = р2.
Результаты решения этой системы нелинейных уравнений при различных значениях р:
Р Х1 х2 х3 Xi ?.2 Z
0,4 0,265 0,237 -0,183 0,108 0,084 0,275
1,0 0,699 0,659 -0,217 0,054 0,027 0,241
1,3 0,908 0,895 -0,256 0,035 0,025 0,226
1,4 0,968 0,981 -0,248 0,032 0,025 0,217
Наименьший припуск Z получен при р=1,4 (xi = 0,968; х2=0,981 и х3= = —0,248). Расчетное значение h при этом равно 2,04 мм, что близко к заданному. При переводе в натуральный масштаб получаем следующие оптимальные значения уровней факторов: аэ= 108,4 м/ч, цн=60,9 м/ч, /=3,75 мм.
240
6.6.3. Методы прямого поиска при оптимизации с ограничениями [40]
До тех пор, пока точка поиска находится внутри области Q, все процедуры, характерные для методов, описанных в § 6.3, 6.4 и 6.5, в принципе используются без изменения. Единственным отличием является необходимость на каждом шаге осуществлять проверку выполнения заданных ограничений: аналитически — для ограничений первого и второго типов, экспериментально — для ограничений третьего типа. И только если окажется, что имеет место нарушение одного или нескольких ограничений, требуется изменить алгоритм определения направления движения последующего шага поиска.
При поиске методом градиента вблизи критической точки Хкр, где нарушено ограничение, проводится эксперимент с целью определения градиентов параметра оптимизации У и того ограничения, которое нарушено. Центр плана такого эксперимента, как правило, относят от критической точки внутрь области Q, чтобы при варьировании факторов во время его реализации не были нарушены ограничения.
Если нарушено одно из ограничений третьего типа, например Z(XKp)< <Zmin или 2(Акр)>2тах, то следующий шаг поиска должен совершаться в компромиссном направлении, где значения параметра оптимизации У продолжают возрастать (или уменьшаться), а точка поиска постепенно смещается вглубь допустимой области Q. Выбор этого направления осуществляется следующим образом.
Реализуется эксперимент для определения составляющих градиента параметра оптимизации У и ограничения Z в точке Ха — центре плана, находящемся вблизи Хкр. Составляющие градиентов вычисляются по формулам (6.6) и (5.33). Затем следует выяснить возможность движения из точки Хо по градиенту параметра оптимизации У. Для этого в линейную модель
k
z = do + 2 dixi
‘=i к
подставляются значения Xi, которые будут получены на j-м шаге движения по градиенту:
Xij=Xoi+jaiAx.
Тогда
k
Z- — Zo -]- /Дх 2 ai^i< (6.28)
где Дх — шаг варьирования нормализованных факторов.
Если после одного-двух шагов нарушается ограничение, т. е. Z3<Zmin или Z3'>Zmax, то следует двигаться в компромиссном направлений, изменяя Xi в соответствии с формулой
(6.29)
где знак (+) относится к случаю, когда Zo<Zmin, а знак ( —), когда Zo> >Zmax.
Реализация движения в компромиссном направлении также сопровождается проверкой ограничений.
При нарушении ограничения второго типа вместо формулы (6.28) используется (6.22), а при нарушении ограничения первого типа фактор хг, по которому оно нарушено, стабилизируется на уровне х,-min (или х< max).
В случае, когда нарушено сразу несколько ограничений различных типов, проверка возможности движения из окрестностей критической точки по
16. Зак. 1001 241
градиенту У проводится с учетом всех ограничений, оказавшихся нарушенными.
Градиентный поиск при наличии ограничений прекращается, когда:
1) координаты градиента а, все близки к нулю; тогда точка поиска находится в окрестности безусловного экстремума параметра оптимизации;
2) нарушено одно из ограничений, но все попытки движения в компромиссном направлении приводят к уменьшению У; тогда условный экстремум находится на границе;
3) нарушено сразу несколько ограничений, и все попытки продвинуться в компромиссном направлении безрезультатны; тогда условный экстремум находится на пересечении нескольких границ.
Результат поиска при наличии ограничений зависит от выбора начальной точки. Иногда формы допустимой области Q и вид функции отклика У таковы, что при некоторых исходных точках возможна остановка процедуры в точке локального экстремума, хотя в области £2 имеются точки с большими значениями У.
7. АВТОМАТИЗАЦИЯ ЭКСПЕРИМЕНТА
7.1. ОСНОВНЫЕ ПОНЯТИЯ [25]
Система автоматизации научно-технических экспериментов (САНТЭ) — это совокупность технических средств, математических методов, схем организации работ и т. д., образующих организованное единое целое и обеспечивающих автоматизированное решение требуемого набора задач эксперимента с заданной точностью и с учетом ограничений по времени и стоимости.
Внешние параметры системы — характеристики ее функционирования, служащие показателями качества работы системы как единого целого. В качестве внешних параметров САНТЭ можно использовать: общую производительность системы по обработке данных; объем перерабатываемой информации; достоверность выходной экспериментальной информации; точность получаемых результатов; количественные характеристики надежности системы; объем используемой в системе аппаратуры (объем памяти, количество преобразователей формы информации, количество внешних устройств и т. д.); время с момента поступления в систему исходных данных до момента выдачи окончательных результатов (во время решения определенной задачи) ; стоимость системы (с учетом разработки математического обеспечения) и т. д.
Внутренние параметры системы — это характеристики, показывающие особенности технических решений, принятых при организации системы в целом, и отдельных технических средств, входящих в ее состав, а также в совокупности влияющие на значения внешних параметров системы. Примерами внутренних параметров САНТЭ являются: вид и характеристики сигналов, сохраняющих и передающих информацию элементам системы по каналам связи, способ кодирования информации, приоритет приема и обработки информации от различных источников, быстродействие отдельных элементов и т. д.
Автоматизация экспериментов позволяет значительно повысить эффективность проводимых исследований, интенсифицировать использование оборудования при проведении экспериментов, сократить сроки получения экспресс-информации по данным опытов и результатов их полной обработки, а во многих случаях получить качественно новые результаты. Автоматизация не только освобождает исследователей от рутинных операций при выполнении расчетов, но и дает возможность проведения сложных, практически неосуществимых без нее исследований.
В настоящее время используются три уровня организации САНТЭ (рис. 7.1). В системе первого уровня ЭВМ, используемая для обработки экспериментальной информации, непосредственно в нее не включена, в силу чего возможности такой системы ограничены. САНТЭ второго уровня предполагает использование ЭВМ в автономном режиме обработки экспериментальных данных, при котором ЭВМ осуществляет управление устройствами сопряжения. На третьем уровне весь комплекс аппаратуры строится как замкнутая автоматическая система, объединенная общей программой функционирования. В такой системе в задачу исследователя (Ис) входит контроль за выполнением программы эксперимента, ее текущая корректировка и интерпре-' тация результатов, получаемых с блока СПИ.
16*
243
САНТЭ включает:
1) экспериментальную установку (ЭУ), предназначенную для проведения опытов над объектом исследования в определенных условиях (часто она сама является объектом исследования). Условия проведения опытов изменяются в соответствии с планом эксперимента;
2) первичные измерительные преобразователи (ИП), реагирующие на изменение того или иного физического параметра и преобразующие эти изменения в форму, удобную для последующего использования (обычно в электрический сигнал);
3) устройства сопряжения (УС), обеспечивающие стыковки всех составных частей системы и осуществляющие такие операции, как усиление и преобразование масштабов аналоговых сигналов, аналого-цифровые и цифро-аналоговые преобразования, временное хранение данных и сигналов управления, синхронизация объема данных и т. д. В САНТЭ, базирующихся на ЭВМ, подобные устройства составляют то, что называют электронным интерфейсом, осуществляющим связь между ЭВМ, экспериментальной установкой и дополнительными средствами отображения, регистрации и накопления информации;
4) средства представления информации (СПИ), предназначенные для выдачи результатов эксперимента в графическом и цифровом виде на экран дисплея, бумажную ленту печатного устройства или графопостроителя;
5) устройство управления (УУ), осуществляющее изменение условий проведения эксперимента, т. е. режим работы ЭУ;
6) ЭВМ — центральную часть САНТЭ.
Программируемые вычислительные системы, имеющие соответствующие устройства связи с процессами, называют управляющими вычислительными машинами. В зависимости от предъявляемых требований для автоматизации
244
эксперимента могут быть использованы свободно программируемые управляющие схемы, микро- и мини-ЭВМ, а также мощные ЭВМ. Однако для решения многих задач в настоящее время предпочтительны мини-ЭВМ, поскольку при этом система чаще всего является оптимальной как по возможностям, так и по стоимости.
Принципиальная блок-схема вычислительной машины показана на рис. 7.2. Центральный блок (ЦБ) состоит из управляющего (УУ) и арифметического (АУ) устройств. Он перерабатывает в арифметическом устройстве информацию, поступающую в оперативное запоминающее устройство (ОЗУ), на основе команд (программ), также вводимых в определенной последовательности в оперативную память и расшифровываемых (декодируемых) управляющим устройством. В зависимости от типа ЭВМ центральный блок способен декодировать примерно 50...100 так называемых машинных команд на выполнение арифметических операций, манипуляций с двоичными разрядами, условных и безусловных переходов в программе, а также команд на передачу информации между вычислительными модулями и оперативной памятью или устройствами для ввода и вывода информации.
Наиболее часто используемые мини-ЭВМ оборудуются блоком памяти емкостью 8...256 К (1 К— 1024 байт). Они работают преимущественно с длиной слова 2 или 4 байта (16 или 32 двоичных разряда), что обеспечивает достаточную точность вычислений.
Запись программ, непосредственно понятных ЭВМ, в форме двоичных чисел (машинный язык) очень громоздка. Поэтому были разработаны языки, более удобные для пользователя (высшего порядка, проблемно ориентированные, не зависящие от типа машин). Программы, написанные на таких языках, переводятся на машинный язык с помощью специальной программы — транслятора, который одновременно выявляет в программе пользователя синтаксические и другие ошибки. Однако часто удобнее пользоваться машинно-ориентированным языком, который носит название Ассемблер. Хотя программа на этом языке получается более длинной, но она отлаживается значительно проще, чем программа, написанная на языке высшего порядка (алгоритмическом).
Программы для управления экспериментальной установкой и решения различных задач статистической обработки результатов эксперимента при помощи таких мини-ЭВМ, как 15 ВУМС-28-025 или ВУМС 001-03, пишутся обычно на алгоритмическом языке Фортран IV или Бейсик (для более простых задач).
Алгоритмическое и программное обеспечение ЭВМ, входящих в САНТЭ, состоит из базовой и прикладной частей. В базовое обеспечение входят операционные системы, управляющие ходом вычислений, вводом и выводом данных в реальном масштабе времени, и трансляторы. Содержание прикладного обеспечения (пакетов прикладных подпрограмм) зависит в значительной степени от типа используемой ЭВМ и от уровня подготовки пользователя пакета в области программирования. Подпрограммы пакета не содержат обычно операторов ввода-вывода, и пользователь должен писать головную программу для ввода исходных данных, вызова подпрограмм пакета и вывода результатов расчета. Подпрограммы могут быть различной вычислительной мощности — от выполнения отдельной вычислительной функции до выполнения определенного вида статистического анализа.
При использовании ЭВМ возможны в основном два способа обработки измерительного сигнала: ‘ непрерывная регистрация и запоминание целой серии измерений с последующим их преобразованием или прямая обработка каждого зарегистрированного значения (в режиме реального времени).
- 7.2. Подготовка измерительных сигналов к автоматическому анализу [31, 83]
Под анализом сигналов следует понимать вычислительную процедуру, позволяющую получить дополнительные сведения об объекте исследования, которые не содержатся непосредственно в множестве зарегистрированных сиг
245
налов. Сюда входит определение средних значений, дисперсий, корреляций, коэффициентов регрессии и т. д. Для решения этих задач используют аналоговые и цифровые управлящие вычислительные машины.
Аналоговые вычислительные машины имеют некоторые существенные преимущества (высокая скорость вычислений в реальном масштабе времени, отсутствие проблем с преобразованием сигнала) по сравнению с цифровыми. И хотя аналоговые вычислительные устройства непрерывно совершенствуются, они непригодны для решения ряда сложных вычислительных задач. Цифровые системы по точности намного превосходят аналоговые и часто обходятся дешевле.
К измерительным сигналам предъявляются требования достоверности и помехозащищенности: измерительный сигнал, подводимый к вычислительному устройству для анализа, должен быть объективным отражением измеряемой величины с минимальными погрешностями измерения и искажения в каналах передачи. Сигнал X(t) должен быть усилен или ослаблен, чтобы имеющийся входной измерительный диапазон был использован по возможности оптимально.
Часто между первичным измерительным преобразователем и аналоговым вычислительным устройством помещают фильтр, позволяющий выделить полезный сигнал и более полно использовать диапазон вычислительного устройства. Однако, если частота полезного сигнала близка к предельной частоте фильтра, то фильтрация сигнала может привести к значительным погрешностям. Ориентировочно наименьшая ожидаемая частота полезного сигнала должна в 5 раз превышать предельную частоту фильтра.
Цифровые сигналы имеют ряд преимуществ перед аналоговыми (например, возможность надежной передачи без помех, простота запоминания и т. д.). Поэтому целесообразно либо сразу получать результаты измерения в цифровом виде, либо возможно раньше преобразовать аналоговый сигнал в цифровой. Для получения цифрового сигнала аналоговый непрерывный сигнал необходимо подвергнуть дискретизации во времени в аналого-цифровых преобразователях (АЦП' « квантованию по амплитуде (рис. 7.3). Последнее
а — аналоговый сигнал; б — набор кван- /—компараторы; 2 — блок перекодирования тованных числовых сигналов
246
необходимо, так как числовое выражение аналоговой величины имеет ограниченное (конечное) число разрядов и должно быть округлено. Число квантов определяется техническими возможностями вычислительного устройства— числом разрядов (бит) преобразователя. Например, 10-разрядный преобразователь разделяет диапазон значений на 210= 1024 кванта. В результате квантования возникает так называемая погрешность квантования. При достаточно большом числе разрядов преобразователя и полном использовании входного диапазона этой погрешностью можно пренебречь. Изменение погрешности квантования во времени называют также шумом квантования.
Правомочность дискретизации во времени обосновывается теоремой Котельникова — Шеннона, согласно которой сигнал с верхней предельной частотой fB полностью описывается дискретными отсчетами, осуществляемыми с частотой ft, по крайней мере вдвое превышающей частоту f3. Хотя при этом вся информация между двумя считываниями остается неучтенной, теоретически возможно по дискретным отсчетам полностью восстановить исходный сигнал. Частоту, составляющую половину частоты считывания, называют также частотой Найквиста. Таким образом, наиболее высокая частота полезного сигнала должна быть ниже частоты Найквиста. Так как считывание не происходит идеально (т. е. существуют конечное время считывания сигнала и погрешность дискретизации), то минимальная частота считывания принимается на 28% большей, чем теоретическая.
При слишком низкой частоте дискретизации возникает так называемый эффект наложения шумовой информации на полезную и искажение последней. Избежать погрешностей, связанных с эффектом наложения, можно двумя путями. Если позволяют технические возможности вычислительного устройства, частоту дискретизации следует принимать вдвое большей, чем максимальная встречающаяся в сигнале (а не максимальная из представляющих интерес) с учетом шума. При этом увеличивается требуемое для расчетов машинное время и появляется избыточная информация. Второй способ заключается в пропускании аналогового сигнала через фильтр, который резко снижает амплитуды при частотах, превышающих его предельную частоту. С учетом того, что фильтр не является идеальным, все же приходится несколько завышать частоту считывания.
АЦП преобразовывает входное напряжение {7В1 (аналоговый сигнал) в кодированный выходной сигнал Da в форме
Da = И a-Y а.\2~1 + а22-2+...+ап2-п,
где Uа — базовое напряжение, с которым сравнивается входное 1/вх; п— число разрядов (бит) АЦП; at — значения отдельных разрядов (0 или 1); е — погрешность квантования, не превышающая по абсолютной величине половины бита; ап — наименьший значащий бит, т. е. бит с наименьшим номером позиции.
Рис. 7.5. Схема инкрементного аналого-цифрового преобразователя:
/ — компаратор; 2 — генератор импульсов; 3 — двоичный счетчик: 4—сигнал «сброс счетчика»; 5—сигнал «данные готовы»; 6 — цифро-аналоговый преобразователь
247
Рис. 7.6. Схема аналого-цифрового преобразователя поразрядного уравновешивания:
/ — компаратор; 2 — логический блок управления; 3 — бинарная память; 4 — цифро-аналоговый преобразова-
тель
По принципу функционирования АЦП подразделяют на параллельные и последовательные. Первые определяют все коэффиценты at одновременно. В последовательных преобразователях коэффициенты определяются один за другим. Такой процесс происходит медленнее, чем в параллельном преобразователе, однако затраты на схемную часть при этом значительно сокращаются.
В параллельных АЦП входной сигнал непосредственно сопоставляется с 2/1—1 сравнительными напряжениями (рис. 7.4). Коэффициенты а, определяются по логическим выходным сигналам компараторов в блоке перекодирования. Ввиду высоких затрат на схемную часть этот способ подходит только для преобразователей с малым числом разрядов (/г = 4...6). Однако одновременное определение всех коэффициентов обеспечивает очень короткое время преобразования (менее 100 нс).
В инкрементном АЦП (рис. 7.5) применяется только один компаратор, а сравнительное напряжение ступенчато повышается. Число приращений напряжения подсчитывается до тех пор, пока выход компаратора логически, не становится равным единице, т. е. пока входной аналоговый сигнал (7ВХ не будет равен сравнительному напряжению. При равенстве обоих напряжений на счетчике будет получен непосредственно выходной сигнал в двоичном коде. Перед следующим преобразованием счетчик должен быть сброшен на нуль. В данном случае время преобразования зависит от числа разрядов и абсолютной величины сигнала.
При способе последовательного приближения (поразрядного уравновешивания) к напряжению Uv (рис. 7.6) на каждом этапе добавляется некоторая часть сравнительного напряжения 11^2*'- (А=1, 2... п). Если после добавле-
ния эквивалентное напряжение Uv станет больше входного UBx, то соответствующий коэффициент ak принимается равным нулю и напряжение U0/2k снова вычитается. Для следующего этапа значение k увеличивается на 1 и повторяется тот же процесс до тех пор, пока не будет определено значение ап. Быстродействие при этом способе для 10-разрядного преобразователя составляет 100 тыс. преобразований в секунду.
Для аналого-цифрового преобразования используются и другие методы (генерирование пилообразных импульсов, простое и двухтактное интегрирование входного напряжения и т. д.).
248
7.3. Аналоговые методы вычислений [46, 31]
Аналоговые методы вычислений часто непосредственно связаны с процессом измерения. Наилучшие результаты дают электронные схемы на базе операционных усилителей (рис. 7.7), которые производят преобразование (усиление) электрического напряжения. Входное и выходное Us напряжения связаны в данном случае уравнением
t/B = /(t/Bx,
где К — коэффициент усиления (К^4 • 104).
Входное и выходное напряжения операционного усилителя (ОУ) имеют разные знаки. В полупроводниковых ОУ максимальное выходное напряжение не превосходит 10...30 В, следовательно, на входе —2,5 мВ.
С помощью электрической схемы, представленной на рис. 7.8, осуществляется суммирование входных напряжений с одновременным их умножением на некоторые постоянные коэффициенты. Операционный усилитель охвачен отрицательной обратной связью с помощью резистора RS. Тогда
k ^в = -2 /=1
где a.i = RS/Ri —коэффициент передачи по i-му входу.
На структурных схемах сумматор изображается в виде треугольника, к которому подводятся несколько входов Xi и от которого отходит один выход (рис. 7.9). Если у сумматора только один вход и а=1, то он лпшь изменяет знак входной переменной Xi. Такой сумматор называется инвертором. Схема, показанная на рис. 7.10, позволяет проводить вычитание без инвертора. В дан-дом случае
t/B = a(t/i-t/2).
Схемы с операционными усилителями дают возможность проводить операции умножения и деления. Для умножения, например, можно использовать метод двух парабол (рис. 7.11), который основан на тождестве
*У = “7 г(* + У)2 — (* — У) 2] • 4 [
Возведение в квадрат можно осуществить при помощи функционального преобразователя, у которого входное напряжение представляет аргумент х, а выходное — значение нёкоторой функции f(x). Функциональный преобразователь будет универсальным, если путем соответствующей настройки его можно использовать для воспроизведения произвольной функциональной зависимости. Специализированный функциональный преобразователь всегда настроен на воспроизведение конкретной функциональной зависимости. В схеме умно-
Рис. 7.7. Схематичное изображение операционного усилителя
249
Рис. 7.9. Схематичное изображение аналогового сумматора
Рис. 7.10. Схема анало-
гового вычитания
жения применяют специализированные функциональные преобразователи — квадраторы.
Схемы для аналогового дифференцирования и интегрирования показаны на рис. 7.12. Чтобы уменьшить влияние помех на результат дифференцирования, включается последовательно с конденсатором С дополнительный резистор R (рис. 7.12, а). При отсутствии этого резистора между U\ и t/2 имеет место зависимость
dU±
а при использовании схемы, показанной на рис. 7.12, б,
(t) dt+UQ:
где t — время; Uo—постоянная интегрирования, равная UB при ?=0.
При обработке сигнала иногда требуется получать только его модуль без учета знака. В таких случаях применяется схема, показанная на рис. 7.13. Основу схемы составляет операционный усилитель 1, охваченный двумя параллельными цепями обратных связей. В обратных связях диоды включены в противоположных направлениях. Поэтому в зависимости от знака входного напряжения ток проводит только одна цепь, которая играет роль резистора обратной связи. На выходе сумматора 2 напряжение U2= [ U\ (t) |.
При анализе ряда сигналов иногда требуется выделить из них тот, который в данный момент времени имеет наибольшее (или наименьшее) значение. Для иллюстрации на рис. 7.14 показана совокупность четырех сигналов, линейно изменяющихся во времени, и проведено выделение максимального сигнала. Схема, необходимая для такого выделения, показана на рис. 7.15. Из че-
Рис. 7.11. Схема аналогового умно- Рис. 7.12. Схемы аналогового диффе-жения ренцирования (а) и интегрирования
(б)
250
VD R
Рис. 7.13. Схема выделения модуля сигнала)
Рис. 7.14. Изменение совокупности четырех сигналов во времени
Рис. 7.15. Схема выделения максимального из четырех сигналов.)
тырех входных диодов будет открыт лишь тот, на входе которого действует наибольшее напряжение Uj. Тогда U3 = Uj. На этом же принципе можно построить схему, выделяющую минимальный по значению сигнал.
7.4. АВТОМАТИЗАЦИЯ РЕГРЕССИОННОГО АНАЛИЗА [46]
На вход аналогового или цифрового электронного устройства подаются сигналы, пропорциональные изменяющимся во времени значениям фактора X и отклика У. Значения X могут изменяться случайным образом (при реализации пассивного эксперимента) или по заданному закону (активный эксперимент). Входные сигналы можно рассматривать как реализации стационарных случайных процессов, эргодических по отношению к модели регрессии (см. § 3.2). Схема получения выборок для вычисления оценок условных математических ожиданий, соответствующих заданному ряду значений X, показана на рис. 7.16. В моменты времени когда X(ti)=x, подается сигнал
251
Рис. 7.16. Схемы получения выборок для вычисления оценок- условных математических ожидании
Рис. 7.17. Блок-схема аналогового ре-грессиографа
Рис. 7.18. Блок-схема цифрового регресснометра.
для регистрации текущего значения УДх. Вычисление оценок условного математического ожидания производится либо ио обычной формуле (см. § 3.7)г либо ио рекуррентной:
Vt (*) = W — -у- [yi (*)]. (7-1)
где у,(х)—оценка условного математического ожидания при учете i-й выборки; —та же оценка, полученная на основании i— 1 предыдущих
выборок; yi — значение отклика при i-й выборке.
На рис. 7.17 показана блок-схема аналогового регрессиографа, самопишущий прибор (СМП) которого выдает график регрессии. В схеме сравнения (СС) сигнал X(i) сравнивается с сигналом уровня х, который вырабатывается в источнике напряжения уровня (ИУ). При их совпадении формирователь импульсов (ФИ) вырабатывает сигнал для модулятора Afi, который выдает при этом имиульс, пропорциональный значению Y(t). В схеме вычитания (СВ) из этого импульса вычитается среднее значение Уг—i, рассчитанное ио всем предыдущим сигналам интегратором (ИН) и усилителем постоянного тока (У). Таким образом, схема для каждого значения х формирует значение у согласно формуле (7.1). В качестве источника напряжения, задающего уровень х, можно применять устройство, линейно изменяющее напряжение, причем скорость этого изменения устанавливается столь малой, чтобы в течение интервала усреднения уровень х оставался практически постоянным. Достоинством данного регрессиографа является непрерывность формирования и записи исследуемой кривой. Однако продолжительность снятия кривой регрессии этим прибором велика, так как каждая ее точка определяется последовательно за время t(M), зависящее от требуемой точности оценки и средней частоты изменения X(i). Время /(М) определяется по формуле (5.4).
Значительно быстрее можно получить кривую регрессии на дисплее (Д) цифрового регрессиометра (рис. 7.18). Этот прибор работает согласно алгоритму, вытекающему из формулы (3.5). При одновременном определении У координат кривой регрессии необходимо задаться У значениями х в диапазоне 252
изменения реализации X(t), причем удобнее значения х, задавать через рав ные интервалы Дх:
Xi = Xo + iAx,
где х0—минимальное значение X(t); 1=1, 2, N.
Поэтому АЦП1 преобразует аналоговый сигнал X(t) в число, т. е. проводит дискредитацию и квантование сигнала. Когда число, сформированное в АЦПЬ совпадает с одним из данных значений х<, блок управления (БУ) вырабатывает сигнал, по которому сигнал 1, из АЦП] указывает адрес Z-й ячейки памяти микропроцессора (МП), с содержимым которой будет складываться число, выработанное АЦП2. Это число, пропорциональное У|х;, подается по каналам 2. По истечении достаточно большого числа опросов N в каждой ячейке памяти МП накапливается число, пропорциональное оценке условного математического ожидания. Так, в i-й ячейке получается число
N[
Et=hy 2
z=i
где Nt — число подключений i-й ячейки памяти; hy — коэффициент пропорциональности.
Числа N{ фиксируются специальным счетчиком. По окончании цикла измерений вычисляются все у(х,) =Ej/Ni. Эти ординаты кривой регрессии отражаются дисплеем в цифровой форме либо в виде кривой на экране.
7.5. АВТОМАТИЗАЦИЯ КОРРЕЛЯЦИОННОГО АНАЛИЗА [46]
Для измерения корреляционных и взаимных корреляционных функций применяют специальные приборы — коррелометры. С их помощью получают либо отдельные ординаты корреляционной (взаимной корреляционной) функции при определенных значениях аргумента, либо график функции — коррелограмму. Коррелометры реализуют различные методы измерения, которые характеризуются неодинаковой статистической точностью.
Метод перемножения, или мультипликативный метод, позволяет проводить измерение временных корреляционных функций в соответствии с их математическим определением. Корреляционную функцию можно представить в виде
т—г
= j k(0-M(A')] [х (t + т) - М (X)] dt, ' (7.2) о
где х(/)—реализация случайной функции; Л1(У)—математическое ожидание стационарной случайной функции; т — сдвиг (принимает дискретные значения от 0 до Tmax<7'); Т — продолжительность измерения.
Оценка взаимных корреляционных функций вычисляется по формуле т—т .
= J U(O-M(X)][z/(^+t)-M(K)]zW, (7.3)
о
где г/(/ + т) —значение отклика в момент времени / + т.
Согласно выражениям (7.2) и (7.3), для измерения значения корреляционной (взаимной корреляционной) функции необходимо осуществить относительный сдвиг (задержку) напряжения реализации на время т, перемножить напряжения х(1) и х(/+т) или x(Z) и y(t+x), а затем усреднить произведение в течение достаточно продолжительного интервала времени.
Переход от непрерывных реализаций к дискретным выборкам из них позволяет существенно упростить аппаратурные решения при построении кор-
253
Рис. 7.19. Принципы перемножения в коррелометрах:
а — последовательного действия при сдвиге на ЗТо; б — параллельно-последовательного действия с помощью некоррелированных парных выборок
релометров, так как в этом случае значительно проще устройства задержки и перемножения.
Вычислительные операции при аналоговом методе перемножения с дискретизацией времени производятся по формулам:
у—t
Кх (Ч) = [*(l\))-M(X)][x(t\ + 4)-M(X)]: (7.4)
£=]
N—k
KXY P4) = I* (*0) - M W1 ly <4 + **o) - 44 (У)], (7.5)
где To — дискрета времени; йт0 — интервал сдвига; й = 0, 1, 2, и; п — число измеряемых ординат корреляционной функции; N—общее число выборок (измерений X или X и У) за время измерения.
В коррелометрах последовательного действия сначала вычисляется ордината корреляционной функции, соответствующая нулевому сдвигу, т. е. дисперсия исследуемого процесса. При этом каждое значение реализации х (it0) умножается само на себя. Затем вводится задержка (йт0) и определяются значения Кх (йт0) при k — 1, 2, ..., п. Операции перемножения при k = 3 иллюстрирует рис. 7.19, а (стрелками соединены перемножаемые значения x(iT0) и х((’т0+ + йт0) реализации).
Параллельно-последовательный метод анализа позволяет осуществить вычисления по принципу определения среднего значения произведений некоррелированных пар выборок. Его сущность заключается в следующем. Реализация разбивается во времени на N циклов длительностью Гц, большей или равной максимальному интервалу (сдвигу) корреляции. При этом выборки с одинаковыми порядковыми номерами в соседних циклах практически не корре-
254
лированы. Перемножение проводится внутри циклов (рис. 7.19, б) —в каждом цикле первая ордината последовательно умножается на все остальные. Пары произведений ординат с одинаковым сдвигом суммируются в соответствующих ячейках памяти и затем усредняются. Способ оценки корреляционных функций при цифровом варианте обработки соответствует формулам (7.4) и (7.5), только значения х(Г) и y(t) подвергаются квантованию.
Аналого-цифровой метод перемножения позволяет строить экономичные схемы гибридных коррелометров, обладающих хорошей точностью. Их особенность заключается в том, что при определении взаимной корреляционной функции двух случайных процессов квантуется напряжение реализации только одного из них, а у второго сохраняется в аналоговой форме. При этом допустимо квантование по малому числу уровней. Так, применение квантующего устройства с тремя двоичными разрядами (восемь уровней квантования) обеспечивает измерение корреляционных функций с хорошей точностью.
Свойство инвариантности стационарных процессов во времени позволяет заменить операцию перемножения значений x(t) и х(<+т) при определении корреляционной функции их сложением и вычитанием с последующим возведением суммы (разности) в квадрат. Остальные операции, необходимые для вычисления корреляционной функции, остаются такими же, как и при осуществлении перемножения. Оценка корреляционной функции в данном случае производится согласно формуле
т
(т) = Dx— j1 [х (0 — х (I — т)]2 di, о
где Dx— дисперсия случайного процесса X (t).
Аналогично можно определить и взаимную корреляционную функцию.
На рис. 7.20 изображена структурная схема аналогового коррелометра последовательного действия, работающего методом перемножения. Входное устройство (ВхУ) прибора, предназначенного для анализа стационарных и эргодических случайных процессов, реализации которых заданы в форме электрического напряжения, состоит из аттенюатора, эмиттерного повторителя, фильтра нижних частот и усилителя. Для центрирования реализаций во входной цепи прибора предусматривают центрирующую схему.
Узел регулируемой задержки (СРЗ) — это устройство, «запоминающее» на некоторое время напряжение исследуемой реализации. Выходной сигнал подобного узла воспроизводит форму входного сигнала через определенный промежуток времени Ат, называемый интервалом задержки. Узел задержки должен передавать сигнал с минимальными искажениями, т. е. модуль его коэффициента передачи должен быть близок к единице во всем спектре частот исследуемого процесса, а фазочастотная характеристика близка к линейной.
Для задержки высокочастотных сигналов служат линии задержки, а низкочастотных — магнитные или другие запоминающие устройства. Магнитная запись позволяет изменять в значительных пределах время задержки случай-
гового коррелометра последователь- Рис. 7.21. Структурная схема цифроного действия вого коррелометра
255
ных процессов. Сравнительно простые и компактные схемы задержки строятся на элементах микроэлектроники. Эффективны также аналоговые линии задержки, выполненные на основе приборов с переносом заряда.
Перемножители (П), встречающиеся в корреляционных анализаторах, аналогичны применяемым в вычислительной технике и радиоэлектронике (см. рис. 7.11). Современная микроэлектроника располагает аналоговыми пере-множителями, выполненными в виде отдельных микросхем.
Результаты перемножения усредняются в усреднителе (УС) и передаются на показывающий или регистрирующий прибор (ПРУ).
Работа цифрового коррелометра (рис. 7.21) при измерении взаимной корреляционной функции заключается в следующем. В момент 1Т0 поступления тактового импульса из блока управления (БУ) на управляющие входы (ВхУ| и ВхУ2) аналого-цифровых преобразователей (АЦП] и АЦП2) напряжения x(iTa) и y(t) преобразуются в числа — соответственно /1; и г,. Число Л, (т-разрядное) подается на первую группу входов микропроцессора (МП), а г, — в схему задержки, состоящую из m регистров сдвига, каждый из которых состоит в свою очередь из п триггеров (по числу параллельно вычисляемых ординат взаимной корреляционной функции). В регистр поступают сдвигающие импульсы от тактового генератора, входящего в состав БУ. С появлением каждого нового сдвигающего импульса «единица» данного разряда числа гг- продвигается в соседний триггер. Так как сдвигающие импульсы повторяются через интервалы То, равные периоду следования импульсов тактового генератора, то появление сигнала на выходе k-ro триггера регистра равносильно задержке сигнала на время kTa. Максимальная продолжительность задержки составляет пТ0. Регулируя период То, можно изменять интервал задержки в широких пределах.
Число которое определяется состоянием триггеров одинаковых номеров (в данном случае номера k) во всех m регистрах, поступает в МП, содержащий перемножители и усреднители. Здесь осуществляется перемножение чисел 1г( и гг_|_£, а результат направляется в й-й канал усреднителя. Накоп-N
ленное в этом канале за цикл измерения число, равное Л£.гг_|_А, пропорцио-6=1
нально оценке ординаты функции взаимной корреляции КХу.
К концу цикла измерения соответствующие числа накапливаются во всех п каналах усреднителя. Показывающий или регистрирующий прибор (например, дисплей Д) индицирует значения ординат функции взаимной корреляции и дает изображение коррелограммы.
7.6. АВТОМАТИЗАЦИЯ ВВОДА В ЭВМ ГРАФИЧЕСКОЙ ИНФОРМАЦИИ [83]
Во многих случаях результаты эксперимента представляют в виде графиков, записанных фотоспособом (осциллограммы) или чернилами (тушью). Часто на одном носителе (пленке, фотобумаге или бумажной ленте) находятся несколько графиков, которые могут пересекаться или касаться в отдельных точках.
Устройства автоматического ввода графической информации в ЭВМ должны отвечать следующим требованиям: 1) быстродействие; 2) достоверность и неизбыточность вводимой информации; 3) универсальность — возможность ввода информации с носителей различной ширины и длины; 4) компенсация помех, вызванных изменениями толщины, контрастности и наклона линий записи; 5) синхронный ввод нескольких графиков с взаимной коммутацией (пересечения, касания); 6) автоматическая поднастройка при изменении фона носителя или контраста линий записи относительно фона носителя; 7) автоматический контроль и устранение сбоев.
В настоящее время создан ряд серийных (Силуэт) и опытных (АСМО) образцов автоматических устройств для считывания и ввода в ЭВМ графиче-256
Рис. 7.22. Схема оптико-электронного преобразователя
ской информации. Общей характерной особенностью таких автоматов является принцип преобразования световой энергии, поступающей на вход, в энергию электрических сигналов на выходе. Схема такого преобразователя включает объект (реализацию), поле восприятия, оптический узел, фотоэлектрический приемник, на вход которого вместе с сигналом X (t) может поступать помеха Z(t), и усилитель-формирователь. Фотокатод приемника и усилитель-формирователь создают шум №(/), который добавляется к выходному сигналу приемника. Так как помеха и шум не коррелированы между собой, то их энергетические спектры можно складывать.
Отношение сигнала к помехе и шуму зависит от толщины линий записи d, диаметра фоточувствительного элемента А, скорости сканирования vB и энергетических спектров яркости линий записи и фона, а также фотоприемника и шума. Оно тем больше, чем выше контрастность записи, меньше h и vc и больше чувствительность приемника.
Если быстродействие устройства ввода меньше, чем ЭВМ, то функции программы ввода могут быть расширены. В этом случае параллельно с вводом выполняются некоторые операции по предварительной обработке поступающей информации: вычисление математического ожидания, исправление грубых сбоев при чтении графика и т. д.
Важнейшей частью устройства ввода графической информации является оптико-электронный преобразователь (ОЭП), вырабатывающий электрические сигналы, временное положение которых определяется ординатой считываемого графика (рис. 7.22). ОЭП включает широкоугольный объектив, преобразователь оптического изображения в электрические сигналы с фокусирующей и отклоняющей системой (ФОС) и усилитель видеосигналов. В качестве преобразователя оптического изображения в электрические сигналы применяется телевизионная передающая трубка — видикон типа ЛИ-23 или ЛИ 415-2.
Изображение считываемого графика (Г) проецируется при помощи фотообъектива (О) на светочувствительный слой видикона (В). Поток электронов, исходящих из электронной пушки видикона, сфокусированный в узкий луч током, протекающим через фокусирующую катушку ФОС, попадает на мишень видикона (его светочувствительный слой).
Мишень видикона состоит из микроэлементов, эквивалентная схема которых может быть представлена в виде резисторов и конденсаторов, соединенных параллельно (рис. 7.23). При освещении мишени сопротивление резистора резко уменьшается. Если через отклоняющие катушки ФОС пропустить линейно изменяющийся ток (например, пилообразной формы), то электронный луч, условно изображенный на рис. 7.23 в виде переключателя, будет последовательно и поочередно замыкать контакты Z, Z+1 и т. д. Благодаря этому
17. Зак. 1001
257
Рис. 7.23. Эквивалентная электрическая схема элементов мишени видикона!
конденсаторы С, будут заряжаться до определенного потенциала, обусловливаемого напряжением источника питания и сопротивлением резистора
На мишени видикона при проецировании считываемого графика имеются освещенные и неосвещенные участки. За промежуток времени между воздействиями луча электронной пушки конденсаторы мишени на освещенных местах разряжаются быстро, а не неосвещенных медленно. Поэтому при повторных циклах воздействия луча на освещенный элемент каждый раз возникает ток, сообщающий новый заряд разрядившемуся конденсатору С,. При прохождении этого же луча по «темным» элементам, заряды которых еще существуют, ток заряда будет незначительным. Следовательно, темным местам (т. е. считываемой линии) соответствует минимум тока электронного пучка или положительный П-образный импульс на мишени видикона. Длительность этого импульса прямо пропорциональна толщине d считываемой кривой и зависит от угла ее наклона к вектору скорости сканирования vc (рис. 7.24):
ti=d/(ve sin а,), где а. — угол наклона кривой для t-й дискреты.
Время сканирования определяется тактом старт-импульсов 1 (рис. 7.25) и сдвигом стоп-импульсов 2 относительно старт-импульсов. П-образный видеосигнал 3 запускает счетчик, который формирует число г<, пропорциональное периоду времени 7,- от видео- до стоп-сигнала. Если на считываемом графике нет нулевой линии для отсчета ординат кривых, то ее заменяют стоп-импуль-сы, определяющие временное расположение П-образных импульсов. Стоп-им-пульсы соответствуют положению точки К (см. рис. 7.22) на поле считываемых графиков.
Статистическое распознавание пересекающихся или соприкасающихся графиков можно осуществить на основе теоремы предсказания, из которой следует:
1) мера предсказания будущей ординаты х(/+т) стохастического процесса определяется коррелированной составляющей рх(т)х(0, где рДт)—нормированная корреляционная функция процесса x(t);
Рис. 7.24. Длительность импульса в зависимости от толщины считываемой линии и угла наклона графика
Рис. 7.25. Схема формирования координирующих импульсов,
258
2) точность предсказания статистического среднего значения х(/+т) увеличивается с приближением рх(т) к единице;
3) чем меньше т, тем точнее предсказание;
4) если т0 — длительность корреляции, то при т>т0 предсказание (распознавание) пересекающихся графиков становится невозможным.
Экстраполяция значения х производится по формуле
х (t + т) = рх (т) х (0 + [1 — р2 (Т)]0-5 и (/), (7.6)
где U(t)—некоррелированная с x(t) составляющая, характеризующая меру непредсказуемости процесса.
Если разница между прочитанным и рассчитанным по формуле (7.6) значениями х статистически незначима, то принимается гипотеза о принадлежности точки данному графику.
Для распознавания пересекающихся графиков можно применять также экстраполирование при помощи интерполяционных полиномов или полиномов наилучшего приближения. Удобной для практического применения является вторая интерполяционная формула Ньютона для равноотстоящих координат, которая после преобразования имеет вид
Ут+\ — ВтУт ^т — 1Ут — { + ...4- В^у 1, где i/m+i — значение экстраполяционной ординаты; т — число ординат, взятых для экстраполяции (т=4...8).
Коэффициенты Bt, В2, ..., Вт вычисляются по формуле = <— 1)"1-*
где С^-1 — число сочетаний из т по k — 1.
Значения Вь для некоторых т приведены ниже:
т Bi В, Вз в4 Bs в( ! В7 в»
4 -1 3 -3 1 0 0 0 0
5 1 — 4 6 — 4 1 0 0 0
6 -1 5 -10 10 -5 1 0 0
7 1 -6 15 -20 15 -6 1 0
8 -1 7 -21 35 -35 21 — 7 1
Для экстраполирования лучше всего использовать ортогональные поли
номы Чебышева. Тогда
Ут + 1 =АтУт + Лт-1(/т-1 + ...+Л 1Z/],
где Ak — коэффициенты, значение и знак которых зависят от степени полинома и числа точек, взятых для экстраполяции (сумма этих коэффицентов не зависит ни от степени полинома, ни от числа точек и равна 1).
При т=7 значения Ak следующие:
Степень At Л2 А3 А4 А$ А6 Ai полинома
3 -1,8810 1,9286 1,8571 -0,0952 -1,9286 -1,6429 2,7619
4 -1,2298 0,4091 2,0742 1,2072 -1,7115 -3,1624 3,4131
Эти значения вычислены по формуле
Р/Рл
Ajn = -
где pj — числа Чебышева (см. табл. П.12);
п2 (т2 — па)
Рл+1 = Р\Рп — 4 (2ге _ 1) (2п +1) ’
Ро=1; Pi = (ffi-l)/2; Л70=1/т.
17*
259
ПРИЛОЖЕНИЕ 1
Табл. П.1 Критические значения критерия Стьюдента t(P,m)
т Доверительная вероятность Р
0,90 0,95 0,975 | 0,99
3 2,920 4,303 6,205 9,925
4 2,353 3,183 4,177 5,841
5 2,132 2,776 3,495 4,604
6 2,015 2,571 3,163 4,032
7 1,943 2,447 2,969 3,707
8 1,895 2,365 2,841 3,500
9 1,859 2,306 2,752 ‘ 3,355
10 1,833 2,262 2,685 3,250
11 1,813 2,228 2,634 3,169
12 1,796 2,201 2,593 3,106
13 1,782 2,179 2,560 3,055
14 1,771 2,160 2,533 3,012
15 1,761 2,145 2,510 2,977
16 1,753 2,132 2,490 2,947
18 1,739 2,110 2,458 2,898
20 1,729 2,093 2,433 2,861
22 1,721 2,080 2,414 2,831
24 1,714 2,069 2,398 2,807
25 1,711 2,064 2,391 2,797
30 1,699 2,045 2,364 2,756
40 1,684 2,021 2,329 2,705
60 1,671 2,000 2,299 2,660
120 1,658 1,980 2,270 2,617
00 1,645 1,960 2,241 2,576
Табл. П.2. Критические значения критерия Пирсона %2 (P.f)
Доверительная вероятность Р
f 0,9 | 0,95 0,975 0,99
1 2 3 4 5
1 2,706 3,841 5,024 6,635
2 4,605 5,991 7,378 9,210
3 6,251 7,815 9,348 11,345
4 7,779 9,488 11,143 13,277
260
Окончание
1 2 3 4 5
5 9,236 11,070 12,833 15,086
6 10,645 12,594 14,449 16,812
7 12,017 14,067 16,013 18,475
8 13,362 15,507 17,535 20,090
9 14,684 16,919 19,023 21,666
10 15,987 18,307 20,483 23,209
И 17,275 19,675 21,920 24,725
12 18,549 21,026 23,337 26,217
13 19,812 22,362 24,736 27,688
14 21,064 23,685 26,119 29,141
15 22,307 24,996 27,488 30,578
16 23,542 26,296 28,845 32,000
17 24,769 27,587 30,191 33,409
18 25,989 28,869 31,526 34,805
19 27,204 30,144 32,852 36,191
20 28,412 31,410 34,170 37,566
22 30,813 33,924 36,781 40,289
24 33,196 36,415 39,364 42,980
26 35,563 38,885 41,923 45,642
28 37,916 41,337 44,461 48,278
30 40,256 43,773 46,979 50,892
Табл. П.З. Критические значения критерия v (Р,т)
т Доверительная вероятность Р
0,9 0,95 0,975 0,99
3 1,406 1,412 1,414 1,414
4 1,645 1,689 1,710 1,723
5 1,791 1,869 1,917 1,955
6 1,894 1,996 2,067 2,130
7 1,947 2,093 2,182 2,265
8 2,041 2,172 2,273 2,374
9 2,097 2,238 2,349 2,464
10 2,146 2,294 2,414 2,540
И 2,190 2,343 2,470 2,606
12 2,229 2,387 2,519 2,663
13 2,264 2,426 2,563 2,713
14 2,297 2,461 2,602 2,759
16 2,354 2,523 2,670 2,837
18 2,404 2,577 2,728 2,903
20 2,447 2,623 2,779 2,959
22 2,486 2,664 2,823 3,008
24 2,521 2,701 2,862 3,051
26 2,553 2,734 2,897 3,089
28 2,582 2,764 2,929 . 3,124
30 2,609 2,792 2,958 3,156
35 2,668 2,853 3,022 3,224
40 2,718 2,904 3,075 3,281
45 2,762 2,948 3,120 3,329
50 2,800 2,987 3,160 3,370
261
Табл. П.4. Значения x2/(m—1) для интервальной оценки дисперсии
tn Доверительная вероятность Р
0,9 0,95 0,98 0,99
7 О1 — х 7 еч 04 X (1—и/)/ 7 X 7 •S- х 7 5 сче? X 7 е. 7 S сТсч X
3 2,996 0,052 3,689 0,025 4,605 0,010 5,299 0,005
4 2,605 0,117 3,116 0,072 3,782 0,038 4,279 0,024
5 2,372 0,178 2,786 0,121 3,319 0,074 3,715 0,052
6 2,214 0,229 2,556 0,166 3,017 0,111 3,350 0,082
7 2,099 0,273 2,408 0,206 2,802 0,145 3,091| 0,113
8 2,010 0,310 2,288 0,241 2,639 0,177 2,897 0,141
9 1,938 0,341 2,192 0,273 2,511 0,206 2,744 0,168
10 1,880 0,369 2,114 0,300 2,407 0,232 2,621 0,193
12 1,790 0,416 1,993 0,347 2,248 0,278 2,433 0,237
14 1,720 0,453 1,903 0,385 2,130 0,316 2,294 0,274
16 1,666 0,484 1,883 0,418 2,039 0,349 2,187 0,307
18 1,623 0,510 1,776 0,445 1,965 0,377 2,101 0,335
20 1,587 0,532 1,729 0,469 1,905 0,402 2,031 0,360
22 1,556 0,552 1,690 0,490 1,854 0,424 1,972 0,383
24 1,529 0,569 1,656 0,508 1,810 0,443 1,921 0,403
26 1,506 0,584 1,626 0,525 1,773 0,461 1,877 0,421
28 1,486 0,598 1,600 0,540 1,739 0,477 1,839 0,437
30 1,468 0,610 1,577 0,553 1,710 0,492 1,805 0,452
35 1,430 0,637 1,523 0,583 1,649 0,523 1,734 0,485
40 1,399 0,659 1,490 0,606 1,601 0,549 1,679 0,513
45 1,375 0,677 1,459 0,627 1,562 0,572 1,634 0,536
50 1,354 0,692 1,433 0,644 1,529 0,591 1,597 0,556
55 1,336 0,706 1,411 0,659 1,501 0,607 1,565 0,574
Табл. П.5. Таблица значений dm
для оценки апо размаху
т Доверительная вероятность Р
0,90 0,95 0,98
dml dm2 dtnl dm2 dm>
1 2 3 4 5 6 7 8
2 1,128 2,77 0,09 3,17 0,04 3,64 0,02
3 1,643 3,31 0,43 3,68 0,30 4,12 0,19
4 2,059 3,63 0,76 3,98 0,59 4,40 0,43
5 2,326 3,86 1,03 4,20 0,85 4,60 0,66
6 2,534 4,03 1,25 4,36 1,06 4,76 0,87
7 2,704 4,17 1,44 4,49 1,25 4,88 1,05
8 2,847 4,29 1,60 4,61 1,41 4,99 1,70
9 2,970 4,39 1,74 4,70 1,55 5,08 1,34
10 3,078 4,47 1,86 4,79 1,67 5,16 1,47
И 3,173 4,55 1,97 4,86 1,78 5,23 1,58
12 3,258 4,62 2,07 4,92 1,88 5,29 1,68
13 3,336 4,68 2,16 4,99 1,97 5,35 1,77
14 3,407 4,74 2,24 5,04 2,06 5,40 1,86
262
Окончание
1 2 3 4 5 6 7 8
15 3,472 4,80 2,32 5,09 2,14 5,45 1,93
16 3,532 4,85 2,39 5,14 2,21 5,49 2,01
17 3,588 4,89 2,45 5,18 2,27 5,54 2,07
18 3,640 4,93 2,51 5,22 2,34 5,57 2,14
19 3,689 4,97 2,57 5,26 2,39 5,61 2,20
20 3,735 5,01 2,62 5,30 2,45 5,65 2,25
Табл. П.6. Коэффициент q для оценки а
т р т р
0,95 0,99 0,95 0,99
11 0,59 0,98 40 0,24 0,35
12 0,55 0,90 45 0,22 0,32
13 0,52 0,83 50 0,21 0,30
14 0,48 0,78 60 0,188 0,269
15 0,46 0,73 70 0,174 0,245
16 0,44 0,70 80 0,161 0,226
17 0,42 0,66 90 0,151 0,211
18 0,40 0,63 100 0,143 0,198
19 0,39 0,60 150 0,115 0,160
20 0,37 0,58 200 0,099 0,136
25 0,32 0,49 250 0,089 0,120
30 0,28 0,43 300 0,081 0,109
35 0,26 0,38 350 0,075 0,101
Табл. П.7. Критические значения критерия Фишера F
Р т д
4 6 8 1° 15 1 20 , 30 40 60
1 2 3 4 5 6 7 8 10 11 12
0,90 4 5,39 5,31 5,27 5,24 5,20 5,18 5,17 5,16 5,15
0,95 9,28 9,10 8,89 8,81 8,70 8,66 8,62 8,59 8,57
0,99 29,5 28,2 27,7 27,3 26,9 26,7 26,5 26,4 26,3
0,90 6 3,62 3,45 3,37 3,32 3,24 3,21 3,17 3,16 3,14
0,95 5,41 5,05 4,88 4,77 4,62 4,56 4,50 4,46 4,43
0,99 12,1 11,0 10,5 10,2 9,72 9,55 9,38 9,29 9,20
0,90 8 3,07 2,83 2,78 2,70 2,63 2,59 2,56 2,54 2,52
0,95 4,35 3,87 3,79 3,64 3,51 3,44 3,38 3,34 3,32
0,99 8,45 7,19 6,99 6,62 6,31 6,16 5,99 5,91 5,86
0,90 10 2,81 2,61 2,51 2,44 2,34 2,30 2,25 2,23 2,21
0,95 3,86 3,48 3,29 3,18 3,01 2,94 2,86 2,83 2,79
0,99 6,99 6,06 5,61 5,35 4,96 4,81 4,65 4,57 4,48
0,90 15 2,52 2,24 2,19 2,12 2,01 1,96 1,91 1,89 1,86
0,95 3,34 2,85 2,76 2,65 2,46 2,39 2,31 2,27 2,22
0,99 5,56 4,46 4,28 4,03 3,66 3,51 3,35 3,27 3,18
0,90 20 2,40 2,18 2,06 1,98 1,86 1,81 1,76 1,73 1,70
263
Окончание
1 2 3 4 5 6 7 8 9 10 П
0,95 3,13 2,74 2,54 2,42 2,23 2,16 2,07 2,03 1,98
0,99 5,01 4,17 3,77 3,52 3,15 3,00 2,84 2,76 2,67
0,90 30 2,28 2,05 1,93 1,85 1,72 1,67 1,61 1,57 1,54
0,95 2,92 2,53 2,33 2,21 2,01 1,93 1,84 1,79 1,74
0,99 4,51 3,70 3,30 3,07 2,70 2,55 2,39 2,30 2,21
0,90 40 2,23 2,00 1,87 1,79 1,66 1,61 1,54 1,51 1,47
0,95 2,84 2,45 2,25 2,12 1,92 1,84 1,74 1,69 1,64
0,99 4,31 3,51 3,12 2,82 2,52 2,37 2,20 2,11 2,02
0,90 60 2,18 1,95 1,82 1,74 1,60 1,54 1,48 1,44 1,40
0,95 2,76 2,37 2,17 2,04 1,84 1,75 1,65 1,59 1,53
0,99 4,13 3,34 2,95 2,72 2,35 2,20 2,03 1,94 1,84
0,90 120 2,13 1,90 1,77 1,68 1,55 1,48 1,41 1,37 1,32
0,95 2,68 2,29 2,09 1,96 1,75 1,66 1,55 1,50 1,43
0,99 3,95 3,17 2,79 2,56 2,19 2,03 1,86 1,76 1,66
Табл. П.8. Критические значения критерия Кохрена GK
п т 4 | 5 | 6 | 7 | 8 | 9 1 10 | 17
Р=0,95
3 0,798 0,746 0,707 0,677 0,653 0,633 0,617 0,547
4 0,684 0,629 0,589 0,560 0,537 0,518 0,502 0,437
5 0,589 0,544 0,507 0,478 0,456 0,439 0,424 0,365
6 0,532 0,480 0,445 0,418 0,398 0,382 0,368 0,314
7 0,480 0,431 0,397 0,373 0,354 0,338 0,326 0,276
8 0,438 0,391 0,359 0,336 0,319 0,304 0,293 0,246
10 0,373 0,331 0,303 0,282 0,267 0,251 0,244 0,203
12 0,326 0,288 0,262 0,244 0,230 0,219 0,210 0,174
15 0,276 0,242 0,219 0,203 0,191 0,182 0,144 0,143
20 0,220 0,192 0,174 0,160 Р=0,99 0,150 0,142 5,136 0,111
3 0,883 0,834 0,793 0,761 0,734 0,711 0,691 0,606
4 0,781 0,721 0,676 0,641 0,613 0,590 0,570 0,488
5 0,696 0,633 0,588 0,553 0,526 0,504 0,485 0,409
6 0,626 0,564 0,520 0,487 0,461 0,440 0,423 0,353
7 0,569 0,508 0,466 0,435 0,411 0,391 0,375 0,310
8 0,521 0,463 0,423 0,393 0,370 0,352 0,337 0,278
10 0,447 0,393 0,357 0,331 0,311 0,295 0,281 0,230
12 0,392 0,343 0,310 0,286 0,268 0,254 0,242 0,196
15 0,332 0,288 0,259 0,239 0,223 0,210 0,200 0,161
20 0,265 0,229 0,205 0,188 0,175 0,165 0,157 0,125
гТабл. П.9. Значения критерия тк
т р т р
0,95 0,99 0,95 1 0,99
1 2 3 4 5 6
4 0,390 0,256 19 0,642 0,510
5 0,410 0,269 20 0,650 0,520
6 0,445 0,281 25 - 0,676 0,542
264
О кончайие
1 2 3 4 5 6
7 0,468 0,307 30 0,704 0,508
8 0,491 0,331 35 0,725 0,611
9 0,514 0,354 40 0,742 0,636
10 0,531 0,376 45 0,757 0,658
11 0,548 0,397 50 0,769 0,674
12 0,564 0,414 60 0,789 0,702
13 0,578 0,431 70 0,804 0,724
14 0,591 0,447 80 0,817 0,741
15 0,603 0,461 90 0,827 0,756
16 0,614 0,475 100 0,836 0,767 ’
17 0,624 0,487 НО 0,843 0,778
18 0,633 0,499 120 0,850 0,788
Табл. П.10. Критические значения критерия Линка—Уоллеса Кк при Р=0,95
т V
2 3 4 6 7 9 12 15
3 1,90 1,44 1,14
4 1,62 1,25 1,01
6 1,50 1,17 0,95 0,80 0,69
8 1,49 1,18 0,96 0,81 0,70 0,62
10 1,52 1,20 0,98 0,83 0,72 0,63 0,52
12 1,56 1,23 1,01 0,85 0,74 0,65 0,53 0,42
14 1,60 1,26 1,03 0,87 0,76 0,67 0,55 0,43
16 1,64 1,30 1,06 0,90 0,78 0,69 0,56 0,44 0,37
18 1,68 1,33 1,09 0,92 0,80 0,71 0,58 0,46 0,38
20 1,72 1,36 1,12 0,95 0,82 0,73 0,59 0,47 0,39
30 1,92 1,52 1,24 1,05 0,91 0,81 0,66 0,52 0,43
40 2,08 1,66 1,35 1,14 0,99 0,88 0,72 0,57 0,47
50 2,23 1,77 1,45 1,22 1,06 0,94 0,77 0,61 0,50
Табл. П.11, Квантили U(P) нормированного нормального распределения
р U(P) р U(P) р
0,55 0,12566 0,87 1,12639 0,95 1,64485
0,60 . 0,25335 0,88 1,17499 0,96 1,75069
0,65 0,3853 0,89 1,22653 0,970 1 ,88079
0,70 0,52440 0,90 1,28155 0,975 1,95996
0,75 0,67449 0,91 1,34076 0,980 2,05375
0,80 0,84162 0,92 1,40507 0,985 2,17009
0,85 1,03643 0,93 1,47579 0,990 2,32635
0,86 1,08032 0,94 1,55477 0,995 2,57583
265
Табл. П.12. Значения ортогональных полиномов Чебышева
Количество точек X Ро Р2 р3 Р5 PjM
1 2 3 4 S 6 7 8 9
7 0 1 0 —4 0 6 0 к Pi = Х-, Рг = хг — 4;
2 3 2 3 —<J 0 5 —1 1 —7 3 —4 1 Ps = х3 — 7х; „ 67 72 Р4 = х4 — — х2 + — 7 7
Ъ 7 28 84 36 264 240
9 0 1 1 0 1 —20 —17 0 —9 18 9 0 9 20 Pi = х\ Р3 = х2 ——;
2 2 —8 —13 —11 4 59
3 3 7 —7 —21 —11 Р3 = х3- — х;
4 4 28 14 14 4 5 115 216
V/ 9 60 924 1188 3432 3120 Р4 = х4—— х2 + —
11 0 1 0 —10 0 6 0
1 1 —9 —14 4 4
2 3 4 5 2 3 4 5 —6 —1 6 15 —23 —22 —6 30 —1 —6 —6 6 4 — 1 —6 3 Pi = х\ Рг = х2 — 10; Р3 = х3 — 17,8х; Р4 = х4 — 25х2 + 72
V/ 11 110 858 5148 3432 6240
13 0 1 0 —14 0 84 0
1 1 —13 —1 64 20 Pi = х; Р2 = х2 — 14;
2 2 —10 —7 11 26 Р3 = х3 — 25х;
3 3 —5 —8 —54 11 2
4 4 2 —6 —96 —18 Р4 = X1 — 35 —-х2 + 144
5 5 И 0 —66 —33
6 6 22 11 99 22 у4= 116 688 Vs = 106 080
V/ 13 182 2002 3432 Y4 ?5
15 0 1 0 —56 0 756 0 56 Pi = x-, Р2 = х4 ——;
1 2 1 2 —53 —44 —27 —49 621 251 657 1000
3 3 —29 -61 —249 751 Р3 = х3 — 33,4х;
4 4 —6 —58 —704 —44 2
5 5 19 —35 —868 —979 Р4 = х4 — 47 — х2 + 259,2
6 6 52 13 —429 —1144 7
7 7 91 91 1101 1001 . ?4 = 22 170 772 Vs = 100 776 000
V/ 15 280 12 376 47 736
17 0 1 0 —24 0 36 0
1 1 —23 —7 31 55
2 2 —20 —13 17 88 Pi = х; Р2 = х2 — 24;
3 3 —15 —17 —3 83 Р3 = х3 — 43х;
4 4 —8 —18 —24 36 Р4 = х4 - 61х2 + 432
5 5 1 —15 —39 -39
6 6 12 7 —39 —104
266
Окончание
1 2 3 4 5 6 7 8 9
7 8 7 8 25 40 7 28 —13 52 —91 104 74 = 201 555 7s =2 015 520
V/ 17 408 7752 23256 Vs
19 0 1 2 3 4 5 6 7 8 9 1 0 1 2 3 4 5 6 7 8 9 -30 —29 -26 —21 —14 -5 6 19 34 51 0 —44 —83 —112 —126 —120 —84 —28 68 204 396 352 227 42 —168 —354 —453 —388 -68 612 0 44 74 74 54 3 —58 —98 —68 102 Pi — x; Pa = x2 — 30; Pa = x3 — 53,8x; 3 6 Pi = xi — 76 — x2 + 678 — 7 7 74 = 3 922 512 7, = 3 565 920
V/ 19 570 13 566 255816 V4 Vs
Табл. П.13. Дробнорациональные модели
с двумя параметрами
Номер модели Графики модели Вид модели и спрямляющая подстановка
1 2 3
6о ^1-^
2 = Х/У; (7 = Х;
1 — &о>О, &1>0;
2 — &0>0, 61 <0
6о ЬхХ Z= 1/Y; U = X; 1 — b0>0, 6i>0; 2 — b0>0, 6j<0
Y = --------;
&o + 6jX
Z = X2!Y\ U = X;
1 — 6o>0, &i>0;
2 — b0>0, b±<0
267
Окончание
з
bo + bjX2 ' Z= 1/Y; U = Хг\ 1 — b0>0, bj>0; 2 — b0>0, &!<()
bo + bxX2 1
Z = Х/Yl U = X2; 1—b0>0, bj>0;
2 — b0>0, bx<0
bo + bjX2
Z = X2/V; U = X2;
1 — b0>0, bj>0;
2 — b0>0, b]<0
bo + bjX3 ’
Z = X/r; (7 = X3;
1 —bo>0, bx>0;
2 — b0>0, b2<0
_ 1
bo -f- bxX3 z = 1/V; и = X3; 1—b0>0, bj>0; 2,—be>0, bi<0
268
Табл. П.14. Иррациональные модели с двумя параметрами
Номер модели
Графики модели
Вид модели и спрямляющая подстановка
Y = V ьв + Ь.Х ;
Z = У2; и = X;
1 — Ьо>0, Ь2>0;
2 — Ьо>О, Ь1<0
Y = XV Л + Ь1№ :
Z = (Y/ХУ; и = X2;
1 — Ьо>О, Ь1>0;
2 — 6о>О, &х<0
у -X jZ й0 _|_ ьгх ’ Z = (Y/Xy-, и = X;
1 — 6о>0, 6i>0;
2 — 4>о>0, />1<0'
Ьв Ф М г = Х/У2; U = X;
1 — Ь0>0, &!>(); 2 — ba>0, bi<0
у = Ьохй‘;
Z = 1пУ; и = 1пХ;
60>0;
1 — &i>l;
2—0<£>1<1;
3 —^<0
269
Табл. П,15. Показательные модели с двумя параметрами
Номер модели
Графики модели
Вид модели и спрямляющая подстановка
г 1
Y = b^x;
2 = InK; U = Л; &»>0;
1 — bi>0;
2 —&2<0
У = btXeb,x;
Z = \n(Y/X)- U = Х\ ba>Q-
1 - bi>0;
2 — fc2<0
2 1
Y = boX2eb,X\ Z = In (//№)•, U=.X\ 60>0;
1 — bi>0;
2 — &2<0
Z = 1пУ; U = X2; bo>O;
1 — bj>0;
2 —Z>!<0
Z = 1п(У/Х); U = X2-ba>Q-, 1 — &!>0;
2 — &!<0
270
Окончание
1 2
з
20
У = ЬаХгеь‘хг;
Z = \п (Y/Х2)\ и = Хг\ 6e>0;
1 — 6х>0;
2 —Й!<0
Y = 60ей‘/х;
Z=lnY; 1/Х;
6в>0;
1 — 6х>0;
2 —6х<0
Табл. П.16. Логарифмические модели с двумя параметрами
Номер модели Графики модели Вид модели и спрямляющая подстановка
1 2 3
Y = &01п [61(1 4* X)]; Z= У; l/ = ln(l +Х); 60>0;
1 —61= 1;
2 —6i>l
Y = 601п [61/(1 >Х)];
Z= У; У = 1п(1 ->Х); 60>0; 6Х> 1
Y = 60Х1п (61/Х );
Z = Y/X-, U = ln X;
6в<0; 6х>0
271
Окончание
i 2 3
25 Y Л У=6аХ21п (Jh/X); Z = У/Х2; и = 1пХ; 6а<0; Ьу>0
Табл. П. 17. Тригонометрические модели с.двумя параметрами
Номер модели
Графики модели
Вид модели и спрямляющая подстановка
27
У = 6asin (6jX);
Zz = arccos[y2z/(2yi.)];
U— Х(. = const; йй>0; й(>0
Y = &0Xsin (6,Х); 2/=агссо5[У2г./(4Уг)];
й0>0; 6[>0
Ь»
Y= —sin (йцХ); Л
Z; = arccos (Y^/Y^;
60>0; Z»!>0
Табл. П.18. Комбинированные модели с двумя параметрами
Номер модели Графики модели Вид модели и спрямляющая подстановка
1 2 3
29 Y Z~X 2 /\\ 1\ X . o’ Л 1 « О о -><>< Л Ло j? и л -о V , I1 AV<-в* | 1 СО II сч II
272
Окончание
3
У = (60 + 61Х) ех;
2 = Ye~x; U = X; Ьо > 0; / — &! > 0;
2 — bt < 0
У — Ь0Хь,е~х;
2 = Х + 1пУ; U = In X;
Ьа > 0;
1 - 61 > 1;
2 — 0 < 6Х < 1
Y = Ьох'-ь‘е~ь‘х-,
7 = 1п(У/Х); L/= In X — X;
Ьо > 0;
1 — 0<Ь1< 1;
2 — 6i > 1
У = (6О + 61Х) In (1 + Х);
Z = У/ln (1 + X); U = X;
60 > 0;
/ — 61 >0;
2 — 61 < О
У=60(1-е-ь>х);
zi = in - 1); У, = 60 >0; 61 > О
1 + 6ОХЬ‘ ’ Z.= ln(X/y—1); {7 = 1пХ;
1 — 6в > 0, 6i > 1;
2 — 60 < 0, 6j > О
18. Зак. 1001
273
Табл. П.19. Модели с тремя параметрами
Номер модели Графики модели Вид модели и спрямляющая подстановка
1 2 3
.37
.39
У = b0 + 6tX 4. 62Х2;
Z = (Y-Y0)/(X~XB)-. U = X-l-—bB>0, ii<0, 62>0;
2 — Ьо > 0, 6j > 0, 62 < О
у = х(б0 + Ь1Ха + М'4);
„ Y/X-Yo/Xo х2-х20 '
и = X2;
1 — б0 > о, > о, б2 < °; 2 — Ьо > О, £>1 < О, 62 > О
У= Xs(60 + 6iX + 62X2);
Y/X3-Yolx3o
X —Хо
1/ = Х;
1 — 60 > О, 61 > О, 62 < О;
2 — 60 > 0, 6j < О, 6г > О
60 + 61Х + 61Х2’
1/У-1/П х-хв ’
!-Ьо>О, 2 — Ьа>0, 3 — 6а > О, 4~ 6о>0,
61 > О,
61 < О,
61 > о,
61 < о,
U= X;
6г > О;
62 > О;
62 < О;
63 < О
•274
Продолжение
Окончание
1 2 | 3
43 Y Л к / Й! У = &о+ ; °2 + X 2 = (Х0-Х)/(У-Ув); U = X; Ьо >0; Ьг > 0; / —&1<0; 2 — Ь1>0
/ / г л
Табл. П.20. Планы главных эффектов
Номер плана План Способ построения
Вспомогательная матрица Номера столбцов вспомогательной матрицы
1 2'//8 Da 1...7
2 2и//12 7712 1... 11
3 215//16 Dis 1... 15
4 34//9 d9 1...4
5 45//16 Dm 16...20
6 24 X 4//8 Da 1, 2, 3, 7, 8
7 22Хб//12 7712 12, 13, 14
8 2«х8//16 Dis 4, 7, 9, 10
Табл. П.21. Таблица случайных чисел
1 2 3 4 1 5 1 6 1 2 1 8 1 9 1 10 1 " : 1 12
15 10 45 10 05 93 55 19 23 09 14 35
34 30 14 86 19 65 74 14 58 73 71 16
61 66 87 28 56 01 03 79 07 40 11 14
28 06 44 68 55 06 30 77 51 71 82 76
60 45 37 72 25 79 92 20 95 42 14 51
47 33 29 03 43 28 14 18- 62 47 61 44
08 42 88 62 26 48 46 50 57 60 87 49
06 58 58 71 34 . 67 57 78 96 01 45 85
99 52 35 93 63 09 52 22 68 16 06 16
15 24 22 95 07 56 11 13 61 15 13 65
28 68 71 58 82 42 78 61 16 26 32 38
82 72 06 96 21 24 66 15 83 77 09 05
92 86 89 50 39 06 91 42 90 53 25 24
13 38 93 05 74 99 12 72 79 75 69 39
84 99 52 63 83 94 53 67 78 59 66 63
10 58 91 41 58 04 38 74 71 97 87 07
99 02 82 20 99 93 25 37 49 02 19 79
74 65 74 12 64 62 33 50 19 60 94 86
34 89 71 51 67 95 64 09 08 21 71 30
02 87 58 28 82 92 88 67 07 18 61 12
276
Окончание
1
81
88 38 25
98
01
56 03 07
14
46 17 67
89 05
38 40
76 62
2 з 4 5 6 7 8 9 Ю и 1 12
55 12 84 03 91 23 01 13 32 08 29
52 23 07 72 09 91 35 74 17 54 76
93 98 71 18 69 55 84 35 73 17 46
83 36 86 56 28 33 04 56 11 39 28
99 23 30 17 20 09 87 68 06 84 09
03 62 . 41 90 60 02 62 90 46 77 73
65 70 35 92 35 31 98 43 03 97 02
30 20 29 41 12 88 99 62 21 27 54
86 87 40 32 02 64 03 98 06 41 05
79 88 59 73 91 81 01 42 04 46 88
57 12 50 29 13 51 82 39 24 03 70
65 51 70 50 36 70 60 16 34 87 13
71 37 89 73 26 28 14 45 14 29 78
98 57 53 69 00 44 62 73 97 41 21
25 56 45 64 06 33 77 25 83 65 98
85 52 87 23 87 05 23 65 75 47 61
07 62 24 92 27 51 71 18 27 16 59
32 79 47 42 83 71 45 73 35 33 46
16 49 06 75 51 22 32 85 75 03 21
ПРИЛОЖЕНИЕ 2
Вспомогательные матрицы
Dt =
О 1 2 О 1 2 О 1 12
(ООО 1 о о 0 1 о 1 1 о О о 1 1 0 1 О 1 1
11 1 1
ООО 1 1 О 1 0 1 О 1 1 О 1 1 1 О 1 1 1 О ООО
0 3 D
1 3 °'
О 2
О 1 10
a loii 10001000 0) 01101110001011 1011011 1000110 01011011100101 00101101110002 00010110111013 10001011011 1 12 1 1000101 101 103 11100010 11000 4 01110001011015 10111000101114 00000000000005
о о о
1 1
1 2
2 2
о
1
2
1
2 о
2 о
1
01 1
2 2 О
1 1
2 О
D.
'16 —
0)
1 о
1 о
1 о
1 о
1 о
1 о
1 о и
о о 1 1 о о 1 1 о о 1
1 о о 1 1
о о о о 1 1 1 1 о о о о 1 1 1 I
о о о о о о о о
1 1
1 1
1 1
1 I
о I 1 о о 1 1 о о 1 1 о о 1
1 о
о 1 о 1 1 о 1 о о 1 о 1 1 о 1 о
О 1 о 1 О 1 о 1 1
о о 1 о 1 о 1 о
о о о о 1 1 Г 1 1 1 о о о
1 1
1 1 о о
о о
1 1
1 1 о о 1 1 о о
о о о о
1 1 1
1 1 1 1 1 о о о о
о 1 1 о 1 о о 1 о 1 1 о 1 о о 1
О 1 1 О о 1 1 о 1 о о 1 1 о о 1
о 1 о 1 1 о 1 о 1 о 1 о о 1 о 1
о о
1 1 1 1 о о 1 1 о о о о
1 1
о 1 1 о 1 о о 1 1 о о 1 о 1
1 о
О 2 3 1 О 2 3 1 О 2 3 1 О 2 3
1
о о о о
2 2
2 2
3 3
3 3
1 1
1 1
о 2 3 1 2 о 1 3 3 1 о 2 1 3 2 о
о 1 3 2 3 2 О 1 2 3 1 О 1 О 2 3
о
3
1
2
2
1
3 о
3 о
2
1 1
2 О
3
о
1
2
3
4
5
6
7 О
2
3
4
5
6
71
О О 1 1 1 2
277
ПРИЛОЖЕНИЕ 3
Приборы для экспериментов в машиностроении
Наименование и назначение Марки
1 2
Самопишущие приборы для регистрации сигналов с частотой изменения: от 0 до 45 Гц от 0 до 150 Гц Графопостроители зависимостей Осциллографы светолучевые Анализаторы спектра колебаний Измерительно-вычислительные комплексы Вычислительно - управляющие комплексы Информационные измерительные системы Виброметры Профилометры Микроскоп растровый (для измерения Ra) Проектор измерительный цифровой Устройства цифровой индикации перемещений Микроскопы измерительные Твердомеры Мост цифровой тензометрический Коммутаторы аналоговые Тахометры: часовой стробоскопический электронные Преобразователи: аналого-цифровые цифро-аналоговые графиков в цифровые коды Усилители: постоянного тока для термопар универсальные Измерительные преобразователи: напряжения мощности температуры функциональные вибраций пьезоэлектрические Субблоки: интегрирующий дифференцирующий математический вспомогательных функций Н 3021 Н 338 Н 306; Н 306 К Н 030 А; Н 041; Н 117/1; Н 145; К 12-22; Н 063 Ф 4325; Ф 4327 ИВК-1; ИВК-2 ВУМС 001-03; 15 ВУМС-28-025 К 734; СТК-400-50; К 484 ВМ-1; ИВ-67 Модели 253 и 283 ОРИМ-1 ПИ-360 Ц Ф 5074; Ф 5095; Ф 5134; Ф 5147 УИМ-24; УИМ-29 БТБ-3; ТКС-14-250 ЦТМ-5 Ф 799; Ф 7100 ТЧ 10-Р ТСт 60-4256 ТЭ 30-5Р; ТЭ 250-4А6 Ф 7044; Ф 7077; Ф 4232 Ф 4407; Ф 4810; ДАС Ф 014; Ф 018 Ф 1733; У 5-10 И 37 Ф 1510; Ф 73; У 7-1 В 9-5; В 9-6 П 030; Е 7019 ТПС-302-01 Е 817; Н 818; Е 819; Е 820 Д Ю; Д 11; Д 23 Ф 5192 Ф 5270 Ф 5178 Ф 5206
278
Окончание
I 2
Блоки питания Устройства сопряжения УВК и ЭУ Цифропечатающие устройства Устройства счета Гальванометры вычислительные (для осциллографов) П 133; П 4109 КРЕЙТ № 1; КРЕЙТ № 2 Щ 68000 К; Ф 5033 К Ф 5111; Ф 5112; Ф 5114 М 024; М 026; М 031; М 021; М 022
ЛИТЕРАТУРА
1. Абрамович Б. Г., Картавцев В. Ф. Цветовые индикаторы температуры.— М.: Энергия, 1978.—214 с.
2. Адлер Ю. П. Предпланирование эксперимента.—М.: Знание, 1978.— 87 с.
3. Адлер Ю. П., Маркова Е. В., Грановский Ю. В. Планирование эксперимента при поиске оптимальных условий,—М.: Наука, 1976,—279 с
4. Армейский Е. В., Фалк Г. Б. Электрические микромашины.— М.-. Высш, шк., 1975,—239 с.
5. Бауманн Э. Измерения сил электрическими методами.— М.: Мир, 1978,— 381 с.
6. Березин С. А., Каратыев О. Г. Корреляционные измерительные устройства в автоматике.— Л.: Энергия. Ленингр. отд-ние, 1976.—104 с.
7. Блохин А. В. Аппаратурный анализ характеристик случайных процессов.— М.: Энергия, 1976.—96 с.
8. Браславский Д. А., Петров В. В. Точность измерительных устройств.— М.: Машиностроение, 1976.—312 с.
9. Бродский В. 3. Введение в факторное планирование эксперимента.— М.: Наука, 1976.—224 с.
10. Бурдун Г. Д., Марков Б. Н. Основы метрологии.— М.: Изд-во стандартов, 1972,—336 с.
И. Вапник В. Н. Восстановление зависимостей по эмпирическим данным.— М.: Наука, 1979.—447 с.
12. Веников В. А. Теория подобия и моделирование.— М.: Высш, шк., 1976.— 479 с.
13. Вибрации в технике: Справочник/Под ред. М. Д. Генкина.— М.: Машиностроение, 1981.— т. 5. 496 с.
14. Вознесенский В. А. Статистические методы планирования эксперимента в технико-экономических исследованиях.— М.: Статистика, 1974.—192 с.
15. Вознесенский В. А., Ковальчук А. Ф. Принятие решений по статистическим моделям.— М.: Статистика, 1978.—191 с.
16. Волосов С. С., Педь Е. И. Приборы для автоматического контроля в машиностроении.—М.: Изд-во стандартов, 1975.—335 с.
17. Галушкин А. И., Зотов Ю. Я., Шикунов Ю. А. Оперативная обработка экспериментальной информации.— М.: Энергия, 1972.—360 с.
18. Гебель И. Д. Новые приборы для измерения отклонений от плоскостности.— Измерит, техника, 1981, № 10, с. 22—25.
19. Грибанов Ю. И., Веселова Г. П., Андреев В. Н. Автоматические цифровые коррелометры.— М.: Энергия, 1971.—240 с.
20. Гришин В. К. Статистические методы анализа и планирования экспериментов.— М.: Изд-во МГУ, 1975.—128 с.
21. Горский В. Г., Адлер Ю. П., Талай А. М. Планирование промышленных экспериментов (модели динамики).— М.: Металлургия, 1978.— НО с.
280
22. Джонсон Н„ Лион Ф. Статистика и планирование эксперимента в технике и науке.— М.: Мир, 1981.—516 с.
23 Долинский Е. Ф. Обработка результатов измерений.— М.: Стандарты, 1973,—183 с.
24. Душинский В. В., Пуховский Е. С., Радченко С. Г. Оптимизация технологических процессов в машиностроении.— Киев: Техника, 1977.—175 с.
25. Египко В. М. Организация и проектирование систем автоматизации научно-технических экспериментов.— Киев: Наук, думка, 1978.—232 с.
26. Ермолов И. Н. Теория и практика ультразвукового контроля.— М.: Машиностроение, 1981.—240 с.
27. Зажигаев Л. С., Кишьян А. А., Романиков Ю. И. Методы планирования и обработки результатов физического эксперимента.— М.: Атомиздат, 1978.— 231 с.
28. Закс Л. Статистическое оценивание.— М.: Статистика, 1976.—598 с.
29. Застрогин Ю. Ф. Контроль параметров движения с использованием лазеров,—М.: Машиностроение, 1981.—175 с.
30. Захаров В. П., Снежко Ю. А. Измерение неровностей поверхности при помощи двухканальной фазометрической системы.— Измерит, техника, 1980, № 4, с. 21—23.
31. Измерения в промышленности: Справочник/Под ред. П. Профоса.— М.: Металлургия, 1980.— 648 с.
32. Испытание материалов: Сиравочник/Под ред. X. Блюменауэра.— М.: Металлургия, 1979.—447 с.
33. Испытательная техника: Справочник/Под ред. В. В. Клюева.— М.: Машиностроение, 1982.— Кн. 1. 582 с.
34. Испытательная техника: Справочник/Под ред. В. В. Клюева.— М.: Машиностроение, 1982.— Кн. 2. 560 с.
35. Кацев П. Г. Статистические методы исследования режущего инструмента.— М.: Машиностроение, 1974.—239 с.
36. Кендэл М. Ранговые корреляции.— М.: Статистика, 1974.—214 с.
37. Кириллов А. В., Моисеев В. С. Аналоговое моделирование динамических систем.— М.: Машиностроение, 1977.—228 с.
38. Колпаков И. Ф. Электронная аппаратура на линии с ЭВМ в физическом эксперименте.— М.: Атомиздат, 1974.—231 с.
39. Конюхов Н. Е., Плют А. А., Шаповалов В. М. Оптоэлектронные измерительные преобразователи.— Л.: Энергия, 1977.—159 с.
40. Красовский Г. И., Филаретов Г. Ф. Планирование эксперимента.— Мн.: Изд-во БГУ, 1982,—302 с.
41. Круг Г. К-, Сосулин Ю. А., Фатуев В. А. Планирование эксперимента в задачах идентификации и экстраполяции.— М.: Наука, 1977.—207 с.
42. Куценко А. В., Полосьянц В. А., Ступин Ю. В. Мини-ЭВМ в экспериментальной физике.— М.: Атомиздат, 1975.—285 с.
43. Макаров А. Д. Оптимизация процессов резания,—М.: Машиностроение, 1976,—278 с.
44. Математическая статистика.— М.: Высш, шк., 1981.—371 с.
45. Махаринский Е. И. Ускоренный метод стойкостных испытаний режущих инструментов.— Труды ВТИЛП. Витебск, 1970, с. 165—166.
46. Мирский Г. Я. Характеристики стохастической взаимосвязи и их измерения.— М.: Энергоиздат, 1982.—319 с.
47. Митропольский А. К. Техника статистических вычислений.— М.: Наука, 1971,—576 с.
48. Михайлов О. П., Цейтлин Л. Н. Измерительные устройства в системах активного управления станками.— М.: Машиностроение, 1978.—151 с.
49. Михелькевич В. Н. Автоматическое управление шлифованием.—М.: Машиностроение, 1975.—304 с.
50. Мудров В. И., Кушко В. Л. Методы обработки измерений.— М.: Сов. радио, 1976.—192. с.
51. Налимов В. В. Теория эксперимента.— М.: Наука, 1971.—207 с.
52. Налимов В. В., Голикова Т. И. Логические основания планирования эксперимента.— М.: Металлургия, 1976.—72 с.
281
53. Налимов В. В., Чернова Н. А. Статистические методы планирования экстремальных экспериментов.— М.: Наука, 1965.—398 с.
54. Невельсон М. С. Автоматическое управление точностью обработки на металлорежущих станках.—Л.: Машиностроение, 1982,—180 с.
55. Новик Ф. С., Арсов Я. Б. Оптимизация процессов технологии металлов методами планирования экспериментов,—М.: Машиностроение, 1980,—304 с.
56. Планирование эксперимента в исследовании технологических процессов/Под ред. Э. К. Лецкого.— М.: Мир, 1977.—552 с.
57. Плескунин В. И., Воронина Е. Д. Теоретические основы организации и анализа выборочных данных в эксперименте.—Л.: Изд-во Ленингп ун-та1, 1979.—232 с.
58. Попов С. А., Малевский Н. П., Терещенко Л. М. Алмазно-абразивная обработка металлов и твердых сплавов.— М.: Машиностроение, 1977.—263 с
59. Приборы для неразрушающего контроля материалов и изделий-. Справоч-ник/Под ред. В. В. Клюева —М.: Машиностроение, 1976,—Кн. 1. 391 с.
60. Приборы для неразрушающего контроля материалов и изделий: Справоч-ник/Под ред. В. В. Клюева.— М.: Машиностроение, 1976.— Кн. 2. 326 с.
61. Протодьяконов М. М., Тедер Р. И. Методика рационального планирования экспериментов.— М.: Наука, 1970.—93 с.
62. Пугачев В. С. Теория вероятностей и математическая статистика.— М.-. Наука, 1979.—496 с.
63. Рабинович С. Г. Погрешности измерений.— Л.: Энергия, 1978.—261 с.
64. Растригин Л. А. Статистические методы поиска.— М.: Наука, 1968.—376 с.
65. Рахвагер А. Е., Шевяков А. Ю. Математическое планирование научно-технических исследований.— М.: Наука, 1975.—440 с.
66. Резников А. Н. Теплофизика процессов механической обработки материалов.— М.: Машиностроение, 1981.—279 с.
67. Румшинский Л. 3. Математическая обработка результатов эксперимента.— М.: Наука, 1971.—192 с.
68. Самбурский А. И., Новик В. К. Бесконтактные измерения параметров вращающихся объектов.— М.: Машиностроение, 1976.—142 с.
69. Себер Дж. Линейный регрессионный анализ.— М.: Мир, 1980.—456 с.
70. Сергиенко И. В., Парасюк И. Н., Тукалевская Н. И. Автоматизированные системы обработки данных.— Киев: Наук, думка, 1976.—256 с.
71. Скрибанов Е. В., Братенков А. А., Гришин М. П., Никонов А. С. Устройство для бесконтактного контроля размеров деталей на основе линейного формирователя видеосигнала.— Измерит, техника, 1981, № 6, с. 20—22.
72. Солонин И. С. Математическая статистика в технологии машиностроения.— М.: Машиностроение, 1972.—215 с.
73. Спиридонов А. А. Планирование эксперимента при исследовании технологических процессов.— М.: Машиностроение, 1981.—184 с.
74. Справочник по производственному контролю в машиностроении/Под ред. А. К. Кутая.— Л.: Машиностроение, 1974.—975 с,
75. Тепло- и массообмен, теплотехнический эксперимент: Справочник/Под ред. В. А. Григорьева и В. М. Зорина.— М.: Энергоиздат, 1982.—510 с.
76. Технологические остаточные напряжения/Под ред. А. В. Подзея.— М.: Машиностроение, 1973.— 216 с.
77. Точность производства в машиностроении и приборостроении/Под ред. А. Н. Гаврилова.— М.: Машиностроение, 1973.—567 с.
78. Трофимов А. И. Пьезоэлектрические преобразователи статических нагрузок.— М.: Машиностроение, 1979.—91 с.
79. Уайлд Дж. Методы поиска экстремума.— М.: Наука, 1967.—267 с.
80. Урмаев А. С. Основы моделирования на АВМ.— М.: Наука, 1974.—319 с.
81. Хастингс Н., Пикок Дж. Справочник по статистическим распределениям.— М.: Статистика, 1980.—95 с.
82. Химмельблау Д. Анализ процессов статистическими методами.— М.: Мир, 1975,—975 с.
83. Чеголин П. М., Пойда В. Н. Методы, алгоритмы и программы статистического анализа.— Мн.: Наука и техника, 1971.—223 с.
282
84. Школьник Л. М. Методика усталостных испытаний: Справочник.— М.: Металлургия, 1978.—302 с.
85. Электрические измерения неэлектрических величин/Под ред. П. В. Новицкого.— Л.: Энергия, 1975.— 576 с.
86. Ящерицын П. И., Махаринский Е. И., Кузьменкова Ф. М. Ускоренный метод определения некоторых технологических характеристик самозатачивающихся шлифовальных кругов.— В сб.: Прогрессивная технология машиностроения. Ми.: Выш. шк., 1972. Вып. 3, с. 119—123.
87. Ящерицын П. И., Олендер П. А., Нехамкин Э. Л. Современные методы и средства контроля качества деталей.— Мн.: Беларусь, 1975.—197 с.
ОГЛАВЛЕНИЕ
Предисловие 3
1. Методы и средства измерения в машиностроении 5
1.1. Измерения и измеряемые величины 5
1.2. Методы и средства измерения линейных размеров и углов 7
1.2.1. Шкальные средства для ручного измерения 7
1.2.2. Пневматические измерительные приборы 7
1.2.3. Индуктивные приборы 8
1.2.4. Механотроны 9
1.2.5. Оптико-механичесКие и оптические приборы 10
1.2.6. Акустические приборы 12
1.3. Методы и средства измерения отклонений формы и шероховатости поверхности 14
1.3.1. Измерение непрямолинейности и неплоскостности 14
1.3.2. Измерение некруглости 16
1.3.3. Измерение параметров шероховатости 17
1.4. Методы и средства измерения параметров движения 19
1.4.1. Измерение скоростей движения 19
1.4.2. Измерение характеристик механических колебаний 21
1.5. Методы и средства измерения силовых и энергетических величин 24
1.5.1. Измерение сил 24
1.5.2. Измерение крутящих моментов 30
1.5.3. Измерение мощности 33
1.6. Методы и средства измерения температуры '34
1.6.1. Механические термометры 34
1.6.2. Электрические контактные термометры 36
1.6.3. Бесконтактные методы измерения температуры 40
1.6.4. Цветовые индикаторы температуры 43
1.7. Методы и средства механических испытаний 46
1.7.1. Испытания статическим нагружением 46
1.7.2. Испытания ударной нагрузкой 47
1.7.3. Испытания циклической нагрузкой 48
1.7.4. Измерение твердости 49
1.7.5. Испытания на износостойкость 50
1.7.6. Неразрушающие методы определения механических свойств и структуры конструкционных материалов 53
1.7.7. Методы определения остаточных напряжений 56
1.8. Методы определения обрабатываемости резанием и шлифованием 62
1.8.1. Метод торцевой обточки 62
1.8.2. Метод ступенчатого изменения диаметра 63
1.8.3. Метод ступенчатого изменения скорости резания 64
284
1.8.4. Определение объективных показателей обрабатываемости
1.8.5. Определение обрабатываемости шлифованием
65
66
2. Погрешности измерений 69
2.1. Виды погрешностей измерений 69
2.2. Характеристики средств измерения 70
2.3. Уменьшение систематических погрешностей средств измерений 74
2.4. Расчет погрешностей средств измерений 77
2.5. Описание случайных погрешностей 78
2.6. Числовая оценка случайных погрешностей 80
2.7. Объединение результатов неравноточных измерений 81
2.8. Погрешности косвенных измерений 83
2.9. Обнаружение грубых погрешностей 84
3. Математическое обеспечение эксперимента 86
3.1. Основные определения 86
3.2. Оценка отклика 88
3.3. Статистическая проверка гипотез 93
3.3.1. Основные определения 93
3.3.2. Проверка гипотезы о равенстве математического ожидания заданному значению 93
3.3.3. Проверка гипотезы о равенстве средних значений 94
3.3.4. Проверка гипотезы о равенстве дисперсий 95
3.3.5. Проверка случайности и независимости результатов измерений в выборке 95
3.4. Дисперсионный анализ 96
3.4.1. Однофакторный дисперсионный анализ 96
3.4.2. Двухфакторный дисперсионный анализ 99
3.5. Корреляционный анализ 101
3.5.1. Парная корреляция 101
3-5-2- Многомерный корреляционный анализ 105
3.5.3. Корреляционные уравнения 107
3.6. Регрессионный анализ 108
4. Предпланирование эксперимента 115
4.1. Основные понятия и процедуры 115
4.2. Методы уменьшения числа параметров оптимизации 117
4.2.1. Использование корреляционного анализа 117
4.2.2. Функции желательности 118
4.3. Методы уменьшения размерности факторного пространства 120
4.3.1. Априорное ранжирование факторов 120
4.3.2. Критериальные математические модели 124
4.3.3. Метод насыщенных планов 127
4.3.4. Метод случайного баланса 131
4.3.5. Последовательное отсеивание 134
5. Планирование эксперимента
136
5.1. Основные принципы и понятия 136
5.2. Планирование эксперимента при оценке отклика 138
5.3. Планирование эксперимента при дисперсионном анализе 140
5.4. Планирование при однофакторном регрессионном анализе 145
285
5.4.1. Определение вида линейной по параметрам однофакторной модели 145
5.4.2. Определение вида нелинейной по параметрам однофакторной модели 153
5.4.3. Уточнение параметров однофакторной модели 159
5.5. Планирование при многофакторном регрессионном анализе 165
5.5.1. Определение вида линейной по параметрам многофакторной модели (последовательное планирование) 165
5.5.2. Определение вида нелинейной по параметрам многофакторной модели 178
5.5.3. Уточнение параметров линейной по параметрам многофакторной модели 189
5.6. Планирование эксперимента при идентификации 198
5.6.1. Основные понятия 198
5.6.2. Определение параметров динамических моделей с аддитивным дрейфом 199
5.6.3. Построение динамической линейной модели 202
5.6.4. Построение параметрических моделей временных рядов 204
6. Планирование эксперимента в задачах оптимизации 206
6.1. Основные понятия и процедуры 206
6.2. Планирование однофакторного поиска 208
6.2.1. Метод дихотомии (половинного деления) 208
6.2.2. Метод Фибоначчи 209
6.2.3. Метод «золотого сечения» 210
6.2.4. Поиск по дискретным точкам 211
6.3. Градиентные методы многофакторного поиска 214
6.3.1. Планирование и анализ результатов эксперимента в исходной точке 214
6.3.2. Поиск области оптимума 216
6.3.3. Планирование и анализ результатов эксперимента в области оптимума 220
6.4. Последовательное симплекс-планирование 224
6.5. Методы случайного поиска 233
6.6. Оптимизация при наличии ограничений 237
6.6.1. Основные понятия 237
6.6.2. Оптимизация на базе математических моделей 238
6.6.3. Методы прямого поиска при оптимизации с ограничениями 241
7. Автоматизация эксперимента 243
7.1. Основные понятия 243
7.2. Подготовка измерительных сигналов к автоматическому анализу 245
7.3. Аналоговые методы вычислений 249
7.4. Автоматизация регрессионного анализа 251
7.5. Автоматизация корреляционного анализа 253
7.6. Автоматизация ввода в ЭВМ графической информации 256
Приложения 260
Литература 280
Петр Иванович Ящерицын, Ефим Ильич Махаринский
ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА
В МАШИНОСТРОЕНИИ
Редакторы Э. Н. К а п р о в а, В. Г. Самарина
Мл. редакторы А. П. Берлина,
Е. Г. П о л о й к о Обложка А. Инкина
Худож. редактор И. А. Д.емковский
Техн, редактор Г. М. Романчук Корректор Н. С. Нипикина
IIБ № 1976
Сдано в набор 14.12.84. Подписано в печать 21.10.85. АТ 18787. Формат 60X90716. Бумага тип. № 2. Гарнитура литературная. Высокая печать. Усл. печ. л. 18. Усл. кр.-отт. 18. Уч.-изд. л. 22,49. Тираж 2800 эка. Заказ 1001. Цена 1 р. 60 к.
Издательство «Вышэйшая школа» Государственного комитета БССР по делам издательств, полиграфии и книжной торговли. 220048, Минск, проспект Машерова, 11.
Отпечатано в набора минского ордена Трудового Красного Знамени полиграфкомбината МППО им. Я. Коласа. 220005, Минск, ул. Красная, 23 в типографии им. Франциска (Георгия) Скорины издательства «Наука и техника». 220600, Минск, Ленинский проспект, 68. Зак. 2067.
'Ящерицын П. И., Махаринский Е. И.
Я 97 Планирование эксперимента в машиностроении: [Справ, пособие].— Мн.: Выш. шк., 1985.— 286 с., ил.
В пер.: 1 р. 60 к.
Освещаются вопросы планирования и математической обработки технологических экспериментов в машиностроении; методы построения одно- и многофакторных математических моделей процессов обработки на металлорежущих станках при различных уровнях априорной информации’, методы оптимизации уело -вий проведения операций механической обработки.
Справочное пособие предназначено для инженерно-технических и научных работников, а также студентов вузов машиностроительного профиля.
я
2701010000—147 1П0 а.
--------------1UV—оО
М304(05)—85
ББК 34.4я2