Автор: Елисеева И.И.
Теги: математическая экономика методы экономических исследований статистика эконометрика
ISBN: 5-279-01955-0
Год: 2003
Текст
ЭКОНОМЕТРИКА
Под редакцией члена- корреспондента Российской Академии наук И.И.Елисеевой
Рекомендовано Министерством образования Российской Федерации в качестве учебника для студентов высших учебных заведений, обучающихся по специальности 061700 “Статистика”
Тутки Й ИН С тиУуГ к о но м и к и ] и информатики
библиотека
fl
' к w । ahi. "
МОСКВА “ФИНАНСЫ И СТАТИСТИКА” 2003
УДК 330.43(075.8)
ББК 65в6я73
Э40
АВТОРЫ:
И.И. Елисеева, чл.-кор. РАН — предисловие, главы 1,2, 3 и 4 (разд. 4.6);
С.В. Курышева, д-р экон, наук — главы 2, 3 и 4 (разд. 4.1 — 4.5);
Т.В. Косте ев а, канд. экон, наук — главы 5, 6 и 7 (разд. 7.1,7.2,7.3.1, 7.4,7.5 и 7.6);
И.В. Бабаева — глава 7 (разд. 7.3.2 и 7.3.3);
Б.А. Михайлов, канд. экон, наук — глава 2
РЕЦЕНЗЕНТЫ:
кафедра математической статистики и эконометрики Московского государственного университета экономики, , статистики и информатики (МЭСИ);
П.А. Ватник,
д-р экон, наук, профессор Санкт-Петербургской государственной инженерно-экономической академии
ISBN 5-279-01955-0
© Коллектив авторов, 2001
ПРЕДИСЛОВИЕ
Сегодня деятельность в любой области экономики (управлении, финансово-кредитной сфере, маркетинге, учете, аудите) требует от специалиста применения современных методов работы, знания достижений мировой экономической мысли, понимания научного языка. Большинство новых методов основано на эконометрических моделях, концепциях, приемах. Без глубоких знаний эконометрики научиться их использовать невозможно. Чтение современной экономической литературы также предполагает хорошую эконометрическую подготовку.
Специфической особенностью деятельности экономиста является работа в условиях недостатка информации и неполноты исходных данных. Анализ такой информации требует специальных методов, которые составляют один из аспектов эконометрики. Центральной проблемой эконометрики являются построение эконометрической модели и определение возможностей ее использования для описания, анализа и прогнозирования реальных экономических процессов.
Известный эконометрист Цви Гриллихес (1929—1999) писал: «Эконометрика является одновременно нашим телескопом и нашим микроскопом для изучения окружающего экономического мира». Это определение подчеркивает значение эконометрического подхода как на микроуровне (поведение индивидов, домохозяйств, фирм), так и на макроуровне. В этом смысле можно говорить о микро- и макроэконометрике.
Развитие эконометрики тесно связано с изучением микро- и макроэкономики. Сейчас уже кажется невозможным понять «кривую Филлипса» или «теорему Эрроу», использование ресурсов и эластичность потребления, не прибегая к статистическим данным, моделированию и оценке параметров.
Свидетельством всемирного признания эконометрики является присуждение четырех нобелевских премий по экономике за
3
разработки в этой области: премия 1969 г. была присуждена Р. Фришу и Я. Тинбергену за разработку математических методов анализа экономических процессов; премия 1980 г. — Л. Клейну за создание эконометрических моделей и их применение к анализу экономических колебаний и экономической политике; премия 1989 г. — Т. Хаавельмо за прояснение вероятностных основ эконометрики и анализ одновременных экономических структур; премия 2000 г. — Дж. Хекману за развитие теории и методов анализа селективных выборок и Д. Макфэддену за развитие теории и методов анализа моделей дискретного выбора.
Процесс перехода высшего экономического образования в России на мировые стандарты характеризуется интенсивным внедрением в учебные планы курсов микро- и макроэкономики. Эконометрика также начинает входить в учебные планы, прежде всего в планы обучения будущих экономистов-статистиков.
Предлагаемый учебник подготовлен коллективом преподавателей кафедры статистики и эконометрики Санкт-Петербургского государственного университета экономики и финансов (СПбГУЭФ), в котором преподавание эконометрики включено в учебные планы всех экономических специальностей и всех форм обучения с 1996/97 учебного года. Практические занятия ведутся с использованием пакетов прикладных программ «Statgraphics», «Статистика», а с 1999 г. — «EViews», специального пакета для решения эконометрических задач, разработанного компанией Quantitative Micro Software и переданного сотрудниками Тилбургского университета (Голландия) СПбГУЭФ и ряду других экономических вузов России по итогам проведения международной школы-семинара «Эконометрика: начальный курс» (руководители Я.Р. Магнус, С.А. Айвазян, А.А. Пересецкий, П.К. Катышев).
Принятая в учебнике последовательность изложения базируется на наиболее распространенном понимании содержания эконометрики как науки о связях экономических явлений.
Это понимание эконометрики определило содержание и структуру учебника. Большое место в нем отводится регрессионному анализу как методу, используемому в эконометрике для оценки уравнения, которое в наибольшей степени соответствует совокупности наблюдений зависимых и независимых переменных, и тем самым дающему наилучшую оценку истинного соотношения между этими переменными. С помощью оцененного таким образом уравнения можно предсказать, каково будет значение зависимой переменной для данного значения независимой переменной. Простейшим примером регрессии является парная 4 ' '
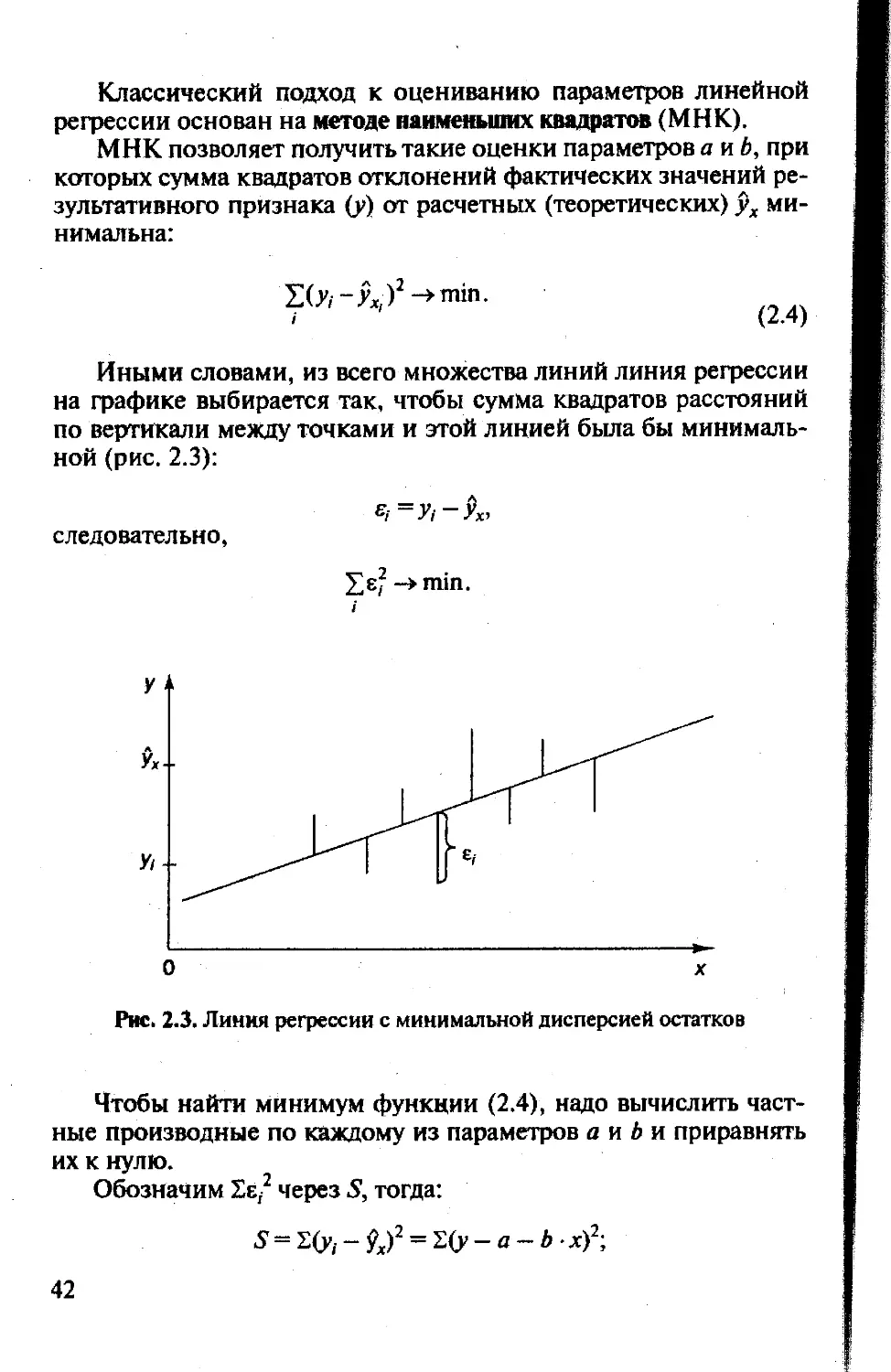
линейная регрессия всего одной независимой переменной и одной зависимой переменной (скажем, располагаемый доход и потребительские расходы). Задача будет заключаться в подборе прямой линии к совокупности данных, состоящих из пар наблюдений дохода и потребления. Линию, которая лучше всего подходит к данным, нужно выбирать так, чтобы сумма квадратов значений вертикальных отклонений точек от линии была минимальной. Этот метод наименьших квадратов применяется при анализе большинства регрессий. Степень приближения регрессионной линии к наблюдениям измеряется коэффициентом корреляции.
Регрессионное уравнение не дает точного прогноза зависимой переменной для любого заданного значения независимой переменной, так как коэффициенты регрессии подвержены случайным искажениям. Чтобы учесть погрешности оцененного уравнения регрессии, отражающего действительные закономерности поведения всего населения на основе выборочного наблюдения, уравнение регрессии обычно записывается как
С = а + by + е.
В уравнении е — дополнительный остаточный член, который отражает остаточное действие случайной вариации и действие других независимых переменных (например, влияние процентных ставок на потребительский кредит), которые воздействуют на потребительские расходы, но в уравнение регрессии явным образом не включены.
Там, где предполагается, что на зависимую переменную существенно влияет более чем одна независимая переменная, используется метод множественной линейной регрессии.
Эти методы взяты эконометрикой из статистики и хорошо знакомы студентам, изучавшим такие дисциплины, как «Статистика», «Математическая статистика». Таким образом обеспечивается преемственность дисциплин. При изложении проблем анализа взаимосвязей на основе пространственных данных в учебнике уделяется внимание спецификации модели. Отмечается, что любое изолированно взятое уравнение регрессии не позволяет раскрыть структуру связей между переменными. Из этого следует естественный переход к изложению структурных моделей и путевого анализа как разновидности такого подхода.
В этой части учебника особое внимание уделяется проблеме идентификации. Поскольку в экономике все большее значение приобретает анализ временных рядов, три главы учебника пос
5
вящены эконометрическим методам работы с временными рядами, начиная с изучения изолированного ряда динамики и его разложения на трендовую, циклическую и случайную компоненты. Затем рассматриваются системы рядов динамики и моделирование взаимосвязей между ними.
Каждая глава завершается перечнем вопросов для повторения. Учебник сопровождается практикумом, подготовленным тем же авторским коллективом. Практикум содержит методические указания по решению эконометрических задач, решению типовых задач, контрольные и тренировочные задания.
Изданию учебника и дополняющего его «Практикума по эконометрике» предшествовала их апробация в СПбГУЭФ и ряде других российских вузов.
Авторы не считают, что становление эконометрики как дисциплины профессиональной подготовки экономистов завершено, и рассматривают свой труд как одну из первых попыток создания российского учебника. Круг охваченных тем и характер подачи материала позволяют отнести его к начальному уровню курса эконометрики.
Авторы благодарят за тщательное рецензирование рукописи Учебно-методическое объединение по статистике. Особую благодарность за ценные замечания, безусловно, способствовавшие улучшению содержания учебника, формы подачи материала, считаем своим долгом выразить рецензенту доктору экономических наук, профессору П.А. Ватнику. Не менее глубокая признательность — коллективному рецензенту - кафедре математической статистики МЭСИ (заведующий кафедрой доктор экономических наук, профессор В.С. Мхитарян). Мы благодарны и кандидату экономических наук С. Б. Макаровой (Европейский университет в Санкт-Петербурге (ЕУСПб)), которая внесла полезные дополнения на завершающем этапе подготовки учебника.
И. И. ЕЛИСЕЕВА
ГЛАВА
ОПРЕДЕЛЕНИЕ ЭКОНОМЕТРИКИ
1.1. ПРЕДМЕТ ЭКОНОМЕТРИКИ
Эконометрика — быстроразвивающаяся отрасль науки, цель которой состоит в том, чтобы придать количественные меры экономическим отношениям.
Термин «эконометрика» был впервые введен бухгалтером П. Цьемпой (Австро-Венгрия, 1910 г.) («эконометрия» — у Цьемпы). Цьемпа считал, что если к данным бухгалтерского учета применить методы алгебры и геометрии, то будет получено новое, более глубокое представление о результатах хозяйственной деятельности. Это употребление термина, как и сама концепция, не прижилось,' но название «эконометрика» оказалось весьма удачным для определения нового направления в экономической науке, которое выделилось в 1930 г.
Слово «эконометрика» представляет собой комбинацию двух слов: «экономика» и «метрика» (от греч. «метрон»). Таким образом, сам термин подчеркивает специфику, содержание эконометрики как науки: количественное выражение тех связей и соотношений, которые раскрыты и обоснованы экономической теорией. Й. Шумпетер (1883—1950), один из первых сторонников выделения этой новой дисциплины, полагал, что в соответствии со своим назначением эта дисциплина должна называться «эко-номометрика». Советский ученый А.Л. Вайнштейн (1892—1970) считал, что название настоящей науки основывается на греческом слове метрия (геометрия, планиметрия и т.д.), соответственно по аналогии — эконометрия. Однако в мировой науке обще-употребимым стал термин «эконометрика». В любом случае, какой бы мы термин ни выбрали, эконометрика является наукой об измерении и анализе экономических явлений.
Зарождение эконометрики является следствием междисциплинарного подхода к изучению экономики. Эта наука возникла в результате взаимодействия и объединения в особый «сплав» трех
компонент: экономической теории, статистических и математических методов. Впоследствии к ним присоединилось развитие вычислительной техники как условие развития эконометрики.
В журнале «Эконометрика», основанном в 1933 г. Р. Фришем (1895—1973), он дал следующее определение эконометрики: «Эконометрика — это не то же самое, что экономическая статистика. Она не идентична и тому, что мы называем экономической теорией, хотя значительная часть этой теории носит количественный характер. Эконометрика не является синонимом приложений математики к экономике. Как показывает опыт, каждая из трех отправных точек — статистика, экономическая теория и математика — необходимое, но не достаточное условие для понимания количественных соотношений в современной экономической жизни. Это — единство всех трех составляющих. И это единство образует эконометрику»1.
Таким образом, эконометрика — это наука, которая дает количественное выражение взаимосвязей экономических явлений и процессов. Нельзя утверждать, что достигнуто однозначное определение эконометрики. Так, Э. Маленво придерживался широкого понимания, интерпретируя эконометрику как «любое приложение математики или статистических методов к изучению экономических явлений»2.
О. Ланге (1904—1965) писал, что эконометрика занимается определением наблюдаемых в экономической жизни конкретных количественных закономерностей, применяя для этой цели статистические методы. Статистический подход к эконометрическим измерениям стал доминирующим. Это положение обусловило содержание настоящего учебника. f
Некоторые сведения об истории возникновения эконометрики
Каждая наука проходит сложный путь зарождения и выделения в самостоятельную область знания. Эконометрика — не исключение. Первоначальные попытки количественных исследований в экономике относятся к XVII в. «Политические арифметики» — В. Петти (1623—1667), Г. Кинг (1648—1712), Ч. Давенант (1656—1714) — вот первая когорта ученых, систематически ис
1 Frisch R. Editorial. Econometrica. — 1933. — № 1. — Р. 2.
*MaUnvaud Е. Statistical Method of Econometrics. — Amsterdam: North-Holland, 1996.
8
пользовавших цифры и факты в своих исследованиях, прежде всего в расчете национального дохода. Круг их интересов был связан в основном с практическими вопросами: налогообложением, денежным обращением, международной торговлей и финансами. Политическую арифметику можно назвать описательным политико-эконометрическим анализом. Это направление пробудило поиск законов в экономике. Одним из первых был сформулирован так называемый «закон Кинга», в котором на основе соотношения между урожаем зерновых й ценами на зерно была выявлена закономерность спроса. Исследователям хотелось достичь в экономике того, что И. Ньютон достиг в физике. Неопределенная природа экономических закономерностей еще Не была осознана. В этот же период все больше учетных данных становятся доступными, создавая основу для измерений.
Существенным толчком явилось развитие статистической теории в трудах Ф; Гальтона (1822-1911), К. Пирсона (1857—1936), Ф. Эджворта (1845—1926). Появились первые применения парной корреляции: при изучении связей между уровнем бедности и формами помощи бедным (Дж. Э. Юл, 1895, 1896); между уровнем брачности в Великобритании и благосостоянием (Г. Хукер, 1901), в котором использовалось несколько индикаторов благосостояния, к тому же исследовались временное ряды экономических переменных. Это были шаги по созданию современной эконометрики.
Параллельно происходил процесс создания маржинали-стской (неоклассической) теории, зарождение которой можно датировать 60-ми годами XIX в. (появление работ СДжевонса, Л. Вальрас а, К.Менгера). С 30-х гг. XIX в. страны с наиболее высоким уровнем развития капитализма стали испытывать спорадические потрясения — упадок деловой активности, возникновение массовой безработицы. Эти явления не находили теоретического объяснения. Быстрая индустриализация выявила огромный диапазон социальных проблем, которые также не согласовывались с теорией. Неоклассическая теория стала восприниматься как слишком удаленная от действительности. Для ее практического значения требовались количественные выражения базовых понятий, таких как «эластичность спроса» или «предельная полезность». Теория спроса могла стать убедительной в том случае, если она смогла бы объяснить и оценить фактические кривые спроса и предложения, продемонстрировать формирование равновесных цен в конкретных условиях.
К этому же времени относится привлечение ученых-экономистов (А. Маршалла, С. Джевонса, К. Менгера) к парламентской деятельности, что подтолкнуло их к анализу макроэкономических проблем на основе временных рядов таких показателей, как, например, валютные курсы и т.п. Это также явилось важным шагом в подготовке развития эконометрики. Многие исследователи признают первой работой, которая могла бы быть названа эконометрической, книгу американского ученого Г. Мура (1869—1958) «Законы заработной платы: эссе по статистической экономике» (1911). Г. Муром были проведены анализ рынка труда, статистическая проверка теории производительности Дж. Кларка, а также изложены основы стратегии объединения пролетариата и т. д. В это время для США решение этих вопросов было безотлагательным: рабочий класс стремительно.рос, возникали такие объединения, как «Индустриальные рабочие мира» и другие радикально настроенные организации. Г. Мур подошел к анализу поставленных проблем с позиций «высшей», как он называл, статистики, используя все достижения теории корреляции, регрессии, анализа динамических рядов. Он стремился показать, что сложные математические построения, наполненные фактическими данными, могли составить основу для разработки социальной стратегии. .
К этому же периоду относится первое применение итальянским ученым Р. Бенини (1862—1956) метода множественной регрессии для оценки функции спроса. Значительным вкладом в становление эконометрики явились исследования по цикличности экономики. К. Жюгляр (1819—1905), французский физик, ставший экономистом, первым занялся исследованием экономических временных рядов с целью выделения бизнес-циклов. Им была обнаружена цикличность инвестиций (продолжительность цикла — 7—11 лет). Вслед за ним С. Китчин, С. Кузнец, Н. Кондратьев, автономно занимаясь этой проблемой, выявили цикличность обновления оборотных средств (3—5 лет), циклы в строительстве (15—20 лет), долгосрочные волны, или «большие циклы» Кондратьева, продолжительностью 45—60 лет.
Значительной вехой в формировании эконометрики явилось построение экономических барометров, прежде всего так называемого гарвардского барометра. Большинство экономических барометров, включая названный, основано на следующей идее: в ' динамике различных элементов экономики существуют такие показатели, которые в своих изменениях идут впереди других, а потому могут служить предвестниками последних. Гарвардский барометр был создан под руководством У. Персонса (1878-1937)
10
и У. Митчелла (1874—1948). В течение 1903—1914 гг. он состоял из
пяти групп показателей, которые в дальнейшем были сведены в
три отдельные кривые: кривая А характеризовала фондовый ры
нок; кривая В — товарный рынок; кривая С — денежный рынок. Каждая из этих кривых представляла среднюю арифметическую из рядов входящих в нее нескольких показателей. Эти ряды пред
варительно статистически обрабатывались путем исключения тенденции, сезонной волны и приведения колебаний отдельных кривых к сравнимому масштабу колеблемости. В основу прогноза гарвардского барометра было положено свойство каждой отдельной кривой повторять движение остальных в определенной последовательности и с определенным отставанием. Так, С 1903 г. и до первой мировой войны поворотные пункты кривой А предшествовали поворотным пунктам кривой В на 6—10 месяцев (в среднем — на 8 месяцев); поворотные пункты кривой В обгоняли аналогичные пункты кривой С на 2—8 месяцев (в среднем на 4 месяца); наконец, колебания кривой С предшествовали колебаниям кривой А следующего цикла на 6—12 месяцев.
Гарвардский барометр представлял собой описание подме-
ченных эмпирических закономерностей и экстраполяции последних на ближайшие месяцы. Однако в построении гарвардского
барометра можно обнаружить и некоторые теоретические предпосылки. Естественно, например, что изменение средних биржевых курсов и показателей фондового рынка (индекс спекуляции А) означало изменение спроса на товары, что влекло за собой, в свою
очередь, изменение в том же направлении индекса оптовых цен, объема производства и товарооборота (индекс В).'Возрастание, например, объема производства вызывало напряжение на денежном рынке, рост учетной ставки и падение курса ценных бумаг с фиксированным доходом (кривая С). Поэтому максимум кривой А обычно должен был совпадать с минимумом кривой С.
Успех гарвардского барометра породил буквально эпидемию таких построений в Других странах (в частности, аналогичный барометр был построен в Великобритании). Несколько лет после первой мировой войны он еще удовлетворительно выполнял свое предназначение. Но затем гарвардский барометр (приблизительно с 1925 г.) потерял чувствительность и сошел со сцены, пережив свою славу. Авторы гарвардского барометра объясняли его крах появлением мощного регулирующего фактора в экономике США. В этих условиях основным методом макроэкономического анализа становится метод «Затраты-выпуск» В.В. Леонтьева (1906-1999).
11
Что касается экономических барометров, то советский математик-статистик Е. Слуцкий (1880—1948) в работе «Сложение случайных причин как источник циклических процессов» (1927), взяв в качестве случайных рядов последние цифры номеров облигаций из тиражных таблиц выигрышного займа, блестяще доказал, что «сложение случайных причин порождает волнообразные ряды, имеющие тенденцию на протяжении большего или меньшего числа волн имитировать гармонические ряды, сложенные из небольшого числа синусоид». Таким образом, никакой закономерности в любом экономическом барометре могло и не существовать.
В этот же период делались эконометрические построения, использующие методы гармонического анализа и периодограмм-анализа (Г.Мур в США, Бэвэридж в Энстром в Швеции). Эти методы перенесены в экономику из области астрономии, метеорологии, физики1.
В основе гармонического анализа и периодограмм-анализа лежит теорема Фурье, согласно которой всякая периодическая функция, произвольно данная в некотором промежутке, может быть разложена на ряд простых гармонических колебаний и в конечном счете представлена тригонометрическим рядом вида
У =Л0 = 4) + A[Sin(kt + е,) + A2sin(2kt + е2) + ....
Каждое слагаемое представляет здесь синусоиду — формулу простого гармонического колебания (гармонику), где 4 — полуамплитуда; et — фаза колебания, т. е. характеризует точку, в которой ордината соответствующей синусоиды имеет нулевое значение; к — связано с периодом колебания равенством
Динамика каждого элемента экономики после исключения из нее тенденции представляется в виде волнообразной кривой. Если бы оказалось возможным эту кривую разложить, хотя бы приближенно, на сумму гармоник, то это дало бы базу для прогноза движения интересующего нас элемента. Следовательно, задача сводится к нахождению коэффициентов искомого ряда — полуамплитуд А/ — по наблюденным значениям, если известны
1 См.: Вайнштейн Л.Л. Эконометрия и статистика//Предисловие к кн.: Тинтнер Г. Введение в эконометрию. — М.: Статистика, 1965. — С. 5—26.
12
периоды отдельных гармоник. Для отыскания периода колебания Г или связанного с ним к применяется метод периодограмм-анализа. Он состоит в том, что в качестве первого приближения берутся два первых члена вышеприведенного ряда, т. е. полагают, что у = Ло + A{sin(kt + «р, и затем испытывают различные произвольные значения Т (целые и дробные). Для каждого из испытываемых периодов вычисляются А, и et. Затем строится периодографик или периодограмма, где на оси абсцисс отмечаются периоды, а на оси ординат откладывается А2, или интенсивность колебания, соответствующая этим периодам. Большей интенсивности колебания отвечает большая вероятность того, что соответствующий ей период колебания не случаен. Затем, выбрав периоды, соответствующие наибольшим интенсивностям, можем представить рассматриваемую волнообразную кривую в виде суммы простых гармоник, имеющих эти периоды, соответствующие А^ Эта сумма может сколь угодно близко подойти к исследуемой кривой. К этому нужно добавить, что при применении гармонического метода и периодограмм-анализа не требуется предварительного исключения тенденции.
К 30-м гг. сложились все предпосылки для выделения эконометрики в отдельную науку. Стало ясно, что специалисты, занимающиеся развитием эконометрической науки, должны использовать в той или иной степени математику и статистику. Возникла необходимость появления особого термина, объединяющего все исследования в этом направлений, подобно биометрике -науке, изучающей биологию статистическими методами.
Выделение эконометрики
В 1912 г. И. Фишер попытался создать группу ученых для стимулирования развития экономической теории путем ее связи со статистикой и математикой. Но тогда эту группу создать не удалось. Тогда Р. Фриш и математик-экономист Ч. Рус обратились с идеей собрать специальный форум экономистов, готовых к использованию математики и статистики.
29 декабря 1930 г. по инициативе И. Фишера (1867—1947), Р. Фриша, Я. Тинбергена (1903—1995), Й. Шумпетера, О. Андерсона (1887—1960) и других ученых на заседании Американской ассоциации развития науки (США, Кливленд, штат Огайо) было создано эконометрическое общество, на котором норвежский ученый Р. Фриш дал новой науке название - «эконометрика».
С самого начала эконометрическое общество было интернациональным. Уже в 1950 г. общество насчитывало почти 1000
13
членов. С 1933 г. под редакцией Р. Фриша стал издаваться журнал «Эконометрика» («Econometrica»), который и сейчас играет важную роль в развитии эконометрической науки. В 30—40-е гг. развитию эконометрики способствовала деятельность Департамента прикладной экономики под руководством Р. Стоуна (Великобритания). В 1941 г. появился первый учебник по эконометрике, который был создан Я. Тинбергеном (1913—1994).
В эти годы вплоть до 70-х гг. XX в. эконометрика понималась как эмпирическая оценка моделей, разработанных экономической теорией. Р. Фриш определял соотношение между теорией и данными наблюдений следующим образом: теория, абстрактно формулирующая количественные соотношения, должна быть проверена множеством наблюдений. Свежие статистические данные и другие факты должны предотвратить теорию от опасного догматизма. Под влиянием лидеров, таких как Р. Фриш, Т. Ха-авелмо, Я. Тинберген, Л. Клейн, экономические модели, построенные в этом периоде, всегда были кейнсианскими.
Все изменилось в 70-е гг. В макроэкономике возникли противоречия между кейнсианцами, монетаристами и марксистами. Формальные методы стали использоваться для доказательства причинности при выборе теоретических концепций. Экономическая теория потеряла свое решающее значение.
Другим важным событием стало появление компьютеров с высоким быстродействием и мощной оперативной памятью. Существенное развитие получил статистический анализ временных рядов. Г. Бокс и Г. Дженкинс создали ARIMA-модель в 1970 г., а К. Симс и другие ученые — VAR-модели, ставшие популярными в начале 80-х гг. Вершиной этой стадии развития явился метод ко-интеграции (см. главу 7), развитый С. Йохансеном и др. (1990 г.).
В настоящее время эконометрика располагает огромным разнообразием типов моделей — от больших макроэкономических моделей, включающих несколько сот, а иногда и тысяч уравнений, до малых коинтеграционных моделей, предназначенных для решения специфических проблем.
1.2. ОСОБЕННОСТИ ЭКОНОМЕТРИЧЕСКОГО МЕТОДА
Становление и развитие эконометрического метода происходили на основе так называемой высшей статистики — на методах парной и множественной регрессии, парной, частной и множественной корреляции, выделения тренда и других компонент вре-14
менного ряда, на статистическом оценивании. Р. Фишер писал: «Статистические методы являются существенным элементом в социальных науках, и в основном именно с помощью этих методов социальные учения могут подняться до уровня наук».
Первый момент — эконометрика как система специфических методов начала развиваться с осознания своих задач — отражения особенностей экономических переменных и связей между ними. В уравнения регрессии начали включаться переменные не только в первой, но и во второй степени — с целью отразить свойство оптимальности экономических переменных: наличия значений, при которых достигается мини-максное воздействие на зависимую переменную. Таково, например, влияние внесения удобрений на урожайность: до определенного уровня насыщение почвы удобрениями способствует росту урожайности; по достижении оптимального уровня насыщения удобрениями его дальнейшее наращивание не приводит к росту урожайности и даже может вызвать ее снижение. То же можно сказать о воздействии многих социально-экономических переменных (скажем, возраста рабочего на уровень производительности труда или влияния дохода на потребление некоторых продуктов питания и т. д.). В конкретных условиях нелинейность влияния переменных может не подтвердиться, если данные варьируют в узких пределах, т.е. являются однородными.
Второй момент — это "взаимодействие социально-экономических переменных, которое может рассматриваться как самостоятельная компонента в уравнении регрессии. Например, имеем регрессию
у — а + bfX + bjZ + byxz.
Конечно, эффект взаимодействия (в данном случае это параметр Ь3) может оказаться статистически незначимым. Поэтому гипотезы о нелинейности и неаддитивности связей не исключают особого внимания к проблеме применимости линейных и аддитивных уравнений регрессии.
Поясним, следуя А. Голдбергеру (A. Goldberger), понятия аддитивности и линейности, часто отождествляемые. Функция у =/(х1, ...рс*) линейна по всем независимым переменным тогда и только тогда, когда dy/dxi не включаетх„ т. е. когда d(dyjdx^ = О, эффект данного изменения по х, не зависит от xt. Мы говорим, что функция у — ДХ|,...л)к) является аддитивной по х, тогда и только тогда, когда dy/dx, не включает xfj i), т. е. тогда, когда didy/dx^dxj = 0, эффект данного изменения по каждой независи
15
мой переменной не зависит от уровня другой переменной. Аддитивность является подходящим определением этой особенности ввиду того, что совместный эффект изменения по всем учтенным независимым переменным может быть получен сложением отдельно вычисленных эффектов изменений по каждой из них.
Примеры оценки линейности и аддитивности ряда функций для случая двух объясняющих переменных приведены в табл. 1.1.
Таблица 1.1
Примеры оценки линейности фу
т
Функция
Линейность
lapq + fljx2
хг/х,
2а^ + ДА
fl2Iogx2
«Л
Лз/х2
тив-ность
ПО X] noxj ПОХ( х2
нет нет нет
нет да нет
нет Да Да
да нет нет
да да нет
Да Нет да
нет нет нет
да да да
В эконометрических исследованиях сами уравнения регрессии стали обосновываться содержательно. Например, зависимость себестоимости (у) от объема производства (х) (количества единиц продукций) может быть представлена как
Затраты на производство
Затраты, не зависящие от объема производства (постоянные затраты) в
Затраты, зависящие от объема производства (переменные затраты) ах
Разделив обе части равенства на объем производства (х), получим:
16
Затраты на произвол- Постоянные ство в расчете на 1 ед. = затраты продукции на 1 ед. продукции
Переменные затраты на 1 ед. продукции
т.е. уравнение имеет вид:
Параметры такого уравнения могут оцениваться методом наименьших квадратов, но особенность его в том, что каждый параметр имеет совершенно определенный экономический смысл.
В ЗО-е гг. XX в. повсеместное увлечение множественной регрессией сменилось разочарованием. Строя уравнение множественной регрессии и стремясь включить как можно больше объясняющих переменных, исследователи все чаще сталкивались с бессмысленными результатами—прежде всего с несоответствием знаков при коэффициентах регрессии априорным предположениям, а также с необъяснимым изменением их значений. Причина заключается в том, что изолированно взятое уравнение регрессии есть не что иное, как модель «черного ящика», поскольку в ней не раскрыт механизм зависимости выходной переменной у от входных переменных а лишь констатируется факт наличия такой зависимости.
Для проведения правильного анализа нужно знать всю совокупность связей между переменными. Одним из первых подходов к решению этой задачи является конфлюэнтный анализ, разработанный в 1934 г. Р. Фришем. Он предложил изучать целую иерархию регрессий между всеми сочетаниями переменных. При этом каждая переменная рассматривалась как зависимая от всех возможных подмножеств переменных, а также от всего множества переменных. Анализируя регрессии с разным числом переменных, Р. Фриш обнаружил «эффект деградации» коэффициентов регрессии. Он проявляется в том, что если в регрессию включается много переменных, имеющих линейные связи друг с другом (мультиколлинеарные переменные), то коэффициенты регрессии имеют тенденцию возвращаться к тем значениям, которые они имели в уравнении с меньшим числом переменных. Напри-
мер, при четырех переменных, вводя разное их число в анализ, Р.Фриш получил следующие коэффициенты регрессии для связи междух/и х2: ЬА2 — — 0,120; bt24 = 0,919; i123 = — 0,112. Это поз-
водило ему сделать вывод о наличии какого-то оптимального 2-1525
17
Тульски й и ист и т ут з ко м ом И Ки
БИБЛИОТЕКА
круга переменных, выход за который не улучшает коэффициенты регрессии, делает их неустойчивыми.
На основе изменения коэффициентов регрессии 6, и множественного коэффициента детерминации Л2 он разделил все переменные на полезные, лишние и вредные. Переменная считалась полезной, если ее включение значительно повышало Л2; когда этого не происходило и ввод новой переменной не изменял коэффициентов регрессии при других переменных, то она рассматривалась как лишняя; если добавляемая переменная сильно изменяла bt без заметного изменения Я2, то переменная относилась к вредным. Надо сказать, что конфлюэнтный анализ не получил большого распространения.
Методы корреляций и регрессий создавались как методы описания совместных изменений двух и более переменных. Совместные изменения переменных могут не означать наличия причинных связей между ними. Потребность в причинном объяснении корреляции привела американского генетика С. Райта к созданию метода путевого анализа (1910—1920) как одного из разновидностей структурного моделирования. Путевой анализ основан на изучении всей структуры причинных связей между переменными, т. е. на построении графа связей и изоморфной ему рекурсивной системы уравнений. Его основным положением является то, что оценки стандартизированных коэффициентов рекурсивной системы уравнений, которые интерпретируются как коэффициенты влияния (путевые коэффициенты), рассчитываются на основе коэффициентов парной корреляции. Это позволяет проанализировать структуру корреляционной связи с точки зрения причинности. Каждый коэффициент парной корреляции рассматривается как мера полной связи двух переменных.
Путевой анализ позволяет разложить величину этого коэффициента на четыре компоненты:
• прямое влияние одной переменной на другую (в этом случае в причинной цепи между одной и другой переменными нет промежуточных звеньев);
• косвенное влияние, т. е. передача воздействия одной переменной на другую через посредство переменных, специфицированных в модели как промежуточное звено в причинной цепи, связывающей изучаемые переменные;
• непричинная компонента, объясняемая наличием общих причин, воздействующих на одну и другую переменную;
18
• непричинная компонента, зависящая от неанализируемой в модели корреляции входных переменных. Если компоненты прямого и косвенного причинного влияния равны нулю, корреляция между переменными является ложной.
Таким образом, путевой анализ С. Райта, так же как и структурные модели, позволил прояснить проблему ложной корреляции, которой занимались многие видные статистики, начиная с К. Пирсона (1857—1936).
При работе с временными рядами разных показателей и при изучении взаимосвязей между ними довольно быстро были осознаны проблема ложной корреляции и проблема лага, т. е. сдвига во времени, который позволял уловить наличие связи между показателями (ВВП и инвестициями, приемом на учебу и выпуском из учебных заведений и т. д.).
Ложная корреляция возникала под влиянием фактора времени, иначе говоря, трендовой компоненты в коррелируемых временных рядах в случаях, если:
у, ~ уровень одного временного ряда во время t,
xt — уровень другого временнбго ряда во время t, то связь между ними выражается графом связей (рис. 1.1).
Рис. 1.1. Граф связей между уровнями временных рядов во время t в
Это привело к идее измерения корреляции не самих уровней х, и yf, а первых разностей: Ах, = xt — хг_], Ду, = yt — yt_t, (при линейных трендах). В общем случае было признано необходимым коррелировать отклонения от трендов (за вычетом циклической компоненты): Еу —у, — yt', Ех = х, — л}, (ул % — тренды временных рядов).
Исходя из структуры уровней временного ряда, которые включают тренд (7), конъюнктурный цикл (К), сезонную компоненту (5) и остаточную компоненту (R), можно представить любой динамический ряд как сумму четырех названных составляющих. Так, временные ряды показателей X и Y можно записать следующим образом:
X, = T(X)i + K(X)i + S(X), + R(X)-,
Y, = T( 1), + K( У), + S( Xb + R( Y), j.
2*
19
О. Андерсон (1887—1960) предложил измерять взаимосвязи между всеми названными компонентами рядов и находить частные корреляции между ними. Значимость каждой из них, конечно, различна: если тренды обоих временных рядов сильно выражены и имеют одинаковую направленность, то соответствующая корреляция получает большое значение; если тренды разнонаправленны, то корреляция может быть более значительной по величине, но отрицательной по знаку; корреляция между остальными компонентами определяется теснотой связи между трендом и конъюнктурными колебаниями, трендом и сезонностью и т. д. О. Андерсон подчеркивал, что невозможно предсказать, какое значение может получить ковариация тех или иных компонент, так как все определяется конкретным экономическим материалом. Он обратил внимание на то, что дисперсии уровней временных рядов также могут быть представлены как многосложные, включающие вариацию тренда, конъюнктурной компоненты, сезонной и остаточной компонент.
Метод оценки разностей разных порядков во временных рядах для подбора наиболее подходящей степени полинома для описания тренда развивался О. Андерсоном одновременно с В. Госсетом (Стьюдент) (1876-1937). Обнаружилось, что нельзя применять классические методы корреляционного анализа к временным рядам, так как не выполняется исходное условие -независимость наблюдений. Так был установлен эффект автокорреляции, выявление и устранение которого составляют одну из важнейших особенностей эконометрического метода.
Исследование динамики социальных и экономических процессов выявило довольно сильную распространенность эффекта насыщения: выхода на асимптоту при достижении определенных значений показателей. В силу этого в эконометрике большое распространение получили так называемые кривые с насыщением. К этому типу кривых относится кривая Гомперца — 5-образная кривая, предложенная Б. Гомперцем (1799—1865), которая имеет вид
у = Kabt, где К,а,Ь — параметры;
t — время (1, 2,...).
Кривая Гомперца используется для аналитического выражения тенденции развития показателя во времени, имеющего ограничения на рост (рис. 1.2).
Если log а < 0, то верхний предел для показателя у равен параметру К, а нижний - 0. Если log а > 0, то кривая имеет лишь нижний предел, равный величине параметра К (рис. 1.2в, г).
20
Рис. 1.2. Кривая Гомперца:
£Г-й£в<Опрн*< l;6-foga<0 при 4 > 1;
*-/aga > 0 приЛ < V,e-toga > 0 при Л < 1.
Для определения параметров тренда а и Ъ может использоваться метод наименьших квадратов, только если задан параметр К. В противном случае возможно лишь приближенное оценивание параметров. Кривая Гомперца применяется в демографических расчетах и страховом деле.
К этому же типу кривых относится логистическая кривая (рис. 1.3), т. е. кривая с насыщением вида
А К
где t - время (1,2, 3, л, Ъ и К — параметры.
21
Рис. 1.3. Логистическая кривая
Эта кривая характеризует развитие показателя во времени,
когда ускоренный рост в начале периода сменяется замедляю-
щимся темпом роста вплоть до полной остановки, что на гра
и-
ке соответствует отрезку кривой, параллельному оси абсцисс.
Используется для описания развития производства новых това
ров, роста численности населения и т. д. Максимум функции со
ответствует параметру если К задано, то параметры а и ft определяются мётодом наименьших квадратов. Впервые такая кривая была применена А. Кетле (1796—1874) для расчета численности
населения.
Большое внимание в эконометрике уделяется проблеме данных — специальным методам работы при наличии данных с про
пусками, влиянию агрегирования данных на эконометрические
измерения. Информация может отсутствовать по единицам сово
купности и быть только на уровне более крупных единиц (агрега
тов) — например, не по отдельным организациям, а по организациям в пределах административного района, т.е. по районам, и т. д. При агрегировании данных во времени опасность искажения результатов измерений (скажем, корреляции между временными рядами), гораздо больше, чем при агрегировании пространственных данных. С одной стороны, добавляется эффект автокорреляции, а с другой — происходит Погашение случайной компоненты. Результаты могут различаться весьма сильно. Например, при из
мерении связи между удельным расходом кокса и величиной суточного проплава по суточным данным коэффициент корреляции составил 0,582, а по четырехсуточным данным — 0,894.
22
Проблемы данных включают и проблемы селективной выбор-
ки в микроэконометрике. Типичные направления исследования в
этой области: рынок труда, выявление факторов, влияющих на ре
шение работать, если «да», то сколько часов; какие экономические стимулы влияют на принятие решения о получении образова
ния, об участии в «трейнинговых» программах, выборе профес
сии, места жительства; какое влияние оказывают различные рынки труда и образовательные программы на доход индивида и принятие им решения о поступлении на работу. При этом выборка может быть не случайной, не репрезентативной, ограниченной
только определенными ситуациями, а не всеми возможными. Скажем, при принятии решения о работе индивид, имеющий определенное образование, стремится получить заработную плату выше определенного минимума. Тогда регрессия, описывающая зависимость заработной платы от образования, будет основана не на всем возможном поле данных (заработная плата выше установленного минимума, ниже его), а только на данных индивидов с заработной платой выше минимальной. Возникает смещение наблюдаемой регрессии от истинной в результате так называемой самоселекции. Селективное смещение связано с поведением индивидов. В 1976-1979 гг. Дж. Хекман предложил двухступенчатый
метод оценивания селективного смещения:
w/=Mi + mi/;
е( =x2(Z>2 + U2I,
где Wf — заработная плата /-го индивида;
х(/ и х2/ — векторы характеристик индивида (возможно, перекрывающиеся);
- ошибки;
— характеристика «участия» индивида (например, его склон-
ность к работе).
При этом мы наблюдаем wf, только если > 0,1.
Эффект самоселекции очень распространен: он возникает, если объективный отбор подменяется «удобной» выборкой, например когда появляются добровольные респонденты, т. е. те, кто сами предлагают, чтобы их опросили. Очевидно, что характеристики добровольцев и недобровольцев могут быть отличны, и это приведет к ошибочному заключению о генеральной совокуп-
£
23
ности.
4
Эконометрический метод складывался в преодолении следующих неприятностей, искажающих результаты применения классических статистических методов:
• асимметричности связей;
• мультиколлинеарности объясняющих переменных;
• закрытости механизма связи между переменными в изолированной регрессии;
• эффекта гетероскедастичности, т. е. отсутствия нормального распределения остатков для регрессионной функции;
• автокорреляции;
• ложной корреляции;
• наличия лагов.
Эконометрическое исследование включает решение следующих проблем:
• качественный анализ связей экономических переменных — выделение зависимых (у.) и независимых переменных (л*);
• подбор данных;
• спецификация формы связи между у и хк;
• оценка параметров модели;
• проверка ряда гипотез о свойствах распределения вероятностей для случайной компоненты (гипотезы о средней, дисперсии и ковариации);
• анализ мультиколлинеарности объясняющих переменных, оценка ее статистической значимости, выявление перемен
ных, ответственных за мультиколлинеарность;
• введение фиктивных переменных;
• выявление автокорреляции, лагов;
• выявление тренда, циклической и случайной компонент;
• проверка остатков на гетероскедастичность;
• анализ структуры связей и построение системы одновременных уравнений;
• проверка условия идентификации;
• оценивание параметров системы одновременных уравнений (двухшаговый и трехшаговый метод наименьших квадратов, метод максимального правдоподобия);
• моделирование на основе системы временных рядов: пробле-
мы стационарности и коинтеграции;
построение рекурсивных моделей, ARIMA- и VAR- моделей;
проблемы идентификации и оценивания параметров.
Эконометрическая модель, как правило, основана на теоре-
тическом предположении о круге взаимосвязанных переменных и характере связи между ними. При всем стремлении к «наилуч
24
шему» описанию связей приоритет отдается качественному анализу. Поэтому в качестве этапов эконометрического исследования можно указать:
• постановку проблемы;
• получение данных, анализ их качества;
• спецификацию модели;
• оценку параметров;
• интерпретацию результатов.
Этот список менее подробен, чем предыдущий, и включает те стадии, которые проходит любое исследование, независимо от того, на использование каких данных оно ориентировано: пространственных или временных.
1.3. ИЗМЕРЕНИЯ В ЭКОНОМИКЕ
Поскольку понятие «эконометрика» включает экономические измерения, остановимся подробнее на этом вопросе. Измерение понимается по-разному. Прежде всего признаками измерения называют получение, сравнение и упорядочение информации. Это определение исходит из того, что измерение предполагает выделение некоторого свойства, по которому производится сравнение объектов в определенном отношении. Так определяется измерение в широком смысле.
Другое понимание измерения исходит из числового выражения результата, т.е. измерение трактуется как операция, в результате которой получается численное значение величины, причем числа должны соответствовать наблюдаемым свойствам, фактам, ка
чествам, законам науки и т. д.
Третий подход к измерению связан с обязательным наличием единицы измерения (эталона). Это определение измерения в узком смысле.
Первый, низший, уровень измерения предполагает сравнение объектов по наличию или по отсутствию исследуемого свойства. На этом уровне измерения используются термины «номинация», «классификация», «нумерация».
Второй уровень предполагает сравнение объектов по интенсивности проявляемых свойств. На этом уровне используются термины «шкалирование», «топология», «упорядочение».
Третий, высший, уровень измерения предполагает сравнение объектов с эталоном (в контексте физического измерения). На этом уровне используются термины «измерение», «квантификация».
25
Все понятия измерения могут быть объединены на базе определения шкалы измерения. Тип шкалы определяется допустимым преобразованием. Допустимое преобразование — это преобразование, при котором сохраняются неизменными отношения между элементами системы — истинные утверждения не становятся ложными, а ложные — истинными.
Для определения любой шкалы измерения необходимо дать название объекта, отождествить объект с некоторым свойством или группой свойств (предприятие промышленное, станок токарный, девушка сероглазая, автомобиль легковой и т.д.). Если это требование оказывается единственным, то шкала называется шкалой наименований или номинальной шкалой.
Измерением в номинальной шкале можно считать любую классификацию, по которой класс получает числовое наименование (например, номер научной или учебной специальности и т.д.).
Следует помнить, что числа на этой шкале играют роль ярлыков и к ним неприменимы обычные правила арифметики.
Номинальная шкала обладает только свойствами симметричности и транзитивности. Симметричность означает, что отношения, существующие между градациями X] и х2, имеют место и междух2 ИХ]. Транзитивность выражается в следующем: если X] = х2, и хг х3, то X] = х3.
Шкала, в которой порядок элементов по уровню проявления некоторого свойства существенен, а количественное выражение различия несущественно или плохо осуществимо, называется порядковой, или ранговой. Шкала порядка, или ординальная шкала, допускает операции «равенство-неравенство», «большеменьше».
Порядковые данные возникают, например, при определении предпочтений избирателей и рейтинга того или иного кандидата, экспертиз качества, при оценке силы землетрясений, измерении полезности, оценке уровня интеллекта, а также при определении потенциала человеческого развития и т. д.
Широкое распространение получили так называемые балльные шкалы. Ординальная шкала единственная с точностью до монотонного преобразования. Кроме номинальной и порядковой шкал для определения измерения используются интервальные шкалы.
Измерения в интервальных шкалах в известном смысле более совершенны, чем в порядковых. Применение этих шкал дает возможность не только упорядочить объекты по количеству свойства, но и сравнить между собой разности количеств. Таким об-26
разом, мы получаем возможность не только указать категорию, к которой относится объект по данному признаку, установить его место в ранжированном ряде, но и описать его отличие от других объектов, рассчитав разность (интервал) между соответствующими позициями на шкале. Примерами интервальных шкал могут служить измерения большинства экономических параметров । производительность труда, себестоимость, рентабельность, ликвидность и т. д.). Формально интервальная шкала определяется как единственная до линейного преобразования шкала вида
у = ах + Ь,
I
где а и b - числа, для которых определены операции сложения и умножения, соответственно а > О, b ф 0. Параметр а называется масштабом, а параметр b — началом отсчета г
V
В случаях, когда на шкале можно указать абсолютный нуль, мы имеем несколько более высокий уровень измерения, а именно шкалу отношений (или пропорциональную шкалу). При измерении на такой шкале можно, например, сделать вывод, что х4 вдвое больше х2, если х4 = 40Л, а х2 = 20Л. Если за нулевую отметку принята некая произвольная точка, то подобное заключение о соотношении отметок не будет справедливым. Например, по шкале температур по Цельсию нельзя утверждать, что вода, нагретая до 40°С, вдвое горячее, чем вода, температура которой +20’С. Шкала температур по Цельсию — это интервальная шкала (в отличие от шкалы абсолютных температур по Кельвину). По шкале отношений можно оценить такие социальные характеристики, как стаж, заработная плата.
Таким образом, по шкале отношений начало отсчета нельзя выбрать произвольно и параметр b = 0. Можно сказать, что шкала отношений — это интервальная шкала с естественным началом.
Под эмпирическим эквивалентом числового нуля подразумевается отсутствие какого-либо свойства у изучаемой системы. В этом случае простейшим и наиболее надежным способом операционального определения шкалы отношений является указание на эталон (эталонный метр и т.п.). Различие между условной и естественной нулевыми точками нередко трактуется как различие между последовательностями значений величин, объективно имеющих некий минимум (например, температура) и не имеющих его (например, время).
27
Пропорциональная шкала допускает операции «равенство-неравенство интервалов», «меньше-больше», операцию деления, на основе которой устанавливается равенство-неравенство отношений.
Шкала отношений — это единственная с точностью до линейных преобразований шкала вида
ь
у = ах при а * О,
где а — масштаб.
Если в интервальной шкале масштаб зафиксирован, то измерение происходит в шкале разностей. Шкала разностей допускает операции «равенство-неравенство», «больше-меньше», «равенство-неравенство интервалов» и операцию вычитания, на основе которой устанавливается величина интервала в фиксированном масштабе. К шкале разностей относятся логарифмические шкалы, а также процентные и аналогичные им шкалы измерений, задающие безразмерные величины. Например, указание года рождения — это представление возраста в шкале разностей.
Шкала разностей существенна с точностью до линейного преобразования вида
у =* х + Ь, где b * 0.
Такое преобразование называется сдвигом. Если зафиксированы масштаб и точка отсчета, то переменная изменяется в абсолютной шкале с точностью до тождественного преобразования вида
у = х.
Эта шкала допускает все операции. В абсолютной шкале изменяются, например, вероятность, число работников и т. д.
Таким образом, в определении шкал участвуют, понятия равенства, порядка, дистанции между пунктами шкалы (интервалы), начала отсчета и единицы измерения. В зависимости от наличия или отсутствия этих элементов возникают различные типы шкал.
В обыденном сознании термин «измерение» используется исключительно применительно к интервальной шкале. С числами проводят различные операции сложения, вычитания, деления, умножения. Однако в общем случае элементы числовой сис
28
темы с отношениями — это не действительные числа, а всего лишь метки, т. е. оцифровки. Для номинальной шкалы при сравнении элементов (объектов), как правило, возникает вопрос: совпадают (подобны, тождественны) они или нет?
Если переменная измерена в ординальной шкале, то неадекватны будут все утверждения о том, во сколько и на сколько одна величина больше другой, но адекватно утверждение, что одна величина больше другой. По отношению к ординальным шкалам лишено смысла использование алгебраических операций, поскольку ординальные данные не аддитивны и не позволяют измерить удаленность одного объекта от другого.
При использовании интервальной шкалы адекватным является сравнение расстояний между парами одной и той же системы.
Переход к измерению в шкале разностей делает адекватными суждения типа «на сколько больше», а измерение в шкале отношений — суждения типа «во сколько раз больше».
Выделение разных уровней измерения дает известное основание говорить о внутреннем единстве задач классификации и измерения. В самом Деле, неупорядоченная классификация есть не что иное, как построение шкалы некоторого признака (фактора), градациями которого являются названия классов. Таким образом, процедура построения неупорядоченной классификации может рассматриваться как процедура измерения по номинальной шкале. В случаях, когда полученные классы могут быть упорядочены по некоторому основанию, например по расстоянию или по мере сходства между собой так, чтобы стоящие рядом в этом ряду классы были более сходны друг с другом, чем отдаленные, говорят о линейно-упорядоченной классификации. В таких случаях построение классификации подобно измерению по порядковой шкале.
В других ситуациях множество объектов может иметь иерархическую структуру (например, по степени взаимного сходства), и мы говорим об иерархической классификации. Если можно указать дистанцию (например, число шагов на дереве разбиения), отделяющую классы друг от друга, то такая классификация в некотором смысле аналогична измерению по интервальной шкале. Заметим, что вариация переменных, измеренных на номинальной шкале, как правило, ниже вариации переменных, измеренных на интервальной шкале.
Любому измерению предшествует качественный анализ, учитывающий цели исследования. Качественный анализ необходим и после того, как измерение произведено, для того чтобы оценить
29
адекватность результатов измерения объектов поставленным целям.
Специфика экономических измерений состоит в наличии большого числа разнородных данных — разнородных ресурсов, разнородных результатов (например, товаров и услуг). Отсюда большое значение имеют стоимостные метрики, далеко не всегда отвечающие поставленным задачам. Это не исключает потребность в натуральных метриках. Количественная определенность функционирования экономики имеет объемные и структурные характеристики. Объемные характеристики определяют масштаб явления, тогда как структурные — его разнообразие, организацию и соподчиненность. Количественные и структурные меры дополняют друг друга. Так, измерение объема теневой экономики дает возможность уточнить ВВП и все производные показатели, а измерение ее удельного веса в ВВП позволяет судить о распространенности этого явления и степени его подконтрольности. Экономические измерения осложняются существованием латентных характеристик, которые непосредственно неизмеримы. Для выражения латентной переменной требуется найти какой-либо индикатор.
Нередко в экономических измерениях возникает задача отражения иерархии измерителей, которая выражается в выделении интегрального и частных показателей. Поскольку экономические меры взаимосвязаны, то следует иметь в виду, что эти взаимосвязи не могут быть точными и однозначными. Они всегда включают случайную компоненту, поэтому при принятии решений необходим учет фактора неопределенности.
Для социально-экономических измерений характерны специфические представления о точности. Экономику относят к «неточным» наукам, так как невозможно произвести измерение с произвольно малой погрешностью. Главное, что определяет специфику точности экономических изменений, — это неконтроли-руемость погрешности наблюдений. Однако, даже имея это в виду, нельзя говорить о «неточных» и «точных» науках, так как неточных наук нет, а есть неточные представления о точности1.
Представления о точности измерений могут быть получены из анализа погрешностей. Обобщая представления о точности измерения, сделаем следующий вывод.
См.: Эйсснер Ю. Н. Организационно-экономические измерения в планировании и управлении. - Л.: Изд-во ЛГУ, 1988. - С. 29.
30
Точность измерения — это его адекватность. Универсальные критерии точности отсутствуют. Критерий точности каждого вида измерения определяется в соответствии с целями этого измерения. Погрешности измерения не сводятся к арифметическим погрешностям.
По объективным причинам для социально-экономических измерений характерна низкая контролируемость их точности. Для проверки адекватности можно использовать ряд простых критериев. Например, оценка, представляющая собой линейную комбинацию величин разной размерности с безразмерными коэффициентами, заведомо не может быть адекватной, если не оговорено заранее совместное преобразование единиц измерения. Неадекватными будут оценки, построенные на основе арифметических операций с рангами (такие операции неприменимы к порядковой шкале).
Для социально-экономических объектов особую трудность представляет выявление эмпирических отношений. Неаддитивность и разнородность свойств остро ставят проблему обобщения (свертки и агрегирования) данных для представления ненаблюдаемых (латентных) переменных.
В естественных науках проблема точности измерения связывается прежде всего с самим процессом измерения.
В области экономических измерений проблема точности связана с:
• определением понятия экономической величины;
• формированием системы принципов, постулатов и других теоретических положений, формирующих базис точности экономических измерений;
• определением экономических показателей;
• разработкой принципов конструирования измерителей и измерений;
• основанием выбора типа шкал при конструировании измерителя;
• разработкой правил формирования систем показателей;
• выявлением типов и определением методов устранения ошибок экономического измерения;
• разработкой правил агрегирования и свертки экономических показателей;
• выявлением условий сравнимости экономических величин (показателей);
• разработкой правил и методов измерений.
31
В теории измерений существуют два основных представления об измерении’.
• измерение понимается как соотношение множества объектов, описываемых некоторой переменной с множеством меток, и выражается теорией соотнесения, представляющей собой теорию шкал;
• измерение понимается как соотношение переменной, непосредственно ненаблюдаемой (латентной), со значениями непосредственно наблюдаемой переменной (индикатора). В этом случае основная проблема состоит в отыскании связи индикатора с латентной переменной.
Поиск измерителя исследуемого признака может происходить в трех направлениях:
• выбор показателя, который может служить индикатором исследуемого признака (патенты);
• определение функциональной зависимости значения исследуемого признака от значений наблюдаемых признаков;
• построение системы признаков, характеризующей исследуемый признак.
Отправной точкой конструирования измерителя является постулат об объективном существовании закономерностей во внутренних и внешних связях объектов.
Основной базой данных для эконометрических исследований служат данные официальной статистики либо данные бухгалтерского учета. Таким образом, проблемы экономического измерения — это проблемы статистики и учета. Используя экономическую теорию, можно определить связь между признаками и показателями, а используя статистику и учет — ответить на следующие вопросы: какие показатели применяются для измерения результатов работы промышленного предприятия — валовая продукция, добавленная стоимость, реализованная продукция? Как оценить остатки оборотных средств — по стоимости первых или последних поставок или по средней стоимости? И т.д.
Контрольные вопросы к главе 1
1. Дайте определение эконометрики.
2. Назовите основные ступени выделения эконометрики в особую науку.
3. Когда возникли эконометрическое общество и журнал «Эконометрика»?
4. С какими науками связана эконометрика?
32
5. Каковы этапы эконометрического исследования? Какие вопросы приходится решать эконометристу?
6. В чем состоит особая роль статистики в формировании эконометрического метода?
7. Почему можно сказать, что эконометрические методы развивались в ответ на преодоление недостатков классических статистических методов?
8. Какие типы данных используются в эконометрическом исследовании? Какие возникают проблемы данных?
9. По каким типам шкал производятся измерения в эконометрике?
10. Каковы допустимые преобразования на каждой шкале измерения?
2” 1525
ГЛАВА
ПАРНАЯ РЕГРЕССИЯ И КОРРЕЛЯЦИЯ В ЭКОНОМЕТРИЧЕСКИХ ИССЛЕДОВАНИЯХ
2.1. СПЕЦИФИКАЦИЯ МОДЕЛИ
Как уже отмечалось, в эконометрике широко используются методы статистики. Ставя цель дать количественное описание взаимосвязей между экономическими переменными, эконометрика прежде всего связана с методами регрессии и корреляции.
В зависимости от количества факторов, включенных-в уравнение регрессии, принято различать простую (парную) и множественную регрессии.
Простая регрессия представляет собой регрессию между двумя переменными — у и х, т. е. модель вида.
У =f(x),
где у — зависимая переменная (результативный признак);
х — независимая, или объясняющая, переменная (признак-фактор).
Множественная регрессия соответственно представляет собой регрессию результативного признака с двумя и большим числом факторов, т. е. модель вида
У -,Хк).
Методам простой или парной регрессии и корреляции, возможностям их применения в эконометрике посвящена данная глава.
Любое Эконометрическое исследование начинается со спецификации модели, т. е. с формулировки вида модели, исходя из соответствующей теории связи между переменными. Иными сло-34
вами, исследование начинается с теории, устанавливающей связь между явлениями.
Прежде всего из всего круга факторов, влияющих на результативный признак, необходимо выделить наиболее существенно влияющие факторы. Парная регрессия достаточна, если имеется доминирующий фактор, который и используется в качестве объясняющей переменной. Предположим, что выдвигается гипотеза . о том, что величина спроса у на товар А находится в обратной зависимости от цены х, т. е. ух = а — b х. В этом случае необходимо знать, какие остальные факторы предполагаются неизменными, возможно, в дальнейшем их придется учесть в модели и от простой регрессии перейти к множественной.
Уравнение простой регрессии характеризует связь между двумя переменными, которая проявляется как некоторая закономерность лишь в среднем в целом по совокупности наблюдений. Так, если зависимость спроса у от цены х характеризуется, например, уравнением у = 5000 — 2 • х, то это означает, что с ростом цены на 1 д. е. спрос в среднем уменьшается на 2 д. е. В уравнении регрессии корреляционная по сути связь признаков представляется в виде функциональной связи, выраженной соответствующей математической функцией. Практически в каждом отдельном случае величина у складывается из двух слагаемых:
У^Уу + Ъ <2Л)
где у^ — фактическое значение результативного признака;
yXf ~ теоретическое значение результативного признака, найденное исходя из соответствующей математической функции связи у и х, т. е. из уравнения регрессии;
£j — случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии.
Случайная величина е называется также возмущением. Она включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения. Ее присутствие в модели порождено тремя источниками: спецификацией модели, выборочным характером исходных данных, особенностями измерения переменных.
Приведенное ранее уравнение зависимости спроса у от цены х точнее следует записывать как
у ~ 5000 — 2 • х + е,
3*
35
ибо всегда есть место для действия случайности. Обратная зависимость спроса от цены не обязательно характеризуется линейной функцией а
ух = а-*х
Возможны и другие соотношения, например:
W Л , Jfx — 1 , Zx ,
х a+b-x
Поэтому от правильно выбранной спецификации модели зависит величина случайных ошибок: они тем меньше, чем в большей мере теоретические значения результативного признака ух подходят к фактическим данным у.
К ошибкам спецификации будут относиться не только неправильный выбор той или иной математической функции для ух, но и недоучет в уравнении регрессии какого-либо существенного фактора, т. е. использование парной регрессии вместо множественной. Так, спрос на конкретный товар может определяться не только ценой, но и доходом на душу населения.
Наряду с ошибками спецификации могут иметь место ошибки выборки, поскольку исследователь чаще всего имеет дело с выборочными данными при установлении закономерной связи между признаками. Ошибки выборки имеют место и в силу неоднородности данных в исходной статистической совокупности, что, как правило, бывает при изучении экономических процессов. Если совокупность неоднородна, то уравнение регрессии не имеет практического смысла. Для получения хорошего результата обычно исключают из совокупности единицы с аномальными значениями исследуемых признаков. И в этом случае результаты регрессии представляют собой выборочные характеристики.
Использование временной информации также представляет собой выборку из всего множества хронологических дат. Изменив временной интервал, можно получить другие результаты регрессии.
Наибольшую опасность в практическом использовании методов регрессии представляют ошибки измерения. Если ошибки спецификации можно уменьшить, изменяя форму модели (вид математической формулы), а ошибки выборки — увеличивая объем исходных данных, то ошибки измерения практически сводят на нет все усилия по количественной оценке связи между признаками. Особенно велика роль ошибок измерения при ис-36
следовании на макроуровне. Так, в исследованиях спроса и потребления в качестве объясняющей переменной широко используется «доход на душу населения». Вместе с тем статистическое измерение величины дохода сопряжено с рядом трудностей и не лишено возможных ошибок, например в результате наличия сокрытых доходов.
Приведем еще один пример: в настоящее время органы государственной статистики получают балансы предприятий, достоверность которых никто не подтверждает. Последующее обобщение такой информации может содержать ошибки измерения. Исследуя, например, в качестве результативного признака прибыль предприятий, мы должны быть уверены, что предприятия показывают в отчетности адекватные реальной действительности величины.
Предполагая, что ошибки измерения сведены к минимуму, основное внимание в эконометрических исследованиях уделяется ошибкам спецификации модели.
В парной регрессии выбор вида математической функции Ух =f(x) может быть осуществлен тремя методами:
• графическим;
• аналитическим, т. е. исходя из теории изучаемой взаимосвязи;
• экспериментальным.
При изучении зависимости между двумя признаками графический метод подбора вида уравнения регрессии достаточно нагляден. Он основан на поле корреляции. Основные типы кривых, используемые при количественной оценке связей, представлены на рис. 2.1.
37
Рис. 2.1. Основные типы кривых, используемые при количественной оценке связей между двумя переменными: а — ух~ а + Л • х; б — )/х = а + Л*х + с-х2;
в — у = д + Л/х; г — ум ч-Л-х+с^+^-х3
д-ух = ахь; е - ух = a Ь*;
Класс математических функций для описания связи двух переменных достаточно широк. Кроме уже указанных используются и другие типы кривых:
Igy =0
+ Ь • х + с х2.
38
Значительный интерес представляет аналитический метод выбора типа уравнения регрессии. Он основан на изучении материальной природы связи исследуемых признаков.
Пусть, например, изучается потребность предприятия в электроэнергии у в зависимости от объема выпускаемой продукции х.
Все потребление электроэнергии у можно подразделить на две части:
• не связанное с производством продукции а;
• непосредственно связанное с объемом выпускаемой продукции, пропорционально возрастающее с увеличением объема выпуска (Ь • х).
Тогда зависимость потребления электроэнергии от объема продукции можно выразить уравнением регрессии вида
$х = а + Ь х.
Если затем разделить обе части уравнения на величину объема выпуска продукции (х), то получим выражение зависимости удельного расхода электроэнергии на единицу продукции
от объема выпущенной продукции (х) в виде уравнения
равносторонней гиперболы:
Аналогично затраты предприятия могут быть подразделены на условно-переменные, изменяющиеся пропорционально изменению объема продукции (расход материала, оплата труда и др.) и условно-постоянные, не изменяющиеся с изменением объема производства (арендная плата, содержание администрации и др.). Соответственно зависимость затрат на производство (у) от объема продукции (х) характеризуется линейной функцией:
у = а + Ь • х, а зависимость себестоимости единицы продукции (?) от объема продукции — равносторонней гиперболой
При обработке информации на компьютере выбор вида уравнения регрессии обычно осуществляется экспериментальным методом, т. е. путем сравнения величины остаточной дисперсии ^ост, рассчитанной при разных моделях.
39
Если уравнение регрессии проходит через все точки корреляционного поля, что возможно только при функциональной связи, когда все точки лежат на линии регрессии ух =Дх), то фактические значения результативного признака совпадают с теоретическими у = ух, т. е. они полностью обусловлены влиянием фактора х. В этом случае остаточная дисперсия = 0. В практичес-
ких исследованиях, как правило, имеет место некоторое рассеяние точек относительно линии регрессии. Оно обусловлено влиянием прочих не учитываемых в уравнении регрессии факторов. Иными словами, имеют место отклонения фактических данных от теоретических (у — ух). Величина этих отклонений и лежит в основе расчета остаточной дисперсии:
Дхя’-ЕО'-.У2. (2.2)
п
Чем меньше величина остаточной дисперсии, тем в меньшей мере наблюдается влияние прочих не учитываемых в уравнении регрессии факторов лучше уравнение регрессии подходит к исходным данным. При обработке статистических данных на компьютере перебираются разные математические функции в автоматическом режиме и из них выбирается та, для которой остаточная дисперсия является наименьшей.
Если остаточная дисперсия оказывается примерно одинаковой для нескольких функций, то на практике предпочтение отдается более простым видам функций, ибо они в большей степени поддаются интерпретации и требуют меньшего объема наблюдений. Результаты многих исследований подтверждают, что число наблюдений должно в 6 — 7 раз превышать число рассчитываемых параметров при переменной х. Это означает, что искать линейную регрессию, имея менее 7 наблюдений, вообще не имеет смысла. Если вид функции усложняется, то требуется увеличение объема наблюдений, ибо каждый параметр при х должен рассчитываться хотя бы по 7 наблюдениям. Значит, если мы выбираем параболу второй степени
у. — а + b х + с х1,
то требуется объем информации уже не менее 14 наблюдений. Учитывая, что эконометрические модели часто строятся по данным рядов динамики, ограниченным по протяженности (10, 20, 30 лет), при выборе спецификации модели предпочтительна модель с меньшим числом параметров при х.
40
2.2. ЛИНЕЙНАЯ РЕГРЕССИЯ И КОРРЕЛЯЦИЯ: СМЫСЛ И ОЦЕНКА ПАРАМЕТРОВ
Линейная регрессия находит широкое применение в эконометрике в виде четкой экономической интерпретации ее параметров.
Линейная регрессия сводится к нахождению уравнения вида
ух = а + b • х или у = а + Ь- х + е.
(2.3)
Уравнение вида ух = а + b-х позволяет по заданным значениям фактора х иметь. теоретические значения результативного признака, подставляя в него фактические значения фактора х На графике теоретические значения представляют линию регрессии (рис. 2.2).
Рис. 2.2. Графическая оценка параметров линейной регрессии
Построение линейной регрессии сводится к оценке ее параметров — а и Ь. Оценки параметров линейной регрессии могут быть найдены разными методами. Можно обратиться к полю корреляции и, выбрав на графике две точки, провести через них прямую линию (см. рис. 2.2). Далее по графику можно определить значения параметров. Параметр а определим как точку пересечения линии регрессии с осью оу, а параметр b оценим, исходя из угла наклона линии регрессии, как dy/dx, где dy — приращение результата у, a dx - приращение фактора х, т. е. Ч|
v Y = а 4- b • х
41
Классический подход к оцениванию параметров линейной
ЛЛИЛВПИ UO иДФПТ1Д naUUAULimiV KTtlO TtltWTVf^B /N>f
>г<
МНК позволяет получить такие оценки параметров а и Ь, при которых сумма квадратов отклонений фактических значений результативного признака (у) от расчетных (теоретических) ух минимальна:
(2.4)
Иными словами, из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной (рис. 2.3):
следовательно
У +
Уе2 ->min.
Рис. 2.3. Линия регрессии с минимальной дисперсией остатков
Чтобы найти минимум функции (2.4), надо вычислить частные производные по каждому из параметров а и b и приравнять их к нулю.
Обозначим Se,2 через S, тогда:
5= 2(у, -$х)2 = £(у-а-Ь -х)2;
42
— = -2Уу+2па + 2ЬУх = 0; da
(2.5)
dS db
= -2'£yx + 2a'£x + 2b'£x2 =0.
Преобразуя формулу (2.5), получим следующую систему нормальных уравнений для оценки параметров а и Ь:
п-а + Ь^х = ^У, а’Х.х+Ь'Ех2 = £у-х.
(2.6)
Решая систему нормальных уравнений (2.6) либо методом последовательного исключения переменных, либо методом определителей, найдем искомые оценки параметров а и Ь. Можно
воспользоваться следующими готовыми формулами:
а = у — b • х. (2.7)
Формула (2.7) получена из первого уравнения системы (2.6), если все его члены разделить на л.
cov(x,y)
где cov (х, у) — ковариация признаков; — дисперсия признака х.
О - -
Ввиду того, что cov(x, у) = ух — у X, а <ГХ = X2 — х , получим
следующую формулу расчета оценки параметра Ь:
(2.8)
Параметр b называется коэффициентом регрессии. Его вели-
чина показы
ет среднее изменение результата с изменением
фактора на одну единицу. Так, если в функции издержек ух — 3000 + 2 • х (у — издержки (тыс. руб.), х — количество единиц продукции), то, следовательно, с увеличением объема продукции
(х) на 1 ед. издержки производства возрастают в среднем на 2 тыс. руб., т. е. дополнительный прирост продукции на 1 ед. потребует увеличения затрат в среднем на 2 тыс. руб.
43
Возможность четкой экономической интерпретации коэффициента регрессии сделала линейное уравнение регрессии достаточно распространенным в эконометрических исследова
ниях.
Формально а — значение у при х = 0. Если признак-фактор х
не имеет и не может иметь нулевого значения, то вышеуказанная трактовка свободного члена а не имеет смысла. Параметр а может не иметь экономического содержания. Попытки экономически
интерпретировать параметр а могут привести к абсурду, особенно при а < 0.
Интерпретировать можно лишь знак при параметре а. Если а > 0, то относительное изменение результата происходит медленнее, чем изменение фактора. Иными словами, вариация ре
зультата меньше вариации фактора — коэффициент вариации по
фактору х выше коэффициента вариации для результата у: Vx> Vy. Для доказательства данного положения сравним относи-
тельные изменения факторах и результата у:
dy dx dy у
— <— или — ;
У х dx х
Откуда 0 < а.
Предположим по группе предприятий, выпускающих один и тот же вид продукции, рассматривается функция издержек: у — a + bx+е. Информация, необходимая для расчета оценок параметров а и Ь, представлена в табл. 2.1.
Таблица 2.1
Расчетная таблица
№ предприятия
Выпуск
Затраты на
изводство,
млн руб. (у)
1
2
3
4
5
6
7 Итого
1 2
4
3 5
3 4
22
30
70
150
о.
170
150
770
30
140
600
300
850
4 4900
2 820
80 99 700
31,1
67,9
141,6
104,7
178,4
104,7
141,6
770,0
33
44
Система нормальных уравнений будет иметь вид (7 а+ 22-b = 770, [22 а+80 Ь = 2820.
Решая ее, получим: а = - 5,79; Ь= 36,84.
Запишем уравнение регрессии:
ух = -5,79 + 36,84 • х.
Подставив в уравнение значения х, найдем теоретические значения у, (см. последнюю графу табл. 2.1)
В данном случае величина параметра а не имеет экономического смысла.
В рассматриваемом примере имеем:
х=3,14; <т, = 1,25; kk = 39,8%; у = 110; ау = 46,29; 1> = 42,1%.
То, что а < 0, соответствует опережению изменения результата над изменением фактора: Vy > Vx.
Если переменные х и у выразить через отклонения от средних уровней, то линия регрессии на графике пройдет через начало координат:
где у = у — у и У = х — х.
Оценка коэффициента регрессии при этом не изменится.
Оценку коэффициента регрессии можно получить проще, не обращаясь к методу наименьших квадратов. Альтернативную оценку параметра b можно найти исходя из содержания данного коэффициента: изменение результата Ду = у„ — у{ сопоставляют с изменением/фактора Дх = х„ — х,.'
В нашем примере такого рода альтернативная оценка параметра bсоставит
.. 170 - 30 _
Эта величина является приближенной, ибо ббльшая часть информации, имеющейся в данных, не используется при ее расчете. Она основана только на мини-максных значениях переменных.
Парная линейная регрессия используется в эконометрике нередко при изучении функции потребления:
C=Ky + L,
где С — потребление;
у - доход;
Кн L — параметры функции.
Данное уравнение линейной регрессии используется обычно в увязке с балансовым равенством:
у = С + 1-г,
где I — размер инвестиций; г — сбережения.
Для простоты предположим, что доход расходуется на пот-
ребление и инвестиции. Таким образом, рассматривается систе
ма уравнений
Наличие в данной системе балансового равенства наклады
ет ограничение на величину коэффициента регрессии, которая не может быть больше единицы, т. е. Кл 1.
Предположим, что функция потребления составила:
С = 1,9 + 0,65-у.
Коэффициент регрессии характеризует склонность к потреблению. Он показывает, что из каждой тысячи дохода на потребление расходуется в среднем 650 руб., а 350 руб. инвестируются. Если рассчитать регрессию размера инвестиций от дохода, т. е. I = а + Ь у, то уравнение регрессии составит: I = 1,9 + 0,35 • у. Это уравнение можно и не определять, ибо оно выводится из функции потребления. Коэффициенты регрессии этих двух уравнений связаны равенством: 0,65 +0,35 = 1.
46
Если коэффициент регрессии оказывается больше 1, то у < (С + 1), т. е. на потребление расходуются не только доходы, но и сбережения.
Коэффициент регрессии в функции потребления используется для расчета мультипликатора:
1
где т — мультипликатор;
b — коэффициент регрессии в функции потребления.
В нашем примере т - 1/(1- 0,65) = 2,86. Это означает, что дополнительные вложения в размере I тыс. руб. на длительный срок приведут при прочих равных условиях к дополнительному доходу в 2,86 тыс. руб.
Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции гх... Существуют разные модификации формулы линейного коэффициента корреляции. Некоторые из них приведены ниже:
cov(x.y)yx-yx
Фу ^Х^у ^X^J?
(2.9)
Как известно, линейный коэффициент корреляции находится в границах: -1 < < 1.
Если коэффициент регрессии b > 0, то 0 < < 1, и, наобо-
рот, при b < 0, -1 < г„ < 0.
По данным табл. 2.1 величина линейного коэффициента корреляции составила 0,991, что достаточно близко к 1 и означает наличие очень тесной зависимости затрат на производство от величины объема выпушенной продукции.
Следует иметь в виду, что величина линейного коэффициента корреляции оценивает тесноту связи рассматриваемых признаков в ее линейной форме. Поэтому близость абсолютной величины линейного коэффициента корреляции к нулю еще не означает отсутствие связи между признаками. При иной спецификации модели связь между признаками может оказаться достаточно тесной.
Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака у,
47
объясняемую регрессией, в общей дисперсии результативного признака: 2
„2 _ ^объясн ------------ (2.10)
/общ
Соответственно величина 1 — г характеризует долю диспер-
сии у, вызванную влиянием остальных не учтенных в модели
факторов.
В нашем примере г = 0,982. Следовательно, уравнением регрессии объясняется 98,2% дисперсии результативного признака, а на долю прочих факторов приходится лишь 1,8% ее дисперсии (т.е. остаточная дисперсия), Величина коэффициента детермина
ции служит одним из критериев оценки качества линейной модели. Чем больше доля Объясненной вариации, тем соответственно меньше роль прочих факторов, и, следовательно, линейная мо
дель хорошо аппроксимирует исходные данные и ею можно воспользоваться для прогноза значений результативного признака. Так, полагая, что объем продукции предприятия может составить 5 тыс. ед., прогнозное значение для издержек производства окажется 178,4 тыс. руб.
2.3. ОЦЕНКА СУЩЕСТВЕННОСТИ ПАРАМЕТРОВ ЛИНЕЙНОЙ РЕГРЕССИИ И КОРРЕЛЯЦИИ
После того как найдено уравнение линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров.
Оценка значимости уравнения регрессии в целом дается с помощью /-критерия Фишера. При этом выдвигается нулевая гипотеза, что коэффициент регрессии равен нулю, т. е. b — 0, и, следовательно, фактор х не оказывает влияния на результат у.
Непосредственному расчету /-критерия предшествует анализ дисперсии. Центральное место в нем занимает разложение общей суммы квадратов отклонений переменной у от среднего значения у на две части — «объясненную» и «необъясненную»:
S(y-y)2 = Х(^-у)2 ' + (2.П)
Общая сумма Сумма квадратов Остаточная сумма квадратов = отклонений, + квадратов
отклонений объясненная отклонений
регрессией
48
Общая сумма квадратов отклонений индивидуальных значений результативного признака у от среднего значения у вызвана влиянием множества причин. Условно разделим всю совокупность причин на две группы: изучаемый фактор х и прочие факторы. Если фактор не оказывает влияния на результат, то линия регрессии на графике параллельна оси ах и у — у. Тогда вся дисперсия результативного признака обусловлена воздействием прочих факторов и общая сумма квадратов отклонений совпадет с остаточной. Если же прочие факторы не влияют на результат, то у связан с х функционально и остаточная сумма квадратов равна нулю. В этом случае сумма квадратов отклонений, объясненная регрессией, совпадает с общей суммой квадратов.
Поскольку не все точки поля корреляции лежат на линии регрессии, то всегда имеет место их разброс как обусловленный влиянием фактора х, т. е. регрессией у по х, так и вызванный действием прочих причин (необъясненная вариация). Пригод
ность линии регрессии для прогноза зависит от того, какая часть общей вариации признака у приходится на объясненную вариацию. Очевидно, что если сумма квадратов отклонений, обусловленная регрессией, будет больше остаточной суммы квадратов, то уравнение регрессии статистически значимо и фактор х оказывает существенное воздействие на результату. Это равносильно тому, что коэффициент детерминации будет приближаться к единице.
Любая сумма квадратов отклонений связана с числом степеней свободы (df — degrees of freedom), т. e. с числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности лис числом определяемых по ней констант. Применительно к исследуемой проблеме число
степеней свободы должно показать, сколько независимых откло
нений из п возможных (О’! — у), (у2 - у),(у„ - у)] требуется для образования данной суммы квадратов. Так, для общей суммы квадратов £(у — у)2 требуется (л — 1) независимых отклонений,
ибо по совокупности из п единиц после расчета среднего уровня свободно варьируют лишь (л — 1) число отклонений. Например, имеем ряд значений у: 1,2, 3,4, 5. Среднее из них равно 3, и тогда л отклонений от среднего составят: —2; —1; 0; 1; 2. Так как Е(у — у) = 0, то свободно варьируют лишь четыре отклонения, а
пятое отклонение может быть определено, если предыдущие че
тыре известны.
При расчете объясненной или факторной суммы квадратов 22(ух — у г используются теоретические (расчетные) значения ре
4-15» 49
зультативного признака ух, найденные по линии регрессии: ух = а + Ь • х.
В линейной регрессии Е(ух — у)2 = Ь2 Е(х — х)2. В этом нетрудно убедиться, обратившись к формуле линейного коэффициента корреляции:
(2.12)
у
Из формулы (2.12) видно, что
2 =Ь2-су и а
(2.13)
где ст2- — общая дисперсия признака у;
о ‘о х— дисперсия признака у, обусловленная фактором х.
Соответственно сумма квадратов отклонений, обусловленных линейной регрессией, составит:
Поскольку при заданном объеме наблюдений по х и у факторная сумма квадратов при линейной регрессии зависит только от одной константы коэффициента регрессии Ь, то данная сумма квадратов имеет одну степень свободы. К. этому же выводу придем, если рассмотрим содержательную сторону расчетного значения признака у, т. е. ух. Величина ух определяется по уравнению линейной регрессии: ух = а + b • х. Параметр а можно определить как а — у — b • х. Подставив выражение параметра а в линейную модель, получим:
$х = у — b • х + b • х=у — b • (х — х).
Отсюда видно, что при заданном наборе переменных у и х расчетное значение ух является в линейной регрессии функцией только одного параметра — коэффициента регрессии. Соответственно и факторная сумма квадратов отклонений имеет число степеней свободы, равное I.
Существует равенство между числом степеней свободы общей, факторной и остаточной суммами квадратов. Число степеней свободы остаточной суммы квадратов при линейной регрессии составляет л — 2. Число степеней свободы для общей суммы
50
квадратов определяется числом единиц, и поскольку мы используем среднюю вычисленную по данным выборки, то теряем одну степень свободы, т. е. df^ = л — 1.
Итак, имеем два равенства:
S(y-y)2 = E6>x-7)2 + S(y-V, л - 1 = 1 + (л - 2).
(2.14)
Разделив каждую сумму квадратов на соответствующее ей число степеней свободы, получим средний квадрат отклонений, или, что то же самое, дисперсию на одну степень свободы D.
"обш —
Х(у-у)2.
л-1 ’
факт * ’
Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F-отношения (F-критерий):
*^факг Дост
(2.15)
где F- критерий для nf
верки нулевой гипотезы Яо:
Если нулевая гипотеза справедлива, то факторная и остаточная дисперсии не отличаются друг от друга. Для Яо необходимо опровержение, чтобы факторная дисперсия превышала остаточную в несколько раз. Английским статистиком Снедекором разработаны таблицы критических значений F-отношений при разных уровнях существенности нулевой гипотезы и различном числе степеней свободы. Табличное значение /’-критерия — это максимальная величина отношения дисперсий, которая может иметь место при случайном их расхождении для данного уровня вероятности наличия нулевой гипотезы. Вычисленное значение F-or-
4*
51
ношения признается достоверным (отличным от единицы), если оно больше табличного. В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи: > /„бд. Но отклоняется.
Если же величина окажется меньше табличной < Е^, то
вероятность нулевой гипотезы выше заданного уровня (например, 0,05) и она не может быть отклонена без серьезного риска сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается статистически незначимым. Яо не отклоняется.
В рассматриваемом примере:
S(y — у )2 “ 'Ey2 — п- у2 = 99700 — 7 • 1102 = 15 000 — общая сумма квадратов;
Ж - У)2 - A2Z(x - X )2 = 36,842 • (80 - 7 -(22: 7)2) = 14 735 - факторная сумма квадратов;
£(у — ух)2 = 15 000 — 14 735 = 265 — остаточная сумма квадратов;
- 14 735;
^остат 265.4- 5 53;
F = 14 735 4-53 = 278;
• 0,05 6,61, Fa а>о,О1 ~ 16,26.
Поскольку Рфюп > F^^, как при 1%-ном, так и при 5%-ном уровне значимости, то можно сделать вывод о значимости уравнения регрессии (связь доказана).
Величина /-критерия связана с коэффициентом детерминации г. Факторную сумму квадратов отклонений можно представить как
Е (Рх - У )2 = f2 • о2,
а остаточную сумму квадратов — как
Е(У-Ух >2= (1 “ - °2, ‘
Тогда значение /-критерия можно выразить как
(2.16)
В нашем примере г2 = 0,982. Тогда F =
0,982
1-0,982
(7-2) = 273
(некоторое несовпадение с предыдущим результатом объясняется ошибками округления).
52
Оценка значимости уравнения регрессии обычно дается в виде таблицы дисперсионного анализа (табл. 2.2).
Таблица 2.2
Дисперсионный анализ результатов регрессии
Источники вариации
Число степеней свободы
Сумма квадратов отклонений
Дисперсия на одну степень свободы
F-отношение
фактическое
табличное при а = 0,05
Общая 6
Объясненная 1
Остаточная 5
15000
14735 14 735 278 6,61
265 53 1
В линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров определяется его стандартная ошибка: ть и та.
Стандартная ошибка коэффициента регрессии определяется по формуле
(2.17)
где о — остаточная дисперсия на одну степень свободы.
Для нашего примера величина стандартной ошибки коэффициента регрессии составила:
ть = л—-— = 2,21.
4 V 10,857
Величина стандартной ошибки совместно с /-распределением Стьюдента при л — 2 степенях свободы применяется для проверки существенности коэффициента регрессии и для расчета его доверительных интервалов.
Для оценки существенности коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т. е. определя-
53
ется фактическое значение /-критерия Стьюдента: tb = — , кото-"ь
рое затем сравнивается с табличным значением при определенном уровне значимости а и числе степеней свободы (л - 2).
В рассматриваемом примере фактическое значение f-критерия для коэффициента регрессии составило:
^^ = 16,67.
2,21
Этот же результат получим, извлекая квадратный корень из найденного ранее /"-критерия, т. е.
/4= V7 = V278 = 16,67.
Покажем справедливость равенства гь = F:
Ь "I / Xfr-*)2 ^(У-Л)2/(«-2)
£(Ух ~У) _ -^факт _ р £(У~~ Ух) -®ост
(Я - 2)
При S а — 0,05 (для двустороннего критерия) и числе степеней свободы 5 табличное значение tb = 2,57. Так как фактическое значение /-критерия превышает табличное, то, следовательно, гипотезу о несущественности коэффициента регрессии можно отклонить. Доверительный интервал для коэффициента регрессии определяется как b±t-mb. Для коэффициента регрессии b в примере 95 %-ные границы составят:
36,84 ± 2,57 • 2,21 = 36,84 ± 5,68, т. е.
31,16^*^42,52.
Поскольку коэффициент регрессии в эконометрических исследованиях имеет четкую экономическую интерпретацию, то доверительные границы интервала для коэффициента регрессии не должны содержать противоречивых результатов, например, —10 £ b < 40. Такого рода запись указывает, что истинное значе
54
ние коэффициента регрессии одновременно содержит положительные и отрицательные величины и даже ноль, чего не может быть.
Стандартная ошибка параметра а определяется по формуле:
т _ 1е(у-Ух)2 Хх2 _ L 5>2 та = -----------------/ Э-------------•
У я-2 п'Е'(х-х) у п-Х(х-х) (2.18)
Процедура оценивания существенности данного параметра не отличается от рассмотренной выше для коэффициента регрес-
сии; вычисляется /-критерий: г = , его величина сравнивается
«о
с табличным значением при df— п — 2 степенях свободы.
Значимость линейного коэффициента корреляции проверяется на основе величины ошибки коэффициента корреляции т/
(2.19)
Фактическое значение /-критерия Стьюдента определяется как
(2.20)
Данная формула свидетельствует, что в парной линейной рег-
рессии Z2,. = F, ибо, как уже указывалось,
Кроме
того, t2/, = F. Следовательно, = ^ь.
Таким образом, проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.
В рассматриваемом примере /г не совпало с tb в результате ошибок округлений. Величина tr = 16,73 значительно превышает табличное значение 2,57 при а = 0,05. Следовательно, коэффициент корреляции существенно отличен от нуля и зависимость является достоверной.
Рассмотренная формула оценки коэффициента корреляции рекомендуется к применению при большом числе наблюдений и если г не близко к + 1 или —1. Если же величина коэффициента
55
корреляции близка к + 1, то распределение его оценок отличается от нормального или распределения Стьюдента, так как величина коэффициента корреляции ограничена значениями от — 1 до +1. Чтобы обойти это затруднение, Р. Фишером было предложено для оценки существенности г ввести вспомогательную величину Z, связанную с коэффициентом корреляции следующим отношением:
(2.21)-
При изменении г от —1 до +1 величина z изменяется от —<х> до +оо, что соответствует нормальному распределению. Математический анализ доказывает, что распределение величины z мало отличается от нормального даже при близких к единице значениях коэффициента корреляции. Стандартная ошибка величины z определяется по формуле
т, =
л-3
(2.22)
где л — число наблюдений.
При г =0,991, z = 0,5 • /л[( 1 + 0,991): (1 - 0,991)] = 2,699, а mz = 1:7(7-3) = 0,5. Величину z можно не рассчитывать, а воспользоваться готовыми таблицами ^-преобразования, в которых приведены значения величины г для соответствующих значений г.
Далее выдвигаем нулевую гипотезу Яо, которая состоит в том, что корреляция отсутствует, т. е. теоретическое значение коэффициента корреляции равно нулю. Коэффициент корреляции зна-
чимо отличен от нуля, если “ = > ^=о,о5> т. е. если фактическое Z
значение tz превышает его табличное значение на уровне значимости а = 0,05 или а = 0,01.
Иными словами, если z Jn-3 > го=0 03, то коэффициент корреляции значимо отличен от нуля, что имеет место в рассмотренном примере:
Z 7^3 = 2,69977 -3 = 5,398 при ta= 003 = 2,57.
56
Ввиду того, что г viz связаны между собой приведенным выше соотношением, можно вычислить критические значения г, соответствующие каждому из значений z- Таблицы критических значений г разработаны для уровней значимости 0,05 и 0,01 и соответствующего числа степеней свободы. Критические значения г предполагают справедливость нулевой гипотезы, т. е. г мало отлично от нуля. Если фактическое значение коэффициента корреляции по абсолютной величине превышает табличное, то данное значение г считается существенным. Если же г оказывается меньше табличного, то фактическое значение г несущественно.
В рассматриваемом примере при числе степеней свободы п — 2 = 5 критическое значение г при а = 0,05 составляет 0,754, а при а = 0,01 составляет 0,874, что ниже фактической величины = 0,991. Следовательно, как было уже доказано, полученное значение г существенно отлично от нуля.
2.4. ИНТЕРВАЛЫ ПРОГНОЗА
ПО ЛИНЕЙНОМУ УРАВНЕНИЮ РЕГРЕССИИ
В прогнозных расчетах по уравнению регрессии определяется предсказываемое (у,) значение как точечный прогноз ух при хр =хк, т. е. путем подстановки в уравнение регрессии ух = а + Ь-х соответствующего значения х. Однако точечный прогноз явно не реален. Поэтому он дополняется расчетом стандартной ошибки т. е. т* , и соответственно интервальной оценкой прогнозного значения (у*)
yx-m}x<y*£yx + mfx.
Чтобы понять, как строится формула для определения величин стандартной ошибки ух, обратимся к уравнению линейной регрессии: ух = а + Ь • х. Подставим в это уравнение выражение параметра а:
а—у — Ь-х, тогда уравнение регрессии примет вид: j>x = y — Ьх + Ь-х=у + Ь-(х — х).
Отсюда вытекает, что стандартная ошибка т* зависит от ошибки у и ошибки коэффициента регрессии Ь, т. е.
mi = + ть2 (х “ х)2-
(2.23)
57
2 _ ° *
Из теории выборки известно, что ту - Используя в каче-
стве оценки сг остаточную дисперсию на одну степень свободы У2, получим формулу расчета ошибки среднего значения переменной у:
2 S2
ту (2-24)
Ошибка коэффициента регрессии, как уже было показано, определяется формулой
2 S2 ть =-------у.
Х(х-х)2
Считая, что прогнозное значение фактора хр = хк, получим следующую формулу расчета стандартной ошибки предсказываемого по линии регрессии значения, т. е. т&:
L(x-x)
(2.25)
Соответственно т$ имеет выражение:
(2.26)
Рассмотренная формула стандартной ошибки предсказываемого среднего значения у при заданном значении хк характеризует ошибку положения линии регрессии. Величина стандартной ошибки /я*, как видно из формулы, достигает минимума при хк = х, и возрастает по мере того, как «удаляется» от х в любом направлении. Иными словами, чем больше разность между хк и х, тем больше ошибка т& с которой предсказывается среднее значение у для заданного значения хк. Можно ожидать наилучшие результаты прогноза, если признак-фактор х находится в центре области наблюдений х и нельзя ожидать хороших результатов прогноза при удалении хк от X. Если же значение хк оказывается за пределами наблюдаемых значений х, используемых при построении линейной регрессии, то результаты прогноза ухудшаются в зависимости от того, насколько хк отклоняется от области наблюдаемых значений фактора х.
58
Для нашего примера т» составит:
। (xt-3,143)2> 10,857 ,
При хк = х
тл = ->/53:7 =2,75. SX
При хк = 4,
(4—3,143)2 10,857
Соответственно т& составит эту же величину и при хк = 2,286. Для прогнозируемого значения ух 95%-ные доверительные интервалы при заданном хк определяются выражением
$хк ' ^Ух’
т. е. ух. ± 2,57 • 3,34, или у,. ± 8,58.
При хк = 4, прогнозное значение у составит:
ур = - 5,79 + 36,84 4 = 141,57, которое представляет собой точечный прогноз.
Прогноз линии регрессии в интервале составит:
S.
132,99 ^у<. 150,15.
На графике доверительные границы для ух представляют собой гиперболы, расположенные по обе стороны от линии регрессии (рис. 2.4).
Рис. 2.4 показывает, как изменяются пределы в зависимости от изменения хк: две гиперболы по обе стороны от линии регрессии определяют 95 % -ные доверительные интервалы для среднего значения у при заданном значении х.
Однако фактические значения у варьируют около среднего значения j)x. Индивидуальные значения у могут отклоняться отух на величину случайной ошибки е, дисперсия которой оценивает-
59
ся как остаточная дисперсия на одну степень свободы э . Поэтому ошибка предсказываемого индивидуального значения у должна включать не только стандартную ошибку тл, но и случайную ошибку S.
У А
Рис. 2.4. Доверительный интервал линии регрессии: а — верхняя доверительная граница; б — линия регрессии; в — доверительный интервал для при xt; г — нижняя доверительная граница
Средняя ошибка прогнозируемого индивидуального значе-
ния у тУы
составит:
/я„
)
1 t (X* -х)2 л Е(х-х)2’
(2.27)
По данным рассматриваемого примера получим:
(4-3,143)2>
10,857 ,
= 8,01.
Доверительные интервалы прогноза индивидуальных значений у при хк — 4 с вероятностью 0,95 составят: 141,57 ± 2,57 • 8,01, или 141,57 ± 20,59, это означает, что 120,98 <>ур £ 162,16.
Интервал достаточно широк прежде всего за счет малого объема наблюдений.
60
При прогнозировании на основе уравнения регрессии следу-
ет помнить, что величина прогноза зависит не только от стандартной ошибки индивидуального значения у, но и от точности прогноза значения фактора х. Его величина может задаваться на основе анализа других моделей исходя из конкретной ситуации, а также из анализа динамики данного фактора.
Рассмотренная формула средней ошибки индивидуального
значения признака
может быть использована также для
оценки существенности различия предсказываемого значения
исходя из регрессионной модели и выдвинутой гипотезы развития событий.
Предположим, что в нашем примере с функцией издержек
выдвигается предположение, что в предстоящем году в связи со стабилизацией экономики при выпуске продукции в 8 тыс. ед. затраты на производство не превысят 250 млн руб. Означает ли это действительно изменение найденной закономерности или же данная величина затрат соответствует регрессионной модели?
Чтобы ответить на этот вопрос, найдем точечный прогноз при х = 8, т. е.
ух .8 = - 5,79 + 36,84 8 = 288,93.
Предполагаемое же значение затрат, исходя из экономической ситуации, — 250,0. Для оценки существенности различия этих величин определим среднюю ошибку прогнозируемого индивидуального значения: г*«
т
Л(х*)
/1 (хк-х)2
5-1 + — + -^--
V п L(x-x)2
(8-3,143)2>
(10,857) ,
= 13,26.
Сравним ее с величиной предполагаемого снижения издержек производства, т. е. 38,93:
-38,93
13,26
= -2,93.
Поскольку оценивается значимость только уменьшения затрат, то используется односторонний /-критерий Стыодента. При ошибке в 5 % с пятью степенями свободы 1табя = 2,015. Следовательно, предполагаемое уменьшение затрат значимо отличается от прогнозируемого по модели при 95 %-ном уровне доверия. Од-
61
нако если увеличить вероятность до 99 %, при ошибке в 1 % фак- Я тическое значение /-критерия оказывается ниже табличного 3,365, и рассматриваемое различие в величине затрат статиста- чески не значимо.
2.5. НЕЛИНЕЙНАЯ РЕГРЕССИЯ 1
Если между экономическими явлениями существуют нели- нейные соотношения, то они выражаются с помощью соответ- fl ствующих нелинейных функций: например, равносторонней ги- перболы у = о+—+£, параболы второй степени у — а + b • х + | х
+ с •х2+ей др. (см. п. 2.1). И
Различают два класса нелинейных регрессий: И
• регрессии, нелинейные относительно включенных в анализ fl
объясняющих переменных, но линейные по оцениваемым па- fl раметрам; Н
• регрессии, нелинейные по оцениваемым параметрам. fl
Примером нелинейной регрессии по включаемым в нее объ- Н ясняющим переменным могут служить следующие функции: Я
• полиномыразных степеней — y = a + b-x + c-xr + E, y = a + bx fl хх + с-хг + (1-х* + е; l fl
• равносторонняя гипербола — У = а+—+Е. Н
К нелинейным регрессиям по оцениваемым параметрам от- Н носятся функции: И
• степенная — у = а-х? е; fl
• показательная — y — a-bf-E', fl
• экспоненциальная — y = ea+bx е. fl
Нелинейная регрессия по включенным переменным не таит Н каких-либо сложностей в оценке ее параметров. Она определяет- Я ся, как и в линейной регрессии, методом наименьших квадратов И (МНК), ибо эти функции линейны по параметрам. Так, в парабо- Я ле второй степени И
у = а0 + а1-х + а2-х2 + е, fl
заменяя переменные х— х,, х2 = х2, получим двухфакторное урав- Н нение линейной регрессии: Я
у = в0 + ах • х( + а2 - х2 4- е, Я
для оценки параметров которого, как будет показано в гл. 3, ис- Я пользуется МНК. Я
62 Я
Соответственно для полинома третьего порядка у = а0 + а, • х + а2 • х2 + а3 х3 + е,
при замене х = Х|, х2 линейной регрессии:
= х3 получим трехфакторную модель
y = a0 + ai Х| + а2-х2 + а3-х3 + е,
а для полинома к-го порядка
получим линейную модель множественной регрессии с к объясняющими переменными:
y = ao + er *i + в2 • х2+...+ак • хк +е.
Следовательно, полином любого порядка сводится к линейной регрессии с ее методами оценивания параметров и проверки гипотез. Как показывает опыт большинства исследователей, среди нелинейной полиномиальной регрессии чаще всего используется парабола второй степени; в отдельных случаях — полином третьего порядка. Ограничения в использовании полиномов более высоких степеней связаны с требованием однородности исследуемой совокупности: чем выше порядок полинома, тем больше изгибов имеет кривая и соответственно менее однородна совокупность по результативному признаку.
Парабола второй степени целесообразна к применению, если для определенного интервала значений фактора меняется характер связи рассматриваемых признаков: прямая связь меняется на обратную или обратная на прямую. В этом случае определяется значение фактора, при котором достигается максимальное (или минимальное) значение результативного признака: приравниваем к нулю первую производную параболы второй степени:
у= а + Ьх + с • х2, т. е. 6 + 2,с,х = 0и х =-.
х 2-с
Если же исходные данные не обнаруживают изменения направленности связи, то параметры параболы второго порядка становятся трудно интерпретируемыми, а форма связи часто заменяется другими нелинейными моделями.
Применение МНК для оценки параметров параболы второй степени приводит к следующей системе нормальных уравнений:
Y,y = na+b'£x+c-'Ex2,
63
Решение ее возможно методом определителей:
где Д — определитель системы;
Д а, Д Ь, Д с — частные определители для каждого из параметров.
При Ь > 0 и с < 0 кривая симметрична относительно высшей точки, т. е. точки перелома кривой, изменяющей направление связи, а именно рост на падение. Такого рода функцию можно наблюдать в экономике труда при изучении зависимости заработной платы работников физического труда от возраста - с увеличением возраста повышается заработная плата ввиду одновременного увеличения опыта и повышения квалификации работника. Однако с определенного возраста ввиду старения организма и снижения производительности труда дальнейшее повышение возраста может приводить к снижению заработной платы работника. Если параболическая форма связи демонстрирует сначала рост, а
затем снижение уровня значений результативного признака, то определяется значение фактора, при котором достигается максимум. Так, предполагая, что потребление товара А (единиц) в зависимости от уровня дохода семьи (тыс. руб.) характеризуется уравнением вида ух = 5 + 6 х — зг. Приравнивая к нулю первую производную ух = 6 — 2 • х = 0, найдем величину дохода, при которой потребление максимально, т. е. при х — 3 тыс. руб.
При b < 0 и с > 0 парабола второго порядка симметрична от-
носительно своей низшей точки, что позволяет определять мини
мум функции в точке, меняющей направление связи, т. е. сниже
ние на рост. Так, если в зависимости от объема выпуска продук-
ции затраты на производство характеризуются уравнением ух — 1200 — 60 • х + 2 • х2, то наименьшие затраты достигаются при выпуске продукции х = 15 ед., т. е. —60 + 2 • 2 х = 0.
В этом можно убедиться, подставляя в уравнение значения х:
X 10 11 12 13 14 15 16 17
У 800 782 768 758 752 750 752 758
Ввиду симметричности кривой парабола второй степени далеко не всегда пригодна в конкретных исследованиях. Чаще исследователь имеет дело лишь с отдельными сегментами параболы, а не с полной параболической формой. Кроме того, парамет
64
ры параболической связи не всегда могут быть логически истолкованы. Поэтому если график зависимости не демонстрирует четко выраженной параболы второго порядка (нет смены направленности связи признаков), то она может быть заменена другой нелинейной функцией, например степенной. В частности, в литературе часто рассматривается парабола второй степени для характеристики зависимости урожайности от количества внесенных удобрений. Данная форма связи мотивируется тем, что с увеличением количества внесенных удобрений урожайность растет лишь до достижения оптимальной дозы вносимых удобрений. Дальнейший же рост их дозы оказывается вредным для растения, и урожайность снижается. Несмотря на несомненную справедливость данного утверждения, следует отметить, что внесение в почву минеральных удобрений производится на основе учета достижений агробиологической науки. Поэтому на практике часто данная зависимость представлена лишь сегментом параболы, что и позволяет использовать другие нелинейные функции. В качестве примера рассмотрим табл. 2.3 (данные заимствованы) .
Таблица 2.3
Зависимость урожайности озимой ппеиицы
По данным табл. 2.3 система нормальных уравнений составит:
5a+15Z»+55c = 50,
П5-о+55-д + 225-с = 167,
55-a+225-i + 979-c = 649. к
----------V--
1 См.: Громыко Г Л. Статистика. — М.: МГУ, 1981.
54525
65
Решая ее методом определителей, получим: Д = 700, Да = 2380, А/> = 2090, Де = —150. Откуда параметры искомого уравнения составят: а = 3,4; b = 2,986; с = —0,214, а уравнение параболы второй степени примет вид
ух = 3,4 + 2,986 • х - 0,214 • х2.
Подставляя в это уравнение последовательно значения х, найдем теоретические значения ух (см. табл. 2.3, гр. 8).
Как видно из табл. 2.3, уравнение параболы второго порядка хорошо описывает рассматриваемую зависимость. Сумма квадратов отклонений остаточных величин Е(у—ух)2 = 0,46. Ввиду того, что данные табл. 2.3 демонстрируют лишь сегмент параболы второго порядка, то рассматриваемая зависимость может быть охарактеризована и другой функцией. Используя, в частности, степенную функцию ух = а • х*, было получено уравнение регрессии ух = 6,136 • х0,474. Для него S(y — ух)2 = 0,43, что означает еще лучшую сходимость фактических и расчетных значений у.
Среди класса нелинейных функций, параметры которых без особых затруднений оцениваются МНК, следует назвать хорошо известную в эконометрике равностороннюю гиперболу: ух =а+—.
Она может быть использована не Только, как уже указывалось в параграфе (2.1), для характеристики связи удельных расходов сырья, материалов, топлива с объемом выпускаемой продукции, времени обращения товаров от величины товарооборота, т.е. на микроуровне, но и на макроуровне. Классическим ее примером является кривая Филлипса, характеризующая нелинейное соотношение между нормой безработицы х и процентом прироста заработной платы у:
b У — QA--НЕ.
X
Английский экономист А. В. Филлипс, анализируя данные более чем за 100-летний период, в конце 50-х гг. XX в. установил обратную зависимость процента прироста заработной платы от уровня безработицы. , .
Для равносторонней гиперболы вида у=а+—+е заменив — х ’ х
на z, получим линейное уравнение регрессии у = а 4- b • z + е, оценка параметров которого может быть дана МНК. Система нормальных уравнений составит:
66
'£у = па + Ь'£г->
При b > 0 имеем обратную зависимость, которая при х -> оо характеризуется нижней асимптотой, т. е. минимальным предельным значением у, оценкой которого служит параметр а. Так, для кривой Филлипса* Ух =0,00679+0,1842 — величина параметра а, равная 0,00679, означает, что с ростом уровня безработицы темп прироста заработной платы в пределе стремится к нулю. Соответственно можно определить тот уровень безработицы, при котором заработная плата оказывается стабильной и темп ее прироста равен нулю.
При b < 0 имеем медленно повышающуюся функцию с верхней асимптотой при х -> оо, т. е. с максимальным предельным b уровнем у, оценку которого в уравнении ух =а+— дает параметр а. х
Примером может служить взаимосвязь доли расходов на товары длительного пользования и общих сумм расходов (или доходов). Математическое описание подобного рода взаимосвязей получило название кривых Энгеля. В 1857 г. немецкий статистик Э. Энгель на основе исследования семейных расходов сформулировал закономерность — с ростом дохода доля доходов, расходуемых на продовольствие, уменьшается. Соответственно с увеличением дохода доля доходов, расходуемых на непродовольственные товары, будет возрастать. Однако это увеличение не беспредельно, ибо на все товары сумма долей не может быть больше единицы, или 100%, а на отдельные непродовольственные товары этот предел может характеризоваться величиной параметра а для уравнения вида
где у — доля расходов на непродовольственные товары;
х — доходы (или общая сумма расходов как индикатор дохода).
'Studenmund A.N. Using Econometrics: A Practical Guide. — 2-nd Edition.-Copyright, 1992 by Harper Collins Publishers Inc. — P. 226.
5*
67
Правомерность использования равносторонней гиперболы
ух=а~— для кривой Энгеля довольно легко доказывается1.
Соответственно можно определить границу величины дохода, дальнейшее увеличение которого не приводит к росту доли расходов на отдельные непродовольственные товары.
Л Ь
Вместе с тем равносторонняя гипербола Ух=а~~ не являет-
ся единственно возможной функцией для описания кривой Энгеля. В 1943 г. Уоркинг и в 1964 г. Лизер для этих целей использовали полулогарифмическую кривуюу = а + 6,1пх + е.
Заменив 1пх на z, опять получим линейное уравнение: у—a + b'z + ь. Данная функция, как и предыдущая, линейна по параметрам и нелинейна по объясняющей переменной х. Оценка параметров а и Ь может быть найдена МНК. Система нормальных уравнений при этом окажется следующей:
|Х> = я-а + £-£1пх, [£у-1пх = о£1пх+6-£(1пх)2.
Применим полулогарифмическую функцию зависимости доли расходов на товары длительного пользования в общих расходах семьи от дохода семьи (табл. 2.4).
Таблица 2.4 Доля расходов на товары длительного пользования в зависимости от дохода семьи
Среднемесячный доход семьи, тыс. долл. США, х 1 2 3 4 5 6
Процент расходов на товары длительного пользования, Y 10 13,4 15,4 16,5 18,6 19,1
1 См., например: Лизер С. Эконометрические методы и задачи / Пер. с англ. — М.: Статистика, 1971. — С. 94.
68
Суммы, необходимые для расчета, составили:
Япх = 6,579251; £> = 93; Z(lnr)* 2 = 9,40991; 1пх= 113,23881.
Решая систему нормальных уравнений
Гб-о + б,57925-6 = 93,
(6,57925 • а+9,40991 Ь = 113,23881,
мы получили уравнение регрессии ух = 9,876 + 5,129 • 1пх, которое достаточно хорошо описывает исходные соотношения дохода семьи и доли расходов на товары длительного пользования, что видно из сравнения фактических и теоретических значений у:
Ух 9,9 13,4 15,5 17,0 18,1 19,1 Сумма
У ~Ух 0,1 0,0 -0,1 -0,5 0,5 0,0 0,0
(У-УхУ 0,01 0,0 0,01 0,25 0,25 0,0 0,52*
*При более точном подсчете ух эта величина составит 0,4864.
Возможны и иные модели, нелинейные по объясняющим переменным. Например, у = а + Ь- ^+г. Соответственно система нормальных уравнений для оценки параметров составит:
Уравнения с квадратными корнями использовались в исследованиях урожайности1, трудоемкости сельскохозяйственного производства. В работе Н. Дрейпера и Г. Смита2 справедливо отмечено, что если нет каких-либо теоретических обоснований в использовании данного вида кривых, то основная цель подобных преобразований состоит в том, чтобы для преобразованных переменных получить более простую модель регрессии, чем для исходных данных.
’См.: Езекил М., Фокс К. Методы анализа корреляций и регрессий. — М.: Статистика, 1966. — С. 393.
2См.: Дрейпер Н., Смит Г. Прикладной регрессионный анализ/Пер. с англ. — М.: Статистика, 1973. — С. 140.
69
Иначе обстоит дело с регрессией, нелинейной по оцениваемым параметрам. Данный класс нелинейных моделей подразделяется на два типа: нелинейные модели внутренне линейные и нелинейные модели внутренне нелинейные. Если нелинейная модель внутренне линейна, то она с помощью соответствующих преобразований может быть приведена к линейному виду. Если же нелинейная модель внутренне нелинейна, то она не может быть сведена к линейной функции. Например, в эконометрических исследованиях при изучении эластичности спроса от цен широко используется степенная функция:
у = ах*е,
где у — спрашиваемое количество;
х — цена;
е — случайная ошибка.
Данная модель нелинейна относительно оцениваемых параметров, ибо включает параметры а и Ь неаддитивно. Однако ее можно считать внутренне линейной, ибо логарифмирование данного уравнения по основанию е приводит его к линейному виду:
Iny = Ina + Ь • 1пх + 1пе.
Соответственно оценки параметров а и Л могут быть найдены МНК. В рассматриваемой степенной функции предполагается, что случайная ошибка & мультипликативно связана с объясняющей переменной х. Если же модель представить в виде у - а • л? + е, то она становится внутренне нелинейной, ибо ее невозможно превратить в линейный вид.
Внутренне нелинейной будет и модель вида
y = a + />-jtc + e
или модель
ибо эти уравнения не могут быть преобразованы в уравнения, линейные по коэффициентам.
В специальных исследованиях по регрессионному анализу часто к нелинейным относят модели, только внутренне нелинейные по оцениваемым параметрам, а все другие модели, которые
70
внешне нелинейны, но путем преобразований параметров могут быть приведены к линейному виду, относятся к классу линейных моделей. В этом плане к линейным относят, например, экспоненциальную модель у = еа+ь х • е, ибо логарифмируя ее по натуральному основанию, получим линейную форму модели
Iny = а + Ь • х + 1пе.
Если модель внутренне нелинейна по параметрам, то для оценки параметров используются итеративные процедуры, успешность которых зависит от вида уравнений и особенностей применяемого итеративного подхода1. Модели внутренне нелинейные по параметрам могут иметь место в эконометрических исследованиях. Однако гораздо большее распространение получили модели, приводимые к линейному виду. Решение такого типа моделей реализовано в стандартных пакетах прикладных программ. Среди них, в частности, можно назвать и обратную модель вида
1
Обращая обе части равенства, получим линейную форму мо-
дели для переменной — :
— = а+Ь-х+г. У
Приводима к линейному виду и логистическая функция
а
или
Обращая обе части равенства, получим:
А .--ОЛ+S ' “
О-в = —
У
Вычитая 1, имеем:
'В данном разделе рассматриваются лишь внутренне линейные модели.
71
Прологарифмировав обе части по натуральному основанию, получим уравнение линейной формы:
или
Z — B — с-х + £, где z = ln —-1 и7?=1п/>.
Среди нелинейных функций, которые могут быть приведены к линейному виду, в эконометрических исследованиях очень широко используется степенная функция у = а • хг е. Связано это с тем, что параметр b в ней имеет четкое экономическое истолкование, т. е. он является коэффициентом эластичности. Это значит, что величина коэффициента b показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1 %. Так, если зависимость спроса от цен характеризуется уравнением вида = 105,56 • то, следовательно, с увеличением цен на 1 % спрос снижается в среднем на 1,12 %. О правомерности подобного истолкования параметра b для степенной функции ух = а можно судить, если рассмотреть формулу расчета коэффициента эластичности
где f(x) — первая производная, характеризующая соотношение приростов результата и фактора для соответствующей формы связи.
Для степенной функции она составит: f'(x) = а- b • лг *. Соот-
ветственно коэффициент эластичности окажется равным:
Коэффициент эластичности, естественно, можно определять и при наличии других форм связи, но только для степенной функции он представляет собой постоянную величину, равную параметру Ь. В других функциях коэффициент эластичности зависит от значений фактора х. Так, для линейной регрессии
= а + Ь • х функция и эластичность следующие:
72
f(x) = ЬмЭ = Ь-
a + bx
В силу того что коэффициент эластичности для линейной функции не является величиной постоянной, а зависит от соответствующего значения х, то обычно рассчитывается средний показатель эластичности по формуле
Для оценки параметров степенной функции у — а • х* • е применяется МНК к линеаризованному уравнению Iny = Ina + Ь • 1пх + + 1пе, т.е. решается система нормальных уравнений:
£1пу=л1па+А£1пх,
£1пу-1пх = 1па-£1пх+/> ^(Inx)2.
Параметр b определяется непосредственно из системы, а параметр а — косвенным путем после потенцирования величины Ina. Так, решая систему нормальных уравнений зависимости спроса от цен, было получено уравнение 1пу = 4,6593 — 1,1214- 1пх. Если потенцировать его, получим:
,4,6593 . х-1,1214=105556.х-1.1214
Поскольку параметр а экономически не интерпретируется, то нередко зависимость записывается в виде логарифмически линейной, т. е. 1пу = 4,6593 - 1,1214 • 1пх. В виде степенной функции изучается не только эластичность спроса, но и предложения. При этом обычно эластичность спроса характеризуется параметром Ь < 0, а эластичность предложения: b > 0.
Поскольку коэффициенты эластичности представляют экономический интерес, а виды моделей не ограничиваются только степенной функцией, приведем формулы расчета коэффициентов эластичности для наиболее распространенных типов уравнений регрессии (табл. 2.5).
73
Таблица 2.5
Коэффициенты эластичности для ряда математических фун
ий
Вид функции, Первая производная, у'х Коэффициент эластич-ности, э = у'х-у
Линейная у — а + Ь- х + с b Э~-4тг-а + b -х
Парабола второго порядка y=a + Z>-x + c- x2 + £ 6 + 2-с-х п +[* И п" •f
Гипербола У = а+ Ьх +е oft 1 3 = b— а -х + b
Показательная y — atfe 1п£ • а -У Э = х • lnZ> L
Степенная у = а • х* • £ а • b V’1 э=ь
Полулогарифмическая у = а + b • 1пх + £ b £ = — ь. a + b • Inx
Логистическая „ = & Г- у {+Ь-е-а*с a - bye в-™ (1 n ex * 1^+1 b
Обратная = 1 У а + Ь- х + е —ь (а + b • х)2 э= a + b- x
Несмотря на широкое использование в эконометрике коэффициентов эластичности, возможны случаи, когда их расчет экономического смысла не имеет. Это происходит тогда, когда для рассматриваемых признаков бессмысленно определение изменения значений в процентах. Например, вряд ли кто будет определять, на сколько процентов может измениться заработная плата с ростом стажа работы на 1 %. Или, например, на сколько процентов изменится урожайность пшеницы, если качество почвы, измеряемое в баллах, изменится на 1 %. В такой ситуации степен-74
ная функция, даже если она оказывается наилучшей по формальным соображениям (исходя из наименьшего значения остаточной вариации), не может быть экономически интерпретирована. Например, изучая соотношение ставок межбанковского кредита у (в процентах годовых) и срока его предоставления х (в днях), было получено уравнение регрессии ух = 11,684 • х0,352 с очень высоким показателем корреляции (0,9895). Коэффициент эластичности 0,352% лишен смысла, ибо срок предоставления кредита не измеряется в процентах. Значительно больший интерес для этой зависимости может представить линейная функция Л = 21,1 + 0,403 • х, имеющая более низкий показатель корреляции 0,85. Коэффициент регрессии 0,403 показывает в процентных пунктах изменение ставок кредита с увеличением срока их предоставления на один день.
В моделях, нелинейных по оцениваемым параметрам, но приводимых к линейному виду, МНК применяется к преобразованным уравнениям. Если в линейной модели и моделях, нелинейных по переменным, при оценке параметров исходят из критерия Z(y—min, то в моделях, нелинейных по оцениваемым параметрам, требование МНК применяется не к исходным данным результативного признака, а к их преобразованным величинам, т. е. 1пу, 1/у. Так, в степенной функции у = а • хг • е МНК применяется к преобразованному уравнению Iny = Ina + Д Inx 1ns.
Это значит, что оценка параметров основывается на минимизации суммы квадратов отклонений в логарифмах.
Z(lny — lnj>x)2—> min.
Соответственно если в линейных моделях (включая нелинейные по переменным) Е(у-ух) = 0, то в моделях, нелинейных по оцениваемым параметрам,
Z(lny-inyJt) = 0, a Tty-anti logyj * 0.
Вследствие этого оценка параметров для линеаризуемых функций МНК оказываются несколько смещенной.
Возьмем, например, показательную кривую: )>х = а • if или равносильную ей экспоненту ух = еа+Ьх. Прологарифмировав, имеем:
Iny = Ina + х 1п/>.
Применяя МНК, минимизируем Z(lny—1пух)2. Система нормальных уравнений составит:
75
|£1пу=л-1па + 1п/>-£.х, [^x-lny = lna-^x+lnft-^x2.
Из первого уравнения видно, что 1 £1пу 1 l Е* £1пу , д -п п п
Предположим, что фактические данные сложились так, что
х = 0. Тогда 1по =— £1пу или а = ^у} у2-...у„,
т. е. параметр а представляет собой среднюю геометрическую из значений переменной у. Между тем в линейной зависимости ух = а + Ь • х при х = 0 параметр
т. е. средней арифметической. Поскольку средняя геометрическая всегда меньше средней арифметической,jjo и оценки параметров, полученные из минимизации Е(1пу-1пух)2, будут несколько смещены (занижены).
Практическое применение экспоненты возможно, если результативный признак не имеет отрицательных значений. Поэтому если исследуется, например, финансовый результат деятельности предприятий, среди которых наряду с прибыльными есть и убыточные, то данная функция не может быть использована. Если экспонента строится как функция выравнивания по динами
ческому ряду для характеристики тенденции с постоянным темпом, то у = а • b‘, где у — уровни д инамического ряда; t — хронологические даты, параметр b означает средний за период коэффициент роста. В уравнении у = е?+1гх этот смысл приобретает вели
чина антилогарифма параметра Ь.
При исследовании взаимосвязей среди функций, использующих In у, в эконометрике преобладают степенные зависимости -это и кривые спроса и предложения, и кривые Энгеля, и произ
водственные функции, и кривые освоения для характеристики
связи между трудоемкостью продукции и масштабами производ
ства в период освоения выпуска нового вида изделий, и зависи
мость валового национального дохода от уровня занятости.
В отдельных случаях может использоваться и нелинейная мо-
дель вида
76
так называемая обратная модель, являющаяся разновидностью гиперболы. Но если в равносторонней гиперболе у = й[+А+е
преобразованию подвергается объясняющая переменная — = г
иу = а + 6- г + е, то для получения линейной формы зависимости в обратной модели преобразовывается у, а именно: 1/у = z и z = a + ft-x + e. В результате обратная модель оказывается внутренне нелинейной и требование МНК выполняется не для фактических значений признака у, а для их обратных
величин —
а именно: 2XZ-2J2 ->min.
Соответственно
но Sy * Sy*.
Проанализируем зависимость рентабельности продукции от ее трудоемкости по данным семи предприятий (табл. 2.6).
Таблица 2.6
Зависимость рентабельности продукции у (%) от ее трудоемкости х (ч/ед.)
1,0
1,2
1,5
2,0
2,5
2,7
3,0
32
28
22
20
16
15
10
0,0312
0,0357
0,0455
0,0500
0,0625
0,0667
0,1000
0,0312 0,0428 0,0682
0,1000 0,1563 0,1800 0,3000
1,44
2,25
©
6,25
7,29
0,0285 0,0341 0,0424 0,0563 0,0703 0,0758 0,0842
35,1 0,0027 -3,1
29,3 0,0016 -1,3
23,6 0,0031 -1,6
17,7 -0,0063 2,3
14,2 —0,0078 1,8
13,2 -0,0091 1,8
11,9 0,0158 —1,9
13,9 143 0,3916 0,8785 31,23 0,3936 145,0 0,0000 -2,0
77
Для оценки параметров исследуемой функции у =-------
а+Ь-х+е
по МНК система нормальных уравнений примет вид:
f I
У
'£- = а'£1х+Ь'£1х1. У
Исходя из данных табл. 2.6, имеем:
7-а+13,9-6 = 0,3916, 13,9-« + 31,23-6 = 0,8785.
Решая эту систему уравнений, получим оценки параметров искомой функции: а = 0,0007; b = 0,0278. Соответственно уравнение регрессии составит:
Ух 0,0007 + 0,0278-х
Сравним последние две графы табл. 2.6. Получим
0, тогда как для обратных значений эта величина равна
нулю. Кроме того, заметим, что положительные отклонения фактических и теоретических обратных значений сменяются на отрицательные значения для аналогичных показателей по исходным данным. Уравнение отражает обратную связь рассматриваемых признаков: чем выше трудоемкость, тем ниже рентабельность. Поскольку данное уравнение линейно относительно
1 ZT 1
величин —, то если обратные значения — имеют экономический у у
смысл, коэффициент регрессии b интерпретируется, так же как в линейном уравнении регрессии. Если, например, под у подразумеваются затраты на 1 руб. продукции, а под х — производительность труда (выработка продукции на одного работника), то обратная величина характеризует затратоотдачу и параметр b имеет экономическое содержание — средний прирост продукции в стоимостном измерении на 1 руб. затрат с ростом производительности труда на единицу своего измерения.
78
I
Уравнение ввда Л = ~7“ характеризует прямую зависимость результативного признака от фактора. Оно целесообразно при очень медленном повышении уровней результативного признака с ростом значений фактора.
Возможно и одновременное использование логарифмирования, и преобразование в обратные величины: у = еа ~ °'х + Е‘ Про-„ 1 логарифмировав, получим: Iny = а — Ь / х + е. Далее заменим —
на z, и тогда для оценки параметров к линейному уравнению Iny = а — Ь • z + 6 может быть применен МНК.
При всех положительных значениях х функция возрастает; при х = Ь/2 кривая имеет точку перегиба — ускоренный рост при х < Ь/2 сменяется на замедленный рост при х > Ь/2. Подобного типа функции используются при анализе статистических данных о бюджетах потребителей, где выдвигается гипотеза о существовании асимптотического уровня расходов, об изменении предельной склонности к потреблению товара, о существовании «порогового уровня дохода»1. В этом случае при х -> со у -> е“ (рис. 2.5).
При использовании линеаризуемых функций, затрагивающих преобразования зависимой переменной у, следует особенно проверять наличие предпосылок МНК (они будут рассмотрены в п. 3, 10), чтобы они не нарушались при преобразовании. При не-
{Джонстон Дж. Эконометрические методы / Пер. с англ. — М.: Статистика, 1980. - С. 60.
79
линейных соотношениях рассматриваемых признаков, приводимых к линейному виду, возможно интервальное оценивание параметров нелинейной функции. Так, для показательной кривой ух = а У сначала строятся доверительные интервалы для параметров нового преобразованного уравнения Iny = 1па + х • 1п/>, т. е. для In а и In Ь. Далее с помощью обратного преобразования определяются доверительные интервалы для параметров в исходном соотношении. В степенной функции ух = а • х* доверительный интервал для параметра b строится так же, как в линейной функции, т. е. b ± ta • ть. Отличие состоит лишь в том, что при определении стандартной ошибки параметра Ь, ть используются не исходные данные, а их логарифмы:
/л* =
Z(lny-lnyx)
i . щи mini
(л-2)£(1пх-1пх)2
(2.28)
2.6. КОРРЕЛЯЦИЯ ДЛЯ НЕЛИНЕЙНОЙ РЕГРЕССИИ
Уравнение нелинейной регрессии, так же как и в линейной зависимости, дополняется показателем корреляции, а именно индексом корреляции (R):
(2.29)
где сгу — общая дисперсия результативного признака у, «Гост — остаточная дисперсия, определяемая исходя из уравнения регрессии ух =fix).
Так как ст2 = -• Е(у-у)2, а = --1(у-К)2, то индекс кор-п п
реляции можно выразить как
(2.30)
80
Величина данного показателя находится в границах: 0 < R < 1, чем ближе к единице, тем теснее связь рассматриваемых признаков, тем более надежно найденное уравнение регрессии.
По данным табл. 2.3 для уравнения регрессии ух = 3,4 + 2,986 • х — 0,214 • х2 индекс корреляции составил:
0,46
530 :5-102
= 0,9609, свидетельствуя о достаточно тесной связи
рассматриваемых признаков.
Парабола второй степени, как и полином более высокого порядка, при линеаризации принимает вид уравнения множественной регрессии. Если же нелинейное относительно объясняемой переменной уравнение регрессии при линеаризации принимает форму линейного уравнения парной регрессии, то для оценки тесноты связи может быть использован линейный коэффициент корреляции, величина которого в этом случае совпадет с индексом корреляции /?„'= А.г, где z — преобразованная величина
признака-фактора, например 1 или Z — 1пх.
Обратимся для примера к равносторонней гиперболе
Л b 1
ух = а+—. Заменив — на z, имеем линейное уравнение
yz = а + b • z, Для которого может быть определен линейный ко-эфициент корреляции: г г = b —. Возводя данное выражение в
Г
квадрат, получим:
з Z(z-z) где ог=----—
_2 ZO-у)2
И ау =------
Л И
Преобразовывая далее, придем к следующему выражению для г 2:
z *
2 b2£(z-Z)2 п Z(y-y)2
6-1S25 ..
(2.31)
81
Как было показано ранее (см. п. 2.3), Ь2 "L(z—z )2 = Е(уг -у)2
и соответственно
ПЛ-у)2
Пу-у)2 ‘
Но так как £(у-у)2 = 2(Л - у)1 + S(y - Л)2 и Е(уг - у)2 = = S(y-y)2 - Цу - £г )2, то
Пу-у)2-Пу-Л)2 Пу-у)2
т. е. приходим к формуле индекса корреляции:
Заменив далее z на 1/х, получим $г = ух , соответственно ?У1 Кух'
Аналогичное положение имеем и для полулогарифмической кривой j>x = а + b • 1пх, ибо в ней, как и в предыдущем случае, преобразования в линейный вид (z — In х) не затрагивают зависимую переменную, и требование МНК S(y — ух)2 -» min выполнимо.
Убедиться в этом можно, обратившись к данным табл. 2.4:
Е(У - У)2 = 58,24; 1(у-рх)2 = 0,4864.
Соответственно индекс корреляции окажется равным:
Я„= /1-^^=0,99581.
у 58,24
Найдем линейный коэффициент корреляции между перемен-нымиуи!пх:
ylnx-ylnx
ГУ1пх 6 •0‘ь. v*lnx
Так как £у • 1пх = 113,23881, £у = 93, Dnx = 6,57925, <ту = 3,11555, Z(lnx)2 = 9,409906, oInx = 0,604908, то ry . 1пх составит:
82
113,23881:6-93:6-6,57925:6
r -----------------------------= 0,99581,
ylnx 3,11555-0,604908
что совпадает с индексом корреляции. Для данной зависимости имеем равенство: А2 • Е(1пх — (Бъс)2 = E(yz —У)2-
По нашим расчетам b = 5,1289; Е(1пх — 1пх)2 =2,19548. Соот-ветственно*£(уг — у )2 = 57,7536. Тогда
Е(у - Л)2 = “У)2“ 2 (Ус -У)2 = 58,24 - 57,7536 = 0,4864,
что совпадает с остаточной суммой квадратов, используемой в расчете индекса корреляции. Таким образом, несмотря на то, что коэффициент корреляции определялся не для у и х, а для у и In х, его величина позволяет определить факторную и остаточную суммы квадратов для признака у:
гк2 • Е(у—у)2 = 62 • Е (1пх—1пх)2 = 57,7536.
Соответственно линейный коэффициент корреляции и индекс корреляции совпадают.
Иначе обстоит дело, когда преобразования уравнения в линейную форму связаны с зависимой переменной. В этом случае линейный коэффициент корреляции по преобразованным значениям признаков дает лишь приближенную оценку тесноты связи и численно не совпадает с индексом корреляции. Так, для степенной функции ух = а-х!’ после перехода к логарифмически линейному уравнению 1пу=1по + 61пх может быть найден линейный коэффициент корреляции не для фактических значений переменных х и у, а для их логарифмов, т. е. Соответственно квадрат его значения будет характеризовать отношение факторной суммы квадратов отклонений к общей, но не для у, а для его логарифмов:
2 = Z(lny-lny)2 _ £(1пу-[пу)2
L(lny-lny)2 L(lny-lny)2
(2.32)
Между тем при расчете индекса корреляции используются суммы квадратов отклонений признака у, а не их логарифмов. С этой целью определяются теоретические значения результативного признака, т. е. ух, как антилогарифм рассчитанной по уравнению величгцты (пу и остаточная сумма квадратов как Е (у — anti log(ln у)2. Индекс корреляции определяется по формуле 6* 83
R
^(y-anti logjln у)2 Z(y-y)2
(2.33)
В знаменателе расчета R2 участвует общая сумма квадратов отклонений фактических значений у от их средней величины, а в расчете участвует Z(lny — 1пу). Соответственно различаются и числители рассматриваемых показателей:
Z (у — anti log(lny)) — в индексе корреляции и
Z(ln у -1пу)2 - в коэффициенте корреляции.
Не совпадают данные показатели и для уравнения регрессии в виде экспоненты, ибо при преобразовании в линейную форму рассчитывается линейный коэффициент корреляции между х и логарифмом у, т. е. опять Z(y — у)2 заменяется на S(Iny — 1пу)2 и £ (у — anti log(lny))2 заменяется на S(lny — 1пу). При использовании в преобразовании нелинейных соотношений в линейную форму обратных значений результативного признака, т. е. 1/у, индекс корреляции R^ также не будет совпадать с линейным коэффициентом корреляции. В этом случае при определении индекса корреляции практически используется формула
R
£(у-1/(1/у) Z(y-y)2
(2.34).
т. е. теоретические значения рх определяются не непосред-ГС .А ственно по данным у и х, а на основе уравнения — -а + ох, ко
торое может быть дополнено линейным коэффициентом корреляции между х и */г
При определении используется сумма квадратов отклонений £(1/у —1/у)2, которая раскладывается на факторную и остаточную. Так, по данным табл. 2.6 £(у — у)2 = 351,714, Z(y - Л)2 = 29,24. Соответственно Ryx = 0,9575, а = 0,9278.
Вследствие близости результатов и простоты расчета с ис-
пользованием компьютерных программ для характеристики тесноты связи по нелинейным функциям широко используется линейный коэффициент корреляции. Несмотря на близость значе
84
ний Ry* й rIn>1IM. или и rlnysX в нелинейных функциях с преобразованием значений признака у, следует помнить, что если при линейной зависимости признаков один и тот же коэффициент корреляции характеризует регрессию как ух = а + b • х, так и
= А + В • у, так как гух = гху, то при криволинейной зависимости Я™ для функции у — J(x) не равен для регрессии х —fly)-Поскольку в расчете индекса корреляции используется соотношение факторной и общей суммы квадратов отклонений, то Я2 имеет тот же смысл, что и коэффициент детерминации. В специальных исследованиях величину Я2 для нелинейный связей назы-
вают индексом детерминации.
Оценка существенности индекса корреляции проводится, так
же как и оценка надежности коэффициента корреляции (см.
п. 2.3).
Индекс детерминации используется для щ
верки существен-
ности в целом уравнения нелинейной регрессии по F-критерию Фишера:
Я2 л-т-1
1-Я2 т
(2.35)
где Я2 — индекс детерминации;
л - число наблюдений;
т — число параметров при переменных х.
Величина m характеризует число степеней свободы для факторной суммы квадратов, а (л — т — 1) — число степеней свободы для остаточной суммы квадратов.
Для степенной функции ух = а х6 т = 1 и формула F-критерия примет тот же вид, что и при линейной зависимости:
р2
Я=-!Ц-(л-2).
1-Я2
Для параболы второй степениу = а + Ь’х + с-х2 + Ет = 2
r R2 п~3 1-Я2 2 ’
Расчет F-критерия можно вести и в таблице дисперсионного анализа результатов регрессии, как это было показано для линейной функции (см. табл. 2.2).
85
Индекс детерминации Я2 можно сравнивать с коэффициентом детерминации г2 для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем величина коэффициента детерминации г2 меньше индекса детерминации Я2 Близость этих показателей означает, что нет необходимости усложнять форму уравнения регрессии и можно использовать линейную функцию. Практически если величина (Я2^ — г2^) не превышает 0,1, то предположение о линейной форме связи считается оправданным. В противном случае проводится оценка существенности различия R2yx, вычисленных по одним и тем же исходным данным, через /-критерий Стьюдента:
(2.36)
где /Я|Д _ - ошибка разности между Я2^ и г2^, определяемая по формуле
(2.37)
Если 4^ > /тайл, то различия между рассматриваемыми показателями корреляции существенны и замена нелинейной регрессии уравнением линейной функции невозможна. Практически если величина t < 2 , то различия между Ryx и /^несущественны, и, следовательно, возможно применение линейной регрессии,
даже если есть предположения о некоторой нелинейности рас-
сматриваемых соотношений признаков фактора и результата.
Предположим, что поданным табл. 2.4, где было найдено уравнение регрессии ух = 9,876 4-5,129- 1пх, была использована линейная функция ух = 9,28 + 1,777 • х, коэффициент корреляции для которой составил 0,97416. Величина коэффициента корреляции
оказалась меньше, чем величина индекса корреляции 0,99581. Оценим существенность различия данных показателей корреляции, используя приведенную формулу: Я2 — г2 = (0,99581)2 — — (0,97416)2 = 0,04265, т. е. применение нелинейной функции увеличивает долю объясненной вариации на 4,3 проц, пункта.
Я2 + г2 = (0,99581)2 + (0,97416)2 = 1,94063;
0,04265 - (0,04265)2 (2 -1,94063)
----------------------------------= U, 10 641,
t = 0,04265 : 0,16841 = 0,25, что < 2.
86
Следовательно, если нет уверенности в правильности выбора полулогарифмической функции, то она может быть заменена линейной функцией.
2.7. СРЕДНЯЯ ОШИБКА АППРОКСИМАЦИИ
Фактические значения результативного признака отличаются от теоретических, рассчитанных по уравнению регрессии, т. е. у и ух. Чем меньше это отличие, тем ближе теоретические значения подходят к эмпирическим данным, лучше качество модели. Величина отклонений фактических и расчетных значений результативного признака (у — ух) по каждому наблюдению представляет собой ошибку аппроксимации. Их число соответствует объему совокупности. В отдельных случаях ошибка аппроксимации может оказаться равной нулю. Отклонения (у — ух) несравнимы между собой, исключая величину, равную нулю. Так, если для одного наблюдения у — ух = 5, а для другого она равна 10, то это не означает, что во втором случае модель дает вдвое худший результат. Для сравнения используются величины отклонений, выраженные в процентах к фактическим значениям. Так, если для первого наблюдения у — 20, а для второго у = 50, ошибка аппроксимации составит 25 % для первого наблюдения и 20 % — для второго.
Поскольку (у — ух) может быть как величиной положительной, так и отрицательной, то ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю.
Отклонения (у — ух) можно рассматривать как абсолютную ошибку аппроксимации, а
100
— как относительную ошибку аппроксимации. Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппрок-
симации как среднюю арифметическую простую:
100.
(2.38)
87
Представим расчет средней ошибки аппроксимации для уравнения ух = 9,876 + 5,129 • 1пх в табл. 2.7. А = • 7,3 = 1,2%, что 6 говорит о хорошем качестве уравнения регрессии, ибо ошибка аппроксимации в пределах 5—7 % свидетельствует о хорошем подборе модели к исходным данным.
Таблица 2.7
Расчет средней ошибки аппроксимации
У Л Ух А У-Ух — • 100 У
10,0 9,9 0,1 1,0
13,4 13,4 0,0 0,0
15,4 15,5 -0,1 0,6
16,5 17,0 -0,5 3,0
18,6 18,1 0,5 2,7
19,1 19,1 0,0 0,0
Итого 93,0 93,0 0 7,3
Возможно и иное определение средней ошибки аппроксима-
ции:
100 У V п .
(2.39)
Для нашего примера эта величина составит:
100
15,5
= 1,9%.
В стандартных программах чаще используется первая формула для расчета средней ошибки аппроксимации.
Контрольные вопросы к главе 2
1. В чем состоят ошибки спецификации модели?
2. Поясните смысл коэффициента регрессии, назовите способы его оценивания, покажите, как он используется для расчета мультипликатора в функции потребления.
88
3. Что такое число степеней свободы и как оно определяется для факторной и остаточной сумм квадратов?
4. Какова концепция F-критерия Фишера?
5. Как оценивается значимость параметров уравнения регрессии?
6. В чем отличие стандартной ошибки положения линии регрессии от средней ошибки прогнозируемого индивидуального значения результативного признака при заданном значении фактора?
7. Какой нелинейной функцией может быть заменена парабола второй степени, если не наблюдается смена направленности связи признаков?
8. Запишите все виды моделей, нелинейных относительно: включаемых переменных;
оцениваемых параметров.
9. В чем отличие применения МНК к моделям, нелинейным относительно включаемых переменных и оцениваемых параметров?
10. Как определяются коэффициенты эластичности по разным видам регрессионных моделей?
11. Назовите показатели корреляции, используемые при нелинейных соотношениях рассматриваемых признаков.
12. В чем смысл средней ошибки аппроксимации и как она определяется?
ГЛАВА
МНОЖЕСТВЕННАЯ РЕГРЕССИЯ И КОРРЕЛЯЦИЯ
3.1. СПЕЦИФИКАЦИЯ МОДЕЛИ
Парная регрессия может дать хороший результат при моделировании, если влиянием других факторов, воздействующих на объект исследования, можно пренебречь. Например, при построении модели потребления того или иного товара от дохода исследователь предполагает, что в каждой группе дохода одинаково влияние на потребление таких факторов, как цена товара, размер семьи, ее состав. Вместе с тем исследователь никогда не может быть уверен в справедливости данного предположения. Для того чтобы иметь правильное представление о влиянии дохода на потребление, необходимо изучить их корреляцию при неизменном уровне других факторов. Прямой путь решения такой задачи состоит в отборе единиц совокупности с одинаковыми значениями всех других факторов, кроме дохода. Он приводит к планированию эксперимента — методу, который используется в химических, физических, биологических исследованиях. Экономист в отличие от экспериментатора-естественника лишен возможности регулировать другие факторы. Поведение отдельных экономических переменных контролировать нельзя, т. е. не удается обеспечить равенство всех прочих условий для оценки влияния одного исследуемого фактора. В этом случае следует попытаться выявить влияние других факторов, введя Их в модель, т. е. построить уравнение множественной регрессии
y = a + bl-xl + b2‘x2 + ... + bf-xp + E. I
Такого рода уравнение может использоваться при изучении потребления. Тогда коэффициенты Ь,- — частные производные потребления у по соответствующим факторам х,-:
90
в предположении, что все остальные х, постоянны.
В ЗО-е гг. XX в. Дж.М. Кейнс сформулировал свою гипотезу потребительской функции. С того времени исследователи неоднократно обращались к проблеме ее совершенствования. Современная потребительская функция чаще всего рассматривается как модель вида
С =7(У, А М, Z),
где С — потребление;
у - доход;
Р — цена, индекс стоимости жизни;
М — наличные деньги;
Z - ликвидные активы.
При ЭТОМ 0<~<1.
dy
Множественная регрессия широко используется в решении проблем спроса, доходности акций, при изучении функции издержек производства, в макроэкономических расчетах и целого ряда других вопросов эконометрики. В настоящее время Множественная регрессия — один из наиболее распространенных методов в эконометрике. Основная цель множественной регрессии -построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель.
Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели. Суть проблемы спецификации рассматривалась применительно к парной зависимости в п. 2.1. Она включает в себя два круга вопросов: отбор факторов и выбор вида уравнения регрессии. Их решение при построении модели множественной регрессии имеет некоторую специфику, которая рассматривается ниже.
91
3.2. ОТБОР ФАКТОРОВ ПРИ ПОСТРОЕНИИ МНОЖЕСТВЕННОЙ РЕГРЕССИИ
Включение в уравнение множественной регрессии того или иного набора факторов связано прежде всего с представлением исследователя о природе взаимосвязи моделируемого показателя с другими экономическими явлениями. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям.
1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность (например, в модели урожайности качество почвы задается в виде баллов; в модели стоимости объектов недвижимости учитывается место нахождения недвижимости: районы могут быть проранжированы).
2. Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи.
Включение в модель факторов с высокой интеркорреляцией, когда Ry*. < Rx „ для зависимости у = а + Ь\ • xt + b2 • х2 + е может привести к нежелательным последствиям — система нормальных уравнений может оказаться плохо обусловленной и повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии.
Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются не-интерпретируемыми. Так, в уравнении у = а + bt • xt + Ь2 • х2 + е предполагается, что факторы х} и х2 независимы друг от друга, т. е. гх • = 0. Тогда можно говорить, что параметр Ь{ измеряет силу влияния фактора х, на результат у при неизменном значении фактора х2. Если же гх „ = 1, то с изменением фактора х, фактор х2 не может оставаться неизменным. Отсюда и Ь2 нельзя интерпретировать как показатели раздельного влияния х( их2 и на у.
Пример. Рассмотрим регрессию себестоимости единицы продукции (руб., у) от заработной платы работника (руб., х) и производительности его труда (единиц в час, г):
у = 22 600 — 5 • х — 10 • z + е.
Коэффициент регрессии при переменной z показывает, что с ростом производительности труда на 1 ед. себестоимость единицы продукции снижается в среднем на 10 руб. при постоянном
92
уровне оплаты труда. Вместе с тем параметр при х нельзя интерпретировать как снижение себестоимости единицы продукции за счет роста заработной платы. Отрицательное значение коэффициента регрессии при переменной х в данном случае обусловлено высокой корреляцией между х иг (гч = 0,95). Поэтому роста заработной платы при неизменности производительности труда (если не брать во внимание проблемы инфляции) быть не может.
Включаемые во множественную регрессию факторы должны объяснить вариацию независимой переменной. Если строится модель с набором р факторов, то для нее рассчитывается показатель детерминации Я2, который фиксирует долю объясненной вариации результативного признака за счет рассматриваемых в регрессии р факторов. Влияние других не учтенных в модели факторов оценивается как 1 — Я2 с соответствующей остаточной дисперсией 5й.
При дополнительном включении в регрессию р + 1 фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться:
Я^йЯ^иа2,^^.
Если же этого не происходит и данные показатели практически мало отличаются друг от друга, то включаемый в анализ фактор хр+/ не улучшает модель и практически является лишним фактором. Так, если для регрессии, включающей пять факторов, коэффициент детерминации составил 0,857 и включение шестого фактора дало коэффициент детерминации 0,858, то вряд ли целесообразно дополнительно включать в модель этот фактор.
Насыщение модели лишними факторами не только не снижает величину остаточной дисперсии и не увеличивает показатель детерминации, но и приводит к статистической незначимости параметров регрессии по /-критерию Стьюдента.
Таким образом, хотя теоретически регрессионная модель позволяет учесть любое число факторов, практически в этом нет необходимости. Отбор факторов производится на основе качественного теоретико-экономического анализа. Однако теоретический анализ часто не позволяет однозначно ответить на вопрос о количественной взаимосвязи рассматриваемых признаков и целесообразности включения фактора в модель. Поэтому отбор факторов обычно осуществляется в две стадии: на первой подбираются факторы исходя из сущности проблемы; на второй -
93
на основе матрицы показателей корреляции определяют /-статистики для параметров регрессии.
Коэффициенты интеркорреляции (т. е. корреляции между объясняющими переменными) позволяют исключать из модели дублирующие факторы. Считается, что две переменных явно коллинеарны, т. е. находятся между собой в линейной зависимости, если гх~. > 0,7.
Поскольку одним из условий построения уравнения множественной регрессии является независимость действия факторов, т. е. Д, = 0, коллинеарность факторов нарушает это условие. Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. Предпочтение при этом отдается не фактору, более тесно связанному с результатом, а тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. В этом требовании проявляется специфика множественной регрессии как метода исследования комплексного воздействия факторов в условиях их независимости друг от друга.
Пусть, например, при изучении зависимости у =J(x, z, v) матрица парных коэффициентов корреляции оказалась следующей:
У X Z V
У 1
X 0,8 1
Z 0,7 0,8 1
V 0,6 0,5 0,2 1
Очевидно, что факторы х и z дублируют друг друга. В анализ целесообразно включить фактор z, а не х, так как корреляция z с результатом у слабее, чем корреляция факторахсу(гуг< г^), но зато слабее межфакторная корреляция < rxv. Поэтому в данном случае в уравнение множественной регресии включаются факторы Z, V.
По величине парных коэффициентов корреляции обнаруживается лишь явная коллинеарность факторов. Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов, когда бо-
94
лее чем два фактора связаны между собой линейной зависимостью, т. е. имеет место совокупное воздействие факторов друг на друга. Наличие мультиколлинеарности факторов может означать, что некоторые факторы будут всегда действовать в унисон. В результате вариация в исходных данных перестает быть полностью независимой, и нельзя оценить воздействие каждого фактора в отдельности. Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью метода наименьших квадратов (МНК).
Если рассматривается регрессия у = д + J'x + y ? + (/• v + e, то для расчета параметров, применяя МНК, предполагается равенство где 5 -С _ ‘“'факт -
общая сумма квадратов отклонений S(y, — У)2;
факторная (объясненная) сумма квадратов отклонений £(Л - у)2;
остаточная сумма квадратов отклонений S(y.- — $/) .
В свою очередь, при независимости факторов друг от друга
fЙИ^ИМО РаВеНСТВО
где Sz, Sv — суммы квадратов отклонений, обусловленные влиянием соответствующих факторов.
Если же факторы интеркоррелированы, то данное равенство нарушается.
Включение в модель мулыпиколлинеарных факторов нежелательно в силу следующих последствий:
• затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов в «чистом» виде, ибо факторы коррелированы; параметры линейной регрессии теряют экономический смысл;
• оценки параметров ненадежны, обнаруживают большие стандартные ошибки и меняются с изменением объема наблюдений (не только по величине, но и по знаку), что делает модель непригодной для анализа и прогнозирования.
95
Для оценки мультиколлинеарности факторов может исполь-
зоваться определитель матрицы парных коэффициентов корреляции между факторами.
Если бы факторы не коррелировали между собой, то матрица парных коэффициентов корреляции между факторами была бы
единичной матрицей, поскольку все недиагональные элементы rXfC.(xt * xj) были бы равны нулю. Так, для включающего три объясняющих переменных уравнения
у^а + ^х, + t>2-x2 + b3-x3 + s
матрица коэффициентов корреляции между факторами имела бы определитель, равный единице.
Det R
гх^
ГХ2Х2
Гхгхг
ТЭК Как ^3x3 1 ’ И Г*1*3 ^*2*3
Если же, наоборот, между факторами существует полная линейная зависимость и все коэффициенты корреляции равны единице, то определитель такой матрицы равен нулю:
Чем ближе к нулю определитель матрицы межфакторной | корреляции, тем сильнее мультиколлинеарность факторов и | ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов.
Оценка значимости мультиколлинеарности факторов может быть проведена методом испытания гипотезы о независимости переменных /10 : Det |Л| = I. Доказано, что величина
(2 т+5) 1g DetR
имеет приближенное распределение
X c-n(n-l)
степенями свободы. Если фактическое значение
96
X превосходит табличное (критическое) х факт > X табл(#,о)> то гипотеза Но отклоняется. Эго означает, что Det |Я| * 1, недиагональные ненулевые коэффициенты корреляции указывают на коллинеарность факторов. Мультиколлинеарность считается доказанной.
Через коэффициенты множественной детерминации можно найти переменные, ответственные за мультиколлинеарность факторов. Для этого в качестве зависимой переменной рассматривается каждый из факторов. Чем ближе значение коэффициента множественной детерминации к единице, тем сильнее проявляется мультиколлинеарность факторов. Сравнивая между собой коэффициенты множественной детерминации факторов
— хр' -*3 — хр И "•)»
можно выделить переменные, ответственные за мультиколлинеарность, следовательно, можно решать проблему отбора факторов, оставляя в уравнении факторы с минимальной величиной коэффициента множественной детерминации.
Существует ряд подходов преодоления сильной межфакторной корреляции. Самый простой путь устранения мультиколлинеарности состоит в исключении из модели одного или нескольких факторов. Другой подход связан с преобразованием факторов, при котором уменьшается корреляция между ними. Например, при построении модели на основе рядов динамики переходят от первоначальных данных к первым разностям уровней Д/ = у, — yf_t, чтобы исключить влияние тенденции, или используются такие методы, которые сводят к нулю межфакторную корреляцию, т. е. переходят от исходных переменных к их линейным комбинациям, не коррелированных друг с другом (метод главных компонент).
Одним из путей учета внутренней корреляции факторов является переход к совмещенным уравнениям регрессии, т. е. к уравнениям, которые отражают не только влияние факторов, но и их взаимодействие. Так, если у =ДХ|, х2, х3), то возможно построение следующего совмещенного уравнения:
12
13
л Л| л3 т и23 л2 л3 . о.
Рассматриваемое уравнение включает взаимодействие первого порядка (взаимодействие двух факторов). Возможно включение в модель и взаимодействий более высокого порядка, если бу
у-1525
97
дет доказана их статистическая значимость по F-критерию Фишера, например, 6)23 • xt х2 х3 — взаимодействие второго порядка и т. д. Как правило, взаимодействия третьего и более высоких порядков оказываются статистически незначимыми, совмещенные уравнения регрессии ограничиваются взаимодействиями первого и второго порядков. Но и эти взаимодействия могут оказаться несущественными, поэтому нецелесообразно полное включение в модель взаимодействий всех факторов и всех порядков. Так, если анализ совмещенного уравнения показал значимость только взаимодействия факторов х, и х3, то уравнение будет иметь вид:
у = а + />| • Xj + b2 х2 + Ь3 х3 + Ьп • Х| • х3 + е.
Взаимодействие факторов х, и х3 означает, что на разных уровнях фактора х3 влияние фактора х, на у будет неодинаково, т. е. оно зависит от значений фактора х3. На рис. 3.1 взаимодействие факторов представляется непараллельными линиями связи с результатом у. И, наоборот, параллельные линии влияния фактора xt на у при разных уровнях фактора х3 означают отсутствие взаимодействия факторов Xj и х3.
У ♦
Рис. 3.1. Графическая иллюстрация взаимодействия факторов:
а
а - Х| влияет на у, причем это влияние одинаково как при х3—Вь так и при Хз=#2 (одинаковый наклон линий регрессии), что означает отсутствие взаимодействия факторов xt и х3;
б — с ростом Х| результативный признак у возрастает при х3 = Вх\ с ростом х, результативный признаку снижается при х3 = В2. Между х( и х3 существует взаимодействие.
98
Совмещенные уравнения регрессии строятся, например, при исследовании эффекта влияния на урожайность разных видов
удобрений (комбинаций азота и фосфора).
Решению проблемы устранения мультиколлинеарности фак-
торов может помочь и переход к уравнениям приведенной формы. С этой целью в уравнение регрессии производится подста
новка рассматриваемого фактора через выражение его из другого
уравнения.
Пусть, например, рассматривается двухфакторная регрессия вида ух = а + Ьх- хх + Ь2 • х2, для которой факторы х} и х2 обнаруживают высокую корреляцию. Если исключить один из факторов, то мы придем к уравнению парной регрессии. Вместе с тем можно оставить факторы в модели, но исследовать данное двухфакторное уравнение регрессии совместно с другим уравнением, в котором фактор (например, х2) рассматривается как зависимая переменная. Предположим, известно, что 22= А + В • у + С • х3. Подставляя это уравнение в искомое вместо х2, получим:
р = а + Ьх -X! + Ь2-(А + Ву + Сх3)
или
VO - b2-B) = (а + b2 - А) + bl xt + С Ь2- х3.
Если (1 — Ь2 • В) * 0, то, разделив обе части равенства на (1 — Ь2 • В), получаем уравнение вида
V -(О+Аг'^)| bf х сьг
Ух (l-h-B) (1-Z>2 -В) 1 (l-fy-B)' 3’
которое представляет собой приведенную форму уравнения для определения результативного признака у. Это уравнение может быть представлено в виде
Ух-а +b'i -X] +b'3-x3. а
К нему для оценки параметров может быть применен метод наименьших квадратов.
Отбор факторов, включаемых в регрессию, является одним из важнейших этапов практического использования методов регрессии. Подходы к отбору факторов на основе показателей кор
1 Приведенная форма модели рассматривается в гл. 4.
99
реляции могут быть разные. Они приводят построение уравнения множественной регрессии соответственно к разным методикам. В зависимости от того, какая методика построения уравнения регрессии принята, меняется алгоритм ее решения на ЭВМ.
Наиболее широкое применение получили следующие методы построения уравнения множественной регрессии:
• метод исключения;
• метод включения;
• шаговый регрессионный анализ.
Каждый из этих методов по-своему решает проблему отбора факторов, давая в целом близкие результаты — отсев факторов из полного его набора (метод исключения), дополнительное введение фактора (метод включения), исключение ранее введенного фактора (шаговый регрессионный анализ)1.
На первый взгляд может показаться, что матрица парных коэффициентов корреляции играет главную роль в отборе факторов. Вместе с тем вследствие взаимодействия факторов парные коэффициенты корреляции не могут в полной мере решать вопрос о целесообразности включения в модель того или иного фактора. Эту роль выполняют показатели частной корреляции, оценивающие в чистом виде тесноту связи фактора с результатом. Матрица частных коэффициентов корреляции наиболее широко используется в процедуре отсева факторов. При отборе факторов рекомендуется пользоваться следующим правилом: число включаемых факторов обычно в 6—7 раз меньше объема совокупности, по которой строится регрессия. Если это соотношение нарушено, то число степеней свободы остаточной вариации очень мало. Это приводит к тому, что параметры уравнения регрессии оказываются статистически незначимыми, а /"-критерий меньше табличного значения.
3.3. ВЫБОР ФОРМЫ УРАВНЕНИЯ РЕГРЕССИИ
Как и в парной зависимости, возможны разные виды уравнений множественной регрессии: линейные и нелинейные.
Ввиду четкой интерпретации параметров наиболее широко используются линейная и степенная функции. В линейной множественной регрессии ух = а + Ьх • + Ь2 • х2 + ... + Ь. • х. параметры при х называются коэффициентами «чистой» регрессии. Они
’Подробнее см.: Дрейпер Н., Смит Г. Прикладной регрессионный анализ. - С. 172-188.
100
характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизмененном значении других факторов, закрепленных на среднем уровне.
Пример. Предположим, что зависимость расходов на продукты питания по совокупности семей характеризуется следующим уравнением:
ух — 0,5 + 0,35 • х( + 0,73 • х2,
где у — расходы семьи за месяц на продукты питания, тыс. руб.;
Х| — месячный доход на одного члена семьи, тыс. руб.;
х2 — размер семьи, человек.
Анализ данного уравнения позволяет сделать выводы — с ростом дохода на одного члена семьи на 1 тыс. руб. расходы на питание возрастут в среднем на 35Q руб. при том же среднем размере семьи. Иными словами, 35 % дополнительных семейных расходов тратится на питание. Увеличение размера семьи при тех же ее доходах предполагает дополнительный рост расходов на питание на 730 руб. Параметр а не подлежит экономической интерпретации.
При изучении вопросов потребления коэффициенты регрессии рассматриваются как характеристики предельной склонности к потреблению. Например, если функция потребления С, имеет вид
С/ в + + ^| * Rf — ।
то потребление в период времени t зависит от дохода того же периода Rt и от дохода предшествующего периода R^. Соответственно коэффициент Ьо характеризует эффект единичного возрастания дохода Rt при неизменном уровне предыдущего дохода. Коэффициент Ьо обычно называют краткосрочной предельной склонностью к потреблению. Общим эффектом возрастания как текущего, так и предыдущего дохода будет рост потребления на b — b0 + bt. Коэффициент b рассматривается здесь как долгосрочная склонность к потреблению. Так как коэффициенты Ло и Ь/ > 0, то долгосрочная склонность к потреблению должна превосходить краткосрочную bG. Например, за период 1905—1951 гг. (за исключением военных лет) М.Фридман построил для США следующую функцию потребления: С( — 53 + 0,58 • R( + 0,32 • Л,_ । с краткосрочной предельной склонностью к потреблению 0,58 и с долгосрочной склонностью к потреблению 0,9*.
1 См.: Маленво Э. Статистические методы эконометрии. — М.: Статистика, 1975. - С. 138.
101
Функция потребления может рассматриваться также в зависимости от прошлых привычек потребления, т. е. от предыдущего уровня потребления С,_р
~ а "4" bfl * Rf "f" b{ * С^_| "4" 6.
В этом уравнении параметр Ьо также характеризует краткосрочную предельную склонность к потреблению, т. е. влияние на потребление единичного роста доходов того же периода Rt. Долгосрочную предельную склонность к потреблению здесь измеряет выражение 6q/(1 — b{).
Так, если уравнение регрессии составило
С, = 23,4 + 0,46 • Rt + 0,20 • С,_{ + е,
то краткосрочная склонность к потреблению равна 0,46, а долгосрочная — 0,575 (0,46/0,8).
В степенной функции $х — а • xfi • х/2-’ х„ьр коэффициенты bj являются коэффициентами эластичности. Они показывают, на сколько процентов изменяется в среднем результат с изменением соответствующего фактора на 1 % при неизменности действия других факторов. Этот вид уравнения регрессии получил наибольшее распространение в производственных функциях, в исследованиях спроса и потребления.
Предположим, что при исследовании спроса на мясо получено уравнение
х1,и
= 0,82 -Xi-2,63 • х/’11 или ух = 0,82• —j-jj-, где у — количество спрашиваемого мяса;
Xi - цена;
х2 - доход.
Следовательно, рост цен на 1 % при том же доходе вызывает снижение спроса в среднем на 2,63 %. Увеличение дохода на 1% обусловливает при неизменных ценах рост спроса на 1,11 %.
В производственных функциях вица
где г — количество продукта, изготавливаемого с помощью т производственных факторов (Г,, Fz,..., Fm);
b — параметр, являющийся эластичностью количества продукции по отношению к количеству соответствующих производственных факторов.
102
Экономический смысл имеют не только коэффициенты b каждого фактора, но и их сумма, т. е. сумма эластичностей: B~bt + b2+-..+ bm. Эта величина фиксирует обобщенную характеристику эластичности производства. Производственная функция имеет вид
Р = 2 • F,0’3
где
выпуск продукции;
стоимость основных производственных фондов;
отработано человеко-дней;
— затраты на производство,
эластичность выпуска по отдельным факторам производства составляет в среднем 0,3 % с ростом Fx на 1 % при неизменном уровне других факторов; 0,2 % — с ростом F2 на 1 % также при неизменности других факторов производства и 0,5 % с ростом F3 на 1 % при неизменном уровне факторов и F2. Для данного уравнения В = b{ + b2 + b3 = 1. Следовательно, в целом с ростом каждого фактора производства на 1% коэффициент эластичности выпуска продукции составляет 1%, т.е. выпуск продукции увеличивается на 1%, что в микроэкономике соответствует постоянной отдаче на масштаб.
m
При практических расчетах не всегда Zfy = 1 • Она может быть ;=1
как больше, так и меньше единицы. В этом случае-величина В фиксирует приближенную оценку эластичности выпуска с ростом каждого фактора производства на 1 % в условиях увеличивающейся (В > 1) или уменьшающейся (В < 1) отдачи на масштаб.
Так, если Р — 2,4 • F?'3 • F2't • F30,2, то с ростом значений каждого фактора производства на 1 % выпуск продукции в целом возрастает приблизительно на 1,2 %.
Возможны и другие линеаризуемые функции для построения уравнения множественной регрессии:
• ’ экспонента—у = e“+^i'х,+^'*2+ ,+Vх/»+е,
• гипербола - у=-------------------------, которая исполь-
а+Р| -X] +р2 -х2+...+рр-хр
зуется при обратных связях признаков.
Стандартные компьютерные программы обработки регрессионного анализа позволяют перебирать различные функции и выбрать ту из них, для которой остаточная дисперсия и ошибка ап-103
проксимации минимальны, а коэффициент детерминации максимален.
Если исследователя не устраивает предлагаемый стандартной программой набор функций регрессии, то можно использовать любые другие функции, приводимые путем соответствующих преобразований к линейному виду, например:
yx = a+bl -X, +1>2 —+Aj-х(2 + />41пх4. х2
Обозначив
1/2, Z4 = 1пх4,
Z/ = Xj, Z2 = 1/Х2, Z3 = Х3
получим линейное уравнение множественной регрессии
у = а + />, • zi + b2 • Z2 + b3 • 23 + Ь4 • Z4 + е.
Однако чем сложнее функция, тем менее интерпретируемы ее
параметры.
При сложных полиномиальных функциях с большим числом факторов необходимо помнить, что каждый параметр преобразованной функции является средней величиной, которая должна быть подсчитана по достаточному числу наблюдений. Если число наблюдений невелико, что, как правило, имеет место в экономе
трике, то увеличение числа параметров функции приведет к их статистической незначимости и соответственно потребует упро
щения вида функции. Если один и тот же фактор вводится в рег
рессию в разных степенях, то каждая степень рассматривается как самостоятельный фактор. Так, если модель имеет вид поли-
нома второго порядка
то после замены переменных Zi — х(, Z2 = х2, z3 — х2, z4 — 25= х}х2 получим линейное уравнение регрессии с пятью факторами:
у = а + Л, • z, + Ь2 z2 + b3 • z3 + b4 • ц + Ь5 z5 + е.
Поскольку, как отмечалось, должно выполняться соотношение между числом параметров и числом наблюдений, для полинома второй степени требуется не менее 30—35 наблюдений.
104
В эконометрике регрессионные модели часто строятся на основе макроуровня экономических показателей, когда ставится задача оценки влияния наиболее экономически существенных факторов на моделируемый показатель при ограниченном объеме информации. Поэтому полиномиальные модели высоких порядков используются редко.
3.4. ОЦЕНКА ПАРАМЕТРОВ УРАВНЕНИЯ МНОЖЕСТВЕННОЙ РЕГРЕССИИ
Параметры уравнения множественной регрессии оцениваются, как и в парной регрессии, методом наименьших квадратов (МНК). .При его применении строится система нормальных уравнений, решение которой и позволяет получить оценки параметров регрессии.
Так, для уравнения у = а + Ь{ • Х| + Ь2 • х2 + ... + Ьр • хр + е система нормальных уравнений составит:
^.У = n a+bt Sxj +/>2-Хх2 +... + Ьр-Ххр,
Ху х\ =a-Z*i +bi -Lx]2 -2>| -х2 +...+bp-X,Xp Х|,
Ху-хр =a-Xxp + bi -Ex! хр +bi-Хх2-хр +... + Ьр-Хх2р.
Ее решение может быть осуществлено методом определителей:
где Д — определитель системы;
Да, Д/>|,..., &Ьр - частные определители.
ft
При этом
105
а Ла, ЛЬ{ Abp получаются путем замены соответствующего столбца матрицы определителя системы данными левой части системы.
Возможен и иной подход к определению параметров множественной регрессии, когда на основе матрицы парных коэффициентов корреляции строится уравнение регрессии в стандартизованном масштабе:
ty Pl * (кj Pl ' ^2 •" ?Хр
У-У < _xi~xi
где ty, tx ,tx — стандартизованные переменные: ty ---, »
1 ₽ °у
для которых среднее значение равно нулю: Ту = Тх. = О, а среднее квадратическое отклонение равно единице:
р — стандартизованные коэффициенты регрессии. .F
Применяя МНК к уравнению множественной регрессии в стандартизованном масштабе, после соответствующих преобразований получим систему нормальных уравнений вида
Rw =Р1 + Рз * Rx-,x + + РD * Rx-X ’
Ryx = Pl Rx,x + Рз +Рз-Лхх +...+Р--Я, . ,
J Л*2 ' 1 *2^1 * ajXj * P х/г^27
“Р1’Лх_х +...4-p«.
Решая ее методом определителей, найдем параметры — стандартизованные коэффициенты регрессии (/3-коэффициенты).
Стандартизованные коэффициенты регрессии показывают, на сколько сигм изменится в среднем результат, если соответствующий фактор X/ изменится на одну сигму при неизменном среднем уровне других факторов. В силу того, что все переменные заданы как центрированные и нормированные, стандартизованные коэффициенты регрессии Д сравнимы между собой. Сравнивая их друг с другом, можно ранжировать факторы по силе их воздействия на результат. В этом основное достоинство стандартизованных коэффициентов регрессии в отличие от коэффициентов «чистой» регрессии, которые несравнимы между собой.
Пример. Пусть функция издержек производства у (тыс. руб.) характеризуется уравнением вида
106
у = 200 + 1,2 • х, + 1,1 • х2 + е,
где Х| — основные производственные фонды (тыс. руб.); хг — численность занятых в производстве (чел.).
Анализируя его, мы видим, что при той же занятости дополнительный рост стоимости основных производственных фондов на 1 тыс. руб. влечет за собой увеличение затрат в среднем на 1,2 тыс. руб., а увеличение численности занятых на одного человека способствует при той же технической оснащенности предприятий росту затрат в среднем на 1,1 тыс. руб. Однако это не означает, что фактор х, оказывает более сильное влияние на издержки производства по сравнению с фактором х2. Такое сравнение возможно, если обратиться к уравнению регрессии в стандартизованном масштабе. Предположим, оно выглядит так:
Это означает, что с ростом фактора х( на одну сигму при неизменной численности занятых затраты на продукцию увеличиваются в среднем на 0,5 сигмы. Так как р{ < Р2(0,5 < 0,8),то можно заключить, что большее влияние оказывает на производство продукции фактор х2, а нех(, как кажется из уравнения регрессии в натуральном масштабе.
В парной зависимости стандартизованный коэффициент регрессии есть не что иное, как линейный коэффициент корреляции г . Подобно тому, как в парной зависимости коэффициенты регрессии и корреляции связаны между собой, так и во множественной регрессии коэффициенты «чистой» регрессии Ь,- связаны со стандартизованными коэффициентами регрессии Р,, а именно:
Это позволяет от уравнения регрессии в стандартизованном масштабе
^у Pl ' (х. Pl ' (г2 ••• Рр ' ^Х-
1 * f*
(3.2)
переходить к уравнению регрессии в натуральном масштабе переменных:
107
Параметр а определяется как
a^y-bl--Xl-b2--X2-...-bp--Xp. (3.3)
Рассмотренный смысл стандартизованных коэффициентов регрессии позволяет их использовать при отсеве факторов — из модели исключаются факторы с наименьшим значением f}j.
Компьютерные программы построения уравнения множественной регрессии в зависимости от использованного в них алгоритма решения позволяют получить либо только уравнение регрессии для исходных данных, либо, кроме того, уравнение регрессии в стандартизованном масштабе.
При нелинейной зависимости признаков, приводимой к линейному виду, параметры множественной регрессии также определяются МНК с той лишь разницей, что он используется не к исходной информации, а к преобразованным данным. Так, рассматривая степенную функцию
мы преобразовываем ее в линейный вид:
Igy = Iga + bt • IgX] + b2 • lgx2 + ... + bp • IgXp + Ige, где переменные выражены в логарифмах.
Далее обработка МНК та же, что и описана выше: строится система нормальных уравнений и определяются параметры Iga, bt, b2,bp. Потенцируя значение Iga, найдем параметр а и соответственно общий вид уравнения степенной функции.
Поскольку параметры степенной функции представляют собой коэффициенты эластичности, то они сравнимы по разным факторам.
Пример. При исследовании спроса на масло получено следующее уравнение:
Igy = — 1,25 — 0,858 • lgX| + 1,126 • lgx2 + е,
где у — количество масла на душу населения (кг);
Xi - цена (руб.);
х2 — доход на душу населения (тыс. руб.).
108
4
Анализируя уравнение, видим, что с ростом цены на 1 % при том же доходе спрос снижается в среднем на 0,858 %, а рост дохода на 1 % при неизменных ценах вызывает увеличение спроса в среднем на 1,126 %. В виде степенной функции данное уравнение примет вид:
у = 0,056 • х,^858 • х2-1’126 • е.
При других нелинейных функциях методика оценки параметров МНК осуществляется так же. В отличие от предыдущих функций параметры более сложных моделей не имеют четкой экономической интерпретации: они не являются/показателями силы связи и ее эластичности. Это не исключает возможности их применения, но делает их менее привлекательными в практических расчетах.
3.5. ЧАСТНЫЕ УРАВНЕНИЯ РЕГРЕССИИ
На основе линейного уравнения множественной регрессии
ь
у = а + Ь{ • х( + Ь2 • х2 + ... + Ьр • хр + е
могут быть найдены частные уравнения регрессии:
= f{xp),
т. е. уравнения регрессии, которые связывают результативный признак с соответствующими факторами х при закреплении других учитываемых во множественной регрессии факторов на среднем уровне. Частные уравнения регрессии имеют следующий вид:
+ Ьр ’ Хр + S,
Ztj-XpXj...Хр а + X | + Ь2 • х2 + Ь3 • х3 + ...
109
При подстановке в эти уравнения средних значений соответствующих факторов они принимают вид парных уравнений линейной регрессии, т. е. имеем:
УЛГ| JCjXj ...Xf ,
где
Ух2.Х|Х3...х, ~ ^2 + ^2*2>
В отличие от парной регрессии частные уравнения регрессии характеризуют изолированное влияние фактора на результат, ибо другие факторы закреплены на неизменном уровне. Эффекты влияния других факторов присоединены в них к свободному члену уравнения множественной регрессии. Это позволяет на основе частных уравнений регрессии определять частные коэффициенты эластичности:
(3.4)
где bj — коэффициенты регрессии для фактора х, в урав-
нении множественной регрессии;
Ух,х1х2...... хр - частное уравнение регрессии.
Пример. Предположим, что по ряду регионов множественная регрессия величины импорта на определенный товар у относительно отечественного его производствах!, изменения запасов х2 и потребления на внутреннем рынке х3 оказалась следующей:
у — — 66,028 + 0,135 • Х| + 0,476 хг + 0,343 • х3.
При этом средние значения для рассматриваемых признаков составили:
У = 31,5, X] = 245,7, Х2 - 3,7, Х3 = 182,5.
НО
На основе данной информации могут быть найдены средние по совокупности показатели эластичности:
Для данного примера они окажутся равными:
— 2457
= 0,135-—= 1,053%, 31,5
т. е. с ростом величины отечественного производства на 1 % размер импорта в среднем по совокупности регионов возрастет на 1,053 % при неизменных запасах и потреблении семей.
Для второй переменной коэффициент эластичности составляет:
Jv -0,476-^- = 0,056%, у‘> 31,5
т. е. с ростом изменения запасов на 1 % при неизменном производстве и внутреннем потреблении величина импорта увеличивается в среднем на 0,056 %.
Для третьей переменной коэффициент эластичности составляет:
— 1825
=0,343-^=1,987%,
т. е. при неизменном объеме производства и величины запасов с увеличением внутреннего потребления на 1 % импорт товара возрастает в среднем по совокупности регионов на 1,987 %. Средние показатели эластичности можно сравнивать друг с другом и соответственно ранжировать факторы по силе их воздействия на результат. В рассматриваемом примере наибольшее воздействие на величину импорта оказывает размер внутреннего потребления товара х3, а наименьшее — изменение запасов х2.
Наряду со средними показателями эластичности в целом по совокупности регионов на основе частных уравнений регрессии могут быть определены частные коэффициенты эластичности для каждого региона. Частные уравнения регрессии в нашем случае составят:
111
Лг| х3 *з О + ij ' Х| + ’ Х2 + 63 ’ Х3,
т- е- Л, Х2«з = -66,028 + 0,135 • *1 + 0,476 • 3,7 + 0,343 182,5 = = —1,669 + 0,135 jq;
Л2 х, х3 = а + *Г х । + Ь2 х2 + Ь3-х3, т. е. Л2 -*1х3“ -66,028 + 0,135 • 245,7 + 0,476 х2 + 0,343 182,5 = = 29,739 + 0,476 • х2;
-х| Х2 ^ + 6| X j + 62 Х2 + Ь3 Х3, т. е. yXj.. ъ = -66,028 + 0,135 • 245,7 + 0,476 • 3,7 + 0,343 х3 = = — 31,097 + 0,343 х3.
Подставляя в данные уравнения фактические значения по отдельным регионам соответствующих факторов, получим значения моделируемого показателя у при заданном уровне одного фактора и средних значениях других факторов. Эти расчетные значения результативного признака используются для определения частных коэффициентов эластичности по приведенной выше формуле. Так, если, например, в регионе х, = 160,2; х2 = 4,0; х3 = 190,5, то частные коэффициенты эластичности составят: fl
или
= 0,135-
160,2 -1,669+0,135-160,2
1,084%;
или
0,476-----------------
29,739+0,476-4,0
= 0,060%;
или
190,5
= 0,343 •
-31,097+0,343-1-90,5
= 1,908%
Как видим, частные коэффициенты эластичности для региона несколько отличаются от аналогичных средних показателей по совокупности регионов. Они могут быть использованы при принятии решений относительно развития конкретных регионов.
3.6. МНОЖЕСТВЕННАЯ КОРРЕЛЯЦИЯ
Практическая значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата — коэффициента детерминации.
112
Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком, или, иначе, оценивает тесноту совместного влияния факторов на результат.
Независимо от формы связи показатель множественной корреляции может быть найден как индекс множественной корреляции:
(3.6)
где — общая дисперсия результативного признака;
<гт — остаточная дисперсия для уравнения у —f(x, х2....Хр).
Методика построения индекса множественной корреляции аналогична построению индекса корреляции для парной зависимости. Границы его изменения те же: от 0 до 1. Чем ближе его значение к 1, тем теснее связь результативного признака со всем набором исследуемых факторов. Величина индекса множественной корреляции должна быть больше или равна максимальному парному индексу корреляции:
^ух[Х2... хр — -^ртДтах) (^ (’/*)•
При правильном включении факторов в регрессионный анализ величина индекса множественной корреляции будет существенно отличаться от индекса корреляции парной зависимости. Если же дополнительно включенные в уравнение множественной регрессии факторы третьестепенны, то индекс множественной корреляции может практически совпадать с индексом парной корреляции (различия в третьем, четвертом знаках). Отсюда ясно, 4TQ, сравнивая индексы множественной и парной корреляции, можно сделать вывод о целесообразности включения в уравнение регрессии того или иного фактора. Так, если у рассматривается как функция х и z и получен индекс множественной корреляции Ry„ = 0,85, а индексы парной корреляции при этом были Ry* = 0,82 и 7?^ = 0,75, то совершенно ясно, что уравнение парной регрессии у = f(x) охватывало 67,2 % колеблемости результативного признака под влиянием фактора х, а дополнительное включение в анализ фактора z увеличило долю объясненной вариации до 72,3 %, т. е. уменьшилась доля остаточной вариации на 5,1 проц, пункта (с 32,8 до 27,7%). 8“ '«а
113
Расчет индекса множественной корреляции предполагает определение уравнения множественной регрессии и на его основе остаточной дисперсии:
Можно пользоваться следующей формулой индекса множественной корреляции:
2 Ш - Ух,х2...
nyxtx2...x “ 1 _
Х(у-у)
(3.7)
При линейной зависимости признаков формула индекса корреляции может быть представлена следующим выражением:
Дух^-х, гух> ' (3.8)
где Дц — стандартизованные коэффициенты регрессии;
гт — парные коэффициенты корреляции результата с каждым фактором.
В справедливости данной формулы можно убедиться, если обратиться к линейному уравнению множественной регрессии в стандартизованном масштабе и определить для него индекс множественной корреляции как
(3.9)
или, что то же самое,
(ЗЛО)
В формуле (3.10) числитель подкоренного выражения представляет собой факторную сумму квадратов отклонений для
стандартизованных переменных: t = .
о,
114
Поскольку Ту = 0 и X(ty—Ту )2 = = п, индекс множествен-
ной корреляции для линейного уравнения в стандартизованном масштабе можно записать в виде
(3.11)
Подставим в эту формулу выражение ty через t у Pxf (х| + Рх2 ^*2 + + Р*р ^хр’
получим:
Л = </—'ЕЛг'СРх ‘^х +₽х *(х + —+ Рх А ) — у П ' ГХ| xi rx2 X1 хр х?
Так как ~'2Х> '1у~гух, то получим формулу индекса множественной корреляции следующего вида (3.8):
"Ж ‘ryxt
Формула индекса множественной корреляции для линейной регрессии получила название линейного коэффициента множественной корреляции, или, что то же самое, совокупного коэффици
ента корреляции.
Возможно также при линейной зависимости определение совокупного коэффициента корреляции через матрицу парных коэффициентов корреляции:
яг,х2 ...х.
(3.12)
где Дг — определитель матрицы парных коэффициентов корреляции;
Ari ] - определитель матрицы межфакторной корреляции.
Для уравнения у = а + bt + b2 • х2 + ... + bp • хр + е опреде-
литель матрицы коэффициентов парной корреляции примет вид:
8* 115
Определитель более низкого порядка /•] ( остается, когда вычеркиваются из матрицы коэффициентов парной корреляции первый столбец и первая строка, что и соответствует матрице коэффициентов парной корреляции между факторами:
Как видим, величина множественного коэффициента корреляции зависит не только от корреляции результата с каждым из факторов, но и от межфакторной корреляции. Рассмотренная формула позволяет определять совокупный коэффициент корреляции, не обращаясь при этом к уравнению множественной регрессии, а используя лишь парные коэффициенты корреляции.
При трех переменных для двухфакторного уравнения регрессии данная формула совокупного коэффициента корреляции легко приводится к следующему виду:
(3.15)
Индекс множественной корреляции равен совокупному коэффициенту корреляции не только при линейной зависимости рассматриваемых признаков. Тождественность этих показателей, 116
как и в парной регрессии, имеет место и для криволинейной зависимости, нелинейной по переменным. Так, если для фирмы модель прибыли у имеет вид
у = а + д| Х| + Ь2 • 1пх2 + Ь3 • lnx3 + 64 • lnx4 + е,
где X] — удельные расходы на рекламу;
х2 — капитал фирмы;
х3 — доля продукции фирмы в общем объеме продаж данной группы товаров по региону;
х4 — процент увеличения объема продаж фирмы по сравнению с предыдущим годом.
Тогда независимо от того,- что фактор х( задан линейно, а факторы х2, х3, х4 — в логарифмах, оценка тесноты связи может быть произведена с помощью линейного коэффициента множественной корреляции. Так, если рассматриваемая модель в стандартизованном виде оказалась следующей:
/ = - 0,4 • L + 0,5 • г + 0,4 • t + 0,3 • t , 1 X J
а парные коэффициенты корреляции прибыли с каждым из ее факторов составили
то коэффициент множественной детерминации окажется равным:
tfyxw, = - 0,4 • (- 0,6) + 0,5 • 0,7 + 0,4 • 0,6 + 0,3 • 0,4 = 0,95. I * J *т
Тот же результат даст и индекс множественной детерминации, определенный через соотношение остаточной и общей
дисперсии результативного признака.
Иначе обстоит дело с криволинейной регрессией, нелинейной по оцениваемым параметрам. Предположим, что рассматри
вается производственная функция Кобба-Дугласа:
Р = а • Lbl • • е,
где Р — объем продукции;
L — затраты труда;
К — величина капитала;
А| + ^2 в
117
Логарифмируя ее, получим линейное в логарифмах уравнение
InP = Ina + b{ ln£ + b2 • InX + Ins.
Оценив параметры этого уравнения по МНК, можно найти теоретические значения объема продукции \Р и соответственно остаточную сумму квадратов Х(Р — Ру, которая используется в расчете индекса детерминации (корреляции):
Я2=1-^--У2.
КР-Р)2
Однако при этом нельзя забывать, что МНК применяется не к исходным данным продукции, а к их логарифмам. Поэтому в индексе корреляции с общей суммой квадратов S(P — Р)2 сравнивается остаточная дисперсия, которая определена по теоретическим значениям логарифмов продукции: Е(Р — антилогарифм (1£>))2, т. е. когда по 1пР путем потенцирования нашли Р.
Индекс детерминации для нелинейных по оцениваемым параметрам функций в некоторых работах по эконометрике принято называть «квази-/г>. Для его определения по функциям, использующим логарифмические преобразования (степенная, экспонента), необходимо сначала найти теоретические значения Iny (в нашем примере InZ’), затем трансформировать их через антилогарифмы: антилогарифм (ту ) = у, т. е. найти теоретические значения результативного признака и далее определять индекс детерминации как «квази- R>>, пользуясь формулой
«квази - Я2» = 1 - 1.(У-^илогаРифм^у))2 (3 16)
Z(y-y)2
г*
Величина индекса множественной корреляции, определенная как «квази-Я2», не будет совпадать с совокупным коэффициентом корреляции, который может быть рассчитан для линейного в логарифмах уравнения множественной регрессии, ибо в последнем раскладывается на факторную и остаточную суммы квадратов не — У)2, a S(lny — Iny) . Аналогичное положение, когда индекс и коэффициент множественной корреляции не совпадают, имеем и для обратной функции:
118
1
a + bf -Xf +...+bp-xp +e’
ибо теоретическое значение результативного признака опре-„ 1
деляется путем обращения расчетной величины —•
В рассмотренных показателях множественной корреляции (индекс и коэффициент) используется остаточная дисперсия, которая имеет систематическую ошибку в сторону преуменьшения, тем более значительную, чем больше параметров определяется в уравнении регрессии при заданном объеме наблюдений п. Если число параметров при Xj равно т и приближается к объему наблюдений, то остаточная дисперсия будет близка к нулю и коэффициент (индекс) корреляцииприблизится к единице даже при слабой связи факторов с результатом. Для того чтобы нс допустить возможного преувеличения тесноты связи, используется скорректированный индекс (коэффициент) множественной корреляции.
Скорректированный индекс множественной корреляции содержит поправку на число степеней свободы, а именно остаточная сумма квадратов £(у —ух.Х2„х )2 делится на число степеней свободы остаточной вариации (п — т — 7), а общая сумма квадратов отклонений L(y —у) — на число степеней свободы в целом по совокупности (л — 1).
Формула скорректированного индекса множественной детерминации имеет вид:
кг , Е(у-у)2:(«-«-1)
" = ‘~ ' (317)
где т — число параметров при переменных х;
п — число наблюдений.
Поскольку £(у -у)/ Е(у -у)2 = 1 — Я2, то величину скорректированного индекса детерминации можно представить в виде
Я2 = 1-(1-Я2)-
(л-1) (л-/п-1)
(3.18)
Чем больше величина т, тем сильнее различия R2 и Jr.
119
Для линейной зависимости признаков скорректированный коэффициент множественной корреляции определяется по той же формуле, что и индекс множественной корреляции, т.е. как корень квадратный из R2. Отличие состоит лишь в том, что в линейной зависимости под т подразумевается число факторов, включенных в регрессионную модель, а в криволинейной зависимости т — число параметров при х и их преобразованиях (х2, In х и др.), которое может быть больше числа факторов как экономических переменных. Так, если у =*/(Х\, х^), то для линейной регрессии т = 2, а для репрессии вида
у = а + bt • X] + bi2 • X]2 +b2 • х2 + b22 х2 + е
число параметров при х равно 4, т. е. т = 4. При заданном объеме наблюдений при прочих равных условиях с увеличением числа независимых переменных (параметров) скорректированный коэффициент множественной детерминации убывает. Его величина может стать и отрицательной при слабых связях результата с факторами. В этом случае он должен считаться равным нулю. При небольшом числе наблюдений скорректированная величина коэффициента множественной детерминации Л2 имеет тенденцию переоценивать долю вариации результативного признака, связанную с влиянием факторов, включенных в регрессионную модель.
Пример. Предположим, что при п = 30 для линейного уравнения регрессии с четырьмя факторами Л2 = 0,7, а с учетом корректировки на число степеней свободы
Rг = 1 - (1 - 0,7) =о,652.
(30-4-1)
Чем больше объем совокупности, по которой исчислена регрессия, тем меньше различаются показатели 7г и Я2. Так, уже при п = 50 при том же значении Я2 и т величина Я2 составит 0,673.
В статистических пакетах прикладных программ в процедуре множественной регрессии обычно приводится скорректированный коэффициент (Индекс) множественной корреляции (детерминации). Величина коэффициента множественной детерминации используется для оценки качества регрессионной модели. Низкое значение коэффициента (индекса) множественной корреляции означает, что В регрессионную модель не включены существенные факторы — с одной стороны, а с другой стороны — рассматриваемая форма связи не отражает реальные соотношения между переменными, включенными в модель. Требуются дальнейшие исследования по улучшению качества модели и увеличению ее практической значимости.
120
3.7. ЧАСТНАЯ КОРРЕЛЯЦИЯ
Как было показано выше, ранжирование факторов, участвующих в множественной линейной регрессии, может быть прове
дено через стандартизованные коэффициенты регрессии
(Д-коэффициенты). Эта же цель может быть достигнута с помо
JlTlf
щью частных коэффициентов корреляции — для линейных
связей. При нелинейной взаимосвязи исследуемых признаков эту функцию выполняют частные индексы детерминации. Кроме
того, частные показатели корреляции широко используются при решении проблемы отбора факторов: целесообразность включения того или иного фактора в модель доказывается величиной показателя частной корреляции.
Частные коэффициенты (или индексы) корреляции характеризуют тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в уравнение регрессии.
Показатели частной корреляции представляют собой отношение сокращения остаточной дисперсии за счет дополнительного включения в анализ нового фактора к остаточной дисперсии, имевшей место до введения его в модель.
Пример. Предположим, что зависимость объема продукции у от затрат труда х1 характеризуется уравнением
= 27,5 + 3,5 • X], гуХ] = 0,58.
Подставив в это уравнение фактические значения х,, найдем теоретические величины объема продукции $>х и соответствующую величину остаточной дисперсии S2:
2
Включив в уравнение регрессии дополнительный фактор х2 — техническую оснащенность производства, получим уравнение регрессии вида
ЛИ2 = 20,2 + 2,8 • Х| + 0,2 • х2.
Для этого уравнения остаточная дисперсия, естественно, меньше. Предположим, что = 3,7, a S1^ = 6. Чем большее число факторов включено в модель, тем меньше величина остаточной дисперсии.
121
Сокращение остаточной дисперсии за счет дополнительного включения фактора х2 составит:
Чем больше доля этого сокращения в остаточной вариации до введения дополнительного фактора, т. е. в З2^., тем теснее связь между У и х2 при постоянном действии фактора х,. Корень квадратный из этой величины и есть индекс частной корреляции, по
казывающий в «чистом» виде тесноту связи у с х2.
Следовательно, чистое влияние фактора х2 на результат у можно определить как
(3.19)
Аналогично определяется и чистое влияние на результат фактора х(: ____________
Гс2_ С2 и с2 ' (3.20)
I >*j
Если предположить, что = 5, то частные показатели корреляции для уравнения у = 20,2 + 2,8 х, + 0,2 • х2 составят
и
г - /6 3>7 =0,619. у 6 ’
Сравнивая полученные результаты, видим, что более сильное воздействие на объем продукции оказывает техническая оснащенность предприятий.
Если выразить остаточную дисперсию через показатель детерминации ^ост = (1 - ?), то формула коэффициента част-
ной корреляции примет вид:
(3.21)
122
Соответственно
1-Я* _ _ 11______
•”2Х1 V |_r2
I Pj
(3.22)
Рассмотренные показатели частной корреляции принято называть коэффициентами (индексами) частной корреляции первого порядка, ибо они фиксируют тесноту связи двух переменных при закреплении (элиминировании влияния) одного фактора.
Если рассматривается регрессия с числом факторов р, то возможны частные коэффициенты корреляции не только первого, но и второго, третьего.(р — 1) порядка, т. е. влияние фактора
х, можно оценить при разных условиях независимости действия других факторов:
Х2 ~ при постоянном действии фактора х2;
rw*2*3 ~ ПРИ постоянном действии факторов х2 и х3;
г • хэ... х ~ при неизменном действии всех факторов, включенных в уравнение регрессии.
Сопоставление коэффициентов частной корреляции разного порядка по мере увеличения числа включаемых факторов показывает процесс «очищения» зависимости результативного признака с исследуемым фактором.
Например, при изучении зависимости себестоимости добычи угля от объема добычи парный коэффициент корреляции оказался равным —0,75, характеризуя довольно тесную обратную связь признаков. Частный коэффициент корреляции этой зависимости при постоянном влиянии уровня производительности труда составил —0,58 и демонстрирует хотя и достаточную, но уже заметно менее тесную связь себестоимости и объема добычи. Закрепив на постоянном уровне также и размер основных фондов, теснота связи рассматриваемых признаков оказывается еще более низкой, т. е. —0,52.
Хотя частная корреляция разных порядков и может представлять аналитический интерес, в практических исследованиях предпочтение отдают показателям частной корреляции самого высокого порядка, ибо именно эти показатели являются дополнением к уравнению множественной регрессии.
В общем виде при наличии р факторов для уравнения
у = а + Ьх х, + Ь2 • х2 + ... + Ьр • Хр + е коэффициент частной корреляции, измеряющий влияние на у фактора х, при неизменном уровне других факторов, можно определить по формуле
123
(3.23)
где Л2^ ... Х/ х — множественный коэффициент детерминации всего комплекса р факторов с результатом;
ч -*/-1 *ж •••*» ~ тот же показатель детерминации, но без введения в модель фактора xt.
При i = 1 формула коэффициента частной корреляции примет вид:
(3.24)
Данный коэффициент частной корреляции позволяет изме-
рить тесноту связи между у и при неизменном уровне всех других факторов, включенных в уравнение регрессии.
Порядок частного коэффициента корреляции определяется количеством факторов, влияние которых исключается. Напри
мер, ч — коэффициент частной корреляции первого порядка. Соответственно коэффициенты парной корреляции называются коэффициентами нулевого порядка. Коэффициенты частной
корреляции более высоких порядков можно определить через коэффициенты частной корреляции более низких порядков по рекуррентной формуле
(3.25)
При двух факторах и / = 1 данная формула примет вид:
Соответственно при / = 2 и двух факторах частный коэффици-
ент корреляции у с фактором х2 можно определить по формуле
124
(3.27)
Для уравнения регрессии с тремя факторами частные коэффициенты корреляции второго порядка определяются на основе частных коэффициентов корреляции первого порядка. Так, по
уравнению
у = а + • х1 + Ь2 • х2 + Ь3 • х3 + е
возможно исчисление трех частных коэффициентов корреляции второго порядка: р
5«т*|*з’
каждый из которых определяется по рекуррентной формуле.
Например, при / = 1 имеем формулу для расчета гт. а именно
* 1 ?
. - '**1*1 **з*2
**|*Л . ''
(3.28)
2
**э*1
Пример. Предположим, изучается зависимость тиража газеты у от ожидаемого дохода от распродажи газеты х,, количества персонала редакции х2, рейтинга газеты среди других газет, распространяемых в регионе х3. В этом случае матрица парных коэффициентов корреляции составила:
1
^=0,69 I
= 0,58 гхл = 0,46 1
^,=0,55 =0,50 гХЛ=0,41 1
Исходя из этих данных, найдем частные коэффициенты корреляции первого и второго порядка.
Приведем частные коэффициенты корреляции первого порядка зависимости у от xj и х2.
0,69 - 0,58 • 0,46 ^1-0,582)(1-0,462)
= 0,585,
125
т. е. при закреплении фактора х2 на постоянном уровне корреляция у и оказывается более низкой (0,585 против 0,69);
ГУХ1х1
0,58 - 0,69 0,46
= 0,409,
т. е. при закреплении фактора х, на постоянном уровне влияние фактора х2 на у оказывается менее сильным (0,409 против 0,58);
0,69-0,55-0,50
EssssssaansssamsEsssssnsss
(1-0,552)-(1-0,502
= 0,574,
т. е. при закреплении фактора х3 на постоянном уровне влияние фактора х( на у несколько снизилось по сравнению с парной корреляцией (0,574 против 0,69) ввиду некоторой связи факторов х, их3;
5*з ~5*э 0,58-0,55-0,41
ft-'Д,) (1 -) 7(1-0,552) (1-0,412)
= 0,465,
т. е. при закреплении фактора х3 на постоянном уровне влияние на у фактора х2 оказалось несколько менее сильным (0,465 против 0,58);
5*з*>
5*> 5*i '5гзх, _ 0,55—0,69*0,50
7(1-^,)-(1-гДХ|) V(l-0.692) (1-0,502)
= 0,327,
т. е. корреляция фактора х3 с у снизилась при фиксированном влиянии на у фактора х( (0,55 и 0,327);
• - ГуХз
0,55-0,58-0,41
7(l-0,582)(l-0,4l2)
= 0,420,
т. е. при закреплении фактора х2 на постоянном уровне влияние фактора х3 на у оказалось менее значительным (0,420 и 0,55).
Приведем частные коэффициенты корреляции второго порядка.
126
0,585-0,420-0,385
pt| XjX,
= 0,505. 1-0,4202)-(1-3852)
При фиксированном влиянии факторов х2 и х3 корреляция у с X] оказалась еще меньше, чем при частной корреляции первого порядка (при закреплении фактора х2): 0,69; 0,585 и 0,505.
0,409-0327 0,234 = Q 362
рсэ-Х|
УХухЛ
УХух\' V 'XjXjXj
Корреляция фактора х2 с у снизилась до 0,409 при элиминировании фактора х( и до 0,362 при элиминировании двух факторов — xt и х3.
*иь-Х|
ГуХуХ\Х2 I
0,327-0,409-0,234 п_,
1 1, ........1.
'1-0,4092)-(1-2342)
x2xrxt
Корреляция у с х3 снизилась с 0,55 в парной регрессии до 0,327 при закреплении на постоянном уровне фактора х( и до 0,261 при одновременном закреплении на постоянном уровне факторов Х| и х2. Частная корреляция второго порядка зависимости у с факторами х(, х2 и х3 оказалась значительно более низкой — 0,505; 0,362 И 0,261 против 0,69; 0,58 и 0,55 для парной регрессии.
Рассчитанные по рекуррентной формуле частные коэффициенты корреляции изменяются в пределах от — 1 до +1, а по формулам через множественные коэффициенты детерминации — от 0 до 1. Сравнение их друг с другом позволяет ранжировать факторы по тесноте их связи с результатом. Частные коэффициенты корреляции, подтверждая ранжировку факторов по их воздействию на результат, на основе стандартизованных коэффициентов регрессии (/^-коэффициентов) в отличие от последних дают конкретную меру тесноты связи каждого фактора с результатом в чистом виде. Если из стандартизованного уравнения регрессии у Рх[' ?х{ + Рх2 («2 + Рх3 ?х3 следует, что > Рх3> т. е. по
силе влияния на результат порядок факторов таков: х1 , х2, х3, то этот же порядок факторов определяется и по соотношению частных коэффициентов корреляции, г^гЯуз > rm.Х[ХЗ > .X[X2.
Согласованность частной корреляции и стандартизованных коэффициентов регрессии наиболее отчетливо видна из сопоставления их формул при двухфакторном анализе. Для уравнения 127
регрессии в стандартизованном масштабе ?>, = /Зх • tx + /3L • /^-коэффициенты могут быть определены по формулам, вытекающим из решения системы нормальных уравнений:
_ 5«i ГУХ1 ' rxi*i
х> 1-г2
‘ *1*2
. ГУХ1 ~ГУХ) 'Г*1*2
Х1 1-г2
*1*2
(3.29)
Сравнивая их с рекуррентными формулами расчета частных коэффициентов корреляции г чиг„.ч, можно видеть, что
(3.30)
Иными словами, в двухфакторном анализе частные коэффициенты корреляции — это стандартизованные коэффициенты ре
грессии, умноженные на корень квадратный из соотношения до
лей остаточных дисперсий фиксируемого фактора на фактор и на
результат.
В эконометрике частные коэффициенты корреляции обычно не имеют самостоятельного значения. В основном их используют
на стадии формирования модели, в частности в процедуре отсева
факторов. Так, строя многофакторную модель, например, мето
дом исключения переменных, на первом шаге определяется уравнение регрессии с полным набором факторов и рассчитывается матрица частных коэффициентов корреляции. На втором шаге отбирается фактор с наименьшей и несущественной по /-критерию Стьюдента величиной показателя частной корреляции. Исключив его из модели, строится новое уравнение регрессии. Процедура продолжается до тех пор, пока не окажется, что все частные коэффициенты корреляции существенно отличаются от нуля. Если исключен несущественный фактор, то множественные коэффициенты детерминации на двух смежных шагах построения регрессионной модели почти не отличаются друг от друга, т. е. /Гр +1» где р — число факторов.
Из приведенных ранее формул частных коэффициентов корреляции видна связь этих показателей с совокупным коэффициентом корреляции. Зная частные коэффициенты корреляции (последовательно первого, второго и более высокого порядка),
128
можно определить совокупный коэффициент корреляции по формуле
р
(3.31)
При полной зависимости результативного признака от иссле-
дуемых факторов коэффициент совокупного их влияния равен
единице. Из единицы вычитается доля остаточной вариации результативного признака (1 — г2), обусловленная последовательно
включенными в анализ факторами. В результате подкоренное выражение характеризует совокупное действие всех исследуемых
ракторов.
В рассмотренном примере с тремя факторами величина ко-
эффициента множественной корреляции составила:
Ryx х ..л = (1 “(I - 0,692) (1 - 0,4092) • (1 - 0,2612))’/2 = 0,770.
Величина множественного коэффициента корреляции всегда больше (или равна) максимального частного коэффициента корреляции, что имеет место в нашем примере: 0,770 по сравнению с 0,505.
3.8. ОЦЕНКА НАДЕЖНОСТИ РЕЗУЛЬТАТОВ МНОЖЕСТВЕННОЙ РЕГРЕССИИ И КОРРЕЛЯЦИИ
Значимость уравнения множественной регрессии в целом, так же как и в парной регрессии, оценивается с помощью /-критерия Фишера:
Дфакг _ R2 п-т-1
Д>ст 1-Я2 т
(3.32)
где Рфап - факторная сумма квадратов на одну степень свободы;
D,,— — остаточная сумма квадратов на одну степень свободы;
/г - коэффициент (индекс) множественной детерминации;
т — число параметров при переменных х (в линейной регрессии совпадает с числом включенных в модель факторов);
п — число наблюдений.
д- ’525
129
Пример. Предположим, что модель урожайности пшеницы у (ц/га) от количества внесенных минеральных удобрений на 1 га X] (ц) и осадков х2 (мм) характеризуется следующим уравнением:
у = —120 + 0,2 • х1 — 0,008 • х(2 + 0,8 • х2 — 0,001 х22 + е.
При этом сг = 2, л = 30, R = 0,85. Результаты дисперсионного анализа оказываются следующими (табл. 3.1).
Таблица 3.1 Результаты дисперсионного анализа
Источники вариации Число степеней свободы Сумма квадратов, 55
Объяснения за счет регрессии 4 86,7
Остаточная 25 33,3
Общая 29 120,0
Дисперсия на одну степень свободы, D ^факт ^табл (0,05)
21,675 16,27 2,76
1,332 1,00
р
^обш = я •о"у = 30-4= 120;
55^ = 55^ Л2 = 120 0,852 = 86,7;
55^ = 53^ • (1 - /г2) = 53^ - 53^ = 120 - 86,7 = 33,3.
Так как фактическое значение /-критерия при а = 0,05 превышает табличное, то уравнение статистически значимо. Этот же результат получим, воспользовавшись приведенной ранее формулой F-критерия:
0,852 1-0,852
30-4-1
4
= 16,27.
Оценивается значимость не только уравнения в целом, но и фактора, дополнительно включенного в регрессионную модель. Необходимость такой оценки связана с тем, что не каждый фак
тор, вошедший в модель, может существенно увеличивать долю объясненной вариации результативного признака. Кроме того,
при наличии в модели нескольких факторов они могут вводиться
130
в модель в разной последовательности. Ввиду корреляции между факторами значимость одного и того же фактора может быть разной в зависимости от последовательности его введения в модель. Мерой для оценки включения фактора в модель служит частный /’-критерий, т. е. Fx
Частный f-критерий построен на сравнении прироста факторной дисперсии, обусловленного влиянием дополнительно включенного фактора, с остаточной дисперсией на одну степень свободы по регрессионной модели в целом. Предположим, что оцениваем значимость влияния как дополнительно включенного в модель фактора. Используем следующую формулу:
1Хух7...хр П-т-1
1-Я* х 1
(3.33)
где
п
т
- коэффициент множественной детерминации для модели с
полным набором факторов;
— тот же показатель, но без включения в модель фактора Х];
- число наблюдений;
— число параметров в модели (без свободного члена).
Если оцениваем значимость влияния фактора хр после включения в модель факторов х19 х^, то формула частного
/’-критерия примет вид:
п2 __ п2
Лрс(х2...хр Лрс(х2...хр_1 Л —Л! —1
х i
(3.34)
В общем виде для фактора х,- частный f-критерий определится как
1>2 __ п2
_ npct...x/...xp /xpct...x/_lx/+l...xp Л-т-1
~ 1 d2 1
1 ^pct...xp..xp (3.35)
В числителе формул (3.33) — (3.35) показан прирост доли объясненной вариации у за счет дополнительного включения в модель соответствующего фактора:
- прирост за счет X!;
р:|Х2..Хр — p^xj.-Xp-i “ 3® счет Хр,
9*
131
yxi-jc^jcj, yxl..jtl^ixi+l..jcp за счет х;.
В знаменателе доля остаточной вариации по регрессионной модели, включающей полный набор факторов. Если числитель и знаменатель Fx умножить на £(у - у)2 или, что то же самое, на п • (Гу, то получим соотношение прироста факторной (объясненной) суммы квадратов отклонений к остаточной сумме квадратов. Чтобы получить величину F-критерия, необходимо эти сум
мы квадратов отклонений разделить на соответствующее число степеней свободы. Так как прирост факторной суммы квадратов отклонений обусловлен дополнительным включением в модель
одного исследуемого фактора (например, X! или хр), то число степеней свободы для него равно: dj\ = 1. Для остаточной суммы квадратов отклонений по регрессионной модели число степеней
свободы, как уже было рассмотрено ранее, равно: df2-n-m — 1.
Соотношение числа степеней свободы приведено в
стного У-критерия в виде дроби:
Фактическое значение частного F-критерия сравнивается с табличным при 5%-ном или 1%-ном уровне значимости и числе степеней свободы: 1 и п — т — 1. Если фактическое значение Fx. превышает Утабл (a, dj\, df2), то дополнительное включение фактора х,- в модель статистически оправданно и коэффициент чистой регрессии Ь, при факторе х; статистически значим. Если же фактическое значение Fx. меньше табличного, то дополнительное включение в модель фактора х,- не увеличивает существенно долю объясненной вариации признака у, следовательно, нецелесообразно его включение в модель; коэффициент регрессии при данном факторе в этом случае статистически незначим.
С помощью частного У-критерия можно проверить значимость всех коэффициентов регрессии в предположении, что каждый соответствующий фактор х, вводился в уравнение множественной регрессии последним.
Пример. Применим частный У-критерий для оценки значимости коэффициентов регрессии в уравнении множественной регрессии, описывающей зависимость объема продукции у от за
трат труда х, и технической оснащенности производства х2:
у = 20,2 + 2,8 • Х[ + 0,2 • х2 + е.
Частный У-критерий для фактора х( определим по формуле
132
!2 -г2 'ухг
1 ~ RyxtX1
(л-m-l).
В рассматриваемом примере = 0,767, г„. = 0,667, Л — 30, V Я ш г £
т — 2. Соответственно имеем величину Fx..
„ 0,7672 - 0,6672
F.= —-------4----(30 - 2 -1)=9,4.
* 1-0,7672
Табличное значение F-критерия при 5%-ном уровне значимости для числа степеней свободы 1 и 27 равно 4,21. Следовательно, включение в модель фактора х, после фактора х2 статистически оправдано — доля объясненной вариации возросла на 14,3 проц, пункта (0,7672 - 0,6672) • 100. Частный F-критерий для фактора х2 определим как
(л-т-1).
1
В рассматриваемом примере гуХ{ == 0,58. Соответственно получим значение Fxr ’
Таблица 3.2
Дисперсионный анализ для оценки существенности фактора х2
Источники вариации Число степеней свободы Сумма квадратов, SS Дисперсия на одну степень свободы, D ^фвкт ^табл (0,05)
Общая 29 270 1^™ 1^™
Регрессия 2 158,8 79,4 19,3 3,35
Обусловленная X] 1 90,8 90,8 22,0 4,21
Обусловленная х2 при данном
68
68
4,21
Остаточная
27
111,2
4,118
133
0,7672 -0,582 i-0,76т2”
(30-2-1) = 16,52.
Фактическое значение F„ больше табличного, и, следовательно, включение в модель фактора х2 после введения в нее фактора х, весьма значимо — доля объясненной вариации возросла на 25,2 проц, пункта (58,8-33,6 %). Коэффициент регрессии в модели статистически значим.
Значения частных /-критериев получаются в результате дисперсионного анализа. Применительно к нашему примеру результаты дисперсионного анализа представлены в табл. 3.2.
В табл. 3.2 приведены три значения /''-критерия. В первой строке показан общий /'-критерий. Он составил 19,3 и характеризует значимость двухфакторного уравнения регрессии в целом. Вторая величина F — 22,0 характеризует значимость парной регрессии у = а + b • Х( при условии, что остаточная дисперсия совпадает с величиной остаточной дисперсии для множественной регрессии. Влияние фактора х( статистически значимо, так как F = 22,0 больше табличного значения /табл = 4,21. Третье значение F = 16,5 - это Мастный /'-критерий, оценивающий значимость дополнительного включения в модель фактора х2 после введения в нее фактора х(. Его величина совпадает с ранее рассчитанной по формуле частного /-критерия /„.
Табл. 3.2 отличается от таблиц результатов дисперсионного анализа, рассматриваемых ранее (см., например, табл.3.1). В ней источник вариации «регрессия» раскладывается на две составляющие: 1) обусловленная влиянием факторах!; 2) обусловленная дополнительным включением в регрессионную модель фактора х2. Соответственно в нашем примере число степеней свободы за счет регрессии, равное 2, также раскладывается на число степеней свободы для каждого фактора, т. е. 1 для фактора х, и 1 для фактора х2. Сумма квадратов за счет регрессии
— v )2 = У?2 л / « у*и2
• Е(у - Г)2 = 0.7672 • 270 = 158,8
соответственно распадается на две суммы. Сумма квадратов, обусловленная включением в модель факторах/, определяется в предположении, что построено лишь парное уравнение регрессии ух = а + b • Х|. Эта величина может быть рассчитана как г* Е(у - у)2, что применительно к нашим данным составит 90,8
134
(0,582 • 270). Сумму квадратов, обусловленную дополнительным включением фактора х2, после того как в модель включен фактор
х(, определим как разность суммы квадратов за счет регрессии по двум факторам и за счет регрессии только фактора хг Эта величина составит 68 (158,8 - 90,8). Далее по известным уже формулам
определяются значения дисперсии на одну степень свободы и
/-критерий.
Чтобы получить частный /’-критерий для фактора хи необхо
димо рассмотреть другую таблицу дисперсионного анализа, в которой оценивается дополнительный вклад фактора xt после включения в модель фактора х2 (табл. 3.3).
> Таблица 3.3
Дисперсионный анализ для оценки существенности фактора х.
Источники вариации
Число степеней свободы
Сумма квадратов, S
Дисперсия на одну степень свободы, D
/-критерий
Общая 29
Регрессия 2
Обусловленная х2 1
Обусловлен-наях] приданном х2 1
Остаточная 27
270
а
158,8 79,4 19,3
120,1 120,1 29,2
I
38,7 38,7 9,4
111,2 4,118 1
Частный F-критерий для фактора составил, как и ранее, 9,4. Если величина частного F-критерия оказывается меньше табличного значения, то дополнительное включение в модель того или иного фактора нецелесообразно.
Частный /-критерий оценивает значимость коэффициентов чистой регрессии. Зная величину Fx , можно определить и /-критерий для коэффициента регрессии при 1-м факторе, tb , а именно:
- 7^
(3.36)
135
В рассматриваемой модели /-критерий для коэффициентов чистой регрессии составит: л =7м= 3,065 и /^ = 716,5 =4,06, что больше табличного значения /табл = 2,05, и подтверждает статистическую значимость включенных в модель факторов.
Если уравнение содержит больше двух факторов, то соответствующая программа PC дает таблицу дисперсионного анализа, показывая значимость последовательного добавления к уравнению регрессии соответствующего фактора. Так, если рассматривается уравнение
у = а + Ь\ • х, + Ь2 х2 + Ь3 • х3 + е,
то определяются последовательно f-критерий для уравнения с одним фактором Х|, далее F-критерий для дополнительного включения в модель фактора х2, т. е. для перехода от однофакторного уравнения регрессии к двухфакторному, и, наконец, f-критерий для дополнительного включения в модель фактора х3, т. е. дается оценка значимости фактора х3 после включения в модель факторов х, и х2. В этом случае F-критерий для дополнительного включения фактора х2 после xt является последовательным в отличие от F-критерия для дополнительного включения в модель фактора х3, который является частным f-критерием, ибо оценивает значимость фактора в предположении, что он включен в модель последним. С /-критерием Стьюдента связан именно частный f-критерий. Последовательный f-критерий может интересовать исследователя на стадии формирования модели.
Оценка значимости коэффициентов чистой регрессии по /-критерию Стьюдента может быть проведена и без расчета частных f-критериев. В этом случае, как и в парной регрессии, для каждого фактора используется формула
(3-37) ть,
где bj — коэффициент чистой регрессии при факторе xf;
ть. - средняя квадратическая ошибка коэффициента регрессии Ь{.
Для уравнения множественной регрессии
у = а + />, -X, + Ь2 х2 + ... Ьр -хр
средняя квадратическая ошибка коэффициента регрессии может быть определена по следующей формуле:
136
— среднее квадратическое отклонение для признака у;
— среднее квадратическое отклонение для признака xz;
(3.38)
— коэффициент детерминации для уравнения множественной
где пу
f
ух\..лр
регрессии;
- коэффициент детерминации для зависимости фактора xf со всеми другими факторами уравнения множественной регрессии;
п - т — 1 - число степеней свободы для остаточной суммы квадратов
отклонений.
Как видим, чтобы воспользоваться данной формулой, необходимы матрица межфакторной корреляции и расчет по ней соответствующих коэффициентов детерминации х . Так, для уравнения
оценка значимости коэффициентов регрессии Ьь Ь2, Ь3 предполагает расчет трех межфакторных коэффициентов детерминации, а ИМеННО. R xj-xycj’ *2*Х1Х3’ ЯЗ’ЯРЯ’
Вместе с тем, если учесть, что
(3.39)
то можно убедиться, что
(3.40)
На основе соотношения b-t и mbi получим:
137
Продемонстрируем это соотношение на примере двухфакторного уравнения регрессии у = а + • х, + Ь2 • х2. Ранее было по-
казано, что коэффициенты регрессии bt могут быть определены как
где Р, — стандартизованный коэффициент регрессии.
В свою очередь для двухфакторного уравнения регрессии
й У*г
Р1 ,2
1—Г 1 4*2
Соответственно параметр Ьх определится как
yxi 'УХ2
। -2
Данное выражение тождественно расчету параметра Ьх исходя из приведенной формулы bh а именно:
р2 2 гух2
1 _2
Иными словами, имеем тождество
У»| -ус, Ч|1; _
1—г2 «1*2
р2 2
гух2
Справедливость данного равенства легко доказывается, если выразить 7г„ „.через парные коэффициенты корреляции:
Тогда имеем:
138
’2 ~r2
У«1*2 'У*2
:(1-^л) =
Следовательно,
При представлении результатов множественной регрессии наряду с уравнением множественной регрессии и скорректированным коэффициентом множественной корреляции или детерминации принято приводить значения tb .
Пример. При зависимости объема продукции у от затрат труда х( и технической оснащенности х2 результаты регрессии оказались следующими:
у = 20,2 + 20,8 • + 0,2 • х2 + е;
^ = 3,1;/^ = 4,1; Я =0,747.
Практически если фактические значения tb] > 3, то совершенно ясно, что значение коэффициента регрессии статистически достоверно. Уравнение может быть использовано для прогнозирования.
Величина F-критерия, оценивая значимость уравнения регрессии в целом, характеризует одновременно и значимость коэффициента (индекса) множественной корреляции. Вместе с тем оценку существенности коэффициента множественной корреляции можно дать и через сравнение скорректированного коэффициента корреляции с его табличным значением при соответствующем уровне вероятности и числе степеней свободы л — т — 1. Так, при п = 30 и т = 2 фактическое значение R должно превышать 0,368 при 5 %-ном уровне значимости, чтобы можно было считать его значение отличным от нуля с вероятностью 0,95.
139
Аналогично можно оценивать и существенность частных показателей корреляции. Фактическое значение частного коэффициента корреляции сравнивается с табличным значением при а = 0,05 или а = 0,01 и числе степеней свободы к = п — h — 2, где л — число наблюдений, h — число исключенных переменных. Так, если л = 30 и оценивается существенность частного коэффициента корреляции второго порядка (например, г то h = 2 и £ = 26. т
Если h является наивысшим порядком расчета частных коэффициентов корреляции для уравнения регрессии, то практически величина к совпадает с числом степеней свободы для остаточной вариации с л — т — 1. Так, в уравнении у = а + Ьх • Xj + Ьг • х2 + Ь3 х х х3 + с, рассчитанном при л = 30, л — т — 1 = 26. Если же уравнение регрессии дополняется расчетом частных коэффициентов корреляции разных порядков (второго, третьего и т. п.), то
к~ л — h — 2.
Если величина частного f-критерия выше табличного значения, то это означает одновременно не только значимость рассматриваемого коэффициента регрессии, но и значимость частного коэффициента корреляции. Существует взаимосвязь между квадратом частного коэффициента корреляции и частным f-крите-рием, а именно:
1-Я
1-^.х
(3-41)
где ?
р
УЧ ...Хр
— частный коэффициент детерминации фактора xf с у при неизменном уровне всех других факторов;
— доля остаточной вариации уравнения регрессии, включающего все факторы, кроме факторах);
- доля остаточной вариации для уравнения регрессии с полным набором факторов.
Пример. Для рассматриваемой регрессии
у = 20,2 + 20,8 • X! + 0,2 • х2 + е;
= °>51; = О’66^ ^14 = °’767-
Тогда
0,512 •1 ~0’667^ .(30-2-1) = 9,4, 1 - 0,7672
что соответствует ранее определенной величине Fx .
140
Взаимосвязь показателей частного коэффициента корреляции, частного /-критерия и /-критерия Стыодента для коэффициентов чистой регрессии может использоваться в процедуре отбора факторов. Отсев факторов при построении уравнения регрессии методом исключения практически можно осуществлять не только по частным коэффициентам корреляции, исключая на каждом шаге фактор с наименьшим незначимым значением частного коэффициента корреляции, но и по величинам tb -и Fx.. Частный F-критерий широко используется и при построении модели методом включения переменных и шаговым регрессионным методом*.
3.9. ФИКТИВНЫЕ ПЕРЕМЕННЫЕ ВО МНОЖЕСТВЕННОЙ РЕГРЕССИИ
До сих пор в качестве факторов рассматривались экономические переменные, принимающие количественные значения в некотором интервале. Вместе с тем может оказаться необходимым включить в модель фактор, имеющий два или более качественных уровней. Это могут быть разного рода атрибутивные признаки, такие, например, как профессия, пол, образование, климатические условия, принадлежность к определенному региону. Чтобы ввести такие переменные в регрессионную модель, им должны быть присвоены те или иные цифровые метки, т. е. качественные переменные преобразованы в количественные. Такого вида сконструированные переменные в эконометрике принято называть фиктивными переменными. В отечественной литературе можно встретить термин «структурные переменные»* 2.
Рассмотрим применение фиктивных переменных для функции спроса. Предположим, что по группе лиц мужского и женского пола изучается линейная зависимость потребления кофе от цены. В общем виде для совокупности обследуемых уравнение регрессии имеет вид:
у — а + Ь- х + е, где у — количество потребляемого кофе;
х — цена.
'Подробнее о разных методах построения уравнения множественной регрессии см.: Дрейпер Н., Смит Г. Прикладной регрессионный анализ. — С. 172-225.
2См., например: Ерина А.М. Математико-статистические методы изучения экономической эффективности производства. — М.: Финансы и статистика, 1983.
141
Аналогичные уравнения могут быть найдены отдельно для лиц мужского пола: у, — а{ + Ь{ • jq + е, и женского пола: У2 = °2 + ^2 ' *2 + е2-
Различия в потреблении кофе проявятся в различии средних у! и у 2 Вместе с тем сила влияния х на у может быть одинаковой, т. е. Ь » « Ь2. В этом случае возможно построение общего уравнения регрессии с включением в него фактора «пол» в виде фиктивной переменной. Объединяя уравнения yj и у2 и вводя фиктивные переменные, можно прийти к следующему выражению:
у = Д| • Zi + а2 • Z2 + b • х + е,
где z, и z2 — фиктивные переменные, принимающие значения:
1 — мужской пол . О — женский пол ’
О — мужской пол 1 — женский пол '
В общем уравнении регрессии зависимая переменная у рассматривается как функция не только цены х, но и пола (z\, z^. Переменная z рассматривается как дихотомическая переменная, принимающая всего два значения: 1 и 0. При этом когда Z\ -1, то z2 — 0 и, наоборот, при Zi — 0 переменная z2 — 1.
Для лиц мужского пола, когда Zi — 1 и z2 = 0, объединенное уравнение регрессии составит: у = а{ + b • х, а для лиц женского пола, когда Zi — 0 и zi — l,y — а2 + b • х. Иными словами, различия в потреблении для лиц мужского и женского пола вызваны различиями свободных членов уравнения регрессии: # а2. Параметр b является общим для всей совокупности лиц, как для мужчин, так и для женщин.
Следует иметь в виду, что при введении фиктивных переменных Z| и z2 в модель у = • q + д2' ф + ‘ * + 6 применение МНК для оценивания параметров а{ и а2, приведет к вырожденной матрице исходных данных, а следовательно, и к невозможности получения их оценок. Объясняется это тем, что при использовании МНК в данном уравнении появляется свободный член, т. е. уравнение примет вид
у = а, • Zi + а2 • Zi + b • х + А.
Предполагая при параметре А независимую переменную, равную 1, имеем матрицу исходных данных:
142
1 1 0 х(
1 1 О х2
I о 1 х3
1 1 О х4
[1 О 1 х.
В рассматриваемой матрице существует линейная зависимость между первым, вторым и третьим столбцами: первый равен сумме второго и третьего столбцов. Поэтому матрица исходных факторов вырождена. Выходом из создавшегося затруднения может явиться переход к уравнениям
или
У = А + А|-£| + 6- х + е у—А + Л2 z2 + b • х + е,
т. е. каждое уравнение включает только одну фиктивную переменную Z] или Z2-
Предположим, что определено уравнение
у — А + Aj • z, + b х + е, где Z| — принимает значения 1 для мужчин и 0 для женщин.
Теоретические значения размера потребления кофе для мужчин будут получены из уравнения
у = А + А[ + Ь • х.
Для женщин соответствующие значения получим из уравнения
у = А + b • х.
Сопоставляя эти результаты, видим, что различия в уровне потребления мужчин и женщин состоят в различии свободных членов данных уравнений: А — для женщин и А + Aj - для мужчин.
Пример. Проанализируем с использованием фиктивных переменных зависимость урожайности пшеницы у от вида вспашки z и количества внесенного органического удобрения х.
143
По 25 наблюдениям уравнение парной регрессии (без учета вида вспашки) составило:
у « 11,463 + 0,326 • х;
8,7; /А - 11,9; t„ - 2,95; - 0,5246.
Для его расчета использовалась следующая система нормальных уравнений:
Г 25д+ 192-6 = 349,1, 1192-0+1914-6 = 2824,2.
Уравнение регрессии статистически значимо — F, tb, превышают табличные значения: при 5 %-ном уровне существенности и числе степеней свободы 23: F — 4,28; tb — 2,069; — 0,398;
при 1 %-ном уровне значимости: F — 7,88; tb — 2,807;
= 0,507).
По виду вспашки поля характеризовались двумя категориями: зяблевая и весенняя. Вид вспашки не влияет на количество внесенных удобрений, но обусловливает различия в урожайности. Чтобы убедиться в этом, введем в уравнение регрессии фиктивную переменную z для отражения эффекта вида вспашки, а именно: z — 1 для зяблевой вспашки и z — 0 для весенней вспашки. Уравнение регрессии примет вид:
y = a + 6- x + c- z + e.
Применяя метод наименьших квадратов для оценки параметров данного уравнения, получим следующую систему нормальных уравнений:
г
Yly = n-a+b-'£tx+c-'£z,
\ '£.У-х = а-'£1х + Ь-'Ех2 +c'£zx,
V
Ввиду того, что z принимает лишь два значения (1 и 0), Zz — «| (число полей с зяблевой вспашкой), Zx • z — Zxt (количество внесенных удобрений на полях с зяблевой вспашкой), Zz2 “ Zz = Л|, Zy • z = ZVi (суммау по полям зяблевой вспашки).
/
144
В рассматриваемом примере вся совокупность из 25 единиц подразделена на две подгруппы: с зяблевой вспашкой - 13 полей и с весенней — 12 полей, т. е. п} = 13 и п2 = 12. Соответственно разделению на эти две группы имеем:
Ex = Ех, + Ех2 = 99 + 93 = 192;
Еу = ЕУ1 + Еу2 = 199,4 + 149,7 « 349,1.
Тогда система нормальных уравнений примет вид:
25-Д+ 192й + 13-с = 349,1, • 192д+1914й+99с = 2824,2, 13д+ 99-6+13с= 199,4.
Решая ее, получим уравнение регрессии
у « 9,908 + 0,331 • х + 2,908 • z.
Уравнение регрессии статистически значимо: F = 15,6; R = 0,766; R — 0,741; ta — 11,8; tb — 3,9; tc — 4,1.
Как видим, добавление в регрессию фиктивной переменной существенно улучшило результат модели: доля объясненной вариации выросла с 27,5 % (г^ = 0,2752) до 58,7 % ~ 0,5867).
При этом сила влияния количества внесенных органических удобрений на урожайность осталась практически неизменной: коэффициенты регрессии, по существу, одинаковы (0,326 в парном уравнении и 0,331 во множественном). Корреляция между видом вспашки и количеством внесенного удобрения на 1 га практически отсутствует: rxz ~ — 0,016.
Применение зяблевой вспышки способствует росту урожайности в среднем на 2,9 ц с 1 га при одном и том же количестве внесенного удобрения на 1 га, что в целом соответствует и различию средней урожайности по видам вспашки (15,3 ц с 1 га для зяблевой вспашки и 12,5 ц с 1 га для весенней вспашки). Частный F-критерий для фактора z составил 16,58, что выше табличного значения при числе степеней свободы 1 и 22 (4,30 при а — 0,05 и 7,94 при а — 0,01). Это подтверждает целесообразность включения фиктивной переменной в уравнение регрессии.
Уравнения парной регрессии по отдельным видам вспашки показывают, практически единую меру влияния количества внесенного удобрения на урожайность:
10-,8И 145
у = 12,678 + 0,349 -х, R- 0,638 - при зяблевой вспашке;
у = 10,148 + 0,300 • х, R- 0,643 — при весенней вспашке.
Поэтому вполне реально предположить единую меру влияния данного фактора независимо от вида вспашки, что и имеет место в уравнении регрессии с фиктивной переменной. Включив фиктивную переменную, удалось измерить ее влияние на изменение урожайности: частный коэффициент корреляции г„. х, оценивающий в чистом виде влияние данного фактора, составил 0,6555, что несколько выше, чем аналогичный показатель для фактора х, т. е. . z — 0,6385.
Частные уравнения регрессии по отдельным видам вспашки составили:
у(г= |) — 12,816 + 0,331 • х — для зяблевой вспашки;
у(г=0) = 9,908 + 0,331 • х — для весенней вспашки.
Как видим, функция урожайности для первой группы (при z = 1) параллельна функции для второй группы, но сдвинута вверх.
В рассмотренном примере качественный фактор имел только два состояния, которым и соответствовали обозначения 1 и 0. Если же число градаций качественного признака-фактора превышает два, то в модель вводится несколько фиктивных переменных, число которых должно быть меньше числа качественных градаций. Только при соблюдении этого положения матрица исходных фиктивных переменных не будет линейно зависима и возможна оценка параметров модели.
Пример. Проанализируем зависимость цены двухкомнатной квартиры от ее полезной площади. При этом в модель могут быть введены фиктивные переменные, отражающие тип дома: «хрущевка», панельный, кирпичный.
При использовании трех категорий домов вводятся две фиктивные переменные: zl и z2- Пусть переменная zt принимает значение 1 для панельного дома и 0 для всех остальных типов домов; переменная z2 принимает значение 1 для кирпичных домов и 0 для остальных; тогда переменные zf и z2 принимают значения 0 для домов типа «хрущевки».
Предположим, что уравнение регрессии с фиктивными переменными составило:
у == 320 + 500 • х + 2200 • zt + 1600 • z2.
146
Частные уравнения регрессии для отдельных типов домов, свидетельствуя о наиболее высоких ценах квартир в панельных домах, будут иметь следующий вид:
• «хрущевки» — у = 320 + 500 • х;
• панельные — у — 2520 + 500 • х;
• кирпичные — у — 1920 + 500 • х;
Параметры при фиктивных переменных Zi и z2 представляют собой разность между средним уровнем результативного признака для соответствующей группы и базовой группы. В рассматриваемом примере за базу сравнения цены взяты дома «хрущевки», для которых Z\ — z2 — 0. Параметр при Zi - 2200 означает, что при одной и той же полезной площади квартиры цена ее в панельных домах в среднем на 2200 долл. США выше, чем в «хрущевках». Соответственно параметр при z2 показывает, что в кирпичных домах цена выше в среднем на 1600 долл, при неизменной величине полезной площади по сравнению с указанным типом домов.
В отдельных случаях может оказаться необходимым введение двух и более групп фиктивных переменных, т. е. двух и более качественных факторов, каждый из которых может иметь несколько градаций. Например, при изучении потребления некоторого товара наряду с факторами, имеющими количественное выражение (цена, доход на одного члена семьи, цена на взаимозаменяемые товары и др.), учитываются и качественные факторы. С их помощью оцениваются различия в потреблении отдельных социальных групп населения, дифференциация в потреблении по полу, национальному составу и др. При построении такой модели из каждой группы фиктивных переменных следует исключить по одной переменной. Так, если модель будет включать три социальные группы, три возрастные категории и ряд экономических переменных, то она примет вид:
у = а + bt • 5, + Ь2 • s2 + b3 • Zi + ' Ъ + *5 • *! + Ь6 Ъ + - ьк • хк + е,
где у - потребление;
1 — если наблюдения относятся к социальной группе (/ = 1,2), 0 — в остальных случаях;
| 1 - если наблюдения относятся к возрастной группе (I == 1,2), [0 — в остальных случаях;
хь х2,..., хк — экономические (количественные) переменные. 10*
147
Фиктивные переменные широко используются для оценки сезонных различий в потреблении. Учет сезонного фактора при построении динамических моделей рассмотрен в главе 5.
Фиктивные переменные могут вводиться не только в линейные, но и в нелинейные модели, приводимые путем преобразований к линейному виду. Так, модель с фиктивными переменными может иметь вид: '
1пу = а + Ь{ • х, + ... + Ьр • хр + с • z + е,
где z — фиктивная переменная.
Целесообразность такого вида модели диктуется характером связи между экономическими переменными:
у — а • bf1 Ь/2... ЬрР е.
Фиктивная переменная вводится в эту модель как очередной сомножитель:
у — а • ft*1 • b/2... bpt • с7 • е.
Логарифмируя данное выражение, получим модель вида
Iny я Inn + • Inft] + х2 * Inftj +... + Хр • Inft^ + z • Inc + Ine, которая равносильна приведенной ранее
Iny == а + ft] • X] + ... + Ьр • Хр + с • z + е, где параметры и случайная составляющая представлены в логарифмах.
Включение в модель фиктивных переменных может иметь цель отразить в модели неоднородность совокупности. Однако нельзя рассматривать фиктивные переменные как панацею при применении методов регрессии к неоднородным данным.
Пример. Рассмотрим зависимость среднего уровня квалификации рабочих от сферы применения ручного труда. Если неоднородность вызвана резкими качественными различиями единиц совокупности, обусловливающими искажения характера рассматриваемой связи признаков у и х, то фиктивные переменные мало изменят результаты анализа. В этом случае более результативным является построение уравнений регрессии по отдельным группам совокупности (табл.3.4).
148
Таблица 3.4
Зависимость среднего уровня
алйфикации рабочих у
от сферы применения ручного труда х
Исследуемая совокупность
Уравнение регрессии
Общая совокупность
в том числе
с включением фиктивной переменной по видам технологий:
Z = 1 — прогрессивная
Z = 0 — традиционная
у =4,2 + 0,01%
г
0,016
у =4,4 + 0,01-%-0,4-г 0,220
Частная совокупность:
а) по заводам с традиционной технологией
б) по заводам с прогрессивной технологией
’• I1
у= 1,6 + 0,08-х
0,941
у =6,8-0,06-х
0,692
Результаты свидетельствуют о целесообразности построения модели по отдельным частным совокупностям. Ввиду разной зависимости уровня квалификации рабочих от уровня занятости ручным трудом по заводам с традиционной и прогрессивной технологиями производства уравнение регрессии по совокупности в целом не позволило выявить наличие связи. Не улучшился результат модели и с введением фиктивной переменной, ибо этот метод предполагает равенство коэффициентов регрессии при х по частным совокупностям и возможность их замены общим коэффициентом регрессии Ь.
До сих пор мы рассматривали фиктивные переменные как факторы, которые используются в регрессионной модели наряду с количественными переменными. Вместе с тем возможна регрессия только на фиктивных переменных. Например, изучается дифференциация заработной платы рабочих высокой квалификации по регионам страны. Модель заработной платы может иметь вид:
у = а + Ь\ • Zt + b2 • z2 + - Ьк • Zk,
где у — средняя заработная плата рабочих высокой квалификации по отдельным предприятиям;
1 — если предприятие находится в Северо-Западном районе
0 — если предприятие находится в остальных районах;
149
1 — если предприятие находится в Волго-Вятском районе, О — если предприятие находится в остальных районах;
1 — если предприятие находится в Дальневосточном районе, О — если предприятие находится в остальных районах.
Поскольку последний район, указанный в модели, обозначен Zic, то в исследование включено к + 1 район.
Ввиду того, что факторы данной регрессионной модели выражены как дихотомические признаки, параметры модели имеют свою специфику по сравнению с традиционной их интерпретацией. Параметр а представляет собой среднее значение результативного признака для базовой группы j70. Параметр bt характеризует разность средних уровней результативного признака для группы 1 и базовой группы 0. Соответственно параметр /*, Представляет собой разность между У,- и Уо. Иными словами, коэффициенты при z отражают величину эффекта соответствующей группы фактора z- Рассмотрим применение данной модели на следующем условном примере (табл.3.5).
Таблица 3.5
Распрострапеппость ручного труда па предприятиях одной отрасли в зависимости от уровня автоматизации производства
Уровень автоматизации производства Число заводов Процент рабочих ручного труда в общей численности рабочих
на каждом заводе данной группы в среднем по группе
Высокий 8 31, 37, 38, 39, 35, 35,0 32, 34, 34 Средний 12 40, 45, 47, 48, 46, 46,5 48, 50, 52, 39, 43, 44,56 Низкий 10 47, 54, 59, 55, 57, 56,6 56,65, 57, 55,61
Итого 30 46,8
По данным этой таблицы рассматривается следующая регрессионная модель:
у - а + bt • zt + Ьг • z2, где у — процент рабочих ручного труда в общей численности рабочих;
z — уровень автоматизации производства;
150
_ г 1 — для предприятий с высоким уровнем автоматизации
~ | производства, Л
t 0 - для остальных предприятий;
fl- для предприятий со средним уровнем автоматизации
z2 “ производства,
О - для остальных предприятий.
В качестве базовой группы, с которой ведется сравнение уровня занятости ручным трудом, выступают предприятия с низким уровнем автоматизации производства.
Регрессионная модель, исходя из средних уровней, приведенных в последней графе табл. 3.5, составит:
у = 56,6 -21,6 • — 10,1 -
Она показывает, что на предприятиях с низким уровнем автоматизации производства средний процент рабочих ручного труда равен 56,6. На предприятиях с высоким уровнем автоматизации производства распространенность ручного труда ниже на 21,6 проц, пункта (У| —у0 =35 —56,6 = — 21,6), а на предприятиях со средним уровнем автоматизации производства — ниже на 10,1 проц, пункта (у2 — у0= 46,5 — 56,6 = — 10,1) по сравнению с предприятиями третьей группы.
В справедливости данного уравнения регрессии можно убедиться, обратившись к методу наименьших квадратов. Применяя МНК, система нормальных уравнений составит:
YIy = n a+bl
£y-Zi =a ^Zt -ZZi +1^-Y.ZiZ2, ^yZi^a-ZZi + bi-^ZiZi+bi-Zzl-
Поскольку переменные z принимают лишь два значения — 1 или 0, в данной системе имеем следующие равенства:
Соответственно система нормальных уравнений составит:
30о+ +12*2 =1404,
8«+ 8-Л| =280,
12в+ 12^=558.
151
Решая систему, получим: а = 56,6; Ьх = — 21.6; Ь2 = —10.1. Уравнение регрессии, как было показано ранее, примет вид:
у = 56,6 - 21,6 •?!- 10,1 z2.
Индекс детерминации для данной модели составит:
ТХу-у)1
513,4
2588,8
= 0,802,
что статистически значимо: f-критерий = 54,6 при а = 0,05 и при степенях свободы 2 и 27, Fn(M = 3,35.
Поскольку коэффициенты при фиктивных переменных в модели, не содержащей других экономических факторов, характеризуют величину эффектов z-го уровня фактора z, то регрессионная модель по своему содержанию тождественна дисперсионной модели. В основе нашего примера лежит дисперсионная модель вида
Уу = У + Ъ +
где у у - у-е наблюдение результативного признака на/-м уровне исследуемого фактора (в примере i - 1, 2, 3;у == 1,30);
У - среднее значение результативного признака в целом по совокупности (в примере у = 46,8);
7} — эффект, обусловленный /-м уровнем фактора (у, - у);
Ъу - случайная ошибка в у-м наблюдении на /-м уровне изучаемого фактора; величина, на которую фактический уровень результативного признака ^отличается от его среднего значения для /-го уровня фактора, т. е.
е</ = У у - (У + ?]) или zv = у у - у,.
1Г J L
В регрессионной модели обычно е; = у,- — у, но так как фиктивная переменная принимает только два значения, то у = у
Так, подставляя в уравнение регрессии z, = 1, = 0, получим у । = у 1 = 35 для каждого завода первой группы по уровню автома
тизации производства, что является средней величиной для данной группы (см. табл. 3.5). Соответственно подставляя в уравнение регрессии Zi = 0, z2 = 1, получим: у2 = У2 = 46,5.
Ввиду того что теоретические значения результативного при-
знака в рассматриваемой модели представляют собой групповые средние (у, = у,), то общая сумма квадратов отклонений Ё(у - у )2
раскладывается на одни и те же составляющие как в регрессион-
152
ном, так и в дисперсионном анализе. Так, для дисперсионного анализа имеем:
ШУУ-У)2 № № / J
= -у)2
i
YL<y,j-y,>2 ' j
Общая сумма квадратов
Факторная сумма квадратов
Остаточная сумма квадратов
Для регрессионной модели данное равенство примет следующий вид:
EU-7)2 /
Общая сумма квадратов
Е(у-у)2
/
Факторная сумма квадратов
Z(y,-y)2
i
Остаточная сумма квадратов
Но так как у, = у,, то факторная и остаточная суммы квадратов, найденные по регрессионной модели и по модели дисперсионного анализа, совпадают (табл. 3.6).
Таблица 3.6
Результаты однофакторного дисперсионного анализа (двухфакторной регрессионной модели с фиктивными переменными)
Источники вариации
Число степеней свободы
Сумма квадратов, 55*
Дисперсия на одну степень свободы, D
/’-отношение
фактиче- табличное, ское а = 0,05
Различия между уровнями фактора (за *
счет регрессии) 2 2075,4 1037,7 54,6 3,35
Различия внутри фактора (остаточная) 27 513,4 19,0 1
Общая 29 2588,8 -
153
Мы рассмотрели модели с фиктивными переменными, в которых последние выступают факторами. Может возникнуть необходимость построить модель, в которой дихотомический признак играет роль результата. Подобного вида модели применяются, например, при обработке данных социологических опросов. В качестве зависимой переменной у рассматриваются ответы на вопросы, данные в альтернативной форме: «да» или «нет». Поэтому зависимая переменная имеет два значения: 1, когда имеет место ответ «да», и 0 — во всех остальных случаях. Модель такой зависимой переменной имеет вид:
а + Л1 • *1 +... + Ьр • хр + е.
Модель является вероятностной линейной моделью. В ней у принимает значения 1 и 0, которым соответствуют вероятности р и 1 — р. Поэтому при решении модели находят оценку условной вероятности события у при фиксированных значениях х. Для
оценки параметров линейно-вероятностной модели применяются методы Logit-, Probit- и Tobit-анализа1. Такого рода модели используют при работе с неколичественными переменными. Как
правило, это модели выбора из заданного набора альтернатив. Зависимая переменная у представлена дискретными значениями (набор альтернатив), объясняющие переменные х- — характеристики альтернатив (время, цена), Zj — характеристики индивидов (возраст, доход, уровень образования). Модель такого рода позволяет предсказать долю индивидов в генеральной совокупности, которые выбирают данную альтернативу. Рассмотрение этих мо
делей выходит за рамки нашего учебника.
Среди моделей с фиктивными переменными наибольшими
прогностическими возможностями обладают модели, в которых
зависимая переменная у рассматривается как функция ряда эко
номических факторов Xj и фиктивных переменных Z,- Последние обычно отражают различия в формировании результативного
признака по отдельным группам единиц совокупности, т. е. в результате неоднородной структуры пространственного или вре
менного характера.
См., например: Аптон Г. Анализ таблиц сопряженности. - Пер. с англ. — М.: Статистика, 1982.
154
з.ю. предпосылки МЕТОДА наименьших КВАДРАТОВ
При оценке параметров уравнения регрессии применяется метод наименьших квадратов (МНК). При этом делаются определенные предпосылки относительно случайной составляющей е. В модели
у = а + bf • х{ + Ь2 • х2 + ... + Ь„ • хр + е
случайная составляющая е представляет собой ненаблюдаемую величину. После того как произведена оценка параметров модели, рассчитывая разности фактических и теоретических значений результативного признака у, можно определить оценки случайной составляющей у — ух. Поскольку они не есть реальные случайные остатки, их можно считать некоторой выборочной ре
ализацией неизвестного остатка заданного уравнения, т. е. е;.
При изменении спецификации модели, добавлении в нее но-
вых наблюдений выборочные оценки остатков е,- могут меняться. Поэтому в задачу регрессионного анализа входит не только построение самой модели, но и исследование случайных отклонений
е„ т. е. остаточных величин.
В предыдущих разделах мы останавливались на формальных проверках статистической достоверности коэффициентов регрессии и корреляции с помощью /-критерия Стьюдента, /'-критерия Фишера и Z-преобразования (для коэффициентов корреляции). При использовании этих критериев делаются предположения относительно поведения остатков е, — остатки представляют собой независимые случайные величины и их среднее значение равно 0; они имеют одинаковую (постоянную) дисперсию и подчиняются нормальному распределению.
Статистические проверки параметров регрессии, показателей корреляции основаны на непроверяемых предпосылках распределения случайной составляющей е,-. Они носят лишь предварительный характер. После построения уравнения регрессии проводится проверка наличия у оценок е,- (случайных остатков) тех свойств, которые предполагались. Связано это с тем, что оценки параметров регрессии должны отвечать определенным критериям. Они должны быть несмещенными, состоятельными и эффективными. Эти свойства оценок, полученных по МНК, имеют чрезвычайно важное практическое значение в использовании ре
зультатов регрессии и корреляции.
155
Коэффициенты регрессии, найденные исходя из системы нормальных уравнений, представляют собой выборочные оценки характеристики силы связи. Их несмещенность является желательным свойством, так как только в этом случае они могут иметь практическую значимость. Несмещенность оценки означает, что математическое ожидание остатков равно нулю. Следовательно, при большом числе выборочных оцениваний остатки не будут накапливаться и найденный параметр регрессии bt можно рассматривать как среднее значение из возможного большого количества несмещенных оценок. Если оценки обладают свойством несмещенности, то их можно сравнивать по разным исследованиям.
Для практических целей важна не только несмещенность, но и эффективность оцЬнок. Оценки считаются эффективными, если они характеризуются наименьшей дисперсией. Поэтому несмещенность оценки должна дополняться минимальной дисперсией. В практических исследованиях это означает возможность перехода от точечного оценивания к интервальному.
Степень реалистичности доверительных интервалов параметров регрессии обеспечивается, если оценки будут не только несмещенными и эффективными, но и состоятельными. Состоятельность оценок характеризует увеличение их точности с увеличением объема выборки. Большой практический интерес представляют те результаты регрессии, для которых доверительный интервал ожидаемого значения параметра регрессии bt имеет предел значений вероятности, равный единице. Иными словами, вероятность получения оценки на заданном расстоянии от истинного значения параметра близка к единице.
Указанные критерии оценок (несмещенность, состоятельность, эффективность) обязательно учитываются при разных способах оценивания. Метод наименьших квадратов строит оценки регрессии на основе минимизации суммы квадратов остатков. Поэтому очень важно исследовать поведение остаточных величин регрессии е,. Условия, необходимые для получения не-- смещенных, состоятельных и эффективных оценок, представляют собой предпосылки МНК, соблюдение которых желательно для получения достоверных результатов регрессии.
Исследования остатков £, предполагают проверку наличия следующих пяти предпосылок МНК:
• случайный характер остатков;
• нулевая средняя величина остатков, не зависящая от %,;
• гомоскедастичностъ — дисперсия каждого отклонения ez одинакова для всех значений х;
156
• отсутствие автокорреляции остатков. Значения остатков б, распределены независимо друг от друга;
• остатки подчиняются нормальному распределению.
В тех случаях, когда все пять предпосылок выполняются, оценки, полученные по МНК и по методу максимального правдоподобия, совпадают между собой. Если распределение случайных остатков б,- не соответствует некоторым предпосылкам МНК, то следует корректировать модель.
Прежде всего проверяется случайный характер остатков е( — первая предпосылка МНК.
С этой целью стоится график зависимости остатков б,- от теоретических значений результативного признака (рис. 3.2).
Если на графике получена горизонтальная полоса, то остатки
£; представляют собой случайные величины и МНК оправдан, те
оретические значения ух хорошо аппроксимируют фактические
значения у.
Возможны следующие случаи: если s, зависит отух, то: • остатки Б, не случайны (рис. 3.3а);
157
в
Рис.3.3. Зависимость случайных остатков е, от теоретических значений ух
• остатки с,- не имеют постоянной дисперсии (рис. 3.3 в);
• остатки Б,- носят систематический характер (рис. 3.3 б), в данном случае отрицательные значения б, соответствуют низким значениям ух, а положительные — высоким значениям.
В случаях а), б), в) (рис. 3.3) необходимо либо применять другую функцию, либо вводить дополнительную информацию и за
ново строить уравнение регрессии до тех пор, пока остатки б,- не
будут случайными величинами.
Вторая предпосылка МНК относительно нулевой средней величины остатков означает, что Е(у - Ух) = 0. Эго выполнимо для линейных моделей и моделей, нелинейных относительно вклю
чаемых переменных. Для моделей, нелинейных по оцениваемым
параметрам и приводимых к линейному виду логарифмировани
ем, средняя ошибка равна нулю для логарифмов исходных дан
ных. Так, для модели вида
у = а • • х2 *2 ... ХрР • Б, Е(1пу — 1пух) = 0.
158
Вместе с тем несмещенность оценок коэффициентов регрессии, полученных МНК, зависит от независимости случайных ос
татков и величин х, что также исследуется в рамках соблюдения второй предпосылки МНК. С этой целью наряду с изложенным
графиком зависимости остатков а от теоретических значений результативного признака ух строится график зависимости случайных остатков е от факторов, включенных в регрессию х,- (рис. 3.4).
E't
2 “ ф ф
1-- • • •
о------1—•—|-------(——♦----------1——|-----►
2 4 6 8 10 12 X;
-2- * •
Рис. 3.4. Зависимость случайных остатков от величины фактора х.
Если остатки на графике расположены в виде горизонтальной полосы (см. рис. 3.4), то они независимы от значений х-. Если же график показывает наличие зависимости 8,- и ху, то модель неадекватна. Причины неадекватности могут быть разные. Возможно, что нарушена третья предпосылка МНК и дисперсия остатков не постоянна для каждого значения фактора ху. Может быть неправильна спецификация модели и в нее необходимо ввести дополнительные члены от ху-, например х-, или преобразовать значения у. Скопление точек в определенных участках значений фактора ху говорит о наличии систематической погрешности модели.
Корреляция случайных остатков с факторными признаками позволяет проводить корректировку модели, в частности использовать кусочно-линейные модели1.
Предпосылка о нормальном распределении остатков позволяет проводить проверку параметров регрессии и корреляции с помощью критериев t, F. Вместе с тем оценки регрессии, найденные с применением МНК, обладают хорошими свойствами даже при отсутствии нормального распределения остатков, т. е. при нарушении пятой предпосылки МНК.
См. подробно: Статистическое моделирование и прогнозирование: Учеб, пособие / Под ред. А. Г. Гранберга. — М.: Финансы и статистика, 1990. - С. 158.
159
Совершенно необходимым для получения по МНК состоятельных оценок параметров регрессии является соблюдение тре
тьей и четвертой предпосылок.
В соответствии с третьей предпосылкой МНК требуется, чтобы дисперсия остатков была гомоскедастичной. Это значит, что
для каждого значения фактора х остатки е,- имеют одинаковую дисперсию. Если это условие применения МНК не соблюдается,
то имеет место гетероскедастичность. Наличие гетероскедастич-ности можно наглядно видеть из поля корреляции (рис. 3.5).
Рис. 3.5. Примеры гетероскедастичности:
а — дисперсия остатков растет по мере увеличения х; б — дисперсия остатков достигает максимальной величины при средних значениях переменной х и уменьшается при минимальных
и максимальных значениях х;
в — максимальная дисперсия остатков при малых значениях х и дисперсия остатков однородна по мере увеличения значений х
160
Гомоскедастичность остатков означает, что дисперсия остатков б(- одинакова для каждого значения х. Используя трехмерное изображение, получим следующие графики, иллюстрирующие гомо- и гетероскедастичность (рис. 3.6, 3.7).
Не) А
Рис. 3.6. Гомоскедастичность остатков Не) А
Рис. 3.7. Гетероскедастичность остатков
1 "1525
161
Рис. 3.6 показывает, что для каждого значения xt распределения остатков е,- одинаковы в отличие от рис. 3.7, где диапазон варьирования остатков меняется с переходом от одного значения Xj к другому. Соответственно на рис. 3.7 демонстрируется неодинаковая дисперсия е,- при разных значениях х,.
Наличие гомоскедастичности или гетероскедастичности можно видеть и по рассмотренному выше графику зависимости остатков б(- от теоретических значений результативного признака Так, для рис. 3.5 а) зависимость остатков отух представлена на рис. 3.8.
Рис. 3.8. Гетероскедастичность: большая дисперсия е, для больших значений ух
Соответственно для зависимости, изображенной на полях корреляции рис. 3,5 б) и в), гетероскедастичность остатков представлена на рис. 3.9 и 3.10.
Для множественной регрессии данный вид графиков является наиболее приемлемым визуальным способом изучения гомо-и гетероскедастичности.
162
Рис. 3.9. Гетероскедастичность, соответствующая полю корреляции рис. 3.5 б)
Рис. 3.10. Гетероскедастичность, соответствующая полю корреляции рис. 3.5 в)
II*
163
Наличие гетероскедастичности может в отдельных случаях привести к смещенности оценок коэффициентов регрессии, хотя несмещенность оценок коэффициентов регрессии в основном зависит от соблюдения второй предпосылки МНК, т. е. независимости остатков и величин факторов. Гетероскедастичность будет' сказываться на уменьшении эффективности оценок bt. В частности, становится затруднительным использование формулы стандартной ошибки коэффициента регрессии ть , предполагающей единую дисперсию остатков для любых значений фактора. Практически при нарушении гомоскедастичности мы имеем неравенства:
и можно записать
При этом величина К(- может меняться при переходе от одного значения фактора xt к другому. Это означает, что сумма квадратов отклонений для зависимости
при наличии гетероскедастичности должна иметь вид:
гетеро
При минимизации этой суммы квадратов отдельные ее слагаемые взвешиваются: наблюдениям с наибольшей дисперсией придается пропорционально меньший вес. Иными словами, вклад каждого сочетания \ с в сумму квадратов остатков должен быть дисконтирован, чтобы учесть систематическое влияние неоднородных элементов К/.
Задача состоит в том, чтобы определить величину К,- и внести поправку в исходные переменные. С этой целью рекомендуется использовать обобщенный метод наименьших квадратов1, который эквивалентен обыкновенному МНК, примененному к преобразованным данным. Чтобы убедиться в необходимости использования обобщенного МНК, обычно не ограничиваются визуальной проверкой гетероскедастичности, а проводят ее эмпирическое подтверждение.
’См.: Джонстон Дж. Эконометрические методы. — С. 207—241.
164
При малом объеме выборки, что наиболее характерно для эконометрических исследований, для оценки гетероскедастич-ности может использоваться метод Гольдфельда - Квандта, разработанный в 1965 г. Гольдфельд и Квандт рассмотрели однофакторную линейную модель, для которой дисперсия остатков возрастает пропорционально квадрату фактора. Чтобы оценить нарушение гомоскедастичности, они предложили параметрический тест, который включает в себя следующие шаги.
1. Упорядочение п наблюдений по мере возрастания переменной х.
2. Исключение из рассмотрения С центральных наблюдений; при этом (л — С): 2 > р, где р — число оцениваемых параметров.
Таблица 3.7
Поступление доходов в консолидированный бюджет Санкт-Петербурга (у — млрд руб.) в зависимости от численности работающих на крупных и средних предприятиях (х —тыс. чел.) экономики районов за 1994 г.*
№ п/п
Районы города
1 Павловский 3
2 Кронштадт 6
3 Ломоносовский 8
4 Курортный 18
5 Петродворец 20
6 Пушкинский 23
7 Красносельский 39
8 Приморский 49
9 Колпинский 60
10 Фрунзенский 74
11 Красногвардейский 79
12 Василеостровский 95
13 Невский 106
4,4 -1,0 5,4
8,1 2,5 5,6
12,9 4,9 8,0
20,8 16,6 4,2
15,5 19,0 -3,5
28,8 22,5 6,3
37,5 41,4 —3,9
48,7 53,2 -4,5
68,6 66,1 2,5
14 Петроградский 112
15 Калининский 115
16 Выборгский 125
17 Кировский 132
18 Московский 149
19 Адмиралтейский 157
20 Центральный________282
Итого 1652
104,6 82,6 22,0
90,5 88,5 2,0
88,3 107,4 -19,1
132,4 120,4 12,0
122,0 127,4 -5,4
99,1 131,0 -31,9
114,2 142,7 -28,5
150,6 151,0 -0,4
156,1 171,0 -14,9
209,5 180,5 29,0
342,9__________327,8________15,1
1855,5 1855,5 0,0
'За строками цифр. — СПб, 1995. — С. 141—145.
165
3. Разделение совокупности из (л - С) наблюдений на две группы (соответственно с малыми и большими значениями фактора х) и определение по каждой из групп уравнений регрессии.
4. Определение остаточной суммы квадратов для первой (5,) и второй (52) групп и нахождение их отношения: R = 5,: S2.
При выполнении нулевой гипотезы о гомоскедастичности отношение R будет удовлетворять f-критерию с (л — С — 2р): 2 степенями свободы для каждой остаточной суммы квадратов. Чем больше величина R превышает табличное значение F-критерия, тем более нарушена предпосылка о равенстве дисперсий остаточных величин.
Пример. Рассмотрим табл. 3.7.
В соответствии с уравнением
ух = —4,565 + 1,178-х (г = 0,9828, F= 510,7) найдены теоретические значения ух и отклонения от них фактических значений у, т. е. е(. Итак остаточные величины е(- обнаруживают тенденцию к росту по мере увеличения х и у (рис. 3.11).
166
Этот вывод подтверждается и по критерию Гольдфельда — Квандта. Для его применения необходимо определить сначала число исключаемых центральных наблюдений С. Из экспериментальных расчетов, проведенных авторами метода для случая одного фактора, рекомендовано при п а 30 принимать С = 8, а при п = 60 — соответственно С = 16. В рассматриваемом примере при п - 20 было отобрано С = 4. Тогда в каждой группе будет по 8 наблюдений [(20 - 4): 2]. Результаты расчетов представлены в табл. 3.8.
Таблица 3.8
Проверка линейной регрессии ив гетероскедастичность
Уравнения регрессии У А Ух £ б2
1 -я группа с 3 4,4 5,7 -1,3 1,69
первыми 8 6 8,1 8,5 -0,4 0,16
районами: 8 12,9 10,3 2,6 6,76
= 2,978+ 18 20,8 19,6 1,2 1,44
+0,921х 20 15,5 21,4 —5,9 34,81
г = 0,979 23 28,8 24,2 4,6 21,16
F= 136,4 39 37,5 38,9 -1,4 1,96
49 48,7 48,1 0,6 0,36
68,34
Сумма
2-я группа с последними 8 районами: ух = 31,142-J + 1,338х г « 0,969
106
112
125
132
149
157
132,4
122,0
99,1
114,2
150,6
156,1
209,5
342,9
110,7 118,7
122,7 136,1
145,4 168,2
178,9 346,1
30,6
470,89
10,89
556,96
479,61
27,04 146,41 936,36
10,24
Сумма
2638,40
Величина R = 2638,4 : 68,34 == 19,3, что превышает табличное значение F-критерия 4,28 при 5 %-ном и 8,47 при 1 %-ном уровне значимости для числа степеней свободы 6 для каждой остаточной суммы квадратов ((20 - 4 — 2 • 2): 2), подтверждая тем самым наличие гетероскедастичности.
167
При построении регрессионных моделей чрезвычайно важно соблюдение четвертой предпосылки МНК — отсутствие автокорреляции остатков, т. е. значения остатков е,- распределены независимо друг от друга. Автокорреляция остатков означает наличие корреляции между остатками текущих и предыдущих (последующих) наблюдений. Коэффициент корреляции между е, и где е; — остатки текущих наблюдений, s., — остатки предыдущих наблюдений (например,у = / - 1), может быть определен как
COV(E,-,£y)
т. е. по обычной формуле линейного коэффициента корреляции. Если этот коэффициент окажется существенно отличным от нуля, то остатки автокоррелированы и функция плотности вероятности Г(е) зависит оту-й точки наблюдения и от распределения значений остатков в других точках наблюдения.
Для регрессионных моделей по статической информации автокорреляция остатков может быть подсчитана, если наблюдения упорядочены по фактору х, как это имеет место в табл.3.7. Коэффициент автокорреляции остатков может быть найден по следующим рядам данных (л = 19):
5,6 8 4,2 -3,5 6,3 -14,9 29,0 15,1
Е/-1 5,4 5,6 8 4,2 -3,5 -0,4 -14,9 29,0
Учитывая, что
cov(e,,£,_,)=£/£“[ - £“,=924,99:19—(—0,2842) (-0,7947) = 48,4578.
az. = 15,1347, _ [ = 14,7663, получим:
ге. гЕ. = 0,2168, что при 17 степенях свободы явно незначимо (г-отношение < 1) и демонстрирует отсутствие автокорреляции
остатков.
Отсутствие автокорреляции остаточных величин обеспечивает состоятельность и эффективность оценок коэффициентов регрессии. Особенно актуально соблюдение данной предпосылки МНК при построении регрессионных моделей по рядам динами
ки, где ввиду наличия тенденции последующие уровни динами
ческого ряда, как правило, зависят от своих предыдущих уров
ней. О специфике исследования остаточных величин по регрес
сионным моделям по временным рядам (см. п. 6.4).
168
Наряду с предпосылками МНК как метода оценивания параметров регрессии при построении регрессионных моделей должны соблюдаться определенные требования относительно переменных, включаемых в модель. Они были рассмотрены ранее при решении проблемы отбора факторов. Это прежде всего требование относительно числа факторов модели по заданному объему наблюдений (отношение 1 к 6—7). Иначе параметры регрессии оказываются статистически незначимыми. В общем виде применение МНК возможно, если число наблюдений п превышает чис
ло оцениваемых параметров т, т. е. система нормальных уравне
ний имеет решение только тогда, когда п>т.
Чрезвычайно важным является и требование относительно матрицы исследуемых факторов. Она должна быть свободна от мультиколлинеарности. Во множественной регрессии предпола
гается, что матрица факторов представляет собой невырожден
ную матрицу, определитель которой отличен от нуля. Наличие мультиколлинеарности мозйет исказить правильную экономиче
скую интерпретацию параметров регрессии (см. п. 3.2).
При несоблюдении основных предпосылок МНК приходится
корректировать модель, изменяя ее спецификацию, добавлять
(исключать) некоторые факторы, преобразовывать исходные данные для того, чтобы получить оценки коэффициентов регрессии, которые обладают свойством несмещенности, имеют мень
шее значение дисперсии остатков и обеспечивают в связи с этим более эффективную статистическую проверку значимости параметров регрессии. Этой цели, как уже указывалось, служит и применение обобщенного метода наименьших квадратов, к рассмотрению которого мы и переходим в п. 3.11.
3.11. ОБОБЩЕННЫЙ МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
При нарушении гомоскедастичности и наличии автокорреляции ошибок рекомендуется традиционный метод наименьших квадратов (известный в английской терминологии как метод OLS — Ordinary Least Squares) заменять обобщенным методом, т. е. методом GLS (Generalized Least Squares).
Обобщенный метод наименьших квадратов применяется к преобразованным данным и позволяет получать оценки, которые обладают не только свойством несмещенности, но и имеют мень
169
шие выборочные дисперсии. Специфика обобщенного МНК применительно к корректировке данных при автокорреляции остатков будет рассмотрена далее. Здесь остановимся на использовании обобщенного МНК для корректировки гетероскедастичности.
Как и раньше, будем предполагать, что среднее значение остаточных величин равно нулю. А вот дисперсия их не остается неизменной для разных значений фактора, а пропорциональна величине Kt, т. е.
где ст2 - дисперсия ошибки при конкретном Лм значении фактора;
<г - постоянная дисперсия ошибки при соблюдении предпосылки о гомоскедастичности остатков;
К — коэффициент пропорциональности, меняющийся с изменением величины фактора, что и обусловливает неоднородность дисперсии.
При этом предполагается, что о2 неизвестна, а в отношении величины К выдвигаются определенные гипотезы, характеризующие структуру гетероскедастичности.
В общем виде для уравнения
yt = а + b • X/ + а,- при о2^ = о2 • К„
модель примет вид:
y^a+Pi-Xi+JKfEj.
В ней остаточные величины гетероскедастичны. Предполагая в них отсутствие автокорреляции, можно перейти к уравнению с гомоскедастичными остатками, поделив все переменные, зафиксированные в ходе /-го наблюдения на '{К,. Тогда дисперсия остатков будет величиной постоянной, т. е. <г = о2.
Иными словами, от регрессии у по х мы перейдем к регрессии на новых переменных: у/4к и х/4к .
Уравнение регрессии примет вид:
170
Исходные данные для данного уравнения будут иметь вид:
*1
Уп
Хп
По отношению к обычной регрессии уравнение с новыми,
преобразованными переменными представляет собой взвешенную регрессию, в которой переменные у и х взяты с весами \/4к.
Оценка параметр
в нового уравнения с преобразованными
переменными приводит к взвешенному методу наименьших квадратов, для которого необходимо минимизировать сумму квадратов отклонений вида
-х,)2.
Соответственно получим следующую систему нормальных уравнений:
л\^
Если преобразованные переменные х и у взять в отклонениях от средних уровней, то коэффициент регрессии Ь можно опреде-
лить как
I
171
При обычном применении метода наименьших квадратов к I уравнению линейной регрессии для переменных в отклонениях ? от средних уровней коэффициент регрессии b определяется по формуле
Т.(х-У)
Z*2 ‘
Как видим, при использовании обобщенного МНК с целью корректировки гетероскедастичности коэффициент регрессии b представляет собой взвешенную величину по отношению к обычному МНК с весами 1/К.
Аналогичный подход возможен не только для уравнения парной, но и для множественной регрессии. Предположим, что рассматривается модель вида
у = а + Ь{ • jq + Ь2 • х2 + е,
для которой дисперсия остаточных величин оказалась пропорциональна К2(. К, - представляет собой коэффициент пропорциональности, принимающий различные значения для соответствующих / значений факторов х, и х2. Ввиду того, что
рассматриваемая модель примет вид
где ошибки гетероскедастичны.
Для того чтобы получить уравнение, где остатки гомоскеда-стичны, перейдем к новым преобразованным переменным, разделив все члены исходного уравнения на коэффициент пропорциональности К. Уравнение с преобразованными переменными составит
Это уравнение не содержит свободного члена. Вместе с тем, найдя переменные в новом преобразованном виде и применяя обычный МНК к ним, получим иную спецификацию модели:
172
Параметры такой модели зависят от концепции, принятой для коэффициента пропорциональности К,-. В эконометрических исследованиях довольно часто выдвигается гипотеза, что остатки е,- пропорциональны значениям фактора. Так, если в уравнении
у = а + b} -X] + b2 • х2 + ... + Ь. • хр + Е предположить, что Е = е • х,, т. е. К = х1 и сг2^ = о2 • х,2, то обобщенный МНК предполагает оценку параметров следующего трансформированного уравнения:
Z=vv^+...+v^+e. Х| X] Х|
Если предположить, что ошибки пропорциональны хр, то модель примет вид:
Применение в этом случае обобщенного МНК приводит к тому, что наблюдения с меньшими значениями преобразованных переменных х/К. имеют при определении параметров регрессии относительно больший вес, чем с первоначальными переменными. Вместе с тем следует иметь в виду, что новые преобразованные переменные получают новое экономическое содержание и их регрессия имеет иной смысл, чем регрессия по исходным данным.
Пример.
Пусть у — издержки производства, х, — объем продукции, х2 — основные производственные фонды, х3 - численность работников, тогда уравнение
у = а + • X, + Ь2 • х2 + Ь2 • х3 + Е является моделью издержек производства с объемными факторами. Предполагая, что <ге. пропорциональна квадрату численности работников х3, мы получим в качестве результативного признака затраты на одного работника (у/х3), а в качестве факторов следующие показатели: производительность труда (xt/x3) и фондовооруженность труда (xj/xJ. Соответственно трансформированная модель примет вид
173
где параметры b}, b2, Ь3 численно не совпадают с аналогичными параметрами предыдущей модели. Кроме того, коэффициенты регрессии меняют экономическое содержание: из показателей силы связи, характеризующих среднее абсолютное изменение издержек производства с изменением абсолютной величины соответствующего фактора на единицу, они фиксируют при обобщенном МНК среднее изменение затрат на работника; с изменением производительности труда на единицу при неизменном уровне фондовооруженности труда; и с изменением фондовооруженности труда на единицу при неизменном уровне производительности труда.
Если предположить, что в модели с первоначальными переменными дисперсия остатков пропорциональна квадрату объема продукции, о2.. = о2 • х2,, можно перейти к уравнению регрессии вида
y.=bl+b2.^+b}.^+e. Xi Xi Xi
В нем новые переменные: у/х{ — затраты на единицу (или на 1 руб. продукции), Хт/х^ — фондоемкость продукции, Xj/X] - трудоемкость продукции.
Гипотеза о пропорциональности остатков величине фактора может иметь реальное основание: при обработке недостаточно однородной совокупности, включающей как крупные, так и мелкие предприятия, большим объемным значениям фактора может соответствовать большая дисперсия результативного признака и большая дисперсия остаточных величин.
При наличии одной объясняющей переменной гипотеза сЛ = а2*2 трансформирует линейное уравнение
y = a + b-x + z'x
в уравнение
у . а — ~Ь~\--Н £,
X X
в котором параметры а и b поменялись местами, константа стала коэффициентом наклона линии регрессии, а коэффициент регрессии — свободным членом.
174
Пример. Рассматривая зависимость сбережений у от дохода х, по первоначальным данным было получено уравнение регрессии1
у = —1,081 + 0,1178х.
Применяя обобщенный МНК к данной модели в предположении, что ошибки пропорциональны доходу, было получено уравнение для преобразованных данных:
-=0,1026-0,8538-—. X X
Коэффициент регрессии первого уравнения сравнивают со свободным членом второго уравнения, т. е. 0,1178 и 0,1026 — оценки параметра b зависимости сбережений от дохода.
Переход к относительным величинам существенно снижает вариацию фактора и соответственно уменьшает дисперсию ошибки. Он представляет собой наиболее простой случай учета гетероскедастичности в регрессионных моделях с помощью обобщенного МНК. Процесс перехода к относительным величинам может быть осложнен выдвижением иных гипотез о пропорциональности ошибок относительно включенных в модель факторов. Например, Incr^. = Incr2 + b • Inx + v, т. e. рассматривается характер взаимосвязи ine2, от Inx. Использование той или иной гипотезы предполагает специальные исследования остаточных величин для соответствующих регрессионных моделей. Применение обобщенного МНК позволяет получить оценки параметров модели, обладающие меньшей дисперсией.
Контрольные вопросы к главе 3
1. Назовите, в чем состоит спецификация модели множественной регрессии.
2. Сформулируйте требования, предъявляемые к факторам для включения их в модель множественной регрессии.
3. К каким трудностям приводит мультиколлинеарность факторов, включенных в модель, и как они могут быть разрешены?
4. Назовите методы устранения мультиколлинеарности факторов.
*См.: Лизер С. Эконометрические методы и задачи/Пер. с англ. — М,: Статистика, 1971. - С. 23.
175
5. Что означает взаимодействие факторов и как оно может быть представлено графически?
б. Как интерпретируются коэффициенты регрессии линейной модели потребления?
7. Какой смысл приобретает ЭД в производственных функциях и что означает ЭД(. >1?
8. Какие коэффициенты используются для оценки сравнительной силы воздействия факторов на результат?
9. В каких случаях рассчитывается «квази-/?2»?
10. От чего зависит величина скорректированного индекса множественной корреляции?
11. Каково назначение частной корреляции при построении модели множественной регрессии?
12. Составьте матрицу частных коэффициентов корреляции разного порядка для регрессионной модели с четырьмя фак
торами.
13. Что такое частный /•’-критерий и чем он отличается от последовательного /’-критерия?
14. Как связаны между собой /-критерий Стьюдента для оценки
15.
16.
значимости Ь, и частные /’-критерии?
При каких условиях строится уравнение множественной рег
рессии с фиктивными переменными?
Как трактуются коэффициенты модели, построенной только
на фиктивных переменных?
17. Сформулируйте основные предпосылки применения МНК
для построения регрессионной модели.
18. В чем сущность анализа остатков при наличий регрессионной модели?
19. Как можно проверить наличие гомо- или гетероскедастично-сти остатков?
20. Как оценивается отсутствие автокорреляции остатков при построении статистической регрессионной модели?
21. В чем смысл обобщенного метода наименьших квадратов?
ГЛАВА
СИСТЕМЫ ЭКОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
4.1. ОБЩЕЕ ПОНЯТИЕ О СИСТЕМАХ УРАВНЕНИЙ, ИСПОЛЬЗУЕМЫХ В ЭКОНОМЕТРИКЕ
Объектом статистического изучения в социальных науках являются сложные системы. Измерение тесноты связей между переменными, построение изолированных уравнений регрессии недостаточно для описания таких систем и объяснения механизма их функционирования. При использовании отдельных уравнений регрессии, например для экономических расчетов, в большинстве случаев предполагается, что аргументы (факторы) можно изменять независимо друг от друга. Однако это предположение является очень грубым: практически изменение одной переменной, как правило, не может происходить при абсолютной неизменности других. Ее изменение повлечет за собой изменения во всей системе взаимосвязанных признаков. Следовательно, отдельно взятое уравнение множественной регрессии не может характеризовать истинные влияния отдельных признаков на вариацию результирующей переменной. Именно поэтому в последние десятилетия в экономических, биометрических и социологических исследованиях важное место заняла проблема описания структуры связей между переменными системой так называемых одновременных уравнений, называемых также структурными уравнениями. Так, если изучается модель спроса как соотношение цен и количества потребляемых товаров, то одновременно для прогнозирования спроса необходима модель предложения товаров, в которой рассматривается также взаимосвязь между количеством и ценой предлагаемых благ. Это позволяет достичь равновесия между спросом и предложением.
Приведем другой пример.
177
При оценке эффективности производства нельзя руководствоваться только моделью рентабельности. Она должна быть дополнена моделью производительности труда, а также моделью себестоимости единицы продукции.
В еще большей степени возрастает потребность в использовании системы взаимосвязанных уравнений, если мы переходим от исследований на микроуровне к макроэкономическим расчетам. Модель национальной экономики включает в себя систему уравнений: функции потребления, инвестиций заработной платы, а также тождество доходов и т.д. Это связано с тем, что макроэкономические показатели, являясь обобщающими показателями состояния экономики, чаще всего взаимозависимы. Так, расходы на конечное потребление в экономике зависят от валового национального дохода. Вместе с тем величина валового национального дохода рассматривается как функция инвестиций.
Система уравнений в эконометрических исследованиях может быть построена по-разному.
Возможна система независимых уравнений, когда каждая зависимая переменная (у) рассматривается как функция одного и того же набора факторов (х):
У| =«n-»1+al2x2+...+almxei+ei, у2 = a2ix1 + а22х2 +...+а2/пхш + е2,
Уп = ап ,Xi + а„2х2 +...+аптхт + е„.
Набор факторов xf в каждом уравнении может варьировать. Так, модель вида
У1 = х2, х3, х4, х5)
У1 =f(xb х3, х4, х5)
Уз х3, х5)
У4 =ftx3,Xt,X5)
также является системой независимых уравнений с тем лишь отличием, что в ней набор факторов видоизменяется в уравнениях, входящих в систему. Отсутствие того или иного фактора в уравнении системы может быть следствием как экономической нецелесообразности его включения в модель, так и несущественности его воздействия на результативный признак (незначимо значение /-критерия или частного /’-критерия для данного фактора).
178
Примером такой модели может служить модель экономической эффективности сельскохозяйственного производства, где в качестве зависимых переменных выступают показатели, характеризующие эффективность сельскохозяйственного производства, -продуктивность коров, себестоимость 1 ц молока, а в качестве факторов - специализация хозяйства, количество голов на 100 га пашни, затраты труда и т. п.
Каждое уравнение системы независимых уравнений может рассматриваться самостоятельно. Для нахождения его параметров используется метод наименьших квадратов. По существу, каждое уравнение этой системы является уравнением регрессии. Поскольку никогда нет уверенности, что факторы полностью объясняют зависимые переменные, то в уравнениях присутствует свободный член а0. Так как фактические значения зависимой переменной отличаются от теоретических на величину случайной ошибки, то в каждом уравнении присутствует величина случайной ошибки.
В итоге система независимых уравнений при трех зависимых переменных и четырех факторах примет вид:
>1 =ао! +ОцХ] +<z12*2 +а]3х3 +а14х4+£,,
у2 =а02 +л21х, +а22х2 +а23х3 +а24х4 +е2,
[Уз = <*03 + <*31*1 + <*32*2 + а33х3 + <*34*4 + Е3-
Однако если зависимая переменная у одного уравнения выступает в виде фактора х в другом уравнении, то исследователь может строить модель в виде системы рекурсивных уравнений:
У1 = <*Н*| +<*12*2 + —+<*1л>*т +S|,
Уз ~^21У1 +<*21*1 +<*22*2 +'" + <*2m*m +е2>
< у3 =*3]У1 +Лз2У2 +<*31*1 +<*32*2 + — + <*3m*m +е3,
Уп =ЬИ\У\ +*Л2У2 + - + *лл-1Ул-1 +<*Л1*1 +<*Л2*2 +- + <*ллЛл + Ел-
В данной системе зависимая переменная у включает в каждое последующее уравнение в качестве факторов все зависимые переменные предшествующих уравнений наряду с набором собственно факторов х. Примером такой системы может служить модель производительности труда и фондоотдачи вида:
12»
179
У1=«11*1 + «12*2 + «13*3+е1.
где у, — производительность труда;
у2 — фондоотдача;
х, — фондовооруженность труда; х2 — энерговооруженность труда; х3 — квалификация рабочих.
Как и в предыдущей системе, каждое уравнение может рассматриваться самостоятельно, и его параметры определяются методом наименьших квадратов (МНК).
Наибольшее распространение в эконометрических исследованиях получила система взаимозависимых уравнений. В ней одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других уравнениях — в правую часть системы:
J’l =*t2 Л'г + ^З Уз +- - + *1л УЯ +«11 *1 +«12 *2 +-- + «lm *т +6,,
У2 = Ь2 Г У\ + *23 • Уз + • • • + *2 л • Уп + «21 • *1 + «22 ' *2 + • • • + «2 т ' хт + Е 2,
.Уп =Ьп\-У\+ЪП2-У2+-+ьт-\-Уп-х+Опх *i +а„2-х2+...+а„т-хт + е„.
Система взаимозависимых уравнений получила название системы совместных, одновременных уравнений. Тем самым подчеркивается, что в системе одни и те же переменные (у) одновременно рассматриваются как зависимые в одних уравнениях и как независимые в других. В эконометрике эта система уравнений называется также структурной формой модели. В отличие от пре
дыдущих систем каждое уравнение системы одновременных
уравнений не может рассматриваться самостоятельно, и для на-
хождения его параметр
в традиционный МНК неприменим. С
этой целью используются специальные приемы оценивания.
Примером системы одновременных уравнений может служить модель динамики цены и заработной платы вида
У1=*12У2 +«11*1+6],
где у! — темп изменения месячной заработной платы;
у2 - темп изменения цен;
Xj — процент безработных;
х2 — темп изменения постоянного капитала;
х3 — темп изменения цен на импорт сырья.
180
4.2. СТРУКТУРНАЯ
И ПРИВЕДЕННАЯ ФОРМЫ МОДЕЛИ
Система совместных, одновременных уравнений (или структурная форма модели) обычно содержит эндогенные и экзогенные переменные.
Эндогенные переменные обозначены в приведенной ранее системе одновременных уравнений как у. Это зависимые переменные, число которых равно числу уравнений в системе.
Экзогенные переменные обозначаются обычно как х. Это предопределенные переменные, влияющие на эндогенные перемен
ные, но не зависящие от них.
сгейшая структурная форма модели имеет вид:
|У1=*12^2+°1А+Е1.
= ^21 У\ +а22х2 +е2»
где у — эндогенные переменные; х - экзогенные переменные.
Классификация переменных на эндогенные и экзогенные зависит от теоретической концепции принятой модели. Экономические переменные могут выступать в одних моделях как эндогенные, а в других как экзогенные переменные. Внеэкономические переменные (например, климатические условия) входят в систему как экзогенные переменные. В качестве экзогенных переменных могут рассматриваться значения эндогенных переменных за предшествующий период времени (лаговые переменные). Так, потребление текущего года (у,) может зависеть не только от ряда экономических факторов, но и от уровня потребления в предыдущем году (у,^).
Структурная форма модели позволяет увидеть влияние изменений любой экзогенной переменной на значения эндогенной переменной. Целесообразно в качестве экзогенных переменных выбирать такие переменные, которые могут быть объектом регулирования. Меняя их и управляя ими, можно заранее иметь целевые значения эндогенных переменных.
Структурная форма модели в правой части содержит при эндогенных и экзогенных переменных коэффициенты д, и ау (Л, — коэффициент при эндогенной переменной, Лу — коэффициент при экзогенной переменной), которые называются структурными коэффициентами модели. Все переменные в модели, выражены в
181
ч
отклонениях от среднего уровня, т. е. под х подразумевается х — х а под у — соответственно у — у. Поэтому свободный член в каждом уравнении системы отсутствует.
Использование МНК для оценивания структурных коэффициентов модели дает, как принято считать в теории, смещенные и несостоятельные оценки. Поэтому обычно для определения структурных коэффициентов модели структурная форма модели преобразуется в приведенную форму модели.
Приведенная форма модели представляет собой систему линейных функций эндогенных переменных от экзогенных:
У1 -5ц Х[ +512 'Х2 + —+^1т ‘Хт’ у2 = 521 -xt +522 х2 +...+52т -xm,
Уп 5Л1 -х, +5д2 х2 +...+5ят 'Хт,
где <5, - коэффициенты приведенной формы модели.
По своему виду приведенная форма модели ничем не отличается от системы независимых уравнений, параметры которой оцениваются традиционным МНК. Применяя МНК, можно оценить 8, а затем оценить значения эндогенных переменных через экзогенные.
Коэффициенты приведенной формы модели представляют собой нелинейные функции коэффициентов структурной формы модели. Рассмотрим это положение на примере простейшей структурной модели, выразив коэффициенты приведенной формы модели (fy) через коэффициенты структурной модели (ау и bt). Для упрощения в модель не введены случайные переменные.
Для структурной модели вида
f-И =^12 'У2 +а1Гх1>
= ^21 ’ У1 + а22 ’ х2
приведенная форма модели имеет вид
(4.2)
в которой у2 из первого уравнения структурной модели можно выразить следующим образом:
182
Тогда система одновременных уравнений будет представлена как
У2-*21‘Л+а22'х2-
Отсюда имеем равенство:
Fl — gllJcl
- ^*21У1 + д22х2
ИЛИ
У1 ~ а11х! ~ ^12^21^1 + ^12а22х2‘
Тогда или
У] — Ь121>21У1 - аПх1 + ^12а22х2
а11 х t д22^12 х 1-^12^21 * 1_^12^21
Таким образом, мы представили первое уравнение структурной формы модели в виде уравнения приведенной формы модели:
Из уравнения следует, что коэффициенты приведенной формы модели представляют собой нелинейные соотношения коэффициентов структурной формы модели, т. е.
1-Ь|2^1
1-^2^21
Аналогично молено показать, что коэффициенты приведенной формы модели второго уравнения системы («^ и ^2) также нелинейно связаны с коэффициентами структурной модели. Для этого выразим переменную у (из второго структурного уравнения модели как
183
У2 ~ д22х2
^21
Запишем это выражение yt в левой части первого уравнения структурной формы модели (4.1):
©21
Отсюда
У1 =
а\Ф1\ 1-^12^21
а22
1-^12^21
что соответствует уравнению приведенной формы модели:
т. е.
5 =_£1А1_ и 5 =_?22_
1-Л|2/>21 1- ^12^21
Эконометрические модели обычно включают в систему не только уравнения, отражающие взаимосвязи между отдельными переменными, но и выражения тенденции развития явления, а также разного рода тождества. Так, в 1947 г., исследуя линейную зависимость потребления (с) от дохода (у), Т.Хавельмо предложил одновременно учитывать тождество дохода. В этом случае модель имеет вид:
с = а+Ьу,
У = с+х,
где х — инвестиции в основной капитал и в запасы экспорта и импорта; а и b — параметры линейной зависимости с от у.
Их оценки должны учитывать тождество дохода в отличие от параметров обычной линейной регрессии.
В этой модели две эндогенные переменные — с и у и одна экзогенная переменная х. Система приведенных уравнений составит:
184
Она позволяет получить значения эндогенной переменной с
через переменную х. Рассчитав коэ
ициенты приведенной
формы модели (Ао, А,, Во, В,), можно перейти к коэффициентам структурной модели а и Ь, подставляя в первое уравнение приве
денной формы выражение переменной х из второго уравнения
приведенной формы модели. Приведенная форма модели хотя и
позволяет получить значения эндогенной переменной через зна
чения экзогенных переменных, аналитически уступает структурной форме модели, так как в ней отсутствуют оценки взаимосвя
зи между эндогенными переменными.
4.3. ПРОБЛЕМА ИДЕНТИФИКАЦИИ
При переходе от приведенной формы модели к структурной исследователь сталкивается с проблемой идентификации. Идентификация — это единственность соответствия между приведенной и структурной формами модели.
Рассмотрим проблему идентификации для случая с двумя эндогенными переменными. Пусть структурная модель имеет вид:
У1 = W2+fliixi +^2х2+-+а1тхт, 1^2 = *21^1 +a2ixi +а22х2 +...+а2тхт,
где и у2 “ совместные зависимые переменные.
Из второго уравнения можно выразить у1 следующей формулой:
У2
*21
а2т
*21
/я*
Тогда в системе имеем два уравнения для эндогенной пере-
менной с одним и тем же набором экзогенных переменных, но
с разными коэффициентами при них:
У| =Ь]2у2+ацХ{+а12х2+...+а1тхт,
®2т
*21
т*
Наличие двух вариантов для расчета структурных коэффициентов одной и той же модели связано с неполной ее идентификацией. Структурная модель в полном виде, состоящая в каждом
185
уравнении системы из п эндогенных и т экзогенных переменных, содержит п(п — 1 + т) параметров. Так, при п “ 2 и т - 3 полный вид структурной модели составит:
(4.3)
Как видим, модель содержит восемь структурных коэффициентов, что соответствует выражению п (п — 1 + т).
Приведенная форма модели в полном виде содержит пт параметров. Для нашего примера это означает наличие шести коэффициентов приведенной формы модели. В этом можно убедиться, обратившись к приведенной форме модели, которая будет иметь вид:
Действительно, она включает в себя шесть коэффициентов бу.
На основе шести коэффициентов приведенной формы модели требуется определить восемь структурных коэффициентов рассматриваемой структурной модели, что, естественно, не может привести к единственности решения. В полном виде структурная модель содержит большее число параметров, чем приведенная форма модели. Соответственно п • (п — 1 + т) параметров структурной модели не могут быть однозначно определены из пт параметров приведенной формы модели.
Чтобы получить единственно возможное решение для структурной модели, необходимо предположить, что некоторые из структурных коэффициентов модели ввиду слабой взаимосвязи признаков с эндогенной переменной из левой части системы равны нулю. Тем самым уменьшится число структурных коэффициентов модели. Так, если предположить, что в нашей модели а13 = 0 и а21 = 0, то структурная модель примет вид:
у, = bi2y2+aiixi+ai2x2, Уг =*21У1 +а22х2 +а23х3.
(4-4)
В такой модели число структурных коэффициентов не превышает число коэффициентов приведенной модели, которое равно 6. Уменьшение числа структурных коэффициентов модели
186
возможно и другим путем: например, путем приравнивания некоторых коэффициентов друг к другу, т. е. путем предположений, что их воздействие на формируемую эндогенную переменную одинаково. На структурные коэффициенты могут накладываться, например, ограничения вида by + = 0.
С позиции идентифицируемости структурные модели можно подразделить на три вида:
• идентифицируемые;
• неидентифицируемые;
• сверхидентифицируемЫе.
Модель идентифицируема, если все структурные ее коэффициенты определяются однозначно, единственным образом по коэффициентам приведенной формы модели, т. е. если число параметров структурной модели равно числу параметров приведенной формы модели. В этом случае структурные коэффициенты модели оцениваются через параметры приведенной формы модели й модель идентифицируема. Рассмотренная выше структурная модель (4.4) с двумя эндогенными и тремя экзогенными (предопределенными) переменными, содержащая шесть структурных коэффициентов, представляет собой идентифицируемую модель.
Модель неидентифицируема, если число приведенных коэффициентов меньше числа структурных коэффициентов, и в результате структурные коэффициенты не могут быть оценены через коэффициенты приведенной формы модели. Структурная модель в полном виде (4.1), содержащая п эндогенных и т предопределенных переменных в каждом уравнении системы, всегда неидентифицируема.
Модель сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае на основе коэффициентов приведенной формы можно получить два или более значений одного структурного коэффициента. В этой модели число структурных коэффициентов меньше числа коэффициентов приведенной формы. Так, если в структурной модели полного вида (4.1) предположить нулевые значения не только коэффициентов а|3 и а21 (как в модели (4.2)), но и а22 = 0’то система уравнений станет сверхццентифицируемой:
/Л = ^12^2 + а1 Iх! +а12х2»
1/2 =Л2|У1 +а23х3' <4’5)
В ней пять структурных коэффициентов не могут быть однозначно определены из шести коэффициентов приведенной фор
187
мы модели. Сверхидентифицируемая модель в отличие от не-идентифицируемой модели практически решаема, но требует для этого специальных методов исчисления параметров.
Структурная модель всегда представляет собой систему совместных уравнений, каждое из которых требуется проверять на идентификацию. Модель считается идентифицируемой, если каждое уравнение системы идентифицируемо. Если хотя бы одно из уравнений системы неццентифицируемо, то и вся модель считается неидентифицируемой. Сверхидентифицируемая модель содержит хотя бы одно сверхидентифицируемое уравнение.
Выполнение условия идентифицируемости модели проверяется для каждого уравнения системы. Чтобы уравнение было идентифицируемо, необходимо, чтобы число предопределенных переменных, отсутствующих в данном уравнении, но присутствующих в системе, было равно числу эндогенных переменных в данном уравнении без одного.
Если обозначить число эндогенных переменных ву'-м уравнении системы через Н, а число экзогенных (предопределенных) переменных, которые содержатся в системе, но не входят в Данное уравнение, — через D, то условие идентифицируемости модели может быть записано в виде следующего счетного правила:
D + 1 = Н— уравнение идентифицируемо;
D + 1 < Н—уравнение нецдентифицируемо;
D + 1 > Н— уравнение сверхидентифицируемо.
Предположим, рассматривается следующая система одновременных уравнений:
У1 = ^2У2+^зУз+аих1 +а12х2,
Уз =*иУ| +ЬпУ2 +аззхз +034X4.
(4.6)
Первое уравнение точно идентифицируемо, ибо в нем присутствуют три эндогенные переменные - у(, у2, у3, т. е. Н= 3, и две экзогенные переменные — *! и х2, число отсутствующих экзогенных переменных равно двум — х3 и х4, D = 2. Тогда имеем равенство: D + 1 = Я, т. е. 2 + 1 = 3, что означает наличие идентифицируемого уравнения.
Во втором уравнении системы Я= 2 Oj и у2) и D = 1 (х4). Равенство D + 1 = Я, т.е. 1 + 1=2. Уравнение идентифицируемо.
188
В третьем уравнении системы Н= 3 (yb у2, у3), a£) = 2(xtH х2). Следовательно, по счетному правилу D + 1 = Н, и это уравнение идентифицируемо. Таким образом, система (4.6) в целом идентифицируема.
Предположим, что в рассматриваемой модели а21 = 0 и а33 — 0. Тогда система примет вид:
>i =bi2y2+bi3y3+anXi+al2x2,
< У2=Ь2\У\+а22х2+а23хЗ’
(4.7)
Л=М1+*}2У2+а34^4-
Первое уравнение этой системы не изменилось. Система по-прежнему содержит три эндогенные и четыре экзогенные переменные, поэтому для него D = 2 при ff= 3, и оно, как и в предыдущей системе, идентифицируемо. Второе уравнение имеет Н = 2 и D = 2 (Х|, х4), так как 2 + 1 > 2. Данное уравнение сверхиденти-фицируемо. Также сверхидентифицируемым оказывается и третье уравнение системы, где Н= 3 (у1( у2, у3) и D = 3 (х1,х2, х3), т.е. счетное правило составляет неравенство: 3 + 1 > 3 или D + 1 > Н. Модель в целом является сверхидентифицируемой.
Предположим, что последнее уравнение системы (4.7) с тремя эндогенными переменными имеет вид:
т. е. в отличие от предыдущего уравнения в него включены еще две экзогенные переменные, участвующие в системе, — х1 и х2. В этом случае уравнение становится неидентифицируемым, ибо при Я = 3, D= 1 (отсутствует только х3) и D + 1 < Н, 1 + 1 < 3. Итак, несмотря на то что первое уравнение идентифицируемо, второе сверхидентифицируемо, вся модель считается неиденти-фицируемой и не имеет статистического решения.
Для оценки параметров структурной модели система должна быть идентифицируема или сверхидентифицируема.
Рассмотренное счетное правило отражает необходимое, но недостаточное условие идентификации. Более точно условия идентификации определяются, если накладывать ограничения на коэффициенты матриц параметров структурной модели. Уравнение идентифицируемо, если по отсутствующим в нем переменным (эндогенным и экзогенным) можно из коэффициентов при них в других уравнениях системы получить матрицу, оп
189
ределитель которой не равен нулю, а ранг матрицы не меньше, чем число эндогенных переменных в системе без одного.
Целесообразность проверки условия идентификации модели через определитель матрицы коэффициентов, отсутствующих в данном уравнении, но присутствующих в других, объясняется тем, что возможна ситуация, когда для каждого уравнения системы выполнено счетное правило, а определитель матрицы названных коэффициентов равен нулю. В этом случае соблюдается лишь необходимое, но недостаточное условие идентификации.
Обратимся к следующей структурной модели:
У1 = *12^2 +W3 + а11Х1 +а12Л2>
W2 “ ^21У1 +^22х2 + а23х3 +а24х4’
„УЗ ~^1У1 +^32У2 +а31х1 +а32х2‘
(4.8)
Проверим каждое уравнение системы на необходимое и достаточное условия идентификации. Для первого уравнения Я = 3 0>1, У2, Уз) и D = 2 (х3 и х4 отсутствуют), т. е. D + 1 = Я и необходимое условие идентификации выдержано, поэтому уравнение точно идентифицируемо. Для проверки на достаточное условие идентификации заполним следующую таблицу коэффициентов при отсутствующих в первом уравнении переменных, в которой определитель матрицы (detA) коэффициентов равен нулю:
0 Уравнения Переменные
х3 х4
2 а23 а24 3 0 0
Следовательно, достаточное условие идентификации не выполняется и первое уравнение нельзя считать идентифицируемым.
Для второго уравнения Н = 2 (у( и у2), D = 1 (отсутствует х0. Счетное правило дает утвердительный ответ: уравнение идентифицируемо (D + 1 = Н).
Достаточное условие идентификации выполняется. Коэффициенты при отсутствующих во втором уравнении переменных составят:
190
Уравнения Переменные
Уз *1
1 Л13 3 —1 л31
Согласно таблице detA * 0 ранг матрицы равен 2, что соответствует следующему критерию: ранг матрицы коэффициентов должен быть не менее чем число эндогенных переменных в системе без одного. Итак, второе уравнение точно идентифицируемо.
Третье уравнение системы содержит Я= 3 и D = 2, т. е. по необходимому условию идентификации оно точно идентифицируемо (D + 1 = Н). Противоположный вывод имеем, проверив его на достаточное условие идентификации. Составим таблицу коэффициентов при отсутствующих в третьем уравнении переменных, в которой detA = 0:
Уравнения Переменные
*3
1 0 0 2 «23 «24
Из таблицы видно, что достаточное условие идентификации не выполняется. Уравнение нецдентифицируемо. Следователь
но, рассматриваемая в целом структурная модель, идентифици
руемая по счетному правилу, не может считаться идентифициру
емой исходя из достаточного условия идентификации.
В эконометрических моделях часто наряду с уравнениями,
параметры которых должны быть статистически оценены, используются балансовые тождества переменных, коэффициенты при которых равны ±1. В этом случае хотя само тождество и не требует проверки на идентификацию, ибо коэффициенты при переменных в тождестве известны, в проверке на идентификацию собственно структурных уравнений системы тождества уча
ствуют.
Например, рассмотрим эконометрическую модель экономики страны:
191
J'l = 4)! +*14^4 4-Sp
^2 ~ А)2 + &23Уз +a2txl +е2> УЗ = 4)3 + ^34>,4 +°31х1 +е3>
1Л = У1 +У2 + х2>
где >>| — расходы на конечное потребление данного года;
у2 — валовые инвестиции в текущем году;
Уз — расходы на заработную плату в текущем году;
у4 — валовой доход за текущий год;
X, — валовой доход предыдущего года;
х2 — государственные расходы текущего года;
А — свободный член уравнения;
е — случайные ошибки.
В этой модели четыре эндогенные переменные (уь у2, у3, у4). Причем переменная у4 задана тождеством. Поэтому практически статистическое решение необходимо только для первых трех уравнений сйстемы, которые необходимо проверить на идентификацию. Модель содержит две предопределенных переменных — экзогенную х2 и лаговую х,.
При практическом решении задачи на основе статистической информации за ряд лет или по совокупности регионов за один год в уравнениях для эндогенных переменных у1( у2, у3 обычно содержится свободный член (Л01, Aq2, Аоз), значение которого аккумулирует влияние неучтенных в уравнении факторов и не влияет на определение идентифицируемости модели.
Поскольку фактические данные об эндогенных переменных
У1, у2, у3 могут отличаться от теоретических постулируемых моде
лью, то принято в модель включать случайную составляющую для каждого уравнения системы, исключив тождества. Случай
ные составляющие (возмущения) обозначены через е1; е2 и е3.
Они не влияют на решение вопроса об идентификации модели.
В рассматриваемой эконометрической модели первое уравнение системы точно идентифицируемо, ибо Н = 3 и D = 2, и вы-
полняется необходимое условие идентификации (D + 1 = Н).
Кроме того, выполняется и достаточное условие идентификации,
т. е. ранг матрицы равен 3, а определитель ее не равен 0 : detA
равен — а31, что видно в следующей таблице:
Уравнения Уг х|
2 —1 <?2i 9 3 0 _а 0 4 1 о 1
192
Второе уравнение системы так же точно идентифицируемо:
Н = 2 и D — 1, т. е. счетное правило выполнено: D + 1 = Я, также
выполнено достаточное условие идентификации: ранг матрицы 3
и detA » — bu:
Уравнения У4 х2
1 -1 0 з ° ьм 0 4 1 _! 1
Аналогично третье уравнение системы также идентифицируемо: Я = 2, D— I, D + 1 = Я и detA * 0, а ранг матрицы А = 3 и detA = 1:
Уравнения У\ У2
1 -1 0 0 2 0-10 4 1 1 1 г
Идентификация уравнений достаточно сложна и не ограничивается только вышеизложенным. На структурные коэффициенты модели могут накладываться и другие ограничения, например, в производственной функции сумма эластичностей может быть равна по предположению 1. Могут накладываться ограничения на дисперсии и ковариации остаточных величин1.
4.4. ОЦЕНИВАНИЕ ПАРАМЕТРОВ СТРУКТУРНОЙ МОДЕЛИ
Коэффициенты структурной модели могут быть оценены разными способами в зависимости от вида системы одновременных уравнений. Наибольшее распространение в литературе получили следующие методы оценивания коэффициентов структурной модели".
Подробное освещение проблемы идентификации см.: Фишер Ф. Про-
блемы идентификации в эконометрии. — М.: Статистика, 1978.
13'152в
193
• косвенный метод наименьших квадратов;
• двухшаговый метод наименьших квадратов;
• трехшаговый метод наименьших квадратов;
• метод максимального правдоподобия с полной информацией;
• метод максимального правдоподобия при ограниченной информации.
Косвенный и двухшаговый методы наименьших квадратов подробно о'писаны в литературе и рассматриваются как традиционные методы оценки коэффициентов структурной модели. Эти методы достаточно легкореализуемы. Косвенный метод наименьших квадратов (КМНК) применяется для идентифицируемой системы одновременных уравнений, а двухшаговый метод наименьших квадратов (ДМНК) используется для оценки коэффициентов сверхйдентифицируемой модели. Перечисленные методы оценивания также используются для сверхидентифицируе-мых систем уравнений.
Метод^Макйимального правдоподобия рассматривается как наиболее обШйй метод оценивания, результаты которого при нормальном распределении признаков совпадают с МНК.- Однако при большом числе уравнений системы этот метод приводит к достаточно сложным вычислительным процедурам. Поэтому в качестве модификации используется метод максимального правдоподобия при ограниченной информации (метод наименьшего дисперсионного отношения), разработанный в 1949 г. Т.Андер-соном и Н.Рубиным. Математическое описание метода дано, например, в работе Дж.Джонстона1.
В отличие от метода максимального правдоподобия в данном методе сняты ограничения на параметры, связанные с функционированием системы в целом. Это делает решение более простым, но трудоемкость вычислений остается достаточно высокой. Несмотря на его значительную популярность, к середине 60-х годов он был практически вытеснен двухшаговым методом наименьших квадратов (ДМНК) в связи с гораздо большей простотой последнего2. Этому способствовала также разработка в 1961 г. Г. Тейлом семейства оценок коэффициентов структурной модели. Для структурной модели Г. Тейл определил семейство оценок класса К и показал, что оно включает три важных оператора оценивания: обычный МНК при К= 0, ДМНК при К= 1 и метод ог
1 См.: Джонстон Дж. Эконометрические методы. — С. 383—386.
См.: Лизер С. Эконометрические методы и задачи. — С. 68.
194
раниченной информации при plimK = 1. В последнем случае решение структурной модели соответствует оценкам по ДМНК.
Дальнейшим развитием ДМНК является трехшаговый МНК (ТМНК), предложенный в 1962 г. А. Зельнером и Г. Тейлом. Этот метод оценивания пригоден для всех видов уравнений структурной модели. Однако при некоторых ограничениях на параметры более эффективным оказывается ДМНК. С концепцией данного метода можно ознакомиться в работе Дж. Джонстона1. %
Косвенный метод наименьших квадратов (КМНК)
Как уже отмечалось, КМНК применяется в случае точно идентифицируемой структурной модели. Процедура применения КМНК предполагает выполнение следующих этапов работы.
1. Структурная модель преобразовывается в приведенную форму модели.
2. Для каждого уравнения приведенной формц модели обычным МНК оцениваются приведенные коэффициенты (8^.
3. Коэффициенты приведенной формы модели трансформируются в параметры структурной модели.
Рассмотрим применение КМНК для простейшей идентифицируемой эконометрической модели с двумя эндогенными и двумя экзогенными переменными:
.Vi _6|2у2 +°ii*i +ei>
Уг - ^21^1 + а22Х2 +е2‘
Пусть для построения данной модели мы располагаем некоторой информацией по пяти регионам:
Регион У\ Уг *1
1 2 ' 5 1 3
2 3 6 2 1
3 4 7 3 2
4 5 8 2 5
5 6 5 4 6
Средние 4 6,2 2,4 3,4
1 См.: Джонстон Дж. Эконометрические методы. — С. 395—4
13*
195
Приведенная форма модели составит:
где U|, и2 — случайные ошибки приведенной формы модели.
Для каждого уравнения приведенной формы модели применяем традиционный МНК и определяем 5-коэффициенты.
Чтобы упростить процедуру расчетов, можно работать с отклонениями от средних уровней, т. е. у = у — уи х = х — X. Тогда для первого уравнения приведенной формы модели система нормальных уравнений составит:
IT
Применительно к рассматриваемому примеру, используя отклонения от средних уровней, имеем:
Гб=5,2*3ц+4,25(2,
И0г=4Д-811+17Д512.
Решая данную систему, получим следующее первое уравнение приведенной формы модели:
У( = 0,852Х( + 0,373*2 + и1-
Аналогично применяем МНК для второго уравнения приведенной формы модели, получим:
J»2 — *" ^22*2 ы2"
Система нормальных уравнений составит: 1
(S.V2X1 = 821Sx? + 822Хх1х2> [2>2х2 = 821Sx1x2 +822Ех2-
Применительно к нашему примеру имеем: 1—0,4 = 5,282| +4,28 22, [-0,4 = 4,2821+17,2822-
196
Откуда второе приведенное уравнение составит: у2 — —0,072г] — О,ОО557х2 + и2.
Таким образом, приведенная форма модели имеет вид: (yt =0,852х| +0,373х2 +И], ly2 =0,072Х]-0,00557х2+«j.
Переходим от приведенной формы модели к структурной форме модели, т. е. к системе уравнений:
\у2=Ь21у1+а22х2+е2.
Для этой цели из первого уравнения приведенной формы модели надо исключить х2, выразив его из второго уравнения приведенной формы и подставив в первое:
„ _ ~0,072х] - у2
2 0,00557
Тогда
у, =0,852Х|+0,37
- 0,072Х| - у2 \
0,00557
у, = —66,966у2 — 3,970Х] — первое уравнение структурной модели.
Чтобы найти второе уравнение структурной модели, обратимся вновь к приведенной форме модели. Для этой цели из второго уравнения приведенной формы модели следует исключить X], выразив его через первое уравнение и подставив во второе:
У] -0,373х2 Ф852
и
у2 = -0,072
°’373*?. I_0,00557х2;
0,852 J
у2 — —0,085у| + 0,026х2 — второе уравнение структурной формы модели.
197
Итак, структурная форма модели имеет вид: (У1 - -66,966у2 - 3,970х, + Б|, |у2 =~О,О85у| +0,026х2 +ег-
Эту же систему можно записать, включив в нее свободный член уравнения, т. е. перейти от переменных в виде отклонений от среднего уровня к исходным переменным у и х.
Свободные члены уравнений определим по формулам:
Ло| =У| ~^\2Уг ~ ai i*i ж 428,717, Лщ ~ У2 ~ &21У1 ~ &22*2 = 6,451.
Тогда структурная модель имеет вид:
Гу, = 428,717 - 66,966у2 - 3,970х, + е,, [у2 = 6,451 - 0,085у! + 0,026х2 + е2.
При обработке по программе DSTAT система приведенных уравнений отсутствует, сразу же выдается структурная модель.
Оценка значимости модели дается через /-критерий и Л2 для каждого уравнения в отдельности. В рассматриваемом примере хороших результатов достичь не удалось: ввиду малого числа наблюдений значения F-критерия Фишера несущественны (при уровне значимости 0,05 F-табличное значение равно 19, а фактическое Г= 7 для первого уравнения).
Если к каждому уравнению структурной формы модели применить традиционный МНК, то результаты будут резко отличаться: а
Гу! =-1,09+0,364у2+ 1.192Х!+6!,
(у2 =5,2+0,533у! -О,333х2 +е2.
Как видим, не совпадают даже знаки коэффициентов при переменных: в первом уравнении структурной формы коэффициенты меньше нуля, а в уравнении регрессии больше нуля; во втором уравнении обратное воздействие у! на у2 в структурной модели сменяется на прямое в уравнении регрессии, а с фактором х2 наоборот.
Различия между коэффициентами регрессии и структурными коэффициентами модели численно могут быть и менее существенными. Так, например, Г.Тинтнер, рассматривая статическую 198
модель Кейнса для австрийской экономики за 1948—1956 гг., получил функцию потребления классическим МНК в виде С — 0,782у + 71,6, а используя КМНК,
С = 0,781у + 73,212*.
При сравнении результатов, полученных традиционным МНК и с помощью КМНК, следует иметь в виду, что традиционный МНК, применяемый к каждому уравнению структурной формы модели, взятому в отдельности, дает смещенные оценки структурных коэффициентов. Как показал Т. Хаавельмо, рассматривая две взаимосвязанные регрессии:
jy = ох+е|, [х = 6у+е2-. i
1 а
коэффициент регрессии отличается от структурного коэффициента и совпадает с ним только в одном частном случае, когда переменная у не содержит ошибок (т. е. е1 = 0), а ошибки переменной х имеют дисперсию, равную единице.
Кроме того, при интерпретации коэффициентов множественной регрессии предполагается независимость факторов друг от друга, что становится невозможным при рассмотрении системы совместных уравнений. Так, в нашем примере уравнение регрессии у I = —1,09 + 0,Зб4у2 + 1,192х, показывает, что с ростом х{ на единицу возрастает в среднем на 1,192 ед. при неизменном уровне значения у2. Между тем в соответствии с системой одновременных уравнений переменная у2 не может быть неизменной, ибо она в свою очередь зависит от у,.
Нарушение предпосылки независимости факторов друг от друга при использовании традиционного МНК в системе одновременных уравнений приводит к несостоятельности оценок структурных коэффициентов; в ряде случаев они оказываются экономически бессмысленными. Опасность таких результатов возрастает при увеличении числа эндогенных переменных в правой части системы, ибо становится невозможным расщепить совместное влияние эндогенных переменных и видеть изолированные меры их воздействия в соответствии с предпосылками традиционного МНК.
См.: Тинтнер Г. Введение в эконометрию / Пер. с нем. — М.: Статистика, 1965. - С 173,176.
199
Компьютерная программа применения КМНК предполагает, что система уравнений содержит в правой части в каждом уравнении как эндогенные, так и экзогенные переменные. Между тем могут быть системы, в которых в одном из уравнений, например, отсутствуют экзогенные переменные. Так, в п. 4.3 рассматривалась модель экономики страны с четырьмя эндогенными и двумя экзогенными переменными, в которой в первом уравнении системы не содержалось ни одной экзогенной переменной. Для такой модели непосредственное получение структурных коэффициентов невозможно. В этом случае сначала определяется система приведенной формы модели, решаемая обычным МНК, а затем путем алгебраических преобразований переходят к коэффициентам структурной модели.
Двухшаговый метод наименьших квадратов (ДМНК)
Если система сверхидентифицируема, то КМНК не используется, ибо он не дает однозначных оценок для параметров структурной модели. В этом случае могут использоваться разные методы оценивания, среди которых наиболее распространенным и простым является двухшаговый метод наименьших квадратов (ДМНК).
Основная идея ДМНК — на основе приведенной формы модели получить для сверхидентифицируемого уравнения теоретические значения эндогенных переменных, содержащихся в правой части уравнения.
Далее, подставив их вместо фактических значений, можно применить обычный МНК к структурной форме сверхидентифицируемого уравнения. Метод получил название двухшагового МНК, ибо дважды используется МНК: на первом шаге при определении приведенной формы модели и нахождении на ее основе оценок теоретических значений эндогенной переменной у t = <5(1 х, + • х2 + ... + • х, и на втором шаге применительно
к структурному сверхидентифицируемому уравнению при определении структурных коэффициентов модели по данным теоретических (расчетных) значений эндогенных переменных.
Сверхидентифицируемая структурная модель может быть двух типов:
• все уравнения системы сверхидентифицируемы;
• система содержит наряду со сверхидентифицируемыми точно идентифицируемые уравнения.
200
Если все уравнения системы сверхвдентифицируемые, то для оценки структурных коэффициентов каждого уравнения используется ДМНК. Если в системе есть точно идентифицируемые уравнения, то структурные коэффициенты по ним находятся из системы приведенных уравнений.
Применим ДМНК к простейшей сверхидентифицируемой модели:
[-V1 = *12 '(У2 +х1) + е1>
|у2 = *21 ’У1 +а22 'х2 + е2-
Данная модель может быть получена из предыдущей идентифицируемой модели:
(я =V-V2+air*i+ei>
[Уг = *2ГУ1 +а22 'х2 +е2’
если наложить ограничения на'ее параметры, а именно:
*12 = 011-
В результате первое уравнение стало сверхидентифицируе-мым: Н= 1 (у^, D = 1 (х2) и D + I > Н. Второе уравнение не изменилось и является точно идентифицируемым: Н — 2 и D = I, D + I = Н.
На первом шаге найдем приведенную форму модели, а именно:
У| -8ц -Х[ +3|2 -х2 +ut, У2 = *21 *! +*22 'х2 +и2-
Предполагая использование тех же исходных данных, что и в предыдущем примере, получим ту же систему приведенных уравнений:
= 0,852 • X] + 0,373 • х2 + ut, у2 =-0,072 •х1 - 0,00557 • х2 +«2.
На основе второго уравнения данной системы можно найти теоретические значения для эндогенной переменной у2, т. е. у 2. С этой целью в уравнение
201
у2 = — 0,072 • X] — 0,00557 • х2 + u2
подставляем значения х{ и х2 (в нашем примере это отклонения от средних уровней). Оценки для эндогенной переменной у2 приведены в табл. 4.1 (гр. 3).
Таблица 4.1
Расчетные данные для второго шага ДМНК
*1 ъ У2 y2+xiez УЯ
1 2 3 4 5 6 7
-1,4 “0,4 0,103 “1,297 —2 2,594 1,682
-0,4 -2,4 0,042 -0,358 -1 0,358 0,128
0,6 -1,4 -0,035 0,565 0 0 0,319
“0,4 1,6 0,020 “0,380 1 “0,380 0,144
L6 .... 2»6, -0,130 1,470 2 2,940 2,161
20 ТО'А- 0 0 0 5,512 4,434
После того как найдены оценки эндогенной переменной у2, обратимся к сверхидентифицируемому структурному уравнению
71 = *12 ’ (У2 + *1)-
Заменяя фактические значения у2 их оценками у2, найдем значения новой переменной
^2+*l=Z-
Далее применяем МНК к уравнению
71 = *12 • г,
е.
b>iZ = bi2
Откуда
*12 “
Z71Z = 5,512 _ Zz2 4,434
Таким образом, сверхидентифицируемое структурное уравнение составит:
202
У1 = 1,243 • (у2 4-Xj).
Ввиду того, что второе уравнение нашей системы не изменилось, то его структурная форма, найденная из системы приведенных уравнений, та же:
у2 = —0,085 • + 0,026 • х2.
В целом рассматриваемая система одновременных уравнений составит:
(У1=1,243 (Уг+хО,
|у2 = -0,085 у1 + 0,026 х2
ДМНК является наиболее общим и широко распространенным методом решения системы одновременных уравнений. Для точно идентифицируемых уравнений ДМНК даеттот же результат, что и КМНК. Поэтому в ряде компьютерных программ, например DSTAT, для решения системы одновременных уравнений рассматривается лишь ДМНК.
Решение сверхидентифицируемой модели на компьютере построено на предположении, что при каждой переменной в правой части системы имеется свой структурный коэффициент. Если же в модель вводятся ограничения на параметры, как в рассмотренном примере 6|2 = ап, то программа DSTAT не работает. Структурная модель может принимать любой вид, но без ограничений на параметры. При этом должно выполняться счетное правило идентификации: D + 1 > Я. Так, если структурная модель имеет вид:
У1=Л01 + 612-у2+а11-х1+е1,
[Уг = А)2+ ^21 ‘У1 + а22 'х2 + а23 ‘х3 + е2>
где первое уравнение сверхидентифицируемо, а второе — точно идентифицируемо, то реализация модели в ППП DSTAT оказывается следующей.
Последовательно ДМНК применяется к каждому уравнению. Эндогенная переменная, находящаяся в левой части системы, рассматривается как зависимая переменная, а переменные, содержащиеся в правой части системы (эндогенные и экзогенные), — как факторы, которые должны быть пронумерованы. Так, при вводе информации о переменных в последовательностную у2, хи
203
х2, х3 для первого уравнения имеем: у2 — фактор 2; х, - фактор 3. Далее отвечаем на следующие вопросы программы DSTAT.
Эндогенная переменная — это фактор №? Ответ: 2.
Экзогенная переменная, входящая в уравнение,— это фактор №? Ответ: 3.
Не входящая в уравнение экзогенная переменная — это фактор №? Ответ: 4.
Не входящая в уравнение экзогенная переменная — это фактор №? Ответ: 5.
По окончании процедуры выдается уравнение ь
и приводится оценка его качества через /'-критерий Фишера, относительную ошибку аппроксимации и оценки значимости структурных коэффициентов модели через /-критерий Стьюдента.
Аналогично поступаем со вторым уравнением системы. В нем соответственно эндогенная переменная рассматривается как фактор 1, а экзогенные переменные х2 и х3 - как факторы 4 и 5. Не входящая в уравнение экзогенная переменная Х| обозначается как фактор 3. В результате получим искомое уравнение
У 2 = ^21 ‘ + а22 ’ х2 + а23 ‘
Несмотря на важность системы эконометрических уравнений, на практике часто не принимают во внимание некоторые взаимосвязи, применение традиционного МНК к одному или нескольким уравнениям также широко распространено в эконометрике. В частности, при построении производственных функций анализ спроса можно вести, используя обычный МНК.
4.5. ПРИМЕНЕНИЕ СИСТЕМ ЭКОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
Под системой эконометрических уравнений обычно понимается система одновременных, совместных уравнений. Ее применение имеет ряд сложностей, которые связаны с ошибками спецификации модели. Ввиду большого числа факторов, влияющих на экономические переменные, исследователь, как правило, не уверен в точности предлагаемой модели для описания экономических процессов. Набор эндогенных и экзогенных переменных модели соответствует теоретическому представлению исследователя о
204
г
моделируемом объекте, которое сложилось на данный момент и может изменяться. Соответственно может меняться и вид модели с точки зрения ее идентифицируемости.
Сверхидентифицируемую модель можно превратить в точно идентифицируемую путем добавления некоторых переменных или отбрасывания некоторых ограничений на параметры. Не исключено, что при правильной спецификации модели она может оказаться неидентифицируемой, и поэтому переходят к с верх-идентифицируемым или точно.идентифицируемым моделям, несколько упрощающим характер взаимосвязей экономических явлений. Отметим, что наличие множества прикладных моделей для решения одного и того же класса задач не случайно. Наиболее ярко это проявляется при построении макроэкономических моделей, когда, например, одна и та же функция потребления может включать в себя разный набор экономических переменных.
Рассмотрим основные направления практического использования эконометрических систем уравнений.
Наиболее широко системы одновременных уравнений используются для построения макроэкономических моделей функционирования экономики той или иной страны. Большинство из них представляют собой мультипликаторные модели кейнсианского типа с той или иной мерой сложности. Статическая модель Кейнса для описания народного хозяйства страны в наиболее простом варианте имеет следующий вид:
С = а+Ь-у+г,
где С — личное потребление в постоянных ценах;
у — национальный доход в постоянных ценах;
I — инвестиции в постоянных ценах;
е — случайная составляющая.'
В силу наличия тождества в модели (второе уравнение системы) структурный коэффициент b не может быть больше 1. Он характеризует предельную склонность к потреблению. Так, если b = 0,65, то из каждой дополнительной тысячи дохода на потребление расходуется в среднем 650 руб. и 350 руб. инвестируется, т. е. С и у выражены в тыс. руб. Если b > 1,тоу < С+ [, т. е. на потребление расходуются не только доходы, но и сбережения. Параметр а Кейнс истолковывал как прирост потребления за счет
205
других факторов. Так как прирост во времени может быть не только положительным, но и отрицательным (снижение), то такой вывод возможен. Однако суждение о том, что параметр а характеризует конкретный уровень потребления, обусловленный влиянием других факторов, неправельно.
Структурный коэффициент b используется для расчета мультипликаторов. По данной функции потребления можно определить два мультипликатора - инвестиционный мультипликатор потребления Мс и инвестиционный мультипликатор национального дохода Му.
Инвестиционный мультипликатор потребления определяется по формуле
Мс = Ь/(\- Ь).
.При ь = 0,65 Мс = 0,65 / (1 - 0,65) = 1,857.
Эта величина означает, что дополнительные вложения в размере 1 тыс. руб. приведут при прочих равных условиях к дополнительному увеличению потребления на 1,857 тыс. руб.
Инвестиционный мультипликатор национального дохода можно определить как Му= 1 / (1 — Ь). В нашем случае он составит:
Му = 1 /(1 — 0,65) = 2,857,
т. е. дополнительные инвестиции в размере 1 тыс. руб. на длительный срок приведут при прочих равных условиях к дополнительному доходу в 2,857 тыс. руб.
Рассматриваемая модель Кейнса точно идентифицируема, и для получения величины структурного коэффициента b применяется КМНК. Это значит, что строится система приведенных уравнений:
С = А + В /+ у = А' + В' I+U2,
в которой А = Д', а параметры В и В1 являются мультипликаторами, т. е. В = Мс и В = Му. Убедиться в этом можно, если выразить коэффициенты приведенной формы модели через структурные коэффициенты. Для этого в первое уравнение структурной модели подставим балансовое равенство:
206
C=a + b-y + E =a + b- (C+ 7) + e = a + b • C + b • I + e; C(l-b) = a + b-J+s;
•e — приведенное уравнение.
Отсюда A = a / (1 - b)\ B= b / (1 - b) = Mc; U{ = (1 / (1 - b)) • s.
Аналогично поступим и co вторым уравнением структурной модели: в тождество у = С + I вместо С подставим выражение первого структурного уравнения, т. е.у = д + 7»-.у + Е + /. Далее, преобразовывая, получим:
т. е. А1 = а/(1 - Ь) = А; В1 = 1/(1 - b) = Му, U2 = (1/(1 - Z>)) • е.
Таким образом, приведенная форма модели содержит муль-
типликаторы, интерпретируемые как коэффициенты линейной
регрессии, отвечающие на вопрос, на сколько единиц изменится
значение эндогенной переменной, если экзогенная переменная изменится на 1 ед. своего измерения. Этот смысл коэффициентов
приведенной формы делает приведенную модель удобной для
прогнозирования.
В более поздних исследованиях статическая модель Кейнса включала уже не только функцию потребления, но и функцию сбережений:
С=а+Ь-у+ъх,
< г = Т+К • (С+1)+е2 >
у = С+/-г,
где С, у и / — те же по смыслу переменные, что и в предыдущей модели; г — сбережения.
Данная модель содержит три эндогенные переменные — С, г, у и одну экзогенную переменную I. Система идентифицируема: в первом уравнении Н=2и D = 1,во втором Я=1иД = 0;С+/ рассматривается как предопределенная переменная (подробное изложение решения данной системы приведено в работе Г. Тинт-нера)1. Наряду со статическими широкое распространение полу-
1 См.: Тинтнер Г. Введение в эконометрию. — С. 175—176, 267—269.
207
чили динамические модели экономики. В отличие от статических они содержат в правой части лаговые переменные, а также учитывают тенденцию (фактор времени). Примером могут служить модели Л. Клейна, разработанные им для экономики США в 1950—1960 гг. В упрощенном варианте модель Клейна рассматривается как конъюнктурная модель1.
где
/, = b4Pt + А5+й|5+62,
5
ункция потребления в период г,
$ Л
t т, 4 Gt
заработная плата в период Г,
прибыль в период Г;
прибыль в период t - 1, т. е. в предыдущий год; общий доход в период
общий доход в предыдущий период;
время;
чистые трансферты в пользу администрации в период г; капиталовложения в период Г,
с административного аппарата, правительственные расхо-
ды в период времени А
Модель содержит пять эндогенных переменных - Cz, It, St, Rt (расположены в левой части системы) и Pt (последняя — зависимая переменная, определяемая по первому тождеству), три экзогенных переменных - Tt, G^tn две предопределенные, лаговые переменные — Pt_{ и Rt_v Как и большинство моделей такого типа, данная модель сверхидентифицируема и решаема ДМНК. Для прогнозных целей используется приведенная форма модели:
’См.: Маленбо Э. Статистические методы эконометрии/Пер. с фр. — М.: Статистика, 1976. ~ С. 230.
208
В данной системе мультипликаторами являются коэффициенты при обычных экзогенных переменных. Они отражают влияние экзогенной переменной на эндогенную переменную. Мультипликаторами в нашей системе выступают коэффициенты при Ти G. Коэффициенты d6, dn, dl6, d2l — мультипликаторы чистых трансфертов в пользу администрации относительно личного потребления инвестиций d6, заработной платы dlh дохода dl6 и прибыли J21. Соответственно коэффициенты d2, d7, dl2, dl7, d22 являются мультипликаторами правительственных расходов относительно соответствующих эндогенных переменных.
Динамическая модель может и не содержать учет тенденции, но лаговые переменные в ней обязательны. Динамическая модель Кейнса представлена следующими тремя уравнениями:
В этой системе три эндогенные переменные:
К — имеющийся в распоряжении доход в период времени г;
С, — частное потребление в период времени /;
Р. - валовой национальный продукт (ВНП) в период времени t.
Кроме того, модель содержит пять предопределенных переменных:
К, - доход предыдущего года;
Gt — общественное потребление;
I. — валовые капиталовложения;
L, -изменение складских запасов;
— сальдо платежного баланса.
Случайная переменная е1 характеризует ошибки в первом уравнении в виду его статистического характера. Параметр а отражает влияние других не учитываемых в данном уравнении факторов потребления (например, цен). Первое уравнение данной системы является сверхидентифицируемым, а второе и третье — определениями.
Если в модели Кейнса доход рассматривается как лаговая переменная, то в других исследованиях функции потребления в виде лаговой переменной используется потребление предыдущего года, т. е. считается, что потребление текущего года зависит не только от дохода, но и от достигнутого в предыдущий период уровня потребления.
Примером динамической модели экономики, учитывающей для каждой эндогенной переменной лаговые переменные соответствующего экономического содержания, может служить мо-14-1525 209
дель открытой экономики с экономической активностью со стороны государства1.
Л -А)+^1 +^2 ‘^-1 +е2’
IMt =кц +кх -Y, +к}-1М{_х +е3,
[Г, = С,+ /,+(?,-ЛИ,.
В этой модели четыре эндогенных переменных:
С, — личное потребление в период времени /;
It — частные чистые инвестиции в отрасли экономики в период времени Г,
IM, -импорт в период времени /;
Yt - национальный доход за период времени t.
Все переменные приведены в постоянных ценах.
Предопределенными переменными в модели являются следующие три переменные:
С,_| — личное потребление за предыдущий период;
Ut_x — доход личных домохозяйств от предпринимательской деятельности за предыдущий период и доход от имущества плюс нераспределенная прибыль предприятий до налогообложения;
1М,_Х — импорт за предыдущий период времени t - 1.
В качестве экзогенной переменной в модели рассматривается переменная G,-общественное потребление, плюс государственные чистые капиталовложения в экономику страны, плюс изменение запасов, минус косвенные налоги, плюс дотации, плюс экспорт.
Первые три уравнения системы являются сверхидентифици-руемыми, а четвертое представляет собой балансовое тождество.
Система одновременных уравнений нашла применение в исследованиях спроса и предложения. Линейная модель спроса и предложения имеет вид:
0^ = fl0 +fl| -Р + Е],
\Qa=b0+bx Р+е2,
где Q1 - спра
II
иваемое количество благ (объем спроса);
О’ — предлагаемое количество благ (объем предложения);
Р — цена.
Описание данной модели на примере Германии за 1950—1959 гг. дано в работе: Иванова В.М. Основы эконометрики. — М.: МЭСИ, 1995. — С. 134-141.
210
В этой системе три эндогенные переменные — Q*, С* и Р. При этом если Q1 и представляют собой эндогенные переменные исходя из структуры самой системы (они расположены в левой части), то Р является эндогенной по экономическому содержанию (цена зависит от предлагаемого и спрашиваемого количества благ), а также в результате наличия тождества ff = Q\
Приравняв первое и второе уравнения, можно показать, что Р — зависимая переменная:
«о + ах Р + е1 = Ьо + • Р+ е2.
Отсюда
A) ~fl0 е2 ~е1 а1 ~&1 а1
Рассматриваемая модель спроса и предложения не содержит экзогенной переменной. Однако чтобы модель имела статистическое решение и можно было убедиться в ее справедливости, в модель вводятся экзогенные переменные.
Одним из вариантов модели спроса и предложения является модель вида
Qd =а0 +а{ Р+а2-Я+е1,
где R — доход на душу населения;
W — климатические условия (предположим, что речь идет о спросе и предложении зерна).
Переменные R и ГК экзогенные. Введя их в модель, получим идентифицируемую структурную модель, оценки параметров которой могут быть даны с помощью КМНК.
Широкий класс моделей в эконометрике представляют производственные функции - Р =ftxl, х2,х„), где Р — объем выпуска (уровень производства); х(, х2, ...,х„ — факторы производства (труд, капитал и др.). Однако реализация такого рода моделей, как правило, не связана с системой одновременных уравнений. Производственная функция в упрощенном виде может быть включена в систему одновременных уравнений. Так, в 1962 г.
14*
211
Б. Хохенбалкен и Г. Тинтнер предложили следующую модель экономики для каждой из одиннадцати стран — членов ОЭС1:
logX = а2 +l>2 -log Д dxldD = Wlp,
Здесь эндогенными переменными являются: )
С — величина личного потребления в текущих ценах;
Y — ВНП в текущих ценах;
X — ВНП в постоянных ценах;
Р — индекс цен;
D — общая занятость.
В качестве экзогенных переменных приняты:
N — численность населения;
средняя годовая заработная плата работника;
К — государственное потребление плюс инвестиции и внешнеторговое сальдо.
В системе имеются только два структурных уравнения — функция потребления (первое уравнение) и производственная функция (второе уравнение). Остальные составляющие модели представляют собой априорно разработанную функцию спроса на труд (третье уравнение) и два тождества, относящиеся к ВНП.
Параметры функции потребления оцениваются с помощью КМНК с учетом тождества Y — С + К, а параметры производственной функции — при комбинации ее с функцией спроса на труд.
Как уже отмечалось, не все эконометрические модели имеют вид системы одновременных уравнений. Так, широкий класс функций спроса на ряд потребительских товаров часто представляет собой рекурсивную систему, в которой с уравнениями можно работать последовательно и проблемы одновременного оценивания не возникают.
1 См.: Лизер С. Эконометрические методы и задачи. — С. 115.
212
4.6. ПУТЕВОЙ АНАЛИЗ
Построение системы структурных уравнений позволяет глубже изучить причины связи, лежащие в основе вариации результирующих переменных. При этом происходят выделение и оценка косвенных (опосредованных) и непосредственных^прямых) влияний признаков. Именно поэтому системы структурных уравнений часто интерпретируются как статистические описания причинно-следственных связей, как причинные модели, объясняющие механизм формирования вариации выходных характеристик системы (результативных признаков). В случае использования аппарата корреляционно-регрессионного анализа структурное моделирование представляет собой попытку преодолеть косвенный характер изучения связей этим методом, подойти к выделению и измерению причинных связей переменных.
Установить направленность связей, их причинный характер можно только лишь на основе содержательного анализа изучаемых связей, в ходе которого формулируются гипотезы о структуре влияний и корреляции. Как уже отмечалось, систему причинных гипотез удобно изображать в виде графа связей, вершинами которого являются переменные — причины или следствия; дуги (ориентированные ребра) соответствуют постулируемым причинным отношениям, а неориентированные ребра — отношениям координированного изменения, не структурируемым в данной схеме.
Для формальной верификации гипотез необходимо соответствие между графом и системой уравнений, его описывающей. Алгебраическая система, соответствующая графу без контуров (петель), является рекурсивной системой, позволяющей рекур-рентно определять значения входящих в нее переменных. В такой системе в уравнения для признака х,- включаются все переменные, за исключением расположенных выше его по графу связей. Формулировка гипотез в структуре рекуррентной модели обычно не вызывает затруднений при использовании данных в динамике. Если же анализируются статистические данные, то следует учитывать зависимость системы от ее прошлых состояний.
В эконометрике рассматриваются структурные модели, включающие уравнения, линейные по отношению к наблюдаемым переменным и имеющие вид
У/ ~ S +uj> (4 9)
где А, В - подмножества эндогенных и воздействующих на них экзогенных переменных соответственно;
/у, Рц — коэффициенты при соответствующих переменных.
213
Одним из наиболее распространенных методов оценки параметров структурных уравнений на ЭВМ является двухшаговый метод наименьших квадратов. На первом шаге этого алгоритма находятся оценки параметров уравнений, описывающих зависимость эндогенных переменных от экзогенных уу- = ZfttpX, + е. На втором шаге вычисленные значения эндогенных переменных уу подставляются в структурные уравнения. Полученные таким образом оценки параметров и Д7 уравнения (4.9) состоятельны.
На основе рекуррентной системы уравнений определяются полные и частные коэффициенты влияния факторов. Коэффициенты полного влияния, иначе говоря — полные коэффициенты регрессии, измеряют роль каждой переменной в структуре. Полные коэффициенты влияния образуют матрицу коэффициентов влияния произвольно задаваемого изменения переменных (независимых приращений) на все остальные переменные:
= Ду? + Z/0/уХ/.
Матрица полных коэффициентов регрессии В находится на основе матрицы коэффициентов частных регрессий (Л):
В = (Е-Л)-1 Дх.
Полному коэффициенту регрессии соответствует сумма показателей связи для каждого пути, связывающего вершины xt и Хр тогда как частный коэффициент представляет собой силу влияния, идущего отх( кх- по соответствующей дуге.
Структурные модели позволяют не только оценить непосредственное и полное влияние переменных, но и прогнозировать поведение системы, определять расчеты значения эндогенных переменных. Если же такая задача не ставится и имеется лишь потребность в уточнении характера связей переменных, то эффективным является применение путевого анализа (р-анализа). Уже в самом названии этого метода отражается активное использование графа связей, изоморфного системе уравнений.
Метод путевого анализа (или путевых коэффициентов) предложен в 20-х гг. XX в. американским генетиком С. Райтом. Сегодня этот метод нашел широкое применение в биометрии, построении социологических причинных моделей, но все еще остается мало знакомым экономистам. Основные положения метода сводятся к следующему. Пусть х2,..., хр — случайные переменные, измеренные в соответствующих единицах. Основным предположением метода является предположение об аддитивности и линейности связей между переменными
214
Xt = T.J gy Xj + gt^, j = TJnJ = T7p- (4.10)
Здесь xul — символ неизмеримого имплицитного фактора uh действующего нах, и обозначающего действие нах, всех переменных, не включенных во множество {х}; gy — некоторые константы; &и — коэффициент влияния хв, на х,.
Будем называть х,у-й причиной, ах,—следствием комбинированного действия всех m-причин. Использование линейных зависимостей между всеми переменными делает p-анализ специальным случаем регрессионного анализа, в котором коэффициенты регрессии интерпретируются в терминах причинно-следственных отношений.
Соотношение (4.10) можно записать также в виде
х, X, - — ^j) 4" CfaXfat (4.11)
где X) — среднее значениеу-й переменной.
Без потери общности можно допустить, что х,в имеет нулевое среднее и единичную дисперсию. В стандартизованной форме уравнение (4.11) будет иметь вид:
X, = XjPyXj + р^, _xi~xi.
где, X,- ,
SJ
Sj - стандартное отклонениеу-й переменной.
(4.12)
Тогда р,у =(sj/s)cv.
Коэффициенты Су являются специальным типом частных коэффициентов регрессии. Коэффициент Ру является стандартизованным коэффициентом р-регрессии. Будем называть ру коэффициентом влияния (согласно С. Райту), понимая при этом, что Ру есть числовая величина, которая измеряет долю стандартного отклонения i-й эндогенной переменной (следствия) с соответствующим знаком, обусловленную влиянием у-й экзогенной переменной (причины) в том смысле, что если произвести измерение этого влияния при измененииу-й переменной в тех же условиях, что и в данных наблюдениях и при неизменных прочих условиях (включая постоянное воздействие фактора хв,), то полученный результат будет равен р„:
PiJ “
SJ У/,12...(У-1)(уЯ)...р.Н _ sl sj. 12..sl
(413)
215
В формуле (4.13) Si.i2...o-i)(i+i)...P.u показывает стандартное отклонение /-Й переменной с учетом влияния переменных от 1 до (/ — 1) и от (/ + 1) дор при постоянном влиянии фактора и.
Из данного определения следует, что квадрат р-коэффициен-та показывает, какая часть общей вариации следствия определяется /-й причиной. Эта величина представляет собой коэффициент детерминации: dx.. — р2у.
Относительно имплицитных переменных хш заметим, что фактор хи1, представляющий постоянное воздействие на следствие х, переменных, не включенных явным образом в модель, считается некоррелированным ни с другими аналогичными факторами хи, ни с экзогенными переменными (входами или причинами) системы х,-.
Входом системы называют переменную Хр при которой ее вариация целиком и полностью определяется фактором х„-, т. е. ру„. = 1, dJU = 1. Входы системы могут быть коррелированы попарно.
Простейшим случаем является модель звена линейной причинной цепи, т. е. детерминации следствия у, всего лишь одной переменной — причиной х. Уравнение этой модели в форме линейной регрессии будет иметь вад (для стандартизованных переменных):
У = Рухх + еу.
Так как х=р,хи., то у = + р^и1, (4.14)
где еу =руи1рсиг а рХИ( = 1 по условию.
Систему (4.14) можно представить в ваде графа связей (рис. 4.1). Встает вопрос об оценке коэффициентов р^, руи . Коэффициент корреляции случайных переменных х и у как первый смешанный момент нормированных случайных величин определяется соотношением
ryx = COV(X,y) = Рух COV(X, х) + Ру^ COV(XXU) = Рух,
так как cov(x, х) = 1, cov(x, хи) = 0 по условию о некоррелированности имплицитных факторов. Но, как известно, в данном частном случае = Д^, где Д^ — стандартизованный коэффициент линейной регрессии. Таким образом, /^-коэффициент (р^) есть 216
стандартизованный регрессионный коэффициент и его оценка методом наименьших квадратов будет являться оценкой эффективности влияния по С. Райту (рис. 4.1 и 4.2).
Рис. 4.1. Граф связи между у и
Рис. 4.2. Граф связей: система с коррелированными входами
Прямая оценка влияний неизмеримых факторов хи невозможна, поэтому ее получают косвенным образом из соотношений для коэффициентов детерминации. В случае модели (4.14) оценку коэффициента , можно получить следующим образом. Соотношение полной детерминации у посредством х и и2 имеет вид:
_2 _ 2 . 2 _ ]
' УУ " ух р уи 2 1 ’
откуда
Pyui
=ф-^ух = = 71-гД-
Обобщение рассмотренной модели на случай л-звенной линейной цепи, а также случай к независимых причин хк одного и того же следствия у могут быть проведены индуктивно.
Широко распространена структурная модель системы с коррелированными входами (случай множества взаимодополняющих причин), изображенная на рис. 4.2. Для этой модели основное уравнение си&гемы записывается следующим образом:
(4.15)
217
а корреляция следствия с <-й причиной определяется из соотношения
ryxi ~ Pyi+^ Pyjrij-j
(4.16)
Соотношение (4.16) демонстрирует важную особенность коэффициента влияния Райта — он может быть как больше, так и меньше соответствующего коэффициента корреляции по абсолютной величине и не совпадать с ним по знаку.
Значения ^-коэффициента заключены в интервале [-<», да]. Положительное значение р-коэффициента указывает на то, что фактор X/ влияет на х,- таким образом, что при изменении Xj в одном направлении (допустим, увеличении) признак х,- изменяется в этом же направлении. Отрицательное значение показывает, что Х( и X, изменяются противоположно. Знак коэффициента влияния получается автоматически в результате решения системы уравнений, связывающей'ГдИ р#. Содержательная интерпретация коэффициентов влияния Райта как показателей интенсивности влияния по дуге графа аналогична интерпретации ^-коэффициентов (как показателей сравнительной силы воздействия факторов) в обычных моделях множественной регрессии.
Выражение полной детерминации у посредством множества взаимокоррелированных причин {х.} имеет вид:
»/
dyy + 2Z Z PyftjPyl = 1 •
\ j i J
Слагаемое называется показателем корреляци-
* j
онной детерминации. Квадрат множественного коэффициента корреляции (коэффициент множественной детерминации):
Ру-I, •• -Хц “ 1 “ = Pyj + 2^ £ Р^ГуРй.
j > i
Таким образом, метод p-коэффициентов позволяет найти наилучшую оценку множественной корреляции Jcy. х .
Подчеркнем, что попарная корреляция входов в модели (4.16) не структурируется. Между тем эта корреляция может быть как следствием координированного изменения двух различных взаи-монезависимых причин — истинной корреляцией, так и ложной — результатом воздействия третьей переменной — общей для этих двух переменных причины.
218
Пусть на рис. 4.3а) изображен граф модели, истинность корреляции входов которой находится под вопросом. Г. Саймон показал, что если корреляция х, и х2 является ложной в отмеченном смысле, то частный коэффициент корреляции первого порядка rx х . v где z — общая для х, и х2 причина — должен быть равен нулю. 2
В самом деле, для такой модели (сравните граф на рис. 4.3, б) с рис. 4.3а)) будут справедливы следующие отношения:
Отсюда
Рис. 4.3. Граф связей: а— общая причина для х, Xj отсутствует; б — общая причина для Xj и х2 присутствует
Первым этапом путевого анализа является идентификация уравнений системы.
219
В современной эконометрической литературе идентификация понимается как структурная спецификация модели, призванная не только определить значения параметров, но и выделить одну-единственную итоговую структурную модель анализируемых данных.
Проблема идентифицируемости в системе структурных уравнений связана с наличием достаточного числа ограничений, накладываемых на него моделью. Применительно к p-анализу—это проблема соответствия между количеством возможных соотношений между rv и ру и числом Ру.
Иначе говоря, проблема идентифицируемости структурных параметров — это проблема достаточности эмпирических данных для оценки всех коэффициентов модели. Необходимым условием идентифицируемости уравнения является отсутствие среди линейных комбинаций оставшихся уравнений, таких, которые удовлетворяли бы всем ограничениям модели, накладываемым на исследуемое уравнение.
Это эквивалентно так называемому условию порядка: для того чтобы уравнение в системе из т линейных структурных уравнений было идентифицируемо, необходимо, чтобы в нем отсутствовало по меньшей мере т — 1 переменных из т + к переменных, встречающихся в модели. Обозначим через т число эндогенных переменных в модели, к — число предопределенных переменных, h — число эндогенных переменных в рассматриваемом уравнении, g — число предопределенных переменных в рассматриваемом уравнении. Тогда условие порядка может быть записано в форме/и— Л — g>m — 1 или Л— g>h — 1.
Структурное уравнение называется идентифицируемым, если оно удовлетворяет условию порядка; в случае точного равенства уравнение называется точно идентифицируемым, при строгом неравенстве — сверхидентифицируемым.
Следующим этапом является оценивание структурных параметров. Для структурных моделей, построенных на основе р-ко-эффициентов, оценка ру производится не методом наименьших квадратов, а с помощью такого приема. Запишем уравнение (4.12) следующим образом:
Хj ~Y.PyXJ + PitPiv
j
или иначе
xi Pi\x\ + Ptyx2 + — + Pl,l- lxl- 1 + PiuH-
(4.17)
220
Используем коэффициенты корреляции между зависимой переменной и каждой из объясняющих переменных:
(4.18)
где л — число наблюдений.
Подставляя в (4.17) вместо х,- правую часть выражения (4.18), получим:
fy = ^lxi(pixl + ...+Pu-iX/,1 + PiuUt)
_ v ZXjXk IхJ IXjUi
я +Py n +Piut я L.Patrjk+Py (4.19)
В этом преобразовании учтено, что корреляция uf с Xj по определению равна нулю. Если учесть, что г у = 1, то соотношение (4.19), называемое основной теоремой путевого анализа, можно записать так:
(4.20)
Здесь j указывает на объясняющую переменную, связь которой с объясняемой переменной i раскрывается в структурной модели, к пробегает по подмножеству всех переменных, непосредственно влияющих на /-ю переменную (на графе эти вершины связаны с вершиной i дугами). Соотношение (4.20) справедливо для любой рекурсивной системы.
Путевой анализ позволяет произвести декомпозицию корреляции Гу. Введем понятия «полная (совокупная) связь», «совокупное влияние», «прямое влияние», «косвенное влияние». Если коэффициент корреляции нулевого порядка г у рассматривать как измеритель полной связи двух переменных, то мерой совокупного влияния j-й переменной на l-ю переменную (fy) будет являться ее часть, не зависящая ни от общих для них переменных — причин, ни от корреляции между общими для у-й и Z-й переменных причинами (компоненты ложной корреляции), ни от наличия не анализируемой в модели априорной корреляции предопределенных переменных — входов.
Таким образом, мы можем разложить полную связь двух переменных на четыре составляющие с учетом постулируемой в модели асимметрии воздействия: на совокупное влияние (причин
221
ное влияние)у-й переменной на 7-ю, на две компоненты, измеряющие эффект ложной корреляции, и на компоненту, еще не имеющую общепринятого названия. В свою очередь, совокупное влияние может быть разложено на две составляющие с учетом того, каким образом оно осуществляется — непосредственно или через другие переменные.
Прямое влияние одной переменной на другую измеряется коэффициентов рд, в этом случае в цепи между объясняющей и объясняемой переменными нет промежуточных звеньев. Косвенное влияние — это влияние тех составляющих совокупного влияния одной переменной на другую, которое образуется при учете эффекта передачи воздействия через посредство переменных, специфицированных в модели как промежуточные звенья в причинной цепи, связывающей изучаемые переменные. Поскольку строение совокупного влияния всецело зависит от постулируемой причинной структуры отношений между переменными, то и все введенные выше понятия имеют смысл только лишь по отношению к причинной модели с заданным графом связей.
Структурные причинные модели в эконометрике и социологии соединяют теорию объекта с эмпирическими данными на основе графа связей. Структурные модели формализуют гипотезы о причинных отношениях. Встает задача выбора гипотез, обозначаемая иногда в эконометрической и социологической литературе как проблема каузального вывода. X. Блейлок, изучая этот вопрос как часть общего вопроса о средствах построения социологических теорий, предложил формальный прием, основанный на идеях Г. Саймона о ложной корреляции и каузальной упорядоченности, иногда называемый процедурой Саймона — Блейлока.
Формальное содержание этого подхода заключается в гипотезе о полностью специфицированной линейной рекурсивной причинной модели, оценке ее параметров, а затем использовании этих значений для воспроизведения эмпирической корреляционной матрицы. Основная идея процедуры — это положение о том, что модель, которая не воспроизводит эмпирических корреляций, должна быть отвергнута.
Очевидна целесообразность использования процедуры Саймона -г Блейлока в двух случаях. Во-первых, когда известен причинный приоритет среди переменных. Если в этом случае имеются две гипотезы, постулирующие различные причинные цепи (структуры графа), то, используя процедуру Саймона — Блейлока, можно воссоздать эмпирические корреляции и отвергнуть ту каузальную цепь, где рассогласование слишком большое. Таким образом, мы можем сравнивать теории.
222
Второй ситуацией является случай с неизвестным каузальным приоритетом среди переменных. Допустим, что мы имеем набор переменных, для которых не известен каузальный порядок причина-следствие, и имеются две гипотезы, каждая по-своему устанавливающая его, постулируя отсутствие тех или иных возможных отношений. Описываемый подход может быть применен как для сравнения этих теорий, так и для их отбрасывания. Заметим, что в процедуре сравнения одна модель-гипотеза может оказаться лучше другой, но никогда — правильной. Более того, если одна из гипотез близка к тому, чтобы описываться полной рекурсивной системой, то обычно она работает, лучше воспроизводя корреляционную матрицу, и, естественно, будет выбираться как более удачная, даже если она весьма далека от истины.
Процедура Саймона — Блейлока является формальным приемом, создающим базис для отвергания гипотез, но никоим образом не представляет собой процедуру для создания новых теорий.
Другим известным приемом является вычеркивание связей в чрезмерно связанном графе с целью изучения поведения системы и ее элементов в новых условиях. Устойчивость системы может означать верность гипотезы. Решение об уничтожении той или иной связи модели может быть принято или на основании критерия статистической значимости, или на основании произвольно установленного порогового критерия величины коэффициента причинного влияния. Проверкой правильности гипотез и корректности модели должно служить ее подтверждение при испытаниях на контрольных данных.
Использование p-анализа в социально-экономических исследованиях связано с рядом трудностей. Прежде всего не всегда можно считать, что линейная зависимость в состоянии удовлетворительно отразить все разнообразие причинно-следственных связей в реальных структурах. Кроме того, следует учитывать, что p-анализ разработан для количественных переменных. Структурные модели и путевой анализ иллюстрируют единство теоретического (качественного) и формально-математического (количественного) подходов. Значимость результатов анализа определяется в первую очередь правильностью построения логического каркаса структурной модели — максимально связанного графа связей, изоморфной математической модели в виде системы уравнений.
223
Контрольные вопросы к главе 4
1. Назовите возможные способы построения систем уравнений. Чем они отличаются друг от друга?
2. Как связаны между собой структурная и приведенная формы модели?
3. В чем состоят проблемы идентификации модели и какие условия идентификации (необходимое и достаточное) вы знаете?
4. Раскройте суть косвенного метода наименьших квадратов.
5. В каких случаях используется двухшаговый метод наименьших квадратов? Раскройте его содержание.
6. Что представляют собой мультипликаторные модели кейнсианского типа? Как интерпретируются коэффициенты приведенной формы такой модели?
7. Приведите пример динамической модели экономики.
8. Как строится структурная модель спроса и предложения?
9. В чем состоит сущность путевого анализа?
10. Как производится оценка путевых коэффициентов?
11. Назовите составляющие коэффициента корреляции, которые выделяются с помощью путевого анализа.
ГЛАВА
МОДЕЛИРОВАНИЕ ОДНОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ1
5.1. ОСНОВНЫЕ ЭЛЕМЕНТЫ ВРЕМЕННОГО РЯДА
Можно построить эконометрическую модель, используя два типа исходных данных:
• данные, характеризующие совокупность различных объектов в определенный момент (период) времени;
• данные, характеризующие один объект за ряд последовательных моментов (периодов) времени.
Модели, построенные по данным первого типа, называются пространственными моделями. Модели, построенные на основе второго типа данных, называются моделями временных рядов.
В главах 5—7 будут рассмотрены модели, построенные по временным рядам данных, а также специальные методы оценки параметров этих моделей, разработанные на основе традиционных методов регрессионного анализа. В заключительной части главы 7 приводится обзор принципиально новых методов, разработанных в 80-е гг.
Временной ряд — это совокупность значений какого-либо показателя за несколько последовательных моментов или периодов времени2. Каждый уровень временного ряда формируется под воздействием большого числа факторов, которые условно можно подразделить на три группы:
• факторы, формирующие тенденцию ряда;
• факторы, формирующие циклические колебания ряда;
• случайные факторы.
’Подготовка глав 5—7 была осуществлена при поддержке Института «Открытое общество».
~В отечественной литературе используются два синонима этого термина: «динамический ряд» и «ряд динамики*.
15-1525
225
При различных сочетаниях в изучаемом явлении или процессе этих факторов зависимость уровней ряда от времени может принимать различные формы. Во-первых, большинство временных рядов экономических показателей имеют тенденцию, характеризующую совокупное долговременное воздействие множества факторов на динамику изучаемого показателя. Очевидно, что эти факторы, взятые в отдельности, могут оказывать разнонаправленное воздействие на исследуемый показатель. Однако в совокупности они формируют его возрастающую или убывающую тенденцию. На рис. 5.1 а) показан гипотетический временной ряд, содержащий возрастающую тенденцию.
Во-вторых, изучаемый показатель может быть подвержен циклическим колебаниям. Эти колебания могут носить сезонный характер, поскольку экономическая деятельность ряда отраслей экономики зависит от времени года (например, цены на сельскохозяйственную продукцию в летний период выше, чем в зимний; уровень безработицы в курортных городах в зимний период выше по сравнению с летним). При наличии больших массивов данных за длительные промежутки времени можно выявить циклические колебания, связанные с общей динамикой конъюнктуры рынка, а также с фазой-бизнес цикла, в которой находится экономика страны. На рис. 5.1 б) представлен гипотетический временной ряд, содержащий только сезонную компоненту.
Некоторые временные ряды не содержат тенденции и циклической компоненты, а каждый следующий их уровень образуется как сумма среднего уровня ряда и некоторой (положительной или отрицательной) случайной компоненты. Пример ряда, содержащего только случайную компоненту, приведен на рис. 5.1 в).
Очевидно, что реальные данные не следуют целиком и полностью из каких-либо описанных выше моделей. Чаще всего они содержат все три компоненты. Каждый их уровень формируется под воздействием тенденции, сезонных колебаний и случайной компоненты.
В большинстве случаев фактический уровень временного ряда можно представить как сумму или произведение трендовой, циклической и случайной компонент. Модель, в которой временной ряд представлен как сумма перечисленных компонент, называется аддитивной моделью временного ряда. Модель, в которой временной ряд представлен как произведение перечисленных компонент, называется мультипликативной моделью временного ряда. Основная задача эконометрического исследования от-
226
в
Рис. 5.1. Основные компоненты временного ряда: а — возрастающая тенденция; б — сезонная компонента; в — случайная компонента
дельного временного ряда — выявление и придание количественного выражения каждой из перечисленных выше компонент с тем, чтобы использовать полученную информацию для прогнозирования будущих значений ряда или при построении моделей взаимосвязи двух или более временных рядов.
5.2. АВТОКОРРЕЛЯЦИЯ УРОВНЕЙ ВРЕМЕННОГО РЯДА И ВЫЯВЛЕНИЕ ЕГО СТРУКТУРЫ
При наличии во временном ряде тенденции и циклических колебаний значения каждого последующего уровня ряда зависят от предыдущих. Корреляционную зависимость между последовательными уровнями временного ряда называют автокорреляцией уровней рада.
Количественно ее можно измерить с помощью линейного коэффициента корреляции между уровнями исходного временного ряда и уровнями этого ряда, сдвинутыми на несколько шагов во времени. Рассмотрим пример.
15*
227
Пример 5.1. Расчет коэффициентов автокорреляции уровней для временного ряда расходов на конечное потребление.
Пусть имеются следующие условные данные о средних расходах на конечное потребление (у„ д. е.) за 8 лет (табл. 5.1).
Таблица 5.1
Расчет коэффициента автокорреляции первого порядка дм временного ряда расходов на конечное потребление, д. е.
(И-1-У2)2
(И-1-У2)2
17 —
2 8 7 -3,29 -3
3 8 8 -3,29 —2
4 10 8 -1,29 —2
5 11 10 -0,29 0
6 12 И 0,71 1
7 14 12 2,71 2
8 16 14 4,71 4
Итого 86 70 -0,03* 0
9,87
6,58
2,58
0,71 5,42 18,84 44,0
10,8241 10,8241 1,6641 0,0841 0,5041 7,3441 22,1841 53,4287
9 4
4 0
1 4 16 38
О
*Сумма не равна нулю ввиду наличия ошибок округления.
Разумно предположить, что расходы на конечное потребление в текущем году зависят от расходов на конечное потребление предыдущих лет.
Определим коэффициент корреляции между рядами yt и y(_t и измерим тесноту связи между расходами на конечное потребление текущего и предыдущего годов. Добавим в табл. 5.1 временной ряду,
Одна из рабочих формул для расчета коэффициента корреляции имеет вид:
^j-x)2-Y.(yj-y)2
В качестве переменной х мы рассмотрим ряд у2, Уз,..., у»; в качестве переменной у — ряду(, у2, Ут- Тогда приведенная выше формула примет вид
Е(Л-Я)-(Я-|-Л)
Г=2
- Л )2 • ЕСИ/-1 - У2)
t=2 t=2
(5.1)
228
где
п
(5.2)
Эту величину называют коэффициентом автокорреляции уровней ряда первого порядка, так как он измеряет зависимость между соседними уровнями ряда t и t — 1, т. е. при лаге 1.
Для данных примера 5.1 соотношения (5.2) составят:
8+8+10+11 + 12+14+16 _ 79 90.
_ 7+8+8+10+11+12+14 70
У2 -------=----------= -=
Используя формулу (5.1), получаем коэффициент автокорреляции первого порядка:
753,42-38
= 0,976.
Полученное значение свидетельствует об очень тесной зависимости между расходами на конечное потребление текущего и непосредственно предшествующего годов и, следовательно, о наличии во временном ряде расходов на конечное потребление сильной линейной тенденции.
Аналогично можно определить коэффициенты автокорреляции второго и более высоких порядков. Так, коэффициент автокорреляции второго порядка характеризует тесноту связи между уровнями у, и у,_| и определяется по формуле
п _ _
1(У/-Л)-(У/-2-У4)
. /=3___________________
2 п п ’
J Е(л - Уз)2 Г(У/-2-у*)2
V/=3 /=з
(5.3)
где
п
п-2'
п
(5.4)
Ддя данных из примера 5.1 получим:
_ 8+10+11 + 12+14+16 V- =----------------
=^ = 11,83; О
229
_ 7+8+8+10+11+12 56
У4 =---—;---------=Т
Построим табл. 5.2.
Подставив полученные значения в формулу (5.3), имеем:
27,3334 /40,8334-19,3334
=0,973.
Таблица 5.2
Расчет коэффициента автокорреляции второго порядка для временного ряда расходов на конечное потребление, д. е.
УгУ^Уг~Уз У,-2-У4
(Уг—Уз) ’ (Уг-2 “У4)
3 8 7 -3,83
4 10 8 -1,83
5 11 8 -0,83
6 12 10 0,17
7 14 11 2,1.7
8 16 12 4,17
Итого 86 56 0,02*
-2,33
-1,33
-1,33 0,67
1,67 2,67
0,02*
8,9239 2,4339 1,1039 0,1139 3,6239
11,1339 27,3334
14,6689 3,3489 0,6889 0,0289 4,7089
17,3889 40,8334
5,4289 1,7689 1,7689 0,4489 2,7889 7,1289
19,3334
‘Сумма равна нулю ввиду наличия ошибок округления.
Полученные результаты еще раз подтверждают вывод о том, что ряд расходов на конечное потребление содержит линейную тенденцию.
Число периодов, по которым рассчитывается коэффициент автокорреляции, называют лагом. С увеличением лага число пар значений, по которым рассчитывается коэффициент автокорреляции, уменьшается. Некоторые авторы считают целесообразным для обеспечения статистической достоверности коэффициентов автокорреляции использовать правило — максимальный лаг должен быть не больше (л/4)1.
Отметим два важных свойства коэффициента автокорреляции. Во-первых, он строится по аналогии с линейным коэффициентом корреляции и таким образом характеризует тесноту только линей
1 См.: Статистическое моделирование и прогнозирование: Учеб, пособие /Под ред. А.Г. Гранберга. - С. 103.
230
ной связи текущего и предыдущего уровней ряда. Поэтому по коэффициенту автокорреляции можно судить о наличии линейной (или близкой к линейной) тенденции. Для некоторых временных рядов, имеющих сильную нелинейную тенденцию (например, параболу второго порядка или экспоненту), коэффициент автокорреляции уровней исходного ряда может приближаться к нулю.
Во-вторых, по знаку коэффициента автокорреляции нельзя делать вывод о возрастающей или убывающей тенденции в уровнях ряда. Большинство временных рядов экономических данных содержит положительную автокорреляцию уровней, однако при этом могут иметь убывающую тенденцию.
Последовательность коэффициентов автокорреляции уровней первого, второго и т. д. порядков называют автокорреляционной функцией временного рада. График зависимости ее значений от величины лага (порядка коэффициента автокорреляции) называется коррелограммой.
Анализ автокорреляционной функции и коррелограммы позволяет определить лаг, при котором автокорреляция наиболее высокая, а следовательно, и лаг, при котором связь между текущим и предыдущими уровнями ряда наиболее тесная, т. е. при помощи анализа автокорреляционной функции и коррелограммы можно выявить структуру ряда.
Если наиболее высоким оказался коэффициент автокорреляции первого порядка, исследуемый ряд содержит только тенденцию. Если наиболее высоким оказался коэффициент автокорреляции порядка т, ряд содержит циклические колебания с периодичностью в г моментов времени. Если ни один из коэффициентов автокорреляции не является значимым, можно сделать одно из двух предположений относительно структуры этого ряда: либо ряд не содержит тенденции и циклических колебаний и имеет структуру, сходную со структурой ряда, изображенного на рис. 5.1 в), либо рад содержит сильную нелинейную тенденцию, для выявления которой нужно провести дополнительный анализ. Поэтому коэффициент автокорреляции уровней и автокорреляционную функцию целесообразно использовать для выявления во временном ряде наличия или отсутствия трендовой компоненты (7) и циклической (сезонной) компоненты (3).
Временной ряд расходов на конечное потребление, рассмотренный нами в примере 5.1, содержит только тенденцию, так как коэффициенты автокорреляции его уровней высокие.
231
Пример 5.2. Автокорреляционная функция и выявление структуры ряда.
Пусть имеются условные данные об объемах потребления электроэнергии жителями региона за 16 кварталов (табл. 5.3).
Таблица 5.3
Потребление электроэнергии:
телямн региона, млн кВт • ч
t л У1 Уf—2 JV-3 Л-4
1 6,0 им им мм
2 4,4 6,0 нм МММ
3 5,0 4,4 6,0 нм мм
4 9,0 5,0 4,4 6,0 мм
5' 7,2 9,0 5,0 4,4 6,0
6 4,8 7,2 9,0 5,0 4,4
7 6,0 4,8 7,2 9,0 5,0
8 10,0 6,0 4,8 7,2 9,0
9 8,0 10,0 6,0 4,8 7,2
10 5,6 8,0 10,0 6,0 4,8
11 6,4 5,6 8,0 10,0 6,0
12 11,0 6,4 5,6 8,0 10,0
13 9,0 11,0 6,4 5,6 8,0
14 6,6 9,0 11,0 6,4 5,6
15 7,0 6,6 9,0 11,0 6,4
16 10,8 7,0 6,6 9,0 11,0
Нанесем эти значения на график (рис.5.2).
с 0 4—।—।—।—।—।—।—।—।—।—।—f—।—।—।—।—т—*-1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 г
Время, квартал
фактические уровни ряда
Рис. 5.2. Потребление электроэнергии жителями региона
232
Определим коэффициент автокорреляции первого порядка (добавим yt_x в табл. 5.3 и воспользуемся формулой расчета линейного коэффициента корреляции). Он составит: = 0,165. Отметим, что расчет этого коэффициента производился по 15, а не по 16 парам наблюдений. Это значение свидетельствует о слабой зависимости текущих уровней ряда от непосредственно им предшествующих уровней. Однако, как следует из графика, структура этого ряда такова, что каждый следующий уровень yt зависит от уровня yf_4 и yt_2 в гораздо большей степени, чем от уровня yt_h Построим ряд yf_2 (см. табл. 5.3). Рассчитав коэффициент автокорреляции второго порядка г2, получим количественную характеристику корреляционной связи рядов уп yt_2. Продол-
жив расчеты аналогичным образом, получим автокорреляционную функцию этого ряда. Ее значения и коррелограмма приведены в табл. 5.4.
Таблица 5.4
Коррелограмма временного ряда потребления электроэнергии
Лаг
Коэффициент автокорреляции уровней
Коррелограмма
1
2
3
4
5
6 7
8
0,165154
0,566873
0,113558
0,983025
0,118711
0,722046
0,003367
0,973848
*♦
*******
************
*
*********
************
Анализ значений автокорреляционной функции позволяет сделать вывод о наличии в изучаемом временном ряде, во-первых, линейной тенденции, во-вторых, сезонных колебаний периодичностью в четыре квартала. Данный вывод подтверждается и графическим анализом структуры ряда (см. рис. 5.2).
Аналогично, если, например, при анализе временного ряда наиболее высоким оказался коэффициент автокорреляции уровней второго порядка, ряд содержит циклические колебания в два периода времени, т. е. имеет пилообразную структуру.
233
5.3. МОДЕЛИРОВАНИЕ ТЕНДЕНЦИИ ВРЕМЕННОГО РЯДА
Одним из наиболее распространенных способов моделирования тенденции временного ряда является построение аналитической функции, характеризующей зависимость уровней ряда от времени, или тренда. Этот способ называют аналитическим выравниванием временного ряда.
Поскольку зависимость от времени может принимать разные формы, для ее формализации можно использовать различные виды функций. Для построения трендов чаще всего применяются следующие функции:
• линейный тренд: у, = а + Ь • Г,
• гипербола: yt = а + b/t\ ।
• экспоненциальный тренд: уt = е°+ь'';
• тренд в форме степенной функции yt = а •
• парабола второго и более высоких порядков
yt = a + bt-t + b2 •? + ... + Ьк • А
Параметры каждого из перечисленных выше трендов можно определить обычным МНК, используя в качестве независимой переменной время t = 1, 2,..., л, а в качестве зависимой переменной — фактические уровни временного ряда у,. Для нелинейных трендов предварительно проводят стандартную процедуру их линеаризации.
Существует несколько способов определения типа тенденции. К числу наиболее распространенных способов относятся качественный анализ изучаемого процесса, построение и визуальный анализ графика зависимости уровней ряда от времени, рас-' чет некоторых основных показателей динамики. В этих же целях можно использовать и коэффициенты автокорреляции уровней ряда. Тип тенденции можно определить путем сравнения коэффициентов автокорреляции первого порядка, рассчитанных по исходным и преобразованным уровням ряда. Если временной ряд имеет линейную тенденцию, то его соседние уровни у, и у1_1 тесно коррелируют. В этом случае коэффициент автокорреляции первого порядка уровней исходного ряда должен быть высоким. Если временной ряд содержит нелинейную тенденцию, например, в форме экспоненты, то коэффициент автокорреляции первого порядка по логарифмам уровней исходного ряда будет выше, чем соответствующий коэффициент, рассчитанный по уровням ряда. Чем сильнее выражена нелинейная тенденция в изучаемом временном ряде, тем в большей степени будут различаться значения указанных коэффициентов.
1 Другая формулировка этой формы тренда имеет вид: у, = а • b'.
234
Выбор наилучшего уравнения в случае, если ряд содержит нелинейную тенденцию, можно осуществить путем перебора основных форм тренда, расчета по каждому уравнению скорректированного коэффициента детерминации Л 2 и выбора уравнения тренда с максимальным значением скорректированного коэффициента детерминации. Реализация этого метода относительно проста при компьютерной обработке данных.
Пример 5.3. Расчет параметров тренда.
Имеются помесячные данные о темпах роста номинальной заработной платы в РФ за 10 месяцев 1999 г. в процентах к уров-ню декабря 1998 г. (табл. 5.5). Требуется выбрать наилучший тип тренда и определить его параметры.
Таблица 5.5 Темпы роста номинальной месячной заработной платы
за 10 месяцев 1999 г.*, % к уровню декабря 1998 г.
Месяц
Январь Февраль Март Апрель Май
Темпы
ста номи-
нальной месячной
заработной платы
82,9
87,3
99,4
104,8 107,2
Месяц
Июнь Июль Август Сентябрь Октябрь
Темпы роста номинальной месячной заработной платы
121,6
118,6
. 114,1
123,0
127,3
•Источник. Оперативная статистика Петербургкомстата.
Построим график данного временного ряда (рис. 5.3).
Время, мес.
фактические уровни ряда
уровни ряда, рассчитанные по линейному тренду
Рис. 5.3. Динамика темпов
ста номинальной заработной платы
за 10 месяцев 1999 г.
235
На графике рис. 5.3 наглядно видно наличие возрастающей тенденции. Возможно существование линейного тренда.
Для дальнейшего анализа определим коэффициенты автокорреляции по уровням этого ряда и их логарифмам (табл. 5.6).
Таблица 5.6
Автокорреляционная функция временного рядя темпов роста номинальной месячной заработной платы за 10 месяцев 1999 г., % к уровню декабря 1998 г.
Лаг Автокорреляционная функция
по уровням ряда по логарифмам уровней ряда ч
1 0,901 0,914 2 0,805 0,832 3 0,805 0,896
Высокие значения коэффициентов автокорреляции первого, второго и третьего порядков свидетельствуют о том, что ряд содержит тенденцию. Приблизительно равные значения коэффициентов автокорреляции по уровням этого ряда и по логарифмам уровней позволяют сделать следующий вывод: если ряд содержит нелинейную тенденцию, то она выражена в неявной форме. Поэтому для моделирования его тенденции в равной мере целесообразно использовать и линейную, и нелинейную функции, например степенной или экспоненциальный тренд.
Для выявления наилучшего уравнения тренда определим параметры основных видов трендов. Результаты этих расчетов представлены в табл. 5.7, согласно данным которой наилучшей является степенная форма тренда, для которой значение скорректированного коэффициента детерминации наиболее высокое. Уравнение степенного тренда можно использовать как в линеаризованном виде, так и в форме исходной степенной функции после проведения операции потенцирования. В исходном виде это уравнение выглядит следующим образом:
Л = g4,39 . f>, 193
ИЛИ
= 80,32 • /°’193.
236
Таблица 5.7
Уравнения трендов для временного ряда темпов роста номинальной месячной заработной платы за 10 месяцев 1999 г., % к уровню декабря 1998 г.
Тип тренда Уравнение Л2 R2
Линейный S, = 82,66 + 4,72/ (0,595)* 0,887 0,873
Парабола второго порядка St =72,9 + 9,599/-0,444? (2,11)* (0,187)* 0,937 0,920
Степенной Iny, = 4,39 + 0,1931п/ (0,017)* 0,939** 0,931**
Экспоненциальный Iny, = 4,43 + 0,045/ (0,006)* 0,872** 0,856**
Г иперболический *В скобках указаны ^Коэффициенты д< регрессии. у, =122,57 - (8,291)* стандартные ошибки коэффиц етерминации рассчитаны по л> 0,758 иентов ре грессм 4неаризованны1 0,728 ги. и уравнениям
Наиболее простую экономическую интерпретацию имеют параметры линейного и экспоненциального трендов.
Параметры линейного тренда можно интерпретировать так: а — начальный уровень временного ряда в момент времени t = 0; Ь — средний за период абсолютный прирост уровней ряда. Применительно к данному временному ряду можно сказать, что темпы роста номинальной месячной заработной платы за 10 месяцев 1999 г. изменялись от уровня 82,66% со средним за месяц абсолютным приростом, равным 4,72 проц, пункта. Расчетные по линейному тренду значения уровней временного ряда определяются двумя способами. Во-первых, можно последовательно подставлять в найденное уравнение тренда значения t = 1, 2^ «««j т. с.
улин, = 82,66 + 4,72 • 1 = 87,38;
= 82 66 + 4д2.2 =92до.
237
Во-вторых, в соответствии с интерпретацией параметров линейного тренда каждый последующий уровень ряда есть сумма предыдущего уровня и среднего цепного абсолютного прироста, т. е.
улин2 = У™Н1 + ь = 87,38 + 4,72 = 92,10;
улин3 = ;ли"2 + ь = 92,10 + 4,72 = 96,82 и т. д.
График линейного тренда приведен на рис. 5.3.
Параметры экспоненциального тренда имеют следующую интерпретацию. Параметр а — это начальный уровень временного ряда в момент времени t = 0. Величина е* — это средний за единицу времени коэффициент роста уровней ряда.
Для нашего примера уравнение экспоненциального тренда в исходной форме имеет вид:
л = е4-43. е°>М5/ или
л =83,96 - 1,046'.
Таким образом, начальный уровень ряда в соответствии с уравнением экспоненциального тренда составляет 83,96 (сравните с начальным уровнем 82,66 в линейном тренде), а средний цепной коэффициент роста — 1,046. Следовательно, можно сказать, что темпы роста номинальной месячной заработной платы за 10 месяцев 1999 г. изменялись от уровня 83,96% со средним за месяц цепным темпом роста, равным 104,6%. Иными словами, средний за месяц цепной темп прироста временного ряда составил 4,6%.
По аналогии с линейной моделью расчетные значения уровней ряда по экспоненциальному тренду можно получить как путем подстановки в уравнение тренда значений t = 1, 2,..., п, так и в соответствии с интерпретацией параметров экспоненциального тренда: каждый его последующий уровень есть произведение предыдущего уровня на соответствующий коэффициент роста:
уЭКСП| = . j 046 = 83 96.1046 = 87>82;
?ксп2 • 1,046 = 87,82 • 1,046 = 91,87 и т. д.
При наличии неявной нелинейной тенденции следует дополнять описанные выше методы выбора наилучшего уравнения тренда качественным анализом динамики изучаемого показателя, с тем чтобы избежать ошибок спецификации при выборе вида тренда. Качественный анализ предполагает изучение проблем 238
возможного наличия в исследуемом временном ряде поворотных точек и изменения темпов прироста, или ускорения темпов прироста, начиная с определенного момента (периода) времени под влиянием ряда факторов, и т. д. В случае если уравнение тренда выбрано неверно при больших значениях /, результаты анализа и прогнозирования динамики временного ряда с использованием выбранного уравнения будут недостоверными вследствие ошибки спецификации.
Иллюстрация возможного появления ошибки спецификации приводится на рис. 5.4.
о t* t
Рис. 5.4. Ошибка спецификации при выборе уравнения тренда
Если наилучшей формой тренда является парабола второго порядка, в то время как на самом деле имеет место линейная тенденция, то при больших t парабола и линейная функция будут по-разному описывать тенденцию в уровнях ряда. При t > . /• парабола второго порядка характеризует убывающую тенденцию в уровнях ряда у„ а линейная функция — возрастающую.
5.4. МОДЕЛИРОВАНИЕ СЕЗОННЫХ И ЦИКЛИЧЕСКИХ КОЛЕБАНИЙ / г
Аддитивная и мультипликативная модели временного ряда
Существует несколько подходов к анализу структуры временных рядов, содержащих сезонные или циклические колебания*.
Простейший подход — расчет значений сезонной компоненты методом скользящей средней и построение аддитивной или мультипликативной модели временного ряда. Общий вид аддитивной модели следующий:
У= T+S + E.
(5.5)
'Моделирование циклических колебаний в целом осуществляется аналогично моделированию сезонных колебаний, поэтому мы рассмотрим
только методы модели
вания последних.
239
Эта модель предполагает, что каждый уровень временного ряда может быть представлен как сумма трендовой (Г), сезонной (5) и случайной (£) компонент. Общий вид мультипликативной модели выглядит так:
У= T-S-E.
(5.6)
Эта модель предполагает, что каждый уровень временного ряда может быть представлен как произведение трендовой (7), сезонной (5) и случайной (£) компонент. Выбор одной из двух моделей осуществляется на основе анализа структуры сезонных колебаний. Если амплитуда колебаний приблизительно постоянна, строят аддитивную модель временного ряда, в которой значения сезонной компоненты предполагаются постоянными для различных циклов. Если амплитуда сезонных колебаний возрастает или уменьшается, строят мультипликативную модель временного ряда, которая ставит уровни ряда в зависимость от значений сезонной компоненты.
Построение аддитивной и мультипликативной моделей сводится к расчету значений Т, S и Е для каждого уровня ряда.
Процесс построения модели включает в себя следующие шаги.
1. Выравнивание исходного ряда методом скользящей средней.
2. Расчет значений сезонной компоненты S.
3. Устранение сезонной компоненты из исходных уровней ряда и получение выравненных данных (Т+ Е) в аддитивной или (Т- Е) в мультипликативной модели.
4. Аналитическое выравнивание уровней (Т+ Е) или (Т - Е) и расчет значений Т с использованием полученного уравнения тренда.
5. Расчет полученных по модели значений (Т+ S) или (Т- S).
6. Расчет абсолютных и/или относительных ошибок.
Если полученные значения ошибок не содержат автокорреляции, ими можно заменить исходные уровни ряда и в дальнейшем использовать временной ряд ошибок Е для анализа взаимосвязи исходного ряда и других временных рядов.
Подробнее методику построения каждой из моделей рассмо- -трим на примерах.
Призер 5.4. Построение аддитивной модели временного ряда.
Обратимся к данным об объеме потребления электроэнергии жителями района за последние четыре года, представленным в табл. 5.3.
240
В примере 5.2 было показано, что данный временной ряд содержит сезонные колебания периодичностью 4. Объемы потребления электроэнергии в осенне-зимний период времени (I и IV кварталы) выше, чем весной и летом (II и III кварталы). По графику, этого ряда (рис. 5.2) можно установить наличие приблизительно равной амплитуды колебаний. Это свидетельствует о возможном существовании в ряде аддитивной модели. Рассчитаем ее компоненты.
Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Для этого:
а) просуммируем уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент времени и определим условные годовые объемы потребления электроэнергии (гр. 3 табл. 5.8);
Ь) разделив полученные суммы на 4, найдем скользящие средние (гр. 4 табл.5.8). Отметим, что полученные таким образом выравненные значения уже не содержат сезонной компоненты;
с) приведем эти значения в соответствие с фактическими моментами времени, для чего найдем средние значения из двух последовательных скользящих средних — центрированные скользящие средние (гр. 5 табл. 5.8).
Таблица 5.8
Расчет оценок сезонной компоненты в аддитивной модели
№ квартала, t
Потребление электроэнергии, Л
Итого за четыре квартала
Скользящая средняя за четыре квартала
4
Центрированная скользящая средняя
5
Оценка сезонной компоненты
6
1 2 3
4 5
6 7
8 9 10
11 12 13 14 15 16
6,0 4,4
5,0 9,0 7,2
4,8 6,0 10,0 8,0
5,6 6,4 11,0 9,0
6,6 7,0 10,8
24,4 25,6
26,0 27,0
28,0 28,8
29,6 30,0
31,0 32,0
33,0 33,6
33,4
6,10 6,40
6,50 6,75
7,00 7,20
7,40 7,50
7,75 8,00 8,25
8,40 8,35
6,250 6,450 6,625
6,875 7,100
7,300 7,450 7,625
7,875 8125
8,325 8,375
-1,250 2,550 0,575
-2,075
2,700 0,550
-2,025
-1,475 2,875 0,675
-1,775
16"1525
241
Шаг 2. Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и центрированными скользящими средними (гр. 6 табл. 5.8). Используем эти оценки для расчета значений сезонной компоненты S (табл. 5.9). Для этого найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты Sf. В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопога-шаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю.
Таблица 5.9
Расчет значений сезонной компоненты в аддитивной модели
Для данной модели имеем:
0,6 - 1,958 - 1,275 + 2,708 = 0,075.
Определим корректирующий коэффициент:
к = 0,075 / 4 = 0,01875. р
Рассчитаем скорректированные значения сезонной компоненты как разность между ее средней оценкой и корректирующим коэффициентом к:
242
Sj — У; — к,
(5.7)
где i = 1:4.
Проверим условие равенства нулю суммы значений сезонной компоненты:
0,581- 1,977 - 1,294 + 2,690 = 0.
Таким образом, получены следующие значения сезонной компоненты:
I квартал: У( = 0,581;
И квартал: У2в —1,979;
III квартал: У3 = —1,294;
IV квартал: У4 = 2,690.
Занесем полученные значения в табл. 5.9 для соответствующих кварталов каждого года (стр. 3).
Шаг 3. Элиминируем влияние сезонной компоненты, вычитая ее значение из каждого уровня исходного временного ряда. Получим величины Т+ Е= Y—S (гр. 4 табл. 5.10). Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту.
Таблица 5.10
Расчет выравненных значений Та ошибок Е в аддитивной модели
8 10,0
9 8,0
10 5,6
И 6,4
12 11,0
13 9,0
14 6,6
15 7,0
16 10,8
0,581 -1,977 -1,294
2,690 0,581
-1,977
-1,294 2,690 0,581
-1,977
-1,294 2,690 0,581
-1,977 -1,294
2,690
5,419 6,337 6,294 6,310 6,619 6,777 7,294 7,310 7,419 7,577 7,694 8,310 8,419 8,577 8,294 8,110
5,902 6,088 6,275
6,461 6,648 6,834
7,020 7,207 7,393
7,580 7,766 7,952
8,139 8,325 8,519
8,698
6,483 4,111 4,981 9,151
7,229 4,857 5,727 9,896 7,974
5,603 6,472
10,642 8,720 6,348 7,218
11,388
-0,483 0,289 0,019
-0,151 -0,029 -0,057
0,273 0,104 0,026
-0,030 -0,072
0,358 0,280 0,252
-0,218 -0,588
0,2333 0,0835 0,0004 0,0228 0,0008 0,0032 0,0745 0,0108 0,0007 0,0009 0,0052 0,1282 0,0784 0,0635 0,0475 0,3457
16*
243
Шаг 4. Определим компоненту Т данной модели.
для этого
проведем аналитическое выравнивание ряда (Т + Е) с помощью
линейного тренда. Результаты аналитического выравнивания
следующие:
Константа
Коэффициент регрессии
Стандартная ошибка коэффициента регрессии
Л-квадрат
Число наблюдений
Число степеней свободы
5,715416 0,186421 0,015188 0,914971 16
14
Таким образом, имеем следующий линейный тренд:
7= 5,715+ 0,186-Л
Подставляя в это уравнение значения t = 1, ..., 16, найдем уровни Т для каждого момента времени (гр. 5 табл. 5.10). График уравнения тренда приведен на рис. 5.5.
Рис. 5.5. Потребление электроэнергии жителями района (фактические, выравненное и полученные по аддитивной модели значения уровней ряда)
Саг 5.
Найдем значения уровней ряда, полученные по адди
тивной модели. Для этого прибавим к уровням Тзначения сезон
ной компоненты для соответствующих кварталов. Графически значения (7+5) представлены на рис. 5.5.
244
Шаг 6. В соответствии с методикой построения аддитивной модели расчет ошибки производится по формуле
£=Г-(Т + 5).
(5.8)
Это абсолютная ошибка. Численные значения абсолютных ошибок приведены в гр. 7 табл. 5.10.
По аналогии с моделью регрессии для оценки качества построения модели или для выбора наилучшей модели можно применять сумму квадратов полученных абсолютных ошибок. Для данной аддитивной модели сумма квадратов абсолютных ошибок равна 1,10. По отношению к общей сумме квадратов отклонений уровней ряда от его среднего уровня, равной 71,59, эта величина составляет чуть более 1,5%:
(1 - 1,10/71,59)-100= 1,536.
Следовательно, можно сказать, что аддитивная модель объясняет 98,5% общей вариации уровней временного ряда потребления электроэнергии за последние 16 кварталов.
Пример 5.5. Построение мультипликативной модели временного ряда.
Пусть имеются поквартальные данные о прибыли компании за последние четыре года (табл. 5.11).
Таблица 5.11
График данного временного ряда (рис. 5.6) свидетельствует о наличии сезонных колебаний (период колебаний равен 4) и общей убывающей тенденции уровней ряда. Прибыль компании в весенне-летний период выше, чем в осенне-зимний период. Поскольку амплитуда сезонных колебаний уменьшается, можно предположить существование мультипликативной модели. Определим ее компоненты.
245
Рис. 5.6. Прибыль компании
Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней. Методика, применяемая на этом шаге, полностью совпадает с методикой аддитивной модели. Результаты расчетов оценок сезонной компоненты представлены в табл. 5.12.
Таблица 5.12
Расчет оценок сезонной компоненты в мультипликативной модели
№ квартала, / Прибыль компании, Л Итого за четыре квартала Скользящая средняя за четыре квартала Центрированная скользящая средняя Оценка сезонной компоненты
1 2 3 4 5 6
72
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
90 64
70 92 80
58 62
80 68 48
52 60
50 30
326 324 316 306 300
292 280 268 258 248
228 210 192
81,5 81,0
79,0 76,5 75,0 73,0 70,0
67,0 64,5 62,0 57,0 52,5
48,0
81,25
1,108
77,75 75,75
74,00 71,50 68,50 65,75 63,25
59,50 54,75 50,25
1,215 1,081 0,811 0,905 1,217 1,075 0,807 0,950
1,194
246
Шаг 2. Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние (гр. 6 табл. 5.12). Используем эти оценки для расчета значений сезонной компоненты .У (табл. 5.13). Для этого найдем средние за каждый квартал оценки сезонной компоненты Sf. Взаимопогашаемость сезонных воздействий в мультипликативной модели выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна числу периодов в цикле. В нашем случае число периодов одного цикла (год) равно 4 (четыре квартала).
Таблица 5.13 Расчет сезонной компоненты в мультипликативной модели
Показатели Год № квартала, i
I II ш ГУ
1 2 3 4 0,900 0,905 0,950 '•X 1,215 1,217 1,194 1,108 1,081 1,075 0,800 0,817 0,807
Итого за /-й квартал (за все годы) 2,755 3,626 3,264 и 2,424
Средняя оценка сезонной компоненты для /-го квартала, 0,918 1,209 1,088 0,808
Скорректированная сезонная компонента, 5J 0,913 1,202 1,082 0,803
Имеем:
0,918 + 1,209 + 1,088 + 0,808 = 4,023.
Определим корректирующий коэффициент:
к = 4/4,023 = 0,9943.
Определим скорректированные значения сезонной компоненты, умножив ее средние оценки на корректирующий коэффициент к.
Sj = У, к, где 1=1:4.
(5.9)
247
верим условие равенства 4 суммы значений сезонной
компоненты:
0,913 + 1,202 + 1,082 + 0,803 = 4.
Получим следующие значения сезонной компоненты:
I квартал:
II квартал:
III квартал:
IV квартал:
= 0,913;
S2 = 1,202;
S3 = 1,082;
У4 = 0,803.
Занесем полученные значения в табл. 5.14 для соответствующих кварталов каждого года (стр. 3).
Шаг 3. Разделим каждый уровень исходного ряда на соответствующие значения сезонной компоненты. Тем самым мы получим величины Т • Е— Y: S (гр. 4 табл. 5.14), которые содержат только тенденцию и случайную компоненту.
Таблица 5.14
Расчет выравненных значений Т н ошибок Е в мультипликативной модели
1 72 0,913
2 100 1,202
3 90 1,082
4 64 0,803
5 70 0,913
6 92 1,202
7 80 1,082
8 58 0,803
9 62 0,913
10 80 1,202
И 68 1,082
12 48 0,803
13 52 0,913
14 60 1,202
15 50 1,082
16 30 0,803
78,86 83,19
83,18 79,70
76,67 76,54 73,94 72,23 67,91
66,56 62,85
59,78 56,96 49,92 46,21 37,36
87,80 85,03
82,25 79,48
76,70 73,93
71,15 68,38 65,60 62,83 60,05 57,28
54,50 51,73
48,95 46,18
80,16 102,20 89,00 63,82
70,03 88,86 76,99
54,91 59,90
75,52 64,98
45,99 49,76
62,18 52,97
37,08
0,898 0,978 1,011
III
1,000 1,035 1,039
1,056 1,035 1,059
1,047 1,044 1,045 0,965 0,944 0,809
-8,16
-2,20
0,18 -0,03
3,14 3,01
3,09 2,10 4,48
3,02 2,01
2,24 -2,18 -2,97 -7,08
66,66
4,86
ill
0,03
III
9,85 9,08 9,57 4,43
20,08 9,14 4,03 5,02 4,73 8,79
50,12
Ш
248
1
Шаг 4. Определим компоненту 7в мультипликативной модели. Для этого рассчитаем параметры линейного тренда, используя уровни (Т Е). Результаты аналитического выравнивания это
го ряда представлены ниже:
Константа 90,585150
Коэффициент регрессии —2,773250
Стандартная ошибка коэффициента регрессии 0,225556
R-квадрат 0,915239
Число наблюдений 16
Число степеней свободы 14
Уравнение тренда имеет следующий вид:
7=90,59-2,773-/.
Подставляя в это уравнение значения t = 1, ..., 16, найдем уровни 7 для каждого момента времени (гр. 5 табл. 5.14). График уравнения тренда приведен на рис. 5.7.
фактические значения тренд (7)
—а— значения (Г• S)
Рис 5.7. Прибыль компании (фактические и выравненные по мультипликативной модели значения уровней ряда)
Шаг 5. Найдем уровни ряда по мультипликативной модели,
умножив уровни Т на значения сезонной компоненты для соот
ветствующих кварталов. Графически значения (7-5) представле
ны на рис. 5.7.
249
Шаг 6. Расчет ошибки в мультипликативной модели производится по формуле
Е=Г:(Т5).
Численные значения ошибки приведены в гр. 7 табл. 5.14. Если временной ряд ошибок не содержит автокорреляции, его можно использовать вместо исходного ряда для изучения его взаимосвязи с другими временными рядами. Для того чтобы сравнить мультипликативную модель и другие модели временного ряда, можно по аналогии с аддитивной моделью использовать сумму квадратов абсолютных ошибок. Абсолютные ошибки в мультипликативной модели определяются как
E = y,-(T-S).
(5.Н)
В данной модели сумма квадратов абсолютных ошибок со-
ставляет 207,40. Общая сумма квадратов отклонений фактичес-
ких уровней этого ряда от среднего значения равна 5023. Таким
образом, доля объясненной дисперсии уровней ряда равна: (1 - 207,40/5023) = 0,959, или 95,9%.
Выявление и устранение сезонного эффекта (в некоторых ис-
точниках применяется термин «десезонализация уровней ряда») используются в двух направлениях. Во-первых, воздействие сезонных колебаний следует устранять на этапе предварительной обработки исходных данных при изучении взаимосвязи нескольких временных рядов. Поэтому в российских и международных
статистических сборниках часто публикуются данные, в которых устранено влияние сезонной компоненты (если это помесячная или поквартальная статистика), например показатели объемов
производства в отдельных отраслях промышленности, уровня безработицы и т.д. Во-вторых, это анализ структуры одномерных временных рядов с целью прогнозирования уровней ряда в буду
щие моменты времени.
Пример 5.6. Прогнозирование по аддитивной модели.
Предположим, поданным примера 5.4 требуется дать прогноз потребления электроэнергии жителями района в течение первого полугодия ближайшего следующего года.
Прогнозное значение Ft уровня временного ряда в аддитивной модели в соответствии с соотношением (5.5) есть сумма трендовой и сезонной компонент.
Объем электроэнергии, потребленной в течение первого полугодия ближайшего следующего, т. е. пятого, года, рассчитыва
250
ется как сумма объемов потребления электроэнергии в I и во II кварталах пятого года, соответственно Г17 и Flg. Для определения трендовой компоненты воспользуемся уравнением тренда
Т= 5,715 + 0,186 -t.
Получим:
Т17 = 5,715 + 0,186 • 17 = 8,877;
Т18 = 5,715 + 0,186- 18 = 9,063.
Значения сезонной компоненты равны: = 0,581 (I квартал);
S2 = —1,977 (II квартал).
Таким образом,
Fn = Т.п + 5, = 8,877 + 0,581 = 9,458;
*18 = Tin + s2 = 9,063 - 1,977 = 7,086.
Прогноз объема потребления электроэнергии на первое полугодие ближайшего следующего (пятого) года составит:
(9,458 + 7,086) = 16,544 млн кВт ч.
Пример 5.7. Прогнозирование по мультипликативной модели.
Предположим, по данным примера 5.5 необходимо сделать прогноз ожидаемой прибыли компании за первое полугодие ближайшего следующего года.
Прогнозное значение Ft уровня временного ряда в мультипликативной модели в соответствии с соотношением (5.6) есть произведение трендовой и сезонной компонент. Для определения трендовой компоненты за каждый квартал воспользуемся уравнением тренда
Т = 90,59 - 2,773 t.
Получим:
Т17 = 90,59 - 2,773 • 17 = 43,401;
Ги = 90,59 - 2,773 18 = 40,626.
Значения сезонной компоненты равны = 0,913 (I квартал);
S2 = 1,202 (II квартал).
251
Таким образом,
F„ = Т17 • = 43,401 • 0,913 = 39,626;
Ля = Г18 • s2 = 40,626 • 1,202 = 48,832.
Прогноз ожидаемой прибыли компании на первое полугодие ближайшего следующего года составит:
(39,626 + 48,832) = 88,458 тыс. долл. США.
Применение фиктивных переменных для моделирования сезонных колебаний
Рассмотрим еще один метод моделирования временного ряда, содержащего сезонные колебания, — построение модели регрессии с включением фактора времени и фиктивных переменных. Количество фиктивных переменных в такой модели должно быть на единицу меньше числа моментов (периодов) времени внутри одного цикла колебаний. Например, при моделировании поквартальных данных модель должна включать четыре независимые переменные — фактор времени и три фиктивные переменные. Каждая фиктивная переменная отражает сезонную (циклическую) компоненту временного ряда для какого-либо одного периода. Она равна единице для данного периода и нулю для всех остальных периодов.
Пусть имеется временной ряд, содержащий циклические колебания периодичностью к. Модель регрессии с фиктивными переменными для этого ряда будет иметь вид:
yt = а + b • t + C]Xj + ... + cjxj + ... + <*_!**_[ + е„ (5.12)
_ J 1 для каждого у внутри каждого цикла, где Xj, - | q всех остальных случаях.
Например, при моделировании сезонных колебаний на основе поквартальных данных за несколько лет число кварталов внутри одного года к = 4, а общий вид модели следующий:
yf = а + b t + cpq + с^с2 + с^х3 + е„
(5-13)
где xt =
1 для первого квартала, 0 во всех остальных случаях.
гдех2 =
1 для второго квартала, 0 во всех остальных случаях.
252
где х3 =
1 для третьего квартала, О во всех остальных случаях.
Уравнение тренда для каждого квартала будет иметь следующий вид:
для I квартала: для II квартала: для III квартала: для IV квартала:
у, = а + 6-г + С| +
у, = а + b • I + с2 + е,;
yt = а + Ь • t + с3 + Б,; yt = а + Ь • t + Ef.
(5.14)
(5.15)
(5.16)
(5.17)
Таким образом, фиктивные переменные позволяют дифференцировать величину свободного члена уравнения регрессии для каждого квартала. Она составит:
для I квартала (а + с,);
для II квартала (а + с2);
для III квартала (а + с3); для IV квартала а.
Параметр b в этой модели характеризует среднее абсолютное изменение уровней ряда под воздействием тенденции. В сущности, модель (5.13) есть аналог аддитивной модели временного ряда, поскольку фактический уровень временного ряда есть сумма трендовой, сезонной и случайной компонент.
Пример 5.8. Построение модели регрессии временного ряда с фиктивными переменными.
Построим модель регрессии с включением фактора времени и фиктивных переменных для данных о потреблении электроэнергии из примера 5.4. В данной модели четыре независимые переменные: t, х1( х2, х3 и результативная переменная у. Составим матрицу исходных данных (табл. 5.15).
Оценим параметры уравнения регрессии (5.13) обычным МНК. Результаты оценки приведены в табл. 5.16.
Уравнение регрессии имеет вид:
у, = 8,33 + 0,19/ - 2,09х1 - 4,48х2 - 3,91х3.
253
Таблица 5.15
Исходные данные для расчета параметров уравнения регрессии
с фиктивными переменными но временному ряду потребления электроэнергии
1
2 3
4 5
6 7
8 9
10
11
12
13
14
15
16
1 0 0 о 1 о о о
1 о о о
1 о о о
о 1 о о о 1 о о о
1 о о о
1 о о
о о
1 о о о
1 о о о
1 о о о
1 о
6,0
4,4
5,0
9,0
7,2
4,8
6,0
10,0
8,0
5,6
6,4
11,0
9,0
6,6
7,0
10,8
Таблица 5.16
Уравнение регрессии с фиктивными переменными для временного ряда потребления электроэнергии
Переменная
Коэффициент
Стандартная ошибка
/-критерий
Константа
8,3250
0,1875
-2,0875
-4,4750
-3,9125
0,227261
0,016939
0,220208
0,216926
0,214933
36,6318
11,0691
-9,4797
-20,6292
-18,2034
Л2 = 0,985
Проанализируем эти результаты. Влияние сезонной компоненты в каждом квартале статистически значимо (фактические значения r-критерия по модулю больше 2 для параметров при переменных х(, х2, х3 и константы а). Параметр а = 8,33 есть сумма начального уровня ряда и сезонной компоненты в IV квартале. 254
Сезонные колебания в I, II и III кварталах приводят к снижению этой величины, о чем свидетельствуют отрицательные оценки параметров при переменных хь х2 их3. Отметим, что эти параметры не равны значениям сезонной компоненты, поскольку они характеризуют не сезонные изменения уровней ряда, а их отклонения от уровней, учитывающих сезонные воздействия в IV квартале. Положительная величина параметра Ь = 0,19 при переменной времени свидетельствует о наличии возрастающей тенденции в уровнях ряда. Его абсолютное значение говорит о том, что средний за квартал абсолютный прирост объема потребления электроэнергии составляет 0,19 млн кВт • ч, или 190 тыс. кВт * ч. Поскольку фактическое значение 7-критерия Стьюдента равно 11,1, можно утверждать, что существование в уровнях ряда тенденции установлено надежно.
Коэффициент детерминации в данной модели Л2 = 0,985. Общая сумма квадратов уровней ряда у, составляет:
собш = ^0’/-У)2 = 67>3-
Определим остаточную сумму квадратов:
= (1 - Л2) • = (1 - 0,985) 67,3 = 1,01.
Остаточная сумма квадратов по аддитивной модели (сумма квадратов абсолютных ошибок) была рассчитана ранее (табл. 5.10) и составляет 1,10. Следовательно, модель регрессии с фиктивными переменными описывает динамику временного ряда потребления электроэнергии лучше, чем аддитивная модель.
Основной недостаток модели с фиктивными переменными для описания сезонных и циклических колебаний — наличие
большого количества переменных. Если, например, строить мо-
дель для описания помесячных периодических колебаний за не
сколько лет, то такая модель будет включать 12 независимых пе-
ременных (11 фиктивных переменных и фактор времени). В та
кой ситуации число степеней свободы невелико, что снижает ве
роятность получения статистически значимых оценок параметров уравнения регрессии.
5.5. МОДЕЛИРОВАНИЕ ТЕНДЕНЦИИ ВРЕМЕННОГО РЯДА
ПРИ НАЛИЧИИ СТРУКТУРНЫХ ИЗМЕНЕНИЙ
От сезонных и циклических колебаний следует отличать единовременные изменения характера тенденции временного ряда, вызванные структурными изменениями в экономике или иными фак-
255
торами. В этом случае, начиная с некоторого момента времени /*, происходит изменение характера динамики изучаемого показателя, что приводит к изменению параметров тренда, описывающего эту динамику. Схематично такая ситуация изображена на рис. 5.8.
Рис. 5.8. Изменение характера тенденции временного ряда
о
Момент (период) времени t* сопровождается значительными изменениями ряда факторов, оказывающих сильное воздействие на изучаемый показатель уг Чаще всего эти изменения вызваны изменениями в общеэкономической ситуации или факторами (событиями) глобального характера, приведшими к изменению структуры экономики (например, начало крупных экономических реформ, изменение экономического курса, нефтяные кризисы и прочие факторы). Если исследуемый временной ряд включает в себя соответствующий момент (период) времени, то одной из задач его изучения становится выяснение вопроса о том, значимо ли повлияли общие структурные изменения на характер этой тенденции.
Если это влияние значимо, то для моделирования тенденции данного временного ряда следует использовать кусочно-линейные модели регрессии, т. е. разделить исходную совокупность на две подсовокупности (до момента времени /• и после момента /*) и построить отдельно по каждой подсовокупности уравнения
256
линейной регрессии (на рис. 5.8 этим уравнениям соответствуют прямые (1) и (2)). Если структурные изменения незначительно повлияли на характер тенденции ряда у„ то ее можно описать с помощью единого для всей совокупности данных уравнения тренда (на рис. 5.8 этому уравнению соответствует прямая (3)).
Каждый из описанных выше подходов имеет свои положительные и отрицательные стороны. При построении кусочно-линейной модели происходит снижение остаточной суммы квадратов по сравнению с единым для всей совокупности уравнением тренда. Однако разделение исходной совокупности на две части ведет к потере числа наблюдений и, следовательно, к снижению числа степеней свободы в каждом уравнении кусочно-линейной модели. Построение единого для всей совокупности уравнения тренда, напротив, позволяет сохранить число наблюдений п исходной совокупности, однако остаточная сумма квадратов по этому уравнению будет выше по сравнению с кусочно-линейной моделью. Очевидно, что выбор одной из двух моделей (кусочнолинейной или единого уравнения тренда) будет зависеть от соотношения между снижением остаточной дисперсии и потерей числа степеней свободы при переходе от единого уравнения регрессии к кусочно-линейной модели.
Таблица 5.17
Условные обозначения для алгоритма теста Чоу
№ уравнения Вид уравнения Число наблюдений в совокупности Остаточная сумма квадратов Число параметров в уравнении1 Число степеней свободы остаточной дисперсии
Кусочно-линейная модель
(1) y(l) = 0J + + />,/ «1 С* ост Л,-£|
(2) ут = а2 + "Ь b2t л2 ^ост к2 п2 — к2
Уравнение тренда по всей совокупности
(3) у(3) — а3 + “Ь Ь3/ п ^ост ^3 п — ку = («| + + п2) - к3
1В рассматриваемой нами формулировке число параметров всех уравнений к} — к2 = — к3 = 2. В общем случае число параметров в каждом уравнении может различаться.
J7-1525
257
Формальный статистический тест для оценки этого соотношения был предложен Грегори Чоу*. Применение этого теста предполагает расчет параметров уравнений трендов, графики которых изображены на рис. 5.8 прямыми (1), (2) и (3). Введем систему обозначений, приведенную в табл. 5.17.
Выдвинем гипотезу Но о структурной стабильности тенденции изучаемого временного ряда.
Остаточную сумму квадратов по кусочно-линейной модели (С^ост) можно найти как сумму С1^ и С2^:
(5.18)
Соответствующее ей число степеней свободы составит:
(«! — Л|) + (и2 — Л2) = (п — Л| — kJ). (5.19)
Тогда сокращение остаточной дисперсии при переходе от единого уравнения тренда к кусочно-линейной модели можно определить следующим образом2:
(5.20)
Число степеней свободы, соответствующее с учетом соотношения (5.19) будет равно:
п — к3 — (п — кх — к2) = кх + ко. —к3. (5.21)
Далее в соответствии с предложенной Г. Чоу методикой определяется фактическое значение /-критерия по следующим дисперсиям на одну степень свободы вариации:
факт ~
Ддс &Cw‘-(ki+k2-k3)
Дкл C^n-kt-ki) '
(5.22)
Найденное значение сравнивают с табличным, получен-
ным по таблицам распределения Фишера для уровня значимости а и числа степеней свободы (кх + Л2 — к3) и (л — кх — Л2).
‘Chow Gregory С. Tests of equality between sets of coefficients in two linear regressions I I Econometrica — \bl. 28. — № 3. — 1960. — C. 591—605.
2B методике расчетов предполагается, что С3^ всегда больше, чем
258
Если > /^абл, то гипотеза о структурной стабильности тенденции отклоняется, а влияние структурных изменений на динамику изучаемого показателя признают значимым. В этом случае моделирование тенденции временного ряда следует осуществлять с помощью кусочно-линейной * модели. Если /фай. < /"табл, то нет оснований отклонять ноль-гипотезу о структурной стабильности тенденции. Ее моделирование следует осуществлять с помощью единого для всей совокупности уравнения тренда.
Отметим следующие особенности применения теста Чоу:
1. Если число параметров во всех уравнениях (1), (2), (3) (см. рис. 5.8 и табл. 5.17) одинаково и равно к, то формула (5.22) упрощается:
г. _ ДСост: к
2. Тест Чоу позволяет сделать вывод о наличии или отсутствии структурной стабильности в изучаемом временном ряде. Если /факт < Лабл> то 3110 означает, что уравнения (1) и (2) описывают одну и ту же тенденцию, а различия численных оценок их параметров а1 и а2, а также и Ь2 соответственно статистически незначимы. Если же /^kt > /табл, то гипотеза о структурной стабильности отклоняется, что означает статистическую значимость различий оценок параметров уравнений (1) и (2).
3. Применение теста Чоу предполагает соблюдение предпосылок о нормальном распределении остатков в уравнениях (1) и (2) и независимость их распределений.
Если гипотеза о структурной стабильности тенденции ряда у, отклоняется, дальнейший анализ может заключаться в исследовании вопроса о причинах этих структурных различий и более детальном изучении характера изменения тенденции. В принятых нами обозначениях эти причины обуславливают различия оценок параметров уравнений (1) и (2).
Возможны следующие сочетания изменения численных оценок параметров этих уравнений (рис. 5.9):
• изменение численной оценки свободного члена уравнения тренда а2 по сравнению с а} при условии, что различия между и Ь2 статистически незначимы. Геометрически это означает, что прямые (1) и (2) параллельны (рис. 5.9 а). В данной ситуации можно говорить о скачкообразном изменении уровней ряда у, в момент времени /* при неизменном среднем абсолютном приросте за период;
17»
259
• изменение численной оценки параметра Ь2 по сравнению с при условии, что различия между а( и а2 статистически незначимы. Геометрически это означает, что прямые (1) и (2) пересекают ось ординат в одной точке (рис. 5.9 б). В этом случае изме-
нение тенденции связано с изменением среднего абсолютного прироста временного ряда, начиная с момента времени /*, при неизменном начальном уровне ряда в момент времени t = 0;
• изменение численных оценок параметров at и а2, а также Ь\ и Ь2. Геометрически эта ситуация изображена на рис. 5.9 в. Она
означает, что изменение характера тенденции сопровождается изменением как начального уровня ряда, так и среднего за период абсолютного прироста.
Рис. 5.9. Изменение тенденции временного ряда при различном сочетании статистической значимости изменений параметров с, и а2, Ь{ и Ь2. а — статистически значимым является различие только между а, и а2; б — статистически значимым является различие только между и Ь2, в — статистически значимым является различие между а, и в2, а также между bt и Ь2
260
Один из статистических методов тестирования при применении перечисленных выше ситуаций для характеристики тенденции изучаемого временного ряда был предложен американским экономистом Дамодаром Гуйарати1. Этот метод основан на включении в модель регрессии фиктивной переменой которая принимает значения 1 для всех t < /*, принадлежащие промежутку времени до изменения характера тенденции, далее — промежутку (1), и 0 значения для всех t > t*, принадлежащие промежутку времени после изменения характера тенденции, далее — промежутку (2). Д. Гуйарати предлагает определять параметры следующего уравнения регрессии:
yt = а + b • Zt + с t + d (Zt • /) + ег (5.24)
Таким образом, для каждого промежутка времени получим следующие уравнения:
Промежуток (1) Z = 1
Промежуток (2) Z О
^ = (a + 6) + (c + d)/ + e,;
yt = а 4- с • 14-
Сопоставив полученные уравнения с уравнениями (1) и (2), нетрудно заметить, что
«1 = (а + Ь);
@9
(5.25)
Параметр b есть разница между свободными членами уравнений (1) и (2), а параметр d — разница между параметрами bt и Ь2 уравнений (1) и (2). Оценка статистической значимости различий а( и а2, а также bt и Ь2 эквивалентна оценке статистической * значимости параметров b и d уравнения (5.24). Эту оценку можно провести при помощи /-критерия Стьюдента.
Таким образом, если в уравнении (5.24) b является статистически значимым, a d — нет, то изменение тенденции вызвано только различиями параметров а, и а2 (рис. 5.9 а). Если в этом уравнении параметр d статистически значим, а Ь — незначим, то изменение характера тенденции вызвано различиями параметров 6, и Ь2 (рис. 5.9 б). Наконец, если оба коэффициента b и d являются статистически значимыми, то на изменение характера тенденции повлияли как различия между а, и а2, так и различия между 6, и Ь2 (рис. 5.9 в).
1 Gujarati D.N. Basic Econometrics. — McGraw-Hill, Inc, 1995. — C. 509 — 513.
261
Этот метод можно использовать не только в дополнение к тесту Чоу, но и самостоятельно для проверки гипотезы о структурной стабильности тенденции изучаемого временного ряда. Основное его преимущество перед тестом Чоу состоит в том, что нужно построить только одно, а не три уравнения тренда.
Мы рассмотрели простейший случай применения теста Чоу для моделирования линейной тенденции. Однако этот тест (а также модель (5.24) с фиктивной переменной) может использоваться (и действительно используется во многих прикладных исследованиях) при проверке гипотез о структурной стабильности и в более сложных моделях взаимосвязи двух и более временных рядов.
Контрольные вопросы к главе 5
1. Перечислите основные элементы временного ряда.
2. Что такое автокорреляция уровней временного ряда и как ее можно оценить количественно?
3. Дайте определение автокорреляционной функции временного ряда.
4. Перечислите основные виды трендов.
5. Какова интерпретация параметров линейного и экспоненциального трендов?
б. Выпишите общий вид мультипликативной и аддитивной модели временного ряда.
7. Перечислите этапы построения мультипликативной и аддитивной моделей временного ряда.
8. С. какими целями проводятся выявление и устранение сезонного эффекта?
9. Как структурные изменения влияют на тенденцию временного ряда?
10. Какие тесты используют для проверки гипотезы о структурной стабильности временного ряда?
11. Какова концепция теста Чоу?
12. Изложите суть метода Гуйарати. В чем его преимущество перед тестом Чоу?
ГЛАВА
ИЗУЧЕНИЕ ВЗАИМОСВЯЗЕЙ ПО ВРЕМЕННЫМ РЯДАМ
6.1. СПЕЦИФИКА СТАТИСТИЧЕСКОЙ ОЦЕНКИ ВЗАИМОСВЯЗИ ДВУХ ВРЕМЕННЫХ РЯДОВ
Изучение причинно-следственных зависимостей переменных, представленных в форме временных рядов, является одной из самых сложных задач эконометрического моделирования. Применение в этих целях традиционных методов корреляционно-регрессионного анализа, рассмотренных в главах 2 и 3, может привести к ряду серьезных проблем, возникающих как на этапе построения, так и на этапе анализа эконометрических моделей. В первую очередь эти проблемы связаны со спецификой временных рядов как источника данных в эконометрическом моделировании. В главе 5 было показано, что каждый уровень временного ряда содержит три основные компоненты: тенденцию, циклические или сезонные колебания и случайную компоненту. Рассмотрим подробнее, каким образом наличие этих компонент сказывается на результатах корреляционно-регрессионного анализа временных рядов данных.
Предварительный этап такого анализа заключается в выявлении структуры изучаемых временных рядов. Если на этом этапе было выявлено, что временные ряды содержат сезонные или циклические колебания, то перед проведением дальнейшего исследования взаимосвязи необходимо устранить сезонную или циклическую компоненту из уровней каждого ряда, поскольку ее наличие приведет к завышению истинных показателей силы и тесноты связи изучаемых временных рядов в случае, если оба ряда содержат циклические колебания одинаковой периодичности, либо к занижению этих показателей в случае, если сезонные или
263
циклические колебания содержат только один из рядов или периодичность колебаний в рассматриваемых временных рядах различна.
Устранение сезонной компоненты из уровней временных рядов можно проводить в соответствии с методикой построения аддитивной и мультипликативной моделей, рассмотренной в п. 5.4. При дальнейшем изложении методов анализа взаимосвязей в этой главе мы примем предположение, что изучаемые временные ряды не содержат периодических колебаний. Предположим, изучается зависимость между рядами х и у. Для количественной характеристики этой зависимости используется линейный коэффициент корреляции. Если рассматриваемые временные ряды имеют тенденцию, коэффициент корреляции по абсолютной величине будет высоким (положительным в случае совпадения и отрицательным в случае противоположной направленности тенденций рядов х и у). Однако из этого еще нельзя делать вывод о том, что х причина у или наоборот. Высокий коэффициент корреляции в данном случае есть результат того, что х и у зависят от времени, или содержат тенденцию. При этом одинаковую или противоположную тенденцию могут иметь ряды, совершенно не связанные друг с другом причинно-следственной зависимостью. Например, коэффициент корреляции между численностью выпускников вузов и числом домов отдыха в РФ в период с 1970 по 1990 г. .составил 0,8. Это, естественно, не означает, что увеличение количества домов отдыха способствует росту числа выпускников вузов или увеличение числа последних стимулирует спрос на дома отдыха.
Для того чтобы получить коэффициенты корреляции, характеризующие причинно-следственную связь между изучаемыми рядами, следует избавиться от так называемой ложной корреляции, вызванной наличием тенденции в каждом ряде. Обычно это осуществляют с помощью одного из методов исключения тенденции, которые будут рассмотрены в п. 6.2.
Предположим, что по двум временным рядам xt и у, строится уравнение парной линейной регрессии вида
yt = а + b • xt + ег
(6.1)
Наличие тенденции в каждом из этих временных рядов означает, что на зависимую yt и независимую xt переменные модели оказывает воздействие фактор времени, который непосредственно в модели не учтен. Влияние фактора времени будет выражено 264
в корреляционной зависимости между значениями остатков е, за текущий и предыдущие моменты времени, которая получила название «автокорреляция в остатках».
Автокорреляция в остатках есть нарушение одной из основных предпосылок МНК — предпосылки о случайности остатков, полученных по уравнению регрессии. Один из возможных путей решения этой проблемы состоит в применении к оценке параметров модели обобщенного МНК. При построении уравнения множественной регрессии по временным рядам данных, помимо двух вышеназванных проблем, возникает также проблема мультиколлинеарности факторов, входящих в уравнение регрессии, в случае если эти факторы содержат тенденцию.
6.2. МЕТОДЫ ИСКЛЮЧЕНИЯ ТЕНДЕНЦИИ
Сущность всех методов исключения тенденции заключается в том, чтобы устранить или зафиксировать воздействие фактора времени на формирование уровней ряда. Основные методы исключения тенденции можно разделить на две группы'.
• методы, основанные на преобразовании уровней исходного ряда в новые переменные, не содержащие тенденции. Полу-
ченные переменные используются далее для анализа взаимосвязи изучаемых временных рядов. Эти методы предполагают непосредственное устранение трендовой компоненты Т из каждого уровня временного ряда. Два основных метода в данной группе — это метод последовательных разностей и метод отклонений от трендов;
• методы, основанные на изучении взаимосвязи исходных уровней временных рядов при элиминировании воздействия фактора времени на зависимую и независимые переменные модели. В первую очередь это метод включения в модель регрессии по временным рядам фактора времени.
Рассмотрим подробнее методику применения, преимущества и недостатки каждого из перечисленных выше методов.
Метод отклонений от тренда
Пусть имеются два временных ряда xt и yt, каждый из которых содержит трендовую компоненту Т и случайную компоненту е. Проведение аналитического выравнивания по каждому из этих рядов позволяет найти параметры соответствующих уравнений трендов и определить расчетные по тренду уровни xt и yt соответ
265
ственно. Эти расчетные значения можно принять за оценку трендовой компонент^ Т каждого ряда. Поэтому влияние тенденции можно устранить путем вычитания расчетных значений уровней ряда из фактических. Эту процедуру проделывают для каждого временного ряда в модели. Дальнейший анализ взаимосвязи рядов проводят с использованием не исходных уровней, а отклонений от тренда х, — 5it и у, — yt при условии, что последние не содержат тенденции.
Пример 6.1. Измерение взаимосвязи расходов на конечное потребление и совокупного дохода.
Вернемся к примеру 5.1. Пусть помимо расходов на конечное потребление имеются данные о совокупном доходе (д. е). Исходные данные за 8 лет представлены в табл. 6.1. Требуется охарактеризовать тесноту и силу связи между временными рядами совокупного дохода xt и расходов на конечное потребление
Таблица 6.1
Расходы на конечное потребление и совокупный доход (усл. е. д.)
Год 1 2 3 4 5 6 7 8
Расходы наконечное потребление,^ 7 8 8 10 И 12 14 16
Совокупный доход, xt 10 12 11 12 14 15 17 20
Корреляционно-регрессионный анализ, проведенный по исходным данным рядов, приводит к следующим результатам:
yt = -2,05 + 0,92 • х„ г2^ = 0,965, = 0,982.
Как было показано в примере 5.1, коэффициент автокорреляции первого порядка по ряду расходов на конечное потребление = 0,976. Аналогично можно рассчитать, что коэффициент автокорреляции первого порядка временного ряда совокупного дохода г* = 0,880. Можно предположить, что полученные результаты содержат ложную корреляцию ввиду наличия в каждом Из рядов линейной или близкой к линейной тенденции. Применим метод устранения тенденции по отклонениям от тренда. Результаты расчета линейных трендов по каждому из рядов представлены в табл. 6.2.
266
Таблица 6.2
Результаты расчета параметров л инейных трендов расходов на конечное потребление и совокупного дохода
Показатели
Расходы на конечное потребление
Совокупный доход
Константа
Коэффициент регрессии Стандартная ошибка коэффициента регрессии R-квадрат Число наблюдений
Число степеней свободы
5,071428 1,261904
0,101946 0,962315
8 6
8,035714 1,297619
0,179889 0,896611
8 6
По трендам у t == 5,07 + 1,26 • t и xt = 8,04 + 1,3 • t определим расчетные значения yt и х{ и отклонения от трендов yt — и — xt (табл. 6.3).
Таблица 6.3
Трендовая компонента я ошибка для временные радов расходов па конечное потребление и совокупного дохода
Время, t У, Л Л У' Л xt л-Л
1 7 10 6,33 9,34 0,67 0,66
2 8 12 7,59 10,64 0,41 1,36
3 8 11 8,85 11,94 -0,85 -0,94
4 10 12 10,11 13,24 -0,11 -1,24
5 11 14 11,37 14,54 -0,37 -0,54
6 12 15 12,63 15,84 -0,63 -0,84
7 14 17 13,89 17,14 0,11 -0,14
8 16 20 15,15 18,44 0,85 1,56
Проверим полученные отклонения от трендов на автокорреляцию. Коэффициенты автокорреляции первого порядка по отклонениям от трендов составляют:
= 0,254, rf* = 0,129.
Следовательно, временные ряды отклонений от трендов можно использовать для получения количественной характеристики тесноты связи исходных временных рядов расходов на конечное
267
потребление и общего дохода. Коэффициент корреляции по отклонениям от трендов Гдгд,, = 0,860 (сравните это значение с коэффициентом корреляции по исходным уровням рядов = 0,982). Связь между расходами на конечное потребление и совокупным доходом прямая и тесная.
Результаты построения модели регрессии по отклонениям от трендов следующие:
Константа
Коэффициент регрессии
Стандартная ошибка коэффициента регрессии /{-квадрат Число наблюдений Число степеней свободы
0,017313 0,487553 0,117946 0,740116 8 6
Содержательная интерпретация параметров этой модели за-
труднительна, однако ее можно использовать для прогнозирова
ния. Для этого необходимо определить трендовое значение фак
торного признака х, и с помощью одного из методов оценить ве
личину предполагаемого отклонения фактического значения от трендового. Далее по уравнению тренда для результативного признака определяют трендовое значение х„ а по уравнению регрес
сии по отклонениям от трендов находят величину отклонения yt—yt. Затем находят точечный прогноз фактического значения yt по формуле
У1 = У1 + (У1-У1)-
Метод последовательных разностей
В ряде случаев вместо аналитического выравнивания временного ряда с целью устранения тенденции можно применить более простой метод — метод последовательных разностей.
Если временной ряд содержит ярко выраженную линейную тенденцию, ее можно устранить путем замены исходных уровней ряда цепными абсолютными приростами (первыми разностями).
Пусть
yt = У t+ (6.2)
где е, — случайная ошибка;
yt = а + Ь • t. (6.3)
Тогда
Л
Л, = У, ~ Л-i = а + b • t + е, - (а + b • (t - 1) +е,_,) =
= Ь+ (е,-е,-е,_|). (6.4)
268
Коэффициент b — константа, которая не зависит от времени. При наличии сильной линейной тенденции остатки et достаточно малы и в соответствии с предпосылками МНК носят случайный характер. Поэтому первые разности уровней ряда А, не зависят от переменной времени, их можно использовать для дальнейшего анализа.
. Если временной ряд содержит тенденцию в форме параболы второго порядка, то для ее устранения можно заменить исходные уровни ряда на вторые разности.
Пусть имеет место соотношение (6.2), однако
= а + • t + b2 • t1. (6.5)
Тогда
Л, = У,-УГ_1 =a + /»i -^ + />2 +е,-(о + Л| • 0 +
+ Ь2 • (Г-I)2 + е,_,) = й| - Ь2 + 2 Ь2 • t + (е, - е,_|). (6.6)
Как показывает это соотношение, первые разности А, непосредственно зависят от фактора времени t и, следовательно, содержат тенденцию.
Определим вторые разности:
“ Е/-1) -
- (*i - Ь2 + 2 • Ь2 • (/ — 1) + (е,_, - е,_2)) =
(6.7)
Очевидно, что вторые разности А2, не содержат тенденции, поэтому при наличии в исходных уровнях тренда в форме параболы второго порядка их можно использовать для дальнейшего анализа. Если тенденции временного ряда соответствует экспо-- ненциальный или степенной тренд, метод последовательных разностей следует применять не к исходным уровням ряда, а к их логарифмам.
Пример 6.2. Изучение зависимости расходов на конечное потребление от совокупного дохода по первым разностям.
Обратимся вновь к данным о расходах на конечное потребление у, и совокупном доходе xt (табл. 6.1). Проанализируем зависимость между этими рядами, используя для этого первые разности (табл. 6.4).
269
Таблица 6.4
Первые разности временных рядов расходов на конечное потребление и совокупного дохода
t Д,х
1 7 10
2 8 12 1 2
3 8 И 0 -1
4 10 12 2 1
5 11 14 1 2
6 12 15 1 1
7 14 17 2 2
8 16 20 2 3
Коэффициент автокорреляции первого порядка —0,109 -0,156
Результаты проверки временных рядов первых разностей на автокорреляцию приведены в последней строке табл. 6.4. Поскольку полученные ряды не содержат автокорреляции, будем использовать их вместо исходных данных для измерения зависимости между расходами на конечное потребление и совокупным доходом. Коэффициент корреляции этих рядов по первым разностям составляет гА 0,717. Это подтверждает вывод о наличии
тесной прямой связи между расходами на конечное потребление и совокупным доходом, приведенный в примере 6.1.
Построение уравнения регрессии зависимости расходов на конечное потребление от совокупного дохода по первыми разностям привело к следующим результатам:
Константа 0,676471
Коэффициент регрессии 0,426471
Стандартная ошибка коэффициента регрессии 0,184967
R-квадрат 0,515219
Число наблюдений 7
Число степеней свободы 5
Таким образом, уравнение регрессии имеет вид: \у « 0,68 + 0,43 • Дд; Л2 = 0,515.
В отличие от уравнения регрессии по отклонениям от тренда, параметрам данного уравнения легко дать интерпретацию. При изменении прироста дохода на 1 д. е. прирост потребления изменяется в среднем на 0,43 д. е. в ту же сторону. При всей 270
своей простоте метод последовательных разностей имеет два существенных недостатка. Во-первых, его применение связано с сокращением числа пар наблюдений, по которым строится уравнение регрессии, и, следовательно, с потерей числа степеней свободы. Во-вторых, использование вместо исходных уровней временных рядов их приростов или ускорений приводит к потере информации, содержащейся в исходных данных.
г ’
Включение в модель регрессии фактора времени
В корреляционно-регрессионном анализе устранить воздействие какого-либо фактора можно, если зафиксировать воздействие этого фактора на результат и другие включенные в модель факторы. ЕНот прием широко используется в анализе временных рядов, когда тенденция фиксируется через включение фактора времени в модель в качестве независимой переменной.
Модель вида
у, = а + • xt + b2 t + e, (6.8)
относится к группе моделей, включающих фактор времени. Очевидно, что число независимых переменных в такой модели может быть больше единицы. Кроме того, это могут быть не только текущие, но и лаговые значения независимой переменной, а также лаговые значения результативной переменной.
Преимущество данной модели по сравнению с методами отклонений от трендов и последовательных разностей в том, что она позволяет учесть всю информацию, содержащуюся в исходных данных, поскольку значения yt и х, есть уровни исходных временных рядов. Кроме того, модель строится по всей совокупности данных за рассматриваемый период в отличие от метода последовательных разностей, который приводит к потере числа наблюдений. Параметры а и b модели с включением фактора времени определяются обычным МНК. Расчет и интерпретацию параметров покажем на примере.
Пример 6.3. Построение модели регрессии с включением фактора времени.
Вернемся к данным табл. 6.1. Построим уравнение регрессии, описывающее зависимость расходов на конечное потребление у( от совокупного дохода х, и фактора времени. Для расчета параметров уравнения регрессии (6.8) воспользуемся обычным МНК. Система нормальных уравнений имеет вид:
271
n-a + bl'£xt+b2-'£.f = l.yn а^Х'+Ь^х? +b2'£txt =Xxt -yt, a-Yt + bi-^tx, + b2-'£x?='£t-y,.
(6.9)
Рассчитав по исходным данным необходимые величины, по-
лучим:
8a + lll/»i +36*2 =86,
lll-a+1619^ +554 *2 =1266, Зб-а + 554-ft, +204 *2 =440.
Решив эту систему относительно a, bt и Ь2, находим: а = 1,15; *! = 0,49; *2 = 0,63. Следовательно, уравнение регрессии имеет вид:
yt = 1,15 + 0,49 • xt + 0,63 •/ + £,.
Интерпретация параметров этого уравнения следующая. Параметр *! = 0,49 характеризует, что при увеличении совокупного дохода на 1 д. е. расходы на конечное потребление возрастут в среднем на 0,49 д. е. в условиях существования неизменной тенденции. Параметр Ь2 = 0,63 означает, что воздействие всех факторов, кроме совокупного дохода, на расходы на конечное потребление приведет к его среднегодовому абсолютному приросту на 0,63 д. е.
6.3. АВТОКОРРЕЛЯЦИЯ В ОСТАТКАХ. КРИТЕРИЙ ДАРВИНА - УОТСОНА
Рассмотрим уравнение регрессии вида
(6.10)
где к — число независимых переменных модели.
Для каждого момента (периода) времени t = 1 : п значение компоненты е, определяется как
(6.П)
или к
z^y.-^a+Ybj-x^. (6.12)
272
Рассматривая последовательность остатков как временной ряд, можно построить график их зависимости от времени. В соответствии с предпосылками МНК остатки ег должны быть случайными (рис. 6.1 а). Однако при моделировании временных рядов нередко встречается ситуация, когда остатки содержат тенденцию (рис. 6.1 б) и в)) или циклические колебания (рис. 6.1 г)). Это свидетельствует о том, что каждое следующее значение остатков зависит от предшествующих. В этом случае говорят о наличии автокорреляции остатков.
б
Рис. 6.1. Модели зависимости остатков от времени а— случайные остатки; б — возрастающая тенденция в остатках; в — убывающая тенденция в остатках; г — циклические колебания в остатках
Автокорреляция остатков может быть вызвана несколькими причинами, имеющими различную природу. Во-первых, иногда она связана с исходными данными и вызвана наличием ошибок измерения в значениях результативного признака. Во-вторых, в ряде случаев причину автокорреляции остатков следует искать в формулировке модели. Модель может не включать фактор, оказывающий существенное воздействие на результат, влияние которого отражается в остатках, вследствие чего последние могут оказаться автокоррелированными. Очень часто этим фактором
18~1525
273
является фактор времени t. Кроме того, в качестве таких существенных факторов могут выступать лаговые значения переменных, включенных в модель. Либо модель не учитывает несколько второстепенных факторов, совместное влияние которых на результат существенно ввиду совпадения тенденций их изменения или фаз циклических колебаний.
От истинной автокорреляции остатков следует отличать ситу-
ации, когда причина автокорреляции заключается в неправиль
ной спецификации функциональной формы модели. В этом слу
чае следует изменить форму связи факторных и результативного
признаков, а не использовать специальные методы расчета пара
метров уравнения регрессии при наличии автокорреляции остатков.
Существуют два наиболее распространенных метода определения автокорреляции остатков. Первый метод — это построение графика зависимости остатков от времени и визуальное определение наличия или отсутствия автокорреляции. Второй метод — использование критерия Дарбина — Уотсона и расчет величины
(6.13)
Таким образом, d есть отношение суммы квадратов разностей последовательных значений остатков к остаточной сумме квадратов по модели регрессии. Практически во всех статистических ППП значение критерия Дарбина — Уотсона указывается наряду с коэффициентом детерминации, значениями t- и /’-критериев.
Коэффициент автокорреляции остатков первого порядка определяется как
где
(6.14)
(6.15)
274
Так как е, — остатки, полученные по уравнению регрессии, параметры которого определены обычным МНК, то в соответствии с предпосылками МНК их сумма и среднее значение равны
нулю:
(6-16)
Следовательно, без уменьшения общности можно предположить, что
ё1=ё‘2 = 0. (6.17)
Предположим также
Ёе? « Ёе?-1-
t~2 t=2
(6.18)
С учетом соотношений (6.17) и (6.18) формула для расчета коэффициента автокорреляции остатков (6.14) преобразуется следующим образом:
(6.19)
Преобразуем теперь формулу (6.13) расчета критерия Дарвина — Уотсона следующим образом:
л п * Л Л *
Ё (е< - е<-1 )2 Ё е» - 2 • Ё eA-i + Ё е/-1
л л -
2а Ул2
/=1 /=1
(6.20)
С учетом (6.18) имеем:
(6.21)
18*
275
Сравнив выражения (6.19) и (6.21), нетрудно вывести следующее соотношение между критерием Дарвина — Уотсона и коэффициентом автокорреляции остатков первого порядка:
rf«2(l
(6.22)
Таким образом, если в остатках существует полная положительная автокорреляция и rcl = 1, то d = 0. Если в остатках полная отрицательная автокорреляция, то = -1 и, следовательно, d = 4. Если автокорреляция остатков отсутствует, то г£1 = 0 и d = 2. Следовательно,
Алгоритм выявления автокорреляции остатков на основе критерия Дарбина — Уотсона следующий. Выдвигается гипотеза Но об отсутствии автокорреляции остатков. Альтернативные гипотезы Я] и Я*! состоят, соответственно, в наличии положительной или отрицательной автокорреляции в остатках. Далее по специальным таблицам. (см. приложение) определяются критические значения критерия Дарбина — Уотсона dL и ^для заданного числа наблюдений п, числа независимых переменных модели к и уровня значимости а. По этим значениям числовой промежуток [0;4] разбивают на пять отрезков. Принятие или отклонение каждой из гипотез с вероятностью (1 — а) рассматривается на рис. 6.2.
Есть положительная автокорреляция остатков. Но отклоняется. С вероятностью Р = (1-«) принимается .
Зона неопределенности
Нет оснований отклонять Но (автокорреляция остатков отсутствует)
Зона неопределенности
Есть отрицательная автокорреляция остатков. Но отклоняется. С вероятностью Р=(1-а) принимается Н/.
О
2
du
Рис. 6.2. Механизм проверки гипотезы о наличии автокорреляции остатков
Если фактическое значение критерия Дарбина — Уотсона попадает в зону неопределенности, то на практике предполагают существование автокорреляции остатков и отклоняют гипотезу Яо.
Пример 6.4. Проверка гипотезы о наличии автокорреляции в остатках.
276
Проверим гипотезу о наличии автокорреляции в остатках для модели зависимости расходов на конечное потребление от совокупного дохода, построенной по первым разностям исходных показателей, используя данные примера 6.2.
Было получено следующее уравнение регрессии: ф
А,у = 0,68 + 0,43 • Дре + £г
Исходные данные, значения е, и результаты промежуточных расчетов представлены в табл. 6.5.
Таблица 6.5
Расчет критерия Дарбина — Уотсона
для модели зависимости потребления от дохода
t Ду Дд д^ £, = Ду- (Er-Sr-!)2
1 — и rt*
2 1 2 1,54 -0,54 rt* rt* 0,2916
3 0 -1 0,25 -0,25 0,29 0,0841 0,0625
4 2 1 1,11 0,89 1,14 1,2996 0,7921
5 1 2 1,54 -0,54 -1,43 2,0449 0,2916
6 1 1 1,11 -0,11 0,43 0,1849 0,0121
7 2 2 1,54 0,46 0,57 0,3249 0,2116
8 2 3 1,97 0,03 -0,43 0,1849 0,0009
Сумма 9 10 9,06 -0,06 0,57 4,1233 1,6624
*Сумма не равна нулю ввиду наличия ошибок округления.
Фактическое значение критерия Дарбина — Уотсона для этой модели составляет:
</ = 4,1233/1,6624 = 2,48.
Сформулируем гипотезы:
Яо — в остатках нет автокорреляции;
Н{ — в остатках есть положительная автокорреляция;
Нх — в остатках есть отрицательная автокорреляция.
Зададим уровень значимости а = 0,05. По таблицам значений критерия Дарбина — Уотсона определим для числа наблюдений п = 7 и числа независимых переменных модели к' = 1 критические значения dL = 0,700 и dv = 1,356. Получим следующие промежутки внутри интервала [0;4] (рис. 6.3).
277
о
dt = 0,700 tiu= 1,356
4-du= 2,644 4-<4 = 3,300
4
Рис. 6.3. Промежутки внутри интервала [0; 4]
Фактическое значение d = 2,48 попадает в промежуток от d(j до 4 — d(j. Следовательно, нет оснований отклонять гипотезу Яо об отсутствии автокорреляции в остатках.
Есть несколько существенных ограничений на применение критерия Дарбина — Уотсона.
Во-первых, он неприменим к моделям, включающим в качестве независимых переменных лаговые значения результативного признака, т. е. к моделям авторегрессии. Для тестирования на автокорреляцию остатков моделей авторегрессии используется критерий h Дарбина. Подробнее эта проблема будет рассмотрена в п. 7.5.
Во-вторых, методика расчета и использования критерия Дарбина — Уотсона направлена только на выявление автокорреляции остатков первого порядка. При проверке остатков на автокорреляцию более высоких порядков следует применять другие методы, рассмотрение которых выходит за рамки данного учебника.
В-третьих, критерий Дарбина — Уотсона дает достоверные результаты только для больших выборок. В этом смысле результаты примера 6.4 нельзя считать достоверными ввиду чрезвычайно малого числа наблюдений п = 7, по которым построена модель регрессии.
6.4.ОЦЕНИВАНИЕ ПАРАМЕТРОВ УРАВНЕНИЯ РЕГРЕССИИ ПРИ НАЛИЧИИ АВТОКОРРЕЛЯЦИИ В ОСТАТКАХ
Обратимся вновь к уравнению регрессии (6.1). Примем некоторые допущения относительно этого уравнения:
• пусть yt и xt не содержат тенденции, например, представляют собой отклонения выравненных по трендам значений от исходных уровней временных рядов;
• пусть оценки а и b параметров уравнения регрессии найдены обычным МНК;
• пусть критерий Дарбина — Уотсона показал наличие автокорреляции в остатках первого порядка.
Чтобы понять, каковы последствия автокорреляции в остатках для оценок параметров модели регрессии, найденных обычным МНК, построим формальную модель, описывающую авто-278
корреляцию в остатках. Автокорреляция в остатках первого порядка предполагает, что каждый следующий уровень остатков е, зависит от предыдущего уровня е,_Р Следовательно, существует модель регрессии вида
6^ С + d 1
(6.23)
где с и d - параметры уравнения регрессии.
В соответствии с рабочими формулами МНК имеем:
c = E,-d-Et.i; d = г-
e,_, - e,_.
(6.24)
С учетом соотношений (6.16) и (6.17) получим:
(6.25)
где - коэффициент автокорреляции остатков первого порядка.
Таким образом, имеем:
Е, = Е,-1 + «И
где и, ~ случайная ошибка.
(6.26)
Заметим, что |^(| < 1.
Учитывая соотношение (6.26), уравнение (6.1) можно переписать в виде
yt = a + b-xt + ^t - Et_i + ur
(6.27)
Найденные соотношения показывают, что текущий уровень ряда у, зависит не только от факторной переменной хр но и от остатков предшествующего периода е,_].
Допустим, мы не принимаем во внимание эту информацию и определяем оценки параметров а и b уравнения (6.1) обычным МНК. Тогда можно показать, что полученные оценки неэффективны, т. е. они не имеют минимальную дисперсию. Это приво
279
дит к увеличению стандартных ошибок, снижению фактических значений r-критерия и широким доверительным интервалам для коэффициента регрессии. На основе таких результатов можно сделать ошибочный вывод о незначимом влиянии исследуемого фактора на результат, в то время как на самом деле его влияние статистически значимо.
Отметим, что при соблюдении прочих предпосылок МНК автокорреляция остатков не влияет на свойства состоятельности и несмещенности оценок параметров уравнения регрессии обычным МНК, за исключением моделей авторегрессии. Применение МНК к моделям авторегрессии ведет к получению смещенных, несостоятельных и неэффективных оценок.
Рассмотрим основной подход к оценке параметров модели регрессии в случае, когда имеет место автокорреляция остатков. Для этого вновь обратимся к исходной модели (6.1). Для момента времени t — 1 эта модель примет вид:
y,_i =в + /»-х,_1 + е,_1. (6.28)
Умножим обе части уравнения (6.28) на
^ГУ,_1 = Л -a + ^i b-x^i + rf\ (6.29)
Вычтем почленно из уравнения (6.1) уравнение (6.29):
Уг “ Л ‘ yt-i = а “ Л а + b • х, - • b • х,_{ + е, - (6.30)
Проведя тождественные преобразования в (6.30), имеем:
У, ~ ’ yt-i = а • (I - 6) + b • (х, - • x,_j) + е, - /t • ег_! (6.31)
или
y't = a +bx, + ur
(6.32)
В формуле (6.32):
ut = ег “ П ’ Ez-а = а(1 — /®|).
(6.33)
(6.34)
(6.35)
(6.36)
Поскольку «, — случайная ошибка, то для оценки параметров уравнения (6.32) можно применять обычный МНК.
280
Итак, если остатки по исходному уравнению регрессии со-
держат автокорреляцию, то для оценки параметров уравнения
используют обобщенный МНК. Для его реализации необходимо
выполнять следующие условия.
1. Преобразовать исходные переменные yt и xt к виду (6.33) и (6.34).
2. Применив обычный МНК к уравнению (6.32), определить оценки параметров а и Ь.
3. Рассчитать параметр а исходного уравнения из соотношения (6.36) как
а = а7(1-/]).
(6.37)
4. Выписать исходное уравнение (6.1).
Обобщенный метод наименьших квадратов аналогичен методу последовательных разностей. Однако мы вычитаем из у, (или х,) не все значение предыдущего уровня yt^x (или х,_|), а некоторую его долю — ге| • yt_x или гЕ, • х,_(. Если гЕ| = 1, данный метод есть просто метод первых разностей, так как
У t ~Vt~ yt-\
(6.38)
и
(6.39)
Поэтому в случае, если значение критерия Дарбина — Уотсона близко к нулю, применение метода первых разностей вполне обоснованно. Если гЕ1 = — 1, т. е. в остатках наблюдается полная отрицательная автокорреляция, то изложенный выше метод модифицируется следующим образом:
y't =yt ~ (-1) ’ Л-i = Л + Л-i- (6-4°)
Аналогично
xt =xt ~ (— О ‘ Л-i ~ xt + Л-г (6.41)
Поскольку
а = а(1 — /*]) = 2 • а, (6.42)
имеем:
yt + Л-I = 2 • а + Ъ • (Л + Л-1) + «г
(6-43)
281
Следовательно,
(У, + = а + b(xt + xt_x)/2 + иД. (6.44)
В сущности, в модели (6.44) мы определяем средние за два периода уровни каждого ряда, а затем по полученным усредненным уровням обычным МНК рассчитываем параметры л и Ь. Данная модель называется моделью регрессии по скользящим средним.
Основная проблема, связанная с применением данного метода, заключается в том, как получить оценку /*|. Существует множество способов оценить численное значение коэффициента автокорреляции остатков первого порядка. Однако основными способами являются оценка этого коэффициента непосредственно по остаткам, полученным по исходному уравнению регрессии, и получение его приближенного значения из соотношения между коэффициентом автокорреляции остатков первого порядка и критерием Дарбина — Уотсона: /*| = 1 — d/2.
Расчет параметров уравнения регрессии при наличии автокорреляции остатков показан в примере 6.5.
6.5. КОИНТЕГРАЦИЯ ВРЕМЕННЫХ РЯДОВ
Общий недостаток методов исключения тенденции заключается в том, что эти методы предполагают некоторую модификацию модели (6.1) вследствие либо замены переменных, либо добавления в эту модель фактора времени. Однако большая часть соотношений, постулируемых экономической теорией, верификацией которых занимается эконометрика, сформулирована в терминах уровней временных рядов, а не их последовательных разностей или отклонений от трендов и предполагает измерение взаимосвязи переменных без включения в модель каких-либо дополнительных факторов (например, переменной времени).
В ряде случаев наличие в одном из временных рядов тенденции может быть следствием именно того факта, что другой ряд, включенный в модель, тоже содержит тенденцию, а не просто результатом прочих случайных причин. Поэтому одинаковая или противоположная направленность тенденций рядов может иметь устойчивый характер и наблюдаться на протяжении длительного промежутка времени, а коэффициент корреляции, рассчитанный по уровням временных рядов, может соответственно не содержать ложной корреляции и характеризовать истинную причинно-следственную зависимость между ними.
282
Начиная с 70-х гг. XX в. высказанные выше предположения были положены в основу новой теории о коинтеграции временных рядов. Под коинтеграцией понимается причинно-следственная зависимость в уровнях двух (или более) временных рядов, которая выражается в совпадении или противоположной направленности их тенденций и случайной колеблемости.
Не останавливаясь детально на положениях и концепциях теории коинтеграции (глубокое ее рассмотрение требовало бы подготовки отдельного учебного пособия), в данном параграфе мы кратко охарактеризуем основные статистические методы и критерии, применяемые для проверки гипотез о наличии коинтеграции временных рядов данных.
В соответствии с этой теорией между двумя временными рядами существует коинтеграция в случае, если линейная комбинация этих временных рядов есть стационарный временной ряд (т. е. ряд, содержащий только случайную компоненту и имеющий постоянную дисперсию на длительном промежутке времени)1.
Рассмотрим уравнения регрессии вида (6.1). Остатки е, в этом уравнении представляют собой линейную комбинацию рядов yt их/
е, = у, — а — b • xt. (6.45)
Одним из методов тестирования гипотезы о коинтеграции временных рядов yt и х, является критерий Энгеля — Грангера. Алгоритм применения этого критерия следующий.
1. Выдвигается ноль-гипотеза об отсутствии коинтеграции между рядами yt и xt.
2. Рассчитывают параметры уравнения регрессии вида
Де, = а + Ь • е,_|. (6.46)
где Де, — первые разности остатков, полученных из соотношения (6.45).
3. Определяют фактическое значение /-критерия для коэффициента регрессии а в уравнении (6.46).
4. Сравнивают полученное значение с критическим значением статистики т. Критические значения т, рассчитанные Энгелем
'Статистические критерии, предназначенные для проверки гипотезы о коинтеграции, основаны не на проверке стационарности остатков, а на проверке менее жесткой гипотезы — гипотезы об отсутствии во временно'м ряде единичного корня.
283
и Грангером для уровня значимости 1, 5 и 10%, составляют 2,5899; 1,9439; 1,6177*. Если фактическое значение t больше критического значения т для заданного уровня значимости а, ноль-гипотезу об отсутствии коинтеграции исследуемых временных рядов отклоняют и с вероятностью (1 — а) принимают альтернативную гипотезу о том, что между рядами yt и х, есть коинтегра-ция. В противном случае гипотеза об отсутствии коинтеграции между исследуемыми рядами не отклоняется.
Другой метод тестирования ноль-гипотезы об отсутствии коинтеграции между двумя временными рядами основан на использовании величины критерия Дарбина — Уотсона, полученной для уравнения (6.1). Однако в отличие от традиционной методики его применения в данном случае проводят проверку гипотезы о том, что полученное фактическое значение критерия Дарбина — Уотсона в генеральной совокупности равно нулю.
Ряд авторов называют следующие критические значения критерия Дарбина — Уотсона, подученные методом Монте-Карло* 2 для следующих уровней значимости: 1% — 0,511; 5% — 0,386; 10% — 0,322. Если результаты тестирования показали, что фактическое значение критерия Дарбина — Уотсона нельзя признать равным нулю (т. е. оно превышает критическое значение для заданного уровня значимости), ноль-гипотезу об отсутствии коинтеграции временных рядов отклоняют.
Если фактическое значение критерия Дарбина — Уотсона меньше критического значения для заданного уровня значимости, то ноль-гипотеза об отсутствии коинтеграции не отклоняется.
Коинтеграция двух временных рядов значительно упрощает процедуры и методы, используемые в целях их анализа, поскольку в этом случае можно строить уравнение регрессии и определять показатели корреляции, используя в качестве исходных данных непосредственно уровни изучаемых рядов, учитывая тем самым информацию, содержащуюся в исходных данных, в полном объеме. Однако поскольку коинтеграция означает совпадение
'Gujarati D.N. Basic Econometrics. — С. 727. Некоторые критические значения т для критерия Энгеля — Грангера можно также найти в учебнике: Davidson R., MacKinnon J.C. Estimation and Inference in Econometrics. — New York: Oxford University Press, 1993. — C. 722.
2Sargon J.D., BhargavaA.S. Testing Residuals from Least Squares Regression for Being Generated by the Gaussian Random №lk // Econometrica — \Ы. 51, 1983. — C. 153—174; или Gujarati D.N. Basic Econometrics. — C. 727—728.
284
динамики временных рядов в течение длительного промежутка времени, то сама эта концепция применима только к временным рядам, охватывающим сравнительно длительные (например, в несколько десятилетий) промежутки времени. При наличии коротких временных рядов данных, даже если формальные критерии показали наличие их коинтеграции, моделирование взаимосвязей по уровням этих рядов может привести к неверным результатам ввиду нарушения предпосылок теории коинтеграции.
Пример 6.5. Анализ взаимосвязи временных рядов среднедушевого располагаемого дохода и среднедушевого расхода на конечное потребление.
Пусть имеются данные о среднедушевом располагаемом доходе и среднедушевом расходе на конечное потребление в США в период с 1960 по 1991 г. (табл. 6.6).
Требуется охарактеризовать тесноту связи между изучаемыми временными рядами и определить предельную склонность к потреблению в США за рассматриваемый период.
Построим графики временных рядов среднедушевого дохода и потребления (рис. 6.3). Графический анализ показывает, что тенденции этих рядов совпадают. Проведем тестирование временных рядов среднедушевого дохода и расхода на потребление на коинтеграцию.
YfXt
15000--
10000--
5000--
t
I I I I I I I I I I I I+4 4 4-I-4 I I I M l I I I I I I I I.....I>
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
—$— ДОХОД
—— расходы на конечное потребление
Рис. 6.3. Динамика среднедушевого дохода и расходов на конечное потребление в США с 1960 по 1991 г.
Ноль-гипотеза состоит в том, что коинтеграция между этими рядами отсутствует.
По имеющимся исходным данным определим обычным МНК параметры уравнения регрессии зависимости среднедушевых расходов на конечное потребление yt от среднедушевого дохода xt.
285
Год, t
1960 1961
1962 1963
1964 1965 1966
1967 1968
1969 1970 1971
1972 1973
1974 1975
1976 1977 1978
1979 1980
1981 1982
1983 1984
1985 1986
1987 1988
1989 1990
1991
Таблица 6.6
Среднедушевой располагаемый доход и среднедушевые расходы
на конечное потребление в С
и
[А в период с I960 по 1991г.
(в сопоставимых ценах 1987 г.)1
Среднедуше-
вой располагаемый доход (долл. США), xt
Среднедушевые расходы на конечное потребление (долл. США) У1
Остатки, £f
Скорректированные на коэффициент автокорреляции остатков значения
дохода,
расхода, y't
3
7264 7382 7583
7718
8140
8508
8822
9114
9399 9606 9875
10 111 10 414 11013
10 832 10 906 11 192
11406 11 851
12 039 12 005
12 156
12 146 12 349 13 029
13 258
13 552
13 545
13 890 14030 14154
13 987
6698 6740
6931
7089 7384
7703 8005
8163 8506
8737
8842 9022
9425 9752
9602 9711
10 121 10 425
10 744 10 867
10 746 10 770
10 782 11 179 11617 12 015
12 336
12 568
12 903 13 027
13 051
12 889
173,80
106,98
112,61
146,12
51,94
31,57
43,99
—67,29
12,88
52,98
—90,10
-127,74
-4,17
-229,57
—212,65
-171,90
-25,65
ill]
-10,39 -51,76
-150,41 -265,66
-244,44
-34,65 -223,75
-36,94 112,93 251,39 268,22 263,11 172,76 164,77
2092,87 2207,95 2196,60 2520,30 2581,03 2627,08 2690,45 2762,83 2762,32 2880,59 2920,73 3051,89 3430,27 2813,12 3018,91 3251,03 3256,78 3545,96 3409,94 3239,06 3414,81 3294,86 3505,15 4037,34 3771,21 3898,47 3677,40
4027,49 3916,29 3938,35 3681,06
1862,99 2023,41
2042,34 2222,29
2326,50 2396,22 2334,33 2562,28 2543,54 2480,34
2583,88 2855,82 2889,38
2501,29 2719,51
3050,14 3055,61
3153,26 3052,98 2826,87
2945,43 2940,05
3328,31 3477,25
3556,33 3587,53
3585,80 3751,88
3631,95 3565,66
3386,19
1 Источник. Economic Report of the President. - \№ishington: US Government Printing Office, 1992. - C. 327.
286
Регрессионный анализ зависимости среднедушевых расходов на конечное потребление от среднедушевого располагаемого дохода показал следующее:
Константа
Коэффициент регрессии
Стандартная ошибка коэффициента регрессии
R-квадрат
Число наблюдений
Число степеней свободы
Критерий Дарбина — Уотсона
-174,746 0,922212 0,012837 0,994221
32
30
0,521
Уравнение регрессии имеет вид:
у, = -174,75 + 0,922 • xt + е,.
Применим критерий Энгеля — Грангера. Воспользовавшись полученным уравнением регрессии, определим остатки е( (гр. 3 табл. 6.6). Определим параметры уравнения регрессии (6.46):
Константа —1,7293
Коэффициент регрессии — 0,2724
Стандартная ошибка коэффициента регрессии 0,126806
R-квадрат 0,137319
Число наблюдений 31
Число степеней свободы 30
Де, = -1,729-0,272
Фактическое значение /-критерия, рассчитанное по данным уравнения регрессии, равно —2,154. Так как полученное фактическое значение по абсолютной величине превышает критическое значение т0 05 — 1,9439, то с вероятностью 95% можно отклонить ноль-гипотезу и сделать вывод о коинтеграции временных
рядов среднедушевого дохода и среднедушевых расходов на ко
нечное потребление.
Этот же вывод подтверждается и другим критерием. Полученное значение критерия Дарбина — Уотсона для уравнения регрессии, рассчитанного по уровням временных рядов, d = 0,521 пре
вышает для уровня значимости 0,01 его критическое значение, равное 0,511, и тем более превышает его критические значения при повышении уровня значимости. Это свидетельствует о том, что в генеральной совокупности критерий Дарбина — Уотсона не
287
равен нулю и, следовательно, временные ряды дохода и потребления коинтегрируют. Для определения показателей силы и тесноты их взаимосвязи можно работать с уровнями рядов.
Коэффициент корреляции, рассчитанный по уровням временных рядов, равен 0,997. Это говорит об очень тесной прямой связи между расходами на конечное потребление и среднедушевым доходом в CILIA в период с 1960 по 1991 г. Однако при расчете параметров уравнения регрессии мы сталкиваемся с другой проблемой — автокорреляцией в остатках (фактическое значение критерия Дарбина — Уотсона составляет 0,521, что свидетельствует о наличии положительной автокорреляции в остатках). Поэтому найденные оценки параметров уравнения регрессии — 174,75 и 0,922 не являются эффективными ввиду нарушения предпосылок МНК в этом уравнении.
Для получения новых оценок параметров, для которых не нарушается свойство эффективности, воспользуемся методом расчета параметров уравнения регрессии при наличии автокорреляции в остатках, изложенным в п. 6.4.
1. Найдем оценку коэффициента автокорреляции остатков первого порядка. Ее можно получить двумя способами. Воспользовавшись приближенным соотношением между критерием Дарбина — Уотсона и коэффициентом автокорреляции остатков первого порядка, которое описывается формулой (6.21), имеем:
гЕ( = 1 -0,521/2 = 0,739.
Приблизительно этот же результат можно получить, если рассчитать коэффициент автокорреляции уровней первого порядка по временному ряду остатков (гр. 3 табл. 6.6): = 0,728.
2. Произведем пересчет исходных данных в соответствии с формулами (6.33) и (6.34). Новые переменные х'1 и у\ приведены в гр. 4 и 5 табл. 6.6 соответственно. При пересчете данных мы использовали величину коэффициента автокорреляции 0,728. Однако в равной степени допустимо применять и другую его оценку 0,731, полученную из соотношения между коэффициентом автокорреляции остатков и критерием Дарбина — Уотсона.
3. Определим параметры уравнения регрессии у, на x't обычным МНК (уравнение 6.32). Получим:
y't =—89,427.3- 0,934 • х’( + ut.
4. Воспользуемся формулой (6.35) для расчета параметра а исходного уравнения (6.32):
а = -89,427/(1 - 0,728) = -328,776.
288
5. Уравнение регрессии зависимости среднедушевых расходов на конечное потребление от среднедушевого располагаемого дохода имеет вид:
у, = - 328,776 + 0,934 • х, +
Коэффициент детерминации для этого уравнения равен 0,997. Для коэффициента регрессии /-критерий составил 35,2. Полученные результаты можно считать статистически значимыми.
Следовательно, предельная склонность к потреблению в США в период с 1960 по 1991 г. была равна 0,934. Это означает, что с увеличением среднедушевого располагаемого дохода на 1 долл. США среднедушевые расходы на конечное потребление возрастали в среднем на 93,4 цента.
Контрольные вопросы к главе 6
1. В чем состоит специфика построения моделей регрессии по временным рядам данных?
2. Что такое ложная корреляция и как ее избежать?
3. Перечислите основные методы исключения тенденции. Сравните их преимущества и недостатки.
4. Изложите суть метода отклонений от тренда.
5. В чем сущность метода последовательных разностей? Какова интерпретация параметров уравнения регрессии по первым разностям уровней рядов?
6. Какова интерпретация параметра при факторе времени в моделях регрессии с включением фактора времени?
7. Охарактеризуйте понятие автокорреляции в остатках. Какие методы ее выявления вам известны?
8. Что такое критерий Дарбина — Уотсона? Изложите алгоритм его применения для тестирования модели регрессии на автокорреляцию в остатках.
9. Перечислите основные этапы обобщенного МНК.
10. Что такое коинтеграция временных рядов? Какие методы тестирования двух временных рядов на коинте грацию вам известны?
19-1525
289
ГЛАВА
ДИНАМИЧЕСКИЕ ЭКОНОМЕТРИЧЕСКИЕ МОДЕЛИ
7.1. ОБЩАЯ ХАРАКТЕРИСТИКА МОДЕЛЕЙ С РАСПРЕДЕЛЕННЫМ ЛАГОМ И МОДЕЛЕЙ АВТОРЕГРЕССИИ
В эконометрике к числу динамических относятся не все модели, построенные по временным рядам данных. Термин «динамический» в данном случае характеризует каждый момент времени t в отдельности, а не весь период, для которого строится модель. Эконометрическая модель является динамической, если в данный момент времени t она учитывает значения входящих в нее переменных, относящиеся как к текущему, так и к предыдущим моментам времени, т. е. если эта модель отражает динамику исследуемых переменных в каждый момент времени.
Можно выделить два основных типа динамических эконометрических моделей. К моделям первого типа относятся модели авторегрессии и модели с распределенным лагом, в которых значения переменной за прошлые периоды времени (лаговые переменные) непосредственно включены в модель. Модели второго типа учитывают динамическую информацию в неявном виде. В эти модели включены переменные, характеризующие ожидаемый или желаемый уровень результата, или одного из факторов в момент времени t. Этот уровень считается неизвестным и определяется экономическими единицами с учетом информации, которой они располагают в момент (г — 1).
В зависимости от способа определения ожидаемых значений показателей различают модели неполной корректировки, адаптивных ожиданий и рациональных ожиданий. Оценка параметров этих моделей сводится к оценке параметров моделей авторегрессии.
290
При исследовании экономических процессов нередко приходится моделировать ситуации, когда значение результативного признака в текущий момент времени t формируется под воздействием ряда факторов, действовавших в прошлые моменты времени/— 1,/ —2, — Например, на выручку от реализации или прибыль компании текущего периода могут оказывать влияние расходы на рекламу или проведение маркетинговых исследований, сделанные компанией в предшествующие моменты времени. Величину /, характеризующую запаздывание в воздействии фактора на результат, называют в эконометрике лагом, а временные ряды самих факторных переменных, сдвинутые на один или более моментов времени, — лаговыми переменными.
Разработка экономической политики как на макро-, так и на микроуровне требует решения обратного типа задач, т. е. задач, определяющих, какое воздействие окажут значения управляемых переменных текущего периода на будущие значения экономических показателей. Например, как повлияют инвестиции в промышленность на валовую добавленную стоимость этой отрасли экономики будущих периодов или как может измениться объем ВВП, произведенного в периоде (/+ 1), под воздействием увеличения денежной массы в периоде /?
Эконометрическое моделирование охарактеризованных выше процессов осуществляется с применением моделей, содержащих не только текущие, но и лаговые значения факторных переменных. Эти модели называются моделями с распределенным лагом. Модель вида
у, = а + Ьй-х, + 6| -х,_| + Ь2-х,_2 + е, (7.1)
является примером модели с распределенным лагом.
Наряду с лаговыми значениями независимых, или факторных, Переменных на величину зависимой переменной текущего периода могут оказывать влияние ее значения в прошлые моменты или периоды времени. Например, потребление в момент времени t формируется под воздействием дохода текущего и предыдущего периодов, а также объема потребления прошлых периодов, например потребления в период (/ — 1). Эти процессы обычно описывают с помощью моделей регрессии, содержащих в качестве факторов лаговые значения зависимой переменной, которые называются моделями авторегрессии. Модель вида
yt = а + Ъй • х, + q • у,_| + е, (7.2)
относится к моделям авторегрессии. 19*
291
Построение моделей с распределенным лагом и моделей авторегрессии имеет свою специфику. Во-первых, оценка параметров моделей авторегрессии, а в большинстве случаев и моделей с распределенным лагом не может быть произведена с помощью обычного МНК ввиду нарушения его предпосылок и требует специальных статистических методов. Во-вторых, исследователям приходится решать проблемы выбора оптимальной величины лага и определения его структуры. Наконец, в-третьих, между моделями с распределенным лагом и моделями авторегрессии существует определенная взаимосвязь, и в некоторых случаях необходимо осуществлять переход от одного типа моделей к другому.
7.2. ИНТЕРПРЕТАЦИЯ ПАРАМЕТРОВ МОДЕЛЕЙ С РАСПРЕДЕЛЕННЫМ ЛАГОМ
Рассмотрим модель с распределенным лагом в ее общем виде в предположении, что максимальная величина лага конечна:
У, “ О + X, + ' Х,_| + ... + Ьр Xf_p + Ер (7.3)
Эта модель говорит о том, что если в некоторый момент времени / происходит изменение независимой переменной х, то это изменение будет влиять на значения переменной у в течение / следующих моментов времени.
Коэффициент регрессии Ьо при переменной xt характеризует среднее абсолютное изменение yt при изменении х, на 1 ед. своего измерения в некоторый фиксированный момент времени t, без учета воздействия лаговых значений фактора х. Этот коэффициент называют краткосрочным мультипликатором.
В момент (/+ 1) совокупное воздействие факторной переменной х, на результату, составит (Ьо + /»,) усл. ед., в момент (/+2) это воздействие можно охарактеризовать суммой (Ьо + Ь{ + Ь2) и т. д. Полученные таким образом суммы называют промежуточными мультипликаторами.
С учетом конечной величины лага можно сказать, что изменение переменной х, в момент t на 1 усл. ед. приведет к общему изменению результата через / моментов времени на (Ьо + Ь{ +...+ 6Z) абсолютных единиц.
Введем следующее обозначение:
ь0 + ь
+...+Ь[—Ь;
(7.4)
292
Величину b называют долгосрочным мультипликатором. Он показывает абсолютное изменение в долгосрочном периоде t +1 результата у под влиянием изменения на 1 ед. фактора х.
Предположим
Р] = Ь}/Ь, /-0:1.
(7.5)
Назовем полученные величины относительными коэффициентами модели с распределенным лагом. Если все коэффициенты bj имеют одинаковые знаки, то для любого /
0<Р; <1 И £₽у=1. /=0
В этом случае относительные коэффициенты ру являются весами для соответствующих коэффициентов bj. Каждый из них измеряет долю общего изменения результативного признака в мо
мент времени (/ +/).
Зная величины ру, с помощью стандартных формул можно
определить еще две важные характеристики модели множественной регрессии: величину среднего лага и медианного лага. Сред-
ний лаг определяется по формуле средней арифметической взве-
шенной:
/ = £/•₽, /=0
(7.6)
и представляет собой средний период, в течение которого будет происходить изменение результата под воздействием изменения фактора в момент времени /. Небольшая величина среднего лага свидетельствует об относительно быстром реагировании результата на изменение фактора, тогда как высокое его значение говорит о том, что воздействие фактора на результат будет сказываться в течение длительного периода времени. Медианный лаг — это
величина лага, для которого Р,-« 0,5.
7=0
Это тот период времени, в течение которого с момента времени t будет реализована половина общего воздействия фактора на результат.
Рассмотрим условный пример.
Пример 7.1. Интерпретация параметров модели с распределенным лагом.
293
По результатам изучения зависимости объемов продаж компании в среднем за месяц от расходов на рекламу была получена следующая модель с распределенным лагом (млн руб.):
Я = —0,67 + 4,5 х, + 3,0 • х,_| + 1,5 • х,_2 + 0,5 • xt_3.
В этой модели краткосрочный мультипликатор равен 4,5. Это означает, что увеличение расходов на рекламу на 1 млн руб. ведет в среднем к росту объема продаж компании на 4,5 млн руб. в том же периоде. Под влиянием увеличения расходов на рекламу объем продаж компании возрастет в момент времени t на 1 млн руб., (/ + 1) — на 4,5 + 3,0 = 7,5 млн руб., (t + 2) — на 7,5 + 1,5 = 9,0 млн руб. Наконец, долгосрочный мультипликатор для данной модели составит: b = 4,5 + 3,0 + 1,5 + 0,5 = 9,5.
В долгосрочной перспективе (например, через 3 месяца) увеличение расходов на рекламу на 1 млн руб. в настоящий момент времени приведет к общему росту объема продаж на 9,5 млн руб.
Относительные коэффициенты регрессии в этой модели равны:
Р, = 4,5/9,5 = 0,474; Р2 = 3,0/9,5 - 0,316;
Рз = 1,5/9,5 = 0,158; р4 = 0,5/9,5 = 0,053.
Следовательно, 47,4% общего увеличения объема продаж, вызванного ростом затрат на рекламу, происходит в текущем моменте времени; 31,6% — в момент (t+ 1); 15,8% — в момент (/+ 2); и только 5,3% этого увеличения приходится на момент времени (/ + 3).
Средний лаг в этой модели определяется как
7 = 0- 0,474 + 1 ♦ 0,316 + 2 • 0,158 + 3 • 0,053 = 0,791 мес.
Небольшая величина лага (менее 1 месяца) еще раз подтверждает, что большая часть эффекта роста затрат на рекламу проявляется сразу же. Медианный лаг в данном примере также составляет чуть более 1 месяца.
Изложенные выше приемы анализа параметров модели с распределенным лагом действительны только в предположении, что все коэффициенты при текущем и лаговых значениях исследуемого фактора имеют одинаковые знаки. Это предположение вполне оправдано с экономической точки зрения: воздействие одного и того же фактора на результат должно быть однонаправленным независимо от того, с каким временным лагом измеряет-294
ся сила или теснота связи между этими признаками. Однако на практике получить статистически значимую модель, параметры которой имели бы одинаковые знаки, особенно при большой величине лага I, чрезвычайно сложно.
Применение обычного МНК к таким моделям в большинстве случаев затруднительно По следующим причинам.
Во-первых, текущие и лаговые значения независимой переменной, как правило, тесно связаны друг с другом. Тем самым оценка параметров модели проводится в условиях высокой мультиколлинеарности факторов.
Во-вторых, при большой величине лага снижается число наблюдений, по которому строится модель, и увеличивается число ее факторных признаков. Это ведет к потере числа степеней свободы в модели.
В-третьих, в моделях с распределенным лагом часто возникает проблема автокорреляции остатков. Вышеуказанные обстоятельства приводят к значительной неопределенности относительно оценок параметров модели, снижению их точности и получению неэффективных оценок. Чистое влияние факторов на результат в таких условиях выявить невозможно. Поэтому на практике параметры моделей с распределенным лагом проводят в предположении определенных ограничений на коэффициенты регрессии и в условиях выбранной структуры лага.
Обратимся теперь к модели авторегрессии. Пусть имеется следующая модель:
y, = a + b0-x,J<-cl-yt_i +ег (7.7)
Как и в модели с распределенным лагом, Ьо в этой модели характеризует краткосрочное изменение у, под воздействием изменения х, на 1 ед. Однако промежуточные и долгосрочный мультипликаторы в моделях авторегрессии несколько иные. К моменту времени (t + 1) результату, изменился под воздействием изменения изучаемого фактора в момент времени t на Ь$ ед., a yt + ( под воздействием своего изменения в непосредственно предшествующий момент времени — на с( ед. Таким образом, общее абсолютное изменение результата в момент (f + 1) составит ЬдС, ед. Аналогично в момент времени (t+2) абсолютное изменение результата составит /»ос|2 еД- и т. д. Следовательно, долгосрочный мультипликатор в модели авторегрессии можно рассчитать как сумму краткосрочного и промежуточных мультипликаторов:
b ~ 1>о + й0 с, + с|2 "** *о
(7.8)
295
Учитывая, что практически во все модели авторегрессии вво-
ггся так называемое условие стабильности, состоящее в том, что
коэффициент регрессии при переменной у,_t по абсолютной величине меньше единицы |cj < 1, соотношение (7.8) можно преобразовать следующим образом:
ft = ft0-(l+Ci+q2
(7.9)
где IcJ < 1.
Отметим, что такая интерпретация коэффициентов модели
авторегрессии и расчет долгосрочного мультипликатора основаны на предпосылке о наличии бесконечного лага в воздействии
текущего значения зависимой переменной на ее будущие зна
чения.
Пример 7.2. Интерпретация параметров модели авторегрессии.
Предположим, по данным о динамике показателей потребления и дохода в регионе была получена модель авторегрессии, описывающая зависимость среднедушевого объема потребления за год (С, млн руб.) от среднедушевого совокупного годового дохода (У, млн руб.) и объема потребления предшествующего года:
С, = 3 + 0,85 • Yt + 0,10 Сг_|. 1
. Краткосрочный мультипликатор равен 0,85. В этой модели он представляет собой предельную склонность к потреблению в краткосрочном периоде. Следовательно, увеличение среднедушевого совокупного дохода на 1 млн руб. приводит к росту объема потребления в тот же год в среднем на 850 тыс. руб. Долгосрочную предельную склонность к потреблению в данной модели можно определить в соответствии с формулой (7.9) как
ft = 0,85/(1 -0,1) = 0,944.
В долгосрочной перспективе рост среднедушевого совокупного дохода на 1 млн руб. приведет к росту объема потребления в среднем на 944 тыс. руб. Промежуточные показатели предельной склонности к потреблению можно определить, рассчитав необходимые частные суммы за соответствующие периоды времени. Например, для момента времени 0+1) получим:
(0,85+ 0,85-0,1) = 0,935.
296
Это означает, что увеличение среднедушевого совокупного дохода в текущем периоде на 1 млн руб. ведет к увеличению объема потребления в среднем на 935 тыс. руб. в ближайшем следующем периоде.
7.3. ИЗУЧЕНИЕ СТРУКТУРЫ ЛАГА И ВЫБОР ВИДА МОДЕЛИ С РАСПРЕДЕЛЕННЫМ ЛАГОМ
Текущее и лаговые значения факторной переменной оказы-
вают различное по силе воздействие на результативную переменную модели. Количественно сила связи между результатом и значениями факторной переменной, относящимися к различным моментам времени, измеряется с помощью коэффициентов регрессии при факторных переменных. Если построить график зависимости этих коэффициентов от величины лага, можно получить графическое изображение структуры лага, или распределения во времени воздействия факторной переменной на результат (рис. 7.1). Структура лага может быть различной. На рис. 7.1 Представлены основные ее формы.
Если с ростом величины лага коэффициенты при лаговых значениях переменной убывают во времени, то имеет место линейная (ее еще называют треугольной — рис. 7.1 а)) или геометрическая структура лага (рис. 7.1 б)). Если лаговые воздействия фактора на результат не имеют тенденцию к убыванию во времени, то имеет место один из вариантов, показанных на рис. 7.1 в) — е). Структуру лага, изображенную на рис. 7.1 в), называют «перевернутой» V-образной структурой. Основная ее особенность — симметричность лаговых воздействий относительно некоторого среднего лага, который характеризуется наиболее сильным воздействием фактора на результат. Графики, представленные на рис. 7.1 г), д) и е), свидетельствуют о полиномиальной структуре
лага.
Аналогичным образом графический анализ структуры лага можно проводить и с помощью относительных коэффициентов регрессии ty. Основная трудность в выявлении структуры лага состоит в том, как получить значения параметров bj (или ty). Выше уже отмечалось, что обычный МНК редко бывает полезным в этих целях. Поэтому в большинстве случаев предположения о структуре лага основаны на общих положениях экономической теории, на исследованиях взаимосвязи показателей либо на результатах проведенных ранее эмпирических исследований или иной априорной информации.
297
Рис. 7.1. Графическое изображение структуры лага а — линейная; б — геометрическая; в — перевернутая V-образная; г —, д —, е — полиномиальная
7.3.1. Лаги Алмон
Рассмотрим общую модель с распределенным лагом, имеющую конечную, максимальную величину лага I, которая описывается соотношением (7.3). Предположим, было установлено, что в исследуемой модели имеет место полиномиальная структура лага, т. е. зависимость коэффициентов регрессии bt от величины лага описывается полиномом k-Vi степени. Частным случаем полиномиальной структуры лага является линейная модель (рис. 7.1 а)). Примерами лагов, образующих полином 2-й степени, явля-298
ются варианты рис. 7.1 г) и д). Перевернутая V-образная структура лага также может быть аппроксимирована с помощью полинома 2-й степени. Наконец, график, представленный на рис. 7.1 е), является примером модели лагов в форме полинома 3-й степени. Лаги, структуру которых можно описать с помощью полиномов, называют также лагами Алмон, по имени Ш. Алмон, впервые обратившей внимание на такое представление лагов'.
Формально модель зависимости коэффициентов bj от величины лага J в форме полинома можно записать в следующем виде:
• для полинома 1-й степени: bj = с0 + с{ j;
• для полинома 2-й степени: Ь, = с0 + cj + c2j,
• для полинома 3-й степени: b, — c0 + clJ + c2f + c^j и т. д.
ч
В наиболее общем виде для полинома Л-й степени имеем2:
— со + + <*/•
(7Л0)
Тогда каждый из коэффициентов bj модели (7.3) можно выразить следующим образом:
ИТ. д.
*0 “ с0»
“ *0 + С1 +•••+
= с0 + 2 с{ + 4 с2 +...+ 2* ск; й3 = с0 + 3 q + 9 с2 +...+ 3* q;
bj Cq + / Cj + Р с2
(7.11)
Подставив в (7.3) найденные соотношения для Ьр получим:
Перегруппируем слагаемые в (7.12):
1 Almon S. The distributed lag between capital appropriations and capital expenditures// Econometrica. — Xbl. 33. — 1965. — № 1 (January). — C. 178—196.
2B данной модели предполагается, что степень полинома к меньше максимальной величины лага /.
299
Обозначим слагаемые в скобках при с,- как новые переменные:
(7.14)
Перепишем модель (7.13) с учетом соотношений (7.14):
у, = а + с0 • Zq + q • zt + с2 • z2 + - + ск zk + s(. (7.15)
Процедура применения метода Алмон для расчета параметров модели с распределенным лагом выглядит следующим образом.
1. Определяется максимальная величина лага /.
2. Определяется степень полинома к, описывающего структуру лага.
3. По соотношениям (7.14) рассчитываются значения переменных Zq,—, Zk-
4. Определяются параметры уравнения линейной регрессии (7.15).
5. С помощью соотношений (7.11) рассчитываются параметры исходной модели с распределенным лагом.
Применение метода Алмон сопряжено с рядом проблем.
Во-первых, величина лага /должна быть известна заранее. При ее определении лучше исходить из максимально возможного лага, чем ограничиваться лагами небольшой длины. Выбор меньшего лага, чем его реальное значение, приведет к тому, что в модели регрессии не будет учтен фактор, оказывающий значительное влияние на результат, т. е. к неверной спецификации модели. Влияние этого фактора в такой модели будет выражено в остатках. Тем самым в модели не будут соблюдаться предпосылки МНК о случайности остатков, а полученные оценки ее парамет-300
ров окажутся неэффективными и смещенными. Выбор большей величины лага по сравнению с ее реальным значением будет означать включение в модель статистически незначимого фактора и снижение эффективности полученных оценок, однако эти оценки все же будут несмещенными.
Существует несколько практических подходов к определению реальной величины лага, например построение нескольких уравнений регрессии и выбор наилучшего из этих уравнений1 или применение формальных критериев, например критерия Шварца1. Однако наиболее простым способом является измерение тесноты связи между результатом и лаговыми значениями фактора. Кроме того, оптимальную величину лага можно приближенно определить на основе априорной информации экономической теории или проведенных ранее эмпирических исследований.
Во-вторых, необходимо установить степень полинома к. Обычно на практике ограничиваются рассмотрением полиномов 2-й и 3-й степени, применяя следующее простое правило: выбранная степень полинома к должна быть на единицу больше числа экстремумов в структуре лага. Если априорную информацию о структуре лага получить невозможно, величину к проще всего определить путем сравнения моделей, построенных для различных значений к, и выбора наилучшей модели.
В-третьих, переменные z, которые определяются как линейные комбинации исходных переменных х, будут коррелировать между собой в случаях, когда наблюдается высокая связь между самими исходными переменными. Поэтому оценку параметров модели (7.15) приходится проводить в условиях мультиколлинеарности факторов. Однако мультиколлинеарность факторов Zo>—, Zk в модели (7.15) сказывается на оценках параметров b0,..., bt в несколько меньшей степени, чем если бы эти оценки были получены путем применения обычного МНК непосредственно к модели (7.3) в условиях мультиколлинеарности факторов х„..., x,_z. Это связано с тем, что в модели (7.15) мультиколлинеарность ведет к снижению эффективности оценок с0,..., ск, поэтому каждый из параметров Z>0,.„, bh которые определяются как линейные комбинации оценок с0,..., ск, будет представлять собой более точную
* Davidson R., MacKinnon J.G. Estimation and Inference in Econometrics. — C. 675-676.
2GuJarati D.N. Basic Econometrics. — C. 615,632.
301
оценку, а стандартные ошибки этих параметров не будут превышать стандартные ошибки параметров, полученных по модели (7.3) обычным МНК1.
Метод Алмон имеет два неоспоримых преимущества.
• Он достаточно универсален и может быть применен для моделирования процессов, которые характеризуются разнообразными структурами лагов.
• При относительно небольшом количестве переменных в (7.15) (обычно выбирают к = 2 или к = 3), которое не приводит к потере значительного числа степеней свободы, с помощью метода Алмон можно построить модели с распределенным лагом любой длины.
Пример 7.3. Построение модели с распределенным лагом.
В табл. 7.1 представлены данные об объеме выпуска продукции в бизнес-секторе экономики США (в % к уровню 1982 г.) и общей сумме расходов на приобретение новых заводов и оборудования в промышленности за 1959—1990 гг. (млрд долл. США).
Построим модель с распределенным лагом для I = 4 в предположении, что структура лага описывается полиномом второй степени. Общий вид этой модели:
yt == а + Ьо • х, + bl- xt_i + b2 Xf_2 + b3 x,_3 + b4 • xt_^ + er
Для полинома второй степени имеем:
bj = с0 + с, -J + с2 -j2, j = 0:4.
Для расчета параметров этой модели необходимо провести преобразование исходных данных в новые переменные Zq, Z\ и 22-Это преобразование в соответствии с (7.14) выглядит следующим образом:
3 • х,_3 + 4 • х/-4;
Z2 = V-1 + 4 • Х,_2 + 9 • Х,_3 + 16 • Х,_4.
'Доказательство этого утверждения достаточно сложное и в данном учебнике не приводится. Подробнее эта проблема рассматривается в: Gujarati D.N. Basic Econometrics. — С. 617/628.
302
Таблица 7.1
Динамика объемов ВВП США (у, в ценах 1987 г., млрц долл- США) и валовых внутренних инвестиций в экономику США (х, в ценах 1987 г., млрд долл. США)*
Год
1959 1931,3 296,4
1960 1973,2 290,8
1961 2025,6 289,4
1962 2129,8 321,2
1963 2218,0 343,3
1964 2343,3 371,8
1965 2473,5 413,0
1966 2622,3 438,0
1967 2690,3 418,6
1968 2801,0 440,1
1969 2877,1 461,3
1970 2875,8 429,7
1971 2965,1 481,5
1972 3107,1 532,2
1973 3268,5 591,7
1974 3248,1 543,0
1975 3221,7 437,6
1976 3380,8 520,6
1977 3533,2 600,4
1978 3703,5 664,6
1979 3796,8 669,7
1980 3776,3 594,4
1981 3843,1 631,1
1982 3760,3 540,5
1983 3906,6 599,5
1984 4148,5 757,5
1985 4279,8 745,9
1986 4404,5 735,1
1987 4540,0 749,3
1988 4781,6 773,4
1989 4836,9 789,2
1990 4884,9 744,5
1991 4848,4 ' 672,6
1541,1
1616,5 1738,7 1887,3 1984,7
2081,5 2171,0 2187,7 2231,2
2344,8 2496,4
2578,1 2586,0
2625,1 2693,3
2766,2
2892,9 3049,7
3160,2 3100,3 3035,2
3123,0
3274,5 3378,5
3587,3 3761,2
3792,9 3796,5
3734,0
2958,0 3017,1
3179,6 3471,3 3752,6
4020,8 4243,3
4349,3 4347,0 4485,2
4629,5 4819,4 5249,0
5427,5 5391,6
5126,4 5177,6 5882,5
6329,2 6478,4
6264,7 5951,4
6102,4 6221,4
6897,4 7487,2
7460,9 7524,3
7645,3
8838,4 8885,5 9266,2 10129,1 10929,0 11836,4 12664,5 12997,1 12993,4 13393,6 13706,3 13929,2 15403,6 16450,1 16625,2 15309,2 14753,2 17061,3 18861,0 19669,6 19129,7 17951,8 18117,6 17819,4 20128,2 22522,8 22320,9 22388,1 22855,7
* Источник. Economic Report of the President. — Washington: US Government Printing Office, 992. - C. 300.
303
Таблица 7.1
Динамика объемов ВВП США (у, в ценах 1987 г., млрд долл. США) и валовых внутренних инвестиций в экономику США (х, в ценах 1987 г., млрд долл. США)*
Год
1959 1931,3 296,4
1960 1973,2 290,8
1961 2025,6 289,4
1962 2129,8 321,2
1963 2218,0 343,3
1964 2343,3 371,8
1965 2473,5 413,0
1966 2622,3 438,0
1967 2690,3 418,6
1968 2801,0 440,1
1969 2877,1 461,3
1970 2875,8 429,7
1971 2965,1 481,5
1972 3107,1 532,2
1973 3268,5 591,7
1974 3248,1 543,0
1975 3221,7 437,6
1976 3380,8 520,6
1977 3533,2 600,4
1978 3703,5 664,6
1979 3796,8 669,7
1980 3776,3 594,4
1981 3843,1 631,1
1982 3760,3 540,5
1983 3906,6 599,5
1984 4148,5 757,5
1985 4279,8 745,9
1986 4404,5 735,1
1987 4540,0 749,3
1988 4781,6 773,4
1989 4836,9 789,2
1990 4884,9 744,5
1991 4848,4 ' 672,6
1541,1
1616,5
1738,7
1887,3
1984,7
2081,5
2171,0
2187,7
2231,2
2344,8
2496,4
2578,1
2586,0
2625,1
2693,3
2766,2
2892,9
3049,7
3160,2
3100,3
3035,2
3123,0
3274,5
3378,5
3587,3
3761,2
3792,9
3796,5
3734,0
2958,0 3017,1
3179,6 3471,3 3752,6
4020,8 4243,3 4349,3
4347,0 4485,2 4629,5
4819,4
5249,0 5427,5
5391,6
5126,4
5177,6
5882,5 6329,2
6478,4
6264,7
5951,4
6102,4 6221,4
6897,4 7487,2 7460,9
7524,3 7645,3
8838,4 8885,5 9266,2 10129,1 10929,0 11836,4 12664,5 12997,1
12993,4 13393,6 13706,3
13929,2 15403,6 16450,1 16625,2
15309,2 14753,2 17061,3
18861,0 19669,6 19129,7 17951,8 18117,6
17819,4 20128,2 22522,8 22320,9
22388,1 22855,7
* Источник. Economic Report of the President. — Washington: US Government Printing Office, 992. - C. 300.
303
Значения переменных z$, Zi и z2 приводятся в табл. 7.1. Отметим, что число наблюдений, по которым производился расчет этих переменных, составило 28 (четыре наблюдения было потеряно вследствие сдвига факторного признаках, на четыре момента времени).
Расчет параметров уравнения регрессии (7.15) обычным МНК для нашего примера приводит к следующим результатам:
у, = 300,010 + 1,922 • щ - 0,921 • zt + 0,184 • z2; Л2 = 0,990.
(66,200) (0,205) (0,299) (0,073)
В скобках указаны значения стандартных о
II
ибок коэффици-
ентов регрессии. Воспользовавшись найденными коэффициен
тами регрессии при переменных z,, i = 0, 1, 2 и соотношениями (7.11), рассчитаем коэффициенты регрессии исходной модели:
Ьо = 1,922;
= 1,922 - 0,921 + 0,184 = 1,185;
b2 = 1,922 + 2 • (-0,921) + 4 • 0,184 = 0,814;
Ь3 = 1,922 + 3 (-0,921) + 9 • 0,184 = 0,811;
Ь4 = 1,922 + 4 • (-0,921) + 16 0,184 = 1,176.
Модель с распределенным лагом имеет вид:
yt = 3000,01 + 1,922 'Х,+ 1,185 •х,_1 + 0,814 х/_2 + 0,811 -х,_3 + + 1,176 х,^; Л2 = 0,990.
(66,200) (0,205) (0,100) (0,142) (0,096) (0,208)
В скобках указаны стандартные ошибки коэффициентов (ta, tbl) регрессии. Нанесем полученные значения на график (рис. 7.2).
Рис. 7.2. Структура лага в модели зависимости объема ВВП от объема инвестиций в экономику
304
Анализ этой модели показывает, что рост инвестиций в экономику США на 1 млрд долл, в текущем периоде приведет через 4 года к росту ВВП в среднем на (1,922 + 1,184 + 0,814 + 0,811 + + 1,176) =5,908 млрд долл. США.
Определим относительные коэффициенты регрессии:
Ро = 1,922 / 5,908 = 0,325; р( = 1,184 / 5,908 = 0,200;
Р2 = 0,814 / 5,908 = 0,138; р3 = 0,811 / 5,908 = 0,138;
р4= 1,176/5,908 = 0,199.
Более половины воздействия фактора на результат реализуется с лагом в 1 год, причем 32,5% этого воздействия реализуется сразу же, в текущем периоде.
Средний лаг в данной модели составит:
Т = 0,325 + 0,200 • 1 + 0,138 • 2 + 0,138 • 3 + 0,199 • 4 = 1,686.
В среднем увеличение инвестиций в экономику США приведет к увеличению ВВП через 1,69 года.
Для сравнения приведем результаты применения обычного МНК для расчета параметров этой модели:
yt = 296,56 + 2,082 • xt + 0,784 • х,_} + 1,298 • xt_2 + 0,428 • x,_3 +
(67,7) (0,314) (0,428) (0,439) (0,432)
+ 1,323 -x,_4, R2 = 0,991.
(0,324)
Хотя коэффициент детерминации по модели, параметры которой были рассчитаны обычным МНК, несколько выше, однако стандартные ошибки коэффициентов регрессии в модели, полученной с учетом ограничений на полиномиальную структуру лага, значительно снизились. Кроме того, модель, полученная обычным МНК, обладает более существенным недостатком: коэффициенты регрессии при лаговых переменных этой модели х,_( их,_3 нельзя считать статистически значимыми.
7.3.2. Метод Койка
Рассмотренные выше модели были построены в предположении конечной величины лага /. Предположим теперь, что для описания некоторого процесса используется модель с бесконечным лагом вида:
yt = а = Ьо • х, + • х,_! + Ь2 xt_2 + ... + е,. (7.16)
Очевидно, что параметры такой модели обычным МНК или с помощью иных стандартных статистических методов определить нельзя, поскольку модель включает бесконечное число факторных переменных. Однако, приняв определенные допущения относительно структуры лага, оценки ее параметров все же можно получить. Эти допущения состоят в наличии геометрической структуры лага, т. е. такой структуры, когда воздействия лаговых значений фактора на результат уменьшаются с увеличением величины лага в геометрической прогрессии. На рис. 7.1 геометрической структуре лага соответствует вариант 7.1 б).
Впервые изложенный в этом разделе подход к оценке параметров моделей с распределенным лагом типа (7.16) был предложен Л.М. Койком1. Койк предположил, что существует некоторый постоянный темп к (0 < X < 1) уменьшения во времени лаговых воздействий фактора на результат. Если, например, в период t результат изменялся под воздействием изменения фактора в этот же период времени на bQ ед., то под воздействием изменения фактора, имевшего место в период (/ - 1), результат изменится на Ьо к ед.; в период (/ - 2) - на Ьо • к • к = Ьо к2 ед., и т. д. Для некоторого периода (t — I) это изменение результата составит й0 • к ед. В более общем виде можно записать:
bj =ьо- X; у = 0,1,2,..., 0<Х< 1. (7.17)
Ограничение на значения X > 0 обеспечивает одинаковые знаки для всех коэффициентов bj > 0, а ограничение X < 1 означает, что с увеличением лага значения параметров модели (7.16) убывают в геометрической прогрессии. Чем ближе X к 0, тем выше темп снижения воздействия фактора на результат во времени и тем большая доля воздействия на результат приходится на текущие значения фактора хг
Выразим с помощью (7.17) все коэффициенты Ь, в модели (7.16) через Ьо и X:
yt = а + Ьо • xt + b0 • к • х,_1 + Ьо • X2 • х,_2 + ... + £,. (7.18)
Тогда для периода (/ — 1) модель (7.18) можно записать следующим образом:
y,_i = а + bQ • x,_i + b0 • X • х,_2 + Ьо • X2 • х,_3 + ... + ем. (7.19)
Умножим обе части модели (7.19) на X:
'Коуск L.M. Distributed Lags and Investment Analysis. — Amsterdam: North Holland Publishing Company, 1954.
306
Нетрудно заметать, что при А. = 0,5 средний лаг Т = 1, а при I < 0,5 средний лаг / < 1, т. е. воздействие фактора на результат в среднем занимает менее одного периода времени. Величину (1 - Л) интерпретируют обычно как скорость, с которой происходит адаптация результата во времени к изменению факторного признака. Для расчета медианного лага необходимо выполнение следующего условия:
(7.25)
Поэтому медианный лаг в модели Койка равен1:
In 0,5 1пЛ ‘
(7.26)
Пример 7.4. Построение модели Койка.
Исследуя взаимосвязь реальной заработной платы и уровня безработицы, Джеффри Сакс и Майкл Бруно использовали следующую модель2:
Ut = 80 + 8! • Ц_! + 62 • t- 83 w, + е„
где UhUt^f — уровень безработицы в периоды t и /—1, соответственно;
wt — превышение реальной заработной платы над ее уровнем в условиях полной занятости;
t — время;
50, — параметры модели;
Е, — ошибка.
Значения переменной и>, были получены расчетным путем.
Для экономики Канады по данным за 1961-1981 гг. авторы получили следующее уравнение регрессии3:
и, = 80 + 0,63 • и,_{ + 0,07 • t + 15,72 w„ R1 = 0,85.
t - критерий (5,46) (2,82) (2,23)
!Если
2Bruno М., Sachs J.D. Economics of Worldwide Stagflation. — USA Harvard University Press, Cambridge, Mass, 1985. — C. 185.
З3начение параметра 50 в источнике не указано.
308
Переменная wt в этой модели является одним из факторов, определяющих спрос на труд. Если предположить, что переменная w, оказывает влияние на уровень безработицы с бесконечным временным лагом в условиях геометрической структуры лага, то в соответствии с методом Койка мы получим следующую модель с распределенным лагом:
Ut = а + Ьо • wt + b0 • к • w(_, + b0 • X2 • wz_2 + ... + с • t + sz.
Данная модель отличается от модели (7.16) тем, что, помимо текущего и лаговых значений факторного признака, она учитывает фактор времени t. Проведя алгебраические преобразования в соответствии с методом Койка, нетрудно убедиться, что эта модель сводится к следующей модели авторегрессии:
U, = {а • (1 - X) + К • с) + (1 - X) • Ut_{ + с • (1 - X) • t + b0 w, + м„ т. е. 80 = а • (1 - X) + X • с; 8Z = 1 - X; 82 = с • (1 - X); 83 = 60-В модели Сакса и Бруно X = 0,63.
Рассчитаем параметры модели Койка:
с = 0,07/(1-0,63) = 0,189;
а =80/(1 - 0,63) + 0,189 • 0,63 = 0,119 + 2,703 • 80;
Ьо = 15,72;
Ь{ = 15,72 0,63 = 9,904;
b2= 15,72 -(0,63)2 = 6,239;
Ь3 = 15,72 • (0,63)3 = 3,931 и т. д.
Модель Койка имеет следующий вид:
U, = (0,119 + 2,703 • So) + 15,72 • w, + 9,904 • wz l + 6,239 • wt_2 + + 3,931 • w,_3+ ... +0,189/.
Средний лаг в этой модели согласно (7.24) составит:
/ = 0,63/(1 -0,63)= 1,703.
Величину медианного лага в соответствии с формулой (7.26) можно определить как
I s JePzL = ~0’69314 = 1,500203.
Ме In0,63 -0,46203
Таким образом, в среднем воздействие разницы между реальной заработной платой в экономике Канады и ее величиной в условиях полной занятости проявляется в течение относительно
309
короткого промежутка времени — 1,7 года, причем половина этого воздействия реализуется в течение первых 1,5 лет с момента изменения wt.
7.3.3. Метод главных компонент
Пример 7.5. Построение модели инфляции с использованием рас-пределения Койка и метода главных компонент.
Инфляция как экономическое явление определяется множеством одновременно и совокупно действующих причин и имеет долговременный характер. Например, увеличение денежной массы или рост цен на сырье приведет к повышению уровня цен не сразу, а спустя несколько периодов времени. Зарождение нового витка инфляции обусловлено динамикой факторов с некоторым временным запаздыванием.
Пусть модель инфляции описывается уравнением:
где
- сводный индекс потребительских цен на товары и услуги;
— индекс оптовых цен на промышленную продукцию;
— стоимость ресурсов;
индекс тарид
в на транспорт;
— индекс капитальных вложений;
- розничный товарооборот;
— состоящие на учете в службе занятости;
- среднесуточный выпуск промышленной продукции;
— средневзвешенный курс доллара;
— прожиточный минимум всего населения;
- денежные доходы на душу населения;
— стоимость набора из 19 основных видов продуктов питания;
- денежный агрегат М2;
— сальдо внешней торговли;
310
х14 — общая кредиторская задолженность;
xt_j' — , /== О,..., si9 лаговые значения /-го фактора.
Од,..., а14 — параметры (коэффициенты) регрессии;
а.о — константа регрессии; е, — случайные остатки.
Исходные данные представлены в табл. 7 2.
Возникает вопрос: как определить значение временного запаздывания для каждого показателя? Для определения соответствующих временных лагов используем корреляционный анализ
динамических рядов данных. Основным критерием для опреде-
ления временного лага является наибольшая величина коэ
и-
циента взаимной корреляции временных рядов показателей с
различным периодом запаздывания их влияния на показатель инфляции. В итоге уравнение примет следующий вид:
+п1’г|(> + о10 г10 +™1()Г1() + г?1 г“ + а“ г11 +
та дХ , т а !-* ч- а jX ,_2 т а gX t -г а [X f_t т
+„п „п +„п „и +„и „н +„п „н +„чгч + ^а jX /_2 та jx (-з + а $х +• а $х + а ^х +•
+а12 х12 + а12 г12 + „12г12 +а12г12 + а12х13 +
qa t -г а [X т а t~2 ’ сс ус • а ус t ।
+„13 „13 + „14 „14 i 14 14 ,
та [X -г а gX , + а т е,.
Для того чтобы получить хорошие в статистическом смысле оценки параметров, необходимо, чтобы факторные признаки бы
ли независимы. Наличие в уравнении лаговых значений для каж
дого фактора, а также зависимость факторов между собой вслед
ствие экономической специфики задачи приводят к тому, что объясняющие переменные оказываются мультиколлинеарными. Для решения этой проблемы использован, во-первых, метод Койка; во-вторых, метод главных компонент.
311
Таблица 7.2
Темпы роста основных макроэкономических показателей за 1997—1998 гг. (в % к предыдущему периоду)
Период
1997 г.
Январь 102,30 101,10 101,10 99,90 37,60 91,50 100,40 71,70 101,20 100,10 79,50 101,60 100,00 95,70 102,00
Февраль 101,50 101,60 100,40 97,60 106,50 92,80 101,50 117,40 100,80 102,50 100,30 101,30 100,60 101,30 95,50
Март 101,40 101,30 101,30 100,80 113,40 104,30 99,80
Апрель 101,00 100,80 101,20 99,90 97,50 101,50 99,00
Май 100,90 100,50 101,20 100,50 101,60 97,90 95,60
Июнь 101,10 100,80 100,60 101,70 121,40 98,70 95,30
Июль 100,90 100,20 101,50 100,70 102,10 100,80 96,40
103,20 100,90 101,00 102,90 101,20 103,30 105,00 102,90 98,90 100,60 101,00 106,60 101,00 102,10 96,10 99,50 93,50 100,20 101,20 92,50 100,80 103,90 95,90 103,30 105,20 100,20 101,40 110,10 101,40 103,30 101,40 101,60 103,80 100,30 100,90 96,60 100,80 107,20 101,70 104,30
Август
99,90 1
,50 100,20 101,10 106,20 103,70
96,90
103,30 100,50 97,90
Сентябрь 99,70 100,10 98,30 98,40 110,70 104,60 96,00 97,30 100,50 97,30
97,10 100,30 103,10 101,60 100,10
98,50 99,50 100,40 100,30 101,30
Октябрь 100,20 100,10 99,70 99,90 92,10 100,30 97,50 115,70 100,50 99,00 105,70 100,00 99,60 106,00 105,50
Ноябрь 100,60 100,20 100,40 101,40 107,30 101,50 99,20 91,90 100,50 101,00 97,40 100,50 101,60 97,70 102,60
Декабрь 101,00 100,20 100,90 99,10 160,10 116,00 100,10 93,40 100,70 101,00 129,90 100,70 96,90 102,00 102,40
21“
Продолжение
11 с рис Ш
1998 г.
Январь Февраль Март Апрель Май Июнь Июль Август Сентябрь Октябрь Ноябрь Декабрь
100,50 100,10 109,70 103,40
99,70
100,50
97,70
104,20
119,80
100,30
99,20
99,00
98,60 65,20 101,10 100,70 63,90 101,10 104,70 93,20 103,80 100,70 107,50 100,80 100,40 104,30 100,80 96,60 101,20 80,00 98,80 98,90 96,20 96,00 98,70 99,20 100,00
103,10 102,70 99,70 103,80 107,80 104,80 106,50 100,10 144,10
108,80 100,60 100,70 101,70 100,40 100,50 104,80 101,90
85,50 100,40 101,20 105,50 99,70 99,30 95,80
110,00 100,50 100,70 91,30 100,20 102,10 93,20
98,00
95,30
96,70
78,80 203,20 122,60 81,50 114,80
©
102,80
102,30 99,70
103,10
99,70
104,20
101,50 100,90 100,20 101,20 34,70 82,30
100,90 100,50 101,50 100,00 106,50 91,60
100,60 99,90
100,40 100,00
100,50 99,10
100,10 100,00 101,20
100,20 99,20 100,40
103,70 98,80 103,50 100,60 107,00 106,80
138,40 107,40 119,60 106,80 106,70 96,70
104,50 105,90 103,80 101,00 92,90 92,70
105,70 105,10 105,30 100,70 107,60 100,40 103,40 98,80 111,70 108,00 69,70 103,10 103,20 100,00 91,00
111,60 104,80 109,40 102,00 152,10 108,10 103,10 100,30 115,50 115,80 122,80 109,10 105,10 107,10 105,40
98,50
99,90
90,20
116,40 103,40 102,30
О
100,60 100,20 102,60 100,30 100,50 100,90
100,60 100,40 102,60 99,90
126,70 102,70 96,60 102,20
99,60
97,70
95,40
94,50
99,30
96,90
Для расчета параметров по методу Койка исходные данные были преобразованы в новые переменные z1, z2.г14 согласно
формуле
х^ + 8 • + 8 • х/,_2 + ... + 8^ dt_p,
где р — количество лаговых значений переменной, включенных в уравнение.
Полученная матрица векторов — значений z, представлена в табл. 7.3.
Следовательно, от оценки параметров исходной модели переходим к оценке параметров следующего уравнения: а
yt = Ро + Р1 • Z1 = р2 • ? + Рз • ? + р4 • ? + р5 • ? + р6 • ? + р7 • Z7 + +Рв ? + Р9 • г9 + Рю • ?° + Рп • г11 + Р12 • ?2 + Р13 • г13 + Рм • г14 +
Экономический смысл заключается в следующем: в уравнении z! (1= 1,..., 14) отражает совокупное влияние х'-го фактора с учетом инерционности, задержки во времени влияния на показатель инфляции уг
Снова возникает задача оценки параметров уравнения множественной регрессии. Действительно, исходя из экономического смысла значения ? (/ = 1,..., 14) представляют собой агрегированные экономические показатели, которые находятся в тесной взаимосвязи и взаимозависимости. Изменение одного из них ведет к изменению всех остальных. Это выводит на проблему мультиколлинеарности, вызванную экономическим содержанием задачи. Для разрешения этой проблемы используется метод главных компонент. Суть метода — сократить число объясняющих переменных до наиболее существенно влияющих факторов.
Метод главных компонент также применяется для исключения или уменьшения мультиколлинеарности объясняющих переменных регрессии. Основная идея заключается в сокращении числа объясняющих переменных до наиболее существенно влияющих факторов. Это достигается Путем линейного преобразования всех объясняющих переменных х* (/ = 0,..., л) в новые переменные, так называемые главные компоненты. При этом требуется, чтобы выделению первой главной компоненты соответствовал максимум общей дисперсии всех объясняющих переменных х1 (/ = 0,..., л). Второй компоненте — максимум оставшейся дисперсии, после того как влияние первой главной компоненты исключается ит. д.
314
ю
Матрица векторов — значений z
Таблица 7.3
Показатели
2 3 4 5 6 7 8 9 10 11 12 13 14
131,60
132,00
131,50
130,90
130,70
130,90
130,30
130,50
130,10
130,20
130,20
130,30
131,10
130,50
129,90
129,70
129,10
111,14
110,53
111,42
111,32
111,26
110,75
111,52
110,03
108,27
109,74
110,49 110,92
110,35 111,55
110,47
109,75
110,62
99,90
100,50 101,70
100,70
101,10 98,40
99,90
101,40 99,10
101,20 100,00
100,10 98,50
99,90
90,20 116,40
100,60
296,38
361,60
371,95
361,70
370,98
380,01
354,49
358,65
397,22
343,65
357,14
357,57
290,63
360,33
369,37
363,90
373,78
227,01 233,70
242,89 239,12
237,16 240,00
244,52 245,93
244,16 240,65
241,71
241,40 216,70
231,96 242,24
238,92 238,24
125,67
126,37
124,37
122,89
119,48
119,41
120,59
120,99
120,46
122,33
124,16
124,83
123,67
125,37
123,39
122,96
120,33
93,50
105,20
103,80
103,30 97,30.
115,70
91,90
93,40
65,20
107,50 108,80
85,50
110,00
98,00
95,30
96,70
396,68 396,45
396,71
397,14 397,48
397,59 397,68
397,82 398,03
398,03 404,38
432,74 441,31
455,42 473,92 466,65
457,57
244,89
244,53
243,60
241,69
239,34
240,43
243,28
245,16
244,58
244,59
246,03
247,06
248,15
251,15
251,58
251,96
253,11
279,25
273,76
279,03
269,83
275,69
263,77
271,36
272,52
298,57
266,06
271,89
240,14
281,28
270,60
270,77
266,74
200,30 200,20
200,30 199,30
198,60 198,30 199,10 199,70 199,90
200,00 199,40
199,10 199,00 200,20 201,60 202,70
205,50
306,22
307,94
306,45
304,93
299,18
294,72
296,50
295,59
293,94
297,14
292,83
296,74
296,30
296,27
291,55
293,34
295,02
186,87
195,80 191,49
182,41
187,16
192,93
193,14
191,87
195,70
193,93
189,50
185,88 184,28
195,52
191,02 179,68
184,01
187,95 188,11
192,45
192,47 194,74
195,47
194,39 191,27
196,25 197,84 194,76
195,12 175,80
171,71
194,42 194,87
192,03
Таким образом, выполненное преобразование содействует уменьшению мультиколлинеарности новых выделенных переменных по сравнению с мультиколлинеарностью набора исходных переменных х, (i = 0,л).
Процедура вычислений по методу главных компонент состоит из следующих шагов.
Строится матрица, элементами которой являются отклонения результатов наблюдений над п переменными от соответствующих средних (Ху — xt), i = 0,..., m\j = 0,п:
(7.27)
Определяется матрица дисперсий и ковариаций объясняющих переменных:
(7.28)
Матрица имеет размерность п х п.
Главные компоненты Zj (/ = 0,..., л) являются линейными комбинациями объясняющих переменных х* (/ - 0,..., п) и могут быть записаны в общем виде как
Zj = Xj'^-jJ = V. (7.29)
Они должны удовлетворять упомянутому выше требованию: каждый раз выделенная главная компонента должна воспроизводить максимум дисперсии. На неизвестные векторы коэффициентов aj в (7.29) накладываются дополнительные ограничения:
ajaj=l,j=^Jf (7.30)
(т. е. они должны быть нормированы) и
aj'ak = 0,J* к, J = , к = (7.31)
(т. е. они должны быть некоррелированы).
Дисперсия главной компоненты Zj
316
(7.32)
должна принимать наибольшее значение при соблюдении условий (7.30), (7.31). Для решения проблемы максимизации функции, связанной дополнительными ограничениями, пользуются методом множителей Лагранжа. В конечном итоге задача сводится к определению собственных значений матрицы и соответствующих собственных векторов а,.
Собственные значения матрицы определяются из уравнений, которые в общем виде записываются как
is» - М - °,
(7.33)
где А — множитель Лагранжа;
I — единичная матрица.
Подставляя последовательно собственные значения, начиная с наибольшего, в уравнение
(5^ — А/) • Оу — 0, j = 0,л
(7.34)
получим собственные векторы матрицы Sxx, соответствующие этим собственным значениям. Собственные векторы затем используются для построения искомых векторов коэффициентов в формуле (7.29).
Так как собственные векторы известны, по формуле (7.29) можно определить главные компоненты. При этом обычно довольствуются меньшим, чем л, числом главных компонент, но достаточным, чтобы воспроизвести большую часть дисперсии. По мере вьщеления главных компонент доля общей дисперсии становится все меньше и меньше. Процедуру вычисления главных компонент прекращают в тот момент, когда собственные значения, соответствующие каждый раз наибольшим дисперсиям, становятся пренебрежимо малыми. Количество выделенных главных компонент г в общем случае значительно меньше числа объясняющих переменных л:. По г главным компонентам строится матрица Z. С помощью главных компонент оцениваются параметры регрессии
B={ZTZ)~\ZTY)
(7.35)
и вычисляются значения регрессии
Y —” Z * В,
(7.36)
317
При всех своих преимуществах (уменьшение высокой мультиколлинеарности объясняющих переменных) метод главных компонент обладает и недостатками. Во-первых, главным компонентам, как правило, трудно подобрать экономические аналоги. Поэтому вызывает затруднение экономическая интерпретация оценок параметров регрессии, полученных по формуле (7.35). Во-вторых, оценки параметров регрессии получают не по исходным объясняющим переменным, а по главным компонентам. В итоге можно сказать, что метод главных компонент применяется в основном для оценки значений регрессии и для определения прогнозных значений зависимой переменной, что также является целью регрессионного анализа.
В данной задаче ограничились двумя главными компонентами:
К, = cto + cqC1, + ajC2,,
где
С1, = 0,3131 •? + 0,2308 • z2 - 0,0930 • ? - 0,3490 • ? -
- 0,3704 •? +0,31
• / + 0,0993 • г7 + 0,3625 • ? + 0,2093 • ? -
- 0,2460 • ?°+ 0,3628 •?’ +
- 0,0605 • г13 - 0,3222 • z14;
С2, = 0,1244 • ? + 0,4067 • г2 - 0,1337 • ? + 0,2158 •? + + 0,2240 • ? - 0,1696 • ? + 0,4243 • ? - 0,2906 • ? + 0,3651 • ? + + 0,0144 • ?° + 0,3143 • z“ + 0,3812 • ?2 + 0,0569 • ?3+ + 0,1736 ?4.
Итоговая модель имеет вид:
yt = 1
,8 + 0,1 • ? + 0,1 • ? - 0,04 • ? - 0,07 • z4
0,07 • ? +
+ 0,06 • ? + 0,07 • Ц + 0,06 • ? + 0,09 • ? - 0,06 • ?° + 0,13 • г“ + +
0,04 г12-0,01 • ?3 - 0,06 • ?4.
Построенное уравнение регрессии выявило следующую особенность инфляции, присущую российской экономике. Такие показатели, как стоимость потребительской корзины и прожиточный минимум населения, обнаружили высокое влияние на индекс потребительских цен. Об этом свидетельствуют высокие значения коэффициентов взаимной корреляции этих факторов с темпом роста индекса потребительских цен и значения весовых
318
коэффициентов при этих показателях. Так, весовой коэффициент при факторе, отражающем стоимость потребительской корзины, равен 0,13, что является наибольшим значением весового коэффициента во всем регрессионном уравнении; и 0,09 при показателе прожиточного минимума населения.
7.4. МОДЕЛИ АДАПТИВНЫХ ОЖИДАНИЙ
И НЕПОЛНОЙ КОРРЕКТИРОВКИ
В последние годы эконометрические методы, разработанные для построения и анализа моделей авторегрессии и моделей с распределенным лагом, широко используются для эмпирической верификации макроэкономических моделей, в которых учитываются ожидания экономических агентов относительно значений экономических показателей, включенных в модель, в момент времени t.
В зависимости от положенной в основу модели гипотезы о механизме формирования этих ожиданий различают модели адаптивных ожиданий, неполной корректировки и рациональных ожиданий. Поскольку эмпирические расчеты по моделям рациональных ожиданий достаточно сложные и требуют знания специальных методов математической статистики, рассмотрение которых выходит за рамки нашего учебника, подробнее остановимся на двух более простых моделях — адаптивных ожиданий и неполной корректировки — и покажем, что оценку параметров каждой из этих моделей можно проводить, используя обычную модель авторегрессии.
Модели адаптивных ожиданий
Рассмотрим модель вида у, = а +/> - х*(+1 + е„ (7.37)
где у, — фактическое значение результативного признака; х*,+| — ожидаемое значение факторного признака.
Механизм формирования ожиданий в этой модели следующий:
Xt+i - x*t = а • (х, - Xt) (7.38)
или
х‘ж = ах,+ (1 — а)х*,), (7.39)
с
где 0 < а < 1.
319
Таким образом, ожидаемое значение факторной переменной х* в период t есть средняя арифметическая взвешенная ее фактического и ожидаемого значений в предыдущий период. Иными словами, как показывает соотношение (7.38), в каждый период времени t + I ожидания корректируются на некоторую долю о разности между фактическим значением факторного признака и его ожидаемым значением в предыдущий период. Параметр а в этой модели называется коэффициентом ожиданий. Чем ближе коэффициент ожиданий а к 1, Тем в большей степени реализуются ожидания экономических агентов. И, наоборот, приближение величины а к нулю свидетельствует об устойчивости существующих тенденций. При а = 0 из соотношения (7.38) или (7.39) мы получим, что х* = х„ т. е. «условия, доминирующие сегодня, сохранятся и на все будущие периоды времени. Ожидаемые будущие значения показателей совпадут с их значениями текущих периодов»1.
Подставим в модель (7.37) вместо х*,+1 соотношение (7.39):
yt = а + b • (а • х, + (1 — а) • х*,) + е, = = а + а • b • xt + (1 — а) • Ь • xt + ег
(7.40)
Если модель (7.37) имеет место для периода /, то она будет иметь место и для периода (/—1). Таким образом, в период (Л-1) получим:
у,_, = а + b • х* + еж.
(7.41)
Умножим (7.41) на (1 — а):
(1 - а) • yr_| = (1 - а) • а + (1 - а) • b • x*z + (1 - а) • £,„! (7.42)
Вычтем почленно (7.42) из (7.40):
yt — (1 - а) • yt-l = а — (1 — а) • а + а • b • xt + е, — (1 — а) • е,_ь. (7.43)
или
где
yt = а • а + а • b • х, + (Г- а) • у,_{ + и„
(7.44)
— Е, — (1 —" ct)
lShaw G.K. Rational Expectations: An Elementary Exploration. — New York: St.-Martin’s Press, 1984. — C. 19 — 20.
320
Мы получили модель авторегрессии, определив параметры которой можно легко перейти к исходной модели (7.37). Для этого с помощью коэффициента при у,_] сначала надо определить значение коэффициента ожиданий а, а затем рассчитать параметры а и Ь модели (7.37), используя полученные значения свободного члена и коэффициента регрессии при факторе х, модели (7.44).
Основное различие моделей (7.37) и (7.44) состоит в том, что модель (7.37) включает ожидаемые значения факторной переменной, которые нельзя получить эмпирическим путем. Поэтому статистические методы для оценки параметров модели (7.37) неприемлемы. Модель (7.44) включает только фактические значения переменных, поэтому ее параметры можно определять на основе имеющейся статистической информации с помощью стандартных статистических методов. Однако, как и в случае с моделью Койка, применение ОМНК для оценки параметров уравнения (7.44) привело бы к получению их смещенных оценок ввиду наличия в правой части модели лагового значения результатив
ного признака j.
Модель (7.37), характеризующая зависимость результативного признака от ожидаемых значений факторного признака, называется долгосрочной функцией модели адаптивных ожиданий. Модель (7.44), которая описывает зависимость результата от фактических значений фактора, называется краткосрочной функцией модели адаптивных ожиданий.
Пример 7.6. Расчет и интерпретация параметров модели адаптивных ожиданий.
Вернемся к модели из примера 7.4. Предположим теперь, что разница между реальной заработной платой и ее уровнем в условиях полной занятости есть не наблюдаемая, а ожидаемая величина, механизм формирования ожиданий для которой определяется соотношением (7.39) модели адаптивных ожиданий, т. е.
и» ж = а • wt + (1 — ct) • w ж,
где 0 < а < 1.
Долгосрочная функция для уровня безработицы имеет вид: Uf ~ а + b •»/,+! + с • t + е,.
Выполнив алгебраические преобразования, аналогичные изложенным выше при получении краткосрочной функции в моде-321
ли адаптивных ожиданий, получим краткосрочную функцию для данной модели:
«. -
и,ж (о • а +(1 — а) • с) + (1 — а) • Ut_t + а • b • wt + а • с-1 + v„ р
J • , .
где v, - е, - (1 - а) • e,_t.
В соответствии с моделью Сакса и Бруно имеем:
а • а + с • (1 - а) = 50 ;а = 2,703 • 80 — 0,189;
1 — а = 0,63; а = 0,37;
а- Ь— 15,72; с = 0,189;
а • с = 0,07; Ь = 42,486.
Выпишем долгосрочную функцию модели адаптивных ожиданий:
U, = (2,703 • 80 - 0,189) + 42,486 • <+1 + 0,189 • t + v,.
В соответствии с интерпретацией коэффициента ожиданий а, который в данной модели составил 0,37, можно сказать, что около 37% различий между фактическими и ожидаемыми значениями w, и w*t+1 реализуется в течение одного года.
Модель неполной корректировки
Б отличие от модели адаптивных ожиданий в модели неполной корректировки эмпирически ненаблюдаемой переменной является результативный признак. Общий вид этой модели следующий: «I
yt == а + b • xt + ег (7.45)
1 . ’ , 1 • ' > г
Формирование ожиданий экономических агентов относительно значений у* происходит по следующей схеме:
yt - yt-i я yt-i)+vt> (7-46)
где 0 < р < 1.
В этой модели предполагается, что абсолютное изменение фактических уровней результата есть некоторая доля его ожидаемого абсолютного изменения. Параметр Р в этой модели называют корректирующим коэффициентом. Чем ближе величина 0 к 1,
322
тем в большей степени реальная динамика показателя отвечает ожиданиям экономических агентов. Чем ближе 0 к 0, тем менее реальное изменение показателя соответствует его ожидаемому изменению. При 0 = 0 значение результативного признака является константой, на которую ожидания агентов не оказывают никакого воздействия.
Модель (7.45) называется моделью неполной корректировки.
Запишем гипотезу о формировании у* в виде:
yt = 0 • y*t+ О - 0)Ул-1+Ъ- (7.47)
Таким образом, фактическое значение результата текущего периода yt есть средняя арифметическая взвешенная его ожидаемого значения текущего периода у,* и фактического значения за предыдущий период времени у,.,.
Подставим уравнение (7.45) в найденное выражение для yt (7.47). Получим:
у,= 0• (а + bxt + е,) + (1 - 0)-y,_i = 0• а + 0 • b-xt +
+ (1-0)-7г-| + «г. (7-48)
где и, = 0 • e,+v,.
Соотношение (7.48) есть основное уравнение модели неполной корректировки. Его называют краткосрочной функцией модели. Как и в модели адаптивных ожиданий, уравнение (7.48) включает только фактические значения переменных. Зная оценки параметров этого уравнения, можно найти 0. Затем путем алгебраических преобразований рассчитать параметры а и b уравнения (7.45), описывающего зависимость ожидаемого значения результата от значений факторного признака. Уравнение (7.45) называют долгосрочной функцией модели неполной корректировки.
Пример 7.7. Построение модели неполной корректировки.
На основе поквартальных данных за 1950—1960 гт. по Великобритании Ф. Бречлинг получил следующее уравнение регрессии, характеризующее спрос на труд1:
ДЕ, = 14,22+0,172(2,-О,О28/-О,ООО7?-0,297Е,.,,
(2,61) (0,014) (0,015) (0,0002) (2,61)
'Brechling F.P.R. The relationship between output and employment in British manufacturing industries // Review of Economic Studies. — \Ы. 32. — 1965. — July.
323
где &£, =
Et - уровень занятости;
Qt — объем выпуска продукции;
t — время.
В скобках указаны значения стандартных ошибок коэффициентов регрессии.
В основу этой модели была положена предпосылка о том, что в долгосрочной перспективе существует определенный желательный уровень занятости £„ который есть функция от объема выпуска Q и времени t. Кроме того, механизм формирования ожиданий относительно значения Е* определяется соотношением
Д - E<-iш Р * (Д ~
где 0 < р < I — корректирующий коэффициент.
Данная модель относится к типу моделей неполной корректировки. Гкпотезу о формировании ожиданий можно переписать в виде:
£,я Р • £,* +(1 — Р) -£м. (7.49)
Поскольку
А£, = имеем:
Е, -14,22 + 0,172 • Q, - 0,028 • t - 0,0007 • ? +
+ (1 - 0,297) • £^. (7.50)
Учитывая, что желательный уровень занятости есть функция от объема выпуска Q, и переменной времени t, в результате сравнения (7.49) и (7.50) получим, что
Р • £,*- 14,22 + 0,172 • Qt - 0,028 • t - 0,0007 • ? и
1-Р = 1-0,297.
Следовательно, р = 0,297. Эго означает, что фактическое изменение уровня занятости (£, — £г-1) составляет 0,297 от его желательного изменения (£, - Et_x).
Функция спроса на труд в долгосрочной перспективе есть зависимость желательного уровня занятости Е* от независимых переменных модели Qt и t. Так как
р • Е*я 14,22 + 0,172 -0,- 0,028 • t - 0,0007 • И,
324
то
= 14,22 0,172 0 0,028 ( 0,0007 /2 ' 0,297 + 0,297 ’ й 0,297 *1 0,297 ’
или
Ё\ = 47,879 + 0,5790, - 0,0943/ - 0,0024?.
7.5. ОЦЕНКА ПАРАМЕТРОВ МОДЕЛЕЙ АВТОРЕГРЕССИИ
Описанные выше преобразование Койка, модель адаптивных ожиданий и модель неполной корректировки сводятся к модели авторегрессии вида (7.2). Однако при построении моделей авторегрессии возникают две серьезные проблемы.
Первая проблема связана с выбором метода оценки параметров уравнения авторегрессии. Наличие лаговых значений резуль
тативного признака в правой части уравнения приводит к нарушению предпосылки МНК о делении переменных на результа
тивную (стохастическую) и факторные (нестохастические).
Вторая проблема состоит в том, что поскольку в модели авто-
регрессии в явном виде постулируется зависимость между теку
щими значениями результата у, и текущими значениями остатков и„ очевидно, что между временными рядами у,_, и также существует взаимозависимость. Тем самым нарушается еще одна предпосылка МНК, а именно предпосылка об отсутствии связи между факторным признаком и остатками в уравнении регрессии. Поэтому применение обычного МНК для оценки параметров уравнения авторегрессии приводит к получению смещенной оценки параметра при переменной у,_(.
Одним из возможных методов расчета параметров уравнения авторегрессии является метод инструментальных переменных. Сущность этого метода состоит в том, чтобы заменить переменную из правой части модели, для которой нарушаются предпосылки МНК, на новую переменную, включение которой в модель регрессии не приводит к нарушению его предпосылок. Применительно к моделям авторегрессии необходимо удалить из правой части модели переменную у,_(. Искомая новая переменная, которая будет введена в модель вместо у,_(, должна иметь два свойства. Во-первых, она должна тесно коррелировать с у,_(, во-вторых, она не должна коррелировать с остатками
Существует несколько способов получения такой инструментальной переменной. Поскольку в модели (7.2) переменная у, за-
325
висит не только оту,_|, но и отх„ можно предположить, что имеет место зависимость у,_ । отх,_,, т. е.
У,-1 = d0 + dt • х,_! + и,.
(7.51)
Таким образом, переменную у,_] можно выразить следующим образом:
Уг-1 “ Л-1 + «г.
где y,-t d0 + dt • xt_j.
(7.52)
(7-53)
Найденная с помощью уравнения (7.53) (его параметры можно искать обычным МНК) оценка Л-i может служить в качестве инструментальной переменной для фактора уг Эта переменная, во-первых, тесно коррелирует с во-вторых, как показывает соотношение (7.53), она представляет собой линейную комбинацию переменной х,_ь для которой не нарушается предпосылка МНК об отсутствии зависимости между факторным признаком и остатками в модели регрессии. Следовательно, переменная Л-i также не будет коррелировать с ошибкой ut.
Таким образом, оценки параметров уравнения (7.2) можно найти из соотношения
y^a + bo-Xt + c^y^ + Vf,
(7-54)
предварительно определив по уравнению (7.53) расчетные значения Л-1-
Допустимо использовать также следующую модификацию этого метода. Подставим в модель (7.2) вместо его выражение из уравнения (7.51):
yt = а + • х, + q • (Jo + di • xt-i + ut) + er
(7.55)
Получим следующую модель:
yt = (a + Cl • </0) + b0 • X, + q • di • x,_! + (q • и, + e,). . (7.56)
i
Уравнение (7.46) представляет собой модель с распределенным лагом, для которой не нарушаются предпосылки обычного МНК, приводящие к несостоятельности и смещенности оценок параметров. Определив параметры моделей (7.51) и (7.56), можно рассчитать параметры исходной модели (7.2) а, Ьо и q. Модель 326
(7.56) демонстрирует еще одно важное свойство изложенного выше метода инструментальных переменных для оценки параметров моделей авторегрессии: этот метод приводит к замене модели
авторегрессии на модель с распределенным лагом.
Отметим, что практическая реализация метода инструментальных переменных осложняется появлением проблемы мультиколлинеарности факторов в модели (7.54): функциональная связь между переменнымиyt_t их,ч приводит к появлению высокой корреляционной связи между Переменными и хг В некоторых случаях эту проблему можно решить включением в модель (7.54) и соответственно в модель (7.2) фактора времени в качест
ве независимой переменной.
Еще один метод, который можно применять для оценки параметров моделей авторегрессии типа (7.2), — это метод максимального правдоподобия, рассмотрение которого выходит за рамки
данного учебника.
Пример 7.8. Расчет параметров модели авторегрессии.
Обратимся к данным о среднедушевом располагаемом доходе и среднедушевых расходах на конечное потребление в США в период с 1960 по 1991 г., представленным в табл. 6.7 (пример 6.5).
Определим по этим данным Параметры модели авторегрессии
вида
у, = а + *0-х, + С|-yr_t + г„
где х, — среднедушевой располагаемый доход (долл. США); у. — среднедушевые расходы на конечное потребление (долл. США). • ' * 1 %
Применение обычного МНК для расчета параметров этой модели приводит к получению следующих результатов:
У'= -21,43 + 0,522х, +0,435у,_,; R1 =0,996.
(131,987) (0,098) (0.105)
В скобках указаны стандартные ошибки параметров уравнения регрессии.
Однако, как было показано выше, оценка параметра равная 0,440, является смещенной. Для получения несмещенных оценок параметров этого уравнения воспользуемся методом инструментальных переменных. Определим параметры уравнения регрессии (7.43) обычным МНК: * и
>С1 =-139,065+0,918хм; R1 =0,994.
(146,406) (0,013)
327
I
скобках указаны стандартные ошибки параметров уравне-
ния регрессии. Определим по этому уравнению расчетные значения а затем параметры уравнения регрессии (7.44). Получим
следующие результаты:
yt =-184,578+0,827х, +0,107-у,_1;
(172,967) (0,155) (0,166)
R2 =0,994. №
В скобках указаны стандартные ошибки параметров уравнения регрессии. Применение метода инструментальных переменных привело к статистической незначимости параметра С] = 0,109 при переменной уг_(. Эго произошло ввиду высокой мультиколлинеарности факторов х, и у,_,. Несмотря на то что результаты, полученные обычным МНК, на первый взгляд лучше, чем результаты применения метода инструментальных переменных, результатам обычного МНК вряд ли можно доверять вследствие нарушения в данной модели его предпосылок. Поскольку ни один из методов не привел к получению достоверных результатов расчетов параметров, следует перейти к получению оценок параметров данной модели авторегрессии методом максимального правдоподобия. ,
При оценке достоверности моделей авторегрессии слеДует учитывать специфику тестирования этих моделей на автокорреляцию остатков.' В п. 6.4 мы уже упоминали, что для проверки гипотез об автокорреляции остатков в моделях авторегрессии нельзя использовать критерий Дарбина — Уотсона. Это объясняется тем, что применение критерия Дарбина — Уотсона предполагает строгое соблюдение предпосылки о разделении переменных модели на результативную и факторные (точнее — о нестохастической природе факторных признаков уравнения регрессии). При наличии в правой части уравнения регрессии лаговых значений результата и, следовательно, несоблюдении этой предпосылки фактическое значение критерия Дарбина — Уотсона приблизительно равно 2 как при отсутствии, так и при наличии автокорреляции остатков. Происходит это по следующей причине.
Предположим, в уравнении (7.2) имеет место автокорреляция остатков, т. е.
Etя 6* 6/-1 + up (7-57)
где ut - случайные остатки,
тогда
Л«л + ^-х) + сг7м+Лчы+«г (7.58)
328
Для периода (t — 1) уравнение (7.2) примет вид:
y,-i = а + Ьо х^, +ct • у,_2 + (7-59)
Как следует из соотношения (7.59), переменные у,_| и е,_, взаимосвязаны. Поэтому в соотношении (7.58) часть воздействия е,_| / на у, будет объясняться взаимодействием факторов yt_t и е,_|, поэтому чистое воздействие е,_( на yt будет невелико. Критерий Дарбина — Уотсона в данной ситуации будет в основном характеризовать случайные остатки и„ а не остатки е, в модели (7.2).
Для проверки гипотезы об автокорреляции остатков в моделях авторегрессии Дарбин предложил использовать другой критерий, который называется критерием h Дарбина. Его расчет производится по следующей формуле1:
A=(1~f) <7-60>
где d — фактическое значение критерия Дарбина - Уотсона для модели авторегрессии;
п — число наблюдений в модели;
V — квадрат стандартной ошибки при лаговой результативной переменной.
Распределение *этой величины приблизительно можно аппроксимировать стандартизованным нормальным распределением. Поэтому для проверки гипотезы о наличии автокорреляции остатков можно либо сравнивать полученное фактическое значение критерия h с табличным, воспользовавшись таблицами стандартизованного нормального распределения, либо действовать в соответствии со следующим правилом принятия решения.
1. Если h > 1,96, нуль-гипотеза об отсутствии положительной автокорреляции остатков отклоняется.
2. Если h < — 1,96, нуль-гипотеза об отсутствии отрицательной автокорреляции остатков отклоняется.
3. Если —1,96 < h < 1,96, нет оснований отклонять нуль-гипотезу об отсутствии автокорреляции остатков.
Пр имер 7.9. Проверка гипотезы о наличии автокорреляции остатков в модели авторегрессии.
Вернемся к модели авторегрессии из примера 7.8, параметры которой были получены методом инструментальных переменных:
'Расчет этого критерия возможен только в случаях, когда л • У< 1.
22"”а
329
yt = -184,578+0,827x, +0,107%.,; R2 = 0,994.
(172,967) (0,155) (0,166)
Протестируем эту модель на автокорреляцию остатков. Сформулируем нуль-гипотезу:
Но — отсутствует автокорреляция в остатках.
Но* — отсутствует отрицательная автокорреляция в остатках.
Рассчитаем по формуле (7.60) величину критерия h Дарбина: поскольку полученное значение h = 4,69, следует отклонить нуль-гипотезу об отсутствии положительной автокорреляции остатков.
V
7.6. НОВЫЕ НАПРАВЛЕНИЯ В АНАЛИЗЕ МНОГОМЕРНЫХ ВРЕМЕННЫХ РЯДОВ
Векторная авторегрессия
Временные ряды — основной источник данных для построения эконометрических моделей в форме систем одновременных уравнений. Однако методы построения структурных моделей (особенно крупных моделей, содержащих большое количество уравнений и переменных) достаточно сложны, поэтому в последние десятилетия был разработан и получил широкое распространение еще один подход — построение моделей векторной авторегрессии. В разработку этого подхода внесли большой вклад Р. Лукас, Т. Сарджент, К. Симс и ряд других макроэкономистов.
Одна из основных проблем, которую приходится решать на этапе оценкй параметров систем одновременных уравнений, -это проблема идентификации. Именно эта проблема наряду с разделением переменных эконометрической модели на эндогенные и предопределенные послужила основным поводом для критики стандартного подхода к системам одновременных уравнений.
Во-первых, в больших эконометрических моделях, содержащих сотни переменных и уравнений, иногда трудно определить некоторые переменные как чисто экзогенные. Например, управляемые переменные экономической политики часто считают экзогенными. Однако в ответ на макроэкономические условия правительство может внести изменения в эти управляемые переменные и параметры. В этом смысле все переменные экономической политики являются эгдогенными.
Во-вторых, ряд проблем иного рода существует даже в небольших моделях, построенных по принципу систем одновременных уравнений. Например, стандартная практика посгрое-330
ния этих моделей — включение лаговой эндогенной переменной в правую часть некоторых уравнений с целью увеличения числа предопределенных переменных модели. Между тем иногда этот шаг не подтверждается веским теоретическим обоснованием.
Таким образом, пытаясь найти решение проблемы идентификации, многие ученые вынуждены снижать обоснованность структурной формы исходной эконометрической модели.
Следует отметить и другой аспект. Одним из основных направлений использования эконометрических моделей является прогнозирование значений эндогенных переменных на будущие периоды. Между тем, как справедливо отмечал Р. Лукас, когда прогноз сделан и доведен до сведения экономических единиц, последние могут изменить свое поведение, если они считают этот прогноз достоверным. Это изменение поведения в свою очередь приводит к изменению значений ряда переменных; например предельной склонности к потреблению, инфляционных ожиданий и т. д., которые использовались в структурной модели при составлении прогноза. Таким образом, если критика Р. Лукаса верна, все экономические переменные потенциально являются эндогенными и эконометрическая идентификация теоретически невозможна.
Одним из результатов подобного рода дискуссий является разработка моделей векторной авторегрессии (VAR). В моделях VAR не делается попыток воссоздать реальную структуру экономики, в них не проводится различий между эндогенными и экзогенными переменными. Каждое уравнение модели VAR описывает зависимость одной из переменных модели от лаговых значений всех переменных модели. Таким образом, каждое уравнение модели есть комбинация модели с распределенным лагом и модели авторегрессии. Число уравнений модели VAR равно числу ее переменных.
Примером простейшей модели векторной авторегрессии является модель, предложенная в 1984 г. Уеббом для прогнозирования процентных ставок (R) и процентного изменения денежной массы (М):
[X =а! +А X-i +<?1 Лч +6,
t п • (7.61)
=а2 +/>2 +с2 ‘Rf-l
Основная характеристика этой модели — симметрия переменных; обе переменные появляются по обе стороны каждого уравнения.
22* 331
Реальные модели VAR имеют более длительные лаги и большее число переменных. Однако по сравнению со структурными моделями модели VAR имеют меньшее число параметров и менее строгие ограничения на их значения, что делает модели векторной авторегрессии чрезвычайно полезными при возникновении трудностей со сбором исходной информации.
Несомненно, модели векторной авторегрессии имеют недостатки. Например, в ряде случаев трудно подвести теоретическое обоснование и дать экономическую интерпретацию параметрам модели VAR. Однако определенная теоретическая база заложена в начальный выбор переменных, которые войдут в модель.
Другой недостаток моделей векторной авторегрессии — необходимость принятия решения относительно величины лага, адекватных методов оценки параметров модели, поскольку обычный МНК, как было показано выше, чаще всего неприменим при оценке параметров моделей с распределенным лагом и тем более неприменим для оценки параметров моделей авторегрессии. Поэтому методы оценки параметров моделей VAR очень громоздки, и в настоящее время далеко не все статистические пакеты прикладных программ имеют эту функцию. Однако в целом модели VAR потенциально значительно проще структурных моделей.
Модели рациональных ожиданий
Теория рациональных ожиданий оказывает все большее воздействие на макроэкономическую теорию и прикладную экономику. В наиболее упрощенной форме рациональные ожидания означают, что экономические агенты имеют доступ ко всей адекватной информации и наилучшим образом ее используют при формировании ожиданий относительно будущих значений экономических переменных. Адекватная информация предполагает знание целей экономической политики государства. Формально в моделях рациональных ожиданий предполагается следующее: экономические агенты на основе прошлого опыта и существующего уровня знаний убеждены, что для любого момента времени t каждая переменная х определяется следующим образом:
(7.62)
где z — экзогенная переменная, которая, по убеждению экономических агентов, влияет на х;
е, — случайная ошибка.
332
Предполагается, что в момент времени t экономические агенты ничего не знают о переменных xt и Z/, поэтому правая часть уравнения содержит только лаговые переменные.
В момент времени (t — 1) экономические агенты формируют свои ожидания относительно xt на базе уравнения (7.62):
£,_i(x,) = а + Ь • + с ♦ zt-i. (7.63)
Эта величина и есть рациональные ожидания относительно переменной хг Таким образом, имеем: и
х, - £,_((х,) = ег (7.64)
В сущности, е, является ошибкой прогноза экономической единицы. Относительно этой ошибки делаются две предпосылки. Во-первых, ее среднее значение должно быть равно нулю. Во-вторых, это должна быть действительно случайная, т.е. непрогнозируемая ошибка. Например, в этих ошибках не может наблюдаться автокорреляция. Прогнозируемость ошибки означала бы наличие информации, которая не использовалась экономическими агентами при формировании ожиданий, что противоречит гипотезе о рациональных ожиданиях. В случае когда возможно получить прогноз ошибки е„ экономические агенты могли бы просто переформулировать исходное уравнение до тех пор, пока ошибка не станет непрогнозируемой.
В настоящее время рациональные ожидания часто используются в прикладных исследованиях как альтернатива адаптивным ожиданиям. Например, предполагается, что переменная у определяется, как и в модели адаптивных ожиданий, в соответствии с уравнением (7.37). Однако вместо предпосылки об адаптивных ожиданиях относительно будущих значений переменной х/ используются рациональные ожидания.
у, - а + b • Et_^x^ + ег (7.65)
Проблема получения оценок параметров а и Ь состоит в том, что данные о рациональных ожиданиях периода (Z — 1) относительно величины х, отсутствуют.
Процедура эмпирического оценивания этих параметров состоит из двух шагов.
II
х,«с0 + с,-х,_, +с2-^|, (7.66)
333
а также расчетные значения хг Эти значения принимают за аппроксимацию
Шаг 2. В исходном уравнении ожидаемые значения Е,_|(х*,) заменяют на х, и определяют оценки параметров а и b обычным МНК.
Коинтеграция временных рядов и механизм исправления ошибок1
Давая обобщающую характеристику проблемы коинтеграции временных рядов, мы отмечали, что сама коинтеграция имеет место только для длительных промежутков времени, или в долгосрочной перспективе. Рассмотрим модель регрессии по двум временным рядам у, и х„ между которыми существует коинтеграция:
yt = а + Ь • х, + ег (7.67)
Из этой модели мы получаем следующее выражение для ошибки:
et = yt — а — b • Xf. (7.68)
Соотношение (7.68) описывает механизм расчета случайной ошибки в модели (7.67) в долгосрочной перспективе. Д. Сарган предложил называть совпадение тенденций (коинтеграцию) рядов х, и у, в долгосрочной перспективе их равновесным состоянием, а ошибку ер описываемую соотношением (7.68), — равновесной ошибкой2.
Очевидно, что при рассмотрении коротких временных рядов данных, или краткосрочной перспективы, равновесное состояние может не достигаться, и коинтеграции между рядами х, и yt может не быть. Поэтому каждый уровень временного ряда случайных ошибок ef, или остатков, можно считать корректирующей компонентой модели (7.67), характеризующей степень достижения равновесного состояния динамики рядов х, и у, в долгосрочной перспективе. Основываясь на этих рассуждениях, Сарган выдвинул предположение о том, что на формирование уровней ряда у, (точнее — на их цепные абсолютные приросты) оказы-
Англоязычная версия этой модели имеет название: «error correction mechanism».
2Sargan J.D. Wges and Prices in the United Kingdom: A Study in Econometric Methodology // K.F. Wilis and D.F. Hendry, eds. Quantitative Economics and Econometric Analysis. Basil Blackwell, Oxford, 1984.
334
вают влияние два фактора — изменение, или цепные абсолютные приросты, ряда х„ который является причиной у„ и величина ошибки предыдущего периода е,^. Формально это предположение можно описать с помощью следующей модели:
byt = а + bt • Дх, + Ь2 et_, + и„
(7.69)
где Ау,, Ах, — первые разности изучаемых рядов;
ez_t - ошибка предыдущего периода в модели (7.67);
и, — случайная ошибка уравнения-(7.69).
Модель регрессии (7,69) называют механизмом корректировки посредством ошибок. Если коэффициент Ь2 статистически значим, то его величина характеризует долю неравновесного состояния временно'го ряда yt, которая корректируется в каждом следующем периоде. Поскольку Ау, в модели (7.69) есть первые разности исходных уровней ряда, можно сказать, что коэффициент Ь2 характеризует скорость корректировки ряда yt во времени по направлению к достижению равновесного состояния.
Таким образом, механизм корректировки посредством ошибок позволяет количественно охарактеризовать взаимосвязь между краткосрочной и долгосрочной динамикой во временных рядах экономических показателей. Впервые этот механизм был описан Сарганом, дальнейшая его разработка и эмпирическая проверка проводились также Энгелем и Грангером.
Контрольные вопросы к главе 7
1. Приведите примеры экономических задач, эконометрическое моделирование которых требует применения моделей с распределенным лагом и моделей авторегрессии.
2. Какова интерпретация параметров модели с распределенным лагом? Перечислите абсолютные и относительные показатели силы связи модели с распределенным лагбм.
3. Какова интерпретация параметров модели авторегрессии? В чем специфика долгосрочного лага в этой модели?
4. В чем сущность метода Алмон? При какой структуре лага он применим? *
5. Опишите методику применения подхода Койка для построения модели с распределенным лагом. При какой структуре лага он применим?
335
6. Изложите методику применения метода главных компонент для построения модели с распределенным лагом.
7. В чем сущность модели адаптивных ожиданий? Какова методика оценки ее параметров?
8. В чем сущность модели неполной корректировки? Какова методика оценки ее параметров?
9. Изложите методику применения метода инструментальных переменных для оценки параметров модели авторегрессии.
10. Изложите методику тестирования модели авторегрессии на автокорреляцию в остатках. Почему в этих целях не рекомендуется использовать критерий Дарбина — Уотсона?
11. Изложите основную идею моделей векторной автогрессии. Каковы преимущества и недостатки этих моделей?
12. В чем сущность моделей рациональных ожиданий? Какова специфика оценки их параметров?
ЛИТЕРАТУРА
1. Айвазян С.А., Мхитарян В,С. Прикладная статистика и основы эконометрики: Учебник. — М.: ЮНИТИ, 1998.
2. Джонстон Дж. Эконометрические методы. — М.: Статистика, 1980.
3. ДоугертиК Введение в эконометрику. — М.: Финансы и статистика, 1999.
4. Елисеева И.И., ЮзбашевММ. Общая теория статистики.- 4-е изд., перераб. и доп. — М.: Финансы и статистика, 2001.
5. Кейн Э. Экономическая статистика и эконометрия. Введение в количественный экономический анализ. — М.: Статистика, 1977. — Вып. 1.
6. Ланге О. Введение в эконометрику / Пер. с польсК. -М.: Прогресс, 1964.
7. Лизер С. Эконометрические методы и задачи. — М.: Статистика, 1971.
8. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика: Начальный курс. — М.: Дело, 1998.
9. Маленво Э. Статистические методы эконометрии. — М.: Статистика, 1976.
10. Тинтнер Г. Введение в эконометрию. — М.: Финансы и статистика, 1965.
11. Фишер Ф. Проблема идентификации в эконометрии. — М.: Статистика, 1978.
12. Четыркин Е.М. Статистические методы прогнозирования. — М.: Статистика, 1977.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Автокорреляция:
в остатках 157, 265, 272-278
уровней временного ряда 227
Автокорреляционная функция 231 Аддитивность 15-16, 216, 239 Альтернативная оценка регрессии 128
Анализ остатков регрессии 155-166, 272-278, 282
Векторная авторегрессия (VAR) 14, 330-332
Визуальная оценка гомо- и гетероскедастичности 157-163 Возмущение 35
Временной ряд 225, 263-264
Гарвардский барометр 10-11 Гармонический анализ 12-13 Гетероскедастичность 24, 162-166 Гомоскедастичность 156, 160-162 Граф связей 18, 213-214'
Динамические модели 290-291, 319, 322, 330, 332
Дисперсионный анализ 53, 130-135 Дисперсия 39-40, 48-51
Дисперсия на одну степень свободы 51
Доверительные интервалы:
коэффициента регрессии 54 линии регрессии 59-60 предсказываемого:
индивидуального значения 57-60
результативного признака 57-60
Значимость:
коэффициентов корреляции 55-56
коэффициентов регрессии 53-55, 136-139
параметров регрессии 48-53, 129-132
уравнения регрессии 47-48, ЮЗ-104, 112-120
Идентификация модели 24, 185, 219-220
Идентифицируемость модели 187-188, 205
Измерения:
допустимые преобразования 26
признаки 25
шкала 26
Индекс:
детерминации 84-86, 113-125
корреляции:
множественный 113-125 парный 80-84, 113-117 частный 121-125
Интервальное оценивание 57-60
Интерпретация:
коэффициента детерминации 47-
48
коэффициентов регрессии 41,43-
45
коэффициентов эластичности 72-75
Источники вариации 49-50
Квази - R2118
Коинтеграции временных рядов
282-285, 334-335
Коллинеарность факторов 92
Конфлюэнтный анализ 17
Коррелограмма 231
Корреляционная матрица 112
Корреляция 10, 12,14, 20
Коэффициент:
автокорреляции 274-276
влияния 18, 215, 218, 223
338
детерминации 47,52, 112,217-218 корреляции: множественный 112-120 парный 18, 50 скорректированный с учетом числа степеней свободы: частный 121-125 эластичности 72-74, 111-112
Коэффициенты регрессии 43, 100 Кривая:
Гомперца 20-21 логистическая 21 с насыщением 20-21, 79 Филлипса 66 Энгеля 67
Критерий:
Дарбина (h-критерий) 329-330 Дарбина -ь Уотсона 272-278, 282, 284
Стьюдента (t-критерий) 54-55, 136, 155 точности измерений 155 Фишера (Р-гоитерий): общий 48-52, 129, 155 последовательный 136 частный 131-132, 136
Энгеля — Грангера 283
Лаг 19, 230, 291, 293, 297, 307, 309 Лаговые переменные 291, 307, 311 Линеаризация 62-63, 66, 69-71, 103 Линейная модель множественной регрессии 90 Линейность 15-16, 70-71 Ложная корреляция 19, 222
Математическая статистика 5 Метод:
Гольдфельда - Квандта 165 инструментальных переменных 325-327 исключения тенденции: включения фактора времени 265, 271-272 отклонений от тренда 265-266 последовательных разностей 265, 268-269
наименьших квадратов: двухшаговый (ДМНК) 200-204, 214 обобщенный (ОМНК) 169 традиционный (обычный) (МНК) 21-22, 42-43, 63-64, 95, 180,217 трехшаговый 195
оценки параметров модели с распределенным лагом:
Алмон Ш. 291-302
Койка Л. М. 305-311,314 главных компонент 310,314, 316-317 скользящего среднего 282
Механизм исправления ошибок 334-335
Модель: авторегрессии 290-291, 307, 309 адаптивных ожиданий 290, 319-321
временного ряда: аддитивная 226, 239-245 мультипликативная 226, 239-240, 245-250
неполной корректировки 290, 319,322-323
рациональных ожиданий 290, 319, 332-334
регрессии по скользящим средним 282
с распределенным лагом 290-291, 306-309
Сакса и Бруно 308-309
Мультиколлинеарность 24, 95, 311
Мультипликативность 240
Мультипликатор: долгосрочный 293 краткосрочный 292 промежуточный 292 инвестиционный 206
Неидентифицируемость модели 187-188
Несмещенность оценок параметров регрессии 156
Нормальность регрессионных остатков 157-159
Отношение дисперсий 293
Относительные коэффициенты 293
Оценивание 35,41-43, 105-106, 193 Ошибка:
аппроксимации 87-88 выборки 36 измерений 36 спецификации 36-37 стандартная коэффициентов 55-
56
регрессии 53, 55, 57-59, 136-137
339
Периодограмм анализ 12-13
Поле корреляции 37, 39
Построение уравнения регрессии 41,43
Предопределенные переменные 220
Процедура Саймона-Блейлока 222-223
Преобразование переменных 62-71 Приведенная форма модели 182-185
Прогноз:
интервальный 59-62
точечный 59
Производственная функция: множественная 103, 117
Путевой анализ 18, 203-215
Путевой коэффициент 18
г
Регрессионный анализ 34
Регрессия:
гиперболическая 62
линейная 41
логарифмически линейная 70
множественная 14,90 нелинейная 62-63 обратная 71
оценка параметров 41-44,62-64
парная 14
полиномиальная 62-63
полулогарифмическая 68
с фиктивными переменными 141-143
Рекурсивные системы 18
Сверхидентифицируемость модели
187-188, 205
Система уравнений: одновременных 180, 204 независимых 178
рекурсивных 178 Состоятельность оценок параметров регрессии 156 Спецификация модели 34,90 Стандартизованные коэффициенты регрессии 216 Статистическая гипотеза 5 Структурная форма модели 180, 181,214,217, 220 Структурные коэффициенты модели 181-183, 185
Сумма квадратов отклонений см. Метод наименьших квадратов
Тест Чоу 258-259
Таблица дисперсионного анализа 53, 130, 133, 135
Теоретическая линия регрессии 41 Теснота связи см. Коэффициент корреляции
Уравнение регрессии: натуральный вид 34-40 стандартизованный вид 106
Уровни временного ряда 225 Условия идентификации системы: достаточное 189-190 необходимое 188-189
Фиктивные переменные 141-143, 252-253
Число степеней свободы 49 Частные уравнения регрессии 109
Шкала:
интервальная 26-28 наименований (номинальная) 26, 29
отношений 27-28 порядковая (ординальная) 26 пропорциональная 28 разностей 28
Экзогенные переменные 181, 212, 216,220
Эконометрика 7-8, 10, 13-15 Эконометрические модели: этапы построения 24-25
Элементы временного ряда: случайная составляющая 19, 225, 239-240, 263-264 тенденция (трендовая составляющая) 19, 225, 231, 234-235, 239-240, 263-264 циклические колебания (сезонная составляющая) 19, 225, 231, 239-240, 263-264
Эндогенные переменные 212, 181 Эффективность оценок параметров регрессии 156
ОГЛАВЛЕНИЕ
Предисловие.................................................
Глава 1. Определение эконометрики.......................... 7
1.1. Предмет эконометрики.......................... 7
1.2. Особенности эконометрического метода......... 14
1.3. Измерения в экономике ....................... 25
Контрольные вопросы............................. 32
Гл а в а 2. Парная регрессия и корреляция в эконометрических исследованиях............................ .........
2.1. Спецификация модели ........................
2.2. Линейная регрессия и корреляция: смысл и оценка параметров.......................................
2.3. Оценка существенности параметров линейной регрес-
сии и корреляции.............................
2.4. Интервалы прогноза по линейному уравнению регрес-
сии ..........................................
2.5. Нелинейная регрессия........................
2.6. Корреляция для нелинейной регрессии.........
2.7. Средняя ошибка аппроксимации ...............
34
34
41
48
57
62
801
87
88
Контрольные вощ
сы...........................
Гл а в а 3. Множественная регрессия и корреляция........ 90
3.1. Спецификация модели ...................... 90
3.2. Отбор факторов при построении множественной регрессии ........................................ 92
3.3. Выбор формы уравнения регрессии........... 100
3.4. Оценка параметров уравнения множественной регрессии............................................. 105
3.5. Частные уравнения регрессии............... 109
3.6. Множественная корреляция ................. 112
3.7. Частная корреляция........................ 121
3.8. Оценка надежности результатов множественной регрессии и корреляции............................. 129
3.9. Фиктивные переменные во множественной регрессии 141
3.10. Предпосылки метода наименьших квадратов... 155
3.11. Обобщенный метод наименьших квадратов .... 169
Контрольные вопросы............................. 175
Гл а в а 4. Системы эконометрических уравнений ......... 177
4.1 Общее понятие о системах уравнений, используемых в эконометрике ................................... 177
4.2. Структурная и приведенная формы модели ... 181
341
4.3. Проблема идентификации.......................... 185
4.4. Оценивание параметров структурной модели..... 193
4.5. Применение систем эконометрических уравнений ... 204
4.6. Путевой анализ ................................. 213
Контрольные вопросы.................................. 225
Глава 5. Моделирование одномерных временных рядов . 225
5.1. Основные элементы временного ряда.......... 225
5.2. Автокорреляция уровней временного ряда и выявление его структуры .............................. 227
5.3. Моделирование тенденции временного ряда.... 234
5.4. Моделирование сезонных и циклических колебаний . 239
5.5. Моделирование тенденции временного ряда при наличии структурных изменений .................... 255
Контрольные вопросы............................ 262
6. Изучение взаимосвязей по временным рядам ..
6.1. Специфика статистической оценки взаимосвязи двух временных рядов.................................
6.2. Методы исключения тенденции ................
6.3. Автокорреляция в остатках. Критерий Дарбина — Уотсона ............................................
6.4. Оценивание параметров уравнения регрессии при наличии автокорреляции в остатках................
6.5. Коинтеграция временных рядов ...............
Контрольные вопросы...............................
263
263
265
272
278
282
289
Глава 7. Динамические эконометрические модели ............... 290
7.1. Общая характеристика моделей с распределенным лагом и моделей авторегрессии......................... 290
7.2. Интерпретация параметров моделей с распределенным лагом......................................... 292
7.3. Изучение структуры лага и выбор вида модели с распределенным лагом.................................. 297
7.3.1. Лаги Алмон.................................. 298
7.3.2. Метод Койка ................................ 305
7.3.3. Метод главных компонент...................... 310
7.4. Модели адаптивных ожиданий и неполной корректировки .............................................. 319
7.5. Оценка параметров моделей авторегрессии ....... 325
7.6. Новые направления в анализе многомерных временных рядов.......................................... 330
Контрольные вопросы ................................ 335
Литература .................................................. 337
Предметный указатель.....................................
338
Эконометрика: Учебник/Под ред. И. И. Елисеевой. - М.: Э40 Финансы и статистика, 2003. - 344 с.; ил. ' /
ISBN 5-279-01955-0
Рассмотрены краткая история возникновения эконометрики, ее задачи и методы. Излагаются условия и методы построения эконометрических моделей по пространственным данным и временнйм рядам. Описываются структурные модели, включая путевой анализ, а также автокорреляционная функция и методы выявления структуры временного ряда. При изучении взаимосвязей между временными рядами уделяется внимание теории коинтеграции, моделям с распределенным лагом (метод Койка) и моделям авторегрессии, включая VAR-модели.
Для преподавателей, аспирантов, студентов экономических вузов, слушателей институтов повышения квалификации.
1602090000 - 125 010(01) - 2003
243 - 2002
УДК 330.43(075.8)
ББК 65в6я73
J г
Учебное издание
Елисеева Ирина Ильинична
Курышева Светлана Владимировна
Костеева Татьяна Владимировна и др.
ЭКОНОМЕТРИКА
Заведующая редакцией JLА. Табакова Редактор Е.В. Стадниченко Художественный редактор Ю.И. Артюхов Технический редактор ТС. Маринина Корректоры Т.М. Колпакова, Г. В. Хлопцева Обложка художника Е.К. Самойлова
ИБ№ 3852
Подписано в печать 23.04.2003. Формат 60x88 !/ 6. Гарнитура «Таймс». Печать офсетная.
Усл. п. л. 21,07. Уч.-изд. л. 19,62. Тираж 5000 экз.
Заказ 1525. «С» 125
Издательство «Финансы и статистика» 101000, Москва, ул. Покровка, 7 Телефон (095) 925-35-02, факс (095) 925-09-57 E-mail: mail@finstat.ru httpy7www.finstat.ru
ГУП «Великолукская городская типография» Комитета по средствам массовой информации Псковской области,
182100, Великие Луки, ул. Полиграфистов, 78/12
Телефакс: (811-53) 3-62-95 E-mail: VTL@MART.RU
ЭКОНОМЕТРИКА
Учебник для вузов под ред. чл.^кор. РАН И.И.Елисеевой
►
i
1
5
Рассматриваются краткая история возникновения эконометрики, ее задачи и методы, условия построения экономических моделей по пространственным данным и временным рядам.
Излагается метод фиктивных переменных прослеживается его аналогия с дисперсионным анализом. Описываются структурные модели, включая путевой анализ.
Анализируются
автокорреляционная функция и структура временного ряда. При рассмотрении взаимосвязей между временными рядами уделяется внимание теории коинтеграции, моделям с распределенным лагом (метод Койка) и моделям авторегрессии, Включая VAR-модели.
Учебник Предназначен для студентов экономических вузов и ориентирован на прикладные задачи моделирования и прогнозирования I в экономике.
Учебник сопровождается
В ЭК Gt Учебн практикумом по эконометрике, Подготовленным Т0ми же авторами.
I .
I
1
♦