АКАДЕМИЯ НАУК СССР
Научно-популярная серия
В.П.ЛИШЕВСКИЙ
ПОПУЛЯРНАЯ
МЕХАНИКА
В
ИЗДАТЕЛЬСТВО «НАУКА»
Москва 1979
Л 67 Лишевский В. П. Популярная механика.— М.: Наука,
1979.— 104 с.
Книга посвящена теоретической механике. В ней
на отдельных примерах в популярной и занимательной
форме рассматриваются основные законы этой науки.
Читатель познакомится с действием и разложением
сил, трением, кинематикой, динамикой точки и си-
стемы, другими разделами механики. Книга дает перво-
начальное представление о механике — теоретической
базе всей техники.
17.3.2
Ответственный редактор
член-корреспондент АН УССР
А. Н. БОГОЛЮБОВ
© Издательство «Наука», 1979 г.
„ 20302—015
Л 054(021-79 3~78 НП 1703020000
Предисловие
С механическими явлениями мы встречаемся на каждом
шагу, но каждый ли сможет объяснить, почему вытекаю-
щая из крана струя воды разделяется в дальнейшем на
отдельные капли; почему ни один трос или веревку нельзя
натянуть строго горизонтально; почему, если двигаться
по лодке в одном направлении, она перемещается в про-
тивоположную сторону, и т. д.
Механика — один из интереснейших разделов физики.
Ученые-механики изучают проблемы управления механиз-
мами и космическими полетами, рассчитывают устойчи-
вость различных инженерных сооружений, составляют
уравнения взаимодействия воздушных течений с поверх-
ностью океана, занимаются теорией плазмы и разрежен-
ного газа. К ним обращаются за помощью медики и биоло-
ги, автомобилисты и железнодорожники, нефтяники и ра-
диотехники. Механика — одна из старейших и в то же
время вечно молодая наука. Она зародилась в глубокой
древности, но по-прежнему с успехом служит людям
и в наш век — век научно-технической революции.
По характеру решаемых задач механика делится на
три части: кинематику, которая изучает движение с гео-
метрической точки зрения, динамику, рассматривающую
движение тел под действием сил, и статику — учение о
равновесии.
Предлагаемая книга посвящена так называемой по-
вседневной механике. Как, располагая только часами, оп-
ределить глубину колодца; чем порочен способ путешест-
вия к Луне, предложенный Сирано де Бержераком —
героем комедии Ростана; почему парусный корабль мо-
жет плыть против ветра; как лучше тормозить: юзом или
чтобы колеса немного проворачивались?
На эти и многие другие вопросы читатель найдет ответ
в данной работе, разумеется, не всегда исчерпывающий.
3
Год рождения теоретической механики как науки точно
указать невозможно. Уже в Древней Греции и в Древнем
Египте мы встречаем довольно сложные механизмы и ма-
шины, сооружение которых было бы невозможно без эле-
ментарных механических знаний. Это говорит о том, что
подобно большинству современных научных дисциплин,
механика ведет свое начало от исследований античных
ученых.
«Отцом механики» принято считать Архимеда (287—
212 гг. до н. э.). Он первым открыл законы, лежащие в ос-
нове работы простых машин. В частности, он нашел законы
действия рычага, который употреблялся при построй-
ках за много тысяч лет до Архимеда.
Гениальный сиракузский математик и механик был
не только великим ученым, но и блестящим инженером.
Описание некоторых военных машин Архимеда мы нахо-
дим у Полибия (201—120 гг. до н. э.) в его «Всеобщей ис-
тории».
«Архимед,—пишет Полибий,—соорудил машины при-
способительно к метанию снарядов на любое расстоя-
ние. Так, если неприятель подплывал издали, Архимед
поражал его из дальнобойных камнеметальниц тяжелыми
снарядами или стрелами... Если же снаряды начинали
летать поверх неприятеля, Архимед употреблял в дело
меньшие машины, каждый раз сообразуясь с расстоянием,
и наводил на римлян такой ужас, что они никак не ре-
шались идти на приступ или приблизиться к городу на
судах.
...Некоторые машины метали камни весом не менее
10 талантов (1 талант ~ 26 кг), другие выбрасывали гру-
ды свинца. Каждый раз, как только приближались сам-
бики (штурмовые машины для подъема воинов на стены
крепости), жерла архимедовых машин отклонялись вме-
сте с подставкою вправо или влево, смотря по надобности,
и при помощи задвижки метали камни в неприятельское
сооружение».
Действие других оборонительных машин Архимеда
Полибий описывает так: «...с машины спускалась прикреп-
ленная к цепи железная лапа. Управляющий жерлом
машины захватывал этой лапой нос корабля в каком-
нибудь месте и потом внутри стены опускал нижний конец
машины. Когда нос судна был таким образом поднят и суд-
но поставлено на корму, основание машины утвержда-
4
лось неподвижно, а лапа и цепь при помощи веревки отде-
лялись от машины. Вследствие этого некоторые суда ло-
жились на бок, другие опрокидывались, третьи — в
большинстве — от падения на них передних частей со зна-
чительной высоты погружались в море, наполнялись водой
и приходили в расстройство».
То же самое рассказывает Плутарх (около 46—126 гг.):
«Тяжелые когти и клювы захватывали суда, подымали
их в воздух и затем кормою вниз погружали в воду.
Иногда корабль перевертывался и, кружась в воздухе,
ударялся о скалы. Под конец страх римлян сделался
так велик, что, как только увидят конец веревки или
бревно над стенами, тотчас обратятся в бегство, крича:
,,Архимед направляет на нас еще какую-то машину!”».
Древним было известно многое в механике, например
то, что в пустоте все тела падают с одинаковой скоростью.
Тит Лукреций Кар (I в. до н. э.) в своей замечательной
поэме «О природе вещей» (примерно 60 г. до н. э.) пишет:
Всякое тело, что падает вниз через воду и воздух,
Собственной тяжестью это падение всегда ускоряет,
Жидкой воды вещество, как и воздух весьма легковесный,
В равном размере падения тел всех замедлить не могут,
А уступают скорее дорогу телам тяжелейшим.
Но пустота никакому пределу, нигде, ни откуда
Не в состоянии вовсе оказывать сопротивления,
Так как всему поддаваться должна уж по самой природе;
Вследствие этого вещи, которые разнятся весом,
Падать должны одинаково все в пустоте неподвижной.
Этот вывод, как мы знаем, впоследствии эксперимен-
тально подтвердил Галилей.
В средние века развитие механики, как и всех наук,
замедлилось. Прогресс строительного дела, военного ис-
кусства, торговли, начавшийся в эпоху Возрождения, по-
требовал дальнейшего развития механики, и ученые, как
всегда, ставят свои знания на службу обществу. Вот только
один пример. Когда враги угрожают Венеции — родине
великого итальянского ученого Никколо Тарталья
(1499—1557), он пишет правителям города: «Я не могу
молчать! Я знаю, что дальность полета стрелы наилучшая
при 45°».
Очень многое для развития механики сделал Галилео
Галилей. Он родился 15 февраля 1564 г. в Пизе. Его
5
отец — известный музыкант и историк музыки — оказал
большое влияние на формирование способностей маль-
чика. В 1581 г. Галилей поступил в Пизанский универси-
тет, в котором стал изучать медицину, но, увлекшись
механикой, ушел из университета и вернулся во Флорен-
цию, где в то время жила семья. Четыре года Галилей
посвятил изучению математики. Он читал Евклида, Ар-
химеда, Витрувия и других греческих и римских авто-
ров, написал первые научные работы, которые принесли
ему известность. В 1589 г. Галилей получил кафедру
математики в Пизе, а в 1592 г.— в Падуе. Здесь он про-
жил 18 лет, и это был наиболее плодотворный период в
творчестве Галилея. С 1610 г. ученый живет во Флорен-
ции. В этом городе в 1632 г. выходит из печати знамени-
тый «Диалог о двух главнейших системах мира», который
подвергается запрещению, а сам автор в феврале 1633 г.
предстает перед судом инквизиции. После отречения от
учения Коперника Галилей последние 9 лет жизни на-
ходится под домашним арестом на своей вилле Арчетри
под Флоренцией. Ему запрещено писать, видеться с
друзьями. Второй основной труд Галилея «Беседы и ма-
тематические доказательства, касающиеся двух новых
отраслей науки» выходит в 1638 г. в Голландии. Умер
Галилей 8 января 1642 г.
Основные результаты получены Галилеем в механике
и астрономии. Он первый выдвинул идею об относитель-
ности движения, сформулировал законы свободного па-
дения тел и движения их по наклонной плоскости, пока-
зал, что период колебаний маятника не зависит от массы
и амплитуды, открыл спутники Юпитера, фазы Венеры,
вращение Солнца и пятна на нем.
Историю любой науки и биографии ученых, внесших
свой вклад в развитие данной области знания, целесооб-
разно рассказывать одновременно с изложением основ-
ного материала. Именно так сделано в этой книге. Сей-
час мы перейдем к непосредственному знакомству с пред-
метом, а экскурсы в историю механики будем совершать
по мере надобности.
Эта книга — не учебник по механике. В ней расска-
зано о некоторых понятиях механики и показано как
можно решать различные механические задачи.
Для тех, кто захочет продолжить знакомство с меха-
никой, в конце книги рекомендована литература.
КИНЕМАТИКА
КИНЕМАТИКА ТОЧКИ
Под движением в механике понимают любое перемеще-
ние тела в пространстве с течением времени. Механичес-
кое движение всегда относительно: мы следим за пере-
мещением данного тела, отмечая его положение относите-
льно некоторого другого тела, которое в этом случае
носит название тела отсчета.
Движение в кинематике изучается только с геометри-
ческой точки зрения: нас интересует, как, с какой скоро-
стью, с каким ускорением движется данный материальный
объект, и не интересуют те физические причины, которые
вызвали, поддерживают или изменяют это движение.
Кинематика делится на два больших отдела — кине-
матику точки и кинематику твердого тела. Так как любое
материальное тело можно рассматривать как совокуп-
ность некоторых малых частиц — материальных точек,
то естественно, что изучению движения тела предшест-
вует изучение движения материальной точки.
Линия, которую описывает в пространстве материаль-
ная точка при своем движении, называется траекторией.
В зависимости от вида траектории движение может быть
прямолинейным или криволинейным. Здесь мы рассмот-
рим только прямолинейное движение материальной точ-
ки, и сделать это лучше всего можно на примерах.
Рассказывают, что одному абитуриенту на приемных
экзаменах в вуз был задан следующий вопрос: «У вас есть
часы и амперметр. Не могли бы вы при помощи этих двух
физических приборов определить глубину ущелья?»
Поступающий легко справился бы с поставленным воп-
росом, если бы знал решение другой известной задачи.
Камень падает в шахту без начальной скорости. Звук
от удара камня о дно шахты слышен через 5 секунд после
момента начала его падения. Найдите глубину шахты>
принимая скорость звука равной 330 м/с,
7
Давайте решим эту задачу. Пусть — время падения
камня, t2 — время распространения звука, h — глуби-
на шахты, с = 330 м/с — скорость звука и т = 5 с.
Камень падает в шахту равноускоренно. Для такого
вида движения справедлива формула
S = vQt + at2/2,
где S — путь, v — скорость, а — ускорение, t —
время. Так как начальная скорость камня равна нулю,
а ускорение равно ускорению свободного падения тел,
то мы можем написать, что h = gt\/2.
Звук распространяется равномерно. Для равномерного
движения справедлива формула S = vt, поэтому, с другой
стороны, мы можем написать, что h = ct2.
Получаем систему двух уравнений с двумя неизвест-
ными: + t2 = т и gt^/2 = ct2,
из которой находим или t2, а затем — h. Глубина шахты
примерно равна 100 м.
Зная решение этой задачи, абитуриент должен был от-
ветить на заданный ему вопрос так: «Бросим амперметр
в ущелье и измерим время от начала падения до того мо-
мента, когда придет звук от удара амперметра о дно
ущелья. Затем составим и решим систему уравнений».
Рассказанный эпизод с абитуриентом — это видимо
анекдот, но вы действительно всегда можете определить
глубину колодца, шахты, ущелья, если у вас есть камень,
часы с секундной стрелкой, карандаш и бумага.
Капли воды вытекают из отверстия вертикальной тру-
бочки одна после другой с интервалом в 0,1 секунды и па-
дают вниз с ускорением свободного падения тел g — 9,8 м!&.
Какое расстояние будет между первой и второй каплями
через секунду после момента истечения первой капли?
Путь, проходимый каплей в свободном падении, вы-
числяется по формуле S = gt2/2 (v0 = 0). За одну секунду
капля пройдет путь S± = 4,9-12 м, а за 0,9 секунды—S2 =
= 4,9 • 0,92 м, т. е. расстояние между первой и второй кап-
лями через секунду после момента истечения первой кап-
ли будет равно — S2 = 4,9- (I2 — 0,92) = 0,935 м.
Теперь давайте вычислим, какое расстояние было ме-
жду каплями в самый первый момент времени, т. е. когда
первая капля уже падала 0,1 секунды, а вторая капля
только начала выходить из трубочки. Понятно, что рас-
стояние между первой и второй каплями в этом случае бу-
8
дет равно тому расстоянию, которое успеет пройти первая
капля за 0,1 секунды, т. е. S = 4,9-0,12 м = 4,9 см. Мы
видим, что если вначале расстояние между каплями было
примерно 5 см, то через секунду оно в 19 раз больше.
Этим объясняется одно явление, которое мы неодно-
кратно наблюдаем в повседневной жизни. Если вода выте-
кает из крана небольшой струей, то вблизи крана она пред-
ставляет собой одно целое, тогда как в раковину уже па-
дают отдельные капли. Происходит это потому, что, номере
движения частиц жидкости вниз, расстояние между ними
увеличивается. Соответственно струя становится все бо-
лее тонкой, и силы поверхностного натяжения разбивают
ее на отдельные капли.
Можно ли по стуку колес определить скорость поезда?
Да, можно. Для этого надо подсчитать количество ударов
колес на стыках рельсов за 45 секунд. Оно равно величине
скорости поезда в километрах в час.
Дело в том, что обычная длина рельсов 12,5 метра.
Если за 45 секунд вы услышали п стуков, значит, за это
время поезд прошел расстояние 12,5 п метров. А за час
он пройдет Збвв. -12,5п = 1000 п метров, или п километров.
На некоторых железнодорожных магистралях уложе-
ны рельсы длиной 25 метров. Такие участки пути легко
распознаются по редким ударам колес на стыках. В этом
случае, чтобы узнать скорость поезда, нужно число уда-
ров за 45 секунд умножить на 2.
Как быстро идет поезд, можно узнать еще при помощи
телеграфных столбов. Среднее расстояние между ними
50 метров. Заметьте время, которое понадобится, чтобы
в поле зрения окна вагона один столб сменил другой.
v = l/t, где I — расстояние между столбами, a t —
время, за которое поезд «пробежал» от одного столба до
другого. Если прошло п секунд, то v = 50/лг м/с;
л лп-ч л л /оялл	50«10“3*3600
так как 1 м = 10 3 км, а 1 с = 1/3600 ч, то v =-----=
П
= 151 Кмч. Пусть п = 3 с, тогда v = 60 км/ч.
Способ определения скорости поезда по телеграфным
столбам, о котором только что было рассказано, весьма
приближенный, так как расстояние между столбами не
всегда точно 50 м. Оно зависит от рельефа местности, кли-
матических условий и многих других причин. Точным
9
и всегда неизменным остается расстояние между кило-
метровыми столбами. Если это расстояние поезд «пробе-
гает» за п секунд, то скорость поезда находится по фор-
3600 км
муле v =	.
Отвесно падающий дождь оставляет на боковых
стеклах автомобиля, движущегося по горизонтальной до-
роге со скоростью 72 км/ч. полосы, наклоненные к верти-
кали под углом 40°. Давайте по этим данным вычислим
скорость падения дождевых капель.
Движение одной и той же материальной точки можно
одновременно рассматривать относительно разных тел
отсчета, которые и сами могут двигаться друг относитель-
но друга. Пусть нам известна скорость точки относитель-
но какого-либо тела отсчета y0TH (относительная скорость)
и скорость 17Пер места нахождения этой точки в теле от-
счета относительно другого, которое мы принимаем за не-
подвижное (переносная скорость). Тогда найти скорость
материальной точки относительно неподвижного тела от-
счета очень просто. Для этого нужно геометрически сло-
жить относительную и переносную скорости.
Скажем, вы сбегаете вниз по эскалатору метро, дви-
жущемуся тоже вниз. Тогда ваша скорость уабС относи-
тельно неподвижных стенок туннеля складывается из
относительной скорости уотн (скорости перемещения от-
носительно движущегося эскалатора) и переносной скоро-
сти уПер (скорости перемещения эскалатора). Если бы вы
просто стояли на эскалаторе, то он переносил бы вас на
себе вниз и ваша абсолютная скорость равнялась бы ско-
рости эскалатора. Но вы еще сами спускаетесь по лест-
нице, поэтому ваша абсолютная скорость увеличивается.
В этом случае она равна сумме двух скоростей: относитель-
ной и переносной.
Аналогично скорость капли дождя относительно земли
складывается из двух скоростей: из относительной скоро-
сти движения капли по стеклу движущегося автомобиля
и переносной, которая равна скорости автомобиля. Рис. 1
помогает вычислить скорость падения дождевых капель:
у = упер ctg 40° = 20 м/с 1,192 = 23,8 м/с.
Допустим, что вам надо переправиться на противопо-
ложный берег реки с сильным течением. Понятно, что
если вы будете плыть перпендикулярно берегам, то лод-
ку снесет и вы пристанете к берегу много ниже по тече-
10
нию. Чтобы попасть в точку, находящуюся перед вами,
надо грести против течения под некоторым углом к нему.
Как находится этот угол, покажем, решая конкретную
задачу.
Берега реки параллельны. Лодка вышла из точки А
(рис. 2) и, держа курс перпендикулярно к берегам, достиг-
ла противоположного берега через t± = 10 мин после от-
правления. При этом она попала в точку С, лежащую на
I = 120 м ниже точки А по течению реки.
Рис. 1. Капли дождя, перемеща-
ющиеся по боковому стеклу
движущегося автомобиля, ос-
тавляют косые следы
Чтобы попасть из точки А в точку В, лежащую на
прямой АВ, перпендикулярной к берегам, лодке надо дер-
жать курс под некоторым углом к прямой АВ и против
течения. В этом случае лодка достигнет противополож-
ного берега через t2 = 12,5 мин. Определите ширину реки
d, относительную скорость v1 лодки по отношению к
воде и скорость v2 течения реки.
Так как мы знаем, что за 10 мин лодку сносит вниз по
течению реки на 120 м, то можем определить скорость те-
чения реки: у2 = 120/10 = 12 м/мин. Кроме того, заме-
тим, что ширина реки АВ равняется относительной ско-
Рис. 2. При переправе через реку лодку сносит течением
11
рости умноженной на время необходимое для пере-
правы в первом случае, т. е. d =
Теперь рассмотрим второй случай. Итак, чтобы попасть
в точку В, надо грести, держа направление на некоторую
точку!) (рис. 3). Строим треугольник сложения скоростей:
v — ^отн + упер, где рпер — это р2« Если умножить все
скорости на время переправы во втором случае, то полу-
чится прямоугольный треугольник ABD, у которого сторо-
на BD известна (BD = v2t2 = 12-12,5 = 150 м), а сторо-
ны АВ и AD выражаются через относительную скорость
Рис. 3. Чтобы переправиться
перпендикулярно к берегам, на-
до грести против течения под
некоторым углом
р1. Записав для треугольника ABD теорему Пифагора,
найдем скорость лодки по отношению к воде:
№ -	= BD*.
Отсюда найдем, что = 20 м/мин. Теперь определим ши-
рину реки: d = 200 м.
Угол а, под которым надо грести, чтобы попасть в точ-
ку В, можно вычислить разными способами. Например,
так: cos а =	= туг == 0,8 и, следовательно,
а ж 37°. Заметим, что скорость лодки относительно бере-
га в первом и во втором случаях разная.
ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛА
Кинематика делится на два больших раздела — кинема-
тику точки и кинематику твердого тела. Чем принципиаль-
но кинематика тела отличается от кинематики точки?
Знать движение точки — это значит знать по какой траек-
тории и с какой скоростью в каждый момент времени дви-
жется данная точка. Знать движение тела — это значит
знать, по какой траектории и с какой скоростью движется
12
каждая точка тела. А так как тело состоит из бесчисленного
множества точек, то на первый взгляд задача усложняется
в бесконечное число раз. Но это не так.
Твердое тело (т. е. такое тело, расстояния между точ-
ками которого не меняются ни при каких условиях) мо-
жет двигаться по-разному. Простейший вид движения те-
ла — поступательное. Так называется движение, при ко-
тором любая прямая, жестко связанная с телом, во все
время движения остается параллельной самой себе.
Примеры поступательного движения привести нетруд-
но. Так движутся рама и педали велосипеда, кузов авто-
мобиля на горизонтальной дороге, вагоны поезда, кабины
аттракциона «колесо обозрения» и т. д.
При поступательном движении все точки тела описы-
вают одинаковые траектории и в каждый момент времени
имеют одинаковые скорости. Следовательно, если мы
знаем, как движется одна точка тела, то мы знаем, как
движутся все точки этого тела. Таким образом, кинема-
тика поступательного движения тела просто сводится к ки-
нематике точки. Поэтому при решении задач на кинематику
точки и кинематику поступательного движения тела ис-
пользуются одни и те же формулы, методы, приемы и т. п.
При определении поступательного движения очень
важны слова «любая прямая». Представьте себе вращаю-
щийся вал и на нем мелом нарисована прямая, параллель-
ная оси вала. Во время движения прямая остается па-
раллельной самой себе, но здесь мы имеем дело с враща-
тельным движением, а не с поступательным.
ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ
Вращение — тоже распространенный вид механического
движения. Вращаются пропеллеры самолетов и гребные
винты судов, лопасти гидротурбин и роторы электродви-
гателей, диски телефонов и антенны радиолокаторов. По
круговым траекториям движутся протоны в синхрофазо-
троне, кордовые модели, люди на карусели. Вращаются
стрелки часов, колеса автомобилей и т. п.
Как изучают вращательное движение в кинематике?
Пусть некоторое тело вращается вокруг неподвижной
оси. Проведем через эту ось две плоскости, одну из кото-
рых закрепим неподвижно, а другую жестко свяжем с те-
13
лом. Двугранный угол между этими двумя плоскостями
называется углом поворота и обозначается греческой бук-
вой ср (рис. 4). Когда тело вращается, угол поворота ме-
няется. Уравнение ф = / (£), показывающее, как угол
поворота меняется с течением времени, называется урав-
нением вращательного движения.
Помимо угла поворота, вращательное движение ха-
рактеризуется еще двумя величинами: угловой скоростью
Рис. 4. Вращение тела вокруг
о и угловым ускорением е. При
равномерном вращении угло-
вая скорость показывает, на
какой угол изменяется величи-
на ф в единицу времени. В об-
щем случае угловая скорость
приближенно равна отношению
Дф к Д£, где Дф — угол пово-
рота тела за весьма малый про-
межуток времени Д^ Угло-
вое ускорение — это скорость
изменения угловой скорости.
Чтобы решать задачи на вра-
щательное движение, надо знать
ряд формул. Часть из них легко
неподвижной оси	запомнить при помощи анало-
гин между прямолинейным и
вращательным движениями. Эта аналогия заключается в
следующем.
Основные характеристики прямолинейного движения—
путь S, скорость и, ускорение а и время t. При вра-
щении им соответствуют угол поворота ф, угловая скорость
о, угловое ускорение 8 и время t. Пусть нам нужно напи-
сать уравнение равномерного вращательного движения.
Вспоминаем формулу S = vt, справедливую для прямо-
линейного равномерного движения, и по аналогии пишем
уравнение равномерного вращательного движения ф =
•-= (dt. Для равномерно ускоренного (или замедленного)
вращения справедливы формулы: угол поворота ф =
=	± &Ч/2 и угловая скорость со = ю0 =Ь st (по ана-
логии cS = vQt ± сЛ*Ч2 и р = р0 ± at). В этих формулах
знак «плюс» относится к случаю равномерно ускоренного
движения, знак «минус» — равномерно замедленного.
Давайте решим задачу.
Ротор электромотора начинает вращаться из состоя-
14
ния покоя равноускоренно и за первые 5 секунд делает
25 оборотов. Вычислите угловую скорость ротора в конце
пятой секунды.
Если вращающееся тело сделало один оборот вокруг
оси, то угол поворота равен 2л (в радианах). Если тело
сделало N оборотов, то угол поворота в N раз больше.
Таким образом, ср = 2 л N, где N — число оборотов.
В задаче сказано, что ротор вращается равноускорен-
но, следовательно, для решения можно применить фор-
мулы равноускоренного вращательного движения:
ф = to$t Н-8^/2 и 0) = (00 + et
Здесь ф = 2л-25 = 50 л, соо “ 0- Из уравнений находим,
что 8 =	= 4л Дг и to = 20 л — .
си	с
Решим еще одну задачу.
Пропеллер самолета вращается с угловой скоростью,
соответствующей 1200 об/мин. В некоторый момент вре-
мени выключают мотор. Сделав 80 оборотов, пропеллер
останавливается. Сколько времени прошло с момента вы-
ключения мотора до остановки, если считать вращение
пропеллера равнозамедленным?
Угловая скорость — это угол поворота в секунду. Ес-
ли известно число оборотов в секунду п, то угловая ско-
рость вычисляется по формуле со = 2лп. Если п дано
в оборотах в минуту, то угловая скорость в 60 раз мень-
2лп т 1	,,,
ше: to = —gg- = -эд- —. (Угловая скорость выражается в ра-
дианах в секунду. Наименование угловой скорости 1/с.)
Для решения задачи используем формулы равномер-
но замедленного вращательного движения. После под-
становки в них данных задачи получим: 160л = 40л£—
и 0 = 40л — st, где t выражено в секундах, а 8 — в 1/с2.
Решая уравнения, найдем, что t — 8 с.
Угловые характеристики ф, о, 8 тела, вращающегося
вокруг неподвижной оси, позволяют вычислить линей-
ную скорость и линейное ускорение любой точки вращаю-
щегося тела, нужно только знать расстояние R от этой
точки до оси вращения, иначе говоря, надо знать ра-
диус той окружности, которую описывает точка при
своем движении.
Линейные характеристики вычисляются по следую-
щим формулам: линейная скорость v = toR, касатель-
15
ное ускорение, направленное по касательной к траекто-
рии, ах = &R, нормальное (центростремительное) уско-
рение ап = o*R, полное линейное ускорение
а = ах + а* = R ]Ле2 + со4.
Формулы показывают, что все линейные характери-
стики прямо пропорционально зависят от расстояния R.
Чем точка расположена дальше от оси вращения, тему
нее линейная скорость и линейное ускорение больше;
чем точка ближе лежит к оси
Рпс. 5. Чем точка дальше рас-
положена от оси вращения, тем
ее линейная скорость больше
вращения, тем все линейные
характеристики меньше.
Покажем на примерах, как
этой зависимостью линейных
характеристик от расстояния
пользуются при решении задач.
Колесо вращается вокруг
неподвижной оси. Точка А, ле-
жащая на его ободе, движется
со скоростью 40 см/с, а некото-
рая точка В, расположенная на
одном радиусе с точкой А, дви-
жется со скоростью 10 см/с.
Расстояние АВ = 15 см. Определите угловую скорость
и диаметр колеса.
Если мы нарисуем в некотором масштабе скорость точ-
ки Л и скорость точки В (рис. 5), то концы изображаю-
щих их векторов будут лежать на одной прямой, так как
скорость v прямо пропорционально зависит от радиу-
са R. Из подобия треугольников следует, что : v2 =
R : (R — 15). Отсюда находим, что R = 20 см, следователь-
но, диаметр колеса d = 40 см. Угловая скорость колеса
со = vr/R = 2 1/с. И еще одна задача.
Угол наклона полного ускорения точки обода махового
колеса к радиусу равен 60°. Касательное ускорение точки
в данный момент времени ах = )Лз м/с*. Какое нормаль-
ное ускорение в этот же момент времени имеет точка,
отстоящая от оси вращения на расстоянии г = 0,5 м?
Радиус махового колеса R = 1 м.
Полное ускорение — это геометрическая сумма ка-
сательного и нормального ускорений. Пользуясь рис. 6,
можно написать, что ап = ах ctg 60° = 1 м/с2. Такое
16
Рис. 6. Касательное, нормаль-
ное и полное ускорения точки,
лежащей на ободе вращающего-
ся колеса
нормальное ускорение имеют все точки, расположенные
на ободе колеса. Точка, лежащая в два раза ближе к оси
вращения (г = R : 2), имеет в два раза меньшее нормаль-
ное ускорение. Следовательно, искомое ускорение равно
0,5 м/с2.
В заключение вычислим средние угловые скорости стре-
лок часов. Пренебрегая фактически прерывистым движе-
нием стрелок, будем считать, что они вращаются равно-
мерно. Тогда для них справедлива формула ср = (at.
Секундная стрелка часов дела-
ет один оборот (360° или 2 л
радиан) за 60 секунд. Следова-
тельно, ее угловая скорость
равна 2л/60 = 0,1047 1/с. Со-
ответственно угловая скорость
минутной стрелки часов равна
2 л/60 • 60 = 0,001725 1/с, а
часовой —	2л/12-60-60 =
= 0,0001455 Ш
Так как наша планета дела-
ет один оборот вокруг своей
оси за 24часа, угловая скорость
Земли в два раза меньше
угловой скорости часовой стрелки. Несмотря на не-
большую угловую скорость Земли (0,0000727 1/с), каждая
точка на ее экваторе движется с линейной скоростью
v = о/? = 0,0000727 1/с-6370000 м = 473 м/с. Как ви-
дите, скорость значительная. Мы не ощущаем ее лишь по-
тому, что атмосфера вращается вместе с Землей с такой
же скоростью. В противном случае на нашей планете всег-
да свирепствовал бы ураганный ветер и жить на ней было
бы практически невозможно (вспомните фантастический
рассказ Г. Уэллса «Чудотворец»).
ПЛОСКОЕ ДВИЖЕНИЕ
«Паровоз мчался на всех парах... Поршни делали 120 хо-
дов в минуту... Бешено вращались колеса...» Эта послед-
няя фраза верна только в том случае, если рассматривать
движение колес относительно паровоза. Как уже было
сказано, под вращательным движением понимают враще-
ние тела вокруг неподвижной оси. Для стороннего наб-
людателя оси колес паровоза не неподвижны, а соверша-
ют поступательное движение вперед с большой скоростью.
17
11
Рис. 7. Перемещение плоской фигуры в ее плоскости можно рассматривать
как совокупность двух перемещений: поступательного (отрезок перехо-
дит » Л2В') и вращательного (поворот вокруг точки Л2)
Колеса участвуют как бы в двух движениях: поступатель-
ном и вращательном. Такой вид движения в механике на-
зывается плоскопараллельным, или плоским.
Плоскопараллельное — это такое движение твердого
тела, при котором все точки тела описывают траектории,
лежащие в плоскостях, параллельных некоторой непо-
движной плоскости. Положите книгу на стол и перемещай-
те ее произвольным образом по поверхности стола. Это
простейший пример плоскопараллельного движения: все
точки тела (книги) движутся параллельно некоторой не-
подвижной плоскости (крышке стола). Таким же обра-
зом (плоскопараллельно) движутся колеса вагонов на
прямолинейных участках пути, линейка эллипсографа —
прибора, который служит для вычерчивания эллипсов,
шатун паровой машины, детали многих других механиз-
мов. Плоское движение так же часто встречается в тех-
нике, как поступательное и вращательное. Существуют
два метода изучения плоскопараллельного движения. Один
из них рассматривает плоское движение как совокупность
двух движений: поступательного и вращательного. Дру-
гой — как вращение в каждый данный момент времени
относительно некоторых неподвижных точек.
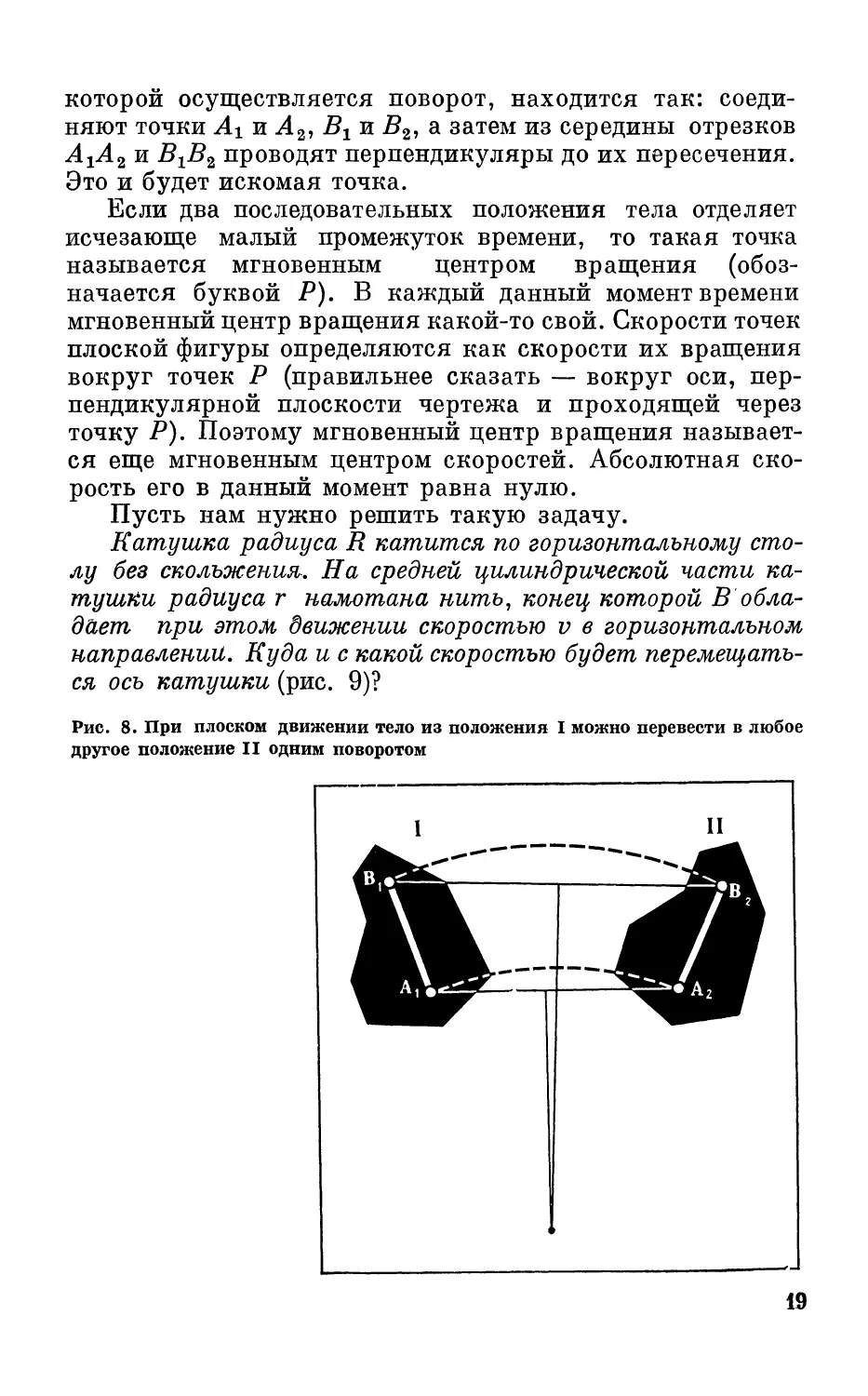
Сказанное поясняют рис. 7 и 8. Тело, движущееся
плоскопараллельно, из одного положения в другое мож-
но перевести или при помощи двух перемещений: посту-
пательного и вращательного (рис. 7), или при помощи од-
ного вращения (рис. 8). В этом случае точка, относительно
18
которой осуществляется поворот, находится так: соеди-
няют точки Ai и Л2, В1 и В2, а затем из середины отрезков
и BrB2 проводят перпендикуляры до их пересечения.
Это и будет искомая точка.
Если два последовательных положения тела отделяет
исчезающе малый промежуток времени, то такая точка
называется мгновенным центром вращения (обоз-
начается буквой Р), В каждый данный момент времени
мгновенный центр вращения какой-то свой. Скорости точек
плоской фигуры определяются как скорости их вращения
вокруг точек Р (правильнее сказать — вокруг оси, пер-
пендикулярной плоскости чертежа и проходящей через
точку Р), Поэтому мгновенный центр вращения называет-
ся еще мгновенным центром скоростей. Абсолютная ско-
рость его в данный момент равна нулю.
Пусть нам нужно решить такую задачу.
Катушка радиуса R катится по горизонтальному сто-
лу без скольжения. На средней цилиндрической части ка-
тушки радиуса г намотана нить, конец которой В обла-
дает при этом движении скоростью v в горизонтальном
направлении. Куда и с какой скоростью будет перемещать-
ся ось катушки (рис. 9)?
Рис. 8. При плоском движении тело из положения I можно перевести в любое
другое положение II одним поворотом
19
Рис. 9. Движение катушки ниток
Катушка движется плоскопараллельно: все точки ее
перемещаются параллельно плоскости, перпендикуляр-
ной крышке стола. Известно, что при плоском движении
распределение скоростей таково, как будто плоская фигу-
ра вращается вокруг некоторой неподвижной точки —
мгновенного центра вращения. Катушка катится по
неподвижному столу. Следовательно, в каждый момент
времени та точка катушки, которая касается неподвиж-
ного стола, тоже имеет скорость, равную нулю. Таким
образом, мы нашли мгновенный центр вращения (Р)
для катушки.
Рис. 10. Распределение скоростей точек колеса, катящегося по неподвижному
рельсу
20
После того как точка Р найдена, определить скорость
любой точки тела просто. Она такова, как будто бы тело
вращается вокруг неподвижной оси, проходящей через
точку Р, Известно, что чем точка тела расположена дальше
от оси вращения, тем ее линейная скорость больше, и
наоборот. Пользуясь рис. 9, мы можем написать уравне-
ние Vq : v = R : (7? — г), откуда найдется величина
скорости оси катушки v0 = vR/(R г). Рис. 9 показы-
вает, что катушка движется в ту же сторону, в которую
тянут нитку.
Это легко проверить на опыте. Поставьте на стол ка-
тушку ниток так же, как на рис. 9, и потяните за нитку
вправо. Вы увидите, как катушка тоже пока-
тится вправо, наматывая на себя нить. Только тянуть
нитку нужно не особенно сильно, чтобы не было проскаль-
зывания между катушкой и поверхностью стола.
Поезд мчится на всех парах вперед. Есть ли у него
такие точки, которые в данный момент времени неподвиж-
ны? Да, есть. Это точки касания колес с неподвижными
рельсами. И, наконец, последняя задача.
Колесо радиуса R катится без скольжения по прямо-
линейному участку пути; скорость центра его постоянна
и равна vQ. Найти скорости концов вертикального и гори-
зонтального диаметров колеса: точек Мг, М2, М3 и М^.
Когда колесо катится без скольжения по неподвиж-
ному рельсу, мгновенный центр скоростей в каждый дан-
ный момент времени совпадает с точкой соприкосно-
вения колеса с рельсом, т. е. мгновенный центр скоро-
стей совпадает с точкой поэтому скорость точки Мг
равна нулю.
Точка М3 расположена в два раза дальше от точки Mi,
чем точка О, поэтому ее скорость в два раза больше ско-
рости центра колеса и равна 2z?0 (рис. 10).
Скорости точек М2 и М4 равны по величине (так как
они расположены на одинаковом расстоянии от точки Р)
и направлены по касательным к окружностям, которые
эти точки описывали бы во вращательном движении во-
круг оси, проходящей через неподвижную точку Р, т. е.
р2 и р4 перпендикулярны к радиусам РМ2 и РМ±. Поль-
зуясь тем, что линейные скорости во вращательном дви-
жении прямо пропорционально зависят от расстояния до
оси вращения, мы можем написать, что р2 : vQ = R ]Л2 : R.
Отсюда р2 = Ро/2.
ДИНАМИКА
ЗАКОНЫ НЬЮТОНА
В каждой науке есть самые общие, самые главные, самые
важные законы. В механике — это законы Ньютона.
Великий английский ученый Исаак Ньютон родился
4 января 1643 г. в местечке Вулсторп. Первоначальное
образование он получил в семье, а в двенадцатилетнем
возрасте его отдали в частный пансион города Гран-
тема.
Первое время в школе Ньютон учился посредственно.
Однажды Исаака обидел лучший ученик класса. Малень-
кий Ньютон долго думал, как отомстить обидчику, кото-
рый был физически сильнее его, и решил отобрать у свое-
го врага лавры первого ученика. Сделать это, имея спо-
собности Ньютона, было нетрудно. Вскоре Исаака ста-
вили в пример товарищам по классу. Главным же резуль-
татом вышеописанного эпизода было то, что Ньютон при-
обрел вкус к учебе, к процессу получения знаний.
Когда Ньютону было 16 лет, его мать, желавшая ви-
деть своего сына фермером, забрала Исаака из школы.
Но юношу не интересовало сельское хозяйство. По на-
стоянию дяди, обратившего внимание на исключительное
стремление своего племянника к учебе, Исаака отправили
в Тринити-колледж — один из колледжей Кембриджского
университета.
Научный гений Ньютона проявился очень рано. Еще
будучи студентом, Исаак получил формулу, выражающую
степень суммы двух слагаемых, которая теперь во всех
учебниках называется формулой бинома Ньютона, вплот-
ную подошел к установлению закона всемирного тяго-
тения. В 1665 г. 22-летнему Исааку присвоили первую
ученую степень бакалавра, а в 1668 г.— звание магистра
наук.
Ньютон многое сделал для развития математики, аст-
рономии, механики, физики. Во всех этих областях чело-
22
веЧеского знания ему принадлежат основополагающие
работы. Одновременно с другими учеными он разрабатывал
основы дифференциального и интегрального исчислений;
благодаря закону всемирного тяготения, открытому Нью-
тоном, астрономы получили возможность рассчитывать
движение небесных тел; классическую механику назы-
вают механикой Ньютона, потому что он первым сформу-
лировал общие законы движения тел и ввел в механику
такие понятия, как «масса» и «сила».
Величайшая слава пришла к Ньютону еще при жизни.
Весь мир преклонялся перед его гением. Он был избран
почетным членом многих научных обществ и академий.
Ему было пожаловано рыцарское звание. Последние
24 года своей жизни Ньютон бессменно возглавлял Лон-
донское королевское общество (английскую Академию
наук). Несмотря на оказываемые ему почести, Ньютон
оставался очень скромным человеком. «Не знаю, чем я
кажусь миру, но сам себе я представляюсь ребенком,
играющим на морском берегу и развлекающимся тем,
что отыскиваю более гладкие камешки или более краси-
вую раковину, чем обыкновенно, в то время как великий
океан истины расстилается передо мной совершенно не-
разгаданный». Эти слова принадлежат одному из вели-
чайших ученых всех времен и народов Исааку Нью-
тону.
Умер Ньютон 31 марта 1727 г. На его могильном кам-
не выбита надпись: «Здесь покоится сэр Исаак Ньютон,
который... впервые объяснил... движения и формы пла-
нет, пути комет, приливы и отливы океана. Он первый ис-
следовал разнообразие световых лучей и проистекающие
отсюда особенности цветов... Пусть смертные радуются
тому, что в их среде жило такое украшение рода челове-
ческого».
Основную задачу механики Ньютон определяет сле-
дующим образом: «Из рассмотрения совершающихся яв-
лений движения найти силы природы и по найденным си-
лам доказать и объяснить прочие явления», т. е., иначе
говоря, Ньютон считал, что перед механиками стоят сле-
дующие задачи: 1) даны силы; спрашивается, как будет
двигаться тело под действием этих сил; 2) дано движение;
надо определить, какие силы вызвали (породили) данное
движение. В решении главной задачи механики Ньюто-
ну помогали сформулированные им три закона.
23
«Всякое тело упорствует в своем состоянии покоя или
равномерного и прямолинейного движения, пока и по-
скольку оно не принуждается приложенными силами из-
менить свое состояние».
«Изменение количества движения пропорционально
приложенной движущей силе и происходит по направ-
лению прямой, по которой эта сила действует».
«Действию всегда есть равное и противоположное про-
тиводействие, иначе — взаимодействия двух тел друг на
друга всегда между собой равны и направлены в противо-
положные стороны».
Древние не знали принципа инерции. Они считали,
что тело может двигаться только под действием силы. Это
заблуждение объяснялось тем, что ученые древности не
принимали в расчет сил сопротивления, которые в обы-
денной жизни останавливают любое тело, движущееся
по инерции. Чтобы тело двигалось равномерно, на него
должна действовать постоянная по величине сила — так
считали философы античного мира. (Как мы знаем, под
действием постоянной силы в отсутствие других сил тело
движется не равномерно, а равномерно ускоренно.)
Вот, например, как Аристотель (384—322 гг. до н. э.)—-
этот величайший мыслитель древности — объяснял, по-
чему движется брошенный камень. Когда летит камень,
говорил Аристотель, за ним образуется пустота. При-
рода не терпит пустоты. Воздух устремляется в об-
разовавшееся пустое пространство и подталкивает
камень.
Первые высказывания о наличии у тел инерции мы
находим у Леонардо да Винчи (1452—1519), Галилея
(1564—1642) и Декарта (1596—1650). Наиболее полно
принцип инерции сформулировал Галилей в своей книге,
которая вышла в 1632 г. и носила принятое по тем време-
нам такое длинное название: «Диалог Галилео Галилея
академии Линчеи экстраординарного математика Пизан-
ского университета и первого философа и математика
светлейшего Великого Герцога Тосканского, в котором
в беседе в течение четырех дней велось обсуждение по по-
воду двух основных систем мира Птолемеевой и Копер-
никовой, предлагались неокончательные философские
и физические аргументы как с одной, так и с другой
стороны». Вот то место «Диалога», где речь идет об
инерции.
24
«Салъвиати. Скажите, что будет с телом на плоскости,
которая ни вниз не опускается, ни вверх не поднимается?
Симпличио. Если нет никакого склона, то нет и естест-
венного стремления к движению, а если нет подъема, то
нет противодействия движению. Значит, тело безразлич-
но должно быть и к тому, чтобы приходить в движение,
и к тому, чтобы противиться движению. Оно должно, ка-
жется мне, по природе оставаться в покое.
Салъвиати, Таково и мое мнение, предполагая, что по-
ложено оно тихо, без толчка. А если дать ему толчок в ту
или другую сторону — что будет?
Симпличио. Не вижу никакого основания ни к уско-
рению, ни к замедлению, так как нет ни спуска, ни
подъема.
Салъвиати. Хорошо. Но если нет основания к замед-
лению, то тем менее основания к полной остановке.
Сколько же времени будет тело продолжать двигаться?
Симпличио. Сколько хватит плоскости, не представляю-
щей ни спусков, ни подъема.
Салъвиати. Если, значит, длина ее будет бесконечна,
то и движение будет без границ, то есть вечно. Не так ли?
Симпличио. Так, по крайней мере, мне кажется, пред-
полагая, что тело из прочного материала».
Свой первый закон — закон инерции — Ньютон пояс-
няет следующими словами: «Брошенное тело продолжает
удерживать свое движение, поскольку его не замедляет
сопротивление воздуха и поскольку сила тяжести не
побуждает это тело вниз. Волчок, коего части, вследствие
взаимного сцепления, отвлекают друг друга от прямоли-
нейного движения, не перестает вращаться (равномерно),
поскольку это вращение не замедляется сопротивлением
воздуха. Большие же массы планет и комет, встречая
меньшее сопротивление в свободном пространстве, сохра-
няют свое как поступательное, так и вращательное дви-
жение в продолжении гораздо большего времени».
Можно указать очень много примеров движения по
инерции. Так движется автомобиль с выключенным мото-
ром, планер в горизонтальном полете, снаряд в горизон-
тальном направлении после вылета из ствола орудия.
Благодаря инерции и тяготению не прекращается движе-
ние нашей Земли и планет вокруг Солнца. Инерцию ис-
пользуют, формируя железнодорожные составы на сорти-
ровочных горках; она позволяет экономить бензин при
25
движении автомобиля накатом; в технике широко приме-
няются различные инерционные механизмы. Но не надо
думать, что инерция — всегда лишь благо. Часто она не
только не нужна, но и вредна. Например, из-за инерции
нельзя мгновенно остановить любой транспорт (иногда
для остановки тяжелогруженого железнодорожного со-
става нужны километры пути).
С инерцией как с физическим явлением мы встречаемся
постоянно. В подтверждение этого еще несколько при-
меров.
Вы прыгаете с обрыва. Каждый знает, что лучше при-
землиться на кучу песка или мягкий дерн, чем на камни.
Песок плавно погасит движение тела, чего не сделают
камни.
Как известно, кузов автомобиля связан с колесами при
помощи рессор или амортизаторов. Такое нежесткое креп-
ление кузова уменьшает его перемещения в вертикальной
плоскости (вследствие инерции), когда колеса наезжают
на неровности дороги.
Через некоторое время после раскрытия парашюта
сила притяжения парашютиста к Земле уравновешива-
ется силой сопротивления воздуха, и далее парашютист
движется по инерции равномерно и прямолинейно.
Теперь о втором законе. Ньютон не дает его математи-
ческой записи, а ограничивается пояснением: «Если какая-
нибудь сила производит некоторое количество движения,
то двойная сила произведет двойное, тройная — тройное,
будут ли они приложены разом все вместе или же после-
довательно и постепенно. Это количество движения, кото-
рое всегда происходит по тому же направлению, как и
производящая его сила, если тело находилось уже в дви-
жении, при совпадении направлений прилагается к коли-
честву движения тела, бывшему ранее, при противопо-
ложности — вычитается, при наклонности — прилага-
ется наклонно и соединяется с бывшим ранее сообразно
величине и направлению каждого из них».
В настоящее время второй закон Ньютона принято
записывать так: та = F, где т — масса тела, а — уско-
рение, сообщаемое силой, a F — сила, действующая на
тело.
Третьему закону Ньютон дает следующее объяснение:
«Если что-либо давит на что-либо другое или тянет его,
то оно само этим последним давится или тянется. Если кто
36
нажимает пальцем на камень, то и палец его также на-
жимается камнем. Если лошадь тащит камень, привя-
занный к канату, то и обратно (если можно так выра-
зиться) она с равным усилием оттягивается к камню, ибо
натянутый канат своей упругостью производит одинаковое
усилие на лошадь в сторону камня и на камень в сторону
лошади, и насколько этот канат препятствует движению
лошади вперед, настолько же он побуждает движение вперед
камня. Если какое-нибудь тело, ударившись в другое те-
ло, изменяет своей силой его количество движения на
сколько-нибудь, то оно претерпит от силы второго тела
в своем собственном количестве движения то же самое
изменение, но обратно направленное, ибо давления этих
тел друг на друга постоянно равны. От таких взаимодей-
ствий всегда происходят равные изменения не скоростей,
а количеств движения, предполагая, конечно, что тела
никаким другим усилиям не подвергаются. Изменения
скоростей, происходящие также в противоположные сто-
роны, будут обратно пропорциональны массам тел, ибо
количества движения получают равные изменения».
Третий закон Ньютона говорит о том, что сила —
понятие дуальное. Такие понятия нам известны из лите-
ратуры. Мы произносим одно слово: дуэль, переписка,
дружба, беседа, любовь, а предполагаем участие двух
людей. Так и при слове сила в сознании должно сразу же
возникать представление о двух силах. Действию всегда
есть равное и противоположно направленное противодей-
ствие. Сила никогда не бывает одна, а только в союзе
с другой силой. Раз есть действие, то есть и противодей-
ствие, т. е. силы всегда выступают «двойками».
На трех законах Ньютона основывается вся динамика.
ОСНОВНЫЕ ТЕОРЕМЫ
ДИНАМИКИ ТОЧКИ
Движение материальной точки можно описывать двояким
образом: пользуясь количеством движения — произве-
дением массы точки на ее скорость (ти) — и пользуясь
кинетической энергией — полупроизведением массы точ-
ки на квадрат ее скорости (V2 та^2)- Первая величина —
векторная (в результате произведения скалярной вели-
чины — массы на векторную — скорость получается век-
торная величина), вторая величина — скалярная (квэд-
27
рат вектора скорости, т. е. произведение вектора самого
на себя есть скалярная величина).
Действие постоянной по величине силы также можно
описать двумя величинами: или импульсом силы — произ-
ведением силы на время ее действия (Ft), или работой —
произведением абсолютного значения силы на путь и на
косинус угла между направлением силы и направлением
прямолинейного движения (FS cos а). Импульс — век-
торная величина, работа — скалярная.
Основные теоремы динамики точки — это не формаль-
ные математические записи, а физические законы, которые
устанавливают соотношения между импульсом тела и
импульсом силы и между работой силы и кинетической
энергией тела.
«Теорема количества движения» ти — mvQ = Ft фор-
мулируется так: изменение количества движения мате-
риальной точки за некоторый промежуток времени рав-
няется импульсу силы, действующей на точку, за тот же
промежуток времени. (Теорема количества движения —
это второй закон Ньютона, записанный и сформулирован-
ный несколько иначе.)
Математическая запись «теоремы кинетической энер-
гии» такова:
mvo т. а
-у- — -5- — FS cos а.
£ z
Или словами: изменение кинетической энергии мате-
риальной точки на некотором участке пути равняется
работе всех сил, действующих на точку, на том же участке
пути.
Давайте посмотрим, как при помощи этих теорем ре-
шаются различные механические задачи.
Для определения массы груженого железнодорожного
состава между тепловозом и вагонами установили дина-
мометр. Среднее показание динамометра за 2 мин 1000 кН.
За это же время состав набрал скорость 57,64 км!ч (вна-
чале он стоял на месте). Коэффициент трения равен
0,02. Требуется найти массу состава.
Воспользуемся «теоремой количества движения». Эта
теорема векторная. Условимся векторам, направленным
по движению поезда, приписывать знак «плюс», в проти-
воположную сторону — знак «минус». Тогда теорема об
изменении количества движения в применении к движу-
28
Щбмуся железнодорожному составу запишется так:
mv = (F —kmg) t.
Здесь F = 1000 кН — сила, с которой тепловоз тянет
состав; т — масса состава, a kmg — сила трения, равная
коэффициенту трения, умноженному на силу нормального
давления (она равна весу состава). Перед силой трения
стоит знак «минус», так как она направлена в сторону,
противоположную движению поезда. В записи теоремы
отсутствует член mvQl так как состав начинает свое дви-
жение из состояния покоя (р0 = 0).
Из записанной теоремы найдем т = Ft/(у + kgt).
Для того чтобы вычислить массу железнодорожного
состава, необходимо подставить в полученную формулу
данные в условии задачи величины, выразив их в одной
системе единиц — СИ: F = 1 000 000 Н,
57,6-1000 м ла м ,
v =	oann— “ = 16 — , t = 120 с.
3600 с с
В результате получим
т =
1 000 000-120
16 + 0,02-9,8-120
3 000 000 кг.
Эта задача показывает, что взвесить железнодорожный
состав можно, не загоняя вагоны на весы.
Автомобиль движется по горизонтальному участку
пути со скоростью 12 км/ч. В некоторый момент времени
шофер начинает тормозить. Через 6 секунд после начала
торможения автомобиль останавливается Каков коэф-
фициент трения колес заторможенного автомобиля о
дорогу?
В условии задачи дано время, поэтому естественно для
решения задачи применить теорему об изменении количе-
ства движения. Конечная скорость автомобиля равна
нулю, а в начале торможения его скорость была 72 км/ч =
— 20 м/с. Автомобиль останавливает сила трения, которая
равна коэффициенту трения, умноженному на силу нор-
мального давления: F = kN. Так как автомобиль движет-
ся по горизонтальной дороге, сила нормального давления
равна весу автомобиля (N = Р), следовательно,
F = kP — kmg.
Теорема об изменении количества движения в приме-
нении к тормозящему автомобилю запишется так:
29
О — mvQ = —kmg t. (Знак минус перед импульсом по-
явился потому, что сила трения направлена в сторону,
противоположную начальной скорости.) Отсюда
* = 5 = тег=0’34-
Материальная точка движется под действием неко*
торой силы с постоянной скоростью vQ по горизонтальной
плоскости с коэффициентом трения к0. Затем точка
переходит на участок плоскости с коэффициентом трения
к (к Ао)« Какой путь пройдет точка до остановки?
Найдем вначале силу F, действующую на точку. Так
как на участке плоскости с коэффициентом трения /г0
т-очка движется с постоянной скоростью р0, то, следова-
тельно, на этом участке сила F уравновешивается силой
трения: F = kQP.
Нам надо найти путь, пройденный точкой до остановки,
поэтому для решения задачи применим теорему об измене-
нии кинетической энергии материальной точки, которую за-
mv
пишем для второго участка пути: 0-— k^ngS-kingS.
(Конечная скорость точки равна нулю. Перед выражением
kmgS стоит знак минус, так как угол между силой трения
и направлением движения равен 180°, a cos 180° = —1.)
Таким образом, до остановки точка прошла путь
2g(k-k0) 
Как видите, решать задачи при помощи основных тео-
рем динамики точки несложно. Надо только помнить, что
если в задаче дано время (или его надо найти), для реше-
ния применяется теорема об изменении количества дви-
жения. Если ищется путь (или он дан в условии зада-
чи), для нахождения ответа используется теорема об из-
менении кинетической энергии.
РАБОТА И МОЩНОСТЬ
Лестницы двух одинаковых эскалаторов движутся вверх.
На одной лестнице человек стоит неподвижно, а на дру-
гой — поднимается. Одинаковую ли работу совершают
двигатели эскалаторов?
30
Понятно, что движущийся человек раньше достигнет
верха. Следовательно, путь, пройденный эскалатором за
время подъема человека, меньше, чем в том случае, когда
человек неподвижен. А значит, двигатель эскалатора,
на котором находится движущийся человек, произведет
меньшую работу (часть работы совершит сам человек).
Часто для решения задач на работу достаточно вот
таких простых рассуждений. Для подсчета величины
работы обычно пользуются формулой А = FS cos а,
т. е. работа равна произведению абсолютного значения
силы на путь и на косинус угла между силой и переме-
щением. Такое выражение стоит в правой части теоремы
об изменении кинетической энергии материальной точки.
Поэтому для вычисления работы еще применяют формулу
А = ти*/2 — mv*/2. В это выражение можно подставлять
значения скоростей, не обращая внимание на то, как они
направлены, так как кинетическая энергия — скалярная
величина.
Решим несколько задач на вычисление работы.
Материальная точка массой 3 кг двигалась по гори-
зонтальной прямой налево со скоростью = 5 м/с. В не-
который момент времени к точке приложили постоянную
по величине силу, направленную вправо. Сила действовала
30 секунд. После окончания ее действия оказалось, что
теперь точка движется направо со скоростью v2 = 55 м/с.
Найдите величину силы и совершенную ею работу.
Вначале найдем силу, для чего применим «теорему
количества движения». «Теорема количества движения»
представляется векторным равенством, поэтому в форму-
ле величинам, направленным вправо, приписываем знак
«плюс», влево — знак «минус». Получаем ти2 — т
= Ft- Отсюда
р = ^(^2+^1) = 3»60 = g н
Теперь вычислим совершенную силой работу
л mv* mvf	«I (г^+ »1)(ra-r1)
Л ~ 2	2 “	2	—	2	—
3-60-50 /r-АА TT
-----x---= 4500 Дж.
Следующая задача такая. Главную часть прибора
для испытания материалов на прочность ударом состав-
ляет тяжелая стальная отливка М (рис. 11), прикреплен-
ная к стержню, который может вращаться вокруг не-
подвижной горизонтальной оси О. Пренебрегая массой
стержня, рассматриваем отливку М как материальную
точку, для которой расстояние ОМ — 0,981 м. Опреде-
лите скорость отливки в наинизшем положении В, если
отливка падает из наивысшего положения А с ничтожно
малой начальной скоростью
(р0 = 0). Трением в оси О
пренебречь.
Для решения задачи приме-
ним теорему об изменении кине-
тической энергии материальной
точки. В правой части формулы
будет стоять работа силы тяже-
сти. Эта работа всегда вычисля-
ется по формуле А = mg (Ло — Л),
где т — масса тела, Ло — высо-
та начального положения точки,
отсчитываемого от какого-то
выбранного заранее уровня,
h — конечная высота. В данной
Рис. 11. прибор для испытания задаче /z0 h АВ 2 ОМ.
материалов на прочность ударом Следовательно, mv^/2=mg-AB.
Отсюда v —^fAg-OM = 6,2 м/с.
Решим еще две задачи такого рода. Панель дома,
изображенная на рис. 12, имеет массу 1000 кг. АВ = CD =
— 8 м, AD = ВС = 6 м. Определите работу, которую
надо затратить на опрокидывание панели вращением
вокруг ребра D. Считаем, что центр тяжести панели
совпадает с центром прямоугольника, ограничивающего
панель.
Центр тяжести панели расположен в точке пересечения
диагоналей АС и BD. При вращении панели вокруг
ребра D центр тяжести О перемещается по дуге окружно-
сти ОО Чтобы опрокинуть панель, надо переместить
центр тяжести из положения О в точку О1. Далее панель
будет двигаться сама. Следовательно, работа, затрачивае-
мая на опрокидывание панели, равна работе, которую
необходимо совершить, чтобы поднять 1000 кг на высоту
OrE. OJD = OD = -J/33 + 42 = 5 м, OJE = OrD-ED =
= 5—4 — 1 м, А = mg-O^E = 9800 Дж.
32
При ходьбе на лыжах на дистанцию S = 20 км по го-
ризонтальному пути центр тяжести лыжника совершал
гармонические колебания с амплитудой а = 8 см и с перио-
дом Т = 4 с. Масса лыжника т = 80 кг, а коэффициент
трения лыж о снег к = 0,05. Определите работу лыжника
на марше, если всю дистанцию он прошел за 1,5 часа.
Примечание. Считать, что работа торможения при
опускании центра тяжести лыжника составляет 0,4 рабо-
ты при подъеме центра тяжести на ту же высоту.
Лыжник затрачивает работу, преодолевая трение, а
также поднимая и опуская свой центр тяжести. Работа
силы трения = kmgS.
Теперь вычислим работу, которую совершает лыжник,
поднимая и опуская центр тяжести. Так как лыжник про-
ходит всю дистанцию за полтора часа ил;и за 5400 с, то
за это время его центр тяжести поднимается и опускается
п = 5400 : 4 = 1350 раз. Следовательно, вторая состав-
ная часть всей работы А2 = 1,4-2 amgn. Окончательно:
А = Аг + А2 = mg (kS + 2,8 an) = 10210816 Дж.
Теперь — о мощности. Мощность — это отношение
работы ко времени, в течение которого она совершена,
т. е. мощность — работа в единицу времени.
Рис. 12. Опрокидывание панели дома вращением вокруг ребра D
2 В. П. Лишевский
33
Представьте себе, что на пятый этаж дома надо поднять
мешок с песком. Выполняя эту работу, человек, согнув-
шись под тяжестью ноши, взберется по лестнице за не-
сколько минут. Ту же работу при помощи лифта можно
сделать за несколько секунд, а муравей, таская по одной
песчинке, проканителится несколько лет. Во всех трех
случаях одна и та же работа будет выполнена в разное
время. Разделив работу на время, которое было затрачено
на ее выполнение, мы получим мощность человека, лифта,
муравья. Понятно, что вычисленные значения мощностей
будут значительно отличаться друг от друга.
Вы, наверное, замечали, что, когда автомобиль въез-
жает на гору, его скорость уменьшается. Но задумывались
ли вы над тем, почему так происходит? Дело в том, что
мощность мотора постоянна. Для того чтобы втянуть авто-
мобиль на гору, нужна большая сила тяги, чем при дви-
жении по ровной дороге. Увеличить же силу тяги при
постоянной мощности можно, только уменьшив скорость
движения.
Обычно работу измеряют в джоулях. Работа в 1 Дж —
это работа, которую надо затратить, чтобы поднять гирьку
в 1,02 кг на высоту 1 м.
За единицу измерения мощности принят ватт — ра-
бота в 1 Дж, выполняемая в течение 1 секунды. Мощность
двигателей автомобилей и тракторов обычно выражают
в лошадиных силах (л.с.): 1 л.с.= 736 Вт.
Средняя мощность человека 0,1 л.с. С такой мощностью
человек может работать длительное время. Небольшое
время человек может развивать значительные мощности.
Например, мощность бегуна на короткие дистанции до-
стигает 7—8 л.с.
Решим две задачи.
Для того, чтобы поднять 5000 м3 воды на высоту 3 м,
поставлен насос с двигателем в 2 л. с. Сколько времени по-
требуется для выполнения этой работы, если коэффициент
полезного действия насоса 0,8?
Надо поднять 5000 м3 воды или 5 000 000 кг на высоту
3 м, то есть совершить работу 15 000 000 кгм. В одну секун-
ду насос может поднять 0,8-2-75 = 120 кгм/с. Следователь-
но, вся работа может быть выполнена за время: 15 000 :
: 120 =125 000 секунд или 34 часа 43 минуты и 20 секунд.
В Древнем Риме жернова мельниц приводились во вра-
щение при помощи лошадей (рис. 13). Определите силу
34
Рис. 13. Мельница в Древнем Риме
тяги лошади, принимая ее мощность равной 1 л. с. Ло-
шадь равномерно движется по окружности радиуса 3 м,
делая 4 об/мин.
Как'уже было сказано, мощность — это работа в еди-
ницу времени, т. е. N = A/t. Так как Л = FS, a S = vt9
то N = Fv. Если сила выражена в ньютонах, а скорость —
в метрах в секунду, то мощность в ваттах находится do
формуле N = Fv. Отсюда F = N/v. N нам известна.
Она равна 1 л.с., или 736 Вт.
Линейная скорость v = <о7?, где о — угловая скорость,
a R — радиус. Зная число п оборотов в минуту, угловую
у	2пп 1
скорость можно вычислить по формуле со =-gQ-— , где
п —число оборотов, совершенных за минуту. Таким об-
разом, v == соR = 4^- R. Следовательно,
ои
р =	= 30Д6 ~ 600 н.
mR 3,14-4-3
2*
35
ПРИНЦИП Д’АЛАМБЕРА
Задачи по динамике решать сложно. Каждая динамическая
задача требует индивидуального подхода, применения
для ее решения какого-то своего определенного приема.
Но есть один метод, который может быть использован
для решения большого класса задач динамики материаль-
ной точки. Он получил название принципа Д’Аламбера —
по имени впервые сформулировавшего его великого фран-
цузского ученого-просветителя Жана Лерона Д’Аламбера
(1717-1783).
Д’Аламбер внес заметный вклад в многие отрасли зна-
ния. Он доказал существование воздушных приливов
(наподобие океанских), обосновал теорию возмущения
планет и объяснил предварение равнодействий и нута-
цию. Основные результаты получены Д’Аламбером в
математике и механике. Он дал метод решения дифферен-
циального уравнения второго порядка с частными произ-
водными, выражающего поперечные колебания струны
(волнового уравнения). Эта работа вместе с последующи-
ми исследованиями Л. Эйлера и Д. Бернулли легла в
основу математической физики. Для решения некоторых
дифференциальных уравнений Д’Аламбер впервые при-
менил функции комплексного переменного. Его имя но-
сят широко применяющиеся в алгебре признак сходимо-
сти рядов и принцип решения механических задач, о
котором речь пойдет ниже.
Д’Аламбер был широко образованным человеком,
ученым-энциклопедистом. Он был избран во все суще-
ствовавшие тогда Академии наук (в Петербургскую —
в 1764 г.). Свой знаменитый принцип, позволяющий сво-
дить динамические задачи к статическим, Д’Аламбер
сформулировал в «Трактате о динамике» (1743 г.), когда
ему было всего 26 лет.
Математически принцип Д’Аламбера легко вывести
из второго закона Ньютона: F = та. Если перенести
член та в левую часть уравнения, то данное выражение
можно переписать в виде F + (—та) = 0. Это и есть
принцип Д’Аламбера. Величина, стоящая в скобках,
условно называется силой инерции. Поэтому принцип
Д’Аламбера читается так: при движении материальной
точки действующие на нее силы и сила инерции взаим-
но уравновешиваются.
3G
Принцип Д’Аламбера говорит о том, что добавление
Силы инерции к силам, действующим на движущуюся
точку, дает взаимно уравновешивающуюся систему сил,
т. е. такое добавление позволяет рассматривать динами-
ческую задачу как статическую. А тогда для ее решения
можно воспользоваться общим методом решения задач
на равновесие.
Давайте посмотрим на примерах, как принцип Д’Алам-
бера помогает решать динамические задачи.
Парашютист массой 70 кг выпрыгнул из самолета и,
пролетев 100 м, раскрыл парашют. Байдите равнодей-
ствующую сил натяжения строп, на которых человек под-
вешен к парашюту, если в течение первых 5с с момента рас-
крытия парашюта, при постоянной силе сопротивления
движению, скорость парашютиста уменьшилась до 4,3 м/с.
Сопротивлением воздуха движению человека до раскры-
тия парашюта пренебречь.
Найдем вначале, какую вертикальную скорость имел
человек, пролетев 100 м, не раскрывая парашюта. Так как
в задаче сказано, что сопротивлением воздуха движению
человека пренебречь, то эту скорость можно вычислить
по формуле свободного падения тел:	2gh- (Началь-
ная скорость парашютиста по вертикали равна нулю, так
как в первый момент времени скорость человека равна
скорости самолета, который летит горизонтально.)
Итак, = ]Л2-9,8-100 = 44,3 м/с.
Теперь вычислим, с каким ускорением (а точнее, с за-
медлением) движется человек после раскрытия парашюта.
Для расчета ускорения можно воспользоваться формулой
равномерно замедленного движения, так как по усло-
вию задачи сила сопротивления движению постоянна:
,	гц —44,3 — 4,3 м о м
= У1 — at, откуда а =	g---— = 8	.
Какие силы действуют на парашютиста? На него дей-
ствует сила тяжести Р = mg, направленная вертикально
вниз, и равнодействующая сил реакций строп Т, нап-
равленная вверх. Так как мы хотим решить задачу при
помощи принципа Д’Аламбера, надо указать на рисунке
еще силу инерции Q.
Парашютист движется вниз. Но это движение замед-
ленное, т. е. ускорение направлено вверх. Так как
сила инерции направлена в сторону, противоположную
ускорению, то ее следует направить вниз.
37
То есть можно написать, что Т — Р — Q — 0.
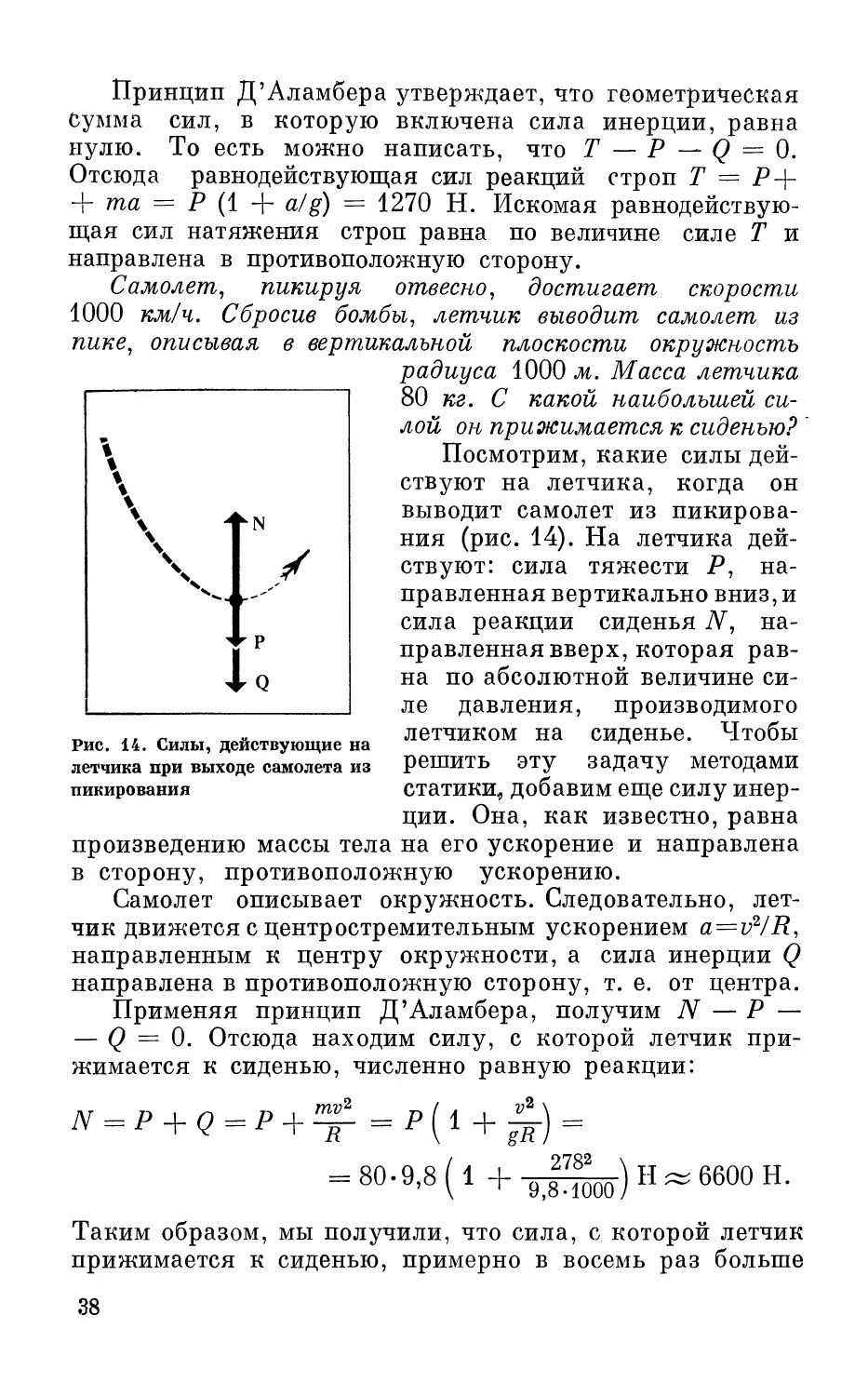
Рис. 14. Силы, действующие на
летчика при выходе самолета из
пикирования
Принцип Д’Аламбера утверждает, что геометрическая
Сумма сил, в которую включена сила инерции, равна
нулю. То есть можно написать, что Т — Р — Q = 0.
Отсюда равнодействующая сил реакций строп Т = Р-\-
4- ma = Р (1 + а/g) = 1270 Н. Искомая равнодействую-
щая сил натяжения строп равна по величине силе Т и
направлена в противоположную сторону.
Самолет, пикируя отвесно, достигает скорости
1000 км/ч. Сбросив бомбы, летчик выводит самолет из
пике, описывая в вертикальной плоскости окружность
радиуса 1000 м. Масса летчика
80 кг. С какой наибольшей си-
лой он прижимается к сиденью?
Посмотрим, какие силы дей-
ствуют на летчика, когда он
выводит самолет из пикирова-
ния (рис. 14). На летчика дей-
ствуют: сила тяжести Р, на-
правленная вертикально вниз, и
сила реакции сиденья N, на-
правленная вверх, которая рав-
на по абсолютной величине си-
ле давления, производимого
летчиком на сиденье. Чтобы
решить эту задачу методами
статики, добавим еще силу инер-
ции. Она, как известно, равна
произведению массы тела на его ускорение и направлена
в сторону, противоположную ускорению.
Самолет описывает окружность. Следовательно, лет-
чик движется с центростремительным ускорением a-=v4R,
направленным к центру окружности, а сила инерции Q
направлена в противоположную сторону, т. е. от центра.
Применяя принцип Д’Аламбера, получим N — Р —
— Q = 0. Отсюда находим силу, с которой летчик при-
жимается к сиденью, численно равную реакции:
N = P + Q = Р + ^=Р(1 + £г) =
= 80'9.ф+ттеР1=<66О0Н-
Таким образом, мы получили, что сила, с которой летчик
прижимается к сиденью, примерно в восемь раз больше
38
его веса на земле (он равен 784 Н), или, как говорят, лет-
чик испытывает восьмикратную перегрузку.
Шарик М, масса которого т, привязан нитью AM к
неподвижной точке А и описывает горизонтальную ок-
ружность с постоянной скоростью (рис. 15). Зная длину
I нити и ее угол с вертикалью а, определите натяжение
нити Т7, скорость шарика v и время t, в течение которого
он описывает полную окружность.
На шарик действуют две силы: сила тяжести Р = mg
и сила Т, численно равная силе натяжения нити. Так как
шарик движется по окружнос-
ти с постоянной скоростью, то
у него есть только нормальное
(центростремительное) ускоре-
ние. Следовательно, сила инер-
ции Q направлена по радиусу
от центра и равна по величине
mv*/R.
Принцип Д’Аламбера утвер-
ждает, что геометрическая сум-
ма всех сил, действующих на
движущуюся точку, включая
силу инерции, равна нулю,
Т. е. равна нулю сумма Рис. Конический маятник
проекций всех этих сил на
любое направление.
Спроектируем все силы на оси х и у. Получим
mv*/R — Т sin а = О,
Т cos а — mg = 0.
Из второго уравнения системы можно сразу найти
натяжение нити: Т = mg/cos а.
Теперь из первого уравнения находим скорость шарика
v — sin а gl/zos а .
Так как vt = 2л2?, то, следовательно, t = 2л ]/7 cos a/g.
Камень, находящийся на вершине гладкого полусфери-
ческого купола радиуса R, получает начальную горизон-
тальную скорость vQ (рис. 16). В каком месте камень по-
кинет купол? При каких значениях vQ камень сойдет с ку-
пола в начальный момент? Трением пренебречь.
Когда камень движется по куполу, на него действуют
две силы: сила тяжести Р и нормальная реакция N. Ус-
39
корение точки представляет собой геометрическую сумму
двух составляющих — касательной и нормальной. Соответ-
ственно на рис. 16 изображаем две силы инерции: каса-
тельную Qr и нормальную (?2.
Применяя принцип Д’Аламбера, проектируем все силы
на нормаль п\ Q2 + N — Р cos а = 0.
Когда камень покидает купол, он перестает давить на
него, следовательно, в той точке, в которой камень по-
Рис. 16. Шарик, движущийся по
сферическому куполу
кидает купол, обращается в нуль нормальная реакция N.
Таким образом, угол ос, при котором камень сходит с ку-
пола, находится из уравнения mv*/R — Р cos а = 0.
В этом уравнении v — скорость камня в той точке,
где камень покидает купол. Величину этой скорости
можно вычислить, воспользовавшись теоремой об изме-
нении кинетической энергии материальной точки:
ти*/2 — mv%/2 = mg (R — R cos a).
Отсюда находим значение скорости v и подставляем его в
уравнение mvNR—mg cos a = 0. Получаем, что cos a=2/3+
+ v*/?gR.
Последняя формула позволяет определить, в какой
точке камень покидает купол при заданной начальной
скорости. Эта же формула позволяет вычислить, с какой
начальной скоростью был пущен камень, если известно,
что он сошел с купола в данной точке. Таким образом,
чтобы камень покидал купол сразу же (а =0), необходи-
мо выполнение условия:
2/3 + v^ZgR = 1 (cos 0 = 1), т. е. vQ = УgR.
Разумеется, камень покидает купол и при скорости
v>VgR, так как сила давления N не может быть отри-
цательной.
40
На горизонтальных участках железнодорожного пути
йри повороте наружный рельс возвышают над внутренним,
для того чтобы избежать бокового давления колес на ре-
льсы из-за центробежной силы. На прямолинейных участ-
ках рельсы, естественно, укладываются на одной высоте.
Давайте определим, какова должна быть величина h возвы-
шения наружного рельса над внутренним, для того чтобы
давление движущегося поезда на рельсы было направлено
перпендикулярно к полотну до-
роги. Известно, что радиус за-
кругления 400 м, скорость поез-
да 10 км/ч, расстояние между
рельсами I = 1,6 м.
Нарисуем все силы, дейст-
вующие на поворачивающий
вагон (рис. 17). К нему прило-
жены сила тяжести Р и сила
реакции N. Если приложить
еще центробежную силу Q (си-
лу инерции), тогда геометриче-
ская сумма всех сил будет рав-
на нулю (принципД’Аламбера).
Итак, сумма всех сил, дейст-
вующих на вагон, включая силу
инерции, равна нулю. Спроек-
тируем все силы на горизон-
тальное направление — ось х.
Получим Q — N sin а = 0. Так
величине равна силе давления
D = P/cos а, то, следовательно,
Из треугольника ABC tg а = у-^2 __ д2 ' . Таким образом,
mv2	h
— — ? ур — № • Подставив в эту формулу числовые дан-
ные, найдем, что возвышение рельса в рассматриваемом
случае равно 4,1 см.
При строительстве железной дороги внешний рельс
постепенно возвышают над внутренним — по миллиметру
подъема на каждый погонный метр пути. По техническим
нормам возвышение не должно превышать 12,5 см, а ра-
диус закругления должен быть не менее 600 м. Лишь в слу-
чае сложного рельефа местности, например в горах, ве-
личина радиуса поворота может быть снижена до 300—
200 м. Но это только как исключение.
Рис. 17. Силы, действующие на
поворачивающий вагон
как сила реакции N по
D вагона на рельсы, а
Q — Р tg а.
h
41
ДИНАМИКА СИСТЕМЫ
Как известно, барон Мюнхаузен вытащил себя из болота
за волосы. Другой шутник, герой комедии Э. Ростана
Сирано де Бержерак, утверждал, что добраться до Луны
можно следующим образом:
Лечь на железный лист и сильными рывками
Магнит подбрасывать, он лист железный с вами
Подтянет кверху. Вы опять.
Так до Луны и упражняйтесь!
Почему мы улыбаемся, читая о подвиге барона Мюн-
хаузена или о предложении Сирано де Бержерака?
Да потому, что все это невозможно! А почему невозможно?
На этот вопрос уже, видимо, ответит не каждый. Дело
в том, что авторы этих двух историй грешат против зако-
нов механики, связанных с внутренними силами.
Для одной материальной точки все силы яв-
ляются внешними. В динамике системы (системой назы-
вается совокупность материальных точек или тел, находя-
щихся во взаимодействии между собой) различают две
группы сил: внешние и внутренние. Внешние силы дей-
ствуют на тела системы со стороны других тел, не входя-
щих в данную систему, а внутренние силы — это силы
взаимодействия между телами системы. Они всегда вы-
ступают попарно, равны по величине и направлены
противоположно, поэтому геометрическая сумма всех
внутренних сил системы всегда равна нулю.
Внутренние силы играют в механике роль своеобраз-
ных «регулировщиков»: они как бы запрещают некото-
рые механические процессы и явления и, наоборот, раз-
решают другие.
Наверное, каждый из вас катался на лодке. Замечали
ли вы, что когда движешься по лодке в одну сторону,
лодка отъезжает в противоположную? Это явление объяс-
няется законом движения центра масс системы — точки,
аналогичной центру масс (центру тяжести) твердого тела.
Теорема о движении центра масс системы записыва-
ется так: Мас = R. Здесь М — масса всей системы, то
есть сумма масс всех объектов, образующих данную си-
стему, ас—ускорение центра масс системы, a R—векторная
сумма всех внешних сил, действующих на систему. Закон
движения центра масс системы очень похож на второй закон
42
Ньютона для материальной точки, поэтому теорема
о движении центра масс системы формулируется так:
центр масс системы движется так же, как материаль-
ная точка, в которой сосредоточена масса всей системы,
под действием силы, равной геометрической сумме внеш-
них сил, приложенных к системе. Внутренние силы не
могут изменить движение центра масс системы.
Вернемся теперь к задаче о лодке. В горизонтальном
направлении никакие силы на систему человек—лодка не
действуют, следовательно, центр масс системы в горизон-
тальном направлении двигаться не может. Перемещаясь
по лодке, вы отталкиваетесь ногами от лодки, т. е.
действуете на лодку, а лодка (с такой же по абсолют-
ной величине силой по третьему закону Ньютона) дей-
ствует на вас. Это внутренние силы. Так как они не
могут двигать центр масс системы, то, когда человек идет
по лодке в одну сторону, лодка отъезжает в противопо-
ложную, чтобы их общий центр тящести остался на преж-
нем месте.
Именно потому, что внутренние силы не могут изменить
положение центра масс системы, нельзя вытащить себя
за волосы из болота и путешествовать к Луне, подбрасы-
вая магнит.
По той же причине нельзя двигать лодку, упираясь в
мачту или дуя на парус, как это делает Волк в одной из
серий мультфильма «Ну, погоди!».
Внутренние силы не могут изменить также количество
движения системы, которое можно вычислять двояким
образом: или как геометрическую сумму количеств дви-
жения всех точек, образующих данную систему, или как
произведение массы всей системы на скорость центра
масс (MvJ. Второй способ удобнее в случае, если скорость
центра масс системы легко найти, как, например, в такой
задаче.
Вычислите количество движения изображенной на
рис. 18 ременной передачи. Все необходимые для вычисле-
ния данные считаются известными. Центры тяжестей
каждого из шкивов лежат на их осях вращения.
Вращаются шкивы, но их центры тяжести неподвиж-
ны, следовательно, общий центр тяжести двух шкивов
тоже неподвижен. Верхняя часть ремня бежит вправо,
нижняя — влево, что также оставляет в покое общий
центр тяжести системы шкив—ремень—шкив. Так как
43
центр масс данной системы не движется (рс = 0), количе-
ство движения ременной передачи равно нулю.
Тем, что внутренние силы не могут изменить количе-
ство движения системы, объясняется откат (отдача) орудия
при выстреле. Так как вначале снаряд и орудие непо-
движны, количество движения системы снаряд—орудие
равно нулю. Пороховые газы с одинаковой силой давят
и на снаряд и на орудие — это внутренние силы. Когда
Рис. 18. Задача о шкивах
снаряд начинает двигаться в одном направлении, орудие
движется в противоположную сторону, чтобы сумма ко-
личеств движения снаряда и орудия по-прежнему остава-
лась равной нулю.
Давайте решим задачу, иллюстрирующую это явление.
Ствол горизонтально расположенного орудия имеет
массу 1100 кг. Масса снаряда равна 5,4 кг. Скорость сна-
ряда у дульного среза v = 900 м/с. Чему равна скорость
свободного отката орудия в момент вылета снаряда?
(Предполагается, что орудие не имеет противооткатного
устройства.}
В горизонтальном направлении на снаряд и орудие
не действуют никакие силы, кроме сил давления порохо-
вых газов, образующихся при выстреле. (Сопротивлением
воздуха пренебрегаем.) Но силы давления пороховых
газов — это внутренние силы. Они не могут изменить
количество движения системы снаряд—орудие, которое
складывается из количества движения снаряда и коли-
чества движения орудия. Так как вначале количество
движения системы снаряд—орудие равно нулю (до выстре-
ла снаряд и орудие неподвижны), то, следовательно, оно
равно нулю и в любой последующий момент времени:
mv + тр^ = 0. Здесь т — масса снаряда, v — его ско-
рость, тг — масса орудия, — скорость отката. Таким
образом, = —mv/m1 = —5,4*900/1100 = —4,42 м/с,
44
т. е. скорость отката равна 4,42 м/с и направлена в сто-
рону, противоположную движению снаряда.
Решим другую задачу.
Граната, имевшая массу 3 кг и летевшая горизонталь-
но со скоростью 15 м/с, разорвалась в воздухе на две части.
Скорость осколка массы 2 кг возросла в направлении дви-
жения до 25 м/с. Какова скорость второго осколка? Сопро-
тивлением воздуха пренебречь.
Силы, разрывающие гранату,— внутренние силы. Они
не могут изменить количество движения гранаты. А силы
притяжения к Земле — внешние силы, действующие на
гранату и осколки, не проектируются на горизонтальное
направление, поэтому количество движения гранаты
в этом направлении измениться не может. Какое оно было
вначале (до разрыва), таким оно останется и после разрыва
гранаты на два осколка. Вначале граната массы т летит
со скоростью v, а затем два осколка с массами т± и т2
движутся со скоростями г?! и г2. Следовательно,
mv =	+ ^2р2-
Подставив в это выражение числа, получим, что скорость
второго осколка и2 = —5 м/с. Знак минус показывает, что
второй осколок движется в сторону, противоположную
движению первого осколка.
Летящий снаряд (или граната) — это тело, брошенное
под углом к горизонту. Такое тело, как известно, движется
по параболе, следовательно, траектория центра тяжести
снаряда — всегда парабола. Внутренние силы, разры-
вающие снаряд, не могут изменить характер движения
центра тяжести. Поэтому после разрыва снаряда центр
масс осколков продолжает перемещаться по параболе.
Осколки летят в разные стороны, а центр масс осколков
как ни в чем не бывало продолжает двигаться по параболе.
И так продолжается до тех пор, пока хотя бы один осколок
не коснется земли или не попадет в цель. Тогда появля-
ются внешние силы, и центр масс осколков сходит с па-
раболы.
Какая причина заставляет двигаться ракету? Та же,
которая заставляет орудие откатываться назад. Ракета—
та же пушка, только покидают ее не снаряды, а газы.
В связи с последним возникает такой вопрос: может
ли скорость ракеты быть больше скорости истечения га-
зов? Да, может. Скорость ракеты возрастает до тех пор,
45
пока происходит истечение газов (пока работает двига-
тель). Поэтому может наступить такой момент, когда ра-
кета будет двигаться вперед быстрее, чем газы отлетать
от нее назад. В этом случае продукты сгорания будут дви-
гаться за ракетой, постепенно отставая от нее.
При помощи простейших подручных средств можно
провести опыты, иллюстрирующие реактивное движение.
Возьмите внешнюю часть спичечного коробка и вырежь-
те для него из картона донышко. Вставьте донышко в ко-
робок на глубину примерно одного миллиметра и залейте
пазы расплавленным стеарином. На высоте 1—2 мм от
донышка с разных сторон коробка проделайте отверстия
диаметром 2 мм. В верхней части коробка друг напротив
друга проколите небольшие дырочки и привяжите нитки.
Подвесьте коробок на нитках. Если теперь налить в коро-
бок воду, то, вытекая, она заставит коробок поворачи-
ваться вокруг вертикальной оси (рис. 19).
Это устройство подобно сегнерову колесу, которое слу-
жит для демонстрации реактивного действия вытекающей
воды. Оно было изобретено в 1750 г. венгерским ученым
Я. Сегнером и явилось прообразом гидравлической турби-
ны. В настоящее время применяется для орошения полей.
Для следующего опыта необходимы фольга, в которую
заворачивают шоколадные конфеты, и спички. Вырежьте
полоску фольги размером примерно 2x6 см и оберните ею
головку спички так, чтобы из фольги получилась малень-
кая блестящая «ракета» (рис. 20). Эта «ракета» должна
плотно облегать спичку, но «сидеть» на ней свободно. Под-
несите горящую спичку к «ракете». Когда фольга прогре-
ется, головка спички вспыхнет, и образовавшиеся газы
сообщат «ракете» движение.
«Ракета» пролетает по воздуху всего 1—2 м, темпера-
тура ее невысока, поэтому опыт безопасен, но все-таки луч-
ше, если в той стороне, куда полетит «ракета», не будет
людей.
Реактивное движение можно также демонстрировать
при помощи детского воздушного шарика. Если его на-
дуть, а затем дать возможность воздуху выходить из ша-
рика, он будет двигаться в противоположную сторону.
В разделе «Кинематика» было рассказано об аналогии,,
существующей между поступательным и вращательным
движениями. Кинематическим характеристикам S, v, a, t
поступательного движения соответствуют характеристики
46
Ф, со, 8, t вращательного движения. Эта аналогия рас-
пространяется и на динамику. При вращении тела вокруг
оси роль массы т играет момент инерции 7, а роль
силы F — момент силы L.
Внутренние силы не могут менять также момент коли-
чества движения системы 7со (по аналогии с количеством
движения системы mv). Момент инерции системы зависит
не только от масс, входящих в систему, но и от расстоя-
Рис. 20. Из фольги и спички можно смастерить ракету
Рис. 19. Сегнерово колесо, изготовленное из спичечного коробка
ний этих масс до оси вращения. Момент инерции системы
тем больше, чем больше массы тел, входящих в нее, и чем
дальше они расположены от оси вращения.
Вы видели, наверное, что, раскручиваясь, фигурист
держит руки расставленными в стороны. Затем он при-
жимает их к туловищу и начинает вращаться быстрее.
Почему так происходит?
Дело в том, что силы трения коньков о лед малы (ими
можно пренебречь), а две другие внешние силы: сила тя-
жести и нормальная реакция, действующие на фигуриста,
вертикальны. Поэтому они не дают моментов вокруг вер-
тикальной оси, и, следовательно, момент количества дви-
жения фигуриста вокруг вертикали не может измениться.
Прижимая руки к туловищу, фигурист уменьшает момент
инерции своего тела. А так как момент количества движе-
ния — произведение момента инерции на угловую ско-
рость — должен остаться тем же, угловая скорость воз-
растает: фигурист начинает вращаться быстрее. Наоборот,
47
чтобы замедлить вращение, фигурист разводит руки в
стороны, увеличивая тем самым момент инерции своего
тела и уменьшая угловую скорость*
Аналогично поступают парашютисты* При прыжке из
самолета парашютист может начать вращаться. В этом
случае, прежде чем открыть парашют, надо остановить
вращение, иначе стропы могут перепутаться при выходе
парашюта из ранца, и парашют не раскроется. Чтобы это
сделать, парашютисты разводят руки и ноги в стороны.
А затем используют их как своеобразные «рули».
Космонавты в условиях невесомости проводили сле-
дующий опыт. Они вращали рукой в одну сторону, а сами
поворачивались в противоположную. Этот опыт показал,
что закон независимости момента количества движения си-
стемы от внутренних сил можно использовать для управ-
ления своим телом в состоянии невесомости. (Между про-
чим, о такой возможности управления телом в состоянии
невесомости писал еще К. Э. Циолковский в своих замет-
ках «Жизнь в межзвездной среде».) Тот же закон может
быть использован для управления космическим кораблем.
Если вращать массивный маховик, расположенный внут-
ри космического корабля, в одну сторону, корабль будет
поворачиваться в противоположную. Несколько махови-
ков, установленных под углом друг к другу, позволят
поворачивать космический корабль в любом направ-
лении.
Как видите, внутренние силы системы не только мно-
гое не позволяют: нельзя вытащить себя за волосы из бо-
лота, нельзя двигать лодку, упираясь в мачту, и т. п.,
но и многое разрешают: стрельбу из орудия, реактивное
движение, управление своим телом в космическом полете,
управление космическим кораблем и т. д. А знать то, что
могут и чего не могут внутренние силы, невредно каждо-
му, и в частности писателям научно-фантастических произ-
ведений и их редакторам.
В одном научно-фантастическом романе герои наде-
вают башмаки, делающие людей невесомыми, и идут по
воздуху, как по тротуару. Но ведь каждому, знакомому с
механикой, ясно, что идти, не отталкиваясь от чего-либо,
нельзя. Двигаться при помощи «башмаков невесомости»—
это все равно, что вытащить себя за волосы из болота или
совершить путешествие к Луне, подбрасывая магнит. Раз-
ница здесь только в одном: создатели «Барона Мюнхау-
48
Зёна» и «Сирано де Бержерака» понийалй невозМоЩйосДЁ
того, о чем писали, а автор упомянутого романа, к сожа-
лению, нет.
ДИНАМИКА ТВЕРДОГО ТЕЛА
Твердое тело можно рассматривать как систему материаль-
ных точек, расстояния между которыми не меняются ни
при каких условиях. Поэтому динамика твердого тела —
частный случай динамики системы. Все теоремы и форму-
лы, справедливые для динамики системы, применимы и к
задачам динамики твердого тела (но не наоборот).
Как уже было сказано, при поступательном движении
все точки твердого тела движутся одинаково, поэтому
динамика поступательного движения твердого тела просто
сводится к динамике точки.
Задачи динамики вращательного движения помогает
решать аналогия, существующая между поступательным
и вращательным движениями. О ней уже было рассказано.
Посмотрим теперь, как это осуществляется на практике.
Пусть нам нужно решить такую задачу. Тяжелый одно-
родный стержень ОВ (рис. 21) длиной Z, надетый своим
концом О на ось, вокруг которой он может вращаться в
вертикальной плоскости, находится в положении устойчи-
вого равновесия. Какую скорость надо сообщить концу В
стержня для того, чтобы он сделал четверть оборота?
Эту задачу можно решить при помощи теоремы об из-
менении кинетической энергии, которая для вращающе-
гося тела записывается так: 7<о2/2 — 7(Оо/2 = А, где А —
работа (по аналогии с теоремой об изменении кинетиче-
ской энергии материальной точки тиЧ2 — тт%/2 = Л).
Линейная скорость связана с угловой соотношением
v = в)В, поэтому начальная угловая скорость стержня
равна v/Ц а конечная — нулю, так как, сделав четверть
оборота, стержень остановится. Совершенная работа бу-
дет равна работе, которую надо затратить, чтобы поднять
центр тяжести стержня на высоту Z/2 (сила тяжести при-
ложена в середине стержня), т. е. Р1/2. Значение момента
инерции стержня, вращающегося вокруг оси, проходя-
щей через его конец, можно взять из справочника: I —
= mZ2/3, где т — масса стержня, a Z — его длина. Таким
образом, теорема об изменении кинетической энергии
49
Рцс. 22. Задача о цилиндре
Рис. 21. Стержень, вращающийся вокруг горизонтальной оси
вращающегося стержня запишется так:
1	1	/2 г>2	I
откуда v = У'3gl.
Плоскопараллельное движение представляет собой
сумму двух движений: поступательного и вращательного,
поэтому при решении задач динамики плоского движения
приходится использовать формулы, относящиеся к обоим
движениям.
Поясним сказанное примером. Тяжелый круглый ци-
линдр О (рис. 22) массы т обмотан посередине тонкой
нитью, конец которой В закреплен неподвижно. Цилиндр
падает без начальной скорости, разматывая нить. Опре-
делите скорость оси цилиндра в тот момент, когда эта ось
опустится на высоту h, и найдите натяжение нити.
Для определения скорости оси цилиндра воспользуем-
ся теоремой об изменении кинетической энергии: W —
— Wq = А (разность кинетических энергий равна рабо-
те). Так как цилиндр движется плоскопараллельно, то его
кинетическая энергия складывается из кинетической энер-
гии поступательного движения со скоростью центра масс
(mv2/2) и кинетической энергии вращения вокруг центра
масс (Zco2/2), т. е. W = mv2/2 + 7со2/2. Поэтому теорема
об изменении кинетической энергии цилиндра при паде-
нии с высоты h запишется следующим образом: ти2/2 +
50
+ Zco2/2 = mgh (WQ — 0, так как вначале цилиндр не-
подвижен, а А есть работа силы тяжести mg на пути й).
Момент инерции цилиндра I относительно оси О равен
т7?2/2 (из справочника), а его угловая скорость со = v/R.
Следовательно, mv2/2 + mR2v2/iR2 — mgh, откуда v =
= 2/3 V3gh.
Цилиндр одновременно участвует в двух движениях:
поступательном и вращательном, т. е. для него справедли-
вы две формулы: та = F и 78 = L (второе соотношение
написано по аналогии с первым). Эти формулы для цилинд-
ра будут иметь вид
та = mg —Т,	(1)
г = TR,	(2)
так как на цилиндр действуют две силы: сила тяжести
и сила реакции нити, причем сила тяжести не дает мо-
мента относительно оси О. Подставив значение углового
ускорения 8 = a/R в соотношение (2), получим, что а =
= 2Т1т. Теперь из уравнения (1) можно найти реакцию
нити: Т = mg/З, следовательно и натяжение нити равняет-
ся одной трети веса цилиндра.
МЕХАНИКА В ЦИРКЕ
Обычно, смотря представление в цирке, мы отмечаем мас-
терство артиста, непринужденность, с которой исполняет-
ся номер, красоту номера и совершенно не задумываемся
над тем, какие физические законы лежат в основе того или
иного номера. Это естественно. Мы приходим в цирк не для
того, чтобы изучать механику. Но давайте «посетим»
цирк именно с этой целью: давайте попробуем разгадать
«механические секреты» некоторых цирковых номеров.
Играет музыка. На арене — два клоуна. Один из них
бросает шляпы, и они точно «садятся» на голову второго
клоуна.
Если вы присмотритесь, то заметите, что, бросая шля-
пы, клоун закручивает их вокруг вертикальной оси. За-
чем он это делает? В данном случае вращающееся тело
сохраняет в пространстве нёизменной ось, вокруг кото-
рой вращается. Вспомните, например, волчок. Если бы
клоун, бросая шляпы, не закручивал их вокруг оси, то
51
Рис. 23. Прижимая руки к туло-
вищу, гимнаст уменьшает свой
момент инерции и начинает вра-
щаться быстрее
шляпы, летя, кувыркались бы в воздухе и могли опустить-
ся на голову второго клоуна своей верхней, а не нижней
частью.
Следующий номер — гимнасты под куполом цирка. Вот
один из артистов прижимает руки к туловищу и начинает
быстрее вращаться вокруг своей оси (рис. 23). Почему это
происходит, вы теперь знаете. Прижимая руки к туловищу,
гимнаст уменьшает момент инерции своего тела. А так как
момент количества движения
гимнаста — произведение мо-
мента инерции на угловую
скорость вращения — не может
измениться (сила тяжести не
дает момента относительно вер-
тикальной оси), угловая ско-
рость возрастает.
Вы все, конечно, видели ки-
нофильм «Цирк» и помните ис-
полняемый там Л. Орловой но-
мер «Из пушки на Луну». Арти-
стку подбрасывает вверх сила
сжатой пружины, а взрываю-
щаяся при этом петарда создает
иллюзию выстрела.
Давайте подсчитаем, какую
перегрузку в момент «выстрела»
испытывает артист, исполняю-
щий данный номер.
Пусть пружина подбрасы-
вает человека вверх на высоту
20 м. Тогда из пушки он выле-
тает с начальной скоростью
Vq = 20 м/с. Зная начальную
скорость, можно определить
ускорение, которое сообщает
цирковому артисту пружина. Если длина пушки 5 м, то
формула и0 = У2aS показывает, что среднее ускорение
а = v*J2S = 40 м/с2, то есть артист испытывает при
«выстреле» четырехкратную перегрузку.
Почему канатоходцы, двигаясь по проволоке, балан-
сируют, отклоняя свое тело вправо — влево? Для сох-
ранения равновесия необходимо, чтобы перпендикуляр,
52
опущенный из центра тяжести тела, все время проходил
через опору — канат. Добиться этого трудно. Но можно
сделать так, что центр тяжести будет совершать колебания
около положения равновесия. При небольшой амплитуде
колебаний такие движения вправо — влево надежно пре-
дохраняют актера от падения.
...Замолкает музыка, и под барабанную дробь испол-
Рис. 24* Цирковой номер «Мертвая петля»
53
няется «смертельный» номер. Артист на велосипеде раз-
гоняется по наклонной дорожке и делает «мертвую пет-
лю» (рис. 24).
Давайте подсчитаем, с какой высоты должен начать
движение велосипедист, чтобы пройти всю окружность
петли, не отделяясь от нее.
Самая опасная точка — точка С. Запишем для нее
принцип Д’Аламбера (велосипедиста и его велосипед бу-
Рис. 25. Разомкнутая «Мертвая
петля»
дем считать точкой, перемещающейся без трения по се-
редине дорожки): Q — N — mg = 0. Здесь Q — сила
инерции, равная mv^R, N — нормальная реакция, a mg—
сила тяжести. Велосипедист проедет всю петлю, не отде-
ляясь от нее, если во все время движения велосипед будет
давить на дорожку, то есть будет существовать реакция N.
Поэтому предельный случай — это N =0. Таким образом,
условие безопасности номера mvNR = mg или, еще луч-
ше, mvMR >> mg.
Скорость велосипедиста в точке С можно найти при
помощи теоремы об изменении кинетической энергии:
mv2!2—mvQ2J2 = mg (h — 27?).
Если велосипедист начинает движение из точки А без
начальной скорости (z;0 — 0), то mv2 = 2mg (h — 27?).
Таким образом, 2mg (h—2R)lR > mg. Отсюдаh 2,57?.
Следовательно, чтобы номер был безопасным, велосипе-
дист должен начать движение с высоты, превышающей
высоту петли не менее чем на половину радиуса петли.
(Приведенный расчет справедлив лишь в том случае, если
велосипедист, скатываясь, не вращает педали, то есть если
его скорость возрастает только благодаря действию
силы тяжести.)
Велосипедный номер «Мертвая петля» был изобретен в
1902 г. одновременно двумя цирковыми артистами: Дья-
вол о (Джонсоном) и Мефисто (Нуазеттом). Вся трудность
54
его в том, чтобы при исполнении не съехать с дорожки
(скорость достигает 60 км/ч). В книге «Велосипедные ат-
тракционы» Бостоне пишет: «Сам по себе велосипедный
трюк при правильном расчете и прочной конструкции ап-
парата не опасен. Опасность трюка лежит в самом артис-
те. Если рука артиста дрогнет, если он будет взволнован,
потеряет самообладание, если ему неожиданно сделает-
ся дурно, то можно ожидать всего».
Бельгиец Шарль Нуазетт
был неплохим механиком-кон-
структором. Он автор вообще
первого в мире циркового атт-
ракциона «Круг смерти», соз-
данного в конце XIX в.: внут-
ри огромной корзины из дере-
вянных реек, без дна, на боль-
шой скорости катались велоси-
педисты.
«Мертвую петлю» можно
сделать внешне еще более эф-
фектной, еслиразомкнутьпетлю
в точке С. Тогда часть пути
велосипедист будет пролетать
по воздуху, двигаясь по пара-
боле. В этом случае высота, с
которой необходимо начать
движение, чтобы номер был
безопасным, вычисляется по
формуле h — R (1 + cos а +х/2
cos а), где а — половина угла
сектора, вырезанного из петли
(рис. 25).
Другой «смертельный» номер — езда на мотоцикле или
автомобиле по вертикальной стене. Давайте подсчитаем,
с какой скоростью надо ехать, чтобы не свалиться вниз.
От движения вниз мотоцикл (или автомобиль) удер-
живает сила трения. Следовательно, сила трения должна
быть равна сумме сил тяжести мотоцикла и артиста:
kN = mg (рис. 26). Сила нормального давления N опре-
деляется силой инерции: N — mv4R. Таким образом,
kmvNR = mg. Отсюда v — ]/"Rglk.
Если, скажем, радиус R = 5 м, а коэффициент трения
Рис. 26. Езда на мотоцикле по
вертикальной стене
55
k = 0,5, то скорость мотоцикла должна быть приблизив
тельно равна 10 м/с, или 36 км/ч. (Здесь приведен
простейший расчет. На самом деле разобранное явление
сложнее: сила трения и сила тяжести образуют пару сил,
вращающиеся колеса создают гироскопический эффект
и т. д.)
Есть цирковой номер, который объединяет в себе и
«мертвую петлю» и «вертикальную стену». Это — езда на
мотоцикле внутри сетчатого шара. С таким номером высту-
пают артисты Маяцкие. Их мотоциклы движутся внут-
ри шара во всех направлениях.
Как видите, смотреть цирковое представление можно»
еще с бумагой и карандашом в руке. В этом случае пе-
ред вами раскрываются секреты некоторых цирковых
номеров, а так называемые смертельные номера оказы-
ваются не такими уж опасными. Конечно, в езде по верти-
кальной стене есть элемент риска. Но он не так велик, как
кажется на первый взгляд. Знание законов механики
позволяет делать подобные номера безопасными, какими
они и должны быть.
МЕХАНИКА И ПРИРОДА
Мы не знаем, кто изобрел колесо. Считают, что оно впер-
вые появилось у степных народов. Можно предположить,
что идея колеса родилась в голове древнего кочевника
в тот момент, когда он наблюдал за перекати-полем, го-
нимым по степи ветром. Или, скажем, парус. Разве
мысль о нем не могла возникнуть при виде быстро мчащего-
ся по реке под действием ветра ветвистого дерева?
Наш предок присматривался и к живой природе. Идею
копья (заостренной палки) мог подсказать рог буйвола,
а мысль о ноже могла появиться после знакомства с ост-
рыми зубами акулы или какого-либо другого животного.
Итак, человек давно изучает природу, заимствуя у
нее все полезное для себя. Любая естественная наука —
это исследование, объяснение и использование явле-
ний природы. Недавно появившаяся новая наука бионика
провозгласила своим девизом «учиться у живой природы».
Название «бионика» происходит от греческого слова
«бион», что означает элемент (ячейка, атом) жизни. Подоб-
но биологии, бионика изучает жизнь, но делает это не-
сколько с других позиций. Бионику интересует, в чем
56
создания природы умнее, совершеннее, экономичнее, луч-
ше творений рук человека. Поняв это, бионика сможет дать
в руки инженеров и конструкторов идеи и методы для ре-
шения стоящих перед ними задач. (А учиться есть чему—
ведь природа совершенствовала свои организмы многие
миллионы лет.) Следуя девизу: «живые прототипы — ключ
к новой технике», бионика моделирует приборы и машины,
приближающиеся по своим свойствам к живым организ-
мам. В частности, бионика моделирует органы чувств жи-
вотных: органы ориентации, локации, движения и т. п.
Давайте посмотрим, что может заимствовать у живой
природы механика.
Как известно, кальмары для своего перемещения ис-
пользуют принцип реактивного движения. Медленно втя-
гивая в себя воду, кальмар затем с силой выталкивает ее
через отверстие и движется в сторону, противоположную
испущенной струе. При длине в 20 см кальмар может раз-
вивать скорость до 40 км/ч. Можно предположить, что
крупные кальмары плавают с еще большими скорос-
тями.
Изучение движения кальмара, возможно, позволит
повысить скорости кораблей, снабженных водометными
двигателями. Скажем, изучение движения дельфина по-
казало, что высокая скорость плавания этого животного
объясняется тем, что дельфин испытывает малое сопротив-
ление при движении из-за вибрации кожи. Можно пред-
ставить себе, что когда-нибудь будет создан корабль (над-
водный или подводный) с вибрирующим корпусом, кото-
рый будет развивать большую скорость, чем корабль та-
кого же класса, но с обычным корпусом.
У современного автомобиля многолетняя история раз-
вития и совершенствования, но инженеры продолжают
искать иные возможные конструкции самодвижущегося
экипажа. Одно из решений в этом направлении —
«шагающий» автомобиль. Действующую модель его по-
строил чешский инженер Ю. Макерле.
Шагая, человек все время как бы падает вперед
то на правую ногу, то на левую. На этом же принци-
пе основано устройство «шагающего» колеса. Внутри не-
го вращается золотник, который распределяет воздух,
нагнетаемый компрессором в эластичные камеры (рис. 27).
Когда камера, находящаяся за точкой касания колеса с
грунтом, раздувается? воздух из камеры, находящейся
57
Рис. 27. «Шагающее» колесо
А — втулк а колеса, в которой
перемещается золотник В, рас-
пределяющий давление возду-
ха по камерам 1, 2, 3, . . .
перед точкой касания, выходит. Появляется опрокиды-
вающий момент, который перемещает колесо. Скорость
движения прямо пропорциональна быстроте наполнения
камер. Чем скорее раздуваются камеры, тем быстрее
перекатывается колесо.
«Шагающий» автомобиль, конечно, не вытеснит обыч-
ные колесные, но он найдет применение там, где требуются
специальные машины высокой проходимости: строитель-
ные, экспедиционные, военные.
Испытание модели показало,
что она легко преодолевает
препятствия и трудные грунты.
Австралийский кенгуру раз-
вивает скорость до 80 км/ч. Не-
льзя ли построить прыгающий
автомобиль? Такую задачу по-
ставил перед собой советский
инженер В. Турик и решил ее.
«Прыгающий» автомобиль
опирается на два башмака, в
каждом из которых расположе-
на коробка с двумя вращающи-
мися навстречу друг другу
грузиками (рис. 28). Предста-
вьте себе, что грузики вращают-
ся в вертикальной плоскости.
Тогда развивающиеся при этом
центробежные силы то прижи-
мают коробку (башмак) к земле, то стремятся под-
бросить ее вверх. При определенной скорости вра-
щения центробежные силы становятся настолько боль-
шими, что начинают отрывать башмак от земли: он начи-
нает подпрыгивать. Так как плоскость вращения грузи-
ков в башмаках расположена под некоторым углом к го-
ризонту, то при каждом обороте грузиков башмаки не
только подпрыгивают вверх, но и немного перемещаются
вперед. У работающей модели «прыгающего» автомобиля
башмаки все время совершают небольшие прыжки вперед.
Корпус же автомобиля, укрепленный на башмаках при
помощи хороших амортизаторов, движется сравнительно
плавно.
Прыгающий автомобиль имеет ряд преимуществ по
сравнению с обычным. Например, чтобы остановиться? до-
статойно выжать сцеплёнйё, т. ё. отключить двигатель от
привода к грузикам. Но прыгающий автомобиль имеет
и ряд существенных недостатков, основным из которых
является вибрация корпуса при движении.
Пингвин... Как будто медлительное, неповоротливое
существо. Вот он бредет, переваливаясь с боку на бок, со
скоростью 3—4 км/ч. Но знаете ли вы, что в случае опас-
ности пингвин может двигаться со скоростью до 30 км/ч!
Как это ему удается? Оказывается, пингвин ложится на
снег и, отталкиваясь крыльями и лапами, быстро сколь-
зит на брюхе вперед.
Профессор Горьковского политехнического института,
доктор технических наук А. Ф. Николаев был в свое вре-
мя в Антарктиде и возглавлял легендарный поход к По-
люсу относительной недоступности. Именно там, в Антарк-
тиде, у него появилась идея создать снегоход, используя
принцип движения пингвина. Такая машина построена
(рис. 29).
Вездеход — автомобиль высокой проходимости. Обыч-
но подобные машины — это или колесные, у которых все
оси ведущие, или гусеничные. Встречаются и смешанные
конструкции. Колесные вездеходы могут двигаться с боль-
шой скоростью по твердому грунту, но вязнут в снегу.
Происходит это потому, что у колесных вездеходов велико
удельное давление на грунт (0,8—2 кг/см2). Гусеничные
Рис. 28. «Прыгающий» автомобиль
I — двигатель, 2 — коробка с грузиками, 3 — башмак, 4 — амортизаторы
59
машины обладают небольшим удельным давлением (0,1 —
0,3 кг/см2), но они тяжелы и медлительны. Снегоход
«Пингвин» свободен от недостатков, присущих колесным
и гусеничным вездеходам. Он может двигаться с большой
скоростью по земле, снегу и воде.
У снегохода «Пингвин» герметичное обтекаемое днище
и колеса, как у старых колесных пароходов, только плицы,
укрепленные вдоль обода колеса, не плоские, а имеют
форму лап пингвина. По ободу колеса расположены шесть
плиц. Они металлические, с резиновыми накладками. Угол
наклона плиц к ободу колеса можно менять. Тем са-
мым обеспечивается различная сила сцепления колес с
грунтом.
Когда вездеход разгоняется, колеса выпущены на мак-
симальную величину, поэтому корпус не касается снега.
Затем с помощью гидравлического устройства колеса под-
жимаются, и вездеход ложится на днище. Теперь «Пинг-
вин» скользит вперед на «брюхе», отталкиваясь от снега
почти убранными плицами-«лапами».
Днище «Пингвина» покрыто синтетическим материа-
лом, который не примерзает к снегу даже в самый лютый
Рис. 29. Снегоход «Пингвин»
1 —плицы, 2 — гидропривод подъема колеса, 3 — цепная передача от мотора
60
мороз. Вода вездеходу также не страшна. Если, скажем,
«Пингвин» провалится в полынью, он не утонет — корпус
водонепроницаем. Гребя плицами, снегоход может плыть
и сам взобраться на берег.
Масса вездехода около 1,5 т. С грузом в 300 кг он раз-
вивает скорость по снегу до 50 км/ч, а по воде — до 15 км/ч.
Вот только несколько примеров использования меха-
никами «патентов» природы. Несомненно, что в будущем
мы станем свидетелями создания многих удивительных
машин и механизмов, подсказанных окружающей нас жи-
вой и неживой природой.
АЭРОМЕХАНИКА
Аэромеханика — это наука о равновесии и движении раз-
личных газообразных сред, а также твердых тел в газах,
и прежде всего в воздухе. В зависимости от того, что яв-
ляется предметом исследования: покой или движение,
аэромеханика делится на два больших раздела: аэроста-
тику и аэродинамику.
Аэромеханика — теоретическая основа воздухопла-
вания. Она очень обширна по объему изучаемых ею явле-
ний, и здесь будет рассказано только о механических коле-
баниях тел, вызываемых потоком воздуха.
История мостостроения полна описаниями катастроф,
которые были вызваны ветром. Вот некоторые из них.
В 1816 г. во время бури обрушился висячий мост близ
Филадельфии (США). В следующем году под порывами
ураганного ветра рухнул висячий мост через реку Твид
во Франции. Очевидцы рассказали, что, перед тем как рух-
нуть, мост совершал такие сильные поперечные колеба-
ния, что был способен сбросить в реку каждого, кто отва-
жился бы вступить на него. В 1833 г. во время бури
обрушился висячий мост в Брайтоне (США). Этот мост отно-
сился к числу наиболее значительных мостовых сооруже-
ний того времени: он имел четыре пролета, длина каждого
из которых достигала 78 м. Мост восстановили, но через
три года он был снова разрушен бурей.
В 1850 г. во Франции рухнул висячий мост через ре-
ку Мэн. Этот мост с пролетом в 102 м обрушился во время
сильного ветра, когда по нему проходил полк солдат, ко-
торые шли не в ногу. В 1852 г. во Франции обрушился мост
с пролетом в 198 м. Мост был восстановлен и снова рухнул
61
в 1871 г. Обе эти катастрофы были вызваны ветром. Перед
обрушением центральная часть моста совершала верти-
кальные колебания с амплитудой, доходящей до 1 м, и
боковые колебания с амплитудой до 25 см.
В 1940 г. произошла грандиозная катастрофа с висячим
мостом через пролив Такома (США). Этот мост по длине
центрального пролета, равной 853 м, был в то время вто-
рым в мире *. Он уступал только мосту через залив в Сан-
Франциско. Такомский мост просуществовал всего четы-
ре месяца. 7 ноября 1940 г. под действием ветра, дувшего
со скоростью 67 км/ч, мост начал колебаться и через пол-
часа рухнул по всей длине между пилонами. Одновремен-
но были засвидетельствованы значительные повреждения
береговых пролетов, а также изгиб пилонов. Техничес-
кие журналы тех лет расценили эту катастрофу как вели-
чайшую в истории мостостроения.
Какие же причины вызывают обрушение мостов?
Когда какое-либо тело обдувается потоком воздуха, за
телом образуются вихри. Срываясь попеременно то с од-
ной, то с другой стороны, они раскачивают тело, застав-
ляют его колебаться. Частота, с которой срываются вих-
ри, зависит от скорости воздушного потока: чем больше
скорость, тем больше частота срыва вихрей. Если эта
частота совпадет с собственной частотой колебаний тела,
то наступит явление, известное в физике под названием
резонанса. При резонансе амплитуда колебаний возраста-
ет и может увеличиться настолько, что сооружение раз-
рушится. Именно это и происходило с висячими мостами.
Когда известна причина, ясно, как с ней бороться. Ес-
ли в данной местности скорость ветра никогда не бывает
больше 50 км/ч, то надо рассчитать мост так, чтобы резо-
нанс наступал при большей скорости, скажем при 100 км/ч,
и сооружение будет стоять надежно.
Под влиянием ветра колеблются деревья и провода
линий электропередач, трубы заводов и высотные здания,
радиомачты и нефтяные вышки. Эти колебания вредны.
Например, известны случаи, когда под действием ветра
падали фабричные трубы и радиомачты. В результате ко-
лебаний проводов линий высоковольтных передач, как
* В настоящее время самый большой висячий мост (длина цент-
рального пролета 1298 м)—через нью-йоркскую бухту Веррацано
(США).
62
легко догадаться, может произойти схлестывание прово-
дов или даже обрыв их. Это приведет к тому, что на неко-
торое время многие промышленные предприятия прекра-
тят работу из-за отсутствия электроэнергии.
Чтобы уменьшить колебания проводов, к ним подве-
шивают различные гасители колебаний — так называе-
мые демпферы. Устроены они просто. К проводу при по-
мощи зажима крепится гибкий тросик, на концах кото-
рого — два грузика. Когда провод начинает колебаться,
грузики тоже приходят в движение. Система рассчитана
таким образом, что колебания грузиков гасят колебания
провода. Это механический способ гашения колебаний.
А не существуют ли аэродинамические методы гашения
колебаний, то есть нельзя ли так изменить форму тела,
чтобы оно не колебалось в потоке воздуха?
Был проведен следующий опыт. Круглый цилиндр по-
местили в аэродинамическую трубу и подвесили его там
на упругой пластинке, которая позволяла цилиндру со-
вершать колебания поперек потока (рис. 30). В воздуш-
ном потоке цилиндр равномерно колебался с постоянной
амплитудой. Эта амплитуда очень сильно возрастала (в не-
сколько раз), если к цилиндру сбоку прикрепляли другой
маленький цилиндр под углом 45° к скорости потока. На-
оборот, колебания почти совершенно прекращались, если
тот же угол составлял 105°.
Этот опыт показал, что форма тела существенно влияет
на характер возникающих колебаний, что возможны аэро-
динамические способы гашения колебаний.
Подобные опыты проводились и на настоящих соору-
жениях. Например, оказалось, что колебания высокой
мачты можно погасить, если вокруг нее обернуть «змей-
кой» (по винтовой линии) достаточно толстый трос.
В одном американском техническом журнале расска-
зывалось, как с помощью аэродинамических методов уда-
лось избавиться от опасных колебаний газопровода, пере-
брошенного через реку Колорадо в Калифорнии. Газо-
провод был подвешен на мачтах и первоначально совер-
шал колебания с амплитудой, достигавшей 1,5—1,8 м.
Пришлось усилить главные несущие тросы и добавить бо-
ковые расчалки. Размах колебаний уменьшился, но все
равно оставалась опасность перенапряжения конструк-
ции за счет вибраций.
При колебаниях был слабый ветер, поэтому причину
их сначала искали в другом: в нагревании конструкции
солнцем, в пульсации газа и т. п. Но тщательные измере-
ния частот, амплитуд и форм колебаний показали их связь
с направлением и скоростью ветра. Колебания газопрово-
да вызывали обычные вихри, о которых рассказывалось
выше. Бороться с колебаниями можно было тремя спосо-
бами: 1) закрепить тягами места наибольших перемеще-
ний на пролете газопровода, 2) применить различные
Рис. 30. Колебания цилиндра
в аэродинамической трубе
механические гасители колебаний и 3) устранить аэроди-
намические силы, вызывающие вибрации.
Наиболее заманчивым был третий, аэродинамический
путь. Решили к трубе газопровода в горизонтальной плос-
кости приварить по обеим сторонам треугольные панели
(рис. 31). Модель была испытана в аэродинамической тру-
бе. Испытания подтвердили правильность расчетов. И дей-
ствительно, после установки панелей на подвесном газо-
проводе его вибрации прекратились.
В последнее время аэродинамические методы гашения
колебаний все больше и больше начинают интересовать
инженеров и конструкторов. Ведь действительно заманчи-
во: немного изменили форму тела, и ветер из врага
превращается в союзника.
В начале 30-х годов по всем технически развитым
странам мира прокатилась волна загадочных авиацион-
ных катастроф. Самолет, находившийся в спокойном
горизонтальном полете, вдруг начинал вибрировать с
такой силой, что разваливался в воздухе на куски. Это
новое грозное явление, с которым столкнулись авиа-
конструкторы и летчики-испытатели, получило название
«флаттер» (от английского flutter — бить крыльями,
трепетать).
64
Рис. 31. Треугольные панели^
приваренные к газопроводу, из-
бавили его от колебаний
Что порождает флаттер? Почему он возникает на впол-
не определенной для данного самолета скорости полета?
Как бороться с ним? Эти и многие другие вопросы встали
перед авиаконструкторами. Те немногие летчики, которым
удалось выбраться из стремительно летящих к земле, бес-
порядочно вертящихся обломков самолета и воспользо-
ваться парашютом, могли рассказать очень мало. Чтобы
изучить флаттер, пришлось организовать на него настоя-
щую «охоту». Вот как описы-
вает «охоту» и сам флаттер
известный летчик-испытатель
М. Л. Галлай в своей книге
«Через невидимые барьеры».
«...Очередной полет проте-
кал в уже ставшем привычным
порядке: взлет, подъем, выход
на горизонталь, регулировка
триммера руля высоты «на да-
вление», включение аппарату-
ры, постепенное увеличение обо-
ротов моторов и соответствую-
щее ему медленное, «ступень-
ками» по пять-шесть километ-
ров в час, приращение скоро-
сти. Все шло, как обычно...
И вдруг — будто огромные
страшной силой забарабанили по самолету. Все затряс-
лось так, что приборы на доске передо мной стали неви-
димыми, как спицы вращающегося колеса. Я не мог видеть
крыльев, но всем своим существом чувствовал, что они
полощутся, как вымпелы на ветру. Меня самого швыряло
по кабине из стороны в сторону — долго после этого не
проходили на плечах набитые о борта синяки. Штурвал,
будто превратившийся в какое-то совершенно самостоя-
тельное живое и притом обладающее предельно стропти-
вым характером существо, вырвался у меня из рук и ме-
тался по кабине так, что все попытки поймать его ни к
чему, кроме увесистых ударов по кистям и пальцам, не при-
водили. Грохот хлопающих листов обшивки, выстрелы
лопающихся заклепок, треск силовых элементов конструк-
ции сливались во всепоглощающий шум.
Вот он флаттер!»
Галлая спасло то, что руль высоты его самолета был
невидимые кувалды со
1/23 В. П. Лишевский
65
отрегулирован определенным образом: чтобы держать са-
молет в горизонтальном полете, надо было все время от-
жимать штурвал от себя. Как только летчик отпускал руч-
ку управления, она отклонялась назад, и самолет набирал
высоту Когда штурвал выбило из рук Галлая, самолет
сделал «горку», скорость уменьшилась, и флаттер прекра-
тился.
Поначалу, столкнувшись с флаттером, летчики и авиа-
конструкторы думали, что они имеют дело с совершенно
новым явлением, которое дотоле никогда и никому не
встречалось. Но оказалось, что это не так. Изучение флат-
тера показало, что он порождается теми же причинами,
которые вызывают обрушение висячих мостов. Правда,
флаттер самолетов — явление более сложное, и здесь бу-
дет рассказано о нем в самых общих чертах.
Крыло самолета может совершать колебания двух ви-
дов: изгибные и крутильные. При колебаниях изгиба крыло
движется вверх — вниз. Это движение как бы умень-
шает или увеличивает угол атаки крыла самолета. Подь-
емная сила, которая зависит от угла атаки, также умень-
шается или увеличивается. Причем изменение подъем-
ной силы таково, что оно гасит возникающие колебания:
если крыло движется вверх, подъемная сила уменьшается,
и наоборот. Таким образом, в потоке воздуха не могут
возникнуть чисто изгибные колебания крыла. Аналогич-
но в потоке воздуха не могут возникнуть и чисто крутиль-
ные колебания крыла. Это следует из того, что возникаю-
щие при крутильных колебаниях аэродинамические мо-
менты направлены против угловых скоростей вращения
крыла.
Для объяснения явления флаттера необходимо рассмот-
реть сложные изгибно-крутильные колебания крыла. Де-
ло в том, что один вид колебаний, возникнув, обязательно
порождает другой. Происходит это потому, что центр
тяжести крыла не совпадает с центром жесткости. Что
такое центр тяжести — известно, центром жесткости на-
зывается точка приложения равнодействующей упругих
сил, возникающих при деформации крыла.
Когда крыло при изгибных колебаниях движется вниз,
сила упругости направлена вверх, а сила инерции — вниз
(рис. 32). Эти две силы образуют пару сил, которая за-
кручивает крыло по часовой стрелке. Следовательно, из-
гибные колебания порождают крутильные. Возникшие
66
крутильные колебания изменяют угол атаки так, что те-
перь уже подъемная сила увеличивается при движении
крыла вверх. Происходит усиление изгибных колебаний,
которые в свою очередь увеличивают крутильные колеба-
ния, и т. д.
Аналогично можно показать, что возникшие крутиль-
ные колебания обязательно вызывают изгибные колеба-
ния. Крыло самолета — система с двумя колебательными
степенями свободы. Как всегда, в такой системе наблюда-
ются две собственные частоты (для изгибных и для кру-
тильных колебаний), которые несколько отличаются от
собственных частот для чисто изгибных и чисто крутиль-
ных колебаний. (Набегающий поток воздуха как бы при-
соединяет свою массу к массе крыла, тем самым меняя его
собственную частоту.) Новые собственные частоты колеба-
ний различны, но они имеют тенденцию к сближению с рос-
том скорости самолета. Это явление также играет опреде-
ленную роль при возникновении флаттера.
Итак, возникшие изгибные колебания крыла самолета
(скажем, из-за неоднородности воздушного потока) обя-
зательно приведут к крутильным колебаниям, так как
центры тяжести и жесткости не совпадают. Крутильные
колебания в свою очередь усиливают колебания изгиба,
и наоборот. Так образуется замкнутая автоколебательная
система с отчетливо выраженной обратной связью.
Энергия, которую колеблющееся крыло черпает из на-
бегающего потока воздуха, быстро растет с увеличением
скорости полета. При определенной скорости, называе-
мой критической, поступление энергии становится равным
цотерям и возникают автоколебания. У правильно рассчи-
3*
67
тайного самолета критическая скорость значительно выше
максимальной скорости полета, и это надежно предохра-
няет самолет от возникновения флаттера
В настоящее время авиаинженеры умеют довольно-
таки точно рассчитывать критическую скорость самолета
по его конструктивным параметрам и данным продувок
модели крыла в аэродинамической трубе. (Критическая
скорость должна быть много выше любой скорости полета,
включая такие особые режимы, как пикирование и што-
пор.) Но скорости самолетов все время растут, и это застав-
ляет ученых думать о том, как вообще избавиться от уг-
розы возникновения флаттера. Задача трудная, но важная.
В последнее время ученые и конструкторы столкну-
лись с новым видом флаттера, который можно назвать
флаттером управления. Он возникает у больших автома-
тически управляемых ракет.
Чтобы держать ракету на курсе, рули совершают ко-
лебательные движения с различными периодами. При
этом корпус ракеты, если она имеет достаточную протя-
женность, начинает изгибаться и возникают колебания
тела ракеты, вызванные колебаниями рулей. Так как кор-
пус ракеты не особенно жесткий (ракета должна быть по
возможности легкой), может произойти его разрушение.
Флаттер встречается и в природе. Наиболее характер-
ный пример — трепетание на ветру листьев деревьев.
Особенно подвержен флаттеру лист осины, который висит
на ветке па длинном черенке и обладает малой боковой
жесткостью.
В заключение — немного о сопротивлении воздуха.
Давайте решим такую задачу.
Требуется найти наибольшую скорость падения шара,
масса которого т = 10 кг, а радиус 8 см, принимая,
что сопротивление воздуха равно R — kSv2, где v — ско-
рость падения, S — площадь проекции падающего тела
на плоскость, перпендикулярную к направлению его дви-
жения, к — численный коэффициент, зависящий от фор-
мы тела и имеющий для шара значение 0,24Я-с2/ж4.
Скорость падающего шара возрастает до тех пор, по-
ка увеличивающаяся сила сопротивления воздуха R, ко-
торая растет с ростом скорости, не уравновесит силу тя-
жести Р = mg. Как только R и Р сравняются, дальше
шар будет двигаться равномерно (с постоянной скоро-
стью). Следовательно, максимальную скорость падения
68
можно найти из уравнения Р = R, или mg = kSv2. Под-
ставив сюда числа, получим v = УmglkS = 144 м/с.
Когда парашютист-спортсмен совершает затяжной пры-
жок, его скорость тоже не возрастает беспредельно. Она
увеличивается только до тех пор, пока сила сопротивле-
ния воздуха не уравновесит вес парашютиста. Дальше
он будет двигаться с постоянной скоростью (равномерно).
Скорость свободного падения парашютиста зависит от
многих причин (веса спортсмена, положения тела и т. п.).
Обычно она равна 40—60 м/с, т. е 140—210 км/ч.
Если спортсмен раскроет парашют, его скорость па-
дения уменьшится, так как увеличится площадь S попе-
речного сечения. У различных марок парашютов скорость
опускания разная. Средняя составляет 4 м/с.
Сила сопротивления воздуха — основная причина, ог-
раничивающая скоростные возможности самолета, поезда,
автомобиля У многих транспортных средств значитель-
ная часть мощности мотора расходуется на преодоление
сопротивления воздуха
Если у движущегося поезда одновременно открыть
все окна, то обтекание его воздухом настолько ухудшит-
ся, что сила сопротивления возрастет примерно на 25%.
Соответственно уменьшится и скорость. Именно поэтому
в экспрессах окна или совсем не открываются или откры-
ваются чуть-чуть. По той же причине гоночным автомоби-
лям придают как можно более обтекаемую форму.
СТАТИКА
СИЛЫ И ИХ ПРОЯВЛЕНИЯ
Силой называется мера воздействия на данное материаль-
ное тело со стороны других тел Она измеряется динами-
ческим или статическим методами. Динамический метод
позволяет найти силу F, если известны масса тела т и его
ускорение a (F = та). Статический способ основан на
уравновешивании измеряемой силы другой, ранее извест-
ной (сравнение с эталоном).
Силы — векторные величины. Они складываются или
раскладываются по правилу параллелограмма, которое
гласит: равнодействующая двух сил, приложенных водной
точке абсолютно твердого тела, определяется диагональю
параллелограмма, построенного на векторах, изображаю-
щих силы. И наоборот чтобы разложить силу но двум
направлениям, надо через конец вектора силы провести
прямые, параллельные этим направлениям
Познакомимся с параллелограммом сил поближе,
а для этого решим ряд задач.
Можно ли из одной силы в 1 Н «сделать» две силы по
ЮН каждая? Можно ли силу el Н разложить на две силы
по 100 Н и т. д.?
Возьмем силу в 1 Я и разложим ее по двум направле-
ниям, которые проведем под одинаковыми углами а к на-
правлению силы (рис. 33). Как уже было сказано, для это-
го надо через конец вектора силы провести линии, парал-
лельные этим направлениям. Выполнив это построение,
мы вместо одной силы будем иметь две. Рис. 33 показыва-
ет, что при увеличении угла а сила в 1 Н превращается
в две все большие и большие силы. В пределе, когда угол а
становится равным 90°, сила в 1 Н раскладывается на две
бесконечно большие силы. Таким образом, из одной силы
в 1 Н можно «сделать» две силы по 10 Н, по 100 Н и т. д.,
вообще две любые по величине силы; для этого надо толь-
ко соответствующим образом выбрать угол а. (Слова
70
«можно сделать» не надо понимать буквально. Они озна-
чают, что при помощи одной небольшой силы можно об-
разовать две какие угодно большие силы.)
Определить угол а можно так. Сначала выберем не-
который масштаб для изображения сил. Пусть, к приме-
ру, 1 см на чертеже соответствует силе в 1 Н. Нарисуем
отрезок АВ длиной 1 см и, отмерив циркулем на линейке
10 см, сделаем засечки, ставя одну из ножек циркуля в
концы сантиметрового отрезка АВ (рис. 34). Через точки
А, В и засечки проведем прямые линии, которые и опреде-
Рис 33. Силу в 1 Н можно разложить на две любые по величине силы
Рис. 34. Графический метод определения угла а
ляют искомые направления действия сил. Угол а измеря-
ется транспортиром. Его можно также вычислить, восполь-
зовавшись теоремой, которая позволяет найти сторону
треугольника через другие стороны и косинус противоле-
жащего угла: 102 = I2 + 102—2*1*10 X cos а. Из это-
го уравнения легко находится cos а, а затем при помощи
тригонометрических таблиц — угол ос.
Таким образом, из любой по величине силы (сила
в 1 Н была взята произвольно) «можно сделать» две ка-
кие угодно большие силы. Так утверждает теория. А так
ли это на самом деле, на практике, в жизни? Ответить на
этот вопрос пам поможет решение следующей задачи.
Уличный фонарь подвешен в точке В к середине троса
АВС, прикрепленного концами к столбам в точках А и С,
которые находятся на одной горизонтали (рис. 35). Мас-
са фонаря 15 кг. Длина всего троса АВС 20 м, а отклоне-
ние точки подвеса фонаря от горизонтали В К составляет
10 см. Пренебрегая массой троса, надо определить его на-
тяжение.
Так как на фонарь действует сила тяжести Р = mg,
трос растягивается. Строим параллелограмм сил. Полу-
71
лившиеся силы Т численно равны силе натяжения троса.
Из подобия заштрихованных треугольников следует, что
т Р-АВ 15-9,8.10	о-
1 "" 2ВК ~	2-0,1	~
т. е. натяжение троса равно 7350 Н. Это в 50 раз больше
веса фонаря! Понятно, что, чем меньше будет провис ВК,
тем больше натяжение троса.
На этом основано то, что ни один трос, провод, верев-
ку нельзя натянуть строго горизонтально — всегда будет
некоторый провис. Пусть даже на тросе ничего не висит,
но ведь он имеет собственный вес, который можно условно
приложить в середине. Получается тот же самый па-
раллелограмм сил. Если натягивать трос, то его провис
уменьшается, и, следовательно, натяжение возрастает.
Для того чтобы трос занял строго горизонтальное поло-
жение, нужно приложить бесконечно большие силы. Та-
ких сил нет в нашем распоряжении, но если бы мы даже
умели их получать, все равно ни один трос не выдержал
бы очень большого натяжения. Он лопнул бы прежде,
чем стал горизонтальным.
То,что провод нельзя натянуть строго горизонтально,—
вредное явление. Представьте себе, что строится высоко-
72
вольтная линия для передачи электроэнергии из одного
города в другой. Работа эта очень трудоемкая. Надо рас-
чистить просеку, подготовить фундаменты для опор, ус-
тановить ажурные металлические вышки, подвесить
«гирлянды» изоляторов, а к ним провода. Все это требу-
ет больших затрат, поэтому всегда хочется поставить как
можно меньше опор. Но, увеличивая расстояние между
опорами, мы тем самым увеличиваем провис проводов,
при этом возрастает вероятность их схлестывания под
действием ветра, что ведет к аварии. Вот инженерам и
приходится думать: с одной стороны, надо поставить как
можно меньше опор, чтобы не выбрасывать деньги на ве-
тер, а с другой стороны, если опор будет мало, тот же ве-
тер может столкнуть два провода и вызвать короткое за-
мыкание. Пока авария будет ликвидирована, пройдет не-
сколько часов, в течение которых целые промышленные
районы будут отключены от подачи электроэнергии. Это
нанесет значительный ущерб народному хозяйству.
Как было бы хорошо, если провод был бы невесомым.
Тогда его можно было бы натянуть строго горизонтально
при значительном расстоянии между опорами. (Очень да-
леко друг от друга опоры невозможно поставить из-за
кривизны Земли.) Но, к сожалению, этого нельзя сделать,
и проектировщикам приходится в каждом конкретном
случае рассчитывать оптимальное (наилучшее) расстоя-
ние между опорами.
А вот два примера положительного использования
свойств параллелограмма сил.
Буксировка корабля во время волнения на море —
очень сложное дело. Отбросит волной судно, туго натянет
трос, и он может лопнуть. Чтобы этого не случилось, на
трос вешают груз: якоря, тяжелые металлические бол-
ванки, цепи и т. п.
Зачем это делают, понятно. Висящий груз увеличивает
провис троса. Кроме того, висящий груз не позволяет тро-
су резко уменьшать свой провис при ударах волн. Это
предохраняет трос от обрыва.
Следующий пример был образно описан в одном поль-
ском научно-популярном журнале.
На глинистой дороге увяз автомобиль. Водитель и его
два товарища вышли из машины, печально посматривая
друг на друга. Человек, стоящий неподалеку, спросил:
— А трос у вас есть?
4 В. П. Лишевский
73
— Есть, а что толку-то? Ведь все равно тянуть неко-
му. Нас с вами только четверо, а тут и десять человек не
справятся. Впрочем, может быть, вы знаменитый силач? —
пошутил один из путешественников.
— Нет, я не силач. Просто знаю один способ.
— Не верю я в чудеса,— сказал водитель, доставая
трос.— Но если хотите, то пожалуйста...
Незнакомец привязал один конец троса к шасси авто-
мобиля, а второй — к придорожному дереву, предвари-
тельно натянув трос. Шофер и его товарищи недоверчиво
следили за работой незнакомца.
— Подойдите сюда,— сказал «чудотворец», указывая
на середину троса.— Теперь оттягивайте трос в какую-
нибудь сторону. Ну, раз, два — взяли!
Четверо сильных мужчин налегли на трос, и автомо-
биль заметно сдвинулся с места.
После этого они опять натянули трос и снова оттяну-
ли его в сторону. Автомобиль еще немного подался вперед,
а через пятнадцать минут уже стоял на ровном и сухом
месте.
— Вы шофер? — спросил водитель.
— Нет,— ответил незнакомец.— Я учитель физики
в здешней школе... (Рис. 36 объясняет, в чем здесь дело.)
То, что силы складываются и раскладываются по пра-
вилу параллелограмма, первым установил замечательный
голландский ученый и инженер Симон Стевин (1548—
1620). Сначала он был конторщиком у одного антверпен-
ского купца, потом много лет провел в далеких путешест-
виях, затем работал в Лейденском университете и, наконец,
состоял инспектором водных сооружений.
Стевипу принадлежит много замечательных открытий.
Он разработал основы гидростатики, изобрел десятичные
дроби, построил первый «автомобиль» (рис. 37). Правда,
он был парусный, но все равно казался современникам
чудом. Так как испытания проводились близ Гааги, то
жители назвали повозку Стевина «Гаагское чудо».
В. Лебедев в книге «Исторические опыты по физике»
пишет, что ветряная повозка Стевина развивала довольно
значительную скорость — до 34 км/ч. При первом испыта-
нии в экипаже сидели 28 человек. В своем устройстве по-
возка имела любопытную особенность. Ось задних колес
можно было поворачивать при помощи особого «руля»
и таким образом управлять повозкой.
74
Рис. 36. Так можно вытащить застрявший автомобиль
Рис. 37. Ветряная повозка Стевина (1600 г.)
4*
Немного другие данные о «ветряном автомобиле» Сте-
вина приводят П. Лакур и Я. Аппель в книге «Историче-
ская физика». Они сообщают, что во время испытания 18
человек за 2 часа проехали 4 голландские мили.
Несмотря на эти несколько отличающиеся сведения,
можно сделать вывод, что ветряная повозка Стевина была
действительно замечательным для своего времени инже-
нерным сооружением. Она мог-
ла двигаться даже против ветра.
Кстати, а каким образом па-
русные суда могут плыть против
ветра или, как говорят моряки,
идти в бейдевинд (от голланд-
ского bij de wind)? Объясне-
ние этому — опять-таки в парал-
лелограмме сил.
Строго говоря, плыть точно
навстречу ветру парусный ко-
рабль не может. Он способен
двигаться только под острым
углом к направлению ветра. Но
и такое движение на первый
взгляд кажется загадочным.
(Этот угол может составлять
Рис. 38. Силы, действующие на всего 22 .) Давайте разберемся,
парус (1) при встречном ветре В чем Тут Дело.
Сила давления ветра R
(рис. 38) раскладывается на две
силы. Одна из них Q не оказывает на парус никакого
действия (ветер просто скользит вдоль паруса), а вторая
сила Р давит на парус. Сила давления Р в свою очередь
тоже раскладывается на две силы. Одна из них Т стремит-
ся сдвинуть корабль вбок. Эта сила встречает сильное
сопротивление воды и гасится им. Вторая же сила S дви-
жет судно вперед. Она максимальна, когда парус распо-
ложен так, что делит точно пополам угол между направ-
лением ветра и направлением движения судна. Так парал-
лелограмм сил позволяет двигаться против ветра.
Двигаясь против ветра, буер может развить значитель-
ную скорость — более 100 км/ч. Абсолютный рекорд ско-
рости на буере, равный 225 км/ч, установил канадец Прайс.
Он воспользовался штормовой погодой, когда дул силь-
ный ураганный ветер.
76
Рис. 39. Построив параллелограмм сил, инженер видит, что нижнюю часть
стрелы подъемного крана надо крепить на упор, а верхнюю — на вырыв
Буера — это не только спорт. В 1921 г. они помогали
в подавлении Кронштадтского мятежа: провели ледовую
разведку и проложили дорогу для десанта. А в Великую
Отечественную войну буера были первым транспортом
на «Дороге жизни», проложенной по Ладожскому озеру.
Две недели под бомбежкой и обстрелом два десятка буе-
ров перевозили в осажденный Ленинград продовольствие,
медикаменты, почту. Это были большие буера грузоподъ-
емностью до полутора тонн. Управляли каждым буером
три человека.
Уметь строить параллелограмм сил должен каждый
инженер. Как, например, нужно крепить стрелу подъем-
ного крана? Построив параллелограмм сил, инженер сра-
зу видит, что нижнюю часть стрелы подъемного крана на-
до крепить на упор, а верхнюю — на вырыв (рис. 39).
Теперь несколько слов о паре сил.
Пусть есть две параллельные или антипараллельные
силы Р и Q (рис. 40), Равнодействующая двух таких сил
Рис. 40. Сложение двух парал-
лельных и двух антипараллель-
ных сил
77
равна или их сумме (в случае двух параллельных сил),
или их разности (когда силы антипараллельны): R = Р ±
±Q, а точка приложения равнодействующей делитрасстоя-
ние между линиями действия сил Р и Q в отношении
Р : а = Q : Ъ = R : I. Так складываются параллельные
и антипар аллельные силы.
Теперь представьте себе, что мы уменьшаем силу Р
(или, наоборот, увеличиваем силу Q) в случае антипарал-
лельных сил. Тогда равнодействующая уменьшается, а точ-
ка приложения ее отодвигается все дальше и дальше от
сил Р и Q. В пределе, когда сила Р становится равной си-
ле Q, равнодействующая обращается в нуль, а точка при-
ложения ее уходит в бесконечность.
Так получается математически. А что это означает фи-
зически? Опыт показывает, что, когда на тело действуют
две равные антипараллельные силы, приложенные к раз-
ным точкам тела (такая система сил называется парой),
тело вращается. Например, заворачивая гайку,ввинчивая
или вывинчивая шуруп, мы прикладываем пару сил
(рис. 41).
Когда имеются две неравные антипараллельные силы,
их можно свести к одной силе — равнодействующей,
которая действует так же, как две данные силы.
Как только силы Р и Q сравниваются, равнодействующая
исчезает. Получается пара сил, которая будет вращать
тело вокруг его центра масс.
Рис. 41. Завертывая гайку или вывинчивая шуруп из стены, мы приклады-
78
Действие пары сил на тело измеряется моментом, т. е.
произведением одной из сил, образующих пару, на плечо
(расстояние между линиями действия сил). Например,
на рис. 41 момент М равен Р1.
Вокруг какой точки вращает пара сил? Иногда счита-
ют, что пара сил вращает тело вокруг середины плеча.
Это неверно. Пара сил вращает тело вокруг его центра тя-
жести. В этом легко убедиться на опыте.
Рис. 42. Опыт, показывающий,
что пара сил вращает тело во-
круг его центра тяжести
Вырежьте из плотного картона фигуру произвольной
формы и определите, где у нее находится центр тяжести.
Для этого подвесьте фигуру последовательно за две раз-
личные точки и проведите через точки подвеса вертикаль-
ные линии. Пересечение их даст центр тяжести.
Привяжите теперь к двум любым точкам фигуры кус-
ки ниток, а на их концах укрепите два одинаковых грузи-
ка. Затем положите фигуру на гладкую поверхность и пре-
доставьте гирькам возможность свободно опускаться вниз
(рис. 42). Вы увидите, что фигура поворачивается вокруг
своего центра тяжести (точки С).
То, что пара сил вращает тело вокруг центра тяжести,
станет еще более очевидным, если одну из ниток при-
вязать в центре тяжести фигуры. Она по-прежнему будет
поворачиваться вокруг своего центра тяжести, создавая
впечатление, будто бы в этой точке вбит гвоздь, и фигура
вращается вокруг него под действием только одного гру-
за, а другой — не играет никакой роли.
79
ТРЕНИЕ
Полезно или вредно трение? Многие, не задумываясь, от-
вечают: «Конечно, вредно!» Но ведь, если бы не было тре-
ния, мы не могли бы ходить по земле (вспомните, как
скользят ноги на льду), нельзя было бы ездить на велоси-
педе, автомобиле, мотоцикле (колеса вертелись бы на мес-
те), нам нечего было бы носить (нитки в ткани держатся
силами трения). Если не было бы трения, вся мебель в
комнате сбилась бы в один угол, тарелки, стаканы и блюд-
ца соскальзывали бы со стола, гвозди и шурупы не держа-
лись бы в стене, ни одной вещи нельзя было бы удержать
в руках и т. д. и т. п. Известный швейцарский физик лау-
реат Нобелевской премии Ш. Гийом (1861—1938) писал:
«Вообразим, что трение может быть устранено совершенно.
Тогда никакие тела, будь они величиною с каменную глы-
бу или малы, как песчинка, никогда не удержатся одно
на другом: все будет скользить и катиться, пока не окажет-
ся на одном уровне. Не будь трения, Земля представляла
бы шар без неровностей, подобно жидкому». К этому мож-
но добавить, что если бы не было трения, неизвестно, как
пошло бы развитие цивилизации на Земле — ведь наши
предки добывали огонь трением.
Перечень подобных «ужасов» можно продолжать до
бесконечности, но и так ясно, что трение — явление от-
нюдь не вредное. Оно вредно только в машинах, и инже-
неры борются там с ним, применяя шарикоподшипники,
смазку и т. п.
Что же такое трение?
При перемещении одного тела по поверхности другого
всегда возникает сила, препятствующая движению. Она-
то и называется силой трения.
Трение — следствие многих причин, но основными
из них являются две. Во-первых, поверхности тел всегда
неровны, и зазубрины одной поверхности цепляются за
шероховатости другой. Это так называемое геометриче-
ское трение. (Даже самые гладкие на глаз поверхности
оказываются под микроскопом шероховатыми, с впадина-
ми и выступами.) Во-вторых, трущиеся тела очень близко
соприкасаются друг с другом, и на их движении сказыва-
ется взаимодействие молекул (молекулярное трение).
Опыт показывает, что для максимально возможных
значений силы трения справедлива формула F — kN. Она
80
читается так: сила трения пропорциональна силе нормаль-
ного давления. Коэффициент пропорциональности к на-
зывается коэффициентом трения.
Можно проверить на опыте, что сила трения зависит
только от качестве трущихся поверхностей и силы нор-
мального давления, а от площади соприкосновения не
зависит. Если положить деревянный брусок на книгу сна-
чала плашмя, а затем ребром (узкой стороной) и подни-
Рис. 43. Брусок начинает сколь-
зить вниз всегда при одном и
том же значении угла а. Это го-
ворит о том, что коэффициент
трения не зависит от площади
соприкосновения тел
мать один конец книги, то брусок начинает скользить
вниз практически всегда при одном и том же значении
угла а (рис. 43). Это говорит о том, что сила трения не
зависит от площади контакта.
Вместо бруска можно взять спичечный коробок, в ко-
торый для тяжести насыпан песок. Только спичечный
коробок надо вначале обязательно обклеить бумагой,
чтобы все стороны коробка были одинаковы в смысле
трения.
Коэффициент трения определяют так. Замеряют дина-
мометром силу, необходимую для перемещения одного
тела по поверхности другого, и делят полученное значе-
ние силы на вес тела. Найденные коэффициенты вносят
в справочники по физике. Если вам для решения той или
иной практической задачи понадобится величина коэффи-
циента трения, ее можно взять из таблицы. Нужно только
помнить, что приведенные там значения коэффициентов
трения приблизительные. Ведь трущиеся поверхности,
как правило, загрязнены. На них бывает ржавчина, окис-
лы и другие посторонние включения, что, естественно,
влияет на величину трения. Так как степень загрязнения
поверхностей при опытном определении коэффициента
81
трения точно неизвестна, то, строго говоря, нам неизвест-
но, что же за коэффициент трения мы получили. Скажем,
указанный в справочнике коэффициент трения меди по
меди — на самом деле не коэффициент трения между дву-
мя медными поверхностями, а коэффициент трения при
наличии каких-то загрязнений, имеющихся на меди.
Теперь познакомимся с конусом трения.
Пусть тело массы т движется под действием силы Т
по шероховатой поверхности (рис. 44). С одной стороны,
Рис. 44. Конус трения
Рис. 45. Явление самоторможения
поверхность не позволяет телу падать вниз под действием
силы тяжести Р = mg. С другой стороны, поверхность
мешает свободному перемещению тела под действием си-
лы Т.
Таким образом, сила трения так же, как и нормаль-
ная реакция, вызвана к жизни поверхностью, т. е. сила
трения — это тоже реакция. Нормальная реакция и сила
трения складываются в полную реакцию /?, которая от-
клонена от нормалина угол <р. Этот угол называется углом
трения. С помощью рис. 44 легко вычислить, чему равен
тангенс угла трения: tg ср = F/N = kN IN ~ к, т. е. тан-
генс угла трения численно равен коэффициенту трения.
Теперь представьте себе, что вы вращаете вектор пол-
ной реакции вокруг нормали к поверхности. В этом слу-
чае сила R описывает конус, который называется конусом
трения. Он интересен тем, что область, ограниченная ко-
нусом трения, определяет область равновесия для тела:
если линия действия силы проходит внутри конуса трения,
сила не сдвинет тело, как бы велика ни была; если же ли-
82
ния действия силы расположена вне конуса трения, сила
сдвигает тело, как бы мала ни была.
Пусть сила Q (рис. 45) действует внутри конуса трения.
Она стремится сдвинуть тело влево, а сила трения F дер-
жит (не пускает) тело. «Запас торможения» F— Qr — kN-^
— Q sin a = tg cp Q cos a — Q sin a = Q sin (cp — <z)/cos cp.
Величины ср и a постоянны. Следовательно, «запас тор-
можения» прямо пропорционален Q. Чем сильнее сила Q
давит на тело, тем больше сила F — препятствующая
движению. Это явление называется самоторможением.
Конус трения построить очень просто. Пусть, напри-
мер, нам надо построить конус трения для стального стерж-
ня, опирающегося на чугунную плиту. Смотрим в справоч-
ник и находим коэффициент трения для стали по чугуну.
Он равен 0,16. Следовательно, надо построить конус,
в котором образующая была бы наклонена к нормали под
углом 9°, так как тангенс 9° примерно равен 0,16 (tg 9° =
= 0,1584). Понятно, что чем больше коэффициент трения,
тем больше угол в конусе трения, и наоборот.
Инженерам часто приходится строить конус трения,
чтобы определить, будет ли находиться в равновесии дан-
ная конструкция или нет. Но с конусом трения имеют де-
ло не одни только инженеры. Каждый из нас ежедневно
сталкивается с этим физическим явлением.
Чтобы пробраться к выходу в переполненном автобу-
се или троллейбусе, приходится «извиваться ужом». Де-
лаем мы это бессознательно, не задумываясь, что таким
образом мы выходим из конусов трения в местах касания
с другими пассажирами.
Катаемся ли мы на коньках, идем ли на работу, пере-
ворачиваем ли страницу в книге — всюду мы сталкиваем-
ся с трением, и в частности с конусом трения.
Рассказывая о трении, нельзя не упомянуть о формуле,
которая носит имя известного математика и механика Лео-
нарда Эйлера (1707—1783)г
Видели ли вы, как сдерживают ход корабля, подошед-
шего к пристани? С парохода на пристань бросают канат,
на конце которого сделана широкая петля. Человек, стоя-
щий на пристани, надевает петлю на причальную тумбу,
а матрос на корабле быстро укладывает канат между кнех-
тами (так называются небольшие тумбы, укрепленные
на борту судна). Сила трения между канатом и кнехтами
останавливает движение судна.
83
Неужели сила трения в этом случае так велика?
Представьте себе, что вы поднимаете из шахты груз при
помощи веревки, переброшенной через неподвижно за-
крепленный блок (рис. 46). Если бы трение отсутствовало,
то, поднимая груз, пришлось бы прикладывать силу, в
точности равную весу поднимаемого груза. Но так как меж-
ду веревкой и блоком существует трение, то, чтобы поднять
груз массы тп, придется приложить силу Т mg. Сила
Рис. 46. Сила Г, необходимая
для поднятия груза Р, вычис-
ляется по формуле Эйлера
Т, необходимая для поднятия груза, вычисляется по фор-
муле Эйлера: Т = mge^. Здесь е — основание натураль-
ных логарифмов, к — коэффициент трения, а ф — угол ох-
вата блока веревкой, выраженный в радианах.
Давайте подсчитаем, какую силу надо приложить, что-
бы удержать корабль у пристани.
Пусть движущийся корабль тянет канат с силой
100 кН. Коэффициент трения каната о железную тумбу
известен. Он равен 0,35. Предположим, что матрос обер-
нул канат вокруг тумбы три раза. Тогда угол охвата тум-
бы канатом ср = 3-2л = 6л. Подставив значения Т, к
и ср в формулу Эйлера, получим
__ Т __	100 000 и
откуда найдем силу F. Она равняется примерно 150 Н.
Следовательно, чтобы сдержать бег судна, матрос должен
удерживать канат всего с силой в 150 Н. Обычно матрос,
обернув канат несколько раз вокруг кнехтов, просто при-
держивает свободный конец каната ногой, прижимая его
к палубе.
Итак, если корабль тянет с силой в 100 кН, матросу
достаточно приложить силу в 150 Н, чтобы остановить
84
движущееся судно (при условии, что канат три раза обер-
нут вокруг тумбы). Остальные 99850 Н гасятся силой тре-
ния!
Приведенный расчет показывает, какие значительные
силы трения развиваются между канатом и кнехтами при
швартовке. Раньше, когда причальные тумбы делались
из дерева, они, нагреваясь, иногда даже начинали дымить-
ся. По этой причине причальные тумбы называли еще ог-
нивами. Чтобы во время швартовки огнива не загорались,
их обливали холодной водой.
В романе Жюля Верна «Матиас Шандор» выведен си-
лач Матифу. Он совершает много подвигов, среди которых
есть такой. Готовился спуск на воду трабаколо — неболь-
шого судна с двумя мачтами и парусами трапециевидной
формы. Плотники начали выбивать из-под киля клинья,
удерживающие трабаколо на спусковой дорожке. В этот
момент в гавань влетела нарядная яхта. Плотники пре-
кратили свою работу, чтобы дать возможность яхте без по-
мех пройти мимо места спуска трабаколо, но оно неожи-
данно заскользило по спусковой дорожке в воду. Трабако-
ло неминуемо должно было врезаться в борт плывущей
мимо верфи яхты.
«Вдруг из толпы зрителей выскакивает какой-то чело-
век. Он хватает трос, висящий на носу трабаколо. Но тщет-
но старается он, упираясь в землю ногами, удержать трос
в руках. Его не страшит мысль, что трабаколо может ув-
лечь его за собою. Поблизости врыта в землю швартовая
пушка. В мгновение ока неизвестный набрасывает на нее
трос, который начинает медленно разматываться, а храб-
рец, рискуя попасть под него и быть раздавленным, сдер-
живает его со сверхчеловеческой силой. Это длится секунд
десять. Наконец трос лопнул. Но этих десяти секунд
оказалось достаточно. Трабаколо... прошло за кормой
яхты на расстоянии не более фута...
Яхта была спасена.
А неизвестный, которому никто не успел помочь,—
до того неожиданным оказался его поступок — был не
кто иной, как Матифу».
Жюль Верн, видимо, не был знаком с формулой Эйле-
ра. Иначе он понял бы, что эпизод с трабаколо не может
свидетельствовать о силе Матифу. Ведь если канат был
обернут несколько раз вокруг швартовой пушки, то удер-
жать трабаколо мог даже ребенок.
85
Каждый из нас по крайней мере раз в день пользуется
формулой Эйлера. Происходит это тогда, когда мы завя-
зываем шнурки на ботинках. Ведь что такое узел, как не
веревка, обвитая вокруг другой части той же веревки?
И крепость узла тем больше, чем больше изгибов делает
шнурок в узле.
Теперь, когда мы познакомились с трением, решим
несколько задач, иллюстрирующих это физическое яв-
Н—ь —я
Рис. 47. Определение высоты
ручки двери, отодвигающейся
вбок
ление.
На какой высоте h нужно
поставить ручку двери купе
вагона, чтобы при отодвигании
двери вбок ее не заклинивало?
Ширина двери 0,8 м, коэффи-
циент трения 0,5.
Посмотрим, какие силы дей-
ствуют на дверь. Если мы по-
тянем за ручку вправо с силой
Т, дверь может начать враща-
ться вокруг точки А, где будут
действовать сила нормального
давления 7V, численно равная
весу двери Р, и сила трения
kN (рис. 47). Дверь упрется точ-
кой В в верхний паз, и про-
изойдет заклинивание: теперь
уже никакая сила ее не от-
кроет.
Чтобы дверь можно было отодвинуть в сторону,
необходимо, чтобы момент силы Р относительно точки А
был больше или в крайнем случае равен моменту, соз-
даваемому силой Т. Напомним, что момент силы равен
произведению силы на плечо, т. е. расстояние от точки,
относительно которой вычисляется момент, до линии дей-
ствия силы. Математически это условие записывается
так: PU2 Th. Так как сила Т должна быть несколько
больше силы трения, а сила нормальной реакции равна
весу, то PU2 > kPh, откуда h U2k. Таким образом,
ручку двери можно ставить на высоте, не превышающей
ширину двери, деленную на удвоенный коэффициент
трения. В нашей задаче h 0,8/(2-0,5) = 0,8 м.
Если вы будете делать в своей квартире раздвижные
двери, то помните о только что решенной задаче. Иначе
86
вы можете укрепить ручку на такой высоте, что дверь не
будет открываться.
Какой длины нужно взять веревку, чтобы усилие, не-
обходимое для перемещения санок, было наименьшим?
Пусть груз массы т движется под действием силы Q
по шероховатой горизонтальной поверхности (рис. 48).
Если движение равномерное, то это означает, что все си-
лы, действующие на тело, взаимно уравновешиваются,
Рис. 48. tga = к — условие, не-
обходимое для того, чтобы уси-
лие при перемещении груза было
наименьшим
т. е. геометрическая сумма всех сил в данном случае рав-
на нулю.
Спроектируем все силы на горизонтальное и верти-
кальное направления. Получим два уравнения: Q cos а —
— kN — О и N + Q sin а — Р — 0, где Р = mg. Из
первого уравнения найдем, что нормальная реакция
TV — c°sa Подставив это значение во второе уравнение
и заменив к на tg ср, получим
Q СО ЗСС I z~i •	о
-4------k Q since = Р.
tgcp 4
Отсюда, выполнив простейшие тригонометрические пре-
образования, определим силу Q : Q — (ц^ср) ’ ®°РмУла
показывает, что сила Q минимальна, если cos (a — ср)
максимален, т. е. равен единице, а, следовательно, а =
= <р. Иначе говоря, веревка должна быть наклонена
к горизонтали под углом трения. Зная значение угла тре-
ния и высоту а до вашей руки от поверхности земли, не-
трудно вычислить оптимальную длину веревки, решив
обыкновенный прямоугольный треугольник, в котором
известен катет и противолежащий ему угол: I = a/sin ср,
где ср — угол трения.
87
Если по наклонным доскам втаскивается груз в кузов
автомобиля, то доски тоже должны составлять с горизон-
том угол, равный углу трения. В этом случае усилие,
необходимое для перемещения груза, будет минимальным.
В заключение — немного о трении качения. Так назы-
вают сопротивление, которое испытывает катящееся коле-
со. Трение качения обусловлено тем, что колесу прихо-
дится все время взбираться на небольшой бугорок, обра-
зующийся перед движущимся колесом, которое несколько
Рис. 49. При торможении сколь-
жением (1) автомобиль до оста-
новки пройдет бблыпий путь,
чем при торможении качением {2}
вдавливается в полотно дороги. Чем дорога тверже, тем
сопротивление качению меньше. Поэтому автомобильные
и мотоциклетные заезды на побитие мировых рекордов
скорости проводят обычно по дну высохших соленых озер,
которые обладают очень твердой поверхностью. Так, на-
пример, абсолютный рекорд скорости 1001,253 км/ч был
установлен американским гонщиком Гарри Габеличем
на треке высохшего соленого озера Бонневилл в США.
(Рекорд скорости на грузовике составляет 212 км/ч, а на
мотоцикле — 487,74 км/ч.)
В гонках участвует далеко не каждый, а вот ездить на
автомобиле, мотоцикле, велосипеде приходится очень
многим. Как лучше тормозить, если перед вами возника-
ет препятствие? На поставленный вопрос отвечает график,
изображенный на рис. 49. Если вы тормозите скольжением
(так называемый юз), то тормозной путь будет длиннее,
чем при торможении качением (колеса заторможены, но
поворачиваются). Зато при торможении скольжением
скорость вначале падает более резко. Поэтому при опас-
ности наезда надо всегда тормозить юзом. Лучше ударить
88
с меньшей скоростью, так как энергия удара пропорцио-
нальна квадрату скорости. Во всех остальных случаях
надо тормозить качением: и тормозной путь будет короче,
и шины меньше изнашиваются.
ЗАДАЧИ НА РАВНОВЕСИЕ
Давайте посмотрим на конкретных примерах, как реша-
ются задачи на равновесие тела, если на него действует
плоская система сил, т. е. такая система сил, линии дей-
ствия которых расположены в одной плоскости.
Пусть нам надо решить такую задачу.
Однородная балка АВ массой 60 кг и длиной 4 м опира-
ется одним концом на гладкий пол, а некоторой промежу-
точной точкой С — на выступ высотой 3 м, образуя с вер-
тикалью угол а — 30° (рис. 50). Балка удерживается
в таком положении веревкой АК, протянутой по полу и
привязанной в точке К. Пренебрегая трением, определите
натяжение веревки Т и реакции пола Rr и выступа R2-
Нарисуем вначале все силы, действующие на балку.
На нее действует, во-первых, сила тяжести Р = mg. Так
как балка однородная, сила Р приложена в середине бал-
ки и направлена вертикально вниз. В точках А и С балка
опирается на гладкие пол и выступ. Если тело опирается
на гладкую поверхность, возникает реакция, перпенди-
Рис. 50. Задача о равновесии балки
89
кулярная этой поверхности; если балка опирается на выс-
туп («угол»), возникает реакция, перпендикулярная бал-
ке. Пользуясь этими правилами, рисуем реакции в точках
А и С. Наконец, в точке А на балку действует сила реак-
ции веревки. Если веревку перерезать, то конец А бал-
ки начнет двигаться вправо, т. е. сила реакции верев-
ки Т удерживает конец А от движения вправо.
Итак, балка АВ находится в равновесии под действи-
ем четырех сил: силы тяжести Р, реакции веревки Г,
реакции пола R± и реакции выступа Н2. Все эти силы рас-
положены в одной плоскости (плоскости чертежа), т. е.
образуют плоскую систему сил. Так как балка находится
в равновесии, то, следовательно, все силы, действую-
щие .на балку, и все моменты, образуемые этими силами,
взаимно уравновешиваются. Иначе говоря, если тело на-
ходится в равновесии под действием плоской системы сил,
то выполняются три условия равновесия: суммы проек-
ций всех сил на два взаимно перпендикулярных направ-
ления равны нулю, и сумма моментов всех сил относитель-
но любой произвольной точки тоже равна нулю. Записав
эти три условия равновесия, мы решим задачу.
Спроектируем все силы на горизонтальное направле-
ние — ось х. Силам, проектирующимся стрелочкой впра-
во, приписываем знак «плюс», влево — знак «минус». Мы
видим, что силы Р и Rr на ось х не проектируются (проек-
тируются в точку), сила реакции веревки Т проектиру-
ется на горизонтальное направление в натуральную вели-
чину, но со знаком «минус» (стрелочкой влево), а проек-
ция силы Т?2 на ось х положительна (направлена вправо)
и по величине равна Т?2 cos Таким образом, первое
уравнение записывается так: —Т + Т?2 cos а = 0.
Теперь спроектируем все силы на вертикальное на-
правление — ось у. Силам, проектирующимся стрелочкой
вверх, приписываем знак «плюс», вниз — знак «минус».
Сила реакции Т на ось у не проектируется, сила Rr
проектируется в натуральную величину со знаком «плюс»,
сила тяжести Р — в натуральную величину, но со
знаком «минус», а проекция Т?2 на вертикаль положи-
тельна и равна /?2 sin а. Второе уравнение: R± — Р +
+ R2 sin а = 0.
Наконец, запишем последнее уравнение — уравнение
моментов. Моментом силы относительно некоторой точки
называется произведение силы на плечо — расстояние от
90
данной точки до линии действия силы. Если сила вращает
вокруг точки против часовой стрелки, момент считается
положительным, по часовой стрелке — отрицательным.
Направление вращения определяется следующим обра-
зом. Ставят мысленно одну ножку циркуля в ту точку,
относительно которой вычисляется момент, а другую —
на линию действия силы и начинают поворачивать цир-
куль вокруг точки в ту сторону, в которую указывает
стрелочка силы. Направление вращения циркуля показы-
вает, по или против часовой стрелки вращает сила.
Вернемся к задаче и вычислим моменты всех сил отно-
сительно какой-нибудь точки, скажем точки А. Прирав-
няв нулю сумму моментов всех сил, действующих на бал-
ку, вычисленных относительно точки А, мы получим пос-
леднее, третье уравнение.
Относительно точки А силы и Т моментов не дают,
так как проходят через эту точку (плечо равно нулю). Си-
ла Р дает положительный момент, величина которо-
го равна Р (А5/2) sin а, а сила Т?2 дает относительно точ-
ки А отрицательный момент, величина которого
равна R2KC/zos ос. Итак, последнее уравнение:
л АВ .	D КС р.
Р —х—since — R2------= 0.
2	z cosa
Таким образом, мы получили систему трех уравнений
с тремя неизвестными:
— Т -f- Т?2 cosa = 0,
Ri — Р + Rz sina = 0,
тэ АВ . D КС л
Р —х— since — R2-----= 0.
2	6 cosa
Из последнего уравнения — уравнения моментов —
находим реакцию выступа R2 = 169 Н. Подставив значе-
ние Т?2 в первое уравнение системы, получим, что Т =
= 147 Н. Сила натяжения веревки численно равна силе Т и
направлена в противоположную ей сторону. Наконец, из
второго уравнения системы определяем R± = 503 Н.
Решим еще одну задачу.
Однородный стержень АВ массой т = 100 кг опирает-
ся одним своим концом на гладкий горизонтальный пол,
а другим — на гладкую плоскость, наклоненную под уг-
лом 30° к горизонту (рис. 51). Конец В стержня поддержи-
91
вается веревкой, перекинутой через блок С и несущей груз
массой М. Часть веревки ВС параллельна наклонной плос-
кости. Пренебрегая трением на блоке, определите массу
груза М и реакции пола Rr и наклонной плоскости R2.
Вначале расставим силы. Сила тяжести Р = mg при-
ложена в середине (стержень однородный) и направлена
вертикально вниз. В точках А и В стержень опирается
на гладкие поверхности, следовательно, в точках возни-
кают реакции, перпендикулярные к поверхностям: Rx
и Т?2- И, наконец, груз, стремясь опуститься, тянет конец
В стержня вдоль наклонной плоскости вверх, т. е. на точ-
ку В действует сила Q = Mg. Итак, на стержень АВ
действуют четыре силы: Р, Р2 и Q-
Так как стержень находится в равновесии, выполня-
ются три уравнения равновесия. Первые два — суммы
проекций всех сил на оси х и у — запишутся так:
R2 cos 60° — Q cos 30° = 0 и R2 sin 60° + Q sin 30° —
- P + R, = 0.
Осталось написать последнее уравнение — уравнение
моментов. Обычно точку для вычисления моментов сил
выбирают таким образом, чтобы через нее проходило как
можно больше неизвестных сил. Тогда уравнение полу-
Рис. 51. Стержень удерживается в равновесии грузом ЛГ
92
чается наиболее простым, так как силы, проходящие че-
рез точку, моментов относительно нее не дают. В рас-
сматриваемой задаче такой «удобной» точкой является
точка В. Если ввести угол а — угол между стержнем и
горизонтальной плоскостью, то уравнение моментов всех
сил относительно точки В примет следующий вид:
АВ
2?i АВ cosa — Р —g- cosa = 0. Отсюда, разделив обе ча-
сти уравнения на АВ cos ос, найдем, что = Z72 = 490 Н.
Рис. 52. Задача о лестнице
Затем из первых двух уравнений вычислим: Q = 245 Н,
М = Q/g = 25 кг, а R2 = 424 Н.
И, наконец, последняя задача на три уравнения рав-
новесия.
Под каким углом к стене надо поставить лестницу
массы т, чтобы по ней мог подняться до самого верха че-
ловек, масса которого М? Стена гладкая. Коэффициент
трения лестницы о пол равен к.
Нарисуем все силы, действующие на лестницу (рис. 52).
Это, во-первых, сила тяжести Р = mg. Будем считать,
что она приложена в середине АВ и направлена верти-
кально вниз. К точке А лестницы будет приложена сила
веса человека Q (так как человек должен подняться до
самого верха лестницы). Она равна Mg.
Если тело опирается на гладкую поверхность, то всегда
возникает реакция, перпендикулярная этой гладкой
поверхности. Поэтому в точке А будет действовать сила
реакции R, перпендикулярная стене. Если бы в точке В
лестница опиралась на гладкий пол, то там возникла бы
одна нормальная реакция N. Но так как пол негладкий,
то в точке В на лестницу действует еще сила трения
F = kN.
93
Итак, лестница находится в равновесии под действи-
ем пяти сил: силы тяжести человека (?, силы тяжести стерж-
ня Р, нормальных реакций R и N и силы трения F.
Запишем три уравнения равновесия. Спроектировав
все силы на оси х и z/, мы получим, что R — kN = 0 и
N — Р — Q = 0. Сумму моментов всех сил вычислим от-
носительно точки В:
д R
Q АВ sina + Р —since — РАВ cosa = 0.
Рис. 53. Шарик, висящий на
нитке
Теперь решим эту систему трех уравнений с тремя не-
известными. Сначала из второ-
го уравнения найдем нормаль-
ную реакцию: N = Р + Q. За-
тем из первого уравнения вы-
числим R: R = kN = к (Р +
+ Q). Наконец, из последнего
уравнения (уравнения момен-
тов) определим, что
etgee =
== Р + 2Q _ т + 2М
~~~2k(P + Q) — 2к(т + М) ’
Пусть, например, масса ле-
стницы 10 кг, масса человека
70 кг, а коэффициент трения
лестницы о пол равен 0,5.
Тогда etg а = 1,87. Если по-
смотреть в таблицу, то увидим,
что такому значению котангенса соответствует угол.при-
близительно 28°. Следовательно, если поставить лест-
ницу под углом, несколько меньшим расчетного, то она
будет находиться в равновесии, даже если по ней под-
няться до самого верха.
Как видите, решать задачи на равновесие при помо-
щи трех уравнений просто. Единственная трудность, с
которой здесь можно встретиться,— это сложность вычи-
сления плеч. Но человек, знакомый с математикой, спра-
вится с ней без труда.
Мы познакомились с тем, как решаются задачи на рав-
новесие, когда на тело действует любая плоская система
сил. Их может быть 10, 100, 1000 и т. д. А если на тело
действуют только три силы? Тогда задачи на равновесие
94
можно решать при помощи треугольника сил. Как это
делается, покажем на конкретных примерах.
К вертикальной гладкой стене АВ подвешен однород-
ный шар массы т (рис. 53). Веревка АС составляет со сте-
ной угол а. Определите натяжение веревки Т и силу Q,
реакции стены.
Кроме сил Q и Т, на шар действует сила тяжести Р =
= mg. Сумма этих трех сил должна быть равна нулю. Сле-
довательно, равнодействующая R сил Р и Q должна быть
равна —Т.
Из любого из прямоугольных треугольников, состав-
ляющих параллелограмм сил, следует, что Q — Plga,
а Г = P/cos а.
Электрическая лампа массой 2 кг подвешена к потол-
ку на шнуре АВ, а затем оттянута к стене веревкой ВС
(рис. 54). Определите натяжение Тг шнура АВ и ве-
ревки ВС, если известно, что угол а = 60°, а угол [3 = 135°.
Массами шнура и веревки пренебречь.
Висящая лампа растягивает шнур и веревку. Силу
тяжести Р = mg, действующую на лампу, можно разло-
жить на две составляющие 7\ и 72, которые равны по
величине силам натяжения шнура и веревки. Треуголь-
ники, из которых состоит параллелограмм сил, не примо-
рие. 54. Электрическая лампа, висящая на шнуре и веревке
95
угольные. В этом случае для решения задачи применяет-
ся «теорема синусов»: стороны в треугольнике относятся
так же, как синусы противоположных углов. Применяя
данную теорему, получим
р
sin 45°	sin 30° sin 105°
Отсюда следует, что Тх = —= 14,3 Н, а Т2 —
= 10,2 Н.
Груз массы m поддерживается двумя шнурами, пере-
кинутыми через блоки в точках А и В. На концах шнуров
висят грузы с массами тг и т2 (рис. 55). Определите углы
а и |3 при равновесии.
Построим параллелограмм сил и воспользуемся из-
вестной из тригонометрии теоремой о стороне, лежащей
против острого угла: Q2 = Р2 + Т2 — 2РТ cos а, где
Q = Т = m2g и Р = mg. Отсюда
Р* _ Q2
cosa =----2рг 
Аналогично
Р2 + Q2 __ Т2
cosp = ----L ------
2PQ
о 2	2
т^ -j- m2 —• mi
2т т2
2 I 2	2
т* + ^2 — т\
2т тг
Однородный стержень АВ прикреплен к вертикальной
стене посредством шарнира А и удерживается под углом
60° к вертикали при помощи веревки ВС, образующей с ним
угол 30° (рис. 56). Определите величину и направление ре-
акции В шарнира, если известно, что масса стержня
равна 2 кг.
96
Нарисуем все силы, действующие на стержень. Сила
тяжести приложена в середине (стержень однородный)
и направлена вертикально вниз. Конец В стержня поддер-
живается веревкой, следовательно, к точке В приложена
сила реакции веревки Т, Как направлена реакция в
шарнире, сразу сказать нельзя, но известно, что если тело
находится в равновесии под действием трех сил, то ли-
нии действия их обязательно пересекаются в одной точке.
Поэтому находим точку пересе-
чения линий действия сил Р и
Т и реакцию В в шарнире на-
правляем так, чтобы ее линия
действия также проходила че
рез эту точку К.
Так как стержень находится
в равновесии, силы Р, Т и В
обязательно образуют замкну-
тый треугольник. Самое трудное
в подобных задачах — опреде-
лить, чему равны углы в этом
треугольнике. Когда углы най-
дены, дальнейшее просто: за-
дача решается при помощи про-
стейших геометрических или
тригонометрических соотноше-
ний.
Попробуем определить углы
в получившемся треугольнике.
Сначала определим угол между
силами Р и Т. Обозначим его а. Так как угол 1 (см.
рис. 56) равен 60°, то угол 2 равен 30°. Сумма углов 2 и 3
равна 60°, следовательно, угол 4 равен 30°, и поэтому
угол а тоже равен 30°.
Теперь определим угол |3 — угол между силами Т и
R. Так как угол 3 равен углу 4, то треугольник АВС рав-
нобедренный. Линия действия силы Р проходит через се-
редину стороны АВ параллельно стороне АС, поэтому
точка К — середина стороны ВС, т. е. линия АК — ме-
диана. Но медиана, проведенная на основание в равно-
бедренном треугольнике, является вместе с тем биссект-
рисой и высотой, поэтому угол (3 равен 90°, т. е. треу-
гольник, образованный силами Р, Т и R, прямоуголь-
ный.
Рис. 56. Определение реакции
в шарнире
97
Таким образом, реакция шарнира R = Р sin 30° =
= 9,8 Н, а направление ее можно указать при помощи
угла САК. который равен 60°.
Так решаются задачи на равновесие при помощи тре-
угольника сил.
ПРОСТРАНСТВЕННАЯ СТАТИКА
В этом разделе механики изучается равновесие тела, ког-
да силы, действующие на него, расположены как угодно
в пространстве. В этом случае для равновесия тела необхо-
димо и достаточно, чтобы суммы проекций всех сил, дей-
ствующих на него, на оси координат х. у. z равнялись
нулю и суммы моментов всех сил относительно трех ко-
ординатных осей х. у. z также равнялись нулю, т. е. для
равновесия тела, находящегося под действием произволь-
ной пространственной системы сил, необходимо и доста-
точно выполнение шести уравнений (условий) равновесия:
Ж = 0,	Зтж(/?) = 0,
Efy = o,	S^(f) = o,
3Fz==0,	3/nz(F) = 0.
Что такое момент силы относительно оси? Ответ на этот
вопрос дает рис. 57. Ясно, что сила Fr будет вращать те-
ло вокруг оси, а сила F2 не будет. Таким образом, чтобы
вычислить момент силы относительно оси, надо вначале
спроектировать силу на плоскость, перпендикулярную
оси, а затем взять момент этой проекции относительно
98
точки пересечения оси с плоскостью проекций. (Как вычис-
ляется момент силы относительно точки, было рассказано
и показано ранее.)
Давайте решим такую задачу.
Однородная горизонтальная прямоугольная пластинка
ABCD со сторонами а и Ъ и массы т лежит на трех то-
чечных опорах в вершинах прямоугольника А и В и некото-
рой точке Е. Давления на опоры в точках А и В соответ-
ственно равны mg/^ и mg/b. Найдите давление на опору
в точке Е и координаты этой точки.
Рис. 58. Задача о
с тремя опорами
Пластинка находится в равновесии под действием че-
тырех сил: силы тяжести Р = mg и реакций 7V1, TV2, Nz
в точках А, В и Е (рис. 58). Спроектируем все силы на вер-
тикаль — ось z. Получим N\ + N2 + N3 — Р = 0. Из
этого уравнения можно вычислить, чему равно давление
Р Р 11
на опору в точке Е\ N3 = Р----------Р .
Чтобы найти координаты х и у точки Е, надо написать
уравнения моментов всех сил относительно осей х и у.
Относительно оси у реакции N\ и N2 моментов не дают как
силы, проходящие через ось (плечо равно нулю). Поэтому
уравнение моментов относительно оси у запишется так:
Nzx — Ра/2 = 0. Отсюда координата х точки Е равна
10а/11. Составив уравнение моментов всех сил относитель-
но оси х\ N2b + 7V3y — РЪ/2 = 0, мы найдем координату
у точки Е: у — 6/п&.
Для решения этой задачи потребовалось записать все-
го три условия равновесия. В общем же случае для реше-
ния задач пространственной статики приходится писать
шесть уравнений равновесия: три уравнения проекций и
три уравнения моментов.
99
ЦЕНТР ТЯЖЕСТИ
В рассказе о паре сил было показано, как можно просто
найти центр тяжести плоской фигуры. Но его можно вы-
числить и математически. Особенно легко это сделать,
если плоская фигура может быть представлена как сумма
или разность простейших геометрических образов: тре-
угольников, прямоугольников и т. п. Делается это при
помощи так называемого метода площадей. Познакомим-
ся с ним на конкретных примерах.
Рис. 59. Нахождение центра тяжести уголка
Рис. 60. Вычисление центра тяжести диска с отверстием
Пусть нам надо найти центр тяжести однородного
уголка, размеры которого указаны на чертеже (рис. 59).
Разобьем уголок OABCDE линией КС на два прямоуголь-
ника: OKDE и КАВС. Тогда координата хс центра тяже-
сти уголка найдется по следующей формуле:
т	Х1 ^2^2
^1 + У2 •
Здесь и 52 — площади прямоугольников КАВС и
OKDE, а и х2 — координаты их центров тяжести, от-
считываемые по оси х. Получим
_ (Ь —d) d d/2 + ad a/2   a2 bd — d2
(b — d) d + ad	2 (a b — d) '
100
Чтобы найти координату Центра тяЖестй уголка по
вертикали, удобнее разбить уголок на два прямоугольни-
ка: ОАВМ и С MED, проведя вертикальную линию СМ:
Ъ2 + ad — d2
Ус = 2(а + 6 —d) •
В следующей задаче плоское тело представляет собой
не сумму простейших геометрических фигур, а их раз-
ность (рис. 60). Имеющийся диск с отверстием получился
как бы в результате того, что из круга радиуса R вырезали
круг радиуса г, В этом случае в формулах для вычисления
центра тяжести вместо знака «плюс» надо поставить знак
«минус» (площадь полости считается отрицательной).
Понятно, что имеющееся тело (диск с отверстием) сим-
метрично относительно оси х, поэтому вертикальную ко-
ординату центра тяжести вычислять не надо: ус = 0.
Вычислим координату центра тяжести по оси х:
— ^2 х2 nR2O— лг2И/2	Rr2
Хс ~	Sx — S2	=	л Я2 - л г2	=	2 (Я2 —г2) ’
Получившийся знак «минус» показывает, что центр тя-
жести диска с отверстием смещен влево от точки О (начала
координат) на величину хс.
Если тело не плоское, а имеет произвольную форму,
то, для того чтобы найти его центр тяжести, оно разби-
вается на такие геометрические тела, у которых располо-
жение центров тяжести известно, а затем применяется так
называемый метод объемов. Он аналогичен методу площа-
дей, только в формулах для вычисления координат центра
тяжести вместо площадей Sx, S2, 83, . . . стоят объемы Уг,
У2, У3, . . . Естественно, что для объемного тела надо
найти не две координаты центра тяжести, а три — хс,
Ус zc.
* * *
Конечно, теоретическая механика много сложнее того,
о чем здесь было рассказано. Совершенно не были
затронуты те разделы механики, которые для своего объяс-
нения требуют привлечения высшей математики. Напри-
мер, приведенные теоремы динамики точки справедливы
101
только в случае постоянных по величине сил. Если силы
переменные, то эти теоремы надо записывать в иной
(дифференциальной или интегральной) форме.
Материалт с которым вы познакомились, дает первое
представление о предмете. Для тех, кого заинтересовала
механика и кому захочется более подробно познакомиться
с нею, ниже рекомендована литература.
ЛИТЕРАТУРА
Боголюбов А. И. Механика в истории человечества. М., 1978.
Бухгольц II. II. Основной курс теоретической механики. М., 1972.
Бухгольц Н. Н., Воронков И. ММинаков А. П. Сборник задач по
теоретической механике. М.—Л., 1949.
Григорьян А. Т. Механика от античности до наших дней. М., 1974.
Дерягин Б. В. Что такое трение? М., 1963.
Кирпичев В. Беседы о механике. М., 1951,
Космодемьянский А. А. Теоретическая механика и современная тех-
ника. М., 1969.
Лакур П., Аппель Я. Историческая физика. М,— Л., 1929.
Ландау Л. Д., Китайгородский А. И. Физика для всех. М., 1963.
Лебедев В. И. Исторические опыты по физике. М.— Л., 1937.
Лойцянский Л. Г., Лурье А. И. Курс теоретической механики. М.,
1957.
Льоцци М. История физики. М., 1970.
Маковецкий П. В. Смотри в корень! М., 1966.
Мещерский И. В. Сборник задач по теоретической механике. М.,
1975.
Некрасов А. И. Курс теоретической механики. М., 1956.
Орир Дж. Популярная физика. М., 1964.
Перельман Я. И. Занимательная физика. М.— Л., 1947.
Перельман Я. И. Занимательная механика. М.— Л., 1951.
Тульчинский М. Е. Сборник качественных задач по физике. М.,
1961.
Ушаков С. 3. Законы движения. М., 1961.
Эллиот Л., Уилкокс У. Физика. М., 1963.
ОГЛАВЛЕНИЕ
Предисловие...................................... 3
Кинематика ...................................... 7
Кинематика точки................................. 7
Поступательное движение тела.................... 12
Вращательное движение........................... 13
Плоское движение................................ 17
Динамика........................................ 22
Законы Ньютона.................................. 22
Основные теоремы динамики точки................. 27
Работа и мощность............................... 30
Принцип Д’Аламбера.............................. 36
Динамика системы................................ 42
Динамика твердого	тела.......................... 49
Механика в цирке................................ 51
Механика и природа.............................. 56
Аэромеханика..................................   61
Статика......................................... 70
Силы и их проявления............................ 70
Трение.......................................... 80
Задачи на равновесие............................ 89
Пространственная статика........................ 98
Центр тяжести.................................. 100
Литература......................................102
Володар Петрович Лишевский
ПОПУЛЯРНАЯ МЕХАНИКА
Утверждено к печати редколлегией
научно-популярной литературы Академии наук СССР
Редакторы И. Ш. Слободецкий и Л. М. Киселевская
Редактор издательства С. С. Матвеев
Художник А. В. Пушкарный
Художественный редактор И. Разина
Технический редактор Л. И. Куприянова
Корректоры Е. Н. Белоусова, В. А. Шварцер
ИБ № 7374
Сдано в набор 11.08.78. Подписано к печати 21.03.79.
Т-01488., Формат 84 х 108*/32
Бумага типографская № 2
Гарнитура обыкновенная. Печать высокая
Усл. печ. л. 5,5. Уч.-изд. л. 5,2. Тираж 25000 экз. Тип. зак. 896
Цена 20 коп.
Издательство «Наука»
117864 ГСП-7, Москва, В-485, Профсоюзная ул., 94а
2-я типография издательства «Наука»
121099, Москва, Г-99, Шубинский пер., 10