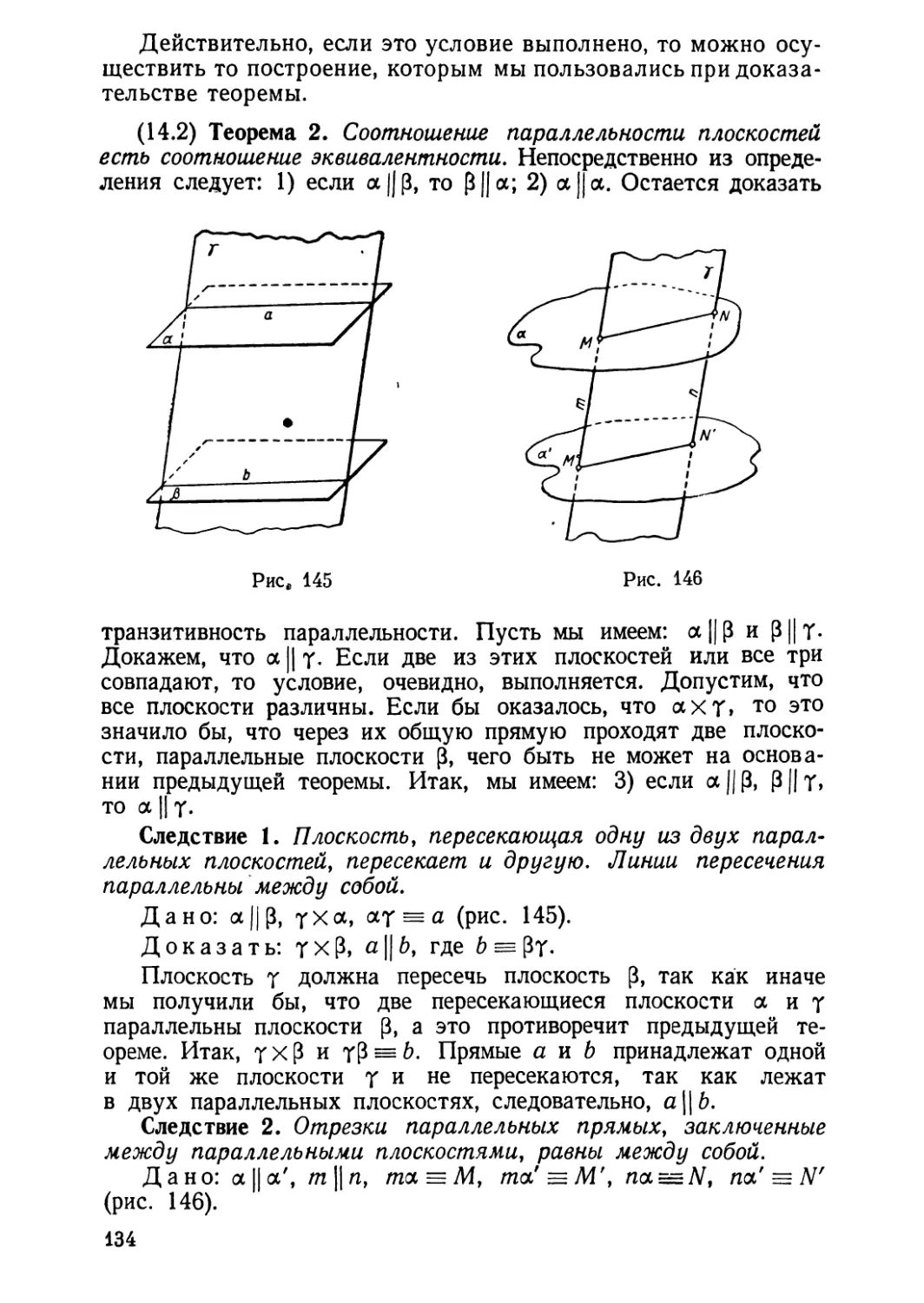
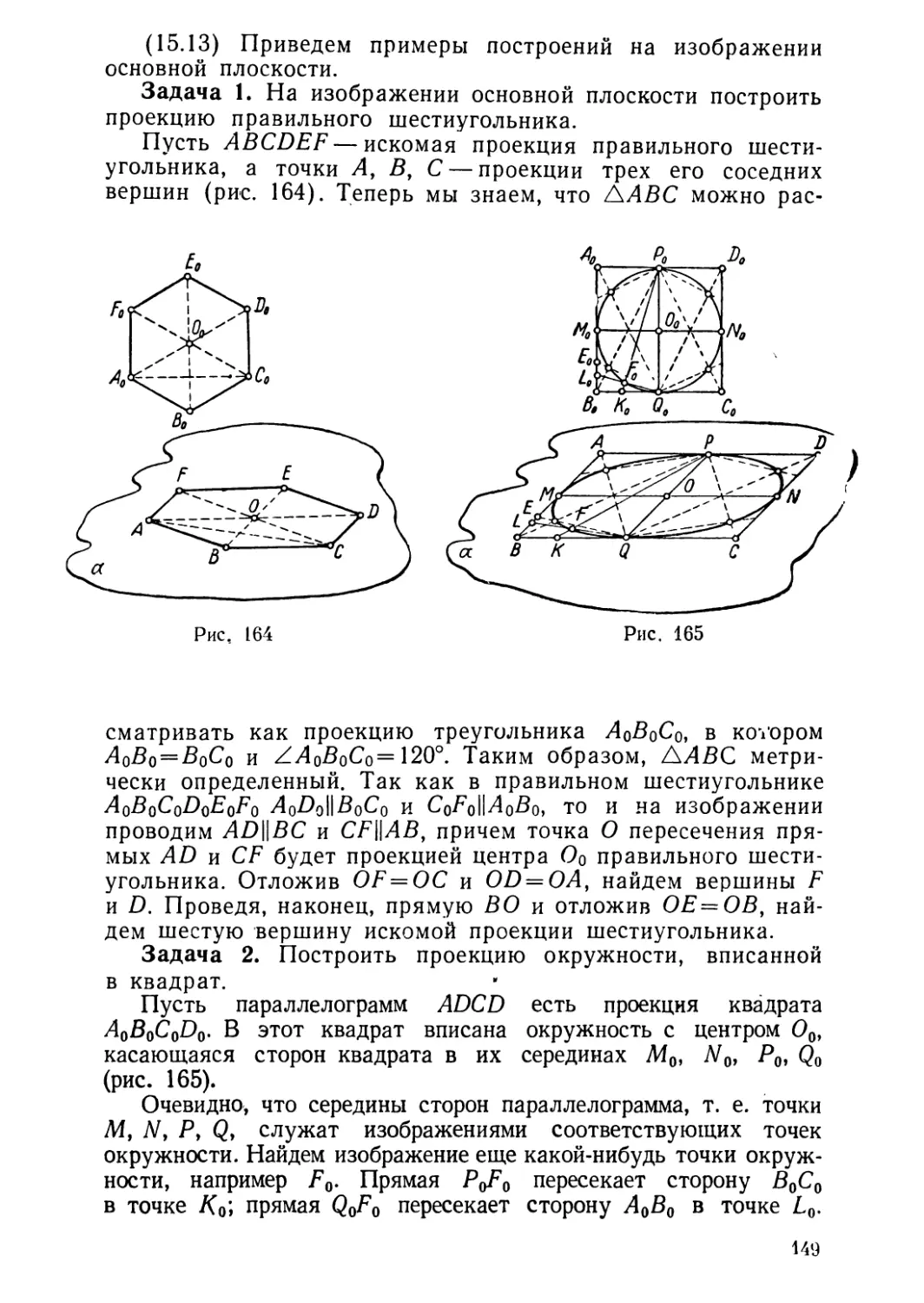
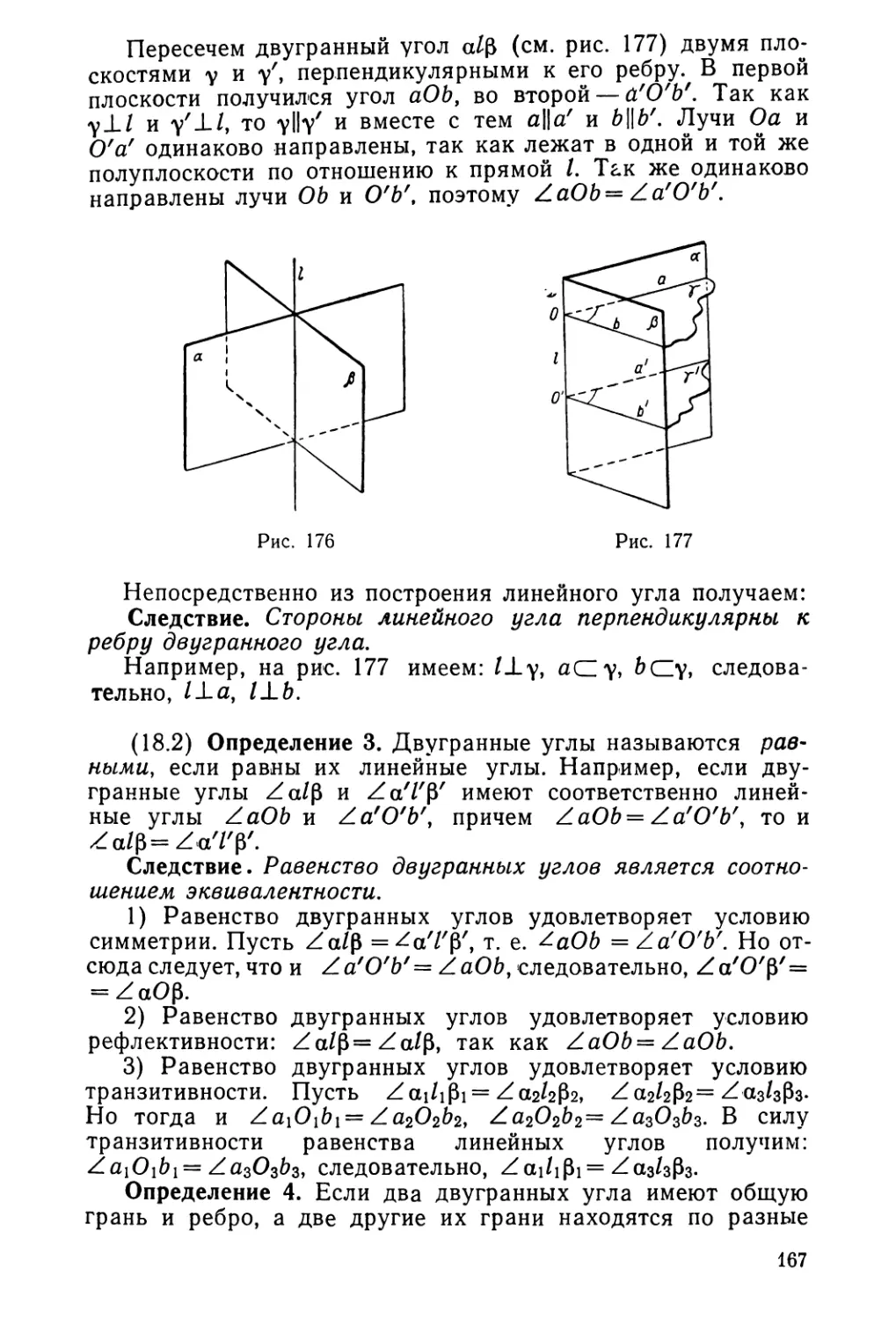
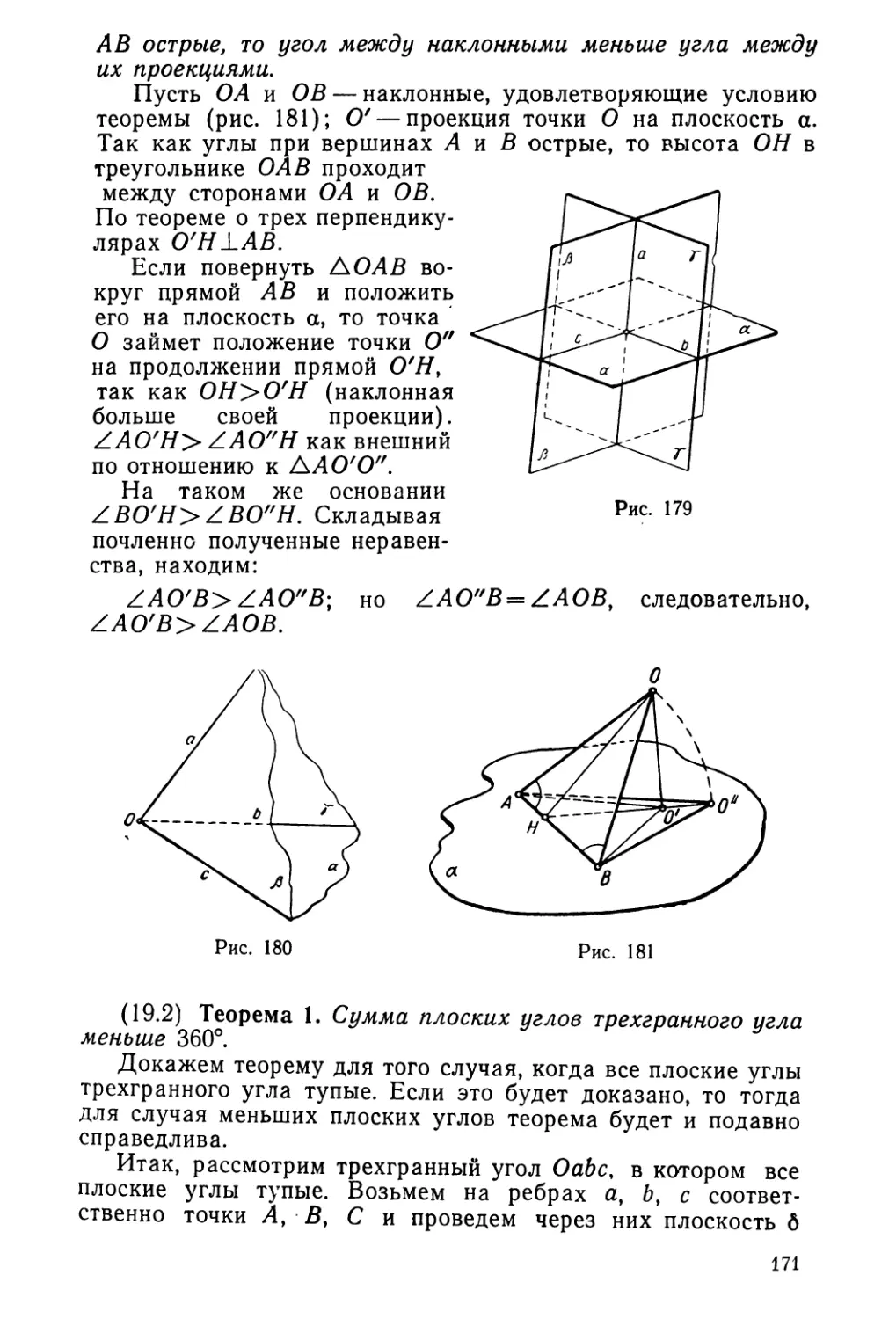
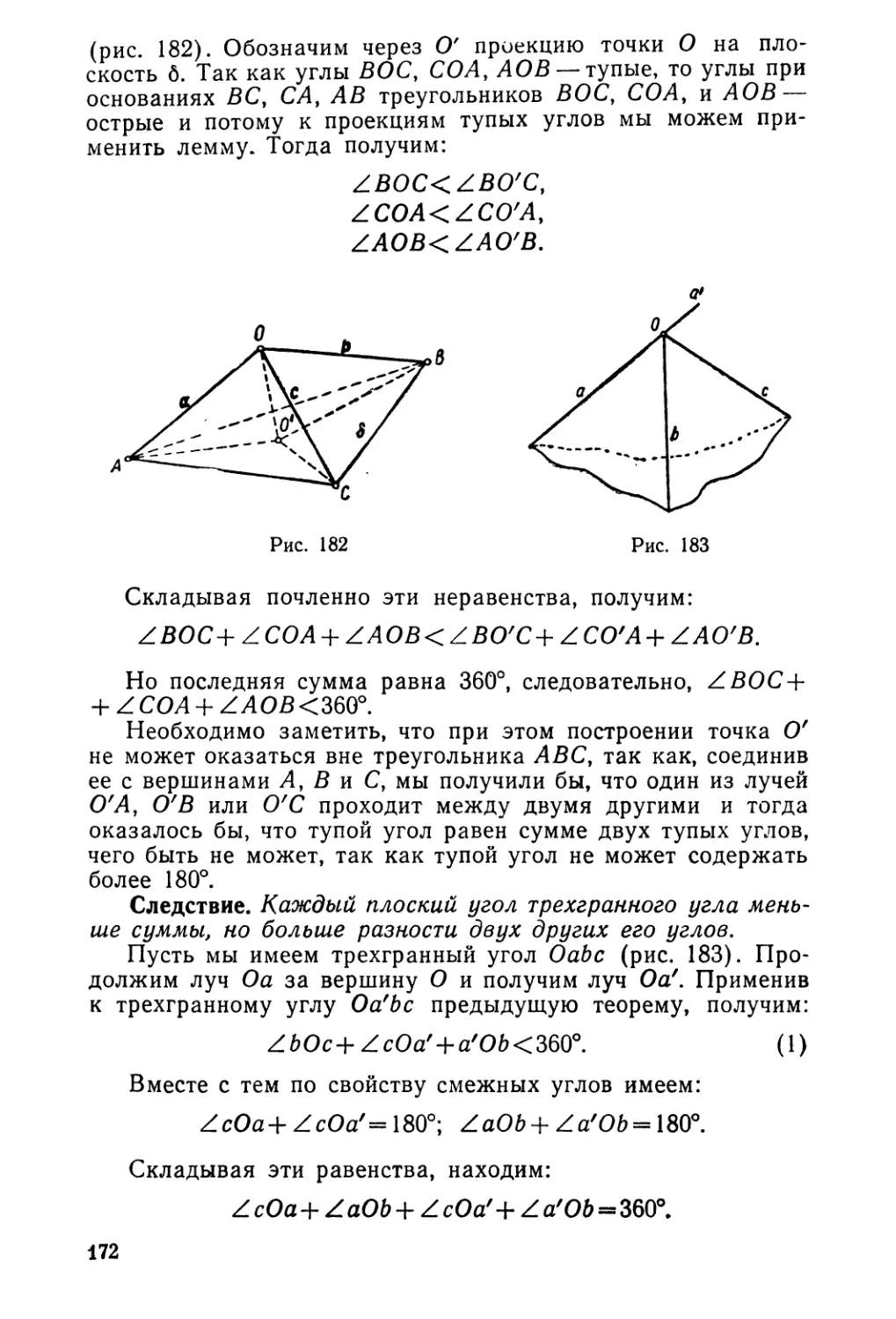
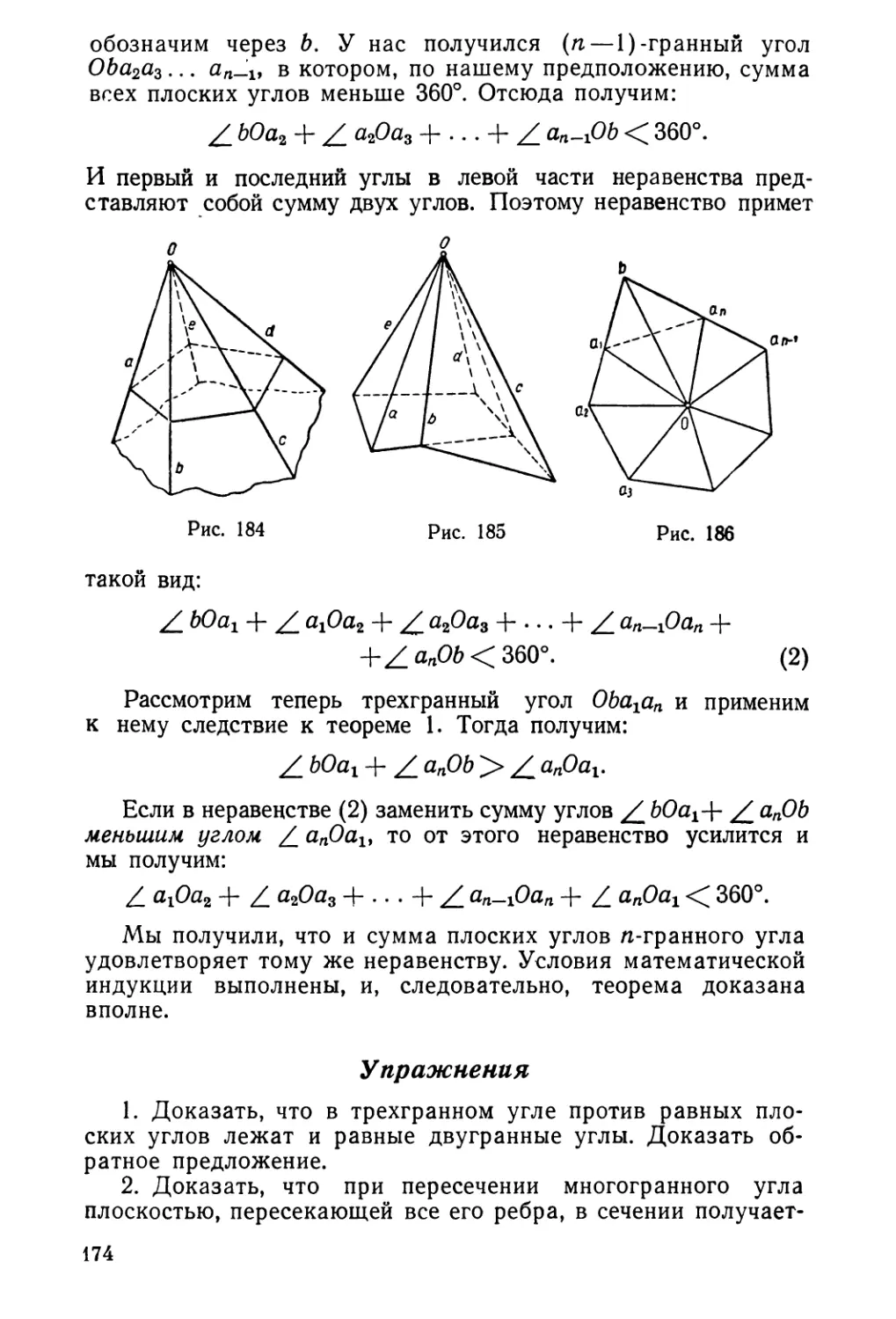
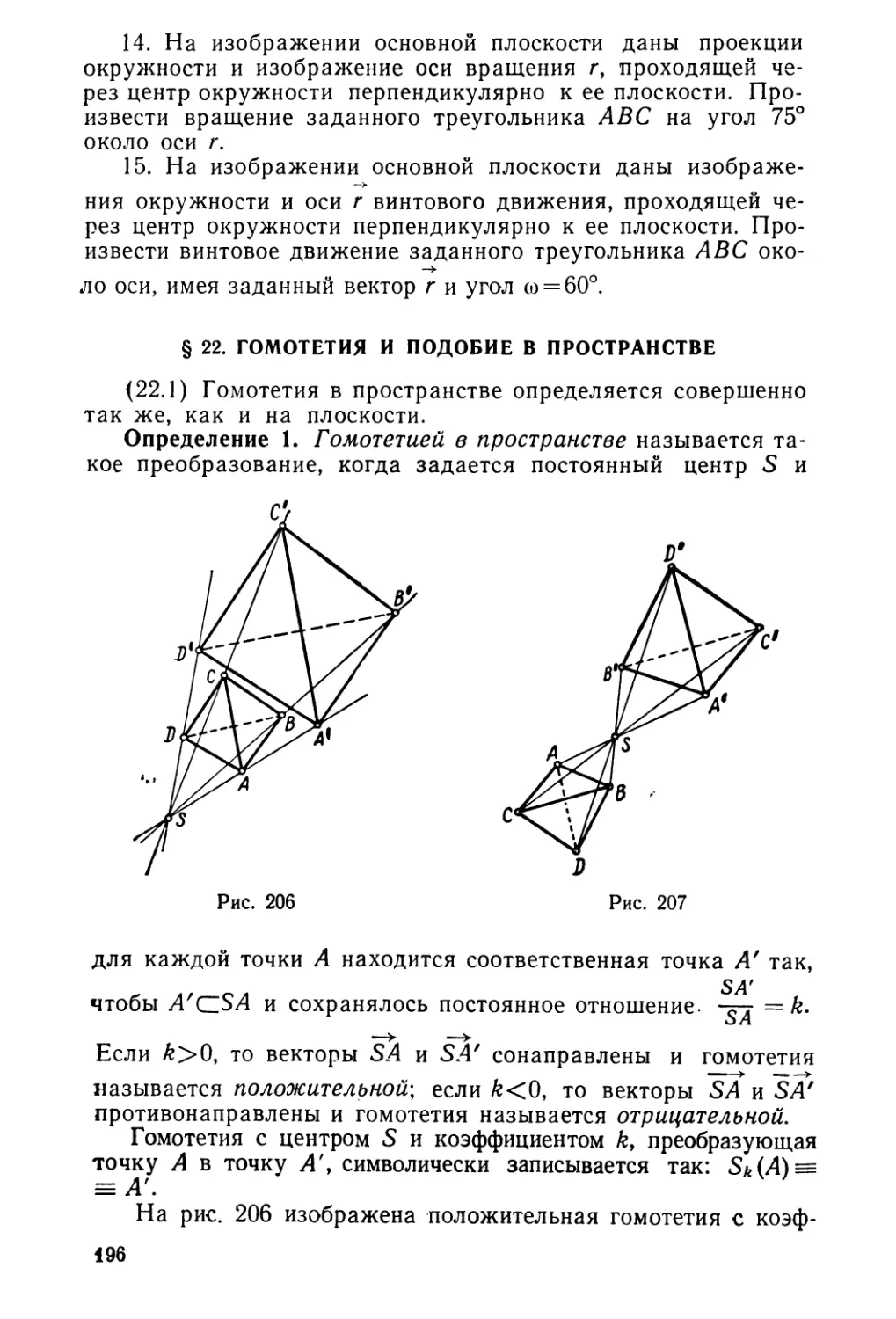
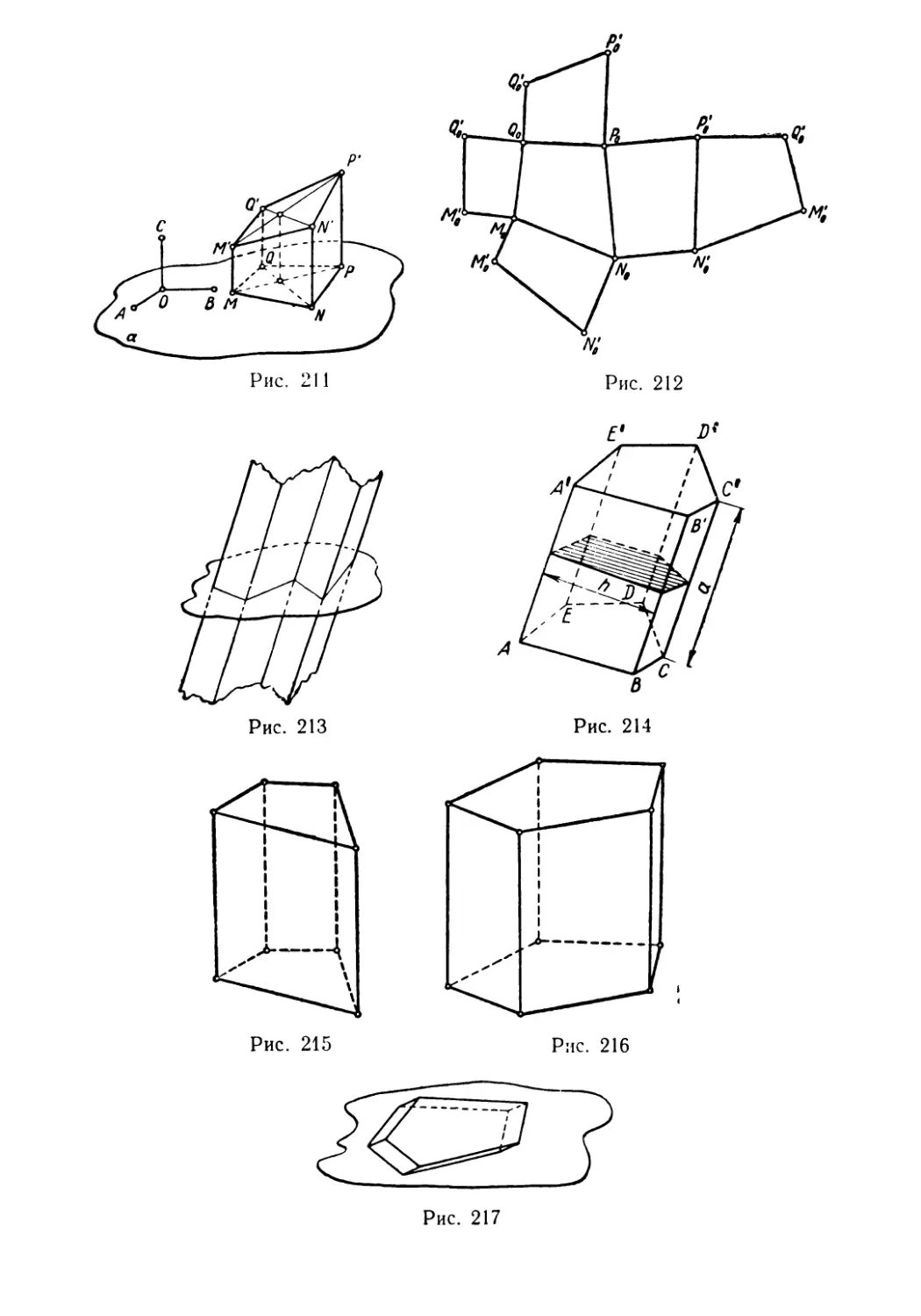
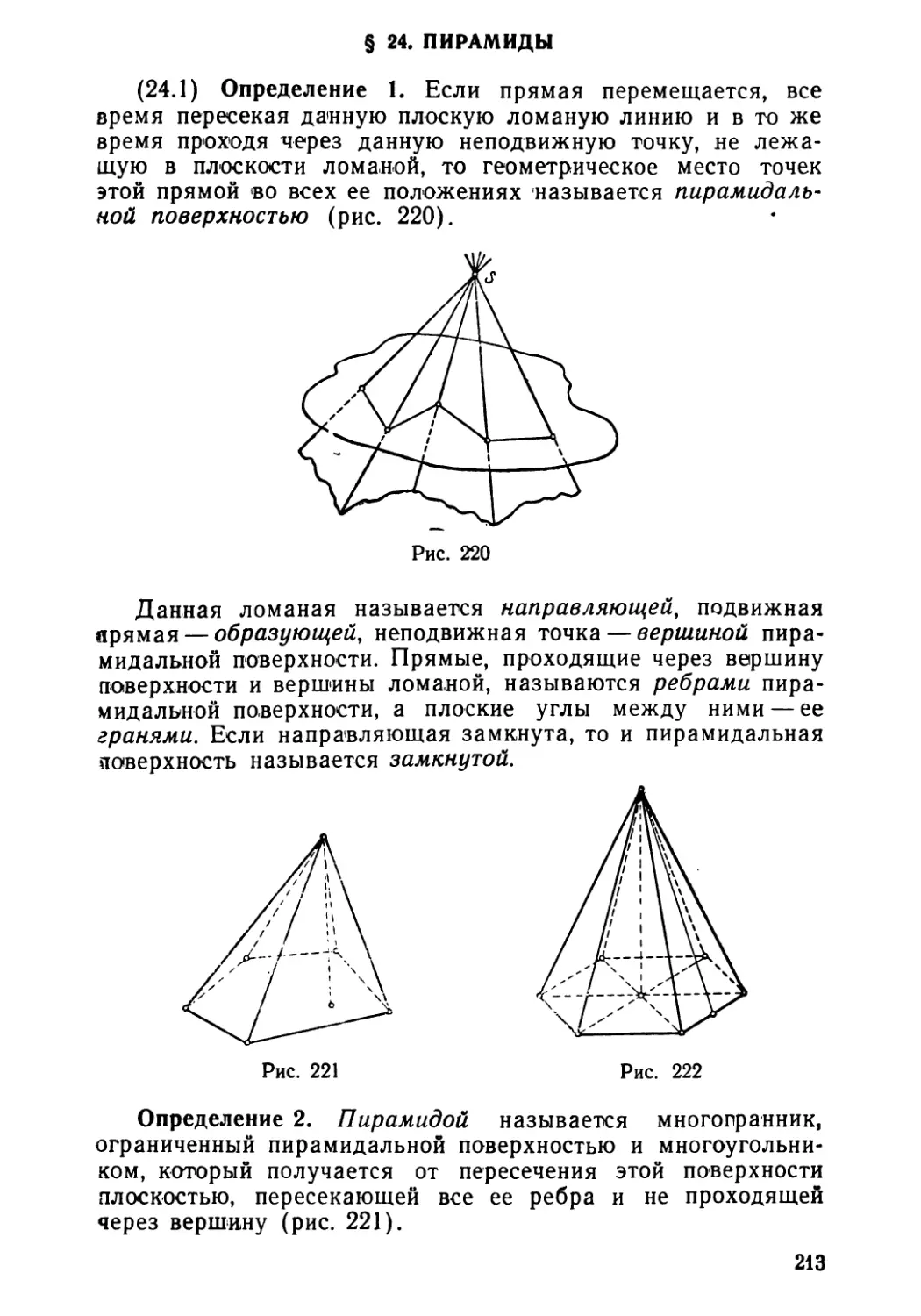
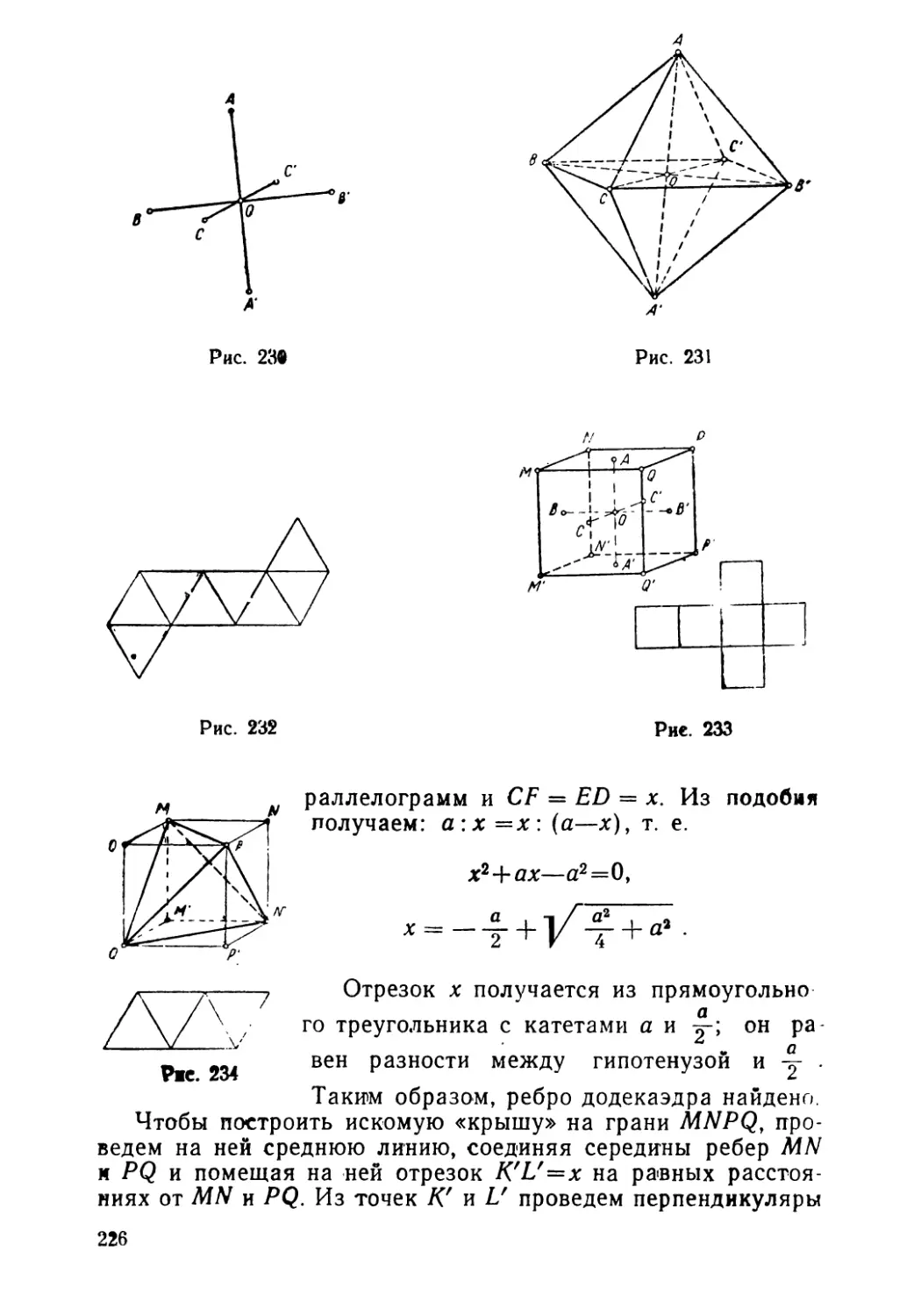
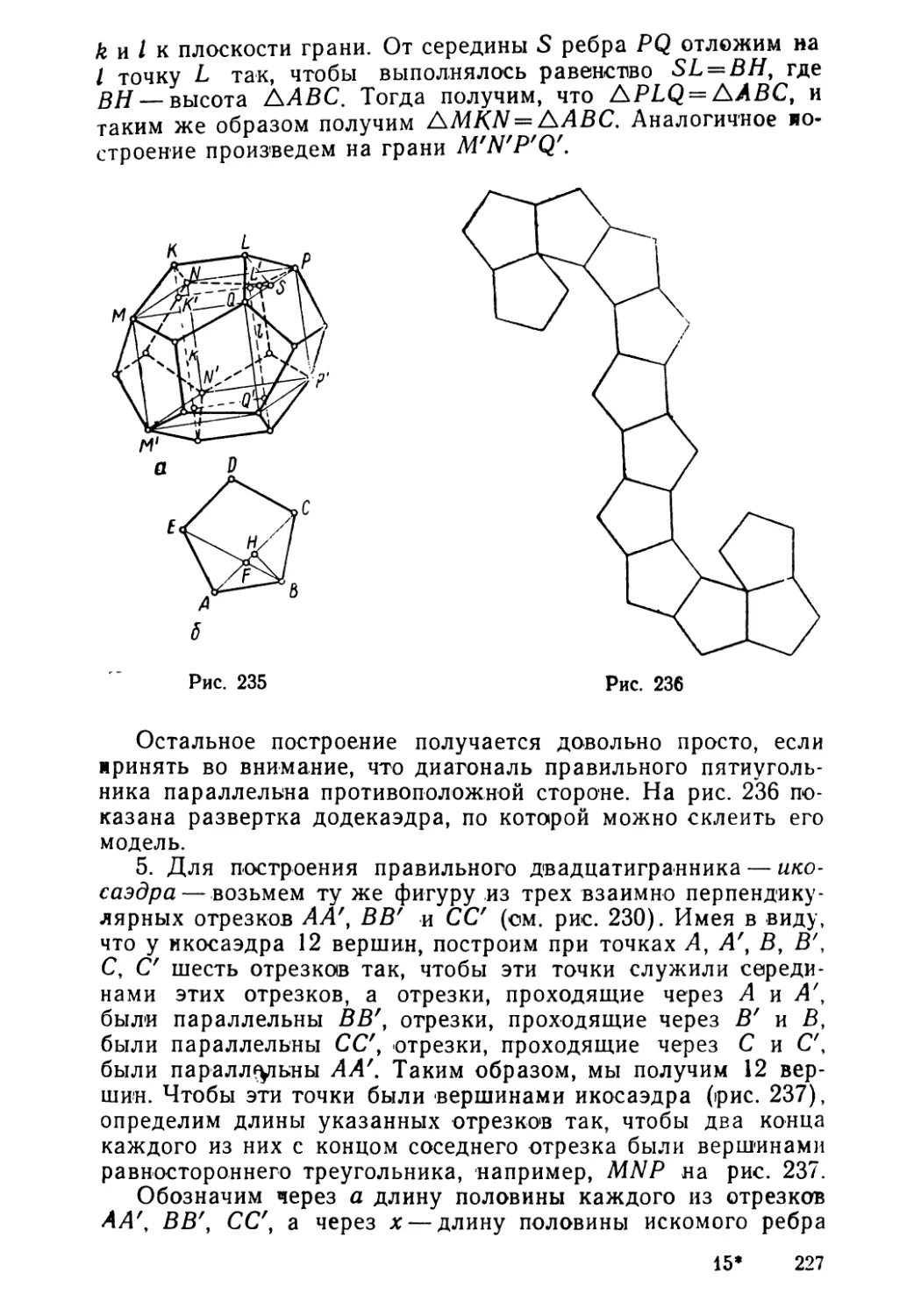
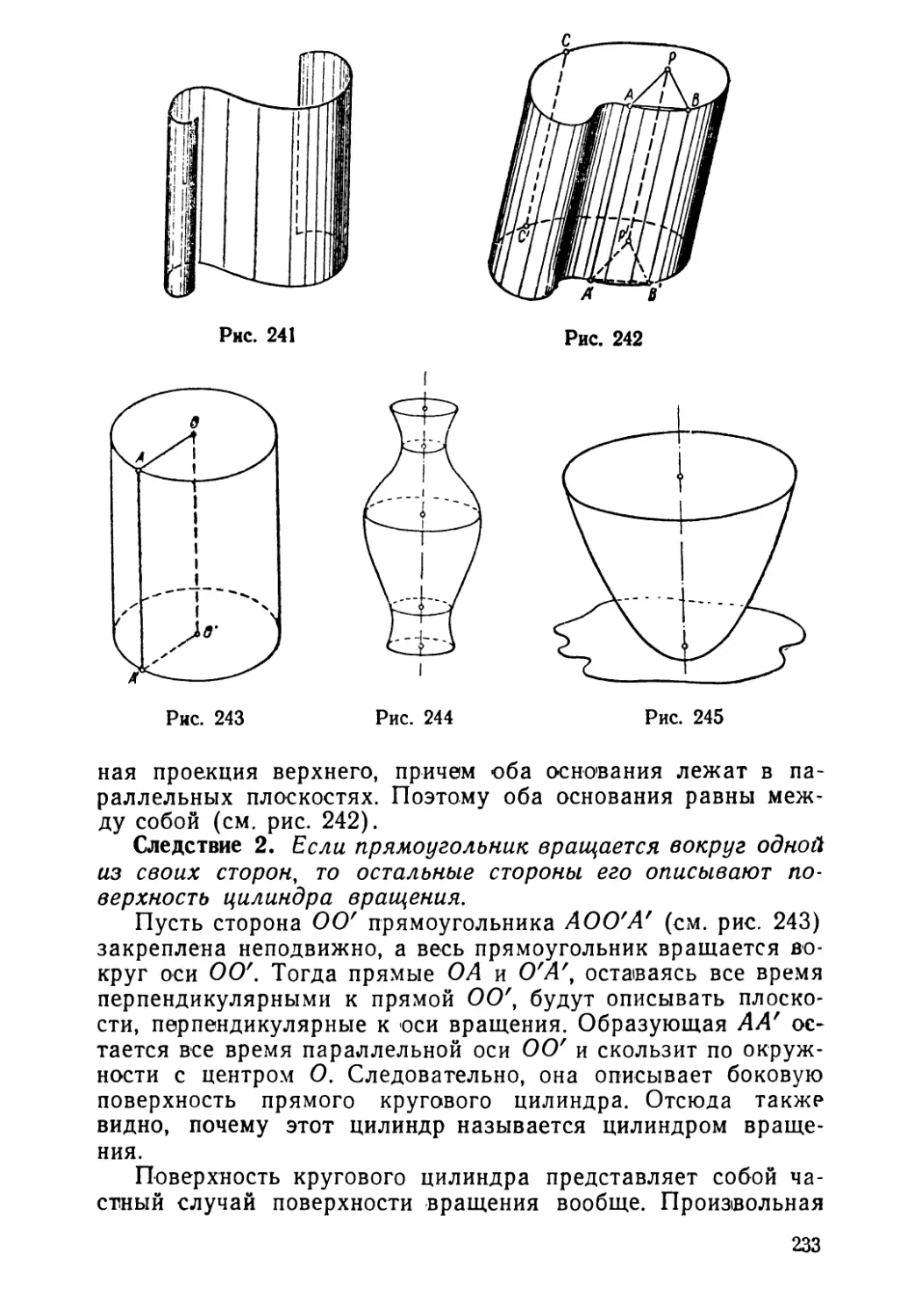
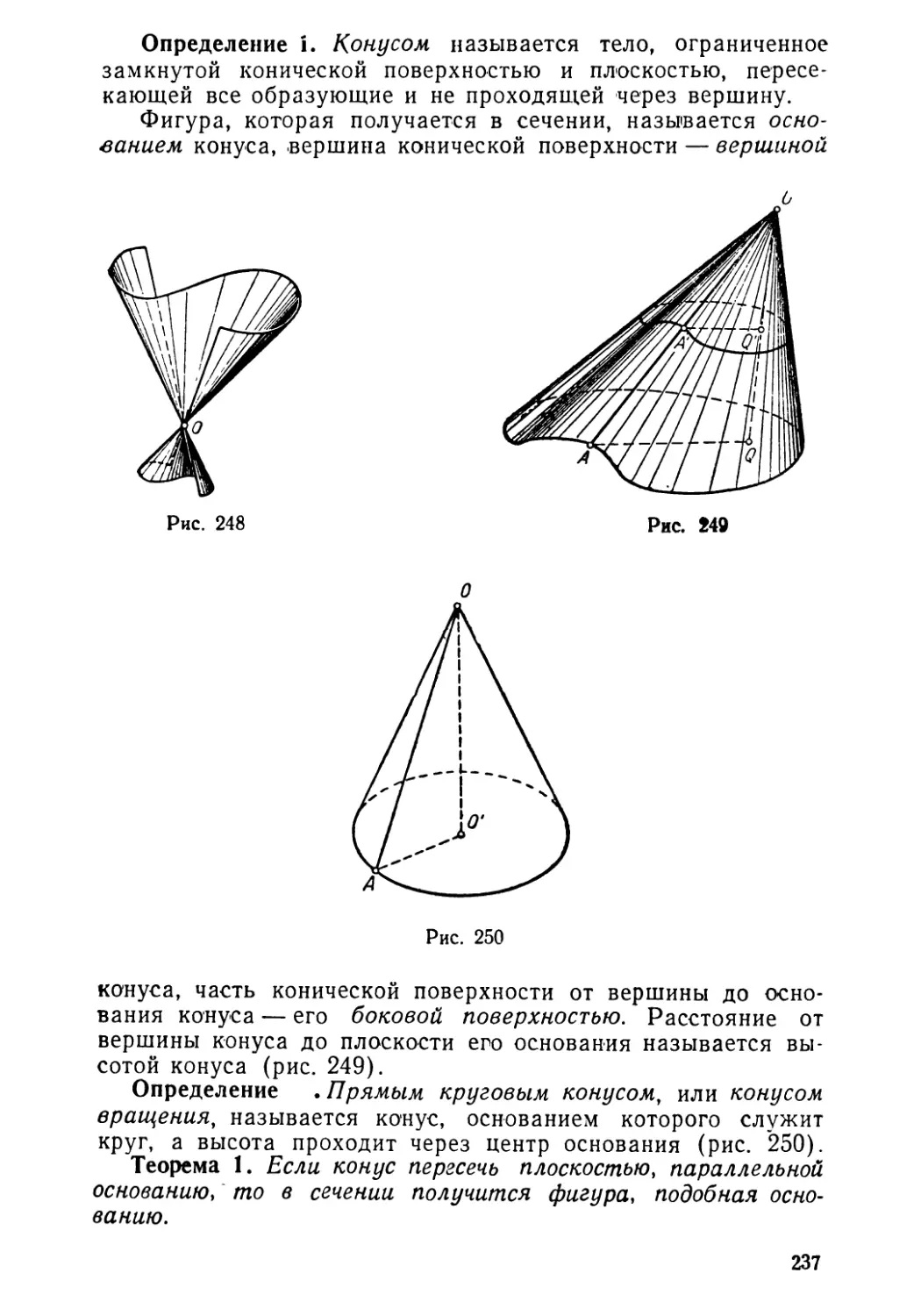
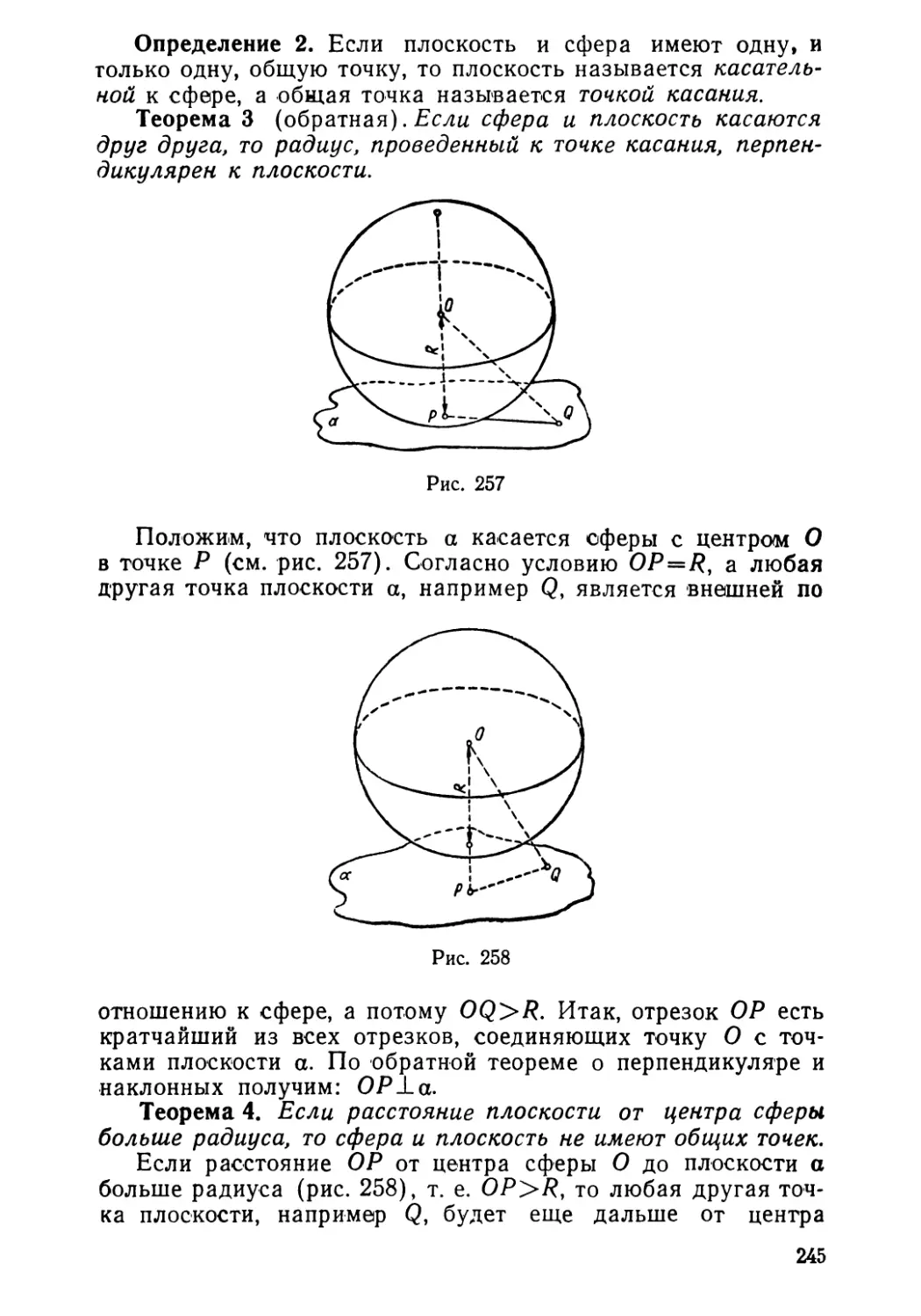
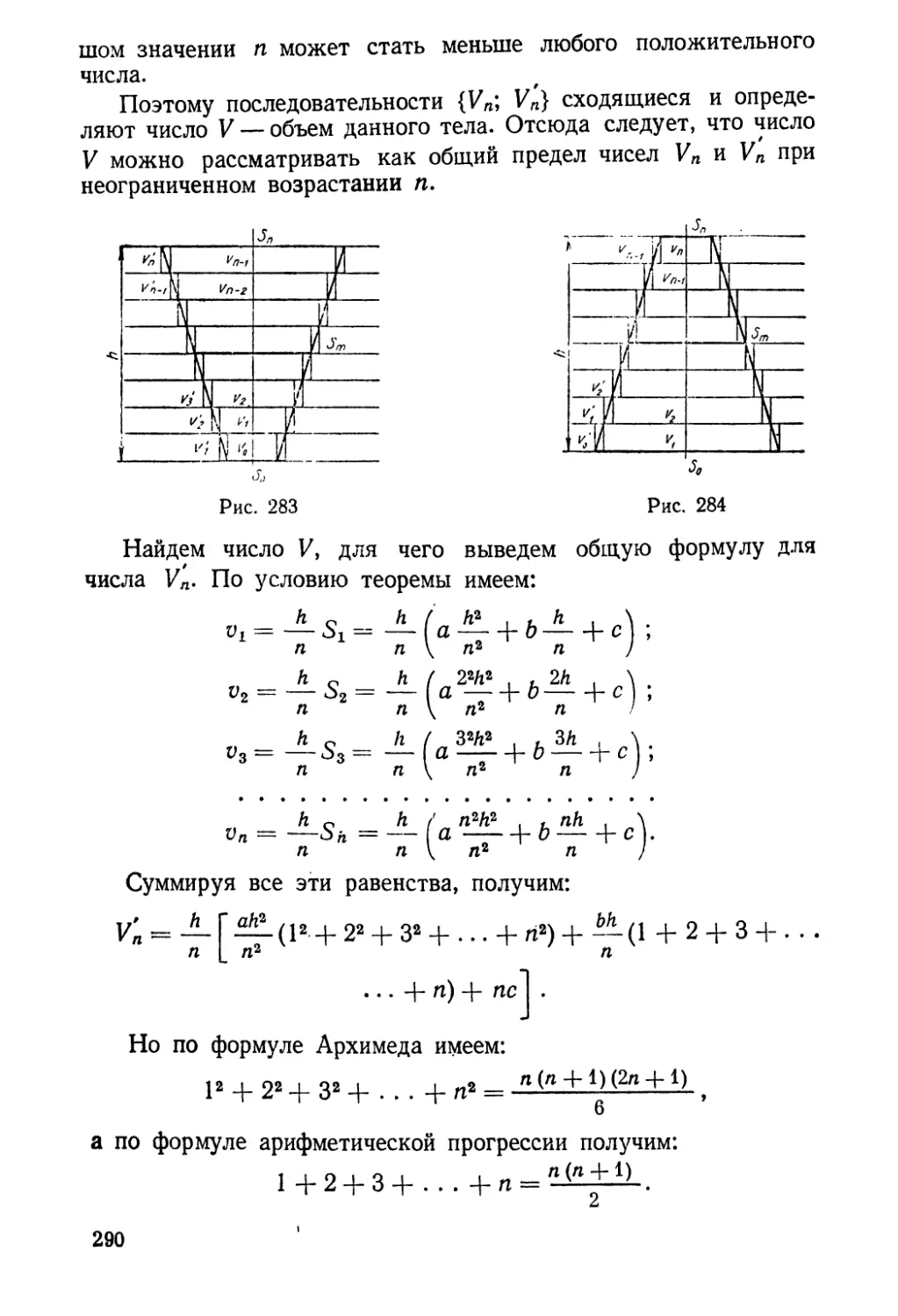
Текст
.,.
А.И.ФЕТИСОВ .
1
I ....
"
""
'
rЕОМЕТРИЯ
J
.I ;
, '
АКАДЕМИЯ ПЕДАrоrИЧЕСКИХ НАУК РСФСР
Институт обlЦеrо и политехническоrо образования
А. И.ФЕТИСОВ
rЕОМЕТРИЯ
УЧЕБНОЕ ПОСОБИЕ
по проrРАММЕ СТАРШИХ КЛАСССJВ
ИЗДАТЕЛЬСТВО АКАДЕМИИ ПЕДАrоrИЧЕСКИХ НАУК РСФСР
Москва 1963
Печатается по решению Ученоzо совета
Института общеzо и по.литехническоzо образованиll
А"адеАСии педаzоzичес"и% нау" РСФСР
Книеа содержит .м.атериал дАЯ в"сп ри.м.ентальное(J
учебника и задачника по zeoACeTpuu д.ля старших к.Аассо.
средней школы.
Все доказате.льства теоре.м. и решения задач осно-
ваны на .м.етоде zео.метрических преобразований: си.м..м.ет-
pии пepeнoca вращения и подобия что значительно
упрощает в сравнении с учебнико.м А. П. Киселева из.ло-
жение и усвоение учебноzо .материала.
Выде.лен специальный раздел посвященный теории
nарал.ле.льной nроекции и построения.м. на nроекциОННОJ4
'4е ртеже
В иэ.ложении .м.етрической части курса используетс.
nонятие вектора"
Пособие окажет 60.льшую по.мощь д.ля са.Alообра-
ЭОВQния учите.ля Q также с успехоАС .м.ожет быть испОАЬ-
зовано Il КРУЖICОllоа работ,_
r л А В А ПЕР В А Я
ПРЕОБРА30ВАНИЯ НА ПЛОСКОСТИ
s 1. КРАТКИ Я ОБЗОР ПРОЯДЕнноrо
(1.1) rеометрия есть наука о пространственных отноше-
ниях и формах тел материальноrо мира. В rеО lетрии изуча-
ются такие свойства предметов, которыми определяется их
форма, величина и взаимное положение.
Основное оодержание курса rеометрии состоит из предло-
жений, в которых описываются свойства rеометрических фи-
ryp. Важнейшими видами rеометрических предложений яв-
ляются определения, аксиомы и теоремы.
Определения предложения, при помощи которых точно
устанавливается, какой именно предмет или кл асс предметов
или взаимоотношений между ними мы будем иметь в виду,
употребляя данное слово. НаПРИ lер, мы даем определение:
«Параллелоrраммом называется четырехуrодьник, противопо-
л'ожные стороны KOToporo попарно параллельны». Этим пред-
ложением мы из всех четырехуrольников выделяем класс та-
ких четырехуrольников, у которых параллельны обе пары
противоположных сторон. Имея это определение, человек.
знающий, что такое четырехуrольник и какие прямые назы-
ваются параллельными, сумеет безошибочно сказать, являет-
ся ли данная фиrура параллелоrраммом или нет.
Аксиомы предложения, принимаемые без доказатель-
ства и отображающие действительно существующие взаИl\'lО-
отношения между изучаемыми объектами. Все остальные
rеометрические предложения при их обосновании опираются
на определения и аксиомы, поэтому и те и друrие являются
настоящим фундаментом, на котором строится вся rеометрия.
Теоремы предложения, истинность которых устанавли-
вается путем рассуждений, называемых доказательством. До-
казательства необходимы не только для установления истин-
ности теорем, но и для Toro, ч'Т'обы ,обнаружить связь между
различными rеометрическими предложениями. Блаrодаря до-
казательствам rеометрия становится научной системой, все
предложения которой объединяются в единое целое в силу
их взаимной обусловленности.
5
к числу rеометрических предл'Ожений отНОсятся также
следствия непосредственные ВЫ1ВОДЫ из предшествующих
предложений и леммы вспомоrательные предложения, He
обходимые для доказательства какой-нибудь теоремы.
(1.2) Припомним теперь некоторые важнейшие предложе-
ния rеометрии. Рассматривая в первую очередь определения,
обратим внимание на то, что, определяя какое нибудь поня-
тие, мы непременно ,р'пираемся на некоторые друrие понятия,
которые предполаrаются уже известными. Так, в приведенном
выше (1.1) примере с параллелоrраммом мы опирались на
уже известные понятия четырехуrольника и параллельности.
Друrими словами, эти понятия были определены раньше при
.
помощи понятии, определенных еще раньше, и Т. Д.
Ввиду Toro что такую цепь последовательных определений
нельзя продолжать бесконечно, мы должны некоторые наибо
лее простые и общие понятия принять без определения.
Такие понятия называются основны}ли. В rеометрии OCHOBHЫ
ми понятиями являются: точка, прямая и плоскость.
Эти понятия достаточно просты и наrлядны, и каждый
человек без особых пояснений понимает, что они
()значают.
Точки обозначаются большими (прописными) латинскими
буквами А, В, С,..., прямые малыми (строчными) латин-
скими буквами а, Ь, С,..., а также двумя буквами, обозна
чающими точки, через которые прямая проходит, например,
АВ, MN. Точки ин'Оrда тоже обозначаются двумя буквами,
например аЬ, обозначающими две пряrvlые (а и Ь), которые
через эту точку проходят.
К числу 'Основных понятий относятся И такие, при помощи
которых устанавливается взаимосвязь между точками, пря-
мыми и плоскостями. В первую очередь сюда надо отнести
понятие nрUflадлежности которое мы выражаем словаrvlИ:
«точка лежит на прямой», «прямая проходит по плоскости)
И 'Т. д. Принадлежность обозначается знаК1ОМ включения С,
например запись М Са обозначает: «точка М лежит на пря-
мой а», или, что то же: «прямая а проходит через точку М».
С понятием принадлежности связаны следующие а«сиомы'
1. Прямой и плоскости принадлежит бесконечное множест-
во точек.
2. Через две точки можно провести одну, u только одну.
прямую.
Друrим основным понятием, определяющим соотношения
между точками на одной и той же прямой, является понятие
н-аnравленuя. Чтобы определить направление на прямой, бе.
рут на неи две произвольные точки А и В и какую-либо из
них, например А, называют предшествующей; тоrда точка В
будет nоследУЮ1-l{ей, чем и lопределится направление на пря
мои (рис. 1).
е
о точках, которые следуют за А и предшествуют В, rOBO
рят, что они лежат между А и В (например, точка С на
рис. 1).
Часть прямой, содержащая в себе точки А и В и все точки,
находящиеся между А и В, называется' отрезком АВ. Отре-
ЗОК АВ в отличие от прямой АВ можно обозначить АВ .
А
о
с
о
в
а
Рис. I
Каждая точка А на данной прямой разделяет эту пря-
\IYIO на две полупрямые, или на два луча. Одному лучу при
надлежат все точки, предшествующие А, друrому все точ-
ки, следующие за А. Сама точка А является общим началом
roro и друrоrо луча.
Подобно тому как Лlобая точка, лежащая на прямой,
делит эту прямую на две полупрямые, так и любая прямая
1, проходящая в плоскости, делит эту плоскость на две полу
плоскости (рис. 2). Основным свойством этих ПО.тIуплоско.
м
1,
l.
РИG. 2
стей является то, что отрезок, концы KOToporo лежат в oд
ной и той же ПОЛУПЛОСКiQСТИ, не пересекает 1, а отрезок, кон...
IIЫ KOToporo лежат в разных полуплоскостях, пересекает 1.
Две пересекающиеся прямые разделяют плоскость на че-
rbIpe части, каждая из которых называется УеЛОМ. 060б..
u.{ая это понятие, мы даем определение: усол есть чаСI'Ь пло-
скости, Оераниченная двумя лучами (СТОРОНЫ уела), име
ющими общее начало (вершина уела). Уrол можно обозна
чить одной буквой, означающеЙ вершину, или тремя буква
\IИ, означающими точки, через которые проходят стороны
уrла, или двумя буквами, означающими ПРЯl\1ые, которые
образуют уrол. Например, LA, LBAC, Lab. Если стороны
уrла принадлежат одной и той же прямой, то такой уrол,
равный полуплоскости, называется развернутым. Половина
развернутоrо уrла, т. е, уrол, равный четверти плоскости,
7
называется прямым. Стороны прямоrо yr ла nерnендикуляр
нь! друr к друrу.
Две прямые называются взаимно nараллеЛЬНblми, если
они принадлежат одной и той же плоскости и не пересека
ются. Важнейшее свойство параллельных прямых выражает-
ся следующеЙ аКСИОМ1ОЙ;
Аксиома параллельности. Через данную точку можно
провести одну, и только одну, прямую, nараллельную дан-
ной прямой.
(1.3) Наиболее важным из основных понятий rеометрии
является понятие равенства. Наrлядно равенство плоских
фиrур проверяется наложением одной фиrуры на друrую:
если при наложении фиzуры совпадают всеми своими точка-
ми, то такие фиzуры равны между собой.
РавенсТ1ВО rеоме'f1рических фИlrур обладает
с.педую.щими СВОЙС'f!вами:
1) каждая фиrУlра равна самой себе;
2) если первая фиrура равна второй, то и
вторая равна пер'вой;
3) если первая ,фиrура равна второй, а
вторая pa BHa третьей, то и первая фиr)'1ра
равна третьей.
Для равенства двух отрезков достаточно.
чтобы совпали их концы, а для равенства yr
лов достаточно, чтобы совпали их стороны.
Равные отрезки можно построить при по
Рис. 3 мощи циркуля, равные уrлы при помощи
малки (рис. 3). При помощи циркуля можно
построить сумму двух отрезков, при помощи малки сумму
двух уrлов.
Суммы отрезков и уrлов обладают следующими OCHOA
ными свойствами:
Если АВ==А'В' и ВС==В'С', то АВ+ВС==А'В'+В'С'.
Если L. аЬ == L. а'Ь' и L. Ьс == L. Ь' с',
o L аЬ + L. Ьс== L а'Ь' + L Ь'с'.
Словами это свойство 'сложения выражается так: если
к каждому из двух равных отрезков (уzлов) nрuбавить COO'Т
ветственно равные отрезки (У;!Лbt), то в сумме получим
тоже равные отрезки (уzлы).
Указанное свойство суммы .отрезков и уrлов в точности
соответствует свойству суммы чисел. Это сходство идет и
дальше: суммы отреЗКОR и уrлов подчиняются перемести-
тельному и сочетательному законам.
8
в заключение припомним еще одно важное свойство CYM
мы отрезК!ов.
Если три точки А, В и С лежат на одной и той же прямой
и В лежит между А и С, то имеем равенство:
АВ + ВС == АС .
Если же точки А, В и С не лежат на одной и той же пря
мой, то имеем неравенство:
АВ + ВС > АС .
r""
dTO неравенство можно выразить друrими словами: CYМ,
ма двух сторон треУ20льника всесда больше третьей сторо"
ны ezo.
Указанное неравенство иноrда называют неравенством
треуrольника. Непосредственным следствием ero является
то, что периметр ломаной линии всеrда больше отрезка, стя
rивающеrо ее концы, а также и то, что периметр объемлемой
выпуклой ломаной линии меньше периметра объемлющей ло
маной линни.
2. ОСЕВАЯ СИММЕТРИЯ
(2.1) Одним из наиболее важных понятий современной
rеОIv!етрии является понятие nреобразования.
Определения.
1. П реобразованием в rеометрии называется всякая опе
рация (например, построение), позволяющая по данной фи
rype получить новую фиrуру.
2. Преобразование называется точечным, если оно позво
ляет по данной точке найти друrую точку. Если каждая дaH
ная точка преобразуется в единственную точку и, обратно,
каждой преобразованной точке соответствует единственнач
точка, которая в нее преобразовалась, то такие точки называ
ются соответственными, а самое соответствие называется
взаuмнооднозначным.
:tlаПРИl\-lер, коrда по данному треуrольнику АВС мы по
строим равный ему треуrольник А'В'С', в котором В'С'==ВС,
С'А'==СА и А'В'==АВ, то этим мы выполним точечное'преобра
зование. В этом преобразовании каждой точке первоrо тре..
уrольника (например, середине стороны АВ) соответствует
одна, и только одна, точка BToporo треуrольника (середина
стороны А' В'). И, обратно, каждой точке BToporo треуrольни"
ка соответствует одна, и только одна, точка первоrо треуrоль..
ника. Поэтому такое построение является точечным преобра
зованием со взаимнооднознаЧНЫl\1 С'оответствием между точ
ками.
9
3, Если в точечном преобразовании какая нибудь точка
преобразуется сама в себя, то такая точка называется непод-
ви?lCНОU (или двойной) точкой преобразования. Если все точки
какой"нибудь фиrуры преобразуются в точки той же сам'оя
фиrуры, то такая фиrура тоже называется неnодвижной.
Если, наконец, каждая точка плоскости окажется неподвиж-
ной, то все преобразование назыIаетсяя тождественным.
В изучаемом нами курсе будет показано, ЧТ10 вся reOMeT
рия, включая и ранее изученные предложения, может быть
обоснована свойствами точечных преобразований.
(2.2) Одним из наиболее простых преобразований являет..
ся осевая симметрuя. Чтобы наrлядно представить себе это
преобразование, возьмем лист БУ 1аrи и
!Проведем по нему прямую ось симметрии.
Переrнув бумаrу по этой оси, мы совместим
каждую точку одноrо полулиста с одной, и
только одной, точкой цруrоrо полулиста.
Проколов оба 'полулиста булавкой и разо
rHYB лист, мы получим представление о двух
точках, симметричных относительно данной
оси (рис. 4). Если на одном полулисте очер-
тить контур какой"нибудь фИ'rуры И, пере..
rHYB лист, ПРОИЗlвести по этому контуру ряд
частых проколов булавкой, то, разоnнув
лист, мы увидим две симметричные фи2УРЫ,
в которых .каждая точка одной фиrуры вза
имнооднозначно соответствует ТОЧI{е дру-
rой фИlrуры.
Симметричность одно из очень распро
страненных свойств предметов в окружающем нас 1ире: СИМ
метричны лиlстья и цветки мноrих растений, симметричны
крылья Iбабочек, симметричны снежинки, opiHaMeHTbI, архитек-
турные украшения и т. д. (рис. 5 6).
J
А
o--
А'
- -o
$
Рис. 4
Рис. 5
Рис. 6
{О
ОпредеJlение. 1) Осевая симметрия есть точечное преобра-
зование, при котором остаются неподвижными все точки по-
v v
стояннои прямои оси симметрии;
2) каждая точка одной из полуплоскостей, определяемых
осью, взаимнооднозначно преобразуется в очку друrой полу-
плоскости. При этом если точка А ,преобразуется в А', то эта
же симметрия прео6разует обратно А' в А;
3) осевая симметрия преобразует прямую- линию в пря-
\1УЮ, отрезок в равный отрезок; уrол в равный уrол.
Из определения осевой симметрии получаем:
СJlедстви . Две фИ2УРЫ, симметричные относительно оси,
оавны между собой.
Равенство симметричных фиrур обусловлено тем, что если
.
плоскость свернуть по оси симметрии, то каждая точка однои
s
с
:
А I
'1 В
I I I
I I '.s
I I I
I I !
1: I
I I I
:: 8'
I
А'
С'
Рис. 7
АЗ симметричных фиrур совпадет с соответствующей точкой
друrой фиrуры. Отсюда следует, что при осевой симметрии
прямая преобразуется в прямую, отрезок в равный отрезок,
уrол в равный уrол, окружность в равную окружность
и т. д.
Однако равенство симметричных фиrур обладает одной
важной особенностью. Пусть А, В и С точки одной фиrу-
ры, не лежащие на IО'ДНОЙ и той же прямой (рис. 7); ИМ соот-
ветствуют симметричные точки А', В' и С', тоже не лежащие
на одной и той же прямой. Если мы будем обходить контур
АВС от А к В, от В к С и от С к А, то всякий раз третья точ-
ка остается слева от направления движения. Если же мы бу
дем в таком же порядке обходить контур А' В'С', то третья
точка всякий раз будет справа от направления движения. ro
ворят также, что обход контура в первом случае совершается
против движения часовой стрелки, а во втором по
авижению часовой стрелки. Поэтому две симметричные фиrу-
ры называют равными, но противоположно ориентирован-
н'ыми.
1!
Равнь!е и одинаково ориентированные фиrуры (например,
6АВС и LA'B'C' на рис. 8) можно совместить друr с друrоМ.
непрерывно перемещая одну из них 'по данной плоскости. Ec
ли же мы захотим совместить друr с друrом равные и проти-
воположно ориентированные фиrуры (например, LABC и
с
A
А.
/
8"
С'
Рис. 8
6А'В'С' на рис. 7), то одну из них нужно вынуть из пло
скости в пространство, перевернуть на друrую сторону и толь
ко после этоrо фиrуры можно будет совместить.
Если точка А симметрична с точкой':А' по отношению к
оси s, то это будем записывать так 1:
s(A) == A'.
Словами эта запись читается так: ось симметрии s nреобра-
зуеm точку А в симметричную с ней точку А'. Аналоrично
записывается симметрия прямых:
s(a) == a',
т. е. ось симметрии s nреооразуеm прямую..а в симметричную с
ней прямую а'.
(2.3) Отметим основные свойства осевой симметрии, которые
вытекают непосредственно из определения.
1. Ввиду Toro что осевая симметрия есть преобразование
взаимное, получаем:
если s (А) == А', то s (А') == А;
если s (а) =. а', то s (а') == а.
2. Как было сказано в определении, точки самой оси сим-
метрии неподвижны. Из определения также следует, что, кроме
точек оси, apyzux неподвижных точек в осевой симметрии нет.
1 Знак = есть знак тождества. Наличие ero указывает на то, что сим-
волы, стоящие слева и справа от Hero, обозначают один и тот же предмет.
12
Поэтому будем иметь: если М С s, то s (М) == М, и обратно:
если s(M) == M, то Mcs.
3. Если две прямые, взаимно симметричные относительно
оси, пересекаются, то точка их пересечения лежит на оси
симметрии ·
Пусть s (а) == а'; обозначим символом аа' точку пересечения
прямых а и а'. Тоrда получим (рис. 9):
( ' ) ' , ,
s аа == а а, но а а == аа ,
поэтому, на основании предыдущеrо свойства,
аа' С s.
4. Из Toro, что симметрия преобразует уrол в равный yroJi',
следует, что ОСЬ симметрии проходит по биссектрисе У2ла,
о'
с\
\
\ , s
\
\
\
\
\М
\
\
\
\
\
\
\
"&"
5
Рис. 9
Рис. 1 О
образуемоrо двумя взаимно симметричными прямыми. И обратно:
биссектриса Уела есть ОСЬ симметрии для любых двух moчек,
расположенных на есо сторонах на равных расстояниях от
вершины.
5. ОСЬ симметрии nерnендикулярна к nря.lИОЙ, проходящей
через две взаимно симметричные точки, и делит пополам отрезок
между этими точками.
Пусть s (А) == А' (рис. 10). Так как по определению симмет..
рии точки А и А' лежат в разных полуплоскостях относительно
прямой s, то отрезок АА' пересекает ось s. ОбознаЧИl\i буквой М
точку пересечения. Тоrда получим: s (АМ) == А' М. Отсюда сле..
дует, во..первых, что s есть биссектриса развернутоrо уrла АМА',
т. е. s АА', и, во"вторых, что отрезок АМ == А'М.
Этим свойством можно ВОСПQльзоваться для построения точки
А', симметричной с точкой А по отношению к оси s: из точки
А проводим перпендику ляр АМ к прямой s и продолжаем ero
на такое же расстояние, чтобы получилось А' М == АМ.
13
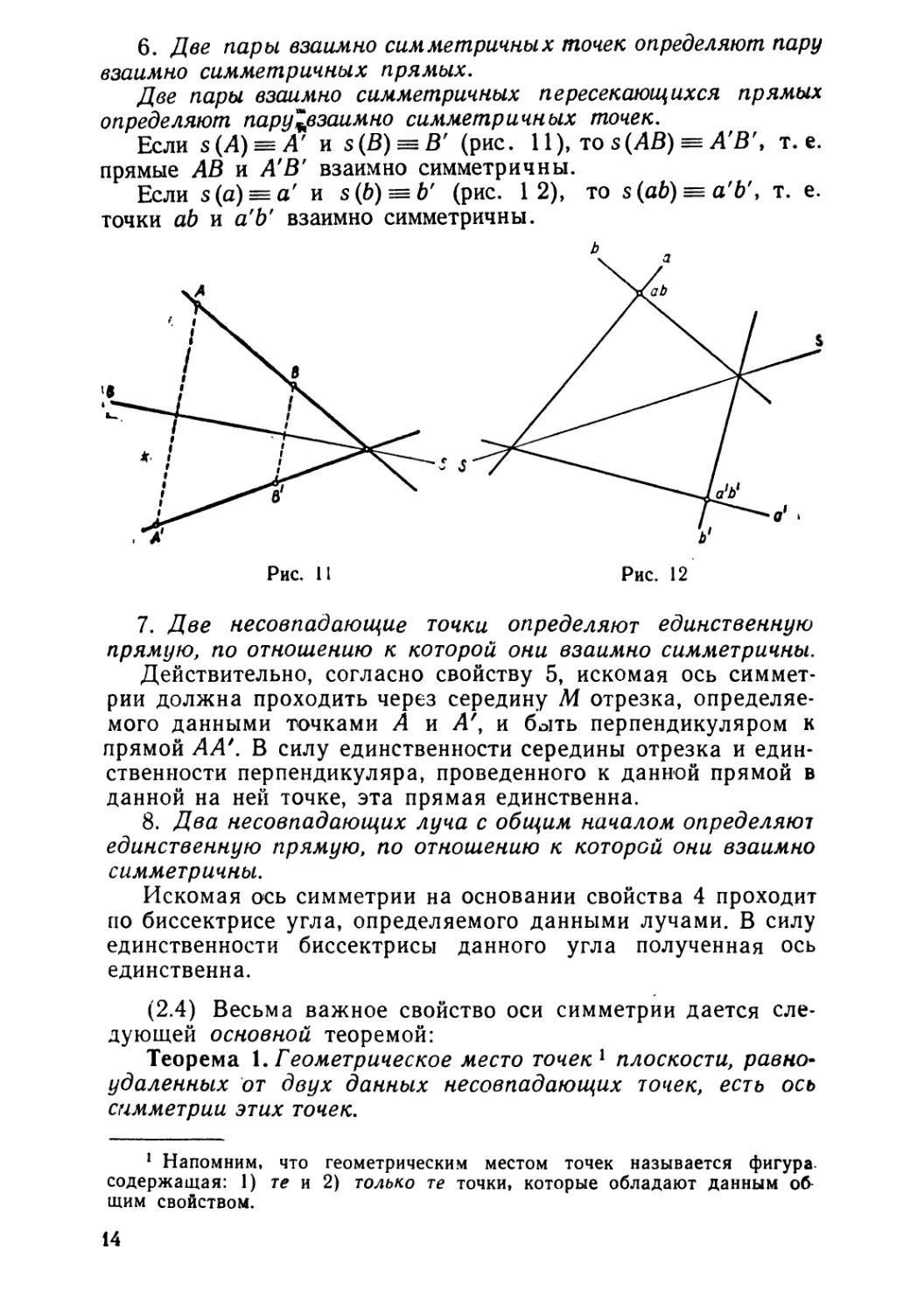
6. Две пары взаимно симметричных точек определяют пару
взаимно симметричных прямых.
Две nарь/' взаимно симметричных nересекающихся nрЯМь/,Х
определяют nару;взаимно симметричных точек.
Если s (А) == А' и s (В) == В' (рис. 11), то s (АВ) == А'В', т. е.
прямые АВ и А' В' взаимно симметричны.
Если s (а) == а' и s (Ь) == Ь' (рис. 1 2), то s (аЬ) == а' Ь', т. е.
точки аЬ и а'Ь' взаимно симметричны.
$ J
ь
Рис. 11
Рис. 12
7. Две несовпадающие Точки определяют единственную
прямую, по отношению к которой они взаимно симметричны.
Действительно, соrласно свойству 5, искомая ось симмет
рин должна проходить через середину М отрезка, определяе
Moro данными очками А и А', и БDIТЬ перпендикуляром к
прямой АА'. В силу единственности середины отрезка и един..
ственности перпендикуляра, проведенноrо к данной прямой в
данной на неЙ точке, эта прямая единственна.
8. Два несовnадающих луча с общим началом определяют
единственную прямую, по отношению к которой они взаимно
симметричны.
Искомая ось симметрии на основании свойства 4 проходит
по биссектрисе уrла, определяемоrо данными лучами. В силу
единственности биссектрисы данноrо уrла полученная ось
единственна,
(2.4) Весьма важное свойство оси симметрии дается сле
дующей основной теоремой:
Теорема 1. rеометрическое место точек 1 плоскости, равно-
удаленных 'от двух данных несовnадающих 10 t leK, есть ось
симметрии этих точек.
I Напомним, что rеометрическим местом точек называется фиrура.
содержащая: 1) те и 2) только те точки, которые обладают данным об.
щим СВОЙСТВоМ.
14
д о к а з а т е л ь с т в о. Пусть А и А' данные точки (рис.
13). Соrласно своЙству 7 существует единственная ось сим-
метрии s данных точек. Возьмем любую точку Р на оси. Так
как s (АР ) == А'Р , то АР == А'Р , чем доказано первое условие
в определении rеометрическоrо места.
Пусть теперь точка Q не принадлежит .оси s и положим
для определенности, что она лежит в одной полуплоскостн С
точкой А. Тоrда 'отрезок QA' пересечеr ось s в некоторой точ-
ке М. Следовательно, АМ ==А' М. В силу неравенства Tpe
уrольника [см. п. (1.3)] имеем:
AM + MQ > AQ , или A'M + MQ>AQ , т. е. A'Q > AQ .
Итак, точка Q не равноудалена от ,точек А и А', чем ДOKa
зано второе условие в определении rеометрическоrо места
точек,
Из доказательст,ва
этой Teope ы, в частности,
ел едует: если точка Не де..
жит На оси симметрии, то
она ближе к той из двух
взаимно симметричных.s
точек, с которой находит-
ся в одной полуплоско-
СТИ.
Рассмотренные нами
свойств а осевой си м ! ет..
рин ПОЗlволяют весьма
просто обосновать ряд
важных rеометрических предложений. У'кажем прежде Bcer8
на следующее свойство окружности.
Теорема 2. Окружность симметрична относительно любой
своей диаметральной прямой 1.
Д О К а з а т е л ь с т в о. Возьмем 10КРУЖНОСТЬ с центром О
и проведем ее диаметральную прямую s. Пусть А какая-
нибудь точка окружности. Найдем точку А', симметричную с
А относительно s. По свойству оси симметрии, установлен
ному предыдущей теоремой, ОА ' == ОА , значит, точка А' при-
адлежит той же окружности.
Итак, каждой точке одной полуокружности соответствует
симметричная с ней точка друrой полуокружности, т. е. обе
полуокружности взаимно симметричны по отношению к раз
деляющей их диаметральной прямой.
Опираясь на свойство окружности и осевой симметрии,
можно решить некоторые основные задачи на построение.
А
,
\ '.....
/ , ..........
/ \ "
" " '.., Q
, \ I
\'
\ I
Р / , /
с( '1
, /М
" I
, I
, I
, I
, /
, I
, I
, I
''6
А'
.s
Рис. 1 3
1 Диаметральной прямой окружности называется всякая прямая, про-
ходящая через tleHTp.
15
Задача 1. Построить точку, симметричную с данной точкой
по 'отношению к данной пряrvlОЙ.
Реш е н и е. Пусть А данная точка и s данная прямая
(рис, 14). Возьмем на прямой s произвольную точку М. Обо
значим буквой А' искомую то чку, с имм етричную с А. По oc
новному свойству IОСИ S имеем МА' ==МА. Значит, если из точ
ки М как из центра описать окружность радиусом МА, то
искомая точка А' должна лежать на этой окружносТlИ. Возь.,
,.
о
.
о
Рис. 14
Рис. 15
мем теперь на прямой s друrую точку N, отличную от М.
При помощи Toro же рассуждения получим, что точка А'
должна лежат и на окружности, описанной из центра N pa
диусом NA. Итак, точка А' находится в пересечении обеих
окружностей. Задача, очевидно, всеrда разрешима и имеет
единственное решение.
Ввиду Toro что АА' ..Ls, тем же построением решается за
дача: «Из данной точки А опустить перпендикуляр на данную
ПрЯl\lУЮ s».
Задача 2. Найти ось симметрии двух данных точек.
Реш е н и е. Пусть А и А' данные точки (рис. 15). Для
отыскания оси s достаточно найти две ее точки. Положим.
Р какая"нибудь точка оси s, отличная от середины отрезка
АА'. Тоrда РА ==РА' и в силу неравенства треуrольника
РА+РА'>АА', Т. е. 2РА>АА' иРА> A' .
Поэтому, описав из центра А окружность радиусом, б6ль
шим половины А..4', мы получим, что на этой окружности
будет лежать точка Р оси s, отличная от середины отрезка
АА'. Если теперь тем же радиусом опишем окружность И1
центра А', то эта же точка Р должна лежать и на второЙ
окружности. 11TaK, искомая точка лежит в пересечении обеих
16
окружностей. Вторая точка пересечения этих окружностей.........
точка р' симметрична с Р по отношению к прямой АА'.
Точками р и р' вполне спределяется ось s. Задача всеrда раз
решима и имеет единственное решение.
Этим же построением решается задача о делении данноrо
отрезка пополам.
Задача 3. Найти ось симметрии двух лучей, имеющих
общее начало.
Реш е н и е. Положим, что даны лучи Оа и аа' с оБЩИ 1
началом а (рис. 16).
Мы знаем (свойст..
во 3), что точка а при..
надлежит искомой оси.
Поэтому если мы от ло
жим на лучах соответст"
венно равные отрезки:
ОА == ОА', то точки А и
А' будут симметричными
относительно Ptскомой оси.
Теперь остается только к
точкам А и А' применить
построение '1 предыдущей
задачи и найти хотя бы одну точку р, равноудаленную от TO
чек А и A' Прямая аР = s и будет искомой осью симмет
рии. Задача тоже всеrда разрешима и имеет единственное
решение.
Этим же построением решается задача о делении данноrо
уrла пополам. В частности, это построение можно применить
к решению задачи: «Провести перпендикуляр к прямой из
данной на ней точки». Действительно, данную точку мо}кно
принять за вершину развернутоf'О уrла. Тоrда искомый пер..
пендикуляр будет биссектрисой этоrо уrла.
При помощи указанных выше основных задач решаются
более сложные задачи на построение. Приведем пример.
Задача. Провести окружность через данные три точки, не
лежащие на одной и той }ке прямой.
Реш е н и е. Если А, В и С данные точки, то искомый
центр О окружности должен лежать одновременно и на оси
симметрии s точек А и В, и на оси s' точек В и С. Параллель
ными прямые s и s' быть не MOryT, так как тоrда три точки
.4, В, С лежали бы на общем перпендикуляре, проведенном
через точку В к параллельным прямым s и s'. Итак, ИСКО fая
точка О есть точка пересечения прямых s и s', так как она
находится на равных расстояниях от точек А, В и с. Решение
единственно, так как центр всякой окружности, пр'оходящей
через А, В и С, должен лежать одновременно и на прямой s,
и на прямой s'. Через ту же точку а пройдет, очевидно, и ось
симметрии точек С и А.
2 A И. Фетисов
s
а'
А'
Рис. 16
17
Заметим, что для построения всех трех осей СИМlVlеТРИII
достаточно из ка)кдой точки А, В и С как из центра описать
три окружности радиусом, большим половины наибольшеrо из
отрезков ВС, СА и АВ.
(2.5) ПрИl\fеним теперь осевую симметрию к решению HeKO
торых теоретических вопросов rеометрии. Докажем при по
мощи 'Осевой симметрии основную теорему о перпендикуляре
и наклонных.
Теорема. Если из точки, не принадлежащей прямой, npo
вести к ней nерnендикуляр и наклонные, то: 1) этот nерnенди..
куляр единственный; 2) nерnендикуляр короче .всякой на..
А клонной, nроведенной из той
же точки; 3) наКАонные,
имеющие раВные nроекции,
равны; 4) наклонная, имею
щая большую nроекцию,
больше.
, Д о к а з а т е л ь с т в о.
- 1) Пусть А данная точка
и s данная прямая
(рис. 17). Проведем перпен"
дикуляр АР к прямой s и
продолжим ero на такое же
расстояние до точки А'. Так
как AA'..Ls и АР==А'Р, то
s(A) -=:А'.
Если мы допустим, ЧТО
можно провести еще перпендикуляр, отличный от АР, то, по
вторив предыдущее построение, мы получили бы еще одну
точку, симметричную с А и отличную от А', что противоречит
однозначности построения симметричной точки. Итак, перпен"
дикуляр АР единственный. .
2) Пусть АМ наклонная. АМ==А'М и АР==А'Р. В силу
неравенства треуrольника имеем:
АМ +А'М>АА', т. е. 2АМ>2АР, откуда АЛ1>АР.
3) Положим, что дана еще наклонная АМ', причем РМ ==
== РМ'. Тоrда М и М' симметричны относительно оси АА' и,
значит, АМ ==АМ'.
4) Пусть, наконец, PN>PM, тоrда ломаная АМА' будет
выпуклой объемлемой, а ломаная ANA' объемлющей. По
этому
AM+A'M<AN+A'N, т. е. 2AM<2AN и AM<AN.
Ме'f10ДОМ от протИвноrо леrко доказать предложения, 06
ратные предложениям 2), 3) и 4).
На основании доказанноrо предложения дается определе
нне расстояния. За расстояние от точки до прямой npиHи
J
н'
N
А'
Рис, 17
18
.мается отрезок nерnеllдuкуляра, npOBeaeHHOZO из этой точки.
/( прямой.
Установив это, мы можем решить следующую задачу.
Задача. Найти rеометрическое место точек, равноудален..,
ных от двух пересекающихся прямых,
Реш е н и е. Пусть а и а' данные прямые, пересеКающие....
ся в точке О (рис. 18). Проведем биссектрисы всех четырех
I
I
\ I ,
\1,' о
'y'N
r
5'
'J
Рис. 18
уrлов и покажем, что СОВ1ОКУПНОСТЬ полученных двух прямых
s и s' и будет искомым rеометрическим местом. Возьмем на
какой"нибудь биссектрисе произвольную точку М И проведем
из нее перпендикуляры мр и МР' к прямым а и а'.
Точки Р и Р' будут симметричны относительно биссектри-
сы ОМ. Действительно, прямая а' симметрична с а относи..
тельно ОМ. Прямая, симметричная с МР относительно ОМ,
должна быть перпендикулярной к а', так как при осевой сим..
метрии сохраняетоя величина уrлов. Значит, эта прямая сов-
падает с МР', а потому Р и Р' симметричны как точки пере..
сечения симметричных прямых. Итак, А1Р == МР'.
Предположим теперь обратное: некоторая точка N одина..
ков о удалена от обеих прямых а и а', т. е. равны соответст"
вующие перпендикуляры: NQ == NQ'. Покажем, что N лежит
на биссектрисе.
Ось симметрии точек Q и Q' проходит через точку N. Пря..
мая а, перпендикулярная к NQ, преобразуется в прямую, про..
ходящую через точку Q' и перпендикулярную к lVQ',
т. е. в прямую а'. Поэтому полученная ось симметрии должна
пройти через точку аа' = О, значит, она проходит по биссект-
рисе уrла.
Мы видим, что обе прямые удовлетворяют условию
задачи, Они перпендикулярны между собой, так как
2* 19
перп.ендикулярны биссектрисы двух смежных уrлов 1. Ввиду
Toro что эти прямые идут по биссектрисам, будем называть
их 6иссекторнымu nрямыми. Отсюда следует предложение:
Биссектриса ВЫnУКЛ020 У2ла есть 2еом,етрическое место
е20 внутренних точек, равноудаленных от сторон.
При помощи найденноrо rеометрическоrо места решается
еще одна основная задача:
Задача. Провести окружность, касающуюся трех данных
несовпадающих прямых: ВС, СА, АВ.
Реш е н 'и е. Так как прямые не совпадают, то точки А, В
и С не лежат (на одной 'и той же прямой (рис. 19). Если окруж
"
...... ,/ п' ,., Р
" ",,
"...... ......
...,." ..,., / ........
./
/
\.\
'
\'\ "-
........
'\ ....... т'
\ ,
\ '
\ "
р. \ \ ........ ,
\ \ п "
\ \ ........
\ \
\ \
\ \
\ \N
\
\
"
"
"
р"
/
lm
Рис. 19
ность касает'ся двух прямых, то центр 'ее находится на одина..
KOBO расстоянии 'От этих прямых, так ,как радиусы, прове..
денные в точки каса l НИЯ, перпендИ'кулярны к ка1сательным и,
значит, ими определяется расстояние от центра до ка,сатель..
ной. Поэтому центр ИСl{.омой окружности леж.ит на биссек..
орной rnрямой. Но через каждую из точек А, В !и С прохо..
дит по две взаимно перпендикулярных биссекторных прямых,
Биесекторную 'прямую, проходящую через точку А и пере..
секающую отрезок ВС, оБОЗ1начим т; проходящую через В
и пересекающую отрезок СА n; проходящую через С и
1 См. упражнение 2 на стр. 29 учебника rеометрии Н. Н. Никитина
(издание 1961 r.).
20
пересекающую АВ р. Перпендикулярные к ним биссектор-
ные прямые обозначим 'соответственно т', п', р'. Точки пере-
сечения 'прямых т, п, р С прот,ивоположными отреЗ'ка\ми обо-
значим 'соответственно М, N, Р. Так как отрезок BN соеди-
няет точки, лежащие ,на двух ,сторонах уrла АСВ, то луч СР
пересекает этот ,о резок в некоторой точке 1. Это есть точка
пересечения прямых пир. По свойству ,биссекторных пря-
мых точка 1 одинаково удалена от IПрЯМЫХ ВС, СА и АВ, зна-
чит, и прямая m 1I1РОХОДИТ через эту же точку, В точке I пере-
секаются три биосектрисы 'внутренних уrлов треуrольнИ'ка..........
она есть центр окружности, вписанной в этот треуI'ОЛЬНИК.
Прямые п' и р' также пересекаются, так как если бы они
оказались па1раллельными, то то:r.да параллельными оказа-
лись бы и прямые п 'И р, пересечение которых мы уже дока-
зали. Обозначим через Iа точку их пересечения. Она тоже
одинаково удалена от прямых ВС, СА и АВ, и потому через
нее проходит еще и прямая т. Iа есть точка пересечения двух
внешних Iи одной внутренней биссектрис 'OHa есть центр вне-
вписанной 'окружности треуrольника. Аналоrично получим
точку 1 ь , В которой пересекаются прямые р', т' n, и точку 1 с,
в которой пересекаются прямые т', п', р.
Итак, rJlbI д'оказали, что существует четыре окружности,
касающиеся трех данных прямых, причем одна из них впи
са'на, а три вневписаны в 6.АВС.
(2.6) Посмотрим, как применяется осевая симметрия к
метр'ическим соотношениям в т,реуrольнике. УстаНОВИ 1 \сна-
чала соотношения между ,сторонами и уrлами треуrольника.
Теорема. В одном и том же треУ20льнике: 1) против рав-
ных сторон лежат и равные уzлы; 2) против большей сторо-
ны лежит и больший уzол.
Д о к а з а т е л ь с т во. 1) Пусть в треУl'ольнике АВС АВ==
==АС (/рис, 20). Проведем ось симметрии s точек В и С. ТаК
как АВ == АС, то ПО основной теореме {см. (2.4)] ACs и, зна-
чит, L. В == L С как взаимно симметричные,
2) Пусть в треутольнике АВС АВ>АС (IРИС. 21). Про.ве-
дем ось симметрии s точек В и с. Так как точка А ближе к
точке С, то А лежит в одной полуплоскости С точкой С ПО от-
ношению к s. Значит, отрезок АВ пересекает s в точке М;
L.MBC== LMCB 'как симметричные. Уrол МСВ есть часть
уrла АСВ, поэтому LACB> L.MCB, или L.ACB> L,MBC, т. е.
L.C>L.B.
Теорема (обратная). В одном и том же треуzольнике:
1) против равных уzлов лежат и равные стороны; 2) против
большеzо уzла лежит u большая сторона.
Д о к а з а т е л ь с т в о обратной теоремы можно провести
методом от про'Тивноrо, НО можно доказать и непосред-
ственно.
21
1) Пусть в треуrольнике АВС L. В == L. С (IРИС. 20). Прове..
дем ось симметрии s точек В и С. У'rлы L. В и L. С равны и
противопол'ожно ор,иентированы, поэтому прямые АВ 'и АС
симметричны относительно s и, значит, А Cs. Поэтому АВ==
==АС.
2) Пусть в треуrольнике АВС L.C>L.B (рис. 21). Про.ве..
дем ось симметрии s точек В и С. Тоrда уrол, симметричный с
А
в с I
I , С
I I
I
I ,
s s
Рис. 20 Рис. 21
уrлом В относительно оси s, окажется внутри большеrо
уrла С, и сторона ero пересечет сторону АВ в точке М, лежа..
щей на ос'и s. Отсюда Iследует, что точка А будет лежать в
ОД'НОЙ полупло'Скост,и С точкой С относительно оси s. П,оэтому
АВ>АС.
Так же леrко при помощи осевой симметрии доказывают..
ся ПрIIзнаки равенства треуrольников.
Теорема. Два треУ20льника равны, если выполняется одно
из следующих трех условий: 1) три стороны одНО20 треУ20ЛЬ..
ника соответственно равны трем сторонам apY20Z0; 2) две сто..
роны u заключенный между ними У20Л OaHOZO треУ20льника
соответственно равны двум сторонам u заключенному между
ними У2ЛУ apyzozo; 3) сторона u два nриле2ающих к ней У2ла
одно€!о треуzольника соответственно равны стороне и двум
nриле2ающим к ней У2лам apYZ020..
Д О К а з а т е л ь с т в 'О, 1) Пусть в треуrольниках АВС и
А'В'С' дано: ВС==В'С'; СА==С'А' и АВ==А'В' (рис. 22).
Приложим 6.А' В'С' к 6.АВС так, чтобы с.овпали стороны
ВС и В'С', а точка А' заняла поло}кение точ и А". По усло..
вию теоремы А"В==АВ, З1начит, точка В лежит на оси симмет..
рии точек А и А". Т,очно так же в силу ,равенства А"С==АС
точка С тоже лежит на оси симметрии точек А и А". Значит,
ВС есть о.'сь сим'метрИ'и точек А и А". Поэтому A"BC==
22
== 6АВС как симм,етричные. Следовательно, и A' В'С' ==
== 6АВС.
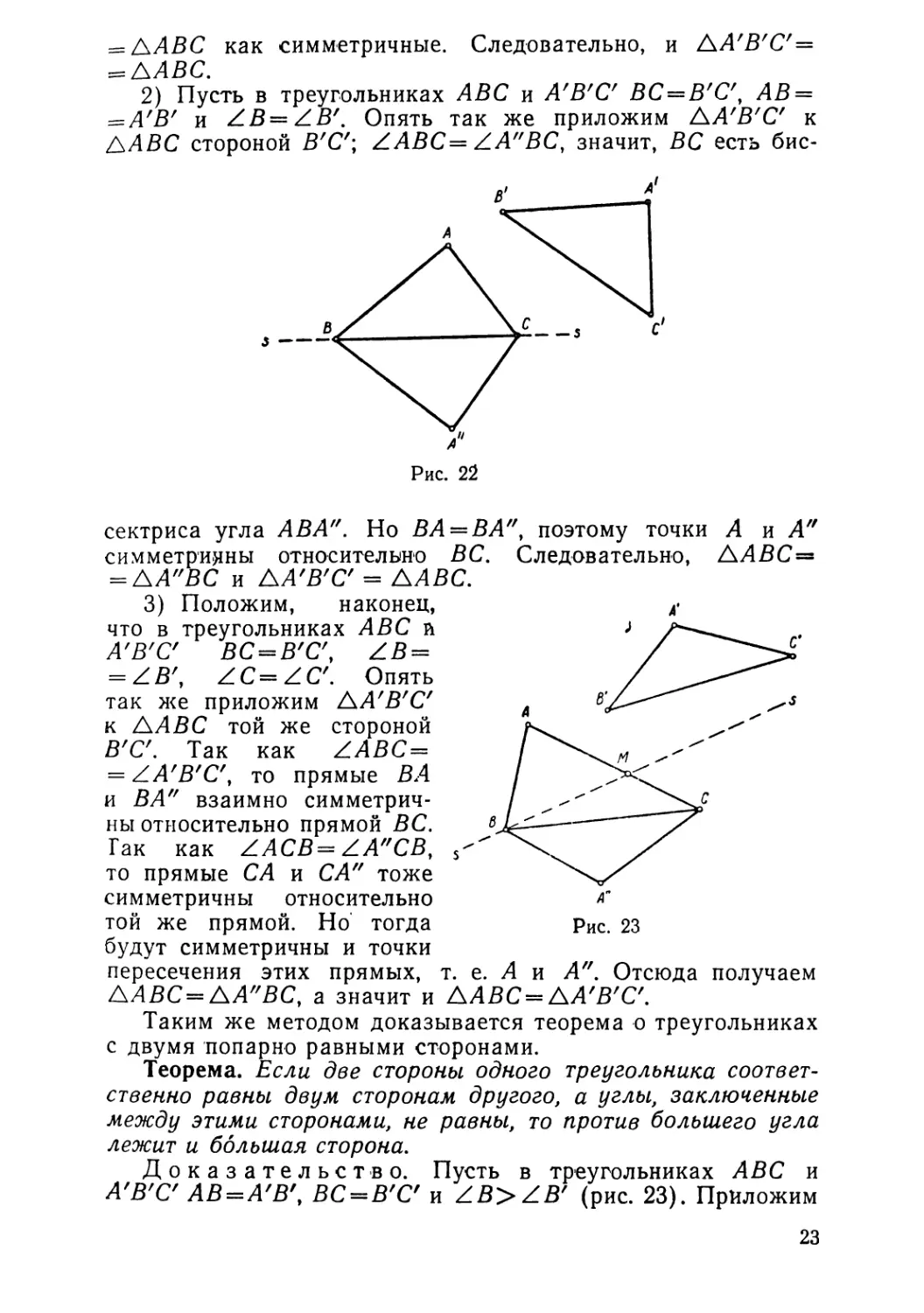
2) Пусть в треу ольниках АВС и А' В'С' ВС==В'С', АВ ==
==А'В' и LB== L.B'. Опять так же приложим A'B'C' к
Ь.АВС стороной В'С'; LABC== L-A" ВС, значит, Ве есть бис
8'
А'
в
J """"'"
А
с ..... s
с'
Рис. 22
сектриса уrла АВА". Но ВА ==ВА", поэтому точки А и А"
симметр'и ны отно,сителыно ВС. След,овательно, ABC==
== A"BC и A'B'C' == ABC.
3) Положим, наконец,
что в треуrольниках АВС 1\
А'В'С' ВС==В'С' LB==
,
==L.B', L-C==L.C'. Опять
так )I{е приложим A' В'С'
к L.ABC той же стороной
В'С'. Так как L-ABC==
== L-A' В'С', то прямые В..4
и ВА" взаимно симметрич
ны относительно прямой ВС.
Так как L-ACB== L.A"CB, s........-
то прямые СА и СА" тоже
симметричны относительно
той же прямой. Но' тоrда
будут симметричны и точки
пересечения этих прямых, т. е. А и А". Отсюда получаем
6ABC== A"BC, а значит и L.ABC== A'B'C'.
Таким же методом доказывается теорема о треуrольниках
с двумя 'попарно равными сторонами.
Теорема. Если две стороны одНО20 треУ20льника COOTвeT
ствеН,но равны двум сторонам дРУ2020, а У2Лbl, заключенные
между этими сторонами, не равны, то против больше20 У2ла
лежит и большая сторона.
Д о к а з а т е л ь с т 'в о. Пусть в тр'еуrольниках АВС и
А'В'С' АВ==А'В', ВС==В'С' и L.B>LB' (рис. 23). Пр"ложим
23
А'
8
J
8'
/$
А
,/
",
",
./
t1 ............
./'
А"
Рис. 23
6.А' В'С' к 6.АВС так, ч обы сторона В'С' совпала с ВС, а
точка А' заняла положение А". Ось симметрии точек А,А"
пройдет через точку В ввиду paBeH'C'f,Ba ВА == ВА". Вместе с
тем s делит пополам LABA" и ,потом'у проходит внутри ero
большей части. Значит, 'Ось s перееекает сторону АС в неко"
торой точке М. Точка А" оказала'сь в одной и той же полу"
8 плоскости С точкой С ПО ОТ-
t ношению к прямой s. Следова-
тельно, АС>А"С, т. е. АС>
>А'С'.
Совершенна тем же спосо..
бом можно доказать и обрат..
ную теорему.
Все предложения, доказан-
ные в этом параrрафе, опи..
1 рались только на основные оп-
Рис. 24 ределения и аксиомы и на ус-
. тановленные наlМИ свойства
осевой симметрии. Этим же методом можно вывести ,и ряд
друrих Iпредложений, например теорему .0 том, что внешний
уrол треуrольника больше всякоrо BHYTpeHHero, несмежноrо с
ним, 'признаки равенства прямоуrольных треу ольников и т. д.
(2.7) Рассмот,рим теперь применение осевой симметрии к
решению задач.
Задача 1. Дана прямая 1 и вне ее две точки А и В. Найти
на прямой 1 !акую точку М, чт,обы сумма АМ +МВ была наи..
меньшая.
Реш е н и е. В то'м случае, коrда точки А и В находятся
по разные стороны 'от прямой 1, задача решае ся очень про..
сто: кратчайшим путем от А к В является отрезок АВ, пере..
секающий 1 в искомой точке М. Положим теперь, что А и В
находятся по одну ,сторону 'от 1 (рис. 24).
Этот ,случай 'Нетрудно привести к предыдущему: возьмем
Т'О'Ч'ку В', симметричную с В отнооительно 'оси [. Кратчайшим
путем от А к В' являе ся отрезок АВ', пересекающий 1 в
искомой точке М. Действительно, путь АМВ Ipa\BeH АМ + ВМ ==
==АМ+МВ'==АВ'. ДЛЯ лю/бой друrой точки N на прямой 1
получим: AN +NB ==AN +N В'>АВ' в силу неравенства тре..
уrольника. Итак, путь АМВ деЙствительно кратчайший.
3амет,им, что в форму этой rеометрической задачи .10ЖНО
облечь весьма разнообразные практические ,вопросы. Пр иве..
дем примеры.
а) Полож,им, что 1 'цр'оекция плоскоrо зеркала, постав..
ленноrо 'перпендИ'куляр'но к пл,оскости чертежа. В точке А
находится источник света. В какую точку зеркала нуж'но на..
править луч света из А, чтобы он, отразившись, попал в В?
24
Такой точкой является точка М, так как для нее выпол
няе-rся закон .отражения: уrол ,наклон,ной АМ с 1 равен уrлу
ВМ с той же прямой.
б) П'усть 1 есть береr судоходной реки. В точках А и В
расположены населенные пункты. В каком месте нужно по
строить пристань, чтобы сумма расстояний АМ и МВ была
наименьшая?
Решением, 'Конечн'о, будет точка М.
в) Пусть 1 борт бильярда. В точках А и В находятся
два шара. В каком направлении нужн'о уда1РИТЬ шар А, чтобы
он, оттол нувшИ'сь от борта 1, попал в шар В?
Ответом является тоже точ
ка М, так как закон отражения
Уlпруrоrо шара при ударе о He
подвижную стенку такой же,
как и для отражения света.
r) Положим, что 1 rлад
кий стержень, по которому
скользит кольцо М. Через это
кольцо пропущена Tyro натя
нутая эластичная нить, закре
пленная 8 точках А и В. KaKO
ва будет Iфиrура равновесия?
Ввиду Toro что нить CTpe
мится сокра1"ИТЬСЯ д'о мини
rvrальной длины, фиrура равновесия имеет вид, указанный на
рис. 24.
Задача 2. Дана окружность с центром О и не принадле
жащие ей точки А и В. Пользуясь одним только циркулем,
найти точки пересечения прямой АВ 'с данной окруж'ностью.
Реш е.н и е. П,оложим, что задача решена и мы нашл.И
точки пересечения М и N прямой АВ с ,данной ОКРУЖ1НОСТЬЮ
(рис. 25). Примем прямую АВ за ось симметрии. Тоrда задан
ная оюружность с цент,ром О преобразуе ся в новую окруж
ность С центром О' и проходящую через те же точки М и N
(так как М и N принадлежат оси АВ и потому являю ся
непод'вижными точками). Отсюда мы поспучаем искомое по
строение. Находим точку О', 'СИ Iметричную с точкой О OTHO
сительно прямой АВ, дЛЯ чеrо проводим из центров А и В
окружности радиусами АО и ВО. Этим определится точка О'.
Далее из центра О' проводим окружность радиусом, paBHЫ 1
радиусу данной окружности. Полученная окружность пересе
кает данную окружность в искомых точках М и N. Точки
.А1 и N принадлежат прямой АВ, так как они должны лежать
на оси симметрии точек О и О'. .
В зависимости от расположения данной окружности и
данных точек мы можем получить две точки пересечения,
одну или ни одной.
"
А ,,"
р
,,""
Рис. 25
25
Приведенное в этой задаче построение я.вляется 'Примером
так называемых «построений Маlскерони» итальян,с.коrо reo
метра, доказаншеrо, ч'foо в'се rеометрические построения, осу.
ществляемые пр.и помощи циркуля и линейки, MorYT быть 'Вы
полнены пр'И помощи одноrо лишь циркуля.
Задача 3. Доказать, что три ЫCOTHыe прямые 1 треуrоль
ника пересекаются в ОДIНОЙ и той же точке.
Реш е н и е. Рас,смотрим сначала остроуzольный ABC
(рис. 26). Проведем через вершину А ВЫ1СОТНУЮ прямую, I{O
'})орая пересечет сторону Ве в
точке М, лежащей между точка-
ми В Iи С; если бы, например,
N ....:: Ml точка М оказалась левее точки В,
... ,.,./' то В AMB внешний острый уrол
,." при вершине В оказался бы м,eHb
ше BHYTpeHHero прямоrо уrла при
вершине М.
Найдем точки М} и М2, симмет
ричные с М относите.,lЬНО прямых
АВ и АС. Уrол M 1 AM 2 вдвое
больше уrла ВАС, TalK как в силу СИМJметрии LMAB==
== L ВАМ}, LMAC== L САМ 2 , причем LMAB + LMAC== L ВАС.
Отсюда следует, что LM}AM 2 меньше pa BepHYToro, так как
LBAC острый. Поэтому отрезок М 1 М 2 пересекает лучи АС и
АВ, идущие внутри этоrо уrла, в точках, которые мы о'бозна
чим соответственно N и Р.
Расс'мотрим теперь треуrольник MNP. П,рямые АВ и АС
являются биссеКl'р'Исами внеш'них уrлов этоrо треуrольника,
поэтому 'Через точку А их пересечения проходит и \биссектриса
BHYTpeHHero уrла, т. е. МА есть биссектриса уrла NMP. fIря-
мая Ее перпендикулярна к АМ, 'поэтому она является 'внеш-
ней биссекторной прямой треуrольника MN Р.
В точке В пересекаю1'СЯ биссеК11РИСЫ 'внешних yr лов Tpe
уrольника MNP, поэтому прямая BN будет БИС1секторноЙ
прямой BHY'f'peHHero уrла MNP; вместе с тем она перпендику
лярна к биссектрисе внешнеrо уrла, Т. е. BN .lAC. Точно так
же РС есть биссеКТР1иса BHYTpeHHero уrла MPN и потому
перпенд\икулярна к биссектрисе внешнеrо 'уrла, т. е. к прямой
АВ. Итак, АМ, BN и СР биссектрисы внутренних уrлов
треуrольника MNP и потому 'Пересекаются в одной и той же
точке Н. Н,о эти же прямые АМ, BN и СР являются BЫCOT
ными прямыми В треуrольнике АВС, чем и доказано предло
жение для ос'Т'роуrольноrо треуrольника. Точка Н пересе
че.ния этих прямых называется ортоцентром, треуrольника.
А
,.
"
"
"
,.
,.
,.
"
,,11 Р
"
м ...
, .......
8
м
с
Рис. 26
1 Высотной прямой называется прямая, проходящая через вершину
треуrольника перпендикулярно к противоположной стороне.
26
Если 6.АВС прямоуrольный с верши'ной прямоrо уrла
в точке С, то ВЫ1СОТНЫМ,и прямым,и будут ВС и СА, ИДУll{ие
по катетам. Они пересекаются 'В точке, через которую прохо
дит также и высотная прямая, перпендикулярная к rипоте
нузе АВ. Таким образом, ортоцентр'ом прямоуrольноrо Tpe
уrольнИ'ка IСЛУЖИТ вершина С прямоrо уrла,
Пусть теперь 6.АВС тупоуrольный, причем вершина
тупоrо уrла находится в точке А (рис. 27). Высотные прямые
BN и СР пересекаются в некоторой н
точке Н. Эти прямые не MorYT быть ,t,
параллельными, так как тоrда были /, ",
б б u " ,
ы параллельны между сО' ои и пер.. I ,
, I '"
пендикулярные к ним прямые СА и АВ. Н..... '",/'
Полученный 6.ВСН остроуrоль А
ный, TaI{ как каждый из ero уrлов
L-BHC, LCBH и LBCH является OCT
рым уrлом соответственно в одном из
прямоуrоль'ных треуrольников ВРН,
BNC, РВС. Но как уже доказано, вы..
сотные прямые остроуrольноrо треуrОЛЬНИtка пересекаются в
одной и тдй же точке. В треуrольнике ВСН высотными прямы
МИ являются АВ и АС, пересекающиеся в точке А. Поэтому
через очку А должна пройти и третья высотная прямая Н М,
проходящая через точку Н перпендикулярно к ВС.
Вместе с тем мы установили, ч о и в тупоуrольном Tpe
уrольнике вы,с.отные 'прямые АМ, BN и' СР проходят через
один и тот же ортоцентр Н.
н
с
Рис. 27
Упражнения
1. Найти 'rеометрическое место центров окружностей, Пiро
ходящих через две данные точки,
2. На сторонах уrла 'от вершины О отложены соответст-
венно равные О'трезки: ОА == ОА' и ОВ == ОВ'. П1рямые АВ' .н
А' В пересекаются в т,очке Р. Доказать, ЧТО Р лежит на бис
сект'рисе уrла.
3. До'казать: если дана ось 'и д,ве симметричные друт с
ApyroM точки, то всякую друrую точку плоскости можно пре
образовать в симметричную, пользуясь только линейкой (не
прибе1rая к циркулю).
4. Пользуясь только линей ой и чертежным треуrольни-
ком, найти ось симметрии двух данных точек.
5. Какой наименьшей величины д:олжно быть зеркало,
чтобы чело'век Mor видеть в нем себя во весь 'рост?
6. ПQrС рОИТЬ равнобедренный треуrольиик так, чтобы Дlве
вер'шины ero основания ,наХОДИЛIИСЬ в двух данных точках,
U U
а третья на данном расстоянии от третьеи даннои точки.
27
7. Какое наименьшее числ,о осевых симме1iРИЙ нужно Пlро
извести, чтобы преобразовать данный отрезок АВ в равный
ему дан'ный 'отрезок А' В'?
8. Какое на.именьшее чи,сло ,осевых 'симметрий нужно про
извести, чтобы даlННЫЙ 1'реуrольник АВС преобраз'овать в
равный ему данный треуrольник А' В'С'?
Рас,смотреть Iслучаи, коrда треуrольники ориентированы
одинаково и коrда противоположно.
9. Пос роить треуrольник по основанию, уrлу при OCHO
вании и сумме (или разности) двух друrих ero сторон.
10. Через две данные точки А и В 'провести две пря'мые
так, чтобы уrол между ними делился данной прямой 1 попо..
лам.
11. На п'рямой 1 найт,и точку М, 'разность расстояний к'ото"
рой от двух даlННЫХ точек А и В была бы наибольшая.
12. На бильярде, два борта KOToporo наклонены друr к
друrу под произвольным уrлом, лежат ша1ры А и В. В каком
направлении нуж/но толкнуть шар А, чтобы -он после дву"
KpaTHoro отражения от обоих бортов попал в шар В?
13. На прямоуrольном' бильярде лежит шар Р. В каком
направлении ero нуж'но толкнуть, чтобы после четырехК!рат
Horo отражения от четырех ,стенок он вернулся в исходное
положение?
14. Дана прямая 1 и точки А и В вне ее. Найти на прямой
такую точку М, чтобы уrол луча МА с прямой 1 был вдвое
больше уrла, образуемо'rо лучом МВ с той же прямой.
15. Внутри OCTporo уrла дана точка Р. Найти 'на двух CTO
ранах ero с.оответственно точки А и В такие, чтобы пер'имеrр
треуrольника АР В был Iнаименьший.
16. Постр,оить четьvpехуrольник по четырем сторонам, зная,
что одна из ero диа оналей есть биссектриса 'BHYTpeHHero
yr л а .
17. Провести бflесектрису уrла, верш,ина Koroporo Heдo
ступна.
18. Дана одна из вершин треуrольника и две прямые, на
которых лежат биссектрисы этоr,о треуrольника, не прохо
дящие через эту верш,ину. Построить этот 11реуrолЬ'ник,
19. Лицевая сторона 'плоскости окрашена в красный цвет,
изнанка в зеленый. На пл'оскости начерчен разносторонний
треуrольник. Предлаrается вырезать этот треуrольник и, раз..
резав ero на 'наименьшее число частей, уложить их на преж..
нее место так, чтобы получил'ся такой же треуrольни'к зеле..
ной стороной 'сверху.
20. Два плоских зеркала наклонены друr к друrу под не..
которым уrл,ом. Луч света, идущий параллельно nepBO:vIY
зеркалу, отражает.ся от BToporo, потом от первоrо, потом
опять от BToporo, потом 'опять от пер'воrо и, наконец, после
28
.отражения от 'BTop,o'ro возвращается по прежнему пути. Опре-
делить уrол между зеJркалами.
21. Провести прямую через данную точку М и точку пере..
-сечения прямых а и Ь, которая недоступна (использовать
пересечение высот треуrольника).
22. Точки А и В 'на местности ,разделены препят,ствием (на..
пример, между ними наХОД1ИТСЯ корпус здания). Пользуясь
осевой симметр.ией, измерить расетояние между точками
А и В.
23. Точка А находит,ся на одном 'б реrу реки, точки В и
С на друrом. Пользуя.сь уrломерным инструментом, найти
-точку А', симметричную ,с А относительно прямой ВС.
24. Точки А IИ В находя ся IHa одном береrу реки, точки
М и N на друr,ом. Пользуясь уrломерным ин,струментом и
решением предыдущей задачи, н,айти расстояние между не-
ДОСТУПJНЫМИ точками А и В.
3. ЦЕНТРАЛЬНАЯ СИММЕТРИЯ ,
(3.1) Qпределения.
1 ) Центральной симметрией 'называется точечное 'Пре..
'Образование, Пlри которо'м в плоскости дается 'неподвижная
-точка О центр симметрии и каждой точке А ставится в
А
с
с'
Рис. 28
Рис, 29
соотве ствие точка А' так, чтобы точка О была Iсерединой от..
резка АА' (рис. 28). Преобрззование точки А в точ'ку А' отно"
сительно центра О записывается так:
о (A) A'.
2) J?:сли между точкаi\1И двух фиrур установлено взаим'но"
одно начное ,соответ,ствие таким образом, что кажд,ой точке
однои фиrуры с-оответствует симмет1ричная с ней точка друrой
фиrуры по отношению к одному .и том'у же центру, то такие
29
фиrуры называют,ся центральн'О сu.мметричН,ыми относ,итель..
но этоrо центра.
ЦеН'f1рально симметри'Чные фиrуры можно 'получить, за..
крепив плоскость данн<>й фиrуры в неП'одвижной точке О, а
потом повернув ее на 1800 BOKpyr этой точки (рис. 29).
Непосредственно .из определения центральной симмет,рии
получаем следующие выводы.
Следствие 1.. В центральной симметрии единственной не..
подвижной точкой является центр симметрии.
Действительно, -Б,сякая точка, 'отличная от центра, пре..
образуется 'в точку, лежащую по Д'р'уrую сторону от цеН1'ра,
и совпадать эти точки не MorYT.
Следствие 2. Всякая прямая, проходящая через центр
симметрии, симметрична сама с собой, так как каждая точка
этой прямой COOTBe'f1CTByeT l'очке той же прямой. Поэтому
прямые, проходящие через центр, являются неnодвижнымu
пРЯМblми.
СJIедствие 3. Ввиду тozo что центральной симметрией
точки взаимно преобразуются apyz в apyza, из соотношения
О (А) == А' следует О (А') == А.
Все основные свойства центральной симметрии можно полу
чить, установив ее связь с осевой симметрией.
s
А
Q.
\
\
\
\
\
А 1
Р
/
1
/
I
I
I
S
s'
,
\
,
,
'о,
А
5
Рис. 30
Теорема. Две nоследоватеЛЬн'ые осевые симметрии со взаимно
перnеН,дикулярными осями тождественны с одной центральн'ОЙ
симметрией, центр которой совпадает с точкой пересечения
осей.
Д о к а з а т е л ь с т в о. Пусть s и s' две оси симметрии,
пересекающиеся в точке О, причем s.l s' (рис. 30). Возьмем
в плоскости произвольную точку А и пусть s (А) == Al и
s'(A1) == A'. Докажем, что О(А) == А'.
30
ПО свойству оси симметрии ОА == ОА 1 И ОА 1 == ОА'. Значит.
ОА === ОА'. Обозначим через rJ., и острые уrлы, образуемые
лучом ОА 1 с осями S и s'. Так как s s', то rJ.,+ ==90°.
в силу симметрии луч ОА образует с осью s уrол, равный rJ.,.
а луч ОА' образует с осью s' уrол, равный . Поэтому
L АОА' == rJ., + rJ., + + ==2 (rJ., + ) == 1800. Кроме Toro, мы
получили, что ОА == ОА', следовательно, точка О есть центр
СИ lIметрии точек А и А', т. е. О(А) == А'.
Теорема (обратная). Всякая центральная симметрия тож-
дественна с двумя последовательными осевыми симметриями,
оси которых взаимно nерnендикулярны и проходят через центр,
nричелt одну из них М,ожно провести nроuзвольно.
Доказательство. Пусть О(А) == А'. Проведем через
центр О произвольную ось s И положим, что s (А) = А 1 . По ус-
ловию теоремы ОА' =::: ОА, а в силу осевой симметрии ОА == ОА 1 .
Поэтому ось симметрии s' точек А 1 и А' проходит через центр О
и, кроме Toro, s s' как биссектрисы смежных уrолов. Итак,
центральную симметрию с центром О можно заменить двумя
осевыми симметриями с осями s и s'.
ОТСЮД,а можно получить все осн.овные свойства централь..
ной симметрии:
1. ЦеН'f1раль'но симметричные фиrуры равны и -одинаково
ориентированы, Так как центральная симметр,ия тождествен..
на двум осевым, а при каждой осевой симметрии сохра'няется
;j
,\. /
S' S'
о
\\.
s
Рис. 31
равенство фиrур, то оно сохранится и при двух последова
тельных осевых симметриях. Вместе с тем каждая осевая
СИ метрия l\1еняет 'ориентацию фиrуры на обратную. Поэто..
МУ после двух осевых симметрий 'Ориентация фиrуры будет
сов'падать с первоначальной (рис. 31).
2. Две пары центрально симметричных точек определяют
пару центрально ,симметричных прямых.
Две пары центрально симметричных прямых опредеЛЯJОТ
пару ценТ'рально симметричных точек.
31
В первом случае имеем: О (А) == А', О (В) == В', следовательно,
О (АВ) == А' В' (рис. 32).
Во втором случае имеем: О (а) == а', О (Ь) == Ь', следовательно,
О (аЬ) == а'Ь' (рис. ...33).
(3.2) Одним из наиболее важных свойств центральной сим-
метрии является параллельность симметричных между собой
прямых.
Теорема. Централь но сuм,м,етрuчные nрям,ые взаим,но nа-
раллель ны.
Д о К а з а т е л ь с т в о. Положим, прямая а, не проходящая
через центр симметрии О, симметрична с прямой а'. Если до-
;'
;'
",.
'"
/
'"
",.
'"
'"
'"
;'
0,,/
--. ....
'" ..........
'" ........
'"
'"
'"
'"
",.
,
/
Рис. 32
Рис. 33
пустим, что прямые а и а' имеют точку пересечения аа', то
получим О (аа') == а'а. Но аа' и a'a OДHa и та же точка.
Однако известно, что в центральной симметрии единственной
неподвижной точкой является центр и друrих неподвижных
точек не существует. Полученное прьтиворечие показывает,
что а и а' пересечься не MorYT. Следовательно, а 11 а'.
Если бы прямая а прох'од.ила через центр О, то симмет
ричная 'с ней прямая а' тоже проходила бы через центр и
совпала с ПрЯ fОЙ а. Поэтому совпадение двух прямых иноr
да бывает целесообразно рассматривать как частный (пре
деЛЬ1НЫЙ) случай параллельности.
Определение 1. Часть плоскости, заключенная между
двумя параллельными прямыми, называется полосой. Па
раллельные прямые называют,ся сторонами полосы. Отрезок,
соединяющий точку од'ной ,стороны полосы С точкой дJруrой
ст.ороны, называется поперечным отрезком.
Из предыдущей теоремы и определения получаем:
Следствие. Середина ВСЯКО20 поnереЧНО20 отрезка есть
центр симметрии nолосы.-
32
Пусть а 11 а', Ас а и А'са', О середина АА ' (рис. 34).
Прямая, центрально симметричная с а относительно О, парал-
лельна а и проходит через точку А'. Следовательно, на осно"
ванИН аксиомы Iпараллель..
насти эта прямая совпадает
с а'. Итак, О (а) :ай'.
Из этоrо следствия сразу
.
получаlОТСЯ все своиства yr..
лов, образующих,ся от пере..
сечения двух параллельных
прямых любой се ущей, так
как внутренние и внешние а-
накрестлежащие уrлы равны
как центральна симметрич"
ные ,относительно середины поперечноrо отрезка, .образуемоrо
секущей. И обратно, равенство накрестлежащих уrлов об..
условливает центральную СИМl\fетрию их относительно той
же середины.
Определение 2. Попе-
речный отрезок, пер,пен
дикулярный к сторонам
l полосы, называется ши
риной полосы.
Следствие. LUupUHa
полосы везде одинакова.
Действительно, если
дано, что 1111', АА' и
ВВ' две ширины, при
чем А cl, BCl, A'cl'
и В'с1' (рис. 35), то от..
резки АА' и ВВ' симмет..
оси симметрии s точек А и В. П,оэтому
ричны относительне
АА'- == ВВ'.
1-'1з этоrо оСлед,ствия леrко получается предложение: 2eo
tеТрllческое место точек удаленных от данной прямой на
расстояние, равное данному отрез..
ку, есть две прямые, nараллельные
данной.
Найдеl\I еще одно rеометриче.. Q
ское место точек.
Задача. Найти rеомет р ическое
'"''''''
место центров симметрии полосы.
Реш е н и е. Пусть полоса. опре-
делена условием аН а', АА' один
из поперечных отрезков и точка О ----- .
ero середина. Как уже доказано, О
есть центр симметрии пол,осы (рис. 36).
Пр,оведем через точку О прямую l, параппелыную старо..
нам ПОJIОСЫ. Докажем, что 1 и есть ИСКО fое rеометр.ическое
l
А
V
I
I
I
I
I
I
,
А
s
I
,
I
I
I
,
I
I
I
I
I
I
I
I
I
I
l'
s
Рис. 35
3 А.. И. Фет сов
а
А
;r
""
,
""
""
""
""
"
о ,,'
/4
/'
"
1';
А'
О'
Q
"'-.
Рис. 34
в
9
I
I
I
I
I
I
I
8'
l'
Q
l
а'
Рис. 36
33
место. Действительно, ширина полосы, проходящая через
точку О, делится в ней п'ополам, так как О центр симмет
рии полосы. Значит, О находится на равных расстояниях от
стор,он полосы. А так как ширина 'полосы ,везде одинакова,
то все точки прямой [ одинаково удалены от сторон полосы,
т. е. в-сякая точка [ есть середина проходящей через нее ши
t рины, и, значит, она
.;0,.;0'" а, есть центр симметрии
А, полосы. Наlконец , ника..
.;о.... а 1
A кая точка вне пnямой 1
... QJ r
А[ центром симметрии по
Л0СЫ быть не l\'[ожет,
так как тоrда проходя
щая через нее шир,ина
,имела бы две середи
ны: одну в данной точ
ке, а друrую на пря
:'vf о Й 1.
Из этоrо доказа
тельства следует, что
ПРЯ1Vtая 1 есть ось сим
метрии полосы. Поэто
му она называется
осью полосы.
Полученные Iсвойства полосы дают 'возможность очень
просто доказать одну из основных теорем rеомеТfрИИ Teope
му Фалеса 1.
Теорема Фалеса. Если на прямой [отложить последОGа
тельно ряд равных отрезков: А 1 А 2 == А 2 А з == А з А 4 ==...== Aп lAп
и через их концы провести параллельные: а 1 11 а 2 11 аз . . . " а п ,
то на любой прямой [', пересекающей эти параллельные, точ
ками пересечения определится тоже ряд равных отрезков
(рис. 37):
........
..........
.;о .... .....
.;о......
....;0
.......
............
.........
.......;0
.....-;...
........
............;0
.............
.;о....
аn.....
'- z,
Рис. 37
" " " "
А 1 А 2 == А 2 А з А з А 4 == . . . == Aп lAп.
Д о к а з а т е л ь с т в о. Рассматривая а 1 и аз как стороны
полосы, мы видим, что а 2 ось этой полосы, поэтому она дe
" "
лит пополам любой поперечный отрезок. Значит, А 1 А 2 == A 2 A:J.
Далее а 2 и а 4 определяют ПQЛОСУ с осью аз, откуда следует,
" "
что А 2 А з ==А з А4' и Т. д.
Частным случаем теоремы Фалеса является предложе
ние: если на одной стороне уzла отложить от вершины nосле
аовательно ряд равных отрезков, то nараллельные прямые,
ftpOBeaeHHble через точки деления, отсекают на apyzou CTO
роне уzла тоже ряд равных отрезков.
,1 Фалес Милетский (конец VII начало УI в. до н. э.) древнеrре
ческий философ, установивший ряд теорем элементарной rеометрии
34
Справедливо It обратное предложение: если на каждой
стороне уzла отложить от вершины ряд равных отрезков и
через соответственные концы их провести прямые, то эти
прямые будут между собой параллельны. .
От,сюда следует евойство 'средней линии треуrольника и
трапеции, а также решение основной задачи о делении дaH
Horo о резка на n равных частей.
(3,3) Свойствами полосы определяются свойства различ
ных видов па раллелоrраммов.
Определения. Часть плоскости, общая двум пересекаю
щимся полосам, называется nараллелоzраммом. Е-сли эти по
лосы взаимно перпендикуляр'ны, 1'0 'параллелотрамм назы
вается прямоуzольником. Если полосы равны между собой, то
параллелоrрамм называется ромбом. Если полосы и равны
и перпендикулнрны между 'с.О'бой, то параллелоrрамм, являю
щийся ОДНОВJременно и прямоуrольником и ромбом, называет
ся квадратом.
Из этих определений следуют все основные свойства
указанных четырехуrольников:
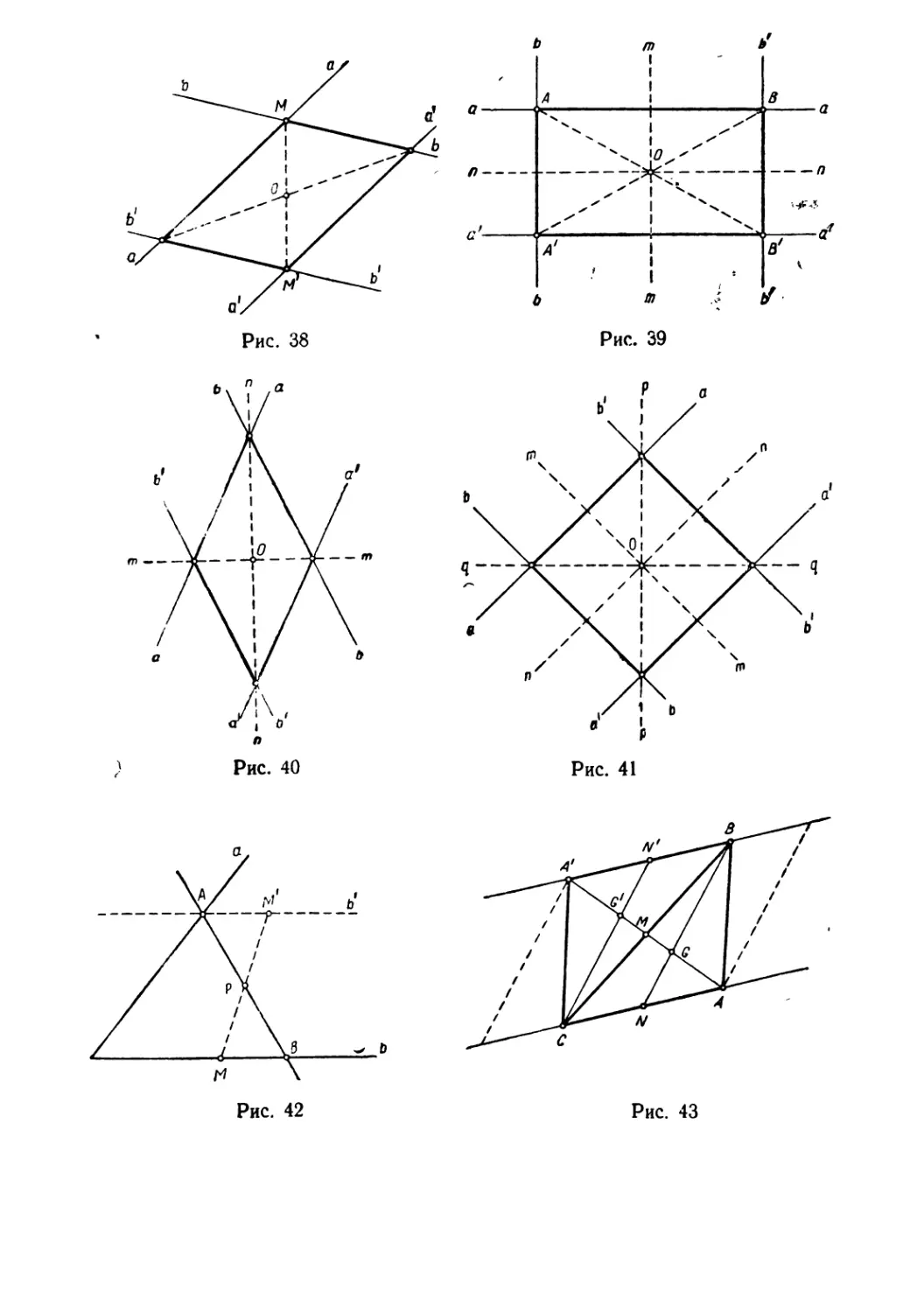
1. Диаrональ параллелоrрамма есть общий попереч'ный
отрез'ок обеих пол'ос (рис. 38), 'поэт,ому середина диаrонали
есть центр сим:метрии всей фиrуры. 01'Сюда следует совпа
дение середин обеих диаrоналей, равенство противопол'ожных
сторон, равенство пр,отивоположных уrлов.
2. у прямоуrолЬ'ника оси .определяющих полос являются
осями симметрии в'сей фиrуры, откуда ,следует равен-ство
диаrоналей (рис. 39).
3. В силу равенсТ'ва полос, определяющих ромб, биссект-
рисы ero уrлов с.ов'падают с осями -симметрии Вrсей фиrуры и
также с ее диаrоналями. Отсюда следует перпендикуляр-
ность диаrоналей (рис. 40).
4. Квадрат обладает всеми свойствами прям'оуrольника и
ромба и является наиболее симме'f1РИЧНЫМ четырехуrольни
ком: осями ,симме-nрии квадрата служат и оси определяющих
ero полос, и диаrонали (рис. 41).
Приведенные при меры показывают, какое значение имеет
центральная симметрия для обоснования важнейших пред
,,10)кений rеометрии.
Рассмотрим применение центральной С'имметрии к реше
нию задач.
Задача 1. Внутри данноrо уrла дана точка Р. Провести
через точку Р прямую так, чтобы отрезок этой п;рям,ой между
сторонами уrла делился этой тачкой пополам.
Реш е н и е. Обозначим через а и Ь стороны данноrо уrла
(рис. 42), а через А и В концы искомоrо отрезка. По усло
вию задачи точка Р есть центр си метрии для точек А и В.
Поэтому если найдем прямую Ь', симrvfетричную с Ь
З* 35
Ри с. 38
ь'
/
Q
\
i
Рис. 40
I ,
{у1 Ь
T
/
I
I
I
..J Ь
Рис, 42
ь
J,'
Q
т
I
I
I
! 8
I //
I /
...... I ",
......,...... 10 /'"
:::- п
", .....;.
// I ............
// I .............
/ I .............
", , ......
А
.....,
,
......
а
п
а'
..+-< ,
8' а"
\.
if.
А'
I
I
I
т
,,"
ь
Рис. 39
а
ь
q
Рис. 41
/
I
I
/
I
,
,
I
I
I
,
I
I
I
I
,
I
I
I
I
I
/
I
Рис. 43
относительно центра Р, то эта црямая пройдет через искомую
точку А. ДЛЯ построения Пlрямой Ь' достаточно взять на
прямой Ь произвольную точку М, найти ей симметричную от..
носителыно Р точку м' и через М' провести b'llb. Задача
всеrда разрешима 'И имеет единствеНlное решение.
Задача 2. Доказать, что три медианы треуrольника пере-
секаются в одной и той же точке.
Реш е н и е. Пусть дан треуrоль,ник АВС с медиакой АМ
(рис. 43). Пrримем точку М за центр симметрии И найдем
A'CB, симметричный с данным, цричем А' М будет медиа-
ной 'Hoaoro треуrолЬ'ника. Отрезок АА' являетс д\иаrональю
параллелоrрамма АВА'С, Пр.оведем ,в ABC вторую медиа-
ну BN, которой в A'CB с,оответствует параллельная ей
1едиана CN'. Если через точки А и А' проведем примые,
параллельные медианам BN и CN', то получим три равные
\тежду собой полосы. По теореме Фалеса эти па1рал:лельные
делят диаrональ АА' на 3 равные части. Отсюда следует, что
\lедиана BN отсекает на медиане АМ две llрети, считая от
вершины А. Ввиду Toro что это же рассуждение мы можем
применить и к третьей медиане треуrольника АВС, то мы
увидим, что и эта медиана отсечет от медиз-ны АМ тоже две
трети, считая от вершины А, т. е. пройдет через эту же точ-
ку а.
Точка пересечения медиан является центром тяжеСТ1i
треуrольника, что можно доказать на основЗ'нии законов
статики.
Упражнения
1. Через данную точку Р 'провести прямую так, чт.обы ее
u u u
отрезок между даннои прямои и даннои окружностью разде..
лился этой точкой пополам.
2. Через противоположные вершины параллелоrрамма
проводят две пары взаимно параллеJIbfНЫХ прямых. С полу"
ченным параллелоrраммом вновь производят такое же по..
строение и т. д. Доказать, чт.о все полученные таким образом
параЛJIелоrраммы имеют один и OT же центр (закон постоян..
ства центров). I
3. Пользуясь одной только линейкой, найти цeH !) тяжести
ф'иrуры, состоящей из двух прямоуrольников, сложенных
друr с друrом в виде буквы r.
4. Двое иrрают в следующую иrру: каждый по очереди
кладет монету на круrлый стол. Монеты должны быть оди..
HaKoBor,o д,остоинства, причем их нельзя класть друr на
друrа. Выиrрывает тот, кто положит последнюю монету. I,aK
нужно иrрать, чтобы неIIlременно выиrрать?
5. Найти rеометрическое место точек, сумма расстояний
37
КО1'орых ОТ д,вух данных перосекающихся прямых постоянна
и равна данному отрезку.
6. Отрезок постоянной длины скользит своими концами по
двум взаимно перпендикулярным прямым. Какую линию
описывает середина отрезка?
7. Доказать, что середины стор,он четырехуrольника суть
вершины па(раллел,оrрамма; середины диаrоналей ЭТОf'О че
тырехуrольника и середины двух против.оположных сторон
так)ке ЯВЛЯЮ1Х:я вершинами параллелоrрамма. Все три па
раллелоrрамма имеют общий центр.
8. Доказать, что, пользуясь только линейкой с параллель
ными краями, М'ОЖ1НО: а) построить биссектрису данноrо уrла;
б) найти 'Т'Очку, симме-"f1РИЧНУЮ с да'нной точкой относительно
данной оси; в) раз,дел'ить данный ,ОТlрез,ок пополам; r) про
вести перпендикуляр из данной очки к данной прямой.
9. Через точку, данную внутри уrла, провести секущую
так, чтобы получился треуrольник 'наименьшей площади.
10. На окружности даны точки А и В, на прямой l дана
точка М. Найти на окружности такую точку Р, чтобы прямые
АР и ВР пересекли прямую l 'в точках, находящихся на .paB
ных рас,стояниях от М.
11. ВНУl'ри треуrольника дана точка. Провести через нее
прямую так, чтобы отрезок, полученный внутри треуrольни
ка, разделился этой точкой пополам.
12. Даны два параллел.оrрамма: ABCD и A'B'C'D'. ДOKa
зать, что середИ'ны отрезков АА', ВВ', СС', DD' тоже явля
ются вершинами параллелоrрамма.
13. Доказать, что биссектрисы уrлов параллелоrрамма
образуют своим пересечением прямоуrольник.
14. На сторонах АВ и АС в треуrольнике АВС ИЗВlне по
строены квадраты ABDE и Асра (вершины D и F противо
положны А). Доказать: а) Еа перпендикулярна к медиане,
проведенной из точки А, и вдвое больше ее; б) если построить
параллелоrрамм AEJG, rде EJIIAG и JGIIAE, то /А проходит
по высоте треуrоль'ника АВС; J В 1.. CD, [С 1.. ВР.
4. ПАРАЛЛЕЛЬНЫй ПЕРЕНОС
(4.1) Прежде чем перейти к изучению преобразования
переноса, 'необходимо познакомиться с понятием вектора 1.
Определение 1. Если на данном отрезке установить опреде
ленное направление, то такой направленный отрезок называ тся
вектором. В каЖДОI\1 векторе различают ero начало и конец.
Если точка А начало вектора, а точка В ero конец, то
вектор обозначается символом АВ. Иноrда для обозначения
1 Слово «вектор» происходит от латинскоrо rлаrола :\'ecto везу,
влеку.
за
вектора мы будем пользоваться одной буквой, но также со
--+- --+-
стрелкой вверху: а, т, r и т. д.
Понятие вектора иrрает большую роль в математике и фи
зике. Векторными величинами являются сила, скорость, YCKope
нне, момент силы и т. д.
Определение 2. Абсолютной величиной, или модулем, вектора
называется длина соответствующеrо отрезка. Обозначается так:
-+
I т 1, , А В 1.
Определение 3. Параллельные векторы называются также кол
линеарными. Коллинеарные векторы называются сонаправлен
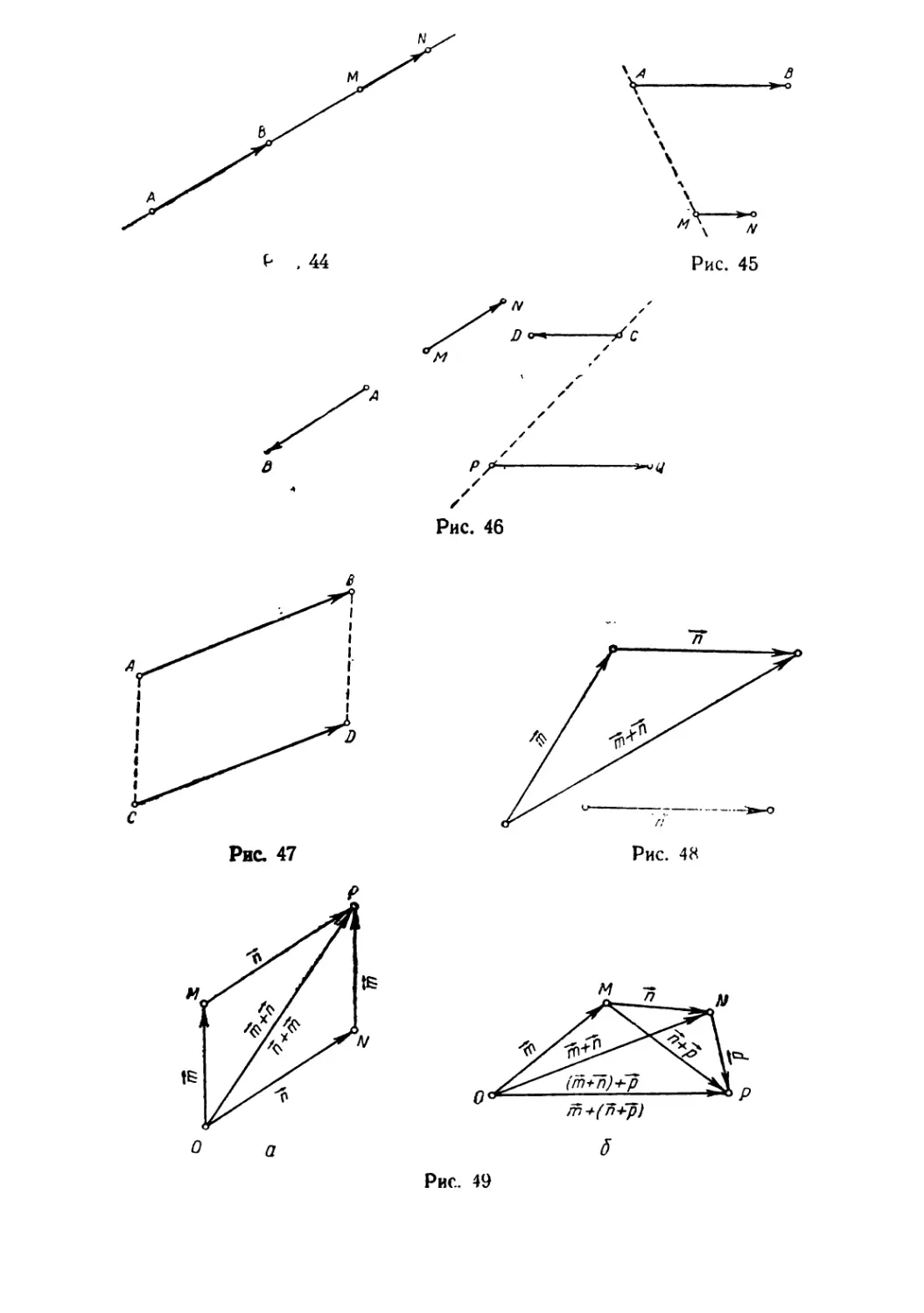
ными, если они принадлежат одной и той же прямой и имеют
одно и то же направление (рис. 44); или если они не принад..
лежат одной и той же прямой, но находятся в одной и той же
полуплоскости относительно прямой, проходящей через их Ha
чала (рис. 45).
Коллинеарные векторы, не удовлетворяющие этим условиям,
называются проmивонаправленнымu (рис. 46).
Определение 4. Два вектора считаются равными, если они
сонаправлены и если равны их абсолютные величины (на рис. 47
АВ == CD).
--+- --+- --+--4
Из этоrо определения следует: 1) т === т; 2) если а == Ь,
.. --+- --+- --+- --+- --+-+
ТО И Ь == а; 3) если а == Ь, Ь == С, то и а == с.
Операции над векторами являются обобщением соответству-
r{)ЩИХ операций над отрезками, что можно видеть из следующеrо
определения.
Определение 5. Для Toro чтобы сложить два вектора, от
конца первоrо вектора отложим вектор, равный второму вектору.
Тоrда суммой будет вектор, началом KOToporo служит начало
первоrо вектора, а концом конец BToporo (рис. 48).
Следствие. При любом расположении точек А, В и С
имеем:
......
АВ ВС == АС.
CY:VIMa векторов подчиняется тем же законам, что и CYMl'vlbI
чисел и отрезков.
Теорема. Сумма векторов подчиняется: 1) переместитель
ному и 2) сочетательному закона/ t.
д о к а з а т е л ь с т в о. 1) Пусть т и n неколлинеарные
векторы (рис. 49, а). Отложим от произвольной точки а вектор
+
ОМ, равный пz, и от конца ero М ОТЛОЖИ!\1 вектор мр == п.
Тоrда ар == т п. Отложим теперь от точки а вектор aN == п.
Четырехуrольник аЛJРN параллелоrрамм, так как мр == aN
за
, 44
/; O
м
,
/А ,/
"
,/
"
,/
/
,/
"
lJ р /.
.. /
/
Рис. 46
8
,
I
I
1
А 1"
I
I f
I I
I
I
,
.
.
.
с
РиСе 47
Р
'. A .
\
\
\
\
\
,
\
'\
\
-\ :. о
М \ N
Рис. 45
'"
/
,/
;l c
/
/
,
:'-t.J IJ
7r
u
. .. . . -...o
(:
Рис. 4R
м
tE:
О р
О а О
РИС. 49
........ ........--+
И, значит,:N Р == т. Итак, ОР == п + т, следовательно,
........ ........
т + п == п + т.
........ ........
Если т и n сонаправлены, то сложение их осуществляется
так же, как сложение отрезков, и потому тоже подчиняется
переместительному закону.
........ )o
Если т и n противонаправлены, то при любой последователь-
ности операций мы из большеrо отрезка вычитаем меньший и
полученной разности даем направление вектора, большеrо по
абсолютной величине. Итак, и в случае l{оллинеарных векторов.
имеем:
.. ---+ ...
т + n == n + т.
-+ -+ -+
2) Пусть даны векторы т, пир (рис. 49,6). Отложим от
.
точки О вектор ОМ == т, потом от точки lYl вектор MN == п
..
и, наконец, от; точки N: вектор N p == р и получим:
-+........
OM+MN==ON, ON+NP==OP, т. е, (m+п)+р==ОР.
С руrой стороны:
'!' --4........ ---+
MN + NP === МР, OJ\t1 + мр == ОР, т. е. т + (п + р) === ОР.
Итак,
--+ --+ --+ ---+
(т + п) + р === т + (п + р).
Определение 6. Если у данноrо вектора переменить направление
на обратное, то полученный вектор называется протuвоnолож....
ным первоначальному. Так, BeKTOp ВА противоположен вектору
........
АВ. Вектор, противоположный вектору т, обозначается симво-
..-.+
лом т.
Сумма двух взаимно противоположных векторов дает нуль-век-
тop точку: АВ + ВА ==0, т + ( т) ==0.
Сtl1едствие. При сложении вСЯКО20 вектора с нуль-вектором.
данньш вектор остается 6ез изменения.
Действительно, мы имеем:
АВ+О ==АВ+ ВС+СВ==АС+СВ==АВ.
41'
...... -+
Определение 7. Чтобы вычесть из вектора тlвектор.п, при..
....... -+
6авляют к вектору m вектор п, т. е.
....... -+.......
т п == m + ( п).
Из этоrо определения следует: 1) Основная определяющая
формула вычитания чисел остается справедливой для вычита
ния векторов:
....... -+.......
т п + п == т + ( п) + п == т + о == т,
-+
т. е. m п + п == т.
2) Если два данных вектора привести к общему началу
и, проведя через концы их параллельные, построить парал
лелоrрамм, то диатональ, идущая из общеrо начала, дает
в'
N
,
,
\
,
,
\
\
\
\
\
,
м
с'
А
Рис. 50
с
Рис. 51
СУ1\IМУ векторов, а диаrональ, 'соединяющая их концы, дает
разность, 'Причем вектор..разность направлен 'от вычитаемоrо
к У 1еныпаемому (рис. 50).
(4.2) Определение 1. Если для каждой точки А плоскости
наЙти соответствующую точку А' таКИ 1 образом, чтобы BeK
.......
тор АА' был равен OДHO Y и тому же постоянному вектору
........
т, то такое преобраЗ1ование называется параллеЛЬНblМ пере..
НОСОМ ИcllИ трансляцией (рис. 51).
Так как параллельный перенос вполне ОI]ределяется зада
........
ние"f вектора т то это преобразование записывается так:
........
т(А) = 4/.
42
с параллельным перенос,о:vl мы довольно часто в-стречаем"
ся на практике. Например, про/водя параллельные прямые
при помощи линейки и реуrольника, мы перемещаем тре-
уrольник так, чтобы одна из ero сторон скользила по линейке.
Это движение и есть па.раллельный перенос, вектор KOToporo
направлен вдоль края ли.нейки. Параллельным переносом
является движение мноrих инструментов, например рубанка
и фуrанка при обработке поверхности дерева, движение тис.
ков при их разведении или сведении и т. д.
Из оп,ределения 1 получаем:
Следствие 1. Неподвижных точек при параллельном nере-
носе нет. Н еnодвижными nрямыми являются прямые, парал.
лельные вектору переноса.
Отсутствие неподвижных точек есть следствие Toro, чта
каждая точка плоскости смещается в нов'ое положение.
Если прямая параллельна вектору переноса, то всякая
точка этой прямой переходит .в точку той же прямой, сама же
прямая 'остается неподвижной.
Следствие 2. Фuzуры, nреобразующиеся дРУ2 в дРУ2а па..
ралельным переносом, равны и одинаково ориентированы
( рис. 51).
Это видно из Toro, что такие две ,фиrуры можно совместить
друr с друrом, передвинув одну из них на BeK Op переноса.
Это же предложение следует из зависимости, существую-
щей между параллельным переносом и осевой симметрией.
Именно, имеют место теоремы:
Теорема 1. Две последовательные осевые симметрии со
взаимно nараллельными осями тождественны с параллель..
ным переносом, вектор КОТОр020 по абсолютной величине
вдвое больше расстояния между осями и направлен от первой
оси ко второй.
Д о к а з а т е л ь с т в о. Пусть мы имеем две оси симметрии
s и s', причем s " s' (рис. 52).
Положим, что s(A) == A 1 И s'(A1) == A', причем отрезок
АА 1 пересекает ось s в точке М, а отрезок A1A' пересекает
ось s' в точке N. Так как АА 1 s, A1A' s' и
s 11 s', то перпендикуляры АА 1 и А 1 А' совпадают и точки А, Al
И А' лежат на одной прямой. При любом расположении осей и
>-
точки А будем Иl\1еть: А М === М А 1 И А 1 N === N А'. Следовательно,
--.............L..............
АЛ1 + MAl A1N + N А' == АМ + MN+N А' == 2MN == АА'.
Здесь MN вектор, направленный по ширине полосы между
осями s и s', АА' вектор переноса.
Теорема l' (обратная). Каждый nараллельный перенос тож-
дествен с двУ.;14,Я последовательными осевыми сим/ еmриями,
43
оси которых перпендиКУЛЯРНbl к вектору переноса и расстоя-
ния .между ни.ми вдвое .меНЫllе абсолютной величины этоео
вектора, nриче.м одну из осей можно взять произвольно.
Рис. 52
........
Доказательство. Пусть мы имеем т(A) == A'. ПрОБе-
дем произвольно ось s перпендикулярно к вектору т. Положим,
что s (А) == А 1 0 Так как s АА', то точки А, Al И А' лежат
на одной и той же прямой. Ось симметрии s' точек А] и А'
8'
А
Рис. 53
перпендикулярна к той же прямой АА'. Итак, мы имеем
s(A) = A 1 ,s'(A 1 ) A', Т. е. параллельный перенос заменен
двумя осевыми симметриями.
Дальнейшее доказательство идет, как Б предыдущей теореме,
и вновь получаем, что АА' 2MN о
Из обеих теорем тотчас же следует, что перенос преобразует
фиrуру в равную и одинаково ориентированную.
44
Отметим еще oд o важное свойство параллельноrо переноса.
Теорема 2. Параллельный перенос nреобразуеm каждый
.,
вектор в равньш ему вектор.
д о к:а 3 а т е л ь с т в о. Пусть АВ данный вектор, т век-
-+ ....
тор переноса (рис. 53). Имеем: т(А) = А'; т(В) = В'. Так как
АА'==ВВ'==т, то А'А+ВВ'==Ои, значит,
АВ ==z А'А + АВ + ВВ' == А'В + ВВ' == А'В'.
Итак, АВ == А' В'.
Из этой теоремы также 'следует, что параллельный пере
нос преобразует всякую прямую в прямую, ей параллельную.
(4.3) При помощи перен.оса можно решить MHoro разно
образ.ных задач. Приведем примеры.
А
,...G, ,
,
,
,
....
.......
'»А'
/
/
/1,
/
/
/
8 /
,/ /
,/ /
,
/ ,
'0(
р 6--- ""' --"'-- -- С
Рис. 54
D
/
А
..'
м
Рис. 55
Задача 1. Построить четырехуrольник по четырем CTOpO
нам и уrлу между двумя противоположными сторонами.
Реш е ,н и е. Пол'ожи.М, что четырехуrольник ABCD
искомый (рис. 54), причем :нам из'вестны ero стороны АВ, ВС,
CD и DA, а также LAPD, rде Р точка пересечения сторон
АВ и CD. Приня.в ВС за вектор переноса, перенесем отрезок
АВ в положение А'С. LA'CD== L.APD, и потому этот уrол
нам известен. Поэтому, начав построение с отрезка CD, мы
можем построить ,отрезок СА', так как нам известна ero дли
на и уrол, который он образует с отрезком CD. Построив
этот 01lрезок, мы определим положение точки А'. Далее нам
известно, что точка А находится от точки D на известном
расстоянии DA, а от точки А' тоже на известном расс1'ОЯ
нии АА'==ВС.
Итак, точка А найдется в пересечении двух дуr окруж
ностей: первая с центром D и радиусом DA, вторая с
центром А' и радиусом ВС. Найдя точку А, проведем через
45
нее -прямую, параллельную А'С, и отложим на ней отрезок
АВ. Этим будут найдены все вершины четырехуrольника.
Задача будет ра3lрешима лишь в том случае, если отрезки
CD, АВ и A'D удовлетворяют неравенст,ву треуrольника, так
как только при этом условии м'ожно найти точку А.
Задача 2. Доказать, что две последовательные централь
ные симметрии относительно двух различных центров TO
ждоствен.ны параллельному переносу.
Реш е н и е. Пусть О и О' два данных центра (рис. 55)
.........
......... ...............
.........
о (А) = A 1 ; О' (А 1 ) = А'; АА 1 == АО + ОА 1 ==20А 1 ;
.......... -.......... t .......
А 1 А' == А 1 О' + О'А' ==2А 1 О'.
......... ......... ......... ......... .
Итак, АА' == АА 1 + А 1 А' ==20А 1 +2А 1 О'.
И, наконец, так как средняя линия треуrольника равна по
.........
ловине основания, то АА' == 200'.
Итак, мы получили перенос, вектор KOTopor,o вдвое боль
'пе вектора, направленноrо от первоrо центра ко второму.
Упражнения
1. Постр.оить трапецию по четы,рем ее сторонам.
2. Постр'оить трапецию по двум основаниям и двум диа
rоналям.
3. Построить треуrольник по трем ero медианам.
4. Внутри полосы дана точка Р. Построить окружность
проходящую через точку Р и касающуюся сторон полосы,
5. Данный :вектор поместить так, чтобы начаЛ1О ero лежа
ло на одной из двух данных ОI<lружностей, а конец на
друrой.
6. Доказать, что никакая оrраниченная фиrура не может
иметь двух центров симметрии.
7. Построить четырехуrольник по четыре?\1 сторонам и
1едиане (медианой четырехуrольника называется отрезок,
соединяющий середины противопо.п'ожных сторон).
8. По разные ,стороны реки на различных Iрас,стояниях от
ее береrов находятся два селения. Предполаrая, что береrа
реки прямолинейны и параллельны, найти, в каком месте
нужно по'строить мост, чтобы дороrа между селениями была
кратчайшей.
9. Доказать, что плоскость можно замостить паркетоr..l из
равных между собой четырехуrОJ1ЬНИКОВ ПрОИЗВОJ1ЬНОЙ
формы.
46
10. Построить параллелоrрамм, зная, что две вершины
ero должны находиться в двух данных точках, а две дpy
rие на данной окружности (paCCM10TpeTb два случая).
11. ПОС'f1роить п уrольник, зная середины n ero сторон.
12. Даны три центра 'симметрии 01, 02, 03. ПРОИЗ1воль'ная
точка плоскости преобразуется в новую точку относительно
01, полученная точка преобразуется относительно 02, новая
точка относительно 0з, далее 'О'-rноситель-но 01, потом OTHO
сительно 02 и, наконец, относительно оз. Доказать, что
после шести преобразований каждая точка возвращается в
исходное пдложение.
13. Дан треуrольник АВС и прямая 1. Провести секущую
параллельную 1, так, чтобы пересечь сторону АВ в точке М,
а сторону АС в точке N и чтобы .был,о AM==CN.
14. Дана ОКРУЖ1НОСТЬ и уr.ол. Провести секущую прямую
перпендикулярно к би.с.сектрисе уrла так, чтобы полученная
хорда в ОКlружности и отрезок секущей В'нутри уrла были
равны между собой.
15. Через две точки 'окружности провести две параллель
ные хорды, 'CY 1Ma или разность которых равнялась бы дaH
ному отрезку.
5. ВРАЩЕНИЕ (ПОВОРОТ)
(5.1) Для Toro чтобы определить понятие 'вращения, 'Нe
обходимо предварительно дать определение направлеННО20'
(или ориентироваННО20) уrла.
При определении понятия вектора мы рассматривали Ha
правленный отрезок, в котором ,один из концов считается Ha
чальной точкой, а друrой конечн,ой, а самый вектор можно
представить как след движения точки 'от начала к концу.
По аналоrии с этим даДИ\f определение ориентированно,rо
vr ла.
.. Опреде.аение 1. Если одну из сторон уrла принять за Ha
чальную, а руrую за конечную, а самый уrол рассматривать
как след движения (вращения) начальноrо луча до ero совпа
дения с конечным, то такой уrол называется ориентирован'
НЫМ У2ЛО.м или версоро.м 1. Два версора считаются paBHbLJr!U,
если равны соответствующие уrлы и одинаковы их направле
ния. Если уrлы двух вер'соров 'равны, а направления их пр'о
тивоположны, то вер'соры называются противоположными.
На \рИ'с. 56, а показаны равные версоры L. аЬ == L а'Ь', так
как равны 'соответствующие уrлы, а лучи ОЬ и О'Ь' Ha
ходятся в левой полуплоскости относительно лучей Оа и О' а'.
1 СЛОБО «версор» происходит от латинскоrо r..1аrо.ла yerso враluаю.
В дальнеЙшем ,будем иметь дело ТО"lЬКО с ориентированными уrлами.
Обозначать их будем обычным знаком «L» и называть просто «уrлом».
47
На рис. 56, б показаны противоположные версоры L. тп==
== L.т'n', так как их уrлы равны, 'но луч Оп находится в ле..
вой полуплос'кости относительно луча От, а луч О'n' в пра-
u О , ,
В'ои полупл<Ускости относительно луча т .
Так как по .отношению к 'начальной стороне уrла вторая
сторона ero может находиться либо в левой, либо в правой
полуплоскости, то отсюда следует, что ориентированный уrол
ь
а
о
о
б
Рис. 56
может иметь два, и только два, различных IнаправлеНИh. Одно
u
из этих направлении считае1'СЯ положительным, друrое
-отрицательным. Обычно в качестве положитель'Ноrо наI1'равле
ния вы'бирают 'fiO, при котор'ом конечный луч уrла лежит в ле
вой полуплоскости по отношению к начальному лучу. В этом
-случае движение от начальноrо луча к конечному называют
вращением в положительном направлении (противопол,ожно
дви)кению часовой -стрелки), а самый уrол считается nоложи
тельным. Пр,отивоположное движение считает,ся вращением в
отрицательном направлении (п,о часовой стрелке), а самый
уrол считается отрицательным.
Сложение уrлов определяется а'налоrично сложению BeK
тор.ов.
Определение 2. . Чтобы сложить два уrла, строят при KO
нечном луче первоrо .слаrаемоrо уrол, равный второму слаrае
мому. Уrол"'Сумма имеет начальным лучом начальный луч
первоrо слаrаемоrо, а конечным лучом конечный луч BTOpO
ro слаrаемоrо. Из этоrо определения следует формула:
L. аЬ+ L. Ьс== L. ас.
Вычитание уr.пов определяется как сложение уrла YMeHЬ
шаемоrо с уrлом, противопол,ожным вычитаемому.
48
Операции над уrла 1И можно представить себе наrЛЯДIН'О
следующим образом. П,оло)ким, что луч, вращаясь в опреде-
ленном направлении, покрывает плоскость какой нибудь
краской, например Кlрасной. При вращении в ПРОТИВОПО.пож
ном направлении этот же луч покрывает ПJIОСКО'СТЬ краской
лруrоrо пнета, наПРИNlер .синей. Положим, 'наконец, что е,сли
эти две краски покроют друr друrа, то они взаимно уничто
жатся.
При ПОМ1ОЩИ этоrо наrлядноrо представления нетрудно
пр,оверить справедливость переместительноr-о и сочетатель'ноrо
законов при СЛО}l{ении уrлов, а также справедливость опреде..
Jlяющей формулы вычитания
Lab Lbc+ L-bc== L-ab.
(5.2) Если 'вершину утла поместить в центре окружности,
то I\10ЖНО установить взаимнооднозначное соответствие меж..
ду уrлами и направленными дуrами одной и той же окруж"
ности. ПоложитеЛЬНО 1У уrлу L аЬ при этом соответствует по..
ложительная направленная дуrа, обозначаемая vAB, rде А
и В С'оответственно точки пересечения лучей Оа и ОЬ с
ОКРУ)I{НОСТЬЮ. Операции над направленны .1И дуrами опреде
ляюrся в соответствии 'с операциями над уrлами. CYM 1a
уrлов Lab+ Lbc соответствует сумме дуr vAB+vBC, и при
любом расположении точек А, В и С на окружности имеет
место формула:
vAB+vBC==vAC.
Две ра'вные, но противоположно направленные дуrи назы-
ваются противоположными. Например, если в окружности
.... .......
проведены параллельные хорды: AA'IIBB', причем векторы
.......
АА' и ВВ' сонапраВJIены, то дуrе АВ противоположна дуrа
А' В', так как они 'Симметричны по отношению к диаметраль..
ной прям,ой, перпендикулярной к хордам (рис. 57). Осевая же.
симметрия меняет ориентацию фиrур на обратную.
Если же ММ' и N N' два диаметра одной и той же
окружности, то L-MON==LM'ON' и vMN==vM'N', так как
эти уrлы и дуrи центрально симметричны относительно
центра О, а центральная симметрия не меняет ориентации
фиrур. На основании этих выводов нетрудно установить со..
ответствие между величиной уrла, стороны KOToporo пересе..
кают окружность, и дуrами этой окружности. Условимся f'O
ворить, что уrол «опирается» на дуrу окружности, если ко'Нцы
дуrи лежат на сторонах уrла или на их продолжении, а все
точки дуrи принадлежат внутренней области уrла или ВНУТ"
ренней области уrла, вертикальноrо с дaHHЫ 1.
.t А. И. Фетисов
49
Теорема 1. Если стороны уzла пересекают окружность или
касаются ее, то этот уzол измеряется полусуммой направлен-
ных дуz, на которые он опирается.
Рассмотрим L. аЬ (рис. 58) и обозначим буквами А, А' и
В, В' точки пересечения окружности соответственно с прямы
ми а и Ь, IИ притом так, чтобы дуrи АВ и А'В' принадлежали
внутренней области уrла (рис. 58, а) либо внутренней об
2
м
.5
в
А'
s
Рис. 57
а
"
Рис. 58
ласти данноrо уrла и вертикальноrо с ним (рис. 58, б). Про
=>
ведем диаметры М'М и N'N, сонаправленные с лучами Sa и
Sb. Тоrда ПОЛУЧИl\1:
vMN==vM'N'; uMA== vM'A'; uBN== vB'N'.
Припоминая формулу vAB + vBC== vAC, получим:
vMN == uMA + vAB + vBN,
vM'N'== vM'A' + vA'B' + vB'N'.
Складывая почленно эти равенства, получим, прин'имая ВО
8нимание 'вышеустановленные 'соотношения между дуrами:
2vMN==vAB+vA'B', или vMN== vAB+vA'B' .
2
Это значит, что направленная дуrа центральноrо уrла,
paBHoro данному уrлу, равна полусумме дуr, определяемых
даННЫ 11 уrл,ом на окружно,сти. И'наче это выражается слова-
1И: уrол измеряется полусуммой направленных дуr, на KOT'O
рые он опирается.
Если, в ча'стности, вершина уrла ле)l(ИТ на окружности, то
дуrа А' В' обращается в нуль и мы получаем, что вписанный
уzол измеряется половиной ayzu, на которую он опирается.
На основании этих выводов можно 'решить следующую
задачу.
50
Задача. Даны две постоянные точки А и В. Найти reo..
метрическое место таких точек О, чтобы Уf'ол АОВ был равен
данному уrлу а.
Реш е н и е. Из вершин А и В проведем два луча Аа, ВЬ,
перпендикулярных к прямой АВ (рис. 59), причем поместим
их в левой полуплоскости относитель,но АВ, если уrол а поло
жительный, и в правой в противоположном случае. При
луче Аа построим L та, равный уrлу а, и обозначим буквой
Рис. 59
о точку пересечения луча Ат с луч,ом ВЬ. В прямоуrольном
треуrольнике АОВ медиана ВМ \равна половине ,rипотенузы,
поэтому окружность .с центром в точке М и радиусом МВ
пройдет через точки А и о; Lma== LAOB как центрально
симметричные относительно центра М.
Вместе 'с тем всякий уrол .с вершиной на дуrе АОВ и СО
сторо:нами, проходящими через точки А и В, равен данному
уrлу а, так как он измеряется половиной направленной дуrи
АВ, которой измеряется и LAOB==a.
Кроме точек этой дуrи, никакие друrие точки плоскости
этим свойством не обладают, так как уrол с вершиной О', не
u u u V AB+vA' В '
лежащеи на этои дуrе, измеряется полусуммои 2 ' ко..
vAB
торая не равна в этом случае v А' В' =1= о.
2
Заметим, что описанное в этой задаче построение назы
вае-rся построением се2Jиента, вмещающе20 данный уzол.
(5.3) Определение. Вращением называется такое преоб
раз-ова'ние, коrда в плоскости дается непод,вижная точка О
центр вращения и каждая друrая точка плоскости А пре
образуется в с,оответственную точку А' так, что выполняются
4* 51
у,словия: ОА==ОА' ,н LАОА'==оо
постоянному уzлу враще
ния (рис. 60).
Условимся считать эквивалентными с точки зрения Bpa
щения уrлы, отличающиеся друr 'от друrа на 3600, так как и
поворот на уrол 00, и поворот на уrол (J) + 3600 все (равно при-
'водит к Iсовмещению точки А с точко А'.
8
Рис. 60
(Iреобразование точки А в точку А' посред'ством враще
пия с центром О и уrлом 00 Зflписывается так:
000 (А) = А'.
11з 'Определения вращения получаем 'ряд след'ствий.
Следствие 1. Единственной' неnодвижной точкой в nреоб
разовании вращения при условии 0<ы<360 0 является центр
вращения о.
Это есть очевидное след-ствие T0f'10, что LAOA'==oo и что ы
отличается и от нуля и от 3600, в сlИЛУ чеrо точки А и А' COB
пасть не MorYT, поэтому никакая точка, отличная от точки О,
не будет неподвижной.
Обратно, из у'словия 000 (А) =---
А мы заключаем, что 00==
==n. 360 0 (n==0,1,2,...).
Следствие 2. При 00 == 1800 вращение TOJjCaeCTBeHHO с цент-
ральной симметрией.
Следствие 8. Каждая фиzура nреобразуется вращением в
равную u одинаково ориентированную. При этом каждый BeK
тор nреобразуется в новый вектор} а уzол MeJlcay ними будет
равен уzлу вращения.
Равенство и 'одинаковую ориентацию фиrур леrко YCTaHO
вить, закрепив плоскость в цеИ'f1ре О и повернув ее на уrол 00
в'О'юруr этой 'точки. Тоrда каждая точка первой фиrуры COBMe'C
ТИТСЯ с еоответственной точкой второй фиrуры (рис. 61).
52
Чтобы установить взаимосвязь между .векторами, пре бра.
зующимися один В друrой вращениеМ,:рассмотр'им вектор АВ,
начало KOToporo не совпадает 'с центром О, и положим, что
000 (А В) -=== А' .8'
(рис. 62).
.. .......
Построим векторы 01\;1 == А В и О М' :::::1 А I В'. 'Так КаК при
враLЦении сохраняется равенство векторов, то
000 (ОМ) == ОМ'
..........
И, значит, LMOM' == со, т. е. yrOJI междувекторами АВ и А'В'
равен уrлу враLЦения.
Как и в предыдущих СJlучаях, это предложение можно ДО-
казать, установив связь между вращением и осевой симметрией.
Она дается в следующих теоремах.
8
':)1
L
с.
с'
n
Рис. 61
Рис. 62
Теорема. Две последовательные осевые симметрии о пере..
секающимися ося.лtи тождественны с вращением, центр кот 0-
рО20 совпадает с точкой пересечения осей, а У20Л (i) вдвое
больше, че,,1( У20Л между осями. '
Д о к а з а т е л ь с т в о. Пусть даны оси 5 и 5', пересекающиеся
в точке О (рис. 63). Выберем на прямой s какой нибудь луч 05,
а луч 08' выберем так, чтобы L sOs' был положительный и: не
больше развернутоrо. Для любой точки А будем иметь:
8(А) = А 1 и s'(A 1 ) = A'.
Далее получим:
L АО5 == L sOA 1 ; L A 1 0s' == L sJOA
53
и вместе с тем:
L АОА' LAOs + L sOA 1 + LA 1 0s' + Ls ОА
2 L sOA 1 + 2L A 1 0s' ===
t:::2(LsOA 1 + LA 1 0s') ==2LsOs'.
Итак, L АОА' ===2L sOs' == ю.
Вместе'с тем в 'силу симметрии OA==OA 1 и OAl OA', еле..
дова ельно, О (i) (А) = А'.
L
Рис. 63
Теорема (обратная). Всякое вращение тождественно с дву-
Аtя последовательными осевыми симметриями, оси которых
проходят через центр вращения, а У20Л между осями равен
половине У2ла вращения. (Пр.и этом одну из осей можно взять
произвольно. )
Доказательство. Пусть мы имеем Ош(А) = А'. Прове
дем через точку О произволыно .ось 5 И пусть 5(А) = Al. Тоrда
по свойству 'симметрии ОА == OA 1 , а по свойству вращения
ОА ОА'. ОТСIода 'следует, что OA 1 == ОА' и потому ось сим
метрии 5 точек А 1 и А' проходит через точку О. Далее анало
rично предыдущему докажем, что 2 L. 50s' == ю.
Этим доказано, что в\ращение можно. заменить двумя oce
выми симметриями s и 5'.
Следствием этих теорем является то, что вращением каж
дая фиrура преобразуется в равную и 'Одинаково ориентиро
ванную фиrуру.
(5.4) Приведем при м еры задач, решаемых при помощи
вращения.
Задача 1. В данный квадрат вписать равносторонний Tpe
уrольник так, чтобы три вершины треуrольника лежали на
сторонах квадрата, притом C)дJHa .из них в данной точке.
54
Реш е н и е. Пусть ABCD данный квадрат, Р данная
точка на стороне AD (рис. 64). Положим, что IvlN Р искомый
равносторонниЙ треуrольник. Произведем вращение всей
4)иrуры BOKpyr центра Р на уrо.п U) == 600. Получим: Р 60 . (А) =
= А'; Рво. (8) = В'; Р вО . (С) = С'; Р 60 . (D) D'; Р вО . (М) = N.
Вместе с тем мы ВИДИ I, что точка N лежит на пересече
нии отрезков CD и А/ В/. Этим 'определяется вторая вершина
ИСК'ймоrо треуrольника. Для получения точки М вер'нем KBaд
с '
с
А
м 8
Рис. 64
рат А' В/С/ D' в первоначальное положение, тоrда точка М
займет надлежащее ПО.пожение на стороне АВ; MNP рав-
носторонний, так как РМ PN и, кроме Toro, L-MPN 600.
Задача 2. Построить квадрат так, чтобы одна ero вершина
находилась в да!нной 'f.очке Р, а соседние вершины: одна на
данной прямой, друrая на данной окружности.
Реш е н и е. Пусть даны: точка Р, прямая [ и окружно,сть
С центром О (рис. 65). Одна из искомых вершин М находит
ся на окружности с центром О, друrая N на прямой [.
Четвертую вершину Q леrко построить, зная вершины М,
N, Р.
Повернем весь чертеж на уrол 900 BOKpyr центра Р. Тоrда
точка М перейдет в точку N, а окружность преобразуется в
новую .окружность с центром 0/. Положение точки N на пря-
мой [ оцределяет-ся пересечением окружности с центром 0/ и
прямой [. Чтобы получить точку М, возвращаем фиrуру в И'с
ходное положение, при этом точка N обратно преобразуется в
М. L-MPN==90°, РМ PN и потому MNP равнобедренный
и прямоуrольный, чем вполне определяется искомый квадрат.
Так как .окружность с центром О' может пересечь пря-
мую [ еще 'в одной точке, то мы можем получить еще один
квадрат, удовлетворяющий условию задачи (на ,рис. 65 по
казан пунктиром кваДlрат P}v!lQ 1 N 1 ).
55
Если бы мы ра'СС fотрели очки пересечения прямой [', в
которую преобразует.ся прямая 1, и окружн,ости С центр.ом О,
ТО !\fоrли бы получить еще решение (на рис. 65 [' не пересе
кает окружность с центром О).
Рис. 65
Задача 3. На стор,онах ВС, СА и АВ треуrольника АВС
построены извне равносторонние треуrольники: А/ВС, В'СА и
С' АВ. Доказать, что: 1) отрезки АА', ВВ/, СС' равны между
собой; 2) они пересекаюrся в одной и той же точке; 3) каж
дый из этих отрезков образует 'с друrим уrол в 1200.
в'
.Рис. 66
Реш е н и е. На рис. 66 построена соотве'I'ствующая фиrу
ра. Проведем сначала только два отрезка ВВ' и СС'. По
вернем отрезок ВВ' b-окруr центра А на уrол 600. Тоrда точка
В' перейдет в точку С, а точка В 'B точку С'. Таким обра
зом, отрезок ВВ' преобразуется в -отрезок С'С, значит. ВВ' ==
== СС'.
56
............... ...............
Кроме Toro, уrол между векторами ВВ' и С'С равен уrлу
.......... .............
аращения, т. е. 60°. По"этому уrол между .векторами ВВ' и СС'
равен 120°.
РаСС 10ТрИМ теперь четырехуrольник РВА' С, в кот,ором
L:A'==60°, L.BPC==120°. Около этоrо четырехуrольника можно
описать окружность (она не показа,на на чертеже). П'О свой..
СТВУ вписанных уrлов L ВРА/ == L. ВСА/ 600. Далее, в четы
рехуrольнике АРВС' L. ВРС/ == L. ВАС' ==60°. Значит, и ОКОJl.О
1Toro четырехуrольника можно описать окружность. Поэтому
L-APC'==L.ABC'==60°. Итак, мы получили: L.A'PB+L.BPC'+
+LC'PA 60o+60o+600==180°, т. е. LА/РА развернутый и
rочки А, Р, А' лежат на одной и той же прямой и, значит,
отрезок АА' проходит через ту же точку Р и образует с отрез-
ками ВВ' и СС/ уrлы в 120°.
Т"очка Р принадлежит к числу так называемых «замеча
тельных точек треуrольника». Она называется точкой Toppи
челли 1 и обладает мноrими интересными С'в'ойствами. Так, на-
пример, можно доказать, что если она лежит внутри треуrоль
ника или на ero стороне, то сумма ее РЗ'С'СТОЯ1НИЙ от трех Bep
шин треуrОЛblника есть величина наименьшая по сравнению с
такоЙ же суммой для любой друrой точки пл'оскости.
\
(5.5) С теоретической и практической очек зрения пред
ставляет большой интерес вопрос о взаимоотношении между
параллельным переносоrvl и вращением. Здесь необходимо в
первую очередь доказать следующую теорему.
Теорема J (Бернулли Шаля 2). Всякие две равные и
одинаково ориентированные фиzуры на одной и той же плос-
кости можно nреобразовать apyz в apyza либо одним перено-
сом, либо oдHи.. вращением.
Д о к а 3 а т е л ь с т в о. Пусть А и В точки одной фиrуры
А' и [З' соответствующие точки друrой. Возможны два иск-
oI1Iочающих друr друrа случая: 1) АВ,==А'В'; 2) AB=I=A'B t .
Рассмотрим сначала пер вый с л у чай. Если А В == А' В'
-+
(рис. 67), то перенос с вектором АА' == n1 преобразует точку
А в А' п точку В в В' в силу Toro, что всякий перенос пре-
образует вектор в равный вектор. Если С какая-нибудь точка
I э. Торричелли (1608 1647) итальянский ученый. Известен свои
ми работами по физике и математике.
2 И. Бернулли (1667 17 48) выдающийся математик, профессор rpo-
Нинrенскоrо (rолландия) и Бззельскоrо (UПвейцария) университеТО9
.\1. Шаль (1793 1880) французский ученый, один из крупнейших reoMeT-
ров Х IX столетия.
51
первой фиrуры, а С' соответствующая ей точка второй, то в
силу равенства и одинаковой ориентации фиrур будем иметь
L САВ == L С'А' В', СА С'А' и потому СА === С'А' и, зна-
чит, точка С преобразуется в С'. Итак, этим переносом каждая
точка первой фиrуры преобразуется в соответствующую точку
второй фиrуры.
Рассмотрим второй случай: пусть AB=I=A'B' (рис. 68).
Найдем вращение, преобразующее первый вектор во второй.
Центр О этоrо вращения может быть найден по следующим
условиям: 1) уrол вращения ю == LAOA' равен уrлу, образуе-
р]
8'
с'
с
в
А
А
Рис. 67
Рис. 68
......
МОМУ вектором А В с вектором А' В'; 2) центр вращения О на-
ходится на оси симметрии точек А иIА', так как ОА == ОА' .
Поэтому для определения центра О строим на отрезке АА'
cerMeHT, вмещающий уrол ю, и проводим ось симметрии точек
А и А'. Искомый центр будет найден в пересечении дуrи cer-
,мента с этой осью симметрии. Очевидно, вращение BOKpyr
центра О на уrол АОА' === ю преобразует точку А в А'. Вместе
с тем вектор, в который преобразуется АВ, образует с АВ уrол.
равный ю, и потому должен совпадать с вектором А ; В', так
как АВ == А' В' и фиrуры одинаково ориентированы.
Итак, найденное вращение преобразует точку А в А' и В
в В'. Если С и С' третья пара соответственных точек, то в
силу равенства и одинаковой ориентации фиrур вектор А'С' O
'
разует с А' В' такой же уrол, как АС с АВ, а значит, и уrол
.....
между АС и А'С' равен уrлу ю. Поэтому найденное вращение
58
преобразует точку С в С'. Таким образом, мы нашли вращение.
преобразующее первую фиrуру во вторую. Задача эта все2да
разреши'м'а, так как всеrда можно определить уrол между со-
ответственными векторами фиrур, построить cerMeHT, вмещаю-
LЦИЙ этот уrол, и найти точку пересечения дуrи cerMeHTa с ее
осью симметрии.
Решение будет единственны'м', так как если бы оказался
еще 'один центр Iв'ращения 0/, то через Hero должны были бы
пройти и О'с.и симметрии пар А и А/, В И В/, С И С/ И т. д., а
также все дуrи cerMeHToB, построенных на АА/, ВВ', СС'
и т. д. И ,вмещающих тот же уrол ы. Но все эти линии должны
пройти и через точку о. Поэтому О/ = о.
8
Рис. 69
Теорема Бернулли Шаля 'ИМ1еет большое практическое
значение при изучении различных плоских движений. Она же
дает возможность выяанить, какое преобразование может по-
лучиться в результате двух последовательных Пlреобразова
ний переноса или вращения. Докажем следующую теорему.
Теорема 2. 1) Два последовательных переноса тожде..
ственны с одним nереносо'м'; 2) перенос и последующее враще
н'ие, а также вращение и последующий перенос дают враще
ние; 3) два последовательных враv.{ения мосут дать либо вра..
щение, либо перенос.
Д о к а 3 а т е л ь 'с т в о. 1) Пусть А и В две различные
точ.ки первой фиrу\ры. Первый перенос преобразует их в точки
А' и В', а второй п ренос преобразует 'Точки А' и В' COOT
ветственно в точки А" и В" (рис. 69). Соrласно доказанному
раньше И lеем:
АВ == А' В'; А' В' === А" В", Т. е. АВ === А" В".
59
Но такое же равенство имеет место для любых соответст--
венных векторов первой и третьей фиrур, поэтому по теореме
Бернулли Шаля СУlцествует перенос, преобразующий пеРВУIО
>
фиrуру в третью. Кроме Toro, равенство АА' + А' А" АА"
показывает, что вектор результuрующеzо переноса равен CYM
м,е векторов данных переносов.
2) Положим теперь, что некоторая фиrура преобразована
.....
переносом с вектором т во вторую фиrуру, которая вращением
с центром О и уrлом о) преобразована в третью фиrуру. Пусть
вектор АВ преобразован в А' В', а вектор А' В' в вектор
А"В". Так как первое преобразование перенос, то АВ === А'В'.
Так как второе преобразование вращение, то вектор А' В' o
разует с А" В" уrол 0). Следовательно, по теореме Бернулли
Шаля первая фиrура преобразуется в третью вращение l с yr..
...!..
лом (», так как вектор А В образует с вектором А" В" тот же
уrол о) (рис. 70). Для построения центра HOBoro вращения про-
ведем через центр О прямую l, перпеНДИКУЛЯРНУiО к вектору
.......
переноса т, и приме 1 ее за ось полосы, ширина которой равна
.......
величине вектора т. По обе стороны от О проведем симмет
(J)
ричные лучи под yr лом ........... к оси [. Пусть левый луч пересе
2
кает сторону полосы в точке О', а правый в точке О". Точка
О' и будет новым центром вращения, так как перенос переве
дет точку О' в О", а вращение переведет О" обратно в О'.
Итак, точка О' осталась на l'vleCTe после двух преобразований"
т. е. О' центр результирующеrо враlI. ения.
ПодоБНЫ 1 же способом нетрудно IIоказать, что врап ение с
последующим переносом дает вращение на тот же уrол, но
с новым центром.
3) Положим, наконец, что мы имеем два вращения с цент..
рами 01 и 02 И С уrлами 0)1 и 0)2 (рис. 71). Первым вращением
> .
вектор АВ преобразуется в вектор А' В', а вторым вращением
......
вектор А' В' преобразуется в вектор А"В". Так как вектор АВ
[ ......
образует с вектором А' В' уrол 0)1' а вектор А' В' с А" В" ........
60
уrол (а)2 и так как оба положительны, то вектор АВ образует
с вектором А" В" уrол 001 + ffi2, который будет yr лом HOBoro
вращения. Если 001 + 002 :.:= п. 3600 (n == О, 1, 2, . . .), то резуль.
-тирующее преобразование будет. переносом.
6
I
,
......."0
t
Рис. 70
в
Рис. 71
СJ]И же ОО} +0О2Фп. 3600 (при n==0,1,2,...), то в результа-
-те мы будем иметь вращение. Для нахождения центра этоrо
вращения строим при веРШИlне 01 уr.ол (()1 так, чтобы луч
0102 был биссектрисой этоrо уrла. При вершине 02 строи
Уf10Л 002 так, чтобы луч 0201 был бы ero биссектрисой. Пра-
вые лучи этих уrло,в пересекаются ,в точке О, левые в точ-
ке 0/. Первое вращение переводит О в О' (01 0== 01 О' В силу
-симметрии относительно 0102). Второе враIцение переводит
О' обратно в о. Итак, О есть единственная неподвижная
точка окончательноrо преобразования, т. е. центр HOBoro
,вращения.
(5.6) Приведем примеры задач, решаемых с помощью
.предыдущих теорем.
Задача 1. Столяру заказан ломберный столик, крышка
KOToporo с.остоит из двух половин. В закры'f.ОМ положении
крышка расположена на рамке стола так, как показано на
рис. 72, а, ,в раскрытом на рис. 72, б. Спраши'вается: в ка-
ком месте 'Столяр должен уи:репить шип, поворотом около
KOToporo крышка ст,ола переходила 'бы из первоrо положе
.ния во второе?
Реш е,н и е. rеометрическиЙ смысл задачи заключается в
'том, чтобы найти центр вращения, преобразующеrо прямо-
61
уrольник ABCD в A'B'C'D' (рис. 73). Центр вращения О леr
ко найти в пересечении IОсей симме'DРИИ пар А и А', В и В'.
В эт,ой именно точке и дол)кен быть закреплен шип, обеспе
чивающий нужный поворот.
r '
8'
с'
б
f
, 8
А I
,
7 ;
f....... I I
I О
i ....
I ....
. ,
А Т 1 I 1 'О,
.,
1.
'.
, .
L .....J
,])
с
"" I
Q
I
I
.
I
I
.
I L ..J
I
I
I I
I I
L j
L
Рис. 72
Рис. 73
Задача 2. На сторонах ВС, СА и АВ треуrольника АВС
извне построены три квадрата с центрами О}, 02 И ОЗ
(рис. 74). Как построить LABC, если даны центры О}, 02, Оз?
Рис. 74
Реш е н и е. Произведем последовательно три вращения
BOK'Pyr центров 01, 02 'и ОЗ каiКДЫЙ раз на 900. Как уже БЫи'IО
доказано, эти три вращения тождественны с одним вращением
на 2700. Центр эт,оrо вращения является Iнеподвижной точкой
преобраз-ования. Найде 1 этот центр. При первом вращении
точка В переходит в точку С, при втором вращении очка С
62
перейдет в точку А, при третьем вращении точка А перейдет
в точку В. Итак, точка В после трех вращений вер\нется в ис
ходн:ое положение, следовательно, она будет непод.вижной
точкой преобразования. Остается найти эту точку.
Заметим прежде Bcero, что два первых вращения с уrла
ми поворота в 900 дают в результате вращение с уrлом пово
р.ота в 1800, т. е. центральную симметрию. Так как этой сим
метрией точка В п(реобразует,ся в точку А, т,о ее центр О COB
падает с серединой сторо"Ны АВ. Зная, кр,оме Toro, что враще
нием на 900 BOKpyr центра Оз точка А должна перейти в
точку В, мы получим ЭТИ точки, строя прямоуrольный Tpe
уrольник с вершиной прямоrо уrла в точке Оз и серединой rи-
п.оте,нузы в точке о.
Итак, построение и,скомоrо llреуr'ольника производится в
такой по,следовательности: 1) Соrласно вышеуказанному пра-
вилу построения на отрезке 0102 как на rипотенузе строим
равнобедренный прямоуrольный треуrольник и притом так,
чтобы вершина прямоrо утла была справа от ,направления
0102. Эта вершина и есть точка о. 2) Ilроведем через точку О
прямую, перпендикуля/рную к ООз, Iи отложим на ней 'вправо
и влево от точки О отрезки ОА == ООз и ОВ == ООз (при этом
А лежит вправо от ОзО, В влево). Для получения точки С
до'статочно по.вернуть точку В 'На 900 ,aoKpyr 'f.очки 01. Полу-
ченная точка С вращением на 900 Bo pyr точки 02 должна
перейти в точку А, так как два вращения на 900 BOKpyr цeHT
ров 01 и 02 эквивалентны центральной симметрии, преобра
зующей А в В.
Решение это единственное, так как если допу.стить, что су"
ществует удовлетворяющий условию задачи треуrольник
А/ В/С/, у KOToporo хотя бы одна из вершин не совпадает с
вершинами ранее полученноrо треуrольника АВС, то, по,вто
рив те же ра.ссуждения, мы придем к выводу, ч о три после-
довательных 'вращения не определяют .однозначно центр ново..
ro вращения.
Упражнения
1. На данной прямой или .на данной окружности найти
точку, соединив которую с концами данн'оrо 'Отрезка, мы
получили бы данный уrол.
2. Дана окружность и две точки. Вписать в эту окруж-
ность прямоуrольный треуrольник так, чтобы ero катеты (или
их продолжения) проходили через эти точки.
3. ВrНУТРИ остроуrольноrо треуr.ольника 'найти точку, из
которой*' ero стороны были бы видны под .одним и тем же
уrлом.
4. Построить т'реуrольник по основанию, противолежа-
щему уrлу и высоте, про.веденной к боковой стор'оне.
(13
5. В данный квадрат вписать друrой квадрат так, чтобы
OLLHa из сторон вписанноrо квадрата проходила через данную
точку внутри данноrо квадрата.
6. Построить равнос оронний треуrольник, стороны КОТО-
p'oro проходили бы через три данные точки и имели бы наи.
большую длину.
7. Построить равносторонний треуrольник, вершины кото-
poro лежали бы на трех данных параллельных прямых или
на трех данных концентрических окружностях.
8. Система из п Iразличных зубчатых колес представляет
собой замкнутую цепь, в которой каждое колесо сцепляется
с двумя 'сосед.НИМИ. Указать необходимое и достаточное уе-
л,овие Toro, чтобы все эти зубчатые колеса моrли одновре-
менно двиrатЬ'ся.
9. Прямоуrольный треуrольник движется по плоско,сти
так, что вершины острых уrлов ero скользят по двум взаим.
но перпендикулярным прямым. KaKYIo линию описывает вер-
ш.ина прямоrо уrла? .
10. Ilлоскость. движется по друrой плоскости так, что ДВt
ее точки скользят по двум пересекающимся прямым непод-
вижной плоскости. ДОI<азать: а) что в подвижной П.поскости
существует бесконечное множество точек, описывающих пря-
молинейные отрезки; б) что на ней также существует бес-
конечное множество точек, описываIОЩИХ окру)кности.
11. Доказать, что если на сторонах параллелоrрамма по-
строить извне квадраты, то центры этих квадратов являют-
ся вершинами HOBoro квадрата.
12. Доказать, что центры равносторонних треуrо.ПЬНИКОВ.
пос роенных извне ,на сторонах произвольноrо треуrольника
являются вершинами paBHocTopoHHero треуrольника.
13. Дана окруж'ность и не лежащая на ней точка Р. Про-
вести через эту точку секущую так, чтобы полученная хорда
имела данную длину.
14. Дан -rреуrольник АВС. Произведем последовательно
три вращения: около центра А на уrол САВ, около центра
В на уrол АВС, около центра С на уrол ВСА. rде будет
центр и каков будет уrол вращения, которое получится в
результате?
6. rОМОТЕТИЯ
(6.1) Все pa'ccmo-rреННbIе нами преабразоваlНИЯ осевая
симметрия, центральная симметрия, параллельный перенос и
вращение изменяли только положение фиrУ'Р, оставляя без
изменения их величину.
Перейдем теперь к изучению преобразований, производя-
щих более rлубокие изменения в rеО 1етрических фиrурах. Но
64
для этоrо нам нужно будет предварительно познакомиться с
некоторыми новыми преДЛО:iкениями. Рас,смотрим прежде в,се-
ro две ак'сиомы, называемые аксиомами непрерывности.
Аксиома Архимеда 1. Если имеем два неравных отрезка,
то, повторяя меньший из них слаzаемым достаточное число
раз, мы всеёда можем получить отрезок, больший ВТОрОёО от..
резка.
Иначе rоворя, е,сли мы имеем a> b, TO в,сеrда существует
такое целое число n, при котором nЬ>а.
Следствие. Если имеем два неравных отрезка, 1'0, деля
60льший из них на некоторое число равных частей, мы всеёда
можем получить отрезок, меньший ВТОр020 отрезка.
АI
Рис. 75
Рис. 76
Пусть п'о прежнему а>Ь. По аксио ме Ар химеда суще-
ствует такое целое число n, при котором nЬ>а. Де.пя обе час-
ти ЭТОI'о нера.венства на n, мы и получим то, что нужно ДOKa
зать:
.... а
Ь>n.
Аксиома r. Кантора 2. Если на прямой имеется не02рани-
ченный ряд отрезков А l В 1, А2В2, АзВ з , ..., А п В п , ..., в котором
каждый последующий находится внутри nредыдуще20, при-
чем эти отрезки уменьшаются так, что величина их может
стать меньше лю6020 даНН020 отрезка, то существует един-
ственная точка, nринадлеalсащая всем этим оrреЗКQ.Ч (точка М
на рис. 75 ).
1 Архимед (ок. 287 212 rr! дО Н. э.) ....... величайшиЙ математик и меха-
ник древней rреции. Им были открыты законы рычаrа, определена длина
окру}кности, площадь Kpyra и Т. д.
2 r., Кантор (1845 1918) известный немецкий .математик, основопо-
ложник теории бесконечных множеств.
5 А. и. Фетисов
65
Совокупность отрезков, удовлетворяющих аксиоме KaHTO
ра, называют системой вложенных СТЯ2ивающuхся отрезков.
На основании этих предложений мы можем доказать сле
ДУЮlltую ле 1МУ.
Лемма. Если из обще20 начала S исходят три пары BeK
торов SA u SA', SB и SB', SC и SC' и векторы каждой пары
сонаправлены дРУ2 с дРУ20М и если, кроме ТО20,
АВIIА'В', ACIIA'C', то и ВСНВ'С'.
Д О К а з а т е л ь с Т В о. Разделим отрезок SA (рис. 76) на
10 .равных частей. Если одна из точек деления попадет в точ-
ку А', то, проведя через все точки деления прямые, парал
лельные прямым АВ и АС, увидим, что отрезок SB разделит-
ся тоже на 10 равных частей, причем одна из точек деления
совпадет с В', и на столько же частей разделится отрезок SC
и одна из точек деления ,совпадет с С'. Но тоrда на основании
следствия из теоремы Фалеса прямые, 'ооединяющие точки де-
ления на сторонах уrла BSC, будут па1раллельны прямой ве,
в чаlСТНОСТИ получим, что В'С'I/ВС.
П'ОJIОЖИМ теперь, что ни одна из точек деления не сов-
падет с А'. Разделим тоrда отрезqк SA на 100 равных частей.
Е'СJJИ .одна из новых точек деления совпадет с А', то, по-
.в оряя rnредыдущее раесуждение, мыI вновь получим, что
B'C'IIBC. Если и при этом ни одна из точек деления не С'ов-
падет с А', то разделим SA на 1000 равных частей, и если в
ЭТ 1 ОМ 'Случае точка деления совпадет с А', то опять будем
иметь B'C'IIBC. Если опять не произойдет 'совпад'ения, то раз
деЛИ 1 SA на 1 О 000 равных частей и т. д.
Однако может случиться, что, как бы далеко мы ни про-
должали .этот процесс, ни одна из точек деления не совпадет
с А'. Такой случай будет, например, при SA' === SA. Тоr,в.а в
. 3
силу неравенств:
111
0,3 < ......... < 0,4; 0,33< < 0,34; 0,333 < < 0,334 и Т. В.
3 3 i
ни одна из точек десятичноrо деления не совпадет с А'.
в этом случае точка А' будет находиться внутри отрезка Be
u SA б В
личинои при лю ом натуральном n. месте с тем и точка
10n
В , б u SB
удет находиться внутри отрезка величинои , а точка
10 n
С , о SC Т
внутри отрезка величинои . ак как при неоrраничен-
10 n
ном увеличении n каждый из этих отрезков (следствие, из ак-
сиомы Архимеда) может стать меньше любоrо данноrо отрезка,
66
ТО при n == 1, 2, 3, . . . мы получим на каждой прямой систему
вложенных отрезков, стяrивающихся к точкам А', В', С'.
Докажем, что и при этом будем иметь В"С' 11 ВС. Действи-
тельно, если бы В'С' была не параллельна ВС, то через точку
В' можно было бы провести прямую, параллельную ВС, кото-
рая пересекла бы SC в точке си, лежащей вместе с точкой с'
u sc б Н
на том же отрезке величинои ............... при лю ом n. о это проти-
10n
воречит аксиоме Кантора о еДИНСТ2енности точки, определяемой
системой вложенных стяrивающихся отрезков. Итак, С" = с'
и, значит, В' с' 11 ВС во всех случаях.
а
б
Рис. 77
(6.2) Определение. То.мотетией 1 называется преобразование.
коrда задается неподвижная точка S (центр rомотетии) и ПО
заданной паре коллинеарных векторов SA и SA' дЛЯ каждой
точки В находят соответственную точку В' так, чтобы векторы
SB и SB' были коллинеарны, а прямые АВ и А'В' параллель..
ны (рис. 77).
Если векторы SA и SA' сонаnравлены (рис. 77, а), то rOMO
тетия называется nоложительн'ОЙ, а если противонаправлеНbl
(рис. 77, б) оmрицательн'ОЙ. Если у векторов АВ и А'В' Ha
чальные точки А и А' и конечные В и В' являются COOTBeT
С1'венными в данной rомотетии, то и векторы называются сооm-
ветсmве Н,Н,ыМ,и.
Из этоrо определения получается основное свойство rOMoTe.
ТИН, котор ое дано в следующей теореме:
1 СЛО20 «rомотетия» (французское homothetie) происходит от rреческоrо
" f.LO подобный и {tet'o расположенный, что значит подобное распо
Л8жение::..
5* 67
Теорема. 1) Соответственные векторы в аомотетии колла-
неарны; в положительной 20.мотеmии они сонаnравлены, а 8
опzрицатеЛЬflОЙ nротивонаnравлеНbl. 2) Отношение! nреоб-
разоваННО20 вектора к nервоначальному выражается одним а
тем же числом, характеризующим данную еомотетию и на-
.зываемым коэффициентом 20мотетии.
...... ............
д о к а э а т е л ь с т в о. 1) Если векторы SA и SA' сонаправ"
-11ены, то центр S (рис. 77, а) находится вне полосы, определяе-
мой параллеJ1ЬНЫМИ, проходящими через точки А и А'. Поэтому
--- .
векторы SB и SB' тоже сонаправлены, так же как и векторы
8С и SC'.
По определению rомотетии АВ IJ А' В' и АС lJ А'С', а на oc
новании леммы также и 8С fI В'С'. Значит, пары векторов АВ
и А'В', АС и А'С', ВС и В'С' -----коллинеарны. Вместе с тем
J
векторы АВ и А' В' проходят внутри уrла ASB И, значит, на-
ходятся в одной полуплоскости по отношению к прямой SA.
следовательно, они сонаправлены. Это же можно сказать и о
.....
векторах АС и А'С', ВС и В'С'.
Отсюда следует, что для пострgения соответственных тачек
в rО1\fотетии l\10ЖНО в качестве исходных брать любую пару
соответственных точек В и В', С и с' и т. п. .
Если векторы SA и SA' противонаправлены, то точка S Ha
ходится DНУТРИ полосы, определяемой параллельными прямыми,
проходящими через А и А' (рис. 77, 6). Поэтому векторы SB
---
и SB', SC и SC' противонаправлены. По опредеJIению имеем
.........
далее А' В' 11 АВ, А'С' 11 АС. Векторы АВ и А' В' противонаправ-
лены, так как точки В и В' находятся в разных полуплоскос-
тях относительно прямой AS. Аналоrичным рассуждением леrко
доказать противонаправленность векторов ВС и В'С', АС и
А'С' и т. д.
2) Для доказательства равенства отношений рассмотрим сна-
......... ............
чала векторы SA и SA', SB и SB' (рис. 78). Поступая так же,
как при доказательстве леммы, разделим SA на 10 n равных
частей и п оложим, что на векторе SA' таких частей отложится
1 Отношенuе.м, двух коллинеарных векторов называется число. равное
отношению длин соответствующих отрезков. При этом для сонаправлен-
ных векторов это число берут со знаком +, а для противонаправленных
.со знаком s
68
ровно р. Тоrдз, проведя параллельные через точки деления, мы
.....
разделим SB тоже на lOn равных частей и на векторе SB'
таких частей отложится ровно р. Это мы запишем так:
---
SA'
C:J8 L ·
,
1()'1
SB' р
== ............... t
sв 1011
.....
SA' SB'
Т. е.
SA SB
SA
Если окажется, что вектор SA' ни для KaKoro n не будет
СОJlержать целоrо числа делений, то положим, что р делений
д
РИСе 78
дают меньmий отрезок, чем отрезок SA', а р + 1 больший,
тоrда число L называется приближенным значением отноше..
10"
аня по недостатку, а число р + 1 приближенным значением
10"
9тoro отношения по избытку, что записывается в виде нера-
венства
..... ........
L < SA' < р + 1 .
10" 10 п
SA
Как и в преZ1ыдущем случае, леrко доказать, что и atЛЯ
..... ........
SB'
ОТНОIПения будем иметь такое же неравенство
SB
L < SB' < р + 1 .
10 п 10 п
SB
Это значит, что при любом числе десятичных знаков оба
отношения будут выражаться одним и тем же числом по не-
аостатку и по избытку, Т. е. одной и той же бесконечной
69
l1есятичной дробью.
SA' SB'
SA SB
Отсюда ааключаем, что и в этом случае
Найдем теперь отношение
А'В'
. Для этоrо построим век-
АВ
---+
торы SB 1 == АВ и SB == А' В'. Так как они равны коллинеар-
ным векторам, то они сами коллинеарны. Кроме Toro,
ВВ! fI В' B , так как ABBlS и А' В' B S параллелоrраммы. Зна-
ЧИТ, по доказанному,
,
SB 1
SB'
---+
SA'
=::1
SB 1
SB
SA
а потому и для равных им векторов будем иметь:
....
А' В' SA'
.
АВ SA
Теорема доказаlна вполне.
Ввиду Tor,o что -при пол'ожительной rомотетии CO'OTBeT
ственные векторы сонаnравлены, коэффициент rомотетии по-
ложителен. При отрицательной rомотетии соответственные
векторы nротивонаnравлены, и потому в этом случае К1ОЭф-
фициент rомотетии отрицателен.
Следствие 1. Fомотетия вполне определяется заданием
центр'а S и коэффициентом k, который может быть задан
либо числом, либо двумя отрезками, отношение которых рав-
но k.
П,оэтому преобразование rомотетии с центром S и коэф
фициенто:м k точки А в точку А' записывается так:
Sk (А) = А'.
Следствие 2. Е ели k == 1, каждая точка плоскости преоб..
разуется 20мотетией в самое себя и мы имеем тождественное
nреобразование. Если k== l, zомотетия тождественна с цeHT
ральной симметрией при центре s. .
Следствие 3. В nреобразовании ZOMOTeTUU неnодвижнымu
образами являются центр ZOMOTeTuu и прямые, проходящие
через центр.
70
Следствие 4. Инвариантами I 20мотетии являются отноше
ние соответственных векторов, величина У2ла между двумя
векторами и ориентация фи2УР.
То, что отношение ооответственных векторов постоянно,
уже доказано в предыдущей теореме. Если вектор АВ пpe
......
образован rомотетией в А'В', а вектор CD в C'D', то АВ
'>-
коллинеарен с А' В', а CD с C'D' и обе пары либо OДHOBpe
менно сонаправлены, либо противонаправлены. По свой-
ству уrлов, стороны которых взаимно параллельны, мы по-
лучим, чт,о И В том и ,в друrом случае уrол между векторами
.....
АВ и CD равен yr лу между векторами А' В' и С' в' (рис. 79, а
и б).
а
Б
Рис. 79
Вместе с тем мы з,наем, что при ПОЛ1ожительной rOMoTe-
тии все векторы первой фиrуры сонаправлены с векторами
второй фиrуры и, значит, фиrуры одинаково ориентированы.
При отрицательной же rомотетии все векторы первой фиrуры
противонаправлены с векторами второй фиrуры. Но отсюда
следует, что векторы второй фиrуры сонаправлены с BeKTopa
ми фиrуры, центрально симметричной с первой. Но центрально
симмеТРИЧ1ные фиrуры одинаково ориеНТИРlованы. Итак, во
всех случаях rомотетичные фиrуры одинаково ориентированы.
(6.3) ОпредеJlеlПfе. Если между точками двух фиrур сущест-
вует взаимнооднозначное соответствие и притом такое, что
каждая точка одной фиrуры получена rомотетией из соответ-
ствующей точки друrой фиrуры, то фиrуры называются 20м'О-
тетиЧНblМ,И. Если rомотетия с центром S и коэффициентом k
преобразует точку А в А', то rомотетия с тем же центром,
преобразую щая А' в А, называется обратной zoAtomeтuea по
1 Величина, остающаяся неизменноа в каком"либо процессе, назы.
вается инвариантом.
71
1
отношению к первоначальной. Ее коэффициент равен k' так
---+
SA' SA 1
как из равенства =:::1 k следует} ............
SA SAI k
Весьма важные свойства rомотетии приведены в следующих
теоремах:
Теорема 1. Всякая прям,ая nреобразуеmсв вомотетиеа в
nараллельную прямую.
Д о к а з а т е л ь с Т В о. Если прямая проходит через центр
rомотетии, то всякая точка этой прямой преобразуется в точку
той же самой прямой, т. е. прямая преобразуется в самое себя.
Но совпаде:е:ие прямых мы условились принимать за частный
случай параллельности.
о. М
tf
а' м'
а
. (
РИС 4 80
Положим теперь, что прямая а не проходит через центр
rомотетии S (рис. 80). Пусть М и N......... точки этой прямой,
причем Sk(M) = М', Sk(N) = N'. Обозначим через а' прямую
M'N'. Докажем, что каждая точка на ПJ?ЯМОЙ а преобразуется
в точку на прямой а'. Так как M'N'IIMN, то alla'. Если
р С а, Sk (Р) = Р', то м' Р' )1 МР, т. е. М' р' 11 а. По аксиоме
параллельности прямая М' р совпадает с а', поэтому Р' С а' .
Итак, Sk (а) = а', причем а If а'.
Теорема 2. [ом,отетия nреобразует окружность 8 окруж-
ность; через центр 20м,отетuи проходят общие к,асательные
к, этuм окружностям.
Д о к а з а т е л ь с т в о. Пусть мы имеем окружность с цент-
ром О и центр rомотетии S (рис. 81). Положим, что Sk(O) = O'.
Возьмем на окружности точки А и В и пусть Sk(A) = А',
Sk(B) = В'.
---+ ---+
Есл,и векторы ОА и 08 ,не колл.инеарны, то мы имеем ра,в-
нобедренный Д ОАВ, в котором ОА == ОБ. В силу инвариант-
72
ности В'еличины уrла в rомотетии O'B'C' тоже равнобед..
ренный и потому О' А' О' В'. Если теперь произвольная точка
..\1 первой окружности будет д'виrаться по этой окружности,
то соответственная точка М' будет тоже .описывать окруж-
ность, так как уже указа:нным спое,обом можно доказать, что
О'М'==О'А'==О'В'. Итак, окружность с центром О преобразо.
б
Рис. 81
валась в окружность с центром О'. Если из ценТ'ра rOM.QTe-
тин S провести касательную ST к первой окружност,и, то эта
же прямая будет ка,сательной и ко второй окружности, так
как единственной общей точке первой окружности с прямой
ST может соответствовать одна, и только одна, общая точ-
ка Т' той же прямой со второй окружностью.
Если rомотетия положительная, то касательные, пр'оходя-
щие через центр S, внешние, если же rомотетия отрицатель..
ная, то эти касательные внутренние.
Признак rомотетичности д'вух фиrур дается в следующей
теореме:
Теорема 3. Если в каждой из двух данных Фи2УР имеется
по крайней мере три точки, не лежащие на одной и той же
прямой, то эти Фи2УРЫ 20мотетичны при условии, что между
их точками можно установить взаимнооднозначное COOT8eT
ствие так, чтобы каждая прямая первой Фи2УРЫ была пllрал..
лельна соответственной прямой дРУ20Й Фи2УРЫ и чтобы 8
первой фиzуре имелся вектор, не равный соответственному
вектору второй фиzуры.
Доказательство. Пусть А, В, С точки од'ной фиrу..
ры, А', В', с' соответственные точки друrой, причем со..
73
rла,сно условию А'В'IIАВ, A'C'IIAC, B'C'IIBC (IРИС. 82) И, кроме
Toro, АВ=I=А'В'. Ввиду oro что векторы не равны, прямые
АА' и ВВ' пересекаются в точке s. Примем эту точку за центр
rомотетии, преобразующей точку А в А'. Тоrда эта же rOMO
тетия преобразует "и В в В'. Положим, что точка С не при
надлежит прямой АВ. Точка, соответственная точке С в этой
rомотетии, лежит на прямой, Пlроходящей через точку А' и па
раллельной АС, т. е. на прямой А'С'. Но эта же точка лежит
и на прямой, проХ'одящей через точку В' и параллельной пря
мой ВС, т. е. на прямой В/С'. Следовательно, эта точка COB
а'
А В
D'
Рис. 82
дl
в'
с
Рис. 83
падает с точкой С'. Та'ким же образом можно доказать, что
и всякая точка D первой фиryры преобразуется в COOTBeTCT
венную точку D' второй фиrуры. Итак, обе фиrуры rOMoTe-
тичны относительно центра s. Этот центр единственный, так
как при любой rомотетии, определяе:мой соответствием тех
же точек, через Hero должны пройти прямые АА' и ВВ'.
Е,сли бы оказалось, что АВ==А'В', то мы получили бы, ЧТО
АА'IIВВ'. НО тоrда и СС'IIАА', так как если бы эти прямые
пересекались, то точку пересечения мож!но было бы принять
за центр rомотетии и, повторив предыдущие рассуждения, мы
вновь пришли бы к тому, что через эту же точку пройдет и
прямая ВВ', а это противоречит нашему предположеНИJО.
в этом 'случае леrко установить, что АА'==ВВ'==СС'==...==
==т (рис. 83) и у нас получился бы перенос с вектор,ом т. П"о
этому в нек'оторых вопросах целесообразно рассматривать
перенос как предельный случай rомотетии с бесконечноуда
ленным, или «несобственным», центром.
В частности, отсюда получаем:
Следствие. Любые две окружности zом.отетичны друс
дРУ2У.
14
Пусть даны окружности С центрами О и О' (см. рис. 81).
Положим сначала, что окружности не раБНЫ. Будем paCCMaT
ривать точки О и О' как соответственные в иском,ой rOMoTe
тии. Соответственными мы будем также считать концы OOHa
f]равленных (см. рис. 81, а) или противонаправленных (СМ.
рис. 81, б) радиусов. Тот да мы получим по 'определению:
OAIIO'A', ОВIIО'В'. НО треуrольники ОАВ и О'А'В' ра.внобед
ренные 'и LAOB== LA'O'B' (стор'оны /их или обе сонаправле-
ны или обе противо!направлены). П,оэтому равны и уrлы при
их основании. Атак как LOAB LO'A'B' и ОА 11 О'А', то и
ABIIA' В'. Итак, выполнены все у,словия предыдущей теоремы
14, значит, оюружности rомотетичны. В случаях rНepaBHЫx
окружностей эта rомотетия может быть как положительной,
так и отрицательной.
С'
в
с
('
Е
А
Рис. 84
Рис. 85
Коrда 'окружност/и ка'саются из.нутри, то точка касания
является центром положительной rомотетии, преобразующей
эти окружности друт В друrа, а если они касаются извне, то
точка касания есть центр 'отрицательной rомотетии, преобра
зующей эти окружности друr в друrа.
Если же рассматривать равные .окружности, то положи..
тельная rомотетия приводится к переносу, а отрицательная
к центральной симметрии, которая, как уже было укаэано,
есть ча,стный случай f'омотетии.
(6.4) Предыдущие рассуждения показы,вают, что для по..
строения фиrуры, rомотетичной с данной прямолинейной
фитурой (например, с мноrоуrольником ABCDE на рис. 84),
достаточно иметь только линейку и треуrольник, так как все
постр'оение .осуществляется проведением параллелыных пря
мых. Е,сли же даны два соответственных векТ'ора первой и
второй фиrур (например, векторы АВ и А' В' на рис. 84), то
для построения ФиrУ'рЫ A'B'C'D'E', rомотетичной с данной.
Можн,о даже не нах'одить центра .rомотетии.
75
Однако в случае фиrуры, оrраlниченной более СЛОЖ}IЫМ
контуром, приход.ится прибеrать к специальному инструмен"
ту пантоzрафу. Панто раф представляет С'обой шарнирный
параллелоrрамм MNPM' (рис. 85)). Положим, что инструмент
закреплен в точке S, BOKpyr которой 'Он может вращаться.
В точке А укреплен штифт, в точке А' караJндаш, а точки А
и А' выбраны так, чтобы S, А и А' находились на одной и той
же прямой.
Рассмотрим теперь rом'отетию с центром S и оэффициен-
том k:
SM'
k==
.......
SA'
.
3М SA
Ввиду Toro что при всех положениях ИНlстрvмента мы
имеем MN == М'Р и MM'==NP, четырехуrольник MNPM' бу-
дет всеrда параллелоrраммом, в силу чеrо будем иметь
MNIIM'P или MAIIM'A'. При любом положении прямой SM
с
А
Рис 86
точки А и А' будут соответственными в этой rомотетии, так
как М и М' всеrда можно рассматривать как центры двух ro-
мотетичных окружностей, раДИУСbI которых параллельны и
сонаправлены И, значит, концы их являются точками, соответ-
ственными в этой rомотетии.
Если теперь штифтом в точке А обводить контур какой.
нибудь фиrуры, то карандаш в точке А' будет описывать фи..
rypy, rомотетичную с данной.
Пантоrраф используется при копировании рисунков, черте-
жей, rеоrрафических карт и т. д.
Важным практическим применением rомотетии является
использование ее при .мензульной съемке плана полярным
способом. Положим, что нам нужно с'нять на план участок
имеющий вид мноrоуrольника ABCDEF (рис. 86). Мензула,
76
предста'вляющая собой квадратный планшет размером 50 Х
Х 50 см, установленный на TpeHore, помещается в такой точ
ке S участка, из которой были бы видны все ето верш,ины. OT
метив на планшете точку S, мы приставляем к ней визирную
u
линеику .и последовательно визируем на в'се вершины MHoro
уrольника, проводя направленные IHa них лучи и откладывая
на этих лучах от точки S в данном масштабе соответственные
точки А', В', С', D', Е', F'. Очевидно, что преобразование есть
rомотетия с центром S и коэффициентом k, который опреде
Jlяется ПрИНЯ'fым на!\fИ масштабом.
Для более точ:ных rеодезических. iра'бот вместо визирноЙ
линейки употребляется кunреzель, представляющий собой rvle
таллическую линейку, на котороЙ 'ук'реплена зрительная TPy
ба. Труба Nlожет двиrаться в плоскости, проходящей через
край линейки. Окулярный конец этой трубы снабжен дальн'О
мером', позволяющим при визировании на специальную рейку,
поста.вленную у ,вершины поли она, Qразу отсчитать расстоя
ние от этой вершины до точки S.
(6.5) Рассмотрим теперь применение rомотетии к реш нию
различных видов ,rеО:Vlетрических задач.
Задача 1. Даны две прямые а I}{ Ь, точка пересечения KO
торых недоступна. Дана также не принадлежащая этим пря
мым точка с. Нужно провести прямую через точку С и Heдo
ступную точку пересечения данных прямых.
ь
Рис. 87
Реш е н и е (рис. 87). Пересечем прямые а 'и Ь двумя па..
ралле.пьными прямыми 1111', которые будем раосматривать как
соответственные в rомотетии с центром в точке пересечения
прямых а .и Ь. Прямая 1 пересекает прямую а в точке А, а пря-
мую Ь в точке В. Прямая [' пересекает прямую а в точке А',
а прямую Ь в точке В'. Пары А и А', В и В' являются ооот-
ветст,венными в rомотетии. Найдем теперь очку С', соответ-
77
ственную точке С. ДЛЯ эторо I1IрО'ведем через А' прямую, па
раллель ую АС, а через В' прямую, параллельную ВС.
Пересечением этих прямых, как уже было доказано, опреде-
лится точка С'. Прямая СС' должна проходить через недо-
ступный центр rомотетии. .
Задача 2. Построить окружность, которая касалась бы
двух данных пересекающих'ся прямых и данной окружноости.
Реш е:н И е. Пусть даны прямые а и Ь, пересекающиеся
в точке Р, и окружность с центр,ом О' (рис. 88). Примем ис-
й'
"
.
Рис. 88
комую точку S касания двух 'Окружностей за центр rOMore-
тии, преобразующей их друr в друrа. Эта rомотетия пре.обра-
зует прямые а и Ь соответственно в а' и Ь', причем a'lIa и b'llb,
и эти прямые должны в то же время касаТЬ1СЯ данной окруж-
ност,и, так как касание окружности 'с прямой сохраняет,ся при
rомотетии. Прямые а' и Ь', очевидно, мож но постр'оить, про-
ведя к даlННОЙ окружности касательные, параллельные данным
прямым а и Ь. Найдя точку Р', проведем прямую РР', которая
пересечет данную окружность в центре rомотетии S. Эта же
точка является точкой касания окружностей. Так как точка
касания окружностей ле}l{ИТ на линии центров, то центр ис-
комой окружности точка О лежит на прямой SO'. в то Ж
время она лежит на биссектрисе уrла аРЬ. Итак, точка О ле-
жит в пересечении этих прямых. На рис. 88 окружности в точ-
ке S касаются извне.
Предлаrается исследовать условия разрешимости задачw
и найти число решений.
Задача 3. Доказать, ЧТО в треуrольнике ортоцентр, центр
78
rяжеСТII и центр описаlННОЙ окружности лежат на одной и
той же прямой. (Это так называемая «прямая Эйлера» 1.)
Реш е н и е. Пусть АВС данный треуrольник. Обозна
ЧИМ через А', В', С' соответственно середины сторон ВС, СА
и АВ (рис. 89). По свойствх с'редней ЛИНИИ треуrольника
будем иметь: В'С'!lВС, С' А 11
11 СА, А' В'!lАВ, откуда следует
на основании теоремы 3, что
треуrольники АВС и А'В'С' ro
мотетичны. Прямые АА', ВВ',
СС' должны проходить через
одну и ту же точку G центр
этой rомотетии. Этим еще раз
доказано, что медианы Tpe
уrольника пересеКdЮТСЯ в oд
ной и тоЙ же точке. Обозначим
буквой f{ ортоцентр треуrоль
ника АВС. Точке f{ в этой ro
мотетии соответствует точка
Н' ортоцентр треуrольника
А' В'С'. Чтобы получить этот ортоцентр, проведем через точки
А', В', С' перпендикуляры к сторонам В'С', С' А' и А' В'. Но
эти же перпендикуляры являются осями симметрии точек В
8 и С, С и А, А и В, так как
проходят через середины
сторон и перпендикулярны
к ним. А мы знаем, что эти
оси СИl\1метрии пересекаются
в одной и той же точке
центре описанной окружно
сти. Итак, точка f{' есть в то
же время и центр окружно
сти, описанной около Tpe
уrольника АВС.
Так как Н и н' соот-
ветственные точки в rOMoTe
тии, то прямая Н Н' прохо
Д T через центр о. Коэффи
циент r()мотетии k== 1/2, так как каждая сторона в 6.А'В'С'
вдвое меньше соответственной стороны в 6.АВС. Поэтому
центр описанной ОКРУЖНОСТИ вдвое ближе к центру тяжести,
чем ортоцентр.
Задача 4. Доказать, что две последовательные rомотетии
эквивален -r,ны либо одной rомотет,ии, либо одному переносу.
1 Леонард Эйлер великий математик XVIII в., член Петербурrской
w БерлинскоЙ академий наук. Родился в 1707 r. в Базеле (Швейцария).
С 1727 по 1741 r. жил в Петербурrе, потом до 1766 r. в Берлине и, HaKO
нец, снова в Петербурrе, rде и умер в 1783 r. Ему принадлежат крупнеw
ПJwе работы по математике, физике, 8СТРОНОМИII.
р.
р не. 90
6
.\ "
\ "
\ ""
,
\
,
. ... ".,
,,,,," \
\
\
\ в'
\
\
\ I
, I
А
Рис. 89
79
В первом случае центры трех rом,отетий лежат на од'ной и т,ой
я(е прямой, а коэффициент результирующей rомотетии равен
произведению коэффициентов данных rомотетий.
Реш е н и е. Положим, что первая rомотетия преобразует
1 очки А, в, С,... ,соответственао в А', В', С',..., а вторая пrе
образует точки А', В', С,...
/ А " В"
'. ! 5,2" /' соответственно в , ,
\ I С",... (рис. 90) 1. Уlстановим
взаИМIlооднозначное OOTBeT
511, \ ствие между точками первой
.. и последней фиrуры так, что
бы точкам А, В , С,... COOTBeT
ствовали точки А", В", С",...
По основным свойствам ro
мотетии имеем: i-\BIIA' В',
А' B'IIA" В"; BCIIB'C', B'C'II
IIB"C"; ACIIA'C', А'С'IIА"С"
и т. д. Из этих соотношений
сейчас же следует, что и
ABIIA"B", BCIIB"C", ACII
IIA"C" и т. д. А отсюда мы
получаем (теорема 3), что преобразование А, В, С,... в А", В",
С",... есть rомотетия, если АВ ФА" В", или перенос, если
АВ ==А" В".
Положим, что все преобраЗ'Jвания rомотетии. Пусть 5
центр первой rомотетии, S' центр второй rомотетии, S"
центр третьей rОi\10тетии. Прямая 88' как проходящая через
центры является неподвижной и в первой и во второй rOMo
тетии. Итак, эта прямая останется неподвижной при обеих
rомотетиях, а значит, и при результирующеЙ 'rОI\10тетии, пото
му прямая S5' пройдет через центр S".
Если
Рис. 91
А'В' == k, А"В" == Il',
.....
АВ А'В'
то
А'В' А"В" А"В" k"
,
---
АВ А'В' АВ
rде k" коэффициент результирующей rомотетии. Итак, kk' ==k fl .
Интересным следствием этоrо предложения является то, что
u u
если центры трех неравных окружностеи не лежат на однои
u u u
И тои же прямои, то шесть центров rомотетии этих окружно-
стей находятся по три на четырех прямых, называемых осям,u
подобия эт их окружностей (рис. 91).
1 Так как rомотетия вполне определена двумя парами соответствен-
ных точек, то на рис. 90 точки С и С' не покзззны.
80
Упражнения
1. Внутри yr ла дана точка Р. Построить окружность, про-
ходящую через точку Р и касающуюся сторон уrла.
2. Дана окружность и 'вне ее точка Р. Провести из точки
р секущую так, чтобы отношен.ие хорды к внешней ча'сти секу-
щей был'о равно 'отношению двух даlННЫХ отрезков.
3. Найти rеометрическое место ,середин отрезков, которые
получаются на прямых, пересекающих треуroльник и па'рал
лельных 'одной из ero сторон.
4. Найти rеометрическое место точек, отношение расстоя-
ний которых до двух данных пересекающихся прямых по-
стоянно.
5. Через 'Точку S проведены три прямые. Провести через
даТiНУЮ точку Р секущую прямую так, чтобы одна из полу-
ченных l1рех точек была серединой 'отрезка, определяемото
двумя друrими точкам.и.
б. Доказать, что прямая, проходящая через точку пересе-
чения непараллельных сторон трапеции и через точку пересе-
чения ее диаrоналей, делит основания трапеции пополам.
7. Даны две параллельные прямые и .отрезок АВ на одной
из 'них. Пользуясь 'Только линейкой, найти середину отрез..
ка АВ.
8. Дана прямая АВ, середина М отрезка АВ и точка Р вне
этой прямой. П1ОЛЬЗУЯСЬ только линейкой, провести через точ-
ку Р прямую, параллельную АВ.
9. В окружности дана хорда. Провести к этой хорде парал..
.пеJIЬНУЮ хорду так, чт,абы радиусы, проведенные к KOHцa '
данной хорды, разделили полученную хорду (на llрИ равные
"1 асти.
10. Построить параллел'оrраМi\1 по ст,оронам и уrлу между
диаrоналями.
11. В данный треуrольник вписать полуокружность так,
чтобы 'она касалась осн,ования треуrольника, а диаметр был
бы параллелен ос'нО'ванию.
12. Дан ABC. Прямая пересекает прямые ВС, СА и АВ
соответственно в точках Х, У, z. Доказать, что иrvlеет место
равенство
.
.
ZA
== 1.
ХВ УС
ХС
УА
ZB
Доказать обратное предложение: если имеет место выше
указанное равенство, то точки Х, У, Z лежат на одной и той
же прямой (теорема Менелая) .
13. Доказать, что три точки пересечения биссектрис внеш
'НйХ уrлов треуrольника с противоположными .сторонами ле
жат на одной и той же прямой.
6 л. и. Фетисов
81
14. Дан ABC. Прямые, проходящие через вершины А,
В, С и одну и ту же точку Р, пересекают прямые ВС, СА и
АВ соответственно в точках Х, У, Z. Доказать, что имеет Mec
то равенство:
ХВ УС
.
ZA == l.
ZB
ХС УА
Доказать обратное предложение: если имеет место выше
указанное равенство, то прямые АХ, ВУ и CZ проходят через
одну и ту же точку (теорема Чевы 1).
15. Доказать, что прямые, соединяющие вершины Tpe
уrольника с точками касания вписанной окружности, проходят
через одну и ту же точку.
7. ПОДОБИЕ
(7.1) Понятие о подобии фиrур мы получаем из непосред
cTBeHHoro опыта, наблюдая предметы, одинаковые по форме,
но различные по размерам. В качестве примеров можно при-
вести различные копии
с одной картины, планы
одной и той же MeCTHO
сти, выполненные в
разных масштабах, и
811
т. д.
Совершенно точное
представление о подо
бии фиrур дают две
rомотетичные между
собой фиrуры (напри
мер, мноrоуrольники
BCDEF и A'B'C'D'E'F'
и рис. 92). Существен-
но, однако, заметить,
что rомотетия фиrур
является частным слу
чаем подобия, так как если в приведенном только что примере
мноrоуrольник А' В' С' D' Е' F' переместить в положение
A"B"C"E"D"F", то он уже не будет rомотетичен с мноrоуrоль
ником ABCDEF, а в то же время он остается ему подобным
(рис. 92).
Какие же соотношения между фиrурами сохранились при
этом преобразовании? Очевидно, установив взаимнооднознач-
с'
['
А'
5
Рис. 92
1 Дя{ованни Чева (1 б48 1734) итальянский математик, работав-
ший в области rеометрии.
Заметим, что предложение упражнения 14 остается справедливым и
для Toro случая, коrда прямые, проходящие через вершины, параллельны
82
ное соответствие между точками так, чтобы точке А соответ-
ствовала А", B B", C C" И т. д., мы получим, что при этом
сохраняется: 1) равенство соответственных уrлов: LABC==
== LA"B"C", LBCD== LB"C"D" и т. д. И 2) равенство OTHO
шений соответственных отрезков:
А"В"
В"С"
С" D"
............ . . .
АВ
ВС
CD
Исходя из этих общих соображений, мы можем дать таКое
определение подобия.
Определение. Если между двумя фиrурами можно устано..
вить такое взаимнооднозначное соответствие, при KOTOpO 1
будут равны соответственные уrлы и равны отношения COOT
ветственных отрезков (т. е. отрезки одной фиrуры пропорцио-
нальны соответственным отрезкам друrой), то это соответ-
ствие (преобразование) называется подобием, а фиrуры
подобными.
Общее числовое значение отношений соответственных ОТ-
резков подобных фиrур называется коэффициентом подобия.
Заметим, что в подобии соответственные элементы обеих
фиrур обычно называются сходственными.
Для обозначения подобия фиrур употребляют знак cп
повернутое изображение латинской буквы S, с которой начи
нается слово siтilis подобный.
Если фиrура с точками А. В, С, D,... подобна фиrу..
ре с соответственными точками А', В', С', D',..., Т. е.
(ABCD...)C/) (A'B'C'D'...) , то это значит, что LABC== LA'B'C'J
L-BCD==LB'C'D' и т. д. И что
А'В'
АВ
B'D'
== . . . == k,
BD
В'С'
ВС
rде k коэффициент подобия.
Непосредственно из определения подобия следует:
1. Равенство и rомотетия фиrур суть частные случаи
подобия; в случае равенства фиrур k == 1.
2. Соотнощение подобия обладает свойствами: а) каждая
фиrура подобна самой себе; б) если первая фиrура подобна
второй, то и вторая подобна первой; в) если первая фиrура
подобна второй, а вторая подобна третьей, то и первая подоб..
v
на третьеи.
Свойства а) и б) очевидны; свойство в) леrко доказать.
Пусть мы имеем соотношения подобия между тремя фиrу-
рами:
(ABCD...) (/J(A'B'C'D'...); (A'B'C'D'...) "",'(A"B"C"D"...) .
Из первоrо соотношения имеем LABC== LA'B'C'; из
BToporo L А'В'С' == L А"В"С". Следовательно, L АВ С=:
== LA"B"C", т. е. сходственные уrлы первой и третьей фиrур
6* 83'
равны, если точкам А, В, С, D,... привести в соответствие
А " В " С " D "
точки , , , ,...
Если в первом случае коэффициент подобия равен k, то
А' В' == k. Если во втором случае коэффициент подобия равен
АВ
k', то А" В" == k'. Отсюда получаем:
А'В'
А"В"
=== k'k.
А"В"
А'В'
А'В' АВ АВ
. .
и так, отношение сходственных отрезков третьеи и первои
фиrур постоянно и равно k'k.
Важной особенностью преобразования подобия является
то, что подобные фиrуры MorYT быть ориентированы и oдиHa
КОдО и противоположно.
с \ 5 С
. \ q"
I В 1 '
\
,,'
\
lY911
s
Рис. 93
Ркс. 94
Например, фиrуры АВС... и А" В"С"... на рис. 92 подобны
и одинаково ориентированы: АВС... и А' В'С'... одинаково ори
ентированы, так как они rомотетичны, а А' В'С'... и А" В"С"...
одинаково ориентированы, так как преобразуются друr в
друrа вращением.
Если же одну из двух rомотетичных фиrур преобразовать
в новую фиrуру осевой симметрией, то полученная фиrура
будет противоположно ориентирована с каждой из перво
начальных фиryр. Например, на рис. 93 фиrуры А ВС и А' В' С'
rомотетичны, а фиrура А"В"С" симметрична с А'В'С' относи
тельно оси s, следовательно, она противоположно ориентиро
вана с фиrурой АВС. Вместе с тем (А"В"С") == (А'В'С') ,
A'B'C')",,(ABC) и, значит, (A"B"C")C/J(ABC). На рис. 94
дан еще пример подобных, но противоположно ориентиро
ванных фиrур.
84
Подобие фиrур с одинаковой ориентацией называется
собственным, а с противоположной несобственным. Из
определения подобия получаются два важных следствия:
Следствие 1. Фи ура, подобная прямой линии, есть прямая.
Действительно, пусть 1 данная прямая. Возьмем на ней
две точки А и В, которым в преобразовании подобия соответ-
ствуют точки А' и В'. Проведем через А' и В' прямую 1'. Если
на прямой 1 возьмем точку М между точками А и В, то
LAMB развернутый;
он равен развернутому
уrлу А'М'В', rде М'
точка, в которую преоб
разуется точка М. По
этому М' С 1'. Если бы
М лежала вне отрезка м
АВ, то LAMB был бы
нулевым; но тоrда HY /
левым был бы и .
LA'M'B' и опять точка
М' была бы на прямой Рис. 95
1'. Итак, всякая точка прямой 1 преобразуется в точку прямой
['. Тем же способом леrко доказать и обратное: всякой точке
прямой [' соответствует точка прямой 1.
Следствие 2. Фu ура, подобная окружности есть окруж-
ность. Пусть мы имеем окружность с центром О (рис. 95).
Возьмем на ней точки А и М. В подобной фиryре точке О
соответствует О', А А' и М М'. AOM равнобедрен-
ный, поэтому LMAO== LAMO. Вместе с тем по свойству
подобия LMAO == LM'A'O' и LAMO == LA'M'O', т. е.
LM'A'O'== LA'M'O', и, значит, A'O'M' тоже равнобедрен
ный и потому О'М'==О'А'. Если теперь точка М будет описы-
вать окружность с центром. О, то соответственная точка М'
будет перемещаться так, что ее расстояние от точки О' будет
постоянно равно отрезку О' А'. Следовательно, точка М' тоже
опишет окружность. Обратно, тем же путем можно доказать,
что каждой точке ОКiружности с центром О' соответствует
точка окружности 'с центром о.
В предыдущем изложении мы видели, что любые две
окружности rомотетичны друr друrу; теперь мы можем также
сказать, что любые две ОКРУЖНОсти подобны дpy apyzy.
(7.2) Рассмотрим теперь случаи подобия треуrольников.
Теорема 1. Два треу ольнuка подобны, если:
1) два у ла одНО20 соответственно равны двум у лам дру-
2020;
2) две стороны одНО20 соответственно nроnорцuонаЛЫtЬt
двум сторонам дРУ2020, а У2ЛЫ, заключенные между этими
сторонами, равны;
85
::3) три стороны одНО20 пропорциональны трем сторонам
apY20Z0.
Д о К а з а т е л ь с т в о. Пусть треуrольники АВС и А' В'С'
удовлетворяют какому"нибудь одному из условий теоремы
(рис. 96). .
Построим отрезок А" В", равный отрезку А' В' и парал
лельный отрезку АВ. Проведя через А" прямую, параллель
ную АС, а через В"
прямую, параллельную
ВС, найдем в их пересече
нии точку С". Треуrольни
ки АВС и A'fB"C" rOMOTe..
тичны (на основании Teo
ремы 3 предыдущеrо па..
раI'рафа). Поэтому
6.A"B"C"cnlJ.ABC. Если
мы докажем, что во всех
трех случаях 6A"B"C"
A'B'C', то отсюда бу
дет следовать, что
6А' В'С'С/) ABC.
1) Пусть LA LA',
L,B LB'. На основании построения имеем: L,A" LA и
'L, В" L В, откуда следует, что L,A' == L,A" и L В' L, В".
Вместе с тем А'В'==А"В" значит 6А"В"С"==6 А 'В'С' по
, ,
стороне и двум прилеrающим уrлам. Итак, 6A'B'C'C/) ABC.
2) Пусть
о
в'
(' А 1
Рис. 96
LA===LA' А'В' А'С'
и
АВ АС
ПО свойству rомотетии имеем:
LA"==LA, А"В" А"С"
АВ АС
Но А" В" === А' В', значит,
А'В' А"С" А'С' А"С"
или
АВ АС АС АС
Т. е. А'С' == А"С". Следовательно, 6 А"В"С" == 6 А' В'С' по
gBYM сторонам и уrлу между ними. Значит, A' B'C'cп ABC.
3) Пусть
В'С'
ВС
С'А'
СА
86
А'В'
АВ
П свойству rомотетии имеем:
В"С"
ВС
С"А"
А"В Ь
АВ
СА
110 А"В"==А'В', отсюда получаем:
В"С" В'С'
ВС ВС
т. е. В"С" == В'С'; и точно так же
т. е. С"А" == С' А'. Следовательно, 6 А" В"С" == 6 А' В" С' по
трем сторонам. Итак, 6 А' В' С' (/) 6 АВС.
Из теоремы о приз- С
наках подобия треуrоль-
ников получаются важ-
ные предложения.
Теорема 2. Два MHO
20У20льнuка подобны,
если oIчежду их вершина-
ми [Аtожно установить
8заи.м,ноод нознаЧflое co
оmвеmствие и если при
эmо.lЧ сходственные 8НУ"
mренние У2ЛЫ их равны,
а сходственные cтopo
ны nроnорциональны.
Д о к а з а т е л ь с т в о.
Пусть мноrоуrольники.
А BCDEF И A ' B ' C ' D ' E ' F ' 97)
рис. удовлетворяют условиям
теоремы, т. е.
С"А" С'А'
СА СА
Е
п'
с'
F'
Рис. 97
LA==LA', LB==LB',...,LF==LF',
А' В'. В"С' Е' Р' Р' А'
k
АВ ВС ... ЕР F А .
Проведем отрезок АIВl' параллельный отрезку АВ и равный
отрезку А' В', и построим на нем мноrоуrольник AIBICIDIEIFl'
равный мноrоуrольнику A'B'C'D'E'F' и одинаково ориентиро-
ванный с мноrоуrольником ABCDEF.
В силу условий теоремы будем иметь:
L Аl == L А, L В 1 === L в, · · · , L F 1 == L Р,
AIBl
АВ
B1C 1
ВС
...
EIFl
ЕР
FIAl
== k.
РА
87
Проведем диаrонали АС, А'С' и A 1 C 1 ; LJ.A 1 B 1 C 1 ==6A'B'C'
(по двум сторонам и уrлу между ними) и в то же вреrvlЯ
6 A1B1C1cnLJ. АВ С, так как LB==LB 1 и AIBl B1C}
АВ ве
Поэтому L ВАС == L B1A1C 1 И L A1C1B 1 == L АСВ. Но
AIBllt АВ и фиrуры одинаково ориентированы, поэтому B1C111 ВС,
C1A 1 U СА и, значит, треуrольники A 1 B 1 C 1 и АВС rомотетичны
при центре s. Отсюда далее следует, что L C1AIFl == L САР.
Проведя диаrонали C1Fl' CF и C'F', 'получим, что LJ. A}C1F 1 :::=
== L А'С'Р' и LJ. A1C1F 1 cn LJ. ACF, так как C1A 1 == FI A l И yr
СА FA
ЛЫ, заключенные между этими сторонами, равны. Отсюда
получим: LA1C1F1==LACF, LA1F1C1==LAFC, а так как
C1A111 СА и фиrуры одинаково ориентированы, то C1F 111 CF,
AtFl Н AF. Значит, 6 AtCIFl И 6 ACF rомотетичны при том
же центре s.
Далее, проведя диаrонали C1El' СЕ, С' Е', мы таким же
способом докажем rомотетичность треуrольников C 1 F 1 E 1 с CFE
и C1EIDl с CED при том же центре. Итак, мноrоуrольники
ABCDEF и AIB1C1DIEIF 1 rомотетичны и, значит AIB} C1DIE}F l(/)
cnABCDEF, откуда следует, что A'B'C'D'E'P'cnABCDEF.
Следствие 1. Подобные МНО20уzольники .можно разбить
на одинаковое число соответственно подобных u сходственно
расположенных треуzольников.
Справедливо и обратное положение:
Слепствие 2. Если данные МНО20У20льники можно разбить
на одно и то же число соответственно подобных и сходственно
расположенных треУ20льников, ТО такие .мНО20У20льниКll
подобны.
Доказательство проводится совершенно так же, как в пре
дыдущей теореме: строят мноrоуrольник, равный одному и
одинаково ориентированный с друrим из данных мноrоуrоль
ников. Разбивая l\1ноrоуrольники на треуrольники, показы
вают, что они rомотетичны.
(7.3) На основании ДОI<азанных предложений решаются
различные rеОl\fетрические задачи.
Оснозная задача. На даННО:\1 отрезке А'В' построить !\tHO
rоуrольник, подобныЙ данному мноrоуrольнику ABCDE
(рис. 98).
Реш е н и е. Опираясь на следствие 2 к предыдущей Teo
реме, разбиваем данный мноrоуrольник на треуrольники.
После этоrо на отрезке А' В' строим .6А' В'С', подобный
.6АВС. ДЛЯ этоrо при вершине А' строим L. В'А'С' == L. ВАС,
а при вершине В' строим LA'B'C'== L.ABC. A'B'C'C/)LJ.ABC
по первому признаку. В зависимости от Toro, ХОТИl\1 ли мы
построить мноrоуrольник, одинаково или противоположно
ориентированный с данным, выбираем и ориентировку Tpe
88
уrольника А'В'С'. Далее на отрезке А'С' строим A'C'D',
подобный треуrольнику ACD и также с соответствующей
ориентировкой и т. д.
В результате получен мноrоуrольник А' В' С' D' Е', который
разбит на треуrольники А'В'С', A'C'D', A'D'E', соответственно
подобные треуrольникам
АВС, ACD, ADE; поэтому
A'B'C'D'E' C"/).ABCDE.
Метод подобия, приме..
няе ый при решении за..
дач на построение, заклю D
чается в 'Сом, что, поль..
зуясь данными задачи,
строят сначала фиrуру,
подобную искомой, после
чеrо, имея данные о HeKO
торых линейных элемен..
тах искомой фиrуры, пре
образуют с помощью подобия полученную фиrуру в новую
фиrуру с заданными линейными элементами. Приведе 1 при..
меры.
Задача 1. Построить треуrольник по двум уrлам и ме-
диане.
L
I ·
;;,
с
Е
8'
lJ
о'
с'
Рис. 98
(,
А
м
8
Рис. 99
Реш е н и е. Пусть а и данные уrлы искомоrо Tpe
уrольника с вершинами в точках А и В, т медиана, coe
диняющая вершину С с серединой стороны АВ (рис. 99).
Построим сначала на произвольном отрезке .А' В' треуrоль-
ник А'В'С, подобный искомому треуrольнику АВС. ДЛЯ этоrо
при вершинах А' и В' строим соответственно уrлы а и .
Медиана СМ' полученноrо треуrольника не будет, вообще
rоворя, равна данному отрезку т. Поэтому на луче СМ' от
начала С отложим отрезок СЛ1 == т. Через точку М проведем
прямую, параллельную А'В', которая пересечет СА' и СВ'
соответственно в точках А и В. LABC искомый, так как
89
LA==LA'==a, LB==LB'== . Кроме Toro, треуrольники АВС
и А'В'С' rомотетичны относительно центра С; поэтому
МА: МВ
M'A" М'В' ,
или
МА
МВ
М'А'
=== 1.
М'В'
Так как М'А'===М'В', то и МА=-=МВ, т. е. отрезок СМ===m
есть медиана.
Рассмотрим несколько более сложную задачу на построение.
Задача 2. 1l0СТРОИТЬ треуrольник по трем ero высотам.
Реш е н и е. IlYCTb h a , h b ,
hc три высоты искомоrо тре-
уrольника (рис. 100). Дока-
жем прежде Bcero, что дли
ны высот треуrольника обрат
но пропорциональны длинам
r ero соответствующих сторон.
Действительно, если в Tpe
уrольнике АВС проведем вы-
соты АМ === ha и BN == h b ,
то получим LAMCC/:>LBNC,
так как у них L с общий
и оба треуrольника прямо-
уrольные. 1l0ЭТОМУ
ho
А'
hb
hc
А
8
iJ1
Рис. 100
АА1
В1У
СА
ВС
или
ha Ь
,
hb а
т. е.
1 1
a.b .
· ha . h ь ·
Так как это же предложение можно доказать и для тре-
тьей высоты h c , то имеем вообще:
111
a'b.c . .
. . ha · hb . hc .
Построим теперь из отрезков h a , h b , hc вспомоrательный
, , ,
треуrольник А' В' С'. Ero высоты h a , h b , hc будут обратно про-
порциональны сторонам h a , hb И h c , т. е.
'. '...' 1. 1 . 1
ha . hb . hc === . . .
\. ha hb hc
, , ,
Но это значит, что новые высоты h a , h b , hc прямо пропор-
циональны сторонам искомоrо треуrольника, т. е.
, , ,
ha : hb : hc == а : Ь : с.
Отсюда следует, что если построить треуrольник АВ"С" со
сторонами В"С" === h , С" А == h , АВ" == h;, то он будет подобен
90
искомому треуrольнику АВС по третьему признаку подобия.
Чтобы получить искомый треуrольник, проведем из вершины А
высоту АМ" к стороне В"С" и на луче АМ" отложим отрезок
АМ == ha. Проведя через точку М прямую, параллельную В"С",
найдем в пересечении ее с лучами АВ" и АС" соответственно
точки В и С. 6 АВС искомый, так как он подобен искомому
треуrольнику и вместе с тем коэффициент подобия k равен
АМ
== 1, т. е. в этом случае имеем равенство. Этим способом
ha
задача разрешима при условии, что данные отрезки h a , hb, hc
удовлетворяют неравенству треуrольника, т. е. если по ним
мо>кно построить треуrольник.
Приведем еще примеры решения задач на доказательство.
Задача 3. Доказать, что если даны две собственно подоб
ные фиrуры, то существует в плоскости единственный He
подвижный центр, поворотом BOKpyr KOToporo одну из этих
фиrур можно сделать rомотетичной с друrой относительно
Toro же центра.
Реш е н и е. Пусть АВС... и А' В'С'... данные фиrуры
)
(рис. 101). Положим, что векторы АВ и А'В' не коллинеарны,
так как если бы оказалось, что
АВ 11 А/В', то это означало бы, что
фиrуры rомотетичны и тоrда полу
ченный центр был бы центром ro..
мотетии и вращения на нулевой
уrол. Пусть прямые АВ и А' В' пере
секаются в точке Р. Проведем две
окружности: через три точки А,А',Р
и через три точки B B',P. Так как
окружности имеют общую точку Р,
то они имеют и еще одну общую
точку S 1. По свойству вписанных
yr лов, опирающих'ся на одну и ту
же дуrу, будем иметь: LASA' +
+LA'PA==1800; LA'PA+ LBPB'== 180°, поэтому LASA'==
==ВРВ' и L BSB' L ВРВ', следовательно,
С'
\
\
\
\
\
\
\
\
\
\
А'
Рис. 101
LASA' == LBSB' == 00,
rде (() уrол между векторами АВ и А'В'.
Если произвести вращение фиrуры АВС... на уrол (() ВОК-
............
pyr иентра S, то вектор АВ преобразуется в вектор AIBl, кол
............
линеарный с вектор'ом А'В'. Вместе с тем, блаrодаря одина-
1 Доказательство остается в силе, если точка S совпадает с Р (окруж
насти будут касаться). Предлаrаем этот случай самостоятельно разобрать
vчащимся.
91
ковой ориентации фиrур А'В'С'... и AtBtCt... Iи все остальные
векторы полученной фиrуры будут коллинеарны с COOTBeT
ственным,и векторами фиrуры А' В'С'... 01'сюда следует, что
обе фиryры rомотетичны относительно центра s.
Полученный центр единственный, так как в силу paBeH
ства уrлов LASA'== LBSB'== LCSC'==...==oo точка S есть
единственная точка плоскости, из которой все отрезки АА',
ВВ', СС'... видны под одним и тем же уrлом 00.
41
с
А
l
Рис. 102
Задача. 4. Доказать, что если даны две несобственно по
добны'е фиrуры, то в плоскости существуют две, и только две,
взаимно...перпендикулярные оси симметрии, каждая из KOTO
рых преобразует одну из данных фиrур в новую, rомотетичную
со второй относительно точки пересечения обеих осей.
Решение. Пусть АВС... и A'B'C'... дaHHыe несоб
ственно подобные фиrуры (рис. 102). В этих фиrурах всеrда
существуют два соответственных неколлинеарных вектора, по-
ложим А В и А' В' (если бы таких векторов не было, т. е. если
бы все соответственные векторы были коллинеарны, то мы
имели бы одинаково ориентированные фиrуры, что противоречит
условию). Проведем через точку А' прямую 1, параллельную АВ,
и произведем осевую симметрию фиrуры А' В'С' . .. относитель
но биссектрисы 81 одноrо из уrлов, образуемых прямой 1 с век-
...... , , ,
тором А' В'. Пусть 81 (А' В'С' ...) = А' В 1 С 1 ... При этом В 1 С 1,
, , ,
и потому А' В 1 \\ АВ. А так как фиrура А' B 1 C 1 . .. одинаково
ориентирована с АВС. . . , то эти фиrуры rомотетичны OTHO
сительно центра 81.
Итак, фиrура Аве... преобразуется в фиrуру А' В' с' . . .
двумя преобразованиями: rомотетией относительно центра SI и
симметрией относительно оси 81. Неподвижной прямой в этом
92
преобразовании служит прямая 8, проходящая через центр 51
и перпендикулярная к оси 81' так как эта прямая не изменяет-
ся ни при первом, ни при втором преобразовании.
Проведем теперь биссектрису 82 BToporo уrла, образуемоrо
, ,
прямой 1 и вектором А' В'. Пусть 82 (А' В'С' . . .) = А' В,С,. · · .
, ,
Фиrура А' В,С, . .. будет тоже rомотетична с А 8С . .. относи-
тельно центра 82. В этом преобразовании неподвижной будет
прямая 8', проходящая через 82 и перпендикулярная к 82.
Пересечение прямых 8 и 8,......... точка 8.......... единственная не-
подвижная точка преобразования. Так как биссектрисы смеж-
ных уrлов взаимно перпендикулярны, то 8 8'.
Если бы оказалось, что в этом преобразовании существует
Е-ще одна неподвижная точка S', отличная от S, то из этоrо
следовало бы, что отрезок SS' преобразуется в caMoro себя,
Т. е. что при любом преобразовании этоrо типа коэффициент
подобия равен единице, что противоречит определению по
добия.
Упражнения
1. Построить rреуrольник по двум уrлам и сумме двух ero
сторон.
2. Построить равносторонний треуrольник по сумме (или
разности) стороны и высоты.
3. Построить треуrольник по двум уrлам Iи расстоянию
между центрами вписанной и описанной окружности.
4. В да.нный четырехуrольник вписать друrой четырех-
уrольник так, чтсбы ero стороны были параллельны четырем
данным прямым.
5. Через четыре данные точки провести четыре прямые так,
1{Iобы они своим пересечением определили четырехуroльник,
подобный данному.
6. Доказать, что если мноrоуrольник, оставаясь постоянно
подобным себе, перемещается так, что три ero вершины опи..
сывают 'прямые линии, то и каждая из остальных вершин
тоже описывает прямую линию.
7. В данный четырехуrольник вписать друrой четырех
уrольник, подобный данному.
8. Построить треуrольник, подобный данному, так, чтобы
одна из ero вершин лежала в данной точке, друrая на дaH
ной прямой, третья на данной окружности.
9. Даны отрезки АВ и А' В'. Найти такую точку S, чтобы
треуrольники ABS и А' B'S оказались собственно подобны
друr друrу.
10. Даны ОТi>езки АВ и А' В'. Найти такую точку S, чтобы
треуrольники А BS и A'B'S оказались несобственно подобны
друr друrу.
11. Можно ли решить задачу 2 (стр. 90), если данные
высоты не удовлетворяют неравенству треуrольника?
rЛАВА ВТОРАЯ
МЕТРИЧЕGКИЕ СООТНОШЕНИЯ В ТРЕуrОЛЬНИКЕ
И в ОКРУЖНОСТИ
8. МЕТРИ'ЧЕСКИЕ СООТНОШЕНИЯ В ТРЕуrОЛЬНИКЕ
Рис. 103
Выведем некоторые
рами.
Определение 1. Проекцией вектора на ось называется
вектор, началом KOToporo служит проекция начала данноrо
вектора, а концом проекция ero конца на эту ось.
На рис. 103 вектор А' В' есть проекция АВ на ось l.
Проекция вектора считается положительной, если ее Ha
правление совпадает с направлением оси, и отрицательной
в проти вном случае.
Числовым значением проекции вектора называется ее Длина,
взятая с положительным знаком, если проекция положительна,
и с отрицательным, если она отрицательна 1.
(8.1) Этот раздел rеометрии посвящен весьма важному и
в теоретическом и в практическом отношении вопросу о KOC
венном измерении zеометрических величин.
Косвенным измерениеl\1 rеометрических величин называет
ся всякий способ нахождения числовоrо значения какой
нибудь величины, при котором не производят непосредствен
в Horo ее измерения. Возмож
, ность TaKoro нахождения обус-
" ловливается тем, что существу
" ют зависимости, которые позво
,
, ляют, зная числовые значения
" одних величин, вычислить по
,
, ним числовые значения друrих.
Только блаrодаря косвенному
измерению были найдены раз
меры Земли, определены рас-
стояния до Солнца, Луны, пла-
нет, звезд, определены разме
ры молекул, атомов и т. д.
числовые зависимости между BeKTO
А
I В некоторых руководствах вектор А' В' называют rеомеТf)И11еской..
а ero числовое значение алrебраической проекцией вектора Ад.
9
Следствие. П роекция суммы нескольких векторов равно
сумме nроекций слаzаеМbLХ.
Пусть, например, мы имеем: АМ == АВ + ве + CD + DM
(рис. 104). Проектируя эти векторы на ось [, получим по опре
де.пению суммы векторов:
)
А'В' + В'С' + C'D' + D'M' == А'М'.
Припомним определение триrонометрических функций. Рас-
смотрим ПРЯl\10уrольные сси координат Ох и Оу (рис. 105).
Проведем произвольный вектор DP и найдем ero проекции ОХ
на Ох и ОУ на Оу.
!I
м
А I I I r
I I I
I I I I
I I I I
I I I I
I I
I I I I
I I I I
"' 6 Ь 1 b A .. Ь l
А' :о' r/ с' м'
Рис. 104 Рис. 105
."..... .. ... !I
, ,
1 !i
,
%
Определение 2. Отношение числовоrо значения проекции
ОХ к длине вектора ОР называется косинусом уrла CJ.. (rде CJ..
уrол, на который нужно повернуть Ох в положительном на..
правлении, чтобы она пошла по направлению вектора ОР). От..
ношение числовоrо значенияj проекции ОУ к той же длиые
вектора ОР называется синусом Toro же уrла rlv.
Известно, что iвеличина косинуса и синуса определяется
I
только уrлом <х и не зависит ,от величины вектора ОР, так
как для любоrо сонаправленноrо вектора ОР' мы будем иметь
в силу rомотетии:
ох' ох . оу' оу
cos rlv == == и SlП rlv === .
ОР' ОР ор' ор
Из определения;косинуса получаем:
Сле,Аствие. Числовое значение nроекции вектора. на ось
равно длине вектора, умноженной на к,осинус У2ла между
осью и вектором.
95
Если т есть вектор, т' ero проекция на ось 1, т ........... длина
вектора, т' числовое значение ero проекции, сх уrол между
осью l и т, то получим:
т' ,
........ == cos сх, поэтому т 1::: т cos (Х.
т
(8.2) Определение. Скалярным nроuзведением двух ве/(,moров
...
а и Ь называется произведение длины а одноrо вектора на чи
словое значение Ь' проекции на ero ось! друrоrо вектора. Ска-
--+ .....
лярное произведение обозначается а.Ь. Таким образом,
...... .....
а · Ь === аЬ'.
Следствие 1. Если векторы сонаnравлеНbl, то их скаляр
ное nроuзведение равно произведению их длин. Если ве/(,торы
nерnендиКУЛЯРНbl то их CKa
лярное произведение равно HY
лю.
Это объясняется тем, что в
первом случае проекция вектора
равна самому вектору, а во BTO
ром случае проекция вектора
обращается в нуль.
Следствие 2. С/(,алярное npo
изведение векторов равно произ-
ведению длин этих ве/(,торов на
/(,осинус уела .между ними.
с
10-' I b i I
r= I
I , ,
$' I
I -,
I
Рис. 106
..... .....
а.Ь==аЬ', но b' bcoscx,
откуда
-+ .....
а · Ь == аЬ cos .
Теорема. С/(,алярное nроизведенuе подчиняется перемести-
тельному и распределительному за/(,онам.
...... ..... -+
Д О К а з а т е л ь с т в о. 1) Если а · Ь аЬ cos сх, то Ь · а ==
=== Ьа cos ( cx). Но аЬ === Ьа и cos ( cx) == cos (сх), поэтому
-+ .....-+
а. Ь == Ь. а.
..... -+
2) Пусть а + Ь == т (рис. 1062). Умножим эту сумму на
I ОСЬЮ вектора называется прямая, проходящая по этому вектору и
сонаправленная с ним.
..... -+
2 На рис. 106 векторы а' и Ь' сонаправлеН_I, поэтому числа (J' и Ь'
одинаковы по знаку и а' + Ь' == т'. Проверьте справедливость этоrо равен-
-+ .....
ствв, коrда а' и Ь' противонаправлены.
96
.....
вектор с. Обозначим через а, Ь, т, с соответственно длины
векторов а, Ь, т, с, а через а', Ь', т' числовые значения
проекций векторов а, Ь, m на ось вектора с. Получим:
--+ --+
с.т == ст' == с (а' + Ь') == са' + сЬ' == с.а + с.Ь,
или
--+ --+
с. (а + Ь) == с.а + с.Ь.
Из этой теоремы следует, что при скалярном умножении
векторных сумм или разностей можно пользоваться обычными
правилами алrебры, которые
применяются при умножении
мноrочленов.
(8.3) Пользуясь свойствами
скалярноrо произведения,
можно получить все основные
метрические соотношения в
треуrольнике.
Теорема косинусов. Kвaд А
рат стороны треУ20льника pa
вен сумме квадратов двух
дРУ2их е20 сторон минус' удвоенное произведение этих сторон
на косинус У2ла между ними.
Д о к а з а т е л ь'с т в о. Пусть нам дан треуrольник АВС
(рис. 107). Обозначим длины ero сторон ВС, СА и АВ
через а, Ь, с. По правилу вычитания векторов имеем:
ь
Рис. 107
--+
BC==AC AB или a==b c.
Умножая каждую часть этоrо равенства на самое себя,
получим:
--+ --+ --+ .....
а 2 == (b c)2==b2+c2 2b. с и окончательно,
a2==b2+c2 2bc cos а. (1)
Это и есть формула, выражающая теорему косинусов.
Если уrол а прямой, то cos 900==0, и тоrда мы получим
reopeMY Пифаrора:
а 2 ==Ь 2 +с 2 ,
f. е. квадрат rипотенузы равен сумме квадратов катетов.
Теорема косинусов дает возможность определить сторону
rреуrольника, если известны две друrие ero стороны и уrол,
аключенный между ними.
Эта же теорема позволяет определить любой уrол тре-
уrольника, если известны три ero стороны. Действительно, из
7 A и. Фетисов
97
rой же формулы (1) можно получить значение cos а:
Ь ! + с 2 а 2
СО5 (J., .
2Ьс
Чтобы получить формулы для остальных уrлов, примеНЯЮ1
так называемое «правило циклической замены». Соrласно этому
правилу во всякой формуле, связывающей стороны а, Ь, с и
уrлы (J." , r треуrольника, можно букву а заменить буквой Ь,
букву Ь буквой с и букву с буквой а. И точно так же
букву (J., заменить буквой , букву буквой r, букву r бук
вой (Х. Пользуясь правилом, леrко получим:
(2)
c2+a2 bl а 2 +Ь 2 """,",",с'
COS == ; cos r == .
2са 2аЬ
Из формулы (2) можно получить также формулы, определй-
ющие синусы уrлов треуrольника по ero сторонам. Введем пред-
варительно обозначения: периметр треуrольника со сторонаМЕ
а, Ь, с обозначим через 2р. Итак
2р == а + Ь + с.
Вычитая последовательно из обеих частей этоrо paBeHCTB
00 2а, 2Ь, 2с, получим:
2 (р а) == ........ а + Ь + с; 2 (р Ь) === а Ь + с:
2 (р с) =:J а + ь с.
Далее получаем:
1 2Ьс Ь 2 с 2 + а 2
....... С05 (J., =-
2Ьс
а 2 (Ь с)2
=-
2Ьс
(а Ь + с) (а + ь с)
-
2Ьс
4 (p' !b) (р с)
2Ьс
Итак, имеем:
1 2 "(р Ь) (р с)
COS а == .
Ьс
(;j\
Аналоrично получаем:
1 + cos (J., == 2Ьс + Ь 2 + Cl: а 2
2Ьс
(Ь + c)21 а 2
==
2Ьс
_ (а + Ь + с) ( a + ь + с) ...... 2р (р а)
2Ьс .... Ьс ·
в8
()тсюдаl
1 +cos(X == 2p(p a) .
Ьс
(4)
Перемножая ФОРМУЛБI (3) и (4), находим:
1 cos l (Х sin2 (Х =- 4р (р ----4 а) (р Ь) (р с)
Ь 2 с 2
е окончательно:
2
sin (Х ...... у р (р а) (р Ь) (р с).
Ьс
Так как синусы уrлов треуrольника всеrда положительны
ro радикал берется со знаком плюс. Обозначая ero величину
через S, получим:
. 28. 28. 28
В1П сх ::8 ; 51n ; 51n r =::1 .
Ьс са а Ь
(5)
Из формул (5) получаем теорему синусов.
Теорема СИНУСОВ. CrnopOHbl треу ольнuк,а относятся как
синусы противоположных уалов.
Д о к а з а т е ль с т в о. Из формул (5) получим:
. . 28 28 Ь
Sln (Х : 51П == : == а: ;
Ьс са
fОЧНО так же:
. . 28 28 Ь
51n : 51П r :::::1 : : С.
са аЬ
Окончательно:
5in (Х : 5in : 5in r а : Ь : С.
Эroй формулой выражается теорема синусов.
(8.4) Пользуясь полученными формулами, можно вычис",
лить стороны И уrлы треуrольника, зная друrие ero стороны и
уrлы. Эти вычисления называются решением TpeYZOAbHUKa.
Рассмотрим основные случаи решения треуrольника. В даль-
нейшем условимся длины сторон ВС, СА и АВ в треуrоль
нике Аве обозначать соответственно буквами й, Ь, с, а вели-
чины уrлов А, В и е буквами а, р, у.
1 а.учаА решения треуrОJlьника. Даны й, р, у; определить
Ь, с и а.
Пользуясь теоремой о сумме внутренних уrлов треуrоль-
е:икз, сразу получаем:
g == 1800..... (Р + у) .
(6)
7* 99
L{алее по теореме синусов определяем:
ь sin
...............
. ,
а slnCL
Ь а sin
откуда ,
sin <х
и аналоrично:
с sfп r
,
а SlП <х
а sin r
откуда с == .
s in <х
Этот случай решения треуrольника часто применяется на
практике для вычисления расстояний до недоступной точки.
Пусть, например, нам нужно измерить расстояние от доступ
ной точки В до недоступной точки А (рис. 108).
На некотором расстоянии от В выбираем третью точку С
так, чтобы из нее были видны точки А и В. Далее возможно
тщательнее измеряем длину ВС (<<базис») и одновременно при
помощи уrломерных инструментов из-
меряем уrлы при вершине В и r
при вершине С треуrольника АВС. По
в уже выведенной формуле получаем окон-
чательно:
1I случай решения треуrольника.
Даны Ь, с и (J.,; найти , r и а.
Пользуясь теоремой косинусов, на-
ходим прежде Bcero сторону а по фор
муле:
Рис. 108 а === у Ь 2 + с 2 2Ьс cos (J.,.
После Toro как определена сторона а, находим уrлы и ,..
опять-таки по теореме косинусов:
с 2 + а2 Ь 2 а 2 + Ь 2 с 2
cos == ; cos r ==
2са 2аЬ
АВ а sin r
c .
sin<x
или по теореме синусов:
sin == ь sin CL ; sin т == ' sin <х
а а
111 случай решения треуrольника. Даны а, Ь, с; найти (J." , Т
Для решения вновь применяем TeOpel\1Y косинусов:
cos (J., ===
Ь 2 + с2 а 2 с 2 + а2 Ь 2
; cos == ;
2Ьс 2са
а 2 + Ь 2 с 2
CoS r ....:.. 2аЬ
100
После Toro как по косинусам будут определены уrлы а, f3 и
\', производим проверку, пользуясь теоремой о сумме BHYTpeH
них yr лов треуrольника. Мы должны получить а +
+ v
180°.
Однако, ввиду Toro что всякое измерение дает лишь прибли
женное значение чисел а, Ь и с, то и результаты вычислений
дают лишь приближенное значение уrлов. Поэтому сумма
а+ l3+v может отличаться от 180°, но эта разница не должна
превышать допустимой ошибки. Например, если относитель-
ная ошибка при измерении длины сторон достиrает 1 о/о, то
ошибка при определении уrла может достичь 20'. Допуская
возможность такой ошибки на каждом из уrлов, мы получим,
что сумма уrлов может отличаться от 180° на целый rрадус.
IV случай решения треуrОJlьника. Даны а, Ь, а; требуется
найти
, у, с.
Пользуясь теоремой синусов, находим:
ь sin
. ь sin а
....... ==
, откуда sln
== ·
а Sln CL а
Определив по таблицам yrол
, находим уrол r по формуле:
r == 1800
«(Х +
).
Сторона с определяется либо по теореме синусов:
а sin r
с== ,
sin CL
либо по теореме косинусов:
с == у а 2 + Ь 2
2аЬ cos r.
При решении треуrольника в этом случае необходимо иссле-
Il0вать формулу:
.
ь sin
sln
== ,
а
так как от результатов, полученных из нее, зависят все даль-
нейшие вычисления. Здесь возможны следующие случаи:
Ь siп
1 ) > 1. Так как синус yr ла не может быть больше
а
единицы, то в этом случае решение невозможно.
Ь sin а ...
2) == 1. Если Sln
== 1, то
=== 900, т. е. треуrольник
а
прямоуrольный. Задача в этом случае имеет единственное
решение.
Ь siп
О
3) < 1. В этом случае задача также разрешима. !!ре-
а
делим число решений. Так как sin(J., == sin(180°
rlv), то для
101
вычисления уrла по ero синусу мы получаем два значения: rx 11
1800 ........ <Х. Если один уrол острый, то друrой тупой. Рассмотрим
следующие случаи: а) а < ь, тоrда и (х < , поэтому уrол
может быть и острым и тупым и, аначит, задача имеет два
решения в зависимости от дву" значений yr ла: либо (х, либс
1800 ........ <х; б) а == Ь, тоrда (х == и задача имеет единственное
решение, если <х < 900; в) а > ь, значит, (Х > и уrол l\ДОЖt:Т
быть только острым, так как если бы уroл был тупым, то
и <х должен быть тупым, но т'реуrольника с цвумя тупыми
yr лами не существует. Следовательно, и в этом случае задача
имеет единственное решение.
Все эти случаи можно наrлядно иллюстрировать rеометри.
ческим построением. Построим АВС по данным а, Ь, <Х. Для
этоrо построим сначала сторону АС == Ь (рис. 109) и при вер.
Рис. 109
шине А построим уrол, равный (Х. Чтобы получить третыо сто
рону, опишем из центра С окружность радиусом, равным а
Точка ее пересечения с друrой стороной уrла (Х и бу ет TpeTbeii
вершиной искомоrо треуrольника.
Варьируя величину а, мы можем получить все рассмотрен.
H Ie случаи. Если а взять очень маЛЫ А, то окружность може1
не пересечь сторону уrла, что бу,пет соответствовать С.Т1учаю.
коrда
ь sin (1 > 1,
а
f. е. треуrольник построить нельзя.
Увеличивая й, мы получим такой CJIучай, коrд.а окрУЖ'НОСТi:
коснется стороны уrла, что соответствует равенству
Ь sin (1 === 1,
а
'. е. уrол при вершине В (точка касания) бу ет прямым.
102
При дальнейшем у,величении а окружно'сть будет пересе..
кать сторону уrла в двух точках Bl Iи B 1 ', т. е. задача будет
иметь два решения. Увеличивая а еще больше, мы получи.м
окружность, которая пройдет через ,ве.ршину А, и -будем иметь
единственную точку (кроме А) пересечения на стороне уrла.
При дальнейшем увеличении а окруж,нtQ'СТЬ -будет пере.секать
сторону уrла только в одной точке, тоrда как друrая точка
пересечения 82' будет лежать на продолжении стороны. Все
'Ти случаи показаны на рис. 109.
(8.5) Выведем теперь формулы для вычисления некото-
рых друrих величин в треуrольнике. Найдем прежде B'cero
формулы, определяющие площадь. Мы знаем, что площадь
rреуrольника равна половине произведения длины ero осно-
вания на длину высоты:
a А
S. == 2 '
с
rде а Длина основания ВС,
ha.' длина опущенной на Hero
высоты (рис. 110). Но высоту ha
можно выразить через одну из
сторон треуrольника и уrол при
основании, прилеrающий к этой
TopOHe. Например, мы имеем:
ha == Ь sin Т,
rде Ь длина стороны СА, r величина уrла с. Заменяя ha
а формуле для площади треуrольника полученным выра}кением,
qаХОДИl\f:
Рис. 110
S аЬ.
== 2" Sln Т,
(7)
f. е. площадь треУ20льника равна половине nроизведенuя двух
тOpOH е20 на синус У2ла между ними.
Если в формулу (7) подставить значение sin r из формул (5).
ro получим:
sin r == ! -v р (р а) (р Ь) (р с),
аЬ
s == -v р (р а) (р Ь) (р с).
(8)
Эта формула, известная под названием формулы rep'OHa l
дает возмо жность определить площадь треуrольника по трем
1 repOH Александрийский..... rреческий reOMeTp, живший в 1 В. дО Н. э.
Ему принадлежит ряд работ по практической rеометрии ..... !емлемерию
iОЗ
ero сторонам. Практическое значение этой формулы заклю-
чается в том, что, зная ее, мы можем вычислить площадь лю-
боrо мноrоуrольника, не прибеrая к уrломерным .инструмен.
там. Для этоrо достаточно ра3'бить этот МНОI'оуrольник на тре.
уrольники и измерить длины их сторон. Площадь мноrоу'rоль.
ника определится как сумма пло.
с щадей составляющих треуrольни,
ков.
Очень простую формулу для
определения площади треуrоль-
ника 10ЖНО получить, рассматри-
вая окружность, вписанную в тре.
уrольник (рис. 1]1). Если соеди'
А тз t нить центр / этой окружности со
все IИ вершинами, то треуrольник
Рис. 111 АВС разобьется на три треуrоль.
ника: ВС/, СА! и АВ!. Беря сто-
роны данноrо треуrольника за основания, а радиус r вписан-
ной окружности за BbIrCOTY, получим:
s == + br + cr == а + ь + с r
4 2 2 2 2'
и окончательно:
s l1 == pr.
(9)
Эта же формула дает возможность определить радиус впи-
санной окружности по трем сторонам треуrольника. Действи-
тельно, из формулы (9) находим:
r == s 4 == V Р (р ..... а) (р ..... Ь) (р с ) == J I (р ..... а) (р ..... Ь) (р с) ,
р р р
Т. е.
r == Y (p a)(p;Ь)(P C) .
( 10)
Из этой же формулы нетрудно получить новые формулы
для вычисления уrлов треуrольника по ero сторонам. Пусть
т 1, Т 2, Т 3 точки касания вписанной окружности со сторонами
ВС, СА, АВ (рис. ]11), х, у, z длины касательных:
х == АТ 2 == АТ з ; у == ВТ з == BT l ; z == CT l == СТ 2 .
104
Имеем уравнения:
у + z == а,
z + х Ь,
х + у с.
Сложив их почленно, получим:
2 (х + у + z) == а + Ь + с, или х + у + z р.
Отсюда х + а р, х р а, аналоrично у
Из треуrольника А Т 2/ получаем:
'"
сх r
t g ....... == ...............,
2 p a
а путем циклической замены найдем
еще:
r
tg ...... == ;
2 p b
tg .r.. r
2 p c
== p Ь, z==p c
р'
Очень полезным при вычислении
некоторых элементов треуrольника
является также следующее предло- Рис. 112
жение:
Теорема. Длина хорды окружности равна про изведению
длины диаметра на синус впuсаННО20 У2ла, опuрающе20СЯ на
эту хорду. .
Д о к а з а т е л ь с т в о. Возьмем окружность с центром О
(рис. 112) и на ней хорду MN дл.иной а. Проведем диаметр
Л1Р == 2R и соединим ero конец Р с точкой N. Обозначим через
а величину уrла MPN. Так как MN Р П/рямоуrольный, то
П'олучим:
a==2R sin а.
( 11 )
Величину друrоrо уrла, опирающеrося на ту же хорду ('на.
пример, МР/ N), обозначим а'. По свойству вписанных уrлов.
опирающихся на одну и ту же х'орду, но ра,споло)кенных пn
разные стороны от нее, имеем: а' == 1800 a, поэтому
sin а' == sin (1800 а) == sin а.
Значит, и в этом случае получаем:
a==2R sin а'.
Следствие 1. Сторона треУ20льника равна произведеНU1()
диаметра описанной окружности на синус противоnоложносо
У2ла:
а == 2R sin CJ..
( 12)
1.0;)
Отсюда также следует уже доказанная теорема синусов'
а
sin
ь
sin
с
== 2R.
sin r
Следствие 2. Радиус описанной окружности равен проаэ-
едению трех сторон треуzольника, деленному на учетверен.
ч,ую площадь еао.
Подставим в формулу (12) выражение sin сх через площадь
· 28 u 2R 28
41 стороны треуrольника: SlП сх == и наидем а == · , ОТКУ.
Ьс Ьс
с да получаем
R == аЬс . ( 13 )
48
(8.6) Рассмотрим метричеСКИЕ
соотношения в некоторых друrи:х
q прямолинейных фиrурах. Докажем
следующее предложение:
Рис. 113 Теорема. Сумма квадрато,
дuаzоналей nараллелоарам,м,а рав.
н,а сумме квадратов всех еао сторон.
Д о к а з а т е л ь с т в о. Пусть мы им ем параллелоrрамм ABCD
......
(рис. 113) со сторонами АВ == р, AD == q и диаI'ОНалями АС ==т
и DB == n. Как уже было доказано [см. (4.1), рис. 50]:
--+ ....
т == р + q,
.
n==p q.
Веря скалярные произведения каждоrо из этих равенств на
aMoro себя, получим:
....
т 2 == р2 + 2pq + q2,
--+
п 2 == р2 2pq + q'J.
Почленным сложением этих равенств ПОЛУЧИlvf д.оказываемое
crредложение:
т 2 + n 2 == 2р2 + 2q2.
( 14)
Если же выражения для т и n скалярно умножить почлен
dO друr на друrа, то получим:
Следствие 1. Произведение дuаzоналей параллелоара.мм,а нй
косинус уzла .между ними равно разности квадратов двy
смеЖНblХ сторон еао.
{06
Мы имеем:
...... --+ --+ --+....
т. п (р + q) (р q),
flЛИ
тп cos q> == р2 q2.
Равенство (14) позволяет вычислить медиану треуrольиик
по трем ero сторонам. Действительно, если мы возьмеы "тре-
уrольник АВС (рис. 114) с ме-
дианой АМ == та, то, продолжая
медиану на ее длину за точку
/И, найдем точку А', соединив
которую с точками В и С, по-
лучим параллелоrрамм АВА'С.
В нем диarональ ВС == й, диаrо-
валь АА' == 2т а . Применяя фор- А
м.у лу (14), получим:
4т: + а l =- 2Ь 2 + 2с 2 ,
откуда
,.
ь
с
Рис. 114
I 2ы + 2с l а 2
та ==
4
и
та == !. У2Ь 2 + 2с 2 а 2 .
2
(8.7) Приведем примеры задач, решаемых с помощью фор
мул.
А
8
р
N
q
с
Рис. 115
Задача 1. Найти отношение отрезков, на которые биссектри.
са BHYTpeHHero yr ла треуrольника делит противоположную сто..
рону ero.
Решение. Пусть AN биссектриса уrла А в треуrОЛЬНI1'
ке АВС (рис. 115). Обозначим отрезки BN и CN COOTBeT TBeH
но через р и q. По теореме синусов имеем:
CI СХ
sin sin
2 2
Р == С. , q Ь
s in 6 == s in 6 '
101
rде и ' соответственно уrлы AN В и ANC. Но б' == 180 0 ..........Ь,
поэтому sin б' == sin б. Почленным делением обоих равенств по..
лучаем:
Итак, мы доказали, что биссектриса внутренне20 У2ла тре.
1j20льника делит противоположную сторону на части l nроnор.
циональные nриле2ающим. боковым. сторонам..
Задача 2. Даны две недо-
ступные точки А и В и точка
М, из которой видны точки А
и В. Определить расстояние
между точками А и В (рис
116).
Реш е н и е. Выбираем на
местности доступную точку N J
из которой видны точки AI В
И А1, и тщательно измеряем
расстояние MN==p (базис). По.
сле этоrо помещае!\'1 уrломер.
ный инструмент в точку М И,
визируя на точки А и В, из-
меряем уrол АМВ==<р. Обозначая буквами а, Ь и х соответ-
ственно длины отрезков MA 1 МВ и ABI получим по теореме
косинусов:
Р'
\
\
......, \
" rc h '
а ,\
N
Рис. 116
р с
- -.
q ь
х 2 == а 2 + b2 2ab COS ср.
Остается определить длины а и Ь.
ДЛЯ этоrо измеряем уrломерным ,инструмен'f.ОМ L BMN == р.
i10TOM перемещаем инстру,мент в точку N и измеряем уrлы'
L-МNА==а и LANB==v. По теореме синусов из AMN по.
п'учим:
а
sin (1
р
sin (1800 с1 q»
'Jткуда находим:
sin с1
,
sin (С1 + + q»
р sin с1
а==
sin (С1 + + q»
Далее из BMN находим:
sin (С1 + '1) sin (C1+r)
р sin (180;) C1 r) sin (C1+ +a)
Окончательно:
Ь===
108
р sin «(1 +r)
sin (С1 + + r)
Таким образом, мы получили все необходимые данные для
определения длины х.
Задача 3. Доказать, что площадь всякоrо четырехуrольника
равна половине произведения ero диаrоналей на синус yr ла
между ними.
Реш е н и е. Пусть ABCD....... произвольный четырехуrольник
с диаrоналями АС == т и BD == n (рис. 117). Проведем через
\ \
,', I
У \,'
, \ ' I
" '('
, I ,
J l' \ /"
" 1"
, l'
м
А
I
r Ь
А
\
с р \
..
Рис. 117 Рис. 118
вершины ABCD прямые, параллельные диаrоналям, и получим
параллелоrрамм MNPQ, в котором MN == QP == DB, NP=== MQ=:II
== АС, Перенесем вершину А в точку М, а вершину С в точ-
ку Q. Так как SABD == 5MBD И SCBD == SQBD, то пло-
щадь треуrольника BMQ равновелика площади данноrо четырех-
уrольника. Если теперь перенесем вершину В в точку Р, то
получим новый треуrольник MPQ с такой же площадью, так
как SMPQ == SBMQ. Итак, SMPQ == SABCD. Но В треуrольнике MPQ
MQ 11 АС, PQ 11 BD и, значит, L MQP == (j), rде ер уrол между
диаrоналями. Кроме Toro, MQ == т и PQ == n. По формуле для
площади треуrольника получим:
S тп s i п qJ .
MPQ 2 '
поэтому и площадь четырехуrольника ABCD выражается фор-
мулой:
S тп sin qJ
ABCD == ·
2
За..в.ача 4. Найти rеометрическое ме.сто точек, раз,нoQ,СТЬ
KBaдpaTO расстояний которых от ДBY данных точ к равна
постоянному числу k 2 .
Реш е н и е. Пусть А и В данные точки (IРИС. 118). Най.
дем прежде Bcero на прямой АВ такую точку М, чтобы
109
, довлетворялось условие:
MA2 MB2==k2.
0бознач,им длину АВ через т, а дли'ну МВ через х, тоrдс
.'ОJIУЧ,И м:
иля
(т........х) 2_____х 2 == k 2 ,
(m X)2==X2+k21
(1 )
Т. е. длина МА равна rипотенузе прямоуroльноrо треуrоль..
ника, катеты KOToporo имеют длины k и х.
Чтобы 'найти х, проведем через В перпендикуляр к АВ :и
)тложим на нем iQтрезок ВА', длина K'OToporo равна k. Тотда,
очевидно, MA'2==k 2 +x 2 . В то же время мы имеем, что и
MA2::::k 2 +x 2 , откуда следует, что МА'==МА, т. е. точка М
лежит на оси симметрии точек А и А'. Проведем эту ось, и
МЫ получим искомую точку М. Перпf'НДИКУЛЯР, проведенный
1(ерез М к пря'мой АВ, и есть иском,ое rеометрическое место.
Действительн'О, если мы возьмем на Э'rом перпендикуляр
:IРОИз.вольную точку Р, то получим:
РА2....... РВ2== (МА2+Мр2) (МВ2+МР2) ==МА2 ----- MB2==k2.
r. е. каждая 1'очка перпендикуляра МР удовлетворяет усло
ВИЮ.
Если же 'возьмем точку р' вне этоrо перпендикуляра, то)'
беря ее проекцию М' 'на прямую АВ, получим, как и рань'ше,
р' A2 p' В2==М' А 2........ М' В2.
Эта разность не может равняться k 2 , так как из у,равнения (1)
\{IMeeM: т 2 ........2mx==k 2 , или m2 k2==2mx, откуда
х==
т2 kt
2т
Мы видим, что получилось уравнение первой степени, ко-
eHЬ KOTop'oro х одноз,начно определяет точку М и потом}
никакой друrой точки М', удовлетворяющей уравнению (1) I
qa прямой АВ 'быть не может.
Упражнения
1. На ,высоте 390 над rоризонтом блеснула молния. Чере.:
\3 секунды ПOCJIе этоrо послыш'ался rp'OM. На какой BЫCOT '
над землей находится nрозовая туча? (Скорость звука равн&
340 м/сек.)
2. От, звезды а в созвездии Большой Медведицы свет ид
к ,нам 96 лет, а от з'везды р в том же созвездии 76 Ле1'
Уrловое расстояние между звездами а и р равно 5023'. Сколь..
ItO лет идет свет от звезды а к звезде р?
tfO
J. Доказать, что если биссектриса Iвнешнеl'О уrла при вер..
шине А в треуrольнике АВС пересекает прямую ВС в точке Р»
1'0 отрезки РВ и РС пропорциональны стор'онам АВ и АС:
РВ РС
АВ == АС .
4. Доказать, что если в треуrольнике отношение квадратов
двух ero сторон равно отношению их проекций на третью
С"ОРОНУ, то этот треуrольник прямоуrольный или равнобед.
ренный.
5. Доказать, что во всяком треуroльнике раССТОЯ1ние от
вершины до точки касания противоположной вневписаlННОЙ
)кружности равно полупериметру.
6. Через данную точку провести 'секущую, которая отсекла
бы от данноrо уrла треуrольник даН'ноrо периметра.
7. Найти отношение суммы квадрато.в медиан треуrОЛЬНИ а
ка к сумме квадратов ero сторон.
8. На прямой даны точки А, В. С и точка Р вне этой
'lРЯМОЙ. Доказать равенство (теорема Стьюарта):
РАI · ве + РС2. АВ РВ2. АС == АВ. ВС. АС.
9. Применить теорему Стьюарrа к ,вычислению длины ме.
дианы или биссектрисы треуrольника по длине трех ero
сто.рон.
10. Найти теометрическое место точек, сумма квадратов-
расстояний которых от двух да/нных точек есть ве..rIичина по.
стоянная.
I 9. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ОКР)'ЖНОСТИ
(9.1) Теорема 1. Если через точку М в плоскости окруж.
OCTи провести прямую, nересекающую окружность в точках
.4 и А', то произведение МА · МА' есть число, постоянное для
1анной точки, независимо ОТ положения секущей.
Д о к а з а т е л ь с т в о. Проведем к данной окружн'ости че-
Jез точку М две секущие, пересекающие ОКРУЖ1Н'ость в точках
4: А' и В, В' (рис. 119,а и б), и докажем, что МА.МА'==
.....
-;:МВ. МВ', Соединим точки А с В' и В с А'; дАВ' М '"
и ВА'М, так как у них равны уrлы при вершине М и L-A==
== L- В, так как они вписанные и опираются на одну и ту же
Iyry А' В'.
Из подобия треуrольников получаем пропорцию:
МА МВ'
МВ МА' ,
11'
откуда по r лавному свойству пропорции получаем: МА. МА' lZ8
МВ.МВ', а следовательно, будем иметь:
МА .МА' == МВ. МВ'.
Определение. Ilостоянная величина скалярноrо произведения
коллинеарных векторов, направленных от данной точки к точ
кам пересечения с окружностью, называется степенью точкu
по отношению к данной окружности.
А
8'
а.
н
в
о
Рис. 119
м
А
Рис. 120
Следствие. Если точка находится вне окружности, то tJ
произведении МА.МА' векторы сонаправлены и потому оно
положительно и равно произведению их длин:
МА.МА' == р2.
Если точка находится внутри окружности, mo в произве-
дении МА. МА' векторы противонаправлеНbl и потаму про-
изведение отрицательно:
МА .МА' == р2.
Если точка находится на окру>кности, то ее степень по от-
ношению к окру>кности равна нулю, так как при этом длина
одноrо из векторов обращается в нуль.
Теорема 2. 1) Степень внешней точки равна квадрату
длины касательной от данной точки до окружности. 2) Сте-
пень внутренней точки равна по абсолютной величине квад-
рату половины длины наименьшей хорды, проведенной через
9ту точку.
Д о к а з а т е л ь с т в о. 1) Ilроведем в окру>кности секущую
А1А'А t1 касательную МТ (рис. 12Q). АМАТ сп A1T А', так как
112
у них равны уrлы при вершине М и LMTA'==LMAT, так
как каждый из них измеряется половиной дуrи А'Т. Отсюда
получаем пропорцию:
МА МТ
мт МА"
а потому
МА.МА' == МТ2.
2) Если М....... внутренняя точка, то из всех хорд, проходя-
щих через М, наименьшей будет та, которая перпендикулярна
к радиусу, проходящему через эту точку, так как эта хорда
находится на наибольшем расстоянии от центра. На рис. 121
хорда ТТ' OM. Хорда АА' находится от центра на расстоянии
ON, но ОМ> ON, так как rипотенуза больше катета в тре-
уrольнике OMN. Итак, мы имеем:
---+
МА.МА' === МТ.МТ' == lИТ2.
Если М внешняя точка, то, описав из центра М окруж-
ность, радиусом, равным МТ, получаем окружность, для кото-
рой радиус ОТ будет касательной. Такую окружность называ-
ют ортО20нальной по отношению к данной, так как уrол между
касательными к ним в точке их пересечения прямой (рис. 122).
Если же М внутренняя точка, то, описав из центра М
окружность радиусом, равным МТ, получим новую окружность,
которую называют диаметральной по отношению к данной,
так как данная окружность пересекает новую по диаметру
(рис. 123).
Величина степени точки по отношению к окружности может
быть выражена через радиус и расстояние точки от центра.
Проведем сеКУЩУIО через центр и получим:
для внешней точки (рис. 124):
---+ ---+
р2 == МА. МА' == (МО + ОА). (МО ОА) == МО2 .......... ,2;
для внутренней точки (рис. 125):
---+ --+ --+ --+ ---+ ---+
....... р2 === МА. МА' == (ОА + МО). (ОА ...... МО) == , 2 ......МО2.
Итак, во всех случаях степень точки М по отношению
к окружности с центром О и радиусом, выражается формулой
р2 == МО2 ....... , 2 .
Из этой формулы видно, Ч'f.о если М внешняя точка, то
МО>, и степень положительна, если М точка ОКРУЖtности,
то MO==r и степень равна нулю. если МО<'1 то точка внут-
ренняя и степень отрицательна.
8 А. и. ФеТIIСОВ
113
Рис. 121
Рис. 122
м
Рис. 123
Рис. 124
А
8
Рис. 125
Рис. 126
(9.2) Рассмотренные нами свойства окружности позволяют
решить большое число разнообразных задач. Приведем при-
меры.
Задача 1. Найти среднее пропорциональное двух данных
отрезков.
Реш е н и е. Напомним,
что средним пропорциональ-
ным двух чисел а и Ь назы-
вается число х, удовлетворяю-
щее пропорции а : х == х : Ь,
или, что все равно, равенству
х 2 =: аЬ.
Если даны два отрезка
длиной а и Ь, то средним про t1
порциональным будет отрезок,
длина KOToporo х удовлетворя-
ет предыдущему равенству.
Для получения такото тр ез ка можно использовать сле-
дующее построение. Пусть а и Ь дЗ'нн.ые отрезки (рис. 126).
Отло ж им на пр я мой 'От точки М по разные стороны отрезки
МА == а и МВ == Ь. На .отрезке АВ, как на диаметре, постро.им
окружность и проведем через точку М хорду ТТ' перпендику-
лярно к АВ. Так как
Рис. 127
МА.МВ:=: МТ.МТ' и мт == ........МТ',
то длина х каждоrо из этих отрезков удовлетворяет условию
х 2 == аЬ.
Эту же задачу можно решить: откладывая отрезки МА и
М В в одном и том же направлении (рис. 127). Если провести
окружность через точки А и В, то касательная МТ удовлетво-
ряет условию МА. М В == Л1Т2 И отрезок МТ имеет искомую
.,
длину.
Задача 2. Найти rеометрическое место точек, имеющих одну
и ту же степень относительно двух данных окружностей.
Реш е н и е. Пусть имеем две окружности с центрами 01 и
02 И радиу ами '1 и '2 (рис. 128). Полощим, что Р есть точка,
удовлетворяющая данному условию. Припоминая общую фор.
мулу для степени, получим равенство:
PO , == РО: ':.
Отсюда находим:
PO ....... РО: :=: ' ....... ':.
Так как разность , ,; постоянна, то, очевидно, искомое
rеометрическое место есть то же самое, что уже было опреде-
8* {15
лено при решении задачи 4 в предыдущем параrрафе. Это есть
rеометрическое место точек, разность квадратов расстояний
которых от двух данных точек 01 и 02 постоянна. Там было
доказано, что этим rеометрическим местом является прямая,
перпендикулярная к прямой, проходящей через данные точки.
В нашем случае это будет прямая,
перпендикулярная к линии центров.
Она называется радикальной осью
двух окружностей.
Ес,пи окру)кности пересекаются, то
их радикальная ось проходит по об
щей хорде, так как точки пересечения
окружностей имеют одну и ту же CTe
пень, равную нулю, относительно обе-
их окружностей (см. рис. 128, а).
Если окружности касаются, то pa
дикальная ось совпадает с касатель
ной, проведенной через точку их Kaca
ния друr с друrом (рис. 128, б).
Если одна окружность лежит вне
друrой, то радикальная ось проходит
через точку, делящую пополам OTpe
зок общей касательной между точка-
ми касания (рис. 128, 8).
Каждая внешняя точка радикаль
ной оси есть центр общей ортоrональ
ной окружности для двух данных OK
ружностей (СМ. рис. 128, 8). Каждая
внутренняя точка радикальной оси
eCTb 1 центр общей диаметральной ок.
ружности (см. рис. 128, а).
Задача 3. Доказать, что если центры трех окружностей не
лежат на одной и той же прям'Ой, то их радикальные оси пере
секаются 'в одной и той )l.{e точке, называемой радикальным
центром трех rOкружн'О'стей.
Реш е н и е. Рассмотрим окружности .с центрами 01, 02, 0з,
не лежащими {на одной и той же ПрЯ iОЙ ('рис. 129, а, б). Обо
значим через 11 радикальную ось ОКlружностей с центрами 02
и 0з, а через 12 радикальную ось ОКРУЖrностей С центрами
ОЗ и 01. По определению радикальной оси имеем:
а
8
Рис. 128
11.1020з И [2.10з01.
Точки 01, 02, Оз не лежат на 'Одной и той же прямой, по
этому прямые 11 и 12 пересекаются в некоторой точке s. Эта
точка имеет одну и ту же 'степень по lотношению ко в-сем трем
{)кружностям. Отсюда следует, что и третья ось 13 окружно
етей с центрами 01 и 02 пройдет через ту же точку s.
116
Если S 'в!нешняя точка, то она служит центром един-
ственной ортоrональной окружности к данным окружностям
а
5
Рис. 129
(рис. 129, а). Если S внутренняя точка, то она служит цент-
u u
ром единственнои окружно,сти, диаметральнои к данным
(рис. 129, б).
Задача 4. Провести через две точки окружность, касаю-
щуюся данной окружности.
Рис. 130
Р е е н и е. Пу.сть даны точки А и В и окружность с цент-
ром О (IРИС. 130). Положим, что задача решена и мы нашли
окружность с центром 01, касающуюся дан!ной в точке Т. Об-
щая ка'сательная, проходящая через эту точку, есть в то же
время и радикальная ось окружностей. Она пересекает пря-
мую АВ в точке s. Проведем через точки А и В вспомоrа-
тельную окружность с центром О' так, чтобы она пересекла
данную окружность в точках М и N. Так как через точку S
проходят радикальные оси АВ и TS, то через нее же должна
пройти и третья ось MN. Если из радикальноrо центра S
117
провести ОКРУЖJНОСТЬ радиусом ST, то эта окружность будет
ортоrональной окружностью для всех трех окружностей.
Отсюда мы получаем следующий порядок построений. Сна..
чала проведем через точки А и В вспомоrательную окруж"
ность и найдем точки М и N. Пересечение прямой MN с пря..
мой АВ определяет точку S. П'роведя через S ка,сательные ST
и ST', определим радиус OIртоrональной окружности и вместе
с тем искомые точки касания. Если точки А и В находятся
одновремен'но в'не или внутри данной окружности, то задача
имеет два решения. Если же одна находится вне, а друrая
внутри, то задача неразрешима. Если бы оказалось, что
MNIIAB, то точки Т ,и Т' лежали бы ,на оси симметрии точек
А и В и на данной окружности.
Упражнения
1. Доказать, что если выполняется равенство МА. МА':=
.........
==МВ · МВ', rде вектор МА' коллинеарен с МА, а МВ' колли..
неарен с МВ, ТО точки А, А', В, В' лежат на одной ,и той же
окруж,ности.
2. Найти rеомеТРiическое ,место точек, степень которых
ОТНОС'ительно данной окружности равна данному числу.
3. Высота маяка над у'р'овнем моря равна h М. Каков ра..
д'иус rориз'Онта, ,ВИДИiм'оrо с этоrо маяка? (Радиу.с Земли
приблизительно равен 6370 КМ.)
4. Доказать, что если раlвнобедренная ТР1апеция описана
около окрУЖ1НОСТИ, то диа l ме1р есть средняя 'пропорцИ'ональ..
ная между основа'ниями трапеции.
5. Если о руж'ности касают'ся извне, то отрезок общей
внешней ка'сательной между точками касания есть среднее
пр'опорциональное между диаlметрами ОКРУЖJНОСТИ.
6. Принимая 'вершины треуrольника за центры, описать
три окруж'ности, к'оторые пересекали бы Дlруr друrа opToro"
нально.
7. Дана окружность с цeHTpo О и прямая 1 с точкой М
на ней. Про'вести окружность, касающуюся прямой 1 в точке
М и пересекающую окружность О ортоrQiнально.
8. Окружности 'с цеНllрами О 'и О' имеют центр положи..
тельной rомотетии в точке s. Доказать, что точки касания
ОКРУЖ'НQiСТИ, ка1сающ,еЙся ИЗlвне данных окружностей, лежат
на о ной и той же Пр'Яiмой с цeHTp'o s.
9. Точка S центр rомотетии окружностей с центрами
О и О'. Т и т' точки касания общей касательной, проходя..
щей через S. Секущая, проходящая через центр rомотетии,
встречает окружности IB соответственных точках А и А', В и
В'. Доказать, :что точки А, В', Т, Т' лежат на одной и той
же ОКРУ)I{НОСТИ, так же как и точки А', В, Т, Т'.
10. Через да,нную точку Пlровести' окружность, касаю..
u
щуюся двух данных ОКРУЖlностеи.
, .. ..
, ..
. . , . , .. . .
.' С , о" .. .... . , Ч::А c-r-b . , В , 'Т,.О р А я
, ТЕ РЕ ОМЕ ТРИ Я
rЛАВА ТРЕТЬЯ
ВВЕДЕНИЕ
10. ОСНОВНЫЕ ПОНЯТИЯ СТЕРЕОМЕТРИИ
Во второй части rеометрии стереОм'етрии I ----- 'Изучаются
е,вой'ства фиrур, не \Бсе точки которых принадлежат одной
и той же плоскости. Такие фитуры называются простран..
ственныМ,и, а стереометри'я называется также zеОм'етрией
пространства.
ОIСНО,В,ными элементам'и в rеометрии пл'оскости плани"
метрии были точки и прямые. В стереометрии к эти(м ос-
новным элем,ентам П'рlИСlQединяются еще 'и плоскости, кото-
рые о,БОЗ1начаются малы1ии rреческими 'буквами а, , 'У,...
Для изображения пр'остран,с'Лвенных ф'иrур приходится
пользоватыся ри,сункам'и, 'на которых некоторые чаlСТИ фиrур
получаются искаженными, не такими, к,ак-овы 'они в деЙстви-
телЬ'ности. Например, на изображении стола (рис. 131) пря-
моуrольная рышка ero п'редстаfвляется в ,виде косоуrольно-
ro параллелоrраМlма.
Плоскость не имеет zраниц, поэтому для изображения ее
на чертеже приходится пользоваться условными фиrурами,
пред,ставляющими собой ее часть. Иноrда эта фиrура берет-
ся в 'виде прямоуrольника, иН'оrда 'Б !виде куска неопреде..
ленной ф'ормы (рис. 132).
/
/
Рис. 131
Рис. 132
1 Слово стереометрия составлено из двух rреческих слов: a'tepe6
(стереос) ..... «пространственный» И Il.e'tp (J) (метрео)..... «мерю».
121
11. АКСИОМЫ СТЕРЕОМЕТРИИ И ИХ СЛЕДСТВИЯ
( 11.1) Соотношения между основными элементами про-
CТfpaHcTBa дают,ся слеДУЮ1Щ'ИМИ аксиомами.
Аксиома 1. Через три точки не лежащие на одной и той
же прЯ.А-IОЙ, Аtожно провести плоскость, и притом только одну.
Указанным в этой аксиоме свой-
ством плоскости мы постоянно поль-
зуемся на практике. Например, за-
пертую на замок дверь нельзя ОТ-
крыть потому., что в ней имеются три
неподви)кные точки: две петли и за-
мок.
Аксиома 2. Если две различные
плоскости и./vtеют общую точку, то
через эту точку проходит единствен-
ная общая прямая этих пЛОС1\,остей.
Две плоскости, имеющие только
одну общую прямую, называются
Рис. 133 пересекающимис.я, а их общая пря-
fая линией их пересечения.
Аксиома 3. Если две различные точки прямой принадле-
жат плоскости то и вся прямая принадлежит этой плоско..
сти.
Этим IСВОЙСТВОМ часто пользуются на практике: если хо-
тят проверить, плоская ли данная поверхность, vo прикла..
дывают к ней линейку в различных направлениях и смотрят,
с'овпадает ли л'инейка с поверхностью всеми своими точками.
Аксиома 4. В пространстве Bcezaa существуют четыре
точкu не принадлежащие одной и той же плоскости.
Из этой ак,с.иомы следует, что если дана какая-нибудь
плоскость а, то в,сеrда существуют точки, лежащие \Вне этой
плоскости.
Возьмем П'р'оизвольную точку А 'на плоскости а (рис. 133);
и,мее'flСЯ еще и точка А', не принадлежащая э ой плоскости.
Прямая а, проходящая че'Рез точки А и А', имеет € плос-
костью одну, и только одну, общую точку А. В этом случае
rо'ворят, что прямая а и плоскость а пересекают,я 'в точке А.
В дальнейшем для еокращен'ия запис.и мы буд'ем пользо-
ваться следующими условными знаками:
1) Знак пересечения Х; .например, аХ Ь ПРЯ1мая а пере-
-секает прямую Ь; аХа прямая а пересекает плоскость а;
а Х плоскость а пересекает плоскость .
2) Знак тождества = употребляется, коrда хотят обозна-
чить, что два данных символа оБОЗ1начают один и тот же
предмет. Напри,мер, З1апись а = MN ОЗ1начает, что символам'и
а и MN 'Обозначена одна и та же прямая; запись А = тn
означает, что символами А и тn обозначена одна и та же
точка.
122
Заметим, что тождеств,о о'бладает свойствами:
1) симметрии: если А = В, то и В = А;
2) рефлективности: А = А (каждый преД/мет тождествен
с сам:им собой);
3) транзитивности: еслиА = В, В = С, то А = С.
Эти своЙства 'вместе назы'ваются условиями эквивалент
ности. Условиям эквивалентности удовлетворяют мноrие
соотношения. Напри/мер, соотношения palBeHcl1Ba чисел: если
т, п, р lобозначают чи!сла, то, очевидно, будем иметь:
1) если т==n, то и n==т;
2) m==т;
3) ес.тIИ m == n, n== р, то т == р.
ЭКВИ1валент,ными ЯIВЛЯЮТСЯ 'СiQ,отношения равенства и по
добия фиrур в rеометрии [см. (1.3) и (7.1)].
Соотношения же неравенства 'не являются эквивалентны
1И. Действительно, из а>Ь не следует, что и Ь>а.
(11.2r Неп'осред,ственно из аК1СИ,ом получаем следствия.
Следствие 1. Через прямую и точку, не принадлежащую
этой прямой, можно провести плоскость, и притом только
одну.
РаСС:\10ТРИМ пря\мую а .и .не при.надлежащую ей точку А
(рис. 134). На прямой а возьмем две различные точки М и
N. Соrласно аксиоме 1 ,существует плоскость а, проходящая
через три точки А, М и N. По аксиоме 3 аСа. Если допустим,
что через 'прямую а и точку 'проходит еще од'на плос-
кость а', то, очевидно, она проходит через точки М и N.
Н'о через три точки А, М и N, 'не принадлежащие одной и
тоЙ же прямой, можно ПР'OIвести только одну пЛ'оскость
(аксиома 1), сл'ед:овательно, а' = а.
Рис. 134
Рис. 135
Следствие 2. Через две nересекающиеся прямые можно
провести плоскость, и притом только одну. .
Расс'мотрим две прямые т и n, пересекающиеся в точке
А (рис. 135). На прямой m 'возьмем т,очку М, отличную от А,
а на прямой n ,возьмем точку N, отлич,ную от А. Точки М,
N и А не лежат на 'одной и той же Пр1ЯМОЙ, и соrласно
аксио е 1 существует пл'оскость а, проходящая через эти
123
точки. По аксиоме 3 прямые т и n принадлежат этой
пл\оскости. Если ДОПУ'СТИ I, что существует д'руrая плоскость
а/, проходящая через те. же прямые т и n, то эта плоскость
проходит и через точки М, N и А. Но через три точки, не
лежащие на одной и той же прям'ой, мож\но провести только
одну плоскость, следовательно, а' = а.
Есл'и числ,о элементов, 'определяющих плоскость, недоста-
точно, то задача о проведении плоскости становится неопре-
деленной. Например, через две данные точки (или, что все
palBHo, через даНlНУЮ пр,Я'мую) можно провести бесконечное
множество плоскостей. Дейст:вительно, если дана прямая a t
то, беря вне ее еще точку А 1 , пр'оведем через прямую и точку
плоскость аl. Беря вне этой плоскости еще точку А2, про..
ведем через нее и прямую а еще плоскость а2. Повт,оряя
этот процесс, мы получим плоскости аз, а4, ..., ап, ...
Дверь, закрепленная на двух петлях, лист книrи или
теТ1ради, 'крыш,ка рояля дают наrлядные преД1ставления о
плоскости, ,В'ращающейся около неПОДIНИЖ1НОЙ прямой и мо-
rущей занимать бесконечное множество различных поло..
жений.
Упражнения
1. Как расположены в пространстве n прямых, каждая из
которых пересекает ,все остальные и никакие три не проходят
через одну и ту же точку? ,
2. На сколько lотдельных обла.стей разделяют плоскость
n прямых, удо!влеТlВОрЯЮЩИХ у,сл,овию предыдущей задачи?
з. На сколько отдельных ,областей разделяют ПрОСТlранст-
u
во п плоскостеи, из к'оторых каждая пересекает все осталь-
\Ные и никакие три не проходят через одну и ту же прямую?
4. Найти rеометрическое 'место точек, принадлежащи,f
двум данным пересекающим,ся пря'мым, а также и принадле-
жащих любой прямой, пересекающей одновременно обе дан-
ные прямые l но не проходящей через 1'очку их пересечения.
rЛА8А ЧЕТВЕРТАЯ
ПАР АЛЛЕЛЬНОСТЬ В ПРОСТРАНСТВЕ
12. ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ
(12.1) Припомним, что параллельными назы'ваю'Тся пря-
мые, принадлежащ'ие одной и той же плоскости и не пересе-
кающиеся друr с друrом. Если раС1сматривать с'овпадение
двух прямых как ча,стный случай параллельности (коrда
раС'стояние 'между параллельны,ми равно нулю), т,о соотно-
шение параллель.ности получает ,uвойст.во э вивалеНТНQlСТИ.
Действительно, для параллельных прямых на плоскости
имеем:
1) если аНЬ, то blla (Iсимметричность);
2) alla (рефлективность);
3) если аНЬ, ЬНс, то аНе (траНЗИТИВНQlСТЬ).
Основное IСВОЙСТВО параллельности на плоскости выражает-
ся аксиомой параллельности: Через данную точку 1(, дан..
ной прямой можно провести одну, и только одну, параллель..
НУЮ прямую (1.2). Это предложение остается в силе и для
пространства.
В самом деле, положим, что в пространстве дана прямая
а и вне ее точка Р. Так как искомая прямая должна лежать
в одной плоскости с прямой а и проходить через точку Р,
то такой плоскостью может быть только единственная плос-
OCTЬ а, проходящая через прямую а и точку Р. А tВ ПЛ'ОСКО-
сти а через точку Р можно провести еДИНС1'1венную прямую
р, параллельную прямой а. Итак, прямая р............. единс.твенная.
Если бы точка Р лежала на прямой а, то единственной па-
раллельной была бы сама прямая а.
Возможные 'случаи положения двух прямых в простран-
стве устанавливаются следующей теоремой.
Теорема 1. Две прямые в пространстве MOZYT находиться
по отношению apyz 1(, apyzy только в одном из следующих
трех положении: 1) прямые пересекаются; 2) прямые парал-
дельны; 3) прямые скрещиваются, Т. е. не принадлежат
однои и той же плоскости.
125
Существова.ние пересекающихся и параллель.НЫХ ПРЯ1МЫХ
совершенно 'Очевидно. Чтобы доказать существование скре-
щивающихся прямых, ра,ссмотrрим четыре точки А, В, С, D
(IРИС. 136), ле лежащие в 'одной и той же плоскости (аксио-
ма 4).
Прямые АВ и CD
'БыI они перосекались,
не имеют общей точки, так как е.сли
то через них можно бы ТIО бы про-
вести плоскость, а тоrда точки А, В,
С, D лежали бы в одной плоскости.
Но прямые АВ и CD не MorYT быть
и параллельными, так как и тоrда
они лежали бы в одной плоскости и
в этой плоскости находились бы и
точки А, В, С, D. Итак, прямые АВ
и CD не имеют общих точек и не MO
rYT принадлежать одноЙ и той же
плоскости.
Следствие. Через две несовnада..
ющие nараллельные nРЯАtые можно
провести одну, и ТОЛЬКО одну, nЛОС"
КОСТЬ.
Существование плоскости, в которой ле)l{ат обе параллель-
ные прямые, есть следствие определения параллельности. Эта
плоскость единственная, так как если взять одну из этих па
раллельных и точку на друrой из
них, то данная плоскоС'ть проходит
и через эту прямую и через эту точ-
ку. Всякая плоскость, проходящая
через эти параллельные, будет со-
держать ту же прямую и ту же
точку, т. е. совпадет с первоначаль-
u
нои плоскостью.
Рис. 136
./
""
, ./
, ""
, ""
, ./
" ;'
, ""
, "
, ./
I ./
" А,,"" t
(12.2) Посмотрим теперь, каки-
ми признаками определяется парал-
лельность прямых в пространстве,
иначе rоворя, каким существенным
свойством отличаются две парал-
лельные прямые от двух пересекаю-
щихся и от двух скрещивающихся
прямых.
Теорема 2. Если две прямые параллельны, ТО все nлоско
сти, nересекающuе одну из них, nересекаl0Т и друzую.
ПУ'СТЬ дано: аН Ь и 6 Х а (рис. 137). По определению пря-
мые а и Ь лежат в 'Одной и той же плоскости у. ПОЛОЖИ f,
Ч'rО плоскость 6 пересекает прямую а в точке А. Следова-
тельно, плоскости 'у и 6 имеют общую точку А и по аксиоме 2
они имеют и общую прямую 1. Прямая 1, принадлежащая
126
Рис. 137
плоскости ,"" пересекает прямую а в точке А, поэто у она
ДОЛ)I{lна пересекать и прямую Ь, так как если бы оказ'алось,
что 111Ь, то через т'очку А проходили бы две параллельные
прямой Ь, что противоречит аксиоме параллельности. Итак,
ПРЯ1мые 1 и Ь имеют lобщую точку, кот,орую обозначим через
В. Эта т,очка является еди.НСllвенной 'общей точк,ой прямой Ь
и плоскости б. Итак, БХЬ.
Теорема 3 (обратная). Если все плоскости} nересекающие
одну из двух данных прямых, пересекают и друzую} ТО эти
прямые параллельны.
Две прямые а и Ь, удовлетворяющие условию теоремы,
не MorYT быть пересекающимися, так как в этом случае
в,сеrда можно найти плоскость, пересекающую одну из н'их И
не пересекающую друrую. Например, на рис. 137 плоскость б
пересекает прямую а, но 'не пересекает прямой [. Пря ые а
и Ь не MorYT Iбыть и .сК'рещи'вающимися, так как и /в этом
случае 'ПЛОСКОСТЬ, пересекающая ,од,ну из них, может и не
пересекать друrую. Например, на рис. 136 плосК'о.сть а п ре-
секает прямую CD, но не пересекает ПРЯМОЙ АВ. Итак, воз-
можно только, что аНЬ.
Т'олько что доказаiнные теоремы (прямую и обратную)
МОЖН1О соединить в одну, применяя условия необходимости и
достаточности, КОТОРЫМ1И весьма чаlСТО пользуются в матема-
тике.
Условие 'наЗЫlвае ся необходимым, если без выполнения
ero данное предложение Qказыlаетсяя безусловно неверным.
Таковы, ,например, У1СЛОВИЯ: «для Toro чтобы прямые были
параллельны, необходимо, чтобы они принадлежали одной и
той же плоскости»; «для Toro чтобы четырехуrольник был па-
раллелоrрамм,ом, необходимо, rч'f'обы две противополож'ные
стороны ero были pa.BIHbI между собой».
Условие называется достаточным, если при ero выполне-
нии данное предложение безусловно верно. Достаточными
например, являются условия: «для Toro чтобы cYl\IMa двух
уrлов равнялась 180°, достаточно, чтобы они были СIvlеж-
ными»; «для Toro чтобы выпуклый четырехуrольник был
параллелоrраММО I, достаточно, чтобы ero вершины совпа-
дали с серединами сторон какоrо-нибудь четырехуrольника».
Обратим внимание на то, что вышеуказанные необходимые
условия не являются в то же время достаточными: принад-
лежность двух прямых к одной и той же плосКОсти не доста-
точна для их параллельности (они MorYT пересекаться); ра-
венство только двух сторон н'едостаточно для Toro, чтобы
четырехуrольник был параллелоrраммом (он может быть и
равнобочной трапецией).
В то же время в двух приведенных выше примерах ДOCTa
точные условия не являются необходимыми: чтобы сумма
двух уrлов равнялась 180°, нет необходимости, чтобы они
127
были смежными (например, они MOrYT быть противополож
ными уrлами вписанноrо четырехуrольника); для Toro чтобы
получить параллелоrрамм, не обязательно брать ero вершины
на серединах сторон четырехуrольника.
Особенно важное значение имеет тот случай, коrда в
предложении объединяются одновременно и необходимое и
достаточное условия. Это имеет место всеrда, если OДHOBpe
менно истинны и прямая и обратная теоремы.
Например, две теоремы о равнобедренном треуrольнике
можно объединить в одну: «для Toro чтобы треуrольник был
равнобедренным, необходимо и достаточно, чтобы уrлы при
ero основании были равны между собой». Здесь необходи
мому условию соответствует прямая теорема: «Если треуrоль
ник равнобедренный, то уrлы при ero основании равны между
собой». Достаточному же условию соответствует обратная
теорема: «Если уrлы при основании треуrольника равны
между собой, то треуrольник равнобедренный».
Таким же образом признак параллельности прямых в про
странстве может быть сформулирован так: чтобы две прямые
былu nараллельн'Ы, н'еобходuмо и достаточН,о, чтобы все nлос
кости, nересекаЮЩие одН,у из н'их, пересекал и и друсую.
Можно очень наrлядно показать практическое значение
этоrо признака параллельности. Представим себе поле, по
u u
крытое хорошо выколосившеися и нормально развившеися
рожью или пшеницей, коrда стебли всех растений располо
жены параллельно друr к друrу.. При этих условиях любая
режущая плоскость (косы или ножей жатвенной машины),
пересекшая один стебель, пересечет и все паралле.пьные ему
стебли и уборка происходит нормально. Если же в результате
какоrо-нибудь стихийноrо бедствия (rрад, ливень с ветром)
часть растений поляжет, то плоскость, пересекшая некоторые
стебли, не пересечет друrие и мноrие растения останутся He
скошенными, что приводит К потери части урожая.
(12.3) Теорема 4. СоотН,ошеН,ие nараллельН,ости прямых
в nростран'стве есть соотН,ошеН,uе эквuвалеН,тН,ости, Т. е. оно
удовлетворяет условиям симметрии, рефлектuвн'ОСТИ и Tpaп
зuтuвности.
Условие симметрии, заключающееся в том, что ИЗ COOTHO
шения allb следует Ь//а, вытекает непосредственно из опреде
ления параллельности, так же как и условие рефлективности:
alla. Остается доказать транзитивность, т. е. что из условиЙ
allb и bllc следует аНс (рис. 138).
Пересечем прямую а произвольной плоскостью 6. ПО Teo
реме 2 эта плоскость пересечет и прямую Ь, а по той же Teo
реме она пересечет и прямую с. Но тоrда мы имеем, что все
плоскости, пересекающие прямую а, пересекают и прямую с,
следовательно, по теореме 3 allc.
128
Теорема 5. Если у двух уzлов, расположенных в пpOCTpaH
стве, стороны параллельны и одинаково направлены 1, ТО та"4
кие У2ЛЫ равны между собой.
Рассмотрим два уrла в пространстве: один с вершиной О
и сторонами а и Ь, друrой с вершиной О' и сторонами а' и
а IJ
с
Рис. 138
Рис. 139
Ь', причем alla' и Ыlb' и направления каждой пары сторон
одинаковы (рис. 139).
Отложим на сторонах а и а' соответственно отрезки
ОА==О'А', а H сторонах Ь и Ь' отрезки ОВ==О'8' и соеди"
ним отрезками точки А и В, А' и B , А и' А', В и В', О и О'.
Так как отрезки ОА и О'А' равны и параллельны, то четырех-
уrольник ОАА'О' параллелоrрамм, т. е. АА' == 00' и
AA'IIOO'. Точно так же ОВ==О'В' и OBIIO'B', значит, четы"
рехуrольник ОВВ'О' тоже параллелоrрамм, поэтому ВВ'==
== 00' и ВВ'" 00'. На основании теоремы 4 получим отсюда:
AA'IIBB', а ввиду равенства этих отрезков одному и тому же
отрезку 00' получим: АА' == ВВ'. Следовательно, четырех-
уrольник АА'В'В тоже параллелоrрамм, поэтому АВ==А'В'.
Итак, в треуrольниках АОВ и А'О'В' три стороны одноrо
соответственно равны трем сторонам друrоrо, поэтому
LAOB== A'O'B', следовательно, L-AOB== L-A'O'B'.
(12.4) На основании предыдущей теоремы мы можем
определить меру У2ла, определяемоrо скрещuвающuмuся пря-
мыми. Пусть мы имеем скрещивающиеся прямые а и Ь, на
которых выбраны определенные направления (рис. 140). Из
произвольной точки О проведем лучи m и п, сонаправленные
с данными прямыми. Величина этоrо уrла не зависит от вы-
бора точки о. Действительно, если мы возьмем любую друrую
1 Два параллельных луча называются одинаково направленными (со..
направленными), если они находятся в одной и той же полуплоскости по
отношению к прямой, проходящей через их начало.
9 А. и. Фетисов
129
точку О' и из нее проведем лучи т' и n', сонаправленные
с прямыми а и Ь, ТО получим mlla и m'IIa, т. с. т!lт', n//Ь,
п'llb, т. е. nlln/. Очевидно также, что лучи m и т', п и п'
сонаправлены. Значит, L-mОn=== L.m'Q'n'. Отсюда получаем:
Определение. За меру У2ла, определяемоrо скрещиваю-
щимися прямыми, принимается величина уrла, образуемоrо
двумя лучами, имеющими общую вершину и сонаправлен
ными с данными прямыми.
IJ
f l
.......
о
0<
nL
о
Рис. 140
Рис. 141
Если уrол между скрещивающимися прямыми равен gov
то прямые называются перnендu1(,УЛЯРНЫМU.
Следствие. Прямая nерnендU1(,улярная 1(, одной uз двух
параллеЛЬНblХ nРЯМblХ перпендU1(,улярна u 1(, дРУ20Й.
Дано: а"Ь; l..La (рис. 141).
Доказать: I1.Ь.
Найдем уrол, определяемый прямыми 1 и Ь, дЛЯ чеrо из
произвольной точки О проведем mllb и nlll. Уrол тОn есть
уrол, определяемый прямыми 1 и Ь. Вместе с тем т 11 а, так
как а"Ь и mflb, следовательно, L. тОn есть в то же время и
уrол, определяемый прямыми 1 и а. Но l а, следователЬНf),.
L. тОn=== 900 и, значит, 11. Ь.
Упражнения
1. На модели куба указать пересекающиеся, параллельные
и скрещивающиеся прямые.
2. Доказать, что если у двух уrлов со взаимно параллель-
ными сторонами обе пары сторон противоположно направ
лены (противонаправлены), то такие уrлы равны между
собой.
3. Доказать, что если у двух уrлов со взаимно параллель-
ными сторонами одна пара сторон сонаправлена, а друrая
противонаправлена, то такие уrлы дают в сумме 1800.
130
4. Для TOrO чтобы Два уrла в пространстве были равны,
достаточно, чтобы обе пары их сторон были сонаправлены.
Является ли это условие необходимым?
5. Т,очки А, В, С и D не лежат в одной и той же плоскости.
Доказать, что середины отрезков АВ, ВС, CD и D..4 я'вляются
вершинами параллелоrрамма.
6. Плоскость пересекается с плоскостью V по ПрЯ IОЙ а;
плоскость 'у пересекаеТ'ся с плоскостью а по прямой Ь; плос-
кость а пересекается с плоскостью р по прямой с. Доказать,
что если аХ Ь, то через точку их пересечения проходит и пря-
1\1 а я с. ЕrCЛ И Ж е а 11 ь, то с 11 а.
7. ТреуrОЛЬНИJ{И АВС и А'В'С', не лежащие в одной и той
iKe плоскости, расположены так, что прямые ВС и В/С' пере-
секаются в точке Х, СА и С'А' в точке У, АВ и А'В'.........
в точке z. Доказать: 1) точки Х, У, Z лежат на одной и той
же прямой; 2) прямые АА', ВВ', СС' проходят через одну и
ту же точку или АА'IIВВ'I!СС'.
8. Найти rеометрическое место точек, принадлежащих
всем прямым, пересекающим одновременно две данные па-
р.аллельные прямые.
9. Дана прямая 1 и вне ее точка Р. Найти rеометрическое
м.есто точек, принаДJlежащих прямым, проходящим через Р
и пересекающим 1, а также принадлежащих прямой, прохо-
дящей через Р параллельно l.
13. ПАРАЛЛЕЛЬНОСТЬ ПРЯМОЯ И ПЛОСКОСТИ
Определение. Прямая, не пересекающая плоскость, назы-
вается параллельной к этой плоскости.
Если прямая 1 параллельна плоскости а, то это записы-
вается так: lll,a или, что все равно, al1l.
Заметим, что и тот случай, Kor..
да прямая принадлежит плоскости,
мы будем раСtсматривать как част..
u .
ныи случаи параллельности.
Существование прямой, парал-
v
лельнои плоскости, доказывается
., u
следующеи теоремои, которая дает
также признак nараллельности nря-
м'ой и плоскости.
Теорема. Если прямая парал.. Рис. 142
лельна КQк,оu"нибудь прямой при..
надлежащей плоскости, то она параллельна и самой nлй..
скости.
Д а н о: 11\ а; а С (рис. 142).
Доказать: 111 .
Допустим обратное, положим, что 1 х (1,. Но тоrда, cor ласно
теореме 2 предыдущеrо параrрафа, мы получим, что (1, Х а, а
это противоречит условию (а С (1,). Итак, 111 (1,. '
Следствие 1. Если через какую-нибудь точку плоскости
.,
провести прямую, nараллельную этоu плоскости, то получен-
ная nРЯ'мая будет принадлежать данной
плоскости.
Дано: 11)(1,; Рс(1,. Ре а, alll.
д о к а 3 а т ь: а С (1,.
Допустим, что ах (1" но тоrда по
теореме 2 предыдущеrо параrрафа (J., Х 1,
что противоречит условию: 1/1 (1,. Итак,
а С (1,.
Следствие 2. Прямая, nараллельная
двум nересекающи'мСЯ nлоскостя'м, парал-
дельна линии их пересечения.
Д а н о: I11 (J.,; 1/1 , (J., = т (рис. 143) 1.
Д о К а 3 а т ь: 111 т. Возьмем какую-ни..
бу дь точку Р на прямой т и проведем
через нее прямую, параллельную 1. Пь
предыдущему следствию эта прямая должна одновременно
при надлежать и плоскости (J." И плоскости , значит, она сов..
падает с линией их пересечения, т. е. т 111. Предложение, ко-
нечно, остается в силе и для Toro случая, коrда данная пря-
мая' лежит в данной плоскости (например, прямая n на рис. 143
принадлежит плоскости ).
т
р
л
'""
......
Рис. 143
l
Упражнения
1. Доказать, что всякая прямая, параллельная прямой,
которая параллельна плоскости, тоже параллельна этой
плоскости.
2. Доказать, что если а и Ь скрещивающиеся прямые,
то существует единственная плоскость, проходящая через а и
параллельная Ь.
з. Доказать, что если прямые а и Ь не параллельны, ТО
через любую точку пространства 'можно провести единствен-
ную плоскость, параллельную одновременно обеим прямым.
4. Найти rеометрическое место точек, принадлежащих
прямым, которые пара.ТIлельны одной из скрещивающихся
прямых и пересекают друrую.
5. Точка А д'Вижется с постоянной скоростью по прямой а,
Т,очка В движется с постоянной скоростью по прямой Ь. Ка-
кую линию описывает середина отрезка АВ?
1 СИМВОЛОМ ар обозначают прямую пересечения плоскостей а и ...
132
14. ПАРАЛЛЕЛЬНОСТЬ ПЛОСКОСТЕЯ
(14.1) Определение. Н еnересекающuеся пЛОСКОСти назы-
ваются параллеЛЬНblМ,и.
Здесь, как и в предыдущих случаях параллельности, со-
впадение плоскостей мы -будем рассматривать как частный
случай параллель ости. Если плоскОсть а параллельна плос-
кости , то это записывается так: all .
Следствие. Если две плоскости nараллеЛЬНbl м'ежду собой,
то каждая из них параллельна всем прямым, принадлежащим
второй плоскости.
Действительно, если (/., 11 и ас(/."
причем (/., и различны, то плоско-
сти не MorYT иметь общих точек
и, значит, а I' . Если же (/., = , то
а C , значит, и в этом случае а \1 .
Теорема 1. Через всякую moчку
пространства можно провести един-
ственную плоскость, nараллельную
данной плоскости.
Пусть (/., данная плоскость, Q
данная точка. Если Q с (/." то иско-
мая единственная плоскость есть
сама плоскость (/.,. Положим, что Q cj:. (/.,
(рис. 144). Проведем на плоскости (/.,
прямые т и n, пересекающиеся в Т,очке Р. Через точку Q проводим
прямые т' и n', соответственно параллельные т и n. Через
пересекающиеся прямые т' и n' проведем плоскость . Дока..
жем, что 11 (/.,.
Допустим противное. Положим, что Х сх и 1..... прямая их
пересечения. Соrласно признаку параллельности прямой и пло-
скости, в силу условий: т 1I т' и n 11 n', получим, что т I и
п II . А на основании следствия 2 предыдущеrо параrрафа т 111
и n 111. Но пересекающиеся прямые не MorYT быть параллельны
одной и той же прямой (аксиома параллельности). Поэтому
плоскость не пересекает плоскости (/., и, значит, 11 (/.,. Пло-
скость единственная, так как если допустим, что суще-
ствует вторая плоскость ', параллельная (/., и проходящая через
точку Q, то соrласно следствию 1 предыдущеrо параrрафа по-
лучим, что т' C ' и n' С '. Но через две пересекающиеся
прямые можно провести только одну плоскость, следовательно,
' = .
fIепосредственно из доказательства этой теоремы получаем:
Следствие (признак параллельности двух плоскостей). Две
плоскости параллельны, если одна из них параллельна двум
nересекаЮlЦИМСЯ прямым дРУ20Й плоскости.
.
Рис. 144
133
Действительно, если это условие выполнено, то можно осу-
ществить то построение, которым мы пользовались при доказа-
тельстве теоремы.
(14.2) Теорема 2. Соотношение nараллельности плоскостей
есть соот1:l0шение эквивалентности. Непосредственно из опреде-
ления слеJlует: 1) если aH , то 11 сх; 2) а. JI а.. Остается доказать
,... ...... ..
,
/
,
" ь
а
.
РИС. 145
РИС. 146
транзитивность параллельности. Пусть мы имеем: all и 11 у.
Докажем, что all у. Если две из этих плоскостей или все три
совпадают, то условие, очевидно, выполняется. Допустим, что
все плоскости различны. Если бы оказалось, что а Х Т, то это
значило бы, что через их общую прямую проходят две плоско-
сти, параллельные плоскости , чеrо быть не может на основа-
нии предыдущей теоремы. Итак, мы имеем: 3) если а и , 11 у,
то (1., 11 у.
СJIедствие 1. Плоскость, nересекающая одну из двух nарал-
лельных плоскостей, пересекает и друzую. Линии пересечения
параллельны . м'ежду собой.
Д а н о: (1., II , r х а, (1.,Т == а (рис. 145).
Доказать: yx , allb, rде b == y,
Плоскость r должна пересечь плоскость , так как иначе
мы получили бы, что две пересекающиеся плоскости (1., и r
параллельны плоскости , а это противоречит предыдущей те-
ореме. Итак, r х и y == Ь. Прямые а и Ь при надлежат одной
и той же плоскости r и не пересекаются, так как лежат
в двух параллельных плоскостях, следовательно, а 11 Ь.
СJIедствие 2. Отрезки nараллельных прямых, заключенные
между nараллельными плоскостями, равны между собой.
Д а н о: (1., 11 (1.,', т 11 n, т(J., = М, т(1.,' = М', n(1., == N, nrJ.,' = N'
(рис. 146).
134
Доказать: MM'==NN'.
Так как т 11 n, то эти прямые лежат в одной и той же
плоскости r. Она пересекает плоскости <х И <х' по параллельным
прямым (соrласно предыдущему следствию). Итак, MN В М' N'
и, значит. четырехуrольник MNN'M' параллелоrрамм, по-
этому мм' с::: NN'.
Упражнения
1. Доказать, что, д я Toro чтобы две плоскости были па
раллельны, необходимо и достаточно, чтобы все прямые,
пересекающие одну из них, пересекал и и друrую.
2. Доказать, что через две скрещивающиеся прямые
IОЖНО провести одну, и только одну, пару параллельных
между собой плоскостей.
3. Доказать, что три параллельные между собой плоскости
определяют на двух секущих прямых соответственно пропор
циональные отрезки.
4. Доказать, что если даны. попарно скрещивающиеся пря
мые а, Ь, и с, то существует единственная прямая, пересекаю..
щая а и Ь и параллельная с.
5. Найти rеометрическое место тс>чек, принадлежащих
всем прямым, проходящим через одну и ту же точку и парал..
лельным данной плоскости.
6. Найти rеометрическое, место точек, делящих в данном
отношении 'все отрезки, соединяющие точки данной плоскости
с точкаrvIИ параллельной плоскости.
7. Прямая движется параллельно постоянной плоскости
и одновременно пересекает две данные скрещивающиеся пря
мые. Какую линию описывает точка этой прямой, делящая
в данном отношении отрезок между .скрещивающимися пря..
lv1ЫМИ?
8. На плоскости а начерчена окружность и вне этой плос..
кости дана точка Р. Найти rеометрическое место середин
всех отрезков, соединяющих точку Р с точками окружности.
15. ЗАДАЧИ НА ПОСТРОЕНИЕ В ПРОСТРАНСТВЕ
(15.1) В планиметрии задачи на построение решаются при
помощи известных инструментов, линейки, циркуля, уrоль
ника. Значительно сложнее обстоит дело в пространстве, так
как мы не раС!10лаrаем 'соответствующим набором инструмен..
тов, при помощи которых rvtожно отмеча ть точки, чертить
прямые, проводить плоскости, определять линии их пересече..
ния и Т. д. .
Для осуществления rеометрических построений в CTepeo
метрии при меняются следующие способы: 1) эффективные
135
построения; 2) воображаемые построения; 3) построения на
проекционном чертеже.
Рассмотрим каждый из этих способов в отдельности.
Эффективным называется такое построение, коrда полу..
чается. действительная пространственная lVlодель какой..либо
rеометрической фиrуры. Для осуществления эффективных по..
строений пользуются различными материальными средствами.
Нити, реЗ'иновые шнуры, проволока применяются для изобра..
жения прямых; картон, фанера, пластмассовые ИЛИ стеклян..
ные пластинки служат для изображения плоскостей. Име..
ются специальные наборы для пространственных построе..
ний так называемые «стереометрические ящики». Напри..
мер, если мы по развертке куба склеим из картона куб, то это
будет эффективным построением, так как в результате ero
получил ась действительная пространственная фиrура, обла..
дающая всеми признаками данноrо тела.
Эффективные построения дают очень живые и наrлядные
представления о соответствующих пространственных формах,
однако систематически применять их на протяжении Bcero
курса rеометрии не представляется возможным ввиду боль..
шой- сложности некоторых фиrур.
(15.2) Воображаемые, или условные, построения, как по..
казывает само название, не требуют для cBoero осуществле..
ния никаких материальных объектов, так как все построение
производится только в нашем воображении. При этом зара..
нее предполаrается, что мы можем каким..либо способом вы..
полнить ряд некоторых основных построений и любое данное
построение считается выполненным, если ero можно расчле..
нить на эти элементарные построения.
Будем считать, что мы можем выполнить следующие
основные построения:
1. Задать положение точки в пространстве.
2. Провести прямую через две данные точки.
3. Провести плоскость через три точки, не лежащие на
одной и той же прямой.
4. Найти точку пересечения прямой с плоскостью.
5. В каждой плоскости производить все планиметрические
построения.
Приняв за основу эти построения, нетрудно убедиться, что
при их помощи мы можем выполнить следующие построения:
6. Провести плоскость через прямую и точку вне ее. Для
этоrо нужно еще задать две точки на данной прямой.
7. Провести плоскость через две пересекающиеся прямые.
Для этоrо достаточно взять еще по точке на данных прямых.
8. Найти прямую пересечения двух плоскостей. Для этоrо
достаточно на одной из этих плоскостей провести две прямые
(ПО,строение 5) и найти две точки пересечения этих прямых со
136
второй плоскостью (построение 4). Прямая, проходящая че..
рез эти точки, и будет иском я.
9. Через данную точку провести прямую, параллельную
данной прямой. Построение указано в начале параrрафа 12.
10. Через данную точку провести плоскость, параллельную
данной плоскости. ,
Построение указано в теореме 1 предыдущеrо параrрафа.
Приведем теперь пример решения более сложной задачи
способом воображаемых построений.
3адача. Даны две скрещивающиеся прямые а и Ь и вне
их точка Р. Провести через точку Р такую прямую с, чтобы
она пересекал а и прямую а и прямую Ь.
Реш е н и е. Через прямую а и точку Р можно провести
плоскость а (построение 6). Находим точку N, в которой пря..
мая Ь пересекает плоскость а (построение 4). По плоскости а
проводим прямую PN и находим точку М, в которой эта пря..
мая пересекает прямую а (построение 5). Прямая MN будет
искомая, так как проходит через точку Р и пересекает пря..
!\'lые а и Ь соответственно в точках М и N.
Полученное решение единственное, так как если бы суще..
ствовала вторая прямая, пересекающая прямые а и Ь в новых
точках М' и N' и проходящая через ту же точку Р, то через
прямь е РМ и РМ' можно было бы провести плоскость, в ко..
торой лежали и точки N и N', т. е. находились прямые а и Ь,
ero не может быть, так как а и Ь не лежат в одной и той же
плоскости.
Задача не имеет решения, если окажется, что blla, так ка,К
в этом случае нельзя найти точку N. Задача также H€ имеет
решения, если ПрЯ lая PN окажется параллельной прямой а.
В этом случае нельзя найти точку М.
Решение приведенной задачи показывает, что, ПОЛЬЗУЯСl>
только одними лоrическими рассуждениями, можно дать ис..
черпывающее решение задачи на построение в пространстве.
Однако найти это построение и провести соответствующие'
раССУJКдения, доказательство и исследование довольно труд..
но ввиду отсутствия наrлядных образов.
В связи с трудностями, возникающими и при эффектив
ных, и при воображаемых построениях, появляется необходи..
мость в отыскании TaKoro метода пространственных построе..
ний, который qыл бы одновременно и наrлядным, и леrко'
выполнимым при помощи привычных инструментов. Таким
условиям удовлетворяют построения на проекционном чер..
теже.
(15.3) ПроеКЦUОflflЫЙ чертеж представляет собой резуль..
тат преобразования пространственной фиrуры в плоскую.
При этом на полученной фиrуре оказывается возможным про..
изводить построения, которым соответствуют определенные
137.
построения ,в пространстве. Вместе с тем проекционный чер-
теж дает возможность с помощью обратноrо преобразования
найти ту фиrуру, из которой он получен.
Преобразование, посредством KOToporo получается проек-
ционный чертеж, называется nроектированием'. Из различных
способов проектирования мы рассмотрим nараллельное nро-
ектирование, которое имеет очень большое значение в тех-
нике. Чтобы дать наrлядное пред-
ставление об этом преобразовании,
возьмем проволочную (каркасную)
модель какой-нибудь пространствен
ной фиrуры, нацример куба, Ii в сол
u u
нечныи день рассмотрим тень этои
фиrуры на стене или на экра-
не. Эта тень и есть nараллельная
nроекцuя куба на данную плоскость,
так как солнечные лучи можно
считать параллельными друr друrу
(рис. 147).
Сравнивая тень куба с ero мо-
делью при различных положениях
куба и экрана, мы можем сделать
ряд выводов о свойствах этоrо преобразования. Прежде Bce
ro мы можеr\i сказать, что это преобразование точечное, так
как тень точки есть тоже точка. Прямая, очевидно, nреобра
зуеТGЯ в прямую. Исключением является тот случай, коrда
прямая параллельна лучам солнца (<<проектирующим» лу
чаl'll). При этом проекция прямой становится точкой (<<вырож
дается» в точку). Таковы, например, проекции четырех ребер
куба на рис. 147, а. Параллельные прямые преобразуются в
параллельные: на рис. 147 мы видим, что параллельные реб
ра куба изобразились параллельными отрезками. И, наконец,
если фиrура находится в плоскости, параллельной плоскости
экрана, то она преобразуется в равную фuzуру. На рис.
147, а и 6 передняя :и задняя rрани куба параллельны плос-
кости экрана, и потому их изображение получилось в виде
квадрата, paBHoro этим rраням.
Вместе с тем важно заме-vить, что на проекции мноrие
элементы фиrур оказываются изменившимися. На рис.
147, в и 2 все rрани куба преобразовались в косоуrольные
параллелоrраммы снеравными сторонаl\-IИ. Это значит, чтu,
вообlце rоворя, величина отрезков и уrлов при этом преобра-
зовании изменяется.
о
а
I
о
Рис. 147
2
(15.4) Уточним теперь определение параллельной проек
ции и дадим обоснование ее важнейших свойств.
Определение. П араллельной nроекцuей фируры называется
совокупность точек, которые получаются от пересечения дaH
138
НОЙ плоскости со всеми прямыми, проходящими через точки
этой фиrуры и параллельными одной и той же прямой.
Само преобразование называется nараллельныМ, npoeKTи
рованиеМ,. Постоянная плоскость называется плоскостью пpo
.екции, а прямые, осуществляю 8
щие проекцию, называются про..
ектuрующuм'U nРЯМ,ЫМ,U.
Теорема 1. Если пРЯм'ая не
параллельна nрое/{,тuруюu{uм' nря..
MЫм' ТО ее nроекцuя есть тоже
пРЯм'ая.
Пусть 1 данная прямая, а
плоскость проекции (рис. 148).
Через точку А на ПрЯl\iОЙ 1 про..
ведеl\f проектирующую ПрЯМУIО
а, которая пересечет плоскость а
в точке А' проекции точки А.
Через пересекающиеся прямые 1 и а проведем плоскость у.
JIинию пересечения плоскостей .а и V обозначим через 1'. Что..
бы найти проекцию какой"нибудь друrой точки прямой [, на..
ПрИl\1ер В, проведем через В проектирующую прямую Ь. Так как
blla, то ЬСу и ПОТО fУ пересечет
плоскость а в точке В', принадле..
жащей 1'. 11TaK, проекции всех то-
чек прямой 1 лежат на прямой ['.
Обратно, если взять точку С'
на прямой [', то, проведя через
нее проектирующую прямую,
увидим, что она пересечет пря-
мую 1 в точке С, проекцией KOTO
рой служит С'. Таким образом,
между точками прямых 1 и l'
установлено взаимнооднозначное
соответствие. Однако эта взаим..
насть будет нарушена в rOM слу-
чае, если прямая l будет проектирующей. В этом случае про..
екцией всех точек этой прямой будет только одна точка пе-
ресечения ее с плоскостью проекции. Такое соответствие, оче..
видно, не будет взаИl\-fнооднозначным.
"/
Рис. 149
,
I
I
,
,
l' ,
В'
Рис. 148
(15.5) Теорема 2. Прое/{,цuu nараллеЛЬНblХ (не проектирую
щих) прям'ЫХ nараллеЛЬНbl м'ежду собой.
Пусть а 1\ ь, r плоскость проекции, а' и Ь' соответственно
проекции а и Ь (рис. 149). Докажем, что а' 11 Ь'. Проведем через
точку А на прямой а проектирующую прямую АА' и через
пересекающиеся прямые а и АА' проведем плоскость ct, KOTO
рая пересечет плоскость r по прямой а'. Точно так же через
точку В на прямой Ь проведем проектирующую прямую ВВ'
139
и через пересекающиеся прямые Ь и ВВ' проведем плоскость
, которая пересечет плоскость r по прямой Ь'. Так как а 11 ь
и АА' 11 8В', то на основании признака параллельности плоско-
стей получим, что ('J., II . НО две параллельные плоскости пере-
секаются третьей плоскостью по па.
раллельным прямым, следовательно,
а' \\Ь'.
Теорема 3. Отношение отрезков,
лежащих на одной и той же прямой
или на двух nараллеЛЬНblХ прямых,
.,
равно отношению их nроекции.
На рис. 148 в одной и той же-
плоскости r три параллельные пря-
мые АА', ВВ' и СС' пересекают пря-
мые 1 и 1'. По известной теореме
планиметрии получим:
АС А ' С '
Рис. 150
ВС В' С'
Если отрезки лежат на двух параллельных прямых, как АС
и BD на рис. 149, то, проведя в плоскости параллельнbIX пря..
мых а и Ь прямую DM "АВ, получим, что ABDM параллело--
rpaMM, поэтому BD == АМ. Так как проекции параллельных
прямых параллельны, то А' В' D' М' ........ тоже параллелоrрамм
И, значит, B'D' == А'М'.
Итак, мы имеем:
АС А'С'
Ам А'М'
Заменяя отрезки АМ и А' М' равными отрезками, получим:
АС А'С'
==
BD. В' D'
(15.6) Теорема 4. Если фи2ура находится в плоскости,.
nараллельной плоскости npoeKции ТО nроекцuя Фи2УРbl равна
самой фuеуре.
На рис. 150 треуrольник АВ С находится в плоскости 6,
параллельной плоскости проекции у; А', В', С' COOTBeTCT
венно проекции точек А, В, С; АА'==ВВ'==СС' как отрезки
параллельных прямых между параллельными плоскостями..
поэтому четырехуrольник АА' В' В параллелоrрамм и, зна
чит, АВ==А'В'. Таким же образом докажем, что ВС==В'С' и
АС==А'С'; следовательно, 6АВС== LA' В'С', т. е. треуrольник
равен своей проекции.
140
Положим теперь, что в плоскости 6, параллельной плос..
кости 'У, начерчена произвольная фиrура. Между ее точками
и точками ее проекции существует взаимнооднозначное соот-
ветствие. При этом любым точкам А, В, С, D, ...этой фиrуры
.соответствуют точки А', В', С', D', ... ее проекции. Вместе с
тем мы имеем равенства: АВ==А'В', АС==А'С', ВС==В'С',
AD==A'D' и т. Д.
Поэтому если мы будем приближать плоскость 6 к плос-
ости 'У, сохраняя их параллельность, то в конце концов точ-
ка А совпадет с А', а в силу равенства отрезков и точка В
(совпадет с В', С с С' и т. д. Друrими словами, фиrура со-
впадет со своей проекцией всеми своими точками, т. е. фиrура
равна своей проекции.
(15.7) Опираясь на свойство па раллельной проекции, по-
-смотрим теперь, как можно производить построения на проек-
.ционном чертеже. Для этоrо нужно в первую очередь пока-
зать, как разрешаются указанные в разделе (15.2) основные
задачи на построение в простран'стве: 1) задать положение
точки в пространстве; 2) провести прямую через две точки;
З) провести плоскость через три точки, не лежащие на одной
и той же прямой; 4) найти точку пересечения прямой с плос-
костью; 5) производить В любой плоскости 'все планиметри-
'ческие построения.
А &
Рис. 151
Рис. 152
Рассмотрим последовательно, как решаются эти основные
задачи.
1) Для Toro чтобы задать положение точки в простран-
.стве, возьмем изображение некоторой постоянной плоскости а,
которую назовем основной (рис. 151) и, кроме изображения
некоторой точки А, будем пользоваться также изображением
'ее параллельной проекции А' на основную плоскость. Если
дано изображение точки и изображение ее проекции, то та-
кую точку мы будем называть заданной. Изображение любой
.фиrуры называется nолным" если все точки этой фиrуры явля-
Iют'ся заданными.
141
Такое задание точек в пространстве при помощи проек
ционноrо чертежа дает нам достаточно наrлядное представле..
ние о действительном расположении точек относительно друr
друrа и основной плоскости. Например, на рис. 151 мы видим,
что точка С находится ближе к плоскости a чем точки А и
В) точка М находится на плоскости, точка D под плоскостью.
2) Пусть заданы точки А и в.
А (РИ1С. 152). Проведем прямую {
через точки А и в. Мы получим
изображение ее проекции пря
мую [', проходящую через точки
А/ и В/. Изображение прямой l
будет nОЛНЫМ 1 так как для любой
точки на прямой 1 ле ко найти
ее проекцию на прямой 1', т. е.
любая точка прямой 1 является
заданной. Точка Р пересечения
прямых 1 и l' есть изображе
Рис. 153 ние точки пересечения заданной
прямой с основной плоскостью.
Точка Р называется следом прямой l на плоскости а.
(15.8) 3) Пусть заданы три точки А, В и С, не принадле..
жащие одной и той же прямой (рис. 153). Изображение пло..
скости, проходящей через эти точки, дано треуrольником АВ С
и ero цроекцией А'В/С' на OCHOB
ную плоскость. Точки X,Y,Z дa Q
ют соответственно изображения
следов прямых ВС, СА, АВ на oc
иовной плоскости а. Прямая
l = XYZ является изображ'ением
линии пересечения плоскости
АВС с плоскостью а.
Изображение плоскости ABC
полное. Действительно, все точ
ки пря {ых ве, СА и АВ являют..
ся заданными, ПОЭТО}\.IУ полным
будет изображение любой прямой Рис. 154
в плоскости АВС, так как такая
прямая всеrда пересечет по крайней мере две из прямых ВС,.
СА и АВ и потому пройдет через две заданные точки. Вместе
с тем прямую можно провести через любую точку плоскости
Аве и, значит, всякая тачка этой плоскости заданная.
Заметим, что для получения полноrо изображения плос
кости достаточно задать изображение ее следа и какую"ни
будь точку вне основной плоскости.
4) Построение точки пересечения прямой с плоскостью мы
рассмотрим сначала для частноrо случая. Решим такую за-
1ч2
дачу: найти точку пересечения заданной плоскости с проекти-
рующей прямой.
Пусть плоскость \ задана своим следом 1 и точкой Р; q "
проектирующая прямая (рис. 154). Проведем плоскость через
параллельные прямые РР' и q. Следом этой плОСкости слу-
жит прямая P'Q', rде Q' след прямой q. Обозначим через М
точку пересечения следов 1 и P'Q'. Эта точка принадлежит
обеим плоскостям и РР'М. Вторая их общая точка есть Р.
Поэтому МР линия пересечения этих плоскостей. Наконец,
точка Q пересечения прямых МР и q и есть искомая точка
пересечения прямой q с плоскостью .
(15.9) Приведем примеры задач, которые MorYT быть ре-
lпены на проекционном чертеже при помощи полученных по..
строений. Решим прежде Bcero задачу, которая была решена
нами способом воображаемых построений в пункте (15.2).
Рис. 155
Рис. 156
Задача 1. Даны скрещивающиеся прямые а и Ь и вне их
точка Р. Провести через эту точку прямую с так, чтобы она
пересекла и прямую а, и прямую Ь.
ДЛЯ решения этой задачи примем за основную плос..
кость а, проходящую через точку Р и прямую а (рис. 155).
Прямая Ь задана своим следом N и точкой В. Очевидно, иско..
мая прямая с есть прямая NP, переС'екающая прямую а в
точке М. Доказательство единственности решения и ero ис-
следование остаются прежними.
Задача 2. Найти линию пересечения двух плоскостей, каж-
дая из которых задана своим следом и точкой.
Пусть плоскость а задана следом а и точкой А, а плос.
кость следом Ь и точкой В; V основная плоскость
(рис. 156). Для определения линии пересечения достаточно
найти две общие точки данных плоскостей. Одна из этих то..
чек уже найдена, это точка Р, 'в которой пересекаются
следы. Для отыскания еще одной общей точки проведем плос..
143
кость б через параллельные прямые АА' и ВВ'. След А' В'
этой плоскости пересекает следы плоскостей а и соответ"
ственно в точках М и N. Прямые МА и N В линии пересе..
чения плоскостей а и с плоскостью б. Значит, PQ есть иско..
мая линия пересечения плоскостей а и .
(15.1 О) Рассмотрим теперь задачи, в которых нужно про..
изводить построения на изображениях тел.
Задача з. На изображении четырехуrольной призмы по-
строить сечение ее плоскостью, заданной тремя точками на
боковых ребрах.
Рис. 157
8
Рис. 158
На рис. 157 дано изображение призмы и точек А, В, С на
€e боковых ребрах. Если плоскость основания призмы при-
нять за основную, а боковые ребра за проектирующие пря-
rvlbIe, то изображение призмы будет полным и вершины А', В',
С' нижнеrо основания будут изображениями проекций то-
чек А, В. С на основную плоскость.
Припоминая построение 3, найдем след 1 плОскости АВС.
Далее при помощи построения 4 находим точку D пересече-
ния ПЛОСКОСТИ АВС с проектирующей прямой четвертым
боковым ребром nризмы. Таким образом мы получили всю
фиrуру сечения. Этот способ построения сечения, называемый
способом следов, может оказаться неприменимым, если от-
резки АА', 8В' и СС' мало отличаются друr от друrа по вели-
чине. Секущая плоскость при этом будет очень близка к па-
раллельности с плоскостью основаlfIИЯ, и след 1 может на чер-
теже не получиться.
В этом случае для построения сечения применяют так на-
зываемый способ соответствия. Пусть мы имеем по-прежнему
четырехуrольную призму с данными точками А, В, С на ее
боковых ребрах (рис. 158). Как и раньше, вершины основа..
ния А', 8', С' мы будем считать проекциями точек А, В
и с. Четвертая вершина основания D' есть проекция ис-
144
комой точки D сечения. Пересечение диаrоналей А'С' и B'D'
определяет точку Р' проекцию общей точки Р диаrоналей
сечения. Проведя через Р' проектирующую прямую, найдем
в пересечении ее с диаrональю АС точку Р. Наконец, проведя
прямую ВР, находим вторую диаrональ искомоrо сечения.
Так же решается задача на
построение сечения пирамиды.
Задача 4. На изображении че-
тырехуrольной пирамиды постро-
ИТЬ сечение ее плоскостью, задан-
ной тремя точками на боковых
ребрах.
На рис. 159 дано изображение
четырехуrольной пирамиды с вер-
шиной S и точками А, В и С на
боковых ребрах. Рассматривая
вершину А' основания как про-
екцию точки А на плоскость ос-
нования, увидим, что вершина S является заданной точкой и
потому изображение будет полным. Диаrонали основания
А'С' и B'D' являются ОБ то же время следами диаrональных
плоскостей пирамиды A'C'S и B'D'S. Точка р' пересечения
диаrоналей основания определяет ПРЯМУIО SP', по которой пе-
ресекаются диаrональные плоскости. На этой прямой лежит
точка Р, в которой пересекаются диаrонали сечения. Вместе
с тем эта точка лежит и на диаrонали АС, т. е. она есть пе-
ресечение SP' и АС. Четвертая вершина сечения D опре-
деляется пересечением прямой ВР с ребром SD'.
s
Рис. 159
(15.11) Во всех предыдущих задачах мы находили пересе-
чения прямых и плоскостей между собой. Такие задачи, в
которых приходится определять построением только пересече-
ния основных элементов, называются nозициОННbl tи.
Перейдем теперь к решению задач, в которых требуется
построить фиrуру, удовлет.воряющую некоторым определен-
ным условиям в отношении величины ее элементов. В таких
задачах приходится откладывать отрезки и строить уrлы дан-
ной величины, проводить перпендикуляры, биссектрисы уrлов,
строить окружности и т. д. Задачи, в которых требуется по-
строить фиrуру по заданной величине ее элементов, назы-
ваются метрическими.
Для решения метрических задач необходимо прежде Bcero
уметь производить пятое из УI<азаиных выше основных по-
строений, т. е. производить все планиметрические построения
на изображении любой плоскости.
Рассмотрим сначала построения на изображении основной
плоскости, так как построения на изображении любой друrой
плоскости выполняются такими же приемами.
10 А. И" Фетисов
145
Обратим внимание на то, что в силу сохранения парал
лельности и отношения отрезков при параллельной проекции
проведение параллельных и перенесение отрезка с одной па.
раллельной на друrую можно производить обычным плани..
метрическим построени.ем. Например (рис. 160), на изобра..
жении основной плоскости а через точку Р проведен ПРНО
мая Ь, параллельная ПрЯlvlОЙ а. На прямой Ь отложен отре-
зок PQ, равный отрезку MN на прямой а, причем отрезок PQ
получаем обычным построением при помощи циркуля. Однако
если бы нужно было построить
изображение перпендикуляра.
проведенноrо через точку Р
прямой а, то строить ero обыч
ным способом было бы непра
вильно, так как при парал
лельной проекции величина
уrла изменяется; изображсни
перпендикуляра будет, вообще
rоворя, не перпендикулярно и
ПРSiмой а.
Вuзможность всех п"п ани-
метрических построений на
изображении плоскости ОС'НО
Ba a на следующеЙ теореме.
Теорема 5. Если на uзоБРQ
жении основной плоскости да.
ны точки AI В и C 1 не лежащие на одной и тои же прямой lJ
являющиеся изображением точек Ай, ВО, СО дан'НОЙ пЛОС1\,ои
фиеУРbl, ТО, зная истинный вид треуzольника АоВоС о , АtОЖ-
но установить взаuмнооднозначн-ое соответствие .междц .,.ОЧ
ками фU2УРЫ и точками ее изображения.
Это значит, что при этих условиях по каждой точке Д3(lНОЙ
фиrуры можно построить точку ее изображения, а по кажлой
точке изображения построить точку данной фиrуры.
Пусть на "изображении основной ;. плоскостиr. (J., даны точки
А, В, С изображения точек А.,:В о , СО (рис. 161). ПО ТОЧКt'
148
Рис. 160
с.
,.
......... р " А
'''О.... М,".,.,
,, :'
с .., ....., ,,/' ..... ..... '"
о
8
Рис. 161
р на иsображении основной плоскости найдем соответстаующую
fОЧКУ Р. на данной фиrуре. Проведеf\1 прямую ЕР, которая
оересечет прямую АС в точке М. Точку Мо, соответстаующую
rочке М. найдем из пропорции АоМо == АМ , указывающей, что
МоС о МС
дя этоro нужно разделить отрезок АС в данном отношении
АМ
ИС ·
Точно так же для отыскания точки Pg воспользуемся про-
u В D O ВР
оорциеи ==............
ВоМо ВМ
Таким образом, каждую точку с изображения фиrуры на
основной плоскости можно перенести на проектируемую фи-
('уру и таким путем найти истинный вид этой фиrуры. Обрат-
но: тем же способом можно каждую точку проектируемой фи-
суры перенести на ее изображение на основной плоскости.
rаким образом, устанавливается взаимнооднозначное соответ.
ствие между точками данной фиrуры и точками ее изобра..
жения.
На основании полученноrо соответствия можно произво.
дить все планиметрические построения на изображении основ-
ной плоскости. Пусть, наПРИ Iер, требуется построить изобра-
жение перпендикуляра, проведенноrо через точку М к пря.
\10Й ВС (рис. 161). Для этоrо на данной фиrуре из точки Мо
проnедем перпендикуляр MoQo к прямой ВоС о . Зная, в каком
">тношении точка Qo делит отрезок ВоС о , разделим в TOl\1 же
отношении отрезок ве и найдем точку Q изображение точ.
ки Qo. Прямая MQ и есть искомое изображение перПендИ-
куляра.
Если по изображению фиrуры можно определить ее истии-
'iый вид, то это изображение называется -метрuческu опре-
деленным.
(15.12) Практически при изучении стереометрии чаще
ясеrо приходится начинать с построения какой нибудь опред€-
,,1енной фиrуры. При этом, естественно, возникает вопрос:
8 какой 1epe произвольными MorYT быть полученные изобра-
жения? Например, можно ли любой треуrольник принять за
rIзображение paBHQCTOpOHHero треуrольника? Ответом на ЭТО1
зопрос служит следующее предложение.
Теорема 6. Любой треУ20ЛЬНU1\, JrtОЖНО рассматривать как
'1араллелыlюю nрQекцuю треУ20льнuка, подобноео любому
1анному треУ20ЛЬНUКУ.
Пусть на изображении основной плоскости мы начертили
произвольный треуrольник А'В'С' (рис. 162) и вместе с тем
имеется некоторый данный треуrольник АоВоС о . Построим
дАне так, чтоБЬJ сторона 8С равнялась стороне В'С'.
10' t47
уrол АВС равнялся уrлу АоВоС о , а уrол АСВ равнялся
уrлу АоСоВо. Тоrда получим, что .LABCcп.LAoBoC o . Поместим
тепеrь LABC так, чтобы ero сторона ВС совпала со CTOpO
ной В'С' треуrольника А/ В/С/, а точка А оказалась вне плос..
кости треуrольника А' В/С/. Если прямую АА' принять за про
ектирующую, то .LA' 8./ С/ будет параллельной проекцией тре..
уrольника АВС, подобноrо данному треуrольнику АоВоС о .
,
A В.
,
,
,
,
,
,
,
,
,
,
Р, с
8
IJ
Рис. 162 .
Рис. 163
Из этой теоремы, в частности, следует:
Следствие 1. Любой треУ20льник можно рассматривать
как параллельную nроекцию равносторонне20 треУ20льника.
Действительно, доказательство предыдущей теоремы ни-
чем не изменится, если треуrольник АоВоС о будет равносто-
ронним.
Следствие 2. Любой nараллелоерамм можно рассматрu"
вать как nараллелъную проекцию квадрата.
Пусть на изображении основной плоскости начерчен па-
раллелоrрамм ABCD. Рассмотрим квадрат AoBoCoDo и прове..
дем в обоих четырехуrольниках диаrонали А С и АоС о
(рис. 163). Соrласно теореме 6 6АВС можно рассматривать
как проекцию треуrольника, подобноrо треуrольнику АоВоС о ,
Т. е. равнобедренному прямоуrольному треуrольнику. Тоrда
прямые CD и AD будут служить изображениями прямых,
параллельных катетам этоrо треуrольника, т. е. прямых CoDo
и AoDo. Но тоrда и весь параллелоrрамм ABCD будет слу-
жить изображением квадрата.
Вместе с тем необходимо заметить, что, приняв какой-
нибудь треуrольник за изображение paBHOCTopoHHero тре-
уrольника или какой-нибудь параллелоrрамм за изображение
квадрата, мы тем самым делаем фиrуру метрически опреде-
ленной и все остальные построения Приходится производить,
сообразуясь с полученным соответствием между фиrурами.
148
(15.13) Приведем примеры построений на изображении
основной плоскости.
Задача 1. На изображении основной плоскости построить
проекцию правильноrо шестиуrольника.
Пусть ABCDEF искомая проекция правильноrо шести
уrольника, а точки А, В, С проекции трех ero соседних
вершин (рис. 164). Т,еперь мы знаем, что 6АВС можно рас-
СО
п о
[(}
fo
D,
)
(
Рис 164
Рис. 165
сматривать как проекцию треуr()JIьника АоВоС о , в KO..I.'OpOM
АоВо==ВоС о и LAOBoCo== 120°. Таким образоrvl, 6АВС метри
чески определенный. Так как в правильном шестиуrольнике
AoBoCoDoEoFo AoDoIIBoC o и CoFoIIAoBo, то и на изображении
проводим ADIIBC и CFIIAB, причем точка О пересечения пря
мых AD и СР будет проекцией центра 00 правильноrо шести
уrольника. Отложив ОР==ОС и OD==OA, найдем вершины F
и D. Проведя, наконец, прямую ВО и отложив ОЕ==ОВ, най
дем шестую 'вершину искомой проекции шестиуrольника.
Задача 2. Построить проекцию окружности, вписанной
в квадрат.
Пусть параллелоrрамм ADCD есть проекцня квадрата
AoBoCoDo. В этот квадрат вписана окружность с центром 00'
касающаяся сторон квадрата в их серединах Мо, N о' РО, Qo
(рис. 165).
Очевидно" что середины сторон параллелоrрамма, т. е. точки
М, N, Р, Q, служат изображениями соотвеТСТВУЮIЦИХ точек
окружности. Найдем изображение еще какой-нибудь точки окруж-
ности, например РО. Прямая РoFо пересекает сторону ВоС о
в точке Ко; прямая QoFo пересекает сторону АоВо в точке [о.
149
6PoKoQo сп QoLoBo, так как. оба они прямоуrольные и
L. KoPoQo== L. LoQoBo как уrлы со взаимно перпенднкулярными
сторонами (PoQol.QoBo и PoKo.lQoLo, так как L.PoFoQo пря-
мой, вписанный, опирающийся. на диаметр). Итак,
PoQo KoQo 2
== .........
Qol3o LoBo 1
Это значит, что отрезок LoBo вдвое меньше отрезка K.Q,
Чтобы по данной точке Ко найти точку Lo, надо отрезок ВоЕ._
равный половине отрезка QoBo, разделить точкой Lo в том же
отношении, в каком точка Ко делит отрезок QoBo. Так KaI{ при
параллельной проекции сохраняется отношение отрезков, то для
tIолучения точки F изображения окружности берем. на отрезке
ВQ....тОчкУ К И находим точку L, пользуясь пропорцией:
KQ BL
:::::::1 ..
BQ ВЕ
Изображение точки окружности точку F най;хем в пересе-
qении прямых РК и QL.
В частности, изображением точки окружности будет точка
пересечения прямых РВ и QE, т. е. коrда точка К совпа)le'r
с В, а точка ,..L с Е.
Построив достаточное число точек изображения, соединим
их плавной кривой от руки или по лекалу и получим изобра.
жение окружности.
'Параллельная проекция окружности называется зллиn-
COJ;t. Проекция центра окружности....- точка О называется
центром эллипса, проекция диаметра окружности диамет-
pO t эллипса, проекция хорды окружности хордой эллunса.
Проекции двух взаимно перпендикулярных диаметров ОК-
ружности называются сопряженными диаметрами эллипса,
ra!l{OBbI, например, диаметры MN и PQ на рис. 165. Каждый
из них есть rеометрическое место середин хорд, параллельных
друrому диаметру. Это объясняется тем, что каждый из двух
взаимно перпендикулярных диаметров ОКРУЖНОС,!и. есть reo.
?iн:трическое место середин хорд, пара.плельных друrому диа-
метру.
(15.14 ) При помощи изображения окружности можно на
изображении основной п.носкости производить все планимет-
рические построения, не пользуясь соответствием между фи-
rурой и ее проекцией. Приведем примеры.
Задача 3. На изображении основной плоскости даны про-
екции окrужности, прямой и точки. Построить проекцию пер..
пендику.пярна к данной прямой, проходящеrо через данную
точку.
,!)О
На изображении основной плоскости даны: эллипс, ЯВJIЯ.
ЮЩИЙСЯ проекцией окружности, прямая l и точка Р
(рис. 166). Проведем прямую 1', параллельную прямой 1 и
пересекаЮJДУЮ эллипс в точках А и М, но не проходящую
через ero центр о. Далее проводим диаметр АВ и соединим
rочки М и В. Уrол АМВ есть проекция прямоrо уrла, так каи
соответствующий уrол в подлиннике является вписанным yr.
ЛО
I. опирающимся на диаметр. ПОЭТОl\IУ, ПрОБОДЯ через точ.
КУ р прямую, параллельную ВМ, получим прямую PQ, KOTO
рая будет искомой проекцией перпендикуляра.
I
Рис. 166
Рис. 167
Задача 4. Пользуясь изображением окружности, найти
проекцию биссектрисы уrла.
На рис. 167 эллипс с центром О есть проекция окру}к.
ности, L. аРЬ
проекция данноrо уrла. Проводим Oa/lla И
Ob/llb. Тоrда L.a'Ob' есть проекция уrла, paBHoro данному.
Если лучи Оа' и ОЬ' пересекают эллип'с соответственно в
rочках А' и В/, то проекция биссектрисы уrла А'ОВ' должна
пройти через середину М' хорды А'В'. Итак, ОМ' есть проек-
ция биссектрисы уrла А/ОВ/. Проведя луч Рт параллельно
лучу ОМ', найдем проекцию биссектрисы данноrо уrла.
Подобным образом проекция окружности используется и
АрИ решении друrих метрических задач на построение.
Упражнения
Поз и ц и о н н ы е з а Д а ч и н а п о с т р о е н и е.
1. Через заданную точку провести ПрЯl\IУIО, параллельную
iаданной прямой.
2. Через заданную точку провести плоскость, параллель-
. . u
ную друrои плоскости, заданноя своим с.педом и точкаи.
3. Через заданную точку провести плоскость:. параллель-
"'ую двум задаННЫ
1 прямым.
\ 51
4. Заданы три попарно скрещивающиеся прямые а, Ь и с..
Провести прямую, пересекающую а и Ь и параллельную с.
5. Найти точку. .пересечения заданной прямой с заданной
плоскостью.
6. Данную треуrольную призму пересечь плоскостью, за
данной следом и точкой на одном из боковых ребер призмы.
7. Данную пятиуrольную призму пересечь плоскостью, за
данной !ремя точками на ее боковых ребрах.
8. Данный куб пересечь плоскостью, заданной тремя точ
ками на трех ero попарно скрещивающихся ребрах.
9. Данную четырехуrольную призму пересечь плоскостью,
заданной тремя точками на трех ее боковых rранях.
10. Найти линии пересечения rраней треуrольной призмы
с заданной плоскостью.
Метрические задачи на построение
11. Точки А, В и С проекции вершин paBHocTopoHHero'
треуrольника. Построить проекцию окружности, вписанной
в этот треуrольник.
12. Точки М, N и Р проекции несмежных вершин пра
вильноrо шестиуrольника. Построить проекцию окружности,
вписанной в этот шестиуrольник.
13. Дан эллипс, являющийся проекцией окружности.
Найти построением ero центр.
14. Дана проекция окружности. Найти проекцию правиль
Horo восьмиуrольника, вписанноrо в эту окружность.
15. Параллелоrрамм ABCD есть проекция квадрата. По
строить проекцию окружности, описанной около этоrо KBaд
рата.
16. Дана проекция окружности и на ней точка. Построить
проекцию вписанноrо в эту окружность paBHocTopoHHero
треуrольника с вершиной в данной точке.
17. Для Toro чтобы две пря:мые были параллельны, необ-
ходимо, чтобы были параллельны их проекци,И. Является ли
это условие достаточным?
rЛАВЛ ПЯТАЯ
ПЕРПЕНДИКУЛЯРНОСТЬ В ПРОСТРАНСТВЕ
16. ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЯ И ПЛОСКОСТИ
(16.1) Определение 1. Прямая, перпендикулярная ко всем
прямым, принадлежащим данной плоскости, называется nep
nендикулярной к этой плоскости. Взаимно, эта плоскость Ha
зывается перnендИl(,УЛЯРНОЙ к данной прямой. Перпендику
лярность прямой р И плоскости а записывается так: р 1.. а или,
Ч10 все равно, а1..р.
Примером перпендикуляра к плосКОсти может служить
вертикальная нить отвеса, которая перпендикулярна к плос
кости пола.
Iiепосредственно из определения получаем:
Следствие 1'. ПрЯАtая пересекает плоскость, к которой она
nерnендикулярна.
Действительно, если бы перпендикуляр не пересекал дaH
ной плоскости, то в этой плоскости нашлась бы прямая, ему
параллельная, а это противоречит определению перпендику
ляра.
Точка пересечения перпендикуляра с плоскостью назы
вается основанием перпендикуляра.
Следствие 2. Прямая р', nараллельная nерnендикуляру р
к плоскости, тоже nерпендикулярна к этой плоскости.
Пусть р1..а, Р'''р и lCa. По определению 'p1..l, а в силу
параллельности и р' l..l. Итак, прямая р' перпендикулярна
к любой прямой плоскости а, значит, р' 1.. а.
Следствие 3. Прямая, nерnендикулярная к плоскости, nер-
nендикулярна и ко всякой плоскост nараллельной данной.
Пусть р1..а, "a. Проведем в плоскости I произвольную
прямую Ь. Тоrда в плоскости а можно найти прямую а, па
раллельную Ь. По определению р 1.. а, а в силу параллельности
p b. Итак, прямая р перпендикулярна к любой прямой плос
кости , поэтому р 1..\ .
153
(16.2) Существование плоскости, перпендикулярной пря
'\10Й, доказывается следующей теоремой.
Теорема 1. rеО.Аtетрическое /vteCTo точек, равноудаленных
.от двух данных точек, есть плоскость nерпен,дuкулярная
прямой, проходящей через эти точки, и делящая nоnола-м
отрезок между ними.
. Пусть Р и Р' данные точки (рис. 168). Середина О от-
.резка рр' принадлежит искомому rеометрическому месту.
Если в любой плоскости, прохо..
дящей через прямую Р Р', провес..
ти к этой прямой перпендикуляр
т, проходящий через точку О, то
все точки этоrо перпендикуляра
будут одинаково удалены от то-
чек Р и Р', так как т есть ось
симметрии этих точек. Проведем
таким же образом еще прямую 11
через точку О перпендикулярно
к РР'. Все точки ПрЯfvlОЙ n тоже
одинаково удалены от точен
р иР'.
Плоскость а, проходящая че..
рез пересекающиеся прямые т и
n, и есть ИСКО'мое Irеометрическое
",,(есто. Чтобы доказать это, покажем, во первых, что каждая
rочка плоскости а одинаково удалена от точек Р и Р', а во-
TOpЫX, что каждая точка, не принадлежащая плоскости а,
не одинаково удалена от точек Р иР'. возы\емM в плоскости
.-(1 произвольную точку Q и проведем через нее прямую, пере-
секающую прямые т и n соответственно в точках М и N. Со-
единим точки Р и Р' с точками М, N и Q; LPMN==6P'MN,
raK как РМ==Р'М, PN==P'N и сторона MN общая. Следо..
· вательно, L-PMN== LP'MN. ОТСlода находим, что и PMQ==
== P'MQ, так как РМ==Р'М, еторона MQ общая и LPMQ==
==L-P'MQ. Значит, и PQ==P'Q, т. е. все точки плоскости о
одинаково уда\лены от Р иР'.
Возьмем теперь точку А вне плоскости а и соединим ее
с Р и Р'. Пусть отрезок АР' пересекает плоскость а в точке К.
По доказанному РК==Р'К. Из 6.АРК имеем: jDK+KA>PA,
или Р'К+КА>РА, т. е. Р'А>РА. Итак, точка, не принадле-
жащая плоскости а, не одинаково удалена от Р иР'. Следо-
аательно, плоскость а и есть искомое rеометрическое место.
Остается показать, что al..PP'. Прямая р = рр' перпенди-
кулярна ко всякой прямой, проходящей в плоскости а через
rочку О, так как все точки такой прямой одинаково удалены
от Р и р' и, значит, она есть ось симметрии этих точек. Та-
кова, например, прямая q, проходящая через точки О и Q.
,НО прямая р перпендикулярна и к любой прямой, лежащеl
'z
Рис. 168
.54
'8 плоскости а и не проходящей через точку О (например
i{ прямой MN). Чтобы обнаружить это, достаточно через точ-
ку О провести прямую, параллельную к этой прямой. Тоrда
ПРЯ 1ая РР', перпендикулярная к одной из параллеЛЬНЫХ 1 бу-
дет перпендикулярна и }(, друrой. Итак, Р Р' ..L а.
(16.3) Определение 2. rеометрическое lecTO точек, равно.
удаленных от двух данных точек, называется плоскостью
СU"и'метрuи этих точек, а сами точки называются сuмметрuч-
чымll относительно этой плоскости.
Е,сли: между точками двух фиrур существует взаимноодно-
начное соответствие, и притом такое. что каждые две соот-
ветственные точки симметричны от-
носительно одной и той же плоско-
сти, то фиrуры называIОТСЯ симмет-
ричн.ым,и относительно этой плоско-
сти.
Наrлядным примером 'Симметрии
является отражение Пр ,L{меrа в
плоском зеркале. ПРИ 1еры еиммет-
ричных предметов мы lоже 1 встре-
чать на каждом lпаrу: мебель, по-
суда, некоторые инструменты и при-
боры, украшения зданий и Т. д.
Из теоремы 1 получаем следст-
-RИЯ.
СJlедствие 1. Плоскость симметрии есть zеометричеСlСое
if,eCTO точек, принадлежащих прямым, перпендuкулярным к
аанной прямой в данной на ней точке.
Следствие 2. Каждые две точки определяют единственную
flЛОСКОСТЬ, относительно которой они симметричны.
р
l
Рис. 169
(16.4) Признак перпендикулярности прямой и плоскости
Аается ь слеДУЮlней Teope 1e, которую иноrда называют тео-
ремой о двух перпендuкулярах.
Теорема 2. Чтобы данная прямая была neрпендИКУЛЯРн'а
IC пЛОСКОСТU J необходuмо и достаточно, чтобы она была nер-
n.ендuкулярна к двум пересекающuм,ся прямым, llРUн'адлежа
.,
щим, этоu плоскости.
УСЛОllие н е о х о Д и м о. Если l..L (J." т С с1 И n С (х, то ll..m
.g l..L п по определению.
Условие д о с т а т о ч н о. Пусть мы имеем: т С (х, .n С С1,
т Х п, 1 т и L n. Докажем, что 1 (J., (рис. 169). Проведем
через точку О пересечения прямых m и п прямую р П 1. Так как
l т и '11 р, то и р т. (1а таком же основании р 1.. n. Но
ror)ta. соrласно следствию 1 (п. 16.3). прямые т и n ПРИНЗJле-
i55
жат плоскости, перпендикулярной к прямой р. Итак, (1., р.
Но р" [, поэтому, cor ласно следствию 2 (п. 16.1), и l.l (1.,.
(16.5) Теорема 3. Существует единственная nлоскость
проходящая через данную точку u nерпендикулярная к дaH
ной прямой.
Рассмотрим два случая:
. 1. Данная точка О принадлежит данной прямой р. Прове
дем через точку О два перпендикуляра к прямой р, а через
эти перпендикуляры проведем пло кость а. По предыдущей
теореме a.lp. Кроме Toro, а единственная перпендикуляр"
ная плоскость к прямой р, проходящая через точку О, так
. как плоскость а есть rеометрическое место всех прямых, IIрО
ходящих через точку О перпендикулярно к прямой р.
2. Данная точка О не принадлежит прямой р. Тоrда через
точку О к прямой р проведем перпендикуляр ОМ (М ер) и
через точку М проведем к прямой р перпендикулярную плос-
кость а, как показано в предыдущем случае. Эта плоскость
содержит перпендикуляр ОМ, а вместе с ним и точку о.
Плоскость а единственна, так как точка М определяется OДHO
значно.
Следствие. Две плоскости, nерnендUКУЛЯрНbtе 1\, одной II
той же прямой, nараллеЛЬНbt между собой.
Д а н о: a.lp; (3.lp.
Д о к а з а т ъ: 'aH .
Положим, что а не параллельна . Тоrда через точку Mt
принадлежащую , можно провести отличную от плос
кость ', параллельную а, т. е. 'II а. Соrласно ,следствию 3
к определению 1, получаем, что ' .lp. Но тоrда мы получим,
что через точку М к прямой р проведены две перпендикуляр
ные плоскости, что противоречит теореме 3. Итак, all .
(16.6) Теорема 4. Существует единственная прямая, пpo
ходящая через данную точку и nерnендикулярная к данной
плоскости.
Пусть р данная точка и а данная плоскость
(рис. 170). Проведем в плоскости а произвольную прямую а
и через точку Р проведем к этой прямой перпендикулярную
плоскость , как показано в предыдущей теореме. Плос..
кость В пересечет плоскость а по прямой т, а прямую а
в точке А. Если через точку Р провести к прямой m перпен"
дикуляр р в плоскости , то р и будет исКомым перпендику
ляром к плоскости а, проходящим через точку Р.
Действительно, по построению a.l , следовательно, a.l р.
Итак, p.lm и p.la, причем ахт, так как a.lm. По теореме
о двух перпендикулярах получаем, что p.la.
Построение остается тем же, независимо от Toro, принад
лежит или не принадлежит точка Р плоскости а.
156
Если мы допустим, что через точку Р проходит друrой
перпендикуляр р' к той же плоскости а, ТО через пересекаю-
щиеся прямые р и р' можно провести плоскость ". Эта плос-
кость пересекает плоскость а по некоторой прямой с. Так как
сСа, p a, р' a, то p c и р' ..Lc. Мы получили, что в плос-
кости 'у через одну и ту же точку Р проходят два различных
перпендикуляра к прямой С, что противоречит известным. тео-
ремам планиметрии. Итак, перпендикуляр р ед'Инственный.
Следствие. Две прямые, пер-
пендUКУЛЯРНblе к одной и той же
плоскости, параллельны .между
собой.
Д а н о: p.l а; q.l а.
Доказать: pllq.
Допустим, что q не паралле'ль-
на р. Тоrда через каI<ую-нибудь
точку Q на прямой q можно про-
вести отличную от q прямую q',
параллельную р. Так как p.la и
q'llp, то и q' а на основании
. следствия 2 к определению 1. Мы
получили, что через точку Q к
плоскости а проведены два раз-
.личных перпендикуляра q и q', а это противоречит предыду-
щей теореме. Поэтому прямые q' и q совпадают и, значит, qllp.
р
Рис. 170
Упражнения
1. Является ли куб симметричной фиrурой? Сколько в нем
можно провести плоскостей симметрии?
2. Являются ли симм:етричными преД:\1етами стол, стул,
диван, чайник? Как проходит в них плоскость симметрии?
Приведите примеры друrих симметричных предметов.
3. Какова должна быть наименьшая величина зеркала,
чтобы человек Mor видеть себя во весь рост?
4. Доказать, что прямая, перпендикулярная к двум сторо-
нам треуrольника, перпендикулярна и к третьей стороне ero.
5. Доказать, что существует единственная точка, симмет-
ричная с данной точкой по 'отношению к данной плоскости.
6. Доказать, что прямая, перпендикулярная к плоскости,
перпендикулярна ко всем прямым, параллельным этой плос-
кости.
7. Доказать, что прямая и плоскость, перпендикулярные
к одной и той же прямой, параллельны между собой.
8. Доказать, что существует единственная прямая, прохо-
дящая через данную точку и перпендикулярная к двум дан-
ным скрещивающимся прямым.
9. Дана плоскость а и 'Вне ее точки А, В и С, не лежащие
на одной и той же прямой. Точки А', В', С' соответ,ственно
157
симметричны с ними относительно плоскости а. Доказать, что
6АВС== LA' В'С'.
10. Для Toro чтобы прямая была перпендикулярна к плос-
кости, необходимо, чтобы она была перпендикулярна к двум
прямым, параллельным этой плоскости. Является ли это УСЛО 4
вие и достаточным?
11. Найти rеометрическое место точек, принадлежаJЦИХ
прямым, проходящим через данную точку и перпендикуляр.
ным к данной прямой.
12. Найти rеометрическое место точек, равноудаленных 01
u u .
трех данных точек, не лежащих на однои и тои же прямои.
13. Дана прямая 1 и плоскОсть а. Найти rеометрическое
место точек, симметричных с точками прямой 1 относительно
плоскости а. Рассмотреть различные с.лучаи взаимноrо поло.
жения прямой 1 и плоскости а.
14. Найти точку, равноудаленную от четырех данных то.
чек, не принадлежащих одной и той же плоскости.
17. ПЕРПЕНДИК)'ЛЯРНОСТЬ ПЛОСКОСТЕR И ортоrОНАЛЬНыt
ПРОЕКЦИИ
(17.1) Определение 1. Плоскость, проходящая через пер-
пендикуляр к друrой плоскости, называется перпендuкуляр-
ной к этой плоскости, т. е. если p a, pC , то a.
Следствие 1. Перnендuкулярность nЛfJскосmeй есть свойство
взаимное; т. е. если а , то и а.
Если а. , то существует в плоскости сх прямая й, перпен..
дикул ярная к:':'плоскости , т. е. а С <х И a...L . Обозначим че..
рез 1 линию пересечения (Х и , а
через М точку пересечения а с 1
(рис. 171). Проведем в плоскости че-
рез точку М перпендикуляр Ь к пря-
мой l. По" определению а b, по
построению. Ь l. Итак, прямая Ь
перпендикулярна к двум пересекаю.
щимся прямым 1 и а в Пl10СКОСТИ (%9
следовательно, Ь (%. Но Ь c ,
значит, f3 а..
L Следствие 2. Если две плос/(,осnta
nерnендUКУЛЯрНbl друа к друау Q
если через точку одной из них про-
Рис. 171 вести nерnендикуляр к дРУ20Й, то
этот nерnендuкуляр принадлежит
.,
nервои nлоскостu.
Д а н о: а 1.. , Ре сх, Ре р, p.l .
Д о к а з а т ь: ре «.
Так как CI _, то существует прямая а, принадлежащая
158
н перпендикулярная к , Т. е. а С й, а 1.. ; но так как р .1. >
то р 11 а. Параллельные прямые р и а лежат в ОДНОЙ и той же
плоскости, определяемой прямой а и точкой Р, Т. е. в плоско-
СТИ сх, следовательно, р С (Х.
Следствие з. Если две nересекающueся плоскости nерnен.
дuкулярны к третьей, то 1(, ней aJCe nерnендикулярна u ЛUНUВ
их пересечения.
Дано: (х r, {3 У, (Х X , схр = р.
д о к а 3 а т ь: р у.
Возьмем произвольную точку Р на прямой р и проведем
через нее перпендикуляр к плоскости ,",. Соrласно предыду-
щему следствию этот перпендикуляр должен одновременно
принадлежать и плоскости а и плоскости . Следовательно.
он совпадает. с линией их пересечения. Итак, р 1.. 'У.
(17.2) Определение 2. Если при параллельной проекции
ароектирующие прямые перпендикулярны к плоскости проек-
.,
иии, то такая проекция называется ОРТО20нальноu.
В изложении этоrо параrрафа мы часто вместо сл()в «орта-
rональная проекция» будем для сокращения употреблять
одно слово «проекция».
Так как ортоrональная проекция является частным ви.
дом параллельной проекции, то она обладает ,всеми свойст--
вами этой проекции, рассмотренными в параrрафе 15.
Определение 3. Прямая, пересекающая плоскесть, но не
u ., u
перпендикулярная к неи, называется наклонН,оu к этои плос-
кости.
В изложении следующей теоремы мы словом «перпенди
куляр» будем называть отрезок перпендикуляра от данной
rочки до ero основания, а словом «наклонная» отрезок на.
клонной от данной точки до ее пересечения с плоскостью.
р
Рве. 172
Теорема 1. Если из одной u тои же точки провести к пло(-
I\,ости перпендuкуляр и наклонные ТО 1) nерnендикуляр коро-
че всякой наклонной; 2) наклонные, имеющие равные npoe1(
ц.uи равны между собой; 3) наклонная, имеющая большую
nроекцuю, больше наклонной с меньшей nроекцuей.
,r)
1) Пусть РО а (рис. 172), Р А наклонная. POA
'прямоуrольный с прямым уrлом при вершине о. Поэтому
катет РО меньше rипотенузы РА, т. е. РО<РА.
2) Пусть ОА проекция наклонной РА, ОВ проекция
,наклонной Р Б. Если ОА == ОБ, то прямоуrольные треуrоль-
ники РОА и РОБ равны между собой, так как катет РО у них
общий и равны еще катеты ОА и ОБ, следовательно, РА ==РБ.
3) Пусть ОС проекция наклонной РС больше ОА
проекции наклонной Р А. Отложим на ОС отрезок ОА' == ОА.
Тоrда по доказанному РА'==РА. Соrласно теореме планимет-
рии о наклонных и их проекциях будем иметь: ОС>ОА', сле-
довательно, РС>РА', т. е. РС>РА.
Теорема 2 (обратная). 1) Кратчайший из всех отрезков,
соединяющих данную точку с точками плоскости, перпенди-
кулярен' к этой плоскости; 2) равные накЛОнные имеют и рав-
ные nроекциu; 3) большая нак/tонная имеет и большую nро-
екцию.
1) Пусть отрезок РО (см. рис. 172) короче всех друrих
отрезков, соединяющих точку Р с точками плоскости а. Допу-
стим, что РО не перпендикуляр, а наклонная. Тоrда сущест-
вует перпендикуляр РО', проведенный из той же точки Р.
Но тоrда по доказанному РО' <РО и отрезок РО уже не
будет самым коротким, что противоречит условию. Итак,
PO.l. а.
2) Если имеем равные наклонные РА и РБ, то OPA==
==.60РБ по катету (общий катет РО) и rипотенузе (РА==
==РБ), следовательно, ОА==ОВ.
3) Если РС>РА, то, ДОПУС1ИВ, что ОС<ОА, мы получили
бы, что и РС <РА, а это противоречит условию. Если допу
стить, что ОС== ОА, то получим, что РС==РА, а это тоже про
тивореч т условию. Поэтому остается допустить, что ОС>ОА.
(17.3) Определение 4. Расстоянием от точки ДО плоскости
называется длина перпендикуляра, проведенноrо из этой точ-
ки к плоскости.
Целесообразность TaKoro определения обусловлена тем,
что перпендикуляр короче всех друrих отрезков, соединяю-
щих данную точку с точками плоскости.
Следствие 1. Расстояние между двумя nараллеЛЬНbl.JtИ
плоскостями везде одинаково.
Пусть alla'. Возьмем на плоскости а точки М и N и прове-
дем из них перпендикуляры ММ' и N N' к плосКОсти а'
MM'IINN' соrласно следствию к теореме 4 предыдущеrо пара-
rрафа. Отрезки же параллельных прямых между параллель-
ными плоскостями равны между собой, следовательно,
ММ' == N N'.
Следствие 2. Точки прямой, nараллельной плоскости, нахо-
дятся на одинаковых расстояниях от этой плоскости.
.160
Пусть all , а' ортоrональная проекция прямой а на
плоскость . В силу параллельности прямой а с плоскостью
имеем a'lla. Поэтому расстояния между точками этих ПРЯl\tIЫХ
везде одинаковы. А так как проекдия ортоrональная, то эти
же расстояния являются расстоянием от точек прямой а до
плоскости .
СJlедствие 3. Fеометрическим местом точек, отстоящих от
данной плоскости на расстояние, равное данному отрезку,
служат две плоскости, параллельные данной.
Пусть а данная плоскость, MN данный отрезок. Возь
мем произвольную точку О В плоскости а, проведем через нее
перпендикуляр р к плоскости и отлОжим на нем по обе сто-
роны от точки О отрезки OP==OP'==MN. Через точки Р и Р'
соответственно проведем плоскости и ', параллельные
плоскости а. Эти плоскости и являются искомым rеометриче
ским местом. Действительно, соrласно следствию 1 точка
каждой из этих плоскостей отстоит от плоскОсти а на рас-
стояние, равное отрезку MN.
Если же точка не принадлежит плоскостям и ' и лежит
между ними, то ее расстояние от а меньше MN, если же она
не находится между плОскостями и ' и лежит вне их, то
ее расстояние от а больше MN.
(17.4) Теорема 3. Если одна из двух взаимно перnендику-
лярных прямых параллельна данной плоскости, а дРУ2ая
к ней не перпендuкулярн то ОРТО20нальные nроекции этих
nрЯJJtЫХ на данную плоскость перпендикулярны дРУ2 дРУ2У.
Д а н о: а1.Ь, ally, Ь не перпендикулярна к 'У, а' проек-
дия а на у, Ь' проекдия Ь на у.
Рис. 173
Доказать: а'1.Ь' (рис. 173).
Пусть а проеКТИРУЮIцая плоскость, проходящая через а
и а', а проектирующая плоскость, проходящая через Ь
и Ь'. Очевидно, а1.у и l..y, откуда следует, что l линия
пересечения а и перпендикулярна к у. Так как [1. у, то
[1.а'; но a'lla, поэтому a.ll. Итак, a.ll и а1.Ь, значит, a1.
и, значит, а1. Ь'. Вместе с тем a'lla, следовательно. а' 1. Ь'.
l' А. и. Фетисов
161
Теорема 4 (обратная). Если одна из двух данных прямых
параллельна данной плоскости, а дРУ2ая к этой плоскости не
перпендикулярна и если ОРТО20нальные проекциu этих пря
A-tblХ перпендикулярны, то перпендикулярны и данные прямые.
Д а н о: ally, ь не перпендикулярна к 'У, а' проекция а
на 'у, Ь' проекция Ь на у, a'..L Ь'.
Д о к а 3 а т ь: a..Lb.
Сохраняя те же обозначения, что и на рис. 173, получим:
а' 1.. Ь', а' 1..[, следовательно, а' 1.. и, значит, а' 1.. Ь. НО аl!а',
поэтому а 1.. Ь.
В том частном случае, коrда прямая а принадлежит плос
кости, Т. е. совпадает со своей проекцией, теорема 3 читается
так:
Прямая, принадлежащая плоскости и перпендикулярная
к наклонной, перпендuкулярна и к ее проекции.
В этом частном случае предложение называется теореАtОЙ
о трех перпендикулярах. Это название объясняется тем, что
здесь имеется соотношение перпендикулярности между тремя
прямыми а, Ь и Ь': если а 1.. Ь, то а 1.. Ь'. ДЛЯ Toro же частноrо
случая обратная теорема формулируется так:
Прямая, лежащая в плоскости и перпендикулярная к пpo
екции наклонной, перпендикулярна и к самой наклонной.
(17.5) Рассмотрим теперь вопрос об определении уrла
между прямой и плоскостью.
Теорема 5.0стрый У20Л между наклоннЬй и ее ОРТО20наль
ной проекцией на плоскость есть наименьший из всех У2ЛОВ
между наклонной и прямыми, проходящими в плоскости через
точку пересечения этой наклонной с плоскостью.
Пусть [ данная наклонная, [' ее проекция на плос
кость й, О точка пересечения наклонной с плоскостью. Про-
ведем через О в плоскости произвольную прямую а и из
точки Р на прямой [ проведем перпендикуляр р к плоскости й.
Он пересечет проекцию [' в точке Р' (рис. 174). На прямой а
от точки О отложим отрезок ОА, равный ОР'. Сравним
LOPP' и .60РА. У них сторона ОР общая, ОА == ОР', но
РА>РР', так как наклонная больше перпендикуляра. Но если
две стороны одноrо треуrольника соответственно равны двум
сторонам друrоrо, а третьи стороны не равны, то против боль
шей стороны л жит И больший уrол, т. е. L. РОА > L. РОР'.
ОпредеJlение 5. Уrол между наклонной и ее проекцией на
плоскость в зывается У2ЛОМ между наклонной и плоскостью.
(17.6) Теорема 6. Существует единственная прямая, пepe
секающая две данные скрещивающиеся прямые и п.epпeHди
кулярная. к ним.
Пусть а и Ь скрещивающиеся прямые (рис. 175). Через
какую нибудь точку на прямой а проведем прямую mllb.
162
Через пересекающиеся прямые а и т проведем плоскость а.
Обозначим буквой Ь' ортоrональную проекцию прямой Ь на
плоскость а. Прямая Ь' пересекает прямую а в точке А, явля"
ющейся проекцией точки В прямой Ь. Прямая АВ перпенди"
кулярна к прямым а и Ь' на плоскОсти а, так как АВ ..La. НО
Ь'II Ь, следовате-пьно, AB.l Ь. Итак, прямая АВ пересекает дан-
ные прямые а и Ь и перпендикулярна к той и к друrой. АВ
единственная прямая, пересекающая а и Ь и перпендикуляр"
р
Рис. 174
р
Рис. 175
ная к ним. Чтобы доказать это, возьмем точку М на прямой а
и точку N на прямой Ь и докажем что прямая MN не мо"
жет быть одновременно перпендикулярна к прямым а и Ь.
l1ействительно, если допустим, что MN.l а и MN.l Ь, то полу-
чим, что MN.l Ь', т. е. MN.l а, следовательно, MNIIAB. Вместе
с тем проекция N' точки N находится на прямой Ь' и по-тому
N N'IIAB. МЫ получ ли, что через точку N к прямой АВ про..
ходят две различные параллельные, что противоречит аксиоме
параллельности. Итак, прямая MN не может быть одновре..
менно перпендикулярна к прямым а и Ь и, значит, прямая
АВ единственная.
Следствие. Отрезок обще20 nерRендикуляра между скре..
щивающимися прямыми короче люБО20 дРУ2020 отрезка, со-
единяюще20 точку одной из этих прямых с точкой дРУ20Й.
Действительно, из доказательства предыдущей теоремы
следует, что отрезок N N' есть перпендикуляр, а отре..
зок MN наклонная к плоскости а. Поэтому MN>lVN'. Но
N N' ==АВ, так как расстояния между параллельными равны
rvlежду собой; следовательно, MN>AB.
Определение 6. Отрезок общеrо перпендикуляра между
скрещивающимися прямыми называется расстоянием между
этими nрямыми.
Понятие о расстоянии между скрещивающимися прямыми
и об уrле между ними иrрает важную роль в элекродина-
11 · 1 63
мике. Известно, что если по двум прямолинейны'м непересе-
кающимся проводникам проходит электрический ток, то
влияние одноrо тока на друrой зависит от расстояния провод
ников и от уrла между ними. Наибольшее влияние оказывают
друr на друrа токи в параллельных проводниках. При это 1\1
оказывается, что одинаково направленные токи притяrивают
друr друrа, а противоположно направленные отталкивают,
причем сила притяжения или отталкивания обратно 'пропор
циональна ра,ССТОЯНИЮ между проводниками. Если скрещива
ющиеся проводники перпендикулярны друr к друrу, то токи
не влияют друr на друrа.
Упражнения
1. Плоскость, перпендикулярная к rоризонтальной плос-
кости, вертикальна. А как расположена плоскость, перпенди-
кулярная к вертикальной плоскости?
2. В полдень 21 июня в Москве телеrрафный столб длинор
6 М отбрасывает тень длиной 3,8 М. Вычислить «высоту солн-
ца» над rоризонтом, т. е. уrол, образуемый лучами солнца
с rоризонтальной плоскостью.
з. При изображении куба в так называемой кабинетной
проекции передняя rpaHb куба помещается параллельно плос.
кости проекции и потому изображается без искажения
в виде квадрата. Ребра, перпендикулярные к этой rрани, изо
бражаются отрезками, проходящими под уrлом в 450 к изо-
бражениям ребер передней rрани, причем длина уменьшается
вдвое по сравнению с истинной длиной. Какой уrол образуют
проектирующие прямые с плоскостью проекuии?
4. .В эллипсе, являющемся ортоrональной проекцией ок-
ружности, найти наибольший и наименьший диаметры. Дока-
зать, что эти диаметры сопряженные и что они Перпендику-
лярны друr к друrу. Заметим, что наибольший диаметр назы
вается большой осью эллипса, а наименьшей ero малой
осью.
5. Доказать, что тупой уrол между наклонной прямой и
продолжением ее проекции на плоскость есть наибольший из
всех уrло.в, образуемых этой прямой со всеми прямыми, про-
ходящими по плоскости через точку ее пересечения с этой
плоскостью.
6. Доказать, что если прямая перпендикулярна к плос-
кости, то ее ортоrональная проекция перпендикулярна к следу
этой плоскости на плоскости проекции.
7. Доказать, что если из одной и той же точки проведены
к плоскости две равные наклонные, то уrол между наклон-
ными меньше уrла между их проекциями.
164
8. Доказать, что длина проекции отрезка равна длине дан-
Horo отрезка, умноженной на косинус уrла между отрезком
и плоскостью проекции.
9. Найти rеометрическое место точек плоскости, находя-
щихся от данной точки, не принадлежащей этой плоскости,
на расстоянии, равном данному отрезку.
10. От вершины О данноrо уrла отложим на ero сторонах
равные отрезки: ОА == ОА'. Доказать, что плоскость симмет-
рии точек А и А' есть rеометрическое место точек, принадле-
жащих прямым, проходящим через точку О и образующим
равные уrлы со сторонами уrла.
11. Найти rеометрическое место точек, расстояния которых
от двух данных пересекающихся плоскостей равно данному
отрезку.
12. Найти rеометрическое место точек, равноудаленных
от двух данных пересекающихся прямых.
13. Отрезок постоянной длины скользит сВОими концами
по двум взаимно перпендикулярным скрещивающимся пря..
мым. Какую линию описывает середина отрезка?
14. Найти rеометрическое место ортоrональных проекций
данной точки на все плоскости, проходящие через данную
прямую, при условии, что точка не лежит на этой прямой.
15. Дана плоскость а и точка Р вне ее. Найти rеометриче-
ское место точек плоскости, расстояния которых от данной
точки Р не больше данноrо отрезка.
16. На изображении куба к вершине О проходят реб-
ра ОА, ,ОВ, ос. Построить изображение ортоrональной иро-
екции точки О на плоскость АВС.
17. На изображении куба построить расстояние между
двумя непараллельными диаrЬналями противоположных ero
rраней. ·
18. На изображении куба построить раССТОЯНИft между
двумя непересекающимися диаrоналями соседних rраней
куба.
19. Куб с ребром а пересечь плоскостью, проходящей
через ero центр перпендикулярно к диаrонали, и найти пло-
щадь полученноrо сечения.
20. Дана плоскость а и наклонная 1. Через точку Р на
этой плоскости провести прямую, образующую данный уrол
с прямой 1. Показать, при помощи каких элементарных по-
строений можно найти решение.
rЛАВА ШЕСТАЯ
llByrPAHHbIE И MHOrOrPAHHbIE уrлы
t 18. ДВУfРАННЫЕ УfЛЫ
(18.1) Из планиметрии известно, что каждая прямая, при
надлежащая плоскости, разделяет эту плоскость на две об
ласти, называемые полуnлоскостями. Разделяющая прямая
является общим ребром этих полуплоскостей. Отрезок, соеди
u u U
няющии две точки однои и тои же полуплоскости, не пepece
кает ребра. Отрезок, соединяющий две точки, принадлежащие
разным полуплоскостям, пересекает ребро. Две пересекаю
щиеся прямые разделяют плоскость на четыре области, каж
дая из которых называется уелом.
Совершенно аналоrичные соотношения мы имеем в про
странстве. Каждая плоскость разделяет пространство на две
области, называемые полуnространствами. Отрезок, соеди
няющий две точки одноrо и Toro же полупространства, не
пересекает разделяющую плоскость. Отрезок, Iсоединяющий
две точки, принадлежащие разным полупространствам, пepe
секает эту плоскость. Две пересекающиеся плоскости разде-
ляют пространство на четыре области, каждая из которых
называется дВУ2ранным У2ЛОМ (рис. 176).
Определение 1. ДВУ2ранным У2ЛОМ называется часть про-
странства, оrраниченная двумя полуплоскостями, имеющими
общее ребро. Полуплоскости эти Iназываются 2ранями ДBY
rpaHHoro уrла, а их общее ребро ребром двуrранноrо уrла.
Двуrранный уrол мы будем обозначать, указывая назва
ния rраней и линии их пересечения. Например, на рис. 176
изображен двуrранный уrол, обозначение Koтoporo нужно за
писать так: L 1 all13.
Определение 2. Линейным У2ЛОМ двуrранноrо уrла назы
u u
вается уrол, которыи получается в плоскости, пересекающеи
двуrранный уroл перпендикуля!рно к ero ребру.
Например, на рис. 177 двуrранный уrол al пересечен пло
скостью ", причем V l, av = a, v = b, L-аОЬ и есть линейный
yroп данноrо двуrранноrо уrла.
Теорема 1. Все линейные У2ЛЫ одноео и ТО20 же дBY2paH
Н020 У2ла равны между собой.
1.66
Пересечем двуrранный уrол al(3 (СМ. рис. 177) двумя пло
скостями V И 'У', перпендикулярными к ero ребру. В первои
плоскости по.nучил'ся уrол аОЬ, во второй а'О'Ь'. Так как
'Y 1 и 'У' 1, то 'YII,,' и вместе с тем alla' и bllb'. J}Учи qa и
О'а' одинаково направлены, так как лежат в однои и тои же
полуплоскости по отношению к прямой 1. TGK же одинаково
направлены лучи ОЬ и О'Ь'. поэтому L аОЬ == L а'О'Ь'.
о
l
..,
I
а
I
,
,
,
,
"
"
Рис. 176
Рис. 177
Непосредственно из построения линейноrо уrла получаем:
Следствие. Стороны JtинеЙНО20 У2ла nерпендикулярны 1\,
ребру дВУ2раННО20 уzла.
Например, на рис. 177 имеем: 11.. у, аС 'У, bCV, следова
тельно, l a, lJ..b.
(18.2) Определение 3. Двуrранные yr лы называются рав-
ными, если равны их линейные уrлы. Напр,имер, если дву-
rpaHHbIe уrлы L. a1 и L a'l' ' имеют соответственно линей
ные уrлы L.aOb и L.a'O'b', причем L.aOb==La'O'b', то и
al == L.\a'l' '.
Следствие. Равенство дВУ2ранных У2ЛОВ является COOTHO
шением эквивалентности.
1) Равенство двуrранных уrлов удовлетворяет условию
симметрии. Пусть L.alP ==La'l' ', т. е. LaOb ==La'O'b'. НО ОТ-
сюда следует, что и L а'О'Ь' == L. аОЬ, 'следовательно, L a'O' ' ==
== L. aO .
2) Равенство двуrранных уrлов удовлетворяет у,словию
рефлективности: L. al == L. al , так как L аОЬ == L. аОЬ.
3) Равенство двуrранных уrлов удовлетворяет условию
транзитивности. Пусть L. al1l l == L. a2l2 2, L. a2l2 2 == L.,азlз з.
Но тоrда и L.alOlbl==L.a202b2, Lа202Ь2==L.азОзЬз. В силу
транзитивности равенства линейных уrлов ПОЛУЧИl\-1:
L. al 01 Ь 1 == L. азОзЬз, следовательно, L. al l l l == L. азlз з.
Определение 4. Если ДВа двуrранных уrла имеют общую
rpaHb и ребро, а ДВе друrие их rрани находятся по разные
167
"., u
стороны от оощеи rрани, то такие уrлы называются nрuле
2ающими. Двуrранный уrол, определяемый несовпадающими
rранями этих уrлов, называется их суммой, а самые уrлы Ha
зываются слаrаемыми.
На рис. 178 имеем: Lal +L lv==
== L al'V.
Теорема 2. Линейный У20Л СУММЫ дBY
2ранных У2лов равен сумме линейных
У2ЛОВ слаzаемых.
Пусть мы имеем сумму (рис. 178):
Для получения линейных уrлов прове
дем плоскость 6, перцендикулярную к об-
щему ребру [. Тоrда в этой плоскости по-
лучатся линейные уrлы: L. аОЬ, L ЬОс,
Ри 178 LaOc, причем LaOb+ L.bOc== L-аОс.
(18.3) Теорема 3. Каждому плоскому У2ЛУ однозначно со-
ответствует дВУ2ранный У20Л, линейным У2ЛОМ к'ОТОрО20 слу-
жит этот плоский У20Л.
Пусть мы имеем плоский уrол аОЬ. Проведем через точ
ку О перпендикуляр 1 к плоскости аОЬ. Прямая 1 и луч Оа
определяют полуплоскость а. Прямая 1 и луч ОЬ определяют
полуплоскость ; L al искомый двуrранный уrол, линей
ным уrлом KOToporo служит данный уrол аОЬ; L al опреде
ляется однозначно, ввиду Toro что прямая 1 является един-
ственным перпендикуляром, проходящим через точку О, к
плоскости аОЬ.
Доказанные предложения ПОЗ1ВОЛЯЮТ привести измере
ние двуrранных уrлов к измерению соответствующих линей
ных уrлов. За единицу измерения принимается двуrранный
уrол в один rрадус, т. е. такой уrол, линейным уrлом KOTO
poro служит у ол в 10.
Определение 5. Двуrранный уrол в 900 называется пря
,MblJr!. Уrлы, меньшие прямоrо, называются острыми, большие
прямоrо тупыми.
Следствие. Трани прямоzо aByzpaHHo20 У2ла nepneHдик'Y
лярны apyz К, дРУ2У.
Действительно, если L al(3 прямой, то ero линейный уrол
LaOb тоже прямой, т. е. aJ...b. Вместе с тем lJ...a, поэтому
aJ... . Но аСа, следовательно, aJ... .
Упражнения
1. Дан 'Острый двуrранный уrол al . На rрани а взята точ-
ка А. Доказать, что из всех прямых, проходящих в rрани а
через точку А, наибольший уrол с плоскостью (3 образует пр я-
мая, перпендикулярная к ребру [.
168
l
О
'"
."
"
"
"
"
L al + L lV== L aly.
Заметим, что указанная н этой задаче прямая называетсн
линией наибольшеzо уклона или линией ската, так как по
этой линии скатывается тяжелый шар, положенный на rpaHb
а при условии, что плоскость (3 rОРИЗ0нтальна.
2. Шар весом в р KZ положен на rладкой плоскости, обра
зующей с rоризонтальной плоскостью уrол в 550. Какую нуж
но приложить силу, направленную по линии ската, чтобы
удержать этот шар в равновесии?
3. Какой уrол должна образовать наклонная плоскость с
rоризонтальной, чтобы сила, удерживающая положенный на
наклонную плоскость тяжелый шар, равнялась половине веса
тел а ?
4. Два плоских зеркала служат rраням,и двуrранноrо
уrла. Луч света, перпендикулярный к ребру и пара.ллельный
первому зеркалу, отражается от BToporo, потом отражается
от первоrо, потом вновь от BToporo, потом вновь от первоrо и,
наконец, отразившись в последний (пятый) раз от BToporo
зеркала, возвращается обратно по той же прямой. Какова
величина двуrранноrо уrла между зеркалами? (Заметим, что
"
при отражении света от плоскоrо зеркала отраженныи луч
образует с плоскостью такой же уrол, как и луч падаю-
щий) .
5. Прилеrающие двуrранные уrлы называются смежными,
u u
если несовпадающие rрани их принадлежат к однои и тои же'
плоскости. Доказать, что если смежные двуrранные уrлы рав-
ны, то rрани их перпендикулярны.
6. Если rрани одноrо двуrранноrо уrла служат продолже
нием rраней друrоrо, то такие двуrранные уrлы называются
вертикальными. Доказать, что верти.кальные двуrранные
уrлы равны между собой.
7. Полуплоскость, имеющая своим ребром ребро двуrран-
Horo уrла и делящая ero на две равные. части, называется-
бuссекторной. Доказать, что биссекторные плоскости двух
смежных уrлов перпендикулярны между собой.
8. Доказать, что площадь ортоrональной проекции пло-
cKoro мноrоуrольника рав-на площади этоrо мноrоуrольника,
умноженной на косинус уrла между плоскостью мноrоуrоль-
ника и плоскостью проекции.
9. Найти rеометрическое место точек, находящихся внутри
"
двуrранноrо уrла и равноудаленных от ero rранеи.
10. Найти rеометрическое место точек, равноудаленных
от двух данных плоскостей. Рассмотреть два случая:
1) коrда плоскости параллельны и 2) коrда они пересека
ются.
11. Найти rеометрическое место точек, ортоrональными
проекциями KOToporo на две пересекающиеся плоскости слу-
жат две прямые линии.
169
12. Найти rеометрическое место точек, принадлежащих
прямым, образующим равные уrлы с двумя пересекающими
ся прямыми и проходящим через точку их пересечения.
13. Найти rеометрическое место точек, равноудаленных от
трех данных пересекающихся прямых, не принадлежащих к
одной и той же плоскости.
14. Найти rеометрическое место точек, принадлежащих
прямым, пересекающим данную прямую под данным уrлом
и образующим с данной плоскостью уrол, равный данному.
Какие элементарные построения нужно произвести, чтобы
решить следующие задачи?
15. Дан двуrранный уrол a[ и полуплоскость а'['. Пост
роить двуrранный уrол a'l' ', равный даННОl\rIУ двуrранному
уrлу a .
16. По rрани а двуrранноrо уrла al проведена прямая 0.,
пересекающая ребро [ в точке о. Провести по rрани чер'ез
точку О прямую Ь, перпендикулярную к а.
17. На rранях а и {3 двуrранноrо уrла a[ даны соответ-
ственно точки А и В. Найти на прямой АВ точку, одинаково
удаленную от rраней.
18. На rранях а и двуrранноrо уrла a[ даны COOTBeT
ственно точки А и В. Найти на ребре [ такую точку М, чтобы
уrол АМ8 ,был прямой.
19. Дана плоскость а и наклонная т, пересекающая эту
плоскость в точке А. Провести через прямую т такую пло
скость , чтобы уrол между плоскостями а и был равен дан-
ному линейному уrлу.
19. MHOrOrPAHHbIE уrлы
(19.1) Если две пересекающиеся плоскости пересечь Tpe
тьей так, чтобы она пересекла и линию их пересечения, то
пространство разделится на восемь областей, каждая из ко-
торых называется TpexrpaHHbIM уrлом (рис. 179). '
Определение 1. Часть пространства, оrраниченная тремя
плоскими уrлами, имеющими общую вершину и попарно об
щие стороны, называется треХ2ранным У2ЛОМ.
Плоские уrлы оrраничивающие трехrранный уrол, назы
ваются ero 2ранями, их стороны ero ребрами, их общая
.,
вершина ero вершинои.
На рис. 180 показан трехrранный уrол с вершиной О, rpa
иями 'а, и у и ребрами: а = 13y, Ь = 'Уа, с = a . Трехrранный
уrол с вершиной О и ребрами а, Ь, с мы будем обозначать
символом ОаЬс.
Чтобы установить соотношения между плоскими уrлами
TpexrpaHHoro уrла, докажем следующее предложение:
Лемма. сли из точки О проведены наклонные ОА и 08 к
плоскости, причем в треУ20льнике ОАВ У2ЛЫ при основании
{70
АВ острые, то У20Л между наклонными .меньше У2ла между
их nроекциями.
Пусть ОА и ОВ наклонные, удовлетворяющие условию
теоремы (рис. 181); О' проекция точки О на плоскость а.
Так как уrлы при вершинах А и В острые, то I\bICOTa ОН в
треуrольнике ОАВ проходит
между сторонами ОА иОВ.
По теореме о трех перпендику
лярах О' Н l.AB.
Если повернуть OAB BO
Kpyr прямой АВ и положит
ero на плоскость а, то точка
О u О "
заимет положение точки
на продолжении прямой О' Н,
так как ОН>О'Н (наклонная
больше своей проекции).
LAO'H> L.AO"H как внешний
по отношению к AO'O".
На таком }ке основании
L. ВО' Н> L. ВО" Н. Складывая
почленно полученные неравен-
ства, находим:
L.AO'B> L.AO"B; но L.AO"B== LAOB, следовательно,
L.AO' В> L.AOB.
о
Рис. 180
Рис. 179
о
Рис. 181
(19.2) Теорема 1. Сумма плоских У2ЛОВ треХ2раНН020 У2ла
меньше 3600.
Докажем теорему для Toro случая, коrда все плоские уrлы
TpexrpaHHoro уrла тупые. Если это будет доказано, то тоrда
для случая меньших плоских уrлов теорема будет и подавно
справедлива.
Итак, рассмотрим трехrранный уrол ОаЬс, в котором все
плоские уrлы тупые. Возьмем на ребрах а, Ь, с COOTBeT
ственно точки А,' В, С и проведем через них плоскость 6
171
(рис. 182). Обозначим через О' прuекцию точки О на пло-
скость б. Так как уrлы ВОС, СОА, АОВ тупые, то уrлы при
основаниях ВС, СА, АВ треуrольников ВОС, СОА, и АОВ
острые и потому к проекциям тупых уrлов мы можем при
l\'lениrь лемму. Тоrда получим:
L.BOC< L.BO'C,
L. СОА< L. СО' А,
L.AOB< L.AO'B.
(JI
А
8
Рис. 182
Рис. 183
Складывая почленно эти неравенства, получим:
L.BOC+ L. СОА + L.AOB< L.BO'C+ L. СО'А+ L.AO'B.
Но последняя сумма равна 3600, следовательно, L. ВОС +
+ L.COA+ L.AOB<360°.
Необходимо заметить, что при этом построении точка О'
не может оказаться вне треуrольника АВС, так как, соединив
ее с вершинами А, В и С, мы получили бы, что один из лучей
О'А, О'В или О'С проходит между двумя друrими и тоrда
оказалось бы, что тупой уrол равен сумме двух тупых уr.пов,
чеrо быть не может, так как тупой уrол не может содержать
более 180°.
Следствие. Каждый плоский У20Л трехеранноео уела мень-
ше суммы, но больше разности двух дРУ2их еео У2ЛОВ.
Пусть мы имеем трехrранный уrол ОаЬс (рис. 183). Про
должим луч Оа за вершину О и ПОЛУЧИl\f луч Оа'. Применив
к TpexrpaHHoMY уrлу Оа'Ьс предыдущую теорему, получим:
L ЬОс+ L. сОа' + а'ОЬ<360°. (1)
Вместе с тем по свойству смежных уrлов имеем:
L сОа+ L. сОа' == 1800; L. аОЬ + L. а'ОЬ == 180°.
Складывая эти равенства, находим:
L. сОа + L аОЬ + L. сОа' + L. а' ОЬ == 3600.
172
Вычитая отсюда неравенство (1), найдем:
L.cOa+ L.aOb L.bOc>O,
откуда сразу получаем:
L. сОа+ L. аОЬ> L. ЬОс,
L. сОа> L. bOc L. аОЬ
{предполаrая, что L-аОЬ<L.ЬОс).
(19.3) Мноrоrранный уrол представляет собой обобщенное
понятие TpexrpaHHoro уrла.
Определение 2. Часть Iпространства, оrраниченная не-
колькими плоскими уrлами, имеющими общую верllIИНУ и
попарно общие стороны, называется MH020zpaHHblM У2ЛОМ.
Плоские уrлы называются 2ранями MHororpaHHoro уrла, их
стороны ero ребрами, общая вершина ero вершиной. По
числу rраней MHororpaHHbIe уrлы называются трехrранными,
четырехrранными, пятиrранными,..., n rранными.
Мноrоrранный уrол с вершиной О и ребрами а, Ь, С,..., п
()бозначается символом ОаЬс...п.
На рис. 184 изображен пяrnrранный уrол Oabcde.
Два MHororpaHHbIx уrла 'считаются равными, если между
их ребрами можно установить взаимнооднозначное COOTBeT
-ствие и если при этом равны соответствующие плоские и co
-ответствующие двуrранные уrлы.
Определение 2. Мноrоrранный уrол называется выпуклым,
-если все ero rрани находятся в одном и том же полупрост-
ранстве по отношению к плоскости любой rрани. MHororpaH-
вые уrлы, не удовлетворяющие этому условию, называются
невыпуклыми.
На рис. 184 показан выпуклый мноrоrранный уrол. Мы ви
дим, что он находится в одном и том же полупространстве
по отношению, например, к плоскости rрани аОЬ. На рис. 185
показан невыпуклый пятиrранный уrол Oabcde. Плоскость
уrла аОЬ разделяет этот уrол на две части, находящиеся по
"
разные стороны от этои плоскости.
Теорема 2. Сумма всех плоских У2ЛОВ выпУКЛ020 MHOZO
.2раНН020 уzла меньше 3600.
Докажем эту теорему методом математической индукции.
Для TpexrpaHHoro уrла теорема уже доказана. Предполаrая,
что теорема справедлива для (п 1) rpaHHoro уrла, ДOKa
же f, что она будет справедлива и для п rpaHHoro уrла.
Пусть мы имеем выпуклый п-rранный уrол Оа 1 а2 а з. . . aп laп
{рис. 186). Ввиду Toro что уrол выпуклый, он находится по одну
сторону от плоскости rрани а 1 Оа 2 и также по одну сторону
от плоскости rрани aп 10aп. Эти две плоскости имеют общую
точку О, и, следовательно, имеют общую прямую, которую
173
обозначим через Ь. У нас получился (п 1) rранный уrол
ОЬа2аз. .. aп l' в котором, по нашему предположению, сумма
B ex плоских уrлов меньше 3600. Отсюда получим:
L ЬОа 2 + L а2 0а з + . . · + L an lOb < 3600.
И первый и последний уrлы в левой части неравенства пред-
ставляют собой сумму двух уrлов. Поэтому неравенство примет
о
Рис. 184
о
Рис. 185
ь
Рис. 186
такой вид:
L ЬОа 1 + L а 1 Оа 2 + L а 2 Оаз + · · · + L an lOan +
+ L апОЬ < 3600. (2)
Рассмотрим теперь трехrранный уrол ОЬа 1 а п и применим
к нему следствие к теореме 1. Тоrда получим:
L ЬОаl + L апОЬ > L а п Оа 1 .
Если внеравенстве (2) заменить сумму уrлов L ЬОа 1 + L апОЬ
.меньшиМ, У2ЛОМ, L anOal' то от этоrо неравенство усилится и
мы ПОЛУЧИl\1:
L а 1 Оа 2 + L а 2 О а з + . . · + L aп 10aп + L а п Оа 1 < 3600.
Мы получили, что и сумма плоских уrлов n rpaHHoro уrла
удовлетворяет тому же неравенству. У'словия математической
индукции выполнены, и, следовательно, теорема доказана
вполне.
Упражнения
1. Доказать, что в TpexrpaHHoM уrле против равных пло-
ских уrлов лежат и равные двуrранные уrлы. Доказать об-
ратное предложение.
2. Доказать, что при пересечении MHororpaHHoro уrла
плоскостью, пересекающей все ero ребра, в сечении получает-
174
ся выпуклый мноrоуrольник, если мноrоrранный уrол был вы'
пуклый, И невыпуклый, если мноrоrранный уrол был невы-
пуклый.
3. Если четыре точки А, В, С и D не лежат в одной пло-
скости, то четырехуrольник ABCD называется пространствен
ным (иноrда ero называют «косым»).
Доказать, что сумма уrлов АВС, BCD, CDA и DAB в
этом четырехуrольнике меньше 3600.
4. Доказать, что если в TpexrpaHHoM уrле два плоских
уrла прямые, то и противоположные им двуrранные уrлы
тоже прямые.
5. Рассмотрим трехrранный уrо.п ОаЬс и обозначим буква-
ми а, , V соответственно плоскости ЬОс, сОа, аОЬ. Проведем
через вершину О лучи: Oa'l..a, Ob'l.. , Oc'l..v. Обозначим
а', ', ,,' соответственно плоскости Ь'Ос', сОа', а'ОЬ'. Tpex
rpaHHbIe уrлы ОаЬс и Оа'Ь'с' называются взаимно полярными.
Доказать, что
L.b'Oc'==180o L. a" и L.bOc==180o L. 'a',,',
и вывести аналоrичные равенства для остальных уrлов.
6. Пользуясь результатами предыдущеrо упражнения, до-
казать, что сумма двуrранных уrлов TpexrpaHHoro уrла боль-
ше 1800.
7. Трехrранный уrол, в котором все плоские уrлы прямые,
называется ОрТО20flаЛЬflЫМ. Доказать, что: а) если все rрани
ортоrональноrо TpexrpaHHoro уrла пересечь плоскостью, то
о
В сечении может получиться только остроуrольныи треуrоль-
ник; б) проекция вершины ортоrональноrо TpexrpaHHoro уrла
совпадает с ортоцентром треуrольника, который получается
в сечении.
8. Доказать, что если равны два TpexrpaHHbIx уrла, то
равны также и соответствующие им полярные TpexrpaHHbIe
уrлы.
9. Доказать, что TpexrpaHHbIe уrлы равны, если: а) два
плоских уrла и заключенный между ними двуrранный уrол
одноrо соответственно равны двум плоским уrлам и заклю-
ченному между ними двуrранному уrлу друrоrо; б) три пло
ских уrла соответственно равны трем плоским уrлам друrоrо;
в) плоский уrол и прилеrающие к нему двуrранные уrлы oд
Horo соответственно равны плоскому уrлу и прилеrающим к
нему двуrранным уrлам друrоrо; r) три двуrранных уrла oд
Horo соответственно равны трем двуrранным уrлам друrоrо.
10. Найти rеометрическое место точек, равноудаленных от
rраней TpexrpaHHoro уrла.
11. Найти rеометрическое место точек, равноудаленных от
ребер TpexrpaHHoro уrла.
12. Ряд параллельных плоскостей пересекает данный
трехrранный уrол. Найти rеометрические места: а) точек
175
пересечения медиан треуrольников, получающихся в сечениях;
б) ортоцентров этих треуrольников; в) точек пересечения их
биссектрис.
13. Данный трехrранный уrол пересечь плоскостью, обра
зующей равные уrлы со всеми ero ребрами.
14. Данный трехrранный уrол пересечь плоскостью, обра
зующей равные уrлы со всеми ero rранями.
15. Данный выпуклый четырехrранный уrол пересечь пло
,скостью так, чтобы в сечении получился параллелоrрамм.
Выполнить построение на проекционном чертеже.
16. Построить трехrранный уrол по двум плоским уrлам
'и двуrранному уrлу Me дy ними.
17. Построить трехrранный уrол по трем 'плоским уrлам.
18. Ортоrональный трехrранный уrол пересечь плоскостью
raK, чтобы в сечении получился остроуrольный треуrольник,
равный данному. (Для трех последних задач изrотовить мо-
дели из картона.)
ПРЕОБРАЗОВАНИЯ В ПРОСТРАНСТВЕ
э 20. СИММЕТРИЯ В ПРОСТРАНСТВЕ
(20.1) Подобно тому как в планиметрии за осНОВНое пре
образование мы приняли симмеТРИI{) относительно ПрЯl\'10Й, oc
новным преобразование 1 в пространстве будеl\f считать СИI\I
иетрию относительно плоскости, называеl\IУЮ также отраже
нием. В rлаве о перпендикулярности прямой и плоскости было
уже Д,ано определение симметричных точек и плоскости сим
:метрии. Напомним это определение.
Определение 1. Симметрией относительно плоскости а,
или отражение-м, называется такое преобразование, коrда для
каждой точки пространства А находят соответственную точку А',
причем такую, что АА' а и ОА' ::=: ОА, rде О точка пересе
чения АА' с а..
Символически симметрия относительно плоскости а (или
отражение) записывается так: а (А) = А'.
Напомним также, что в той же rлаве было доказано, что
две несовпадающие точки А и А' опредеЛЯIОТ единственную
плоскость а, относительно которой они симметричны друr с
ApyroM.
Отсюда вытекают важнейшие свойства отражения:
1. Симметрия точек относительно плоскости преобразо-
вание взаимное:
если а(А) = А', то а(А') = А.
2. Точки плоскости сим,М,етрии являются неподвиЖНЫ)1dи
(двОЙНЫ'м'и) точка'м'и nреобразования:
если М С а, то а (М) = М. И обратно, если а (М) = М, то М С а.
3. l1ря,М,ая линия nреобразуеmся си'м''м'етрией в прямую,
причем точка пересечения симметричных nря'м'ЫХ принадлежит
плоскости симметрии.
Пусть 1 не перпендикулярна к а. Находя точки, симметрич-
ные с точками [, мы убедимся, что все полученные перпендику-
ляры к плоскости а лежат в одной и той же плоскости сх,
12 А. И Фетисов
177
перпендикулярной к о (рис. 187). Обозначив буквой s проекцию l
на <1, увидим, что наше преобразование есть осева,Я СИМl'vlетрия
в плоскости (1., относительно оси s. Но s (l) 1 , поэтому и
(j (l) l'. Обратно, (j П = l. Обознач я си волом а' ,точку пере-
сечения ПрЯl'vIЫХ 1 и 1 , получим: о (ll ) = 1 [, т. е. II С о. Если
l" 0', то 111 s и l' 11 s, значит, l' 110'. Если 1 0', то она преобра-
зуется в самое себя: O' (l) 1.
Рис. 187
р
Рис. 188
4. Плоскость nреобразуется отражением в плоскость,
nричеJ.! линия пересечения плоскостей принадлежит плоскости
СUJ1tметрuи.
Пусть (1., не перпендикулярна к О' (рис. 188). Возьмем в плос
кости (1., точку Р и проведем через нее в этой плоскости прямые
т и n. Пусть O'(P) P', О'(т) т', О'(п) = n'.
Проведем через пересекающиеся прямые т' и п' плоскость (1., и
покажем, что ка)кдая точка Q плоскости (1., преобразуется в точку
Q' плоскости (1.,'. Проведем через Q прямую q, пересекающую
т и п соответственно в точках М и N; О' (М) = М'; О' (N) = lV',
O'(q) q', причем M'cq', N'Cq' и вместе с тем М'сm',
N' С n', следовательно, М' С (1.,'; N' С (1.,', значит, q' С \1.,'. Если
Q с q и О' (Q) = Q', то Q' с q', т. е. Q' с \1.,'.. Итак, любая точка
плоскости (1., преобразуется в точку плоскости (1.,'. Таким же пу-
тем можно показать, что и любая точка плоскости \1.,' преобра-
зуется в точку плоскости (1." поэтому 0(\1.,) = \1.,' и, взаимно,
о' (a') \1.,. Обозначим буквой 1 линию пересечения \1., и \1.,', т. е.
1 == (1.,(1.,'. Тоrда получим: О' (\1.,\1.,') == (1.,'(1." следовательно, \1.,\1.,' С 0',
т. е. 1 С 0'. Если (1., 11 0', то и (1.,' \1 0', т. е. \1., 11 \1.,'. Если \1., 0', то,
очевидно, \1., преобразуется в самое себя: О' (\1.,) = \1.,.
(20.2) При изучении осевой симметрии на плоскости было
установлено, что взаимно симметричные фиrуры равны, но проти-
воположно ориентироваНБI.
178
Понятие о равенстве и ориентации пространственных (h'И
u П 1
ryp дает нам повседневным опыт. ри современном серийном
ПРОизводстве наша промышленность выпускает в большом
числе различные детали, причем детали одной и той же серии
должны быть одинаковы по форме и размерам. Для достиже-
ния наиболее совершенноrо равенства таких деталей произ
водятся тщательные и всесторонние измерения их как в про
иессе производства, так и при окончательной отделке.
А
А.
А
А'
с с'
8'
Рис. 189
Рис. 190
Равенство пространственных фиrур определяется совер"
шенно так же, как и равенство плоских фиrур.
Определение 2. Две пространственные фиrуры называют-
ся равными, если между их точками можно установить вза-
имнооднозначное соответствие и если все соответствующие
друr друrу отрезки фиrур равны между собой.
Практически в некоторых простейших случаях равенство
пространственных фиrур можно проверить, вкладывая одну
в друrую. Так, например, имея две картонные модели paBHbIX
TpexrpaHHbIx уrлов, можно проверить их равенство, ВЛОЖИВ
один уrол в друrой.
Понятие о равных, но противоположно ориентированных
пространственных фиrурах дает нам сравнение предмета с
ero отражением в зеркале. Например, на изображении чело.
века в зеркале правая рука становится левой, левая пра
вой. Зеркальное изображение человека пишет левой рукой и
справа налево. Пара ботинок дает нам также пример равных,
но противоположно ориентированных фиrур.
Определение 3. Две равные пространственные фиrуры на-
зываются одинаково ориентированными, если четыре не лежа
щие в одной плоскости точки первой фиrуры А, В, С, D и co
ответствующие им точки А', В', С', D' второй фиrуры распо
ложены так, что для наблюдателя, смотрящеrо из точек D и
D' на треуrольники АВС и А'В'С', они окажутся одинаково
ориентированными. Если же при этих условиях треуrольни
ки АВС и А'В'С' будут противоположно ориентированы, то и
фиrуры называются противоположно ориентированными.
На рис. 189 показаны равные и одинаково ориентирован
ные фиrуры ABCD и A'B'C'D'. На рис. 190 показаны равные
и противоположно ориентированные фиrуры. Можно дока-
12. 179
зать, что если две произвольно взятые соответственные чет
верки точек равных фиrур окажутся одинаково ориеНТИрОI3ан
ными, то тоrда окажутся одинаково ориентированны,ми и все
соответственные четверки точек этих фиrур.
Для двух фиrур, симметричных относитеJ1ЬНО плоскости,
имеет место следующая теорема.
Теорема 1. Две фиzуры, симметричные относительно пло
скости, равны, но противоположно ориентированы.
Пусть фиrура Ф с точ
ками А, В, С, D, Е, Р,...
симметрична с фиrурой ф'
с соотвеТСТВУIОЩИ 1И точка
ми А', В', С', D', Е', Р',...
Из caMoro определения OT
ражения слсдует, что меж
ду точками фиrур сущест
вует взаимнооднозначное
соответствие. РаС'С 10ТрИМ
любую пару COOTBeTCTBeH
ных отрезков, наПРИ Iер EF
и Е' Р'. Онн равны мс}кду
собой, так I\:ак симметричны
относительно прямой s, по
которой плоскость EF Р' Е' пересекает плоскость симметрии <1.
Итак, симметричные фиrуры равны между собой.
Положим теперь, что точки А, В и С лежат в плоскости
симметрии (1. Тоrда А = А', B В', С = С'. Точка D ле}кит
вне плоскости (1, поэтому и симметричная точка D' лежит вне
плоскости <1. Но эти точки лежат по разные стороны (1. Поэто-
му для наблюдателей, находящихся в точках D и D' ориенти
ровка треуrольников АВС и А' В'С' будет противоположной.
Например (рис. 191), для наблюдателя, сrvl0трящеrо на 6.АВС из
точки D, обход по контуру происходит в направлении движения
стрелки часов, а для наблюдателя, СI\lотрящеrо из D', тот }I{e
обход совершается в противоположном направлении. Итак, сим-
метричные фиrуры противоположно ориентированы.
JJ
Рис. 19]
(20.3) Рассмотрим теперь осевую симметрию в пространстве,
которая называется также транспозицией.
Определение 4. Осевой СUМJ.tеmрuей в пространстве называет-
ся такое преобразование, коrда задается постоянная прямая s
и для каждой точки А находится соответственная точка А',
причем АА' 1.. s, о А == О А' '. rде О точка пересечения АА' с s
(рис. 192).
Важнейшие свойства осевой симметрии в пространстве можно
получить, если установить связь между осевой симметрией и
отражением.
{80
Теорема 2. Осевая симметрия в пространстве эквивалентна
дву.М, последоваmельны/';(, отражения.м. относитеЛЬflО двух взаим-
но перпеflдUКУЛЯРНblХ плоскостей, проходящих через ОСЬ СИМ..
ме/nрии.
Пусть s (А) А' (рис. 193). Проведем через s произвольную
плоскость а и плоскость а', перпендикулярную к а. Положим,
s
.D'
А
.... ...
s
Рис. 192 Рис. 193
что а (А) = А 1 и а' (А 1 ) = А 2 . Докажем, что А 2 = А'. Дей
ствительно, так как АА 1 а, то АА 1 s, а AIA2 а', следо..
вательно AIA2 s. Итак, s перпендикулярна к плоскости AA 1 A 2 ,
пересекающей s в той же точке О, в которой ее пересекает АА'.
Плоскость AAIA2 пересекает плоскости а и а' по взаИ IНО пер..
пендикулярным прямым [ и [', так как L asa' прямой. В силу
симметрии имеем: L.. AOl L lOAl' L A10l' === L l'OA 2 . Но
L lOA] + L А 1 О[' === L lOl' == 900, следовательно, L АОА2 ==
== 2 L [0[' == 180°, т. е. точки Аl И А 2 лежат на одной и той
же прямой и AIA2 s. Вместе с тем ОА == ОА 1 === ОА 2 , следо..
вательно, ОА2 == ОА', т. е. А 2 = А'.
Необходимо заметить, что если сначала были бы даны две
взаимно перпендикулярные плоскости а и а', пересекающиеся
по прямой s, то тем же построением мы доказали бы, что по-
следовательные отражения точки от обеих плоскостей экви"
валентны осевой симметрии относительно прямой s.
Следствие. Пространственные фU2УРЫ, симметричные ОТ-
носительно ОСИ, равны и одинаково ориентированы.
Так как любая осевая симметрия эквивалентна двум OT
ражениям и так как при каждом отр,ажении фиrура преобра
зуется в равную, то равными будут и фиrуры, полученные
после двух отражений (в силу транзитивнрсти равенства).
Ввиду Toro что каждое отражение меняет ориентировку
фиrуры на обратную, мы заключаем, что после двух отраже
ний, на которые разлаrается данная осевая симметрия, ориен
тация фиrуры будет тождественна с первоначальной
(см. рис. 192).
181
(20.4) Центральная симметрия в пространстве определяет-
ся совершенно так же, как и на плоскости.
Определение 5. Центральной симметрией в пространстве
называется такое преобразование, коrда дается постоянная
точка О (центр симметрии) и для каждой точки А находится
соответственная точка А' так, чтобы точка О была середи-
ной отрезка АА' (рис. 194).
I ,
I "
I А ' "
I "
I / .n'
I / . ",," .JJ
# //"
О /
",,//
..."" / I
Л'" / I
и / I
/\ A I
, 1)/ 8
с-
В'
Рис. 194
Рис. 195
Непосредственно из этоrо определения получаем следую-
щие предложения.
Следствие 1. Центральная симметрия прео6разует каждую
прямую в прямую, ей параллельную.
В силу определения каждая прямая, проходящая через
центр симметрии О, преобразуется в самое себя, т. е. в парал
.пельную прямую, так как каждая прямая параллельна самой
себе.
Пусть теперь прямая 1 не проходит через центр о. Тоrда
qерез эту прямую и центр О можно провести плоскость CJ., и этим
привести центральную симметрию прямой 1 в пространстве к цент-
ральной симметрии относительно Toro же центра в плоскости а.
Но ранее было доказано, что этим преобразованием прямая 1
преобразуется в параллельную прямую ['. Итак, О (l) = [' и,
взаимно, О (l') = [.
Следствие 2. Центральная симметрия преобразует плос-
кость в параллельную плоскость.
Если плоскость CJ., проходит через центр симметрии о, то по
определению О (О') = а. Но каждая плоскость параллельна саl\10Й
себе, и потому для этоrо случая предложение доказано. Положим
теперь, что плоскость сх не проходит через центр О (рис. 195).
80зьмем на плоскости сх произвольную точку А и проведем через
нее в плоскости а всевозможные прямые аl' а 2 , аз,. . . , а n . . .
182
Центральной симметрией эти прямые преобраЗУIОТСЯ соответ-
, " ,
ственно в прямые а 1 , а 2 , аз,. · ., а n ,. · · , проходящие через точ
КУ А', симметричную с А. При этом a 11 а 1 , a 11 а2' a IJ аз, . . .
a 11 а n , ..., поэтому все эти прямые параллельны плоскости а.
Но rеометрическое место точек, принадлежащих прямым, прохо
Дящим через одну и ту же точку и параллельным данной пло
скости, есть плоскость, паралле-
льная этой плоскости. Итак,
О (ех) = ех', причем ех' 11 ех. Взаимно:
О(ех') == ех.
(20.5) Связь центральной сим-
метрии с отражением дается сле-
дующей теоремой:
Теорема 3. ЦеНlпральная сим-
метрия в пространстве экви-
валентна трем последовательным
отражениям относительно трех Рис. 196
взаимно перпендикулярных плос-
костей, проходЯlцих через центр симметрии.
Пусть О данный центр симметрии и О (А) = А' (рис. 196).
Проведе?\f через О произвольную плоскость ех и через ту же
точку О перпендикулярную к ней плоскость . Обозначим
через С линию пересечения ех и . Проведем, наконец, через
точку О плоскость Т, перпендикулярную к с. Тоrда получим:
c.l Т, значит, exl.. r и т.
Пусть ех (А) = Аl' (А 1 ) = А2' Т (А 2 ) = Аз. Докажем, что
Аз = А'. Введем еще обозначения: T = а, тех = Ь. Первые два
отражения относительно двух взаимно перпендикулярных плос-
костей ех и эквивалентны симметрии относительно оси с. Обоз-
начим через Р, Р 1 , Р 2 соответственно проекции А, Аl' А 2 на
плоскость Т. Тоrда прямая РР2 = s, проходящая через точку О,
есть проекция прямой АА 2 на плоскость, r 1 . Отражение точки
А 2 от плоскости r тождественно с осевой СИI\iметрией относи-
тельно прямой s, следовательно, s (А 2 ) Аз. B leCTe с тем
L РОА + L АОА 2 + L А 2 ОР 2 === 1800. Кроме Toro, L РОА
L А 2 ОР 2 L Р 2 ОА з в силу симметрии, поэтому L АОА 2 +
+ L А 2 ОР 2 + L Р 2 ОА з === 1800, или L АОА з === 1800, т. е. точки
А, О, Аз лежат на одной и той же прямой. Но ОА === ОА 1 =='
=== ОА 2 == ОА з , т. е. ОА == ОА з , значит, Аз == А'.
Обратно, если первоначально даны три взаимно перпенди-
кулярные плоскости (х, и f, пересекающиеся в точке О, то
тем же самым построением можно доказать, что последователь-
ное отражение любой точки от плоскостей ех, и f эквивалент-
но центральной симметрии относительно точки О.
Для упрощении чертежа прямая AAs на рис. 196 не показана.
{83
Следствие. Центральная симметрия преобразует данную
фИ2УРУ В равную, но противоположно ориентированную.
Это есть результат Toro, что -центральная симметрия эк
вивалентна трем отражениям. Каждое отражение сохраняет
равенство фиrур, но меняет их ориентацию. Поэтому после
трех отражений фиrура преобразуется в равную, но противо
положно ориентированную.
Упражнения
1. Дана плоскость о' и не принадлежащие ей точки А и
В. Найти на плоскости о' такую точку М, чтобы сумма отрез
!{ов МА и МВ была наименьшая. Рассмотреть случаи, коrда
точки А и В находятся по разные стороны и ПО одну сторону
ОТ плоскости.
2. В условиях предыдущей задачи найти такую точку N
на плоскости а, чтобы разность отрезков NA NB была наи
большая.
3. Доказать, что центральная симметрия эквивалентна
осевой симметрии и последующему отражению, причем ось
симметрии и плоскость СИ lметрии взаимно перпендикулярны
и проходят через центр 'СИМl\1етрии.
4. Если ребра TpexrpaHHoro уrла продолжить за ero Bep
шину, то получим новый трехrранный уrол, «вертикальный» I
С первоначальным. Будут ли вертикальные TpexrpaHHbIe уrлы
равны? Как они ориентированы' относительно друr друrа?
5. Доказать, что середина любоrо отрезка, соединяющеrо
точки двух парал.пельных плоскостей, есть центр симметрии
этих плоскостей. i
6. Найти rеометрическое место центров симметрии двух
параллельных плоскостей.
7. При осевой симметрии прямая преобразуется в пря
мую. Рас.смотреть различные случаи, коrда данная прямая:
а) пересекает ось симметрии; б) паралле.пьна ей; в) скрещи
вается с ней. В последнем случае указать, как проходит об
щий перпендикуляр к данной прямой и к симметричной с ней.
8. Осевая симметрия преобразует плоскость в плоскость.
PaccrvloTpeTb случаи, коrда плоскость: а) пересекает ось СИМ
метрии, б) параллель а ей. Как проходит линия пересечения
симм:етричных плоскостей, если они пересекаются?
9. Внутри двуrранноrо уrла дана точка. Провести через
эту точку прямую, перпендикулярную к ребру уrла, и притом
так, чтобы отрезок этой прямой между сторонами уrла дe
u «.о
лился это и точкои пополам.
1 Термин «вертикальные уrлы» происходит от LТIатинскоrо слова ver-
tex вершина. У вертикальных уrлов общая вершина.
{84
10. в пространстве даны равные отрезки АВ и А' В'. Най
ти наименьшее число отражений, преобразующих отрезок
АВ в А'В'.
11. В пространстве даны равные треуrольники АВС и
А' В'С'. Найти наименьшее число отражений, преобразующих
первый треуrольник во второй.
12. Дано изображение основной плоскости <1 И двух точек
А и А', симметричных относительно этой плоскости. ДOKa
зать, что построить точку, симметричную с любой заданной
точкой В, можно при помощи только одной линейки.
21. ДВИЖЕНИЯ В ПРОСТРАНСТВЕ
(21.1) В планиметрии мы неоднократно пользовались
ва)I{НЫМ понятием вектора. Не менее значительную роль иr--
рает это понятие и в стереометрии.
Определения, основные операции
и свойства операций над векторами
остаются теми же, что и в планимет
рии [см. (4.1)].
ПростеЙшим пространственным
u
движением является параЛJIеJIЬНЫИ
перенос, или трансляция.
Определение 1. П араллеЛЬНblМ В
переносом, или трансляцией, в про-
странстве называется такое преоб
разование, коrда каждой ТОЧI<е А
данной фиrуры приводится в COOT А
веТСТIЗие такая ТОЧI{а А', что В'ектор
АА' равняется постоянному BeKTO Рис. 197
ру т вектору переноса (рис. 197).
Символически преобразование записывается так:
(А) == А'.
Заметим, что, в отличие от ранее изученных преобразова--
ний, перенос не обладает CBO CTBOM взаимности:
если т (А) = А 1, то m (А ') фА.
Непосредственно из определения получаем следующее СВОЙ
СТВО переноса.
Следствие. Переное nрео6разует вектор в равный вектор.
--+
Пусть АВ данный вектор, т вектор переноса. По опре-
---+
Аелению m (А) = А', m (В) = В', причем АА' == ВВ' === т. При..
18
бавим к обеим частям полученноrо равенства вектор А'В
и получим:
.
АА'+А'В==А'В+ВВ', или АВ==А'В'.
(21.2) Связь параллельноrо переноса с отражением дается
следующей теоремой.
Теорема 1. Всякий перенос эквивалентен последовательным
отражениям от двух nараллельных плоскосmей, nерnендику-
ЛЯрНbLХ к вектору переноса и
находящuхся дРУ2 Oln дРУ2а на
расстоянии, вдвое ./ e ньшел1, мо-
дуля этО20 вектора.
Пусть мы иrvlеем перенос с
---+
вектором т и, положим, т(А) ==
== А' (рис. 198). Возьмем про-
извольную плоскость а.1. т и
пусть а (А)==А 1 . Так как AA' a
и АА 1 .1. а, то точки А,
А 1 И А I лежат на одной и той
Рис. 198 же прямой. Проведем теперь
плоскость СИl\lметрии а' .точек А 1 и А', т. е. а' (A 1 ) = А'. Так
.как a...L АА', то а 11 а'. Пусть S и S' соответственно точки
пересечения прямой А А I С плоскостями а и а'. По определе-
нию отражения получрм:
AS==SA 1 ; A 1 S'==S'A'.
В!\lесте с тем, по определению сложения векторов, имеем:
. ..... ....
AS + SA 1 + A1S' +S' А' == т, или 2SA} + 2A 1 S' == т,
> ---+
2 (SA 1 + A1S') == т, 2SS' == т и окончательно:
---+
т
SS'== .
2
11так, плоскости а и а' параллельны и вектор расстояния
от (J к а' равен половине вектора переноса.
Обратно, такими же рассуждениями нетрудно доказать,
что последовательное отражение от двух взаимно параллель
ных плоскостей эквивалент о переносу, вектором KOToporo
является удвоенный вектор расстояния между плоскостями.
Следствие 1. Перенос в пространстве преобразует даННУ10
ФU2УРУ в ФU2УРУ, равную и одинаково ориентuрованную.
18 6
Так как перенос эквивалентен двум отражениям и каждое
отражение сохраняет равенство, но меняет ориентацию фи..
ryp, то при двух отражениях, очевидно, сохраняется и равен-
ство, и ориентаuия фиrур.
Следствие 2. Два последовательных переноса эквивалент
ны одному переносу, вектор КОТОРО20 равен сумме векторов
составляющих переносов.
Пусть первый перенос определяется вектором т, второй
I ""'"*
вектором n. Тоrда т (А) ==А', n (А') ==А". Но АА'==т; А'А"==
.... ""'"* ....
==n, АА' +А'А" ==АА" ==т+n, следовательно, (т+n) (А) = А".
Заметим, что перенос фиrур весьма часто ВСТQечается в
производственной практике. Это имеет место всеrда, коrда
данное тело совершает так называемое поступательное дBи
жение. Такое движение, например, производят строrающие
инструменты рубанок и фуrанок, таково же движение Ba
rOHa, коrда он двиrается по прямолинейному участку желез
нодорожноrо пути.
(21.3) Вторым видом пространственноrо движения являет..
ся вращение ВОКРУ2 оси.
Определение 2. Вращением ВОКРУ2 оси называется такое
преобразование, при котором задается постоянная прямая
r ось вращения и для каждой точ-
ки А определяется соответствующая
точка А', лежащая в плоскости а, про
ходящей через А и перпендикулярной
к " и притом так, чтобы уrол АОА'==
==00 (rде о точка пересечения а с ')
был постоянным по величине й Ha
правлению (рис. 199).
Чтобы определить направление Bpa
щения, устанавливают сначала поло
жительное направление на оси r и счи-
тают вращение положительным, если
для наблюдателя, находящеrося с той
стороны плоскости а, куда направлен
луч оси " движение от А к А' проис
ходит в направлении, противоположном движению стрелки
часов.
Преобразование точки А в А' вращением с осью, и уrлом
U) записывается символически так: r (А) А'.
Вращение представляет собой движение, которое осуще..
ствляется в очень большом числе механизмов, начиная от
вращения зубчатых колес в карманных часах и кончая rи..
rантскими роторами турбин на rидроэлектрических станциях.
Основные свойства вращения определяются ero связью с
симметрией относительно плоскости.
r
Рис. 199
187
Теорема 2. Вращение ВОКРУ2 оси эквивалентно последова
тельным отражениям от двух плоскостей, пересекающихся по
оси вращения; линейный У20Л между плоскостями равен пo
ловине У2ла вращения.
Пусть r 00 (А) = А' (рис. 200). Проведем через r произволь
ную плоскость а. Пусть А 1 точка, СИ ,Iметричная с А OTHO
сительно 0', Т. е. о' (А) == А 1 .
При этом получим: ОА == ОА',
ОА == ОА 1 , следовательно, ОА' == ОА 1 .
6 Вместе с тем АА 1 а, значит, АА 1 r
и, значит, точка А 1 lIТ}ежит в той же
плоскости а, которой принадлеясат
точки А, А', о.
Проведем терерь плоскость симмет
рии о' точек А 1 и А', т. е. о' (А 1 ) == А'.
Так как ОА 1 == ОА', то ОС 0", а так
как о' l.. C:J, и r с/." то r С о'. Итак,
два последовательных отражения точки
А от о' и 0" преобразуют ее в точкуА'.
Пусть S и S' соответственно точ-
ки пересечения АА 1 с о И А 1 А' с а'. В силу симметрии по-
лучим:
.......
,.
А'
'"
,
,
I
\ с1.
,
"
....
"-
"
о
l'
Рис. 2l)O
L AOS == LSOA 1 , LA 1 0S' == LS'OA'.
Далее имеем:
LAOS + LSOA 1 + LA 1 0S' LS'OA' == ю,
т. е.
2 LSOA 1 + 2 LA 1 0S' 00, или 2 (LSOA 1 + LA 1 0S') == (О.
И окончательно:
(J)
LSOS' ==т.
Обратно, два последовательных отражения от двух пере
секающихся плоскостей эквивалентны вращению BOKpyr пря
мой их пересечения на уrол, равный удвоенному ли ейному
уrлу между плоскостями. Это можно доказ ть такими же
рассуждениями, какими мы ПОЛЬЗ0вались при доказательстве
теоремы.
Следствие. Вращение преобразует данную фИ2УРУ в paB
ную и одинаково ориентированную.
Так же как и в случае переноса, это обусловлено тем, что
каждое вращение эквивалентно двум последовательным OT
ра} ениям, в силу чето сохраняется и равенство, и ориентация.
(21.4) И перенос, и вращение в пространстве эквивалент
ны также двум последовательным симметриям относительно
оси.
188
Теорема 3. Перенос эквивалентен. двум последовательным
симметриям относительно двух взаимно параллельных oce
перпендикулярных к вектору переnоса.. При ЭТОJt расстояние
JteJ.'Cay осями равно половине вектора переноса.
Пусть m (А) = А'. Проведем произвольную прямую s 1.. m
(рис. 201). Через эту прямую проведем плоскость о также
...
перпен икулярно к т. Далее через эту же прямую s проведем
,
две совпадающие плоскости о и
01' перпендикулярные к плоско
сти о. Наконец, проведем еще
, .
плоскость 01' параллельную пло
скости о, так, чтобы расстояние
между ними было равно \
ПОЛОВ:1не длины вектора переноса.
Пусть s' линия пересечения пло
,
скости <11 С совпадающими пло
СКОСТЯl\lИ (1' И <11.
Произведя по ледовательные
отражения точки ,,4. от всех че..
TЫp X плоскостей, мы убедимся,
что преобразование это приве
дет к двум последовательным
отражениям от параллельных
,
плоскостей о и <1 н так как отра)кение от двух совпадающих
плоскостей друr друrа взаимно уничтожают. Но, как было уже
доказано, два последовательных отражения от параллельных
, -+
плоскостей о и (11 эквивалентны переносу с вектором т, пре-
образующему А в А'.
Кроме Toro, последовательные отражения от двух перпен-
дику.лярных плоскостей о и о' эквивалентны симметрии с осью
d '
S, а последовательные отражения от плоскостеи 01 и 01 экви-
валентны симметрии с осью s'. Итак, этот же переное эквива-
лентен ДВУ11 последовательным симметриям с параллельными
осями s и s', перпендику лярными к вектору переноса. При
этом расстояние между осями равно половине длины вектора
переноса и одну из осей можно провести произвольно.
Очевидно, это же Cal\10e построение показывает, что две
последовательные симметрии относительно любых двух па
раллельных осей эквивалентны переносу, длина вектора КОТО-
poro вдвое больше расстояния между осями.
(21.5) Ана.поrично доказывается, что и вращение эквива
лентно двум последовательным осевым симметриям.
Теорема 4. Вращение с осью r и У2ЛОМ U) эквивалентно
двум последовательным симметриям относительно двух осей,
.s
т
Рис. 201
189
nересекающих ось враlцения в одной и той же точке и пер"
nендикулярных к ней. при этом У20Л .Аtежду осями вдвое
меньше У2ла вращения и имеет одинаковое с ним направле-
ние. Одну из осей симметрии можно провести произвольно.
Рассмотрим вращение с осью r и уrлом (о и пусть 'ro (А) =
= А' (рис. 202). Возьмем на оси вращения произвольную точку
О И проведем через нее перпен-
дикулярно к r ПРОИЗВОЛЬНУIО
ось симметрии s. Через оси r и
s проведем плоскость а, а пер
пендикулярно к (J через прямую
s проведем две совпадающие
плоскости (J 1 И а'. П роведем, Ha
конец, через r еще одну пло..
,
скость а1 И притом так, чтоБыl
,
уrол (Jr(J1 по величине и направ
(J)
лению был равен """"2' т. е. поло-
вине уrла вращения. Пусть s' ли-
,
ния пересечения аl с совпадаlОЩИ ПI
плоскостями а' и <11.
Производя последовательные отражения точки А от всех
четырех плоскостей, мы убедимся, что это преобразование при
,
ведет к двум отражениям от плоскостей (J и <11, так как по-
следовательные отражения от совпадающих плоскостей а' и а]
друr друrа взаимно уничтожаIОТ. Но последовательные отраже
,
ния от пересекающихся плоскостей (J и а1, как мы уже виде
ли, эквивалентны враIIl,ению с осью r и yr лом ((), преобразую
ЩИМ точку А в А'.
Отражения же от двух перпендикулярных плоскостей а и
а' эквивалентны симметрии с осью s; а отр жения от перпен-
,
дикулярных плоскостеЙ а 1 и а1 эквивалентны симметрии с осыо
5'. Уrол sOs' есть не что иное, как линейный уrол двуrранноrо
, <о И
уrла ara 1 , Т. е. равен 2"". так, наше вращение можно заме-
,
нить двумя осевыми симметриями с осями s и s, пересекаю-
щимися в точке О на оси вращения. При этом s.l (, s' ..1 r и
w
LsOs' "2. Кроме Toro, одну из осей можно провести про-
извольно.
Обратно, из Toro же caMoro построения нетрудно убедить
ся, что всякие две симметрии с перееекаЮЩll 1 нея осями
квивалентны одному вращению, ось KOToporo перпенд'ику
лярна к осям симметрии и проходит через точку их пересече
ния, а уrол вращения вдвое больше уrла между осями СИМ--
метрии.
,
r
Рис. 202
t !JO
11TaK, мы видим, что каждое днижение в пространстве,.
Т. е. каЖДЫЙ перенос и каждое вращение, может быть разло
жено как на два последовательных отражения, так и на две
последовательные осевые симметрии.
(21.6) В планиметрии было доказано (теорема Вернул-
ли Шаля), что две равные и одинаково ориентированные
фиrуры на плоскости всеrда можно преобразовать друr в
друrа одним движением, т. е. либо переносом, либо вращени
ем. В стереО Iетрии наиболее общим ВИДОl\I движения, при по
fОЩИ KOToporo всетда можно преобразовать одну из двух
равных и одинаково ориентированных фиrур в друrую, яв-
ляется винтовое движение, объединяющее перенос и вра-
щение.
Определение 3. Винтовое движение есть вращение, соеди"
ненное с переносом, вектор KOToporo сонаправлен с осью вра-
щения.
Таким образом, винтовое движение вполне определяется за-
данием оси и уrла вращения и вектором переноса. Так как
направления оси вращения и вектора переноса совпадают, то
...
все преобразование можно записать так: r ro (А) = А', rде СИl\I-
вол r обозначает и направление оси вращения, и величину ве-
ктора переноса, а символ U) величину и направление уrла
вращения. Например, обозначение
5 п (А) == А'
з
показывает, что для преобразования точки А в точку А' НУ)К-
-+
НО переместить А в направление оси r на 5 единиu длины и
n
повернуть около то/1 же оси на уrол 3" (600) в поло}китель
ном направлении.
Винт совершает винтовое движение, коrда ero ввинчивают
в какой нибудь предмет. Различают правые винты с поло-
жительным уrлом вращения и левые с отрицательным.
В большинстве случаев на практике применяются правые
винты.
Направление электрическоrо тока, идущеrо по прямоли
нейному проводнику, и окружающие ero KpyroBbIe силовые
линии маrнитноrо поля образуют правую винтовую систему.
Теорема 5. ДЛЯ ТО20 чтобы данную nространственную фи
2УРУ преобразовать в фИ2УРУ, равную u одинаково ориентu
рованную, достаточно применить не более четырех последова-
тельных отражений.
Пусть мы имеем фиrуру Ф с точками А, В, С, D, Е,...,
которые не при надлежат одной и той же плоскости, и равную
{91
и одинаково ориентированную с ней фиrуру ф' с COOTBeTCTBeH
ными точками А', В', С', D', Е',... Проведем плоскость сим
метрии 0"1 точек А и А'. Тоrда получим фиrуру Ф 1 с точками
А', В1' С 1 , Dl' Еl'...' rде 0"1 (В) В 1 , 0"1 (С) == С 1 , 0"1 (D)
== Dl' 0"1 (Е) Е 1 ... При этом фиrура Ф 1 равна, но противо
положно ориентирована с фиrурой Ф'.
Проведем плоскость симметрии 0"2 точек В' и 81. Так как
А' В ' == А' В 1 В силу равенства фиrур, то эта плоскостр пройдет
через, точку А'. Мы получим: O" (A') == A', 0"2(81) == В',
0'2(С 1 ) == С 2 , 0"2 (D 1 ) D2' 0"2 (Е 1 ) == Е 2 , . . . , rде точки А', В', С 2 ,
D2' Е2' · . · принадлежат новой фиrуре Ф 2 , равной и одинаково
ориентированной с Ф. Проведем плоскость симметрии О"З точек
С' и С 2 . Так как А'С' == А'С 2 И В'С' == В'С 2 , то плоскость О"З
пройдет через точки А' и В' и мы получим: О"з(А') = А',
(Jз(В') В', О"З (С 2 ) = С', О"з (D 2 ) == D з , О"З (Е 2 ) == Е з , . . ., rде
точки А', ,В', С', D з , Е з , . . . принадлежат фиrуре ф з , равной,
но противополо»сно ориентированной с фиrурой Ф.
Точки А', В', С' не лежат на одной и той же прямой, так
как если бы было, что А' С В'С', то тоrда точки А', В', С',
D' лежали бы в одной и той же плоскости, определяемой этой
прямой и точкой ' D'. I-Iтак, А' g:. В' С', следовательно, точки
А', В', С' определяют проходящую через них плоскость 0"4.
Так как фиrуры Ф и Ф З противоположно ориентированы, то
точки D' и D з лежат по разные стороны от 0"4. Вместе с тем
в силу равенства фиrур имеем: А' D' == А' D з , В' D' ==В' Dз,
C'D' == С'D з , т. е. плоскость симметрии точек D' и D3 прохо-
дит через точки А', В' и с' и, значит, совпадает с плоскостью
. 0"4. На том »се основании 0"4 есть плоскость симметрии точек
Е' и Е з и вообще Лlобой пары соответственных точек фиrур
ф' и Фз.
Итак, четвертое отражение от плоскости 0". преобраэует
фиrуру Ф З в Фитуру Ф'.
Следствие. ДЛЯ ТО20 чтобы данную nространственную фи
2УРУ nреобразовать в равную и одинаково ориентированную,
достаточно произвести не более двух последовательных дви-
жений.
В предыдущей теореме было доказано, что для преобраэо
вания фиrуры Ф в равную и одинаково ориентированную, дo
статочно произвести отражение от четырех плоскостей 0"1, 0"2,
аз, 0"4. Но отражения от плоскостей 0"1 и 0"2 дают одно движе
иие, а отражение от плоскостей О"З и 0"4 дают друrое движение.
При этом возможны такие комбинации:
1) Оба движения переносы. Тоrда 'соrла'сно следствию к
теореме 1 все преобразование приводится к одному переносу.
2) Первое движение перенос, второе вращение.
3) Первое движение вращение, второе перенос.
4) Оба движения вращения.
192
(21.7) Выводы, полученные в предыдущем пункте, позво-
ляют доказать наиболее общее предложение о движении в
пространстве.
Теорема 6. Существует единственное винтовое движение
nреобразующее одну из двух равных и одинаково ориентиро:
ванных фИ2УР в дРУ2УЮ.
Доказательство этой важной теоремы мы разобьем на не-
сколько частей.
-\
"
Рис. 203
Рис. 204
1) Докажем сначала, что достаточно не более двух осе-
вых симметрий, чтобы преобразовать данную фиrуру в paB
ную и одинаково ориентированную. Действительно, соrласно
предыдущему следствию, для TaKoro преобразования необхо
димо не более двух двмженин. Если оба движения nepeHO
СЫ, то они приводятся К одному переносу, который разлаrает
ся на д'ве осевые симметрии.
......
Положим, первое движение перенос с вектором т, BTO
рое движение вращение с осью r и уrлом ы. Разложим пер
вое движение на две симметрии относительно осей 5} и 52,
второе на две симметрии относительно осей 5з и 54 (рис. 203).
При этом, пользуясь известным произволом в выборе осей,
мы проведем ось 52 так, чтобы она была перпендикулярна к
т и в то же время пересекал а бы ось вращения r и была бы
перпендикулярна к ней. Для этоrо достаточно через какую
нибудь точку О оси r провести прямую, параллельную т, и че-
рез эту же точку провести перпендикуляр к плоскости, опре-
деляемой этой прямой и осью вращения. Ось 5з пусть совпа-
дает к осью 52. Ось 5} проведем параллельно оси 52 так, чтобы
т
вектор расстояния от 51 к 52 был бы равен 2:. Ось 54 прове
дем через ту же точку О на оси , и перпендикулярно к ней
(J)
и под уrлом 2 к оси 53. Произведя последовательные симмет
1 3 А. и. Фетисов
193
рии относительно осей 51' 5 z , 5з, 54' МЫ УВИДИМ, что симметрии
52 и 8з друr друrа взаимно уничтожают и остаются лишь две
симметрии 8} и 84.
Случай вращения и переноса совершенно таким же путем
приводится к двум осевым симметриям.
,
Рассмотрим, наконец, два вращения r о) и r 0)' (рис. 204).
Разложим первое на симметрии 81' 52' а второе на симметрии
8з, 84. При этом оси 52 И 5з проведем по общему перпендику-
u , u ,
ляру осеи вращения r и r , которыlи пересекает оси r и r со-
ответственно в точках О и О'. Ось 81 проведем через О пер-
(J)
пендикулярно к r под уrлом 2'""" к 53. Ось 54 проведем через
(J)'
О' перпендикулярно к " под уrлом 2 к oc 53. Производя по-
следовательно симметрии к осям 81, 52' 5з, 54, увидим, что сим-
метрии 82 и 8з друr друrа взаимно уничтожают и остаются
лишь две симметрии с осями 81 И 84.
2) Всякие две осевые симметрии эквивалентны винтовому
движению.
Пусть мы имеем две симметрии с осями 51 И 54. Проведем
к ним общий перпендикуляр " пересекающий пер'вую ось в
точке О, вторую в точке О'. Проведем через точку О две
совпадающие оси 82 и 8з, парал-
,.' лельные оси 8!. Тоrда симметрии с
пересекающимися в точке О осями 51
И 82 дают вращение с осью r и
уrлом ffi == 2 L8 1 08 2 , а симметрии с
параллельными ОСЯ 1И 8з И 84 даю'l'
......
перенос с вектором т == 200', направ-
ленным по оси r (рис. 205).
Если это же построение прои
вести при точке О', то наше преоб..
разование разложится на винтовое
движение с той же осевой симмет-
рией сначала и с тем же вращением
РIIС. 205 потом. Отсюда мы заключаем, что
lН Р ZaOK вращения и переноса в вин-
товом движении безразличен.
......
Итак, существует винтовое движение r ю , прео6разующее
данную фиrуру Ф в равную и одинаково ориентированную фи-
rypy Ф'. Если, в частности, оси симметрии 81 и 54 параллельны,
то движение приводится к переносу (ы == О). Если оси 8. И 5.
---+
пересекаются, то движение приводится к враlцению (' == О).
3) Это Винтовое движение единственно. Действительно, в
винтовом движении есть одна, и только одна, неподвижная
прямая ось '. Поэтому если мы допустим, что существует
tl.t
Jtpyroe винтовое движение, осуществляющее это же преобра...
зование с друrой осью ,', то, следовательно, преобразование
имеет две неподвижные прямые, а это противоречит определе-
нию в'Интовоrо движения.
Упражнения
1. Какому преобразованию эквивалентны две последова..
rельные центральные симметрии?
2. Не прибеrая к замене осевых симметрий отражениями,
доказать, что две симметрии с параллельными осями эквива-
лентны переносу, а две симметрии с пересекаЮЩИ IИСЯ осями
эквивалентны вращению.
3. Доказать, что если даны две равные и одинаково ори...
ентированные фиrуры с соответственными точками А и А', В
и В', С и С', в которых АВ==А'В' и АС==А'С', то существует
единственный перенос, преобразующий эти фиrуры друr в
друrа.
4. Доказать, что если две равные и одинаково ориентиро..
ванные фиrуры имеют совпадающую пару соответственных
rочек, то существует единственное вращение, преобразующее
эти фиrуры друr в друrа.
5. Доказать, что если оси двух. вращений пересеl{аютс ,
то два таких последовательных вращения эквивалентны одно--
му вращению.
6. Вращение с осью, преобразует плоскость а в плоскость
а'. Какие положения может занимать линия пересечения этих
плоскостей относительно оси '?
7. Вращение с осью r преобразует прЯ..мую 1 В прямую 1'.
I(aKoe положение по отношению друr к друrу занимают об...
щие перпендикуляры, определяющие расстояние между 1 и r
и :r-,1ежду l' и '?
8. Доказать, что ось вращения есть rеометрическое MeCТ(J
точек, равноудаленных от двух соответственных точек в этом
вращении.
9. Найти достаточное число отражателей, прео'бразующих
данную фиrуру в равную, но противоположно ориентированную.
10. Доказать, что два последовательн ых винтовых движе-
ния эквивалентны одному винтовому движению.
11. Доказать, что достаточно двух осевых симметрий и oд
Horo отражения, чтобы преобразовать данную фиrуру в ра....
ную противоположно ориентированную.
12. Доказать, что. достаточно одноrо отражения и одноr.
вращения, чтобы преобразовать данную фиrуру в равную' 11
противоположно ориентирова ную.
13. На проекционном чертеже задан вектор переноса т jJ
llABC. Построить изображение треуrольника А' В'С', в KOTO
рый заданный треуrольник преобразуется этим переносом.
\
13* '115
14. На изображении основной плоскости даны проекции
окружности и изображение оси вращения " проходящей че
рез центр окружности перпендикулярно к ее плоскости. Про
извести вращение заданноrо треуrольника АВС на уrол 750
около оси /".
15. На изображении основной плоскости даны изображе-
.
ния окружности И оси , винтовоrо движения, проходящей че
рез центр окружности перпендикулярно к ее плоскости. Про
извести винтовое движение заданноrо треуrольника АВС OKO
---+
ЛО оси, имея заданный вектор r и уrол (О == 60°.
22. rОМОТЕТИЯ И ПОДОБИЕ В ПРОСТРАНСТВЕ
(22.1) rомотетия в пространстве определяется совершенно
так же, как и на плоскости.
Определение 1. Fомотетией в пространстве называется Ta
кое преобразование, коrда задается постоянный центр S и
с
D
Рис. 206
Рис. 207
для каждой точки А находится соответственная точка А' так,
SA'
чтобы A'CSA и сохранялось постоянное отношение. SA == k.
Если k>O, то векторы S.4 и S.4' сонаправлены и rомотетия
---
называется положитеЛ!;JНОЙ; если k<O, то векторы SA и SA'
противонаправлены и rомотетия называется отрицательной.
rомотетия с центром S и коэффициентом k, преобразующая
точку А в точку А', символически записывается так: Sk (А) ==
= А'.
На рис. 206 изображена положительная rомотетия с коэф-
{96
фициентом k==2; на рис. 207 изображена отрицательная rOMO-
1
тетия с коэффициентом k == 1 2. Заметим, что центральную
симметрию можно рассматривать как частный случай отрица-
тельной rомотетии, коrда коэффициент k == 1.
Следствие. Единственной неnодвижной точкой 20мотетии
является центр S. НеnодвИЖНblМИ являются также прямые
и плоскости, проходящие через
центр.
Это утверждение непосред-
ственно следует из определения.
Действительно, по определению
точки всякой прямой, прохо-
дящей через центр, преобразу-
ются в точки той же прямой.
Если через центр S проходит
плоскос ть (1." то, беря на ней
точку А и проведя прямую SA,
мы увидим, что точка А', соот-
ветствующая А, лежит на пря-
мой SA, т. е. принадлежит (1.,.
Итак, любая точка плоскости (1., Рис. 208
преобразуется в точку той же
плоскости, т. е. плоскость преобразуется сама в себя.
Теорема 1. Томотетия преобразует всякую прямую в nа-
раллельную прямую и всякую плоскость в параллельную
плоскость.
1) Пусть мы имеем rомотетию с центром S и прямую /.
Есл S С /, то / преобразуется сама в себя, т. е. / \1/. Поло-
жим поэтому, что S Ф. /. Тоrда через S и / можно пр вести
плоскость (1., и в этой плоскости осуществить rомотетию при
том же центре и коэффициенте. Мы это можем сделать, так
как любая прямая, проходящая через центр S и точку прямой
1, принадлежит плоскости (1.,. Но мы знаем, что rомотетия в
плоскости преобразует прямую / в параллельную прямую l'.
Итак, Sk (/) == l', rде l' \\ /.
2) Если дана rомотетия с центром S и плоскость а, то в том
случае, коrда S С (1." Sk «(1.,) = (1." получим, что (1.," (1.,. Положим,
что S Ф. (1.,. Возьмем в плоскости (1., три точки М, N и Р, не
лежащие на одной и той же прямой, и проведем прямые MN
и мр (рис. 208). rомотетия преобразует прямые MN и мр со-
ответственно в прямые М' N' и М' Р', удовлетворяющие усло-
виям: MN 11 М' N' и МР 11 М' Р'. Проведем через пересекающие-
ся прямые М' N' и м' Р' плоскость а', которая в силу парал-
лельности M'N' с MN и М'Р' с МР будет параллельна (Х.
Докажем, что любая точка Q плоскости (1., преобразуется в
197
roчку Q' плоскости r;t'. Проведем через точку Q прямую q,
которая пересечет прямые MN и мр соответственно в точках
Х и У. Sk(q) q', Sk(X) == X',Sk(Y) Y', Sk(Q) == Q', rде
X'Cq', X'cM'N', Y'Cq', У'СМ'Р'. Но M'Crx', N'crx',
следовательно, q' С (х', Q' с q', значит Q' с rJ.,'. Ит.ак, rOMoTe
ия преобразует плоскость в параллельную плоскость:
Sk( ) == r;t'.
(22.2) Теорема 2. При еомотеmиu сохраняется равенство
сходственных уелов и nропорциональность сходственных om
реЗКО8.
Возьмем три точки А, В и С, не лежащие на ОДНОЙ и той
же прямой. Пусть Sk (А) == А', Sk (8) В', Sk (С) == С'. Так
..........
K ABjA'B' и ВСIIВ'С' и вместе с тем векторы АВ и А'В',
ВС и В'С' сонаправ.пены при поло,кительной rомотетии и про..
rивонаправлены при отрицательной, то LABC == LA'B'C'.
Точки S, А, В, А', В' лежат в одной и той же плоскости.
Поэтому мы можем использовать известное свойство плоской
rомотетии, cor ласно которому
А' В' SA' 3В'
АВ SA == 5В == k.
Следствие. Положительная еОAlотетия nреобразует данную
фисуру в одинаково ориентированную. Отрицательная ео,М,оте..
muя преобразуепz данную фиеУР!J в ФИ2УРУ, противоположно
ори е нт и рованн у ю.
Рассмотрим rомотетию с центром S и коэффициентом k > о.
Возьмем треуrольник АВС, расположенный так, что ero плос
Кость не проходит через центр S (см. рис. 206). Sk ( ABC) ==
e= А'В'С', а в силу предыдущей теоремы A'B'C'(/) ABC.
Наблюдатель, смотрящий из точки S на эти треуrольники, уви
Аит их совместившимися и, значит, одинаково ориентированны
ми. Поэтому и фиrуры SABC и SA' В'С' являются одинаково
ориентированными.
I1YCTb теперь k < о. Возьмем треуrольник АВС, плоскость
KOToporo не прс>ходит через центр S (см. рис. 207), и пусть
опять Sk ( ABC) == A' В'С'. В этом случае для наблюдателя.
находящеrося в точке S, треуrольник А' В'С' одинаково ориен
tиропан с треуrОJlЬНИКОМ AtBtCt, центрально симметричным с
треуrо ,ьником А ВС относительно иентра S. Но мы знаем, что
фиrуры SABC и SAtBtC. ПРОТИВОПОЛО)I{НО ориентированы. По
этому противоположно ориентированы и фиrуры SABC и
SA' В/С'.
(22.3) Условие, необходимое и достаточное для Toro, чтобы
Be фиrуры в пространстве были rомотетичны относительно
ДРУI"' друrа, дается следующей теоремой.
198
Теорема 3. ДЛЯ тоео чтобы две пространственные
ФU2УРЫ были 20AlотетичН,ы отН,осительН,о дРУ2 дРУ2а, необхо-
димо u достаточно, чтобы: 1) .между точками фИ2УР было
установлено взаUм'ноодН,озН,ачН,ое соответствие; 2) сходствен-
ные прямые были параллельН,ы; 3) для двух сходственных
вектОР18 АВ u А' В' выполнялось условие АВ =1= А' В' (при
А' <t= АВ).
1) У с л о в и е н е о б х о д и м о, так Как в силу определения
между точками обеих фиrур установлено взаимнооднозначное
соответствие, а в силу теоремы 1 сход-
ственные прямые параллеЛЬНbl. Кроме J}'
>
Toro, если бы было АВ == А' В', то пря-
мые АА' и ВВ' были бы параллеЛЬНbl- с
ми и несовпадающими и не Mor ли бы
проходить через одну и ту )Ке точку s.
2) У с л о в и е Д о с т а т о ч н о. Пусть
мы имеем фиrуры ФиФ' с соответст-
венными парами точек А и А', в и В',
с и С', D и D', Е и Е' (рис. 209), rде
АВ 11 А' В', АС 11 А'С', ВС \\ В'С',...
Так как АВ" А' В', то через эти
прямые можно провести плоскость, а
........
так как векторы АВ и А' В' не равны IJ
и не лежат на одной и той же прямой, Рис. 209
ТО прямые АА' и ВВ' пересекаются
в некоторой точке s. Примем эту точку за центр rомотетии
SA'
с коэффициентом k == . Точка С при этом преобразуется
SA
в точку с" и А' С" 11 АС, следовательно, прямая А' С" тождест",
венна с прямой А'С'. Вместе с тем В'С" 11 ас, значит, прямая
В'С Н тождественна с прямой В' С', поэтому тождественны и
точки пересечения этих прямых, т. е. С" = С'. Подобным же
образом дока/кем, что rомотетия с центром S и коэффициентом
k преобразует точку D в D', Е в Е' и т. д.
Полученная rомотетия будет положительной, если векторы
АВ и А' В' сонаправлены. Если же эти векторы противонаправ-
пены, то rомотетия будет отрицательной (на рис. 209 она отри-
цательна).
Следствие. rомотетuя в просmран'стве вполне определена,
если заданы два коллuН,еаРНblХ, Н,еравных между собой вектора,
к,оторые должны соответствовать apyz apyzy в этой zoMome-
mии.
Пусть мы имеем неравные коллинеарные векторы АВ и
А' B i . Положим сначала, что А' С/= АВ. Тоrда в силу параллель-
ности прямых АВ и А' В' через них можно пр?вести плоскость.
199
Так как АВ =1= А' В', то прямые АА' и ВВ', лежащие в этой
плоскости, пересекутся в иекоторой точке S, которая и буде'r
SA'
центром искомой rомотетии с коэффициентом k == . Коэффи-
SA
циент k> О при сонаправленных векторах АВ и А' В'; k < О
при противонаправленных векторах АВ и А' В'. Если векторы
АВ и лежат на одной и той же прямой (рис. 210), то
s
Рис. 2JO
через точку А можно провести в RРОИЗВОЛЬНОМ направлении
вектор АС, равный по абсолютной величине вектору АВ, а через
точку А' провести коллинеарный с А С вектор А' С', равный по
абсолютной величине вектору А' В'. Векторы АС и А'С' должны
быть сонаправлены, если сонаправлены АВ и А' В', и противо-
направлены в противоположном случае. Точка S определяется
пересечением прямых АА' и СС', причем определяется одно-
SA' А'С' А' В'
значно, так как == == , откуда видно, что положе-
SA АС АВ
иие точки S вполне определено отношением векторов А' В' и АВ.
(22.4) Как и в планиметрии, преобразование подобия яв-
ляется обобщением преобразования rомотетии. Относительно
двух rомотетичных фиrур было доказано, что между их ТОЧ
ками существует взаимнооднозначное соответствие и уrлы
между сходственными лучами равны. Вместе с тем xapaKTep
ной особенностью rомотетии является то, что все прямые,
проходящие через пару соответственных точек, пересекаются
в одной и той же точке S центре Ifомотетии. Если отбросить
это последнее требование, то получим определение подобия.
200
Определение 2. Две пространственные фИ2УРЫ называют-
ся подобными, если между их точками существует взаимно-
однозначное соответствие и У2ЛЫ, образуемые сходственными
лучами, равны между собой.
Соотношение подобия фиrур обозначается, как и в плани-
метрии, знаком (/), т. е. Ф(/)Ф'.
Существование подобных фиrур доказывается наличием
фиrур rомотетичных. Если одну из двух. rомотетичных фиrур
движением перевести в друrое место, то rомотетичность фи
ryp нарушится, а подобие их сохранится.
На практике мы на каждом шаrу встречаемся с примера
ми подобных фиrур. Такими примерами являются модели
всевозможных машин, предметов обихода, архитектурных co
оружений и т. д. Подобными фиrурами являются модел'и ис
кусственных спутников Земли. rлобус является подобным
изображением земноrо шара.
Непосредственно из определения получаем следующее
предложение.
Следствие 1. Если в подобных фИ2урах существует пара
равных между собой сходственных отрезков, то такие фИ2У-
ры равны между собой.
Пусть мы имеем фиrуру Ф с точками А, В, С, D,... и подоб
ную ей фиrуру Ф' с соответствующими точками А', В', С', D',...
и еще дано, что АВ==А'В'. Так как фиrуры пространственные,
то в первой фиrуре существует точка С, не принадлежащая
прямой АВ, а во второй
соответствующая точка С', не при
надлежащая прямой А' В'. Ввиду Toro что по определению по
добия L.ABC==L-A'B'C' и L-BAC==L-B'A'C', то .6АВС==
== .6А' В'С', сл'едовательно, BC
В'С' и АС ==А'С'. Подобным
же образом мы докажем, что AD==A'D', BD==B'D' и т. д.,
т. е. что все сходственные отрезки фиrур равны между собой
и, значит, фиrуры не только подобны, но и равны друr дру-
ry. Таким образом, равенство фиrур есть частный случай по-
добия.
Следствие 2. Соотношение подобия удовлетворяет услови-
ям эквивалентности.
Непосредственно из определения подобия следует:
1. Закон симметрии в подобии: если Ф 1 C/JФ 2 , то и Ф2(/)Фl.
2. Закон рефлективности в подобии: Ф(/) Ф. Всякая фиrу
ра подобна самой себе.
3. Закон транзитивности в подобии: если Ф 1 C/JФ2, Ф 2 (/)ФЗt
то Ф 1 (/)Ф з .
Действительно, если А 1, В 1, С 1,...
точки первой фиrуры,.
А2, В2, С 2 ,...
соответственные им точки второй фиrуры,
Аз, В з , с з ,...
соответственные точкам второй фиrуры точки
третьей фиrуры, то между точками первой и третьей фиrур
СО()'Рветствие установим по схеме:
А 1
А2.....Аз, В 1 .....В 2 .....В з , С 1
с2
Сз,...
201:
При этих условиях получим:
L А}В} С 1 == LA 2 B 2 C 2 , LA 2 B 2 C 2 ==АзВзС з , т. е. LA 1 B 1 C 1 ==
== L АзВзС з ,...,
LB}C 1 A 1 == LB 2 C 2 A 2 ; LВ2С2А2==ВзСзАз, т. е. LB 1 C 1 A) ==
== L ВзСзА з ...,
Т. е. все уrлы первой Фиrуры равны сходственным уrлам
второй фиrуры. Поэтому ФiC/JФз.
Ввиду Toro что две rомотетичные фиrуры MorYT быть кау
одинаково, так и противоположно ориентированными, в об
щем случае подобия две подобные Фиrуры MorYT быть и оди"
иаково ориентированными и противоположно ор'Иентирован
ныи..
Следствие 3. В подобных фи2урах отношение сходственных
отрезков есть постоянное число, наЗblваемое коэффициентом
подобия.
, , ,
Если А 1 , В 1 , С 1 , D 1 , ...
точки первой фиrуры, Аl' 81' С 1 ,
,
D 1 , ...
соответственные точки второй фиrуры, то, ввиду Toro
что мы рассматриваем пространственные фиrуры, предполаrаеТСЯ t
что эти точки не лежат на одной и той }ке прямой. Рассмотрим
треуrольники АВС и А' В'С'. По определению подобия LABC===
r==LA'B'C' и LBCA==LB'C'A', следовательно,
ABC(/)
'" 6. А'В'С', откуда следует, что
А' В' В'С' С' А'
==
с:= == k.
АВ ВС СА
Подобным }ке образом, рассматривая треуrольники BCD и
В' С' D', получим:
С'О'
CD
В'О' В'С' ,
== ............... 1:::= k J И Т . д.
BD ВС
(22.5) Связь между rомотетией и подобием определяется
сп:еДУЮfЦИМ предложением.
Теорема 4. Для тО20 чтобы преобразовать друа в друаа
две подобные пространственные фU2УРЫ, достаточно nроuз-
вести одну 20мотетию и одно вращение.
Пусть Ф (А, В, С, D, Е, ... )e/:JФ' (А', В', С', D', Е', ...)
предполаrается, что А и А', В и В' и т. д.
пары соответст"
веннь[х точек данных фиrур.
Произведем rомотетию с центром S, преобразующую точку
А в точку А', причем коэффициент k rомотетии возьмем по
абсолютной величине равным коэффициенту подобия, определя
А'В'
.емому отношением . Знак k возьмем положительным, если
АВ
202
ФиФ' одинаково ориентированы, и отрицательным, если они
противополо>кно ориентированы. Тоrда получим:
Sk (А) == А', Sk (В) == 81' Sk (С) == C 1 , Sk (О) == D 1 .
Sk (Е) == Е 1 . · ·
,
Фиrура Ф} (А , В 1 , С 1 , Dt, Е 1 , ...) равна и одинаково ори{н
тирована с фиrурой ф' (А', В', С', D', Е', ...). ДействитеЛI:НО:
В'С' B1C 1 k В ' С ' В С
ВС- == k, ве == ,следовательно, === 1 1.
Таким же путем можно доказать равенство и всех друrих
сходственных отрезков. Итак, Ф' == Фl. Вместе с тем выбор
знака k обусловливает одинаковую ориентировку фиrур ф' и Фl.
Ввиду Toro что А' есть общая точка обеих фиrур, А' В' ===А' Вl'
плоскость симметрии <11 точек В' и В 1 пройдет через точку At
И мы получим:
<11 (81) == В', 0'1 (С 1 ) == С 2 , 0'1 (D 1 ) == D2' 0'1 (Е 1 ) ==== Е,., ...
Полученная фиrура Ф 2 (А', В', С 2 , D 2 , Е 2 , ...) равна и про-.
тивоположно ориентирована с фиrурой ф' и имеет с ней общую
прямую А' В'. В силу Toro что С 2 А' == С' А', С 2 В' == С' В', плос-
кость симметрии 0'2 точек С' и С 2 пройдет через прямую А' В'
и мы получим:
02 (А') === А', 02 ('В') == В', 0'2 (С 2 ) == С', 0'2 (D 2 ) == Ds,
02 (Е 2 ) == Е з ...
Мы получили фиrуру Ф З (А' В'С' D
Ез, .. .), равную и одинаково
ориентированную с фиrурой ф'. Докажем, что Ф З == Ф', для
чеrо установим, что D
== D', E
== Е', ...
Допустим, что D з не совпадает с D'. Тоrда плоскость сим",
метрии о' точек D' и D з должна пройти через точки А', В', С'
ввиду равенств: D'A' == D з А', D' В' == D з 8', D'C' == DзС', значит
а == А' В'С', чеrо не может быть, так как в силу одинаковой
ориентаuии фиrур ф' и фз точки D' и D3 лежат по одну сто-
рону от плоскости АВС. А в силу Toro что о'
плоскость сим-
метрии точек D' и D з , эти точки должны лежать по разные
стороны от нее. Это противоречие показывает, что D' не может
не совпада ть с D3. Итак, D з == D', Е з == Е' И' т. д. Следова-
тельно, Ф З = ф'.
Но два отражения с плоскостями 0'1 И O'
эквивалентны
.одному вращению с осью r == <110'2. Таким образом, преобразо-
вание подобия в общем случае оказывается эквивалентным одной
rомотетии и одному вращению.
2Q
(22.6) На основании доказанной теоремы можно решить
следующую задачу.
Задача. Данную .пространственную фиrуру Ф (А, В, С, D,
Е,...) преобразовать в подобную так, чтобы А, В, С преобра..
зовывались в данные точки А', В', С' при условии, что
ABCC/)6A'B'C'.
Для решения этой задачи произведем сначала rомотетию
с центром S, преобразующую точку А в А'. Коэффициент ro
А'В'
мотетии k определяется равенством k == АВ . Число k берем с
положительным знаком, если требуется построить фиrуру,
одинаково ориентированную с Ф, и с отрицательным
в про-
тивном случае. В результате этоrо получим фиrуру
Фl (А', В}, С},...), равную искомой фиrуре Ф'. Остается найти
ось вращен'ия " преобразующую фиrуру Ф} в фиrуру Ф'.
Эта ось определяется пересечением плоскостей симметрии то-
чек В' и В}, с' и С 1 . Таким образом, определены все элемен
ты искомоrо преобразован
я.
Упражнения
1. Доказать, что две последовательные rомотетии эквива-
лeHTHы одной rомотетии (ил'и одному переносу) , а центры
всех этих rомотетий лежат на одной и той же прямой, назы-
ваемой осью rомотетии. Чему равен коэффициент результи"
рующей rомотетии?
2. При каких условиях две последовательные rО
10тетии
эквивалентны одному переносу? l,aK расположена в этом
случае ось rомотетии?
3. При каких условиях две последовательные rомотетии
эквивалентны одной центральной симметрии?
4. Даны четыре пространственные фиrуры, из которых
первая
омотетична со второй, вторая
с третьей, третья
с четвертой. Доказать, что все эти фиrуры попарно rOMOTe
тичны между собой и что шесть центров этих rомотетий ле..
жат в одной и той же плоскости. Как расположены оси этих
rомотетий?
5. Если первая фиrура подобна второй, а вторая подобна
третьей, то первая подобна третьей. Чему равен коэффициент
подобия м'ежду первой и третьей фиrурами, если два данных
коэффициента подобия равны k} и k 2 ?
6. Доказать, что все кубы подобны между собой.
7. На проекционном чертеже задано изображение четы-
рехуrольной призмы и задано положение центра rомотетии
s. Преобразовать эту призму в rомотетичную с коэффициен"
204
том k == 2. На друrом чертеже дать изображение rомотетии с
. 3
коэффициентом k ==
2 ·
8. На проекционном чертеже заданы изображения трех
колл'инеарных неравных между собой векторов A 1 B 1 , А2В2,
.......
АзВ з . Построить изображения осей rомотетий, преобразую..
щих эти векторы друr в друrа.
9. На проекционном чертеже задано изображение трех
пара.плельных инеравных друr друrу отрезков. Для каждой
пары из них существует две rомотетии, преобразующие их
друr в друrа. Как расположены шесть центров этих rOMoTe..
тий? Построить соответствующее изображение.
10. Доказать, что у двух подобных между собой простран..
ственных фиrур равны сходственные двуrранные и CXOДCTBeH
ные TpexrpaHHbIe уrлы.
rпABA ВОСЬМАЯ
м HO.rO rp А н ни I<И
i 23. ПРИЗМЫ
(23.1) Определение 1. М ноzоzранником. называется тело
оrраннченное мноrоуrольниками.
Эти мноrоуrольники называются zранямu, их стороны
ребрамu, их вершины
вершинами мноrоrранника. Отрезок,
соединяющий две вершины, не принадлежащие одной и той
же rрани, называется дuа20налью мноrоrранника.
Мноrоrранник называется выпуклым, если О'н находится в
одном полупростраНСТ1ве по отношению к каждой из своих
rра'ней. В противном случае мноrо
ранник называет,ся невы.
nУКЛblМ.
Нам уже известны примеры простейших мноrоrраН'никО'в
куб, призма, пирамида. Нетрудно убедиться в том, что, на-
.ример, куб является выпуклым мноrоrранником.
Практически IВЫПУКЛЫЙ мноrоrранник можно охарактери-
зовать тем, что ero можно поставить на плоскую повеРХНОСТЬj>
например 'на стол, любой rранью.
Чтобы изображение мноrоrранника на проекционном чер..
теже было. полным, необходимо, чтобы все ero вершины были
38данными точками. Для Toro чтобы изображение MHoro-
rранника было метричеСКll определенным, необходимо уста..
.овить М,етрику nространствеННОёО изображения, подобно
1'Ому как это было сделано для изображения на основной
влоскости.
Можно доказать, что для определения метрики простран-
с"венной фиrуры' ОоАоВоС о достаточно иметь четыре задан-
ные точки ее изображения О, А, В, С, не лежащие в одной и
той же плоскости, и знать истинную величину отрезков ОоАо,
ОоВо и ОоС о и истинную величину уrлов между нимиз
L ВоОоС о , L СоОоАо и LAoOuCo. Тоrда совершенно так же,
как это делалось на изображении основной плоскости [тео-
рема 5 из пункта (15.11)], можно доказать, что по любой за-
данной на изображении точке Р можно найти ее истинное
Rол,ожение РО на пространсТ'венной фиrуре.
J06
Обычно при этом заданные точки, например О, А, В, бе-
рутся на изображении основной плоскости, а чеТ'вертая точ-
ка С берется вне этой плоскости.
Рассмотрим в качестве примера рис. 211, на КО1'ором OA J
tJB, ОС изображают три взаимно перпендикулярных отрез-
ка, каждый из которых 'имеет длину, равную единице.
MNPQM'N'P'Q' изображение мноrоrранника, ребра ко-
roporo ММ', NN', рр' и QQ' перпендикулярны к основной
плоскости. По этому изображению мы совершенно точно мо-
жем изrото'вить модель мноrоrРанника, проекцией KOToporo
CJIужит это изображение.
Действительно, так как метрика основной плоскости r:J., уже
определена, то мы можем определить истинный вид мноrоуrоль"
, , , ,
ника MoNJJoQo. Далее, ввиду Toro что ММ'" N N' 11 рр' /1 QQ' 11 ос,
мы можем определить истинную длину этих ребер по отноше-,
иию к единичному отрезку ос. Отсюда следует, что мы можем
, , ,
построить ребра МоМо, N oN о, роро И этим найти вершины Мо.
N о, Р О' Q о. Практически обычно строят так называемую развертку
поверхности мноrоrранника. Для этоrо \ представляют себе, что
эта поверхность разрезана по некоторым ребрам и затем развер-
нута в плоскую фиrуру. По чертежу этой фиrуры на картоне
или каком-либо друrом материале можно склеить мноrоrранник,
соединяя друr с друrом те ребра, по которым были произве-
р:еиы разрезы.
На рис 212 показана развертка данноrо мноrоrранника
, , , , ,
!\1oNoPoQoMoNoPoQo. Разрезы произведены по ребрам момо'
, , , " " "
NoN o , PoPo,QoQo, MoQo, QoMo, MoN o .
(23.2) Рассмотрим теперь некоторые виды мноrоrранни
ков.
ПредстЗ'вим себе, что ,на ПЛОСКОСl'и начерчена произволь-
ная ломаная линия, а прямая, не принадлежащая этой плос-
кости, движется по этой ломаной, постоянно ее пересекая и
nставаясь параллельной одной и той же прямой (рис. 213).
rеометрическое rMecTo точек, принадлежащих подвижной пря-
МОЙ во всех ее положениях, называется nрuзматuческой по-
верхностью. Данная ломаная ЛI1НИЯ называется направляю-
щей призматической поверхнос1'И, а подвижная прямая ее
образующей. Прямые, проходящие через вершины ломаной,
называются ребрами призматической поверхности, а полосы
между ребрами ее rранями. Если направ.пяющая ломаная
замкнута, то и призматическая поверхность называется
.,
за.мкнутои.
Определение 2. П ризмой. J:I зывается . мноrоrра'нник, orpa..
ниченный замкнутой призматической поверхностью и двумя
мноrоуrольниками, которые получаются от пересечения этой
207
Р'
11.'
,
М'
I
Рис. 211
Рис. 212
А
п '
Рис. 213
Рис. 214
I
I I
I I
I I
I .
I I
I .
I I
;......... 4
,."" \
\
\
\
.................... ..
Рис. 215
P:iC. 216
РИС. 217
поверхности двумя параллельными пло'скостями, пересекаю-
ЩИМИ ее ребра.
Мноrоуroльн,ики, получающие.ся в ,сечении, называются
основаниями ПрИ3iмы, а расстояние между секущими плоско-
стям'И высотой призмы. rрани и ребра, П1ринадлежащие
призматической поверхности, называются боковыми rраня,ми
и ребра'ми призмы (ри'с. 214).
По числу ст,орон ,основания ПР1изма называется треуrоль-
ной, четырехуrолЬ'ной, пятиуrольной, ..., п-у ольной.
Призма называется прямой, если плоскости оснований
перпендикулярны к ее боковым ребрам (рис. 215). Непрямая
призм а называется наклонной (ом. ри,с. 214).
Прямая призма называется правильной, если ее о.снова-
нием служит правильный мно оуrолЬ'ник. На рис. 216 показа-
на праlвильная пятиуrольная призма.
Из определения призмы получаю'ОСя следующие основные
ее своЙства:
1. Все боковые rрани призмы параллелоrраммы, так
как боковые ребра параллельны между .ообой IB силу опреде-
ления, а СООТlВетствующие друr друrу ребра основания па-
раллельны как прЯ'мые, полученные от пересечения плоско-
стью параллельных плоскостей.
Кроме Toro, боковые ребра ра,вны между /Собой как отрез-
ки параллельных прямых между параллельньrми плоскостяrvfИ.
2. Основа.ния призмы palB.HbI между 'Собой в с'илу равен-
ства соответствующих СТ;ОРОН и уrл'ов. Если принять ребра за
проектирующие прямые, то каждый из этих мноrоуrольник,ое
я.вляе-ося па раллельной проекцией друrоrо.
3. у прямой ПР1ИЗМЫ боковые лра:ни прЯ'моу ольни,ки, так
как боковые ребра перпендикулярны к основаниям.
(23.3) Для определения площади боковой по.верх,ности
призмы пользуются следующей теоремой.
Теорема 1. Площадь боковой поверхности призмы равна
произведению периметра перпендикулярноzо сечения на длину
60ковоео ре6ра.
В данной призме ABCDEA'B'C'D'E' ('см. ри,с. 214) про..
изведем сечение, перпендикулярное к боковым ребрам. Все бо-
ковые ребра имеют одну и ту же дл'ину а. В перпендикуляр-
ном сечении получился п..уrольник с длинами сторон h 1 , 122,...,
h п . Каждая f'paHb есть параллелоrрамм, основанием KOToporo
является боковое ребро, а высотой одна из сторон перпен-
ди,кулярноrо сечения. Поэтому боковая поверх'Н'ость опреде-
ляе!tСЯ суммой:
Sб === ah} + ah 2 + · · · + ah п === а (h} + h 2 + . . . + h n ), или
Sб == ар,
rде р периметр перпендикулярноrо сечения.
14 А. и. Фет.сов
209
Для получения площади полной повеРХ1НОСТИ призмы нуж-
но К полученному числу ар ПР1ибавить площади обоих осно-
ваний.
Заметим, что для ,некоторых призм доказа.нная теорема
может оказаться практически неприrодной. Это будет 'в том
случае, коrда при очень Iмалой ,высоте призмы боковые ребра
наклонены к плоскости оенования под очень малым уrлом
(рис. 217). В такой призм:е перпендикулярное сечение может
не пересечь в,сех бо.КrQ,ВЫХ ребер, и тоrда прих'Оди'ОСя вычис-
лять площадь каждой rрани 'в отдель:ности и суммир'О'вать по-
лученные результаты.
Следствие. Площадь боковой поверхности прямой пРИЗМbl
равна произведению периметра основания на длину высоты.
Очевидно, .в прямой призме само основание СJlУЖИТ пер-
пендикулярным ,сечением, а вы,сота параллелына боковым реб-
palM и потому равна им.
(23.4) Определение 3. Параллелеnиnедом называется
призма, основанием которой служит параллелоrрамм.
Параллелепипед оrраничен шестью параллелоrраммами)
имеет IВOQeMb вершин и двенадцать ребер (р1ИС. 218).
С'
r
Рис. 218
Теорема 2. Параллелеnиnед есть центрально симметрич-
ная фиzура по отношению к середине каждой из ezo auazo-
налей.
Рассмотрим параллелепипед с основаниями ABCD и А' В'С' D',
rде точки А и А', В и В', С и С', D и D' попарно являются
концами одной и той же диаrонали (см. рис. 218). Примем
середину О диаrонали АА' за центр симметрии. Эта симметрия
преобразует плоскость rрани ABCD в параллельную плоскость,
проходящую через точку А', т. е. в плоскость rрани A'B'C'D'.
Так как АВ == CD, CD == А'В', то АВ А'В'. Центральная сим-
метрия, преобразующая отрезок АВ в равный и параллеJIЬНЫЙ.
210
преобразует точку В в В'. Таким же образом докажем, что
О (С) == С', О (D) -::= D'. .
Итак, О (ABCD) == А' В'С' D', О (АВС' D') == А' B'CD
O(BCD'A')==B'C'DA, т. е. противоположные еранu паралле..
лепипеда равны и параллельны. Отсюда также заключаем:
дuazонали параллелепипеда пересекаются в одной и moй же
точке и делятся ею пополам.
Блаrодаря центральной с-имметрии параллелепипеда и
тому, ч,.,о er,o противоположные rрани ра.вные и параллель-
ные между собой параллелоrраммы, любую ero rpaHb мож'но
при,нять за основание.
(23.5) Определение 4. Прямой параллелепипед называет..
ся пРЯМОУZОЛЬНIJlМ, если основаниями ero служат прямоуrоль..
ники .
Д'
С'
А'
, I
, ,
'i,
I "
I ,
I ,
I '
I '
I ,1
.o Jc
/
/
/ ". ., ".
А
...,
Рис. 219
Прям.оуrольный параллелепипед Яlвляется наиболее рас-
пространенной формой среди предметов ,окружающей нас об..
становки: корпуса зданий, кирпичи, из которых эти здания
сл'ожены, к,ом.наты, ящики и кор'обки, шкафы, сундуки, чемо..
даны, футляры для книr и т. д. 'Blce это 'имеет форму Пlрямо
уrольно о параллелепипеда.
Длины трех ребер, выходящих из одной и той же вершины
прямоуrолыоrоo параллелепипеда, называются также ero из..
мерениями a/J,UHOU, шириной и высотой. Например, на
рис. 219 ребро АВ ОПlределяет длину, AD ширину, АА'
высоту прямоуrОЛl>.ноrо па-раллелеnипеда.
Определение 5. Кубом называется прямоуrольный парал
лелепипед, все измерения KOToporo равны ежду собой.
Между измерениями прямоуrольноrо параллелепипеда и
ero диаrональю сущеСТ1вует С1оотношение, аналоrичное с'оот'"
ношению между сторонами и диаrональю прямоуrолЬ!ника.
Теорема 3. Квадрат диаzонали прямоуzольноzо параллеле.,
пипеда равен сумме квадратов трех вео измерений.
14* 21t
в прямоуrольном параллелепипеде ABCDA'B'C'D' (СМ.
рис. 219) обозначим: АВ == а, AD == Ь, АА' == с, диаrональ А'С ==d,.
диаrональ основания АС==т. По теореме Пифаrора из прямо...
уrольноrо треуrольника АВС получим: т 2 ==а 2 +Ь 2 . Далее из
прямоуrольноrо треуrольника АА'С получим: d 2 ==т 2 +c 2 или
d 2 == а 2 + Ь 2 + с 2 .
Следствие. Все дuа20На,лu nрЯМОУ20ЛЬНО О параллелепu-
педа равны между собой. '
Это есть результат Toro, что каждая диаrональ имее1'
длину
d== Уа 2 +Ь 2 +с 2 .
Упражнения
1. Сколько плоскостей сим'метрии можно провести IB пря.
моуrольном параллелепипеде?
2. Каков должен быть косоуrольный параллелепипед, что-
бы в нем можно было провести плоскость Iсимметрии?
3. Существует ли косоуrольный параллелепипед, все rрани
Ko-roporo равны между с'обой?
4. Доказать, что д'ва прнмоуrоль'ных параллелепипеда рав"
ны между собой, если COOTBe "BeHHO ра.вны их ,измерения.
5. Доказать, что если диаrонали паlраллелепипеда раВ'ны
между с,обой, то этот параллелепипед прямоуrольный.
6. Прямоуrольный параллелепипед имеет измерения, palB-
ные 9, 12 и 16 линейным единицам. Разрезать ero на такие
две части, чтобы из них можно было сложить равновеликий
куб.
7. Доказать, что плоскость, проходящая через концы трех
ребер параллелепипеда, имеющих общую ,вершину, o-rсекает
t u u
3 диаrонали, ,выходящеи из тои же веРШИIНЫ.
8. Доказать, что сумма квадра-rов диаrаналей всякоr-о па-
раллелепипеда ,равна сумме квадратов всех ero ребер.
9. Косоуrольный параллелепипед пересечен плоскостью,
не параллельной основа'нию, так, что отрезки трех боковых
ребер от основания до сечения ,palHHbI соответст,венно 3 см,
8 см и 11 СМ. Чему равна длина отрезка четвертоrо боковоrо
ребра от основания д-о сечения?
Предполаrая, что метрика пространства задана изображе..
нием трех взаимно перпендикуляр,ных единичных отрезков.
два из которых лежат в основной плоскости, решить следую..
щи е задачи на построение:
IC>. Построить прямую "реуrольную пр,изму, если заданы
1'ри ребра основания и высота.
11. Построить прнмоуrольный параллелепипед по данному
основанию и диаrонали.
12. Построить куб по Дз'нной диаrонали.
212
)
24. ПИРАМИДЫ
(24.1) Определение 1. Если прямая перемещается, все
время пересекая даlННУЮ пл,оскую ломаную линию и в то же
время ПРiQХ'ОДЯ ч,ерез данную неподвижную 'rочку, не лежа-
щую в плоскости лома.ной, ТО rеометрическое место точек
зтой прямой 'во всех ее пол'ожениях (называется пuрамuдаль-
н'ой поверхностью (рис. 220).
Рис. 220
Дан,ная ломаная называе-rся направляющей, ПQдвижная
прямая образующей, неподвижная точка вершиной пира-
мидальн,ой по'верхности. Прямые, проходящие через вершину
П1оверх,ности и веРШ1ИНЫ лома.ной, называются ребрами пира-
мидальной по,верхности, а пло'ские уrлы между ними ее
ранямu. Если напраlВЛЯIощая замкнута, то и пирамидальная
п'оверхность называется замкнутой.
Рис. 221
Рис. 222
Определение 2. П ирамидой называе-ося мноrоnранник,
оrраниченный пирамидальной поверхностью и мноrоуrольни"
ком, КO'J'Iорый получается от пересечения этой ПО1верхности
плоскостью, пересекающей все ее ребра и не проходящей
qерез верШ1ИНУ (рис. 221).
213
Вершина, ребра и rра.ни пирамидальной поверхн'ости на-
зываю'f1СЯ вершиной, БОКОВЫм'и ребрам'и и БОКОВЫм'и zраняМ,u
пирамиды. Перпендикуляр, проведенный из вершины к пло'С-
кости основа\ния, называется высотой пирамиды (с'м. рис. 2 1).
П,о числу боковых rраней пирамиды разделяются на тре-
уrольные, четырехуrольные, пятиуrольные, ..., n..уrольные.
Если основанием пирамиды IСЛУЖИТ правильный M:Horo-
уrольник и проекция вершины попадает в u,eHTp основа.ния)
то пирамида называется правильной (рис. 222).
Треуrольная пирамида представляет собой мно оrранник,
<>rра'ниченный наименьшим числом rраней четырьмя тре-
уrольниками, поэтому она назы.вается также тетраэдром' (че-
тырехrранник). Лю'бую rpaHb тетраэдра можно принять за
основание треуrольной пирамиды.
Форму пирамиды имеют наиболее J1рандиозные сооруже-
ния древности rробниuы еrипет,ск'ИХ фараонOIВ. Величайшая
из 'них пирамида Хеопса, имеющая 146 м, BЫCOTЫ, по-
строена в третьем тысячелетии до н. э. Необычайная проч-
ность И УСТОЙЧИ1ВОСТЬ сооружения (центр тяжести пирамиды
f
находится на 4' ее высоты, считая от основания) обеспечили
с'охран'ность ero до наших дней.
Следствие. Боковые срани правильной пирам'иды рав-
ные м'ежду собой равнобедренные треуzольники.
Боковые ребра правильной пираlМИДЫ рав,ны между С'обой,
так как равны их проекции на основание. Стороны основания
palBHbI между собой как СТОр'О'ны праlв\ильноrо ,мноrоуrольни-
ка. Итак, в-се ,стороны одной боковой rрани pa'BIHbI coo-rвет-
с-rвующим сторонам друrой. Поэтому все боковые rра'ни ара-
виль.ной пирамиды равны между собой и являются в o же
время равнобедренными треуrольниками.
Определение 2. Высота боковой rрани правильной пира-
миды, проведенная к ребру основания, наЗЫIваеТС1Я ее апофе-
м'ой.
Теорема 1. Площадь боковой поверхности правильной пи.
рам'иды равна половине произведения периМ,етра основания
на апофему.
Обозначим через а длину стороны основания правильноА
п-уrольной пирамиды, а через k......... длину ее апофемы. Тоrда
б u Ф u S ak
площадь оковон rрани выразится ормулои: == .
2
Так как пирамида ,.n-уrольная, то площадь всей боковой
Ф u s паk и
поверхности выразится ормулои: б ==: . О па есть пери-
2
метр основания па ==р, следовательно,
pk
Sб == ·
2
214
(24.2) Теорема 2. Если пирамиду пересечь пЛОСКОСТЬЮ t
параллельной основанию, то полученное сечение будет обла..
дать следующими свойствами: 1) боковые ребра и высота
пирамиды разделяются сечением на соответственно пропор..
циональные отрезки; 2) в сечении получается мноzоуzольник,
подобный МНО20уzольнику основания; 3) площадь сечения
прямо пропорциональна квадрату расстояния плоскости се..
чения от вершины.
о
8
А
Рис. 223
Рассмотрим пирамиду 'с 'верIIIИНОЙ О и ОСНОlванием ABCD
(,рис. 223).
Секущая плоскость, параллельная основанию, определяет
в сечении м,ноrоуrольник A'B'C'D'. Принимая 'верш/ину О за
центр rомотетии, убедимся, Ч'f10 ,мноrоуrолыник ABCD пре..
образуе'f1СЯ в /мноrоуrольник А' В'С' D' и коэффициент rOMoTe-
rии k определяется равенством
ОА'
k == ОА ·
Этому же числу равно, очевидно, и отношение сходственных
сторон мноrоуrольников и отношение высот:
OQ'
== k.
OQ
Так как rомотетичные фиrуры подобны, то ABCDGп
",А' В' С' D'. Отношение площадей подобных мноrоуrольников
равно квадрату коэффициента подобия. Поэтому
SA'B'C'D' == k 2 == ( OQ' ) 2.
SABCD OQ
На основании доказаlННОЙ теоремы выводитС'я физичеСКtИЙ
закон о том, чт.о освещенность -плоской повеРХ1НОСТИ, пере.се-
кающей световые лучи, обратно пропорциональна КlBaдpaTY
раlССТОЯНИЯ от источника света до освещенной поверхности.
215
Предста'вим себе, что 'в вершине пирамиды (точка О на
рис. 223) помещен источник совета. Поток свето,вой энерrиrи,
ра.спространяющийся Вiну"ри MHororpaHHoro уrла с верши-
ной О, может быть перехвачен Лlибо площадкой A'B'C'D't
либо площадкой ABCD. К,оличество световой энерrии, прихо-
дящейся 'На единицу площади, обратно пропорционально ве-
личине этой площади, т. е. .обратно пропорциональн,о квадра-
ту 'ра'сстоянИ'я площадки ОТ Iвершины О ИСl'очника света.
Заметим, ч о на ос.новании этоrо закона были определены
расстояния до самых отдаленных объектов Вселенной вне.
rала,ктических туман'ностей.
(24.3) Определение 3. Усеченной пира.мидой называется
часть пирамиды, за.ключенная между ос,нованием и секущей
плоскостью, параллельной основанию (р,ис. 224).
Рис. 224
Мноrоуr.ольник сечения называется верхним основанием
у,сеченной пирамиды, а основа,ние полной пираМ1ИДЫ ниж-
ним оснtQ,вани'ем усечен'ной пирамиды. Расстояние между
пл'оскостя,ми оснований ,называет,ся высотой усеченной пира-
миды.
Если полная пирамида была правильной, то и полученная
из нее усеченная ПИ1рамида наЗЬJ1вается правuльной.
Следствие. БоковЫе 2рани усеченной nupaMudbl тра-
пеции; у правuльной усеченной пирамиды они являются рав-
ными между собой равнобедреннымu траnецuямu.
Боковые rрани трапеции ,в силу Toro, что стороны па.
раллельноrо сече.ния параллельны соотве-r,ствующим сторо-
на'м основания. У правилыной усеченной пирамиды уrлы п'ри
основании трапеций равны между собой, поэтому эти rрани
равнобедренные трапеции. Эти трапеции равны между со-
бой в силу равенсТ'ва соотвеТСl1ВУЮЩИХ 'Сторон и уrЛiQВ.
Определение 4. Высота боковой rрани усеченной пирами.
ды назы'вается апофемой этой пирамиды.
216
Теорема 3. Площадь БОКО80Й поверхности правильной усе-
ченной пирамиды равна произведению полусуммы перимет..
ров оснований на длину апофемы.
Пусть а длина стороны нижнеrо основания, а' длина
стороны BepXHero основания правильной n"уrольной усеченной
пирамиды; k длина пофемы. Тоrда площадь одной rрани
а +а'
будет равна 2 "k. Вся (же боковая поверхность, состоящая
И3 n rраней, будет равна
Sб == n а + а' k == па + па' k.
2 2
Но па == р периметру нижнеrо основания, па' == р' пери.
метру BepXHero основания. Ilоэтому окончательно:
S р + р' k
б 2 ·
Упражнения
\ 1. Д'оказать, что три отрезка, соедИlняющие середины про-
rИВОПОЛ1ОЖIНЫХ ребер тетраэдра, пересекаю1'СЯ ,в одной и той
\Ке точке и делятся ею попола,м.
2. Доказать, что боковое ребро п'равильной треуrоль'Ной
пирам иды перпендикулярно к пр'отивополож,ному реб.ру осно-
вания.
3. Доказать, что шесть плоскостей симметрии четырех
веРШИIН тетраэдра перосекаются в одной и той же точке.
4. Доказать, что шесть плоск,остей симметр,ии четы'рех
rраней тетраЭДlра перосекаю1'СЯ в одной и той же 'I'очке.
5. Д'оказать, что четыре ,отрезка, С'оединяющие вершины
тетраэдра с точкой пересечения медиа,н ПРОТИВОПОЛ1ОЖJ,il'ОЙ rpa-
ни, пересекаются 'в одной и той же точке. Эта точка находит-
ся на 1/4 длины каждоrо отрезка. (Замечание: если тетраэдр
с.делан из какоrо-нибудь однородноr.о материала, то точка.
оп'ределяемая у,словием этой задачи, Я1вляется центром тяже.
сти тетраэдра.)
6. Доказать, что в сечении тетраэдра плоскостью, парал-
пельной двум ero противоположным ребрам, получается па-
раллелоrра,мм.
\ 7. Д1оказать, что боковая поверх,ность правильной пира..
миды равна площади оенова,ния, деленной на косинус уrла
между пл,оскостью боко8'ОЙ rрани и плоскостью о,сН'ования.
8. Доказать, что боковая поверхность правильной усечен-
ной пирамиды ра.в,на разаости площадей нижнето и BepXHero
ОС'80ва I НИЙ, деленной на кос,инус уrла между бок'овой rранью
и осаованием.
217
9. Доказать, что два одинаково ориентирова.нных тетра.
эдра равны между собой, е.сли: а) д,ве rрани ОДНОРО соответ-
ственно равны двум rраням друrоrо и равны двуrранные
уrлы, заключенные между этими rранями; б) три ребра од-
Horo соответственно равны трем ребрам друrоrо и равны трех..
rpa.HHbIe уrлы, имеющие эти \ребра.
. 10. Доказать, что Дlва одинаково ориеН'f.ир'ова,нных тетра-
эдра подобны между собой, если между их ребрами уста,н,ов"
лен'о взаимнооднозначное соответствие и четыре двуrра.нных
уrла oд.HO O соответ,ственно равны четырем д,вуrраIН,ным уrлам
друrоrо.
11. Данный тетраэдр пересечь плоскостью так, чтобы в
сечении получился ,ромб.
12. П'остроить теrраэд'р по данным шести e o ребрам. На-
черТ1ИТЬ развертку и ПО1СТрОИТЬ ero м,одель.
, 13. Построить пра.вильную треуrольную пирам:иду по реб-
ру осно!вания и вы,соте.
I 14. Построить праlВИЛЬНУЮ четыреху оль'ную пирамиду по
ребру 'Основания и IBbICOTe.
15. Начер,-,ить развертку и построить модели пирамид,
указа,нных в двух предыдущих задачах.
16. Построить правильную треуrо.пьную пирамиду, если
дано основание и двуrранные уrлы, образуемые бо:юовыми
rранями с 'ос'нованием. Начертить ра3ВЕ:рТ ку и по,с'rроить мо-
дель этоrо тела.
'. 17. В да ную пр ав ильную четырехуrольную пира'миду
вписать куб так, чтобы одна из rраней куба лежала на осно"
вании пирамиды, а четыре вершины на четырех ее боковых
ребрах.
18. В правильной треуrольной пирамиде ребро основа.ния
равно а, а боковые rрани образуют с плоскостью основания
уrол в 300. Найти построением и вычислением рас,стоя.ние от
вершины о.снования до плоскости противополож,ной rрани.
\ 19. Найти rеометрическое ,место точек, рав'ноудаленных от
в,сех боковых rраней правильной пираlМИДЫ.
25. ПРАВИЛЬНЫЕ мноrоrРАННИКИ
(25.1) Определение 1. Мноrоrранник называется nравuль-
НЫм', если ,в.се rрани ero правильные и ра,вные между с'обой
мноrоуrОЛЬ1НИКИ и если все ero MHoronpaHHbIe уrлы равны
между ,собой.
Для Toro чтобы разрешить IВОПрОС о сущес"вовании и виде
л'равильных I,но оrра'Нников, необходимо предварительно ус-
танvвить IС1оот,ношение между числом rраней, ребер и 'ве'ршИ'н
мноrоrранника. Непоеред,ственный подсчет этих ''Чисел дает
следующие результаты. В п"уrольной призме число верши,н
218
равно 2 п (п вершин BepxHero и п вершин нижнеrо основа-
НИЯ), число ребер ра.вно 3 п (п сторон BepxHero, п сторон
нижнеrо ос'Н,ования и п боковых) ; число rраней ра'вно
п+2 (п боковых rраней и 2 основания).
В п-уrольной пирам,иде число Iвершин palBHo п+ 1 (п вер-
шин ос,нова'ния и вершина пирамиды) , числ.о ребер рав,но 2 п
(п сторон основания и n боковых ребер), число rраней рав-
но п + 1 (п боковых rp а.ней и основание).
Рис. 225
Рис. 226
Е,сли сложить основаниями две равные .между С'обой пи-
рамиды, то получи/М мноrоrранник, назы,ваемый бunuра.м.u-
дой (рис. 225). В нем число вершин равно п +2, ЧИcJIО ребер
равно 3 п, .число nраlней 2 п.
Если на обоих ос'нованиях п..уrольной призмы построить
п'о п..уrольной пирамиде, то получим м,ноrоrранник, наЗЫlвае-
мый комбинацией призмы с пирамидами (рис. 226). В нем
число вершин равно 2 п+2, число ребер равно 5 п, число rpa-
ней palHHo 3 п.
Положим теперь, что на каждой rрани куба по.строены
rnравильные четыреху ольные пирамиды. В Э'f10М мноrоrра:нни-
ке, называемом пирамидаЛЬНbtм кубом, число вершин равно
14, ч'исл.о ребер 36, число rраней 24.
Сводя вместе 'результаты всех этих под,счето'в, получим
:ледующую таблицу, ,в которой В обоз,начает число вершин,
р число ребер, r число rраней.
Мноrоrранник В Р r
Призма 2п 3п п+2
Пирамида п+1 2п п+1
Бипирамида п+2 3п 2п
Комбинация призмы спирамидами 2п+2 5п Зп
Пирамидальный куб 14 36 24
219
Рассмотрение этой таблицы позволяет установить зависи
мость между числами вершин, ребер и раней ,во всех эти
мноr,оrра'нниках. Эта завис'имость заключается IB 1'ОМ, чro
су.мма чи.сел 'верш-ин и rра,ней на 2 боль'ше числа ребер В +
+r===p+2. Нетрудно проверить правильность этоrо вывода It
на М'НО1rоrран.никах, которые можно получить из расс.мотрен.
ных путем срезы/вания плоскими сечениями .нескольких МНО-
rоrрз<нных уrлов. Например, срезая все TpexrpaHHble уrлы
куба, ,мы получим четыр,надца"иrранн'ик (рис. 227) 'с 24 вер.
шинами и 36 'ребрами. По-прежнему мы получи'м: 24 + 14
36 == 2.
/J
Рис. 227
Рис. 228
O Ha'KO необходим,о за.мет,ить, что существуют. ,мноrоrра'и...
ники, для к.оторых у.становленная зависимость не имеет мес...
ra. Возымем, например, четьrрехуrольную бипирамиду (О,К.
rаэдр 'восьмиrранник) и срежем д'ва противопол'ож'ных че.
Tbl'pexrpaHHbIx уrла пл,оскостя'ми, параллельными общему ос-
нованию (рис. 228). После этоrо удалим из мноrоrранникз
приз,му ABCDA'B'C'D', т. е. просверлим этот мноrолра.ннин
так, 'Чтобы IB 'нем получилось сквозное отверстие. Подсче1'
qисл,а вершин, ребер и rраней этоrо мноrоrранника дает еле.
дующие цифры:
В==12, Р==24, r==12, т. е. B+r p==12+12 24==O.
Полученное различие объясняется тем, что по,веРХНОСТR
ранее ра,ос,мотренных мноrоrранников и пО'верхность MHoro..
nраlнника .на рис. 228 сущес венно 'отличаются друr от друrа.
РаЗlница эта заключается в том, что любой замкнутый раз.
рез поверхности первых мноrоrранников разделяет эту по..
верх'ность на д,ва отдельных куска. Например, произведя та-
к:ой разрез по l\o.HTYPY какой-нибудь rрани куба, призмы ил'н
пира'миды, мы можем удалить эту rpaHb и поверхность ,рас-
падется на два отдельных куска. На поверхности же MHoro-
rранника на рис. 228 мы можем произвести такой замкнутый
раз,рез (например, по контуру ABCD), что поверх'ность H
два отдельных куска не распадеreя.
120
(25.2) Определение 2. Поверхности, расnадающиеся 11,4
два отдельных куска при любом замкнутом разрезе, назы- .
ваются односвязными.
Уста'новленная 'ра.нее зависимость между числами rраней.
ребер ,И вершин имеет место только для МIноrоrра.нников.
оrра,ниченных односвязной поверхностью. Это обосновано в
следующей теореме.
Теорема 1 (теорема Эйлера). Если МНО202раннак 02рани",
чен односвязной поверхностью, то CYMAta чисел е20 вершин u
ераней на 2 больше числа ребер.
РаlССМОТРИМ какой-нибудь мноrоrранник с ОДНОQВЯЗ'НОЙ по.
верхностью, которая с,одеРЖ1ИТ В Iвершин, r rра.ней и Р ребер.
А
.... .......... l' С
I
f /
I
I
I
I
I
в
Рис. 229
Произведем за'мкнутый ра3'рез этой поверхности по контуру
какой-либо rрани. Ввиду TOf'O что поверхность односвязная,
мы можем эту rpa'Hb удалить. Предс'тав,им себе теперь, что ос-
тавшаяея часть поверхности сделана из эластичноrо материа-
ла (например, из 'резины), .споообноrо ра.стяrиваться. И'мея
это в виду, растянем оставшуюся часть поверхности так, что
бы при С'охра'нени.и числа ее ребер, 'вершин и rраней ее М1ОЖНО
было бы наложить на плоскость. Тоrда на плоскости получит-
ся прямолинейная сетка (рис. 229). Обоз,начим числ'о jвершин
этой сетки буКlВОЙ р, число отд'ельных областей " число ОТ-
резков между вершинами а. Очевидно, р == в, f == r 1,
й== Р. Докажем, что при некоторых преобразованиях сетки
число р + f а остается неизменным.
Прежде Bcero это число остается неизменным, если про-
вести диаf'ональ 'В любом из мноrоуrольников сетки. Дейст,ви-
rельно, пр:и этой операции число р 'остается неизменным, чис-
ло f увеличивается на 1 и число а тоже увеличивается на 1, а
общее значение выражения p+f a останется ,неиз'менным.
Пользуясь этим, мы м,ожем, проведя диаrонали, разбить
нашу ,сетку на l1реуrольники, как показано на рис. 229. Вы'ра-
жение p+f a сохранит неиз,менную величину. Эта \величи-
на остане-r,ся неизменной, если мы к одному 'из отрезков на
221
OHType сетки пристроим из.вне еще треуrольник (например,
дАВС к отрезку АВ). В эrом случае число р увеличится 'На 1,
числ,о f тоже 'на 1, число а у'величится на 2, а выражение
p+f a ,не изменит,ся.
Не изменится это выражение и 'в том случае, если по.
строить новый треуrlОЛЬНИК при 'входящем уrле (например,
ДLМN), так как число р в этом случае не изменится, число f
увеличится на 1 и число а тоже увеличится на 1.
Очевид'но, 'Что число p+f a не из,менит,ся и при обра ной
операции последовательном уничтожении поrраничных тре-
уrольников. НаПРИ Iер, на рис. 229 можно последовательно
лиК!видировать треуrольники, помеченные номерами с l-ro по
13-й. В результате от сетки останется еДИ'НСl'венный тре-
уrольни.к 14, для KOToporo р==3, f== 1 и а===З.
Следовательно, имеем:
р + f a === 1.
Восстанавливая пер,в.оначальную 'сетку, мы не изменим
qислово о значения этоrо выражения. П'осле этоrо свернем
сетку в первоначальную поверхность и добавим к ней удален-
ную rpaHb. Окончательно получим:
B+r p==2.
(25.3) Опираясь на теорему Эйлера, м.ожно установ,нть
число воз,можных видов правилыных мноrоrраННИКОIВ.
Теорема 2. Мосут существовать не более пяти различных
видов праВUЛЬНblХ мнососранников.
С'оrлаlС'НО определению все J1рани правильноrо MHororpaH-
ника ДОЛЖIНЫ быть правильными m..уrольникаlМИ и все M'Horo.
rpaHHbIe уrлы долж,ны быть п-rран.ным,и.
Вместе с тем, очевидно, т> 3 и п;> 3. Положим, что число
вершин искомоrо мноrоrранника равно В, число rраней r, число
ребер Р. По теореме Эйлера имеем:
в + r р == 2.
Подсчитаем число ребер по rраням. Если все rрани т-уrоль.
ники и число rраней равно r, то произведение т r дает удвоен-
ное число ребер, так как каждое ребро прилеrает к двум
мноrоуrольникам и потому будет сосчитано дважды. Итак, имеем:
mr 2Р
Р == , или r == .
2 т
Сосчитаем число ребер по вершинам. Так как при каждой
вершине сходится п ребер, а число вершин равно В, то произ-
ведение n В дает удвоенное число ребер, потому что каждое
(1)
222
ребро соединяет две вершины. Поэтому получим:
пВ 2Р
р == ..........., или В == .
2 n
(2)
Подставляя полученные значения для В и r в формулу
Эйлера, находим:
2Р 2Р ( 2 2 )
.......... + р == 2, или + 1 Р == 2.
n т 'п т
2 2
Так как р > О и 2> о, то и + 1 > о.
п т
Итак, для определения чисел т, п, В, r и р
веравенства:
(3)
мы имеем
2 i2
+ > 1; т:;> 3, п:;> 3.
п т
(4)
Эти три неравенства дают возможность определить допусти-
мые значения для т и п.
1. Подставляя значения т == 3 и п == 3 в равенстве (3),
получим:
( 1 ) Р == 2; [ Р == 2; Р == 6.
Из формул (1) и (2) имеем: В == 4 и r == 4.
Мы получили мноrоrранник, оrраниченный четырьмя тре-
уrольными rранями, имеющий четыре вершины и шесть ребер.
Он называется правильный тетраэдр.
22127
2. Положим т === 4, п === 3; + == + ...... > 1.
4 3 236
Равенство (3) дает в этом случае:
( I)P==2, P==2, P==12.
Из равенств (1) и (2) получаем: В === 8, r === 6.
Этот мноrоrранник оrраничен шестью квадратами, имеет
восемь вершин с трехrранными yr лами при них и двеиадцать
ребер. Он называется zексаэдр (шестиrранник......... куб).
3. Положим, наоборот: т === 3, п === 4. Тоrда тем же путем
получим: Р == 12, В == 6, r === 8. Полученный мноrоrранник,
оrраниченный восемью треуrольниками, имеет шесть вершин
с четырехrранными yr лами при них и 12 ребер. Он называется
октаэдр (восьмиrранник).
2 2
4. Значения т == 4 и п 4 не rодятся, так как 4 + 4=== 1.
2 2
Положим поэтому т == 5, n === 3. Тоrда получим: 5" + 3'"
223
16 /16 ) l'
_ ..... > 1. Из равенства (3) находим: I ........ 1 P:::II 2, ....... Р::::= 2,
15 \15 15
Р == 30.
Из (1) и (2) получим:
В 20, r == 12.
Полученный мноrоrранник, оrраниченный двенадцатью пяти..
уrольниками, имеет 20 вершин с трехrранными уrлами при них
и 30 ребер. Он называется додекаэдр (двенадцатиrранник).
5. Положим, обратно, т == 3, n == 5. Тоrда из тех же ра-
венств получим: Р == 30, В == 12, r == 20. Этот мноrоrранник
оrраничен двадцатью треуrольниками, имеет 12 вершин с пяти-
rранными уrлами при них и 30 ребер. Он называется и"осаэдр
(двадцатиrранник).
Сочетания т == 3 и n == 6 или т == 6, n::::::::J 3 не ПОДХОДЯТ.
так как
2 2
...... + == 1.
3 6
Не rодятся также сочетания т == 4, n == 5 или т::=8 5, n - 4,
так как
22129
...... + ........ == ....... + < 1.
4 5 2 5 10
Дальнейшее увеличение чисел т и. n будет, очевидно, еще более
2 2
уменьшать левую часть неравенства ...... + ....... > 1, и потому даль-
т n
нейшие пробы уже не имеют смысла.
Таким образом, мы видим, что MorYT существовать B,ce o
лишь пять IВ,ИДОIВ правильных мноrоrранников. В этом отно-
шении трех'мерное Пр1ос'ЛрансТtВО СУЩОС'f.венны.м образом ото.
JIичает,ся от двухмер,ноfoО (плоскости), так ,как на плоскости
мож:но построить бесконечное множе.ство :видов праВ1ИЛЬНЫХ
мноrоуrольников 'с каким уrодно числом равных сторон, Tor-
да как 'в простраlнстве может быть не более пяти видов пра-
вильных мноrоrран:ников.
Результат нашеrо ис.следования мож,но изобразить сле-
дующей таблицей.
т n В r р мноrorранника
3 3 4 4 6 I тетраэдр
4 3 8 6 12 reксаэдр
3 4 6 8 12 октаэдр
5 3 20 12 30 додекаэдр
3 5 12 20 30 икосаэдр I
Название
224
(25.4) Полученные выводы показывают только, что IB про..
странстве может -существовать не более пяти видов пра.виль"
ных м'ноrоrранникО'в. Для Toro чтобы решить вопрос, суще..
ствуют ли они 'в действительности, необходимо показать, ка..
"ими построениями они MorYT быть получены.
В основу построения всех пяти праlВИЛЬНЫХ мноrоrранни"
ков мо)кет быть поло)кена одна и та же фиrура: три взаимно
перпендикулярных равных отрезка АА', ВВ' и СС' с общей
серединой в точке О (рис. 230). Из этой фиrуры 1\1Ы можен
получить правильные мноrоrранники следующими построе..
ниями.
1. Соединяя концы этих отрезков, получим восемь рав"
ных между собой ра.вностороiнних треуrольникD'В: АВС, АВ'С,
АВС', АВ'С', А' ВС, А' В'С, А' ВС', А' В'С' (рис. 231), так как
LOBC== 60СА, следовательно, ВС== СА ==АВ и т. д.
Итак, мы получили правильный мноrоrран:ник, оrраничен
ный восемью равносторонними треуrольниками, октаэдр. На
рис. 232 дана также развертка TaKoro мноrоrранника, по KOTO
рой леrко изrотовить модель октаэдра.
2. Если через концы отрезков АА', ВВ', СС' провести
шесть плоскостей, каждая из которых перпендикулярна к
данному отрезку и параллельна двум друrим, то в результате
получ'им мноrоrра'нник, оrраниченный шестью квадрата.ми,
zе"саэдр (куб ,рис. 233) MN PQM' N' P'Q'. На этом же чер
теже дана также раз-вертка куба.
3. Если в полученном кубе MNPQM'N'P'Q' провести диа
rонали rраней МР, PQ', Q'M, MN', N'P и Q'N' (рис. 234),
то в силу равенства диаrоналей получим мноrоrранник,
оrраниченный четырьмя равносторонними треуrольниками:
MPQ', MPN', MN'Q' и Q'PN', тетраэдр. Ero же леrко
получить iИ из очень простой развертки (см. рис. 234).
4. Для построения правильноrо двенадцатиrранника дo
де1\,аэдра заметим, что число ребер куба (12) равно числу
rраней додекаэдра. ПОЭТО IУ постаlВИМ своей задачей провес
ти через ребра куба двенадцать плоскостей так, чтобы они
Clвоим пересечением определили двенадцать правильных пяти
уrольников. 8 вершин куба при этом будут вершинами
додекаэдра, остальные 12 вершин ero должны попарно Haxo
диться над шестью rранями куба. Таким образом, на Ka)l{..
дой rрани куба ДОЛ)I(на быть построена «четырехскатная ]{pы
ша», две rрани которой треуrольники и две трапеции
(рис. 235). Такой треуrольник и трапецию получим, проводя
одну диаrональ в правильном пятиуrольнике ABCDE (рис.
235), диаrональ KOToporo ра'вна ребру куба. Чтобы опреде..
лить ребро додекаэдра х, обозначим буквой а ребро куба
и пnоведем еще диаrональ ВЕ, которая пересечет АС в точ-
ке Р; 6АВС(/)6АВР, так как L.A обший и L.ABF== L.AEB==
LACB. Вместе с тем ACIIDE и BEIICD, Т. е. CDEF па..
t 5 А. и. Фетисов
225
А
6
А'
Рис. 2аl
Рис. 2 2
м
()
о
4
с'
8
8'
"
А'
Рис, 231
/'/
f)
м
11'
I О
I I ('
Bo---- l B'
ct 1°
N'!
I"-
.,.".,,-' 6 A 1
О'
,.
l
j
J
Ри . 2ЗЗ
N
раллелоrраым и СР == Еп == х. Из подобll"
получаем: а: х ==х: (a x), т. е.
x2+ax a2==O,
а У а2
х == + + а 2
2 4
Отрезок х получается из прямоуrольно
а
ro треуrО.lIьника с катета 1И а и '2; он ра
, . Q
вен разности между rипотенузои и 2" .
TaKWM образом, ребро додекаэдра найдено.
Чтобы построить искомую «крышу» на rрани MNPQ, про
Еедем на ней среднюю линию, соединяя середины ребер MN
м PQ и помещая на ,ней отрезок K'L'==x на ра,вных расстоя
"иях от MN н PQ. ИЗ точек К' и [' проведем перпендикуляры
61\ )/ /
"-е. 234
2 6
k и l к плоскости rрани. От середины S ребра PQ ОТЛQЖИМ на
1 точку L так, чтобы выпол,нялось равенсТ1ВО SL==BH, rде
ВН высота ABC. Тоrда получим, что p LQ == ABC, и
таким же образом получим MKN == ABC. Аналоrич'ное .0-
строение произ!ведем на rрани М' N' P'Q'.
t
с
L
D
Рис. 235
Рис. 236
Остальное построение получается довольно просто, если
JlрИНЯТЬ во внима.ние, что диаrональ правильноrо пятиуrоль
ника параллель:на противополож,ной стороне. На рис. 236 п()
казана развертка додекаэдра, по которой можно склеить ero
модель.
5. Для постр,оения правильно о д'вадцатиrра,нника ИКО
саэдра ,возьмем ту же фиrуру ,из трех 'взаимно перпенд'ику
JlЯрНЫХ отрезков АА', ВВ' 'и СС' (см. рис. 230). Имея в .виду,
что у икосаэдра 12 вершин, построим при точках А, А', В, В',
С, С' шесть отрезкOIВ так, чтобы эти точки служили середи
нами этих отрезков, а отрезки, проходящие через А и А',
были параллельны ВВ', отрезки, прох,одящие через В' и В,
были параллель'ны СС', ,отрезки, проходящие через С и С',
были пар'алл ь;ны АА'. Таким образом, мы получим 12 Bep
ши/н. Чтобы эти точки были 'вершинами икосаэдра ('рис. 237),
определим длины указанных отрезк,ов так, чтобы два конца
каждоrо из них с концом соседнеrо отрезка бы.пи верш'инами
paBHOCTOpo.HHer.o треуrольника, 'например, MN Р на рис. 237.
Обозначим 1tJерез а длину половины каждоrо из стреЗк<m
АА', ВВ', СС', а через х длину половины искомоrо ребра
15* 227
икосаэдра. П1роведя 'отрезок АР и отрезок PDII СО, получим
1) из ПРЯМ:ОУl'ольноrо треуrольника АМР: АР2+х 2 ==4 х 2 , т. е.
АР2==3х 2 ; 2) из прямоуrольноrо треуrольника ADP: (a x)2+
.. a2==AP2, или a2 2ax+x2+a2==3x2, т. е. 2x2+2ax 2a2==O И,
Рис. 237
Рис. 238
наконец: x2+ax a2==O. l\'\bI видим, что х может быть получен
из а тем же построением, каким из ребра куба получено ребро
додекаэдра.
Отложив длину х на соот,ветсТtВУЮЩИХ отрезках, ,найдем
двенадцать вершин икосаэдра, IСооединив которые получим
иско'мый праlВИЛЬНЫЙ мноrоуrольник. Для построения ero 'MO
дели на р.ис. 238 дана развертка этоrо 'м'ноrоrранника.
(25.5) Определение 3. ОСЬЮ симметрии п..ео порядка Ha
3600
зывается пря.мая, пр,и Iв'ращении около КО1'орой на уrол
тело совмещается с самим Сlобой.
Рассмотри:м, например, праlВИЛЬНУЮ ПЯТИУflОЛI>НУЮ пира
миду (рис. 239). Повернем ее на уrол в 720 около высоты 00'.
При таком повороте (если произвести ero 'в положительном
направлении) точка А попадет 'на мест.о, зЗ'нимаемое точкой В.
точка В займет положение точки С, C D, D E и, наконец.
3600
Е займет положение точки А. Так как 72 0 ==:. 5 ' -ro мы за
ключаем, что 00' есть ось симметрии 5..ro порядка 'в пра
вильной пятиуrольной пирамиде.
Мож'но произвес1'И еще четыре таких поворота около оси
00', после чеrо точка А вернется в исходное положение, со-
вершив полный оборот около оси 00'.
Каждое положение м'ноrоrра.нника, при котором он со-
вмещается с некоторым исходным положением, называется
ero СQмосовмещением. К числу самосовмещений относят и
rтервоначальное ПQложение тела. Так, в приведенном примере
,
228
п
с пятиуrольной пирамидой мож,но убедиться, что этот MHoro-
rранник имеет пять самосовмещений. Вообще нетрудно уста-
новить, что правильная п..уrольная пирамида имеет ось сим-
метрии п..ro порядка и п сам'осовмещений.
Число .о,сей симметрии и связанное с ним число calMoCioB-
мещений определяют сu"иметрuю данноrо мноrоrранника.
Симметрия м.ноrоrра\нника иrрает о,сновную роль в к'ристалло-
rрафии науке о кристаллах. По степени симметрии произ-
водится классификация кристаллических форм.
1J
,
I
I
I
I
I
A
./ ,
,
о
А
в
Рис. 239
Рис. 240
Дад'им еще примеры -определения числа осей симметрии и
чи.сла самосовмещений.
В правиль'Ной шестиуrольной призме (рис. 240) прямая,
rrрох.одящая через центры оснований, служит осью симметрии
6..ro порядка. Т'ри оси симметрии BToporo порядка проходят
через середины противоположных ребер и еще три оси сим-
метрии 2..ro 1l0рядка пр'оходят через центры противоположных
раней. Призма ,самосовмещаеТ1СЯ двенадцатью различ,нымн
способа/ми.
Куб (см. рис. 233) имеет три оси 4..ro порядка, проходящие
через центры противоположных rраней (10 самосовмещений).
Четыре оси симметрии 3..ro порядка проходят по диаrоналям
куба, что дает 8 новых самосовмещений. Наконец, шесть
осей 2..ro порядка проходят через середины противоположных
ребер (t) новых самосовмещений) . Bcero для куба существует
24 различных самосовмещения.
Совершенно такой )ке симметриай обладает октаэдр. Три
оси симметрии 4..ro порядка проходят через протИ\воположную
вершину, четы'ре оси симметрии 3..ro порядка проходят через
центры противо.п,оложных rраней, шесть осей -симметрии
2.. o порядка проходят через середины ПРОТИ1ВОПОЛОЖНЫХ ре-
бер. От'сюда следует, что октаэдр тоже имеет 24 caMOCO,B e-
щения (см. рис. 231).
229
Тетраэдр имеет четыре оси симметрии 3"РО по'рядка, про
ходящие через вершину Iи центр противоположной rрани, н
три оси симметрии 2..ro порядка, проходящие через середи.ны
противоположных ребер. Bcero тетраэдр допускает .и.вена
дцать самосовмещений.
Упражнения
1. СущеС11вует ли мноr.оrранник, и tfеющий 7 ребер?
2. Доказать, что число Р ребер lноrОIlранника выражаеТСJ1
ФВР'МУЛОЙ:
,2 Р==3 r з +4 r..+5 rs+...,
rде r з ЧИ'СЛQ трехуrольных rра'Ней мноrоrранника, r. Ч1И,с"
ло четырехуrольных rра.ней и Т. д.
3. Доказать, что число Р ребер мноrоrранника определяет..
ся формулой:
2 Р==3 Вз+4 В4+5 В5+...,
rAe В, ЧI1СЛО T,pexrpaHHbIX уrлов м;ноrоrранника, В. число
четырехrранных уrло,в и Т. д.
4. Доказ,ать, что ЧИ1СЛО плоских уrлов мноrоnранника вдвое
()ольше 'Числа ero ребер.
5. Доказать, что число самосовмещений праlВИЛЬНОro 'М'НО"
rоrранника ВДIВ,ое больше числа ero .ребер.
6. Установить числ'о и порядок осей симметрии у додекаэд
ра и и осаэдра и найти число их самос'овмеще.ний.
7." Сколько осей симметрии и каково число самосовмеще..
инА у правильной п уrолыной бипирамиды?
8. Сколько плоскостей симметрии можно провести 'в каж
ДОМ из пяти пра!виль'ных мН'оrоrран:ников?
9. Доказать, чт.о если точка ле)кит на поверхности пра..
вильноrо тетраэдра ил,и находится внутри Hero, то сумма ее
ра.сстояний от четырех rраней есть величина по'стоянная.
I(). Будет ли предложение предыдущей задачи справедл'и"
'50 для остальных правильных м'ноrоrра.нников?
11. Доказать, что центры rраней куба служат вершинами
октаэдра, а центры r,раней октаэдра вершинами куба.
12. Доказать, что середины ребер пра.вильно о тетраэдра
служат вершинами октаэдра.
13. Доказать, что центры rраней додекаэдра служат Bep
ш'инами икосаэдра, а центры rраней икосаэдра служат верши..
нами додекаэдра.
14. Сколько различных кубов 'можно ,вписать в додекаэдр
так, чтобы вершины каждоrо куба были в то же время и Bep
шинами да:нноrо додекаэдра?
15. В данный октаэдр ,вписать куб так, чтобы вершины
куба лежали на ребрах октаэдра.
16. Построить тетраэдр по данному ребру ero.
23()
17. Построить октаэдр по данному ребру ef'o.
18. Данный октаэдр пересечь плоскостью так, 1f?Oбы в се-
. .
че",ИИ получился правильныи шестиуrольни,к.
19. Найти точки, симметрич,ные с центро.м куба ОТНОСII-
тель,но 'всех ero rраней. Полученные 6 т'очек с 8 ,вершинами
куба определяют 14 вершин мноrоrранника, называемоro
ромбическим додекаэдром. Определить числ,о ero rраней Jl
ребер, число и порядок о'сей симметрии и число с a.M,OCOBIM е..
щений. (Заметим, что та ими ,мноrОl1ранниками являются
кристаллы ,некоторых минералов, например rpaHaTa.) Приrо..
ТО вить модель ромбическоrо додекаэдра.
20. Срезать у куба TpeXf'paHHbIe yr'nbI так, чтобы полу
чился uноrоrранник, оrраниченный шестью праlВИЛЬНЫМИ
8,осьмиуrольниками и во'с-емью раlВНОСТО'РОННИМИ треуrолыни"
камн. Приrотовить модель мноrоrранника.
21. Срезать у октаэдра четырехrранные уrлы так, чтобы
получился м,ноrоrранник, Оl1раниче'нный восемью правиль..
ВЫМИ ш стиуrольниками и шестью квадратами. Прнrотовить
'''10дель' TaKoro мноrоrранника.
rЛЛВЛ ДЕВЯТЛJI
KPyr ЛЫЕ ТЕЛА
.
I 26. ЦИЛИНДР
(26.1) Если через каждую точку какой"н.ибудь линии про-
вести прямую, параллельную одной и той же прямой, то reo-
метрическое место всех этих прямых называется цилиндриче-
ской поверхностью (рис. 241).
Данная линия называется направляющей цилиндрической
поверхности; параллельные прямые, KO OpЫM I1Iринадлежат
все точки поверхности, назы'ваются ее образцющими. Еслн
направляющая Л'И'ния замкнута, то и цилиндрическая поверх
ность назыIаетсяя замкнутой.
М'ожно предста.вить, что образующая движется, оставаясь
все время параллельной одной и той же прямой и скользя
при этом по направляющей. При таком непреРЫJВНОМ дви}ке
нии она опишет цилиндрическую поверхность.
Из этоrо определения мы видим, что призматическая по..
верхность есть частный случай цили.нд'рической, коrда на..
лравляющая является ломаной линией. Если же наlпра,вляю"
щая будет прямая, то поверхность, очевидно, станет плос
костью.
Определение. Цилиндром называется тело, оrраниченное
замкнутой цилиндрической поверхностью и двумя параллель
ными между ,собой плоскостями, пересекающими образующие
(рис. 242).
Фиrуры, полученные в сечении, называются основаниями
Ilилиндра. Расстояния между секущими плоскостя'ми назы-
ваются высотой цилиндра. Если секущие ПЛО1СКОСТИ перпенди-
кулЯ'р'ны к образующим, то цилиндр называется прямым.
В противном 'случае он называется наклонны/..t. Если направ'"
..1яющая прямоrо цилиндра окружность, ТО цилИ'ндр назы-
вается прямым КРУ20ВЫМ или цилиндром вращения (рис. 243).
Следствие 1. Основания цилиндра равны между собой.
Действительно, если направление образующих цилиндриче-
ской по ерхности принять за Iнаправление параллельной про-
екции, то мы увидим, что нижнее основание есть параллель-
232
Рис. 241
I
I
I
,
I
l ...
..,-- I ....."
f "
.
"
"
"
Рис. 243
Рис. 244
Рис. 242
Рис. 245
ная проекция BepxHero, пр.ичем 'Оба оснО'вания лежат в па
раллельных плоскостях. Поэтому оба основания равны меж
ду собой (см. рис. 242).
Следствие 2. Если nРЯМ,ОУ20ItьниК, вращается 80круе одноЙ
из своих сторон, ТО остальные стороны е20 описывают пo
верхность цилиндра вращения.
Пусть сторона 00' прямоуrольника АОО'А' (СМ. рис. 243)
закреплена неподвижно, а ве,сь прямоуrольник вращается BO
Kpyr оси 00'. Тоrда прямые ОА и О' А', остаlваясь все вреМЯ
перпендикулярными к прямой 00', будут описывать ПJ]ОСКО
сти, перпендикулярные к 'оси вращения. Образующая АА' oc
тается в'се время параJlлельной оси 00' и скользит по окруж"
ности С цeHTpO 1 о. Следовательно, она описывает боковую
поверхность прямоrо KpyroBoro цилиндра. Отсюда такжр
ВИДНО, почему этот ЦИЛИНДР называется цилиндром враще
ния.
Поверхность KpyroBoro цилиндра представляет собой ча
с"ный случай поверхности ,вращения вообще. Произ\вольная
2ЗЗ
ипос.кая ли-ния, вращающаяся 'BoKpyr оси, лежащей в той же
плоскости, опи-сы'вает поверхность ,вращения (рис. 244). На..
пример, парабола, вращаясь \BoKpyr .своей оси, описывает
поверхность, называемую параболоидом вращения (рис. 245).
Поверхностями вращения оrраничены мноrие предметы
домашнеrо обих'ода и техники: /вазы, стаканы, rрафины, нра..
щающиеся детали м,но их машин. Па1раболоидом вращения
является ,поверхность жидкости, налитой св цилиндрический
сосуд, вращающийся B'oKpyr вертикальн'ой оси. Такую же по..
верхность имеют отражающие зеркала телескопов рефлек"
то р о в.
(26.2) Теорема 1. Площадь боковой поверхности цилинд..
ра вращения равна проuзведению длины окружности основа..
ния на длину высоты:
Sб == 21tRH.
в этой формуле R обозначает длину радиуса основания
'цилиндра, Н.......... длину ero высоты.
Боковая поверхность цилиндра является кривой поверхностью.
Площадь ее может быть определена тем же методом последо-
,нательных приближений, каким пользуются при определении
АЛИНЫ окружности и площади Kpyra.
Разделим окружность основания цилиндра на п равных
цастей и, соединив последовательно точки деления, впишем
в эту окружность правильный п-уrольник. Примем этот n-уrоль-
НИК за основание правильной n-уrольной призмы, боковыми
ребрами которой будут образующие, проходящие через вершины
n-уrольника, а основания лежат в плоскости оснований цилиндра
(рис. 246). Такая призма называется вписанной в цилиндр.
Площадь боковой поверхности вписанной призмы примем за
приближенное значение площади боковой поверхности цилиндра.
При неоrраниченном увеличении числа n площадь боковой
поверхности призмы стремится к пределу. Действительно, обоз-
начая через Sn эту площадь, а через Р п .......... периметр основания,
получим: Sn == РпН, но lim Р п == 2nR, поэтому:
п...оо
lim РпН == 2nRH.
n--+оо
Как известно из планиметрии, число 2nR не зависит от
выбора исходноrо правильноrо мноrоуrольника. Поэтому и число
2л,R Н не зависит от выбора исходной правильной призмы. Это
число по определению принимается за площадь боковой поверх-
ыости цилиндра:
56 == 2nRH.
34
TO.lbKO что Д'йказанное 'предложение можно сделать впоп
не наrлядным, если рассмотреть развертку боковой поверх
ности цилиндра (,рис. 247). Представим себе модель цилИ'нд
ра, сделанную из пл,отной бумаrи. Разрежем бо.ковую поверх
и(ость цилиндра по образующей АВ и раз\вернем ее на плос
КОС1'К. МЫ получим прямоуrоль'ник AIA2B2BI. Основанием
11,
.41
Ь,'
!3 !
Рис. 246
Рис. 247
nрямоуrольника служит отрезок 8182, длина KOTop'oro ра'внз
,Длине окружности основания, Т. е. 2тcR, а высотой служит
отрезок А181, рав'ный вы,соте цилиндра Н. ПJl,ощадь получен
Horo прям,оуrольника 'равна площади боковой поверхности
цилиндра, т. е. числу 2nRH.
Понятно, что полученный выlодд формулы для площади
бокО'в'ой поверхности цилИ'нд'ра является лишь практическим
приемо,u, делающим наrлядной найденную формулу и не MO
жет за fенить при.веденно о выше доказатель'ства.
Упражнения
1. Почему с,оприкасающаяся с землей поверхность Iвсякоrо
колеса я,вляет'ся поверхностью вращения?
2. Доказать, что если через какую-'нибудь точку .на окруж
ности ,основания цилИ'ндра вращения провести к этой оК'руж
ности касательную, то плоскость, проходящая через эту Kaca
тельную и образующую цилиндра в этой точке, не пересекает
поверхность цилиндра. Эта плоскость называется касатель
'ной плоскостью к цилиндру.
3. Доказать, что если расстояние от точки до осе.вой пря
мой цилИ'ндра вращения больше ero :радиуса, то [через эту
точку проходят две касательные плоскости к цилиндру. Дать
.соответствующее построение на проекционном чертеже.
4-. Разделим 'Окружность основания круrлоrо цилиндра на
п равных частей и построим праlВИЛЫНЫЙ описанный n..уrоль-
235
ник. Построив на этом основании правильную п"уf'ОЛЬНУЮ
призму с высотой, равной высоте цилиндра, получим Пiризму.
описанную около цилиндра. Доказать, что пределом площади'
боковой поверхности этой призмы при n, стремящемся к бес
конечности, является площадь боковой ПOlверхности цилиндра.
5. Заданную на пр'оекционном чертеже боковую поверх
ность цилиндра 'вращения пересечь пл'оско,стью, заданной'
следом на ПЛОСК1О'СТИ основания и точкой на оси цилиндра.
6. Доказать, Чl'О фиrУ'ра сечения в предыдущем упраж'не
нии есть эллипс. Вычислить ero большую и малую 'ось, если
секущая плоскость образует с плоскостью сечения уrол ЧJ,
а радиус цилиндра равен R.
7. Доказать, что если ПРЯ1моуrольник Iв,ращается около оси.
паралл'ельной еро стО'р,оне и не пересекающей ero, то пол'ная
. ПОrверхность полученноrо тела вращения равна произведению,
пери: етра этоrо прямоуrольника на длину окружности, KO
торую описы,вает ero цен'Dр.
8. Что являе ся rеометрическим местом точек, находя
щихся ОТ да:нной ,прямой на расстоянии, равном данному
отрезку?
9. В куб с ребром а 'вписан цилиндр так, что ero OCHOBa
иия леж,ат на ПРОТИ1ВОПОЛОЖНЫХ rранях куба. Определить.
полную поверхность цилиндра.
10. Оси двух цилиндрических поверхностей вращения па
раллельны между собой. П'ровести к этим поверхностям об
щую касате.пыную пл'оск,ость. Дать построение на проекцион
ном чертеже.
11. П ровесТ'и плоскость, касательную к цилинд,рической
поверхности в'ращения 'и параллельную данн.ой прямой. Дать.
построе'ние на проекционном чертеже.
f 27. КОНУС
(27.1) Если через каждую точку какой",нибудь линии про
вести пря'мую, проходящую через постоянную точку, не ле
жащую на этой линии, то rеомеТ'рическое место всех этих
прямых пред,ставляет собой поверхность, называемую KOHи
ческой (рис. 248).
Данная линия наЗЫ1вается направляющей конической ло
верхности, постоянная точка вершиной, прямые, проходя
щие через точки направляющей и вершину, образующими
конической поверхности.
Если направляющая замкнута, то коническая поверхность.
называется замкнутой.
Из этоrо определения следует, что боковая поверхность
пирамиды есть ча.стный случай конической поверхности, Kor..
да напра.вляющая замкнутая ломаная линия.
236
Определение i. Конусом называется тело, оrраниченное
замкнутой !{онической поверхностью и ПЛ1ОСКОСТЬЮ, пересе
кающей все образующие и не ПРОХОДЯll ей 'Через вершину.
Фиrура, которая получает.ся в сечении, наЗЫlвается OCHO
t/3aHueM кону,са, ,вершина конической поверхности вершиной
и
Рис. 248
Рис. !4g
о
Рис. 250
конуса, часть конической поверхности от вершины до осно"
вания кО'ну,са ero боковой поверхностью. Расстояние от
вершины конуса до плоскости ero ос.нования называется BЫ
сотой конуса (рис. 249).
Определение . Прямым КРУ20ВЫМ конусом, или конусом
вращения, называется КО'НУС, основанием KOToporo служит
Kpyr, а высота проходит через центр основания (рис. 250).
Теорема 1. Если конус пересечь плоскостью, параллельной
основанию, то в сечении получится фиzура, подобная ОСНО..
ванию.
237
Рассмотрим сечение конуса плоскостью, параллельной OCHO
ванию (СМ. рис. 249). При помощи лучей с началом в точке О.
можно установить взаимнооднозначное соответствие между
точками сечения и точками основания. Пусть, например, точке
А соответствует точка А', точке В точка В' и т. д. в силу
параллеJ1ЬНОСТИ плоскостей будем иметь, что АВ 11 А' В', а это
значит, что фиrура основания и фиrура сечения rомотетичны,
ОА' ОБ' OQ'
причем == == == ... k, rде k коэффициент rOMo
ОА ОВ OQ
тетии. А так как rомотетичные фиrуры подобны, то, значит,
в сечении получилась фиrура, подобная основанию, и коэффи
циент подобия равен k.
Так же как и круrовой цилиндр, круrлый конус является
телом вращения. Пусть прямоуrо.пьный треуrольник АОО' (см.
рис. 250) вращается около катета 00'. Коrда второй катет,
будучи перпендикулярным к оси вращения, опишет Kpyr, пер..
пендикулярный к этой оси, точка А опишет окружность этоrо,
Kpyra. rипотенуза ОА служит образующей, которая описывает
боковую поверхность конуса. Поэтому круrовой конус называет
('я также конусом вращения.
(27.2) Теорема 2 . Площадь боковой поверхности конуса равна
n.пловuне nроuзведеflUЯ длины окружности основания на длин у
образующей:
s, == nRl.
Здесь R длина радиуса окружности основания, l.......... длина
образующей.
Для доказательства разделим окружность основания на n
равных частей (рис. 251) и проведем через точки деления Kaca
тельные к окружности, которыми определится правильный
описанный n..уrольник. Соединяя вершины этоrо мноrоуrольника
с вершиной конуса, получим правильную n..уrольную пирамиду,
описанную около конуса. Апофемы этой пирамиды совпадают
с образующими конуса.
При неоrраниченном увеличении n площадь боковой поверх
ности описанной пирамиды стремится к пределу. Обозначив
эту площадь через Sn' получим:
t
Sn == P"l,
rде Р" периuетр основания, а 1 длина апофемы, совпадаю-
щей с gбразующей конуса.
liт .!.. P lI l === ..!.. 2nRl == nRl.
,..... _ 2 2
2: 8
Этот предел по определению принимается за площадь бокv,
вой поверхности конуса вращения:
Sб == лRl.
Если сравнить это число c площадью основания конус а
S == пR2, то получим:
S лR2 R
.............. == == == cos (J."
Sб nRI 1
L
r,ite сх........ уrол наклона обраЗУlощей конуса к плоскости OCHOBa
мия. Отсюда можно получить еще одну формулу для ВЫЧИС.Jf€'--
вия площади боковой.;_поверхности конуса:
Sб == лR2 .
OS а
Форму лу боковой поверхности КРУ r лоrо- конуса можно попу-.
чить, рассматривая развертку конуса (рис. 252). Для этоrо раз
')
Ij
PII . 251
Рис. 252
режем боковую поверхность по образующей и развернем ее H3
плоскость. При этом получается круrовой сектор с центром О'
,
1( радиусами О' А 1 и О' А;, длина которых равна длине образук)
щей l.
Площадь сектора равна половине произведения длины ero
2адиуса на длину дуrи. Радиус равен 1, а длина дуrи равна
pnR. Итак, площадь боковой поверхности выражается формулой:
Sб == 1/ 2 '2лRl == лRl.
(27.3) Определение 3. Jlсеченным конусом называется часть
конуса, заключенная между основанием и секущей плоскостыо,
параллельной основанию.
239
TeOpel\1a 3 Площадь БОКО80Й поверхности усечеННО20 Конуса
вращzния выражается формулой:
Sб == л; (R + ') 1.
rде r длина радиуса BepxHero основания, R длина радиуса
нижнеrо основания, 1 ......,. Длина образующей боковой поверхности
(рис. 253).
Соrласно по ледней формуле в предыдущей теореме площадь
боковой поверхности полноrо конуса равна nR' , а площадь
cos «
Рис. 253
боковой поверхности отделившейся верхней части ero равна
nr'
. Площадь боковой поверхности усеченноrо конуса равна
cos с1
разности:
nR2
Sб ==
cos с1
==:
п (R + ,) (R ,>
п,2
cos с1
cos с1
R r
Но cos (J., == , следовательно:
1
Sб == л; (R + ') 1.
Упражнения
1. Вывести формулу для площади боковой поверхности
конуса вращения, раС1сматривая ее как предел площади бо-
ковой поверхности правильной п..уrольной пирамиды, вписан
ной в этот конус.
2. Начертить развертку боковой поверхности усеченноrо
конуса вращения и из рассмотрения ее вывести фор,мулу для
площади боковой поверхности усеченноrо конуса.
3. На проекционно черте)l(е найти сечение заданноrо KO
нуса плоскостью, заданной следом и точкой на оси конуса.
4. В конус ,вращения вписать равносторонний 1 цилиндр
так, чтобы основание цилиндра лежало на основании конуса.
1 Kpyr лый цилиндр называется равностороынuм., если высота ero paB
на диаметру основания.
24.0
5. Вычислить полную повер ность конуса 'вращения, нпи-
ca,HHoro ,в правильный тетраэдр, ,ребро Koтroporo 'равно а.
6. У ол между вы.сотой конуса вращения ,и образующей
равен а. Вычислить уrол между rpадиусами, оrраничивающи-
ми сектор в ero развертке.
7. Через данную точку провести ка1с,ательную ПЛОСКОIСТЬ 1<
боко.вой поверхности конуса .вращения.
8. П'р.Qlвести ,плоскость, ка.сателЬ!нУю к боковой поверхно-
сти данноrо конуса 'вращения и па.раллельную данной пря,мой.
9. Равносторонний треуroльник со ст,ор'оной а вращается
BOKpyr одной из своих сто,рон. Определ,ить площадь получен-
Н'ОЙ поверхн,ости вращения.
10. Данный конус вращения пересечь плоскостью, парал-
лельной о-снованию, так, чтобы ero боко,вая п,оверхность раз-
делила,сь на две равн.овеликие ча.сти.
11. Три прямые, не леж,ащие в 'одной и той же плоскости,
имеют 'Общую точку. Сколько к'онических -поверхностей враще-
ния М'оЖ'Н:о провести через эти пря'Мые?
12. Доказать, что 'в -вы.пуклом четырехrра.нн'ом уrле, Iвпи-
санном 'в ко.ническую поверхность 'вращения, сум\ма двух про-
тивоположных двуrранных уrлов равна сумме двух друrих
ll,ByrpaHHbIx yr лов.
13. Доказать теорему, обратную предложению предыдущей
задачи.
14. В данный трехrраlННЫЙ у ол вписать коническую П'о-
верх.ность вращения.
15. Коническая поверхность 'вращения вписана 'в четырех-
rранный уrол. Д-оказать, что сумма двух противоположных
плоских уrлов этоrо четырехrтра'нн'оrо уrла равна сумме двух
друrих ero плоских уrло.в.
16. Прямая, имеющая одну, и только одну, общую точку с
цил,индрической или конической поверхностью 'в'ращения, на..
зывается касательной к эт.ой поверхности. Найтrи rеометриче-
ское 'место точек, принадлежащих всем касательным, прох'О..
дящим через данную точку цилиндрической или конической
поверхности вращения.
s 28. СФЕРА И ШАР
(28.1) Определение 1. rеометрическое место точек про..
странства, 'ра.естояние которых от данной точки равно дан-
ному отрезку, называется сферой.
Данная точка наЗЫ1вается центром сферы, расстояние от
'rочки ,сферы до центра 'называется ее радиусом. Отрез,ок,
соединяющий две точки сферы и проходящий через центр.
называется ее диаметром.
16 А,. и. Фетисов
241
Т,очки, раест,ояния кот,орых от центра сферы меньше pa
диуса, наЗЫlваются внутренними по .отношению к С'фер ; ТОЧ
ки, ра,сстояния которых от центра больше ,радиуса, называ
Ю'rСЯ внешними по отношен,ию к 'Сфере. Часть пространства,
оrраниченная сферой (Т. е. сов,окупность IВcex :не в'нешних
точек сферы) называет,ся шаром. .
Нетрудно убедить,ся .в том, что сфера является частным
случаем поверхнос1'И вращения. ПОЛfОЖИМ, 'полуокружность С
центром О (рис. 254) 'нращается 'BoKpyr диаметра РР'. Тоrда
Рис. 254
Рис. 255
каждая точка полуокружности (например, точка А), нахо-
дясь на постоянном рас,стоянии от центра О, будет находить
ся в.се время и на поверхности сферы. Поэтому лолуокруж"
ность при С'воем Iвращении описывает сферу.
Определение сферы вполне а'налоr,иЧНО определению OK
РУЖНОtСТИ ,в планимет,рии. П'оэтому ,и мноrие свой,ства сферы
аналоrичны свойствам окруж!ности. Например, в пла'ниметрии
мы без доказатеЛЬС'frва принимали предлО'жение о том, что
нсякий 'отрезок, соединяющий внутреннюю точку ,окружности
с внешней, пересекает окружность в одной, и толькО' одной,
т,очке. Подобное предложение ОКrазывается СПlраведл'ивым и
для сферы.
Отрезок, соединяющий внутреннюю точку сферы с внеш..
ней, пересекает сферу в одной, и только в одной, точке.
На основании этоrо свойс-r.ва сферы ,м,ожно доказать сле-
дующую теорему.
Теорема 1. Если расстояние плоскости от центра сферы
меньше радиуса, то плоскость и сфера имеют общие точки,
zеометрическим местом которых служит окружность.
Пусть мы имеем сферу с радиусом R и плосК!ость а, при
чем ра'сстоЯ'ние ОР ЭТОЙ пл.оскости от центра меньше радиу-
са: OP<R (рис. 255). П,ровед.ем из точки Р ПО пл,оскости (]
лроизвольный луч И отложим на нем отрез'ок PQ==R. С,оеди
нив точки О и Q, получим прямоуrольный OPQ. Так как
ОР l..a. то, значит, OQ>PQ, Т. е. OQ>R. Следовательно, Q'
242
есть внешняя точка относительно .сферы. В то же время Р
есть внутренняя точка (OP<R), поэтому отрезок PQ п,ере-
секает -сферу 'в некoQТОрОЙ точке А. Е,сли из центра Р по
ал'оскости а радиусом Р А опишем ОКlружность, то все точ,ки
этой 'окружности принадлежат .одновременно и ,плоскости, и
сфере. Действительно, всякая точка В на окружности нахо-
дится от центра О на расстоЯ'нии радиуса R, так как проек-
ции наклонных ОА и ОВ равны между собой (РА==РВ)
И, значит, OB==OA==R. Внутренние точки Kpyra являются
и внутренними точками шара, так как их расстояния от
центра Р меньше радиуса РА, а значит, и расстояния от
центра О меньше ОА. Подобным же образом внешние TO
чки относительно Kpyra будут внешними и относительно
шара. В этом случае плоскость а называется секущей, а ок-
ружность ОКРУЖНОСТЬЮ сечения.
Е,сли, -в частности, секущая плоскость ПрОХОд'ит через
центр сферы, то радиус окружности сечения ра,вен радиусу
сферы и Kpyr сечения называется большим КРУ20М, а концы
диаметра, перпендикулярноrо к плоскости этоrо Kpyra, назы-
ваются ero полюсами. Очевидно, во ,всех сечениях, не прохо
дящих через центр, радиусы сечений меньше радиуса сферы
(например, на рис. 255 Р А < ОА).
Следствие. Если две точки сферы не являются концами
одНО20 и ТО20 же диаметра, то ими определяется eдиHCT8eH
"lЫЙ большой КРУ2.
Дей,ствительно, ли точки М и N лежат на с'фере, а центр
О не лежит на прямой MN, то этими Тlремя т,очкаlМИ опреде-
ляется единственная ПЛoQСК1ОСТЬ. А так как она ,проходит через
центр, то, значит, в сечении получится большой Kpyr.
(28.2) Форма шара является 'весьма 'распространенной IВ
природе и в окружающей нас обстановке. Земля, Луна, па-
дающая капля дождя, ,масляная капля в Clмеси 'воды и спир-
та (опыт Плато) и Т. д. имеют форму, близкую к ша.ровой;
сферическую форму имеет мыльный пузырь.
Шар,ообразность этих тел объясняе ся тем, что 8нутрен-
ние силы, действующие на их частицы (сила тяжести .для
пебесных тел, молекулярное притяжение для небольш'их масс
жид ости), стремя1'1СЯ у,меньшить поверхность тела. Из всех
же тел данноrо объема наименьшую поверхность имеет шар.
Следует обратить Iвнимание на то, что при изображении
сферы Iна ПР1оекцианном чертеже ,пр-их,одится пользоваться
тольюо ОРТО20нальной проекцией. Это объясняется тем, что
любая Iк,осоуrольная параллельная проекция дает .изображе
яие сферы в виде эллипса, а не в виде окружности, что co
'Вершенно .не соответствует привычному восприятию сфериче
ской формы нашим rлазом, так как нашему rлазу сфера Bcer
да предстаВJlяется Kpyr,oM. Причиной этоrо служит ТО, что
1'- 243
лучи, идущие от преД!\-fетов ,к нашему rлазу, падают на сет-
чатку rлаза перпендикуляр,но к ее поверхности.
Если мы будем проектировать шар параллельньrми луча
ми (рис. 256), '1'0 лучи, проектирующие внутренние точки
шара, будут проХ'одить 'внутри цилиндрической поверхности
вращения, напраВЛЯIощей которой 'служит окруж'ность боль-
шоrо Kpyra, перпендикулярноrо к направлению лучей, а обра-
зующими лучи, идущие из точек этой окружности. Пере-
секая полученную цилиндрическую поверхность плоскостью,
мы получим в сечении проекцию контура Т. е. Irраницу, ОТ-
Рис. 256
деляющую проекции внутренних точек шара от остальных
точек плос'кости проекции). Эта проекция будет окружностью
только в том случае, если 'секущая плоскость перпендикуляр-
на к направлению проектирующих лучей, т. е. при opToro-
нальной проекции.
Ч1'обы изображение шара не смешать с изображением
окружности, на изображении шара даются еще проекuии
пл'о'ских сечений ero.
(28.3) Теорема 2. Если расстояние плоскости от центра
сферы равно ее paдиycy то эта сфера и плоскость имеЮ1
oдHY и только oдHY общую точку.
Пусть мы имеем сферу с центром О и плоскость а, рас-
стояние которой от центра сферы равно 'радиусу R, т. е,
OP==R (рис. 257). ,По условию теоремы OP.la, причем точка
р принадлежит одновре lенно и сфере, и плоскости а. Возь-
мем какуюоонибудь друrую точку Q пл,оскости а. Так как ОР
перпендикуляр к плоскости, то OQ наклонная и, значит,
OQ>OP, т. е. OQ>R. Следовательно, все точки плоскости а,
за ,исключением точки Р, являются внеLUНИМИ по отношению
к сфере. Итак, Р единственная общая точка сферы и плос-
кости.
244
Определение 2. Если плоскость и сфера имеют одну, и
только одну, общую точку, то плоскость называется касатель-
ной к сфере, а ,0БИl.ая точка наЗЫ1вает,ся точкой касания.
Теорема 3 (обратная). Если сфера и плоскость касаются
друе друеа, то радиус, проведенныа к точке касания, перпен"
дикулярен к плоскости.
Рис. 257
Пол'ожим, 'Что плоскость а ка,сается сферы с центрО'М О
в точке Р (см. 'рис. 257). С.оrласно условию OP==R, а любая
д'руrая точка плоскости а, например Q, является 'внешней по
Рис. 258
отношению к сфере, а пот,ому OQ>R. Итак, отрезок ОР есть
кратчайший из всех отрезков, соединяющих точку О с точ"
ками плос ости а. По 'обратной теореме о перпендикулЯ'ре и
наклонных получим: ОР a.
Теорема 4. Если расстояние плоскости от центра сферы
больше радиуса, то сфера и плоскость не имеют общих точек.
Если рас,стояние ОР от центра сферы О до плоскости а
больше радиу.са (рис. 258), Т. е. OP>R, то любая друrая точ-
ка ПЛОС1КОСТИ, например Q, бу,п,ет еще дальше от центра
245
OQ>OP>R. Значит, Blce точки плоскости а Iвнешнне отно-
сительно с.феры, и ,потому сама плоскость а тож,е называется
внешней.
(28.4) При определении площади сферы и ее частей мы
будем ПОЛЬЗ'Qваться тем же способом последовательных при-
ближений, каКИIМ пользовались для вычи,сления площадей
боковых поверхностей цилиндра и кону,са вращения.
Определение 3. Сферическим поясом 'наЗЫlвается часть
сферы, заключенная между двумя параллельными плоско-
стями, которые MorYT быть секущими и касательными. Рас-
стояние между этими плоскостями называется высотой
пояса.
Рис. 259
Теорема 5. Площадь сферическоzо пояса равна произве.
дению длины окружности большоzо круеа на высоту пояса.
Будем рассматривать сферу как поверхность, полученную
враrцением полуокру>кности с центром О BOKpyr диаметральной
прямой d. Тоrда сферический пояс МО>КНО рассматривать как
поверхность вращения, описываемую дуrой АоАn (рис. 259).
Разделим эту дуrу на п равных частей и, соединив точки
деления, получим правильную ломаную линию АоАl ... Аn......1АII,
все звенья которой равны между собой и имеют одну и ту
же длину [. Расстояние каждоrо звена от центра обозначим
через k ll (так как равные хорды равноудалены от центра),
а середины звеньев через М 1 , М 2 , ..., М n ...... 1 , М n . Пусть
" , , " "
Ао, А 1 , ..., А n...... 1 , Аn, М l' Мэ, ..., М n ...... 1 , М n ----
проекции соответствующих точек на ось d.
При вращении BOKpyr оси d ломаная AoAl А п описы-
вает поверхность вращения, которая тем ближе прилеrае'J
246
к поверхности сферы, чем меньше каждая из дуr АоАl'
41A2' ..., An lAn, т. е. чем больше число п. Поэтому примем
за площадь сферическоrо пояса предел, к которому стремится
площадь полученной поверхности вращения Sn при неоrрани-
ченном увеличении п.
Чтобы определить величину этой площади, заметим, что она
u u
есть сумма площадеи n поверхностеи вращения, описываемых
каждым звеном ломаной:
S,. == 51 + 52 + ... + 5 n ......l + 5 п .
Вычислим площадь поверхности, описываемой первым звеном.
По формуле для площади боковой поверхности усеченноrо ко-
нуса получим
, ,
51 == 1tl (АоАо + А I А 1 ).
Но по свойству средней линии трапеции имеем:
, ,
АоАо+ A1Al М М ,
== 1 1 == '1'
2
, ,
или АоАо + AI A l :=: 2'1. А из прямоуrольноrо треуrольника
, ,
OM I M 1 имеем '1 == k n cos (1" rде (1,......... величина уrла М 1 ОМ 1 ,
klJ расстояние хорды от центра. Итак, мы получим:
51 =z: 21tk n l cos (1,.
,
Но LM I OM 1 L АI А оР ::;IZI сх. Поэтому 1 cos (1, == h l , rде h l
Алина проекции первоrо звена на ось вращения. Итак, оконча-
тельно: 81 == 21tk n h l .
Подобным же образом для остальных звеньев получим:
В:! == 21tk n h a ; 5з 21tk n h з , ..., 8п 1 21tk n h n ...... 1 ; 5 п ::::= 21tk n h n .
Суммируя все эти равенства, получим:
Sn === 21tk n (h l + h 2 + ... + h n ...... 1 + h n ) с:::: 21tk n H,
rge Н......... высота пояса.
Переходя к пределу, получим площадь сферическоrо пояса:
Sсф. п == Нт Sn с:2 Нт 21tk n H ::::::1 21tR Н,
п п
так как известно, что Вт k n == R.
n--+оо
Следствие 1. Полная nлоu,адь сферы равна учеmверенноt2
nАощади 60льшоао круеа: Sсф:::::l 41tR2.
247
Для доказательства достаточно рассмотреть случай, коrда
две параллельные плоскости, определяющие сферический пояс,
становятся касательными к сфере. Тоrда в формуле 8 сф . п==2тr,RН
надо будет положить: Н == 2R и мы получим:
8 с ф. == 2nR. 2R == 4nR2.
Следствие 2. Площади двух сфер относятся м,ежду собой,
как квадраты их радиусов.
Пусть мы имеем сферы с радиусами R 1 и R 2 . Тоrда для
площадей их поверхностей получим:
81 == 4nR ; 82 === 4тr,R:.
СлеJlовательно:
81 == 4лR
82 4лR 2
2
R 2
1
.
R"
2
(28.5) Приведе.м теперь примеры решения Iважнейших за
дач ,на построение на изображении сферы в ортоrональной
проеКЦиrи.
Задача 1. На изображении сферы задано поло!Жение по-
люса. ПОС11рОИТ изображе.ние 'с,оответс'Лвующеrо большоrо
Kpyra.
А
о
6
Рис. 260
Реш е н и е. ПреДПОЛJОЖИМ, что на изображении сферы
даны точки Р и Р' проекции концов диа\ме-r.ра (рис. 260).
Чтобы найти проекцию окруж'ности больш.оrо 'Kpyra,
перпендикулярноrо к этому диаметру, рассмотрим вид той же
фиrуры сбоку (в профиль) . Для этоrо найдем проекцию той
же фиrуры на плоскость, параллельную диаметру РР'. В си
лу параллелЬ'ности проекция диаметра рр' равна самому
диаметру (см. рис. 260, б, ,на котором все точки рис. 260, tl
обозначены теми же буквами). На рис. 260, б большой Kpyr,
перпендикулярный к диаметру Р Р', изобразится отрезком
MN, перпендикуляр.ным к РР'. Отсюда следует, что 'На
248
рис. 260, а окружность изобразит-ся эллипсом, большой ОСЫО
KOTOp0f10 СЛУ)I{ИТ отрез-ок АВ, а малой отрезок MN.
На Пlрактике можно не прибеrать к построению вспомоrа.
rельноrо рис. 260, б и все необх,одимые построения произ
вести rсразу 'на рис. 260, а. Для этоrо д,остаточно ПрОlвест.}t
полухорду PP 1 , перпендикулярную к РР', и найти диа'метр
P1P 1 '. Радиус ON', перпендикулярный к диаметру P1P 1 ', опре-
делит точку N'. Наконец, полухордой N'N определится точка
N конец малой .оси искомоrо эллипса. В силу равенства
прямоуrольных треуrольников OPP 1 и N'NO можно не делать
и этоrо построения, а просто найти отрезок PP 1 и ОТЛОЖИТЬ
раВfIЫЙ е,му отрезок ON.
Е
а
6
Рис. 261
Если нужно решить обратную задачу, Т. е. 'по дЗ'нному
и'зображению большоrо 'Kpyra (например, на рис. 260, а) по..
строить из.ображение ero полюса, то до-статочно через конеll
N малой оси эллипса ПРОlвести полух.орду NN' параллельно
болышйй .о,С'и. Тоrда отрезок NN' определит расстояние ОР
l'очки Р от центра о.
Задача 2. На изображении сферы построить изображениt'
окружности сечения, пер'пендикулярно о к данному иаметру
в данной на нем точке.
Реш е н и е. Пусть мы имеем изображение сферы с цент-
ром О и проекцию диаlметра РР' с заданной .на нем точкой М
(рис. 261, а). Как и при решении предыдущей задачи, по.
строим вид этой фиrуры сбоку (рис. 261, б). На этом изобра
жении диаметр РР' получается без искажения. Проекция ce
чения, проходящеrо через т.очку М перпендикулярно к диа-
метру, изобразится в виде хорды ЕР, перпендикулярной к
РР'. На рrИС. 261, а точки Е и F определяют концы малой оси
эллипса, являющеrося изображением окружности сечения.
Х1орда ЕР на рис. 261, б определяет длину большой оси этоrо
эллипса. Точка Т на рис. 261, 6 есть проекция точки пересе-
чения окружности большоrо Kpyra, перпендикулярноrо к пло-
скости проекции, и окружности искомоrо сечения. На
рис.' 261, а точке Т соответствуют точки Т и Т', в которых
эллипс, изображающий ,окруж'ность сечения, касается окруж-
ности, изображающей 'контур сферы.
24
Как .и в предыдущей задаче, можн,о J3ce .построение сделать
на рис. 261, а (rде эт,о ноказано штриховыми ЛИН1ИЯМИ).
(28.6) Задача 3. На изображении сферы построить изо-
'{)раж,ение окружности больш.оrо Kpyra, проходящей через
концы да'нноrо диаметра.
Реш е 'н и е. Пусть мы имеем 'ИЗ1ображение сферы с цент-
.ром О (рис. 262). Как уже было указано при решении первой
задачи, по заданны'м концам диаметра Р и Р' находим
эллипс, изобра'жающий о.круж,но,сть большоrо Kpyra, перпен-
дикулЯ'рноf'О к этому диаметру. Пол,ожим, что и,скомое сече-
.ние должно перосечь болышой Kpyr по диаметру ММ'. Про..
ведя через т,Qlчки М 'и М' ПРЯ1мые, параллельны,е диаметру
РР', а через точки Р и Р' прямые, параллельные ММ', мы
получим из-ображение квадрата, лежаще о в плоскости иско-
Рис. 262
Рис. 263
Moro сечения. Окруж'ность больш,оrо Kpyra, (изображение ко-
орой МЫ должны построить, вписана 'в этот квад'рат. Поль-
зуясь IpaHee указанным Iспособом, мы можем вписать в полу-
ченный параллелоrрамм эллипс, являющийся и,ск.()lмым
изображением окружности больш,оrо Kpyra.
Ч-rобы найти большую -ось этоr-о эллипса, а ,вместе с тем
получить точки касЗ'ния ero с окружностью, из'ображающей
контур сф'еры, построим диаlметр, ,перпендикулярный к
плоскости сечения. Он изобразится диаметром QQ', сопря-
женным с диаме'fiрОМ ММ'. Диаметр NN', перпендикуля'р'ный
к QQ', и есть искомая большая ось эллипса, так как в про-
странстве диаметр QQ' перпендикулярен к N N', а диаметр
(VN' параллелен плоскости проекции, следовательно, и на
из-ображе'Нии N N' ..L QQ'.
На рис. 263 изображена сфера с системой сечений,
перпендикулярных к диаметру РР', и с системой сечений,
crроходящих через РР'.
2S()
Упражнения
1. Как определить при помощи линейки и циркуля диа..
eTp да,нной модели шара?
2. Три точки, не лежащие на одной пря'мой, ,вполне опре-
деляют проходящую через них окружность. Сколько нужно
задать т,очек в пространстве, чтобы ,вполне определить поло-
жение прох'Одящей через них сферы?
3. Доказать, что если 'рас,стояние между цеН'fIрами ДIВУХ
.сфер меньше суммы, ;но боль'ше ,разности их радиус'ов, 1"0 эти
феры пересекаются по окружности.
4. Доказать, что с'фера симметрична относителЬ'но всякой
пл.оскости, проходящей через центр этой оферы.
5. Доказать, что если расстояние 'между центрами сферы
равно CYMIMe их 'радиусов, 1'0 с,феры Iимеют одну, и только
одну, .общую точку. В этом случае rов.орят, что сферы каса-
ются друе друеа извне.
6. Д.оказать, что если расстоЯ'ние между центрами двух
фер равн.о раз.Н'ости ,их радиус'ов, то эти сферы .имеют одну,
и только 'одну, общую точку. rоворят, что ,в Э'f10М случае сфе-
ры касаются друе друеа изнутри.
7. Доказать, что если ра,сст.ояние прямой .от центра с'феры
меньше 'радиу,са, то прямая пересекает сферу в д'вух точках.
Если ра,сстоЯ'ние прямой от центра сферы равно радиусу, 1'0
прямая .и сф.ера имеют одну, и только одну, 'Общую точку и
rtрямая назы,вается касательной к сфере. Если ра,с,ст.оя'ние
прямой от центра сферы больше 'радиуса, ,,0 .прямая и сфера
не имеют общих точек.
8. Найти rеометрическое место
очек, принадлежащих всем
rтрямым, касающимся сферы 'в одной и той же точке.
9. Найти rеометрическое 'место точек пространства, из ко-
[орых данный отрезок 'виден под прямым уrл.ом.
10. Найти rеометрическ.ое мест.о прямых, проходящ'их Ч
-
рез данную точку и касающихся данной сферы.
11. Доказать, Ч1'О если через данную точку провести к
'фе'ре секущую прямую, то произведение длин отрезк'ов от
данной точки до точек пересечения со сферой есть вели..
чина постоянная, не зависящая от положения секущей.
Эта величина называется степенью точки по отношению к
сфере.
12. Доказать, что если сферы пересекаются, то степень
любой точки, лежащей в плоскости .окружности пересечения,
одна и та же по отношению к обеим сферам.
13. Доказать, что около правильной призмы и около пра-
вильной пирамиды можно описать .сферу, и притом только
одну.
14. Доказать, что около всякоrо тетраэдра мож'но опи,сать
сферу.
251
15. Доказать, что 'во всякий тетраэдр мож'но вписать
еф,еру.
16. Каковы необходимые и достаточные условия для Toro
чтобы около пр'из'мы м,ожно было описать сферу?
17. Доказать, что фиrура, rомотетичная сфере, есть
сфера.
18. Доказать, что Две еферы всеrда :rомотет.ичны между
собой.
19. Найти rеометрическое место середин IBcex отрезков,
соединяющих данную точку с точками сферы.
20. Через данную прямую провести плоскость, .касатель
ную ,к данной сфере.
'21. Через да'нную точку провести плоскость, касательную
к двум данным сферам. .
22. Пlровести пло'С'кость, касатеЛЬНУIО к Tp M данным
сферам.
23. Найти rеометрическое место центров всех сфер, про
ходящих через ТрlИ данные точки, не лежащие на одной и
той же прямой.
24. Дано 'изображение сферы 'в ортоrональной проекц'ии.
Построить изображение праIВИЛЬНОf'О тетраэдра, вписанноrо
в эту сферу.
25. Каков радиус 'ВИДИМОllО :на море r,оризонта с маяка
ВЫIСОТОЙ :В 70 м, если диам:етр земноrо шара приблизительно
равен 12 700 км?
26. Сферическим. сектором 1 называе-r-ся часть сферы, за.
ключенная ,ме}кду Д'ВУIМЯ ,секущими плоскостями, прох,одящи-
ми через диаlметр. Уrол между этими плоскостями наЗЫ1вает-
ся У2ЛОМ сектора. Доказать, что площадь поверхности секто-
ра выражае ся формулой: S с== 2 R2 а, rде R радиус сферы.
а ,величина уrла ,сектора в радиЗ'нной ,мере.
I Сферический сектор называют также сферическим двууrольником.
rЛАВА ДЕСЯТАЯ
ИЗМЕРЕНИЕ rЕОМЕТРИЧЕСКИХ ВЕЛИЧИН
29. ДЕйСТВИТЕЛЬНЫЕ ЧИСЛА
(29.1) Задача измерения rеометрических величин заклю-
ttается в том, чтобы установить взаимнооднозначное CO'OTBeT
С11ние между множеством данных rеометрических величин и
множеством дейс'Т'вительных чисел. Это С'ОО'tветствие должно
удовлетворять следующим УСЛQlВИЯМ: 1) 'существует величина.
КОl'орой соответствует число единица; 2) равны'м величинам'
соответствуют равные числа; 3) сумме двух величин COOT
вет.ствует сумма относящихся к НИl\1 чисел.
Припомним 'в с\вяз'и .с этим основные определения и свой
ства дейс-лвительных чисел.
ПеРlвоначальное понятие 'о числе мы получаем в резуль-
тате счета предметов. Таким образом у нас получаются Ha
туральные числа 1, 2, 3, 4, 5, ... П'рименяя к натуральным
числам операции сложения, 'вычитания, умножения и деле-
ния (исключая деление на нуль), мы получим все виды pa
циоН,альных чисел, т. е. нуль, положителЬ'ные" отрицательные.
целые и дробные числа. Кажд'ое не целое рациональное число
может быть изображено десятичной дробью, .fIибо конеч-
н/ой, либо бесконечной периодической.
Бесконечные деСЯТ1ичные дроби дают нам примеры бес
конечных числовых последовательностей. Напрwмер, обращая
в десятичную дробь 1/з, мы получим периодическую дробь
0,3333... Числа 0,3; 0,33; 0,333;... дают приближенное значе-
ние числа 1/3 по недостатку.
Если в этих числах увеличить последний десятичный знак
на единицу, то получим приближенные значения 'roro же
числа 1/3 по избытку: 0,4; 0,34; 0,334;... Отсюда получаем не-
р а в ен с ТlB а:
0,3<0,33<0,333< ... < 1/3<...; 0,334<0,34<0,4.
И слева и справа мы имеем бесконечные по,следователЬ'но-
сТ'и, в каждой из которых можно указать, Ka oe число нахо-
253
дится на 1 1, 2 'M, 3 M, (вообще на n M месте. Часто эти по
сл.едовательности записывают 'в виде двух с олбцов:
0,3
0,33
0,333
0,3333
0,4
0,34
0,334
0,3334
. . .
Будем пару таких последовательностей обозначать общим
символом:
,
{а n ; а n }, rде n == 1, 2, 3, . . .
Рассматривая всевозмо)Кные последовательности бесконечных
периодических десятичных дробей, дающих приближенные зна-
чения данноrо рациональноrо числа по недостатку и по избыт
ку, нетрудно .установить следующие основные свойства таких
последовательностей.
1. Каждое число первой последовательности не больше лю-
,
боrо числа второй последовательности: ар < a q .
2. Числа первой последовательности не уменьшаются, числа
второй не возрастают: аР+l > ар; а;+1 < а;.
3. Каково бы ни было положительное число 8, всеrда най..
дется такое число n, для KOToporo будем иметь:
,
aп aп<8.
Эти три условия называются условиями сходимости двух
числовых последовательностей, а числовые последовательности..
удовлетворяющие этим трем условиям, называются сходящими..
ея. Сходящиеся последовательности обладают важным свойст
вом, которое выражено следующей теоремой.
Теорема 1. Если существует рациональное число, которое
не меньше люБО20 числа первой из двух сходящихся nоследо
вательностей и не больше люБО20 числа второй, то это ра-
циональное число единственное.
,
Пусть мы имеем последовательности {а п ; а п }, удовлетворя-
ющие трем условиям сходимости. Положим, что существует
число <х, удовлетворяющее условию:
,
а п < <х -< а п
(1 )
аля любоrо n.
Допустим, что существует еще число , не равное <х (поло-
жим > сх), удовлетворяющее тому же условию:
,
а п < < Qll.
(2)
Z54
Из условий (1) и (2) получим: a > ; а п < а. Вычитая второе'
неравенство из первоrо, получим:
,
а п a п > ......... сх.
Но ЭТо противоречит третьему условию сходимости: разность
,
а п а п при достаточно большом n должна стать меньше любо-
ro положительноrо числа В, а мы получили, что она не может
стать меньше а. Следовательно, число а......... единственное.
На ,основании доказанной теоремы М'ОЖ1НО с'казать, что в
зтом случае сходящиеся последовательности определяют
единствен'ное рациональное число. Например, последователь-
Н1ОСТ'И 0,3; 0,33; 0,333; 0,3333; ...и 0,4; 0,34; 0,334; 0,3334; ...
оп,ределяют единственное число 1/3. П,ослеДOlвательности 0,7;
0,77; 0,777,...и 0,8; 0,78; 0,778;...определяют единственное 'число
7/9 и т. д.
В'ообще можно ,доказать, что любая периодическая беско-
нечная десятичная д'робь определяет еДИНС11венное рацио-
нальное число.
Заметим еще, что частным случаем IСХОДЯЩИХСЯ последо.
вательностей являются последовательност,и, 'в которых беско
нечно повторяет,ся одно и то же числ,о. TaK10BbI J !наПрlимер.
оследовательности:
2
2
2
2
2,1
2,01
2,001 или
2,0001
5
5
5
5
5
5
5
5
С,овершенно ,очевидно, что первая пара послед,овательно
стей опре'деляет чи,сло 2, а вторая число 5.
(29.2) Весьма важным математическим фактом является
то обс оятельство, что сущесТ1ВУЮТ сходящиеся последова
rеЛI>Но.сти, ко орыми не определяет,ся никакое рациональное
число. Рассмотрим, например, числ'овые по.слеДОlвате.лыности
приближенных значений, которые получим, извлекая корень
к;вадратный из 5. Т,оrда получатся следующие числа:
2
2,2
2,23
2,236
2,2360
2,23606
3
2,3
2,24
2,237
2/2361
2,23607
255
рациональное число су-
L. При этом для лю-
q
6oro числа ап, первой последовательности и любоrо числа a
второй последовательности будем иметь неравенства:
Числа первой последователь'н,ости (левой) при воз'ведении
в квадрат дают числа, меньшие 5, а числа 'Второй последо-
вательности (правой) при возведении в К/вадрат дают числа.
большие 5. Докажем, что не существует рациональноrо чис..
ла, большеrо чисел пер-вой последоватеЛЬ1НОСТИ и меньшеrо
чисел IВТОРОЙ последовательности.
Допустим обратное, Т. е. что такое
ществует и равно несократимой дроби
р ,
а п < < а п ·
q
Аналоrичные неравенства будем иметь и для квадратов ЭТИХ
-чисел:
2 р2 '1
а п < < а п ·
q2
Последовательности {a ; a 2} тоже СХ:1дящиеся, потому что
'1 2 '
1) а п > а п (так как а п > а п ),
s 2 '1'2'
2) а п + l > а п (так как а п +l > а п ) и J n + 1 < а п (так как а п + l <
-
<а п ) и
'1 2' ,
3) а п а п == (а п аn)(а п + а n ). Но при Лlобом пимеем:
, ,
а п < 3 и а п < 3, поэтому а п + а п < 6, и мы можем взять для
.любоrо положительноrо числа 8 число n таким, чтобы у довдет"
, 8
норить неравенству: а п а п < 6' откуда получим:
'1 l' е '1 2
а п а п < 6 (а п а п ) < 6 ==: 8, т. е. а п а п < 8.
6
Итак, сходящимися последовательностями {а:; a l} определяет-
.СЯ единственное рациональное число L. Вместе с тем мы
q2
1 '1
имее f, что а п < 5 < а п , т. е. этими же последовательностями
определяется и число 5. В силу теоремы 1 это значит, что
р2 == 5. Но дробь J!...... по условию несократима, а значит, не-
q2 q
сократима и дробь L. МЫ пришли к противоречию: целое чис-
q2
ДО 5 равно несократимой дроби. Полученное противоречие пока.
зывает, что не суще.ствует рациональноrо числа, определяемоrо
этими последовательностями.
256
(29.3) В том случае, коrда две сх'одящиеся последова-
rельности рациональных чисел не определяют рационально-
ro числа, условились Роворить, ЧТО они определяют ирра-
циональное число.
Необходимо замет.ить, что иррациональность числа должна
быть у.становлена специальны'м доказательством, как ЭТ1О и
было СiI.елано 'в предыдущем примере. В зависимости от ПРiО"
исхожден'Ия данноrо иррациональноrо числа оно получает
специальное обозначение. Например, МОЖ1НО доказать (см.
упражнение 20), чт,о последовательности приведеннО'rо при..
мера определяют числ.о, квадрат KoTop'oro ра,вен 5, а потому
соответствующее и'ррациональное число обоз'начается симво-
Л'ОМ VБ.
Подобными же последовательностя и определяют и число
11: отношение длины окруж.ности к дл'ине диаметра:
3
3,1
3,14
3,141
3,1415
3,14159
3,141592
4
3,2
3,15
3, 142
3,1416
3,14160
3,141593
ВIВИДУ Toro что всяк.ое рациональное число обращается в
конечную или бе.с'конечную периодическую десятичную дробь
и .обратно, всякая бесконечная периодическая десятичная
др,обь определяет единственное рациональное число, которое
в эту др,обь обращается, мы заключаем, что бесконечная
неперuодическая десятичная дробь определяет единственное
иррациональное число.
Рациональные и иррационалыные числа вместе образуют
множестВ'о действительных чисел.
Для сраlвнения двух чисел, заданных сходящимися двой-
ными последовательностями, применяю я правила:
,
1. Число , заданное последовательностями {а n ; а n }, мень-
,
ше числа , заданноrо последовательностями {Ь n ; Ь n }, если ка..
кое"нибудь приближенное значение числа rJ., по избытку меньше
приближенноrо значения числа по недостатку:
,
rJ., < , если ар < b q .
2. Если неравенства rJ., < и rJ., > не имеют места, то от.
СЮДа следует, что (J., == .
На основании этих определений выводится следующая основ.
н,ая теорема.
17 А. и. Фетисов
257
Теорема 2. Если числа (J., II , заданные последовательнос..
, ,
тямu {а n ; а п } и {Ь п ; Ь п }, таковы, что всесда справедливы не..
, ,
равенства: ар < b q и ар> b q , то (J., === .
,
Действительно, допустим, что (J., > , тоrда получим ар> b q ,
но это противоречит первому условию теоремы. Если же допус..
,
тим, что (J., < , то получим, что ар < b q , а это противоречит
второму условию теоремы. Итак, на основании BToporo прави...
ла сравнения' получим (J., == .
Приведем при м е р. Выше мы рассматривали сходящиеся последователь
ности десятичных дробей, в которых квадраты чисел первой последователь
ности меньше 5, а квадраты чисел второй последовательности больше 5. Пост
роим последовательности недесяmичных дробей, обладающих тем же самым
свойством.
Число х, квадрат KOTOpOro равен 5,
должно удовлетворять равенству:
1
х 2 ----- 4 == 1., или' (х ----- 2) (х + 2) == 1., т. е. х ----- 2 == , и наконец:
х+2
f
х==2+
х+2
(1)
Если в правую часть этоro равенства подставить вместо х число, KBaд
ра т KOTOpOro меНhше 5, то в левой части получим число, квадрат KOToporo
больше 5, так как при уменьшении знаменателя дробь увеличивается. Если
же в правую часть подставить число, квадрат KOTOpOro больше 5, то в ле
вой части получим число, квадрат KOTOpOro меньше 5, так как при увеличе-
нии знаменателя дробь уменьшается.
Примем за первое приближение число ы 1 == 2 < х (так как b < 5). Под-
ставив это значение в правую часть равенства (1), получим приближенное
, 9
значение по избытку: ы 1 == . Подставив снова это значение в правую
4
38
часть равенства (1), получим приближенное значение по недостатку: Ь 2 == .
17
161
Новой подстановкой получим новое приближенное значение по IIзбытку: .
72
Продолжая далее этот процесс, получим последовательности:
9 Можно показать, что полученные последовательности
2 ,
4 {Ь п ; Ь п } сходящиеся. Сравнивая их с последовательностями {а п ;
, ,
38 161 а n }, рассмотренными в п. (29.2), мы видим, что ар < b q , так
'1 '
17 72 как a < 5, а b q > 5-. В то же время ар> b q , так как
682 2889 a 2 > 5, а ь: < 5. Итак, обе пары последовательностей YДOB
305 12 92 летворяют условиям доказанной теоремы и потому опреде
ляют одно и то же число.
12238 51841
5473 23184
. . .
(29.4) Ввиду Toro что десятичные дроби более удобны при
вычислениях, для определения иррациональноrо числа пред'"
258
почитают пользоваться сходящимися последовательностями
десятичных дробей. При этом обычно не выписывают обеих
последовательностей, а берут одно приближенное значение
по недостатку .с достаточно большим числом десятичных зна-
ков. Например, число 1[ записывается так:
1[ == 3, 141 592 653 589 793...
Мноrоточие в конце указывает, что за последней цифrрой
следует бесконечное множество десятичных знак,ов. Из этой
записи нетрудно получить обе СХОДЯlЦиеся последовательно-
сти в том. виде, как они были ПРИlведены в примере 'в п. (29.3).
Сколько десятичных знаков надо взять в каждом отдель.
ном случае, мы определяем по степени точ'ности, требуемой
нашими вычислениями. Например, измерив диаметр окруж-
ности в метрах с точностью до сантиметра и получив 2,15 .м,
мы для получения длины окружности умножаем это число на
приближенное значение 1[ 3,14 и получаем 6,75 М. Если бы
мы умножили на более точное значение 1[, например на
3,141 592, то получили бы 6,75442 280. Однако последние
6 цифр нам придется отбросить, так как нельзя узнать длину
окружности с точностью большей, чем до 1 СМ, если при
измерении диа 1етра мы моrли допустить ошибку около сан.
тиметра. П'оэтому, ч обы не делать бесполезных вычислений,
мы в приближенном значении 1[ удерживаем лишь те цифры,
которые M.orYT повлиять на второй знак после запятой.
Напомним, как производятся операции над действительными
числами. Если действительное число С/., определяется последова-
,
тельностями {а n ; а п }, а число последовательностями
{b + b }, то можно доказать, что п.оследовательности {aп+b ;
" ,
а n + Ь n } тоже СХОДЯlЦиеся. Определяемое ими число назы-
вается СУММОЙ и обозначается a+ . Далее доказывается, что
эта сумма подчиняется переместительному и сочетательному
законам:
С/., + == + С/., и С/., + ( + r) == ( + ) + Т.
,
Если у всех членов последовательностей {а n ; а n }, определя
ющих число С/." переменить знаки на обратные, а сами последо-
вательности поменять местами, .то вновь получим сходящиеся
последовательности, КОТОРЬП fИ определяется число (х, обратное
по знаку с числом (Х. Нетрудно показать, что rJ., + ( (X) == о.
Вычитание определяется как сложение уменыпаемоrо с чис-
лом, обратным по знаку с вычитаемым: rJ., == (Х + ( ).
Если действительные числа (Х и , определяемые последов а-
, ,
тельнсстями {а п ; а п } и {Ь n ; Ь n }, положительны, то nроuзведенu-
ем их наЗЫЕается число (1. , определяемое сходящимися после-
, ,
Довательнсстями {апЬ n ; апЬ п }.
17* 259
Произведение действительных чисел подчиняется перемести-
тельному и сочетательному законам:
ct == ; ( y) === ( )y.
По отношению к сложению и умножению имеет место закон
распределительный:
( + у) == + y.
Если положительное число определено последова-
, { 1 1 }
тельностями {а n ; а п }, то последовательности ; тоже
аn qn
. 1
сходящиеся и определяемое ими число обозначается и на.
сх
зывается обратным числу по величине. Далее доказывается.
что про изведение двух взаимно обратных по величине чисел
1
равно единице: . == 1.
сх
Действие деления определяется как умножение делимоrо на
1
число, обратное делителю: : == . .
При операциях над положительными и отрицательными дей.
ствительными числами заменяют все отрицательные числа рав.
ными им по абсолютной величине положительными числами.
Знак результата определяется обычными правилами знаков ум.
ножения и деления.
Заметим в заключение, что действительное число можно оп-
ределить сходящимися последовательностями каких yzoaHO дей.
ствительных чисел. Можно доказать, что последовательности
,
любых действительных чисел { n; n}, удовлетворяющие усло-
виям сходимости, определяют единственное действительное чис-
ло, которое не меньше любоrо числа первой последовательности
и не больше любоrо числа второй.
Упражнения
1. Доказать транзитивный закон неравенства действитель-
ных чисел: если (Z < , < у, то (Z < у.
2. При помощи бесконечной rеометрической проrрессии:
1 1 1 ( 1 ) n l
1 T+4 8+...+ 2 +...
построить сходящиеся последовательности и найти определяемое
ими число.
3. Какое число определяют сходящиеся последовательности
{а п ; a }, если все a положительны, а все а п отрицательны?
260
,
4. Последовательности {а n ; а n } определяют число а. Удалим
из этих последовательностей все члены, стоящие на четных ме-
стах. Будут ли последовательности оставшихся членов сходя-
щимися? Какое они определяют число?
, ,
5. Последовательности рациональных чисел {а n ; а n } и {Ь n ; Ь n }
, ,
сходящиеся. Доказать, что последовательности {а n + Ь n ; а n + Ь n }
тоже сходящиеся.
,
6. Доказать, что если последовательности {а n ; а n } сходящие-
,
ся, то последовательности { an; а n } тоже сходящиеся.
7. Доказать, что а + ( a) == о.
8. Доказать, что rx +0 == а.
9. Доказать переместительный и сочетательный законы сло-
1Кения действительных чисел.
1 о. Последовательности положительных рациональных чисел
, ,
{а n ; а n } и {Ь n ; Ь n } сходящиеся. Доказать, что последовательности
, ,
{аnЬ n ; аnЬ n } тоже сходящиеся.
11. Доказать переместительный и сочетательный законы ум-
ножения действительных чисел.
12. Доказать, что (х. 1 == а.
,
13. Доказать, что если последовательности {а п ; а n } опреде-
дяют положительное число а, то последовательности { ; ..!.. }
а n а n
тоже сходящиеся.
1
14. Доказать, что а. === 1.
(х
,
15. Доказать, что если последовательности {а n ; а n } опреде-
,
ляют число а, то последовательности {ka n ; ka n }, rде k рацио-
нальное число, определяют число krx.
16. Может ли сумма двух иррациональных чисел быть чис-
лоМ рациональным?
17. Может ли произведение двух иррациональных чисел
быть числом рациональным?
18. Каким числом является сумма рациональноrо числа с
иррациональным?
19. Каким числом является произведение иррациональноrо
qисла на рациональное?
,
20. Доказать, что сходящиеся последовательности {а n ; аn}.
,1
удовлетворяющие условию a <5, а n > 5, определяют иррацио-
нальное число, квадрат KOToporo равен 5 и которое можно по-
зтому обозначить символом "У5.
21. Доказать, что если два действительных числа rx и
удовлетворяют неравенству: rx < , то всеrда существует: ра-
ци нальное число k, удовлетворяющее неравенствам:
rx < k < .
2f1f
22. Пусть даны последовательности каких YZOaHO действи-
, ,
тельных чисел {(Хn; (Хn}, удовлетворяющих условиям: 1)(Xn <(Хп;
, ,
2) (Хn+l> (Хп; (Хn+l < (Хn; 3) для всякоrо положительноrо числа
е можно найти такое число п, что будет удовлетворяться не-
, .
равенство: (ХN (ХN < В. Рассмотреть последовательности рацио-
, .
нальных чисел {а п ; а n }, удовлетворяющих неравенствам:
, , ,
(Xn l < а n < (Хn; (ХN < а n < (Xn 1'
и доказать, что эти последовательности будут сходящимися.
,
23. Пусть последовательности {а п ; а n }, рассмотренные в пре-
дыдущем упражнении, определяют число (Х. Доказать, что при
любом п имеют место неравенства: (Хп < (Х < (X , и показать,
что число (Х единственное, удовлетворяющее этим неравенст-
вам.
30. ИЗМЕРЕНИЕ ЛИНИЯ
(30.1) Задача определения длины отрезка заклю'чае-reя в
том, чтобы каждому отрезку поставить в соответствие дей-
ствительное число ero длину, которое удовлетворяло бы
условиям: 1) существует отрезок, длина KOToporo равна еди-
нице; 2) равные от,резки имеIОТ palBHbIe длины; 3) длина
суммы двух отрезков равна сумме длин составляющих.
Измерение отрезков основывается на двух аксиомах, на-
зываемых аксиомами непрерывности: ак,сиоме АРХ1имеда и
аксиоме KaH opa.
Аксиома Архимеда. Если даны два отрезка а и Ь 1,
причем Ь <а, то существует такое целое число п, при котором
пЬ > а.
В этой аксиоме утверждается очевидная истина, что лю-
бой отрезок, будучи пов орен слаrаемым достаточно больш.ое
число раз, может превзойти по величине любой данный отре-
зок. Например, отрезок в 1 см очень мал по сравнению с рас-
стоянием от Земли до Луны. Однако если пов орить ero сла-
raeMbIM 40 000 000 000 раз, то получим отрезок в 400 000 К-М,
который больше рас'стояния от Земли до Луны, paBHoro в
среднем 384 000 К'м.
- ,...... ......
Следствие. Если даны два отрезка а и Ь и а>Ь, то уще"
а
ствует такое целое число п, при KO'J'lOP'OM Ь> -; .
I Символами а, ь обозначены отрезки, чтобы отличить их от обозна-
чения чисел а, Ь.
262
ДеЙСТlвительно, по теореме р хи меда существует такое
целое число п, при котор.ом пЬ>а. Деля каждый из этих
..... а
отрезков на п равных частей, получим: b> .
n
Из этоrо след'ствия мы заключаем, что каков бы ни был
отрезок, ero можно разделить на столь большое число paB
ных частей, что каждая часть будет меньше любоrо 'да'нноrо
отрезка.
Аксиома r. Кантора. Если на данной прямой имеется после-
довательносtnb отрезков AIB1' А2В2' АзВ з , ..., АпВ п , ..., в ко-
торой каждый последующий отрезок находится внутри nре-
дыдущеzо, и если в этой последовательности Bcezaa можно
найти отрезок, меньший люБО20 aaHHOZO отрезка, то суще-
ствует точка, принадлежащая всем этим отрезкаАt.
Непосредственно из этой аксиомы заКЛlочаем:
1. П оследоваtпельность отрезков, удовлетворяющих усло-
виям аксиомы, бесконечна.
. Q"
I 1 111 f I -+
А, Az Аз h д} lh д,
Рис. 264
Действительно, если бы в последовательности был послед
пий отрезок, например АnВn, то это означило бы, что в после-
довательности нет отрезка, меньшеrо чем АпВ n , а это противо
речит второму условию аксиомы.
2. Точка, при надлежащая всем отрезкам последовательно-
сти, единственная.
Действительно, если мы допустим, что существуют две та-
кие точки, например М и N, то и все точки отрезка MN при-
надлежали бы всем отрезкам последовательности и, значит, в
этой последовательности нельзя было бы найти отрезка, мень-
шеrо MN, что опять таки противоречит второму условию аксиомы.
Пример. Возьмем отрезок AIBl и отложим на нем отрезки
А 1 А 2 ==I/ з А"IВ I и BIB2==I/3AIBlo Отрезок А 2 В 2 будет Haxo
диться внутри отрезка AIBl' и величина ero равна I/ з А 1 В 1 .
Повторим такое же построение на отрезке А 2 В 2 и получим от-
резок АзВз, равный l/зА2В2, и будем неоrраниченно продол
жать этот процесс (рис. 264). Нетрудно убедиться в том, что
точка М середин.а AIB I является общей серединой всех
отрезков последовательности, т. е. она и есть точка, определя-
емая данной последовательностью.
Последовательность отрезков, удовлетворяющих условиям
аксиомы [. Кантора, называется системой вложенных стяzи-
ваЮЩllХСЯ отрезков.
2f
(30.2) Для определения длины отрезка выбираем прежде
u u
Bcero некоторыи постоянныи отрезок, длину KOToporo прини-
маем за единицу. Если нанести на линейке единичные деления,
то получим .масшта611,УЮ линейку. Для определения длины ОТ-
резка MN (рис. 265) накладываем на Hero масштабную линейку
и считаем число единичных отрезков, которые всеми своими
точками принадлежат отрезку MN. Полученное число а о дает
приближенное значение длины по недостатку. Одновременно
,
считаем число а о единичных отрезков, которые хотя бы одной
точкой принадлежат отрезку MN. Это число дает приближен-
ное значение длины по избытку.
Рис. 265
После этоrо делим каждый единичный отрезок на 1 О рав-
ных частей и вновь производим такой же подсчет. В результате
,
получим приближенные значения al и аl длины по недостатку
и по избытку с большей степенью точности. Затем делим каж
дую десятую долю вновь на 10 равных частей и вновь пр<?изво
дим такой же подсчет. В результате ПОЛУЧИI последовательно-
,
сти чисел {а п ; а п }, удовлетворяющие всем условиям сходимости.
Действительно:
,
1) а п не может быть больше а п в силу определения, так как
,
отрезки а n находятся внутри отрезка MN, а отрезки а n ero
перекрывают.
2) При дроблении единичных отрезков на более мелкие доли
,
числа а п MorYT только уве.ТIИЧИТЬСЯ, а а п ..........тольКо уменьшаться.
, , ,
3) а о .......... а в == 2; а 1 .......... аl == 0,2; а 2 .......... а2 == 0,02, ..., вообще
, 2
а п ........ а п == . Очевидно, при увеличении числа n дробь
10 n
2 может стать меньше Лlобоrо данноrо числа.'
10 п
2п.4
Например, на рис. 265 получаем последовательности:
,
а п й п
3 5
3,6 3,8
3,65 3,67
Число а, определяемое полученными последовательностями
(а п ; a }, называется длиной отрезка.
Найденное нами число обладает следующими основными
двумя свойствами:
1. Длина отрезка не зависит от способа наложения м'ас-
штабной линейки.
Положим, что мы на тот же отрезок наложили масштабную
линейку с такими же единичными делениями, но как нибудь
иначе. Произведя вновь такие же подсчеты, опять ПОЛУЧИ!\I схо.
nящиеся последовательности {Ь n ; b }, определяющие число Ь.
Однако самый способ получения чисел Ь п и b показывает.
, ,
QTO всеrда Ь n < а n и Ь п > а n . По основной теореме отсюда
следует, что а Ь.
Вместе с тем отсюда же следует, что равные отрезки иМ,еют
равные длины, так как результат измерения не зависит от Toro.
будем ли мы перемещать масштабную линейку по отрезку или
отрезок по масштабной линейке. При измерении на практике
обычно . улевое деление линейки совмещают с концом отрезка.
2. Длина СУм'мы двух отрезков равна СУМм'е длин слаzае-
.f,(blX.
Пусть на прямой нам дана сумма отрезков: АВ + ВС АС
(рис. 266). Наложим на эти отрезки масштабную линейку и
проведем измерение, в результате чеrо получим последовательно.
сти:
, , ,
{а п ; а n }, {Ь п ; Ь п } и {сп; Сп},
которыми соответственно определяется длина а отрезка АВ.
длина Ь отрезка ВС и длина с отрезка АС. Найдем сумму чи-
сел а + Ь, дЛЯ чеrо рассмотрим последовательности {а п + bn
, ,
а п + Ь п }. Так как деления а п и Ь п находятся внутри отрезка АС.
,
а деления сп ero перекрывают, то при любом пимеем:
,
а п + Ь п < Сп.
Например, на рис. 266 аl 5а, Ь 1 == 6, С l == 12. Аналоrично
, , , , ,
а п + Ь п > сп (на рис. 266 a 1 7, Ь 1 ==8, С l 14). Поэтому в си-
пу основной теоремы а + ь == с.
265.
(30.3) Применим теперь метод последовательных приближе-
ний к отысканию длины выпуклой и rладкой кривой. Кривая
называется выпуклой, если отрезок, соединяющий две ее любые
точки, друrих общих точек с этой кривой не имеет. Например,
на рис. 267,а показана выпуклая, а на рис. 267,6 невыпук-
лая кривая.
\.
Рис. 266
Кривая называется 2ладкой, если в каждой ее точке суще-
ствует единственная касательная. На рис. 267 изображены rлад-
кие кривые. На рис. 268 изображена неrладкая кривая, так как
в точке Р она имеет две касательные. Заметим, что известные
нам из курса алrебры и rеометрии кривые окружность, эллипс,
парабола и rипербола являются выпуклыми и rладкими кривыми
и потому к ним применимы все дальнейшие выводы о длине
кривой.
Рассмотрим дуrу АВ выпуклой и rладкой кривой (рис. 269)
и найдем ее длину. Для этоrо разделим дуrу АВ на п частей
и, соединив последовательно точки деления, получим ломаную
линию, вписанную в дуrу АВ. Если же через точки деления
проведем касательные к дуrе, то получим ломаную линию,
" ,
описанную около дуrи АВ. Обозначим буквами аl, а 2 , ..., а 2п
длины отрезков касательных от вершин описанной ломаной до
точек касания, а буквами аl, а 2 , ..., а 2п длины проекций от-
резков этой ломаной на звенья вписанной ломаной. Тоrда пе-
,
риметры: Р п описанной и Р п вписанной ломаных выразятся
формулами:
, " ,
Р п == а l + а?, + + й2п,
Р п == al + а 2 + ... + а 2п .
2f)f\
Если неоrраниченно увеличивать число n, вводя новые точки
,.аеления, притом так, чтобы длина каждоrо звена в обеих ло-
маных Mor ла стать меньше длины любоrо данноrо отрезка, то
,
последовательности {Р п ; Рn} будут удовлетворять условиям схо-
димости.
/
.0
Рис. 267
Рис. 268
a а.
А
Рис. 269
Рис. 270
, "
Действительно, мы имеем: 1) Р п < Р п, так как ak + ak+l>
> ak + ak+l в силу Toro, что сумма двух сторон треуrольника
больше третьей стороны (см. рис. 270, на котором отдельно по-
казана одна из дуr кривой вместе с соответствующими частя-
ми ломаных). 2) При увеличении n периметр Рn увеличивается
(на рис. 270 вместо отрезка PR берется ломаная PTR), а пери-
,
метр Рn уменьшается (на рис. 270 ломаная MQN заменяется
,
отрезком MN). 3) Для оценки разности Рn Рn при неоrрани-
,
ценном увеличении п заметим, что ak === ak COS (/.,k, rде (/.,k уrол
между касательной и хордой (k:=: 1,2, ..., 2п). Поэтому Р п ===
" ,
== а l cos (/.,1 + а 2 COS (/.,2 + ... + а 2п COS (/.,2п.
26i
Заменяя в этом равенстве все уrлы (1.,k наибо.пьшим 'из них,
который обозначим (1." мы уменьшим правую часть равенства
(так как при увеличении oCTporo уrла косинус ero Уl\lеньшается)
и получим:
", ,
Рn> (а l + а 2 ... + а 2n ) cos (1." или: Рn> Рn cos (Х.
Отсюда находим:
, " , ,
Р п Рn < Рn Рn cos (Х, или Рn Рn < Рn (l cos (1.,),
Т. е.
, , 2
Р n Р n < 2Р n sin .
2
,
Ввиду Toro что при увеличении n периметр Р n уменьшается,
а уrол (1., между касательной и хордой стремится к нулю, мы
можем для данноrо положительноrо числа е взять n настолько
большое, чтобы одновременно выполнялись неравенства:
, . в
2Р п < N и S1n 2 < .
2 N
Тоrда получим:
, 8 '
Pn Pn.<NN' ИJI'И Pn Pn< 8.
Итак, все условия сходимости выполнены, и последовательно-
,
сти {Р n ; Р п } определяют действительное число s, которое по
определению принимают за длину дуzи к,ривой.
Полученное число обладает следующими свойствами:
1. Оно не зависит от способа разбиения дуrи на части, лишь
бы при неоrраниченном увеличении n длина каждоrо звена
обеих ломаных стремилась к нулю.
Действительно, положим, что при друrом разбиении дуrи мы
,
получили последовательности {Qn; Qn}, которые также будут
сходящимися и которыми определится число s'. Имея ввиду,
что периметр объемлемой выпуклой ломаной линии всеrда мень-
,
ше периметра объемлющей, имеем неравенства: Qn < Р п И
,
Qn > Рn. В силу основной теоремы отсюда следует, что 5' == s.
2. Равные дуrи имеют равные длины.
Это следует из Toro, что в эти дуrи. можно вписать и около
них можно описать соответственно равные ломаные.
3. Если кривая состоит из нескольких выпуклых и rладких
qастей, '1'0 ее длина равна сумме длин составляющих ее частей.
4. Если две кривые подобны между собой, то отношения их
длин равно коэффициенту подобия.
Действительно, если длина 5 первой кривой определяется
,
последовательностями {Р п ; Р п }, то, впцсывая во вторую кривую
268
и описывая около нее соответственно подобные ломаные, мы
увидим, что длина этой кривой определяется последовательно-
,
стями {kP n ; kP n }, rде k коэффициент подобия, следовательно,
она равна ks. Отсюда, в частности, следует, что длины двух ок-
ружностей относятся друr к друrу, как длины их диаметров:
С D С С'
== или == ............
С' D" D D' ,
т. е. отношение длины окружности к длине диаметра есть число
постоянное. Таким образом, мы получаем определение числа л
и известные формулы:
с ===:лD и С ==21tR.
Упражнения
1. Рассмотрим числовую ось, т. е. прямую, на которой от
начальной (нулевой) точки О отложены последовательно еди..
ничные отрезки: вправо с положительными номерами 1, 2, 3,...,
влево с отрицательными 1, 2, 3, ... Доказать (пользуясь
аксиомой Кантора), что на числовой оси существует единствен-
ная точка, соответствующая данному действительному числу а.
,
определяемому последовательностями {а п ; а п }.
В качестве примера использовать последовательности:
0,3333...; 2,23606 ...
2. Пусть длина отрезка а при не оторой единице длины
ра,вна а, длина же отрезка е при ой же единице palB Ha е.
Доказать, что если за единицу длины при'нять отрезок е, то
а
длина отрезка а будет равна .
3. Отношением двух отрезков называется частное от де-
ления друr на друrа их длин (при усл-овии, что отрезки из-
мерены о дной и той же единицей). Д'оказ ат ь, что отношение
отре'3ка а к отрезку Ь есть длина отрезка а при условии, что
()трезок Ь принят за единицу.
4. Доказать, Ч'f10 отношение д'вух отрезков не зависит от
roro, какой единицей определены их длины.
I 5. Впишем в окружность правиль'ный n У ОЛDНИК. Деля
каждую из n полученных дуr пополам, строи'м вершины пра-
вильноrо вписанноrо 2n уrольника. Соединив последователь
но середины сторон этоrо 2n уrольника, получим новый 2n-
уrольник. Доказать, что периметр HOBoro 2n уrольника равен
периметру первоначальноrо n уrольника.
6. ОбознаЧ1ИМ буквами ,} и k 1 соответственно радиус и
апофему правильноrо n уrольника, pacOMOTpeHHoro в пр еды-
2t)g
дущей задаче, а буквами '2 и k 2 соответственно радиус и
апофему правильноrо 2п уrольника, имеющеrо с п уrольни
ком одинаковый периметр. Доказать, что
k l + '1
k 2 == И '2 == V 'l k 2'
2
7. Возьмем какой нибудь правильный n уrольник. Получим из
Hero правильный 2n уrольник с таким же периметром, как это
сделано- в задаче 5. Из этоrо 2п уrольника получим правильный
4n уrольник с таким же периметром и т. д. Пусть k 1 , k 2 , k з ,. . . t
k p , . . .......... соответственно апофемы этих мноrоуrольников, r 1, '2'
, 3, · . · , r р, . . . их радиусы. Имея в виду выведенные в пре
дыдущей задаче формулы:
k 1 + , р "1 r
k p + l == " Р+l == У r pk p + l ,
2
доказать, что последовательности {k p ; ( р } сходящиеся.
8. Рассматривая число " определяемое последовательностями
{k p ; , р} предыдущей задачи как длину радиуса предельной OK
ружности, к которой стремятся мноrоуrольники с одним и Te1t
v 1 2
же периметром, наити число как отношение , к постоян
Л
ному периметру р. В качестве исходноrо мноrоуrольника при
нять квадрат с периметром, равным 2 единицам.
3 v 1
аметим, что указанныи метод вычисления числа носит
л
название метода изопериметров, так как он основан на pac
смотрении последовательности правильных мноrоуrольников е
одним и тем же периметром.
i 31. ПЛОЩАДИ
(31.1 ). Площадью фиrуры называется действительное число,
которое приводится в соответствие с данной фиrурой и которое
удовлетворяет условиям: 1) существует фиrура с площадью,
равной единице; 2) равные фиrуры имеют равные площади
3) если фиrура состоит из нескольких частей, то площадь этой
фиrуры равна сумме площадей составляющих ее частей.
Чтобы измерить площадь фиrуры, поступают так же, как и
при измерении длины. Сначала выбирают единицу площади.
За единицу измерения площади принимают квадрат, сторона
KOToporo равна единице длины. Если стороны единичноrо квад-
рата разделить на 1 О равных частей и через точки деления
провести прямые, параллельные сторонам, ТО единичный квад-
рат разобьется на 100 равных квадратов, причем площадь ка:н,..
270
1
доrо будет равна единицы. Каждый из новых квадратов
100
можно также разбить на 100 равных квадратов и т. д.
Если провести по плоскости систему параллельных прямых,
расстояния между которыми равны единице, и пересечь ее
такой же системой перпендикулярных к ней параллельных пря-
мых, то получим плоскую масштабную сетку, посредством KO
торой вся плоскость разбивается на единичные квадраты. На-
неся масштабную сетку на кальку, целлофан или стекло,
мы получили nалетк,у инструмент для непосредственноrо
измерения площадей.
Чтобы найти площадь какой-нибудь фиrуры, наложим на нее
масштабную сетку (рис. 271) и сосчитаем число квадратов, при-
надлежащих фиrуре всеми своими точками (внутренние квад-
раты). Обозначим это число буквой 50. Сосчитаем также число
квадратов, которые хотя бы одной точкой принадлежат фиrуре
,
(накрывающие квадраты), и обозначим число их 80. Заметим,
что число накрывающих квадратов равно числу внутренних
квадратов плюс число квадратов, пересекаемых rраницей фиrу-
ры. Разобьем теперь каждый квадрат, пересекаемый контуром,
на 100 равных квадратиков и прибавим к 80 число сотых долей,
равное числу внутренних квадратиков, заполняющих промежу-
ток между контуром и rраницей области внутренних квадратов.
Мы получим число Sl' Если к 81 прибавить число сотых долей,
равное числу квадратов, пересекаемых контуром, то получим
число 8 . Продолжая далее этот процесс, мы получим число-
вые последовательности {8 п ; S }. Здесь 8 п обозначает п",о-
щадь внутренних квадратов n ro разбиения, а 8 площадь
накрывающих квадратов. Если эти последовательности сходятся,
то определяемое ими число и будет площадью фиrуры.
При определении палеткой числовоrо значения площади
фиrуры считают число внутренних квадратов и прибавляют
к нему половину числа квадратов, пересекаемых контуром
фиrуры. Очевидно, это число равно среднему арифмети
ческому между числом внутренних и накрывающих квад.
ратов.
(31.2) Определять площади путем подсчета числа BHYT
ренних и накрывающих квадратов весьма кропотливо и уто-
мительно. Поэтому основная задача теории измерения пло
щадей заключается в оты'скании к,освеННО20 способа, при по-
мощи KOToporo измерение площадей сводится к измерению
отрезков.
Для Toro чтобы определить площадь nРЯМ,0У20Л , ьник,а нало-
жим на Hero масштабную сетку так, чтобы линии сетки ОКаза-
лись параллельными сторонам прямоуrольника. Пусть длина
прямоуrольника равна а и ширина Ь (рис. 272). Для подсчета
27J
внутренних квадратов нужно перемножить числа а о и Ь о , кото.
рые дают приближенные значения длины и ширины прямоуrоль-
ника по недостатку (на рис. 272 а о == 8, Ь О == 6, а о · Ь О == 48).
Аналоrично для получения числа накрываюIЦИХ квадратов
достаточно умножить приближенное значение длины по избыт-
ку на приближенное значение ширины по избытку (на рис. 272
, , "
а о == 10, Ь О == 8, ао. Ь О =z: 80). Производя десятичное дробление
сетки, мы получим новые приближенные значения: a1b 1 ,
" " , ,
а 2 Ь 2 , . · . , аnЬ п , . · · , а l ы 1 ' a S b 2 , · · · , аnЬ n , . .. Последовательно-
сти {аnЬ n ; a b } СХОДЯIЦиеся (соrласно правилу умножения дей.
ствительных чисел), и определяемое ими число есть произведе.
ние чисел а и Ь, определяемых сходящимися последовательно-
, ,
стями {а n ; а n }, {Ь n ; Ь n }. Итак, мы получили, что если длина и
ширина прямоуrольника выражаются числами а и Ь, то ero
/......... ....... k
, \. .J \
;".J )
J
("
\ J
\.., I
\. 1------ I
\. ........v
I I I I .
I I ; I 1; I
:. ь
I
.. I
Рис. 271
Рис. 272
ПЛОIЦадь выражается числом аЬ. Таким образом, для ПЛОIЦади
прямоуrольника имеем формулу:
S == аЬ.
Полученное число не изменится, если прямоуrольник под.
seprHYTb преобразованию параллельноrо переноса. При этом
стороны прямоуrольника 'останутся параллельны линиям сетки
и длина сторон останется пре>кней, так как длина отрезка не
зависит от способа наложения масштабной линейки. Поэтому
сохранится прежняя формула площади:
S аЬ.
(31.3) Возьмем теперь произвольный мноrоуrольник и, на-
ложив на Hero масштабную сетку, подсчитаем число внутрен-
,
них квадратов So и число накрываюIЦИХ квадратов So (рис. 273).
Произведя десятичное дробление сетки и повторяя такой же
,
подсчет, мы получим последовательности {Sn; Sn}. Докажем.
,
что они будут СХОДЯIЦимися. Действительно, мы имеем: 1) Sn<Sn.
так как по самому определению число накрывающих квадратов
72
равно числу внутренних квадратов плюс числn квадратов, пере-
секаемых контуром фиrуры. 2) При дроблении квадратов на
более мелкие доли число Sn увеличивается, так как к преж-
ним квадратам присоединяются более мелкие квадраты, запол-
няющие промежутки между контуром сетки и областью, по-
крытой квадратами предыдущеrо деления (см., например, квад-
рат а на рис. 273). Таким же путем получим, что при эти:xi
,
условиях число S,. уменьшается (см. квадрат Ь на рис. 273).
,
3) Разность S,. S,. равна площади квадратов, пересекаемыJCi
контуром мноrоуrольника.
Покажем, что при неоrраниченном' увеличении числа n эта
разность становится меньше любоrо положительноrо числа.
Возьмем какую-нибудь сторону мноrоуrольника, образующую
с rоризонтальной линией сетки уrол, не больший 450 (например"
сторону АВ на рис. 273), и спроектиру-
ем ее на эту линию сетки. К этой же
линии перенесем по вертикальному направ-
лению все квадраты, пересекаемые сторо-
ной АВ (на рис. 273 эти квадраты заштри-
хованы). Тоrда все эти квадраты помес-
тятся внутри прямоуrольника, длина кото-
poro равна приближенному значению по
избытку длины проекции А' В', а ширина
равна двум единицам, так как прямая,
образующая с rоризонталью уrол, не
больший 450, в вертикальном направле-
нии может одновременно проходить не
более чем в двух квадратах. Итак,
площадь всех квадратов, пересекаемых отрезком А В, не больше
, 2 '
числа а п , rде а п ....... П р иближенная длина А' В' по избытку, а
10 п
длина стороны квадрата при n-м разбиении сетки. При
10 п
,
неоrраниченном увеличении n длина а п не увеличивается, а
2 u
длина 10n становится сколь уrодно малои, следовательно, сколь
уrодно малой становится и площадь прямоуrольника, а вместе
с тем и площадь квадратов, пересекаемых стороной АВ.
Это же рассуждение мы сможем повторить для всех сторон
мноrоуrольника, образующих с rоризонталью уrол, не больший
450. Остальные же стороны мы спроектируем на вертикальную
линию сетки, и тоrда к ним можно будет применить те же
выводы.
Итак, мы можем взять n настолько большим, чтобы для
каждой из k сторон нашеrо мноrоуrольника площадь пересе-
8
каемых ею квадратов была меньше Тоrда получим
k
18 А. и. ФеТНСО8
Рис. 273
273
окончательно:
, е
Sn Sn < k . == 8.
k
,
Отсюда следует, что последовательности {Sn; Sn} сходящи-
еся и ими определяется действительное число S площадь дан-
Horo мноrоуrольника.
(31.4) Если МНО20У20льник состоит из нескольких м'НО20-
У20льников, ТО е20 площадь равна сумме площадей COCTa8
ляющих МНО20У20льников.
Рассмотрим мноrоуrольник (рис. 274), состоящий из двух
мноrоуrольников, и наложим на Hero масштабную сетку. Про
изводя подсчет внутренних и накрывающих квадратов и повто
ряя такой же подсчет при дальнейшем дроблении сетки, мы
найд-ем для одноrо из составляющих lноrоуrольников последова
теJIЪНОСТИ {Sn; s }, определяющие число s, а для BTOpOrO MHO
,
rоуrольника последовательности {Sп; Sn}, определяющие чис
ло S. Наконец, для Bcero мноrоуrольника найдем последователь
,
ности {Zn; zп}, определяющие число Z. Покажем, что
Z == S + S.
Сравнивая области внутренних и накрывающих квадратов,
получим неравенства:
, , ,
Sn + 811 < Zn < Zп < Sn + Sn'
Первое неравенство справедливо потому, что при подсчете
квадратов Sn И Sn мы не считаем квадраты, пересекаемые rpa
ницей составляющих мноrоуrольников, тоrда как эти же KBaд
раты входят в состав области Zn. Последнее неравенство
, ,
справедливо потому, что в сумме Sn + Sn квадраты,
пересекаемые rраницей составляющих мноrоуrольников, считают-
ся дважды. Итак, мы имеем:
, "
Sn + 8 п < Zn И Zn < Sn + Sn.
Поэтому, соrласно основной теореме, получмм:
Z == S + S.
Из этоrо равенства следует, что если какой нибудь MHoro-
уrольник есть часть друrоrо мноrоуrольника, то площадь части
М,еньше площади целоrо.
(31.5) Равные МНО20У20льники и},(еют и равные площади.
Докажем прежде Bcero, что равны площади мноrоуrольников
П 1 и П 2 , которые преобразуются друr в друrа параллельным
274
переносом. Для этоrо наложим на первый мноrоуrОЛЬНI1К мас-
штабную сетку и, произведя С,оответствующие подсчеты, полу
чим последовательнос-:и {Sn; Sn}, Если при помощи параллель-
Horo переноса первыи мноrоуrольник с наложенной на Hert)
сеткой совместить с мноroуrольником П 2 , то числа Sn И S fle
изменятся, так как они определяют плоп ади областей, состо-
ящих из прямоуrольников, а площадь прямоуrольника при парал-
лельном переносе не изменяется. Итак, площадь MHoroyroJfo-
I I q J
[........
..,/ "r--...,
",,'7 "\
(1
\
\
I j
l I \ -
/, 7 ,
I
(
, 1\ .............
,\ :..,.........""
\ l...----:'"
v i
I v.......
'1"
h
.
b
а
Рис. 274
Рис. 275
ника П 2 определяется теми же самыми последовательностями
{Sn; S } и, значит, равна площади мноrоуrольника П..
ПОЛО)l{ИМ теперь, что квадрат со стороной с повернут на
некоторый уrол по отношению к линиям сетки. как это пока..
зано на рис. 275. Коrда стороны ero бы.пи параллельны линиям
сетки, ero П.пощадь была равна с 2 . Чтобы определить ero пло-
шадь в новом положении, проведем через ero вершины прямые,
параллельные линиям сетки, и получим новый квадрат. кота..
рый получается из первоrо присоединеннем к нему четырех
равных прямоуrольных треуrольников с катетами а и Ь и rи-
потеНУ30Й с. Площадь HOBoro квадрата равна
(а + Ь)2 == а 2 + 2аЬ + Ь 2 .
Чтобы получить площадь первоначальвоrо квадрата, вычтем
из этоrо числа сум лу площадей четырех прямоуrольных тре-
уrольников. Параллельным переносом (при котором значение
площади не меняется) можно соединить первый треуrольник с
третьим, а второй с четвеРТЫl\1. В обоих случаях мы получим
прямоуrольники со сторонами а и Ь, сумма площадей KOTOpЫ
равна 2аЬ. Вычитая эту площаJlЬ из площади большоrо
18* 27r.
квадрата, получим:
а 2 + 2аЬ + Ь 2 2аЬ == а 2 + Ь" == с 2 (по теореме Пифаrора).
Итак, площадь данноrо квадрата осталась прежней.
Возьмем теперь мноrоуrольники П 1 и П 2 , расположенные
произвольным образом. Наложим на первый мноrоутольник мас-
,
Illтабную сетку и получим последовательности {Sn;Sn}, опреде-
ляющие ero площадь S. Совместим теперь первый мноrоуrоль-
ник со вторым, сохраняя наложенную на первый мноrоуrольник
,
масштабную сетку. Тоrда площади Sn и Sn останутся неизмен-
ными, так как соответствующие области состоят из квадратов,
..а площадь квадрата, как уже доказано, остается неизменной
при повороте. Итак, площадь мноrоуrольника П 2 определяется
,
теми же ПОСJlедовательностями {Sn; Sn} и имеет то же значе-
ние) s. Отсюда также следует, что площадь мноzоуzольника не
.зависит от способа наложения масштабной сетки, так как
перемещение мноrоуrольника по сетке эквивалентно перемеще-
RИЮ сетки по мноrоуrольнику.
(31.6) Установленные нами свойства площадей мноrоуrоль-
ников позволяют получить все косвенные методы измерения
площадей прямолинейных фиrур.
J и
I .. Q I
I 2 /l1
14 Q J
а
Рис. 276
Рис. 277
Всякий параллелоrрамм можно разрезать на две части, из
которых можно сложить прямоуrольник (рис. 276). Таким пу
тем мы получаем, что площадь пар а л л е л о r р а м м а равна
произведению длины основания на длину высоты:
S == ah.
Дополняя любой треуrольник до параллелоrрамма (рис. 277),
получим, что площадь т р е у r о л ь н и к а равна половине про-
изведения длины основания на длину высоты:
S == ah .
2
:276
Наконец, разбивая любой м н о r о у r о л ь н и к на треуrоль..
ники, мы можем найти ero площадь как сумму площадей со..
ставляюIИ.ИХ треуrольников. Таким путем, в частности, riолуча...
ются формулы:
Площадь трапеции:
s== a+b h
2 '
rде а и Ь......... длины оснований, h длина высоты.
Площадь описанноrо мнorоуrольника:
S pr
,
2
rде р периметр, r длина радиуса вписанной окружности о..
(31.7) Для определения площади фиrуры, оrраниченной про..
извольным контуром, можно использовать следующий метод.
Рассмотрим систему мноrоуrольников с площадями SI' S2' . . . ,
Sn, . . ., каждый из которых принадлежит фиrуре всеми своими-
точками. Одновременно рассмотрим друrую систему мноrоуrоль
" ,
ников с площадями S1' S2'...' Sn,..., каждому из которых
данная фиrура принадлежит всеми своими точками. Если по..
,
следовательности {Sn; Sn} сходящиеся, то определяемое ими'
число S и есть площадь данной фиrуры.
Для доказательства наложим на данную фиr.уру квадратную
масштабную сетку и обозначим через Zm площадь квадратов,
находящихся внутри мноrоуrольника с площадью Sn, а через-
,
Zm площадь квадратов Toro же разбиения сетки, покрывающих
,
мноrоуrольник с ПJIощадью Sn.
Докажем, что при одновременном возрастании n и т после-
,
овательности {Zm; Zт} будут сходящимися. 1) Очевидно, что-
,
Zm < Zm. 2) При возрастании n и т Zm увеличивается, так как
, ,
увеличивается, sп, а Zm уменьшается, так как уменьшается Sn.
З) Возьмем n настолько большим, чтобы выполнялось неравен"
, 8 О
ство Sn Sn < , rде 8 Лlобое положительное число. дно-
3
временно можно взять т настолько большим, чтобы выполня-
в ' , 8 Z
JIИСЬ неравенства: Sn Zm < И Zm........ Sn < , так как m
3 3
есть приближенное значение площади мноrоуrольника Sn, а Z
приближенное значение площади мноrоуrольника S . Сложив все-
,
три неравенства, получим: Zm........ Zm < 8.
,
Итак, последовательности {Zn; Zn} сходящиеся и определяют
ействительное число l. В то же время из неравенств,
277
, , "
Zm < Sn < Sn < Zm имеем: Zm < Sn И Sn < Zm' откуда по ос-
новной теореме следует, что Z == s. Значит, число, определяю-
щее площадь данной фиrуры, будет тем же и при общем спо..
собе измерения с помощью масштабной сетки.
Пользуясь той же основной теоремой, нетрудно доказать,
что число S, выражающее площадь данной фиrуры, останется
тем же, какие бы мы ни брали системы внутренних и накры"
вающих мноrоуrольников, лишь бы последовательност их пло-
щадей были сходящимися.
(31.8) Полученные выводы можно применить к определеНИIО
площади Kpyra. Если вписать в Kpyr и OДHOBpe 1eHHO описать
около Hero правильные п..уrольники, то при неоrраниченном
удвоении числа их сторон площади этих мноrоуrольников дадут
,
сходящиеся последовательности {Sn; Sn}. Действительно, пло..
щадь вписанцоrо мноrоуrольника определяется формулой:
Sn == 1/ 2 Р п К п ,
rде Р n периметр мноrоуrольника, Кn апофема. Площадь опи-
caHHoro мноrоуrольника определяется формулой:
, ,
Sn == 1/2 P nR,
,
rде Р n периметр описанноrо мноrоуrольника, R радиус Kpyra.
Таким образом, наши последовательности принимаlОТ вид
,
{1/2 P пК n ; 1/ 2 Р nR}.
,
Но последовательности {Р п ; Р п } определяют длину окруж-
ности, Т. е. число 2лR, а последовательности {Кn; R} опреде-
ляют длину радиуса, т. е. число R. По правилу умножения
,
действительных чисел получим, что последовательности {Sn; Sn}
определяют число S == 1/2 2лR. R == лR2.
Окончательно для площади Круёа получаем:
S == лR2.
Так же как и для мноrоуrольников, нетрудно доказать, что
в более общем случае, коrда можно определить площадь фи-
rypbI, равные фиrуры имеют равные плоu ади и если фиrура со-
стоит из нескольких фиrур, то ее площадь равна сумме пло-
щадей всех составляющих ее частей.
На основании этоrо мы находим, что площадь секmoра, уrол
KOToporo выра>кается в радианной мере числом а, равна
Sa == 1/2R 2 cx.
278
Площадь ceZMeHтa получается как разность между пло-
щадыо сектора 1/2R 2 rx и площадью треуrольника, оrраниченноrо
двумя радиусами и ХОРДОЙ, т. е. 1/2R2 sin (х:
ScerM == 1/2R2 (rx sin (х).
Заметим в заключение, что если фиrура имеет площадь S,
то подобная ей фиrура имеет' площадь k 2 S, rде k коэффици-
ент подобия. Для доказательства наложим
на данную фиrуру квадратную масштабную 11
сетку, а потом эту фиrуру вместе с нало-
)кеиной на нее сеткой подверrнем преобразо-
ванrnu подобия с коэффициентом k (рис. 278).
ТОlда на новую фиrуру будет наложе-
на квадратная масштабная сетка, причем
сторона каждurо единичноrо квадрата будет
равна уже не единице, а k и площадь ero
будеr равна не единице, а k 2 . Поэтому если
П 10щадь S прежней фиrуры определялась
,
последовательностями {Sn; SI1}' то площадь
новой фиrуры будет определяться последо- Рис. 278
,
взтельностями {k 2 S n ; k 2 S n }, значит, соответствующее число
равно k 2 S.
Итак, при изменении линейных размеров фиrуры в k раз
площадь ее из'меняется в k 2 раз.
Упражнения
1. Фиrуры, имеющие равные площади, называются равно..
великими. Дlве фиrуры называются равносоставлеНН,blМU, если
их можно разрезать на одно и то же число cooTBeTc'r.BeHHo
равных частей. Доказать, что равносоставленные фиrуры
paB'h-овелики.
2. Доказать, что два параллелоrрамма, JfIмеющие равные
основания и равные 'высоты, равносоставлены.
3. Доказать, что два равновеликих параллелоrрамма ра'в-
нососта,влены.
4. Доказать, что д'ве фиrуры, равносоставленные с одной
и той же третьей, равносоставлены между собой.
5. Построить квад'рат, равновеликий данному прямоуrоль-
HtiKY.
6. Данный прямоуr.ольник разрезать на такие части, из
которых мож:но было бы сложить равновеликий квадрат.
7. Квадраты, построенные на катетах лрямоуroль,ноrо
rреуr.ольни.ка, разрезать на такие части, из коroрых можно
было бы сложить BaдpaT, построенный на rипотенуэе.
279
8. Докаэать, что из всех треуrольников с данным оС'но-
ванием н данным периметром наибольшую площадь имеет
равнобедреыный треуrольник.
9. В данную окружность ,вписат'ь треуrольник наибольшей
площади.
10. На сторонах прямоуrольноrо треуrольника как на диа-
метрах построены три окружности. Доказать, что площадь
Kpyra, построенно о на rипотенузе, равна сумме площадей
Kpyr,oB, построенных на катетах.
11. На rипотенузе прямоуrольноrо треуrольника как на
диаметре построена полуокружность, проходящая через вер-
шину прямоrо уrла. На катетах также построены полуокруж-
ности вне треуrольника. Доказать, чтЬ
сумма площадей двух получившихся лу-
ночек равна площади прямоуrольноrо
треуrольника (на рис. 279 эти луночки
заштрихованы) .
12. Вычислить площадь треуr,ольника,
одна из вершин KOToporo совпадает с
началом координат, а две друrие верши-
ны находятся соответственно в точках с
координатами (хl, Уl), (Х2, У2).
13. Вычислить площадь треуrольника,
Рис. 279 вершины KOToporo заданы координата и:
(хl, Yl), (Х2, У2), (хз, Уз).
14. Вычислить площадь любоrо мноrоуrольника, если
заданы координаты всех ero вершин.
15. Доказать, что площадь ортоrональной проекции плос-
кой фиrуры равна площади этой фиrуры, умноженной на
косинус уrла между плоскостью фиrуры и плоскостью про-
екции.
16. Рассматривая эллипс как ортоrональную проекцию
Kpyra, доказать, что площадь ero выражается формулой:
S == nаЬ, rде а большая полуось, Ь малая полуось
эллипса.
17. Через вершину треуrольника провести прямую, кото-
рая делит площадь треуrольника на части, плошади КОТОРЫХ
()тносятся как т: n (т и n данные отрезки).
18. Через точку, 'данную на стороне треуrольника, про-
вести прямую, которая разделила бы площадь треуrольника
на две равновеликие части.
19. Данный параллелоrрамм разделить на три равнове-
ликие части прямыми, проходящими через одну из ero вер-
шин.
20. Данный треуrольник разделить на две равновеликие
части прямой, параллельной основанию.
280
21. Данный треуrольник разделить на три равновеликие
части ПРЯМЫ1МИ, параллельными данному направлению.
22. Доказать, что площадь ,Б-сякоrо четырехуrольника ра'В-
на половине произведения ero диаrаналей на синус уrла
между ними.
23. Даны две концентрические окружности. Хорда внеш..
ней окружности, имеющая длину а, касается внутренней
окружности. Определить площадь кольца, оrраниченноrо
окружностями.
24. На сторонах ВС, СА и АВ треуrольника АВС отло"
жены отрезки: А'В==I/ з ВС, В'С==I/ з СА И С'А==l/ з АВ. Опре..
делить отношение площад'и BHYTpeHHero треуrольника, опре..
деляе.моrо пересечением прямых АА', ВВ' и СС', к площади
Bcero треуrольника АВС.
25. Данный равносторонний треуrольник разрезать на
такие части, из которых можно было бы сложить равнове..
ликий к,вадрат.
. 32. ОБЪЕМЫ ТЕЛ
(32.1) Объемом тела называется действительное число,
которое ПрИВoQДИ1'Ся в соответствие с дЗ'нным телом икото"
рое должно удовлетворять условиям: 1) СУЩ&'f.вует тел
объеNI KOToporo равен единице; 2) равные тел(! имеют равны€;
объемы; 3) если тело состоит из нескольких частей, то
объем этоrо тела равен сумме объемов составляющих ef"o
частей.
За единицу измерения объемов принимают куб, ребро
KOToporo равно единице длины. Если ребра ед'И'ничноrо куба
разделить H 10 равных частей и через точки деления про-
вести плоскости, параллельные ero rраням, то единичный куб
разобьется на 1000 равных кубов, пр.ичем объем каждоrо
t
из них будет равен 1000 единицы. Каждый из Н'овых кубов
можно также разбить на 1000 равных кубов и т. д.
Подобно тому как на пл,оскости мы СТРОИЛ1И КlBaдpaT-
ную масштабную сетку, для измерения объемов построим в
пространстве кубическую масштабную сетку. Для этоrо про..
nедем ряд паралле.пьных между собоЙ плоскостей так, чтобы
рас.стояние между с.оседними плоскостями было ра'вно еди
нице. Далее проведем такой же ряд параллельных плоскостей,
перпендикулярных к плоск'остям перв'оrо ряда. Наконец,
проведем такой же ряд параллельных пл'оскостей, перпенди-
кулярных к плоскостям первоrо и BToporo ДOB. В резуль
тате все пр.остранство окажется разбитым на единичные
кубы (рис. 280) и мы получим кубическую масштабную сетку.
Чтобы определить объем какоrо нибудь тела, поместим
281
ero внутри кубической сетки (предползrая, что все тело про-
низывается линиями сетки) и сосчитаем число единичных
кубов, принадлежащих телу всеми овоими точками (ВНУТ-
ренние кубы). Обозначим буквой V o число внутренних кубов.
Сосчитаем теперь число кубов, которые хотя бы одной точкой
принадлежат данному телу (накрывающие кубы). Очевидно,
что это число pa HO числу внутренних кубов плюс число ку-
бов, пересекаемых поверхностью тела. Это число обозна-
чим V a '.
Рис. 2ВО
Рис. 2Вl
Разобьем теперь каждый из кубов, пересекаемых поверх-
ностью тела, на 1000 кубиков и прибавим к числу V о тысячные
доли, число которых равно числу внутренних кубиков, заполняю-
щих ПрОl\1ежуток между областью внутренних единичнЫХ кубов
и поверхностью тела. В результате получим число V 1 . Прибав-
ляя к нему тысячные доли, число которых равно числу кубиков,
,
пересекаемых поверхностью тела, получим число V 1 , определяю-
щее новый объем накрывающих кубов. Кубики, пересекаемые
поверхностью тела, мы вновь разделим на 1000 новых кубиков
и снова произведем такой же подсчет. Продолжая этот проuесс,
,
мы получим последователь.насти {V n; V п}. Если эти последова-
тельности сходящиеся, то определяемое ими число V и БУJl-ет
()бъемом данноrо тела.
(32.2) Непосредственнае определение объемов при помощи
наложения масшта(>ноЙ кубической сетки встречает на практике
еще БОЛЫlIие затруднения, чем определение площадей при по-
мощи палетки. Поэтому основной uелью теории измерения объ-
емов является отыскание KocBeHHoro способа, при помощи кото-
poro измерение объемов сводится к измерению отрезков.
Рассмотрим пре)кде Bcero цилиндр, площадь основания ко-
Toporo равна S, а высота h, причем образующие цилиндра
перпендику лярны к плоскости ero основания, Т. е. ЦИJlИн.u.р
282
nрям-ой. Поместим этот цилиндр в кубическую масштабную сетку
так, чтоБыI одна из плоскостей сетки совпала с плоскостью ос-
нования цилиндра (рис. 281). Тоrда для подсчета числа кубов
внутренней области мы сначала подсчитаем число квадратов
сетки, всеми своими точками принадлежащих основанию. Это
число равно So приближенному значению площади основания
по недостатку. На каждом из этих квадратов построим колонку
кубов (одна из этих колонок показана на рис. 281); число вну-
тренних кубов в ней равно ho длине высоты по недостатку.
Итак, число кубов внутренней области определится формулой:
V o == Soho.
Подобным же образом для числа накрывающих кубов полу-
чим формулу:
, "
У О == Soho,
,
rде So приближенное значение площади основания по избытку,
,
ho приближенное значение длины высоты по избытку. Произ-
ведя дробление поrраничных кубов на тысячные доли, получим
новые приближенные значения:
, " " ,
V 1 == Slhl И V l == Slhl; V 2 == S2h2 И V 1 == Slh l И Т. д.
ЭтИМ путем мы получим последовательности
, , "
{V n ; V n }, rде V n == Snhn и V n == Sпhn. Но последовательности
, ,
{Sn; Sn} определяют число S, а последовательности {h n ; h п } оп-
ределяют число h. По правилу умножения действительных чи-
, ,
сел последовательности {Snhn; Snhn} определяют число Sh. Этим
числом выражается объем прямоrо цилиндра.
Итак, мы получили: объем прямоrо цилиндра равен произ-
ведению площади основания на длину высоты:. V == Sh.
Отсюда можно получить целый ряд следствий:
1. Объем- прям-ой призм-ы равен произведению площади ос-
нования на длину высоты. Это следует из Toro, что призму
мо.жно рассматривать как частный случай цилиндра, у KOToporo
направляющей служит замкнутая ломаная линия.
2. Объем- пРЯМОУ20ЛЬНО20 параллелепипеда равен произве-
дению трех е20 измерений. Прямоуrольный параллелепипед есть
частный случай прямой призмы, коrДа основанием служит пря-
моуrольник. Если длина основания равна а, ширина ero Ь, вы-
сота параллелепипеда равна с, то S == аЬ; h == с и V == аЬс.
3. Объем- цилиндра вращения выражается фо рм-улой:
V == nR 2 h,
rAe R длина радиуса основания, h лина высоты.
28з
Заметим, наконец, что объем nрЯМО20 цuлиндра не uзме-
Plится, если перенести е20 nараллельно линиям сетки или
повернуть около оси, nараллельной образующей. Это объяс-
няется тем, что как площадь основания, так и длина высоты не
изменяются от изменения способа наложения масштабной сетки.
Поэтому формула V === Sh сохранится при любом перемещении
цилиндра по сетке, лишь бы ero образующие оставались парал-
nельными линиям сетки.
(32.3) Докажем теперь существоваяuе объема любоrо МНО-
rоrранника и найдем основные свойства этоrо объема.
Представим себе, что мноrоrранник помещен внутри куби-
ческой масштабной сетки и линии этой сетки ero пронизывают.
Пользуясь ранее описанным общим приемом последовательноrо
подсчета внутренних и накрывающих кубов, найдем последова-
, ,
тельности {V n ; V n } И докажем, что они сходящиеся.
Из CaMOrO процесса получения внутренних и накрывающи
, "
кубов имеем: 1) V n < V n; 2) V п+l > V n; V n+l < V n' 3) Для оценки
,
разности V n .......... V n спроектируем каждую rpaHb мноrоrранника
на ту плоскость сетки, с которой эта rpaHb образует двуrран-
вый уrол, не превышающий 450. Возьмем одну из этих rраней
и положим для определенности, что она проектируется на одну
из rоризонтальных плоскостей сетки. Перенесем на эту плос-
кость в вертикальном направлении все кубы, пересекаемые дан-
ной rранью, подобно тому как это было сделано с пересекае-
МtJМИ квадратами на рис. 273. В результате мы получим тело,
оt7ъем KOToporo не превышает объема призмы с площадью осно-
Вt1НИЯ, равной площади проекции rрани по избытку, и высотой,
равной высоте двух кубов (так как при уrле, не большем 450,
с кущая плоскость может проходить одновременно не более чем
в двух расположенных друr над друrом кубах). Итак, объем та-
кой призмы равен
, 2
sn. ,
10 зп
,
rде Sn.......... приближенное значение площади проекuии rрани по
избытку. При неоrраниченном увеличении n этот объем может
,
стать меньше любоrо положительноrо числа 8. Действительно, Sn
не возрастает, и потому это число остается меньше HeKoToporo
2
положительноrо числа N. Число же при неоrраниченном
10 зп
е
возрастании n становится меньше . Поэтому мы получим:
N
,
2S n 8
< N · == 8.
10 зп N
284
Итак, объем кубов, пересекаемых любой rранью, становится
и остается коль уrодно малым. Если число rраней MHororpaH-
ника равно k, то можно взять n настолько большим, что объем
кубов, пересекаемых каждой rранью, станет меньше Е Тоrда
k
получим:
, е
Vn Vn<k. ==8.
k
Таким образом, выполнены все условия сходимости для по
,
следовательностей {V n ; V n } и, значит, СУ1,цествует число V,
оnределяющ е объем МНО202ранника.
(32.4) Положим, что мноrоrранник составлен из двух мно-
rоrранников, причем объем ero определяется последовательно-
,
стями {W п; W n}, а объемы составляющих мноrоrранников опре-
, ,
деляются последовательностями {V n ; V n } И {V n ; V n } И равны
соответственно V и V. Полученные числа связаны неравенствами:
, , ,
V п + V n < W n < w n < V n + V n .
Первое из этих неравенств обусловлено тем, что в сумму
V n + v n не входят кубы, пересекаемые rраницей между состав-
ляющими мноrоrранниками, а в число W n они входят. Последнее
,
же неравенство обусловлено тем, что в сумме W п эти же rpa-
, ,
ничные кубы счи r ,. .1.ются один раз, а в сумме V n + V n они счи-
, ,
таются 1 ажды один раз в V п, друrой в V n . Итак, имеем:
, "
V n + V n < W n ; W n < V n + V N ,
OTKYД по основной теореме следует, что
V + V == W,
т. е. если МНО202ранН,ик составлен' из нескольких МНО202ран-
н'икой, то е20 объем' равен сумме объемов составляющих е20
часrrей.
Непосредственно отсюда следует, что если один MHororpaH-
ник составляет часть друrоrо, то объем цеЛО20 МНО202ранН,ика
больше объема любой е20 части.
1/1, наконец, докажем, что объем М,Н,О202ранника не изме-
няется, если е20 произвольным образом перемещать в прост-
ранстве.
.Действительно, ранее (32.2) мы доказали, что объем цилиндра
(а начит, и призмы) не изменяется ни при параллельном пере-
носе, ни при повороте около оси, параллельной образующей.
Эт.. выводы можно применить к объему единичноrо куба, кото-
19 A и. Фетисов
285
рый также можно переносить паралле.пьно и поворачивать около
ЛlобоЙ: оси, параллельной ero ребру. Не l Ы знаеI\I, что всякое
движение в пространстве можно заменить вращением и парал-
лельным переносом. Следовательно, ни при каком движении
объем куба не изменяется. Поэтому если мы поместим MHoro-
rранник в кубическую сетку и найдем ero объем V при помоlЦИ
,
последовательностей {V n ; V n }, то, переместив этот мноrоrранник
вместе с сеткой в любое друrое положение, ПОЛУЧИ!\f, что зна-
,
чение чисел V n И V n не изменится, а потому не изменится и
объем v.
Этот вывод, очевидно, остается в силе и для любоrо тела,
lIмеЮlцеrо объем.
Итак, во всех случаях равные тела имеют и равные объ-
емы, или, что то же самое, объем тела не зависит от способа
наложения масшпшбной сетки.
(32.5) Перейдем теперь к вьшоду формул для определения
объемов различных тел.
Докажем прежде Bcero следующее предложение.
Теорема 1. П усть .мы имеем систему тел с объемами V о,
У 1 , V 2 , . . ., V n , . . ., находящихся внутри данносо тела, и си-
, " ,
стему тел с объемами V о, V l' V 2, . . . , V п, . . ., внутри ко-
торых содержится данное ,тело. Если последовательности
,
{V п; V п} сходящиеся, то определяемое ими число V есть
об?Jем данносо тела.
Для доказательства наложим на тело кубичеСI{УЮ масштаб..
ную сетку, и пусть \\7 т .......... число кубов m-ro разбиения, находя-
,
щихся внутри объема V п, W т число кубов m-ro разбиения,
,
накрывающих объем V п' 8......... данное положительное число. Возь-
мем n настолько большим, чтобы выполнялось неравенство:
, 8
V п .......... V n < ·
3
Установив это, возьмем
полнились неравенства:
8
Vn Wm<
3
т настолько большим, чтобы вы-
, , е
И Wт Vn < ,
.. 3
что всеrда возможно, так как W т приближенное значение
,
объема мноrоrранника V n по недостатку, а W т. приближенное
,
значение ero объема V п по избытку. Складывая почленно три
полученных неравенства, находим:
,
Wт Wт<e
286
А это значит, что последовательности {\V т; \rl } при не-
оrраниченном возрастании пz и п сходяrциеся.
Действительно: 1) W т < tV , так как объем W т составляет
часть объема w:п. 2) При увеличении n и т W т увеличивается,
. ,
так как увеличивается V n , И при. тех же условиях объем W т
,
уменьшается, так как уменьшается V n. 3) Наконец, мы}уже дo
казали, что для любоrо ПОЛО}l{ительноrо 8 можно найти такие
т и n, при которых будет иметь место неравенство:
,
Wm W m <8.
,
Положим, что последовательности {W т; W т} определяют
число w. Вместе с тем мы имеем неравенства:
, ,
W т < V n И Wm>V n ,
так как объем W т- есть часть V , а объем V n ........ 3CTЬ
довательно, по основной теореме W == V. I
Опираясь на основную теорему [см.
п. (29.3)], таким же путем нетрудно по
казать, что объе.М V не зависит от Toro,
каковы будут последовательности тел
внутренних и накрывающих данное тело,
лишь бы последовательности их объемов
были СХОДЯIЦИl'vIИСЯ.
,
w т' Сле-
,
ffi
(32.6) Теорема 2 (nринцип Б. Ka Рис. 282
вальери 1). Если при пересечении двух тел
плоскостями, nараллельными одной и той
же плоскости, в сечении все2да получаются фи2УРЫ, равно..
великие между собой, то объемы этих тел равны.
Допустим, что сечения, указанные в теореме, параллельны
rоризонтальной плоскости (рис. 282). Наложим на оба тела
кубичеСКУIО масштабную сетку так, чтобы одна из плоскостей
сетки была rоризонтальна. Положим, что объем первоrо тела
,
равен V и определяется последовательностями {V n ; V n }, а объем
BToporo тела равен W и определяется последовательностями
,
{W n ; W n }.
Рассмотрим два сечения, определяемых rоризонтальными
плоскостями, расстояние между которыми равно еди ице. Пусть
число единичных внутренних квадратов, помещающихся на пло-
щади первоrо сечения в первом теле, равно Sm, а число еди-
,
ничных кв адратов, накрывающих ту же площадь, равно Sm.
1 Бонавентура Кавальери (159 1647)....... выдающиАся ИТ8J1bЯВСКИЙ
математик. Ero «метод неделимых весьма близок к открытым позднее
методам анализа бесконечно малых.
19* 2В7
Поэтому число единичных внутренних кубов, помещающихся
на той же площади, будет не больше S т, а число накрывающих
,
кубов, помещающихся на той же площади, не меньше Sm. Пусть
,
Zn И Zn соответственно числа внутренних и накрывающих
квадратов на площади Toro же сечения во втором теле. Так
как площади обоих сечений равны, то будем иметь неравенства:
, ,
Sт<Zm, Sm>Zm.
Отсюда следует, что число внутренних кубов, помещающихся
на данной площади в первом теле, меньше числа накрывающих
кубов, помещающихся на этой же плоскости во втором теле.
Число же накрывающих кубов на этом сечении в первом теле
больше числа внутренних кубов Toro же сечения во втором
теле. А так как это же рассуждение можно повторить для
любоrо сечения, то будем иметь вообще:
, ,
V 1 <W 1 ; У 1 > W 1 .
Аналоrично получим:
" " ,
V 2 <W 2 ; V 2 >W 2 ; Vз<W з ; Vз>W з ,..., Vn<W n ;
,
V n > w n.
Соrласно основной теореме отсюда сл дует, что V == W, т. е.
что объемы тел равны между собой.
(32.7) Теорема 3 (Симпсона 1). Если площадь сечения тела
плоскостью, nерnендикулярной к высоте этО20 тела, есть
функция не выше второй степени от расстояния сечения до
постоянной (начальной) точки на высоте, то объем тела вы-
ражается формулой:
h
V == (So + 4S m + Sn),
6
еде h......... высота тела, So площадь нижне20 основания, sп ......... nло
щадь верхне20 основания, Sm......... площадь средне20 сечения.
Положим, что площадь S сечения, находящеrося на рассто-
янии х от начальной точки, выражается формулой:
S(x) === ах 2 + Ьх + с.
При этом мы будем пока предполаrать, что функция S (х)
монотонно возрастает от начальной точки до конечной.
1 Томас Симпсон (1710 1761) анrлийский математик. Был сначала
ткачом и школьным учителем в Дерби, а потом профессором математики
в военной школе в Вульвиче.
288
Для вывода формулы Симпсона рассмотрим тело вращения,
у KOToporo площадь сечения, перпендикулярноrо к оси, равна
ах 2 + Ьх + с. Очевидно, в сечении получится Kpyr, радиус ко-
Toporo леrко определить из уравнения:
"1 / ах 2 + Ьх + с
nr 2 == ах 2 + Ьх + с, откуда r V л: .
Cor ласно принципу Кавальери объем этоrо тела вращения
будет равен объему любоrо тела, площадь перпендикулярноrо
сечения KOToporo выражается той же формулой:
8 ах 2 + Ьх + с.
Итак, рассмотрим тело вращения с высотой h (на рис. 283
показан разрез тела вращения по оси; площадь сечения выра-
жается формулой: 8 == х 2 + 3х + 7). Разделим высоту на n
равных частей и через точки деления проведем секущие плоско-
сти перпендику лярно к высоте. На каждой из полученных пло
щадок построим внутренние и накрыIающиеe цилиндры с общей
высотой, равной . Объемы внутренних цилиндров обозначим
n
через v o , V 1 , V 2 , . . ., Vn l' Объемы накрывающих цилиндров
, " ,
обозначим через V l , V 2 , V з , . . . , V n . Сумму объемов внутренних
цилиндров обозначим через V п, а сумму объемов накрывающих
,
цилиндров через V n. Докажем, что при неоrраниченном уве-
,
личении n последовательности {V n; V п} будут сходящимися..
Действительно, из caMoro определения чисел V п И V имеем:
, "
1) V n -< V п; 2) V п+l > V n; V п+l < V п' 3) Для оценки разности
, ,
V п ......... V п заметим, что V п V o + V 1 + V 2 + . · · + Vn l; V n ==
, " , , ,
== V 1 + V 2 + V з + . . · + V п . Но Vl == V 1 ; V 2 V 2 , . . ., Vп l ==
V l' так как у каждой пары этих цилиндров общее основа-
h '
вне и одинаковые высоты................ Следовательно, Vn Vn Vп Vo,
n
при ЭТОМ V п > V o ввиду предполаrаемоrо MOHoToHHoro возраста-
ния функции 8 (х).
h h
Но V o === So · , V n == 8 п , rде 80 площадь начальноrо,
n n
Sп площадь конечноrо сечения. Итак,
, h(Sп So)
Vn Vn .
n
Так как h, 80 и 8n постоянные числа, а число n Heorpa.
,
ниченно возрастает, то разность V N V n пр достаточно боль-
289
шом значении n может стать меньше любоrо положительноrо
числа.
,
Поэтому последовательности {V n; V п} сходящиеся и опреде-
ляют число V ........ объем данноrо тела. Отсюда следует, что число
,
V можно рассматривать как общий предел чисел V n И V n при
неоrраниченном возрастании n.
У";
J n
ос::
I
I
= {
I
У
t5,}
.50
Рис. 283
Рис. 284
НаЙД7М число V, ДЛЯ чеrо выведем оБLЦУЮ формулу Д.ТlЯ
числа V n. По условию теоремы имеем:
vl::=: 81== ( .a h2 +b +C ) ;
n n n 2 n
V 2 == 82 == ( а 22h2 + Ь 2h + с \ ;
n n n 2 n )
V З 8з == ( а 32h2 + Ь 3h t С ) ;
n n n 2 n
.............
...... ..
h h ( ' n2h2 nh )
v n == 8п == а + ь + с .
n n п 2 n
Суммируя все эти равенства, получим:
v: == [ a 2 (12. + 22 + 32 + . . . + ( 2 ) + (1 + 2 + 3 + . . .
ппп
· .. + п) + пс ] .
Но по формуле Архимеда и еем:
12+22+32+... + n 2 == n(n+1)(2n+1)
6 '
а по формуле арифметической проrрессии получим:
1 + 2 + 3 + . . . + n == n (n + 1) .
2
290
Поэтому
V == аh З . n(n+1)(2n+1) + bh2 . п(n+1) + ch
па 6 п 2 2 '
или
V === а: э (1 + + ) (2 + ) + b: Z (1 + ) + ch
И, наконец:
. ' аll З bh 2
V === 11т V п == + + ch,
n 3 2
так. как Нт == о. Итак, мы получили для объема данноrо
n---+оо n
тела фОр 1У лу:
v == аh З -Т bh 2 + ch.
3 2
Эта формула выведена в предположении, что функция S(x)
монотонно возрастает. Если бы оказалось, что на данном про-
межутке функция 8 (х) == ах 2 r- Ьх + с монотонно убывает, то
достаточно верхнее основание принять за нижнее, а нижнее
за верхнее и повторить прежние рассуждения (см. рис. 284, на
котором 8 (х) == х 2 19х + 65).
Если, наконец, функция 8 (х) от О до h 1 изменяется в одном
направлении, в точке h 1 достиrает максимума или минимума,
а от точки h 1 до h изменяется в друrом направлении, то, вы-
числяя сначала объеl'Л от О до h 1 , а пото:м от h 1 до h и сум-
мируя оба объема, мы вновь получим ту же формулу:
V === аh З + bh 2 + ch.
3 2
Если теперь в формулу ах 2 + Ьх + с подставить последова-
h
тельно х == О, х === и х == h, то получим:
2
80 == с;
ah 2 bh
8 т == 4 +Т+ С ;
8 п == ah 2 + bh + с.
h h
Умножая первое из этих равенств на 6' второе.......... на 4 6'
h
третье на 6 и суммируя, получим:
8 == ch ·
6 о 6'
4 8 == ah 3 + bh2 + 4ch .
6 т 6 3 '6'
291
5 аh З + bh 2 + ch
6 n 6 6 6
h a b
(50 +45 т +5 п ) == + + ch V
632
и окончательно
h
V == (50 + 45 т + 5n).
6
(32.8) Применим теперь доказанные теоремы к вычислению
объемов различных тел.
1. Объем вСЯКО20 цилиндра и всякой призмы равен произве-
дению площади основания на длину высоты.
Рис. 285
Рис. 286
Соrласно принципу Кавальери, объем наклонноrо цилиндра
равен объему прямоrо цилиндра, если равны площади их OCHO
ваний и высоты. Действительно, подставив оба тела на rори
З0нтальную плоскость (рис. 285), нетрудно убедиться, что в ce
чении этих тел любой rоризонтальной плоскостью получатся
фиrуры, равные основаниям, а потому равновеликие между собой.
Такие два тела удовлетворяют условиям принципа Кавальери
и, значит, объемы их равны между собой. А для прямоrо ци-
линдра и прямой призмы была уже выведена формула:
V == 5h.
11. Объем всякой пирамиды и вСЯКО20 конуса равен одной
трети проuзведения площади основания на длину высоты.
Если конус или пирамиду пересечь плоскостью, параллель..
ной основанию, то в сечении получается фиrура, rомотетичная
основанию; центром rомотетии служит вершина, а коэффициент
rомотетии равен отношению расстояний этих фиrур (сечения
и основания) от вершины (рис. 286). А так как отношение пло..
292
щадей подобных фиrур равно квадрату коэффициента подобия,
то мы получим:
s х 2 Qx 2
== , или 8 == ,
Q h 2 h 2
rде Q площадь основания, 8 площадь сечения, h длина
высоты, х расстояние плоскости сечения от вершины. Мы
видим, что площадь сечения выражается квадратной функцией
от расстояния х. Если расстояние брать не от вершины, а от
основания, то формула площади сечения ПРИНИlVlает друrоЙ
вид:
(1)
Q (h х)2
8== ,
h 2
(2)
но функция по-пре}l{нему остается квадратной. Поэтому мы мо-
жем для определения объема использовать формулу Симпсона:
h
V == (80 + 48 т + 8n).
6
Q
Здесь So == о; 8 т == , Sn == Q [по формуле (1)]. Поэтому по
4
лучим: V == + (О + Q + Q) == Q: . Итак,
V == Qh .
3
Для конуса вращения с высотой h и радиусом основания R'
по этой фюрмуле получим:
V == п R 2 h .
3
111. Объем усечеННО20 конуса, а также и усеченной nира
миды выражается формулой:
V == .!!:.. (Q + -V Qq + q),
3
rде h высота тела, Q площадь нижнеrо основания, q
площадь BepXHero основания.
Формула (2) показывает, что к этим телам применима фор
мула Симпсона. Применяя ее, получим:
h
V == (Q + 4S m + q).
6
293.
Следовательно, V == n R (3R2 + 3RI1R R2). Но этот
3
же объем заключен между двумя сферами с радиусами R + R'
и R. Площадь первой сферы обозначим буквой s', второй ,-f;),
причем S' > S. Если бы понадобилось вычислить количество
краски, покрывающей сферу, то естественно принять за прибли-
женное ero значение произведение площади сферы на толщину
слоя краски. Таким образом, с одной. стороны, это приближен..
ное значение будет меньше истинноrо объема краски, так как
площадь сферы меныпе внешней поверхности слоя, с друrой
стороны, произведение внешней поверхности на толщину слоя
даст приближенное значение объема краски по избытку. Сле..
довательно, мы получим неравенства:
s · R < v < S' R,
т. е.
s · R < n R (3R2 .+ 3R R + I1R2).
3
Деля обе части неравенства на R, получим:
s < n (3R2 + 3R I1R + R2) < S'.
3
Если R будет стремиться к нулю, то S' будет стремиться
к S, а следовательно, и заключенная между ними переменная
величина будет тоже стремиться к S. Итак, мы имеем:
s == liт n (3R2 + 3R R + R2) == n 3R2 == 4nR2,
R O 3 3
Т. е. вновь получили ранее выведенную формулу для площади
сферы
s == 4nR2.
,
Упражнения
1. Доказать, что объем наклонной призмы ра,вен объему
такой прямой ПрrИЗ1МЫ, у которой 'основанием служит перпен-
дикулярное 'сечение ,наклонной приз ы, а высотой боковое
ребро этой призмы.
2. Доказать, что объем треуrольной призмы palBeH поло
Бине произведения ПЛОLЦади ее боковой rрани на расстояние
от этой rрани до ПРoQтивоположноrо ребра.
3. Какие измерения нуж'но произ,вести на модели праIВJИЛЬ-
ной четырехуrольной пирамиды, чтобы вычислить ее объем?
Тот же вопрос для праlВ,ильной шестиуrоль'ной пирамиды.
296
4. Д.оказать, что объем пирамиды или конуса не изменит
ся, если их вершину переместить параллельно плоскости OCHO
ван.ия.
5. Даны две 'скрещИ'вающиеся прямые т и п. На пеРIВОЙ
даны точки А и В, на ,второй точки С и D. Доказать, что
объем тетраэдра ACBD не изменится, если отрезки АВ и CD
будут перемещаться по прямым т и п, сохраняя свою длину.
6. Вычислить .объем праlвильноrо тетраэдра, длина ребра
KOToporo ршвна а.
7. Доказать, 'Что объемы двух тетраэдров, имеющих общий
трехrранный уrол, относятся, как произведения длин ребер,
принадлежащих этим TpexrpaHHbI'M уrлам.
8. Найти объем пра'вильноr,о октаэдра, длина ребра KOTO
pa o равна а.
9. Тетраэдр срезан четырьмя секущим,и плоскостями, каж
дая из которых про,х'одит через середины трех ero ребер.
Найти отношение объема оставшеrося тела к объему TeTpa
эдра.
10. TpexrpaHHbIe уrлы ку.ба срезаны В'осемью секущими
плоскостями, проходящими через .середины трех ребер, ИМею
щих общую вершину. Определ'ить .отношение объема o,cTaB
ше ося тела ,к ,объему ,куба.
11. Определ,ить ,объем помещения под четырехскатной
крышей, если основанием ее служит прямоуrоль'Ник со CTO
ронами дл,иной а и Ь, длина «конька» крыши palBHa С, а pac
.стояние e o от основания рав'но h.
12. Вычислить объеrvl тетраэдра, ec
ли известна площадь параллелоrрам
a, вершинами KOToporo служат cepe
дины четырех ребер, и если дано pac
стояние между двумя друrими ребра
1И.
13. Сечение тела плоскостью, пер
пендикулярной к высоте, ИМеет пло
щадь S==ax 2 +bx+c, rде х расстоя
ние сечения от нижнеrо основания. Bы
-сота тела равна h. Функция MOHOTOH Рис. 2ВВ
но возрастает от О до h 1 , а от }ll до h
rvfOHoTOHHO убывает. Доказать, что и в ЭТОl\f случае объем BЫ
ражается формулой Симпсона. '
]4. Доказать, что если тело можно разбить на несколько
тел, и еющих общую вы,соту, и если каждое из Э'f.их тел
удовлетворяет у,словиям теоремы Симпсона, то и объем IBcero
тела можно выrчислить по фор'муле Симпсона.
15. Два различных мноrоуrоль'ника находятся в парал
лельных плоскостях. Сьединяя ,вершины ,одноrо с Iвершинами
дру оrо, получим тело, назы'ваемое прuзматоuдом (рис. 288).
297
Для определения площади среднеrо сечения Sm заметим, что
линейные размеры среднеrо сечения являются средним арифме-
тическим линейных раЗ Iеров BepXHero и нижнеrо основа-
ний. В то же время эти размеры пропорциональны корням
квадратным: из соответствующих .площадей. Поэтому И lеем:
"Jf([ -yq "1 rc-- "1 rп "1 r:;-
== 2, или 2 у Sm == у Q + у q ,
.
11, наконец,
4S m ==Q+2 +q.
t?'
...... ----........ "
, ', \
I ...... '- \
I '\ .
I
/t u
/
/ I
/ I
/' J
",/ '
:'
Рис. 287
Подставляя это значение в фОрl\lУЛУ объема, получим:
h ...r
V == (2Q + 2 у Qq+2q).
6
Окончательно:
v == (Q + + q).
3
Для усеченноrо конуса вращения с высотой h, радиусом
BepXHero основания r и радиусом нижнеrо основания R получим:
V == 1t: (R2 + Rr + r2).r!
IV. Объем шара с радиусом R (диаметр D) выражается
формулой:
4 tCD3
V == 1t R 3 ил и' V == ............... .
3 6
Обозначим буквой r радиус сечения, находящеrося на рас-
стоянии х от конца Р диаметра (рис. 287). Тоrда из прямо-
294
уrольноrо треуrольника 00/ А, в котором ОА == R, 00/ === R х,
О' А === " получим: ,2 == R! (R х)2 == 2Rx х 2 . Площадь
этоrо сечения равна:
n,2 == 2тr.Rx тr.x 2 .
Мы видим, что эта площадь есть квадратная функция от
расстояния х. Поэтому объем шара можно вычислить по фор-
муле Симпсона. .
В данном случае мы имеем: 80 === о; Sm === nR2; 8n === О,
,h == 2R, и формула Симпсона нам дает:
V == 2R (О + 4тr.R2 + О) == :rtR3.
6 . 3
D
Подстав'пЯЯ вместо R . равную ему величину 2 ' получим:
'ЛD3
v== .
6
(32.9) Для Toro чтобы по объему данноrо тела вычислить
объе 1 подобноrо ему тела, можно пользоваться следующим
предложением:
Теорема 4. Отношение объемов подобн,ых тел равно кубу
коэффициента подобия.
Пусть объем V данноrо тела определяется последовательно-
, u
стями {V n ; V n }. Подверrнем эту фиrуру вместе сналоженнои
на нее масштабной сеткой преобразованию подобия с коэффи-
циентом k. Тоrда объем каждоrо куба масштабной сетки станет
равен k 3 . Поэтому объе HOBoro тела определится последова-
тельностями {k 3 V n ; k3V } И потому будет равен k 3 V. Отсюда,
в частности, следует, что объемы двух шаров относятся apyz
к друzу как кубы их радиусов или диаметров.
Ввиду Toro что фJрМУЛЫ для вычисления объемов тел полу-
чены нами независимо от измерения их поверхностей, покажем
как из формулы для определения объема тела можно получить
формулу для определения площади ero поверхности.
Выведем, например, формулу площади сферы, зная формулу
объема шара. Представим себе, что сфера радиуса R покрывает-
ся слоем краски равномерной толщины I1R. Объем V всей
краски можно получить, вычитая из объема шара с радиусом
R + I1R объем шара с радиусом R. Произведя соответствующие
преобразования, получим:
v == тr. (R + I1R)3 тr.R3 == тr. (R 3 + 3R 2 11R + 3R R2 +
333
+ R3 R3).
295
,.[Т,оказать, что объе!\ п И.j lатоида IОЖНО /вЫЧИСЛИТЬ по фор
муле Спмпсона.
16. Деревянный цилиндр вращения плавает в воде так.
что ero ось вращения rоризонтальна. Насколько он поrру
зит-ся в iВОДУ, если удельный вес дерева ра'вен 0,7, а диамет,р.
ра,вен 20 см?
17. Цилиндр ,вращения пересечен плоскостью, не парал
лельной основанию. Какие нужно произвести измерения, что
бы найти объем ero части между основанием .и плоскостью.
сечения?
18. Доказать, что объем тела, полученноrо от 'вращения-
прямоуrольника около оси, параллельной одной из ero CTO
рон и не пересекающей ero, palBeH произведению площади
прямоуrольнИ'ка на длину окружности, описываемой ero цeHT
ром.
19. Две 'цилиндрические поверхности с одинаковыми ра-
диусами распол,ожены так, что их оси пересекаются под пря"
мым уrлом. Определить объем ПОДУШI{ообразноrо тела,
оrраниченноrо обеими поверхностями вращения.
20. Определить объем конуса вращения, если уrол ero
развертки ра,вен: а, а длина образующей равна 1.
21. Определить объем конуса вращения, вписанноrо в
тетраэдр, дл,ина ребра KOToporo равна а.
22. Данную пирамиду (и.Jl 1 И конус) разделить на две рав-
новеликие части плоскостью, параллельной основанию.
23. Вычислить отношение объема шара, вписанноrо в куб,
к объему шара, описанноrо около куба. Такое же задание
для октаэдра и тетраэдра (правильных) .
24. Шаровым сеzмеНТОJи, называют часть Iшара, заключен.
ную между двумя параллельными плоскостями, которые o
rYT пересекать шар или касаться ero. Определ.ить объем ша
p'OBO O cerMeHTa, если радиусы сечений paiBHbI '1 и '2, а pac
стояние между пл,оскостями равно h.
25. Парабола, уравнение которой у==ах 2 , вращается!
BOKpyr 'оси Оу. Определить объем параболоида /Вращения от-
вершины д'о перпендикулярноrо сечения 'на расстоянии h от'
верш.ины.
26. Даны две скрещивающиеся пря\мые а и Ь' l rол между
которыми равен ер, а расстояние ОА==а (ОсЬ, са). Пря
:мая а, вращаясь BOKpyr Ь, описывает поверхность, называе
мую одНОnОЛОСТНblМ 2unерболоuдом вращения. Определить
объем, оrраниченный этой поверхностью и д'вумя плоскостя
МИ, проходящими на ра.сстоянии h от точки О перпендикуляр"
но к прямой Ь.
I
оrЛАВЛЕНИЕ
Часть 1. Планиметрия
r л а в а 1. Преобрэзования на плоскости
1. Краткий обзор пройденноrо
2.' Осевая симметрия .
3. Центральная симметрия
4. Параллельный перенос
5. Вращение (поворот)
6. rомотетия .
7. Подобие
.
.
.
.
.
r л а в а 11. Метрические соотношения в треуrольнике и в окружности
В. !r1.етрические соотношения в треуrольнике
Э 9. .l\'\етрические соотношенlIя в окружности
Часть 11. Стереометрия
r л а ва 111. В'ведение
10. Основные понятия стереометрии .
11. Аксиомы стереометрии и их следствия .
r л а в а IV. Параллельность в пространстве
12. Параллельные прямые . . . .
13. Параллельность прямой и плоскости
14. Параллельность плоскостей. . .
э 15. Задачи на построение в пространстве
r л а в а V. Перпендикулярность в пространстве
16. l1ерпендикулярность прямой и плоскости . . . . .
17. Перпендикулярность плоскостей и ортоrональные проекции
r л а в а VI. Двуrранные и MHororpaHHbIe yrпbI
lВ. Двуrранные уrлы .
19. MHororpaHHble уrлы .
r л а в а V.II. Преобразования в пространстве
20. Симметрия в пространстве
21. Движ:ения в пространстве . . .
22. rомотетия и подобие в пространстве
5
9
29
38
47
64
28
94
111
121
122
125
131
133
135
153
158
.
166
170
177
185
196
r л а в а VIII. Мноrоrранники
23. Призмы
24. Пирамиды
25. Правильные мноrоrранники .
r л а в а IX. Kpyr лые тела
26. Цилиндр
27. Конус .
28. Сфера и шар
r л а в а Х. Измерение rеометрических величин
29. Действительные числа
Э 30. Измерение линий.
31. Площади .
32. Объемы тел
Антонин Иванович Фетисов
rЕОМЕТРИЯ
Редактор В. С. Капустина. Оформление художника Л. И. Конвиссера
Техн. редактор Е. К. Полукарова Худож. редактор Т. И. Добровольнова
Корректоры Е. А. Блuнова l В. А. Седова
Сдано в набор lNI 1963 r. Подписано к печати 27j1Х 1963 r.
Формат БОХ92 J / J6 Бум. Л. 9,38 Печ. Л. 18,75 .Ч. ИЗД. п. 16,3
Тираж 34800 ЭКЗ. Заказ 5719
Цена 54 коп.
Изд-во АПН РСФСР, Москва, Поrодинская Y.'I., 8.
2-я Типоrрафия АН СССР. Шубинский переулок, 10
206
213
218
232
2 5
241
253
262
270
281
ОПЕЧАТКИ
Строка
Стр. CBepxyl СННЗУ Напечатано Следует читать
'15 4 5 ( АР ) == А' Р 5 ( АР ) = А'Р
87 8 I 6 I АВС. 6 АВС.
"178 17 плоскость сх. плоскость (1'
187 7 , (А) = А' r (а) (А) = А'
195 13 отражателей отражений
247 17 '1 == k n cos (1, rде (1 'l == k n cos (1', rде (1'
величина уrла М 1 ОМ 1 ' величина уrла ОМ I М 1 '
247 19 51 == 2пk n l cos (1. 51 == 2пk n l cos (1'.
247 20 L. М I ОМ 1 '== LA 1 A o P==(1. L. О м 1М l' == L. АIАоР == (1' .
Поэтому l COS :l == h l Поэтому l COS (1' == h l
265 3 5а 5а
А. И. Фетисов «rеометрия»