Факультет вычислительной математики и кибернетики МГУ имени М. В. Ломоносова
ПОДГОТОВИТЕЛЬНЫЕ КУРСЫ
проводят обучение по
МАТЕМАТИКЕ ФИЗИКЕ ИНФОРМАТИКЕ РУССКОМУ ЯЗЫКУ
учащихся 9-х (трехгодичная программа), 10-х (двухгодичная программа) и 11 -х классов (девятимесячная, шестимесячная и трехмесячная программы) в целях подготовки к сдаче школьных выпускных экзаменов (ЕГЭ) и вступительных испытаний в вузы.
Для жителей Подмосковья и ближайших областей организуются группы выходного дня (только для 11-х классов) с занятиями по субботам.
Занятия на подготовительных курсах проходят в вечернее время с 18.00 до 21.10
в учебных аудиториях факультета вычислительной математики и кибернетики в группах по 15-16 человек (метро «Университет»).
Набор на трехгодичную, двухгодичную и на девятимесячную программы проходит с 10 по 20 мая и с 1 сентября по 20 сентября, на шестимесячную программу - в конце декабря, на трехмесячную - в конце марта.
http://www.vmk-edu.ru
Справки по телефону (495) 932-98-08 с 16 часов до 19 часов в рабочие дни.
Учащимся, не имеющим возможности приезжать на занятия, предлагаются дистанционные подготовительные курсы:
http://ecmc.cs.msu.ru


ВМК МГУ-ШКОЛЕ
Б. А. Будак, Н. Д. Золотарёва, М. В. Федотов
ГЕОМЕТРИЯ
УГЛУБЛЕННЫЙ КУРС
с решениями и указаниями
Учебно-методическое пособие
6-е издание
Под редакцией М. В. Федотова
4W
Москва Лаборатория знаний


УДК 514
ББК 22.151.0я721.9 Б90
Будак Б. Л.
Б90 Геометрия. Углубленный курс с решениями и указаниями : учебно-методическое пособие / Б. А. Будак, Н. Д. Золотарёва, М. В. Федотов ; иод ред. М. В. Федотова. -- 6-е изд. — М. : Лаборатория знаний, 2020. — 596 с. : ил. — (ВМК МГУ ~~ школе). ISBN 978-5-00101-237-5
Настоящее пособие составлено преподавателями факультета ВМК МГУ имени М. В. Ломоносова на основе задач вступительных экзаменов по математике в МГУ и задач Единого государственного экзамена. Пособие содержит теоретический материал, подборку задач, а также идеи, указания (подсказки) и решения задач.
Рекомендуется школьникам при подготовке к сдаче Единого государственного экзамена, абитуриентам при подготовке к поступлению как в МГУ, так и в другие вузы, учителям математики, репетиторам, руководителям кружков и факультативов, преподавателям подготовительных курсов.
УДК 514
ББК 22.151.0я721.9
Учебное издание Серия: «ВМК МГУ — школе»
Будак Борис Александрович Золотарёва Наталья Дмитриевна Федотов Михаил Валентинович
ГЕОМЕТРИЯ.
УГЛУБЛЕННЫЙ КУРС С РЕШЕНИЯМИ И УКАЗАНИЯМИ Учебно-методическое пособие
Ведущий редактор М. С. Стригунова Технический редактор Т. Ю. Федорова
Подписано в печать 13.08.19. Формат 70x100/16.
Уел. печ. л. 48,75. Заказ № ВЗК-05005-19.
Издательство «Лаборатория знаний»
125167, Москва, проезд Аэропорта, д. 3 Телефон: (499) 157-5272 e-mail: info@pilotLZ.ru, http://www.pilotLZ.ru
Отпечатано в АО «Первая Образцовая типография», филиал «Дом печати - ВЯТКА» в полном соответствии с качеством предоставленных материалов.
610033, г. Киров, ул. Московская, 122.
(с) Б. А. Будак,
Н. 	Д. Золотарёва,
М. В. Федотов, 2020
ISBN 978-5-00101-237-5 © Лаборатория знаний, 2020


Оглавление
От редактора 5
Предисловие 6
Часть I. Теория и задачи 7
1. Треугольники 7
1.1. Прямоугольные треугольники 7
1.2. Теоремы синусов и косинусов 19
1.3. Биссектриса, медиана, высота 29
1.4. Подобие треугольников 41
1.5. Площадь треугольника 53
2. Окружности 64
2.1. Углы в окружностях 64
2.2. Касательные, хорды, секущие 75
3. Четырёхугольники и многоугольники 86
3.1. Параллелограммы 86
3.2. Трапеции 94
3.3. Четырёхугольники и многоугольники общего вида 106
4. Задачи на доказательство 120
4.1. Треугольники 120
4.2. Многоугольники 125
4.3. Окружности 128
4.4. Площади 132
5. Задачи на построение 134
5.1. Алгебраический метод 134
5.2. Метод геометрических мест точек 138
5.3. Метод симметрии и спрямления 145
5.4. Метод параллельного переноса 149
5.5. Метод подобия 155
5.6. Метод поворота и смешанные задачи 160
6. Стереометрия 164
6.1. Введение в стереометрию 164
6.2. Многогранники 167
6.3. Тела вращения 173
6.4. Комбинации тел 180
Часть II. Указания и решения 181
1. Треугольники 181
1.1. Прямоугольные треугольники 181
1.2. Теоремы синусов и косинусов 208
1.3. Биссектриса, медиана, высота 238
1.4. Подобие треугольников 265
1.5. Площадь треугольника 287
2. Окружности 317
2.1. Углы в окружностях 317
2.2. Касательные, хорды, секущие 347


4
3. Четырёхугольники и многоугольники 384
3.1. Параллелограммы 384
3.2. Трапеции 413
3.3. Четырёхугольники и многоугольники общего вида 446
4. Задачи на доказательство 473
4.1. Треугольники 473
4.2. Многоугольники 484
4.3. Окружности 489
4.4. Площади 493
5. Задачи на построение 495
5.1. Алгебраический метод 495
5.2. Метод геометрических мест точек 503
5.3. Метод симметрии и спрямления 514
5.4. Метод параллельного переноса 524
5.5. Метод подобия 534
5.6. Метод поворота и смешанные задачи 545
6. Стереометрия 554
6.2. Многогранники 554
6.3. Тела вращения 560
6.4. Комбинации тел 568
Задачи ЕГЭ последних лет 578
Варианты ДВИ МГУ последних  лет 580
Ответы 587
Список литературы 596


От редактора
Уважаемый читатель, Вы держите в руках одну из книг серии «ВМК МГУ - школе». Учебно-методические пособия, входящие в эту серию, являются результатом более чем десятилетнего труда коллектива авторов, работающих на подготовительных курсах факультета вычислительной математики и кибернетики (ВМК) МГУ имени М. В. Ломоносова. Сначала были созданы пособия для очных подготовительных курсов, затем были разработаны электронные версии учебников, используемые при дистанционном обучении. На основе этого опыта подготовлена серия книг для старшеклассников, одной из которых и является настоящее пособие.
Сейчас изданы пособия по алгебре, геометрии и физике. По каждому предмету вышли два пособия: основной курс и углубленный курс, содержащий сложные задачи единого государственного экзамена и нестандартные задачи вступительных экзаменов в вузы (в основном это задачи различных факультетов МГУ имени М.В. Ломоносова). Основной курс содержит все разделы соответствующего предмета, необходимые для решения задач первой части ЕГЭ и некоторых задач второй части, а также первой половины задач вариантов вступительных экзаменов в вузы. Углубленный курс содержит задачи, научившись решать которые, вы сможете решать все задачи ЕГЭ и все или почти все задачи олимпиад и вступительных экзаменов в вузы (за отведённое время можно просто физически не успеть решить все задачи).
В серии «ВМК МГУ - школе» вышли два пособия по информатике. Первое рекомендуется в качестве пособия при подготовке к ЕГЭ по информатике и ИКТ. Разделы этого пособия соответствуют темам, включенным в ЕГЭ. Второе - пособие по программированию - поможет вам подготовиться к экзамену по информатике, научиться решать задачи по программированию на языке Паскаль.
Отличительной особенностью наших пособий является то, что наряду с традиционными составляющими (теоретический раздел, примеры с решениями, задачи для самостоятельного решения) мы предлагаем решения всех предложенных задач с идеями и последовательными подсказками, помогающими решить задачу оптимальным способом без посторонней помощи. Это позволит ученику самостоятельно продвигаться в решении задачи так, как если бы за его спиной стоял учитель и направлял ход его мысли при решении трудных задач. Конечно, мы понимаем, что настоящего учителя не может заменить никакая книга, но если учителя рядом нет, то, как показал опыт наших дистанционных подготовительных курсов, наличие грамотных подсказок помогает учащимся самостоятельно научиться решать задачи. С помощью нашего пособия приобретение такого опыта учениками будет значительно облегчено. С другой стороны, наши пособия помогут молодым учителям вести занятия. Мы знаем на собственном опыте, что не всегда легко направлять ученика так, чтобы он сам догадался, как решить задачу. Второй особенностью наших пособий является спиралевидная схема подачи материала, когда каждая тема повторяется несколько раз, причём каждый раз на более сложном уровне, чем в предыдущий. Это позволяет не забывать пройденный материал и постепенно подходить к сложным задачам.
Заместитель декана по учебной работе факультета ВМК МГУ имени М. В. Ломоносова
М. В. Федотов


Предисловие
Предлагаемый «Углублённый курс» является естественным продолжением «Основного курса» по геометрии и предполагает свободное владение методами и приёмами из «Основного курса».
Каждый раздел пособия содержит теоретические основы, описание методов решения задач, примеры применения методов и набор заданий для решения. Задачи в разделах расположены по принципу « от простого - к сложному». Аналогичная ситуация имеет место и с последовательностью разделов, поэтому сами разделы и задачи в разделах рекомендуется изучать в предложенном порядке. Приступать к решению задач надо, после изучения соответствующего теоретического материала и разбора примеров. Если самостоятельное решение задачи вызывает трудности, рекомендуется воспользоваться системой указаний (подсказок). В случае, если Вам не удалось получить правильный ответ или у Вас возникли сомнения в правильности Вашего решения, рекомендуется изучить решение, предложенное авторами.
Необходимо отметить, что в формулировках задач параллельно с математически более корректной терминологией типа «длина отрезка А В равна 5» и записью \АВ\ = 5 используется школьная терминология типа «отрезок АВ равен 5» и запись АВ = 5.
Рекомендуется школьникам при подготовке к сдаче единого государственного экзамена, абитуриентам при подготовке к поступлению как в МГУ, так и другие вузы, учителям математики, репетиторам, руководителям кружков и факультативов, преподавателям подготовительных курсов.
Желаем удачи!


Часть I. Теория и задачи
1. Треугольники
1.1. 	Прямоугольные треугольники Теоретический материал
Этот раздел всецело посвящен прямоугольным треугольникам. Для успешного решения задач, относящихся к этой теме, необходимо знать и уметь обосновывать все факты, перечисленные ниже по тексту.
1. 	Соотношения между длинами сторон и величинами углов в прямоугольном треугольнике
Рассмотрим прямоугольный треугольник ABC, будем считать, что его угол С прямой (то есть его величина равна 7г/2), длины отрезков АВ, АС и ВС (которые везде в пособии будут обозначены как |АВ|, \АС\,
\ВС\) равны с, Ь и а соответственно. Тогда
а = Ь • tg А = b • ctg В = с • sin А = с • cos В, Ъ = а • tg В = а • ctg А = с • sin В = с • cos Л,
_а_а_6_6
sin Л cos В sin В cos А
Замечание. Полезно знать, что эти формулы на самом деле есть не что иное, как переписанные утверждения, вытекающие из определений тригонометрических функций величин острых углов, а именно:
Синус величины острого угла прямоугольного треугольника равен отношению длины катета, противолежащего этому углу, к длине гипотенузы;
Косинус величины острого угла прямоугольного треугольника равен отношению длины катета, прилежащего к этому углу, к длине гипотенузы;
Тангенс величины острого угла прямоугольного треугольника равен отношению длины катета, противолежащего этому углу, к длине катета, прилежащего к этому углу;
Котангенс величины острого угла прямоугольного треугольника равен отношению длины катета, прилежащего к этому углу, к длине катета, противолежащего этому углу.


8
Теория и задачи
В
2. 	Соотношения между длинами сторон и величинами углов в равнобедренном треугольнике
Пользуясь вышеизложенными фактами, получим непосредственно вытекающие из них важные соотношения между длинами сторон, длиной высоты, проведенной к основанию, и величинами углов в равнобедренном треугольнике. Как показывает практика, при решении задач очень часто возникают различные конфигурации, в которые входят равнобедренные треугольники, и, как следствие, возникает необходимость применять нижеприведённые формулы. Рассмотрим равнобедренный треугольник ABC, в котором \АВ\ = \ВС\, ВН — высота, проведенная к основанию АС. Справедливы следующие утверждения:
I. 	Длина боковой стороны равнобедренного треугольника равна частному длины его основания и удвоенного косинуса величины угла при основании этого треугольника:
\АВ\ = \ВС\ =
\АС\
2 cos ВАС
\АС\ =2\AB\cosBAC.
II. 	Длина высоты равнобедренного треугольника, проведенной к его основанию, равна частному длины этого основания и удвоенного котангенса величины угла при основании этого треугольника:
\вн\ =
\АС\
2 ctg ВАС
\АС\ = 2-\BH\-ctg В АС.
Доказательство этих фактов несложно: ясно, что прямоугольные треугольники АВН и СВН равны по гипотенузе и катету. Из этого равенства вытекает, что \АН\ = \НС\, а, с другой стороны, из прямоугольного треугольника АВН следует, что \АН\ = \АВ\ ■ cos ВАС, \АН\ = \ВН\ • ctg ВАС. Поэтому
\АС\ = 2 • \АН\ = 2 • \АВ\ • cos В АС
\АС\ = 2 • \АН\ = 2 • \ВН\ ■ ctg ВАС
\АВ\ - \ВС\ =
\ВН\ =
\АС\
2 cos ВАС \АС\
2 ctg ВАС
Утверждение доказано.
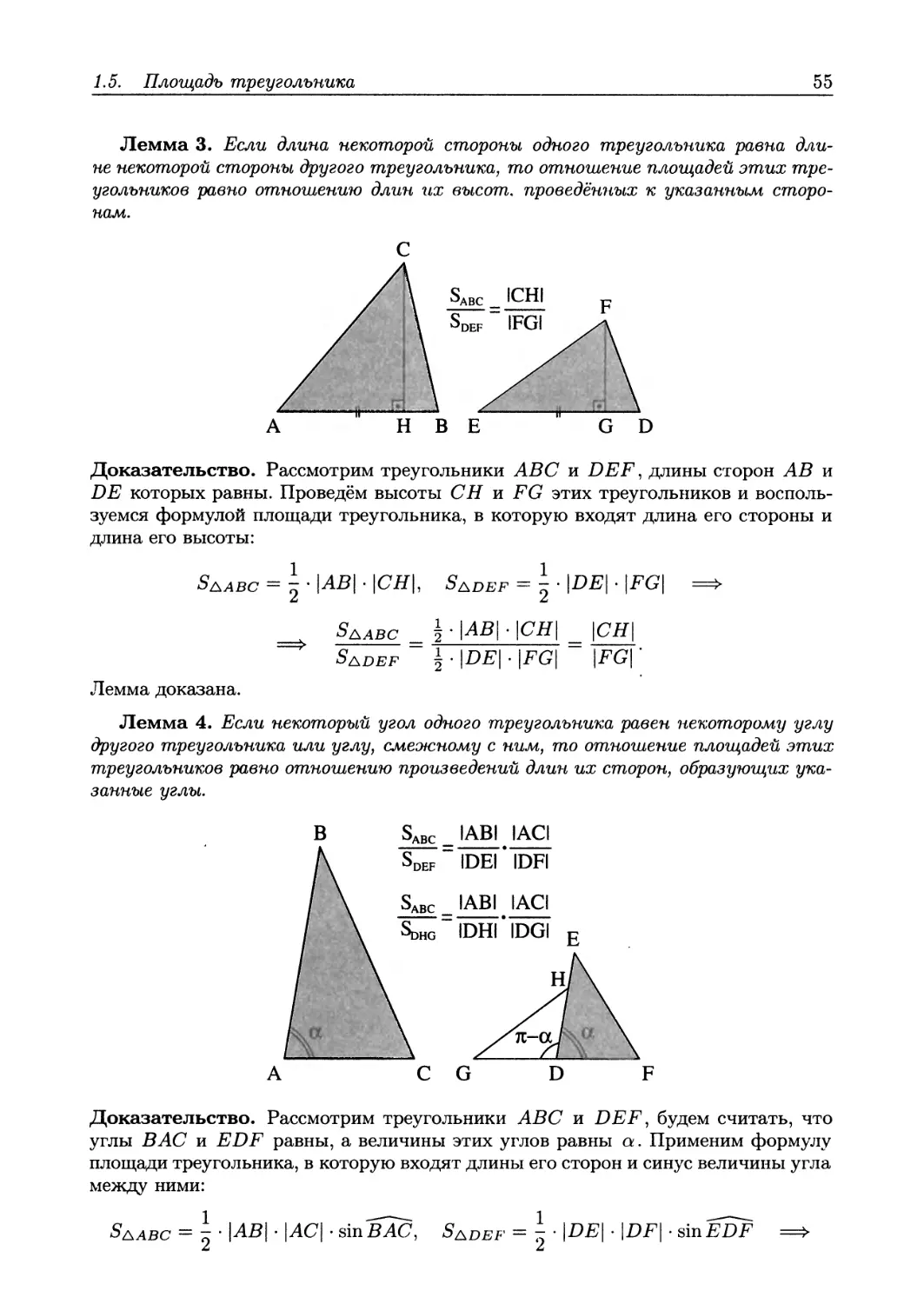
3. 	Формула площади прямоугольного треугольника
Площадь прямоугольного треугольника может быть вычислена как половина произведения длин его катетов (s = у"
Доказательство этого факта практически очевидно - ясно, что если в прямоугольнике, длины сторон которого равны а и 6, провести диагональ, то он будет разделён на два равных прямоугольных треугольника, длины катетов которых


1.1. Прямоугольные треугольники
9
равны а и Ь. Осталось лишь вспомнить, что площадь прямоугольника равна произведению длин двух его смежных сторон, то есть аЬ.
4. Окружность, описанная около прямоугольного треугольника
Центр окружности, описанной около прямоугольного треугольника, находится на середине его гипотенузы; длина радиуса этой окружности равна половине
длины гипотенузы (&= •
Для доказательства этого утверждения воспользуемся тем, что центр окружности, описанной около произвольного треугольника, лежит на пересечении серединных перпендикуляров к его сторонам.
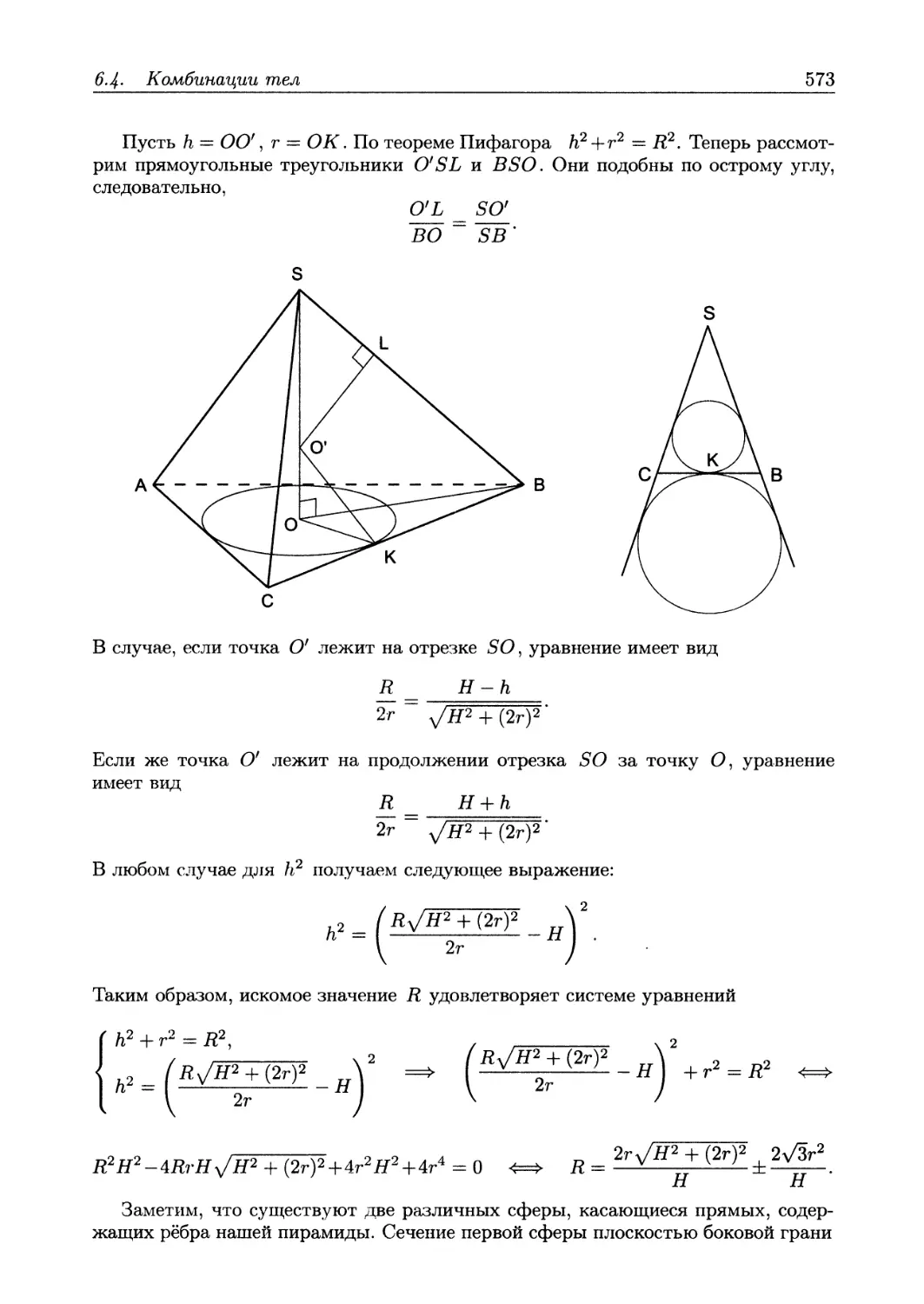
Рассмотрим прямоугольный треугольник ABC (угол С прямой), обозначим буквой К середину его стороны ВС, проведем через точку К прямую га, перпендикулярную ВС (она как раз и будет серединным перпендикуляром к отрезку ВС) и обозначим буквой О точку пересечения т и АВ.
Рассматривая прямоугольные треугольники ABC и ОВК, имеем cos Б = \ВК\ : \ОВ\ = \ВС\ : |АВ|, из чего следует \ОВ\ : \АВ\ = \ВК\ : \ВС\. Но поскольку
\ВК\ : \ВС\ = 1:2, точка О - середина отрезка АВ. Наконец, в силу того, что серединный перпендикуляр к АВ тоже проходит через точку О, точка О есть точка пересечения серединных перпендикуляров к сторонам треугольника ABC, то есть она является центром окружности, описанной около треугольника ABC. Длина радиуса этой окружности, очевидно, равна длине отрезка ОА, то есть половине длины гипотенузы АВ.
Замечание. Верно и обратное утверждение: если у некоторого треугольника центр описанной около него окружности находится на середине одной из его сторон (что эквивалентно тому, что длина радиуса этой окружности равна половине длины одной из его сторон), то этот треугольник прямоугольный.
5. Теорема Пифагора
В прямоугольном треугольнике сумма квадратов длин катетов равна квадрату длины гипотенузы (а2 + Ъ2 — с2).
Приведем доказательство этого факта. Рассмотрим четыре равных между собой прямоугольных треугольника АВР, BCQ, CDR и DAS, будем считать, что
\АВ\ = \ВС\ = \CD\ = \DA\ = с,
\АР\ = \BQ\ = \CR\ = \DS\ = а,
\ВР\ = \CQ\ = \DR\ = | AS | = 6,
и расположим их так, как показано на рисунке. Заметим, что \PQ\ = \QR\ = |Л5| = \SP\ = а + Ь, углы Р, Q, R и S прямые, поэтому PQRS - квадрат. С другой стороны, из теоремы о сумме величин
углов треугольника вытекает, что сумма величин острых углов прямоугольного


10
Теория и задачи
треугольника равна 7г/2. Но тогда величины углов ABC, BCD, CD А и DAB тоже равны 7г/2. Это следует из того, что, например, ABC + АВР + CBQ = 7Г, АВР + CBQ = 7г/2. Пользуясь этим фактом и равенством длин отрезков АВ, ВС, CD и JDA, мы получаем, что ABCD тоже является квадратом.
Наконец, очевидно, что площадь квадрата PQRS равна сумме площади квадрата ABCD и учетверённой площади треугольника АВР. Пользуясь формулами площади квадрата и прямоугольного треугольника, находим
(а + Ь)* = г + *.%
д2 -Ь 2ab -j- 62 — с2 -+■ 2а6
а2 -h Ъ2 = с2
Замечание. Верна и обратная теорема: если в некотором треугольнике сумма квадратов длин двух его сторон равна квадрату длины его третьей стороны, то он прямоугольный.
6. 	Окружность, вписанная в прямоугольный треугольник
Длина радиуса окружности, вписанной в прямоугольный треугольник, равна
. . { а+ Ь-с'
полуразности суммы длин его катетов и длины его гипотенузы
( а + b — с\
С-—а—
В
Доказательство этого факта чуть более сложно, чем предыдущие доказательства. Рассмотрим прямоугольный треугольник ABC (угол С прямой), обозначим центр вписанной в него окружности буквой О, точки её касания со сторонами АВ, ВС и АС - буквами К,
М и L соответственно, а длину её радиуса - буквой г.
Ясно, что О К _L АВ, ОМ _L ВС и OL ± АС. Из этого следует, что OLCM - квадрат (у четырёхугольника OLCM три прямых угла, поэтому он прямоугольник, и равны длины смежных сторон OL и ОМ, поэтому он квадрат), стало быть, \СМ\ = \CL\ — \OL\ = г.
Также заметим, что равны пары прямоугольных треугольников AOL и АО К, ВОМ и ВОК (по гипотенузе и катету), из чего вытекает, что \AL\ = \АК\, \ВМ\ = \ВК\. Наконец, запишем цепочку соотношений
\АВ\ = \АК\ + \ВК\ = \AL\ + \ВМ\ =
= (\АС\ - \CL\) + (\ВС\ - \СМ\) = \АС\ + \ВС\ - 2г, откуда и следует требуемая формула.
Замечание. Обратное утверждение опять-таки верно: если длина радиуса окружности, вписанной в некоторый треугольник, может быть вычислена как по- луразность суммы длин двух его сторон и длины его третьей стороны, то этот треугольник прямоугольный.
7. 	Медианы прямоугольного треугольника
Длина медианы прямоугольного треугольника, проведённой к гипотенузе, рае- на половине длины гипотенузы, длина медианы, проведённой к катету, равна корню из суммы четверти квадрата длины этого катета и квадрата длины другого катета:
с
U о? Г
Ь2


1.1. Прямоугольные треугольники
11
Доказательство этого факта тривиально. Рассмотрим прямоугольный треугольник ABC (угол С прямой), его медианы обозначим как АА\, ВВ\ и СС\. Так как С\ - середина гипотенузы, то С\ - центр окружности, описанной около треугольника ABC, поэтому
\АС1\ = \ВС1\ = \СС1\
\АВ\
Для нахождения длин отрезков АА\ и ВВ\ надо всего лишь применить теорему Пифагора для треугольников АА\С и ВВ\С.
Следствие. Сумма квадратов длин медиан прямоугольного треугольника, проведённых к катетам, в пять раз больше, чем квадрат длины его медианы, проведённой к гипотенузе (5га\ — т\ -f т2).
Замечание. Опять-таки верны обратные утверждения: если в некотором треугольнике длина медианы, проведённой к одной из его сторон, равна половине длины этой стороны или выполнено соотношение 5га;? = га\ + га|, то этот треугольник - прямоугольный.
8. Высоты прямоугольного треугольника
I. Длина высоты прямоугольного треугольника, проведённой к гипотенузе, равна частному произведения длин катетов и длины гипотенузы М)-
II. Квадрат длины высоты прямоугольного треугольника, проведённой к гипотенузе, равен произведению длин отрезков гипотенузы, на которые её делит основание этой высоты (h2 = са • сь).
Доказать эти утверждения несложно: возьмем прямоугольный треугольник ABC (угол С прямой), проведём его высоту СН и с помощью соотношений между длинами сторон и величинами углов в прямоугольном треугольнике выразим двумя способами синус величины угла А (рассмотрев треугольники ABC и АСН):
sin А —
\вс\
| АВУ
\ВС\
sin Л =
\сн\
АС |
\сн\
\сн\ =
\АС\ ■ \ВС\
\АВ\ \АС\ 1 1 \АВ\ '
С другой стороны, из прямоугольных треугольников АСН и ВСН имеем
tg^
\сн\
\АН\ ’
tg В =
\СН\
\вн\
tgA-tgB =
\СН\2
\АН\ ■ \ВН\'
из чего, пользуясь тем, что tgA-tgB — соотношение: |СЯ|2 = \АН\ ■ \ВН\.
\ВС\ \АС[ \АС\ \ВС |
= 1, мы получаем требуемое


12
Теория и задачи
Замечание 1. Верны и обратные утверждения:
I. 	Если в некотором треугольнике длина высоты, проведённой к одной из его сторон, равна отношению произведения длин двух других его сторон и длины стороны, к которой проведена высота, то этот треугольник прямоугольный;
И. Если в некотором треугольнике квадрат длины высоты, проведённой к одной из его сторон, равен произведению длин отрезков, на которые её основание делит эту сторону, то этот треугольник прямоугольный.
Замечание 2. Ясно, что высота прямоугольного треугольника, проведённая к одному из его катетов, совпадает с другим его катетом. То есть ha = 6, Нъ = а.
Отметим, что все приведённые обратные утверждения даны без доказательств. Это сделано по причине того, что их доказательства требуют применения различных фактов, связанных с произвольными треугольниками и впрямую не относящихся к теме этого параграфа, или же решения различных тригонометрических уравнений. Тем не менее, попробуйте их доказать.
Наконец, перечислим некоторые факты, относящиеся к произвольным треугольникам, которые также необходимо знать и уметь использовать при решении задач, в которых встречаются прямоугольные треугольники.
В нижеприведённых формулах а, Ь, с - длины сторон произвольного треугольника, А, В, С - величины соответствующих противолежащих им углов треугольника, ha,hb,hc - длины высот, проведённых к сторонам, длины которых равны а, b и с соответственно, р - полупериметр треугольника, г - длина радиуса вписанной в треугольник окружности, R - длина радиуса описанной около треугольника окружности.
Теорема о сумме величин внутренних углов треугольника
Сумма величин внутренних углов треугольника равна 7г. (Сумма градусных мер внутренних углов треугольников равна 180°.)
Теорема синусов:
а b с
^ = — = — = 2 R.
sin A sin В sin С
Теорема косинусов:
а2 = Ъ2 + с2 — 2bccosA, Ь2 — а2 + с2 — 2accosB, с2 = а2 + Ъ2 — 2abcosC.
Различные формулы площади произвольного треугольника:
5 = i • а • Ъ • sin С = ^ • а • с • sin В = i • b • с • sin А,
2 2 2
s = ! • а • /ia = ^ • 6 • Ль = i • с • Лс, s = л/р{р - а)(р - Ь)(р - с),
S = p-r, S=^£, S = 2R2 • sin A ■ sinB • sinC.
4 R
Теоремы о медианах и высотах треугольника
Медианы треугольника пересекаются в одной точке и делятся этой точкой на отрезки, длины которых относятся как 2:1, считая от вершины.
Прямые, содержащие высоты треугольника, пересекаются в одной точке. Если треугольник остроугольный, то эта точка лежит внутри треугольника. Если он тупоугольный, то эта точка лежит вне него.


1.1. Прямоугольные треугольники
13
Теоремы об описанной и вписанной окружностях
Около всякого треугольника можно описать окружность и притом только одну. Центр этой окружности лежит в точке пересечения серединных перпендикуляров, проведённых к сторонам треугольника. Причем этот центр лежит внутри треугольника, если он остроугольный; вне треугольника, если он тупоугольный; на середине гипотенузы, если он прямоугольный.
Во всякий треугольник можно вписать окружность и притом только одну. Центр этой окружности лежит в точке пересечения биссектрис всех трёх внутренних углов треугольника, причем всегда внутри треугольника.
Примеры решения задач
Пример 1. В треугольнике ABC из вершины В к стороне АС проведены медиана ВМ и высота ВН. Известно, что \АВ\ = \/5, \ВМ\ = 2>/2? \ВН\ = 2. Найдите длину стороны J3C, если ABC -1- АС В < 7г/2.
Решение. При решении этой задачи главное - выяснить, где находится основание высоты ВН. Для этого рассмотрим данное нам про величины углов треугольника соотношение и используем теорему о сумме величин углов треугольника:
В
ВАС
ABC + АС В <
: 7Г - (ABC + АсЩ =>
7Г 7Г
ВАС>*-~ =
Таким образом, угол ВАС тупой. Из этого вытекает, что точка Н лежит на продолжении стороны АС заточку А, поэтому \АН\ + \АМ\ = \НМ\. Применяя теорему Пифагора для треугольников ВАН и ВМН, получаем
\ВН\2 + \АН\2 = \ВА\2 =► 22 + \АН\2 = (л/5)2 =*• \АН\ = 1,
|ВЯ |2 + \МН\2 = \ВМ\2 =*• 22 + \МН\2 = (2\/2)2 =► \МН\ = 2.
Отсюда вытекает, что \АМ\ = \МН\ — \АН\ = 1. Далее, М - середина АС, значит, \АС\ = 2 • \АМ\ = 2, а \СН\ = \АН\ + \АС\ = 3.
Наконец, записываем теорему Пифагора для треугольника В НС:
\вн\2 + \нс\2
Ответ. \ВС\ = л/13.
\ВС\*
\ВС\2 = 22 + З2 = 13.
Пример 2. Вне прямоугольного треугольника ABC на его катетах АС и ВС построены квадраты ACDE и BCFG. Продолжение медианы СМ треугольника ABC пересекает прямую DF в точке N. Найдите длину отрезка CN, если известно, что \АС\ = 1, \ВС\ = 4.
Решение. СМ - медиана треугольника ABC, проведённая к его гипотенузе, значит, \АМ\ = \ВМ\ = \СМ\ и треугольники ACM и ВСМ равнобедренные.


14
Теория и задачи
С учётом этого и того, что углы FCN и MCA вертикальные, получаем
FCN = MCA = MAC = | - МВС.
А из равенства прямоугольных треугольников FCD и ВС А (по двум катетам) вытекает равенство углов CFN и МВС. Отсюда следует, что
D
FCN + CFN = -
й»-|.
То есть С N - высота треугольника FCD. Её длину можно легко вычислить с помощью формулы длины высоты прямоугольного треугольника, проведённой к гипотенузе:
с
■Ж
\ 1
и 1
1
В
G
Ответ.
\DF\ = \f\CF\2 + \CD\2 = л/17; |CW| = 4
у/й'
\CD\ ■ \CF\ \DF\
4
y/Vf'
Пример 3. В прямоугольном треугольнике ABC биссектриса BE прямого угла В делится центром О вписанной окружности в отношении у/3 : л/2, считая от вершины В. Найдите величины острых углов треугольника ABC.
Решение. Проведём из центра вписанной окружности радиусы ОН,ОК и OL в точки д касания её с гипотенузой и катетами, положим \ОН\ = \ОК\ = \OL\ = r.
Поскольку углы OKB,OLB,ABC прямые, а \ОК\ = |OL|, OKBL - квадрат. Поэтому \ВО\ = гу/2. Теперь выразим длину отрезка ОЕ. Так как BE - биссектриса угла ABC, величина угла АВЕ равна 7г/4. Обозначим величину угла А через а, тогда, так как сумма величин углов треугольника АВЕ равна 7Г, величина угла АЕВ равна 37г/4 — а. С учётом этого из прямоугольного треугольника ОНЕ получаем
\ОН\ г
\ОЕ\ =
sinОЕН sin(3f - а)'
Подставляя выраженные нами длины отрезков ВО и ОЕ в соотношение из условия задачи и учитывая тот факт, что, поскольку угол А - острый, то 0 < а < 7г/2 и величина 37г/4 — а может принимать только значения из интервала (7г/4,37г/4), имеем


1.1. Прямоугольные треугольники
15
Мы получили два варианта для величины угла а, в сумме они дают 7г/2. Это и есть величины острых углов треугольника, поскольку, если мы выберем в качестве а одно из двух полученных значений, величина другого острого угла будет равна как раз второму из этих значений.
_ 57Г 7Г
0твет' 12 И 12-
Пример 4. Через точку N проведены две прямые, касающиеся некоторой окружности с центром О. На одной из этих прямых взята точка А, а на другой взята точка В так, что \ОА\ = \ОВ\, \ОА\ > \ON\, \NA\ Ф \NB\. Известно, что \NA\ = a, |iVJ3| = 6, \ОА\ = с. Найдите длину отрезка ON.
Решение. Обозначим точки касания прямых и окружности из условия задачи буквами К и L, без ограничения общности будем считать, что точка А лежит на прямой NK, а точка В - на прямой NL.
Заметим, что ANOK = ANOL и ААОК = ABOL (по гипотенузе и катету), откуда следует, что \NK\ = \NL\ и \АК\ = \BL\. Также отметим, что из данных в условии задачи неравенств \ОА\ > \ON\, \ОВ\ > \ON\ и теоремы Пифагора вытекает, что \АК\ > \KN\ и \BL\ > |LiV|. После этого мы можем сделать вывод о расположении точек А и В. Если предположить, что точка А лежит на луче [NК), а точка В - на луче [NL), то необходимо получается, что точка К лежит на отрезке N А, а точка L - на отрезке NB, то есть
\NA\ = \NK\ + I-AjRTI; \NB\ = \NL\ + \BL\
\NA\ = \NB\.
Это противоречит условию задачи. Аналогично доказывается, что невозможен случай, когда точка А лежит на луче, дополнительном к [NК), а точка В - на луче, дополнительном к [NL). Будем полагать, что А лежит на луче [NК), а В - на луче, дополнительном к [NL). Тогда |ЛГА| = \NK\ + \АК\, = \BL\ — \NL\,
и в силу того, что \NK\ = \NL\, \АК\ = \BL\, мы находим
\NA\ 4- \NB\ = |АЙГ| + \BL\
\АК\ = \BL\ = |ЛГЛГ| = |ЛГ£| =
Теперь запишем теорему Пифагора для треугольников АО К и NOK:
=► \ОА\2 - \АК\2 = \ON\2 - \NK\2
\ОК\2 = \ОА\2 -\АК\2; \ОК\2 = |CW|2 - \NK\2
\ON\2 = \ОА\2 + \NK\2 -\АК\2
с +
а — Ь
с — аЪ.
Случай, когда А лежит на луче, дополнительном к [NK), а В - на луче [NL), рассматривается аналогично.
Ответ. |OiV| = у/с2 — ab.


16
Теория и задачи
Задачи
1. В треугольнике ABC угол ВАС прямой, \АВ\ = 1, \ВС\ = 3. Точка К делит сторону АС в отношении 7:1, считая от точки А. Что больше: \АС\ или \BK\1
2. В прямоугольном треугольнике ABC точки D и Е лежат соответственно на катетах ВС и АС так, что \CD\ = \СЕ\ = 1. Точка О есть точка пересечения отрезков AD и BE. Площадь треугольника BOD больше площади треугольника АОЕ на 0,5. Известно, что \AD\ = у/10. Найдите длину гипотенузы АВ.
3. В равнобедренном треугольнике длины высот, опущенных на основание и на боковую сторону, равны соответственно тип. Найдите длины сторон этого треугольника.
4. В прямоугольном треугольнике длина гипотенузы равна с, а величина одного из его острых углов равна а. Найдите длину биссектрисы прямого угла этого треугольника.
5. В треугольнике ABC угол А прямой, \АВ\ = 1, \ВС\ = 2. Биссектриса угла ABC пересекает сторону АС в точке L. G - точка пересечения медиан треугольника ABC. Что больше: \BL\ или |ВС?|?
6. В треугольнике ABC \АВ\ = с, \ВС\ = а, а медианы AD и СЕ взаимно перпендикулярны. Найдите длину стороны АС.
7. В треугольнике ABC угол А прямой, величина угла В равна 7г/6. В треугольник вписана окружность, длина радиуса которой равна л/З. Найдите расстояние от вершины С до точки касания этой окружности с катетом АВ.
8. В треугольнике ABC величина угла ВАС равна 7г/3, длина высоты, опущенной из вершины С на сторону АВ, равна \/3, а длина радиуса окружности, описанной около треугольника ABC, равна 5. Найдите длины сторон треугольника ABC.
9. В прямоугольном треугольнике отношение длины радиуса вписанной окружности к длине радиуса описанной окружности равно 2/5. Найдите величины острых углов треугольника.
10. В треугольнике ABC угол В тупой, продолжения высот AM и CN пересекаются в точке О, ВАС = а, ВС А = 7, \АС\ = Ь. Найдите расстояние от точки О до прямой АС.
11. В треугольнике, величина одного из углов которого равна разности величин двух других его углов, длина меньшей стороны равна 1, а сумма площадей квадратов, построенных на двух других сторонах, в два раза больше площади описанного около треугольника круга. Найдите длину большей стороны треугольника.
12. В прямоугольном треугольнике KLM проведён отрезок MD, соединяющий вершину прямого угла KML с точкой D, лежащей на гипотенузе KL таким образом, что \DL\ — 1, \DM\ = у/2, \DK\ = 2. Найдите величину угла KMD.


1.1. Прямоугольные треугольники
17
13. В треугольнике ABC угол С прямой, катет ВС разделён точками D и Е на три равные части. Найдите сумму величин углов АЕС, ADC и ABC, если известно, что \ВС\ = 3|А(7|.
14. В прямоугольном треугольнике ABC расстояние от середины гипотенузы А В до катета ВС равно 5, а расстояние от середины этого катета до гипотенузы равно 4. Найдите площадь треугольника ABC.
15. В прямоугольный треугольник ABC вписана окружность, касающаяся его сторон в точках Р, Q и R. Найдите площадь треугольника PQR, если длины катетов треугольника ABC равны 3 и 4.
16. В треугольнике ABC угол С прямой, CD - высота. Найдите длину радиуса окружности, вписанной в треугольник ABC, если длины радиусов окружностей, вписанных в треугольники ACD и BCD, равны 6 и 8 соответственно.
17. Расстояния от центра окружности, вписанной в прямоугольный треугольник ABC, до его вершин А и В равны у/b и \/Гб соответственно. Найдите длины катетов треугольника ABC.
18. В треугольнике ABC точка М расположена на стороне АС таким образом, что \АМ\ : \МС\ — 1 : Зу/З. Величина угла АВМ равна 7г/6, \ВМ\ = 6, угол В прямой. Найдите величину угла ВАС.
19. Дан треугольник KLM. Через точки К и L проведена окружность, центр которой лежит на высоте LF, опущенной на сторону КМ. Известно, что точка F лежит на стороне КМ. Найдите площадь круга, ограниченного этой окружностью, если \KL\ = 1, \КМ\ — \/3/2, \FM\ = у/3/6.
20. В прямоугольнике ABCD длины отрезков АВ и BD равны 3 и 6 соответственно. На продолжении биссектрисы BL треугольника ABD за точку L взята точка N такая, что отношение \BL\ : \LN\ равно 10 : 3. Что больше: длина отрезка BN или длина отрезка CL1
21. В прямоугольном треугольнике ABC угол В прямой, AM - медиана, ВН - высота. Найдите величину угла ВАМ, если известно, что величина угла между прямыми AM и ВН равна (р. При каких задача имеет решение?
22. В треугольнике ABC угол С прямой, отношение длины медианы СМ к длине биссектрисы СL равно у/б : 1, длина высоты СН равна 2. Найдите площадь треугольника ABC.
23. В прямоугольном треугольнике ABC отрезок ED соединяет середины сторон АВ и ВС. Точка F лежит на стороне ВС, отрезки AF и ED пересекаются в точке М. Известно, что отношение площадей четырёхугольника AM DC и треугольника ABC равно 7/10, а длины катетов ВС и АС равны а и Ь соответственно. Найдите длину отрезка AM.
24. В треугольнике ABC проведены высота ВН и медиана ВМ. Найдите \ВМ\, если известно, что \ВН\ = /г, АВН = СВМ, НВМ — 2 • СВМ.


18
Теория и задачи
25. В треугольник ABC вписана окружность, длина радиуса которой равна 2; D - точка касания этой окружности со стороной АС, \AD\ = 2, |iX7| = 4. Найдите длину биссектрисы треугольника ABC, проведённой из вершины В.
26. В прямоугольном треугольнике ABC угол В прямой, AL - биссектриса. Известно, что \АС\ = 5, \AL\ = 5/л/З. Найдите \ЬС\.
27. Треугольники ABC и ABD имеют общую сторону АВ и не имеют общих внутренних точек, углы ВАС и ADB прямые. Найдите \CD\, если \AD\ = 3, \ВС\ = 13, |Ж7| + |В£>| = 16.
28. В треугольнике ABC сторона АВ имеет длину 3, а высота CD, опущенная на сторону АВ, имеет длину л/З - Также известно, что основание D высоты CD лежит на стороне АВ и \AD\ = |ВС|. Найдите длину стороны АС.
29. В прямоугольном треугольнике ЛВС длина катета А В равна 4, а длина катета АС равна 3. Точка D делит гипотенузу пополам. Найдите расстояние между центром окружности, вписанной в треугольник ACD, и центром окружности, вписанной в треугольник ABD.
30. В равнобедренном треугольнике длина боковой стороны равна 20, а длина диаметра описанной около него окружности равна 25. Найдите длину радиуса окружности, вписанной в этот треугольник.
31. Из середины D гипотенузы А В прямоугольного треугольника ABC проведён луч, перпендикулярный гипотенузе и пересекающий один из его катетов. На этом луче отложен отрезок DE, длина которого равна половине длины отрезка АВ. Длина отрезка СЕ равна 1 и совпадает с длиной одного из катетов треугольника ABC. Найдите площадь треугольника ABC.
32. Прямая, параллельная гипотенузе АВ прямоугольного треугольника ABC, пересекает катет АС в точке £>, а катет ВС - в точке Е, причем длина отрезка DE равна 2, а длина отрезка BE равна 1. На гипотенузе взята точка F так, что \BF\ = 1. Известно также, что величина угла FCB равна а. Найдите площадь треугольника ABC.
33. Гипотенуза АВ прямоугольного треугольника ABC является хордой окружности, длина радиуса которой равна 10. Вершина С лежит на диаметре этой окружности, параллельном гипотенузе. Градусная мера угла С А В равна 75°. Найдите площадь треугольника ABC.
34. Длины катетов прямоугольного треугольника равны 36 и 48. Найдите расстояние от центра окружности, вписанной в этот треугольник, до его высоты, проведённой к гипотенузе.
35. Середины высот треугольника лежат на одной прямой. Какое максимальное значение может принимать его площадь, если длина его наибольшей стороны равна 10?


1.2. Теоремы синусов и косинусов
19
1.2. 	Теоремы синусов и косинусов Теоретический материал
Во всех материалах этого параграфа будут использоваться следующие обозначения: а, Ь, с - длины сторон произвольного треугольника, а, /3,7 - величины соответствующих противоположных им углов, р - полу периметр треугольника, R - длина радиуса описанной около треугольника окружности, г - длина радиуса вписанной в треугольник окружности. ha,hb,hc - длины высот, проведённых к сторонам, длины которых равны а,Ь и с соответственно.
Приведем некоторые базовые факты, касающиеся общих треугольников. Часть из них приводится без доказательства, поскольку их подробное обоснование можно найти в любом школьном учебнике геометрии.
1. Различные формулы площади произвольного треугольника
5 = - • а • Ь • sin 7 = ^ ■ а • с • sin В — ~ • Ъ • с • sin а,
2 1 2 2
S = \-a-ha = yb-hb = ±-c-hc, S = р -г, S=^^,
S = у/р • (р — а) • (р — Ь) • (р — с) (формула Герона).
2. Теорема синусов
Отношение длины любой стороны треугольника к синусу величины внутреннего угла треугольника, противолежащего этой стороне, равно удвоенной длине радиуса окружности, описанной около этого треугольника:
sin a sin р sin 7
Отметим, что теорема синусов является одним из наиболее часто используемых средств для решения задач на треугольники. Однако для нахождения величины угла треугольника лучше пользоваться теоремой косинусов. Это соображение можно пояснить так: с помощью теоремы синусов можно найти лишь синус величины угла треугольника, а вот однозначно найти эту величину нельзя, так как
уравнение sin а = а (0 < а < 1) имеет два решения, лежащих в интервале (0, тг). То есть некоторому значению синуса величины угла треугольника соответствуют два угла, острый и тупой, сумма величин которых равна 7г.
3. Теорема косинусов
Квадрат длины любой стороны треугольника равен разности суммы квадратов длин двух других его сторон и удвоенного произведения длин этих сторон и косинуса величины внутреннего угла треугольника, заключенного между ними:
а2 = Ь2 + с2 — 26с cos а, Ь2 — а2 + с2 — 2accos/3, с2 = а2 + b2 — 2abcos'y.


20
Теория и задачи
4. 	Окружность, вписанная в треугольник
В произвольный треугольник можно вписать окружность, причем только одну. Центр этой окружности лежит в точке пересечения биссектрис внутренних углов треугольника, причем всегда расположен внутри треугольника.
Рассмотрим произвольный треугольник ABC, буквой О обозна- С
чим центр вписанной в него окружности, буквами D,E и F обозначим точки, в которых она соответственно касается его сторон АВ, АС и ВС. Сформулируем и докажем важное утверждение, связывающее длины сторон треугольника ABC и длины отрезков, на которые они разбиты точками £), Е и F. В
Теорема. Длина любого из отрезков, на которые стороны треугольника разбиваются точками их касания с вписанной в этот треугольник окружностью, может быть вычислена как разность полупериметра треугольника и длины стороны треугольника, не содержащей ни один из концов этого отрезка:
\AD\ = \АЕ\ =
\АВ\ + \АС\ - \ВС\
= Раавс - \ВС\;
\BD\ = |BF| =
\АВ\ + \ВС\ -\АС\
— Раавс - \AC\-,
1СЩ = 1СР1^лс1±1вс1-Ш=рлАвс_1АЩ
Доказательство. Равенство длин пар отрезков AD и АЕ, BD и BF, СЕ и CF следует из равенства по гипотенузе и катету пар прямоугольных треугольников AOD и АОЕ, BOD и BOF, СОЕ и COF соответственно. С учётом этого положим \AD\ = \АЕ\ = ж, \BD\ = \BF\ = г/, \СЕ\ = \CF\ = z и составим систему уравнений:
\АВ\ = \AD\ + \BD\, \АС\ = \АЕ\ + |C7JS7|, \ВС\ = \BF\ + \CF\
\АВ\ = х + у, \АС\ = х + z, \ВС\ = у + z
х —
У =
z =
\АВ\ + \АС\ - \ВС\ 2
\АВ\ + \ВС\ -\АС\ 2
\АС\ + \ВС\ - \АВ\
х=\щ±1лс\+т _ |вс|_
„=ма±ф±ма_ИС|, z _ |АВ|.
Теорема доказана.


1.2. Теоремы синусов и косинусов
21
5. 	Окружность, описанная около треугольника
Около произвольного треугольника можно описать окружность, причем только одну. Центр этой окружности лежит в точке пересечения серединных перпендикуляров к сторонам треугольника, причем расположен вне треугольника, если треугольник тупоугольный, и внутри треугольника, если треугольник остроугольный.
Рассмотрим произвольный треугольник АВС, буквой О обозначим центр описанной около него окружности.
Теорема. Величина угла, образованного стороной треугольника и радиусом описанной около этого треугольника окружности, проведённым в один из концов этой стороны, может быть вычислена как модуль разности числа п/2 и величины угла, противолежащего этой стороне:
О АС = ОСА =
’--ABC
; ОВС = ОС В =
*--Шс
ОАВ=ОБА=
'--АО в
Доказательство. Поскольку О А, О В и ОС - радиусы окружности, описанной около треугольника ABC, имеем \ОА\ = \ОВ\ = \ОС\, поэтому треугольники АОВ, АОС и ВОС равнобедренные. Из этого факта вытекает, что О АС = ОСА, ОВС = ОС В, ОАВ = О В А. Введем обозначения О АС = tp, ОВС = ф, ОАВ = в и рассмотрим два варианта.
Если треугольник ABC остроугольный, то точка О лежит внутри него и
ОАВ + О АС = ВАС, ОВА + ОВС = ABC, { ОСА + ОСВ = АСВ
' e + tp = BAC,
е + Ф = 'авс,
k •ф + <р = АС В
ч> =
ф = в =
ВАС + АС В - АВС
АВС + АС В - ВАС
АВС + ВАС - АС В
Наконец, с учётом того, что АВС + АС В + ВАС = 7г, и того, что АВС < п/2,


22
Теория и задачи
ВАС < 7г/2, АС В < 7г/2, мы получаем
ОАС = <р= ^ ~ АВС^ ~ = тг/2 - АВС = |тг/2 - АВС|,
< ОВС = ф=^~ ВАС^ ~ ВАС = тг/2 - ВАС = |тг/2 - ВАС\,
ОАВ = в= ТЛ(7.? = тг/2 - ЛСБ = |тг/2 - АСВ|.
2
Если же треугольник ЛВС тупоугольный (будем считать, что угол С тупой), то точка О лежит вне треугольника, поэтому
' ОАС-ОАВ = ВАС, ( ОАС = тг/2- АВС = \я/2-АВС\,
< ОВС -ОВА = АВС, =► < ОВС = тг/2 - ВАС = \ж/2-ВАС\, k ОСА + ОСВ = АСВ [ ОАВ = ЛСВ - тг/2 = |тг/2 - АСВ\.
Теорема доказана.
Замечание. Эту теорему можно доказать и более простым способом, используя соотношения между величинами центральных и вписанных углов. Попробуйте сделать это самостоятельно.
Примеры решения задач
Пример 1. В треугольнике АВС дано \ВС\ = 6, \АС\ = 5, АВС = 7г/6. Найдите площадь треугольника АВС, если расстояние от вершины А до прямой ВС меньше 1/л/2-
Решение. В этой задаче данным из условия задачи соответствуют два различных треугольника АВС. В самом деле, можно построить отрезок ВС длины б, отложить из точки В два симметричных относительно прямой ВС луча, составляющих с лучом [ВС) угол величины 7г/6, и построить окружность с центром в точке С, длина В радиуса которой равна 5. Точка А - одна из точек пересечения лучей и этой окружности. Таких точек будет, вообще говоря, четыре, но поскольку лучи симметричны, треугольники получатся тоже попарно симметричными. Так что различных треугольников будет все-таки два.
Для того чтобы найти площадь треугольника АВС, нам необходимо найти либо длину стороны АВ, либо синус угла АС В. \АВ\ найти попроще, для этого достаточно написать теорему косинусов:
\АС\2 = \АВ\2 + \ВС\2 - 2 • |АВ| • |ВС| • cos ABC =>
25 = |АВ|2 + 36 — 12 • |АВ| • => |AB|ii2 = 3-\/3 ± 4.


1.2. Теоремы синусов и косинусов
23
Как и ожидалось, мы получили два различных варианта длины стороны АВ. Меньшей из этих длин на чертеже соответствует точка А\ (Аз), большей - ^(А*).
Осталось проверить условие, что расстояние от вершины А до прямой ВС меньше 1/у/2. Это расстояние есть длина перпендикуляра, опущенного из точки А на прямую ВС. Ясно, что оно может быть вычислено как произведение длины отрезка А В на синус угла ABC:
\АВ\ = Зл/З + 4 =► р(А, (ВС)) = > 2 > 1
\АВ\ = Зл/З — 4
Р(А,(ВС))
2
Зу/З — 4
>/2’
<
V2'
Значит, \АВ\ = Зу/З — 4. Наконец, найдём искомую площадь
Saabc = \ • \АВ\ ■ \ВС\ ■ sin ABC = 1 • (3\/3 - 4) • 6 • i = ^(3^ - 4).
Ответ. -(3\/3 —4). z
Пример 2. В остроугольном треугольнике ABC известно, что \ВС\ \АС\ = 6, АС В = а. Найдите длину высоты CD и величину угла ABC.
Решение. Длину высоты С£> можно посчитать как с помощью формулы площади, так и через синус угла ABC.
В любом случае нам понадобится длина стороны АВ, найдем её с помощью теоремы косинусов:
\АВ\2 = \АС\2 + \ВС\2 - 2 • \АС\ ■ \ВС\ • cos АСВ =►
=► \АВ\ = Va2 +Ь2- 2аЬ cos а.
Теперь запишем формулу площади треугольника ABC :
Saabc = \ • \АС\ • \ВС\ • sin Адв = ± ■ \АВ\ • \CD\
a\
7
*1
\a
ab sin а = \CD\ • \/а2 + Ь2 — 2ab cos а
|CD| =
D
ab sin а
у/а2 + b2 — 2ab cos а
Самым простым способом определения величины угла ЛВС здесь является, конечно, выражение его синуса из прямоугольного треугольника CDB и использование того факта, что треугольник ABC остроугольный. Однако лучше сразу привыкать к тому, что для нахождения величины угла треугольника следует искать его косинус, поскольку по косинусу угол треугольника определяется однозначно. Так и поступим:
\АС\2 = \АВ\2 + \ВС\2
2 \АВ\ \ВС\ cos ABC =* b2 = а2 + b2 — 2abcosa 4- a2 — 2ay/a2 + b2 — 2ab cos a • cos ABC cos ABC
a- b cos a
\/a24-62^2abcosa
Ответ. \CD\ =
ab sin a
у/a2 -\-b2 — 2ab cos a
ABC = arccos
a — b cos a
у/a2 + b2 — 2ab cos a


24
Теория и задачи
Пример 3. Окружность, вписанная в треугольник АВС, касается его стороны ВС в точке М. Найдите площадь треугольника АВС, если \АС\ =21, \ВМ\ = 9, а градусная мера угла АВС равна 60°.
л
Решение. Воспользуемся теоремой о длинах отрезков, на которые окружность, вписанная в треугольник, делит точками касания его стороны:
\ВМ\ = Раавс ~ \ АС\ ==» 9 = раавс - 21 ==>
=> Раавс = 30, Раавс = 60.
Теперь обозначим длины сторон АВ и ВС через х и у соответственно, запишем теорему косинусов для треугольника АВС и заметим, что поскольку
1 /я
Saabc = g * 1^£| • |ВС| • sin ABC =
нам надо найти не сами хиу,а лишь значение произведения ху.
Г |ЛС|2 = \АВ\2 + |ВС|2 - 2 • |АВ| • |ВС| • cos ABC,
\ |АВ| + |ВС| + |АС| = Раавс ^
( 212 = ж2 + у2 - ху, Г 212 = (я + ?/)2 - Зжу,
я -f у + 21 = 60 ^ ж + т/ = 39
=» 3ху = 392 - 212 = (39 - 21)(39 + 21) = 18-60 => ху = 360.
л/3
Наконец, площадь треугольника АВС равна • 360, то есть 90\/3.
Ответ. 90\/3.
Пример 4. Внутри треугольника АВС выбрана точка О таким образом, что sin ВОС = 1/4, sin АОС = 1/3. Найдите расстояние между центрами окружностей, описанных около треугольников АОС и ВОС, если известно, что |ВО| = 2, |ВС| = 3, \АС\ =4.
Решение. Обозначим центры окружностей, описанных около треугольников ВОС и АОС, буквами Ох и О2 соответственно и заметим, что точки 0\ и О2 обе лежат на прямой, проходящей через середину отрезка ОС перпендикулярно ему (поскольку центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к его сторонам).
Далее по теореме синусов
|OiO| = \0\C\ = Raboc = = 6;
2 sin БОС 1/2
|020| - |02C| = Raaoc = lA^L = A = 6. 2 sin AOC 2/3


1.2. Теоремы синусов и косинусов
25
Таким образом, АО\ОС = ДО2ОС (по трем сторонам). Если точки 0\ и О2 лежат в одной полуплоскости относительно прямой ОС, то они совпадают, из чего вытекает, что все четыре точки А, В, С и О лежат на одной окружности, что невозможно. Поэтому точки 0\ и О2 лежат в разных полуплоскостях относительно прямой ОС, то есть О1ОО2С - ромб. Мы знаем длину его стороны, просят же нас найти длину его диагонали O1O2.
Очевидно, что для её нахождения необходимо вычислить длину второй его диагонали, ОС. Её легко найти из треугольника ВОС по теореме косинусов, если знать cos ВОС.
Для начала попробуем выяснить, острый или тупой угол ВОС. Ясно, что
ВОС + АОС + АОВ = 2тг; АОВ < тг =» ВОС + АОС > тг.
Если угол ВОС острый, то есть его величина равна arcsin 1/4, то даже если угол АОС тупой, то есть АОС = тг — arcsin 1/3, будем иметь:
ВОС + АОС = тг — arcsin 1/3 4- arcsin 1/4 < тг.
—>/15
Значит, угол ВОС тупой, поэтому cos ВОС = —. Теперь запишем теорему
косинусов для треугольника ВОС:
\ВС\2 = \ВО\2 + \ОС\2 - 2 • \ВО\ ■ \ОС\ • cos ВОС =►
=► 9 = 4 + \ОС\2 + л/15|ОС7| =» {|ОС|>0} =» | ОС\ = .
£d
Наконец, воспользуемся тем, что в ромбе диагонали перпендикулярны и точкой пересечения делятся пополам. Из этого следует, что
|0,0г|. 2^c?-\\ocv - f= ]/Щ^ _ Щ±1.
п 5V21 + 1
Ответ. .
Задачи
1. Длина стороны АС треугольника АВС равна 3, синусы величин его углов А и В равны \/3/2 и у/2/2 соответственно. Найдите длину стороны АВ.
2. В треугольнике АВС известно, что \АВ\ = с, А = а, В = 0. Найдите площадь треугольника АВС.
3. Внутри треугольника АВС взята точка К так, что треугольник АВК равносторонний. Известно, что расстояние от точки К до центра окружности, описанной около треугольника АВС, равно 6, а величина угла АС В равна arcsin(5>/l3/26). Найдите длину стороны АВ.
В


26
Теория и задачи
4. В треугольнике ABC \АС\ = 3, ВАС = 7г/6, длина радиуса окружности, описанной около треугольника ABC, равна 2. Докажите, что площадь треугольника ABC меньше 3.
5. В треугольнике ABC найдите величину угла САВ, если произведение квадрата длины стороны ВС на сумму длин сторон АС и АВ равно сумме кубов длин сторон АС и АВ.
6. В треугольнике ABC длины сторон А В и АС равны 3 и 2 соответственно. На стороне АВ выбрана точка М, а на стороне АС - точка N так, что \АМ\ = 2, \AN\ = 1,5. Найдите площадь треугольника AMN, если длина стороны ВС больше длины отрезка MN в б/л/17 раз.
7. В треугольнике ABC \АВ\ = 4, \ВС\ = 5. Из вершины В проведен отрезок ВМ (М € АС), причём АВМ = 7г/4, МВС = 7г/6.
а) В каком отношении точка М делит сторону АС?
б) Вычислите длины отрезков AM и МС.
8. В треугольнике ABC \ВС\ = 4, \АВ\ + \АС\ = 6. Найдите площадь треугольника ABC, если cos АС В = 5/12.
9. В треугольнике ABC градусная мера угла АС В равна 75°, а длина высоты, опущенной из вершины этого угла, равна 1. Найдите длину радиуса окружности, описанной около треугольника ABC, если его периметр равен 4 -{- л/6 — \/2.
10. Внутри треугольника ABC взята точка К таким образом, что |АЙГ| = 1,
\КС\ = v/з, АКС = 120°, АВК = 15°, КВС = 15°. Найдите длину отрезка В К.
11. Величины углов тупоугольного треугольника ABC удовлетворяют соотношению sin (^A — B^j = sin2 А — sin2 В. Найдите периметр этого треугольника,
если длина радиуса описанной около него окружности равна Д, а величина одного из его углов равна п/8.
12. В треугольник ABC вписана окружность с центром в точке О. Площадь треугольника АО В относится к площади треугольника ВОС как л/3 : 2, АС В = 7г/3, \АС\ = 2. Найдите длину радиуса окружности, описанной около треугольника ABC.
13. В треугольнике ABC известно, что ВАС = a, ABC = /3, \ВС\ = а. На стороне А В взята точка Р так, что \АР\ : \РВ\ = 1:2. Через точку Р проведена окружность, касающаяся стороны ВС в точке D, причём AD - высота треугольника ABC. Найдите длину радиуса этой окружности.
14. Через центр окружности, вписанной в треугольник ABC, провели прямую MN параллельно основанию АВ (М лежит на ВС, N лежит на АС). Известно, что \АВ\ = 5,\MN\ = 3. Найдите периметр четырёхугольника ABMN.


1.2. Теоремы синусов и косинусов
27
15. В треугольнике АВС даны длины сторон \АВ\ — у/2, \ВС\ = у/b и \АС\ = 3. Сравните градусную меру угла ВОС и 112,5°, если О - центр вписанной в треугольник АВС окружности.
16. В треугольнике АВС известно, что \ВС\ — \АВ\ = 0,1Ъ\АС\. Чему равно произведение tg (^BAC'j • ctg ^ACB^j ?
17. Окружность, вписанная в треугольник АВС, касается его сторон АС, АВ и ВС в точках К, М и N соответственно. Известно, что \АК\ = \КС\,
KMN = 75°, а произведение длин всех сторон треугольника KMN равно 9 -f 6^3. Найдите длины сторон треугольника АВС.
18. Точка О лежит на отрезке АВ так, что \АО\ = 13, \ОВ\ = 7. С центром в О проведена окружность, длина радиуса которой равна 5. Из А и В к ней проведены касательные, пересекающиеся в точке М, причём точки касания лежат по одну сторону от прямой АВ. Найдите длину радиуса окружности, описанной около треугольника AM В.
19. Периметр треугольника АВС равен 40/3, косинусы углов АВС и АС В равны 0,6 и 0,28 соответственно. Найдите площадь треугольника АВС.
20. Известно, что для величин углов треугольника АВС выполнено соотношение cos2 А+cos2 Б-f-cos2 С — 1. Найдите площадь этого треугольника, если длины радиусов вписанной в него и описанной около него окружностей равны у/3 и 3V2 соответственно.
21. Площадь треугольника равна 6\/6, периметр его равен 18, расстояние от центра вписанной в него окружности до одной из его вершин равно у/56/3. Найдите длину наименьшей стороны этого треугольника.
Бу/2 5>/5
22. В треугольнике АВС \АВ\ = —^-,\ВС\ = ——. Точка М лежит на сто-
3
роне АВ, точка О лежит на стороне ВС, причём \ВМ\ = - \АМ\, а прямые
МО и АС параллельны. Биссектриса угла ВАС пересекает прямую МО в точке Р, лежащей между точками М и О, причём длина радиуса окружности, описанной около треугольника АМР, равна у/2 + у/2. Найдите длину стороны АС.
23. В треугольнике АВС величина угла при вершине В равна 7г/3, а длины отрезков, соединяющих центр вписанной окружности с вершинами А и С, равны 4 и 6 соответственно. Найдите длину радиуса окружности, вписанной в треугольник АВС.
24. Известно, что длина радиуса окружности, вписанной в треугольник АВС, равна 1. Эта окружность касается его сторон АВ, ВС и АС в точках К, М и N соответственно, MKN = АВС = 45°. Найдите длины сторон треугольника АВС.
25. Через центр О вписанной в треугольник АВС окружности проведена прямая, параллельная стороне ВС и пересекающая стороны АВ и АС в точках


28
Теория и задачи
М и N соответственно. \ВС\ = \/2, периметр треугольника AMN равен 3^2, а длина отрезка АО втрое больше длины радиуса вписанной в треугольник ABC окружности. Найдите площадь треугольника ABC.
26. В треугольник KLM вписана окружность, которая касается его стороны КМ в точке А. Известно, что \АК\ = 10, \АМ\ = 4, KLM = 7г/3. Найдите длину отрезка AL.
27. В равностороннем треугольнике ABC проведена окружность с центром в точке О, проходящая через точку пересечения медиан треугольника ABC и касающаяся его стороны ВС в её середине D. Из точки А проведена прямая, касающаяся этой окружности в точке Е так, что градусная мера угла ВАЕ меньше 30°. Найдите отношение площадей треугольника АВЕ и четырёхугольника BEOD.
28. В треугольнике длина стороны АВ равна 2\/2, а длина радиуса окружности, описанной около него, равна 2. Отношение длин сторон АС и ВС равно \/8, длина стороны ВС больше 1. Найдите площадь треугольника ABC.
29. В треугольнике ABC даны длины сторон: \АВ\ = \ВС\ = 13, \АС\ = 10. Найдите расстояние между центрами окружностей, вписанной в него и описанной около него.
30. В равнобедренном треугольнике ABC (\АВ\ = \ВС\) отношение расстояний от центра вписанной в этот треугольник окружности до вершин В и С соответственно равно к. Найдите величины углов треугольника ABC. При каких значениях к задача имеет решение?
31. В равнобедренном треугольнике ABC с основанием АС проведена биссектриса угла С, которая пересекает боковую сторону АВ в точке D. Точка Е лежит на основании АС так, что DE _L DC. Вычислите длину отрезка AD, если \СЕ\ = 2.
32. В треугольнике ABC \АВ\ = 4, \АС\ = 3, угол С острый. Известно, что sin ^АС В — ABc'j =7/25. Найдите площадь треугольника ABC.
33. В треугольник ABC, в котором длина стороны ВС равна 9, вписана окружность, касающаяся стороны ВС в точке D. Известно, что \AD\ = |DC\,
cos ВС А = 2/3. Найдите длину стороны АС.
34. Треугольник ABC со стороной АВ, длина которой равна 4, и углом А, градусная мера которого равна 60°, вписан в окружность с длиной радиуса 2у/3. Найдите длину средней линии этого треугольника, параллельной АС, и расстояние между точками, в которых её продолжение пересекает окружность.
35. В треугольнике ABC проведена биссектриса AD. В треугольники ADC и ADB вписаны окружности с длинами радиусов 3 и 8 соответственно, касающиеся отрезка AD в точках М и N. Найдите расстояние между центрами этих окружностей, если \ND\ = 4.


1.3. Биссектриса, медиана, высота
29
36. 	В треугольнике КLM отношение длин радиусов описанной около него и вписанной в него окружностей равно к. Окружность, вписанная в треугольник KLM, касается его сторон в точках А, В и С. Найдите отношение площадей треугольников ABC и KLM.
1.3. 	Биссектриса, медиана, высота Теоретический материал
1. 	Биссектриса треугольника
Определение. Биссектрисой треугольника называется отрезок биссектрисы внутреннего угла треугольника, заключённый между его вершиной и противолежащей ей стороной треугольника.
Рассмотрим треугольник ABC, проведём его биссектрисы АК, BL и CN. Длины сторон АВ, АС и ВС обозначим через с, Ъ и а соответственно, длины биссектрис АК, BL и CN обозначим через 1а, 1ь и 1С соответственно, точку их пересечения обозначим буквой О. Также введём обозначения для длин отрезков, на которые биссектрисы разбивают стороны: \ВК\ = ас, \СК\ = аъ, \BN\ = са, \AN\ = cb, \AL\ = bc, \CL\ = ba.
С IABI = с IACI = b IBCI = a
Приведём несколько важных фактов, связанных с биссектрисами треугольника. Основное свойство биссектрисы треугольника. Отношение длин двух сторон треугольника равно отношению длин прилежащих к ним отрезков, на которые биссектриса треугольника разбивает третью его сторону:
а са b аъ с Ьс
b съ с ас a bd
Первая формула длины биссектрисы треугольника. Длина биссектрисы треугольника, проведённой к некоторой его стороне, равна частному удвоенного произведения длин двух других сторон треугольника на косинус половины величины угла между ними и суммы длин этих сторон:
26ccost5t , 2accosl , 2abcos?
la = -г--—; lb = ——lc = ——и-
o-fc a + c a + o


30
Теория и задачи
Вторая формула длины биссектрисы треугольника. Квадрат длины биссектрисы треугольника, проведённой к некоторой его стороне, равен разности произведения длин двух других его сторон и произведения длин отрезков, на которые она делит сторону треугольника:
l2~bc- аъас', 1ь = ас - babc; I* = аЬ - сась.
Точка пересечения биссектрис. Бгьссектрисы треугольника пересекаются в одной точке, эта точка является центром окружности, вписанной в этот треугольник. Эта точка делит каждую биссектрису на отрезки, отношение длин которых, считая от. вершины треугольника, равно частному суммы длин сторон, образующих угол, из вершины которого она проведена, и длины стороны, к которой она проведена.
Докажем все эти факты, начнем с основного свойства биссектрисы треугольника. Для этого запишем теорему синусов для треугольников ACN и BCN, предварительно обозначив величины смежных углов BNC и ANC через <р и 7г — <р соответственно:
|A/V| \АС\ сь b сь sin
sin ACN sin ANC sin^ sin(7r - <p) b sin(7r - <p)'
2 2
|ВЛГ| \BC\ ca a ca sin?
sin BCN sin BNC sin 2 sin<P a sin<^'
Воспользовавшись тем, что sin(7r — <p) = sin<£, получим
ca Cb a Ca
— = T *=► T = —•
a b b сь
Оставшиеся два соотношения доказываются абсолютно аналогично.
Для доказательства первой формулы длины биссектрисы выпишем формулы площади для треугольников ABC, AN С и BNC и воспользуемся тем, что площадь треугольника АВС равна сумме площадей треугольников ACN и BCN:
Saabc = ~ * \ АС\ • \ВС\ • sin ACS = ^absin7,
S&ANC = \ ■ \AC\ • \CN\-sin ACN = ±aJc sin 2 =*
Sabnc = \ • \BC\ • |CW| • sin ВСЛГ = |ыс sin 2
/■у /у /у /у /у
ab sin 7 = alc sin ~ + blc sin — <=> 2 ab sin — cos — = (a + b)lc sin — =>
z z z z z
2ab cos ?
^ lc = ТГ1-
(2 *f 0
Формулы для длины la и /б доказываются таким же образом.
Для доказательства второй формулы длины биссектрисы запишем теорему косинусов для треугольников ANС и BNC:
Г |АС|2 = \AN\2 + \CN\2 - 2 • |A7V| . \CN\ • cos ANC,
\ \BC\2 = |£A/f 4- |C7V|2 - 2 • |£7V| • |CiV| • cosШС


1.3. Биссектриса, медиана, высота
31
Г Ь2 = cl + 12с - 2Cblc cos(7T - ф),
| а2 = cl + l2- 2Calc cos <£.
Домножим первое из этих соотношений на са, второе на сь и сложим их. Пользуясь тем, что cos(7r — (р) = — cos<^, получим
а2Сь 4" b2Ca = C2Cfe + 1ссЬ Н“ сЬса + 1ссЬ•
Из доказанного выше основного свойства биссектрисы вытекает, что ась = Ьс0. С помощью этого факта преобразуем левую часть последнего равенства:
аЬса+Ьасъ = с2асъ+12ссь+с2са+12ссъ => аЬ{са+съ) = сась(са+сь)+11(са+сь) =>
===> ab = сась 4- I2 => I2 = ab — сась.
Формулы для /а и /ь доказываются аналогично.
Наконец, для обоснования последнего утверждения предварительно выразим величины аь, ас, Ьа, 6С, са, сь через длины сторон треугольника ABC. Воспользуемся основным свойством биссектрисы:
\АВ\ = |ЛЛГ| + |ВЛГ|,
\AN\ \BN\ =>
\АС\ ~ \ВС\
Абсолютно аналогично получаем, что
ас
са — “Г’
а 4" b
Ъс
сь = —т.
а 4* о
ab be ab ас
Ud ' ) Ос ----------- ^
I ’ — ) **0 — , . у — 1 .
а 4- с а 4- с о 4~ с о 4” с
Теперь рассмотрим треугольник A/VC • АО - его биссектриса, поэтому
\СО\ \АС\ Ъ Ь а + Ь \ON\ ~ \AN\ ~ cb~ J>c_ ~ с ’ а 4- Ь
Рассуждая таким же образом, находим
\АО\ b 4~ с \ВО\ а Л- с |ОК\ = ]оЦ = "Т“‘
Замечание. С учётом полученных выражений для аь, ас, Ьа, £>с, са, сь вторая формула длины биссектрисы может быть записана в виде
l2a = bc(l- (6 + с)2)’ *ь=ас ^1- (а + с)2)> ,2с=аЬ (1_ (а + 6)2) '
2. 	Медиана треугольника
Определение. Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противолежащей этой вершине стороны.
Рассмотрим треугольник ABC, проведём его медианы АР, BQ и CR. Длины сторон АВ, АС и ВС обозначим через с, b и а соответственно, длины медиан АР, BQ и Ci? обозначим через та, ть и тс соответственно.


32
Теория и задачи
В
Точка пересечения медиан. Медианы треугольника пересекаются в одной точке, эта точка является его центром тяжести. Она делит каждую медиану на отрезки, отношение длин которых, считая от вершин треугольника, равно 2:1.
Формула длины медианы треугольника. Учетверённый квадрат длины медианы треугольника, проведённой к некоторой его стороне, равен разности удвоенной суммы квадратов длин двух других сторон треугольника и квадрата длины стороны, к которой проведена медиана:
4Шд = 2 Ь2 + 2с2 — а2; Ат2 = 2а2 + 2с2 — Ь2; 4га2 = 2а2 + 2 Ъ2 — с2.
Для доказательства этого утверждения запишем теорему косинусов для треугольников ABQ и CBQ, предварительно обозначив величины смежных углов AQB и CQB через ip и 7г — ip соответственно:
Г \АВ\2 = \AQ\2 + \BQ\2 - 2 • \AQ\ • \BQ\ • cos AQB, \ \BC\2 = \CQ\2 + \BQ\2 - 2 • \CQ\ • \BQ\ • cos CQB ^
2 & 2 _ c = — -f- mb — оть cos ip;
^ 2 Ъ2 2 т
a = — H- rag — оть cos(7r — <^J.
Сложив эти равенства и учитывая то, что cos(7r — ip) = — cos<^, получим
а2 + с2 — 2га2 4- ~ => 4га2 = 2а2 -f 2с2 - Ь2.
Для двух других медиан треугольника АВС доказательство проводится так же.
Замечание. Доказанные соотношения можно переписать в таком виде:
1 , 1 ______________ 1 ________________
та = - \/2Ъ2 -f 2с2 — а2, ть — - у/2a2 + 2с2 — Ь2, гас = - \/2а2 + 2Ь2 — с2.
Zd Zi Jd


1.3. Биссектриса, медиана, высота
33
3. 	Теорема о наибольшем угле треугольника
В треугольнике против большей стороны лежит больший угол, против меньшей - меньший.
Без ограничения общности будем считать, что длины сторон треугольника связаны соотношением а ^ с.
Тогда по теореме синусов
и
=> sin а ^ sin /3 ^ sin 7.
sin a sin /3 sin 7
А поскольку величины углов треугольника находятся в интервале (0, тг), из этого следует а ^ /3 ^ 7. В самом деле, если предположить, что а > /3, то, пользуясь свойствами синуса, мы получаем, что либо а и /3 тупые, что невозможно, либо а тупой, /3 острый, но тогда а 4- /3 > 7г, что тоже невозможно. Поэтому а ^ /3. Аналогично доказывается, что /3^7.
4. 	Критерий остроугольности (тупоугольности) треугольника
Рассмотрим произвольный треугольник, будем считать, что длины его сторон равны а, b и с, причем с ^ а, с ^ 6.
Ддл того чтобы треугольник являлся тупоугольным (остроугольным) [прямоугольным], необходимо и достаточно, чтобы выполнялось следующее условие:
с2 > а2 + b2 или тс < ^ ^с2 < а2 4* Ь2 или тс > ^
2 2 I l2
с = а 4- о или гас ^
Для обоснования этого факта заметим, что тупоугольность или остроугольность треугольника зависит только от того, является ли тупым или острым наибольший из его углов, напротив которого лежит наибольшая сторона треугольника. Ответ на этот вопрос проще всего получить с помощью косинуса этого угла - если он отрицательный, то угол тупой, если же он положительный, то угол острый. Воспользуемся этим фактом и теоремой косинусов:
7 - тупой cos 7 < 0 <=> а2+Ъ2—2abcosj > a2+b2 <==> с2 > а24-62,
7 - острый <£=> COS7 > 0 а2 4- Ъ2 — 2a6cos7 < а2 4- Ь2 <==> с2 < а2 4- Ъ2,
7 - прямой COS7 = 0 <=> а2 4- Ь2 — 2a6cos7 = а2 4- Ь2 <=> с2 = а2 4- Ь2.
Теперь задействуем формулу длины медианы, предварительно переписав ее в виде 4т2 4- с2 = 2(а2 4- Ь2):
с2 > а2 + Ь2 <=>■ с2 > 4тос + с с2 > 4ТО2 Тос < с
с2 < а2 4- 62 <=> с2 < 4?7\+ С <=> с2 < 4т2 гас >
2 , , ~ ^ —с . 2,
с 2*
2 2 12 2 4т2 4- с2 2 2 С
с = а 4- Ь <^=> с = с = Атс тс —
Утверждение доказано.
2 Геометрия


34
Теория и задачи
Замечание. В основном эта теорема, конечно же, применяется, когда надо по длинам сторон треугольника понять, является ли он тупоугольным или остроугольным. Действовать надо просто - взять квадрат длины наибольшей стороны треугольника и сравнить его с суммой квадратов длин двух остальных его сторон. Однако в ряде задач применима и вторая часть этой теоремы.
5. 	Высота треугольника
Определение. Высотой треугольника называется отрезок, соединяющий его вершину и прямую, содержащую противолежащую ей сторону треугольника, перпендикулярный этой прямой.
Точка пересечения высот. Прямые, содержащие высоты треугольника, пересекаются в одной точке, эта точка называется ортоцентром треугольника.
Отметим, что в остроугольном треугольнике все высоты попадают на его стороны и лежат внутри треугольника, поэтому его ортоцентр является точкой пересечения высот. В тупоугольном треугольнике высоты, проведённые из вершин двух его острых углов, попадают на продолжения сторон и лежат вне треугольника. Поэтому его ортоцентр есть точка пересечения прямых, содержащих высоты.
Для вычисления длин высот треугольника используется либо формула площади, либо соотношения между длинами сторон и величинами углов различных прямоугольных треугольников, сторонами которых являются эти высоты.
Примеры решения задач
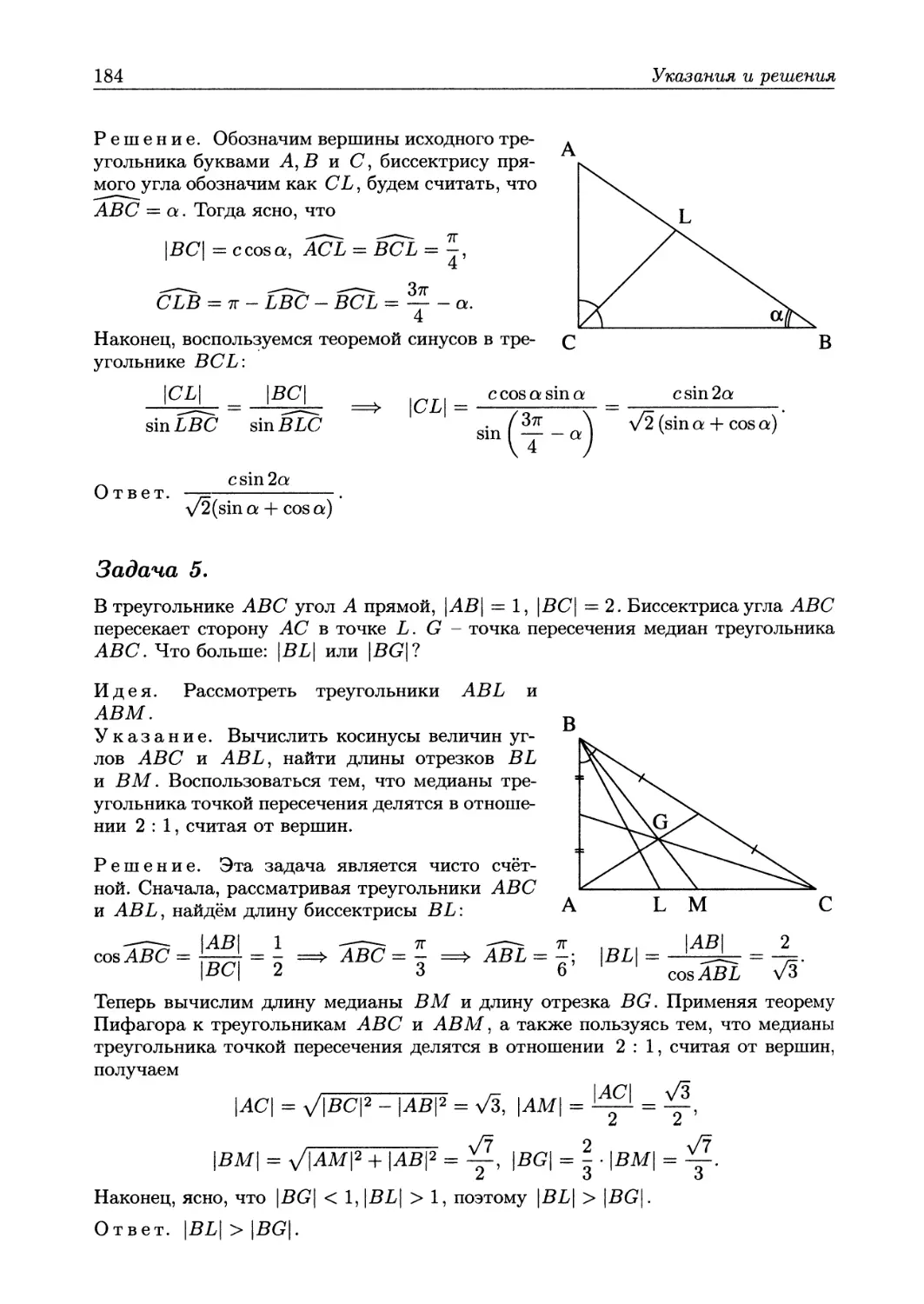
Пример 1. В треугольнике АВС градусная мера угла С равна 60°, длина биссектрисы, проведённой из вершины С, равна 5\/3, \АС\ : \ВС\ =5:2. Найдите тангенс величины угла А и длину стороны ВС.
Решение. По условию задачи \АС\ : \ВС\ =5:2, поэтому если принять длину отрезка ВС за 2х, то длина отрезка АС равна Ъх. Обозначим буквой L точку пересечения биссектрисы угла С со стороной АВ и воспользуемся первой формулой длины биссектрисы треугольника:
В
\сц —
2 • \АС\ ■ \ВС\ • cos \АС\ + \ВС\
5\/3 :
2 • 5х • 2х • & 5х + 2х
7
Х=2•
Значит, \ВС\ = 7. Теперь если величину угла А обозначить через а, то по теореме о сумме градусных мер углов треугольника В = 180° — А — С = 120° — а. Запишем теорему синусов для треугольника АВС:
И<?| _ |вс|
sin В sin А л/З
5 sin а = у/3 cos а + sin
а
Vs
tga=—.
Ответ. tgA=—, \ВС\ = 7.


1.3. Биссектриса, медиана, высота
35
Пример 2. В треугольнике ABC длина стороны АВ равна 21, длина биссектрисы BD равна 8\/7, а длина отрезка DC равна 8. Найдите периметр треугольника ABC.
Решение. Для ответа на вопрос задачи нам надо найти длины отрезков AD и ВС. Обозначим их длины через х и у соответственно, после чего, воспользовавшись основным свойством биссектрисы треугольника и второй формулой её длины, мы получим два уравнения для введённых неизвестных:
\АВ\ \AD\ v 21 х
\BC\~ \DC\ ^ у~ 8;
|В£>|2 = \АВ\ • \ВС\ -\AD\ ■ \DC\ =
448 = 21у - 8х.
Теперь решим полученную систему уравнений, учитывая, что х и у положительные:
ху — 168,
21 у = 8х + 448
х(8х + 448) = 168 • 21, 21 у = 8х + 448
Наконец, периметр треугольника ABC равен сумме длин отрезков АВ, AD, DC и ВС, то есть 60.
Ответ. 60.
Пример 3. В равнобедренном треугольнике ABC с основанием АС точка D делит сторону ВС в отношении 2:1, считая от вершины В, а точка Е - середина
v^23
стороны АВ. Известно, что длина медианы CQ треугольника СED равна —— и \/23
\DE\ — ——. Найдите длину радиуса окружности, описанной около треугольника ABC.


36
Теория и задачи
Решение. В этой задаче нам придётся немедленно вводить какие-то неизвестные величины, поскольку по данным в условии задачи длинам ничего явно вычислить нельзя. Обозначим \АВ\ = \ВС\ = 6х, АВС = 2а. Тогда 0 < а < 7г/2,
\CD\ = 2х, \DB\ = 4ж, \АЕ\ = \ЕВ\ = Зж,
САВ = тг/2 — а, \АС\ = 12xsina.
Для того чтобы составить два уравнения с введёнными неизвестными, поступим следующим образом. Сначала рассмотрим треугольник DBE и запишем для него теорему косинусов:
| DE\2 = \DB\2+\ЕВ\2 -2-\DB\-\EB\-cos В = => 100х2 — 96х2 cos 2а = 23
В
23
16х2+9ж2 —24х2 cos 2а
4х2 + 192a;2 sin2 а = 23.
После этого воспользуемся формулой длины медианы в треугольнике СDE и применим теорему косинусов к треугольнику АСЕ:
|CQ|2 = 2\СЕ\2 + 2\СР\2-\РЕ\2_
\СЕ\2 = \АС\2 + \АЕ\2 - 2 ■ \АС\ • \АЕ\ • cos Л
2|Ж7|2 + 2\АЕ\2 - 4 ■ \АС\ • \АЕ\ • cos А + 2\CD\2 - \DE\2 = 4\CQ\2 =►
144х2 sin2 а + 26х2 = ~23.
4
23
=> 288ж2 sin2 а + 18х2 — 1Мх2 sin2 а + 8х2 —- = 23 =
4
Решая полученную систему уравнений, получаем
4ж2 + 192ж2 sin2 а — 23;
144х2 sin2 а + 26х2 = ^ • 23 4
Ъх2 + 240ж2 sin2 а = 144ж2 sin2 а + 26ж2 =Ф
_ 25
7
96х2 sin2 а = 21х2
sin а =
32
cos2 а ■
32’
4х2 + 192ж2 • — = 23
oZ
cos а
4V2'
Наконец, запишем теорему синусов в треугольнике АВС: I ВС\ л Зх
2Raabc
sin CAB
Raabc = —
Зх
sin(7r/2 — a) cos a
_1_
V2‘
V2 12
5 5 '
4sf2
Ответ.
12


1.3. Биссектриса, медиана, высота
37
Пример 4. Из точки М, расположенной внутри остроугольного треугольника ABC, опущены перпендикуляры на его стороны. Длины сторон и опущенных на них перпендикуляров соответственно равны а и fe, бит, сип. Вычислите отношение площади треугольника ABC к площади треугольника, вершинами которого служат основания этих перпендикуляров.
Решение. Обозначим основания перпендикуляров, опущенных из точки М на стороны треугольника ABC как Р, Q и В, без ограничения общности будем считать, что \АВ\ = с, \МР\ = п; |ЛС| = 6, |MQ| = га;
|ВС| = а, |МР| = fc.
Наметим путь решения. С площадью треугольника ABC всё понятно, её можно вычислить, например, по формуле Герона. В треугольнике же PQR нам не даны ни длины сторон, ни величины углов. Поэтому представим его площадь как сумму площадей треугольников MPQ, MPR и MQR, после чего найдём связь между величинами углов PMQ, РМЛ, QMR и величинами углов треугольника ABC.
Sampq = \ ’ \МР\ • \MQ\ • sin PMQ = ^ran sin PMQ;
Sampr = \ * \MP\ • \MR\ • sin PMR = ^nfc sin PMR;
& z
Samqr = ~ |MP| • sinQMR = ^-kmsinQMR ==>
z z
=> Sapqr = ^ (wirc- sin PMQ + nk sin PMR + km sin QMR^j . (*)
Теперь заметим, что, поскольку сумма величин углов четырёхугольника равна 27т, а в каждом из четырёхугольников PMQA, PMRB и QMRC есть по два прямых угла, имеем
PMQ = 7г - A, PMR = тг - Б, QMP = тг - С =»
=> sin PMQ = sin Л, sin PMR = sin В, sin QMR = sin C.
В задаче нас просят найти не сами площади треугольников ЛВС и PQP, а их отношение. Поэтому поступим таким образом: выразим синусы величин углов Л, В и С через площадь треугольника ЛВС.
sin Л
ABC
sin В
2Saabc
\АВ\ • |ЛС|’
2Saabc
=> sin Л =
' |лв|.|всг
. в 2 Saabc sm В =
sin С =
Ъс ас
Подставив полученные соотношения в (*), получаем
sin С =
2Saabc \АС\ • |ВС|
2Saabc
ab
- I %S&abc , 7 2Saabc . 7 25длвс^
Sapqr = г шп г Ь fen h rafe —
2 V be ас ab J


38
Теория и задачи
/ тп кп гпк\
=> SAPQR = SAABC^ + - + -^) Saabc 1 а&с
Ответ.
Sapqr ^ ^ aran -f bkn + стк *
abc
атп + bkn + стк Задачи
1. В остроугольном треугольнике площади 5 известны величины а и /3 углов А и В. Найдите длину высоты, опущенной на сторону, прилежащую к углам А и В.
2. В треугольнике KMN, в котором sinifTVM = у/3/2, cos KMN =1/3, проведены высоты iVP и MQ. Найдите значение отношения |iVP| : \MQ\.
3. Длины сторон АВ, ВС и АС треугольника АВС образуют в указанном порядке геометрическую прогрессию. Найдите знаменатель этой прогрессии, если известно, что отношение длины высоты треугольника АВС, проведённой из вершины А, к длине радиуса вписанной в этот треугольник окружности равно 3.
4. В равнобедренном треугольнике ABC \АВ\ = |ВС|, AD - биссектриса, \BD\ = 6, \DC\ = с. Найдите длину биссектрисы AD.
5. Известно, что длины высот треугольника равны hi, h,2 и J13. Найдите его площадь.
6. Точка М лежит внутри равнобедренного треугольника АВС с основанием АС на расстоянии 6 от его боковых сторон и на расстоянии \/3 от его основания. Найдите длину этого основания, если В = 27г/3.
7. В треугольнике ВСЕ известно, что \СЕ\ : \ВС\ = 3, а величина угла ВСЕ равна 7г/3. Отрезок С К - биссектриса треугольника. Найдите \КЕ\, если длина радиуса окружности, описанной около треугольника ВСЕ, равна 8\/3.
8. В треугольнике АВС градусная мера угла В равна 30°, |AJ3| = 4, \ВС\ = 6. Биссектриса угла В пересекает сторону АС в точке D. Найдите площадь треугольника ABD.
9. В треугольнике АВС проведена биссектриса CD, при этом величины углов ADC и CDB относятся как 7:5. Найдите длину отрезка AD, если известно, что \ВС\ — 1, ВАС = 7г/6.
10. В треугольнике АВС биссектрисы J3D и СЕ пересекаются в точке О, \АВ\ = 14, |ВС| = 6, |АС| = 10. Найдите длину отрезка OD.
11. В тупоугольном треугольнике АВС на стороне АВ длины 14 выбрана точка L, равноудаленная от сторон АС и ВС, а на отрезке AL - точка К, равноудаленная от вершин А и В. Найдите синус величины угла АС В, если \KL\ = 1, CAB = 7г/4.


1.3. Биссектриса, медиана, высота
39
12. Величины углов Л, В и С треугольника ABC составляют арифметическую прогрессию с разностью п/7. Биссектрисы этого треугольника пересекаются в точке D. Точки А', В' и С' находятся на продолжениях отрезков DA, DC за точки А, В, С соответственно на одинаковом расстоянии от точки D. Доказать, что величины углов Л', В', С' треугольника А'В'С' также образуют арифметическую прогрессию. Найдите её разность.
13. В треугольнике ABC биссектриса угла ABC пересекает сторону АС в точ-
3 у/2
ке К. Известно, что \ВС\ = 2, \КС\ = 1, \ВК\ = -. Найдите площадь
треугольника ABC.
14. Треугольник ABC вписан в окружность, длина радиуса которой равна л/З — 1. Градусная мера угла ВАС равна 60°, а длина радиуса окружности, касающейся стороны ВС и продолжений сторон АВ и АС, равна 1. Найдите градусные меры углов ABC и АС В.
15. Величина одного из углов треугольника равна 27г/3, длина противолежащей ему стороны равна б, а длина одного из отрезков, на которые она разделена проведённой к ней биссектрисой этого треугольника, равна 2. Найдите величины двух других углов треугольника.
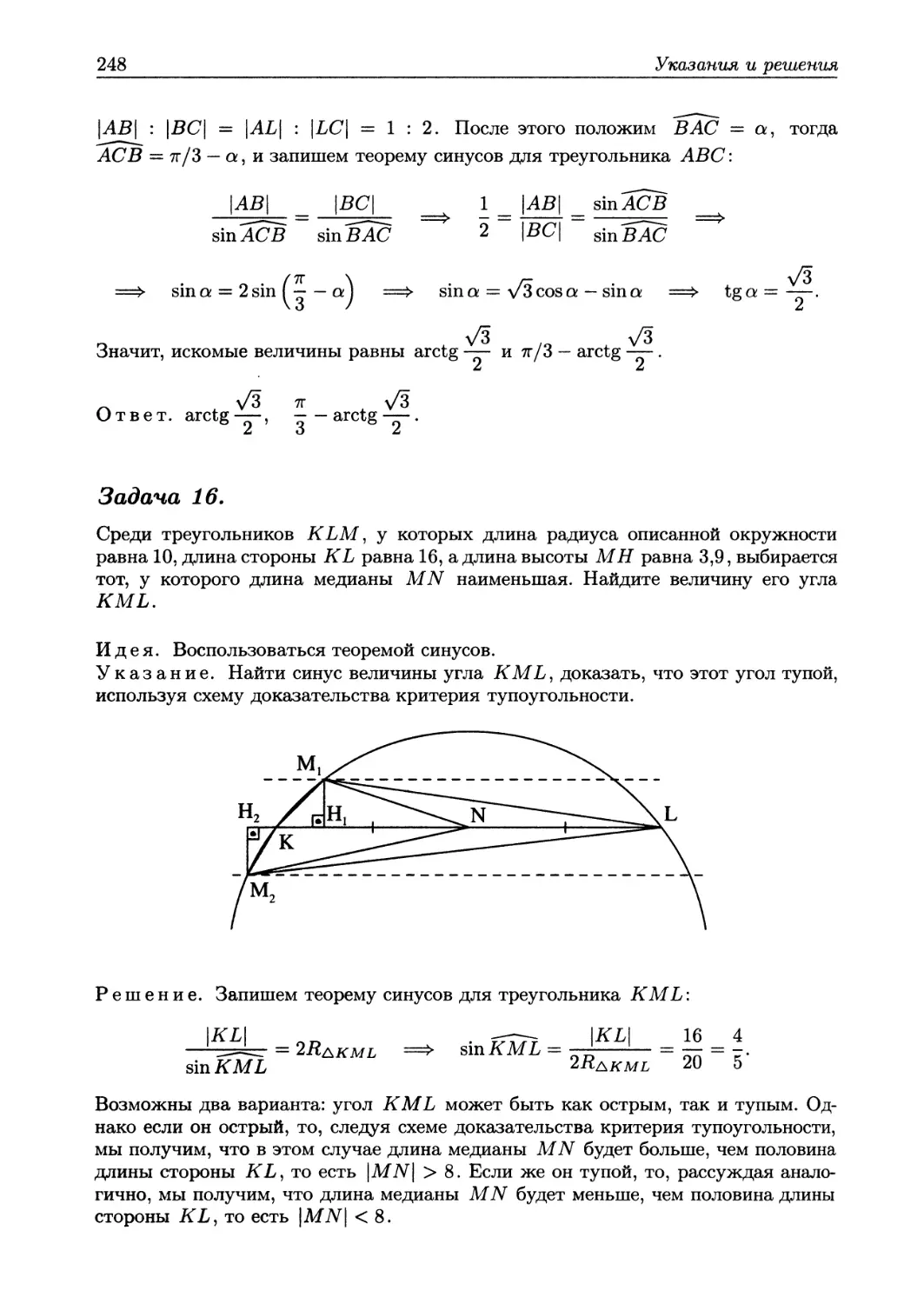
16. Среди треугольников KLM, у которых длина радиуса описанной окружности равна 10, длина стороны KL равна 16, а длина высоты МН равна 3,9, выбирается тот, у которого длина медианы MN наименьшая. Найдите величину его угла KML.
17. В треугольнике ABC проведена медиана AD, \AD\ = га, \ АВ\ = с, \ АС\ = Ь. Найдите ВАС.
18. Найдите величину угла А треугольника ABC, если известно, что \АВ\ = 2, \АС\ = 4, а длина медианы AM равна у/7.
19. В треугольнике ABC проведена медиана AM. Найдите площадь треугольника ABC, если \АВ\ = |ВС| = 2|ЛС|, \АМ\ = 4.
20. Найдите величины углов, образованных медианой ВВ\ треугольника ABC со сторонами АВ и ВС, если \АВ\ = 6, \ВС\ — 8, \ВВ\ \ = 5.
21. В треугольнике ABC проведена прямая, пересекающая стороны АВ и ВС в точках Р и Q соответственно. Известно, что \АВ\ = 3, \АС\ = \/5, длина медианы, проведённой из вершины А к стороне ВС, равна \/б? а длины отрезков АР, PQ и QC равны между собой. Найдите длину отрезка PQ.
22. В треугольнике ABC проведены биссектриса В К и медиана ВМ. Найдите длину отрезка КМ, если АВМ = 7г/4, СВМ — 7г/6, |AftT| = 6.
23. В треугольнике ЛВС проведены биссектриса BD и медиана Л#. Известно, что \АВ\ = 8, |ВС| = |BU| = 6. Найдите длину медианы АЕ.
24. В треугольнике ABC проведены биссектриса AL и медиана AM. Известно, что \AL\ = 6, |ЛМ| = 8, |ЛС| = 2 • |ЛВ|. Найдите длину стороны ВС.


40
Теория и задачи
25. В треугольнике KMN проведены высота N А, биссектриса NB и медиана NC, которые делят угол KNM на четыре равные части. Найдите длины высоты N А, биссектрисы NB и медианы NC, если длина радиуса описанной около треугольника KMN окружности равна R.
26. В треугольнике АВС проведены высоты СН и АК. Найдите длину стороны АС, если \АВ\ = с, \СН\ = h, |ЛЯГ| = Jfc.
27. В треугольнике АВС проведена высота ВН, при этом оказалось, что длины отрезков СН и ЛЯ относятся как 10 : 3. Найдите площадь треугольника АВС, если известно, что \ВН\ = Д, АВС = 7г/6.
28. В треугольнике ЛВС проведена биссектриса BL, длина которой равна I. Найдите длины сторон треугольника АВС, если известно, что расстояния от точек Л и С до прямой BL равны р и q соответственно.
29. Вычислите величину угла Л треугольника АВС, если величина угла В равна 7г/5 и известно, что биссектриса угла при вершине С делит пополам угол между медианой и высотой, проведёнными из этой вершины.
30. На продолжении стороны ВС треугольника АВС за точку В расположена точка Е так, что биссектрисы углов АЕС и АВС пересекаются в точке К, лежащей на стороне АС. Длина отрезка BE равна 1, длина отрезка ВС равна 2, градусная мера угла ЕКВ равна 30°. Найдите длину стороны АВ.
31. В треугольнике АВС известно, что |ЛС| = |ВС| = 12, |ЛВ| = 6, AD - биссектриса. Найдите длину радиуса окружности, описанной около треугольника ADC, и сравните эту длину с числом 13/2.
32. В треугольнике АВС на сторонах АВ и ВС отмечены точки М и N соответственно, причем \ВМ\ = \BN\. Через точку М проведена прямая, перпендикулярная ВС, а через точку N - прямая, перпендикулярная АВ. Эти прямые пересекаются в точке О. Продолжение отрезка ВО пересекает сторону АС в точке Р, |ЛР| = 5, |РС| = 4. Найдите длину отрезка ВР, если известно, что |ВС| = 6.
33. Вокруг треугольника МКН описана окружность с центром в точке О, длина её радиуса равна г. Длина стороны НМ равна а. Известно, что справедливо равенство \НК\2 — \НМ\2 = \НМ\2 — \МК\2. Найдите площадь треугольника OLK, где L - точка пересечения медиан треугольника МКН.
34. В треугольнике KLM проведены биссектрисы КА и MB, которые пересекаются в точке О. Диагонали четырехугольника AOBL пересекаются в точке С. Найдите численные значения отношений |ВС| : |СЛ| и \ЬС\ : |СО|, если известно, что \KL\ = т, \КМ\ = I, \LM\ = к.
35. Отрезки AM и ВР являются медианами треугольника АВС. Известно, что угол АР В равен углу ВМА, |ВР| = 1, косинус величины угла АС В равен 4/5. Найдите площадь треугольника АВС.
36. Внутри прямоугольного треугольника АВС с прямым углом С взята точка О таким образом, что |ОЛ| = |OJ3| = b. CD - высота треугольника АВС, точка Е - середина отрезка ОС, \DE\ — а. Найдите |CJ57|.


1.4. Подобие треугольников
41
1.4. 	Подобие треугольников Теоретический материал
В этом параграфе рассматриваются задачи, при решении которых ключевую роль играет подобие треугольников.
Определение. Два треугольника называются подобными, если у них попарно равны все углы, а длины соответствующих сторон пропорциональны. То есть
ААВС ~ ААгВгСг, если ZA = ZAU ZB = ZBU ZC = ZCU \AB\ \BC\ \AC\
\AiBi\ ~ \BiCi\ ~ \AXCi|'
B,
в
A\ А С A! C!
Численное значение отношения длин соответствующих сторон называется коэффициентом подобия треугольников. Имеется в виду следующее: если нам дано, что ААВС ~ AAiBiCi, то k = \АВ\ :
Замечание. У подобных треугольников пропорциональны не только стороны, но и все соответствующие линейные элементы (например, длины радиусов описанных около них окружностей или длины биссектрис, проведённых к соответственным сторонам). Отношение площадей подобных треугольников равно квадрату коэффициента их подобия.
Сформулируем три признака подобия треугольников:
1. Если два угла одного треугольника равны двум углам другого треугольника, то эти треугольники подобны.
2. Если некоторый угол первого треугольника равен некоторому углу второго треугольника, а длины прилежащих к этим углам сторон треугольников пропорциональны, то эти треугольники подобны.
3. Если длины трех сторон одного треугольника пропорциональны длинам трех сторон другого треугольника, то эти треугольники подобны.
Замечание. Подобие треугольников необходимо записывать правильно, то есть порядки появления соответственных вершин треугольников в записи их подобия должны совпадать. Если, например, про треугольники ABC и MKN известно,


42
Теория и задачи
что А = К и С = М, то правильной записью их подобия будет А АС В ~ AKMN. После этого, глядя на эту запись, можно легко выписать пропорцию
|АС| |АВ| |СВ|
\КМ\ ~ \KN\ ~ \MN\ ’
Теорема Фалеса. Если при пересечении сторон угла параллельными прямыми на одной стороне угла отсекаются равные между собой отрезки, то и на другой стороне угла отсекаются также равные между собой отрезки (левый рисунок).
Обобщенная теорема Фалеса. При пересечении сторон угла параллельными прямыми на сторонах угла отсекаются пропорциональные отрезки (правый рисунок):
\АО\ \АВ\ \ВС\
\АгО\ ~ \AXBX\ “
Теперь рассмотрим несколько классических ситуаций, в которых возникает подобие треугольников.
Утверждение 1. Пусть на сторонах АВ и ВС треугольника АВС взяты точки М и N (М £ [AB],N е [АС]) таким образом, что MN\\AC. Тогда треугольники АВС и MBN подобны.
В
Доказательство. Углы ВАС и BMN являются парой соответственных углов при параллельных прямых АС и MN. Поэтому ZВАС = A.BMN. Аналогично получаем, что /.ВСА = /.BNM. Значит, треугольники АВС и MBN подобны по первому признаку подобия треугольников.
Утверждение 2. Пусть отрезки АС и BD пересекаются в точке О, причём AB\\CD. Тогда треугольники АОВ и COD подобны.


1.4• Подобие треугольников
43
А
В
Доказательство. Углы ОАВ и OCD образуют пару внутренних накрест лежащих углов при параллельных прямых АВ и CD и секущей АС. Поэтому /.ОАВ = Z.OCD. С другой стороны, углы АОВ и COD вертикальные, значит, /АОВ = /.COD. Таким образом, треугольники АОВ и COD подобны по первому признаку подобия треугольников.
Утверждение 3. Пусть в треугольнике ABC проведены высоты ВВ\ и СС\. Тогда треугольники АВ\С\ и ABC подобны с коэффициентом подобия | cos ВАС |, а также подобны треугольники АВВ\ и АСС\.
С
Доказательство. При доказательстве этого утверждения необходимо рассмотреть два различных случая. Если угол А острый, то точки В\ и С\ попадают либо на стороны АС и АВ, либо на их продолжения за точки С и В. Независимо от этого из прямоугольных треугольников АВВ\ и АСС\ вытекает, что
1АСА сссПЛС
\АВ\ -соеВЛС’ |Ж'| -соиВАС.
Пользуясь этим фактом и тем, что угол А - общий угол треугольников АВ\С\ и ABC, мы получаем, что AABiCi ~ A ABC по второму признаку подобия треугольников, причём коэффициент их подобия равен отношению длин их соответствующих сторон, то есть косинусу угла ВАС. Подобие треугольников АВВ\ и АСС\ вытекает из того, что углы АВ\В и АС\С прямые, а угол А - их общий угол. Стало быть, они подобны по первому признаку подобия треугольников.


44
Теория и задачи
Если же угол А тупой, то точки В\ и С\ попадают на продолжения сторон АС и АВ за точку А. Тогда из прямоугольных треугольников АВВ\ и АСС\ получаем
Так же как и в предыдущем случае, с учётом того, что углы В\АС\ и ВАС равны как вертикальные, мы заключаем, что ААВ1С1 ~ A ABC по второму признаку подобия треугольников, причём коэффициент их подобия равен — cos ВАС. Таким образом, в любом случае треугольники АВ\С\ и ABC подобны с коэффициентом подобия | cos ВАС |.
Подобие треугольников АВВ\ и АСС\ вытекает их того, что углы АВ\В и АС\С прямые, а углы В\АВ и С\АС вертикальные.
Утверждение 4. Пусть окружность проходит через вершины В и С треугольника ABC и пересекает его стороны АВ и АС в точках С\ и В\ соответственно. Тогда треугольники АВ\С\ и ABC подобны.
А
Доказательство. Для доказательства этого утверждения воспользуемся тем фактом, что сумма величин противоположных углов четырёхугольника, вписанного в окружность, равна тг. Применяя её к четырёхугольнику ВС\В\С, получаем, что
СгВС = тг - СВ^Сг; В^СВ = тг - ВСХВХ.
С другой стороны, по свойству смежных углов
AB^Ci = тг - АС^Вг = тг - BCJ3l.
Их этих двух пар соотношений следует, что
СхВС = АВГСЬ В^СВ^АС^Вг.
Таким образом, треугольники АВ\С\ и ABC подобны по первому признаку подобия треугольников.
Замечание. Утверждение 3 является частным случаем утверждения 4. В самом деле, если ВС - диаметр окружности, а угол А острый, то точки В\ и С\ лежат на сторонах АС и АВ соответственно, углы ВС\С и СВ\В опираются на диаметр, поэтому они прямые. То есть отрезки ВВ\ и СС\ являются высотами треугольника ABC. Однако, в отличие от утверждения 3, утверждение 4 не дает никакой информации о коэффициенте подобия треугольников АВ\С\ и ABC.


1.4. Подобие треугольников
45
Утверждение 5. Пусть СН - высота прямоугольного треугольника АВС, проведённая из вершины его прямого угла С. Тогда треугольники АСН, СВН и АВС попарно подобны.
С
Доказательство. Если обозначить величину угла ВАС через а, то из прямоугольных треугольников АСН, АВС и СВН вытекает, что
ТГ ТГ ТГ f ТГ \
АСН = - - а; АВС = - - а; ВСН = — — ог)=аг.
2 2 2 V 2 /
Поэтому любая пара перечисленных в формулировке утверждения треугольников подобна по первому признаку подобия треугольников.
Приведём еще две важные теоремы, которые часто используются для решения задач. Их доказательство проводится с использованием подобия треугольников.
Теорема Менелая. Пусть прямая пересекает произвольный треугольник АВС, причём В\ - точка её пересечения со стороной АС, А\ - точка её пересечения со стороной ВС и С\ - точка её пересечения с продолжением стороны
АВ. 	Тогда
\АСг\ | ВАг\ \СВг\
\СгВ\ ’ \АгС\ ' \ВгА\ *
С С
Доказательство. Могут возникнуть две различные ситуации: либо точка С\ лежит на продолжении стороны А В за вершину В (левый рисунок), либо же она лежит на продолжении стороны АВ за вершину А (правый рисунок).


46
Теория и задачи
Рассмотрим первый из этих случаев. Проведем отрезок В К (К лежит на прямой А\С\), параллельный стороне АС. Тогда по утверждению 1
дВ*С1~л.ад - Ш-gg} _
а по утверждению 2
* 1 ПК - \гп — ,iMll - — 1ИК-1 - ^ •|СВ11
AAtBK-AAtCB, ^ с I I '
Из двух полученных соотношений вытекает, что
\ABt\-\BCx\ _ \BAx\-\CBx\ \АСг\ \ВАХ\ \СВХ\ =
\ACi\ \САХ\ \C\B\ ' \A\C\ ' \ВгА\ ‘
Второй случай рассматривается абсолютно аналогично.
Теорема Чевы. Пусть в треугольнике АВС точки А\, В\ и С\ лежат на сторонах ВС, АС и АВ соответственно, причёлг отрезки АА\, ВВ\ и СС\ пересекаются в одной точке. Тогда
\АСг| \ВАг\ \СВг\
\СгВ\ ' \A\C\ ' \B\A\ *
В
Доказательство. Обозначим точку пересечения отрезков АА\, ВВ\ и СС\ буквой О и применим теорему Менелая для треугольников АВВ\ и СВВ\:
\B\0\ \ВСг\ \АС\ , ч \ВгО\-\АС\
\ОВ\ ' \C\A\ ' \CBi\ \ВСг\ \ОВ\ ’
\ВгО\ \ВАг\ \СА\ _ _ \АВХ\ ■ \АгС\ _ \ВхО\ • \АС\
\ОВ\ ' \АгС\ ' \АВ\\ \ВАг\ \ОВ\ '
Приравняем левые части полученных соотношений:
\CiA\-\CBi\ _\АВ1\-\А1С\ _ \АСх\ \ВАХ\ \СВг|
\ВСг\ \ВА!\ \СгВ\ ‘ \АгС\ ‘ \ВХА\ '
Теорема Чевы доказана.


1.4. Подобие треугольников
47
Примеры решения задач
Пример 1. В прямоугольном треугольнике ABC, длины катетов А В и АС которого равны 4 и 3, расположен прямоугольник ЕКМР так, что сторона ЕК лежит на гипотенузе ВС, а вершины М и Р - на катетах АС и АВ соответственно. Найдите длины сторон прямоугольника ЕКМР, если его площадь равна 5/3, а периметр меньше 9.
А
Решение. Обозначим длины сторон ЕР и МК прямоугольника ЕКМР через х. Треугольники МКС и ВАС подобны по первому признаку подобия, поскольку углы МКС и ВАС прямые, а угол С является их общим углом. Значит,
\МК\ \КС\ \МК\ ■ \АС\ Ъх
\АВ\ \АС\ 11 \АВ\ 4 ‘
Аналогично получаем, что АР ЕВ ~ АСАВ, что даёт нам
\ВЩ = \ЕР\_ \EP\-\AB\ 4х
\АВ\ \АС\ 11 \АС\ 3 '
Далее заметим, что по теореме Пифагора \ВС\ = 5. Поскольку точки Е и К лежат на стороне ВС, получаем
\ЕК\ = \ВС\ - \ВЕ\ - \КС\ = 5 - Щ - у = = \МР\.
Теперь можно воспользоваться условием задачи про площадь и периметр прямоугольника ЕКМР.
Sekmp = \ЕК\ ■ \ЕР\;
Рекмр = \ЕК\ + \ЕР\ + \МР\ + \МК\ ^
60 — 25х
То > Г 5а:2 — \2х + 4 = 0;
11 — 1 ^ * = 2.
25х < 9 I 60 ~ 13х < 54
60 — 2е) • 2
Таким образом, \ЕР\ = \МК\ = 2, \ЕК\ = \МР\ = — = -.
Ответ. \ЕР\ = \МК\ = 2, \ЕК\ = \МР\ = |.
О


48
Теория и задачи
Пример 2. В треугольнике ABC на сторонах А В и АС взяты точки К и М соответственно. Найдите отношение, в котором точка пересечения прямых КС к ВМ делит отрезок ВЫ, если \АК\ : \КВ\ = 2:3, \АМ\ : \МС\ =4:5.
Решение. В такого сорта задачах, то есть в задачах, где даны какие-либо отношения длин отрезков, традиционно вводят по одной неизвестной на каждое отношение. Обозначим точку пересечения прямых КС и ВМ буквой О и положим \АК\ = 2х, \КВ\ = Зх, \АМ\ = 4у, \МС\ = 5у, тогда |АВ| = 5х, |Ж7| = 9?/.
Первый способ решения заключается в следующем: применим теорему Менелая к треугольнику АВМ и секущей КО.
\АК\ \ВО\ \МС\ \КВ\ ’ \ОМ\ ‘ \СА\
= 1
JBOI
|ОМ|
9у
5у
Зх
2х
27
10*
Минусом этого способа решения является то, что теорема Менелая не входит в школьную программу и при использовании её в решении задач на экзаменах придется привести её доказательство.
Однако можно предложить другой способ решения, который использует идею, с помощью которой доказывается теорема Менелая. Раз мы ищем численное значение отношения \ВО\ : |ОМ|, проведём из точки М отрезок ММ', параллельный КС (М' £ АВ). Тогда по утверждению 1 треугольник АМ'М подобен треугольнику АКС, а треугольник В КО подобен треугольнику ВМ'М. Из этих подобий мы находим
\АМ'\ \АМ\ \АК\ ~ \АС\
| АМ'\ _
2х 9 у
\АМ'\ = Щ;
\ВМ\ _ \ВМ'\ _ \АВ\ -\АМ'\ _ 5х - у _ 37 \ВО\ ~ \ВК\ ~ \ВК\ Зх 27'
Теперь получить нужное нам отношение совсем просто:
\ВМ\ 37 \ВО\ _ \ВО\ _ 1 1 _ 27
\ВО\ ~ 27 ^ \OM\~ \BM\-\BO\~ \ВМ\
\ВО\ 27
Пример 3. Длины отрезков, соединяющих основания высот остроугольного треугольника, равны 5, 12 и 13. Найдите площадь треугольника.
Решение. Обозначим вершины треугольника буквами А, В и С и проведём его высоты АР, BQ и CS. Без ограничения общности будем считать, что \SP\ = 13,
|pg| = 12, |QS| = 5.


1.\. Подобие треугольников
49
Пользуясь утверждением 3, мы находим три пары подобных треугольников: ACPQ ~ АСАВ, ABSP ~ АВС А и AAQS ~ А АВС, причём коэффициенты этих подобий в силу остроугольности треугольника АВС равны cos АС В, cos ABC и cos CAB соответственно. Так что если нам удастся найти величины этих углов, то задача фактически будет решена, поскольку
\PQ\
cos АС В,
]SP\
= cos ABC,
\QS\
cos CAB,
\AB\ ’ \AC\ ’ \BC\
то есть мы сможем найти длины сторон треугольника АВС. Заметим, что, помимо этого, эти подобия дают нам следующие соотношения на величины углов:
CPQ = Шв, CQP = СВА, BSP = ВСА, BPS = ВАС,
AQS = ABC, ASQ = АСВ.
Теперь мы легко получаем связь между величинами углов треугольника АВС и величинами углов треугольника PQS:
QPS = тг - CPQ - BPS = тг - 2ВАС PSQ = тг - BSP - ASQ = тг - 2АСВ SQP = тг - AQS - CQP = тг - 2АВС
ВАС
7Г
2
АВС = -~
QPS 2 ’
PSQ 2 5 SQP
Осталось посчитать необходимые нам косинусы. Заметим, что треугольник PQS прямоугольный (поскольку 132 = 122 -f 52). Тогда
c°s«PS=!f|l = g, cosPSO=M = A, -Хвс=1,
п QPS\ . QPS JI-cobQPS 1 cos ВАС = cos - - — U sin— = y-— =
cos ЛСВ = cos U - ^ * ll-cosPSQ
sin -
N , V 2 v^'
Таким образом, мы вычислили все коэффициенты подобия. Осталось найти длины нужных нам сторон треугольника АВС:
™ -«*/13, \вс\ = 1051
\АВ\ =
cos АСВ
cos ВАС
= 5\/26;
Saabc = J • \АВ\ ■ \ВС\ • sin ABC = \ • 6^ • 5\/26 • 4= = 195.
2 2 у/2
Ответ. 195.


50
Теория и задачи
Пример 4. В остроугольном треугольнике ABC на высоте AD взята точка М, а на высоте ВР - точка N так, что углы ВМС и AN С - прямые. Известно, что MCN = 30°, \MN\ = 4 + 2\/3. Найдите длину биссектрисы CL треугольника MCN.
Решение. В условии этой задачи даны лишь два элемента треугольника MCN. Это означает, что нам надо каким-то образом из условий про расположение точек N и М получить ещё одно соотношение на элементы треугольника MCN. Заметим, что по утверждению 5 треугольник NCP подобен треугольнику ACN, треугольник CMD подобен треугольнику СВМ, и воспользуемся этими подобиями:
В
\CN\ \СР\
\АС\
\см\
|CJV|
\CD\
\CN\2 = \AC\-\CP\;
/ /
n\
/ /!А
ЛАо
> 1
\СМ\2 = \BC\-\CD\.
\вс\ \см\
С другой стороны, из утверждения 3 вытекает, что треугольники ADC и ВРС также подобны, поэтому
\СР\ \АС\ \СР\ \вс\
Таким образом, \СМ\2 = |C7JV|2, ник MCN равнобедренный, CL этого находим
=» \АС\ • \СР\ = \ВС\ • \CD\.
то есть \СМ\ = \CN\. Следовательно, треуголь- - его биссектриса, медиана и высота. С учётом
\СЬ\ = \ • \MN\ • ctg 15° = (2 + V3). 1 ^°° =7 + 4^3.
Ответ. 7 + 4\/3.
Задачи
1. В прямоугольном треугольнике ABC из вершины прямого угла В опущена высота BD на гипотенузу АС. Известно, что \АВ\ = 13, \BD\ = 12. Найдите площадь треугольника ABC.
2. В треугольнике ABC длина высоты BD равна 11,2, а длина высоты АЕ равна 12. Точка Е лежит на стороне ВС, причём \ВЕ\ : \ЕС\ = 5:9. Найдите длину стороны АС.
3. В треугольнике ABC длина стороны А В равна 8, величина угла АС В равна 7г/3. Прямая, параллельная стороне АВ, пересекает сторону АС в точке D, а сторону ВС в точке Е. Известно, что \ВС\ = |iX7|, |jD£?| = 3. Найдите |J5C|.


1.4. Подобие треугольников
51
4. Окружность, центр которой лежит на гипотенузе прямоугольного треугольника, касается его катетов. Найдите длину радиуса этой окружности, если длины катетов треугольника равны 3 и 4.
5. Окружность, центр которой лежит на гипотенузе АВ прямоугольного треугольника АВС, касается катетов АС и ВС в точках Е и D соответственно. Найдите величину угла АВС, если |^4JE7| = 1, \BD\ = 3.
6. В параллелограмме ABCD длина стороны АВ равна 6, а длина высоты, проведённой к основанию AD, равна 3. Биссектриса угла BAD пересекает сторону ВС в точке М так, что \МС\ = 4; N - точка пересечения отрезков AM и BD. Вычислите площадь треугольника BNM.
7. В равнобедренный треугольник АВС с основанием АС вписана окружность, длина радиуса которой равна 3. Прямая р касается этой окружности и параллельна прямой АС, но не совпадает с ней. Расстояние от точки В до прямой р равно 3. Найдите расстояние между точками, в которых данная окружность касается сторон АВ и ВС.
8. В ромбе ABCD проведены высоты ВР и BQ. Они пересекают диагональ АС в точках М и N соответственно (М между А и N). Известно, что \АМ\ = р, \MN\ = q. Найдите \PQ\.
9. На сторонах острого угла с вершиной О взяты точки А и В. На луче О В взята точка М на расстоянии 3- |Ол4| от прямой О А, а на луче О А - точка N на расстоянии 3|OjB| от прямой О В. Длина радиуса окружности, описанной около треугольника АОВ, равна 3. Найдите \MN\.
10. В треугольнике АВС угол С тупой, D - точка пересечения прямой DB, перпендикулярной к АВ, и прямой DC, перпендикулярной к АС. Высота треугольника ADC, проведённая из вершины С, пересекает А В в точке М.
Известно, что \АМ\ = а, \МВ\ = Ь. Найдите \АС\.
11. На стороне PQ треугольника PQR взята точка 7V, а на стороне PR - точка L, причем \NQ\ = \LR\. Точка пересечения отрезков QL и NR делит отрезок QL в отношении т : п, считая от точки Q. Найдите значение отношения |PiV| : \PR\-
12. В треугольнике АВС на стороне АС взяты точки Р и Q таким образом, что \АР\ > \AQ\. Прямые ВР и BQ делят медиану AM на три равные части. Известно, что \PQ\ = 3. Найдите длину стороны АС.
13. В треугольнике АВС взяты точка К на стороне АВ и точка М на стороне АС так, что \АК\ : \КВ\ = 3:2, \АМ\ : \МС\ =4:5. Найдите отношение, в котором прямая, проходящая через точку К параллельно стороне ВС, делит отрезок ВМ.
14. В треугольнике АВС взяты точка N на стороне АВ и точка М на стороне
АС. 	Отрезки CN и ВМ пересекаются в точке О. Вычислите \СО\ : |OJV|,
если известно, что \AN\ : |ATJ5| =2:3, |jB0| : \ОМ\ = 5:2.


52
Теория и задачи
15. В треугольнике ЛВС точка D делит сторону АВ пополам, а точка Е лежит на стороне ВС, причем \ВС\ = 3\ВЕ\. Отрезки АЕ и CD пересекаются в точке О, \АЕ\ = 5, \ОС\ = 4, АОС = 120°. Найдите длину стороны АВ.
16. В треугольнике ABC точки D, Е и F расположены на сторонах АВ, ВС и АС соответственно. Известно, что \AD\ : \DB\ = 1:2, \ВЕ\ : \ЕС\ = 2:3, |ЛР| : |РС| = 1:1. Отрезки DE и BF пересекаются в точке К. Вычислите отношение |Bif| :
17. В треугольнике ABC длина высоты BD равна 6, длина медианы СЕ равна 5, расстояние от точки пересечения отрезков BD и СЕ до стороны АС равно 1. Найдите длину стороны АВ.
18. В треугольнике ABC из вершин А и В проведены отрезки AD и BE, причём точки D и Е лежат на сторонах ВС и АС соответственно. Отрезки AD и BE пересекаются в точке Q таким образом, что \AQ\ : \QD\ = х, \BQ\ : \QE\ = у. Найдите значения отношений \АЕ\ : \ЕС\ и \BD\ : |ВС|.
19. В треугольнике PQR точка Т лежит на стороне PR так, что QTR = PQR. Известно, что \РТ\ = 8, \TR\ = 1. Найдите:
а) длину стороны QR;
б) величину угла QRP, если длина радиуса описанной около треугольника PQT окружности равна 3\/3-
20. Через вершины А и В треугольника ЛВС проведена окружность с длиной радиуса 2\/5, отсекающая от прямой ВС отрезок длины 4%/5 и касающаяся прямой АС в точке А. Из точки В проведён перпендикуляр к прямой ВС до пересечения с прямой АС в точке F. Найдите площадь треугольника ЛВС, если \BF\ = 2.
21. Медианы AM и BE1 треугольника ABC пересекаются в точке О. Точки О, М, В, С лежат на одной окружности, |ВВ| = \АМ\ = 3. Найдите |АВ|.
22. На сторонах ЛВ, ВС и ЛС треугольника ABC взяты точки D, Е и F соответственно. Отрезки АЕ и DF проходят через центр вписанной в треугольник ЛВС окружности, а прямые DF и ВС параллельны. Найдите длину отрезка BE и периметр треугольника ЛВС, если известно, что |ВС| = 15, \BD\ = 6, \CF\ = 4.
23. Прямая, параллельная медиане А£) прямоугольного треугольника ЛВС, пересекает его гипотенузу ВС в точке F, катет ЛВ в точке В и прямую ЛС в точке Н. Известно, что |BF| = 1, |ВВ| = 3. Найдите длину гипотенузы ВС.
24. На сторонах Л В и ЛВ прямоугольника ABCD выбраны точки Р и Q (Р Е ЛВ) так, что ZCQD = ZAQP = ZBPC. Вычислите длину отрезка ЛР, если |АВ| = 6, |АВ| = d (b>d).
25. Прямые, содержащие высоты треугольника ЛВС, пересекаются в точке В. Известно, что |ВВ| = 6, ЛВС = 7г/3. Найдите длину стороны ЛС.


1.5. Площадь треугольника
53
26. В треугольнике АВС расположен прямоугольник PQRS так, что сторона PQ лежит на отрезке АС, а вершины R и 5 - на отрезках ВС и АВ соответственно. Найдите длину отрезка PS, если известно, что \АР\ = 1, \PQ\ — 5, \QC\ = 2, а периметр треугольника равен 15.
27. На продолжении биссектрисы AL треугольника АВС за точку А взята точка D таким образом, что В DC = BAL = 7г/3, |AD| = 10. Найдите площадь треугольника АВС.
28. В прямоугольном треугольнике АВС проведена биссектриса BD, а на гипотенузе ВС взята точка Н так, что DH _L BD. Найдите площадь треугольника АВС, если известно, что \СН\ = 1, \CD\ = 2.
29. На стороне АВ выпуклого четырёхугольника ABCD выбрана точка М так, что /.AMD = /ADB и /АСМ — /АВС. Утроенный квадрат отношения расстояния от точки А до прямой CD к расстоянию от точки С до прямой AD равен 2, \CD\ = 20. Найдите длину радиуса вписанной в треугольник ACD окружности.
30. На сторонах АВ и ВС треугольника АВС взяты точки М и N соответственно таким образом, что ВАС = BNM = 7г/6. Также известно, что \АМ\ = \CN\. Найдите отношение периметра треугольника АВС к сумме длин его медиан.
31. Найдите пару подобных треугольников, длины всех сторон которых выражаются целыми числами, если известно, что длины двух сторон первого треугольника равны длинам двух сторон второго треугольника, а длины их третьих сторон отличаются на 61.
1.5. 	Площадь треугольника Теоретический материал
В этом разделе рассматриваются различные факты, связанные с площадями треугольников. Для успешного решения задач, относящихся к этой теме, необходимо знать и уметь обосновывать все леммы, приведённые ниже.
Сначала сформулируем два утверждения, которые следует воспринимать как аксиомы.
Утверждение 1. Равные фигуры имеют одинаковые площади.
Утверждение 2. Если фигура F состоит из двух непересекающихся фигур F\ и i*2, то площадь фигуры F равна сумме площадей фигур F\ и F2.
Теперь докажем пять лемм, с помощью которых решается большинство задач, связанных с площадями треугольников и многоугольников.
Лемма 1. Если два треугольника имеют общую вершину, а их стороны, противолежащие этой вершине, лежат на одной прямой, то отношение площадей этих треугольников равно отношению длин указанных сторон.


54
Теория и задачи
Доказательство. Рассмотрим треугольники ABC и DEC, стороны АВ и DE которых лежат на одной прямой. Опустим из точки С перпендикуляр СН на эту прямую, тогда, очевидно, отрезок СН будет являться как высотой треугольника ABC, так и высотой треугольника DEC. Наконец, воспользуемся формулой площади треугольника, в которую входят длина его стороны и длина его высоты:
Saabc = \ • \АВ\ ■ \СН\, Sadec = \ • \DE\ ■ \СН\ =► = И||.
Лемма доказана.
Лемма 2. Если некоторая вершина и противолежащая ей сторона одного треугольника и некоторая вершина и противолежащая ей сторона другого треугольника лежат на двух параллельных прямых, то отношение площадей этих треугольников равно отношению длин указанных сторон.
А Е G F
Доказательство. Рассмотрим треугольники ABC и DEF, будем считать, что сторона ВС и точка D лежат на одной прямой, а сторона EF и точка А лежат на другой прямой, причём эти прямые параллельны. Проведём высоты АН и DG этих треугольников, тогда длины отрезков АН и DG будут равны, поскольку каждый из них перпендикулярен обеим прямым. После этого воспользуемся формулой площади треугольника, в которую входят длина его стороны и длина его высоты:
Saabc = \ • \ВС\ ■ \АН\, Sadef = \-\EF\-\DG\ => = Щ.
Случай, когда вершины А и D лежат на одной прямой, а стороны ВС и EF лежат на другой прямой, рассматривается аналогично. Лемма доказана.


1.5. Площадь треугольника
55
Лемма 3. Если длина некоторой стороны одного треугольника равна длине некоторой стороны другого треугольника, то отношение площадей этих треугольников равно отношению длин их высот, проведённых к указанным сторонам.
С
Доказательство. Рассмотрим треугольники АВС и DEF, длины сторон АВ и DE которых равны. Проведём высоты СН и FG этих треугольников и воспользуемся формулой площади треугольника, в которую входят длина его стороны и длина его высоты:
Saabc = \-\AB\-\CH\, Sadef = \-\DE\-\FG\ =►
Saabc \ ■ \АВ\ ■ \СН\ \СН\
Sadef \ • \DE\ ■ \FG\ \FG\'
Лемма доказана.
Лемма 4. Если некоторый угол одного треугольника равен некоторому углу другого треугольника или углу, смежному с ним, то отношение площадей этих треугольников равно отношению произведений длин их сторон, образующих указанные углы.
В SABC IABI IACI
Доказательство. Рассмотрим треугольники АВС и DEF, будем считать, что углы ВАС и EDF равны, а величины этих углов равны а. Применим формулу площади треугольника, в которую входят длины его сторон и синус величины угла между ними:
Saabc = ^-\АВ\- \АС\ • sin 'ВАС, Sadef = y\DE\-\DF\• sin EDF


56
Теория и задачи
Saabc _ \ ~ \АВ\ ■ \АС\ - sing _ \АВ\ ■ \АС\
^ Sadef ~ § ■ \DE\ ■ \DF\ • sin а ~ \DE\ • |DF|'
Теперь рассмотрим треугольники ABC и DGH, ясно, что угол ВАС равен углу, смежному с углом GDH. Поскольку сумма величин смежных углов равна 7Г, GDH = 7г — EDF = 7Г — а. Тогда с учётом того, что sin(7r — а) = sin а, получаем
Saabc = \ ■ \АВ\ • \АС\ ■ sin ВАС, SADGH = \ • \DG\ • \DH\ ■ s in GDH =►
Saabc = I • \AB\ ■ \AC\ ■ sin a = \AB\ ■ \AC\
^ Sadgh \ ■ \DG\ ■ \DH\ ■ sin(7r - a) \DG\-\DH\’
Лемма доказана.
Лемма 5. Если два треугольника подобны с коэффициентом подобия к, то отношение их площадей равно к2 .
Доказательство. Рассмотрим подобные треугольники ABC и DEF, пусть
\АВ\ \АС\ _ \ВС\
\DE\ \DF\ \EF\
Поскольку соответственные углы подобных треугольников равны, то применима лемма 4, что дает нам
Saabc _ \АВ\ • \АС\ \АВ\ \АС\ 2
Sadef \DE\ ■ \DF\ \DE\ ' \DF\
Лемма доказана.
Примеры решения задач
Пример 1. На сторонах АВ, ВС и AD параллелограмма ABCD взяты точки К, М и L соответственно. Найдите отношение площадей треугольников KBL и BML, если \АК\ : \КВ\ =2 : 1, \ВМ\ : \МС\ = 1 : 1, \AL\ : \LD\ = 1 : 3.


1.5. Площадь треугольника
57
Решение. Обозначим длину отрезка AL буквой х, а длину отрезка КВ - буквой у. Тогда, в соответствии с условием задачи, \LD\ = Зх, \AD\ = 4х, \АК\ = 2у, \АВ\ = 3?/. Поскольку ABCD - параллелограмм, во- первых, ВСЦАО и, во-вторых, \ВС\ = \AD\ = 4ж, из
чего вытекает, что \ВМ\ = |МС| = ^|SC| = 2х.
В 2х М 2х С
Замечание. Если в задаче требуется найти отношение площадей треугольников, то удобно меньшую площадь обозначить буквой 5 и выразить через неё большую площадь, возможно, используя промежуточные треугольники. Всегда полезно сначала составить план, а только потом проводить вычисления.
Итак, обозначим площадь треугольника KBL буквой 5 и выразим через неё последовательно площади треугольников Sakbl —> Saabl —> Sbml• Теперь, пользуясь леммами 1 и 2, получаем
Saabl _ \АВ\ Sakbl \КВ\
= 3 ==> Saabl = 35;
Sabml _ 1 ВМ\ Saabl \AL\
= 2
Sabml — 65.
Следовательно,
Ответ. 1:6.
Sakbl
Sabml
S_
65
1
6’
Пример 2. В треугольнике ABC длина высоты BD равна 3, длина медианы ВМ равна 5. На стороне ВС взята точка Q так, что \BQ\ = 1, \QC\ = 5. Найдите площадь треугольника AQC, если известно, что она больше трёх.
А М С
Решение. Сначала получим соотношение, связывающее площади треугольников АВС и AQC. Применяя к ним лемму 1, находим
Saaqc \QC\ 5 5
sZmJ = jlcj= ё ^ W = j W
Для вычисления площади треугольника АВС нам необходимо вычислить длину его основания АС, поскольку длина его высоты BD нам уже известна. Поступим следующим образом: сначала запишем теорему Пифагора для треугольников В DM и В DC :
\DM\2 = \ВМ\2 - \BD\2 = 25 - 9 = 16 => \DM\ = 4,
\DC\2 = \BC\2 - \BD\2 = 36 - 9 = 27 ==> \DC\ = 3V3.


58
Теория и задачи
Далее заметим, что возможны две различные конфигурации. Если точка М лежит между точками D и С (правый чертёж), то
\СМ\ = \DC\ - \DM\ = Зл/з - 4, \АС\ = 2\СМ\ = 2 • (3>/3 - 4),
Saabc = \ • |ЛС| • |Ш)| = 3 • (Зл/З - 4), 5ДЛдс = | - (Зл/З - 4) с 3.
Таким образом, эта конфигурация нам не подходит. Если же точка D лежит между точками М и С (левый чертёж), то
\СМ\ = \DC\ + \DM\ = 3>/3 + 4, |Ж7| = 2\СМ\ = 2 ■ (3\/3 + 4),
Saabc = 5 • |ЛС| ■ |ЯЛ| = 3 • (3^3 + 4), Saaqc = \ • (3>/3 + 4) > 3.
15^3 + 20 Ответ. .
Пример 3. В трапеции ABCD на продолжении основания ВС взята точка М таким образом, что прямая AM отсекает от трапеции ABCD треугольник, площадь которого в 4 раза меньше площади трапеции ABCD. Найдите длину отрезка СМ, если \AD\ = 8, \ВС\ = 4.
Решение. Обозначим точку пересечения отрезков AM и CD буквой N. Так как треугольники г
AND и MNC подобны, то для ответа на вопрос 4 задачи нам не хватает отношения \DN\ : \NC\, которое легко получить, используя отношение площадей из условия задачи. Для того чтобы эффективно воспользоваться леммами о площадях треугольников, проведём диагональ АС. Тогда с учётом того, А 8 D что AD\\BC, по лемме 2 мы находим, что отношение площадей треугольников ACD и ABC будет
равно отношению длин отрезков AD и ВС, то есть 2. Таким образом, площадь треугольника ACD равна двум третям площади трапеции ABCD и по лемме 1
Saand _ \DN\ \SAbcd _ \DN\ ]£Wj = 3 |DiV| _ 3
Saacd \CD\ | Sabcd \CD\ \CD\ 8 |JVC| 5
Наконец, из подобия треугольников AND и MNC получаем
\АЩ \DN\ 3 = 5 40
|СМ| |ЛГС| 5 11 3 11 3 '
Ответ. —.


1.5. Площадь треугольника
59
Пример 4. В треугольнике АВС проведена биссектриса BL. Известно, что \АС\ = 8, а площади треугольников ABL и BLC относятся как 3:1. Найдите длину биссектрисы BL, при которой длина высоты, опущенной из вершины В на основание АС, будет наибольшей.
В
\ / \ /
Решение. По лемме 1 и основному свойству биссектрисы мы получаем, что 0 Saabl \AL\ \АВ\
3 = — = т = ——т. Далее можно рассуждать по-разному.
OABLC |ЬС| \ВС\
Первый способ. Положим \ВС\ = х, тогда \АВ\ = Зх, раавс = 2х + 4. Применим формулу Герона:
Saabc = л/(2х + 4)(2х + 4 — 8)(2х + 4 — Зх)(2х + 4 — х) — yj(4х2 — 16)(16 — х2).
Используя свойства квадратичной функции, мы получаем, что максимум правой части достигается при х2 = 10, то есть \ВС\ = \/10, \ АВ\ = Зл/То. Теперь осталось лишь воспользоваться формулой длины биссектрисы:
\BL\2 = \АВ\ ■ \ВС\ - \AL\ ■ \LC\ = 30 - 12 = 18 =► \BL\ = Vl8.
Второй способ. Докажем, что геометрическое место точек В, удовлетворяющих условию \АВ\ : \ВС\ = 3, есть окружность, диаметром которой является отрезок LL', где V - точка пересечения биссектрисы угла, смежного с углом АВС, и прямой АС. В самом деле, точки L и V принадлежат этому геометрическому месту, так как по основному свойству биссектрисы внутреннего угла треугольника \AL\ : \LC\ = 3, а по свойству биссектрисы внешнего угла треугольника (которое доказывается точно так же, как и свойство биссектрисы внутреннего угла, - надо дважды применить теорему синусов) \AU\ : \LfC\ = 3. При этом расположение точек L и U никак не зависит от расположения точки В. Наконец, заметим, что угол LBU прямой, так как он является углом между биссектрисами смежных углов. Отсюда и следует наше утверждение.
После этого из свойств биссектрис внутреннего и внешнего угла мы получаем \CL\ = 2, \CL'\ = 4, \LL\' = 6, то есть длина радиуса окружности, на которой лежит точка В, равна 3. Отметим, что так как
Saabc = \ • \ВИ\ • \АС\ = 4\ВН\,
то площадь треугольника АВС будет максимальна тогда, когда максимальна длина высоты ВН. Из геометрических соображений понятно, что наибольшая возможная длина высоты ВН равна 3, причём точка Н является центром нашей


60
Теория и задачи
окружности, то есть \LH\ = 3. Наконец, применяя теорему Пифагора в треугольнике BLH, мы находим нужную нам величину: |JE?L| = у/\ВН\2 + \LH\2 = y/lS.
Ответ, л/18.
Задачи
1. На стороне КМ треугольника KLM, площадь которого равна 4, взята точка N таким образом, что \КМ\ = 4\MN\. Найдите длину отрезка LN, если длина стороны KL равна 2\/3, a KLN = 7г/3.
2. Центр О окружности, длина радиуса которой равна 3, лежит на гипотенузе АС прямоугольного треугольника ABC. Его катеты касаются этой окружности. Найдите площадь треугольника ABC, если известно, что \ОС\ = 5.
3. Внутри прямоугольного треугольника ABC (угол ABC прямой) взята точка D таким образом, что площади треугольников ABD и BCD соответственно в три и в четыре раза меньше площади треугольника ABC. Найдите длину отрезка BD, если \AD\ = a, \DC\ = с.
4. В трапеции ABCD \CD\ = 12, боковая сторона AD перпендикулярна основаниям, а её длина равна 9. Длина отрезка АО, где О - точка пересечения диагоналей трапеции ABCD, равна 6. Найдите площадь треугольника ВОС.
5. Прямая, проходящая через вершину основания равнобедренного треугольника, делит его площадь пополам, а периметр делит на части 5 и 7 м. Найдите площадь треугольника.
6. В равнобедренном треугольнике ABC длина основания АС равна 2, величина угла АС В равна 7г/6. Из вершины А к боковой стороне ВС проведены медиана AD и биссектриса АЕ. Найдите площадь треугольника ADE.
7. В треугольнике FGH угол G прямой, \FG\ = 8, \GH\ = 2. Точка D лежит на стороне FH, А и В - точки пересечения медиан треугольников FGD и DGH соответственно. Найдите площадь треугольника GAB.
8. Дан треугольник ABC, площадь которого равна 2. На его медианах АК, BL и CN взяты соответственно точки Р, Q и R так, что \АР\ = \РК\, \QL\ = 2\BQ\, \CR\ : = 5:4. Найдите площадь треугольника PQR.
9. Точка N лежит на гипотенузе АС прямоугольного равнобедренного треугольника ABC. Точка М расположена на катете АВ таким образом, что угол MNC прямой. Известно, что площадь треугольника MNC составляет три восьмых площади треугольника ABC. Вычислите отношение |АЛГ| : \NC\.
10. 	Прямоугольные треугольники ABC и ABD имеют общую гипотенузу АВ, длина которой равна 5. Точки С и D расположены по разные стороны от прямой АВ, \ВС\ = \BD\ = 3. Точка Е лежит на стороне АС, \ЕС\ = 1. Точка F лежит на стороне AD, \FD\ = 2. Найдите площадь пятиугольника ECBDF.


1.5. Площадь треугольника
61
11. В треугольнике АВС медиана AD и биссектриса BE перпендикулярны и пересекаются в точке F. Найдите площадь треугольника АВС, если площадь треугольника DEF равна 5.
12. В ромбе ABCD перпендикуляр к стороне AD, восстановленный из её середины, пересекает диагональ АС в точке М, а перпендикуляр к стороне CD, восстановленный из её середины, пересекает диагональ АС в точке N. Найдите отношение площадей треугольника MND и ромба ABCD, если BAD = тг/З.
13. Основание А В трапеции ABCD вдвое длиннее основания CD и вдвое длиннее боковой стороны AD. Найдите площадь трапеции ABCD, если известно, что \АС\ = а, \ВС\ =Ь.
14. На сторонах KL и LM треугольника KLM взяты точки А и В соответственно. Отрезки КВ л МА пересекаются в точке С. Найдите площадь треугольника ALC, если известно, что площади треугольников К АС, МВС и КСМ равны соответственно 12, 50 и 45.
15. В параллелограмме ABCD на диагонали АС взята точка Е, а на стороне AD взята точка F, причём |Ж7| = 3|АЕ?|, \AD\ = 4|AF|. Найдите площадь параллелограмма ABCD, если площадь четырёхугольника ABGE, где G - точка пересечения прямой и отрезка БС, равна 8.
16. В треугольнике АВС на стороне АВ взята точка К, а на стороне взята точка L так, что \АК\ : \ВК\ = 1:2, |CL| : |SL| = 2:1. Пусть Q - точка пересечения прямых AL и С К. Найдите площадь треугольника АВС, если дано, что площадь треугольника BQC равна 1.
17. В равнобедренный треугольник АВС с основанием АС вписана окружность, которая касается боковой стороны АВ в точке М. Через точку М проведён перпендикуляр ML к стороне АС треугольника АВС (точка L - основание этого перпендикуляра). Найдите величину угла ВС А, если известно, что площадь треугольника АВС равна 1, а площадь четырёхугольника LMBC равна S.
18. Через вершины А к В треугольника АВС проведена окружность, пересекающая стороны ВС и АС в точках D и Е соответственно. Площадь треугольника CDE в 7 раз меньше площади четырёхугольника ABDE. Найдите \DE\ и длину радиуса окружности, если \АВ\ = 4, С = 45°.
19. На стороне АВ треугольника АВС взята точка Е, а на стороне ВС - точка D так, что \АЕ\ = 2, \CD\ = 1. Прямые AD и СЕ пересекаются в точке О. Найдите площадь четырёхугольника В DOE, если \АВ\ = \ВС\ = 8, \АС\ = 6.
20. На плоскости лежит равнобедренный прямоугольный треугольник, у которого катеты имеют длину а. Поворотом в этой плоскости данного треугольника вокруг вершины его прямого угла на угол 45° получается другой равнобедренный прямоугольный треугольник. Найдите площадь четырёхугольника, являющегося общей частью этих двух треугольников.


62
Теория и задачи
21. Длина радиуса вписанной в равнобедренный треугольник ABC окружности равна 4, \АС\ = \ВС\. Ha. прямой АВ взята точка D, удалённая от прямых АС и ВС на расстояния 11 и 3 соответственно. Найдите cos DBC.
22. Площадь трапеции ABCD равна 30. Точка Р - середина боковой стороны АВ. Точка R на боковой стороне CD выбрана так, что 2\CD\ = 3|i?D|. Прямые AR и PD пересекаются в точке Q. Найдите площадь треугольника APQ, если известно, что \AD\ = 2\ВС\.
23. В трапеции ABCD стороны АВ и CD параллельны, причём \CD\ = 2|АВ|. На сторонах AD и ВС выбраны соответственно точки Р и Q таким образом, что \DP\ : \РА\ =2:1, \BQ\ : \QC\ =3:4. Найдите отношение площадей четырёхугольников ABQP и CDPQ.
24. Точки Р и Q расположены на стороне ВС треугольника ABC таким образом, что \ВР\ : \PQ\ : \QC\ = 1:2:3. Точка R делит сторону АС этого треугольника таким образом, что |AR| : \RC\ = 1:2. Чему равно отношение площади четырёхугольника PQST к площади треугольника ABC, если S и Т - точки пересечения прямой BR с прямыми AQ и АР соответственно?
25. В треугольнике ABC, площадь которого равна 5, проведены биссектриса СЕ и медиана BD, пересекающиеся в точке О. Найдите площадь четырёхугольника ADOE, если \ВС\ = а, \АС\ = Ь.
26. Длина высоты трапеции ABCD равна 7, а длины оснований AD и ВС равны соответственно 8 и 6. Через точку Е, лежащую на стороне CD, проведена прямая BE, которая делит диагональ АС в точке О в отношении |-АО| : \ОС\ =3:2. Найдите площадь треугольника О ЕС.
27. В прямоугольном треугольнике величина меньшего из углов равна а. Прямая, перпендикулярная гипотенузе, делит этот треугольник на две части, равные по площади. Найдите, в каком отношении она делит гипотенузу.
28. Через вершину А и середину М стороны ВС параллелограмма ABCD, площадь которого равна 1, проведена прямая, пересекающая диагональ BD в точке О. Найдите площадь четырёхугольника OMCD.
29. В треугольнике ABC градусная мера угла А равна 45°, а угол С острый. Из середины стороны ВС на сторону АС опущен перпендикуляр MN. Найдите градусные меры углов треугольника ABC, если площади треугольников MNC и ABC относятся как 1:8.
30. Точка О является центром окружности, вписанной в прямоугольный треугольник ABC с прямым углом В. Известно, что отношение площадей треугольников АОС и ABC равно к : к + 1. Найдите величины острых углов треугольника ABC. При каких к задача имеет решение?
31. В треугольнике ABC точка D лежит на стороне АС, \AD\ = 2\DC\. На стороне ВС взята точка Е таким образом, что площадь треугольника AED равна 1. Отрезки АЕ и BD пересекаются в точке О. Найдите отношение площадей треугольников АВО и OED, если площадь треугольника ABD равна 3.


1.5. Площадь треугольника
63
32. На отрезке АВ лежат точки С и D, причём точка С - между точками А и D. Точка М взята так, что перпендикулярны прямые AM и MD, а также перпендикулярны прямые СМ и MB. Найдите площадь треугольника CMD, если известно, что CMD = а, а площади треугольников AMD и СМ В равны Si и 52 соответственно.
33. Точка F лежит на продолжении за точку С стороны ВС параллелограмма ABCD. Отрезок AF пересекает диагональ BD в точке Е и сторону CD в точке G. Известно, что \GF\ = 3, \АЕ\ = \EG\ + 1. Какую часть площади параллелограмма ABCD составляет площадь треугольника AED ?
34. Отрезок BL является биссектрисой треугольника АВС. На продолжении его стороны АС за точку С взята точка М таким образом, что угол LBM прямой. Найдите площадь треугольника CBL, если известно, что площади треугольников ABL и СВМ равны 10 и 15 соответственно.
35. Точки D и Е являются соответственно серединами сторон АС и ВС равностороннего треугольника АВС. Точка F лежит на отрезке CD, отрезки BF и DE пересекаются в точке М. Найдите длину отрезка MF, если известно, что площадь четырёхугольника ABMD составляет пять восьмых площади треугольника АВС, а \АВ\ = а.
36. На стороне ВС треугольника АВС выбраны точки К и L таким образом, что \BL\ = \LC\, \ВК\ = \KL\. Точки D и F лежат соответственно на продолжениях отрезков AL и АК за точки L и К так, что \KF\ = 2|AL|, |LjD| = lAK]. Вычислите отношение площадей четырёхугольника KLDF и треугольника АВС, если известно, что АВС = /3, АСВ = 7.


64
Теория и задачи
2. 	Окружности
2.1. 	Углы в окружностях Теоретический материал
1. Центральные углы
Центральный угол измеряется дугой окружности, на которую он опирается: АОВ=АВ.
Этот факт вытекает из определения радианной меры угла. В самом деле, если взять окружность единичного радиуса, то ра- дианная мера центрального угла будет в точности равна длине отсекаемой им дуги. Если же длина радиуса окружности не равна единице, то радианная мера центрального угла будет равна отношению длины дуги, отсекаемой этим углом, и радиуса окружности. Видно, что в любом случае есть взаимно однозначное соответствие между радианной мерой угла и длиной дуги окружности, поэтому в дальнейшем под словами «мера ду- В ги» мы будем понимать отношение её длины и длины радиуса окружности.
2. Вписанные углы
Вписанный угол, т.е. угол, образованный двумя хордами, исходящими из одной точки окружности, равен по величине половине центрального угла, опирающегося на ту же дугу окружности (измеряется половиной дуги окружности, на
которую он опирается): АС В — ^АОВ = - АВ.
Для доказательства этого утверждения обозначим величину центрального угла АОВ через 2а и рассмотрим три случая: центр окружности может лежать внутри вписанного угла, вне его или на одной из его сторон.
Если центр окружности попадает на сторону угла АС В (левый чертёж), то из того, что углы АОВ и ВОС смежные, вытекает, что ВОС = 7г — 2а, а из того, что треугольник ВОС равнобедренный, имеем АС В = ~(7г — ВОС) = а.
Если центр окружности попадает внутрь угла АС В (центральный чертёж), то в этом случае АС В = ВСОЛ-АСО. Треугольники ВОС и АОС равнобедренные,


2.1. Углы в окружностях
65
поэтому
ВСО = I(тг — ВОС), АСО = АОС) =►
Z Z
=► ВСд + АСд = 7г-^(вдС + АдС) = п-1(21г-Адв) = 1АЗв = а.
Z Z Z
Наконец, если центр окружности лежит вне угла АСВ (правый чертёж), то тогда АСВ = АСО — J3CO. Треугольники ВОС и Л ОС равнобедренные, значит,
ВСО = i(7T - ВОС), АСО = ~(тг - АОС) =►
Z Z
=► ЛСО-ВСО = i(BOC-ЛОС) = ^АОВ = а.
Z Z
Утверждение доказано.
Отметим важные следствия этого факта:
• Вписанные углы, опирающиеся на одну и ту же дугу (или на равные по величине дуги), равны.
• Если вписанные углы равны, то равны и дуги, на которые они опираются.
• Если две параллельные прямые пересекают окружность, то заключенные между ними дуги равны.
• Если две прямые пересекают окружность и заключенные между ними дуги равны, то прямые параллельны.
Первые два утверждения просто следуют из доказанного выше утверждения, а для доказательства двух последних достаточно вспомнить свойства и признаки параллельных прямых.
3. 	Углы между хордой и касательной
Угол между хордой и касательной равен по величине половине меры заключённой внутри него дуги окружности:
ВАК = I АВ= ^ЛОВ.
2 2
Для обоснования этого факта разберём два случая. Если угол ВАК острый, то
ОАВ = | - ВЛХ,
ЛОВ = тг - 2 • ОАВ = 2 • ВАК.
Поскольку АОВ —АВ (по свойству центрального угла), ВАК = \ АВ.
Если угол ВАК тупой, то ОАВ = ВАК— ^ , АОВ = тг — 2 ОАВ = 2тг—2 ВАК.
Но АВ= 2п — АОВ. Таким образом, ВАК = \ АВ. Третий случай, когда угол ВАК прямой, очевиден. Утверждение доказано.
3 Геометрия


66
Теория и задачи
4. 	Углы между пересекающимися хордами
Угол между пересекающимися хордами равен по величине полусумме мер дуг окружности, которые отсекают на окружности эти хорды:
АКБ = -(АВ + CD) = АС В + CBD.
Доказательство этого утверждения очевидно. Угол АКВ является внешним углом треугольника СКВ, поэтому его величина равна сумме величин углов АС В и СBD. Но по свойству вписанных углов
АСВ = i АВ, CBD = i CD .
2 2
Утверждение доказано.
5. 	Углы между секущими
Угол между секущими, выходящими из одной точки, равен полуразности мер дуг окружности, заключенных между ними:
D
АКС = i(ic - BD) = ABC - BCD.
Доказательство этого утверждения также весьма просто. Угол ABC является внешним углом треугольника СКВ, поэтому его величина равна сумме
величин углов В КС и ВС К. Применяя свойство V /Ч/_—
вписанных углов, получаем
ABC = I АС, ВСК = BCD =\bD.
2 2
Отсюда и вытекает нужное нам соотношение.
Приведём некоторые важные следствия рассмотренных утверждений:
• Синусы вписанных углов, опирающихся на одну и ту же хорду (или на равные хорды), равны.
• Вписанный угол, опирающийся на диаметр окружности, является прямым.
• Если вписанный угол является прямым, то он опирается на диаметр окружности.
• Сумма величин противоположных углов выпуклого четырехугольника, вписанного в окружность, равна 7г.
• Равные хорды отсекают равные дуги.
6. 	Теорема о четырёх точках
Укажем ещё один важный факт.
Геометрическим местом точек, из которых данный отрезок АВ виден под углом заданной величины а, являются две дуги окружностей радиуса длины , проходящих через точки А и В.


2.1. Углы в окружностях
67
На чертеже эти дуги обозначены толстыми сплошными линиями, а произвольные точки этих дуг обозначены буквами С. Нетрудно догадаться, что геометрическое место точек, из которых данный отрезок АВ виден под углом величины 7Г — а, есть оставшиеся дуги этих окружностей, на рисунке они обозначены штриховыми линиями, а произвольные точки этих дуг обозначены буквами D. Обоснование этого факта можно легко провести с помощью теоремы синусов и свойств вписанных углов.
Из этого утверждения непосредственно вытекает крайне важная для решения задач
Теорема о четырёх точках. Для того чтобы точки А, В, С и D лежали на одной окружности, необходимо и достаточно, чтобы выполнялось одно из двух утверждений:
1. Точки А и В лежат в одной полуплоскости относительно прямой CD и при этом CAD = CBD.
2. Точки А и В лежат в разных полуплоскостях относительно прямой CD и выполнено CAD + CBD = 7Г.
В В
Наконец, рассмотрим ещё одну полезную теорему. Конфигурация, ею описываемая, встречается в случае, когда биссектриса внутреннего угла произвольного треугольника продолжается до пересечения с описанной около него окружностью.
Теорема. Пусть четырёхугольник ABCD вписан в окружность с центром О, К - точка пересечения его диагоналей. Тогда равносильны следующие утверждения:
1. АС - биссектриса угла BAD.
2. \ВС\ = \DC\.
3. Касательная, проведённая к окружности в точке С, параллельна прямой BD.
4. Треугольники К DC и DAC подобны (подобны и треугольники К ВС и ВАС).
5. Отрезок ОС перпендикулярен отрезку BD (делит его пополам).
Доказательство. Сначала докажем, что из утверждения 1 вытекают все остальные.


68
Теория и задачи
По свойствам вписанных углов,
'ВАС = i ВС= BDC, DAC = I DC= DBC.
2 2
Поскольку величины углов ВАС и DAC равны, равны и величины углов В DC и DBC.
Стало быть, треугольник BDC равнобедренный,
\ВС\ = \DC\, утверждение 2 вытекает из утверждения 1.
Далее, по свойству угла между касательной и хордой
DCE = I DC= DBC = BDC.
2
Так как углы В DC и DCE - внутренние накрест лежащие при прямых СЕ и BD, а их величины равны, то по признаку параллельных прямых CE\\BD, то есть утверждение 3 следует из утверждения 1.
Справедливость утверждения 4 получается почти автоматически: мы уже доказали, что равны величины углов ВАС, В DC, DAC и DBC, поэтому нужные нам пары треугольников подобны по двум углам.
Наконец, поскольку CE\\BD, получаем ОС _1_ СЕ, то ОС _L BD. Треугольник OBD, очевидно, равнобедренный, поэтому из того, что ОС ± BD вытекает, что точка пересечения отрезков ОС и BD делит отрезок BD пополам.
Теперь докажем, что из каждого из утверждений 2-5 следует утверждение 1. Это завершит доказательство теоремы.
Если \ВС\ = \DC\, то треугольник В DC равнобедренный, В DC = DBC, но по свойствам вписанных углов В DC = ВАС, DBC = DAC. Таким образом, iMC = DAC, т.е. утверждение 1 следует из утверждения 2.
Далее, если CE\\BD, то углы DCE и CDB равны как внутренние накрест лежащие, а углы iDCE и DBC равны в силу свойств вписанных углов и углов между касательной и хордой. Таким образом, треугольник В DC равнобедренный, \BD\ = \DC\. То есть утверждение 2 (и, по доказанному выше, утверждение 1) вытекает из утверждения 3.
Тот факт, что утверждение 1 следует из утверждения 4, практически очевиден: из подобия треугольников К DC и DAC вытекает равенство углов К DC и DAC, но, с другой стороны, углы К DC и КАВ равны как вписанные углы, опирающиеся на одну и ту же дугу ВС.
Наконец, если ОС _L BD, то в силу того, что ОС _L СЕ, мы получаем BD\\CE. Итак, из утверждения 5 вытекает утверждение 3, из которого, в свою очередь, вытекает и утверждение 1. Теорема доказана.
Примеры решения задач
Пример 1. В окружности проведены две пересекающиеся хорды АВ и CD. Найдите длину диаметра этой окружности, если АВ _L CD, \AD\ — га, \ВС\ = п.
Решение. Обозначим точку пересечения хорд АВ и CD буквой К.


2.1. Углы в окружностях
69
Первый способ. Обозначим величину угла ABD буквой а , тогда величина угла В DC равна 7г/2 — а. Треугольники ABD и BCD оба вписаны в данную окружность, поэтому R&bcd = Raabd — Во - Запишем для этих треугольников теорему синусов:
2Raabd
I АР\^
sin ABD 2Rabcd =
\AD\ = 2Rq • sin a;
\BC\
sin В DC
\BC\ = 2R0 • sin — a) = 2R0 • cos a.
Наконец, возведём эти соотношения в квадрат и сложим:
I Л Т~Н2 I I о/^|2 а г?2 Л2 . ___2 _ \ _
Значит, искомая длина диаметра окружности равна у/т2 + п2.
Второй способ. Применим свойство угла между пересекающимися хордами:
1 = акЪ = \£Ь+\вс
AD + тг.
Отложим на окружности дугу AF, равную дуге ВС (точка F берется так, чтобы точка А лежала между точками D и F). Тогда \AF\ = \ВС\, поскольку равные хорды стягивают равные дуги и наоборот, а, с другой стороны,
DAF= 7г, значит, FD - диаметр. Отсюда получаем, что угол FAD прямой. Наконец, из треугольника ADF по теореме Пифагора получаем, что |jFjD| = у/т2 + п2.
Ответ, у/т? + п2.
Пример 2. Касательная, проведённая через вершину С вписанного в окружность 7 треугольника ABC, пересекает продолжение стороны А В за вершину В в точке D. Известно, что длина радиуса окружности 7 равна 2, \АС\ = л/12 и ADC + АС В = 2 • ВАС. Найдите длину секущей AD.
Решение. Положим ВАС = a, ABC = (3. Тогда АС В = тт — а — /3 и по свойству угла между касательной и хордой BCD = а. Далее заметим, что углы ABC и CBD смежные, поэтому CBD = тт — /3, и из треугольника BCD находим ADC = 7г — CBD — BCD = /3 — а. Теперь воспользуемся условием задачи:
7Г
4‘
ADC + АС В = 2 • ВАС
— a-f-7T — а — /3 = 2а
а = —.


70
Теория и задачи
После этого применим к треугольнику АВС теорему синусов:
|ЛС| - 2 Raabc => sin ABC = |ЛС| - ^
sin ABC ZRaabc 2
Таким образом, возможны два случая (оба они представлены на чертеже):
„ . 7Г 7Г —ТГ —27Г
1. АВС = /3 = —, ВАС — а — - =» ADC = —, ЛСО = —;
О Tt 1Z о
—1 Tw^." 27Г 7Г —' " 57Г —гт% ТГ
2. ЛВС = /0 — —, ВЛС = а = — => ADC = —, ЛС£) = —.
3 4 12 3
Из треугольника ADC по теореме синусов получаем
\AD\_ = \ЛС^ ^ = |ЛС[ sinACD
sin ACD sin ADC sin ADC
Подставляя в эту формулу известную нам длину отрезка АС и найденные значе-
3
ния величин углов ACD и ADC, находим, что \AD\ = —-=. j= — 3(\/б ± \/2).
уб =F v2
4
Ответ. 3(\/б±\/2).
Пример 3. В окружности проведены хорды АС и BD, пересекающиеся в точке Е, причем касательная к окружности, проходящая через точку В, параллельна АС. Известно, что площадь треугольника DCS равна 16, \ЕА\ : |-DA| =3:4. Найдите площадь треугольника ВСЕ.
Решение. Поскольку отрезок АС параллелен касательной, проведённой через точку В, то, во-первых, углы ВС А и BDC равны, а треугольники ВСЕ и BDC подобны, и, во-вторых, DB - биссектриса угла ADC, a DE - биссектриса треугольника ACD. Пользуясь основным свойством биссектрисы треугольника и полученным подобием, имеем
\СЕ\ = \ЕА\ = 3 SAbce = (\СЕ\\2 = 9 \CD\ \DA\ 4’ Sabdc \\CD\) 16'
В
/ 9 \2 9
Наконец, Sabce = ( ^6 / Sabdc = • 16 = 9.
Ответ. 9.
Пример 4. Две окружности пересекаются в точках А и В. Через точку В проведена прямая, пересекающая окружности в точках С и D, лежащих по разные стороны от прямой АВ. Касательные к этим окружностям, проведённые в точках С и D, пересекаются в точке Е. Найдите длину отрезка АЕ, если \АВ\ = 10, \АС\ = 16, \AD\ = 15.


2.1. Углы в окружностях
71
Решение. По свойству угла между касательной и хордой
BDE = DAB, ВСЕ = СА£.
После этого заметим, что
CAD = CAB + DAB, СяВ = тг - ВСЕ - BDE,
стало быть, CAD + CED = тг. Но поскольку сумма величин внутренних углов четырёхугольника равна 2тг, получаем АСЕ -f ADE = тг. С учётом того, что точки С и D лежат в разных полуплоскостях относительно прямой АВ, они попадают и в разные полуплоскости относительно прямой АЕ. Таким образом, выполнены все условия теоремы о четырёх точках и вокруг четырёхугольника ACED можно описать окружность.
Теперь, воспользовавшись свойствами вписанных углов, мы находим, что AED = ACD, DCE = DAE. Из этого вытекает подобие треугольников AED и АС В, что даёт нам
\ЛЕ\ | АР\ \АС\ \АВ\
\АС\ ■ [АР| \АВ\
24.
Ответ. 24.
Задачи
1. В треугольнике ABC известно, что \АВ\ = 6, \АВ\ = \ВС\. На стороне АВ, как на диаметре, построена окружность, пересекающая сторону ВС в точке D так, что \BD\ : \DC\ = 2:1. Найдите длину стороны АС.
2. Найдите длину радиуса окружности, если вписанный в неё угол со сторонами, длины которых равны 1 и 2, опирается на дугу меры 2тг/3.
3. Около треугольника ABC описана окружность. Продолжение биссектрисы С К треугольника ABC пересекает эту окружность в точке L, причём CL - диаметр данной окружности. Найдите отношение длин отрезков BL и АС, если известно, что sin ВАС = 1/4.
4. Диаметр АВ окружности 7 продолжили за точку В и на этом продолжении отметили точку С. Из точки С провели секущую, пересекающую окружность в точках D и Е, считая от точки С. Известно, что \DC\ = 3, градусные меры углов DAC и ACD равны 30° и 7° соответственно. Найдите длину диаметра окружности 7.
5. На катете АС прямоугольного треугольника ABC как на диаметре построена окружность, которая пересекает гипотенузу АВ в точке К. Найдите площадь треугольника СКВ, если \АС\ = 6, ABC = /3.
6. В окружность, длина радиуса которой равна 7, вписан выпуклый четырёхугольник ABCD. Длины сторон АВ и ВС равны. Площадь треугольника ABD относится к площади треугольника BCD как 2 : 1, a ADC = 120°. Найдите длины всех сторон четырёхугольника ABCD.


72
Теория и задачи
7. В треугольнике АВС \АВ\ = 3, \АС\ = 3\/7, АВС = 7г/3. Биссектриса угла АВС пересекается в точке D с окружностью, описанной вокруг треугольника АВС. Найдите длину отрезка BD.
8. Диагональ BD четырёхугольника ABCD является диаметром окружности, описанной около него. Вычислите длину диагонали АС, если \BD\ = 2, |АВ| = 1, ABD .DBC = 4:3.
9. В треугольнике ABC AN и СМ - медианы, АВС = 27г/3. Окружность, проходящая через точки А, М и iV, проходит также и через точку С. Длина радиуса этой окружности равна 7. Найдите площадь треугольника АВС.
10. На окружности 7 расположены четыре точки А, В, С, D. Продолжение хорды АВ за точку В и продолжение хорды CD за точку С пересекаются в точке 25, причём AED = 7г/3. Величина угла ABD в три раза больше величины угла ВАС. Докажите, что А22 - диаметр окружности 7.
11. Вершины В,С и jD четырёхугольника ABCD расположены на окружности с центром О, которая пересекает сторону АВ в точке F, а сторону AZ) - в точке Е. Известно, что угол BAD прямой, длина хорды EF равна длине хорды FB, а также равны длины хорд В С, CD и ED. Найдите величину угла АВО.
12. На стороне АВ треугольника АВС как на диаметре построена окружность, пересекающая стороны АС и ВС в точках D и Е соответственно. Прямая DE делит площадь треугольника АВС пополам и образует с прямой АВ угол величины 7г/12. Найдите величины углов треугольника АВС.
13. На сторонах острого угла с вершиной В взяты точки А и С. Одна окружность касается прямой АВ в точке В и проходит через точку С. Вторая окружность касается прямой ВС в точке В и проходит через точку А. Точка D - вторая общая точка этих окружностей. Известно, что |АВ| = с, |ВС| = a, \CD\ = d. Найдите \AD\.
14. В окружность 7 с центром в точке О вписан выпуклый четырёхугольник ABCD, диагонали которого перпендикулярны. Известно, что величина угла АОВ в три раза больше величины угла COD. Найдите площадь круга, ограниченного окружностью 7, если \CD\ = 10.
15. Биссектрисы углов треугольника АВС, площадь которого равна 2, продолжены до точек пересечения с описанной около треугольника АВС окружностью, отличных от точек А, В, С. Эти точки образуют новый треугольник. Найдите его площадь, если величины углов треугольника АВС равны 7г/6, 7г/3 И 7г/2.
16. В окружность, длина радиуса которой равна 2у/7, вписана трапеция ABCD, причём её основание AD является диаметром, a BAD = 7г/3. Хорда СЕ пересекает диаметр AD в точке Р такой, что \АР\ : \PD\ = 1:3. Найдите площадь треугольника ВРЕ.


2.1. Углы в окружностях
73
17. Из вершины тупого угла А треугольника ABC опущена высота AD. Проведена окружность с центром в точке D, проходящая через точку А и пересекающая стороны треугольника АВ и АС в точках М и N соответственно. Вычислите длину стороны АС, если известно, что \АВ\ = с, \АМ\ = п, \AN\=m.
18. Через точку С проведены две прямые, касающиеся окружности в точках А и В. На большей из дуг АВ взята точка D так, что sin ACD sin BCD = 1/3. Найдите расстояние от точки D до хорды АВ, если известно, что \CD\ = 2.
19. В треугольнике ABC точка О - центр описанной окружности, точка L лежит на отрезке АВ и \AL\ = \LB\. Описанная около треугольника ALO окружность пересекает прямую АС в точке К. Найдите площадь треугольника ABC, если AOL = 7г/4, \LK\ = 8, \АК\ = 7.
20. В окружности проведены диаметр MN и параллельная ему хорда АВ. Касательная к окружности в точке М пересекает прямые N А и N В соответственно в точках Р и Q. Известно, что \МР\ = р, \MQ\ = q. Найдите длину диаметра MN.
21. Продолжение медианы треугольника ABC, проведенной из вершины А, пересекает описанную около треугольника ABC окружность в точке D. Найдите длину отрезка ВС, если длины отрезков АС и DC равны 1.
22. Выпуклый четырёхугольник ABCD вписан в окружность. Диагональ АС является биссектрисой угла BAD и пересекается с диагональю BD в точке К. Найдите длину отрезка КС, если известно, что \АК\ = 6, \ВС\ = 4.
23. Длина стороны АВ треугольника ABC равна 3, Е - точка пересечения продолжения биссектрисы CD треугольника ABC с описанной около него окружностью, \ВС\ = 2 • \АС\, \DE\ = 1. Найдите длину стороны АС.
24. В треугольнике ABC ВАС = 57г/12, \АВ\ = с, \АС\ = Ь. На стороне ВС выбрана точка М так, что ВАМ = 7г/6. Продолжение прямой AM пересекает окружность, описанную вокруг треугольника, в точке N. Найдите длину отрезка AN.
25. Окружность с центром в точке О, лежащей на гипотенузе АС прямоугольного треугольника ABC, касается его катетов АВ и ВС. Найдите длину АС, если известно, что \АМ\ = 20/9, \AN\ : \MN\ =6:1, где М - точка касания АВ с окружностью, а N - точка пересечения окружности с АС, расположенная между точками А и О.
26. Четырёхугольник ABCD вписан в окружность с центром в точке О. Радиус О А перпендикулярен радиусу О В, а радиус ОС перпендикулярен радиусу OD. Длина перпендикуляра, опущенного из точки С на прямую AD, равна 9, \AD\ = 2\ВС\. Найдите площадь треугольника АОВ.
27. В треугольнике ABC \АВ\ = 3, АС В = arcsin|. Хорда KN окружности, описанной около треугольника ABC, пересекает отрезки АС и ВС в точках


74
Теория и задачи
М и L соответственно. Известно, что АВС = С ML, площадь четырёхугольника ABLM равна 2, \LM\ — 1. Найдите длину высоты треугольника KNC, опущенной из вершины С, и площадь этого треугольника.
28. В треугольнике АВС точка D лежит на стороне ВС, прямая AD пересекается с биссектрисой угла АСВ в точке О. Известно, что точки С, D и О лежат на окружности, центр которой находится на стороне АС, величина угла DAC в три раза больше величины угла DAB, \АС\ : \АВ\ =3:2. Найдите косинус величины угла АСВ.
29. В треугольнике АВС проведена средняя линия MN, соединяющая стороны АВ и ВС. Окружность, проведенная через точки M,N и С, касается стороны АВ, а длина её радиуса равна \/2- Найдите sin Л СВ, если \АС\ = 2.
30. В треугольнике ЛВС длина стороны ВС равна 4, а длина стороны АВ равна 2\/19. Известно, что центр окружности, проведённой через середины сторон треугольника АВС, лежит на биссектрисе угла С. Найдите длину стороны АС.
31. Диагонали выпуклого четырёхугольника ABCD пересекаются в точке Е, С А - биссектриса угла С, |АВ| = |AD|, BAD = 77г/9, BE А = 117г/18. Найдите величину угла CDB.
32. В треугольнике АВС биссектриса AZ) угла А и биссектриса BL угла В пересекаются в точке F. При этом оказалось, что LFA = 7г/3.
1. Найдите величину угла АСВ.
2. Зная, что \АВ\ = 2, CLD = 7г/4, найдите площадь треугольника АВС.
33. В выпуклом четырёхугольнике ABCD проведены диагонали АС и BD. При этом оказалось, что ВАС = В DC, а площадь круга, описанного около треугольника BCD, равна 257г/4.
1. Найдите длину радиуса окружности, описанной около треугольника АВС.
2. Зная, что |ВС| = 3, \АС\ = 4, BAD — 7г/2, найдите площадь четырёхугольника ABCD.
34. В трапеции KLMN LM\\KN, KLM = п/2. Окружность проходит через точки М и N и касается прямой KL в точке А. Найдите площадь треугольника AMN, если известно, что |LM| = Z, |ifiV| = fc, |МАГ| = а.
35. Две окружности пересекаются в точках А и К. Их центры расположены по разные стороны от прямой, содержащей отрезок АК. Точки В и С лежат на разных окружностях. Прямая, содержащая отрезок АВ, касается одной окружности в точке А. Прямая, содержащая отрезок АС, касается другой окружности также в точке А. \ВК\ = 1, \СК\ = 4, а тангенс величины угла САВ равен 1/\/15. Найдите площадь треугольника АВС.
36. В треугольнике АВС величина угла В равна 7г/6. Через точки А и В проведена окружность, длина радиуса которой равна 2, касающаяся прямой АС в точке А. Через точки В и С проведена окружность, длина радиуса которой равна 3, касающаяся прямой АС в точке С. Найдите |АС|.


2.2. Касательные, хорды, секущие
75
2.2. 	Касательные, хорды, секущие Теоретический материал
1. Площадь круга, сектора, сегмента
Приведём формулы площади круга, сектора и сегмента:
• Площадь круга с длиной радиуса г равна пг2.
• Площадь сектора величины а круга с длиной радиуса г
Г2 OL
{АОВ) равна ——.
• Площадь сегмента величины а круга с длиной радиу-
Г2 (a- sin а) са г (CD) равна .
Отметим, что формулу для площади круга стоит принять за аксиому, из которой уже можно вывести формулы площади сектора и сегмента.
2. Касательные, проведённые из одной точки
Отрезки касательных к окружности, проведённые из одной точки, имеют равные длины и составляют равные углы с прямой, проходящей через эту точку и центр окружности: \AL\ = \АК\, OAL = ОАК.
Доказательство этого утверждения тривиально: в силу того, что АО - общая сторона треугольников ОАК и OAL, углы ОКА и OLA прямые, а длины отрезков О К и OL равны (они оба являются радиусами окружности), прямоугольные треугольники ОАК и OAL равны по гипотенузе и катету.
Из этого следует, что \AL\ = OAL = OAK. Отметим,
что фактически мы обосновали и такое утверждение: центр окружности, вписанной в угол, лежит на его биссектрисе.
3. Свойство пересекающихся хорд
Произведения длин отрезков двух пересекающихся хорд равны:
\АК\ • \КВ\ = \СК\ • \KD\.
Для обоснования этого факта заметим, что углы BAD и BCD являются вписанными углами, опирающимися на одну дугу. Значит, они равны, поэтому с учётом того, что углы AKD и ВКС равны как вертикальные, мы получаем, что треугольники AKD и СКВ подобны (по двум
ч „ . \АК\ \KD\
углам). Из этого подобия вытекает = <==>
\АК\ • \КВ\ = \СК\ • \KD\, что и требовалось доказать.
4. 	Свойство секущих
Произведение длины отрезка секущей на длину её внешней части для всех секущих, проведённых из одной точки, есть величина постоянная. Эта величина равна квадрату длины отрезка касательной, проведённой из этой же точки:


76
Теория и задачи
\АВ\ ■ \АС\ = \AD\ ■ \АЕ\ = \АК\2.
Рассмотрим произвольную секущую АС. Угол АКБ является углом между касательной и хордой, поэтому он измеряется половиной дуги КВ и равен углу КС В. Отсюда вытекает подобие треугольников АКВ и АС К, что даёт нам
К
\АК\ \АВ\ \ЛС\ \АК\
*=> \АВ\ ■ \АС\ = \АК\2.
Ясно, что для другой секущей АЕ, проведённой из точки А, можно повторить такие же рассуждения и получить тот же результат. Или можно действовать так: заметим, что углы BCD и BED равны в силу свойств вписанных углов, поэтому треугольники ACD и АЕВ подобны. Из этого подобия вытекает
IAC\ = \AD\ \АЕ\ \АВ\
\АВ\ ■ \АС\ = \AD\ ■ \АЕ\.
Утверждение доказано.
5. Свойство описанного около окружности четырёхугольника
В любом описанном около окружности четырёхугольнике суммы длин противоположных сторон равны, а центр этой окружности лежит на пересечении его биссектрис.
Для доказательства этого факта воспользуемся теоремой о равенстве длин отрезков касательных. Она даёт нам следующие соотношения:
\АР\ = |AS|, \ВР\ = \BQ\,
\CQ\ = \CR\, \DR\ = \DS\,
ZO AS = Z.OAP, ZOBP = ZOBQ,
ZOCQ = ZOCR, Z.ODR = ZODS.
Отсюда сразу вытекает, что центр вписанной в четырёхугольник окружности лежит на пересечении его биссектрис. Получить равенство сумм длин противоположных сторон тоже совсем нетрудно: р
\АВ\ + \CD\ = \АР\ + \ВР\ + \CR\ + \DR\ =
= \AS\ + |DS| + \BQ\ 4- \CQ\ = \AD\ + \BC\.
6. Свойство хорды, перпендикулярной диаметру
Если диаметр окружности проходит через середину некоторой хорды этой окружности, то он перпендикулярен этой хорде. Верно и обратное утверждение: если диаметр окружности перпендикулярен пересекающейся с ним хорде этой окружности, то он делит её пополам.


2.2. Касательные, хорды, секущие
77
Доказать эти утверждения совсем нетрудно: если известно, что некоторая хорда делится диаметром окружности пополам, то есть \СК\ = \DK\, то треугольники СОК и DO К равны по трем сторонам, из чего вытекает равенство углов С КО и DKO. Но эти углы смежные, поэтому они оба прямые, стало быть,
АВ LCD.
Если же известно, что некоторая хорда перпендикулярна диаметру, то есть АВ _L CD, то прямоугольные треугольники СОК и DO К равны по гипотенузе и катету, из чего следует равенство длин отрезков С К и DK.
7. 	Свойство общей хорды двух пересекающихся окружностей
Общая хорда двух пересекающихся окружностей перпендикулярна прямой, содержащей их центры, и делится этой прямой пополам.
Обосновать этот факт просто: поскольку |AOi| = \ВО±\, а \А02\ = |-ВО219 обе точки Oi и О2 лежат на серединном перпендикуляре к отрезку АВ, поэтому 0\02 JL АВ, \АН\ = \ВН\.
8. 	Свойства касающихся окружностей
Если две окружности касаются (внутренним или внешним образом), то их центры и точка касания лежат на одной прямой.
Справедливость этого утверждения вытекает из того, что радиус окружности, соединяющий её центр с точкой её касания с некоторой прямой, перпендикулярен этой прямой.
Если две окружности касаются внешним образом, то длина отрезка их общей внешней касательной, заключённого между точками касания, равна удвоенному корню из произведения длин их радиусов, а их общая внутренняя касательная делит его пополам:
|Я!Я2| = 2y/\0\Hi\ ■ |02ff2|, \HiM\ = \Н2М\.


78
Теория и задачи
Докажем это утверждение. Положим \0\Н\\ = Д,
Юг#21 = г, будем считать, что R ^ г. Проведём отрезок 02N, параллельный #i#2- Тогда NH1H2O2 - прямоугольник,
|Я!Я2| = \NO2l \NHi \ = \02н2\ = г,
стало быть, |ОхАГ| = |Oi#i| — |-/V#i| = R — г. Также Н{ М Н2
заметим, что в силу того, что точки 0\, О2 и К лежат на одной прямой,
• IO1O2I = \OiK\ + \02к\ = R + г.
Записывая теорему Пифагора для треугольника O1O2N, получаем
|#1#2| = \N02\ = VIO1O2I2 - |OiAT|2 = y/(R + r)2 ~{R-r)2 = 2VRr.
После этого заметим, что в силу свойства касательных, проведённых из одной точки к окружности, \КМ\ = \H\M\, \КМ\ = \Н2М\, поэтому \H\M\ = |ЯгМ|. Утверждение доказано.
Примеры решения задач
П р и м е р 1. Касательная к окружности (К - точка касания) параллельна её хорде LM. Известно, что \LM\ = б, \КМ\ = 5. Найдите длину радиуса этой окружности.
Решение. Проведём диаметр этой окружности, проходящий через точку К. Поскольку К - точка касания, он будет перпендикулярен касательной из условия задачи, а поскольку хорда LM ей параллельна, он будет перпендикулярен и этой хорде. Обозначим точку пересечения хорды LM с этим диаметром буквой Н, центр окружности обозначим буквой О, а второй конец этого диаметра обозначим буквой Р.
Так как \LM\ = 6, а хорда, перпендикулярная диаметру, делится им пополам, то \LH\ = \НМ\ = 3. Из прямоугольного треугольника МКН находим
\КН\2 = \КМ\2 - \НМ\2 = 16 =» \КН\ = 4.
Теперь обозначим длину радиуса окружности буквой R, тогда
\КР\ = 2Д, \НР\ = \КР\ - \КН\ = 2R - 4.
Применяя теорему о произведении длин отрезков пересекающихся хорд, получаем
25
\LH\-\HM\ = \KH\-\HP\ => 9 = 4- (2R- 4) =» #=^-.
8
р
Ответ. —.


2.2. Касательные, хорды, секущие
79
Пример 2. Две окружности, длины радиусов которых равны 4 и 3, касаются друг друга внешним образом. К этим окружностям проведены общие касательные PQ и RS таким образом, что точки Р и S принадлежат большей окружности, а точки Q и R принадлежат меньшей окружности. Найдите длину радиуса окружности, касающейся отрезков RS, SP и PQ.
Решение. Центр окружности, касающейся отрезков RS, SP и PQ, лежит на пересечении биссектрис углов RSP и SPQ. Этот факт и будет отправной точкой решения.
Обозначим через О' и О" центры данных окружностей. Рассмотрим прямоугольную трапецию O’PQO". Поскольку окружности касаются друг друга, О10" = 7,
cos РОЮ"
\OfP\ - \OnQ\
sinPO'O" = i/l - — =
_1_
49
4^3
\0'0"\
Теперь строго обоснуем некоторые утверждения, которые почти очевидны из-за симметрии. Пусть L - точка пересечения прямых PQ и RS. Тогда обе окружности вписаны в угол PLS, поэтому точки О' и О" лежат на биссектрисе этого угла, \LP\ = |LS|. Значит, треугольник PLS равнобедренный, его биссектриса, проведённая из вершины L, является также его медианой и высотой. Это означает, что прямая О'О" перпендикулярна отрезку PS и проходит через его середину (обозначим её буквой Н).
С другой стороны, углы RSP и SPQ равны. Значит, если обозначить буквой О точку пересечения их биссектрис, то углы OSP и OPS также равны. Это означает, что \ОР\ = \OS\, так что точка О лежит на серединном перпендикуляре к отрезку PS, то есть на прямой О'О", и, кроме того, точка Н есть точка касания отрезка PS и окружности, длину радиуса которой мы ищем. Это легко доказать от противного. Пусть эта точка касания не есть точка Н, тогда обозначим её К. Треугольники ОКР и OKS равны (по гипотенузе и катету), значит \КР\ = \KS\. Противоречие с тем, что К - не середина PS.
Теперь осталось немного посчитать и найти искомую величину - \ОН\.
tgOPtf = tgQ(
f 7Г ,2
\PH\ = \PO'\smP'OH =
n 24
Ответ. —.
vph)) = tg \poh =
4 2 1 + cos PO’H 2
16V3
\OH\ - \PH\ tg OPH =
16л/3 у/з 24
Пример 3. В треугольнике ABC дано ВАС = а, ВС А = /3, \АС\ = Ь. На стороне ВС взята точка D так, что \BD\ — 3|£>С|. Через точки В и D проведена окружность, касающаяся стороны АС или её продолжения за точку А. Найдите длину радиуса этой окружности.


80
Теория и задачи
Решение. Для наглядности на чертеже отображены оба случая: точка касания прямой АС с окружностью (обозначим её буквой Н) может как попадать на отрезок АС, так и не попадать. Видно, что в этой задаче сразу даны базовые элементы треугольника ABC, просят же найти достаточно экзотическую величину. Искать её будем из равнобедренного треугольника DHO. Надо найти величину угла DOH и длину отрезка DH. Будем действовать последовательно и сначала определим длины сторон треугольника ABC, записав для него теорему синусов:
\АС 1 _ \АВ\ _ \ВС 1 sin ABC sin АС В sin ВАС b _ \AB\_ _ \BC\ sin(7r — a — /3) sin (3 sin a
\AB\
b sin/3 sin(a: + /3) ’
\BC\
6 sin a sin(a + /3) ’
Для сокращения записи полученную нами длину стороны ВС обозначим буквой Q. Далее, поскольку \BD\ = 3|-DC|, получаем \DC\ = -Q. Применяя теорему о произведении длины секущей на длину её внешней части, получаем
\СН\2 = \CD\ • \ВС\
\ch\2 = Q.q
\СН\ =
Теперь из треугольника CDH, используя теорему косинусов, найдём длину стороны DH и величину угла CHD:
\DH\2 = \CD\2 + \СН\2 -2-\CD\- \СН\ ■ cos DCH =»
\DH\ = ^ +
Q2 , Q2 Q2 cos/3
Q
16 4 4
|CD|2 = \CH\2 + \DH\2 - 2 • \CH\ ■ \DH\ ■ cos CHD
91
i6
2 — cos /3
D#| = ^ — 4cos/3;
4 16 4
Q2 cos /3 Q2 • \/5 — 4cos/3
cosCHD
cosCHD
sin CHD =
1 — cos2 /3
sin/
\/5 — 4 cos /3 y5 —4cos/3 У5 - 4 cos /3
Наконец, пользуясь свойством угла, образованного касательной и хордой, имеем DOH — 2CHD, где О - центр окружности. С учётом этого из равнобедренного треугольника DOH находим длину радиуса окружности:
\\РН\ _ \РН\ _ Д V5-4cosl _ Q(5 — 4cos/3)
sin \DOH
2 sin CHD
8sin/3
\/5—4 cos
Подставляя в эту формулу полученное ранее выражение для Q, получаем ответ. Из решения видно, что ответ не зависит от того, где находится точка А.
b sin a(b — 4cos/3)
Ответ.
8sin/3sin(a + /3)


2.2. Касательные, хорды, секущие
81
Пример 4. На стороне ВС треугольника АВС взята точка D такая, что CAD = 2 • BAD. Длины радиусов окружностей, вписанных в треугольники ACD и ABD, равны соответственно 8 и 4, расстояние между точками касания этих окружностей с прямой ВС равно у/129. Найдите \AD\.
А
Решение. Обозначим центр окружности, длина радиуса которой равна 4, буквой О, центр второй окружности обозначим буквой О'. Точки их касания с отрезком ВС обозначим как Н и Hf соответственно, а точки их касания с отрезком AD обозначим буквами J и 7. Выразим длину отрезка IJ двумя способами.
Рассмотрим прямоугольные треугольники AOJ и АО'1. Обозначим величину угла BAD через 2а, тогда по условию величина угла CAD равна 4а. Точки О и О' - центры вписанных в треугольники ABD и ACD окружностей, поэтому АО и АО' - биссектрисы углов BAD и CAD, стало быть, OAD = а, OfAD = 2а и
\AJ\ = \OJ\ctgOAJ = 4 ctg а,
—■*ctcr2 а — 1 4
IAZ1 = lO'JI ctg O'AI = 8 ctg 2а = 8 • — = 4 ctg о; < 4 ctg a = \AJ\.
2 ctg a ctg a
Значит, \DI\ > \DJ\. Теперь заметим, что DO - биссектриса угла ADB, а DO' - биссектриса угла ADC. Известно, что угол между биссектрисами смежных углов прямой, то есть О DO' = 7г/2. Поэтому ODJ = DO'I. Следовательно, треугольники ODJ и DO'I подобны, из чего вытекает
т _ т
\DJ\ \ОЧ\
\DJ\ ■ \DI\ = 32.
С другой стороны, |DH\ — \DJ\ и \DH'\ = \DI\ по теореме об отрезках касательных, проведённых из одной точки к окружности. С учётом этого мы имеем \DJ\ + \DI\ = \DH\ + \DH'\ = \HH\f = у/129. Решая полученную систему уравнений, находим
|Ш|. 2^1. т =


82
Теория и задачи
Поэтому \IJ\ = \DI\ — \DJ\ = 1. С другой стороны, \IJ\ = \AJ\ — \А1\ и получаем
4 ctg а — 8 ctg 2а = 1 => ■а + 4 ctg а = 1 => ctga = 4.
2 ctg а
Откуда \DJ\ = —-, |А/| = 4 ctg a = 16, \AD\ = \ AJ\ + \DJ\ = 31 +^129
31 + л/Т29
Ответ. .
2
Задачи
1. На боковой стороне ВС равнобедренного треугольника ABC как на диаметре построена окружность, пересекающая основание этого треугольника в точке D. Найдите расстояние от её центра до точки А, если \AD\ = \/3, ABC = 2тг/3.
2. В треугольнике ABC \АВ\ = 4, градусные меры углов ВАС и ABC равны 30° и 130° соответственно. На стороне АВ как на диаметре построен круг. Найдите площадь части этого круга, лежащей внутри треугольника ABC.
3. Из точки М на окружности проведены три хорды MN, МР и MQ таким образом, что \MN\ = 1, \МР\ = 6, \MQ\ = 2. При этом величины углов NMP и PMQ равны. Найдите длину радиуса этой окружности.
4. В треугольнике ABC с периметром 2р длина стороны АС равна а и величина острого угла ABC равна а. Вписанная в треугольник ABC окружность с центром О касается стороны ВС в точке К. Найдите площадь треугольника ВОК.
5. В треугольник ABC вписана окружность, которая касается его сторон АВ, ВС и АС в точках М, D и N соответственно. Вычислите длину отрезка MD, если известно, что \NA\ = 2, |iVC| = 3, БСМ = 7г/3.
6. Окружность касается сторон АВ и PC треугольника ABC соответственно в точках D и Е. Найдите длину высоты треугольника ABC, опущенной из вершины А, если |АВ| = 5, \АС\ = 2, а точки A,D,E и С лежат на одной окружности.
7. Две окружности касаются друг друга внешним образом в точке А. Их общая касательная касается первой окружности в точке Р, а второй в точке С. Прямая, проходящая через точки А и В, пересекает вторую окружность в точке D. Известно, что \АВ\ = 5, \AD\ = 4. Найдите \CD\.
8. В окружности, длина радиуса которой равна 4, проведены хорда АВ и диаметр АК, причём ВАК = 7г/8. В точке В проведена касательная к этой окружности, пересекающая продолжение диаметра АК в точке С. Найдите длину медианы AM треугольника ABC.


2.2. Касательные, хорды, секущие
83
9. 	В треугольнике АВС на стороне АС как на диаметре построена окружность, которая пересекает сторону АВ в точке М и сторону ВС в точке N. Известно, что длина отрезка АВ равна 3, длина отрезка АС равна 2, \АМ\ : \МВ\ =2:3. Найдите длину отрезка AN.
10. Окружность проходит через вершины А и С треугольника АВС, пересекает сторону А В в точке D и сторону ВС в точке Е. Найдите величину угла CDB, если \AD\ = 5, \АС\ = 2у/7, \ВЕ\ = 4, \BD\ : |СЯ| =3:2.
11. В четырёхугольник ABCD вписана окружность, длина радиуса которой равна 2. Угол DAB прямой, \АВ\ — 5, |ВС| = 6. Найдите площадь четырёхугольника ABCD.
12. Окружность, проходящая через вершину А треугольника АВС, касается стороны ВС в точке М и пересекает стороны АС и АВ в точках L и К соответственно. Найдите отношение |АС| : |АВ|, если известно, что длина отрезка CL в два раза больше длины отрезка В К, \СМ\ : \ВМ\ =3:2.
13. В круге с центром О хорда АВ пересекает радиус ОС в точке £), причём величина угла ADC равна 27г/3. Найдите длину радиуса окружности, касающейся отрезков AD,DC и дуги АС, если \ОС\ = 2, \OD\ = у/3.
14. Две окружности с радиусами разной длины касаются в точке А одной и той же прямой и расположены по разные стороны от неё. Отрезок АВ - диаметр окружности меньшего радиуса. Из точки В проведены две прямые, касающиеся окружности большего радиуса в точках М и N. Прямая, проходящая через точки М и А, пересекает меньшую окружность в точке К. Известно, что \МК\ = \/2 + \/3, ВМА = 7г/12. Найдите площадь фигуры, ограниченной отрезками касательных BM,BN и той дугой MN большей окружности, которая не содержит точку А.
15. Две окружности, длины радиусов которых относятся как (9 — 4у/3) : 1, касаются друг друга внутренним образом. Проведены две равные по длине хорды большей окружности, касающиеся меньшей окружности. Одна из этих хорд перпендикулярна отрезку, соединяющему центры окружностей, а другая нет. Найдите величину угла между этими хордами.
16. Две окружности, длины радиусов которых равны 6 и 8, пересекаются в точках А и В. Через центры Ог и О2 этих окружностей проведена прямая; Ci и С2 - две из четырёх точек пересечения этой прямой с окружностями, причём точка С\ лежит на окружности с центром Oi, а длина отрезка С1С2 больше 20. Найдите расстояние между точками 0\ и О2, если произведение площадей треугольников С1О1А и С2О2В равно 336.
17. В круге, длина радиуса которого равна 1, проведены хорды АВ и ВС. Найдите площадь части этого круга, лежащей внутри угла АВС, если угол ВАС острый, |АВ| = у/2 и |ВС| = 10/7.
18. Длина радиуса окружности, описанной около треугольника KLM, равна R. Через вершину L проведена прямая, перпендикулярная стороне КМ. Эту прямую пересекают в точках А и В серединные перпендикуляры к сторонам KL и LM. Известно, что \AL\ = а. Найдите \BL\.


84
Теория и задачи
19. В окружности, длина радиуса которой равна Д, проведены хорда АВ и диаметр АС. Хорда PQ, перпендикулярная диаметру АС, пересекает хорду А В в точке М. Известно, что \АВ\ = а, \РМ\ : \MQ\ = 1:3. Найдите длину отрезка AM.
20. Диаметр АВ и хорда CD окружности пересекаются в точке Е таким образом, что \СЕ\ = |<Di?| • Через точки В и С проведены две касательные к этой окружности, которые пересекаются в точке К. Отрезки А К и СЕ пересекаются в точке М. Найдите площадь треугольника С КМ, если \АВ\ = 10, |АБ| = 1.
21. Дана окружность с центром в точке О, длина радиуса которой равна 2. Из конца отрезка О А, пересекающегося с окружностью в точке М, проведена касательная АК к окружности. Величина угла ОАК равна 7г/3. Найдите длину радиуса окружности, касающейся отрезков А К, AM и дуги М К.
22. Площадь треугольника ABC равна 3\/Т5, а длина радиуса вписанной в него окружности равна \/15/3. Окружность, длина радиуса которой равна 5л/Т5/9 , касается лучей, образующих угол АС В, и вписанной в треугольник ABC окружности. Найдите tg ABC, если наибольшей из сторон треугольника ABC является сторона АС.
23. В треугольник ABC вписана окружность 7. Касательная к этой окружности, параллельная стороне ВС, пересекает сторону АВ в точке D и сторону АС в точке Е. Периметры треугольников ABC и ADE равны соответственно 40 и 30, ABC = 2/3. Найдите длину радиуса окружности 7.
24. В угол с вершиной А, величина которого равна 7г/3, вписана окружность с центром в точке О. К этой окружности проведена касательная, пересекающая стороны угла в точках В и С. Отрезок ВС пересекается с отрезком АО в точке М. Найдите длину радиуса окружности, вписанной в треугольник ABC, если \АМ\ : \МО\ =2:3, \ВС\ = 7.
25. Две окружности, длины радиусов которых равны Лиг, пересекаются в точках А и В и касаются некоторой прямой в точках С и D ; N - точка пересечения прямых АВ и CD (В между А и N). Найдите:
1) длину радиуса окружности, описанной около треугольника ACD ;
2) отношение длин высот треугольников N АС и NAD, опущенных из вершины N.
26. В треугольнике ABC ВАС = а, \АС\ = Ь. Вписанная в него окружность касается сторон АВ и ВС в точках М и N, биссектриса угла ВАС пересекает прямую MN в точке К. Найдите расстояние от точки К до прямой АС.
27. В угол вписано несколько окружностей, радиусы которых возрастают. Каждая следующая окружность касается предыдущей окружности. Найдите сумму длин второй и третьей окружностей, если длина радиуса первой равна 1, а площадь круга, ограниченного четвёртой окружностью, равна 647г.
28. На стороне О К острого угла КОМ взята точка L (L между О и К). Окружность проходит через точки К и L и касается луча ОМ в точке М.


2.2. Касательные, хорды, секущие
85
На дуге этой окружности LM, не содержащей точку К, взята точка N. Расстояния от точки N до прямых ОМ, О К и КМ равны га, к и I соответственно. Найдите расстояние от точки N до прямой LM.
29. На прямой взяты три точки L,M и N (М между L и JV, |LM| ф \MN\). На отрезках LM, M7V и LiV как на диаметрах построены полуокружности, серединами которых являются точки А, В и С соответственно. Точка С лежит по одну сторону, а точки А и В - по другую сторону от прямой LN. Найдите отношение площади фигуры, ограниченной этими тремя полуокружностями, к площади треугольника АВС.
30. В окружности 7 проведены хорды KL, MN, PS. Хорды KL и PS пересекаются в точке О, хорды KL и MN пересекаются в точке А, а хорды MN и PS пересекаются в точке В, причём \AL\ = \СК\, \АМ\ = |BiV|, \BS\ = 5, \ВС\ = 4. Найдите длину радиуса окружности 7, если величина угла ВАС равна 7г/4.
31. Дана окружность, длина диаметра MN которой равна 16. На касательной к этой окружности в точке М отложен отрезок МР, длина которого больше 15. Из точки Р проведена вторая касательная к окружности, пересекающая прямую MN в точке Q. Найдите площадь треугольника MPQ, если его периметр равен 72.
32. На стороне ВС остроугольного треугольника АВС (АВ ф АС) как на диаметре построена полуокружность, пересекающая высоту AD в точке М, Н - точка пересечения высот треугольника ABC, \AD\ = a, \MD\ = b. Найдите \АН\.
33. Три круга с центрами в точках Р, Q и R попарно касаются друг друга внешним образом в точках А, В и С. Известно, что PQR = 2 arcsin(l/3), а сумма длин радиусов всех трёх кругов равна 12\/2. Какую наибольшую длину может иметь окружность, проходящая через точки А, В, С?
34. Окружность, вписанная в равнобедренный треугольник АВС, касается его основания АС в точке D и боковой стороны АВ в точке Е. Точка F - середина стороны АВ, а точка G - точка пересечения окружности и отрезка FD, отличная от D. Касательная к окружности, проходящая через точку G, пересекает сторону АВ в точке Н. Найдите величину угла ВС А, если известно, что |Pjff| : |НЕ\ = 2:3.
35. Из точки А проведены к окружности две касательные (М и N - точки касания) и секущая, пересекающая эту окружность в точках В и С, а хорду MN в точке Р. Известно, что \АВ\ : \ВС\ =2:3. Найдите \АР\ : |РС|.
36. Две окружности с центрами А и В и длинами радиусов соответственно 2 и 1 касаются друг друга. Точка С лежит на прямой, касающейся каждой
3\/5
из окружностей, и находится на расстоянии от середины отрезка А В.
Найдите площадь 5 треугольника АВС, если известно, что S > 2.


86
Теория и задачи
3. 	Четырёхугольники и многоугольники
з.1. Параллелограммы Теоретический материал
Ломаной AiA2A^...An называется фигура, состоящая из точек А\, А2, ... , Ап (вершин ломаной) и соединяющих их отрезков А\А2, А2А$, ... , Ап-\Ап (звеньев ломаной).
Простым многоугольником называется замкнутая ломаная без самопересечений, соседние звенья которой не лежат на одной прямой.
Поскольку в элементарной геометрии рассматриваются только простые многоугольники, в дальнейшем по умолчанию под многоугольником будет подразумеваться простой многоугольник. Случаи, когда имеется в виду многоугольник с самопересечениями, будут оговариваться отдельно.
Определение. Параллелограммом называется четырёхугольник, противоположные стороны которого попарно параллельны.
Заметим, что параллелограмм является выпуклым четырёхугольником (то есть лежит в одной полуплоскости относительно любой прямой, содержащей его сторону), его диагонали пересекаются и (как диагонали любого выпуклого многоугольника) лежат внутри него.
1. 	Свойства параллелограмма
Если четырёхугольник является параллелограммом, то
1. Величины его противоположных углов равны.
2. Длины его противоположных сторон равны.
3. Его диагонали пересекаются и точкой пересечения делятся пополам.
4. Треугольники, на которые он разбит диагоналями, имеют равные площади.
5. Сумма квадратов длин его диагоналей равна сумме квадратов длин его сторон.
Рассмотрим параллелограмм ABCD, точку пересечения его диагоналей обозначим буквой О. Поскольку AB\\CD и AD\\BC, в силу свойств внутренних накрест лежащих углов при параллельных прямых
АСВ = CAD, ACD = САВ,
ABD = BDC, CBD = ADB.
Из этого вытекает, что, во-первых,
ABC = ABD + CBD = CDB + ADB = ADC,
ШЗ = ШС + CAD = ACD + ACB = BCD
и, во-вторых, треугольники ABC и CD А равны по второму признаку равенства треугольников. Значит, \АВ\ = \CD\ и \ВС\ = \AD\. Но тогда треугольники
В С


3.1. Параллелограммы
87
АОВ и COD также равны по второму признаку равенства треугольников, поэтому \АО\ = \ОС\ и \ВО\ = \OD\. Из этих равенств с учётом того, что синусы величин углов АОВ, ВОС, COD и AOD равны (так как эти углы смежные/вертикальные), мы получаем и равенство площадей всех треугольников, на которые параллелограмм разбит своими диагоналями.
Последнее свойство проще всего доказать так: углы АВС и BAD являются внутренними односторонними при параллельных прямых ВС, AD и секущей АВ, поэтому сумма их величин равна 7г, а косинусы их величин противоположны по знаку. Записывая теорему косинусов для треугольников АВС и BAD, учитывая, что \AD\ = \ВС\, \АВ\ = |C.D|, и складывая полученные соотношения, получаем
\BD\2 = \АВ\2 + \AD\2 - 2 • \АВ\ ■ \AD\ ■ cos BAD = = \CD\2 + \AD\2 + 2 • \AB\ ■ \BC\ ■ cos ABC, \AC\2 = \AB\2 + \BC\2 - 2 • |AB| • \BC\ • cos ABC =>
=► \AC\2 + |B£>|2 = \AB\2 + | BCf + \CD\2 + \AD\2.
Свойства параллелограмма доказаны.
2. 	Признаки параллелограмма
Если для четырёхугольника выполнено хотя бы одно из утверждений:
1. Величины его противоположных углов равны.
2. Длины его противоположных сторон равны.
3. Две его противоположные стороны параллельны и равны по длине.
4. Его диагонали делятся пополам точкой их пересечения, то он является параллелограммом.
В дополнение к этим четырём основным признакам параллелограмма докажем ещё два вспомогательных признака.
Если для выпуклого четырёхугольника выполнено хотя бы одно из утверждений:
а) Треугольники, на которые он разбит диагоналями, имеют равные площади.
б) Сумма квадратов длин диагоналей равна сумме квадратов длин его сторон, то он является параллелограммом.
Рассмотрим выпуклый четырёхугольник ABCD.
а) 	Пусть площади треугольников АОВ,
ВОС, COD и DO А равны. Запишем формулы площади для треугольников АОВ и ВОС:
Saaob = ^ • \ АО\ ■ \ОВ\ • sin АОВ, Saboc = \ ■ \ВО\ ■ \ОС\ ■ sin ВОС.
Теперь заметим, что синусы смежных углов АОВ и ВОС равны, и почленно поделим друг на друга полученные соотношения. Получим \АО\ = |ОС|. Аналогично доказывается, что \ВО\ = |OD|, значит, в силу доказанного ранее, ABCD - параллелограмм.
В С


88
Теория и задачи
б) 	Доказательство последнего признака посложнее, чем предыдущие. Введем обозначения \АО\ = а, \ВО\ = 6, \СО\ = с, \DO\ = d, АОБ = а. Тогда
COD = a, ВОС = AOD = TT-a, \АС\ = а + с, \BD\=b + d.
Запишем теорему косинусов для треугольников ЛОВ, ВОС, COJ9 и DO А:
|АВ|2 = а2 + Ь2 — 2a6cosa, |J5C|2 = 62 + с2 + 26с cos а,
|CD|2 = с2 + d2 — 2cdcosa, |AD|2 = а2 + d2 + 2adcosa.
После этого, сложив полученные соотношения и воспользовавшись тем, что
\АВ\2 -f \ВС\2 + \CD\2 + \AD\2 = \АС\2 + \BD\2,
мы получаем
2(a2 -f Ь2 + с2 + (i2) + 2(ad + Ъс — ab — cd) cos a = (a + c)2 + (b -f c?)2
(a — c)2 + (b — d)2 — 2(a — c)(b — d) cos a = 0.
Если b = d, то из полученного уравнения вытекает, что а = с, то есть диагонали четырёхугольника ABCD точкой пересечения делятся пополам и по доказанному выше он является параллелограммом. Если b ф d, то, деля обе части уравнения на (b — d)2, находим
а — с D о
— 2 cos а • + 1 = 0, — — cos а — 1 ^ 0 => а = 7ггг, n € Z.
b — d 4
Но величина угла АОВ лежит в интервале (0, тг), поэтому в случае Ъ ф d уравнение решений не имеет. Признаки параллелограмма доказаны.
3. Площадь параллелограмма
Площадь параллелограмма ABCD может быть вычислена по формулам S-\AB\-\AD\-wiBAD, S = \AD\ ■ hi = \АВ\ ■ h2, S = | • \AC\ ■ \BD\ ■ sin a,
где hi и /12 - длины высот параллелограмма ABCD, проведенных к его сторонам AD и А В соответственно, а а - величина угла между его диагоналями.
4. Вписанная и описанная окружности
В параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом.
Около параллелограмма можно описать окружность тогда и только тогда, когда он является прямоугольником.
Примеры решения задач
Пример 1. Периметр параллелограмма ABCD равен 26, величина угла ABC равна 27г/3, а длина радиуса окружности, вписанной в треугольник BCD, равна у/З. Найдите длины сторон параллелограмма ABCD, если известно, что длина стороны AD больше длины стороны АВ.
b-d


3.1. Параллелограммы
89
Решение. Поскольку ABCD - параллелограмм, имеем \АВ\ = \CD\,
\AD\ = \ВС\. С учётом этого из того, что периметр ABCD равен 26, вытекает, что \ВС\ + \CD\ = 13. Поэтому, если обозначить длины отрезков AD и ВС через у, то длины отрезков АВ и CD равны 13 — у. По условию задачи \AD\ > \АВ\, то есть у > 13 — у <=Ф у > 13/2.
Далее, поскольку прямые АВ и CD параллельны, по свойствам внутренних односторонних углов BCD = п — АВС = 7г/3. Записав для треугольника BCD теорему косинусов, имеем
\BD\2 = \BC\2 + \CD\2-2-\BC\-\CD\-сое BCD => \BD\ = у/3 у2 - 39 у + 169.
Теперь обозначим центр окружности, вписанной в треугольник BCD, буквой О, а точку её касания со стороной ВС обозначим буквой К. Тогда СО - биссектриса угла BCD, то есть ОС К = 7г/6 и по свойствам отрезков, на которые окружность, вписанная в треугольник, делит его стороны, \СК\ = pabcd — \BD\. Наконец, из прямоугольного треугольника ОС К имеем
\ок\ = \ск\-ьёдск => V3 = 13~ \/%2~39^ +--•? • 4= =►
2 л/3
y/Зу2 - 39у + 169 = 7.
Возводя в квадрат полученное уравнение, находим
3у2 - 39у + 169 = 49 => у2 — 13у + 40 = 0 => у = 8 или у = 5.
Ну а поскольку у > 13/2, получаем
\AD\ = |ВС| = у = 8, |АВ| = |СТ>| = 13 — у = 5.
Ответ. |i4D| = |BC|=8, |АВ| = |С£)| = 5.
Пример 2. В плоскости даны квадрат ABCD и точка О. Известно, что площадь квадрата ABCD больше 225, \ОВ\ = \OD\ = 13, \ОС\ = 5у/2. Найдите длину стороны А В и выясните, где расположена точка О - вне или внутри квадрата ABCD.
Решение. Обозначим середину диагонали BD буквой К и заметим, что точка О по условию задачи равноудалена от точек В и D. Это означает, что она лежит на серединном перпендикуляре к отрезку BD, то есть на прямой, проходящей через точку К и перпендикулярной BD. С другой стороны, ABCD - квадрат, поэтому его диагонали перпендикулярны и пересекаются в точке К. Из этих двух фактов следует, что точка О лежит на прямой АС.
К


90
Теория и задачи
Далее, поскольку площадь квадрата равна g квадрату длины его стороны, из условия задачи вытекает, что \АВ\ = \ВС\ > 15. Теперь учтем, что АВ, ВС и О В - наклонные, опущенные из вершины В на прямую АС, \АВ\ = \ВС\ > \ОВ\, из чего вытекает, что \АК\ = |C7f| > |ОХ|, стало быть, точка О лежит внутри квадрата ABCD.
Вообще говоря, точка О может лежать как на отрезке КС (этот вариант обозначим буквой СУ), так и на отрезке АК (этот вариант обозначим буквой О"). Положим \ВК\ = х > 0, тогда \КС\ = х,
\АВ\ = V\BK\2 + |АГС|2 = *V2,
|0'tf| = = V\OB\2 - \ВК\2 = \/169 — ж2.
Рассмотрим оба варианта расположения точки О. Для варианта O' в силу равенства \КС\ = \0'К\ -f |0'С| получаем уравнение х = \/169 — х2 + 5\/2, ИЗ которого нетрудно получить х = 17/ч/2- Тогда |ЛВ| = 17, что удовлетворяет условию задачи. В другом варианте \КС\ = \OffC\ — \0"К\, что дает нам уравнение х = \/169 — х2 — 5л/2. Решением этого уравнения является х = 7/\/2, но тогда
|АВ| = 7, что противоречит условию задачи.
Ответ. 17, точка О лежит внутри квадрата.
Пример 3. В параллелограмме ABCD точки Е и F лежат соответственно на сторонах АВ и ВС таким образом, что \АЕ\ = 2\ВЕ\, \BF\ = 3|CF|. М - точка пересечения прямых AF и DE. Найдите численное значение отношения \АМ\ : \MF\.
Решение. Конфигурация, описанная в этой задаче, является довольно стандартной: даны какие- то отношения длин отрезков и отношение же просят найти. В таких случаях, как правило, применяют подобие или теорему Менелая. Однако, если мы ограничимся тем, что изобразим параллелограмм ABCD и построим отрезки AF и DE, то на чертеже не найдется ни подобных треугольников, ни д ^
конструкции, к которой можно будет применить теорему Менелая. Поэтому придется делать дополнительное построение, а именно продолжим прямую DE до пересечения с прямой ВС в точке N.
Введём обозначения \ВЕ\ = х, \CF\ = у, тогда по условию задачи \АЕ\ = 2х, \BF\ = 3у, \ВС\ = 4у и по свойствам параллелограмма \AD\ = 4у. Треугольники ADE и BNE подобны, что даёт нам


3.1. Параллелограммы
91
Треугольники ADM и FNM подобны, что даёт нам
\АМ\ \AD\ _ \АМ\ 4 у 4
\MF\ ~ |FJV| ^ \MF\ ~ Ьу ~ 5'
Ответ. 4:5.
Пример 4. В треугольник АВС вписан квадрат, две вершины которого лежат на стороне АС, одна на стороне АВ и одна на стороне ВС. Через середину D стороны АС и центр этого квадрата проведена прямая, которая пересекается с высотой ВН треугольника АВС в точке Е. Найдите площадь треугольника DEC, если \АВ\ = 6, \ВС\ = 5 и \АС\ = 7.
Решение. При первом взгляде на условие этой задачи может показаться, что она чисто счётная. В самом деле, даны все длины сторон треугольника АВС, поэтому рано или поздно, так или иначе, можно вычислить все величины, присутствующие в этой задаче. Однако такой лобовой путь приведет к весьма большому объёму работы. Поэтому будем рассуждать так: запишем формулы площади треугольников АВС и DEC и вычислим их отношение:
Saabc = \ • \АС\ ■ \ВН\,
Sadec = j ' \DC\ ■ \ЕН\
Sadec \ЕН\ \DC\ \ЕН\
Saabc \ВН\ \АС\ 2\ВН[
Итак, фактически нам надо лишь найти, в каком отношении точка Е делит высоту ВН. Обозначим вершины квадрата буквами К, L, М и N таким образом, что точка L лежит на стороне ВС, точка М лежит на стороне АВ, а его центр обозначим буквой О.
Проведем отрезок BD, точку его пересечения с отрезком LM обозначим буквой Q'. Так как LM\\AC, треугольник BLM подобен треугольнику ВС А, и поскольку BD - медиана треугольника ВС A, BQ' - медиана треугольника jBLM, то есть Q' - середина LM. Из
этого следует, что если мы опустим перпендикуляр Q'Q на сторону АС, то он будет содержать точку О, причем \QrO\ = \OQ\.
Далее, так как QQ'WBH, треугольник DQQ' подобен треугольнику DHB, и поскольку DO - медиана треугольника DQQ', DE - медиана треугольника DHB, то есть Е - середина ВН, или \ЕН\ : |ВН\ = 1:2. Осталось получить ответ:
Раавс
= = 9, Saabc = V9 • 2 • 3 • 4 = бл/б, Sadec — тSaabc —
Зх/б
Ответ.
3V6


92
Теория и задачи
Задачи
1. Найдите площадь равностороннего треугольника, сторона которого равна стороне ромба с диагоналями длины 10 и 12.
2. В квадрат, площадь которого равна 18, вписан прямоугольник так, что на каждой стороне квадрата лежит одна вершина прямоугольника. Длины сторон этого прямоугольника относятся как 1:2. Найдите площадь прямоугольника.
3. В параллелограмме ABCD биссектриса угла BAD пересекает сторону CD в точке М таким образом, что \DM\ : \МС\ = 2. Найдите величину угла BAD, если известно, что САМ = а.
4. В прямоугольнике ABCD сторона А В втрое длиннее стороны ВС. Внутри него лежит точка iV, причём |A/V| = \/2, \BN\ = 4л/2, |£W| = 2. Найдите косинус величины угла BAN и площадь прямоугольника ABCD.
5. В ромбе ABCD величина угла при вершине А равна 7г/3. Точка N делит сторону АВ в отношении 2:1, считая от точки А. Найдите tgDNC.
6. В ромбе ABCD, длина стороны которого равна б, на стороне ВС взята точка Е таким образом, что \СЕ\ = 2. Найдите расстояние от точки Е до центра ромба, если BAD = 7г/3.
7. Площадь прямоугольника ABCD равна 48, а длина его диагонали равна 10. На плоскости, в которой расположен прямоугольник ABCD, выбрана точка О так, что \ОВ\ = \OD\ = 13. Найдите расстояние от точки О до наиболее удалённой от нее вершины прямоугольника ABCD.
8. В выпуклом четырёхугольнике ABCD точки Е, F, Н и G являются соответственно серединами отрезков АВ, ВС, CD и AD \ О - точка пересечения отрезков ЕН и FG. Известно, что \ЕН\ = a, \FG\ = 6, FOH — а. Найдите длины диагоналей четырёхугольника ABCD.
9. Выпуклый четырёхугольник ABCD описан вокруг окружности с центром в точке О. Найдите его периметр, если известно, что \АО\ — \ОС\ = 1, \ВО\ = \OD\ = 2.
10. В ромб, одна из диагоналей которого имеет длину 10, вписан круг площади 97г . Вычислите площадь части ромба, расположенной вне круга.
11. В параллелограмме ABCD длины диагоналей АС и BD равны d\ и d2 (di "ф- d2)• Найдите площадь параллелограмма ABCD, если ABC = а.
12. Через вершину А и середину М стороны ВС параллелограмма ABCD, площадь которого равна 1, проведена прямая, пересекающая диагональ BD в точке О. Найдите площадь четырёхугольника OMCD.
13. В параллелограмме ABCD \АВ\ = \BD\ = 1, а длины его диагоналей относятся как 1 : УЗ. Найдите площадь той части круга, описанного около треугольника В DC, которая не принадлежит кругу, описанному около треугольника ADC.


3.1. Параллелограммы
93
14. В параллелограмме PQRS биссектриса угла при вершине Р, градусная мера которого равна 80°, пересекает сторону RS в точке L. Найдите длину радиуса окружности, касающейся отрезка PQ и лучей QR и PL, если известно, что \PQ\ = 7.
15. В параллелограмме ABCD величина угла BCD равна 57г/6, а длина основания AD равна 8. Найдите длину радиуса окружности, касающейся прямой CD и проходящей через вершину А, а также пересекающей основание AD на расстоянии 2 от точки D.
16. Окружность, длина диаметра которой равна \/Тб, проходит через соседние вершины А и В прямоугольника ABCD. Длина касательной, проведённой из точки С к этой окружности, равна 3, а \АВ\ = 1. Найдите все возможные значения, которые может принимать длина стороны ВС.
17. В прямоугольнике ABCD, в котором \AD\ = 3+3\/2/2, а \АВ\ = 6, расположены две окружности. Окружность с центром в точке К, длина радиуса которой равна 2, касается сторон А В и AD. Окружность с центром в точке L, длина радиуса которой равна 1, касается стороны CD и первой окружности. Найдите площадь треугольника СLM, если М - основание перпендикуляра, опущенного из вершины В на прямую, проходящую через точки К и L.
18. Окружность, проходящая через вершины В, С и D параллелограмма ABCD, касается прямой AD и пересекает прямую АВ в точках В и Е. Найдите длину отрезка АЕ, если \AD\ = 4 и |CJ5| = 5.
19. В параллелограмме проведены биссектрисы всех внутренних углов. Четырёхугольник, образованный точками пересечения этих биссектрис, имеет площадь, равную двум третям площади исходного параллелограмма. Найдите отношение длин большей и меньшей сторон исходного параллелограмма.
20. Через вершины А, В и С параллелограмма ABCD проведена окружность, пересекающая прямую BD в точке Е таким образом, что \ВЕ\ = 9. Найдите |£D|, если \АВ\ = 3, \ВС\ =5.
21. Стороны ромба EFGH являются гипотенузами прямоугольных равнобедренных треугольников EAF, PDG, GCH и НВЕ, причём все эти треугольники имеют общие внутренние точки с ромбом EFGH. Сумма площадей четырёхугольника ABCD и ромба EFGH равна 12. Найдите \GH\.
22. В параллелограмме лежат две окружности, касающиеся трех его сторон и другой окружности каждая. Длина радиуса одной из них равна 1. Также известно, что длина одного из отрезков стороны параллелограмма от вершины до точки касания с одной из окружностей равна л/3. Найдите площадь параллелограмма.
23. В ромб ABCD, у которого \АВ\ = I и BAD = 2а, вписана окружность. Касательная к этой окружности пересекает сторону АВ в точке М, а сторону AD в точке N. Известно, что \MN\ = 2а. Найдите длины отрезков MB и ND, если известно, что \МВ\ < |iV\D|.


94
Теория и задачи
24. На стороне АВ треугольника ABC взята точка D таким образом, что |CD\ = л/13 и sin ACD : sin BCD = 4:3. Через середину отрезка CD проведена прямая, пересекающая стороны АС и ВС в точках М и N соответственно. Известно, что АС В = 27г/3, площадь треугольника MCN равна 3\/3, а расстояние от точки М до прямой АВ в два раза больше расстояния от точки N до этой же прямой. Найдите площадь треугольника ABC.
25. В параллелограмме ABCD диагонали пересекаются в точке О, а длина диагонали BD равна 12. Расстояние между центрами окружностей, описанных около треугольников AOD и COD, равно 16. Длина радиуса окружности, описанной около треугольника АОВ, равна 5. Найдите площадь параллелограмма ABCD.
26. В параллелограмме ABCD величина угла между диагоналями АС и BD равна 7г/6. Известно, что \АС\ : \BD\ = 2 : \/3 * Точка В\ симметрична точке В относительно прямой АС, а точка С\ симметрична точке С относительно прямой BD. Найдите отношение площадей треугольника АВ\С\ и параллелограмма ABCD.
27. Дан параллелограмм ABCD, \АВ\ = 3, \AD\ = л/3 + -BAD = 7г/3. На стороне АВ взята точка if таким образом, что \АК\ : \КВ\ = 2 : 1. Через точку К параллельно AD проведена прямая. На этой прямой внутри параллелограмма ABCD выбрана точка L, а на стороне AD выбрана точка М так, что \АМ\ = \KL\. Прямые ВМ и CL пересекаются в точке N. Найдите величину угла BKN.
3.2. 	Трапеции Теоретический материал
Определение. Трапецией называется четырёхугольник, две противоположные стороны которого параллельны. Эти стороны называются основаниями трапеции, а две другие его стороны называются боковыми сторонами трапеции.
Отметим, что трапеция является выпуклым четырёхугольником и, согласно этому определению, параллелограмм является частным случаем трапеции.
Замечание.В некоторых учебных пособиях под трапецией подразумевается четырёхугольник, у которого две противолежащие стороны параллельны, а две другие не параллельны.
1. 	Средняя линяя трапеции
Средняя линяя трапеции параллельна её основаниям, а её длина равна полусумме длин оснований трапеции.
Для доказательства этого факта рассмотрим трапе- A DM
цию ABCD с основаниями AD и ВС, К - середина АВ, L - середина CD. Продолжим отрезок BL за точку L до пересечения с прямой AD в точке М. Тогда углы BLC и DLM равны как вертикальные, а углы BCL и LDM равны как внутренние накрест лежащие при параллельных прямых AD и ВС и секущей CD. Учитывая тот факт, что


3.2. Трапеции
95
\CL\ = |ZXL|, мы получаем, что треугольники BCL и MDL равны по второму признаку равенства треугольников, что даёт нам \ВС\ = \DM\, \BL\ = \LM\.
Стало быть, отрезок KL является средней линией треугольника АВМ, поэтому, во-первых, KL\\AD (из чего сразу следует, что KL\\BC) и, во-вторых, \KL\ = \\АМ\ = ^(\AD\ + \DM\) — \(\AD\ 4-1ВС\). Утверждение доказано.
2. 	Высота трапеции
Длины боковых сторон трапеции можно вычислить с помощью деления длины высоты трапеции на синус величины соответствующего угла при основании трапеции:
\PQ\ . ,_nl \PQ\
\АВ\ =
\CD\ =
sin BAD sinCDA
Площадь трапеции равна произведению полусуммы длин её оснований и длины её
высоты:
Sabcd = W t|ДС| • \pQ\ = \KL\ • \pQ\■
в
I
>
С
к/
•1
V
/,
F
I7
D
Рассмотрим трапецию ABCD с основаниями AD и ВС,
К - середина АВ, L - середина CD, PQ - её высота. Для доказательства первого из приведенных утверждений достаточно опустить перпендикуляры из точек В и С на основание AD и рассмотреть соответствующие прямоугольные треугольники, учитывая, что длины проведённых перпендикуляров равны длине высоты PQ. Второе утверждение легко обосновывается с помощью рассмотрения треугольников ABD и BCD, площади которых равны | • \AD\ • \PQ\ и | • \ВС\ • \PQ\ соответственно. Ну а сумма их площадей как раз равна площади трапеции ABCD.
3. 	Диагонали трапеции
Теорема. Диагонали трапеции делят её на четыре треугольника, два из которых
подобны (AAOD ~ АСОВ), а два других равновелики (S&aob = S&cod)• При
этом справедливы следующие соотношения:
Saaod __ f\AD\\2 Saaod _ \AD\
Sacob ~ \\BC\J 5 SAAOB “ \BC\'
Доказательство. Поскольку прямые AD и ВС параллельны, а АС - секущая, углы CAD и АСВ равны, как внутренние накрест лежащие.
С другой стороны, углы AOD и СОВ равны, как вертикальные, поэтому треугольники AOD и СОВ подобны по двум углам. Это дает нам следующее соотношение:
\АО\ \РО\ \АР\
\ОС\ \ОВ\ I всу
где к - коэффициент подобия этих треугольников. Первое из соотношений теоремы немедленно вытекает из того, что площади подобных треугольников относятся как квадрат коэффициента их подобия.


96
Теория и задачи
Теперь опустим из точек В и С на прямую AD перпен- В С
дикуляры ВН и С К. Длины этих отрезков равны (каждая из этих длин фактически есть расстояние между параллельными прямыми AD и ВС). С учётом этого, записывая формулы площади треугольников ABD и ACD, получаем д
S&abd = -\AD\-\BH\; S&acd = \-\AD\-\CK\ =► Saabd = Saacd-
Осталось заметить, что
Saaob — Saabd - Saaod; Sacod = Saacd - Saaod,
поэтому Saaob = Sacod • Наконец, воспользуемся тем, что углы AOD и АОБ смежные, поэтому сумма их величин равна 7г, а их синусы равны. Значит,
Saaod _ \ • [ЛО[ • |£>Q[ sin ЛОР _ |1Ю| _ ]AD|
Saaob ~~ I • |АО| • |ОВ| • sinAOB ~ \ОВ\ ~ \ВС\'
Теорема доказана.
4. 	Свойства точки пересечения диагоналей и точки пересечения боковых сторон трапеции
Теорема. Пусть в трапеции ABCD стороны AD\\BC, Е - точка пересечения
прямых АВ и CD, Р и Q - середины оснований AD и ВС соответственно, О -
точка пересечения диагоналей. Тогда точки Р, Q, О и Е лежат на одной прямой.
Доказательство. Докажем, что прямая, проходящая через точки Е и О, проходит также и через середины оснований трапеции. р
Изначально будем считать, что точки Р и Q являются всего лишь точками пересечения этой прямой с основаниями трапеции.
Поскольку прямые AD и ВС параллельны, треугольник АЕР подобен треугольнику BEQ, а треугольник DEP подобен треугольнику CEQ. Из этих подобий находим
\АР\ _ \ЕР\ \DP\ _ \ЕР\ \АР\ _ \DP\
\BQ\ ~ \EQ\ ’ \CQ\ ~ \EQ\ ^ \BQ\ ~ \CQ\' A " P " D
С другой стороны, треугольник АОР подобен треугольнику COQ, а треугольник DOP подобен треугольнику BOQ. Из этих подобий вытекает
\АР\ _ \ОР\ \DP\ _ \ОР\ \АР\ _ \DP\
\CQ\~\OQ\' \BQ\~ \OQ\ \CQ\~ \BQ[
Почленно разделив друг на друга полученные соотношения, получаем = |щ => \BQ\ = \CQ\ => \AP\ = \DP\, то есть Р и Q - середины оснований AD и ВС соответственно. Теорема доказана.


3.2. Трапеции
97
5. Вписанная в трапецию окружность
В трапецию можно вписать окружность тогда и только тогда, когда сумма длин оснований трапеции равняется сумме длин её боковых сторон.
Теорема. Если в трапецию ABCD (AD\\BC) можно вписать окружность с центром в точке О, то точка О является точкой пересечения биссектрис всех внутренних углов трапеции, длина высоты трапеции ABCD равна удвоенной длине радиуса этой окружности, углы АОВ и COD - прямые.
Доказательство. Точки касания окружности, вписанной в ABCD, со сторонами АВ, ВС, CD и AD обозначим буквами К, L, М и N соответственно.
Тогда \ОК\ = \OL\ = \ОМ\ = |OiV|, то есть точка О равноудалена от отрезков АВ, ВС, CD и AD, из чего следует, что точка О лежит на биссектрисе каждого из углов ABC, BCD, CD А и DAB.
Заметим, что OL ± ВС и OTV _L AD. Из этого с учётом параллельности прямых AD и ВС вытекает параллельность прямых OL и ON. Но у этих прямых есть общая точка О, поэтому они совпадают, то есть точки L, О и N лежат на одной прямой, перпендикулярной основаниям трапеции. Стало быть, LN - высота трапеции ABCD и \LN\ = \OL\ + \ON\ = 2г, где г - длина радиуса окружности, вписанной в ABCD.
Наконец, углы АВС и DAB являются внутренними односторонними при параллельных прямых AD и ВС и секущей АВ, поэтому ABC + DAB = 7г.
АО и ВО - биссектрисы углов DAB и АВС, значит,
OAB + OBA = lDAB + lABC = ^; АОВ = тг — (ОАВ + ORA) = £.
Zi Zi Zi z
To, что угол COD тоже прямой, доказывается абсолютно аналогично. Теорема доказана.
6. Равнобедренная трапеция
Определение. Равнобедренной трапецией называется трапеция, боковые стороны которой равны по длине и непараллельны.
Отметим, что, давая такое определение, мы не берём в рассмотрение параллелограммы. Для всех параллелограммов, за исключением прямоугольников, приведённые ниже свойства не будут выполняться. Тем не менее, для единообразия прямоугольники мы тоже исключим из рассмотрения.
Рассмотрим равнобедренную трапецию ABCD (AD||BC), будем считать, что |AD| > |ВС|. Пусть ВН и С К - её высоты.
Теорема. Следующие утверждения эквивалентны:
1. Трапеция ABCD равнобедренная.
2. Величины углов при каком-либо из оснований трапеции ABCD равны.
3. Длины диагоналей трапеции ABCD равны.
4. Величины углов CAD и ADB (или CBD и АСВ ) равны.
5. Длины отрезков АН и KD равны (полуразности длин оснований AD и ВС).
6. Около трапеции ABCD можно описать окружность.
В L С
4 Геометрия


98
Теория и задачи
Доказательство. Сначала докажем все свойства равнобедренной трапеции, то есть тот факт, что из утверждения 1 вытекают все остальные.
Поскольку \АВ\ = \CD\, \ВН\ = \СК\, прямоугольные треугольники АВН и DC К равны по гипотенузе и катету, что дает нам равенство длин отрезков АН и KD. Заметим, что ВНКС - прямоугольник, поэтому \НК\ = \ВС\. Отсюда с учётом того, что \АН\ + \НК\ + \KD\ = |AD|, немедленно вытекает \АН\ = \KD\ = \{\AD\ — \ВС\). Таким образом, 1 => 5.
Далее, из равенства треугольников АВН и DC К вытекает и равенство углов BAD и ADC. Ну а поскольку сумма величин углов BAD и ABC равна 7г и сумма величин углов ADC и BCD равна п (по свойствам односторонних углов), равны и углы ABC и BCD, стало быть, 1 => 2.
Раз равны углы BAD и ADC, то равны и треугольники ABD и DC А (по двум сторонам и углу между ними). Поэтому \АС\ = \BD\ и /ADB = /CAD. Но угол ADB равен углу CBD, а угол CAD равен углу АС В (по свойствам внутренних накрест лежащих углов), значит, равны и углы АС В и CBD. Итак, 1 => 3 и 1 =* 4.
Наконец, заметим, что прямая, соединяющая середины оснований трапеции ABCD, им перпендикулярна. Это вытекает из того, что она проходит через точку пересечения прямых АВ и CD, и равнобедренности треугольника, образованного этой точкой и точками А и D. Точка О пересечения этой прямой и серединного перпендикуляра к стороне АВ и будет центром окружности, описанной около трапеции ABCD, так как О по построению равноудалена от всех вершин трапеции. Свойства равнобедренной трапеции доказаны.
Теперь докажем признаки равнобедренной трапеции. Пусть величины углов при каком-либо из оснований трапеции ABCD равны. Тогда неминуемо равны углы BAD и ADC, что даёт нам равенство прямоугольных треугольников АВН и DC К по катету и острому углу. Отметим, что равенство этих треугольников вытекает и из того факта, что \АН\ = \KD\. Ну а раз треугольники равны, то и \АВ\ = \CD\. Значит, 2 => 1 и 5 => 1.
Если равны длины отрезков АС и BD, то треугольники АС К и DBH равны по гипотенузе и катету, а если /CAD = ZADB /АСВ = /CBD, то они
равны по катету и острому углу. Поэтому в любом случае \АК\ = \HD\, но поскольку \АК\ = \АН\ + \НК\ и \HD\ = \НК\ + \KD\, получаем \АН\ = \KD\. Таким образом, 3=>5=^1 и 2=^5=> 1.
Наконец, если около трапеции ABCD можно описать окружность, то по свойствам вписанных углов ABC + ADC = 7г и по свойствам односторонних углов ABC + BAD — 7г. Значит, углы ADC и BAD равны, то есть 6 => 2 =Ф- 1. Теорема доказана.
Приведём также два свойства, касающиеся произвольных четырёхугольников, которые будут полезны при решении задач этого раздела.
I. 	Площадь произвольного выпуклого четырёхугольника равна половине произведения длин его диагоналей на синус величины угла между ними.
И. Если диагонали выпуклого четырёхугольника перпендикулярны, то суммы квадратов длин его противоположных сторон равны между собой.


3.2. Трапеции
99
Примеры решения задач
Пример 1. В трапеции ABCD стороны AD и ВС параллельны, \АВ\ — с и расстояние от середины отрезка CD до прямой АВ равно d. Найдите площадь трапеции ABCD.
Решение. Обозначим середину отрезка CD буквой К, а основание перпендикуляра, опущенного из точки К на прямую АВ, обозначим буквой Н. Приведём три способа решения этой задачи: первый способ основан на леммах о площадях, два других используют дополнительные построения.
Первый способ
Из того, что дано в условии, можно легко найти д D
площадь треугольника АВК:
Saabk = \ • \АВ\ ■ \КН\ = у.
Попробуем выразить площадь трапеции через площадь треугольника АВК. Из того, что |СК\ = \KD\, следует, что
Saakd = g * и S&bck = g ' Sabcd-
Поэтому
Saakd + Sabck = * (Saacd + Sabcd) =
= \ ■ (;ИР| ■ h + i ■ |BC| ./,)=!.|j4P|+ m -h=\- S*BCD,
где h - высота трапеции. Поэтому и Saabk — \ • Sabcd • Следовательно,
Sabcd = 2 Saabk = cc!.
Второй способ
Проведем через точки В и К прямую до пересечения с прямой AD в точке Е. Поскольку прямые AD и ВС параллельны, углы KDE и КС В равны как внутренние накрест лежащие. Углы В КС и DKE равны как вертикальные. Тогда в силу того, что \СК\ = \KD\, получаем равенство треугольников КС В и KDE (по стороне и двум прилежащим углам).
Поэтому, во-первых, \ВК\ — \КЕ\ и, во-вторых,
Sakcb = Sakde => Sabcd = Saabe•
Найдём высоту треугольника АВЕ. Обозначим основание высоты, проведенной из точки Е на сторону АВ, буквой N. Тогда, очевидно, АВКН ~ ABEN =>
{Uplift2 ^ \EN\ — 2d =► SAABE = \-\AB\.\EN\=cd.
В С
4*


100
Теория и задачи
Третий способ
Проведём через точку К прямую, параллельную прямой АВ, и обозначим буквами Е и F точки пересечения этой прямой с прямыми ВС и AD соответственно. Заметим, что ABEF - параллелограмм. Поскольку прямые AD и ВС параллельны, углы КСЕ и KDF равны как внутренние накрест лежащие. Углы СКЕ и DKF равны как вертикальные. Тогда в силу того, что \СК\ = \KD\, получаем равенство треугольников СКЕ и DKF (по стороне и двум прилежащим углам). Поэтому
Sacke = Sadkf => Sabcd = Sabef = \ЛВ\ • \KH\ = cd. Ответ, cd.
В СЕ
Пример 2. В трапеции длина средней линии равна 4, градусные меры углов при одном из оснований равны 40° и 50°. Найдите длины оснований трапеции, если длина отрезка, соединяющего их середины, равна 1.
Решение. Обозначим вершины трапеции буквами А, В, С и D, середины сторон АВ, ВС, CD и AD обозначим буквами М, К, N и L соответственно. Будем считать, что AD\\BC, BAD = 40° и ADC = 50°, тогда по условию задачи \MN\ = 4, \KL\ = 1. Если обозначить буквой Е точку пересечения прямых АВ и CD, то
AED = 180° - EAD - EDA = 90°,
то есть треугольники ВЕС и AED прямоугольные. Далее заметим, что ЕК и EL - медианы прямоугольных треугольников ВЕС и AED, проведённые к их гипотенузам, значит,
\ЕК\ = |£НГ| = |tfC| = И |SL| = |AL| = |L£>| =
Наконец, точки Е, К и L лежат на одной прямой, поэтому
\KL\ = \EL\ - \ЕК\ = 1Л£>1 ~ 1ДС1 |AD| - |ВС| = 2.


3.2. Трапеции
101
Второе уравнение пишется совсем просто: воспользуемся тем, что длина средней линии трапеции равна полусумме длин её оснований:
\MN\ = 1А£>1 + \ВС\ ^ \AD\ + \ВС\ = 8-
Наконец, из полученных уравнений находим \AD\ = 5, \ВС\ = 3.
Ответ. 3 и 5.
ПримерЗ. В трапеции АВСЕ длина основания АЕ равна 16, а длина боковой стороны СЕ равна 8л/3. Окружность, проходящая через точки А, В, С, пересекает прямую АЕ в точке Н. Величина угла АН В равна 7г/3. Найдите длину отрезка ВН.
Решение. Поскольку АВСЕ - трапеция, а СЕ - её боковая сторона, прямые АЕ и ВС параллельны, значит, и АН\\ВС. По условию задачи точки А, В, С и Н лежат на одной окружности, стало быть, АВСН - трапеция, вписанная в окружность. Из этого вытекает, что она равнобедренная, что, в свою очередь, даёт нам следующие соотношения:
\АС\ = \ВН\, ZAHB = АСАН.
Таким образом, нам достаточно найти длину отрезка АС, что легко делается путём применения теоремы косинусов к треугольнику АСЕ :
\СЕ\2 = \АС\2 + \АЕ\2 - 2 • \АС\ ■ \АЕ\ • cos CAE =»
=> 192 = \АС\2 + 256 - 2 • \АС\ • 16 • ^ =s> \АС\ = 8.
Ответ. 8.
Пример 4. В трапеции ABCD стороны AD\\BC, \АВ\ = 9, \CD\ = 5, биссектриса угла D пересекает биссектрисы углов А и С в точках М и N соответственно, а биссектриса угла В пересекает те же две биссектрисы в точках L и К, причем точка К лежит на основании AD.
а) В каком отношении прямая LN делит сторону АВ, а прямая МК сторону ВС1
б) Найдите отношение \MN\ : \KL\, если \LM\ : \KN\ = 3:7.
Решение. Обозначим величины углов ABC и BCD через 2а и 2/3 соответственно. Тогда BAD = 7г — 2а и ADC = 7г — 28 (по свойству односторонних углов при параллельных прямых). Поскольку AL и В К - биссектрисы углов BAD и ABC, имеем BAL = п/2 — а, АВК = а, поэтому ALB — тг — а — (тг/2 — а) = тг/2. Таким образом, AL - высота и биссектриса треугольника АВК, стало быть, во- первых, треугольник АВК — равнобедренный, \АВ\ = |^4jRT| = 9, и, во-вторых,


102
Теория и задачи
L - середина отрезка В К. Абсолютно аналогично доказывается, что DN - высота и биссектриса треугольника CDK, \CD\ = \KD\ = 5 и N - середина отрезка
Теперь заметим, что LN - отрезок, соединяющий середины сторон В К и С К треугольника ВС К, поэтому LN - его средняя линяя, из чего следует параллельность прямых LN, ВС и AD. В таком случае прямая LN проходит и через середину стороны АВ. Действительно, отрезок, концами которого являются точка L и точка пересечения прямых LN и АВ, во-первых, параллелен прямой АВ и, во-вторых, одним из его концов является середина отрезка В К. Значит, он является средней линией треугольника АВК, поэтому второй его конец - середина отрезка АВ. Итак, прямая LN делит сторону АВ в отношении 1:1.
Для ответа на вторую часть первого вопроса задачи заметим, что поскольку \АВ\ ф \CD\, ABCD - не параллелограмм, из чего вытекает, что прямые АВ и CD пересекаются в точке Е. Теперь докажем, что точки М и К лежат на биссектрисе угла AED.
С одной стороны, точка М лежит на биссектрисе угла EAD, поэтому она равноудалена от сторон этого угла, то есть от прямых АЕ и AD. С другой стороны, точка М лежит на биссектрисе угла ADE, поэтому она равноудалена от сторон этого угла, то есть от прямых DE и AD. Значит, точка М равноудалена от прямых АЕ и DE, то есть лежит на биссектрисе угла AED. Аналогично доказывается, что точка К тоже лежит на биссектрисе угла AED.
Обозначим буквой Р точку пересечения прямой ЕК и отрезка ВС. Тогда ЕР - биссектриса треугольника ВЕС, а ЕК - биссектриса треугольника AED. Следовательно, по свойству биссектрисы треугольника
СК.
Е
В Рj Х.С
А
К
D
\ВР\ _ \ВЕ\ \АК\ \АЕ\
\РС\ | СЕ\' \KD\ \DE\ *
Но так как треугольники ADE и ВСЕ подобны, то
\ВЕ\ \СЕ\ \DE\ \СЕ\
\АЕ\ _ \DE\ ^ ^ \АЕ\ \ВЕ\
, '-Г', — 7^7777 ■■ - ■■■ ■ =
и мы имеем


3.2. Трапеции
103
Для ответа на второй вопрос задачи рассмотрим четырёхугольник MNKL. Так как из приведенных выше рассуждений следует, что углы MLK и MNK прямые, их сумма равна 7г и, значит, вокруг четырёхугольника MNKL можно описать окружность. Тогда по свойству вписанных углов углы MNL и MKL равны, а углы MNL и NDK равны в силу параллельности прямых LN и AD. Следовательно, равны углы MKL и NDK. Поэтому прямоугольные треугольники MKL и KDN подобны. Отсюда получаем
\ML\ \МК\
\KN\ ~ \KD\ '
Аналогично показывается подобие треугольников KNM и ALK. Тогда
\MN\ _ \МК\ \MN\ _ \МК\ \KD\ _ \ML\ \KD\ 3 5 _ 5
\KL\ ~ \AK\ ^ \KL\ ~ \KD\ ’ \AK\ ~ |/£ГЛГ| ' \AK\ ~ 7 ' 9 ~ 21'
Ответ, a) 1: 1; 5:9; 6) 5:21.
Задачи
1. В трапеции KLMN отрезки KN и LM являются основаниями, а также
известно, что \KL\ = 36, \MN\ = 34, \LM\ = 10. Найдите длину диагонали
LN, если косинус величины угла KLM равен —1/3.
2. В трапецию вписана окружность. Точка касания делит одну из боковых сторон этой трапеции на отрезки длиной 12 и 3, длина её меньшего основания равна 9. Найдите площадь трапеции.
3. В трапеции ABCD отрезки АВ и CD являются основаниями. Диагонали трапеции пересекаются в точке Е. Известно, что \АВ\ = 30, \CD\ = 24, \AD\ = 3, DAB = 7г/3. Найдите площадь треугольника ВЕС.
4. В трапеции ABCD даны длины оснований \AD\ = 4, \ВС\ = 1 и углы BAD и ADC, величины которых равны соответственно arctg 2 и arctg 3. Найдите длину радиуса окружности, вписанной в треугольник ВЕС, где Е - точка пересечения диагоналей трапеции.
5. В трапеции ABCD известны длины оснований \AD\ = 39 и \ВС\ = 26, а также известны длины боковых сторон \АВ\ = 5 и \CD\ = 12. Найдите длины её диагоналей.
6. В трапеции ABCD с основаниями AD и ВС длина боковой стороны А В равна 2. Биссектриса угла BAD пересекает прямую ВС в точке Е. В треугольник АВЕ вписана окружность, касающаяся стороны АВ в точке М и стороны BE в точке Н, \МН\ = 1. Найдите величину угла BAD.
7. В трапецию ABCD с основаниями ВС и AD вписана окружность с центром О. Найдите площадь трапеции, если угол DAB прямой, \ОС\ = 2, \OD\ = 4.
8. В выпуклом четырёхугольнике MNLQ углы при вершинах N и L прямые, а тангенс величины угла при вершине М равен 2/3. Найдите длину диагонали NQ, если известно, что длина стороны LQ вдвое меньше длины стороны MN и на 2 больше длины стороны LN.


104
Теория и задачи
9. 	В трапеции ABCD сторона АВ параллельна стороне CD. Диагонали трапеции пересекаются в точке О, причём треугольник ВОС является равносторонним. Найдите длину стороны ВС, если \АВ\ = 5, \CD\ = 3.
10. В трапеции KLMN KN\\LM, LA - биссектриса угла KLM, точка А - середина отрезка MN. Длина средней линии трапеции KLMN равна у/Ь, \АК\ = 4. Найдите \AL\.
11. В трапеции ABCD AD\\ВС, биссектриса угла BAD пересекает сторону CD в точке М. Найдите длину отрезка AM, если известно, что треугольники ACM и ADM имеют одинаковую площадь, \ВМ\ = 8, \ВС\ + \ AD\ = 17.
12. Непараллельные стороны трапеции перпендикулярны друг другу. Длина одной из них равна 3, а градусная мера угла, образованного ею и одной из диагоналей, равна 40°. Другая сторона образует с одним из оснований такой же угол. Найдите длину средней линии этой трапеции.
13. Найдите площадь трапеции ABCD, если AB\\CD, CAB = 2DBA, \АС\ = 5, |В£>| =7.
14. Длины боковых сторон описанной около окружности трапеции равны 3 и 5. Известно, что средняя линия этой трапеции делит её на две части, отношение площадей которых равно 5/11. Найдите длины оснований трапеции.
15. В трапеции ABCD с основаниями AD и ВС диагонали пересекаются в точке Е. Около треугольника ЕС В описана окружность, а касательная к этой окружности, проведённая в точке Е, пересекает прямую AD в точке F таким образом, что точки A, D,F лежат последовательно на этой прямой. Известно, что \AF\ = a, \AD\ = b. Найдите длину отрезка EF.
16. В трапеции ABCD длина основания AD больше длины основания ВС. Известно, что \AD\ = \CD\ = 14/3, BAD = тт/2, BCD = 57г/6. На основании AD построен треугольник AED так, что точки В и Е лежат по одну сторону от прямой AD, причём \АЕ\ = \DE\. Длина высоты этого треугольника, проведенной из вершины Е, равна 7/5. Найдите площадь общей части трапеции ABCD и треугольника AED.
17. В трапеции ABCD длина основания AD равна 4, длина основания ВС равна 3, длины сторон АВ и CD равны. Точки М и N лежат на диагонали BD, причём точка М расположена между точками В и N, а отрезки AM и CN перпендикулярны диагонали BD. Найдите длину отрезка CN, если \BM\:\DN\ = 2:3.
18. Около окружности, длина радиуса которой равна R, описана трапеция. Хорда, соединяющая точки касания этой окружности с боковыми сторонами трапеции, параллельна основаниям трапеции. Длина этой хорды равна Ь. Найдите площадь трапеции.
19. В трапеции BCDE (CD\\BE) проведена средняя линяя LN (точка L лежит на стороне ВС). Прямая, проходящая через точку В и перпендикулярная к стороне DE, пересекает отрезок LN в точке М, \LM\ : \MN\ = 2 : 1. Также известно, что \ВЕ\ = 14, \CD\ — 10, ВС _L BE. Найдите площадь трапеции BCDE.


3.2. Трапеции
105
20. В трапеции ABCD (AD\\BC) \AD\ = 8, \ВС\ = 6, а величина угла между прямыми АВ и CD равна arctg 0,25. Найдите площадь трапеции ABCD, если известно, что её диагонали перпендикулярны.
21. Трапеция ABCD с основаниями ВС и AD вписана в окружность. На дуге CD взята точка Е и соединена со всеми вершинами трапеции. Известно, что величина угла CED равна 27г/3, ABE — ВАЕ = 8. Найдите отношение периметра треугольника АВЕ к длине радиуса вписанной в него окружности.
22. Точка М лежит на боковой стороне CD трапеции ABCD. Найдите длину отрезка ВМ, если известно, что BCD = CBD = ABM = arccos(5/6), \AB\ = 9.
23. В трапеции ABCD BC\\AD, \BC\ < |AD|, длина диагонали BD в 4/3 раза больше длины радиуса окружности, описанной около ABCD. Найдите отношение длин CD и радиуса этой окружности, если отношение площадей треугольников ABD и BCD равно 5.
24. Дана трапеция, в которую вписана окружность и около которой описана окружность. Отношение длины высоты этой трапеции к длине радиуса описанной около неё окружности равно >/2/3. Найдите величины углов трапеции.
25. В окружность с центром О вписана трапеция ABCD с основаниями АВ и CD, \АВ\ = 5, |iX7| = 1, ABC = 7г/3. Точка К лежит на отрезке АВ таким образом, что \АК\ = 2. Прямая С К пересекает окружность в точке F, отличной от точки С. Найдите площадь треугольника OF С.
26. На основаниях AD и ВС трапеции ABCD построены квадраты ADEF и BCGH, расположенные вне трапеции. Диагонали трапеции ABCD пересекаются в точке О. Найдите длину отрезка AD, если \ВС\ = 2, |6?0| = 7, а \GF\ = 18.
27. Известно, что трапеция ABCD равнобедренная, AD\\BC и \ВС\ > \AD\. Трапеция ECDA также равнобедренная, причём AE\\CD и \АЕ\ > \CD\. Найдите \ВЕ\, если известно, что \DE\ = 7, a CDE + BDA = arccos(l/3).
28. В равнобедренной трапеции, длины оснований которой равны 1 и 4, расположены две окружности, каждая из которых касается двух боковых сторон трапеции, другой окружности и одного из оснований трапеции. Найдите площадь этой трапеции.
29. В трапеции ABCD диагонали пересекаются в точке Е, а величины углов AED и BCD равны. Окружность, длина радиуса которой равна 17, проходит через точки С, D и Е, пересекает основание AD в точке F и касается прямой BF. Найдите длины оснований и высоты трапеции ABCD, если \CD\ = 30.
30. На боковой стороне АВ трапеции ABCD взята точка М таким образом, что \АМ\ : \ВМ\ =2:3. На противоположной стороне CD взята такая точка N, что отрезок MN делит трапецию на части, одна из которых по площади втрое больше другой. Найдите отношение \CN\ : \ND\, если известно, что \ВС\ : \AD\ = 1:2.


106
Теория и задачи
31. В трапеции ABCD BC\\AD, ABC — п/2. Прямая, перпендикулярная стороне CD, пересекает сторону АВ в точке М, а сторону CD в точке N. Известно, что расстояние от точки D до прямой МС равно с, \МС\ = а, |-BiV| = 6. Найдите расстояние от точки А до прямой BN.
32. В окружность, длина радиуса которой равна \/Т, вписана трапеция. Длина её меньшего основания равна 4. Через точку этой окружности, касательная в которой параллельна одной из боковых сторон трапеции, проведена хорда, параллельная основаниям трапеции. Длина этой хорды равна 5. Найдите площадь трапеции и длину её диагоналей.
33. В окружность вписана трапеция ABCD, AD\\BC, \AD\ > \ВС\. На дуге AD, не содержащей вершин В и С, взята точка S. Точки Р, Q, М и N являются основаниями перпендикуляров, опущенных из точки S на прямые AD, ВС, АВ и CD соответственно. Известно, что \SP\ = a, |5Q| = 6, \SN\ = с. Найдите отношение площадей треугольников MQS и NQS.
34. Дана трапеция ABCD, сторона А В которой перпендикулярна основаниям AD и ВС. На стороне АВ как на диаметре построена окружность, касающаяся стороны CD. Длина радиуса этой окружности равна л/б- Другая окружность, длина радиуса которой равна \/2, касается сторон AD и CD и пересекает первую окружность так, что длина их общей хорды равна \/б, а центры окружностей расположены по разные стороны от этой хорды. Найдите площадь трапеции ABCD.
3.3. 	Четырёхугольники и многоугольники общего вида Теоретический материал
Сначала приведём некоторые факты и утверждения, относящиеся к четырёхугольникам.
1. Сумма величин углов четырёхугольника
Сумма величин внутренних углов четырехугольника равна 2п .
Для доказательства этого факта достаточно сложить суммы величин внутренних углов двух треугольников, на которые разбивается четырёхугольник одной из своих диагоналей. Для выпуклого четырёхугольника можно рассмотреть любую из его диагоналей, для невыпуклого надо рассмотреть ту диагональ, которая содержится внутри него.
2. Формула площади четырёхугольника
Площадь четырёхугольника равна половине произведения длин его диагоналей на синус величины угла между ними.
Для доказательства этого факта рассмотрим два случая. Если четырёхугольник ABCD выпуклый (левый рисунок), то точка О пересечения его диагоналей


3.3. Четырёхугольники и многоугольники общего вида
107
лежит внутри него и его площадь может быть представлена как сумма площадей треугольников АОВ, ВОС, COD и AOD.
Заметим, что синусы величин всех четырех углов АОВ, ВОС, COD и AOD равны, так как эти углы являются либо смежными, либо вертикальными друг с другом. Обозначая величину любого из этих углов буквой а и пользуясь формулой площади треугольника, мы получаем
Sabcd = Saaob + Saboc + Sacod + Saaod = ^ ' \BO\ • sina +
+ i • \BO\ ■ \CO\ ■ sina + \ ■ \CO\ • \DO\ • sina + \ ■ \AO\ ■ \DO\ • sina = z z z
= \ ■ (\AO\ + \CO\) ■ (IBO\ + \DO\) • sina = \ ■ \AC\ ■ \BD\ ■ sina. z z
Если же четырёхугольник ABCD невыпуклый (правый рисунок), то точка О (точка пересечения прямых, содержащих его диагонали) лежит вне него. Будем считать, что она попадает на продолжение диагонали BD за точку В. Тогда площадь четырёхугольника ABCD равна разности площадей треугольников ACD и АВС, каждая из которых может быть представлена как сумма площадей соответствующих треугольников. Углы АОВ и СОВ смежные, поэтому синусы их величин равны. Обозначая величину любого из них буквой а и рассуждая аналогично предыдущему случаю, мы получаем
Sabcd = Saaod + Sacod — Saaob — Sacob = ^ * \ AO\ • \DO\ • sina +
+ i • \CO\ • \DO\ • sina - ^ • \AO\ • \BO\ • sina — ^ • \CO\ • |J30| • sina = z z z
= ^ ' (\AO\ + \CO\) ■ {\DO\ — \BO\) ■ sina
Формула площади четырёхугольника доказана.
Если использование доказанной формулы по каким-либо причинам затруднительно, то, если четырёхугольник выпуклый, можно поступать следующим образом: провести какую-либо из его диагоналей и посчитать по отдельности площади полученных треугольников.
Такой подход дает нам еще две формулы:
Sabcd = \ • \АВ\ ■ \AD\ ■ sin BAD + i •
Sabcd = \ • \AB\ ■ \BC\ ■ sin ABC + ± ■
Если четырёхугольник оказался невыпуклым, то можно поступить аналогично и провести ту его диагональ, которая лежит внутри него.
Отметим, что в силу того, что синус величины угла не превосходит 1, из этих формул вытекает следующее утверждение:
= i • \АС\ • \BD\ • sina. z
в в
D D
\ВС\ • |С£>| - sin ВСД
\AD\ ■ \CD\-sin ADC.


108
Теория и задачи
Площадь четырёхугольника не превосходит полусуммы произведений длин двух пар его смежных сторон и равна этой полусумме тогда и только тогда, когда углы, образованные этими парами, прямые.
3. 	Окружность, описанная около четырёхугольника
Если около четырёхугольника можно описать окружность, то суммы величин его противоположных углов равны п. Верно и обратное утверждение: если сумма величин двух противоположных углов четырёхугольника равна тг , то около него можно описать окружность.
Доказательство этих утверждений легко проводится с помощью свойств вписанных углов и теоремы о четырёх точках. Отметим также, что возможность описать окружность около четырехугольника эквивалентна тому факту, что серединные перпендикуляры к его сторонам пересекаются в одной точке.
Докажем ещё одно красивое свойство вписанного четырёхугольника, а именно теорему Птолемея.
Теорема. Произведение длин диагоналей вписанного в окружность четырёхугольника равно сумме произведений длин его противоположных сторон.
С’
Доказательство. Рассмотрим вписанный в окружность четырёхугольник ABCD обозначим буквой К точку пересечения его диагоналей.
Сначала заметим, что по свойствам вписанных углов
CAD = CBD, ABD = ACD, BCA = BDA, CDB = CAB
и по свойству угла между пересекающимися хордами
АКВ = CKD = ADB + CAD, ВКС = AKD = ВАС + ACD.
Вводя обозначения CAB = a, CBD — /3, ACD — 7, ADB = S, ВКС = с учётом вышесказанного имеем = а + 7, 7г — = /3 + 6.
Теперь рассмотрим четырёхугольник ABC'D, получающийся из четырёхугольника ABCD переворотом треугольника BCD, то есть \ВС'\ = \CD\, \C'D\ = \ВС\. Ясно, что треугольники BC'D и BCD равны по трем сторонам, поэтому, во-первых, C'BD = CDB = a, C'DB = CBD = (3 и, во-вторых, площади четырёхугольников ABCD и ABC'D равны.
Наконец, заметим, что
Sabcd — ^ • \АС\ • \BD\ • sin (р,


3.3. Четырёхугольники и многоугольники общего вида
109
Sabcd = SAABc + SAadc> = \-\AB\■ \ВС'\-sin АВС' + \ • |AD| • \DC'\smADC' =
Zi z
= ^-\AB\-\CD\- sin (a + 7) + | • | AD\ ■ \BC\ • sin (/? + S) = | • | AB| • \CD\ ■ sin <p +
+ I ■ \AD\ ■ \BC\ • sin(7r -¥>) = £. (\AB\ ■ \CD\ + \AD\ ■ \BC\) • sin tp. z z
Приравнивая друг другу правые части этих соотношений, получаем \АС\ • \BD\ = |i4B| • \CD\ + |AD| • |J5C|.
Теорема Птолемея доказана.
4. 	Окружность, вписанная в четырёхугольник
Если в четырёхугольник можно вписать окружность, то он выпуклый и суммы длин его противоположных сторон равны. Верно и такое утверждение: если суммы длин противоположных сторон выпуклого четырёхугольника равны, то в него можно вписать окружность.
Доказательство первого из этих утверждений легко вытекает из теоремы о равенстве длин отрезков касательных, проведенных из одной точки к окружности. Второе утверждение доказывается по следующей схеме: обосновывается тот факт, что все четыре биссектрисы внутренних углов рассматриваемого четырёхугольника пересекаются в одной точке, которая лежит во внутренней области четырёхугольника. Эта точка и будет центром вписанной в четырёхугольник окружности. Отметим, что возможность вписать окружность в четырёхугольник эквивалентна тому факту, что все биссектрисы его внутренних углов пересекаются в одной точке.
Докажем ещё одно свойство описанного четырёхугольника, а именно теорему о его площади.
Теорема. Площадь описанного около окружности четырёхугольника равна произведению длины радиуса этой окружности на его полупериметр.
Доказательство. Рассмотрим описанный около окружности четырёхугольник ABCD, обозначим буквой О её центр, длину её радиуса обозначим буквой г, а буквами К, L, М и 7V обозначим точки её касания со сторонами АВ, ВС, CD и AD соответственно.
Тогда \ОК\ = \OL\ — \ОМ\ = \ON\ — г и, кроме того,
OK _L АВ, OL _1_ ВС, ОМ ± CD, ON _L AD. Поскольку четырёхугольник ABCD выпуклый, его площадь равна сумме площадей треугольников ОАВ, ОВС, OCD и В OAD. Записывая формулы площадей этих треугольников, получаем
К
Sabcd = Saoab + Saobc 4- Saocd + Saoad =
= \ • \AB\ • \OK\ + \ ■ \BC\ • \OL\+ A
С
+\ ■ \CD\ ■ \OM\ + | • |AD| • \ON\ =


110
Теория и задачи
= | • (\АВ\ + \ВС\ + \CD\ + \AD\) ■ г = рАВСо • г,
что и требовалось доказать.
5. 	Диагонали четырёхугольника
Если прямые, содержащие диагонали четырёхугольника, перпендикулярны, то суммы квадратов длин его противоположных сторон равны.
В
В
В
Доказательство этого факта практически очевидно. Рассмотрим четырёхугольник ABCD \ точку пересечения прямых, содержащих его диагонали, обозначим буквой К. На чертеже изображены все возможные случаи: выпуклый четырёхугольник, невыпуклый четырёхугольник с непересекающимися сторонами и невыпуклый четырёхугольник с пересекающимися сторонами. Записывая теорему Пифагора для треугольников АВК, ВС К, CDK и ADK, получаем
\АВ\2 = \АК\2 + |ВК\2, \CD\2 = \СК\2 + \DK\2,
\ВС\2 = \ВК\2 + \СК\2, \AD\2 = \АК\2 + \DK\2.
Наконец, складывая попарно эти соотношения, получаем
\АВ\2 + \CD\2 = \AD\2 + \ВС\2 = \АК\2 + \ВК\2 + \СК\2 + \DK\2.
Утверждение доказано.
Диагонали выпуклого четырёхугольника разбивают его на четыре треугольника таким образом, что произведения площадей противоположных треугольников равны.
Справедливость этого утверждения вытекает из следующих соображений: заметим, что синусы величин углов АОВ,
ВОС, COD и AOD равны в силу того, что эти углы либо смежные, либо вертикальные друг с другом. Обозначая любую из этих величин через а и пользуясь формулой площади треугольника, получаем
В
о.
с .с _о .с АОВ COD~ ВОС AOD
D
1
1
Saaob = ^ ‘ 1^1 * \в®\ * sina> Sacod = ^ ' \@0\ ‘ \DO\'sina; Saboc — 2 ‘ \ВО\ ‘ \СО\ • sin a, Saaod = * \АО\ • \DO\ • sin а.


3.3. Четырёхугольники и многоугольники общего вида
111
Перемножив попарно эти соотношения, получаем
Saaob • Sacod = Saboc • Saaod = j • \AO\ • \BO\ • \CO\ • \DO\ • sin2 a,
что и требовалось доказать.
6. 	Теорема Вариньона
Четырёхугольник, вершины которого являются серединами сторон произвольного четырёхугольника, есть параллелограмм.
Рассмотрим произвольный четырёхугольник ABCD, буквами К, L, М и N обозначим середины сторон АВ, ВС, CD и AD соответственно. На чертеже изображены все возможные случаи: выпуклый четырёхугольник, невыпуклый четырёхугольник с непересекающимися сторонами и невыпуклый четырёхугольник с пересекающимися сторонами. Заметим, что отрезок KL является средней линией треугольника ABC, поэтому KL\\AC, \KL\ = ||А(7|. Отрезок же MN является средней линией треугольника ADC, поэтому MN\\AC, \MN\ =
Из вышесказанного следует, что отрезки KL и MN, во-первых, параллельны и, во-вторых, равны по длине. Значит, четырёхугольник KLMN является параллелограммом. Также отметим, что, рассуждая абсолютно аналогично, мы получим \LM\ = \KN\ = ^\BD\. Теорема Вариньона доказана.
Замечание. Если стороны четырёхугольника ABCD пересекаются, то не исключен случай совпадения середин сторон АВ и CD. Тогда четырёхугольник KLMN выродится в отрезок.
Теперь приведем некоторые формулы и факты, относящиеся к произвольным многоугольникам.
Т. Сумма величин углов произвольного многоугольника
Сумма величин всех внутренних углов произвольного выпуклого п-угольника равна (п — 2)7г.
Это утверждение доказывается точно так же, как и утверждение о сумме величин внутренних углов четырёхугольника. Отметим, что приведенный факт будет справедлив и для произвольного невыпуклого многоугольника.
8. 	Свойства правильных многоугольников
Определение. Многоугольник, у которого равны между собой длины всех сторон и равны между собой величины всех его внутренних углов, называется правильным.


112
Теория и задачи
Отметим, что, в отличие от треугольников, в этом определении приходится требовать и равенство длин сторон, и равенство величин углов. Например, не любой ромб (так же как и не любой прямоугольник) является правильным четырехугольником. Правильным будет четырёхугольник, который одновременно является и ромбом, и прямоугольником, то есть квадрат.
Докажем несколько соотношений, устанавливающих зависимость между величинами стандартных элементов правильных многоугольников.
(п — 2)7Г
1. 	Величины всех внутренних углов правильного п-угольника равны
п
2. 	Около правильного п-угольника можно описать окружность. Если длина его стороны равна а, то длина радиуса описанной около него окружности равна
2 sin ^
3. В правильный п-угольник можно вписать окружность. Если длина его
а тг
стороны равна а, то длина радиуса вписанной в него окружности равна — ctg — .
2 п
4. Площадь правильного п-угольника, длина стороны которого равна а, равна па2 тг
~Г ctS ~ •
4 п
Доказать все эти утверждения достаточно просто. Рассмотрим правильный п- угольник А1А2 ... Ап. Ясно, что у него п внутренних углов, их величины равны между собой, сумма этих величин равна (п — 2)7г, стало быть, величина каждого
(п — 2)тг
из его внутренних углов равна .
п
Далее проведём биссектрисы углов АпА\А2 и А\ Л2 As, точку их пересечения обозначим буквой О.
Поскольку эти углы равны, равны и углы ОА\ А2 и ОА2А1, то есть треугольник ОА\А2 равнобедренный. Теперь проведём биссектрису угла А2А3А4.
Пусть R - точка, в которой она пересекается с биссектрисой угла А1А2А3. Рассуждая аналогично, мы получим, что треугольник RA2A3 тоже равнобедренный. Но поскольку углы ОА2А1 и RA2A3 равны, равны и треугольники ОА1А2 и RA2A3. Из этого равенства вытекает, что IOA2I = \RA2\. А так как точки О и R обе лежат на биссектрисе угла А1А2А3, то они совпадают. Продолжая эти рассуждения, мы, очевидно, получим, что все биссектрисы
внутренних углов рассматриваемого многоугольника проходят через точку О, эта точка равноудалена от всех его сторон, стало быть, в А\ А2 ... Ап можно вписать окружность и О - её центр. Отметим также, что попутно мы установили равенство длин всех отрезков ОА\, ОА2, ..., ОАп. Но это означает, что точка О равноудалена от всех вершин рассматриваемого многоугольника и является центром описанной около него окружности.
Наконец, рассмотрим треугольник ОА1А2, проведём его высоту ОР, которая является также его биссектрисой и медианой. Ясно, что отрезок ОА2 является радиусом описанной около А\А2...Ап окружности, а отрезок ОР есть радиус вписанной в него окружности.
Поскольку все треугольники ОА\ А2, ОА2А3, ..., ОАпА\ равны между собой, равны и углы А1ОА2, А2ОА3, ..., АпОА\. Этих углов п штук, сумма их


3.3. Четырёхугольники и многоугольники общего вида
113
величин равна 2п, стало быть, величина каждого из них равна 2тг/п. После этого из прямоугольного треугольника ОА2Р мы находим
\ОА I - ]РМ = = а
sin А2ОР sin(^f^) 2sinT
А\ОА2\ а Л я-
j=2°tgn'
Наконец,
SAAnOAi = . . . = SaA2OA3 = S&a1OA2 = ТГ ‘ * |OJP| = — Ctg —,
z 4 n
na2 7Г
^AiA2-..An = оAA1OA2 + ^>AA2OA3 + • • • + b&A^OAx = Z Ctg —.
4 n
Свойства правильных многоугольников доказаны.
9. 	Многоугольник, описанный около окружности
Площадь описанного около окружности многоугольника равна произведению длины радиуса этой окружности на его полупериметр.
Доказательство этой формулы абсолютно аналогично доказательству формулы площади четырехугольника, описанного около окружности.
Примеры решения задач
Пример 1. В четырёхугольник ABCD можно вписать окружность, К - точка
пересечения его диагоналей. Известно, что \АВ\ > \ВС\ > \КС\, \ВК\ = 4 + \/2,
а периметр и площадь треугольника ВКС равны соответственно 14 и 7. Найдите длину стороны CD.
Решение. В этой задаче достаточно трудно найти путь решения. Тем не менее, ясно, что в треугольнике ВКС нам известно три элемента, поэтому мы можем вычислить величины его углов и длины его сторон. Положим \ВС\ — х,
\КС\ = у, причём по условию задачи х > у. Пользуясь данным нам значением периметра треугольника ВКС и формулой Герона, получаем систему уравнений
х + у + 4 + >/2 = 14,
< ф -(7-х) -(7 -у) -(7— (4 + V2)) = 7,
, X > 2/,
решая которую, находим \ВС\ = х = б, \КС\ = у = 4 — у/2.
На первый взгляд кажется, что мы не сильно приблизились к отысканию искомой величины. Однако (и это главный шаг в решении) заметим, что в силу того, что
\ВС\2 = 36 = (4 + V2)2 + (4 - у/2)2 = \ВК\2 + \КС\2,
\ОР\ = \РА2\ ■ ctgА2ОР = ^\АгА2\ • ctg


114
Теория и задачи
угол В КС прямой. Запишем свойства четырёухгольника с взаимно перпендикулярными диагоналями и четырёхугольника, описанного около окружности:
\АВ\ + \CD\ = \AD\ + \ВС\, \АВ\2 + \CD\2 = \AD\2 + \ВС\2.
Возводя в квадрат первое из этих равенств и вычитая его из второго, предварительно умноженного на 2, получаем
(\AB\-\CD\)2 = (\AD\-\BC\)2 ^ \\AB\-\CD\\ = \\AD\-\BC\\.
Раскрывая модули и пользуясь тем, что \АВ\ + \CD\ = \ AD\ + |jBC|, имеем
\АВ\ - \CD\ = \AD\ - \ВС\, \АВ\ + \CD\ = \AD\ + \ВС\;
\АВ\ - \CD\ = \ВС\ -\AD\, \АВ\ + \CD\ = \AD\ + \ВС\
\АВ\ = \AD\, \CD\ = \ВС\; \АВ\ = \ВС\, \CD\ = \AD\.
Итак, мы доказали, что описанный около окружности четырёхугольник с перпендикулярными диагоналями обязательно является дельтоидом, то есть четырёхугольником, у которого есть две пары смежных сторон, равных по длине. В нашей же задаче по условию \АВ\ > \ВС\, поэтому нам подходит только вариант \АВ\ = |AD|, |СТ>| = \ВС\ = 6.
Ответ. 6.
П р и м е р 2. Пятиугольник ABCDE вписан в окружность, длина радиуса которой равна 1. Известно, что \АВ\ = \/2, АВЕ = тг/4, EBD = 7г/б, а \ВС\ = \CD\. Чему равна площадь пятиугольника ABCDE1
Решение. Для вычисления площадей многоугольников, как правило, используется следующий подход: многоугольник делится на несколько треугольников или простых четырёхугольников, площади которых считаются по отдельности и затем суммируются.
Сначала заметим, что треугольник АВЕ также вписан в окружность из условия задачи. Применяя к нему теорему синусов, получаем
sin АЕВ =
\АВ\ 2 R
В
и величина угла АЕВ равна либо 7г/4, либо 37г/4.
Второй из этих вариантов невозможен в силу того, что сумма величин углов АВЕ и АЕВ должна быть меньше, чем 7г. Итак, АЕВ = 7г/4, поэтому треугольник ВАЕ прямоугольный и равнобедренный, \АВ\ = \ВЕ\ = \/2, площадь этого треугольника равна 1, а BE - диаметр окружности.
Далее отметим, что угол BDE прямой, поскольку он опирается на диаметр, поэтому величина угла BED равна 7г/3, величина угла BCD равна 27г/3 в силу


3.3. Четырёхугольники и многоугольники общего вида
115
свойств вписанного в окружность четырехугольника BCDE, а величины углов CBD и CDB равны 7г/6 (поскольку треугольник BCD равнобедренный по условию задачи). Пользуясь формулой площади треугольника через длину радиуса описанной около него окружности и синусы величин его углов, находим
Sabde = \ ■ \ВЕ\ ■ \BD\ • sin DBE = i • 2 • 2 • sin ^ • sin ^
2 2 6 О z
Sabcd - \ • \BD\ ■ \BC\ • sin CBD = ^ • 2 • sin ^ • 2 • sin ^ • sin ^
2 I 6 о о 4
з
Наконец, Sabcde = S&bde + S&bcd + S&abe = 1 + j
3
Ответ. 1 -f 7%/3.
4
Пример 3. Известно, что площадь выпуклого четырёхугольника ABCD равна среднему арифметическому произведений \АВ\ • \CD\ и \AD\ • \ВС\, \ВС\ = 4, Л£)С = 7г/3, BAD = 7г/2. Найдите длину стороны CD.
Решение. Условие про площадь четырёхугольника ABCD, данное в условии задачи, напоминает уело- 0
вие из разобранного в теоретических материалах факта о том, что площадь выпуклого четырёхугольника не превосходит полусуммы произведений его смежных сторон. Будем рассуждать следующим образом: возьмём в той же полуплоскости относительно прямой BD, где находится точка С, точку С' таким образом, что \ВС\ — \C'D\, \CD\ — \ВС'\. Тогда треугольники BCD и DC'В равны по трем сторонам, поэтому равны и их площади, а, стало быть, равны и площади четырёхугольников ABCD и ABC'D. Значит,
S ABC'D —
\АВ\ ■ \CD 1 + \AD 1 • |ВС\ 1 АВ\ • \ВС'\ + \AD\ • \C'D\
из чего следует, что углы ABC' и ADC' прямые.
Далее все достаточно просто. Поскольку угол BAD тоже прямой, четырёхугольник ABC'D является прямоугольником, поэтому BCD = BC'D = 7г/2, \АВ\ = |C'jD|. Но тогда прямоугольные треугольники ABD и CBD равны по гипотенузе и катету, значит, равны и углы ADB и СDB. Сумма же их величин равна величине угла ADC, то есть 7г/3. Итак, CDB = 7г/6, и из прямоугольного треугольника CDB мы находим \CD\ = \ВС\ • ctg В DC = 4\/3.
Ответ. 4\/3.
Пример 4. Величины всех внутренних углов шестиугольника ABCDEF равны. Известно, что \АВ\ = 3, \ВС\ = 4, \CD\ = 5, \EF\ — 1. Найдите длины сторон DE и AF.


116
Теория и задачи
Решение. Сразу вычислим величины всех внутренних углов нашего шестиугольника. Сумма этих величин равна 7г-(6 — 2) = 47г, поэтому величина каждого из этих углов равна 27г/3.
Опираясь на этот факт, можно заметить, что любой треугольник, до которого достраивается шестиугольник ABCDEF, будет равносторонним.
Действительно, если обозначить буквой К точку пересечения прямых АВ и EF, буквой L - точку пересечения прямых АВ и CD, а буквой М - точку пересечения прямых CD и EF, то в силу того, что ABC = BCD = 27г/3, мы получаем, что LBC — LCB = 7г/3, поэтому L — 7г/3
и треугольник BLC равносторонний. Рассуждая аналогично, мы заключаем, что треугольники AKF и DEM тоже равносторонние, К = М = 7г/3. Стало быть, треугольник KLM также равносторонний.
Теперь обозначим \AF\ = х, = у. Тогда из вышесказанного вытекает
|АК1 = |#F| = х, |DAf | = |AfJE7| = у, |ВС| = |BL| = |LC| = 4.
Наконец, выписывая длины сторон треугольника KLM и приравнивая их друг к другу, получаем
\KL\ = х 4- 3 + 4, |1/М| =44-5 + 2/,
- {
Ответ. |£>£| =6, |AF|
ж + 7 = ж + 2/ + 1, 9 + у = х4-^/4-1
|i^Af | = х 4-1 4- 2/ у = 6, х = 8.
Задачи
1. В окружность, длина радиуса которой равна 17, вписан четырёхугольник, диагонали которого взаимно перпендикулярны и находятся на расстоянии 8 и 9 от центра окружности. Найдите длины сторон этого четырёхугольника.
2. В выпуклом четырёхугольнике ABCD точка Е - точка пересечения диагоналей. Известно, что площадь каждого из треугольников АВЕ и DCE равна 1, площадь четырёхугольника ABCD не превосходит 4, \AD\ = 3. Найдите длину стороны ВС.
3. В выпуклом четырёхугольнике длины диагоналей равны 1 и 2. Найдите его площадь, зная, что длины отрезков, соединяющих середины его противоположных сторон, равны.
4. В выпуклом четырёхугольнике ABCD длина отрезка, соединяющего середины диагоналей, равна длине отрезка, соединяющего середины сторон AD и ВС. Найдите величину угла между прямыми АВ и CD.
5. В выпуклом четырёхугольнике ABCD величина угла, под которым пересекаются отрезки, соединяющие середины противоположных сторон, равна 7г/3, а длины этих отрезков относятся как 1:3. Чему равна длина меньшей диагонали четырёхугольника ABCD, если длина большей равна л/39?


3.3. Четырёхугольники и многоугольники общего вида
117
6. В остроугольном треугольнике ABC из основания D высоты BD опущены перпендикуляры DM и DN на стороны АВ и ВС. Известно, что \MN\ — а, \BD\ — b. Найдите величину угла ABC.
7. В выпуклом четырёхугольнике ABCD длина стороны AD равна 4, длина стороны CD равна 7, косинус величины угла ADC равен 1/2, синус величины угла ВС А равен 1/3. Найдите длину стороны ВС, если известно, что окружность, описанная около треугольника ABC, проходит также и через точку D.
8. Четырёхугольник PQRS вписан в окружность. Его диагонали PR и QS перпендикулярны и пересекаются в точке М. Известно, что \PS\ = 13, \QM\ = 10, \QR\ = 26. Найдите площадь четырёхугольника PQRS.
9. В выпуклом четырёхугольнике ABCD диагонали пересекаются в точке О. Площади треугольников ВОС, COD и AOD равны соответственно 20, 40 и 60. Найдите градусную меру угла В АО, если известно, что \АВ\ = 15, \АО\ = 8, а градусная мера угла ВО А больше 31°.
10. Диагонали четырёхугольника PQRS, вписанного в окружность, пересекаются в точке D. На прямой PR взята точка А, SAD = 50°, PQS = 70°, RQS = 60°. Где расположена точка А: на диагонали PR или на её продолжении? Ответ обосновать.
11. В трапецию, длины оснований которой равны 3 и 5, можно вписать окружность и около неё можно описать окружность. Вычислите площадь пятиугольника, образованного радиусами вписанной окружности, перпендикулярными боковым сторонам трапеции, её меньшим основанием и соответствующими отрезками боковых сторон.
12. Точки К, L, М, JV, Р расположены последовательно на окружности, длина радиуса которой равна 2у/2. Найдите площадь треугольника KLM, если известно, что LM\\KN, KM\\NP, MN\\LP, a LOM = 7г/4, где О - точка пересечения хорд LN и МР.
13. В окружность вписан четырёхугольник ABCD, диагонали которого взаимно перпендикулярны и пересекаются в точке Е. Прямая, проходящая через точку Е и перпендикулярная к прямой АВ, пересекает сторону CD в точке М. Докажите, что ЕМ - медиана треугольника СED, и найдите её длину, если \AD\ = 8, \АВ\ = 4 и CDB = а.
14. В четырёхугольнике ABCD диагонали АС и BD пересекаются в точке К. Точки L и М являются соответственно серединами сторон ВС и AD. Отрезок LM содержит точку К. Четырёхугольник ABCD таков, что в него можно вписать окружность. Найдите длину радиуса этой окружности, если \АВ\ = 3, \АС\ = VT3 и \LK\ : \КМ\ = 1:3.
15. В трапеции BCDE CD\\BE, |ВЕ\ = 13, \CD\ = 3, \СЕ\ = 10. На описанной около BCDE окружности взята отличная от Е точка А так, что \АС\ = 10. Найти длину отрезка АВ и площадь пятиугольника ABCDE.


118
- Теория и задачи
16. В четырёхугольнике ABCD диагонали перпендикулярны и пересекаются в точке Р. Точка М является серединой отрезка AD, длина отрезка СМ равна 5/4. Расстояние от точки Р до отрезка ВС равно 1/2, \АР\ = 1. Найдите длину отрезка AD, если известно, что около четырёхугольника ABCD можно описать окружность.
17. Параллелограммы ABCD и A'BCD' имеют общую сторону ВС и расположены симметрично относительно прямой ВС (точка А! симметрична точке А, точка D' симметрична точке D). Диагональ BD первого параллелограмма и сторона В А' второго параллелограмма лежат на одной прямой. Величина угла между диагоналями АС и А'С двух параллелограммов равна 7г/4, площадь пятиугольника ADCD'A' равна 15 у/2. Найдите длины сторон параллелограмма ABCD.
18. Точки К, L и М расположены на сторонах АВ, ВС и CD выпуклого четырёхугольника ABCD соответственно, причём выполнены соотношения \АК\ : \ВК\ = \CL\ : \BL\ = \СМ\ : \DM\ = 1:2. Длина радиуса окружности, описанной около треугольника KLM, равна 5/2, |ifL| = 4, |LM| = 3. Чему равна площадь четырёхугольника ABCD, если известно, что \КМ\ < \KL\1
19. В выпуклом четырёхугольнике ABCD отрезок СМ, соединяющий вершину С с точкой М, расположенной на стороне AD, пересекает диагональ BD в точке К. Известно, что |СЛГ| : |#М| = 2:1, |С£>| : \DK\ = 5:3, ABD + ACD = 7г. Найдите отношение длин стороны А В и диагонали АС.
20. В окружность вписан четырёхугольник ABCD, Р - точка пересечения его диагоналей, |АВ| = |С£)| = 5, \AD\ > \ВС\. Длина высоты, опущенной из точки В на сторону AD, равна 3, а площадь треугольника ADP равна 25/2. Найдите длины сторон AD и ВС, а также длину радиуса окружности.
21. В выпуклом четырёхугольнике ABCD известно, что угол DAB острый, угол ADC тупой, sin DAB = 3/5, cos ABC = —63/65. Окружность с центром в точке О касается сторон PC, CD и AD. Найдите длину отрезка ОС, если \АВ\ = 25/64, \ВС\ = 793/64, \CD\ = 25/4.
22. В окружность, длина радиуса которой равна 2, вписан правильный шестиугольник ABCDEF. Из точки К, лежащей на продолжении стороны AF таким образом, что \КА\ < \KF\ и \КА\ = у/П— 1, проведена секущая ХЯ, пересекающая окружность в точках N и Н, причём точка 7V лежит между точками К и if. Известно, что |ifiV| = 2, а угол NFH тупой. Найдите величину угла HKF.
23. В выпуклом пятиугольнике ABCDE диагонали BE к СЕ являются биссектрисами внутренних углов при вершинах В и С соответственно, А = 35°, D = 145°, а площадь треугольника ВСЕ1 равна 11. Найдите площадь пятиугольника ABCDE.
24. Продолжения сторон AD и ВС выпуклого четырёхугольника ABCD пересекаются в точке М, а продолжения сторон АВ и CD - в точке О. Отрезок МО перпендикулярен биссектрисе угла AOD. Найдите отношение площадей


3.3. Четырёхугольники и многоугольники общего вида
119
треугольника AOD и четырёхугольника ABCD, если \ОА\ = 12, \OD\ = 8, \CD\ = 2.
25. В четырёхугольнике ABCD, вписанном в окружность, биссектрисы углов А и В пересекаются в точке Е, лежащей на стороне CD. Известно, что отношение длины отрезка CD к длине отрезка ВС равно га. Найдите:
1) отношение расстояний от точки Е до прямых AD и ВС,
2) отношение площадей треугольников ADE и ВСЕ.
26. Диагонали вписанного в окружность четырёхугольника ABCD пересекаются в точке Е, причём \AD\ • \СЕ\ = \DC\ • |АЕ|, |Ш)| = 6, ADB = 7г/8. Найдите площадь четырёхугольника ABCD.
27. На одной стороне угла О взяты точки К, L и М, а на другой его стороне - точки Р, Q и R таким образом, что ifQ -L P/2, PL ± КМ, ЬД _L PQ, QM A. KL. Известно, что отношение расстояния от точки О до центра вписанной в четырёхугольник KPRM окружности к длине отрезка КР равно 17 : 6. Найдите величину угла О.


120
Теория и задачи
4. 	Задачи на доказательство
Задачи, приведённые в этом разделе, очень редко можно встретить на письменном экзамене. Однако такие задачи позволяют узнать много интересных и полезных для решения задач письменных экзаменов фактов. Они также позволяют научиться видеть и доказывать полезные соотношения в треугольниках, многоугольниках и окружностях.
4.1. 	Треугольники Теоретический материал
Напомним основные формулы и теоремы, связанные с треугольниками.
• Условие существования треугольника: если даны три отрезка с длинами а, 6, с, то для того, чтобы существовал треугольник со сторонами а, Ь, с, необходимо и достаточно выполнение следующих условий:
а + Ъ> с, а + с > 6, Ъ + с> а.
Здесь и ниже а, 6, с - стороны треугольника, а, /3,7 - соответствующие противоположные им углы.
• Монотонно возрастающая зависимость сторон от углов: если даны стороны треугольника а, 6, с, то для того, чтобы они удовлетворяли неравенствам а > Ь > с, необходимо и достаточно выполнение неравенств a > /3 > 7.
• Теорема о сумме углов треугольника: для углов треугольника а, /3,7 справедливо равенство а + /3 -f 7 = 7Г.
• Теорема о биссектрисах: все биссектрисы треугольника пересекаются в одной точке. Эта точка есть центр вписанной окружности.
• Теорема о медианах: все медианы треугольника пересекаются в одной точке и делятся ею в соотношении 2:1, считая от вершины.
• Теорема о высотах: все высоты треугольника пересекаются в одной точке.
• Теорема о серединных перпендикулярах: все серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. Эта точка есть центр описанной окружности.
• Теорема косинусов: для сторон и углов треугольника имеет место равенство
а2 = Ъ2 + с2 — 2Ьс • cos а.
• Теорема синусов: для сторон и углов треугольника имеют место равенства
sina sin/3 sin 7
где R - радиус описанной около треугольника окружности.


4.1. Треугольники
121
• Теорема о биссектрисе: биссектриса угла а треугольника делит противолежащую сторону а на прилежащие к сторонам бис отрезки аъ и ас, которые пропорциональны Ъ и с:
• Теорема Фалеса: если при пересечении сторон угла параллельными прямыми на одной стороне угла отсекаются равные между собой отрезки, то и на другой стороне угла отсекаются также равные между собой отрезки.
• Обобщенная теорема Фалеса: при пересечении сторон угла параллельными прямыми на сторонах угла отсекаются пропорциональные отрезки.
• Формулы длины биссектрисы:
здесь аъ,ас - отрезки из теоремы о биссектрисе. • Формула длины медианы:
• Признаки подобия треугольников: два треугольника подобны по двум углам; по двум сторонам и углу между ними; по трём сторонам.
Напомним, что в подобных треугольниках отношение длин соответствующих сторон, биссектрис, медиан, высот равно к - коэффициенту подобия. Отношение площадей подобных треугольников равно к2.
Примеры решения задач
Пример 1. Дан треугольник ABC. Доказать, что
аъ Ъ
ас с
та
V2Ь2 + 2с2 - а2 2
Решение. Пусть Z.A = а, ZJ5 = /3, Z.C = у = п — а — /3, тогда
cos а + cos /3 Н- cos 7 = cos a -f cos /3 — cos (a + /3) =
a — /3
2
+ --COS
что и требовалось доказать.


122
Теория и задачи
Пример 2. Существует ли треугольник с углами
arctg 2, arcsin (—1= j , arccos ( |?
\Vio)' V bs/2)
Решение. Для того чтобы существовал такой треугольник, надо, чтобы arctg2 4- arcsin (~i= j 4- arccos ( ^7= j = тг.
\VioJ V 5V2J
Для того чтобы доказать равенство
arctg 2 4- arcsin ( —) = тг — arccos ( \=) ,
\VTdJ V 5\/2/
достаточно показать, что косинус левой части равен косинусу правой и обе части лежат в пределах от нуля до тг. Для левой части равенства справедливо
ТГ . ( 1 \ 27Г
— < arctg 2 + arcsin —= < —,
4 & V vToy з
поскольку
• ( М w
sm —= <
V\/l0 У 6
Для правой части равенства справедливо
7Г 7Г . ,
— < arctg2 <2’) 0 < arcsm |
О < 7г — arccos Г ~= ) < так как х < arccos ( ^7= ) < 7г.
V 5у/2/ 2’
7Г ( 1
W2.J
Теперь вычислим значение косинуса от левой и правой частей равенства, получим
cos | arctg 2 -Ь arcsin ( —) J = = и cos (тг — arccos ( \=. j ) = —^7=.
V \л/10)) 5v/2 v V 5V2JJ 5V2
Следовательно, такой треугольник существует.
Ответ. Существует.
Пример 3. В прямоугольном треугольнике длины сторон - натуральные взаимно простые числа. Доказать, что длина гипотенузы - нечётное число, а длины катетов имеют разную чётность.
Решение. Пусть m и к - длины катетов прямоугольного треугольника, п - длина гипотенузы, т, п, к - взаимно простые числа и г? — тп2 + к2.
Пусть п - чётное число, то есть п = 21. Из равенства тп2 + к2 = 412 следует, что га и к имеют одинаковую чётность. Причём чётными они быть не могут, так как по условию являются взаимно простыми.
Значит, га = 2/i -Ь 1, к = 2/2 + 1 и
412 = (2/i + 1)^ -Н (2/2 4" 1)^ 412 = 412 4" 4/2 4- 4Zi 4- 4/2 4- 2.
Это невозможно, так как левая часть уравнения делится на 4, а правая нет.
Следовательно, п = 2/4-1, но тогда числа га и к должны иметь разную чётность.


4.1. Треугольники
123
Пример 4. Доказать, что если в треугольнике из одной вершины проведены медиана, биссектриса и высота, то биссектриса лежит между медианой и высотой.
Решение. Рассмотрим треугольник ABC, где высота СН, биссектриса СL и медиана CD проведены к стороне АВ. Если ВС = АС, то СН, CL и CD совпадают. Пусть для определенности ЛС > ВС.
По свойству биссектрисы
ВС
АС
< 1
BL < AL,
следовательно, точка L лежит между точками В и D, так как BD = AD. Поскольку
АС> ВС
/СВА > /кСАВ,
/ВСН < /АСН, следовательно, /ВСН < /BCL и точка лежит между точками J5 и L, так как /BCL = /АСЬ.
Пр и мер 5. Докажите, что площадь треугольника меньше единицы, если длины всех биссектрис меньше единицы.
Решение. Поскольку высота в треугольнике с
всегда меньше соответствующей биссектрисы,
ha la 1, hb <С l\) 1, 1%q <с Iq ^ 1»
Докажем, что все стороны треугольника меньше двух. Пусть биссектрисы AL и i?iV треугольника ABC пересекаются в точке О.
Из неравенства треугольника для ДАВ О следует, что
АВ < АО + ВО < AL -f BN < 2.
Аналогично получаем, что ВС < 2 и АС < 2. Оценим площадь ААВС
Sabc = т;а * ^ ' 2 * 1 = 1,
то есть 5лвс < 1-
Задачи
1. Какого вида треугольник, у которого высоты 3,4,5?
2. Доказать, что если в треугольнике две высоты равны, то он равнобедренный.
3. Медиана треугольника совпадает с его биссектрисой. Доказать, что этот треугольник равнобедренный.


124
Теория и задачи
4. Доказать, что если у треугольника равны две медианы, то он равнобедренный.
5. Пусть длины сторон прямоугольного треугольника - натуральные числа. Доказать, что длина одного из катетов кратна трём.
6. Доказать, что все прямоугольные треугольники, стороны которых образуют арифметическую прогрессию, подобны «египетскому» треугольнику (длины его сторон равны 3, 4, 5).
7. Пусть а, Ь, с - длины сторон треугольника. Доказать, что
2 (а2Ь2 + Ь2с2 + с2а2) > а4 + Ь4 + с4.
8. Доказать, что если медиана и высота, проведенные из одной вершины треугольника, делят его угол на три равные части, то треугольник прямоугольный.
9. Доказать, что в любом треугольнике большей стороне соответствует меньшая биссектриса.
10. Две биссектрисы у треугольника равны. Доказать, что он равнобедренный.
11. Доказать, что в равнобедренном треугольнике сумма расстояний от любой точки основания до боковых сторон равна боковой высоте.
12. В треугольнике АВС угол А прямой. Из вершины А проведены медиана AM, высота АН и биссектриса AL. Доказать, что AL - биссектриса в треугольнике АМН.
13. Доказать, что из всех треугольников с данным основанием и данным углом, противолежащим основанию, равнобедренный треугольник имеет наибольшую площадь.
14. Доказать, что из всех треугольников с данным основанием и данным углом, противолежащим основанию, равнобедренный треугольник имеет наибольший периметр.
15. Доказать, что сумма медиан треугольника
а) меньше Р,
3
б) больше -Р, где Р - периметр треугольника.
16. Доказать, что сумма расстояний от любой точки, взятой внутри (или на стороне) треугольника, до трех его сторон заключена между наибольшей и наименьшей его высотами. Найти точку в треугольнике, сумма расстояний от которой до сторон наибольшая.
17. Какого вида треугольник, у которого медианы 3, 4 и 5?
18. Пусть а, /3,7 - углы треугольника. Доказать, что
sin а • sin /3 • sin 7 <


4.2. Многоугольники
125
19. 	Доказать, что для любого треугольника справедливо неравенство
к < \/р-(р- о)-
20. 	Доказать, что для любого треугольника справедливо неравенство
1 1 1 /1 1 1
+ г + >2[ - + Т + -
р — а р — Ъ р — с \а Ъ с
4.2. Многоугольники Теоретический материал
Напомним основные формулы и теоремы.
У параллелограмма
• противоположные стороны равны;
• противоположные углы равны;
• диагонали пересекаются и точкой пересечения делятся пополам;
• сумма квадратов диагоначПей равна сумме квадратов сторон.
У трапеции
• средняя линия параллельна основаниям и равна их полусумме;
• сумма углов, прилежащих к боковой стороне, равна 7г.
У прямоугольника
• диагонали равны.
У ромба
• диагонали перпендикулярны и являются биссектрисами соответствующих углов.
У произвольного выпуклого п-угольника
• сумма углов равна тг(п — 2).
Признаки параллелограмма. Четырехугольник является параллелограммом, если выполнено хотя бы одно из следующих условий:
• противоположные стороны попарно равны;
• противоположные углы попарно равны;
• диагонали пересекаются и точкой пересечения делятся пополам;
• две противоположные стороны равны и параллельны.


126
Теория и задачи
Примеры решения задач
Пример 1. Внутри выпуклого четырехугольника найти точку, сумма расстояний от которой до вершин четырехугольника минимальна.
Решение. Рассмотрим четырехугольник ABCD, диагонали которого пересекаются в точке О.
С
Расстояние от точки О до вершин четырехугольника равно
АО + ВО + СО + DO — АС + BD.
Рассмотрим произвольную точку О', лежащую внутри четырехугольника. Имеем АО' + О'С > АС, ВО' + O'D > BD,
следовательно,
АО' + (УС + ВО' 4 O'D > АС + BD,
то есть точка пересечения диагоналей четырехугольника есть та точка, сумма расстояний от которой до вершин минимальна.
Ответ. Точка пересечения диагоналей.
Пример 2. Доказать, что если соединить середины сторон выпуклого четырехугольника, то получится параллелограмм. Когда этот параллелограмм будет ромбом? Квадратом?
Решение. Пусть точки K,F,M и N - середины соответственно сторон АВ, ВС, CD и AD четырехугольника ABCD.
В


4.2. Многоугольники
127
Отрезок KF - средняя линия треугольника ABC, отрезок MN - средняя линия треугольника ADC, значит,
KF || AC, KF = \АС, MN || AC, MN = \аС, следовательно,
KF || MN, KF = MN
и четырехугольник KFMN - параллелограмм.
Если диагонали четырехугольника равны (АС = BD), то параллелограмм KFMN будет ромбом. Если диагонали еще и взаимно перпендикулярны, то ромб KFMN будет квадратом.
Задачи
1. Доказать, что если каждая из диагоналей выпуклого четырехугольника делит его на равновеликие треугольники, то этот четырехугольник - параллелограмм.
2. В равнобедренной трапеции диагональ имеет длину 8 и является биссектрисой одного из углов. Может ли одно из оснований этой трапеции быть меньше 4, а другое равно 5?
3. Доказать, что из всех прямоугольников с данной диагональю наибольшую площадь имеет квадрат.
4. Какой четырехугольник с диагоналями d\ и d2 имеет максимальную площадь?
5. Доказать, что если отрезок, соединяющий середины двух противоположных сторон выпуклого четырехугольника, равен полусумме двух других сторон, то этот четырехугольник - трапеция.
6. Доказать, что биссектрисы углов, прилежащих к одной из непараллельных сторон трапеции, пересекаются под прямым углом в точке, лежащей на средней линии трапеции (или её продолжении).
7. В выпуклом четырехугольнике ABCD с диагоналями АС и BD на стороны CD и АВ опущены соответственно высоты АЕ и DF. Известно, что АЕ > BD, DF > АС, AD = 2 • АВ. Найти меры углов четырехугольника ABCD.
8. В выпуклом четырехугольнике KLMN с диагоналями LN и ХМ на стороны MN и КL опущены соответственно высоты КР и NQ. Известно, что КР > LN, NQ > КМ, KL = 3, KN = 5. Найти КМ.
9. Дан выпуклый четырехугольник ABCD, у которого АВ + BD < АС -Ь CD. Сравните длины отрезков АВ и АС.


128
Теория и задачи
4.3. 	Окружности Теоретический материал
Напомним основные утверждения об углах в окружностях:
• центральный угол равен по величине мере дуги окружности, на которую он опирается;
• вписанный угол равен по величине половине меры дуги окружности, на которую он опирается;
• угол, составленный секущими к окружности, равен полуразности мер дуг, на которые он опирается;
• угол, составленный пересекающимися хордами, равен полусумме мер дуг, на которые он опирается;
• угол, составленный касательной и хордой, измеряется половиной меры дуги, стягиваемой этой хордой.
Полезные следствия:
• вписанные углы, опирающиеся на одну и ту же дугу, равны;
• вписанные углы, опирающиеся на одну и ту же хорду (или на равные хорды), равны или в сумме равны 7г;
• вписанный угол является прямым тогда и только тогда, когда он опирается на диаметр.
Теоремы о касательных, хордах и секущих:
• отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности;
• произведения длин отрезков двух пересекающихся хорд равны;
• квадрат длины отрезка касательной равен произведению длины отрезка секущей на длину её внешней части.
Теоремы о вписанных и описанных окружностях:
• вокруг произвольного треугольника можно описать окружность, центром этой окружности является точка пересечения серединных перпендикуляров к сторонам треугольника;
• в произвольный треугольник можно вписать окружность, центром этой окружности является точка пересечения биссектрис треугольника;
• для того чтобы около четырехугольника можно было описать окружность, необходимо и достаточно, чтобы суммы противоположных углов были равны 7г;


4.3. Окружности
129
• для того чтобы в четырехугольник можно было вписать окружность, необходимо и достаточно, чтобы суммы длин противоположных сторон были равны;
• для того чтобы около трапеции можно было описать окружность, необходимо и достаточно, чтобы эта трапеция была равнобедренной.
Примеры решения задач
Пример 1. Доказать, что если из вершины А неравнобедренного треугольника АВС проведена биссектриса, а из середины ВС восстановлен перпендикуляр, то точка их пересечения лежит на окружности, описанной около треугольника АВС.
Решение. Пусть D - точка пересечения биссектрисы угла ВАС треугольника АВС с описанной окружностью. Из равенства углов BAD и CAD следует, что BD = CD и треугольник В DC равнобедренный. Следовательно, перпендикуляр, опущенный из точки D на отрезок J5C, делит его пополам.
Пример 2. Доказать, что расстояние от точки окружности до хорды есть среднее пропорциональное между расстояниями от концов хорды до касательной к окружности в этой точке.
Решение. Если хорда АВ параллельна касательной, проведенной в точке М, то все три расстояния равны и утверждение задачи справедливо. Рассмотрим случай, когда продолжение хорды А В и касательной в точке М пересекаются. Обозначим точку пересечения S; MN - расстояние от точки М до хорды АВ; АК и BF - расстояния от концов хорды до касательной. Требуется доказать, что MN = VBF • АК.
АК
пи АК SM
SAK подобен треугольнику SMN, следовательно, —— = и MN = -—АК.
OiVi JVL iV
5 Геометрия


130
Теория и задачи
По свойству касательной и секущей
SM = VSA ■ SB.
Откуда получаем, что
—АК = VBF ■ АК. АК
Пример 3. Доказать, что, если четырехугольник вписан в окружность, то про- изведение его диагоналей равно сумме произведений его противоположных сторон (теорема Птолемея)!
Решение. Рассмотрим четырехугольник ABCD с диагоналями АС и BD. Введём обозначения:
Надо доказать, что d\d2 = ас Н- bd. Проведём отрезок АА\, параллельный BD, тогда четырехугольник AA\DB - трапеция и A\D = АВ = 6, А\В = AD = а. Треугольник DA\B равен треугольнику DAB по трём сторонам. Тогда
АВ = 6, AD = а, ВС = с, CD = d, AC = db ££> = d2-
Sdayb = SdAB,
Sabcd = Sbcd + Sbad, Saxbcd = Sbcd +
то есть Sabcd = Saxbcd• Пусть ZDOA = (p, тогда, с одной стороны,
Sabcd = -did2sin</?
и, с другой стороны,
Sabcd = SUiBCD = Sa^bc + Saxcd =
= ^Л1В • BC • sin ZAiBC + \axD ■ CD • sin t'.AXDC =


4-3. Окружности
131
Для того чтобы доказать равенство d\d2 = ас+ bd, нам достаточно показать, что ZAiDC = ф. Обозначим
АВ = AiD = а, ВС = /3, ААг = 7, тогда по свойству вписанных углов
а по свойству углов между пересекающимися хордами получаем
ZAOD = <p=a + % + 7.
Значит, Z.A\DC = (р. Тогда Sabcd = ^ (ас + Ьб?) • sin<£>, откуда следует, что d\di = ас + bd.
Задачи
1. Докажите, что в прямоугольном треугольнике сумма длин катетов равна сумме длин диаметров вписанной и описанной окружностей.
2. В круг вписаны две трапеции с соответственно параллельными сторонами. Докажите, что диагонали этих трапеций равны.
3. Может ли у треугольника со сторонами меньше 1 радиус описанной окружности быть больше 100?
4. Доказать, что касательные к двум пересекающимся окружностям, проведенные из любой точки продолжения их общей хорды, равны между собой.
5. В окружности проведены равные пересекающиеся хорды. Доказать, что соответствующие части этих хорд, на которые они делятся точкой пересечения, равны.
6. Через точки пересечения двух окружностей Р и Р' проводятся произвольные прямые, пересекающие окружности. Через точки пересечения этих прямых с окружностями проводятся прямые га и га'. Доказать, что га параллельна га'.
7. К двум неггересекающимся окружностям проведены две общие внешние касательные и внутренняя. Точки М и N - точки касания внешней касательной с окружностями, а Р и Q - точки пересечения внутренней касательной с внешними. Доказать, что MN = PQ.
8. 	К двум окружностям с центрами 0\ и О2, касающимся внешним образом в точке Л, проведена общая касательная ВС (В и С - точки касания). Доказать, что угол ВАС прямой.


132
Теория и задачи
4.4. Площади Теоретический материал
Напомним основные формулы.
• Площадь треугольника:
S=^a-ha, 5=ia-6-sin7, S = p-r, S =
S = \Jp ■ (p - a) ■ (p - b) ■ (p - c),
где a, fe, с - стороны треугольника, a, /3,7 - соответствующие противоположные им углы, ha,hb,hc - высоты, проведенные к сторонам, р - полу периметр треугольника, г - радиус вписанной в треугольник окружности, R - радиус описанной около треугольника окружности.
• Площадь параллелограмма:
S = а • ha, S = а • Ъ • sin 7,
где а и Ъ - стороны параллелограмма, 7 - угол, образованный сторонами а и b,ha - высота, проведенная к стороне а.
Площадь трапеции:
S=±(a + b)-h,
где a, b - длины оснований трапеции, а h - её высота.
• Площадь произвольного четырехугольника:
S = • с?2 • sin </?,
где di, с!г ~ длины диагоналей четырехугольника, а ip - угол между ними. Примеры решения задач
Пример 1. Существует ли треугольник, у которого две высоты больше 100, а площадь меньше 1?
Решение. Пусть ha > 100 и hb > 100. Так как а > Нъ, то а > 100 и
S = ]-а ■ ha > \ ■ 100 • 100 = 5000.
Ответ. Не существует.


4-4' Площади
133
Пример 2. Пусть а, 6, с, d - последовательные стороны произвольного выпук-
ac + bd
лого четырехугольника. Доказать, что его площадь Ь < —-—.
Решение. Пусть в четырехугольнике ABCD стороны АВ = а, ВС = 6, CD = с, AD = d.
Построим треугольник BDCi такой, что ВС\ — CD = с, DC\ = ВС = Ь. Площадь четырехугольника ABC\D равна площади четырехугольника ABCD. Пусть /.АВС\ — ol, ZADCi = 7, тогда
Sabcd = SabcxD = Sabcx + Sadci = 2 ' ^ ' sina + 2 ’ * sin7 =
_ ac • sin a + • sin 7 ^ ac -f bd
Задачи
1. В выпуклом четырехугольнике ABCD известно, что АВ = a, J3C = 6, CD = с, .ОЛ = d. Доказать, что для его площади S имеет место неравенство
S < ~(ab + cd). В каких случаях это неравенство обращается в равенство?
2. Все стороны выпуклого четырехугольника меньше 7. Доказать, что его площадь строго меньше 50.
3. В треугольнике АВС заданы длины двух его сторон а и Ь. Доказать, что
а2 -j- b2
для его площади 5 справедливо неравенство S < —j—В каком случае это неравенство обращается в равенство?
4. Может ли уменьшиться площадь треугольника при увеличении всех его сторон?


134
Теория и задачи
5. 	Задачи на построение
Задачи на построение нельзя встретить на письменном экзамене. Однако такие задачи позволяют узнать много интересных и полезных для решения задач письменных экзаменов фактов. Они также позволяют научиться видеть и доказывать полезные соотношения в треугольниках, многоугольниках и окружностях.
5.1. 	Алгебраический метод Теоретический материал
Решение задачи на построение состоит в описании последовательности операций, которые надо проделать циркулем и линейкой, чтобы получить нужную фигуру.
С помощью циркуля можно
• провести окружность с центром в любой точке плоскости радиусом, равным длине заданного отрезка;
• найти точки пересечения проведённой окружности с любым заданным объектом плоскости (прямой, окружностью и т.п.).
С помощью линейки можно
• провести прямую через две заданные точки;
• найти пересечение проведённой прямой с любым заданным объектом плоскости.
Общая схема решения задач на построение такова.
• Анализ — считаем, что искомая фигура построена, рисуем её, исследуем геометрические свойства, которые могут подсказать способ её построения.
• Построение — указывается последовательность действий, дающих искомую фигуру.
• Доказательство — приводится обоснование того, что построено именно то, что требовалось (в большинстве случаев это следует из самого построения).
• Исследование — определяются условия, при которых существует решение задачи, анализируется число различных решений.
Приведём список элементарных построений, которые будут использоваться при решении задач:
1) поделить отрезок на п равных частей;
2) поделить угол пополам;
3) провести через данную точку перпендикуляр к данной прямой;
4) провести через данную точку прямую, параллельную данной прямой;
5) построить треугольник по трём сторонам;
6) построить треугольник по двум сторонам и углу между ними;
7) построить треугольник по стороне и двум прилежащим к ней углам.


5.1. Алгебраический метод
135
Если какое-либо из элементарных построений вызывает у вас трудности, повторите соответствующий материал в школьном учебнике.
Алгебраический метод решения задач на построение заключается в построении искомых элементов по формулам, выражающим их зависимость от заданных элементов.
Большинство задач этого вида решается с помощью комбинирования основных четырёх формул, приведённых ниже.
Примеры решения задач
Пример 1. Построение отрезка х = у/а2 + Ь2, где а и Ь - заданные отрезки.
Решение. Построим прямой угол и на его сторонах отложим катеты а и Ь. Соединив полученные точки А и В, по теореме Пифагора получим
х = АВ = \Лг2 + R
Пример 2. Построение отрезка х = \Jа2 — Ь2.
где а и Ъ - заданные отрезки.
Решение. Построим прямой угол и на одной из его сторон отложим катет Ь. Из полученной точки С раствором циркуля, равным а, сделаем засечку на другой стороне угла. Второй катет построенного треугольника по теореме Пифагора равен
х — \Jа2 — Ъ2.
Пример 3. Построение отрезка х = у/ab, где а и b - заданные отрезки.
Решение. Отложим на прямой отрезки АК — а, КВ = Ъ (точки А и В находятся по разные стороны от точки К) и построим окружность на отрезке АВ как на диаметре.


136
Теория и задачи
Из точки К восстановим перпендикуляр до пересечения с окружностью в точке D. В прямоугольном треугольнике ADB отрезок DK будет высотой, проведённой из прямого угла к гипотенузе. Следовательно, DK = у/АК • В К = y/ab.
ab
Пр и м е р 4. Построение отрезка х = —, где а, о и с - заданные отрезки.
с
Решение. На сторонах произвольного угла с вершиной О отложим отрезки О А = с, АВ = Ь, ОС = а. Через точку В проведём прямую, параллельную АС, которая пересечёт другую сторону угла в точке D.
_ _ с a ab
По теореме Фалеса имеем - = —, откуда х — —.
b х с
Пример 5. Найти геометрическое место точек, расстояния от которых до двух данных точек А и В находятся в заданном отношении т\пф 1.
Решение. В следующем разделе будет предложено геометрическое решение этой задачи. Сейчас решим её с помощью алгебраического метода.
Обозначим длину отрезка АВ через а, отношение т : п через к. Примем точку А за начало координат и прямую АВ за ось х.
Точка М с координатами (ж, у) принадлежит искомому ГМТ
AM
MB
= к
х2 +у2
= кг
(х - а)2 + у2
Домножим равенство на знаменатель и сгруппируем слагаемые по степеням х. Поделив полученное уравнение на коэффициент перед х2, получим
2
х2-
2ак2 к2- 1
• х + Г +
а2 к2 к2 — 1
О
х —
ак2 к2- 1
+ У2 =
а2 к2
(fc2-l)2’
М(х,у)


5.1. Алгебраический метод
137
ак
Мы получили уравнение окружности радиуса —^ гг с центром на прямой АВ
\к — 1|
ак2
на расстоянии —т—— от точки А справа, если к > 1, и слева, если к < 1. \кг — 1|
Полученная окружность называется окружностью Аполлония.
Пример 6. Построить треугольник по двум сторонам и медиане, выходящей из общей вершины данных сторон.
Решение. Пусть даны а, 6, тс, тогда
тс2 =
а2 -f Ь2 с2
2 4
—, откуда с = д/2 а2 + 2 Ь2 — 4 т2.
Для того чтобы построить отрезок длины с, сначала построим отрезки х = у/2а, у = у/26, потом 2 = у/х2 у2 и, наконец, с = yjz2 — (2mc)2. В результате осталось построить треугольник по трём сторонам.
Замечание. Геометрическое решение этой задачи будет приведено в одном из следующих разделов.
Задачи
1. 	Дан отрезок а. Построить отрезок х = а • >/n, п £ N.
2. Даны отрезки а, 6, с. Построить отрезок х = \/&2 + Ь2 4* с2.
3. Дан отрезок а. Построить отрезок х = а • v^.
а1995
4. Даны отрезки а, 6. Построить отрезок х =
£1994 ‘
5. Даны два отрезка: длины 1 и длины а. С помощью циркуля и линейки построить отрезок длины х = v^a3 — 4a2 -f 3a.
-f-
6. Даны отрезки a, b. Построить отрезок x = —r——.
a1 H- bz
7. Построить треугольник ABC, если известна биссектриса BD и отрезки AD и DC, на которые она делит противоположную сторону.
8. Построить треугольник по основанию a, ha и у/b2 — с2.
9. Построить окружность, проходящую через две данные точки и касающуюся данной прямой.
10. Построить прямоугольный треугольник по гипотенузе с и сумме катетов s.
11. Дан угол в 19°, построить угол в 1°.
12. Дан отрезок длины а и угол, равный а. Построить отрезки длины a cos а,
а а
asina, , — , a-tga, a-ctga.
cos a sin a


138
Теория и задачи
13. Дан равносторонний треугольник АВС со стороной 1. Через вершину А с помощью циркуля и линейки провести такую прямую, что сумма расстояний от точек В и С до этой прямой равна \/2.
14. Дан ААВС. Построить отрезок DE с концами на сторонах АВ и ВС так, что DE || АС и DE виден из середины АС под прямым углом.
15. Построить угол, равный трём градусам.
16. С помощью циркуля и линейки разделите угол 54° на три равные части.
17. Провести прямую, параллельную диагонали и пересекающую две смежные стороны данного прямоугольника так, чтобы его площадь разделилась в отношении 1:3.
5.2. 	Метод геометрических мест точек Теоретический материал
Геометрическим местом точек плоскости (пространства) с данным свойством называется множество всех точек плоскости (пространства), обладающих этим свойством.
При решении задач на геометрические места точек (сокращённо ГМТ) должно быть предъявлено множество и доказано, что каждая точка этого множества обладает заданным свойством, а любая другая точка не обладает.
В дальнейшем под ГМТ в данном пособии будет подразумеваться ГМТ плоскости. Простейшими примерами ГМТ являются следующие:
• ГМТ, удалённых на расстояние R от данной точки О, - это окружность радиуса R с центром в точке О;
• ГМТ, равноудалённых от точек А и В, - это серединный перпендикуляр к отрезку АВ;
• ГМТ, из которых данный отрезок АВ виден под данным углом а, - это объединение двух дуг окружностей радиуса R = ^4^-- с центрами на серединном перпендикуляре к отрезку АВ, лежащими на расстоянии R cos а от прямой АВ.
При построении ГМТ бывает удобно разбить данное свойство на более простые и найти соответствующие более простые ГМТ. Пересечением этих множеств будет множество точек, для которых одновременно выполняются все свойства, то есть искомое ГМТ.
Помимо задач на нахождение ГМТ в этом разделе будут рассмотрены задачи на построение циркулем и линейкой, решаемые методом ГМТ.


5.2. Метод геометрических мест точек
139
Примеры решения задач
Пример 1. По сторонам прямого угла скользит отрезок заданной длины а. Какую кривую при этом описывает середина этого отрезка?
Решение. Пусть М - середина отрезка А В = а, скользящего по сторонам прямого угла.
Так как медиана в прямоугольном треугольнике равна половине гипотенузы, то ОМ = АВ/2 = а/2. То есть точка М удалена от точки О на расстояние а/2 и, следовательно, принадлежит четверти дуги окружности радиуса а/2 с центром в точке О.
Теперь покажем, что произвольная точка этой дуги является серединой гипотенузы длины а некоторого прямоугольного треугольника.
Для этого из произвольной точки М данной дуги сделаем засечку радиусом а/2 на стороне прямого угла. Получим точку А. Обозначим через В точку пересечения прямой AM со второй стороной прямого угла. Покажем, что А В = а. Пусть /.ОАВ = а, тогда /АОМ — а и /.МОВ = 90° — а — /АВО. Следовательно,
АО MB равнобедренный и MB = ОМ = а/2. То есть ААВО имеет гипотенузу
длины а, что и требовалось доказать.
Пример 2. По данной дуге окружности «бегает» точка М. Хорда АВ фиксирована. Какие кривые при этом пробегает в треугольнике AM В точка пересечения медиан треугольника?
Решение. Пусть дуга АВ вмещает углы, равные а. Обозначим через К точку пересечения медиан треугольника AM В и проведём через неё прямые, параллельные сторонам угла AM В. Получим /А'К В' = /АМВ = а.
Так как медианы точкой пересечения делятся в отношении 2 : 1, то по теореме Фалеса
АА' = \АВ и ВВ' = )-АВ,
3 3
следовательно, А'В' = АВ/3. Таким образом, точка пересечения медиан лежит на дуге A! Bf, вмещающей углы, равные а.
Верно и обратное. Если взять произвольную точку на дуге А'В' и рассмотреть два соответствующих подобных треугольника, то эта точка будет точкой пересечения медиан большего из них.
Следовательно, дуга А'В* есть геометрическое место точек пересечения медиан треугольника АМВ.


140
Теория и задачи
Пример 3. Построить прямоугольный треугольник по гипотенузе и высоте, опущенной на гипотенузу.
Решение. Построим окружность с диаметром, равным гипотенузе, и проведём прямую параллельно диаметру на расстоянии, равном высоте. Точка пересечения этой прямой с окружностью даст вершину В\ треугольника АВ\С, причём угол АВ\С будет прямым, так как опирается на диаметр.
При h = с/ 2 получим единственную точку В\.
При 0 < h < с/2 получим две точки и, следовательно, два равных симметричных треугольника АВ\С и АВ2С.
Если h > с/2, то задача не имеет решения.
Пример 4. Найти геометрическое место точек, расстояния от которых до двух данных точек А ж В находятся в заданном отношении т : п.
Решение. В предыдущем разделе было приведено решение этой задачи, полученное алгебраическим методом. Сейчас решим задачу геометрически.
Пусть т > п (при т — п искомое ГМТ является серединным перпендикуляром к отрезку АВ).
Рассмотрим точки Е G АВ и С ф АВ такие, что АЕ : ЕВ = АС : СВ = т : п.
Отрезок СЕ является биссектрисой A ABC, так как делит противолежащую сторону в отношении прилежащих сторон. Проведём CD А. СЕ и ВМ || CD. Треугольник АВМС равнобедренный, так как его биссектриса СЕ будет одновременно и высотой. Следовательно, СВ = СМ и
AD АС АС т DB~ СМ~ СВ~~ п
то есть положение точки D на прямой АВ не зависит от выбранной нами точки С. Важно только, что АС : СВ = т : п. Поскольку ZECD = 90°, точка С лежит на окружности с диаметром ED. Значит, если АС : СВ = т : п, то точка С лежит на окружности, построенной на ED как на диаметре.
Теперь возьмём произвольную точку С' на этой окружности и покажем, что АО :С'В = т:п.


5.2. Метод геометрических мест точек
141
С"
Обозначим длину отрезка АС' через d и рассмотрим треугольник А АС" В, у которого
AC" = d и ВС" = d -
т
Так как АС" : С"В = т : п, точка С" лежит на построенной окружности. Но в верхней полуплоскости существует только одна точка на окружности с диаметром ED, находящаяся на расстоянии d от точки А. Следовательно, точки С" и С" совпадают, что и требовалось доказать.
Таким образом, искомое ГМТ - окружность, построенная на отрезке ED как на диаметре.
Замечание. Полученную окружность называют окружностью Аполлония, а точки А, Е, В и D, лежащие на одной прямой и удовлетворяющие равенству
АЕ . ЕВ = AD : DB,
называют гармоническими точками.
Пример 5. Доказать, что геометрическим местом точек, разность квадратов расстояний от которых до двух данных точек М и N есть величина постоянная, является прямая, перпендикулярная отрезку MN.
Решение. Пусть точка D такова, что
MD2 - ND2 = а2
(где а2 есть заданная в условии постоянная величина), и Е - её проекция на отрезок MN.
Из прямоугольных треугольников MDE и NDE получим
ME2 = MD2 - DE2, NE2 = ND2 - DE2
и, следовательно,
ME2 - NE2 = MD2 - ND2 = а2.
Таким образом, мы нашли на отрезке MN точку Е такую, что MLТ2 — EN2 = а2. Так как D - произвольная точка из искомого ГМТ, то все точки ГМТ лежат на перпендикуляре к отрезку МN, восстановленному из точки Е.
Аналогично (с помощью теоремы Пифагора) показывается, что любая точка на перпендикуляре обладает требуемым свойством.
D


142
Теория и задачи
Замечание. Для того чтобы получить точку Е (основание перпендикуляра), построим вспомогательный прямоугольный треугольник АВС с катетом а. Гипотенузу и второй катет выберем такими, чтобы выполнялось условие с + b > MN.
По теореме Пифагора а2 = с2 — Ь2. Сделаем засечки радиусами b и с из точек N и М. Обозначим точку пересечения этих дуг через D и опустим перпендикуляр из D на MN.
Основанием этого перпендикуляра будет искомая точка Е.
П ример 6. Доказать, что геометрическим местом точек, касательные из которых к двум данным окружностям равны, является прямая, перпендикулярная линии центров этих окружностей (эта прямая называется радикальной осью двух окружностей).
Решение. Рассмотрим окружности с центрами 0\ и О2 радиусов R\ и Т?2- Пусть DA\ и DA2 - равные касательные, проведённые к окружностям из точки D.
D
Из прямоугольных треугольников AO\A\D и AO2A2D получим A\D2 = O1D2 — RJ, A2D2 = O2D2 — R2, откуда
0\D2 - 02D2 — R\- R\.
Следовательно, точка D такова, что разность квадратов расстояний от неё до 0\ и О2 есть величина постоянная.
Согласно предыдущей задаче, множество всех таких точек есть прямая, перпендикулярная отрезку O1O2.
Замечание. Три радикальные оси любых трёх попарно взятых окружностей пересекаются в одной точке, называемой радикальным центром.
Для объяснения этого факта достаточно рассмотреть точку пересечения двух радикальных осей. Поскольку она принадлежит двум радикальным осям, касательные из неё ко всем трём окружностям равны. Следовательно, она принадлежит и третьей радикальной оси.
Рассмотрим способы построения радикальной оси в зависимости от взаимного расположения окружностей.


5.2. Метод геометрических мест точек
143
1) 	Если окружности касаются друг друга, то радикальная ось проходит через точку касания, так как в этом случае касательные, проведённые из точки D, равны отрезку общей касательной DА.
Следствие. Три общие касательные трёх попарно касающихся окружностей пересекаются в одной точке.
2) 	У пересекающихся окружностей радикальная ось проходит через точки пересечения. В этом случае касательные, проведённые из точки D, равны в силу того, что квадрат касательной равен произведению длин секущих, то есть
DA\ = DB ■ DC = DA\.
Следствие. Три общие хорды трёх попарно пересекающихся окружностей пересекаются в одной точке.
3) 	Если окружности не пересекаются, то для построения радикальной оси будем использовать вспомогательную окружность, пересекающую две данные. Пусть М - точка пересечения прямых, содержащих общие хорды АВ и CD. Это есть радикальный центр трёх окружностей. Следовательно, точка М принадлежит радикальной оси двух данных окружностей. Найдя таким же образом ещё одну точку или опустив перпендикуляр на линию центров 0\02, найдём искомую радикальную ось.


144
Теория и задачи
Задачи
1. По данной дуге окружности «бегает» точка М. Хорда АВ фиксирована. Какую кривую при этом пробегает в треугольнике AM В точка пересечения высот?
2. Построить треугольник по заданной стороне, противолежащему ей углу и проведённой к ней высоте.
3. По сторонам прямого угла скользит гипотенуза прямоугольного треугольника. Найти геометрическое место вершин прямого угла этого треугольника.
4. Построить треугольник по двум сторонам и высоте, опущенной на одну из этих сторон.
5. Построить треугольник по а, а, г.
6. Построить треугольник по а, г, R.
7. Построить треугольник по а, г, R.
8. Построить треугольник по а, /3, г.
9. Построить треугольник по заданной стороне а, противолежащему ей углу а и проведенной к ней медиане та-
10. Построить параллелограмм по углу и диагоналям.
11. Построить треугольник по стороне, высоте, опущенной на эту сторону, и медиане другой стороны.
12. Дана окружность и точка А, лежащая вне круга, ограниченного окружностью. Построить касательные к окружности, проходящие через эту точку.
13. Построить треугольник по заданным a, ha,la>
14. Построить треугольник по заданным а, а, b : с.
15. Провести общую внешнюю касательную к двум данным окружностям (то есть даны их центры и радиусы).
16. На сторонах угла даны два отрезка А В и CD и точка М внутри угла. Найти геометрическое место точек N таких, что Sabn + Scdn = Sabm + Sc dm-
17. По окружности «бегает» дуга данной длины CD, хорда АВ задана, CD < АВ. Найти геометрическое место точек пересечения прямых АС и BD.
18. Через точку А внутри окружности проводятся всевозможные хорды. Найти геометрическое место середин этих хорд.
19. Найти на стороне угла точку, из которой данный отрезок АВ, лежащий на другой стороне угла, виден под наибольшим углом.


5.3. Метод симметрии и спрямления
145
5.3. 	Метод симметрии и спрямления Теоретический материал
В случаях, когда нужную фигуру сразу построить затруднительно, бывает удобно преобразовать её в другую фигуру, которую построить легче.
В этом разделе будут рассмотрены задачи, решаемые с помощью преобразования фигур методом симметрии и спрямления.
Точки А и В называются симметричными относительно прямой га, если отрезок АВ JL га и делится этой прямой пополам. Прямую га называют осью симметрии. Точку В называют отражением точки А и наоборот.
m
Фигуры, все точки которых являются симметричными относительно прямой га, называются симметричными относительно этой прямой.
Метод симметрии заключается в следующем. Считаем, что нужная фигура построена, и отражаем часть фигуры (точку, прямую, окружность) относительно некоторой оси. Изменённую фигуру подчиняем тем же условиям, которым должна удовлетворять исходная фигура, и решаем новую задачу уже известными способами.
В ряде задач метод симметрии приводит к спрямлению ломаных линий в прямые. Метод спрямления состоит в следующем. Считаем задачу решённой и в полученном чертеже некоторую ломаную линию заменяем прямой. Таким образом исходная задача заменяется новой - более простой. После построения новой фигуры определяется, в какой точке надо согнуть выпрямленную линию, чтобы вернуться к исходной задаче.
Метод спрямления особенно часто применим в задачах, где дана сумма или разность частей некоторой ломаной линии.


146
Теория и задачи
Примеры решения задач
п р и м е р 1. Дана прямая т и две точки А и В по одну сторону от неё. Найти на прямой т точку X такую, что сумма расстояний АХ и ВХ минимальна.
Решение. Рассмотрим точку А', симметричную точке А относительно прямой га. Обозначим через X точку пересечения отрезка А!В о, прямой га. Имеем
АХ + ХВ = А'Х + ХВ = А'В.
в
Для любой другой точки X’ £ га будет выполняться
АХ' + Х'В = А'Х' + Х'В > А'В.
Следовательно, искомая точка X - это точка пересечения отрезка А'В с прямой га.
П ример 2. Построить треугольник по периметру Р и двум углам а и /3.
Решение. Пусть треугольник ABC с данными ZА = a, ZC = /3, Рдвс = -Р уже построен. На прямой АВ отложим отрезки АА' = АС и В В' = ВС.
С
Треугольники АА'С и ВВ'С равнобедренные с углами при основании соот- а (3
ветственно — и Следовательно, у треугольника А'В'С сторона А'В' = Р и
/.А! = Z.B' - 2 2
Таким образом, для того чтобы построить A ABC, сначала нам надо построить АА'В'С по стороне и двум прилежащим углам, потом провести к сторонам А'С


5.3. Метод симметрии и спрямления
147
и В'С серединные перпендикуляры, которые пересекут А!В' соответственно в точках А и В.
Построенный треугольник АВС будет удовлетворять заданным условиям, то есть Равс = Р и ZВАС = а, /.ВСА = /3.
Пример 3. Даны отрезок АВ и прямая, пересекающая его. Построить треугольник АВС, биссектриса которого принадлежит данной прямой.
Решение. Построим отражение точки А относительно прямой га. Проведём через В и полученную точку А! прямую, которая пересечёт исходную прямую га в точке С.
Пусть Н - точка пересечения отрезка АА’ с прямой га. Прямоугольные треугольники А АСН и АА'СН равны друг другу и, следовательно, /АСМ — /ВСМ.
Пример 4. Внутри угла дана точка А. Найти такое положение точек X и Y на сторонах угла, чтобы периметр треугольника AXY был минимальным.
Решение. Пусть А! и А!' - отражения точки А относительно сторон угла. Длина ломаной А'ХУА" равна периметру AAXY.
Так как ломаная имеет минимальную длину в случае, когда является отрезком, то искомые точки X, Y - это точки пересечения отрезка А! Ап со сторонами угла.


148
Теория и задачи
Пример 5. Построить треугольник, зная а, с и а+ 6.
Решение. От отрезка AD = а + b отложим под углом а отрезок А В = с. В качестве вершины С возьмём точку пересечения серединного перпендикуляра к отрезку BD с отрезком AD.
В
Так как отрезки ВС и DC равны между собой, построенный треугольник A ABC удовлетворяет всем данным в условии задачи требованиям.
Задачи
1. Построить треугольник, зная Р, а и ha-
2. Даны две окружности и между ними прямая. Начертить равносторонний треугольник так, чтобы две его вершины были на окружностях, а одна из высот лежала на данной прямой.
3. Дана прямая т и две точки А и В по одну сторону от неё. Найти на т такую точку X, чтобы АХ составлял с т угол, вдвое больший, чем ВХ.
4. Внутри угла даны точки А и В. Построить равнобедренный треугольник, основание которого лежит на одной стороне угла, вершина - на другой, а боковые стороны проходят через точки А и В.
5. Дана прямая АВ и две окружности, лежащие по одну сторону от прямой. Найти на прямой АВ точку, касательные из которой составляют с этой прямой равные углы.
6. Точки А и В расположены между параллельными прямыми тип. Постройте точки М Е ш, N £ п так, чтобы длина ломаной AMNB была наименьшей.
7. В данную окружность вписать прямоугольник, зная разность основания и высоты.
8. Построить треугольник по стороне, прилежащему углу и разности остальных сторон.
9. Построить четырёхугольник ABCD, зная его стороны, если диагональ АС делит угол А пополам.
10. 	Найти сумму перпендикуляров, опущенных на стороны равнобедренного треугольника из точки, взятой на основании.


5.4• Метод параллельного переноса
149
11. Найти сумму перпендикуляров, опущенных из точки, взятой внутри равностороннего треугольника, на его стороны.
12. На окружности даны точки А и В. Отыскать на ней точку X такую, что АХ + ВX = а, где а - заданный отрезок.
13. На окружности даны точки А и В. Отыскать на ней точку X такую, что АХ — ВХ = а, где а - заданный отрезок.
14. Найти геометрическое место точек, сумма расстояний от которых до двух данных пересекающихся прямых равна заданному отрезку.
15. На данной прямой найти такую точку, что разность расстояний от неё до сторон данного угла равна данному отрезку.
16. Провести окружность, касающуюся двух данных окружностей, так, чтобы радиусы, проведённые из центра искомой окружности к точкам касания, образовывали данный угол.
17. Построить равнобедренный треугольник, зная его боковую сторону а и сумму высоты с основанием s.
18. Построить треугольник по а, ть + Ь и /(га*,, Ъ).
19. Построить треугольник по Ь, си /3 — 7.
5.4. 	Метод параллельного переноса Теоретический материал
В этом разделе будут рассмотрены задачи, решаемые с помощью параллельного переноса. В таких задачах часть фигуры переносят параллельно самой себе так, чтобы новую фигуру было легче построить, чем искомую.
После построения новой фигуры надо сделать обратный параллельный перенос, чтобы вернуться к исходной задаче.
Многие задачи на построение четырёхугольников можно решить с помощью построения вспомогательного параллелограмма, стороны которого параллельны и равны диагоналям искомого четырёхугольника. Рассмотрим четырёхугольник ABCD. Перенесем диагональ АС параллельно самой себе в отрезки ВХ и DY. Полученный параллелограмм BXYD будет обладать следующими свойствами.
X


150
Теория и задачи
1) Стороны и угол параллелограмма BXYD равны диагоналям и углу между ними в исходном четырёхугольнике.
2) Расстояния от точки С до вершин параллелограмма BXYD равны сторонам исходного четырёхугольника.
3) Углы между отрезками, соединяющими точку С с вершинами параллелограмма BXYD, равны углам исходного четырёхугольника.
4) Площадь параллелограмма вдвое больше площади четырёхугольника.
5) Диагонали параллелограмма вдвое больше отрезков, соединяющих середины сторон АВ и CD, ВС и AD; угол между диагоналями равен углу между этими отрезками.
6) Углы /XCD и Z.BCY дополняют углы между противоположными сторонами АВ и CD, ВС и AD до 180°.
Докажем эти свойства.
1) Стороны параллелограмма параллельны и равны диагоналям четырёхугольника, следовательно, угол параллелограмма равен углу между этими диагоналями.
2) Отрезки ВС и CD являются сторонами четырёхугольника. Отрезки СХ и CY параллельны и равны сторонам АВ и AD, поскольку АВХС и ACYD - параллелограммы.
3) Углы ZВСХ = /АВС и ZDCY = /LCDА как внутренние накрест лежащие при параллельных прямых. Углы /XCY = /.BAD как углы с параллельными сторонами.
4) Обозначим диагонали ABCD через d\,d2 и угол между ними через а. Тогда
Sabcd = -dicfesina, Sbxyd = did2sina, откуда Sbxyd = 2Sabcd •
5) Пусть отрезок MN соединяет середины сторон А В и CD.
X


5-4- Метод параллельного переноса
151
Так как диагонали параллелограмма точкой пересечения делятся пополам, то N есть точка пересечения диагоналей параллелограмма ACYD, а отрезок MN есть средняя линия ДABY.
Следовательно, MN = BY/2, что и требовалось доказать.
6) 	Пусть С' есть точка пересечения продолжений сторон АВ и CD, а В! взята на продолжении ВС1 за точку С'. Равенство углов ZXCD = ZCC'B' следует из параллельности прямых АВ' и СХ.
Замечание. В случае, когда стороны ВС и AD параллельны (то есть ABCD трапеция), ломаная BCY выпрямляется.
Примеры решения задач
Пример 1. Построить четырёхугольник, зная его углы и две противоположные стороны.
Решение. Пусть в четырёхугольнике ABCD даны углы а, /3,7, S и стороны ВС и AD. Перенесём ВС параллельно самой себе в АЕ.
В AAED стороны АЕ и AD известны, а угол ZEAD = a—ZBAE = а — (тг — (3). Следовательно, этот треугольник мы построить можем.
Точку С можно получить как точку пересечения луча, отложенного от прямой AD под углом 5, и луча, отложенного от прямой АЕ под углом /3. Затем, переместив отрезок АЕ вдоль ЕС, получим точку В.


152
Теория и задачи
Пример 2. Построить отрезок, равный
и параллельный данному так, чтобы один конец лежал на данной прямой, другой - на данной окружности.
Решение. Пусть даны прямая га, отрезок А В и окружность.
Сдвинем прямую т на вектор АВ, получим прямую га' || га.
Через точки пересечения га' с окружностью проведём прямые, параллельные АВ. Четырёхугольник PQQ'P' - параллелограмм, причём РР1 || QQ' || АВ и PPr = QQ' = АВ. Следовательно, РР' и QQf - искомые отрезки.
Задача может иметь одно решение, два решения или не иметь решений вообще.
П р и м е р 3. Построить трапецию по двум диагоналям и двум основаниям.
Решение. Рассмотрим трапецию ABCD с диагоналями АС и j3D. Перенесём диагональ BD вдоль основания ВС. Получим параллелограмм BCED.
В треугольнике АСЕ стороны АС и СЕ равны диагоналям, основание АЕ равно сумме оснований трапеции. Следовательно, А АСЕ можно построить по трём сторонам. После этого отложим отрезок ED (равный ВС) и найдём вершину D. Потом, достроив ACDE до параллелограмма, получим вершину В.
П р и м е р 4. Построить треугольник по трём его медианам.
Решение. Пусть медианы ВМ = гаь, AN = та и С К = гас треугольника АВС пересекаются в точке О. Перенесём отрезок ВО параллельно самому себе в отрезок А! С.


5.4• Метод параллельного переноса
153
Так как медианы в треугольнике точкой пересечения делятся в отношении 2 : 1, то в параллелограмме О В А'С стороны
ОВ = -гпь, В А' — ОС = \шс.
о о
В
Кроме того, поскольку в параллелограмме диагонали точкой пересечения делятся пополам,
О А’ = 2 ON = ^ma.
О
Таким образом, треугольник О В А' мы можем построить по трём сторонам. Затем, достроив его до параллелограмма О В А'С, получим вершину С. Далее, отложив отрезок АО = О А!, получим вершину Л.
Пример 5. Построить четырёхугольник, зная две диагонали, угол между ними и две противолежащие стороны.
Решение. Зная две диагонали и угол между ними, мы можем построить вспомогательный параллелограмм BXYD. Согласно свойству 2 (сформулированному в теоретической части) отрезки ВС к CY равны противолежащим сторонам четырёхугольника и точку С мы можем найти как точку пересечения дуг соответствующих радиусов. Достроив ACYD до параллелограмма, получим вершину А.
X


154
Теория и задачи
Пример 6. Через две точки, данные на окружности, провести две параллельные хорды, разность которых равна данной величине.
Решение. Пусть А и В - заданные на окружности точки, а А А! || В В' - хорды, с заданной разностью. Трапеция АВВ'А' является равнобокой, так как она вписана в окружность. Перенесём АА' параллельно в отрезок ВС. Получим параллелограмм АВСА!. В итоге получаем АВ — А!С = А'В'.
Треугольник, равный треугольнику АА'В'С, можно построить по трём сторонам. После этого надо отложить от АВ угол, равный углу /.А'С В'. Так мы найдем точку В'. Точку А' можно получить как точку пересечения прямой, параллельной В В', с окружностью.
Замечание. Если в условии задачи дана сумма (разность) отрезков или углов, надо так преобразовать исходную фигуру, чтобы эта величина входила в преобразованную фигуру.
Задачи
1. Построить трапецию по четырём сторонам.
2. Между двумя окружностями1 провести отрезок, делящийся пополам в данной точке А.
3. Построить треугольник, зная гаа, гас, /(га*,, а).
4. Через точку А внутри угла провести прямую так, чтобы отрезок, заключённый между сторонами, делился точкой А пополам.
5. Построить трапецию, зная диагонали, угол между ними и одну из боковых сторон.
6. Построить четырёхугольник, зная две диагонали, две противолежащие стороны и угол между ними.
7. Через данную точку М провести прямую так, чтобы разность расстояний до неё от двух данных точек А и В была равна данной длине.
1 Имеется в виду, что один конец отрезка лежит на одной окружности, второй - на другой.


5.5. Метод подобия
155
8. В данный остроугольный треугольник вписать прямоугольник с наименьшей диагональю (одна сторона прямоугольника лежит на основании треугольника) .
9. Даны три параллельные прямые. Провести через данную точку секущую так, чтобы разность отрезков между параллелями была равна заданной величине.
10. Построить трапецию ABCD, зная боковую сторону CD, угол между диагоналями, расстояние между параллельными сторонами и отрезок, соединяющий середины боковых сторон.
11. Построить треугольник по 6, с и та.
12. Построить четырёхугольник, зная его стороны и отрезок, соединяющий середины двух противоположных сторон.
13. Построить четырёхугольник, зная четыре его стороны и угол между двумя противоположными сторонами.
14. Построить биссектрису угла, вершина которого недоступна.
15. Даны две точки А и В и между ними две параллели тип. Провести между этими параллелями в данном направлении отрезок CD так, чтобы сумма АС + CD -f BD была минимальной.
16. На окружности даны две точки А и В. В данном направлении провести хорду XY так, чтобы сумма хорд АХ и BY была равна заданной величине.
17. Построить прямоугольник с данной стороной так, чтобы его стороны проходили через четыре заданные точки.
18. Даны две окружности и прямая. Провести параллельно этой прямой секущую, отсекающую в окружностях хорды, сумма которых равна заданному отрезку длины s.
5.5. 	Метод подобия Теоретический материал
Два многоугольника называются подобными, если равны их соответствующие углы, а соответствующие стороны пропорциональны.
Если два подобных многоугольника расположены так, что их соответствующие стороны параллельны, то прямые, соединяющие вершины равных углов, пересекаются в одной точке. Эта точка называется центром гомотетии или центром подобия, а многоугольники называются гомотетическими. Отношение расстояний от центра подобия до соответствующих вершин гомотетических многоугольников равно коэффициенту их подобия.
Центр подобия может лежать внутри многоугольников, может - вне, может совпадать с одной из вершин или принадлежать одной из сторон.


156
Теория и задачи
Центром подобия двух окружностей называется точка пересечения их общих внешних касательных. Центр подобия лежит на линии центров окружностей. Отношение расстояний от центра подобия до центров окружностей равно отношению радиусов.
Точка пересечения внутренних касательных к двум окружностям называется обратным центром подобия, который обладает аналогичными свойствами.
Любые две секущие, проведённые через центр подобия окружностей, пересекают окружности таким образом, что треугольники АВО и А!В'О' будут гомо- тетическими (соответствующие радиусы и хорды параллельны).
Метод подобия заключается в том, что сначала мы строим фигуру, ещё не удовлетворяющую всем условия задачи, но подобную искомой фигуре. Потом, используя остальные условия, преобразуем построенную фигуру в искомую.


5.5. Метод подобия
157
Примеры решения задач
Пример 1. Построить треугольник по двум углам и биссектрисе третьего угла.
Решение. Пусть даны углы а,/3 и отрезок 1С. Построим произвольный треугольник ДА'В'С с двумя данными углами.
А'
Проведём в нём биссектрису СЬ' и отложим на ней отрезок CL = 1С. Через точку L проведём прямую, параллельную А'В'. Углы и биссектриса полученного треугольника А АВС равны заданным.
Пример 2. Построить треугольник по се, /3 и а + ha.
Решение. Построим ААВ'С' по двум углам а,/3 и высоте ha> = а + fta, проведённой к стороне В' С' = а'. Искомый треугольник АВС подобен треугольнику AB'Cf и
ha (х -h ho, ha' Oj -f-
A
fl2,
Следовательно, ha = —:——■—. Построим точку H на прямой AH' на рассто- а' + har
янии ha от точки А и через точку Н проведём прямую, параллельную прямой В'С'. Построенный треугольник АВС удовлетворяет заданным условиям.


158
Теория и задачи
Пример 3. Построить треугольник по трём высотам ha,hb,hc.
Решение. Возьмём произвольный отрезок р и построим А А' В' С" со сторонами / р2 р2 , р2
а = т~1 о = — И с =
tla hb
25 25
Пусть 5 - площадь искомого треугольника, тогда его стороны а = —, Ь = —,
ha hb
25
с = —. Следовательно, искомый треугольник и ААГВ'С* подобны.
he
А'
Для того чтобы построить искомый треугольник АВС с высотами ha^hb,hC) достаточно в треугольнике А'В'С' на прямой А! Н* отложить отрезок AfH = ha и через точку Н провести прямую J5C, параллельную В*С'.
Задача имеет решение, если существует треугольник, построенный из отрезков J_ J_ _1_
h-a kb he
Пример 4. Дан отрезок длины у/b. С помощью циркуля и линейки построить отрезок длины 2.
Решение. Построим прямоугольный треугольник АВС с катетами АВ = а, ВС = 2а, где а - произвольный отрезок. Тогда гипотенуза АС = ау/5.
На гипотенузе АС отложим отрезок CD, равный л/5, и из точки D опустим пер-
СН DC
пендикуляр DН. Из подобия треугольников DHC и АВС получаем —— = -т-р; >
ВС АС
следовательно, СН = 2.


5.5. Метод подобия
159
Пример 5. В круговой сектор вписать квадрат.
Решение. Пусть точка О - центр заданного сектора. Построим вспомогательный квадрат ABCD, две вершины которого (А и D) лежат на радиусах сектора на равном расстоянии от точки О.
Проведём прямые О В и ОС, они пересекут дугу сектора в точках В' и С'.
Далее проведём В'А'±.В'С' и C'D' А-В'С'.
Четырёхугольники ABCD и A'B'C'D' подобны (один получается из другого с помощью гомотетии с центром в точке О), следовательно,
A'B'C'D' также является квадратом, причём квадратом, вписанным в данный сектор.
Задачи
1. Построить треугольник по двум углам и высоте, проведенной из третьего угла.
2. Построить окружность, касающуюся сторон данного угла и проходящую через заданную внутри него точку.
3. Дан треугольник АВС со сторонами А В = 5, ВС = 6, АС = 7. Построить точку S £ ВС, точку Q Е АС и точку Р Е АВ так, чтобы треугольник SQP был равносторонним.
4. В данный треугольник вписать квадрат.
5. Построить треугольник по а,/3,г.
6. Через данную точку провести прямую, отсекающую от двух данных окружностей хорды, пропорциональные их радиусам.
7. Дан угол АВС и точка М внутри него. Найти на стороне ВС точку X, равноудалённую от АВ и точки М.
8. Даны три точки А, В и С, не лежащие на одной прямой. Провести прямую, пересекающую отрезок АС в точке X, а отрезок ВС в точке Y таким образом, что АХ = XY = YB.
9. Даны две окружности и на них по точке. Провести две равные окружности, касающиеся друг друга и двух данных окружностей в заданных точках.
10. Через данную точку А провести к двум данным окружностям секущую, отсекающую в окружностях
а) равные хорды;
б) хорды, длины которых находятся в заданном соотношении.
11. Построить треугольник, зная /3,1ь и AD : DC, где BD - высота.


160
Теория и задачи
12. Даны три концентрические окружности. Провести секущую АВС так, чтобы точки А, В и С лежали на разных окружностях и АВ = ВС.
13. Через две точки, лежащие вне данной окружности, провести окружность, касающуюся заданной окружности.
14. Даны две окружности с центрами в точках О и О'. Через центр их подобия S проведены касательная и секущая. Касательная касается окружностей в точках С и С" соответственно, секущая отсекает от окружностей хорды АВ и А!В9. Доказать, что CS • СS = AS • B'S = BS • A'S.
15. Через данную точку А провести окружность, касающуюся двух данных окружностей.
5.6. 	Метод поворота и смешанные задачи Теоретический материал
В этом разделе рассматриваются задачи, решаемые с помощью поворота фигуры (или её части) относительно некоторой неподвижной точки плоскости (центра поворота).
Также приводятся задачи, не попадающие однозначно ни под один из предложенных ранее типов задач, и задачи, решение которых требует комбинирования нескольких методов.
Примеры решения задач
П ример 1. Даны две окружности и точка А. Построить равнобедренный треугольник АВС (АВ = АС) с данным углом при вершине А так, чтобы вершины В и С лежали на окружностях.
Решение. Пусть 0,0' - центры данных окружностей и а - данный угол. Повернём окружность в центром О' относительно точки А на угол а. Обозначим через В и В' точки пересечения новой окружности с окружностью с центром в О и совершим обратный поворот новой окружности в окружность с центром в О'. Точки В и В' перейдут при этом в некоторые точки С и С'. Таким образом, мы получили два треугольника ААВС и ААВ'С', удовлетворяющих условиям задачи.
Замечание. Если точки В и В' совпадают, то задача имеет одно решение. Если построенная окружность не пересекает окружность с центром в точке О, то решений нет.


5.6. Метод поворота и смешанные задачи
161
Пример 2. Даны две окружности, треугольник и точка А. Построить треугольник АВС, подобный данному, так, чтобы вершины В и С лежали на окружностях.
А
Решение. Пусть 0,0'- центры данных окружностей и пусть дан треугольник с углом а и прилежащими сторонами бис. Сначала для окружности с центром в О' построим гомотетичную окружность с центром гомотетии в точке А и коэффициентом гомотетии к = с/Ь. Эту окружность повернём относительно точки А на угол а и, как и в предыдущем примере, получим точки В и В'. Совершив обратный поворот, получим точки D и D', а совершив обратную гомотетию, найдём искомые С и С".
Пример 3. Построить равносторонний треугольник, вершины которого лежат на трёх данных параллельных прямых.
Решение. Пусть а, 6, с - три данные параллельные прямые.
а А/
с'
6 Геометрия


162
Теория и задачи
Рассмотрим произвольную точку В Е Ъ и повернём относительно неё прямую с на 60°, получим прямую с' и точку A Е а. При обратном повороте А перейдёт в С Е с. Треугольник АВС равносторонний, так как по построению В А = ВС и /В = 6 0°.
Пример 4. В треугольнике найти точку, сумма расстояний от которой до вершин минимальна.
Решение. Рассмотрим произвольную точку Р внутри треугольника АВС. Повернем ААВР относительно точки А на 60°, получим ДАВ'Р'. При этом В'Р' = ВР и РР' = АР (так как ДАРР* равносторонний), следовательно,
ВР + АР + СР = В'Р1 + Р'Р + PC,
то есть сумма расстояний от точки Р до вершин треугольника равна длине ломаной В'Р'PC > В'С. Минимальное значение длины ломаной равно В'С при Р,Р' Е В'С.
В В
Следовательно, для построения искомой точки Р надо сначала построить точку В' (повернуть отрезок АВ относительно А на 60°). Точки Р и Р' должны быть расположены на отрезке В'С таким образом, чтобы треугольник АРР1 был равносторонним, поэтому они должны лежать на лучах, отложенных от перпендикуляра АН под углом 30°.
Замечание. Если один из углов исходного треугольника больше 120°, то луч, отложенный от АН под углом 30°, пересекает отрезок В'С в точке, не лежащей внутри треугольника. В этом случае искомая точка Р совпадает с вершиной тупого угла.
Пример 5. Построить треугольник по заданным отрезкам медианы, биссектрисы и высоты, проведённым из одной вершины.
Решение. Рассмотрим треугольник АВС с данными высотой В#, биссектрисой BL и медианой ВМ. Продолжим биссектрису BL до пересечения с описанной окружностью в точке В' (так как ZABB' = ZCBB', то В' - середина дуги АС).
Теперь через точку М проведём перпендикуляр к хорде АС. Точка В' (середина дуги) и точка О (центр описанной окружности) принадлежат этому серединному перпендикуляру.


5.6. Метод поворота и смешанные задачи
163
Таким образом, для того чтобы построить ДАВС, сначала надо построить треугольник ВНМ (по заданным гипотенузе ВМ и катету ВН), потом на отрезке МН отметить точку L (биссектриса всегда лежит между медианой и высотой) и найти точку В' как точку пересечения перпендикуляра к прямой НМ в точке М и прямой BL.
Центр окружности О есть точка пересечения прямой MB' и серединного перпендикуляра к хорде В В'. Вершины А и С есть точки пересечения этой окружности с прямой НМ.
Задачи
1. Даны три параллельные прямые. Построить квадрат, три вершины которого лежат на этих прямых.
2. Даны прямая и окружность. Построить окружность, касающуюся данной окружности и прямой в данной точке.
3. Даны две окружности. Провести к ним через заданную точку две секущие, пересекающиеся под заданным углом и отсекающие
а) равные хорды;
б) хорды, длины которых находятся в заданном отношении.
4. В данный параллелограмм ABCD вписать равнобедренный треугольник APQ (АР = AQ) с данным углом при вершине А.
5. Построить четырёхугольник, вписываемый в окружность, зная его стороны а,6, с и d.
6. Провести через заданную точку прямую, отсекающую от данной окружности хорду заданной длины.
7. При помощи циркуля и линейки построить окружность, проходящую через две данные точки и отсекающую от данной окружности хорду данной длины.
8. Провести через точку В пересечения двух окружностей прямую, высекающую из окружностей равные хорды.
9. Через точку А внутри угла провести прямую, отсекающую от угла треугольник минимального периметра.
10. Даны три точки. Построить окружности, попарно касающиеся в этих точках.
11. Построить треугольник, зная о,Ла и Z(mb,c).
12. Через вершину выпуклого четырёхугольника провести прямую, которая делит его площадь пополам.


164
Теория и задачи
6. 	Стереометрия
6.1. 	Введение в стереометрию
Приведём основные стереометрические определения, связанные с взаимным расположением прямых и плоскостей в пространстве.
Параллельность прямых и плоскостей в пространстве
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Прямая и плоскость называются параллельными, если они не пересекаются.
Две плоскости называются параллельными, если они не пересекаются.
Скрещивающиеся прямые
Прямые, которые не лежат в одной плоскости и не пересекаются, называются скрещивающимися.
Угол между скрещивающимися прямыми определяется как угол между параллельными им прямыми, проходящими через одну точку.
Общим перпендикуляром двух скрещивающихся прямых называется отрезок, концы которого лежат на этих прямых, перпендикулярный к ним (такой отрезок существует и притом только один).
Расстоянием между двумя скрещивающимися прямыми называется длина их общего перпендикуляра (оно же является и расстоянием между параллельными плоскостями, содержащими эти прямые).
Двугранный угол
Двугранным углом называется фигура, образованная двумя полуплоскостями (гранями) с общей ограничивающей их прямой (ребром двугранного угла).
Двугранный угол измеряется своим линейным углом, то есть углом между перпендикулярами к ребру, восстановленными в обеих плоскостях из одной точки.


6.1. Введение в стереометрию
165
Многогранный угол
Трехгранным углом (abc) называется фигура, составленная из трех плоских углов (ab), (Ъс) и (ас), не лежащих в одной плоскости. Эти углы называются гранями трехгранного угла, а их стороны - ребрами. Общая вершина плоских углов называется вершиной трехгранного угла. Двугранные углы, образованные гранями трехгранного угла, называются двугранными углами трехгранного угла.
Аналогичным образом определяется понятие п-гранного угла (aia2-..an) - как фигуры, составленной из п плоских углов (ахаг), (азаз), ... , (anai).
Многогранный угол называется выпуклым, если он лежит по одну сторону каждой из ограничивающих его плоскостей.
Замечание 1. Каждый плоский угол трехгранного угла меньше суммы двух других плоских углов.
Замечание 2. Сечением выпуклого n-гранного угла плоскостью, не проходящей через вершину, является выпуклый п-угольник.
Замечание 3. В выпуклом многогранном угле сумма плоских углов не превосходит 360°.


166
Теория и задачи
Перпендикулярность прямых и плоскостей в пространстве
Прямая перпендикулярна плоскости, если она перпендикулярна любой прямой в этой плоскости.
Две плоскости перпендикулярны, если соответствующий двугранный угол является прямым.
Наклонная
Наклонной, проведенной к данной плоскости, называется прямая, пересекающая плоскость, но не перпендикулярная ей. Точка пересечения наклонной и плоскости называется основанием наклонной.
Проекцией точки на плоскость называется основание перпендикуляра, опущенного из данной точки на данную плоскость.
Проекцией наклонной на плоскость называется прямая, состоящая из проекций всех точек наклонной на данную плоскость.
Углом между наклонной и плоскостью называется угол между наклонной и её проекцией.
Теоремы о параллельности прямых и плоскостей
• Две прямые, параллельные третьей прямой, параллельны друг другу (транзитивность параллельности прямых).
• Ели прямая, не лежащая в плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости (признак параллельности прямой и плоскости).
• Если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны (признак параллельности плоскостей).
• Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны (теорема о параллельных плоскостях).
• Если плоскость содержит прямую, параллельную другой плоскости, и пересекает эту другую плоскость, то линия пересечения плоскостей параллельна первой прямой.


6.2. Многогранники
167
Теоремы о перпендикулярности прямых и плоскостей
• Если прямая перпендикулярна двум пересекающимся прямым в плоскости, то она перпендикулярна этой плоскости (признак перпендикулярности прямой и плоскости).
• Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны (признак перпендикулярности плоскостей) .
• Прямая, лежащая в плоскости, перпендикулярна проекции наклонной на эту плоскость тогда и только тогда, когда эта прямая перпендикулярна самой наклонной (теорема о трех перпендикулярах).
• Два различных перпендикуляра к одной и той же плоскости параллельны.
• Две плоскости, перпендикулярные одной и той же прямой, параллельны.
• Перпендикуляр к одной из двух взаимно перпендикулярных плоскостей, проходящий через линию пересечения этих плоскостей, целиком лежит во второй плоскости.
Замечание. Последняя теорема имеет важное следствие: если каждая из двух непараллельных плоскостей перпендикулярна третьей плоскости, то прямая пересечения этих двух плоскостей также перпендикулярна этой третьей плоскости.
6.2. 	Многогранники Теоретический материал
Многогранником называется тело, ограниченное в пространстве конечным числом плоскостей.
Многогранник называется выпуклым1, если он лежит по одну сторону от каждой из ограничивающих его плоскостей.
Общая часть поверхности многогранника и ограничивающей его плоскости называется гранью многограннике?, стороны граней - ребрами многогранника, а вершины - вершинами многогранника.
*В дальнейшем мы будем рассматривать только выпуклые многогранники.
2Все грани выпуклого многогранника являются выпуклыми многоугольниками.


168
Теория и задачи
Основные определения, связанные с призмами
N -угольной призмой называется многогранник, две грани которого - равные п-угольники, лежащие в параллельных плоскостях (основания призмы), а остальные грани - параллелограммы (боковые грани).
Призма называется прямой, если её боковые ребра перпендикулярны основаниям; в противном случае призма называется наклонной.
Прямая призма называется правильной, если её основаниями являются правильные многоугольники.
Призма, основанием которой является параллелограмм, называется параллелепипедом.
Прямой параллелепипед, у которого основанием является прямоугольник, называется прямоугольным параллелепипедом.
Прямоугольный параллелепипед с равными ребрами называется кубом.
Высотой призмы называется перпендикуляр, проведенный из какой-либо точки плоскости одного основания к плоскости другого основания.
Основные утверждения, связанные с призмами
Объем произвольной призмы: V = SH, где S - площадь основания, Н - высота призмы.
Объем прямоугольного параллелепипеда: V = аЪс, где а, 6, с - длины трех ребер, выходящих из одной вершины.
Объем куба: V = а3, где а - длина ребра куба.
Свойства параллелепипеда:
• противолежащие грани попарно равны и параллельны;
• все четыре диагонали пересекаются в одной точке (центре симметрии параллелепипеда) и делятся этой точкой пополам.
В отличие от прямой призмы, ребра наклонной призмы не перпендикулярны основаниям, поэтому иногда бывает удобно провести сечение призмы плоскостью, перпендикулярной ребрам. В этом случае справедливы следующие формулы.


6.2. Многогранники
169
Объем наклонной призмы: V = SnL, где Sn - площадь перпендикулярного сечения, L - боковое ребро призмы.
Площадь боковой поверхности: 5бок = PnL, где РП - периметр перпендикуляр¬
ного сечения.
А' В1
Замечание. Приведенные формулы справедливы и для прямой призмы, причем в качестве перпендикулярного сечения можно использовать основание призмы.
Основные определения, связанные с пирамидами
N -угольной пирамидой называется многогранник, одной гранью которого является п -угольник (основание пирамиды), остальными - треугольники (боковые грани), у которых только одна общая вершина (вершина пирамиды).
Высотой пирамиды называется перпендикуляр, проведенный из вершины пирамиды к плоскости основания пирамиды.
Пирамида называется правильной, если её основание - правильный многоугольник, а основание высоты совпадает с центром этого многоугольника.
Высота боковой грани правильной пирамиды, проведенная из её вершины, называется апофемой.
Усеченной пирамидой называется многогранник, отсекаемый от пирамиды плоскостью, параллельной основанию, и расположенный между плоскостью сечения и плоскостью основания исходной пирамиды.
Усеченная пирамида называется правильной, если она является частью правильной пирамиды.
Высотой усеченной пирамиды называется перпендикуляр, проведенный из какой-либо точки плоскости одного основания к плоскости другого основания.
Апофемой правильной усеченной пирамиды называется высота боковой грани (трапеции).


170
Теория и задачи
Основные утверждения, связанные с пирамидами
Объем произвольной пирамиды: V — \;SH,
о
где S - площадь основания, Н - высота пирамиды.
Объем произвольной усеченной пирамиды: V = \-Н (5i + y/SiS^ + S2),
о
где Si и 5г - площади оснований, Н - высота пирамиды.
Площадь боковой поверхности правильной пирамиды: 5б<ж =
где Р - периметр основания, I - апофема.
Площадь боковой поверхности правильной усеченной пирамиды:
5бок = 7^ (^1 + ^2) h гДе А и ?2 " периметры оснований, I - апофема.
Основные сведения о тетраэдрах
Тетраэдром называется треугольная пирамида.
Тетраэдр называется правильным, если все его ребра равны.
Тетраэдр называется прямоугольным, если все три плоских угла при какой- либо его вершине прямые.
Два ребра, имеющие в качестве одного из своих концов общую вершину, называются смежными. Два не смежных ребра называются противоположными (или скрещивающимися).
Медианой тетраэдра называется отрезок, соединяющий вершину тетраэдра с точкой пересечения медиан противоположной грани. Медианы тетраэдра пересекаются в одной точке, называемой центроидом, и делятся этой точкой в отношении 3:1, считая от вершины.
Бимедианой тетраэдра называется отрезок, соединяющий середины противоположных ребер. Бимедианы пересекаются в одной точке (центроиде тетраэдра) и делятся этой точкой пополам.


6.2. Многогранники
171
D
С
Высотой тетраэдра называется перпендикуляр, опущенный из вершины на противоположную грань. Если высоты (или их продолжения) пересекаются в одной точке, то тетраэдр называется ортоцентрическим.
Приведём также некоторые полезные сведения относительно расположения основания высоты тетраэдра.
• Основание высоты тетраэдра является центром окружности, описанной около основания, тогда и только тогда, когда длины всех боковых ребер равны между собой (или все боковые ребра наклонены к плоскости основания под одним углом).
• Основание высоты тетраэдра является центром окружности, вписанной в основание, тогда и только тогда, когда все боковые грани наклонены к плоскости основания под одним углом.
Замечание. Приведённые утверждения справедливы и для произвольной пирамиды.
Примеры решения задач
Пример 1. Высота прямой призмы 1м, её основанием служит ромб со стороной 2м и острым углом 30°. Через сторону основания проведена секущая призму плоскость, наклоненная к плоскости основания под углом 60°. Найти площадь сечения.
Решение. Рассмотрим прямую призму ABCDA!В'С'D', в основании которой лежит ромб ABCD с углом ZBAD = 30° и стороной, равной 2 м. Высота ромба ВН = АВ • sin 30° = 1. Отложим на прямой В В' отрезок ВР = \/3, тогда в прямоугольном треугольнике ВНР ZВНР = 60°.
Заметим, что отрезок ВН является проекцией наклонной HP и ВН _L AD, следовательно, по теореме о трёх перпендикулярах HP J_ AD. Это значит, что плоскость, проходящая через прямые AD и HP, наклонена к плоскости основания под углом 60°. Построим сечение призмы этой плоскостью.


172
Теория и задачи
Так как секущая плоскость должна пересекать две параллельные плоскости по параллельным прямым, то искомая плоскость пересекает верхнее основание призмы по отрезку ML || AD || A'D'.
Из параллельности противолежащих сторон четырёхугольника A'D'LM следует, что он является параллелограммом и ML = A'D' = 2. А из параллельности и равенства отрезков ML и AD следует, что искомое сечение ADLM также является параллелограммом.
Для того чтобы найти его площадь, нам необходимо вычислить длину высоты КН, где К есть точка пересечения отрезков ML и HP. Опустим из точки К перпендикуляр на отрезок ВН и рассмотрим точку К' - основание этого перпендикуляра. Из прямоугольного треугольника К'КН получим:
К'К
КН
= sin 60°
1
КН
v/3
2
КН = —=.
Уз
В результате искомая площадь равна
Sadlm = AD • КН = 2
_2_ _ А_ у/% ~ \/з’
Ответ.
_4_
V3'
Задачи
1. В прямоугольном параллелепипеде диагональ, равная d, образует с боковыми гранями углы /3 и 7. Найти объём параллелепипеда.
2. Объём правильной треугольной призмы равен V. Угол между диагоналями двух боковых граней, проведёнными из одной вершины, равен а. Определить сторону основания призмы.
3. Дан прямоугольный параллелепипед ABCDA!В'С'D', у которого AD = 6, АВ = 3 и А А' = 2. Найдите угол между прямой АС' и прямой, проходящей через середины ребер А А' и В'С'.


6.3. Тела вращения
173
4. Дан куб ABCDA' В'С' D', в нём через вершину В' проведена диагональ. Найти отношение площади сечения этого куба плоскостью, перпендикулярной указанной диагонали и проходящей через её середину, к площади его полной поверхности.
5. В основании пирамиды лежит треугольник со сторонами 7, 8, 9. Боковые рёбра пирамиды наклонены к плоскости основания под углом 60°. Найти высоту пирамиды.
6. Дана правильная четырехугольная пирамида SABCD с вершиной S. Через точки А, В и середину ребра SC проведена плоскость. В каком отношении эта плоскость делит объём пирамиды?
7. В правильной треугольной пирамиде SABC с вершиной S проведена высота SD. На отрезке SD взята точка К так, что SK : KD = 1 : 2. Известно, что
двугранные углы между основанием и боковыми гранями равны —, а рас-
6
4
стояние от точки К до бокового ребра равно —= . Найти объём пирамиды.
v 13
8. Основанием пирамиды SABC является равносторонний треугольник АВС, длина стороны которого равна Ау/2. Боковое ребро SC перпендикулярно плоскости основания и имеет длину 2. Найти величину угла и расстояние между скрещивающимися прямыми, одна из которых проходит через точку 5 и середину ребра ВС, а другая проходит через точку С и середину ребра АВ.
6.3. 	Тела вращения Теоретический материал
В этом разделе собраны задачи на вычисление элементов цилиндра, конуса, шара и задачи, связанные с описанными и вписанными цилиндрами, конусами, шарами. Приведём основные определения и теоремы.
Основные определения, связанные с цилиндром
Цилиндром (точнее, прямым круговым цилиндром) называется фигура, полученная вращением прямоугольника вокруг одной из его сторон.
Поверхность цилиндра состоит из оснований цилиндра - двух равных кругов, лежащих в параллельных плоскостях, и боковой поверхности.
Отрезок с одним концом на окружности одного основания и другим концом на окружности другого основания, перпендикулярный плоскостям оснований, называется образующей цилиндра.
Высотой цилиндра называется расстояние между плоскостями оснований.
Осью цилиндра называется прямая, проходящая через центры оснований. Сечение цилиндра плоскостью, проходящей через ось, называется осевым сечением.


174
Теория и задачи
Плоскость, проходящая через образующую цилиндра и перпендикулярная осевому сечению, проходящему через эту образующую, называется касательной плоскостью цилиндра.
Цилиндр называется вписанным в призму, если его основания вписаны в основания призмы, и грани призмы касаются его боковой поверхности. В этом случае призма называется описанной около цилиндра (левый рисунок).
Цилиндр называется описанным около призмы, если его основания описаны около оснований призмы и ребра призмы являются его образующими. В этом случае призма называется вписанной в цилиндр (правый рисунок).
Основные утверждения, связанные с цилиндром
Площадь боковой поверхности: SeOK = 2nRH.
Объем цилиндра: V = 7гR2H.
Здесь R - радиус основания цилиндра, Н - высота цилиндра.
Напомним также, что
• сечением цилиндра плоскостью, параллельной оси цилиндра, является прямоугольник;
• плоскость, перпендикулярная оси цилиндра, пересекает его боковую поверхность по окружности, равной окружности основания.
Основные определения, связанные с конусом
Конусом (точнее, прямым круговым конусом) называется тело, полученное вращением прямоугольного треугольника вокруг одного из катетов.
Поверхность конуса состоит из основания конуса (круга) и боковой поверхности (кругового сектора).
Отрезок с одним концом в вершине конуса и другим концом на окружности основания называется образующей конуса.
Высотой конуса называется перпендикуляр, опущенный из вершины конуса на плоскость основания. Основание высоты прямого кругового конуса совпадает с центром основания.


6.3. Тела вращения
175
Осью конуса называется прямая, проходящая через вершину конуса и центр основания. Сечение конуса плоскостью, проходящей через ось, называется осевым сечением.
Плоскость, проходящая через образующую конуса и перпендикулярная осевому сечению, проходящему через эту образующую, называется касательной плоскостью конуса.
Конус называется вписанным в пирамиду, если его основание вписано в основание пирамиды и грани пирамиды касаются его боковой поверхности. В этом случае пирамида называется описанной около конуса (левый рисунок).
Конус называется описанным около пирамиды, если его основание описано около основания пирамиды и боковые ребра пирамиды являются его образующими. В этом случае пирамида называется вписанной в конус (правый рисунок).
Плоскость, перпендикулярная оси конуса, отсекает от него меньший конус. Оставшаяся часть называется усеченным конусом.
Основные утверждения, связанные с конусом
Площадь боковой поверхности: вбок = kRL.
Объем конуса: V = -7rR2H.
о
Здесь R - радиус основания, L - образующая, Н - высота конуса.
Напомним также, что
• сечением конуса плоскостью, проходящей через вершину конуса, является равнобедренный треугольник;
• плоскость, перпендикулярная оси конуса, пересекает его боковую поверхность по окружности.


176
Теория и задачи
Основные определения, связанные с шаром
Шаром называется тело, состоящее из всех точек пространства, находящихся от данной точки (центр шара) на расстоянии, не большем данного (радиус шара).
Замечание. Шар, так же как цилиндр и конус, является телом вращения. Он получается при вращении полукруга вокруг его диаметра.
Граница шара называется шаровой поверхностью или сферой.
Плоскость, проходящая через точку, лежащую на сфере, и перпендикулярная радиусу, проведенному в эту точку, называется касательной плоскостью.
Прямая, проходящая через точку сферы перпендикулярно к радиусу, проведенному в эту точку, называется касательной прямой или просто касательной.
Многогранник называется вписанным в шар, если все его вершины лежат на поверхности шара. В этом случае шар называется описанным около многогранника.
Многогранник называется описанным около шара, если все его грани касаются шара. В этом случае шар называется вписанным в многогранник.
Основные теоремы, связанные с шаром
Касательная плоскость имеет с шаром только одну общую точку - точку касания. Через любую точку сферы проходит бесконечное число касательных, причем все они лежат в касательной плоскости шара.
Любая диаметральная плоскость (плоскость, проходящая через диаметр) является плоскостью симметрии шара. Центр шара является его центром симметрии.
Площадь поверхности сферы: S = АпД2, где R - радиус сферы.
4
Объем шара: V = -7ГR3.
о
Центром шара, вписанного в многогранник, является точка пересечения плоскостей, делящих двугранные углы многогранника пополам.
Если многогранник вписан в шар, то вокруг каждой из его граней можно описать окружность. Центр описанного шара есть точка пересечения перпендикуляров к граням, проведенных через центры этих окружностей.
Для каждого тетраэдра существует вписанный и описанный шар, причем
V = isr,
где V - объем тетраэдра, S - площадь его полной поверхности, г - радиус вписанного шара.
Вокруг любой правильной пирамиды можно описать шар, причем центр описанного шара будет лежать на высоте пирамиды.
о


6.3. Тела вращения
177
В любую правильную пирамиду можно вписать шар. Причем центр вписанного шара будет лежать на высоте пирамиды, а точки касания шара с боковыми гранями - на соответствующих апофемах.
Вокруг любой правильной призмы можно описать шар, причем центром этого шара будет середина высоты, проведенной через центры оснований призмы.
Сечением шара плоскостью является круг. Его центр есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.
Линия пересечения двух сфер есть окружность.
Части шара
Шаровым сегментом называется часть шара, отсекаемая от него плоскостью.
Шаровым слоем называется часть шара, расположенная между двумя параллельными плоскостями, пересекающими шар.
Шаровым сектором называется тело, ограниченное сферической поверхностью шарового сегмента и боковой поверхностью конуса, который имеет общее основание с сегментом и вершину в центре шара.
Замечание. Шаровой сектор получается из шарового сегмента и конуса следующим образом. Если шаровой сегмент меньше полу шара, то он дополняется конусом, у которого вершина в центре шара, а основанием является основание сегмента. Если же сегмент больше полушара, то конус из него удаляется.
Основные формулы для шарового сегмента:
• площадь боковой поверхности: 5 = 2,kRH\
• объем: V = ттН2 ^R —
где R - радиус шара, Н - высота сегмента.
Основные формулы для шарового слоя:
• площадь боковой поверхности: S = 2ttRH;
7Г Tf
• объем: У = — (ЗД? + ЪЩ + Я2),
где R - радиус шара, Ri и i?2 радиусы оснований, Н - высота слоя.


178
Теория и задачи
Основные формулы для шарового сектора:
• площадь боковой поверхности: S = 2nRH;
• объем: V = \vR2H,
О
где R - радиус шара, Н - высота сектора.
Примеры решения задач
Пример 1. Дан конус с вершиной М, радиус основания которого равен 6. На окружности его основания выбраны точки А, В, С так, что углы ВМА, AM С, СМ В равны 90° каждый. Точка F выбрана на дуге ВС окружности основания конуса, не содержащей точки А, так, что объём пирамиды MABFC наибольший. Найдите расстояние от точки F до плоскости МАВ.
Решение. Рассмотрим конус с радиусом основания R = 6, высотой h и наклонной I. Пирамида АВСМ вписана в конус, следовательно, её боковые рёбра равны I.
М
Так как по условию задачи углы при вершине М равны 90° каждый, то боковые грани являются равными равнобедренными прямоугольными треугольниками. Следовательно, рёбра основания пирамиды АВСМ равны между собой и треугольник АВС равносторонний.
Определим положение точки F на окружности основания конуса из условия максимальности объёма пирамиды MABFC:
Vmabfc = J • Sabfc = J • I • вс • AF ■ sm Z(BC, AF)<^BC- 2 R.
6 6 1 D
Максимум достигается в случае, когда AF является диаметром и угол между диагоналями четырёхугольника ABFC прямой.
Для того чтобы найти искомое расстояние от точки F до плоскости МАВ, подсчитаем объём тетраэдра ABFM двумя способами. С одной стороны,
h 0 VI2 - R2 BF • АВ
*ABFM ^ * ААВF з*2’
где отрезки BF = Д, АВ = \/3R (как катеты прямоугольного треугольника ABF с острым углом Z.AFB = 60° и гипотенузой AF — 2Л), а образующая конуса


6.3. Тела вращения
179
АВ
V2
=*vf . Следовательно,
г У2Д2 R2 R-VZR R3 yg
Vabfm = j — = = 18л/5.
С другой стороны,
X
Vabfm = g * Samab,
12 ЗЛ2
где Ьамав = тг = —— =27, а ж - искомое расстояние от точки .F до плоскости МАВ, следовательно,
Vabfm = | ■ 27 = 18>/б => * = 2V&
«J
Ответ. 2\/б.
Задачи
1. 	Плоское сечение SAB, проходящее через вершину 5 прямого кругового конуса, имеет площадь 60 см2. Точки А и В, лежащие на окружности основания конуса, делят её длину в отношении 1:5. Найти объём конуса, если
угол SAB равен arccos
(л/2э)'
2. Основание пирамиды - правильный треугольник со стороной 6. Одно из боковых ребер перпендикулярно плоскости основания и равно 4. Найти радиус шара, описанного вокруг пирамиды.
3. Угол в осевом сечении прямого кругового конуса равен а. Через его вершину
а
под углом /3 к оси конуса (/3 < —) проведена плоскость. Найти угол х между
двумя образующими конуса, по которым проведенная плоскость пересекает его поверхность.
4. Ребро куба равно а. Найти объем прямого кругового цилиндра, вписанного в куб так, что осью его является диагональ I куба, а окружности оснований касаются тех диагоналей граней куба, которые не имеют общих точек с диагональю I куба.
5. Дана правильная треугольная пирамида со стороной основания, равной 2л/7. Центр основания пирамиды является вершиной конуса, окружность основания которого вписана в боковую грань пирамиды. Найдите радиус основания конуса.
6. В треугольной пирамиде длины двух непересекающихся рёбер равны 12 и 4, а остальные рёбра имеют длину 7. В пирамиду вписана сфера. Найти расстояние от центра сферы до ребра длины 12.
7. Три параллельные прямые касаются в точках А, В и С сферы радиуса 4 с центром в точке О. Найти угол ВАС, если известно, что площадь треугольника ОВС равна 4, а площадь треугольника АВС больше 16.


180
Теория и задачи
6.4. 	Комбинации тел Задачи
1. В сферу радиуса R вписан прямой круговой цилиндр. Найти наибольшее значение площади боковой поверхности цилиндра и отношение его высоты к радиусу сферы в этом случае.
2. В прямой круговой конус вписан шар. Отношение объёмов конуса и шара равно двум. Найти отношение полной поверхности конуса к поверхности шара.
3. В правильную треугольную пирамиду помещены три шара так, что первый шар касается всех боковых граней пирамиды и второго шара, второй шар касается боковых граней пирамиды и третьего шара, а третий шар касается боковых граней, основания пирамиды и второго шара. Какую долю объёма пирамиды занимают три шара, если её боковые грани наклонены к основанию под углом а ?
4. Сфера радиуса 2 касается плоскости в точке А. В той же плоскости лежит основание конуса. Прямая, проходящая через центр основания конуса (точку С) и точку сферы, диаметрально противоположную точке А, проходит через точку М. Точка М является точкой касания сферы и конуса (их единственная общая точка). Найдите высоту конуса, если АС — 1.
5. Основанием правильной пирамиды является равносторонний треугольник со стороной а, а высота, опущенная на это основание, равна Н. причём все шесть рёбер пирамиды касаются некоторой сферы. Найти радиус этой сферы.
6. Внутри правильного тетраэдра ABCD расположен конус, вершина которого является серединой ребра CD. Основание конуса вписано в сечение тетраэдра, проходящее через середину ребра ВС параллельно прямым CD и АВ. Площадь боковой поверхности конуса равна 9тгл/3. Найдите длину ребра тетраэдра.
7. В треугольной пирамиде ABCD ребро DC = 9, ребро DB — AD, а ребро АС перпендикулярно грани ABD. Сфера радиуса 2 касается грани АВС, ребра DC, а также грани ABD в точке пересечения её медиан. Найти объём пирамиды.
8. Отрезок PN - диаметр сферы. Точки М, L лежат на сфере так, что объем пирамиды PNML наибольший. Найдите синус угла между прямой NT и плоскостью PMN, если Т - середина ребра ML.


Часть II. Указания и решения
1. Треугольники
1.1. 	Прямоугольные треугольники
Задача 1.
В треугольнике АВС угол ВАС прямой, \АВ\ = 1, \ВС\ = 3. Точка К делит сторону АС в отношении 7:1, считая от точки А. Что больше: \АС\ или \BK\1
Идея. Воспользоваться теоремой Пифагора.
Указание. Вычислить длину катета АС, g затем найти длины отрезков АК и В К.
Решение. Сначала с помощью теоремы Пифагора определим длину катета АС:
\АС\2 + |АВ|2 = \ВС\2 =►
А 7х К х С
=> \АС\2 + 1 = 9 =► \АС\ = 2л/2.
Теперь вычислим длины отрезков АК и В К:
\АК\ = \ • \АС\ = \ВК\ = ч/\АК\2 + |АВ\* = ]/f + 1 = \/Ц-
Наконец, сравним найденные длины:
\АС\ V \ВК\
2V2 V 8 V
64 V 57.
Так как 64 > 57, то \АС\ > \ВК\.
Ответ. \АС\ > \ВК\.


182
Указания и решения
Задача 2.
В прямоугольном треугольнике АВС точки D и Е лежат соответственно на катетах ВС и АС так, что \CD\ = |СЕ\ = 1. Точка О есть точка пересечения отрезков AD и BE. Площадь треугольника BOD больше площади треугольника АОЕ на 0,5. Известно, что \AD\ = у/10. Найдите длину гипотенузы АВ.
Идея. Сравнить площади треугольников ACD и ВСЕ.
Указание. Применить теорему Пифагора для вычисления длины отрезка АС, затем, рассмотрев треугольники ACD и ВСЕ, получить условие, связывающее их площади.
Указание. Воспользоваться тем, что площадь треугольника ACD равна сумме площадей треугольника АОЕ и четырёхугольника С DOE, а площадь треугольника ВСЕ равна сумме площадей треугольника BOD и четырёхугольника С DOE. Применить формулу площади прямоугольного треугольника.
Решение. Сначала найдём длину катета АС:
\АС\2 + \CD\2 = \AD\2 =» \АС\2 + 1 = 10 =► \АС\ = 3.
Заметим, что в условии задачи дано соотношение на площади треугольников BOD и АОЕ, которым достаточно трудно воспользоваться напрямую из-за того, что в этих треугольниках нам известно слишком мало элементов. Тем не менее, с его помощью мы можем получить условие, связывающее площади удобных для нас треугольников ACD и ВСЕ.
Saaoe = Sabod — 2 Saaoe + Scdoe — Sabod + Scdoe - ^
<=> Saacd = Sabce — ^ •
Записывая формулы для площадей треугольников ACD и ВСЕ, получаем
\-\AC\-\CD\ = \-\BC\-\CE\-± <=* Z-=l-.\BC\-\ =► \ВС\ = 4.
Наконец, воспользуемся теоремой Пифагора в треугольнике АВС:
\АС\2 + \ВС\2 = \АВ\2 => 9 + 16 = \АВ\2 =» \АВ\ = 5.
Ответ. \АВ\ = 5.
Задача 3.
В равнобедренном треугольнике длины высот, опущенных на основание и на боковую сторону, равны соответственно тип. Найдите длины сторон этого треугольника.
А


1.1. Прямоугольные треугольники
183
В
Идея. Воспользоваться формулой площади треугольника.
Указание. Применить в исходном треугольнике формулу площади треугольника через высоту и основание, записать теорему Пифагора для одного из треугольников, на которые исходный треугольник разделен высотой, проведённой к основанию.
Решение. Обозначим вершины треугольника из условия задачи буквами А, В и С, будем полагать, что А В и ВС - его боковые стороны. Их длины обозначим через х, а длину основания АС через 2у. Основания высот, опущенных на стороны АС и ВС, обозначим буквами Н и
К соответственно. Известно, что высота ВН, проведённая к основанию, является также и медианой треугольника АВС, поэтому \АН\ = \НС\ = у.
Сначала записываем теорему Пифагора для треугольника В НС:
\вн\2 + \нс\2 = \вс\2 =*•
Далее два раза выразим площадь треугольника АВС:
2.2 2 у -Ь га = х .
Saabc = \ ■ \АС\ ■ \ВН\ = ± • \АК\ ■ \ВС\ Решаем полученную систему уравнений:
4га2
: т2 т" =
? А i
2ту = пх
2 ту = пх.
т2 = —2~У2~У21 пz
2 га
х = у
п
У =
ran
х —
л/4 га2 — п2 ’ 2га2
у/Ат2 — п2
Осталось не забыть, что длина основания равна 2у, и выписать ответ.
2га2
Ответ. Длины боковых сторон равны 2 ran \/4га2 — п2
\/4га2 — п2 ’
длина основания равна
Задача 4-
В прямоугольном треугольнике длина гипотенузы равна с, а величина одного из его острых углов равна а. Найдите длину биссектрисы прямого угла этого треугольника.
Идея. Рассмотреть один из двух треугольников, на которые биссектриса делит исходный.
Указание. Выразить длины катетов исходного треугольника, воспользоваться теоремой синусов.


184
Указания и решения
Решение. Обозначим вершины исходного треугольника буквами А, В и С, биссектрису прямого угла обозначим как CL, будем считать, что АВС = а. Тогда ясно, что
\ВС\ = с cos a, ACL = BCL Ж
4’
CLB = тг - LBC - BCL
Зтг
— а.
Наконец, воспользуемся теоремой синусов в треугольнике BCL:
\CL\ \ВС\ с cos asm а
sin LBC sin BLC
\СЦ =
c sin 2a
sin
37Г
— a
\[2 (sin a + cos a)
Ответ.
с sin 2a
Vasina + cos a)
Задача 5.
В треугольнике ABC угол А прямой, \AB\ = 1, \BC\ = 2. Биссектриса угла ABC пересекает сторону АС в точке L. G - точка пересечения медиан треугольника АВС. Что больше: \BL\ или |BG|?
Идея. Рассмотреть треугольники ABL и АВМ.
Указание. Вычислить косинусы величин углов АВС и ABL, найти длины отрезков BL и ВМ. Воспользоваться тем, что медианы треугольника точкой пересечения делятся в отношении 2:1, считая от вершин.
Решение. Эта задача является чисто счётной. Сначала, рассматривая треугольники АВС и ABL, найдём длину биссектрисы BL:
\АВ\ _ 1 ТГ
= 2
В
cos ABC
ABC = - =*> ABL
о
\bl\
\AB\
2_
V3'
\BC\ 2 3 в ■ ■ cos ABL
Теперь вычислим длину медианы ВМ и длину отрезка BG. Применяя теорему Пифагора к треугольникам АВС и АВМ, а также пользуясь тем, что медианы треугольника точкой пересечения делятся в отношении 2:1, считая от вершин, получаем
\АС\ S 2 ~ 2 ’
\АС\ = v/IBCI2 - \АВ\2 = V3, |АМ|
|ВМ| = у/\АМ|2 + |АВ|2 = -V, |BG|
Наконец, ясно, что \BG\ < 1, \BL\ > 1, поэтому \BL\ > \BG\. Ответ. \BL\ > \BG\.


1.1. Прямоугольные треугольники
185
Задача 6.
В треугольнике АВС \АВ\ = с, \ВС\ = а, а медианы AD и СЕ взаимно перпендикулярны. Найдите длину стороны АС.
Идея. Рассмотреть прямоугольные треугольники, образованные точкой пересечения медиан, основаниями медиан и вершинами исходного треугольника.
Указание. Обозначить длины медиан AD и СЕ как Зх и 3у соответственно. Воспользоваться тем, что медианы треугольника точкой пересечения делятся в отношении 2:1, считая от вершин, применить теорему Пифагора.
В
Решение. В этой задаче из-за перпендикулярности медиан AD и СЕ возникает несколько прямоугольных треугольников. Их мы и будем
рассматривать, заметив, что через длины этих медиан можно выразить длины всех сторон треугольника АВС.
Обозначим длины медиан AD и СЕ как Зх и 3у соответственно, а точку их пересечения обозначим буквой О. Поскольку медианы треугольника точкой пересечения делятся в отношении 2:1, считая от вершин,
\АО\ = 2х, \OD\ = х, \СО\ = 2у, \ОЕ\ = у.
После этого, записывая теорему Пифагора для треугольников АОЕ, COD и АОС, находим
|ЛО|2 + | ОЕ\2 = \АЕ\2, \СО\2 + \OD\2 = \CD\2, \АО\2 + \СО\2 = \АС\2
4х2 +у2 —
4г/2 + х2 —
Ах2 + Ау2 = \АС\2
2 + с2
П2 Г2
5*2 + 5,2 = т + т,
4х2 + Ау2 = \ АС\2
Замечание. Вообще говоря, во всех задачах после введения неизвестных сначала имеет смысл выразить с их помощью искомую величину. Зачастую получается так, что значения самих переменных находить не надо, а достаточно найти лишь значение некоторой их комбинации. Видно, что в только что рассмотренной задаче значения самих переменных х и у нам не понадобились.
/ Q2 4- с2
Ответ. \AC\ = J-~--.


186
Указания и решения
Задача 7.
В треугольнике АВС угол А прямой, величина угла В равна 7г/6. В треугольник вписана окружность, длина радиуса которой равна л/3 - Найдите расстояние от вершины С до точки касания этой окружности с катетом АВ.
Идея. Провести радиусы из центра вписанной окружности в точки её касания с катетами треугольника АВС, воспользоваться тем, что центр вписанной в треугольник окружности находится в точке пересечения биссектрис треугольника.
Указание. Рассмотреть прямоугольный треугольник, образованный точкой С, центром вписанной в треугольник АВС окружности и точкой её касания с катетом АС.
Решение. Так как величина угла В равна 7г/6, величина угла ВС А равна 7г/3. Центр окружности, вписанной в треугольник АВС, обозначим буквой О, точки её касания с катетами АВ и АС обозначим буквами D и Е соответственно. Из того, что центр окружности, вписанной в произвольный треугольник, лежит на пересечении его биссектрис, вытекает, что ОС - биссектриса угла ВС А, поэтому величина угла ОСЕ равна 7г/6.
Рассмотрим прямоугольный треугольник ОСЕ. В нем нам известны величины катета ОЕ и угла ОСЕ - сих помощью выражаем длину отрезка СЕ:
\СЕ\ = \ОЕ\ • ctg ОСЕ = л/3 V3 = 3.
Поскольку OEAD - квадрат, \АЕ\ = |ОЕ\ = \AD\ = \/3. Точка Е лежит на катете АС, следовательно, \АС\ — \АЕ\ + \СЕ\ = 3 4- \/3.
Наконец, применим теорему Пифагора для треугольника CAD:
\АС\2 + \AD\2 = \CD\2 =► \CD\2 = (3 + л/3)2 + (л/З)2 = 15 + бл/3.
Ответ. \/l5 + 6т/3-
Задача 8.
В треугольнике АВС величина угла ВАС равна 7г/3, длина высоты, опущенной из вершины С на сторону АВ, равна \/3, а длина радиуса окружности, описанной около треугольника АВС, равна 5. Найдите длины сторон треугольника АВС.
Идея. Применить теоремы синусов и косинусов. с
Указание. Рассмотрев прямоугольный треугольник, образованный вершинами А, С и основанием высоты, опущенной из С на АВ, вычислить \АС\.
Указание. Применить теоремы синусов и косинусов в треугольнике АВС.
АН В
С


1.1. Прямоугольные треугольники
187
Решение. Обозначим основание высоты, опущенной из С на АВ, буквой Н. Вообще говоря, точка Н может находиться как на стороне АС, так и на её продолжении за точку В. Куда именно она попадет, станет понятно только после вычисления длин сторон треугольника АВС. Тем не менее, вне зависимости от расположения точки Н из прямоугольного треугольника АСН находим
|ЛС| = = _E£L = ^ = 2.
sin НАС sin ВАС &
Далее, записывая теорему синусов для треугольника АВС, получаем
lBSL = 2RABac =► IВС\ = 10 ~ = 5л/3. sin ВАС 2
Наконец, для определения длины стороны АВ воспользуемся теоремой косинусов: \ВС\2 = \АВ\2 + \АС\2 - 2 • \АВ\ ■ \АС\ • cos ВАС =►
=> 75 = |АВ|2 + 4 — 2\АВ\ ==> \АВ\2 - 2\АВ\ + 71 = 0.
Полученное квадратное уравнение имеет два корня: 1 + 6\/2 и 1 — 6\/2- Второй из них меньше нуля и нам не подходит.
Замечание. В большинстве задач, где в условии дана длина радиуса окружности, описанной около треугольника, так или иначе задействуется теорема синусов.
Ответ. |Л£| = 1 +6л/2, \ВС\=Ьу/Ъ, \АС\=2.
Задача 9.
В прямоугольном треугольнике отношение длины радиуса вписанной окружности к длине радиуса описанной окружности равно 2/5. Найдите величины острых углов треугольника.
Идея. Выразить длины сторон треугольника через радиусы вписанной и описанной окружностей.
Указание. Обозначить длины радиусов вписанной и описанной окружностей через 2а, 5а и с помощью теоремы Пифагора получить уравнение с одной неизвестной.
Решение. Обозначим через Р, Q и R точки касания окружности с центром О со сторонами прямоугольного треугольника АВС. Пусть длины радиусов вписанной и описанной окружностей равны соответственно 2а и 5а.
Выразим стороны треугольника через а и вычислим косинусы острых углов.
Так как в прямоугольном треугольнике гипотенуза равна двум радиусам описанной окружности, то АВ = 10а.
Обозначим через х длину отрезка РВ и составим уравнение для этой неизвестной.


188
Указания и решения
Из того, что четырёхугольник CPOQ является квадратом, следует равенство отрезков CP = OP = OQ = QC = 2а. А из равенства отрезков касательных, проведённых из одной точки, следует, что BR = РВ = х и AQ = AR = 10а — х. Теперь применим теорему Пифагора к треугольнику АВС:
(10а)2 = (2а + х)2 + (12а - х)2 <=> х2 - 10а + 24а2 = 0,
откуда х — 4а или ж = 6а. В обоих случаях получается египетский треугольник
3 4
со сторонами 6а, 8а, 10а с острыми углами arccos- и arccos-.
5 5
п 3 4
Ответ, arccos- и arccos-.
5 5
Задача 10.
В треугольнике АВС угол В тупой, продолжения высот AM и CN пересекаются в точке О, ВАС = а, ВС А = 7, \АС\ = Ь. Найдите расстояние от точки О до прямой АС.
Идея. Рассмотреть треугольник АОС. Воспользоваться тем, что расстояние от точки О до прямой АС есть длина его высоты, опущенной из точки О на АС. Указание. В прямоугольном треугольнике сумма величин острых углов равна 7г/2, отношение длин катетов равно котангенсу соответствующего острого угла.
Решение. Искомое расстояние есть длина пер- д пендикуляра, опущенного из точки О на сторону АС. Общим подходом к решению такого сорта задач является нахождение некоторого треугольника, в котором бы этот перпендикуляр оказался высотой, и последующее вычисление его длины. В этой задаче мы будем рассматривать треугольник АОС, соответственно нам необходимо вычислить длину его высоты ОЕ. Можно заметить, кстати, что поскольку отрезки AN и СМ также являются его высотами и пересекаются в точке В, отрезок ОЕ также проходит через эту точку.
Поскольку угол В тупой, точка Е попадает на ® отрезок АС, то есть \АС\ = \АЕ\ 4- |C7JE7|. Далее,
рассматривая прямоугольные треугольники ACM и ACN, можно вычислить величины углов САМ и ACN:
САМ = -- ACM = - - 7, ACN = -- CAN = --<*.
2 2 2 2
После этого обозначим длину отрезка ОЕ буквой h и рассмотрим прямоугольные треугольники АОЕ и СОЕ. Из них мы находим
\СЕ\ = \ОЕ\ ■ ctg ECO = h ctg - a) = h tg a,


1.1. Прямоугольные треугольники
189
|АЕ\ — \ОЕ\ • ctgЕАО = hctg (^ — 7^ = htg'y.
Подставляя полученные выражения в соотношение, связывающее длины отрезков
АС, АЕ и СЕ, имеем b = htga -f htg'y => h = .
tg a -f tg 7
Ответ. - .
tg а -h tg 7
Задача 11.
В треугольнике, величина одного из углов которого равна разности величин двух других его углов, длина меньшей стороны равна 1, а сумма площадей квадратов, построенных на двух других сторонах, в два раза больше площади описанного около треугольника круга. Найдите длину большей стороны треугольника.
М
Идея. Доказать, что треугольник, данный в условии задачи, прямоугольный.
Указание. Использовать тот факт, что сумма величин углов треугольника равна 7Г, и условие задачи, связывающее величины углов треугольника.
Указание. Воспользоваться тем, что центр окружности, описанной около прямоугольного треугольника, лежит на середине его гипотенузы.
Решение. Прежде всего необходимо разобраться, что даёт нам условие задачи, связывающее величины углов треугольника.
Обозначим вершины треугольника как А, В и С, без ограничения общности будем считать, что 1 = \АВ\ < \ВС\ < \АС\. Поскольку в любом треугольнике против большей стороны лежит больший угол, АС В < ВАС < АВС.
Рассмотрим данное нам соотношение на величины углов треугольника, используем теорему о сумме величин углов треугольника и сложим полученные соотношения:
Г АВС - ВАС = АСВ, тг
< _ =* 2 АВС = ж => АВС = —.
[ АВС + АС В + ВАС = 7г 2
Таким образом, треугольник АВС прямоугольный. Обозначим длину отрезка АС буквой х, тогда по теореме Пифагора |J3C| = у/\АС\2 — |АВ|2 = у/х2 — 1.
Далее ясно, что площади квадратов BCLK и ACNM равны х2 — 1 и х2 соответственно. Также учтём тот факт, что длина радиуса круга, описанного около треугольника АВС, равна половине длины гипотенузы АС, следовательно, площадь этого круга равна пх2/А. С учётом всего этого, пользуясь условием задачи, получаем
^ 9 Л 7ГХ2
2х -1 = 2- —— => х =
4 V 4 — 7Г
Ответ. Длина большей стороны треугольника равна
4 — 7Г


190
Указания и решения
Задача 12.
В прямоугольном треугольнике KLM проведён отрезок MD, соединяющий вершину прямого угла KML с точкой D, лежащей на гипотенузе КL таким образом, что \DL\ = 1, \DM\ = \/2, \DK\ = 2. Найдите величину угла KMD.
Идея. Доказать, что MD - высота треугольника KLM.
Указание. Применить теорему косинусов для треугольников KMD и LMD.
Решение. В теоретических материалах к этому разделу было приведено следующее свойство высоты прямоугольного треугольника, проведённой к гипотенузе: она делит гипотенузу на части, произведение длин которых равно квадрату длины этой высоты. Заметим, что \MD\2 = \DK\ • \DL\, и докажем, что в этой задаче отрезок MD действительно будет высотой треугольника KLM. Это можно сделать, например, так: обозначим величины углов К DM и LDM через а и 7г — а и запишем теорему косинусов для треугольников KMD и LMD:
\КМ\2 = 6 - 4\/2cosa, \LM\2 = 3 + 2-s/2cosa
=► \КМ\2 + \LM\2 = 9- 2V2cosa.
С другой стороны, \КМ\2 + \LM\2 = \KL\2 = 9, поэтому cos a = 0, а = 7г/2. Тогда из прямоугольного треугольника KMD получаем tg KMD = \DK\ : \DM\ = \/2- Замечание. Справедливо следующее утверждение: если точка D лежит на гипотенузе ВС прямоугольного треугольника АВС и \AD\2 = \BD\ • |CD|, то либо AD - высота треугольника АВС, либо AD - медиана треугольника АВС. Попробуйте доказать его сами.
Ответ, arctg\/2.
Задача 13.
В треугольнике АВС угол С прямой, катет ВС разделен точками D и Е на три равные части. Найдите сумму величин углов АЕС, ADC и АВС, если известно, что
|ВС| = 3|ЛС|. С D Е В
Идея. Использовать тангенсы углов АЕС, ADC и АВС,
Указание. Рассмотреть прямоугольные треугольники ABC, ADC и АЕС. Указание. Найти тангенс суммы величин углов АЕС и АВС.
Решение. Если положить |ЛС| = ж, |ВС| = Зх, то \CD\ = = |ЯВ| = х.
Ясно, что tg ADC = 1, tgi4J5C = 1/2, tg ЛВС = 1/3. Тогда
ADC = j; tg (аЕС + АВС) = tS^fl^tgABC^ = t ^
4 V ' 1 — tg АЕС • tg ABC


1.1. Прямоугольные треугольники
191
АЕС + АВС — ^ =► AEC + ABC + ADC=
4 2
~ тг
Ответ. —.
2
Задача 14-
В прямоугольном треугольнике АВС расстояние от середины гипотенузы АВ до катета ВС равно 5, а расстояние от середины этого катета до гипотенузы равно 4. Найдите площадь треугольника АВС.
Идея. Вычислить величины углов треугольника АВС.
Указание. Расстояние от середины гипотенузы А В до катета ВС есть длина одной из средних линий треугольника АВС.
Решение. Обозначим буквой D середину гипотенузы А В и возьмем на катете ВС точку Е так, что DE J. ВС. Тогда \DE\ = 5 по условию задачи и, кроме того, DE\\AC, так как DE ± ВС и AC _L ВС. Поэтому DE - средняя линяя треугольника АВС и \АС\ = 10. Теперь возьмем точку F на гипотенузе АВ таким образом, что EF АВ. Тогда, по условию задачи, \EF\ = 4. Далее, sin EDF = \EF\ : \ED\ = 4/5, cos EDF = 3/5, tgEDF = 4/3. Наконец, ясно, что DBE = 7г/2 — EDF, поэтому
|BC| = |AC|.ctg(|-g5F) = y; SAABc = W 2]BCl = ™.
Ответ.
Задача 15.
В прямоугольный треугольник ABC вписана окружность, касающаяся его сторон в точках Р, Q и R. Найдите площадь треугольника PQR, если длины катетов треугольника АВС равны 3 и 4.
Идея. Вычислить длины отрезков, на которые точки Р,
Q и R разбивают стороны треугольника АВС.
Указание. Найти длину радиуса окружности, вписанной в треугольник АВС, вычислить площади треугольников, дополняющих треугольник PQR до треугольника АВС.
Решение. Будем считать, что Р G [ВС], Q € [АС],
R € [АВ], \АС\ = 3, \ВС\ = 4. Путем элементарных вычислений находим, что
Saabc = 6, \АВ\ = 5, sin RAC = 1 sin ABC =
5 5


192
Указания и решения
\АС\ + \ВС\-\АВ\
r&ABC = 2 1> 1^1 '^-П = ГААВС = 1)
\AR\ = |AQ| = \АС\ - \CQ\ = 2, |ВД| = |ЯР| = \ВС\ - \СР\ = 3.
Наконец, пользуясь формулой площади треугольника через длины двух его сторон и синус величины угла между ними, получаем
<? 1 с 8 с 27 с А 1 8 27 6
JACQP = 2> *ДЛ(ЗЯ - ]Г, OABPR = Yq => bAPQR _2_5_Io = 5'
0
Ответ. -.
5
Задача 16.
В треугольнике ABC угол С прямой, CD - высота. Найдите длину радиуса окружности, вписанной в треугольник АВС, если длины радиусов окружностей, вписанных в треугольники ACD и BCD, равны 6 и 8 соответственно.
Идея. Выразить длины отрезков AD, АС, BD и А ВС через длину высоты CD и величину одного из острых углов треугольника АВС.
Указание. Воспользоваться формулой длины радиуса окружности, вписанной в прямоугольный треугольник.
Решение. Положим \CD\ = /г, ВАС = а. Тогда q ABC = 7г/2 — a, BCD = а и
\AD\ = h ctg а, \АС\ = -Д-, ШХ>| = htga, \ВС\ =
sin а cos а
Записывая формулу длины радиуса окружности, вписанной в прямоугольный треугольник, применительно к треугольникам ADC и В DC, получаем
Г h Н- Л, ctg а — hj sma = 12; Г /i(sina + cos а: — 1) = 12 sin а;
у h + htga — /г/cos а = 16 \ h( sin а + cos а — 1) = 16 cos а.
Поделив первое из полученных уравнений на второе, мы легко находим tg а = 4/3, sin a = 4/5, cos се = 3/5, h = 24. Наконец,
\АС\ = 30, \ВС\ = 40, |АВ| = 50, гЛАВС = ИС1 + l,-gg| ~ |А5| = щ
Замечание. Если использовать подобие, то эту задачу можно решить значительно проще, но подобие мы пока «не знаем».
Ответ. 10.


1.1. Прямоугольные треугольники
193
Задача 17.
Расстояния от центра окружности, вписанной в прямоугольный треугольник АВС, до его вершин А и В равны у/Ъ и л/ГО соответственно. Найдите длины катетов треугольника АВС.
Идея. Воспользоваться тем, что центр окружности, вписанной в треугольник, лежит на пересечении его биссектрис.
Указание. Рассмотреть прямоугольные треугольники, образованные вершинами острых углов, центром окружности, вписанной в треугольник АВС, и точками её касания с катетами.
Решение. В этой задаче необходимо рассмотреть два случая: вершины А и В могут оказаться вершинами острых углов, а могут оказаться вершинами прямого и острого углов. Сначала рассмотрим первый случай.
Пусть ВАС = 2а. В силу того, что ВАС + АВС = 7г/2, а д АО и ВО - биссектрисы углов ВАС и АВС соответственно, имеем OAQ = а, ОВР = 7г/4 — а. Заметим, что OQCP - квадрат, поэтому \OQ\ = \QC\ = \СР\ = \ОР\. Наконец, из прямоугольных треугольников AOQ и ВОР получаем
ч. R
71/ (Р4^
\OQ\ = \AO\sinOAQ, \ОР\ = \BO\sinOBP
В
=> \/2sin(7r/4 — а) = since.
Решая это уравнение, находим tga = 1/2, sina = 1/л/б, cos a = 2/VE, после чего получаем \OQ\ = \QC\ = \СР\ = \ОР\ = 1, \AQ\ = 2, \ВР\ = 3, \АС\ = 3, \ВС\ = 4.
Рассмотрим второй случай. Если \ОС\ = л/10, то, так как OQCP - квадрат, имеем |OQ| = \ОР\ = л/5 = \ОА\(\ОВ\), что невозможно, поскольку длина перпендикуляра меньше длины наклонной.
Если же \ОС\ = л/Е, \ОВ\ = \Д0, то
А
\OQ\ = \ОР\ = \1 -, \ВР\
, \вс\
tg ОВР = ~^=, tg ABC = tg (2 • OBp) = л/з;
ч/З
|AC| = |BC| -tgABC
Ответ. 3 и 4 или
7 Геометрия


194
Указания и решения
Задача 18.
В треугольнике АВС точка М расположена на стороне АС таким образом, что \АМ\ : \МС\ = 1 : Зл/З. Величина угла АВМ равна 7г/6, \ВМ\ = 6, угол В прямой. Найдите величину угла ВАС.
Идея. Найти соотношение между длинами отрезков AM и МС и величиной угла ВАС.
Указание. Применить теорему синусов для треугольников АВМ и СВМ.
Решение. Ясно, что СВМ = 7г/3. Пусть ВАС = а, тогда АС В = 7г/2 — а. Запишем теорему синусов для треугольников АВМ и СВМ :
\АМ\ \ВМ\ . \ВМ\
:===г = ==> smа = . ■■ ;
sin АВМ sin В AM 2\АМ\
\МС\ \ВМ\ Уз\ВМ\
■■и....ни — _______ ■% COS су — -
sin СВМ sin ВСМ 2\МС\
Почленно поделив полученные соотношения друг на друга, находим tg а = 3.
Ответ, arctg3.
Задача 19.
Дан треугольник KLM. Через точки К и L проведена окружность, центр которой лежит на высоте LF, опущенной на сторону КМ. Известно, что точка F лежит на стороне КМ. Найдите площадь круга, ограниченного этой окружностью, если \KL\ = 1, \КМ\ = у/3/2,
\FM\ = л/3/6.
Идея. Воспользоваться тем, что треугольник KOL равнобедренный (О - центр окружности).
Указание. Рассмотреть прямоугольные треугольники KLF и К OF, где О - центр окружности.
Решение. Точка F лежит на стороне КМ, стало быть, \KF\ = \КМ\ — \FM\ = х/3/3. Далее, применяя теорему Пифагора к треугольнику KLF, находим \LF\ = у/2/3. Введём обозначение \ОК\ = \OL\ = R, тогда \OF\ = у/2/3 — R. Запишем теорему Пифагора для треугольника К OF:


1.1. Прямоугольные треугольники
195
Задача 20.
В прямоугольнике ABCD длины отрезков АВ и BD равны 3 и 6 соответственно. На продолжении биссектрисы BL треугольника ABD за точку L взята точка N такая, что отношение \BL\ : \LN\ равно 10 : 3. Что больше: длина отрезка BN или длина отрезка СL ?
Идея. Найти величину угла LBA и длину отрезка LD. q j)
Указание. Воспользоваться теоремой Пифагора и соотношениями между длинами сторон и величинами углов в прямоугольном треугольнике.
Решение. Приведём различные величины, легко вычисляемые в этой задаче:
ABD=l> ABl = l, \BL\ = 2л/3, |£JV| = —;
\AD\ = 3V3, \AL\ = V3, \LD\ = 2y/3, \CL\ = >/21.
Ответ. |ВЛГ| < \CL\.
Задача 21.
В прямоугольном треугольнике ABC угол В прямой, AM - медиана, ВН - высота. Найдите величину угла ВАМ, если известно, что величина угла между прямыми AM и ВН равна ip. При каких ip задача имеет решение?
Идея. Найти условие, связывающее величины данного в условии и искомого углов. д
Указание. Рассмотреть треугольники ВАМ и АВС.
Указание. Положить |J3M| = х, выразить двумя способами длину отрезка АВ.
Решение. Углом между прямыми называется меньший из углов, ими образованных. Поэтому величина угла MAC равна тт/2 — ip. Обозначим величину угла ВАМ через а, тогда величина угла ВАС равна 7г/2 — (ip — а). Рассматривая прямоугольные треугольники ВАМ и АВС и вводя обозначения \ВМ\ = х, \ВС\ = 2х, имеем
\АВ\ = .xctga = 2a:ctg(7r/2 — (ip — а)) ==> 2tg2a - tgtptga + 1
/tg^>± vtgV-eA
о
tga
2 tg(y> — a) tg a = 1 tg cp± V'tg2 if-
Ответ, arctg
4>
G [arctg2л/2;тг/2).
т


196
Указания и решения
Задача 22.
В треугольнике АВС угол С прямой, отношение длины медианы СМ к длине биссектрисы CL равно \/б : 1, длина высоты СН равна 2. Найдите площадь треугольника АВС.
Идея. Выразить все элементы треугольника АВС через длину биссектрисы CL и величину одного из его острых углов.
Указание. Применить теорему синусов в треугольнике ALC.
Решение. Введём обозначения \CL\ = х, ВАС = а. Тогда, с учётом условия задачи и того факта, что медиана прямоугольного треугольника, проведённая к гипотенузе, равна половине её длины, \СМ\ = \АМ\ = \ВМ\ = л/бх. Далее, пользуясь соотношениями между длинами сторон прямоугольного треугольника и тем, что биссектриса треугольника делит угол пополам, находим
\АВ\ = 2у/бх, \АС\ = 2у/бх cos а, \ВС\ = 2\/бх sin a, ALC = 37г/4 — а.
С
АН L М В
Теперь, записывая теорему синусов для треугольника ALC, получаем \АС\ _ \CL\ 2\/§xcosa х
sin ALC sin CAL sin (3f - a) sin a
sin = 2л/б sin a cos a <=>• sin о + cos a: = 4\/3 sin cos a.
Полученное тригонометрическое уравнение надо возвести в квадрат, после чего мы легко получаем sin 2а = 1/3. Наконец, воспользуемся формулой для длины высоты прямоугольного треугольника, проведённой к гипотенузе:
\СН\ = ===^ 2\/6xsinacosQ: = 2 => х sin 2а = -^= => х — л/б;
\АВ\ V6
Saabc = \ • \АВ\ ■ \СН\ = 2у/бх = 12.
Ответ. 12.
Задача 23.
В прямоугольном треугольнике АВС отрезок ED соединяет середины сторон АВ и ВС. Точка F лежит на стороне ВС, отрезки AF и ED пересекаются в точке М. Известно, что отношение площадей четырёхугольника AM DC и треугольника АВС равно 7/10, а длины катетов ВС и АС равны а и Ъ соответственно. Найдите длину отрезка AM.


1.1. Прямоугольные треугольники
197
Идея. Рассмотреть треугольники ABF и MDF, записать для них формулы
х, \MD\ = у. Рассмотреть прямоуголь-
площади.
Указание. Ввести неизвестные |BF| ный треугольник ACF.
Решение. Очевидно, что ED - средняя линяя треугольника АВС, поэтому ED\\AC, из чего следует, что ED JL ВС. Положим \BF\ = х, \MD\ = у, тогда ясно, что \FD\ = а/2 — х. Из условия задачи следует, что сумма площадей треугольников ABF и MDF составляет 3/10 площади треугольника АВС, поэтому
!/ /о ч 3 1
2 2 _ Х = 10 2
С другой стороны, |М£>|
tg AFC =
|ЛС|
|DF| |CF|
а/2-
а — х
У = Ь•
а/2 — х а — х
Подставляя это выражение в первое уравнение, находим х = а/6, у = 26/5. После этого для нахождения длины AM проведём отрезок ММ'||£?С\ Понятно, что MM'CD - прямоугольник, \СМ'\ = 26/5, |АМ'| = 36/5, \ММ'\ = а/2. Наконец,
Ответ.
\АМ\ = л/|МЛ/'|2 + |ЛМ'|2 - v/25a2T3662
a2 962 _ у/25а2 -f 3662 4 + 25 10
10
Задача 24-
В треугольнике АВС проведены высота ВН и медиана ВМ. Найдите \ВМ\, если известно, что \ВН\ = /г, АВЯ - С13М. НВМ = 2 • СБМ.
Идея. Найти величину угла АВС.
Указание. Записать теорему синусов для треугольников АВМ и СВМ, найти величины углов треугольника АВС.
Решение. Найдём величину угла АВС. Положим
\АМ\ = \МС\ = х, |BAf| = т, ЛВЯ = СВМ = а, ЯВМ = 2а.
Если предположить, что точка Н лежит на продолжении стороны АС за точку А (нетрудно убедиться, что на продолжение за точку С она вообще попасть не может), то из условия задачи будет вытекать, что АВМ = СВМ = а, то есть медиана AM является также и биссектрисой треугольника АВС. Но тогда треугольник АВС равнобедренный, точки Н и М совпадают. Противоречие.


198
Указания и решения
Если же точка Н лежит на стороне АС, то она попадает на отрезок AM, ВАН = 7г/2 — а, ВСН = 7г/2 — За. Также заметим, что, поскольку угол СВН острый, 0 < а < 7г/6. Запишем теорему синусов для треугольников ВАМ и ВСМ:
т
х
sin(7r/2 - га
а)
sin За ’
х
В
га
х
cos а cos За
sin За sin а
sin 2а = sin 6а
ol = -
sin(7r/2 — За) sin а
Стало быть, АВС = 4а = 7г/2. Тогда из прямоугольного треугольника ВМН находим
|ЯЯ|
|ВМ|
cos 2а
hV2.
Замечание. Отметим, что из условия АВН = СВМ и того, что точка Н лежит на стороне АС, вытекает, что треугольник АВС либо прямоугольный (угол В прямой), либо равнобедренный (\АВ\ = \ВС\). Имеет смысл попробовать доказать этот факт отдельно. Схема доказательства точно такая же, как и в решении задачи, надо два раза записать теорему синусов, полагая НВМ = /3.
Ответ, hy/2.
Задача 25.
В треугольник АВС вписана окружность, длина радиуса которой равна 2; D - точка касания этой окружности со стороной АС, \AD\ = 2, \DC\ = 4. Найдите длину биссектрисы треугольника АВС, проведённой из вершины В.
Идея. Воспользоваться тем фактом, что центр окружности, вписанной в треугольник, лежит на пересечении его биссектрис. Указание. Рассмотреть прямоугольные треугольники AOD и COD, найти величины углов треугольника АВС.
Решение. Обозначим центр окружности, вписанной в треугольник АВС, буквой О и воспользуемся тем фактом, что центр окружности, вписанной в треугольник, лежит на пересечении его биссектрис. Сначала, рассмотрев прямоугольный треугольник AOD, находим
С
tg0AD = W\=l =* OAD = J =► =


1.1. Прямоугольные треугольники
199
Затем из прямоугольного треугольника COD получаем
tg ОСD =
\OD\
tg АС В =
2 tg ОСD
\ОС\ 2 -to"— 1 - 1
Теперь найдём стороны и третий угол треугольника АВС:
_ii
1 - tg2 OCD i _ I
4
4
3‘
\AB\ = \AC\ • tg ACS = 8, |BC| = 10, cos ABC = -.
5
Наконец, обозначим биссектрису треугольника ABC, проведённую из вершины В, как BL. Найдём величину угла ABL и, рассматривая прямоугольный треугольник ABL, найдём :
Ответ.
cos ABL 8-v/lO
' 1 + cos ABC
VTo1
\BL\
\AB\ 8>/l0
cos ABL
Задача 26.
В прямоугольном треугольнике ABC угол В прямой, AL - биссектриса. Известно, что \АС\ = 5, \AL\ = 5/л/З- Найдите \LC\.
CAL.
Указание. Рассмотрев треугольники siuu п АВС, двумя способами выразить длину отрез-
11 дея. Найти величину угла CAL.
Указание. Рассмотрев треугольники ABL и АВС, двvm я способами выпазить ллину отпез- ка АВ.
Решение. Обозначим величины углов BAL и CAL буквой а. Тогда ВАС = 2а. Пользуясь соотношениями между длинами сторон и величинами углов в прямоугольных треугольниках ABL и АВС, получаем
\АВ\ = |AL| • cos BAL = |АС| • cos ВАС 5 cos с*
V3
= 5 cos 2a
2л/3
cos2 a
cos a
Уз = о
cosa : cosa :
V3/2,
-l/y/3.
Поскольку углы BAL и CAL острые, нам подходит только положительный косинус. Значит, а = 7г/6. Наконец, заметим, что АСВ = 7г/2 — 2а = 7г/6, поэтому треугольник ALC равнобедренный, \AL\ = \LC\ = 5/л/3-
5


200
Указания и решения
Задача 27.
Треугольники АВС и ABD имеют общую сторону АВ и не имеют общих внутренних точек, углы ВАС и ADB прямые. Найдите |CD|, если \AD\ = 3, \ВС\ = 13, \AC\ + \BD\ = 16.
Идея. Найти длину отрезка АС и косинус величины угла CAD.
Указание. Применить теорему Пифагора для треугольников АВС и ABD.
Решение. Положим \АС\ = х, тогда \BD\ = 16 — х. Записывая теорему Пифагора для треугольников АВС и ABD, имеем
\АВ\2 = \ВС\2-\АС2\,
\АВ\2 = \AD\2 + \BD\2 ^
=*> 169-х2 = 9 +(16-х)2.
Решая это уравнение, получаем два варианта.
1. 	\АС\ — х = 12 (левый чертёж). Тогда ясно, что
\BD\ — 4, \АВ\ = 5, cosCAD = cos (^ + BAD^j = -sinBAD =
Применяя теорему косинусов для треугольника ACD, находим
\CD\2 = 144 + 9 + 2-12-3 - - =
1053
|OD| =
9л/65
2. 	|Ж7| = х = 4 (правый чертёж). В этом случае, рассуждая абсолютно аналогично, имеем
\BD\ = 12, \АВ\ = 3\/l7, cosCAD = -^=5 1^1 = l/25 +
9\/б5 / 96
Ответ. —-— или 4/254—т=.
5 V VT7
Задача 28.
В треугольнике ЛВС сторона АВ имеет длину 3, а высота CD, опущенная на сторону АВ, имеет длину у/3. Также известно, что основание D высоты CD лежит на стороне АВ и \AD\ = \ВС\. Найдите длину стороны АС.
Идея. Выразить длины отрезков BD и ВС через длину отрезка AD. Указание. Применить теорему Пифагора для треугольника BCD.


1.1. Прямоугольные треугольники
201
Решение. Точка D лежит на отрезке АВ, стало быть,
\AD\ + \BD\ = \АВ\. Обозначим длину отрезка AD через ж, тогда длина отрезка BD равна 3 — ж, длина отрезка ВС по условию также равна х. Записывая теорему Пифагора для треугольника BCD, получаем
|ДО|2 + \CD\2 = IВС\2 =* (v/з)2 + (3 - х)2 = X2 <=> х = 2.
Наконец, записываем теорему Пифагора для треугольника ACD:
|AL>|2 + \CD\2 = \АС\2 => \АС\2 =4 + 3 = 7 =► |Ж7| = уП.
Ответ. \АС\ = л/7 -
Задана 29.
В прямоугольном треугольнике АВС длина катета АВ равна 4, а длина катета АС равна 3. Точка D делит гипотенузу пополам. Найдите расстояние между центром окружности, вписанной в треугольник ACD, и центром окружности, вписанной в треугольник ABD.
Идея. Рассмотреть треугольник, вершинами которого являются точка D и центры окружностей, фигурирующих в условии.
Указание. Воспользоваться тем, что центр окружности, вписанной в произвольный треугольник, лежит на пересечении его биссектрис, а также тем, что угол между биссектрисами двух смежных углов прямой.
Указание. Вычислить длины радиусов окружностей, вписанных в треугольники ACD и ABD.
Решение. Обозначим центры окружностей, вписанных в треугольники ABD и ACD, буквами 0\ и О2 соответственно. Сначала докажем, что угол O1DO2 прямой. Поскольку DO\ и DO2 ~ биссектрисы углов ADB и ADC, величина угла ADOi равна половине величины угла ADB, а величина угла ADO2 равна половине величины угла ADC. Следовательно,
бЗбг = ADOi + AD02 = \ADB + \ADC = \ (ADB + ADC) = J.
jL £ Z ' / Z
Так как D - середина гипотенузы, то \AD\ = \BD\ — \CD\, треугольники ABD и ACD равнобедренные. Отрезки DE и DF являются их биссектрисами, поэтому они являются также их высотами и медианами, из чего вытекает DE _L АВ, DF _L АС, \АЕ\ = \ВЕ\, \AF\ = \CF\. Таким образом, DE и DF - средние линии
С
D В


202
Указания и решения
треугольника АВС, значит, \DE\ = 3/2, \DF\ =2 и, кроме того, отрезки 0\Е и 02F являются радиусами соответствующих вписанных окружностей. (Если мы предположим, что окружность, вписанная в треугольник ABD, касается его стороны АВ не в точке Е, а в некоторой отличной от неё точке К, то 0\К JL АВ и 0\Е _L АВ. А это противоречит тому, что из точки на прямую, не содержащую эту точку, можно опустить единственный перпендикуляр.)
Теперь посчитаем длины радиусов окружностей. Имеем
Saabd = \ ■ \АВ\ ■ \DE\ = 3, Saacd = \ • \АС\ ■ \DF\ = 3;
\АВ\2 + \АС\2 = \ВС\2 =► \ВС\ = 5, \AD\ = \BD\ = \CD\ =
9 2 3
Paabd = т, Paacd = 4; 7'aabd — \0\E\ = -, r^ACD = \02F\ = -.
После этого вычисляем длины отрезков DOi и DO2 •
iDOil = |£>S| - \0\E\ = I - I = |, |D02| = |£>F| - |02F| = 2 - | .
Наконец, применяем теорему Пифагора для треугольника 0\ D02:
\dox\2 + \do2\2 = \o1o2\2 =* |о1о2|2 = || + || = |||. о 5ч/1з
Ответ. ———.
12
Задача 30.
В равнобедренном треугольнике длина боковой стороны равна 20, а длина диамет- ра описанной около него окружности равна 25. Найдите длину радиуса окружности, вписанной в этот треугольник.
Идея. Высота в равнобедренном треугольнике, проведённая к основанию, является также медианой и биссектрисой. Центр вписанной окружности лежит на этой высоте.
Указание. Воспользоваться теоремой синусов, затем рассмотреть треугольник, образованный одной из вершин основания исходного треугольника, центром вписанной в него окружности и серединой основания.
А Н В
Решение. Обозначим вершины треугольника из условия задачи буквами А, В и С, будем считать, что \АС\ = \ВС\, проведём его высоту СН. Заметим, что она является медианой и биссектрисой треугольника АВС, поэтому центр окружности, вписанной в треугольник АВС, лежит на пересечении СН
С


1.1. Прямоугольные треугольники
203
и биссектрисы угла В. Обозначим его буквой О. Так как ОН _L АВ, то ОН - радиус окружности, вписанной в треугольник АВС.
Теперь найдём длину отрезка ВН. Запишем теорему синусов для треугольника АВС:
2Raabc = |y^L =► sin ABC = 7fc = t
sin ABC 25 5
Поскольку угол ABC острый,
cos ЛВС = v^1-sin2 ABC = |Btf | = |BC| • cos ABC = 12.
О
После этого найдём тангенс величины угла НВО и \ОН\:
НВО = ^АВС => | = cos ABC = -1~-tg--^£g
2 5 1 + tg2 НВО
tg2нвд = ] =► tgHBd = \\ \он\ = \BH\ tgHBd = 6.
Ответ. 6.
Задача 31.
Из середины D гипотенузы АВ прямоугольного треугольника АВС проведён луч, перпендикулярный гипотенузе и пересекающий один из его катетов. На этом луче отложен отрезок DE, длина которого равна половине длины отрезка АВ. Длина отрезка СЕ равна 1 и совпадает с длиной одного из катетов треугольника АВС. Найдите площадь треугольника АВС.
Идея. Построить окружность, описанную около треугольника АВС, и провести радиусы из её центра к точкам С и Е.
Указание. Найти величину одного из острых углов треугольника АВС путем рассмотрения треугольников DC A, DC В и DCE.
Решение. Заметим, что точка D является центром А окружности, описанной около треугольника АВС. Поскольку \DE\ = \DA\ по условию задачи, точка Е также лежит на указанной окружности, причём, поскольку луч DE пересекает один из катетов, располагается на той же из полуокружностей АВ, что и точка С.
Рассмотрим два случая.
1) 	Пусть \СЕ\ = \АС\ = 1. Тогда получаем, что AADC = ACDE (по трём сторонам), из чего вытекает равенство углов ADC и CDE. А поскольку угол ADE прямой,


204
Указания и решения
Теперь посчитать площадь треугольника АВС совсем просто.
14* cos - I , /о
\ВС\ = \АС\ ■ ctg - = = 1 + у/2, Saabc =
й sin - *
4
2) 	Пусть \СЕ\ = \ВС\ = 1. Тогда получаем, что ABDC = ЛCDE (по трём сторонам), т.е. они совпадают. Это противоречит тому, что DE _L АВ.
Ответ.
2
Задача 32.
Прямая, параллельная гипотенузе АВ прямоугольного треугольника АВС, пересекает катет АС в точке D, а катет ВС - в точке Е, причём длина отрезка DE равна 2, а длина отрезка BE равна 1. На гипотенузе взята точка F так, что \BF\ = 1. Известно также, что величина угла FCB равна а. Найдите площадь треугольника АВС.
Идея. Принять за неизвестную величину /3 величину угла АВС.
Указание. Выразить из треугольника CDE длину отрезка СЕ, затем применить теорему синусов в треугольнике FCB.
Решение. Поскольку DE\\AB, получаем DEC = ABC. Обозначим величины этих углов буквой /3, тогда величина угла CFB равна 7Г — а — /3. Из прямоугольного треугольника DEC вытекает, что
\СЕ\ = \DE\ • cos DEC = 2 cos/? =* |BC| = \BE\ 4- |CJS| = 2 cos/ Теперь запишем теорему синусов для треугольника FCB:
[BF| _ \ВС\ 1 _ 2 cos /3 4-1
sinFCB ~~ sin CFB sina ~ sin(ir - a - /3)
*<=> sin(a 4-/3) = 2 sin a cos /3 4- sin a.
Раскрывая скобки в левой части полученного уравнения, получаем
sin a cos /3 4- sin /3 cos a = 2 sin a cos /3 4- sin a <==>
<=$> sin /3 cos a — sin a cos /3 = sin a <*=> sin(/3 — a) = sin a. Так как a и /3 - острые углы, то /3 — а = а <£=> /3 = 2а. Поэтому
|ВС| = 2 cos 2a 4- 1, \АС\ = |ВС| • tg АВС = (2 cos 2а 4-1) tg2a.


1.1. Прямоугольные треугольники
205
Наконец, считаем площадь треугольника АВС:
Saabc = \ ■ \АС\ ■ \ВС\ = | tg2a(2cos2a + I)2.
Ответ. ^ tg2a(2cos2a + l)2.
Задача 33.
Гипотенуза АВ прямоугольного треугольника АВС является хордой окружности, длина радиуса которой равна 10. Вершина С лежит на диаметре этой окружности, параллельном гипотенузе. Градусная мера угла САВ равна 75°. Найдите площадь треугольника АВС.
Идея. Обозначить длину гипотенузы через 2х, расстояние между диаметром и хордой через h. Составить два уравнения с этими неизвестными.
Указание. Рассмотреть треугольник, образованный центром окружности, точкой В и серединой гипотенузы, выразить длину высоты исходного прямоугольного треугольника через длину его гипотенузы и величину одного из острых углов.
Решение. Проведём высоту СН треугольника АВС и отрезок О К, перпендикулярный АВ (К € АВ). Тогда очевидно, что \ОК\ = \СН\. Далее, поскольку треугольник ОАВ равнобедренный, ОК является его медианой, биссектрисой и высотой, значит, \АК\ = \ВК\.
Обозначим \ВК\ через ж, \ОК\ через Л, тогда \АВ\ = 2ж, \СН\ = h. Применим теорему Пифагора для треугольника ОВК:
\ОК\2 + \ВК\2 = |ОВ|2
с2 + h2 = 100.
Далее,
\АС\ = \АВ\ • cos CAB, \СН\ = \АС\ • sin CAB
=> h = \СН\ = |АВ| • sin CAB • cos CAB = 2x • sin 75° cos 75° = —.
z
Решая систему из двух полученных уравнений, находим, что х = 4\/5, h = 2\/5. Наконец,
Saabc = \ • \АВ\ ■ \СН\ = xh = 40.
Ответ. Saabc = 40.


206
Указания и решения
Задача 34-
Длины катетов прямоугольного треугольника равны 36 и 48. Найдите расстояние от центра окружности, вписанной в этот треугольник, до его высоты, проведённой к гипотенузе.
Идея. Воспользоваться параллельностью высоты, опущенной на гипотенузу, и радиуса вписанной окружности, проведённого в точку её касания с гипотенузой. Указание. Рассмотреть прямоугольник, вершинами которого являются центр вписанной окружности, точка её касания с гипотенузой, основание высоты, опущенной на гипотенузу, и основание перпендикуляра, опущенного из центра вписанной окружности на высоту.
Решение. Без ограничения общности будем считать, что \АВ\ — 48, \ВС\ — 36.
Поскольку ВН J_ АС и О К _L АС, а также ОЕ _L ВН, ОЕНК - прямоугольник. Таким образом, для нахождения длины отрезка ОЕ достаточно найти длину отрезка КН. Обе точки К и Н лежат на гипотенузе, поэтому длина отрезка КН равна модулю разности длин отрезков АК и АН, поскольку, вообще говоря, мы заранее не знаем, который из отрезков АК и АН длиннее, то есть лежит ли точка Н между точками А и К или, наоборот, точка К лежит между точками А и Н. Именно поэтому берётся модуль.
Теперь немного посчитаем. По теореме Пифагора находим \АС\ = 60. По известной формуле через катеты и гипотенузу прямоугольного треугольника находим длину радиуса окружности, вписанной в него, \ОК\ = 12.
Длину отрезка АН найдём из прямоугольного треугольника АВН:
cos ВАН
\АВ\ 4 , . 4 192
щ = 5> ИЯ| = ИВ|.си,ВУ1Я = 48.- = —
Для нахождения длины АК удобно использовать равенство длин касательных, проведённых к окружности из одной точки:
\АК\ = \AL\ = \АВ| - \BL\ = 48 - 12 = 36
\КН\ = \\АК\ -\АН\\ = у.
л 12
Ответ. —.
5


1.1. Прямоугольные треугольники
207
Задача 35.
Середины высот треугольника лежат на одной прямой. Какое максимальное значение может принимать его площадь, если длина его наибольшей стороны равна 10?
Идея. Доказать, что треугольник из условия задачи прямоугольный. Указание. Воспользоваться тем фактом, что середины высот треугольника лежат на прямых, содержащих его средние линии, и аксиомой Паша.
Решение. Докажем, что треугольник из условия задачи прямоугольный. Для этого нам потребуется такой факт:
Аксиома Паша.
Если прямая, лежащая в одной плоскости с треугольником, проходит через внутреннюю точку одной из его сторон, то она имеет общие точки хотя бы с одной из двух других его сторон.
Следствие.
Если прямая, лежащая в одной плоскости с треугольником, проходит через внутренние точки двух его сторон, то она не имеет общих точек с третьей его стороной.
В В
Рассуждаем так: если треугольник АВС остроугольный, то середины Р, Q, R его высот АА!, ВBf, СС' суть внутренние точки его средних линий, поэтому они не могут лежать на одной прямой в силу следствия из аксиомы Паша. Если же треугольник АВС тупоугольный (угол А тупой), то середина Р его высоты АА! есть внутренняя точка его средней линии, параллельной ВС, а середины Q и R высот В В1 и СС' лежат на продолжениях двух других средних линий. Но прямая PQ по аксиоме Паша должна проходить через точку, лежащую на средней линии, параллельной АВ, то есть она не может содержать точку R. Для прямоугольного же треугольника, как нетрудно убедиться, условие задачи выполнено.
Далее всё просто. Если угол А прямой, то ВС - наибольшая сторона. Положим \АВ\ = х, тогда \АС\ = \/100 — х2,
Saabc = ^ж2(100 — х2) ^ 625,
равенство достигается при х2 = 50.
Ответ. 25.


208
Указания и решения
1.2. 	Теоремы синусов и косинусов
Задача 1.
Длина стороны АС треугольника АВС равна 3, синусы величин его углов А и В равны л/3/2 и л/2/2 соответственно. Найдите длину стороны АВ.
Идея. Воспользоваться теоремой синусов.
Указание. Найти величины углов треугольника АВС, рассмотреть все случаи.
Решение. Исходя из данных задачи, величина угла А может быть равной либо 7г/3, либо 27г/3, а величина угла В может быть равна только 7г/4. (Если она равна 37г/4, то сумма величин углов А и В будет в любом случае больше 7г.) Значит, величина угла С равна либо 7г/12, либо 57г/12. Применяя теорему синусов, находим (можно отдельно вычислить sin 7г/12 и sin 57г/12)
\АВ\ = \АС\ • ^2 = 3 • sin В
\/б ± \/2
В”
3(\/3 =Ь 1)
V2
2
Ответ.
3(n/3±1)
Задача 2.
В треугольнике АВС известно, что \АВ\ = с, А = а, В = 3. Найдите площадь треугольника АВС.
Идея. Найти длину стороны АС или ВС.
Указание. Воспользоваться теоремой синусов.
Решение. Поскольку нам известны величины двух углов треугольника АВС, уместно применить теорему синусов. Сумма величин углов треугольника равна 7Г, стало быть, С = 7г — а — /3. Записывая теорему синусов, находим
|ЛД1 = 1ЛС| ; ,ЛС| = csin/3 sin С sinB sin (а + /3)
Наконец, воспользуемся формулой площади треугольника:


1.2. Теоремы синусов и косинусов
209
Задача 3.
Внутри треугольника АВС взята точка К так, что треугольник АВК равносторонний. Известно, что расстояние от точки К до центра окружности, описанной около треугольника АВС, равно 6, а величина угла АСВ равна arcsin(5\/l3/26). Найдите длину стороны АВ.
Идея. Воспользоваться тем фактом, что центр окружности, описанной около треугольника АВС, и точка К лежат на серединном перпендикуляре к стороне В К, причём обе внутри треугольника.
Указание. Оценив величины углов треугольника АВС, показать, что он остроугольный. Выразить расстояние, данное в условии задачи, через искомую длину.
Решение. Сначала докажем, что точка О (центр окружности, описанной около треугольника АВС) лежит внутри него. Для этого достаточно доказать, что он остроугольный. В самом деле, из того, что точка К лежит внутри треугольника АВС, а величины углов ВАК и АВК равны 7г/3, вытекает, что величины углов ВАС и АВС больше, чем 7г/3. С другой стороны, из свойств функции арксинус вытекает, что величина угла АСВ лежит в пределах от 7г/6 до 7г/3. Объединяя эти рассуждения, получаем, что треугольник АВС остроугольный.
Далее все просто. Обозначим длину стороны АВ через 2х. Тогда по теореме синусов мы находим
\АО\ = \ВО\
\АВ\
2ж\/ТЗ
2 sin ЛСВ 5 Затем из прямоугольных треугольников АКМ и АОМ получаем
\КМ\ = ху/з, \ОМ\ = ^х.
5
Наконец, в силу того, что точки О и К лежат внутри треугольника АВС, мы имеем
е = \ок\ = \\км\
Ответ. 10л/3.
\ОМ\\ =
=
\АВ\ = 10\/3.
Задача 4 •
В треугольнике АВС \АС\ = 3, ВАС = 7г/6, длина радиуса окружности, описанной около треугольника АВС, равна 2. Докажите, что площадь треугольника АВС меньше 3.


210
Указания и решения
Идея. Найти длину стороны ВС.
Указание. Воспользоваться теоремой синусов, применить формулу площади треугольника через длины двух его сторон и синус величины угла между ними.
Решение. Обратим внимание на то, что в этой задаче не просят вычислить точное значение площади треугольника АВС, а всего лишь просят доказать, что она меньше трёх. Этим и займемся. Поскольку нам дана длина радиуса окружности, описанной около треугольника АВС, применим теорему синусов:
• ^ = 2 Raabc => \ВС\ = 2.
sin ВАС
Теперь воспользуемся формулой площади треугольника через две стороны и синус угла между ними:
Saabc = ^ • \АС\ • \ВС\ • sin АС В = 3sin АС В < 3, так как sin АС В ^ 1.
Осталось доказать, что площадь треугольника АВС не может равняться 3. Если бы это было так, то синус величины угла АС В обязан бы был равняться 1, то есть угол АС В был бы прямым. Но в таком случае тангенс величины угла ВАС равнялся бы отношению длин отрезков ВС и АС, то есть 2/3. Однако по
условию ВАС = 7г/6, а значит, tg В АС = 1/л/З* Противоречие. Итак, площадь треугольника АВС меньше 3.
Замечание. На самом деле данным из условия задачи соответствует два различных треугольника АВС. Геометрически это объясняется так: сначала можно построить окружность радиуса 2, потом провести её хорду длины 3. Это будет отрезок АС. Точка В обязана, с одной стороны, лежать на окружности, с другой стороны, лежать на луче, образующем с АС угол величины 7г/6. Но такой луч можно построить двумя способами, что и отражено на чертеже.


1.2. Теоремы синусов и косинусов
211
Задача 5.
В треугольнике АВС найдите величину угла САВ, если произведение квадрата длины стороны ВС на сумму длин сторон АС и АВ равно сумме кубов длин сторон АС и АВ.
Идея. Проанализировать соотношение, данное в условии.
Указание. Преобразовать условие, данное в условии задачи. Воспользоваться теоремой косинусов.
Решение. Выпишем и преобразуем соотношение, данное в условии:
|Ж7|2 • {\АС\ + \АВ\) = \АС\3 + |ЛВ|3 <=> \ВС\2 = \АС\2 + \АВ\2 -\АС\ ■ \АВ\.
Так как по теореме косинусов
\ВС\2 = \АС\2 + |АВ|2 - 2 • \АС\ ■ \АВ\ • cos Л,
получаем
2 cos А — 1 => А —
о
г* п
Ответ. —.
о
Задача 6.
В треугольнике АВС длины сторон АВ и АС равны 3 и 2 соответственно. На стороне АВ выбрана точка М, а на стороне АС точка N так, что \АМ\ = 2, \AN\ = 1,5. Найдите площадь треугольника AMN, если длина стороны ВС больше длины отрезка MN в 6/-ч/Т7 раз.
Идея. Найти величину угла ВАС.
Указание. Положить ВАС = а, записать теорему косинусов для треугольников АВС и AMN.
Решение. Понятно, что для нахождения площади треугольника AMN нам не хватает только значения синуса величины угла ВАС. Обозначим величину угла ВАС через а, длину отрезка MN через ж, тогда длина отрезка ВС равна 6ж/\/Т7, и запишем теорему косинусов для треугольников АВС и AMN:
\ВС\2 = \АВ\2 + \АС\2 - 2 • \АВ\ • \АС\ • cos ВАС^ \MN\2 = \АМ\2 -f \AN\2 - 2 • \АМ\ • \AN\ • cos MAN
36ж2
17
= 94-4 — 2-3- 2 cos а,
х2 = 4 + 2,25 — 2 • 2 • 1,5cosa
36# 13--пГ 6,25 - х2
= 12 cos а, 6 cos а


212
Указания и решения
=> 13 —- = 12,5 — 2х2 => х2 = — => cos а = -.
17 4 3
Теперь осталось найти синус величины угла ВАС и записать формулу площади для треугольника АВС :
sine* = y/l — cos2а = Saamn = ~ • \АМ\ • |AiV| • sina = у/2.
О А
Ответ, у/2.
Задача 7.
В треугольнике АВС \АВ\ = 4, \ВС\ = 5. Из вершины В проведен отрезок ВМ
(М G АС), причём АВМ = 7г/4, МВС = 7г/6.
а) В каком отношении точка М делит сторону АС?
б) Вычислите длины отрезков AM и МС.
Идея. Записать теорему синусов для треугольников AM В и СМ В, воспользоваться тем, что синусы величин смежных углов равны. Указание. Поделив полученные соотношения, вычислить отношение \АМ\ : \МС\. Указание. С помощью теоремы косинусов найти длину стороны АС.
Решение. Для получения ответа на первый вопрос задачи используется та же схема, что и при доказательстве свойства биссектрисы, а именно, запишем теорему синусов для треугольников AM В и СМ В:
В
\АВ\
\АМ\
sin AM В sin АВМ
\вс\ _ \мс\
sin AM В =
sin СМВ =
\АВ\ • sin АВМ \АМ\ '
\BC\-sin МВС
sin СМ В sin МВС \мс\
Поскольку углы AM В и СМ В смежные, синусы их величин равны. Отсюда следует, что
\AB\- sin АВМ _ \BC\-sin МВС
\АМ\
\МС\
\АМ\ _ \AB\-sin АВМ _ 4\/2 \МС\ ~ \BC\ -sin МВС ~ 5
Теперь, когда мы знаем отношение длин отрезков AM и МС, для получения ответа на второй вопрос задачи достаточно вычислить длину отрезка АС. Это легко делается с помощью теоремы косинусов.


1.2. Теоремы синусов и косинусов
213
=* \АС\2 = 16 + 25-40cos(^ + Л = 41 - 10(>/Б - V2).
V 4 6 /
Таким образом, \АС\ = у 41 — 10(л/б — \/2). Наконец, найдём длины отрезков AM и МС:
’ \АМ\ + \МС\ = \АС\,
\АМ\ 4у/2 \МС\ ~ 5
4^2
\МС\ + \МС\ = \АС\,
\АМ\ = ^ф.\МС\
\МС\ =
\АС\
1 +
4^2’
Ответ, а)
4 Л/о
\АМ\ = -т-\МС\ 5
\АМ\ _ 4\/2
\МС\ = \АМ\ =
5^41 - 10(л/6 — л/2)
5 + 4 д/2 ’
4^2^41-10(4/6-4/2)
5 + 4 т/2 '
|МС| 5 ’
б) |ЛМ| = у41 - 10(л/6 - V2), |МС| =
5 + 4\/2
•^/41 — 10(\/б — \/2).
Задача 8.
В треугольнике АБС |2?С| = 4, |АВ| + |АС| = 6. Найдите площадь треугольника АВС, если cos АСВ = 5/12.
Идея. Вычислить длину стороны АС.
Указание. Положить \АС\ = х, записать теорему косинусов для треугольника АВС.
Решение. Примем длину стороны АС за х. Тогда \АВ\ = б — х. Теперь можно записать теорему косинусов для треугольника АВС:
\АВ\2 = \АС\2 + \ВС\2 - 2 • \АС\ • \ВС\ • cos АСВ
(6 — х)2 = х2 + 16 — 8х •
20 =
26ж
12
30
=* * = 1з-
После этого нам осталось только вычислить синус величины угла АСВ и записать формулу площади треугольника АВС:
/ГТэ
sin АСВ
1 - cos2 АСВ =
12 ’
Здлвс = \ '\АС\ • \BC\-sinACB = ± ^ -4- ^ = ^л/Й9.
Ответ, —л/119.
1о


214
Указания и решения
Задача 9.
В треугольнике АВС градусная мера угла АС В равна 75°, а длина высоты, опущенной из вершины этого угла, равна 1. Найдите длину радиуса окружности, описанной около треугольника АВС, если его периметр равен 4 4- л/б — \/2.
Идея. Вычислить длину стороны АВ треугольника АВС. г
Указание. Обозначить длины отрезков АС, ВС и АВ буквами х, у и z, воспользоваться теоремой косинусов и формулой площади треугольника.
Решение. Сначала посчитаем синус и косинус 75°:
sin 75° = sin(45° 4- 30°) = cos 75° = cos(45° 4- 30°) =
\/б + у/2 4 5
s/6-y/2
В этой задаче по данным из условия невозможно непосредственно найти значения каких-либо других величин. Поэтому возникает необходимость введения неизвестных. Обозначим длины отрезков АС, ВС и АВ буквами х, у и z соответственно. Поскольку мы знаем синус угла АС В, для нахождения длины радиуса окружности, описанной около треугольника АВС, нам достаточно найти длину отрезка А В, то есть z. Воспользуемся теоремой косинусов, формулами площади (для того, чтобы задействовать данную нам длину высоты) и определением периметра треугольника АВС:
\АВ\2 = \АС\2 + \ВС\2 - 2 • \АС\ • \ВС\ • cos АСВ,
Saabc = \ • \АВ\ ■ \СН\ = i • \АС\ ■ \ВС\ ■ sin АСВ, =►
Раавс = \АВ\ + \ВС\ + \АС\
= X2 + у2 - 2ху •
1.2.1 =1.ху.&ьй,
4 + \/б — \/2 = х + у + z
z2 = (x + y)2-2xy4+^--*3
хУ = 7072=г
(4 + >/б - V2 - z)2 - 2 • z ■ (>/б - у/2) ■
(у/6-у/2), X + у = 4 + \/б — — 2
4 + л/6- у/2
Для того чтобы быстрее решить это уравнение, положим Р = 4 + у/б— у/2. Получаем
Р
z — (Р — zf - 2z(P - 4)
z2 - р2 - 2Pz + z2- \Pz{P - 4)
0 = P-2z- -z{P-A)
0 = 2Р — 4z — Pz + 4z
z = 2.


1.2. Теоремы синусов и косинусов
215
Осталось воспользоваться теоремой синусов:
\АВ\ _ 2
2 Raabc =
sin АС В
Ответ. V6-V2.
Raabc =
2 ■ л/2
= \/б — \pi.
Задача 10.
Внутри треугольника АВС взята точка К таким образом, что \АК\ = 1, \КС\ = \/3, AifC = 120°, АВК = 15°, К ВС = 15°. Найдите длину отрезка ВК.
Идея. Вычислить сумму градусных
мер углов В АК и ВС К, воспользовать- ^
ся теоремой синусов.
Указание. Воспользоваться теоремой о сумме градусных мер углов треугольника.
Указание. Записать теорему синусов для треугольников АВК и СВК.
Решение. Идея решения заключается в следующем: для нахождения дли-
градусную меру одного из двух углов - ВАК или ВСК. Мы можем написать
три уравнения: две теоремы синусов (для треугольников АВК и СВК) и одно соотношение, связывающее градусные меры углов ВАК и ВСК.
Сначала запишем теорему о сумме градусных мер углов треугольника для треугольников АВК и СВК:
ВАК + АВК + АКВ = 180°, ВСК + КВС + ВКС = 180° =>
=* ВАК + 15° + АКВ + ВСК + 15° + ВКС = 360°.
Теперь заметим, что
АКСЛ-ШСЛ- АКВ = 360° =» ВКС + АКВ = 240°.
Стало быть,
ВАК + ВСК = 90°.
Обозначим градусную меру угла ВАК через а, тогда ВСК — 90° — а. После чего запишем теоремы синусов для треугольников АВК и СВК:
\вк\
\АК\
sin ВАК sin АВК
\вк\ _ \ск\ _
sin ВСК sin КВС
=> \ВК\ sin 15° = sin а;
\ВК\ sin 15° = л/38ш(90° — а).


216
Указания и решения
Из этих двух соотношений вытекает, что sina = \/3sin(90o —a) то есть a = 60°. Наконец,
tga = л/3,
ч/З
2
= sma = 2 = 2^3 = у/6
1 sin 15° у/Ь-у/2 у/Ъ-у/2 \/3-Г
Ответ.
V5-1 ‘
Задача 11.
Величины углов тупоугольного треугольника ЛВС удовлетворяют соотношению
sin ^4 — = sin2 А — sin2 В. Найдите периметр этого треугольника, если длина
радиуса описанной около него окружности равна Д, а величина одного из его углов равна 7г/8.
Идея. Понять, что скрывается за соотношением sin (^А — В^ = sin2 А — sin2 В.
Указание. Преобразовать данное в условии задачи соотношение, воспользоваться теоремой синусов.
Решение. Преобразуем правую часть данного нам соотношения: sin2 А — sin2 В = ^sin А — sin B^j • ^sin А -f sin B^j =
Л . A-В А + В . А + В А-В = 2 sm —-— cos —-— • 2 sin —-— cos —-— =
' . Ал- В А + В
2 sin —-— cos
2 2 A-В A — В
Л . 2 sin;—-— cos ——
2 2 I { 2 2
= sin + B^ • sin
С учётом этих преобразований из условия задачи и того факта, что величины углов А и В лежат в интервале (0,7г), мы получаем
sin ^А — В^ = sin — В^ sin ^A -h b'J
sin (А — в\ = 0,
" А = В,
V / sin (^А ■+■ В^ = 1;
'Т С: 7Т
А + В=-;
А = В, С=
Поскольку по условию задачи треугольник АВС тупоугольный, нам подходит только вариант А = В, то есть треугольник АВС равнобедренный, угол С тупой, а углы А и В острые. Их величины равны 7г/8, стало быть, величина угла С равна 37г/4.


1.2. Теоремы синусов и косинусов
217
Осталось всего лишь записать теорему синусов: |ЛС| \АВ\ \ВС\
т-» ^ 2Ддлвс
sin В sin С sin А
\АС\ = |ВС| = 2#sin^- = 2R
\АВ\ = 2i?sin^ =RV2]
« „„/1
Paabc = r(V2 + 21/2-4/2) .
Ответ. R ^\/2 + 2\/2 — л/2^ .
Задача 12.
В треугольник ЛВС вписана окружность с центром в точке О. Площадь треугольника АОВ относится к площади треугольника ВОС как \/3 : 2, АС В = 7г/3, |ЛС| = 2. Найдите длину радиуса окружности, описанной около треугольника АВС.
Идея. Вычислить отношение длин сторон АВ и ВС.
Указание. Воспользоваться формулами площади, затем теоремами синусов и косинусов.
Решение. Поскольку центр окружности, вписанной в треугольник, лежит на пересечении его биссектрис, углы А ВО и С ВО равны. Записывая формулы площади для треугольников АОВ и ВОС, получаем
Saaob
Saboc
V3
2
\ • \АВ\ • \OB\ -sin ABO _ V3 \ ■ \BC\ ■ \OB\ ■ sinCBO ~ 2
\AB\ V3 \BC\ ~ 2 '
После этого положим \BC\ = 2х. \АВ\ = л/Зх и применим теорему косинусов:
Зх2 = 4х2 + 4 — 2 • 2х ■ 2 • -
х — 2, \АВ\ - 2л/3.
Наконец, длину радиуса окружности, описанной около треугольника ЛВС, найдём по теореме синусов:
Raabc
\АВ\
2 sin ЛСВ
= 2.
Ответ. 2.


218
Указания и решения
Задача 13.
В треугольнике АВС известно, что ВАС = а, АВС = /3, \ВС\ — а. На стороне АВ взята точка Р так, что \АР\ : \РВ\ = 1:2. Через точку Р проведена окружность, касающаяся стороны ВС в точке D, причём AD - высота треугольника АВС. Найдите длину радиуса этой окружности.
Идея. Рассмотреть равнобедренный треугольник ODP, где О - центр окружности из условия задачи.
Указание. Найти длины отрезков ВР и BD.
Указание. Воспользоваться теоремами синусов и косинусов в треугольниках АВС и BPD.
Решение. Идея решения заключается в следующем: если провести отрезок DP, затем обозначить центр окружности из условия задачи буквой О и соединить его с точками Р и D, то треугольник OPD будет равнобедренным, поскольку \ОР\ = |OjD|, а точка А будет лежать на прямой OD в силу того, что OD ± ВС и AD _L ВС. С учётом этих рассуждений становится ясно, что нам достаточно найти длину отрезка DP и величину угла ADP, после чего из треугольника OPD мы найдём и длину радиуса нашей окружности.
Запишем теорему синусов для треугольника АВС:
\АС\
\АВ\
\ВС\
\АВ\
sin ABC sin АСВ sin ВАС Значит,
ИС| = \лв\ =
smc*
{
\АВ\ = \АР\ + \РВ\, \РВ\ = 2\АР\
\АС\ _
sin j3 sin(7r — a — /3) sin a
asin(a + j3)
asin(a + f3)
sma
1,
\AP\ = -z\AB\ = ,
o 6 sm a
\PB\ = Ьав\ =
3 3 sin a
Также из прямоугольного треугольника ABD вытекает, что
asin(a 4- /3) cos (3
\BD\ = \AB\cosABD
sma
a sin(a + 0)
Для сокращения записи введем обозначение с = и запишем теорему
sma
косинусов для треугольника BPD:
\DP\2 = \BD\2 + \РВ\2 -2-\BD\- \DP\ ■ cos DBP =>
\DP\2 = c2 cos2 /3 + c2 — ^ c2 cos2 j3 У о
\DP\ = - \/4 — 3 cos2 /?.
О


1.2. Теоремы синусов и косинусов
219
Теперь запишем для него же теорему синусов:
\DP\ \РВ\ . —\PB\smDBP 2 sin /3
— —" sm В DP = —
sin DBP sin В DP \DP\ ^/4 - 3cos2/3'
Последний шаг: из треугольника OPD с учётом того, что ODP = тг/2 — BDP, получаем
IOP1 1£>£L l^4-30082^ с(4 — 3 cos2 /3)
2 cos ODP 2 sin BDP 2sin^ 12sin/3
\/4 — 3 cos2 /3
Осталось подставить выражение для с и получить ответ. asin(a: + /3)(4 — 3cos2 /3)
Ответ.
12 sin a sin /3
Задача 14-
Через центр окружности, вписанной в треугольник ЛВС, провели прямую МАГ параллельно основанию ЛВ (М лежит на ВС, iV лежит на АС). Известно, что \АВ\ = 5, \MN\ = 3. Найдите периметр четырёхугольника ABMN.
Идея. Доказать, что длина отрезка MN равна сумме длин отрезков ВМ и AN.
Указание. Рассмотреть треугольники AON и ВОМ, где О - центр окружности из условия задачи.
Указание. Воспользоваться определением биссектрисы и свойством внутренних накрест лежащих углов при параллельных прямых.
Решение. Обозначим центр окружности, вписанной в треугольник ЛВС, буквой О.
Тогда ОВ и О А — биссектрисы углов ЛВС и ВАС соответственно, значит,
ЛВО = МВО, ВАО = NAO.
С другой стороны, поскольку прямые Л В и MN параллельны, по теореме о равенстве внутренних накрест лежащих углов при параллельных прямых получаем, что
ЛВО = ВОМ, ВАО = AON.
Стало быть, ВОМ — МВО, AON = NAO, поэтому треугольники AON и ВОМ равнобедренные, причём |ВМ| = |МО|, \AN\ = |iVO| - Сложив эти равенства, мы имеем |ВМ| -f \AN\ = \МО\ + \NO\ = \MN\. Теперь можно посчитать периметр четырёхугольника ABMN:
Pabmn = \АВ\ + \MN\ + |ВМ| + \AN\ = \АВ\ + \MN\ + \MN\ = 11.
Ответ. 11.
С


220
Указания и решения
Задача 15.
В треугольнике АВС даны длины сторон \АВ\ = \/2, \ВС\ = у/Ъ и |Ж7| = 3. Сравните градусную меру угла ВОС и 112,5°, если О - центр вписанной в треугольник АВС окружности.
Идея. Воспользоваться тем, что центр окружности, вписанной в треугольник, лежит на пересечении его биссектрис.
Указание. Выразить градусную меру угла ВОС через градусные меры углов треугольника АВС, воспользовавшись теоремой о сумме градусных мер углов треугольника.
Решение. Поскольку О - центр окружности, вписанной в треугольник АВС, О В и ОС - биссектрисы углов АВС и АСВ соответственно. Поэтому
Таким образом, ВОС = 90° + —- = 112,5°.
Ответ. ВОС — 112,5°.
Задана 16.
В треугольнике АВС известно, что \ВС\ - \АВ\ = 0.15|ЛС|. Чему равно произ-
ВОС = 180°
(ОВС + ОС в) = 180° - (\лвс + \асв\
с
в
А
Величину угла ВАС можно легко найти по теореме косинусов: |ВС|2 = \АВ\2 + \АС\2 - 2 • \АВ\ ■ \АС\ ■ cos ВАС =*
=► 5 = 9 + 2 — 6л/2 cos ВАС =» cosJВАС = ~^= => ВАС = 45°.
V2
45°


1.2. Теоремы синусов и косинусов
221
Идея. Воспользоваться тем, что центр окружности, вписанной в треугольник, лежит на пересечении его биссектрис.
Указание. Воспользоваться теоремой о длинах отрезков, на которые окружность, вписанная в треугольник, делит точками касания его стороны.
Решение. Пусть О - центр вписанной в треугольник В
АВС окружности, Н - точка её касания со стороной АС.
Заметим, что
ta/ЪпгЛ 1°я1 \сн\_\сн\
tg {2BACj • ctg \jACBj |ЛЯ| • 10Я| |АЯ|.
По теореме о длинах отрезков, на которые окружность, вписанная в треугольник, делит его стороны, находим
\АС\ + \ВС\ - \АВ\
\СН\ _ 2 _ |^С1 + 0,15|Ж7| _ 23
\АН\ ~ \АС\ + \АВ\ - \ВС\ “ \АС\ - 0,15\АС\ ~ 17*
2
п 23
Ответ. —.
Задача 17.
Окружность, вписанная в треугольник АВС, касается его сторон АС, АВ и ВС в точках К, М и N соответственно. Известно, что \АК\ = \КС\, KMN = 75°, а произведение длин всех сторон треугольника KMN равно 9 4- 6\/3. Найдите длины сторон треугольника АВС.
Идея. Доказать, что треугольники АВС и KMN равнобедренные, найти градусные меры всевозможных углов.
Указание. Воспользоваться теоремой о длинах отрезков, на которые окружность, вписанная в треугольник, делит точками касания его стороны, а также теоремой синусов.
Решение. По теореме о длинах отрезков, на которые окружность, вписанная в треугольник, делит точками касания его стороны, имеем
\АК\ = \АМ\ = раавс ~ \ВС\, \КС\ = |Ж7| = раавс ~ \АВ\ =►
==> Раавс - \ВС\ = раавс - \АВ\ =*> \АВ\ = \ВС\.
Таким образом, треугольник АВС равнобедренный, ВАС = АСВ, треугольники AM К и CNK равнобедренные и равны (по двум сторонам и углу между ними),


222
Указания и решения
из чего вытекает, что \КМ\ — |jFsTiV|, АКМ = CKN = AM К = CNK. Значит, треугольник KMN тоже равнобедренный, причём
KNM = KMN = 75°, MKN = 180° - KNM - KMN = 30°.
Теперь найдём длины сторон треугольника KMN. Обозначим длины отрезков КМ и KN буквой ж, тогда \MN\ = 2х • cos75°. Подставляя эти величины в соотношение из условия задачи, находим
2хз У6-У2 ^ ^ 18 + 12у/3 _ (18 + 12>/3)(л/б + у/2)
4 s/G-y/2 4
Наконец, вычислим длины сторон треугольника АВС, пользуясь соотношениями между длинами сторон и величинами углов в равнобедренном треугольнике.
—- - 180° - MKN - -—-
АМК = АКМ = CKN = = 75°, ВАС = Ш°-АМК-АКМ = 30°,
\АК\ = = -7^—г = = 3 + 2^’
2cos АКМ у/б-у/2 уД-1 2 \АС\ = 2 • \АК\ = 6 + 4л/3, |АЯ| = |ВС| = —^SL. = 4 + 2^3.
2 cos В ЛС
Ответ. |ЛВ| = |ВС| = 4 + 2>/5, |Ж7| = 6 + 4>/5.
Задача 18.
Точка О лежит на отрезке А В так, что \АО\ = 13, \ОВ\ = 7. С центром в О проведена окружность, длина радиуса которой равна 5. Из А и В к ней проведены касательные, пересекающиеся в точке М, причём точки касания лежат по одну сторону от прямой АВ. Найдите длину радиуса окружности, описанной около треугольника AM В.
Идея. Вычислить синус величины угла AM В.
Указание. Провести радиусы ОН и О К, рассмотрев прямоугольные треугольники ВОН и АО К, найти величины углов А и В, затем воспользоваться теоремой синусов.
Решение. Ясно, что \АВ\ = \АО\ + \ОВ\ = 20.
Теперь для нахождения длины радиуса окружности, описанной около треугольника AM В, нам достаточно найти синус угла AM В. Проведём радиусы ОН и О К, после чего, рассмотрев


1.2. Теоремы синусов и косинусов
223
прямоугольные треугольники ВОН и АО К, можно вычислить синусы и косинусы величин острых углов МАВ и MBA:
втШё = М| = 1 =*. С0»ДШ=|,
&тМВА = ^щ = ^ =*■ со
Далее, поскольку АМВ = 7г — МАВ — MBA, получаем
л 10^ + 60
sin АМВ = sin (МАВ + MBA) Наконец, по теореме синусов
91
АВ 20-91 _ „ 91(6-76)
4Г1ААМВ — —- — /— _ * -К>ААМВ — '
sin AM В 10V6 + 60 30
91(6 - л/6)
Ответ.
30
Задача 19.
Периметр треугольника АВС равен 40/3, косинусы углов АВС и АСВ равны 0,6 и 0,28 соответственно. Найдите площадь треугольника АВС.
Идея. Найти синусы величин всех углов треугольника АВС.
Указание. Вывести формулу площади треугольника через его периметр и синусы величин его углов.
Решение. Для начала найдём синусы величин всех углов треугольника АВС:
sin ABC = \] 1 — cos2 ABC = sin^CJE? = д/1 — cos2 АСВ =
5 25
sinlL4C = sin (АСВ + ABC) = 0,8 • 0,28 + 0,6 • 0,96 = 0,8 = |.
Теперь выведем ещё одну формулу для площади треугольника, в которую входят его периметр и синусы величин его углов, полагая, что длины его сторон и величины противоположных им углов равны а и а, 6 и ^ с и 7 соответственно.
а Ъ с . _ Р sin а
— ~—п — ~—, а + b + с = Р => а = — . .—,
sina smp sin 7 sin a + sin p + sm 7
P sin /3 P sin 7
Q — Q — _
sin a + sin /3 + sin 7 ’ sin a + sin /3 + sin 7 *
Подставляя эти выражения в стандартную формулу площади, имеем
_ 1 , . Р2 sin a sin /3 sin 7
Ь — -aosin7 = —— ;— : -г.
2 2(sm a + sin p + sin 7)^


224
Указания и решения
Осталось лишь подставить сюда данные из нашей задачи.
1600 • 4 • 4 • 24 25
Saabc
642 3
2. д. 5. 5-25-^
п 25
Ответ. —.
о
Задача 20.
Известно, что для величин углов треугольника АВС выполнено соотношение cos2 А 4- cos2 В -f cos2 С = 1. Найдите площадь этого треугольника, если длины радиусов вписанной в него и описанной около него окружностей равны у/3 и Зу/2 соответственно.
Идея. Проанализировать данное в условии соотношение.
Указание. Преобразовать данное в условии соотношение.
Указание. Воспользоваться формулами для длин радиусов окружностей, вписанной в прямоугольный треугольник и описанной около него.
Решение. Преобразуем данное нам в условии соотношение, пользуясь тем, что А +В + С = тг:
9 - о - 9 - 1+ cos 2А 1 + cos 2 В 9 -
cos А 4- cos В 4- cos С — 1 <*=> 1 = 1 — cos С <==>
£ Z
<=> cos2A + cos2B = — 2cos2 С Ф=> cos(A-f-В) cos(A — В) = — cos2 С
' А-В + б'
х
cos С ^cos С — cos( А — = 0 2 cos С sin
. (А-В-С\ л я й 7 л
х sm I 1=0 cos С cos В cos А = 0.
Очевидно, что один их косинусов обязан равняться нулю, поэтому наш треугольник прямоугольный. Укажем формулу для вычисления его площади через длины радиусов вписанной в него (г) и описанной около него (R) окружностей. Пусть а и Ъ - длины его катетов, с - длина гипотенузы. Тогда с = 2Д, а + Ь = 2R + 2г, р = 2R 4- г, S = рг = г2 + 2Rr. Подставляя сюда данные из условия задачи, получаем 5 = 3 + 6\/б.
Ответ. 34-6\/б.
Задача 21.
Площадь треугольника равна 6\/б, периметр его равен 18, расстояние от центра вписанной в него окружности до одной из его вершин равно у/5б/3. Найдите длину наименьшей стороны этого треугольника.


1.2. Теоремы синусов и косинусов
225
Идея. Найти длину радиуса окружности, вписанной в треугольник, и величину одного из его углов.
Указание. Воспользоваться формулой площади треугольника через его полупериметр и формулой длин отрезков, на которые вписанная в треугольник окружность делит его стороны.
Указание. Применить теорему косинусов.
Решение. Обозначим вершины треугольника буквами Л, Б и С, центр вписанной в него окружности обозначим буквой О, а точку её касания со стороной АВ обозначим буквой Н. Без ограничения общности будем считать, что \ВО\ = а/56/3. Поскольку нам известны площадь и периметр треугольника АВС, то, воспользовавшись формулой площади треугольника, мы можем найти длину радиуса вписанной в него окружности, то есть длину отрезка ОН. После этого из треугольника ВОН можно найти \ВН\ и величину угла ОВН:
]^TJl Saabc бл/б 2\/б , , /56 24 о
|0Я| ~ = ~Г = —■ \BH\ = ^-^ = i,cosOBH = 2^ и.
После этого, применив формулу для длин отрезков, на которые вписанная в треугольник окружность делит его стороны, находим \АС\ = Раавс ~ \ВН\ = 5. Также заметим, что величина угла АВС в два раза больше величины угла ОВН, поэтому cos ABC = 2cos2 ОВН — 1 = 5/7, sin ЛВС = 2>/б/7. Наконец, введя обозначения \АВ\ = ж, |ВС| — у и воспользовавшись формулой площади тре-
1 2>/б г
угольника АВС, составляем систему уравнений ж + у + 5 = 18; - • ——ху = буб,
Z I
решением которой являются пары (6,7) и (7,6).
Ответ. 5.
Задача 22.
5\/2 Ъу/Ъ
В треугольнике АВС \АВ\ = —— ,|ВС| = ——. Точка М лежит на стороне
Z “Г
з
АВ, точка О лежит на стороне ВС, причём \ВМ\ = -|ЛМ|, а прямые МО и
Л С параллельны. Биссектриса угла ВАС пересекает прямую МО в точке Р, лежащей между точками М и О, причём длина радиуса окружности, описанной около треугольника АМР, равна у/2 + л/2. Найдите длину стороны АС.
Идея. Рассмотреть треугольник АМР, доказать, что он равнобедренный.
Указание. Из треугольника АМР найти величину угла ВАС, воспользоваться теоремой косинусов в треугольнике АВС, проверить, лежит ли точка Р на отрезке МО.
Решение. Ясно, что, поскольку нам дана длина радиуса окружности, описанной около треугольника АМР, необходимо искать ещё какие-то элементы этого треугольника.
В
8 Геометрия


226
Указания и решения
Достаточно просто находится длина отрезка AM:
3
\АВ\ = \АМ\ + \ВМ\, \ВМ\ = \\АМ\
\ВМ\ = -\АВ\, ^ Г \вМ\ = \у/2,
\АМ\ = у\АВ\ [ \АМ\ = у/2.
О
Далее заметим, что из параллельности прямых АС и МО вытекает равенство углов РАС и АРМ, а из того, что АР - биссектриса, следует равенство углов РАМ и РАС. Значит, углы АРМ и РАМ равны, то есть треугольник АМР равнобедренный.
Обозначим величину углов РАМ и АРМ буквой а, тогда величина угла ВАС равна 2а. Запишем теорему синусов для треугольника АМР:
\АМ | OD . \АМ\ у/2 у/2-у/2
= 2R&AMP => sm а— — -
sin АРМ 2RAAmp 2у/2 + у/2 2
Значит,
cos ВАС = cos 2а = 1 — 2 sin2 а = 1 — -——^ ^ => Б Л С — ~.
2 2 4
Теперь задача сведена к более-менее стандартной. Для нахождения \АС\ воспользуемся теоремой косинусов для треугольника АВС:
|ВС\2 = \АВ\2 + |АС|2 - 2 • |АВ| • \АС\ • cosBAC =>
=► ^ = Ц + \АС\2-5\АС\ =► |ЛС|2 - 5|ЛС<| + g = 0.
5 15
У этого уравнения два положительных корня: \АС\ = -, \АС\ — — (на чертеже
изображены оба варианта). При решении задачи может показаться, что они оба подходят под условие задачи. Однако это не так. Мы не проверили, что точка Р лежит между точками М и О, что эквивалентно тому, что длина отрезка МР (которая равна длине отрезка AM, то есть у/2) меньше длины отрезка МО.
3
Воспользуемся тем, что \МО\ = — (для обоснования этого факта можно
5
5
использовать подобие треугольников или теорему Фалеса). Если \АС\ — -, то
3 15 9
\МО\ = - < у/2, а если \АС\ = —, то \МО\ = - > у/2. Поэтому нам подходит
только второй вариант.
п 15
Ответ. —.
4
Задача 23.
В треугольнике АВС величина угла при вершине В равна 7г/3, а длины отрезков, соединяющих центр вписанной окружности с вершинами А и С, равны 4 и б соответственно. Найдите длину радиуса окружности, вписанной в треугольник АВС.
Идея. Вычислить величину угла АОС, воспользоваться теоремой косинусов.


1.2. Теоремы синусов и косинусов
227
Указание. Воспользоваться тем, что центр О окружности, вписанной в треугольник, лежит на пересечении его биссектрис.
Применить теорему о сумме величин углов треугольника.
Указание. Заметить, что искомая длина есть длина перпендикуляра, опущенного из точки О на АС.
Решение. Пусть О - центр вписанной в треугольник АВС окружности, Н - точка её касания со стороной АС. Заметим, что
гГл?ч глг^л ВАС АС В 1 / 2'Л’
АОС — 7г - ОАС — ОСА = 7г — = 7г — - • (7г — АВС) = —.
2 2 2 V /3
После этого запишем теорему косинусов для треугольника АОС и воспользуемся формулами площади:
|Ж7|2 = 36 + 16-2-6-4- =76 =► \АС\ = 2л/19;
\ОА\ ■ \OC\ smAOC
\он\
\АС\
Ответ,
Задача 24-
Известно, что длина радиуса окружности, вписанной в треугольник АВС, равна 1. Эта окружность касается его сторон АВ, ВС и АС в точках К, М и N соответственно, MKN = АВС = 45°. Найдите длины сторон треугольника АВС.
Идея. Вычислить градусные меры углов треугольника АВС, воспользоваться формулами площади. г
Указание. Использовать тот факт, что треугольники AKN и ВКМ равнобедренные.
Решение. Положим А — 2а. Заметим, что треугольники AKN и ВКМ равнобедренные, поэтому AKN = 90° - а, ВКМ = 67,5°. Далее,
B^+MKN+AKN = 180° =» а = 22,5°, А = 45°, С = 90°.
Значит, треугольник АВС является прямоугольным и равнобедренным. Положим \АС\ = \ВС\ = х, тогда \АВ\ = ху/2, и воспользуемся формулами площади треугольника:
_ х2 2х + ху/2 . г-
Saabc = — = 1 => х — 2 v2.
Ответ. \АС\ = \ВС\ = 2 + у/2, \АВ\ = 2 + 2у/2.


228
Указания и решения
Задача 25.
Через центр О вписанной в треугольник АВС окружности проведена прямая, параллельная стороне ВС и пересекающая стороны АВ и АС в точках М и N соответственно. \ВС\ — периметр треугольника AMN равен 3v^2, а длина отрезка АО втрое больше длины радиуса вписанной в треугольник АВС окружности. Найдите площадь треугольника АВС.
Идея. Доказать, что периметр треугольника AMN равен сумме длин сторон АВ и АС.
Указание. Рассмотреть треугольники jВ МО и С NO, доказать, что они равнобедренные.
Указание. Найти косинус угла ВАС, воспользоваться теоремой косинусов.
Решение. Заметим, что равны углы МВО и ОВС (так как ОВ - биссектриса), а также равны углы ОВС и МОВ (как внутренние накрест лежащие углы при параллельных прямых MN и ВС). Из этого вытекает, что МВО = МОВ, а значит, тре- В
угольник ВМО равнобедренный. Отсюда получаем, что \ВМ\ = \МО\.
Аналогично заключаем, что \CN\ = \ON\. Но тогда мы можем легко доказать, что периметр треугольника AMN равен сумме длин сторон АВ и АС:
Paamn = \АМ\ +1 A/V| + \МО\Н-\ON\ = \AM\ + \BM\ + \AN\ + \CN\ = \АВ\ + \АС\.
Далее из прямоугольного треугольника АОН имеем
• \°Н\ 1 sm0AH=т= з-
С учётом того, что АО - биссектриса угла ВАС, получаем
cos ВАС = 1 - 2 sin2 ОАН = J; sin ВАС = ^l-cos2 ВАС = —.
У У
Раз мы нашли синус угла ВАС, то площадь треугольника АВС логично искать с помощью формулы Saabc = -|AB|-|AC|*sin.Bj4C7. Найдём \AB\-\AC\, применяя теорему косинусов к треугольнику АВС:


1.2. Теоремы синусов и косинусов
229
=> ур2 = 9у/2 —— • \АВ\ • \АС\ ==> \АВ\ • \ АС\ = ■ ■■■.
1 V2 4v^ ,
Значит, Saabc = ^ = 1.
Ответ. 1.
Задача 26.
В треугольник KLM вписана окружность, которая касается его стороны КМ в точке А. Известно, что \АК\ = 10, \АМ\ = 4, KLM = 7г/3. Найдите длину отрезка AL.
Идея. Воспользоваться теоремой об отрезках, на которые вписанная окружность делит точками касания стороны треугольника.
Указание. Записать теорему косинусов для треугольников KLM и ALM.
Решение. Пользуясь теоремой о длинах отрезков, на которые вписанная окружность делит точками касания стороны треугольника, мы находим \АК\ = \ВК\ = 10, \АМ\ = \СМ\ = 4.
Введём обозначение \LB\ = \LC\ = х, тогда ^
\KL\ = ж-f 10, \LM\ = x-f-4. Записывая теорему косинусов для треугольника KLM, получаем:
142 = (х + 10)2 -f (х + 4)2 — 2(х + 10)(х + 4) • ~ => ж = 6.
Далее, записывая ещё раз теорему косинусов для треугольника KLM, получаем cos КМL = 1/7, а из треугольника ALM с её же помощью находим \АЬ\ = 2у/Ш/7.
Ответ. 2
Задача 27.
В равностороннем треугольнике АВС проведена окружность с центром в точке О, проходящая через точку пересечения медиан треугольника АВС и касающаяся его стороны ВС в её середине D. Из точки А проведена прямая, касающаяся этой окружности в точке Е так, что градусная мера угла В АЕ меньше 30°. Найдите отношение площадей треугольника АВЕ и четырёхугольника BEOD.
Идея. Выразить все необходимые длины и величины углов через длину радиуса окружности из условия задачи.
Указание. Используя свойство точки пересечения медиан и соотношения в прямоугольном треугольнике, выразить отрезки АО, AD, АЕ и АВ через длину радиуса окружности из условия задачи.
А М


230
Указания и решения
Указание. Площадь четырёхугольника BEOD найти как разность площадей треугольников.
Решение. Отрезок AD является высотой и медианой треугольника АВС, поэтому центр окружности из условия задачи лежит на нём. Обозначим длину её радиуса буквой г, тогда, поскольку медианы треугольника делятся точкой пересечения в отношении 2:1, считая от вершины, \AD\ = 6 г, \АО\ = 5г. Из прямоугольного треугольника АОЕ находим
\ОЕ\ = г, \АЕ\ = 2V6r, sin ОЛЕ
1
cos ОАЕ
2%/б
5’ 5
Затем из прямоугольного треугольника ABD получаем
аое — \/бг2.
\АВ\ = 4\/3г, \BD\ = 2л/3г, Saabd = 6^3 г2.
После этого найдём площадь треугольника АВЕ:
2\/б-\/3
— / 7Г
sin В ЛЯ = sin Наконец,
ОЛЕ!
10
24\/3 — 6\/б 2
ОААВЕ = Г .
С С, С С бл/з + у/б 2
JBEOD = JAABD ~ ЪааВЕ ~ *ААОЕ = : Г
С учётом вышесказанного искомое отношение равно 78 - 30л/2
78-
5
30\/2
17
Ответ.
17
Задача 28.
В треугольнике длина стороны АВ равна 2\/2, а длина радиуса окружности, описанной около него, равна 2. Отношение длин сторон АС и ВС равно л/8, длина стороны ВС больше 1. Найдите площадь треугольника АВС.
Идея. Вычислить величину угла АС В, затем найти длины сторон АС и ВС. Указание. Воспользоваться теоремой синусов, затем теоремой косинусов.
Решение. По теореме синусов сразу находим
sinACJ5 = \АВ\ : 2Raabc — 1/л/2-
Значит, величина угла АС В либо равна 7г/4, либо равна 37г/4, а косинус этой величины равен либо 1 /у/2, либо — 1 /у/2.


1.2. Теоремы синусов и косинусов
231
Далее положим \ВС\ = х, тогда по условию задачи х > 1, \АС\ Выразим искомую величину через х:
Saabc = \ • |Ж7| • \ВС\ • sin АСВ = х2,
после чего воспользуемся теоремой косинусов для нахождения х
,2.
8 = х2 + 8х2 ± 4х2
2 ® 2
х = - или ж =
13
Под условие ж > 1 подходит лишь вариант х2 = 8/5
g
Ответ. -.
5
Задача 29.
В треугольнике АВС даны длины сторон: \АВ\ = \ВС\ = 13, |Ж7| = 10. Найдите расстояние между центрами окружностей, вписанной в него и описанной около него.
В
Идея. Воспользоваться тем, что у равнобедренного треугольника центры вписанной в него и описанной около него окружностей лежат на высоте, опущенной на основание.
Указание. Воспользоваться нужными формулами для вычисления длин радиусов окружностей.
Решение. Поскольку отрезок ВМ является как биссектрисой треугольника АВС, так и серединным перпендикуляром к стороне АС, центры окружностей лежат на нём. Найдём длины их радиусов:
Раавс = 18; Saabc — л/18 • 5 • 5 • 8 = 60;
\AB\-\AC\-\BC\ 169. Saabc Ю
\ВО\ = Raabc = = тгг. \МР\ = гаавс = = ~г-
4Ьаавс ^4 Раавс о
Наконец,
\ВМ\ = у/\АВ\2 -\АМ\2 = 12; \ОР\ = \\ВМ\ - \ВО\ - \МР\\ =
39
24'
Ответ.
39
24'
Задача 30.
В равнобедренном треугольнике АВС (\АВ\ = \ВС\) отношение расстояний от центра вписанной в этот треугольник окружности до вершин В и С соответственно равно к. Найдите величины углов треугольника АВС. При каких значениях к задача имеет решение?


232
Указания и решения
Идея. Воспользоваться тем, что центр окружности, вписанной в треугольник, лежит на пересечении его биссектрис. Указание. Опустить из центра вписанной в треугольник АВС окружности перпендикуляр на боковую сторону, рассмотреть получившиеся прямоугольные треугольники.
Решение. Пусть О - центр вписанной в треугольник АВС окружности, Н - точка её касания со стороной ВС. Положим АС В = 2а, тогда 0 < а < 7г/4 (так как угол АСВ острый), АВС = 7г-4а, ОСЯ = а, ОВН = тг/2-2а. Из прямоугольных треугольников ОВН и ОСН получаем
В
\ОВ\
\он\^
sin ОВН
\ос\ =
\ОН\^
sin ОСН
к =
sina
\ОВ\
\ОС\ cos 2а
2к sin а + sin а — к = 0.
Решая это уравнение, находим
ч -1 - VSk2 + 1 ч -1 + y/Sk2 4-1
(sma)i = , (sm a)2 = -
4 к
4 к
У нас 0 < a < 7г/4, поэтому 0 < sina < 1/\/2. Очевидно, что к может быть только положительным числом, стало быть, первый из полученных корней всегда меньше нуля и нам не подходит. Легко проверить, что второй корень удовлетворяет нашим условиям при всех fc > 0.
Ответ. АСВ = ВАС = 2 arcsin задача имеет решение при всех к > 0.
у/ШТТ-1
4 к
АВС = 7г — 4 arcsin
VSk2 + 1-1 4 к
Задача 31.
В равнобедренном треугольнике АВС с основанием АС проведена биссектриса угла С, которая пересекает боковую сторону АВ в точке D. Точка Е лежит на основании АС так, что DE ± DC. Вычислите длину отрезка AD, если \СЕ\ — 2.
Идея. Воспользоваться теоремой синусов и соотношениями в прямоугольном треугольнике.
Указание. Рассмотреть треугольники ADC и EDC.
Решение. В этой задаче главное - понять, между какими геометрическими элементами есть зависимость. Если посмотреть, какие величины мы знаем и что нам нужно найти, то становится ясно, что нужно рассматривать треугольники ADC и EDC, поскольку, во-первых, их углы связаны друг с другом, а во-вторых, в них входят как отрезок AD, так и отрезок СЕ.


1.2. Теоремы синусов и косинусов
233
Примем величину угла ACD за а, тогда с учётом того, что CD - биссектриса, и того, что треугольник АВС равнобедренный, имеем DAC = 2а. Запишем теорему синусов в треугольнике ADC:
JADi_ _ ;< />! _ lADI = ]0D] sina _ \CD\
sin ACD sin DAC sin2“ 2cosa
С другой стороны, из прямоугольного треугольника EDC вытекает, что
\CD\ = \СЕ\ • cos ACD = 2 cos а.
Таким образом,
_ 2cosa = L
2 cos a
Ответ. 1.
Задача 32.
В треугольнике АВС \АВ\ = 4, \АС\ = 3, угол С острый. Известно, что sin {^АСВ — ABC^J =7/25. Найдите площадь треугольника АВС.
Идея. Проанализировать соотношение на углы из условия.
Указание. Используя теорему синусов и условие, получить два уравнения на углы АСВ и АВС.
Решение. Введём обозначения 7 = АСВ, /3 = АВС. По теореме синусов получаем
Ав № , . о о .
—— = ——- => 4smp=3sm7. sm 7 sm р
Так как угол АСВ острый, из условия sin(7 — /3) = 7/25 следует, что
.7 Л . 7
7 — р = arcsin — ==> 7 = р -f arcsin —.
Подставим это выражение для 7 в полученное выше соотношение:
( 7 \ 24
4 sin [3 = 3 sin (/3 -f arcsin — J Ф=> 4 sin /3 = 3 sin /3 • — + 3 cos /3 •
\ 25 / 25
25
Приводя подобные слагаемые, имеем 4sin/3 = 3cos/3. Учитывая соотношение 4sin/3 = 3sin7, получаем:
(7Г \ 7Г 7Г
/3J=sin7 — “ Р — 7 /3 -f 7 = —.
Следовательно, ВАС = то есть треугольник прямоугольный и его площадь равна 6.
Ответ. 6.


234
Указания и решения
Задача 33.
В треугольник АВС, в котором длина стороны ВС равна 9, вписана окружность, касающаяся стороны ВС в точке D. Известно, что \AD\ = \DC\, cos ВС А = 2/3. Найдите длину стороны АС.
Идея. Воспользоваться теоремой д
косинусов.
Указание. Обозначить длину отрезка AD буквой х, воспользоваться теоремой косинусов и тем, что D - точка касания стороны ВС с окружностью, вписанной в треугольник АВС.
Решение. Обозначим длины отрезков AD и DC буквой х. Тогда \BD\ = 9 — ж, а из равнобедренно- g го треугольника ADC мы получаем |ЛС| = 2 • |£>С| • cos ACD = Ах/3.
Поскольку D - точка, в которой окружность, вписанная в треугольник АВС, касается стороны ВС, справедливо соотношение
|РС| = 1»С| + |ВС|-ИД| ^ ив|
Z О
Теперь заметим, что
ADB = тг - ADC = тг - (тг - 2 • ACD) = 2 • ACD.
Поэтому cos ADB = 2 cos2 ACD — 1 = —1/9.
Наконец, запишем теорему косинусов для треугольника ABD:
\АВ\2 = \AD\2 + |BD|2 - 2 • |AD| • \BD\ • cos ADB =ф
=>• ^9 - у ^ = x2 + (9 - ж)2 + у • (9 - x) => x = 3, \AC\ = у = 4.
Ответ. 4.
Задача 34-
Треугольник ЛВС со стороной ЛВ, длина которой равна 4, и углом Л, градусная мера которого равна 60°, вписан в окружность с длиной радиуса 2\/3. Найдите длину средней линии этого треугольника, параллельной АС, и расстояние между точками, в которых её продолжение пересекает окружность.
Идея. Рассмотреть треугольник, образованный центром окружности и точками, в которых продолжение средней линии треугольника ЛВС, параллельной ЛС, пересекает окружность.


1.2. Теоремы синусов и косинусов
235
Указание. Для ответа на первый вопрос воспользоваться теоремами синусов и косинусов для треугольника АВС.
Указание. Для ответа на второй вопрос найти расстояния от центра окружности до АС и средней линии треугольника АВС, параллельной АС.
Решение. Обозначим середины сторон А В и ВС буквами М и N соответственно, тогда MN - средняя линяя, длину которой нам надо найти. Точки, в которых её продолжение пересекает окружность, описанную около треугольника АВС, обозначим буквами К и L.
Длину MN найти достаточно просто: она равна половине длины АС. Нахождение \АС\ является в общем-то стандартной задачей, необходимо всего лишь записать теоремы синусов и косинусов для треугольника АВС:
Щ = 2RAABC => \вс\ = 2 • 2уД • ^ = 6; sin Л *
| ВС\2 = \АВ\2 + I АС\2 -2-\АВ\- \АС\ - cos А =►
=> 36 = 16 + \АС\2 — 2 • 4 • \АС\ • ^ => \АС\ = 2 + 2л/б.
Таким образом, |M7V| = 1 -f \/б-
Нахождение \KL\ является более сложной задачей, требующей довольно тонких рассуждений. Во-первых, заметим, что треугольник АВС остроугольный, поскольку АС - его наибольшая сторона и |АС|2 = 28 4- 8л/б < \АВ\2 -f \ВС\2 = 52. Из этого вытекает, что точка О - центр окружности, описанной около треугольника АВС, - лежит внутри него.
Проведём через точку О отрезок QP (Q е KL,P Е АС), перпендикулярный АС и XL. Тогда AOQK = AOQL (поскольку \ОК\ — |OL|, QO - общая, углы OQL и OQK прямые), из чего следует, что \KQ\ = ^\KL\. Аналогично можно получить, что \АР\ = ||АС|. Тогда
\ОР\ = у/\АО\2 - \АР\2 = 12- (7 + 2\/ё) = \]ь-2у/Ъ = л/3 - у/2.
Теперь с учётом того, что точки О и Q лежат в одной полуплоскости относительно прямой АС, имеем
\QP\ = \АМ\ • sin А = уД; \QO\ = \QP\ - \ОР\ = у/2.
Наконец, \KQ\ = у/\ОК\* ~ \Q°? = vTO =► \KL\ = 2y/l0.
Ответ. 1 + \/б, 2y/l0.


236
Указания и решения
Задача 35.
В треугольнике АВС проведена биссектриса AD. В треугольники ADC и ADB вписаны окружности с длинами радиусов 3 и 8 соответственно, касающиеся отрезка AD в точках М и N. Найдите расстояние между центрами этих окружностей, если \ND\ = 4.
Идея. Выяснить, в каком порядке расположены точки А, М, N и D. Указание. Рассмотреть прямоугольные треугольники, каждый из которых образован точкой А, центром одной из окружностей из условия задачи и точкой её касания с отрезком AD.
Указание. Рассмотреть треугольник, образованный точкой D и центрами окружностей из условия задачи, доказать, что он прямоугольный.
Решение. Будем считать, что Р - центр окружности, вписанной в треугольник ADC, a Q - центр окружности, вписанной в треугольник ADB. При решении этой задачи особое внимание надо обратить на тот момент, что в условии не сказано, какая из точек М и N является точкой касания какой окружности с отрезком AD. Поэтому придется рассматривать два случая.
Первым этапом решения является рассмотрение конфигурации, образованной точками Л, Р, Q и точками М и N. Поскольку центр окружности, вписанной в треугольник, лежит на пересечении его биссектрис, a AD - биссектриса угла А, углы PAD и QAD равны. Поэтому точка касания отрезка AD и окружности, вписанной в треугольник ADC, лежит между точкой А и точкой касания отрезка AD и окружности, вписанной в треугольник ADB (для обоснования этого факта достаточно рассмотреть прямоугольные треугольники APM(N) и AQN(M)).
Вторым этапом решения является рассмотрение конфигурации, образованной точками D, Р, Q и точками М и N. Поскольку DP и DQ - биссектрисы смежных углов ADB и ADC, угол PDQ прямой, из чего (по формулам приведения) вытекает, что тангенс величины угла PDA равен котангенсу величины угла QDA. Далее, если считать, что точка М - точка касания отрезка AD и меньшей окружности (как изображено на чертеже), то мы получаем
А
\DM\ = 6,
что соответствует полученному ранее результату, гласящему, что точка М лежит между точками А и N. Если же мы будем полагать, что точка М есть точка


1.2. Теоремы синусов и косинусов
237
касания отрезка AD и большей окружности, то, рассуждая аналогично, мы находим
тсЬл^-ш\ |DM|='6'
что, невозможно. Наконец, по теореме Пифагора мы находим
\DP\ = у/З2 + 62 = 3V5, \DQ\ = у/%2 + 42 = 4\/5,
|PQ| = Л/|РРрТ|РО|2 = 5^5.
Замечание. Длину отрезка PQ можно было найти из прямоугольного треугольника PQK, где К - основание перпендикуляра, проведённого из точки Р к прямой NQ:
PQ2 = у/РК2 + QK2 = л/22 + II2 = 5л/5.
К
Ответ. 5\/б.
Задача 36.
В треугольнике KLM отношение длин радиусов описанной около него и вписанной в него окружностей равно к. Окружность, вписанная в треугольник KLM, касается его сторон в точках А, В и С. Найдите отношение площадей треугольников АВС и KLM.
Идея. Выразить площади треугольников АВС и KLM через синусы углов треугольника KLM и длины радиусов данных окружностей.
Указание. Площадь треугольника АВС найти как сумму площадей треугольников АОВ, АОС и ВОС, где О - центр описанной около треугольника АВС окружности.
Указание. Для вычисления площади треугольника KLM воспользоваться формулой S = рг, предварительно выразив стороны треугольника через радиус описанной окружности и синусы соответствующих углов углов.
Решение. Пусть KLM — а, LKM = /3, KML = 7, г - длина радиуса вписанной окружности, О - её центр, a R - длина радиуса описанной окружности.


238
Указания и решения
Заметим, что
АОВ = 7г—а, АОС = 7г—/3, ВОС = 7г—7, Saabc = Saaob + Saaoc + Saboc =
= ~r2(sirm + sin/3 + sin 7),
Saklm = rpAKLM = r#(sin a -f sin /3 + sin 7).
Saabc _ 1 r _ 1 Saklm 2 R 2k
Следовательно,
M
Ответ. —.
2k
1.3. 	Биссектриса, медиана, высота Задача 1.
В остроугольном треугольнике площади 5 известны величины а и /3 углов А и В. Найдите длину высоты, опущенной на сторону, прилежащую к углам А и В.
Идея. Воспользоваться формулой площади треугольника через длины его стороны и проведённой к ней высоты. п
Указание. Выразить длину стороны АВ через длину высоты, проведённой к ней, и величины его углов.
Решение. Поскольку по условию треугольник АВС - остроугольный, основание высоты, опущенной из вершины С на АВ (обозначим его Н), лежит на стороне АВ.
Поэтому \АВ\ = \АН\ + \НВ\.
Обозначим длину высоты СН буквой h. Из прямоугольных треугольников АСН и ВСН вытекает
\АН\ = \СН\ • ctg НАС = h ctg а, \НВ\ = \СН\ • ctg НВС = /ictg/З.
Значит, \АВ\ = h(ctg о; + ctg/З). Наконец, воспользуемся формулой площади треугольника через его основание и высоту:
Saabc = \-\АВ\-\СН\
S = - Л2 (ctg а+ctg Р)
25
ctg а + ctg /J
Замечание. Полученная выше формула \АВ\ = h(ctgа + ctg/3) очень полезна. Запомните её. Она вам ещё не раз пригодится.
Ответ.
25
ctg а + ctg /3


1.3. Биссектриса, медиана, высота
239
Задача 2.
В треугольнике KMN, в котором smKNM = \/3/2, cos KMN = 1/3, проведены высоты NP и MQ. Найдите значение отношения \NP\ : |MQ|.
Идея. Найти величины углов треугольника KMN.
Указание. Выразить длины высот NP и MQ через длину стороны MN.
К
Решение. Поскольку синус величины угла KNM равен л/3/2, вообще говоря, величина угла KNM может быть равна как 7г/3, так и 27г/3. Однако, поскольку косинус величины угла KMN равен 1/3, величина угла KMN больше, чем 7г/3, но меньше, чем 7г/2 (это следует из свойств арккосинуса). Из этого вытекает, что величина угла KNM не может равняться 27г/3, гак как в таком случае сумма величин углов треугольника KMN окажется больше чем 7г. Значит, треугольник АВС остроугольный, точки Р и Q лежат на сторонах КМ и KN.
Из прямоугольных треугольников MNP и MNQ находим
Г \NP\ = |МЛГ| • sin NMP, \NP\ _ sin NMP _ sin KMN
\ \MQ\ = \MN\-sin MNQ \MQ\ sin MNQ sin KNM'
sin KMN = \/1 - cos2 KMN = J1 - i ^ =► ^
v у О Q I Л/Г/П1 ./5 о /о
n 4v/®
Ответ. ——.
9 3 \MQ\ & Зл/З*
Задача 3.
Длины сторон АВ, ВС и АС треугольника АВС образуют в указанном порядке геометрическую прогрессию. Найдите знаменатель этой прогрессии, если известно, что отношение длины высоты треугольника АВС, проведённой из вершины А, к длине радиуса вписанной в этот треугольник окружности равно 3.
Идея. Воспользоваться различными формулами площади.
Указание. Ввести обозначения \АВ\ = с, \ВС\ = qc, |Ж7| = q2c.
Решение. Положим \АВ\ = с, \ВС\ = qc, |Ж7| = #2с. Тогда, записывая двумя разными способами площадь треугольника АВС, получаем
\АВ\ + \ВС\ + \АС\ 1 _
ОААВС = ^=>
. / . , 2 \ 1 . О ^АВ 1 + q + q2
=> (с + qc + qLc) • Г&АВС = qc • hAB => 3= = g = 1.
ГААВС q
Ответ. 1.


240
Указания и решения
Задача 4-
В равнобедренном треугольнике ABC \АВ\ = \ВС\, AD -биссектриса, \BD\ = 6, \DC\ = с. Найдите длину биссектрисы AD.
Идея. Воспользоваться основным свойством биссектрисы треугольника и второй формулой её длины.
Указание. Вычислить длину основания АС.
Решение. Так.как \АВ\ = \ВС\ = 6-1-с, для вычисления длины основания АС воспользуемся основным свойством биссектрисы:
Ш. = \Ш =± МП - 1лд1-1-рс'1 с(ь + с)
\АВ\ \BD\ 11 \BD\ b '
Для нахождения \AD\ воспользуемся второй формулой длины биссектрисы треугольника:
\AD\ = у/\АВ\ • \АС\ - \BD\ ■ \DC\ = ^/c(b + СУ _ b~ = ^2c2 + j.
Ответ, у2c2-f—.
Задача 5.
Известно, что длины высот треугольника равны h\, и /13. Найдите его площадь.
Идея. Выразить длины сторон треугольника через его площадь и длины его высот.
Указание. Воспользоваться формулой Герона.
Решение. Обозначим площадь треугольника буквой S. Тогда длины его сторон равны 2S/hi, 2S/h,2 и 2S/h%. Записывая формулу Герона, получаем


1.3. Биссектриса, медиана, высота
241
Задача 6.
Точка М лежит внутри равнобедренного треугольника АВС с основанием АС на расстоянии 6 от его боковых сторон и на расстоянии \/3 от его основания. Найдите длину этого основания, если В = 27г/3.
Идея. Воспользоваться тем, что точка М лежит на биссектрисе ВН треугольника АВС.
Указание. Найти длину отрезка ВМ.
Решение. Поскольку точка М равноудалена от боковых сторон треугольника АВС и лежит внутри него, она лежит на его биссектрисе ВН, которая является также медианой и высотой этого треугольника.
Поэтому АВН = СВН = 7г/3, а дли- А Н С
на отрезка МН фактически и есть расстояние от точки М до основания АС. После этого из прямоугольного треугольника MBS мы находим \МВ\ = \MS\ : sin MBS = 4>/3, стало быть, \ВН\ = 5л/3- Наконец, \АС\ = 2\ВН\ • tg АВН = 30.
Ответ. 30.
Задача 7.
В треугольнике ВСЕ известно, что \СЕ\ : \ВС\ = 3, а величина угла ВСЕ равна 7г/3. Отрезок С К - биссектриса треугольника. Найдите \КЕ\, если длина радиуса окружности, описанной около треугольника ВСЕ, равна 8у/3.
Идея. Воспользоваться основным свой- В
ством биссектрисы треугольника.
Указание. Применить теорему синусов и найти \ВЕ\.
Решение. Сначала по теореме синусов находим \ВЕ\:
2Raabc = - =► \ВЕ\ = 16л/3 ~ = 24.
sin ВСЕ 2
Затем, применяя основное свойство биссектрисы треугольника, находим \КЕ\:
{И}=|^§1==3, \КЕ\ + \ВК\ = \ВЕ\ = 24 =* \КЕ\ = 1Ъ.
Ответ. 18.


242
Указания и решения
Задача 8.
В треугольнике АВС градусная мера угла В равна 30°, \АВ\ = 4, \ВС\ = 6. Биссектриса угла В пересекает сторону АС в точке D. Найдите площадь треугольника ABD.
Идея. Вычислить длину отрезка BD. Указание. Воспользоваться первой формулой длины биссектрисы.
Решение. Идея решения проста - для нахождения искомой площади нам не хватает только длины отрезка BD, которую мы можем легко вычислить путем применения первой формулы длины биссектрисы:
2 • \АВ\ ■ \ВС\ • cos (|АВС)
\BD\ =
24 cos 15°
Saabd = 2 * \АВ\ ’ \BD\ ' sin ABD
\AB | + |BC|
48 sin 15° cos 15°
24 sin 30°
12 5 ’
n 12
Ответ. —.
5
Задача 9.
В треугольнике ABC проведена биссектриса CD, при этом величины углов ADC и CDB относятся как 7:5. Найдите длину отрезка AD, если известно, что \ВС\ = 1, ВАС = 7г/6.
С
Идея. Найти длины сторон и величины углов треугольника АВС.
Указание. Воспользоваться теоремой о сумме величин углов треугольника, теоремой синусов и основным свойством биссектрисы. В D А
Решение. Сначала вычислим величины всех углов треугольника АВС. Примем величины углов ADC и CDB за 7а и 5а соответственно. Эти углы являются смежными, поэтому сумма их величин равна 7г. Значит, 12а = 7г, а — тг/12, ADC = 77г/12. Далее, пользуясь теоремой о сумме величин углов треугольника, из треугольника ACD находим ACD = 7г — ADC — CAD = 7г/4.
Стало быть, АСВ = 2 • ACD = тг/2, АВС = тг - ЛСБ - ВАС = тг/З. Дальнейшее просто: треугольник АВС оказался прямоугольным, поэтому
\АС\ = |£С| • tg ABC = у/3, \АВ\ = = 2.
cos ABC


1.3. Биссектриса, медиана, высота
243
Осталось лишь применить формулу для вычисления длин отрезков, на которые биссектриса треугольника делит сторону, к которой она проведена:
Ответ. 3 — VS.
Задача 10.
В треугольнике АВС биссектрисы BD и СЕ пересекаются в точке О, \АВ\ — 14, \ВС\ — 6, \АС\ = 10. Найдите длину отрезка OD.
Идея. Вычислить длину биссектрисы BD.
Указание. Воспользоваться формулой для отношения длин отрезков, на которые биссектрисы делятся точкой пересечения.
Решение. Воспользуемся формулой длины биссектрисы по трем сторонам: |ВГ>|2 = \АБ\ ■ \ВС\ ■ (l - (pgjTpjgqp) ” 63 - =
С другой стороны,
\ВО\ \АВ\ + \ВС\ п , 1
1Ш\- \АС\ ~2 ^ \OD\--\BD\-V7.
Ответ, у/7.
Задача 11.
В тупоугольном треугольнике АВС на стороне АВ длины 14 выбрана точка L, равноудаленная от сторон АС и ВС, а на отрезке AL - точка К, равноудаленная от вершин А и В. Найдите синус величины угла АСВ, если \KL\ = 1,САВ = п/4.
Идея. Воспользоваться тем, что CL и С К - соответственно биссектриса и медиана треугольника АВС.
Указание. Применить основное свойство биссектрисы и теорему синусов.
Решение. Поскольку точка L равноудалена от сторон АС и ВС, она лежит на биссектрисе угла АСВ. Таким образом, CL - биссектриса треугольника АВС. А поскольку точка К равноудалена от вершин А и В, С К - медиана треугольника АВС. Из этого вытекает, что
\АК\ = \КВ\ = 7, \AL\ = \АК\ + \КЬ\ = 8, \LB\ = \АВ\ - \AL\ = 6.
Теперь применим основное свойство биссектрисы треугольника и воспользуемся теоремой синусов:
\АС\ \AL\ 4 \АС\ \ВС\ . -г5?, \АС\ . ^ГХЪ
= 77-^7 = х; —= - => sm ABC = f-—7 • sin CAB — ——.
\BC\ \LB\ 3 sin ЛВС sin CAB \BC\ 3


244
Указания и решения
Возможны два варианта: либо угол АВС острый, тогда по условию задачи угол АСВ обязан быть тупым, либо угол АВС тупой. Однако выше мы получили, что \АС\ > \ВС\, а следовательно,
АВС > ВАС = т 4
АВС + ВАС > |.
Поэтому угол АСВ не может быть тупым. Значит, угол АВС тупой. Вычислим синус угла АСВ:
АВС>\
cos ABC
1 — sin2 ЛВС = —7-;
sin АСВ = sin (тг - ABC - CAB) = sin (ABC + CAB^ = = sin ABC cos CAB + cos ABC sin CAB = -—.
Ответ.
4- y/2
Задача 12.
Величины углов А, В и С треугольника АВС составляют арифметическую прогрессию с разностью 7г/7. Биссектрисы этого треугольника пересекаются в точке D. Точки А', В' и С" находятся на продолжениях отрезков DA, DB, DC за точки А, В, С соответственно на одинаковом расстоянии от точки D. Доказать, что величины углов А!, ВС" треугольника А’В'С' также образуют арифметическую прогрессию. Найдите её разность.
Идея. Найти величины углов А!, В’, С".
Указание. Воспользоваться тем, что биссектриса треугольника делит его угол пополам, и теоремой о сумме величин углов треугольника.
Решение. Обозначим величины углов А, В и С как а, /3 и 7. Исходя из условия задачи и определения арифметической прогрессии, будем считать, что
/3 — 0/ = 7-/3 = тг/7.
Из треугольника ADC с учётом того, что AD и CD - биссектрисы, вытекает, что
ADC = *-(l + T)


1.3. Биссектриса, медиана, высота
245
А поскольку треугольник A'DC' равнобедренный по условию задачи,
= DOS' = i (,-(*-(f + 1))) = ^±1.
С’
Рассуждая абсолютно аналогично, можно легко получить, что
-——- а + в -—- - /3 + 7
DA'Bf = DB'A' = —pS DB'C' = £>C"£' = ^-4 4 4
Далее ясно, что В'A'С' = DA'B' + DA!С' = ■ . Таким же
7Г + /3 7Г + 7
способом находим, что А'В'С1 — —-—; A'C'B' = —-—. Наконец, из равенств
7г + /3 7г + а /3 — а п 7Г + 7 7г + /3 7 — /3 7г
“1 Г” = 4 = 28’ 4 4 = 4 = 28
следует, что величины углов А', В', С' образуют арифметическую прогрессию с
разностью —, что и требовалось доказать.
28
Задача 13.
В треугольнике АВС биссектриса угла АВС пересекает сторону АС в точке К.
3 у/2
Известно, что \ВС\ = 2, \КС\ = 1, \ВК\ = ——. Найдите площадь треугольника АВС.
Идея. Воспользоваться основным свойством биссектрисы треугольника и второй формулой её длины.
Указание. Обозначить длины отрезков А В и АК буквами х и у, написать два уравнения, в которые входят эти величины.


246
Указания и решения
Решение. Обозначим длины отрезков А В и АК буквами х и у, воспользуемся основным свойством биссектрисы треугольника и второй формулой её длины:
\АВ\ = \АК\ х = у
\ВС\ \КС\ 2 1 У’
\ВК\2 = \АВ\ ■ \ВС\ -\АК\ ■ \КС\ =► ^ = 2 х-у.
Решая полученную систему уравнений, находим х = \АВ\ — 3, у — \АК\ =3/2, стало быть, длина отрезка АС равна 5/2. Теперь, зная длины всех сторон треугольника АВС, мы можем посчитать его площадь по формуле Герона:
2 + 3+| 15 _ /15 7 3 5 15 г-
Рлавс = 2 = Т’ Saabc = VT'i'4'4= 16v
15 г-
Ответ. — V7.
16
А
Задача 14-
Треугольник ЛВС вписан в окружность, длина радиуса которой равна у/3 — 1. Градусная мера угла ВАС равна 60°, а длина радиуса окружности, касающейся стороны ВС и продолжений сторон АВ и АС, равна 1. Найдите градусные меры углов АВС и АСВ.
Идея. Воспользоваться тем, что центр окружности, вписанной в угол, лежит на его биссектрисе.
Указание. Выразить длину стороны ВС через длины радиусов окружностей из условия задачи.
Указание. Рассмотреть прямоугольные треугольники, образованные центром окружности, касающейся стороны ВС и продолжений сторон АВ и АС, точкой её касания со стороной ВС и вершинами В и С, применить теорему синусов.
Решение. Обозначим центр окружности, касающейся стороны ВС и продолжений сторон АВ и АС, буквой О, точки касания её со стороной ВС и продолжениями сторон АВ и АС обозначим буквами М, L и К соответственно, а градусную меру угла АВС обозначим 2а°. Тогда
АСВ = (120—2а)°, КСВ = (60+2а)°, CBL = (180-2а)°.


1.3. Биссектриса, медиана, высота
247
Далее заметим, что СО - биссектриса угла КС В, а ВО - биссектриса угла CBL, поэтому
ОСВ = (30 + а)°, ОВС = (90 - а)°.
Из прямоугольных треугольников ОВМ и ОСМ вытекает, что (вспомните замечание к задаче 1)
\ВМ\ = |ОМ| • ctg ОВМ = ctg(90 - а)° = tga°,
|СМ| = \OM\ ctgOCM = ctg(30 + a)°; |ВС| = |ВМ| + \СМ\ = tga° + ctg(30 + a)°. С другой стороны, по теореме синусов для треугольника АВС:
|ВС| -2Raabc => |ВС| - 2(ч/3 - 1) ~ = 3 - л/3.
sin ВЛС 2
Решим полученное уравнение:
о чо « sina0 cos(30 + a)° о г-
tga + ctg(30 + a) = 3 — v3 <=> + v_- r- = 3 — v3 -<=>
toV J cos a° sm(30 + a)°
cos(30 -f- a — a)° /- 0 . 0 \/3
— 3 — v3 <*=> cos a sm(30 -f a) =
cos a° sin(30 + a)° 2(3 — \/3)
^(sin(2a + 30)° + sin 30°) = sin(2a + 30)° =
2 2*6 2
Наконец, из этого простейшего уравнения мы получаем два варианта:
1) (2а + 30)° = 120° =» 2а° = АВС = 90° =» АСВ = 30°;
2) (2а + 30)° = 60° => 2а° = АВС — 30° => АСВ = 90°.
Ответ. 30°,90°.
Задача 15.
Величина одного из углов треугольника равна 27г/3, длина противолежащей ему стороны равна 6, а длина одного из отрезков, на которые она разделена проведённой к ней биссектрисой этого треугольника, равна 2. Найдите величины двух других углов треугольника.
Идея. Вычислить значение отношения \АВ\ : \ВС\, воспользоваться теоремой синусов.
Указание. Воспользоваться основным свойством биссектрисы треугольника.
Решение. Будем считать, что |АС| = 6, A L
\AL\ = 2. Тогда \LC\ = 4 и по основному свойству биссектрисы треугольника
С


248
Указания и решения
\АВ\ : \ВС\ = \AL\ : \LC\ = 1:2. После этого положим ВАС = а, тогда АСВ = 7г/3 — а, и запишем теорему синусов для треугольника АВС:
|АВ| _ \ВС\ 1 _ |j4B| _ sin АСВ
sin АС В sin ВАС 2 \вс\ sin ВАС
=> sina = 2sin — a) => sina = \/3cosa — sina => tga =
y/3 ln y/3
Значит, искомые величины равны arctg —- и 7г/3 — arctg .
Z Zi
Ответ, arctg^, f-arctg^.
Задача 16.
Среди треугольников KLM, у которых длина радиуса описанной окружности равна 10, длина стороны KL равна 16, а длина высоты МН равна 3,9, выбирается тот, у которого длина медианы MN наименьшая. Найдите величину его угла KML.
Идея. Воспользоваться теоремой синусов.
Указание. Найти синус величины угла К ML, доказать, что этот угол тупой, используя схему доказательства критерия тупоугольности.
Решение. Запишем теорему синусов для треугольника KML:
^ -2RAKml => Sin KML= \КЬ\ - 16 - 4
sin KML ZRakml 20 5
Возможны два варианта: угол KML может быть как острым, так и тупым. Однако если он острый, то, следуя схеме доказательства критерия тупоугольности, мы получим, что в этом случае длина медианы MN будет больше, чем половина длины стороны KL, то есть \MN\ > 8. Если же он тупой, то, рассуждая аналогично, мы получим, что длина медианы MN будет меньше, чем половина длины стороны KL, то есть \MN\ < 8.


1.3. Биссектриса, медиана, высота
249
Значит, треугольник KLM, удовлетворяющий условию задачи, - это тот, у которого угол KML тупой. Косинус его величины равен, очевидно, —3/5, а его величина равна arccos(—3/5).
Замечание. Числовое значение длины высоты МН мы использовали только для определения количества треугольников, удовлетворяющих условию задачи. Так, при \МН\ £ (0; 4] существует два треугольника: остроугольный и тупоугольный, а при \МН\ £ (4; 16] возможен только один вариант - остроугольный треугольник. В первом случае в ответ идёт тупой угол, во втором - острый.
Ответ, arccos (—^V
Задача 17.
В треугольнике АВС проведена медиана AD, \AD\ = m, |AJ5| = с,\АС\ = Ь. Найдите ВАС.
Идея. Воспользоваться формулой длины медианы треугольника.
Указание. Найти длину стороны ВС, применить теорему косинусов.
Решение. Применим формулу длины медианы треугольника:
4\AD\2 = 2\АВ\2+ 2\АС\2-\ВС\2 <=>
•Ф=> \ВС\2 = 2Ь2 + 2с2 - 4т2.
Теперь воспользуемся теоремой косинусов:
\ВС\2 = \АВ\2 + \АС\2 - 2 • \АВ\ ■ \АС\ ■ cos RAC =*•
Am2 — h2 — г2
2b2 -f 2c2 — 4m2 = b2 + c2 — 2be cos ВАС => cos ВАС =
Значит, величина угла ВАС равна arccos Ответ, arccos
2 be
4 т2 — b2 — с2
2 be
4 т2 — Ь2 — с2
26с
Задача 18.
Найдите величину угла А треугольника АВС, если известно, что \АВ\ = 2, \АС\ = 4, а длина медианы AM равна у/7.
Идея. Вычислить длину стороны ВС.
Указание. Воспользоваться формулой длины медианы.


250
Указания и решения
Решение. Воспользовавшись формулой длины медианы, мы получаем
4\АМ\2 = 2\АВ\2 + 2\АС\2 - \ВС\2 => \ВС\2 = 12.
Теперь заметим, что \АВ\2 + \ВС\2 = |Ж7|2, поэтому треугольник АВС прямо- угольный, угол В прямой, стало быть,
cosl=j4^} = i =► А = ^-.
\АС\ 2 3
у-ч ТГ
Ответ. —.
о
Задача 19.
В треугольнике АВС проведена медиана AM. Найдите площадь треугольника АВС, если \АВ\ = \ВС\ = 2\АС\, \АМ\ = 4.
Идея. Воспользоваться формулой длины медианы.
Указание. Положить \АС\ = х.
Решение. Положим \АС\ = х, \АВ\ = \ВС\ = 2х.
Применяя формулу длины медианы, получаем
4\АМ\2 = 2\АВ[2 + 2\АС\2 - \ВС\2
=> 64 = 6х2 ==> х2 = Щ-.
После этого площадь треугольника АВС можно легко найти по формуле Герона:
Ответ.
,Ъх Зх х х х2у/ТЕ 8\/15
ААВС - у у • у • 2 ‘ 2 “ 4 “ 3 *
8л/15
Задача 20.
Найдите величины углов, образованных медианой ВВ\ треугольника АВС со сторонами АВ и ВС, если \АВ\ = б, |ВС| = 8, \ВВг \ = 5.
Идея. Найти длину стороны АС.
Указание. Использовать формулу длины медианы.


1.3. Биссектриса, медиана, высота
251
Решение. Записывая формулу длины медианы, находим 4\BBi\2 = 2|АВ|2 + 2\ВС\2 — |Ж7|2 =►
=Ф 100 = 200 -\АС\2 => \АС\ = 10.
Далее можно записать теорему косинусов для треугольников АВВ\ и СВВ\, но в нашем случае можно заметить, что треугольник АВС прямоугольный, угол АВС прямой, поэтому треугольники АВВ\ и СВВ\ равнобедренные:
IABI 3
АВВ\ = ВАВ\ — arccos ——- = arccos
| AG I 5
____ I qc\ 4
CBB\ = BCB\ = arccos ——■ = arccos -.
I AC I 5
n 3 4
Ответ, arccos -, arccos -.
5 5
Задача 21.
В треугольнике ABC проведена прямая, пересекающая стороны АВ и ВС в точках Р и Q соответственно. Известно, что \АВ\ = 3, |АС| = л/5, длина медианы, проведённой из вершины А к стороне ВС, равна л/б, а длины отрезков АР, PQ и QC равны между собой. Найдите длину отрезка PQ.
В
Идея. Воспользоваться формулой длины медианы и теоремой косинусов.
Указание. Вычислить |J3C|, выразить длины всех сторон треугольника BPQ через искомую длину.
Решение. Записывая формулу длины медианы, находим 4|АМ|2 - 2|АР|2 + 2|АС|2 - |£С|2 =»
=> 24 = 18 + 10 — \ВС\2 =* \ВС\ = 2.
После этого положим |АР| = \PQ\ — \QC\ — х, тогда |РР| = 3 — х, \BQ\ = 2 — ж, затем, вычислив косинус величины угла АВС с помощью рассмотрения треугольника АВС, мы можем записать теорему косинусов для треугольника BPQ:
cos ABC =
\АВ\2 + |БС|2 - |АС|2
2
з;
2 • \АВ\ • \ВС\
\PQ\2 = \ВР\2 + \BQ\2 - 2 • \ВР\ ■ \BQ\ ■ cos ABC v2 = (3 — х)2 + (2 — х)2 — ^(2 - х)(3 — х) => а
О
= 2V10-5.
Ответ. 2-\/10 — 5.


252
Указания и решения
Задача 22.
В треугольнике АВС проведены биссектриса В К и медиана ВМ. Найдите длину отрезка КМ, если АВМ = 7г/4, СВМ = 7г/6, | = 6.
Идея. Вычислить значение отношения |АЙГ| : \КС\. в
Указание. Записать теорему синусов для треугольников АВМ и СВМ.
Решение. Дважды записывая теорему синусов, получаем
А К. М С
\АМ 1 _ \АВ\ \СМ 1 _ \ВС |
sin АВМ sin АМВ sin СВМ sin СМ В Поделив эти соотношения, с учётом свойства биссектрисы находим
sin СВМ _ \АВ\ \АК\ _ \АВ\ _ 1
sin АВМ ~ \ВС\ ^ \кс\ ~ \ВС\ ~ уД-
Таким образом, \КС\ = у/2 • \АК\ = 6\/2,
\АМ\ = + 1^С1 = з + 3л/2, = \АМ\ -\АК\ = 3\/2 - 3.
Ответ. 3(у/2 — 1).
Задача 23.
В треугольнике АВС проведены биссектриса BD и медиана АЕ. Известно, что \АВ\ = 8, \ВС\ = |JB-D| = 6. Найдите длину медианы АЕ.
Идея. Вычислить длину стороны АС.
Указание. Воспользоваться второй формулой длины бис- R
сектрисы, затем формулой длины медианы.
Решение. Поскольку по основному свойству биссектрисы \AD\ : \DC\ = \АВ\ : \ВС\ =4:3, полагая \AD\ = 4х,
|DC| = Зж и записывая формулу длины биссектрисы, мы получаем уравнение
62 = б • 8 — 4ж • Зх 12х2 = 12 х = 1.
Значит, \АС\ = 7х = 7, и по формуле длины медианы мы находим
у/Ш
\АЕ\ = -V2|j4B|2 + 2|AC|2-|BC|2
_ УТ90
Ответ. —-—.


1.3. Биссектриса, медиана, высота
253
Задача 24•
В треугольнике АВС проведены биссектриса AL и медиана AM. Известно, что \AL\ = 6, \АМ\ = 8, \АС\ = 2 • \АВ\. Найдите длину стороны ВС.
Идея. Воспользоваться формулой длины медианы и второй формулой длины биссектрисы.
Указание. Ввести обозначения \АВ\ = х, \АС\ = 2х, \ВС\ = Зг/.
Решение. Положим |АВ| = х, тогда д |ЛС| = 2ж по условию задачи. Пользуясь основным свойством биссектрисы треугольника, имеем \АВ\ : \АС\ = \BL\ : \CL\ = 1 : 2, с учётом этого введём обозначения \BL\ = у,
|СХ| = 2у, тогда |Ж7| = Зг/. После этого воспользуемся формулой длины медианы и второй формулой длины биссектрисы:
4\АМ\2 = 2|АВ|2 + 2|Ж7|2 - \ВС\2 =*• 10х2 - 9t/2 = 256;
|Л£,|2 = \АВ\ ■ \АС\ - \BL\ ■ \CL\ =* 2х2 - 2у2 = 36.
Решая полученную систему из двух уравнений с двумя неизвестными, находим у = 2\/19, х = \/94, стало быть, \ВС\ = 6л/19.
Ответ, бл/19.
Задача 25.
В треугольнике KMN проведены высота N А, биссектриса iVi? и медиана iVC, которые делят угол KNM на четыре равные части. Найдите длины высоты N А, биссектрисы NB и медианы NC, если длина радиуса описанной около треугольника KMN окружности равна Д.
Идея. Найти величину угла KNA.
Указание. Выразить длины отрезков КА, АС, СМ через длину высоты N А и величину угла KNA и составить уравнение.
Решение. Поскольку биссектриса треугольника расположена между его медианой и высотой, проведёнными из той же вершины, точка В лежит между точками А и С. Обозначим величины углов KNA, AN В, BNC и CNM через а, длину высоты NA обозначим через h. Из прямоугольных треугольников NAK, NAB, N АС и N AM вытекает, что
N
NKM = £ - a, iVMAT = J - За, |АГА| = \АВ\ = htga,


254
Указания и решения
\АС\ = h tg2a, \АМ\ = /itg3a.
Ясно, что \КС\ = \КА\ + |Ж7|, |СМ| = \АМ\ — |Ж7|. А поскольку NC - медиана, имеем \КС\ = \СМ\. Подставляя сюда выраженные нами длины отрезков, получаем уравнение
h tg a + h tg 2a = h tg 3a — h tg 2a.
Оно решается достаточно просто:
h(tga + tg2a) = /i(tg3a — tg2a) <=> tg3a — tga = 2 tg2a <£=>>
sin 2a 2 sin 2a r . Л
<=> = — <=> {sm2a f 0} <=> cos 2a = 2 cos a cos 3a <*=>•
cos a cos 3a cos 2a
7Г
<£=>• cos 2a = cos 2a + cos 4a cos 4a = 0 <==> 4a = —.
z
Таким образом, a = 7г/8, угол KNM, величина которого равна 4a, прямой, NKM = 37г/8, NMK = 7г/8. Длина медианы iVC находится сразу: в прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы, стало быть, \КС\ = \МС\ = |М7| = R.
Далее из прямоугольного треугольника AN С найдём длину высоты NA, а затем из прямоугольного треугольника AN В найдём длину биссектрисы NB:
\NA\ = |Ж7| • cos2a = \NB\ = ^1 = • 2 = R\/2-yfl.
2 cosc* 2 V2 + V2
Ответ. |ЛГЛ| = A \NB\=rJ2-V2, \NC\ = R.
V2
Задача 26.
В треугольнике ABC проведены высоты СН к АК. Найдите длину стороны АС, если \АВ\ = с, \СН\ = h, \АК\ = к.
Идея. Вычислить косинус величины угла АВС.
Указание. Используя формулу площади, найти длину стороны ВС. Рассмотреть треугольник АВК и вычислить синус величины угла АВС.
Указание. Вычислить косинус величины угла АВС и применить теорему косинусов.
Решение. Сначала найдём длину стороны ВС. Записывая двумя способами площадь треугольника АВС, находим
Saabc = \ • \АВ\ ■ \СН\ = i • \ВС\ ■ \АК\ => \ВС\ = у.
После этого, рассматривая прямоугольный треугольник АВК, мы получаем sin АВК = |A/f| : \АВ\ = fc/c. Заметим, что в зависимости от того, лежит ли точка К на отрезке ВС или нет, угол АВС либо совпадает с углом АВК, либо


1.3. Биссектриса, медиана, высота
255
является смежным с ним. Из этого вытекает, что синусы углов АВС и АВК в любом случае равны. Наконец, учитывая тот факт, что угол АВС может оказаться как острым, так и тупым, получаем
cos ABC = ±y/l — sin2 ABC = ±— —;
\AC\ = \J\AB\2 + | BC\2 - 2 • \AB\ ■ \BC\ • cos ABC =
[~0 c2h2 2chy/c2 — W у/c2k2 H- c2h2 ± 2ckh\Jс2 —=W
= V + ~^± к = к '
Замечание. Можно проиллюстрировать геометрически тот факт, что у этой задачи два различных ответа. После того, как мы нашли длину стороны ВС, можно легко построить треугольники АВС' и АВС", удовлетворяющие условиям задачи. Для этого надо построить отрезок АВ, на расстоянии h от него провести параллельную ему прямую, после чего построить с центром в точке В окружность, длина радиуса которой равна найденной нами длине отрезка ВС. Точки пересечения её и построенной ранее прямой и есть точки С' и С".
у/с2к2 + c2h? ± 2ckhVc2 - к2
Ответ. .
к
Задача 27.
В треугольнике АВС проведена высота ВН, при этом оказалось, что длины отрезков СН и АН относятся как 10 : 3. Найдите площадь треугольника АВС, если известно, что \ВН\ = h, ABC = 7г/6.
Идея. Рассмотреть прямоугольные треугольники АВН и СВН.
Указание. Полагая АВН = а, выразить длины отрезков АН и СН.


256
Указания и решения
В
Решение. В этой задаче возможны два различных случая: точка Н может лежать на продолжении стороны АС за точку А, а может лежать на стороне АС. Попасть на продолжение стороны АС за точку С она не может, так как тогда \АН| > \СН\, что противоречит условию задачи.
Если точка Н лежит на продолжении стороны АС за точку А, то, полагая АВН = а и рассматривая прямоугольные треугольники АВН и С ВН, получаем
\AH\ = htga, |Cff| = fttg(o + |)
tg (« + f) = 10
tga 3
10 tg2 a — Tv^tga + 3 = 0
tga =
\/3
V3
или tg a = —-.
5
Ясно, что единственным требованием к ограничениям на величину а является то, что она лежит в интервале (0,7г/3), то есть тангенс этой величины лежит в интервале (0, \/3). Оба полученных ранее тангенса удовлетворяют этому условию. Теперь выразим искомую площадь и подставим в полученную формулу найденные тангенсы:
\АС\ = \СН\ - \АН\ = j\АН\ - \АН\ = \\АН\ =
1 ют 7ft2tSa 7^2 7^2
Saabc = ^ ’\АС\ * \вн\ = —g— = ~2~ или —зо“*
Если же точка Н лежит на стороне АС, то, опять-таки полагая АВН = а и рассуждая аналогично, получаем
\АН\ = htga, \СН\ = htg - a) =► tg(f-a) 10 /1 \ / tga\
— - 3 (тз_ tga)= sa ( w) ^
-13л/3± л/627
tga 3
10tg2 a + 13\/3tga -3 = 0
tga =
20
Из полученных тангенсов нам подходит лишь положительный. Наконец, считаем искомую площадь:
\ЛС\ = \СИ\ + \АН\ = “|.4Я| + \АН\ = у|.4Я| = 15^;
- 1 ■ ИС| • \ВН\ _ _ ИМ + УЯН*».
2 о
120
Ответ.
7л/3/г2 7\/3/г2 (—13л/3 + \/б27)Л2
12
30
120


1.3. Биссектриса, медиана, высота
257
Задача 28.
В треугольнике АВС проведена биссектриса BL, длина которой равна I. Найдите длины сторон треугольника АВС, если известно, что расстояния от точек А и С до прямой BL равны р и q соответственно.
Идея. Рассмотреть треугольники АВН и СВК (Н и К - основания перпендикуляров, опущенных на прямую BL из точек А и С соответственно). Указание. Воспользоваться первой формулой длины биссектрисы.
Решение. Обратим внимание на то, что во всех задачах, где фигурирует расстояние от точки до прямой, надо всего лишь опустить перпендикуляр из этой точки на эту прямую. Его длина и будет этим расстоянием. У нас расстояния от точек А и С до прямой BL будут не чем иным, как длинами перпендикуляров АН и С К. Далее положим АВС = 2/3, рассмотрим прямоугольные треугольники АВН и СВК, после чего воспользуемся первой формулой длины биссектрисы:
В
\АВ\
\АН |
Р
sin АВН sin/3’
\вс\ =
I ск\^ = q
sin СВК sin/3’
2 • \АВ\ ■ \ВС\ ■ cos\АВС Zpqctg/3 l(p + q)
т = \АВ\ + \вс\ =* i = _FT7~ с'ё/г = '2Й~'
Теперь, зная ctg/З, мы можем с помощью тригонометрических формул найти sin /3 и cos2/3, после чего найти |АВ|, \ВС\ и \АС\:
Л 2ра Л 12(р -Ь о)2 — 4р2а2
Sin/З = -7. , COS 2/3 = 5
\/l2{p + q)2 + 4p2q2 l2(p +q)2 + 4p2q2
[ЛТ>[ л/12(р + q)2 + 4p2q2 \/l2{p + q)2 +4p2q2
\AB\ = - , \BC\ = .
Наконец, применяя теорему косинусов, получаем
\АС\ = \J \АВ\2 + \ВС\2 - 2 ■ \АВ\ ■ \ВС\ ■ cos ABC = \/^2(р2 q2f* + 4p2q2{p + W
2pq
Ответ, \AB\ = + |fic| = VPfr + ^ + W.
= a//2(p2 - g2)2 + Ap2q2{p + g)2 2pq
9 Геометрия


258
Указания и решения
Задача 29.
Вычислите величину угла А треугольника АВС, если величина угла В равна 7г/5 и известно, что биссектриса угла при вершине С делит пополам угол между медианой и высотой, проведёнными из этой вершины.
Идея. Доказать, что треугольник АВС либо равнобедренный, либо прямоугольный.
Указание. Ввести обозначение АСВ = 27, выразить величины углов ВАС, AM С, ВМС. Указание. Записать теорему синусов для треугольников ACM и ВСМ (М - основание медианы СМ).
Решение. Отметим, что биссектриса треугольника всегда лежит между его медианой и высотой, проведёнными из той же вершины. Доказательство этого факта можно провести самостоятельно, воспользовавшись основным свойством биссектрисы.
Ясно, что в нашей задаче случай, когда основание Н высоты СН лежит на продолжении стороны АС за точку А, невозможен, так как тогда из геометрических соображений мы получим, что величина угла HCL будет больше половины величины угла АСВ, а величина угла MCL будет меньше половины угла АСВ, что противоречит условию. Далее положим АСВ = 27, HCL = MCL = ф. Тогда, рассматривая прямоугольные треугольники АСН и ВСН, мы имеем ВАС = 7г/2 — 7 + v?, АВС = 7г/2 — 7 — ф. После этого запишем теорему синусов для треугольников ACM и ВСМ и поделим друг на друга полученные соотношения:
\АМ\
\СМ\
\ВМ\
\СМ\
sin(7 + ф) sin(f - 7 + ф) ’
sin(7 — ф) cos(7 4- ф)
sin(7 4- ф) cos(7 — ф)
sin(7 — ф) sin(| — 7 — ф)
sin(27 — 2ф) = sin(27 4- 2ф)
27 - 2ф = 27 4- 2ф,
27 — 2ф = 7Г — 27 — 2ф
Ф = О,
27 = тт/2.
Эти соотношения говорят о том, что условие задачи может выполняться в двух случаях. Если ф = 0, то медиана СМ, биссектриса CL и высота СН совпадают, треугольник АВС равнобедренный. Однако из условия следует, что угол между медианой и высотой ненулевой. Поэтому этот случай нам не подходит. Если же 27 = 7г/2, то треугольник АВС прямоугольный, ВАС = 7Г — 7г/2 — 7г/5 = 37г/10.


1.3. Биссектриса, медиана, высота
259
Задача 30.
На продолжении стороны ВС треугольника АВС за точку В расположена точка Е так, что биссектрисы углов АЕС и АВС пересекаются в точке К, лежащей на стороне АС. Длина отрезка BE равна 1, длина отрезка ВС равна 2, градусная мера угла ЕКВ равна 30°. Найдите длину стороны АВ.
Идея. Вычислить градусную меру угла ВАЕ, найти значение отношения \AB\-.\AE\.
Указание. Воспользоваться основным свойством биссектрисы треугольника и теоремой о сумме градусных мер углов треугольника.
Указание. Рассмотреть треугольники АВС и ЕАС, показать, что ЕВ С
\АВ\ : \АЕ\ = \ВС\ : \ЕС\.
Решение. Поскольку отрезки В К и ЕК являются биссектрисами треугольников АВС и ЕАС соответственно, то, записывая основное свойство биссектрисы треугольника, мы получаем
\АВ\ _ \АК\ \АЕ\ _ \АК\ \АВ\ _ \АЕ\ \АВ\ _ \ВС\ _ 2
\ВС\ ~ \КС\' \ЕС\ ~ \КС\ ^ \ВС\ ~ \ЕС\ ^ \АЕ\ ~ \ЕС\ ~ 3‘
Далее обозначим градусные меры углов АВС и АЕС через 2а° и 2/?° соответственно. Тогда из треугольника ЕКВ мы находим
/3° + (180° - а°) + 30° = 180° =* а° — /3° = 30°,
и, с учётом полученного соотношения рассматривая треугольник АВЕ, мы получаем
ВАЕ = 180° - 2/3° - (180° - 2а°) = 2(а° - /3°) = 60°.
Наконец, положим \АВ\ = 2ж, \АЕ\ = Зх и запишем теорему косинусов для треугольника АВЕ:
\ВЕ\2 = \АЕ\2 + \АВ\2 - 2 ■ \АЕ\ ■ \АВ\ ■ cos ВАЕ => 1 = 7х2 =$■ х = ~^=.
V7
Осталось учесть, что \АВ\ = 2х, и выписать ответ.
2
Ответ. —
V7
Задача 31.
В треугольнике АВС известно, что \АС\ = \ВС\ = 12, \АВ\ = 6, AD - биссектриса. Найдите длину радиуса окружности, описанной около треугольника ADC, и сравните эту длину с числом 13/2.
а*


260
Указания и решенья
Идея. Воспользоваться основным свойством биссектрисы и второй формулой длины биссектрисы треугольника.
Указание. Вычислить длины отрезков CD и AD.
Указание. Используя теорему косинусов, найти косинус величины угла ACD.
Решение. Вычислим длины отрезков CD и AD, пользуясь основным свойством биссектрисы и второй формулой длины биссектрисы треугольника:
\BD\ \АВ\
\BD\
\DC\ \ВС\ 2 \AD\2 = \AB\-\AC\-\BD\-\DC\
4, \DC\ = 8;
=► \AD\ = 2-ч/То.
Далее из треугольника ADC по теореме косинусов найдём косинус величины угла ACD, после чего, найдя синус величины угла ACD, применим теорему синусов:
cos ACD =
|АС\2 + |DC\2 - \AD|2 144 + 64-40 7
2 • \АС\ • \DC\ R&adc =
\AD\
2-12-8
2л/Ш-8 2VT5
sin ACD
VIE
8л/6
2 sin ACD
Наконец, проведём требуемое сравнение.
8л/6
3
64-6 9
128-4 512
Поскольку все преобразования были равносильными, длина радиуса окружности, описанной около треугольника ADC, больше, чем 13/2.
V
13
V
2
169
V
4
169-3
>
507.
Ответ. Raadc =
8\/б
13
ttAADC > ~2~ •
Задача 32.
В треугольнике АВС на сторонах АВ и ВС отмечены точки М и N соответственно, причём |J3M| = |ВЛГ|. Через точку М проведена прямая, перпендикулярная ВС, а через точку N - прямая, перпендикулярная АВ. Эти прямые пересекаются в точке О. Продолжение отрезка ВО пересекает сторону АС в точке Р, \АР\ = 5, \РС\ = 4. Найдите длину отрезка РР, если известно, что \ВС\ — 6.


1.3. Биссектриса, медиана, высота
261
В
Идея. Рассмотреть различные прямоугольные треугольники с вершиной В.
Указание. Доказать, что ВР - биссектриса треугольника АВС, воспользоваться основным свойством биссектрисы треугольника и второй формулой её длины.
Решение. Пусть К - точка пересечения ВС и прямой, перпендикулярной ВС и проходящей через точку М; L - точка пересечения АВ и прямой, проходящей через точку N перпендикулярно АВ.
Заметим, что треугольник МКВ равен треугольнику NLB, так как по условию \ВМ\ = |J5iV|, угол В у них общий, углы МКВ и NLB прямые. Из этого равенства следует, что \ВК\ = \BL\.
Но тогда равны и прямоугольные треугольники В КО и BLO, поскольку \ВК\ = \BL\, ВО - общая. Стало быть, углы ОВК и OBL равны, то есть прямая О В - биссектриса угла АВС, а ВР - биссектриса треугольника АВС.
Теперь воспользуемся основным свойством биссектрисы треугольника и второй формулой её длины:
\АВ\ = \АР\
\ВС\ \РС\
\ВР\2 = \АВ\ • \ВС\ - \АР\ • \РС\
\АВ\
\АР\ • \ВС\ \РС\
\ВР\2
\АВ\ =
15 2 ’
15
2
-6-5-4
\ВР\ = 5.
Ответ. 5.
Задача 33.
Вокруг треугольника МКН описана окружность с центром в точке О, длина её радиуса равна г. Длина стороны НМ равна а. Известно, что справедливо равенство \НК\2 — \НМ\2 = \НМ\2 — \МК\2. Найдите площадь треугольника OLK, где L - точка пересечения медиан треугольника МКН.
Идея. Рассмотреть треугольник РКО, где Р - середина стороны НМ. Указание. Найти длину отрезка KL, вычислив предварительно с помощью формулы длины медианы и соотношения из условия задачи длину отрезка КР. Указание. Используя теорему косинусов, найти косинус величины угла РКО.
Решение. Для нахождения площади треугольника OLK нам понадобится найти три каких-то его элемента. Нам уже известна длина его стороны ОК - она равна г. Длину стороны KL мы сможем найти, вычислив длину медианы КР и умножив её на 2/3 (медианы треугольника делятся точкой пересечения в отношении 2:1, считая от вершин). Применим формулу длины медианы и воспользуемся условием задачи:


262
Указания и решения
4\КР\2 = 2\НК\2 + 2\МК\2 - \НМ\2, \НК\2 + \МК\2 = 2\НМ\2
• А\КР\2 = 4|ЯМ|2 - \НМ\2 = 3|ЯМ|2
\КР\ = £\НМ\ = «£
Теперь нам осталось найти синус величины угла РКО. Это можно сделать, рассмотрев треугольник КОР. Заметим, что поскольку центр описанной около треугольника окружности лежит на пересечении серединных перпендикуляров, проведённых к сторонам треугольника, OP JL НМ. Из прямоугольного треугольника ОРН следует, что
|ОР|2 = \ОН\2 - |ЯР|2 = г2 - ==►
\KL\
ау/3
\ОР\ =
у/Ат
Далее, по теореме косинусов
\ОР\2 = \ОК\2 + \КР\2 - 2 • \ОК\ • \КР\ • cos РКО
9 а о За ау/3
Т= +Т" т
• cos РХО
cos РКО =
V5’
sin РХО = \/1 — cos2 РКО = Наконец, считаем искомую площадь:
л/Зг2 — о2
1 —\/<\гГ2 /72
= j ' l^l' |O^I sin РКО = .
Ответ, а
\/Зг2 — а2 "б
Задача 34-
В треугольнике KLM проведены биссектрисы ХА и MB, которые пересекаются в точке О. Диагонали четырёхугольника АО В L пересекаются в точке С. Найдите численные значения отношений \ВС\ : \СА\ и \LC\ : |С70|, если известно, что \KL\ = ш, \КМ\ = /, \LM\ = к.


1.3. Биссектриса, медиана, высота
263
Идея. Доказать, что LO - биссектриса угла KLM.
Указание. Первое отношение найти из треугольника ABL, используя свойство биссектрисы и формулу для вычисления длин отрезков, на которые биссектриса треугольника делит сторону, к которой проведена.
Указание. Рассмотреть треугольники LAB и LAK, воспользоваться основным свойством биссектрисы треугольника, первой формулой её длины, формулой для вычисления длин отрезков, на которые биссектриса треугольника делит сторону, к которой проведена.
Решение. Заметим, что поскольку биссектрисы треугольника пересекаются в одной точке, LO - биссектриса угла KLM, таким образом, LC - биссектриса треугольника ALB, a LO - биссектриса треугольника LAK. Тогда, пользуясь основным свойством биссектрисы и формулой для вычисления длин отрезков, на которые биссектриса треугольника делит сторону, к которой проведена, находим
\KL\ • \LM\ mk
\ВС\ \LB\ \КМ\ + \LM\ i + k m + l
\CA\~\LA\ \LM\-\KL\ km к + Г
\KL\ + \KM\ m + l
Для вычисления отношения \LC\ : \CO\ рассмотрим треугольники LAB и LAK и с помощью первой формулы длины биссектрисы треугольника найдём отношение \LC\ к \LO\-.
2 • \LA\ ■ \LB\ • cos(\KLM)
ILC\ = \LA\ + \LB\ = \LB\ • (\LA\ + \KL\) =
IL°\ ~ 2 • \LA\ ■ \KL\ ■ cos(%KLM) \KL\' (\LA\ + \LB\) ~
\LA\ + \KL\
\LB\ ax m + l ( km \
= \LA\ ' + 11^ = ~k+J' (^~+7+mJ = к+ m +I
tr/Tt (■, , Л , m + l\ к + m + 2l
|KL4I + MlJ m41+bnJ
Наконец, с помощью полученного значения мы можем вычислить интересующее нас отношение:
\LC\_
\LC\ _ \LC\ _ \LO\ _k + l + m \CO\ ~ \LO\ - \LC\ ~ \LC\ ~ I
\LO\
M
\BC\ l + m \LC\ k + l + m °TBeT- ]CA\=TTk’ ]coi = —I—


264
Указания и решения
Задача 35.
Отрезки AM и ВР являются медианами треугольника АВС. Известно, что угол АР В равен углу ВМА, \ВР\ = 1, косинус величины угла АСВ равен 4/5. Найдите площадь треугольника АВС.
Идея. Доказать, что А АВС равнобедренный.
Указание. Воспользоваться формулой длины медианы и теоремой косинусов.
Решение. Заметим, что поскольку равны углы АР В и ВМА, равны и смежные с ними углы СРВ и СМ А.
Но тогда в силу теоремы о сумме величин углов треугольника равны и углы СВР и САМ. Запишем теорему синусов для треугольников ВСР и ACM :
\СР\ _ \СВ\ \СМ\ _ \СА\
В
sin СВР sin СРВ sin САМ sin СМ А
Деля друг на друга эти соотношения и учитывая тот факт, что \СР\ = ~|(L4|, \СМ\ — ~|СВ|, получаем
\СР\ _\СВ\ _ \СА\2 \СВ\2 _
]СМ\~]СА\ ^ \CA\-\CB\.
Итак, треугольник АВС равнобедренный. Далее положим \СА\ = \СВ\ = а, тогда по теореме косинусов получаем
Ол2
\АВ\2 = \СА\2 + \СВ\2 - 2 • \СА\ • \СВ\ • cos АСВ = —
5
и по формуле длины медианы треугольника находим а2:
А\ВР\2 = 2\АВ\2 + 2\СВ\2 - \СА\2 => 4 = =>. а2 = 20
9
Наконец,
sin АСВ = Saabc = I • |СЛ| • |СВ| • sin АСВ =
5 2 3
Замечание. При доказательстве равнобедренности треугольника АВС мы использовали теорему синусов, хотя проще было бы просто сказать, что треугольники САМ и СВР подобны по двум углам. Однако про подобие мы поговорим чуть позже.
Ответ. -.


1.4- Подобие треугольников
265
Задача 36.
Внутри прямоугольного треугольника АВС с прямым углом С взята точка О таким образом, что \ОА\ = \ОВ\ = b. CD - высота треугольника АВС, точка Е - середина отрезка ОС, \DE\ = а. Найдите |СЕ\.
Идея. Воспользоваться свойством высоты прямоугольного треугольника, проведённой к гипотенузе, и формулой длины медианы.
Указание. Рассмотреть треугольники АКО и ^
OKD, доказать, что \CD\2 — \АО\2 — \OD\2.
Решение. Проведём перпендикуляр О К к гипотенузе АВ. Поскольку длины отрезков О А и О В равны, то К - середина АВ, |АК"| = |#Х|. После этого, применяя свойство высоты прямоугольного треугольника, проведённой к гипотенузе, получаем С В
\CD\2 = |AD|-|B£>| = (|А^|-|/£Т>|)(|В^|+|ИГ1)|) = \AK\2-\KD\2.
Далее, по теореме Пифагора
\АК\2 = \АО\2 - \ОК\2, \KD\2 = \OD\2 - |<Ж|2,
поэтому
\CD\2 = \АО\2 - |OD|2 = Ь2 - \OD\2.
Наконец, запишем формулу длины медианы:
4\DE\2 = 2\CD\2+ 2\OD\2-\ОС\2 => 4а2 = 2b2 - \ОС\2 =► =* \ОС\ = V2b2 - 4а2 =► \CE\ = \\OC\ = sJb^-cfi.
Ответ, у——а2.
1.4. 	Подобие треугольников Задача 1.
В прямоугольном треугольнике АВС из вершины прямого угла В опущена высота BD на гипотенузу АС. Известно, что \АВ\ = 13, \BD\ = 12. Найдите площадь треугольника АВС.
Идея. Воспользоваться подобием треугольников АВС и ADJ3.
Указание. Найти длину отрезка AD.


266
Указания и решения
Решение. Для нахождения площади треугольника АВС нам достаточно найти длину его гипотенузы АС или длину его катета ВС. Это можно сделать из подобия треугольников АВС и ADB (два прямоугольных треугольника с общим углом), так как треугольник ADB полностью определён своими гипотенузой и катетом. Для начала из треугольника ADB с помощью теоремы Пифагора находим длину AD:
\AD\2 = \АВ\2 - \BD\2
D
В
\AD | = 5.
Далее используем подобие треугольников АВС и ADB, из которого следует
\ВС\ \АВ\ \BD\ \AD\
Наконец,
Saabc = ^
\ВС\ =
\АВ\ • \ВС\ =
\BD\ • \АВ\ 156 \AD\ ~ 5 ’
13 • 156 2028
25
10
Ответ. 202,8.
Задача 2.
В треугольнике АВС длина высоты BD равна 11,2, а длина высоты АЕ равна 12. Точка Е лежит на стороне ВС, причём \ВЕ\ : \ЕС\ — 5:9. Найдите длину стороны АС.
Идея. Доказать, что ААЕС ~ ABDC.
Указание. Рассмотреть треугольник А ЕС.
Решение. Обозначим длину отрезка BE как Ъх, тогда по условию задачи длина отрезка ЕС равна 9ж, а длина стороны ВС равна 14х. По утверждению 3 (см. теоретический материал) треугольники АЕС и BDC подобны (прямоугольные треугольники с общим углом), поэтому
\АС\ _ \ЕС\ \АЕ\
\АС\
12
\ВС\ = 15х.
\ВС\ \CD\ \BD\ r‘~' 11,2'
Записывая теорему Пифагора для треугольника АЕС, получаем
Ш
D
\АЕ\2 = \АС\2- Ответ. 15.
•| ЕС\2
144 = 225х —81х
1
\АС\ = 15.
Задача 3.
В треугольнике АВС длина стороны АВ равна 8, величина угла АСВ равна 7г/3. Прямая, параллельная стороне АВ, пересекает сторону АС в точке D, а сторону ВС в точке Е. Известно, что \ВС\ = \DC\, \DE\ = 3. Найдите \ВС\.
Идея. Воспользоваться подобием треугольников АВС и DEC.
Указание. Применить теорему косинусов.


1.4. Подобие треугольников
267
Решение. Положим \ВС\ = |£>С| = ж, |АС| = г/. Треугольники АВС и DEC подобны, поэтому
\РЕ\ ; |РС| |ЛБ| |Ж7|
Ж
2/
С другой стороны, записывая теорему косинусов для треугольника АВС, получаем
\АВ |2 = |ЛС|2 + | ВС\2 - 2 • \АС\ ■ \ВС\ • cos АСВ
64 = у2 + х2 — ху.
р 24 64
Решая систему полученных уравнении, находим ж = —, у = —.
п 24
Ответ. —.
7
Задача 4-
Окружность, центр которой лежит на гипотенузе прямоугольного треугольника, касается его катетов. Найдите длину радиуса этой окружности, если длины катетов треугольника равны 3 и 4.
Идея. Провести отрезки, соединяющие центр окружности и точки её касания с катетами.
Указание. Найти пару подобных прямоугольных треугольников.
Решение. Пусть в прямоугольном треугольнике АВС даны катеты \АС\ = 3, \АВ\ = 4. Соединим центр окружности и точки её касания с катетами отрезками OL и О К. Поскольку OL _L АС, ОК _!_ АВ, AC _L АВ и \OL\ = \ОК\, четырёхугольник OKAL является квадратом. Поэтому, если ввести обозначение \OL\ = \ОК\ = г, то |ВАГ| = 4 — г, |СХ| = 3 —г. Заметим, что треугольники OLC и ВАС подобны по первому признаку подобия треугольников, стало быть,
\ОЦ \АВ\ \CL\ \АС\
3 — г
4
3
Зг = 12 — 4г
12 7 ’
Ответ.
12
Задача 5.
Окружность, центр которой лежит на гипотенузе АВ прямоугольного треугольника АВС, касается катетов АС и ВС в точках Е и D соответственно. Найдите величину угла АВС, если \АЕ\ = 1, |BD| =3.
Идея. Доказать, что А АОЕ ~ AOBD (О - центр окружности).
Указание. Используя подобие, найти \OD \.
Указание. Рассмотреть треугольник OBD.


268
Указания и решения
Решение. Обозначим центр данной в условии окружности буквой О. Заметим, что, поскольку ОЕ JL АС, OD ± ВС, АС ± ВС и \ОЕ\ = |0£>|, OECD - квадрат. Положим \ОЕ\ = |OZ>| = х и воспользуемся тем, что 02?||ВС и OjD||AC7. Из этого по первому признаку следует , что ААОЕ ~ AOBD. Поэтому
\АЕ\ _ \ОЕ\
1
х
3
v/5.
|0£>| |BD|
Затем из прямоугольного треугольника OBD находим
\0D\ _ у/%
tg ABC
\BD\
ABC=\.
6
~ 7Г
Ответ. —.
6
Задача 6.
В параллелограмме ABCD длина стороны АВ равна 6, а длина высоты, проведённой к основанию AD, равна 3. Биссектриса угла BAD пересекает сторону ВС в точке М так, что \МС\ = 4; N - точка пересечения отрезков AM и BD. Вычислите площадь треугольника BNM.
Идея. Воспользоваться подобием треугольников AND и BNM. Указание. Доказать, что треугольник AM В равнобедренный, найти длины отрезков ВМ и AD.
В К М С
и 1-^
А Н D
Решение. Заметим, что углы AM В и MAD равны, как внутренние накрест лежащие при параллельных прямых ВС и AD и секущей AM. А так как равны и углы MAD и МАВ, то угол AM В равен углу МАВ, то есть треугольник AM В равнобедренный и |АВ| = \ВМ\ = 6. Далее, |AD| = |J3C| = \ВМ\ + \МС\ = 10. Теперь воспользуемся тем, что треугольники AND и BNM подобны по первому признаку подобия треугольников, что даёт нам
\NK\ \ВМ\ 3 _ |Y/f|_3 9
]Щ~Ш~ 5 ^ W --|Я*| -
1 27
Наконец, Sabnm = ^ ■ \ВМ\ ■ |JV2f| = у.
Ответ. —.
8


1.4- Подобие треугольников
269
Задача 7.
В равнобедренный треугольник АВС с основанием АС вписана окружность, длина радиуса которой равна 3. Прямая р касается этой окружности и параллельна прямой АС, но не совпадает с ней. Расстояние от точки В до прямой р равно 3. Найдите расстояние между точками, в которых данная окружность касается сторон АВ и ВС.
В
Идея. Найти расстояния от точки В до центра О окружности, вписанной в треугольник АВС, и до точки М её касания со стороной АВ.
Указание. Доказать, что треугольники МОТ и ВОМ подобны (Т - точка пересечения отрезка ВО и отрезка, концами которого являются точки касания вписанной в треугольник АВС окружности с его сторонами АВ и ВС).
Решение. Обозначим буквой О центр вписанной в треугольник АВС окружности, буквой R — точку касания прямой р и этой
окружности, буквами Q и Р обозначим точки пересечения прямой р со сторонами АВ и ВС соответственно. Точки касания вписанной в треугольник АВС окружности с его сторонами обозначим буквами М, N и Н (М Е АВ, N Е ВС, Не АС).
Поскольку треугольник АВС по условию задачи равнобедренный, то есть его биссектриса BL, проведённая из вершины В, является также его высотой и медианой, то, с одной стороны, OL _L АС, но, с другой стороны, ОН _L АС. Поэтому точки L и Н совпадают.
Далее, р || АС, поэтому треугольник QBP подобен треугольнику АВС. Стало быть, \QB\ = |J3P|. Заметим, что АМОВ = ANOB (по гипотенузе и катету), что даёт нам равенство длин отрезков MB и NB. Тогда \MQ\ = |iVP|, а из этого, с учётом того, что AMOQ = AROQ и AROP = ANOP, вытекает, что \QR\ = \RP\. Но ВН — биссектриса угла АВС, следовательно, она проходит через середину отрезка PQ и перпендикулярна ему. Итак, все четыре точки В, Р, О, Н лежат на одной прямой, поэтому
\BR\ = 3, \ВО\ = |ВД| + |ДО| = 6, \ВМ\ = у/\ВО\2 - \ОМ\2 = Зл/з.
Аналогичными рассуждениями получаем, что ВН проходит через середину отрезка MN (обозначим её Т) и перпендикулярна ему. По утверждению 5 треугольники МОТ и ВОМ подобны (прямоугольные треугольники с общим углом), из чего вытекает
\мт\ \мо\ \вм\ ~ \во\
Наконец, \MN\ = 2 • \МТ\ = Зл/З.
\мт\ =
Зл/З
Ответ. Зл/3-


270
Указания и решения
Задача 8.
В ромбе ABCD проведены высоты ВР и BQ. Они пересекают диагональ АС в точках М и N соответственно (М между А и N). Известно, что \АМ\ = р, \MN\ = q. Найдите \PQ\.
Идея. Доказать, что треугольник АМР подобен треугольнику СМ В, а треугольник BMN подобен треугольнику BPQ.
Указание. Найти отношение \ВР\ : \ВМ\.
D
Решение. Поскольку четырёхугольник ABCD - ромб, \АВ\ = \ВС\, /BAD = /.BCD. Из этого вытекает равенство прямоугольных треугольников АВР и CBQ (по гипотенузе и острому углу), стало быть,
\ВР\ = \BQ\, /АВР = /CBQ. Так как треугольник АВС равнобедренный, то ZВАС = /.ВСА. Значит, треугольники АВМ и CBN равны по стороне и двум углам, поэтому \ВМ\ = \BN\, \АМ\ = |CW| = q, \СМ\ = \CN\ -f \MN\ = р + q.
Далее заметим, что треугольники BMN и BPQ подобны по второму признаку подобия треугольников. Действительно, отношения \ВМ\ : \ВР\ и \BN\ : \BQ\
равны в силу полученных ранее фактов, а угол В у них общий. Из этого подобия вытекает, что
\PQ\ \ВР\ _ |Д,ЛП \ВР\
\MN\ \ВМ\
\PQ\ = |AfJV|
| ВМ[
Для нахождения отношения \ВР\ : \ВМ\ заметим, что AD\\BC. Из этого следует равенство углов CAD и АСВ (они внутренние накрест лежащие) и перпендикулярность отрезков ВР и ВС. Но тогда треугольники АМР и СМ В подобны по первому признаку подобия треугольников, стало быть,
\МР\ \АМ\ р \ВР\ \ВМ\ + \МР\
\ВМ\ \МС\
1 +
р
p + q’ \ВМ\ 2p + q
p+q p+q
\ВМ\
\PQ\
i +
\МР\
\вм\
2pq + q2 p + q
Ответ.
2 pq + q2 Р + Я
Задача 9.
На сторонах острого угла с вершиной О взяты точки А и В. На луче О В взята точка M на расстоянии 3 • | О А | от прямой О А, а на луче О А - точка N на расстоянии 3 • \ОВ\ от прямой О В. Длина радиуса окружности, описанной около треугольника АОВ, равна 3. Найдите \MN\.


1.4. Подобие треугольников
271
Идея. Доказать, что треугольник АОВ подобен треугольнику MON, воспользовавшись вторым признаком подобия треугольников.
Указание. Выразить синус величины угла АОВ из треугольников OKN и OLM. Доказать, что треугольник АОВ подобен треугольнику MON.
Указание. Применить теорему синусов к треугольнику АОВ.
Решение. Заметим, что конфигурация, получающаяся в этой задаче, кое-чем напоминает конфигурацию из
утверждения 3. Для решения этой задачи нам придётся провести рассуждения, похожие на доказательство этого утверждения.
Положим АОВ = а, основания перпендикуляров, опущенных из точек М и N на прямые О А и О В, обозначим буквами L и К. Тогда из Л OKN и AOLM получаем
\KN\ 3\ОВ\ \ОВ\ sina
sma =
sma
\ON\
\LM\
\ON\
3-\OA\
|OiV|
\OA\
3 ’ sina
\OM\ \OM\ ^ \OM\ 3 Следовательно, АЛОВ ~ ЛMON по второму признаку подобия треугольников,
причём коэффициент их подобия равен \АВ\
sma
. Отсюда вытекает, что
sina
=> \MN\ =
3 • \АВ\
\MN\ 3 sma
Теперь, записывая теорему синусов для треугольника АОВ, мы находим
\АВ\ = 2Raaob • sina.
3 • 2Raaob • sina
Наконец, ответим на вопрос задачи: \MN Ответ. 18.
sina
6Raaob = 18.
Задача 10.
В треугольнике АВС угол С тупой, D - точка пересечения прямой DB, перпендикулярной к АВ, и прямой DC, перпендикулярной к АС. Высота треугольника ADC, проведённая из вершины С, пересекает АВ в точке М. Известно, что \АМ\ = а, \МВ\ = Ъ. Найдите \АС\.
Идея. Доказать, что треугольник АСН подобен треугольнику ADC, а треугольник АМН подобен треугольнику ADB.
Указание. Выразить двумя способами произведение длин отрезков AD и АН.


272
Указания и решения
Решение. Самое трудное в этой задаче - найти связь между известными нам величинами и той величиной, которую просят вычислить. Заметим, что известные нам величины входят в пару треугольников АМН и ADB, при этом АНМ = ABD — п/2, а угол МАН - общий угол этих треугольников. Поэтому А АМН ~ AADB. Неизвестная нам величина \АС\ входит в три треугольника: в А АВС,
А АСН и AADC. Заметим, что поскольку АНС = ACD, а угол CAD является общим углом треугольников АСН и ADC, то А АСН ~ AADC. Из найденных подобий мы получаем
/1
14
—
Н
D
\АМ\ \АН\ \AD\ ~ \АВ\
\АС\ \АН\ \AD\ \АС\
Сравнивая полученные соотношения, получаем
ААМН ~ AADB
AACH ~ AADC
\AD\ ■ \АН\ = \АВ\ ■ \AM\-,
\AD\ • \АН\ = |Ж7|2.
|ЛС|2 = |АВ| • \АМ\ = (а+ Ь) ■ а
\АС\ = VaF+ab.
Ответ. Vа2 + ab.
Задача 11.
На стороне PQ треугольника PQR взята точка N, а на стороне PR - точка L, причём \NQ\ = \LR\. Точка пересечения отрезков QL и NR делит отрезок QL в отношении т : п, считая от точки Q. Найдите значение отношения |PiV| : |PiZ|.
Идея. Воспользоваться теоремой Менелая.
Указание. Рассмотреть треугольник LQP.
Решение. Обозначим точку пересечения отрезков QL и NR буквой О. Из условия задачи следует, что \QO\ : \OL\ — т : п. Применим теорему Менелая к треугольнику LQP и секущей N0 :
\LO\ \QN\ \PR\ _ |PJV| \LO\ \QN\ n
\OQ\ ' |iVP| ' \RL\ ~ ^ |РД| _ \OQ\ ' \LR\ ~ m
Ответ, n : m.
Задача 12.
В треугольнике ABC на стороне АС взяты точки Р и Q таким образом, что \АР\ > \AQ\. Прямые ВР и BQ делят медиану AM на три равные части. Известно, что \PQ\ — 3. Найдите длину стороны АС.


1.4. Подобие треугольников
273
Идея. Применить теорему Менелая в A ACM.
Указание. Показать, что ВР - медиана треугольника АВС. Указание. Применить теорему Менелая к треугольнику ACM.
Решение. Обозначим точки пересечения медианы AM с отрезками BQ и ВР буквами R и S соответственно. Так как AM - медиана, а отрезок ВР разделил её точкой пересечения S в отношении 2:1, считая от вершины, то ВР - тоже медиана. Положим \AQ\ = х, тогда \РС\ — \АР\ = х 4- 3. Применяя теорему Менелая к треугольнику ACM и секущей QR, получаем:
\MR\ \AQ\ \СВ\ _ 2 ж 2 _
|ДА| '\QC\'\ВМ\ ~ ^ Гх + 6'l “ ^
Ответ. 10.
\
/ R
Q
' Р 1
= 2
\АС\ = 10.
Задача 13.
В треугольнике АВС взяты точка К на стороне АВ и точка М на стороне АС так, что |ART| : \КВ\ = 3:2, \АМ\ : \МС\ =4:5. Найдите отношение, в котором прямая, проходящая через точку К параллельно стороне ВС, делит отрезок ВМ.
Идея. Воспользоваться теоремой Менелая. Указание. Используя теорему Фалеса, найти отношение \AL\ : \LC\, где L - точка пересечения прямой, проходящей через точку К параллельно стороне ВС, и отрезка АС.
Указание. Применить теорему Менелая к треугольнику АВМ и секущей KL.
В
Решение. Пусть L - точка пересечения прямой, проходящей через точку К параллельно стороне ВС, и отрезка АС, а N - точка пересечения отрезков KL и
ВМ. Поскольку KL\\BC, по теореме Фалеса \AL\ : \LC\ = \АК\ : \КВ\ = 3:2.
Положим \АС\ = z, тогда
\AM\ = ±z, |AL| = |*, \LM\ = \AL\ — \AM\ — -~z.
Наконец, применяя теорему Менелая к треугольнику АВМ и секущей KN, находим
3
\MN\ \ВК\ \AL\ _ Л |BJV| _ 2 lz _ 18
^ |JVM| “ 3 ' _7 7 ‘
|iVB| |/£ГЛ| |LM| Ответ. 18 : 7.
45


274
Указания и решения
Задача 14-
В треугольнике АВС взяты точка N на стороне АВ и точка М на стороне АС. Отрезки CN и ВМ пересекаются в точке О. Вычислите \СО\ : \ON\, если известно, что \AN\ : |ЛГ£| = 2:3, \ВО\ : \ОМ\ =5:2.
Идея. Воспользоваться теоремой Менелая.
Указание. Найти отношение \АМ\ : \МС\.
Решение. Применяя теорему Менелая к треугольнику АВМ и секущей CN, получаем:
\МО\ \BN\ \АС\ _ \АС\ _ 5
\ОВ\ ' |ЛМ| ' \см\ ~ ^ \см\ ~ 3'
Положим \АС\ = Ьу, \СМ\ = 3у, |АЛГ| = 2х, |ЛГВ| - Зх, тогда \АМ\ -- 2у, \АВ\ = 5х. Наконец, применим теорему Менелая к треугольнику АС N и секущей ВМ:
|ЛГО| \СМ\ \АВ\ _ \СО\ _ 3у 5х _ 5
|ОС| ' \МА\ ' ^ \ON\ ~ 2у ' Зх ~ 2'
Ответ. 5:2.
В
Задача 15.
В треугольнике АВС точка D делит сторону АВ пополам, а точка Е лежит на стороне ВС, причём \ВС\ = 3|J3J5|. Отрезки АЕ и CD пересекаются в точке О, \АЕ\ — 5, \ОС\ = 4, АОС = 120°. Найдите длину стороны АВ.
Идея. Воспользоваться теоремой Менелая. Указание. Найти длины отрезков О А и DO.
Решение. Так как точка D делит сторону АВ пополам, достаточно найти длину отрезка AD. Для этого нам надо найти длины отрезков О А и DO. В соответствии с условием задачи положим \AD\ = \DB\ = х, \ВЕ\ = ?/, \ВС\ = 3у. Тогда \ЕС\ = 2у. Для того чтобы найти длины отрезков О А и DO, дважды применим теорему Менелая - сначала к треугольнику АВЕ и секущей DO, затем к треугольнику CBD и секущей ЕО:
= 1
|JE70| \AD\ \ВС\
\ОА\ ’ |DjB| ’ \СЕ\
\DO\ \СЕ\ \ВА\ \ОС\ ■ \ЕВ\ * \AD\
\ЕО\
\ОА\
В
х 2у _ 2 х 3 у 3
|ЯО|=2, \ОА\ = 3;
= 1
\DO\ _ х У _ 1
4 2х 2г/ 4
|£>0| = 1.


1.4- Подобие треугольников
275
Теперь все просто: заметим, что AOD = 180° — АОС = 60°, и запишем теорему косинусов для треугольника AOD:
| ADf = \ОА\2 + \DO\2 - 2 • \ОА\ ■ \DO\ • cos ADD = 9 + 1-3 => \AD\ = у/7.
Наконец, \АВ\ = 2|Л£>| = 2у/7.
Ответ. 2>/7.
Задача 16.
В треугольнике АВС точки £>, Е и F расположены на сторонах АВ, ВС и АС соответственно. Известно, что \AD\ : \DB\ = 1:2, \ВЕ\ : \ЕС\ =2:3,
|AF| : \FC\ = 1:1. Отрезки DE и BF пересекаются в точке К. Вычислите
отношение \ВК\ : \KF\.
Идея. Продолжить прямую ED до пересечения с прямой АС.
Указание. Использовать теорему Менелая.
Решение. Поскольку по условию задачи \ВЕ\ : \ЕС\ < \BD\ : \DA\, прямая ED пересекает прямую АС в точке L, причём точка А лежит между точками L и С. Записывая теорему Менелая для треугольника АВС и секущей ED, находим
\AD\ \ВЕ\ |CL\ ч
\DB\ \ЕС\ \LA\ \LA\
Положим \LA\ = х, тогда \CL\ = Зж, \АС\ = 2х, \AF\ = \FC\ = х. Ещё раз применяя теорему Менелая для треугольника ABF и секущей KD, получаем
\АР | \ВК\ \FL\ \ВК\=1 ± = х
\DB\ \KF\ \LA\ \KF\ 1 2x
Ответ. 1:1.
Задача 17.
В треугольнике ABC длина высоты BD равна 6, длина медианы СЕ равна 5, расстояние от точки пересечения отрезков BD и СЕ до стороны АС равно 1. Найдите длину стороны АВ.
Идея. Применить теорему Менелая к AABD и А АСЕ.
Указание. Найти расстояние от точки пересечения отрезков BD и СЕ до точек С и Е.
Указание. Дважды применить теорему Пифагора.
В
\CL\


276
Указания и решения
Решение. Для нахождения искомой длины нам надо найти длину отрезка AD. Пусть О - точка пересечения отрезков BD и СЕ. Поскольку OD 1_ АС, длина отрезка OD и есть расстояние от точки D до прямой АС, значит, \OD\ = 1, \ВО\ = 5. Также положим \ЕА\ = \ВЕ\ = х. Дважды применим теорему Менелая - сначала к треугольнику ABD и секущей ЕО, затем к треугольнику АСЕ и секущей DO:
\DO\ \ВЕ\ \АС\ \OB\\EA\\CD\
\ЕО\ \CD\ \АВ\
= 1
= 1
\АС\ _хЪ_ \CD\ ~xl~
\АС\ = 5|С£>|, \AD\=4\CD\;
\ЕО\
4|СР\ х
10 ^ ВД = у, |ОС| = |.
\ОС\ \DA\ \ВЕ\ \ОС\ \CD\ 2х
Теперь, записывая теорему Пифагора в треугольнике О DC, получаем
\CD\ = V\OC\2 - \OD\2 = ^-1 = 1
Наконец, из A ABD находим \АВ\ = y/\AD\2 -f \BD\2 =
Ответ. ~\/l45.
IACI = f.
256
_+36= —
Задача 18.
В треугольнике АБС из вершин А и В проведены отрезки AD и BE, причём точки D и Е лежат на сторонах ВС и АС соответственно. Отрезки AD и BE пересекаются в точке Q таким образом, что \AQ\ : |QZ)| = х, |£?Q| : |Qi?| = ?/. Найдите значения отношений |AJE7| : \ЕС\ и |BjD| : \DC\.
Идея. Применить теорему Менелая.
Указание. Рассмотреть треугольники ADC и ВЕС.
Указание. Ввести неизвестные и — \АЕ\ : \ЕС\, v = \BD\ : \DC\.
Решение. Введём неизвестные
u= |AJS| : \ЕС\, v= \BD\ : \DC\.
Положим \ЕС\ = k, \DC\ = /, тогда
\АЕ\ = ик, | АС| = (и + 1)Л, | BD| = vl, \ВС\ = (v + 1)1.
Применяя теорему Менелая к треугольникам ACD и ВСЕ, получаем
\DQ 1 \АЕ\ \СВ\ \QA\ \ЕС\ \BD\
= 1
1 ик (v +1)/ х к vl
= 1 <==> u(v -f 1) = vx\


1.4■ Подобие треугольников
277
\m,\BD\.\CA\=l 1 (a+l)fc ^ „(U + 1) = „V
|<ЗВ| 0С\ \ЛЕ\ у I ик
Решая полученную систему уравнений, находим
и = \АЕ\ : \ЕС\ = v = \BD\ : \DC\ = ху ~ 1
у + 1 х + 1
Ответ. \АЕ\ : \ЕС\ = ——\BD\ : \DC\ = ХУ '
у+1 х+1
Задача 19.
В треугольнике PQR точка Т лежит на стороне PR так, что QTR = PQR. Известно, что \РТ\ = 8, \TR\ = 1. Найдите:
а) длину стороны QR ;
б) величину угла QRP, если длина радиуса описанной около треугольника PQT окружности равна 3\/3.
Идея. Рассмотреть треугольники QTR и PQR, доказать, что они подобны.
Указание. Вычислить значение отношения \QT\ : \PQ\ и длину отрезка QR.
Указание. Для нахождения длины отрезка PQ воспользоваться в треугольнике PQT формулой Герона и формулой пло- аЬс
■цади S=—.
Решение. Заметим, что треугольники QTR и PQR подобны по первому признаку подобия треугольников, так как угол R у них общий, а углы QTR и PQR равны по условию задачи. Из этого подобия получаем
\QT\ \QR\ \TR\ \PQ\ \PR\ \QR\
|<ЭД|2 = |ТД|-|РД| = 9
\QR\ = 3;
\QT\
\PQ\
С учётом полученного только что соотношения положим \QT\ = х, \PQ\ = Зх. Для ответа на второй вопрос задачи нам достаточно найти х, поскольку, применяя теорему косинусов для треугольника PQR, мы имеем
cos QRP =
\QR\2 + \PR\2 - \PQ\2 10 -x2
2 • |Qfl| • \PR\
Численное значение x можно найти, например, пользуясь формулой Герона и фор-
„ с аЪс мулои Ь = :
АН
х •Зх • 8
Sapqt = V (2ж + 4)(2ж — 4)(ж + 4)(4 — х) = => х4 - 15х2 + 48 = 0
х2 =
12у/3 15 ± л/33


278
Указания и решения
Подставляя найденные значения х2 в полученную ранее формулу, находим
7^75 5±л/33 г^пЪ ($±у/3з\
cos QRP = ——— => QRP = arccos I ——— J .
\ 1Z J
Ответ. \QR\ = 3, QRP = arccos | ---J •
Задача 20.
Через вершины А и В треугольника ABC проведена окружность с длиной радиуса 2\/5, отсекающая от прямой ВС отрезок длины 4\/5 и касающаяся прямой АС в точке А. Из точки В проведён перпендикуляр к прямой ВС до пересечения с прямой АС в точке F. Найдите площадь треугольника АВС, если \BF\ = 2.
Идея. Доказать, что прямая АВ проходит через центр окружности. Указание. Рассмотреть два случая расположения точки В.
Указание. Использовать подобие треугольников АОС и BFC (О - центр окружности).
Решение. Заметим, что если прямая пересекает окружность, то отрезок максимальной длины (эта длина равна длине диаметра этой окружности) будет отсечён от этой прямой в случае, когда она проходит через центр окружности. Верно и обратное утверждение: если прямая проходит через центр окружности, то отсекаемый от неё отрезок будет иметь ц А С
максимальную длину среди всех тех отрезков,
которые получаются при пересечении этой окружности какой-либо другой прямой.
Поэтому прямая ВС проходит через центр окружности, данной в условии задачи. Обозначим этот центр буквой О. Возможны два случая: либо точка О лежит на отрезке ВС (на чертеже этому случаю соответствует точка В\), либо точка В лежит на отрезке ОС (на чертеже этому случаю соответствует точка Въ). Первый случай невозможен, так как по условию задачи \ОА\ > \BF\, но
\ОА\ = \ОС\ • sin С < |BiC| • sin С < \ВгС\ • tg С=
Поэтому условию задачи соответствует второй случай. Треугольники АОС и B2F2C подобны по первому признаку подобия треугольников, так как угол С - их общий угол, а С АО = F2B2C = тг/2. Поэтому
JO£[ \AO\_ \AC\_ \АС\ = Л\ИС\
\f2c\ \b2f2\ \в2с\ ^ |лс|
Положим \В2С\ = ж, тогда \ОС\ = \ОВ2\ + \В2С\ = х + 2\/5. Применяя к треугольнику АОС теорему Пифагора, получаем
\ОС\2 = \АС\2 + \АО\2 =► (х + 2у/b)2 = {\/Ьх)2 Л- {2у/Ъ)2.


1.4. Подобие треугольников
279
Решая это уравнение, получим х = у/Ъ = \В2С\. Тогда |АС| = 5, \ОС\ = Зл/5. Теперь для нахождения площади треугольника АВС нам не хватает лишь синуса величины угла С. Из прямоугольного треугольника О АС находим
. я \ОА\ 2\/Ь 2 1 1D^, . я 5V5
“ jOC| = 3^ = 3 => *лдгС = 2-ИС|'|ВС|-».пС=—.
Ответ.
3
Задача 21.
Медианы АЛ/ и BE треугольника АБС пересекаются в точке О. Точки О, М, Е, С лежат на одной окружности, |Б.Е| = \АМ\ = 3. Найдите |АБ|.
Идея. Доказать, что треугольник АБС равносторонний.
Указание. Используя равенство медиан, показать, что треугольник АСВ равнобедренный.
Указание. Доказать, что ЛБОМ ~ АВСЕ.
Решение. Так как О - точка пересечения медиан и \ВЕ\ = | АМ\, то \ВО\ = \АО\ = 1\ВЕ\ = 2, \ОМ\ = |ОЯ| = l\BE\ = 1.
Также заметим, что углы АО# и ВОМ равны, поскольку они вертикальные. Следовательно, треугольники ВОМ и АОЕ равны по первому признаку равенства треугольников. Отсюда вытекает, что |AjE7| = \ВМ\ => |АС| = |БС|, то есть треугольник АБС равнобедренный.
Тогда треугольники ОМС и ОЕС равны по тре- q
тьему признаку равенства треугольников, из чего вытекает, что ОМС = ОЕС. Далее, в силу того что точки О, М, С и Е лежат на одной окружности,
АВОМ ~ АВСЕ (по утверждению 4 из теоретических материалов). Поэтому В МО = ВЕС.
Сравнивая последние два соотношения, получаем, что углы ОМС и ВМО равны. Но эти два угла смежные. Значит, они прямые, то есть AM - медиана и высота. Стало быть, |АБ| = |АС|, треугольник АБС равносторонний, величина угла АВМ равна 7г/3. Наконец, из прямоугольного ААМВ получаем
\АВ\ =
\АМ\
= 2>/3.
Ответ. 2>/3-


280
Указания и решения
Задача 22.
На сторонах АВ, ВС и АС треугольника АВС взяты точки D, Е и F соответственно. Отрезки АЕ и DF проходят через центр вписанной в треугольник АВС окружности, а прямые DF и ВС параллельны. Найдите длину отрезка BE и периметр треугольника АВС, если известно, что \ВС\ = 15, \BD\ = 6, \CF\ = 4.
Идея. Центр вписанной окружности лежит в точке пересечения биссектрис. Указание. Используя определение биссектрисы, найти DO и FO. Указание. Воспользоваться подобием треугольников АВС и ADF для нахождения AD и AF.
Указание. Использовать свойство биссектрисы АЕ для нахождения BE.
Решение. Обозначим центр вписанной в треугольник д
АВС окружности буквой О. Поскольку точка О лежит на отрезке АЕ, АЕ - биссектриса треугольника АВС, и для ответа на первый вопрос задачи нам желательно найти отношение \АВ\ : \АС\, чтобы воспользоваться основным свойством биссектрисы.
Отрезки ВО я СО являются отрезками биссектрис соответствующих углов треугольника АВС. Поэтому OBD = ОВЕ, но в силу параллельности прямых DF и ВС получаем DOB = ОВЕ. Следовательно, OBD = DOB и треугольник BDO равнобедренный. Аналогично доказывается, что треугольник CFO равнобедренный. Поэтому \DO\ = \BD\ = 6, \FO\ = \CF\ = 4.
Ясно, что треугольники ADF и ABC подобны. Из этого следует, что
\АВ\ _ \АС\ _ \ВС\ \AD\ + \BD\ _ |AF| + \CF\ __ 3
|AD| “ |AF| ~ \DF\ ^ \AD\ ~ |^F| _ 2'
Следовательно, \AD\ = 12, \AF\ = 8, Paabc = 45. Теперь найдём \BE\:
\BE\ \AB\ 3
\EC\ “ \AC\ “2’ => \BE\ = 9, |JS?C| = 6.
|БЕ| + |JSC| = \BC\ = 15
Ответ. IBE1! = 9, периметр треугольника ABC равен 45.
Задача 23.
Прямая, параллельная медиане AD прямоугольного треугольника АВС, пересекает его гипотенузу ВС в точке F, катет АВ в точке £ и прямую АС в точке Н. Известно, что \EF\ = 1, \ЕН\ = 3. Найдите длину гипотенузы ВС.


1.4- Подобие треугольников
281
Идея. Доказать, что треугольники ЕАН и ВАС подобны, воспользоваться подобием треугольников BEF и BAD.
Указание. Воспользоваться свойством медианы прямоугольного треугольника, проведённой к гипотенузе.
Решение. Положим \AD\ = х. По свойству медианы прямоугольного треугольника, проведённой к его гипотенузе,
\BD\ = \CD\ = х, DAC = DC А.
Поскольку EF\\AD, во-первых, подобны треугольники BEF и BAD и, во- вторых, в силу того, что углы DAC и ЕНС равны как соответственные, подобны треугольники ЕАН и ВАС. Из этих подобий вытекает
\EF\ _ \ВЕ\' \ЕН\ _ \АЕ\
\AD\ ~ \АВ\У \ВС\ ~ \АВ\ ’
Складывая полученные соотношения, получаем
- + — “ х 2х
\ВЕ\ + \АЕ\ \АВ\
= 1 =►
* = -, \ВС\ = 5.
Ответ. 5.
Задача 24-
На сторонах АВ и AD прямоугольника ABCD выбраны точки Р и Q (Р € АВ) так, что ZCQD = ZAQP = ZBPC. Вычислите длину отрезка АР, если |AJ5| = 6, \AD\ = d (b>d).
Идея. Воспользоваться тем, что треугольники AQP, j) q
ВРС и DQC попарно подобны.
Указание. Ввести обозначения \АР\=х, \AQ\=y.
Решение. Положим |АР| = х, \AQ\ = у. Тогда ясно, что \ВР\ = Ь—х, \DQ\ — d—у. Заметим, что треугольник AQP подобен треугольнику ВРС и треугольник DQC подобен треугольнику AQP. Из этих подобий вытекает
\AQ| _ \АР|
dy = х(Ъ—х)\
\AQ\ _ \АР\
by = x(d—y).
\ВР\ \ВС\ * 4 у’ \DQ\ \DC\
Выражая у из первого уравнения и подставляя его во второе, находим
х(Ь — х) ( , х(Ь — х)
— х- \ а
Ь-
d
b2—bx = d2—bx+x2
= Vb2 -d2.
Ответ. \/b2 — d2.


282
Указания и решения
Задача 25.
Прямые, содержащие высоты треугольника АВС, пересекаются в точке Н. Известно, что \ВН\ = 6, АВС = 7г/3. Найдите длину стороны АС.
Идея. Доказать, что треугольники ВНК и АСК подобны (К — основание высоты, опущенной на АС).
Указание. Воспользоваться теоремой о сумме величин углов треугольника и соотношениями между длинами сторон и величинами углов в прямоугольном треугольнике.
Решение. Сначала рассмотрим случай, когда углы ВАС и АСВ острые. Тогда точка Н лежит внутри треугольника АВС и КНВ = — —НВК = АСК. Из этого вытекает, что прямоугольные треугольники ВНК и АСК подобны, поэтому
\BH\jm . МП |ШЛ \АК\ Г 1 :Ж С Л
\АС\ \АК\ I ' I' '' \ВК\ 6 t%ABK 6л/3-
Если предположить, что угол ВАС тупой, то конфигурация несколько изменится, но тот факт, что КНВ = 7г/2 — НВК = АСК, остаётся неизменным. Поэтому опять-таки прямоугольные треугольники ВНК и АСК подобны, и, проводя аналогичные рассуждения, мы приходим к тому же ответу. Случай, когда угол АСВ тупой, рассматривается аналогично.
Ответ. 6>/3.
Задача 26.
В треугольнике АВС расположен прямоугольник PQRS так, что сторона PQ лежит на отрезке АС, а вершины R и S - на отрезках ВС и АВ соответственно. Найдите длину отрезка PS, если известно, что \АР\ = 1, \PQ\ = 5, \QC\ = 2, а периметр треугольника BRS равен 15.
Идея. Воспользоваться подобием треугольников SBR и АВС и равенством длин отрезков PS и RQ.
Указание. Используя подобие треугольников SBR и АВС, найти отношения |ВД| : \ВС\ и \BS\ :
Указание. Применить теорему Пифагора для ACRQ и A AS Р.


1.4. Подобие треугольников
283
Решение. Из того, что PQRS - прямоугольник, вытекает, что \PQ\ = \RS\ = 5, \PS\ = |RQ\, RS\\PQ. Значит, треугольники SBR и ABC подобны, поэтому
|RR| \BS\ |AS| 5 \BC\ “ \BA\ “ \CA\ ~ 8*
Положим \BC\ = 8x, \AB\ = 8у, тогда |J55| = 5y,
\BR\ = 5x, |AS| = Зу, |СД| = Зх. Далее, во-первых,
5 + 5х + by = 15 ==> х + у = 2 и, во-вторых,
\RQ\2 = |СД|2 - |CQ2| = 9х2 - 4; |Р5|2 = \AS\2 -\АР\2 = 9у2 - 1,
стало быть, 9х2 = 9у2 + 3. Решая полученные уравнения, находим х = У — 11/12, \PS\ = у/Ш/4.
13/12,
Ответ.
\/105
Задача 27.
На продолжении биссектрисы AL треугольника АВС за точку А взята точка D таким образом, что В DC = BAL = 7г/3, \AD\ = 10. Найдите площадь треугольника АВС.
Идея. Найти произведение \АВ\ • \АС\.
Указание. Доказать, что треугольники ACD и ADB подобны.
Решение. Ясно, что поскольку величины углов BAL и CAL равны 7г/3, величины смежных с ними углов BAD и CAD равны 2ж/Ъ. Положим ACD = а, тогда
ADC = тг - ACD - CAD = - - а,
о
ADB = J2ZX7 - ADC = а.
Значит, треугольники ACD и ADB подобны по первому признаку подобия треугольников, что
даёт нам
\АС\ \АР | ИД| \АВ\
\AB\-\AC\ = \AD\2 = 100.
Наконец, Saabc = \ • \АВ\ ■ \АС\ • sin ВАС = 25\/3.
D
Ответ. 25\/3.


284
Указания и решения
Задача 28.
В прямоугольном треугольнике АВС проведена биссектриса BD, а на гипотенузе ВС взята точка Н так, что DH 1_ BD. Найдите площадь треугольника АВС, если известно, что \СН\ = 1, \CD\ = 2.
Идея. Доказать, что ACDH ~ ACBD.
Указание. Доказать, что углы DBC и HDC равны. Используя подобие, найти длину отрезка ВС.
Указание. Воспользоваться основным свойством биссектрисы и теоремой Пифагора для нахождения катетов.
Решение. Положим ABD = CBD = /3, тогда ADB = | - /3, HDC = тг - ADB - BDH = 0.
Значит, треугольники CDH и CBD подобны по двум углам, из чего следует
\CD\ \СН\ \СР\2
\ВС\ \CD\ 11 \СН\
Для нахождения остальных элементов треугольника АВС проще всего поступить так: по основному свойству биссектрисы имеем \AD\ : \АВ\ = \CD\ : \ВС\ = 1:2, после чего положим \AD\ = у, \АВ\ = 2у и воспользуемся теоремой Пифагора:
\ВС\2 = \АВ\2 + \АС\2 =► 16 = Ау2 + {у + 2)2 =► у = 6/5.
Наконец, |АВ| = 12/5, |ЛС| = 16/5, Saabc ^ 96/25.
Ответ. 96/25.
Задача 29.
На стороне Л В выпуклого четырёхугольника ABC D выбрана точка М так, что /.AMD = /ADB и /АСМ = /АВС. Утроенный квадрат отношения расстояния от точки Л до прямой CD к расстоянию от точки С до прямой AD равен 2. \CD\ = 20. Найдите длину радиуса вписанной в треугольник ACD окружности.
Идея. Использовать равенство углов для нахождения пар подобных треугольников.
Указание. Используя равенство углов из условия, показать, что A AMD ~ AADB, A ACM ~ А АВС.
Указание. Доказать, что треугольник ACD равнобедренный.
Указание. Найти отношение высот треугольника ACD.
Указание. Для нахождения радиуса вписанной окружности использовать формулу Герона и формулу S = рг.
В


1.4. Подобие треугольников
285
Решение. В задачах, условие которых содержит равенство каких-либо углов, как правило, надо искать пары подобных треугольников. Заметим, что подобны треугольники AMD и ADB (угол А у них общий и по условию задачи равны углы AMD и ADB), а также подобны треугольники ACM и АВС (угол А у них общий и по условию задачи равны угла ACM и АВС). Из этого вытекает, что
\АМ\ \AD\ \AD\ ~ \АВ\ \АС\ \АМ\ \АВ\ ~ \АС\
\AD\2 = \АМ\ ■ \АВ\;
\АС\2 = \АМ\ ■ \АВ\.
Таким образом, \АС\ = \AD\, треугольник ACD равнобедренный. Далее все более-менее просто. Расстояния от точки А до прямой CD и от точки С до прямой AD суть не что иное, как длины высот треугольника ADC (обозначим эти длины как hcD и Had)- Из условия задачи находим
зГ—V = 2 =► ^ = л/?.
\ h-AD) h-AD V 3
После этого запишем двумя способами площадь треугольника ACD :
Saacd = \ ■ \CD\ ■ hCD = \ • \AD\ ■ hAD =» \AD\ = \CD\ ■ ^ = 20^. Наконец, применяя формулу Герона и формулу S = рг, получаем
Paacd = 20 ^ ; Saacd = 100taacd = 4\/l0 - 2у/\Ъ.
Ответ. 4\/l0 — 2л/15.
Задача 30.
На сторонах АБ и ВС треугольника АВС взяты точки М и N соответственно таким образом, что ВАС = BNM = 7г/6. Также известно, что \АМ\ = \CN\. Найдите отношение периметра треугольника АВС к сумме длин его медиан.
Идея. Доказать, что треугольник АВС равнобедренный.
Указание. Пользуясь тем, что треугольники АВС и NBM подобны, доказать, что треугольник АВС равнобедренный.
Указание. Выразить стороны и медианы треугольника АВС через радиус описанной окружности.


286
Указания и решения
Решение. Введём обозначения \АМ\ — |CN\ — г, \МВ\ — р, \NB\ = q. Треугольники ABC и NBM подобны по двум углам, поэтому
\АВ\ \ВС\ p + r q + r 2 2
1 1 - 1 1 —" - <=> р2 + pr = qz + qr
|ЛГВ| \МВ\ q р
<=> р2 - q2 + pr - qr = 0 <*=> (р - q){p + q + г) = 0 => р = q.
Значит, треугольник АВС равнобедренный,
ВАС — АСВ = 7г/6, АВС = 27г/3. Дальше мож¬
но поступить, например, так. Пусть длина радиуса окружности, описанной около треугольника АВС, равна R, тогда по теореме синусов
\АВ\ = \ВС\ = 2i?sin £ = Д, |Ж7| = 2Д sin ^ = Д>/3.
6 3
После этого по формуле длины медианы находим
•I D /у Г>
тАв — тпвс = 2 у2ДМ-бД2ТГд2 = ___ t тАс = Ь,Ас = -^-
Наконец,
Раавс _ /2 -Ь i? -Ь Ry/b _ 4 + 2\/3 тлв + тле + rnBc Ry/7 + § 2>/7 + 1 *
4 + 2ч/3
Ответ. —т= .
2л/7 + 1
Задача 31.
Найдите пару подобных треугольников, длины всех сторон которых выражаются целыми числами, если известно, что длины двух сторон первого треугольника равны длинам двух сторон второго треугольника, а длины их третьих сторон отличаются на 61.
Идея. Использовать целочисленность сторон треугольников и рациональность коэффициента подобия.
Указание. Ввести коэффициент подобия треугольников. Использовать целочисленность сторон треугольников и рациональность коэффициента подобия. Указание. Доказать, что длины меньшей стороны первого треугольника и большей стороны второго треугольника - кубы целых чисел.
Решение. Пусть длины сторон первого треугольника равны а, Ь и с, причём а < b < с. Будем считать, что коэффициент подобия треугольников равен к, тогда длины сторон второго треугольника равны ка, кЬ и кс соответственно. Из условия задачи мы получаем ка — 6, kb = с, кс — а = 61, стало быть, с = к2а, (к3 — 1)а = 61. Далее, поскольку а, £>, с - целые числа, число к рациональное, то есть к = ш/п, где тип- натуральные числа. Тогда мы имеем


1.5. Площадь треугольника
287
Отметим, что в силу простоты числа 61 дробь сократима, только если а
а
делится на 61. Но тогда а = 61 d, — Ф . Противоречие. Значит,
а ап6
га3 = а -1-61, п3 = а => ш3 — п3 = 61 <<=> (m — п)(т2 + тп + п2) = 61.
Возможны два варианта: т — п— 1, га2 -Ь тп + п2 = 61, тогда т — 5, п — 4, либо т — п = 61, т2 + тп + п2 = 1, что не выполняется ни при каких целых тип. Итак, к = 5/4, а — 64.
Ответ. 64,80,100 и 80,100,125.
1.5. 	Площадь треугольника Задача 1.
На стороне ХМ треугольника KLM, площадь которого равна 4, взята точка iV таким образом, что \КМ\ = 4|MiV|. Найдите длину отрезка LiV, если длина стороны KL равна 2л/3, a KLN = п/3.
Идея. Найти площадь треугольника КLN.
Указание. Воспользоваться леммой 1 о площадях для нахождения площади треугольника KLN.
Указание. Использовать формулу площади треугольника для нахождения длины отрезка L N.
Решение. Пользуясь леммой 1 о площадях, получаем
Sakln \KN\ 3 0
~Б Ti777i = 1 ==>' bAKLN — О.
Saklm \КМ\ 4
Теперь применим формулу площади треугольника через полупроизведение сторон на синус угла между ними:
Sakln = ^-\KLI-\LN\-smKLN => 3 = |-2%/3-|LiV| ~ =» \LN\ = 2.
Ответ. 2.
Задача 2.
Центр О окружности, длина радиуса которой равна 3, лежит на гипотенузе АС прямоугольного треугольника АВС. Его катеты касаются этой окружности. Найдите площадь треугольника АВС, если известно, что \ОС\ = 5.
Идея. Воспользоваться подобием треугольников АВС и ОКС, где К - точка касания окружности и катета ВС.
Указание. Найти длины отрезков КС и ВС.


288
Указания и решения
Решение. Четырёхугольник OKBL является квадратом, поэтому \ВК\ — \ОК\ = 3. По теореме Пифагора находим \КС\ = 4. Из этого вытекает, что \ВС\ = 7, а площадь треугольника О КС равна 6. Наконец, треугольники АВС и ОКС подобны, поэтому
Saabc (\ВС\\2 49
Saokc VltfCi; 16
n 147
Ответ. ——.
с 49 « 147
Saabc = ^-Q = —.
Задача 3.
Внутри прямоугольного треугольника АВС (угол АВС прямой) взята точка D таким образом, что площади треугольников ABD и BCD соответственно в три и в четыре раза меньше площади треугольника АВС. Найдите длину отрезка BD, если \AD\ = a, \DC\ = с.
Идея. Опустить из точки D перпендикуляры DK и DL на стороны ВС и АВ, найти отношения \ВК\ : \КС\ и \BL\ : \LA\.
Указание. Воспользоваться леммой 3.
Указание. Записать теорему Пифагора для треугольников ADL, С DK и BDL.
Решение. Опустим из точки D перпендикуляры q DK и DL на стороны ВС и АВ соответственно, будем считать, что \DK\ = ж, \DL\ = у. Поскольку угол АВС прямой, BKDL - прямоугольник, из чего следует \ВК\ = \DL\ — у и \BL\ = \DK\ = х. Для того чтобы найти \BD\, достаточно найти \DL\ и \BL\, то есть хну. Тогда по теореме Пифагора из треугольника BDL получим \BD\2 = х2 + у2. Следовательно, нам не надо знать сами х и у, достаточно найти их квадраты.
Далее воспользуемся леммой 3. Получим
1 _ Saabd _ \DL\
3 1
4
Saabc
Sabcd
\BC\
\DK\
\BC\ = Зу, \КС\ = \ВС\ - \ВК\ = 2у; \АВ\ = 4х, \LA\ = \АВ\ - \BL\ = Зх.
Saabc \АВ\
Теперь, записав теорему Пифагора для треугольников ADL, CDK, мы получим систему из двух уравнений с двумя переменными:
\AD\2 = \LA\2 + |DL|2, \DC\2 = \KC\2 + \DK\2,
a2 — 9x2 + y2, c2 = 4 y2 + x2,
x2 =
4a2 - <
35
2 9c2 — a2
У =-35“-
Наконец, |jBD|2 p- /
|SL|2 + \DL\2 = x2 + y2 =
3 a2 + 8c2 35
Ответ.
За2 + 8c2
35


1.5. Площадь треугольника
289
Задача 4-
В трапеции ABCD \CD\ = 12, боковая сторона AD перпендикулярна основаниям, а её длина равна 9. Длина отрезка АО, где О - точка пересечения диагоналей трапеции ABCD, равна 6. Найдите площадь треугольника ВОС.
Идея. Доказать, что площади треугольников AOD и ВОС равны.
Указание. Используя лемму 2, доказать, что площади треугольников AOD и ВОС равны. ^ ®
Указание. Используя лемму 1, выразить Saaod через Saacd•
Решение. По условию задачи треугольник ACD прямоугольный, поэтому
Saacd = \ • \AD\ ■ \CD\ = 54, \АС\ = y/\AD\2 + \CD\2 = 15.
Далее заметим, что по лемме 2 площади треугольников ACD и BCD равны. А из этого вытекает и равенство площадей треугольников AOD и ВОС, поскольку
Saaod = Saacd Наконец, по лемме 1 Saaod \АО\ б 2
Saacd
Ответ.
\АС\
108
~5~’
15
Sacod, Saboc — Sabcd — Sacod•
Saboc = Saaod = Saacd • - = 54 • - = .
Задача 5.
Прямая, проходящая через вершину основания равнобедренного треугольника, делит его площадь пополам, а периметр делит на части 5 и 7 м. Найдите площадь треугольника.
Идея. Доказать, что эта прямая проходит через середину боковой стороны треугольника.
Указание. Используя лемму 1 о площадях, показать, что эта прямая проходит через середину боковой стороны треугольника.
Указание. Рассмотреть два случая деления периметра на части 5 и 7 м. Указание. Воспользоваться формулой Герона.
Решение. Обозначим вершины треугольника буквами А, В и С, будем считать, что \АВ\ = \ВС\. Предположим, что прямая из условия задачи проходит через вершину А, точку её пересечения со стороной ВС обозначим буквой D. Пользуясь леммами о площадях, получаем
1 = = - iBD| = |C!D|'
10 Геометрия


290
Указания и решения
Теперь положим \АВ\ — \ВС\ = х, тогда \BD\ = \CD\ = х/2, а длину отрезка АС обозначим буквой у. Поскольку нам не известно, какая из частей периметра треугольника АВС равна 5 м, придётся разобрать два случая:
Г \AB\ + \BD\ = 5, \АС\ + \CD\ = 7;
х +
5,
У+2 = 7;
10
16
у=т;
Г \АВ\ + \BD\ = 7, \ \АС\ + \CD\ = 5;
х
*+2=7.
X
2/+2 =5;
14
3 ’
v=3-
С с
Для вычисления площади нашего треугольника можно воспользоваться, например, формулой Герона (так как нам известны длины всех его сторон). В первом случае получаем S = 16/3 м2, во втором - S = 8>/5/3 м2.
16
3
Ответ. ^ м2 или —г— м2
8у/Е
Задача 6.
В равнобедренном треугольнике АВС длина основания АС равна 2, величина угла АСВ равна 7г/6. Из вершины А к боковой стороне ВС проведены медиана AD и биссектриса АЕ. Найдите площадь треугольника ADE.
Идея. Найти отношение \ED\ : \ВС\, применить леммы о площадях.
Указание. Воспользоваться основным свойством биссектрисы треугольника.
Решение. Так как треугольник равно- А бедренный, то
\АВ\ = \ВС\ =
1 2
cos АСВ у/3' Пользуясь основным свойством биссектрисы, находим
|CS| _ IAC7I _ ^ ]ВЕ] _ |В<7|
\ВЕ\ \АВ\ 1 1 у/3 + l'
\ВС\ \ВС\ (>/5-1)|ВС|
\ED\ = \BD\ - \ВЕ\ =
у/3+1 2(^+1)


1.5. Площадь треугольника
291
Наконец,
1 SAADE _ \ED\ (х/3-1) ^ 0 2у/3 — 3
Sa*bc~js; sZibc - |Щ - £(Л7Т) ”*■ S^E~ 6 '
2\/3 — 3 Ответ. .
Задача 7.
В треугольнике FGH угол G прямой, \FG\ = 8, \GH\ = 2. Точка D лежит на стороне FH, А и В - точки пересечения медиан треугольников FGD и DGH соответственно. Найдите площадь треугольника GAB.
Идея. Провести отрезки GL и GK - медианы треугольников FGD и DG# соответственно. Найти отношение \KL\ : \FH\.
Указание. Медианы треугольника делятся точкой пересечения в отношении 2:1, считая от вершины.
Применить леммы 1 и 4.
Решение. Проведём отрезки GL и GK - медианы треугольников FGD и DGH соответственно. Заметим, что \DK\ — - \DH\, \DL\ — -\DF\, поэтому
\KL\ = \DK\ + \DL\ = \\DH\ + \\DF\ = | • (|ЯЯ| + |PF|) = \\FH\.
Теперь можно составить план действий. Поскольку площадь исходного треугольника мы легко можем посчитать, надо протянуть цепочку от треугольника GAB к треугольнику FGH. Вот план, который мы можем реализовать:
Sagab —> Sagkl —> Saghf-
Сначала воспользуемся тем фактом, что медианы треугольника делятся точкой пересечения в отношении 2:1, считая от вершины:
\GA\ = \\GL\, \GB\ = 1\GK\.
Применяя лемму 4 к треугольникам GAB и GLK, находим
Sagab _ \GA\ • \GB\ _ \\GL\ ■ %\GK\ _ 4 ^ c 4 c
Saglk ~ \GL\ • \GK\ ~ \GL\ ■ \GK\ 9 AGAB 9b^GLK'
Далее, применяя лемму 1 к треугольникам GLK и FGH, получаем
Saglk _ \KL\ 1
Safgh \FH\ 2
Saglk = Isafgh
Sagab = qSafgh-
Так как Safgh = \ • \FG\ ■ \GH\ = 8, to Sagab = у •


292
Указания и решения
Задача 8.
Дан треугольник АВС, площадь которого равна 2. На его медианах АК, BL и CN взяты соответственно точки Р, Q и Д так, что |АР| = |PjRT| , \QL\ = 2|PQ|, |СД| : |PiV| =5:4. Найдите площадь треугольника PQR.
Идея. Представить площадь треугольника PQR как сумму площадей треугольников PMR, PMQ и QMR (М - точка пересечения медиан).
Указание. Воспользоваться леммами о площадях.
Решение. Поскольку нам известны все отношения на медианах, можно составить план действий.
Обозначим точку пересечения медиан треугольника АВС буквой М. Заметим, что, во-первых, точка М находится внутри треугольника PQR (это вытекает из соотношений, данных в условии), поэтому площадь треугольника PQR есть сумма площадей треугольников PMR, PMQ и QMR, и, во-вторых, площади треугольников AM В, AMС и ВМС одинаковы (это вытекает из того, что медианы треугольника делят его на шесть равных по площади треугольников, докажите самостоятельно этот факт) и равны, исходя из условия задачи, 2/3. Поэтому нам надо найти, в каких отношениях точки Р, Q и R делят отрезки AM, ВМ И СМ соответственно. Для этого воспользуемся отношениями, данными в условии, и тем фактом, что медианы треугольника делятся точкой пересечения в отношении 2:1, считая от вершины. Положим \АК\ = 6х, \BL\ = 6у, \CN\ = 9z. Тогда
\АМ\ = 4х, \АР\ = Зх, \РМ\=х; \ВМ\ = 4у, \BQ\ = 2у, \QM\=2y;
\СМ\ = 6z, \CR\ = 5z, \RM\ = z.
Теперь осталось лишь воспользоваться леммами о площадях:
Sapmr \РМ\ • \RM\ 1
Saamc \АМ\ ■ \СМ\ 24
Sapmr —
36
Sapmq \РМ\ • \QM\ _ 1
Saamb \АМ\ • \ВМ\ 8
Sapmr —
Saqmr \QM\ • \RM\ 1
Sabmc \BM\ ■ \CM\ 12
Sapmr = jg
Значит, площадь треугольника PQR равна 1/6.


1.5. Площадь треугольника
293
Задача 9.
Точка N лежит на гипотенузе АС прямоугольного равнобедренного треугольника АВС. Точка М расположена на катете АВ таким образом, что угол MNC прямой. Известно, что площадь треугольника MNC составляет три восьмых площади треугольника АВС. Вычислите отношение |АЛГ| : |А^С7|.
Идея. Воспользоваться формулой площади прямоугольно- д го треугольника.
Указание. Ввести обозначения \AN\ = ж, \АВ\ = а. Используя условие на площади, выразить ж через а.
М
Решение. Введём обозначение \АВ\ = \ВС\ = а. Треугольник АВС прямоугольный и равнобедренный, поэтому \АС\ = ау/2. Ясно, что треугольник AMN тоже пря- ^ моугольный и равнобедренный. Положим \AN\ = ж, тогда \MN\ = ж, \АМ\ = ху/2, \CN\ = ау/2 — ж. Применяя формулу площади прямоугольного треугольника, из условия получаем
3 1 3 1
Sacmn = оSaabc => --х-(ау/2 — х) = - --а2 => 8х2-8у/2ах+3а2 = 0.
о 2 о 2
_ as/2 3 as/2
Решая это однородное уравнение, находим ж = —— или ж = —~—. Нам подходит
меньший их этих корней, так как, в силу того что точка М лежит на катете А В, длина отрезка AM меньше длины отрезка А В, то есть ху/2 < а.
Наконец, находим требуемое отношение |АЛГ| : \NC\ = ж : (ау/2 — ж) = 1 : 3.
Ответ. 1:3.
Задача 10.
Прямоугольные треугольники АВС и ABD имеют общую гипотенузу АВ, длина которой равна 5. Точки С и D расположены по разные стороны от прямой АВ, \ВС\ = \BD\ = 3. Точка Е лежит на стороне АС, \ЕС\ = 1. Точка F лежит на стороне AD, \FD\ = 2. Найдите площадь пятиугольника ECBDF.
Идея. Искомую площадь представить как разность площадей четырёхугольника ACBD и треугольника AEF.
Указание. Воспользоваться подобием треугольников, лемма- g ми 4 и 5.
Решение. Заметим, что треугольники АВС и ABD равны по гипотенузе и катету. Значит, \ВС\ = \BD\, \АС\ = И^|, поэто- ^ му точки А и В лежат на серединном перпендикуляре к отрезку CD. Но поскольку через две точки можно провести только одну прямую, прямая АВ и есть серединный перпендикуляр к отрезку CD. Обозначим точку их пересечения буквой Р, тогда \СР\ = \DP\, а треугольник АРС равен треугольнику APD.


294
Указания и решенья
Искомую площадь удобнее всего искать как разность площадей четырёхугольника ACBD и треугольника AEF. Площадь четырёхугольника ACBD найти просто:
|Ж7|2 - \АВ\2 - \ВС\2 = 16 =► \АС\ — 4, Saabc = \ • \АС\ ■ \ВС\ = 6,
Sacbd — Saabc + Saabd, ААВС = AABD => Sacbd = 2 • Saabc — 12.
Для отыскания площади треугольника AEF сначала найдём площадь треугольника ACD, пользуясь подобием треугольников и леммой 5:
А ,РГ Л ИС| 4 Яллрс ,2 16 . „ 16 96
ДЛРС ~ ДЛСВ, *=Ц5| = 5, g^ = k = 25 =*■ = 25 25’
192
Saacd = + ААРС = AAPD => Saacd = %’S аарс =
Zo
Теперь, учитывая, что |AF| = |АС| — |FC| = 3, |AF| = |AD| — |FD| = 2, применим лемму 4:
Saasf _ \АЕ\ ■ [AF| _ 3 • 2 _ 3 _ 3 с _72
б'длсо |Ж7| • \AD\ 4-4 8 AAiSF 8' AACD 25'
Наконец,
72 228
Secbdf — Sabcd — Saaef = 12 — — = —
zo zo
n 228
Ответ. ——.
25
Задача 11.
В треугольнике ABC медиана AD и биссектриса BE перпендикулярны и пересекаются в точке F. Найдите площадь треугольника АВС, если площадь треугольника DEF равна 5.
Идея. Найти соотношения между площадями треугольников DEF, DAE и DAC.
Указание. Доказать, что треугольник ABD равнобедренный.
Указание. Используя определение медианы и свойство биссектрисы, найти \АЕ\ : \ЕС\.
Указание. Составить план и воспользоваться леммой 1.
Решение. Заметим, что в треугольнике ABD отрезок BF является одновременно биссектрисой и высотой. Из этого следует, что треугольник ABD равнобедренный, \АВ\ = \BD\, а отрезок BF является медианой этого треугольника, то есть \AF\ — \DF\. Далее, поскольку AD - медиана треугольника АВС,


1.5. Площадь треугольника
295
\BD\ = |iX7|. Обозначим длины отрезков АВ и AF через х и у соответственно, тогда из вышесказанного вытекает, что \DF\ = у, \DC\ = ж, |AD| = 2у, \ВС\=2х.
Теперь, пользуясь основным свойством биссектрисы треугольника, находим
\АЕ\ \АВ\ х 1
\ЕС\ \ВС\
поэтому если положить \АЕ\ = г, то \ЕС\ вить план:
Sadef —> Saade —> Применяя лемму 1, получаем:
Saade
\AD\
-
— о
Sadef
\DF\
У
— L
Saadc
\AC\
3 z
— Q
Saade
\AE\
z
— u
Saabc
\BC\
_ 2x
= 2
Saadc
\DC\
X
Ответ. 60.
2х 2 ’
2г, \АС\ = 3z. Теперь можно соста- Saadc —> Saabc•
=> Saade = Ю;
=> Saadc = 30;
=> Saabc = 60.
Задача 12.
В ромбе ABCD перпендикуляр к стороне AD, восстановленный из её середины, пересекает диагональ АС в точке М, а перпендикуляр к стороне CD, восстановленный из её середины, пересекает диагональ АС в точке N. Найдите отношение площадей треугольника MND и ромба ABCD, если BAD = п/3.
Идея. Доказать, что точки М и N являются точками пересечения медиан треугольников ABD и CBD, найти значение отношения \MN\ : |АС|.
Указание. Воспользоваться тем, что треугольники ABD и СBD рав- д посторонние.
Решение. В этой задаче сначала стоит заметить, что ромб ABCD фактически составлен из двух равносторонних треугольников ABD и CBD. Обосновать этот факт легко: \АВ\ = \AD\, поэтому треугольник ABD равнобедренный, а из того, что величина угла BAD равна п/3, следует, что и ABD = ADB = 7г/3, то есть треугольник ABD равносторонний, \BD\ = \АВ\. Значит, \BD\ = \ВС\ = \CD\ и треугольник CBD также равносторонний.
В


296
Указания и решения
Далее обозначим точку пересечения диагоналей ромба ABCD буквой Р. Известно, что диагонали ромба перпендикулярны и делятся точкой пересечения пополам. Это вытекает, например, из того, что треугольники АВС и ADC равны по трем сторонам, поэтому равны углы ВАС и DАС, значит, АР - биссектриса, медиана и высота равнобедренного треугольника ABD. Для нас же из вышесказанного актуальным является то, что АР и СР - медианы треугольников ABD и CBD, а площадь треугольника ACD равна половине площади ромба ABCD.
Теперь обозначим буквами Q и R середины сторон AD и CD соответственно. Поскольку \АВ\ = \BD\, точка В лежит на прямой, перпендикулярной стороне AD и проходящей через её середину, то есть на прямой из условия задачи. Итак,
точка М есть точка пересечения прямых BQ и АР, а с учётом того, что BQ
и АР - медианы треугольника ABD, она является точкой пересечения медиан треугольника ABD. Аналогично доказывается, что N - точка пересечения медиан треугольника CBD.
Наконец, воспользуемся тем, что медианы треугольника делятся точкой пересечения в отношении 2:1, считая от вершины, и леммой 1:
\АМ\ : \МР\ =2:1, \АМ\ + \МР\ = \АР\ =► \МР\ = i|AP|;
О
|СЛГ| : \NP\ =2:1, \CN\ + |7VP| = \СР\ =*> \NP\ = ^|СР|,
О
\MN\ = \МР\ + |iVP| = |(|АР| + \СР\) = \\АС[,
Samnd _ \MN| _ 1 Saacd _ 1 Saacd \AC I 3’ Sabcd 2
Ответ. 1:6.
Задача 13.
Основание А В трапеции ABCD вдвое длиннее основания CD и вдвое длиннее боковой стороны AD. Найдите площадь трапеции ABCD, если известно, что \АС\ =а, \ВС\ =Ь.
с D
Идея. Доказать, что треугольник АВС прямоугольный.
Указание. Воспользоваться критерием прямоугольности треугольника и доказать, что угол АСВ прямой.
Указание. Применить лемму 2. в Е А
Решение. Поскольку ABCD - трапеция, AB\\CD. Из этого вытекает, что углы ВАС и ACD равны, обозначим их величины буквой а и положим \AD\ = \CD\ = ж, \АВ\ = 2х. Предложим два различных способа решения этой задачи.
Первый способ. Из равнобедренного треугольника ACD имеем а = 2xcosa и, записывая теорему косинусов для треугольника АВС, получаем
\ВС\2 = \АВ\2 + \АС\2 - 2 • \АВ\ • \АС\ • cos RAC =»
=> b2 — а2 + 4ж2 — 2а-2х cos а => Ь2 = а2 + 4х2 — 2а2 => 4х2=а2 + Ь2.
о
Samnd _ 1 Sabcd 6


1.5. Площадь треугольника
297
Из последнего равенства следует, что треугольник АВС прямоугольный, поэтому ab _
его площадь равна —. 1огда, применяя лемму 2, находим
Saabc \АВ\ ab 3 ab
Saadc = \CD\ = adc = ~^\ &abcd = эаавс + jaadc =
Второй способ. Обозначим середину стороны AD буквой Е. Тогда \АЕ\ = х, поэтому треугольники АСЕ и СAD равны по двум сторонам и углу между ними, что даёт нам \СЕ\ = \AD\ = х. Таким образом, длина медианы СЕ треугольника АВС равна половине длины его стороны АВ, стало быть, по критерию прямо- угольности треугольник АВС прямоугольный, угол АСВ прямой. Дальнейшие рассуждения совпадают с рассуждениями из первого способа.
3 аЪ
Ответ. —-.
4
Задача 14-
На сторонах KL и LM треугольника KLM взяты точки А и В соответственно. Отрезки КВ и МА пересекаются в точке С. Найдите площадь треугольника ALC, если известно, что площади треугольников К АС, МВС и КСМ равны соответственно 12, 50 и 45.
Идея. Воспользоваться леммами о площадях. к
Указание. Найти \АС\ : \СМ\, \ВС\ : \СК\.
Указание. Обозначить площади треугольников ALC и BLC буквами S\ и S2 соответственно и применить леммы о площадях к парам треугольников ALC и МLC, BLC и KLC.
Решение. Сначала заметим, что
\АС\ _ Sakac _ \ВС\ _ Sambc _ 10 \СМ\ Sakcm 15’ \СК\ Sakcm 9
Далее обозначим площади треугольников ALC и BLC буквами S\ и S2 соот¬
ветственно и воспользуемся леммами о площадях:
Saalc = \АС\ Si = 4 Sablc = \ВС\ S2 = 10
Samcl \СМ\ ^ 52 + 50 15’ Sakcl \СК\ ^ Si +12 9'
Решая полученную систему уравнений, находим S\ = 24, S2 = 40.
Ответ. 24.
Задача 15.
В параллелограмме ABCD на диагонали АС взята точка Е, а на стороне AD взята точка F, причём \АС\ = 3|АЕ|, \AD\ = 4\AF\. Найдите площадь параллелограмма ABCD, если площадь четырёхугольника ABGE, где G - точка пересечения прямой FE и отрезка ВС, равна 8.


298
Указания и решения
Идея. Площадь четырёхугольника ABGE представить в виде разности площадей треугольников АВС и С EG.
Указание. Используя подобие, найти отношение \CG\-.\BC\.
Указание. Воспользоваться леммами 4 и 2.
Решение. Положим \AF\ = х, \АЕ\ = у. Тогда по условию задачи \АС\ = 3у, \ЕС\ = 2у, \AD\ = Ах,
\FD\ = Зх. Далее, поскольку ABCD - параллелограмм, \ВС\ = \AD\ = Ах, AD\\BC, треугольники AEF и С EG подобны. Стало быть,
= №С\=\ =* \CG\=2\AF\ = 2x => \BG\ = \BC\-\CG\ = 2x.
Теперь заметим, что данная нам в условии площадь четырехугольника ABGE может быть представлена в виде разности площадей треугольников АВС и С EG. Обозначим площадь треугольника С EG через 5, тогда площадь треугольника АВС равна S Н- 8. Воспользуемся леммой 4:
Saceg \СЕ\ • \CG\ _S_ = 2yj2x = l
Saabc \AC\-\BC\ S + 8 Зу4с 3
Стало быть, площадь треугольника АВС равна 12. Наконец, из леммы 2 вытекает, что площади треугольников АВС и ACD равны, поэтому площадь параллелограмма ABCD равна 24.
Ответ. 24.
Задача 16.
В треугольнике АВС на стороне АВ взята точка К, а на стороне ВС взята
точка L так, что |АЙГ| : \ВК\ = 1:2, \CL\ : \BL\ = 2:1. Пусть Q - точка
пересечения прямых AL и С К. Найдите площадь треугольника АВС, если дано, что площадь треугольника BQC равна 1.
Идея. Вычислить отношение |jFsTC7| : \QC\, применить в
леммы о площадях.
Указание. Воспользоваться теоремой Менелая.
Решение. План перехода от треугольника BQC к треугольнику АВС очевиден:
Sabqc —> S&bkc —>• Saabc• А С
Не хватает только отношения \КС\ : \QC\. Положим \АК\ = ж, \ВК\ = 2ж,
\BL\ = у, \CL\ = 2у. Применяя теорему Менелая к треугольнику ВСК и секущей LA, находим
\KQ\ \CL\ \ВА\ \KQ\=y_ x_=l
\QC\ ' \LB\ ' \AK\ \QC\ 2y 3x 6‘


1.5. Площадь треугольника
299
В соответствии с этим обозначим \KQ\ = z, \QC\ = бz, тогда \КС\ — 7z. Наконец, применяя лемму 1 о площадях, находим
Sabkc _ \КС\ _ 7 ^ с _ 7 Saabc _ \АВ\ _ 3 ^ а _ 7
Sabqc “ \QC\ ~ 6 =* 5двкс ” б5 5лбкс ~ \вк\ ” 2 =* “ 4-
7
Ответ. -.
4
Задача 17.
В равнобедренный треугольник АВС с основанием АС вписана окружность, которая касается боковой стороны АВ в точке М. Через точку М проведён перпендикуляр ML к стороне АС треугольника АВС (точка L - основание этого перпендикуляра). Найдите величину угла ВС А, если известно, что площадь треугольника АВС равна 1, а площадь четырёхугольника LMBC равна S.
Идея. Воспользоваться леммой 4 и формулой длины отрезков, на которые окружность, вписанная в треугольник, разбивает точками касания его стороны. Указание. Выразить длины отрезков AM, AL и АС через длину стороны АВ и величину угла ВС А.
Решение. Пусть ВАС = АСВ — а, \АВ\ = р, тогда \ВС\ = р, \АС\ = 2pcoso;. Пользуясь формулой длины отрезков, на которые окружность, вписанная в треугольник, разбивает точками касания его стороны, находим \АМ\ = раавс — \ВС\ = рcosa, после чего из прямоугольного треугольника AML получаем
\AL\ = \АМ\ • cos В АС — р cos2 a.
Наконец, применяя лемму 4, имеем
Saaml = |АМ\ • \AL\
Saabc \АВ\ • \АС\
Ответ, arccos л/2 — 25.
cos3 а 2 cos а
cos а = д/2 — 2S.
Задача 18.
Через вершины А и В треугольника АВС проведена окружность, пересекающая стороны ВС и АС в точках D и Е соответственно. Площадь треугольника CDE в 7 раз меньше площади четырёхугольника ABDE. Найдите \DE\ и длину радиуса окружности, если \АВ\ = 4, С = 45°.
Идея. Воспользоваться подобием треугольников АВС и DEC.
Указание. Используя подобие треугольников АВС и DEC, найти \DE\. Указание. Выразить величину угла BE А через величину угла С BE. Указание. Применить теорему синусов к треугольникам BDE и АВЕ.


300
Указания и решения
Решение. Заметим, что треугольники АВС и DEC подобны. Тогда, вводя в соответствии с условием задачи обозначения Sadec — S, Sabde — 7S, получаем
Sadec = (\DE\\2 S (\DE\\2
Saabc V|A£|/ S + 7S \ 4 J
=» \DE\ = V2.
Для нахождения длины радиуса окружности поступим следующим образом: обозначим её через R, а градусную меру угла С BE обозначим через /3°. Тогда градусная мера угла АЕВ, в силу того что это внешний угол треугольника С BE, равна (/9 + 45)°. Наконец, треугольники BDE и АВЕ оба вписаны в нашу окружность, поэтому, записывая теорему синусов, получаем
\АВ\ _2R_ \DE\_ ^ 4 у/2 2Л
sin АЕВ sin DBE sin(/3 + 45)° sin£°
sin(ff + 45)° = ^ ^cosff° + ^sinft0 = ^
sin /3° sin /3°
Значит, sin /3° = 1 / y/lO, R = y/E.
Ответ. |jDjE7| = л/2, длина радиуса окружности равна у/Е.
Задача 19.
На стороне АБ треугольника АВС взята точка Е, а на стороне - точка D так, что |АЕ| = 2, |CD| = 1. Прямые AD и СЕ пересекаются в точке О. Найдите площадь четырёхугольника В DOE, если \АВ\ = \ВС\ = 8, |АС| = 6.
Идея. Площадь четырёхугольника В DOE искать как разность площадей треугольников, например ABD и АОЕ.
Указание. Применяя теорему Менелая к треугольнику ABD и секущей ЕС, найти отношение \АО\ : \OD\.
Указание. Воспользоваться леммами о площадях.
Решение. Площадь четырёхугольника В DOE лучше искать как разность площадей треугольников, например ABD и АОЕ. Тогда, поскольку площадь треугольника АВС мы можем найти по формуле Герона, план действий выглядит так:
Saabc —> Saabd —> Saaoe•
Для последнего перехода нам не хватает значения отношения \АО\ : \AD\. Ясно, что \BD\ = 7, |ВЕ\ = 6, Saabc = Зу/ЕЕ. Применяя теорему Менелая к треугольнику ABD и секущей ЕС, находим
\DO\ \АЕ\ \ВС\ _ \DO\ _ 3 \АО\ _ 8
\ОА\ ' \ЕВ\ ' \CD\ ~ ^ \ОА\ ~ 8’ \AD\ ~ 11'
В
=»
ctg /3° = 3.


1.5. Площадь треугольника
301
После этого, применяя леммы о площадях, получаем
Saabd = \BD\_ = 7 Saaoe = \АО\ \АЩ=2_ Saabc \ВС\ 8’ Saabd \AD\ ‘ \АВ\ 11
7 7
==> Saabd = oS&abci Saaoe — тт^л авс,
8 44
63 0 189V55
OBEOD = OAABD ~ &ААОЕ = ~gg&AABC = gg •
Ответ.
189%/55 88 ‘
Задача 20.
На плоскости лежит равнобедренный прямоугольный треугольник, у которого катеты имеют длину а. Поворотом в этой плоскости данного треугольника вокруг вершины его прямого угла на угол 45° получается другой равнобедренный прямоугольный треугольник. Найдите площадь четырёхугольника, являющегося общей частью этих двух треугольников.
Идея. Представить искомую площадь в виде разности площади исходного треугольника и суммы площадей отсекаемых треугольников. Указание. Воспользоваться соотношениями между длинами сторон и величинами углов в прямоугольном треугольнике.
В
Решение. Обозначим вершины исходного треугольника буквами А, В и С, вершины треугольника, полученного при повороте, обозначим В' и С'. Точку пересечения отрезков АВ и В'С' обозначим буквой М, точку пересечения отрезков ВС и В'С' обозначим буквой L, точку пересечения отрезков ВС и АС' обозначим буквой К. Ясно, что треугольники АКС и BML также прямоугольные и равнобедренные, причём
\АК\ = \АМ\ = -2L \ML\ = \ВМ\ = \АВ\ - \АМ\ = a (l -
Наконец,
Saabc = Saakc = ~р Sabml =
Samlk = Saabc - Saakc - Sabml =
(3 - 2y/2)a2
(y/2 — l)a2
Ответ.
(ч/2-1)а2


302
Указания и решенья
Задача 21.
Длина радиуса вписанной в равнобедренный треугольник АВС окружности равна 4, \АС\ = \ВС\. На прямой АВ взята точка D, удалённая от прямых АС и ВС на расстояния 11 и 3 соответственно. Найдите cos DBC.
Идея. Представить площадь треугольника АВС в виде суммы или разности площадей треугольников ADC и В DC (в зависимости от того, где лежит точка D).
Указание. Воспользоваться различными формулами площади треугольника.
В D А
Решение. При решении этой задачи необходимо разобрать все три случая возможного расположения точки D. Обозначим длины сторон АС и ВС буквой х, длину стороны АВ обозначим буквой у. Если точка D лежит на стороне АВ (см. рисунок), то, во-первых, угол DBC совпадает с углом АВС и, во-вторых, площадь треугольника АВС равна сумме площадей треугольников ADC и В DC. Заметим, что расстояние от точки D до прямой АС равно длине высоты треугольника ADC, опущенной из точки D, а расстояние от точки D до прямой ВС есть длина высоты треугольника jBDC, опущенной из точки D. Осталось лишь воспользоваться теми формулами площади, в которые входят эти длины:
1 11т* 1 *\т
Saadc = j '\АС\ ■ \DL\ = —; SABdc = ^ • \ВС\ • \DK\ = у;
Их Зх 3
Saabc = Раавс • гаавс = Ах + 2у =>■ -у + — — Ах+ 2у => у - -х\
cos DBC = cos ABC = Jj- =
2x A
Теперь предположим, что точка D лежит на продолжении стороны А В за точку А. Этот случай отличается от предыдущего тем, что площадь треугольника АВС теперь будет равна разности площадей треугольников В DC и ADC. Рассуждая абсолютно аналогично, мы получим уравнение Зж/2 — Их/2 = 4х + 2у, т которого следует, что числа х и у разного знака. Значит, этот случай невозможен.
Наконец, если предположить, что точка D лежит на продолжении стороны АВ за точку В, то угол DBC станет смежным с углом АВС, а площадь треугольника АВС будет равна разности площадей треугольников ADC и В DC. Опять-таки рассуждая аналогично, мы приходим к равенству Их/2 — Зх/2 = 4х Н- 2у, из которого вытекает, что у = 0. Таким образом, и этот случай невозможен.
3
Ответ. -.
4
Задача 22.
Площадь трапеции ABCD равна 30. Точка Р - середина боковой стороны АВ. Точка R на боковой стороне CD выбрана так, что 2\CD\ = 3|jRJD| . Прямые AR и


1.5. Площадь треугольника
303
PD пересекаются в точке Q. Найдите площадь треугольника APQ, если известно, что \AD\ =2\ВС\.
Идея. Достроить трапецию до треугольника, приме- Е
нить свойства средней линии треугольника. /'^
Указание. Воспользоваться теоремой Менелая для / \
нахождения отношения \AQ\ : \QR\.
Указание. Воспользоваться леммами о площадях.
Решение. Отметим, что классическим способом решения задач такого сорта является достроение трапеции до треугольника. Обозначим \АР\ = х, \RD\ = 2г/, тогда, в силу условия задачи, |J3P| = х, \АВ\ = 2х, \CD\ = 3у.
Далее продлим боковые стороны АВ и CD до пересечения в точке Е и заметим, что, поскольку AD\\BC и \AD\ = 2\ВС\, ВС - средняя линяя треугольника AED. С учётом этого факта находим | АЕ\ = 4х, \ED\ = 6 у. Теперь можно составить план действий:
Sabcd —> Saade —> Saaer —> Saapq•
Для последнего перехода нам не хватает отношения \AQ\ : \AR\. Найдём его, пользуясь теоремой Менелая для треугольника AER и секущей PQ:
\RQ\ \АР\ \ED\ = 1 ^ \QA\ _ х 6у _Л \AQ\ _ 1
\QA\ \РЕ\ \DR\ \RQ\ Зх 2 у \AR\ 2*
Теперь немного посчитаем. Треугольники ЕВС и EAD подобны, стало быть,
аевс _ /IJA _ Saade — Saebc = 30 => Saade = 40.
Saade \\AD\J 4
Используя леммы о площадях, получаем
Заляя \ER\ 2 Saapq \АР\ • \AQ\ 1 с 10
“ ~ ‘ ~ ~ &AAPQ ~ —
Saade \ED\ 3’ Saaer \AE\-\AR\ 8 3
10
Ответ.
О
Задача 23.
В трапеции ABCD стороны А В и CD параллельны, причём \CD\ = 2\АВ\. На сторонах AD и ВС выбраны соответственно точки Р и Q таким образом, что |£>Р| : |РА| = 2:1, \BQ\ : \QC\ =3:4. Найдите отношение площадей четырёхугольников ABQP и CDPQ.
Идея. Достроить трапецию до треугольника, применить леммы о площадях. Указание. Площади четырёхугольников искать через разность площадей треугольников.
Указание. Воспользоваться свойствами средней линии треугольника для нахождения нужных отношений.


304
Указания и решения
Решение. Обозначим \РА\ = ж, |J5Q| = Зу, тогда в силу условия задачи
\DP\ = 2х, \AD\ = 3®, \QC\ = 4у, |ВС| = 7у.
Е
N
/ N*
Продлим боковые стороны AD и ВС до пересечения в точке Е и заметим, что, поскольку AB\\CD и \CD\ = 2|АВ|, АВ - средняя линяя треугольника CED, поэтому |АЕ| = Зх, |££| = 7у. Положим Saeab = S. Площади четырёхугольников будем искать через разность площадей треугольников. Теперь составим план действий:
Saeab —> Saepq, Saeab —> Saedc•
Для нахождения Saepq воспользуемся леммой 4 о площадях:
Saepq _ \РЕ\ • \QE\ _ 40 „ 40 „
Saeab \АЕ| • |Б£| 21
*>AEPQ
21
19,
=>* Sabqp = Saepq - Saeab = ^5.
Для нахождения Saedc воспользуемся леммой 5 о площадях (АЕАВ ~ AEDC):
ч2
Saecd _ ПРС\\ _ Saeab \\AB\J
Saecd — 45
44
Scdpq = Saedc — Saepq = ^j-5. Таким образом, искомое отношение равно 19 : 44.
19
Ответ.
44'
Задача 24-
Точки Р и Q расположены на стороне ВС треугольника АВС таким образом, что \ВР\ : \PQ\ : \QC\ = 1:2:3. Точка R делит сторону АС этого треугольника таким образом, что \AR\ : \RC\ = 1:2. Чему равно отношение площади четырёхугольника PQST к площади треугольника АВС, если 5 и Т - точки пересечения прямой BR с прямыми AQ и АР соответственно?
Идея. Площадь четырёхугольника PQST искать через разность площадей треугольников APQ и ATS.
Указание. Применить теорему Менелая для нахождения отношений \АТ\ : \АР\ и \AS\ : \AQ|.
Указание. Воспользоваться леммами 1 и 4.


1.5. Площадь треугольника
305
Решение. Площадь четырёхугольника PQST лучше всего искать через разность площадей треугольников APQ и ATS. Поэтому план действий таков:
Saabc —> Saapq —> Saats —> Spqst-
Для реализации этого плана нам не хватает отношений \АТ\ : \АР\ и \AS\ : \AQ\. Найдём их, пользуясь теоремой Менелая для треугольников АРС и AQC:
\РТ\ \АЩ \СВ\= ИИ = * ^ \АТ\ 3-
\ТА\ \RC\ \ВР\ \РТ\ \АР\ 4’
\QS\ \AR\ \СВ\= Ш = 1 JM = I
\SA\ \RC\ \BQ\ |5Q| \AQ\ 2'
Далее положим Saabc — S и, пользуясь леммами 1 и 4 о площадях, находим
Saapq __ \PQ\ _ 1 ^ _1с
Saabc \ВС\ 3 AAPQ 3 ’
Saats \АТ\ • |Л5| 3 _ 0 1, _ р 5 0
__ = = => 5P(3sr = -5.
5
Ответ. —.
24
Задача 25.
В треугольнике АВС, площадь которого равна S, проведены биссектриса СЕ и медиана BD, пересекающиеся в точке О. Найдите площадь четырёхугольника ADOE, если \ВС\ = а, \АС\ = Ъ.
Идея. Площадь четырёхугольника ADOE искать в
через разность площадей треугольников ABD и ЕВО.
Указание. Используя леммы о площадях, выразить площадь четырёхугольника ADOE через площадь треугольника АВС.
Указание. Используя основное свойство биссектрисы, найти отношения |J5JE7| : \ЕА\ и |J30| : \OD\.
Решение. Площадь четырёхугольника ADOE лучше всего искать через разность площадей треугольников. Но у нас есть две такие возможности. Поскольку СЕ - биссектриса в треугольниках АСВ и DC В, пользуясь основным свойством биссектрисы, можно найти отношения \ВЕ\ : \ЕА\ и \ВО\ : \OD\. Поэтому площадь четырёхугольника ADOE будем искать как разность площадей треугольников ABD и ЕВО. Теперь можно составить план действий:
Saabc —> Saabd —> Saebo —> Saadoe-


306
Указания и решения
Сначала, пользуясь леммами 1 и 4 о площадях, выразим площадь четырехугольника ADOE через площадь треугольника АВС:
Saabd \AD\ 1 с 1 с
S^ = W\=* Saabd = ^Saabc,
Saebo _ \BE\ • \BO\ Q _ 1 \BE\ \BO\ _
Saabd \AB\ • \BD\ AEBO 2 ' \AB\ ' \BD\ AABC’
Sadoe = Saabd - Saebo = ^ ^ ~ |ab| \bD\ ) ^aabc-
Теперь посчитаем отношения, входящие в полученную нами формулу. Применяя основное свойство биссектрисы для треугольников АСВ и DC В, получаем
\ВЕ\ _ \ВС\ _ а \ВЕ\ _ а
\АЕ\ \АС | Ъ \АВ\ а + Ь’
\ВО\ \ВС\ 2 а ^ \ВО\ 2 а
\OD\ ~ \DC\ Ъ ^ \BD\ “2а + Ь'
Итак,
1 / а 2а \ _ Ь2 -f 3ab
Sadoe 2 ^1 a + b 2a + b) Saabc 2(a + b)(2a + b)S'
S b2 + 3 ab
Ответ.
2 (a -f- Ь){2а -j- b)
Задача 26.
Длина высоты трапеции ABCD равна 7, а длины оснований AD и ВС равны соответственно 8 и 6. Через точку £*, лежащую на стороне CD, проведена прямая BE, которая делит диагональ АС в точке О в отношении \АО\ : \ОС\ = 3:2. Найдите площадь треугольника О ЕС.
Идея. Продлить отрезок BE до пересечения с прямой AD g q
в точке F.
Указание. Использовать подобие треугольников AOF и СОВ для нахождения длины отрезка DF.
Указание. Использовать подобие треугольников DEF и СЕВ для нахождения значения отношения \СЕ\ : \CD\.
Указание. Воспользоваться леммами о площадях.
Решение. Поскольку площадь треугольника ACD мы можем посчитать исходя из условия, для нахождения площади треугольника О ЕС нам не хватает отношения \СЕ\ : \CD\. Продлим отрезок BE до пересечения с прямой AD в точке F. Ясно, что точка D окажется между точками А и F. Треугольники AOF и СОВ подобны, что даёт нам \AF\ : \ВС\ = \АО\ : \ОС\ =3:2 => \AF\ = 9, \DF\ = 1. Далее заметим, что треугольники DEF и СЕВ также подобны, поэтому
\СЩ = \ВС[= \СЕ\ = 6
\ED\ \DF\ \CD\ 7‘


1.5. Площадь треугольника
307
Наконец, пользуясь тем фактом, что высота трапеции ABCD является также и высотой треугольника ACD, и леммой 4 о площадях, получаем Saacd = 28,
Saoec \OC\-\CE\ 2 6 12 48
— — — v ОАОЕС =
Saacd \AC\-\CD\ 5 7 35 5
n 48
Ответ. —.
5
Задача 27.
В прямоугольном треугольнике величина меньшего из углов равна а. Прямая, перпендикулярная гипотенузе, делит этот треугольник на две части, равные по площади. Найдите, в каком отношении она делит гипотенузу.
Идея. Доказать, что прямая из условия задачи пересекает больший катет.
Указание. Воспользоваться подобием треугольников и леммами о площадях.
Решение. Будем считать, что угол АСВ меньший. Обозначим точку пересечения прямой из условия задачи и гипотенузы ВС буквой D, а точку её пересечения с прямой АС (таковая обязательно есть) буквой Е. Вообще говоря, заранее не известно, попадет ли точка Е на катет АС или нет, поэтому сначала необходимо ответить на этот вопрос. Проведём высоту АН, тогда
Saach _ \СН\ _ \AH\ctga 2
Saabh \ВН\ |,4tf|ctg(|-a) °S
Но поскольку угол АСВ наименьший, а < 7г/4, ctg а > 1. Значит, площадь треугольника АСН больше площади треугольника АВН. Из этого следует, что точка Е должна лежать на отрезке АС.
Тогда площадь треугольника СED по условию равна половине площади треугольника АВС. Далее ясно, что треугольники CED и СВ А подобны. Из этого подобия находим
\CD\ ISaced 1 ■ , \АС\
\АС\ у S^bc ч/2 11 у/2 '
Но, с другой стороны, из прямоугольного треугольника АВС:
\АС\ \АС\
ШС\ = \АС\ \BD\ = \ВС\ ~ \CD\ _ cosa V2 = V2-COSа
1 1 cosa ^ \CD\ \CD\ \АС\ cos а '
у/2
Ответ. (v2 — cosa ): cosa.


308
Указания и решения
Задача 28.
Через вершину А и середину М стороны ВС параллелограмма ABCD, площадь которого равна 1, проведена прямая, пересекающая диагональ BD в точке О. Найдите площадь четырёхугольника OMCD.
Идея. Площадь четырёхугольника OMCD искать через разность площадей треугольников CBD и МВО.
Указание. Используя подобие треугольников AOD и МОВ, найти \ВО\ : \BD\.
Указание. Воспользоваться леммами о площадях.
A D
Решение. Площадь четырёхугольника OMCD лучше всего искать через разность площадей треугольников CBD и МВО. Поэтому план действий таков:
Sabcd —> Sacbd —> Sambo —> Somcd•
Для реализации этого плана не хватает только отношения \ВО\ : \BD\. Его легко найти. Поскольку противоположные стороны параллелограмма параллельны и
равны по длине, \ВМ\ = = 2^^’ а тРеУгольники ^OD и МОВ подобны.
Из этого подобия вытекает, что
\BO\.lBD\--.
Начнём реализацию плана. Из-за равенства треугольников ABD и CBD площадь треугольника CBD равна половине площади параллелограмма ABCD, то есть 1/2. По лемме 4 получаем
Sambo _ \ВМ\ • |ВО\ _ 1 с 1 о _ 1 _ 1 _ А
Sacbd \BC\-\BD\ 6 АМВО 12 OMCS 2 12 12'
5
Ответ. —.
12
Задача 29.
В треугольнике АВС градусная мера угла А равна 45°, а угол С острый. Из середины стороны ВС на сторону АС опущен перпендикуляр МN. Найдите градусные меры углов треугольника АВС, если площади треугольников MNC и АВС относятся как 1:8.
Идея. Использовать подобие и леммы о площадях.
Указание. Провести высоту ВН. Используя подобие, вычислить отношение \CN\ : \СН\.
Указание. Используя леммы о площадях, вычислить отношение \CN\ : \АС\. Доказать, что ВН - медиана треугольника АВС, т.е. треугольник АВС равнобедренный.


1.5. Площадь треугольника
309
Решение. Проведём высоту ВН треугольника АВС. Ясно, что треугольники CMN и СВН подобны с коэффициентом подобия 1/2, поэтому
\CN\ = -\СН\. Используя лемму 4 о площадях, находим
1 = Sacmn = \CN\ • \СМ| 8 5длвс \СА\ • \СВ\
\СЩ
\СА\
1
4’
В
Стало быть, \АС\ = 4|CiV| = 2|СБ|, то есть ВН - медиана треугольника АВС. Таким образом, треугольник АВС равнобедренный, АСВ = ВАС = 45°, АВС = 90°.
Ответ. АСВ = 45°, АБС = 90°.
Задача 30.
Точка О является центром окружности, вписанной в прямоугольный треугольник АВС с прямым углом В. Известно, что отношение площадей треугольников АОС и АВС равно к : к +1. Найдите величины острых углов треугольника АВС. При каких к задача имеет решение?
Идея. Выразить все необходимые величины через длину гипотенузы АС и величину угла ВАС.
Указание. Ввести обозначения: ВАС = а, |АС\ = 2R, а длину радиуса окружности, вписанной в треугольник АВС, обозначить буквой г. Выразить площади данных треугольников через эти величины.
Решение. Положим ВАС = а, |АС| = 2R, а длину радиуса окружности, вписанной в треугольник АВС, обозначим буквой г. Тогда, пользуясь соотношениями между длинами сторон и величинами углов в прямоугольном треугольнике, а также формулой площади треугольника, включающей в себя длину радиуса вписанной в треугольник окружности, получаем
\АВ\ = 2i?cosa, \ВС\ = 2i?sina; Saabc = Rr(l + sina + cosa).
С другой стороны, Saaoc = Rr. Значит,
1
к
1 -f sin a + cos a к + 1 Поскольку a G (0; n/2), имеем
sin a -f cos a = — к
7Г
a + — E 4
(7Г 37Г \ 1 . / 7Г \
U;tJ => 7!<smVa+4)
< i
A: €


310
Указания и решения
Следовательно, задача имеет решение при k Е 1
а = arcsin
у/2к
7Г
4
или
а
а;1)и
Зтг . / 1 \
= — arcsin -=- .
4 \V2kJ
Полученные величины в сумме дают тг/2 и являются ответом в задаче.
• / 1 \ * 37Г • / М I Г 1 Л
Ответ, arcsin —- и — arcsin - ; /с G -7=; 1 .
\V2kJ 4 4 \V2kJ _л/2 )
Задача 31.
В треугольнике АВС точка D лежит на стороне АС, |^4Z>| = 2|iX7|. На стороне ВС взята точка Е таким образом, что площадь треугольника AED равна 1. Отрезки АЕ и BD пересекаются в точке О. Найдите отношение площадей треугольников АВО и OED, если площадь треугольника ABD равна 3.
Идея. Доказать, что AB\\DE, воспользоваться леммой 5.
Указание. Найти отношение \ВЕ\ : \ЕС\, предварительно вычислив площади треугольников BED и CED с помощью леммы 1.
Указание. Доказать, что АВ|\DE.
Указание. Воспользоваться леммой 5.
Решение. Идея решения достаточно проста - с помощью утверждений из теоретических материалов связать площади всевозможных треугольников. Сначала заметим, что по лемме 1
Saaed \AD\ 1 Saabd \AD\ 3
S^ = \DC\=2 =*■ S*CSD = 2; = IDCf = 2 =*
После этого мы получаем, что Sabed = Sacbd — Saced = 1 и, кроме того,
|ВЕ\ : \ЕС\ = Sabed • Saced = 2.
Теперь заметим, что так как \AD\ : \DC\ = \ВЕ\ : \ЕС\ — 2, то по теореме, обратной теореме Фалеса, прямые АВ и DE параллельны, из чего вытекает подобие треугольников АОВ и EOD. Коэффициент их подобия равен численному значению отношения \АВ\ : \ED\, найти же эту величину мы можем из того факта, что треугольники CDE и САВ также подобны, и леммы 5. Итак,
\АВ\ \AC\ \AD\ + \DC\_3\DC\ SAAOB 2
\ED\ \DC\ \DC\ \DC\ Saeod
В
Ответ. 9.


1.5. Площадь треугольника
311
Задача 32.
На отрезке АВ лежат точки С и D, причём точка С - между точками А и D. Точка М взята так, что перпендикулярны прямые AM и MD, а также перпендикулярны прямые СМ и MB. Найдите площадь треугольника CMD, если известно, что CMD = а, а площади треугольников AMD и СМ В равны Si и 52 соответственно.
Идея. Доказать, что
Saamc * SaBMD 2
= cos а.
Saamd • Sacmb
Указание. Воспользоваться формулой площади треугольника через длины двух его сторон и синус величины угла между ними.
Решение. Заметим, что величины углов AM С и BMD равны 7г/2 — а. Также обозначим искомую площадь треугольника CMD через х, тогда Saamc — Si— х, Sabmd = S2 — х. Запишем формулы площади этих треугольников:
Saamc = \ • \АМ\ ■ \МС\ ■ sin АМС = ± ■ \АМ\ ■ \МС\ ■ sin (| - а) ;
Sabmd = \ • \ВМ\ ■ \MD\ • sin BMD = i • |BM| • |MD| • sin (| - a) . Перемножив полученные соотношения, получаем
(Si - *)(S2 - ж) = J • ИМ| • \MC\ ■ \ВМ\ ■ \MD\ • cos2 a.
С другой стороны,
Si = ~\AM\-\MD\, S2 = -\BM\-\MC\ =► S1S2 = ~\AM\-\MD\-\BM\-\MC\
Таким образом,
(Si -x){S2 -x) = Si S2 cos2 a => x2 - a: (Si + S2) + SiS2 sin2 a = 0.
Sx+S2± J{S1+S2)2-‘iSxSzsix^a Решая это уравнение, находим xi^ = • Из
полученных корней выбираем меньший, так как из того, что х < Si, х < S2,
следует, что х < ^ ^ —■. Отметим, что больший корень есть не что иное, как
площадь треугольника АМВ.
Sx + S2 - J (Si + S2)2 - 4SiS2 sin2 a Ответ. .


312
Указания и решения
Задача 33.
Точка F лежит на продолжении за точку С стороны ВС параллелограмма ABCD. Отрезок AF пересекает диагональ BD в точке Е и сторону CD в точке G. Известно, что \GF\ = 3, \АЕ\ = \EG\ + 1. Какую часть площади параллелограмма ABCD составляет площадь треугольника AED1
Идея. Воспользоваться тем, что треугольник AGD подобен треугольнику FGC, а треугольник ЕАВ подобен треугольнику EGD.
Указание. Ввести обозначение \EG\ — х, выразить двумя способами отношение \CD\ : \CG\.
Указание. Показать, что Sabcd — 5дabf Указание. Воспользоваться леммой 4.
Решение. Обозначим длину отрезка EG через х. Тогда по условию задачи \АЕ\ = х + 1, \AG\ = 2х -Ь 1, \AF\ = 2х + 4. Далее, поскольку ABCD - параллелограмм, \АВ\ = \CD\, AD\\BC и AB\\CD. Поэтому подобны треугольники AGD и FGC, а также подобны треугольники ЕАВ и EGD. Из этих подобий мы получаем
\AG\ _ |G£>| 2ж + 1 __ \GD\ _ \CD\ - \CG\ _ |CD| \CD\ _ 2x-f 4_
|GF| _ ICG| ^ 3 |CG| “ |CG| “ |CG| ^ |CG| ~ 3 ;
\CD\
\AE\ _ \AB\ x +1 _ \AB\ _ \CD\ _ \CD\ _ |CG|
|JSG| _ |G£»| ^ a: |G£»| _ |GD| “ |C£»| - |CG| “ |CD|
|CG|
Подставляя первое из этих соотношений во второе, приходим к уравнению
1
2х -Ь 4
х +1 о х -f 1 2х + 4
2х + \ х 2х +1
1.
Теперь мы знаем все необходимые для ответа на вопрос задачи величины. Проще всего было бы воспользоваться явными формулами площади параллелограмма, но мы пока обойдёмся без них. Итак, у нас \EG\ = 1, \АЕ\ = 2, \AG\ = \GF\ = 3, поэтому треугольники AGD и FGC равны (коэффициент их подобия оказался равным единице). Исходя из этого, заметим, что
Sabcd — Sabcg + Saagd = Sabcg + S&fgc = S^abf',
\AD\ = \CF\ => \BF\ = \BC\ + \CF\ = 2\AD\.
Saaed S^aed \AE\ • \ AD\ 2 • \ AD\ 1
Наконец, по лемме 4 находим
Sabcd Saabf \AF| • |J5F| 6 • 2 • \ AD\ 6
Ответ. -.
6


1.5. Площадь треугольника
313
Задача 34-
Отрезок BL является биссектрисой треугольника АВС. На продолжении его стороны АС за точку С взята точка М таким образом, что угол LBM прямой. Найдите площадь треугольника CBL, если известно, что площади треугольников ABL и СВМ равны 10 и 15 соответственно.
Идея. Доказать, что справедливо соотношение \АМ\ :\СМ\ = \AL\ : \LC\. Воспользоваться леммами о площадях.
Указание. Записать теорему синусов для треугольников АВМ и СВМ. Использовать основное свойство биссектрисы.
Решение. Заметим, что, в силу лемм о площадях
\LC\
Sacbl
\AL\
\СМ\
Saabl
Sacbm
2
з;
. Таким образом, для вычисления искомой величины нам до-
\СМ\ Sacbm
статочно найти отношение \LC\ : \СМ\. Обозначим величины углов ABL и CBL через а, тогда величина угла СВМ равна тг/2 — а, а величина угла АВМ равна тт/2 + а. Записывая теорему синусов для треугольников АВМ и СВМ, получаем
\АМ\
\АВ |
\СМ\
\вс\
sin(7r/2 + a) gin АМВ' sin(7r/2 -a) sin СМВ’
после чего, почленно деля эти соотношения друг на друга и учитывая тот факт, что sin(7r/2 + а) = sin(7r/2 — а), мы находим \АМ\ : \СМ\ = \АВ\ : \ВС\.
С другой стороны, \AL\ : \CL\ = \АВ\ : \ВС\ по основному свойству биссектрисы треугольника. Стало быть, \АМ\ : \СМ\ = \AL\ : \LC\. Далее положим \AL\ = 2х, \СМ\ = Зх. Тогда
Ъх + \LC\ _ 2х
Зх
\LC\
\LC\2 + bx\LC\ - 6х2 = 0
\LC\ = ж.
Наконец, Sacbl = ^Sacbm = 5.
Замечание. Отметим, что отрезок ВМ является биссектрисой внешнего угла треугольника АВС (смежного с углом АВС). Полученное нами в ходе решения соотношение \АМ\ : \СМ\ = \АВ\ : \ВС\ есть не что иное, как основное свойство биссектрисы внешнего угла треугольника, которое, как нетрудно заметить, очень похоже на основное свойство биссектрисы внутреннего угла треугольника.
Ответ. 5.


314
Указания и решения
Задача 35.
Точки D и Е являются соответственно серединами сторон АС и ВС равностороннего треугольника АВС. Точка F лежит на отрезке CD, отрезки BF и DE пересекаются в точке М. Найдите длину отрезка MF, если известно, что площадь четырёхугольника ABMD составляет пять восьмых площади треугольника АВС, а \АВ\ = а.
Идея. Использовать теорему косинусов для AABF, предварительно вычислив \AF\ и отношение \MF\ : \BF\.
Указание. Найти 5дв£;м-
Указание. Применяя лемму 4 о площадях, найти отношение \DM\ : \МЕ\.
Указание. Используя подобие треугольников DFM и AFB, вычислить \AF\ и отношение \MF\ : \BF\.
Указание. Используя теорему косинусов для AABF, найти \BF\.
Решение. Ключевым моментом в решении этой задачи является вычисление значения отношения \DM\ : \МЕ\ и, как следствие, длин входящих в него отрезков. Это можно сделать, например, так. Заметим, что DE — средняя линяя треугольника АВС, поэтому DE\\AB и \DE\ = а/2. Из этого вытекает, что треугольники CDE и САВ подобны с коэффициентом подобия 1/2, поэтому площадь треугольника CDE составляет 1/4 площади треугольника АВС, площадь четырёхугольника BADE составляет 3/4 площади треугольника АВС, а площадь треугольника В ЕМ, с учётом условия задачи, составляет 1/8 площади треугольника АВС.
Теперь, пользуясь леммой о площадях, находим
Наконец, треугольники DFM и AFB также подобны, стало быть,
\MF\jmjDM\ = l |MF| = W
\BF\ \AF\ \AB\ 4 11 4
\DF\ = ±\AF\ = \(1 + \DF\) =► \DF\ = 1, \AF\ = y.
Нам осталось лишь применить теорему косинусов в треугольнике ABF:
lBFf=a1 + ^-2a-^1- = 74 =*■ \BF\ = |Л№| = вч/?
Ответ.
12
3 2 9 3 ’ 1 1 12
ау/7


1.5. Площадь треугольника
315
Задача 36.
На стороне ВС треугольника АВС выбраны точки К и L таким образом, что \BL\ = \LC\, \ВК\ = \KL\. Точки D и F лежат соответственно на продолжениях отрезков AL и АК за точки L и К так, что \KF\ — 2\AL\, \LD\ = |АЙГ|. Вычислите отношение площадей четырёхугольника KLDF и треугольника АВС, если известно, что АВС = /3, АСВ = 7.
Идея. Площадь четырёхугольника KLDF искать через разность площадей треугольников ADF и AKL.
Указание. Применить леммы о площадях. Выразить искомое отношение через отношение \AK\:\AL\.
Указание. Используя теоремы синусов и косинусов, найти отношение \АК\ : \AL\.
Решение. План действий в этой задаче очевиден:
Saabc
Saakl
Saadf
Sakldf•
Обозначим \KL\ = x, \AL\ = Z, \AK\ = k. Тогда, в соответствии с условием задачи, \ВК\ = х, \LC\ = 2х, \LD\ = k, \KF\ = 21. Применяя леммы о площадях, находим
Saakl _ \KL\ Saabc ~ \ВС\
Skldf
Saakl
1. Saakl _ 4’ Saadf
kl
(k + 2l)(k + l) kl
(k + 2l)(k + l)
\AK\ ■ \AL\ \AF\ • \AD\
kl
1 -
(fc + 20(fc + 0 (
k2 + 2 kl + 212
+ 2'T + 2
kl
к
I
Skl
DF
Saabc
(j)
+ i+ 1 к i . к 4 ' I + 2 +
7
1
Таким образом, для вычисления искомой величины нам достаточно найти отношение длин отрезков АК и AL. Это можно сделать, например, так: сначала, применяя теорему синусов, получаем
\АВ\
\ВС\ sin АСВ 4xsin7
sin ВАС sin(/3 + 7)'
Затем, пользуясь теоремой косинусов для треугольников ABL и АВК, находим
\AL\2 - 4х2 + 4
16х2 sin2 7 16х2 sin 7 cos в
sin2(/3 + 7) sin(/? + 7)


316
Указания и решения
. . о 16x2sin27 8х2 sin 7 cos/3
lAK'=X+^WTV)~ si°№ + 7) ' Наконец, поделив полученные соотношения, получаем
\АК\ _ / sin2(/3 4- 7) 4- 16 sin2 7 — 8sin7cos/3sin(/3 4- 7)
\AL\ у 4sin2(/3 4-7) 4- 16 sin2 7 — 16sin7cos/3sin(/3 + 7)
Обозначим a = sin(/3 4-7), b = cos/3, с = sin7, d = 1 + 16c
4a2 4- 16c2 — 16afrc Тогда
Skldf _ d 1
Saabc A 2 2d
1 d 1
Ответ. 2 4 + й’
. /о ч j Л , , a2 4- 16с2 - 8abc
где a = sin(p 4- 7), b — cos p, с = sin 7, d -
4a2 4- 16c2 — 16abc


2.1. Углы в окружностях
317
2. Окружности
2.1. 	Углы в окружностях
Задача 1.
В треугольнике АВС известно, что \АВ\ = б, \АВ\ = \ВС\. На стороне АВ как на диаметре построена окружность, пересекающая сторону ВС в точке D так, что \BD\ : \DC\ = 2:1. Найдите длину стороны АС.
Идея. Воспользоваться тем, что угол, опирающийся на £
диаметр, прямой.
Указание. Рассмотреть прямоугольные треугольники ADB и CDB, применить теорему Пифагора.
Решение. Угол ADB является вписанным углом, опирающимся на диаметр, значит, он прямой. Далее, поскольку |J3C| = б, \BD\ : |ZX7| =2:1, имеем \BD\ = 4, \DC\ = 2. Применяя теорему Пифагора к треугольникам ADB и CDB, получаем
|i4D|2 = \АВ\2 - \BD\2 = 36 - 16 = 20,
\АС\2 = \AD\2 + \DC\2 = 20 + 4 =
Ответ. 2\/б.
В
\АС\ = 2>/б.
Задача 2.
Найдите длину радиуса окружности, если вписанный в неё угол со сторонами, длины которых равны 1 и 2, опирается на дугу меры 27г/3.
Идея. Воспользоваться свойством вписанного угла.
Указание. Применить теоремы синусов и косинусов.
Решение. Обозначим данный нам угол ВАС {А - вершина угла). Будем считать, что \АВ\ = 1, \АС\ = 2. Тогда, поскольку вписанный угол измеряется половиной дуги, на которую опирается, получаем, что радианная мера угла ВАС равна 7г/3. Далее воспользуемся тем, что треугольник АВС вписан в окружность, длину радиуса которой нам надо отыскать. Запишем для него теоремы косинусов и синусов:
\ВС\2 = \АВ\2 + \АС\2 - 2 • \АВ\ ■ \АС\ • cos В АС
ZRaabc=
\BC\_ sin ВАС
Raabc =
л/3
2'#
\ВС\ = л/3; = 1.
Ответ. 1.


318
Указания и решения
Задача 3.
Около треугольника АВС описана окружность. Продолжение биссектрисы С К треугольника АВС пересекает эту окружность в точке L, причём СL - диаметр данной окружности. Найдите отношение длин отрезков BL и АС, если известно, что sin ВАС = 1/4.
Идея. Применить свойство вписанных углов, опирающихся на диаметр окружности.
Указание. Доказать равенство треугольников ACL и BCL.
Решение. Углы CAL и CBL - вписанные углы, опирающиеся на диаметр окружности. Поэтому CAL = CBL — 7г/2. С учётом этого получаем, что треугольники СAL и CBL равны (по гипотенузе и острому углу), значит, \АС\ — \ВС\, \AL\ — \BL\.
Таким образом, треугольник АВС равнобедренный,
значит, его биссектриса С К является также его высотой и медианой, то есть \АК\ = \ВК\, СКВ = 7г/2, и, кроме того, угол ВАС острый, из чего вытекает положительность его котангенса.
Теперь искомое отношение ищется элементарно:
\m = \AL| \АС\ \АС\
Ответ. у/IE.
= tg ACL = tg (| - ВАС) = ctg ВАС
1
sin2 ВАС
- 1 = л/15.
Задача 4-
Диаметр АВ окружности 7 продолжили за точку В и на этом продолжении отметили точку С. Из точки С провели секущую, пересекающую окружность в точках D и Е, считая от точки С. Известно, что \DC\ = 3, градусные меры углов DAC и ACD равны 30° и 7° соответственно. Найдите длину диаметра окружности 7.
Идея. Использовать свойство вписанных углов, опирающихся на диаметр окружности, и соотношения в прямоугольных треугольниках.


2.1. Углы в окружностях
319
Указание. Найти величину угла CBD и, используя теорему синусов для треугольника BCD, найти \BD\.
Указание. Из прямоугольного треугольника ABD найти \АВ\.
Решение. Угол ADB является вписанным углом, опирающимся на диаметр, поэтому он прямой. С учётом этого имеем
ABD = 180° - ADB - DAB = 60°, CBD = 180° - ABD = 120°.
Теперь запишем теорему синусов для треугольника BCD:
J5£L = JML ^ |BD|Hi>c|.^^l£g = 2^.si„r.
sin DBC sin BCD sin DBC
Из прямоугольного треугольника ABD получаем
\AB\ = —= 4>/5sin70. sin DAB
Ответ. 4\/3sin70.
Задача 5.
На катете AC прямоугольного треугольника ABC как на диаметре построена окружность, которая пересекает гипотенузу АВ в точке К. Найдите площадь треугольника СКВ, если \АС\ = Ь, АВС = /3.
Идея. Использовать свойство вписанных углов, опи- ® рающихся на диаметр окружности, и соотношения в прямоугольных треугольниках.
Указание. Рассмотреть прямоугольные треугольники АКС и ВКС. Найти \СК\ и \ВК\.
Решение. Угол АКС является вписанным углом, ^ опирающимся на диаметр, значит, он прямой. После этого остается только рассмотреть прямоугольные треугольники АКС и ВКС и провести некоторые подсчёты:
\ВС\ = \АС\ • ctg ABC = bctg/?; \СК\ = \ВС\ • sin ABC = 6cos/?;
\ВК\ = \ВС\ • cos АВС = Ъ ■ SACkb = \ • 1^1 • \СК\ =
sinp 2 2sinp
b2 cos3 /3 Ответ. ————.


320
Указания и решения
Задача 6.
В окружность, длина радиуса которой равна 7, вписан выпуклый четырёхугольник ABCD. Длины сторон АВ и ВС равны. Площадь треугольника ABD относится к площади треугольника BCD как 2 : 1, a ADC = 120°. Найдите длины всех сторон четырёхугольника ABCD.
Идея. Использовать свойство вписанных углов, тео- q
рему синусов и теорему косинусов.
Указание. Найти величину угла ADB, затем, за- /
писав теорему синусов для треугольника ADB, най- / s'
ТИ \АВ\. в/
Указание. Используя теорему синусов для тре- | / ,
угольника ACD, найти АС. Записав для него теорему \ 1 / /
косинусов, найти \CD\ и |AD|. \ ]/ /
Решение. Поскольку |АВ\ = |J5C|, величины углов А
ADB и CDB равны. Значит, DB - биссектриса угла
ADC. Таким образом, CDB = ADB = 7г/3. Треугольники ABD и BCD оба вписаны в данную нам окружность, поэтому применим теорему синусов:
J4SL = 2Raabd =» |АВ| = 2 • 7 • sin £ = 7>/3; |ВС| = |АВ| = 7>/3.
sin ADB 3
Теперь воспользуемся условием про отношение площадей треугольников ABD и BCD:
После этого для нахождения длин отрезков AD л CD достаточно рассмотреть треугольник ACD. Сначала, с учётом того, что и он тоже вписан в данную нам окружность, воспользуемся теоремой синусов:
Наконец, запишем для него теорему косинусов, положив |CD| = х, \AD\ = 2х:
\AD\=2\CD\.
27Г
\АС\ = 2 • 7 • sin — = 7 о
Ответ. \АВ\ = \ВС\ = 7у/3, \CD\ = 4/2Т, \AD\ = 2^21.
Задача 7.
В треугольнике АВС \АВ\ — 3, \АС\ = 3\/7, АВС = 7г/3. Биссектриса угла ЛВС пересекается в точке D с окружностью, описанной вокруг треугольника АВС. Найдите длину отрезка BD.


2.1. Углы в окружностях
321
Идея. Использовать свойство вписанных углов и теорему синусов.
Указание. Записывая теорему синусов для треугольника АВС, найти Raabc и sin ЛСВ. Доказав, что угол АСВ острый, найти cos АС В.
Указание. Применив теорему синусов для треугольника ABD, найти \BD\.
Решение. Так как \АС\ > \АВ\, то АСВ < АВС, поэтому угол АСВ острый. Запишем теорему синусов для треугольника АВС:
\АВ |
\АС\
sin АСВ sin ABC
= 2Raabc ==>
Raabc = V2l, sin АСВ =
х/3
cos АСВ =
2ч/7’ 2y/l'
Также заметим, что вписанные углы ADB и АСВ опираются на одну дугу, значит, ADB = АСВ. С учётом этого из треугольника ABD получаем
DAB = тг- ABD - ADB = тг --АВС
ADB =
Ьтг
"б~
ADB.
Наконец, очевидно, что треугольники АВС и ABD вписаны в одну и ту же окружность. Для подсчёта длины BD осталось применить теорему синусов для треугольника ABD :
I ВР\^
sin DAB
= 2 Raabd
\BD\ — 2Raabc • sin
_ 2VST (i • -5- + ^ = 1^31
h 2V7 2 2^7) 4Vf
= 4\/3.
Ответ. 4л/3•
Задача 8.
Диагональ BD четырёхугольника ABCD является диаметром окружности, описанной около него. Вычислите длину диагонали АС, если |J3jD| = 2, \АВ\ = 1, ABD:DBC = 4:3.
Идея. Использовать свойство вписанных углов, опирающихся на диаметр, соотношения в прямоугольном треугольнике и теорему синусов.
Указание. Из прямоугольного треугольника ABD найти угол ABD. Используя условие, найти величину угла DBC.
Указание. Используя теорему синусов для треугольника АВС, найти \АС\.
11 Геометрия


322
Указания и решения
Решение. Поскольку углы BAD и BCD являются вписанными углами, опирающимися на диаметр, они прямые. Из треугольника ABD находим
cos ABD =
\АВ[
\BD\
ABD =
Тогда
DBC
4 4
Наконец, в силу того, что ВD - диаметр окружности, из треугольника АВС с помощью теоремы синусов получаем
\АС\ = 2 ЯЛАвс • sin ABC = \BD\ • sin ABC = 2 sin (| + =
л/б +
л/б + >/2
Ответ.
Задача 9.
В треугольнике ABC AN и CM - медианы, ABC = 2тт/3. Окружность, проходящая через точки А, М и N, проходит также и через точку С. Длина радиуса этой окружности равна 7. Найдите площадь треугольника АВС.
Идея. Использовать свойство вписанных углов, свойство медианы треугольника, соотношения в прямоугольном треугольнике, формулу для медианы треугольника и теорему синусов.
Указание. Используя свойство вписанных углов и свойство медианы треугольни- // ка, показать, что треугольник АВС равнобедренный (\АВ\ = \ВС\).
Указание. Выразить длину стороны АС через длину стороны АВ. Используя формулу длины медианы треугольника, выразить длину медианы AN через длину стороны АВ.
Указание. Использовать теорему синусов для треугольника AN С.
Решение. Поскольку MN - средняя линяя треугольника АВС, имеем MN\ \АС. Тогда величины углов ANM и NAC равны (так как они внутренние накрест лежащие), поэтому равны меры дуг AM и NC. Но тогда равны и длины отрезков AM и NC, стало быть, треугольник АВС равнобедренный (\АВ\ = \ВС\), а величины углов АСВ и САВ равны 7г/6.
Положим \АВ\ = \ВС\ = х. Тогда \АС\ = 2-|AB|-cos7r/6 = х\/3. Воспользуемся формулой длины медианы:
|ЛЛГ|2 = 2\АС\2 + 2[АВ|2 — \ВС\2 = 7^2
|A7V| =


2.1. Углы в окружностях
323
Теперь применим теорему синусов для треугольника AN С:
2Raanc = =» \AN\=2-7-l = 7 =► ж = 2у/7.
sin ACN 2
Наконец, найдём искомую площадь:
Saabc = \ • \АВ\ ■ \ВС\ - sin ABC = i • 28 — = 7л/3. Ответ. 7\/3.
Задача 10.
На окружности 7 расположены четыре точки А, В, С, £>. Продолжение хорды АВ за точку В и продолжение хорды CD за, точку С пересекаются в точке F, причём AED = 7г/3. Величина угла ABD в три раза больше величины угла ВАС. Докажите, что AD - диаметр окружности 7.
Идея. Использовать свойство вписанных углов и углов между секущими.
Указание. Показать, что угол ABD прямой.
Решение. Обозначим величину угла ВАС через а, тогда величина угла ABD будет равна За. Применим свойство угла между секущими:
AED = \ AD-i ВС=АВ6-ШС => 2 2
ТГ 7Г
=> — = За — а ==> а = —.
3 6
Таким образом, угол ABD прямой. Из этого и вытекает, что AD - диаметр окружности 7.
Задача 11.
Вершины В, С и D четырёхугольника ABCD расположены на окружности с центром О, которая пересекает сторону АВ в точке F, а сторону AD - в точке Е. Известно, что угол BAD прямой, длина хорды EF равна длине хорды FB, а также равны длины хорд ВС, CD и ED. Найдите величину угла АВО.
Идея. Использовать свойство центральных углов, опирающихся на равные хорды, и свойство углов между секущими.
Указание. Показать, что ВОС = COD = DOE и BOF = EOF.
Указание. Используя то, что сумма величин всех центральных углов в окружности равна 27Г, и свойство углов между секущими, получить систему для нахождения величин центральных углов.
Е


324
Указания и решения
Решение. Поскольку длины хорд EF и FB равны, треугольники EOF и BOF равны по третьему признаку равенства треугольников. Стало быть, BOF = EOF. Аналогично доказывается, что ВОС = COD = DOE.
Обозначим величины углов BOF и ВОС через а и /3 соответственно. Первое уравнение, связывающее эти неизвестные, составляется просто:
BOC + COD + DOE + EOF + BOF = 2тг => 2а + 3/3 = 2п. Далее воспользуемся свойством угла между секущими:
BAD
i BCD - i FE= i(BOC + COD) - \eOF
7Г
2
Решив полученную систему уравнений, получаем а = 7г/7, /3 = 47г/7. Наконец, из равнобедренного треугольника BOF находим
FBO =
тг —
Зтг 7 '
п 37Г
Ответ. —.
7
Задача 12.
На стороне АВ треугольника АВС как на диаметре построена окружность, пересекающая стороны АС и ВС в точках D и Е соответственно. Прямая DE делит площадь треугольника АВС пополам и образует с прямой АВ угол величины 7г/12. Найдите величины углов треугольника АВС.
Идея. Использовать свойство вписанных углов, опирающихся на диаметр, свойство углов между секущими и подобие треугольников.
Указание. Используя то, что BD и АЕ - высоты q
треугольника АВС, показать, что треугольники EDC и АВС подобны с коэффициентом подобия cos АСВ.
Указание. Используя свойство отношения площадей подобных треугольников, найти величину угла АСВ.
Указание. Используя свойство углов между секущими и свойство суммы углов треугольника, найти оставшиеся углы. Не забудьте рассмотреть два случая пересечения прямых DE и АВ.
Решение. Заметим, что углы ADB и АЕВ прямые, поскольку они являются вписанными углами, опирающимися на диаметр окружности. Поэтому BD и АЕ - высоты треугольника АВС, стало быть, во-первых, угол АСВ острый, во-вторых,


2.1. Углы в окружностях
325
треугольники EDC и АВС подобны с коэффициентом подобия cos АСВ. Из этого вытекает, что
Sacde
Saabc
cos2 АСВ
АСВ = j. 4
Тогда ВАС + АВС = 37г/4. Далее обозначим точку пересечения прямых АВ и DE буквой М и воспользуемся свойством угла между секущими:
ЕМ В
\ВЕ
1
AD
| ВАЕ - ABD |
(| - ABE) - - BAD) | = \BAD - ABE\
7Г
\BAC-ABC\ = —
Модуль возник из-за того, что, вообще говоря, мы не знаем, где находится точка пересечения прямых А В и D Е. Если она лежит на продолжении АВ за точку А (см. рисунок), то модуль раскроется с плюсом. Если же наоборот, то соответственно с минусом.
Наконец, решая полученную систему уравнений, находим
АВС + ВАС = Зтг/4; \BAC- АВС\ = тг/12,
: 5тг/12;
: тг/З, АВС = 5тг/12;
ВАС = тг/3.
Ответ. ВАС=АВС=^,
О -L Jd
АСВ = — или 4
= АВС
7Г
з’
Задача 13.
На сторонах острого угла с вершиной В взяты точки А и С. Одна окружность касается прямой АВ в точке В и проходит через точку С. Вторая окружность касается прямой ВС в точке В и проходит через точку А. Точка D - вторая общая точка этих окружностей. Известно, что \АВ\ = с, \ВС\ = a, \CD\ = d. Найдите \AD\.
Идея. Использовать свойства вписанных углов и углов между касательной и хордой, подобие треугольников.
Указание. Используя свойство вписанных углов и углов между касательной и хордой, показать, что треугольники ABD и BCD подобны по двум углам.


326
Указания и решения
Решение. Обозначим меру дуги BD окружности, содержащей точки А, В и D, через а, а меру дуги BD окружности, содержащей точки В, С и D, через /3. Пользуясь свойством угла между касательной и хордой, получаем
ABD = i -Р = ВСД CBD = i • а = SAB.
Из этого следует, что треугольники ABD и подобны по двум углам. Из
этого подобия находим
|Л£?! _ |ЛР| _ 1-В-Р| |ЛД| • [С£>1 erf |ЛД|-|ДД| _ c2d
|5С| |BD| |CD| 11 |ВС| а ’ 11 \ВС\ а2 '
. . , 2
Ответ, d
(!)■
Задача 14-
В окружность 7 с центром в точке О вписан выпуклый четырёхугольник ABCD, диагонали которого перпендикулярны. Известно, что величина угла АОВ в три раза больше величины угла COD. Найдите площадь круга, ограниченного окружностью 7, если \CD\ = 10.
Идея. Использовать свойство углов между пересекающимися хордами и теорему косинусов.
Указание. Используя свойство углов между пересекающимися хордами, найти величину угла COD.
Указание. Используя теорему косинусов для треугольника COD, найти длину радиуса окружности.
Решение. Обозначим точку пересечения диагоналей четырёхугольника ABCD буквой Н. Тогда по свойству угла между пересекающимися хордами
f = ®b = \ab+\cd=
= ^AOB + ^COD => АОВ + COD = тг.
С учётом того, что АОВ = 3 • COD, получаем АОВ = 37г/4, COD = п/4. Далее, поскольку \ОС\ = \OD\ = i?7, применив теорему косинусов для A COD, найдём длину радиуса окружности:
\CD\2 = \OD\2 + |ОС\2 - 2 • \OD\ • |ОС| • cos COD
=► 100 = 2Д2 • (l-cos^) =► Д2 = тг—----г
7 V 4J 7 (i_cos|)
^ о 50тг 1007Г . /-ч
=> S7 = nR = ■= — = 507t(2 + y/2).
7 2-л/2
Ответ. 507г(2 + \/2)-


2.1. Углы в окружностях
327
Задача 15.
Биссектрисы углов треугольника АВС, площадь которого равна 2, продолжены до точек пересечения с описанной около треугольника АВС окружностью, отличных от точек А, В, С. Эти точки образуют новый треугольник. Найдите его площадь, если величины углов треугольника АВС равны 7г/6, 7г/3 и тт/2.
Идея. Использовать свойство вписанных углов, определение биссектрисы и теорему синусов.
Указание. Используя свойство вписанных углов и определение биссектрисы, найти величины углов нового треугольника.
Указание. Используя теорему синусов, записать площади треугольников через длину радиуса окружности и величины известных углов.
Решение. Обозначим вершины нового треугольника Q
буквами Ai, В\ и С\ (А\ лежит на биссектрисе угла
ВАС, В\ лежит на биссектрисе угла АВС, и С\ лежит на биссектрисе угла АСВ). Без ограничения общности будем считать, что САВ = 7г/3, АВС = 7г/6, АСВ = 7г/2. Тогда по свойствам вписанных углов
В^МСх = \ ВгС, = | В?А + i ACi = B^BA + ACCl = + J = J;
MFhCi = i A?Ci = \ MB + i BCX = MAB + C^CB = £ + £ =
ЛТсГВ! = 7Г - ЛТК&1 - B^MC1 = =
Теперь выразим площади треугольников АВС и AiBiCi через радиус описанной окружности и синусы их углов (эти соотношения элементарно получаются путем подстановки в формулу площади треугольника через две стороны и синус величины угла между ними длин этих сторон, выраженных с помощью теоремы синусов через длину радиуса описанной окружности):
SaAiBiCi = ^RaAiBiCi ' sinBjAiCi • sill A1B1C1 • sinAiCiBi.
2 = Saabc = 2 R\Abc ‘ sin В AC • sin ЛВС • sin АСВ.
Почленно деля эти равенства, с учётом того, что оба треугольника АВС и А\В\С\ вписаны в одну и ту же окружность, получаем
SaaiBiCi = sinВ^МСх • sin ATfhCi • sinМС\ВХ = зф . . зф. = Уз + 1
2 sin ВАС sin ABC sin ЛСВ & ■ 1 ■ \ 2
Ответ. х/З -f 1.


328
Указания и решения
Задача 16.
В окружность, длина радиуса которой равна 2\/7, вписана трапеция ABCD, причём её основание AD является диаметром, a BAD = 7г/3. Хорда СЕ пересекает диаметр AD в точке Р такой, что \АР\ : \PD\ = 1:3. Найдите площадь треугольника ВРЕ.
Идея. Использовать параллельность прямых ВС и AD, свойство центральных углов и свойства равнобедренного треугольника.
Указание. Используя параллельность прямых ВС и AD и то, что AD является диаметром, найти меры дуг АВ, ВС и CD.
Указание. Показать, что треугольники АОВ, ВОС и COD равносторонние.
Указание. Доказать, что Р - середина отрезка АО.
Решение. Поскольку ABCD - трапеция, AD\\ВС.
Из этого вытекает равенство мер дуг АВ и CD. Далее, поскольку BAD = 7г/3, мера дуги BCD равна 27г/3. С другой стороны, AD - диаметр, поэтому мера дуги ABCD равна 7г. С учётом всего вышесказанного получаем, что
2тг
CD=AB= тг
_ = - =* вс= -
3 3 3
АОВ = ВОС = COD = |, Шс
7Г
6*
Далее заметим, что треугольники АОВ, ВОС и COD равносторонние (они равнобедренные, а угол при вершине каждого из них равен 7г/3). Из этого вытекает, что
\АО\ = \OD\ = |АВ| = \ВС\ = \CD\ = 2>/7.
Поскольку 3|АР| = |P.D|, имеем \АР\ = j|AD|. С другой стороны, \АО\ = |\А1)\. Значит, Р - середина отрезка АО, ВР - медиана равностороннего треугольника АВО, поэтому ВР _L |SP| = |АВ| • sin ОАВ = л/2Т. Из параллельности AD и ВС следует, что ВР _1_ ВС, стало быть,
tg ВРС
\вс\
\ВР\
—7=, COS В PC =
ч/з
1
1 + tg2 ВРС
Л-
cos ВРЕ
cos В PC
4
sin EBP = sin (ВРЕ + ВЕР)
sin ВРЕ = \/l — cos2 BPS -
_2_
7?’
A ^
y/l ' 2
V3
л/г
_\/3_
2\/7'
Наконец,
Sabpe = 2 ’ \BP\2
sinBPE1 • sin .EBP _ 21 sin ВЕР ^
2 .
л/7 ’ 2 л/7 1 2
Зл/З.
Ответ. 3^3.


2.1. Углы в окружностях
329
Задача 17.
Из вершины тупого угла А треугольника АВС опущена высота AD. Проведена окружность с центром в точке D, проходящая через точку А и пересекающая стороны треугольника АВ и АС в точках М и N соответственно. Вычислите длину стороны АС, если известно, что \АВ\ = с, \АМ\ = п, |АЛГ| = га.
Идея. Использовать свойство вписанных углов, свойство равнобедренного треугольника и подобие треугольников.
Указание. Используя свойство вписанных углов, свойство равнобедренного треугольника и свойство суммы острых углов прямоугольного треугольника, показать, что AM N = ACD.
Указание. Использовать подобие треугольников AMN и АСВ.
Решение. Проведём отрезки DM, DN и MN. Заметим, что угол AMN является вписанным углом, опирающимся на дугу AN, поэтому AMN = ^ADN. С другой стороны, треугольник AND равнобедренный, треугольник ADC прямоугольный, поэтому
DAN = £ - ]-ADN, ACD = £ - DAN = ^ADiV. 2 2 2 2
Итак, мы доказали, что AMN = ACD. Таким образом, треугольники AMN и АСВ подобны по двум углам (угол А у них общий), из чего вытекает
\ЛВ\_=\т \AB\-\AM\ пс
\АС\ \АМ\ 11 |АЛГ| т'
пс
Ответ. —.
т
Задача 18.
Через точку С проведены две прямые, касающиеся окружности в точках А и В. На большей из дуг АВ взята точка D так, что sin ACD sin BCD = 1/3. Найдите расстояние от точки D до хорды АВ, если известно, что \CD\ =2.
Идея. Сделать дополнительное построение. Использовать свойство вписанных углов и углов между касательной и хордой. Использовать подобие и соотношения в прямоугольном треугольнике.
Указание. Опустить из точки D перпендикуляры на прямые АВ, АС и ВС. Указание. Используя свойства вписанных углов и углов между касательной и хордой, показать, что AADH ~ ABDL и ЛADK ~ ABDH.
Указание. Использовать соотношения в прямоугольном треугольнике.
А


330
Указания и решения
Решение. Опустим из точки D перпендикуляр на прямую АВ. Основание этого перпендикуляра обозначим буквой Н. Длина отрезка DH и будет ответом на вопрос задачи. Проведём дополнительное построение: на сторонах угла АВС возьмем точки К и L (К на АС, L на ВС) таким образом, что DK _L АС, DL JL ВС. Тогда по свойству угла между касательной и хордой DBL = BAD и DAK = ABD. Следовательно, AADH ~ ABDL и AADK ~ ABDH по двум углам.
Из этих подобий имеем
\AD\ _ \DH\ \AD\ _ \DK\ \DH\ _ \DK\
\BD\ ~ \DL\ ’ \BD\ ~ \DH\ ^ \DL\ ~ \DH\
\DH\2 = \DK\ ■ \DL\.
Наконец, заметим, что \DK\ = |CJD| • sinKCD, \DL\ = \CD\ • sin LCD. С учётом этого
Ответ.
|L>#|2 = \CD\2 • sin КСD • sin LCD = -
о
2y/3
\DH\ =
Vs'
Задача 19.
В треугольнике ABC точка О - центр описанной окружности, точка L лежит на отрезке А В и \AL\ = \LB\. Описанная около треугольника ALO окружность пересекает прямую АС в точке К. Найдите площадь треугольника АВС, если AOL = тг/4, \LK\ = 8, \АК\ = 7.
Идея. Доказать, что К - середина отрезка АС, a sin AOL = sin АСВ.
Указание. Доказать, что АО - диаметр окружности, описанной около треугольника ALO, воспользоваться свойством углов, опирающихся на диаметр. Указание. Не забудьте рассмотреть оба случая расположения точек О и К относительно прямой АВ.


2.1. Углы в окружностях
331
Решение. Поскольку точка О является точкой пересечения серединных перпендикуляров треугольника ABC, a L - середина АВ, получаем OL _L АВ. Таким образом, угол OLA прямой. Из этого следует, что АО - диаметр окружности, описанной около треугольника ALO. Но тогда угол АКО тоже прямой, поскольку он опирается на диаметр этой окружности. Значит, О К _L АС, из чего вытекает равенство длин отрезков АК и С К. В самом деле, если предположить, что К - не середина АС, то мы придём к тому, что из точки О можно опустить два различных перпендикуляра на прямую АС: один проходит через середину АС, а второй - через точку К. Таким образом, \АС\ — 2 • \ АК\ — 14. Отметим также, что KL - средняя линия треугольника АВС, поэтому \ВС\ = 2 • \LK\ = 16 и АСВ^АКЬ.
Заметим, что в этой задаче возможно два различных случая, а именно, точки О и К могут лежать как в одной полуплоскости относительно прямой АВ, так и в разных. В первом из этих случаев мы получим, что углы AOL и AKL опираются на одну дугу, значит, их величины равны, а во втором они будут опираться на дуги, дополняющие друг друга до полной окружности, то есть сумма величин этих углов равна 7г. Таким образом, независимо от расположения точек О и К верно равенство sin AOL = sin AKL.
Наконец, Saabc = \ • \BC\ ■ \AC\ • sin ACB = 112 • sin AOL = 56>/2.
Ответ. 5бл/2-
Задача 20.
В окружности проведены диаметр MN и параллельная ему хорда АВ. Касательная к окружности в точке М пересекает прямые NA и NB соответственно в точках Р и Q. Известно, что \МР\ = р, \MQ\ = q. Найдите длину диаметра MN.
Идея. Использовать свойство вписанных углов, до
углов между касательной и секущей, подобие.
Указание. Используя свойство вписанных углов, углов между касательной и секущей, показать, что MNQ = MPN.
Указание. Использовать подобие прямоугольных треугольников MNQ и MPN. М Q Р
Решение. Из того, что MN\\AB, вытекает равенство дуг MB и AN. Также заметим, что, во-первых, мера дуги MB AN равна 7г и, во-вторых, MN _L МР. С учётом этого, применяя свойство вписанных углов, получаем
MNQ = - MB, MPN = £ - АШЛ = £ - ]■ АВМ= \(ъ- АВМ 2 2 2 2 2 V
Значит, MNQ = MPN. Поэтому прямоугольные треугольники MNQ и MPN подобны, что даёт нам щщ = ЩЩ \MN\2 = \MP\-\MQ\ => \MN\ = y/pq.
Ответ, y/pq.


332
Указания и решения
Задача 21.
Продолжение медианы треугольника АВС, проведённой из вершины Л, пересекает описанную около треугольника АВС окружность в точке D. Найдите длину отрезка ВС, если длины отрезков АС и DC равны 1.
Идея. Использовать теорему о продолжении биссектрисы треугольника до пересечения с описанной около него окружностью.
Указание. Доказать, что треугольники CMD и CDB подобны.
Решение. Обозначим середину отрезка ВС буквой М.
Из равенства длин отрезков АС и DC и свойства вписанных углов вытекает, что CBD = СВ А = CD А. Следовательно, треугольники CMD и CDB подобны. Значит,
\МС\ _ \DC\ _
\DC\ \ВС\
|DCY = \МС\ ■ \ВС\.
С другой стороны, по условию задачи \МВ\ = \МС\, то есть \МС\ = \ВС\/2. Подставляя это соотношение в полученное нами равенство, находим
1 = I DC\2 = =ф \вс\
у/2.
Ответ, у/2.
Задача 22.
Выпуклый четырёхугольник ABCD вписан в окружность. Диагональ АС является биссектрисой угла BAD и пересекается с диагональю BD в точке К. Найдите длину отрезка КС, если известно, что \АК\ = 6, \ВС\ = 4.
Идея. Использовать теорему о продолжении биссектрисы треугольника до пересечения с описанной около него окружностью.
Указание. Доказать, что треугольники ВКС и АВС подобны.
Решение. Обозначим искомую длину отрезка КС через х, тогда \АС\ = х + 6. Поскольку АС - биссектриса угла jBAD, треугольники ВКС и АВС подобны, что даёт нам
|fq ^ \ВС\* = \АС\-\КС\ =* 16 = (х + 6)-х => *2 + 6х —16 = 0.
Решая полученное квадратное уравнение и отбрасывая отрицательный корень, получаем \КС\ —2.
Ответ. 2.


2.1. Углы в окружностях
333
Задача 23.
Длина стороны АВ треугольника АВС равна 3, Е - точка пересечения продолжения биссектрисы CD треугольника АВС с описанной около него окружностью, \ВС\ = 2 • \АС\, \DE\ = 1. Найдите длину стороны АС.
Идея. Использовать теорему о продолжении биссектрисы треугольника до пересечения с описанной около него окружностью.
Указание. Используя свойство биссектрисы и соотношение \ВС\ = 2 • |Ж7|, найти \AD\ и \DB\.
Указание. Используя теорему косинусов для треугольников ADE и BDE, найти величину угла ADE, \АЕ\ и \ВЕ\.
Указание. Используя подобие треугольников ADE и ЕАС, найти \АС\.
Решение. По свойству биссектрисы внутреннего угла треугольника \AD\ : \DB\ = \АС\ : \ВС\ = 1 : 2. С другой стороны, \AD\ -f \DB\ = \АВ\ = 3, поэтому \AD\ = 1,
\DB\ = 2.
Далее из того, что СЕ - биссектриса угла АСВ, вытекает, что \АЕ\ = |J3JE7|, а треугольник ADE подобен треугольнику ЕАС (так как EAD = ЕС А). Обозначим величину угла ADE буквой а и воспользуемся теоремой косинусов для треугольников ADE и BDE:
Г |АЕ|2 = \AD\2 + \DE\2 - 2 • |AD| • \DE\ • cos ADF,
1 |£F|2 = |J5D|2 -f |jDF|2 - 2 • |BD| • \DE\ • cosBDE
\AE\2 = 2 — 2 cos a,
|£F|2 = 5 — 4cos(7r — a)
Наконец, подобие треугольников ADE и FAC даёт нам \AD\ \DE\
cosa = -i, |АБ| = = л/3.
|ЛЕ| |AC|
Ответ, v/3-
Задача 24-
В треугольнике ABC ВАС = 57г/12, |-AJ5| = с, |ЛС| = Ь. На стороне ВС выбрана точка М так, что ВАМ = 7г/6. Продолжение прямой ЛМ пересекает окружность, описанную вокруг треугольника, в точке N. Найдите длину отрезка AN.
Идея. Использовать свойство вписанных углов, теорему синусов и теорему косинусов.
Указание. Используя теорему косинусов для треугольника АВС, найти длину отрезка ВС и значения косинуса и синуса величины угла АВС.
Указание. Применить к треугольникам АВС и ABN теорему синусов.


334
Указания и решения
Решение. При решении этой задачи можно рассуждать, например, так: в треугольнике ЛВС нам известны три элемента, поэтому мы можем найти длину радиуса описанной около него окружности. Треугольник ABN также вписан в неё, поэтому для нахождения длины AN нам надо найти синус величины угла ABN.
Поступим следующим образом: сначала с помощью теоремы косинусов найдём длину отрезка ВС и значения косинуса и синуса величины угла АВС:
|ВС\2 = \AB\2+\AC\2-2-\AB\-\AC\-cosBAC =» \ВС\ = \jb2 + с2 - 26ccos
\АС\2 = \АВ\2 + | ВС\2 - 2 • \АВ\ ■ \ВС\ • cos АВС =►
57Г
62 = с2 + 62 + с2 — 26с cos ^ — 2су 62 + с2 — 26с cos ^ • cos ABC
A Zd V
cos ЛВС
с — 6 cos
yjb2 + с2 — 26c cos
sin ЛВС =
bsinjf
^Jb2 + c2 — 26c cos
Далее, так как вписанные углы СЛА" и CBN опираются на одну дугу, а величина угла CAN равна разности величин углов ВАС и BAN, то CAN = СВАТ = 7г/4,
sinAR/V = sin Q + ABC) =
с — 6 cos + 6 sin
л/2 • yjb2 + с2 — 26с cos Наконец, применяя к треугольникам АВС и ABN теорему синусов, получаем
|ВС| _ \]ь2 + с2 -26сcos ff
2sinff
Ответ.
|AV| = 2Д • sin ЛВЛГ = 2с+\/2Ь
2 • sin В АС
с — 6cosттг -Ь 6sin2c-f\/26
12 \/2sin
v%/2 V3 + 1 ’
2 л/2
Задача 25.
Окружность с центром в точке О, лежащей на гипотенузе АС прямоугольного треугольника ЛВС, касается его катетов АВ и ВС. Найдите длину ЛС, если известно, что \АМ\ = 20/9, |ЛАГ| : |MiV| =6:1, где М - точка касания ЛВ с окружностью, а ЛГ - точка пересечения окружности с Л С, расположенная между точками Л и О.
Идея. Обозначить величину угла AMN буквой а и, используя свойство углов между касательной и хордой, выразить угол MAN через а.


2.1. Углы в окружностях
335
Указание. Применив теорему синусов для треугольника AMN, найти а. Указание. Используя соотношения в прямоугольном треугольнике, найти \АС\.
Решение. Для нахождения \АС\ достаточно найти \ВМ\ и cos ВАС. Поскольку М - точка касания окружности и АВ, треугольник АОМ прямоугольный, поэтому угол МОА острый и МАО = 7г/2 — МОА. По свойству угла между касательной и хордой AMN = | MN= -МОА.
Обозначим величину угла AMN буквой а, тогда МОА = 2а, 2а < 7г/2 а < 7г/4, и применим к треугольнику AMN теорему синусов:
\AN\ _ \MN\ sin AMN sin MAN
sina
i^i
\MN\ sin(f - 2a)
6 cos 2a = sin a
12 sin a -f sin a — 6 = 0
sina
3
4
Второй из полученных корней нам, очевидно, не подходит, так как синус угла треугольника всегда положителен. Таким образом, с учётом того, что a < 7г/4, получаем a = arcsin 2/3 и, следовательно,
cos а
cos ВАС = cos — 2 а^ = tg В АС
4х/5*
Наконец, примем во внимание тот факт, что |МО| = |MJ3|. Это вытекает из того, что четырёхугольник, образованный точками касания окружности с катетами, точкой О и точкой В, - квадрат. С учётом этого из треугольника АОМ получаем \МО\ = \МВ\ = \АМ\ tgBAC = л/5/9. Наконец,
\АВ\ = |АМ| + |МБ|
20 + у/Ъ
\АС\
-^SL = V5+1-.
cos РЛС ^
Ответ, л/5 + -.
4
Задача 26.
Четырёхугольник ABCD вписан в окружность с центром в точке О. Радиус О А перпендикулярен радиусу О В, а радиус ОС перпендикулярен радиусу OD. Длина перпендикуляра, опущенного из точки С на прямую AD, равна 9, \AD\ = 2\ВС\. Найдите площадь треугольника АОВ.
Идея. Использовать свойство вписанных углов и соотношения в прямоугольном треугольнике.
Указание. Положив ВОС = а, из равнобедренных треугольников ВОС и AOD, используя соотношение \AD\ = 2\ВС\, найти а.


336
Указания и решения
Указание. Используя свойство вписанного угла, найти ADC. Далее, используя соотношения в прямоугольном треугольнике, найти длину радиуса окружности.
Решение. Поскольку величины углов АОВ, ВОС, COD и DO А в сумме дают 2тг, а углы АОВ и COD прямые, ВОС + DO А = тг. Введём обозначения ВОС = а, \ОА\ = \ОВ\ = \ОС\ = \OD\ = Д, тогда DO А = тг —а. Из равнобедренных треугольников ВОС и AOD получаем
\ВС\ = 2 • |ОВ| • sin = 2Л sin
|AD| = 2 • |0£>| • sin ( 2D0A;
Далее, по свойству вписанного угла
тг — а
Л а
~ \ВС\ ~ Ctg 2'
а
ADC = I АС = I АВ + I ВС = I АОВ + I ВСЮ =
2 2 2 2 2 4 2
Теперь обозначим буквой Н основание перпендикуляра, опущенного из точки С на прямую AD. По условию задачи \СН\ = 9, и из прямоугольного треугольника
CDH мы легко находим \CD\ = \СН\/ sinCDH = 9/ sin -I- .
Прямоугольные треугольники АОВ и COD, очевидно, равны и являются равнобедренными. Поэтому \АВ\ = |CD|, ЛБО = БЛО = 7г/4,
81 81
Saaob = \ • |ОЛ| • |ОВ| = | • \АВ\2 sin j cos J =
4sin2(f+ f)
Осталось чуть-чуть посчитать:
се . 2 ctg f
ctg •
=>■ sin a =
45
1 + ctg2 f
= -, 2 — 2 cos
(sH-
2 — 2cos(| + a)*
Л . 18
2 -f 2 sin a = — .
5
Значит, Saaob = — •
n 45
Ответ. —.
2
Задача 27.
В треугольнике ABC \АВ\ = 3, АСВ = arcsin |. Хорда KN окружности, описанной около треугольника АВС, пересекает отрезки АС и ВС в точках М и L соответственно. Известно, что ABC = CML, площадь четырёхугольника ABLM равна 2, |LM| = 1. Найдите длину высоты треугольника KNC, опущенной из вершины С, и площадь этого треугольника.


2.1. Углы в окружностях
337
Идея. Использовать подобие, леммы о площадях, свойство вписанных углов и углов между хордами, теорему синусов и теорему Пифагора. Указание. Используя подобие треугольников АВС и LMC (по двум углам) и леммы о площадях, найти длину высоты треугольника KNC, опущенной из вершины С.
Указание. Используя свойство угла между пересекающимися хордами и свойство вписанного угла, доказать, что треугольник KNC равнобедренный.
Указание. Используя теорему синусов и теорему Пифагора, найти сторону KN треугольника KNC.
Решение. Заметим, что из равенства величин углов АВС и CML вытекает подобие треугольников АВС и LMC (по двум углам). Из этого следует, что
Salmc _ /\LM\\2 _ 1 Saabc \ \АВ\) 9’
1 9
Salmc + Sablm = Saabc => Salmc = ^ Saabc =
Теперь мы в состоянии ответить на первый вопрос задачи. Ясно, что высоты треугольников KNC и LMC, опущенные из вершины С, совпадают. Поэтому, обозначая основание искомой высоты буквой Р, с помощью формулы площади мы находим \СР\ = 2Salcm/\LM\ = После этого для нахождения площади треугольника KNC нам достаточно найти длину его стороны KN. Для этого сначала докажем, что треугольник KNC равнобедренный. Воспользуемся свойством угла между пересекающимися хордами и свойством вписанного угла:
CMN = ~ (NC + АК) , ABC = | АС= ^ (АК + СА-) =>
\
=» CK=NC => \СК\ = \NC\.
Таким образом, высота СР является и медианой треугольника KNC, то есть серединным перпендикуляром к стороне KN. Центр окружности тоже лежит на
этой прямой. Тогда, обозначая его буквой О, получаем \ОК\ — —5
2 sin АСВ 2
\ОР\ = \ОК\ - \КР\ = 2, \КР\ = |РЛГ| = у/\ОК\* - \ОР\2 =
Стало быть, \KN\ = 3, SAKNC = | • \KN\ ■ \СР\ = §.
1 3
Ответ. fiKN =-, S&knc = j-


338
Указания и решения
Задача 28.
В треугольнике АВС точка D лежит на стороне ВС, прямая AD пересекается с биссектрисой угла АСВ в точке О. Известно, что точки С,D и О лежат на окружности, центр которой находится на стороне АС, величина угла jDAC в три раза больше величины угла DAB, \АС\ : \АВ\ =3:2. Найдите косинус величины угла АСВ.
Идея. Использовать свойство вписанных уг- д лов и теорему синусов.
Указание. Обозначив величину угла АСВ через 2а, используя свойство вписанных углов, выразить все углы треугольника АВС через а.
Указание. Применить теорему синусов для треугольника АВС.
Решение. Поскольку дано отношение сторон в треугольнике АВС, а требуется найти косинус угла против одной из этих сторон, надо выразить угол, лежащий против другой стороны, g £)ч^ / ^
через искомый угол и применить теорему си- " - ^ ^ ^
нусов.
Обозначим центр окружности, проходящей через точки С,D и О, буквой R. Величину угла АСВ обозначим через 2а, величину угла ВАС обозначим через 4/3. Тогда по условию задачи OCD = ОСА = a, CAD = 3/3.
Далее, углы OCD и ORD являются вписанным и центральным углами, опирающимися на дугу OD. Значит, ORD = 2 • OCD = 2а. С другой стороны,
\RC\ = \RD\ = |ДО|, то есть треугольники RCD и ROD равнобедренные. Это
даёт нам следующие соотношения:
RCD = RDC = 2а, RDO = ROD = i (тг - ORD^j = | - а.
Теперь воспользуемся теоремой о сумме величин углов треугольника:
RCD + RDC Н- RDO + OAR = 7г => 2а + 2а Н- — — а -I- 3(3 = 7г => а + (3 = —.
2 6
Исходя из этого, получаем
'ВАС = 40 = ^ - 4а, АВС = тг - ВЖ7 - ЛОВ = J + 2а.
О о
Наконец, воспользуемся теоремой синусов:


2.1. Углы в окружностях
339
Задача 29.
В треугольнике АВС проведена средняя линия МN, соединяющая стороны АВ и ВС. Окружность, проведённая через точки M,N и С, касается стороны АВ, а длина её радиуса равна у/2. Найдите sin АСВ, если \АС\ = 2.
Идея. Использовать свойство средней линии треугольника, свойство вписанных углов, углов между касательной и хордой, подобие и теорему синусов. Указание. Доказать, что ВАС = BMN = MCN. Для этого применить свойство средней линии треугольника, свойства вписанных углов и углов между касательной и хордой.
Указание. Записав для треугольника MCN теорему синусов, найти sin ВАС. Указание. Используя подобие треугольников MBN и СВМ (по двум углам), показать, что \АВ\ = у/2\ВС\.
Указание. Применить к А АВС теорему синусов для нахождения sin АСВ.
Решение. Поскольку MN - средняя линяя треугольника АВС, соединяющая стороны АВ и ВС, имеем MN\\AC, \MN\ — |АС|/2 = 1. Теперь заметим, что углы BMN и ВАС равны, как соответственные при параллельных прямых, а углы BMN и MCN равны по свойству угла между касательной и хордой. Применив к треугольнику MCN теорему синусов, находим
smBAC = smMCN = 'MN' -- 1
2^окр. 2у/2
Из всего вышесказанного вытекает и подобие треугольников MBN и СВМ (по двум углам). Из этого подобия получаем
ilq = ji£i ^|вм|2 = lBCl'|ВЛГ| ^ = ^1ЛВ] = ^BCl
Наконец, применим к треугольнику АВС теорему синусов:
\АВ\ _ \ВС\ зщАСВ = J4S • sinBAC = I.
sin АСВ sin ВАС \вс\ 2‘
Замечание. Существует два различных треугольника АВС, удовлетворяющих условию задачи. У одного из них АСВ = 7г/6, а у другого АСВ = 57г/б. Оба они изображены на чертеже. Отметим, что приведённое решение не зависело от конфигурации.
1


340
Указания и решения
Задача 30.
В треугольнике АВС длина стороны ВС равна 4, а длина стороны АВ равна 2л/19. Известно, что центр окружности, проведённой через середины сторон треугольника АВС, лежит на биссектрисе угла С. Найдите длину стороны АС.
Идея. Использовать свойство вписанных углов, теоремы синусов и косинусов, свойство средней линии треугольника и неравенство треугольника.
Указание. Обозначить середины сторон АС, ВС и АВ треугольника АВС буквами L, К и М соответственно, центр окружности, проходящей через эти точки, обозначим буквой О. Используя теорему синусов для треугольников КОС и LOC. показать, что sin О КС = sin OLC.
Указание. При рассмотрении случая О КС = OLC показать, что равны треугольники КОС и LOC (по стороне и двум углам). Использовать неравенство треугольника при изучении получившегося результата.
Указание. При анализе случая ОКС -f- OLC = тг, показать, что KCL = 7г/3.
Решение. Обозначим середины сторон АС, ВС и АВ треугольника АВС буквами L, К и М соответственно, центр окружности, проходящей через эти точки, обозначим буквой О. Запишем теорему синусов для треугольников КОС и LOC, заметив, что у них много равных элементов (\ОК\ = |OL|, АОСК = ZOCL):
рк\ \OC\_ _ sin ОКС = sin OLC =*
sin ОС К sin ОКС sin ОСЬ sin OLC
=> ОКС = OLC или ОКС + OLC = тг.
Разберем поочерёдно эти варианты. Если углы ОКС и OLC равны, то равны и треугольники КОС и LOC (по стороне и двум углам). Из этого вытекает, что \СК\ = \CL\ <=> \АС\ = \ВС\ = 4. Но тогда \АС\ + |JBC| = 8 < 2>/l9 = \АВ\, то есть для треугольника АВС не выполнено неравенство треугольника. Стало быть, величины углов ОКС и OLC в сумме дают тг.
Теперь заметим, что поскольку сумма величин углов четырёхугольника CKOL равна 2тг, то и KCL + KOL = тг. Это соотношение является ключевым. Действительно, из того, что КМ и LM - средние линии треугольника АВС, следует, что четырёхугольник CKML - параллелограмм. Поэтому KML — KCL. А так как угол KOL центральный, то KOL = 2 • К ML. С учётом всего этого имеем
КСЬ + 2КС1 = ж ==» KCL=\.
О
Дальнейшее очевидно. Запишем теорему косинусов для треугольника АВС:


2.1. Углы в окружностях
341
=> 76 = \АС\2 + 16 - 4 • \АС\ =► \АС\ = 10.
Ответ. 10.
Задача 31.
Диагонали выпуклого четырёхугольника ABCD пересекаются в точке Е, С А - биссектриса угла С, \АВ\ = \AD\, BAD = 77г/9, BE А — 117г/18. Найдите величину угла CDB.
Идея. Использовать свойство вписанных углов, свойство биссектрисы и свойство серединного перпендикуляра к отрезку.
Указание. Описать окружность вокруг треугольника BCD и доказать, что точка А совпадает с серединой дуги BD.
Указание. Используя свойство вписанных углов, свойство вертикальных углов и свойство суммы углов треугольника, найти величину угла CDB.
Решение. Опишем окружность около треугольника BCD. Так как \АВ\ = |AD|, точка А и середина дуги BD лежат на биссектрисе угла BCD и на серединном перпендикуляре к отрезку BD. Поэтому точка А совпадает с серединой дуги BD. Значит, BAD + BCD = 7г. Тогда
BCD = тг - BAD Следовательно, из треугольника CED получаем
ECD = \bCD = ^, CED = BEA =
9 2 9 18
CDB = CDE = тг - ECD - CED = — = —.
9 18 18
5ti-
Ответ. —.
18
Задача 32.
В треугольнике ABC биссектриса AD угла А и биссектриса BL угла В пересекаются в точке F. При этом оказалось, что LFA = 7г/3.
1. Найдите величину угла АСВ.
2. Зная, что \АВ\ = 2, CLD = 7г/4, найдите площадь треугольника АВС.
Идея. Использовать свойство внешнего угла треугольника и определение биссектрисы угла. Использовать теорему о четырёх точках, свойство вписанных углов, свойство суммы углов треугольника.
Указание. Используя свойство внешнего угла треугольника и определение биссектрисы угла, найти величину угла АСВ.


342
Указания и решения
Указание. Используя теорему о четырёх точках, показать, что четырехугольник DFLC вписан в окружность.
Решение. Ответить на первый вопрос задачи просто: обозначим величины углов ВАС и АВС через 2а и 2/3. Тогда ABF = /3, BAF = а, АСВ = 7г—2а—2/3. Угол LFA - внешний угол треугольника ABF, поэтому
LFA = ABF+BAF
АСВ = тг-(2а+2/3) =
О
Для ответа на второй вопрос задачи заметим, что угол DFL - смежный с углом LFA, значит, его величина равна 27г/3 и DFL + DCL = тт. Поскольку точки А и В лежат в одной полуплоскости относительно прямой DL, а точка С в этой полуплоскости не лежит, точки С и F находятся в разных полуплоскостях относительно прямой DL. Таким образом, выполнены все условия теоремы о четырёх точках и вокруг четырехугольника DFLC можно описать окружность.
Далее, точка F - точка пересечения биссектрис, поэтому CF - биссектриса угла АСВ, ACF = BCF = 7г/6. По свойствам вписанных углов величина угла FLD тоже равна тт/6. С учётом этого находим
CLB = CLD + FLD = CBL = тг - CLB - BCL = АВС = 2 СВ1 = ~.
12 4 2
Итак, треугольник АВС прямоугольный. Из него мы легко находим
\ВС\ = \АВ\ ctg АСВ = , Saabc = \ • \АВ\ ■ \ВС\ = .
—■ 7Г 2
Ответ. АСВ = -, Saabc = •
Задача 33.
В выпуклом четырёхугольнике ABCD проведены диагонали АС и BD. При этом оказалось, что ВАС = В DC, а площадь круга, описанного около треугольника BCD, равна 257г/4.
1. Найдите длину радиуса окружности, описанной около треугольника АВС.
2. Зная, что \ВС\ = 3, \АС\ = 4, BAD = 7г/2, найдите площадь четырёхугольника ABCD.
Идея. Использовать теорему синусов. Использовать теорему о четырёх точках, свойство вписанных углов, теоремы косинусов и Пифагора.


2.1. Углы в окружностях
343
Указание. Используя теорему синусов, показать, что радиусы окружностей, описанных около треугольников BCD и АВС, равны.
Указание. Используя теорему о четырёх точках, показать, что вокруг четырёхугольника ABCD можно описать окружность, для которой BD - диаметр.
Указание. Искать площадь четырёхугольника ABCD как сумму площадей двух прямоугольных треугольников ABD и BCD. При этом использовать теоремы косинусов и Пифагора.
Решение. Сначала ответим на первый вопрос задачи. Поскольку
\вс\ . _ _ \вс\
Rabcd =
2 sin В DC
Raabc =
2 sin ВАС
очевидно, длины радиусов окружностей, описанных около треугольников АВС и BCD, равны. Применяя формулу площади круга, получаем
Raabc = Rabcd = у к-^--а = 2 •
Для ответа на второй вопрос задачи заметим, что поскольку четырёхугольник ABCD выпуклый, точки А и D лежат в одной полуплоскости относительно прямой ВС. Стало быть, выполнены все условия теоремы о четырёх точках, поэтому четырёхугольник ABCD вписан в окружность.
Дальнейший ход решения достаточно прост. Так как BAD = 7г/2, то BD диаметр этой окружности. Длина её радиуса нами уже найдена в пункте 1, стало быть, \BD\ = 5. Исходя из этого, угол BCD также прямой (он опирается на диаметр). Поэтому проще всего искать площадь четырёхугольника ABCD как сумму площадей двух прямоугольных треугольников ABD и BCD.
Из прямоугольного треугольника BCD имеем \CD\ = 4, cos В DC — 4/5. С учётом того, что ВАС = В DC, запишем теорему косинусов для треугольника АВС:
\ВС\2 = \АВ\2 + \АС\2 - 2 • \АВ\ ■ \АС\ ■ cos ВАС =>
\АВ\ — 5,
QO
9 = \АВ\2 + 16 - ^-|АВ|
Ъ\АВ\2 — 32|АВ| + 35 = О
|АВ| =
Первый из этих вариантов нам не подходит, поскольку длина катета прямоугольного треугольника должна быть меньше длины его гипотенузы. Наконец,
, 24 1 «4
\AD\ = y/\BD\2 - \АВ\* = SAAbd = ^ • \АВ\ • \AD\ =
1 84 2Я4
Sabcd = ^ ‘ \ВС\ ■ |CD\ = 6, Sabcd = 6 + — = -^г.
Ответ. Raabc = я> Sabcd =
I 25


344
Указания и решения
Задача 34-
В трапеции KLMN LM\\KN, KLM = тг/2. Окружность проходит через точки М и N и касается прямой KL в точке А. Найдите площадь треугольника AMN, если известно, что \LM\ = I, |JRriV| = /с, |MiV| = а.
Идея. Использовать свойства вписанных углов, углов между касательной и хордой и подобие треугольников.
Указание. Показать, что подобны пары треугольников К AN и НМ A, LAM и HNА, где Н - основание высоты, опущенной из точки А.
Указание. Не забудьте рассмотреть все случаи касания окружности с прямой KL.
Решение. Поскольку мы знаем длину отрезка MN, для нахождения площади треугольника AM N нам необходимо найти длину его высоты, опущенной из точки А. Обозначим основание этой высоты буквой Н.
Далее нам придётся рассмотреть два случая: точка А может либо попасть на отрезок KL, либо не попасть. Если она на него попадает, то, во-первых, углы К AN и LAM будут обязательно острыми, поскольку диаметр, проходящий через точку А, лежит между прямыми KN и LM, и, во-вторых, по свойству угла между касательной и хордой
KAN = AMN, LAM = ANM.
Из всего этого вытекает, что точка Н обязательно попадает на отрезок MN и, кроме того, подобие пар треугольников К AN и НМ A, LAM и HNA. Из этих подобий вытекает
IJRTjYI \an\ \lm\ \ам\
\АН\ ~ \АМ\ ’ \АН\ ~ \AN\ ■
Перемножая эти равенства, получаем
= 1 *=* \АН\ = V\KN\ ■ \LM\ = Vkl,


2.1. Углы в окружностях
345
Saamn = \ • \MN\ ■ \АН\ =
Теперь разберем случай, когда точка А не попадает на отрезок KL. Для определенности будем считать, что L лежит между А и К. Тогда углы К AN и LAM снова будут обязательно острыми и, по свойству угла между касательной и хордой, выполнено
KAN = AMN, тг - LAM = AN М.
Значит, угол AMN тупой, точка Н попадает на продолжение отрезка MN за точку iV, поэтому ANH = 7г — ANM = LAM. Итак, мы опять получили подобие пар треугольников К AN и НМ A, LAM и HNA. Дальнейшие вычисления проводятся аналогично.
_ Va2kl
Ответ. —-—.
Задача 35.
Две окружности пересекаются в точках А и К. Их центры расположены по разные стороны от прямой, содержащей отрезок АК. Точки В и С лежат на разных окружностях. Прямая, содержащая отрезок АВ, касается одной окружности в точке А. Прямая, содержащая отрезок АС, касается другой окружности также в точке А. \ВК\ = 1, \СК\ = 4, а тангенс величины угла САВ равен 1/\/15. Найдите площадь треугольника АВС.
Идея. Использовать свойства вписанных углов и углов между касательной и хордой, подобие, свойство суммы углов треугольника, теорему косинусов.
Указание. Используя свойство вписанных углов и углов между касательной и хордой, показать, что треугольники АСК и ВАК подобны по двум углам. Найти \АК\.
Указание. Используя теорему о сумме величин углов треугольника, показать, что АКВ — АКС = тг - САВ.
Указание. Пользуясь теоремой косинусов для треугольников ВАК и АСК, найти \АВ\ и \АС\.
Решение. Обозначим величины углов ВАК и САК буквами а и /3 соответственно. По свойству угла между касательной и хордой ВАК = АСК, САК = АВК. Из этого следует, что треугольники АСК и ВАК подобны по двум углам. С учётом этого получаем
Щ = *=* \АК\* = \ВК\-\СК\ =► |АЙГ| = 2.


346
Указания и регйения
Далее заметим, что
САВ = ВАК + САК = а + /3
tg(a + /3) =
у/15
л/15
cos(a + /3) =
АЙГВ = тг - ВАК - = тг - (а + 0), ЛКС = тг - СЛХ - Л(Ж = тг - (а + /3).
Теперь воспользуемся теоремой косинусов для треугольников ВАК и АС К:
|АВ\2 = \АК\2 + \КВ\2 - 2 • |ЛЯГ| • \КВ\ • cos АЮ? =►
=>■ | АВ\2 = 5 — 4 cos(tг — (а + /3)) — 5 + 4 cos(a + /3) =Ф- | АВ| = \f 5 + vT^;
|ЛС|2 = |vUf|2 + IJsTC'l2 - 2 • |ЛЙГ| • |КС| • cos АКС =>
=>■ |Ж7|2 = 20 — 16cos(tt — (а + /3))
Наконец,
|Ж7| = 2\] 5 + л/15. 5 +VT5
Ответ.
sin(a + /3) = i, 5длВС = | • \АВ\ ■ \АС\ • sinCAB = 5 + л/15
Задача 36.
В треугольнике АБС величина угла В равна 7г/6. Через точки А и В проведена окружность, длина радиуса которой равна 2, касающаяся прямой АС в точке А. Через точки В и С проведена окружность, длина радиуса которой равна 3, касающаяся прямой АС в точке С. Найдите |АС|.
Идея. Использовать свойство вписанных углов и углов между касательной и хордой, теорему синусов. Указание. Обозначить центр окружности, длина радиуса которой равна 3, буквой О, центр другой окружности обозначить за О', величину угла ВАС обозначить буквой а. Используя свойство вписанных углов и углов между касательной и хордой, выразить углы АО'В и ВОС через а.
Указание. Выразить \АВ\ и |БС| через а. Записывая в треугольнике АВС теорему синусов, найти Raabc •
Решение. Обозначим центр окружности, длина радиуса которой равна 3, буквой О, центр другой окружности обозначим за О', величину угла ВАС обозначим буквой а. Тогда АСВ = 7г — ВАС — АВС = 57г/6 — а.
По свойству угла между касательной и хордой величина угла АО'В треугольника АО'В будет равна либо 2а (если а < 7г/2), либо 2п — 2а (если а > 7г/2).


2.2. Касательные, хорды, секущие
347
Рассуждая аналогично, получаем, что величина угла ВОС треугольника ВОС равна либо 57г/3 — 2а, либо 2а4-7г/3. Тем не менее, независимо от этих вариантов
\ВС\ = 2|OB|sin — 6 sin , \АВ\ = 2|0'B|sin ~ 4 sina.
Записывая в треугольнике АВС теорему синусов, получаем
\АВ\ \ВС\ ^ 4 sin a 6sin(f-a) _
ЛКаавс = = ===== => бПААВС = -—JTZ Г = : =>
sin АСВ sin В AC sin(^-a) sina
( sina \ _ 3 sina [3 _ /З _ /^
=* ^sin(^_a)J “2 ^ sin(f-a)_V 2 ^ RaABC V 2 ^
И, наконец, по теореме синусов находим
\АС\ = 2 • Raabc * sin ЛВС = \/б.
Ответ, л/в.
2.2. 	Касательные, хорды, секущие Задача 1.
На боковой стороне ВС равнобедренного треугольника АВС как на диаметре построена окружность, пересекающая основание этого треугольника в точке D. Найдите расстояние от её центра до точки Л, если \AD\ = \/3, АВС = 27г/3.
Идея. Определить, какая из сторон^треугольника д АВС является его основанием, воспользоваться свойством угла, опирающегося на диаметр.
Указание. Найти длины всех сторон треугольника.
Указание. Воспользоваться теоремой косинусов для треугольника АВО, где О - центр окружности.
Решение. Заметим, что угол АВС тупой, поэтому он не может быть углом при основании равнобедренного треугольника АВС. Стало быть, ЛС - его основание, \АВ\ = |ВС|, ВАС = АСВ = тг/6.
Далее, поскольку ВС - диаметр окружности, угол BDC прямой. Таким образом, BD - высота равнобедренного треугольника ЛВС, проведённая к его основанию. Поэтому она также является медианой и биссектрисой треугольника ЛВС, то есть \AD\ = \DC\, \АС\ = 2\AD\ = 2^5.
Наконец, из прямоугольного треугольника BCD получаем
\РС\ . Уз 2
cos DCB &


348
Указания и решения
Итак, в треугольнике АВС нам известны длины всех его сторон: \АВ\ = \ВС\ = 2, \АС\ = 2л/3. Обозначим центр окружности буквой О, тогда О - середина отрезка ВС. Воспользуемся теоремой косинусов для треугольника АВО:
\АО\2 = |АВ|2 + \ВО\2 - 2 • \АВ\ ■ \ВО\ ■ cos АВО = 7 =► \АО\ = у/7.
Ответ, у/7.
Задача 2.
В треугольнике АВС \АВ\ = 4, градусные меры углов ВАС и АБС равны 30° и 130° соответственно. На стороне АВ как на диаметре построен круг. Найдите площадь части этого круга, лежащей внутри треугольника АВС.
Идея. Доказать, что сторона ВС не имеет общих точек с кругом, отличных от точки В. Искомую площадь представить в виде суммы простых фигур. Указание. Представить искомую площадь в виде суммы площадей треугольника АО К и сектора ВОК, где О - центр круга, К — точка пересечения окружности и стороны АС.
Решение. Поскольку градусная мера угла АВС равна 130°, отрезок ВС не имеет общих точек с кругом, отличных от точки В. Обосновать этот факт просто: если предположить противное, то, обозначая точку пересечения отрезка ВС и окружности буквой Л, мы получим, что угол ARB прямой и тогда ARB -f ABR > 180°, что невозможно. Отрезок же АС, напротив, пересекает окружность. Точку их пересечения обозначим буквой К, а буквой О обозначим центр окружности.
Искомую площадь, очевидно, можно найти как сумму площадей треугольника АО К и сектора ВОК. Треугольник АО К равнобедренный, |АО| = \ОК\ — 2,
ОАК = АКО = 30°, АОК = 120°. Тогда ВОК = 60°,
Saaok = \ • \АО\ • \ОК\ • sin 120° = у/з, SceKTOpaBOK = \ • \ОВ\2 = у.
Осталось сложить полученные значения и выписать ответ.
3\/3 + 27Г Ответ. .
Задача 3.
Из точки М на окружности проведены три хорды MN, МР и МQ таким образом, что \MN\ = 1, \МР\ = 6, \MQ\ = 2. При этом величины углов NMP и PMQ равны. Найдите длину радиуса этой окружности.
Идея. Доказать, что |iVP| = \PQ\.


2.2. Касательные, хорды, секущие
349
Указание. Воспользоваться теоремами синусов и коси- ^
нусов.
Решение. Обозначим величины углов NMP и PMQ через а. Поскольку треугольники MNP и MPQ вписаны в одну и ту же окружность, используя теорему синусов для этих треугольников, мы сразу получаем, что \NP\ = \PQ\ — 2,Rsina (за R обозначена длина радиуса окружности).
Запишем теорему косинусов для этих треугольников:
\NP\2 = \MN\2 + \МР\2 - 2 • \MN\ ■ \МР\ • cos NMP = 37- 12 cos a;
|PQ|2 = |Af<3|2 + \MP\2 - 2 • \MQ\ ■ \MP\ • cos PMQ = 40 - 24 cos a. Приравнивая правые части полученных соотношений, находим, что
cos <* = т =>• sina = ~J~> \NP\ = y/M => R = = 2\[^.
4 4 1 1 2 sina V 15
Ответ. 2\/т^.
V 15
Задача 4-
В треугольнике АВС с периметром 2р длина стороны АС равна а и величина острого угла АВС равна а. Вписанная в треугольник АВС окружность с центром О касается стороны ВС в точке К. Найдите площадь треугольника ВОК.
Идея. Воспользоваться теоремой о длинах отрезков, на которые окружность, вписанная в треугольник, делит его стороны, и тем, что центр этой окружности лежит на пересечении биссектрис треугольника.
Указание. Найти длину отрезка В К, затем рассмотреть прямоугольный треугольник ВОК.
Решение. Пользуясь теоремой о длинах отрезков, на которые окружность, вписанная в треугольник, делит его стороны, находим
\вк\ = Р&АВС -\АС\ = р-а.
Далее, О - центр вписанной в треугольник АВС окружности, поэтому ВО - биссектриса угла АВС. Таким образом, ОВК = а/2. Наконец, К - точка касания окружности, вписанной в треугольник АВС, и стороны ВС, поэтому О К _L ВС, и из прямоугольного треугольника ВОК находим
В
\ОК\ — \ВК\ ■ tg ВОК = (р-a) tg Saabc = \ • \ВК\ ■ \ОК\ = \(р-a)2 tg |.


350
Указания и решения
Задача 5.
В треугольник АВС вписана окружность, которая касается его сторон АВ, ВС и АС в точках М, D и N соответственно. Вычислите длину отрезка MD, если известно, что |iV^4| = 2, \NC\ = 3, ВС А = 7г/3.
Идея. Воспользоваться теоремой о равенстве длин отрезков касательных, проведённых к окружности из одной точки.
Указание. Обозначить \BD\ = \ВМ\ —х. Воспользоваться теоремой косинусов для треугольника АВС, найти х и cos ABC.
Решение. Поскольку отрезки касательных, проведённых к окружности из одной точки, равны,
\АМ\ = |-АЛГ| = 2, \CN\ = \CD\ = 3, \BD\ = \ВМ\.
Обозначим длины отрезков BD и ВМ буквой х и запишем теорему косинусов для треугольника АВС:
\АВ\2 = \АС\2 + |ВС\2 - 2 • |Ж7| • |ВС| • cos АСВ =►
=>• (ж + 2)2 = 25 + (ж + 3)2 — 5(а;+3) => ж = 5 ==> |ЛВ| = 7, |j5C|=8.
Теперь ещё два раза воспользуемся теоремой косинусов для треугольников АВС и В DM:
\АС\2 = \AB\2 + \BC\2-2-\AB\-\BC\-cosABC =» cos ABC = —= 77;
2*7*8 14
\MD\2 = \BM\2 + \BD\2-2-\BD\-\BM\-cosABC =>• |MI?| = \/50_ ^ = 5\/|'
/З*
Ответ. 5y -.
Задача 6.
Окружность касается сторон АБ и ВС треугольника АБС соответственно в точках D и Е. Найдите длину высоты треугольника АВС, опущенной из вершины А, если |АВ| = 5, \АС\ = 2, а точки A, D, Е и С лежат на одной окружности.
Идея. Выяснить, что даёт то, что точки A, D, Е и С лежат на одной окружности.
Указание. Воспользоваться теоремой о равенстве длин отрезков касательных, проведённых к окружности из одной точки, и свойством выпуклого четырёхугольника, вписанного в окружность.


2.2. Касательные, хорды, секущие
351
Указание. Для нахождения длины высоты воспользоваться двумя формулами площади треугольника.
Решение. Поскольку отрезки касательных, проведённых к окружности из одной точки, равны, \BD\ = \ВЕ\, значит, треугольник BDE равнобедренный, из чего вытекает BDE = BED. Далее, четырёхугольник ADEC выпуклый и вписан в окружность, поэтому ADE -f АСЕ — DAC -I- DEC.
А так как углы ADE и DEC смежные с равными углами BDE и BED, их величины также равны. Значит, равны и величины углов АСЕ и DAC, то есть треугольник АВС равнобедренный, \АВ\ = \ВС\ = 5.
Наконец, найдём длину высоты треугольника АВС, опущенной из вершины А, с помощью формул площади:
Saabc = yjРаавс{раавс - \АВ\)(раавс ~ \ВС\)(раавс ~ \ЛС\) = 2\/б;
2 Saabc 4\/б
Ьвс =
\ВС\
Ответ.
4\/б
Задача 7.
Две окружности касаются друг друга внешним образом в точке А. Их общая касательная касается первой окружности в точке В, а второй в точке С. Прямая, проходящая через точки А и В, пересекает вторую окружность в точке D. Известно, что \АВ\ — 5, \AD\ = 4. Найдите \CD\.
Идея. Доказать, что CD J_ ВС.
Указание. Обозначить центры окружностей буквами О и О'. Рассмотрев равнобедренные треугольники АОВ и AO'D, доказать, что OB\\OfD.
Указание. Воспользоваться теоремой о произведении длины секущей на длину её внешней части.
Решение. Обозначим центр первой окружности буквой О, а центр второй - буквой О'. Заметим, что треугольник АОВ равнобедренный (\АО\ = \ОВ\), поэтому ZОАВ = ZOBA. Треугольник AO'D тоже равнобедренный (|j40'| = \OfD\), значит, ZO'AD = ZO'DA. Далее, поскольку окружности касаются друг друга, точки О, А и О' лежат на одной прямой, то есть углы ОАВ и О'AD вертикальные.
Из всех этих рассуждений следует, что Z.OBA = ZO'DA. Эти углы являются внутренними накрест лежащими при прямых О В и О'D и секущей BD, значит, 0B\\0'D. Тогда с учётом того, что ОВ _1_ ВС, мы получаем, что OD _1_ ВС, но О'С _L ВС, поскольку С - точка касания. Поэтому точки D, О' и С лежат на одной прямой и треугольник BDC прямоугольный.


352
Указания и решения
Теперь воспользуемся теоремой о произведении длины секущей на длину её внешней части:
\ВС\2 = \BD\ • \ВА\ =» \ВС\2 = (\АВ\ + \AD\) ■ \АВ\ = 45.
Наконец, запишем теорему Пифагора для треугольника BCD:
\CD\2 = \BD\2 — |БС|2 =81-45 =>■ \CD\ = 6.
Ответ. 6.
Задача 8.
В окружности, длина радиуса которой равна 4, проведены хорда АВ и диаметр АК, причём ВАК = 7г/8. В точке В проведена касательная к этой окружности, пересекающая продолжение диаметра АК в точке С. Найдите длину медианы AM треугольника АВС.
Идея. Найти величины углов треугольника АВС. Указание. Воспользоваться тем, что треугольник АОВ равнобедренный, где О - центр окружности. Указание. Воспользоваться теоремой о произведении длины секущей на длину её внешней части. Применить теорему косинусов.
Решение. Обозначим центр окружности буквой О, середину отрезка ВС обозначим буквой М. Тогда \АО\ = \ОВ\ = \ОК\ = 4, треугольник АОВ равнобедренный. Значит,
ВАО = ОВА=1, ВОК = Шд + ОВА = ^, АОВ =
8 4 4
Поскольку ВС _L ОБ, получим ВСО — — — ВОК = Таким образом, треугольник ОВС тоже равнобедренный, \ВС\ = |ОБ| = 4. По свойству секущей получаем: \СК\ • \СА\ = |СБ|2 =>
\СК\2 + 8\СК\ - 16 = 0 ==► \CK\ = 4V2-4 => \АС\= 4 +4V2.
Наконец, пользуясь теоремой косинусов, найдём \АМ\ из треугольника ACM:
\АМ\2 = \АС\2 + |СМ|2 - 2 • \АС\ ■ \СМ\ ■ cos ACM = 36 + 24л/2
=» |АМ| = V^ + 2V2 = 2V3-(V2 +1) = 2V6 + 2V3. Ответ. 2(4/64-4/3).


2.2. Касательные, хорды, секущие
353
Задача 9.
В треугольнике АВС на стороне АС как на диаметре построена окружность, которая пересекает сторону АВ в точке М и сторону ВС в точке N. Известно, что длина отрезка АВ равна 3, длина отрезка АС равна 2, \АМ\ : \МВ\ =2:3. Найдите длину отрезка AN.
Идея. Воспользоваться тем, что вписанные углы, опирающиеся на диаметр окружности, являются прямыми.
Указание. Рассмотреть прямоугольные треугольники AM С, ВМС и AN В.
Решение. По условию задачи АС - диаметр окружности, поэтому углы АМС и ANС прямые. Найдём длины отрезков AM и MB: пусть \АМ\ = 2ж, тогда \МВ\ = Зж, \АВ\ = 3 = \АМ\ + \МВ\ = 5я :
* = |, \АМ\ = \, \МВ\ = 9-.
Теперь рассмотрим прямоугольные треугольники АМС, ВМС и AN В:
|МС|2 = |ЛС|2-|ЛМ|2=4-| = |
81 64 145
\вс\ = \МВ\ + \МС\ = - + - =
25
Ответ.
sin ABC =
24
[МС[ _ 8
\ВС\ ~ л/145’
\МС\ - \ВС\ =
5’
л/145
|ЛЛГ| = \ AB\smABC =
24
>/145'
В
Задача 10.
Окружность проходит через вершины Л и С треугольника АВС, пересекает сторону АВ в точке Z) и сторону ВС в точке Е1. Найдите величину угла CDB, если |А£| = 5, \АС\ = 2-ч/7, |В£?| = 4, |В£>| : |СЕ| =3:2.
Идея. Воспользоваться теоремой о произведении длины секущей на длину её внешней части.
Указание. Применить теорему косинусов к треугольникам ADC и В DC.
Решение. Положим \BD\ — Зх, \СЕ\ = 2х и воспользуемся теоремой о произведении длины секущей на длину её С Е В
внешней части:
\BD\ • \ВА\ = \ВЕ\ • \ВС\ =*
12 Геометрия


354
Указания и решения
=* 3х (3х + 5) = 4-(4 + 2х) => ж = 1, \ВС\ = б, |АВ| = 8.
Положим CDJ9 = а, |С£)| = г/ и запишем теорему косинусов для треугольников В DC и ADC:
Г |ВС|2 = |Я£|2 + |CD|2 - 2 • |В£>| • |С£>| • cosa,
1 \АС\2 = \AD\2 + |СТ>|2 - 2 • |AD| • |С£>| • cos(tг - a); ^
=> u = 3\/2 =£• cosa = =.
2уД
Ответ, arccos
36 = 9 -f у2 — 6у • cos а,
28 = 25 + у2 4- 10у • cos а;
Значит, CDB = arccos 1
2у/2
Задача 11.
В четырёхугольник ABCD вписана окружность, длина радиуса которой равна 2. Угол DAB прямой, \АВ\ = 5, \ВС\ = 6. Найдите площадь четырёхугольника ABCD.
Идея. Использовать свойство касательных и формулу площади выпуклого четырёхугольника через полу периметр и радиус вписанной окружности. Указание. Используя свойство касательных и тот факт, что величина полного угла равна 27т, найти длины всех сторон четырёхугольника.
Решение. Обозначим центр вписанной в четырёхугольник ABCD окружности буквой О, точки её касания со сторонами АВ, ВС, CD и AD обозначим буквами К, L, М и JV соответственно. Тогда, во-первых, OK _L АВ, OL _L ВС, ОМ _L CD, ON ± AD, во-вторых, \АК\ = \AN\, \ВК\ = \BL\, \CL\ = \СМ\, \DM\ = \DN\ и, в-третьих, \ОК\ = \OL\ = \ОМ\ = \ON\ = 2.
Из этих фактов и из условия задачи вытекает, что AKON - квадрат. Действительно, у этого четырёхугольника три угла прямые, следовательно, прямым является и четвёртый его угол, поэтому он - прямоугольник. А раз у него равны две соседние стороны, то он - квадрат. Из этого мы получаем, что \АК\ = \AN\ = 2, тогда \ВК\ = \BL\ = 3 и \CL\ = \СМ\ = 3 и, кроме того, К ON = тг/2.
Теперь для ответа на вопрос задачи нам достаточно найти длины отрезков DM и DN, после чего воспользоваться тем фактом, что площадь любого выпуклого многоугольника, описанного около окружности, равна произведению длины радиуса А К В
этой окружности и его полупериметра.
Треугольники К ВО, LBO, LCO и МСО равны между собой (по двум катетам). Поэтому равны между собой углы КОВ, LOB, LOC и МОС. Аналогично


2.2. Касательные, хорды, секущие
355
равны треугольники MOD и NOD, а, стало быть, равны между собой углы MOD и NOD. Положим КОВ = a, MOD = /3.
Из треугольника КОВ получаем tga = \ВК\ : \ОК\ = 3/2. Далее, ясно, что
4а + 2/3 + ^ = 27Г => /3 — ~~ — 2а =>
в - 1 + 2с* — 1 + 2 tg а ~tg2 а _ _L
^ l-tg2a tg2a + 2tga-l 17*
Наконец, из треугольника DOM находим
\DM\ = |OAf | tg/З = 14/17, \DN\ = \DM\ =>
n n , 0 14 300 п Л 1 300 300
=> Pabcd = 2- 2 + 4*3 + 2‘ — = —, Sabcd = 2 • - • — = —.
300
Ответ. -.
17
Задача 12.
Окружность, проходящая через вершину А треугольника АВС, касается стороны ВС в точке М и пересекает стороны АС и АВ в точках L и К соответственно. Найдите отношение \АС\ : \АВ\, если известно, что длина отрезка CL в два раза больше длины отрезка ВК, |СМ| : |ВМ| =3:2.
Идея. Воспользоваться теоремой о произведении длины секущей на длину её внешней части.
Указание. Рассмотреть секущие В А и С А и касательные ВМ и СМ.
Решение. Дважды применяя теорему о произведении длины секущей на длину её внешней части, получаем
\АС\ • \CL\ = \СМ\2, \АС\ \CL\ _ ПСМ\\2 о \АС\ _ 9
\АВ\ ■ \ВК\ = \ВМ\2 ^ \АВ\'\BK\~ \\ВМ\) ^ ' \АВ\ ~ 4‘
Таким образом, |j4C| : \АВ\ =9:8.
Ответ. 9:8.
А
Задача 13.
В круге с центром О хорда АВ пересекает радиус ОС в точке D, причём величина угла ADC равна 2п/3. Найдите длину радиуса окружности, касающейся отрезков AD.DC и дуги АС, если \ОС\ = 2, \OD\ = \/3-
12*


356
Указания и решения
Идея. Воспользоваться тем, что центр окружности, вписанной в угол, лежит на его биссектрисе, и тем, что точка касания двух окружностей и их центры лежат на одной прямой.
Указание. Рассмотреть треугольник 00\К, где 0\ - центр окружности, касающейся отрезков AD, DC и дуги АС, а К - точка касания этой окружности и отрезка DC.
Указание. Воспользоваться тем, что DO\ - биссектриса угла ACD, а длина отрезка 00\ равна разности длин радиусов окружностей.
Решение. Обозначим центр окружности, касаю- q в
щейся отрезков AD, DC и дуги АС, буквой 0\.
Поскольку эта окружность касается отрезков AD и DC, она вписана в угол ADC, стало быть, её центр лежит на биссектрисе этого угла. С учётом этого, обозначив буквой К точку касания этой окружности с отрезком DC, мы получаем, что величина угла Oi DK равна половине величины угла ADC, то есть 7г/3.
С другой стороны, окружности из условия задачи касаются друг друга, поэтому их центры и точка касания лежат на одной прямой. Таким образом, длина отрезка 00\ может быть вычислена как разность длин радиусов окружностей.
Обозначим искомую длину буквой х. Тогда, исходя из вышесказанного,
\ООх | = 2 - ж, \ОгК\= х, \DK\ = \ОгК\ • ctgOxDK
х
7з’
\ОК\ = \OD\ + \DK\ = V3 +
х -j- 3
■у/З V3 '
Записывая для треугольника 00\К теорему Пифагора, получаем
|OOi|2 = \OiK\2 + \OK\*
{2-х)2 = х2 + ^-(х+3)2
О
х + 18х — 3 = 0.
Полученное квадратное уравнение имеет два корня х\^ = — 9 ± 2у/21, из которых нам подходит только положительный.
Ответ. 2\/21 — 9.
Задача 14>
Две окружности с радиусами разной длины касаются в точке А одной и той же прямой и расположены по разные стороны от неё. Отрезок АВ - диаметр окружности меньшего радиуса. Из точки В проведены две прямые, касающиеся окружности большего радиуса в точках М и N. Прямая, проходящая через точки М и А, пересекает меньшую окружность в точке К. Известно, что \МК\ = у/2 + л/3, ВМА = 7г/12. Найдите площадь фигуры, ограниченной отрезками касательных ВМ, BN и той дугой MN большей окружности, которая не содержит точку А.


2.2. Касательные, хорды, секущие
357
Идея. Воспользоваться свойством угла между касательной и секущей, найти длину радиуса большей окружности.
Указание. Рассмотреть прямоугольные треугольники МКВ и МОВ, искомую площадь представить как сумму площадей треугольников ВОМ, BON и площади сектора MON.
Решение. Обозначим центр окружности большего радиуса буквой О. По теореме о величине угла между касательной и секущей угол ВМА измеряется половиной дуги AM. Таким образом, мера дуги AM равна 7г/6. С другой стороны, центральный угол АОМ измеряется дугой AM, поэтому АОМ = п/б.
Далее, поскольку угол АКВ опирается на диаметр меньшей окружности, он прямой. Из прямоугольного треугольника МКВ получаем
\ВМ\ =
\мк\
cos ВМК
V2 + V3
cos
л/3+l
У2
12
cos(f - I) V3 + i
(Уз+ip
(V2)»
cos j cos | -f sin j sin ^
л/3 + 1
4/24/3,4/21
2*22*2
л/3+l
2
2.
V2 •
Так как ВМ - касательная к окружности большего радиуса, то угол ВМО прямой. Из прямоугольного треугольника ВМО находим
\ОМ\ = R= \ВМ\ ■ ctg ВОМ = 2 • ctg | = 2\/3.
Наконец, искомую площадь можно представить как сумму площадей треугольников ВОМ и BON и сектора MOiV, не содержащего точку А. Треугольники ВОМ и BON, очевидно, равны, поэтому
Sabom 4- Sabon = 2S&bom = 2 • - • |J3M| • |ОМ| = 4л/з.
Величина угла МОiV (опирающегося на дугу МN, содержащую точку А) равна удвоенной величине угла ВОМ, то есть 7г/3, поэтому величина центрального угла сектора, площадь которого нам надо найти, равна 27г — 7г/3, то есть 57г/3. Исходя из этого,
^сектора MON — В
Ответ. 4\/3 + 107Г.
5-7Г
3
2
(2\/3)2 • у = Ютг.
Задача 15.
Две окружности, длины радиусов которых относятся как (9 — 4\/3) : 1, касаются друг друга внутренним образом. Проведены две равные по длине хорды большей


358
Указания и решения
окружности, касающиеся меньшей окружности. Одна из этих хорд перпендикулярна отрезку, соединяющему центры окружностей, а другая нет. Найдите величину угла между этими хордами.
Идея. Рассмотреть четырёхугольник, образованный центрами окружностей и их проекциями на хорду, не перпендикулярную отрезку, соединяющему центры окружностей. Доказать, что один из его углов равен искомому.
Указание. Выразить длины сторон четырёхугольника, образованного центрами окружностей и их проекциями на хорду, не перпендикулярную отрезку, соединяющему центры окружностей, через длину радиуса меньшей окружности. Указание. Доказать, что равные хорды окружности равноудалены от её центра.
Решение. Обозначим хорду, перпендикулярную отрезку, соединяющему центры окружностей, CD, а вторую хорду - АВ. Центр большей окружности обозначим
О,
О
3 1 т?
е
Q Р
Обозначим радиус меньшей окружности буквой R, тогда радиус большей окружности равен (9 — 4\/3)R. Заметим, что (9 — 4\/3)R > 2Д, поэтому точка О лежит вне меньшей окружности.
Пусть S - точка пересечения меньшей окружности с отрезком 00\. Тогда она является точкой касания меньшей окружности с хордой CD, поскольку в противном случае радиус меньшей окружности, соединяющий её центр с этой точкой касания, также перпендикулярен хорде CD, но из одной точки можно провести только один перпендикуляр к прямой.
Наконец, обозначим точку касания хорды АВ с меньшей окружностью буквой Q, точку пересечения хорд буквой Т и середину хорды АВ буквой Р, тогда OP LAB.
Так как величиной угла между отрезками (прямыми) называется величина острого или прямого угла, образованного ими, то в нашем случае это будет величина угла QTC, смежного с углом QTS. Поскольку сумма величин углов четырёхугольника равна 2п, из четырёхугольника 0\ QTS вытекает, что величина угла QO\S равна величине угла QTC. Поэтому будем искать QO\S.
буквой О, меньшей окружности - 0\.
С


2.2. Касательные, хорды, секущие
359
Поскольку \АВ\ = \CD\, равны равнобедренные треугольники ОАВ и OCD (по трём сторонам). Из этого равенства вытекает, что равны и высоты этих треугольников, опущенные на стороны АВ и CD, то есть \ОР\ = |05|.
Теперь проведём некоторые подсчёты. Ясно, что
|OiQ| - |OiS| = R, \ОР\ = |05| = (9 - AVZ)R -2R = (7- 4\/3)R,
|OOi| = (9 - 4л/3 )R -R= (8- 4уД )R.
Из четырёхугольника POO\Q находим (см. отдельный чертёж), что
пп7) \°iQ\-\Op\ Д-(7-4ч/3)Д (4у/3-6)Д 2Уз(2-лД) Уз
с°ь 1У |00i| (8-4л/3)R (8-4\/3)R 4(2 — >/3) 2 ’
Поэтому величина угла 00\Q, а следовательно, и искомого угла равна 7г/6.
^ п Ответ. —.
Задача 16.
Две окружности, длины радиусов которых равны б и 8, пересекаются в точках А и В. Через центры Oi и Oz этих окружностей проведена прямая; С\ и С2 ~ две из четырёх точек пересечения этой прямой с окружностями, причём точка С\ лежит на окружности с центром 0\, а длина отрезка С1С2 больше 20. Найдите расстояние между точками 0\ и О2, если произведение площадей треугольников С\0\А и С2О2В равно 336.
Идея. Воспользоваться тем, что общая хорда двух окружностей перпендикулярна прямой, соединяющей их центры, и делится ею пополам.
Указание. Выяснить порядок расположения точек 0\, О2, С\ и С2 •
Указание. Выразить площади треугольников С\0\А и С2О2В через длину хорды АВ и длины радиусов окружностей.
Решение. Всего, очевидно, возможно четыре варианта взаимного расположения точек С\ и С2, однако под условие задачи подходит только один - тот, когда отрезок С1С2 содержит обе точки 0\ и О2. В противном случае длина отрезка С\С2 не будет превышать удвоенную длину большего из радиусов окружностей, то есть 16.
Далее, поскольку отрезок АВ перпендикулярен прямой O1O2 и делится ею пополам, обозначая буквой Н точку их пересечения, получаем, что |А£Г| — \ВН\ и, кроме того,
5дс101л = \ • IC1O1I • \АН\ = 3|ЛЯ|, Sac2o2b = \ • \С202\• \ВН\ = 4\ВН\.


360
Указания и решения
Пользуясь условием задачи, имеем 12 • \АН\ • \ВН\ = 336 => \АН\ = \ВН\ = 2у/7. После этого запишем теорему Пифагора для треугольников АО\Н и АО2Н:
\0\H\2 + \АН\2 = \АО\\2 => \0\H\ — 2\/2,
\02Н\2 + \АН\2 = \А02\2 ==► |02Я| = 6.
Наконец, ещё раз воспользуемся тем, что длина отрезка С\Сч больше 20. Вообще говоря, мы заранее не знаем, попадает ли точка Н на отрезок O1O2. Поэтому возможно два варианта: либо точка Н лежит на отрезке O1O2, либо точка Н лежит вне отрезка O1O2. Первый из этих вариантов даёт нам
|0i021 = \0\H\ + \02Н\ = 2у/2 + 6 =►
=► IC1C2I = IC1O1I + IO1O2I + \с202\ = 20 + 2V2 > 20.
Для второго же варианта получаем
\0102\ = \02H\-\0iH\ = 6-2^2 =>
=► \CiC2\ = IC1O1I + \0г02\ + \С202\ = 20-2V2< 20.
Ответ. 2л/2 + 6.
Задача 17.
В круге, длина радиуса которого равна 1, проведены хорды А В и ВС. Найдите площадь части этого круга, лежащей внутри угла АВС, если угол ВАС острый, \АВ\ = у/2 и \ВС\ = 10/7.
В
Идея. Искомую площадь представить в виде суммы простых фигур.
Указание. Доказать, что точки А и С лежат по разные стороны от прямой, проходящей через точку В и центр окружности (О). Найти площади треугольников АОВ и ВОС и площадь сектора АОС.
Решение. Обозначим центр круга буквой О. Заметим, что в треугольнике АОВ \АО\ — \ВО\ = 1,
\АВ\ = л/2, поэтому он прямоугольный и равнобедренный, и величина угла АОВ равна 7г/2.
Проведём прямую через точки В и О. Она делит окружность на две равные дуги, точка А попадает на середину одной из них. Поскольку точка С удалена от точки В на расстояние, равное 10/7, точка С есть точка пересечения окружности с центром в точке В, длина радиуса которой равна 10/7, и нашей исходной окружности. Ясно, что они пересекаются в двух точках, то есть точка С может лежать как на дуге, на которой лежит точка А (на рисунке этот вариант представлен точкой Ci), так и на дуге, на которой не лежит точка А (на рисунке этому варианту соответствует точка С2). В первом из этих случаев вписанный угол ВАС, очевидно, опирается на дугу, мера которой больше тг, значит, его мера


2.2. Касательные, хорды, секущие
361
больше 7г/2, что противоречит условию, а во втором случае он опирается на дугу, мера которой меньше 7Г, значит, его мера меньше 7г/2.
Итак, нам подходит случай, когда точки А и С лежат по разные стороны от прямой ВО. Тогда искомая площадь может быть посчитана как сумма площадей треугольников АОВ и ВОС и сектора АОС. Сначала вычислим площади треугольников:
1,-1 12 _ /12 2 5 5 Юу'б
э&АОВ = 2 2’ РАВОС ~ У’ ь&вос = у -у ■ J ■ -j ■ J — "4g- •
Теперь с помощью теоремы косинусов найдём величину угла ВОС:
\ВС\2 = \ВО\2+ \ОС\2-2 \ВО\\ОС\-cos ВОС =► cos ВОС =
Тогда АОС = 2тт — АОВ — ВОС — — arccos ( — j = ? + arccos j-.
TT r* ,2 ^ П 1 \ 7Г 1 1
Наконец, SceKTOpaiAOC = 1 ‘ 2 ( 2 + arccos 49 7 4 + 2 arccos 49 *
Складывая полученные выражения, получаем ответ.
49 + 20л/6 я* 1 1
Ответ. — Ь — + - arccos — . Возможны и другие формы его записи.
Уо ^ sL “ri/
Задача 18.
Длина радиуса окружности, описанной около треугольника KLM, равна R. Через вершину L проведена прямая, перпендикулярная стороне КМ. Эту прямую пересекают в точках А и В серединные перпендикуляры к сторонам KL и LM. Известно, что \AL\ — а. Найдите \BL\.
Идея. Рассмотреть треугольники LAP и LBQ, Р - середина KL, а Q - середина LM.
Указание. Выразить произведение \AL\ • \BL\ через длины сторон KL и LM и синусы величин углов KLM и LKM. Использовать теорему синусов.
Решение. В этой задаче надо рассмотреть два случая: основание перпендикуляра, опущенного из вершины L на прямую КМ, попадает на отрезок КМ (левый чертёж) или не попадает (правый чертёж).
Обозначим середину отрезка KL буквой Р, а середину отрезка LM - буквой Q. В первом случае из прямоугольных треугольников LAP и LBQ получаем
H£|=-i^U= . , =
cos ALP cos ( § - LKM) 2 sin LK M


362
Указания и решения
\вц = \L®\ - _ \Ш\
cos BLQ cos (§ - LMK^J 2 sin LMK
Перемножая эти равенства, получаем \AL\ ■ \BL\ = Ji=4!— Ho no
2 sin LKM ■ 2 sin LMK
теореме синусов для треугольника KLM
\KL\ -2R, \L^\^ = 2r ==* \AL\ ■ \BL\ = R2 => \BL\ = —.
sin LMK sin LKM
Во втором случае будем действовать абсолютно аналогично. Единственная разница с первым случаем возникнет при рассмотрении треугольников LAP и LBQ:
]АЦ= \LP\ _ WKL\ _ \КЦ .
cos ALP cos ( § ~ LKM^j 2 sin LKM
\BL\ = \LSL = =
cos BLQ cos (f - (7Г - LMK)^ 2sin LMK Дальнейшие выкладки полностью совпадают с первым случаем.
n R2
Ответ. —.
а
Задача 19.
В окружности, длина радиуса которой равна R, проведены хорда АВ и диаметр АС. Хорда PQ, перпендикулярная диаметру АС, пересекает хорду АВ в точке М. Известно, что \АВ\ = а, \РМ\ : \MQ\ = 1:3. Найдите длину отрезка AM.
Идея. Применить теорему о произведении длин отрезков пересекающихся хорд.
Указание. Найти величину угла ВАС, выразить длины отрезков, на которые хорда PQ делит диаметр АС, через длину отрезка РМ.
Указание. Применить теорему о произведении длин
отрезков пересекающихся хорд АС и PQ.
Решение. Обозначим буквой Н точку пересечения Q
диаметра АС и хорды PQ, длину хорды PQ положим
равной 4х. Поскольку PQ _1_ АС, получаем \РН\ = \HQ\ = 2х. Из условия задачи вытекает, что \РМ\ = х, \MQ\ = Зх, поэтому \МН\ = х.
Угол АВС опирается на диаметр, поэтому он прямой. Из прямоугольного треугольника АВС, в котором нам известна длина гипотенузы (2R) и длина катета (а), находим
\вс\2 = \ас\2-\ав\2 =* \вс\ = V4R2 - «2; Ctg ВАС = =-^=1=


2.2. Касательные, хорды, секущие
363
Теперь рассмотрим прямоугольный треугольник МАН :
ах
\АН\ = \MH\-ctgMAH =
y/4R2 - а2
\НС\ = \AC\-\AH\ = 2R-
ах
vW
Наконец, применим теорему о произведении длин отрезков пересекающихся хорд:
\АН\ ■ \НС\ = \РН\ ■ \HQ\
ах
2 R = х
у/Ш1
+
4у/4R2 -а2'
= ■ (2R- -=^=Л =
а2 V у/4 R2-a2)
4х
2aRV4R2 - а2
х = —-■■ ■ = \МН\.
a* a J 16i?2 — За2
Осталось выразить AM. Для этого из треугольника АВС найдём
\ВС\ у/т2 - а2
sin ВАС =
\АС\
и из треугольника АМН находим
\АМ\ =
2 R
4aR2
sin
\МН\
МАЙ !6Д2 - За2'
Ответ.
4aR
16R2 - За2 ’
Задача 20.
Диаметр АВ и хорда CD окружности пересекаются в точке Е таким образом, что \СЕ\ = |DE\. Через точки В к С проведены две касательные к этой окружности, которые пересекаются в точке К. Отрезки АК и СЕ пересекаются в точке М. Найдите площадь треугольника С КМ, если \АВ\ = 10, \АЕ\ = 1.
Идея. Найти длины отрезков КВ и СМ. Воспользоваться тем, что CD\\KB, поэтому длина отрезка BE равна длине высоты треугольника СКМ. Указание. Рассмотреть треугольник СОЕ, где О - центр окружности. Найти \СЕ\ и величину угла СОЕ.
Указание. Найти величину угла ВОС и длину отрезка КВ.
Указание. Воспользоваться подобием треугольников АМЕ и АКВ для нахождения \МЕ\.
Решение. Поскольку \СЕ\ = \DE\, хорда
CD перпендикулярна диаметру АВ. Обозначим центр окружности буквой О, тогда
\АО\ = \ОВ\ = \ОС\ = 5, \ЕО\ = \АО\ -\АЕ\ = 4.


364
Указания и решения
После этого из прямоугольного треугольника СОЕ можно найти длину отрезка СЕ и величину угла СОЕ:
\СЕ\ = У\ОС\2 - \ЕО\2 = 3, cos СОЕ = = £ =► СОЕ = arccos
\ОС\ 5 5
Далее, треугольники КОВ и КОС равны между собой (по катету и гипотенузе), поэтому равны и углы КОВ и КОС. Если обозначить их величины буквой а, то
cos [кОВ + KOC^j = cos ^7г — COE^j ==> cos2a=—^ => cosa=--L=.
Теперь из прямоугольного треугольника КОВ находим
\ОК\ = - 5л/То, \ВК\ = ч/|<Ж|2 - |ОВ|2 = 15.
cos а
Наконец, прямые КВ и CD перпендикулярны отрезку АВ, поэтому КВЦСВ и треугольники МАЕ и КАВ подобны. Из этого подобия получаем
“щ} =» 'М£' = 11Г = | ICMI = |С£| - IMEI = !•
Площадь треугольника С КМ можно легко найти, заметив, что длина отрезка BE равна длине высоты этого треугольника, опущенной из вершины К. Значит,
Sackm = \ ■ \СМ\ • \ВЕ\ = Ц.
ъ 27
Ответ. —.
4
Задача 21.
Дана окружность с центром в точке О, длина радиуса которой равна 2. Из конца отрезка О А, пересекающегося с окружностью в точке М, проведена касательная АК к окружности. Величина угла ОАК равна 7г/3. Найдите длину радиуса окружности, касающейся отрезков АК, AM и дуги МК.
Идея. Рассмотреть треугольник, образованный центрами окружностей и точкой А.
Указание. Воспользоваться тем, что центр окруж- ^ ^
ности, длину радиуса которой надо найти, лежит как f \
на биссектрисе угла К AM, так и на прямой, проходя- / о
щей через точку О и через точку касания окружностей. I N
Указание. Выразить стороны треугольника НОО' \ \МУ
через искомый радиус, где О' - центр искомой окруж- ности, а Н - точка касания этой окружности с отрез- £ д
ком AM. Записать теорему Пифагора.


2.2. Касательные, хорды, секущие
365
Решение. Обозначим центр окружности, касающейся отрезков АК, AM и дуги МК, буквой О', точку касания этой окружности с отрезком AM обозначим буквой Н. Ясно, что О'Н _1_ AM.
Поскольку окружность, длину радиуса которой нам нужно найти, касается отрезков АК и AM, она вписана в угол К AM, стало быть, её центр лежит на биссектрисе этого угла. Из этого вытекает, что О'АО = 7г/6. С другой стороны, она касается окружности с центром в точке О, поэтому их центры и точка их касания лежат на одной прямой, то есть длина отрезка ОО равна сумме длин радиусов окружностей. Обозначим искомую длину буквой г, тогда
Далее, АК - касательная, поэтому АК _1_ ОК. Из треугольника АО К находим
Какой же из этих ответов нам подходит? Так как \ОН\ > 0, то г < 4/3. Поэтому подходит только меньшее из значений г. Оно и является ответом к задаче. Большее же из полученных значений соответствует окружности, которая касается продолжений отрезков AM и АК за точки М и К и исходной окружности внешним образом.
окружности равна л/15/3. Окружность, длина радиуса которой равна 5\/15/9, касается лучей, образующих угол АСВ, и вписанной в треугольник АВС окружности. Найдите tg ABC, если наибольшей из сторон треугольника АВС является сторона АС.
Идея. Найти ещё один элемент треугольника АВС.
Указание. Рассмотреть прямоугольную трапецию, образованную центрами окружностей и точками их касания с одной из сторон угла, найти величину угла
Указание. Воспользоваться формулами площади и теоремой косинусов для нахождения сторон треугольника АВС.
\ОСУ\ =г + 2, \0'Н\ = г, \АН\ = \0'Н\ • ctg O'АО = \/3г.
Теперь запишем теорему Пифагора для треугольника НОО' :
\оо'\2 = \НО\2 + \НО'\2 =>
Задача 22.
Площадь треугольника АВС равна Зл/15, а длина радиуса вписанной в него
АСВ.
Решение. По условию даны два элемента в треугольнике АВС, не хватает ещё одного. Здесь легко найти величину угла АСВ.


366
Указания и решения
Обозначим центр окружности, вписанной в треугольник АВС, буквой О, центр второй окружности - буквой О', точки их касания с лучом С А обозначим буквами Я и Я' соответственно. Поскольку обе они вписаны в угол АСВ, точки О и О' лежат на биссектрисе этого угла, а из того, что они касаются друг друга, вытекает, что длина отрезка ОСУ равна сумме длин их
радиусов. Наконец, заметим, что длина радиуса окружности с центром O' больше, чем длина радиуса окружности с центром О, стало быть, точка О лежит между точками С и О'.
Рассмотрим прямоугольную трапецию ОО'Н'Н. Проведём OF\\CA, тогда
\0'F\ = \0'Н'\ - \ОН\ = OOF = ОСА,
У
sm бдр-^-^-- = -
loo'i ш + 4"
3 9
Таким образом,
sin ^ АСВ^ = J => cos ^ACB^j = —sin АСВ = cos ACВ =
Теперь задача сведена к классической: по трем элементам треугольника АВС надо определить величину одного из его углов. Положим \ВС\ = х, \АС\ = у, |АВ| = г и запишем для треугольника АВС две формулы площади и теорему косинусов:
с , 2Saabc 10
Ьаавс — Раавс • гаавс => x + y + z= = 18;
гаавс
Saabc = I • \АС\ • |ВС| • sin АСВ =► ху = = 48;
^ sin АСВ
|АВ|2 = |АС|2 + |ВС|2 - 2 • |АС| • |ВС| • cos АСВ => z2 = х2 + у2- 7-ху.
Решим полученную систему:
х + у = 18 -г,
ХУ = 48> _ г2 = (18—г)2—180 =» г = 4; \ Х + УТЯ Н
9/49^7 v ' ’ I ху = 48.
^ = (х + у)г - 2ху - -ху к
Поскольку АС - наибольшая сторона, у > х. Поэтому у — 8, х = 6. Для нахождения искомой величины осталось ещё раз воспользоваться теоремой косинусов:


2.2. Касательные, хорды, секущие
367
Задача 23.
В треугольник АВС вписана окружность 7. Касательная к этой окружности, параллельная стороне ВС, пересекает сторону АВ в точке D и сторону АС в точке Е. Периметры треугольников АВС и ADE равны соответственно 40 и 30, АВС = 2(3. Найдите длину радиуса окружности 7.
С
Идея. Воспользоваться подобием треугольников ADE и АВС и свойством касательных к окружности.
Указание. Используя свойство касательных, найти \АР\, где Р - точка касания окружности и отрезка А В.
Указание. Используя подобие треугольников найти отношение \AD\ : \АВ\. Указание. Выразить длины отрезков AD и АВ через длину радиуса окружности и величину угла АВС.
Решение. Рассмотрим четырёхугольник BCED, описанный около окружности, вписанной в треугольник АВС. Обозначим точки её касания с отрезками ВС, СЕ, ED и DB буквами Q, R, S и Р соответственно, а её центр обозначим буквой О. Точка О является точкой пересечения биссектрис углов ВСЕ, CED, EDB и DBC (это вытекает из того, что точка О равноудалена от сторон этих углов). Тогда с учётом того, что BC\\ED, получаем
ОВР = OBQ = /3, ODP = ODS = | - 0.
По свойству касательных \DS\ = \DP\, |i?S| = \ER\ и \AP\ = |AR|. Поэтому
Paade = \AP\ + \AR\ = 2|AP| =» \AP\ = 15.
Поскольку ED || ВС, треугольники ADE и ABC подобны, причём коэффи¬
циент их подобия равен отношению их периметров, то есть 3/4. Таким образом, |AD| : |АВ| =3:4. Обозначим искомую длину буквой г и выразим \AD\ и |АВ| через г. Для этого надо выразить \ВР\ и |PjD| через г.
Рассматривая прямоугольные треугольники ВРО и DPO, находим
\ВР\ = гctg/3, \DP\ = rctg(^ -/З) =rtg/8.
Теперь, используя отношение \AD\ : \АВ\ =3:4, получим
3 \АР\ \AP\-\PD\ 15-rtgff 15
4 \АВ\ \АР\ + \ВР\ 15 + г ctg Р Г Sctg/3 + 4tg/?’
15
Ответ.
3 ctg /3 + 4 tg /3


368
Указания и решения
Задача 24-
В угол с вершиной А, величина которого равна 7г/3, вписана окружность с центром в точке О. К этой окружности проведена касательная, пересекающая стороны угла в точках В и С. Отрезок ВС пересекается с отрезком АО в точке М. Найдите длину радиуса окружности, вписанной в треугольник АВС, если \АМ\ : \МО\ =2:3, \ВС\ = 7.
Идея. Использовать две формулы площади треугольника АВС.
Указание. Записав площадь треугольника АВС двумя способами, выразить искомый радиус через периметр треугольника и его высоту, проведённую к стороне ВС.
Указание. Используя подобие, выразить высоту треугольника АВС через радиус окружности с центром в точ- А В Н
ке О.
Указание. Используя свойство касательных и соотношения в прямоугольном треугольнике, выразить периметр треугольника АВС через радиус окружности с центром в точке О.
Решение. Поскольку \АМ\ < \АО\, конфигурация такая, как приведено на рисунке. Радиус г окружности, вписанной в треугольник, можно искать из формулы площади треугольника, записав её двумя способами:
Saabc = Равс * Л Saabc = г * \ВС\ • \ AL\ ==> г = — -,
2 ГАВС
где AL - высота треугольника АВС. Обозначим точки касания окружности с лучами АВ,АС и отрезком ВС буквами Н, N и К соответственно, длину её радиуса обозначим буквой R. Треугольники AML и ОМ К подобны. Поэтому
\Щ=\АМ\_ = 2 иг|=2Д
\ОК\ \ОМ\ 3 1 1 3 ■
По свойству касательных \СК\ = \CN\, \ВК\ = \ВН\ и \AN\ = \АН\. Поэтому
Pabc = \AH\ + \AN\ = 2-\AH\.
Окружность вписана в угол ВАС, поэтому её центр лежит на биссектрисе этого угла. С учётом этого из прямоугольного треугольника АОН получаем
ОАН = 7г/6, \АН\ = \ОН\ ■ ctgOAH = V3R =» PABc = 2V3R. Следовательно, 7 • Щ 7\/3 Г-2^3R~ 9 '
Ответ. Ьр.
9


2.2. Касательные, хорды, секущие
369
Задача 25.
Две окружности, длины радиусов которых равны R и г, пересекаются в точках А и В и касаются некоторой прямой в точках С и D \ N - точка пересечения прямых А В и CD (В между А и N). Найдите:
1) длину радиуса окружности, описанной около треугольника ACD \
2) отношение длин высот треугольников N АС и NAD, опущенных из вершины N.
Идея. Выразить длины сторон АС и AD через длины радиусов окружностей и величины углов ACD и ADC, доказать, что |iVC| = |iVZ)|.
Указание. Применить теорему синусов для треугольника AC D, теорему о произведении длины секущей на длину её внешней части и формулу площади треугольника, в которую входит длина его высоты.
Решение. Обозначим величину угла ACD через а, а величину угла ADC через /3, центры окружностей обозначим буквами О (центр окружности, длина радиуса которой равна R) и О' (центр окружности, длина радиуса которой равна г). Тогда по теореме об угле, образованном касательной и хордой,
ACD =\аС, ADC — - AD .
2 2
С другой стороны,
АОС —AC, AOD —AD,
поэтому если а < ^, /3 < |, то АОС = 2а, АО'D = 2/3. Ну а если один из углов ACD или ADC тупой (для определённости будем считать, что это будет угол ADC), то АОС = 2а, AOD = 2тг - 2/3.
Далее из равнобедренных треугольников АОС и АО'D выразим длины сторон АС и AD. Важно, что независимо от того, будут ли углы ACD и ADC острыми или тупыми, результат получится один и тот же (за счёт формул приведения):
\АС\ = 2\АО\ ■ sin iАОС = 2i?sina, \AD\ = 2\АО'\ • sin ^АОЧЭ = 2rsin/3.
Теперь запишем теорему синусов для треугольника ACD:
\АС\ _ \AD\ 2Rsina _ 2rsin/3 sina _ PF
sin ADC ~ sin ACD sin/? ~ sina sin/3 ~ \ R’


370
Указания и решенш
п _ \АС\ * р _ ^sina _ TJ
Maacd — :===: => Maacd — —:—77“ — ti •
2 sin ADC 81П0
Ответ на первый вопрос задачи нами получен. Для ответа на второй вопрос задачи нам понадобятся формулы площади и теорема о произведении длины секущей на длину её внешней части. Запишем её, заметив, что N А - секущая для обеих окружностей:
|NC\2'= \NB\ • |iVi4|, |iVD|2 = \NB\ • \NA\ => \NC\ = \ND\.
Ну а поскольку высоты треугольников AN С и AND, опущенные из точки А, совпадают, их площади равны (это следует из того, что площадь треугольника равна половине произведения длины его стороны и длины его высоты, опущенной на эту сторону). Наконец, обозначим длины высот из второго вопроса задачи через h ас и Had и ещё раз запишем площади треугольников AN С и AND:
Saanc = ' IАС\ • Нас, S&and = ^ * 1-^1 • had ==>
h>AC \AD\ 2rsin/3 r [R Гг
Had \AC\ 2i2sina R V r \J R Ответ. 1 )VR/r; 2)y^*
Задача 26.
В треугольнике ABC ВАС — a, \AC\ = b. Вписанная в него окружность касается сторон АВ и ВС в точках М и N, биссектриса угла ВАС пересекает прямую MN в точке К. Найдите расстояние от точки К до прямой АС.
В
Идея. Доказать, что треугольники AM К и АОС подобны, где О - центр окружности, вписанной в треугольник АВС.
Указание. Обозначить величину угла В через /3, воспользоваться равенством длин отрезков ВМ и BN, посчитать величины углов, входящих в треугольники AM К и АОС.
Решение. Обозначим величину угла АВС через ft, центр окружности, вписанной в треугольник АВС, обозначим буквой О. Докажем, что треугольники AMN и АОС подобны. Пользуясь теоремой о сумме величин углов треугольника, тем фактом, что треугольник BMN равнобедренный (\ВМ\ — |JBiV|), а также тем, что центр окружности, вписанной в треугольник, лежит на пересечении его биссектрис, получаем
BMN = BNM = £-?, ОСА = — 2 2’
АВС - ВАС
7Г
2
Р
2
а
2*
AMN = тг - BMN = £ + ЛЛГМ = тг - АШГ - tfAM = £ _ | - 2 2 2 2 2 2


2.2. Касательные, хорды, секущие
371
Таким образом, треугольники AMК и АОС подобны по двум углам. Из этого подобия, с учётом того, что треугольник АОМ прямоугольный, получаем
\АК\ \АМ\ а , л ту\ и ^
ЙС|=ЙО|=СШ2 => И«| = Ьсо8-.
Наконец, искомое расстояние есть длина отрезка КН. Из прямоугольного треугольника АКН находим
iT^rn \ ats\ • I а . a Ьsina
\КН\ = \АК\ • sm К АН = b cos — sin — =
Ответ.
2 2 2 b sin а
Задача 27.
В угол вписано несколько окружностей, радиусы которых возрастают. Каждая следующая окружность касается предыдущей окружности. Найдите сумму длин второй и третьей окружностей, если длина радиуса первой равна 1, а площадь круга, ограниченного четвёртой окружностью, равна 647Г.
Идея. Доказать, что длины радиусов окружностей образуют геометрическую прогрессию.
Указание. Рассмотреть несколько подобных прямоугольных треугольников, гипотенузами которых являются отрезки с концами в центрах окружностей.
Решение. Обозначим центры окружностей буквами 0\, О2, О3, О4, вершину угла обозначим буквой А, точки касания окружностей с одной из сторон угла обозначим как Н1, #2, #з» #4- Построим отрезки OiP, O2Q, O3R, параллельные стороне угла, на которой лежат точки Hi, Н2, Щ, Я4, так, что Р G 02Н2)


372
Указания и решения
Q 6 О3Н3, R € О4Н4. Тогда, если принять длины радиусов окружностей за П,Г2,Г3,Г4, то
IO1O2I = П + г2, |0203| = г2 + r3, |03О4| =г3 + г4,
|02P| = r2-ri, |03Q| = r3-r2, |04Д| = г4 — г3.
Далее ясно, что ДО1РО2 ~ AO2QO3, AO2QO3 ~ AO3RO4. Из первого из этих подобий получаем
|02Р| = IO1O2I г2 - Г1 Г2 + Г1 2
|Оз<5| |020з| г3-г2 г3 + г2 Г2 ПГз‘
Аналогичным образом задействовав второе подобие, получаем г2 = ?’2г4. Таким образом, числа Г1,т*2,Гз образуют геометрическую прогрессию и числа т*2,гз,г4 образуют геометрическую прогрессию. Из этого вытекает, что и все четыре числа 5 ^4 образуют геометрическую прогрессию.
По условию задачи г\ = 1, 7гг| = 647т г4 = 8. Тогда ясно, что 7*2 = 2, гз = 4, длина второй окружности равна 4тг, длина третьей окружности равна 87т.
Ответ. 127Г.
Задача 28.
На стороне О К острого угла КОМ взята точка L (L между О и К). Окружность проходит через точки К и L и касается луча ОМ в точке М. На дуге этой окружности LM, не содержащей точку К, взята точка N. Расстояния от точки N до прямых ОМ, О К и КМ равны m,k и Z соответственно. Найдите расстояние от точки N до прямой LM.
Идея. Найти две пары подобных треугольников.
Указание. Опустить из точки N перпендикуляры на прямые О К, ОМ, КМ и LM.
Указание. Воспользоваться свойствами вписанных углов и свойством угла между касательной и хордой.
Указание. Доказать, что NMO = NKM и, с другой стороны, NKO = NML.
Решение. Опустим из точки N перпендикуляры на прямые О К, ОМ, КМ и LM, их основания обозначим буквами А, В, С и D соответственно. Тогда по условию задачи \AN\ = k, \BN\ = га, \CN\ = I, a |ZW| - величина, которую нужно найти.
Теперь, с учётом того, что
NMO = NKM = i MN, NKO = NML = i ZJV,


2.2. Касательные, хорды, секущие
373
заметим, что ABMN ~ ACKN и ADMN ~ AAKN (по двум углам). Из этих подобий получаем
' \BN 1 _ |MJV|
\CN\ \KN\ ’ ^ \Вщ _ |DAT|
\DN\_\MN\' ^ \CN\~ \AN\
. \AN\ “ \KN\5
<=► \DN\ - |АЛГ|' ^
11 IC7VI I ’
Задача 29.
На прямой взяты три точки L,M и N (М между L и N, |LM| ^ |MiV|). На отрезках LM, МАГ и LN как на диаметрах построены полуокружности, серединами которых являются точки А, В и С соответственно. Точка С лежит по одну сторону, а точки А и В - по другую сторону от прямой LN. Найдите отношение площади фигуры, ограниченной этими тремя полуокружностями, к площади треугольника АВС.
Идея. Искать площадь треугольника как разность площади прямоугольника и прямоугольных треугольников. Указание. Обозначим середины отрезков LM,MN и LN буквами О', О" и О соответственно. Положим \LM\ = 2Д, \MN\ = 2г. Провести через точки А и С прямые, параллельные прямой LN, до пересечения с прямыми АО' и ВО". Выразить искомые площади через R и г.
Указание. Площадь фигуры, ограниченной полуокружностями, равна сумме их площадей.
D
HN
Решение. Обозначим середины отрезков LM,MN и LN буквами О', О" и О соответственно. Положим \LM\ = 2R, \MN\ = 2г, тогда \LN\ = 2(i? + r). Проведём отрезки О'А, О"В и ОС. В силу того, что А,ВиС- середины полуокружностей, все эти отрезки будут перпендикулярны прямой LN, \СУА\ = Я, \ОпВ\ = г, |ОС| = Д + г.
Площадь фигуры, ограниченной полуокружностями, очевидно, равна сумме их площадей, то есть
Зфиг. = + ^7Г?’2 + +г)2 = 7Г(д2 + Rr +г2)-
Для нахождения площади треугольника АВС проведём через точки А и С прямые, параллельные прямой LN, до пересечения с прямыми AOf и ВО" в точках Л, D и F, Е соответственно. Тогда площадь треугольника АВС можно выразить через разность площади прямоугольника ADEF и площадей прямоугольных треугольников ADC, ВСЕ и ABF:
SUbc = Sadef — Sadc — Sbce — Sabf =


374
Указания и решения
= (2R+r) • (R+r) - i • ((2R + г) ■ г + (R +2r) ■ R + (R +г) ■ (R -г)) = R2 + Rr+r2.
Таким образом, искомое отношение равно 7Г.
Ответ. 7Г.
Задача 30.
В окружности 7 проведены хорды KL, MN, PS. Хорды KL и Р5 пересекаются в точке С, хорды KL и МАГ пересекаются в точке Л, а хорды МАГ и PS пересекаются в точке В, причём |AL| = |Cif|, |АМ| = |ВЛГ|, \BS\ = 5, |ВС| = 4. Найдите длину радиуса окружности 7, если величина угла ВАС равна 7г/4.
Идея. Доказать, что центры окружности 7 и окружности, описанной около треугольника АВС, совпадают.
Указание. Воспользоваться теоремой о произведении длин отрезков пересекающихся хорд и доказать, что \ВР\ = |С5|.
Указание. Воспользоваться свойством хорды, перпендикулярной диаметру, и доказать, что центры окружности 7 и окружности, описанной около треугольника АВС, совпадают.
Указание. Рассмотреть все случаи взаимного расположения точек К и L, М и iV, Р и 5.
Решение. В этой задаче возможно достаточно большое количество случаев. Связано это с тем, что пары точек К и L, М и N, Р п S могут располагаться произвольным образом. Этот факт отражен на чертеже.
Будем рассуждать следующим образом: каждая из хорд KL, MN и PS точками пересечения с двумя другими хордами делится на 3 отрезка: два «крайних» и один «средний». Поскольку \АМ\ = \BN\, в любом случае (т.е. независимо от того, как конкретно расположены точки М и N) длины «крайних» отрезков хорды MN равны. Обозначим эти длины через х. Аналогично из того, что \AL\ = \СК\, вытекает равенство длин «крайних» отрезков хорды KL, эти длины мы обозначим через у. Длины же «крайних» отрезков хорды PS обозначим через b и с.


2.2. Касательные, хорды, секущие
375
Трижды применяя теорему о произведении длин отрезков пересекающихся хорд, получаем
( х-(\АВ\+х)=у-(\АС\+у),
{ х-(\АВ\+х) = Ь-(\ВС\+с), => Ъ ■ {\ВС\ + с) = с ■ (\ВС\ + Ь) <==> Ь = с.
{ у(\АС\ + у) = с-(\ВС\+Ъ)
Таким образом, длины «крайних» отрезков хорды PS также равны. Теперь самое интересное: если мы опустим из центра окружности 7 (обозначим его буквой О) перпендикуляры на хорды KL, MN и Р5, то их основания попадут на середины этих хорд. А поскольку длины «крайних» отрезков каждой хорды равны, середины хорд будут также являться и серединами их «средних» отрезков. Таким образом, точка О есть точка пересечения серединных перпендикуляров треугольника АВС, то есть является центром описанной около него окружности.
Наконец, немного посчитаем. Поскольку угол ВОС является центральным углом, опирающимся на дугу ВС, получим ВОС = 2 • ВАС = 7г/2. Обозначим середину отрезка ВС буквой Н, заметим, что треугольник ВОС прямоугольный и равнобедренный. Из этого вытекает, что \ОН\ = \ВН\ = \\ВС\ — 2. Осталось не упустить из виду, что точки Р и S могут расположиться двумя способами (см. чертёж). В одном из этих случаев мы получим, что
\SH\ = |В5| + \ВН\ = 7, |05| = \Z\SH\2 + |ОЯ|2 = >/53,
а во втором случае имеем
\SH\ = |BS| - \ВН\ = 3, |05| = V\SH\2 + |ОЯI2 = >/13.
Ответ. >/53 или у/й.
Задача 31.
Дана окружность, длина диаметра MN которой равна 16. На касательной к этой окружности в точке М отложен отрезок МР, длина которого больше 15. Из точки Р проведена вторая касательная к окружности, пересекающая прямую MN в точке Q. Найдите площадь треугольника МPQ, если его периметр равен 72.
Идея. Выразить длины сторон треугольника MPQ через длину отрезка MN и величину угла MPQ.
Указание. Рассмотреть прямоугольные треугольники МОР и MPQ, где О - центр окружности.
Решение. Поскольку МР и PQ - касательные к окружности, во-первых, окружность вписана в угол MPQ, из чего следует, что её центр лежит на биссектрисе угла MPQ, и, во-вторых, МР _L МАГ, то есть МР _L MQ. Обозначим центр окружности буквой О, величину острого угла ОРМ обозначим через а. Тогда \ОМ\ = \\MN\ = 8, MPQ = 2а.
Далее из прямоугольных треугольников ОМР и QMP получаем
|МР| = \ОМ\ • ctg ОМР = 8 ctg a, \MQ\ = \МР\ • tg MPQ = 8 ctg a tg 2а,


376
Указания и решения
\PQ\
\МР\
8 ctg а
cos MPQ cos2<*
По условию задачи \МР\ > 15, значит, ctg а > 15/8. Пользуясь тем, что периметр треугольника MPQ равен 72, мы получаем уравнение
8 ctg а + 8 ctg a tg 2а -Ь - — -f а = 72 cos 2а
Путем применения формул
ctg2 а —1 2 ctg а
cos 2а = —о г, tg 2а =
ctg а ( 1 -f tg 2а +
cos2a
ctg2 а + 1 ’ ctg2 а — 1
наше уравнение преобразуется к виду
a ^1
ctg a ( 1 +
2 ctg a ctg:
+
ctg2 a — 1 ctg2 <
2 ctg2 a(l-fctga) = 9(l+ctga)(ctga—1).
Поскольку a < 7г/2, имеем ctg a > 0 и ctg a + 1 ф 0. С учётом этого получаем
2 ctg2 a — 9 ctg a -f 9 = 0
9.
ctg a — 3 или ctg a = -.
Второй из полученных котангенсов меньше 15/8, стало быть, нам подходит только вариант ctg a = 3. Тогда tg2a = 3/4 и, значит,
Наконец,
Ответ. 216.
\МР\ = 8 • 3 = 24, \MQ\ = 8 • 3 • - = 18.
Sampq = * \МР\ • \MQ\ = 216.
Задача 32.
На стороне ВС остроугольного треугольника АВС (АВ ф АС) как на диаметре построена полуокружность, пересекающая высоту AD в точке М, Н точка пересечения высот треугольника ABC, \AD\ = a, \MD\ = b. Найдите \AH\.
Идея. Воспользоваться теоремой о произведении длины секущей на длину её внешней части.
Указание. Точку пересечения стороны АС с окружностью обозначить буквой Е. Пользуясь теоремой о произведении длины секущей на длину её внешней части, найти |^4JE7| • \АС\ = а2 — Ь2.
Указание. Из прямоугольных треугольников АЕН и ACD выразить произведение \АЕ\ • \АС\ через произведение \АН\ • \AD\.


2.2. Касательные, хорды, секущие
377
Решение. Достроим полуокружность из условия задачи до полной окружности и продлим высоту AD за точку D до второго пересечения с этой окружностью.
Полученную точку пересечения обозначим М\. Точку пересечения стороны АС с окружностью обозначим буквой Е. Угол ВЕС опирается на диаметр, стало быть, он прямой, значит, BE - высота треугольника АВС и Я - точка пересечения отрезков AD и BE.
Далее заметим, что, поскольку хорда ММ\ перпендикулярна диаметру ВС, \DM\ \ = \DM\ = Ь. Тогда
\АМ\| = |AD| + \DMX\ = а + Ъ, \АМ\ = \AD\- \DM\ = а-Ъ.
Теперь воспользуемся теоремой о произведении длины секущей на длину её внешней части. Получим
\АЕ\ ■ \АС\ = \АМ\ ■ \ АМ\ \ = (а- Ь)(а + Ь) = а2- Ь2.
С другой стороны, из прямоугольных треугольников АЕН и ACD вытекает
\AD\
|АЕ\ ■ \АС\ = \АН\ • cos DAC ■
Значит, а2 — b2
cos DAC
\АН\ • а. Осталось выписать ответ.
\АН\ • \AD\.
Ответ.
-Ь2
Замечание. Для доказательства того, что \АЕ\ • \АС\ = |АйГ| • |AD|, можно было использовать подобие треугольников АЕН и ADC.
Задача 33.
Три круга с центрами в точках Р, Q и R попарно касаются друг друга внешним образом в точках А, В и С. Известно, что PQR = 2arcsin(l/3), а сумма длин радиусов всех трёх кругов равна 12у/2. Какую наибольшую длину может иметь окружность, проходящая через точки А, В, С?
И дея. Доказать, что окружность, проходящая через точки А, В и С, является вписанной в треугольник PQR. Доказать, что окружность наибольшего радиуса будет вписана в равнобедренный треугольник, если в треугольнике заданы угол и полу периметр.
Указание. Центр окружности, проходящей через точки Л, В и С, лежит в точке пересечения серединных перпендикуляров к отрезкам ВС, АС и АВ. Но в силу равнобедренности треугольников BRC, AQC и АР В эти серединные перпендикуляры являются также и биссектрисами углов В RC, AQC и АР В. Указание. Пусть PQR - равнобедренный треугольник и в него вписана окружность, a P'QR' - неравнобедренный треугольник, в который вписана та же окружность и у которого угол P'QR' равен углу PQR. Показать, что тогда его периметр больше, чем периметр треугольника PQR.


378
Указания и решения
Решение. Сначала докажем, что окружность, проходящая через точки Л, В и С, является вписанной в треугольник PQR. Это можно сделать, например, так. Очевидно, что точки А, В и С лежат на отрезках PQ, РЯ и QR соответственно. Центр окружности, проходящей через точки Л, В и С, лежит в точке пересечения серединных перпендикуляров к отрезкам ВС, АС и АВ. Но в силу равнобедренности треугольников BRC, AQC и АР В эти серединные перпендикуляры являются также биссектрисами углов ВRC, AQC и АРВ. Поэтому центр окружности, описанной около треугольника АВС, является также центром окружности, вписанной в треугольник PQR. Значит, окружность, проходящая через точки Л, В и С, является вписанной в треугольник PQR.
Теперь докажем, что окружность наибольшего радиуса будет вписана в равнобедренный треугольник, если в треугольнике заданы угол и полу периметр.
Пусть PQR - равнобедренный треугольник и в него вписана окружность, a P\QR\ - неравнобедренный треугольник, в который вписана та же окружность и у которого угол PiQRi равен углу PQR. Покажем, что тогда его периметр больше, чем периметр треугольника PQR.
Пусть К - точка пересечения отрезков P\R\ и PR. Проведём RR2WP1P. Тогда треугольники KPPi и КRR2 подобны по двум углам, причём |-^Д| > \кр\, так как \РВ\ = \BR\. Поэтому
SaKRR2 > SakPPx => SaKRRi > S^KPPi ==>
=> SAQPiRi > Saqpr.
25
Следовательно, PaqPxRi > Paqpr ? так как P = —. Значит, если мы возьмём
неравнобедренный треугольник такого же периметра, что и APQR, то в него можно будет вписать окружность меньшего радиуса, а следовательно, и меньшей длины.
Таким образом, мы доказали, что окружность наибольшего радиуса будет вписана в равнобедренный треугольник, если в треугольнике заданы угол и полупе- риметр. Осталось найти этот радиус.
Положим \РВ\ = х. Тогда \PQ\ = \2у/2 — х. Из прямоугольного треугольника PBQ получаем
Q
\РВ\
\PQ\
= sin PQB
12\/2 ■
1
3
= 3V2 => \QP\ = 9\/2
r = - = i-
(9>/2)2 • sin РОД
12V2
81.2.1.2^1
12\/2
^окр. — 67г.
Ответ. 67г.


2.2. Касательные, хорды, секущие
379
Задача 34-
Окружность, вписанная в равнобедренный треугольник АВС, касается его основания АС в точке D и боковой стороны АВ в точке Е. Точка F - середина стороны АВ, а точка G - точка пересечения окружности и отрезка FD, отличная от D. Касательная к окружности, проходящая через точку G, пересекает сторону АВ в точке Н. Найдите величину угла ВС А, если известно, что \FH\ : \НЕ\ = 2:3.
Идея. Найти треугольник, в который входят величины, данные в условии или равные им.
Указание. Рассмотреть два различных случая: \АС\ > \АВ\ и \АС\ < \АВ\, выразить величины углов треугольника FGH через величину угла ВС А. Указание. Воспользоваться тем, что D - середина АС, и теоремой о равенстве длин отрезков касательных, проведённых из точки к окружности.
Решение. Обозначим величину угла ВС А буквой а и попытаемся найти треугольник, в который входят величины, данные в условии или равные им. Треугольник АВС равнобедренный, поэтому величина угла ВАС также равна а, a D - середина АС. Тогда DF - его средняя линяя, поэтому DF\\BC, FDA = ВС А = а, AFD = 7г — 2а, BFD = 2а.
Далее нам придётся рассмотреть два различных случая: либо точка Е попадает на отрезок BF, либо точка Е попадает на отрезок AF. Заметим, что первый из этих случаев возникает, если \АС\ > \АВ\, а второй возникает, если \АС\ < \АВ\.
В первом из этих случаев прямая HG пересечёт отрезок АС в точке J. Поскольку отрезки касательных, проведённых из точки к окружности, равны, \GJ\ = \JD\, \НЕ\ = \HG\. Таким образом, треугольник DGJ равнобедренный, DGJ = JDG = а. Углы DGJ и FGH вертикальные, значит, и величина угла FGH равна а. Наконец, положим \FH\ = 2х, \НЕ\ = Зж, тогда \HG\ = Зх и нам удалось свести все необходимые величины в один треугольник FGH. Запишем для него теорему синусов:
\FH\ \HG\ 2х Зж 2 3 3
! ==» = = — => cos а = -.
sinFG# sin HFG sin о: sm2a sma 2 sma cos a 4
Проверим, выполнено ли условие \АС\ > \АВ\. Это сделать очень просто: ясно, что \АС\ = 2\AB\cosa — ||АВ|. Таким образом, этот случай даёт нам ответ к задаче.


380
Указания и решения
Во втором из этих случаев прямая HG пересечёт продолжение отрезка АС за точку А в точке J. Рассуждая аналогично, получим \GJ\ = \JD\, \НЕ\ = \HG\, DGJ = JDG = а. Углы DGJ и FGH смежные, значит, FGH = 7г — а. Опять положим \FH\ = 2х, = Зх, тогда \HG\ = Зх, и запишем для треугольника
FGH теорему синусов:
\FH\ _ | HG\ 2х _
sin FGH ~ sin HFG «“fr - a) ~
2 3
<*=> -— = — =>•
sin a 2 sin a cos a
Значение а получилось такое же, поэтому условие Таким образом, этот случай невозможен.
3
Ответ, arccos-.
4
Задача 35.
Из точки А проведены к окружности две касательные (М и N - точки касания) и секущая, пересекающая эту окружность в точках В и С, а хорду MN в точке Р. Известно, что \АВ\ : \ВС\ = 2:3. Найдите \АР\ : \РС\,
Идея. Рассмотреть схемы доказательства теорем о квадрате длины касательной и о равенстве произведений длин отрезков пересекающихся хорд. С их помощью доказать, что \ВМ\ : \СМ\ = \BN\ : |CW|,
\ВР\ : \СР\ = (\BN\ : |CW|)2.
Указание. Полностью разобрать подобия пар треугольников АВМ и АМС, ABN и AN С, МРВ и CPN, МРС и BPN, вычислить отношение |JBiV| : \CN\.
Решение. В этой задаче достаточно сложно понять, какие свойства имеет данная геометрическая конструкция. Сначала докажем, что \ВМ\ : \СМ\ = \BN\ : \CN\. Одним из способов проведения доказательства этого утверждения является более внимательное рассмотрение схемы, используемой в теореме о квадрате длины касательной.
Для того чтобы наши рассуждения имели наиболее общий вид, будем считать, что \АВ\ : \ВС\ = а : 6, положим \АВ\ = ах, \ВС\ = Ьх, \АС\ = (а + Ь)х. Как известно, треугольники АВМ и АМС подобны (так как угол А у них общий, углы AM В и ACM равны по теореме об угле, образованном касательной и хордой). Из этого подобия мы получаем
\АМ\ \АВ\ \ВМ\
\АС\ = \АМ\ ~ \СМ\'
Зх
— —г <=>
sin(7г — 2а)
3
cos а = -.
4
\АС\ < \АВ\ не выполнено.


2.2. Касательные, хорды, секущие
381
Из этих соотношений вытекает, что \АМ\2 = \АВ\ • \АС\ (известный факт), стало быть, \АМ\ = х\/а2 + аЪ. Тогда \ВМ\ : \СМ\ — у/а2 + ab : (а + Ь). После этого аналогичные рассуждения необходимо применить для треугольников ABN и AN С, отношение длин отрезков BN и С N получится таким же. Утверждение доказано.
Теперь внимательно рассмотрим схему доказательства свойства пересекающихся хорд. Известно, что АМР В ~ ACPN, AM PC ~ ABPN. Полностью записывая отношения длин соответственных сторон этих пар треугольников, мы имеем
\ВР\ \ВМ\ \МР\ \СР\ \СМ\ \МР\
|МР| ” \CN\ “ \СР\ ’ \NP\ “ \BN\ “ \ВР\ ’
откуда получаем
\BM\-\NP\ __ \СМ\ • |NP\ \ВР\ \ВМ\ • |BN\ (а2 + аЬ)
1 1 |СЛГ| ’ 1 1 \BN\ \СР\ \СМ\ ■ \CN\ (а + Ь)2 '
Теперь осталось подставить числа из условия задачи. У нас а = 2, 6 = 3, значит, \АВ\ =2х, \ВС\ — Зх,
]вр]: |СР| = = 1 ^ = |СР| = ^,
|ЛР| : \АС\
\АВ\ + |ВР\ _ 2х+Щ- _ 4 \АВ\ }-ВС<| 2х -Ь Зх Т
Ответ. 4:7.
Задача 36.
Две окружности с центрами А и В и длинами радиусов соответственно 2 и 1 касаются друг друга. Точка С лежит на прямой, касающейся каждой из окружностей,
3\/3
и находится на расстоянии —-=. от середины отрезка АВ. Найдите площадь Ь
2у/2
треугольника АВС, если известно, что S > 2.
Идея. Рассмотреть все способы касания окружностей, учесть, что точка С может лежать как на общей внешней, так и на общей внутренней касательной. Указание. Для случая внутреннего касания окружностей и для случая, когда окружности касаются внешним образом, но точка С лежит на общей внутренней касательной, найти длину стороны АВ и длину высоты, опущенной на эту сторону (или её продолжение).
Указание. Для случая, когда окружности касаются внешним образом, а точка С лежит на общей внешней касательной, рассмотреть трапецию, образованную точками Л, В и их проекциями на общую внешнюю касательную к окружностям. Площадь треугольника АВС представить как разность площади указанной трапеции и двух треугольников.


382
Указания и решетя
Решение. В этой задаче есть три принципиально различных случая. Пер» q вый случай возникает, когда окружности касаются внутренним образом и точка С лежит на единственной их общей К касательной. Второй и третий же случаи возникают, если окружности касаются внешним образом, тогда точка С лежит либо на их общей касательной, проходящей через точку их касания, либо лежит на их общей касательной, не проходящей через точку их касания. Все эти случаи представлены на чертеже.
Обозначим точку касания окружностей буквой К, тогда |ART| = 2, \ВК\ = 1, середину отрезка А В обозначим буквой М и разберём по очереди все варианты, заметив предварительно, что в первых двух случаях искомая площадь может быть вычислена как половина произведения длин отрезков АВ и С К.
Первый случай. Если окружности касаются внутренним образом, то
\АВ\ = \АК\ - \ВК\ = 1, \АМ\ = \ВМ\ = \КМ\ = \ВК\ + \ВМ\ =
Из прямоугольного треугольника С КМ получаем
\СК\ = V\CM\* _ lKMl2 = | = ^2,
3v/2
тогда площадь треугольника АВС равна ——, что меньше, чем 2. Значит, кон-
8
фигурация, получающаяся в этом случае, не удовлетворяет условию задачи.
Второй случай. Если окружности касаются внешним образом и точка С лежит на их общей касательной, проходящей через точку К, то
\АВ\ = |АЙГ| + \ВК\ = 3, \АМ\ = \ВМ\ = | \КМ\ = \ВМ\ - \ВК\ = ^
Из прямоугольного треугольника С КМ находим
\СК\ = V\CM\* - \KM\1 = \/| - i =
стало быть, площадь треугольника АВС равна —, что больше, чем 2. Таким
8
образом, этот случай удовлетворяет условию задачи.
Третий случай. Окружности касаются внешним образом, и точка С лежит на их общей касательной, не проходящей через точку К. Здесь придется провести несколько более сложные рассуждения, нежели в первых двух случаях. Обозначим буквами Р и Q соответственно точки касания большей и меньшей окружностей с прямой, на которой лежит точка С. Тогда APQB - прямоугольная трапеция, \АР\ — 2, \BQ\ = 1, \АВ\ = 3. Найдём длину отрезка PQ:
\PQ\2 = \АВ\2 - (\АР\ - \BQ\)2 = 8 ==► \PQ\ - 2у/2.


2.2. Касательные, хорды, секущие
383
Далее введём на прямой PQ систему координат. Координатой точки Р положим число 0, координатой точки Q положим число 2\/2, а координату точки С обозначим за х. Тогда \РС\ — \х\у \CQ\ = \2у/2 — х\. Ясно, что если х < 0 или х > 2\/2, то точка С не попадает на отрезок PQ.
По теореме Пифагора из треугольников АРС и BQC получаем
\АС\2 = \АР\2 + |РС\2 = х2 + 4, \ВС\2 = \BQ\2 + \CQ\2 = х2 - 4л/2х + 9,
после чего воспользуемся формулой длины медианы для треугольника АВС:
07
4|СМ|2 = 2\АС\2 + 2\ВС\2 -\АВ\2 => — = 4а;2 - 8^2х + 17.
Решая полученное квадратное уравнение, находим х\ = \/2/4, Х2 = 7л/2/4. Оба этих значения лежат в промежутке [0,2у/2], что означает, что есть два различных положения точки С, удовлетворяющих условию задачи (на рисунке они обозначены как С" и С"), причём в обоих этих случаях точка С попадает на отрезок PQ. Из этого вытекает, что площадь треугольника АВС может быть посчитана как разность площади трапеции APQB и суммы площадей треугольников АРС и BQC.
Проведём эти подсчёты. Сначала найдём площадь трапеции APQB:
Sapqb = \ • (\АР\ + \BQ\) • \PQ\ = 3>/2.
Теперь разберемся с каждым из положений точки С:
1. 	\РС\ = ^ => \CQ\ = 7-^, SbAPC = y\AP\-\PC\ = ^,
Sacqb = \ • \CQ\ ■ \BQ\ = Saabc = 3^2- ^ ^ ^ > 2;
2. 	\PC\ = 7-^ =» \CQ\ = ^, Saapc = \-\AP\.\PC\ = ^,
Sacqb = ^ • |CQ| • \BQ\ = 5длвс = 3v/2-^-^ = ^<2.
Таким образом, под условие задачи подходит только первый из этих двух вариан-
. _ _ 15л/2
тов и площадь треугольника АВС равна —-—.
8
п 15^
Ответ. —-—.


384
Указания и решения
3. Четырёхугольники и многоугольники
3.1. 	Параллелограммы
Задача 1.
Найдите площадь равностороннего треугольника, сторона которого равна стороне ромба с диагоналями длины 10 и 12.
Идея. Доказать, что диагонали ромба перпендикулярны друг другу и делятся точкой пересечения пополам.
Указание. Воспользоваться теоремой Пифагора и формулой площади треугольника.
Решение. Рассмотрим ромб ABCD, будем считать, что \АС\ = 12, \BD\- = 10, буквой О обозначим точку пересечения его диагоналей. По определению ромб - это четырёхугольник, длины сторон которого равны, значит, \АВ\ = \CD\ и \AD\ = \ВС\. А это значит, что по признаку параллелограмма ромб является параллелограммом, поэтому его диагонали точкой пересечения делятся пополам. Но тогда треугольники АОВ и СОВ равны по трём сторонам, что даёт нам равенство углов АОВ и СОВ. Эти углы являются смежными, стало быть, они прямые.
Наконец, по теореме Пифагора находим \АВ\ = ^\АО\2 + \ОВ\2 щадь же равностороннего треугольника, длина стороны которого равна на \ ■ (\/б1)2 • ^, то есть
D
>/61. Пло- л/бГ, рав-
Ответ.
61д/3
Задача 2.
В квадрат, площадь которого равна 18, вписан прямоугольник так, что на каждой стороне квадрата лежит одна вершина прямоугольника. Длины сторон этого прямоугольника относятся как 1:2. Найдите площадь прямоугольника.
Идея. Доказать, что треугольники, отсеченные прямоугольником от квадрата, подобны друг другу. Найти длины отрезков, на которые стороны квадрата разбиты вершинами прямоугольника.
Указание. Воспользоваться тем, что внутренние углы прямоугольника и квадрата прямые.
Решение. Обозначим вершины квадрата буквами А, В, С и D, вершины прямоугольника обозначим буквами К, L, М и N, причем К £ [АВ], L Е [ВС], MG [CD], N £ [AD], \KL\ = 2\KN\. Величину угла AKN обозначим буквой а,
В L С


3.1. Параллелограммы
385
тогда с учётом того, что угол LKN прямой, имеем BKL = тг — а — 7г/2 = 7г/2 — а. Далее, угол АВС также прямой, поэтому BLK = 7г — 7г/2 — (7г/2 — а) = а. Продолжая цепочку этих рассуждений, получаем
AKN = BLK = CML = DNM = a, BKL = CLM = DMN = ANK = | - а.
Из этих равенств вытекает подобие треугольников AKN, BLK, С ML и DNM. Полагая | APT | = ж и | A/V| = у и рассмотрев эти подобия, находим
ЦК| _ |АЛГ| _ IKJVJ _ 1 ^ |B£|=i2ii =
|Ш,| |JCX-| 2
|CM| | CL | |LM| 1
\CM\ = X, \CL\ = y.
\BL\ \BK\ \KL\ 2 Ho ABCD - квадрат, поэтому
\AB\ = \BC\ *=> \AK\ + \BK\ = \BL\ + \CL\ =» x + 2y = 2x + y =► я = y.
Наконец, если обозначить длину стороны квадрата ABCD через а и воспользоваться формулой площади прямоугольника и теоремой Пифагора, мы получим
Sabcd \АВ\ • \ВС\ а2 = 18 =¥ а — Зл/2;
\АК\ + \ВК\ = \АВ\ => Зх = Зл/2 =► as = л/2;
|ATJV| = у/\АК\2 + \AN\2 = 2 ==» \KL\ = 4, = \KL\ • |KW| = 8.
Ответ. 8.
Задача 3.
В параллелограмме ABCD биссектриса угла BAD пересекает сторону CD в точке М таким образом, что \DM\ : \МС\ = 2. Найдите величину угла BAD, если известно, что САМ = а.
К
Идея. Продолжить отрезок AM до пересечения с продолжением прямой ВС за точку С в точке К. Доказать, что треугольники АВК и AMD равнобедренные.
Указание. Выразить длины сторон параллелограмма и длину отрезка АК через длину отрезка МС и величину угла BAD, воспользоваться теоремой синусов.
Решение. Обозначим точку пересечения прямой AM с продолжением прямой ВС за точку С буквой К. Поскольку АК - биссектриса угла BAD, углы ВАК и KAD равны. С другой стороны, прямые AD и ВС параллельны, АК - секущая, поэтому углы АКВ и KAD равны как внутренние накрест лежащие. Таким
13 Геометрия


386
Указания и решения
образом, угол ВАК равен углу АКВ, стало быть, треугольник АВК равнобедренный, \АВ\ = \ВК\.
Также отметим, что из параллельности прямых AD и ВС вытекает подобие треугольников AMD и КМС. Обозначим длину отрезка AD через 2х, учтём, что \AD\ = \ВС\. Из этого подобия имеем
]Щ = Щс\=2 =* \СК\ = Х’ \AB\ = \BK\ = \BC\ + \CK\ = Zx.
Теперь обозначим величины углов KAD, ВАК и АКВ буквой 7. Тогда, во- первых,
BAD = 27, AB# = п-ВАК-АКВ = тг-27, ЖЖ = п-САК-АКС = тг-а-7
и, во-вторых, из равнобедренного треугольника АВК находим |АЙГ| = 2|AB|cos7. Наконец, запишем теорему синусов для треугольника АСК:
\АК\ \СК\ 6х cos 7 х
sinACTf sinСА/Г sin(7r - а - 7) sina
6 sin a: cos 7 = sin(a + 7) <=> 6 sin a cos 7 = sin a cos 7 + sin 7 cos a =
tg7 = 5tga => 7 = arctg(5 tga) => BAD = 2 arctg (5 tga).
Ответ. 2 arctg(5 tg a).
Задача 4-
В прямоугольнике ABCD сторона AB втрое длиннее стороны ВС. Внутри него лежит точка JV, причём \AN\ = у/2, \BN\ = 4\/2, \DN\ = 2. Найдите косинус величины угла BAN и площадь прямоугольника ABCD.
Идея. Положить |AD| = ж, BAN = а, воспользоваться теоремой косинусов. Указание. Рассмотреть треугольники BAN и DAN.
Решение. Обозначим длину стороны А В через Зх, тогда по условию задачи \ВС\ = \AD\ = х, а величину угла BAN обозначим буквой а, что с учётом того, что угол BAD прямой, даёт нам DAN — тт/2 — а. Запишем теорему косинусов для треугольников BAN и DAN:
|J5iV|2 = \АВ\2 4- \AN\2 - 2 • \АВ\ • |A/V| • cos BAN = \DN\2 = \AD\2 + \AN\2 - 2 • \AD\ • \AN\ • cos DAN =
30 = 9ж2 — 6\/2^cosa,
2 = ж2 - 2у/2:
:x sina.
Для того чтобы решить эту систему, умножим её второе уравнение на 15, вычтем из него первое и подставим полученное выражение для х во второе уравнение:
15х2 — ЗОл/2# sin a — 9#2 + 6л/2ж cos a = 0
= 5\/2sina — \/2cos a;


3.1. Параллелограммы
387
2 = (5\/2 sin а — \/2 cos а)2 — 2л/2(5л/2 sin а — V2 cos a) sin а =>
. 2 „ • 4 . 4 7 13\/2
=>■ 28sin а = 16 sma cos а => tga = -, sma = —=, cosa = —=, ж = —■=-.
7 V65 v/65 \/б5
78
Наконец, Sabcd = |АВ| • | AD| = Зх2 = —.
5
—7 78
Ответ, cos BAN = —==, Sabcd = •
V65 5
Задача 5.
В ромбе ABCD величина угла при вершине А равна 7г/3. Точка N делит сторону АВ в отношении 2:1, считая от точки А. Найдите tg DNC.
Идея. Выразить длины отрезков DN и CN через длину стороны ромба.
Указание. Воспользоваться теоремой косинусов.
Решение. Положим |A/V| = 2х, \BN\ = х. Тогда длины всех сторон ромба равны Зх. Величина угла BAD равна
7г/3, значит в силу того, что ромб является параллелограммом, величина угла АВС равна 2п/3. Выразим длины отрезков DN и CN, воспользовавшись теоремой косинусов:
\DN\2 = \AN\2+\AD\2-2-\AN\-\AD\-cosBAD => |£>JV|2 = 7х2, \DN\ = \ftx;
\CN\2 = \BN\2+\BC\2-2-\BN\-\BC\-cosABC =► |CiV|2 = 13a;2, |C7JV| = Vr3x.
Наконец, запишем теорему косинусов в треугольнике CDN :
\CN\2 + |£>iV|2 - \CD\2 _ Их2 _ И
cos DNC
2 • \CN\ ■ \DN\ 2V91x2 2^91
Ответ. ^
sinDNC= Jl- = -^2= => tgDNC=^.
V 364 2y/91 И
9\/3
Задача 6.
В ромбе ABCD, длина стороны которого равна б, на стороне ВС взята точка Е таким образом, что \СЕ\ = 2. Найдите расстояние от точки Е до центра ромба,
если BAD = 7г/3.
Идея. Использовать теорему косинусов для треугольника СОЕ.
Указание. Найти \ОС\ из прямоугольного треугольника ВОС.
13*


388
Указания и решения
Решение. Воспользуемся тем фактом, что центр ромба - это точка пересечения его диагоналей. Обозначим её буквой О. Поскольку диагонали ромба перпендикулярны друг другу и являются биссектрисами его внутренних углов, а величины его противоположных углов равны, имеем
В
ВОС=J, BCD =J, Wo=1-Wd = ^.
2 3 2 6
Используя соотношения в прямоугольном треугольнике, найдём \СО\:
\СО\ = \ВС\ • cos ВСО = 3\/3 и затем по теореме косинусов из треугольника СОЕ находим |OjE7| :
\ОЕ\2 = \СЕ\2+ \СО\2-2-\СЕ\-\СО\-cos ЕСд = 13 \ОЕ\ = у/П.
Ответ. >/13.
Задача 7.
Площадь прямоугольника ABCD равна 48, а длина его диагонали равна 10. На плоскости, в которой расположен прямоугольник ABCD, выбрана точка О так, что \ОВ\ = \OD\ = 13. Найдите расстояние от точки О до наиболее удалённой от неё вершины прямоугольника ABCD.
Идея. Найти длины сторон прямоугольника, воспользоваться тем, что точка О лежит на серединном перпендикуляре к BD.
Указание. Рассмотреть треугольники АО К и СОК, где К - точка пересечения диагоналей прямоугольника. Для нахождения величины угла ОКС предварительно найти величину угла ВКС.
Решение. Сначала найдём длины всех сторон прямоугольника ABCD. Обозначим длины отрезков А В к CD через ж, длины отрезков AD и ВС обозначим через у, без ограничения общности будем считать, что х ^ у. Воспользуемся формулой площади прямоугольника и теоремой Пифагора:
Sabcd = \АВ\ ■ \AD\ =► ху = 48, \BD\2 = \АВ\2 + \AD\2 => *2 + у2 = 100.
Решив полученную систему уравнений, находим х = 6, у = 8. Далее обозначим точку пересечения диагоналей прямоугольника ABCD буквой К. Поскольку диагонали прямоугольника равны по длине и делятся пополам точкой пересечения, \АК\ = \ВК\ = \СК\ = \DK\ = 5. Точка О равноудалена от вершин В и D, поэтому она лежит на прямой, проходящей через точку К и перпен- дикулярной BD. Применяя теорему Пифагора к треугольнику ОВК, находим \ОК\ = у/\ОВ\2 -\ВК\2 = 12.
О


3.1. Параллелограммы
389
Ясно, что возможно два варианта расположения точки О - либо она лежит в той же полуплоскости относительно прямой BD, что и точка С, либо в другой. Рассмотрим первый из этих вариантов. Длины отрезков О А и ОС проще всего искать из треугольников АО К и СОК, в которых мы уже знаем длины двух сторон. Для нахождения величин углов О КС и ОКА обозначим величину угла ВКС буквой а и запишем теорему косинусов для треугольника ВСК:
|£С|2 = \В К\2+ \СК\2-2-\BK\-\CK\-cos ВКС =*■ соя а = 25 + 25 ~ 64 = __1
2*5*5 25
Таким образом, угол ВКС тупой, поэтому
ОКС = ВКС - со8<ЖС = сов(а-|) =sina = Wl—
|ОС| = ^\ОК\2 + \СК\2 - 2 • \ОК\ ■ \СК\ ■ cosOKC = ^144 + 25 - ^
Для вычисления длины отрезка О А можно рассуждать аналогично, а можно заметить, что О К - медиана треугольника АОС, поэтому
|CJ,|2 2\ОА\2 + 2\ОС\2-\АС\2 ^ |ел|2 4\ОК\2-2\ОС\2 + \АС\2 ^
576 - ^ + 100
=► \ОА\2 = = ^ 1ОА\ = ]/Щ^
Очевидно, что \ОА\ > \ОВ\ > \ОС\, поэтому ответом к задаче будет длина отрезка О А.
Если рассмотреть второй вариант расположения точки О, то из соображений симметрии очевидно, что численное значение ответа останется таким же, единственная разница будет заключаться в том, что наиболее удаленной от точки О вершиной окажется не вершина А, а вершина С.
Ответ. 7\
Задача 8.
В выпуклом четырёхугольнике ABCD точки Е, F, Н и G являются соответственно серединами отрезков АВ, ВС, CD и AD; О - точка пересечения отрезков ЕН и FG. Известно, что \ЕН\ = a, \FG\ = 6, FOH = а. Найдите длины диагоналей четырёхугольника ABCD.
Идея. Доказать, что четырёхугольник EFHG - параллелограмм, а длины его сторон равны половинам длин диагоналей четырёхугольника ABCD. Указание. Используя свойства средней линии треугольника, доказать, что четырёхугольник EFHG - параллелограмм.
Указание. Использовать теорему косинусов для нахождения \EF\ и \FH\.


390
Указания и решения
Решение. Поскольку точки Е и F являются серединами сторон АВ и ВС, ЕЕ является средней линией треугольника АВС, из чего вытекает EF\\AC и \EF\ = ||Ж7|. С другой стороны, точки G и Н являются серединами сторон AD и CD, поэтому GH - средняя линяя треугольника ACD, что даёт нам GH\\AC и \GH\ = \\АС\.
Из полученных фактов вытекает, что EF\\GH,
\EF\ = \GH\, поэтому EFHG - параллелограмм. Но тогда отрезки ЕН и FG, являющиеся его диагоналями, точкой пересечения делятся пополам, то есть
\OG\ = \OF\ = \\FG\ = | \OE\ = \OH\ = \\EH\ =
A G D
Теперь нам надо всего лишь записать теорему косинусов
для треугольников EOF и FOH и ещё раз учесть тот факт, что \EF\ = ^|АС|, a \FH\ = t}\BD\ (в силу того, что FH - средняя линяя треугольника BCD):
\EF\2 = \ОЕ\2 + \OF\2 - 2 • \ОЕ\ ■ \OF\ • cos EOF =<j + j + abc°sa;
\FH\2 = \OF\2 + \OH\2 - 2 • \OF\ ■ \OH\ • cos FOH + -у—;
\AC\ = 2\EF\ = 2\J = ^a2 + 62 + 2ab cos a,
|jBD| = 2|РЯ| = ^\J~^— + = \/a2 + 62 - 2a6cosa.
Ответ. л/«2 + Ь2 — 2abcosa и \/a2 + 62 + 2abcosa.
Задача 9.
Выпуклый четырёхугольник ABCD описан вокруг окружности с центром в точке О. Найдите его периметр, если известно, что \АО\ = \ОС\ — 1, \ВО\ = \OD\ = 2.
Идея. Доказать, что четырёхугольник ABCD - ромб.
Указание. Обозначить буквами Р и Q точки касания окружности со сторонами А В и ВС, рассмотреть треугольники АОР, COQ, ВОР и BOQ.
Решение. Докажем, что четырёхугольник ABCD - ромб. Для этого обозначим буквами Р и Q точки касания окружности со сторонами АВ и ВС. Тогда \ОР\ = \OQ\ и ясно, что, во-первых, прямоугольные треугольники АОР и COQ равны по гипотенузе и катету и, во-вторых, прямоугольные треугольники ВОР и BOQ равны по гипотенузе и катету. Из этого следует \АР\ = \CQ\, \ВР\ = \BQ\, стало быть,
\АВ\ = \АР\ + \ВР\ = \CQ\ + \BQ\ = \ВС\.


3.1. Параллелограммы
391
Далее, рассматривая точки касания окружности со сторонами CD и AD и проводя совершенно аналогичные рассуждения, мы можем доказать, что \АВ\ = \AD\, \ВС\ = \CD\. Значит, ABCD - ромб. Но тогда его диагонали являются биссектрисами его внутренних углов, поэтому точка О и есть точка пересечения его диагоналей (поскольку центр окружности, вписанной в многоугольник, лежит на пересечении биссектрис его внутренних углов). Наконец, диагонали ромба перпен- дикулярны друг другу, \АВ\ = у/\АО\2 + \ВО\2 = \/5, a Pabcd = 4л/5.
Ответ. 4>/5.
Задача 10.
В ромб, одна из диагоналей которого имеет длину 10, вписан круг площади 97г. Вычислите площадь части ромба, расположенной вне круга.
Идея. Воспользоваться тем, что центр круга, вписанного в ромб, лежит на пересечении его диагоналей.
Указание. Провести радиус круга в одну из точек его касания со сторонами ромба, учесть, что диагонали ромба перпендикулярны, рассмотреть полученные прямоугольные треугольники.
В
Решение. Обозначим вершины ромба буквами А, В, С и D, точку пересечения его диагоналей обозначим буквой О, опустим перпендикуляр ОН на сторону ВС. Без огра- д< ничения общности будем считать, что \АС\ = 10.
Далее заметим, что поскольку диагонали ромба делятся пополам точкой их пересечения и являются биссектрисами ^
его внутренних углов, во-первых, \АО\ = \ОС\ = 5 и, во- вторых, точка О является центром круга, вписанного в ромб ABCD. Но тогда отрезок ОН является радиусом этого круга, а его длина равна л/Этг/тг, то есть 3.
Теперь заметим, что для нахождения площади ромба нам достаточно найти длину его второй диагонали BD, поскольку площадь ромба равна половине произведения длин его диагоналей. Это можно легко сделать, рассмотрев прямоугольные треугольники ОСН и ВОС :
sin ВСЮ = = I =► cos ВСО = I, tg ВСО = 7, \ВО\ = \ОС\ ■ tg ВСО =
\ОС\ 5 5 4 4
Таким образом,
1 с: 1 7 г. 7с
\BD\ = 2\ВО\ = у, Sabcd = ^ ■ \АС\ ■ \BD\ = SABcd Округа — т~97Г-
\Н
° )/
75
Ответ. ——97г. 2
Задача 11.
В параллелограмме ABCD длины диагоналей АС и BD равны d\ и {d\ ^ с^). Найдите площадь параллелограмма ABCD, если АВС = а.


392
Указания и решения
Идея. Воспользоваться тем, что сумма квадратов длин диагоналей параллелограмма равна сумме квадратов длин всех его сторон.
Указание. Записать теорему косинусов в треугольнике АВС. Учесть, что площадь параллелограмма равна произведению длин двух его соседних сторон и синуса величины угла между ними.
Решение. Обозначим длины сторон АВ и АС буквами х и у соответственно, будем считать, что \АС\ = d\, \BD\ = d2- Учтём, что площадь параллелограмма равна произведению длин двух его соседних сторон и синуса величины угла между ними, то есть нам надо искать не сами величины х и у, а их произведение. Воспользуемся тем, что сумма квадратов длин диагоналей параллелограмма равна сумме квадратов длин всех его сторон, а также запишем теорему косинусов в треугольнике АВС, предварительно заметив, что из того, что длины диагоналей параллелограмма различны, следует, что он не является прямоугольником и cos а ф О:
d2 + 4 = 2х2 + 2у2, ( *2+У2 = № + 4), _d2_d2
d2 = x2 + y2-2xycosa =* | *2 + ?;2 - oif =» ХУ ~ 4 C0SQ'
V 2 cos а
d2 — d2
Наконец, площадь параллелограмма ABCD равна ху sin а, то есть —- tg а.
4-4
Ответ. —-—tga.
Задача 12.
Через вершину А и середину М стороны ВС параллелограмма ABCD, площадь которого равна 1, проведена прямая, пересекающая диагональ BD в точке О. Найдите площадь четырёхугольника OMCD.
Идея. Представить площадь четырёхугольника OMCD ВМС как разность площадей треугольника BCD и треугольника ВОМ.
Указание. Воспользоваться леммами о площадях треугольников.
АН D
Решение. Проведём высоту ВН параллелограмма ABCD. Заметим, что
Sabcd = \ВС\ ■ \ВН\, SABCd = \ • \ВС\ • \ВН\,
поэтому площадь треугольника BCD равна половине площади параллелограмма ABCD, то есть 1 /2.


3.1. Параллелограммы
393
Далее положим \ВМ\ - \МС\ = х. Тогда \AD\ = 2х. Треугольники ВОМ и DO А подобны, стало быть,
\ВО\ \ВМ\ 1 \OD\ ~ \AD\ ~ 2'
Наконец, заметим, что
Sabom _ \ВМ\ ■ \ВО\ _ х 1 _ 1 „ _ 1
Sabcd ~ \ВС\ ■ \BD\ ~ 2х ' 3 ~ 6 ЛВОМ “ 12'
Значит, Somcd — Sabcd — Sabom = 5/12.
5
Ответ. —.
12
Задача 13.
В параллелограмме ABCD \АВ\ = \BD\ = 1, а длины его диагоналей относятся как 1 : v/З. Найдите площадь той части круга, описанного около треугольника В DC, которая не принадлежит кругу, описанному около треугольника ADC.
Идея. Найти длины сторон и величины углов параллелограмма ABCD, вычислить длины радиусов и расстояние между центрами окружностей, описанных около треугольников В DC и ADC.
Указание. Рассмотреть два случая.
Указание. Отбор случаев провести, используя неравенство треугольника.
Указание. Доказать, что В - центр окружности, ^ описанной около треугольника ACD, а треугольник BCD равносторонний, искомую площадь вычислить как разность площадей двух сегментов.
Решение. Поскольку в условии задачи не сказано, какая из диагоналей параллелограмма ABCD длиннее, нам придётся рассмотреть два случая. Сначала будем считать, что \АС\ = 1/л/З- Обозначим буквой К точку пересечения диагоналей параллелограмма. Тогда в треугольнике АВК известны все стороны: \АВ\ = 1, \ВК\ = \АК\ = Но такой треугольник не существует, поскольку не выполняется неравенство треугольника.
Пусть теперь \АС\ = \/3. В этом случае \АВ\ = 1, \ВК\ = \АК| = &. Но тогда треугольник АВК прямоугольный и, значит, диагонали параллелограмма перпендикулярны, т.е. ABCD - ромб и, кроме того, треугольники ABD и CBD равносторонние. Из всего этого вытекает, что точка В лежит, во-первых, на серединном перпендикуляре к АС и, во-вторых, на серединном перпендикуляре к AD. Значит, точка В - не что иное, как центр окружности, описанной около треугольника ADC, а длина радиуса этой окружности равна длине отрезка ВС, то есть 1. Центром же окружности, описанной около равностороннего треугольника BCD будет точка О, которая является точкой пересечения его медиан. Длину


394
Указания il решения
её радиуса посчитать легко (например, с помощью теоремы синусов) - она равна 1/д/З.
Итак, перед нами стоит следующая задача: даны два круга, известны длины их радиусов и расстояние между их центрами. Необходимо найти площадь той части одного из них, которая не лежит внутри другого круга. Решение этой задачи в общем случае рекомендуем провести самостоятельно.
В нашей же задаче ясно, что CD - общая хорда этих двух кругов и искомая площадь может быть вычислена как разность площадей сегмента CD круга, описанного около треугольника BCD и сегмента CD круга, описанного около треугольника ACD. Поскольку величина угла CBD равна 7г/3, величина угла COD равна 2тг/3 (по свойствам центральных и вписанных углов). Наконец, пользуясь формулой площади сегмента, получаем
Задача 14•
В параллелограмме PQRS биссектриса угла при вершине Р, градусная мера которого равна 80°, пересекает сторону RS в точке L. Найдите длину радиуса окружности, касающейся отрезка PQ и лучей QR и PL, если известно, что \PQ\ = 7.
Идея. Рассмотреть треугольник, образованный точками Р, Q и точкой пересечения прямой PL с продолжением прямой QR за точку Д, доказать, что он равнобедренный, а окружность из условия задачи в него вписана.
Указание. Для доказательства равнобедренности треугольника воспользоваться свойствами внутренних накрест лежащих углов при параллельных прямых.
Указание. Воспользоваться тем, что центр окружности, вписанной в треугольник, лежит на пересечении его биссектрис.
Решение. Обозначим точку пересечения прямой PL с продолжением прямой QR за точку R буквой М. Поскольку РМ - биссектриса угла QPS, имеем Z.QPM = Z.SPM. С другой стороны, прямые PS и QR параллельны, РМ - секущая, поэтому углы PMQ и SPM равны, как внутренние накрест лежащие. Таким образом, угол PMQ равен углу QPM, стало быть, треугольник PQM равнобедренный, \PQ\ = \QM\ = 7, PMQ = QPM = 40°.
Далее, окружность, касающаяся отрезка PQ и лучей QR и PL, является вписанной в треугольник PQM, поскольку она касается всех его сторон. Если обозначить её центр буквой О, а точку её касания со стороной РМ буквой К, то из равнобедренности треугольника PQM вытекает, что К - середина РМ, а поскольку центр окружности, вписанной в треугольник, лежит на пересечении его


3.1. Параллелограммы
395
биссектрис, градусная мера угла ОРК равна 20°. Наконец, из прямоугольных треугольников PQK и ОРК мы получаем
\РК\ = \PQ\ • cos QPK = 7 cos 40°, \OK\ = \PK\ • tg ОРК = 7cos40° • tg20°. Ответ. 7 cos 40° • tg 20°.
Задача 15.
В параллелограмме ABCD величина угла BCD равна 57г/б, а длина основания AD равна 8. Найдите длину радиуса окружности, касающейся прямой CD и проходящей через вершину А, а также пересекающей основание AD на расстоянии 2 от точки D.
Идея. Рассмотреть треугольники AKL и KLD, применить теорему синусов. Указание. Воспользоваться теоремой о произведении длины секущей на длину её внешней части. Найти длину отрезка KL и синус величины угла LKD. Указание. Длину радиуса окружности искать по теореме синусов для треугольника AKL. Воспользоваться свойством угла между касательной и хордой для нахождения величины угла LAK.
Указание. Рассмотреть оба варианта расположения точки К.
Решение. В этой задаче возможно два различных случая: К - точка касания прямой CD и окружности из условия задачи может лежать на луче [DC) (этому случаю на чертеже соответствует точка К\), а может лежать на луче, дополнительном к нему (этому случаю на чертеже соответствует точка К2). Обозначим точку пересечения окружности и основания AD буквой L, тогда по условию \LD\ = 2, \AD\ = 8и независимо от расположения точки К по теореме о квадрате длины касательной мы находим
Дальше будем рассуждать следующим образом. Опять-таки независимо от расположения точки К углы LKD и LAK равны по теореме об угле между касательной и хордой. Обозначим величину этих углов через а, тогда, записывая теорему
В
С
\KD\2 = \LD\ ■ \AD\ = 16 => \KD\ = 4.


396
Указания и решения
синусов для треугольника AKL, вписанного в нашу окружность, мы получаем
\KL\ | KL\
°КР 2 sin KAL 2 sin а'
С другой стороны, применение теоремы синусов к треугольнику LKD даёт нам
\KL\ \LD\ . \LD\sin KDL
— —w sina =
sin KDL sin LKD \KL\
Но по свойствам углов параллелограмма величина угла KDL равна либо 7г/6 (в первом случае), либо Бтг/6 (во втором случае). Это означает, что sin KDL независимо от конфигурации равен 1/2, стало быть,
2± = J_ \KL\ \KL\2
\KL\ \KL\’ Яокр 2-^ц 2 •
Квадрат длины отрезка KL ищется элементарно: надо всего лишь воспользоваться теоремой косинусов для треугольника KDL. Для первого случая (точки К\) мы имеем
k[d~L = \KiL\2 = \KXD\2 + \LD\2 - 2 • \Кф\ ■ \LD\ ■ cos KDL = 20 - 8\/3,
а для второго случая получаем
K^DL = \K2L\2 = \K2D\2 + \LD\2 - 2 • \K2D\ ■ \LD\ ■ cosK^DL = 20 + 8л/3.
6
Осталось поделить пополам полученные величины и выписать ответ.
Ответ. 10±4л/3.
Задача 16.
Окружность, длина диаметра которой равна \/10, проходит через соседние вершины Ап В прямоугольника ABCD. Длина касательной, проведённой из точки С к этой окружности, равна 3, а | АВ\ = 1. Найдите все возможные значения, которые может принимать длина стороны ВС.
Идея. Воспользоваться свойствами вписанных углов и теоремой о произведении длины секущей на длину её внешней части.
Указание. Доказать, что прямая ВС пересекается с окружностью из условия задачи в двух точках, найти длину отрезка, отсекаемого от этой прямой окружностью.
Указание. Рассмотреть оба возможных варианта расположения точки С.


3.1. Параллелограммы
397
Решение. В этой задаче возможны две различные конфигурации, а именно: окружность из условия задачи может не пересекать сторону ВС (этому случаю на чертеже соответствуют прямоугольник ABC\D\ и касательная С\К\), а может и пересекать (этому случаю на чертеже соответствуют прямоугольник ABC2D2 и касательная С2К2). Теперь заметим, что прямая ВС не является касательной к окружности. В противном случае мы бы получили, что она перпендикулярна как диаметру окружности, проведённому через точку В, так и отрезку АВ, который этим диаметром не является (его длина не равна длине диаметра), что невозможно. Поэтому прямая ВС пересекает окружность ещё и в некоторой точке F, отличной от В.
Далее заметим, что треугольник ABF прямоугольный, поэтому AF окружности, \AF\ = л/10 и по теореме Пифагора \BF\ = \/10 — 1
диаметр 3. Наконец,
обозначим искомую длину стороны ВС буквой х и воспользуемся теоремой о квадрате длины касательной. В первом случае |Ci.F| = \ВС\\ -Ь \BF\ = х -f 3,
ICiifil2 = |CiB| • \C\F\ =* ф + 3) = 9
а во втором случае \C2F\ = \BC2\ — \BF\ = x — 3,
\C2K2\2 = \C2B\ ■ \C2F\ => x(x - 3) = 9
3(л/5±1)
Ответ. .
x =
-3 + 3^5
3 + 3\/5
Задача 17.
В прямоугольнике ABCD, в котором \AD\ = 3 + Зл/2/2, а \АВ\ = 6, расположе- ны две окружности. Окружность с центром в точке К, длина радиуса которой равна 2, касается сторон АВ и AD. Окружность с центром в точке L, длина радиуса которой равна 1, касается стороны CD и первой окружности. Найдите площадь треугольника CLM, если М - основание перпендикуляра, опущенного из вершины В на прямую, проходящую через точки К и L.
Идея. Доказать, что точки A,K,L лежат на одной прямой, площадь треугольника СLM искать как половину произведения длины отрезка LM на длину перпендикуляра СН, опущенного из точки С на прямую KL.
Указание. Провести через точку L прямую, параллельную AD, опустить на неё перпендикуляр KR. Показать, что сумма величин углов AKR и LKR равна 7Г.
Указание. Обозначить буквой F точку пересечения прямой KL и стороны CD, воспользоваться тем, что треугольники ADF, CFH и АВМ прямоугольные и равнобедренные.


398
Указания и решения
Решение. Отправной точкой для реше- Н
ния этой задачи является доказательство того, что точки А, К, L лежат на одной прямой. Обозначим точку касания окружности с центром в точке К со стороной АВ буквой S. КА - биссектриса угла BAD, поэтому ICAS = AKS = тг/4, \KS\ = 2,
\АК\ = 2у/2. Проведём через точку L прямую PQ, параллельную AD (Р лежит на прямой АВ, Q лежит на прямой CD), и опустим на неё перпендикуляр KR. Тогда ADQP - прямоугольник, у которого \PQ\ — \AD\ = 3 + Зл/2/2, a Q - точка касания второй окружности и отрезка CD, стало быть, \LQ\ = 1.
С другой стороны, KRPS - тоже прямоугольник, то есть \PR\ = |jFsTiS| = 2, \LR\ = \PQ\ — \LQ\ — |РД| = Зу/2/2. Окружности касаются друг друга, поэтому длина отрезка KL равна сумме длин их радиусов, то есть \KL\ = 3. Из прямоугольного треугольника KLR мы находим sin LKR = у/2/2, то есть LKR = 7г/4.
Но тогда AKS+ SKR+ LKR — 7г, а это означает, что угол AKL развёрнутый, точки А, К и L лежат на одной прямой, \AL\ = |AftT| + \KL\ = 3 + 2y/2.
Второй ключевой идеей решения является следующее: площадь треугольника СLM проще всего искать как половину произведения длины отрезка LM на длину перпендикуляра, опущенного из точки С на прямую KL. Мы выяснили, что прямая КL проходит через точку А и является биссектрисой угла BAD. Поэтому треугольник АВМ прямоугольный и равнобедренный, \АМ\ = \АВ\/у/2 = Зу/2. Значит, \LM\ = \AL\ — \АМ\ = 3 — у/2.
Наконец, обозначим буквой F точку пересечения прямой KL и стороны CD, а буквой Н обозначим основание перпендикуляра, опущенного из С на KL. Треугольник ADF прямоугольный и равнобедренный, \DF\ = \AD\ = 3 + 3\/2/2, \CF\ = \CD\ - \DF\ = 3 - Зл/2/2. Треугольник CFH тоже прямоугольный и равнобедренный, поэтому \СН\ = \CF\fу/2 — (Зу/2 — 3)/2.
Теперь можно найти площадь треугольника CLM:
1 ^ За/2-З 12л/2 —15
Saclm - g ' 1СЯ1 • \ЬМ\ = 2 '(3 ~ ^ 2 = 4 '
12\/2 — 15 Ответ. .
Задача 18.
Окружность, проходящая через вершины В, С и D параллелограмма ABCD, касается прямой и пересекает прямую АД в точках В и Е. Найдите длину отрезка АЕ, если |AD| = 4 и |С2?| = 5.
Идея. Использовать теорему о квадрате длины касательной и теорему об угле между касательной и хордой. Рассмотреть два случая.


3.1. Параллелограммы
399
D
Указание. Показать, что треугольник DBC равнобедренный.
Указание. Использовать то, что четырёхугольник BCDE (BDCE) является трапецией, вписанной в окружность.
Решение. Заметим, что в этой задаче возможны два случая: окружность пересекает отрезок АВ и окружность пересекает продолжение отрезка АВ за точку В. Причём большая часть рассуждений одинакова для обоих случаев.
Сразу отметим для себя, что по условию задачи AD - касательная к окружности. Это означает, что нам могут пригодиться две классические теоремы: теорема о квадрате длины касательной и теорема об угле между касательной и хордой. Первая из них даёт нам соотношение | AD\2 = \АЕ\ • \АВ\, из чего мы
делаем вывод, что для решения задачи нам достаточно каким-то образом найти длину стороны АВ.
Далее, использовав вторую из перечисленных теорем, мы получаем, что углы ADB и DC В равны (оба они измеряются половиной дуги DB). Но, с другой стороны, AD\\BC, поэтому углы ADB и DBC равны в силу свойств внутренних накрест лежащих углов. Значит, угол DBC равен углу DC В, стало быть,
ADBC равнобедренный, \BD\ = \CD\.
Единственным не использованным нами фактом является то, что прямые А В и CD также параллельны. Исходя из этого заметим, что в первом случае четырёхугольник BCDE является трапецией, вписанной в окружность, а во втором случае четырёхугольник BDCE является трапецией, вписанной в окружность. Но вписанная в окружность трапеция является равнобедренной, а у равнобедренной трапеции равны не только боковые стороны, но и диагонали. Таким образом, в обоих случаях получаем, что \BD\ = \СЕ\ = 5 и длина отрезка CD по доказанному выше также равна 5, ну и поскольку \АВ\ = \CD\ в силу свойств параллелограмма, получаем \АВ\ = 5.
В первом случае получаем \AD\2 = \АЕ\ • \АВ\ => 16 = 5|АЕ| => \АЕ\ =
Второй же случай невозможен, так как длина отрезка касательной, проведённой из точки к окружности, всегда больше длины внешней части секущей, проведённой из этой точки к той же окружности, т.е. в нашем случае должно выполняться условие \AD\ > \АВ\, но \AD\ = 4, \ АВ\ = 5.
п 16
Ответ. —.
5
Задача 19.
В параллелограмме проведены биссектрисы всех внутренних углов. Четырёхугольник, образованный точками пересечения этих биссектрис, имеет площадь, равную двум третям площади исходного параллелограмма. Найдите отношение длин большей и меньшей сторон исходного параллелограмма.


400
Указания и решения
В
Идея. Доказать, что четырёхугольник (PQRS), образованный точками пересечения биссектрис всех внутренних углов исходного параллелограмма (ABCD), является прямоугольником.
Указание. Показать, что биссектрисы двух соседних углов параллелограмма пересекаются под прямым углом.
Указание. Выразить длины сторон четырёхугольника PQRS через длины сторон параллелограмма ABCD и величину одного из его внутренних углов, рассматривая различные прямоугольные треугольники.
Решение. Обозначим вершины параллелограмма буквами А, В, С и D, точку пересечения биссектрис углов BAD и АВС обозначим буквой Р, точку пересечения биссектрис углов АВС и BCD обозначим буквой Q, точку пересечения биссектрис углов BCD и ADC обозначим буквой R, а точку пересечения биссектрис углов ADC и BAD обозначим буквой S.
Ключевым моментом в решении этой задачи является доказательство того, что четырёхугольник PQRS - прямоугольник. Поступим следующим образом: обозначим величину угла BAD через а, тогда по свойствам параллелограмма и условию задачи
BCD = a, ABC = ADC = тг - а,
ВАР = DAP — BC7R = DCR =
abp = cbp = 'Wr = cdr = ^: -
2 2
С учётом этого, применяя теорему о сумме величин углов треугольника к треугольникам АВР, BCQ, CDR и DAS, мы получаем, что все четыре угла Р, Q, R и S прямые. Значит, PQRS - прямоугольник.
Теперь нам надо связать между собой площади параллелограмма ABCD и прямоугольника PQRS. Обозначим длины сторон АВ и AD через bud соответственно. Рассматривая прямоугольные треугольники АВР и DAS, находим
|AS| = \AD\ • cos DAS = dcos | AP| = \AB\ • cos BAP = bcos
Отметим, что мы, вообще говоря, не знаем, как точно расположены точки А, Р и 5. Однако мы можем утверждать, что точка А никак не может лежать между точками Р и 5, поэтому
\PS\ = \\AP\-\AS\\ = \b-d\cos^.
Далее, проводя аналогичные рассуждения для треугольников АВР и BCQ, получаем


3.1. Параллелограммы
401
а
Стало быть, \PQ\ = \\ВР\ — \BQ\ \ = \b — d\ sin —. Теперь воспользуемся формулами площади:
Sabcd — \ЛВ| • \ AD\ • sin BAD = bdsina, .
Spqrs = \PQ\ ■ |P5| = \b — d\2 sin ^ cos ^ = ^(6 - d)2 sina.
Деля друг на друга полученные соотношения, имеем 2 _ Spqrs _ (b-d)2 м
Sabcd 2bd
Ш = 3{b2 - 2bd + d2) <=> 3b2 - 1Ш -h 3d2 = 0.
Решая последнее уравнение как квадратное относительно Ь, находим b = 3d или Ъ = -. Ясно, что в любом случае отношение длин большей и меньшей сторон
О
параллелограмма ABCD равно 3.
Ответ. 3:1.
Задача 20.
Через вершины А, В и С параллелограмма ABCD проведена окружность, пересекающая прямую BD в точке Е таким образом, что \ВЕ\ = 9. Найдите \BD\, если \АВ\ = 3, \ВС\ = 5.
Идея. Использовать свойство пересекающихся хорд и свойство параллелограмма, связывающее диагонали и стороны параллелограмма.
Указание. Выяснить взаимное расположение точек В, D и Е.
Указание. Обозначить половины диагоналей параллелограмма через хм у. Использовать свойство пересекающихся хорд и свойство параллелограмма, связывающее диагонали и стороны параллелограмма.
Решение. Для начала отметим, что \CD\ = 3, \AD\ = 5, и попытаемся понять, где находится точка Е: на отрезке BD или на его продолжении за точку D. Это сделать достаточно просто. Если Е G BD, то \BD\ > \ВЕ\ = 9, но, с другой стороны, по неравенству треугольника \BD\ < \АВ\ -Ь \AD\ =■ 8. Противоречие. Итак, точка Е лежит вне параллелограмма ABCD.
Теперь, когда мы определились с конфигурацией, немного порассуждаем. В общем-то ясно, что отрезок BD, длину которого просят найти, является частью хорды BE. Поэтому мы должны каким-то образом использовать свойство пересекающихся хорд.
Проведём диагональ АС и обозначим буквой F точку пересечения диагоналей. Так как диагонали параллелограмма делятся точкой пересечения пополам, положим \AF\ = \FC\ = х, \BF\ = \FD\ = у. Теперь используем свойство пересекающихся хорд и одно из свойств параллелограмма, связывающее диагонали и стороны параллелограмма:
/ \AF\-\FC\ = \BF\-\FE\,
{ \АС\2 + \BD\2 = 2{\АВ\2 + \ВС\2)]
Г х2 = у ■ (9 - у),
\ 4х2 + 4у2 = 2(32+52У, ^


402
Указания и решения
х2 + у2 х2 + у
9 у, 2 - 17;
=>
17
У“Т
\BD\=2y=™.
Ответ.
34
Задача 21.
Стороны ромба EFGH являются гипотенузами прямоугольных равнобедренных треугольников EAF, FDG, GCH и НВЕ, причём все эти треугольники имеют общие внутренние точки с ромбом EFGH. Сумма площадей четырёхугольника ABCD и ромба EFGH равна 12. Найдите \GH\.
Идея. Доказать, что четырёхугольник ABCD яв- р
ляется квадратом.
Указание. Показать, что равнобедренные треугольники ABE, ВСН, CDG и DAF равны и ADC = n/2. Ц ]
Указание. Выразить площади квадрата ABCD и ромба EFGH через длину стороны ромба и величину его острого угла.
Решение. Обозначим длину стороны ромба EFGH через ау/2, тогда длины отрезков АЕ, AF,
ВН, CiJ, CG, DF, DG будут равны а. Помимо этого, величину угла FEH обозначим буквой а, без ограничения общности будем считать, что а ^ тг/2. Ясно, что тогда
FGtf = a, EFG = EHG = тг - а.
Далее заметим, что величины всех углов AEF, AFE, ВЕН, ВНЕ, CHG, CGH, DFG, DGF равны тг/4 и
А&В = AEF + В£Я - Р£Я = £ - a, CGD = DGF + CGH - FGH = J - a;
= £FG - AFE - = £ - а, CtfB = £я5 - ВНЕ - CHG = £ - a.
2 2
Из этого вытекает, что все четыре равнобедренных треугольника АВЕ, ВСН, CDG и DAF равны по двум сторонам и углу между ними, стало быть, ABCD - ромб. Более того, с учётом этого равенства мы находим, что
ADC = FDG + ADF-CDG = FDG =
то есть ABCD - квадрат.
Теперь немного посчитаем.
. * ~ . АЕВ л . /тг а\
\АВ\ = 2 ■ \АЕ\ • sin —— = 2asin - -J ,
Sabcd — = 4a2sin2 (^ — ^) = 2a2(l — cos(7r/2 — a)) = 2a2(l — sincc),


3.1. Параллелограммы
403
Sefgh = \EF\ • \EH\ sin FEH = 2a2 sin a\
12 = Sabcd + Sefgh — 2 a2 =>• a = л/б => |С?-НГ| = ау/2 = 2\/3.
Ответ. 2\/3.
Задача 22.
В параллелограмме лежат две окружности, касающиеся трех его сторон и другой окружности каждая. Длина радиуса одной из них равна 1. Также известно, что длина одного из отрезков стороны параллелограмма от вершины до точки касания с одной из окружностей равна у/3. Найдите площадь параллелограмма.
Идея. Доказать, что обе окружности касаются одной и той же пары противоположных сторон параллелограмма.
Указание. Показать, что окружности одинаковые, воспользоваться тем, что центр окружности, вписанной в угол, лежит на его биссектрисе.
Указание. Рассмотреть все отрезки сторон параллелограмма, концами которых являются вершина параллелограмма и точка касания с одной из окружностей.
Решение. Основная трудность в этой задаче заключается в однозначном определении конфигурации, удовлетворяющей условию задачи. Будем рассуждать следующим образом: у параллелограмма всего четыре стороны, а каждая окружность касается трёх их них. Это означает, что есть как минимум две стороны параллелограмма, касающиеся обеих окружностей.
Если эти стороны смежные, то обе окружности вписаны в угол, ими образованный, поэтому их центры лежат на биссектрисе этого угла. Учитывая тот факт, что окружности ещё и касаются друг друга, мы получаем, что касаться они могут только внешним образом и одна из окружностей будет больше другой. Но тогда ясно, что меньшая окружность не может иметь общих точек с двумя другими сторонами параллелограмма (на чертеже пунктирными прямыми показаны варианты расположения этих других сторон). Противоречие.
Итак, эти стороны противоположные.
Но противоположные стороны параллелограмма параллельны, поэтому длины диаметров обеих окружностей будут равны между собой (и равны расстоянию между этими сторонами). Стало быть, окружности одинаковые, поэтому касаются они ^ внешним образом, а конфигурация выглядит так, как показано на чертеже. Обозначим вершины параллелограмма буквами А, В, С и D, центр первой окружности обозначим буквой 0\, точки её касания со сторонами АВ и CD обозначим буквами Р и S соответственно. Центр второй окружности обозначим буквой О2, точки её касания со сторонами А В и CD обозначим буквами Q и R соответственно. Ясно, что |OiО21 = I^PQI — 2, \PS\ = 2, PQRS - квадрат.
R С


404
Указания и решения
Теперь надо понять, длина какого из отрезков может равняться у/3. В силу того, что длины отрезков касательных, проведённых из одной точки к окружности, равны, нам достаточно перебрать отрезки АР, AQ, ВР и BQ. Понятно, что \AQ\ > \PQ\ = 2 > \/3 и \ВР\ > \PQ\ = 2 > \/3 и возможны всего два варианта: \АР\ = у/3 или \BQ\ = у/3.
Если \АР\ = л/3, то, учитывая, что центр окружности, вписанной в угол, лежит на его биссектрисе, мы находим
‘8бг;5?=т = 75
ABC = n-DAB = у, б^Щ=^АВС = ^, \BQ\ = \02Q\ • ctg®Q = -Ь
\AB\ = \AP\ + \PQ\ + \BQ\ = SABcd = \AB\ • |PS| = 8^ + 12.
Если же \BQ\ = л/З, то, проводя аналогичные вычисления, мы приходим к тому же ответу. Причём приведённый рисунок соответствует второму случаю, поскольку на нём угол DAB тупой, а АВС острый.
4(3 + 2л/3)
Ответ. .
Задача 23.
В ромб ABCD, у которого \АВ\ = I и BAD = 2а, вписана окружность. Касательная к этой окружности пересекает сторону АВ в точке М, а сторону AD в точке N. Известно, что \MN\ = 2а. Найдите длины отрезков MB и ND, если известно, что \МВ\ < \ND\.
Идея. Искать не длины отрезков MB и ND, а длины их дополнений до сторон ромба, т.е. длины отрезков AM и AN.
Указание. Применить теорему косинусов к треугольнику AMN. Указание. Рассмотреть треугольник AM N. Доказать, что его периметр равен удвоенной длине отрезка с концами в точке А и точке касания окружности из условия задачи со стороной АВ. Воспользоваться свойством отрезков касательных, проведённых из одной точки к окружности, а также тем, что центр окружности из условия задачи лежит в точке пересечения диагоналей ромба. D С
Решение. Заметим, что отрезки, длины которых требуется найти, очень неудобно расположены. Поэтому искать лучше не их, а их дополнения до сторон ромба, т.е. длины отрезков AM и AN, особенно если учесть тот факт, что в треугольнике AMN известны сторона и угол. Значит, одно уравнение, связывающее длины отрезков AM и AN, уже есть - теорема косинусов. Осталось найти ещё одно.
М Р В


3.1. Параллелограммы
405
Обозначим буквой О центр вписанной в ромб ABCD окружности, а буквами Р, Q и R - точки её касания с отрезками АВ, AD и MN соответственно. Поскольку диагонали ромба являются биссектрисами его внутренних углов, точка О является точкой их пересечения. Также заметим, что угол АОВ прямой. Тогда из прямоугольных треугольников АОВ, АОР и AOQ мы находим
\АО\ = \АВ\cos В АО = / cosa, \АР\ = \AQ\ = \АО\ cos ОАВ = / cos2 а.
Далее, \MR\ = \МР\ и \NR\ = \NQ\ по свойству отрезков касательных, проведённых из одной точки к окружности. Положим \АМ\ = х и \AN\ = у (из условия следует, что х ^ у). С учётом этого получаем
Для того чтобы получить второе уравнение, связывающее хну, запишем теорему косинусов для треугольника AMN:
\MN\2 = \AM\2 + \AN\2-2-\AM\-\AN\-cosMAN =» x2+y2-2xycos2a = 4а2. Осталось решить полученную систему:
В этом месте стоит применить теорему, обратную теореме Виета. Она утверждает, что х и у являются корнями квадратного уравнения
21 cos2 a = | АР| + \AQ\ = \AM\ + \MP\ + |ЛЛГ| + \NQ\ =
= \AM\ + |Af Д| + \AN\ + \NR\ =x + y + 2a.
t2 — 2(1 cos2 a — a)t + I2 cos2 a — 2a/ = 0.
Вычислим его дискриминант:
— = (/ cos2 a — a)2 — (I2 cos2 a — 2a/) = a2 + 2al sin2 a — I2 sin2 a cos2 a. Значит, с учётом условия х ^ у, получаем
х = I cos2 a — a + \Л*2 + 2al sin2 a — I2 sin2 a cos2 a, 2/ = I cos2 a — a — у/a2 + 2al sin2 a — I2 sin2 a cos2 a.
Наконец, |MP| = \AB\ - \AM\ =l-x и |iV£>| = |AD| - \AN\ = I -y.
\MB\ = a + I2 sin2 a — \/a2 + 2al sin2 a — I2 sin2 a cos2 a, |7V\D| = a + I2 sin2 a -f \/a2 -j- 2a/ sin2 a — I2 sin2 a cos2 a.


406
Указания и решения
Задача 24-
На стороне АВ треугольника АВС взята точка D таким образом, что \CD\ = \/Гз и sin : sin BCD = 4:3. Через середину отрезка CD проведена прямая,
пересекающая стороны АС и ВС в точках М и N соответственно. Известно, что АСВ = 27г/3 , площадь треугольника MCN равна 3\/3, а расстояние от точки М до прямой АВ в два раза больше расстояния от точки N до этой же прямой. Найдите площадь треугольника АВС.
Идея. Доказать, что четырёхугольник CMDN - параллелограмм, а треугольники AMD и DNB подобны.
Указание. Показать, что \CM\ = \DN\, \CN\ = \DM\.
Указание. Найти величины углов ACD и BCD.
Указание. Представить площадь треугольника MCN как сумму площадей треугольников МСО и 7VCO, воспользоваться формулой площади. Найти \СМ\ и \CN\.
Указание. Применить теорему косинусов в треугольниках MCD и NCD. Найти \DN\ и \DM\.
Решение. Это довольно трудная задача. Явно не хватает данных, чтобы составить план решения задачи. А это значит, что в численных значениях, которые мы можем получить в этой задаче, скрыта дополнительная информация. Поэтому сначала вычислим все, что можно, а потом подумаем, какие выводы можно будет сделать из полученных результатов.
Начнем с вычисления величин углов ACD и BCD. Введём обозначение ACD = а, тогда по условию задачи BCD = 27г/3 — а. Пользуясь данным нам соотношением на синусы величин углов ACD и BCD, имеем
sina 4 0 /л/3 1
—^ - = - 3 sin а = 4 I —- cos а + -
sin(4?- — а) о \ 2 2
3sina = 4 [ —- cos а: + - sina ] => tga = 2v/3
sin ACD = sina = ^=1, sinBCD = - sin ACD =
Vl3 4 2VT3
После этого мы можем вычислить длины сторон треугольника MCN. Обозначим середину отрезка CD буквой О, тогда по условию задачи \СО\ = л/ТЗ/2. Положим \СМ\ = ж, |САГ| = у и дважды выразим площадь треугольника MCN:
Samcn = \ ■ \СМ\ • |CW| . sin ЛСВ => 3\/3 = =► ху = 12;
Samcn — S&mco + S&nco =


3.1. Параллелограммы
407
Решая полученную систему уравнений, мы находим \СМ\ = х = 3, \CN\ = у = 4. Дальше наиболее логичным будет вычислить длины отрезков DM и DN, чтобы хоть как-то подобраться к условию про расстояния от точек М и N до прямой АВ. Вспомним, что тангенс величины угла ACD равен 2л/3, поэтому она лежит в пределах от 7г/3 до тт/2. Из этого вытекает, что величина угла BCD лежит в пределах от 7г/6 до 7г/3, стало быть, углы ACD и BCD острые,
cos ACD = у 1 — sin2 ACD = —L=, cos BCD — у 1 — sin2 BCD — —%=> v д/й’ V 2VT3
После этого, записывая теорему косинусов для треугольников MCD и NCD, находим
|Г>М|2 = |СМ|2 + |СТ>|2 - 2 • |СМ| • |СТ>| • cos ACD =16 =* \DM\ = 4;
|D7V|2 = |CW|2 + |CT>|2 - 2 • \CN\ • |CZ?| • cos BCD = 9 =» |Z>AT| = 3.
Теперь, собственно, наступает ключевой момент решения. Совершенно неожиданно получилось, что \СМ\ = \DN\, \CN\ = \DM\. Из этого следует, что четырёхугольник CMDN - параллелограмм, стало быть, DM\\BC, DN\\AC. Но тогда треугольники AMD и DNB подобны по двум углам (угол ADM равен углу DBN, а угол DAM равен углу BDN по свойствам соответственных углов при параллельных прямых). А тот факт, что расстояние от точки М до прямой АВ в два раза больше расстояния от точки N до этой же прямой, означает то, что коэффициент подобия этих треугольников равен 2, поскольку эти расстояния суть не что иное, как соответствующие друг другу высоты этих треугольников.
Наконец, из этого подобия мы получаем
|Щ = ТЩ = 2 ^ 1^1 = 6, \BN\ = 2 =► \АС\=9, \BC\=Q
и, применяя формулу площади треугольника, находим
Saabc = I • \АС\ • \ВС\ ■ sin АСВ = \ • 9 • 6 • ^ = 2?V^
Ответ.
2 2 2 2 27л/3
Задача 25.
В параллелограмме ABCD диагонали пересекаются в точке О, а длина диагонали BD равна 12. Расстояние между центрами окружностей, описанных около треугольников AOD и COD, равно 16. Длина радиуса окружности, описанной около треугольника АОВ, равна 5. Найдите площадь параллелограмма ABCD.
Идея. Доказать, что четырёхугольник, образованный центрами окружностей, описанных около треугольников АОВ, ВОС, COD и AOD, - параллелограмм, причём длины его высот равны половинам длин диагоналей параллелограмма ABCD, длина одной из диагоналей равна удвоенной длине радиуса окружности,


408
Указания и решения
описанной около треугольника АОВ, а один из углов между его сторонами равен углу между диагоналями параллелограмма ABCD.
Указание. Воспользоваться тем, что центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к его сторонам, а также равенством треугольников АОВ и COD.
Указание. Воспользоваться формулами площади параллелограмма и теоремой косинусов.
Решение. Обозначим буквами Р, Q, R и S центры окружностей, описанных около треугольников АОВ, ВОС, COD и AOD соответственно. Воспользуемся тем, что центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к его сторонам. Значит, точки Р и S лежат на прямой, проходящей через середину отрезка АО и перпендикулярной ему, а точки Q и R лежат на прямой, проходящей через середину отрезка ОС и перпендикулярной ему. Итак, PS _L АС, А QR _L АС, стало быть, PS\\QR. Рассуждая абсолютно аналогично, мы получаем, что PQ\\RS, поэтому PQRS - параллелограмм, причём по условию задачи |Д5| = 16.
Далее заметим, что треугольник АОВ равен треугольнику COD. Из этого следует, что, во-первых, длины радиусов описанных около них окружностей также равны, то есть \OR\ = \ОР\ = 5, и, во-вторых, равны и углы РОВ и ROD, из чего вытекает, что точки Р, О и R лежат на одной прямой (для обоснования этого факта достаточно воспользоваться свойством вертикальных углов). Таким образом, \PR\ = \ОР\ + \OR\ = 10, точка О является серединой диагонали PR параллелограмма PQRS.
Обозначим середины отрезков АО, ВО, ОС и OD буквами К, L, М и N соответственно. Диагонали параллелограмма точкой пересечения делятся пополам, поэтому \АК\ = \ОК\ = \ОМ\ = \СМ\, a \BL\ = \OL\ = |07V| = \DN\ = 3. Так как PQ _L BD и RS _L BD, отрезок LN является высотой параллелограмма PQRS, а его длина равна 6. Также отметим, что отрезок КМ, длина которого равна половине диагонали АС, тоже является высотой параллелограмма PQRS. Наконец, учтём ещё и тот факт, что углы АОВ и PSR равны, как углы с взаимно перпендикулярными сторонами.
Подводя итог всем этим рассуждениям, делаем вывод: площадь параллелограмма ABCD уместно искать по формуле Sabcd = \ * \АС | • \BD\ • sin АОВ,
причём недостающие величины \АС\ и sin ЛОВ мы можем найти, рассматривая параллелограмм PQRS, в котором нам известно \RS\ = 16, \PR\ = 10, \LN\ = б. Введём обозначения АОВ = PSR = а, \КМ\ = х. Пользуясь формулой площади параллелограмма и учитывая тот факт, что независимо от того, где лежит точка N, \LN\ = \PS\ • sin PSR, имеем
96
Spqrs = \RS\ • \LN\ = 96= |PS| • \KM\ => \PS\ = —;
В С
— -sina = 6 => x = 16 sin a.
x


3.1. Параллелограммы
409
После этого запишем теорему косинусов для треугольника PRS:
|РД|2 = |PS|2 + |PS|2 - 2 • \PS\ • IД5| • cos PSR ==►
/ 96\2 96
===> 100 = ( — ) + 256 — 2 • — • 16 • cos а.
\ X ) X
Подставляя в это уравнение х, получаем
36 /9ч
100=—5 Ь 256 — 192 ctg а Ф=Ф 9(ctg а + 1) — 48ctga + 39 = 0 <==>
sin a
3 ctg2 a — 16 ctg a + 16 = 0.
Это уравнение имеет два корня: ctg a = 4/3 и ctg a = 4. Тот факт, что мы получили два разных значения, можно проиллюстрировать следующим образом: для того чтобы построить параллелограмм PQRS, удовлетворяющий условиям \RS\ = 16, \PR\ = 10, \LN\ = 6, надо провести две параллельные прямые на расстоянии 6 друг от друга, на одной из них отложить отрезок Д5, длина которого равна 16, и построить окружность, длина радиуса которой равна 10, с центром в точке R. Точки её пересечения со второй прямой и дадут два варианта расположения точки Р - на чертеже они обозначены как Р\ и Р2. Точки Q\ и Q2 достраиваются из условия \PQ\ = 16. В данном случае получилось так, что точки Р2 и Q\ совпали - это случайность.
Наконец, заметим, что
1 192
Sabcd = - • 2х • 12 • sina = 16sina • 12 sin a = 192 sin2 a = —5 •
2 ctgJ a + 1
Подставляя в эту формулу полученные значения ctg a, находим ответ:
1728 192
Ответ. ------ или —-.
25 17
Задача 26.
В параллелограмме ABCD величина угла между диагоналями АС и BD равна 7г/6. Известно, что \АС\ : \BD\ = 2 : у/3. Точка В\ симметрична точке В относительно прямой АС, а точка С\ симметрична точке С относительно прямой BD. Найдите отношение площадей треугольника АВ\С\ и параллелограмма ABCD.
Идея. Выразить длины отрезков АВ\ и АС\ через длины сторон параллелограмма ABCD, вычислить величину угла В\АС\. Рассмотреть два случая: АОВ — 7г/6 и AOD = 7г/6.


410
Указания и решения
Указание. Принять половины длин диагоналей параллелограмма ABCD за 2х и у/Зх, с помощью теоремы косинусов выразить длины сторон параллелограмма и найти величины различных углов.
Указание. Воспользоваться тем, что |AJ3i| = \АВ\, В\АС = ВАС. Рассмотреть треугольник АСС\.
Решение. В этой задаче возможны два различных случая. Поскольку углом между прямыми по определению является меньший из образованных ими углов, может оказаться, что АОВ = 7г/6 (первый случай, левый чертёж), а может оказаться, что AOD = 7г/6 (второй случай, правый чертёж). Также сразу отметим, что понятие «две точки симметричны относительно прямой» подразумевает тот факт, что отрезок, их соединяющий, перпендикулярен этой прямой и делится ею пополам.
В
Сначала рассмотрим первый случай. Обозначим точку пересечения диагоналей параллелограмма ABCD буквой О. Поскольку диагонали параллелограмма точкой пересечения делятся пополам, \АО\ : \ВО\ = 2 : у/3. Введём обозначения \АО\ = \ОС\ = 2ж, \ВО\ = \OD\ = у/Зх. Записывая теорему косинусов для треугольника АОВ, мы можем выразить длины сторон АВ и CD и найти величины различных углов:
|AjB|2 = Ах2 + Зх2 — 2 • 2х • у/Зх • = х2
\АВ\ = \CD\ = х,
cos ABO =
х2 + Зх2 — Ах2
0
АВО =
7Г
2 • х • у/Зх 2
Итак, мы получили, что АВ _L BD. Это означает, что и CD _L BD. Стало быть, точки С, D и Ci лежат на одной прямой, |CCi| = 2\CD\ = 2х. AB\\CD, поэтому ACD = ВАО = 7г/3, и из треугольника ACCi мы находим
|ACi| = \J\AC\2 + IC'C'il2 - 2 • \АС\ ■ |CCi| • cosACCi =
cos Сi AC —
\АС\2 + |ACi|2 - IC’C'il 16x2 + 12ж2 - 4x2
0
2 • |AC| • |ACi| 2 • Ax • 2\/Зж
Далее, AC - серединный перпендикуляр к отрезку ВВ\. Из этого вытекает, что |AjE?i| = |AJ3| = ж, В\АС = J5AC = тт/3. Наконец,


3.1. Параллелограммы
411
sABco - i ■ ис • до sinAoB - avb*. _ I,
Рассуждения для второго случая похожи на рассуждения для первого случая. Положим \АО\ = \ОС\ = 2х, \ВО\ = |OD| = y/Зх. Записывая теорему косинусов для треугольника ВОС, мы находим |РС| = |AD| = х, СРО = 7г/2, ВСО = 7г/3, а из треугольника ЛОР мы имеем
| АВ|2 = 4х2 + Зх2 - 2 • 2х • л/Зх • = 13х2 =>• \AB\ = \CD\ = у/Пх,
13х2 4- 4х2 — Зх2 7
cos В АО =
2 • у/ТЗх • 2х 2VT3*
Далее в силу того, что CP _L BD, точки С, В и Ci лежат на одной прямой,
|jBCi| = |РС| = х. Отметим, что BC\\\AD, \ВС±\ = |AD|, поэтому AC\BD - параллелограмм, |i4Ci| = |PD| = 2у/3х. Более того, ВС\ _L BD, поэтому AC\BD - прямоугольник, угол ACiC прямой,
2у/3х у/3 п
cosC'AC = Не = — = Т => ClAC = f
Теперь опять воспользуемся тем, что АС - серединный перпендикуляр к отрезку ВВ\. Значит, |ABi| = \АВ\ = \/ТЗх, В\АС = ВАС = arccos(7/2v^3) • Наконец,
sin thAC = \Д “ cos2 ВхАС = = BiACi — BiAC + C\AC
=Ф> sin Вi ACi — sin Вi AC • cos C\ AC + cos B\ AC • sin C\ AC
2л/Тз’
SaabiCi = \ ■ \AB\ \ • |ACi | • sinC4Ci - ^x2,
- | ■ HCI ■ № .si„30B _ 2^, - *
П 1 5
Ответ. - или -.
4 4
Задача 27.
Дан параллелограмм ABCD, |АВ| = 3, |AD| = л/3 + 1, PAD = тт/3. На стороне АВ взята точка К таким образом, что \АК\ : |ifP| = 2 : 1. Через точку К параллельно AD проведена прямая. На этой прямой внутри параллелограмма ABCD выбрана точка L, а на стороне AD выбрана точка М, |АМ| = \KL\. Прямые ВМ и CL пересекаются в точке N. Найдите величину угла BKN.
Идея. Ввести обозначение \KL\ = х, выразить через х величины углов АВМ и BCL, рассмотреть треугольники BKN и BCN.


412
Указания и решения
Указание. Записать теорему синусов для треугольников АВМ, CLP, BKN и BCN (Р - точка пересечения прямых KL и CD), выразить котангенс величины угла BKN через котангенсы величин углов АВМ и BCL.
Указание. Использовать формулу
sin(x ± у)
: = sm ж ctg у ± cos х.
sin у
Решение. Из условия задачи следует, что |АК\ = 2, \КВ\ = 1. Обозначим буквой Р точку пересечения стороны ВС с прямой, проходящей через точку К и параллельной AD. Ясно, что К PC В - параллелограмм, \СР\ = 1, \КР\ = \/3+1. С другой стороны, \АМ\ = \KL\, AM||jRTL, поэтому AMLK - тоже параллелограмм, ML\\AB.
Поскольку мы не знаем, где точно расположе- ^ PC
на точка L, введём обозначение \KL\ = \АМ\ = ж и попытаемся каким-то образом выразить длины различных отрезков и величины различных углов, присутствующих на чертеже, через эту переменную.
Так как точка L расположена внутри параллелограмма ABCD, то \LP\ = \КР\ — \KL\ = л/З-fl —ж.
Понятно, что единственным разумным способом нахождения искомой величины является рассмотрение
треугольника BKN. В нём мы можем попытаться выразить длину отрезка BN и величину угла АВМ - для этого воспользуемся теоремой синусов. Для сокращения записи отметим, что справедлива формула
sin(x ± у)
: = sin х ctg у ± cos ж,
sin у
которой мы будем постоянно пользоваться при решении задачи. Сначала рассмотрим треугольник АВМ, поскольку в нём мы знаем величину угла BAD - она равна 7г/3, и длины двух сторон. Пусть АВМ = а, тогда AM В = 27г/3 — а,
\АМ\ \АВ\ х
sin АВМ sin AM В sina sin(^ - а)
л/5 1 3 6-
<*=> — ctg а + - = - <£=> ctg а =
2 2 х у/Зх '
После этого рассмотрим треугольник CLP, в котором мы знаем величину угла CPL - она, очевидно, равна 27г/3, и длины двух сторон. Пусть CLP = /3, тогда LCP = 7г/3 - /3,
|СР| _ |LP| 1 _v/3 + l-x
sin CLP sin LCP sin(f-/3)
^ „ 1 , , „ 2\/3 + 3 - 2z
— ctg/?-- = V3 + 1-ж ctg/3=: -^= .
Теперь обозначим величину искомого угла BKN через <£. Тогда KNB = 7г—а-(р. Величина угла АВС равна 27г/3, поэтому величина угла NBC равна 27г/3-а,


3.2. Трапеции
413
a BNC = 7г/3 + а — /3. Записывая теорему синусов для треугольников BKN и BCN, имеем
\BN\ _ \КВ\ |PiV| _ 1
sin BKN sin BN К sin<^ sin(a + <p) ’
|jBAT| _ \BC\ \BN\ _ V3 + 1
sin BCN sin BNC sin/3 sin(f+a-/3)'
Поделив полученные соотношения, получаем
sin/3 _ sin(| + а -/3) siny> (\/3 + 1) sin(a + ip)
<=> (V3 + l)(sinactgi£ + cosa) = sin ^ + cxj ctg/3 — cos ^ + a) <=
(/3 2 \ ^ /3
— ctga+ - J ctg/3 — — ctg a + —.
Наконец, подставим сюда полученные ранее выражения для ctg а и ctg /3:
/ к f 6-х\ 3 2л/3 + 3-2а: 6-х л/З
я vs* + ir —
^ _ _ 12\/3 +12 - 8ж 6-х _ (у/3-3)х _1-у/3
^ Ct8<P ~ (л/З + 1) • 2\/3x ~~ у'Зх ~~ (v% + 1) • л/Зх _ V3 + 1 ’
(l - ч/З \ 7тг ^
Отметим, что arcctg I J = —. Докажите это самостоятельно.
п 7п
Ответ. —.
12
3.2. 	Трапеции Задача 1.
В трапеции KLMN отрезки KN и LM являются основаниями, а также известно, что \KL\ = 36, \MN\ = 34, \LM\ = 10. Найдите длину диагонали LN, если косинус величины угла KLM равен —1/3.
Идея. Провести высоты LH и AfP трапеции KLMN. Рассмотреть два случая расположения точки N.
Указание. Используя теорему Пифагора и соотношения между сторонами и углами прямоугольного треугольника, вычислить длины отрезков LH, МР, if#, ЯР и РЛГ.


414
Указания и решения
Решение. Проведём высоты LH и МР трапеции KLMN. Тогда LMPH - прямоугольник, стало быть, \НР\ = \LM\ = 10. Так как углы LKN и KLM - односторонние при параллельных прямых KN и LM и секущей KL, то сумма их величин равна 7г, поэтому cos LKN = — cos KLM = 1/3. С учётом этого из прямоугольных треугольников LKH и MPN находим
\КН\ = |ЯХ| • cos LKH = 12,
[Ltf | = s/\KL\2 - |АГЯ|2 = 24>/2 = |МР|;
|iVP| = y/\MN\2 - \МР\2 = 2.
Далее заметим, что возможны два варианта расположения точки N: она либо попадает на отрезок КР, либо нет. На чертеже эти варианты обозначены как Ni и N2 соответственно. Длину диагонали LN найти совсем просто:
М
^мярцрлт^в,
ILATjI2
y\LH\2 + \HN!\2 = 8л/19;
\HN2\ = |ЯР| + |PiV2| = 12, |iiV2|2 = y/\LH\2 + \HN2\2 = 36.
Ответ. 36 или 8\/l9.
Задача 2.
В трапецию вписана окружность. Точка касания делит одну из боковых сторон этой трапеции на отрезки длиной 12 и 3, длина её меньшего основания равна 9. Найдите площадь трапеции.
Идея. Воспользоваться тем, что треу голь- D КС
ник, образованный центром вписанной в трапецию окружности и концами боковой стороны, которая делится на отрезки длиной 12 и 3, прямоугольный.
Указание. Найти длину радиуса окружности, вписанной в трапецию, воспользоваться теоремой о равенстве длин отрезков касательных, проведённых из одной точки к окружности. AM В
Решение. Так как в трапецию вписана окружность, то высота трапеции равна диаметру вписанной окружности, а сумма оснований трапеции равна сумме её боковых сторон.


3.2. Трапеции
415
Обозначим вершины трапеции буквами А, Я, С и D (-АЯЦCD), точки касания окружности, вписанной в ABCD, со сторонами ЛЯ, ЯС, CD и AD обозначим буквами М, Я, К и L соответственно, а центр этой окружности обозначим буквой О. Будем считать, что \ВН\ = 12, |ЯС| = 3. Тогда угол ВОС прямой. Из прямоугольного треугольника ВОС получаем
\ОН\2 = \ВН\ • |СЯ| = 36 => \ОН\ = 6 =► \МК\ = 12.
Далее воспользуемся теоремой о равенстве длин отрезков касательных, проведённых из одной точки к окружности. Она даёт нам
\МВ\ = |ЯЯ| = 12, |ЯС| = \СК\ = 3.
Видно, что длина основания АВ не меньше 12, поэтому CD - меньшее основание, \CD\ = 9, \KD\ = \CD\ — \СК\ = 6. Далее, треугольник OKD прямоугольный, \ОК\ = \ОН\ = 6, \KD\ = 6, поэтому ODK = 7г/4. С учётом того что OD - биссектриса угла ADC, из этого вытекает, что угол ADC прямой, стало быть, трапеция ABCD прямоугольная, \AD\ = |Mif| = 12. Наконец,
\АВ\ + |СТ>| = |AD| + \ВС\ =27 =► SABcd = ^ ^ ' \мк\ = 162-
Ответ. 162.
Задача 3.
В трапеции ABCD отрезки АВ и CD являются основаниями. Диагонали трапеции пересекаются в точке Е. Известно, что \АВ\ = 30, |С£>| = 24, \AD\ = 3, DAB = 7г/3. Найдите площадь треугольника ВЕС.
Идея. Найти соотношение между площадями треугольника ВЕС и трапеции ABCD.
Указание. Найти длину высоты трапе- ^ ^
ции ABCD, затем воспользоваться свой- /■—-—-—
ством треугольников, на которые трапеция
делится своими диагоналями. ^ В
Решение. Опустим перпендикуляр DH из точки D на основание АВ. Он будет являться высотой трапеции, его длину можно легко найти из прямоугольного тре-
. ^ 3\/3
угольника ADH : \DH\ = \AD\ • sin DAB = ——. После этого вычислим площадь трапеции ABCD :
sABCD=
Обозначим площадь треугольника CED буквой S. Тогда, используя свойства треугольников, на которые трапеция делится своими диагоналями, получаем
о . с. \АВ\ а __ (\АВ\\2 _ 255
AED &АВЕС \CD\ 4 ’ АЕВ y|CD|y CED •


416
Указания и решения
С учётом этих соотношений имеем
о 81>/3 0 55 55 255
OABCD = bAAEB + OABEC + b&CED + OAAED => —“— = Ь + —+ —+ ——
2 4 4 16
=>• 5 = 8л/3 => Sabec — т ■ 8\/3 = 10л/3.
4
Ответ. 10л/3 •
Задача 4-
В трапеции ABCD даны длины оснований \AD\ = 4, |ВС| = 1 и углы BAD и ADC, величины которых равны соответственно arctg 2 и arctg 3. Найдите длину радиуса окружности, вписанной в треугольник ВЕС, где Е - точка пересечения диагоналей трапеции.
Идея. Вычислить площадь и полупериметр треугольника ВЕС.
Указание. Провести из точек В и С высоты трапеции ABCD, найти её площадь, рассмотрев получившиеся прямоугольные треугольники.
Указание. Воспользоваться свойствами треугольников, на которые трапеция делится своими диагоналями.
Указание. Для нахождения периметра треугольника ВЕС использовать подобие.
Решение. Проведём высоты трапеции В К и СН, их длины обозначим буквой h. Отметим, что углы при основании AD трапеции ABCD острые, поэтому точки К и Н будут лежать на основании AD и \AD\ = \АК\ + \КН\ + \HD\. Далее, ВС НК - прямоугольник, стало быть, \КН| = 1, а из прямоугольных треугольников АВК и CDH мы получаем, что \АК\ = hj2, \HD\ = /г/3. С учётом всего вышесказанного имеем
В
.. 18 I <1-1 9
Н = T' Иг?| = б1
\HD\ = \АН\ = И, |КВ| = j-.
После этого вычислим площадь трапеции ABCD:
Теперь обозначим площадь треугольника ВЕС буквой 5. Тогда
Saaeb — Saced = j^yj • Sabec = 45, Sadea = ^ j д ffj ^ ‘ Sabec = 165.


3.2. Трапеции
417
Пользуясь тем, что Sabcd = Saaeb 4- Sabec + Saced + Sadea > получаем
9 = 5 + 45 + 45+165 =► S=^~.
25
Для ответа на вопрос задачи нам осталось найти полупериметр треугольника ВЕС. Это можно сделать, например, следующим образом: с помощью теоремы Пифагора найдём длины отрезков АС и BD, после чего воспользуемся подобием треугольников DEA и ВЕС:
\BD\ = V\BK\2 + \KD\2 = \АС\ = у/\СН\2 + \АН\2 =
О о
\АЕ\ \DE\ \AD\ , 1 ,/520 1 v®5
ilcf “ ]Щ “ jscf “ ^ |£C| “ ~ IT' |£B| - s|BD| -
Наконец,
Sabec A
tabec = — —
Ответ.
Pabec I. Л + iJlo + 25 + 2>/130 +v/445’
2 V 25 25 у
18
25 + 2\/Т30 + \/i45 '
Задача 5.
В трапеции ABCD известны длины оснований \AD\ = 39 и |J9C| = 26, а также известны длины боковых сторон \АВ\ = 5 и \CD\ = 12. Найдите длины её диагоналей.
Идея. Обозначить величины углов при одном из оснований трапеции буквами а и /3, воспользоваться теоремой косинусов.
Указание. Записать теорему косинусов для треугольников ABD и BCD, затем для треугольников АВС и ACD, применив предварительно свойство внутренних односторонних углов.
В С
A D
Решение. Введём обозначения BAD = a, ADC = /3. Тогда, поскольку AD||i?C, по свойствам внутренних односторонних углов мы имеем АВС = 7г — а, BCD = 7г — /3. Далее запишем теорему косинусов для треугольников ABD, BCD, ABC и ACD :
\BD\2 = 392 + 52 - 2 • 39 • 5cosa = 262 + 122 - 2 • 26 • 12cos(tt - /?); |AC\2 = 392 + 122 - 2 • 39 • 12cos£ = 262 + 52 - 2 • 26 • 5cos(tt - a).
14 Геометрия


418
Указания и решения
Приводя подобные слагаемые, получаем
Г 195 cos а + 312 cos (3 — 363, Г cosa = 5/13,
65 cos a + 234 cos /3 = 241 ^ cos /3 = 12/13.
Подставляя найденные значения косинусов в выражения для \АС\2 и \BD\2, находим \АС\ = 3\/89, — 2%/349.
Ответ. \АС\ = Зл/89, |Я£| = 2\/349.
Задача 6.
В трапеции ABCD с основаниями АЯ и ЯС длина боковой стороны АВ равна 2. Биссектриса угла BAD пересекает прямую ВС в точке Е. В треугольник АВЕ вписана окружность, касающаяся стороны АВ в точке М и стороны BE в точке Я, \МН\ = 1. Найдите величину угла BAD.
Идея. Доказать, что треугольник АВЕ равнобедренный, после чего найти величины его углов.
Указание. Воспользоваться свойством внутренних накрест лежащих углов.
Указание. Применить формулу для вычисления длин отрезков, на которые окружность, вписанная в треугольник, точками касания делит его стороны, а также использовать подобие треугольников АВЕ и МВН.
Решение. Поскольку АЕ - биссектриса угла BAD, углы ВАЕ и DAE равны. С другой стороны, прямые AD и ЯС параллельны, АЕ - секущая, поэтому углы DAE и АЕВ равны как внутренние накрест лежащие. Из этого следует, что ВАЕ = АЕВ, то есть треугольник АВЕ равнобедренный, \АВ\ = |ЯЯ| = 2.
Теперь надо рассмотреть треугольник АВЕ. Длину отрезка ВН обозначим буквой х, длину отрезка АЕ обозначим буквой у.
Заметим, что отрезки ВН и ВМ тоже равны, как отрезки касательных, проведённых из одной точки к окружности, поэтому МН\\АЕ по теореме, обратной к теореме Фалеса, что даёт нам подобие треугольников АВЕ и МВН. Используя это подобие и применяя формулу для вычисления длин отрезков, на которые окружность, вписанная в треугольник, делит его стороны, получаем
|ЯЯ| \мн\ \ВЕ\ ~ \АЕ\
х
2
1
У
\вн\
\АВ\ + \ВЕ\ + \АЕ\
-\АЕ\
4-у
Полученную систему уравнений решить совсем нетрудно: она имеет единственное решение х — 1, у = 2. Таким образом, треугольник АВЕ равносторонний, поэтому величина угла ВАЕ равна 7г/3, а величина угла BAD равна 27г/3.
2тг


3.2. Трапеции
419
Задача 7.
В трапецию ABCD с основаниями ВС и AD вписана окружность с центром О. Найдите площадь трапеции, если угол DAB прямой, \ОС\ = 2, \OD\ = 4.
Идея. Воспользоваться тем, что треугольник, образованный центром вписанной в трапецию окружности и концами боковой стороны прямоугольный.
Указание. Найти длину радиуса окружности, вписанной в ABCD, длины её боковых сторон и высоты, воспользоваться свойством четырёхугольника, описанного около окружности.
В
N
Решение. Обозначим точки касания вписанной в трапецию ABCD окружности со сторонами ВС, CD и AD буквами N, М и L соответственно, а центр этой окружности обозначим буквой О. Тогда \ОМ\ = \ON\ = |OL|, а угол COD прямой. Из прямоугольного треугольника COD получаем
\CD\2 = \ОС\2 + \OD\2 = 20
|СС| = 2^5, |ОМ| = ^™ = ±.
Далее, поскольку угол DAB прямой, трапеция ABCD прямоугольная и ABNL - прямоугольник, кроме того, по свойству четырёхугольника, описанного около окружности, |АВ\ + \CD\ = \AD\ 4- \ВС\. С учётом всего этого находим
\АВ\ = ]NL\ = 2\ОМ\ =
О О 1 о
75' 'AD' + 'BC' = 2V~5+VS = Tb'
\AD\ + \ВС\ 9 8 72
Sabcd j |WL| =
n 72
Ответ. —.
5
Задача 8.
В выпуклом четырёхугольнике MNLQ углы при вершинах N и L прямые, а тангенс величины угла при вершине М равен 2/3. Найдите длину диагонали NQ, если известно, что длина стороны LQ вдвое меньше длины стороны MN и на 2 больше длины стороны LN.
Идея. Доказать, что четырёхугольник MNLQ - трапеция, провести высоту QH.
Указание. Рассмотреть прямоугольные треугольники MQH и NLQ.


420
Указания и решения
Решение. Поскольку MN _L LN и LQ _L LN, получаем MN\\QL, значит,
MNLQ - прямоугольная трапеция. Обозначим длину отрезка LN через ж, тогда по условию \LQ\ = ж + 2, \MN\ = 2х + 4.
После этого проведём высоту QH, тогда QHNL - прямоугольник,
\QH\ = \LN\ = ж, \LQ\ = |ЛГЯ| = ж + 2, |МЯ| = |MiV| - |ЛГЯ| = ж + 2.
Рассматривая прямоугольный треугольник MQH, получаем
1<2Я|
\мн\
tg м
х + 2
2
3
4.
Стало быть, |I/iV| = 4, LQ j = 6. Осталось записать теорему Пифагора для треугольника NLQ:
|ATQ|2 = \LN\2 + \LQ\2 = 52
\NQ\ = 2V13.
Ответ. 2\/l3-
Задача 9.
В трапеции ABCD сторона АВ параллельна стороне CD. Диагонали трапеции пересекаются в точке О, причём треугольник ВОС является равносторонним. Найдите длину стороны ВС, если \АВ\ = 5, \CD\ = 3.
Идея. Воспользоваться подобием треугольников АОВ и COD.
Указание. Применить теорему косинусов к треугольнику АОВ.
Решение. Треугольники АОВ и COD подобны, что даёт нам
\АО\ \ВО\ \АВ\ 5 \ОС\ “ \OD\ “ |СТ>| “ 3‘
Обозначим \ОС\ через Зж, тогда из последнего соотношения вытекает, что \АО\ = 5ж. Треугольник ВОС равносторонний, значит, \ВО\ = \ВС\ = Зж,
ВОС = 7г/3. Углы АОВ и ВОС смежные, поэтому АОВ = 7Г — ВОС = 27г/3. Наконец, применим теорему косинусов к треугольнику АОВ:
D С


3.2. Трапеции
421
Задача 10.
В трапеции KLMN KN\\LM, LA - биссектриса угла KLM, точка А - середина отрезка MN. Длина средней линии трапеции KLMN равна \/б, \АК\ = 4. Найдите |AL|.
Идея. Доказать, что треугольник LAB равнобедренный.
Указание. Воспользоваться свойством внутренних накрест лежащих углов. Применить формулу длины медианы.
Решение. Проведём среднюю линию АВ трапеции KLMN. Тогда AB\\LM, поэтому углы LAB и ALM равны, как внутренние накрест лежащие при параллельных прямых АВ, LM и секущей AL. С другой стороны, поскольку LA - биссектриса угла KLM, углы ALM и ALB тоже равны. Итак, треугольник LAB равнобедренный,
\АВ\ = \LB\ = у/5.
Далее отметим, что В - середина отрезка KL, поэтому \KL\- 2 >/5, А В - медиана треугольника AKL. Наконец, воспользуемся формулой длины медианы треугольника:
4|АВ|2 = 2|AL|2 + 2\АК\2 — \KL\2 =► 20 = 2\AL\2 + 32 - 20 =► \AL\ = 2.
Ответ. 2.
Задача 11.
В трапеции ABCD AD\\BC, биссектриса угла BAD пересекает сторону CD в точке М. Найдите длину отрезка AM, если известно, что треугольники ACM и ADM имеют одинаковую площадь, \ВМ\ — 8, \ВС\ -f \AD\ = 17.
Идея. Доказать, что М - середина CD, продлить отрезок AM за точку М до пересечения с прямой ВС в точке Е.
Указание. Воспользоваться леммами о площадях треугольников.
Указание. Рассмотреть треугольник АВЕ, доказать, что он равнобедренный.
Решение. Сначала заметим, что из того, что треугольники ACM и ADM имеют одинаковую площадь, вытекает, что \СМ\ = \DM\, то есть М - середина CD. Далее, продлим отрезок AM за точку М до пересечения с прямой ВС в точке Е. Тогда треугольники СЕМ и DAM равны по второму признаку равенства треугольников (углы СМЕ и DMA равны, как вертикальные, углы MCE и MDA равны, как внутренние накрест лежащие при параллельных прямых AD, ВС и секущей CD). Из этого равенства следует, что \СЕ\ = \AD\, \АМ\ = \МЕ\.
L М


422
Указания и решения
Далее заметим, что точка Е обязательно попадает на продолжение отрезка ВС за точку С, поэтому \ВЕ\ = \ВС\ + \СЕ\ = |ВС7| + \AD\ = 17. Наконец, в силу того, что углы СЕМ и DAM равны, как внутренние накрест лежащие при параллельных прямых AD, ВС и секущей АЕ, а углы ВАМ и DAM равны, так как AM - биссектриса, мы получаем, что равны углы ВАМ и ВЕМ. Значит, треугольник АВЕ равнобедренный, \АВ\ = |ВЕ\ = 17, ВМ - медиана этого треугольника. Но тогда она является и его высотой, значит, \АМ\ = у/\АВ\2 — \ВМ\2 = 15.
Ответ. 15.
В
Задача 12.
Непараллельные стороны трапеции перпендикулярны друг другу. Длина одной из них равна 3, а градусная мера угла, образованного ею и одной из диагоналей, равна 40°. Другая сторона образует с одним из оснований такой же угол. Найдите длину средней линии этой трапеции.
Идея. Рассмотреть различные варианты, понять, какую конфигурацию описывает условие задачи.
Указание. Обозначить вершины трапеции буквами А, В, С и D, считая, что \AD\ > \ВС\, доказать, что если BAD = 40°, то BDC = 40°.
Указание. Воспользоваться свойствами внутренних накрест лежащих углов и теоремой о сумме градусных мер углов треугольника.
Указание. Применить теорему синусов.
Е
Решение. При решении этой задачи основная трудность заключается в однозначном определении конфигурации, удовлетворяющей условию. Обозначим вершины трапеции буквами Л, В, С и D, будем считать, что AD - её большее основание, то есть прямые А В и CD пересекаются в точке Е, лежащей на продолжении отрезков АВ и CD за точки В и С соответственно. Тогда по условию задачи AED = 90°.
Будем считать, что длина стороны CD равна 3. Тогда сторона АВ образует с одним из оснований угол, градусная мера которого равна 40°. Это может быть лишь основание AD, поскольку треугольник AED прямоугольный, углы EAD и EDA острые, а углы АВС и BCD тупые. Итак,
BAD = 40°
ADC = 50°, ABC = 140°, BCD = 130°.
Далее нам надо понять, с какой конкретно из диагоналей сторона CD образует угол, градусная мера которого равна 40°. Если мы предположим, что это диагональ АС, то тогда ACD = 40°, CAD = 180° — ADC — ACD = 90°. Но точка С


3.2. Трапеции
423
лежит внутри угла BAD, поэтому градусная мера угла CAD меньше градусной меры угла BAD, то есть 40°. Противоречие.
Итак, под условие задачи подходит лишь один вариант, а именно В DC = 40°. Тогда CBD = 10°, ADB = 10°, ABD = 130°. Записывая теорему синусов для треугольников ABD и BCD, находим
\CD^ \ВС\^ IВР\^ _ 3 sin 40° 3 sin 130°
sin CBD sin В DC sin BCD sin 10° ’ sin 10°
\BD\ _ \AD\ . _ \BD\ sin 130° _ 3 sin2130°
sin BAD ~ sin ABD ~ sin 40° ~ sin 10° sin 40°'
Наконец, длина l средней линии трапеции равна полусумме длин её оснований, то есть
г _ 3 sin2 130° + sin2 40° _ 3 sin2 50° + cos2 50° 3
~ 2 sin 10° sin 40° ~ 2 sin 10° sin 40° ~~ 2 sin 10° sin 40°'
з
Ответ. .
2 sin 10° sin 40°
Задача 13.
Найдите площадь трапеции ABCD, если AB\\CD, CAB = 2DBA, \AC\ = 5, \BD\ = 7.
Идея. Воспользоваться тем, что треугольники АОВ и COD подобны (О - точка пересечения диагоналей трапеции).
Указание. Применив теорему синусов к треугольнику АОВ, найти величину угла между АС и BD.
Указание. Площадь трапеции ABCD вычислить с помощью формулы площади произвольного четырёхугольника.
Решение. Обозначим буквой О точку пересечения диагоналей трапеции ABCD. Тогда треугольники АОВ и COD подобны, из чего вытекает
\АО\ _ \ВО\ _ \АО\ _ \ОС\
\ОС\ ~ \OD\ ’ \ВО\ ~ \OD\
D С
С другой стороны,


424
Указания и решения
Теперь положим величины углов САВ и DBA равными 2а и а соответственно и воспользуемся теоремой синусов для треугольника АОВ:
\АО\ \ВО\ \АО\ sin АВО 5 sina 7
I I _ I I ^^ I L — —V _ _ —^ cos a = —
sin АВО sin В АО \в0\ sin В АО 7 sin2<* 10
Теперь для нахождения площади трапеции ABCD проще всего воспользоваться общей формулой для площади четырёхугольника:
1 _ 35 35
Sabcd = ^ ‘ \АС\ ’ \BD\ ‘ sin АОВ => Sabcd = у sin(7r - За) = — sin За. Осталось применить формулы тригонометрии:
7 . s/51 . „ . з Зу'бТ 204>/51 12>/5Т
<=““=10 =>■ зто = —;8,n30 = 3sm0-4sm a = —-^г = —.
Подставляя это значение в формулу для площади ABCD, получаем ответ.
„ 42\/5l
Ответ. ———.
25
Задача Ц.
Длины боковых сторон описанной около окружности трапеции равны 3 и 5. Известно, что средняя линия этой трапеции делит её на две части, отношение площадей которых равно 5/11. Найдите длины оснований трапеции.
Идея. Воспользоваться тем, что средняя линяя трапеции делит её на две трапеции, длины высот которых равны половине длины высоты исходной трапеции.
Указание. Воспользоваться свойством описанной около окружности трапеции, применить формулу площади трапеции.
Решение. Обозначим вершины трапеции буквами А, В, С и D (AB\\CD), её среднюю линию обозначим KL (К € AD). Проведём высоту трапеции СН, точку её пересечения с KL обозначим буквой Р. Поскольку KL\\AB, получаем, что AKLB и KDCL - трапеции, СН 1. KL, а треугольники CPL и СНВ подобны, поэтому
тгт - ^ =*■ №=т
Теперь обозначим длины оснований А В и CD через х и у соответственно, бу-
х ~\~ у
дем считать, что х > у. Тогда \KL\ = —-— и, кроме того, Saklb > Skdcl-
D С


3.2. Трапеции
425
Воспользуемся формулой площади трапеции:
Saklb = * ]КЦ ■ \РИ\ = ■ |РЯ |,
Wl = m±M.|CP |_£±а-.|сп
т-r 5 Skdcl х + 3 у
Поделив друг на друга эти соотношения, получаем — = — = . С дру-
11 ОАКЬВ ОХ + у гой стороны, трапеция ABCD описана около окружности, поэтому
\АВ\ + \CD\ = \AD\ + |J5C| => х + у = 8.
Наконец, решим полученную систему уравнений:
х + 3 у 5
3 х + у 11’
х + у = 8;
Ответ. 1 и 7.
5(3# + 8 — х) = 1\(х + 3(8 — х)), J х = 7,
2/ = 8 — ж; 1 2/ = 1-
Задача 15.
В трапеции ABCD с основаниями AD и ВС диагонали пересекаются в точке Е. Около треугольника ЕС В описана окружность, а касательная к этой окружности, проведённая в точке Е, пересекает прямую AD в точке F таким образом, что точки A, D,F лежат последовательно на этой прямой. Известно, что \AF\ = а, \AD\ = b. Найдите длину отрезка EF.
Идея. Доказать, что треугольники AEF и EDF подобны.
Указание. Доказать, что углы EAF и DEF равны.
Решение. Обозначим буквой К точку пересечения прямой AF с отрезком АВ. Заметим, что угол EAF равен углу ЕС В в силу параллельности прямых AD и ВС. Угол ЕС В равен половине меры дуги BE и, следовательно, он равен углу ВЕК, который равен углу DEF. Поэтому углы EAF и DEF равны. Значит, треугольники AEF и EDF подобны. Из этого подобия получаем
{И| = и^! ^ \EF\2 = \AF\-\DF\ = a-(a-b) =» \EF\ = Va2 - ab.
Ответ, у/a2 — ab.


426
Указания и решения
Задача 16.
В трапеции ABCD длина основания AD больше длины основания ВС. Известно, что \AD\ = \CD\ = 14/3, BAD = п/2, BCD = 57г/6. На основании AD построен треугольник AED так, что точки В и Е лежат по одну сторону от прямой AD, причём | АЕ\ = \DE\. Длина высоты этого треугольника, проведённой из вершины Е, равна 7/5. Найдите площадь общей части трапеции ABCD и треугольника AED.
Идея. Доказать, что отрезок АЕ пересекается с отрезком CD, то есть общая часть трапеции ABCD и треугольника AED - треугольник, образованный точками A, D и точкой пересечения АЕ и CD.
Указание. Опустить из точки Е перпендикуляр ЕН на AD, показать, что \ЕН\ < \АВ\ и EDA > CD А.
Указание. Нужную площадь выразить через \AD\, CD А и EAD.
Решение. Из условия задачи вытекает, что трапеция ABCD прямоугольная. Опустим из точки С высоту трапеции СР, тогда из того, что \AD\ > \ВС\, мы получаем, что точка Р лежит на основании AD, то есть \AD\ = \АР\ + \PD\. Также заметим, что АВСР - прямоугольник, поэтому \АР\ = \ВС\.
Далее, с учётом того, что CDP = 7Г — BCD = 7г/6, из прямоугольного треугольника CDP находим
\PD\ = \CD\ cosCDP=j • ^ \СР\ = \CD\ sinCDP=j • \
Теперь, если опустить из точки Е перпендикуляр ЕН на основание AD, мы видим, что 7/5 = \ЕН\ < \СР\ = 7/3. Из этого вытекает, что точка Е лежит между прямыми AD и ВС.
Рассмотрим треугольник AED. Он равнобедренный, поэтому точка Н - середина отрезка AD. С учётом этого находим
%gШD = tgШA=¥тTK^=\>}Ч- =► EDA>CDA.
2\AV\ о о
Итак, с одной стороны, точки Аи Е лежат в разных полуплоскостях относительно прямой CD, ас другой стороны, точка Е лежит между прямыми AD и ВС. Из этого вытекает, что отрезки АЕ и CD пересекаются в некоторой точке К и площадь общей части трапеции ABCD и треугольника AED есть площадь треугольника ADK. В нем нам известны следующие величины: \AD\ = 14/3, AD К = 7г/6, KAD = arctg 3/5. Площадь его можно найти, например, так:
S&ADK = \ ■ \AD\ [ADl 6- = 49 Л/5 - .
2 ctg ADK + ctg KAD 9(v/3+ §) V 3 J
В С


3.2. Трапеции
427
Задача 17.
В трапеции ABCD длина основания AD равна 4, длина основания ВС равна 3, длины сторон А В и CD равны. Точки М и N лежат на диагонали BD, причём точка М расположена между точками В и N, а отрезки AM и CN перпендикулярны диагонали BD. Найдите длину отрезка CN, если \ВМ\ : \DN\ =2:3.
Идея. Воспользоваться подобием треугольников AMD и CNB.
Указание. Найти соотношение между длинами отрезков ВМ, MN и DN, применить теорему Пифагора для треугольников AM В, CND и CNB.
Решение. Поскольку AD\\ВС, углы ADB и DBC равны, как внутренние накрест лежащие при параллельных прямых AD и ВС и секущей BD. Это даёт нам подобие прямоугольных треугольников AMD и CNB (по двум углам). Из этого подобия мы находим
\BN\ \CN\ \ВС\ \DM\ ~ \АМ\ ~ \AD\
В
= 3:4.
С учётом полученного соотношения введём обозначения: \BN\ = Зх, \DM\ = 4х, \CN\ = 3?/, \АМ\ = 4у. Поскольку точка М расположена между точками В и N, получаем \ВМ\ = |-BJV| — \ MN\, |£W| = \DM\ — \ MN\. Используя условие задачи, имеем
\ВМ\
|Щ
За; - \MN\ 4х - \MN\
\MN\ = х, \ВМ\ = 2х, |LW| = Зх.
Теперь учтем, что трапеция ABCD равнобедренная. Применим теорему Пифагора к треугольникам АМВ и CND и воспользуемся тем, что \АВ\ = \CD\:
\АВ\2 = \АМ\2 + \ВМ\2, \CD\2 = \CN\2 + |£W|2
7 у2 5 '
=> 16 у2 + I.)'2 = 9у2 + 9х2 =>• а
После этого запишем теорему Пифагора для треугольника CNВ:
7 у2
\ВС\2 = |£Af+|САГ|2
Наконец, \CN\ = 3у
9у2+9х2
1
У2+-
2\/3
у/15


428
Указания и решения
Задача 18.
Около окружности, длина радиуса которой равна R, описана трапеция. Хорда, соединяющая точки касания этой окружности с боковыми сторонами трапеции, параллельна основаниям трапеции. Длина этой хорды равна Ъ. Найдите площадь трапеции.
Идея. Доказать, что трапеция из условия задачи равнобедренная, вычислить величины её углов.
Указание. Рассмотреть треугольник, образованный центром окружности, вписанной в трапецию, и точками её касания с боковыми сторонами трапеции, воспользоваться тем, что он равнобедренный.
В
R
Решение. Обозначим вершины трапеции буквами А, В, С и D (AD\\BC), центр окружности, вписанной в эту трапецию, обозначим буквой О, а её точки касания со сторонами АВ, ВС, CD и AD обозначим буквами Р, Р, Q и S соответственно. Также обозначим буквой К точку пересечения отрезка PQ и прямой RS.
Тогда, во-первых, \ОР\ = \OR\ = \OQ\ = |OS| = Р, \PQ\ = Ь и, во-вторых, прямая RS перпендикулярна основаниям трапеции. Но тогда она перпендикулярна и отрезку PQ, поскольку по условию задачи PQ\\AD\\BC. Из этого вытекает, что О К - высота равнобедренного треугольника OPQ, значит, она является и его биссектрисой и медианой. Таким образом, POR = QOR. Но тогда равны и углы PBR и QCR, поскольку в каждом из четырёхугольников PBRO и QCRO есть два прямых угла, и поэтому POP + PBR = QOR + QCR = тг. Итак, трапеция ABCD равнобедренная.
Наконец, заметим, что BAD — тг — АВС = 7г — (7г — POP) = РОД, и произведём необходимые подсчёты, воспользовавшись тем, что, в силу того, что трапеция ABCD описана около окружности, \AD\ + \ВС\ = \АВ\ 4- \CD\.
sin POR = sin QOR =
\PK\
Ответ.
Sabcd : 8RS
\OP\ \AD\ + \BC\
—; \AB\ = \CD\ =
2 R
\RS\
\RS\_
sin BAD
\RS\
\AB\
±^-\RS\ = ^.2R
sin POR 8R? b
4 Д2 6 ;
Задача 19.
В трапеции BCDE (CD\\BE) проведена средняя линяя LN (точка L лежит на стороне ВС). Прямая, проходящая через точку В и перпендикулярная к стороне DE, пересекает отрезок LN в точке М, \LM\ : \MN\ = 2 : 1. Также известно, что \ВЕ\ — 14, \CD\ — 10, ВС -L BE. Найдите площадь трапеции BCDE.


3.2. Трапеции
429
Идея. Воспользоваться тем, что трапеция ABCD прямоугольная, провести её высоту DH.
Указание. Найти \LM\ и \НЕ\, доказать, что треугольники DEH и MBL подобны.
Указание. Введя обозначение |J3C| = = \DH\ = х, составить уравнение с этой неизвестной.
Решение. Из того, что ВС ± BE, а BE\\CD, следует, что ВС ± CD, трапеция BCDE прямоугольная. Таким образом, если мы проведём её высоту DH, то четырёхугольник BCDH окажется прямоугольником, поэтому = \CD\ = 10, \НЕ\ = |J3JE7| — \ВН\ = 4. Также
отметим, что \LN\ = \{\ВЕ\ + \CD\) = 12, \LM\ = \\LN\ = 8.
Z о
Ясно, что для ответа на вопрос задачи нам достаточно вычислить длину высоты трапеции BCDE. Проще всего это сделать так: положим |J3C| = \DH\ = х, тогда |J3L| = х/2, и заметим, что прямоугольные треугольники DEH и MBL
подобны по двум углам, поскольку DEH = МBL = — — МВЕ. Из этого подобия получаем
\НЕ[=\ВЦ 4 _ х/2
\DH\ \LM\ х 8
Наконец, Sbcde = 5 ■ (1^1 + 1^1)' \DH\ = 96. Ответ. 96.
Задача 20.
В трапеции ABCD (AD\\BC) \AD\ = 8, |JBC| = 6, а величина угла между прямыми АВ и CD равна arctg 0,25. Найдите площадь трапеции ABCD, если известно, что её диагонали перпендикулярны.
Идея. Продлить стороны АВ и CD до пересечения в точке Е, площадь трапеции ABCD представить как разность площадей подобных треугольников ADE и ВСЕ.
Указание. Воспользоваться теоремой косинусов и свойством четырёхугольника с перпендикулярными диагоналями.
Решение. Это довольно сложная задача. Обозначим длины боковых сторон А В и CD буквами х и у соответственно, а также продлим эти стороны до пересечения в точке Е. Тогда треугольники ЕВС и EAD подобны, что даёт нам
\AD\ __ \АЕ\ _ \DE\ 8 _ \АВ\ Л- \ВЕ\ _ \DC\ + \СЕ\
\ВС\ ~ \ВЕ\ ~ \СЕ\ ^ 6 “ \ВЕ\ СЕ ^


430
Указания и решения
I= Цт~ = у+сеЩ 1ВЩ = Зх> 1СЩ=1ЛЩ=4ж’1ПЩ=Ау-
После этого заметим, что площадь трапеции ABCD может быть вычислена как разность площадей треугольников ADE и ВСЕ, то есть
Sabcd — Saade — Sabce = ^ sin Е — \ВЕ\ • \СЕ\ - sin Е =
16xysinE 9xysinE 7 . ^
2 j =
Таким образом, поскольку мы знаем величину угла Е, нам надо вычислить ху. Это можно сделать, воспользовавшись свойством четырёхугольника, диагонали которого перпендикулярны, и записав теорему косинусов для треугольника ВСЕ:
\AD\2 + \ВС\2 = \АВ\2 + \ВС\2 =► х2 + у2 = 100;
|ВС|2 = |ВЯ|2 + |С£?|2-2-|ВЯ|-|СЯ|-совЕ ==» х2 + у2 - 2xycosE = 4.
Вычитая второе из полученных уравнений из первого, имеем ху = 48/ cos Е. Подставляя это значение в выражение для площади трапеции ABCD, находим
7 48
Sabcd = « • sini? = 168tg£7 = 42.
* cos £7
Ответ. 42.
Задача 21.
Трапеция ABCD с основаниями ВС и AD вписана в окружность. На дуге CD взята точка Е и соединена со всеми вершинами трапеции. Известно, что величина угла CED равна 27г/3, АВЕ — ВАЕ = 8. Найдите отношение периметра треугольника АВЕ к длине радиуса вписанной в него окружности.
Идея. Найти величины всех углов треугольника ABE. jj q
Указание. Воспользоваться свойствами вписанных углов и равнобедренностью трапеции ABCD.
Указание. Используя теорему синусов, выразить стороны треугольника АВЕ через радиус окружности, описанной около треугольника АВЕ.
Решение. Поскольку трапеция ABCD вписана в окружность, она равнобедренная, что даёт нам равенство длин сторон АВ и CD и равенство дуг CED и АВ (не содержащей точку Е). Так как вписанный угол измеряется половиной дуги, на которую опирается, то мера дуги С BAD равна 47г/3, тогда мера дуги CED равна 27г — 47г/3 = 27г/3. Но дуги CED и АВ равны, поэтому мера дуги АВ также равна 27г/3, из чего вытекает, что АЕВ = 7г/3. Таким образом,
7Г 8


3.2. Трапеции
431
Теперь задача свелась к вычислению отношения элементов треугольника АВЕ, в котором нам известны величины всех его углов. Обозначим буквой R длину радиуса окружности, описанной около этого треугольника, тогда, пользуясь теоремой синусов и формулами площади треугольника, находим
\АВ\ = 2i?sin | = RV3, \АЕ\ = 2Rsm ^ + 0 , \ВЕ\ = 2Rsm (| - 0 ;
Saabe = 2R? • sin § • sin (| + 0 ' sin (| - 0 = VZR2 (cos2 8- - 0 ;
Paabe = r(^Y+ sin (| + 0 + sin (^-|)) cos 0 ;
_ д, c°fJ, -| = д, Лр8 £ _ 1V ^aabe_ _ 2^/g 2 cos f + 1
^ A /4 R R -*■ Ь ' '"i S' JLV ~ I KsVJO „ “ I . Л V U с •
Paabe I + cos I V 2 2y/ taabe 2cos|-l
^ /-2 cos | + 1
Ответ. 2\/3 1 .
2 cos | - 1
Задача 22.
Точка M лежит на боковой стороне CD трапеции ABCD. Найдите длину отрезка ВМ, если известно, что BCD = CBD = АВМ = arccos(5/6), \АВ\ = 9.
Идея. Доказать, что треугольники ABD и МВС подобны.
Указание. Найти две пары равных углов в треугольниках ABD и МВС и, используя подобие этих треугольников, выразить длину отрезка ВМ через 1
отношение длин отрезков ВС и BD.
Указание. Найти отношение длин отрезков ВС и BD из треугольника BCD.
Решение. Заметим, что в условии этой задачи присутствует равенство нескольких углов. Как часто бывает в таких случаях, идея решения этой задачи заключается в нахождении пары подобных треугольников. Заметим, что углы ADB и CBD равны, как внутренние накрест лежащие при параллельных прямых AD, ВС и секущей BD, а углы CBD и BCD равны по условию задачи, поэтому ADB = BCD. С другой стороны,
ABD = АВМ - DBM, СВМ = CBD - DBM,
из чего, с учётом равенства углов АВМ и CBD, мы получаем ABD = СВМ. Таким образом, треугольники ABD и МВС подобны по первому признаку подобия треугольников, стало быть,
WJBD\ \ВС\ \ВС\
\ВМ\ \ВС\ I I I I |Б£)| |Б£)|-


432
Указания и решения
Наконец, отношение длин отрезков ВС и BD элементарно считается из треугольника BCD, который является равнобедренным по условию задачи:
COs55S = S {ПН =* 1ВА1Ч = 9 - ! = 15.
Ответ. 15.
Задача 23.
В трапеции ABCD BC\\AD, \ВС\ < \AD\, длина диагонали BD в 4/3 раза больше длины радиуса окружности, описанной около ABCD. Найдите отношение длин CD и радиуса этой окружности, если отношение площадей треугольников ABD и BCD равно 5.
В
Идея. Вычислить отношение длин оснований трапеции ABCD, выразить длины всех её сторон и диагоналей через длину радиуса описанной около неё окружности.
Указание. Воспользоваться тем, что длины высот треугольников ABD и BCD, проведённых к сторонам AD и ВС, равны. Применить теорему синусов и свойства равнобедренной трапеции.
Решение. Сначала выясним, что нам даёт условие про отношение площадей треугольников ABD и BCD.
Ясно, что высоты этих треугольников, проведённые к сторонам AD и ВС, равны между собой (и обе являются высотами трапеции ABCD). Поэтому, если провести высоту В К трапеции ABCD, то
Saabd i ‘\AD\ * \вк\ \AD\
Sabcd
\ВС\
\AD\
\ВС\
= 5.
\ • \вс\ • \вк\
Далее, поскольку трапеция ABCD вписана в окружность, она равнобедренная и, кроме того, треугольник ABD вписан в эту же окружность. Применяя к нему теорему синусов и учитывая тот факт, что углы BAD и ADC острые (это вытекает из того, что \AD\ > \ВС\), находим
sin BAD =
Rabcd
\BD\
ZRaabd 2Rabcd
2
3
tsBAD = 7s-
Теперь обозначим длины оснований AD и ВС трапеции ABCD через Ъх и х соответственно. По свойствам равнобедренной трапеции
1АЩ = т^ш=2х,
\KD\ = \AD\ - \АК| = Зх,
а из прямоугольного треугольника АВК мы имеем \ВК\ = |AJf| • tg ВАК = Наконец, запишем теорему Пифагора для треугольников АВК и BDK:
Ах
ТГ
\АВ\2 = \АК\2 + \ВК\2 = Щ-х2, \BD\2
5
\KD\2 + \ВК\2 = х2.
5


3.2. Трапеции
433
Осталось разделить полученные соотношения и ещё раз вспомнить, что трапеция ABCD равнобедренная:
ш.»ив|_|CD|_ • ,|BD|.4,4-iWo- |CD|
\BD\2 61 y/Ql у/б! 3 Rabcd \/6l
g
Ответ. —7=.
VST
Задача 24 •
Дана трапеция, в которую вписана окружность и около которой описана окружность. Отношение длины высоты этой трапеции к длине радиуса описанной около неё окружности равно д/2/3. Найдите величины углов трапеции.
Идея. Воспользоваться свойствами равнобедренной трапеции и свойством четырёхугольника, описанного около окружности.
Указание. Выразить длину диагонали этой трапеции через длину её высоты и синус величины угла при основании, воспользоваться теоремой синусов.
Решение. Обозначим вершины трапеции буквами А, В, С и D. Будем считать, что AD\\BC, \AD\ ^ \ВС\. Поскольку трапеция ABCD вписана в окружность, она равнобедренная, то есть \АВ\ = \CD\ и ZBAD = ZADC, а поскольку она описана около окружности, \AD\ + \ВС\ = \ АВ\ + \CD\, из чего вытекает, что
\АВ\ = \CD\ =
\AD\ + \ВС\
Далее опустим высоту ВН этой трапеции, обозначим её длину буквой h, а величины углов BAD и ADC обозначим буквой а. Поскольку \AD\ ^ \ВС\, имеем О < а ^ 7г/2, точка Н попадает на отрезок AD и по свойствам равнобедренной трапеции
\АН |
\AD\ - \ВС\
\HD\ = \AD\ - \АН\ =
\AD\ + \ВС\
то есть \HD\ = \АВ\ = \CD\.
Теперь рассмотрим треугольники АВН, BDH и ABD. Первые два из них прямоугольные, поэтому
\HD\ = \АВ\
\ВН\
h
sin BAD sina
\BD\ = V\BH\2 + \HD\2 = h ■
V sin2 a + 1
sina
а третий вписан в ту же окружность, что и трапеция ABCD. Применяя к нему теорему синусов и обозначая длину радиуса окружности, описанной около трапеции ABCD, буквой R, находим
R
1Д-РЦ
2 sin BAD
h•
\Jsin2 a + 1 2 sin2 a


434
Указания и решения
Таким образом,
[2 h 2 sin2 а 4 sin4 а _ 2
V 3 R yjsjn2 а + 1 sin2 а -f 1 3
6 sin а — sin а — 1 = 0.
Решая полученное биквадратное уравнение с учётом того, что sin а ^ 0, находим sina = у/2/2. Значит, a = 7г/4. Величины углов при другом основании трапеции ABCD равны, очевидно, 37г/4.
_ 7Г 7Г 37Г ЗТГ
4’ 4’ Т' Г'
Задача 25.
В окружность с центром О вписана трапеция ABCD с основаниями Л В и CD, \АВ\ = 5, |jDC| = 1, АВС = 7г/3. Точка К лежит на отрезке АВ таким образом, что \АК\ = 2. Прямая С К пересекает окружность в точке F, отличной от точки С. Найдите площадь треугольника OFC.
D
Идея. Доказать, что DK 1_ АВ, найти длины всех сторон треугольника OF С.
Указание. Воспользоваться теоремой Пифагора, теоремой синусов и свойством пересекающихся хорд.
Решение. Поскольку трапеция ABCD вписана в окружность, она равнобедренная и ABC = BAD. Заметим, что если опустить высоту трапеции ABCD из точки D и обозначить её основание через К', то
\АК'\ = \{\АВ\ - \CD\) = 2 = \АК\. Таким обра-
зом, К - основание высоты, опущенной из точки D,
DK LCD, DK LAB.
Из прямоугольных треугольников ADK, СDK и BDK получаем
\DK\ = \АК\ • tg BAD = 2\/3, \СК\ = y/\DK\2 + |CD|2 =
\КВ\ = \АВ\ -\АК\ = 3, |RD| = V\DK\2 + |А"5|2 = V21.
Теперь можно найти длину радиуса окружности, описанной около трапеции ABCD, применив теорему синусов к треугольнику ABD:
|ОС| = \OF\
\BD\
у/7.
2 sin ZBAD
После этого с помощью свойства пересекающихся хорд найдём \KF\:
6
\АК\ • \КВ\ = \СК\ ■ \KF\
19
|Ю?| = 71з; +


3.2. Трапеции
435
Наконец, вычислим площадь равнобедренного треугольника OFC, предварительно отыскав длину его высоты, опущенной из точки О:
лсГ = \/|ОС12-ег! = \/ b
Wc-i-pn.Ac, 1 19 ^ 19V5
Ответ.
52
2 1 1 2 у'ХЗ V 52 52 '
19л/3
Задача 26.
На основаниях AD и ВС трапеции ABCD построены квадраты ADEF и BCGH, расположенные вне трапеции. Диагонали трапеции ABCD пересекаются в точке О. Найдите длину отрезка AD, если \ВС\ = 2, \GO\ = 7, a |GF| = 18.
Идея. Доказать, что точки G, О и F лежат на одной прямой.
Указание. Рассмотреть треугольники С GO и AFO, доказать, что они подобны.
Решение. Для решения этой задачи необходимо доказать, что точки G, О и F лежат на одной прямой. Сначала воспользуемся тем, что треугольники AOD и
тп * и * \AD\ 1Л°1
СОВ подобны. Из этого подобия имеем ——- = -.
\вс\ \ос\
F А
Далее заметим, что, поскольку по условию задачи ADEF и BCGH - квадраты, во-первых, AF _L AD и CG _L ВС, поэтому AF\\GC и углы GCO и FAO равны, как внутренние накрест лежащие при параллельных прямых AF и GC и секущей АС, и, во-вторых, \AF\ = \AD\ и \GC\ = \ВС\. Из всего вышеперечисленного следует подобие треугольников С GO и AFO (по двум сторонам и углу между ними). Это подобие даёт нам равенство углов COG и AOF, из которого и следует, что точки G, О и F лежат на одной прямой. В самом деле, если предположить противное, то мы получим, что луч OF и продолжение луча GO за точку О, во-первых, не совпадают, во-вторых, лежат в одной полуплоскости относительно прямой АС и, в-третьих, образуют одинаковые углы с лучом О А, что невозможно.


436
Указания и решения
Наконец, из доказанного нами факта и подобия треугольников С GO и AFO вытекает, что
!§} = {i} = y ~
П 11 22
=► \AD\ = |AF| = - ■ \GC\ = - • \ВС\ = у.
л 22
Ответ. —.
7
Задача 27.
Известно, что трапеция ABCD равнобедренная, AD\\BC и \ВС\ > \AD\. Трапеция ЕС DA также равнобедренная, причём AE\\CD и \АЕ\ > \CD\. Найдите \ВЕ\, если известно, что \DE\ = 7, a CDE + BDA = arccos(l/3).
Идея. Воспользоваться тем, что длины диагоналей равнобедренной трапеции равны.
Указание. Доказать, что треугольник BDE равнобедренный, найти величину его угла BDE.
Решение. Заметим, что поскольку трапеции ABCD и ECDA равнобедренные, длины их диагоналей равны: \АС\ = \BD\ и \АС\ = \DE\.
Значит, во-первых, треугольник BDE равнобедренный, \BD\ = \DE\ = 7, и, во-вторых, треугольник BDA равен треугольнику CAD, а треугольник CAD равен треугольнику EDC (по трём сторонам). Из этих равенств вытекает, что jBDA = CAD, a ACD = CDE. Также отметим, что АСВ = CAD в силу свойств внутренних накрест лежащих углов, а ADC = 7г — BCD в силу свойств внутренних односторонних углов. Пользуясь этими фактами, имеем
АСВ = BDA-, BDE = AJDC - BDA - CDE = тг - BCD - BDA - CDE =
= тг - (АСВ + ACD^j - (BDA + CDE^j = тг - 2 (BDA + сБЩ = тг - 2 arccos^. Наконец, из равнобедренного треугольника BDE получаем
\ВЕ\ = 2 • |-DJE7| • sin BDE = 14 • sin ^ — arccos ^ = 14 • cos ^arccos ^ =
n 14
Ответ. —.
о
14
¥’
Замечание. Условия |2?С| > |AD| и |АЕ| > |CD|, не использованные нами при решении задачи, нужны для того, чтобы конфигурация, описываемая условием, существовала. В этом легко убедиться, попробовав нарисовать чертёж.


3.2. Трапеции
437
Задача 28.
В равнобедренной трапеции, длины оснований которой равны 1 и 4, расположены две окружности, каждая из которых касается двух боковых сторон трапеции, другой окружности и одного из оснований трапеции. Найдите площадь этой трапеции.
Идея. Доказать, что окружности касаются оснований в их серединах, воспользоваться теоремой о равенстве длин отрезков касательных, проведённых из одной точки к окружности, найти длину боковой стороны трапеции.
Указание. Рассмотреть два треугольника, каждый из которых образован центром одной из окружностей, точкой её касания с основанием и одной из вершин трапеции. Доказать, что они подобны.
Указание. Рассмотреть трапецию, образованную центрами окружностей и точками их касания с одной из боковых сторон.
Решение. Обозначим вершины трапеции буквами A, J5, С и D, будем считать, что \AD\ = 4, \ВС\ = 1. Сначала докажем, что окружности из условия задачи касаются оснований в их серединах. Это сделать достаточно просто: обозначим центр окружности, касающейся основания AD и боковых сторон, буквой О2, точку её касания с AD обозначим буквой Р. Поскольку она вписана в углы BAD и ADC, её центр лежит на пересечении биссектрис этих углов. Но трапеция ABCD равнобедренная, стало быть, углы BAD и ADC равны. Значит, равны и углы O2AD и O2DA, то есть треугольник AO2D равнобедренный. Отрезок О2Р является его высотой, поэтому он будет и его медианой, то есть Р - середина AD, \АР\ = \DP\ = 2.
После этого обозначим центр окружности, касающейся основания ВС и боковых сторон, буквой 0\, а точку её касания с основанием ВС обозначим буквой Q. Проводя абсолютно аналогичные рассуждения, мы получаем, что Q - середина ВС, \BQ\ = \CQ\ = 1/2. Далее рассмотрим треугольники DO2P и 0\CQ. Положим |Oi<2| = г, \С>2Р\ = Д, ADC = а. Тогда O2DP = а/2', BCD = 7г — а в силу свойств внутренних односторонних углов, 0\CQ = 7г/2 — а/2, CO\Q = а/2. Значит, треугольники DO2P и 0\CQ подобны по двум углам, из чего вытекает
!2j£[ = JS3. ^ _и=? вг = 1
\CQ\ \0,Q\ 1/2 г
Теперь обозначим точки касания окружностей с боковой стороной CD буквами Н\ и Н2 соответственно. Четырёхугольник О1Н1Н2О2 является прямоугольной трапецией, \0\Hi\ = г, |02#2| = а |OiО21 = R + г, так как окружности касаются друг друга. Поэтому
|Я1#2| = V\Oi02\2 - (\02н2\ - \OiHr\y = у/(R + r)2-(R-r)2 = = 2.


438
Указания и решения
Наконец, заметим, что по теореме о равенстве длин отрезков касательных, проведённых из одной точки к окружности, \CHi\ = \CQ\ = 1/2, \DH2\ = \DP\ = 2. Стало быть, \CD\ = \CHi \ + \H\H2\ + \DH2\ = 9/2. Теперь всё просто:
\QP\ = y/\CD\2 - (\DP\ - \CQ\Y = 3^2; SABCD = ^ W ' \QP\ =
n 15
Ответ, —=.
V2
Задача 29.
В трапеции ABCD диагонали пересекаются в точке Е, а величины углов AED и BCD равны. Окружность, длина радиуса которой равна 17, проходит через точки С, D и Е, пересекает основание AD в точке F и касается прямой BF. Найдите длины оснований и высоты трапеции ABCD, если \CD\ = 30.
Идея. Доказать, что ВС - касательная к окружности из условия задачи, треугольники CDF и BCF равнобедренные и подобны друг другу.
Указание. Воспользоваться свойствами вписанных углов и углов между касательной и хордой.
Указание. Воспользоваться соотношениями между длинами сторон и величинами углов в равнобедренном треугольнике.
Указание. Пользуясь теоремой о произведении длины секущей на длину её внешней части, доказать, что \ВС\ • \ AD\ = \BD\2 — \ВС\2.
В С С’
Решение. Возьмём произвольную точку С1 на продолжении отрезка ВС за точку С. Тогда углы С'CD и CED равны, как смежные с равными углами BCD и AED, из чего вытекает, что ВС - касательная к окружности, проходящей через точки С, D и Е. Это легко доказать от противного: если она таковой не является, то проведём прямую, касающуюся в точке С рассматриваемой окружности. По


3.2. Трапеции
439
свойству угла между касательной и хордой угол между этой касательной и отрезком CD будет равен углу CED. Значит, через точку С проходят две различные прямые, образующие одинаковые углы с отрезком CD. Противоречие.
Итак, ВС - касательная. Поскольку AD\\BC, CD - секущая, углы С'CD и CD А равны, как внутренние накрест лежащие. С другой стороны, углы CED и CFD равны, как опирающиеся на одну дугу. Стало быть, угол CD А равен углу CFD, поэтому треугольник CDF равнобедренный, \CD\ = \CF\ = 30, длина радиуса описанной около него окружности равна 17.
Проведём высоту СН этого треугольника, величины углов CD А и CFD (заметив, что они острые) обозначим через а и воспользуемся теоремой синусов:
lCFl op _ • 15 8 \пт • 450
= 2 licDF => sina = —, cos а = —, \CH\ = \CD\ sina =
sin CDF 17’ 1Г 1 1 1 1 17*
На один вопрос задачи ответ получен. Для нахождения длины основания ВС заметим, что ВС и BF - отрезки касательных, проведённых из одной точки к окружности. Значит, \ВС\ = \BF\, треугольник BCF также равнобедренный, а величины его углов BCF и BFC тоже равны а, поскольку углы BCF и CDF равны по свойствам углов между касательной и хордой и вписанных углов. Значит,
]ВС\=jigi=^
cos BCF Tf 8
Нахождение длины основания AD - более сложная задача. Для начала воспользуемся подобием треугольников AED и СЕВ, а также теоремой о произведении длины секущей на длину её внешней части:
ДО|=|§1р lBCf = \BD\ ■ \ВЕ\ =► \BC\-\AD\ = \BD\-\DE\.
Преобразуя правую часть полученного соотношения, находим
\ВС\ ■ \AD\ = \BD\ ■ (\BD\ - \ВЕ\) = \BD\2 - \BD\ ■ \BE\ = \BD\2 - \BC\2.
Но по теореме косинусов из треугольника BCD вытекает
\BD\2 - \ВС\2 = \CD\2 - 2 • \ВС\ ■ \CD\ - cos BCD = \CD\2 + 2 • \BC\ ■ \CD\ ■ cos a.
Наконец, вспомним, что \BC\ = СD\/2 cos a. С учётом этого имеем
• \AD\ = \CD\2 + 2- . \cd\ -cosa \AD\ = 4\CD\cosa =
2 cos a 1111 2 cosa 11 i i i i 17
255 960 450
Ответ. Длины оснований равны и -у^г, длина высоты равна .
Задача 30.
На боковой стороне АВ трапеции ABCD взята точка М таким образом, что \АМ\ : \МВ\ = 2:3. На противоположной стороне CD взята такая точка N, что отрезок MN делит трапецию на части, одна из которых по площади втрое больше другой. Найдите отношение \CN\ : |iVD|, если известно, что \ВС\ : \AD\ = 1:2.


440
Указания и решения
Идея. Продлить боковые стороны трапеции до пересечения в точке Е, представить площади частей, на которые трапеция делится отрезком MN, как разности площадей треугольников.
Указание. Воспользоваться леммами о площадях треугольников.
Указание. Выразить всевозможные площади через площадь треугольника AED.
Решение. В задачах, где известно отношение длин оснований трапеции, как правило, надо достраивать трапецию до треугольника. Обозначим точку пересечения прямых АВ и CD буквой Е. Ясно, что треугольники ВЕС и AED подобны, причём
Е
/\
\ВЕ\ \СЕ\ \ВС\
\АЕ\ \DE\ \AD\ 2'
Из этого вытекает, что \АВ\ = |ВЕ\, \CD\ = \СЕ\. Введём обозначения
\АМ\ = Зх, \МВ\ = 2х, \CN\ = ky, \ND\ = у.
Тогда к - величина, которую нас просят отыскать,
\АВ\ = \ВЕ\ = 5х, \CD\ = \СЕ\ = (к + 1 )у, \МЕ\ = 8х, \NE\ = (2 к + 1)у.
Далее заметим, что Smbcn = Samen ~ Sabec , Samnb = Saaed — Samen • Положим Saaed — S и с помощью лемм о площадях треугольников выразим всевозможные площади через эту величину:
Sabec _ Saaed
стало быть,
(\ВС\ у
1. Samen _ \МЕ\ ■ \NE\ _ 8х 4’ 5длес |А£|-|£>Я| 10®
(2fc + 1)^/ 4Л: + 2
(2к + 2 )у = 5fc -Ь 5’
С _ * о с ^ + 2 о.
ВЕС и ’ &AMEN г; . г ’
4 5/с + 5
Smbcn
(Ак + 2 _ 1\ V5fc + 5 4У ’
Samnd = ( 1
Ак + 2 5fc + 5
S.
Наконец, по условию задачи либо Smbcn — 3Samnd, либо 3Smbcn = Samnd- В первом из этих случаев мы имеем
4fc + 2 5fc + 5
-з)5=30
Ак + 2 5к + 5
11 к -|- 3 Зк 9
4(5к + 5) 5/с -f 5
к = -33.
Понятно, что к > 0, стало быть, этот случай невозможен. Рассматривая второй случай, мы получаем
= U _ ^±1)
V 5fc + 5 J
33k + 9
к 3
4(5А: + 5) 5А: + 5
29'
Ответ. 3 : 29.


3.2. Трапеции
441
Задача 31.
В трапеции ABCD BC\\AD, ABC = тг/2. Прямая, перпендикулярная стороне CD, пересекает сторону АВ в точке М, а сторону CD в точке N. Известно, что расстояние от точки D до прямой МС равно с, \МС\ = a, \BN\ = b. Найдите расстояние от точки А до прямой BN.
Идея. Доказать подобие треугольников ABN и DC М.
Указание. Показать, что вокруг четырёхугольников ADNM и MBCN можно описать окружности. Указание. Показать, что углы МAN и MDN равны, как опирающиеся на одну дугу. Поэтому равны углы BAN и МDC наших треугольников.
Указание. Показать, что углы MBN и MCN равны, как опирающиеся на одну дугу. Поэтому равны углы ABN и MCD наших треугольников.
D
Решение. Опустим из точек А и D перпендикуляры на прямые BN и СМ, основания этих перпендикуляров обозначим буквами Q и Р соответственно. Тогда \DP\ = с, a \AQ\ - величина, которую нам необходимо вычислить.
В этой задаче достаточно нелегко найти связь м^жду величинами, данными в условии, и величиной, которую надо найти. Но если внимательно присмотреться, то видно, что отрезки BN и AQ являются основанием и высотой в треугольнике ABN, а отрезки МС и DP являются основанием и высотой в треугольнике DCM. Если бы эти треугольники оказались подобными, то \AQ\ мы бы легко нашли. Попробуем доказать подобие треугольников ABN и DCM.
Рассмотрим четырёхугольник ADNM. Так как углы DAM и DNM прямые, то вокруг четырёхугольника ADNM можно описать окружность. Тогда углы MAN и MDN равны, как опирающиеся на одну дугу. Поэтому равны углы BAN и MDC наших треугольников.
Теперь рассмотрим четырёхугольник MBCN. Так как углы МВС и MNC прямые, то вокруг четырёхугольника М ВС N можно описать окружность. Тогда углы MBN и MCN равны, как опирающиеся на одну дугу. Поэтому равны углы ABN и MCD наших треугольников.
Следовательно, треугольники ABN и DCM подобны. Поэтому
|ДЛН \AQ\ \СМ\ \DP\
\AQ\ =
\BN\ ■ \DP\ be \CM\ ~ a '
_ be
Ответ. —.
a


442
Указания и решения
Задача 32.
В окружность, длина радиуса которой равна у/7, вписана трапеция. Длина её меньшего основания равна 4. Через точку этой окружности, касательная в которой параллельна одной из боковых сторон трапеции, проведена хорда, параллельная основаниям трапеции. Длина этой хорды равна 5. Найдите площадь трапеции и длину её диагоналей.
Идея. Доказать, что длина хорды из условия задачи равна длине диагоналей трапеции. Воспользоваться теоремой синусов.
Указание. Доказать, что хорда из условия задачи либо проходит через середины дуг, отсекаемых боковыми сторонами, либо равна ей по длине. Рассмотреть дугу, заключённую между противоположными основаниями трапеции, и дугу, заключённую между серединами дуг, отсекаемых боковыми сторонами, показать, что они равны.
Указание. Найти синус величины угла при меньшем основании, вычислить длину боковой стороны, затем найти длину высоты и большего основания.
Решение. Обозначим вершины трапеции буквами А, В, С и D, будем считать, что ВС - меньшее основание, то есть \ВС\ = 4. Поскольку трапеция ABCD вписана в окружность, она равнобедренная, \АВ\ = \CD\. Центр окружности, описанной около ABCD, обозначим буквой О.
Рассмотрим некую точку окружности, касательная в которой параллельна АВ. Заметим, что касательная к окружности перпендикулярна диаметру, проходящему через точку касания, поэтому А В также будет перпендикулярна этому диаметру и в силу свойства хорды, перпендикулярной диаметру, будет делиться им пополам. Из этого следует, что у нас есть два варианта расположения этой точки - она в любом случае является концом диаметра, проходящего через середину стороны АВ и ей перпендикулярного. На рисунке они обозначены буквами К и К\. Отметим, что точка К лежит на дуге АВ, не содержащей других вершин трапеции.
Рассмотрим хорды KL и K\L\, параллельные AD. Обе они удовлетворяют условию задачи. Однако ясно, что они параллельны друг другу, поэтому углы LKO и L\K\0 равны, как внутренние накрест лежащие, из чего следует равенство равнобедренных треугольников KOL и K\OL\. Стало быть, \KL\ = |jKiIq|. А это значит, что вне зависимости от того, какая хорда (KL или К\Ь\) имелась в виду в условии задачи, длина хорды KL равна 5.
Теперь докажем, что длина хорды KL равна длине диагоналей трапеции ABCD. Для этого заметим, что треугольник АОВ равнобедренный, О К JL АВ, поэтому О К - биссектриса угла АОВ. Из этого вытекает, что дуги АК и КВ равны. Далее, KL\\BC, поэтому KBCL - трапеция, вписанная в окружность, стало быть, она равнобедренная, \КВ\ — \СЬ\. Но равные хорды стягивают равные дуги, поэтому дуги КВ и CL также равны. Сопоставляя эти факты, имеем
АВС—АК + КВ + ВС=СЬ + КВ + BC=KBCL .
Итак, мы доказали, что дуги АВС и KBCL равны. А из этого следует, что длины хорд АС и KL, стягивающих эти дуги, тоже равны. Значит, \АС\ — 5. Ну а так как длины диагоналей равнобедренной трапеции ABCD равны, то и \BD\ = 5.


3.2. Трапеции
443
Для нахождения площади трапеции ABCD поступим следующим образом: сначала, для того чтобы задействовать длину радиуса описанной около неё окружности, рассмотрим треугольник АВС, также вписанный в эту окружность. Записывая для него теорему синусов, имеем
sin ABC
2 R
sin ABC
2 VY'
D
Поскольку ВС - меньшее основание, угол ABC тупой, cos ABC = — yj 1 — sin2 ABC = Теперь воспользуемся теоремой коси¬
нусов:
| АС\2 = |.АВ\2 + \ВС\2-2-\AB\-\BC\-cos ABC
25 = \АВ\2 + т + ^-\АВ\.
Решая это квадратное уравнение, находим \АВ\ — . Наконец, проведём высоту
ВН и учтём, что sin ВАС = sin АВС. Тогда
З-у/З 5
\ВН\ = \АВ\-BinАВС =
= И«1 = ^Ивр-|вяр = ^
\АН\
\AD| - \ВС\
\AD\ + \ВС\
= \АН\ + \ВС\
65
14’
sABCD = rn±m.m] = ^
Ответ. Длины диагоналей равны 5, площадь равна
196
975\/3 196 '
Задача 33.
В окружность вписана трапеция ABCD с основаниями AD и ВС, \AD\ > \ВС\. На дуге AD, не содержащей вершин В и С, взята точка S. Точки Р, Q, М и N являются основаниями перпендикуляров, опущенных из точки 5 на прямые AD, ВС, АВ и CD соответственно. Известно, что \SP\ = a, |SQ| = 6, \SN\ = с. Найдите отношение площадей треугольников MQS и NQS.
Идея. Доказать, что искомое отношение равно отношению длин отрезков SM и SN. Доказать, что треугольники SMQ и SPN подобны.
Указание. Воспользоваться леммами о площадях треугольников. Показать, что точки S', М, В и Q лежат на одной окружности, а точки S, N, D и Р лежат на другой окружности.


444
Указания и решения
Указание. Воспользоваться теоремой о четырёх точках и свойствами вписанных углов.
Решение. Сразу заметим, что трапеция ABCD является равнобедренной в силу того, что она вписана в окружность. Из этого следует, что углы АВС и BCD равны. Значит, из того, что SM _L АВ, SQ -L ВС и SN _L CD, вытекает равенство углов MSQ и NSQ. Поэтому ■ =
Sanqs
±-\SM\-\SQ\-ffaMSQ _ \SM\ ±-\SN\-\SQ\-sinNSQ ~ W
В этой задаче серьёзным препятствием при решении является тот факт, что существует весьма большое количество вариантов расположения точек М, Q и N. Тем не менее, по теореме о четырёх точках в любом случае точки 5, М, В и Q лежат на одной окружности, а точки S, N, D и Р лежат на другой окружности. Из этого следует, что угол SNP равен углу SDP, а угол SQM равен углу SBM в силу свойств вписанных углов. Но углы SDP и SBM опираются на дугу AS, стало быть, они равны. Значит, равны и углы SNP и SQM. Таким образом, треугольники SMQ и SPN подобны по двум углам,
И = Ш <=* ,од,| \SP\-\SQ\ \SM 1 \SP\ • \SQ\ ab
|SP| \SN\ 11 |S7V| \SN\ |5iV|2 с2'
Ответ.
с2
Задача 34-
Дана трапеция ABCD, сторона АВ которой перпендикулярна основаниям AD и ВС. На стороне АВ как на диаметре построена окружность, касающаяся стороны CD. Длина радиуса этой окружности равна у/б. Другая окружность, длина радиуса которой равна у/2, касается сторон AD и CD и пересекает первую окружность так, что длина их общей хорды равна у/б, а центры окружностей расположены по разные стороны от этой хорды. Найдите площадь трапеции ABCD.
Идея. Доказать, что центр О первой окружности лежит на пересечении биссектрис углов ADC и BCD, вычислить величину угла ADC, затем, рассматривая треугольники ADO и ВСО, найти длины оснований трапеции.
Указание. Доказать, что центры обеих окружностей лежат на биссектрисе угла ADC, рассмотреть четырёхугольник, образованный центрами окружностей и точками их пересечения, найти расстояние между центрами окружностей. Указание. Для нахождения величины угла ADC рассмотреть треугольники AOD и HQD (Q - центр второй окружности, Н - проекция Q на AD).
Решение. Обозначим буквами О и Q центры первой и второй окружностей соответственно.


3.2. Трапеции
445
В
Сразу заметим, что поскольку прямая AD перпендикулярна диаметру первой окружности АВ, она является касательной к ней. Поэтому обе окружности касаются сторон AD и CD, то есть обе они вписаны в угол ACD и их центры О и Q лежат на биссектрисе этого угла.
Также отметим, что первая окружность касается и стороны ВС (это обосновывается так же, как и её касание со стороной AD), поэтому она вписана и в угол BCD, стало быть, СО - биссектриса угла BCD. Ясно, что для ответа на вопрос задачи нам достаточно найти величину угла ADC, потому что тогда, рассмотрев треугольники AOD и ВОС, мы сможем найти и длины оснований трапеции.
Понятно, что О - середина АВ, \АО\ = \ВО\ = у/б, \АВ\ = 2у/б. Обозначим буквами R и S точки пересечения первой и второй окружностей, тогда по условию задачи \OR\ = |05| = у/б, \QR\ = \QS\ = у/2, a \RS\ = л/б; а буквой Т обозначим точку пересечения отрезков RS и OQ (они пересекаются в силу того, что точки О и Q лежат по разные стороны от RS по условию задачи). Треугольники ORQ и OSQ, очевидно, равны по трём сторонам, поэтому углы ROQ и SOQ равны. Стало быть, OQ - биссектриса угла ROS. Но треугольник ORS равнобедренный, значит, OQ JL RS, \RT\ = \TS\ = \/б/2. Пользуясь теоремой Пифагора и тем, что \OQ\ = \ОТ\ + \QT\, находим
\ОТ\ = y/\OR\2 - |ЯГ|2 =
Зл/2
\QT\ = vlQW
V2
\RT\2 = \OQ\ = 2V2.
Далее проведём отрезок QH, перпендикулярный стороне AD (Н £ AD), и обозначим величину острого угла ADO буквой а. Из прямоугольных треугольников AOD и HQD мы получаем
J42U = ^-, iqdi = = -А
sin ADO sina
|OZ?| =
sin ADO sma
\OQ\ = |OD| - |QD|
2\/2:
V6-V2 . >/3-1
— => sm a = —-—, cos a =
sma 2
Наконец, пользуясь свойствами внутренних односторонних углов и рассматривая треугольники AOD и ВОС, получаем
ADC = 2ADO = 2a, BCD = тг - ACD = тг - 2a, SCO = ^BCD = J - a; |AD| = |j40| • ctg ADO = \/6ctga, |BC| = |BO| • ctg BCO = >/6tga;
4^
\AD\ + \BC\ y/6,
Чг = -rr(tga + ctgQ:) = 7T~- >
2 2 2 sin a cos a
sABCD = \M±m.lAB 1
vs
2 sin a cos a
•2>/6:
6
y/S-1 .
2 ' y/2
6(-\/6 + y/2)
V3
Ответ.
6(v/6 + л/2)
V3


446
Указания и решения
3.3. Четырёхугольники и многоугольники общего вида Задача 1.
В окружность, длина радиуса которой равна 17, вписан четырёхугольник, диагонали которого взаимно перпендикулярны и находятся на расстоянии 8 и 9 от центра окружности. Найдите длины сторон этого четырёхугольника.
Идея. Воспользоваться свойством хорды, перпендикулярной диаметру. Указание. Опустить из центра окружности перпендикуляры на диагонали четырёхугольника, воспользоваться теоремой Пифагора.
Решение. Обозначим вершины четырёхугольника буквами А, В, С и D, центр окружности обозначим буквой О, точку пересечения его диагоналей обозначим буквой К, опустим перпендикуляры OQ и ОР на диагонали АС и BD соответственно. Будем считать, что диагональ BD находится ближе к центру окружности, чем диагональ АС. Тогда по условию задачи \ОС\ = \OD\ = 17, \ОР\ = 8, \OQ\ = 9.
Заметим, что, во-первых, KQOP - прямоугольник, поэтому \ОР\ = \KQ\ = 8, \OQ\ = \КР\ = 9, и, во- вторых, по свойству хорды, перпендикулярной диаметру, \AQ\ = \QC\, \ВР\ = \PD\. После этого по теореме Пифагора находим
\AQ\ = \QC\ = V\OC\2 - \OQ\2 = 4\/T3, \BP\ = \PD\ = y/\OD\2 - |OP|2 = 15. Значит,
\АК\ = \AQ\ - \KQ\ = 4\/l3 - 8, |ATC| = |QC| + |ATQ| = 4\/l3 + 8;
|£#| = \BP\ - \KP\ = 6, \KD\ = \PD\ + \KP\ = 24.
Наконец, применяя теорему Пифагора в треугольниках АКВ, ВКС, CXZ) и AKD, получаем
- \/з08-64\Лз, |ВС| = \/308 Ч- 64л/13,
|СТ>| = \/848 + 64л/Гз, |AD| = ^848 - 64\/1з.
Ответ. 848 ± 64VT3, \/з08 ± 64%/Тз.
Задача 2.
В выпуклом четырёхугольнике ABCD точка Е - точка пересечения диагоналей. Известно, что площадь каждого из треугольников АВЕ и DCE равна 1, площадь четырёхугольника ABCD не превосходит 4, \AD\ = 3. Найдите длину стороны ВС.


3.3. Четырёхугольники и многоугольники общего вида
447
Идея. Доказать, что четырёхугольник ABCD - параллелограмм.
Указание. Воспользоваться свойством площадей треугольников, на которые выпуклый четырёхугольник делится диагоналями, доказать, что площади треугольников ВСЕ и ADE равны 1.
Решение. Пользуясь свойством площадей треугольников, на которые выпуклый четырёхугольник делится диагоналями, и условием задачи, получаем
Sabce * Saade = Saabe • Sadce = 1,
Sabce + Saade + Saabe + Sadce ^ 4 1 „ 1
В
Sabce
Saade+
^2.
Saade’ ' Saade
С другой стороны, сумма двух положительных взаимно обратных чисел всегда больше либо равна двум, поэтому
1
Saade+
Saade
Saade = 1, Sabce = 1-
Итак, треугольники, на которые четырёхугольник ABCD поделен диагоналями, равновелики, поэтому он параллелограмм, \ВС\ = \AD\ = 3.
Ответ. 3.
Задача 3.
В выпуклом четырёхугольнике длины диагоналей равны 1 и 2. Найдите его площадь, зная, что длины отрезков, соединяющих середины его противоположных сторон, равны.
В
Идея. Доказать, что диагонали четырёхугольника из условия задачи перпендикулярны. Указание. Воспользоваться теоремой Вариньона.
Решение. Обозначим вершины четырёхугольника буквами А, В, С и D, середины его сторон АВ, ВС, CD и AD обозначим как Р,
Q, R и S соответственно. С одной стороны, четырёхугольник PQRS по теореме Вариньона является параллелограммом, а с другой стороны, длины его диагоналей равны по условию задачи. Из этого вытекает, что четырёхугольник PQRS - прямоугольник. Но поскольку PQ\\AC, а QR\\BD, величина угла между диагоналями АС и BD четырёхугольника ABCD равна величине угла PQR, то есть 7г/2. Наконец, применяя формулу площади четырёхугольника, находим
SABCD = y\AC\-\BD\-em^ = l.
Ответ. 1.


448
Указания и решения
Задача 4-
В выпуклом четырёхугольнике ABCD длина отрезка, соединяющего середины диагоналей, равна длине отрезка, соединяющего середины сторон AD и ВС. Найдите величину угла между прямыми АВ и CD.
Идея. Доказать, что четырёхугольник, вершинами которого являются середины диагоналей и середины двух противоположных сторон произвольного четырёхугольника - параллелограмм.
Указание. Воспользоваться тем, что параллелограмм, длины диагоналей которого равны, - прямоугольник.
Решение. Обозначим середины сторон AD D
и ВС буквами Р и Q, а середины диагоналей
АС и BD обозначим буквами R и S соответственно. Будем рассуждать так же, как и при доказательстве теоремы Вариньона. Поскольку R - середина АС, a Q - середина ВСполучаем, что RQ - средняя линяя треугольника АВС, стало быть, RQ\\AB. Рассуждая абсолютно аналогично, мы находим, что PS\\AB, PR\\CD, QS\\CD. Из этих параллельностей мы получаем, что противоположные стороны четырёхугольника PRQS параллельны, поэтому он является параллелограммом. Далее, по условию задачи длины его диагоналей равны, стало быть, четырёхугольник PRQS - прямоугольник. Наконец, поскольку RQ\\AB, a QS\\CD, величина угла между прямыми АВ и CD равна величине угла RQS, то есть п/2.
гл п
Ответ. —.
2
Задача 5.
В выпуклом четырёхугольнике ABCD величина угла, под которым пересекаются отрезки, соединяющие середины противоположных сторон, равна 7г/3, а длины этих отрезков относятся как 1:3. Чему равна длина меньшей диагонали четырёхугольника ABCD, если длина большей равна \/39?
Идея. Воспользоваться теоремой Вариньона.
Указание. Выразить длины диагоналей четырёхугольника ABCD через длины отрезков, соединяющих середины его противопо- D ложных сторон.
Решение. Обозначим середины сторон АВ, ВС, CD и AD буквами Р, Q, R и S соответственно, точку пересечения отрезков PR и QS обозначим буквой К. Без ограничения общности будем считать, что \PR\ : \QS\ = 1:3, PKQ = 7г/3, QKR = 27г/3. По теореме Вариньона мы заключаем, что четырёхугольник PQRS


3.3. Четырёхугольники и многоугольники общего вида
449
является параллелограммом, причем \PQ\ = ^|АС| и \QR\ = \\BD\. Положим \PR\ = х, |Q5| = Зх, тогда по свойствам параллелограмма \РК\ = \KR\ = х/2, |QK| = Зх/2 . Пользуясь теоремой косинусов, находим
I-PQI2 = |-РЙ"|2 + \QK\2 -2-\РК\ - \QK\ ■ cosPKQ = =► \PQ\ = ^;
1 Чг2 Гл/ГЧ
\QR\2 = |Qi^|2 -f |ХД|2 - 2 • |QX| • \KR\ • cosQKR = — => \QR\ = -yA
С учётом вышесказанного получаем |Ж7| = х\/7, |BJ5| = х\/ТЗ. Очевидно, что |RD| > |Ж7|, стало быть, \BD\ = \/39, х = \/3, |Ж7| = л/2Т.
Ответ, л/21.
Задача 6.
В остроугольном треугольнике АВС из основания D высоты BD опущены перпендикуляры DM и DN на стороны АВ и ВС. Известно, что \MN\ = а, |£.D| = Ь. Найдите величину угла АВС.
Идея. Доказать, что четырёхугольник BMDN вписан в окружность с диаметром BD.
Указание. Воспользоваться теоремой синусов.
В
Решение. Заметим, что поскольку BMD = 7г/2,
BND = 7г/2, а точки М и N лежат в разных полуплоскостях относительно прямой BD, четырёхугольник BMDN является выпуклым и сумма величин его противоположных углов равна 7г. Значит, он вписан в
окружность, причём отрезок BD является её диаметром. Поскольку треугольник MBN вписан в ту же окружность, по теореме синусов получаем
\BD\ = 2R&mbn =
\MN\
sin MBN =
sin MBN
Так как треугольник ABC остроугольный, то ABC
\MN\
\BD\
a
b'
■ arcsin |.
Ответ, arcsin-.
b
Задача 7.
В выпуклом четырёхугольнике ABCD длина стороны AD равна 4, длина стороны CD равна 7, косинус величины угла ADC равен 1/2, синус величины угла ВС А равен 1/3. Найдите длину стороны ВС, если известно, что окружность, описанная около треугольника АВС, проходит также и через точку D.
Идея. Воспользоваться свойством четырёхугольника, вписанного в окружность. Указание. Применить теоремы синусов и косинусов.
15 Геометрия


450
Указания и решения
Решение. Из условия вытекает, что величина угла ADC равна 7г/3, а четырёхугольник ABCD вписан в окружность. Таким образом, в неё же вписан и треугольник ADC.
Пользуясь теоремами синусов и косинусов, вычислим длину её радиуса:
\АС\ = yj\CD\2 + \AD\2 - 2 • \CD\ ■ \AD\ • cos ADC = >/37;
\AC\ /37
■lLabcd — — \ 0 •
2sinADC V 3
Далее, пользуясь свойством выпуклого четырёхугольника, вписанного в окружность, находим АВС — тг — ADC = 27г/3. Поскольку сумма величин углов треугольника АВС равна 7Г, величина угла ВС А должна быть меньше 7г/3, то есть ВС А = arcsin 1/3. Наконец,
ВАС = тг - ABC - ВСА = £ - arcsin \ВС\ = 2Rabcd • sin ВАС =
О о
„ /37 . /тг . 1\ „ /37 (V3 2уД 1 l\ >/37(2л/§-1)
= V IT 8Ш \ з ~ агс8ш 3^ = у *з^ ~~3 2 Зу =
0твет.
3V3
Задача 8.
Четырёхугольник PQRS вписан в окружность. Его диагонали PR и Q5 перпендикулярны и пересекаются в точке М. Известно, что \PS\ = 13, \QM\ = 10, |Qi2| = 26. Найдите площадь четырёхугольника PQRS.
Идея. Доказать, что треугольники MPS и MQR подобны.
Указание. Воспользоваться теоремой Пифагора и формулой площади четырёхугольника, в которую входят длины его диагоналей.
Решение. Записывая теорему Пифагора для треугольника MQR, находим
\MR\ = y/QR2 - MQ2 = 24.
После этого заметим, что треугольники MPS и MQR подобны по первому признаку подобия треугольников (углы PMS и QMR прямые, а углы SPM и RQM равны, как вписанные углы, опирающиеся на одну дугу). Из этого подобия мы получаем
\РМ\ \MS\ |Р5| \QM\ ~ \MR\ ~ \QR\
\РМ\ = = 5, \MS\ = = 12.
\QR\
\QM\


3.3. Четырёхугольники и многоугольники общего вида
451
Наконец, пользуясь формулой площади четырёхугольника, находим
Spqrs = \ • \QS\ • \PR\ = \ • (|М5| + \QM\) • (\РМ\ + \MR\) = 11 • 29 = 319. Ответ. 319.
Задача 9.
В выпуклом четырёхугольнике ABCD диагонали пересекаются в точке О. Площади треугольников ВОС, COD и AOD равны соответственно 20, 40 и 60. Найдите градусную меру угла ВАО, если известно, что \АВ\ = 15, \АО\ = 8, а градусная мера угла ВО А больше 31°.
Идея. Применить свойство площадей треугольников, на которые четырёхугольник разбивается своими диагоналями.
Указание. Найти площадь треугольника АОВ, записать формулу его площади.
Решение. Пользуясь свойством площадей треугольников, на которые четырёхугольник разбивается своими диагоналями, находим
Saaob • Sacod = Saboc • Saaod => Saaob = —тт;— = 3U.
40
После этого, применяя формулу площади треугольника, получаем
1 ^2-^0 1
Saaob = 7: *\АО\ • \АВ\ • sin ВАО =» sin ВАО = —— = -.
Z о • 15 Z
Таким образом, градусная мера угла ВАО равна либо 30°, либо 150°. Второй из этих вариантов невозможен, поскольку сумма градусных мер углов ВО А и ВАО не может превосходить 180°.
Ответ. 30°.
Задача 10.
Диагонали четырёхугольника PQRS, вписанного в окружность, пересекаются в точке D. На прямой PR взята точка Л, SAD = 50°, PQS = 70°, RQS = 60°. Где расположена точка А: на диагонали PR или на её продолжении? Ответ обосновать.
Идея. Найти величины углов SPR, SRP и PSR.
Указание. Воспользоваться свойствами вписанных углов, сравнить длины отрезков АН, RH и PH, где Н - основание высоты SH треугольника SPR.
А 15 В
D
20 • 60
15*


452
Указания и решения
Решение. Поскольку четырёхугольник PQRS вписан в окружность, пользуясь свойствами вписанных углов, мы находим
SRP = SQP = 70°, SPR = SQR = 60°, PSR = 180° - RQP = 50°.
Теперь можно обосновать, что точка А в любом случае лежит на продолжении диагонали PR (за точку R или за точку Р). Треугольник PRS оказался остроугольным, поэтому если мы проведём его высоту SH, то точка Н попадет на основание PR. Наконец, выразим длины отрезков АН, PH и RH:
\АН\ = \SH\ ctg 50°, \RH\ = \SH\ ctg 70°,
Q
|Ptf| = \SH\ ctg60°.
Поскольку ctg 50° > ctg 60° > ctg 70°, получаем \AH\ > \PH\ > \RH\.
Ответ. На продолжении.
Задача 11.
В трапецию, длины оснований которой равны 3 и 5, можно вписать окружность и около неё можно описать окружность. Вычислите площадь пятиугольника, образованного радиусами вписанной окружности, перпендикулярными боковым сторонам трапеции, её меньшим основанием и соответствующими отрезками боковых сторон.
Идея. Представить искомую площадь как сумму площадей треугольников. Указание. Воспользоваться свойствами четырёхугольников, описанных около окружности, и четырёхугольников, вписанных в окружность.
Решение. Обозначим вершины трапеции буквами А, В, С и D, точки касания окружности, вписанной в эту трапецию, со сторонами АВ, ВС и CD обозначим буквами К, L и М соответственно, а центр этой окружности обозначим буквой О. Будем считать, что AD\\BC, \AD\ = 5, \ВС\ = 3. Сразу заметим, что по свойству четырёхугольника, описанного около окружности, \АВ\ + |СТ>| = \AD\ + \ВС\ = 8.
Далее, поскольку трапеция ABCD вписана в окружность, она равнобедренная. Значит, длины сторон А В и CD равны, поэтому с учётом предыдущего соотношения \АВ\ — \CD\ =4.
После этого воспользуемся тем, что длина радиуса окружности, вписанной в трапецию, равна половине длины её высоты. По свойствам равнобедренной трапеции
hABCD = \J\AB\Z- = ^15 =» \ок\ = \OL\ = \ОМ\ =


3.3. Четырёхугольники и многоугольники общего вида
453
Наконец, искомая площадь может быть представлена в виде суммы площадей треугольников ВОК, BOL, COL и СОМ. Они все являются прямоугольными, причем АВО К = ABOL и A COL = АСОМ (по гипотенузе и катету). Тогда
^пятиугольника == 2(»SABOL “Ь 5дCOl) = 2SАВОС =: |-®^| * l^-^l =: 7^ *
л 3v^
Ответ. —-—.
Задача 12.
Точки К, L, М, N, Р расположены последовательно на окружности, длина радиуса которой равна 2у/2. Найдите площадь треугольника KLM, если известно, что LM\\KN, KM\\NP, MN\\LP, a LOM = 7г/4, где О - точка пересечения хорд LN и МР.
Идея. Воспользоваться тем, что четырёхугольники KLMN, KMNP и LMNP - трапеции, вписанные в окружность.
Указание. Пользуясь тем фактом, что равные хорды стягивают равные дуги, найти величины различных углов.
Решение. Ключевым шагом в решении этой задачи яв- l
ляется использование того факта, что четырёхугольники KLMN, К MNP и LMNP по условию задачи являются трапециями, вписанными в окружность. Из этого вытекает, что все они равнобедренные, \KL\ = \MN\,
\MN\ = \КР\, \LM\ = \PN\. Далее, пользуясь тем, что ^ равные хорды стягивают равные дуги, мы имеем
KL=MN=KP, LM==PN .
Р
Теперь положим KL= а, LM= /3, воспользуемся тем, что
сумма мер всех пяти упомянутых дуг равна 27т, и свойством угла между пересекающимися хордами:
^ = ЮМ = \-(£м + PN) % = I ■ 2/3 «=► 0 = За + 2/3 = 2тг =>> а = Ц.
4 2V/42 4 2
После этого по свойствам вписанных углов получаем
—1 т 2а + в 5тг 1 Р тг
KLM = - • KPNM= —= —, LKM = - • LM= £ = -,
2 2 8 2 2 8
1 а 7Г
tfML = ± • KL- х = т- 2 2 4
Наконец, с помощью формулы Saklm = 2$aklm ' sin KLM • sin LKM • sin KML находим


454
Указания и решения
Задача 13.
В окружность вписан четырёхугольник ABCD, диагонали которого взаимно перпендикулярны и пересекаются в точке Е. Прямая, проходящая через точку Е и перпендикулярная к прямой АВ, пересекает сторону CD в точке М. Докажите, что ЕМ - медиана треугольника CED, и найдите её длину, если \AD\ = 8, \АВ\=4 и CDB = а.
Идея. Доказать, что треугольники DEM и СЕМ равнобедренные. Указание. Воспользоваться свойствами вписанных углов.
Решение. Заметим, что
ACD = £ - CDB = £ - а,
2 2
и по свойствам углов, вписанных в окружность,
CAB = CDB = а. С другой стороны, если обозначить буквой Н точку пересечения прямой ЕМ и стороны АВ, то
МЕС = АЕН = £ - НАЕ = £
а,
DEM =
7Г
Таким образом, треугольники DEM и СЕМ оба равнобедренные, |£>М| = |£М|, |СМ| = \ЕМ\. Значит, М - середина CD. Дальнейшие рассуждения достаточно просты. Сначала из прямоугольного треугольника АВЕ мы легко находим \АЕ\ = \АВ\ • cos ВАЕ = 4 cos а, затем из прямоугольного треугольника AED по теореме Пифагора получаем \DE\ — y/\AD\2 — \АЕ\2 = 4\/4 — cos2 а и, наконец, рассматривая прямоугольный треугольник CED, имеем
\CD\ =
\DE\ 4л/4"
= 4
cos CDB cosa V cos q
\EM\ = \DM\ = \CM\ = \\CD\ = 2^/4tg2a + 3.
Ответ. 2\JA tg2 a + 3.
\JA tg2 a
-f 3;
Задача 14-
В четырёхугольнике ABCD диагонали AC и BD пересекаются в точке К. Точки L и М являются соответственно серединами сторон J3C и AD. Отрезок LM содержит точку if. Четырёхугольник ABCD таков, что в него можно вписать окружность. Найдите длину радиуса этой окружности, если \АВ\ = 3, \АС\ = л/13 и \LK\ : \КМ\ = 1:3.


3.3. Четырёхугольники и многоугольники общего вида
455
Идея. Доказать, что четырёхугольник ABCD является трапецией. Указание. Рассмотреть треугольники АКМ, DKM, BKL и CKL, записать для них формулу площади. Вывести из этого, что треугольники AKD и CKD подобны.
Указание. Ввести обозначения
\ВС\ = х, |AD| = Зх, CAD = АСВ = а.
Записать теорему косинусов для треугольников АВС и ADC.
Решение. Ключевым шагом в решении этой задачи является доказательство того факта, что четырёхугольник ABCD является трапецией. На эту мысль нас наводит свойство произвольной трапеции: отрезок соединяющий середины оснований трапеции, проходит через точку пересечения её диагоналей.
Так как отрезки KL и КМ являются ме- q
дианами треугольников ВКС и AKD соответственно, площадь треугольника АКМ равна площади треугольника DKM, а площадь треугольника BKL равна площади треугольника CKL. Записывая формулы площадей этих треугольников, имеем
S&akm — Sad км
\-\АК\ \КМ\ -sin АКМ £
— - • \DK\ • \КМ\ • smDKM £
Sackl = Sabkl
1
= -\BK\\KL\sinBKL
\AK\ • sin АКМ = \DK\ • sin DKM; у \CK\ ■ \KL\ sm CKL =
\CK\ • sin CKL = \BK\ ■ sin BKL
и, почленно деля эти соотношения, с учётом того, что в силу свойства вертикальных углов угол BKL равен углу DKM, а угол CKL равен углу АКМ, получаем \АК\ : \СК\ = \DK\ : \ВК\. Это означает, что треугольники AKD и СКВ подобны по второму признаку подобия треугольников, поэтому угол KAD равен углу КС В и \ВС\ : \AD\ = \LK\ : \КМ\ = 1 : 3. Эти углы являются внутренними накрест лежащими при прямых AD и ВС и секущей АС, стало быть, AD\\BC, то есть четырёхугольник ABCD - трапеция.
Исходя из этого введём обозначения \ВС\ = х, \AD\ = Зх, CAD = АСВ = а. Трапеция ABCD описана около окружности, значит,
\АВ\ + |СТ>| = \AD\ + \ВС\ = 4х, \CD\ = 4х - 3.
Запишем теорему косинусов для треугольников АВС и ADC:
|Л£|2 = \АС\2 + \ВС\2 - 2 • \АС\ • \ВС\ • cos АСВ => 9 = х2 + 13 - 2>/l3a;cosa; \CD\2 = \AC\2+\AD\2—2 \AC\ \AD\-cosCAD =*> (4x—3)2 = 9x2+13—бл/ТЗхсоэа.


456
Указания и решения
Умножая первое из этих уравнений на 3 и вычитая его из второго, получаем
2
(4х — З)2 — 27 — 6х2 — 26 => 10х2 — 24х + 8 = 0 => х = 2 или х = -.
о
Заметим, что х = 2/5 - посторонний корень в силу того, что тогда длина отрезка CD будет равна —7/5, что невозможно. Итак, х = 2, поэтому
ж2+ 4 2 . 3
cos а = —==- = —= => sm а =
2VT3# >/1з л/Тз’
Так как диаметр окружности, вписанной в трапецию, является высотой трапеции, то
2гавси = |АС| • sina = 3 ==> tabcd = -•
3
Ответ. -.
2
Задача 15.
D
В трапеции BCDE CD\\BE, |В£?| = 13, |С£)| = 3, |CJE| = 10. На описанной около BCDE окружности взята отличная от Е точка А так, что \АС\ = 10. Найти длину отрезка АВ и площадь пятиугольника ABCDE.
Идея. Доказать, что \АВ\ = \CD\. Площадь пятиугольника ABCDE представить как сумму площадей треугольников АВС, АСЕ и CDE.
Указание. Воспользоваться тем, что равные хорды стягивают равные дуги.
Решение. Поскольку трапеция BCDE вписана в окружность, она является равнобедренной,
\ВС\ = \DE\ и \BD\ = \СЕ\ = 10. По условию задачи \АС\ = \СЕ\, поэтому \АС\ = \BD\, стало быть, равны дуги АС и BD (не содержащие точку Е), что дает нам равенство углов АЕС и BED.
Заметим, что дуга ВС меньше дуги BCD, значит, она меньше и дуги АС, то есть точка А лежит на дуге BE, не содержащей точки С и D. Тогда ясно, что
АЕВ = АЕС - ВЕС, CED = BED - 'ВЕС
АЕВ = CED,
и, кроме того, АЕВ = АСВ, поскольку углы и АСВ опираются на одну ду¬
гу. Итак, АСВ = CED, |jBC| = |Di£|, |АС| = |#£|, поэтому треугольники АВС и CDE равны по первому признаку равенства треугольников. Из их равенства мы получаем, что |АВ| = \CD\ =3.
Для нахождения площади пятиугольника ABCDE разобьём его на треугольники АВС, АСЕ и CDE и немного посчитаем. Проведём высоту DH трапеции BCDE, тогда по свойствам равнобедренной трапеции
\НЕ\
\ВЕ\ - \CD\
5, \ВН\ = \ВЕ\ - \НЕ\ = 8.


3.3. Четырёхугольники и многоугольники общего вида
457
После этого, обозначив величины равных углов АЕС и BED буквой а, из прямоугольных треугольников BDH и DEH находим
\DH\ = \f\BD\2 - \ВН\2 = 6, \DE\ = V\HE\* + |£>tf|2 - у/б1,
\НЕ\ 5 . |£>Я| 6 . Л „ 5 6 60
cos а = ——г = —=, sin а = • = —= => sm 2а = 2 • —= • —7= = —.
\DE\ л/бТ |£>£| \/б! \/бТ 61
Наконец, длина высоты треугольника CDE, опущенной из вершины JS, равна длине отрезка а треугольник АСЕ равнобедренный, при этом нам в нем
известны длины боковых сторон и величина угла при основании. Значит,
Saabc = Sacde = J • |CD| • |£>Я| = 9; = J ■ |АС| • |С7£7| • sin(7r - 2а) =
Z 2 Ы
Sabcde = Saabc + Saace + Sacde = 9 + ——h 9 =
Ответ. \AB\ = 3, Sabcde =
61 61 4098
61
Задача 16.
В четырёхугольнике ABCD диагонали перпендикулярны и пересекаются в точке Р. Точка М является серединой отрезка AD, длина отрезка СМ равна 5/4. Расстояние от точки Р до отрезка ВС равно 1/2, \АР\ = 1. Найдите длину отрезка AD, если известно, что около четырёхугольника ABCD можно описать окружность.
Идея. Доказать, что точки М, Р и Н лежат на одной g
прямой.
Указание. Показать, что угол АРМ равен углу НРС. Воспользоваться свойствами вписанных углов.
Решение. Обозначим величину угла СAD буквой а, тогда величина угла ADB равна тг/2 — а и по свойству медианы прямоугольного треугольника, проведённой к гипотенузе, \АМ\ = \РМ\, АРМ = МАР = а. После этого заметим, что по свойствам углов, вписанных в окружность, АСВ = ADB = 7г/2 — а. С другой стороны, если обозначить буквой Н основание перпендикуляра, опущенного из точки Р на сторону ВС (тогда, по условию, \РН\ = 1/2), то НРС = 7г/2 — АСВ = а. Значит, углы АРМ и НРС равны, поэтому точки М, Р и Н лежат на одной прямой.
Положим \AD\ = х, тогда из вышесказанного вытекает, что \РМ\ = х/2, \МН\ = \РМ\ + \РН\ = х/2 -К 1/2. Заметим, что прямоугольные треугольники APD и РНС подобны, что дает нам
1
1^1 - \1М1 ^ \РС\ = 1ря1 • \AD\ -1
\AD\ \РС\
\АР\
О • х X = 2'


458
Указания и решения
Наконец, воспользуемся теоремой Пифагора:
\СН\2 = \СМ\2 — \МН\2 — \РС\2 — \РН\2 =* + =*
=> ?1-я2-2х-1=а?-1 =» 2х2 + 2х-^=0 =»
4 4 4
V54-2
Ответ. .
4
Задача 17.
Параллелограммы ABCD и AfBCD' имеют общую сторону ВС и расположены симметрично относительно прямой ВС (точка А симметрична точке А, точка D' симметрична точке D). Диагональ BD первого параллелограмма и сторона В А! второго параллелограмма лежат на одной прямой. Величина угла между диагоналями АС и А'С двух параллелограммов равна 7г/4, площадь пятиугольника ADCD' А' равна 15л/2. Найдите длины сторон параллелограмма ABCD.
Идея. Доказать, что параллелограммы из условия задачи равны, площадь пятиугольника ADCD' А! представить в виде суммы площадей равных трапеций ADCM и A'D'CM, где М - точка пересечения отрезка А А' и прямой ВС.
Указание. Рассмотреть треугольники BCD,
АВМ и ACM, положив \АВ\ = х, DBC = а.
Составить два уравнения с этими неизвестными.
Решение. Обозначим точку пересечения отрезка АА! и прямой ВС буквой М. Тогда из того, что точки А и А' симметричны относительно прямой ВС, мы имеем \АМ\ = \А'М\, А А! ± ВС. Из этого следует, что прямоугольные треугольники АМВ и AfMB равны по двум катетам, \АВ\ = \А!В\, /.АВМ — Z.A!BM. Далее заметим, что поскольку по условию задачи диагональ BD и сторона В А' лежат на одной прямой, углы А! ВМ и DBC равны, как вертикальные. А поскольку ABCD - параллелограмм, \АВ\ = |CjD|, AB\\CD и углы АВМ и BCD равны, как соответственные при параллельных прямых АВ и CD и секущей ВС. Суммируя все вышесказанное, получаем, что треугольник BCD равнобедренный, \АВ\ = \BD\ = \CD\.
Далее отметим, что углы А'ВС и АВС также равны (как смежные с равными углами АВМ и А'ВМ), поэтому параллелограммы ABCD и A'BCD' равны, \А'С\ = \АС\. Положим \АВ\ = х, DBC = а. Тогда из равнобедренного треугольника BCD мы находим \ВС\ = 2xcosa, а из прямоугольного треугольника АВМ мы имеем \АМ\ = ж sin a, \ВМ\ = xcosa. Треугольник А!АС также равнобедренный, стало быть, MCA = 7г/8, и из прямоугольного треугольника ACM мы находим


3.3. Четырёхугольники и многоугольники общего вида
459
Данную нам в условии задачи площадь пятиугольника ADCD' А! представим в виде суммы площадей равных трапеций ADCM и AID1 СМ. Пользуясь формулой площади трапеции, получаем
15л/2 = 2Sadcm = (\AD\ + \СМ\) • \АМ\ = 5xcosa • xsina => х2 sin 2а = б\/2.
Осталось немного посчитать:
. 2tga 3(\/2 —1)
tga — 3(л/2 — 1) =► sm2a — 1 + tg2^ - U_Q^
x2 = _6^ = 6V2(14-9v^)= ^ X = 2^W2;
sin 2a 3(v^-l)
cosa
Vtg2 a + 1 >/28 - 18л/2
=> IBCI — 2xcosa = 4\ ——= 2W^2 + V2.
V 28 - 18\/2 v
Ответ. |AI>| = |BC| = 2^2+^, |AB| = \CD\ = 2у/ь-2у/2.
Задача 18.
Точки К, L и М расположены на сторонах А#, ВС и CD выпуклого четырёхугольника ABCD соответственно, причём выполнены соотношения \АК\ : =
= \CL\ : |SL| = |CM| : |DM| = 1:2. Длина радиуса окружности, описанной около треугольника KLM, равна 5/2, = 4, |LM| = 3. Чему равна площадь
четырёхугольника ABCD, если известно, что \КМ\ < \KL\1
Идея. Доказать, что треугольник АВС подобен треугольнику KBL, а треугольник BCD подобен треугольнику LCM, найти длины диагоналей четырёхугольника ABCD.
Указание. Воспользоваться вторым признаком подобия треугольников, показать, что угол между диагоналями четырёхугольника ABCD равен углу KLM.
Решение. Заметим, что из того, что \АК\ : \ВК\ = \CL\ : \BL\ = 1:2, вытекает, что \АВ\ : \ВК\ = \ВС\ : \BL\ =3:2. Это означает, что треугольники АВС и KBL подобны по второму признаку подобия треугольников. Тогда мы имеем \АС\ : \KL\ = 3 : 2, \АС\ = 6. Далее, рассуждая совершенно аналогично, мы получаем \ВС\ : \CL\ = \CD\ : \СМ\ = 3:1, треугольники BCD и LCM подобны по второму признаку подобия треугольников, \BD\ : \LM\ = 3:1, \BD\ = 9. Таким образом, мы нашли длины диагоналей четырёхугольника ABCD, поэтому


460
Указания и решения
для нахождения его площади нам достаточно вычислить синус величины угла между ними.
Это можно сделать, например, так: из найденных нами подобий также следует, что KL\\AC, LM\\BD, поэтому siп(АС, BD) = sin KLM. Обозначим величину угла KLM буквой а и воспользуемся теоремами синусов и косинусов применительно к треугольнику KLM :
\КМ\
= 2Raklm
\КМ\ = 5 sina;
sin KLM
\КМ\2 = \KL\2 + \LM\2 - 2 • \KL\ • \LM\ • cos KLM 25 sin2 a = 16+9—24 cosa: => 24 cos a = 25 cos2 a
cos a = 0,
24
cosa = —.
25
Если cosa = 0, то треугольник KLM прямоугольный, \KM\ = 5 > \KL\, что противоречит условию задачи. Если же cosa = 24/25, то \КМ\ = 7/5 < \KL\. Итак, cosa = 24/25, поэтому sina = 7/25 и
Sabcd = ^ ‘ 1^1 • \BD\ sina
189 25 ’
n 189
Ответ. ——.
25
Задача 19.
В выпуклом четырёхугольнике ABCD отрезок СМ, соединяющий вершину С с точкой М, расположенной на стороне AD, пересекает диагональ BD в точке К. Известно, что \СК\ : \КМ\ = 2:1, \CD\ : \DK\ = 5:3, ABD + ACD = тг. Найдите отношение длин стороны АВ и диагонали АС.
Идея. Рассмотрев треугольники ABD и ACD, до- С
казать, что
\АВ\ _ sin АРБ \ЛС\ ~ sin ADC'
Указание. Воспользоваться теоремой синусов. Рассмотрев треугольники MKD и MCD, найти отношение синусов величин углов ADB и ADC.
Решение. Начнем решать задачу с конца, а именно, попытаемся понять, с помощью каких теорем можно подобраться к искомой величине. Как правило, отношение длин отрезков, являющихся сторонами некоего треугольника, вычисляют с помощью теоремы синусов. Однако формальное применение её к треугольнику АВС ничего не даст, так как нам придется искать отношение синусов величин углов АВС и АСВ, а эти углы никак не относятся к данным нам в условии задачи отношениям. Главным шагом в решении этой задачи является рассмотрение треугольников ABD и ACD, в которые входят как интересующие нас отрезки


3.3. Четырёхугольники и многоугольники общего вида
461
АВ и АС, так и углы ABD и ACD, синусы которых по условию задачи равны. Применяя к этим треугольникам теорему синусов и почленно деля полученные соотношения, получаем
IЛВ\^ IАР^ ]ЛС|^ _ |АР^ ^
sin ADB sin ABD sin ADC sin ACD
\AB\ sin ADC |AB| sin АРД
I^C| sin ADB ~~ I^C| ~ sin ADC'
Итак, нам надо найти отношение синусов величин углов ADB и ADC. Это легко сделать, применяя теорему синусов к треугольникам MKD и MCD, в которые входят как отрезки, отношения которых даны в условии, так и эти углы, и опять- таки деля почленно полученные соотношения:
1 КМ\ _ \РК\ \СМ\ _ \СР\ sin ADB sin CMD sin ADC sin CMD
\KM\ sin ADC _ \DK\ sin ADB __ \CD\ \KM\ _ 5 15
^ \CM\ ' shlADB ~ \CD\ =* sinADC ~ \DK\ \CM\ ~ 3 ' 3 ~ 9’
Ответ. 5:9.
Задача 20.
В окружность вписан четырёхугольник ABCD, Р - точка пересечения его диагоналей, \АВ\ = \CD\ = 5, \AD\ > \ВС\. Длина высоты, опущенной из точки В на сторону AD, равна 3, а площадь треугольника ADP равна 25/2. Найдите длины сторон AD и ВС, а также длину радиуса окружности.
Идея. Доказать, что четырёхугольник ABCD является трапецией, воспользоваться свойством треугольников, на которые трапеция делится своими диагоналями.
Указание. Выразить площадь трапеции ABCD двумя способами.
Указание. Воспользоваться теоремой синусов.
Решение. Сначала докажем, что четырёхугольник ABCD является трапецией. Это можно сделать, например, так: поскольку длины отрезков АВ и CD равны, то равны и дуги АВ и CD, из чего, по свойствам вписанных углов, вытекает равенство углов CAD и АСВ. Но эти углы являются внутренними накрест лежащими при прямых AD и ВС и секущей АС, стало быть, AD\\BC и четырёхугольник ABCD - трапеция.
Далее опустим из точек В и С перпендикуляры ВН и С К на прямую AD. Тогда по условию задачи \ВН\ = 3, и, записывая теорему Пифагора для прямоугольного треугольника АВН, мы находим |А£Г| = yJ\AB\2 — \ВН\2 = 4. Также заметим, что, поскольку AD\\BC, имеем |-В#| = |CiiT|, треугольники АВН и


462
Указания и решения
DC К равны по гипотенузе и катету, поэтому \АН\ = \DK\ = 4. Четырёхугольник ВСКН, очевидно, является прямоугольником, значит, \ВС\ = \НК\. Обозначим длины этих двух отрезков буквой х и вспомним, что по условию задачи \AD\ > \ВС\, из чего следует, что точки Н и К попадают на отрезок AD и \AD\ = \АН\ + \НК\ + \DK\ = х + 8.
После этого воспользуемся свойствами треугольников, на которые трапеция разбивается своими диагоналями:
f\BC\\2 fх2 _|ВС\ _ fX
& ABC Р 1|ч гл1 I AADP / о\о > ААВ Р ^ AC DP i л ^AADP
\\AD\J (х + 8)2’ \AD\ х + 8’
Sabcd — Sabcp + Saadp + Saabp + Sacdp = _|_ g)2 + 2X ^ g^ •
С другой стороны, Sabcd = \BH\ ■ —— = Зх + 12.
Теперь найдём х, приравнивая полученные выражения для площади трапеции ABCD:
25 /, х2 х \ . . 25 / х \
Зх-Ы2-т(1+(^ + 2—j <*=► 3(х + 4)_-(1 + —)
2
<=► 3(х + 4) = <=> 3(х + 8)2 = 50(х + 4) <s=4> Зх2 - 2х - 8 = 0 => х = 2.
{х + 8)^
Итак, \ВС\ = х = 2, |AD| = х + 8 = 10. Наконец, для нахождения длины радиуса окружности, описанной около трапеции ABCD, применим теорему синусов для треугольника ADB, вписанного в эту же окружность:
\BD\ = у/\ВН\* + \DH\2 = Зл/5; sinBAD = Ц|| = Д = |g^L =
\АВ I 5 2 sm BAD 2
Ответ. |AZ>| = 10, \ВС\ = 2, R=^.
Задача 21.
В выпуклом четырёхугольнике ABCD известно, что угол DAB острый, угол ADC тупой, sin DAB = 3/5, cos ABC = —63/65. Окружность с центром в точке О касается сторон ВС, CD и AD. Найдите длину отрезка ОС, если \АВ\ = 25/64, \ВС\ = 793/64, |С£>| = 25/4.
Идея. Воспользоваться тем, что окружность, касающаяся сторон ВС, CD и AD, является вписанной в треугольник DEC, где Е - точка пересечения продолжений сторон AD и ВС за точки А и В соответственно.
Указание. Найти длины сторон треугольника DEC, пользуясь теоремами синусов и косинусов.
Указание. Длину радиуса вписанной окружности искать по формуле S = рг.


3.3. Четырёхугольники и многоугольники общего вида
463
Решение. Основой решения этой задачи является тот факт, что окружность, касающаяся сторон ВС, CD и AD, является вписанной в треугольник DEC, где Е - точка пересечения продолжений сторон AD и ВС за точки А и В соответственно. Обоснуем, почему эти продолжения действительно пересекаются. Из условия задачи следует, что
cos DAB
1 — sin2 DAB = -, sin ABC 5
cos2 ABC = ;
65
Таким образом, сумма величин углов ABC и DAB больше, чем п. Из этого и вытекает нужный нам факт.
Дальнейший ход решения заключается в вычислении длин сторон треугольника DEC. Сначала рассмотрим треугольник АВЕ и найдём длины отрезков АЕ и BE. Ясно, что
О ^ ^ ^ 1 g
sin ВАЕ = sin DAB = -, sin AB# = sinAJ5C = —;
5 65
sin AEB = sin ^BAE + ABE^j — sin ^7r — DAB + ж — ABC^ =
= sin (2tt - (ABC + DAB)) = - sin (ABC + DAB^j = A Теперь, применяя теорему синусов, находим
\АВ\
\ВЕ\
1 \ВЕ\
_5_ — 3
13 5
QQ
\ВЕ\ = \СЕ\ = \ВЕ\+\ВС\ = 13.
sin АЕВ sin ВАЕ
После этого перейдём к вычислению длины стороны DE. Ясно, что угол ВАЕ тупой, поэтому угол АЕВ острый, значит, cos АЕВ — \f\
12
r 1 — sin2 АЕВ — ^. Положим \DE\ — х и запишем теорему косинусов для треугольника DEC:
||2 _ I гытч2 , |/-ч ц!|2 - I ^ -^7^, 625
\CD\2 = \DE\2 + \СЕ\2 -2-\DE\-\CE\-cos DEC
16
13
= х2 + 169 —24х
о 625
=> х2 - 24х + 144 = — - 25
16
225
-1б =*
X =
33 4 ’ _ 63
х“ 4 •


464
Указания и решения
Вспомним, что по условию задачи угол ADC тупой. По критерию тупоугольности треугольника это эквивалентно тому, что
\СЕ\2 > |DE\2 + \CD\2 =» 169 > х2 + ^ х2 <
16 16
Этому условию удовлетворяет лишь меньший из полученных корней. Итак, \DE\ = 33/4, длины всех сторон треугольника DEC найдены. Теперь обозначим буквой К точку касания стороны CD к окружности, вписанной в треугольник DEC, и воспользуемся формулами длины радиуса окружности, вписанной в треугольник, и длин отрезков, на которые вписанная в треугольник окружность делит его стороны:
\CD\ + \DE\ + \CE\ 55 |рр| П.
PADEC = ^I ^ I — ~ \Dtj\ — —,
Sadec = \ • \СЕ\ ■ \DE\ • sin DEC = \ОК\ = tadec = = t
4 о PADEC 6
Наконец, \ОС\ = \/\ОК\2 + \КС\2 = у/Ш/2. л/130
Ответ. —-—.
Задача 22.
В окружность, длина радиуса которой равна 2, вписан правильный шестиугольник ABCDEF. Из точки К, лежащей на продолжении стороны AF таким образом, что \КА\ < \KF\ и \КА\ = у/ll — 1, проведена секущая КН, пересекающая окружность в точках N и Н, причём точка N лежит между точками К и Я. Известно, что \KN\ =2, а угол NFH тупой. Найдите величину угла HKF.
Идея. Найти расстояние от точки К до центра окружности.
Указание. Записать теорему о произведении длины секущей и длины её внешней части для секущих КН и KF.
Указание. Провести прямую через точку К и центр окружности, записать теорему о произведении длины секущей и длины её внешней части для этой прямой и секущей КН.
Указание. Искомую величину представить как разность величин двух углов, воспользоваться теоремой косинусов.
Решение. Ясно, что нам придётся вычислить длину стороны шестиугольника ABCDEF. Найти её очень просто: положим обозначим |AF| = х и, пользуясь формулой длины радиуса окружности, описанной около правильного п-угольника, имеем
2 =
2 sin |
х = 2.


3.3. Четырёхугольники и многоугольники общего вида
465
Итак, \AF\ = 2, \KF\ = \КА\ + \AF\ = л/ГТ + 1. Теперь воспользуемся теоремой о произведении длины секущей на длину её внешней части:
\KA\-\KF\ = \KN\-\KH\ =» (vTT-l)(\/ll + l) = 2-\КН\ =» \КН\ = Ъ.
Отметим, что секущую КН, вообще говоря, можно провести двумя способами. Однако по условию задачи угол NFH тупой. Это означает, что мера дуги NH, не содержащей точку F, больше чем 7г. Поэтому, если мы проведём прямую через точку К и центр окружности О (точки её пересечения с окружностью обозначим через К' и К", К' лежит между точками К и К"), то точки N, F и Н лежат в одной полуплоскости относительно неё (на рисунке пунктиром обозначен вариант секущей КН, не удовлетворяющий условию задачи).
Дальнейший ход решения построен на сделанном нами дополнительном построении (прямой КО). Соединим точку О с точками А и Н. Отрезки О А, ОН, О К' и О К" - радиусы окружности, поэтому их длины равны 2. Искомую величину с учётом вышесказанного мы будем искать как разность величин углов ОКА и ОКН, для их нахождения нам понадобится длина отрезка КО. Положим \КО\ = у, тогда \КК'\ = \КО\ - \ОК'\ = у - 2, \КК"\ = \КО\ + \ОК"\ = у + 2. Ещё раз применяя теорему о произведении длины секущей на длину её внешней части, имеем
\КК'\ ■ \КК"\ = \KN\ • \КН\ =*> (у — 2)(у + 2) = 2 • 5 =4- у = у/й.
Теперь осталось лишь записать теорему косинусов для треугольников КО А и КОН:
|АГО|2 + |Ю1|2 - \ОА\2 14+(VTI-I)2-4
cos OK Л =
cos ОКН =
2 ■ \КО\ ■ \КА\ 2л/14(\/ТТ - 1)
\КО\2 + \КН\2 - \ОН\2 14 + 25-4 7
2 • \КО\ ■ \КН\ Юл/14 2у/й'
Итак,
[П ~ 7
ОКА = arccos \ —, ОКН = arccos ■
14’ 2>/14’
HKF = ОКА — ОКН = arccos л /тт — arccos - 7
14 2л/ТТ
7
Ответ, arccos \ — — arccos —7=.
2v/l4
Задача 23.
В выпуклом пятиугольнике ABCDE диагонали BE и СЕ являются биссектриса- ми внутренних углов при вершинах В и С соответственно, А = 35°, D = 145°, а площадь треугольника ВСЕ равна 11. Найдите площадь пятиугольника ABCDE.
Идея. Доказать, что АВНЕ = АВКЕ, ДСК£ = ACLE, а ДЛЯЯ = ADLE. Указание. Воспользоваться тем, что любая точка биссектрисы угла равноудалена от его сторон. Разбить пятиугольник ABCDE на треугольники.


466
Указания и решения
Решение. Поскольку диагонали BE и СЕ являются биссектрисами углов АВС и BCD соответственно, то по основному свойству биссектрисы угла точка Е, во- первых, равноудалена от прямых АВ и ВС и, во-вторых, равноудалена от пря- А мых ВС и CD. Из этого вытекает, что она равноудалена от всех трех указанных прямых. Опустим на прямую АВ перпендикуляр ЕН, на прямую ВС перпендикуляр ЕК, и на прямую CD - перпендикуляр EL. Из вышесказанного следует, что \ЕН\ = \ЕК\ = \EL\.
После этого нам необходимо уточнить, как расположены точки Н, К и L. Поскольку пятиугольник ABCDE выпуклый, величины всех его внутренних углов лежат в интервале (0,7г). Из этого следует, что углы АВЕ, С BE и ВСЕ острые. Также заметим, что угол ВАЕ, градусная мера которого равна 35°, тоже острый. Таким образом, в треугольнике АВЕ углы ВАЕ и АВЕ острые, поэтому точка Н лежит на стороне АВ, а в треугольнике ВСЕ углы С BE и ВСЕ острые, поэтому точка К лежит на стороне ВС. Угол же CDE по условию является тупым, поэтому точка L лежит на продолжении стороны CD за точку D.
Далее заметим, что треугольники ВНЕ и ВКЕ равны по гипотенузе и катету,
поэтому их площади также равны. То же самое верно и для треугольников СКЕ и CLE. С другой стороны, треугольники АНЕ и DLE тоже равны (по катету и острому углу), так как градусная мера угла LDE равна 180° — 145°, то есть 35°.
Наконец, разбивая пятиугольник ABCDE на треугольники и пользуясь установленными ранее фактами, мы получаем
Sabcde = Saahe + Sabhe + Sabke + Sacke + Sacde —
= Saahe + 2 Sabke + Sacke + Sacle — Sadle =
= 2 Sabke + 2Sacke = 2 Sabce = 22.
Ответ. 22.
Задача 24-
Продолжения сторон AD и ВС выпуклого четырёхугольника ABCD пересекаются в точке М, а продолжения сторон АВ и CD - в точке О. Отрезок МО перпендикулярен биссектрисе угла AOD. Найдите отношение площадей треугольника AOD и четырёхугольника ABCD, если \ОА\ = 12, \OD\ = 8, \CD\ = 2.
Идея. Показать, что луч МО является биссектрисой угла, смежного с углом AOD. Доказать, что
\АМ\ \AL\ \АО\ \DM\ “ \DL\ “ \OD\'
Указание. Воспользоваться теоремой синусов.
Указание. Записать теорему Менелая для треугольника AOD и секущей ВМ. Воспользоваться леммами о площадях треугольников.
L


3.3. Четырёхугольники и многоугольники общего вида
467
Решение. Поскольку отрезок МО перпендикулярен биссектрисе угла AOD, он является биссектрисой угла, смежного с углом AOD, т.е. является биссектрисой внешнего угла треугольника AOD. Но тогда по свойству биссектрисы внешнего угла треугольника (оно доказывается аналогично свойству биссектрисы треугольника)
\АМ\ \AL\ \АО\
\DM\ ~ \DL\ ~ \OD\
Теперь положим \ОВ\ = х, тогда \ВА\ = 12 — х, и запишем теорему Менелая для треугольника AOD и секущей ВМ:
\DC\ \ОВ\ \АМ\ _
\СО\ ' \ВА\ ’ \MD\ ~ '
Подставляя в это равенство выраженное ранее отношение \АМ\ : \DM\ и учитывая, что \ОС\ = б, получаем
\Ср\\ОВ\\Ю\ 2 12 _ 2 . т„
\ОС\ \ВА\ \OD\ 6 12-х 8 12-х
Наконец, воспользуемся соотношениями между площадями треугольников:
Saaod _ \ОА\ • \ОР\ _ 12 • 8 _
Saboc \ОВ\ • \ОС\ 8 • б
Итак, площадь треугольника ВОС равна половине площади треугольника AOD, из чего вытекает, что площадь четырёхугольника ABCD также равна половине площади треугольника AOD, то есть искомое отношение равно 2.
Ответ. 2.
Задача 25.
В четырёхугольнике ABCD, вписанном в окружность, биссектрисы углов А и В пересекаются в точке Е, лежащей на стороне CD. Известно, что отношение длины отрезка CD к длине отрезка ВС равно т. Найдите:
1) отношение расстояний от точки Е до прямых AD и ВС,
2) отношение площадей треугольников ADE и ВСЕ.
Идея. Доказать, что точка Е равноудалена от прямых AD и АВ. Выразить искомое отношение и данное в условие отношение через синусы величин углов АВЕ и ВАЕ.
Указание. Воспользоваться тем, что любая точка биссектрисы угла равноудалена от его сторон.
Указание. Записать теорему синусов для треугольников ВСЕ, АВЕ и ADE.
О


468
Указания и решения
Решение. Ответить на первый вопрос этой задачи совсем просто. Поскольку точка Е лежит на биссектрисе угла Л, она равноудалена от сторон этого угла, то есть от прямых AD и АВ. А так как она лежит и на биссектрисе угла В, она равноудалена и от сторон этого угла, то есть от прямых ВС и В А. Значит, она равноудалена от прямых AD и ВС, то есть ответом на первый вопрос задачи будет 1:1.
Получить ответ на второй вопрос этой задачи гораздо сложнее. Для начала отметим, что расстояния от точки Е до прямых AD и ВС суть не что иное,
как длины высот ЕН и ЕК треугольников ADE и ВСЕ соответственно. Ранее мы доказали, что \ЕН\ = \ЕК\, поэтому
Saade _ | • \ЕН\ • \АР\ _ \АР\
Sabce £ • \ЕК\ ■ \ВС\ \ВС\'
Итак, фактически нам надо вычислить отношение \AD\ : \ВС\. Введём обозначения ___
DAE = ВАЕ = a, ABE = СВЕ = /3.
Тогда, пользуясь свойствами вписанных углов и теоремой о сумме величин углов треугольника, имеем
5 = тг - 2/3, С = тг - 2а, 'ВЕС = 2а - /3, AED = 2/3 - а.
Теперь, записывая теорему синусов для треугольников ВСЕ, АВЕ и ADE, выразим длины всех отрезков через длину отрезка ВС:
|ВС| |В£| |С£|
sin ВЕС sin С sin СВЕ
\ВЕ\ = \ВС\- . У?,,, \СЕ\ = |ВС| Sill,i
sin(2a — /3) ’ sin(2a — /3)5
J££U = J4SL —. ИЕ| = |BE| . Eig = |BC|.
smBAE sin ABE sm« sm a sm(2a — p)
\AD\ _ \AE\ _ \DE\
sin AED sin D sin DAE
, um i л z74 sin(2 p-а) ID„, sin2asin/3sin(2/3 — a)
=* m = ]AEl ‘ sin 2/3 ' |BC| ' sin a sin(2a - /3)sin2/3 “
_ |nC| cos a sin(2/3 — a) = sin 2/3 - sin(2a - 2ff)
sin(2a — /3) cos /3 sin 2a + sin(2a - 2/3) ’
|DB| = |A£| ■ = \BC\ ■ , = \BC\ • Si”2"
sin 2/3 sin(2a — /3) sin 2(3 2 sin(2a — /3) cos /3 ’
|CZ>| = IDEI + \CE\ = |BC| • + 2sln(2S:",2;)cos^,) =


3.3. Четырёхугольники и многоугольники общего вида
469
sin 2а + sin 2/3 sin 2а + sin 2(3
= \ВС \ ' О 'z'fW' oT^ZTo = 1^°1
2 sin(2a — /3) cos /3 sin 2а -f- sin(2a — 2/3)
Итак, мы получили, что
\CD\ _ sin 2а + sin 2/3 |AD| _ sin 2/3 — sin(2a — 2/3)
|J5C| sin 2a + sin(2a - 2/3) ’ |BC7| sin 2a + sin(2a — 2/3)'
Вычитая второе из этих соотношений из первого, имеем
\CD\ \AD\ sin 2a -I- sin(2a — 2/3)
\BC\ \BC\ sin 2a + sin(2a - 2/3)
1.
\AD\ \CD\ л Таким образом, = -щщ - 1 = т - 1.
Ответ. 1)1:1, 2) т — 1.
Задача 26.
Диагонали вписанного в окружность четырёхугольника ABCD пересекаются в точке Е, причём \AD\ • \СЕ\ = \DC\ • \АЕ\, \BD\ = 6, ADB = 7г/8. Найдите площадь четырёхугольника ABCD.
Идея. Доказать, что отрезок DE является биссектрисой треугольника ADC. Указание. Записать теорему синусов для треугольников ADE и С DE. Указание. Воспользоваться формулой площади четырёхугольника и свойствами вписанных углов.
Решение. Первым шагом в решении этой задачи является обоснование того факта, что отрезок DE является биссектрисой треугольника ADC. Заметим, что из соотношения, данного в условии задачи, вытекает, что
\AD\ : \DC\ = \АЕ\ : \СЕ\,
то есть фактически нам надо установить справедливость утверждения, обратного к основному свойству биссектрисы треугольника. Записывая теорему синусов для треугольников ADE и CDE, имеем
\АР\ _ | АЕ\ \РС\ _ \СЕ\
sin AED sin ADE sinC^D sin CDE
Почленно деля эти соотношения и учитывая, что sin^^D = smCED в силу того, что углы AED и CED смежные, получаем


470
Указания и решения
Ясно, что сумма величин углов ADE и CDE не может быть равна 7Г, поэтому ADE = CDE, что, собственно, нам и нужно было получить.
После этого отметим, что в силу свойств вписанных углов
ADE = CDE = АСВ = ВАС =
7Г
8’
№
поэтому ADC = 7г/4, треугольник АВС является равнобедренным, \АВ\ = \ВС\. После этого можно рассуждать двумя способами.
Первый способ. Логично предположить, что для вычисления площади четырёхугольника ABCD, раз уж мы знаем длину диагонали BD, надо воспользоваться формулой
Sabcd = \ • \АС\ ■ \BD\ • sin АЕВ.
Заметим, что, с одной стороны, по свойству внешнего угла треугольника
АЕВ — АЛЕ + ГУАЕ = 1)АЕ + —
и, с другой стороны, BAD = ВАЕ + DAE = DAE + |, то есть BAD = АЕВ. После этого выразим длину диагонали АС, пользуясь теоремой синусов для треугольников ABD и ACD, вписанных в одну и ту же окружность:
2R =
\BD\
\АС\
\АС\ = \BD\ sin BAD sin ADC
Наконец, пользуясь тем, что BAD = АЕВ, находим
3\/2
sin ADC
3%/2
Sabcd = \ • \АС\ ■ \BD\ ■ sin АЕВ = ±
sin BAD sin BAD
• 6 • sin АЕВ = 9\/2.
sin BAD
Второй способ. Сделаем дополнительное построение: отложим на продолжении отрезка AD за точку А точку F таким образом, что |AF| = \CD\.
Заметим, что, с одной стороны, BAF = it — BAD и, с другой стороны, в силу свойств вписанных углов BCD = тг — BAD. Значит, углы BAF и BCD равны.
Помимо этого нами ранее было получено, что \АВ\ ~ \ВС\. Поэтому треугольники BAF и BCD равны по первому признаку равенства треугольников. Из этого следует, что
\BF\ = \BD\=6,
7Г
37Г
Т’
AFB = CDB = ~, DBF 8
Поэтому
Sabcd = Saabd+Sabcd = Saabd+Sabaf = Sabdf;
Sabdf = I ■ \BD\ ■ \BF\ ■ sin DBF = 9y/2.
Ответ. 9\/2.


3.3. Четырёхугольники и многоугольники общего вида
471
Задача 27.
На одной стороне угла О взяты точки К, L и М, а на другой его стороне - точки Р, Q и R таким образом, что KQ J_ PR, PL _L KM, LR _L PQ, QM _L KL. Известно, что отношение расстояния от точки О до центра вписанной в четырёхугольник KPRM окружности к длине отрезка КР равно 17 : 6. Найдите величину угла О.
Идея. Доказать, что четырёхугольник KPRM - трапеция.
Указание. Воспользоваться теоремой о высотах.
Указание. Показать, что центр окружности, вписанной в четырёхугольник KPRM, лежит на биссектрисе угла О.
Решение. Решение этой задачи достаточно трудное и состоит из двух этапов. Сначала выясним, какими свойствами обладает четырёхугольник KPRM. Ясно, что угол О острый (в противном случае отрезки KQ и PR не смогут быть перпендикулярны). Заметим, что по условию задачи отрезки PL и QK являются высотами треугольника ОРК.
Из этого по теореме о высотах следует, что
ОРК = OLQ, ОКР = OQL, |^§j=cos<5.
С другой стороны, отрезки LR и QM являются высотами треугольника OQL, что по той же самой теореме о высотах дает нам
бш = бщ, 6mr = 6qL, M = cosa
\QL\
Объединяя полученные соотношения, мы находим
ОРК = ORM, ОКР = OMR, = cos2 б.
Ну а поскольку углы ОРК и ORM являются соответственными при прямых КР и MR, эти прямые параллельны. Итак, четырёхугольник KPRM - трапеция.
Далее сразу отметим, что по условию задачи трапеция KPRM вписана в окружность, из чего вытекает, что она равнобедренная. Значит, углы ОРК, ОКР, ORM и OMR равны, а треугольники ОРК и ORM равнобедренные, \ОР\ = \ОК\, \OR\ = \ОМ\.


472
Указания и решения
После этого будем рассуждать следующим образом. Проведём биссектрису угла О, точки её пересечения с отрезками MR и КР обозначим буквами Т и S соответственно. Тогда, в силу того, что биссектриса равнобедренного треугольника, проведённая к основанию, является также его медианой и высотой, \МТ\ = \RT\,
\KS\ = \PS\, OS _L MR, OS _L KP. Таким образом, прямая TS является серединным перпендикуляром к сторонам MR и КР трапеции KPRM. Учитывая тот факт, что центр окружности, описанной около произвольного многоугольника, лежит на пересечении его серединных перпендикуляров, мы находим, что центр окружности, описанной около трапеции KPRM (обозначим его буквой N), лежит на прямой TS, а отрезок, соединяющий точку N и середину Н стороны МК, перпендикулярен прямой О К.
Теперь в соответствии с условием задачи положим \ON\ = 17х, \КР\ = 6х, а, искомую величину угла О обозначим через 2а. Тогда с учётом вышесказанного
OKS = - - а.
\KS\ = \SP\ = Zx, \MR\ = Gx cos2 2a, KOS - a,
Затем, рассматривая AOS К и A ONH, а также трапецию KPRM, мы получаем |iC5| За;
\OK\ =
\мк\
sin К OS smc* \КР\ - \MR\
\ОН\ — |07V| • cos NOH = 17xcosa, 6x — 6x cos2 2a 3a: sin2 2 a
sma
2cosOPK 2cos(f -a)
Наконец, пользуясь тем, что \ОН\ = \ОК\ — \КН\ = \ОК\ — \ \МК\, получаем
Зх Зх sin2 2а
17xcos а
sma
Л <
2 sin a
34 sin a cos а — б — 3 sin"* 2а <==> 3 sin2 2а + 17 sin 2a — б = О,
откуда sin 2a = 1/3 и в силу того, что угол О - острый, О = 2а — arcsin(l/3). Ответ, arcsin(1/3).


4-1. Треугольники
473
4. Задачи на доказательство
4.1. Треугольники
Задача 1.
Какого вида треугольник, у которого высоты 3,4,5?
Идея. Сравнить квадрат одной стороны треугольника с суммой квадратов двух других сторон.
Указание. Выразить стороны треугольника через его высоты и площадь.
Решение. Пусть а,6,с - стороны треугольника и соответствующие им высоты равны ha = 3, hb = 4, hc = 5. Для площади треугольника имеем
aha bhb chc ^ 2 5 25 25 5 25 25
= ~~2~~ = ~2 = ^ а^К= Т’ =^= 2’ С=Л7 = Т’
2 452 ,2 52 2 4S2
откуда az = “g“> 4 ’ ~25~* результате получаем
.. , 41S2 , 4 S1
ь +г = 1оо<а
следовательно, треугольник тупоугольный.
Ответ. Тупоугольный.
Задача 2.
Доказать, что если в треугольнике две высоты равны, то он равнобедренный.
Идея. Использовать формулу площади треугольника через высоту. Указание. Приравнять два выражения для площади.
Решение. Рассмотрим треугольник со сторонами а, 6, с и высотами ha,hb,hc. Площадь треугольника равна 5 = aha/2 = bhb/2. Следовательно, если ha = /i&, то и а = Ь.
Задача 3.
Медиана треугольника совпадает с его биссектрисой. Доказать, что этот треугольник равнобедренный.
Идея. Использовать свойство биссектрисы.
Указание. Биссектриса угла а делит сторону а на отрезки аь и ас, которые пропорциональны сторонам бис:


474
Указания и решения
Решение. Поскольку медиана совпадает с биссектрисой, в равенстве
аь _ Ь ас с
отрезки аь и ас равны. Следовательно, - = 1, то есть b = с.
Задача 4-
Доказать, что еслй у треугольника равны две медианы, то он равнобедренный.
Идея. Доказать, что А АОЕ = ABOD.
Указание. Использовать то, что медианы точкой пересечения делятся в отношении 1:2.
Решение. Пусть медианы AD — BE = га, тогда
АО = ВО = \т, ЕО = DO = \т.
о «5
Так как углы при вершине О вертикальные, то ААОЕ = ABOD по первому признаку.
Следовательно, АЕ = BD и сторона АС (равная 2АЕ) равна стороне ВС (равной 2BD).
Задача 5.
Пусть длины сторон прямоугольного треугольника - натуральные числа. Доказать, что длина одного из катетов кратна трём.
Идея. Перебрать остатки от деления на 3.
Указание. Применить теорему Пифагора.
Решение. Предположим, что длины катетов не кратны трём, то есть
а — 3fc ± 1, b = 31 ± 1, fe, / 6 N.
По теореме Пифагора
с2 = а2 + Ь2 = 9к2 + 9/2 ± 6к ± Ы + 2,
то есть с2 при делении на 3 дает остаток 2. Переберем возможные варианты:
1) Если с делится на 3, то остаток у с2 равен нулю.
2) Если с не делится на 3, то с = Зга ±1, га Е N, и остаток у с2 равен 1.
В любом случае остаток не равен 2, следовательно, наше предположение неверно и длина одного из катетов кратна трём.


4-1. Треугольники
475
Задача 6.
Доказать, что все прямоугольные треугольники, стороны которых образуют арифметическую прогрессию, подобны «египетскому» треугольнику (длины его сторон равны 3, 4, 5).
Идея. Использовать теорему Пифагора.
Указание. Выразить все стороны треугольника через среднюю сторону и разность прогрессии.
Решение. Пусть длина большего катета равна 6, тогда длины гипотенузы и меньшего катета равны соответственно b + d и Ъ — d, где d > 0 - разность арифметической прогрессии. По теореме Пифагора получаем
(b + d)2 = b2 + (b-d)2 *=> 4 bd = b2 b = 4d.
Следовательно, стороны треугольника равны Sd, 4d, 5d, что и требовалось доказать.
Задача 7.
Пусть а, Ь, с - длины сторон треугольника. Доказать, что 2 (а2Ъ2 + Ъ2с2 -I- с2а2) > а4 4- Ь4 + с4.
Идея. Использовать неравенство треугольника.
Указание. При каждом возведении неравенства в квадрат проверять неотрицательность обеих частей неравенства.
Решение. Пусть в треугольнике со сторонами а,6,с угол напротив b острый и с > а. Тогда из неравенства треугольника следует, что с — а<Ъ. После возведения в квадрат (обе части неотрицательны, так как с > а) получим
с2 — 2са + а2 < Ь2 с2 + а2 — Ъ2 < 2са.
После возведения в квадрат (обе части неотрицательны, так как угол напротив b острый) получим
с4 + а4 4- 2с2а2 + Ь4 - 2с2Ь2 - 2а2Ь2 < 4с2а2 <=>
2 (а262 + Ь2с2 + с2а2) > а4 + 64 + с4.
Задача 8.
Доказать, что если медиана и высота, проведенные из одной вершины треугольника, делят его угол на три равные части, то треугольник прямоугольный.
Идея. Обозначить одну из равных частей через а, выразить углы треугольника через а и с помощью теоремы синусов получить уравнение для а.
Указание. Применить теорему синусов к двум треугольникам, на которые медиана разбивает исходный треугольник.


476
Указания и решения
Решение. Пусть ВН и ВМ - соответственно высота и медиана А АВС и /АВН = ZHBM = ШВС = а, тогда АВАН = £ - a, /ВС А = £ - 2а.
A Z
в
Применим к треугольникам АВМ и ВМС теорему синусов: AM ВМ МС ВМ
sin2а sjn ^ sina sin ^ — 2a^
Разделим одно равенство на другое, учитывая, что AM = МС, получим
cos 2a sin a cos a sin 2a
sin 4a = sin 2a sin 2a • (2 cos 2a — 1) = 0.
1 7Г
Так как 0 < 3a < 7г, то sin2a ф 0. Следовательно, cos2a = -, откуда a = —
2 6
и /.ABC = 3a = |.
Задача 9.
Доказать, что в любом треугольнике большей стороне соответствует меньшая биссектриса.
Идея. Воспользоваться формулой для биссектрисы, содержащей косинус половинного угла.
Указание. Использовать то, что в треугольнике напротив большей стороны лежит больший угол.
Решение. Пусть а - наибольшая сторона треугольника, тогда лежащий против
этой стороны угол а - наибольший угол треугольника. Биссектрисы, проведенные
а
2 ос • cos —
к сторонам а и Ъ треугольника, вычисляются по формулам 1а = — — и
о + с
2ас • cos ^
1ь = —. Сравним их:
а + с


4-1. Треугольники
477
Так как а > /3 и Ь < а, тоО< cos — < cos — < 1 и ba+bc < ba-\-ас. Следовательно,
Z Z
(у, (3
Ь (а + с) • cos — < а (Ь + с) • cos — и 1а < 1ь.
Задача 10.
Две биссектрисы у треугольника равны. Доказать, что он равнобедренный. Идея. Воспользоваться результатом предыдущей задачи.
Указание. В любом треугольнике большей стороне соответствует меньшая биссектриса.
Решение. Пусть la = lb. Предположим, что треугольник не является равнобедренным. Следовательно, Za ф Z/3. Для определенности пусть /.a > Z/3 и а > Ь. Так как в треугольнике большей стороне соответствует меньшая биссектриса, то 1а < 1ь. Получили противоречие, значит, наш треугольник равнобедренный.
Задача 11.
Доказать, что в равнобедренном треугольнике сумма расстояний от любой точки основания до боковых сторон равна боковой высоте.
Идея. Разрезать исходный треугольник на две части и использовать формулу площади через высоту.
Указание. Sabc — Sakb + Sbkc •
В
Решение. Пусть дан равнобедренный треугольник АВС, АВ = ВС, АН - высота и произвольная точка К на его основании АС. Проведем из точки К перпендикуляр КМ к стороне ВС и перпендикуляр KN к стороне АВ.
Sabc = Sakb + Sbkc <=>
<?=*■ \ah ■ вс = \nk ■ AB + \km ■ BC.
// Zi Zd
Так как AB = ВС, получим AH = NK -f KM. a
Задача 12.
В треугольнике ABC угол А прямой. Из вершины А проведены медиана AM, высота АН и биссектриса AL. Доказать, что AL - биссектриса в треугольнике АМН.
Идея. Выразить ZHAL, Z.MAL через углы треугольника.
Указание. ZH AL = ZM AL = ?-- ZABC.
4


478
Указания и решения
Решение. В любом треугольнике биссектриса лежит между медианой и высотой. Так как AM - медиана А АВС, проведенная из вершины прямого угла к гипотенузе, то AM = - ВС и ААВМ, ААСМ равнобедренные, тогда
/АВМ = /ВАМ = а и /MCA = /MAC = J - а.
Zt
А
Поскольку АН - высота треугольника, ZНАС = с*. Тогда /HAL = /LAC - /НАС =j-a,
/MAL = /MAC - /LAC = ^- а- т = т - а-
2 4 4
Следовательно, ZHAL = ZMAL, го есть AL - биссектриса угла MAH.
Задача 13.
Доказать, что из всех треугольников с данным основанием и данным углом, противолежащим основанию, равнобедренный треугольник имеет наибольшую площадь.
Идея. Наибольшую площадь будет иметь треугольник с наибольшей высотой. Указание. Геометрическим местом точек, из которых заданный отрезок виден под заданным углом, является дуга окружности.
Решение. Пусть даны сторона а и противолежащий ей угол а. Рассмотрим А АВС со стороной АВ = а и углом ZC = а. Опишем вокруг него окружность.
Найдём геометрическое место точек (в верхней полуплоскости относительно отрезка АВ), из которых данный отрезок а виден под заданным углом а.
Для любой точки лежащей на дуге АСВ,
Z.AC\B = а, для любой точки С\, лежащей вне окружности, ZАС\В < а, для любой точки С\, лежащей внутри окружности, Z.AC\B > а.
Следовательно, геометрическое место точек, из которых заданный отрезок виден под заданным углом, есть дуга окружности АСВ. Среди треугольников с вершинами на этой дуге наибольшую высоту, а, следовательно, и наибольшую площадь будет иметь равнобедренный треугольник АМВ.


4.1. Треугольники
479
Задача 14-
Доказать, что из всех треугольников с данным основанием и данным углом, противолежащим основанию, равнобедренный треугольник имеет наибольший периметр.
Идея. Использовать результат предыдущей задачи.
Указание. Использовать теорему косинусов и формулу площади треугольника через произведение сторон и синус угла.
Решение. Пусть даны сторона а и противолежащий ей угол а. По теореме косинусов
а2 — 62 + с2 — 26с cos а,
отсюда
62 + с2 + 26с = а2 + 26с(1 + cosa).
Так как площадь А АВС равна 5 = ~ 6с sin а, то 26с = -г—. И, следовательно,
2 sma
(6 + с)2 = a2 + -"^--(1 + cosa). sina
Значит, чем больше площадь, тем больше сумма сторон 6 и с, то есть наибольший периметр (как и наибольшая площадь) будет у равнобедренного треугольника.
Задача 15.
Доказать, что сумма медиан треугольника
а) меньше Р,
3
б) больше -Р, где Р - периметр треугольника.
Идея. Использовать неравенство треугольника.
Указание.
а) Достроить треугольник до параллелограмма.
б) Рассмотреть треугольник, образованный одной из сторон и отрезками медиан. Решение.
а) Достроим А АВС до параллелограмма АС ВС' (левый рисунок) и запишем неравенство треугольника для ААСС':
СС' < AC-V АС' <=> 2тс < а + 6.
Аналогичным образом можно получить неравенства 2ть < а + с, 2та < 6 + с. Сложив три эти неравенства и поделив на 2, получим
та + mb + тс < Р
б) Пусть медианы пересекаются в точке О (правый рисунок).


480
Указания и решения
Запишем неравенство треугольника для А АС О:
АС < СО + АО
b < -^(.ГПс + ТПа)
Аналогично можно получить неравенства для сторон а и с, сложив которые, получим
-{та + тъ + тс) > Р
та + тъ + тс> -Р,
что и требовалось доказать.
Задача 16.
Доказать, что сумма расстояний от любой точки, взятой внутри (или на стороне) треугольника, до трех его сторон заключена между наибольшей и наименьшей его высотами. Найти точку в треугольнике, сумма расстояний от которой до сторон наибольшая.
В
Идея. Разбить треугольник на три и записать его площадь через расстояния от точки до сторон.
Указание. В треугольнике из условия на длины сторон а > Ь > с следует условие на длины высот На<Нь< Нс.
Решение. Пусть На,Нь,Нс - высоты треугольника, опущенные на стороны а, Ь, с. Пусть для определенности а > b > с, тогда На < Нь < Нс и
clHq — *2Sаавс — ahd -J- bhb ^hq 5^ hb -t~ he),
cHc = 2Saabc = aha -b bhb + chc > c(ha -f- hb + hc).
Следовательно, Ha < ha -f hb + hc < Hc. Сумма расстояний от точки О до сторон треугольника принимает свое наибольшее значение, равное Нс, тогда, когда О совпадает с вершиной С.


4.1. Треугольники
481
Задача 17.
Какого вида треугольник, у которого медианы 3, 4 и 5?
Идея. Вычислить длины сторон треугольника.
Указание. Использовать формулы длины медианы.
Решение. Для трех медиан имеем
4тп2 = 2Ь2 + 2с2 - а2,
Ат2 - 2 а2 + 2с2 - Ь2,
Ат2 = 2а2 + 262 - с2.
Найдем а,Ь,с. Сложив второе и третье уравнения, получим
A(ml + тп2) = 4а2 + (Ь2 + с2).
Выразив отсюда (b2 + с2) и подставив в первое уравнение, получим
4то2 = 8(m2 + т2) - 9а2,
откуда
а2 = + 2т2 - т2).
Аналогичные формулы справедливы для b и с. В результате
а2 = ^ • 73, Ь2 = ^ • 52, с2 = ^ • 25.
9 9 9
Поскольку для квадрата большей стороны треугольника выполняется а2 < Ь2 + с2, треугольник является остроугольным.
Ответ. Остроугольный.
Задача 18.
Пусть а,/3,7 - углы треугольника. Доказать, что sina • sin/3 • sin7 <
Идея. Использовать оценку у/аЬс < — - .
о
Указание. С помощью тригонометрических преобразований доказать, что
• о • ^ 3\/3
sma + smp + sm7 < ——.
jL
16 Геометрия


482
Указания и решения
Решение. Покажем, что для углов треугольника справедливо неравенство
• « • ^ з>/5
sm а + sm р + sin 7 < —у.
Преобразуем левую часть неравенства следующим образом:
f Р +1\ {— l\ {Р +1\
sina -f sinp + sin7 = sina -f 2sin ( —-— J • cos ( —-— J < sina -f 2sin I —-— 1 =
^ к — a\ n . ol a Л a a/, a \
= sm a 4- 2 sm ( —-— 1 = 2 sm — cos — + 2 cos — = 2 cos — ( sm — + 11 .
\ z / z z z z \ z /
_ 3V3 __. a
Докажем, что это выражение не превосходит —у. Положим t = sin — и возведем
_ a / . а \ Зл/3 ___
неравенство 2 cos — ^sm — -f-1J < -у в квадрат. Получим
27 11
4(1 — £2)(t2 + 2£ + 1) < — <=> t4 + 2t3 - 2t + — > 0 «=»
(,-1)2.(12 + 3( + Н)>° (l-j)2>0.
Таким образом, доказана справедливость вспомогательного неравенства
• „ • _ 3%/3
sm a + sm р 4- sm 7 < ——.
Теперь перейдем к доказательству основного неравенства. Так как для трех
1 згт~ ^ а + b + с
положительных чисел а, о, с выполняется неравенство V аос < , то
о
3 Г :—Ъ—:— ^ sin а + sin /? + sin7 л/3 . . . / \/з\
ysma • sinp • sm7 < < —- <=$■ sma-smp-sin7 < I —
o 2 \ Z I
Задача 19.
Доказать, что для любого треугольника верно неравенство ha < у р ■ (р — а). Идея. Воспользоваться формулой Герона.
Указание. Приравнять друг другу выражения для площади через высоту и полупериметр и выразить из этого равенства высоту.
Решение. Площадь произвольного треугольника равна
s = оЛ« = (р — Ь)(р — С),
а + Ь + с
где р = . Отсюда получаем, что


4.1. Треугольники
483
гг 2л/(р — Ь) (р — с) __
Докажем, что —1 меньше единицы. Имеем
а
у/(р — Ь) (р — с) < - Ф=> (а + с — Ъ)'{а + Ъ — с)<а2 <=> а2 — (6 — с)2 < а2.
Получили верное неравенство, следовательно, ha < yjp • (р — а).
Задача 20.
Доказать, что для любого треугольника справедливо неравенство
Р
1 1 1 1 Л
1 г Н > 2 ( —Ь - Н— ) .
— а р — о р — с \а о с)
Идея. Воспользоваться формулой площади через высоту и формулой Герона. Указание. Использовать оценку предыдущей задачи для высоты: Л2 < р(р—а).
Решение. Домножим левую часть неравенства на S2 = р(р — а)(р — Ь)(р — с), первое слагаемое правой части на S2 = |/г2а2, второе на S'2 = \h2b2, третье на S2 = \h2c2. Получим
р{р — Ь)(р — с) + р(р — а)(р — с) + р(р -а)(р-Ь)>1 (ah\ + bhj + chi).
Поскольку h2 < р(р—a), h2 < p(p — b), h2 < р(р—с) (см. предыдущую задачу), нам достаточно доказать более сильное неравенство
Р(Р ~ Ь)(Р ~ с) +Р(Р “ °){Р ~ с) +Р(Р -а)(р-Ь)> ^(ар(р - а) + Ьр(р - Ъ) + ср(р - с)).
Поделим неравенство на р/2, перенесём всё в одну сторону и вынесем общие множители:
(р — а)(2р — 2с — а) + (р — Ь)(2р — 2а — Ъ) + (р — с)(2р — 26 — с) > 0.
Заменим во втором множителе каждого слагаемого 2р на а + b + с, получим
(р - а)(Ь -с) + (р- Ь)(с -а) + (р- с)(а - Ь) > 0.
Теперь заменим р на (а + b + с)/2 в первом множителе каждого слагаемого и приведём подобные члены. Получим 0 > 0. Таким образом, поскольку все преобразования были эквивалентными, неравенство доказано.


484
Указания и решения
4.2. 	Многоугольники Задача 1.
Доказать, что если каждая из диагоналей выпуклого четырехугольника делит его на равновеликие треугольники, то этот четырехугольник - параллелограмм.
Идея. Доказать, что диагонали четырехугольника точкой пересечения делятся пополам.
Указание. Показать, что перпендикуляры, опущенные из противолежащих вершин на диагональ, равны.
Решение. Пусть диагонали АС и BD четырехугольника ABCD пересекаются в точке О, Sabc = Sacd,
Sabd — Sbcd• Опустим перпендикуляры из точек В и D на диагональ АС.
Так как Sabc = \аС ■ ВН и Sacd = ^АС ■ DK, то А
ВН = DK. Отсюда следует, что АВН О — ADKO по катету и острому углу, следовательно, ВО = OD.
Аналогично доказывается, что АО = ОС. То есть диагонали четырехугольника ABCD точкой пересечения делятся пополам и, следовательно, он является параллелограммом.
Задача 2.
В равнобедренной трапеции диагональ имеет длину 8 и является биссектрисой одного из углов. Может ли одно из оснований этой трапеции быть меньше 4, а другое равно 5?
Идея. Для получения противоречия использовать неравенство треугольника и теорему синусов.
Указание. Рассмотреть отдельно случаи, когда диагональ является биссектрисой угла при большем основании трапеции и когда при меньшем.
Решение. Возможны два варианта: либо АС - в х с
биссектриса угла при большем основании трапе- /
ции, либо - при меньшем. / \
1) 	Пусть АС - биссектриса угла BAD и AD = 5, / s' Л
тогда \
/.ВАС = /CAD = /ВС А g * D
и ААВС равнобедренный, АВ = ВС. Следовательно, если ВС < 4, то
АВ + ВС < 8 = АС, то есть треугольник АВС не может существовать и этот вариант невозможен.


4.2. Многоугольники
485
2) 	Пусть АС - биссектриса угла BCD и AD = 5, тогда
ZBC А = ZACD = ZCAD = а
и AACD равнобедренный, следовательно, AD = CD = АВ = 5. Из AACD имеем cosa = 4/5, тогда
32 7
cos ZBCD = cos 2a = — — 1 = — >0,
25 25
то есть ZBCD острый, что противоречит условию.
Ответ. Нет.
Задача 3.
Доказать, что из всех прямоугольников с данной диагональю наибольшую площадь имеет квадрат.
Идея. Использовать формулу площади четырёхугольника через произведение диагоналей на синус угла между ними.
Указание. Из формулы площади четырёхугольника через произведение диагоналей на синус угла между ними следует, что максимальную площадь будет иметь прямоугольник, диагонали которого перпендикулярны.
Решение. Используем формулу площади через произведение диагоналей на синус угла между ними:
S = \d2 • sina < \d2.
2 “2
Следовательно, наибольшую площадь будет иметь прямоугольник, диагонали которого перпендикулярны, то есть квадрат.
Задача 4•
Какой четырехугольник с диагоналями d\ и б?2 имеет максимальную площадь?
Идея. Использовать формулу площади четырехугольника через диагонали и угол между ними.
Указание. S = -dic^sina.
Решение. Пусть a - угол между диагоналями четырехугольника ABCD, тогда
Sabcd = -di^sina < ~dic?2*
Следовательно, площадь четырехугольника ABCD достигает своего максималь-
_ 7Г
ного значения при sm a = 1. То есть a = — и диагонали четырехугольника взаимно перпендикулярны.
Ответ. Четырехугольник, у которого диагонали взаимно перпендикулярны.


486
Указания и решения
Задача 5.
Доказать, что если отрезок, соединяющий середины двух противоположных сторон выпуклого четырехугольника, равен полусумме двух других сторон, то этот четырехугольник - трапеция.
В
Идея. Разрезать четырехугольник на два треугольника и использовать свойство средних линий.
Указание. Средние линии полученных треугольников составляют отрезок, соединяющий середины двух противоположных сторон данного четырехугольника.
Решение. Рассмотрим четырехугольник ABCD, у которого точка М - середина стороны АВ, точка N - середина CD к точка О - середина диагонали BD.
Отрезки МО и NO - средние линии AABD и ABCD соответственно, следовательно,
МО = \aD, MO\\AD И NO = \вС, NO\\BC,
Zd £
то есть МО + NO = j- (AD + ВС). Но по условию задачи MN = ^ (AD + ВС),
значит, точки М, О и N лежат на одной прямой. Следовательно, MN\\AD и MN\\BC, то есть ABCD - трапеция.
Задача 6.
Доказать, что биссектрисы углов, прилежащих к одной из непараллельных сторон трапеции, пересекаются под прямым углом в точке, лежащей на средней линии трапеции (или её продолжении).
Идея. Использовать то, что сумма внутренних односторонних углов при параллельных прямых равна 180°.
Указание. Геометрическим местом точек, g
равноудаленных от двух параллельных пря- мых, является прямая, параллельная данным / \
и находящаяся на равном от них расстоянии. м / \
/ к
Решение. Рассмотрим трапецию ABCD.
Пусть АК и В К - биссектрисы углов BAD
и АВС соответственно. Пусть /.BAD = а, тогда /АВС = 7г — а и
/АКБ = п- 1/BAD - \/.АВС =
2 2 2
Осталось доказать, что точка К лежит на средней линии трапеции MN. Так как точка К лежит на биссектрисах углов А и В, то она равноудалена от сторон


4-2. Многоугольники
487
АВ, AD и ВС. Поскольку геометрическим местом точек, равноудаленных от двух параллельных прямых, является прямая, параллельная данным и находящаяся на равном от них расстоянии, точка К принадлежит средней линии MN трапеции ABCD (или её продолжению).
Задача 7.
В выпуклом четырехугольнике ABCD с диагоналями АС и BD на стороны CD и АВ опущены соответственно высоты АЕ и DF. Известно, что АЕ > BD, DF > АС, AD = 2 • АВ. Найти меры углов четырехугольника ABCD.
Идея. Точка Е совпадает с точкой С, точка F совпадает с точкой В. Указание. Использовать то, что перпендикуляр короче наклонной.
Решение. Рассмотрим выпуклый четырехугольник ABCD, отрезок АЕ перпендикулярен CD, отрезок DF перпендикулярен АВ.
В
АС > АЕ > BD и BD > DF > АС,
следовательно, АС = АЕ = DF = BD и точка Е совпадает с точкой С, точка F совпадает с точкой В. Следовательно, ZABD = Z.ACD = 90° и AABD равен AACD по гипотенузе и катету. Так как высоты, опущенные на гипотенузы, тоже равны, то AD || ВС и четырехугольник является трапецией.
По условию AD = 2 • АВ, значит,
ZBAD = ZCDA = 60° и ZABC = ZBCD = 120°.
Ответ. ZBAD = ZCDA = 60°, ZABC = ZBCD = 120°.
Задача 8.
В выпуклом четырехугольнике KLMN с диагоналями LN и КМ на стороны MN и KL опущены соответственно высоты КР и iVQ. Известно, что КР > LN, NQ > КМ, KL = 3, KN = 5. Найти КМ.
Идея. Как и в предыдущей задаче, показать, что все неравенства должны обратиться в равенства. Попробуйте доказать это самостоятельно.
Указание. Использовать то, что перпендикуляр короче наклонной.


488
Указания и решения
Решение. Пусть KLMN - данный четырехугольник. Так как перпендикуляр короче наклонной, справедливы неравенства
КМ > КР > LN и LN >NQ>KM,
следовательно, КМ = КР = LN = NQ и точка Р совпадает с точкой М, точка Q совпадает с точкой L.
М
N
Следовательно, Z.KLN = Z.KMN = 90 и AKLN равен AKMN по гипотенузе
и катету.
По теореме Пифагора LN = \/52 — З2 = 4. В результате КМ = LN = 4.
Ответ. КМ = 4.
Задача 9.
Дан выпуклый четырехугольник ABCD, у которого АВ + BD < АС + CD. Сравните длины отрезков АВ и АС.
Идея. Доказать вспомогательное неравенство: в любом выпуклом четырехугольнике сумма диагоналей больше суммы двух противоположных сторон. Указание. Использовать неравенство треугольника.
В
Решение. Пусть диагонали четырехугольника ABCD пересекаются в точке О.
Из неравенства треугольника для ААВО и ACDO следует, что
АВ < АО + ВО, CD < СО + DO.
Сложив эти неравенства, получим
AB + CD<AC + BD.
Теперь сложим исходное неравенство АВ + BD < АС + CD с полученным неравенством и приведём подобные члены:
{АВ + CD) + (АВ + BD) < {АС + BD) + (АС + CD) Ответ. АВ < АС.
АВ < АС.


4-3. Окружности
489
4.3. 	Окружности Задача 1.
Докажите, что в прямоугольном треугольнике сумма длин катетов равна сумме длин диаметров вписанной и описанной окружностей.
Идея. Использовать теорему о равенстве касательных, проведённых из одной точки.
Указание. Гипотенуза прямоугольного треугольника равна диаметру описанной окружности.
Решение. Рассмотрим треугольник АВС. Пусть М, N,
К - точки касания вписанной в треугольник окружности со сторонами, a R и г - радиусы описанной и вписанной в треугольник окружностей.
Четырехугольник OMCN - квадрат и, следовательно,
СМ = CN = г. По теореме о равенстве касательных, проведённых из одной точки к окружности, имеем ВК = BN,
AM = АК. Тогда получаем, что
АС + ВС = г + AM + г + BN = 2г + АК + ВК = 2г + АВ.
Так как гипотенуза прямоугольного треугольника равна диаметру описанной окружности, то АС + ВС = 2г + 2R.
В
Задача 2.
В круг вписаны две трапеции с соответственно параллельными сторонами. Докажите, что диагонали этих трапеций равны.
Идея. Выразить диагонали с помощью теоремы синусов.
Указание. Рассмотреть треугольники, на которые диагональ разбивает трапецию.
Решение. Пусть стороны трапеции ABCD параллельны соответствующим сторонам трапеции A'B'C'D'. Рассмотрим AABD.
Обозначим /.BAD через а. По теореме синусов
BD
= 2 R <£=> BD = 2Rsina.
sina
Теперь рассмотрим треугольник А! В' D'. У него ZB'A'D' = /.BAD = а, следовательно, по теореме синусов B'Df = 2i2sina = BD.


490
Указания и решения
Задача 3.
Может ли у треугольника со сторонами меньше 1 радиус описанной окружности быть больше 100?
Идея. Привести соответствующий пример.
Указание. Сначала построить окружность, потом вписанный в неё треугольник.
Решение. Рассмотрим окружность радиуса больше 100 и произвольную точку А на ней. Отложим на окружности от точки А точки В и С на расстоянии 1/2. Стороны полученного треугольника будут меньше 1.
Ответ. Да.
Задача 4-
Доказать, что касательные к двум пересекающимся окружностям, проведённые из любой точки продолжения их общей хорды, равны между собой.
Идея. Использовать свойство касательных и секущих, проведённых из одной точки.
Указание. Квадрат длины отрезка касательной равен произведению длины отрезка секущей на длину её внешней части.
Решение. Пусть окружности пересекаются в точках А и В. Рассмотрим произвольную точку М на прямой АВ и проведем касательные МС и МО.
Так как квадрат длины отрезка касательной равен произведению длины отрезка секущей на длину её внешней части, то
МС2 = МА ■ MB и МС'2 — МА ■ MB =>
Задача 5.
В окружности проведены равные пересекающиеся хорды. Доказать, что соответствующие части этих хорд, на которые они делятся точкой пересечения, равны.
Идея. Использовать свойство пересекающихся хорд.
Указание. Произведения длин отрезков двух пересекающихся хорд равны.
МС = МС'.
Решение. Пусть хорды АВ и CD пересекаются в точке Q и А В — CD = а.


4.3. Окружности
491
Положим AQ = х, CQ = ?/, тогда PQ = а — х, DQ = а — у. По свойству пересекающихся хорд получаем
AQ • BQ = CQ х{а - х) = у(а - у) а(х - у) = х2 - у2 (.х - у) (а - х - у) = О
А
D
То есть либо х = у, либо х = а — у, что и требовалось доказать.
Задача 6.
Через точки пересечения двух окружностей РиР' проводятся произвольные прямые, пересекающие окружности. Через точки пересечения этих прямых с окружностями проводятся прямые шит'. Доказать, что т параллельна ш'.
Идея. Рассмотреть два случая: отрезки прямых, проходящих через точки Р и Р', лежащие внутри окружностей, не пересекаются и пересекаются. В первом случае доказать, что сумма внутренних односторонних углов при пересечении секущей прямых шит' равна 180°. Во втором случае доказать, что внутренние накрест лежащие углы при пересечении секущей прямых шит' равны. Указание. Использовать то, что у вписанного четырехугольника сумма противоположных углов равна 180°.
Решение. Рассмотрим два случая: отрезки прямых, проходящих через точки Р и Р', лежащие внутри окружностей, не пересекаются и пересекаются.
1 случай (отрезки А А' и В В' не пересекаются).
Покажем, что ZАВР' + /.А'В'Р' = 180°.
Пусть /.А'В'Р1 = а. Так как у вписанного четырехугольника сумма противоположных углов равна 180°, то /Л'РР' = 180° — а и смежный с ним угол ZAPPf = а. Поскольку четырехугольник АРР'В также является вписанным, /АВР' = 180° — а.
Мы доказали, что /АВР' + /.А'В'Р' = 180°, и, следовательно, прямые т и т' параллельны.
2 случай (отрезки А А! и В В' пересекаются).
Покажем, что /АВР' = /А!В'Р'.
т’
т


492
Указания и решения
Пусть /А'В'Р' = а. Так как у вписанного четырехугольника сумма противоположных углов равна 180°, то /А'РР' = 180° — а и смежный с ним угол /АРР' = а. Поскольку угол АВР' опирается на ту же дугу, что и угол АРР', то /.АВР' = а.
Мы доказали, что /.АВР' = /А'В'Р', и, следовательно, прямые шит' параллельны.
Задача 7.
К двум непересекающимся окружностям проведены две общие внешние касательные и внутренняя. Точки М и N - точки касания внешней касательной с окружностями, а Р и Q - точки пересечения внутренней касательной с внешними. Доказать, что MN = PQ.
Идея. Использовать равенство касательных, проведенных из одной точки. Указание. Продолжить внешние касательные до пересечения и выразить MN и PQ через отрезки касательных.
Решение. Продолжим две внешние касательные до пересечения в точке S. По свойству касательных, проведённых из точки 5, имеем SN = ST и SM = SK, откуда MN = КТ.
По свойству касательных, проведенных из точек Р и Q, имеем PM = РР', PN = PQ',
QT = QQ', = QP', откуда следует, что
2-MN = МИЛ-КТ = MP+PW+tfQ+QT = PP'+PQ'+QP'+QQ' = 2PQ. Следовательно, MiV = PQ.
Задача 8.
К двум окружностям с центрами Oi и О2, касающимся внешним образом в точке А, проведена общая касательная ВС (В и С - точки касания). Доказать, что угол ВАС прямой.
Идея. Использовать то, что угол между касательной и хордой измеряется половиной меры дуги, стягиваемой этой хордой.
Указание. Сделать дополнительное построение - провести общую внутреннюю касательную.
Решение. Через точку А касания окружностей проведем их общую внутреннюю касательную АК.


4-4- Площади
493
Так как O1BWO2C, то ZВО\А + ZAO2C = 7г. По свойству угла между касательной и хордой получим
ZBAK = \zBOiA, ZCAK = -ZA02C.
2 2
Тогда
ZBAC = ZBAK + ZCAK = i {ZBO^A + ZA02C) = J-
z z
4.4. 	Площади Задача 1.
В выпуклом четырехугольнике ABCD известно, что АВ = а, ВС = 6, C-D = с, DA = d. Доказать, что для его площади S имеет место неравенство
S < | (ab + cd).
В каких случаях это неравенство обращается в равенство?
Идея. Разрезать четырехугольник на два треугольника и у каждого из них оценить площадь.
Указание. Максимум достигается, когда синусы соответствующих углов равны 1.
Решение. Проведем диагональ АС в четырехугольнике ABCD. Имеем
Sabcd = Sabc + Sacd =
= ^ (ab sin ZB + cd sin ZD) < - (ab + cd). z z
Равенство достигается, когда оба синуса рав- м d и
ны 1, то есть ZB = ZD = 90°.
Ответ. Равенство достигается, когда ZB = ZD = 90°.
Задача 2.
Все стороны выпуклого четырехугольника меньше 7. Доказать, что его площадь
строго меньше 50.
Идея. Воспользоваться результатом предыдущей задачи.
Указание. S<-(ab + cd).
Решение. В предыдущей задаче было доказано, что у четырехугольника со сторонами а, Ь, с, d площадь
S < i (ab + cd).
Следовательно, 5 < 49 < 50, что и требовалось доказать.


494
Указания и решения
Задача 3.
В треугольнике АВС заданы длины двух его сторон а и 6. Доказать, что для его
а2 4- Ь2
площади Ь справедливо неравенство Ь < —-—. В каком случае это неравенство обращается в равенство?
Идея. В качестве S взять половину произведения сторон на синус угла между ними.
Указание. Для получения оценки площади воспользоваться неравенством, связывающим среднее арифметическое и среднее геометрическое двух чисел.
Решение. Пусть а - угол между сторонами а и Ь. Тогда
о 1 7 . 1 7 а2 + Ь2
Ь = -absina < -ab < —.
2 ~ 2 - 4
Здесь мы воспользовались тем, что среднее геометрическое двух чисел не превосходит среднего арифметического. Первое неравенство обращается в равенство
при sina = 1, второе - при а = Ь. Следовательно, S = — У равнобедренного
прямоугольного треугольника.
Ответ. Неравенство обращается в равенство, если а и b - равные катеты прямоугольного треугольника.
Задача 4-
Может ли уменьшиться площадь треугольника при увеличении всех его сторон? Идея. Привести соответствующий пример.
Решение. В качестве первого треугольника возьмем равносторонний треугольник со стороной а = 1 и площадью S\ = В качестве второго треугольника
возьмем равнобедренный треугольник со сторонами а = 2, Ь = с = 1,01 и площадью 52 = х/0,0201 < Si.
Ответ. Может.


5.1. Алгебраический метод
495
5. Задачи на построение
5.1. 	Алгебраический метод
Задача 1.
Дан отрезок а. Построить отрезок х = а • у/п, п £ N.
Идея. Использовать построение отрезка х = у/аЬ.
Указание. Сначала построить отрезок b = п • а.
Решение. Сначала надо построить отрезок b = п • а, потом х = \/а6. В результате получим, что х = а • у/п.
Задача 2.
Даны отрезки а, Ь, с. Построить отрезок х = у/о? + Ь2 + с2.
Идея. Использовать построение отрезка х = у/а2 + Ъ2.
Указание. Построить прямоугольный треугольник с катетами а и 6. Его гипотенуза d равна л/а2 + 62 •
Решение. Построим прямоугольный треугольник с катетами а и Ъ. Его гипотенуза d равна \/а2 + Ь2. Теперь построим прямоугольный треугольник с катетами d и с. Искомым отрезком будет гипотенуза этого треугольника.
Задача 3.
Дан отрезок а. Построить отрезок х = а • у/2.
Идея. Использовать построение отрезка х = y/ab, где 6 = л/2 • а.
Указание, b = л/2 • а - гипотенуза равнобедренного прямоугольного треугольника с катетами, равными а.
Решение. Построим прямоугольный треугольник с катетами, равными а. Его гипотенуза b будет равна у/2-а. Теперь, построив отрезок х = y/ab, получим, что х = а • ^2.
Задача 4-
а1995
Даны отрезки а, Ь. Построить отрезок х = .
Идея. Использовать построение отрезка ^.
Указание. Построить отрезок .
О


496
Указания и решения
а3
Указание. Построить отрезок и т.д.
ег
^ ^ т ас
Решение. По трем известным отрезкам а,о,с мы умеем строить отрезок —, значит, мы умеем домножать отрезок на отношение известных отрезков.
а о? _
Домножив отрезок ана - , получим отрезок длины —. Домножив полученный
b о
а а3
отрезок на -, получим отрезок длины —г. Проделав эту процедуру 1994 раза, о bz
получим искомый отрезок.
Замечание. При решении этой задачи, так же как и остальных задач на построение, не надо проводить все построения, достаточно рассказать схему.
Задача 5.
Даны два отрезка: длины 1 и длины а. С помощью циркуля и линейки построить отрезок длины х = v^a3 — 4а2 -Ь За.
Идея. Использовать построение отрезка х = л/ab.
Указание. Разложить подкоренное выражение на множители:
х = у/а3 — 4 a2 + 3a = у/а - (а — 3) • (a — 1) • 1.
Указание. Построить сначала отрезки у = у/а (а — 3) и z = у/(а — 1) • 1.
Решение. Разложим подкоренное выражение на множители:
х = у/а3 — 4а2 + За = у/а • (а — 3) • (а — 1) • 1.
Построим сначала отрезки у = у/а • (а — 3) и z = а потом отрезок
х = VF7*- Задача 6.
тт г-, а3 + Ь3
Даны отрезки а, о. Построить отрезок х = —5—рг.
аг + о
Идея. Использовать все четыре приведенные в теоретической части формулы. Указание. Разложить числитель дроби на множители
а3 + Ъ3 (а + Ь) (а2 — ab + b2)
* = = '
Указание. Последовательно построить отрезки:
с = \/a2 Н- 62, d=Vab, е= у/с2 — d2, / = -
с


5.1. Алгебраический метод
497
Решение. Разложим числитель дроби на множители
а3 4- Ь3 (а + b) (а2 — ab + Ь2)
а2 + Ъ2 а2 + 62
и будем последовательно строить отрезки:
с = у/а2 Л- b2, d = \/а6, е = \/с2 — d2, / = ^Q ~^~ ^е.
с
Искомый отрезок х = —.
Задача 7.
Построить треугольник АВС, если известна биссектриса BD и отрезки AD и DC, на которые она делит противоположную сторону.
Идея. Сначала построить две другие стороны треугольника.
Указание. Пусть биссектриса BD равна Z, отрезки AD = р, DC = q. Тогда по свойству биссектрисы боковые стороны АВ = кр, ВС = fcg. По формуле для биссектрисы:
/2 12
12 = k2pq — pq <=> — = k2q — q <=> k2q = b <?.
Указание. Построить боковую сторону fcg = yjk2q •q.
Решение. Пусть биссектриса BD равна I, отрезки AD = р, DC = <7. Тогда по свойству биссектрисы боковые стороны А В = кр, ВС = kq.
По формуле для биссектрисы имеем
Z2 = k2pq — pq
12
12 I*
— = kq
P
Отрезок длины — мы можем построить, следователь- Р
но, можем построить и
,2 12 k2q = t-q.
Р
Теперь построим боковую сторону kq = \/k2q • q. Аналогично строим сторону кр. Осталось построить треугольник по трём сторонам.
Замечание. Эту задачу можно было решить и чисто геометрически, например с помощью окружности Аполлония.


498
Указания и решения
Задача 8.
Построить треугольник по основанию a, ha и у/Ь2 — с2.
Идея. Сравнить а и у/Ь2 — с2, чтобы определить, где лежит основание высоты: на стороне ВС или на продолжении стороны ВС.
Указание. Найти расстояние от точки В до основания высоты.
Указание. Рассмотреть три случая возможного расположения основания высоты относительно отрезка ВС.
Решение. Пусть точка Н - основание высоты ha •
Положим ВН = х, d = у/Ь2 — с2. Рассмотрим три случая расположения точки Н на прямой ВС.
1) 	Если Н G ВС, то СН = а — х. По теореме Пифагора
b2 = h2a + (a-x)2, c2 = h2a+x2,
откуда
Ь2 — с2 = а2 — 2 ах
х =
l-d2 2 а
Для неотрицательности х достаточно, чтобы а > d.
В этом случае сначала надо построить отрезок у = у/а2 — d2, потом х =
У- У
2а
2) Точка Н не может лежать левее С, так как тогда нарушается условие неотрицательности подкоренного выражения у/b2 — с2, поскольку в этом случае b < с.
3) Если Н лежит правее В, то СН = а + х.
По теореме Пифагора А
Ъ2 = h2 + (а + ж)2, с2
Л2 + *2,
d2-a2
2 а
откуда Ь2 — с2 = а2 + 2ах ж =
Для неотрицательности ж достаточно, чтобы а < d. В этом случае сначала надо построить отрезок у = л/d2 — а2, потом
^ 2/ * 2/ ж = ——.
2 а
В результате общая последовательность действий такова.
а) Если d = у/Ь2 — с2 = 0, то Ь = с и нам надо построить равнобедренный треугольник по основанию и высоте (восстановленной из середины основания).
б) Если а = d, то х = 0 и, следовательно, точки В и Н совпадают; нам надо построить прямоугольный треугольник по двум катетам а и ha-
в) Если а > d, то основание высоты лежит на отрезке ВС и построение надо выполнять согласно пункту 1.
г) Если а < d, то построение надо выполнять согласно пункту 3.


5.1. Алгебраический метод
499
Задача 9.
Построить окружность, проходящую через две данные точки и касающуюся данной прямой.
Идея. Найти точку касания окружности и данной прямой. Рассмотреть два случая: прямая, проходящая через две данные точки, параллельна данной прямой и не параллельна.
Указание. Если прямая, проходящая через две данные точки, не параллельна данной прямой, то точку касания найти, используя свойство секущей и касательной, проведённых к окружности из одной точки.
Решение. Пусть даны точки А, В и прямая га. Рассмотрим два случая.
1) Отрезок АВ не параллелен прямой га. Пусть С - точка касания, а К - точка пересечения прямых га и АВ. По свойству секущей и касательной, проведённых к окружности из одной точки, имеем С К2 = АК • ВК. Следовательно, от точки К на прямой га надо отложить отрезок С К = VАК • В К и построить окружность по трём точкам А, В и С.
2) Если отрезок АВ параллелен прямой га, то точка касания С есть точка пересечения серединного перпендикуляра к АВ с прямой га. Осталось построить окружность по трём точкам А, В и С.
Задача 10.
Построить прямоугольный треугольник по гипотенузе с и сумме катетов s.
Идея. Используя теорему Пифагора, выразить длину одного из катетов через гипотенузу и сумму катетов.
Указание. Пусть х - длина одного из катетов, тогда длина другого s — x и по теореме Пифагора
с2 = х2 -f (s — х)2 <==> 2х2 — 2sx + s2 — с2 = О х = - ± ^ \/2с2 — s2.
Решение. Пусть х - длина одного из катетов, тогда длина другого s — x и по теореме Пифагора
с2 = х2 + (s — х)2 <=> 2х2 — 2sx + s2 - с2 = О,
s 1
откуда при 2с2 > s2 имеем х = - ± -\/2с2 — «2, а такие отрезки мы уже умеем строить. Осталось по катету и гипотенузе построить прямоугольный треугольник.


500
Указания и решения
Задача 11.
Дан угол в 19°, построить угол в 1°.
Идея. 192 = 361.
Указание. Отложить от произвольного луча 19 раз угол 19°.
Решение. Отложим от произвольного луча 19 раз угол 19°. Острый угол между исходным и полученным лучами будет равен 1°.
Задача 12.
Дан отрезок длины а и угол, равный а. Построить отрезки длины
а а
a cos о;, a since, , — , а- tga, a-ctg а.
cos a sm а
Идея. Использовать соотношения в прямоугольном треугольнике.
Указание. Построить прямоугольный треугольник по гипотенузе а и острому углу, равному а. Его катеты будут равны a cos а и a sin а.
Решение. 1) Построим прямоугольный треугольник по гипотенузе а и острому углу, равному а. Его катеты будут равны a cos а и a sin а.
2) Построим прямоугольный треугольник по катету а и прилежащему углу, рав-
_ ^ а
ному а. Тогда его гипотенуза будет равна , а второй катет а • tg а.
cos a
3) Построим прямоугольный треугольник по катету а и противолежащему углу,
а
равному а. Тогда его гипотенуза будет равна — , а второй катет а • ctg а.
sina
Задача 13.
Дан равносторонний треугольник АВС со стороной 1. Через вершину А с помощью циркуля и линейки провести такую прямую, что сумма расстояний от точек В и С до этой прямой равна у/2.
Идея. Расстояние от основания высоты АН до этой прямой равно у/2/2. Указание. На АН как на диаметре построить окружность. С центром в точ-
тт \/2
ке Н провести окружность радиусом . В пересечении двух окружностей получится вторая точка прямой.


5.1. Алгебраический метод
501
Решение. Пусть нужная прямая уже построена, а С", В' ,Н' - проекции на неё точек С, В и Н, где Н - основание высоты АН.
В прямоугольной трапеции С'СВВ' отрезок НН' будет средней линией и, следовательно,
НН' = (СС' + В В')/2 = у/2/2.
На АН как на диаметре строим окружность. С центром в точке Н проводим окруж-
^ R
ность радиусом . В пересечении двух окружностей получим две искомые точки Н'.
Задача 14-
Дан ААВС. Построить отрезок DE с концами на сторонах АВ и ВС так, что DE || АС и DE виден из середины АС под прямым углом.
Идея. Предположить, что отрезок DE построен, и найти, на каком расстоянии от точки В он пересекает медиану ВМ, выражая это расстояние через элементы треугольника.
Указание. Используя подобие, выразить длину отрезка медианы от вершины до точки пересечения с отрезком DE через половину основания АС и длину медианы ВМ.
Решение. Пусть отрезок DE уже постро- В
ен. Обозначим медиану ВМ = Ь и половину основания AM = а и выразим длину DE через а и Ь.
Из параллельности прямых АС и DE следует равенство соответствующих углов ААВС и ADBE. Следовательно, они подобны с некоторым коэффициентом к. Тогда DL = ка, BL = и, так как медиана прямо¬
угольного треугольника равна половине гипотенузы, LM = DL — ка.
В результате получаем А
b Ь2
ВМ = BL+LM <=> Ъ = kb+ka <=> к = => BL = -.
a -j- о а + о
Для того чтобы построить отрезок DE, надо на медиане ВМ отложить отре- Ъ2
зок BL = и провести через точку L прямую параллельно АС. Она пересечёт
а + о
стороны АВ и ВС в точках D и Е.


502
Указания и решения
Задача 15.
Построить угол, равный трём градусам.
Идея. Построить углы, равные 15° и 18°.
Указание. 15 = - • - • 60. В равностороннем треугольнике все углы равны 60°.
Указание. Для вычисления sin 18° использовать равенство sin36° = cos54°.
Решение. Сначала построим угол 15°. Для этого построим равносторонний треугольник и дважды поделим один из его углов пополам.
Теперь построим угол 18°. После этого, отняв от него угол 15°, получим искомый угол 3°.
Для вычисления sin 18° используем равенство
sin(2 • 18°) = sin36° = cos(90° - 36°) = cos54° = cos(3 • 18°).
Распишем синус двойного угла и косинус тройного угла
2 sin 18° cos 18° = 4 cos3 18° — 3 cos 18°.
Сократив на cos 18° и заменив cos2 18° на 1 — sin2 18°, получим
4 sin2 18° + 2 sin 18° -1 = 0,
у/b — 1
откуда, с учётом положительности sin 18°, находим sin 18° = —-—.
Построим угол с таким синусом. Возьмём произвольный отрезок длины а и построим отрезок длины с = (у/b + 1 )а. Потом построим прямоугольный треугольник с гипотенузой с и катетом а. Синус угла против катета а будет равен л/5 — 1
—-— . Отняв от него угол 15°, получим искомый угол 3°.
Замечание. Теперь, имея угол 3°, мы сможем построить любой, кратный ему угол.
Задача 16.
С помощью циркуля и линейки разделите угол 54° на три равные части.
Идея. Построить угол 18°.
Указание. Вычислить sin 18°.
Указание. Смотри предыдущую задачу.
Решение. Проведём внутри исходного угла два луча, составляющие со сторонами угла 18° (см. пред. задачу). Эти лучи разделят угол на три равные части.
Задача 17.
Провести прямую, параллельную диагонали и пересекающую две смежные стороны данного прямоугольника так, чтобы его площадь разделилась в отношении 1:3.


5.2. Метод геометрических мест точек
503
Идея. Использовать подобие. g С' С
Указание. Прямая отсекает треугольник, площадь которого в два раза меньше площади половины прямоугольника.
Указание. Стороны получившегося треугольника относятся к сторонам прямоугольника как 1 : у/2. д.
Решение. Пусть А! С' - искомая прямая. Из условия следует, что A q
Sa'bc' = т Sabcd = -Sabc•
4 2
Из параллельности прямых АС и А'С' следует подобие треугольников А'ВС' и АВС. Так как их площади относятся как 1 : 2, то коэффициент подобия равен 1/у/2. Пусть АВ = a, J9C = 6, тогда = а/у/2, Ж7' = Ь/у/2. Отрезок длины а/\/2 можно получить, построив равнобедренный прямоугольный треугольник с гипотенузой а. Катеты такого треугольника будут иметь длину а/у/2.
Аналогично строится отрезок ВС' — Ь/у/2. Прямая, проходящая через точки А! и С", будет искомой прямой, то есть будет делить площадь прямоугольника в отношении 1:3.
5.2. 	Метод геометрических мест точек.
Задача 1.
По данной дуге окружности «бегает» точка М. Хорда АВ фиксирована. Какую кривую при этом пробегает в треугольнике АМВ точка пересечения высот?
Идея. Найти угол между высотами, опущенными из точек А и В.
Указание. Угол треугольника при вершине М постоянный.
Решение. Если точка М принадлежит дуге окружности, то угол АМВ постоянен. Обозначим его через а. Пусть Р и Q — основания высот, опущенных из точек А и В, а Н — точка их пересечения.
Из четырёхугольника PHQM получим:
ZPHQ = 180° - а.
Следовательно, /.АНВ — /PHQ = 180° — а, как вертикальный. Значит, ГМТ пересечения высот - это дуга, опирающаяся на отрезок АВ и содержащая вписанные углы с градусной мерой 180° - а.
С’


504
Указания и решения
Задача 2.
Построить треугольник по заданной стороне, противолежащему ей углу и проведённой к ней высоте.
Идея. Найти ГМТ, из которых данный отрезок виден под данным углом. Указание. Используя высоту, найти требуемый треугольник. Провести анализ: при каких соотношениях между данными задачи такой треугольник существует.
Решение. Пусть дана сторона А В, равная с, и противолежащий ей угол 7. Сначала построим дугу, из каждой точки которой отрезок А В виден под углом 7 (см. замечание).
Для того чтобы найти точку С, проведём параллельную АВ прямую т на расстоянии, равном высоте h.
о
В случае h <
2tg|
эта прямая пере¬
сечёт окружность в двух точках С и С" и мы получим два симметричных треугольника АВС и АВС', обладающих заданными элементами. Л
Если h
При h >
2 tg
7
, то треугольник будет единственным.
решении нет.
Замечание. Для того чтобы построить дугу, из каждой точки которой отрезок длины с виден под углом 7, достаточно описать окружность вокруг прямоугольного треугольника, построенного по катету АВ — с и острому углу ZАСВ — 7.
Из всех точек дуги АСВ отрезок АВ будет виден под углом 7.
Задача 3.
По сторонам прямого угла скользит гипотенуза прямоугольного треугольника. Найти геометрическое место вершин прямого угла этого треугольника.
Идея. Вокруг получившегося четырёхугольника можно описать окружность. Указание. Вписанные углы, опирающиеся на одну хорду, равны.
Решение. Пусть АВМ — заданный прямоугольный треугольник. Рассмотрим четырёхугольник AM ВО. Так как у него ZM + /О = 180°, то вокруг него можно описать окружность.
Тогда ZМОВ = /.МАВ = а, как опирающиеся на одну дугу, то есть отрезок MB виден из О под постоянным углом а.


5.2. Метод геометрических мест точек
505
L
Искомое ГМТ - это отрезок PQ на луче OL, где Р и Q - крайние положения точки М, когда гипотенуза треугольника оказывается на одной из сторон данного угла.
Задача 4-
Построить треугольник по двум сторонам и высоте, опущенной на одну из этих сторон.
на расстоянии, равном высоте.
Решение. Пусть даны стороны а,Ь и высота ha. Построим отрезок ВС = а и проведём прямую га || ВС на расстоянии, равном ha. Теперь из точки С раствором циркуля, равным 6, сделаем засечки на прямой га.
При b> ha мы получим две точки А' и А" и, следовательно, два треугольника А'ВС и А"ВС. Если b = /г0, то треугольник будет единственным. При b < ha решений нет.
Задача 5.
Построить треугольник по а, а, г.
Идея. Построить треугольник ВОС, где ВС = а, О - центр вписанной окружности.
Указание. В АВОС известны сторона ВС = а, высота, равная г, и угол
Указание. ГМТ вершин треугольников с данными основанием и высотой - прямая, параллельная основанию и находящаяся от него
Идея. Найти ГМТ вершин треугольников с данными основанием и высотой.


506
Указания и решения
Решение. Рассмотрим треугольник АВС со стороной ВС = а и углом ВАС, равным а, в который вписана окружность с центром в точке О радиуса г. Пусть /.АВС — /3, /АСВ — 7, тогда /3 4- 7 = 7г — а.
Так как ВО и СО - биссектрисы углов АВС и АСВ соответственно, то
в 4- тг 4-су
/ВОС = тг - /ОВС - /ОСВ = тг - = -4—.
2 2 А
В треугольнике ВОС известны сторона ВС = а, вы- сота ОК = г и /ВОС =
2
Следовательно, АВОС можно построить по стороне, противолежащему ей углу и высоте, опущенной на эту сторону. Потом от отрезков О В и ОС надо отложить углы, равные /О В К и /ОС К, стороны которых пересекутся в вершине А треугольника АВС.
Задача 6.
Построить треугольник по а, г, R.
Идея. Свести задачу к предыдущей.
Указание. Вписать в окружность радиуса R угол, равный а. Длина хорды, на которую он будет опираться, будет равна а.
Решение. Впишем в окружность радиуса R угол, равный а. Длина хорды, на которую он будет опираться, будет равна а. Таким образом, задача свелась к предыдущей.
Задача 7.
Построить треугольник по а, г, R.
Идея. Свести задачу к предыдущей.
Указание. Из произвольной точки окружности радиуса R раствором циркуля, равным а, отложить хорду. Угол, опирающийся на неё, равен а.
Решение. Рассмотрим окружность радиуса R. Из произвольной точки окружности раствором циркуля, равным а, отложим хорду. Угол, опирающийся на неё, равен а. Таким образом, задача свелась к предыдущей.
Задача 8.
Построить треугольник по а, /3, г.
Идея. Построить треугольник по двум углам а/2, /3/2 и высоте, равной г.


5.2. Метод геометрических мест точек
507
Указание. Пусть О - центр вписанной в треугольник АВС окружности. В треугольнике АВО известны два угла а/2, /3/2 и высота, равная г.
Решение. Пусть О - центр вписанной в треугольник АВС окружности. Мы можем построить треугольник АВО по двум углам а/2, /3/2 и высоте, равной г.
Для того чтобы построить точку С, достаточно отложить от отрезка АВ углы, равные а и /3.
Задача 9.
Построить треугольник по заданной стороне а, противолежащему ей углу а и проведённой к ней медиане та.
Идея. Построить геометрическое место точек, из которых отрезок а виден под углом а.
Указание. Рассмотреть три случая: угол а - прямой, острый, тупой. Провести анализ: при каких соотношениях на данные задачи есть решение.
Решение. Построим отрезок АВ, равный а, и дугу, из любой точки которой отрезок виден под углом а. Обозначим через М середину отрезка АВ. Рассмотрим следующие случаи.
1) 	Если угол а прямой и та ф ^, то решений нет. При та = ^ решений бесконечно много, так как любой треугольник с вершиной С, взятой на окружности с диаметром АВ, удовлетворяет
С
аК Цв
2) Пусть угол а острый. Сделаем засечки радиусом, равным та, из точки М на
_ а а а .
дуге, вмещающей угол а. При - < та < — ctg — мы получим две точки С и С
такие, что оба треугольника АВС и АВС' обладают заданными элементами. При а а
тпа — 2С^~2 точки и совпадают.
3) Если угол а тупой, то засечки из М радиусом та на дуге, вмещающей угол
^ а а а _ а а
а, дадут две точки С и С при - ctg — < та < —. При та = - ctg — точки С и
Z Z Z Z Z
С' совпадут. В противном случае решений не будет.
условиям задачи.
С'
В А
М
i В
С


508
Указания и решения
Задача 10.
Построить параллелограмм по углу и диагоналям.
Идея. Использовать результат предыдущей задачи.
Указание. Построить треугольник по углу, противолежащей ему диагонали и половине второй диагонали.
Решение. Пусть даны отрезки di,d2 и Za. Отрезок АО будет медианой в AABD. После того, как мы построим AABD по стороне BD = б?2, медиане АО = di/2 и углу а (см. пред. задачу) нам останется построить точку С. Для этого достаточно отложить отрезок ОС — d\/2 от точки О на прямой АО.
Задача 11.
Построить треугольник по стороне, высоте, опущенной на эту сторону, и медиане другой стороны.
Идея. Построить прямую, на которой лежит основание медианы.
Указание. Основание медианы лежит на прямой, параллельной известной стороне и отстоящей от неё на расстоянии, равном половине высоты.
Решение. Пусть даны a, ha, гпь. Сначала построим отрезок ВС длины а и параллельно ему прямую т на расстоянии, равном ha/2. На этой прямой раствором циркуля, равным тъ, сделаем две засечки М*, % — 1;2. Отложив от точки Мг отрезок длины С Mi, получим точку Ai, отстоящую от прямой ВС на расстоянии ha.
Ai А2
Таким образом, мы получили два треугольника AAiBC и ДА2ВС с заданными элементами. Задача имеет решение при гщ > ha/2.
Замечание. В случае, когда ть = haj2, точки А\ и .42 совпадают.


5.2. Метод геометрических мест точек
509
Задача 12.
Дана окружность и точка А, лежащая вне круга, ограниченного окружностью. Построить касательные к окружности, проходящие через эту точку.
Идея. Использовать свойство касательной.
Указание. Касательная перпендикулярна радиусу. На отрезке АО как на диаметре построить окружность (О - центр окружности).
Решение. Для начала найдём центр окружности. Возьмём произвольно три точки на окружности и проведём серединные перпендикуляры к полученным отрезкам. Они пересекутся в точке О, которая является центром описанной вокруг построенного треугольника окружности.
Теперь, когда найден центр окружности, построим на отрезке АО как на диаметре другую окружность. Получим точки В и В'. Углы ZАВО = /АВ'О = 90° как опирающиеся на диаметр АО. Следовательно, отрезки АВ и АВ' перпендикулярны радиусам исходной окружности и являются искомыми касательными.
Задача 13.
Построить треугольник по заданным a, ha,la.
Идея. Построить прямоугольный треугольник, у которого ha - катет, 1а - гипотенуза. Указание. Построить отрезок АН длины ha и прямую, ему перпендикулярную и проходящую через точку Н. На этой прямой сделать засечку радиусом 1а с центром в точке А.
Решение. Построим отрезок АН длины ha и прямую, ему перпендикулярную и проходящую через точку Н. На этой прямой сделаем засечку радиусом 1а с центром в точке А. Получим точку L. От отрезка AL отложим два луча под углом а/2. Они пресекут прямую LH в точках В и С. Треугольник АВС (а также


510
Указания и решения
симметричный ему треугольник, у которого L лежит правее, чем Н) обладает заданными элементами.
ol h
Задача имеет решение при la>ha и — -f arccos < 90°.
Задача 14-
Построить треугольник по следующим данным: а, а, b : с.
Идея. Использовать окружность Аполлония.
Указание. Вершина А лежит на пересечении окружности Аполлония, построенной для отрезка ВС = а и соотношения b : с, и дуги окружности, из точек которой отрезок ВС виден под углом а.
Решение. Пусть даны угол а, сторона ВС = а и отрезки Ь' и с' такие, что bf Ъ
— = - ф 1 (в случае Ъ — с задача сводится к построению равнобедренного трест с
угольника по основанию и противолежащему углу). Для определенности пусть
АС Ь
b > с. Построим ВС = а. Вершина А должна быть выбрана так, что -г-=- = -.
АВ с
Геометрическим местом таких точек является окружность, построенная на отрезке LL' как на диаметре, где точки L и V лежат на прямой СВ и
CL
LB
СУ
LfB
Сначала построим точку L G СВ такую, что = -. Для этого из точки С под произвольным углом к отрезку СВ проведём луч, на котором отложим отрезки СМ = bf и MN = с'.
Проведём через точку М прямую, параллельную N В. Она пересечёт отрезок
г CL b' Ъ
С В в точке L, причем по теореме Фалеса —- = -» = -.
LB с с
N
N
L’
CL* ь
Теперь построим точку L' £ СВ такую, что Для этого из точки С
под произвольным углом к лучу СВ проведём второй луч, на котором отложим отрезки СМ — Ь'—с' и MN = с'. Проведём через точку N прямую, параллельную
MB. Она пересечёт луч СВ в точке Z/, причём по теореме Фалеса —— = — = -.
Lj 13 с с
Теперь построим на отрезке LL' как на диаметре окружность Аполлония, а на отрезке СВ - дугу, из точек которой отрезок СВ виден под углом а. Они пересекутся в точке А.


5.2. Метод геометрических мест точек
511
Таким образом, мы получили ААВС, у которого ВС = а, /.ВАС = а и АС относится к АВ как 6 : с.
Задача 15.
Провести обшую внешнюю касательную к двум данным окружностям (то есть даны их центры и радиусы).
Идея. Предположить, что касательная уже проведена и проанализировать рисунок.
Указание. Предположить, что касательная уже проведена, провести радиусы в точки касаний и опустить перпендикуляр О2Н из центра меньшей окружности на радиус большей окружности 0\ А.
Указание. Прямоугольный треугольник О1О2Н легко построить по гипотенузе O1O2 и катету 0\Н, равному R — г.
Решение. Пусть окружности с центрами 0\ и О2 имеют радиусы R и г такие, что R > г. Пусть А и В - точки касания окружностей с их общей касательной, а Н - основание перпендикуляра, опущенного на АО\ из точки О2 •
Для того чтобы построить точки А и В, надо сначала построить прямоугольный треугольник О1О2Н по гипотенузе O1O2 и катету, равному R — r. Пересечение прямой 0\Н с первой окружностью даст нам точку А. Прямая, параллельная 0\А, проведённая через точку О2, пересечёт вторую окружность в точке В. Прямая АВ (так же, как и симметричная ей относительно линии центров) будет внешней касательной к двум данным окружностям.
Замечание. В случае, когда R = г, точки 0\ и Н совпадают и точка А находится как точка пересечения перпендикуляра к линии центров, проведённого из точки 0\, с первой окружностью.


512
Указания и решения
Задача 16.
На сторонах угла даны два отрезка А В и CD и точка М внутри угла. Найти геометрическое место точек N таких, что Sabn + Scdn = Sabm + Sc dm-
Идея. Сдвинуть отрезки АВ и CD по соответствующим сторонам угла до вершины.
Указание. Пусть О - вершина угла. Взять точки В' и D' на сторонах угла ОВ и OD так, что OB' = АВ, OD' = CD. Следовательно,
Sabm — Sob'm, Scdm = Sod'm и Sabm + Scdm = Sob'md'-
Указание. Через точку М провести прямую т || B'D' и рассмотреть произвольную точку N € т.
Решение. Сдвинем отрезки А В и CD по соответствующим сторонам угла до вершины. Получим OB' = АВ, OD' = CD. Следовательно,
Sabm = Sqb'm, Scdm = Sqd'm и Sabm + Sc dm = Sob'md'-
Теперь через точку M проведём прямую т || B'D' и рассмотрим произвольную точку N G т. Заметим, что
SoB'MD' = SoB'D' + Sb'MD' = SoB'D' + Sb'ND' = SoB'ND' =>
==> Sabn + Scdn = Sabm + Scdm•
Следовательно, эта прямая m и есть искомое ГМТ.
Задача 17.
По окружности «бегает» дуга данной длины CD, хорда АВ задана, CD < АВ. Найти геометрическое место точек пересечения прямых АС и BD.
Идея. Использовать свойство угла между секущими.
Указание. Рассмотреть три случая взаимного расположения точек А, В, С, D.


5.2. Метод геометрических мест точек
513
Решение. Рассмотрим три случая.
1) 	Пусть точки С и D обе лежат на большей дуге А В данной окружности. Тогда по свойству углов между секущими ф = а—/3. Следовательно, в этом случае искомое ГМТ - это дуга, вмещающая угол ф — а — (3.
2) Если точки С и D обе лежат на меньшей дуге данной окружности, то по свойству углов между секущими ф = (тг — а) — /3. Следовательно, в этом случае искомое ГМТ - это дуга, вмещающая угол ф = 7г — а — /3.
3) Рассмотрим случай, когда одна из точек С или D лежит на большей дуге окружности, другая - на меньшей. Имеем
ф = Z.BDC - /.DBA = (/BDA - /С DA) - (ZDBC - /ABC) = a-f3.
To есть мы получили один из уже рассмотренных случаев.
В результате получаем: искомое ГМТ - это две дуги, опирающиеся на отрезок АВ и вмещающие углы а — (3 и 7г — а — /3.
Задача 18.
Через точку А внутри окружности проводятся всевозможные хорды. Найти геометрическое место середин этих хорд.
Идея. Соединить точку М - середину произвольной хорды ВС, проходящей через точку А, с центром окружности О.
Указание. По свойству отрезка, соединяющего центр окружности с серединой хорды, ОМ J_ ВС.
Решение. Проведём через точку А хорду ВС.
Пусть точка М - середина ВС.
По свойству отрезка, соединяющего центр окружности с серединой хорды, ОМ _1_ ВС.
Следовательно, угол ОМА прямой и геометрическим местом середин хорд, проходящих через точку А, будет окружность, построенная на отрезке АО как на диаметре.
17 Геометрия


514
Указания и решения
Задача 19.
Найти на стороне угла точку, из которой данный отрезок АВ, лежащий на другой стороне угла, виден под наибольшим углом.
И дея. Использовать свойства вписанного в окружность угла и угла между секущими.
Указание. Провести через точки А и В окружность, касающуюся другой стороны угла.
Решение. Проведём через точки А и В окружность, касающуюся другой стороны угла. Обозначим через С точку касания и рассмотрим любую другую точку С' на этой стороне.
Так как угол между секущими равен по- луразности соответствующих дуг, то
ZAC’B = Щ-~ < ZACB =
Zi Jd £
Следовательно, точка С - искомая точка.
Замечание. Точку С легко найти, используя свойство касательной и секущей, проведённых из одной точки.
5.3. 	Метод симметрии и спрямления
Задача 1.
Построить треугольник, зная Р, а и /га.
Идея. Развернуть треугольник на прямую.
Указание. Пусть треугольник АВС уже построен. На прямой ВС отложить отрезки В В' = АВ и С С' = АС.
Указание. ААВ'С' легко построить по стороне, противолежащему углу и высоте.
Решение. Пусть треугольник АВС уже построен. На прямой ВС отложим отрезки В В' = АВ и СО = АС.
А


5.3. Метод симметрии и спрямления
515
Треугольники ВВ'А и СС'А равнобедренные с углами при основании соот-
(3 'У
ветственно — и —. Следовательно, у треугольника АВ'С' сторона В'С' — Р и
= = г + *
2 2 2 2
Таким образом, для того чтобы построить ААВС, сначала нам надо построить А АВ'С' по стороне, противолежащему углу и высоте.
Серединные перпендикуляры к сторонам А В' и АС' пересекут В' С' в точках В и С.
Задача 2.
Даны две окружности и между ними прямая. Начертить равносторонний треугольник так, чтобы две его вершины были на окружностях, а одна из высот лежала на данной прямой.
Идея. Отразить одну из окружностей относительно прямой.
Указание. Точка пересечения окружностей - одна из вершин искомого треугольника.
Решение. Пусть даны окружности с центрами 0\ и 02 и прямая га. Отразим первую окружность относительно прямой. Пусть А - точка пересечения отражённой окружности со второй окружностью, а В - симметричная ей точка на первой окружности.
Теперь отметим на прямой га точку С так, чтобы АС = АВ. Треугольник АВС будет равносторонним, и его высота будет лежать на га.
В зависимости от числа точек пересечения окружностей задача может иметь одно, два или ни одного решения.
Задача 3.
Дана прямая га и две точки А и В по одну сторону от неё. Найти на га такую точку X, чтобы АХ составлял с га угол, вдвое больший, чем ВХ.
Идея. Построить окружность, касающуюся прямой га с центром в точке В.
17*


516
Указания и решения
Указание. Отразить построенную окружность относительно прямой т и провести к отражённой окружности касательную через точку А.
Решение. Построим окружность, касающуюся прямой га с центром в точке В. Отразим её относительно прямой га и проведём к отражённой окружности касательную через точку А.
Точка пересечения этой касательной с прямой га и есть искомая точка (см. рисунок).
Задача 4•
Внутри угла даны точки А и В. Построить равнобедренный треугольник, основание которого лежит на одной стороне угла, вершина - на другой, а боковые стороны проходят через точки А и В.
Идея. Отразить точку А симметрично относительно прямой ОМ в точку А, где О - вершина угла, а М - вершина искомого равнобедренного треугольника. Указание. Выразить /.А'MB через величину данного угла.
Решение. Пусть О - вершина данного угла а, МН - высота искомого треугольника. Отразим точку А относительно прямой ОМ, получим А!. Имеем
ZA'MB = 2ZOMH = 2 (| - а) = ж - 2а.
Следовательно, для того чтобы определить вершину М, надо найти точку пересечения дуги, опирающейся на отрезок А'В и вмещающей угол 7г — 2а, со стороной данного угла.
Задача 5.
Дана прямая АВ и две окружности, лежащие по одну сторону от прямой. Найти на прямой АВ точку, касательные из которой составляют с этой прямой равные углы.
Идея. Отразить одну из окружностей относительно прямой АВ.
Указание. Провести внутреннюю касательную ко второй окружности и отражённой окружности.


5.3. Метод симметрии и спрямления
517
Решение. Пусть даны окружности с центрами 0\ и 02 и прямая АВ. Рассмотрим отражение первой окружности относительно прямой АВ. Внутренняя касательная к окружностям с центрами 0'х и 02 пересечет прямую АВ в точке X. Обозначим через M,N,N' точки касания окружностей с центрами 02,0\,0'х с касательными, проведёнными из точки X.
Заметим, что /.NXВ = /N'XB, как симметричные, и /МХА = /N'XB, как вертикальные. Следовательно, точка X есть искомая точка.
Задача 6.
Точки А и В расположены между параллельными прямыми тип. Постройте точки М € га, N Е п так, чтобы длина ломаной AMNB была наименьшей.
Идея. Отразить точки А и В относительно прямых тип соответственно. Указание. Соединить получившиеся точки А' и В'.
Решение. Рассмотрим А' -- отражение относительно т точки А и В' - отражение относительно п точки В.
Ломаные AMNB и A'MNB' имеют одинаковую длину. Эта длина принимает своё минимальное значение в случае, когда точки М и N лежат на отрезке А'В'. Следовательно, искомые М и N суть точки пересечения прямых типе отрезком А! В'.
В’
Задача 7.
В данную окружность вписать прямоугольник, зная разность основания и высоты.
Идея. Диагональ прямоугольника является диаметром окружности.
Указание. Отложить на большей стороне прямоугольника известную разность сторон.
Решение. Рассмотрим прямоугольник ABCD, вписанный в окружность. Отметим на А В точку С" такую, что ВС = ВС'.


518
Указания и решения
Треугольник ВСО равнобедренный с углами при основании 45°. Следовательно, Z.AOC — 180° — 45° = 135° и треугольник АОС можно построить по сторонам АС (равна 2R), АС' (равна данной в условии разности) и углу ААОС = 135°.
Точку В можно получить как точку пересечения прямой АО с окружностью, а вершину D как точку, симметричную В относительно центра окружности.
Задача 8.
Построить треугольник по стороне, прилежащему углу и разности остальных сторон.
Идея. Предположить, что искомый треугольник построен, и проанализировать данные.
Указание. Отложить на большей из двух неизвестных сторон отрезок, равный меньшей стороне.
Решение. Пусть требуемый треугольник АВС построен по известной стороне АВ = с, углу А, равному а, и разности двух других сторон, равной Ь—а. Отложим на стороне С А отрезок СО, равный СВ. Тогда АС' = Ь — а. Треугольник АВС' легко построить по сторонам с, Ь — а и углу между ними а.
Так как треугольник ВСО равнобедренный, точку С можно найти как точку пересечения серединного перпендикуляра к ВО с прямой АО.
Задача 9.
Построить четырёхугольник ABCD, зная его стороны, если диагональ АС делит угол А пополам.
Идея. Отразить вершину D относительно прямой АС.
Указание. Треугольник BCD' легко построить по трём сторонам.


5.3. Метод симметрии и спрямления
519
Решение. Рассмотрим четырёхугольник ABCD. Так как Z.CAD = ZCAB, то D' (отражение точки D относительно АС) будет лежать на прямой АВ. В треугольнике BCD' стороны
ВС, CD' = CD, BD' = АВ-AD
выражаются через данные стороны четырёхугольника. Следовательно, мы можем построить его по трём сторонам.
Вершину А можно получить, отложив от В на прямой BD' отрезок, равный В А. Вершина D есть отражение D' относительно прямой АС.
В
Задача 10.
Найти сумму перпендикуляров, опущенных на стороны равнобедренного треугольника из точки, взятой на основании.
Идея. Отразить основание одного из перпендикуляров относительно основания.
Указание. Показать, что искомая сумма равна высоте, проведённой к боковой стороне треугольника.
Решение. Пусть DM и DN - перпендикуляры, опущенные на боковые стороны из точки D. Рассмотрим М' - отражение точки М относительно основания АС. Из равенства углов ZM'AD — AM AD = Z.NCD следует параллельность прямых AM' || ВС.
Так как M'D и DN перпендикулярны параллельным прямым, точки M',D и N лежат на одной прямой и их сумма равна расстоянию между этими прямыми.
В результате сумма DM + DN = DM' + DN равна расстоянию от точки А до стороны ВС, то есть высоте, проведённой к боковой стороне треугольника.
Задача 11.
Найти сумму перпендикуляров, опущенных из точки, взятой внутри равностороннего треугольника, на его стороны.
Идея. Воспользоваться результатом предыдущей задачи.


520
Указания и решения
Указание. Провести через точку, из которой опущены перпендикуляры, прямую, параллельную одной из сторон треугольника.
Решение. Пусть даны равносторонний треугольник АВС и точка D внутри него. Обозначим через М, N, К основания перпендикуляров, опущенных из D на стороны АВ, ВС, АС.
Проведём через D отрезок А'С' || АС. Согласно утверждению предыдущей задачи,
DM + DN = ВН',
где ВН' - одна из равных высот равностороннего треугольника АА'ВС'.
Так как DK = Н'Н, то
DM + DN + DK = ВН' + Н'Н = ВН,
то есть сумма перпендикуляров из точки внутри равностороннего треугольника равна высоте исходного треугольника.
В
Задача 12.
На окружности даны точки А и В. Отыскать на ней точку X такую, что АХ + ВХ = а, где а - заданный отрезок.
Идея. Пусть задача решена и точка X уже найдена. Отложить на прямой ВХ отрезок ХС = АХ.
Указание. Треугольник АВС легко построить.
Решение. Пусть задача решена и точка X уже найдена. Отложим отрезок ХС = АХ на прямой ВХ. Заметим, что угол АХ В = а известен как угол, опирающийся на известную дугу. Тогда в равнобедренном треугольнике АХ С углы при основа- а
нии равны —.
Следовательно, треугольник АВС мы можем построить по основанию АВ, противолежащему
углу ~ и боковой стороне, равной а. Его сторона
ВС пересечёт окружность в искомой точке X.
Задача 13.
На окружности даны точки А и В. Отыскать на ней точку X такую, что АХ — ВХ = а , где а - заданный отрезок.


5.3. Метод симметрии и спрямления
521
Идея. Пусть задача решена и точка X уже найдена. Отложить на отрезке АХ отрезок ХС = ВХ.
Указание. Треугольник АВС легко построить.
Решение. Пусть задача решена и точка X уже найдена. Отложим на отрезке АХ отрезок ХС = ВХ. В равнобедренном треугольнике
а
ВХС углы при основании равны 90° — —, где
Z
угол а = ZAXB известен как угол, опирающийся на известную дугу.
Рассмотрим треугольник АВС. У него известны основание АВ, сторона АС = а и угол
OL
ZACB = 90° -Ь —. Построив треугольник АВС
и продолжив его сторону АС до пересечения с окружностью, мы получим искомую точку X.
Задача 14-
Найти геометрическое место точек, сумма расстояний от которых до двух данных пересекающихся прямых равна заданному отрезку.
Идея. Использовать одну из предыдущих задач про сумму расстояний от точки на основании равнобедренного треугольника до боковых сторон.
Указание. Отложить от точки пересечения прямых во все четыре стороны отрезки, равные заданному отрезку.
Указание. Соединить последовательно получившиеся четыре точки на прямых и показать, что получившийся прямоугольник - искомое ГМТ.
Решение. Пусть прямые тип пересекаются в точке О. Отметим на прямой т точку А, находящуюся на заданном расстоянии d от прямой п. Отложим отрезки, равные О А, на других лучах, выходящих из О. Получим четыре точки А, В, С и £), которые являются вершинами четырёх равнобедренных треугольников с общей вершиной О.
Согласно одной из предыдущих задач, сумма расстояний от любой точки на основании равнобедренного треугольника до боковых сторон равна высоте, проведённой к боковой стороне. Следовательно, искомое ГМТ есть четыре отрезка, являющиеся сторонами прямоугольни
ABCD.


522
Указания и решения
Задача 15.
На данной прямой найти такую точку, что разность расстояний от неё до сторон данного угла равна данному отрезку.
Идея. Провести прямую, параллельную одной из сторон угла и отстоящую от неё на расстоянии, равном длине данного в условии задачи отрезка.
Указание. Показать, что биссектриса нового угла пересечёт данную прямую в искомой точке.
Решение. Пусть дана прямая т и угол со сторонами кип. Построим прямую п' || п на расстоянии d, равном длине данного в условии задачи отрезка. Биссектриса угла со сторонами кип' пересечёт прямую т в искомой точке М.
Действительно, если через К, N и N' обозначить основания перпендикуляров на соответствующих прямых, то
MN-MK = MN'+N'N-MK = N'N = d.
Задача 16.
Провести окружность, касающуюся двух данных окружностей, так, чтобы радиусы, проведённые из центра искомой окружности к точкам касания, образовывали данный угол.
Идея. Предположить, что искомая окружность уже построена, и проанализировать, что известно.
Указание. В треугольнике, вершинами которого являются центры трёх окружностей, известны сторона, угол против этой стороны и разность двух других сторон.
Указание. Использовать одну из предыдущих задач.
Решение. Рассмотрим окружности с центрами 0\, Оч и радиусами R\, R2. Пусть искомая окружность с центром О уже построена.
В треугольнике O1O2O известны основание O1O2? противолежащий угол а и разность сторон 0\0 — О2О = R\ — i?2- Для того чтобы построить этот треугольник, надо на отрезке 0\ О2 построить дугу, вмещающую угол а, а на этой дуге найти точку О такую, что разность получившихся хорд будет равна
i?i — i?2- А такую задачу мы умеем решать (см. одну из предыдущих задач).


5.3. Метод симметрии и спрямления
523
Задача 17.
Построить равнобедренный треугольник, зная его боковую сторону а и сумму высоты с основанием s.
Идея. Отложить от основания высоты BD на её продолжении отрезок DE, равный основанию АС треугольника.
Указание. Треугольник ВСЕ легко построить по
1
двум сторонам и углу, равному arctg - .
Решение. Пусть в А АВС с высотой BD стороны АВ = ВС = а, BD + АС = s. Отложим на продолжении BD отрезок DE = АС. Так как DE = 2DC, то tg Z.DЕС = 1/2.
Для того чтобы построить треугольник ЛВС, сначала построим отрезок BE = s, отложим от него угол
а = arctg -, потом на стороне этого угла сделаем засечку из точки В радиусом а. Так мы получим точку С. Вершину А можно получить как отражение точки С относительно прямой BE.
Задача 18.
Построить треугольник по а, тъ + Ь и /(ш^, Ъ).
Идея. Отложить от основания медианы BD на её продолжении отрезок DE, равный стороне АС треугольника.
Указание. Зная угол Ь), легко построить угол DEC.
Указание. Треугольник ВСЕ легко построить по двум сторонам и углу ВЕС.
О z
/
2 z /
Е


524
Указания и решения
Решение. Пусть в ААВС с медианой BD сторона ВС = a, BD + АС = 5. Отложим на продолжении BD отрезок DE = АС.
Определим углы а = /.DEC и /3 = Z.DCE в треугольнике DEC. Для этого на одной стороне угла О, равного 180° — /(га*,, 6), отложим отрезок произвольной длины z, на другой - отрезок длины 2z. Углы напротив сторон длины z и 2z будут равны а и /3.
Итак, для построения треугольника АРС сначала надо построить отрезок BE = s, потом отложить от него угол о: и на стороне этого угла сделать засечку из точки В радиусом а. Из полученной точки С под углом /3 к ЕС проведём луч. Он пересечёт BE в точке D. Отложив AD = DC, найдём вершину А.
Задача 19.
Построить треугольник по 6, с и /3 — 7.
Идея. Рассмотреть треугольник, симметричный данному, с общей третьей стороной.
Указание. Пусть в А АВС стороны АС = b, А В = с. Рассмотреть А А ВС, симметричный исходному, со сторонами А!В = 6, А'С = с.
Указание. Треугольник А А' В легко построить по двум сторонам и углу между ними.
Решение. Пусть в треугольнике АВС стороны АС = Ь, АВ = с. Рассмотрим А А'ВС, симметричный исходному, со сторонами А'В = b, А'С — с. В треугольнике А А'В получаем А В = с, А'В = Ь и ZABA' = /5 — 7.
Следовательно, треугольник А А'В мы можем построить по двум сторонам и углу между ними. Для того чтобы построить вершину С, проведём через В прямую параллельно АА' и отложим на ней С так, что АС = Ь.
5.4. 	Метод параллельного переноса Задача 1.
Построить трапецию по четырём сторонам.
Идея. Произвести параллельный перенос боковой стороны трапеции.
Указание. После параллельного переноса боковой стороны трапеции получится треугольник, который легко построить по трём сторонам.


5.4• Метод параллельного переноса
525
Решение. Пусть даны стороны трапеции ВС = a, AJ3 = fo, CD = с, AD = d. Перенесём боковую сторону Ь вдоль основания а, получим параллелограмм АВС А'.
Отрезок A'D = d — а. Следовательно, треугольник A'CD можно построить по трём сторонам. Для того, чтобы получить точки А и В, достаточно перенести отрезок А1 С вдоль прямой A!D на расстояние, равное а.
Задача 2.
Между двумя окружностями провести отрезок, делящийся пополам в данной точке А.
Идея. Предположить, что искомый отрезок построен, и воспользоваться параллельным переносом.
Указание. Рассмотреть окружности с центрами О и СУ. Пусть XY - искомый отрезок. Продолжить ХО до X' и перенести первую окружность так, чтобы X' совместилась с Y.
Указание. Так как XY'YX' - параллелограмм с диагональю XY, то точка А - её середина.
Решение. Рассмотрим окружности с центрами О и О'. Пусть XY - искомый отрезок. Продолжим ХО до X' и перенесём первую окружность так, чтобы X' совместилась с Y. Получим параллелограмм XY'YX' с диагональю XY, серединой которой будет точка А.
Для решения задачи надо перенести первую окружность вдоль прямой О А на расстояние 00" = 20А. Проведя прямую через полученную точку пересечения Y и точку А, найдём точку X.
Задача может иметь одно, два или ни одного решения.
Задача 3.
Построить треугольник, зная ma,mc и
Идея. Предположить, что треугольник построен, и провести дополнительное построение.
Указание. Пусть даны медианы AN = та и С К = тс треугольника АВС и угол МВС = а. Пусть медианы пересекаются в точке О. Достроить АВОС до параллелограмма ВОС А'.
Указание. Сначала построить треугольник АО В А'. Для этого на отрезке О А! — | та отметить середину N и получить вершину В как точку пересечения двух дуг: дуги, опирающейся на отрезок ON и вмещающей угол а, и дуги, проведённой из точки А! радиусом \тс.


526
Указания и решения
Решение. Пусть даны медианы AN = та и С К = тс треугольника АВС и угол МВС = а. Пусть медианы пересекаются в точке О. Достроим АВОС до параллелограмма ВОС А'.
Общая последовательность действий такова.
1) Сначала построим треугольник О В А'. Для этого на отрезке О А' = | та отметим середину N и получим вершину В как точку пересечения двух дуг: дуги, опирающейся на отрезок ON и вмещающей угол а, и дуги, проведённой из точки А! радиусом \тс.
2) Вершину А получим, отложив на прямой О А' отрезок О А = О А'.
3) Вершину С получим, отложив на прямой BN отрезок NC = NB.
Задача
Через точку А внутри угла провести прямую так, чтобы отрезок, заключённый между сторонами, делился точкой А пополам.
Идея. Диагонали параллелограмма делятся точкой пересечения пополам.
Указание. Отложить на прямой О А отрезок АВ = О А. Через точку В провести прямые, параллельные сторонам угла.
Решение. Отложим на прямой О А отрезок А В = О А. Через точку В проведём прямые, параллельные сторонам угла. Получим параллелограмм OCBD.
Так как диагонали параллелограмма точкой пересечения делятся пополам, то С А = AD. Следовательно, CD - искомая прямая.
Задача 5.
Построить трапецию, зная диагонали, угол между ними и одну из боковых сторон.
Идея. Использовать параллельный перенос одной из диагоналей трапеции.
Указание. Пусть даны длины диагоналей АС и BD и длина боковой стороны CD. Перенести диагональ BD в отрезок СЕ вдоль основания ВС.
Указание. Треугольник АСЕ легко построить по двум сторонам и углу между ними.
В


5.4• Метод параллельного переноса
527
Решение. Пусть даны длины диагоналей АС и BD и длина боковой стороны CD. Перенесём диагональ BD в отрезок СЕ вдоль основания ВС.
В треугольнике АСЕ боковые стороны равны диагоналям трапеции, а угол АСЕ равен углу между диагоналями. Следовательно, этот треугольник мы можем построить. Для того чтобы найти вершину D, надо сделать засечку циркулем из С на прямой АЕ радиусом, равным длине боковой стороны CD. После этого, достроив ACDE до параллелограмма, получим вершину В.
Задача 6.
Построить четырёхугольник, зная две диагонали, две противолежащие стороны и угол между ними.
Идея. Использовать параллельный перенос одной из диагоналей четырёхугольника.
Указание. Пусть даны стороны АВ = a, CD = с, угол между ними ZAC'D = а и две диагонали четырёхугольника. Тогда ZB'C'D = 7г — а. Достроить А АВС до параллелограмма АВХС.
Указание. Треугольник XCD можно построить по двум сторонам и углу между ними.
Указание. Треугольник BDX легко построить по трём сторонам.
Решение. Пусть даны стороны АВ = а,
CD = с, угол между этими сторонами ZAC'D = а и две диагонали четырёхугольника. Тогда ZB'C'D = 7г — а. Достроим ААВС до параллелограмма АВХС.
Тогда СХ = а и ZXCD = ZB'C'D = тг-а.
Следовательно, АХ CD мы можем построить по двум сторонам и углу между ними. Поскольку отрезки ВХ и BD равны диагоналям трапеции, мы можем построить ABDX по трём сторонам. Так получим вершину В. Достроив АВСХ до параллелограмма, найдём вершину А.
Задача 7.
Через данную точку М провести прямую так, чтобы разность расстояний до неё от двух данных точек А и В была равна данной длине.
Идея. Предположить, что прямая проведена, опустить на неё перпендикуляры из данных точек и использовать параллельный перенос.
Указание. Пусть А! и В' - основания перпендикуляров, опущенных из точек Л и В на искомую прямую. Перенести отрезок AfВ* параллельно в отрезок АС. Указание. Прямоугольный треугольник АВС легко построить по гипотенузе АВ и катету СВ, равному данной в условии задачи разности расстояний.


528
Указания и решения
Решение. Пусть А' и В' - основания перпендикуляров, опущенных из точек А и В на искомую прямую. Перенесём отрезок А'В' параллельно в отрезок АС.
Треугольник АВС является прямоугольным с известной гипотенузой А В и катетом СВ, равным данной в условии задачи разности расстояний.
Для того чтобы построить нужную прямую, надо сначала построить треугольник АВС по катету и гипотенузе, а потом провести через точку М прямую, параллельную отрезку АС.
А’
М
В'
У
\
J
\
и
Л
с
Задача 8.
В данный остроугольный треугольник вписать прямоугольник с наименьшей диагональю (одна сторона прямоугольника лежит на основании треугольника).
Идея. Вершину треугольника перенести параллельно основанию так, чтобы получился прямоугольный треугольник.
Указание. Пусть в треугольник АВС вписан прямоугольник KLMN. Перенести вершину С параллельно АВ так, чтобы треугольник АВС' был прямоугольным. Так как LL' = КК', прямоугольник KLMN при этом перейдёт в равный ему прямоугольник К'Ь'М'А.
Указание. Диагональ прямоугольника К'Ь'М'А будет принимать минимальное значение в случае, когда АЬ' ± ВС'.
Решение. Пусть в треугольник АВС вписан прямоугольник KLMN. Перенесём вершину С параллельно АВ так, чтобы треугольник АВС' был прямоугольным. Так как LU = К К', прямоугольник KLMN при этом перейдёт в равный ему прямоугольник К'Ь'М'А.
Диагональ прямоугольника К'Ь'М'А будет принимать минимальное значение в случае, когда AL' JL ВС'. То есть в А АВС' надо провести АЬ' _L ВС' и построить прямоугольник К'Ь'М'А с такой диагональю. Этот прямоугольник и будет искомым прямоугольником.
Осталось совершить обратный параллельный перенос прямоугольника вдоль АВ на расстояние Ь'Ь.
Задача 9.
Даны три параллельные прямые. Провести через данную точку секущую так, чтобы разность отрезков между параллелями была равна заданной величине.
Идея. Использовать методы симметрии и параллельного переноса.


5.4• Метод параллельного переноса
529
Указание. Пусть даны прямые га || п || fc, точка А и отрезок d, равный разности отрезков между параллелями. Провести прямую га', симметричную прямой га относительно п.
Указание. Пусть секущая пересекает параллельные прямые в точках М, N, М', if. Из равенства отрезков MN = M'N следует, что КМ' = KN — MN, то есть является разностью отрезков секущей.
Решение. Пусть даны прямые га || п || fc, точка А и отрезок d, равный разности отрезков между параллелями. Проведём прямую га/, симметричную прямой т относительно п. Пусть секущая пересекает параллельные прямые в точках М, N, М',К.
Из равенства отрезков MN = M'N следует, что КМ' = KN — MN, то есть является разностью отрезков секущей.
В целом построение выглядит так: сначала строим га', потом из произвольной точки К прямой к делаем засечку на га' радиусом, равным d. Так мы получим точку М'. Осталось провести через данную точку А прямую, параллельную построенной секущей.
Задача 10.
Построить трапецию ABCD, зная боковую сторону CD, угол между диагоналями, расстояние между параллельными сторонами и отрезок, соединяющий середины боковых сторон.
Идея. Пусть трапеция построена. Перенести диагональ BD в отрезок СЕ параллельно вдоль основания ВС.
Указание. Треугольник АСЕ можно построить по основанию, высоте и известному углу.
Решение. Пусть нам дана высота трапеции, длина средней линии и длина боковой стороны CD. Перенесём диагональ BD в отрезок СЕ параллельно вдоль основания ВС.
Рассмотрим треугольник АСЕ. Так как средняя линия трапеции равна полусумме оснований, отрезок АЕ равен двум средним линиям, угол АСЕ равен углу между диагоналями, а высота А АСЕ равна высоте трапеции. Следовательно, этот треугольник мы можем построить по основанию, высоте и известному углу. Для того чтобы найти вершину D, надо сделать засечку циркулем из С на прямой АЕ радиусом, равным длине боковой стороны CD. После этого, достроив ACDE до параллелограмма, получим вершину В.


530
Указания и решения
Задача 11.
Построить треугольник по 6, с и та.
Идея. Использовать вспомогательное построение: достроить треугольник до параллелограмма.
Указание. Предположить, что треугольник АВС с данными сторонами АС = 6, АВ — с и медианой AM — та построен. Отложить точку А; на прямой AM так, что MAf = AM.
Указание. Построить ААВА' по трём известным сторонам.
Решение. Рассмотрим треугольник АВС с данными сторонами АС = Ь, АВ — с и медианой AM = та. Отложим точку Л' на прямой ЛМ так, что МА! — AM. Четырёхугольник АВА'С будет параллелограммом со сторонами, равными b и с, и диагональю АА' = 2та.
Для построения ААВС надо сначала построить ААВА! по трём известным сторонам, а потом, достроив его до параллелограмма, получить вершину С.
В
А’
Задача 12.
Построить четырёхугольник, зная его стороны и отрезок, соединяющий середины двух противоположных сторон.
Идея. Использовать вспомогатель- X
ный параллелограмм, стороны которого параллельны и равны диагоналям искомого четырёхугольника.
Указание. Пусть ABCD - искомый четырёхугольник, а точки X и Y взяты таким образом, что четырёхугольники АВХС и ACYD являются параллелограммами. Цель - построить вспомогательный параллелограмм BXYD, а потом восстановить четырёхугольник ABCD. д Указание. Построить ABCY по трём сторонам.
Указание. Построить ACXD по медиане и двум сторонам.
Решение. Пусть ABCD - искомый четырёхугольник, а точки X и Y взяты таким образом, что четырёхугольники АВХС и ACYD являются параллелограммами. Наша цель - построить вспомогательный параллелограмм BXYD, а потом восстановить четырёхугольник ABCD.


5.4• Метод параллельного переноса
531
В теоретической части было показано, что диагонали параллелограмма BXYD вдвое больше средних линий исходного четырёхугольника.
Рассмотрим ABCY. У него стороны ВС и CY (CY = AD) равны сторонам исходного четырёхугольника, а сторона BY вдвое больше отрезка, соединяющего середины сторон АВ и CD. Следовательно, ABCY мы можем построить по трём сторонам.
Теперь построим точки X и D. Обозначим через Е середину стороны BY и рассмотрим ACXD. Точки С и Е уже построены. То есть в ACXD дана медиана и стороны СХ (СХ = АВ) и CD, которые равны данным в условии задачи сторонам четырёхугольника. Построив ACXD по медиане и двум сторонам (см. пред. задачу), мы определим точки X и D. А достроив АВСХ до параллелограмма, получим вершину А.
Задача 13.
Построить четырёхугольник, зная четыре его стороны и угол между двумя противоположными сторонами.
Идея. Использовать вспомогательный параллелограмм, стороны которого параллельны и равны диагоналям искомого четырёхугольника.
Указание. Построить сначала вспомогательный параллелограмм BXY D, стороны которого параллельны и равны диагоналям искомого четырёхугольника ABCD.
Указание. Построить ACXD по двум сторонам и углу между ними. Указание. Построить ABCY по медиане СЕ и двум сторонам ВС и CY.
Решение. Построим сначала вспомогательный параллелограмм BXYD, стороны которого параллельны и равны диагоналям искомого четырёхугольника ABCD.
Угол XCD равен углу между прямыми, содержащими стороны АВ и CD (см. теоретическую часть). Следовательно, в ACXD стороны СХ (СХ = АВ) и CD равны сторонам исходного четырёхугольника и Z.XCD известен. Построив ACXD, мы определим точки X и D. Для того чтобы построить точки В и Y, построим ABCY по медиане СЕ и двум сторонам ВС и CY (CY = AD), которые равны сторонам четырёхугольника А ABCD. Достроив АВСХ до параллелограмма, получим вершину А.


532
Указания и решенная
Задача 14-
Построить биссектрису угла, вершина которого недоступна.
Идея. Предположить, что биссектриса построена, и провести из любой точки биссектрисы две прямые, параллельные сторонам угла.
Указание. Расстояния от построенных прямых до соответствующих сторон угла будут одинаковыми.
Решение. Пусть стороны угла лежат на ^
прямых к и п, пересекающихся в точке О. /
Через точку О', лежащую на биссектрисе т, проведём прямые, параллельные сторонам угла.
В силу равенства углов при параллельных прямых биссектрисой построенного угла будет также прямая т. Отметим, что расстояния между параллельными прямыми будут равными.
Следовательно, если вершина О недоступна, то надо провести две прямые на равном расстоянии от сторон исходного угла и для угла с уже доступной вершиной построить биссектрису.
Задача 15.
Даны две точки А и В и между ними две параллели тип. Провести между этими параллелями в данном направлении отрезок CD так, чтобы сумма АС+ + CD -f BD была минимальной.
Идея. Использовать параллельный перенос отрезка CD.
Указание. Пусть отрезок CD с концами на параллелях тип проведён в заданном направлении. Перенести его параллельно в отрезок С'В, тогда
АС + CD + BD = AC + СС' + ВС'.
Решение. Пусть отрезок CD с концами на параллелях тип проведён в заданном направлении. Перенесём его параллельно в отрезок С' В, тогда
AC + CD + BD = AC + СС' + ВС'.
Следовательно, задача свелась к отысканию на прямой т точки С такой, что сумма АС + С С1 минимальна. Значит, в качестве точки С надо взять точку пересечения прямой т с отрезком АС'.


5.4- Метод параллельного переноса
533
Задача 16.
На окружности даны две точки А и В. В данном направлении провести хорду XY так, чтобы сумма хорд АХ и BY была равна заданной величине.
Идея. Провести хорду А А' параллельно заданному в условии направлению и использовать метод симметрии и спрямления для нахождения точки Y. Указание. Надо построить точку Y такую, что BY -f YА' имеет заданную длину, а эта задача была решена в предыдущем разделе методом симметрии и спрямления.
Решение. Пусть X, Y - искомые точки. Проведём хорду АА! в заданном в условии направлении. Отрезок A'Y — АХ, так как у вписанной трапеции AA'YX боковые стороны равны.
Итак, всё свелось к построению точки Y такой, что BY -f YА! имеет заданную длину, а эта задача была решена нами в предыдущем разделе методом симметрии и спрямления.
Задача 17.
Построить прямоугольник с данной стороной так, чтобы его стороны проходили через четыре заданные точки.
Идея. Пусть прямоугольник построен. Проанализировать, что нам известно. Указание. Пусть даны точки А, В, С, D и отрезок длины а. Рассмотреть перпендикуляр АН, опущенный из точки А на противоположную сторону искомого прямоугольника.
Указание. Треугольник АСН можно построить по известной гипотенузе АС и катету АН = а.
Решение. Пусть даны точки A,B,C,D йот- А
резок длины а. Рассмотрим перпендикуляр АН, опущенный из точки А на противоположную сторону искомого прямоугольника.
Треугольник АСН мы можем построить по известной гипотенузе АС и катету АН — а. Для того чтобы построить искомый прямоугольник, надо через точки D и В провести прямые, параллельные АН, а через А и С - прямые, параллельные НС. Точки пересечения этих прямых и будут вершинами искомого прямоугольника.


534
Указания и решения
Задача 18.
Даны две окружности и прямая. Провести параллельно этой прямой секущую, отсекающую в окружностях хорды, сумма которых равна заданному отрезку длины S.
Идея. Предположить, что искомая прямая проведена, и провести параллельный перенос одной из окружностей.
Указание. Рассмотрим две окружности с центрами 0\ и О2 и прямую га. Пусть AD || га и AB + CD = s. Перенести вторую окружность так, что хорда CD перейдёт в хорду BE.
Указание. Пусть Р и Q - основания перпендикуляров, опущенных из точек Oi и 0'2 на прямую AD. Отрезок PQ = s/2.
Решение. Рассмотрим две окружности д —р
с центрами 0\ и О2 и прямую га. Пусть /С | \
AD || га и AB+CD = s. Перенесём вторую / н f—Vj-—+
окружность так, что хорда CD перейдёт в / V \ 2 J
хорду BE. I
Пусть Р и Q - основания перпендику- \ J
ляров, опущенных из точек 0\ и О2 на У
прямую AD. Отрезок PQ — s/2.
В целом построение выглядит следующем образом. Проведём через О2 прямую параллельно т и через 0\ прямую перпендикулярно т. Так мы найдём точку Н. Отложив от неё отрезок Н(У2 = s/2, получим центр перенесённой окружности О2. Эта окружность пересечёт первую окружность в точке В. В результате осталось провести прямую через В параллельно прямой т.
5.5. 	Метод подобия Задача 1.
Построить треугольник по двум углам и высоте, проведённой из третьего угла.
Идея. Построить треугольник, подобный искомому.
Указание. По двум данным углам построить АА'В'С'.
Решение. Сначала по двум данным углам построим АА'В'С'.
Для того чтобы построить искомый треугольник А'ВС с высотой ha, достаточно в треугольнике А'В'С' на прямой, содержащей высоту А'Нотложить отрезок А'Н — ha и через точку Н провести прямую ВС, параллельную В'С'.
К


5.5. Метод подобия
535
Задача 2.
Построить окружность, касающуюся сторон данного угла и проходящую через заданную внутри него точку.
Идея. Построить вспомогательную окружность с центром СУ, касающуюся сторон угла.
Указание. Соединить вершину угла S с заданной точкой А.
Решение. Построим вспомогательную окружность с центром СУ, касающуюся сторон угла.
Соединим вершину угла S с заданной точкой А. Пусть А' — точка пересечения прямой SА с окружностью. Проведём через А прямую параллельно отрезку А*О*. Она пересечёт луч SO' в точке О - центре искомой окружности.
Замечание. Если через А! обозначить вторую точку пересечения прямой SA со вспомогательной окружностью, го, действуя аналогично, получим вторую окружность, проходящую через точку А и касающуюся сторон угла.
Задача 3.
Дан треугольник АВС со сторонами АВ = 5, ВС — 6, АС — 7. Построить точку S £ ВС, точку Q £ АС и точку Р £ А В так, чтобы треугольник SQP был равносторонним.
Идея. Построить треугольник (со вписанным в него равносторонним треугольником), подобный данному, а потом с помощью гомотетии преобразовать вписанный треугольник в искомый.
Указание. Вписать в угол А равносторонний AP'Q'S'.
Решение. На сторонах угла А возьмём произвольно точки Р', Q' и построим равносторонний AP'Q'S'. Если точка S' попала на сторону ВС, то наша задача выполнена. Если нет, то проведём прямую через точку S' параллельно ВС. Пусть В', С' - точки пересечения этой прямой с лучами АВ и АС соответственно.


536
Указания и решения
Заметим, что треугольники АВС и АВ'С' подобны с коэффициентом подобия к = ——, поэтому если мы
применим гомотетию с этим коэффициентом с центром в точке А, то А АВ'С' перейдёт в А АВС, а вписанный в него равносторонний треугольник S'Q'P' перейдёт в искомый треугольник SQP. Для того чтобы построить точку Р Е АВ, достаточно отложить от точки А отрезок длины
. АВ , ч .
АР • - - (это мы умеем делать). Ана-
/\.jD
логично строятся точки Q и S.
Задача 4-
В данный треугольник вписать квадрат.
Идея. Построить вспомогательный квадрат и воспользоваться преобразованием гомотетии.
Указание. Пусть дан треугольник К LM. Построить вспомогательный квадрат ABCD такой, что А,Ве КМ, D £ KL.
Указание. Провести прямую К С до пересечения со стороной ML.
Решение. Пусть дан треугольник KLM. Построим вспомогательный квадрат ABCD такой, что А, В £ КМ,
D £ KL. Проведём прямую КС, она пересечёт сторону ML в точке С'. Далее проведём В'С'±КМ,
C'D'LB'C' и D'A'±.D'C'. Четырёхугольники ABCD и A'B'C'D' подобны (один получается из другого с помощью гомотетии с центром в точке К), следовательно, A'B'C'D' также является квадратом.
Задача 5.
Построить треугольник по а, /3,г.
Идея. Вписать окружность данного радиуса в треугольник, подобный данному. Указание. По двум данным углам построить А А' ВС', подобный искомому. В угол В вписать окружность данного радиуса.
L
В


5.5. Метод подобия
537
Решение. По двум данным углам построим ДА'ВС', подобный искомому. В угол В впишем окружность данного радиуса. Из центра О опустим перпендикуляр ОН' на сторону А'С', на котором отложим ОН = г. Через точку Н проведём АС1.0Н. Полученный треугольник АВС удовлетворяет заданным условиям.
Замечание. Задача решается аналогичным образом, если вместо угла а задано отношение сторон а и с.
Задача 6.
Через данную точку провести прямую, отсекающую от двух данных окружностей хорды, пропорциональные их радиусам.
Идея. Использовать свойства центра подобия окружностей.
Указание. Воспользоваться тем, что любая секущая, проведённая через центр подобия окружностей, отсекает от окружностей хорды, пропорциональные радиусам.
Решение. Воспользуемся тем, что любая секущая, проведённая через центр подобия окружностей, пересекает окружности таким образом, что треугольники АВО и А'В'О' являются гомотетическими. Проведём через центр подобия 5 и данную точку Р прямую. Из подобия треугольников АВО и А'В'О' следует пропорциональность соответствующих отрезков.
Задача 7.
Дан угол АВС и точка М внутри него. Найти на стороне ВС точку X, равноудалённую от АВ и точки М.
Идея. Использовать преобразование гомотетии.
Указание. Из произвольной точки X' £ ВС опустить перпендикуляр X'Y' на прямую АВ и отметить на луче ВМ точку М' такую, что Х'М' = X'Y'. Указание. Провести через точку М прямую, параллельную прямой М'Х'.


538
Указания и решения
Решение. Из произвольной точки X' Е ВС опустим перпендикуляр X'Y' на прямую АВ и отметим на луче ВМ точку М' такую, что Х'М' = X'Y'. Теперь проведём через точку М прямую, параллельную прямой М'Х', и получим искомую точку X. Треугольник MXY (где Y - основание перпендикуляра, опущенного из X на АВ) гомотетичен треугольнику M'X'Y' и, следовательно, также является равнобедренным.
Замечание. Задача решается аналогичным образом, если вместо перпендикуляра XY требуется провести отрезок, образующий с АВ заданный угол и находящийся в известном отношении к MX.
Задача 8.
Даны три точки А, В и С, не лежащие на одной прямой. Провести прямую, пересекающую отрезок АС в точке X, а отрезок ВС в точке Y таким образом, что АХ = XY = YB.
Идея. Построить четырёхугольник, подобный четырёхугольнику AXYB. Указание. На стороне АС отложить отрезок АХ' произвольной длины d, а на стороне ВС - отрезок BY' = АХ' = d. Провести окружность с центром в X' радиусом d и прямую через Y' параллельно АВ. Пусть Y" - точка их пересечения. Провести через неё прямую параллельно ВС и получить точки В' и С'.
Указание. Четырёхугольник AX'Y"B' (AX' = X'Y" — Y"B' = d) подобен искомому.
Решение. Построим четырёхугольник, подобный искомому четырёхугольнику AXYB. На стороне АС отложим отрезок АХ' произвольной длины d, а на стороне ВС - отрезок BY' = АХ' = d. Проведем окружность с центром в X' радиусом d и прямую через Y' параллельно АВ. Пусть Y" - точка их пересечения. Проведём через неё прямую параллельно ВС, получим точки В' и С'. Треугольник


5.5. Метод подобия
539
АВ'С' подобен ААВС, а четырёхугольник AX'Y"B' (AX' = X'Y" = Y"B' = d) подобен искомому.
Проведём прямую через точки А и Y" до пересечения со стороной ВС - получим точку Y. Теперь через точку Y проведём прямую, параллельную X'Y", до пересечения со стороной АС - получим точку X.
Замечание. Задача решается аналогичным образом, если вместо равенства отрезков задано отношение АХ : XY :YB.
Задача 9.
Даны две окружности и на них по точке. Провести две равные окружности, касающиеся друг друга и двух данных окружностей в заданных точках.
Идея. Использовать замечание к предыдущей задаче.
Указание. Рассмотреть треугольник АВС, где А и В - точки, данные на окружностях с центрами О и O', а С точка пересечения прямых О А и О'В.
Решение. Пусть О и О' - центры данных окружностей, а А и В - данные на них точки. Обозначим через С точку пересечения прямых О А и О'В.
В треугольнике АВС нам надо отыскать точки X Е АС и Y Е ВС такие, что АХ : XY :YB = 1:2:1, которые и будут центрами искомых окружностей. Точки X и Y строятся способом, указанным в предыдущей задаче.
Замечание. Если прямые О А и О' В параллельны, то радиусы искомых окружностей равны половине расстояния между этими прямыми.
Задача 10.
Через данную точку А провести к двум данным окружностям секущую, отсекающую в окружностях
а) равные хорды;
б) хорды, длины которых находятся в заданном соотношении.
Идея, а) Предположить, что секущая построена, и параллельно перенести одну из окружностей, б) Использовать результат пункта а).
С


540
Указания и решения
Указание, а) Пусть О и О' - центры данных окружностей, R и R' - их радиусы, а га - искомая прямая. Перенести вторую окружность вдоль этой прямой так, чтобы хорды совпали.
Указание. Построив вспомогательную окружность с центром в О", найти точки Р и Р', через которые проходит искомая секущая.
Решение. Пусть О и О' - центры данных окружностей, R и R' - их радиусы, а га - искомая прямая.
а) 	Перенесём вторую окружность вдоль этой прямой так, чтобы хорды совпали. Заметим, что, построив вспомогательную окружность с центром в СУ', мы найдем точки Р и Р', через которые проходит искомая секущая.
А
Для начала построим отрезок длины АО". Это есть гипотенуза прямоугольного треугольника с катетами длины R' и АС, где АС = АВ. Теперь точку О" можно построить как пересечение окружности с центром в А радиусом, равным уже построенному отрезку длины АО", и окружности, построенной на 00' как на диаметре (так как ZOO"О' = 90°).
б) 	Преобразуем первую окружность с помощью гомотетии с центром в точке А с коэффициентом, равным данному в условии отношению. Теперь для второй окружности и этой преобразованной окружности построим секущую, отсекающую равные хорды (см. пункт а).
Задача 11.
Построить треугольник, зная /3,1ь и AD : DC, где BD - высота. Идея. Построить треугольник, подобный требуемому.


5.5. Метод подобия
541
Указание. На произвольном отрезке А! С' построить дугу, вмещающую угол /3. Из точки D' е А'С такой, что A'D' : D'Cf = AD : DC, восстановить перпендикуляр к отрезку А'С'.
Решение. На произвольном отрезке А'С' построим дугу, вмещающую угол /3. Из точки D' е А'С' такой, что A! D’ : D’C9 = AD : DC, восстановим перпендикуляр к отрезку А'С'. Он пересечёт дугу в точке В. На биссектрисе угла В треугольника А'ВС' отложим отрезок BL = 1ь и проведём через точку L прямую параллельно А'С'. Получим точки А и С. Построенный таким образом треугольник АВС удовлетворяет заданным условиям.
Задача 12.
Даны три концентрические окружности. Провести секущую АВС так, чтобы точки А, В и С лежали на разных окружностях и АВ = ВС.
Идея. Использовать окружность Аполлония.
Указание. Используя окружность Аполлония, построить треугольник, подобный треугольнику АОС, где О - центр окружностей.
Решение. Пусть радиусы данных окружностей R\ < R2 < Дз- Рассмотрим произвольный отрезок А'С' с серединой в точке В'. Построим геометрическое место точек, расстояния от которых до А' и В' относятся как Rs : R2 (окружность Аполлония). Затем пересечём его с геометрическим местом точек, расстояния от которых до В' и С" относятся как R2 : Ri, и получим точку О' такую, что АА'С'О' подобен искомому ААСО. Для построения точек А и С достаточно построить угол, равный ZA'O'C', с вершиной в центре данных окружностей О.


542
Указания и решения
Задача 13.
Через две точки, лежащие вне данной окружности, провести окружность, касающуюся заданной окружности.
Замечание. Эта задача не на метод подобия, она потребуется для решения одной из следующих задач.
Идея. Использовать свойство секущих к окружности.
Указание. Провести через заданные точки А, В произвольную окружность, пресекающую данную в точках С, D. Пусть S - точка пересечения прямых СD и АВ. Провести касательные SL и SL' к заданной окружности.
Указание. По свойству секущих имеем SA • SB = SC • SD = SL2 = SL'2.
Решение. Проведём через заданные точки А, В произвольную окружность, пресекающую данную в точках С, D. Обозначим через S точку пересечения прямых CD и АВ. Рассмотрим касательные SL и SL' к заданной окружности. По свойству секущих имеем
SA ■ SB = SC ■ SD = SL2 = SL’2.
Теперь проведём окружность через точки А, В и L. По свойству секущих длина касательной, проведённой к этой новой окружности, равна y/SA • SB, следовательно, отрезок SL будет касаться этой окружности, а построенная окружность будет касаться данной окружности (внешним образом). Окружность, проведённая через точки А, В и L', также будет касаться данной окружности (внутренним образом) .
S
Задача 14-
Даны две окружности с центрами в точках О и O'. Через центр их подобия S проведены касательная и секущая. Касательная касается окружностей в точках С и С' соответственно, секущая отсекает от окружностей хорды АВ и АВ'. Доказать, что CS ♦ C'S = AS • B'S = BS • A'S.


5.5. Метод подобия
543
Замечание. Эта задача не на построение, она потребуется для решения следующей задачи.
Идея. Использовать подобие окружностей и свойство секущих.
Указание. Используя подобие окружностей, доказать второе равенство. Указание. Используя свойство секущих и доказанное равенство, доказать первое равенство.
Решение. Пусть к есть коэффициент подобия окружностей, тогда
AS _ BS _ h A'S ~~ B'S ~ ’
откуда AS • B'S = BS • A'S, и второе требуемое равенство доказано.
Для доказательства первого равенства воспользуемся свойством секущих:
CS2 = AS ■ BS, C'S2 - A’S ■ B'S =>
=> (CS ■ CS)2 = (AS ■ B’S) ■ (BS • AS) = (AS ■ B'S)2 = (BS ■ A'S)2
=» CS • C'S = AS ■ B'S = BS ■ A'S.
Задача 15.
Через данную точку А провести окружность, касающуюся двух данных окружностей.
Идея. Использовать результаты двух предыдущих задач.
Указание. Предположить, что окружность построена, и провести две прямые - одну через точки касания и вторую через центры данных окружностей. Указание. Показать, что точка пересечения этих прямых есть центр подобия данных окружностей.
Указание. Для нахождения второй точки, лежащей на искомой окружности, использовать результат предыдущей задачи.
Указание. Для построения искомой окружности использовать задачу 13.


544
Указания и решения
Решение. Пусть О и О' - центры данных окружностей, R и R! - их радиусы, О" - центр искомой окружности, Р и Q - точки касания искомой окружности с данными, S - точка пересечения прямой PQ с линией центров ОО'.
Из равенства вертикальных углов и равенства углов при основаниях равнобедренных треугольников PQO" и QP'O' следует, что
ZSPO = ZQPO" = ZPQO" = ZP'QO' = ZQP'O'.
О"
Таким образом, треугольники 5РО и SP'O' подобны по двум углам и коэффициент их подобия равен k = R/R'. Следовательно, точка 5 лежит на линии центров двух данных окружностей и
SO _ R SO' ~ R' ;
значит, S есть центр подобия этих окружностей. Используя результат предыдущей задачи и свойство секущих, получим
CS • С'S = PS • QS = AS • AS,
где С, С' - точки касания данных окружностей с касательной, проходящей через точку S, а В - точка пересечения секущей SА с искомой окружностью.
Итак, для построения искомой окружности сначала надо найти центр подобия данных окружностей 5, потом построить точку J5, отложив на отрезке 5А отрезок длины BS = CS С'S/AS. Далее через точки А и В (см. задачу 13) провести окружность, касающуюся любой из данных окружностей.


5.6. Метод поворота и смешанные задачи
545
5.6. 	Метод поворота и смешанные задачи Задача 1.
Даны три параллельные прямые. Построить квадрат, три вершины которого лежат на этих прямых.
Идея. Использовать поворот одной из прямых на 90°.
Указание. Взять произвольную точку на средней прямой и повернуть относительно неё одну из крайних прямых на 90°.
Решение. Пусть а, Ь, с - три данные параллельные прямые. Рассмотрим произвольную точку В G b и повернём относительно неё прямую с на 90°, получим прямую с' и точку A G а. При обратном повороте А перейдет в С G с. Осталось достроить равнобедренный прямоугольный треугольник АВС (по построению В А = ВС и ZВ = 90°) до квадрата.
Задача 2.
Даны прямая и окружность. Построить окружность, касающуюся данной окружности и прямой в данной точке.
Идея. Предположить, что искомая окружность построена, и использовать поворот данной окружности относительно центра построенной окружности.
m
18 Геометрия


546
Указания и решения
Указание. Пусть дана прямая т с точкой А и окружность с центром в точке О. Пусть искомая окружность (с центром в СУ) касается данной окружности в точке В, тогда при повороте на угол ZOO'А относительно точки СУ точка В переходит в А, а центр окружности О-в центр повёрнутой окружности О".
Решение. Пусть дана прямая га с точкой А и окружность с центром в точке О и радиусом г. Пусть искомая окружность (с центром в О') касается данной окружности в точке В, тогда при повороте на угол ОСУ А относительно точки СУ точка В переходит в точку А, а центр окружности О-в центр повёрнутой окружности О".
Для того чтобы построить центр искомой окружности СУ, надо сначала построить вспомогательную окружность с центром в точке О" радиуса г, касающуюся прямой га в точке А. Потом к отрезку ОСУ' провести серединный перпендикуляр, он пересечёт перпендикуляр из точки А к прямой га в искомой точке О'.
Задача 3.
Даны две окружности. Провести к ним через заданную точку две секущие, пересекающиеся под заданным углом и отсекающие
а) равные хорды;
б) хорды, длины которых находятся в заданном отношении.
Идея. Использовать поворот и задачу 9 предыдущего раздела.
Указание, а) Повернуть первую окружность относительно заданной точки А на заданный угол. Провести через точку А секущую, отсекающую от второй окружности и этой вспомогательной окружности равные хорды (см. задачу 9 предыдущего раздела).
Указание, б) Преобразовать первую окружность с помощью гомотетии с центром в точке А с коэффициентом, равным данному в условии отношению.
Решение. Пусть О и О' - центры заданных окружностей.


5.6. Метод поворота и смешанные задачи
547
а) Повернём первую окружность относительно заданной точки А на заданный угол. Теперь проведём через точку А секущую, отсекающую от второй окружности и этой вспомогательной окружности равные хорды (см. задачу 9 предыдущего раздела). Получим ВС — KL. С помощью обратного поворота найдём искомые В'С = KL.
б) 	Преобразуем первую окружность с помощью гомотетии с центром в точке А с коэффициентом, равным данному в условии отношению. Теперь для второй окружности и этой преобразованной окружности построим секущие, пересекающиеся под заданным углом и отсекающие равные хорды (см. пункт а).
Задача 4-
В данный параллелограмм ABCD вписать равнобедренный треугольник APQ (АР = AQ) с данным углом при вершине А.
Идея. Повернуть прямую, на которой лежат вершины С и £), на данный в
условии угол относительно точки А. Указание. Повернув прямую, на которой лежат вершины С и D, на данный в условии угол относительно точки А, получить на стороне ВС точку Р.
Решение. Повернём прямую га, на которой лежат вершины С и D, на данный в условии угол а относительно точки А. По- — лучим прямую га'. Пусть она пересекает сторону ВС в точке Р. При обратном повороте точка Р перейдёт в точку Q € га, причём Z.PAQ = а и АР = AQ.
/
Задача 5.
Построить четырёхугольник, вписываемый в окружность, зная его стороны а, 6, с и d.
Идея. Использовать поворот и окружность Аполлония.
Указание. Пусть ABCD - искомый четырёхугольник со сторонами АВ = а, ВС = 6, CD = с, DA = d и A ABC + Z.ADC — 180°. Отложить на прямой А В отрезок ABf = AD = d и провести через В' отрезок В'С' || ВС. Повернуть треугольник АВ'С' относительно точки А на угол /.BAD.
Указание. При таком повороте В' перейдет в точку D, а С' - в точку С", лежащую на прямой CD.
Указание. Для построения искомого четырёхугольника сначала построить треугольник АС С". У него известны
CD = с, AD = d, DC" = b-~, AC : AC" = a : d.
a
18*


548
Указания и решения
С помощью окружности Аполлония можно построить этот треугольник.
Решение. Пусть ABCD - искомый четырёхугольник со сторонами АВ = а, ВС = 6, CD = с, DA = d и ZABC -I- ZADC = 180°. Отложим на прямой АВ отрезок А В' = AD = d и проведём через В' отрезок В* С' || ВС.
Теперь повернём треугольник АВ'С' от- D. В
носительно точки А на угол BAD. При этом В' перейдет в точку D, а С' - в точку С", лежащую на прямой CD, так как
Z.ADC" + Z.ADC = ZABC + Z.ADC = 180°.
Для построения искомого четырёхугольника ~ D и
сначала надо построить треугольник АС С". У него известны
CD = с, AD = d, DC" = 6--, AC:AC"=a:d.
а
С помощью окружности Аполлония можно построить этот треугольник.
Далее от прямой АС надо отложить под углом, равным /.С"AD, отрезок АВ = а.
Задача 6.
Провести через заданную точку прямую, отсекающую от данной окружности хорду заданной длины.
Идея. Предположить, что искомая прямая построена, опустить на неё перпендикуляр из центра окружности и проанализировать рисунок.
Указание. Пусть 5 - данная точка, R - радиус окружности, а - длина отсекаемой хорды CD. Пусть М - середина хорды CD. Построив прямоугольный треугольник с катетом а/2 и гипотенузой Я, получить отрезок длины МО. Указание. Построить прямоугольный треугольник с гипотенузой SO и катетом МО.
Решение. Пусть S - данная точка, R - радиус окружности, а - длина отсекаемой хорды CD. Предположим, что искомая прямая проведена.
Пусть М - середина хорды CD. Построив прямоугольный треугольник с катетом а/2 и гипотенузой R, получим отрезок длины МО. Теперь построим прямоугольный треугольник с гипотенузой SO и катетом МО. Проведем прямую через точки М и 5.


5.6. Метод поворота и смешанные задачи
549
Задача 7.
При помощи циркуля и линейки построить окружность, проходящую через две данные точки и отсекающую от данной окружности хорду данной длины.
Идея. Найти точку, лежащую на прямой, проходящей через точки пересечения окружностей, и воспользоваться результатом предыдущей задачи.
Указание. Провести через заданные точки Л,В произвольную окружность, пресекающую данную в точках С, D. Показать, что местоположение точки S - точки пересечения прямых CD и АВ, не изменится, если через заданные точки Л, В провести другую окружность, пересекающую данную окружность в других точках.
Указание. При доказательстве использовать свойство секущих.
Решение. Проведём через заданные точки Л, В произвольную окружность, пресекающую данную в точках С, D. Обозначим через S точку пересечения прямых CD и АВ.
s
Рассмотрим касательные SK и SL к нашим двум окружностям. По свойству секущих имеем
SA-SB = SC-SD = SK2 = SL2.
То есть 5 - такая точка на прямой АВ, что отрезки касательных, проведенных из неё к заданной и искомой окружностям, равны между собой.
Проведём другую окружность через точки Л, В и покажем, что продолжение общей хорды пересечёт прямую АВ в точке S. Пусть новая окружность пересекает заданную в условии в точке С'. Обозначим через D',D" точки пересечения прямой SC' с заданной и новой окружностями. По свойству секущих имеем
SC' • SD" = 5Л • SB = SK2 = SL2 = SC9 • SD’.
Отсюда SCf • SD" = SC* • SD' и, следовательно, точки D' и D" совпадают.
Для того чтобы построить точку 5, достаточно провести через Л, В произвольную окружность и продолжить общую хорду до пересечения с прямой АВ.


550
Указания и решения
s
Теперь осталось провести через точку S прямую, отсекающую от данной окружности хорду CD заданной длины (см. предыдущую задачу), и описать вокруг четырёхугольника ABDC окружность (то, что это можно сделать, следует из подобия треугольников SAC и SBD).
Задача 8.
Провести через точку В пересечения двух окружностей прямую, высекающую из окружностей равные хорды.
Идея. Предположить, что требуемая прямая проведена, опустить на неё перпендикуляры из центров окружностей и проанализировать рисунок.
Указание. Пусть АС - искомая прямая (АВ = ВС) и Н, Н' - основания перпендикуляров, опущенных на неё из центров окружностей О, О'. Тогда HB = Н'В = АВ/2 = ВС/ 2.
Указание. Четырёхугольник ОНН'О' является прямоугольной трапецией со средней линией BD, где D - середина отрезка ОО'.
Решение. Пусть АС - искомая прямая (АВ = ВС) и Н,Н' - основания перпендикуляров, опущенных на неё из центров окружностей О, О'.
А


5.6. Метод поворота и смешанные задачи
551
Тогда НВ = Н'В = АВ/2 = ВС/2, так как перпендикуляр, опущенный из центра окружности на хорду, делит её пополам. Четырёхугольник ОНН'О' является прямоугольной трапецией со средней линией BD, где D - середина отрезка ОО'.
Для того чтобы построить АС, надо к прямой ВD (где D - середина отрезка ОО') провести перпендикуляр, который пересечёт окружности в точках А и С.
Задача 9.
Через точку А внутри угла провести прямую, отсекающую от угла треугольник минимального периметра.
Идея. Провести через точку А окружность, касающуюся сторон данного угла (см. предыдущий раздел), и провести через точку А касательную к этой окружности.
Указание. Показать, что эта касательная отсекает от угла треугольник минимального периметра.
Указание. Доказательство провести от противного, предположив, что искомая прямая является не касательной, а секущей.
Решение. Проведём через точку А окружность, касающуюся сторон данного угла (см. предыдущий раздел) в точках Р и Q, и проведём через точку А касательную к этой окружности. Покажем, что эта касательная отсекает от угла треугольник ОВС минимального периметра, причём
Ровс = (ОВ + В А) + (ОС + С А) = (ОВ + ВР) + (ОС + CQ) = OP + OQ.
Пусть искомая прямая С"В" является не касательной, а секущей. Проведём параллельно ей касательную С'В'. Получаем
Рос В" > Poc'B' = OP + OQ = Ровс ?
что противоречит нашему предположению. Следовательно, искомая прямая является не секущей, а касательной.
Задача 10.
Даны три точки. Построить окружности, попарно касающиеся в этих точках.


552
Указания и решения
Идея. Предположить, что искомые окружности построены, и провести через точки касания касательные к ним.
Указание. Эти касательные пересекаются в точке, которая по свойству касательных равноудалена от точек касания А, В и С, а значит, является центром описанной вокруг ААВС окружности.
Решение. Предположим, что искомые окружности построены. Касательные к ним, проведенные через точки касания А, В и С, пересекаются в точке О, которая по свойству касательных равноудалена от точек А, В и С. Значит, О - центр описанной вокруг ААВС окружности.
Проведём через точки А, В, С прямые, перпендикулярные радиусам описанной окружности. Точки пересечения этих прямых обозначим через О',О",О'". Покажем, что они являются центрами искомых окружностей.
Отрезок О'С равен отрезку О'В. Это следует из равенства прямоугольных треугольников О'СО и О1 ВО по катету и гипотенузе. Проведём окружность с центром в точке О' радиусом В! — О*С = О'В. Отрезок ОС будет касаться этой окружности, так как он перпендикулярен радиусу. Аналогично показывается, что ОС касается окружности с центром О" с радиусом R" = О"С = О"А. Следовательно, первая и вторая окружности касаются друг друга. Подобным образом показывается, что вторая окружность касается третьей, а третья — первой.
Задача 11.
Построить треугольник, зная a, ha и /(гаь,с).
Идея. Предположить, что треугольник построен, и провести в нём среднюю линию, параллельную стороне а.
Указание. Рассмотреть треугольник, отсекаемый данной медианой и средней линией В'С', параллельной стороне а.
Указание. Треугольник В'ВС' можно построить по основанию, противолежащему углу и высоте.
Решение. Рассмотрим треугольник, отсекаемый данной медианой и средней линией В'С', параллельной стороне а. Угол В'ВС' известен из условия задачи. Основание В'С' — а/2, так как является средней линией ААВС. Высота ВН = ha/2. Сле- С
довательно, АВ'ВС' мы можем построить по основанию, противолежащему углу и высоте.
После этого, отложив на прямой ВС' отрезок С'А = ВС', получим вершину А. Отложив отрезок СВ' = В'А на прямой В'А, построим вершину С.


5.6. Метод поворота и смешанные задачи
553
Задача 12.
Через вершину выпуклого четырёхугольника провести прямую, которая делит его площадь пополам.
Идея. Если середину диагонали четырёхугольника соединить с противолежащими вершинами, то площадь получившегося четырёхугольника будет вдвое меньше площади исходного четырёхугольника.
Указание. Провести прямую через середину диагонали параллельно другой диагонали.
Решение. Пусть О - середина диагонали АС четырёхугольника ABCD.
Проведем через точку О параллельно BD отрезок KF. Прямая BF будет делить площадь четырёхугольника пополам.
Это следует из того, что
-Sabcd = Sabod = Sabd + Sbod = Sabd + Sbdf — Sabfd•
Здесь мы воспользовались тем, что Sbod = Sbdf ? так как у этих треугольников общее основание и одинаковые высоты.
В


554
Указания и решения
6. Стереометрия
6.2. 	Многогранники
Задача 1.
В прямоугольном параллелепипеде диагональ, равная d, образует с боковыми гранями углы /3 и 7. Найти объём параллелепипеда.
Идея. Выразить длины рёбер параллелепипеда через длину диагонали и данные в условии углы.
Указание. Рассмотреть прямоугольные треугольники с гипотенузой d.
Решение. Рассмотрим прямоугольный параллелепипед ABCDА'В'С'D' с диагональю B'D = d, которая образует с гранью COD'D угол /3, а с гранью ADD'А' угол 7. Так как ребро В'С' перпендикулярно плоскости грани COD'D, то В'С' _L C'D и катет прямоугольного треугольника В'С'D равен В'С' = dsin/З. Из аналогичных соображений треугольник A'B'D также является прямоугольным и А'В' = dsin7. Для вычисления объёма параллелепипеда осталось найти DD'. Воспользуемся теоремой Пифагора:
В'
С'
DD' = л/d2 - (B'DО2 = л/d? - ((В'С')2 + (А'В')2) = dyjcoii1 (3 - sin2 7. В результате объём параллелепипеда равен
V = А'В' • В'С' • DD' = d3 sin /3 sin 7 \Jcos2 /3 — sin2
7-
Ответ, d3 sin /3 sin 7 \/ cos2 /3 — sin2 7.
Задача 2.
Объём правильной треугольной призмы равен V. Угол между диагоналями двух боковых граней, проведёнными из одной вершины, равен а. Определить сторону основания призмы.
Идея. Ввести две неизвестные (сторона основания и высота призмы) и составить два уравнения с этими неизвестными.
Указание. Первое уравнение - объём призмы, второе - теорема косинусов для угла а.
Решение. Пусть дана правильная прямоугольная призма АВС А'В'С' со стороной основания а и высотой h. Составим два уравнения с переменными а и h.


6.2. Многогранники
555
По условию задачи объём призмы равен V, следовательно,
/о
V = Sabc • h = ——a2h.
4
Теперь рассмотрим треугольник В'АС'. У него /В'АС' = а по условию, a стороны В' А — С' А = у/a2 -\-h2. По теореме косинусов
а2 = BfA2 + С'А2 - 2 • В'А • С'Л • cosa = 2(а2 + h2)(l - cosa).
Выразив из первого уравнения h
4V
2 16V2\ „
a = 2 ( a + "gQ4"' )(■*■““ COSQ;)
3a6 = 2 (3a6 + 16F2) (1 - cosa)
6 _ 32F2(1 — cosa)
3(2 cos a —1)
y/3a2
и подставив во второе, получим
a =
2y/V sin(a/2) {/3(2 cos a — 1)
Ответ.
2 {/У sin(a/2)
y3(2cosa-=Ty
C'
Задача 3.
Дан прямоугольный параллелепипед ABC DA' B'CfDf, у которого AD = б, AB = 3 и AA' = 2. Найдите угол между прямой АС' и прямой, проходящей через середины ребер А А' и В'С'.
Идея. Перенести прямую, проходящую через середины ребер А А и ВС, таким образом, чтобы она проходила через вершину А.
Указание. Искомый угол равен углу между отрезком АС' и отрезком, соеди¬
няющим вершину А с центром грани В В
Решение. Пусть К и М - середины рёбер А А' и В'С' соответственно. Перенесём отрезок КМ так, чтобы точка К перешла в вершину А. Тогда точка М перейдёт в центр грани В В'С'С - точку О и искомый угол будет равен углу О АС', который можно найти из соответствующего треугольника.
Вычислим длины сторон треугольника О АС':
'С.
В* М с


556
Указания и решения
АС' = у/АС2 + С'С2 = л/З2 + 62 + 22 = 7,
АО = VAB2 + ВО2 = у/З2 + 10 = \/19.
Теперь применим теорему косинусов к А ОАС' и найдём искомый угол:
29
Ю = 72 + 19 - 2 • 7 • \/19 • cos /.ОАС' cos АО АС' = —7=.
7л/19
п 29
Ответ, arccos—=.
Гл/19
Задача 4-
Дан куб ABCDA'В'С'D', в нём через вершину В' проведена диагональ. Найти отношение площади сечения этого куба плоскостью, перпендикулярной указанной диагонали и проходящей через её середину, к площади его полной поверхности.
Идея. Доказать, что искомым сечением будет многоугольник, вершинами которого являются середины рёбер куба, не имеющие общих точек с концами указанной диагонали.
Указание. Использовать то, что отрезок, соединяющий середину каждого из этих рёбер с серединой диагонали, перпендикулярен этой диагонали.
Решение. Рассмотрим куб ABCDА'В'С'D' с ребром а. Пусть К - середина ребра C'D', а О - середина диагонали B'D. Покажем, что OK _L B'D. Для этого рассмотрим треугольник B'KD. Он равнобедренный (равенство сторон В'К — KD следует из равенства прямоугольных треугольников В'С'К и DD'K), и, следовательно, его медиана КО является высотой. Таким образом, точка К (середина ребра C'D') принадлежит плоскости, перпендикулярной диагонали B'D и проходящей через её середину.
Аналогичным образом доказывается, что точки L, М, N, Р, Q (середины рёбер куба, не имеющие общих точек с концами диагонали B'D) также принадлежат указанной плоскости. Заметим, что расстояния от вершин полученного шестиугольника до точки О равны, как медианы соответствующих равных равнобедренных треугольников, а стороны шестиугольника равны а/у/2. Следовательно, он является правильным и состоит из шести равносторонних треугольников со стороной, равной а/у/2. Его площадь равна
6 • Sklo = 6 sin 60° = ^ра2.
Отношение площади сечения к площади полной поверхности куба равно


6.2. Многогранники
557
Задача 5.
В основании пирамиды лежит треугольник со сторонами 7, 8, 9. Боковые рёбра пирамиды наклонены к плоскости основания под углом 60°. Найти высоту пирамиды.
Идея. Воспользоваться тем, что если боковые рёбра наклонены к плоскости основания под одним углом, то основание высоты пирамиды является центром окружности, описанной около основания пирамиды.
Указание. В пирамиде ABCD провести высоту DH и воспользоваться равенством треугольников AHD, BHD и CHD.
Решение. Рассмотрим пирамиду ABCD с высотой DH. Прямоугольные треугольники AHD,
BHD, CHD равны по катету (DH - общий) и острому углу (ZDAH = Z.DBH = ZDCH = 60° по условию). Следовательно, АН = ВН = СН = R, где радиус описанной вокруг ААВС окружности равен
7-8-9
R =
4 5
Найдём площадь ААВС по формуле Герона
S = ^р(р-7)(р-8)(р-9) = л/12 • 5 • 4 • 3 = I2s/S.
В результате
В
DH = R.tg 60- = LJ^.V3=21'/I5
45
10
Ответ.
21у/15
10
Задача 6.
Дана правильная четырехугольная пирамида SABCD с вершиной 5. Через точки А, В и середину ребра SC проведена плоскость. В каком отношешш эта плоскость делит объём пирамиды?
Идея. Разбить отсекаемый пятигранник на две пирамиды (треугольную и четырёхугольную) и выразить объёмы этих пирамид через объём исходной пирамиды. Указание. Использовать формулу объёма пирамиды для нахождения отношений объёмов пирамид.
Решение. Рассмотрим правильную четырёхугольную пирамиду SABCD. Покажем, что плоскость, проходящая через А, В и середину ребра 5С, пересекает ребро 5D в его середине.
Проведём в треугольнике CDS среднюю линию KL. Так как KL || CD, а CD || АВ, то KL || АВ. Следовательно, искомая плоскость содержит прямую KL и пересекает ребро SD в точке L.
Выразим объём пятигранника ABCDKL через объём исходной пирамиды V.


558
Указания и решения
Сначала рассмотрим пирамиду ABCDL. Её объём равен V/2, так как её основание совпадает с основанием исходной пирамиды, а высота, опущенная на плоскость основания, в два раза меньше.
Теперь выразим через V объём пирамиды BCKL. Заметим, что
VbCKL = -jVBCKD,
поскольку длина перпендикуляра, опущенного на плоскость ВС К из точки L, в два раза меньше длины перпендикуляра, опущенного из точки D. Кроме того,
Vbckd = оVbcsd,
поскольку Sbck = ^ Sbcs • В результате получаем
Vabcdkl Ответ. 3:5.
V , Vbckd V , Vbcsd V , V Vabcdl + Vbckl = 2 + 2 = 2 + 4 = ¥ + ¥ =
5V^
Задача 7.
В правильной треугольной пирамиде SABC с вершиной 5 проведена высота SD. На отрезке SD взята точка К так, что SK : KD = 1 : 2. Известно, что двугранные углы между основанием и боковыми гранями равны —, а расстояние от
4 6
точки К до бокового ребра равно —=. Найти объём пирамиды.
\/13
Идея. Рассмотреть сечение пирамиды плоскостью, проходящей через её высоту и боковое ребро.
Указание. Опустить перпендикуляры из точек К и D на ребро SB и воспользоваться подобием полученных прямоугольных треугольников.
Решение. Рассмотрим высоту ВН правильного треугольника АВС, лежащего в основании правильной пирамиды SABC. Так как основание высоты пирамиды совпадает с центром треугольника АВС, то D € ВН и BD — 2HD.
Заметим, что HD является проекцией наклонной HS и HD _L АС. Следовательно, по теореме о трёх перпендикулярах SH J_ АС. Значит, угол между основанием и боковой гранью равен ZSHD = 30°.
х
Пусть HD = ж, тогда BD = 2х и SD = х- tg30° = . По теореме Пифагора
V3
/Тз
из ABDS получим, что SB = ху —.


6.2. Многогранники
559
Теперь проведём высоту DD' в прямоугольном треугольнике BDS. Так как SK : SD — 1 : 3 по условию, то из подобия треугольников SKK' и SDD' следует, что
DD' = 3 • К К' =
12
7Тз'
Найдём х из соотношения подобия треугольников SBD и DBD':
SB
SD
DB
DD'
x
7з
X = 6.
Следовательно, = Зх
Sabc = 3%/3а;2 = 108\/3 и
2х
~12~
7!з = 18,
F = i • 5D • Sabc = J • 2^ • 108\/3
«5 о
= 216.
В
Ответ. 216.
Задача 8.
Основанием пирамиды SABC является равносторонний треугольник АВС, длина стороны которого равна 4\/2. Боковое ребро SC перпендикулярно плоскости основания и имеет длину 2. Найти величину угла и расстояние между скрещивающимися прямыми, одна из которых проходит через точку S и середину ребра ВС, а другая проходит через точку С и середину ребра АВ.
Идея. Перенести одну из скрещивающихся прямых таким образом, чтобы искомый угол можно было найти как угол между двумя пересекающимися прямыми. Указание. Рассмотреть прямую, проходящую через середину отрезка ВС и параллельную прямой С К, где К - середина АВ.
Решение. Пусть К - середина АВ, a L - середина ВС. Перенесём отрезок С К в отрезок PQ вдоль прямой АВ так, что L € PQ. Искомый угол равен Z5LP, который можно найти из соответствующего треугольника. Вычислим длины его сторон SP и PL. Так как SC _L ABC, то треугольник SCP прямоугольный и
SP = yfsc2 + СР2 = у 22 + =^22+(V2)2 = V6.
Поскольку С К - медиана равностороннего треугольника, ZCKQ = 90°, параллелограмм CKQP является прямоугольником и PL = у/CL2 — СР2 = л/б-


560
Указания и решения
Теперь найдём угол SPL. Отрезок СР (проекция наклонной SP) перпендикулярен прямой PL, следовательно, по теореме о трёх перпендикулярах и сама наклонная SP перпендикулярна этой прямой. То есть треугольник SLP является равнобедренным прямоугольным треугольником и искомый ZSLP == 45°.
Осталось найти расстояние между скрещивающимися прямыми С К и SL.
Так как С К || PQ С SLP, то С К || SLP.
Следовательно, искомое расстояние равно расстоянию от прямой С К до плоскости SLP и равно высоте h тетраэдра PCLS, проведённой из вершины С.
Для того чтобы найти эту высоту, воспользуемся формулой объёма тетраэдра. С одной стороны,
Vpcls
SC
3
Sclp = з
2 v/2 - ч/б
С другой стороны,
h h V6-V6
У PCLS = з • &SLP — з • 2 =
_2_
у/з'
h =
_2_
V3'
Ответ. 2/ч/3.
6.3. 	Тела вращения Задача 1.
Плоское сечение SAB, проходящее через вершину S прямого кругового конуса, имеет площадь 60 см2. Точки А и В, лежащие на окружности основания конуса, делят её длину в отношении 1:5. Найти объём конуса, если угол SAB равен
( 2 ^ arccos —= I.
\V29j
Идея. Найти радиус основания конуса из формулы для площади сечения. Указание. Выразить стороны треугольника SAB через радиус основания конуса и приравнять выражение для площади ASAB числу 60.
Решение. Сначала выразим длину отрезка АВ через радиус основания R. Пусть О - центр основания конуса. По условию задачи длина дуги АВ составляет одну шестую всей длины окружности, следовательно, ZАОВ = 60°, треугольник АОВ равносторонний и АВ = R. Теперь выразим через R длину отрезка SA:


6.3. Тела вращения
561
Приравняем выражение для площади ASAB числу 60: Ssab = \ -SA- АВ -sinZSAB = 60 <^=>
* * 60 ^ Я = 4^.
2 4 у/29
Из прямоугольного треугольника AAOS найдём высоту конуса SO:
29 R2 „л/13
SO = y/SА2 - АО2 = \ ~R2 = R^-r- = V78.
V 16 4
В результате объём конуса равен
V = i • тгЛ2 • SO = ^ • 96тг • \/78 = 32тг\/78.
О О
Ответ. З27г\/78см3.
Задача 2.
Основание пирамиды - правильный треугольник со стороной 6. Одно из боковых ребер перпендикулярно плоскости основания и равно 4. Найти радиус шара, описанного вокруг пирамиды.
Идея. Использовать то, что центр описанного шара лежит на перпендикуляре к плоскости основания, проведённом через центр окружности, описанной около основания пирамиды.
Указание. Центр описанного шара лежит на перпендикуляре, проведённом через центр треугольника, лежащего в основании пирамиды.
Указание. Использовать то, что центр шара лежит на серединном перпендикуляре к боковому ребру.
Решение. Пусть боковое ребро SA перпендикулярно плоскости основания пирамиды ABCS. Пусть Н - центр основания АВС, то есть точка Н лежит на 2
медиане AM и АН = -AM.
о
Центр описанного шара лежит на перпендикуляре к плоскости основания, проведённом через точку Н. Следовательно, ОН || SA и центр О лежит в плоскости ASH. Так как центр шара равноудалён от точек А и S, то О принадлежит серединному перпендикуляру к отрезку SA, проведённому в плоскости ASH.
Таким образом, точка О есть точка пересечения этого серединного перпендикуляра и перпендикуляра, проведённого к отрезку AM из точки Н в плоскости ASH. Заметим, что полученный четырёхугольник AHON (см. рисунок) является прямоугольником.


562
Указания и решения
Искомый радиус О А найдём из прямоугольного треугольника АОН, катеты которого равны соответственно
ОН = l-S А = 2, АН = ^АМ = 1- ^- ■ АС = 2--^- ■ 6 = 2ч/3.
По теореме Пифагора
О А2 = ОН2 + АН2 = 22 + 4 • 3 = 16 => О А = 4.
Ответ. 4.
Задача 3.
Угол в осевом сечении прямого кругового конуса равен а. Через его вершину
Ct
под углом /3 к оси конуса (/3 < —) проведена плоскость. Найти угол х между
двумя образующими конуса, по которым проведенная плоскость пересекает его поверхность.
S
Идея. Рассмотреть тетраэдр, основанием которого является указанное сечение, а вершиной - центр основания конуса. Выразить высоту конуса и высоту равнобедренного треугольника, являющегося основанием тетраэдра, через длину образующей.
Указание. Угол между осью конуса и высотой равнобедренного треугольника, получившегося в сечении конуса, является углом между плоскостью сечения и осью конуса.
Решение. Пусть S - вершина прямого кругового конуса,
I - его образующая, О - центр основания, ABS - сечение конуса, проведённое под углом /3 к оси конуса, Н - середина АВ.
Покажем, что Z.HSO = /3. Так как SH JL АВ и ОН _L АВ (как медиана равнобедренного треугольника), то вся плоскость SHO JL АВ и любая прямая этой плоскости при проектировании на плоскость сечения проектируется в прямую SH. Следовательно, SH есть проекция наклонной SO и угол Z.HSO есть угол
между плоскостью сечения ABS и осью конуса, то есть Z.HSO — /3.
х
Найдём cos — из прямоугольного треугольника HSB. Для этого сначала найдём SO из прямоугольного треугольника В SO:
SO — BS • cos ~ = / • cos ~.
2 2
Теперь найдём SH из прямоугольного треугольника HSO:
/ а ОГЛ I • COS —
SH - = -2-.
cos р cos р


6.3. Тела вращения
563
В результате косинус половины искомого угла равен
а
cos —  2
cos/3 а
cos-
Ответ. 2arccos j-.
cos p
/ a orj I • COS —
cos Z# SB = —— = -2-:*
cos p
Задача 4-
Ребро куба равно а. Найти объём прямого кругового цилиндра, вписанного в куб так, что осью его является диагональ I куба, а окружности оснований касаются тех диагоналей граней куба, которые не имеют общих точек с диагональю I куба.
Идея. Для каждого из концов диагонали I рассмотреть треугольник, вершинами которого являются три ближайшие вершины куба, и показать, что основание цилиндра вписано в этот треугольник.
Указание. Доказать, что плоскость этого треугольника перпендикулярна диагонали I.
Решение. Рассмотрим куб ABCDА'В'С'D' сребром, равным а, и диагональю I = DB'. Покажем, что плоскость А'ВС' перпендикулярна диагонали DB'.
Рассмотрим треугольник B'C'D с высотой С'Н.
Он прямоугольный, так как ребро В'С' перпендикулярно плоскости грани CDD'C'. Из аналогичных соображений треугольник В'A'D также является прямоугольным. Из равенства этих треугольников (по катету и гипотенузе) следует равенство проекций катетов на гипотенузу. Следовательно, точка Н является основанием высоты и для А В'A'D.
Поскольку диагональ I перпендикулярна двум пересекающимся прямым плоскости А'НС', плоскость А'НС' JL /. Другими словами, плоскость, перпендикулярная прямой I и проходящая через точку Н, содержит вершину куба А'. Из аналогичных соображений эта плоскость содержит и вершину В.
По условию задачи окружности оснований цилиндра касаются тех диагоналей граней куба, которые не имеют общих точек с диагональю I, в частности диагоналей А'В, ВС' и А'С'. Так как плоскость А'ВС' JL / , то этих диагоналей может касаться только одна из окружностей основания конуса, причём только если она вписана в треугольник А ВС'. Выразим радиус этой окружности и диагональ куба через а:
i • sin 60е о
■^Ч'ТГ
I = B'D = у/(В'С’)2 + CD2 = а\/3.
Для того чтобы найти высоту цилиндра, выразим через а длину отрезка В'II:
sin ZC'DB' = sin ZB'C'H
a
1
B’H
a
B’H =
a\/3


564
Указания и решения
Заметим, что второе основание цилиндра вписано в треугольник ACD', плоскость которого также отсекает от диагонали I одну треть. Следовательно, высота цилиндра равна
^ _ I _ ал/3 _ а 2 т а2 а 7га3\/3
3 3 у^З 6 у/з 18
Ответ. 7га3\/3/18.
Задача 5.
Дана правильная треугольная пирамида со стороной основания, равной 2\/7. Центр основания пирамиды является вершиной конуса, окружность основания которого вписана в боковую грань пирамиды. Найдите радиус основания конуса.
Идея. Рассмотреть сечение пирамиды, проходящее через высоту пирамиды и ось конуса.
Указание. Использовать подобие прямоугольных треугольников и то, что центр основания конуса является точкой пересечения биссектрис соответствующей боковой грани пирамиды.
Решение. Пусть SH - высота пирамиды ABCS, а окружность основания конуса с вершиной Н вписана в боковую грань ABS. В этом случае осью конуса будет являться отрезок НО, где О - центр окружности, вписанной в треугольник ABS. Рассмотрим сечение пирамиды плоскостью, проходящей через высоту пирамиды и боковое ребро SC. Поскольку пирамида правильная, сечение будет проходить через середину ребра АВ, ^ точку М. Центр основания конуса О будет лежать на биссектрисе 5М, причём отрезок ОМ будет радиусом основания конуса г. Положим Z.OAM = а. Так как АО - биссектриса угла ZSAM, то ZSAM = 2а. Выразим tga и tg2a через г и составим соответствующее уравнение для г с помощью формулы тангенса двойного угла.
Из прямоугольного треугольника АОМ получим tg а = • Из пря-
о SM SM
моугольного треугольника ASM получим tg2a = • Для того чтобы
выразить длину отрезка SM через г, воспользуемся подобием прямоугольных треугольников НОМ и SHM. Получим
S


6.3. Тела вращения
565
Теперь составим уравнение для г с помощью формулы тангенса двойного угла:
2tga у/7 _ 2гу/7
1 — tg2 a 3r 7 — г2
tg 2a = —2— => — = у <=> 7 — г = 6 г <==> г = 1,
откуда г = 1. Ответ. 1.
Задача 6.
В треугольной пирамиде длины двух непересекающихся рёбер равны 12 и 4, а остальные рёбра имеют длину 7. В пирамиду вписана сфера. Найти расстояние от центра сферы до ребра длины 12.
Идея. Найти на бимедиане, соединяющей середины неравных рёбер, точку, равноудалённую от всех граней тетраэдра.
Указание. Показать, что любая точка этой бимедианы находится на одинаковом расстоянии от равных граней.
В
Решение. Рассмотрим пирамиду ABCD, у которой рёбра АС = 4, BD = 12, а длины остальных рёбер равны 7. Пусть PQ - бимедиана, соединяющая середины рёбер АС и BD. Найдём точку О £ PQ, равноудалённую от всех четырёх граней тетраэдра. Это и будет центр вписанной сферы.
Заметим, что плоскость BDP _1_ АС и угол ZBPD есть угол между плоскостями ADC и АВС, поскольку DP _L АС (как медиана равнобедренного треугольника ADC), а ВР _L АС (как медиана равнобедренного треугольника АВС).
Так как PQ - биссектриса угла BPD (как медиана равнобедренного треугольника BDP) и PQ ± АС (PQ С BPD _L АС), то /.(ADC, AQC) = Z{ABC,AQC), то есть PQ лежит в биссекторной плоскости и любая точка прямой PQ равноудалена от плоскостей ADC и АВС.
Аналогичным образом показывается, что любая точка прямой PQ равноудалена от плоскостей BAD и BCD. Следовательно, если мы найдём точку О £ PQ такую, что расстояния от неё до плоскостей АВС и BCD равны, то О будет равноудалена от всех четырёх граней тетраэдра.
Рассмотрим точку О G PQ и точку СУ - проекцию точки О на прямую ВР. Так как ОО' С BPD ± АС, то ОО' _L АС. Значит, ОО' перпендикулярна двум пересекающимся прямым плоскости АВС и, следовательно, ОО' JL АВС. Аналогичным образом доказывается, что отрезок ОО" (где О" - основание перпендикуляра, опущенного из О на CQ) перпендикулярен плоскости BCD.


566
Указания и решения
Пусть искомый отрезок OQ = х. Составим уравнение для х, приравняв длины отрезков ОО' и ОО":
РО ■ sin /BPQ = QO • sin /.CQP ^ (PQ - х) • ^ = х •
Иг
Найдём длины отрезков CQ, ВР и PQ:
CQ = у/ВС2 - BQ2 = = у/й,
ВР = у/ВС2 - СР2 = \/72 - 22 = >/45,
PQ = \/С<52 - СР2 - >/13 - 22 = 3.
Подставив эти значения в уравнение, получим
(3 — ж) • —== — х • — Vl3(3 — х) = х\/ъ ■<=>■ х = ^
Ответ.
\/45 л/13 л/13 + л/5 *
Зл/13
\/l3 + л/5
Задача 7.
Три параллельные прямые касаются в точках А, В и С сферы радиуса 4 с центром в точке О. Найти угол ВАС, если известно, что площадь треугольника ОВС равна 4, а площадь треугольника АВС больше 16.
Идея. Рассмотреть сечение сферы, проходящее через центр сферы перпендикулярно данным прямым.
Указание. Найти синус угла ВОС, использовав информацию о том, что площадь треугольника ОВС равна 4. Рассмотреть возможные значения величины угла ВАС. Произвести отбор согласно условию: площадь треугольника АВС больше 16.
Решение. Так как радиусы О А, О В и ОС перпендикулярны данным параллельным прямым и имеют общую точку, то все три отрезка (О А, О В и ОС) лежат в одной плоскости. Рассмотрим сечение сферы этой плоскостью.
По условию задачи Saobc = 4, следовательно,
- • О В ■ ОС • sin /ВОС — 4 <=> sin /ВОС =
2 2
Рассмотрим возможные варианты.
7Г 7Г 11.7Г
1) 	Если ZВОС = —, то ZВАС = — (левый рисунок) или ABAC — (правый
рисунок).


6.3. Тела вращения
567
А
В любом случае будет
Saabc = \-АВ ■ АС ■ sin LB АС < ± • 8 • 8 • | = 16, что противоречит условию.
2) 	Если /.ВОС = -тг и ZВАС = ^ (левый рисунок), то 6 12
Saabc < ^ • ВС • ОА < - • 8 • 4 = 16, что также противоречит условию.
Остаётся единственно возможный вариант (правый рисунок): ZВОС = — и
6


568
Указания и решения
6.4. 	Комбинации тел
Задача 1.
В сферу радиуса R вписан прямой круговой цилиндр. Найти наибольшее значение площади боковой поверхности цилиндра и отношение его высоты к радиусу сферы в этом случае.
Идея. Представить выражение площади боковой поверхности цилиндра в виде функции от радиуса его основания и найти максимум этой функции.
Указание. Рассмотреть осевое сечение цилиндра и с помощью теоремы Пифагора выразить его высоту через радиус основания и радиус сферы.
Решение. Так как осевым сечением цилиндра будет прямоугольник с диагональю 2R и сторонами, равными 2г и /г, где г - радиус основания цилиндра, h - его высота, то
£бок “ 27гг/г = 27гг у/(2R)2 — (2г)2.
Заметим, что функция 5|ок = 167r2r2(i?2 - её максимальное значение достигается при г2 Искомое отношение в этом случае равно
2\2
h
R
y/(2R)2 - 2R2 R
R /2 и равно (2ttR2)
V2.
Ответ. 2ttR2 , y/2.
Задача 2.
В прямой круговой конус вписан шар. Отношение объёмов конуса и шара равно двум. Найти отношение полной поверхности конуса к поверхности шара.
Идея. Составить систему из трёх уравнений с четырьмя неизвестными: высота конуса, образующая, радиус основания и радиус вписанного шара. Выразить все неизвестные через какую-нибудь одну и подставить в искомое выражение. Указание. Рассмотреть осевое сечение конуса.
Решение. Пусть треугольник АВС - осевое сечение конуса, тогда сечение сферы, вписанной в конус, будет окружностью, вписанной в этот треугольник, причём центр О этой окружности будет лежать на высоте ВН. Положим h = ВН, I — ВС, R = НС, г - радиус вписанной окружности и выпишем уравнения, связывающие эти переменные.
1) 	Объём конуса в 2 раза больше объёма вписанного шара:
\'kR2H — 2 • ^7гг3.
3 3


6.4• Комбинации тел
569
2) Теорема Пифагора для треугольника ВСН :
I2 = h2 + R2.
3) Подобие треугольников ОМ В и СНВ:
г h — г R = I ’
Теперь выпишем искомое выражение (отношение площади полной поверхности конуса к площади поверхности шара):
7tR2 -f~ 7ГRl R? -Ь RI
4 7ГГ2 4г2
Заметим, что для всех конусов, подобных нашему, мы получим один и тот же ответ, то есть мы можем рассмотреть наиболее удобный для нас с вычислительной точки зрения конус, например со вписанным шаром радиуса г = 1. В этом случае система примет вид
R2h = 8, l2 = h2 + R2,
< l = R(h- 1), R2 + Rl , 4
Далее можно действовать одним из следующих способов.
1) Честно решить систему из трёх нелинейных уравнений, найти значения всех переменных (R = у/2, h = 4, Z = Зу/2) и подставить эти значения в искомое выражение.
2) Подставить выражение для / в искомое выражение и использовать первое равенство системы:
R2 + Rl _R2 + R2(h - 1) _ R2h _ 8 _ п 4 “ 4 ~ 4 ~ 4 ~ '
Ответ. 2.
Задача 3.
В правильную треугольную пирамиду помещены три шара так, что первый шар касается всех боковых граней пирамиды и второго шара, второй шар касается боковых граней пирамиды и третьего шара, а третий шар касается боковых граней, основания пирамиды и второго шара. Какую долю объёма пирамиды занимают три шара, если её боковые грани наклонены к основанию под углом а ?
Идея. Рассмотреть сечение, проходящее через высоту пирамиды и апофему боковой грани.
Указание. Провести к трём окружностям, полученным в этом сечении, общие касательные и использовать подобие трёх полученных треугольников.
В


570
Указания и решения
Указание. Выразить радиусы шаров, сторону основания пирамиды и её высоту через МН и а, где Н - центр основания пирамиды, а М - середина стороны основания.
Решение. Рассмотрим сечение правильной пирамиды ABCS, проходящее через апофему SM и боковое ребро CS. Поскольку пирамида является правильной, МС 1. АВ и ZSMC есть угол между боковой гранью и основанием, то есть Z.SMC = а.
Заметим, что третий шар касается всех граней пирамиды, то есть является шаром, вписанным в правильную пирамиду, следовательно, точка касания боковой грани принадлежит апофеме. Кроме того, центр шара О лежит на высоте пирамиды SH, причём Н является центром треугольника АВС и точкой касания шара с основанием пирамиды.
Первый и второй шары также вписаны в трёхгранный угол с вершиной 5, следовательно, их центры также принадлежат высоте SH (прямой пересечения бис- секторных плоскостей трёхгранного угла), а точки касания с боковой гранью ABS принадлежат апофеме SM. Поэтому в сечении SMC мы получим три окружности, касающиеся отрезка SM, с центрами на SH. Обозначим через Н' и Н" точки касания третьего шара со вторым и второго с первым. Проведём через них общие касательные, которые пересекут отрезок SM в точках М' и М" соответственно.
М
Пусть а = МН, h\ = SH, h2 — SH', hs = SH", тогда r\ = ОН =
hi = a tga. Выразим радиусы второго и третьего шара через г\ и hi. Треугольники SM'H' и SMH подобны с коэффициентом подобия
a tg
а
2 ’
h2 hi
hi — 2r*i hi
1
2ri
hi
7*2 = kin = n 1
2гЛ
Треугольники SMnHn и SM'H' подобны с коэффициентом подобия
h3 h2-2r2 л 2 r2 f 2r2\ (л 2ri"\2
fe = ^ = -^ = 1“ ЛГ ^ ra = km=r2(l--)=r^.1-—j.
Сумма объёмов всех трёх шаров равна
к+ц+и, = |»(г?+^+г1) = |»гг^1+(1-^) +(1-^) )•


6.4• Комбинации тел
571
_ а
Воспользовавшись тем, что r\ = a tg — и /ii = a tg а, упростим выражение во
внутренних скобках:
а а
2 tg — 2 tg
Л-i tg а 2 tg — ' ^ ^
6 2
Следовательно,
Vi + V2 + V3 = ^тга3 tg3 | (i + tg6 ^ + tg12 .
Теперь выразим через а и а объём пирамиды
/ii МС • АВ h\ За • 2у/3а /— 2 /о з
F = у = у = V3hia2 = v3a tg а.
Искомое отношение равно
у-. + у. + ц Г“3^|(1 + ^| + ^12|) 4va,tg3t/1|U..«»|U.a»\
V у/да3 tg а 9 tga Vi + tS 2 + g г)
4\/37гtg3 ^ / a а\
°ТВеТ' 9tga (1+te 2+tS а)’
Задача 4-
Сфера радиуса 2 касается плоскости в точке А. В той же плоскости лежит основание конуса. Прямая, проходящая через центр основания конуса (точку С) и точку сферы, диаметрально противоположную точке А, проходит через точку М. Точ¬
ка М является точкой касания сферы и Найдите высоту конуса, если АС = 1.
Идея. Рассмотреть сечение, проходящее через высоту конуса и центр сферы. Указание. С помощью теоремы Фалеса показать, что радиус основания конуса равен половине отрезка АС.
Решение. Пусть 5 - вершина конуса, О - центр сферы.
Высота конуса SC и радиус сферы О А параллельны, так как оба отрезка перпендикулярны данной плоскости. Рассмотрим секущую плоскость, проходящую через них. В этой плоскости будут лежать и точка В (диаметрально противоположная точке А), и точка М
конуса (их единственная общая точка).
В


572
Указания и решения
(точка касания сферы и конуса, которая принадлежит прямой СВ по условию задачи).
Обозначим через Р вершину треугольника, являющегося сечением конуса, ближайшую к точке А.
Высоту конуса SC будем искать из прямоугольного треугольника SCP:
SC = СР • tg Z.CPS.
Сначала найдём СР. Пусть угол MBA = а, тогда
ZMOA = 2а, ZPOA = ZMOA = а.
2
Из равенства соответственных углов следует параллельность прямых СВ и РО, а из равенства АО = О В и теоремы Фалеса следует равенство отрезков СР = РА. Так как по условию АС = 1, то СР = РА = 1/2.
Теперь выразим угол CPS через а и найдём длину катета SC:
/CPS = 180° - /АРМ - 180° - (180° - /АОМ) = 2а,
РА V2 1 1 2 tga 4
tga =— = - => SC = CP- tg2a=-- 6
Ответ.
15
АО 2 4 6 2 1 — (tga)2 15'
4
Задача 5.
Основанием правильной пирамиды является равносторонний треугольник со стороной а, а высота, опущенная на это основание, равна Н, причём все шесть рёбер пирамиды касаются некоторой сферы. Найти радиус этой сферы.
Идея. Найти такую точку на прямой, содержащей высоту пирамиды ABCS, что расстояния от неё до ребра ВС и прямой BS равны.
Указание. Опустить перпендикуляры на прямые ВС, BS и получить систему из двух уравнений с двумя неизвестными, применив теорему Пифагора к двум получившимся прямоугольным треугольникам.
Решение. Рассмотрим правильную пирамиду ABCS с высотой 50, в основании которой лежит равносторонний треугольник АВС со стороной a. Поскольку сфера касается рёбер основания пирамиды, сечение этой сферы плоскостью АВС есть окружность, вписанная в треугольник АВС. Так как пирамида является правильной, то основание её высоты (точка О) есть центр этой окружности. При этом центр самой искомой сферы будет лежать на прямой, перпендикулярной плоскости АВС, проходящей через точку О.
Найдём точку О' на прямой 50 такую, что расстояния от неё до ребра ВС и прямой В5 равны. Обозначим основания соответствующих перпендикуляров через К и L соответственно. Заметим, что точка К есть точка касания окружности, вписанной в ААВС, со стороной ВС. Тогда искомый радиус равен R = О'К = O'L.


6-4- Комбинации тел
573
Пусть h = ОО', г = О К. По теореме Пифагора h2+r2 = R2. Теперь рассмотрим прямоугольные треугольники O'SL и BSO. Они подобны по острому углу, следовательно,
O'L SO' ВО ~ SB'
В случае, если точка О' лежит на отрезке SO, уравнение имеет вид
R H-h
2 г у''#2 + (2 г)2
Если же точка О' лежит на продолжении отрезка SO за точку О, уравнение имеет вид
R H + h
2 г y/WTWF
В любом случае для 1г получаем следующее выражение:
/ Ry/H2 + (2 г)2
h
Н
V 2г /
Таким образом, искомое значение R удовлетворяет системе уравнений Г h2+r2 = R2,
h,= (R№
^Ry/H2 + (2r)2
2r
- Я + r2 = Д2 <=*•
R2H2-4RrHy/H2 + (2r)2+4r2tf2+4r4 = 0 Ф=Ф Я = ± .
ii iiz
Заметим, что существуют две различных сферы, касающиеся прямых, содержащих рёбра нашей пирамиды. Сечение первой сферы плоскостью боковой грани


574
Указания и решения
BCS есть окружность, вписанная в треугольник BCS, сечение второй сферы этой плоскостью есть вневписанная окружность.
По условию задачи интересующая нас сфера касается боковых рёбер (а не их продолжений), поэтому в качестве её радиуса возьмём меньшее из полученных значений,
_ 2гУЯ2 + (2 г)2 2уДг2
R- Я Н~'
Осталось выразить ответ через Н и а:
ау/3 „ ау/Ш2 + а2 а2
г = —— => R =
ЗЯ 2у/ЗН
ау/ ЗЯ2 + а2 а2
Ответ.
ЗЯ 2у/3 Я'
Задача 6.
Внутри правильного тетраэдра ABCD расположен конус, вершина которого является серединой ребра CD. Основание конуса вписано в сечение тетраэдра, проходящее через середину ребра ВС параллельно прямым CD и АВ. Площадь боковой поверхности конуса равна 97г\/3. Найдите длину ребра тетраэдра.
Идея. Доказать, что данное сечение является квадратом.
Указание. Показать, что бимедианы правильного тетраэдра перпендикулярны друг другу и равны между собой.
Решение. Пусть плоскость данного сечения а правильного тетраэдра ABCD с ребром длины а проходит через точку К - середину ребра СВ.
Так как по условию задачи а || CD, то а пересекает плоскость BCD по прямой KN || CD, причём KN - средняя линия равностороннего треугольника BCD.
Так как а || АВ, то а пересекает плоскость АВС по прямой KL || АВ, причём KL - средняя линия равностороннего треугольника АВС.
Рассмотрим отрезок MN - среднюю линию треугольника ABD:
MN || АВ, АВ || KL =»
следовательно, сечением данного тетраэдра плоскостью а является четырёхугольник KLMN, вершинами которого являются середины соответствующих рёбер.
С
В
MN || KL =» MN с а,


6.4. Комбинации тел
575
Заметим, что стороны этого четырёхугольника являются средними линиями соответствующих граней тетраэдра, следовательно, KLMN - ромб со стороной а/2. Более того, KLMN - квадрат, поскольку
AD = АС = а, АК — KD — AN — NC (как медианы равных граней тетраэдра) ==> Д AKD = A AN С => MX = LN (как медианы равных треугольников).
Замечание. По ходу дела мы доказали, что бимедианы правильного тетраэдра, во-первых, пересекаются в одной точке и делятся этой точкой пополам (это верно и для любого произвольного тетраэдра), во-вторых, равны и взаимно перпендикулярны.
Получается, что основание конуса вписано в квадрат KLMN со стороной а/2, то есть радиус основания конуса равен Д = а/4. Согласно замечанию, бимедиана PQ проходит через точку О (центр квадрата KLMN) и PQ _L МК, PQ _L LN, следовательно, PQ _L а и РО - высота конуса.
Найдём длину бимедианы PQ из треугольника CDQ со сторонами CD = а, л/З
CQ = DQ — а~2~ и высот°й
PQ = ^DQ2 - DP2 = .
PQ >/2
Следовательно, высота конуса /i = РО = —— = а~~г~ч а площадь боковой поверхности
С D7 D /в2 ". L2 ™ 1а2 , 2а2 тгсг2\/3
5бок - тгД/ - тгД V Д — 4V16 16- 16 *
Приравняв это выражение значению 97г\/3? найдём а:
7га2\/3 /-
——— = 97tv3 <=^ а = 12.
16
Ответ. 12.
Задача 7.
В треугольной пирамиде ABCD ребро DC — 9, ребро DB = AD, а ребро АС перпендикулярно грани ABD. Сфера радиуса 2 касается грани АВС, ребра DC, а также грани ABD в точке пересечения её медиан. Найти объём пирамиды.
Идея. Принять за неизвестные длины рёбер, выходящих из вершины А, и составить систему из трёх уравнений с этими неизвестными.
Указание. Записать теорему Пифагора для AADC. Выразить длину медианы DH треугольника ABD через радиус сферы и записать теорему Пифагора для Д ADH.
Указание. Последнее уравнение можно получить, применив теорему Пифагора к треугольнику ACO"Q, где О" - проекция центра сферы О на плоскость АВС, a Q - проекция точки О" на прямую АС.


576
Указания и решения
Решение. Пусть О - центр данной сферы, а О', О" и Р - точки касания этой сферы с гранями ABD, ABC и ребром DC соответственно.
Рассмотрим плоскость а, перпендикулярную прямой АВ, проходящую через точку О. Так как радиус, проведённый в точку касания, перпендикулярен касательной плоскости, то ОО' С а и ОО" С а. Обозначим через Н точку пересечения прямой А В с плоскостью а.
Покажем, что ОО'НО" - квадрат. Поскольку a _L АВ, отрезки О'Н и 0"Н перпендикулярны АВ. Кроме того, /О'НО" = 90°, так как из перпендикулярности ребра АС и плоскости ABD следует перпендикулярность плоскостей АВС и ABD. Таким образом, углы при вершинах О', О" и Н четырёхугольника ОО'НО" прямые, следовательно, он является прямоугольником. Так как две смежные стороны равны (ОО' = ОО" = 2), этот прямоугольник является квадратом.
Для того чтобы найти площадь основания с тетраэдра, нам надо найти высоту треугольника ABD. Так как по условию задачи О' есть точка пересечения медиан равнобедренного треугольника ABD, то О' Е DH, где DH является медианой и высотой одновременно. Следовательно,
DO' = 2 НО' = 200" = 4 =► DH = 6.
Положим h = АС, а = AD, b = ЛЯ и составим три уравнения с этими неизвестными. По теореме Пифагора из прямоугольных треугольников AHD и ACD получим
В
Ъ2 + 62,
а2 + Л
Теперь запишем теорему Пифагора для треугольника CO"Q, где Q - основание перпендикуляра, опущенного из точки О" на прямую АС. Так как четырёхугольник AHO"Q является прямоугольником, то AQ = НО" = 2, QO" = АН = Ь, следовательно,
О"С2 = (Л - 2)2 + Ь2.
Длину гипотенузы О" С найдём с помощью равенства касательных, проведённых из одной точки:
О" С = СР = 9 - DP Из полученной системы найдём Ь и h:
' а2 = Ь2 + 62, а2 + h2 = 92, ==>
(.h - 2)2 + Ь2 = 52;
Следовательно, объём тетраэдра равен
9 - /ХУ = 9 — 4 = 5.
62 + h2 = 45,
(Л - 2)2 + Ь2 = 52;
6 = 3, /1 = 6.
V = | • | • 66 = 36.
Ответ. 36.


6-4• Комбинации тел
577
Задача 8.
Отрезок PN - диаметр сферы. Точки М, L лежат на сфере так, что объем пирамиды PNML наибольший. Найдите синус угла между прямой NT и плоскостью PMN, если Т - середина ребра ML.
М
Идея. Объём пирамиды PNML максимален в случае, когда отрезки ОМ и OL перпендикулярны диаметру PN и друг другу.
Указание. Показать, что проекцией наклонной NT является отрезок NH, где Н - середина МО.
Решение. Сначала определим положение точек М и L на сфере. Так как расстояние от любой точки сферы до диаметра не превосходит радиуса сферы R, то
VpNML < g • SaPNL • R < g • 2
причём максимум достигается тогда, когда перпендикуляры, опущенные из точки L на прямую PN и из точки М на плоскость PNL, приходят в центр сферы
О. 	Это значит, что грани тетраэдра PNM и PNL являются равными равнобедренными треугольниками с взаимно перпендикулярными высотами МО = R и LO = R соответственно.
Рассмотрим треугольник MOL. Его средняя линия ТН _L PMN, так как ТН || OL, a OL _L PMN. Следовательно, отрезок NH есть проекция наклонной NT и искомый угол между прямой NT и плоскостью PMN есть угол ZSTNH. Для того чтобы вычислить sin ZTNH, нам понадобится найти НТ и NT.
Отрезок НТ - средняя линия треугольника MOL, следовательно,
М
ЯГ =
OL
R 2 ’
Отрезок NT найдём как медиану треугольника MNL. Заметим, что все стороны этого треугольника равны RyJ2, следовательно, его медиана равна
NT = RV2 ■
V3 rVg
В результате sin ZT NH =
HT
Д/2
NT ~ Rs}6/2
ч/б’
Ответ. 1/V6.
19 Геометрия


578
Задачи ЕГЭ последних лет
Задачи ЕГЭ последних лет Планиметрия
1. (ЕГЭ-2013.С4) Окружности радиусов 4 и 13 с центрами 0\ и 02 соответственно касаются в точке L. Прямая, проходящая через точку L, вторично пересекает меньшую окружность в точке К, а большую - в точке М. Найдите площадь треугольника КМО\, если ALM02 = 22,5°.
2. (ЕГЭ-2013.С4) Окружности радиусов 13 и 20 с центрами 0\ и 02 соответственно касаются внешним образом в точке С, АО\ и В02 - параллельные радиусы этих окружностей, причём АА0\02 = 60°. Найдите АВ.
3. (ЕГЭ-2014.С4) В остроугольном треугольнике АВС провели высоту ВН. Из точки Н на стороны АВ и ВС опустили перпендикуляры НК и НМ соответственно.
а) Докажите, что треугольник МВК подобен треугольнику АВС.
б) Найдите отношение площади треугольника МВК к площади четырёхугольника АКМ С, если ВН = 1, а радиус окружности, описанной около треугольника АВС, равен 3.
4. (ЕГЭ-2014.С4) Около остроугольного треугольника АВС описана окружность с центром О. На продолжении отрезка АО за точку О отмечена точка К так, что ABAC + ААКС = 90°.
а) Докажите, что четырёхугольник О В КС вписанный.
б) Найдите радиус окружности, описанной около четырёхугольника ОВКС, если cos ABAC = 5/13, а ВС = 72.
5. (ЕГЭ-2014.С4) Высоты ВВ1 и СС' остроугольного треугольника АВС пересекаются в точке Н.
а) Докажите, что А АН В' = А АС В.
б) Найдите ВС, если АН = 10л/3 и ABAC — 30°.
6. (ЕГЭ-2014.С4) Две окружности касаются внешним образом в точке К. Прямая АВ касается первой окружности в точке А, а второй — в точке В. Прямая В К пересекает первую окружность в точке D, прямая АК пересекает вторую окружность в точке С.
а) Докажите, что прямые AD и ВС параллельны.
б) Найдите площадь треугольника АКВ , если известно, что радиусы окружностей равны 4 и 1.
7. (ЕГЭ-2016.16) В трапеции ABCD боковая сторона АВ перпендикулярна основаниям. Из точки А на сторону CD опустили перпендикуляр АН. На стороне АВ отмечена точка Е так, что прямые CD и СЕ перпендикулярны.
а) Докажите, что прямые ВН и ED параллельны.
б) Найдите отношение ВН : ED, если угол BCD = 135°.


Задачи ЕГЭ последних лет
579
Стереометрия
1. (ЕГЭ-2013.С2) В правильной четырёхугольной пирамиде MABCD с вершиной М стороны основания равны 18, а боковые рёбра равны 15. Точка R принадлежит ребру MB, причём MR : RB = 2:1. Найдите площадь сечения пирамиды плоскостью, проходящей через точки С и R параллельно прямой BD.
2. (ЕГЭ-2013.С2) В правильной четырёхугольной призме ABCDA'В'С'D' сторона основания равна 22, а боковое ребро А А' = 7. Точка К принадлежит ребру В'С' и делит его в отношении 6:5, считая от вершины В'. Найдите площадь сечения этой призмы плоскостью, проходящей через точки В, D и К.
3. (ЕГЭ-2014.С2) В прямоугольном параллелепипеде ABCDA!В'С'D' известны рёбра: АВ = 3, AD = 2, АА! = 5. Точка О принадлежит ребру В В' и делит его в отношении 2:3, считая от вершины В. Найдите площадь сечения этого параллелепипеда плоскостью, проходящей через точки А, О и С'.
4. (ЕГЭ-2014.С2) В правильной треугольной пирамиде МАВС с основанием А ВС стороны основания равны 6, а боковые рёбра равны 8. На ребре АС находится точка D, на ребре АВ находится точка J3, а на ребре AM - точка L. Известно, что CD = BE = LA = 2. Найдите площадь сечения пирамиды плоскостью, проходящей через точки Е, D и L.
5. (ЕГЭ-2014.С2) Радиус основания конуса с вершиной Р равен 8, а длина его образующей равна 9. На окружности основания конуса выбраны точки А и В, делящие окружность на две дуги, длины которых относятся как 1:3. Найдите площадь сечения конуса плоскостью АВР.
6. (ЕГЭ-2014.С2) В треугольной пирамиде МАВС основанием является правильный треугольник АВС, ребро MB перпендикулярно плоскости основания, стороны основания равны 6, а ребро МА равно 6\/2. На ребре АС находится точка D, а на ребре АВ находится точка Е. Известно, что AD = 4, BE = 2. Найдите площадь сечения пирамиды плоскостью, проходящей через точки Е, D и середину ребра МА.
7. (ЕГЭ-2015.16) Все рёбра правильной треугольной призмы АВС А'В'С' имеют длину 6. Точки М и N - середины рёбер А А' и А'С' соответственно.
а) Докажите, что прямые ВМ и MN перпендикулярны.
б) Найдите угол между плоскостями BMN и АВВ'.
8. (ЕГЭ-2016.14) В правильной треугольной призме АВС А'В'С' сторона основания АВ равна 6, а боковое ребро АА! равно 3. На ребре В'С' отмечена точка L так, что B'L = 1. Точки К и М - середины ребер АВ и А'С' соответственно. Плоскость 7 параллельна прямой АС и содержит точки К и L.
а) Докажите, что прямая ВМ перпендикулярна плоскости 7.
б) Найдите объём пирамиды, вершина которой - точка М, а основание - сечение данной призмы плоскостью 7.


580
Варианты ДВИ МГУ
Варианты ДВИ МГУ последних лет
Июль 2011
1 4
1. Вычислите значение функции х2 — 0,625а; — - в точке х — -.
8 5
2. Решите уравнение (sinx -f cosx)2 = 1.
3. Решите уравнение log2 (Зх — 4) = log4 (2 — х).
. Т-. V их -г о — 1
4. Решите неравенство ■■ > 1.
у/Зх + 2-1
5. Медианы AL и ВМ треугольника АВС пересекаются в точке К. Найти
длину отрезка С К, если А В = у/3 и известно, что вокруг четырёхугольника KLCM можно описать окружность.
6. Найдите наибольшее значение функции
9х
4х - 6х + 9х
и точку х, в которой это значение достигается.
7. В закрытой коробке, имеющей форму куба с ребром 5, лежат два шара. Радиус первого из них равен 2. Этот шар касается плоскости основания и двух соседних боковых граней куба. Второй шар касается двух других боковых граней куба, плоскости основания и первого шара. Чему равен радиус второго шара?
8. Решите систему неравенств
Г 2х2 + 4ху + 11 у2 < 1, 4х + 7у > 3.


Варианты ДВИ МГУ
581
Июль 2012 года
4
1. Найдите многочлен второй степени, если известно, что его корни равны —-
5
и -, а свободный член равен —2. о
417
2. Вычислите log2 log81 —.
3. Решите неравенство (9х — Зж+2 + 14)\/4 — 2х < 0.
4. Решите уравнение sin Зх = л/2 cos х — sin х.
5. Найдите площадь фигуры, состоящей из точек (х; у) координатной плоскости, удовлетворяющих уравнению
|ж| + \х + Зу\ + 3|у - 2| = 6.
6. Окружность касается сторон А В и ВС треугольника АВС в точках D и Е соответственно и пересекает сторону АС в точках F, G (точка F лежит между точками А и G). Найдите радиус этой окружности, если известно, AF = 5, GC = 2, AD : DB = 2 : 1 и BE = ЕС.
7. Определите, при каких значениях параметра а уравнение
ау/х + у = у/Зх -I- 2у/у имеет единственное решение (х; у).
8. В основании пирамиды лежит равнобедренный треугольник АВС со сторонами АС = ВС = 5 и АВ = б, боковые рёбра пирамиды AS, BS и CS равны соответственно 7, 7 и 4. Прямой круговой цилиндр расположен так, что окружность его верхнего основания имеет ровно одну общую точку с каждой из боковых граней пирамиды, а окружность нижнего основания лежит в плоскости АВС и касается прямых АС и ВС. Найдите высоту цилиндра.


582
Варианты ДВИ МГУ
Июль 2013 года
1. Старший коэффициент квадратного трехчлена /(х) равен 2. Один из его корней равен 5/2. Найдите второй корень, если известно, что /(0) = 3.
2. Вычислите log12 3 • log9 12.
3. Решите неравенство 9 (1 4- 51-2х) 2 — ^ ([Ъ2х + 5)2 >6^ • 5^.
Л _ sin5x cos5x sinx cosx
4. Решите уравнение — = —— —.
smx cosx sin5x cos5x
5. В 14:00 из села Верхнее вниз по течению реки в сторону села Нижнее отпра¬
вился катер «Быстрый». Когда до Нижнего оставалось плыть 500 метров, ему навстречу из Нижнего вышел катер «Смелый». В этот же самый момент «Быстрый», не желая встречи со «Смелым», развернулся и пошел обратно к Верхнему. В 14:14, когда расстояние по реке от «Быстрого» до Верхнего сравнялось с расстоянием по реке от «Смелого» до «Быстрого», на «Смелом» осознали, что они идут с «Быстрым» на одинаковой скорости, развернулись и направились обратно к Нижнему. В исходные пункты катера вернулись одновременно в 14:18. Найдите расстояние по реке между Верхним и Нижним, если известно, что оба катера движутся равномерно и с одинаковой собственной скоростью.
6. Трапеция ABCD вписана в окружность радиуса R и описана около окружности радиуса г. Найдите г, если R = 12, а косинус угла между диагональю АС и основанием AD равен 3/4.
7. В основании прямой призмы АВС А' В'С' лежит прямоугольный треугольник АВС такой, что АС = ВС = 1. На ребре А'В' верхнего основания (параллельном АВ) отмечена точка D так, что A'D : DB' = 1:2. Найдите радиус сферы, вписанной в тетраэдр ABC'D, если высота призмы равна 1.
8. Найдите все значения параметра а, при которых уравнение
sin ^х + — ^ = х + 1 имеет бесконечно много решений.


Варианты ДВИ МГУ
583
Июль 2014 вода
1. 	Найдите в явном виде натуральное число, заданное выражением
^7-4>/3-(8 + 4л/3).
2. Найдите максимальное значение функции log^ (я2 — 6х + 17).
3. Найдите все положительные х, удовлетворяющие неравенству х3х+7 > х12.
5. Окружности 0,1 и И2 с центрами в точках 0\ и О2 касаются внешним образом в точке А. Общая внешняя касательная к этим окружностям касается
и соответственно в точках В\ и В2. Общая касательная к окружностям, проходящая через точку А, пересекает отрезок А1А2 в точке С. Прямая, делящая угол АСО2 пополам, пересекает прямые 0\В\, O1O2, 02В2 в точках D1, L, D2 соответственно. Найдите отношение LD2 : O2D2? если известно, что CZ>i = COi.
6. Найдите все положительные х, г/, удовлетворяющие системе
7. 	В основании прямой призмы лежит правильный треугольник со стороной 1. Высота призмы равна \/2. Найдите расстояние между скрещивающимися диагоналями боковых граней.
Найдите все значения, которые может принимать хотя бы одна из этих функ¬
ций.
4. Решите уравнение
х3/2 -f у = 16,
х + у2!ъ = 8.
8. 	Пусть
/(х, у) = \/-6х2 - 14у2 - 18х?/ + 6 + у,
д(х,у) = -\/-6х2 - 14т/2 - 18ху + 6 + у.


584
Варианты ДВИ МГУ
Июль 2015 года х 3 1
1. Найдите /(2), если f(x) = - Н h —.
О X 1U
2. Найдите сумму квадратов корней уравнения х2 — 7х + 5 = 0.
3. Решите неравенство cosx -f- \/2cos2x — sin ж > 0.
4. Решите уравнение \ogx \2х2 — 3| = 41og|2x2_3| х.
5. Окружность радиуса 3/2 касается середины стороны ВС треугольника АВС и пересекает сторону АВ в точках D и Е так, что AD : DE : ЕВ = 1:2:1. Чему может равняться АС, если ZВАС = 30° ?
6. Велосипедист Василий выехал из пункта А в пункт Б. Проехав треть пути,
Василий наткнулся на выбоину, вследствие чего велосипед безнадёжно вышел из строя. Не теряя времени, Василий бросил сломавшийся велосипед и пошёл пешком обратно в пункт А за новым велосипедом. В момент поломки из пункта А выехал мотоциклист Григорий. На каком расстоянии от пункта А он встретит Василия, если пункт Б отстоит от пункта А на 4 км, а Василий доберётся до пункта А тогда же, когда Григорий до пункта Б? Скорости велосипеда, мотоцикла и пешехода считать постоянными.
7. В правильную треугольную призму с основаниями АВС, А'В'С' и рёбрами АА!, В В', СС' вписана сфера. Найдите её радиус, если расстояние между прямыми АЕ и BD равно л/13, где Е и D - точки, лежащие на А'В' и
В'С' соответственно, и А'Е : ЕВ' = B'D : DC' = 1:2.
8. Найдите все пары (а, /3), при которых достигается минимум выражения
4 — 3 sin а 2 4- cos 2а (З2 + /3 + 1 \//3 + 1
2 + cos 2а /З2 + /3 + 1 +1 ^ 4 — 3 sin а


Варианты ДВИ МГУ
585
Июль 2016 года
1. Найдите /
| j , если f(x)
2. 	Разность между наибольшим и наименьшим корнями уравнения
х2 + ах — 6 = О
равна 5. Найдите все возможные значения а.
3. Решите уравнение 2 cos2 х + 3 sin 2х = 4 + 3 cos 2х.
4. Решите неравенство log^^ х (1 4- log^ 3) < 1.
5. Две окружности касаются внутренним образом в точке Т. Хорда АВ внешней окружности касается внутренней окружности в точке S. Прямая TS пересекает внешнюю окружность в точках Т и С. Найдите площадь четырёхугольника ТАСВ, если известно, что СВ = ВТ = 3, а радиусы окружностей относятся как 5:8.
6. Ровно в 9:00 из пункта А в пункт Б выехал автомобиль. Проехав две трети пути, наблюдательный водитель автомобиля заметил, что мимо него в сторону пункта А проехал некий велосипедист. В тот самый момент, когда автомобиль прибыл в пункт Б, из пункта Б в пункт А выехал автобус. Когда до пункта А оставалось две пятых пути, не менее наблюдательный водитель автобуса заметил, что он поравнялся с тем самым велосипедистом. Во сколько приедет велосипедист в пункт А, если известно, что автобус прибыл в пункт А ровно в 11:00? Скорости велосипедиста, автомобиля и автобуса считать постоянными.
7. В основании правильной пирамиды с вершиной S лежит шестиугольник ABCDEF со стороной 14. Плоскость 7г параллельна ребру АВ, перпендикулярна плоскости DES и пересекает ребро ВС в точке К так, что В К : КС — 3:4. Кроме того, прямые, по которым 7Г пересекает плоскости BCS и AFS, параллельны. Найдите площадь треугольника, отсекаемого плоскостью 7г от грани CDS.
8. Найдите наименьшее значение выражения
\J 106 + log^ cos ах -(- loga cos10 ax + y^58 -f log^ sin ax — loga sin6 ax +
и все пары (a, x), при которых оно достигается.


586
Варианты ДВИ МГУ
Июль 2017 года
1. Какое число больше: \ - + 7 + - или 3?
V 7 6
2. Известно, что а + Ь + с = 5 и ab + Ьс + ас = 4. Найдите а2 + Ь2 + с2.
3. Решите уравнение sin 7х + sin 6х = sin а:.
4. Решите неравенство х2 log2 х + 3 logg х < х log7 ж • log6 ж4.
5. Через вершины А и В треугольника АВС проведена окружность, касающаяся прямых АС и ВС. На этой окружности выбрана точка D (внутри треугольника), лежащая на расстоянии у/2 от прямой А В и на расстоянии у/Ъ от прямой ВС. Найдите угол ZDBC, если известно, что ZABD = ZBCD.
6. Василий с друзьями решили устроить пикник. Для этого им от пункта А нужно добраться вниз по реке до пункта В, причем в их распоряжении есть два катера. Считая себя самым ответственным, Василий вызвался самостоятельно доехать до пункта В на более быстроходном катере и начать готовить место для пикника. Оба катера вышли одновременно из пункта А. Однако, промчавшись восемь километров, Василий заметил на берегу машущего ему рукой Григория, который просил по старой дружбе довезти его до пункта С. И хоть пункт С Василий уже проехал, он согласился. По пути в пункт С Василий с Григорием встретили идущий навстречу второй катер с друзьями Василия, откуда те крикнули, что им до пункта В осталась треть пути и чтобы Василий нигде не задерживался. Доставив Григория в пункт С, Василий немедленно помчался догонять друзей. Найдите расстояние между пунктами В и С, если известно, что оба катера пришли в пункт В одновременно, скорости катеров постоянны, а Василий, действительно, нигде не задерживался.
7. Из вершины D на плоскость основания АВС пирамиды ABCD опущена высота DH. Найдите объем этой пирамиды, если известно, что площади треугольников АН ВС, АН АС, АНАВ равны соответственно 2/9, 1/3, 4/9, и что все три плоских угла при вершине D прямые.
8. Решите систему уравнений
X /О о \ / 7Г
—г 2Т - У -tg(xJ -у2) = J-,
cos (xz — уг) V 2
<
k cos (J -y2)~X'tg {x2 ~ y2) = '


Ответы
587
Ответы
l.i.
1. \АС\>\ВК\.
2. \АВ\ = 5.
3. Длины боковых сторон равны
2 тг
у/4 т2
:, длина основания
равна
2 тп
4.
у/ 4т2 — п2 с sin 2а
\/2(sina + cosa) 5. |£L|>|BG|.
3. 	|Ж7| = У^
+ С2
7. л/15 + 6л/3.
8. |АВ| = 1 + 6\/2, |Ж7| = 5л/3, |АС| = 2.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
3 4
arccos - и arccos —.
4 — 7Г arctg \/2.
7Г 2 '
200 3 ’
6
5*
10.
arctg 3.
Зтг 8 ‘
\BN\ < \CL\.
21. arctg
tgy?± y/tg2y?-8
4
22.
23.
24.
<p € [arctg 2 л/2; 7г/2). 12.
y/25a2 + 3662
10
hy/2.
25.
26.
8л/10 3 *
5
V5’
9>/65 27. —-— или
28. |AC| = y/7. 5Vl3
25 -f-
96
л/17 *
29.
30. 6.
12
31.
1 + y/2
32. - tg 2a(2 cos 2a + 1)
33. 40.
35. 	25.
1.2.
1.
2.
3.
4.
5.
6. 7.
3(\/3±l)
2
c2 sin a sin (3 2sin(a + p) '
W3.
3 ■ y/2.
a)
\AM\
\MC\
4\/2 5 ’
Зи4илиу|+У^иу/^+у/|. 6)
|AM| =
IMCI = 5"+7^V41 - 1Q(^6 - V2).
9.
10.
11.
12.
13.
s’*®-
\/6-\/2.
V6 ■y/3 — 1
Я (V2 + 2v/2- v^)- 2.
asin(a + /3)(4 — 3cos2 /3) 12 sin a sin /3


588
Ответы
14.
15.
16.
17.
18.
19.
20. 21. 22.
23.
24.
25.
26.
11.
ВОС = 112,5°.
23
17'
\АВ\ = \ВС\ = 4 + 2>/3, \АС\ = 6 + 4>/3.
91(6 - л/6)
30
25 3 *
З + бл/б.
5.
15
к-
\АС\ = \ВС\ = 2 + у/2, \АВ\ = 2 + 2v/2.
1.
9 /Ш
V 7 ’
78 - 30\/2
17
27.
28.
29,
30. ACJ3 = J3.AC = 2 arcsin
8
5'
39
24'
V8 к2 +1-1 4fc
ABC = 7Г — 4 arcsin
л/8Л:2 4-1-1 4/с
31.
32.
33.
34.
35.
36.
задача имеет решение при всех к > 0. 1.
6.
4.
1 Ч- л/5, 2л/Тб.
5л/5.
_1_
2к'
1.3.
25
ctg а 4- ctg /3' 4\/б 9 '
1.
2с2 + т-
5. 5 =
1
где
у/abed ’
а=1 + 1 + 1 + L
а hi ^ h2 ^ h3 » U ~ /4 ^ /г2 /13 ’
J L + -L <7 = L + _I_ + JL
/il /12 /13 1 hi ho hi
. — J,
h2 ^ h3
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
30.
18.
12 5 *
3-V3.
л/7.
4 — \f2
\у/7.
28*
—
161
30°, 90°.
. y/z тг л/З
arctg —, - - arctg — .
16. arccos
17.
18.
(-I)-
4m2 -b2-C2
2 be
19.
20.
21.
22.
23.
24.
25.
26. 27.
3 *
8\/l5
arccos -, arccos —. 5 5
2V10—5.
3(л/2-1).
\/Ш 2 ’ 6\/l9.
\NA\ = -j=, |ЛГВ| = R\j2-V2, |ATC| = R.
у/c2k2 4- c2h2 ± 2ckh\fi? — к2 к
7y/3h2 7y/3h2 (—13л/3 4- V&27)h2
12 ’ 30 ’ 120


Ответы
589
28. \АВ\ =
\ВС\ = \АС\ =
Зтг 10 '
_2_
V7’
y/l2(p + q)2 +4p2q2 2 <?
\/Р(р + g)2 + 4p2g2
18. |АЕ| : \ЕС\ = \BD\ : \DC\ =
ху - 1 У + 1 ’ ху - 1
2р
ж + 1
>//2(р2 - q2)2 + 4рУ(р +"^)2 19. \QR\ = 3, Q#P = arccos (
29.
30.
31.
32.
33.
34.
35.
36.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16. 17.
8\/б 0 13
Jt&ADC ^ ) ■Li'&ADC 2 '
5.
y/3 r2 — a2
a .
6
|BC| _ l + m \LC\ _ k + l + m \CA\ ~ I + к ’ \CO\ ~ I 2
b2
202,8.
15.
24 7 *
12
7 ‘
7Г 6 '
27
8 *
Зл/З.
2p<? + g2
P + 9 18.
л/а2 + ab. n : m.
10.
18 : 7.
5 : 2.
2y/7.
1:1.
§1/145.
1.4.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
1.
2.
3.
4.
5.
6.
7.
8. 9.
10.
11.
12.
13.
5л/5 3 ’
2л/3.
|ЯЯ| = 9, Paabc — 45. 5.
V^-d2.
6>/3.
vlos
4 ‘
25л/3.
96
25’
4\/l0-2>/i5.
4 + 2л/3 2л/7+Г
64,80,100 и 80,100,125.
1.5.
2.
147
/
108
5
16
За2 + 8с2
35
о 8л/5 о — м или —■■■■■■ м .
О • О
2\/3 — 3 6
16 9 *
1
6*
1 : 3.
228 25 ’
60.
1 : 6.
3 ab
Т’
5±>/33\ 12 ;•


590
Ответы
14.
24.
2.1.
15.
24.
7
1.
2 у/Ъ.
16.
4*
2.
1.
17.
arccos y/2 — 2S.
3.
уДБ.
18.
\DE\ = у/2, длина радиуса окружно¬
4.
4\/3sin 7°.
сти равна у/b.
5.
b2 cos3 Р
19.
189\/55
2 sin р
88 *
6.
\АВ\ = \ВС\ = Т-ч/3, |С£>| =
л/5
20.
(у/2-l )а2
\AD\ = 2л/2Т.
2
7.
4л/3.
21.
3
8.
V6 + V2
4 '
о
10
Z
22.
з~*
9.
7\/3.
23.
19
10.
44'
5
11.
37Г
Т‘
24.
24 ’
12.
ВАС = АВС = АСВ
=
25.
S Ъ2 4- Sab
3 12
или
2 (а 4" Ь)(2а -Ь Ь)
ВАС = АВС = АСВ =
7Г
48
12’ 3
4 *
26.
, / С\ 2
5 '
13.
(д) •
27.
^л/2 — cos : cos а.
14.
\ а /
50тг(2 + \/2).
28. ~~
5_
12'
29. АСВ = 45° , АВС = 90° .
30.
31.
32.
33.
34.
35.
36.
( М *
arcsm —— —- и
\V2kJ 4
Зтг . / 1 \
— arcsin —т=— ; к £
4 \V2kJ
9.
Si+ S2- у/(Si + S2)2 -45i52sin2a 2
1
6*
5.
ay/7 12 '
1 d 1
2 4 2d ’ ГД6
15. \/3 + 1-
16. Зл/З.
17.
a = sin(/? 4- 7), b = cos p, с = sin 7,
8abc
4a2 4- 16c2 — 16afec
18.
19.
20. 21. 22.
23.
24.
25.
26.
27.
28.
nc
m
2^3 3 ‘
56v/2.
s/m-
л/5.
2.
л/5.
2с + л/2Ь л/3+1
\/5 + i.
4
45 2 '
/1КЛГ = S/\KNC ~ ~ • 2
уЯ'


Ответы
591
29.
30.
31.
1 2 10. 57Г 18 *
32. АСВ = 7г/3, Saabc =
33.
34.
л/з‘
Raabc = —, Sabcd = -гг-- 2 2Ь
35.
36.
1.
2.
3.
4.
5.
6.
7.
8.
9.
\/а?Ш 2 ’ 54-л/15
у/6.
V7.
Зу/З “Ь 27Г
Чть-
|(р-»)г«81-
2.2.
V?-
4\/б
5
6.
2(л/б + л/3).
24 л/145"
10. arccos
И)
300 17 *
9:8.
2у/21 — 9.
4у/3 4- 107Г.
7Г 6 ’
2\/2 + 6.
49 4- 20\/б 7г 1 ^
gg + 4 2 arCC°S 49 ’ Возмож"
ны и другие формы записи.
В* а
11.
12.
13.
14.
15.
16. 17.
18. —
1
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
35.
36.
1.
2.
3.
4.
5.
6.
7.
8. 9.
10.
4 aR 16Д2 - За2 ’
27 4 ’
6-4\/2
3
-л/15.
15
3 ctg /3 4- 4 tg Р * 7\/3 9 ’
1)л/йг; 2)^J.
6 sin а 2 '
12тг.
тк
~Т'
7Г .
л/53 ИЛИ л/13. 216. а2-Ь2
а
67Г.
(!)■
4 : 7. 15л/2
61>/3
3.1.
2 arctg(5 tg а).
cos BAN = - , Sabcd = -г •
л/65 5
9л/3 11 ’ л/13.
V?-
л/а2 + b2 — 2а6 cos а и л/а2 + Ь2 + 2аЬ cos а 4л/5.


592
Ответы
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26. 27.
d2 - dl
tga.
4 _5_
12'
Зл/З-тг 18 ’
7 cos 40° • tg 20°.
10±4>/3.
3(л/5 ± 1)
2
12^/2 - 15 4
16 5 *
3: 1.
34 9 ‘
2y/3.
4(3 + 2л/3)
3
\MB\ = a -f I2 sin2 a—
— \Ja2 -f 2aZ sin2 a — I2 sin2 a cos2 a, \ND\ = a -f Z2 sin2 a+
+ Va^-f^a/sii^a—I^sin^acos^a.
27\/3 2 '
1728
192
“25" ИЛИ If'
1 5
-7 или -.
4 4
7тг
12 *
3.2.
1. 36 или 8\/l9.
2. 162.
3. 10x/3.
4 I?
25 + 2л/Т30 + у/Ш
5. |AC| = Зл/89, \BD\ = 2n/349.
° I-
8. 2\/l3.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
32.
33.
34.
15 7 ’ 2.
15.
2 sin 10° sin 40° 42>/5l 25 ‘
1 и 7.
y/a2 — ab.
49
M-
VIE 2 ’
SR3 b * 96.
42.
2\/3
2 cos I 4-1 2 cos I — 1
15.
8
•/61 '
7Г 7Г 37Г 37Г
4’4’T’T’
19л/3 52 *
22 7 *
14 3 ‘
_15
\/2
n „ 255 960
Длины оснований равны и -jy.
450
длина высоты равна -jy .
3 : 29.
be
а
Длины диагоналей равны 5,
975л/3
площадь равна
196
ab 72 ■
6(л/6 + у/2) №


Ответы
593
3.3.
4.1
\J848 ± 64\/l3, \/з08±64\/Тз.
10.
11.
12.
13.
14.
3. 1.
7Г
2 '
v^I.
. а arcsm —. о
л/37(2-ч/б — 1) Зл/З
319.
30°.
На продолжении.
Зл/Тб 2 *
4.
2\/4tg2a + 3.
3
2*
15. \АВ\ = 3, Sabcde =
16.
17.
4098 61 '
>/54-2
18.
19.
20.
21.
22.
23.
24.
25.
26. 27.
\AD\ = |ВС| = 2\/2 + >/2,
|АВ| = |СТ>| = 2\jb-2>/2.
189 25 '
5:9.
HZ?! = 10, |ВС| = 2, Я=^.
\/1зо 2 ■
/ТГ 7
arccos \ — ~ arccos —= .
V 14 2-/L4
22. 2.
I) 1 : 1, 2) m- I.
9\/2.
. 1
arcsm -. о
3. Тупоугольный. 20. Остроугольный.
4.2
2. 	Нет. 4
Четырехугольник, у которого диагонали взаимно перпендикулярны.
7. /.BAD = /С DA == 60°,
/АВС = /BCD = 120°.
8. КМ = 4.
9. АВ<АС.
4.3
3. 	Да.
4.4
Равенство достигается, когда /В = /D = 90°.
Неравенство обращается в равенство, если а и 6 равные катеты прямоугольного треугольника.
Может.
6.2
1.
2.
3.
4.
5.
6. 7.
d3 sin /3 sin 7 ycos2/ 2^/F sin(o:/2) <y/3(2cosa: — 1)
29
arccos —=.
7\/l9
VS 8 '
21>/l5 10 ’
3 : 5.
216.
45°, 2/л/З-
— sin 7.
6.3
З27г\/78см3. 4.
2 arccos
cos-
3л/3/18.


594
Ответы
1.
Эх/13 л/13 + л/5 57Г 12 ‘
6.4
2тгД2, л/2.
2.
4^tg3f
9tga V g 2 S 2/'
_£
15*
ау/ЗН2 + a2 a2
ЗЯ 2л/ЗЯ ‘
12.
36.
1Л/5.
Задачи ЕГЭ
Планиметрия
9л/2 ИЛИ 17\/2.
33 или 37.
1/35.
50,7.
10.
3,2.
1 : 2.
Стереометрия
117>/2. 176%/2.
>/1зз.
2\/l0.
28л/2.
%/39.
arcsm 1 / -.
8. 5\/3.
ДВИ МГУ 2011 ГОД
1. 3/200.
2. nk/2, к € Z.
3. 14/9.
4.
[-НМ-И
5. 1.
6. | при X = log2/3 i .
7. 1.
8. (5/9; 1/9).
2012 год
1. 2,1х2 — 2,3ж — 2.
2. -2.
3- [1°6з 1оёз Т] U {2}.
, ТГ | / ^ \fi ТГ 7Г71
4. 2 +7ГП> (-D 8+Т-
5. 6.
6. \/б.
7. (—оо; л/3) U (\/7; +оо). 5л/15
8.
2013 год
1. 3/5.
2. 1/2.
3. 	[0; 1].
7Г 7Гк , 7Г 7Г&
“■ 4+Т' ±6 + Т'
7Г . 7г/с . _
8 *4*’ fc€Z’
5. 2000.
6. 7.
У!)
7. ^/5 + л/5 +1 +
8. (—оо;0) U (0; +оо).
2014 год
1. 4.
2. -3.
n G Z.
1


Ответы
595
(0; l)u(f;+oo).
+ 47Гк, к G Z.
1.
(4;8).
л/2
3 '
[—Зч/2;Зл/2].
2015 год
5. 7г/4.
6. 4 км.
7 ^
9^3‘
2л/3 + ^2
8'
л/3 + 2л/2 г-
2.
39.
57Г л , 7Г л ,
+ 27г/с; - + 2ТГЛ
117Г л , 57Г л .
— + 2пк; — + 2ттк
к £ Z.
4. V3,
1 %/3 + лД7
л/2 ’ 2
5. л/3 ± л/2.
6. 1.
7. 13/6.
8. а = ^ + 27гАг, к 6 Z; /? = 0.
2016 год
1. 29/35.
2. ±1.
7Г
3. — + 7г/с, arctg5 + nk, fceZ.
4. (0; 1/3] U (1; 3).
5. 8\/2.
6. 12:00.
7. 25л/2.
8. 9л/5, а = 2, х = ^ +пк, fceZ.
8
2017 год
1. Первое больше.
2. 17.
Л 7гк 7Г 27гА; , . ^
3. —, - + —я-fc, к ez.
4. {1} U [loge 7; 3 log6 7].


Список литературы
1. Золотарёва Н.Д., Семендяева Н.Л., Федотов М. В. Геометрия. Основной курс с решениями и указаниями. - М.: Лаборатория знаний, 2018. - 302 с.
2. Федотов М. В., Золотарёва Н. Д. Геометрия. Подготовка к вступительным экзаменам в МГУ. - М.: МАКС Пресс, 2009. - 132 с.
3. Федотов М. В., Хайлов Е. Н. Задачи устного экзамена по математике.- М.: МАКС Пресс, 2002. - 144 с.
4. Математика. Задачи вступительных экзаменов по математике в МГУ имени М. В. Ломоносова с ответами и решениями (1999-2004 гг.) Сост. Е. А. Григорьев. - М.: Издательство УНЦ ДО, 2005. - 399 с.
5. Варианты вступительных экзаменов по математике в МГУ (2000-2002, 2003, 2004 гг.). - М.: Механико-математический факультет МГУ.
6. Сергеев И. Н. Математика. Единый государственный экзамен. Задания типа С. - М.: Изд-во «Экзамен», 2009. - 318 с.
7. Денищева Л.О., Бойченко Е.М., Глазков Ю. А. и др. Единый государственный экзамен 2003-2004: Контрольные измерительные материалы: Математика. - М.: Просвещение, 2003. - 191 с.
8. Денищева JI. О., Рязановский А. Р., Семенов П. В., Сергеев И. Н. ЕГЭ 2008. Математика. Федеральный банк экзаменационных материалов. - М.: Эксмо, 2008. - 240 с.
9. Галеев Э. М. Подготовка к ЕГЭ по математике. Задания типа В и С. - М.: Издательство ЦПИ при механико-математическом факультете МГУ, 2009. - 96 с.
10. Ежегодные «Справочники для поступающих в Московский университет». - М.: Издательство Московского университета, 2012-2018 гг.


ВУЗОВСКАЯ И ПРОФЕССИОНАЛЬНАЯ ЛИТЕРАТУРА
ВЫСШАЯ МАТЕМАТИКА
Золотарёва Н. Д. Математика. Полный курс для девятиклассников с решениями и указаниями
учебно-методическое пособие / Н. Д. Золотарёва, Н. Л. Семендяева, М. В. Федотов ; под редакцией М. В. Федотова. - 2017. - 704 с. : ил. - (ВМК МГУ- школе).
Настоящее пособие содержит теоретический материал, подборку задач, а также идеи, указания (подсказки) и решения задач. Пособие составлено преподавателями факультета ВМК МГУ имени М. В. Ломоносова.
Рекомендуется школьникам при подготовке к ОГЭ и ЕГЭ (базовый уровень и первая часть профильного уровня), учителям математики, репетиторам, руководителям кружков и факультативов, преподавателям подготовительных курсов.
ИЗДАТЕЛ ЬСТВО 125167, Москва, проезд Аэропорта, д. 3
„ Телефон: (499)157-5272
«ЛАБОРАТОРИЯ ЗНАНИИ» e-mail: info@pilotLZ.ru, http://www.pilotl_Z.ru


ВУЗОВСКАЯ И ПРОФЕССИОНАЛЬНАЯ ЛИТЕРАТУРА
ВЫСШАЯ МАТЕМАТИКА
Золотарёва Н. Д. Математика. Сборник задач по базовому курсу : учебно-методическое пособие / Н. Д. Золотарёва, Ю. А. Попов, Н. Л. Семендяева, М. В. Федотов ; под ред. М. В. Федотова. -2015. - 238 с. : ил.-(ВМК МГУ-школе).
Настоящее пособие составлено преподавателями факультета ВМК МГУ имени М. В. Ломоносова на основе задач вступительных экзаменов по математике в МГУ и задач Единого государственного экзамена. Пособие содержит теоретический материал, примеры с решениями и подборку задач.
Рекомендуется школьникам при подготовке к сдаче Единого государственного экзамена, абитуриентам при подготовке к поступлению как в МГУ, так и в другие вузы, учителям математики, репетиторам, руководителям кружков и факультативов, преподавателям подготовительных курсов.
ИЗДАТЕЛЬСТВО 125167, Москва, проезд Аэропорта, д. 3
w Телефон: (499)157-5272
«ЛАБОРАТОРИЯ ЗНАНИЙ» e-mail: info@pi!otLZ.ru, http://www.pilotLZ.ai


ВУЗОВСКАЯ И ПРОФЕССИОНАЛЬНАЯ ЛИТЕРАТУРА
ВЫСШАЯ МАТЕМАТИКА
Золотарёва Н. Д. Алгебра. Основной курс с решениями и указаниями : учебно-методическое пособие / Н. Д. Золотарёва, Ю. А. Попов, Н. Л. Семендяева, М. В. Федотов ; под редакцией М. В. Федотова. - 2018.- 568 с. : ил. - (ВМК МГУ- школе).
Настоящее пособие составлено на основе задач вступительных экзаменов по математике в МГУ имени М. В. Ломоносова и задач Единого государственного экзамена преподавателями факультета ВМК МГУ имени М. В. Ломоносова. Пособие содержит теоретический материал, подборку задач, а также идеи, указания (подсказки) и решения задач.
Рекомендуется школьникам при подготовке к сдаче Единого государственного экзамена, абитуриентам при подготовке к поступлению как в МГУ, так и в другие вузы, учителям математики, репетиторам, руководителям кружков и факультативов, преподавателям подготовительных курсов.
ИЗДАТЕЛ ЬСТВО 125167, Москва, проезд Аэропорта, д. 3
„ Телефон: (499) 157-5272
«ЛАБОРАТОРИЯ ЗНАНИИ» e-mail: info@pilotLZ.ru, http://www.pilotLZ.ru


ВУЗОВСКАЯ И ПРОФЕССИОНАЛЬНАЯ ЛИТЕРАТУРА
ВЫСШАЯ МАТЕМАТИКА
Золотарёва Н. Д. Геометрия. Основной курс с решениями и указаниями : учебно-методическое пособие / Н. Д. Золотарёва, Н. Л. Семендяева, М. В. Федотов; под редакцией М. В. Федотова. -2018. -302 с. : ил. - (ВМК МГУ- школе).
Настоящее пособие составлено на основе задач вступительных экзаменов по математике в МГУ имени М. В. Ломоносова и задач Единого государственного экзамена преподавателями факультета ВМК МГУ имени М. В. Ломоносова. Пособие содержит теоретический материал, подборку задач, а также идеи, указания (подсказки) и решения задач.
Рекомендуется школьникам при подготовке к сдаче Единого государственного экзамена, абитуриентам при подготовке к поступлению как в МГУ, так и в другие вузы, учителям математики, репетиторам, руководителям кружков и факультативов, преподавателям подготовительных курсов.
ИЗДАТЕЛЬСТВО 125167, Москва, проезд Аэропорта, д. 3
w Телефон: (499)157-5272
«ЛАБОРАТОРИЯ ЗНАНИИ» e-mail: info@pilotL2.ru, http://www.pilotLZ.ru


ВУЗОВСКАЯ И ПРОФЕССИОНАЛЬНАЯ ЛИТЕРАТУРА
ВЫСШАЯ МАТЕМАТИКА
Математика. Сборник задач по углубленному курсу :
учебно-методическое пособие / Б. А Будак [и др.] ; под ред. М. В. Федотова. - 4-е изд.-2018.- 328 с. : ил. - (ВМК МГУ-школе).
Настоящее пособие составлено преподавателями факультета ВМК МГУ имени М. В. Ломоносова на основе задач вступительных экзаменов по математике в МГУ и задач Единого государственного экзамена. Пособие содержит теоретический материал и подборку задач.
Рекомендуется школьникам при подготовке к сдаче Единого государственного экзамена, абитуриентам при подготовке к поступлению как в МГУ, так и в другие вузы, учителям математики, репетиторам, руководителям кружков и факультативов, преподавателям подготовительных курсов.
ИЗДАТЕЛЬСТВО 125167, Москва, проезд Аэропорта, д. 3
w Телефон: (499)157-5272
«ЛАБОРАТОРИЯ ЗНАНИИ» e-mail: info@pilotl_Z.ru, http://www.pilotL2.ru


ВУЗОВСКАЯ И ПРОФЕССИОНАЛЬНАЯ ЛИТЕРАТУРА
ВЫСШАЯ МАТЕМАТИКА
Алгебра. Углубленный курс с решениями и указаниями учебно-методическое пособие / Н. Д. Золотарёва [и др.]; под ред. М. В. Федотова. - 4-е изд. - 2018. -544 с. : ил. - (ВМК МГУ-школе).
Настоящее пособие составлено преподавателями факультета ВМК МГУ имени М. В. Ломоносова на основе задач вступительных экзаменов по математике в МГУ и задач Единого государственного экзамена. Пособие содержит теоретический материал, подборку задач, а также идеи, указания (подсказки) и решения задач.
Рекомендуется абитуриентам при подготовке к поступлению как в МГУ, так и в другие вузы, при подготовке { к сдаче Единого государственного экзамена, а также учителям математики, репетиторам, руководителям кружков и факультативов, преподавателям подготовительных курсов.
ИЗДАТЕЛЬСТВО 125167, Москва, проезд Аэропорта, д. 3
w Телефон: (499)157-5272
«ЛАБОРАТОРИЯ ЗНАНИИ» e-mail: info@pilotLZ.ru, http://www.pilotLZ.ru


ВУЗОВСКАЯ И ПРОФЕССИОНАЛЬНАЯ ЛИТЕРАТУРА
ВЫСШАЯ МАТЕМАТИКА
Шабунин М. И. Математика пособие для поступающих в вузы / М. И. Шабунин. - 7-е изд., испр. и доп. - 2016. - 744 с. : ил.
Книга предназначена для всех, кто, обладая знаниями основ школьного курса математики, хочет систематизировать свои знания, а также стремится успешно сдать вступительные экзамены в вуз. Пособие окажется полезным студентам педагогических вузов, а также учителям средних школ.
Каждый раздел пособия содержит необходимый справочный материал и подробно разобранные примеры, взятые из практики вступительных экзаменов в вузы, предъявляющие достаточно высокие требования к математической подготовке абитуриентов. Кроме того, в пособие включены задачи для самостоятельной работы учащихся. Ко всем задачам даны ответы, а к некоторым наиболее трудным - краткие указания.
В пособие также включены образцы вариантов вступительных экзаменов в МФТИ разных лет.
ИЗДАТЕЛ ЬСТВО 125167, Москва, проезд Аэропорта, д. 3
„ Телефон: (499)157-5272
«ЛАБОРАТОРИЯ ЗНАНИИ» e-mail: info@pilotLZ.ru, http://www.pilotLZ.ru


Для заметок


Для заметок


Для заметок


Для заметок


Для заметок


Факультет вычислительной математики и кибернетики МГУ имени М. В. Ломоносова
КОМПЬЮТЕРНЫЕ КУРСЫ
Курсы для школьников:
работа на компьютере для школьников 3-5 кл., занимательная логика на компьютере, программирование для школьников младшего возраста, базовая подготовка для начинающих (6-11 кл.), игровые алгоритмы, основы программирования для 6-7 кл., занимательное моделирование в программе Автокад, моделирование в программе 3D-MAX, создание сайтов, компьютерная анимация Flash (основы и программирование), графика (Photoshop), программирование (Паскаль, DELPHI, С, C++, С#, Java), создание домашней компьютерной сети, машинопись.
Организованным группам школьников предоставляется скидка.
Компьютер для начинающих и углубленно:
Windows, офисные программы, Интернет. Компьютер для работы в офисе. Машинопись.
Построение сайтов:
HTML и CSS, JavaScript, управление сайтами, РНР.
Компьютерная графика и верстка:
Photoshop, CorelDraw, Flash, AutoCAD, 3D-MAX, основы цифровой фотографии. Профессиональные курсы:
С, C++, С#, Java, 1C, SQL, Создание малой компьютерной сети для офиса и дома, Управление ИТ-процессами.
Будни и выходные www.vmk-edu.ru
(495) 939-54-29, 939-36-04
м. «Университет»
Занятия в течение учебного года 1-2 раза в неделю Интенсивные курсы в июне