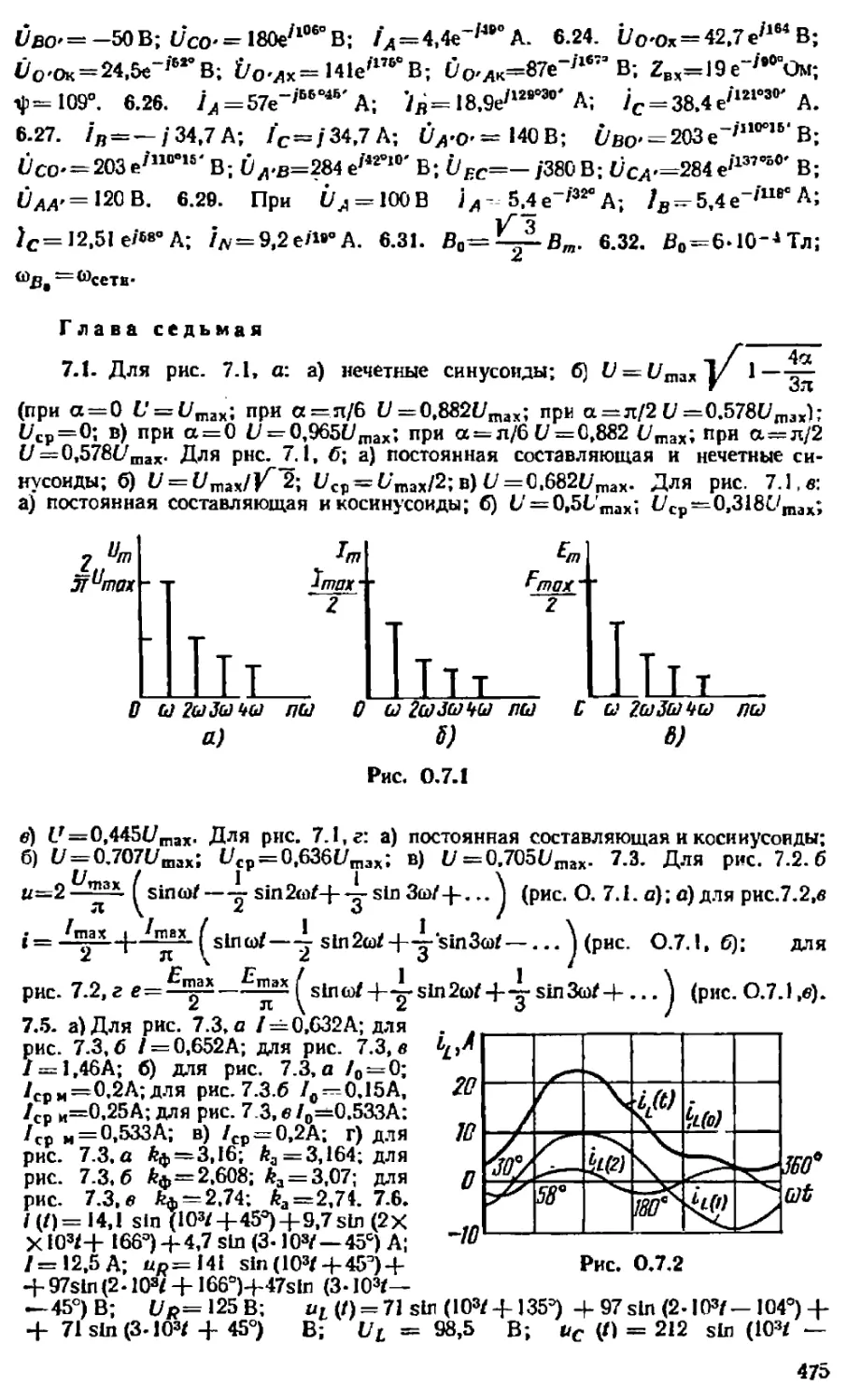
Автор: Бессонов Л.А.
Теги: электротехника электроэнергетика электроника сборник задач
ISBN: 5-06-003795-9
Год: 2003
Текст
Сборник
по теоретическим
основам
электротехники
Издание четвертое, переработанное и исправленное
Под редакцией Л.А.Бессонова
Рекомендовано Министерством образования
Российской Федерации
в качестве учебного пособия для студентов
энергетических и приборостроительных
специальностей вузов
Кик-1 UC.KU
ТОЭ О'|Ц ТЛЭЦ Электротехника
Москва
«Высшая школа» 2003
УДК 621.3
ББК 31.21
С 23
Л. А. Бессонов, И. Г. Демидова, М. Е. Зарудж,
В. И Каневская, С. А. Малеат, С. Э. Ресовская
Рецензент — д-р техн, наук, проф. В. Г. Герасимов
(Московский энергетический институт — ТУ)
Сборник задач по теоретическим основам элсктротех-
С 23 ники: Учеб, пособие для энерг. и приборостр. спец, вузов.—
4-е изд., перераб. и испр./Л. А. Бессонов, И. Г. Демидова,
М. Е. Заруди и др.; Под ред. Л. А. Бессонова. — М.:
Высш, шк.: 2003. 528 с.: ил.
ISBN 5-06-003795-9
В сборнике приведены задачи по всем разделам курса ТОЭ, ляны
решения некоторых из них. Помимо традиционных представлены задачи
по следующим темам: сверхпроводимость, электрические фильтры, устано-
вившиеся режимы и переходные процессы в линиях с распределенными
параметрами, а также включены задачи на матрично-топологические мето-
ды расчета, метод интегральных уравнений для расчета электромагнитных
полей.
Третье издание вышло в 1988 г.
Для студентов технических вузов.
УДК 621.3
ББК 31.21
ISBN 5-06-003795-9
© ФГУП «Издательство «Высшая школа», 2003
Оригинал-макет данного издания является собственностью издательства
«Выйная школа», и его репродуцирование (воспроизведение) любым способом
без согласия издательства запрещается.
ПРЕДИСЛОВИЕ
Предлагаемое вниманию читателя четвертое издание «Сбор-
ника задач по теоретическим основам электротехники» соответ-
ствует программе курса ТОЭ, утвержденной Министерством об-
разования Российской Федерации.
По теории линейных и нелинейных электрических цепей в за-
дачнике рассмотрены следующие группы вопросов: элементная
база электрических цепей, свойства и методы расчета цепей при
постоянных, синусоидальных, периодических несинусоидальных
процессах, матрично-топологическое направление теории цепей,
четырехполюсники взаимные и невзаимные, цепи с операцион-
ными усилителями, имитированные элементы, к, т, RC- и* актив-
ные ЯС-фильтры, расчет переходных процессов классическим,
операторным методами, с помощью интеграла Дюамеля, метод
пространства состоянии, преобразования Фурье и спектральный
метод, синтез двух и четырехполюсников, цепи с распределен-
ными параметрами в установившихся и переходных процессах,
основы теории сигналов, корреляционные функции, направлен-
ные и ненаправленные графы, цепи с переменными во времени
параметрами, устойчивость режимов работы, автоколебания, не-
которые малоизвестные физические явления в нелинейных цепях
и другие вопросы.
По теории электромагнитного поля рассмотрены: методы
расчета электрических, магнитных и электромагнитных полей
при постоянных и синусоидальных во времени процессах в ди-
электрике, проводящих и полупроводящих средах, запаздыва-
ющие потенциалы, излучение электромагнитной энергии, поля
в направляющих системах, объемные резонаторы, основные по-
ложения магнитной гидродинамики, движение заряженных ча-
стиц, сверхпроводящие среды в электрома! нитном поле, метод
интегральных уравнений, метод конформных преобразований.
Структура задачника следующая: сначала представлен раздел
условий задач, затем раздел решений задач, снабженных в усло-
виях буквой р, и в заключение раздел ответов для задач без буквы
р. Всего задач 1000. Из них задач с решениями и подробными
пояснениями 330.
Рисунки в разделе условий имеют двойную нумерацию, на-
пример 10.20. Цифры до точки указывают номер главы, после —
порядковый номер внутри главы. Рисунки в разделе решений
з
и в разделе ответов имеют тройную нумерацию. В разделе
решений с дополнительной буквой Р, например Р. 10.20, в разделе
ответов с дополнительной буквой О, например 0.10.15.
Для облегчения пользования книгой, задачи каждой главы
подразделены на группы с близкой тематикой по 4—7 задач
в каждой.
Работа по написанию сборника задач распределялась между
авторами следующим образом: Л.А. Бессонов — гл. 1, 10, 15, 18,
руководство всей работой и редактирование; И.Г. Демидова —
гл. 19—26; М.Е. Зарудн — гл. 8, 9, 16, 27, 28; В.П. Каменская —
гл. 2, 3, 4, 14; С.А. Миленина — гл. 5, 11, 12; С.Э. Расовская —
гл. 7, 13 ,17; С.Э. Расовская и И.Г. Демидова — гл. 6.
Авторы выражают благодарность рецензенту заслуженному
деятелю науки и техники,профессору МЭИ (ТУ) Герасимову В.Г.
за ценные замечания, учтенные при переиздании.
Замечания по книге просим направлять по адресу: 127994,
Москва, ГСП-4, Неглннная ул., 29/14, издательство «Высшая
школа».
Авторы
Глава первая
Линейные электрические цепи постоянного тока
А. Законы Ома и Кирхгофа. Источники ЭДС и тока.
Разность потенциалов
1.1р . На рис. 1.1,а изображен остов некоторой схемы. Токи
и /3 известны. Найти ток /э.
Рис. 1.1
1.2. Две части Л нВ некоторой электрической цепи (рис. 1.1,6)
соединены тремя проводами. Токи /, = 0,1 А и /2=0ДА, резистор
имеет сопротивление /?=ЮООм. Определить показание вольт-
метра, имеющего внутреннее сопротивление 10000м.
1.3. На рис. 1.2, а изображен участок некоторой цепи. Известны
потенциалы <рв = 5В и <pft = 40B точек а и Ь. Резисторы имеют
сопротивления Я, = 8 Ом и Я.=2Ом, ЭДС Е, — 15 В и£2=25 В.
Найти ток /.
1.4. Найти значения токов /2 и / для участка цепи рис. 1.2,6.
Ток /,= 10 мА, резистор имеет сопротивление /? = 2кОм, ЭДС
5
I
£=15 В, напряжение J7ab==9B. Ветвь, состоящую из резистора
сопротивлением 7? и источника ЭДС £,заменить источником тока
и резистором.
1.5. Для участка цепи (рис. 1.2, в} известна разность потен-
циалов i/eft==120B. Найти ток J, если / = 20мА; /?1==1к0м;
/?, = 2к0м; £=18В.
1.6р . В схеме рис. 1.3, а определить потенциал точки О и
токи /8, /3, если £!=10В; /?1 = 2кОм; £2 = 25В; /?а = 8к0м|
/?а=12кОм; «Pi — —5 В; <р,= 16 В; <р3 = 28В.
Рис. 1.3
1.7. В схеме рис. 1.3,6 определить ток /2 и потенциал точки т.
Известно, что Ц = 20 мА; /а — —10 мА; R.2 = 5 кОм; Е2 = 15 В;
7?а=ЮкОм. Осуществить эквивалентную замену источника ЭДС
на источник тока.
1.8р . В схеме рис. 1.4, а заданы токи Ц и /а, сопротивления
резисторов иЭДС- Определить токи /4, /Б, /в, а также разность
потенциалов Uab между точками а и Ь, если Ц — 10 мА; /3 =—20 мА;
/?4 = 5кОм; £5 = 20В; R.— ЗкОм; £в = 40В, /?в = 2кОм.
1.9. В схеме рис. 1.4,6 определить потенциал точки k, если
/,=5мА; /а——20 мА; /?4=5кОм; /?5=ЗкОм; £ь=20В, 7?в=2кОм.
1.10. В схеме рис. 1.5, а определить ЭДС £, если показание
вольтметра равно нулю. Ток источника тока / =1 мА; R = 1 кОм.
1.11. Составить уравнения по законам Кирхгофа и определить
токи во всех ветвях схемы рис. 1.5,6, если — 1 мА; Ja —2мА;
/а = ЗмА; Я4=4кОм; R6—5 кОм; /?в=6кОм; /?,=7к0м; £4 = 27В.
6
1.12. Схему рис. 1.5,6 преобразовать так, чтобы она не со-
держала источников тока Jt и J*. Для полученной схемы опре-
делить токи и сравнить их с токами в непреобразованной схеме.
1.13. Сколько уравнений следует составить для схемы рис. 1.6
по первому и второму законам Кирхгофа?
1.14р . В схеме рис. 1.7 определить токи во всех ветвях и на-
пряжение Unlt между точками пик. Значение сопротивления
каждого резистора (/?!—/?п) дано в омах и равно номеру соот-
ветствующего резистора, например /?7 = 70м; /?20 = 20Ом. Токи
—/1в даны в амперах, причем значения каждого равно номеру
источника тока, например = 15А. ЭДС Ел =—29 В; Е6 — 10В;
£,= 10 В.
Б. Потенциальная диаграмма. Линейные соотношения
1.15р . Построить потенциальную диаграмму для схемы рис. 1.4,а.
Параметры схемы даны в условии задачи 1.8р.
7
1.16. Построить потенциальную диаграмму для контура abdc
схемы рис. 1.5,6 по данным задачи 1.11.
1.17. На рис. 1.8, а изображен остов некоторой схемы. Буквами
обозначены точки соединения отдельных элементов схемы. На
рис. 1.8, б, в показаны потенциальные диаграммы вдоль контура
Рис. 1.8
oabcfo и вдоль ветви cede соответственно. Определить значение
и направление токов в ветвях и характер элементов, включенных
на различных участках схемы.
1.18р . На рис. 1.9,6 изображена потенциальная диаграмма
вдоль контура oabcdefgo скелетной схемы рис. 1.9, а. Известно,
что в ветвях af и cf включены резисторы. Определить значение
а b с
а д f е d
о)
и направление тока в каждой ветви, а также значения элементов
схемы на всех участках. Потенциалы точек схемы: Фа — 3,175 В;
ФЬ = О,975В; фс = 10,975В; фе= 15,53В; ф/ = 7,53В; Фй=—2.47В.
1.19р . В схеме рис. 1.10, а сопротивление резистора R* из-
меняется от 0 до оо. Записать зависимость тока от тока /а
для двух случаев: 1) £^=0; 2) £*х = 10В. Ток источника тока
J — 1А; /?, = Ю0м; /? = 1Ом.
1.20. На рис. 1.10,6 изображена скрещенная мостовая схема.
Ток источника тока J = 1 A; Rt = 1 Ом; /?2 = 20м; /?3 = ЗОм;
/?4 = 4 0м. Сопротивление резистора Rn изменяется от 0 до оо.
Записать линейную зависимость между токами и /4 для двух
8
случаев: 1) схема рис. 1.10,6 питается от источника тока; 2) нс
точник тока заменен на источник ЭДС Е = 1 В.
/?г 1(
О) 6} в)
Рис. 1.10
1.21. В одной диагрнали мостовой схемы рис. 1.10, в нахо-
дится источник тока J, в другой—резистор, сопротивление кото-
рого R изменяется от 0 до оо, Записать линейное соотношение
между напряжениями на диагоналях Ucd и йлЬ.
В. Входные сопротивления. Преобразование треугольника
в звезду и звезды в треугольник
1.22р . Определить входное сопротивление Rab схемы рис. 1.11 ,а
относительно точек а и 6, если — 2,26 Ом; /?,=ЗОм; /?а=2,170м;
/?4 = 40м; /?5 = 30м; Яв = 20м.
Рис. 1.11
1.23. Решая задачу 1.22р (рис. 1.11, а) по определению вход-
ного сопротивления между точками а и bt студент преобразовал
треугольник, состоящий из резисторов 7?lt R2, RSf в звезду и
точку О звезды, состоящей из резисторов /?4, /?5. Рч. соединил
с точкой О' вновь полученной звезды. Ответ он получил невер-
ный. В чем заключается его ошибка?
1.24. Найти входное сопротивление Rab схемы рис. 1.11,6
относительно точек а и Ь, если J5 и Ja — источники тока.
1.25. В схеме рис. 1.11,6 источник тока заменен на источ-
ник э.д.с. Резисторы имеют сопротивления /?, —10м; /?а=2Ом;
/?3 = 20м; /?4 = 0,6Ом; /?в=0,2Ом. Определить входное сопро-
тивление между точками а и Ь.
9
1.26. В схеме рис. 1.12, а сопротивления резисторов указаны
в омах. Определить входное сопротивление схемы относительно
точек а и Ь.
1.27. В схеме рис. 1.12,6 сопротивления всех резисторов,
кроме двух, указаны в омах. Сопротивления двух резисторов
обозначены х. Чему равно сопротивление х, если входное сопро-
тивление схемы относительно точек а и b Rab =1,5 Ом?
Рис. 1.12
1.28р . Измерение сопротивления R резистора было произведено
с помощью схемы рис. 1.12, в. В этой схеме переключатель может
находиться либо в первом, либо во втором положении. Внутрен-
нее сопротивление вольтметра /?ЕЯ = ЗкОм. Было проведено два
измерения при неизменном входном напряжении U. Когда пере-
ключатель находился в положении /, вольтметр показал 100 В.
При установке переключателя в положение 2 вольтметр показал
90В. Найти сопротивление R резистора.
Рис. 1.13
1.29. На рис. 1.13, а—г изображены четыре схемы, состав-
ленные из проволок. В местах соединений проволоки спаяны.
Определить: а) входное сопротивление между точками а и Ь
схем рис. 1.13,а,б, полагая сопротивление каждой проволоки
равным R; б) входное сопротивление между точками а и 6, с и d
схемы рис. 1.13,в, считая сопротивление каждой проволоки рав-
ным R\ в) потенциалы точек с, d, е, ft g схемы рис. 1-13, г, по-
лагая потенциал точки а равным 18В, а потенциал точки b рав-
ным— 18 В. Считать сопротивление каждой проволоки, кроме
10
проволок, находящихся на линии О—0, равным ЗОм, а распо-
ложенных на линии О—О равным 0,5Я=1,5Ом. Во всех ли
горизонтальных перемычках
схемы рис. 1.13, г будет отсут-
ствовать ток?
1.30р . На рис. 1.14, а изоб-
ражен проволочный куб, каждое
ребро которого имеет сопро-
тивление R = 1 Ом. Найти соп-
ротивление между точками а и
Ь, а и с, d и с.
1.31. Шесть проволочных
колец диаметром d, сечением
S и удельным сопротивлением
р и четыре проволоки длиной
d того же сечения и из того
а)
Рис. 1.14
же материала спаяны, как показано на рис. 1.14,6. Определить
сопротивление между точками а и b проволочной фигуры.
Г. Входные и взаимные проводимости ветвей.
Теорема взаимности. Принцип наложения. Теорема вариаций
1.32р . Для схемы рис. 1.15, я найти входные и взаимные про-
водимости. Значения сопротивлений резисторов в омах указаны
на схеме.
[W
«)
1.33. В схеме рис. 1.15,6 определить входные и взаимные
Проводимости gia, g22, ^23, g-33. Значения сопротивлений
резисторов в омах указаны на схеме.
1.34р . Известны входные и взаимные проводимости ветвей
схемы рис. 1.15, в: gn = 0,454 См; gt2 = 0,273См; gls = 0,182 См;
g>2 — 0,3635См; g2S = 0,091 См. Найти ток /2, если Ех=10мВ;
Е8 = 6мВ; Е3 = 5мВ.
1.35. В схеме рис. 1.15, в ток Л = 4 мА. Значения ЭДС Е2
и Е3 и проводимостей даны в условии задачи 1.34р. Определить
ЭДС Ff.
1.36. 1. На рис. 1.16, а буквой II обозначена пассивная часть
некоторой схемы. Токи в двух ветвях схемы обозначены Jt и /8.
11
Каждый из переключателей 77, и 77, может находиться в одном
из трех положений. В табл. 1.1 приведены данные двух режимов
работы схемы.
Полагая Е” = ЗЕ{ и £Я = 4Е;, найти токи 7f и 7Я в режиме,
когда переключатели 77, и П2 находятся в положении 3.
1
a) 6j
Рис. 1.16
2. Токи в трех ветвях схемы рис. 1.16,6 обозначены 7П 73
и 73. Известны токи в трех режимах работы схемы (табл. 1.2).
Таблица 1.1
Режим Положение 77, Положение 77, нА 7 ,. нА
1 2 1 7; =80 4=40
2 1 2 /; = — 80 96
Таблица 1.2
Режим Положе- ние 77| Положе- ние 77, Положе ш.е 7/, /1. мА I fa МА 7,. мА
1 2 1 1 /1= 200 /2=60 /;=«)
2 1 2 1 /1= —60 4 = —120 Г8=-40
3 1 1 2 /1 = 120 /а" = 60 /Г = 200
Найти токи в четвертом режиме, когда все переключатели нахо-
дятся в положении 3, если £J = 2£J; Е'2=ЗЕ‘2; E'i = 4E‘s.
1.37. На рис 1.17, а изображен активный четырехполюсник А
с двумя выделенными ветвями 7 и 2. В исходном режиме ток
7, = 7А. В ветвь 7 дополнительно включили резистор сопротив-
лением Д/?=1Ом. При этом ток ве7ви 7 стал 5,516 А, не изменив
12
Рис. 1.17
направления. Определить входную проводимость первой ветви и
изменение тока Д/2 второй ветви, полагая, что взаимная прово-
димость между первой и второй ветвями = 0,1153 См.
Д. Метод контурных токов. Метод узловых потенциалов.
Метод двух узлов. Баланс мощностей.
Замена нескольких параллельных ветвей эквивалентной
1.38р . Определить мощность, доставляемую источником тока,
в схеме рис. 1.17,6 при J = Jk= 1 А; /1 = 0,ЗА; R = 10 Ом; Е = ЗВ.
1.39. Найти токи в ветвях схемы рис. 1.18, а методом контур-
ных токов и методом двух узлов. Сравнить результаты. Прове-
рить выполнение баланса мощ-
ности, если J = 1 А; ₽1 = 5Ом;
Я„ = 8Ом; Я3 = 20м; Е2=16В;
Е>4В.
1.40. Вычислить токи в вет-
вях схемы рис. 1.18,6 методом
узловых потенциалов и методом
контурных токов. Составить урав-
нение баланса мощности. Исходные
Рис. 1.19
Рис. 1.18
данные: Ед=25 В; Ег=10В; Ee = 20B; J = 2A; /?2 = 10Ом;
7?3 = 20Ом; /?4 = 10Ом; R. = 8 Ом; Re = 5 Ом.
1.41. В мостовых схемах рис. 1.19, а—г определить токи
в ветвях методом контурных токов и методом узловых потенциа-
лов. В схемах рис. 1.19, а, б в диагонали cd находится источник
тока с J = 1 А, в схемах рис. 1.19, в, г—источник ЭДС с £а = 5,1 В.
13
Схемы рис. 1.19. а и б, виг отличаются полярностью ЭДС
£6 = 1 В. Исходные данные: = 1 Ом; R2 = 2 Ом; Rs — 3 Ом;
/?д = 4Ом; /?5 = 0,6Ом; /?я —30м.
1,42р . Сколько уравнений следовало бы составить для расчета
токов в схеме рис. 1.7, если воспользоваться: а) методом узловых
потенциалов; б) контурных токов?
1.43. В схеме рис. 1.18. а заменить одной эквивалентной вет-
вью: а) ветви 1 и 2; б) ветви 2 и 3. Номер ветви соответствует
номеру резистора.
Е. Активный двухполюсник. Л1етод эквивалентного генератора
1.44. Опытным путем был получен участок зависимости тока Z
на входе некоторого активного двухполюсника в функции от на-
пряжения U на его зажимах (рис. 1.20, а). Рассчитать параметры
схемы замещения этого двухполюсника: а) с источником ЭДС;
б) с источником тока.
1.45. Определить ток /3 в схеме рис. 1.20, б методом эквива-
лентного генератора. если Ег = 20В; J—1 А; 7?х^Ю0м; Я2=100м;
£3 = 50м; /?4=150м; Я3 = 50м; Яя=50м.
1.46. Методом эквивалентного генератора определить ток /5
в диагоналях ab мостовых схем рис. 1.19, а—г. Значения пара-
метров даны в условии задачи 1.41.
Рис. 1.21
1.47р . В схеме рис. 1.21, а с помощью вольтметра с внутрен-
ним сопротивлением Rv и амперметра с внутренним сопротивле-
14
нием RA были проведены измерения для трех сочетаний положе-
ний переключателей и /7,. Результаты измерений приведены
в табл. 1.3.
Таблица 1.3
Режпы Положение пх Положение /7, Показание амперметра. А Показание вольтметра. Б
1 1 2 0,4755 95,3
2 2 1 0,906 0
3 2 2 1,295 86.5
Определить сопротивление R резистора, внутреннее сопротив-
ление амперметра RA, внутреннее сопротивление вольтметра RVt
входное сопротивление двухполюсника R„ab относительно точек
а и 6. напряжение на зажимах а и b при холостом ходе UabT.
1.48р . Переключатель П в схеме рис. 1.21, б может находиться
в трех положениях. Когда он находится в положении /, ток
/ = Л =100 мА, в положении 2 ток / = /, = 50 мА, в положении 3
ток / = /, = 20 мА. Сопротивление резистора /?,= 1кОм. Опреде-
лить сопротивление резистора R9* входное сопротивление двух-
полюсника относительно точек а и b и напряжение холостого
хода ивЬх.
Ж. Передача мощности от активного двухполюсника нагрузке.
Теорема компенсации
1.49. Для двухполюсника рис. 1.22, а при изменении сопро-
тивления нагрузки /?в была получена зависимость мощности Ри,
выделяющейся в нагрузке, от Rn (рис. 1.22,6). Определить:
а) напряжение на зажимах а и b двухполюсника при холостом
ходе; б) входное сопротивление двухполюсника относительно то-
чек а и 6; в) КПД при RK — 0,5 и 2 Ом.
1.50. Определить ЭДС источника, включенного в ветвь ab
(рис. 1.22, а) вместо резистора сопротивлением 2^=1 Ом, и как
она должна быть направлена, чтобы ток / этой ветви не изме-
нился?
15
1.51р . Определить сопротивление резистора нагрузки /?и в схеме
рис. 1.10,6 (вариант 1 примера 1.20), при которохм в нагрузке
выделяется максимально возможная мощность. Найти эту мощ-
ность.
1.52. По двухпроводной линии постоянного тока с напряже-
нием на конпе линии £/2=100В передается нагрузке мощность
Рн=10кВт. При этом КПД передачи -q = 0.9. Чему будет равен
КПД. если при той же передаваемой мощности напряжение на
нагрузке станет 200 В?
3. Задачи на различные темы
1.53р. Для схемы рис. 1.23, а записать два уравнения, связы-
вающие входные gu, g23 и взаимную g12 проводимости ветви
с собственными и взаимными сопротивлениями контуров /?12, /?а2.
1.54. На рис. 1.23,6 изображен активный четырехполюсник.
В ветвях 1 и 2 протекают токи /, и /2, положительные направ-
ления которых указаны на ри-
сунке. В ветвь 2 подключили
резистор сопротивлением Д/?, в
результате чего токи и /2 из-
менились на Д/^ и Д/2. Затем
этот резистор перенесли из вет-
ви 2 в ветвь 1. При этом ток 1Х
изменился на Д/, по сравнению
с его первоначальным значением.
Определить входные проводимос-
ти и и взаимную прово-
димость g12, а также изменение
тока Д/2 в случае, когда резис-
тор сопротивления Д/? включен
в ветвь 1.
1.55. На рис. 1.23. в изобра-
жены два электрических изолиро-
ванных контура. Первый контур образован источником напряже-
ния (ЭДС) t/j и резисторами с сопротивлениями /?т и /?э = 1 Ом.
С резистора /?э снимается выходное напряжение. Второй контур
образован источником напряжения (ЭДС) и резисторами,
имеющими сопротивления и 7?3= 1 Ом. Сопротивления резисто-
ров Ry и Р2 могут изменяться, оставаясь всегда равными друг
другу (движки реостатов жестко соединены). Доказать, что вы-
ходное напряжение (7ВЫХ будет равно UyiU^ если сопротивление
резистора при изменяющемся напряжении Uz варьировать так,
чтобы ток /2 поддерживался неизменным и равным 1 А.
1.56. Для подсчета входных и взаимных проводимостей сим-
метричных схем с перекрестными связями, например схемы
рис. 1.24, я, перекрестные резисторы сопротивлением /?в делят на
неравные части х и у (рис. 1.24,6) так, чтобы точка т имела
нулевой потенциал, а токи /а=/вВсхеме рис. 1.24, а были равны
16
токам 1х = 1и в схеме рис. 1.24,6. После этого симметричную
относительно нулевой линии О—О схему рис. 1.24,6 заменяют ее
половиной (рис. 1.24, в). В укороченной схеме резистор сопротив-
лением R4, расположенный по линии симметрии, отсутствует,
поскольку ток через него в схемах рис. 1.21, о, б не протекает.
Входная или взаимная проводимость укороченной схемы рис. 1.24, в
в два разя больше соответствующей входной или взаимной прово-
димости исходной схемы рис. 1.24, а. Вывести формулы для опре-
деления сопротивлений х и- у и найти взаимную проводимость
между ветвью с резистором сопротивлением /?, и ветвью с рези-
стором сопротивлением RK в укороченной схеме рис. 1.24, в (gHtyKnp).
1.57р . На рис. 1.25, а изображен граф, в котором имеется
пять узлов и восемь ветвей. Выберем дерево графа, изображен-
2
3
4
S)
Рис. 1.25
ное на рис. 1.25,6, обозначим его ветви номерами /, 2, 3, <
а остальным ветвям графа придадим номера 5. 6, 7, 8. Поставим
стрелки на всех ветвях графа (рис. 1.25, в). Сопротивления вет-
вей электрической схемы, которую изображает граф, обозначим
Я]—/?в (проводимости —gp). В ветвях 5 и 7 имеются источ-
ники э.д.с. £5 и £/, кроме того, в схеме имеются два источника
тока Jfl и Зв. Составить узловую матрицу [А], заземлив узел 5,
матрицу Алавных сечений [Qr] и матрицу главных контуров [Аг].
17
1.58. Используя топологические матрицы, составленные при
решении задачи 1.57 р, составить для схемы рис. 1.25, а уравне-
ния по законам Кирхгофа.
1.59. Записать уравнения по методу контурных токов в мат-
рично-топологической форме для схемы рис. 1.25, в, взяв за основу
дерево, изображенное на рис. 1.25,6, обозначив контурные токи
/вв, /вв, /„, /8в, выбрав их положительные направления по стрел-
кам на хордах 5, 6, 7, 8 соответственно.
1.60. Для схемы рис. 1.25, в записать систему уравнений по
методу узловых потенциалов, взяв за основу узловую матрицу [А],
составленную для узлов 1—4t полагая узел 5 заземленным.
1.61. По матрице
Сечения Ветви
5 6 7 8'
—10 0 1
—1 10 0
0—11 0
0 0 1 —1J
для задачи 1.57р составить матрицы [Кг] и [фг].
1.62. Заданы узловая матрица и матрица главных контуров!
[А] = 1 1 “ 1 II — о о о —1 1 0 0 0 0 С 0—1 1 1 0 0 С 0 0 0 —1—1 1 ( 0 0—1 0 1 0—1 0 0 0 0 0 —1 ( гО 0 0 1 —1 1 0 0 Оп 1 0 1 0 10100 о —1 —1 —1 0 0 0 1 0 _1 —1 0 0 0 0 0 0 L 1 О' ) 0 ) 0 0 ) — >
Построить граф, жирными линиями выделить на нем дерево и
показать положительные направления отсчета тока и напряжения
на каждой ветви графа.
1.63. По узловой матрице
[А] = ' 1 0 0 0 0 —1 —1 0 0 О' —1 —1 0 0 0 0 0 —1 0 0 00 —1 0000 1 0 1 0 1110 10 0 10 _ о 0 0 0 —1 0 0 0 —1 —1_
построить граф и для него составить матрицу главных контуров,
взяв в качестве ветвей дерева ветви /, 2, 3, 4, 5.
Глава вторая
Индуктивные и емкостные элементы электрических
цепей
А. Индуктивность и взаимная индуктивность катушек
2.1р . По катушке с числом витков = 6 протекает ток 1 =
= 3,2 А. Картина магнитного поля, возникающая при этом, по-
казана на рис. 2.1. Определить потокосцепление катушки тр и
ее индуктивность L, если картина поля построена так, что каж-
дая магнитная силовая линия соответствует силовой трубке с
одинаковым значением потока ДФ=10“* Вб.
2.2р . Две магнитно-связанные катушки с числом витков w, =
= 100 и u/2= 150 обтекаются соответственно токами 1± = 10 А и
/2 = 20 А. Найти индуктивность катушек L, и L, и взаимную
индуктивность М, полагая, что каждая силовая линия магнит-
ного поля на рис. 2.2 соответствует силовой трубке с потоком
ДФ=10-4 Вб.
2.3р . Вычислить взаимную индуктивность между двухпровод-
ной линией АС и прямоугольной рамкой пт, стороны которой
параллельны проводам линии и равны (/ = 40 см), число витков
tfj=100. Взаимное расположение линии и рамки показано на
19
рис. 2.3. Необходимые размеры на рисунке указаны в санти-
метрах.
2.4. Рассчитать индуктивность кабеля (рис. 2.4) длиной I —
= 10 км, радиусом жилы = 5 мм и внутренним радиусом обо-
лочки Л?я=20 мм, не учитывая потокосцепление в телах жилы и
оболочки.
2.5. Определить взаимную индуктивность между лежащими в
одной плоскости двухпроводной линией АВ и разомкнутым коль-
цевым витком с радиусом г0 (рис. 2.5), если: а) виток неподви-
жен; б) виток вращается вокруг горизонтальной осн О—О' с
частотой со =1000 с"1; r0 = 1 см; 10 см; /?, = 20 см. При
г0</?х приближенно считают, что виток находится в равномер-
ном магнитном поле, индукция которого равна индукции в его
центре.
Б. Индуцированные ЭДС
2.6р . При полете самолета в магнитном поле Земли между
концами его крыльев наводится ЭДС. Определить эту ЭДС,
если поле Земли считать равномерным и имеющим индукцию
fi=l,5-10“s Тл, длину крыла самолета /=10 м, угол между
крыльями 0=120°, скорость движения самолета v =720 км/ч.
Вектор скорости составляет угол а = 60° с вектором магнитной
индукции (рис. 2.6).
2.7. Металлический диск радиусом г0 вращается с частотой
п об/мин в равномерном магнитном поле, направленном за чер-
теж перпендикулярно плоскости диска (рис. 2.7). Вывести фор-
мулу для определения ЭДС. наводимой между щетками, при-
соединенными к точкам Она диска.
20
2.8. Прямоугольная рамка со сторонами а = 2 см, Ь — 5 см и
числом витков w = 1 000 находится в магнитном поле. Магнитная
индукция, пронизывающая рамку, изменяется, как показано на
рис. 2.8,о. Определить наведенную ЭДС. Построить графики
e = и ф=/(/), полагая, что постоянная составляющая пото-
ка равна нулю, а на разомкнутых концах рамки получена ЭДС
прямоугольной формы (рис. 2.8,6) с периодом Т = 5Ю~а с.
2.9. Прямоугольная рамка со сторонами о и & и числом вит-
ков w (рис. 2.9) вращается с угловой частотой ы в равномерном
магнитном поле, имеющем индукцию В. Найти ЭДС, наведен-
ную между разомкнутыми концами обмотки.
2.10. Прямоугольный контур abed движется в неравномерном
магнитном поле, где каждая
вой трубке с потоком ДФ =
= 10-3 Вб. На рис. 2.10 нап-
равление силовой линий выб-
рано за плоскость рисунка.
Определить значение и нап-
равление ЭДС, наводимых
в разомкнутом контуре, если
он переместится за время
А/= 0,01 с: а) из положения
abed в положение
силовая линия соответствует енло-
(рис. 2.10, я); б) из положения abed в положение a2br£2d2 (рис. 2.10.6).
2.11. По данным задачи 2.5 рассчитать ЭДС, наведенную в
разомкнутом вращающемся витке радиусом г0, если по линии
протекает: а) постоянный ток I = 10 А; б) синусоидальный ток
i= lOsin 1000/ А.
В. Механические усилия в магнитном поле
2.12. Определить силу, действующую на сторону т рамки, в
задаче 2.3р, если по проводам линии течет постоянный ток Л =
= 100 А, а по рамке—ток Z2= 1 А.
£1
2.13. На рис. 2.11 показано расположение параллельных про-
водов А, В, С, D двух двухпроводных линий постоянного тока
в каждом из них и проводника М с постоянным током /2.
Указать провода линии с одинаковыми направлениями токов,
при которых усилие на 1 м проводника М было бы: а) мини-
мальным; б) максимальным. Рассчитать эти силы при а = 20 см;
Л = 100 А; /2= 1 А.
2.14. К точкам Она диска (см. условие задачи 2.7) подве-
дено постоянное напряжение £ = 0,25 В. Сопротивление прово-
Рис. 2.11
дов Впр = 2 Ом; сопротивление участка диска между точками О
и a = Ом; радиус диска го=10 см. Определить силу F,
действующую на участке Оа, и частоту вращения диска л, если
В = 0,956 Тл. Как должна быть направлена ЭДС для того,
чтобы диск вращался по часовой стрелке?
2.15. Рамка магнитоэлектрического вольтметра расположена
на ферромагнитном барабане (рис. 2.12) и находится в радиаль-
ном магнитном поле с индукцией В = 0,2 Тл. Найти вращаю-
щий момент рамки, если по ней протекает ток 7 мА. Длина
рамки (размер, перпендикулярный рисунку) а=12 мм, ширина
Ь = 25 мм, число витков ш— 125.
Г. Энергия магнитного поля
2.16. Определить энергию магнитного поля катушки в зада-
че 2.1р.
2.17. Рассчитать энергию магнитного поля двух магнитно-
связанных катушек задачи 2.2р.
2.18. Вычислить внутренние индуктивности на единицу длины
жилы и оболочки L2 кабеля задачи 2.4, если £3 = 22 мм.
2.19р . На одном сердечнике цилиндрической формы с площа-
дью поперечного сечения S = 50 см2 расположены две катушки,
обтекаемые токами (рис. 2.13). Первая катушка неподвижна,
вторая может перемещаться вдоль оси х. Неподвижная катушка
с током создает магнитное поле. Зависимость составляющей
магнитной индукции, направленной вдоль оси х, выражена соот-
ношением В = е~3х Тл. Определить силу, действующую на вторую
катушку, если /а=10 А; и/2 = 20.
22
2.20. Рассчитать энергию, которую необходимо затратить на
создание магнитного поля с индукцией Во=О,8 Тл в тороидаль-
ном сердечнике сечением 5=10 см2 и длиной средней линии
/ср = 25 см. Кривая намагничивания приведена на рис. 2.14.
Рис. 2.13
Д. Емкость как параметр электрической цепи
2.21р . Рассчитать емкость кабеля (см. рис. 2.4) по данным
задачи 2.4, если относительная электрическая проницаемость
диэлектрика кабеля ег = 4.
2.22. Напряженность электрического поля в плоском конден-
саторе Е = 2-104 В/см, площадь пластин 5 = 200 см3, расстояние
между ними d=l см, ег = 4 (рис. 2.15,а). Определить напряже-
ние, заряд и емкость конденсатора.
w
4
Рис. 2.15
2.23. Вычислить емкость конденсатора, если известно, что до
начала его разряда напряжение на нем было 100 В; кривая то-
ка разряда приведена на рис. 2.15,6.
2.24. Найти ток, протекающий через конденсатор емкостью
20 мкФ, если напряжение на н&м изменяется по закону иЩ —
- 100 sin 1000/ В.
2.25. Подсчитать электрическую энергию конденсатора: а) в за-
даче 2.22; б) в задаче 2.23.
2.26. Энергия двух одинаковые параллельно включенных кон-
денсаторов №э=1 Дж (рис. 2.15, в). Напряжение на них U —
— 1 кВ. Определить емкость каждого конденсатора.
23
Глава третья
Электрические цепи однофазного
синусоидального тока
А. Мгновенные значения синусоидального тока
напряжения и мощности. Активные, реактивные,
комплексные сопротивления и проводимости.
Символический метод расчета
3.1. Известно, что в момент времени /=0 мгновенное значе-
ние синусоидального тока i = 5 А и достигает положительного
максимума через /г = 2,5 мс. Период Т = 0,02 с. Определить амп-
литудное значение тока, начальную фазу и угловую частоту.
Записать выражение для *мгновенного значения тока и построить
ее график.
3.2р . По /?С-цепи (рис. 3.1) протекает синусоидальный ток с
амплитудным значением /т=1,41 А; / — 50 Гц. Найти мгновен-
ные значения приложенного к цепи напряжения и, напряжений
на конденсаторе ис и резисторе Ur, если R — 100 Ом; С = 31,8 мкФ.
Построить графики мгновенных значений тока, приложенного к
цепи напряжения и мощности.
3.3р . Катушка, индуктивность которой £ = 100 мГн, включе-
на последовательно с резистором сопротивлением /? = 10 Ом
(рис. 3.2). Рассчитать мгновенные значения тока i и приложен-
ного к цепи напряжения и, если ЭДС самоиндукции eL =
= 100 sin (3142 + 30е) В. Построить графики мгновенных значе-
ний тока, напряжения на катушке индуктивности и ЭДС само-
индукции.
Рис. 3.1
Рис. 3.2
Рис. 3.3
3.4р . Для определения параметров катушки (R, L) измерены
подведенное к катушке напряжение и ток в ней (рис. 3.3) при:
а) Л = 0; ^ = 100 В; Д=1 А; б) /, = 500 Гц; U = 100 В; /2 =
= 0,5 А. Рассчитать R, L и показание амперметра при /3 —
= 1000 Гц; С/я = 100 В.
3.5. В схеме рис. 3.4 протекающий ток отстает от приложен-
ного к цепи напряжения на 45°; /? = 50 Ом; С = 3,18 мкФ; / =
= 500 Гц. Определить индуктивность £, приложенное напряже-
ние Uac и ток в цепи /, если Uab~ 315 В. Записать выражение
для комплексного сопротивления цепи.
24
3.6. В схеме рис. 3.5 при разомкнутом выключателе сдвиг
фаз между током / и напряжением на входе U — 60°. Найти
сдвиг фаз между ними при замкнутом выключателе.
Рис. 3.4
3.7. При каком значении емкости конденсатора С в цепи
рис. 3.6 ток в ветви с катушкой будет в три раза больше тока
в ветви с конденсатором. Определить комплексные значения вход-
ного сопротивления Zex и входной проводимости FBX. Исходные
данные: Rt = 9 Ом; /?2 = 3 Ом; £=1,28 мГн; / = 500 Гц.
3.8. Найти комплексные значения входной проводимости и
входного сопротивления, а также мгновенные значения прило-
Рис. 3.6
Рис. 3.8
женного напряжения и токов в ветвях цепи рис. 3.7, если про-
водимости ветвей £ = 0,01 См, £ = 0,02 См, а действующее значе-
ние тока на входе /=1 А.
3.9. К входным зажимам цепи рис. 3.8 приложено напряже-
ние и —282 sin 30°) В. Ток, протекающий через конденсатор,
ii = 1,41 cosat А; Хс = 73,5 Ом; Xt = 50 Ом. Определить комп-
лексное сопротивление, заменяющее сопротивление Z и состоящее
из последовательно соединенных активного и реактивного сопро-
тивлений. Рассчитать токи /х и 7й, а также активную и реактив-
ную проводимости двух параллельных ветвей, с помощью кото-
рых можно заменить данную цепь.
Б. Векторные и топографические диа! раммы
ЗЛО. Построить векторную диаграмму токов и напряжений
по результатам расчета предыдущей задачи для цепи, приведен-
ной на рис. 3.8.
3.11. Параметры схемы рис. 3.9: /?г=10 Ом; С=159 мкФ;
Ю Ом; £ = 31,8 мГн; Ёт —100 В; / = 50 Гц. Рассчитать
25
токи в ветвях: а) с помощью закона Ома; б) методом контурных
токов; в) методом двух узлов. Построить векторную диаграмму
токов и топографическую диаграмму.
3.12р . В депи рис. 3.4 измерены ток / = 2 А, напряжения на
входе &сс=100 В, на катушке Uab = 173 В, на конденсаторе
Ube— 100 В. Построить векторную диаграмму напряжений и оп-
ределить комплексное сопротивление катушки.
Рис. 3.9
Рис. 3.10
3.13. Определить показания амперметров А2 и А3 по извест-
ным значениям Ait Ait А. (рис. 3.10), если /t = 5,64 А; /4 = 4 А;
/5 = 3 А.
3.14. В цепи рис. 3.11 измерены все токи и напряжения:
/!==/3 = /3 = 2 А; иаЬ = иъс= 100 В; (/вс=141 В. Построить век-
торную диаграмму токов и топографическую диаграмму, приняв
Фь = 0. Найти Zlt Z2, Z3 и ZBX.
Рис. 3.12
Рис. 3.11
3.15. С помощью топографической и векторной диаграмм оп-
ределить в приведенной на рис. 3.12 цепи токи /п /а и напря-
жение на входе цепи если ток /3 = 1 А. Сопротивления эле-
ментов цепи в омах указаны на схеме.
В. Активная, реактивная н полная мощности в цепи
переменного тока
3.16р . Определить активную, реактивную и полную мощности
в цепи по данным задачи 3.2р.
3.17р . Рассчитать параметры схемы замещения пассивного
двухполюсника при замене его: а) последовательно включенными
активными реактивным сопротивлениями; б) параллельно вклю-
ченными активным и реактивным сопротивлениями. Показания
26
приборов в схеме рис. 3.13: U = 80 В; Р = 102 Вт; / = 1,6 А.
Учесть, что при включении конденсатора небольшой емкости
параллельно входным зажимам двухполюсника показание ампер-
метра уменьшается.
3.18. Для увеличения коэффициента мощности cos ср в элект-
рическую цепь включают конденсатор. Определить costp по дан-
ным задачи 3.3р. Для cos ср = 0,865 рассчитать емкость конден-
сатора, который следует включить в цепь: а) последовательно с
источником питания; б) параллельно ему.
Рис. 3.U
3.19. Коэффициент мощности нагрузки, состоящей нз после-
довательно соединенных активного и индуктивного сопротивле-
ний, равен 0,8. Как следует изменить индуктивное сопротивление,
чтобы при его параллельном включении с тем же активным соп-
ротивлением значение cos ср не изменилось?
3.20. Потребляемая активная мощность цепи рис. 3.14 равна
150 Вт. Определить показания приборов и проверить баланс
мощностей, если /? = 50 Ом; X
Рис. 3.15
3.21. Комплексы полных мощностей генераторов в схеме
рис. 3.15 §1 = 250-Ь/1250 В-A; S2 = 375 + /125 В-A; /\ =
= 12,75е-/78°45‘ А; индуктивное сопротивление XL— 10 Ом. Най-
ти Elt /:2, J2, 13, Хс. /?.
3.22. На рис. 3.16 показана часть электрической цепи, для
которой 71=10е/37° А; /3 = 8е-/15°Д; Z, = 2 Ом; Z8= 1,8е-Л*в о.м.
Определить показание ваттметра.
Г. Резонансы и частотные характеристики
3.23р . Конденсатор емкостью С =1000 пФ имеет добротность
<2=1000 и работает на частоте /=1 мГц. Определить параметры
последовательной и параллельной схем замещения этого конден-
сатора.
3.24р . Потери в обмотке катушки на частоте f составляют
10 Вт при напряжении 100 В я токе 1 А. Рассчитать доброт-
ность катушки для данной частоты и параметры последователь-
ной и параллельной схем замещения.
3.25. Чему равна добротность Q’. а) последовательного резо-
нансного контура, если добротности конденсатора и катушки со-
ответственно равны Qi и <2S; б) параллельного резонансного
контура, составленного из тех же элементов? Учесть, что при
резонансе w0L= l/(tooC); эквивалентная проводимость двух ветвей
= + Q== l/[l/(co0Lg,)].
3.26р . В последовательной резонансной цепи /? = 2 Ом; С =
= 100 мкФ; L = 40 мГн. Определить резонансную частоту, доб-
ротность контура, полосу пропускания и зависимость полосы
пропускания от добротности контура. Построить резонансную
кривую = f (и) в относительных единицах, где п=ы/ь)0.
При {/=10 В построить векторные диаграммы напряжений для
частот о)о/2, ю0, 2<оо.
3.27. Выбрать параметры индуктивной катушки для последо-
вательного резонансного контура, обеспечивающие полосу про-
пускания от Д — 148 кГц до [2 = 152 кГц.
Ёмкость конденсатора С=10-8 Ф.
3.28. Для измерения параметров ка-
тушки применяют Q-метр, принцип дей-
ствия которого основан на явлении резо-
нанса напряжении. Схема прибора по-
казана на рис. 3.17. Известно, что при
резонансе напряжений отношение напряжения на конденсаторе к
напряжению на входе UmniUab = 100; С =10 000 пФ; [=10 кГц.
Определить параметры катушки.
3.29. При резонансе ток в цепи рис. 3.17 равен 0,1 А при
напряжении на входе 12 В. Добротность контура <2 = 3. Найти
напряжение на всех элементах и ток в цепи при со = 2(о0 и том
же значении напряжения.
3.30. В резонансном режиме электрическая цепь, собранная
по схеме рис. 3.17, позволяет увеличить подведенное напряже-
ние в Q раз и повернуть его на угол <р = —90’. Напряжение
Umn = UabQe-/90°. Какими должны быть параметры цепи, чтобы
при резонансной частоте <%= 10вс“1, напряжении на входе Uab =
- 10 В и потребляемой мощности I Вт получить на выходе
t/„„=1000 в?
3.31. Параметры цепи рис. 3.18: R = 10 Ом; L = 40 мГн;
С= 100 мкФ; {/=16,6 В. Определить резонансную частоту и по-
строить графики зависимости Д, /2, Uaf> от [.
28
3.32. Рассчитать резонансную частоту цепи, состоящей из па-
раллельно включенных конденсатора емкостью 100 мкФ, катуш-
ки индуктивностью 40 мГн и резистора сопротивлением 10 Ом.
Построить векторную диаграмму токов при (7 = 46 В.
3.33. В цепи рис. 3.19 J — 8 А; /?я = 4 Ом; R2 = 2XL. При
резонансе токов амперметр показывает 5 А. Рассчитать токи в
остальных ветвях, а также сопротивления Хс, XL, R>.
3.34. В цепи рис. 3.20 £,==£., = 20 мГн; С = 200 мкФ; R =
= 2 Ом. Определить резонансные частоты и токи в режиме ре-
зонанса напряжения при [7 = 20 В.
Рис. 3.20 Рис. 3.21
3.35р . Построить частотные характеристики входных сопро-
тивлений и проводимостей для цепей рис. 3.21,0,6, если L =
= 40 мГн; С =100 мкФ. Записать условие возникновения резо-
нансов для этих цепей.
i) В) г)
Рис. 3.22
3.36. Какие двухполюсники из приведенных на рис. 3.22, а—г
имеют одинаковые частотные характеристики? Качественно по-
стройте их.
3.37. Известно, что цепь состоит из четырех реактивных эле-
ментов. В этой цепи возникает три резонанса, причем первым
наступает резонанс токов. Качественно построить частотную ха-
29
рактеристику такой цепи. Составить несколько схем, дающих
такую же характеристику.
3.38. Качественно построить частотные характеристики цепей,
приведенных на рис. 3.23, а, б.
Рис. 3.23
Д. Магнитно-связанные цепи
3.39р . На рис. 3.24 показаны схема соединения и намотка
катушек, имеющих общий сердечник (здесь и далее цепи линей-
ные). Определить одноименные зажимы катушек. Привести элект-
рическую схему цепи с учетом взаимной индуктивности. Вывести
выражение для входного сопротивления цепи, если известны па-
раметры катушек /?lt Llt /?2, £2 и взаимная индуктивность Л1.
Рис. 3.24
Рис. 3.25
Составить эквивалентную схему замещения данной цепи без маг-
нитных связей.
3.40. Определить напряжение и2 в цепи рис. 3.25, если из-
вестны 7ИП, Л124 и = А.
3.41. Активная мощность цепи, состоящей из двух последо-
вательно соединенных магнитно-связанных катушек, при их
встречном включении в 10 раз больше, чем при согласном. Рас-
считать активное сопротивление второй катушки, если /?1 = 2О.м;
= 10 Ом; Х2 = 20 Ом; Ад| —10 Ом.
3.42. Какое сопротивление Z следует включить в схему
рис. 3.26 последовательно с Х2, чтобы напряжение на Х2 было
равно нулю при /3 = 5 А? Построить топографическую диаграм-
му. Определить напряжение на входе схемы и токи в ветвях.
Исходные данные: Rl^X1 — Xi — 5 Ом; Х9^= 4 Ом; Ал;~2 Ом.
3.43р . На рис. 3.27 изображена схема, в которой к входным
зажимам трансформатора, имеющего параметры /^ = 2,3 Ом;
30
Xj==8 Ом; X2=10 Ом; Xw = 8 Ом, присоединена нагрузка Z.
Найти сопротивление нагрузки исходя из условия выделения в
ней максимальной активной мощности. Рассчитать токи транс-
форматора, построить векторную диаграмму, составить баланс
активной мощности и схему замещения трансформатора без маг-
нитной связи при (71=100В.
Рис. 3.26
Рис. 3.27
3.44. Рассчитать токи в ветвях и напряжения Uac, Ubc в це-
пи, приведенной на рис. 3.28, если J = 20 А; Я, = 4,9 Ом; Хс —
= 15,1 Ом; /?2 = 5,1 Ом; Х£( = 6 Ом; Х£>=10 Ом; ХЛ=3 Ом.
3.45. Составить эквивалентную схему замещения цепи рис. 3.29
без магнитных связей, если известны Rlt L,. R,. Rs, a
Mu=M1s = Mm=M.
Рис. 3.30
Рис. 3.31
3.46. Определить показания вольтметра и ваттметра в цепи
рис. 3.30: а) при разомкнутом выключателе; б) при замкнутом
выключателе. 11араметры схемы: Rj = Rt — 10 Ом; Xt = Ха = 10 Ом;
£=141 В; коэффициент связи Х = 0,8. Во втором случае соста-
вить баланс активной мощности для ветви с Rt и X,.
31
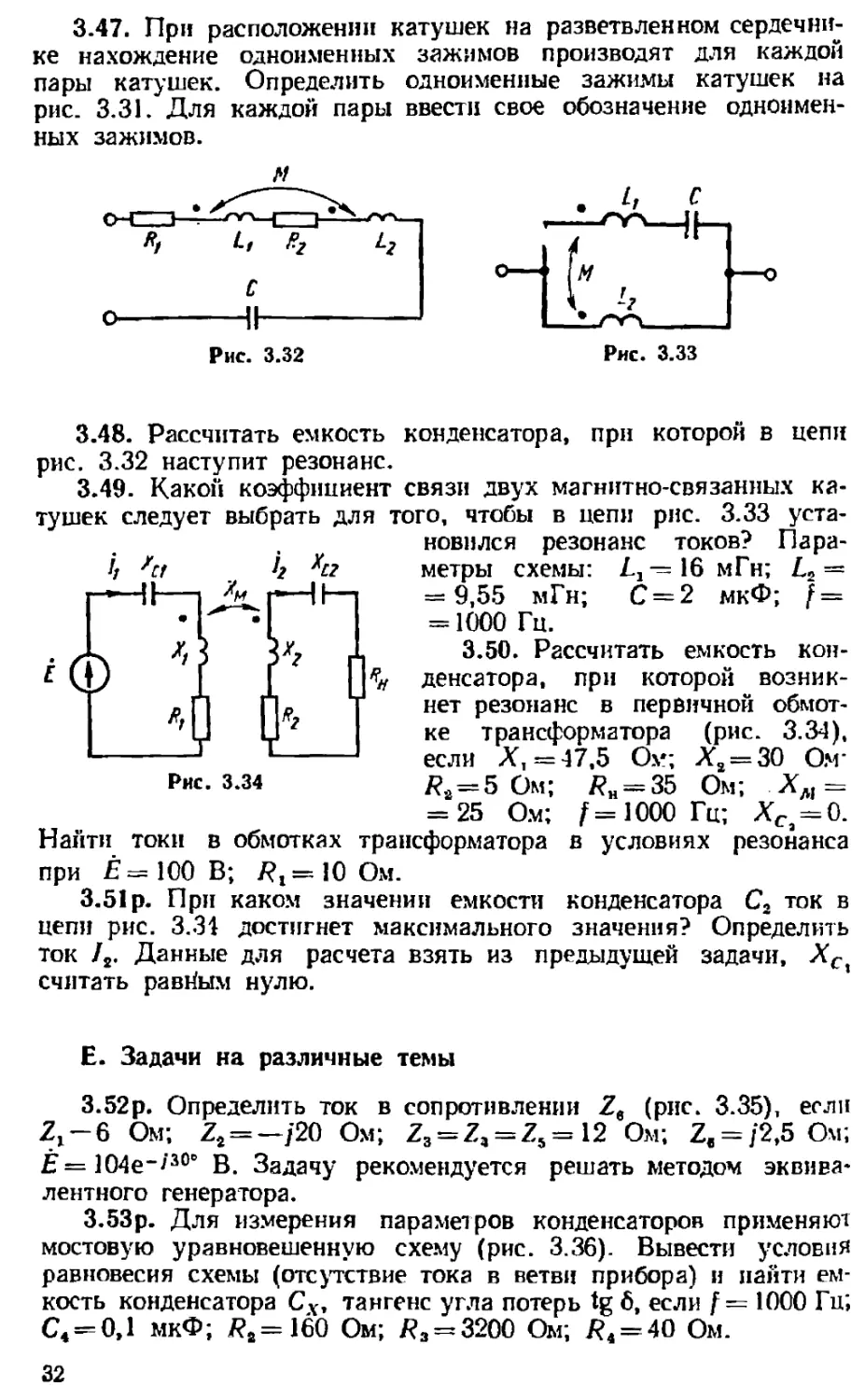
3.47. При расположении катушек на разветвленном сердечни-
ке нахождение одноименных зажимов производят для каждой
пары катушек. Определить одноименные зажимы катушек на
рис. 3.31. Для каждой пары ввести свое обозначение одноимен-
ных зажимов.
Рис. 3.32
Рис. 3.33
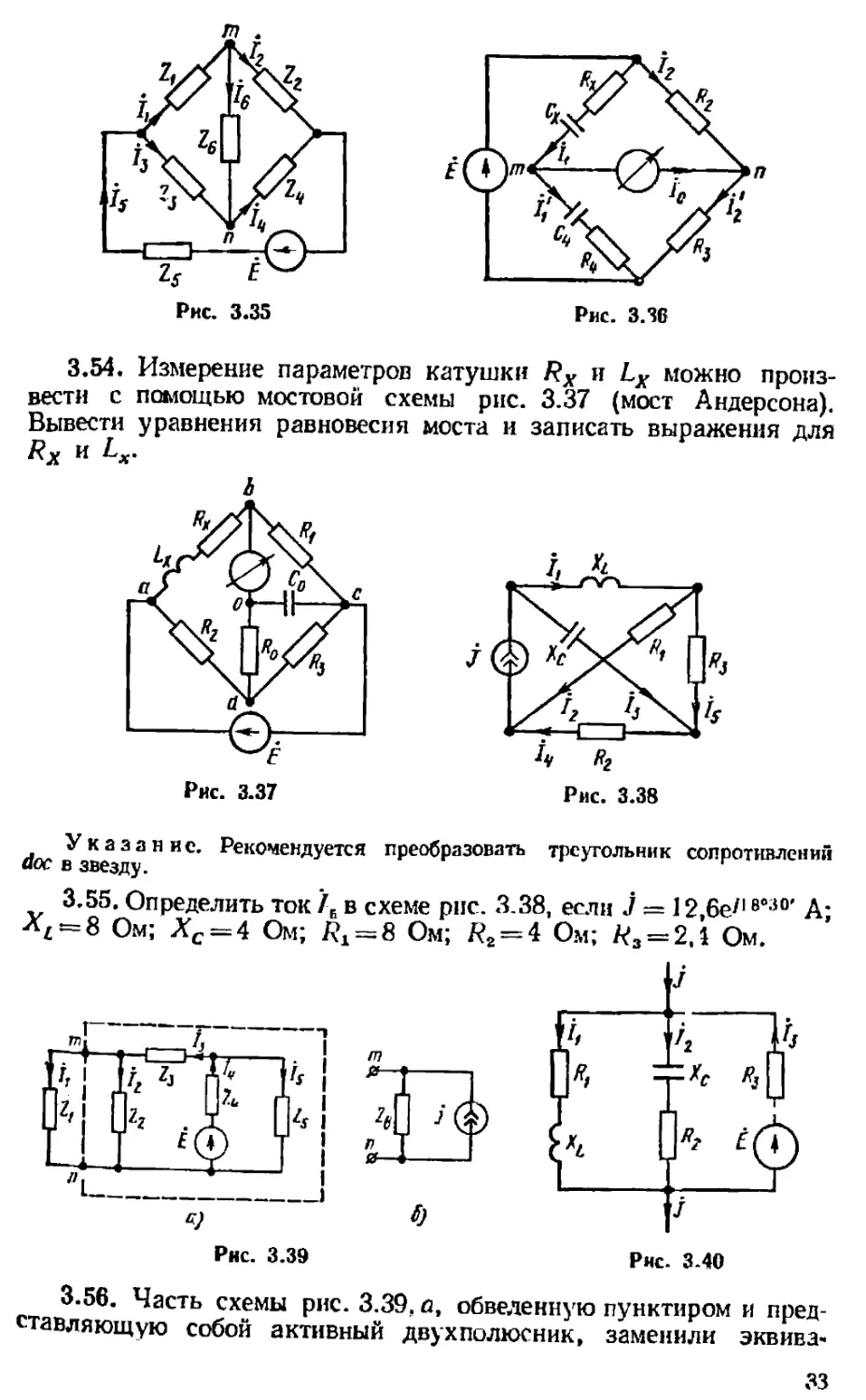
3.48. Рассчитать емкость конденсатора, при которой в цепи
рис. 3.32 наступит резонанс.
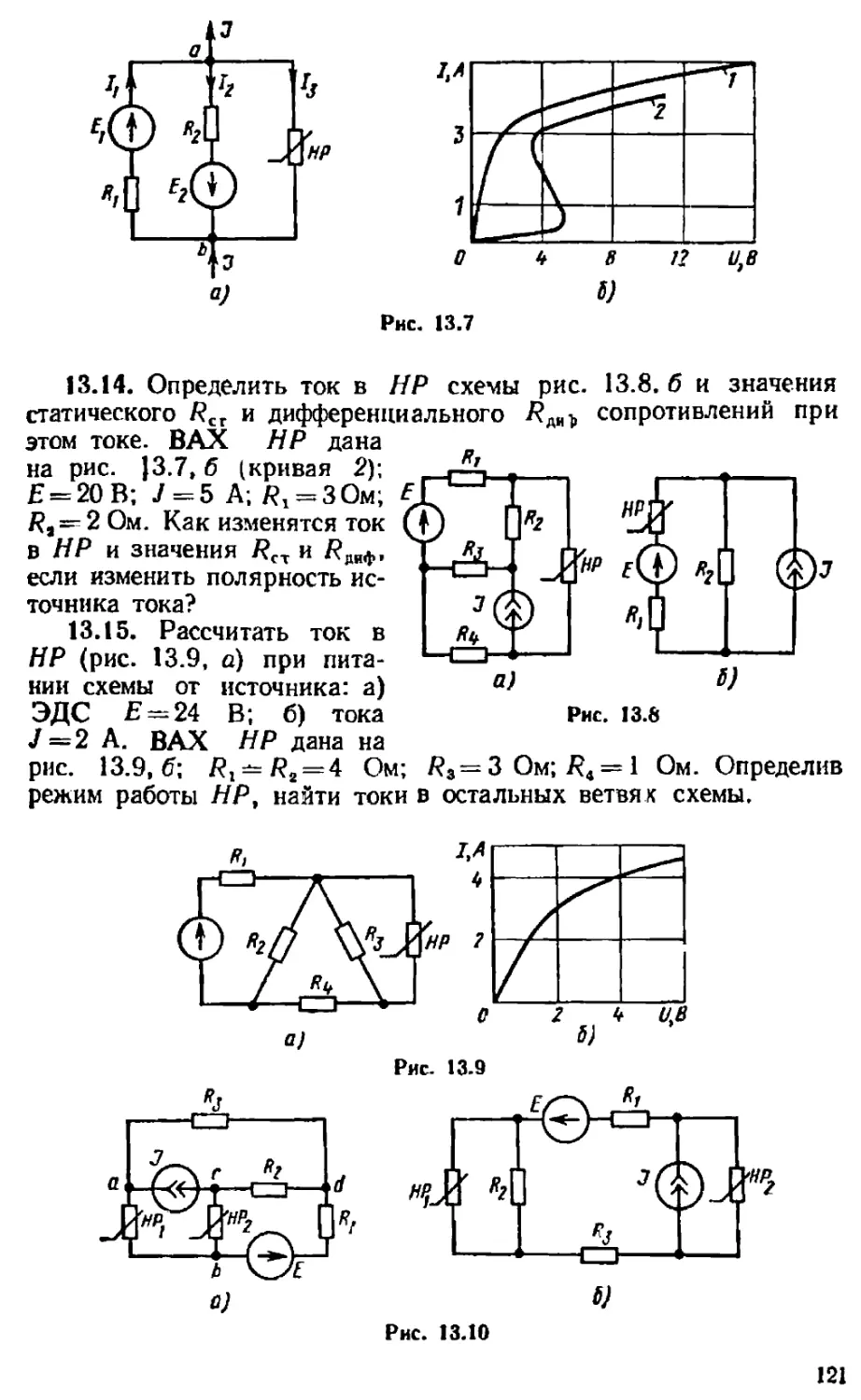
3.49. Какой коэффициент связи двух магнитно-связанных ка-
тушек следует выбрать для того, чтобы в цепи рис. 3.33 уста-
новился резонанс токов? Пара-
метры схемы: 16 мГн; £2 =
= 9,55 мГн; С = 2 мкФ; f =
=1000 Гц.
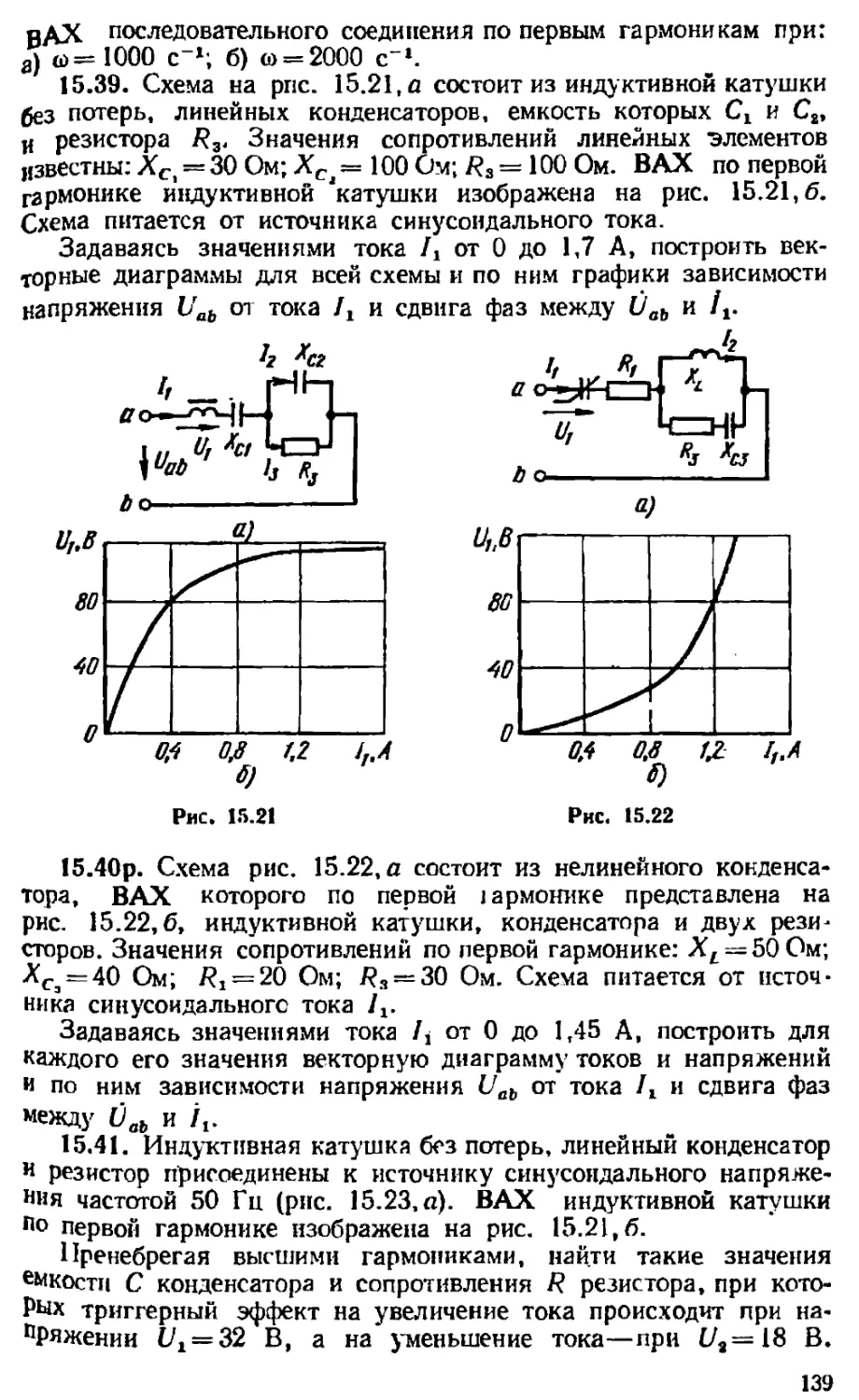
3.50. Рассчитать емкость
денсатора, при которой возник-
нет резонанс в первичной обмот-
ке трансформатора (рис. 3.34),
если Х\=47,5 Оу; Ха = 30 Ом'
7?а = 5 Ом;
= 25 Ом;
Найти токи в обмотках трансформатора
при £=100 В; /?!=10 Ом.
3.51р . При каком значении емкости
цепи рис. 3.31 достигнет максимального
ток Данные для расчета взять из предыдущей задачи, ЛС1
считать равным нулю.
4
—1Ь
Рис. 3.34
кон-
/\н — । -Л д| —
/=1000 Гц; ХСа = 0.
в условиях резонанса
конденсатора С, ток в
значения? Определить
Е. Задачи на различные темы
3.52р . Определить ток в сопротивлении Ze (рис. 3.35), если
Zx —6 Ом; Z2 =—/20 Ом; Z3 = Z4 = Z5=12 Ом; 2в = /2,5Ом;
£=104е“/30° В. Задачу рекомендуется решать методом эквива-
лентного генератора.
3.53р . Для измерения параметров конденсаторов применяют
мостовую уравновешенную схему (рис. 3.36). Вывести условия
равновесия схемы (отсутствие тока в ветви прибора) и найти ем-
кость конденсатора CY, тангенс угла потерь tg 6, если [ = 1000 Гн;
С4 = 0,1 мкФ; £2 = 160 Ом; £3 = 3200 Ом; £4 = 40 Ом.
32
т .
Рис. 3.35
Рис. 3.3G
3.54. Измерение параметров катушки Rx и Lx можно произ-
вести с помощью мостовой схемы рис. 3.37 (мост Андерсона).
Вывести уравнения равновесия моста и записать выражения для
Рис. 3.37
Указание. Рекомендуется преобразовать треугольник сопротивлений
doc в звезду.
3.55. Определить ток /Е в схеме рис. 3.38, если </ —12,66^ 8°30' А;
= 8 Ом; Хс —4 Ом; Йх = 8 Ом; £?2 = 4 Ом; А?3 = 2Д Ом.
Рис. 3.39
Рис. ЗЛО
3.56. Часть схемы рис. 3.39, <з, обведенную пунктиром и пред-
ставляющую собой активный двухполюсник, заменили эквива-
33
лентным генератором, изображенным на рис. 3.39,6. Найти Z2,
£ и токи в ветвях исходной схемы, если J — 8,4е/7°" A; ZB =
= 13,6е-'28°20' Ом; Zi-бе/300 Ом; Z3=10e'37° Ом; Z4 = 3 Ом;
Z6 = 4e/9°° Ом.
3.57, Рассчитать токи в ветвях схемы рис. 3.40, если =
= ЗОм;Х£=4Ом; R2—5 Ом; Хс = 5 Ом; /?3=ЮОм; Ё =
= 120е/30° В; j = 30,6e-/93° А.
3.58. Определить напряжение на зажимах источника тока в
цепи рис. 3.41, если XC — XL = R.
Рис. 3.41 Рис. 3.42 Рис. 3.43
3.59. Построить дуальную цепь по отношению к планарной
(рис. 3.42), у которой £, = 100 В; /?=10 Ом; £ = 31,8 мГн;
С = 636 мкФ; [ = 50 Гц; £2 = /50 В. Рассчитать параметры ду-
альной цепи, приняв /?/£э = £/С9 = £9/С= 1, и убедиться, что за-
кон изменения контурных токов в исходной схеме и узловых
потенциалов в дуальной одинаков.
3.60. Построить дуальную цепь по отношению к цепи, при-
веденной на ряс. 3.43.
Глава четвертая
Четырехполюсники и круговые диаграммы
А. Определение параметров пассивных
и активных четырехполюсников
4.1. Записать уравнения четырехполюсника через Л-, Z-, Y-,
Н-, G-, В-параметры *.
4.2р. Определить A-параметры четырехполюсника, схема ко-
торого приведена на рис. 4.2: а) используя законы Кирхгофа;
б) при режимах холостого хода и короткого замыкания.
* Все задачи в этой главе и их решения предусматривают выбор положи-
тельных направлений токов и напряжений в соответствии с рис. 4.1, а для
A-параметров, с рис. 4.1,6 для Е-, Z-, G-параметров и с рис. 4.1. для
5-параметров.
34
4.3. Рассчитать Z-, Y~, Н-, G- и В-параметры для четырех-
полюсника предыдущей задачи.
4.4. Определить Л-, Z-, //-параметры четырехполюсников, схемы
которых показаны на рис. 4.3,о,б.
Рис. 4.1
4.5р. На рис. 4.4 приведена диаграмма напряжений/710 —t lx;
С/30 = С/2х и тока Ло = Лх симметричного четырехполюсника, рабо-
тающего в режиме холостого хода. Найти Л-параметры четырех-
полюсника, если известно, что по модулю U1Jt = 100 В; L/ax = 200 В;
/1Х = 2,5 А.
4.6р. Рассчитать Z-параметры симметричного четырехполюс-
что в режиме холостого хода при включении
ника, если известно,
четырехполюсника по схеме рис. 4.5, а показания вольтметра и
амперметра на входе = 70,7 В; = 5 А; вольтметра на выходе
(Л =56 В. Показания ватт-
метров: Pt = 250 Вт; Р2 —
= 120 Вт. Определение знака
аргумента произвести по ос-
циллограмме рис. 4.5,6.
4.7. Определить А-пара-
метры трансформатора на
рис. 4,6.
4.8. Рассчитать Z-парамет-
ры трансформатора в задаче
4.7; если 7?! = 10 Ом; =
=60 Ом; /?2 = 8 Ом; А3 =
-40 Ом; ХЛ1 = 30 Ом.
4.9. Рассчитать У-пара-
метры четырехполюсника на
Рис. 4.7. Сопротивления в
омах указаны на схеме.
4.10. Выразить Z-, У-, //-, В-параметры через Л-параметры.
4.11. Выразить Л-, Z-, //-параметры четырехполюсника через
35
сопротивления прямого, обратного холостого хода и короткого
замыкания.
4.12. При питании четырехполюсника со стороны первичных
зажимов были измерены Ult /п в двух режимах: а) в режиме
холостого хода t/lx=100 В; /1Х = 1 А; Р1х = 0; б) в режиме ко-
роткого замыкания Я1К = 100 В; /1К = 1,41 А; Р1Х = 100 Вт. В обоих
случаях характер сопротивлений емкостный. При питании со сто-
роны вторичных зажимов при закороченных первичных UiK = 100 В,
/^ = 1 А; РЛ=100Вт. Известно, что Z^/Z^ = Z1X/Z2X. Рассчи-
тать сопротивления прямого, обратного холостого хода и корот-
кого замыкания. Определить по ним Л-, Z-, Я-параметры четырех-
полюсника. Найти характеристические сопротивления Zcl и Zc2.
Рис. 4.8
Рис. 4.6
Рис. 4.7
4-13. Для симметричного четырехполюсника рис. 4.8 определить
сопротивления холостого хода и короткого замыкания; А- и
Z-параметры четырехполюсника; характеристическое сопротивле-
ние Zf; постоянную передачи £ = д+ jbt если четырехполюсник
нагружен на характеристическое сопротивление.
4.14. Вычислить A-параметры симметричного четырехполюс-
ника, нагруженного на согласованную нагрузку ZH = Zc = 500 Ом,
с помощью которого осуществляется задержка синусоидального
сигнала на четверть периода без его ослабления.
Б. Т- и П-схемы замещения четырехполюсника
4.15. Выразить сопротивления Zlt Z2, Z3 Т-схемы замещения
(см. рис. 4.3, а) и сопротивления Z4, Z5, Z6 П-схемы замещения
четырехполюсника (см. рис. 4.3,6) через Л-параметры.
4.16. Рассчитать сопротивления Т- и П-схем замещения четы-
рехполюсника по Л-параметрам, найденным в задаче 4.5р.
4.17. Заменить четырехполюсник, приведенный на рис. 4.7,
П-схемой замещения.
4.18. Выразить сопротивления Т- и П-схем замещения четырех-
полюсника через Z-параметры.
4.19. Рассчитать сопротивления Т-схемы замещения трансфор-
матора задачи 4.8 по его Z-параметрам.
4.20. Для некоторого симметричного четырехполюсника из-
36
вестны уравнения, записанные в Я-форме:
2<7f; 1
lt = -21\-j0,05Ut. I
Определить сопротивление Т-схемы замещения.
4.21. Для ослабления сигнала в нагрузке между нагрузкой
и источником питания включен симметричный четырехполюсник
(аттенюатор). Вычислить параметры Т-схемы замещения, если он
нагружен на согласованное сопротивление ZU = ZC = 200 Ом, а сиг-
нал нужно ослабить на 0,5 Н (4.34 дБ) без задержки во времени.
В. Схемы соединений четырехполюсников
4.22р . Схему рис. 4.7 можно рассматривать как каскадное
включение двух четырехполюсников, собранных по Т-схеме. Опре-
делить A-параметры эквивалентного четырехполюсника по А-пара-
метрам каждого из них. Сопротивления элементов в омах даны
на рисунке.
Рис. 4.9
4.23. Рассчитать A-параметры результирующего четырехполюс-
ника, которым можно заменить каскадно включенные четырехпо-
люсники по схемам рис. 4.9, а, б, если каждое сопротивление
равно 10 Ом.
Рнс. 4.10
4.24. При параллельном, параллельно-последовательном и по-
следовательно-параллельном соединениях нескольких четырех-
полюсников должно выполняться условие регулярности—токи,
проходящие через оба первичных (а также оба вторичных)
зажима, соотвегсгвенно равны по значению и противоположны по
направлению. Определить, какие из приведенных на рис. 4.10, а—в
четырехполюсников удовлетворяют этому условию.
37
4.25. Два четырехполюсника, каждый из которых соединен
по схеме рис. 4.7, включены параллельно (рис. 4.11). Полагая
известными У-параметры каждого из них, определить У-параметры
эквивалентного четырехполюсника.
Рис. 4.11
Рис. 4.12
4.26. Два четырехполюсника соединены последовательно пз
схеме рис. 4.12, и им соответствуют уравнения
р;1_Г— /loo —/юс 1Г/Л
lid ~ |—ЛОО (100—/100)] |_/а '
Рассчитать Z-параметры эквивалентного четырехполюсника.
4.27. Какую форму записи
уравнений удобнее применить
для отыскания параметров экви-
валентного четырехполюсника,
которым можно заменить два
последовательно-параллельно
соединенных четырехполюсника
по схеме рис. 4.13? Найти соот-
ношения между параметрами
этих четырехполюсников.
Г. Четырехполюсник как согласующее звено
между источником энергии и нагрузкой
4.28р. Источник ЭДС Е —100 В с внутренним сопротивле-
нием 7?в=1 Ом нагружен на резистор сопротивлением RK = 9 Ом.
Чтобы мощность в нагрузке была максимальной, между источни-
ком и нагрузкой включено согласующее звено—симметричный
четырехполюсник.
1, Определить /1-параметры этого четырехполюсника 2. По
полученным значениям Д-параметров рассчитать сопротивления
Т-схемы замещения. 3. Найти мощность, выделяющуюся в на-
грузке, в двух случаях: а) согласующий четырехполюсник отсут-
ствует; б) при наличии согласующего четырехполюсника.
4.29. Какие сопротивления Т-схемы четырехполюсника нужно
взять для согласования сопротивления нагрузки 7Я =? 27 + /6 Ом
38
с внутренним сопротивлением источника ZB = 3+j Ом, чтобы
мощность в нагрузке была максимальной?
Указание. Реактивные составляющие сопротивлений источника и на-
грузки следует рассматривать как части продольных сопротивлений Т-схемы
четырехполюсника.
4.30. Между активной нагрузкой и источником энергии
с внутренним сопротивлением /?в = 2 Ом включен трансформатор,
параметры и сопротивления схемы замещения которого известны
из задачи 4.19. Какие дополнительные сопротивления необходимо
включить в продольные плечи Т-схемы замещения трансформатора,
чтобы мощность в нагрузке была максимальной? Определить RH.
4.31р . Рассчитать комплексное сопротивление нагрузки из
условия выделения в ней максимальной мощности. Внутреннее
сопротивление источника энергии Zu — 1 -г- / Ом. Мещлу нагрузкой
и источником включен идеальный трансформатор
коэффициент связи k — 1) с коэффициентом трансформации п =
= u,lyto2 = l/5, где —число витков первичной и вторичной
обмоток.
4.32. Внутреннее сопротивление генератора ZB = 2~/ Ом, со-
противление нагрузки Z„ = 72-|-/10 Ом. Определить коэффициент
трансформации идеального трансформатора, включенного между
генератором и нагрузкой, а также дополнительное сопротивле-
ние ZflOn, включенное последовательно с нагрузкой, при выделе-
нии в нагрузке максимальной мощности.
Д. Невзаимные и активные четырехполюсники
4.33р. Для активного четырехполюсника (рис. 4.14) найти
Л-параметры, токи /1К, /2к и записать расчетные уравнения для
определения £, и Л, если £. = 100 В; £, = 50 В; £, = /50 В;
Z1 = Z3=10 Ом; Z5 = /10 Ом.
[ управляемых источников: на
управляемый током (ИНУТ);
4.34 . На рис. 4.15 приведены схемы
рис. 4.15,о—источник напряжения, ;
на рис. 4.15, б — источник тока, уп-
равляемый напряжением (ИТУН);
на рис. 4.15,в—источник тока,
управляемый током (ИТУТ); на
рис. 4.15,г—источник напряже-
ния, управляемый напряжением
(ИНУН). Записать уравнения этих
четырехполюсников в матричной
форме.
4.35 р. 1. Записать У-, Z-,
Л-матрицы идеального гиратора,
если проводимость гиратора G. 2. Определить входное сопротив-
ление гиратора, если он нагружен на сопротивление ZH- 1 /(/<оС).
4.36 . Два каскадно включенных идеальных i иратора с прово-
димостями, равными @1 и Gzt нагружены на сопротивление ZH
39
(рис. 4.16). Какую проводимость GL надо выбрать, чтобы входное
сопротивление всей схемы было в 4 раза больше сопротивления
нагрузки, если G2 = 4?
4.37 р. Показать, что четырехполюсник, состоящий из двух
каскадно включенных идеальных гираторов при ZH= оо с прово-
димостями, равными Gt = 1, С.2 — п (рис. 4.16), эквивалентен идеаль-
ному трансформатору, подчиняющемуся уравнениям Ut~nU^
— где п—коэффициент трансформации.
4.38 р. Реализовать гиратор с помощью управляемых источни-
ков ИН УТ и ИТУН.
4.39 р. Связь между малыми приращениями входных и выход-
ных величин электронной лампы (рис. 4.17) задана уравнением
&ia = ДUagf -г Составить схему замещения лампы с помощью
управляемых источников. Сеточным током пренебречь.
Рис. 4.16
Рис. 4.13
4.40 р. Связь между малыми приращениями входных и выход-
ных величин транзистора, включенного по схеме с общей базой
(рис. 4.18), выражается линейными уравнениями, записанными
с помощью Z-параметров:
Д/Zi — ЯцДГгЧ- Я12Л12; (1)
Дм2 = -Ь Я22Д/2. (2)
Составить Т-схему замещения транзистора с управляемыми
источниками и определить сопротивления схемы замещения.
Е. Круговые диаграммы
4.41 р. При постоянных значениях частоты и приложенного
к схеме рис. 4.19 напряжения сопротивление резистора нагрузки
40
меняется от 0 до оо. При этом = 100 В; Х1=10 Ом; =
= 10 Ом.
1. Показать, что для тока в нагрузке /и, тока на входе цепи /\ и
напряжения на катушке UL могут быть построены круговые
п
Рис. 4.19
диаграммы. 2. Рассчитать данные для построения круговых диа-
грамм и Ut. 3. По круговой диаграмме тока /, определить
cos<p, Р, Q при /?н=10 Ом.
4.42р . Схема рис. 4.20 позволяет при постоянном выходном
напряжении Umn менять его фазу от 0 до л. Показать это, если
= — — а модуль Хс меняется от 0 до оо.
Рис. 4.22
Рис. 4.21
4.43. Схема рис. 4.21 питается от источника синусоидального
тока J=20e'4b° A; Z^IO Ом; Z2 = /10 Ом. Построить геометри-
ческое место концов вектора тока /2 при: а) = б) Z„ — /?.
4.44. Построить геометрическое место концов вектора напря-
жения Um„ в схеме рис. 4.22 и определить наибольшее значение
этого напряжения, если известно, что схема питается от источ-
Рис. 4.23
Рис. 4.24
ника э.д.с., Z = 54-/8,65 Ом, а в режиме резонанса напряжение
<Л,„=173 В.
41
4.45. В режиме короткого замыкания (Хс-0) токи в вет-
вях схемы рис. 4.23 по модулю равны; / = 31,5 А; /Х=Ю А;
/2 = 23,5 А. Построить геометрическое место концов вектора тока.
Рассчитать емкость в резонансных режимах, если схема питается
от источника ЭДС ut = 200 sin 31402 В.
4.46. Построить геометрическое место концов вектора тока /х
и напряжения Uab в схеме рис. 4.24 при изменении сопротивле-
ния нагрузки от 0 до оо, если схема питается от источника тока
j=10 А и источников ЭДС £, = 100 В, £„ = /100 В одинаковой
частоты. При этом Zt = Z2 = 5 Ом; Z3 = 10 Ом; Z4 = /10 Ом.
Глава пятая
Электрические фильтры
А. Общая методика анализа фильтрующих свойств
реактивного четырехполюсника
5.1р. Четырехполюсник, изображенный на рис. 5.1, в теории
фильтров называют полузвеном или “| -звеном. Считая Zt и Z2
идеальными реактивными сопротивлениями и пользуясь соотноше-
нием ch g = ch (а + jb) = l^AD, показать, что в полосе прозрач-
ности (а = 0) должно выполняться соотно-
_________________Л „ шение
-1 I1 < о, (5.1)
I lz
U 2 т. е. Zt и Z2 различны по знаку, причем
_________| IZJCIZJ.
/0 1 °/ 5.2р. Пользуясь условием (5.1), опре-
Рис. 5.! делить, к какому типу фильтров по поло-
се прозрачности относятся полузвенья,
изображенные на рис. 5.2, а—е. Выразить граничные частоты через
£н С.
42
5.3. Симметричным четырехполюсник, собранный по Т- или
П-схеме, можно рассматривать в виде каскадного согласованного
соединения двух одинаковых полузвеньев (рис. 5.3, а, б). Полоса
прозрачности такого четырехполюсника
совпадает с полосой прозрачности одного
полузвена.
С учетом решения задачи 5.2р опре-
делить, к какому типу фильтров по по-
лосе прозрачности относятся симметричные
четырехполюсники, изображенные на рис.
5.4, а—г, 5.5,о—г.
5.4. Для четырехполюсника рис. 5.6 °" ! [ZZbo-СП-^т—о
заданы: Г1 = 4-10"3 Гн; £, = 0,410“® Ф; JL Л А 1
L„ = 210-s Гн; С2 = 0,2-10-* Ф.
Найти граничные частоты полосы проз- 0 Т 0 I
рачности. Как они изменятся, если Lif г,
и L2, Cs поменять местами? Рекомен- '
дуется воспользоваться решением задачи Рис- 5-3
5.2р.
5.5. Показать, что характеристические сопротивления полу-
звена (см. рис. 5.1) в области прозрачности имеют активный ха-
рактер. Воспользоваться соотношениями
(5.1а)
где Zlx—входное сопротивление четырехполюсника со стороны
зажимов 1 — Г при разомкнутых зажимах 2—2'\ ZlK — входное
Рис. 5.4
сопротивление со стороны 1 — Г при замкнутых накоротко 2—2*;
22к—сопротивления, аналогичные Zlx и Z1K, но относительно
зажимов 2—2'.
Показать, что в полосе затухания: 1) характеры ZfI=ZT и
продольного сопротивления Z, одинаковы; 2) характеры Zc2 — Zn
и поперечного сопротивления Z2 одинаковы.
43
5.6р . Пользуясь выражением chg = K^D и условием (5.1),
показать, что для реактивного полузвена (см. рис. 5.1) справед-
ливы следующие соотношения:
Рис. 5.6 Рис. 5.7
В
(5.2)
в
полосе прозрачности
я —0; 'I
b = zharcsinKj^i/^2 h J
полосе затухания
а = arch j/| Zx/Z21 (при различных знаках Zt и Z2); , Q.
b =±90° J
a — arch Иj Zt/Z2 | (при одинаковых знаках Zt и Z2). 1
b=0 I (&’4)
5.7р . Для четырехполюсника, изображенного на рис. 5.7, по-
строить зависимости а(<о), d(w), Ztf(w). Параметры элементов:
А^бЮ’8 Гн; Ла=15-10-8 Гн; Cx-U,5-10-e Ф.
Б. Фильтры типа k
5.8. Полузвено (см. рис. 5.1) принадлежит к типу kt если
при чисто реактивных сопротивлениях Zx и Zt выполняется со-
44
отношение
ZxZa = k*=const, (5.5)
где величина, не зависящая от частоты.
Симметричные Т- и П-фильтры принадлежат к типу kt если
они составлены из согласованно включенных полузвеньев типа k
(см. рис. 5.3). Значение k в этом случае совпадает со значением k
составляющего полузвена.
Определить, какие из фильтров, изображенных на рис. 5.2,
5.4, 5.5, 5.6, относятся к типу k. Для каждого фильтра типа k
выразить k через параметры элементов.
5.9. Показать, что для полузвена (см. рис. 5.1) типа k в по-
лосе прозрачности, согласно (5.1),
fZJ<fe; (5.6) |Zs|>fe. (5.7)
5.10. Показать, что для полузвена (см. рис. 5.1) типа k:
a) ZTZn = fe2; (5.8)
б) в полосе прозрачности ZrmiX=k't Znmin = k,
где Zjmax—наибольшее значение характеристического сопротив-
ления Zrt = Zy". Znmin—наименьшее значение характеристического
сопротивления ZeS = Zn-
5.11р . Получить зависимости с (о), &(w), ZT(o), 2п(со) для
полузвеньев, изображенных на рнс. 5.2, б, в; построить графики
этих зависимостей. Принять £ = 510“3 Гн*. С = 0,5-10“в Ф.
5.12. Пользуясь результатами, полученными при решении за-
дачи 5. Пр, построить графики а (со), b (со), Zc(£o) для симметрич-
ных фильтров, изображенных на рис. 5.4, в, г и рис. 5.5, с, б.
Принять £ = 5-10“3 Гн; С-0,5-10е Ф. Построить графики
зависимостей от частоты коэффициента передачи напряжения при
v *41
согласованной нагрузке Ау-тр
Ui IZn=Zp
5.13. Для ФНЧ типа Л, содержащего три каскадно включенных
П-звена, при согласованной нагрузке на частоте со ==2,2-104 рад/с
известно отношение напряжении на входе и выходе */2/*/1 = 0,1.
Определить частоту среза фильтра.
5.14. Сколько Т- илн П-образных звеньев должен содержать
ФНЧ типа k, чтобы на частоте ю = К2ос затухание а >5 Нп?
5.15. ФВЧ собран из двух Т-звеньев типа k, имеет частоту
среза юс=1.104 рад/с. Чему равно затухание фильтра на час-
тоте 0 = 0,5-10* рад/с?
5.16. Показать, что четырехполюсник, изображенный на рис. 5.8,
является фильтром типа k при выполнении соотношения LyCj =
£2С*. Пользуясь условием (5.6), вырази гь граничные частоты
и ширину полосы прозрачности через параметры £t, Ct, £<>, С2.
Определить Zj и Zn на частоте w0 = 1LtCt =- 1
5.17. Из двух полузвеньев (рис. 5.8) собран Т-фильтр. Полоса
прозрачности ограничена частотами ол==Ь 10* рад/с; (оа = 1,25х
45
X 10* рад/'с. Характеристическое сопротивление фильтра на час-
тоте ZT(«o) = 50 Ом. Пользуясь результатами решения
задачи 5.16, рассчитать параметры элементов фильтра.
Рис. 5.8
Рис. 5.9
5.18 . Для полузвена, изображенного на рис. 5.9, при £,£, =
= Л2С2 выразить граничные частоты полосы прозрачности через
параметры элементов. Найти Zt н Zn на граничных частотах и
Рис. 5Л0
при оэ = 0, w = oo; определить
характер Zt и Zn в полосе
затухания.
5.19 . Из двух полузвень-
ев предыдущей задачи (рис.
5.9) собран симметричный
фильтр. Его граничные часто-
ты «1=1-104 рад/с; <о2 =
= 1,25-104 рад/с. Наименьшее
значение характеристическо-
го сопротивления в полосе
прозрачности Zfmin = 50 Ом.
Определить схему фильтра,
значения £it Clf />2, С2, а
также коэффициенты затуха-
ния и фазы для следующих частот: 0,75 а), ; IJwf, 1 1 До/,
5.20 р. Два Т-фильтра типа k—ФНЧ и ФВЧ (рис. 5.10, с, б) —
нагружены на резистор нагрузки сопротивлением Z„ = £ = КZ,Z2.
Для каждого фильтра получить зависимость коэффициента пере-
дачи напряжения от относительной частоты ю/а>0
(соо= 1/И1С). Построить графики этих зависимостей, сравнить
их с аналогичными зависимостями в согласованном режиме.
В. Фильтры типа т
5.21 р. На рис. 5.11,а изображен четырехполюсник, представ-
ляющий собой каскадное соединение двух полузвеньев. Первое
полузвено из сопротивлений Zn Z2 является полу звеном типа Л.
Продольное сопротивление второго полузвена
Ziffl = 7nZj, (5-9)
где т < 1 —положительное число.
46
Сопротивление поперечной ветви второго полузвена
____7 1— /п2
2/Я—
(5.10)
т. е. поперечная ветвь представляет собой последовательное соеди-
нение двух сопротивлений z/^”1 , имеющего тот же характер,
что Zi и Zzfm и совпадающего по характеру с Z2.
Показать, что при выполнении (5.9), (5.10) /с-полузвено
(Zj, Z2) и m-полузвено (Zlfft, Z2m) (рис. 5.11, а) соединены со-
гласованно. Получить выражения для характеристических сопро-
тивлений четырехполюсника рис. 5.11, a Zn и Znm и отношения
Znm/Zn через Zlt Z2, m.
Показать, что полосы прозрачности полузвеньев одинаковы.
Примечание. Полузвено гг с параметрами, определяемыми по (5.9) и
(5.10), называют последовательно-производным, а соответствующее А-полузвено—
его прототипом.
5.22. Для fc-полузвена-прототипа (см. рис. 5.2, б), рассмотрен-
ного в задаче 5.11р, при L — 5-10’3 Гн; С = 0,5-10 ° Ф построить
схему последовательно-производного ги-полузвена (рис. 5.11, с)
и определить параметры ее элементов. Взять ш^-0,6.
Построить частотную зависимость характеристического сопро-
тивления m-полузвена Znm (со) (рис. 5.11, с) в полосе прозрачности;
совместить ее с зависимостью Zn(w) прототипа из задачи 5.11р
(см. рис. Р.5.8 и табл. Р.5.2). Провести сравнение построенных
зависимостей Znw(<j>) и Zn(co) с точки зрения их равномерности
в полосе прозрачности.
Расчет Znm(w) рекомендуется провести по выражению (2) (см.
решение задачи 5.21 р) с учетом того, что в рассматриваемом слу-
чае Z1/Z2 =—l/(io2£C) = — (ct>0/ci))2. где о0—частота среза прото-
типа, а следовательно, и m—полузвена.
5.23. В условиях предыдущей задачи построить зависимость
^пгДсо) в полосе прозрачности при пг = 0,4; 0,8. Сравнить их
с зависимостью Znm(w) при т —0,6 (рис. 0.5.2, б). Какое из
рассмотренных значений m наиболее целесообразно для обеспече-
ния меньшей зависимости характеристического сопротивления Znm
от частоты со в полосе прозрачности?
47
5.24р . На рис. 5.11,6 изображено каскадное соединение Za)
и m(Z1m, 22ст)-полузвеньев. Сопротивления /n-полузвена связаны
с сопротивлениями Л-полузвена следующими соотношениями:
Z2ffl = Z2/m; (5.11)
-----Ц------- (5.12)
т
“i---5* “2
1 —тг
где т < 1 —положительное число, т. е. продольная ветвь т-полу-
звена представляет собой параллельное соединение двух сопро-
тивлений mZx и Zg> причем /nZx имеет тот же характер,
что и Zx; совпадает по характеру с Z2.
Примечание. Полузвено т- с параметрами, определяемыми (5.11) и
(5.12), называют параллельно-производным.
Показать, что полузвенья рис. 5.11,6 при выполнении (5.11)
и (5.12) соединены согласованно. Выразить через Zlt Z2, т ха-
рактеристические сопротивления четырехполюсника рис. 5.11,6
Zfm и ZT, а также отношение ZTm/ZT. Показать, что полосы
прозрачности полузвеньев одинаковы.
5.25. Для &-полузвена-прототипа рис. 5.2,6 (ФВЧ), рассчи-
танного в 5.11р, построить схему параллельно-производного
ги-полузвена (рис. 5.11,6) при /п = 0,6.
Построить график зависимости характеристического сопротив-
ления /n-полузвена от частоты Zt„(co) в полосе прозрачности;
совместить его с графиком Zt(co) для прототипа (см. рис. Р.5.8
или табл. Р.5.2). Сравнить ZTm(co) и ZT (со) с точки зрения мень-
шей зависимости от частоты.
5.26р . Получить зависимости от частоты (графические! коэф-
фициентов затухания ат (со) и фазы Ьт (со) для /п-полузвеньев
задач 5.22 и 5.25 (схемы и параметры элементов полузвеньев
приводятся в ответах к задачам 5.22 и 5.25).
5.27. Симметричный фильтр содержит включенные согласованно
два fe-полузвена и два последовательно-производных ги-полузвена,
рассмотренных в задаче 5.22 (схема прототипа дана на рис. 5.2,6,
схема т-полузвена—на рис. О.5.2,с).
Изобразить схему фильтра, получить для него зависимость
п (со), воспользовавшись известными зависимостями fl* (со) и ст(со)
для составляющих полу звеньев, где с*—коэффициент затухания
Л-полузвена [с*(со), см. рис. Р.5.7 или табл. Р.5.2); ат—коэф-
фициент затухания /п-полузвена [ал (со), см. рис. Р.5.13 или
табл. Р.5.4].
5.28. Изобразить схему симметричного фильтра, составленного
из согласованно включенных двух параллельно-производных
т-полу звеньев задачи 5.25 (схема т-полузвена дана на рис. 0.5.4,а)
и двух Л-полузвеньев-прототипов.
48
5.29. Найти параметры последовательно-производного полу-
звена типа т при т — 0,6 для fc-прототипа рис. 5.2,в (рассмотрен
в задаче 5.Пр).
5.30. Определить схему и параметры последовательно-произ-
водного и параллельно-производного тп-полузвеньев для прототипа
рис. 5.2,г. Для каждого случая построить симметричный фильтр,
содержащий согласованно включенные два 6-полузвена и два
щ-полузвена.
Г. Пассивные /?С-фильтры
5.31р . Для четырехполюсников, изображенных на рис. 5.12,
а—з, получить выражения: а) передаточной функции Н (р) —
= ^2(р)'^А (Р) при разомкнутых зажимах 2—2'; б) передаточной
Рис. 5.12
функции У12(р) ~ /2 (p)/Ui (р) при коротком замыкании зажимов
2—2' (операторной взаимной проводимости)*; в) зависимости от
частоты модуля комплексного коэффициента передачи напряжения
Н (со) = | | при холостом ходе зажимов 2—2'.
Построить графики зависимостей Н (х), где х = ы/?С—относи-
тельная частота; при этом для схем рис. 5.]2,в—ж принять
= R2 — R; С, = С2 = С. Для каждого четырехполюсника выра-
зить через R, С граничные частоты полосы пропускания, приняв,
что на граничной частоте согр Щсогр)//7тах = 1/1Л2 л; 0,707. где
Нта*—наибольшее значение Н в полосе пропускания. К какому
* Положительное направление для 1г(р)— в зажим 2, как это принято
при записи Е-формы уравнений четырехполюсника.
49
типу фильтра по полосе пропускания относится каждый из рас-
смотренных четырехполюсников?
5.32. Однозвенный ФНЧ (рис. 5.12,с) нагружен на резистор
/?н. Получить выражение амплитудно-частотной характеристики
Н (о) — \йг/йt\. Как зависит частота среза фильтра от величины
/?„//? (относительного сопротивления нагрузки)? Сравнить частоты
среза при RH = R и 7?я = оо.
5.33. Для однозвенного ФВЧ (рис. 5.12,6) известны /?—10 кОм;
С — 0,1 • 10"® Ф. Сопротивление нагрузки фильтра может изменяться
в пределах: Rn = оо 4- 20 кОм. Как при этом изменяется ширина
полосы задерживания фильтра?
5.34р . Полосовой фильтр, изображенный на рис. 5.13, является
частным случаем фильтра рис. 5.12,д, рассмотренного в задаче
5.31 р: сопротивления элементов низкочастотного звена в т раз
больше сопротивлений элементов высокочастотного звена (т—пЪ-
ложительное число); частоты квазирезонанса обоих звеньев оди-
наковы и равны ю0 = 1/(/?С).
Оценить влияние параметра tn на избирательные свойства
фильтра: ширину полосы пропускания и эквивалентную доброт-
ность. Построить графики Н (<о) = | U2 г (/©) | при т=0,5; 2; 10.
Рис. 5.13
Рис. 5.14
5.35. Пользуясь данными табл. Р.5.5 (схема е), оценить влия-
ние параметра т (положительное число) на избирательные свой-
ства полосно-пропускающего фильтра, изображенного на рис. 5.14:
эквивалентную добротность и ширину полосы пропускания.
5.36. Передаточная функция полосно-заграждающего фильтра,
собранного по схеме рйс. 5.12,ж, при определенном выборе па-
раметров элементов обладает важным свойством: корни много-
члена числителя (нули передаточной функции) являются ком-
плексно-сопряженными. Благодаря этому свойству данная схема
широко используется при построении активных фильтров с пере-
даточными функциями, обладающими комплексно-сопряженными
полюсами (признак высокой степени избирательности фильтра).
Пользуясь данными табл, Р.5.5 (схема »с), для фильтра, пред-
ставленного на рис. 5.15, получить условие, которому должен
удовлетворять параметр т (пг — положительное число), чтобы
нули передаточной функции фильтра Н (р) = U2 (p)/Uj (р) были
комплексно-сопряженными.
Построить и сравнить графики АЧХ фильтра Я («/(%) при
tn —2: 1/2; 1/9; 1/16. Как зависит от значения tn минимальный
уровень АЧХ Hmin — Н (ы0), а также частота квазпрезонанса w0?
Можно ли, изменяя параметр mt снизить до нуля уровень Hmia?
50
5.37, Исследования схемы полосно-заграждающего фильтра
(рис. 5.15) показывают, что изменением параметра т нельзя сни-
зить до нуля минимальный уровень АЧХ фильтра в полосе за-
держивания (см. ответ к задаче 5.36.)
Эта задача может быть решена путем
включения указанного фильтра в мостовую
схему (рис. 5.16), причем параметры резис-
тивного делителя напряжения удовлетворя-
ют УСЛОВИЮ min- Для Рис-
5.16 A/mill = 2/3 (см. ответ задачи 5.36).
Рис. 5.15
Получить выражение передаточной функ-
ции //„ (р) = (p)/UB* (р) заданного мостового фильтра и
построить соответствующую АЧХ Н„(х), где x = g>RC.
5.38. Полосно-пропускающий фильтр рис. 5.12,е является
составной частью мостового полосно-заграждающего фильтра,
Рис. 5.16
представленного на рис. 5.17. Пользуясь данными табл. Р.5.5
(схема е), получить выражение для передаточной функции мосто-
вого фильтра /7И (р) = 6'вых (p)/U6x (р) и построить график соот-
ветствующей АЧХ.
Д. Активные /?С-фильтры
5.39. Составной частью большого класса активных фильтров
являются усилитель с большим коэффициентом усиления р, (р,=
= 1034-Юь) и RC-четырехполюсник в цепи отрицательной обрат-
ной связи (рис. 5.18,с). Показать, что если усилитель инверти-
рует сигнал (С/вых = — р/7,), то передаточная функция системы
рис. 5.18,а К (р) = (7вых(р)/С/вх(р) связана с передаточной функ-
цией RC-четырехполюсника цепи обратной связи И (р) = (P)/U< (Р)
соотношением
К(р) = -1/Н(р). (5.13)
Считать коэффициент усиления усилителя р,—► ос, входное
сопротивление усилителя (относительно зажимов 1 — Г) RBX — оо,
выходное сопротивление (относительно зажимов 2—2') RBbIX = 0.
Примечание. Из (5.13) следует, что рассматриваемая система позволяет
менять местами нули и полюсы передаточной функции. Это свойство исполь-
зуется при построении активных RC-фильтров.
51
5.40. Известно, что избирательные свойства четырехполюсника
выше, если его передаточная функция обладает комплексно-сопря-
женными полюсами, причем чем ближе полюсы к мнимой оси,
тем избирательность выше. Передаточные функции пассивных
обладают, однако некоторые из
RC-четырехполюсииков при оп-
ределенном выборе параметров
могут иметь передаточные функ-
ции с комплексно-сопряженны-
ми или даже мнимыми нулями
(см. задачи 5.36 — 5.38). При
включении таких четырехполюс-
ников в цепь обратной связи
усилителя по схеме рис. 5.18,а,
согласно (5.13), результирующая
передаточная функция обладает
комплексно-сопряженными или
мнимыми полюсами.
В цепи обратной связи уси-
лителя с коэффициентом усиле-
ния 1 включен полосно-
заграждающий /?С-фильтр (/? =
= 100/2кОм; С=1010-’ Ф)
(рис. 5.18,6). При условии, что
усилитель инвертирует сигнал, а
его параметры RBX->oo, Япых=
= 0, получить выражение пере-
даточной функции и построить
график АЧХ фильтра /С(о) = 1•
Рекомендуется воспользоваться данными табл. Р.5.5 (схема ж).
5.41р. Полосно-пропускающий активный фильтр задачи 5.40
обладает невысокой избирательностью, о чем свидетельствует гра-
фик АЧХ, приведенный на рис. 0.5.8. Это объясняется небольшой
разницей в значении коэффициента обратной связи Н (со) [Н (со) —
модуль комплексного коэффициента передачи /?С-четырехполюсника
цепи обратной связи] в пределах полосы пропускания и вне ее.
В полюсно-нулевом представлении низкая избирательность объ-
ясняется значительной удаленностью полюсов К (р) или нулей
Н (р) от мнимой оси.
Избирательность на квази резонансной частоте можно теоре-
тически неограниченно увеличить за счет частичной компенсации
отрицательной обратной связи положительной обратной связью.
Схема, реализующая такую компенсацию, представлена на рис. 5.19
(предполагается, что усилитель инвертирует сигнал). Напряжение
положительной обратной связи снимается с резистивного делителя
напряжения Ru R,: где у = R!/(R1+R,'i —
коэффициент положительной обратной связи.
52
Построить АЧХ активного фильтра К (w) — ] UBWJUK*J при
Y = 0,4; 0.5. Параметры RC-четырехполюсника те же, что и в
задаче 5.40.
5.42р. На входе активного фильтра задачи 5.40 каскадно
включен двухзвенный ФНЧ (рис. 5.20), выделенный на схеме как
четырехполюсник А в отличие от RC-четырехполюсника цепи об-
ратной связи, обозначен-
ного Б; Ra = R б =
= 100)^2 кОм; СЛ*=СБ=
= 5-10~* Ф.
Получить выражение
для передаточной функции
всего устройства К (р) =
=UbhApWbAp}> пост-
роить его АЧХ К (<о) и
сравнить ее с АЧХ вход-
ного ФНЧ Нл(со).
5.43. При построении
активных фильтров на опе-
рационных усилителях
(ОУ) обратная связь ча-
ще осуществляется пу-
тем включения пассив-
ного RC-четырехполюс-
ника параллельно уси-
лителю (на рис. 5.21
четырехполюсник Б).
Считая коэффициент
усиления ОУ ц- > сю
(действительное значе-
ние 100 000, входное
сопротивление RBX —► оо,
Ряс. 5.21
выходное сопротивление « 0), по-
казать, что комплексный коэффициент передали активного фильтра,
построенного по рис. 5.21,
A (jw)— ^вых/^вх—
(5.14)
53
где КЙЛ, yi2fi—комплексные взаимные проводимости четырех-
полюсников А и Б.
5.44р. В активном фильтре, построенном по схеме рис. 5.21,
в качестве четырехполюсников А и Б взяты четырехполюсники
задачи 5.42р (см. рис. 5.20). С учетом (5.14) получить выражение
Рис. 5.22
передаточной функции фильт-
ра и построить соответствую-
щую АЧХ.
5.45. По структурной схе-
ме рис. 5.21 построить ФВЧ
с передаточной функцией вида
А(р)= >+к°р\--
pJ-bawop4-(i)o
В цепи обратной связи (че-
тырехполюсник Б на рис.
5.21) включить четырехполюс-
ник по схеме рис. 5.12,эс
(табл. Р.5.5) с парамелрами — R<> = 100-К2 кОм; С^Со/2 —
= 2,5.10-® Ф.
Схему четырехполюсника А подобрать из приведенных в
табл. Р.5.5. Найти параметры ее элементов.
5.46. Рассчитать передаточную функцию активного фильтра,
U вых
5Вх ’
изображенного на рис. 5.22, построить его АЧХ А =
где <оо=1/(/?С). Определить
тип фильтра. Рекомендуется
воспользоваться данными
табл. Р.5.5 (схема з).
5.47р . На рис. 5.23,п изоб-
ражен активный фильтр на
ОУ с многоконтурной обрат-
ной связью. Параметры эле-
ментов: Rr = 10 кОм; А2 =
=256,5 Ом; С3 = С4 =
=5*10-6Ф; R5 = 400 кОм.
Па раметры ОУ: р —> со,
АЙХ—>оо (относительно за-
жимов а и 6), Авых ~ 0 (отно-
сительно зажимов с и d).
Получить выражение для
передаточной функции фильт-
ра К(р}= исых (p)lU№ (р),
построить соответствующую АЧХ, назвать тип фильтра, опреде-
лить ширину полосы пропускания.
Рекомендуется иметь в виду, что ОУ может быть представлен
эквивалентной схемой рис. 5.23,6, на которой зажимы ab ра-
зомкнуты, а между зажимами cd включены последовательно иде-
альный источник ЭДС ^ВЫХ и резистор /?вых.
54
5.48. Для фильтра с многоконтурной обратной связью (рис.
5.24) известны: = Рл = Ю/К2 кОм; R3 = 3,535 кОм; С2 =
= 0,8-10“® Ф; С6 = 0,2-10~® Ф. Параметры ОУ: р—> со; /?вх—► оо;
/?ЙЫ* ~ 0.
Определить тип фильтра, граничные частоты полосы пропу-
скания, построить его АЧХ /С(й)) =
tZBX (/«)
б'вых (/&)
5.49. Для активного фильтра, изображенного на рис. 5.25,
получить выражение передаточной функции Л (р) — UBbn (p)/UPK (р),
определить тип фильтра и граничные частоты полосы пропускания.
Параметры элементов: С1 = С3 = С4 = 0,5 мкФ; Я2 = 47,14 кОм;
/?ь = 212 кОм. Параметры ОУ: р^-оо; /?вх-+оо; ^*«0.
Глава шестая
Трехфазные цепи
А. Симметричная нагрузка и режимы,
возникающие при обрывах проводов
6.1. Ламповая нагрузка питается от сети, система линейных
напряжений которой симметрична (С7Я = 220 В). В каждую фазу
включено по одной лампе на номинальную мощность 50 Вт и
номинальное напряжение 220 В (рис. 6.1,с).
Определить фазные и линейные токи, напряжение на каждой
лампе и показания ваттметров и P2t если нагрузка соединена:
55
а) звездой, как показано на рисунке; б) звездой, обрыв фазы С
в точке М: в) треугольником. По найденным показаниям ватт-
метров найти мощность, потребляемую трехфазной нагрузкой в
каждом случае. Для всех случаев построить топографические
диаграммы и векторные диаграммы токов.
6.2. Симметричная нагрузка соединена треугольником и пита-
ется от сети, линейные напряжения которой симметричны и равны
220 В (рис. 6.1 ,б). Сопротивление каждой фазы нагрузки Z =
= 22е'3°с Ом. Определить фазные и линейные токи, напряжения
на каждой фазе и показания
ваттметров и при: а)
нормальной работе, как по-
казано на рисунке; б) обрыве
линейного провода в точке М;
в) обрыве фазного провода в
точке Л7.
По найденным показаниям
ваттметров рассчитать мощ-
ность, потребляемую нагруз-
кой во всех случаях. Пост-
роить топографические диаг-
раммы и векторные диаграм-
мы токов.
6.3. Фазное напряжение
трехфазного генератора про-
мышленной частоты —
= 120 В. Сопротивление каж-
дой фазы приемника = 12 + /16 Ом; сопротивления проводов
линии Z = 4+/2 Ом (рис. 6.2,а). Определить емкость С конден-
саторов каждой фазы, включенных на приемном конце линии
для увеличения coscp приемника до единицы. Найти фазное нап-
ряжение на зажимах приемника при отсутствии конденсато-
ров и напряжение при их наличии.
а)
Рис. 6-3
6.4. Фазное напряжение вторичных обмоток трансформатора,
соединенных треугольником, равно 220 В (рис. 6.2,6). Сопротив-
ление фазы нагрузки Zf = 30 + /60 Ом, сопротивление подводящих
проводов Z = 2+/4 Ом. Считая UАв~-220е'30° В, определить токи
в проводах линии, фазах трансформатора и нагрузки, напряже-
56
ння на фазах нагрузки при: а) нормальной работе; б) обрыве
фазы АВ трансформатора в точке М.
6.5р . Симметричная нагрузка питается от сети, система линей-
ных напряжений которой симметрична; С'л = 220 В. Показание
ваттметра (рис. 6.3,а) составляет 2520 Вт; показание амперметра
равно 20 А. Найти активную, реактивную и полную мощности
трехфазной нагрузки. Определить фазные сопротивления, считая,
что нагрузка соединена: а) звездой, б) треугольником.
6.6. Симметричный приемник электрической энергии соединен
звездой (рис. 6.3,6). Сопротивление фаз приемника Z —6-^-/8 Ом.
Система фазных напряжений нагрузки симметрична; 6^ = 100 В.
Рассчитать показания ваттметра при двух различных положе-
ниях переключателя. Воспользовавшись показаниями ваттметра,
определить активную, реактивную и полную мощности приемника.
6.7. Симметричный приемник соединен треугольником. Система
линейных напряжений симметрична; U3 — 220 В. Ваттметры, вклю-
ченные в цепь рис. 6.3,в, дают показания Рг = 3 кВт; Р2 = 0.
Определить комплекс фазного сопротивления.
Б. Режимы при несимметричном источнике
или несимметричной нагрузке
6.8р . Трехфазиый трансформатор, вторичные обмотки которого
соединены звездой, питает симметричный приемник (рис. 6.4,о).
Сопротивления фаз приемника Z = 4 4- /3 Ом. Фазное напряжение
трансформатора (/ф = 380 В. Найти фазные токи и напряжения,
построить топографические диаграммы и векторные диаграммы
токов, если обмотки трансформатора соединены: а) правильно, как
Рис. 6.4
показано на рисунке; б) ошибочно: концы х и у первой и вто-
рой фаз трансформатора соединены с началом третьей фазы С,
приемник подключен к зажимам А, В и г трансформатора.
6.9. При соединении звездой вторичных обмоток трансформа-
тора, фазные напряжения которого симметричны = 220 В),
допущена ошибка: конец х первой фазы соединен не с концами
У и г последующих фаз, а с началом фазы В (рис. 6 4,6). Тран-
сформатор нагружен на симметричную нагрузку, соединенную
треугольником; Z=10e/30° Ом. Определить фазные, линейные на-
пряжения и токи, построить топографическую диаграмму и век-
торную диаграмму токов.
57
6.10р . Фазные напряжения приемника, соединенного звездой,
<7и = 100 В; UB= Ю0е_/90’ В; йс = 150е/135° В. Сопротивление
фазы В ZB = 8—j8 Ом. Какими должны быть сопротивления ZA
и ZCt чтобы система токов была симметрична? Найти линейные
напряжения. Построить топографическую диаграмму и векторную
диаграмму токов.
6.11. Линейные напряжения приемника, соединенного тре-
угольником: (J АВ — Ю0 + /200 В; =—300 В. Проводимость
фазы СА Усл = 0,4—/0,3 См. Найти проводимости фаз АВ и ВС,
если фазные токи приемника симметричны. Определить линейные
токи, построить топографическую диаграмму и векторную диаграмму
токов.
Рис. 6.5
6.12. Система фазных напряжений генератора, соединенного
звездой, симметрична; Г7ф—120 В. Фазные сопротивления при-
емники ZA = ZB—10 Ом; Zc= 10е~'90° Ом. Сопротивления про-
водов линии и нулевого провода 2Л —2е/бС° Ом; Zo —4е^30° Ом
(рис. 6.5,а).
Определить фазные токи, ток в нулевом проводе, фазные на-
пряжения на нагрузке. Построить топографическую диаграмму и
векторную диаграмму токов. Найти показание ваттметра.
6.13. Фазные напряжения несимметричного источника, соеди-
ненного звездой (рис. 6.5,6), UA = 220 В; UB~220е/'3°э В; Uc —
= 180е/120° В. Сопротивления фаз приемника, соединенного звездой,
гА= 10е-/3°я Ом; гд=10 Ом; Zc-5е-'90° Ом.
Определить показания всех приборов в схеме, если: а) между
нулевыми точками генератора и приемника включен вольтметр
(рис. 6.5,6); б) вольтметр, включенный между нулевыми точками
генератора и нагрузки, заменен амперметром. Для обоих случаев
построить топографические диаграммы и векторные диаграммы
токов.
6.14р . К источнику несимметричной системы линейных напря-
жений присоединена несимметричная нагрузка, соединенная звез-
дой (рис. 6.6,а). Параметры схемы: Uлв = 80 В; (7вс = 60е~/90° В;
ZA— 10е'3°в Ом; Z^ = 5e_/6G° Ом; Zc— 10 Ом. Определить актив-
ную, реактивную и полную мощности нагрузки. Построить век-
торные диаграммы напряжений и токов.
58
6.15. Система фазных напряжений источника, соединенного
треугольником, симметрична; С= 220е'30° В. Симметричная
нагрузка соединена звездой; 7 = 3 +/4 Ом (рис. 6.6,6). Несим-
метричная активная нагрузка соединена треугольником; 100 Ом;
Я2 = 20 Ом; ₽я=50Ом. Сопротивление проводов линии 7Л =
= 3 + /3 Ом. Определить токи в проводах линии.
а)
Рис. 6.6
6.16. К симметричному трехфазному генератору, соединенному
звездой (0А= 100 В), подключены два потребителя, также соеди-
ненные звездой (рис, 6.7,о). Параметры схемы: Zr=10 Ом;
/10 Ом; Z3 = /10Om; Z4=10Om; Z5 = /10Om; Ze = — /10Ом.
Рис. 6.7
Рассчитать токи в цепи и напряжение при разомкнутом
выключателе. Определить ток в перемычке при замкнутом выклю-
чателе, если: a) Z0 = 0; б) Z0=14,6 Ом.
Указание. При выполнении п. а) н б) воспользоваться методом экви-
валентного генератора.
6.17. Проволочный реостат, индуктивная катушка (активное
сопротивление катушки RK = 0) и конденсатор соединены тре-
угольником (рис. 6.7,6). Приборы, включенные в цепь, дали сле-
дующие показания: 6/лд=100 В: 0^ = 150 В; —120 В;
Л,-15 А; /с=12 А; Р^ =—600 Вт. Определить сопротивления
фаз нагрузки. Построить топографическую диаграмму и векторную
Диаграмму токов. Задачу рекомендуется решать графически.
Ь9
В. Цепи с магнитно-связанными ветвями
6.18р . Симметричная нагрузка Z=20 + /20 Ом соединена
треугольником и питается от сети, система линейных напряже-
ний которой симметрична; £/л = 220 В (рис. 6.8,а). Каждый провод
линии обладает индуктивным сопротивлением Х£=10 Ом. Сопро-
тивление, обусловленное взаимной индукцией между любой парой
проводов, ХЛ1 = 5 Ом. Определить линейные и фазные токи,
фазные напряжения нагрузки и падения напряжения в проводах
линии. Построить топографическую диаграмму и векторную
диаграмму токов.
6.19. Решить предыдущую задачу при условии, что в фазе А'В'
нагрузки произошел обрыв.
6.20р . Система линейных напряжений (рис. 6.8,6), к которой
подключен приемник, соединенный треугольником, симметрична;
Д/лв = 200 В. Активное сопротивление резистора /?=10 Ом,
индуктивные сопротивления катушек Х1 = Х2=10 Ом (активные
сопротивления катушек 7?в = 0). Сопротивление, обусловленное
взаимной индукцией, Хл1 = 5 Ом. Найти фазные и линейные
токи. Построить топографическую диаграмму и векторную ди-
аграмму токов.
Рис. 6.9
6.21. Система фазных напряжений генератора симметрична:
0А = 100 В (рис. 6.9,о). Сопротивления фаз приемника, соеди-
ненного звездой. /? = 5 Ом; Х1 = Х2=10 Ом; Хг = 20 Ом. Сопро-
тивление, обусловленное взаимной индукцией, Хлт —8 Ом. Опре-
делить токи в ветвях цепи и показание вольтметра, включенного
между нулевыми точками генератора и приемника. Построить
топографическую диаграмму и векторную диаграмму токов.
60
Г. Круговые диаграммы
6.22р . Система фазных напряжений источника симметрична
(рис. 6.9,6); (7д=100 В. Сопротивления фаз Си В приемника
Я = 30 Ом; Xz =40 Ом. Модуль сопротивления ZH = ze~'60° фазы А
приемника изменяется в пределах от 0 до то. Построить круго-
вые диаграммы тока 1А и напряжения Uq’o между нулевыми
точками приемника и источника.
6.23. Сопротивление резистора R (рис. 6.10,а} меняется от
0 до то. Фазные напряжения источника, соединенного звездой,
симметричны; {/$=100 В. Индуктивные сопротивления приемника
Х£ = 30 Ом. Построить круговую диаграмму смещения нейтрали
и круговую диаграмму тока в фазе А. Чему равны фазные на-
пряжения и ток в фазе А при Я = 5,78 Ом?
6.24. Сопротивления резисторов нагрузки, включенных в фазы
Д, В и С, /?=12 Ом; емкостные сопротивления Xt=16 Ом;
Х? = 9 Ом (рис. 6.10,6). Фазное напряжение симметричного ис-
точника, соединенного звездой, С/д=100 В; индуктивное сопро-
тивление катушки XL меняется от 0 до то. Построить круговую
диаграмму смещения нейтрали и круговую диаграмму напряже-
ния на фазе А нагрузки.
Д. Метод симметричных составляющих
6.25р. Разложить несимметричную систему фазных напряжений
{/л, Uв и йс на симметричные составляющие аналитическим и
графическим методами (рис. 6.II,а). Модули фазных напряжений
(/л=100 В; £7в=150 В;
Uc = 75 В. Найти симмет-
ричные составляющие системы
линейных напряжений.
6.26. Трехфазный электри-
ческий двигатель, соединен-
ный звездой, подключен к
несимметричному источнику,
линейные напряжения ко-
торого йАВ = 320е'22°35' В;
*'|хл
0с
Генератор
А
8
С
а)
Рис. 6.11
V,
61
UBC~26fe~iW> В; UCA = 320е>1Б7*25' В. Фазное сопротивление
двигателя токам прямой последовательности Z1 = 4 + /4 Ом, а то-
кам обратной последовательности Z2 — 0,23+ /0,55 Ом. Рассчи-
тать токи во всех фазах двигателя.
6.27. К симметричному трехфазному идеальному генератору,
соединенному звездой, подключен трехфазный двигатель, также
соединенный звездой. Фазное напряжение генератора Оло — 220 В.
В линейном проводе А произошел обрыв (рис. 6.11,6). Опреде-
лить фазные токи, фазные и линейные напряжения двигателя,
а также напряжение между точками А и А', если фазное сопро-
тивление двигателя токам прямой последовательности Z1 = /9Om,
токам обратной последовательности Za — /2 Ом.
6.28р . В цепи схемы рис. 6.12 фазное напряжение трехфазного
симметричного генератора С/ф=Ю0В. Сопротивления фаз прием-
ника /?д=Ю0м; /?в = 20Ом; /?с = 30 Ом. Сопротивление прово-
дов линии Z, = (! + /) Ом; сопротивление нулевого провода
Zh = 2+j2 0m. Сопротивления каждой фазы генератора токам
прямой, обратной и нулевой последовательностей соответственно
2г1 = /ЗОм; Zr2 = /2 0м; Zrt = /1OM. Пользуясь методом симмет-
ричных составляющих, определить токи в проводах линии.
6.29. Трехфазный симметричный генератор, соединенный звез-
дой, питает симметричную нагрузку, также соединенную звездой
(рис. 6.13). Фазное напряжение генератора U^— 100 В, фазные
сопротивления нагрузки /?ф = 20 Ом. Сопротивление проводов
линии Z, = 2 +/2 Ом; сопротивление заземления нулевой точки
генератора Z3r —5Ом. Сопротивление каждой фазы генератора
токам прямой последовательности Zrl = /3 Ом; токам обратной
последовательности Zr2 = /2O.M; токам нулевой последовательности
ZrQ — Ом. Методом симметричных составляющих определить
токи в проводах при замыкании на землю фазы С в точке М.
Е. Вращающееся магнитное поле
6.30р . Оси двух одинаковых круглых катушек (рис. 6.14,а)
сдвинуты в пространстве на 90°. По катушкам протекают синусо-
идальные токи с равными амплитудами и одинаковой частотой.
62
Доказать» что если токи в катушках: а) совпадают по фазе,
то вектор магнитной индукции результирующего поля в точке О
пульсирует в определенном направлении (найти положение оси
пульсации вектора магнитной индукции); б) сдвинуты по фазе
на 90°, то магнитное поле в точке О характеризуется вращающимся
вектором магнитной индукции Во. Определить Во, если магнитная
индукция по продольной оси первой катушки Bt = Вт sin со/.
6.31. . Оси двух одинаковых катушек сдвинуты в прострастве
на 60° (рис. 6.14,6). По катушкам протекают токи /!==/„ sin со/,
is—/wsin(co/ + 120е). Определить амплитуду вектора магнитной
индукции результирующего магнитного поля в центре катушек,
если амплитуда вектора магнитной индукции каждой катушки
равна Вт.
6.32. Провода круглого сечения трехфазной линии передачи рас-
положены в воздухе, как показано на рис. 6.14, в. Токи в проводах
образуют симметричную систему: ^=7^ sin со/; Zs=/msin(<of—120°);
= sin (со/н-120°). Доказать, что магнитное поле в точке О,
находящейся в центре тяжести треугольника АВС, характери-
зуется вращающимся вектором магнитной индукции Вп. Опреде-
лить Воискорость его вращения, если расстояние между проводами
d = 50 И Зсм, амплитуда тока в проводах 1га = 1000 .4, частота
/ — 50 Гц.
Глава седьмая
Периодические несинусоидальные режимы
в линейных электрических цепях
А. Разложение несинусоидальных токов и напряжений
в ряд Фурье. Действующие и средние значения.
Коэффициенты, характеризующие форму
7.1. Напряжение изменяется по законам, указанным на
Рйс. 7.1,а—г. Для этих рисунков требуется: а) качественно
определить, какие гармоники присутствуют при разложении в ряд
Фурье; б) рассчитать действующее и среднее значения напряжения
63
путем непосредственного интегрирования; в) найти действующее
значение напряжения, учитывая три первых члена ряда Фурье*.
Примечание. Для рис. 7.1,а принять а = 0; л/6; л/2.
7.2р . В схеме двухполупериодного выпрямления, построенной
на тиристорах, напряжение на чисто активной нагрузке имеет
л/г л w/г 2Я wc
6)
7Г/2 Jt Л?/Z 27]
г;
Рис. 7.1
Рис. 7.2
вид, указанный на рис. 7.2, а. Считая а = п/6, разложить кривую
в ряд Фурье, ограничившись тремя первыми гармоническими
составляющими ряда.
7.3. Разложить в ряд Фурье периодические кривые, показан-
ные на рис. 7.2, б—г, предварительно определив, какие гармо-
/,Л
2
1
0
~1
-2
Риг. 7.3
ники присутствуют в разложении. Построить амплитудно-частот-
ный спектр этих функций.
* Разложение кривых дано в кн.: Бессонов Л. А. Теоретически^
основы электротехники.—М.: Высшая школа, 1996, табл. 7.1.
64
7.4р . Определить коэффициенты амплитуды kai формы и
искажения kK для зависимости, показанной на рис. 7.2,6.
7.5. Для кривых, представленных на рис. 7.3, а—в, опреде-
лить: а) действующее значение тока; б) постоянную составляющую
тока и среднее значение тока по модулю; в) для кривой рис. 7.3, а
среднее значение тока за полупериод; г; коэффициенты формы
и амплитуды.
Б. Применение рядов Фурье для расчета электрических цепей,
содержащих несинусоидальные источники тока и ЭДС
7.6. К схеме рис. 7.4,а подведено напряжение, изменяющееся,
как показано на рис. 7.2, б. Ограничившись тремя гармоническими
составляющими воздействующего напряжения, определить мгно-
венные и действующие значения тока в схеме и напряжения на
Рис. 7.4
элементах. Рассчитать мощность (активную, реактивную и полную),
развиваемую источником; £/^ = 314 В; со=103с“1; /?=ЮОм;
£ = 5мГн; С —66,7 мкФ.
7.7р . Схема рис.7.4, б питается от источника периодического
несинусоидального тока частотой / = 50Гц, изменяющегося, как
показано на рис. 7.2, в. Ограничившись тремя составляющими
ряда Фурье в выражении для / (0, найти токи в ветвях схемы,
активную и полную мощности, развиваемые источником. Построить
график iL = /(0; —2А; /?=20Ом; L = 31,8 мГн; С= 159 мкФ.
7.8. Схема рис. 7.4, в питается от источника несинусоидальной
периодической ЭДС, график которой показан на рис. 7.2, г.
Частша источника питания 1,59-103 Гц; Ert = 6 В. Ограни-
чившись тремя составляющими ряда Фурье в выражении для е(0,
определить мгновенное и действующее значения напряжения на
выходе схемы. Построить график этого напряжения в функции
времени. Параметры цепи: С=10-4мкФ; £=10 мГн; Л4=5мГн;
R ~ 10 кОм.
7.9. Рассчитать мгновенное значение тока в индуктивной
Катушке и построить график его в функции времени (рис. 7.5. а),
если e(t) = 100 + 50 sin (со/— 30°) В: / (0 = 10+5 sin2co/A; R2 =
= <о£ = I/(соС) ~ 10 Ом; — 5 Ом.
7.10р . Определить мгновенное значение напряжения
На зажимах источника тока (рис. 7.5, б) и его активную и полную
Мощности, если р(Л — 100 + 50sin (2со/ + 30°) В: j(0 = 6-Ь 1 cosco/ А.
Параметры цепи на частоте со: /?1 = 7?а = со£=10 Ом; 1/(соС) — 20Ом.
65
7.11 р. На вход четырехполюсника, собранного по П-схеме
(рис. 7.5. в), подано напряжение wt(0» изменяющееся по закону,
указанному на рис. 7.1,в; t/CT==50B; /=159,1 Гц. Найти мгно-
венное и действующее значения напряжения на нагрузке
/?и = 20Ом, ограничившись четырьмя гармоническими составляю-
Рис. 7.5
щими воздействующего напряжения. Построить линейные спектры
входного и выходного напряжений. Параметры четырех-
полюсника: R =40 Ом; С = 16,7 мкФ; L = 10 мГн.
В. Резонансные явления при несинусоидальиых токах
и напряжениях. Показания измерительных приборов*
7.12р . На входе цепи рис. 7.6, а действует источник напря-
жения, содержащий первую ((о=103с~1), третью и пятую гармо-
нические составляющие. Между входом и нагрузкой /?н = 80Ом
а) 6) В)
Рис. 7.6
включен электрический фильтр; L, = L2=10 мГн. Подобрать
емкости конденсаторов С, и Сг так, чтобы в нагрузку не прохо-
дили токи третьей и пятой гармоник. Определить отношение
напряжений по первой гармонике.
7.13. На вход цепи рис. 7.6,6 подано напряжение и(/)=5 4*
+ 3 sin (1000£ + 30°) + 2 sin 5000/ В. Подобрать индуктивности ка-
тушек Lt и так, чтобы в нагрузке присутствовала лишь посто-
янная составляющая спектра. Параметры цепи: С1 = С2=10мкФ;
Ra — 0,1 кОм. Рассчитать мгновенные значения токов i1(t) и ха(0
* Приборы магнитоэлектрической системы показывают постоянную состав-
ляющую. приборы электромагнитной и электродинамической систем — дейст-
вующее значение, ваттметр электродинамической системы—среднюю мощность»
66
и показания амперметров и ваттметра электродинамической
системы.
7.14. На вход цепи рис. 7.6,е подано напряжение и(/) = 100+-
+ 50 sin 3000/ 4- 30sin (9000/ —45°) В. Подобрать емкости конден-
саторов С, и Сг так, чтобы в нагрузку не проходили постоянная
составляющая и третья гармоника напряжения, а первая гармо-
ника проходила без искажения. Параметры схемы: £=10 мГн;
/?н = 100 Ом. Определить мгновенные значения токов ц (/); t2(/);
/в(/) и показания приборов электродинамической системы.
Рис. 7.7
7.15. Рассчитать мгновенное значение напряжения на конден-
саторе ис (/) (рис. 7.7, а) и построить его график. Найти показания
вольтметра электромагнитной системы и ваттметра электродина-
мической системы. Параметры схемы: /(/)=5+10sin(1000/-|-30o) А;
е(/) = 50 + 100sin(2000/—45е) В; £1 = 30 мГн; £,= 10 мГн;
С = 33,3 мкФ; /?=ЮОм.
7.16. Резистивно-емкостная нагрузка питается через транс-
форматор от источника тока / (/) = 5 + 6 sin со/ + 3 cos 2<о/ А
(рис. 7.7, б). Определить мгновенное значение напряжения итп (/),
а также показания вольтметра и ваттметра электродинамической
системы. Параметры цепи: со£1 = 8 0м; со£2 = 2Ом; коэффициент
связи обмоток трансформатора k = 0,25; /?„ = 3 Ом; 1/(соСк) = 2 Ом.
a) S)
Рис. 7.8
7.17р . Рассчитать мгновенные значения токов во всех ветвях
схемы рис. 7.8,а, а также активные и полные мощности обоих
Источников. Параметры цепи: (t) =100+60 sin (со/ + 30е) В;
МО = 20 + 30 cos 2с+ В; /? = 6 Ом; ю£. = 1 Ом; со£, = 3 Ом;
1/(<мС) = 4 Ом.
7.18. В цепи рис. 7.8, б ег (/) = 20 + 30 sin (<о/ — 15е) +
+ 20sin(2(o/ + 45°) В; е2(/)= 10 В. Параметры цепи: (о£,=2 0м;
= 1. (wC) _ 6 Ом; R — 10 Ом. Определить показания вольт-
Метра и амперметра электромагнитной системы.
67
Г. Расчет простейших электрических цепей
с несинусоидальными источниками тока
и ЭДС без разложения в ряд Фурье
7.19. Цепь рис. 7.9, а питается от источника тока / (/), изме-
няющегося за период Т = 0,02 с, как показано на рис. 7.96.
Построить график напряжения u(t) на зажимах источника тока
за период Т. Параметры цепи: R — 30 Ом; Л. = 0,1 Гн.
Рис. 7.9
7.20р . Построить = — и ic = f (t) для схемы
рис. 7.9, в, если к ней подводится напряжение, изменяющееся
за период 7=6 мс (рис. 7.9, г). Параметры схемы: 7? =100 Ом;
L = 0,l Гн; С=1 мкФ. При построении считать, что ток в ин-
дуктивной катушке не имеет постоянной составляющей.
7.21. Ток iR(i) в схеме рис. 7.9,6 меняется по периодическому
(7 = 0,02 с) закону (рис. 7.9, е). Определить закон изменения
тока на входе <(/), если 7? = 30 Ом; С =100 мкФ.
Д. Несинусоидальные токи и напряжения в трехфазных цепях
7.22. Фазовая ЭДС симметричного трехфазного генератора,
соединенного звездой, содержит первую, третью и пятую гармо-
ники с амплитудами £1ст = 49,5 В; Е3,л = 42,4 В; Е5ст = 27,4 В.
Определить показания вольтметров электромагнитной системы,
если вольтметр включен на фазовое напряжение, а вольтметр
Уя—на линейное.
7.23. Фазовые токи в симметричной нагрузке, соединенной
треугольником, содержат первую и третью 1 армоники. Амперметры
68
электромагнитной системы, включенные в фазу нагрузки и линей-
ный провод, покажут соответственно /Л1 = 10 А; 1 Аг — 13,85 А.
Рассчитать амплитуду первой и третьей гармоник фазового тока.
7.24р . Определить мгновенное значение напряжения uafi акт ив-
ную и полную мощности трехфазной системы (рис. 7.10, о), если
иАв = (100 sin of + 20sin5w0 В; сопротивления для первой гармо-
ники = 8 Ом; Ад —6 Ом; Хс==30 Ом.
Рнс. 7.10
7.25. Найти токи в линии и нагрузке схемы рис. 7.10, я
(см. задачу 7.24р), если в фазе ab в точке d произошел обрыв.
7.26. Определить показание вольтметра электромагнитной
системы, включенного между нулевыми точками симметричного
трехфазного генератора и симметричной нагрузки (рис. 7.10,6,
выключатель в положении /), если eA(t) = 100 sin со/ 4-2Osin3<of—
— 5sin5tof В, сопротивления для первых гармоник ZA = ZB — ZC =
— 3 4- /4 Ом. Найти показание амперметра электромагнитной
системы, включенного вместо вольтметра (выключатель в поло-
жении 2). Считать внутреннее сопротивление вольтметра беско-
нечно большим, а внутреннее сопротивление амперметра равным
нулю.
7.27. Определить показания вольтметра и амперметров электро-
магнитной системы в схеме рис. 7.11, я. ЭДС фазы А еА имеет
форму, указанную на рис. 7.11, б. Параметры симметричной
нагрузки на основной частоте: со£ = 9 Ом; 1 /(соС) = 30 Ом;
Я=10 Ом; = 1 Ом.
7.28. ЭДС фазы А симметричного трехфазного источника,
соединенного звездой, ед/) — 100 sin tof 4- 50sin(3of 4- 30°) 4-
69
4 30 sin (5<of—45°) 4- 20 sin (7cof 4 60°) 4 10 sin (9co/ 4 45°) В. Чему
равно линейное напряжение «дс(0?
7.29. К симметричному трехфазному источнику, соединенному
звездой, подключен трехфазный двигатель, обмотки которого также
соединены звездой. ЭДС фазы А источника еА (t) — 180 sin о/ 4
4 50 sin В. Сопротивление фазы двигателя на частоте о токам
прямой последовательности Z, = /6 Ом, а токам обратной после-
довательности Za —/1 Ом. Найти мгновенное и действующее зна-
чения тока фазы В.
Е. Амплитудно-модулированные колебания
7.30р . На выходе схемы напряжение изменяется по закону
u(t) — 100 sin 900/ 4 100 sin 1100/ В. Построить график этого на-
пряжения в функции времени и определить период возникающих
биений.
7.31. Источник модулированного напряжения «(/)==
= 10 cos 104/sin 10е! В питает последовательный резонансный
контур, настроенный на частоту со = 106 с”1; добротность контура
Q=100, сопротивление резистора /?=10 Ом. Определить закон
изменения тока в цепи.
7.32. Напряжение, модулированное по амплитуде, имеет вид
tz(0 = 10sin(10V—45°)44sin(9-10V4 45c)—4sin(ll-103/445°) В.
Построить график этого напряжения в функции времени.
7.33. Источник тока /(/) = 0, 1 (1—0,5 sin2-104/)sin50-104/ А
питает последовательный резонансный контур, настроенный на
частоту со = 50-104 с~1. Добротность контура Q — 100; /? = Ю0м.
Рассчитать действующие значения тока и напряжения на зажимах
источника тока.
Глава восьмая
Переходные процессы
в линейных электрических цепях
с сосредоточенными параметрами
А. Классический метод
1. RC-цепи
8.1. Конденсатор емкостью С = 0,1 мкФ разряжается на ре-
зистор сопротивлением /?—1 кОм. Напряжение на конденсаторе
непосредственно до коммутации UCt) —100 В (рис. 8.1, я). Найт
напряжение ис (0+) и ток ic (0+) непосредственно после комму-
тации. Определить закон изменения напряжения нс(/) и тока ic(l)
после коммутации и построить графики этих величин во времени.
Подсчитать энергию, израсходованную в резисторе за время пол-
ного разряда конденсатора.
70
8.2. Конденсатор емкостью С = 2 мкФ (рис. 8.1,6) подклю-
чается через резистор сопротивлением Я = 0,5 кОм к источнику
ЭДСе(0. 1. Полагая ЭДС е (/) = Е — 100 В, найти закон изме-
нения напряжения на конденсаторе uc[t} и тока в цепи
Построить графики этих величин во времени для: а) ис(0_) =
= t/C(l = 0; б) tzc(O_) —t/co—100 В; в) дс(0_) = £/св = —100 В.
2. Решить задачу при условии, что е(/) = 100И25ш(103/-|-45о) В.
Рис. 8.1
8.3. Найти закон изменения во времени напряжения на кон-
денсаторе uc(t) и токов во всех ветвях схемы (рис. 8.2, д) после
коммутации (переключатель переводится из положения 1—0 в по-
ложение 2—0). Построить графики этих величин во времени.
Задачу решить для трех вариантов (табл. 8.1). Считать Я1 = Я2 =
— 1 кОм; С = 20 мкФ.
Таблица 8.1
Вариант е. (О. В е, (/). В
а 200 0
б 200 200
В 200 sin (100/-i-45') 100
8.4. Найти напряжение и ток в ветви с конденсатором С
(рис. 8.2,6) после коммутации при: а) Я1 = Яа = Яэ = Я4= 1 кОм;
a) S)
Рис. 8.2
5 “ Я. = 1 кОм; R2 — Я3 —!»5 кОм. Считать С = 0,66 мкФ;
£^150 В.
71
8.5. Найти напряжение на конденсаторе и токи в ветвях после
подключения к схеме, источника тока / (/). Включение источника
тока на схеме рис. 8.3, а соответствует размыканию выклю-
чателя. Рассмотреть два случая: 1) / (/) = /=! мА; 2) /(/) =
= J/ 2 sin (100/—45°) мА. Данные схемы: R = 20 кОм; С = 0,5 мкФ.
а) б)
Рис. 8.3
8.6. Найти напряжение на конденсаторе uc(t} и ток i(/)
в диагонали схемы (рис. 8.3,6) после коммутации, считая, что
схема питается от источника: а) постоянной ЭДС Е=100 В;
6) постоянного тока 7=0,4 А. Данные схемы: Rt = R4 — 200 Ом;
Я2 = Я3 = 300 Ом; R5 = 250 Ом; С = 20 мкФ.
8.7р . Методом эквивалентного генератора найти ток /(/) в диа-
гонали схемы рис. 8.4, а после коммутации при: а) /\(/) = Jj-
=0,2 A; /2(/) = J2 = 0,l А; б) А (0 = 0; /5(/) = 0,1 sin(104/—16°) А.
Данные схемы: ^г = 300 Ом; R2 = R3 = 200 Ом; С = 0,5 мкФ.
8.8р . Методом эквивалентного генератора рассчитать напря-
жение uab(t) после размыкания контакта, считая, что в схеме
рис. 8.4,6 включены источник постоянной ЭДС и источник тока:
а) £=100 В; /(/)=7=0,5 А; б) £=0; j (0 =0,335sin(101/4- 13°) А.
Данные схемы: Rr = 300 Ом; R2 = Ra = 200 Ом; С = 0,5 мкФ.
8.9р . Простейшее неидеальное интегрирующее звено (RC-це-
почка) (рис. 8.5, а) в момент времени / = 0 подключается к источ-
нику ЭДС Elt а через время / = Т после этого—к источнику
ЭДС Е2. Определить напряжение на выходе звена «,,ыХ(0 = ^с(0
и ток в цепи / (/) после коммутаций и построить графики изме-
нения указанных величин во времени, если: а) £1=100 В;
72
£2 = 0; б) £,-100 В; £2 = 200 В; в) £, = 100 В: £.г = —100 В.
расчеты выполнить для Т = 0,1 и 0,03 с. Данные схемы:
fl == 1 кОм; С = 100 мкФ.
Построить графики изменения напряжения на выходе идеаль-
ного интегрирующего звена (рис. 8.5,6) при выполнении условий
п. а) — в). Идеальное интегрирующее звено получено добавлением
к схеме рис. 8.5, а усилителя с коэффициентом усиления k=l
и введением обратной связи.
б)
Рис. 8.5
8.10р . В цепи при £ = 0 происходит замыкание, а через время
t — T после этого — размыкание выключателя (рис. 8.5, в). 1. Рас-
считать напряжение на конденсаторе и построить график его
изменения во времени после первой и второй коммутаций для
Т = 0,1 и 0,03 с, считая /? = £, = 2 кОм; С— 100 мкФ, £=150 В.
2. Полагая, что включение и отключение периодически повто-
ряются, найти напряжение на конденсаторе в установившемся
режиме. В расчетах считать время включенного и отключенного
состояний одинаковым: Т = 0,1 с.
2. RL-цепи
8.11. В цепи происходит переключение выключателя из поло-
жения 1—0 в 2—0 (рис. 8.6, о). Найти ток и напряжение на
индуктивной катушке после коммутации и построить графики
изменения этих величин
в функции времени, счи-
тая, что: а) е(/) = £ =
100 В; б) б(/) =
=200 sin 104/ В; в) е(/) =
= 200sin(104/ + 45°) В.
Для случая а) подсчи-
тать полный заряд и энер-
гию, выделяющуюся на ре-
зисторе после коммутации.
Данные схемы: К = 10 Ом;
£- 1 мГн.
Рве. 8.6
8.12. В пени (рис. 8.6,6) переключение выключателя проис-
ходит из положения /—0 в 2—0. Рассчитать ток в цепи и напря-
жение на индуктивной катушке и резисторах R и Rx после
73
коммутации. Построить графики этих величин в функции времени.
Задачу решить для трех вариантов (табл. 8.2). Данные схемы:
Ri — 40 Ом; /?=10 Ом; L=1 мГн.
Таблица 8.2
Вариант </). в е, (П. В
а 100 0
б 100 100
В 200 sin (10*74-45=) 100
8.13. Найти ток и напряжение на индуктивной катушке после
коммутации (рис. 8.7, а), построить графики этих величин во вре-
мени, полагая, что: а) е(t) = E = 100 В; /(/) = 0; б) е(1) = Е~ 100 В;
/(/) = J = 10 А; в) г(0 = Е=1ОО В; = J = —10 А; г) e(t} =
~ 200 sin Ю4/; / (/) = J = 10 А. Данные схемы: R — 10 Ом;
L= 1 мГн.
8.14. Определить ток в первичной обмотке и напряжение на
вторичной обмотке воздушного трансформатора (рис. 8.7,6) после
размыкания контакта при: а) /(/) = /=10мА; б) j (/) = 10 2 х
Xsin(10b/4- 45°) мА. Данные схемы: /?=100Ом; L1 = L.2=10“3 Гн;
Л1 = 5-10“4 Гн.
а)
S)
Рис. 8.8
8.15. Рассчитать токи в ветви с индуктивной катушкой iL(i)
и в диагонали схемы t\(Z) (рис. 8.8, я) после коммутации, пола-
гая, что схему питает источник: а) постоянного тока J — 3 А;
б) постоянной ЭДС Е = 10 В. Данные схемы: =/?,=/?3=10 Ом;
£=10Гн.
74
8.16р . Найти токи в ветви с индуктивной катушкой iL(t) и
в диагонали тд(0 схемы рис. 8.8,6 после коммутации, полагая,
что схему питает источник: а) постоянной ЭДС € (/) = £ = 300 В;
б) синусоидальной ЭДС e(t) = 250 sin (200/-}- 45°) В. Данные
схемы: /?=100 Ом; £=1 Гн.
8.17р . Определить напряжение uab(t) после размыкания кон-
такта, полагая, что в схему рис. 8.9, а включены источники,
4 *
Рис. 8.9
у которых^ а) е(0=£=1О В, = 1 А; б) е(0 = Е=1ОВ;
j(0 = 2l 2sin(500/—45е) А. Данные схемы: = /?я = 10 Ом;
/?3==5 Ом; L = 0,01 Гн.
8.18. 1. Простейшее неидеальное дифференцирующее звено
в момент времени / = 0 подключается к источнику ЭДС Е,,
а через время / = Т после этого—к источнику ЭДС Е2 (рис.8.9,6).
Найти ток i(t) и напряжение на выходе ппыу(0 после коммута-
ций, построить графики этих величин в функции времени для:
а) Ех=100 В; Es = 0; б) ^=100 В; £2 = 200 В; в) £\ = 100 В;
Е9 =—100 В. Расчеты выполнить для Т = 10~3; 5-10“4 с. Данные
схемы: #=100 Ом, £ = 0,1 Гн. 2. Построить графики изменения
напряжения на выходе при выполнении условий пунктов а)—в)
для идеального дифференцирующего звена, т. е. если uaiM = duBJldt.
Рис. 8.10
8.19. Пассивный двухполюсник (рис. 8.10, а) при / = 0 под-
ключается к источнику ЭДС ei (0, а через время после этого—
к источнику ЭДС е,(0. Определить ток и построить его зависи-
мость от времени после первой и второй коммутаций, полагая;
а) с, («) = £,. sinг2(0 = 0; /. = Т/2; б) M0 = E,„sin^ /;
75
e„(/) = E2; /х=Т/4. Исходные данные: 7?i=l Ом: Л =10 3 Гн;
Т = 2л-10"3 с; £1/л = 20 В; £2=10 В.
8.20р . На вход пассивного двухполюсника подается напряже-
ние от ннзкоомного потенциометра (рис. 8.10,6). В начальный
момент времени / = 0 подвижный контакт включает первую сту-
пень потенциометра с напряжением «д. Затем через равные про-
межутки времени Г, 2Т, .... kT контакт замыкает вторую,
третью, .... fc-ю ступени потенциометра (рис. 8.10,в). Найти ток
в цепи двухполюсника после первой, второй, третьей и А?-й ком-
мутаций, полагая, что сопротивление резистора R^> Rn. Данные
схемы: /?=1 кОм; Г = 0,1 Гн; «д=1 В; Т— 10~4 с.
3. RCC- и RLL-qenu
8.21. Предварительно заряженный до напряжения Ucw кон-
денсатор подключается к пассивной схеме (рис. 8.11, а).
Рис. 8.11
Рассчитать напряжения на конденсаторах Сх и Са, токи во
всех ветвях и их производные непосредственно после коммутации.
Определить изменения во времени токов и напряжений на кон-
денсаторах и построить графики переходных процессов после
коммутации. Исходные данные: Ri = R2 = 1 кОм; С1 = С2—100 мкФ;
СС1П= 100 В.
8.22. Найти значения напряжений на конденсаторах, токов
во всех ветвях и их производных в схеме рис. 8.11,6 непосред-
ственно после коммутации. Определить uci(t) » ^С2 (О’ *1(0» *2 (О’
|’3(0 при: а) е(t) = E = 10 В; б) e(f) = 22,3 sin (100/—27°). В. Дан-
ные схемы: /?х = Ra = 100 Ом; Cj = C2=100 мкФ.
Рис. 8.12
8.23. Рассчитать напряжения на конденсаторах и токи в вет-
вях схемы рис. 8.12,в после коммутации, полагая: a) (t) = E=
76
= 100 В; б) (0 = 123 sin (100/—43а) В. Данные схемы: Сг =
= 20 мкФ; С2 —30 мкФ; R1 = 500 Ом; /?2 — 400 Ом.
8.24. Рассчитать токи в ветвях и напряжения на индуктив-
ных катушках схемы рис. 8.12,6. Задачу решить для трех вари-
антов (табл. 8.3). Данные схемы: R1=RS = 10 Ом; Ll=Lz=QA Гн.
Таблица 8.3
Вариант С| (Г), в с, <0. в J, А
а 100 0 0
б 100 100 —10
В 300 к 2 sin (102/4-45°) 0 0
8.25. Найти напряжение uab(i) после
график его изменения во времени, если
ключена к источнику: а) постоянной
ЭДС Е = 200 В; б) постоянного тока
J = 2 А. Данные схемы: RZ = RZ~
= 200 Ом; R = 100 Ом;
=L3 = 0,01 Гн; М =0,005 Гн.
коммутации и построить
схема (рис. 8.13)
R
под-
4. RLC-цепи
8.26. Определить ток в контуре,
*2
М
а
\^оЬ
b
напряжения на конденсаторе и ка- Рис. 8.13
тушке после коммутации (рис. 8.14, а).
Построить графики изменения этих величин во времени при:
а) С= 1 мкФ; L = 0,01 Гн; R = 250 Ом; б) С = 1 мкФ; L =
=0,01 Гн; R=100 Ом; в) С=1 мкФ; Г = 0,01 Гн; R-200 Ом.
Для всех случаев ток источника тока J = 1 А.
a) 6)
Рис. 8.14
8.27р . Найти напряжение на конденсаторе и ток в индук-
тивной катушке после коммутации в цепи рис. 8.14,6, полагая:
а) е(/) = Е = 200 В; ис(0) = 0; С = 1 мкФ; 1 = ± Гн;
=R, = R =-2 кОм; б) е(/) = Е=100 В; ис (0) = 100 В; С=5 мкФ;
-'-=0.1 Гн; /?т = 0,1 кОм; R. = RS = O.
77
Таблица 8.4
Вариант *(О. в /<О. А
а 100 0
б 200 10
В 200 cos 103/ 10
г —100 20^2 514 (103—45Э •
8.28. Найти значения начальных (при / = 0+) токов в ветвях
и их производных, а также напряжений на всех элементах цепи
(рис. 8.15, а). Задачу решить для четырех вариантов (табл. 8.4).
Параметры схемы: = Р2 — = Ю Ом; С = 100 мкФ; L = 0,01 Гн.
а}
б)
Рис. 8.15
8.29. Определить корни характеристического уравнения и на-
чальные значения свободных составляющих QCB(0+) и »Ссв(0+)
непосредственно после коммутации, полагая, что схема рис. 8.15,6
питается от: а) источника ЭДС e(t) = E = 160 В; Rl = 0\ б) источ-
ника тока /(/) = /= 10 А; в) источника ЭДС е(0 = 260 В; Rx =
= 10 Ом. Параметры схемы: /?2 = /?3 = /?5 = Т?в = 10 Ом; /?4=5Ом;
£ = 3,75 мГн; С = 88 мкФ.
Указание. Для случая в) характеристическое уравнение рекомендуется
составлять ио определителю системы, найденному из уравнении для свободных
контурных токов.
8.30р . Рассчитать начальные значения (при / = 0+) свободных
составляющих токов в ветвях и напряжения на конденсаторе
после подключения к цепи источника синусоидальной ЭДС
(рис. 8.16, а).
Комплексные амплитуды принужденной синусоидальной состав-
ляющей после коммутации известны: (7Cffl=90e/30° В; //4Л=18е“/3°вА.
Задачу решить для: а) /(/) = 0; б) — А, если 7?х =
= = Ом.
8.31р . Резонансный контур с малым затуханием (рис. 8.16,6)
подключают к источнику синусоидальной ЭДС e(t)=Em sin (юГ-ИДО.
78
Определить напряжение на конденсаторе и ток после комму-
тации при: а) со = с)(| = l/J^LCf Q=: 1» тде 6=
=^/?/(2£); б) o=o0=l//ZC; R=0. Построить графики измене-
ния указанных величин во времени для о = о0 и ф = 0.
8.32. Найти ток в индуктивной катушке ir после замыкания
выключателя и построить график его изменения во времени для
случаев, когда число последовательно включенных одинаковых
ЛС-ячеек: а) п—2\ б) п=4; в) п=оо. Параметры схемы рис. 8.17, а:
/?=100 Ом; С = 0,5 мкФ; £ = 62,5 мГн; 7 = 1 А.
Рис. 8.17
8.33р . Рассчитать напряжение на конденсаторах после комму-
тации при следующих параметрах схемы рис. 8.17,6: a)
=800 Ом; /?3 = Я4 = 100 Ом; £1 = Л2 = 0,01 Гн; С3 = С4 = 1 мкФ;
£ = 60 В; б) ^ = 2^=1600 Ом; /?3 = 4/?4 = 400 Ом; £4 = 2£а =
= 0,02 Гн; С4 = 4С3=1 мкФ; £ = 41,3 В.
5. Цепи с емкостными контурами и индуктивными сечениями
8.34. Составить уравнения и по ним определить начальные
значения: а) напряжений на конденсаторах схемы рис. 8.18, а
при С1 = С2 = С3 = С4 = С; £1=100 В; £ = 50 В; б) токов в ка-
тушках схемы рис. 8.18,6 после размыкания контакта при
£=40 В; J=1 A; /?l=Rt=R,=R4=R=10 Ом; I ^L^L^L^L.
79
Указание. При решении таких задач можно пользоваться обобщенными
ваконами коммутации: законами сохранения (непрерывности) заряда и потоко-
сцепления. При этом следует учитывать, что алгебраическая сумма зарядов
на конденсаторах, присоединенных к любому узлу емкостного контура (или
контура из конденсаторов и источников ЭДС), непрерывна. Аналогично, алгебра-
ическая сумма потокосцепления катушек, входящих в индуктивные сечения
(или сечения из катушек и источников тока), в любом замкнутом контуре,
состоящем из индуктивных катушек, непрерывна.
Рис. 8.18
8.35р . Найти ток в цепи /(/) и напряжение на выключателе
uab(t) после его размыкания, построить графики изменения токов
во времени при следующих параметрах схемы рис. 8.19, a: a)
= 100 Ом; Я2 = 300 Ом; ^ = ^ = 0,01 Гн; М=0; б) RX = R2 =
= 100 Ом; £1 = £а = 0,01 Гн; М=0; в) 7^=100 Ом; Я2=ЗОООм;
£х=£а=0,01 Гн; М = 0,0025 Гн. Во всех случаях ЭДС £=200 В.
Рнс. 8.19
8.36. Рассчитать ток ia(/) во вторичной катушке и напряже-
ние ы1а(0 после коммутации при: а) согласном включении кату-
шек (рис. 8.19,6); б) встречном включении катушек (предполо-
жить, что «вывернута» первая катушка). Данные схемы: ^x=Ra=
= 100 Ом; £1 = £а = 0,01 Гн; М = 0,005 Гн; J = 1 А.
8.37. Определить токи в магнитно-связанных катушках после
коммутации, полагая, что коэффициент связи катушек: а) /г =
= М/Гг£1£а==0,5; б) А = 0; в) А=1 Параметры схемы рис. 8.20,
a: Ri = Ra=150 Ом; £х = £а=150 В.
80
8.38. Найти напряжения на конденсаторах после коммутации
(рис. 8.20,6), полагая, что ЭДС имеют следующие значения:
a) £i=100 В; E2 = Q-, б) Ег=100 В; Е3 = — 100 В; в) ЕХ=Е2=
Рис. 8.20
Рис. 8.21
= 100 В. Параметры схемы: 7^ = 7^=1000 Ом; Сх=1 мкФ;
С., — 3 мкФ.
8.39. Определить напряжения на конденсаторах (рис. 8,21)
после коммутации при: а) Е = 200 В; 7?, =400 Ом; б) Е = 200В;
7?, — оо. Параметры схемы: 7?s =
= 100 Ом; Сх = 4 мкФ; Сг=1 мкФ.
Б. Операторный метод
8.40. Составить в общем ви-
де выражения для операторных
сопротивлений цепей рис. 8.22,
а—г и операторных проводимо-
стей цепей рис. 8.22,6—з. Убедитесь путем расчета, что вход-
ные сопротивления цепей, составленных из параллельно включен-
ных цепочек рис. 8.22, а, б и последовательно включенных цепо-
чек рис. 8.22,6, е при CR = L/R активны и равны R. Будут ли
в таких цепях происходить переходные процессы?
а) б) б) г)
д) е) а; з)
Рис. 8.22
8.41. На вход пассивного четырехполюсника (рис. 8.23, а)
Подключается: а) источник ЭДС е (7) — б) источник тока / (/) =
Найти операторные коэффициенты передачи: а) V
б) У.(р)/Л(р).
81
8.42р . Рассчитать коэффициент передачи пассивной цепи (рис.
8.23, б) и составить ее схему так, чтобы при подключении на вход
источника постоянной ЭДС. е = получить на выходе напря-
жения вида: a) u.2 — Uje-at\ б) ня=(/1(1—е~а9-
8.43. Найти операторное выражение для входного тока /(/?)
и его изменение во времени i(t) после подключения источника
ЭДС e(t) к цепи рис. 8.24, а, полагая: а) е(0 =£= 100 _В;
б) е(0 = 100e“aoof В; в) е(/) = 100/ В; г) e(t) = 100]/"2х
х sin (100/ — 45°) В. Входное операторное сопротивление цепи
ZBX(p) = p + ЮО.
8.44. Найти операторное напряжение на выходе U2(p) схемы
рис. 8.24,6 и его выражение во времени и.2 (0 после коммутации.
Таблица 8.5
/(О. А
Вариант
а
б
в
г
0.1
0,1 (I—е-200*)
О, I coslOO/
0,1 sin 100/
Задачу решить для четырех вариантов (табл. 8.5). Коэффициент
передачи пассивного звена (р) = U2 (p)/I{(р) = 100р/(р +100).
Рис. 8.25
8.45р . Источник постоянной ЭДС Е подключают к цепочке
из п одинаковых линейных четырехполюсников (рис. 8.25), обла-
дающих детектирующим действием (сигналы проходят только от
входа к выходу). Найти коэффициент передачи Un+i(p)/Ut(p)
всей цепи, полагая, что коэффициент передачи /г-го четырех-
полюсника Л* (р)=1/(Т*р +1), где /г=1, 2, ..., п. Определить
82
напряжение на выходе схемы при t = 0 и t—► оо. Для л = 3
найти операторное напряжение на выходе и его выражение во
времени.
8.46р . Операторное выражение для входной проводимоств
двухполюсника (рис. 8.26) имеет вид Увх (/?) = . Найти
приближенное выражение для тока во времени после подключе-
ния к цепи источника постоянной ЭДС Е, используя разложе-
ние изображения тока по обратным степеням /?.
Рис. 8.26 Рис. 8.27
8.47. Операторным методом рассчитать ток на входе схемы
рис. 8.27, а после коммутации. Задачу решить для трех вариан-
тов (табл. 8.6). Данные схемы: Я =100 Ом; L=1 Гн.
Таблица 8.6
Вариант *1 (0. В МО. В
а 100 0
б 100 —100
В 100 100 sin (100/4-45°)
Z
4
а)
8.48р . Определить напряжение на конденсаторе uc(t) и ток
i2(Z) после коммутации операторным методом: а) учитывая внут-
реннюю ЭДС?; б) приведя
сначала задачу к нулевым
начальным условиям. Па-
раметры схемы рис. 8.27, б:
Я£=Я, = 200 Ом; С =
= 10“4“ Ф; Е=100 В.
8.49р . Найти ток в цепи
»(0 и напряжение между
контактами
(/) после
размыкания контакта в рис 8.28
схеме рис. 8.28, а опе-
раторным методом: а) с учетом внутренней ЭДС ; б) приведя
сначала задачу к нулевым начальным условиям. Исходные дан-
ные: J?f = ₽a=l Ом; Е=2 Гн; £=100 В.
83
8.50. Составить уравнения для операторных токов и потен-
циалов в схеме рис. 8.28,6 по методу: а) контурных токов; б) узло-
вых потенциалов. Записать в общем виде операторные выражения
для напряжений на индуктивном и емкостном элементах схемы.
Рис. 8.29
8.51. Составить выражение для операторного напряжения
J7JS(p) (рис. 8.29,о) при: e(t) — E; = б) е(/) = Е; /(0 =
= 7msin(o/ + <p/); в) е(/) = Ewsin((o/ +<р£); /(0 = ^-
8.52р . Найти токи одинаковых магнитно-связанных контуров
после коммутации (рис. 8.29,6) при: а) сильной связи между
контурами (Л«1); б) слабой связи (Л<^1); в) в отсутствие по-
терь (/^ = 0).
В. Метод интеграла Дюамеля
8.53. Для цепей рис. 8.30, о—д найти реакции на действие
единичного ступенчатого напряжения иг (0=1(0» т* е* переход-
ные характеристики цепей по току (переходные проводимости)
£(0 = Ч(0|С|<п=кп и по напряжению k(0 = «2(0L.tn=i<*>- Аля
г) S)
Рис. 8.30
тех же цепей определить реакции на действие единичного им-
пульсного напряжения «1(0 = 6(0» т- е- импульсные передаточ-
ные характеристики М0 = «2(0|Я1(П=б(О-
Указание. Для нахождения переходных характеристик (переходных
функций) цепей необходимо рассчитать переходный процесс, возникающий при
подключении ко входу цепи источника постоянного напряжения Е— 1 В, пола-
84
гая начальные условия нулевыми. Для определения импульсных характеристик
следует рассчитать переходный процесс при воздействии на вход схемы им-
пульсной (в виде fi-функций) ЭДС. Импульсную характеристику можно опре-
делить и как производную во времени от переходной характеристики.
8.54. Для цепей рис. 8.31,с—г при />0 найти реакции
на действие единичного ступенчатого тока <\(0=1 (0> т. е. пере-
е)
Рис. 8.31
ходные характеристики по току Л(0 = 4(01х1и>=*‘Л и напРяже'
НИЮ А, (0 = «а (О |/1(п=1 сп-
Указание. Для определения переходных характеристик необходимо
рассчитать переходный процесс при подключении ко входу схемы источника
постоянного тока J — J А, полагая начальные условия нулевыми.
8.55. Найти взаимную переходную проводимость g12(0 между
первой (ветвь с RJ и второй (ветвь с /?2) ветвями рис. 8.31.0, е.
Указание. Для расчета взаимной переходной проводимости следует
определить переходный ток в ветви с R2 при включении в ветвь с Ri источ-
ника постоянной ЭДС £—I В.
8.56. Рассчитать напряжения на выходе дифференцирующего
Jcm. рис. 8.30, а) и интегрирующего (см. рис. 8.30,6) звеньев.
Задачу решить для пяти вариан-
тов (табл. 8.7). В расчетах счи- Таблица 8.7
тать 6=1 с“1, где 6=1/(/?С)
(см. рис. 8.30, а) или & = R[L
(рис. 8.30,6).
Примечание. Функция /(/)==! (/)
обозначает единичный скачок, т. е.
/(/)=0 прии /(/)= * при/2^50+.
8.57. Определить напряжение
между контактами иРК{1) и ток в
индуктивной катушке iL(t) после
Вариант и( (О. В
а —100-1 (Л
б 100.1 (/ — /о
В 100М (П
Г 100е —1 (/)
Д (100—юо/3).1 (Л
размыкания, считая, что на входе схемы рис. 8.32, а действует
Источник тока: a) 1 (/)—0,1 -1 (/) А: б) / (0=0,1 (e-100f—
—е2009-1(/) А; в) /(0=0,1 sinlOOM (0 А. Параметры схемы:
Я=100 Ом; L=1 Гн.
85
изменения во времени,
аг и
Рис. 8.32
8.58р . Найти ток в цепи рис. 8.32,6 и построить график его
лагая, что входное напряжение имеет
форму, изображенную на рис. 8.33, а—г.
Параметры схемы: R =0,5 кОм; С=1
мкФ.
8.59р . Определить ток в цепи схемы
задачи 8.58р при условии, что началь-
ное напряжение на конденсаторе Uco=
— 100 В. Расчеты выполнить при фор-
мах входного напряжения, изображен-
ных на рис. 8.33, а, в.
8.60р . К последовательному резонансному контуру (рис. 8.34, а)
с малыми потерями (Q^> 1) подключают импульсные источники
ЭДС, графики ЭДС которых показаны на рис. 8.34, б,в. Найти
Рис. 8.34
выходное напряжение u2(t) и построить график его изменения
во времени, полагая, что частота синусоиды, заполняющей им-
пульс, <t)=(t)0 = а время кратно 2л/сй0, т. е.
где k — 1, 2, 3...
Г. Метод дискретных преобразований
8.61р . В цепи рис. 8.35 переключение выключателя происхо-
дит циклически с периодом Т. Первая часть периода, во время
которой конденсатор заряжается (переключатель в положении
О—/), имеет длительность tt, вторая (переключатель в положе-
нии 0—2)— (Г—tj.
Считая сначала конденсатор разряженным, найти закон изме-
нения напряжения на конденсаторе для любого цикла и оценить
минимальное число циклов, при котором достигается установив-
86
шийся, периодически повторяющийся переходный процесс. Пара-
метры цепи: Я1 = 2Яа = 2 кОм; С = 5 мкФ; £=100 В.
8.62. К входу цепи рис. 8.36 начиная с момента времени
/ = 0 на время подключают источник ЭДС ^(Z), а затем на
время —источник ЭДС е2(0. Переключение контакта из поло-
жения /—2 в 1—3 и обратно происходит с периодом
Рис. 8.35 Рис. 8.36
Построить график напряжения на входе цепи uw в функции
времени и найти закон изменения напряжения на выходе и для
любого интервала времени, включая установившийся периоди-
ческий режим, если: а) ех(1) = Е- е2(/) = 0; ^ = 0,8 Г;
б) М0=£; М0=0; /, = г2=о,5 в)М0=2£; М0=£;
^ = /, = 0,5 7\ Принять £=100 В; 7' = 2,5-10“3 с; /?=16 Ом;
£ = 0Л Гн.
8.63. По данным задачи 8.62 определить закон изменения
тока для любого интервала времени, включая установившийся
периодический режим, если (t) =е2 (/) = Ет sin 4- ф); /1=/2=
=Т; = 2л/Г0, где Ет = 100 В; Го = 2Т = 2,5 • 10-3 с. Параметры
схемы: R=2 Ом; £ = 4-10~8 Гн.
Построить графики напряжения на входе и тока в цепи,
если: а) ф = 0; б) ф = л/2; в) установившийся режим наступает
после первой коммутации. Для всех случаев найти среднее зна-
чение тока в установившемся режиме.
Рис. 8.37
8.64. Определить закон изменения напряжения на выходе
иепн (рис. 8.36) при подаче на ее вход дискретно изменяющихся
с интервалом времени Т напряжений we< = Mi0, форма которых
показана на рис. 8,37, а—в.
87
Д. Метод переменных состояния*
8.65. По законам Кирхгофа составить уравнения состояния
цепей рис. 8.38» п. б после коммутации и уравнения связи выход-
ной переменной и2 с переменными состояния и внешними воз-
действиями.
Рис. 8.38
8.66р . Методом приведения к резистивной цепи составить
уравнение состояния цепи рис. 8.39 после размыкания контакта
и уравнение связи выходной переменной и2 с переменными состоя-
ния и внешними воздействиями.
8.67. Составить уравнение состояния цепи рис. 8.40 после
ее переключения с et(f) на е(/) и уравнение связи ic, iL
Рис. 8.39
Рис. 8.40
с переменными состояния и внешними воздействиями. Вычи-
слить коэффициенты уравнений при С —1/16 Ф; £=1/6 Гн;
Я1 = Яа=Я3 = 2 Ом.
8.68р . Для цепи рис. 8.40 (см. условие задачи 8.67) найти
/д(0, <с(0 и ut(0 после коммутации, если: a) ei(0 = £*x = 2O В;
е(0 = 0; б) = «(/) = £ = —20 В; в) ех(0 = Е1 = 2О В;
e(t) = E =—20 В. Параметры цепи: С = 1/16 Ф; £ = 1/6 Гн;
= = 2 Ом.
8.69. Для послекоммутационной цепи рис. 8.41 методом пере-
менных состояния определить uc(i) и iL(i), полагая e(t) = E =
= 10 В; / (0 = J = 10 А; С=1/8 Ф; £=1/2 Гн; Ях=/?2-₽3=2 Ом.
Задачу решить при следующих начальных условиях: а) ыс(0) =
=0; iL (0) = 0; б) ис (0) = 10 В; q=(0)=—5 А.
* Во всех задачах настоящего раздела предполагается, что в качестве пере-
менных состояния выбраны напряжения на конденсаторах и токи в индуктив-
ных катушках.
88
Рнс. 8.4!
8.70. Для послекоммутационной цепи рис. 8.41 методом пере-
менных состояния рассчитать пс(/), х£(0» Ч?(0. 4? (Л и
полагая е(/) = 20е~4г В; / = 0; С =1/16 Ф; £ = 1/6 I н; =
~R3 = 2 Ом.
Решить задачу при следующих начальных условиях: а) цс(0) =
= 10 В; (£(0) = 5 А; б) цс(0) = 40/3 В; iL(0) = 20/3 А; в)ис(0) =
=30 В; it(0) = 15 А; г) цс(0) =
= 40 В; i£(0) = 0.
8.71. Для цепи рис. 8.41 найти
iR(t) и uL(t) при действии толь-
ко одного источника, форма сиг-
нала которого представляет сту-
пенчатую единичную 1 (0 или им-
пульсную 6 (/) функцию, т. е. оп-
ределить переходные и импульсные
характеристики цепи. До подключения источника считать началь-
ное состояние цепи нулевым.
Задачу решить при: a) e(t)
= 1(0; в) е(0 = 6(0; /(0 = 0;
= 1(0; /(/) = 0; б) е(/) = 0; /(/)=
г) е(0 = 0; /(0 = ^(0- Параметры
цепи: С—1/16 Ф; £=1/6 Гн;
Ri = pi = R3^2 Ом.
8.72. Для цепи рис. 8.42 сос-
тавить уравнение состояния, вы-
числить переходную функцию е1л,1f
и найти uci(t), ucz(t) и iL(l) при
следующих условиях: 1) внешние
воздействия после коммутации от-
сутствуют [е (0 = 0; j (/) = 0], на-
чальное состояние задано: (0) =
= 1 В; иС2 (0) = 0; iL (0) = 0 или
Рис. 8.42 uci (0) — 1В; иСо (0)— 1 В; ij (0)
= 0; 2) в цепи действуют импульс-
ные источники: e(t) = 6(f); /(f) = 0 или е(0 =0; /(f) = 6(f).
До включения источников считать состояние цепи нулевым.
Параметры цепи: С] = CZ = 1/3 Ф; £ = 3 Гн; Rt — R2 — 1 Ом.
Е. Численные методы
8.73р. Для послекоммутационной схемы цепи рис. 8.38, а
составить дифференциальное уравнение относительно напряжения
на выходе u2(f). Численно найти закон изменения w,(f) после
коммутации от / = 0 до t = 5 с, полагая Rx — R* —10Е. * 3 Ом; С —
— 10-3 Ф; /(0=0,01/ А.
8.74. Для схемы цепи рис. 8.38,6 составить дифференциаль-
ное уравнение относительно напряжения на выходе и2 (/) и с ша-
гом h = 0,25 с решить его для интервала времени 1 — 0—2,5 с,
полагая Rj = R2 — 0,2 Ом; £ = 0,1 Гн; = е = 54'5е-0,5/ В.
89
8.75. Для схемы цепи рис. 8.40 после ее переключения с
е2(0 на e{t) составить дифференциальное уравнение относительно
напряжения на конденсаторе uc(f) и решить его при /?, = ₽а =
= R3 = 2 Ом; L=l/6 Гн; С=1/16 Ф; et = 20 В; еа = —10 В.
8.76. Для цепи рис. 8.42, образовавшейся после коммутации,
составить дифференциальное уравнение и численно с шагом h —
Рис. 8.43
С,
нии с шагом Л = 0,1
вале t = 0 4- 1 с.
=0,1 с найти изменение тока iL(t) для
интервала времени t = 0— 1 с, полагая
е = 0; /=0; иС1(0) = 1 В; «С2(0) = 0.
Параметры цепи: Cj=Ca=l/3 Ф;
Л = 3 Гн; Rl = Rt=\ Ом. Выполнить
решение задачи с шагом Л = 0,05 с.
Оценить погрешности полученных реше-
ний с шагами h = 0,1; 0,05 с по сравне-
нию с точным решением (см. задачу
8.72).
8.77. Импульс напряжения и (/) (рис.
8.43) воздействует на пассивный двух-
полюсник, переходная характеристика
которого g (/)==!—е“иг. Представив
график u(t) рядом дискретных значе-
найти изменение входного тока в интер-
Глава девятая
Спектральный метод анализа
линейных электрических цепей
А. Частотные характеристики цепей
9.1. Найти выражение для комплексной функции передачи
четырехполюсника К (jv) = t/2 (jo))/^ (fw) (рис. 9.1, а). Построить
графики амплитудно- и фазочасготных характеристик передачи
/?
Рис. 9.1
/С (ш) и <pft при a) R^R^R; б) R2^> Ri=Rt полагая R=10 кОм;
С= 10 мкФ.
9,2. Найти выражения для входной проводимости Y (ju>) —
— h (ММ (jv) и комплексной функции передачи Л (/о) =
90
==UAia)/ViU^ для цепи рис. 9.1,6 при условии, что L)R =
=CR(R = V L/C).
9.3. Показать, что для пассивного двухполюсника, содержа-
щего помимо активных сопротивлений сколько угодно емкостных и
индуктивных накопителей энергии, действительная частотная ха-
рактеристика входного сопротивления R((&)—четная, а мнимая
частотная характеристика А" (со)—нечетная функции со.
9.4р . Пассивные двухполюсники (рис. 9.2, а—г) состоят только
из реактивных элементов. Показать, что угол наклона частотной
характеристики X (со) при любой частоте <о положителен, т. е.
>0.
do
9.5. Определить комплексную функцию передачи К (/«1 =
= С72(/«О)/1/1(Ло) мостовой схемы рис. 9.3, а и убедиться, что ее
а) б)
Рис. 9.3
амплитудно-частотная характеристика К (со) не зависит от частоты.
Найти частотную зависимость времени задержки t3 (<о)= | d<pA.(o))/do) |,
полагая R = 1 Ом; L— 1 Гн.
9.6. Определить фазочастотную характеристику (ш) функции
передачи сигналов напряжения по линии без потерь длиной
согласованной на конце. Используя зависимость <jpfr(co), рассчитать
время задержки t3 сигналов в конце линии. Параметры линии
на единицу длины До и Со считать известными.
9.7. Найти выражения и построить графики амплитудяо- и
фазочастотны к характеристик цепи, пропускающей в диапазоне
частот от 0 до сигналы со входа на выход без искажений
[идеальный фильтр).
9.8р . Для последовательного резонансного контура с большой
Добротностью Q (рис. 9.3,6) рассчитать точное и приближенное
(при Q^> 1) выражения для коэффициента передачи К (j&>) —
91
9.9р . Определить полосу пропускания цепей рис. 9.4, а, б,
полагая R — 1 Ом; L = 0,1 Гн; С=10мкФ.
Указание. Полосой пропускания считают область частот, в которой
К (<о)/К (^)щах меняется в отношении 1/рг 2.
* L L L
О—Г~~>—у о О—rw-y у--О
c=r Пя Пя
о---------* о о-----1-----1—0
а) Ь)
Рис. 9.4
9.10. Комплексное сопротивление нелинейного инерционного
сопротивления (например, дуги, термистора) относительно малых
наложенных синусоидальных колебаний можно представить ли-
v нейным сопротивлением Z (/<о) = ——»где
. ✓ T—постоянная времени, обусловленная тепло-
7 \. выми процессами; ₽с, Ra—статическое и диф-
ференциальное сопротивления для заданного ре-
жима работы (точки /, 2, 3 в. а. х. на рис. 9.5).
____________ Построить годограф Z(/co) при: а) /?я=
1 ==—Юм; Д=3 0м; Т=10-эс; б) Яй=0;
Рис. 9.5 Яс=1Ом; 7=10-3с; в) Яд=0,5 Ом; Rc =
= 1,5Ом; T=10"3c.
Примечание. Под годографом понимают кривую, соединяющую концы
векторов Z (/со) на комплексной плоскости.
(гауссов импульс) выражается такой же по
Б. Спектры периодических и апериодических сигналов
9.11. Показать, что спектр S (ш) напряжения e(t) =
А 1 / t
~ ——— е~ { 7"
у 2л/! г‘
виду функцией. Как связана ширина импульса e(t) с шириной
его спектра 5е(ш)? Определить спектр £е(ю) при a) tx —> 0;
б) ix —► оо, А—>оо, если Л//1 = В1/Г2л = const.
Примечание. Ширина кривой, описываемой функцией Гаусса, опреде-
ляется значениями абсцисс, при которых ее амплитуда изменяется в е~1/2 раз.
9.12. Сигнал e(t) представляет собой периодическую последо-
вательность прямоугольных импульсов напряжения (рис. 9.6).
Представить его рядом Фурье в комплексной форме записи.
9,13. Для периодической последовательности импульсов напря-
жения e(t) (см. условие задачи 9.12) построить графики спектров
амплитуд и фаз. При построении считать время импульса фикси-
рованным, а период Т определить из условия: а) Т = 2гх; б) 7 = 4/р
В) T^t..
9.14. Для последовательности импульсов напряжения, рас-
смотренной в задаче 9.12, построить график спектров амплитуд,
92
полагая фиксированным период 7' = 4л-10~яс. Длительность им-
пульса: а) ^ = 772; б) ^ = 774; в) /i<^7'.
9.15. Найти связь составляющих мощности сигнала в задаче
9.12 с комплексными составляющими спектра.
Рис. 9.7
9.16. Найти спектральную характеристику S(/(d) одиночных
прямоугольных импульсов напряжения (рис. 9.7, а. б). Построить
графики спектров амплитуд и фаз. Показать, что 5(0) опреде-
ляется площадью импульса.
Рис. 9.8
9.17. Найти спектры экспоненциального импульса напряжения
(рис. 9.8, а), скачка напряжения в виде ступенчатой (рнс. 9.8,6)
и 6-функций (рис. 9.8, в).
9.18р . Найти спектры импульсов напряжения, формы которых
приведены на рис. 9.9, а—в.
Рис. 9.9
9.19. Определить распределение энергии в спектре и полную
энергию для следующих апериодических сигналов е (/): а) 6-функ-
иии (рис. 9.8, в); б) прямоугольных импульсов (см. рис. 9.7, а, 6);
В) экспоненциального импульса (рис. 9.8, а); г) спектра, задан-
93
кого аналитически: на участке от ю —0 до = S(w) = 1; на
участке от (1) = ол/2 до <о = шо S(ti)) = K2(l—ш/соо); на участке
w = w0 до (1) = оо S((d) = 0.
9.20р . Приближенно рассчитать ширину спектра Д/х импульс-
ных сигналов конечной длительности (рис. 9.10, а—в).
Рис. 9.10
Примечание. Под шириной спектра понимают полосу частот, в которой
сосредоточена основная энергия сигнала (~ 0.91F).
В. Корреляционные функции детерминированных
и случайных сигналов и их спектры
9.21р . Найти автокорреляционную функцию /?(т) для следую-
щих сигналов: а) е(/) = £0; б) е (/) = Ет cos (со/—ф); в) прямо-
угольного импульса амплитудой Е и длительностью г) e(t) =
= 6(0, где 6(f) —6-функция.
9.22. Определить автокорреляционную функцию периодического
сигнала напряжения е(0» представленного конечным рядом Фурье:
е (1) = Е„ + sin (at + <ь) + Е,т sin (2at + <p8) = 10 +
+10 sin (1001—30°) + 5 sin (2001 + 30°) B.
Вычислить среднеквадратическое значение e- (0, т. e. среднюю
мощность сигнала.
9.23. Случайный стационарный сигнал напряжения опреде-
ляется выражением e(t) = Emsin (ot -}-ф), где Ет, со—постоянные
величины; ф—случайная величина. Най-
ти автокорреляционную функцию сиг-
нала.
9.24р. Автокорреляционная функция
R (т) случайного сигнала напряжения
e(t), полученная в результате обработ-
_______________кн опытных данных, представлена на
~ ° 1 2 рИС 9д 1, Найти среднеквадратическое
₽ис- 9-Ч_______значение е2(0, среднее значение e(f);
приближенно оценить время корреляции
<0
J R (т) dz
___________
0 R (0)____•
9-25. Рассчитать взаимную корреляционную функцию Ret {
сигналов напряжения e(t) и тока »(/), пола!ая: а; е—
94
i sin И+ф(); 6) e (0= Ea cos (о/—<pe); i (0= la cos (2to/—ф,);
в) <?(0 = £mcos(<o/—фе); t(0 = /wcos(o)/—Ф,).
9,26р. Рассчитать взаимную корреляционную функцию /?е</(т)
импульсов напряжения е(/) и тока <(0, представленных на
рис. 9.12, а—г.
Рис. 9.12
9.27 р. Предложить способ определения коэффициента пере-
дачи К (/со) = Us (fatyUi (/to) линейного четырехполюсника, внутри
которого имеется источник помех, значительно превышающих по
амплитуде входное напряжение (0^t/lmsin<ot Считать, что
входной сигнал и помехи не коррелированы
между собой.
9.28 р. Найти энергетический спектр G(co)
детерминированных сигналов следующего ви-
да: a) e(t) = Ea; б) е(/) = £1ст cos(toj —ф,);
АО
В) е(/)=Е<,+ s Eb.costfatf.r—ф»), где
Ео=10В; £^ = 20/£В, fe=l, 2, 3, ....
9.29 р. Определить энергетический спектр
Рис. 9.13
G (со) случайного
процесса, автокорреляционная функция которого представляет
собой «узкий» импульс.
9.30 . Энергетический спектр G (о) случайного стационарного
процесса построен по опытным данным (рис. 9.13). Найти сред-
нюю мощность процесса.
Г. Прохождение периодических, апериодических
и случайных сигналов через линейные цепи
9.31 . Рассчитать напряжение на входе схемы рис. 9.14. а,
к которой подключен источник! периодического тока / (/), изме-
няющегося в соответствии с рис. 9.14, б, считая: а) Т= 2^; б) T=4/v
95
При расчете использовать комплексное представление ряда Фурье.
Параметры схемы: R=IOm; £=1Гн; Т = 6,28с; /СТ = 2А. Рас-
чет ограничить определением пятой гармоники.
9.32р . Рассчитать напряжение на входе схемы рис. 9.14, а при
воздействии импульса тока прямоугольной формы (рис. 9.14, в).
Расчет провести двумя способами: а) по переходной или импульс-
ной характеристике цепи; б) методом периодизации, т. е. полагая,
что импульсы повторяются с периодом При расчете этим
методом ограничиться первыми пятью гармониками разложения
в ряд Фурье периодизированной кривой.
Рис. 9.14
Рис. 9.15
9.33р . На пассивный двухполюсник воздействует импульс тока
малой длительности (рис. 9.15,6). Найти напряжение на входе,
если частотная зависимость активной составляющей входного
сопротивления двухполюсника задана графически (рис. 9.15, а).
При решении использовать графоаналитический метод трапеций.
Исходные данные: ₽0= 1,57 Ом; = 100 рад/с; со2 — 2Ы]; J j (/) dt=
о
=QO=1 Кл.
9.34р . Определить форму сигнала на выходе идеального низ-
кочастотного фильтра при воздействии на входе: а) импульса
напряжения в виде 6-функции Uj (0 = 6(0; б) единичного скачка
напряжения ut (0=1(0- Передаточная функция фильтра К (/«)=
= Ке~/“/» при /Ujco)—-0 при ю>сос. При каких условиях
передача указанных сигналов не будет искажена?
Рис. 9Л6
9.35. На вход четырехполюсника рис. 9.16, а воздействует'
прямоугольный импульс напряжения амплитудой UM = 1 В и дли-
тельностью 0=1 с (рис. 9.16,6). Параметры четырехполюсника:
96
R = 1 МОм; С = 1 мкФ. Определить выражения для модуля и ар-
гумента спектра напряжения на выходе.
9.36. Импульс тока / (t) с заданной в виде графика спектраль-
ной плотностью S, (со) (рис. 9.16, в) проходит по резистору сопро-
тивлением /?=ЮОм. Найти энергию, которая выделится в рези-
сторе при воздействии импульса.
Рис. 9.17
9.37р . Импульс прямоугольной формы амплитудой £ = 2В и
длительностью ^=1с (рис. 9.17,о) воздействует на четырехпо-
люсник (рис. 9.17,6). Определить, какая часть энергии импульса
выделится в нагрузке. Задачу решить, используя теорему Рейли.
Сопоставить решение с результатом, полученным при интегриро-
вании по времени. Параметры четырехполюсника и нагрузки:
С- 1 мкФ; МОм.
9.38р. Импульс прямоугольной формы длительностью
(рис. 9.17,а) подан на вход последовательного резонансного
/^LC-контура (рис. 9.17, в) высокой добротности
Найти выражение для тока в контуре после подачи импульса
в случае, когда период собственных колебаний контура Т =
=2лКГС=2/,.
9.39. Некоторую функцию времени с ограниченным спектром
(ему соответствует полоса частот от 0 до требуется передать
без потери информации с помощью чисел через равные интервалы
времени. Через какие наибольшие интервалы времени следует
изменять и передавать значения функции?
9.40. Для схемы четырехполюсника рис. 9.17,й составить пе-
редаточную функцию К (jw) = (/со)/^! (/®) и 110 ней найги зна-
чение переходной функции четырехполюсника h(t) при /=0, оо,
т. е. й (0) и Л (оо).
9.41. Для пассивного четырехполюсника опытным путем полу-
чена переходная характеристика h (0=1—е_(Х<. Определить пере-
даточную функцию Л (/ш) этого четырехполюсника.
9.42р . На вход цепи рис. 9.18, а поступает случайный сигнал
u(t), энергетический спектр которого можно считать постоянным,
т. е. Gn(w) = Gc В2/с. Найги энергетический спектр Одсо) и кор-
реляционную функцию /?,(т) тока в цепи.
9.43. На вход пассивного четырехполюсника (рис- 9.18,61 по-
ступает случайный сигнал к, (/) с энергетическим спектром СД1 ((d).
выбрать амплитудно-частотную характеристику коэффициента
97
передачи К (to) так, чтобы энергетический спектр выходного на-
пряжения соответствовал спектру белого шума, т. е. Gui (со) — Go.
* Л Л ГЧ 41 Ы ___________
а) 6)
Рис. 9.18
9.44. Линейный четырехполюсник
представляет собой идеальный фильтр
низких частот. Найти энергетический
спектр и корреляционную функцию
выходного напряжения, полагая, что
на вход фильтра подается шумовое
напряжение ux(t) со спектром
Gf;1 (to) =G0 (белый шум). Передаточная
функция идеального фильтра дана в задаче 9.34р.
Глава десятая
Синтез двухполюсников и четырехполюсников
А. Возможность реализации двухполюсников по заданному Z(p).
Определение элементов двухполюсника
10.1. Проверить, удовлетворяют ли приведенные выражения
для входного сопротивления
ческой реализуемости:
двухполюсника Z(p) условиям физи-
. 5р*+1 . рЗ+2ра+4р+8
6p3-J-2p* 4 p»4-3p2-j-24p+18 ’
проверить, выполняется ли условие
р*+рэ+4р®+Зр4-1
' p84-8p24-30p+I6 ’
10.2р . Методом Штурма
Ее/(/о))^0для двухполюсника, у которого7(р)= р^рз^рЪ-^р^ i
10.3. Можно ли осуществить двухполюсник из элементов L
„ \ \ (Р2-Н) (р2+9) _ . (р2-]-0,25)(р24-2)
и С, если, a) Z(p)— I б) Z(p)— P(2pa-f-3) ’
в)
' 6р3-~2р
10.4 р. Может ли двухполюсник состоять иэ элементов R и С,
если: a) Z(p)=-^^-; б) Z(p) = -^2?
10.5. Из каких элементов составлен двухполюсник, если его
нули р,——1, р3 =—3, р6 =—5, а полюсы ра =—2, рА = —4,
Ре - -6?
10.6. Может ли двухполюсник состоять из элементов R и L,
•7 1 \ р(2 + 0,02р) -
если Z(p)= o,3p-i-io ?
10.7р . Является ли двухполюсник с Z (р) — ДВУХП0'
люсником минимального реактивного сопротивления?
10.8. У некоторого двухполюсника пули входного сопротив-
ления pt = — 1, р3 = - 2 и полюсы р2,4 = —1 ± 2/. Является ли
он двухполюсником минимального реактивного сопротивления?
Б. Составление входных сопротивлений двухполюсников
10.9р . Составить входное сопротивление Z(p) двухполюсника
в виде отношений двух полиномов, нуль которого р,=— 1,а по-
люсы А> = 0 и рл — —1,5. Вычет функции Z(p) в полюсе ра = 0
равен 10/3.
10.10. Составить выражение для Z(p) двухполюсника, нуль
которого рг — —I, а полюс ря = —1/3. Вычет функции Z(p) в по-
люсе рг =—1/3 равен 2/9.
10.11р . Составить выражение Z(p) двухполюсника, нули кото-
рого Pi = 0, р3<6 = ±/, полюсы p2i4—±/0,578 и вычет функции
Z(p) в полюсе р2— 0,578 равен 2.’
10.12. Составить У(р) двухполюсника, который имеет два нуля
на мнимой оси ± / и три полюса (0, 2/, —2/). Вычет функции
Y (р) в полюсе р = 0 равен 1, а в полюсе р=2/ равен 1,5.
В. Реализация Z(p) лестничной схемой,
путем последовательного выделения
простейших составляющих и методом Бруне
10.13. На рис. 10.1, а изображена лестничная схема. На ри-
сунке числовые значения индуктивности катушек даны в генри,
емкость конденсаторов—в фарадах, активные сопротивления ре-
зисторов—в омах. Записать выражение для входной проводи-
мости схемы в виде непре-
рывной дроби.
10.14р . У некоторой лест-
ничной схемы выражение для
входного сопротивления пред-
ставлено в виде непрерывной
дроби:
Z(p)=p+--------Ц------.
₽+-------j---
'+-----Г~
2₽+zp + 3
Рис. 10.1
Составить лестничную схему и найти числовые значения ее
элементов.
10.15. Для некоторой лестничной схемы входная проводи-
мость дана в виде непрерывной дроби. Составить схему и найти
числовые значения ее элементов, если
Г(р)=-5---1
Т+Т-
10.16. Реализовать лестничной схемой двухполюсник, для ко-
\ \ ах 'j I \ 1000 ±600р 50р2±р3
торого: a) Z(p) = 5;^__; б) Z(p) =--------
99
10.17. Реализовать двухполюсник с Z(p)=^—2^: а) путем
последовательного выделения простейших составляющих; б) лест-
ничной схемой.
10.18. I. Путем последовательного выделения простейших со-
ставляющих реализовать двухполюсник, имеющий
7 . . ЗОр4 +146,5р3+ЗОр® 4- 48.5р 4
р(Зр®4-1) (p-j-8)
Убедиться в том, что реализация лестничной схемой, в каж-
дой ветви которой имелось бы по одному элементу (/?, L, С), для
данного случая невозможна.
2. Реализовать методом выделения простейших составляющих
Z(P)= 2pit^+1-
V' p*+p
10.19р . Методом Бруне реализовать двухполюсник, входное
сопротивление которого Z (р) ?=
10.20. Реализовать методом Бруне двухполюсники, имеющие
\ 2р®н-р+1 x\4ps+p+1
следующие входные сопротивления: а) ; б) >
хр* Ар-уЪ Р" Т Р Т 1
10.21. Реализовать методом Бруне двухполюсники, заданные
. р»4-5р84-2р+1 . 4р34-4р24-4рЧ-3
входными сопротивлениями: а) - . г • I б) 3v~ j ;
Г. Реализация двухполюсника по временному отклику.
Связь между действительной и мнимой частями
10.22р. При нулевых начальных условиях на вход пассивного
двухполюсника поступает ток *(/)=100/ от источника тока
(рис. 10.1,6). При этом напряжение на входе ц(/) = 10ь/—КРх
Х(1—е~1001). Составить схему двухполюсника и определить его
параметры.
10.23. Для некоторого двухполюсника комплексное сопротив-
ление на частоте Z (/со) = A (to) 4- /В (со). Известно, что А (со) =
= (о2/(1 4-со2). Найти В (со).
Указание. При решении воспользоваться соотношением В(<ос) =
2 Г Л (со)
= — iaw, в котором после интегрирования заменить шс на со.
п со£
10.24. Для некоторого двухполюсника А (со) = . Опре-
делить (нВ (ю) при (О—> оо.
Указание. При решении воспользоваться соотношением соВ (ш) =
41>-*Э0
ОО
2 с
------1 (Л — Дм) dto; Л« = А (со)4
л х Ю-+»
100
Д. Некоторые особенности преобразования треугольника
в звезду и звезды в треугольник. Эквивалентные замены.
Дополняющие и взаимно обратные двухполюсники
10.25р . На рис. 10.2, а изображена Т-схема (звезда), в плечах
которой имеются резистивные, емкостные и индуктивные элементы.
Проводимости лучей звезды Уг = а\ Y^ — jk^a, Y9= — jk3a, где
k£t k3—числовые коэффициенты. Показать, что для этой схемы
Рис. 10.2
физически невозможно реализовать ее П-эквивалеш (схему
рис. 10.2,6) при k2 и k3t одновременно не равных нулю и друг
другу-
10.26. На рис. 10.2,в изображена П-схема, состоящая из ре-
зисторного, индуктивного и емкостного элементов. Сопротивления
элементов схемы указаны на рисунке. Показать, что при любых
значениях числовых коэффициентов k9 и ke, не равных нулю и
друг другу, Т-эквивалент схемы рис. 10.2, г физически реал изо-
Рис. 10.3
10.27р . На рис. 10.3, а изображено последовательно-парал-
лельное соединение сопротивлений, где Z1 и Z2—некоторые ча-
стотно-зависимые сопротивления: а-—числовой коэффициент- Пока-
зать, что для любых частот этому соединению соответствует уча-
сток цепи рис. 10.3,6. Коэффициенты Ь, с, d выражены через
Коэффициент а следующим образом: 6 = а(1-]-а), с=(1-|-д)\
«= 1-Ьа.
10.28. Вывести формулы, которые позволяют осуществить
эквивалентный переход, справедливый для любых частот, от схемы
Рис. 10.3,в к схеме рис. 10.3, г.
101
10.29. Используя преобразование звезды в треугольник, тре-
угольника в звезду и эквивалентные преобразования, рассмотрен-
ные в задачах 10.27р и 10.28, привести к каноническому виду
с минимальным числом индуктивных и емкостных элементов схему
рис. 10.3, д. Параметры схемы: L[ = L'2 = 2,5 Гн; /4=1.25 Гн;
L4=Ls = 0,5 Гн; £в=1 Гн; Llo = 0,25 Гн; С — 2,25 Ф.
10.30. Задан двухполюсник, содержащий в общем случае резис-
тивные, индуктивные и емкостные элементы. Его входное сопро-
тивление Zf. Двухполюсником, дополняющим исходный, называют
двухполюсник с входным сопротивлением Z2, который, будучи
включен последовательно или параллельно с исходным, дополняет
полное входное сопротивление до чисто активного.
В качестве примера на рнс. 10.4, а изображен исходный двухполюсник,
а на рис. 10.4, б—дополняющий. Если их соединить последовательно, то
результирующее сопротивление будет чисто активное. Схема, характер элемен-
тов и числовые значения параметров дополняющего двухполюсника зависят от
схемы, характера элементов и числовых значений параметров исходного двух-
полюсника. Элементы дополняющего двухполюсника дуальны элементам исход-
ного (индуктивный элемент L/ схемы рис. 10.4, а заменен на емкостный Са
в схеме рис. 10.4, б) и по значению таковы, что сопротивление элемента исход-
ной схемы, умноженное на сопротивление соответствующего элемента допол-
няющей схемы, равно /?2, где R—произвольное активное сопротивление. Напри-
мер, откуда Ct=Lt/R2. Параллельное соединение и G
/CDC2
в исходной схеме заменяют последовательным соединением C2 = Li/7?8 и La==
= CtR2 в дополняющей схеме. Последовательное соединение Lj и в исходной
схеме заменяют параллельным соединением C2=bi//?2 н Lz = CiR2 в допол-
няющей схеме. Резистивные сопротивления оставляют без изменения.
Руководствуясь сказанным, убедиться в том, что двухполюс-
ник рис. 10.4, г является дополняющим для двухполюсника
рис. 10.4, в при их последовательном соединении.
10.31р . На рис. 10.4, д изображен двухполюсник в виде после-
довательного соединения элементов /?, и Сг. На рис. 10.4, *
дана схема дополняющего двухполюсника. Убедиться в том, что
параллельное соединение двухполюсников рис. 10.4, д, е имеет
чисто активное сопротивление.
10.32. Составить схему дополняющего двухполюсника для
рис, 10.1, ж так, чтобы при последовательном соединении исход*
102
кого и дополняющего двухполюсника результирующее сопротив-
ление было чисто активным.
10.33р . Два дуальных двухполюсника с входными сопротивле-
ниями Zj и Z2, причем ZjZ.2 = 7?2 (7?—некоторое заданное число
имеющее размерность сопротив-
ления), называют взаимно об-
ратными. Между взаимно дуаль-
ными элементами обратных
двухполюсников существует та-
кое же соотношение, как и между
входными сопротивлениями.
Составить двухполюсник, вза-
имно обратный данному па
рис. 10.5, а. Определить пара-
метры его элементов через параметры исходного двухполюсника
и коэффициент преобразования R. Показать, что произведение
входных сопротивлений дуальных двухполюсников равно R2.
Е. Проверка возможности реализации четырехполюсника
по его параметрам
10.34р . Проверить, могут ли выражения, приведенные для
Z-параметров, соответствовать некоторому физически осуществи-
~ р2-4-2р-Ь1 гу ч р -J-1
мому четырехполюснику: Zu = -—; Z12 = ZC2=i-^—.
10.35. Некоторый четырехполюсник имеет следующие Z-napa-
метры: Zu-=^i^ij-; Z12=Z22^^—.
Проверить, выполняются ли для данного случая условие
Геверца и условие вычетов.
10.36. Некоторый четырехполюсник имеет следующие У-пара-
метры: a) Yn = p- -Yn = p-, б)
__у 2 . у 2-J- Зр*
+ Г22— р3_^р-
Проверить, соответствуют ли они физически осуществимому
четырехполюснику.
Ж. Определение типа четырехполюсника
по его передаточной функции
10.37р . Передаточная функция по напряжению некоторого
согласованно нагруженного четырехполюсника — .
Выяснить, является ли этот четырехполюсник минимально-фа-
зовым.
10.38. Дано выражение для передаточной функции по напря-
жению при холостом ходе на выходе до и после сокращения на
103
общий множитель
К рЧр-М) = р*
А£/х - (р-н 1) (р®4-р+1) р2+р+ 1 *
Проверить, может ли приведенное выражение быть передаточ-
ной функцией неуравновешенного четырехполюсника, в котором
входной и выходной контуры имеют общую точку.
]2ра Х8р-|-1
10.39. Может ли передаточная функция
принадлежать лестничной схеме, состоящей только из элемен-
тов R и С?
10.40р . Задана передаточная функция по напряжению некото-
рого четырехполюсника до и после сокращения на общий мно-
житель:
к р3(р+1)(рЧ рЧ-1) р(р-Н)
Л^-ра(р2-Ь2р4-2)(р^4-р+1) р8Н-2р + 2 ’
Проверить, может ли эта функция быть передаточной функ-
цией лестничной схемы.
3. Реализация четырехполюсника Г-схемой
10.41. Реализовать четырехполюсник с передаточной функцией
по напряжению при холостом ходе Л^х = 6р2^.^р_|_ р в виДе
Г-схемы рис. 10.5, а. Составить эквивалентные схемы, используя
в качестве дополнительных полиномов: a) Q —6р-{- Г, б) Q = p4* I;
в) Q = p 4-0,5.
10.42. Для некоторого четырехполюсника = -^ - f .
Реализовать четырехполюсник в виде Г-схемы рис. 10.5, б. Для
сопоставления с ответом взять дополнительный полином Q —р-4-5.
10.43р . Передаточная функция четырехполюсника задачи 10.42
записана в нормированном виде. Она нормирована при безразмер-
ной частоте w0 = 104 и безразмерном сопротивлении /?0 — 10s.
Схема соответствующего четырехполюсника с нормированными
параметрами изображена на рис. 0.10.5, а. Требуется перейти
от нормированных параметров этой схемы к ненормированным.
10.44. Реализовать передаточную функцию четырехполюсникз
Кик — 4/Л+7р~4 [* полагая, что первый нуль дополнительною
полинома Q (р) находится посередине между нулями а второй
нуль равен сумме полюсов
10.45р . Четырехполюсник рис. 10.6, а служит для амплитудной
коррекции. Он нагружен на сопротивление 7?, его входное сопро-
тивление равно R. Сопротивления Z, и Z, взаимно обратны:
Z,Z2 — R-. Если Zj образовано параллельно соединенными Rt и Li
(рис. 10.6, б), то Z2—это последовательно соединенные R., и С
(рис. 10.6, е). В этом случае затухание четырехполюсника о
104
==lnf/i/i/2 характеризуется кривой рис. 10.6, г. При <о = 0
с ростом со а увеличивается. Если Zj образовано параллельно
соединенными /?t и Сг (рис. 10.6, д), то Z.,—это последовательно
соединенные Т?2 и £« (рис. 10.6, е). Соответствующая зависимость
д=^/(о) изображена на рис. 10.6, ж. Затухание а уменьшается
с ростом со. Вывести формулы для определения Zx и Z2 четырех-
полюсника рис. 10.6, о, полагая заданными сопротивление на-
грузки R и затухание четырехполюсника а при двух значениях
частоты для следующих случаев: а) форма зависимости а = /(со)
Рис. 10.6
соответствует кривой рис. 10.6, г\ значения а заданы при со, [a (wj]
и со2[а(со2)]: б) форма зависимости а —Цы) соответствует кривой
рис. 10.6, ж\ значения а заданы при <о = О [а(0)] и [с(coj].
Учесть, что затухание четырехполюсника рис. 10.6, а опреде-
ляется через его параметры Zx и R (вывод см. в [3]): ес =
- 11 +
И. Задачи на различные темы
10.46р . Напряжение на выходе Г-образного четырехполюсника
рис. 10.7, а при холостом ходе на выходе и подключении его
К единичному напряжению — 1 В изменяется во времени сле-
дующим образом: «,(/) = 0,448 (e“3,63t—е”8®*17*) В. Составить пол-
ную схему четырехполюсника.
10.47. Для четырехполюсника рис. 10.7, б сопротивление Zt
Представляет собой входное сопротивление источника питания,
Подключенного к зажимам/—/; Z2=r3—сопротивление нагрузки,
105
подключенной к зажимам 2—2. Взаимная проводимость между
ветвями 1 и 2 y^ = ^ApWAP)- Вывести формулу для определе-
ния сопротивления Z3 = Z12.
10.48. Для четырехполюсника рис. 10.7, б Zj = l Ом; Za = р\
Найта Zs>
Рис. 10.7
10.49. При аппроксимации по Баттерворсу нормированной
передаточной функции низкочастотного фильтра, изображенной
на рис. 10.7, е, было получено выражение
(Р) = рЗ_|_2р2-1-2р+1 *
где p = jx; x = w/o)o; w0—безразмерная величина, равная частоте
среза фильтра. Найти затухание фильтра а с указанным К (р)
при частотах, равных <оо и 2со0.
10.50. Определить степень полинома Баттерворса, которым
аппроксимирована передаточная функция низкочастотного фильтра
с характеристикой | К (jx) | = f (х) (рис. 10.7, в), если известно,
что при х = 2 затухание а = 42 дБ.
Глава одиннадцатая
Установившиеся процессы в электрических цепях,
содержащих линии с распределенными параметрами
А. Первичные и вторичные параметры линии
11.1р . Для воздушной двухпроводной линии длиной / =
= 500 км известны погонные параметры: 7?О = 2 Ом/км; =
= 0,5-10“" См/км; Со = 5-10“° Ф/км; Lo = 2,5-10“3 Гн/км. Опре-
делить ZB, у = сс + /Р, к и коэффициент передачи напряжения
= | t/j/t/j | при согласованной нагрузке на частотах со1 = О;<о2=
= 314 рад/с; <о3 = 4000 рад/с; со4=104 рад/с. Построить графики
зависимостей а (о), Р(ю), Уф(со), ^(со), | ZB | (<о).
11.2. Для однородной линии на частоте/ = 1000 Гц постоянная
распространения у = (1,5 + /8л)-10“3 км-1, волновое сопротивление
ZB = 600 Ом. Найти у и ZB на частотах f = 50 Гц и f = 0.
11.3. Для кабельных линий ввиду близкого расположения пря-
мого и обратного проводников в диапазоне сравнительно невысо-
ка
ких частот (300 Гц—6 кГц) погонное индуктивное сопротивле-
ние много меньше погонного активного сопротивления, а
емкостная проводимость соСо значительно больше проводимости
утечки Go. Поэтому при приближенных расчетах можно считать
Lg Л/ 0, Gc г^О.
На частоте f=l кГц коэффициент затухания кабельной линии
а = 6Ю~а Нп/км. Чему равны коэффициент фазы на этой же
частоте и постоянная распространения у=а-Н₽< на частоте
f — 4 кГц?
11.4. Определить погонные параметры кабеля, если на частоте
ь>=1000 рад/с Z, = 500e-/“’; ? = (/“2 + j/Д)-10-» км"1.
11.5. Кабельная линия имеет следующие параметры: Ro —
== 10 Ом/км; Go«O; Lo«O; Со = 40-10“* Ф/км. В согласованном
режиме при ю=1000 рад'с источник отдает активную мощность
Л —100 Вт. При этом мощность в нагрузке Ра=5,91 Вт.
Рассчитать длину линии, напряжения и токи на входе Ц
и выходе Z73, /2, а также сдвиг фаз между входным и выходным
напряжениями.
Б. Искажения сигнала, передаваемого по линии.
Линия без искажений
Н.бр. По воздушной линии связи с параметрами /?0=2,5 Ом/км;
Go= Ы0“6 См/км; £с=1,9-10“э Гн/км; Со = 8-10“* Ф/км пере-
дается сигнал в диапазоне 100 Гц—10 кГц (звуковые частоты).
Какова наибольшая длина линии, если допустимое затухание
al ^3,3 Нп? Для найденной длины линии определить время
распространения сигнала по линии. Назвать причины отличия
формы сигналов на выходе и входе линии.
11.7 р. Катушку какой индуктивности необходимо дополнительно
включить на каждом километре длины линии, заданной в за-
даче Н.бр, чтобы она стала неискажающей? Как при этом изме-
нятся дальность передачи /тах (наибольшая допустимая длина
линии при затухании 3,3 Нп) и фазовая скорость? Чему равно
время распространения сигнала по линии длиной 1так?
11.8. На входе кабельной линии с параметрами Ro = 23 Ом/км;
Gd = 0,7-Ю"6 См/км; /^ = 0,6-10“3 Гн/км; Со=36-1О“* Ф/км,
1=50 км действует напряжение (t) = 500 sin 5000/ В.
При условии, что линия работает в согласованном режиме,
определить активные мощности, потребляемую нагрузкой Рн
н теряемую В ЛИНИИ Лотерь» а ТЭКЖв кпд передачи энергии
от источника к нагрузке т}. Как изменятся значения Ря, Рпотсрь.
*1 после включения на каждом километре длины линии дополни-
тельных катушек для обеспечения неискажающей передачи (в согла-
сованном режиме)?
11.9р . Какой наибольшей длины может быть кабельная линия
с параметрами, заданными в предыдущей задаче после включения
Дополнительных катушек, обеспечивающих неискажающую пере-
107
дачу сигнала, чтобы удовлетворялись два условия: 1) затухание
а/тах^3,3 Нп; 2) время распространения сигнала по линии
не должно превышать Л/тах = 0,15 с?
В. Распределение по линии мгновенных
и действующих значений тока и напряжения
11.10. На входе однородной линии с параметрами — 2 Ом км;
Go = 0,5-10“’ См/км действует постоянное напряжение — 1 кВ.
Линия нагружена на резистор /?н = Go- Длина линии / =
= 500 км.
Записать и решить для этого случая телеграфные уравнения
линии. На основании полученных решений построить графики
распределения по линии напряжения и тока U (х), / (х), где х—
расстояние, отсчитываемое от входа линии. Чему равно входное
сопротивление линии? Определить мощность развиваемую
источником, и мощность Ра, потребляемую нагрузкой, а также
КПД передачи энергии от источника к нагрузке 1].
11.11. На входе линии с параметрами, заданными в задаче
11.1 р, и длиной / = 1 действует напряжение (/) = 500 sin 4000/ В.
Линия нагружена на резистор ZH = ZB.
Рассчитать мгновенные значения напряжения и тока в конце
МО. 4(0. а также тока на входе ц(/) линии. Построить гра-
фики распределения по линии мгновенных значений напряжения
для моментов времени 0 = 0, /2 = л/(4ш); /3 = л/(2со); /4 = л/ш.
Рекомендуется воспользоваться результатами решения задачи
11.1р. приведенными в табл. Р.11.1.
11.12. Как изменится режим в нагрузке задачи 11.11, если
длина линии уменьшится вдвое? Изменится ли при этом мощность,
отдаваемая источником и КПД?
11,13. В условиях задачи 11.11 изменилось сопротивление
нагрузки: Z„=2ZB. Рассчитать мгновенные значения напряжения
и тока в конце линии, а также в точках, отстоящих от нагрузки
на расстояниях # = 1/4; 1/2. Определить КПД передачи энер-
гии от источника к нагрузке, сравнить его с КПД в согласован-
ном режиме.
11.14. Для линии с параметрами ZB = 7I3e_'6’e6° Ом; у =
=(1,4 + /14,2)- 10“э км“1, / = 1, нагруженной на резистор Z}I = 2ZB,
известна комплексная амплитуда напряжения на нагрузке (7S» =
= 327,6 В. Записать выражения для мгновенных значений напря-
жения и тока падающей и отраженной волн в середине линии
ипад(/, //2), 4ад(0 Z/2), Un-rp (t. 1/2),
4>тр (^* Z/2).
11.15. Линия с параметрами ZB = 713e~/e° Ом; у =
= (1,4 + /14,2)-10“3 км“1; / = 1 на конце разомкнута. Найти
мгновенные значения напряжения в конце и тока в начале
линии при напряжении на входе (/) =. 500 sin со/ В.
11.16р . На входе кабельной линии длиной / = 55,5 к.м дейст-
вует напряжение ц4(/) = 500 sin 1000/ В. Ток на входе при корот-
108
ком замыкании /1К(/) = 1 sin (1000/4- 21,5°) А, а при холостом
ходе /1Х (0 = 1 sin (1000/ + 68,5°) А.
Определить первичные параметры линии /?0, Ло, Go, Ср и мгно-
венные значения тока и напряжения в конце линии при согласо-
ванной нагрузке. Известно, что длина линии меньше 1/2.
11.17. При каком сопротивлении нагрузки линии с ZB =
==500е~'4Б° Ом; у = 0,02е'4Б° км-1; / = 1/8 в нагрузке выделяется
наибольшая мощность? Чему она равна, если напряжение на
входе и, (0 = 500 sin со/ В, а внутреннее сопротивление источника
близко нулю?
Г. Линия без потерь
11.18. На ‘ входе линии с параметрами £о = 210~3 Гн/км;
Св = 8-10"® Ф/км; 7?о = 0; Go —0; 1= 130 км действует напряжение
их (/) =500 sin(2л-4167) / В. В конце линии: a)ZH = ZB; б) ZH = oo;
в) ZH = 0.
Определить ZB, 1 и записать выражения для мгновенных
значений напряжения и тока в нагрузке п2(/), 4(0 в случаях
а)—в).
11.19. В условиях задачи 11.18 произошло изменение частогы
источника питания на 3 % (новое значение частоты / = 4167-1,03 =
— 4292 Гц). Во сколько раз изменится при этом амплитуда напря-
жения в конце линии, если: a) Z„=ZB; б) ZH = oo?
11.20р . На входе линии без потерь с волновым сопротивлением
ZB = 500 Ом;_Цф = 250- 10а км/с; / = 62,5 км действует напряжение
ut(0 = 500 И 2sin (2л-2500) / В. Линия нагружена на индуктивное
сопротивление = Определить напряжение на нагрузке U„,
ток на входе /г Построить графики распределения по линии
действующих значений напряжения и тока. На какам расстоянии
от нагрузки расположены ближайшая пучности и ближайший
узел напряжения?
11.21. В условиях задачи 11.20 в конце линии включено емкост-
ное сопротивление ZH = — /‘)/~3ZB. Определить напряжение и ток
в нагрузке.
11.22. Входное сопротивление линии без потерь длиной / —
= 62,5 км при ZB = 500 Ом ZBX1 =— /134 Ом. Рабочая длина
волны в линии 1=100 км. Определить модуль и характер сопро-
тивления нагрузки.
11.23. Определить комплексное сопротивление отрезка линии
без потерь с ZB = 500 Ом, нагруженного на Zll = ZB/2t длиной:
а) / = 1/2; б) / = 1/4; в) / = 1/8.
11.24. Входное сопротивление нагруженного отрезка линии
без потерь длиной /=(3/4) 1 с волновым сопротивлением ZB=400 Ом
^вх1 = 200 4-/200 Ом. Определить активную и реактивную состав-
ляющие сопротивления нагрузки.
11.25р . Для согласования линии без потерь, обладающей вол-
новым сопротивлением ZB1= 100 Ом, с нагрузкой (ZB = = 400 Ом)
199
между основной линией и нагрузкой включен четвертьволновый
отрезок линии без потерь с волновым сопротивлением ZB2. В основ-
ной линии наблюдается режим бегущей волны. Определить ZB1
и напряжение на нагрузке (Л, если на входе линии напряжение
t/x = 100 В,
11.26р . Рассчитать входное сопротивление линии без потерь
и сопротивление нагрузки, если известно отношение комплексов
напряжения падающей и отраженной волн (комплексный коэффи-
циент отражения) на входе линии fx = Uorpl/Una;ii — —^e”'46’.
Длина линии / = (9/16)Х, волновое сопротивление ZB = 400 Ом.
Глава двенадцатая
Переходные процессы в цепях
с распределенными параметрами
А. Волновой метод
12.1р. Линия без потерь с волновым сопротивлением ZB=400 Ом
длиной / — 300 км в момент времени t = 0 подключается к источ-
нику постоянной ЭДС £ = 500 В. Скорость распространения
электромагнитной волны в линии считать равной скорости света.
Получить выражения для мгновенных значений напряжения
и тока в конце и середине линии (х = /, х = //2), построить соот-
ветствующие графики. Рассмотреть следующие случаи нагрузки
линии: a) ZH = ZB; б) ZH = oo; в) ZH = 0. В каких режимах пере-
ходный процесс имеет ограни-
V. / 2 L j ценную длительность, а в ка-
—• — ких—протекает теоретически
| бесконечно долго?
rQ) ?в 12.2. В условиях предыдущей
у t , задачи Z„=2ZB. Построить гра-
2 __фики распределения по линии
мгновенных значений напряже-
0______I_________х ния и тока u(x), i(x) для мо-
х мента времени / = 2,5 l/v.
Рис. 12.1 12.3р. Линия без потерь бес-
конечной длины в момент време-
ни 1 = 0 подключается к источнику постоянной ЭДС £ = 400 В.
На расстоянии / = 600 м от входа линии последовательно вклю-
чена сосредоточенная индуктивность 1 = 1,6 мГн (рис. 12.1).
Построить эпюры распределения по линии мгновенных значений
тока и напряжения для момента времени t = 1,5 l/v, если ZB =
= 400 Ом; и = 3-109 м/с.
12.4. В условиях задачи 12.3 на расстоянии I от входа линии
параллельно ей включена сосредоточенная емкость С=0,01 • 10-€ Ф.
Построить графики и(х), i(x) для момента времени / = 3-10“6 с.
НО
12.5р . На вход линии без потерь длиной /=3000 м подклю-
чают источник постоянной ЭДС £ = 500 В с внутренним сопро-
тивлением /?DH = ZB. В исходном состоянии параллельно входным
зажимам линии включен конденсатор емкостью С = 0.04-10-6 Ф.
Конец линии разомкнут (рис. 12.2). Построить графики распре-
деления по линии мгновенных значений напряжения и тока для
моментов времени
tа = 1,5 l/v. Принять Ze=
^500 Ом; и=3*10эм/с.
12.6. В условиях зада-
чи 12.5р линия нагружена
на ZH = ZB. Получить функ-
ции распределения по ли-
нии мгновенных значений
напряжения и тока для
t = 2//и.
12.7. Линия без потерь
длиной I = 1500 м, на конце
которой включен конденсатор емкостью С = 1,25-10"9 Ф, в момент
времени t = 0 подключаются к источнику постоянной ЭДС £=600 В;
ZB = 400 Ом; и = 3-109 м/с. Определить мгновенное значение напря-
жения на конденсаторе в интервале 0 —3//и. Для / = 8-10”® с
построить распределение по линии мгновенных значений напря-
жения.
12.8р . По окончании переходного процесса, рассматриваемого
в задаче 12.7, параллельно конденсатору подключают катушку
индуктивностью £ = 0,8-10~э Гн. Построить эпюры распределения
мгновенных значений напряжения я тока по линии для t=2,5 • 10“G с.
12.9. Линия без потерь длиной /, разомкнутая на конце, в
момент времени t — 0 подключается к источнику постоянной
ЭДС £. Через интервал времени 2т = 2//ц последовательно с
источником £ включают еще один такой же источник. Показать,
что в этом случае переходный процесс имеет органиченную дли-
тельность. Рассчитать, чему она равна. Построить графики вре-
менных зависимостей напряжения и тока в точках х = 0, x—ll2,
х—1. Рекомендуется воспользоваться результатами решения задач
12,1 р или 12.11р.
12.10. На входе линии без потерь длиной I, разомкнутой на
конце, действует прямоугольный импульс напряжения амплитудой
£ и длительностью: а) 2т = 2//и; б) 4т = 4//и. Определить напря-
жение, возникающее в конце линии, построить его графики для
случаев а) и б). Рекомендуется воспользоваться решением задачи
12.1р или 12.11р.
Б. Операторный метод
12.11р . Отрезок линии без потерь длиной / с параметрами
Со нагружен на произвольное операторное сопротивление
(рис. 12.3).
Ill
Определить передаточную функцию отрезка линии Н (р) =
=//2(р)/С\(Р) и операторное входное сопротивление ZBX(p) =
=(/1(р)//1(р). Получить операторные выражения для напряжения
и тока в точке, отстоящей от входа линии на расстоянии х при:
a) ZH = ZB; б) ZH = oo; в) ZH = 0; г) ZH = 2ZB; д)/н=1/(С» (емко-
стная нагрузка). По найденным изображениям записать соответст-
вующие функции времени и (/, л), /(/, х). Для случаев г) и д)
получить временные зависимости напряжения на нагрузке и2(1).
Рис. 12.4
12.12. Линию без потерь длиной / с волновым сопротивлением
ZB, нагруженную на ZH, в момент времени / — 0 подключают к
источнику, обладающему постоянной внутренней ЭДС Е и внут-
ренним сопротивлением ZEH = ZB (рис. 12.4). Показать, что при со-
противлении ZH активного характера переходный процесс имеет
конечную длительность. Получить выражения для мгновенных зна-
чений напряжения и тока в точке х при: a) ZH = ZB; б) Z8 = oo;
в) ZH = 0; г) ZH--2Zn.
12.13. В условиях предыдущей задачи в конце линии включена
катушка индуктивностью L— 0,5-10-3 Гн; /=300 м; Zb = 500 0m;
и = 3-108м/с; £=100 В. Определить напряжение на катушке
u,(t) и ток на входе ц (/) в переходном режиме. Построить эпюру
распределения по линии мгновенных значений напряжения для
/=1,5 т, где т—время прохождения волны по линии.
12.14. Источник, обладающий постоянной внутренней ЭДС
£ = 500 В и внутренним сопротивлением ZBH = ZB, в момент вре-
мени t ~ 0 подключают
к линии без потерь дли-
ной / = 600 м. Линия
нагружена на резистор
2 сопротивлением ZB =
8 =500 Ом. Параллельно
линии в ее середине вклю-
чена сосредоточенная ем-
кость С = 2-10~® Ф (рис.
12.5). Найти напряжения
на нагрузке и2 (/) и конденсаторе ис (/). Построить эпюры распре-
деления по линии мгновенных значений напряжения для ^ = 0,5^,
/2 = 1,5т; z8 = 2t; /4 = 2,5т, где т—время прохождения волной
112
половины длины линии. Скорость распространения волны по ли-
нии 0 = 3-10® м/с.
12.15. Конденсатор емкостью С = 0,01 10"® Ф, заряженный до
напряжения (70= 120 В, в момент времени / = 0 подключают к
двум параллельно соединенным линиям с волновыми сопротивле-
ниями ZBi = 300 Ом; ZB2 = 450 Ом (рис. 12.6). Линии нагружены
согласованно. Скорость перемещения волны в линия х v = 3-10® м/с.
Рис. 12.7
Длина первой линии /, = 300 м, второй /а = 600 м. Рассчитать
напряжения на нагрузках линий uHI (/); н„2(/) и на конденсаторе
иМ-
12.16р . На входе линии без потерь включены последова гельно
источник постоянной ЭДС Е и резистор сопротивлением ZB.
Сопротивление нагрузки также равно ZB (рис. 12.7).
В момент времени / — 0 параллельно нагрузке подключают
незаряженный конденсатор С. Считая, что до коммутации в линии
был установившийся режим, определить напряжение на нагрузке
и входе линии в переходном режиме. Построить эпюры распре-
деления по линии мгновенных значений напряжения для /, = 0,5//и;
/2 = 0,75//и при / = 300 м; ZB = 500 Ом; и = 3-10я м/с; Е=500 В;
С = 410-« Ф.
Рис. 12.8 Рис. 12.9
12.17. Получить выражения u{t, х), i(lt х) для рис. 12.8
после коммутации, считая режим до коммутации установившимся.
Линия потерями не обладает. Принять Е = 500 В; ZB^ 500 Ом;
113
линии без потерь: ZB = 400 Ом;
Рис. 12.10
L — 0,001 Гн; v = 3 - 10s м/с; / = 600 м. Найти зависимость от вре-
мени напряжения на входе иг (/).
12.18. Определить ток через резистор /?в = 2в(рис. 12.9), если
£=1200 В (постоянная ЭДС), /?BH = ZB/2. Параметры отрезка
/ = 300 м; и = 3-10® м/с. До ком-
мутации режим был установив-
шимся.
12.19р. В цепи, изображенной
на рис. 12.10, до коммутации
был установившийся режим.
Линия потерями не обладает,
Е = 500 Ом; /=1500 м; и =
=3-10® м/с; Е = 0,0025 Гн. По-
лучить выражения для мгновен-
ных значений напряжения и
тока в произвольной точке на
линии.
12.20. В условиях задачи 12.19р (рис. 12.10) в момент вре-
мени 1 = 0 к разомкнутому концу линии подключают конденсатор
емкостью С = 10~8Ф, заряженный до напряжения £/с0 = 2Е. Пост-
//2
роить графики и(х), i(x) для ^ = 0; /2 = -^-; t3 = lfv, а также
зависимость от времени напряжения в конце линии п2(/).
В. Формирование импульсов с помощью заряженного
отрезка линии
12.21р . Отрезок линии без потерь длиной/ = 300 м заряжен до
напряжения Uo = 4 кВ (рис. 12.11). В момент времени/ = 0 один
из концов линии (на рис. 12.11 правый; х — 1) замыкается на ре-
зистор сопротивлением RH = ZB = 400 Ом. Скорость распростра-
нения волны в линии v = 3- 10я м/с.
Найти ток /„(/), возникающий в нагрузке, и напряжение на
разомкнутом конце линии и^/), построить их графики.
12.22. В условиях предыдущей задачи в момент времени / = 0
к обоим концам отрезка липин подключают резисторы сопротив-
лением Z?H = ZB (рис. 12.12). Определить форму и длительность
114
t=0 t-0
Рис. 12.13
импульсов тока, ц(/), i2(Z), возникающих в нагрузках. Сравнить
if(/) с импульсом тока в нагрузке предыдущей задачи (см.
пис. Р.12.10, б). Построить графики u(x), i (х) для /х = 0;
; _ № . , . / _ц. / _1
J j у ’ 3 у ’ 4 4 У * 6 V*
12.23. В условиях задачи 12.21 р к правому концу отрезка
линии подключают резистор сопротивлением Z?H = ZB> а левый
конец замыкают накорот-
ко. Найти ток iH(Z) в пе-
реходном режиме, пост-
роить его график.
12-24. В условиях за-
дачи 12.21 р в момент вре-
мени t = 0 к левому концу
отрезка линии подключают
незаряженный конденсатор
С=2,5-10“9 Ф, а к право-
му концу—резистор соп-
ротивлением ZB (рис. 12.13). Определить напряжение на конден-
саторе в переходном режиме uc(t) и построить его график.
Рис. 12.14
Г. Каскадное, последовательное и параллельное
соединения двух линий
12.25р . В момент / = 0к разомкнутому концу линии без по-
терь подключают отрезок линии с теми же параметрами той же
длины, разомкнутый на конце (рис. 12.14).
Построить графики распределения мгновенных значений напря-
f/2 I
жения и тока по линии для /1 = 0; = ; Z3 = —; /4 = 1,5 Z/o;
Z6=3Z/u. Чему равна длительность переходного процесса? При-
нять Е = 500 В; ZB—500 Ом;
/= 1500 м; п=3-10* м/с.
12.26. В условиях задачи
12.25р (рис. 12.14) подключае-
мый отрезок линии на конце
замкнут накоротко. Получить
выражения для мгновенных зна-
чений напряжения и тока в
произвольной точке линии.
12.27. В условиях 12.25р(рис.
12.14) подключаемый отрезок
Построить графики распределе-
ния по линии мгновенных значений напряжения и тока для Z = 0;
t I ГЛ
*----- ; i = — . Определить длительность переходного процесса.
12.28. Линия без потерь длиной 2/ нагружена на ZB. На входе
линии действует источник постоянной ЭДС Е с внутренним
сопротивлением ZB. В момент времени / = 0 в среднем сечении
линии на конце нагружен на ZB.
115
линии параллельно ей подключают: а) незаряженный конденсатор
рис. (12.15, а); б) резистор сопротивлением 2В (рис. 12.15,6); в)
короткозамкнутую перемычку (рис. 12.15, в).
Получить выражения для мгновенного значения напряжения в
первом участке линии (от источ-
ника до места коммутации) рас-
стояние следует отсчитывать от
источника и обозначить на
втором участке—от места ком-
мутации и обозначить х2.
Построить качественно эпюры
распределения мгновенных зна-
чений напряжения по линии для
/=0; /=//»; t = 4liv.
Режим для коммутации считать
установившимся.
12.29. В условиях задачи
12.28 (рис. 12.15, в) выходные
зажииы линии разомкнуты. По-
лучить выражение для мгновен-
ного значения напряжения в
конце линии и2(0, если: а) в
исходном состоянии ключ разом-
кнут, режим установившийся;
в момент времени t — 0 ключ
замыкается; б) в исходном сос-
тоянии ключ замкнут, режим
установившийся, при 7=0 ключ
размыкается. В каком случае
переходный процесс имеет ограниченную длительность? Построить
графики н2(/).
12.30. Две линии без потерь с волновыми сопротивлениями
Ze! и ZB1 каждая длиной I соединены каскадно (рис. 12.16). На
Рис. 12.18
Рис. 12.17
входе первой линии включен источник постоянной ЭДС с внут-
ренним сопротивлением, равным ZB1. Выходные зажимы второй
линии замкнуты накоротко. В исходном состоянии в месте стыка
линий существуег короткозамкнутая перемычка. При £ — 0 про-
116
исходит обрыв перемычки. Получить выражения для мгновенных
значений напряжения на входе первой линии и, (г) и тока в конце
второй линии /,(/). При этом считать скорости распространения
электромагнитных волн в обеих линиях одинаковыми; принять
Zpa ~ ZM/3.
12.31р . К двум одинаковым линиям без потерь с волнозым
сопротивлением ZB длиной /, соединенным последовательно, в
момент времени / = 0 подключают источник постоянной ЭДС
Е (рис. 12.17). Одна линия нагружена на резистор сопротивле-
нием ZF = ZB, зажимы другой замкнуты накоротко. Определить
мгновенные значения напряжения на нагрузке первой линии
и тока в конце второй линии
Чему равна длительность переходного процесса в каждой из
линий? Сравнить их (скорость распространения электромагнитной
волны в линиях v считать извест-
ной).
12.32. В условиях задачи 12.31 р
(рис. 12.17) выходные зажимы вто-
рой линии разомкнуты. Рассчи-
тать мгновенные значения напря-
жений на нагрузке первой линии
tzn(O и разомкнутых зажимах вто-
рой линии u.,(Z).
12.33. Две одинаковые линии
без потерь с волновым сопротив-
лением ZB длиной Z соединены па-
раллельно. Первая линия нагру-
жена на ZB, а зажимы втор<
В момент времени 1 = 0 к входным зажимам линий подклю-
чают источник постоянного тока J. Получить выражения для
мгновенных значений напряжений на входе линий (Z) и на
выходных зажимах линий uH(Z), u2{t).
и*
Рис. 12.18
разомкнуты (рис.
12.18).
Глава тринадцатая
Нелинейные электрические цепи постоянного тока
А. Построение характеристик нелинейных цепей.
Расчет токов и напряжений графическим методом
в цепях с одним источником
13.1р. Построить входную ВАХ U = f(I) схемы рис. 13.Га.
ВАХ нелинейных резистивных элементов НРг и НР2 даны на
рис. 13.16; R = 5 Ом.
13.2. Три одинаковые лампы накаливания соединены, как по-
казано на рис. 13.2, а. Определить ток в неразветвленной части
схемы, если ток в лампе 1 равен 0.3 А. ВАХ одной лампы
Дана на рис. 13.2, а Построить входную ВАХ схемы.
117
13.3р. Туннельный диод, ВАХ которого изображена на
рис. 13.2, б, соединен последовательно с источником ЭДС £ = 1 В
и резистором, сопротивлением R. Сопротивление R изменяется от
Рис. 13.1
13.5. На рис. 13.3, а
измерительного прибора.
О до оо. Построить график
зависимости тока 1 в схеме
рис. 13.2, б от сопротивле-
ния R.
13.4. Схема и ВАХ
HP те же, что и в задаче
13.Зр, но ЭДС изменяет-
ся от О до 1,4 В; /?==
= 100 Ом. Построить зави-
симость /=/(£).
представлена схема термокомпенсации
Сопротивление рамки прибора /?пр,
выполненной из медной проволоки, зависит от температуры
(рис. 13.3, б). Последовательно с рамкой включена цепочка тер-
мокомпенсации, состоящая из параллельно соединенных терми-
стора сопротивлением /?т и манганинового шунта сопротивлением
Зависимости Rr и Rm от температуры Т приведены на
рис. 13.3, б. Построить зависимость общего сопротивления от
П8
температуры и убедиться, что оно будет стабильным в диапазоне
температур 0 < Т < 100° С.
13.6. На рис. 13.3, в представлена схема, используемая для
определения постоянной времени термистора, который включен в
одно плечо моста (ВАХ термистора дана на рис. 13.3, г),
= 30 кОм; #,= 10 кОм; £/вх = 120 В. Определить: а) сопро-
тивление #3, при котором мост сбалансирован, т. е. £/вы?( = 0;
б) напряжение £/вых, если 67ВХ уменьшится на 20 В. В обоих
режимах найти статическое #ст и дифференциальное R^ сопро-
тивления термистора.
Рис. 13.4
13.7р . На рис. 13.4, а представлена цепь, содержащая пози-
стор СТ5-1, ВАХ которого показана на рис. 13.4, б, и рези-
стор сопротивлением R (позистор—терморезистор с положитель-
ным температурным коэффициентом в определенном диапазоне
напряжений U; в данном случае при U > 4 В). Подобрать зна-
чение # так. чтобы цепь могла быть использована как стабили-
затор тока. Построить входную ВАХ 1 = f (U) и определить ток
стабилизации 7СТ.
13.8. Для стабилизации тока в нагрузке RB (рис. 13.4, в)
используются параллельно включенные позистор, ВАХ которо-
го дана на рис. 13.4, г, и резистор сопротивлением R.
Подобрать значение R так, чтобы ток I был постоянен при
изменении напряжения на позисторе от 3 до 10 В. Найти ток
стабилизации /ст. Определить пределы изменения напряжения U
на входе, при котором ток 7 в цепи неизменен; #н = 100 Ом.
13.9. Одна из схем стабилизации напряжения на термисторе
приведена на рис. 13.5, а. Так как ВАХ. используемого терми-
стора ТП6/2 (рис. 13.5,6) не имеет вертикального участка, то
последовательно с ним подключается резистор сопротивлением
Найти сопротивление R2 и стабилизированное напряжение
на нагрузке #н= 1 кОм. Напряжение на входе меняется на
10% от номинального, равного 20 В. Подобрать сопротивле-
119
ние /?х, если при минимальном напряжении на входе ток через
термистор /т=1 мА. Проверить, изменится ли напряжение на
нагрузке при возрастании входного напряжения до максимума.
Рис. 13.5
13.10р . Триод 6С19П включен в цепь по схеме рис. 13.6. а.
Анодные характеристики лампы показаны на рис. 13.6,6. Считая,
что ток сетки весьма мал (/с<^/а), определить ток в анодной
цепи /а, напряжение на аноде Ua и нагрузке сопротивлением
если Еа = 250 В; /^«1210 Ом; Яв = 40 Ом; Яа=2500 Ом.
13.11. Подобрать сопротивление Ra (рис. 13.6, в) так, чтобы
при возрастании напряжения на сетке до Uc = 16 В ток в анод-
ной цепи не превышал 60 мА; Еа = 250 В. Анодные характери-
стики лампы даны на рис. 13.6, б. При наименьшем из выбран-
ных значений /?а построить зависимость напряжения на нагрузке
{/яа от сеточного напряжения £7С.
Б. Метод эквивалентного генератора.
Метод одновременного холостого хода двух ветвей
13.12р . В схеме рис. 13.7, а определить все токи. ВАХ HP
изображена на рис 13.7, б (кривая /). Параметры схемы: Ех = 18 В;
Г2 = 6 В; J = 1 А; 7?х = 3 Ом; /?2 = 6 Ом.
13.13. Рассчитать ток в HP (рис. 13.8, а) и мощность, выде-
ляющуюся в нем. Параметры цепи: Е —ЗОВ; J = 2 А; /?,-4Ом,
R2 = 1 Ом; Rs = 3 Ом; Rt 2 Ом. В. а. х. HP дана на рис. 13.7,6
(кривая /),
120
S)
Рис. 13.7
13.14. Определить ток в HP схемы
статического /?сг и дифференциального
этом токе. ВАХ HP дана
на рис. J3.7, б (кривая 2);
£ = 20 В ; J=5 A; Rt = 30m;
рис. 13.8. б и значения
сопротивлений при
7?9 = 2 Ом. Как изменятся ток
в HP и значения 7?ст и /?йиф,
если изменить полярность ис-
точника тока?
13.15. Рассчитать ток в
HP (рис. 13.9, q) при пита-
нии схемы от источника: а)
ЭДС £ — 24 В; б) тока
J=2 А. ВАХ HP дана на
рис. 13.9,6; Рг —Р2 = 4 Ом;
режим работы HP, найти токи
R3 = 3 Ом; Р4 = 1
в остальных ветвях схемы.
Рис. 13.8
Ом. Определив
Рис. 13.10
121
13.16р . Определить токи во всех ветвях схемы рис. 13.10, а.
ВАХ НРХ и HP* одинаковы и даны на рис. 13.7, б (кривая
/); £=10 В; J = 2 А; £1 = 4Ом; £= = 2Ом; /?э = 30м.
13.17. В схеме рис. 13.10, б рассчитать токи во всех ветвях.
ВАХ двух одинаковых нелинейных элементов даны на рис. 13.7,6
(кривая /); £ = 20 В; J = 3 А; /?1 = £8 = /?3=2 Ом.
В. Замена нелинейного активного двухполюсника
эквивалентным. Метод двух узлов.
Расчет разветвленной цепи
13.18р . Заменить нелинейный активный двухполюсник
(рис. 13.11, с) эквивалентным и определить его параметры. ВАХ
нелинейных элементов даны на рис. 13.11, б; £ = 30 В; 7 = 1 А
Рис. 13.11
13.19. Решить задачу 13.18р, изменив полярность источника
тока 7, т. е. определить: а) ЭДС эквивалентного источника
ЭДС £э и ВАХ нелинейного элемента, соединенного с ним
Рис. 13.12
последовательно; б) ток эквивалентного источника тока 7Э и
ВАХ нелинейного элемента, включенного параллельно ему.
13.20. Заменить две параллельные ветви схемы рис. 13.11, в экви-
валентной, определив ЭДС £э и ВАХ нелинейного элемента
122
рис. 13.11, а, равен нулю.
Рис. 13.13
эквивалентной ветви; Ех=Е2 = 30В. ВАХ ЯРХ и ЯР2даны иа
рис. 13.11, б.
13.21р . Определить токи в задаче 13.18р при условии, что ток,
подтекающий к двухполюснику на
13.22. Рассчитать токи в схеме
рис. 13.12, а, если Е,=30 В;
£2 = 35 В; Я2 = 5 Ом. ВАХ. оди-
наковых элементов HPf и ЯР2
даны на рис. 13.12, б.
13.23. Решить задачу 13.21 р,
изменив полярность источника
тока J (в схеме рис. 13.11, а ток
7 = 0).
13.24р . Определить токи в вет-
вях схемы рис. 13.13. ВАХ
трех одинаковых нелинейных элементов представлена на рис.
13.12, б. Исходные данные: Ех = 10 В; Е2 = 20 В; J = 1 A; R = 5 Ом.
Г. Аналитический расчет нелинейных цепей
13.25. Две лампы накаливания, включенные параллельно че-
рез резистор сопротивлением R = 50 Ом, подсоединены к источ-
нику ЭДС Е = 0,68 В (рис. 13.14). ВАХ ламп можно выра-
Рис. 13.14 Рис. 13.15
зить аналитически: Ц = 0,06Ях 4- 10-5Я;; /2 = 0,04Я2 4- 0,6- 10"3Я£
(ток—в амперах, напряжение—в вольтах). Определить ток и
напряжение в лампах.
13.26р . На рис. 13.15, а представлена схема, позволяющая про-
извести операцию перемножения Ях и Я2. В схеме используют
варисторы (полупроводниковые резисторы) с квадратичной зави-
симостью тока от приложенного напряжения: 1—Виг. Показать,
что при подаче на вход напряжения, как показано па рисунке,
ток через амперметр будет пропорционален произведению напря-
жений и Uz.
13.27. Показать, что напряжение на выходе схемы рис. 13.15, б
пропорционально произведению напряжений Ur и Я2, если ВАХ
Цепочки, состоящей из последовательно соединенных диода Д и
Резистора сопротивлением Я, описывается квадратичной зависи-
мостью / = ЕЯ3(Я=ЯД + ЯЛ).
123
Д. Цепи с идеальными диодами
13.28р. На рис. 13.16, а изображена часть диодного функ-
ционального преобразователя, приблизительно реализующая ВАХ
в виде параболы. Полагая, что диоды имеют идеальные ВАХ
а) Ь)
Рис. 13.16
(рис. 13.17, а), подобрать значения сопротивлений/?, Rlt Rt так,
чтобы ВАХ l = f(U) схемы описывалась зависимостью, которая
аппроксимирует функцию 1 — 10~3£78 в диапазоне 0 < U < 30 В
тремя линейными участками; £,= 10 В; £2 = 20 В.
13.29. На рис. 13.16, б показана часть диодного функциональ-
ного преобразователя. Полагая ВАХ диодов идеальными
г д (рис. 13.17, а), построить
о О -----—------>- ОЛ ВАХ J = f(U) всей схе-
I мы; £, = 20 В; £3=50 В;
- __ I А £ их * I £3 = 40 В; £« = 80 В; /? =
U 14 Ь =Ю0 Ом; /?i=50 Ом;
I Т R3 = 40 Ом; R3 — R* —
о) б) =80 Ом.
Рис. 13.17
13.30. Для функцио-
нального преобразователя,
схема которого дана на рис. 13.16,6, подобрать значения сопро-
тивлений Л, £„ £г, /?3, /?4 так, чтобы ВАХ I=f(U) схемы
описывалась зависимостью, которая аппроксимирует кубическую
параболу 7 = 10“Ч/3 (ток — в амперах, напряжение—в вольтах)
пятью линейными участками в диапазоне—100</7<Ч 100 В;
£* = £3 = ЗО В; £8 = £4 = 60 В. ВАХ диодов идеальны (рис.
13.17, а).
13.31р. К зажимам а и b схемы рис. 13.17,6 от не показан-
ного на рисунке источника ЭДС подводится напряжение Uab-
Сопротивление R и ЭДС £, источника постоянной ЭДС зада-
ны и неизменны. К точке d подтекает, а от точки с оттекает
ток J. Построить зависимость тока / от напряжения Uab. ВАХ
диола идеальна.
13.32. Решить задачу 13.31 р при условии, что ЭДС £i
изменила свое направление на противоположное.
Глава четырнадцатая
Магнитные цепи
А. Не разветвленные магнитные цепи
14.1. На стальном кольцевом магнитопроводе равномерно
намотана обмотка с числом витков w = 300. При / = 0,2 А маг-
нитная индукция внутри обмотки (по длине средней силовой ли-
нии) имеет то же значение, что и при 1 =
=200 А; но без стального сердечника. Оп-
ределить магнитную индукцию, намагничен-
ность и относительную магнитную проницае-
мость стали. Средний диаметр кольца dcp=
=23,9 см.
14.2. На магнитопровод, выполненный из
стали марки Э41 (табл. 14.1), сечением
Рис. 14.1
5 = 5 см1 и длиной средней силовой линии
/ср = 20 см намотана обмотка с числом витков w =100. Найти
ток в обмотке, необходимый для создания в магнитопроводе по-
тока Ф = 6,6-10 * Вб (рис. 14.1).
Таблица 14.1
В, Тл И. дм В, Тл Я. A/и | В, Тл Я-10», А/м В. Тл Я-10», А/м
0.25 50 1.0 210 1.4 15 1,65 10
0.4 64 1.1 250 1,42 20 1.7 13
0,6 88 1.2 390 1,45 28 1,75 18
0,7 113 1,25 530 1,5 42 1,8 23
0,8 138 1,3 700 1.56 60 1.9 34
0,9 170 1,35 1000 1.6 78 2,0 70
14.3. Определить пределы изменения индукции в магнитопро-
воде (см. условие предыдущей задачи), если ток в обмотке изме-
няется от 0,5 до 2,5 А.
14.4р . На магнигопровод, размеры которого в миллиметрах
приведены на рис. 14.2, намотана обмотка с числом витков tt'= 100.
По обмотке протекает ток 2 А. Определить магнитную индукцию
в воздушном зазоре. Площадь сечения воздушного зазора считать
равной площади сечения магнитопровода.
14.5. Как следует изменить зазор магнитопровода в задаче 14.4р,
чтобы поток в нем стал равным Ф = 5,5-10“* Вб?
14.6. Как следует изменить толщину пакета листоь стали маг-
• Если не будет оговорено, то в остальных задачах считать магнитолрово-
Ды выполненными из стали той же марки. Характеристика стали дана в
Табл. 14.1.
125
нитопровода в задаче 14.4р, чтобы поток в нем стал равным Ф =ч
= 5,5.10-4 Вб?
14.7. Левый магнитопровод (рис. 14.3) имеет воздушный зазор
6 = 0,1 мм, правый—без зазора. Размеры магнитопроводов:
Рис. 14.3
= 4 = 20 см; S, = S2 = S6 = 5 см2. Магнитный поток первого маг-
нитопровода Ф, = 1,2-10~4 Вб. Определить МДС обмотки и маг-
нитный поток второго магнитопровода.
Б. Разветвленные магнитные цепи
14.8. На среднем стержне симметричной магнитной цепи рис. 14.4
расположены две обмотки с шг = 250 и w2 = 75, обтекаемые током
2 А. Размеры магнитной цепи в миллиметрах указаны на рисунке.
Толщина пакета листов стали 25 мм. Оп-
Рис. 14.4
нескольких разнородных
и сечением S2 = 24 см2,
ределить магнитные потоки в стержнях
магнитопровода: а) для указанной це-
пи; б) для той же цепи, если ширина
среднего стержня станет равной 10 мм.
14.9. На рис. 14.5, а показан разрез
четырехполюсной машины постоянного
тока. Наличие симметрии позволяет рас-
считать магнитную цепь пары полюсов
как неразветвленную, состоящую из
участков: 1) ярма длиной 4 = 15 см
выполненного из стали марки 10880;
Рис- 14.5
2) двух полюсов длиной /,=4,5 см и сечением S, = 60 см2 каж-
дый; 3) якоря длиной = 1 см и сечением S3 = 36 сма, выполнен-
126
яого из листовой стали Э12; 4) двух воздушных зазоров шириной
6- 0,2 см и сечением Sfl = 66 см2.
Наличие зубцов на якоре учтено увеличением ширины воздуш-
ного зазора. Определить м.д. с. обмотки полюса, если в зазоре
необходимо создать магнитный поток Фс = 10-2 Вб. Коэффициент
рассеяния обмотки Лс=1,2. Расчет вести по потоку Фо, проходя-
щему по якорю и воздушным зазорам, и по потоку ЛсФс/2, про-
ходящему по ярму и полюсам. Кривые намагничивания исполь-
зуемых материалов даны на рис. 14.5,6.
14.10. Магнитопровод (рис. 14.6) изготовлен из материала
с относительной магнитной проницаемостью = 100. Магнитная
индукция в правом (третьем) стержне магнитопровода В — 0,4 Тл.
Рис. 14.7
Найти: а) магнитные сопротивления стержней магнитопровода
Z?Mi, Ruit Ru3\ б) магнитное напряжение £/моЬ; в) магнитные потоки
в стержнях Фп Ф2, Ф3; г) МДС обмотки /2ш2. Толщина пакета
листов стали 20 мм; размеры на рисунке даны в миллиметрах.
14.11. Определить ток /, в обмотке магнитопровода на рис. 14.7,
если ш3 = 100, /1^! = 10,5 А; индукция в воздушном зазоре Вб = 0.
Толщина пакета листов стали 20 мм, ра-
змеры магнитопровода на рисунке указа-
ны в миллиметрах.
14.12р . Построить зависимость потока
Ф от магнитного напряжения UM аЬ (вебер-
амперную характеристику участка магнит-
ной цепи (рис. 14.8), если длина магнит-
ной цепи /ср = 20 см, ширина зазора
6,—0,2 мм, сечение магнитопровода и зазо-
ра S, = S2 = 5 см2; МДС Iw = 200 А. Рас-
смотреть следующие варианты. 1. Поток
направлен от а к Ь: а) ток втекает в
зажим п; б) ток втекает в зажим т. 2. Поток направлен от b
к а: а) ток втекает в зажим п; б) ток втекает в зажим т.
14.13. На рис. 14.9 показана разветвленная магнитная цепь,
размеры которой даны в миллиметрах. Толщина пакета листов
стали равна 20 мм. На первом и третьем стержнях магнитопро-
вода расположены обмотки с числом витков ^=100, к.’3 —40;
Направление токов в обмотках указано на рисунке.
127
Рассчитать магнитные потоки в стержнях и магнитное напря-
жение UMab, если: а) /х = 1,2 Л; /3 = 0; б) /^О; 73= 1 А; в) 71==
= 1,2 А; 73 = 1 А.
14.14р . В магнитной цепи (рис. 14.9) известны /1сг,1= 120 А;
Ф3 = Ф2—0,5 • 10~4 Вб. Определить ток в обмотке третьего стержня
и потоки в стержнях, если оу3=1ОО.
14.15. На средний стержень магнитопровода (рис. 14.9) намо-
тана обмотка, направление МДС которой совпадает с направле-
нием потока Фа. Найти МДС 72^'2, если 73&’s = 20 А; 7^ ~ 120 А;
Ф2-Ф3.
В. Магнитные цепи, содержащие ферромагнитные сердечники
с прямоугольной петлей гистерезиса
14.16р . Тороидальный сердечник прямоугольного сечения
(рис. 14.10, а) выполнен из материала, имеющего петлю гистере-
зиса прямоугольной формы (рис. 14.10,6). Сердечник находится
в состоянии, характеризующем-
ся отрицательной остаточной ин-
дукцией В = — Вг. Построить
график зависимости B = f(R)>
где В—расстояние от оси сер-
дечника до рассматриваемой точ-
ки, если: а) по проводу, прохо-
дящему через отверстие в сер-
дечнике, пропустить ток 7 =
— 15! А; б) этот ток отключить.
Рис. 14.10
Провод и сердечник соосны. Размеры на рис. 14.10, а даны в сан-
тиметрах.
14.17. На рис. 14.11 приведена часть магнитного запоминаю-
щего устройства, выполненного на ферритовых сердечниках пря-
моугольного сечения с ППГ, показанной на рис. 14.10,6. Внешний
Рис. 14.11
диаметр сердечника П = 5 мм, внутренний 6 = 3,0 мм, высота
сердечника h = 2 мм. Магнитное состояние сердечников было таким:
сердечники 1 и 3 имели отрицательную остаточную индукцию
— Вг, сердечники 2 и 4—положительную остаточную индукцию
4- Вг. Каким будет магнитное состояние сердечников, если: а) п°
проводам протекают токи /j = 13 А; 7, = 0; 73 = 3 А; 74 = 8 А>’
6) протекающие токи отключить?
128
14.18р . На рис. 14.12 изображен разветвленный магнитопровод
из материала с ППГ, приведенной на рис. 14.10,6. Под действием
тока /, протекающего по обмотке первого стержня, магнитопровод
перемагничивается от — Вг до + Вг- Построить зависимость маг-
нитны к потоков Ф1т Ф2, Ф3 от тока /, если к» =100. Размеры
магнитопровода на рисунке даны в миллиметрах.
Г. Постоянные магниты
14.19. На рис. 14.13, а показан постоянный магнит из платино-
железного сплава. При намагничивании промежуток между его
полюсами заполняется магнитно-мягким материалом, который вы-
нимается после снятия намагничивающей обмотки. Найти отно-
шение длины воздушного зазора
б к длине средней силовой линии
/ср магнита, при котором индук-
ция в воздушном зазоре В —
= 0,45Тл, считая SM = Se. По-
токами рассеяния пренебречь.
Кривая размагничивания приве-
дена на рис. 14.13,6.
14.20. Постоянный магнит
Рис. 14.13
зазоре часть его заполнили
(рис. 14.13, с) имеет /ср = 20см;
6 = 2,75 см. Для увеличения
магнитной индукции в воздушном
магнитно-мягким материалом. Определить длину оставшегося воз-
душного зазора, если значение индукции увеличено на 0,05 Тл.
Коэффициент возврата материала магнита К = 2- 10~в Гн2/м.
Глава пятнадцатая
Нелинейные электрические цепи
переменного тока в установившемся режиме
А. Цепи с неуправляемыми нелинейными
индуктивными катушками и конденсаторами.
Расчет по мгновенным значениям величин
15.1. На рис. 15.1, а—в изображены вебер-амперные характе-
ристики индуктивной катушки при трех способах кусочно-линей-
ной аппроксимации. Соответствующие им значении потокосцепле-
ния и тока даны в табл. 15.1. К зажимам индуктивной катушки
Подведено напряжение L/racosw/. Полагая активное сопротивление
Индуктивной катушки равным нулю, построить кривую тока в цепи
в Функции в)/ для трех способов аппроксимации. Амплитуда на
Пряжения U,n= 1000 В; ы=1000 с’1.
15.2р . Через индуктивную катушку, зависимость ip = f(t) кото-
Р°и изображена на рис. 15.1,6, в, протекает синусоидальный ток
129
Таблица 15.1
Точки на
Параметры рис. 15.1. а рис. 15.1.0 рис. 15.1. в
а й с d е 1 m л о
чр» В-с i, А 0.9475 0 1 I 0,95 0,05 1 1 —0.945 0,05 0,9525 0,1 1 1 0,945 —0,05 0,9525 -0,1
/fflsinwZ. Построить кривую
ной катушке в функции со/
со == 1000 с-1.
изменения напряжения на индуктив-
для этих двух случаев, если Im = 1 А,
15.3. На рис. 15.2, а—в изображены кулон-вольтные харак-
теристики нелинейного конденсатора при трех способах кусочно-
линейной аппроксимации. Соответствующие значения заряда q
и напряжения и приведены в табл. 15.2. Полагая, что ток, про-
текающий через конденсатор, изменяется по закону Im cos со/, где
Iт — 0,001 А и о)=103 с”1, построить график изменения напря-
жения на конденсаторе в функции со/ для трех способов аппрок-
симации.
15.4. К нелинейному конденсатору, кулон-вольтная характе-
ристика которого показана на рис. 15.2,6, в, подведено синусо-
идальное напряжение £/msinwf = 1 sin 1000/ В. Построить кривую
тока, протекающего через конденсатор, для кривых q — изобра-
женных на рис. 15.2,6, в.
130
Таблица 15.2
Точки на
Параметры рис. 15.2, д рис. 15.2,6 рис. 15.2.в
а ь с d е 1 m п о
0.10е, Кл а. в 0,945 0 1 1 0,95 0,05 1 1 —0,9525 0,05 0,9525 0,1 1 1 0,945 —0,05 —0,9525 0,1
15.5р . Построить кривые изменения во времени потокосцепле-
ния ф тока i и напряжения и на индуктивной катушке в схеме
рис. 15.3, а. Характеристика ф = /(0 изображена на рис. 15.3,6;
ih =0,015 В-с. График действующей ЭДС e = f(0 изображен на
рис. 15.3,в; £ffl=W0 В. Период 7, = 9-10-< с; £ = 1000 Ом.
15.6. Построить кривые изменения во времени заряда q, на-
пряжений ис на нелинейном конденсаторе и тока в цепи рис. 15.4, а,
если е— sincoZ; Ест = 2000 В; ^m=10~$ Кл; £=103 Ом;
to=I05 с"1. Зависимость q = f(uc) показана на рис. 15.4,6.
Рис. 15.5
и/
чп
15.7р . Схема рис. 15.5, а питается от источника синусоидаль-
ного тока = 0,1 sin 10<t А. Характеристика индуктивной ка-
тушки ф = /(0 изображена иа рис. 15.5,6; фт = 0,853-10~? В-с;
£—100 Ом; 1/(<оС)=1ОО Ом. Построить графики iit uCl i, ucd,
i* в функции ш/.
15.8р . На вход схемы рис. 15.6,б! поступает ток zf треугольной
Формы (рис. 15.6,6) с амплитудой /т = 2,29 мА. Период Т = 0,01 с.
ебер-амперная характеристика индуктивной катушки ф = /(<)
°казана на рис. 15.5,6. Исходные данные: фст = 0,0025 В-с;
131
R = 1000 Ом; L = 0,773 Гн. Построить графики uael i, ф,
в функции со/.
15.9. На вход схемы рис. 15.7, а поступает синусоидальный
ТОк ц = /от sin со/; 1т = 6,83 мА; со =10* с-1. Индуктивность ка-
тушки L = 0,1465 Гн; Я = 1465 Ом. Кулон-вольтная характери-
стика нелинейного конденсатора изображена на рис. 15.7,6, где
qm = 10~’ Кл. Построить кривые иас, i, ucd, uabt q в функции cot
Рнс. 15.6 Рис. 15.7
15.10. На вход схемы рис. 15.7, а подается ток /п имеющий
треугольную форму (см. рис. 15.6,6), с амплитудой 1т~
= 1,455-10“а А. Период Т = 6,28-10“4 с; L = 0,1465 Гн; R =
= 1465 Ом; со =104 с“*; ?ст=110~в Кл. Построить графики iLt
*. “at» Я в функции со/.
15.11. На вход схемы рис. 15.8, а воздействует синусоидальное
напряжение uflb = //wsinco/; Um=\ В; /?=1 Ом; со = 371 с-1.
Вебер-амперная характеристика индуктивной катушки изображена
на рис. 15.5,6; фга = 0,00251 В-с. ВАХ нелинейного резистора
дана на рис. 15.8,6. Построить графики изменения токов i2, i
и ii в функции со/.
а) У
Рис. 15.9
15.12р . На вход схемы рис. 15.9, а воздействует синусоидаль*
ное напряжение sin со/; Um= 1 В; со = 474 с-1; R — 3 Ом*
Вебер-амперная характеристика индуктивности катушки изобра*
132
tv.
Ф>
Рис. 15.10
экеиа на рис. 15.5, 6; фст = 0,001 В-с. В. а. х. нелинейного резистора
дана на рис. 15.9,6. Построить графики изменения токов ц, /2
и /, напряжений ис4 и иас и потокосцеп-
ления ф в функции art.
15.13. Магнитный усилитель, схема
которого изображена на рис. 15.10, выпол-
нен на магнитопроводах с идеально пря-
моугольной кривой намагничивания (см.
кривую рис. 15.5,6). Поток насыщения
одного магнитопровода Ф — 1,7 -10—4 В с;
^ = 400; ы0 = 1600; о = 314 c“J; Ео = 3 В;
= 100 Ом; R9 = 50 Ом; Um = 40 В. Опре-
делить законы изменения токов it и ic в
функции со/ и коэффициент усиления по
мощности kp*
Б. Цепи с неуправляемыми нелинейными резисторами.
Расчет по мгновенным значениям величин
15.14. В схеме рис. 15.11, а последовательно включены источ-
ник синусоидальной ЭДС е(/) = Ега81п(ю/-{-ф), где Ест = 127 В
и ф = 45°, источник постоянной ЭДС Ео = 50 В, идеальный полу-
Рис. 15.11
проводниковый диод (рис. 15.11,6) и резистор сопротивлением
R — 1 кОм. Построить графики изменения тока i и напряжения
Цд на диоде в функции со/.
Рис. 15.12
15.15. Условие то же, что и в задаче 15.14, но ЭДС Ео изме-
нила направление на противоположное.
ь * Сч.: Бессонов Л. А. Теоретические основы электротехники.— М.:
“Ысшая школа, 1967. С 328.
133
15.16р . Условие то же, что и в задаче 15.14, но в цепь вклю-
чена индуктивная катушка с L = 1,59 Гн; со = 628 с"1 (рис. 15.11, в).
15.17. В схеме рис. 15.12, а резисторы имеют сопротивления
7?i=100 Ом; Я2 = 120 Ом; (/) = 10 sin со/; ег{()= 17 sin о/ В;
Ео = 5 В. Построить графики токов ц, /2, i3 и напряжений на
диодах ыд1-, ид2 в функции со/.
15.18. Условие то же, что и в задаче 15.17, но e2(t) =
= 17 sin (со/ + 90') В.
15.19р . На рис. 15.12,6 изображена мостовая схема двухполу-
периодного выпрямления. ЭДС источника е (/) = Ет sin со/. На-
грузка образована резистором сопротивлением R и катушкой
индуктивностью L. Вывести формулу, для мгновенного значения
тока в нагрузке и показать, что среднее его значение за полу-
период равно (2/rt)(Em/R) и не зависит от L.
15.20. На рис. 15.12, в показана схема однополупериодного
выпрямления, в которой нагрузка R шунтирована конденсатором
для сглаживания пульсаций. Полагая диод идеальным, а ЭДС
источника е (/) = Ет sin со/, вывести формулы для определения вре-
мени открытия и закрытия диода. Построить кривые изменения
токов 1с, /₽, t и напряжения на конденсаторе ис в функции со/.
Рассчитать значения углов открытия и закрытия диода при К =
= 1 кОм; С=18 мкФ; со = 314 с-1.
15.21р . На рис. 15.13, а изображена схема двух пол у периодного
выпрямления, в которой резистор R шунтирован конденсатором
для уменьшения пульсаций выпрямленного напряжения; е —
— Ет sin со/. Построить графики изменений во времени напряжения
на конденсаторе ис, тока через конденсатор /с, тока через рези-
стор тока с, напряжений на диодах 1 и 2 ил и . Вывести
формулу для среднего значения и напряжения *Ha нагрузке за
период (оно же среднее за полпериода).
15.22р . На рис. 15.13,6 показана схема двустороннего ампли-
тудного ограничителя напряжения, которая состоит из полупро-
водниковых диодов 1 и 2, линейного резистора R и двух источ-
ников постоянного напряжения Et и Е2. Полагая £1 = 3£2>^»
построить график зависимости напряжения на выходе
от напряжения на входе — uab для положительных и отрица-
тельных значений uab. К зажимам ab подключен источник ЭД^
134
15.23. На вход схемы рис. 15.13,6 поступает синусоидальное
напряжение амплитудой 100 В (пунктирная кривая на рис. 15.14, а).
j4a выходе схемы получено напряжение, изображенное сплошной
линией на рис. 15.14, а. Определить Eit Е2 и сопротивление R
резистора схемы рис. 15.13,6, полагая, что токи через полупро-
водниковые диоды не должны превышать 1 мА.
Рнс. 15.14
15.24р . На рис. 15.14,6 изображена схема двустороннего ам-
плитудного ограничителя тока. В ней имеются полупроводниковые
диоды 1 и 2, резистор сопротивлением R и источники тока
и Jt. К зажимам а и b присоединен источник ЭДС, напряжение
которого можно менять. Полагая Ja —2,4Jlt построить зависимость
тока 7 от напряжения иаЬ при положительных и отрицательных
значениях иаЬ.
В. Цепи с управляемыми нелинейными трехполюсниками.
Расчет по мгновенным значениям и линейным схемам
замещения для малых переменных составляющих токов
и напряжений
15.25. Кремниевый транзистор включен по схеме с общим эмит-
тером (рис. 15.15, а) и служит для усиления мощности. Входные
Рис. 15.15
выходные характеристики транзистора показаны на рис. 15.15, б, в.
^противление резистора в цепи базы /?б = 66,6 Ом; £б = 5 В;
и —35 В. Сопротивление нагрузки /?н—140 Ом. Сопротивление
135
резистора Ra в данной задаче положить равным нулю. Определить
ток нагрузки iK и ток базы Гб.
15.26р . Условие то же, что и в предыдущей задаче* но в цепь
эмиттера включен резистор сопротивлением 10 Ом, с помощью
которого в схеме осуществлена отрицательная обратная связь.
Найти токи и tK.
Рис. 15.16
15.27. На рис. 15.16, а изображена схема замещения транзи-
стора с общей базой для малых переменных составляющих токов
и напряжений на низких и средних частотах. Вывести формулы
для расчета сопротивлений гк, гб, г9 и коэффициента усиления а
через //-параметры.
15.28. На рис. 15.16, б показана схема замещения германиевого'
транзистора для малой синусоидальной составляющей при отно-
сительно высоких частотах. Транзистор включен по схеме с общей
базой, внутреннее сопротивление генератора /?г, сопротивление
нагрузки /?н. емкость коллекторного перехода С. Полагая ампли-
туду входной ЭДС Ег достаточно малой, составить уравнение по
методу узловых потенциалов.
Рис. 15.17
15.29. На рис. 15.17, а изображена схема лампового усилителя.
В схеме использована лампз 6С2С, анодные характеристики кото-
рой представлены на рис. 15.17, б. Исходные данные: Ег0~ 180 В;
— 12,85 кОм; ис0 =— 1 В. Определить внутреннее сопротивление
лампы /?,, крутизну характеристики S и коэффициент усиления
для малых по амплитуде переменных составляющих токов и на-
пряжений.
136
15.30р . На рис. 15.17, в изображена схема замещения транзи-
стора для малых переменных составляющих. Транзистор соединен
по схеме с общим эмиттером. Полагая известными проводимости
уб, Уэ, Y* схемы замещения транзистора, ЭДС управления Еу
А коэффициент усиления транзистора по току а, составить сигналь-
ный граф и по нему найти ток в нагрузке.
15.31. Известны параметры схемы замещения транзистора Уа,
Уб, Ук, Ск, включенного по схеме с общей базой (рис. 15.18, а),
коэффициент усиления транзистора по току а и частота ш сигнала
на входе. Вывести формулы для определения /-параметров (Уп,
У22) невзаимного активного четырехполюсника, которым
может быть (в расчетном смысле) заменен транзистор для малых
переменных составляющих.
15.32р . На рис. 15.18,6 дана схема трех полюс ника, где пока-
зано три узла (6, 1 и 2). Базисный узел 6 является общим для
входного (/—0) и выходного (2—0) контуров. Нагрузка, прово-
димость которой Ун, включена между узлами 2 и 0. Приняв поло-
жительные направления токов и потенциалов в соответствии с ри-
сунком, вывести формулы для входного сопротивления, коэффи-
циентов усиления по напряжению и току с использованием формулы
для двойного алгебраического дополнения и матрицы узловых
проводимостей. При составлении матрицы узловых проводимостей
в нее не включать проводимость нагрузки У н.
15.33. Для схемы лампового усилителя с обратной связью
(Рис. 15.19) составить укороченную матрицу узловых проводимостей
11 • воспользовавшись ею, определить коэффициент усиления напря-
137
жени я KUt если Sj — крутизна характеристики первой лампы;
S3—крутизна характеристики второй лампы; УаК, УаК—проводи-
мости анод—катод первой и второй ламп. При решении исполь-
зовать низкочастотную схему замещения лзмпы.
15.34. В схеме рис. 15.17, а в анодную цепь лампы 6С2С
включен источник постоянной ЭДС £дО = 275 В и вместо —
нелинейный резистор, ВАХ которого показана на рис. 15.20, а.
В сеточной цепи имеются источники постоянной —3 В)
и синусоидальной (ac_ = 3sin<oZ В) ЭДС Анодные характеристики
лампы изображены на рис. 15.17, б. Построить зависимость анод-
ного тока 1Л в функции со/.
15.35. В схеме рис. 15.20, б в анодную цепь лампы 6С2С вклю-
чены источник постоянной ЭДС £д0 —235 В, источник синусои-
дальной ЭДС еа(/) = 100 sin ш/ В и нелинейный резистор, в. а. х.
которого изображена на рис. 15.20, a; ——% В. Построить
зависимость
Г. Расчет по первым гармоникам и действующим значениям
15.36. В табл. 15.3 приведены соответствующие друг другу
значения тока и потокосцепления для некоторой катушки со сталь-
ным сердечником, полученные опытным путем при постоянном
токе. Выразить аналитически полученную зависимость i =
и, пользуясь ею, построить ВАХ 1 по первым гармоникам,
полагая, что потокосцепление ф изменяется во времени по сину-
соидальному закону, а частота со— 100 с-1.
Таблица 15.3 Таблица 15.4
В-с 1. мА Е. кВ/см q, мкКл/см*
0 0 0 0
1 1.5 0,067 0,5
Ъ5 4,15 0,208 1
2 9 0,755 1.5
2.5 16,85 2.75 2
15.37. Опытным путем была снята зависимость напряженности
поля Е от заряда q для диэлектрика триглицинсульфата, употреб-
ляемого для нелинейных конденсаторов (табл. 15.4).
1. Считая, что эта зависимость описывается выражением Е =
= aq+bq\ определить коэффициенты а и Ь. 2. Полагая, что пло-
щадь пластин конденсатора S = 10 см3 и заряд конденсатора ме-
няется во времени по закону q = Qmsinco/, где w—1000 с-1; d —
= 0,1 см—расстояние между пластинами, построить ВАХ по
первым гармоникам тока и напряжения.
15.38. Полагая, что конденсатор предыдущей задачи соединен
последовательно с линейным резистором /? = 50 кОм, построить
138
В AX последовательного соединения по первым гармоникам при:
а) со = 1000 с"1; б) « = 2000 с~‘.
15.39. Схема на рпс. 15.21, а состоит из индуктивной катушки
без потерь, линейных конденсаторов, емкость которых Сг и С2,
и резистора R3. Значения сопротивлений линейных элементов
известны: ХС1 = 30 Ом; ХС1 = 100 Ом; R3 = 100 Ом. ВАХ по первой
гармонике индуктивной *катушки изображена на рис. 15.21,6.
Схема питается от источника синусоидального тока.
Задаваясь значениями тока Ц от 0 до 1,7 А, построить век-
торные диаграммы для всей схемы и по ним графики зависимости
напряжения Uab от тока и сдвига фаз между йаЬ и
15.40р . Схема рис. 15.22, а состоит из нелинейного конденса-
тора, ВАХ которого по первой iармонике представлена на
рис. 15.22,6, индуктивной катушки, конденсатора и двух рези-
сторов. Значения сопротивлений по первой гармонике: Х£ = 50Ом;
АСэ = 40 Ом; = 20 Ом; /?я = 30 Ом. Схема питается от источ-
ника синусоидального тока /х.
Задаваясь значениями тока 7, от 0 до 1,45 А, построить для
каждого его значения векторную диаграмму токов и напряжений
и по ним зависимости напряжения Uab от тока и сдвига фаз
между Uab и
15.41. Индуктивная катушка без потерь, линейный конденсатор
и резистор присоединены к источнику синусоидального напряже-
ния частотой 50 Гц (рис. 15.23, я). ВАХ индуктивной катушки
по первой гармонике изображена на рис. 15.21,6.
Пренебрегая высшими гармониками, найти такие значения
емкости С конденсатора и сопротивления R резистора, при кото-
рых триггерный эффект на увеличение тока происходит при на-
пряжении t\ = 32 В, а на уменьшение тока—при У3 —18 В.
139
Построить в масштабе векторную диаграмму до и после скачка
тока для некоторого произвольного значения напряжения, нахо-
дящегося между 4/ж и Ut.
15.42. Феррорезонансный стабилизатор (рис. 15.23,6) состоит
из линейного конденсатора и индуктивной катушки с нелинейной
ВАХ. Емкостное сопротивление по первой гармонике Хс == 237 Ом.
ВАХ по первой гармонике индуктивной катушки показана на
Рис. 15.23
О "о Ч Ч
Рис. 15.24
рис. 15.23,6. К выходным зажимам а и b может быть подключена
нагрузка. Построить зависимость действующего значения напря-
жения первой гармоники на выходе от действующего значения
первой гармоники напряжения на входе для трех случаев: а) хо-
лостого хода; б) когда к зажимам а и b подключена индуктивная
нагрузка 500 Ом; в) когда к зажи-
мам а и b подключена активная наг-
рузка 500 Ом.
15.43. На рис. 15.24 изображена
схема диэлектрического усилителя
На ее вход (зажимы а и б) воздейст-
вует некоторое малое постоянное нап-
ряжение пвх, дополнительное к посто-
янному напряжению £/0. Изменяя пвх,
можно управлять падением напряже-
ния переменного тока на резисторе сопротивлением Rx (на зажимах
с и d). Индуктивность представляет собой большое сопротир-
ление для переменного тока и поэтому практически исключает
прохождение его через источник постоянного напряжения. Кон-
денсатор емкостью Ci препятствует протеканию постоянного тока
через источник синусоидальной ЭДС. Параметры и С\ выбираю^
так, чтобы в контуре, по которому протекает переменный ток
(Llt и нелинейный конденсатор), имел место резонанс на-
пряжений по первой гармонике при «вх=0. Тогда появление
напряжения нвк приводит к выходу схемы из режима резонанса,
что сопровождается резким изменением тока через Rt.
Полагая, что кулон-вольтная характеристика нелинейного кон-
денсатора задана в виде u = ash|ty, значения Uo, Ет, <а, а и ₽
известны, вывести соотношение между Lx и С\, которое должно
выполняться для нормальной работы схемы.
140
15.44. 1. В схеме рис. 15.25, а параллельно соединены управ-
ляемая нелинейная индуктивная катушка и конденсатор С. Схема
питается от источника синусоидального тока J, действующее зна-
чение которого поддерживается неизменным и равным 2А. ВАХ
нелинейной индуктивной катушки при различных значениях тока
управления (тока подмагничивания) /0 изображены на рис. 15.25,6.
Построить зависимость напряжения Uab на зажимах а и b в функ-
ции тока управления /0.
Рис. 15.25
2. В схеме рис. 15.25, в ток источника синусоидального тока
/=2А, сопротивление резистора /? = 42 Ом, емкостное сопротив-
ление Хс=22,7 Ом. Семейство ВАХ управляемой нелинейной
индуктивной катушки изображено на рис. 15.25, б. Ток управле-
ния /в = 0,2А. Определить напряжение Uab на зажимах а и b
источника тока.
15.45р . Индуктивная катушка со стальным сердечником питается
от источника синусоидального напряжения 100 В (действующее
значение). Через нее течет ток / —0,1 А. Мощность, потребляемая
от сети, Р == 1,58 Вт; активное сопротивление обмотки R 20 Ом,
индуктивное сопротивление рассеяния Х$ = 50 Ом. Найти потери
в стали сердечника, обусловленные гистерезисом и вихревыми
токами, ток, вызванный потерями в стали, и намагничивающий ток.
15.46. С повышающим трансформатором, отношение числа вит-
ков которого 00^ — 10, провели опыт холостого хода и опыт
короткого замыкания. Опыт холостого хода проведен при СГ1Х —
= 100 В; /1х=0,2 А; Р|х = 3 Вт (Р1х—мощность холостого хода).
Опыт короткого замыкания вторичной обмотки—при //1К = 10 В;
/,Ж«=ЗА; Р1к—15Вт.
Определить активные сопротивления Pt и Ps первичной и вто-
ричной обмоток, потери в стали сердечника при номинальном
Режиме Рс, индуктивные сопротивления Х51 и л52, обусловлен-
ные потокосцеплеииями рассеяния. При решении полагать, что
Сопротивление вторичной обмотки, приведенное к числу витков
Первичной, равно сопротивлению вторичной обмотки, т. е.
15.47р . Однофазный трансформатор со стальным сердечником
Работает при первичном напряжении 380 В и вторичном—6600 В.
141
Он сконструирован таким образом, что тепловые потери при номи-
нальной нагрузке в первичной и вторичной обмотках практически
равны [при этом Яа = Rx а индуктивное сопротивление
рассеяния вторичной обмотки Х$2, умноженное на квадрат отно-
шения числа витков равно индуктивному сопротивлению
рассеяния первичной обмотки: ХС2(ьу1/щ2)2 = Х51].
Для определения ASI; XS2, Ri и /?2 к первичной обмотке
трансформатора подвели пониженное напряжение 38 В при номи-
нальной частоте, а вторичную обмотку закоротили накоротко,
измерили ток в первичной обмотке и потребляемую из сети
активную мощность Р. Вывести формулы для расчета Rit Rit Xsit XSt
по данным опыта.
Д. Частотные характеристики
15.48. Электрическая цепь рис. 15.26, а состоит из нелиней-
ного конденсатора с кулон-вольтной характеристикой ис
—aq3 (а = 4/3 В/Кл3), линейной индуктивной катушки с индуктив-
ностью L = 1 Гн и источника синусоидальной ЭДС е(/) — Ет sin©/.
Полагая Еда = 2 В, а © —var, построить зависимость амплитуды
первой гармоники заряда нелинейного конденсатора от часто-
ты ©.
15.49р . Для цепи рис. 15.26, в, состоящей из нелинейной ин-
дуктивной катушки и линейного конденсатора емкостью С, в кото-
рой действует источник синусоидальной ЭДС е(/) = £‘ясоьюг,
построить зависимость амплитуды первой гармоники потокосцеп-
ления фя индуктивной катушки от частоты © при неизменных
Ет и С. Считать, что мгновенное значение потокосцепления свя-
зано с мгновенным значением тока через индуктивную катушку
соотношением / =пф3 ([п] = А-В“э-с“3). При построении принять
а=|с. Е„=2В.
142
15.50р . В электрическую цепь рис. 15.26,в дополнительно вклю-
чен резистор сопротивления /? = 0,1 Ом. По-прежнему п=уС;
£т₽2В. Вывести уравнение резонансной кривой фт = ^((о), пола-
гая, что частота со изменяется от 0 до оо. Принять/?С = 0,182 с.
Воспользовавшись резонансной кривой Для чепи без
потерь, полученной при решении предыдущей задачи, построить
резонансную кривую для цепи с потерями.
15.51. В электрическую цепь рис. 15.26, а (см. задачу 15.48)
включен еще резистор сопротивлением R. Считая, что кулон-
вольтная характеристика нелинейного конденсатора описывается
уравнением uc—aq3, где с = 4,3 В/Кл-®, вывести формулу для
частотной характеристики Qm = f (ю) п0 первой гармонике и, при-
няв L=1 Гн; Я = 0,2 Ом и Ет — 2 В, построить эту характе-
ристику.
15.52р . Электрическая цепь та же, что и в задаче 15.49 р
(рис. 15.26, д), но нелинейная индуктивная катушка подмагни-
чивается постоянным током /0 такого значения, что /0/а = 6. Пола-
гая, что обмотка подмагничивания и основная имеют по одному
витку, а вебер-амперная характеристика нелинейной индуктивной
катушки описывается выражением i + /0 = аф®, а а — у С; Ет — 2 В,
-построить зависимость амплитуды первой гармоники потокосцеп-
ления фп, в функции частоты <о.
15.53р . Нелинейные конденсатор с кулон-вольтной характе-
ристикой ис —arf и индуктивная катушка с вебер-амлерной харак-
теристикой 1 = а2ф® присоединены к источнику синусоидального
напряжения e(Z) = £rasin(oZ (рис. 15.26, В). Полагая Fffl = 2B,
построить резонансную зависимость амплитуды Qm первой гармо-
ники заряда на нелинейном конденсаторе от частоты о).
Е. Метод малого параметра
15.54. Схема рис. 15.27, а содержит источник постоянной ЭДС
Е, резисторы сопротивлением R и R* и нелинейный конденсатор
с кулон-вольтной характеристикой uc—aq-i b'q9. До замыкания
выключателя Вх выключатель В2 находился в замкнутом состоя-
нии и в схеме был установившийся режим. Методом малого пара-
метра определить закон изменения заряда q во времени t при
замыкании ограничившись первым приближением и приняв
9(0) = Д (рис. 15.27,6).
15.55р . В схеме рис. 15.27, а выключатели Вг и В2 находятся
в разомкнутом состоянии; в схеме имеют место нулевые началь-
ные условия. При / = 0 выключатель Ва замыкается н нелинейный
конденсатор начинает заряжаться. Как и в предыдущей задаче,
uc=a'q + brqs. Составить дифференциальное уравнение относи-
’вльно заряда q и решить его методом малого параметра, огра-
Вичившись первым (не нулевым) приближением.
15.56р , До замыкания выключателя В в цепи рис. 15.27, в
143
был установившийся режим. Составить дифференциальное урав-
нение относительно потокосцепления ф и решить его методом
малого параметра, ограничившись вторым приближением, т. е.
учитывая члены с р2. Считать, что зависимость потокосцепления ф
от тока i описывается уравнением х==а'ф-}-Ь'ф2.
Рис. 15.27
15.57р . Электрическая цепь состоит из конденсатора емкостью С
и индуктивной катушки, вебер-амперная характеристика которой
описывается формулой t^ashfhp. Обозначив Рф — х, ар/С = <о2
и полагая при малых х sh х та х + х3/3! решить уравнение свобод-
ных колебаний методом малого параметра, ограничившись первым
приближением. Начальные условия: х(0) = Л4; х'(0) = 0.
15.58. Схема рис. 15,27, г состоит из источника постоянного
тока J~Ik, линейных резисторов сопротивлением R и нелинейной
индуктивной катушки. Показать, что переходный процесс в этой
схеме, вызванный замыканием выключателя, описывается уравне-
нием
dx/dt + ах 4 Рх* = 0. (1)
Начальное условие х(0)—1. Через х = ф обозначено потоко-
сцепление. Ток i связан с потокосцеплением ф соотношением
аф-|-Ьф3; = а = а/?/2; p=W?/2. Решить уравнение (1)
методом малого параметра.
15.59. Схема рис. 15.27, д состоит из источника постоянной
ЭДС £, линейного резистора сопротивлением 7?» линейного кон-
денсатора емкостью С, нелинейной индуктивной катушки с вебер-
амперной характеристикой i — «ф4 Ьф3. До размыкания выключа-
теля в схеме был установившийся режим. Приняв некоторое потоко-
сцепление фо нелинейной индуктивной катушки за базисное, выра-
зить потокосцепление в относительных единицах х=ф1=ф/ф0;
показать, что уравнение относительно х при разомкнутом выклю-
144
чателе имеет вид
(Рх < S ( I X3 \ л
4/3 + + g — О»
где too = a/C', -£-ipo= 1/6- Методом малого параметра решить урав-
нение (1) при начальных условиях х(0) = Л и х'(0) = 0, где Л —
корень уравнения А + -g Д3
(1)
Ж* Некоторые энергетические соотношения
15.60р . На рис. 15.28 изображены две петли гистерезиса одного
и того же ферромагнитного материала» полученные при одной
и той же максимальной индукции. Сплошная кривая снята при
Рис. 15.28 Рис. 15.29
бесконечно медленном изменении магнитного поля, пунктирная —
при синусоидально изменяющейся магнитной индукции и частоте
А =100 Гц.
Полагая, что потери на гистерезис пропорциональны первой
степени частоты, а потери на вихревые токи — второй, определить
потери в ферромагнитном сердечнике объемом 10 см3 при частоте
А=200 Гц, считая, что распределение поля по сечению, макси-
мальное значение и форма индукции во времени такие же, как
и при Д = 100 Гц, а потери, обусловленные магнитной вязкостью,
на низких частотах не имеют существенного значения.
15.61. Для некоторого равномерно намагничиваемого ферро-
магнитного материала потери на частоте А(А=1»ЗА) на 50 %
больше, чем на частоте Во сколько раз частота /3 больше А»
если при ней потери в четыре раза больше, чем при А* Во всех
случаях форма индукции и ее амплитуда одинаковы.
15.62. На рис. 15.29, а дана схема электрической цепи, состоя-
щей из источника синусоидальной ЭДС = sinert, резистора
сопротивлением R и нелинейной индуктивной катушки, зависи-
145
мость потокосцепления ф от тока i которой изображена на
рис. 15.29, б. На рис. 15.29, в показан характер изменения тока
во времени. Доказать, что активная мощность, доставляемая
источником синусоидальной ЭДС равна тепловым потерям в ре-
зисторе R за 1 с.
15.63. К нелинейному конденсатору с безгнстерезисной харак-
теристикой подводятся мощность на частоте fa и мощность U?o
на частоте f0. Кроме частот fa и fa в цепи действуют токи и на-
пряжения частот f+ —fi 4- и f_ — fj—f0. Токи остальных частот
подавлены идеальными фильтрами. Пользуясь теоремой Менли
и Роу, вывести формулы для определения мощности W+ на часто-
те f+ и мощности на частоте f_.
15.64 р. К нелинейному конденсатору с безгнстерезисной харак-
теристикой подводится мощность на двух частотах: мощность
на частоте f и мощность 1Г3 на частоте 3[. Выяснить, какая мощ-
ность отдается нелинейным конденсатором на частотах 4f и 2f.
При решении полагать, что токи всех частот, кроме f, 2/, 3f и 4f,
подавлены идеальными фильтрами.
15.65. К нелинейной индуктивной катушке с безгнстерезисной
характеристикой подводятся мощность на частоте / и мощ-
ность Wt на частоте 2/. Показать, что если токи всех частот,
кроме fa 2/, 3/, 5f, подавлены идеальными фильтрами, то исходя
из теоремы Менли и Роу нельзя определить, какие мощности IFS
и отдаются нелинейной индуктивной катушкой на частотах
3/ и 4/.
3. Появление посторонних составляющих потока, заряда
и тока при отсутствии выпрямителей.
Метод гармонического баланса
15.66р. На рис. 15.30, а изображена индуктивная катушка
с замкнутым (без воздушного зазора) ферромагнитным сердечником.
Вебер-амперная характеристика сердечника приближенно может
Рис. 15.30
2 л/со значение тока равно нулю, что
него за период 2л/со потокосцепления
быть описана формулой
i = a sh 0ф. К зажимам а и
b этой катушки подведено
напряжение, содержащее
первую (частота о) и вто-
рую (частота 2со) гармони-
ки: и — Ur„ cos со/ +
4- cos (2<irf 4- ф). Так
как в цепи нет выпрями-
телей, среднее за период
вызывает появление сред-
Ф = Фо4- Фгд sintof-l ф^в1п(2^+ф).
Вывести зависимость ф0 от ф^, ф^ и <р.
146
15.67. По индуктивной катушке с замкнутым ферромагнитным
сердечником (рис. 15.30, а} протекает ток i=/lnsinco/4-
Xsin(2co/ 4- <р2), не содержащий постоянной составляющей. Пока-
зать, что потокосцепление ф будет содержать постоянную состав-
ляющую ф0. Вывести формулу для определения ф0, полагая, что
вебер-амперная характеристика ферромагнитного сердечника при-
ближенно может быть описана выражением ф — ai—bi3f а макси-
мальное значение тока в процессе работы не превышает значения
15.68. Нелинейный конденсатор с кулон-вольтной характеристи-
кой, приближенно описываемой выражением uc = ос shfty, при-
соединен к источнику периодического напряжения, среднее зна-
чение которого за период частоты со равно нулю. Заряд конден-
сатора изменяется во времени так, что содержит первую (Q1JB sin со/)
л четвертую [Q4CTsin(4t)/4- <р*)3 гармоники. Показать, что среднее
значение напряжения на конденсаторе за период 2зт/со равно нулю,
если заряд конденсатора имеет постоянную составляющую Qo;
= Qo 4- Qlm sin со/ 4- Qim sin (4co/ 4- ф4). Вывести формулу зависимо-
сти <?o от Q4m и ф4.
15.69. На нелинейный резистор с симметричной характеристи-
кой i = аи9 воздействует напряжение и — Ulm sin со/ 4 U2m (2со/4-ф).
Показать, что через резистор протекает постоянная составляющая
тока, и вывести формулу для нее.
15.70р . В схеме рис. 15.30, б ЭДС источника содержит пер-
вую и вторую гармоники: е (/) = Eim sin со/ 4- Е^ sin (2со/ 4- Ф)- Не-
линейный резистор имеет симметричную характеристику » =
резистор сопротивлением 7? имеет линейную ВАХ Пренебрегая
гармониками выше второй, составить уравнения для определения
постоянных составляющих токов и напряжений в цепи для пер-
вых и вторых гармоник.
И. Зависимость постоянной составляющей потока (заряда)
от переменной составляющей
В схеме рис. 15.31, а линейные резисторы сопротивле-
индуктивная катушка, источник по-
15.71,
нием Rt ]
стоянкой :
точник
ЭДС
соединены
но. Число
индуктивной катушки w =
— 500, площадь попереч-
ного сечения сердечника
8 = 4 см2, длина средней
Магнитной линии I -= 25 см.
и /?2, нелинейная
ЭДС Ео и не-
си нусои дальней
е (/) = Ет • sin со/
последователь-
। витков обмотки
Рис. 15.31
Кривая намагничивания материала сердечника приближенно описы-
вается формулой Н ash РВ, где Я—в А^ м; а = 7 А/м; р = 6 Тл”1;
В*—к Тл. Определить постоянную составляющую Во> амплитуду
147
первой гармоники Вт переменной составляющей индукции в сер-
дечнике в установившемся режиме при разомкнутом и замкнутом
выключателе, если /?1 = 7?1=100 Ом; ЕЛ = 48 В; о = 314 с-1;
£О=14,3 В.
Указание. Задача сводятся к трансцендентному уравнению.
15.72. Определить постоянную составляющую Qe и амплитуду
первой гармоники Qm заряда на нелинейном конденсаторе в схеме
рис. 15.31, б при замкнутом и разомкнутом выключателе в уста-
новившемся режиме; £в = 200 В; £„ = 341 В; /?х = /?г=5 кОм;
(0=3140 с-1. Кулон-вольтная характе-
ристика нелинейного конденсатора вы-
ражена аналитически: u=30sh(0,4x
X Ю’д), где и—в В; q—в Кл.
15.73р. В схеме рис. 15-32 к ис-
точнику тока j = Jo 4- J„ sin - (art 4 q>)
присоединены три параллельных вет-
ви: ветвь с активной проводимостью
G, конденсатор емкостью С, нелиней-
7
G
Рис. 15.32
ная индуктивная катушка с вебер-амперной характеристикой, опи-
сываемой выражением i = ash|3$. Полагая, что потокосцепление
Ф = Фо + Фстsin вывести формулу, с помощью которой можно
определить зависимость постоянной составляющей потокосцепле-
ния фо от амплитуды первой
гармоники переменной состав-
ляющей потокосцепления ф„,
а также от безразмерных па-
раметров G/(wC), р/(ю2С), a.
К. Исследование
устойчивости положения
равновесия.
Автоколебания
15.74р . На рис. 15.33, a
изображена схема релакса-
ционного генератора на не-
линейном резисторе(неоновой
лампе) с S-образной ВАХ.
На рис. 15.33, б «з—напря-
жение зажигания, иг—напря-
жение гашения. Положим, что
и3 в а раз больше и?, т. е.
ил—аи^ ЭДС Е источника ЭДС в Ъ раз больше иг,т. е. Е—ЬиТ.
Нагрузочная прямая на рис. 15.33, б проходит через точки £, О
и О, Е/R, пересекая падающий участок ВАХ нелинейного рези-
стора в точке п. Примем дифференциальное сопротивление на
участке ef (рис. 15.33, б) равным а/?, где а< 1.
Вывести формулу для определения периода колебаний Т =
= G4 Ч (Рпс« 15.33, в). Схема замещения для зажженного состоя-
Ркс. 15.33
U6
нпя неоновой лампы изображена на рис. 15.33, г. Дополнитель-
ная ЭДС Елоп = тЕ совместно с резистором сопротивлением aR
описывает участок fe ВАХ нелинейного резистора. Считая а = 3;
£ = 6; т=0,166 и положив, что точка п делит отрезок и3—s на
части 1:3, вывести формулы для определения Л
период колебаний составляет Т секунд.
R и С, при которых
Рис. 15.34
(E = RJ).
Рис. 15.35
15.75. На рис. 15.34, а изображена схема, состоящая из источ-
ника тока J, резистора сопротивлением R* индуктивной катуш-
ки L и туннельного диода, ВАХ которого показана на рис JL5.34, б.
Схема рис. 15.34, в эквивалентна схеме рис. 15.34, а
При каких значениях индуктивности ка-
тушки L положение равновесия будет
неустойчивым?
15.76. Релаксационный генератор
на туннельном диоде (рис. 15.34, в)
имеет следующие данные: R =40 Ом;
1=9 мГн; Е = 0,4 В. ВАХ туннель-
ного диода изображена на рис. 15.35.
Вывести формулу для определения ко-
лебаний, считая дифференциальное соп-
ротивление на участке 1—2 ВАХ диода
равным а, а на участке 3—4 равным Ь.
Емкость туннельного диода Са настоль-
ко мала, что напряжение на диоде может
изменяться практически скачком. Пост-
роить в функции времени кривые тока t,
напряжения иа на диоде и напряжения
«£ на индуктивной катушке.
15.77р . На рис. 15.36, а изображена
туннельном диоде. Резисторы Ri и Rs служат для насгройки схемы
по постоянному току (чтобы точка равновесия находилась на падаю-
щем участке характеристики). Емкость блокировочного конден-
сатора Cg достаточно велика, чтобы закорачивать зажимы а и b
ьа частоте генерации. На рис. 15.36, б показана схема замещения
схема ДС-генератора на
149
диода при работе на падающем участке. В этой схеме емкость Сд
конденсатора может составлять от нескольких единиц до несколь-
ких сотен пикофарад, сопротивление резистора R'—от долей ом
до I Ом; ЯДНф« 1 4-500 Ом; г = ЯДИф—R'. Полагая сопротивле-
ния резисторов Rlr Rt и ЭДС Е выбранными таким образом, что
единственная точка равновесия находится на падающем участке
ВАХ диода, и используя эквивалентную схему рис. 15.36, в, вы-
вести формулу для соотношения между параметрами, при которых
наступит самовозбуждение.
15.78. Вывести дифференциальное уравнение для лампового
генератора с колебательным контуром в анодной цепи, воспользо-
вавшись обозначениями на рис. 15.37, а и полагая, что зависи-
мость анодного тока от сеточного напряжение известна. Эта схема
соответствует малым переменным составляющим; на ней не пока-
зан источник ЭДС в анодной цепи.
15.79р . На рис. 15.37, б изображена схема £С-генератора на
транзисторе с трансформаторной обратной связью. На рис. 15.37, в
показана схема замещения его для малых переменных составляю-
щих. Составить уравнения по методу контурных токоз для схемы
рис. 15.37, в. Записать определитель этой системы уравнений Д
и из уравнений 1тД —0 и ReA = 0 найти угловую частоту воз-
никающих автоколебаний и соотношение, которое должно выпол-
няться между параметрами схемы для существования автоколеба-
ний. При решении учесть, что между параметрами схемы заме-
щения имеет место соотношение R^^Re^Ra-
15.80» На рис. 15.38, а изображена схема генератора на тран-
зисторе с емкостной обратной связью. Источник ЭДС смещения
150
рисунке не показан. Схема замещения для исследования усло-
вий возникновения автоколебаний приведена на рис. 15.38, б.
Воспользовавшись этой схемой, составить определитель А системы
уравнений по методу контур-
ных токов, приравнять нулю
его действительную и мни-
мую части и записать выра-
жение для угловой частоты
возникающих автоколебаний.
Вывести условия, наклады-
ваемые на соотношения меж-
ду параметрами схемы, при
которых автоколебания су-
ществуют. При решении учесть, что Rx^-Rb^R^ Rm—aR* принять
равным RK.
Л. Электрические цепи с операционными усилителями*
15.81р . Показать, что схема рис. 15.39 может выполнять функ-
ции конвертора отрицательного сопротивления.
Рис. 15.39
15.82. Показать, что для схемы рис. 15.40 ZBX = — RtRjZ^
т. е. схема может выполнять функции инвертора отрицательного
сопротивления.
15.83. Показать, что входное сопротивление схемы рис. 15.41
Ах » т- е- схема может выполнять функции инвертора
положительного сопротивления.
15.84. Показать, что передаточная функция полосового фильтра
(рис. 15.42)
К (р) =----------^1 + -_____________
‘+«Гт(С1+с’1₽+^Тл7с,С!0
* При решении задач 15.81р—15.89р полагать, что ОУ обладают идеаль-
ными свойствами, т. е. что их входные сопротивления бесконечно велики, вход-
ные токи и входные напряжения стремятся к нулю и ксэффиингнт усиления
(Передаточная функция ОУ) не зависит от частоты и стремится к бесконечности.
151
15.85. Показать, что в схеме рис. 15.43 —ср, (I-У Rj/Rn),
т. е. схема может выполнять функции источника напряжения,
управляемого напряжением. Здесь (рг, <р2—потенциалы точек 1 и 2.
15.86 р. Показать, что с
реализовать отрицательную
помощью схемы рис. 15.44 можно
емкость, равную— ( о~ ь> + Q ).
\ K2 Ki /
если параметры Rlt Rs, Cn С2 таковы,
что квадрат угловой частоты источника
питания <о2= l/fRiCj/^Cj).
15.87 р. Доказать, что входное сопро-
тивление схемы рис. 15.45 ZBX = R4-i-
при
15.88 . Показать, что схема рис. 15.46
позволяет реализовать продольное сопро-
Рис. 15.43 тивление между точками 1 и 2 Z12 = R(l-1-
воляет реализовать продольный
4-pCR2RB, если R, = Rn (т. е. схема поз-
незаземленный индуктивный эле-
мент с потерями).
Рис. 15.45
15.89р. Показать, что схема рис. 15.47 реализует регулируе-
мый одним резистором R, индуктивный элемент с потерями, у кото-
poro L = CR^R-11 4--gi} н R — Rt-i R. + ^.
\ Кз / “ Кз
152
15.90р. На рис. 15.48 изображена схема автоколебательной
системы. Она содержит два ОУ и четыре резистора; k и а—не-
которые числовые коэффициенты (&< 1; а< 1). Устойчивые авто-
колебания в схеме возникают за счет того, что в ней имеются
обратные связи, а ОУ не идеальны (коэффициент усиления каж-
дого из них зависит от частоты: К (р) =Л0/(1 + pi), где kc — коэф-
фициент усиления ОУ при ш = 0; т—величина, по размерности
обратная частоте, при которой коэффициент усиления ОУ умень-
шается на ЗдБ).
Рис. 13.48
Рис. 15.49
Показать, что автоколебания возникают при ~ и частота
J -рос
« Ал -1 Г ka-
автоколебании ю0 = ~ I/ ——.
" т г 1-|-а
15.91р. На рис. 15.49. изображена схема полосового /?-фильтра.
Она содержит ОУ (1 и 2) и пять резисторов Внешних
конденсаторов в схеме нет. Схема выполняет функции фильтра,
так как коэффициент усиления каждого ОУ зависит от частоты:
Л (р) =_А— (учитываем первый доминантный полюс каждого ОУ).
1. Составить схему замещения фильтра, в которой выходная цепь
Каждого ОУ замещена источником напряжения, управляемым
153
напряжением, и малым выходным сопротивлением Явых. 2. Вывести
формулу для передаточной функции фильтра, полагая, что вход-
ное напряжение фильтра создается источником напряжения, а
фильтр работает в условиях холостого хода. 3. При Ло = 2-10ь;
т=0,0307 с; /?!=0,6 кОм; /?2=0,1 кОм; /?3=9,9 кОм; Я4=0,09к0м;
/?5—ЮкОм; ЯВых = 0,075 кОм подсчитать числовое значение пере-
даточной функции при / = 50 кГц.
Глава шестнадцатая
Переходные процессы в нелинейных
электрических цепях
А. Расчет переходных процессов
в целях первого порядка
16.1р. ’•Найти изменения тока и потокосцепления в цепи
рис. 16.1,а после коммутации, используя кусочно-линейную ап-
проксимацию вебер-амперной характеристики нелинейной индук-
тивной катушки. Задачу решить для следующих значений макси-
Рис. 16.1
мального потокосцепления (рис.
В) ’!’»,=
16.2р. Подключение цепи рис.
форма которой показана на рис.
16.1,6): а) = б) ^„=11)»,;
16.1, а к источнику ЭДС е(/),
16.1, в, происходит при тех же
6)
Рис. 16.2
а!
условиях, что и в предыду-
щей задаче. Определить изме-
нения тока и потокосцепле-
ния во времени, полагая
7\<772.
16.3. Определить измене-
ние напряжения на нелиней-
ном резисторе после комму-
тации цепи (рис. 16.2, а).
ВАХ резистора аппрокси-
мирована полиномом вида i (и) = аи Ьи~. Полученное решение
сравнить с решением линейной (Ъ = 0) задачи.
154
16.4. Найти изменение напряжения при разряде нелинейного
конденсатора (рис. 16.2, б), кулон-вольтную характеристику кото-
рого при ис^Е можно представить в виде q(uc) = Couc—
Задачу решить аналитически для: а) а =1/2; б) а = 0 (линейный
конденсатор).
16.5. Рассчитать ток в цепи после коммутации (рис. 16.3, а),
воспользовавшись методом графического интегрирования. ВАХ
нелинейного резистора показана на рис. 16.3, б. Параметры цепи:
Д = 200 0м; £=10 Гн; £= 300 В.
а)
Рис. 16.3
Рис. 16.4
16.6. Методом интегрируемой нелинейной аппроксимации найти
изменения во времени тока и потокосцепления после коммутации
цепи (рис. 16.4). Вебер-амперная характеристика нелинейной ин-
дуктивной катушки задана выражением <=675ф*, где i—в А;
ф—в В-с. Параметры схемы: /?=200 0м; Е=100В.
16.7. Решить предыдущую задачу графоаналитическим методом
Волынкина.
16.8. Решить задачу 16.6 методом последовательных интерва-
лов. Результаты расчета сравнить с аналитическим решением.
а)
16.9. Найти ток через резистор (после коммутации цепи
(рис. 16.5, а). Задачу решить методом последовательных интерва-
лов и сравнить результат с аналитическим решением методом
кусочно-линей ной аппроксимации. ВАХ диода в проводящей
области показана на рис. 16.5, б. Сопротивление диода в непро-
водящей области считать бесконечно большим. Исходные данные:
е(0-100sin314/В; /? = 35,5Ом; С = 70мкФ.
16.10р . Найти изменение во времени напряжения на нелиней-
ном конденсаторе при его разряде (рис. 16.6, а), полагая, что
155
дифференциальная емкость конденсатора определяется выражением
= —a~§~^ • Задачу решить в общем виде методом изоклин
для: а) а =1/2; б) а = 0. Сравнить полученные графические реше-
ния с аналитическими (см. задачу 16.4).
16.11р . Определить изменения тока во времени после комму-
тации цепи рис. 16.6,6. Задачу решить методом изоклин, если:
а) ВАХ резистора линейна, т. е. w(O = /?oi; б) ВАХ резистора
нелинейна u(i) = flim, где/и = 2; 1/2.
Рис. 16.6 Рис. 16.7
16.12. Найти ток после коммутации цепи рис. 16.7, а. Задачу
решить методом изоклин, если: а) ВАХ резистора u(i) — Rj;
б) ВАХ нелинейного резистора w(t) = ots.
16.13. Определить зависимость скорости изменения напряже-
ния на конденсаторе в функции напряжения ducldt=f(uc) и по-
строить фазовые портреты для: a) uc(t)~±Uc^ б) ис(/) = ±а/;'
в) цс(/)=6/8; г) wc=e±a/; д) ис(/) = 1—e~a/; е) «c(/) = sin(o/;
ж) wc(0 = e±a/sinw:.
16.14. Построить фазовые портреты изменения напряжения на
конденсаторе при его разряде (рис. 16.7,6), если: а) емкость кон-
денсатора Со не зависит от напряжения; б) емкость конденсатора
нелинейно зависит от напряжения:
“7 / 1 ис \
due °v 2UCJ'
а)
Рис. 16.8
16.15р . Построить фазовые портреты изменения напряжения
на конденсаторе (рис. 16.8,о), если: а) R(i) = R0 (линейный ре-
зистор); б) ВАХ нелинейного резистора i—au*', в) ВАХ. нели-
нейного резистора задана графически на рис. 16.8, 6.
16.16р . Построить график изменения напряжения на конден-
саторе во времени, используя фазовый портрет генератора релак-
сационных колебаний (см. п. в) предыдущей задачи).
156
16.17р . Показать, что точка равновесия (у = 0) в задаче 16.15р
для случая в) неустойчива в малом.
Б. Расчет переходных процессов
в цепях второго порядка
16.18. Качественно построить фазовые портреты y = f(x)t где
t у=di/dt, полагая зависимость тока известной (рис. 16.9, а—и).
Определить характер особых точек.
Рис. 16.9
16.19. Качественно построить по фазовым портретам у = [(х),
где х = ис, y~duc!dt зависимости во времени напряжения на
конденсаторе и тока в нем. Фа-
зовые портреты y=f(x) приве-
дены на рис. 16.10, а, б.
16.20р . Определить характер
переходного процесса при раз-
ряде конденсатора (рис. 16.11, а).
Задачу решить методом фазовой
плоскости при: а) С (и) = С0-,
б) С(«) = С0, Яо = 0.
Начальные значения: Wc(^) =
= Uco\ q (0) — Qo- Параметры схе-
мы: = 1 Ом; £-о=1 Гн; Со =
-1 Ф; <7(0)=1 Кл.
16.21. Методом фазовой плоскости определить характер пе-
реходного процесса при разряде нелинейного конденсатора
(рис. 16.11,6). Кулон-вольтная характеристика конденсатора по-
казана на рис. 16.11, в. Рассмотреть два случая; а)
157
6) Ro = O. Параметры схемы и начальные условия: Я0=1Ом;
Lo — 1 Гн; q (0) = q0 = 1 Кл.
16.22р. Построить фазовые портреты изменения напряжения
на конденсаторе (рис. 16.12, о) после коммутации, если: а) ВАХ
резистора линейна; б) ВАХ
резистора нелинейна и задана
графически (рис. 16.12,6).
В обоих случаях принять
wc (0) “ ^со-
Примечание. При построе-
нии фазовых траекторий удобно
пользоваться методом Льенара.
ЛЮ
а)
«. с0
Рис. 16.12 16.23р. Найти закон изме-
нения огибающих амплитуд
заряда конденсатора после коммутации (рис. 16.13, а). Задачу решить
методом медленно меняющихся амплитуд при: а) Q =
— 1» б) 7?о=0. Анализ изменения амплитуд во времени
«в
провести с помощью фазовой плоскости.
16.24. Определить закон изменения заряда на нелинейном кон-
денсаторе после коммутации (рис. 16.13,6), полагая wc(g)_ с//С04-
4-РФ*. При решении воспользоваться методом, медленно меняю-
щихся амплитуд. Начальные условия: uc(ty = UCKi’t ?(0) = t/0.
16.25. Найти закон изменения амплитуд вынужденных коле-
баний в контуре без потерь (рис. 16.14, а) при подключении его
к источнику ЭДС • e(t) = Em sin со/, полагая: а) ы = ш0; б) (оу=сос,
где (d0 = \/У L6C0—резонансная частота контура. Задачу решить
методом медленно меняющихся амплитуд.
16.26р . Определить изменение амплитуд напряжения на кон-
денсаторе после коммутации (рис. 16.14,6), если уравнение цепи
описывается выражением L0C0~~—Л/(1—+ = где
ki и k* зависят от параметров управляемого нелинейного актив-
ного двухполюсника. Отношение k^^L0CQ<^. 1.
В. Численные методы
16.27. Для цепи рис. 16.2, а найти закон изменения тока Г й
напряжения и на нелинейном резисторе во времени на интервале
< = 04-0,15 с, полагая £ — 10 В; L = 0,l Гн. ВАХ резистора
158
u(i)—au + bu*t где a=l; 6 = 0,1; i—в A; и—в В. Порученное
решение нелинейной задачи сравнить с решением линейной (6 = 0).
16.28. Рассчитать время, за которое ток в цепи рис. 16.3, а
постигнет после коммутации значения if = 0,8 А. ВАХ нелиней-
ного резистора tt(i) = 200P^; £ = 300 В; £ = 200 Ом; £=10 Гн.
16.29. Для цепи рис. 16.4 численно определить закон изме-
нения потокосцепления катушки ф и тока в ней i во времени на
интервале t = 0 4- 0,3с при Е — 100 В; £ = 200Ом; ВАХ i (ф) =
-=6754?*, где t — в А; ф—в Вб.
16.30. Для цепи рис. 16.5, а численно с шагом h — 1/1200с
найти закон изменения напряжения на конденсаторе после ком-
мутации, полагая, что ВАХ диода задана кусочно-линейной
зависимостью. При этом если ии^0, то £B(iH) = £ВПр = 35 Ом,
если пв<0, то £B(iR) = £вобр= 1000 Ом. Параметры цепи: Е =
= 100 В; £ = 35,5 Ом; С = 70 мкФ.
16.31. Автоколебательная система с мягким возбуждением
рис. 16.14,6 описывается уравнением Ван-дер-Поля
g-e(l-x«)|+x=0,
где х=ис; т=Ыо/; ь)0 = 1/ 1/(£0С0); е = 0,2. Полагая x = a(x)sinT,
где а(т)—медленно меняющаяся амплитуда, определить уравне-
ние для огибающей а(т) и решить его численно с шагом 6 = 0,5
при: 1) 0 < | а01 < 2; 2) |о0|>2 (а0—начальная амплитуда).
16.32. Автоколебательная система с жестким возбуждением
рис. 16.14,6 описывается уравнением вида
^ + е(1—х! + Рх*)^ + х = 0,
где х = ис\ т = (о0/; со0 = И 1/(/0С3). Полагая х — а (т) sin т, где
а(т)—медленно меняющаяся амплитуда, найти уравнение для
огибающей а (г) и возможные установившиеся значения амплитуд
уст» с2Уст’» характеризующие устойчивый н неустойчивый пре-
дельные циклы. Считая е=0,1; 0=0,14, численно с шагом 6 = 0,5
найти законы установления амплитуд (фазовые траектории) при
различных начальных значениях: а) а0 = 2; б) ас = 2,4.
Глава семнадцатая
Анализ линейных электрических цепей
методом графов
А. Направленные графы (линейные графы сигналов)
1. Составление графа и определение передачи схемы
с одним источником энергии
17.1 р. Составить граф схемы рис. 17.1, а и определить взаим-
ную проводимость g14. Проводимость ветвей gx ~g2 — gs = gt ~
= g5z=ge= 1 См. При решении воспользоваться двумя способами:
а) упрощением графа путем последовательного исключения узлов;
б) использованием общей формулы передачи графа (правило Мэ-
зона).
17.2 . Составить граф схемы рис. 17.1,6 и определить ток /3
в диагонали моста при питании цепи от источника: а) синусо-
идальной ЭДС £ = 10 В; б) синусоидального тока J =4 А. Пара-
метры схемы: У,=— /2 См; У8 = У4 = 2См; У8— 1 См; — /4 См.
Рис. 17.1
Рис. 17.2
17.3 . Дана система уравнений, соответствующая некоторой
электрической цепи:
20/,+ Ю/3—5/3 = £,; 1
24/, — 5/, + 4/3=15£1; I
Ю/, + 3/.—4/. = 0. I
Начертить граф этой цепи и определить входную проводимость g^
17.4 . Определить передачи сигнала в графе рис. 17.2: а) от
узла х, к узлу х4; б) от узла х, к узлу хв. Проверить правиль-
ность решения, составив и решив аналитически соответствующие
графу уравнения.
17.5 . Составить граф схемы рис. 17.3, а и определить взаим-
ную проводимость g03, если /?, = 2Ом; Яа = /?3=ЗОм; Т?4—1 Ом;
R5 = 4 Ом.
17.6 . Схема рис. 17.3, б питается от источника синусоидаль-
ного напряжения. Составить граф этой схемы и найти У13. Пара-
метры схемы: 7?1 = 0,8Ом; Ха = ЛС2 = /?8 = 4 Ом; /?я = 2Ом.
160
2. Объединение нескольких истоков графа в один
17.7р. Составить граф схемы рис. 17.4, а без предварительного
составления уравнений, используя метод: а) контурных токов;
б) узловых потенциалов. Определить ток /5, если /?1 = /?2 = /?4 =
3 Ом; У?з = 1 Ом; = 2 Ом; Е = 45 В; J 5 А.
о} 5)
Рис. 17.3
а) б)
Рис. 17.4
17.8. Составить граф схемы рис. 17.4, б, взяв за основу метод:
а) контурных токов; б) узловых потенциалов. Найти для обоих
случаев ток /1. Проверить правильность решения, рассчитав ток
/* методом эквивалентного генератора. Параметры схемы: Et =
-12В;£2=18В; / = ЗЛ; = 7?3 ==/?5 =/?в = ЮОм.
5. Графы четырехполюсников
17.9 р. Начертить графы четырехполюсника, соответствующие
А- и //-формам записи.
17.10 . Начертить графы четырехполюсника, соответствующие
Z- и У-формам записи.
а) б)
Рис. 17.5
17.11 р. Составить граф четырехполюсника, эквивалентного двум
Каскадяо соединенным (рис. 17.5, а), используя //-форму записи
Параметров исходных и эквивалентного четырехполюсников.
161
17.12 . Составить граф четырехполюсника, эквивалентного дву^
каскадно соединенным (рис. 17.5, б), используя Л-форму записи
параметров исходных и эквивалентного четырехполюсников. Опре,
делить передачи ветвей эквивалентного графа.
17.13 . Составить граф, соответствующий двум параллельно
соединенным четырехполюсникам (рис. 17.6, а), воспользовавшись
У-формой записи параметров. Проверить решение аналитически.
Найти передачи ветвей.
17.14 р. Построить граф цепи, состоящей из трех смешанно
соединенных четырехполюсников (рис. 17.6, б).
4. Анализ электронных схем в линейном режиме
17.15р. Для схемы усилительного каскада (рис. 17.7, а) со-
ставить граф и определить коэффициент усиления по напряже-
17.16. Воспользовавшись схемой усиления для малых сигна-
лов, представленной на рис. 17.7, б, составить граф и определить
коэффициент усиления по напряжению kal = uBhtx/uBX. Рассматри-
вая схему как катодный повторитель, найти по составленному
графу коэффициент усиления k^ — uJuBx. Параметры лампы S и
а также сопротивления резисторов схемы /?к н /?к известны-
17.17р. Составить граф для усилительного каскада рис. 17.8Л
и определить коэффициент усиления по напряжению. Параметры
ламп giit SBt git и схемы g0, gt, gR известны.
1Б2
17.18р. Полупроводниковый триод включен по схеме с общей
доой. На рис. 17.8,6 изображена его эквивалентная схема для
переменных составляющих. Составить граф этой схемы и пресс-
разевать его, приводя к //-форме записи.
Рис. 17.8
Б. Ненаправленные графы
17.19р. Рассчитать определитель схемы
шпми способами: а) как сумму величин всех
по узлу;
б) используя разложение определителя
рис. 17.9,0 следую,
возможных деревьев;
в)
используя раз-
4
5)
ложенпе определителя по путям между
зуя разложение определителя по ветви,
видимости каждой ветви, кружка-
ми—узлы схемы.
17.20р. Схема рис. 17.9, б пи-
тается от источника тока. Опре-
делить показание вольтметра, ис-
пользуя теорию ненаправленных
П^афов. Параметры схемы: g, =
=- 1 См; = 2 См; g4 = 0,5 См;
*'==5 А.
17.21. Решить задачу 17.2,
^пользовавшись теорией ненап-
равленных графов.
17.22. Определить входное сопротивление 7?рч
РВС- 17. Ю, а; б) рис. 17.10,6. Проводимости ветвей в
казаны на чертеже.
двумя узлами; г) псполь-
Буквамп обозначены про-
17.10
о)
Рис.
схем: а)
сименсах
163
17.23. Рассчитать входную Уп и взаимную У13 проводимости
лестничной схемы рис. 17.11, а. Параметры схемы:
= соС = 1 См.
а)
Рис. 17.11
Сс
Со
Рис. 17.12
0-----
17.24. Определить показание вольтметра в схеме рис. 17.11,6.
Параметры схемы: Е = 100 В; 7?г = Хл| = 5 Ом; XLi — Хс~ R2 =
— 10 Ом; XLZ~ 15 Ом.
Указание. Рекомендуется предваритель-
но упростить электрическую схему, исключив
магнитную связь между индуктивными катуш-
ками.
17.25р. На рис. 17.12 дана схема уси-
лительного каскада с емкостной связью.
Найти комплексный коэффициент усиле-
ния по напряжению X. Параметры схе-
мы: лампа 6118 (Я, —10 кОм; р = 20);
/?а = 20 кОм; Rc = 500кОм; Сс = 1000 пФ;
со = 100 пФ; f = 2 кГц.
иВых
0
Глава восемнадцатая
Электрические цепи с изменяющимися
во времени параметрами
А. Установившиеся процессы в цепях с периодически
изменяющимися параметрами при наличии источников
электрической энергии
18.1. К источнику постоянной ЭДС £с—1В подключен ре-
зистор, сопротивление которого Ro (1—т sin со/) изменяется во вре-
мени (рис. 181, а). Глубина модуляции гп<0,1. Известно, что
протекающий по цепи ток содержит постоянную составляю-
щую 1,0032 мА и синусоидально изменяющуюся составляющую
0,08 sin о/мА. Определить /?0 и tn.
18.2. Цепь рис. 18.1,6 питается от источника постоянного
тока J. Индуктивная катушка имеет индуктивность £(/), изме-
няющуюся во времени. Сопротивление резистора R постоянно.
Составить дифференциальное уравнение относительно тока i2 через
индуктивную катушку.
164
18.3р . В цепи рис. 18.1, в ток через индуктивную катушку
/ s=s 4- /21 sin со/ -|- /82 cos <0/; L (/) = L0-}- Lt sin 2ю/. Onределнть за-
кон изменения во времени тока /(/).
Рис. 18.1
В цепи рис. 18.2,а £=100 В; £ = 0,1 Гн, а сопротив-
резистора R (/) изменяется во времени в соответствии
18.2, б,; так что /^=200 Ом; R2 = 100 Ом; т = 0,5 мс. Опре-
18.4.
леиие
с рис.
делить изменение тока и нап-
ряжения на индуктивной катуш-
ке в установившемся режиме для
первого (0—т) и второго (т—2т)
интервалов времени.
18.5. Если в цепи рис. 18.2, а
частоту изменения сопротивле-
ния резистора увеличить (т. е.
уменьшить т), то ток будет мало
изменяться в течение каждого
полу периода. Составить транс-
цендентное уравнение для опре-
деления т, исходя из того, что
Рис. 18.2
отношение тока в конце перво-
го полупериода в установившемся режиме работы к току в начале
первого полу периода равно 0,9.
18.6. По данным задачи 18.4 найти активную мощность, по-
требляемую цепью.
18.7р . К источнику постоянного тока J = 10 мА подключены
(рис. 18.2, в) конденсатор емкостью С=1мкФ и резистор сопро-
тивлением R(t). скачкообразно изменяющимся во времени от
₽1 = 2кОм до /?а=1кОм. Время, равное полупериоду измене-
ния R(t), т=1мс (рис. 18.2,6). Составить уравнение для на-
пряжения на конденсаторе ис в установившемся режиме. Снача-
ла решить его в общем виде, затем для заданных значений
параметров.
18.8. Найти активную мощность, доставляемую в цепь источ-
ником постоянного тока по данным задачи 18.7р. Решить задачу
в общем виде.
18.9. В электрической цепи рис. 18.2, г сопротивление резис-
тора R постоянно, индуктивность катушки L(t) — L0(l 4-A sin to/),
где k < 1; «•(/) = £ 4- Ет sin(to/ |- гр). Представив ток в цепи в виде
i = /0 4 /ц sin со/ 4- Лг cos to/ 4- /21 sin 2со/ 4- /22 cos 2ы/ и используя
Метод гармонического баланса, вывести формулы для определения
165
амплитуд гармоник тока /и, fi2, Л,- Найти зависимость по.
стоянной составляющей потокосцепления ф0 в функции /0 при
установившемся режиме.
18.10. Для цепи рис. 18.2, г по данным задачи 18.9 опреде-
лить ток и постоянную составляющую потокосцепления при
Ет = 10 В; Е = 0; R = 2 Ом; w£0 == 10 Ом; со = 1000 с"1.
18.11. По данным задачи 18.10 найти i — f (/) и ф0, считая,
что в цепи кроме синусоидальной ЭДС действует и постоянная
ЭДС £ = 7,06 В.
Б. Параметрические колебания
18.12р . В параметрическом генераторе (рис. 18.3, о) £ =
= 100 мГн. ВАХ нелинейного резистора R (/) характеризуется
табл. 18.1.
Емкость конденсатора меняется во времени
по закону С = Сй—\Ccos2uZ (рис. 18.3,6),
где Со= 10 мкФ. Полагая ДСС0<^1, опреде-
лить: а) минимальное значение ДС, при кото-
ром в цепи возбуждаются параметрические
колебания с частотой со = 1/К£С0= 1000 с-1;
б) амплитуду тока в цепи при w = 1000 с-1;
ДС/Со = 0,08.
18.13 . В параметрическом генераторе задачи 8.12р емкость
конденсатора стала изменяться скачкообразно (рис. 18.3, в).
Рис. 18.3
Емкость конденсатора уменьшается скачком, когда заряд на нем
имеет максимальное значение (положительное или отрицательное),
166
л увеличивается скачком, когда заряд проходит через нулевое
значение (рис. 18.3, г). Полагая ДССо=0,08 и считая, что
амплитуда тока /,л ^0,1635 А, подсчитать энергию, вводимую
D цепь за 1 с, при указанном характере изменения емкости кон-
денсатора.
18.14 р. В параметрическом генераторе (рис. 18.4, а) накачка
энергии осуществляется путем скачкообразного изменения индук-
тивности L на с частотой 2<о, в два раза большей частоты ’
изменения тока. Индуктивность увеличивается скачком на Д£,
когда ток принимает амплитудное значение, и уменьшается скач-
ком на AL, если i = 0 (рис. 18.4, б, в). Данные схемы: С = 10 мкФ;
До-г *х2= 24- 100/=.
Исходя из баланса энергии по первой гармонике определить
значение АЛ, при которой амплитуда первой гармоники тока
в цепи равна 0,1 А, если частота со= 1000 с"1.
Рис. 18.5
18.15 р. На рис. 18.5, а изображена схема параметрического
генератора, где £с—источник постоянной ЭДС смещения, обес-
печивающий работу полупроводникового диода в запертом со-
стоянии; j„—источник синусоидального тока с амплитудой /ят
и частотой шн. Источник тока /и обеспечивает накачку энергии
в колебательный контур на частоте <йк, в два раза большей час-
тоты (0у, генерируемой параметрическим генератором.
Колебательный контур состоит из индуктивности L и емкости
р-л-перехода полупроводникового диода, работающего в запертом
состоянии благодаря наличию Е6. В качестве полупроводникового
Диода часто берут германиевый (кремниевый) диод емкостью
^20 “40 пФ. Емкость диода является функцией напряжения
на нем нд (рис. 18.5,6). Напряжение на диоде ил—— Ес—iKR —
— L~ является функцией времени, вследствие чего зависимость
емкости р-л-перехода также является функцией времени
(рис. 18.5, в). Из-за периодического изменения емкости с часто-
167
той сок генератор тока накачивает энергию в колебательный кон-
тур. Колебательный контур для частоты генерации представлен
на рис. 18.5,2, где —усредненная за период емкость Сл полу-
проводникового диода, гэ—некоторое эквивалентное сопротивле-
ние контура. Колебания будут незатухающими, если гэ = 0. Тре-
буется: а) сформулировать условия, при которых схема рис. 18.5, а
может работать в качестве параметрического генератора; б) за-
писать последовательность расчета схемы при известной харак-
теристике Сл = ^(нд) и заданной частоте Емкость в схема
рис. 18.5,г может изменяться и в соответствии с рис. 18.5, д.
В. Исследование устойчивости режимов работы цепей
с периодически изменяющимися параметрами
18.16 р. На рис. 18.6, а изображена электрическая цепь, со-
стоящая из линейных и неизменных во времени L и R и изме-
няющейся во времени С = С0(1—mcos2(o/).
Полагая т<|1, составить уравнение относительно заряда q
на конденсаторе и свести его к уравнению /Матье ^4-т-
4- 16рсоз2т)т] = 0. За-
писать коэффициенты а в
р уравнения Матье через
£, К, Со, т и со.
18.17. В цепи рис.
18.6, а Со=1О мкФ, £ =
—0,1 Гн; м = 0,05; R =
= 20м (см. задачу 18.16р).
Будет ли режим работы цепи устойчив, если частота изменения
параметра: а) 2й) = 2000 с"*; б) 2ю= 1414 с*'1?
18.18р. На рис. 18.6,6 изображена электрическая цепь, со-
стоящая из линейных и неизменных С, R и изменяющейся во
времени L = LO(1—т cos 2ш/)- Полагая глубину модуляции индук-
тивности гп<^1, составить уравнение относительно заряда q на
конденсаторе, перейти от него к уравнению для приращения за-
ряда и, введя подстановку, аналогичную проведенной в задаче
18.16р, прийти к уравнению Матье для приращений. Выразить
коэффициенты аир уравнения Матье через £0, /?, С, т.
Г. Некоторые явления в цепях с периодически
изменяющимися параметрами
18.19 р. Источник синусоидальной ЭДС ECTsincoZ подсое-
диняют в момент времени / = 0 к индуктивной катушке L без
потерь (рис. 18.7, а). При этом потокосцепление ф = 0. Индук-
тивность L изменяется скачками: во все нечетные полупериоды
она равна L04-AL, во все четные—равна £с—А£ (рис. 18.7,6).
Показать, что в рассматриваемом идеализированном режиме
работы ток, проходящий по цепи, имеет постоянную составляю-
168
щую (среднее за период 2л/со значение)
I =
П’ “ ы [Z.5 — (AL)-’]'
18.20 р. Источник синусоидального тока /(/) = /„ sin со/ в мо-
мент времени t = 0 присоединяют к конденсатору без потерь
(рис. 18.7, в). При этом заряд д = 0. Емкость конденсатора С
изменяется скачками: во все нечетные полу периоды она равна
Св4-ДС, во все четные—равна Со—АС (рис. 18.7, г).
Показать, что в рассматриваемой идеализированной схеме на-
пряжение на конденсаторе имеет постоянную составляющую
(среднее за период 2л/со значение) Uc = —. fmC° .
' 0 ш [Со— (АС)2]
Рис. 18.7
Рис. 18.8
18.21 р. Электрическая цепь рис. 18.8, а образована источни-
ком постоянного тока Jo, источником синусоидальной ЭДС
е(/) = Еад5’1п (со/4-<р), линейными и постоянными во времени R
и С, изменяющейся во времени L(t) = L0(\ 4- "г sin со/). Частота
модуляции индуктивности равна частоте источника е(/). Цепь
обладает примечательным свойством: при определенных условиях
кривая зависимости постоянной составляющей потокосцепления
*|’о индуктивного элемента от протекающего по нему постоянного
тока /0 имеет отрицательный угол наклона (рис. 18.8,6), т. е.
коэффициент b в выражении — а-т-Ы0 отрицателен.
Вывести условия, при которых это явление имеет место. Для
упрощения выкладок достаточно учитывать лишь первую гармо-
нику тока i (высшие гармоники относительно мало сказываются
на числовых результатах). Написать выражения для коэффициен-
тов а и b в уравнении = а-4-
18.22 . Проверить выполнение условий задачи 18.21 р и запи-
сать аналитическое выражение ф0— для цепи рис. 18.8, а
при R ~ 1,4 Ом; со —100 с“’; со£й = 1ОО Ом; 1/(соС) = 97 Ом;
0,3165; Ет = 2 В.
Глава дейятнадцатая
Электростатическое поле
А. Интегральные соотношения между зарядом,
напряженностью поля и потенциалом
19.1. Два точечных заряда = 10“1и К л и q2 располо-
жены на оси х. Их координаты *1 = 0; л\=12 см. Окружающей
средой является воздух. Определить координаты точки /н(л'и),
в которой напряженность электрического поля Е — 0 (точка ветв-
ления силовых линий), и точки п (х„), в которой напряженности
Рис. 19.1
поля, создаваемые каждым зарядом, равны п направлены со-
гласно. Вычислить напряженность поля в точке п(Еп) и силу,
действующую на заряд (Ft). Качественно построить картину
поля. Задачу решить для: а) = 4<у; б) q2 =—lq.
19.2. Электрическое поле создается положительным зарядом
Q=1,6 1O“10 Кл. Электрон (q =—1,6-10~1в Кл) достаточно мед-
ленно перемещается по пути abca (рис. 19.1, а). Подсчитать ра-
боту, которую необходимо затратить на каждом участке пути, а
также полную работу на пути abca. Указать, за счет действия
каких сил может быть совершено такое перемещение на каждом
участке пути. Все расстояния на рисунке даны в сантиметрах.
19.3р . Точечный заряд q помещен в начале сферической сис-
темы координат. Напряжение между точками a (Ra = 3 см;
—45°; ао = 0) и b (Rb = 7 см; 0ь=180°; аь = 90°) Uab = 25 В.
Определить значение напряженности поля в точке с (Rc~5 см;
0с = 270°; ас = 0) и ее направление, если окружающей средой
является воздух.
19.4. Вдоль оси z цилиндрической системы координат распо-
ложена бесконечно длинная заряженная нить. Напряженность
поля в точке р [гр^2Ъ см; а^О) Ер — г°-500 В;м. Рассчитать
напряжение между точками иг (гд=10 см; аж = 270°) и п (гп=-
~ 30 см; а„ — 135°).
19.5. Бесконечно длинный проводящий цилиндр радиусом
го^ЗО мм расположен в диэлектрике (ег = 5). Какой заряд на
единицу длины можно сообщить цилиндру, если пробивная на-
пряженность диэлектрика £‘пр = 20-104 кВ/м?
170
19.6р . У коаксиального кабеля длиной / = 10 м радиус внут-
ренней жилы г, = 2 мм, радиус внешней оболочки г, = 5 мм. Под
какое напряжение можно включить кабель, если максимальная
напряженность поля не должна превышать 2/5 пробивной напря-
женности, равной 210* кВ/м?
19.7. Уединенный прозодящий шар радиусом Яо = 5 см, по-
верхностная плотность заряда которого сг = 0,1-10~* Кл/м2, поме-
щен в минеральное масло (е, = 3). Построить графики изменения
модул я градиента потенциала | grad ф | и потенциала <р внутри и
вне шара в функции расстояния R от его центра, приняв ф = 0
при R = cc. Определить напряжение между точками, одна из
которых лежит на поверхности шара, а другая находится на рас-
стоянии 10 см от его поверхности. Вычислить емкость шара.
19.8р . Заряд равномерно распределен с плотностью р —
= 10~4 Кл/м3 по объему бесконечно длинного цилиндра радиусом
гс = 5 мм. Диэлектрическая проницаемость окружающей среды и
цилиндра бд.
Найти закон изменения потенциала внутри и вне цилиндра и
построить график ф = /(г), приняв ф = 0 при г = 0. Вычислить
разность потенциалов между точками, лежащими: а) на оси
цилиндра и его поверхности; б) на поверхности цилиндра и на
расстоянии а =10 мм от поверхности (а — расстояние по нормали
к поверхности цилиндра).
19.9. Между двумя концентрическими сферическими бесконечно
тонкими проводящими поверхностями, расположенными в ваку-
уме, равномерно распределен заряд, объемная плотность кото-
рого р = 210~® Кл/м3. Радиус внутренней поверхности а — 10 см,
радиус внешней поверхности 6 = 20 см. Найти напряженности
поля в точках А, В и С, если расстояния от центра сфер до
указанных точек /?л = 5 см; /?в=15 см; Rc = 25 см.
19.10. Два длинных разноименно заряженных параллельных
тонких провода расположены в воздухе на расстоянии 2d = 600 см
Друг от друга (рис. 19.1, б). Линейная плотность заряда
т=10“* Кл/м. Считая, что ф = 0 при х = 0, t/ = 0, получить ана-
литические выражения зависимостей ф=Д(х, у, z) и grad(p =
= /г (х> У* г)- Вычислить напряженность электрического поля
в точке В, используя: а) выражение для grad<р; б) теорему
Гаусса. Координаты точки В: хв=0; v^=40 см; za=0. Построить
эквипотенциаль, для которой ф = 25 В.
19.11. Электрический диполь, состоящий из зарядов 4- q —
= 10“в Кл и —<7 = —10~® Кл, расположен в вакууме. Расстоя-
ние между зарядами d=\ мм (рис. 19.1, в). Определить потен-
циалы и векторы напряженностей поля в точках А и В, сфери-
ческие координаты которых /?л=^0,1 м; 6Л = 0°; ал = 0°; RB = 0,1 м;
®а = 30°; ав = 90°. Потенциалы точек, удаленных в бесконечность,
принять равными нулю.
19.12р . Два бесконечно длинных проводящих цилиндра с па-
раллельными осями расположены в воздухе (рис. 19.2, а). Ра-
диусы цилиндров: гх — 2 см; г2 = 4 см; расстояние между геомет-
171
рическнми осями 2Я = 8 см. Напряжение, приложенное к цилинд-
рам, — 100 В. Определить: а) положение электрических осей;
б) напряженность электрического поля в точке т\ в) поверхностную
плотность заряда в точке т\ rj
емкость на единицу длины цилинд-
ров.
19.13. Бесконечно длинный
проводящий цилиндр радиусом
rt = 1 см расположен внутри дру_
гого бесконечно длинного про-
водящего цилиндра радиусом г, =
— 3 см. Расстояние между гео-
метрическими осями цилиндров
6=1,5 см (рис. 19.2,6). Область
между цилиндрами заполнена диэлектриком (ег = 4). К цилиндрам
приложено напряжение t\2 = 200 В. Найти: а) положение элект-
рических осей; б) напряженность поля в точке т\ в) емкость на
единицу длины цилиндров.
Б. Дифференциальные соотношения между плотностью
заряда, напряженностью поля и потенциалом
19.14. Между двумя концентрическими цилиндрическими элек-
тродами, расположенными в вакууме, потенциал меняется по
закону <р = аг3 -{- 61п г-р с, где г—расстояние до оси цилиндров;
Рис. 19.3
п, 6, с—числовые коэффициенты. Найти законы распределения
Е, divE, rot Е и объемной плотности заряда р между электродами.
19.15. Потенциал между плоскими электродами, расположен-
ными в вакууме (рис. 19.3, й), меняется в функции расстояния
х по закону = ах?4-Ьх + г, где а — — 6,28-10'’ В/м3;
=—9,42-106 В/м2; с=—12-10* В/м. Электроды представляют
собой квадраты со стороной / = 0.1 м. Расстояние между ними
d = 0,5-10-a м. Пренебрегая краевым эффектом, найти полный
объемный заряд, скопившийся между электродами.
19.16. Бесконечно длинный слой воздуха (рис. 19.3, б) равно-
мерно заряжен; объемная плотность р = —10~*/(12л) Кл/м3. Тол-
172
niuia заряженного слоя 2й=10мм, ширина h^>a. Построить
графики изменения модуля напряженности поля и потенциала
а функции координаты х при 0<х<оо. Принять <р = 0 при
19.17р . Бесконечно длинный диэлектрическим (ег = 4) цилиндр
кругового сечения радиусом а = 0,5 см заряжен и находится
в воздухе. Объемная плотность заряда р является функцией рас-
стояния от оси цилиндра: р = Лг, где £=1/(4л) К л/м*. Найти
законы изменения потенциала ф внутри и вне цилиндра в функ-
ции расстояния г от оси, приняв ф = 0 прн г = 0. Определить
конфигурацию и положение эквипотенциальной поверхности, для
которой ф = —2 В.
19.18. Шар из диэлектрика (ег = 3) заряжен и расположен
в воздухе. Объемная плотность заряда является функцией рас-
стояния R от центра шара: р = /г/?. где Л= 1/(10л) Кд'м*. Радиус
шара /?о=1 см. Найти законы изменения потенциала ф и на-
пряженности поля Е внутри и вне шара в функции расстояния R
от его центра. Принять <р = 0 при /? = оо. Рассчитать напряже-
ние между точками А и сферические координаты кото-
рых /?и = 5-10’3 м; ал = 180°; 6л = 60°; /?в = 210-“ м;6в = 90°;
ав = 90°.
19.19. Две протяженные тонкие проводящие пластины распо-
ложены в воздухе под углом а0 друг к другу (рис. 19.3, в). По-
тенциал первой пластины Ф3 = 0, второй пластины ф2 = £Л Пре-
небрегая краевым эффектом, определить законы распределения
<р и Е в областях: а) 0 < а < а0; б) а0 < а < л; в) л < а < 2л.
Качественно построить картину поля.
19.20. Две тонкие проводящие конические поверхности рас-
положены в вакууме. Вершины конусов изолированы друг от
Друга (рис. 19.3, г). Потенциал первой поверхности <ря = LZ, вто-
рой поверхности <ра=0. Пренебрегая краевым эффектом, найти
законы распределения <р и Е между поверхностями. Качественно
построить картину поля.
В. Граничные условия. Многослойные диэлектрики
и конденсаторы
19.21. Напряженность равномерного электрического-поля в
трансформаторном масле Ег = 105 В/м. Угол между вектором напря-
женности и нормалью к поверхности стеклянной пластины ~ 30°
(рис. 19.4, а). Размеры пластины в направлении осей у и z до-
статочно велики. Найти напряженности поля, а также углы па-
дения и преломления в стекле и в воздухе (<х2 и аэ). Относитель-
ные диэлектрические проницаемости масла и стекла соответственно
*п-2,5; ег2 = 7.
19.22. Вектор электрического смещения равномерного поля
в воздухе П1 = 1,77 10~7 Кл/м2, а напряженность поля в ди-
электрике £2 = 8-10э В/м (рис. 19.4,6). Определить относитель-
на
ную диэлектрическую проницаемость ег2, если угол падения
а1 = 20о.
19.23. Между одной из пластин плоского конденсатора и на-
полнителем (парафином, ег1 = 4,3) образовался слой воздуха
(рис. 19.4, в). Площадь сечения пластин конденсатора S = 200 см2
толщина слоя парафина <^ = 0,5 см, толщина воздушного слоя*
d3 = 0,l см. Пробивные напряженности для парафина и для воз-
духа соответственно Епр1= 15-103 кВ м; Епр1 = 3-103 кВ/м.
При каком напряжении Z7np этот конденсатор будет пробит?
Какое напряжение выдержит конденсатор без указанного дефекта
(принять • расстояние между плас-
тинами б/ = 0,6 см)? Считая, что
конденсатор включен под посто-
янное напряжение Z7 = Z7np/2, по-
строить графики распределения
Ф, Е, Р и D в функции расстоя-
ния х (расстояние от левого
электрода) для конденсатора: а)
с воздушным зазором; б) без воз-
душного зазора. Принять <р = 0
при л- = 0. Для конденсатора с
воздушным зазором найти плот-
ность связанных зарядов на по-
верхности парафина. Вычислить
емкость конденсатора с воздушным
зазором и без него.
19.24. На рис. 19.4, г при-
веден график потенциала поля
плоского трехслойного конденсатора <₽ = f1(x). Ось х направлена
нормально к пластинам конденсатора. Точка х-~ 0 находится
на внутренней поверхности левой пластины. Построить графики
Е = /2(х); D = /9(x) и определить емкость конденсатора С, если
известно, что в его изоляции (д.= 3) имеется воздушная прослой-
ка, а площадь пластин 5—0,04 м2.
19.25. Радиус внешней жилы цилиндрического конденсатора
г2 —5,44 см, длина конденсатора / = 20 см, относительная ди-
электрическая проницаемость диэлектрика ег = 2. Подобрать опти-
мальное значение радиуса внутренней жилы с тем чтобы кон-
денсатор выдерживал наибольшее напряжение. Вычислить про-
бивное напряжение конденсатора £/пр, если пробивная напряжен-
ность электрического поля Епр = 2-104 кВ м. Найти зависимость
удельной плотности энергии электрического поля в функции рас-
стояния от оси цилиндров w3 = f(r) и вычислить полный запас
энергии поля если напряжение на конденсаторе равно (/пр/2.
19.26. Сферический конденсатор с двухслойным диэлектриком
имеет радиус внутренней сферы с =10 мм, а радиус внешней
сферы fi = 20 мм. Относительная диэлектрическая проницаемость
внутреннего слоя £гХ = 5. Радиус поверхности раздела диэлектри-
ков х. Разрез конденсатора показан на рис. 19.5, а.
174
Требуется: а) подобрать е^ внешнего слоя и толщины слоев
д и Д2 так, чтобы наибольшая напряженность внутреннего слоя
была равна наибольшей напряженности внешнего слоя, а наи-
меньшая напряженность внутреннего слоя—наименьшей напря-
женности внешнего слоя: б) найти наибольшую и наименьшую
напряженности электрического поля в каждом слое, если ди-
электрик с е, = 5 расположен во внешнем слое [радиусы слоев
Рис. 19.5
остаются такими же, как в случае а)], а заряд конденсатора
равен К л. Для случаев а) и б) качественно построить гра-
фики напряженности поля в функции расстояния от центра
сфер E=j(R). Вычислить емкости конденсаторов.
Г. Поля простого и двойного заряженною слоев
19.27. Заряд равномерно распределен с плотное! ью о =
— 10 й Кл/м* по поверхности бесконечно тонкого круглого диска
радиусом —0.1 м, расположенного в воздухе. Для точек на
оси г, нормальной к поверхности диска и проходящей через его
Центр при 2 = 0, определить зависимости потенциала н напряжен-
ности поля и функции координаты г. Построить графики у ==fl(zr,
£ — и указать особенности поля простого заряженного слоя.
19.28р . Диполи, расположенные в вакууме, образуют двойной
заряженный слой, имеющий форму диска радиусом R». Оси ди-
полей перпендикулярны поверхности диска. Плотность положи-
тельных зарядов ст", отрицательных зарядов а расстояние
между ними /. При этом о = const, l<^Rn. Для точек на оси z,
Нормальной к поверхности диска и проходящей через его пентр
При 7 = 0, найти зависимость потенциала и напряженности поля
6 функции координаты z. Качественно построить графики <г =
= А(г>;
175
19.29. Электрет па основе полимера (еа = Е„Ег) имеет форму
диска радиусом /?0 и толщиной d (рис. 19.5, 6). Одна его поверх,
ность металлизирована и заземлена. Средой, окружающей устрой-
ство, является воздух. В расчетном отношении электрет может
рассматриваться как два слоя поверхностных зарядов, распреде.
ленных с плотностями <rt и о2, находящихся на расстоянии I друг
от друга. При этом Oj > 0, о2 < 0; |о21 < |о, |; 1<^а.
Определить зависимость Е = f (г) для: a) Z/2<z<oo; б) — //2 <
< z < Z/2; в) —(d—1/2) <z < —1/2.
Указание. Рекомендуется рассматривать поле электрета как сумму по-
лей двойного и простого заряженных слоев.
Д. Метод изображений
19.30. Какая сила действует на точечный заряд Q= 1О~10 Кл,
расположенный в воздухе на расстоянии d = 5 см от: а) плоской
проводящей поверхности; б) поверхности стеклянной (ег = 6) очень
толстой пластины? Вычислить работу, затрачиваемую при удале-
нии заряда в бесконечность (для обоих случаев).
19.31р . Вблизи безграничной плоской поверхности раздела
двух диэлектриков с ег1 и ег2 расположен точечный заряд
Q — Ю_9 Кл. Необходимые расстояния даны на рис. 19.5, в.
Вычислить напряженность поля в точках а, Ь, с, d. Точку b
следует рассматривать как точку, принадлежащую двум средам.
Построить график E = f(x).
19.32. Электрический диполь (<7=10~10 Кл; I — 20 мм) распо-
ложен нормально к плоской поверхности раздела двух диэлект-
риков (рис. 19.5, г). Доказать, что поле в каждой среде можно.
рассчитывать как поле диполя, расположенного в однородной
среде с соответствующей диэлектрической проницаемостью. Вычис-
лить <рл и £л, если d = 10 см, заряд q находится в среде с ег1.
19.33р . Две плоскости образуют двугранный угол, равный 45е
Область, расположенная внутри это угла, запол-
(рнс. 19.6, а).
йена воздухом. Остальная часть
пространства заполнена проводя-
щей средой. Через точку m (rm -
= 5,22 см; ая = 22,5°) параллель-
но проводящим поверхностям про-
ходит прямой тонкий бесконечно
длинный провод, линейная плот-
ность заряда которого т = 2-10“9
Кл/м. Определить поверхпост-
т
а)
Рис.
Ггп
45
19.6
&т Iff
X
ную плотность заряда в точке а.
19.34р . Две параллельные безграничные проводящие плоско-
сти отделены друг от друга слоем изоляции (ег =3), толщина
которого 1,5 см. Параллельно проводящим поверхностям распо-
ложен тонкий прямолинейный проводник (рис. 19.6, 6), линейная
плотность заряда которого т=10“в Кл/м. Найти напряженность
176
оля и поверхностную плотность связанных зарядов в точке а.
Линейные размеры на рис. 19.6, б даны в сантиметрах.
19.35. Бесконечно тонкий провод, линейная плотность заряда
которого т, расположен в воздухе параллельно заземленному
«поводящему цилиндру радиусом г0 (рис. 19.7, а). Определить
силу» действующую на единицу длины провода, с которой он
притягивается к цилиндру. Вычислить потенциал точки А.
19.36р . Точечный заряд Q=10“® Кл расположен в воздухе
на расстоянии d = 20 см от заземленного металлического шара
радиусом /?о=10 см (рис. 19.7,6). Качественно построить кар-
тину электростатического поля. Найти расстояние h от заряда Q
до точки ветвления Ь. Определить напряженность поля в точке а.
19.37. Заземление шара, описанного в задаче 19.36р, отклю-
чено. Вычислить напряженность поля в точках а и Ь, если рас-
стояние А = 0,512 м. Найти поверхностную плотность заряда
в точках а и с.
Е. Поле системы заряженных тел.
Формулы Максвелла
19.38р . Два цилиндрически к бесконечно длинных провода рас-
положены на изоляторах вдоль проводящей стены (рис. 19.7, е).
Необходимые размеры указаны в сантиметрах. Радиус первого
провода г, = 0,8 см; радиус второго провода г2 = 0,4 см. Окружаю-
щей средой является воздух. Первый провод присоединен к поло-
жительному полюсу источника, ЭДС которого h ==200 В. Отри-
цательный полюс источника ЭДС заземлен. Второй провод изо-
лирован от источника и от земли. Вычислить напряжение
между первым и вторы,м проводами,
19.39. Емкостные коэффициенты трехжильного экранирован-
ного кабеля с симметричным расположением жил pfcJ!r=20- 1010Ф/м;
РЛет = — 510~1с Ф/м. Экран кабеля заземлен. Первая жила при-
соединена к положительному полюсу источника, ЭДС которого
£ = 200 В, а отрицательный полюс заземлен. Вторая жила в ре-
зультате аварии замкнута на экран, а третья — изолирована.
Определить заряды на единицу длины и потенциалы всех жил.
177
19.40. Рассчитать частичные емкости Cu, С22, С12 и рабочую
емкость Ср на 1 м длины двухпроводной воздушной линии. Рас,
положение проводов и необходимые геометрические размеры в сан-
тиметрах даны на рис. 19.7, в. Радиусы проводов: = 0,8 см;
г2 = 0,4 см.
Указание. Под рабочей емкостью Ср понимают отношение абсолютного
значения линейной плотности заряда на одном из проводов линии к напряод.
нию между проводами:Ср^ т С12.
ж. Метод разделения переменных
19.41. В диэлектрике плоского конденсатора (ел = 4) появи-
лось длинное цилиндрическое воздушное включение диаметром
2а =1 мм. Расстояние между пластинами конденсатора d = 20MM
Рис. 19.8
(рис. 19.8, с). Пробивные • напря-
женности для диэлектрика и воз-
духа соответственно равны 12-10*
и ЗЮ3 кВ/м. Определить рабочее
напряжение 6/р, под которое может
быть включен конденсатор, если:
а) в его изоляции есть указан-
ное отверстие; б) отверстие отсут-
ствует. Принять отношение про-
бивного напряжения к рабочему
в обоих случаях равным трем. Качественно построить картины
линий D, Е и Р для поля конденсатора с цилиндрическим отвер-
стием в изоляции.
19.42. В стеклянную изоляцию плоского конденсатора запрес-
сован цилиндрический проводник диаметром d = 2 мм. Ось про-
водника параллельна пластинам конденсатора. Пробивная напря-
женность стекла Елр=1510э кВ/м, а расстояние между пласти-
нами конденсатора й = 40 мм. Под какое напряжение может быть
включен: а) этот конденсатор; б) этот же конденсатор, но без
проводника в изоляции? Принять отношение пробивного напря-
жения к рабочему в обоих случаях равным трем. Качественно
построить картину поля конденсатора с цилиндрическим провод-
ником в изоляции.
19.43р . В равномерное электрическое поле внесен длинный ди-
электрический (ег = 4) цилиндр радиусом г0 = 2 см (рис. 19.86).
Окружающей средой является воздух. Найти напряженность внеш-
него равномерного поля £0 и напряженность поля внутри ци-
линдра если напряжение между точками В и А С/дл = 26 В.
Цилиндрические координаты точек А и В: гА=\ см; ал = 60°;
гв — 4 см; ад = 135°.
19.44. Диэлектрический (еп = 8) цилиндр внесен в равномерное
поле напряженностью £о=1Оэ В/м (рис. 19.8,6). Окружающей
средой является диэлектрик (еге = 2). Определить поверхностную
плотность связанных зарядов <гсв в точке а = 0. Качественно по-
строить графики £ = Д(х); D =/,(*)., £ = f3Q/), D = fA(y).
178
19.45. В равномерное поле напряженностью Е6 = 10s В/м по-
ветей2 длинная стеклянная трубка (ег = 5) так, что ее ось пер-
пендикулярна внешнему полю. Внутренний радиус трубки а=2см,
внешний 6=3 см (рис. 19.9, а). Окружающей средой внутри и
вне трубки является воздух. Внутри стеклянной трубки (вдоль
ее оси) проходит длинный цилиндрический провод радиусом
Рис. 19.9
го = 0,1 см. Вычислить напряженность электрического поля ЕА
на поверхности провода в точке А. Найти напряженность элект-
рического поля в той же точке ЕАл если провод удален.
Указание. Воспользоваться аналогией с расчетом цилиндрического маг-
нитного экрана.
19.46. В равномерное поле напряженностью Ео — 2-10* В/м
внесен проводящий заряженный шар радиусом Ro = 1 см
(рис. 19.9,6). Заряд шара Q= 10-м Кл, окружающей средой яв-
ляется воздух. Получить закон распределения плотности заряда о
в функции полярного угла 0 и построить график о = /(0), Каче-
ственно начертить картину поля и указать на ней точки с наи-
большей и наименьшей напряженностью. При какой напряжен-
ности внешнего поля напряженность поля в одной из точек на
поверхности шара достигает значения пробивной? Пробивная на-
пряженность воздуха £лр = 3-103 кВ/м.
19.47. Диэлектрический (ег/ = 3) шар радиусом а = 2 см рас-
положен во внешнем равномерном поле (рис. 19.9, в}. Разность
потенциалов между точками Л и В —<Гв = 5 В. Сферические
координаты точек А и В\ RA = 1 см; = 60°; ал = 90°; /?в = 4 см;
6д = 30°; ав = 90°. Окружающей средой является воздух. Опре-
делить модули векторов смещения в точках Л и В.
3. Графическое построение картины поля
19.48. На рис. 19.10, а изображена картина электрического
поля у края плоского конденсатора. Линейные размеры на ри-
сунке даны в масштабе 1;1. Напряжение между пластинами коя-
179
денсатора {/=120 В. Определить по картине поля значение £
в точках 1—4.
19.49р . Графическим методом построить картину электриче-
ского поля между двумя параллельными бесконечно длинными прово-
дящими цилиндрами, заряженными разноименно (см. рис. 19.2, о).
Радиусы цилиндров гг = 2 см, гл = 4 см, расстояние между их
геометрическими осями 2Я = 8 см. Полагая диэлектрическую про-
ницаемость среды равной по картине поля найти емкость
между цилиндрами на 1 м длины. Полученный результат сопоста-
вить с результатом решения задачи 19.12р.
Рис. 19.10
о
19.50. Графическим методом построить картину плоскопарал-
лельного поля электродов (рис. 19.10,6), между которыми рас-
положены два диэлектрика (ег1=1; ег2 = 2). По картине поля
определить емкость между электродами на 1 м их длины, считая,
что геометрические размеры даны в масштабе 1:1.
19.51. К электродам, расположенным в воздухе, приложено
напряжение U =300 В (рис. 19.10, а). Размеры на рисунке даны
в миллиметрах. Длина электродов в направлении, перпендику-
лярном чертежу, /=1 м. Графическим методом построить кар-
тину поля и, пользуясь ею, определить: а) £ в точке Л; б)
в) о в точке С; г) потоки векторов Е и D в одной силовой трубке,
т. е. и Д/V^; д) заряд Q, скопившийся на поверхности
электрода.
180
и. Метод конформных преобразований
19.52р . Определить поле на Плоскости г, если поле на плоско-
сти W равномерно и преобразование осуществлено с помощью
функции z = 2 sin 0,5VZ. Выбрать форму электродов и построить
картину поля на плоскости z, полагая, что потенциальной функ-
цией является функция: a) U\ б) V.
19.53. Определить поле на плоскости z и построить семейство
линий U = const и V — const, если преобразование на плоскость
1F осуществляется с помощью функций: a) Wz=l/z; б) IT—
= 2r a2/z, где a —const (преобразование Жуковского). Для случая
а) рассчитать линейный коэффициент преобразования Л4—Л1е/а.
19.54. Определить поле на плоскости z, если преобразование
на плоскость У7 осуществляется с помощью функций: a) z^e^710;
б) z=10/F; в) z — Для случая в) получить уравнения
силовых и эквипотенциальных линий на плоскости z, принимая
за потенциал U.
19.55. Два бесконечно длинных плоских электрода располо-
жены в воздухе под углом 143° (рис. 19.10, а). Размеры в пло-
скости чертежа даны в масштабе т1 == 1 мм/дел. Напряжение
между электродами 50 В. Правый электрод заземлен. Исполь-
зуя преобразование W=101nz, найти напряженность электриче-
ского поля и потенциал в точке fc(xft = 30 мм; t/fc = 40 мм), а
также поверхностную плотность заряда в точке m(xm = —40 мм;
У30 мм).
19.56. Плоскопараллельное поле в областях, изображенных
На рис. 19.11, а—отобразить на верхнюю половину плоско-
JP1
Таблица 19.!
Вариант IV,
Рис. 19.11, а 4 16
Рис. 19.11,6 2 8
Рис. 19.11,в /8 —-4.
сти VF. Определить аналитическую функ-
цию, с помощью которой может быть вы-
полнено это преобразование, учитывая, что
точке Zy соответствует точка а точке
z.,—точка 1FS. Для всех вариантов zt=^C),
VTj =0; значения z, и 1Г2 приведены в
табл. 19.1.
19.57. Составить выражение dz/dlT
для случая, когда поле на плоскости z
создается двумя линейными зарядами в точках at и а2 (рис.
19.11, г), заряженной полоской Ьс и диполем в точке d. В поле
имеется точка ветвления силовых линий е.
К. Метод интегральных уравнений
19.58 р. На расстоянии h от плоской границы раздела двух
сред расположен точечный заряд q. Воспользовавшись методом
интегральных уравнений, определить закон распределения плот-
ности связанных зарядов на поверхности раздела сред <tcb — [(г)
и вычислить связанный заряд qs, находящийся на поверхности
внутри окружности радиусом i\. Расчет выполнить для двух слу-
чаев: а) обе среды являются диэлектриками (ег1 и ег2) (рис. 19.12, о);
б) в нижнем полупространстве диэлектрик (е,2) заменен проводя-
щей средой.
19.59 . Определить аналитическую зависимость и построить
график распределения плотности связанных зарядов на поверх-
ности раздела двух диэлектриков (ег1 = 1; ег2 = 4), если электри-
ческое поле создается точечным зарядом q = 6,28-10-8 Кл. нахо-
дящимся в плоскости %0у, и бесконечно длинной диэлектрической
нитью, расположенной перпендикулярно плоскости чертежа, заря-
женной с линейной плотностью т —3,14-10-6 Кл/м (рис. 19.12,6).
Расстояние h 2 см.
19.60 р. Бесконечно длинный незаряженный полуцилиндр
радиусом а расположен на проводящей плоскости и находится ro
внешнем равномерном поле напряженностью £0 —90 кВ/м. Опре-
182
«слить закон изменения осв па цилиндрической поверхности
р функции координаты а для трех случаев: а) полуцилиндр вы-
ролнен из стекла (ег2 = 5), окружающая среда—воздух (ег1 = 1)
(рис. 19.12, в); б) полуцилиндр заполнен воздухом (fr;=i), окру-
жающая среда—стекло (ег2 = 5) (рис. 19.12,в); в) полуцилиндр
выполнен из меди, окружающая среда—воздух.
19.61 р. Прямолинейный проводящий цилиндр длиной/ = 60 см
и радиусом г0=1 см (рис. 19.13, л) заряжен и расположен в ди-
электрике (ег=4,5). Потенциал цилиндра относительно бесконечно
удаленной точки (ро = 100В. Определить закон распределения
линейной плотности заряда вдоль оси цилиндра т —f (г), его пол-
ный заряд Q и емкость С. Найти аналитическую зависимость и
построить график изменения потенциала поля в диэлектрике
<Р = /(г) при z = 30 см.
19.62 . Два одинаковых цилиндрических электрода, располо-
женных в воздухе, присоединены к источнику постоянной ЭДС
(рис. 19.13,6). Потенциалы электродов фдг=ф0; Чп — — гГо-
Фо = ]00 В. Длина каждого электрода Z = 60 мм, радиус сече-
ния г0 — 1 мм. Расстояние мм. Перемещая электрод В вдоль
оси г/, можно управлять распределением линейной плотности
заряда т(г) на оси электрода А и изменять его полный заряд.
Пренебрегая влиянием соединительных проводов, определить: а) за-
коны распределения т вдоль осн каждого электрода и их заряды
Q4 и Qb- если расположение электродов соответствует рис. 19.13, б;
6) закон распределения т вдоль оси электрода Д, если электрод В
удален в бесконечность.
Глава двадцатая
Электрическое поле постоянного тока
А. Законы Ома, Кирхгофа и Джоуля —Ленца
в дифференциальной форме
20.1. В проводящей среде с удельной проводимостью у ==
= 3 107 См/м потенции л изменяется по закону <р=—4Ю“8х—
—3-10~2^, где хм у—координаты прямоугольной системы коорди-
нат. Подсчитать ток, протекающий через прямоугольную площадку
длиной 2 см и шириной 1 см, которая расположена параллельно
оси z и составляет угол 30° с осью х (рис. 20.1, а).
а) б) В) г)
Рис. 20.!
20.2. Потенциал постоянного электрического поля, созданного
в проводящей среде с удельной проводимостью у = 10“4 См/м,
изменяется по закону (р = сх2—су* Л- d, где х, у—координаты точки
в прямоугольной системе координат; с=1 В/м®; d = 2B— число-
вые коэффициенты.
“> —•
Найти законы изменения плотности тока 6 и div 6 в зависи-
мости от координат точки. Подсчитать ток, протекающий через
квадратную площадку со стороной а = 50 см, которая располо-
жена параллельно плоскости zOy и находится на расстоянии
5=10 см от нее (рис. 20.1,6).
20.3р . Стальная пластина представляет собой 3/4 диска с кон-
центрически вырезанным круглым отверстием (рис. 20.1,в). Внут-
ренний радиус диска = 1 см, внешний /?2 = 2 см. Толщина
пластины постоянна. Между электродами 1 и 2 поддерживается
постоянная разность потенциалов. Найти разность потенциалов
0л—ф2«если наибольшее значение плотности тока б1ГЭХ = 5 10е А/м’,
а удельная проводимость стали у=107См/м.
20.4. Плоская алюминиевая пластина представляет собой */<
диска с концентрически вырезанным круглым отверстием. Внут-
ренний радиус диска = 5 см, внешний/?2 = 10 см (рис. 20.1,?)-
Толщина пластины постоянна. Между краями, ограниченными
радиальными прямыми ab и cd, поддерживается постоянная раз-
ность потенциалов. У края ab потенциал <р = 0. у края cd потен-
184
цнал ф = 0,01 В. Удельная проводимость алюминия у =
-js 3,3-107 См/м. Найти зависимость модуля плотности тока в функ-
ции расстояния от центра диска. Построить график 6 =/(г).
20.5. Пластина в задаче 20.4 имеет толщину Л = 2 мм. Под
действием разности потенциалов между краями ab и cd через
рластину протекает постоянный ток / = 200 А. Вычислить наи-
большие значения плотности тока и удельных тепловых потерь.
20.6. Водоподогреватель представляет собой металли аеский
заземленный цилиндрический бак диаметром D=1 ми высотой/:.
Дно и крышка бака выполнены из изолирующего материала. Для
подогревания воды в бак коаксиально с ним вставляют цилинд-
рический электрод диаметром /Л = 20 см. Водоподогреватель при-
соединен к однофазному трансформатору промышленной частоты,
один полюс которого заземлен.
Построить график зависимости удельной активной мощности
в функции расстояния от оси цилиндров. Считая, что нагрев про-
исходит только за счет токов проводимости, определить время,
необходимое для нагрева воды в баке от 20 до 100 °C, если дей-
ствующее значение приложенного напряжения {7 = 220 В. Удель-
ную проводимость воды (у = 1 См/м) считать не зависящей от
температуры.
Б. Определение проводимостей и токов утечки
20.7. Плоский конденсатор с двухслойным диэлектриком имеет
площадь электродов 5=20 см2, толщины слоев dj = l см, =
=0,5 см, удельные проводимости слоев У]=10'9 См/м, у3 =
= 5-10“9 См/м. Определить проводимость утечки через изоля-
цию конденсатора. Найти напряжение на каждом слое изоляции,
если конденсатор включен под постоянное напряжение U = 200 В.
°) S) 6)
Рис. 20.2
20.8. Цилиндрический конденсатор имеет два слоя
Шенной изоляции. Удельные проводимости внутреннего
него слоев диэлектрика у, = 10~8 См/м; уг = 10"7См/м.
электродов конденсатора (рис. 20.2, а) и цилиндрической поверх-
ности, разделяющей диэлектрики, г, =5 см; г^ег^ г3=сгя
(е—основание натуральных логарифмов). Длина конденсатора
‘ = 50 см. Определить постоянное напряжение, под которое может
несовер-
и внеш-
Радиусы
185
быть включен конденсатор, при котором ток утечки через него
не превышает 1,5 мкА.
20.9. Между цилиндрическими электродами (рис. 20.2,6) рас-
положены два несовершенных диэлектрика с удельными проводи-
мостями ?! = 10~* См/м; ?3 = 2-10-1 См/м. Радиусы электродов
/-!=! см; г2 = 2 см, их длина Z = 20 см. К электродам прило-
жено постоянное напряжение U = 100 В. Определить полный ток
утечки между электродами и плотности тока в точках А и В.
20.10р . Радиус внутреннего электрода сферического конденса-
тора Ri = 2 см, радиус внешнего электрода /?8 = 5 см. Удельная
проводимость диэлектрика ? = 10-10 См/М. К электродам конден-
сатора приложено постоянное напряжение £7 = 3000 В. Найти
зависимость модуля плотности тока в функции расстояния от
центра сфер, подсчитать ток утечки через несовершенную изо-
ляцию и вычислить наибольшие удельные тепловые потери.
20.11. Радиус внешнего электрода сферического конденсатора
/?2 = 10 см. При условии, что плотность тока утечки на поверх-
ности внутреннего электрода должна быть наименьшей при неиз-
менном приложенном напряжении и проводимости среды, опреде-
лить радиус внутреннего электрода Rt. Найти проводимость
утечки через несовершенную изоляцию конденсатора, если удель-
ная проводимость изоляции у = 5-1010 См/м.
20.12. В несовершенной изоляции плоского конденсатора;
обладающей удельной проводимостью у= 10"7 См/м, просверлено
цилиндрическое отверстие диаметром 2d=0,4 см (рис. 20.2, в).
Размеры конденсатора в сантиметрах указаны на рисунке. Кон-
денсатор включен под постоянное напряжение £7 = 200 В.
Пренебрегая краевым эффектом, определить ток утечки, про-
текающий через площадь сечения конденсатора плоскостью A BCD,
если: а) цилиндрическое отверстие в изоляции заполнено возду-
хом (?2 = 0); б) в цилиндрическом отверстии находится изоли-
рующий материал с удельной проводимостью уа= 10"® См/м; в) ци-
линдрического отверстия в изоляции нет. Качественно построить
картины поля для каждого случая.
В. Метод изображений
20.13. Найти радиус Ro полусферического заземлителя, погру-
женного в глинистый грунт, если через него протекает ток 1 =
= 105 А, а максимальное шаговое напряжение не превышает
£7 = 50 В. Шаг человека принять равным 0,8 м. Удельная прово-
димость глинистого грунта ? = 510“8 См/м.
20.14. Для определения удельного сопротивления грунта
в него помещена металлическая полусфера радиусом /?0 = 25 см
(рис. 20.3, а). Через заземлитель пропускают ток / = 5 А. Электро-
статический вольтметр, присоединенный к двум зондам, которые
отстоят от центра полусферы на а = 50 см, £>—100 см, показы-
вает напряжение 40 В. Считая, что второй электрод удален
186
-остаточно далеко и его влиянием можно пренебречь, рассчитать
удельную проводимость грунта.
у 20.15. Заземление выполнено в виде полой металлической
сферы радиусом а = 0,2 м, расположенной в грунте на расстоя-
нии d==10 м от его поверхности (рис. 20.3,6). Удельная прово-
димость грунта у=10-2См/м. Определить сопротивление заземле-
6)
Рис. 20.3
_____I
d
• —
8)
имя /?1, считая заряды сферы и ее зеркального изображения
сосредоточенными в центрах сфер. Сравнить найденное значение
с сопротивлением Ro металлической сферы, расположенной в грунте
на весьма большой глубине от поверхности. Качественно начер-
тить картину линий плотности тока для заземления, изображен-
ного на рис. 20.3,6.
Указание. Под сопротивлением заземления понимают сопротивление
среды между данным электродом н электродом, удаленным в бесконечность.
20.16р . Заземлитель представляет собой цилиндрическую трубу,
расположенную в грунте (рис. 20.3, в). Длина трубы 1=1 м, ее
внешний диаметр d — 40 мм. Удельная проводимость грунта у =
= 210“2 См/м. Определить сопротивление заземления.
а) 8)
Рис. 20.4
20.17. В проводящей среде с удельной проводимостью Yt =
10~6 См/м расположены два длинных проводящих цилиндра,
находящихся под постоянным напряжением. Расположение прово-
дов и необходимые геометрические размеры в миллиметрах ука-
заны на рис. 20.4, а. Найти напряженность электрического поля
® точке а, если ток утечки между цилиндрами на 1 м их длины
составляет 100 мА.
187
20.18. Параллельно безграничной плоскости двух несовершен-
ных диэлектриков с удельными проводимостями yi = 10-10 См/м и
у2 = 4-10’10 См/м расположены два длинных провода круглого
сечения. Радиусы проводов rt = 0,5 мм; G=1 мм. Расположение
проводов и геометрические размеры указаны на рис. 20.4,6
в миллиметрах. Определить проводимость между проводами на
1 м длины. Вычислить ток утечки между проводами, считая, что
линия включена под постоянное напряжение 100 В. Найти плот-
ность тока утечки в точке а.
20.19р . Полусферической заземлитель радиусом располо-
жен в грунте (рис. 20.4, в). Расстояние от центра полусферы до
поверхности раздела двух слоев различного грунта а. Удельные
проводимости слоев грунта и ?2, при этом > *у2. Постоян-
ный ток, стекающий через заземлитель в грунт, Определить
закон изменения потенциала в функции расстояния. Принять
потенциал <р = 0 при /? = оо.
Г. Расчет постоянного электрического поля
в неоднородной проводящей среде
20.20. Коаксильный кабель с радиусом внутренней жилы
Г| = 5 мм, радиусом внешней оболочки г2=20 мм и длиной /= 1 м
включен под постоянное напряжение U = 100 кВ. Вследствие не-
равномерного нагрева изоляции ее удельная проводимость уве-.
личивается от внешней оболочки к внутренней жиле по закону
Y=Vo(l + n/r), где /"1<г<га, у0 = 1б’10См/м.
Подсчитать проводимость изоляции, ток утечки через несовер-
шенную изоляцию кабеля и мощность, идущую на нагрев изо-
ляции.
20.21р . Между электродами сферического конденсатора нахо-
дится диэлектрик, удельная проводимость которого меняется
в функции расстояния R от центра сфер по закону y = y0/R, где
Rl<R<R2; у0=Ю“4 См/м. Радиусы внутренней и внешней сфер
соответственно R\ = 1 см; R2=5 см. Ток утечки через несовершен-
ную изоляцию Z= 0,2 А.
Найти закон изменения потенциала между электродами, если
известно, что внешний электрод заземлен. Определить напряже-
ние между электродами и проводимость утечки конденсатора.
20.22. В плоском конденсаторе с несовершенной изоляцией
вследствие нагрева одного из электродов удельная проводимость
меняется по закону у = у0(1 4-for), где*—координата прямоуголь-
ной системы координат (рис. 20.5, а); у = 10’10См/м; £ = 20м’1-
Относительная диэлектрическая проницаемость ег = 4. Расстояние
между электродами d —0,5 см. Конденсатор подключен к источ-
нику постоянной ЭДС 200 В. Пренебрегая краевым эффектом,
найти закон изменения плотности объемного заряда и закон из-
менения потенциала в зависимости от расстояния х.
20.23. Плоский конденсатор (рис. 20.5, а) заполнен неоднороД'
ным несовершенным диэлектриком, абсолютная диэлектрическая
188
проницаемость которого ев = воем(1 4-Ах1), где вг1 и k—постоян-
ные величины. Удельная проводимость у = const. Конденсатор под-
ключен к источнику постоянного напряжения U. Расстояние
между электродами d. Определить закон распределения плотно-
сти объемного заряда между электродами р(х).
20.24. В жидкий несовершенный диэлектрик помещены два
плоских электрода, к которым приложено постоянное напряже-
ние V=E (рис. 20.5, а). За счет осаждения примеси удельная про-
водимость диэлектрика меняется по закону у=у0(1—/ту), а абсо-
лютная диэлектрическая проницаемость ee = const. Найти закон
распределения плотности объемного заряда между электродами
р(*. у}-
20.25р . В цилиндрическом конденсаторе с несовершенной изо-
ляцией вследствие неравномерного нагрева относительная диэлек-
трическая проницаемость меняется по закону ъг = вг1 (2 4- kr), а
удельная проводимость меняется по закону у = yt (2—jfer), где
ert = 5; yl= 10 См/см; k — 0,1 см"1; г—в см. Радиус внутрен-
него цилиндра с==5см, радиус внешнего цилиндра 6= 10 см.
Длина конденсатора I = 1 м. Конденсатор включен под постоянное
напряжение 1/=1кВ. Найти закон распределения объемного
заряда н закон распределения плотности тока в функции расстоя-
ния от оси цилиндра. Вычислить ток утечки.
Д. Графический метод построения картины
плоскопараллельного электрического поля
20.26. Для исследования электрического поля в электролити-
ческую ванну погружены два металлических электрода (рис. 20.5, б).
Внешний электрод представляет собой полый круглый цилиндр,
а внутренний является эллиптическим цилиндром. Размеры
электродов указаны на рисунке в миллиметрах.
Графическим путем построить картину электрического поля
*«ежду электродами и определить проводимость между электродами
1 м длины, если удельная проводимость электролита у = 2 См/м.
189
Найтп емкость между электродами на 1 м длины, если электроду
расположены в воздухе. Краевым эффектом можно пренебречь,
так как длина цилиндров достаточно велика. Вычислить напря-
жение между точками А и В, если к электродам приложено
постоянное напряжение 300 В. Координаты точек .4 и В:.\л = 0;
tfA = 18 мм: хв = — 34 мм; ул = 0.
20.27. Два металлических электрода выполнены в виде одина-
ковых эллиптических цилиндров и расположены по отношению
друг к другу так, как показано на рис. 20.5. в. Размеры элек-
тродов указаны на рисунке в сантиметрах. Удельная проводи-
мость среды, находящейся между электродами, много меньше
удельной проводимости самих электродов. К электродам подведено
постоянное напряжение. Построить графическим путем картину
электрического поля. По картине поля найти точки, где плотность
тока имеет наибольшее значение.
Глава двадцать первая
Магнитное поле постоянного тока
А. Закон полного тока
21.1. Вдоль прямолинейного цилиндрического полого биметал-
лического провода
протекает постоянный ток / — 200 А. Наруж-
ный п роводник—медный
(ум = 57-10* См м), внут-
ренний проводник—латун-
ный (ул =30- 10* См .м).
Радиус внутренней полос-
ти го=3мм, радиус ци-
линдрической поверхнос-
ти, разделяющей медь и
латунь, ^=6 мм; внеш-
ний радиус г, = 9мм.
Направление тока в
проводе совпадает с поло-
жительным направлением
оси Z цилиндрической сис-
темы координат (рис.
21.1.0).
Найтп зависимость мо-
дуля напряженности, маг-
нитного поля в функции расстояния от оси провода H —
для областей 7, 2, 3 и 4. Пользуясь найденными зависимостями,
определить выражения для rot Н в этих областях и сопоставить
их со значением плотности тока в каждой области. Построить
графики | Н | = f (г) и |rot/7[ = /(r) при 0<г<оо.
190
21.2. Радиус внутренней жилы коаксиального кабеля г0 = 5 мм,
рлутренний радиус оболочки гг=10мм (рис. 21.1,6). Жила и
оболочка выполнены из стали, относительная магнитная прони-
цаемость которой р, = 100. Ток в жиле и оболочке кабеля
/=х31.4А. Направления тока в них указаны на рисунке.
Выбрать внешний радиус оболочки rt так, чтобы плотность
тока в оболочке была такой же, как и в жиле. Найти зависи-
мость модуля магнитной индукции в функции расстояния от оси
кабеля при 0<г<оо.
21.3р. В прямолинейном цилиндрическом проводе радиусом
20 мм имеется цилиндрическое отверстие круглого сечения
радиусом 6 = 5 мм. Расстояние между осями цилиндров d— 10 мм
(рис. 21.1. в). Вдоль провода в направлении «от нас» протекает
постоянный ток плотностью 6 = 5105А/м8. Найти значения век-
тора напряженности магнитного поля внутри отверстия, а также
в точках А и В. Координаты точек А и В: хА = 0; уА =—10 мм;
хв^40мм; ув=0.
21.4. В прямолинейном цилиндрическом проводе радиусом
а = 30 мм имеется цилиндрическое отверстие круглого сечения
(рис. 21.1, е). Вдоль провода протекает постоянный ток 7 = 700 А.
Известно, что напряженность магнитного поля на оси провода
Я = /600А/м, а напряженность магнитного поля на оси отверстия
Я2= /2400 А/м. Найти радиус цилиндрического отверстия и рас-
стояние между осями провода и отверстия.
21.5. Вдоль трех прямолинейных длинных параллельных про-
водов протекают токи 71=/2 = 0,5А; 73=1 А (рис. 21.1, г). Рас-
стояние между проводами d— 1 м. Определить силы, действующие
на единицу длины каждого провода Flt Ft, F3, и индукцию В в
точке 0, если провода расположены в воздухе.
Б. Закон Био — Савара — Лапласа
21.6. Рассчитать и построить графики распределения индук-
ции В по оси х в магнитном поле постоянного тока 1— 1 А, про-
зекающего вдоль: а) отрезка прямолинейного провода длиной
/=0,2м (рис. 21.2, о); б) бесконечно длинного прямолинейного
провода. В обоих случаях расстояние h = 0,1м, окружающей
средой является воздух.
21.7. Вдоль прямоугольной рамки со сторонами а — Зсм.
6 = 4 см, расположенной в воздухе, протекает постоянный ток
7 = 20 А (рис. 21.2,6). Число витков рамки &'= 10. Найти маг-
нитную индукцию в точках р и q по величине и направле-
нию.
21.8. Постоянный ток 7 =10 А протекает вдоль одновиткового
Контура, показанного на рис. 21.2, в. Найти магнитную индук-
цию в точке О. Контур расположен в воздухе. Радиус витка
с= 10 см.
191
21.9р . Постоянный ток I = 5 А протекает вдоль рамки, выпол-
ненной в виде правильного многоугольника, вписанного в окруж-
кость радиусом с=10см. Число сторон многоугольника л = 6,
число витков рамки ш = 5. Определить напряженность магнитного
поля в центре многоугольника.
В. Скалярный магнитный потенциал
и магнитное напряжение
21.10. Вдоль цилиндрического прямолинейного провода проте-
кает постоянный ток /==300 А. Направление тока в проводе пока-
зано на рис. 21.2, г. Ось г цилиндрической системы координат
перпендикулярна плоскости
чертежа и направлена к чи-
тателю. Воспользовавшись
уравнением Лапласа, полу-
чить зависимость скалярного
магнитного потенциала <рм=
=fx (г, a, г) и его градиента
grad <jpM = /а (г, a, z) от коор-
динат. Считать фм=0 в точ-
ках, лежащих на экви потен-
циал и Ох.
21.11. Вдоль цилиндри-
ческого прямолинейного про-
вода протекает постоянный
ток. Направление тока в
проводе показано на рис.
21.3, с. Магнитное напряже-
ние между точками а и b
по пути acb UK ab — 30 А.
Определить напряженность
магнитного поля в точке d. Цилиндрические координаты точек:
га = 30 см; аа — 0; гь= ]0см; аь— 120°; гс=20 см; ас = 30°; rd=45 см;
ad=270°.
21.12. В постоянном равномерном магнитном поле напряж^'
ностью Яв = 1«100А/м расположен медный бесконечно длинн^
192
цилиндрический провод, вдоль которого протекает постоянный
/ = ЮА (рис. 21.3,6). Найти два возможных значения маг-
нитного напряжения между точками А и С и ^мадс)-
рассчитать магнитное напряжение UnAB и градиент скалярного
магнитного потенциала в точке A grad<jpMA. Координаты точек:
*л==10см; уА = 0\ хв=20см; = хс = 0; ус —— 20 см.
21.13р . Вдоль двухпроводной линии протекает постоянный ток
/=:36А. Направление тока в проводах линии показано на рис.
21.3, в. Расстояние между осями проводов d=l м.
Определить магнитное напряжение между точками М и Л\
К и Р. Координаты точек: хл1 = 0,5м; #m=0,5m; л)у = 0;
уv 0,5 м; хр = — 0,5 м; ур = — 0,5 м. Качественно построить
картину магнитного поля двухпроводной линии.
Указание. При решении выбрать путь интегрирования, соединяющий
точки М н N, М и Р так, чтобы он не пронизывал контур с током.
Г. Векторный магнитный потенциал
21.14. В магнитном поле, созданном в неферромагнитной среде
и подчиняющемся цилиндрической симметрии, векторный потен-
циал изменяется по закону A =z°(ar8+61nr-|-c). Определить
законы распределения индукции и
плотности тока в функции коорди- .
нат.
21.15р. Вдоль длинного цилинд-
рического стального провода проте-
кает постоянный ток. Радиус прово-
да г0= 1см. Относительная магнит-
ная проницаемость стали рг = 50.
Средой, окружающей провод, являет-
ся воздух. Проекция векторного маг-
нитного потенциала на ось z меняет-
ся в функции расстояния от оси про-
вода внутри провода по закону А,=
== —6,28г* Вб/м, а вне провода по
закону А3—~ 25,1 10~* 1пг/0,01 —
—6,28-10-* Вб/м.
Найти законы изменения модулей
напряженности поля и вектора на-
магниченности в функции расстояния
оси провода. Построить графики
и Z=fs(r) при 0<Г<ОО.
21.16. Вдоль длинной стальной
Н1ины в направлении оси z проте-
?ает постоянный ток Z—100 А,
2d
№
У
b iC
№•
I
а
did
о)
h
В)
d
в)
Рис. 21.4
дг=300. Толщина шины
4fl==l см, ее высота А—10 см (на рис. 21.4, а даны две ее
проекции). В плоскости zOr, составляющей угол 30° с ппос-
°^ью zOy, находится одновитковая квадратная рамка со
z
о
с
Ь
h
45*
193
стороной ab — 2 см. Сторона ab параллельна оси Oz и находится
на расстоянии I = 1,5 см от поверхности шины.
Найти зависимость проекции векторного магнитного потенциала
на ось z в функции координаты у и построить график А — f (yj
при 0<у<оо. Принять А=0 при у = 0. Пользуясь полученной
зависимостью A~f (y)t подсчитать магнитный поток, сцепленный
с рамкой. Построить след эквипотенциальной поверхности, для
которой А = — 75- 10“* Вб/м.
21.17р . Вдоль длинной плоской стальной шины, показанной
на рис. 21.4, а в двух проекциях, в направлении оси г протекает
постоянный ток I. Толщина шины 2а = 4 мм, высота шины h = 40 мм.
Относительная магнитная проницаемость стали цг = 20. Средой,
окружающей шину, является воздух. Известно, что разность
векторных магнитных потенциалов между точками т и п
Ая—А„ — k- Ю-* Вб/м. Координаты точки т: хя = 0; уя=1мм;
2ж = 0. Координаты точки л: х„ =—10 мм; у„ = 5 мм; г„ — 100 мм.
Считая А = 0 при у = 0, определить ток /, протекающий вдоль
шины.
21.18. Вдоль длинного цилиндрического алюминиевого провода
радиусом г0=2 см протекает постоянный ток / =628 А (рис. 21.4, б).
В радиальной плоскости zOr находится рамка, представляющая
собой трапецию со стороной аб=15см, высотой Л = 5см и уг-
лами adc = 45° и Ы=60°. Сторона ab параллельна оси провода
и находится от нее на расстоянии h = 5 см.
Найти зависимость модуля векторного потенциала в функ-
ции расстояния от оси провода для областей 1 и 2 (внутри
и вне провода) и построить кривую A ~f (г) при О < г <оо. При-
нять Л = 0 при г = 0. Воспользовавшись результатами расчета,
подсчитать магнитный поток Ф, сцепленный с рамкой. Вычислить
разность векторных магнитных потенциалов между точками, нахо-
дящимися на расстоянии 1 см от оси провода, и точками, распо-
ложенными на расстоянии 1 см над поверхностью провода. По-
строить эквипотенциальную поверхность, на которой А —
= -1,78-10“* Вб/м.
21.19. Вдоль длинного цилиндрического провода радиусом
г0 = Змм, расположенного в воздухе, протекает постоянный ток
(рис. 21.4, в). Разность векторных магнитных потенциалов между
точками а и Ь Аа—Ab = ?2,73-10"6 Вб/м.
Найти разность скалярных магнитных потенциалов между
этими же точками. Цилиндрические координаты точек а и Ь:
гс=4мм; ac = 30°; zB = 0; гь = 20мм; ab=150°; zb= 100 мм.
21.20. Радиус внутренней жилы коаксильного кабеля г0=5 мм,
внутренний радиус оболочки п = 10 мм, внешний радиус оболоч-
ки г2 = Н,2 мм (см. рис. 21.1, б). Жила и оболочка кабеля выпол-
нены из меди. Вдоль кабеля протекает постоянный ток, плот'
ность которого в жиле и оболочке 5 = 40-104 А/м2. Направлен^
тока в жиле и оболочке указаны на рис. 21.1, б.
194
Определить зависимость модуля векторного магнитного потен-
циала в функции расстояния от оси кабеля, полагая А=0 при х=0.
21.21. Вдоль проводов двухпроводной линии (рис. 21.5, п) про-
текает постоянный ток / = 50А. Направление тока в проводах
ЛИНИИ показано на рисунке. Линия выполнена из круглого мед-
ного провода диаметром 2а — 4 мм. Расстояние между проводами
линии 2d = 0,5 м.
a} S) в)
Рис. 21.5
Для точек плоскости zOx найти зависимость модуля век-
торного магнитного потенциала как функции координаты х
при изменении х от 0 до d—а. Принять А=0 при х—С. Найти
внешнюю индуктивность линии на 1 км длины, воспользовавшись:
а) выражением для векторного потенциала; б) формулой Ф = J В dS.
s
Указание. Под внешней индуктивностью следует понимать индуктив-
ность, обусловленную магнитным потоком, проходящим в пространстве между
проводами линии.
21.22. Провода высоковольтной линии выполнены из медного
провода диаметром 4о=10мм. Расстояние между проводами
С-Зм. На тех же опорах расположены провода линии связи.
Расположение проводов линий и геометрические размеры в метрах
указаны на рис. 21.5, б.
Найти взаимную индуктивность между высоковольтной линией
в линией связи на 1 км длины. При решении воспользоваться
пависимостью векторного потенциала как функцией расстояния
01 оси провода: A—f(r).
21.23. Вдоль кругового витка радиусом Я = 0,1м протекает
постоянный ток / = 10 А. Поперечные размеры сечения проводника
налы по сравнению с радиусом витка (рис. 2L5, в). Средой, окру-
’«ающей виток, является воздух.
Найти вектор-потенциал точки а. Провести через эту точку
линию равного векторного потенциала. Цилиндрические коорди-
Наты точки a: гв = 0,2м; сса = 60°; ?в = 0,4м. Определить вектор-
магнитный потенциал и магнитную индукцию в центре витка.
195
Д. Метод изображений
21.24. В массивной чугунной плите на расстоянии h = 15 см
от ее поверхности просверлен цилиндрический канал и проложен
изолированный провод, вдоль которого протекает постоянный ток
/—10 А (рис. 21.6, о). Относительная магнитная проницаемость
чугуна рг= 10.
Для точек плоскости у — 0 построить зависимости напряжен-
ности магнитного поля и магнитной индукции от расстояния вдоль
Рис. 21.6
оси х- H — fi(x) и В = /4(х). Найти значение и направление силы,
действующей на 1 м провода. Толщиной изоляционного слоя
между стенками канала и проводом пренебречь.
21.25р . Прямолинейный длинный провод, вдоль которого про-
текает ток / = 60 А, расположен в воздухе параллельно плоской
поверхности стальной (р.г—*-оо) плиты на расстоянии Л = 2см от
нее (рис. 21.6,6). Определить напряженность магнитного поля
в точках а и Ь, координаты которых хв = 0; уа = 0; хь = 3см;
у6 = 2 см.
21.26. Вблизи плоской поверхности стальной (рг —* оо) плиты
в воздухе расположена треугольная рамка, вдоль которой проте-
кает гок ! — 1 А. Расположение рамки и геометрические размеры
в сантиметрах указаны на рис. 21.6, г. Определить магнитную
индукцию в точке А.
21.27. Параллельно безграничной плоскости раздела двух фер-
ромагнитных сред (рг1 = 50; pfS = 150) расположены два изоли-
рованных провода, образующих двухпроводную линию. Располо-
жение проводов и геометрические размеры в миллиметрах указаны
196
на рис. 21.6,в. Радиусы проводов равны I мм. Рассчитать внеш-
нюю индуктивность линии на 1 м ее длины.
21.28. Длинный ферромагнитный цилиндр (рг1=19) радиусом
^ = 3 см и прямолинейный медный провод расположены в воздухе
^=1) на расстоянии d=10cM параллельно друг другу
(рис. 21.6, д). Вдоль провода протекает ток / = 100 А. Вычислить
Н и В в точках 0, а, Ь. Качественно начертить графики зависи-
мостей // = /1(х); В=/2(х). Учесть, что в точке а индукция имеет
два значения.
Указание. При решении рекомендуется использовать аналогию с соот-
ветствующей задачей электростатики, заменив в расчетных формулах % на /,
а на 1/цв.
Е. Метод разделения переменных
21.29. Бесконечно длинный прямолинейный цилиндрический
стержень из магнитодиэлектрика (рг = 9) радиусом а = 5 мм распо-
ложен в равномерном магнитном поле. Ось стержня перпендику-
лярна линиям магнитной индукции внешнего поля Во. Магнит-
ный поток, проходящий через
продольное сечение стержня
длиной 1 см, перпендикуляр-
ное к линиям В, Ф = 510~ь
Вб. Определить индукцию
внешнего поля Во. Вычис-
лить объемную плотность
энергии &’м в цилиндрическом
.стержне.
21.30. Прямолинейный ци-
линдрический стальной про-
вод радиусом а = 5 мм распо-
ложен в равномерном магнит-
ном поле напряженностью
Яо= 1000 А/м (рис. 21.7, я).
Относител ьна я ма гн итна я
проницаемость стали рл — 10.
Вдоль провода протекает пос-
тоянный ток / = 100 А, нап-
равление которого указано
на рисунке. Найти напряжен-
ность магнитного поля в
точках /, 2 и 3. Расстояния
гз= г3 = 10 мм.
Рис. 21.7
точек от оси провода rt = 0;
21.31. Стальной шар (pw = 28) радиусом 2 см обвит витком
тонкой проволоки, плотно прилегающим к поверхности шара,
и помещен в равномерное постоянное магнитное поле напряжен-
ностью /Уо =5000 А/м так. что плоскость витка перпендикулярна
силовым линиям поля (рис. 21.7, б). Окружающей средой является
воздух: р,е=1.
197
Определить потокосцепление витка. Найти напряженность маг-
нитного поля внутри шара Hh а также в точках А, В и С, нахо-
дящихся в воздухе у самой поверхности шара. Координаты точек:
—2 см; ел = 0°, 6д==30°1 ес=90°. Качественно построить кар-
тины линий магнитной индукции В, напряженности поля Н н
намагниченности Л
21.32. Стальной эллипсоид вращения (рг = 31) расположен
в постоянном равномерном магнитном поле напряженностью
7/о = 2ООО0А/м так, что его большая ось а совпадает с направ-
лением поля. Ося эллипсоида а = 5 см; Ь=с = 3см. Окружающей
средой является воздух.
Рассчитать коэффициент размагничивания напряженность
размагничивающего поля Н9О и магнитную индукцию внутри
эллипсоида B9t. Сравнить найденные значения с соответствующими
значениями для шара, выполненного из той же стали (#ш, /7Шез, ВШ1).
Как изменится магнитная индукция внутри эллипсоида, если
его повернуть на 90° вокруг малой оси?
Указание. Напряженность размагничивающего поля На = —Ht.
21.33. Внутри длинной металлической трубы (а = 3 см; & = 5 см)
расположен прямолинейный медный провод радиусом го = О,1см
с током / = 3,14 А (рис. 21.7, в). Ток в проводе направлен «от нас».
Описанное устройство находится во внешнем равномерном поле
напряженностью /70= 1 000 А/м. Определить векторы напряжен-
ности поля в точках р и д, если труба выполнена: а) из стали
(рг = 250); б) из меди. Координаты точек р и q аю = 0, а„ = —90°;
rp=rq= \ см, zp=z4=0. Вычислить запас энергии на единицу
длины магнитного поля, заключенного внутри металлической
трубы, если /7о=0.
21.34. Магнитный экран представляет собой стальную трубу
с внешним диаметром 26= 10 см и внутренним диаметром 2а = 8 см.
Относительная магнитная проницаемость стали рг=100. Внутри
трубы находится медный провод диаметром d—4 мм, вдоль кото-
рого течет постоянный ток / (рис. 21.7, л). Ось провода совпадает
с осью экрана. Экран с проводом находятся во внешнем равно-
мерном магнитном поле напряженностью H0 = i-10000 А/м. Изве-
стно, что в точке с координатами г = 3,11 см, а = 90° напряжен-
ность магнитного поля Н = 0. Определить значение и направление
тока в проводе. Построить график зависимости модуля магнитной
индукции в функции расстояния г от оси провода при а = ±90°
Указание. Сначала построить графики для внешнего поля и пол*’
созданного током /, а затем для результирующего поля.
21.35р . Лабораторная установка для исследования магнитных
экранов представляет собой электромагнит, между полюсами кото'
рого создается равномерное постоянное магнитное поле. В это
поле помещают исследуемый экран (рис. 21.7, г). Экран выполнеН
разъемным. Внутри экрана в плоскости, перпендикулярной сил0*
198
рым линиям, находится круглая рамка, подключенная к бал-
листическому гальванометру, на рисунке не показанному.
С помощью описанной установки был исследован стальной сфе-
рический экран с внешним радиусом 6= 5 см и внутренним радиу-
сом а=4см. Средний диаметр катушки, находящейся внутри
экрана, D = 6cm. Число витков катушки w =10. Относительная
магнитная проницаемость стали рг = 20.
Установить, при каком расположении щели между двумя поло-
винами экрана относительно направления силовых линий экрани-
рование наиболее эффективно. Определить отклонение луча а
баллистического гальванометра при переключении тока в обмотке
возбуждения электромагнита с 4-/ на —/. Баллистическая постоян-
ная установка С$ = ф/а= 1,8-10~* Вб/дел. Напряженность внеш-
него равномерного магнитного поля Яо= 10000 А/м. Расчет про-
вести для случая наивыгоднейшего расположения экрана.
Ж. Графическое построение картины
магнитного поля и ее использование
21.36. На рис. 21.8, а изображена картина магнитного поля
двухпроводной линии постоянного тока, построенная так, что
магнитные потоки всех силовых трубок равны. Линейные размеры
на рисунке даны в масштабе 1:1. Ток в линии / = 16А. Направ-
ление тока в проводах показано на рисунке. Окружающей средой
является воздух.
Приняв <рм = 0 для эквипотенциальной линии, проходящей
через начало координат, указать значение <рм в амперах у каждой
эквипотенциальной линии. Пользуясь картиной поля, определить
разность скалярных магнитных потенциалов между точками А и В,
напряженность поля в точке С; магнитный поток, пронизывающий
пространство между проводами линии на единицу длины.
21.37р . На рис. 21.8,6 изображена картина магнитного поля
трехпроводной линии, расположенной в воздухе; все геометри-
ческие размеры даны в сантиметрах. Для каждой эквипотенциаль-
ной линии указано значение скалярного магнитного потенциала
в амперах.
Определить значение и направление токов в проводах линии.
Пользуясь картиной поля, найти магнитную индукцию в точке А
и сопоставить ее с индукцией в этой же точке, найденной в ре-
зультате сложения трех векторов, определенных по закону пол-
ного тока.
21.38. На рис. 2.18, в изображен разрез магнитной цепи*. Все
размеры даны в миллиметрах. Длина магнитопровода в направ-
лении, перпендикулярном плоскости чертежа, / = 40см. Магнито-
провод выполнен из стали, относительная магнитная проницае-
мость которой принимается равной бесконечности. Обмотка
Расположена на двух полюсах и имеет по 50 витков на каждом.
* При решении магнитное поле считать плоскопараллельным.
199
Пользуясь графическим методом, построить картину магнитного
поля, т. е. семейство эквипотенциальных линий и линий магнит-
ной индукции, так, чтобы магнитные потоки всех силовых тру-
бок были равны.
Рис. 21.8
По картине поля определить:
а) магнитное сопротивление воз-
душного зазора в среднем стерж-
не (с учетом скоса полюса); б) ин-
дуктивность двух последователь-
но соединенных катушек
(2^= 100); в) взаимную индук-
тивность между основной об-
моткой, расположенной на верх-
нем полюсе N (^-50), и вит-
ком а'2, плотно прилегающим
к поверхности нижнего полюса
S 1).
21.39. На рис. 21.8, г изоб-
ражена магнитная цепь элект-
роизмерительного прибора. Все
размеры даны в миллиметрах.
Толщина магнитопровода в нап-
равлении, перпендикулярном
плоскости чертежа, Z = 50 мм.
Магнитная проницаемость стали
магнитопровода принимается
равной бесконечности. Магнит-
ное поле воздушного зазора
создается двумя катушками
по 25 витков в каждой, распо-
ложенных на крайних стерж-
нях. Число витков поворотной
рамки = Пользуясь гра-
фическим методом, построить
картину магнитного поля в воз-
душном зазоре между полюсам»
электромагнита с соблюдением
тех же условий, что и в преды-
дущей задаче.
По картине поля определить:
а) магнитное сопротивление воз-
душного зазора между полюса-
ми; б) взаимную индуктивность
М между обмоткой и пово-
ротной рамкой w2, при а— О*
30, 60, 90°. Построить зависи-
мость При решении
магнитное поле считать плоско-
параллельным.
200
Глава двадцать вторая
Основные уравнения переменного
электромагнитного поля
А. Уравнения Максвелла
22.1. В поле плоского конденсатора помещен несовершенный
диэлектрик с удельной проводимостью у=10-4 Сц/м и относи-
тельной диэлектрической проницаемостью ег = 6. Конденсатор
включен под напряжение u = Umsmtot. Расстояние между пла-
стинами конденсатора d = 3 см. Считая» что и у не зависят от
частоты, вычислить амплитуды плотностей токов смещения
и проводимости б,лпр для следующих частот: 0; 300 Гц; 300 МГц.
Амплитуда приложенного напряжения (7СТ = ЗОООВ.
22.2. К плоскому конденсатору с воздушной изоляцией приложе-
но напряжение, изменяющееся по закону H=6000sin(103/+60") В.
Пластины конденсатора
имеют форму дисков и расположены
на расстоянии d = 2 см
друг от друга. Найти вы-
ражение для мгновенных
значений напряженности
магнитного поля в точках,
лежащих между пластина-
ми конденсатора на рас-
стоянии г от оси симмет-
рии.
22.3. Между электрода-
ми плоского конденсатора
расположено кольцо пря-
Рис. 22.1
моугольного сечения, изго-
товленное из несовершен-
ного диэлектрика (рис.
22.1, а). Относительная диэлектрическая проницаемость несовер-
шенного диэлектрика рг = 4. удельная проводимость у — 2-10“5См/м.
Цилиндрическая область внутри кольца заполнена воздухом. Рас-
стояние между пластинами конденсатора d = 0,5 см, внутренний
радиус кольца г = 2 см, а внешний радиус г2 = 4 см. Средой, ок-
ружающей кольцо, является воздух. Конденсатор подключен к ис-
точнику синусоидального тока i = 0,5 sin (wf-}-47o30') А, частота
которого / = 910* Гц.
Пренебрегая краевыми эффектами внутри и вне конденсатора,
получить выражения для мгновенных значений напряженности
Магнитного поля Н и rot Н в точках, лежащих между пласти-
нами конденсатора на расстоянии г от оси симметрии.
22.4. Цилиндрический конденсатор имеет два слоя несовер-
шенной изоляции. Радиус внутреннего цилиндра г0=1 см. радиус
поверхности раздела двух диэлектриков /^ = 2 см, внутренний
Радиус внешнего цилиндра га = 2,5см. Длина конденсатора
201
1 = 20 см. Относительная диэлектрическая проницаемость внутрен-
него слоя ег1 = 5, его удельная проводимость ^=8,66-10 5 См/м.,
относительная диэлектрическая проницаемость внешнего слоя
erJ = 3, его удельная проводимость у2 = 3-10-6 См/м. Конденсатор
подключен к источнику синусоидального тока i = 0,628sin<о/ А,
частота которого f= 18-10* Гц. Найти выражения для мгновенных
значений Е и D в функции расстояния г от оси цилиндров для
каждого слоя изоляции. Определить мгновенное значение напря-
жения между электродами конденсатора.
22.5. По прямолинейному весьма длинному проводу протекает
постоянный ток 1 =10 А. В одной плоскости с проводом распо-
Рис. 22.2
ложена прямоугольная
одновитковая рамка
(рис. 22.1, б), две сторо-
ны которой параллель-
ны оси провода. Длина
каждой стороны I = 10
см. Две другие стороны,
перпендикулярные оси
провода, имеют длину
с = 2см каждая. Рамка
движется вдоль оси х с
ускорением а = 0,5 м/с2.
Начальное положение'
рамки х0 = 2 см.
Найти зависимость
э.д.с., наводимой в рамке, в функции расстояния от оси про-
вода. Вычислить значение этой э. д. с. в тот момент, когда ближай-
шая сторона находится на расстоянии х = 6см от оси провода.
22.6р . Прямолинейный весьма длинный провод и прямоуголь-
ная одновитковая рамка расположены в одной плоскости
(рис. 22.1, в). Размеры рамки: 6 = 50 см; с=30см. Вдоль провода
протекает синусоидальный ток i=10sinl0/A. Рамка движется
со скоростью v = 80 см/с в направлении, перпендикулярном оси
провода.
Написать выражение для ЭДС, наводимой в рамке, если
в начальном положении при / = 0 ближайшая сторона находится
на расстоянии с=10см от оси провода. Найти мгновенное зна-
чение ЭДС в тот момент, когда ближайшая сторона находится
на расстоянии х=20 см от начального положения.
22.7. Кольцо радиусом Я® = 40 см выполнено из тонкой изо-
лированной проволоки и короткими проводниками (длиной про-
водников можно пренебречь) присоединено к зажимам электромаг-
нитного вольтметра (рис. 22.2, а). Сопротивление вольтметра бес-
конечно велико. Кольцо помещено в равномерное магнитное поле,
индукция которого изменяется по закону B = zc0,l sin 100л/ Тл.
Определить мгновенное значение rot£ и найти показание вольт-
метра.
202
Б. Теорема Умова—Пойнтинга
22.8р . Вдоль цилиндрического прямолинейного полого сталь-
ного провода (у = 5-105 См/м), расположенного в воздухе, про-
текает постоянный ток / = 94,2 А. Внутренний радиус провода
Г1= 1 см, внешний радиус г2 = 2 см. Известно, что тангенциаль-
ная составляющая вектора Пойнтинга на внешней поверхности
провода П(= 1,5 - 10а Вт/м*.
Найти угол <р, который составляет вектор Пойнтинга с нор-
малью к поверхности провода. Построить график зависимости мо-
дуля вектора Пойнтинга в функции расстояния от оси провода
для трех областей: а) внутри провода; б) в теле провода; в) вне
провода.
22.9. Коаксиальный кабель с двухслойным ди электриком имеет
радиус внутренней жилы г0 = 5 мм, радиус поверхности раздела
двух диэлектриков ^ = 21,8 мм, внутренний радиус оболочки
Гз=40 мм. Относительные диэлектрические проницаемости внут-
реннего слоя диэлектрика ег1 = 5, внешнего слоя ег2 = 2. Кабель
находится под постоянным напряжением U = 100 кВ. Вдоль жилы
и оболочки кабеля протекает ток / = 100 А. Подсчитать потоки
вектора Пойнтинга через поперечное сечение каждо.т) из слоев
изоляции и найти мощность, передаваемую кабелем от источника
к приемнику.
22.10. Для кабеля, описанного в задаче 22.9, выбрать толщину
внешней оболочки А так, чтобы потоки вектора Пойнтинга через
боковые поверхности жилы и оболочки были равны. Подсчитать
потоки вектора Пойнтинга через боковые поверхности жилы и
оболочки на 1 м длины кабеля. Жила и оболочка кабеля выпол-
нены из меди (у = 57-10° См м). Вдоль жилы и оболочки протекает
постоянный ток /= 100 А.
22.11. Двухпроводная линия выполнена из медных проводов
радиусом г0=1 см. Расстояние между осями проводов d=200 см
(рис. 22.2, б). Линия находится под постоянным напряжением
LJ—100 кВ Вдоль проводов линии протекает постоянный ток
/ = 200 А.
Построить графики распределения модуля вектора Пойнтинга
в направлении осей х и г: а) П = (х) при —99 см < х < +99 см;
б) n = f2(z) при —со <г < + 00•
22.12. Две длинные параллельные шины служат прямым и
обратным проводами (рис. 22.2, в). Шины находятся под постоян-
ным напряжением U, вдоль них протекает ток /. Геометрические
размеры заданы, при этом 2a<^h; 2b<^h. 1. Пренебрегая поте-
рями в шинах, определить потоки вектора Пойнтинга через попе-
речное сечение диэлектрика, находящегося между шинами —
$SindS, и через квадратный контур klmn — JSandS. 2. Полагая
Удельную проводимость материала шин равной у, найти потоки
вектора Пойнтинга через боковую поверхность шины ПбЗ и
Через вертикальную плоскость MN—IIdS на единицу длины.
203
Глава двадцать третья
Переменное электромагнитное поле
в однородной и изотропной
проводящей среде
А. Установившиеся процессы при распространении
плоской электромагнитной волны в проводящем
полупространстве
23.1. Плоская электромагнитная волна проникает в толстую
металлическую плиту (у = 2-107 См.м; рг=1). Фазовый фронт
волны параллелен поверхности плиты. На глубине z = 1 мм мгно-
венное значение магнитной индукции Bt = 12,56 sin -4-30°) Тл.
Угловая частота w1 = 314 с"1. Записать выражение для мгновен-
ного значения плотности тока на глубине z2 = 5 мм, если угловая
частота станет равной о3 = 2826 с-1.
23.2. Плоская электромагнитная волна проникает из воздуха
в проводящую среду (у=1 См'м; рг=1). Фазовый фронт волны
параллелен поверхности проводящей среды. На расстоянии 10 см
от поверхности напряженность электрического поля меняется по
закону £1 = £CTsin(w^+30°) В/М. В момент времени / = 0 на глу-
бине z = 25 см Е2 =—10 В;м. Частота колебаний /= 107 Гц.
Записать выражения для мгновенных значений напряженности
магнитного поля на поверхности (Но) и на расстоянии Zj=10cm
от поверхности (Н^. Вычислить значения Но и Hi для = 0,5 • 10-т с.
23.3р . Плоская электромагнитная волна проникает из воздуха
в металлическую плиту (у —5-10е См/м; рг=1). Фазовый фронг
волны параллелен поверхности плиты. Частота колебаний f = 5 кГц.
Амплитуда плотности тока на поверхности 6m = 5-K2-10s А/м2.
Определить активную мощность Р, поглощаемую слоем металла
толщиной 0,5 см и площадью 1 м2. Найти эквивалентную глубину
проникновения электромагнитной волны h и ее длину А в металле.
23.4. Какую минимальную толщину А должен иметь медный
лист (у = 5,6-107 См/м), предназначенный для экранирования внеш-
него пространства от электромагнитного поля частотой f = 105 Гц,
если напряженность поля на внешней поверхности должна состав-
лять не более 5% от напряженности поля на внутренней поверх-
ности экрана? Электромагнитную волну считать плоской; отражен-
ной волной пренебречь.
Б. Поверхностный эффект в плоском теле
23.5р . Стальная пластина (у = 4 • 10е См м; рг —200) находится
в переменном магнитном поле, изменяющемся во времени по си-
нусоидальному закону с частотой f—500 Гц (рис. 23.1, о). Ее
поперечные размеры: 2а = 1 мм; й = 50мм. Напряженность маг-
нитного поля на поверхности пластины На — /20е^в* А/м. Найти
204
действующее значение магнитного потока, проходящего через по-
перечное сечение пластины. Построить график зависимости модуля
действующего значения плотности вихревых токов от координаты z.
Д 23.6. Магнитопровод трансформатора собран из листовой транс-
форматорной стали (у = 2- 10е См/м; рг = 500). Толщина листов
2^ = 0,5 мм. Для уменьшения потерь на вихревые токи был собран
другой магнитопровод из листов толщиной 2а = 0,2 мм.
Рис. 23.1
Во сколько раз уменьшились потери на вихревые токи при
той же средней индукции, если синусоидальный магнитный поток
меняется с частотой / = 2 кГц? Во сколько раз изменится при этом
отношение напряженности магнитного поля на поверхности пла-
стин к напряженности магнитного поля в средней плоскости
k — HjHJ
23.7. Для нагрева перед поверхностной закалкой в переменное
магнитное поле помещена стальная (у “5-10“ См'м; рг = ЗОО) по-
лоса размерами 2а = 4 мм; й = 5 см; I = 20 см (рис. 23.1.6). Удель-
ная теплоемкость ста пи с = 0,1 ккал/(кгград), ее удельная плот-
ность g = 7,9-103 кг/м3. Действующее значение напряженности
внешнего магнитного поля 5-103 А/м, частота колебания 1.5 кГц.
Вычислить толщину слоя металла А, в котором модуль плотности
вихревых токов 6Z составляет не менее 20% от модуля плотно-
сти вихревых токов на поверхности 6а. Найти модуль вектора
Пойнтинга на поверхности (Па) и па глубине, равной А (I1J.
Определить время, за которое поверхностный слой полученной
толщины нагреется от 20 до 720 °C. Теплоотдачей пренебречь.
Учесть, что при ра > 2 | sh pa |« sh ka\ th ра ~ 1. где pa=ka -f-
+ jka
23.8. Вдоль уединенной плоской медной (у ~ 5,6- 10т См/м)
Шины в направлении оси х протекает переменный ток i —
111 sin (6280/—8°) А (рис. 23.1, в). Размеры поперечного сече-
ния шины: 2а = 0,2 см; h = 4 см.
205
Найти значение и направление вектора Пойнтинга на поверх-
ности шины (Пс) и вычислить потери мощности в шине на 1 м ее
длины. Записать выражение для мгновенного значения магнит-
ного потока, пронизывающего контур ОАВСО. Определить актив-
ное сопротивление R и внутреннюю индуктивность £ви этой шины
на 1 м ее длины при протекании по ней синусоидальных токов
частотой h = 10э Гц и fa = 10ь Гц. Вычислить сопротивление шины
Rq на 1 м ее длины при постоянном токе.
У
о)
Рис. 23.2
23.9р . В открытом прямоугольном пазу ротора электрической
машины расположен медный (у = 5.6-10’ См/м) провод прямо-
угольного сечения (рис. 23.2, а). Размеры поперечного сечения
провода: Л = 2 мм; а = 20 мм. Вдоль провода в направлении оси х
протекает переменный ток, меняющийся во времени по закону
i = 28,2 sin (wi—30°) А. Частота f = 50 Гц.
Принимая относительно магнитную проницаемость стали ротора
цг=оо и полагая, что провод заполняет лаз полностью, построить
графики распределения действующих значений плотности тока и
напряженности магнитного поля по сечению провода. Определить
активное и внутреннее индуктивное сопротивления провода на 1 м
его длины. Вычислить сопротивление провода на 1 м его длины
при постоянном токе.
23.10. Две медные (у=5,6-107 См/м) плоские шины толщиной
2а — 2 мм и шириной й = 2 см расположены параллельно друг
другу на расстоянии 2Ь = 2 мм (рис. 23.2, б}. По обеим шинам
в направлении оси х протекают одинаковые переменные синусои-
дальные токи. В точках средней плоскости левой шины напря-
женность магнитного поля меняется по закону// = 670 sin (3140/+
+ 46°) А/м.
Построить график зависимости мгновенных значений плотно-
сти тока от координаты z для момента времени, при котором
плотность тока во всех точках внутренней поверхности левой ши-
ны обращается в нуль.
Указание. Сначала получить зависимости /7 —/i(z) и £=А(г) для
случая, когда по двум параллельным шинам протекают равные токи в одно»*
направлении.
206
23.11 - Две латунные шины (у = 3 • 107 См/м) толщиной 2а = 0,2 см
и шириной Л = 3 см расположены параллельно друг другу на
расстоянии 2Ь=0,3 см и служат прямым и обратным проводами
(рис. 23.2, б). Определить комплексное значение полного сопро-
тивления петли длиной 1 м при частоте 2 кГц. Какой ширины hx
вужно взять шины и на каком расстоянии 2bt друг от друга
следует их расположить, чтобы при частоте 5 кГц комплексное
значение полного сопротивления петли длиной 1 м оставалось
прежним? Учесть, что при 2ра>2 th2pa« 1.
В. Поверхностный эффект в цилиндрическом теле
23.12. Вдоль цилиндрического медного провода (у=5,6-107 См/м)
диаметром 2r0 = 1 см протекает синусоидальный ток частотой
f=l кГц. Действующее значение плотности тока на оси провода
64«= 105 А/м1.
Построить в масштабе графики распределения плотности тока
и напряженности магнитного поля в функции расстояния г от
оси провода. Вычислить действующее значение полного тока, про-
текающего через поперечное сечение провода.
23.13р . Вдоль цилиндрического уединенного стального про-
вода (у=2* 10* См/м; рг=100) протекает синусоидальный ток
частотой f = 50 Гц. Радиус провода гв = 5 мм.
Какой ток можно пропустить вдоль провода, если плотность
тока ни в одной точке сечения не должна превышать 10* А/м2?
Вычислить модуль вектора Пойнтинга на поверхности провода и
найти потери мощности на 1 м его длины.
23.14. Вдоль цилиндрического стального провода (у= 107 См/м;
|ir = 20) диаметром 0,5 см протекает синусоидальный ток / = 20 А.
Построить график плотности тока на оси провода от частоты
Для 0,1; 1,0; 10 кГц. Определить частоту, при которой плот-
ность тока на оси в любой момент времени противоположна
плотности тока на поверхности. Найти активное сопротивление
к внутреннюю индуктивность LBB провода при 0,1, 1,0, 10 кГц.
Сравнить их с сопротивлением Ro и индуктивностью Ц при по-
стоянном токе. Построить графики /?//?0 и £/£0 в функции частоты.
Частоту отложить в логарифмическом масштабе.
23.15. Вдоль цилиндрического уединенного медного провода
Радиусом ах = 0,5 см протекает переменный ток, f=0,5 кГц. Мед-
вей провод (у = 5,6* 107 См/м) необходимо заменить стальным
(Т= 107 См/м) так, чтобы при указанной частоте активное сопро-
тивление стального провода было равно активному сопротивлению
Одного провода. Найти радиус стального провода Вычислить
^противления обоих проводов на единицу длины провода при:
а) /=0; б) f = 500 Гц.
Указание. Считать, что входящие в выражение для активного сопро-
стального провода функции Бесселя нулевого и первого порядков
Рвого рода приближенно равны.
207
23.16р . С целью индукционного нагрева длинный ферромаг-
нитный цилиндр (у= 10’ См/м; рг= 10) помещен в переменное маг-
нитное поле, направленное вдоль его оси. Радиус цилиндра а=1см.
Частота переменного поля f = 1 кГц. Действующее значение маг-
нитного потока, проходящего через поперечное сечение цилиндра,
Ф = 3,14-10“» Вб.
Построить график распределения магнитной индукции по сече-
нию цилиндра B = f(r). Вычислить относительную комплексную
магнитную проницаемость.
23.17. Для ферромагнитного цилиндра, описанного в задаче
23.16р, построить график распределения плотности вихревых токов
по сечению цилиндра б = /(г). Определить толщину слоя металла
А, на котором плотность тока уменьшается в е раз, и сравнить
ее с глубиной проникновения h плоской электромагнитной волны
в металл. Найти разность потенциалов между точками т и п,
находящимися на поверхности цилиндра (рис. 23v2, в).
23.18. Длинный ферромагнитный цилиндр (у = 0,5-10’ См/м;
Рг-50) расположен внутри индуктора. Индуктором является
длинная прямая катушка, выполненная из медной трубки, с чис-
лом витков на единицу длины му/=100 витков/м. Действующее
значение тока, протекающего вдоль катушки, I = 50 А; его частота
/ = 0,8 кГц. Радиус ферромагнитного цилиндра г0 = 8мм.
Построить график зависимости модуля вектора Пойнтинга
в функции расстояния г от оси цилиндра. Подсчитать активные
потери на вихревые токи в цилиндре на 1 м его длины.
Г. Переходные процессы при распространении
плоской электромагнитной волны в проводящей среде
23.19р . В результате включения внешнего постоянного во вре-
мени магнитного поля возникает плоская электромагнитная волна,
которая распространяется в проводящем полупространстве Фронт
волны параллелен поверхности проводящей среды. Волна распро-
страняется в направлении оси z прямоугольной системы коорди-
нат. Удельная проводимость среды у, абсолютная магнитная
проницаемость цо, напряженность магнитного поля на поверхно-
сти проводящей среды Но.
Найти законы изменения напряженностей магнитного и элек-
трического полей как функции координат и времени, если внеш-
нее поле включается в момент времени t — 0 при нулевых началь-
ных условиях.
23.20. Рассмотреть процесс установления постоянного магнит-
ного поля (см. рис. 23-1, а), создаваемого внешним источником
в бесконечно длинной проводящей полосе, ширина которой на-
много больше толщины (й^>2а). Удельная проводимость мате-
риала у, абсолютная магнитная проницаемость рв. Внешнее маг-
нитное поле включается в момент времени / = 0. До включения
магнитного поля полоса не была намагничена. Напряженность
магнитного поля на поверхности проводящей полосы На. Найти
208
законы изменения напряженности магнитного и электрического
полей как функции координат и времени.
23.21р . Плоскую медную (у = 5,7-107 См/м; pfl = Po) шину
подключают к источнику постоянного тока / = 0,1А. Ширина
шины ft = 5 см, толщина 2а = 2 мм. Найти законы изменения во
времени напряженности магнитного поля и построить графики
Н=/(/) для точек поперечного сечения шины с координатами
2 = 0; z = 0,5a, г — 0,75а, г = а.
Глава двадцать четвертая
Переменное электромагнитное поле в диэлектрике
и полу проводя щей среде
А. Распространение плоской электромагнитной волны
в однородных и изотропных диэлектрике
и полупроводящей среде
24.1. Плоская электромагнитная волна распространяется в
воздухе в направлении оси 2. Комплексная амплитуда вектора напря-
женности магнитного поля HM = j-10"2 А/м. Определить действую-
щее значение напряжения между концами А и В прямолинейного
стержня длиной /—1м, расположенного в плоскости: а) хОу
(рис. 24.1, а); б) уОг.
24.2. Плоская электромагнитная волна распространяется в
воздухе по направлению оси z. В момент времени / = 0в точке а
напряженность магнитного поля —HCT£in30° = 2А/м. Длина
волны X == 4000 м. Определить мгновенные значения напряженностей
электрического и магнитного полей в точках а и b через tx = 10“ ? с.
Точка b находится на линии движения волны позади точки а на
2 км
24.3. Плоская электромагнитная волна проникает из воздуха
в минеральное масло (8, = 2,25). Фазовый фронт волны паралле-
лен поверхности масла. Длина волны в воздухе А = 1м. Найти
значение модуля вектора Пойнтинга в точке, находящейся на
глубине 33,3см, в момент, когда напряженность магнитного поля
209
на поверхности проходит через положительный максимум и рав-
на 5-10_*А/м. Определить частоту изменения вектора Пойнтинга
во времени.
24.4. Плоская электромагнитная волна проникает из воздуха
в полупроводящую среду. Удельная проводимость среды у =
= 3-10“*См/м, относительная диэлектрическая проницаемость
ег = 3, относительная магнитная проницаемость pr = 1. Фазовый
фронт волны параллелен поверхности среды. Напряженность
электрического поля на поверхности меняется по закону £0 =
= 100 sin (3-104 4-60°) В/м. Записать выражение для мгновенного
значения напряженности магнитного поля Нх (/) в точках, находя-
щихся на расстоянии 0,5 м от поверхности в полупроводящей среде.
24.5р . Плоская электромагнитная волна проникает из воздуха
в морскую воду (у= 1См/м; er = 80; pr= 1). Фазовый фронт волны
параллелен поверхности
Таблица 24.1
А МГц V. См/м
400 53 1.14
1000 50,5 1,3
8500 41 8,83
моря. Определить мгновенное значение
вектора Пойнтинга на поверхности, если
плотность тока проводимости на глуби-
не ?!=10см меняется по закону —
= 10 sin (104 —30°) А/м.
24.6. С целью исследования теплово-
го действия ЭМП диапазона СВЧ на ор-
ганизм человека рассчитать зависимость
удельных тепловых потерь в функции
частоты p = f(f) в слое мышечной ткани
толщиной 1 см, полагая электромагнитную волну плоской и напря-
женность электрического поля на поверхности слоя £0 = 1 В/м.
Построить график p = f(f). Зависимости = и y = ft(f) для
мышечной ткани приведены в табл. 24.1.
Б. Переход плоской электромагнитной волны
из одной среды в другую
24.7р . Плоская линейно поляризованная волна падает из воз-
духа на плоскую поверхность стекла подуглом <р=63°25' (рис. 24.1, б)
и полностью проходит в стекло. Напряженность электрического
поля в воздухе £== 10 мВ/м. Считая стекло идеальным диэлект-
риком, имеющим неограниченную толщину, вычислить среднее за
период значение вектора Пойнтинга в нем. Определить среднее
за период значение П в этом же стекле, если напряженность поля
падающей волны и угол падения останутся прежними, а плоскость
поляризации будет повернута на 90°. Найти волновые векторы
падающей и прошедшей волн (К + и К и), если ш=6' 108 с'1.
Указание. Волновым вектором называют вектор, совпадающий по на-
правлению с вектором Пойнтинга и равный коэффициенту распространения
для данной среды.
24.8. Электромагнитная волна переходит из одного диэлект-
рика (ег1 = 2) в другой (ег1 = 8) через плоскую границу. Плоскость
210
поляризации волны составляет угол 30° с плоскостью падения.
Напряженность электрического поля падающей волны на поверх-
ности раздела сред £+ (0) = 5e/lsC В/м, а угол падения ср = 30°.
Определить модули векторов напряженности электрического и
магнитного полей отраженной и прошедшей волн на той же по-
верхности: Ё~ (0). Й~ (0), £п (0), £п(0). Найти угол падения <plt
при котором отраженная волна не содержит параллельно поля-
ризованной компоненты.
24.9. Плоская электромагнитная волна проникает из воздуха
(гг17- 1) в трансформаторное масло (ег2 = 2.25). в котором распо-
ложена квадратная рамка со стороной d ~ 1 см и числом витков
1 (рис. 24.1,в). Плоскость рамки совпадает с плоскостью
поляризации прошедшей волны. Угол преломления 6 = 23° 10'.
Действующее значение напряжения на зажимах рамки U2= 10 мкВ.
частота f — 10 ГГц. Определить действующее значение напряжения
на зажимах рамки Ut, если она повернута относительно стороны
а и расположена в воздухе так, что ее плоскость совпадает с
плоскостью поляризации падающей волны. Построить фазовые
фронты падающей, отраженной и прошедшей волн.
24.10. С целью исследования электрических свойств стекло-
пластика в диапазоне миллиметровых волн опытным путем най-
ден коэффициент отражения для плоской волны, падающей
на его поверхность из воздуха. При угле падения <р = 45е R±=—0,4.
Считая стеклопластик идеальным диэлектриком, определить его
диэлектрическую проницаемость ег.
24.11р . Электромагнитная волна падает на плоскую границу
раздела двух диэлектриков (рис. 24.1,6). Мгновенное значение
напряженности электрического поля падающей волны при 2 = 0
£+(0,/) = /5-10~asin2nl09/B/M. Угол падения <р = 53°10'. Ди-
электрические проницаемости сред ег1= 4.5, ег, = 2. Записать
выражение для мгновенного значения напряженности поля неод-
нородной поверхностной волны £n (х, г, /). Вычислить фазовую
скорость поверхностной волны ифп и сравнить ее с фазовыми ско-
ростями в первой и во второй средах и иф,. Определить кри-
тический угол полного внутреннего отражения <ркр.
24.12. Диэлектрическая проницаемость стекловолокна сердеч-
ника световода eri — 2,56, а его оболочки ег2=2,25. Определить
критический угол полного внутреннего отражения <ркр. Построить
график зависимости глубины проникновения h неоднородной по-
верхностью волны в оболочку в функции угла падения <р, если
<р меняется от <рхр до 90°. Расчет выполнить для красного свето-
вого луча, приняв его длину волны в вакууме 2^ = О,65мкм.
Вычислить минимальную толщину оболочки Дщ1п> полагая Amin =
Указание. Глубину проникновения h приближенно рассчитать так же.
как для случая падения плоской волны на плоскую поверхность раздела сред:
Л-1/сс.
211
24.13. Плоская электромагнитная волна распространяется
вертикально и проникает из воздуха в дистиллированную воду.
На глубине 10 см мгновенное значение напряженности электро-
магнитного поля Еа(0 = 2-10'esin3-104В/М.
Считая воду диэлектриком (ег = 81), определить мгновенные
значения напряженностей электрического Ег(1) и магнитного //х (/)
полей на высоте 10 см над
поверхностью воды.
24.14. Плоская электро-
магнитная волна распростра-
няется нормально к плоской
границе раздела двух несо-
вершенных диэлектриков
(рис. 24.2, а). Комплексная
амплитуда напряженности
электрического поля на гра-
нице сред Effl(0) = 2 мВ/м,
угловая частота © — 3 • 1 О’ с “1.
Комплексные диэлектрические проницаемости сред на указанной
частоте ёг1 = 2—/0,2; ёгг = 4—/2. Найти комплексные амплитуды
напряженности электрического поля и волновые векторы падаю-
щей, отраженной и прошедшей волн. Вычислить комплексные
показатели преломления (/ij и п2) и фазовые скорости (иф1 и оф2)
для каждой среды.
24.15. Рассчитать используемые в медицине для целей диаг-
ностики коэффициенты отражения R и преломления Т на границе
биологических тканей. Определить R и Т при нормальном паде-
нии плоской волны на поверхность раздела кожи (среда /) и
мышечной ткани (среда //) при частоте/=1 ГГц. Для указанных
сред на заданной частотеег1—45; ега=50; Yt=0f95 См/м;уг— 1 ,ЗСм/м.
В. Расчет электромагнитного поля в слоистых средах
методом направленных графов
24.16р . Плоская электромагнитная волна падает нормально на
поверхность раздела двух сред (рис. 24.2, а), комплексные диэлект-
рические проницаемости которых ём=2—/0,2; ег2 = 4—/2. Соста-
вить направленные графы, предназначенные для расчета напря-
женностей электрического поля отраженной Е~ и прошедшей Е"
волн по заданной напряженности поля падающем волны Ё+, если
волна переходит: а) из среды / в среду //;б) из среды П вере-
ду /. Найти передачи ветвей графов.
24.17р . Плоская электромагнитная волна (рис. 24.2,6) падает
нормально на пластину идеального диэлектрика ег2, окруженную
воздухом (erl = er3= 1). Пользуясь методом направленных графов,
определить коэффициент радиопрозрачности Т и коэффициент
отражения пластины R.
212
Указание. Под коэффициентом радиопрозрачности Т понимают отноше-
ние напряженности поля прошедшей через пластину волны к напряженности
поля падающей волны: Т = Еп!Е*. Под коэффициентом отражения понимают
отношение напряженности поля отраженной от пластины волны к напряжен-
ности падающей волны: /? = Ё“/Ё+.
24.18. Электромагнитная волна проникает из воздуха (ег1=1)
в сосуд с водой (рис. 24.2,6). Стенки сосуда плоские и выпол-
нены из диэлектрика (ег2). Диэлектрическая проницаемость воды
е/Э = 81. Длина волны в воздухе Х=12мм. Определить диэлект-
рическую проницаемость ьг2 и
минимальную толщину стенки
d, при которых отражение от-
сутствует и волна полност ью
проходит в воду. Считать, что
потерями в стенках со-
суда и воде пренебречь.
24.19. Составить направлен-
ные графы для расчета коэффи-
циентов прохождения и отраже-
ния плоской волны при нормальном падении на плоские идеаль-
ные диэлектрики: а) двухслойный (рис. 24.3,а); б) трехслойный
(рис. 24.3.6). Определить передачи ветвей графов, считая угловую
частоту, диэлектрические проницаемости и толщины слоев ди-
электриков заданными.
24.20. Воспользовавшись графом задачи 24.16р [случай а)],
рассчитать напряженность электрического поля прошедшей волны
Еп, если напряженность поля падающей волны Е+ в передачи
ветвей графа известны.
Г. Квазистатическое электрическое поле в вязкой среде
и несовершенном диэлектрике
24.21. Плоский конденсатор, заполненный вязким диэлектри-
ком, включен под напряжение и = 100P<2sin25- 103f В. Расстоя-
ние между пластинами </ = 2,5см. Статический коэффициент поля-
ризуемости диэлектрика а = 5, постоянная времени поляризации
т0=-4-10-6 с. Определить относительную комплексную диэлектри-
ческую проницаемость вязкого диэлектрика ег, ее вещественную
(t'r) и мнимую (е;) части на заданной частоте, при <о = 0 и со=оо.
Построить графики зависимостей от частоты е,‘г и е'Д Вычислить
Удельные активные потери мощности.
Указание. Под статическим коэффициентом поляризуемости понимают
коэффициент поляризуемости диэлектрика в электростатическом поле.
24.22. Цилиндрический конденсатор заполнен вязким днаэлект-
риком, статический коэффициент поляризуемости которого а = 5,
а постоянная времени поляризации т0 = 4 • 10~3 с. Радиус внутрен-
него цилиндра конденсатора а = 5см, внутренний радиус внеш-
него цилиндра 6= 15см, длина конденсатора / = 20см. Конден-
213
сатор подключен к источнику синусоидального напряжения
u = 200 /2sin250f В.
Найти комплексы модулей векторов напряженности электри-
ческого поля, смещения и поляризации у поверхности внутреннего
электрода на заданной частоте и при ш = 0 (£/ = 200 В). Для
частоты со = 250 с'1 построить векторную диаграмму, на которую
нанести D, ес£, Р.
24.23. Двухпроводная линия расположена в воздухе на рас-
стоянии h= 100 см от стены. Расстояние между проводами d=200 см
(рис. 21.4, а). Материалом стены
является диэлектрик с потеря-
ми. Радиусы проводов линии
го = О,4 см. Свойства сред ха-
рактеризуются следующими ве-
личинами: У! = 0; erf=l; уа=
= 2-10_в См/м; ег2 = 2.
Линия находится под нап-
ряжением и = 100 K2sin 1,13 х
X Ю3£В. Определить комплекс-
ную проводимость утечки Уо, активную проводимость Ge и емкость
Со на 1м длины линии. Вычислить плотность полного тока утечки
в точке а (6в).
24.24. Плоский конденсатор заполнен несовершенным диэлект-
риком с удельной проводимостью у= 10“7 См/м и относительной
диэлектрической проницаемостью е, = 5 (рис. 24.4,6). Расстояние
между пластинами d = 2 мм, площадь пластин S= 100 см2. Конден-
сатор подключают через резистор Р = ЗМОмк источнику постоян-
ного напряжения £/0 = ЗкВ. Найти законы изменения во времени
напряженности электрического поля, плотности тока проводимости,
плотности тока смещения, плотности свободных зарядов на плас-
тинах конденсатора и связанных зарядов у пластин в диэлектрике.
Задачу решить классическим методом.
24.25р . Шар из несовершенного диэлектрика, свойства которого
определяются у,- и еО|-, расположен в реальной среде, характери-
зующейся уе и ede (рис. 24.5, а). Радиус шара а. В момент вре-
214
меня f==0 при нулевых начальных условиях включается внешнее
поле с постоянной напряженностью £0. При отсутствии шара
рнешнее поле равномерно. Найти законы изменения потенциалов
внутри и вне шара как функции координат и времени.
24.26. В несовершенном диэлектрике, характеризующемся у,
я еге, оказалось длинное цилиндрическое воздушное включение
(у^—О; ег/=1) радиусом а (рис. 24.5,6). В момент времени /=0
при нулевых начальных условиях включается постоянное внеш-
нее поле, равномерное при отсутствии воздушного включения.
Напряженность поля Ео. Найти законы изменения потенциалов
я плотностей тока проводимости внутри и вне цилиндрического
включения как функции координат и времени.
Глава двадцать пятая
Запаздывающие потенциалы
переменного электромагнитного поля
и излучение электромагнитной энергии
А. Запаздывающие электродинамические потенциалы
25.1. Линейная плотность заряда бесконечно длинной оси,
расположенной в воздухе, меняется по закону т==10‘*х
X sin (3- 104 4-60°) Кл/м. Записать выражение для мгновенного
значения скалярного потенциала <р(/) для точек, находящихся
на расстоянии г> = 82,8 м от заряженной оси, полагая, что при
гв=20м <р = 0.
Рис. 25. t
25.2. Линейная плотность заряда бесконечно длинной заря-
’кенной оси, расположенной в вакууме, меняется во времени по
закону т=тв(1-ьМ). Найти выражения для скалярного ф и век-
торного А электродинамических потенциалов как функций коор-
динат точки и времени. Считать, что А = 0; (р-0 при г = г0.
25.3р . Вдоль отрезка тонкого прямого провода длиной dZ,
Расположенного в воздухе, протекает синусоидальный ток
(Рис. 25.1, а), комплексная амплитуда которого 1№) а длина вол-
215
ны К. Записать выражения для комплексных амплитуд векторного
Ат и скалярного tpm потенциалов для точки а, координаты ко-
торой £с, 6О, аа.
25.4. Вдоль отрезка провода длиной dl = 0,15 м, расположен-
ного в диэлектрике (ег=4), протекает ток i = 10 4- 5- 108z А.
На расстоянии й = 0,15м от него расположен точечный заряд
д=Ю_*Кл (рис. 25.1,6). Найти законы изменения во времени
векторного потенциала А (/) и напряженности поля £ (0 для то-
чек k и т,
Б- Излучение электромагнитной энергии
25.5. Вдоль отрезка тонкого прямоугольного провода длиной
dl = 1 м, расположенного в воздухе, протекает ток t = 15 • sin 2л • 10еА
(рис. 25.1, о). Определить амплитуды напряженностей магнитного
и электрического полей в точках а и Ь. Координаты точек а к Ь:
Яв = 30м; 6e = 30°; аа = 0; /?ь = 30км; 0ь = 30°, аь = 90°. Вычис-
лить комплексную амплитуду векторного потенциала в точке b и
время запаздывания tb.
25.6. Вдоль отрезка провода длиной Л/=10см протекает си-
нусоидальный ток частотой / = 3-10’Гц (рис. 25.1,а). Известно,
что в точке о, сферические координаты которой /?а = 100 м; 6а=903;
ota = 30°, вектор Пойнтинга меняется по закону Па = 510-ах-
X cos2 (со/—30с)Вт/м2. Написать выражение /(о/) для тока в из-
лучающем проводе. Построить полярные диаграммы напряженности
электрического поля £ (0) для точек, находящихся на расстоянии
Rt — 100 м и R2 — 1 м от него.
25.7р . Антенна, расположенная в воздухе и излучающая энер-
гию при частоте /,= 1 МГц, имеет действующую высоту — 20 м.
1. Какой ток нужно пропустить через антенну, чтобы излучаемая
ею мощность была равна Р = 4,4 кВт? 2. Какой высоты следует
взять антенну, чтобы при частоте (2==10МГц и при том же токе
антенной излучалась та же мощность?
25.8. Магнитный излучатель (рис. 25.1, в) представляет собой
круглый экранированный виток радиусом г0=1см, расположен-
ный в воздухе. Вдоль витка протекает синусоидальный ток
«
I = 0,1 X sin (6л • 109Z 4- 60°) А. Определить Ет и Нт для точки я,
сферические координаты которой Ra = 5,55 м; 0а = 30°; 0^ = 90°-
Построить диаграммы направленности магнитного излучателя в
полярной и экваториальной плоскостях для точек, находящихся
на расстоянии R = 5,55 м от него.
25.9. Вдоль круглой рамки радиусом г = 0,1 м, расположенной
в воздухе, протекает синусоидальный ток с частотой f— 10т Гц
(рис. 25.1, в). В точке о, координаты которой 7?а=100м; 0в=ЗО°;
аа = 60°, Ета = 2,06 • 10“4e_/'llfie В/м. Определить мгновенное зна-
чение вектора Пойнтинга П (соГ) в этой точке и полную мощность
излучения Ps,
216
Глава двадцать шестая
Электромагнитные волны
в направляющих системах
А. Электромагнитное поле в волноводах
26.1р . В прямоугольном волноводе (рис. 26.1, а) сечением
ах /> — 8,64x4,32 см требуется возбудить волну типа Н10. Как
для этой цели следует расположить электрический (штырь) и как—-
магнитный (петлю)
ХкР10> длину волны
излучатели? Найти критическую длину волны
в свободном пространстве Л и длину волны в
волноводе при частоте генератора / — 3-10® Гц. Может ли рас-
пространяться в данном волноводе волна типа Н10? Определить
мощность, передаваемую ею вдоль волновода, если максимальная
напряженность магнитного поля Нт = 30 А/м. Вычислить фазовую
и групповую скорости и расстояние, на которое переместится
энергия вдоль оси z за один период колебания.
26.2. Прямоугольный волновод имеет ширину сечения а = 1,07 см
и высоту /> = 0,43 см. Определить типы поперечных электрических
волн, которые могут распространяться вдоль этого волновода,
если частота питающего генератора / = 20- 10е Гц.
26.3. Вдоль прямоугольного волновода (рис. 26.1. а) сечением
8.64x4,32 см распространяется электромагнитная волна типа Н10.
Диэлектриком волновода является воздух. Частота питающего
генератора / = 3-109Гц. Максимальная напряженность магнитного
поля в волноводе Нт = 25 А, м. Рассчитать мгновенные значения
составляющих напряженностей электрического и магнитного полей,
а также плотности тока смещения в диэлектрике.
26.4. В стенках волновода, вдоль которого распространяется
полна //10, сделаны шесть щелей (рис. 26.1,6). Указать, какие
Щели являются непзлучающнми (НИ) и какие—излучающими (И).
26.5. На рис. 26.1,е изображена структура электромагнитного
п°ля для волны, распространяющейся в прямоугольном волноводе
Учением 4,04x2,02 см. Определить тип волны и ее критическую
217
26.6* . В прямоугольном волноводе сечением 4,75x2,2 см воз-
буждается поперечная магнитная волна Еп. Частота питающего
генератора 7=1010Гц. Амплитудное значение продольной состав-
ляющей напряженности электрического поля в центре сечения
волновода Естг = 5-10* В/м. Определить амплитуды составляющих
напряженностей электрического н магнитного полей: Етх, Е
НтХ1 Нтуу Hmz. Найти мощность, переносимую в волноводе вол-
ной Еп.
26.7. В прямоугольном волноводе сечением 4,75x2,2 см воз-
буждается поперечная магнитная волна типа Еи. Частота питаю-
щего генератора /—1010Гц. Амплитуда продольной составляющей
напряженности электрического поля в центре сечения волновода
Emz = 5 -10* В/м. Стенки волновода покрыты серебром, удельная
проводимость которого у = 6,6-10’См/м. Диэлектриком волновода
является воздух. Определить потери мощности в стенках волно-
вода на 1 м длины и вычислить коэффициент характеристического
затухания а. Как следует расположить электрический (штырь) и
как—магнитный (петлю) излучатели для возбуждения волны ука-
занного типа?
Б. Электромагнитное поле в объемных резонаторах
26.8. Объемный резонатор (рис. 26.2, а) имеет форму куба с
ребром 6 см. В резонаторе возбуждается электромагнитная волна
типа ЯМ1. Максимальная амплитуда напряженности электричес-
Рис. 26.2
кого поля Е„,ах = 2-10* В/м. Диэлектриком резонатора является
воздух. Найти резонансную частоту, резонансную длину волны
и максимальную мощность электромагнитного поля.
26.9. Определить, на каком наименьшем расстоянии d следует
расположить поперечные металлические диафрагмы в прямоуголь-
ном волноводе шириной с=13см и высотой Ь = 6,4см, чтобы
превратить его в объемный резонатор, настроенный на частоту
/ = 3.10е Гц для возбуждения электромагнитной волны типа Ец1*
♦ В задачах 26.1—26.6, 26.8, 26.9 считать стенки волноводов и объемна*
резонаторов выполненными из сверхпроводящего материала.
218
26.10. На рис. 26.2,6 приведены графики изменения состав-
ляющих векторов Е и И в функции координат х, у, г для пря-
моугольного резонатора, размеры которого а = 20 см; 6 = 8 см;
^^10 см. Диэлектриком резонатора является воздух. Максималь-
ная амплитуда напряженности электрического поля Етй* = 10* В/м.
Определить тип волны, возбуждаемой в резонаторе. Вычислить
потери мощности в его стенках если добротность резонатора
(?= 10*.
Глава двадцать седьмая
Движение заряженных частиц в электрическом
и магнитном полях
А. Движение заряженных частиц в электрическом поле
27.1. В однородное электрическое поле плоского конденсатора
влетает электрон, скорость которого и0 направлена вдоль оси у
(рис. 27.1). Найти наибольшее напряжение на конденсаторе, при
Рис. 27.1
Рис. 27.2
котором электрон еще пролетит через пространство между плас-
тинами. Расстояние между пластинами d, ширина пластин I. Эф-
фектом искажения поля у кран конденсатора пренебречь.
27.2р . На пути летящей прямолинейно вдоль оси х со ско-
ростью Ц) частицы с зарядом q и массой т находится потенци-
альный барьер, выполненный в виде трех плоских сеток, распо-
ложенных перпендикулярно движению (рис. 27.2). Боковые сетки
заземлены, а на среднюю подан положительный потенциал (pt.
Сумеет ли преодолеть потенциальный барьер, т. е. пролетит ли
насквозь: а) отрицательно заряженная частица (q < 0); б) поло-
жительно заряженная частица (<7>0)? Зависят ли скорость час-
т»п на выходе системы и время их пролета от знака заряда?
27.3. В центре сферического двойного слоя толщиной
помещен источник, испускающий заряженные частицы в радиаль-
ном направлении (рис. 27.3). На внутренней поверхности двойного
219
слоя существует отрицательный заряд с поверхностной плотное-
тью —о, на внешней 4-сг.
Считая обе поверхности слоя проницаемыми для частиц, опре-
делить: а) условие отражения от двойного слоя частицы с заря-
дом 4- q и массой ш, движущейся от центра в радиальном на-
правлении со скоростью uf, б) характер движения частицы, если
условие отражения выполняется; в) скорость движения положи-
тельно заряженной частицы после пролета двойного слоя, если
условие отражения не выполняется.
27.4. Источник задачи 27.3 помещен эксцентрично и испуска-
ет отрицательно заряженные частицы (?<0) массой т, движу-
щиеся со скоростью вдоль оси х (рис. 27.4). Определить ско-
рость и угловое отклонение частицы от первоначальной траектории
после ее пролета через двойной слой, полагая
27.5. Покажите, что изменение кинетической энергии частицы
массой т и зарядом glt движущейся со скоростью и про-
шедшей в электростатическом поле путь между точками 1 и 2,
определяется разностью потенциала между этими точками. Чему
пропорциональна скорость отрицательно заряженной частицы,
начавшей движение из состояния покоя в точке поля, где потен-
циал равен нулю?
27.6. Считая, что скорость отрицательно заряженной частицы
определяется значением потенциала в данной точке (см. зада-
чу 27.5), найти угловое отклонение частицы при прохождении
через проницаемую границу двух эквипотенциальных областей
(рис. 27.5). Такие области можно создать, если на обе стороны
граничной поверхности нанести весьма тонкий двойной слой за-
рядов.
27.7. Определить приближенно траекторию электронов, дви-
жущихся в поле двух коаксиальных цилиндров. До входа в об-
ласть, занятую полем, электроны двигались в плоскости, прохо-
дящей через ось цилиндров, прямолинейно и параллельно осп-
Картина эквипотенциален в плоскости движения показана на
рис. 27.6.
220
Указание. При построении траекторий заменить распределение потен-
циалов ступенчатой функцией и использовать закон преломления, полученный
и предыдущей задаче.
27,8р . Потенциал поля вдоль оси х, созданный двумя парами
противоположно заряженных тонких осей (рис. 27.7), меняется
по закону ф = пх3. Как будет двигаться частица с зарядом + Q
И массой т, имеющая в начале координат скорость vOf направ-
ленную вдоль оси х, если полная энергия частицы №=ти%2<
< (Ь)? Устойчиво ли движение частицы вдоль оси х?
27.9р . Частица зарядом q2 и массой т движется со скоростью
v<gc в поле неподвижного точечного заряда qt. Определить ха-
рактер движения частицы для случаев, когда: а) заряды и q2
имеют разные знаки; б) заряды qt и q2 одного знака.
Б. Движение заряженных частиц в магнитном
и скрещенных полях
27.10. Определить соотношение между кулоновскими и магнит-
ными (электродинамическими) силами для двух точечных зарядов
.ft и qt, движущихся прямолинейно и параллельно друг другу
с одинаковой скоростью и<^с. Расстояние между зарядами г.
Как направлены эти силы, если qt = q2?
27.11р . Источник заряженных частиц создает пучок, в котором
все частицы зарядом q и массой т имеют одно и то же на прав-
ление скорости—вдоль оси х (рис. 27.8). При движении частицы
попадают в зазор постоянного магнита, в котором создано одно-
•->
,родное магнитное поле с индукцией В, направленное перпендику-
лярно движению частиц за плоскость чертежа—«магнитная стен-
ка». 1. При каких наибольших скоростях заряженные частицы
еще отражаются от «магнитной стенки»? 2. Зависит ли условие
отражения от знака заряда? 3. На какой угол отклонится траек-
тория заряженных частиц, движущихся со скоростями и=10итах1
после пролета «магнитной стенки»?
27.12 р. В однородном магнитном поле с индукцией В в точке
О помещен источник, испускающий одинаковые частицы зарядом q
221
и массой т. Источник испускает частицы под углом а к направ-
лению силовых линий (рис. 27.9). 1. Определить траекторию дви-
жения частиц. 2. Показать, что при малых углах а магнитное
поле обладает фокусирующим действием. 3. Будет ли движение
частиц при а = 0 устойчивым?
27.13. По данным задачи 27.12р определить магнитный момент,
создаваемый движущимися заряженными частицами. Зависят ли
значение и направление магнитного момента от знака заряда?
X X 7 X
Xfl X X
X X X X X
X X х X х
X X X х X
5
Рис. 27.8 Рис. 27.9 Рис. 27.10
27.14. По обе стороны плоской границы созданы различные
однородные магнитные поля В^ и В2, силовые линии которых
направлены за плоскость чертежа (рис. 27.10). Найти траекторию
движения частицы зарядом +- q и массой т, испускаемой источ-
ником в точке О, если начальная скорость частицы г0 направлена
перпендикулярно силовым линия и и граничной плоскости. Задачу
решить для: а) Bi — 2Bl’, б) B2=1,25Bj. Зависит ли направление
средней скорости вдоль оси х (скорости дрейфа) от знака заряда?
Рис. 27.11
27.15. Частица зарядом q и массой т движется в однородных
электрическом (Е) и магнитном (В) полях, имеющих одинаковое
направление (рис. 27.11,о) 1. Качественно описать движение по-
ложительно заряженной частицы, если ее начальная скорость
в точке О направлена под острым углом а к силовым линиям.
2. Изменится ли характер движения частицы, если поля В и £
антнпараллельны (рис. 27.11,6)?
222
27.16р . Для определения массы т заряженных частиц исполь-
зуется трохотрон (один из типов масс-спектрометров), названный
так потому, что частицы в нем под действием взаимно перпенди-
кулярных однородных электрического (£) и магнитного (В) полей
движутся по трохоидальным траекториям.
Показать, что пучок частиц с одинаковым отношением q/m при
любых значениях начальной скорости и, вектор которой лежи г
в плоскости уОг (рис. 27.12), под действием скрещенных полей
£ и В вновь пересечет ось у в точке Ог. Найти зависимость фо-
кусного расстояния I от Е, В и q/m. Зависит ли фокусирующее
действие скрещенных полей Е и В от знака заряда?
27.17. Частица зарядом q движется равномерно и прямоли-
нейно со скоростью и<|с в скрещенных электрическом (£) и
магнитном (В) полях. Какие поля (Е' и В') обнаружит наблюда-
тель, движущийся вместе с частицей?
27.18р . В некоторой области пространства (рис. 27.13) создано
аксиально-симметричное нарастающее во времени магнитное поле
5(1)» которое индуцирует вихревое электрическое поле £(/).
Считая, что в момент начала возбуждения поля электрон в точке А
находился в состоянии покоя, найти условие его движения по
круговой орбите со скоростью v<^,c.
Глава двадцать восьмая
Основы магнитной гидродинамики.
Сверхпроводимость
А. Уравнениия магнитной гидродинамики,
равновесные конфигурации, волны, течения
28.1р . При высокой проводимости (у=оо) скорость движения
всей плазмы в скрещенных магнитном и электрическом поляк
совпадает со скоростью дрейфа заряженных частиц—электронов
и ионов. Найти значение и направление составляющей скорости
дрейфа vlt перпендикулярной линиям В. Показать, что направле-
ние Uj совпадает с [ЕВ]. Оценить значение v при В= 1 Тл; Е =
= 1 В/м.
28.2. Показать, что движение плазмы с высокой проводимостью
(у = со) в магнитном поле физически можно объяснить дви жением
вместе с ней магнитных силовых линий, т. е. эффектом «вморо-
женного» в плазму поля. Используя закон электромагнитной ин-
дукции в дифференциальной форме и условие идеальной проводи-
мое] и (у=оо), получить уравнение движения такой плазмы с
«Вмороженным» в нее полем.
28.3р . Показать, что уравнение, описывающее движение иде-
223
ального (у=оо) жидкого проводника с «вмороженным» полем
(см. задачу 28.2), с учетом уравнения непрерывности для сжимае*
d Гв \ / в .-Л
мои жидкости эквивалентно уравнению = где
= + l 1 — материальная (полная) производная, выражаю-
щая изменение В/p выбранного движущегося элемента прово-
дящей жидкости.
Рис. 28.1
плазмы высокой
28.4. Используя результаты решения задачи 28.3р, найти зави-
симости магнитной индукции В и магнитного давления в
функции плотности р жидкой идеаль-
ной проводящей среды (плазмы с
у = оо), если: а) плоский слой плазмы
сжимается поперек магнитного поля;
б) плоский слой плазмы сжимается
вдоль силовых магнитных линий;
в) плазма сжимается изотропно (сфе-
рическое сжатие).
28.5. Приближенно оценить время
проникновения (диффузию) магнит-
ного поля в неподвижный (о = 0)
но конечной (уг/=оо) проводимости
(рис. 28.1,а), если: а) сгусток сферический радиусом б) сгусток
тороидальный с радиусом поперечного сечения г0.
28.6. 1. Оценить время проникновения внешнего магнитного
поля в тороидальный сгусток плотной водородной высокотемпера-
турной плазмы с Т— 15- 10е К, если радиус поперечного сечения
тора г0=1 м (рис. 28.1,6), а средняя проводимость при этой
температуре примерно равна проводимости меди при комнатной
температуре [у = 5-107 (Ом-м)~г]. (Параметрытакой высокотемпе-
ратурной плазмы приближаются к параметрам, при которых мо-
жет начаться реакция термоядерного синтеза.)
2. Найти время затухания магнитного поля Солнца, если его
радиус /?о = 7ООО0О км, а средняя проводимость солнечной плазмы
примерно в 50 раз меньше проводимое и меди при комнатной
температуре. Считать в обоих случаях ро = р0 = 4л-10~7 Гн/м.
28.7р . 1. Определить общие условия, при которых плотная,
хорошо проводящая плазма, находящаяся без движения (а — 0),
в магнитном поле не испытывает действие магнитных сил (усло-
вия «бессилового» поля). Силой тяжести пренебречь. 2. На осно-
вании найденных условий показать, что магнитное поле из силовых
линий в виде спиралей, образованных при определенных усло-
виях наложением однородного поля соленоида и поля тока 0
протяженном цилиндрическом сгустке плазмы (рис. 28.2), явля-
ется «бессиловым», если внутри сгустка Вг = Вт-Ц (Рг);
~BnJx(0r); Вг = 0, где J0(Prj; Jt (₽г)—функции Бесселя; Г, <*«
г—цилиндрические координаты; р—константа.
224
28.8. Высокотемпературная плазма может в течение некоторо-
го времени удерживаться от соприкосновения со стенками силь-
ным магнитным полем. Метод магнитной изоляции плазмы от
стенок реализуется, например, в токамаке (рис. 28.3)—устройстве,
состоящем из тороидальной камеры /, внутри которой в плазмен-
ном сгустке 3, как во вторичной обмотке трансформатора, инду-
цируется ток,- Магнитное поле этого тока вместе с внешним полем
дополнительных катушек 2, намотанных на тороид, создает ре-
зультирующее поле в виде спиральных линий.
Оценить минимальное значение индукции необходимое
для удержания водородной плазмы с концентрацией электронов
и ионов ng = п;— 15-1020 1/м* и температурой 10* К.
28.9. Какая из приведенных на рис. 28.4, а—в равновесных
конфигураций хорошо проводящей жидкости (плазмы) устойчива
в магнитном поле? Считать, что магнитное поле
сосредоточено у границы и не проникает внутрь
плазмы.
Рис. 28.4
28.10. Внутри цилиндрической вертикально расположенной
проводящей трубы с внутренним радиусом R течет жидкая струя
немагнитного металла радиусом г0 (рис. 28.5) По внутреннему
(Жидкому) и внешнему проводникам в противоположных направ-
ления к проходит постоянный ток /. Взаимодействие тока с собст-
венным магнитным полем приводит к радиальному сжат ию жидкого
Проводник а—п инч -эффекту.
1. Найти распределение давления по сечению жидкого провод-
впка. 2. Как изменится распределение давления внутри провод-
225
ника, если ток по внутреннему проводнику потечет в весьма
тонком поверхностном слое? 3. Будет ли равновесие жидкого
проводника устойчивым по отношению к случайно возникшему
изгибу проводника или уменьшению его сечения («перетяжке»),
если: a) r0^ R; б) 4. Предложите способ борьбы с не-
устойчивостью.
28.11. Качественно рассмотреть волновые процессы, происхо-
дящие в плазме с у==оо, находящейся в однородном магнитном
поле Во, при двух различных по типу малых возмущениях поля
(Ь)‘. а) линии поля смещаются (изгибаются) в поперечном направ-
Рис. 28.6
Рис. 28.7
лении (рис. 28.6,о); б) линии поля смещаются параллельно самим
себе (рис. 28.6,6).
Оценить скорости поперечных (альфвеновских) волн [слу-
чай а)] и продольных (магнитозвуковых) волн vM3 [случай б)|.
сравнивая переносимую с волной энергию (в единице объема)
р0иг/2 с магнитной энергией [случай а)] или с суммой магнитной
энергии и энергии, затраченной на сжа-
тие [случай б)]. Процесс сжатия пола-
гать адиабатным с yn — cp!cv^2.
28.12. Простейшая схема магнито-
гидродинамического генератора, позво-
ляющего преобразовать тепловую энер-
гию непосредственно в электрическую,
показана на рис. 28.7.
1. Определить э. д. с., индуцирован-
ную генератором, полагая, что в ка-
нале равномерно со скоростью v движется слабоионизирова-
нный (с проводимостью у) газ. Магнитное поле В направлено
поперек газовой струи. 2. Оценить максимальную удельную (на
единицу активного объема генератора) мощность при Тл.
ц = 500 м/с; у = 40 (Ом-м)”1.
28.13 р. В плоском канале шириной 2 d, длиной L вдоль
оси х движется упорядоченно (ламинарном) в поперечном магнитном
поле В6 проводящая жидкость с проводимостью у, плотностью Р
и кинематической вязкостью v (рис. 28.8).
226
Найти распределение скоростей по сечению канала, полагая
течение жидкости стационарным. Скоростной напор Ад (разность
давлений на входе и выходе) считать известным. Силой тяжести
жидкости пренебречь. В качестве граничного условия принять
условие прилипания жидкости к стенкам канала.
Б. Сверхпроводимость
28.14 р. Как было установлено опытами (Мейснер, Оксенфельд)
массивное тело, находящееся в относительно слабом магнитном
поле (меньшем критического Нкр) (рис. 28.9,о), при переходе его
вещества в сверхпроводящее сос-
тояние «выталкивает» из себя
линии магнитной индукции
(рис. 28.9,6), т. е. ведет себя
как идеальный диамагнетик с
р, = 0 (В,=0).
Показать, что: а) подобное
доведение сверхпроводника не
является следствием того, что
Y _ оо (р = 0); б) условие В( — 0
должно рассматриваться при
построении теории как дополни-
тельное.
28.15 р. Показать, что: а) после удаления сверхпроводящего
односвчзного тела, например шара (рис. 28.9,6). за пределы про-
странства, занятого магнитным полем, в нем не могут существо-
вать какие-либо стационарно протекающие токи; б) токи могут
стационарно протекать, если из области, занятой магнитным по-
лем, удалить двусвязное сверхпроводящее тело, например мас-
сивное кольцо.
28.16 . Внутри массивных сверх проводни?.ов поля Е и В равны
нулю. 1. Сформулировать граничные условия для векторов Е и В
на поверхности сверхпроводника. 2. В условиях задачи 28.14р
найти закон изменения внешнего поля Не у поверхности сверх-
проводящих тел, имеющих форму: а) длинного цилиндра, ось
которого перпендикулярна внешнему однородному полю frc;
б) Длинного цилиндра, ось которого совпадает с полем /70; в) шара.
28.17 . Найтн полный магнитный момент М, созданный поверх-
ностными токами .сверхпроводящего шара радиуса /?0, помещен-
його в практически однородное поле длинного (8i^>2/?j) соленоида
е числом витков и током (рис. 28.10).
Определить индуктивность соленоида с внесенным внутрь него
СаеРХпроводяшнм шаром при
28.18 . Определить распределение индукции по сечению сверх-
Роводящей: а) тонкой пленки (2а 6) тонкой круглой нити
227
Рис. 28.10
Рис. 28.11
(2г0^Л£) (рис. 28.11), где —характерная толщина слоя мас-
сивного сверхпроводника, занятого поверхностными токами.
Решения
Глава первая
1.1 р. Мысленно рассечем схему рис. 1.1 ,а плоскостью, прохо-
дящей через ветви с токами 1и Z2, /я. Все, что находи гея по
одну сторону от этой плоскости, можно рассматривать как неко-
торый узел. Алгебраическая сумма токов, входящих в этот узел,
равна нулю: It 4-1 *— Z3 = 0. Отсюда /3 = Л + Z,.
1.6 р. В соответствии со схемой рис. 1.3,с по закону Ома за-
пишем выражение для каждого тока: /x = (<pi—4-£1)£г; /» =
= (<РЯ—Фо—£2)&; ^«==(фа“Фо)Яз» где gt, gt и g3— проводимости
ветвей.
Учтем, что, по первому закону Кирхгофа, Z14-Z14-Zt = 0.
Отсюда
_ <Г1£1 + ф2£2+фз£з-|-£1₽1—___кос R
=---------Я< + /?5+’Кв “ В-
Подставляя найденное значение <р0 в формулы для токов, по-
лучим /, = — 0,125 мА; /, = —1,78 мА; /3 =—1,905 мА.
1.8 р. Так как /j 4*/34-/3 = 0, то /2 = — —Zs=10 мА. Для
нахождения токов Z4, /5, Ze составим два уравнения по первому
и одно по второму законам Кирхгофа: ZS4-Z4 = Z5; Ze4-Zj=Z4;
Z</?4 + Z5/?6 + = £«—Е5. Отсюда
Et-Eb-]-!1R^isR-a
Я<4-
мА;
Z6= —10 мА; Ze = 0; <po=<pfc—Z,Z?e—Z4/?4=(p6—50В; Uab = — 50 В.
1.14 р. Всего ветвей в схеме е=20, в том числе с источниками
тока ент = 8. Следовательно, неизвестных токов 20—8= 12. Узлов
У в схеме 12. По первому закону Кирхгофа следует составить
у— 1 = 12—1 = 11 уравнении, по второму закону—одно: в—еит—
— (р— 1) = 20—8—(12—1)^1.
Так как в узлах т, n, k, I неизвестно только по одному току,
то, по первому закону Кирхгофа,
/1 — — Ju—Jj7 — 32; ZJ0 — Ч- J12 — 20;
/ц= *^12= 26, /И “ /ц 4" «^17 = 9.
Для узлов gt hf d. b. e, а определим неизвестные токи Zt,
Ze, Z*, Z4, Zj, Z8, ZB, выразив их через найденные ранее и через
ток Z7:
Z. = 27-/,; Ze=2-Z?; /e = 21-Z,; Z4=-34-Z,;
Z, = -14-Z7; Zb = 19-Z?; Z3 = 34-Z,.
229
Убедимся, что для узла с получим тождество /64/к— /1В = 0.
С целью определений тока /7 составим уравнение по второму за-
кону Кирхгофа для контура feacghdbf:
4 Ж4/Д 4 'Л-'Л = 4- Еь4 Еа.
Подставляя в это уравнение токи, выраженные через /7, найдем:
/, = 572/44= 13 А; /9=14 А; /„ = — It А; /в = 8 А;
/4= 10 А; /., = 21 А; /3 = 12 А; /& = 6 А.
Потенциал точки п
Фл ~ Ф* ^11^11 ^10^10 ^8^8 4 ^4^4
-----------------/2^2 4 20^20 4 /1/?1 4 Ев 4 Ez,
Подставляя числовые значения токов и сопротивлений резис-
торов, получим ф„ = <рЛ—37; Unk = — 37 В.
1.15 р. Из решения задачи 1.8р известны токи в ветвях схемы
рис. 1.4,о: /4=10 мА; /6 = —10 мА; /в = 0. Потенциальная диа-
грамма изображена на рис. Р. 1.1,а. Потенциалы Фс = 0; фь—
так как /в = 0; <ри =—Ев = —40 В; ф<? = ф</ + /е/?5 — —40—30 =
= —70 В; Фа = фе4В6 = — 50 В; Фс = Фа4 /4/?, = 0.
1.18 р. В соответствии с рис. 1.9,а, б определим токи в ветвях
и характер включенных элементов. Сопротивление участка оа
Roa = 5 Ом. На этом участке ток
течет от точки а к точке о и сос-
тавляет 3,175/5 = 0,635 А. Сопротив-
ление участка ab Rab = l0 Ом. Ток
течет от с к b и равен (3,175 —
—0,975)/10 = 0,225 А. Между точками
b и с включен источник ЭДС с
Е = 10 В. Сопротивление участка cd
Rcd — 3 Ом. Ток по ветви fedc течет
от точки f к точке с и равен 1,52 А.
Ток диагональной ветви cf течет от
точки с к f и равен 1,31 А (найден по
закону Ома для узла с). Сопротивле-
ние ветви cf /?с/ = 2,63 Ом.
1.19 р. В обоих случаях зависи-
мость между токами /t и /2 линейна
и имеет вид Ц = а 4 Ы2. Коэффициен-
ты а и b определим из опытов корот-
кого замыкания и холостого хода
второй ветви.
При £г = 0 и /?2 = 0/2= I, - 0;
Поэтому 1=д + 0, 0=о + 6-1. Решив
два уравнения совместно, найдем о = 1, t = -l, 1Г = \—/а.
При и /?2 = 0 /2 —2, /i = — 1 А; при /?2=оо /2=0;
/2=1, откуда —1 =о + 2bt 1=о4 0. Ток /t = 1— 1/а.
1.22 р. Звезду, состоящую из резисторов /?4, /?5, /?я, на рис.
1.11,о заменим на треугольник из резисторов /?4.= 13,03 Ом,
Рис. Р.1.1
/4=00 /„ = 0. /. = 1.
230
£5В = 6,52 Ом и /?я1 = 8,67 Ом (рис. Р.1.1,6). Резистор R.2 и
параллельный ему заменим одним, сопротивление которого
равно 2,44 Ом, резистор R3 и параллельный ему /?ба—резисто-
ром сопротивлением 1,63 Ом, резистор Rt и параллельный ему
—резистором сопротивлением 1,79 Ом. Входное сопротивление
/?„,= |'243 Ом.
1.28 р. Обозначим показание вольтметра в положение 2 через
[Jv. В этом положении через вольтметр и резистор R течет оди-
наковый ток, поэтому отношение напряжения на резисторе к на-
пряжению на вольтметре (U — Uv)/Uv — R/Rv. Отсюда R —
= RV[(U/UV)—1] = 3000 (100/90— 1) = 333 Ом.
1.30 р. Для каждого из трех случаев в одном jb ребер, наи-
более удаленном от плоскости симметрии (по обе стороны от ко-
Рис. Р.1.2
торой значения токов по соответствующим ребрам одинаковы),
зададимся произвольным током, например / —1 А. Затем, исполь-
зуя законы Кирхгофа и условия симметрии, найдем токи в осталь-
ных ребрах. После этого определим разность потенциалов между
заданными точками и входной ток. Частное от деления разности
потенциалов на входной ток даст искомое сопротивление.
Распределение токов при питании между точками а и b пока-
зано на рис. Р.1.2,а; —5/6 Ом. Распределение токов при
питании между точками а и с дано на рис. Р.1.2,6; £flf = 3/4 Ом.
На рис. Р.1.2,в показано распределение токов в ребрах куба
при питании между точками d и с; Rdc = 7/12 Ом.
1.32 р. Для определения gu и £12 задаемся током /=1 А
в ветви 2 и подсчитаем, какой источник ЭДС следовало бы для
этого включить в ветвь Г. £t= 1 - 2-}- 1,667-1 — 3,667 В (1,667 А—
ток, текущий в ветви /; 0,667 А—ток, текущий в ветви 5).
Отсюда
= 1,667/3,667 = 0,454 См; g12= 1/3,667 = 0,273 См;
g„ = 0,667/3.667 = 0,182 См.
Для подсчета g2i и g23 исключим из схемы источник ЭДС
£,, а в вегвь 2 подключим некоторый источник ЭДС £2. Зна-
чение этой ЭДС берем таким, чтобы в этом опыте ток lt — 1 А.
При этом /я=0,33 А: /а= 1,333 А; £„= 3,666 В. Следовательно,
£2з= 1,333/3,666 = 0,3635 См; ^ = 0,33/3,666=0,091 См.
23|
1.34 р. В соответствии с рис. 1.15,в запишем выражение для
тока /о. Соответствующие слагаемые правой части берем положи-
тельными, если они создают ток, направленный согласно току /2:
/, = — Etgl2 + Ез&з—E2g22 = —0,273 • 10 4* 5 • 0,091 — 6 • О,3635 =
= —4,445 мА.
1.38 р. В соответствии со схемой рис. 1.17,6 ток / — Л+ J =
= 1,3 А. Разность потенциалов между точками а и b <ра = уь—Е-Ь
4-/7?; Uab — 1R—Е=10 В. Мощность, доставляемая источником
тока, Рнт = UabJ = Ю Вт.
1.42 р. а) В схеме рис. 1.7 всего один контур, не содержащий
источников тока, поэтому для нее можно составить только одно
уравнение методом контурных токов. При записи этого уравнения
следует учитывать падение напряжения, вызванное контурными
токами от имеющихся в схеме восьми источников тока. Ток Jk
каждого источника тока должен замыкаться по ветвям, в которых
не содержится других источников тока, кроме этого, б) По методу
узловых потенциалов следует составить 11 уравнений (число узлов
в схеме равно 12).
1.47 р. Для первого режима составим два уравнения:
0,4755Яи = 95,3; ----= 0,4755.
Для второго режима составим одно уравнение;
D = 0,906.
Для третьего режима имеем два уравнения:
^1,295 = 86,5;
Uab*
RA+R,Mb+-j£^
= 1,295.
Совместное решение пяти уравнений дает R — 100 Ом; Ra =0,5 Ом;
flv = 200 Ом; ЯвхоЬ=Ю Ом; <7вЬх=Ю0 В.
1.48 р. Для первого режима lt=UabjRBXab ;для второго режима
Л=^х/(Я2+ЯвхСь); Для третьего режима Is = UabJ(R9 + RB*ab)-
Следовательно, 100 ^вхОь = VabB)j!x = 1 кОм;
/?3=4 кОм.
1.51 р. Нагрузка RK должна быть согласована с входным со-
противлением RBXab, т.е. Rn = RBXllb. Так как схема питается от
источника тока, то
> __ + /?э) (/?2-Ь Я4)
вхоЬ-
= 2,4 Ом;
П — f #2 I D. р _П1 идр П 1 Г)4 ОТ
J Rl + Ra+Ri+R4 -1 Ь. FH-C/abx/(4/<H)-U,lU4bT.
1.53р. Составим уравнения для схемы рис. 1.23, а по методу
контурных токов, полагая, что в левом контуре имеется э. д. с. Ен»
а в правом ЭДС Egg. Rit^Ri,2.^2t==^ii* Rt2^22==^22‘
232
Определитель Д =
12 сначала раскроем по элементам первой
22 I
строки /?цД1Х+/?18ДИ^= А, а затем по элементам второй строки
/?и1Д214- #22^22 = А. Здесь ДЛ/Я—минор вместе с принадлежащим
ему знаком. Разделим каждую из строчек на Д и учтем, что
д>да/Д=£Ля1. В результате получим искомые зависимости:
^*11^11 "Г ^12^12--- U
^22822 —
1.57р. Узлы 1—4 графа рис. 1.25, в (рис. Р.1.3, а) обведем
кружками и составим [.4]-матрииу, поставив в.ее клетки Ч- 1 для
ветвей, стрелки на которых выходят из соответствующих кружков:
Ветви
Т1
о
о
Узлы г 1 2 3 А
1 —1 0 0 0
[Л] = 2 0 1 0 0
3 0 0 1 0
4 L о 0 0 —]
5 6 7
1 О О
—1 1 О
О —1 1
О 0—1
=1лш-
ij
Для дерева, изображенного на рис. 1.25, б, главные сечения будут
совпадать с кружками, показанными на рис. Р. 1.3, а и исполь-
зованными при составлении [Д]-матрицы. Каждое главное сечение
Рис. Р.1.3
рассекает одну ветвь дерева, а остальные—хорды. Номер главного
сечения соответствует номеру ветви дерева. Плюс 1 в клетках
|(?г]-матрицы ставят для рассекаемой этим сечением ветви дерева
и для всех ветвей связи, стрелки на которых ориентированы отно-
сительно поверхности сечения, так же как и стрелка на рассе-
каемой этим сечением ветви дерева. Поэтому.
Ветви
Сечения г 1
К>г]= 2
3
4
1
0
о
L-0
2 3 4
ООО
1 0 0
0 1 0
0 0 1
5
—1
—1
о
о
6 7
0 0
1 0
— 1 1
0 1
81
—1-J
1
о
о
Для дерева рис. 1.25, б главные контуры изображены на
Рис. Р.1.3, б. Каждый главный контур содержит по одной хорде
233
(остальные его ветви—это ветви дерева). Номер главного контура
соответствует номеру хорды. Направление обхода каждого глав-
ного контура (и направление контурного тока) соответствует
стрелке на хорде этого контура. В соответствии с рис. Р. 1.3, б
Ветви
Контуры Г’ 1 2 3 4 5 6 7 8п
5 1 I 0 0 1 0 0 0
[Кг]= 6 0 —1 1 0 0 1 0 0 =ИН1-
7 0 0 —1 -1 0 0 1 0
8 L—1 0 0 1 0 0 0 1J
Глава в торая
2.1р. Потокосцепление катушки равно алгебраической сумме
потоков, пронизывающих отдельные ее витки:
= £Ф„а»я === ДФ- 4+ ДФ-44- 4ДФ-6 = 32ДФ= 32*10“4 Вб.
Индуктивность катушки L = i|?// —32-10-*/3,2 = 10-э Гн — 1 мГн.
2.2р. Потокосцепление первой катушки
'Г11 = «'1Ф114-И'1ФИ,
где Фл—поток, создаваемый током /1 и пронизывающий только
первую катушку; Ф1а— поток, создаваемый током и пронизы-
вающий обе катушки.
Индуктивность первой катушки определим из равенства гри —
=1,1 й
I, = !]>„//, = а'1(Ф11 + Ф12)//1. (1)
Потокосцепление второй катушки
я|'22 = ^’2Ф22 "Ь ^2Ф21’
где —поток, создаваемый током /а и пронизывающий только
вторую катушку; Фл—поток, создаваемый током /2 и пронизы-
вающий обе катушки.
Индуктивность второй катушки
4,=®5(ФЯ+Ф»№- (2)
Взаимную индуктивность катушек найдем из соотношений
ф12 = Л1/1; 4'21 = М/2, (3)
где il’i2 =^ф12; =
Отсюда
Ф1г//1 = Фа1/Л ИЛИ Ц-’2ф12//1 = (О
Из условия задачи известна сумма потоков
Ф12-г Фг1 = 4-10-1 Вб. (5)
Решив совместно уравнения (4) и (5), получим
Ф12=10"‘ Вб; Ф21 = 3-10~4 Вб.
234
Согласно уравнениям (1), (2) и (3),
£1^ !°?.(!о:^1о-.Ъ=2 мГн.
150-(2-ю-ч-з-10-<)3,75 мГн;
A1=J^Zi=It5 мГн.
2.3р. Взаимная индуктивность
М = ф// = гсФрез/Л
где /—ток линии; w—число витков
щий поток, пронизывающий рамку
сумме потоков от проводов Л и С.
Рамка находится в неравномерном
поле, поэтому сначала ищем поток
через элементарную площадку
рамки ds = ldx от тока линии А:
рамки; Фргз — результирую-
и равный алгебраической
на рис. Р.2.1. Напряженность
где Вл = li0/7а—вектор ма гнитной
индукции от тока / линии Л.
Положительное направление век-
торов ds, ВА и Вс (Вс — вектор
индукции от тока линии С) указано
магнитного поля определим по закону полного тока: ^Hdl = I.
Напряженность на расстоянии R от осн провода находим из выра-
жения H£nR—I, откуда Ял = //(2л7?).
Так как dx = dR/cos а, то
J(DZ = BAds = р0 1 dx cos а ~ —
А а го 2л/? 2л
R 9
Ап
Полный ПОТОК Фд = f -7?^-^- = -^- In-пр- .
А J 2л R 2л А/п
Ат
Аналогично определяем поток от провода С:
Ст
__ С dR __ Ро^ 1г, Сгп
Чс~ 3 ~2л”ТГ~2ji П СГ‘
При указанных на рис. Р.2.1 направлениях ВА, Вс и ds оба
потока положительны (BAds > 0 и Bcds>0), поэтому результи-
рующий поток
Ф»-> = Фл4-<1’с = !^
In
АпСт
АтСп *
235
Взаимная индуктивность
Л1=^1п42$!- = 6,41О-‘ Гн.
2л АтСп
2.6 р. ЭДС, наведенная в проводнике длиной d/, движущимся
со скоростью v в постоянном во времени магнитном поле, е =
—• —>
= B[d/V].
Для равномерного поля e = B/aV„, где В—индукция равномер-
ного поля; /а—длина активной части проводника; V„—нормаль-
ная составляющая скорости движения проводника.
Для данного случая e = Btyn~B2l sin у Vcos(90°—а)=45 мВ.
2.19 р. Сила, действующая на подвижную катушку, может быть
выражена как производная от магнитной энергии двух магнитно-
связанных катушек по координате х. Магнитная энергия двух
магнитно-связанных катушек с учетом направлений токов в ка-
тушках
Следовательно, | F | == dWjdx.
Индуктивности и Ьг не зависят от взаимного расположения
катушек, т. е. не являются функциями координаты х. Функцией
этой координаты будет взаимная индуктивность катушек М =
= = Сила, действующая па вторую
катушку. F = = 3/2tt>2Se”** = 3e“SJt Н.
2.21 р. Емкость между двумя проводящими телами, разделен-
ными диэлектриком,
Ua ’
\Edl
i
где q—заряд на одном из тел; —разность потенциалов.между
ними; Е—напряженность поля; = —абсолютная электри-
ческая проницаемость диэлектрика; ds—элемент поверхности; dl
элемент пути от тела / к телу 2.
Напряженность электрического поля кабеля (и цилиндрического
конденсатора) E = ql(2nrl^. Тогда
^12=£ =1п ** *
<7 2-3,14-10*-4-8,86-10~12 t ft 1п_в ф
Ul2 1п4
236
Глава третья
3.2 р. Расчет проведем по мгновенным значениям тока и напря-
жений. Мгновенное значение тока в цепи
i=/CTsinco/ = 1,41 sin 314/ А.
Мгновенное значение напряжения на резисторе
uR — Ri = RIfJI sin со/ = 141 sin 314/ В;
на конденсаторе
wc=4" f idt =---Jr Im coso/Ч- Cx = 141 sin (314/—90°) B,
G J COG
где 1/(<оС) = хс—емкостное сопротивление; xc = 3i4,3Ig t0-0 =
= 100 Ом.
Постоянная интегрирования Cx — 0, ввиду того что при сину-
соидальном токе и установившемся процессе в цепи напряжение
на конденсаторе, так же как и напряжение на всех остальных
элементах, не имеет постоянной составляющей.
На входе цепи
и = uR н ис = RI„ sin <о/ —cos со/ = zlm sin (<о/ 4- ср),
где z=l''/?2+(l/<uC)!=141 Ом; tg <р ~ — 1; <р = —45°.
Следовательно, и = 200sin (314/—45°) В.
Мгновенное значение мощности в цепи
р = ui = 1,41 sin 314/• 200 sin (314/—45°) =
= [100—141cos(628/—45е)] В-A.
Графики мгновенных значений и, /, р приведены на рис. Р.3.1.
3.3 р. Задачу решаем символическим методом: дифференциаль-
ные уравнения, связывающие мгно-
венные значения тока, напряже-
ния и ЭДС, заменяем алгебраи-
ческими уравнениями относительно
комплексных амплитуд этих вели-
чин.
ЭДС самоиндукции eL свя-
зана с протекающим по катушке
током i соотношением е, = — L ,
* at
или в комплексах ELm=
где g)L=^Xl—индуктивное сопро-
тивление.
Комплексная амплитуда тока
/ _ 100е'30°
m —juL — /314-100-
— = 3,18е/1”в А. (1)
237
Мгновенное значение напряжения на входе цепи
что соответствует алгебраическому уравнению относительно комп-
лексных амплитуд тока 1т и напряжения на входе Um:
й„ = =/„(«+М)=/>е'* = /„z,
где z—модуль комплексного сопротивления; Z—комплексное
сопротивление цепи; —аргумент. Определим z и у>:
г = (wL)‘ = /102 -t- (314 • 100-10’’)2 = 33 Ом; (1)
tg<p=coZ./R = 31,4/lO = 3.14; q, = 72°20'.
Таким образом,
l/CT = 3,18e'120°-33e'72C=0’ = 105е'1о2°20' В. (2)
Для перехода от комплексных амплитуд тока и напряжения
к их мгновенным значениям обе части равенств (1) и (2) умно-
жаем на е'ш/, а затем берем их мнимую часть:
Im [/CTe/td*] = Im [3,18е'1а0°е'ъ/];
t = 3,18 sin (со/4- 120°) A.
Аналогично получим и— 105 sin (со/ 4- 192°20') В.
3.4 р. Комплексное сопротивление цепи Z —ае^ является коэф-
фициентом пропорциональности между комплексами действующих
значений приложенного к цепи напряжения U = Uei4>tt и тока
/ = 7е/<гч
zeJv =
откуда z = U'H\ <Р = <Р«—«Р/.
Комплексное сопротивление катушки запишем как
R + Jco£ = R + jXL = ге'ф,
где z = R- 4- Л’£; tg ср = XjR.
При Л = 0 ю£ = Х£=0 и z1=U1fl1 = R', R= 100/1 = 100 Ом.
При /2 = 500 Гц
z2 = Ujl2 = К#24-= 100/0,5 = 200 Ом;
= /?2 = 173 Ом;
£ = Xju = -3 = 5510~3 Гн = 55 мГн.
При fs = 1000 Гц
z3 = К7?2 4- (2л/3£)2 = 358 Ом.
Показание амперметра /3 = t/3/za= 100/358 — 0,28 А.
3.12 р. На комплексной плоскости отложим произвольно вектор
тока 1 = 1. Вектор напряжения на конденсаторе йЪс отстает от
238
ректора тока 7 на 90°. Положение векторов и ас
из условия Oae = Oab-i- l)bc, делая засечки при
окружностей радиусами Ri = Uab и R2 = Uac1
конца и начала вектора Ubc (рис. Р.3.2).
По теореме косинусов найдем
cos a= 0,865,
— ZUbcUab
откуда а = 30°, ф = 60°. Тогда Uab= 173е'в0° В.
Комплексное сопротивление катушки Z=
^Uablf = 32,3+ /750м.
3.16 р. Под активной мощностью цепи си-
нусоидального тока понимают среднее значение
мгновенной мощности р за период Т:
и Uab определим
построении двух
проведенных из
Рис. Р.3.2
т
R=-i-1 ul dt cos у ~ UI cos<p= 1,41 cos 45° = 100 Вт,
л «1 &
о
т- е. активная мощность равна постоянной составляющей мгно-
венной мощности (см. рис. Р.3.1).
Полная мощность S= U1 (S — P при costp=l); <5=141 В-A.
Реактивная мощность Q — Ul sin ф = 100 ВАр.
В комплексной форме записи
S = L7 = P +/Q= 141е~/46° В-А;
/> = Re[W] = Re[141е-'«"-1] = 141 cos45°= 1бо Вт;
Q = Im [1/7] = Im [141е-<«“-1] = 141 sin 45° = 100 ВАр,
где /—сопряженный комплекс тока.
3.17 р. а) Параметры схемы замещения двухполюсника при
последовательном включении активного и реактивного сопротив-
лений определим по показаниям приборов на основании следующих
зависимостей:
P = {//costp.
cos ф = P/(UI) = 102/(80-1,6) - 0,8;
z = U}I =50 Ом; /? = 2созф = 40 Ом;
Л = 2 sin ф = i' г2— R* = 30 Ом.
Характер реактивного сопротивления уточним по знаку угла ф
из векторной диаграммы на рис. Р.3.3, где Ц и /^—возможные
положения вектора тока относительно напряжения на входе
Цепи Uit соответствующие емкостной (73) и индуктивной (Гг)
нагрузкам.
При включении ветви с конденсатором ток на входе двухпо-
люсника увеличится при емкостном и уменьшится при индуктив-
ном характере нагрузки: 73+/с —Л; |7j > [/^ |; 73Ч- 1С — К\
239
Известно, что при включении конденсатора небольшой емкости
ток на входе цепи уменьшается. Это соответствует индуктивному
характеру нагрузки,
т. е. угол <р > 0. В этом случае двухполюс-
ник может быть заменен последовательно
включенными сопротивлениями: Z = R +
+/Х = 40+/30 Ом.
б) Коэффициент мощности и характер
нагрузки R и X при параллельном вклю-
чении не меняют своих значений. Сле-
довательно, аргумент комплексной прово-
димости цепи равен—<р. Проводимость цепи
равна сумме проводимостей ветвей:
Y=g—jb^ye-Ъ,
откуда у — I/U = 1,6/80 = 0,02 См: g =
cos ф = 0,016 См; b = у sin <р = 0,012 См; Y = 0,016—/0,012 См,
что соответствует параллельно включенным активному (A?=l/g =
= 62,5 Ом) и индуктивному (ХЛ= 1/6 = 83,3 Ом) сопротивлениям.
3.23р. Добротностью конденсатора при последовательной схеме
замещения называют отношение напряжения на емкостном сопро-
тивлении к напряжению на активном сопротивлении:
Qc — U С&R — ^с/^посл— 1/(ыС/?|]осл).
Под добротностью контура при параллельной схеме замещения
понимают отношение тока через емкостное сопротивление к току
через активное сопротивление:
Qc ~ 1 cilR~ ~ ^^/Япар-
Параметры контура: Хс = 159 Ом; 7?ПОСЛ=0,159 Ом; /?пар= 159 кОм.
3.24р. Добротность катушки
СЛ = <о£//?посл; <2/. = /?пв1/((о£)= 1/(со£ЯпаР)-
Параметры контура: А\1ОСЛ=10 Ом; со£ = 99,5 Ом; Q = 9,95;
/?пар= 1000 Ом. _
3.26р. Резонансная частота контура соо = 1/|/£С = 500 с-1.
Добротность контура Q — a)0LlR — 10.
Резонансная кривая может быть построена по уравнению
где или
(рис. Р.3.4)
в относительных единицах—по уравнению
(2)
/ __________1_______
Лпах . __ / 1
у l-hQg(n—
240
ро определению полосы пропускания из уравнения (2) имеем
или */<2=л2— 1/п8; —1/Q=nj —1/пх.
Отсюда п/е—1 или ____
<*)о = К «1Ш2; (3)
п2—nt = (со,—<ож)/<ор = !/<?, (4)
где <Oj и со2—граничные частоты полосы пропускания.
Решая совместно уравнения (3) и (4), находим
®1 = -g-lKl + 4Q-l]«475 с’1;
<оа = ^-|1 + ГГПё]~525 с-*.
3.35р. В электрической цепи, составленной из п реактивных
элементов, возникает не более п—1 резонанса. Резонансы тока
и напряжения чередуются между собой.
Если в цепи есть путь для прохожде- Ц1тВ\ [\
ния постоянного тока, т. е. при со = О
ZHM = 0 (частотная характеристика на-
чинается с нуля), то первым наступает
резонанс токов, если нет (при со = 0
ZBX = оо), то первым наступает резонанс
напряжений.
В рассматриваемых схемах возника-
ет по одному резонансу: резонанс нап-
ряжений в схеме рис. 3.21, а и резонанс
токов в схеме рис. 3.21, б. Частотные характеристики входных
сопротивлений и проводимостей для этих схем приведены со-
ответственно на рис. Р.3.5,атб. Условие возникновения резонансов:
a) u0L = 1/(со0С); б) ю0С = l/(cocL).
Рис. Р.3.5
3.39р. Одноименными зажимами катушек являются зажимы
* и 2. Схема цепи приведена на рис. Р.3.6, а. Входное сопротив-
ление магнитно-связанной цепи ZBX = UjL
241
Запишем уравнения цепи в соответствии с законами Кирхгофа:
7-Л + Л; (1)
й = lt (Ri + jvLJ + jaMIy (2)
(7 = /4 (Яа + /WJ + jtoM 7 lt (3)
или
U — 7iZr + / 2ZM; (1)
I/^AZm + zX (5)
Решив уравнения относительно тока /, получим
z^-zb ’
откуда
7 Z\Zi—Z/л
Подставив значение тока /а из уравнения (1) в (4) и тока /\
из уравнения (1) в (5), найдем
(7 = /Zm + 71(Z,-Zm);
J7=/ZM+/S(ZS-Z«).
Этим уравнениям соответствует схема рис. Р.3.6, б.
Рис. Р.3.6
3.43р. Выделим ветвь тп с сопротивлением Z, а остальную
часть схемы будем рассматривать как активный двухполюсник.
Если обозначить входное сопротивление двухполюсника со сто-
роны выходных зажимов через Z2BX, то передача максимальной
активной мощности от двухполюсника нагрузке происходит при
условии, что активные сопротивления у Z и Z2BX равны, а реак-
тивные сопротивления равны по модулю, но противоположны по
знаку. Значение Z2BX определим из пассивной схемы двухполюсника
(С71 = 0) при Гг = 1/„„.
По законам Кирхгофа,
«/а/хг 7,/Лд^
242
При совместном решении этих уравнений получим
е ; Л-v . Хм \
Zzbx = = 2,12 + /2,6 Ом;
Z = Z«K = 2,12—/2,60м.
Таким образом, сопротивление нагрузки равно сопряженному
комплексу входного сопротивления:
Хм ____ RiXm jXjXm n • v
P-_L»Y. ГЛ 2 , v-2 гл2 , v 2 ~ J ЛВВ'
где /?ЕВ, Хвн—активное и
во вторичную обмотку.
реактивное сопротивления, вносимые
Совместно решая уравнения
= Л (Я1“г jXj) 7(1)
0=/2(Z + jXj?)-/1JX^, (2)
найдем токи в обмотках трансформатора:
4 = 21,94; l2=22t8ei^'A.
Определим баланс активной мощности. Мощность, получаемая
из сети,
Р = UJt cos ф, = 100-21,9 = 2190 Вт.
Мощность, поглощаемая в первичной цепи,
Pt = = 21,92- 2,3 = 1095 Вт.
Мощность, поглощаемая во вторичной цепи,
Р2 = = 22,82 • 2,12 = 1095 Вт.
Мощность, потребляемая во вторичной цепи, передается из
первичной вследствие явления взаимоиндукции и может быть опре-
делена как F2 = /1X,I/acos.(/ljX1I; 1095 Вт.
Векторная диаграмма приведена на рис. Р.3.7, а.
243
Составим схему замещения трансформатора. Прибавим к урав-
нениям (1), (2) соответственно ±/Х^/х и dz/X^/j. Тогда урав-
нения примут вид
С/, = /'Л + ij (Х.-Х,,) + (Л~4) /Хя; (3)
0=Лг+<х,-х„)+(/„-/,) jXK. (4)
Уравнениям (3) и (4) соответствует схема рис. Р.3.7, б, в ко-
торой токи /\ и /о рассматриваются как контурные.
3.51р. Максимальное значение тока /2 (режим частного резо-
нанса) получим при наименьшем значении входного сопротивления
со стороны вторичной обмотки трансформатора. Это достигается
при чисто активном сопротивлении, а именно: если Z2BX = /?2Bxd_
± /Х2вх, то для условия резонанса необходимо, чтобы Х,вх = 0
(метод определения Z2nx рассмотрен в решении задачи 3.43р)_
Совместное решение двух уравнений, записанных для данной цепи,
дает следующие условия:
Яя-г jX2—ХС2) 1 (В
0 = Л(^ + /Х1)-/2/Хм; , (2)
' Г/D т D \ I । • / у у XI \
2ВХ — -Г Кп) ф - Л С2 J J *
Условие резонанса:
X^Xf
(3)
Подставляя числовые значения в уравнения (1) и (3), получим
Са = 9мкФ; /2=1,2А.
3.52р. Выделим ветвь с сопротивлением Ze. Оставшуюся часть
схемы, представляющую собой активный двухполюсник, заменим
эквивалентным генератором. Э. д. с. эквивалентного генератора
равна напряжению холостого хода (ветвь с Ze разомкнута) на
зажимах тпп*Ёъ = От„^. Внутреннее сопротивление генератора
равно входному сопротивлению по отношению к зажимам тп.
Схему рис. 3.35 заменим схемой рис. Р.3.8, а. Искомый ток /в =
=e/(ZBX “Г Ze).
Для определения напряжения холостого хода UmnK следует
сначала рассчитать токи в схеме рис. Р.3.8,6. Ток на входе схемы
t Ё __ ЕД
в “ 7 I (Z3+Z<)(Zt + Zt) -° А-
Токи в ветвях:
/ = / --------------= 4 33е/эо° А.
/й = Л-/с = 2,52е-/в°сА.
Напряжение UmnK = lbZa—/rZ1=52e_y6B°?0' В.
244
Входное сопротивление определим в соответствии со схемой
рис. Р.3.8, в, в которой треугольник сопротивлений Zs, Z4, Z6
предварительно преобразован в звезду:
7
[•^+2» “6ОМ: Ze”
ZtZ
,У1-7 - = 6 Ом;
z3+z4+z6 ~60м;
^ + 27)(Z2+ZC) 09 -13в
z1+z7+z2H-z„ - 1и’у е им-
Искомый ток
52е~/вв’>30'
= 4,87е~/™°А.
!0,9е-/13в-1-/2;5
3.53р. Условия равновесия схемы:
4 =
Отсюда Rx = /у?4//?3 = 20м; СХ = С4Я3/Я2 = 2мкФ.
/77
Рис. Р.3.8
Тангенс угла потерь
tg 6 —г-^гТ = иР.хСх ® 0,025.
Г лава четвертая
4.2р. а) Выберем направление токов и напряжений согласно
рис 4.1, а и составим для данной схемы уравнения по законам
Кирхгофа таким образом, чтобы С\ и были выражены через (7,
и и параметры схемы. Сравним ко)ффициенты в уравнениях,
^писанных через Д-параметры. с коэффициентами в уравнениях,
составленных для данной схемы.
245
Д-форма записи уравнений (основная форма):
/7,-Л.Д+Л^,; \
/,=лгД+л,/,. )
По законам Кирхгофа,
Ut = U, + RJt;
i f , KR + Uz и. , f . , R A f
Л =+ -=7лс- = =prc + u + =цсс г ••
Сравнение коэффициентов в уравнениях (1) и (2) дает
Дн=1; Д12 = /?Ом; Д21 = 1/(-/Хс)См;
А — I 1 — R—jXc
23 1 -Me -Me ’
б) Режим холостого хода (7. = 0). Из уравнения (1)
I
^1х = Лл(73х* I
Из схемы рис. 4.2
f IX ~ ^2х/(— j^c).
откуда Д„= 1; Дп = 1/(—/Хс)См.
Режим короткого замыкания (0^ — 0). Из уравнения (1)
^1к ^12^2к’ \
/1к=д2Л, I
Из схемы рис. 4.2
U^ = l\KR't
(1)
(2)
(3)
(4)
(5)
откуда Д12 = #Ом; Д88 —(₽ —/Хс)/(—/Хс).
4.5р. В режиме холостого хода (/а = 0) при Д-форме записи
уравнении /|Х = Л8ДХ.
Запишем те же зависимости, пользуясь векторной диаграммой:
100 = Д„200;— /2,5 = Д21200,откуда Дп = 0,5; Д21=—/0,0125 См.
Известно, что Д-параметры четырехполюсника подчиняются
уравнению Л„Д22—Д12Д21=1. Для симметричного четырехполюс-
ника Дп — Д-22* поэтому Д2., = 0,5; Д12 = — /60Ом.
4.6р. В режиме холостого хода при Z-форме записи уравнений
^Лх~А1Лх« ^Лх — Z2Jix. Определим комплексные значения тока
и напряжения. Из осциллограммы следует, что £/1х = 70,7В.
Сдвиг фаз между током и напряжением на входе найдем из
соотношения cos <p1 = P1/(t\x/lx) = 0,707, что соответствует углу
Ф1 = 45°.
246
Знак угла уточним из осциллограммы: /1х^5е~'*5'А.
Сдвиг фаз между током и напряжением на выходе получим из
соотношения cos <у = РгД(/8х/1х) = 0,446, что соответствует углу
gt;=60o30'.
Из осциллограммы следует, что (7,х= 56ens°3C'В. Поэтому
Zn = ^1х-'Лх =Ю< /10 Ом;
Z2X= = (5 + /10) Ом.
oe '
Для симметричного четырехполюсника
Z22=Zj, = 10 -г j 10 Ом;
Zjj = Z21 = 5 4 j 10 Ом.
4.22 р. Представим исходный четырехполюсник в виде двух
каскадно включенных четырехполюсников (рис. Р.4.1). Для каж-
дого четырехполюсника запи-
шем расчетные уравнения с
Л-параметрами в матричной
форме записи.
Для первого четырехпо-
люсника
Рис. Р.4.1
л;,’
Л22
для второго четырехполюсника
и; I
Л _“LA\
Г и:
a:J [ /:
(2)
При каскадном включении U’z = lJ\ и Г2 = К- Заменим напря-
жение и ток на выходе первого четырехполюсника напряжением
итоком на выходе второго. Подставив выражение (2) в (1), полу-
чим запись уравнений для результирующего четырехполюсника:
Следовательно, Лп = Л^Л^ 4- Л^Зя —— 0,5; Л12 = Л^.43\-4-
4-Л^2Л22= /30Ом; Лм= Л21.411 ; ЛюЛа1 = /0,025 См; Л2,= .42] • Л>\ +
4~ Л22Л22 = —0,5.
4.28 р. 1. Л-параметры четырехполюсника определим следующим
образом:
а) из условия согласования внутреннего сопротивления источ-
ника с входным сопротивлением четырехполюсника, нагруженного
на Яи:
р __7 __р ____ Л|2.
— ^1вх - А1ЕХ — у' — \ - 7 . - »
4 Aii/Ca-M-a
247
б) из условия согласования нагрузки с входным сопротивле-
нием четырехполюсника со стороны выходных зажимов:
г, р +Д»8 .
ки - к2ВХ - _ (_Л21£71+ - Л„КВ+Л„ *
в) из условия симметрии четырехполюсника: Ди = Д22;
г) из уравнения связи А -параметров: А ir422—
Совместное решение уравнений дает следующие выражения для
Д-параметров: Лп — 0; Д12 =—1/Д21 = + /к /?нЯв-
2 . Расчет сопротивлений Т-схемы замещения:
Z3 = 1/Д21 = zhjP Д и — 1 Z1(/Z3 0,
откуда Zx =—Z3; ZX = Z2 = ±/] г/?н/?в.
Таким образом, сопротивления схемы замещения реактивные
равные по значению, но различные по характеру. Схему можно
рассчитать при Z1=Z2=/p RaRB — /ЗОм; Z3 =—/ЗОм; Zj =Z>=
=—/ЗОм; Zs = /30m.
3 . а) Мощность, выделяющаяся в нагрузке без согласующего
четырехполюсника, Р2 — I2Rn = UjRHJ(Ra + /?н)2 = 900 Вт.
б ) Мощность, выделяющуюся в нагрузке при наличии согла-
сующего четырехполюсника, собранного по Т-схеме с параметрами
Zx = Z2 = /30m; Z3 =— /ЗОм, определим следующим образом:
/______ RA Д • / _/ —___ г — А-
1’-^В + «1вх_ ’ 2 + 73Л’
Р2 =/2/?ч = 2500 Вт.
4 .31р. Из условия согласования источника энергии с нагруз-
кой входное сопротивление четырехполюсника, представляющего
собой идеальный трансформатор, нагруженный на ZH, должно
быть равно сопряженному комплексу сопротивления источника:
Z1DX = Z;=1—/Ом;
ZXbx —^4/Л» Z.n=U2[l2.
У идеального трансформатора потери в обмотках отсутствуют
(/?! = /?а=0) и коэффициент связи обмоток /г=1 (отсутствуют
потоки рассеяния), поэтому
= (1)
UJU, - UjU, = = n (2)
(так как в данном случае = c/2 = to2-^ ; = Ф321;
/;//; - -1 /п=4//.=/х//2. (З)
Тогда Zlm = Ul/ii = Uin/l2/n = U2nz/l2 = Zlin2, т. е. сопротивление
нагрузки имеет такой же характер, как и входное сопротивление:
= (1 — /) 5“ = 25 — /25 Ом.
248
4 .33р. Расчетные уравнения для активного четырехполюсника,
Приведенного на рис. 4.14, запишем с помощью У-параметров:
2К1
(1)
где —часть тока вызванная ЭДС, находящимися
внутри четырехполюсника; ^ЕКУ.»К—часть тока /2, вызванная
теми же ЭДС. Эти токи могут быть определены из условия
одновременного короткого замыкания входных (тп) и выходных
(pq) зажимов четырехполюсника, т. е. при Ui — С\ — 0. Обозначим
SF Y = 1 • У Е Y — I
L'k1 Ik ' 1х» к' 2к 12к-
Для данной схемы /1н — 1,41е_/’82° А; /2К=- 4,06е/113° А. Эти токи
имеют то же направление, что и токи 1г и Л.
Подставим значения токов при коротком замыкании в урав-
нение (1):
Правая часть этих уравнений ничем не отличается от правой
части уравнений, записанных для пассивного четырехполюсника.
Следовательно, YiU У2], У«2—параметры пассивного четырех-
полюсника (при Et = Ё2 — Е3 = 0).
По условию задачи следует определить не У-, а .4-параметры.
Для данной схемы А — D= 1 —j; В — 20—/10 Ом; С = —/0,1 См.
Расчетные уравнения в А-форме записи:
й^Айг + Вй,-^)-
И] =
4 .35р. 1. Гиратор обладает свойством инверсии сопротивления на-
грузки. У гиратора Ап =А22=0. Входное сопротивление гиратора,
нагруженного на ZH, ZBX= Ai2/(AaiZH)= 1/(G2ZH), i де A21=G; 1/412=G.
Тогда — — и матрица гиратора с А-параметрами
‘0 1/G1
G 0
. Уравнения гиратора через У-параметры (с учетом
изменения направления тока /2): ll = GU2t i2 — — GUt. Матрица
с У-параметрами
[У1= 0 G .
L J — G Oj
^-матрица гиратора для Z-параметров
Г 0 — 1/G
1/G О
2. ZM = 1/(G2Z„) = jaCIG1 = jvL„
где L3 = C/G2.
[ZJ =
249
4.37 р. Для определения Л-параметров результирующего четы-
рехполюсника, эквивалентного двум каскадно включенным гира-
торам, используем Л-матрицы гираторов:
[Л] = [Л1][Л2] =
О 11 Го 1/л
/ о] [л О
п О
О 1/п
что соответствует Л-матрице идеального трансформатора.
4.38 р. Z-матрицу гиратора можно представить как сумму двух
матриц:
[Z] =
О — 1/G
1/G О
О О
1/G 0.
0 — 1/G1
О 0 Г
Эти матрицы соответствуют двум последовательно-последовательно
включенным четырехполюсникам, удовлетворяющим уравнениям
С/i = 0; 02 l)s—0и являющимися источниками
напряжения, управляемыми токами. Таким образом, гиратор реа-
лизуется схемой, приведенной на рис. Р.4.2, с. F-матрнцу гира-
тора можно также представить как сумму двух матриц:
rvn 0 G] Г° G1 t Г 0 0]
lrJ = | — G 0] = [0 0j+| — G О]’
Эти матрицы соответствуют параллельно включенным четырехпо-
люсникам, удовлетворяющим уравнениям 71 = G(72; /2 = 0 и /г— 0,
Рис. Р.4.2
— GUX и являющимися источниками тока, управляемыми
напряжением (рис. Р.4.2, б).
4.39 р. Если Диа = £Л; Аь®/.; Д«с = (71; Aic = /,=(), то урав-
нения лампы как четырехполюсника могут быть записаны с по-
мощью Р-параметров:
АКГо о'
L 4. Is J
<А1
L <4 Г
Эти уравнения соответствуют схеме замещения с источником тока,
управляемым напряжением (рис. Р.4.3, а). Внутреннее сопротив-
ление лампы /?-— i/g;. Если источник тока заменяют источником
ЭДС, то получают схему замещения с источником напряжения,
управляемым напряжением (рис. Р.4.3,б). Здесь р — S/g^SRe
250
4.40 р. Транзистор является невзаимным четырехполюсником,
так как /?12#=₽21. Добавим в уравнение (2j ±Z?j,Aij. Тогда
система уравнений будет иметь вид
Д«1 — РпАц + /?12ДС, (О
Лн2 = R12ДГ! /?22ДГ2 + (Я21 — /?12) Дij. (2)
Обозначим /?а1—Ri2 = Rm- В результате получим
0 0П Дц'
Rm 0 J J _ Af2
Г Awt ( /?ц Rlt
| ДПо J R12 R 22
Эти уравнения соответствуют двум последовательно включен-
ным четырехполюсникам: взаимному четырехполюснику, который
может быть представлен
Т-схемой замещения, и ис-
точнику напряжения, уп-
равляемому током (рис.
Р.4.4, о). Сопротивления
Т-схемы замещения Zt =
~гЗУ Z2 = rK, Z3 = r6y они
выражаются через Z-пара-
метры: G=/?u —/?12; гк =
~Ri2 Rl2i^6 = Rl2- ЭДС
управляемого источника
е RmMy = Rm&i3. Источник ЭДС можно заменить на источник
тока (рис. Р.4.4, б). В этом случае /?Л/гк=а—коэффициент усиле-
ния по току.
4.41 р. 1. Если выражение для тока (напряжения) в комплек-
сной форме записи имеет вид
М л • б
8 — । .ТйГ нл и ® — ft Ч________>
где векторы ЛТ, N, О постоянны, коэффициент k меняется от 0
До оо, угол ф постоянен и не равен 0 или ±180°, то геометри-
ческим местом концов вектора тока (напряжения) является дуга
окружности (круговая диаграмма). При ф = 0, il80° геометри-
ческим местом концов вектора тока (напряжения) будет прямая
Диння (линейная диаграмма).
251
Используя метод эквивалентного генератора, заменим схему>
за исключением ветви резистора переменного сопротивления /?п>
эквивалентным генератором с ЭДС Д», равной напряжению хо-
лостого хода йтпк на разомкнутых зажима к резистора перемен-
ного сопротивления Ёа = Umn х = и входным со против-
лением ZaBX = R^jx*
Входное сопротивление схемы относительно зажимов пере-
менного сопротивления определим из исходной схемы при замене
имеющихся в ней источников энергии их внутренними сопротив-
лениями (для источников ЭДС ZB = 0, для источников тока
ZB = oo). Тогда ток в нагрузке
J __ ^9 _______Ё1Т-2 вх___
Z„ + Z2„ 1+&'<’'« “’«•»> ’
т. е. конец вектора тока /н скользит по дуге окружности, хор-
дой которой является вектор а направление касательной
определяется углом гр — <рн—фавх.
В линейных цепях ток (напряжение) в любой ветви связан
с током в другой ветви линейным соотношением. Например, ток
на входе цепи и напряжение на индуктивном сопротивлении свя-
заны с током в нагрузке соотношениями ix — a-\-bIн; U t=c-\-dI
Коэффициенты о, Ь, с, d найдем при режимах холостого хода
(/?н=оо) и короткого замыкания (Ян = 0).
В общем виде получим
0)
(2)
Приведенные выражения свидетельствуют о том, что геометри-
ческим местом концов векторов /т и UL также являются дуги
окружностей.
2. Для построения круговых диаграмм рассчитаем следующие
режимы цепи:
а) режим холостого хода:
/- = ^Тх7 = 7.°7е-'45“ А;
l>lM=/„JX,=7O,7e/‘s’ В;
б) режим короткого замыкания:
/«^t>l/(/Xx) = 10e-/90’ A; ULK = йг = 100 В:
в) режим для определения входного сопротивления Z2FX отно'
252
сительно зажимов тп:
Отсюда
ф = Фв—Ф2 вх = 0—45° = — 45°.
С/1 = 70№° +
io-/9O°_7ia7e-/45»
i+fe->43°
100 — 70,7е'15°
l+fte-/45“ Ь.
А;
Строим круговую диаграмму для 1Х. Окружность проводим
по хорде оЬ, являющейся разностью векторов Ц
тельной, проведенной под углом ф к
ке Ь. Центр окружности О лежит
на пересечении перпендикуляра,
проведенного из середины хорды,
и перпендикуляра к касательной
(рис. Р.4.5.)
Для построения линии перемен-
ного сопротивления (ЛПС) на хорде
от конца вектора тока холостого хода
(точка а} откладываем в масштабе
модуль сопротивления Z.^ (отрезок
ас). Затем от конца этого отрезка
под углом ф проводим ЛПС.
3. При /?в=10 Ом по круго-
вой диаграмме найдем /1=8,95е“,б3*А;
cos ф — 0,46; Рх — их1г cos ф = 400 Вт;
Q — 800 вар.
4.42р. Круговую диаграмму нап-
ряжения Umn строим, исходя из вы-
ражения для дуги окружности в общем виде (см. решение задачи
4.41р):
1К и /тх и каса-
продолжению хорды в точ-
Касательная $
4,
W
Ф г,Я
Рис.
Р.4.5
г*г г'[ । тп к U тп х
тп Uтп х । . /1Ь
Режим холостого хода (хс=оо):
• • • • Ё
4>п ~ Фо» Ф/»х Флх Лх*1 Фпх~ Rj ~
= Флх 2~’ -^/2.
Режим короткого замыкания (хс = 0):
• . . . . . Ё . ё
Фот И.= Фл K_b^jK^8 Фим I ^3==фяк4 2"
Определим входное сопротивление относительно зажимов Ьп:
Ztll = R2 = R.
253
Рис. Р.4.6
Угол ф = <гн—Ф?нх = — 90е —
—0° = — 90ф. Дугу окружнос-
ти строим в соответствии с
выражением
fl == £ £/2-(£/2)
тя 2 1+Ле-'^'
Круговая диаграмма приведе-
на на рис. Р.4.6.
Глава пятая
5.1р. Для рассматриваемого четырехполюсника Л = (Zj 4-Z2) Z ;
D=l. ___ ________________________
Уравнение ch g = l^AD — pr(Zx 4- Z2)/Z2 — V 1 4-Z,/Z, имеет место
при любом направлении передачи.
В области прозрачности (о = 0) g = a + jb = jb; chg = ch jb~
= cosb — |/ 1 TZj Z2. Последнее уравнение имеет смысл лишь
в том случае, когда V1 -j- Z1Z.2—вещественное число, по модулю
не превышающее 1. Для этого подкоренное выражение должно
удовлетворять системе неравенств 0=С 14- 1, откуда — 1
5.2р. Для рис 5.2,q ZX — \^L\ Z2 —— j . Из рассмотрения
частотных зависимостей Z17 и Z2 j, построенных на рис. P.5.L
следует, что зона прозрачности ограничена частотами со, =9 и
со^ = 1 \/"LC (на частоте соо |Zi| = |Z2|), т. е. схема является ФНЧ.
• , 1
f f-
Для рис. 5.2,6 Ze=j [соЛ-1 (соС)]; Z2—-----Лд *
/toL“/«С
Согласно рис. Р.5.2, полоса прозрачности ограничена частотами
254
0 и o2, определяемыми из уравнения |ZJ = |Z2| или
(I)
Рассматриваемая схема является полосно-пропускающим фильтром.
Из аналогичных построений следует» что на рис. 5.2,6 дан
ФВЧ, частота среза wc =соо= на рис. 5.2, г — ПЗФ, гра-
ничные частоты определяются выражениями (1), на рис. 5.2,6 —
ППФ, полоса прозрачности ограничена частотами о\= 1 l^LC;
0,= ^2/KLC, на рис. 5.2,е—ФВЧ, частота среза <ос = р 2,1 LC.
5.6р. Для четырехполюсника рис. 5.1 A^Zj+Z^/Z^ D= 1. Тог-
да chg=ch(a4-/fe)=|/^D=K(Z14-Z2) Z2 = J' l-hZj/Z.,: chacosfc-f-
4-/ sh a sin b = 1 4- Z/Z,. (2)
В полосе прозрачности o = 0; shn = 0, cho=l.
По (2), ch g cosb = p I 4- ZltZ2; cos2b — 1 =Z, Zs — — sin2b;
sinh = ±l —Zt.'Z2. Так как в полосе прозрачности, по условию
(5.1), Zi/Z2<0, то sin6= IZj'Z. |. Таким образом, в полосе
прозрачности коэффициент фазы потузвена связан с комплексами
Zt и Z, выражением b — ± arcsin KlZj/ZJ .
В полосе затухания а^=0. Здесь необходимо выделить два
случая.
1. Знаки Z, и Z2 различны, или ~< 0. Согласно (5.1). для по-
лосы затухания |Z^Z-J > 1, Тогда 1 4- Z^/Z^ 1 —|Z, Z2| < 0 или
I 1 4- Zt/Z2 = ±: j Г |Zj/Z2| — 1. С учетом последнего выражения
в соответствии с (2)
( ch a cos b = 0;
\ shasin Ь = ± J [Z/ZJ—1.
Так как cho^O, то из (3) имеем cos& = 0: &=i90°r
Sinb— 1, Тогда из второго уравнения (3) следует, что sho =
lZvZtJ — I; sbIa=|Z,/ZJ —1; ch= а = 17.//,j.
255
Таким образом, при различных знаках Zx и Z8 в полосе зату.
хания
f a = arch/|Z1/Z8|;
\б=±90°.
2. Знаки Zj и Z2 одинаковы, т.е. ~ > 0. В этом случае 14-~->
_____________ ^2 Z2
> 0, а к 14-Z^Za—вещественное число. Тогда, согласно (2),
shflsin 6 = 0;
ch a cos b — |/1-|-Zi/Z2. ^)
Так как в полосе затухания sho=/:0, то из (5) имеем 6 = 0;
cos6=1; ch а = |/ 1 -f Zj/Zs; ch2a = 1 4-Z,/Z2; sh2a = ZjZ2. Tогда
в полосе затухания
f a = arsh |/Zi/Z2 = arsh К| Zj/Z, |;
(6 = 0.
5.7р. Заданный симметричный фильтр
расщепляется на два полузвена (рис.
Р.б.З.о). Комплексы продольного и попе-
речного сопротивлений полузвена равны
Zj = j<n£j — / ; Z2 = Частотные за-
висимости -5- (ы) и -у- (to) построены на
рис. Р. 5.3. б. Согласно рис. Р.5.3, б, по-
лоса прозрачности полузвена, а следова-
тельно, и заданного симметричного фильт-
ра ограничена частотами и соа. Ниж-
няя граничная частота tot определяется
из условия lZil = IZ>l или Zx =— Z2 (рис.
Р.5.3, б):
1 1
to. = — — - _ — = —г — . ——-- —~ ==
1 У (Li + Ls) ^20-10-3-0,5-Ю ъ
= 1-10* рад/с.
Верхняя граничная частота находится из условия Zx = 0:
<0.Lt-------------т" = 0; в, = -Л= = 21С' рад/с.
Таким образом, данный четырехполюсник является полосовым
фильтром.
Расчет зависимостей а (и), 6 (и) ведем по выражениям (5.2)-"
(5.4), учитывая, что фильтр содержит два лолузвена:
!2 arch V Z-JZ2 | при (знаки Zt и Za Р33'
_______лнчны; рис. Р.5.3,6);
2 arsh К| Zj/Z21 прии2 С to оо (знаки Za и Z2
наковы; рис. Р.5.3, б).
266
Полоса прозрачности
Т а б л и и а Р.5Л
Ш[ (Oj
(о- 104, рад/с 0 0,4 0,8 0.9 1,0 1,2 1.4 1,6 1,8 2,0 2.1 2,4 2,6 3,0
Zi Z1K . 1 —oZ-i — , Ом / 1 1 <оСх ’ — 00 —480 —210 — 177 — 150 —106 —73 45 —21 0 9J 36,7 53 83
Ом / 0 60 120 135 150 180 210 240 270 300 315 360 390 450
Zj»=A±A, o„ J 1 — 00 —420 —90 42 0 71 137 195 249 300 325 397 443 533
| v Z|0Z1K|=|Zc|. Ом 00 450 137 86,5 0 89 100 93 72 0 56 120 153 211
Характер Zc Емкостный Активный Индуктивный
x-/|Z,/Zs| 00 2.8 1,32 1,14 1 0.77 0,56 0,432 0,28 0 0,18 0,32 0,36 0,44
। 2 arch x 0— <Dt; a, Hn=J 0 <i)i— d)2; I 2 arsh x (i)2— oo co 3,4 1,5 1 0 0 0 0 0 0 0,32 0,54 0,6 0,8
r —180° 0—coi*, 6, град=‘* —2arcsinx coi—a)2;’ 0 <i)2—oo. M СП — 180 — 180 —180 — 180 -180 — 100 —70 —52 —31 0 0 0 0 0
В полосе прозрачности при cOj^co^CcOj а = 0, b (со) =
= —2 arcsin И ] Zx/Z2 | . Отрицательный знак в выражении для’б (со)
выбран после качественного построения векторной диаграммы
полузвена в области прозрачности (рис. Р.5.4, б). При ее построе-
нии учитывалось, что в полосе прозрачности (см. рис. Р.5.3,6)
продольное сопротивление Zr име-
ет емкостный, поперечное -
индуктивный, а сопротивление сог-
ласованной нагрузки—активный
характер. Эквивалентная схема
полузвена в полосе прозрачности
изображена на рис. Р.5.4,а.
Сдвиг фаз между Ul н йг на
рис. Р.5.4, б обозначен Ь/2, так
как он соответствует полу звену.
В полосе затухания при OsC
со < (olt когда Zj и Zt имеют
различные знаки (см. рис. Р.5.3, б),
согласно (5.3) и рис. Р.5.4, б,b(со)—
— const = b (о)1) = —2 arcsin 1 =
= —2 90°= —180°. При со > со.,,
когда знаки Zj и Z2 одинаковы, в
соответствии с (5.4)
b (со) = const = 0.
Так как характеристическое сопротивление заданного фильтра
Zc равно характеристическому сопротивлению ZT полузвена (см.
рис. Р.5.3, а), то зависимость Zc (со) строим по выражению
Z,(u)=ZT(<o) = /Z^;
ГД6 ~ Zi~t~ Z2 = j<0 (£rf -f- С'а) j ~ “ J (®C1 ioCi” / *
В полосе затухания характер Zc аналогичен характеру Zx (р>,с-
Р.5.3, б). Расчет зависимостей a (io), b (со), Zf(co) сведен в табл-
p.5.1. По данным табл. Р.5.1 на рис- Р.5.5, а, б построены сооТ'
ветствующие графики.
258
5.11р. Для обеих схем k=^V LiC = 1/ = 100 0м. Гра-
1чные частоты фильтров определяем из условия IZJ^A или
Зависимости а (со) получаем по выражению (5.3), так как для
фильтров знаки Zx и Z2 различны на всех частотах.
Рис. Р.5.7
Рис. Р.5.6
Для фильтра типа k, согласно
Hzg/fc«i=l^Ik*=fc/|z1|.
Зависимости Ь(ы) в поло-
се прозрачности определяем
по выражению (5.2); знак в
(5.2) выбирают после пост-
роения -векторных диаграмм
фильтра, нагруженного сог-
ласованно.
В полосе затухания, сог-
ласно (5.3), b (со) — ±90°.
Знак b (со) в последнем слу-
чае находим по знаку 6 (со)
на граничной частоте.
Зависимости ZT (<о) и Zn («)
строим по выражениям ZT =
“/Z1XZ1K = l^(^i ” ^2)
^VZ?i + Z,Z.t = Vk^—\ Z, Is;
Zn — k^(Z-\. В полосе проз-
рачности ZT и Zn активны,
в полосе затухания характер
ZT совпадает с характером
продольного сопротивления
Zn Zn имеет противополож-
ный характер.
(5.2), (5.3), x-K|Z/Z2| =
Схема рис. 5.2, б (ФВЧ). Согласно рис. 5.1, Zx =— * ^2 —
/со/.; х = Zx/Z21= 1 /(соИ IC) = co0/co, где co0 = 1/KZC = 2 X
104 рад/с; A = |/L/C= 100 Ом.
259
Граничные частоты полосы прозрачности из условия |Zt|^£
определены по рис. Р.5.6, б. На частоте среза <ов=1/И£С;
На рис. Р.5.6, в построена векторная диаграмма фильтра
(рис. Р.5.6, а), согласованного в полосе прозрачности. Согласно
Z,DM
icoC k* nen \
*=-п-7—1/> ,Лп=~7~ (Рис- Р-5.9, а).
/ (oL—1/(соС)] Zi
<9
рис. Р.5.6, в, Ь<0. По-
этому в полосе прозрач-
ности б (со) = —arcsinx; на
частоте среза b (со^) =
=— arcsin 1 = —90°. В по-
лосе затухания b (®) =
= const — b (со0) — —90°.
Зависимости п(ш), b (со),
ZT(®), Zn(o) по данным
табл. Р.5.2 построены на
рис. Р.5.7, Р.5.8.
Схема рис. 5.2, в(ППФ).
Продольное сопротивленца
Z, = /((dL—1/соС); попере-
чное сопротивление Z2 =
Граничные частоты полосы
Рис. Р.5.9
прозрачности из условия | Z, | k найдены по рис. Р.5.9, б, сог-
ласно которому
( ®XL— 1 /((0,0 = — k = — VLiC\
I. (oxL— 1 /(<oxQ — k = V L/C;
0,, = —-^-(/5—1)я?1,236-10« рад/с;
<o2 ——1=г(/5+ 1)« 3,236 -10* рад/с;
260
Полоса затухания
Таблица Р.5.2
©о
(О- IC4, рад/с 0 0,4 0,8 1,2 1.6 1,8 1.9 2.0 2,1 2,4 3,0 3,5 4 5
Х«=(1)о/© 00 5 2,5 1.6 1,25 1,1 1,05 1 0,95 0,8 0,66 0,57 0,5 0,4
a. Hn=|’rchx0-“’: | 0 ©о — » 00 2,3 1,56 1,05 0,67 0,45 0,3 0 0 0 0 0 0 0
/— 90° 0—гп0; Ь, град={ . °’ г 1 — arcsinx ©0~» -90 -90 -90 -90 -90 —90 -90 -90 -72 -55 —42 —35 —31 —24
Z17=I/(wC), Ом — 00 —500 —250 — 166 — 125 — 11! — 105 — 100 -95 -83 —67 —57 -50 —40
|Zr! = |K*2-|Zil’|. ОМ 00 490 230 133 75 50 32 0 30 55 72 74 82 90
Характер Zj Емкостный Активный
|2-п| = Л2/1Ит|. Ом 0 20 43 75 133 203 310 00 330 181 134 122 116 109
Характер 2п Индуктивный Активный
Векторные диаграммы фильтра (нагруженного согласованно) в по-
лосе прозрачности построены на рис. P.5J0, б, г. Диаграмма
рис. Р.5.10, б соответствует области частот <ог—соп, где имеет
емкостный характер (рис. Р.5.9, б), a Z2— индуктивный, Эквива-
лентная схема фильтра на этих частотах (рис. Р.5.10, с) совпа-
дает со схемой ФВЧ.
В диапазоне частот <od—ю2, согласно рис. Р.5.9, б, Z,—имеет
индуктивный характер, a Z2—емкостный. Эквивалентная схема
фильтра при этом (рис. Р.5.10,в) совпадает со схемой ФНЧ. Соот-
ветствующая векторная диаграмма дана на рис. Р.5.10, г.
Согласно рис. Р.5.10, а, г, в полосе прозрачности
Ь(и) =
— arcsin х при сох—tv,
arcsin х при соо—ш2;
b (й1) = — arcsin 1 = —90°;
b (<ог) = 4- arcsin 1 = 4*90°;
в полосе затухания
в диапазоне 0 —<d1 b (со) = const = b (coj == —90°;
в диапазоне <о2 — оо b (со) = const = b (со2) = -|-90э,
где х = V| Zx/Z2| =-1 Zr \/k.
Расчет зависимостей п(со), б(со). ZT(w). Zn(co) сведен в табл. Р.5.3,
по данным которой на рис. Р.5.11» а, б построены соответствующие
графики.
5.20р. Задаемся комплексом [)2. Пользуясь законами Ома и
262
263
104, рад/с 0 0,4 1 1,2
1/(<оС), Ом — 00 —480 — 150 — 106
*«/|Zt/Za| =|21|/й 00 4,8 1.5 1.06
/О он — (0$; °- Hn=1archJ°-“*; V 1 (Og—00 00 2.5 0,95 0,36
b, град = r—90° 0—(Oil — arcsin z »!— (oo: 4-arcsin z (On—ws; k 4-90° (Oj—co —90 -90 -90 —90
|Zt|-|KOm 00 470 112 35
Характер Zt Емкостный
|Zn I-=**/|Zt 1. Ом 0 21,3 89 284
Характер Zn Индуктивный
Таблица Р.5.3
Полоса прозрачности
(Oj £t>0 (i)j
1,236 1,3 2.0 3,0 3,236 3,3 3,5 3,7 4,0 5,0
—100 —89 0 83 100 104 118 131 150 210
1 0,89 0 0,83 1 1,04 1,18 1,31 1.5 2,1
0 0 0 0 0 0,28 0,59 0,77 0.96 1,37
-90 -63 0 55 90 90 90 90 90 90
0 46 100 55 0 30 63 85 112 185
Активный Индуктивный
00 219 100 191 ОО 334 160 119 89 54
Активный Емкостны Ft
Кирхгофа, находим соответствующий комплекс Ut:
= 2 (И ZJZJ3 + 2 (И Z./Z,)1 + 2 (КZjzy + 1.
Для ФНЧ (рис. 5.10, a) fl=j«a>»LC=/»(-£)•; =/^ = /n:
1Z _ I ^2 I_ 1___________ 1 _* I I j
u I Ux I V(1 — 2^2)2-р(2^ —2т]3)2 V i — 4^4-4^ ’ 4 '
Для ФВЧ (рис. 5.10,6)
_ _J____________1 . 1 —___tv-
Zs~~ jWLC ~~ /8(<oM)* ’ V z2 ’to
К _ £г I_________________I__________ 1
U | 1^(1 — 2x*)>+(2x — 2x3)2 V i — 4x44- 4xb ‘
(2)
По выражениям (1) и (2) на рис. P.5.I2,ct,б построены графики
зависимостей с учетом того, что в (1) Т]=ю/С1)0, а в (2)
х = со0/со. Максимальное значение Китах= 1,557 достигается при
т) = х = У 2/3.
На рис. Р.5.12, at б представлены частотные зависимости коэф-
фициента передачи напряжения при согласованной нагрузке
^ul^n-Ze = и~ L _у — е °.
Так как для ФНЧ o = 2arch —, для ФВЧ а —2 arch то
ш0 ’ _____ со ’
с учетом соотношений archx= — ln(x—Rxz—1); e“2archA —(х—
264
—- }гхг— I)2 получим:
для ФНЧ «-«=(£-(3)
для ФВЧ е-« = (-^—^V—iy. (4)
Пунктирные кривые на рис. Р.5.12, д, б построены по выраже-
ниям (3) и (4).
Рис. Р.5.12
5.21р. Характеристические сопротивления полузвеньев, состав-
ляющих четырехполюсник рис. 5.11гд, со стороны зажимов 3—3',
согласно (5.1а),
ZT = У (Z, + ZjZ?; ZT„, ~ K(Z,„ + Z2„) Z,„ =
= ], (mZ, + Z, hz2!+Z,-L.) mZ, = / (Z, + ZJZ, = ZT.
Таким образом, ZT7J = ZT; следовательно, полузвенья рис. 5.11, а
соединены согласованно. В этом случае характеристическое со-
противление четырехполюсника рис. 5.11, а со стороны зажимов
1— Г совпадает с характеристическим сопротивлением А-полу-
звена с той же стороны:
Z =
265
Характеристическое сопротивление четырехполюсника со сто-
роны зажимов 2—2' равно характеристическому сопротивлению
Znm т-полузвена:
^Пт —
С учетом (5.9) и (5.10)
Zn„ - ^£гД1 + (1-т°)^] = Zn [1 + (l-™s) %] 0)
V 1+£
Тогда
ДП2=1 + (1—(2)
Zn Z2
Покажем, что полосы прозрачности полузвеньев при выполне-
нии (5.9) и (5.10) одинаковы. По условию (5.1), в полосах про-
зрачности । для &-полузвена — 1 ZjZ2 0, для zn-полузвена
1 Zlm/Z2rar 0.
На граничных частотах отношения ZjZ2 и Zlm/Z2m обращаются
в 0 либо в —1; согласно (5.9) и (5.10),
Z\m
%2т
mZi
m-Z^ tn~ZifZz
X = z^^l-m^Zt= l+(\-m*)~ZjZi
tn
(3)
В соответствии с (3) при ZjZ2 = $ ZlmlZ2m — 0f при Z1/Z2 = —1
Zlfl,/Z2m = —1, т- е- ZjZ„ и ZlmjZim обращаются в 0 и в —1 при
одних и тех же частотах. Следовательно, граничные частоты рас-
сматриваемых полузвеньев одинаковы.
5.24р. Характеристические сопротивления полузвеньев со сто-
роны зажимов 3—3‘ (рис. 5.11,6) определяются зак:
V ZiZ2 .
V 1 + Z\fZb
Zn —
%Пт —
mZzm
1 -Т- Zirfi/Zim
Подставляем в последнее соотношения (5.11) и (5.12), в результате
получаем Znm~^n- "
Характеристические сопротивления четырехполюсника рис-
5.11,6: со стороны зажимов 1—Г
ZT = ^(Z, + ZJZ, = гZ,Z2 V1 + Z^Z,;
со стороны зажимов 2—2*
Z-rm - V (Zlm + Z2„) Z,„ = /(Z, + Z;)Z,-!--=-;
l + (|_m^SJ
Z.2
(•)
266
В соответствии с (5.11) и (5.12)
Zim _ 1_______т _ тг __ т Zj
Z“ ~ Zi r+(’-m!) l+(l-m=)fl'
m£i пи,% Z] ts
Последнее выражение совпадает с (1) решения 5.21 р; следова-
тельно. здесь также справедливы выводы, сделанные в реше-
нии 5.21 р и позволившие утверждать, что полосы прозрачности
каскадно включенных полузвеньев одинаковы.
5.26р. Расчет зависимостей ат (со) и Ьт (со) для т-полузвена
проведем по методике, рассмотренной в задачах 5.6р, 5.7р. В со-
ответствии с соотношениями (5.2)—(5.4): _________
в полосе прозрачности ат (<о) = 0; bm (со) = ± arcsin И| Z^/Z^ |;
знак в последнем выражении выбираем после построения вектор-
ных диаграмм полу звена в полосе прозрачности, учитывающих
характер ZJm и Z2ra;
в полосе затухания:
при ~~ < 0
*-2т
' И = агс11 V I Z1/a/Z2,J; (2)
< bm (со) = ±90° [знак определяется знаком b (со) на сосед-
ней граничной частоте];
при -ф5- > 0
j О-m 0°) ~ arsh ] Zlm/Z2ffl |,
lbm(«)=0. (3)
В отличие от фильтров 1ипа £. для которых отношение Zj/Z»
всегда отрицательно, у фильтров типа т отношение Zlm/Z2m в по-
лосе затухания может быть и положительным и отрицательным.
Для расчета по выражениям (1) — (3) необходимо знание час-
тотной зависимости ZimfZim (со) *. Последняя в соответствии с (3)
решения задачи 5.21р определяется зависимостью (со) полу-
звена-прототипа :
г Zi о 1 Zi I
7 у т~ I у I
ZiCT _________Zq______ | ^g | П .-лч
7 7 7 I 7 V*J
2m £1 (1-W2) £1 _1 (l^rn2)- £2
Z-g ^2 I
Обычно зависимость |Z1/Zs|((o) или | Z2/Zj | (ио) известна из пред-
варительного расчета полузвена-прототипа.
При нахождении зависимости (со) следует принимать во
внимание то, что отношение Zim/Z2ffl меняет знак на частоте ц*,
* Так как отношение ZimIZ$m (<о) для последовательно-производного и па-
раллельно-производного m-полузвеньев одинаково, то зависимости ат(ь>) и Ьт (ш)
в Обоих случаях одинаковы.
267
при которой знаменатель (4) обращается в нуль:
(1 —m‘) + ^(a>J = O или —
(5)
Поэтому: а) на частоте со,, Zlm/Ztm = со и согласно (2), (3) за-
тухание, вносимое /п-полузвеном при со„, также бесконечно ве-
лико*; б) на частоте зависимость Ьт{<а) изменяется скачком
на ±90° [см. (2), (3)].
Таким образом, рекомендуется такая последовательность рас-
чета ав(ш) и Ья (со):
1) определяем зависимость ^(<о) для полузвена-прототппа.
В рассматриваемом случае ZjZt — (соо/(о)в, где соо—частота среза
для прототипа, а следовательно, и для производного ги-полузвена;
2) по выражению (4) рассчитываем зависимость -f12- (со).
Частоту находим по (5); в рассматриваемом случае на час-
тоте
со
Zj/Zjj = — (<Оо/со_)2 = |m=0 в = —1/0,64;
—0,8wo = 0,8-2-10*= 1,6-10* рад/с;
3) качественно строим частотные зависимости Zlm (ю) и Z2M (ы)
для одного из типов m-полузвена (последовательно-производного
или параллельно-производного). На рис. Р.5 Л 2, а построены Zlm(w)
и Z2/B(o) для параллельно-производного m-полузвена. При по-
строении учтено, что продольная ветвь (Z1IB) содержит параллельно
включенные индуктивный Llm~L и емкостный С‘1ж = С,-/и
элементы, которые на частоте —О,8соо вступают в резонанс
токов; поперечная ветвь Z2m содержит индуктивный элемент LSm =
= L/m\ на частоте среза ц,, по условию (5.1), |Z2ra| = |Zlrt |.
Согласно рис. Р.5.12, в, в полосе затухания 0—при 0 < со <
< <*>« ?ia И имеют индуктивный характер, > 0; при со^ <
< со < й>0 Zlm имеет емкостный характер, a Zim—индуктивный;
Z,
-я-5- < 0 в полосе прозрачности со > со0, Zlm имеет емкостный,
ZZm— индуктивный характер;
4) на основании результатов п. 3 по (2), (3) получаем окон-
чательные расчетные соотношения для а„(со):
{arsh И | ZiJlin |; 0—
arch И| Zlm/Z2m ]; <ото— соо;
0 ; (Do—оо;
• В случае последовательно-производного гп-полузвена бесконечно боль-
шое затухание имеет место при ZZm 0 (резонанс напряжений в поперечной
ветви), а в случае парад лельно-производного полузвена—при 21и=0 (резонанс
токов на продольном участке).
26S
5) для выяснения знака Ья (ю) в полосе прозрачности каче-
ственно строим векторную диаграмму нагруженного согласованно
m-полузвена. При построении учитываем, что в рассматриваемом
случае Zln имеет емкостный, Ztm—индуктивный, а сопротивление
нагрузки—активный характер.
При этом эквивалентная схема m-полузвена совпадает со схе-
мой прототипа в полосе прозрачности (см. рис. Р.5.6, а). Соответ-
ствующая векторная диаграмма представлена на рис. Р.5.6, а,
согласно которому b < 0. Поэтому расчет Ъл (<о) в полосе прозрач-
ности ведем по выражению
(®) =—arcsin^ |Z1/7I/Z2a|;
на граничной частоте Ьа(<оо) ——arcs in 1 =—90°;
в полосе затухания, согласно (5.3), (5.4),
для ы„ Zle/Zan<0; *„(<!>) = 6„(й>0) = —90°;
для 0 Z,^Z,„>0, 6„(о) = 0.
Расчет и 6„(<о) по изложенной методике сведен в табл. Р.5.4,
по данным которой на рис. Р.5.13 построены соответствующие
Графики (сплошные кривые).
5. 31р. Схема рис. 5.12, в. а) При разомкнутых зажимах 2—2'
Задаемся напряжением на выходе и, пользуясь законами
Ома н Кирхгофа, рассчитываем соответствующее напряжение на
269
Т а бл и ца Р.5,4
Полоса затухания
1 w« | (i>0
о- JOS рад/с 0 0,4 0,8 1,2 1,5 1,6 1,7 1.8 1,9 2.0 2.1 2,4 3,2 4 00
^й| 7 W V—f ш V \ 2.10* ) 0 0,04 0,16 0,36 0,56 0,64 0,72 0,81 0,9 1,0 1.1 1,44 2,56 4 00
21а 0.36 ZSm 0,64 — (W/WO)J 0,56 0,6 0,75 1,3 4,64 oo -4,4 -2,1 -1,36 — 1 -0,8 * —0,45 —0,19 —0,11 0
= I 1 0,75 0,78 0,86 1,13 2,15 00 2.1 1.5 1,16 1 0,89 0,67 0,43 0,33 0
farshx 0 —(oe; am, Hn=| archx шм-й0; ( 0 <t)0— 00 0,59 0,7! 0,78 0,97 1.5 00 2,74 1.8 1,13 0 0 0 0 0 0
fO 0— <oM; bm, град = 4 —90° (о*, —ш0; I — arcslnx <o0— oo 0 0 0 0 0 0 —90 -90 —90 -90 —62 —42 —26 — 19 0
входе (/Др):
/?t +
+ Ui(p)Cip^R2-y-~^^ = U1 (py
i
Uo(p) rj r * R1R2^* 1^2
Ui (Д) ~ W - g , RyC^R^2+RtC2 ~ I
P RiR&iCi P*1-/?I/?£CiCi
где
°® RiRtCiC^ 0“
K" RiRzCiC^
б) При коротком замыкании за-
жимов 2—2' задаемся током на вы-
ходе /3(р) (рис. Р.5.14). Соответст-
вующее напряжение на входе
[/,(р)адр+Л(р)]^ +
Рис. Р.5.14
h(p) у (п\ У (п\ RiR^i
i/нл - У21 (Р) - УМ - — j
Р+ г
К, + R, *
в) Комплексный коэффициент передачи четырехполюсника в ре-
жиме холостого хода
н (М=я W |Р=/И = _Ц,+Др+^ =
____________। . 1
1 ( “ V_i_.7 “Ar о—*2)+/₽* ’
+4«r)₽
IЯ (/(О) | = Я (<o) = 1 — ,
1 v ' F(i --x2)4 P2*2
где (i)/£oo^x.
При R,=Rt = R, Ct = C2=C <»,= 1/(₽Q. ₽ = 3,
(1)
По выражению (1) в табл. Р.5.5 построен график Н(х), ха-
рактер этой зависимости свидетельствует о том, что рассматривае-
мая схема является ФНЧ. Найдем частоту среза Xj = b),^C из
Условия И М= 11]/ 2:
й=7-й^—4+/(1У^
©х^олэ/^с).
271
Разновидности
рис. 5.12
# (р). <оо
гг / <_ * .
W~/?Cp4-l~p + a>0 ’
(О0=1/(ЯС)
fj / \_ RCp _ р
^-/еср-н-Я7^?
И„(р)
г12(р)=1//?
Yn&^Cp
(Оо= 1/(ЯС)
• я< W = *г 1 к U2(pl Н(Р)= ; Рг+₽<йор4-<оо <00= 1/(/?1₽2С1С2); P=Wo (/?iCi4-/?2C24-/?|C2) 1 у / X UlRjCl ' 12 (р) ” ] " Р 1 _^l5s_r Я1+Я2 1
*' в) г •
1^1 сННт-ЧН 1W п п I R,T R? J 1 г) г □ о. 2 Я(р) = ; р2 Ч- Р<Оцр -J- со2 ®о= V(^i^aCiC2); Р=(1>о (/?iC j-|-/?2С2-|-J?iC2) с2 и12(р)= С1^-г Р 1 Ri (Ci4-C2)
\ V.6 - -> 6 i i2 г э иг(р) О, 2 Н (Р)= ; Р2+Р«оР+<Оо <о2= 1/(/?1/?2СхС2); (On г— 1/(^?2С2); Р^о^Л+ЯгСгЧ-ЯА) 1 V <12(р)да' " "J Р 1
° и*1 1 1 *) 2 —а К 1—с У/Р) X Р_ - ; Рг Ч~ Р(ОоР+(Оо (o^iaR^GCa); Р=(Оо (/?1С1Ч’/?2С2Ч“^2^1) 1 р Р HJ2(p)— Р 1 RiCt
Таблица Р.5.5
273
Разновидности
рнс. 5.12
Н (р). <во
У12 (Р)
И12(Р) =
р24-сио0р4~Юо
1 . , '
— (р4-оий0)
(А?14-/?г) Ci
RiRjCjCt
Н (р) = РН-омо0р+<оо .
PS 4“ Р<О0р+<йо
<|>о= l/CPiRaCjCa);
Ос—(Do Cjj
(Pf-j-Pg) \
К1К2 Cj
1
RiRiCiCi
Н(р)=----------;
p24-4d)op4-(Oo
<oD=i/(pq
Схема рис. 5.12,3. Эта схема представляет собой параллельное
соединение двух Т-образных четырехполюсников, изображенных
^22 (р) —
на рис. Р.5.15, а, б. При этом через
параметры составляющих четырехпо-
люсников наиболее просто опреде-
ляются У-параметры сложного четы-
рехполюсника.
Для подсхемы рис. Р.5.15, а
У?.(Р) =-----—j—;
* i 1р
Ср Г „ , I
Г?«(д)—j—
Р^2ЯХС
Для подсхемы рис. Р.5.15, б
u(p)- ^(^dp+2)* *
Продолжение к таб.1. Р.5.5
И (х); x==(j>/w0
Г рафик Н (х)
У-параметры сложного четырехполюсника:
У22 (р) = У м (р) 4- П2 (р); У12 (р) = У12 (р) + У?2 (Р).
С учетом R/2, СХ = 2С
. , 4 1
у . ч_ С Р ^RC^R^O _ с р«4 4«оР4(»о .
^22lP}— 2 ! '2 p-;-w0
V C?+R*C*_ С
nW- g । 2p+t)0.
R + RC
где l/(RC) = w„.
Согласно У-форме записи уравнений четырехполюсника,
4(р) - Г21 (р) (р) + Ую (р) f»(p)-
(2)
(3)
(4)
При разомкнутых зажима х 2—2' [/2 (р) — 0] из (2)—(4) следует
^2 (р) = LJ / \ „ У21 (р) ра4~Юб .
Vi (Р) 22 (Р) р* 2 * * 4 4©ор4^ ’
и/. х --(и24*«о 1 —ха . .
Н ^--^+^+<4 ~ •-*г+Ях ’ Х~
И (г)=-yj=!.~/s 1 J~ 1_—. (5)
' 1 /(1—х2)2416ха Г j-i-14x2-px«
275
График Н (х), построенный по выражению (5), дан в табл.
Р. 5.5; схема обладает свойствами полоспо-заграждающегофильтра.
Расчет остальных схем рис 5.12 проводится аналогично. Вы-
ражения Н (р), У12(р), Я (о) для четырехполюсников рис.
5,12,0—з приведены в табл. Р.5.5. Там же даются соответствую-
щие графики Я(х). где x = (o/ti)0 = (o/?C (для схем рис. 5.12,в—ж
при Ri — Rt = Rt Ci = C2 = C).
5.34р. В общем выражении Н (со), полученном для схемы рис.
5.12, д (см. табл. Р.5.5), учитываем, что при Rt = R, Ci — C,
Ri = tnR', Ct~C/nv, we2=ioo= 1/(/?С); P = coe^7?C-r ₽С+/?С^ =
т
1
(!)
Последнее выражение достигает максимального значения при
1 [со== 1/(/?С)], когда знаменатель его минимален, причем
^шах = 2+Т/т ‘ Тогда для граничных частот полосы пропускания
справедливо уравнение
Н(Х}
^Лпах
______________________i______________________ _]
]/ 1 "^“(2-4- 1/m)®
(1а)
или
(х— 1/х)2 —(24- 1/т)2.
Нижнюю граничную частоту (xt < 1) определяем из уравнения
Xi — 1 /х2 = -(24- 1/m), (2)
а верхнюю граничную (ха> 1) — из уравнения
х2— 1/х2 = 24- 1/т. (3)
Из (2) и (3) получаем
х2=+о.5(2+1) +
Ширина полосы пропускания Дх=х8—х2 = 24- 1/т.
Частотная зависимость (1а) по виду сходна с зависимостью
от частоты модуля комплексного коэффициента передачи после-
довательного RLC-контура, если выходное напряжение снимается
276
c R (рис. Р.5.16):
где <^=1/1^10; Q=-~^C-—добротность контура.
В выражении (1а) добротностью является ФЭк = 2-| 1/т' ^ак
же как и для /?£С-контура, в рассматриваемом случае с ростом
кривая Н (w/ti)0) становится острее.
Ширина полосы пропускания Дх=ха—
—х1 = 2 + l/m=l/Q3K обратна эквивалент-*
ной добротности.
При т= 1 Фэк= 1/3, Ах = 3 [этому слу-
чаю соответствует график Н (х) схемы д)
табл. Р.5.5]. С ростом т Q3K увеличивает-
ся, однако она не может быть
Рис. Р.5.16
больше
1/2. Следовательно, относи-
тельная ширина полосы про-
пускания Ах >2 (A(d>2too).
По выражению (1а) на
рис. Р.5.17 построены графи-
ки Я(х)/Нш>ж для /п = 0,5;
2; 10.
5.41р. Передаточная функ-
Рис. Р.5.17 ция /?С-четырехполюснпка
цепи отрицательной обратной
связи согласно данным табл. Р.5.5 (схема ж)
Я(р) =
Р^+У 2(1)0р-|- coj __ U 2 (р) .
р24- 2 К 2 ь)0р+<оо ^вых (Р) *
2l(RC).
В соответствии с рис. 5.19
(Р) = и, (р) - и, (р) = ивых (р) Н (р) -
^вых(Р/
= <Лых (Р)[^(Р)—?]•
Результирующая передаточная функция четырехполюсника цепи
обратной связи Uoc (pWKm (р) = И (р)—у. Передаточная функция
активного фильтра, по (5.13),
К (р) =_____!_________________!________=
Я(р)-у р2+К2й)0рН 4
р*-|-2)/ гсоор+соо
При у = 0,4
__ Р* 4" 2 У 2 (0ор -J- coo I
а । > —, 1 — 2 t—у
Р + * 2 '1 —у “оР
К (р)= 1,66P‘4 2,93,'W’J- ,
р*0,47(0^ + соо
(1)
2П
при у = 0,5
P2-j-wo
(2)
В последнем случае К (р) имеет мнимые полюсы ± М,
A (ы0) = 00 -
Графики К (<о)/Ктзх. соответствующие выражениям (1) и (2),
построены на рис. Р.5.18 (кривые / и 2).
Рис. Р.5.18
5.42р. Передаточную функцию всей системы выразим через
передаточные функции четырехполюсников А и Б НА (р)п НБ(р)1
К(р)=Ял(р)[-^]
при условии, что усилитель инвертирует сигнал.
Согласно данным табл. Р.5.5 (схемы в и ж),
Д (р) о . Q 1 2 *
Г Ч~Рл«оЛР Т ыо.4
(1)
_ 9
где при /?д = ^б;Сл = С£; Рд^Рь=2И2; о^д—«0Б=ш0= 1000 рад^с
и многочлены знаменателей НА(р) и НБ(р) одинаковы: аБ = р 2.
Следовательно,
2 2
= Ы,'А . » °--------------и-Л* а. »• (2)
Р'Ч-ссбсооб-^ сооб Р"+г 2ы0р-|-соо
Хотя выражение (2) для К (р) аналогично выражению (1)для
передаточной функции входного двухзвенного ФНЧ НА(р), но
качество фильтрации активного фильтра выше. НолюсыА(р) —
комплексно-соп ряженные [определяются нулями передаточной
функции НБ(р)], а Нл(р)—вещественные.
На рис. Р.5.19 для сравнения изображены частотные ха ранте-
Г 7 / (1J \ у* / (1) \ _
ристики л л I — 1 и A I — ], 1 де <ос—частота среза, соответствующая
уровню 1/И2. Для НА (со) (ос« 0,4ю0, для К (со) coc = (dfl.
278
5.44р. Согласно табл. Р.5.5 (схемы в и ж) с учетом обозна-
чений рис. 5.16
Y (п\ —_____ .
р + 2//?лСЛ*
(СВ/2)(р«+ ? р^-5-г)
гл / _\ \ ZJl-.fi К Б^Б /
г12Б\Р)~ р + ‘2/ЯбСб
По условию, = Са = Сб. Тогда выражения в знаме-
нателях передаточных функций К12Л(р) и Г1гБ (р) одинаковы
(полюсы К12д (р) и УиБ (р) равны). Следовательно,
2
I/ Z х 12л (р) _ РбСб___________________Wo______
У12Б(Р) 2 ______2. 2 p^ + V ЗсооРЧ-юо’
Р 'КбСьР
где <о„ = 1/Г2,''(₽вС£)= 1000 рад/с.
Полученное для К (р) выражение совпадает с (2) решения 5.4 2р,
поэтому АЧХ К (to/w0), построенная на рис. Р.5.19, справедлива
и в этом случае. Активный фильтр, так же как в фильтр задачи
5.42р, является ФНЧ.
Необходимо иметь в виду, что в рассматриваемом случае ем-
костный элемент Сл/2 четырехполюсника А может быть исключен,
так как он работает в режиме короткого замыкания.
Таким образом передаточная функция вида (2) в задачах 5.42р
в 5.44р реализована по двум различным схемам. Реализация по
схеме рис. 5.17 предпочтительнее по ряду причин. Одной из них
является меньшее число элементов.
5.47р. Переходим от заданной схемы к эквивалентной расчет-
ной схеме (рис. Р.5.20), учитывая рис. 5.23,6. Считаем также,
что входное напряжение 0вх обусловлено идеальным источником
Эде £.х = 1/.х.
Искомая передаточная функция К (р) =
U в х \Р)
27Э
Так как коэффициент усиления ОУ р = т-^вы.х---> оо, а вели-
Фв. ФЬ
чина £вых конечна, то фй—фь = 0 или <pa = (pb1 фс(р) = фь (р).
Таким образом, при заданной ЭДС £Вх(Р) ЭДС £в«х(Р)
такова, что Фа(р)-Фь(р)- Этим условием и определяется пере-
даточная функция системы.
Составляем для эквивалентной схемы рис. Р.5.20 систему
уравнений по методу узловых потенциалов относительно изобра-
жений. При этом принимаем фь(р)=0, а точку а считаем узлом:
Фо (Р) ( С,р + — ф. (р) ф. (р) СзР = 0;
—Фо (р) С,р—фс (р) С ,р + фе (р) ( + Cj> + Csp'j =
= £.х(Р)у^-
При ф.(р) = ф6(р) = 0, фг(р) = {/в„х(Р) система (1) принимает вид
^вых(Р) Фе(Р)^зР
— *Лых (р) С4р + фе (р) (~ + 4; + С4р + с3р) =
= £« (Р)^ = ^вх (р)^«
Делим уравнения системы (2) на Г7ВХ (р) и решаем относительно
^вых(Р)/^вх(Р):
^ВХ (р)
= X (р) =-------------------j--------------------j---------
РЧ~~СзС< „ р+ R1R2 „ ~
СзН-С4 5 R1+R2 3 4
_ Р«>оР
St I 2 *
Р cuijQp -J- <oq
где
С учетом числовых значений параметров схемы получаем
(о0 = 20 рад/с; а(оо=1 рад/с; 0юо = 2О рад/с.
Следовательно, а^=1/20; 0=1;
(Р) ~ р2_|_р4- 400 ’ (
АЧХ, соответствующая (3) и (4), имеет вид
280
сходный с частотной характеристикой фильтра на РГОконтуре
(см. рис. Р.5.16) с добротностью Q = 20.
Таким образом, схема обладает свойствами высокоизбиратель-
ного полосно-пропускающего фильтра с центральной частотой
ь)0 = 20 рад/с (/о = 3,2 Гц). Ширина
полосы пропускания Acd = cd0/Q—
1 рад/с (Af = 0,159 Гц).
График (o)/g)0). построенный по
выражению (5), дан на рис. Р.5.21.
Г лава шестая
6.5р. Показание ваттметра
P\v = Uncf л cos <р1 = UВС1А sin <рн.
Из векторной диаграммы рис. Р.6.1
найдем ф1=90°—<рн. Реактивная
мощность трехфазной нагрузки
ф=ИЗ [7Д/Л sinq)H=lr3Pw,= 4360 вар.
Определим аргумент нагрузки:
sin <рн = Pw/(UaIJ = 0,574; = 35э.
Активная мощность системы
Р = Р 3 ия1д cos фн = 6240 Вт.
Полная мощность системы
5 = /ЗУ,/. =7620 В-А.
а) При соединении нагрузки звездой фазное
сопротивление
7ф^=^е'т»=6,35е«5° Ом.
б) При соединении нагрузки треугольником фазное сопротивление
е*» = 19,05e'’3S’ Ом.
6.8р. а) Фазные наряжения на нагрузке симметричны и равны
фазным напряжениям трансформатора:
йАх = UA0. = 380 В; L?Bi/ = t/BO. = 380e-/l20° В;
L/c^«7co'=380e/l20° В.
Фазные токи также образуют симметричную систему:
/л=«)лО'//ф = 76е-/3^'А;
7B = 76e~/l56°s0' А; 7с = 76е'83°10' А.
векторная диаграмма токов построена на рис. Р. 6.2. а.
28!
б) Электрическая схема показана на рис. Р.6.2, б. Определим
смещение нейтрали нагрузки. Так как УфЛ = УГфВ = УфС = ^Ф» то
U0,x = ^^ф+^яГф-бсУф 254е-/е0° В.
ЗЕф
Рассчитаем фазные напряжения на* нагрузке и токи в каж-
дой фазе:
£/ло.=1)л—и0.л=335е'<'-; С'по- = UB—Uo;=335e-l'6'’ В;
Dx,. = —i7c—1/0.х= 126е-/60* В; /л = iWZ4 = 67e'4"10' А;
/в=1/во-/2ф = 67е/|62‘10- А;
/с = {/г0./2ф = 25,2е-'96°и‘ А.
Векторная диаграмма токов показана на рис. Р.б.2,в.
S)
Рис. Р.6.2
6. Юр. Определим ток в фазе В нагрузки: IB = UBfZB— 10е~'53С А.
При симметричной системе токов /А=а1в, 1с = а*1в, где а—опе-
ратор трехфазной системы.
Найдем токи и сопротивления в фазах А и С:
/л= 10е'67’ А; 7С = 10е-'173° А;
2Л = {7Л//Л = 10е-'67” Ом; Zc = Uc/ic = 15е-/52" Ом.
Рассчитаем линейные напряжения:
Uab = Ua— 141e'4SCB; UBC = UB—UC = 232^^5' В;
йСА=йс—йА=232^°^ в.
Векторная диаграмма токов изображена на рис. Р.6.3, а.
6.14р. Определим линейное напряжение:
Оса = ~ (0лв + 0вс) = 100е/143’ В.
Найдем фазные напряжения на нагрузке:
Оло- = Оао—йо-о -;
,7 л _ ОсаУа +UcbYr
Uc°f Уа + Ув+Ус ‘
282
При этом иАС= 100е-/37°В; Ул = 0,1е-/30° См; Гв = 0,2е'с°в См;
ус = 0,1 См.
Подставив числовые значения, получим Uao- = 57е'2350' В;
Е/яо' = 23е'',73° В; UCo- = 66е'11 <^5' В.
Рис. Р.6.3
Рассчитаем фазные токи:
/л = (/д0 Ул = 5,7е-^7°10'A; /s = 4,6с-/1270 А;
/с = 6,66е'п0°5' А.
Активная мощность трехфазной системы
Р — и АО-1A COS Фл + UboJb C0S Фв + и CG-I с CGS Фс — 777 Вт.
Реактивная мощность трехфазной системы
Q = и АО-I A sin Фл н ^во'7 в sin Фв + f }co-Ic sin Фс = 70*5 ваР-
Полная мощность
S = /P2 + Q2 = 779 В-А.
Векторная диаграмма напряжений и токов изображена на рис.
Р.6.3, б.
6.1Ьр. Заменим треугольник нагрузки А'В'С эквивалентной
звездой:
ZA = Z/\/3 — 6,6 4 /6,6 Ом.
Пусть L//,B = 220ef’30° В. Осуществим развязывание магнитно-
связанной цепи. Получим трехфазную цепь, не содержащую маг-
нитно-связанных элементов (рис. Р.6.3,в). Сопротивление каждого
линейного провода 2Л = /(ХЛ—Хм). Так как нагрузка источника
симметрична (£ф=^л-{ ZA), система фазных напряжений на ней
также симметрична ((/ло'== 220/И 3= 127 В) и расчет токов мож-
но вести для каждой фазы отдельно:
iА = йло-Мь + ZA) = 9,5е~/’ео°15' А.
Зайдем токи в фазах В и С:
= = А; /с =/ла=9,5е/59в-’5' А.
283
Рассчитаем фазные напряжения и токи в нагрузке:
Ua'b- = ЛЛ—/в2* = 155е'14"45' В;
1'л.в. = Va-b-iZ^ = 155e/,4‘4E'/28,2e/4s” = 5,5е-/30"15'А.
Исходя из симметрии нагрузки получим
=7/л.в.е/|20’ = 155е-<' »5”16' В; 1/с-л-=&л-в-е/,20” =
= 155е'134"46’ В; iB-c- = /л-в-е-',го’ = 5,5е^,5<>"15' А;
/см. =/Л,в.е/120»=5>5е/в9"<5- д.
Падение напряжения в линии
йлА’ = I aI^i + в!хм + cixM — i aIxl + 0 в + ^с) 1ХА1 =
=<AiXt-iAiXM^iAuxL-iX„)=47.5ei^ в.
Аналогично, йвв' = 47,5е“/9°в|5‘ В; t7cc' = 47,5e'149’45’ В. То-
пографическая диаграмма и векторная диаграмма токов изобра-
жена на рис. Р.6.4, а.
Рис. Р.6.4
6.20р. По второму закону Кирхгофа,
&АВ ~ ‘abR’» UВС ~ Bci^z
Uca — ^caI^i—I вс! Хм-
Полагая (7лв = 200 В и решая систему уравнений относительно
фазных токов, получим 7^ = ОавЖ — 20 А; 7ВС = —11,5-4 /20 —
= 23е/,20° А; 1СЛ = 11,5 + /20 = 23е/60° А.
Определим линейные токи:
/л=/лв-/сл=21,75е;/”-А; /в = /яс-/ля = 37.3е'"3’3’' А;
с a i вс = 23 А.
Топографическая диаграмма и векторная диаграмма токов по*
строены на рис. Р.6.4, б.
284
6.22р. Строим круговую диаграмму тока /А. При изменении
сопротивления Z„ по модулю в какой-либо ветви от о до ос ток
в любой m-ветви этой схемы
/ __ Г । Ж
^вх
да —ток в т~и ветви при ZH = oo; /ст|1—ток в m-й ветви при
ZH = 0; ZBX—входное сопротивление цепи относительно зажимов,
к которым присоединена нагрузка ZB.
Рис. Р.в.5
Для нашей схемы /Лх = 0. Для определения /Лк воспользу-
емся методом эквивалент кого генератора: = В соот-
ветствии со схемой рис. Р.6.5, а
Uao^ = UAB + l\jXL = 236е-/5°<0' В.
Входное сопротивление в соответствии со схемой рис. Р.6.5, б
7 — _ ои л/37° гк,
^вх — я IXL — \М.
Ток короткого замыкания /Ли = 9,85е~/‘42°40' А. Угол тр =
= фя—Фвх = —60°—37° = —97°. Круговая диаграмма тока JA по-
казана на рис. Р,6.5,а.
Строим круговую диаграмму напряжения Uo’o- При изменении
сопротивления ZH по модулю в какой-либо ветви от 0 до оо на-
пряжение на любом участке этой схемы
• *
I*/ If । UgbK ЦдЬк
иаЪ uabi п у ; {аз . »
1 I Zh 1фн
285
где Uab*—напряжение на зажимах рассматриваемого участка при
ZH = co; UabH—напряжение на зажимах рассматриваемого участка
при ZH = 0.
В соответствии со схемой рис. Р.6.5, a Uo’o^ = EB—1JXL=~
= 138е/17о°10'В. Напряжение t/o'oK = ^=100B. Сопротивление
ZBX = 24e/3?c Ом, угол ф =—97е. Круговую диаграмму напряже-
ния Uo'o совместим с топографической диаграммой потенциалов
(рис. Р.6.5, г). При изменении ZB от 0 до оо точка О' будет
скользить по дуге окружности от точки А до точки т.
6.25р. Запишем фазные напряжения в комплексной форме:
UA = 100е'30° В; U9 = —150 В; Uc = 75е'60° В.
Рассчитаем симметричные составляющие фазного напряжения-
йА0 = Ч3 ФА +йв + Uc) = 1 ОеЛ5°° В;
0Ai = 1/s(UA + aUB + a*Uc) = 105е->5,° В;
УАг = Чз Фа + + а0с) = 39е'«“ В.
Зная симметричные составляющие фазного напряжения UA,
найдем симметричные составляющие фазных напряжений йв я Uc:
i>Bo = t/Co = ^o=10e/15o°B; UBi ^аЧ)А1 = 105е-'171° В;
UB2 = aUAz — 39tfl630 В; Ucl^aUA1 = Юбе'69’ В;
UCi=&UA, = 39e-i77°B.
Симметричные составляющие линейных напряжений получим
по симметричным составляющим фазных напряжений:
Uabo~Uao = U всо
Олв1 = ОЛг-йВ1= 105/Зе-*1" В; йлю=UM-Um~ _
= 39/3е*(|3° В; йВС1 = агйАЙ1 = 105 /Зе'141’ В;
йвсг = айАч. = 39 /Зе'133" В;
UcM = alJABl= 105 /Зе'99" В; UCAt=a^UABl = 39Vr3e-i'В.
Определим графически симметричные составляющие фазного
напряжения йА. На рис. Р.6.6, а показано построение С/Ло: на
рис. Р.6.6, б—построение С/хна рис. Р.6.6,в—построение йА2-
6.28р. Примем фазу А за основную и будем искать токи //с,
/д1, /Л2. Составим три независимые схемы для прямой (рис. Р.6.7, а),
обратной (рис. Р.6.7, б) и нулевой (рис. Р.6.7,в) последователь-
ностей. Так как источник ЭДС симметричный, он не содержит
обратной и нулевой последовательностей; Ulf йг и й0—емммет-
2*6
рнчные составляющие напряжения t/л'О'. По законам Кирхгофа,
IД1 (4i + 2Д) т == ЁА;
4UZr2-FZJ-i-tf2 = 0;
IAo (3ZH 4 Zrt 4- 2Л) -|- (70 = 0. -
(1)
Выразим напряжения на несимметричной нагрузке через со-
ставляющие прямой, обратной и нулевой последовательностей
Рис. Р.6.7
для токов и напряжений:
йдчу=л Кд; 01 + о.+й0=(Ц+/2+М RA\ |
0в'О' — ibRb^ 01<72 4“ Ь 4* Щ = (1 ха- 4- 4* ^о) Кд» | (2)
Oc'O'—^c^ci 4“ <4а24- Uq — (/^4* 4* Л) Re '
Решив систему уравнений (2), найдем:
I; _f Яд4-о2Яв4-о#с t j Я.д4-дЯд 4-я2Яс t / Яд4-Яя4-Яс.
—11-------3-------г ' 2----з------г * о----3----» (о)
Ut = i । j Ra'V-o^Rr-toRc i ц а5Яс .
(г _i Яд4-o#s4~o2Rc । i Яд + /?д-|-₽с . у ₽л4-о*Я/?4-йЯс
= 11------§-------г * j----з-----г 'с-----3-----• (о)
Подставив выражения (3)—(5) в систему уравнений (1) и введя
Дополнительные обозначения Zo = —с; Zx= ^в+а3кс .
£ о
287
*1 R A ”1" 4~^^C
Zt-—^-—--------~, получим
о
/"Д1 (Zrl 4" Zjt + Zo) + Ая^2 ”Ь /доД ~ ^A>
1ai^i ~i~ A2 (^ra 4- Zj| + Zo) 4-1 AbZ2 — 0;
Л Л + iA A + Ло (Zrt+zA+z0+3ZN)-о.
(6)
Подставив числовые значения в систему (6), найдем симмет-
ричные составляющие тока /А:
/Л1 = 5,26е-'‘,б°10’ А; /Л2 = 1,475е’/5°45' А;
/ло= 1,233е“/47'35' А.
Определим искомые токи:
Л = /д1 + Л2Ч /д0=7,75е-/13°,3'А;
1в-1А1аг + /Л2а+/до = 4,8е-^7° А;
/с = /дга + /д2а2 + /до = 3,26е'115 А;
/w = 3/д0 = 3,7е~/47035'А.
Рис. Р.6.8
6.30р. а) Токи ц = Imsin©/; i2 = Imsin©/; следовательно, В, *
s=BOTsin©/; B2 = BOTsin©/.
Диаграмма векторов магнитной индукции показана на рис
Р.6.8 для момента времени / = 774. Результирующая магнитная
индукция B0==VBf-b B| = Braj/2sin©/.
Определим угол, под которым в каждый .мо-
мент времени расположен вектор Во относительно
оси первой катушки: tga= B2/Bl= 1; а = 45°.
Угол а не зависит от времени; следователь-
но, поле не вращающееся, а пульсирующее.
б) Токи tj^/^sin©/; /2 = /OTsin(©/—90°); отсю-
да Bj = Втsin©/; B2 = Bffisin(©/—90°).
Результирующая индукция
Во = VВ{ + Bl = Вт J/rsin2 ы! 4- sin2 (©г—90°) = Вш.
При
В2 Вт sin (о/—90 °) sin (со/—90°)
Bi Вт sin tot cos (w/ — 90 °)
= tg(©/—90c) a—©/—90°.
Угол a меняется с течением времени, поле вращается с угло-
вой частотой ы = 2я/.
Глава седьмая
7.2р. Так как при двухполупериодном выпрямлении период
напряжения на нагрузке в два раза меньше периода напряже-
ния источника питания, то искомая кривая будет содержать по-
стоянную составляющую и четные гармоники синуса и косинуса-
288
Постоянная составляющая
~ Л 2л
^Anax ®1П ©/dw» У ^Anax
n+a
ka
• sir.©/ do/ =
= 1,866 -^
л
2Л
Л“=2л J u(<s>l)dn>t = -^
0
Л
= £™x C sjn t d t _ JJ.щах
л J JI
Л/6
Амплитуда синусной составляющей четной k-н гармоники
2л
J и (of) sin ktotd ©/ =
о
“Л 2Л
sink(i)tdо/— sin®/sinЫ/do/ =
л
я+-б J
О О
ЕАпзх
Л
я/6
__ ^гпах
Л
амплитуда косинусной составляющей четной ^-гармоники
2Л
и (©/) COS k($t d ©/ =;
О
“ Л 2л “
j sin ©/ cos k&t d (dt— У sin©/cosAo/dof
Л Л
-6 лч 6
! cos(*+l)-^- cos(*~ 1)~
m k^\ •
^mix
Л
___ ^trtax
Л
Используя полученные выражения и подставляя значение k =
= 2, 4, получим
ц (ы<) = £вн«. [1,866—(0,166 sin 2со/ + 1,53 cosW +
4- 0,233 sin 4©/ + 0,377 cos 4о/ +...)].
7.4р. Действующее значение напряжения
U==
2л
I u? (art) dart —
Л J
о
^=0,578Д/т„.
л
Среднее по модулю значение £/ср м = У —”ах ©* do/ = —^ах
о
269
Действующее значение первой гармоники U1_==2UmaJ(]^2n)r==
= 0,45L/max. Таким образом, ==_UmajU = ИЗ, Лф = t7t/cp и =
= 2/ИЗ =1,15; k„ = UjU = V 2 / 3; л = 0,78.
7.7р. Мгновенное значение тока источника
/ (/) = Ь- +Ь f sin at ~ sin 2<»/) = 1 + 0,64 sin 314/—0,32sin628/,
где to = 2л/= 314 с-1.
Расчет цепи производим для каждой гармоники в отдельности.
Расчет постоянной составляющей. Параметры цепи- /(0) = 1 А;
R — 20 Ом; <i)L = 0; 1/((оС) = оо.
б)
а)
Рис. Р.7.1
Схема цепи представлена на рис. Р.7.1, а. Ток источника тока
замыкается по ветви с индуктивной катушкой, так как сопро-
тивление этой ветви равно нулю; iL (0) = /(0) = 1 A; iR (0) = 0;/с {0) = 0.
Напряжение на зажимах источника тока ц0> = 0.
Расчет по первой гармонике. Параметры цепи: /1(0 = О,64х
У sin 314/ A; R = 20 Ом; оА — 10 Ом; 1 /(«С) — 20 Ом. Расчет про-
водим в комплексной форме для амплитуд. Схема цепи показана
на рис. Р.7.1,б.
Амплитуда тока источника
tn = 0,64 А.
Напряжение на зажимах источника
г) — J /У______________ГЯ (1)___________0,64 _ 0.64 _
и ш rntul вх — 1— 0,05—/0,1 + /0,05 "" 0,05-/0.05
=------7Г7- =9.1е'“° В.
0,05 У 2е“/*ь
где Увх—суммарная проводимость трех параллельных ветвей.
Ток fRm (1) = UmiiJR = 0,455е/4$ А; ток /Гта} = Um nJjXL =*
*= 0,91е-'«’ А; ток ICm (1> = Um jxc) = 0,455e'i35‘ А.
Расчет по второй гармонике. Параметры цепи: —
= —0.32 sin 628/ А; /? = 20 Ом; 2wL = 20 Ом; 1/(2й)С) = 10 Ом.
Расчет проводим в комплексной форме для амплитуд (рис. Р.7.1, б)-
Амплитуда тока источника Jra(a) =—0,32 = 0,32е/18°в А. Напря-
жение на зажимах источника
• • 1 П Ч9/>/180’
U _____J /у ______n QOP/iaoe_______!_______— _______
v«(2>— U.dze 0,05—/0,05/0,1 0,054-/0.05““
= 4,55e/136° A.
290
Определим токи в ветвях схемы;
/я» ,в=0.227е/>’‘- A; JLm (11 = 0,227е'«‘" А;
4».<я = 0,455е-/‘з»- А.
Найдем мгновенные значения токов:
|> (/) = 0,455 sin (314/+ 45е)+ 0,227 sin (628/ + 135е) А;
»£ (0 = 1 + 0,91 sin (314/—45°) + 0,227 sin (628/ + 45е) А;
«c(0 = 0,455sin(314/+ 135°) +0,455sin(628/ —135°) А.
График тока — показан на рис. Р.7.2. Первая гармоника
Для расчета мощности источника тока вычислим действующие
вначения тока источника и напряжения на его зажимах:
= 1 A; = 0,454 А; = 0,226е/<«’ А;
/ = /•/?«>+^>+/?а= 1,12 А; 1/„, = 0; = 6,44е»*° В;
С'а = 3,22е'131° В; 6' = И^и + 1^,+ ЬЪ> = 7,2 В.
Тогда мощность
Р == U <о)Ло) + cos Ф1 + ^(2)Лг)cos Q's= 6,44 - 0,454 cos 45° -Ь
Н-3.22-0,226 cos 45°-2,587 Вт; <S = tJ-7,2-1,12-8,1 В-А.
7.10р. Расчет ведем для каждой гармоники в отдельности.
Расчет постоянной составляющей. Его осуществим по схеме
рис. Р.7.3, а. Сопротивление постоянному току индуктивной ка-
тушки равно нулю, конденсатора—бесконечности. Схема пред-
ставляет собой единственный контур, по которому течет ток /(0).
Напряжение
Umn (0) — — + /(С> (Pi + Р^ —-100 -J- 6 - 20 = 20 В.
Расчет по первой гармонике. Расчет проводим в комплексных
амплитудах по схеме рис. Р.7.3,б. На частоте о) источник ЭДС
Ке работает; следовательно, в схеме он представлен своим нулевым
291
внутренним сопротивлением (короткое замыкание зажимов
источника Э.Д.С.). Амплитуда тока в комплексной форме /л(1) =
= 1е'»°’ А. Напряжение Umn (1, = Ja U)ZBX где Zmmn = Rt +
+ °30 О»: t/m(U = W-B. Мгновенное зна-
чение иап <п = 30 sin (©/ + 90°) В.
Рис. Р.7.3
Расчет по второй гармонике. Расчет осуществляем в комп-
лексных амплитудах по схеме Р.7.3,а. На частоте 2© источник
тока не работает; следовательно, в схеме он представлен своим
бесконечно большим внутренним сопротивлением (обрыв на зажи-
мах источника тока). Амплитуда ЭДС в комплексной форме
4<«=50е^вВ.
Ток в контуре
/___________ю------------50е^80_____о 54е-/15° Д
1 “ <2> ~ /?x+/2(dL—/Д2соС) — 104-/20—/10 ~ ’
Напряжение ^яя<в) = ^*я(Л (рис. Р.7.3, а); следовательно,
Uan <« = -4 (“ /72«С) = 35,4еЛ«»в- = 35,4e'”‘ В;
нвя <2) = 35,4 sin (2«/ 4 75°) В.
Окончательно напряжение
мЛ« (0 =ип„ м + ияп (1) 4 итп w = 20 + 30 sin (©/ + 90р) +
4 35,4 sin (2©/ 4 75°) В.
Активная мощность источника тока
Р = Uтп (ot^m + cos <Pi — 20-6 + • 1 — 270 Вт
Г * Г
(ток источника тока по второй гармонике равен нулю; <рх = 0).
Полная мощность
s = V U^UL^ + IL* V Jb + J’a, - 38,4-9,3 = 356 В А.
7.11р. Мгновенное значение напряжения на входе четырех-
полюсника
«1 (0=“^2’(у+Jcos<fl^ + 4‘cos^—зк * cos4ft1^ =
= 15,9 + 25 cos at + 10,6 cos 2tot—2,12 cos =
= 15,9 + 25 sin (tot + 90°) 4 10,6 sin (2©Z + 90°) 4 2,12 sin (4©f—90>
292
Выразим Ut через Uit обозначив сопротивления четырехпо*
люсника в комплексной форме: Zi~— jXCt Zb = R, Z^=^jXL:
ft=й,+/А=й,+(/.+/J z,=й, + (Cjz,+Ujr,) zt =>
= ft(l + 2i/Z.+Z<//?„).
Отсюда напряжение на нагрузке
fj йх______йх
“ 1+г4/4+адн i-xc xL-jxC!RH •
Воспользуемся этой формулой при расчете и2 для каждой
составляющей входного напряжения. (Обратим внимание, что
не влияет на значение I7f.)
Расчет постоянной составляющей. Параметры схемы: щт —
= 15,9 В; Хс — с»; Xl — (bL — 0. Напряжение на на-
грузке «а(в> = 0.
Расчет по первой гармонике. Расчет ведем в комплексных
амплитудах; Ulm (1) = 25/ = 25е/в®° В. Параметры схемы: Хс (1> =
= 1/((оС)=60 Ом; X£rt)==G)L=]0 Ом; /?н = 20 Ом. Напряжение
• 25е^®®° 25е/®°° 25₽/в0°
U — _____________________________4 9Qp -/i21» d .
2m <И ”” _52_ . 60 ~ -5 -3/ “ 5,83e/21I° ~
1 JO 1 20
a) (0 = 4,29 sin (wf—12Г) B.
Расчет no второй гармонике. Напряжение на входе =
= 10.6/ — 10,6е/в®° В. Параметры схемы: Хс (2] ]/(2юС) = 30 Ом;
X£(2)~2wL=20 Ом; /?н = 20Ом. Напряжение на нагрузке
• Ю,6е^® to.6e/g° Ю,6е^® g ,1в1 #о
30 30 —0,5—/1.5 — 1,58е/26“6’7е ' В*
1 20 Z20
Ugи) (0“6,7sin (2gjZ—161,6°) В.
Расчет по четвертой гармонике. Напряжение на входе
1АЯ(.п — —/2,12—2,12е~'®°° В. Параметры схемы: ХСН)= l/fW?)—
— 15 Ом; XL (4) = 4<oL — 40 Ом; /?н = 20Ом. Напряжение
^2л» (4) -
2г12е~^°е 2,12е~/0Р* 2,!2е~/>оФ
, t 15 0,625-/0,75 0,976е’/в°*а
40 '20
= 2,17е-/а® ®0 В.
Напряжение на нагрузке
«>«>(0 = 2,17 sin(4^—39,8°) В.
Окончательно напряжение на выходе
Щ (0 = М2 (0) (0 + ^2 (1) (0 + (2) (0 4“ ^2 (4) (0 —
= 4,29 sin (ш/—121°) Ч- 6,7 sin(2co/ — 161,6°) +
4-2,17 sin (4^—39,8°) В.
293
Действующее значение напряжения
2
fJtmtli | ^2m(2> | t/jfft <4< __ 5 gg g
Спектры напряжений на входе пх и выходе иг четырехполюс-
ника показаны на рис. РЛА^а^б.
7Л2р. Для того чтобы в нагрузку не проходили третья и пя-
тая гармоники, оба контура (последовательный и параллельный)
Uf,B
25-
20 -
15
10
О а) 2и Зй) 4й>
должны быть настроены в резонанс: один—
на частоте Зо, другой—на частоте 5gj,
Рассмотрим два решения.
1. Параллельный контур Lfix настроен
в резонанс на частоте Зоэ: 1/(303/,,) —
= 3wСi = 1/30 См. Отсюда Ct — 11,1 мкФ.
На частоте Зо сопротивление параллель-
ного контура Zt (8) = оо (резонанс токов).
Последовальная цепь L2C2 настроена в
резонанс на частоте 5<d: 5ы/2= 1/(5<оС3) =
= 50 Ом. Отсюда С2 = 4 мкФ. На час-
тоте 5<о сопротивление последовательной
0 ь) 2и) Зш цепи Za{5) = 0 (резонанс напряжений);
S) следовательно, пятая гармоника тока прой-
Рис. р.7.4 дет по Z2 минуя /?н
Для определения UxfUm ш найдем зна=
чения Z, и Z2 по первой гармонике:
2‘<»=-7^!- = '* 1,’25 Ом;
Za (П = j 10—/250 = — /240 Ом.
В результате получим
И Я]________________I m I___________1 ОЧ
I "2Ц (1)1
2. Параллельный контур настроен в резонанс на частоте 5<о;
Сх = 4мкФ; последовательный—на частоте 3w: С, = 11,4 мкФ.
Вычислим сопротивления Zx, Za и Z2H на частоте со:
^<1) = /10,4 Ом; —/80Ом; 72к1П=40/2е-'»°Ом.
Тогда
_ I ^гя П) I ___ t । о
^ВХ (1) I ^2Н (1)4-21(1)Г *
7.17р. Расчет постоянных составляющих (® = 0). Расчет про-
водим по схеме рис. Р.7.5,д. Параметры схемы: ех(О}—100 В;
е2(в)=20В; R —6 Ом; со/х=ш/й = О. l, (wC)s=oo. Ток /1<0> =*
& (о) ~ 20 А.
294
Расчет по первой гармонике (частота о). Его проводим по
схеме рис. Р.7.5,6 в комплексной форме. Амплитуда £'inn) =
60е/зв° В; ея(1) не содержит составляющей частоты о>, поэтому
вместо нее в расчетной схеме короткое замыкание (2вн = 0).
Сопротивление параллельного контура Z^ab—oo (резонанс
токов). Определим токи:
Л ci)= 0; 0аЬт = Ё1т w = 60е'30 В; (11 — t)abm Ci>/(/ti)A2) =
= 20е~^° A; Iam (1) = Uabm I J = 2OeJ-120 A.
Расчет no второй гармонике (частота 2co). Его ведем по
схеме рис. Р.7.5, в в комплексной форме. Амплитуда P2«<ae
о -
Рис. Р.7.5
= 30e/fi°e В; ег (/) не содержит составляющей частоты 2ю. Комп-
лексное сопротивление средней ветви Z = j2aL1—2шС = ^—= Q
(резонанс напряжений в ветви); следовательно, ток по левой
ветви не пойдет (левая ветвь шунтирована средней): —0;
1Ят о» — — Л™ (2)—== 5 А. Рассчитаем мгновенные зна-
чения токов:
(/) = 20 А; ц (0 = 20 + 20 sin (at—60°) + 5 sin 2w/ A;
i8 (0 = 20 sin (at + 120°)—5 sin 2wf A.
Определим мощности источников:
ej (0)4! «j) = 2 кВт; Р8=елц (о> + Рь ыЦ с» cos ср£ =s
= 20-20 + 75 cos 90° = 400 Вт.
Проверка. По балансу активных мощностей потребляемая
мощность Р^=4?<о>Р = 2400 Вт равна сумме мощное гей источников
Pi+P». Определим полные мощности:
/F2
«?«>+^211(м = 2.18кВ А; S,=763 В А.
7.20р. По закону Ома, ток iR—ulR. График iR=f(t) дан на
рис. Р.7.6,а. Ток iL—~$uLdt. График iL = f(t) показан на
рис. Р.7.6, б (кривая проведена с учетом отсутствия постоянной
составляющей).
295
Для интервалов времени 0—1, 2—4, 5—бмс график тока
—парабола; для интервалов времени 1—2и4—5 мс—прямая.
Ток График ic — f (t) представлен на рис. Р.7.6,в.
7.24р. Соединение треугольник —
треугольник заменим соединением
звезда—звезда. Определим ЭДС фаз
генератора:
eJ( = yJ=sin(<i>t—30p)+
+y=-sin(5arf + 30,’)B;
ee=-^Lsin(<of—150°) +
г 3
+у= sin (5e>« + 150°) В;
100 . t л .
^=-sin(5<o/—90°) В.
Найдем сопротивление фазы наг-
рузки, соединенной треугольником,
по первой и пятой гармоникам:
= /6-/30 = -/24 Ом;
Zft=j6-5-/f=/24OM.
Рассчитаем сопротивление фазы нагрузки, соединенной звез-
дой, по первой и пятой гармоникам:
4* = -/“------/8 Ом;
4* = /^ = /8 Ом.
Расчет по первой гармонике токов и напряжений:
/ =/' _. — 57»74e“J3fl _ - 1 ,1Ьс Л.
1 Ami * аО mi — 3__/8 «5,1с А,
</«0'т4* = 5.1е'‘'“8е-/‘«° = 40,8е->-‘" В;
t?.tai = /3 Uo-nl е'3»’ = 70,5е-/«° В;
/.tai» I4ta«/4S = 70,5е-/«724е-/"° =2,93е'“’ А;
^™i=4taie-/“«" = 2.93e-/«" А;
= 2,93e-/«"6e'”" + 2,39е'*ь°24е->9«° ₽ 80,7e~“*° B.
296
Расчет по пятой гармонике токов и напряжений:
/ — f о, — ^АтЬ _ 11»6е^а0 _ . Q25e-/16e Д •
Uao-mt =/«o-ralZ&>=- 1,025е-/‘»‘8е'«’=8,2е'«" В;
= /3 йа0 = 14,2е ‘»’ В;
Ata. •= OabmJZ^ = 14,2е/«‘724е/“" = 0,59е-/«* А;
А™. - Ata,*» •••=о,59е'«’ А;
Va,at •= + Ata,ЭД - 15,9е'1“°>0' В.
Мгновенное значение напряжения
иа{ = 80,7 sin (со/ —34°) -г 15,9 sin (5ш/ -г 115°30') В.
Активная мощность
Р = 3 Едт^Ат' cos Ф1 + 3 ЕАт**Ат* cos<р5 = 650 Вт.
Полная мощность
S = 3 у у ъ 800 В • А.
7.30р. С учетом соотношения sina + sin0s=2cos^^* sin
пслучим выражение
и (0 = 200 cos 100/ sin 1000/ В,
где 100 с-1—частота й огибающей колебания и(0; 1000 с”1 —
несущая частота <о. Период
риод несущей Тк = 2п/(а =
— 0,00628 с. График и~
— f (0 показан на рис.
Р.7.7, период биений Тб
равен половине периода
огибающей: 7$ = 0,0314 с.
Глава восьмая
огибающей Т& = 2я/О = 0,0628 с, пе-
8.7р. Применяя метод
эквивалентного генератора, построим расчетную схему замещения
(рис. Р.8.1).
а) По методу наложения:
иаЪ х — + Л (Я1 + — 90 В;
НП = in, (П + i« (t> = + Ае₽.',
где
in,(0 = 0,18A; A = i (0+)-i„,(0+) =
I u°b x j uab x \ Цд& к л / e д.
\ Яз Л1 + Л8 ="U,4&A’
Pi=-l/(₽sQ““i04c-1.
297
Таким образом, i (/) = 0,18-}-0,45e~10*z А.
6) В схеме замещения включен эквивалентный источник сивуч
соидальной ЭДС.
Е _ [) _ J . IQ 5р-/46с В
Соответственно иое,х(/) = 19,5 sin (10*/—45е) В.
После коммутации
i (t) = »„Р (0 + «С. (0 = «в, (0 + Ле<-.‘,
где «ч, (0=й (/) = 0,1 sin (10* t — 16s) А;
Pi=—10*c-1; A = i(0J—inp(0T) =
___________f Uab х (Йо.) i^obx(0+) \ • /л v л ЛДЯ7
₽ I---------------------------------+ ) ~~ '«₽ <0+) = -0*0687-
В результате получим /(/) —0,1 sin(10*/—16е)—0,0687 e“10,/A.
Рис. P.8.1
Рис. P.8.2
8.8р. а) Применяя метод эквивалентного генератора, получим
расчетную схему замещения с эквивалентным источникам тока
(рис. Р.8.2), в которой при /=^0 контакт размыкается и
= tfi-r₽a “ °’4 A’ Uab = U“b п₽ "J" i4e*/»
где
«вЬ пР = Л^з= 80 В; Pi = — L С (R2 -| Я3) = -5 -103 с’1;
(0J = J, = 40 В; А = ил (0 J - uo6DP (0 J = -40 В;
иаЬ = 80—40е-«“,‘В.
б) Решение аналогично п. а), но эквивалентный источник тока
содержит синусоидальную составляющую /в:
=-ft ~1-----------j------- о, 1 A; j, = 0,1 sin 10* t А;
/?1 * /?а"* R,—jxc
/,(0t) = 0; г?аМря = /м> ft-^-^ " 12-7(г11™ В;
««ю,- 12,7sin(10*/—18’30') В; иЛпр(0ч)----4В;
= мйь (0+)"~"Нвьпр (Of.) 4 В.
Следовательно, иаЬ(/) = 12,7 sin(104/— 18с30')Ч- 4е-510,/В.
298
8.9р. а) После первой коммутации при
“c(0 = “cI.p + “cc. = ^i + »ie'’1<; Ах.= ис(0.)—£, =—100 В;
р,= 1,7?С=—Юс";
ис(t) = 100— ЮОе-*»' В; i=C^ = 0.1e"’'А;
«с(Л = 100(1—е-*«г)В.
После второй коммутации при i^T
«с(П = «е.,+ Л(еЛ'’; t' = t-T,
где Uc„p = 0; Aa = uc(T)—uc„p=100(l—е-»”); pt=—I/(/?C) =
= —10c-1.
Таким образом, uc(t)= 100(1—е-1вГ) е~10(/_Г) В; i(t) —
==—0,1 (1—e-x’Oe-^'-^A.
б) При для случаев б) и в) решение аналогично.
При />Т
ис (/) = 200—100 (1 + е-10Г) е-10Кг-п В;
<(0 = 0,1 (1 + е->or)e-i®«-D А.
в) При t^T
ис (t) = — 100 + 100 (2—е-1 “г) е- г> В;
х(0 = —0,1 (2—е-10Г)е-10(/“г>А.
Графики переходных процессов при Т = 0,1 и 0,03 с показаны
для случая а) на рис. Р.8.3, а, б.
Убедимся, что схема рис. 8.5,6 представляет собой интегри-
рующую цепь. Действительно, составляя уравнение для входного
контура, получим Я/4 ис—«ЙЫЖ = мвх.
2У9
Учитывая, что i = C^- и при 6=1 ^Ых = «с> находим
^С~^^=иъх. Следовательно, uFbIX=-^-ju^dt. В соответствии
с этим выражением построены графики на рис. Р.8.3, в—д
для случаев а)—в).
8.10р. 1. Решение аналогично решению первой части задачи
8.9р. При «с(/)=75+25е-1О/В; при t>T uc(i) =
= 100—25 (1— е-*вг)е-’•»<'-*> В.
2. После многократных ком-
мутаций в цепи устанавливается
периодический режим (рис. Р.8.4).
Обозначим через их напряжение
на конденсаторе в момент замыка-
ния выключателя /2н = 2л7', а че-
рез и*—напряжение на конденса-
торе в момент размыкания <1лМ =
= (2rt + l)T, т. е. ut(t9n) и щ =
— иКая+1)-
При рассмотрении установившегося режима целесообразно
вести отсчет времени не после первой коммутации, а от начала
замыкания (размыкания) выключателя.
Если обозначить через t' время, отсчитываемое от момента
замыкания, т. е. от f2n, то напряжение на конденсаторе в этой
области изменяется по закону
^зам (^ ) — ^пр! 4” (^1 ^npl)
где нпр1 = 75В; рг = —Юс-1.
К моменту размыкания (t' — Т) напряжение на конденсаторе
достигнет значения и3, т. е.
кзам G") — Цг == wnpi 4" (^1 Ц1рт) 7 — Цпр! (1 0 4~ uiePi г.
Подставляя в это выражение числовые значения, получим
иг = 47,5 Ц- О.Збви,.
Аналогичные уравнения можно составить, когда выключатель
разомкнут, обозначая через Г время, отсчитываемое от моменга
размыкания:
^раэ (О = Ыпра 4“ (^2 ыпрг) •
где ипр2=100В; р2=—5,7 с"1.
К моменту замыкания (Г=Т) напряжение на конденсаторе
равно ulf т. е.
up„(T) = «i = «np2(l—е₽«т) + и2е^г и ^ = 52,5 + 0,475^.
Решив оба уравнения относительно ut и uv получим ut = 91 В;
«2=81 В. Следовательно, в моменты времени, когда контакт замк-
нут, цзвм=75+16е~1оГ В, а когда разомкнут, то «раэ^
= 100—19е-«гВ.
300
8.16р. а) Ток
it (0 ~ Q пр + св Чпр4" A1ex>*^t
л • /л ч • ЕЕ п г. 37?
ГД₽ 1д (0+) ^£пр 27? 7? *37? 0»*^» Pi 2L
z~!r~
s=i—150c-1’ В результате получим it(/) = 2—0,5e-l60ZA. Ток
/я(/) = 1Дпр Ч Ase₽«z. Значения принужденных токов во всех ветвях
схемы, рассчитанные по схеме замещения (рис. Р.8.5,а), а также
напряжения источников приведены на рисунке в амперах и воль-
тах. Расчет полных токов во всех ветвях схемы непосредственно
после коммутации (/ —0+) выполнен с помощью схемы замещения
(рис. Р.8.5,6) для момента времени / = 0+п* D = 1 А; <«(0+) =
= 0,75 А; А2 = —0,25; iR(/) = 1— 0,25e"16eZ А.
Аналогично решается задача для случая 6)j
i£ (0 = 1 sin (200/—8°) + 0,14е- «« А;
/д (/) = 0,5 sin (200/—8°) 4- 0,07е~“»z А.
8.17р. Применив метод эквивалентного генератора, получим рас-
четную схему замещения (рис. Р.8.6) с нулевыми начальными
условиями, в которой при /=== 0 кон-
такт размыкается. » _
а) Ток эквивалентного источника [ 1
тока О'* (HU*
J.=Ч (0 J = E/R, + J = 2А. TFT IT
Напряжение на выключателе пос- Рис. Р.8.6
ле размыкания контакта
«^(О-Чл^Ю + ^е^.
где А. = и^(0+)-и„,„„ (0+) = (0+) (0 J -^^- = 5 А; /?,=
^RiRJtRi + Я8); Pi — — (Rt 4- R3)'L = — № с~\ Следовательно,
Чгь(/)= 5-ь5е-10’* В. Для случая б) решение аналогично реше-
нию п. а):
(0 s-2,5+ 3,12 sin (500/—71°20') 4 0,45e-i°BZB.
8.20р. Входное напряжение иаЬ (/), заданное в виде ступенча-
той функции (рис. Р.8.7, д), можно представить как сумму после-
301
довательно включаемых постоянных напряжений ид (рис. Р.8.7
б—д). Напряжение в любой момент времени обусловлено суммой
предшествующих напряжений, т. е. ukz = щ-J- ил 4- • • • 4- к*. Для
определения тока в любой момент времени (после коммутация)
используем метод наложения. Найдем ток G, вызванный первой
коммутацией;
11 == Gnp 11св == «Д/R ~T~ i >
где Д, = ц(О+)— Gnp(0+) = —1 мА; рг = —= — 104с-1. Следо.
вательно, i\=l—е-10<#мА.
Рис* Р.8.7
Ток G, вызванный няпряжением ц2, будет таким же, как и
ток ilt но сдвинутым во времени на Т. Таким образом,
Т) = 1— е-1®,/е1°,тмА.
После второй коммутации суммарный ток
Ge = G 4- G=2—e~10’r (1 4- е10<г) мА.
После £-й коммутации при kT^t^(k-^ 1)Т
ikZ =k—е“*0<'[14-е1°4г4-еа10ЛГ + ...
= /г—e-i0’f
1_е10*Г
Выражение в квадратных скобках представляет собой геомет*
рическую прогрессию со знаменателем е10<г.
Возможна и иная запись выражения для тока Де. Если вести
отсчет времени от начала каждого импульса (обозначение Г на
рис. Р.8.7,в—д), то время /, отсчитываемое от первого включе-
ния, можно записать в виде t = (k—1) Т 4- V. В результате получи^
1______________________________е-ю*лг
i*z = k ——-г е- !••<' мА.
1 — е-хо’Г
8.27р. Составим характеристическое уравнение:
Я1 + Яз4" р!~
или
~2 _! ПГ__?___I ^1^3 1 1_J_ ^Э_ О
+ + i^LC' Ях+Кз
302
Пая случая a) ——6-103с-1; —16*10sc”x; для случая б)
Г,₽-6±м~-10’±/108с-\
г' а) Напряжение на конденсаторе и ток в. катушке определим
из выражений
“с (0 = ис пр (0 + А&”‘’ + А^ = ис nt (/) + 2
h (О=«4 пр (0 + В^' + В^ = ц „„ (/) + 2 Bfi°S.
Возможны два способа расчета Л;, Bt.
1. Найдем Лр Bf из уравнений
Л/+Л1=мс(0+)—Испр(О-г); Л^ + Л^ =-j£-(0+)-------^j-^(0+);
Vh+B^h. (0+)-«\ „р (0+); ВЛ + ВЛ = (OJ -(о+);
где
ис (0+) = ис (0_) = 0» wc np (0+) = Uc пр = 100 В;
^«М=0; ^(0+)=*^>;
h (0+) = Ч (0_) = El(Rt + Л.) = 50 • 10- А;
linp((M=/lBp=50.10-A; -f^-(0+)=0; ^(O.)=2^±l.
Значение ic(0+) определим из уравнений, составленных по
законам Кирхгофа для послекоммутационной схемы при / = 0+;
Ra^C (®+) »“ (0+) R1* (0+) =
i (0+) = Q (0+) + ic (0+)>
откуда ic (0+) = 25 -Ю”3 А.
Значение uL(0+) вычислим из уравнения
ul (0+) Rji (0+) ис (0+)— Rs^c (0*) ~ О»
откуда ut(0+) = —50 В. Соответственно = —120; Ла = 20; BL=
•==30-10“*; Вг = —30-Ю"3. Окончательно получим
ис(0= ЮО—120е-«1®*'Ч-20е-1в-10’'В;
^(0 = (50+ ЗОе-®-10*'—ЗОе-1**10’*). 10~3 А.
2, Постоянные Лл Bt- можно определить путем совместного реше-
тя уравнений для uc(t) и iL(t) при f = 04. При этом не тре-
буется рассчитывать производные напряжения на конденсаторе и
Юка в катушке для £ = 0+. В результате получим
Ла = «с(0+) Ц?пр(0+)= 100; (1)
4- В2 = iL (0+) - iL Пр (0+) = 0. (2)
Дополнительные связи между Лп В» и Л£, В2 найдем поурав-
еНию, составленному по закону Кирхгофа для отдельных (/-х)
303
свободных компонент напряжения ис{ и тока iu. Выбрав на по,
слекоммутационной схеме контур, содержащий L и С, получи^
Нд/ 4- — uCi Rtjci —
raeuu-»p/LBje₽''; «1, = В/е'’‘<; ucl=‘Afi',<‘; ici^C^i = p,CAfip.‘,
Таким образом,
(ptLBl+ RJi-A,-p,CR,A,) = 0,
откуда В,— p , Л.-. Из этого уравнения при i = 1, 2
АЯ-ГР/Ь
Rz+piL ~ 4 1U Л1’ (3)
в _ 1+PaCRs л — 3^ io-зл
K2 + p2L 2 1U 712* (4)
Решив совместно уравнения (1)—(4), вычислим —120-
А,= 20; В^ЗО-Ю"8; Bs = —ЗО-Ю’3.
б) В этом случае корни характеристического уравнения комп-
лексно-сопряженные.
1. При этом способе целесообразно искать решение для нс(/)
в виде
ис (0 = ис пр (0 Т 4е-ы sin (w0/ + v),
где нСпр==0; 1£.пр=£//?= 1 А. Определим А и v из уравнений
Л sin v = ис (0+)—ис пр (0+) = Uco = 100;
л (- 8 sin v + co, cos V) = (0+)- (0 „) = -2-10\
Отсюда
Л = 100К2; tgv:-----1; v = + 135°;
ис (/)= 100 /2 е-‘«ч sin (10s# +135°) В.
Аналогично, iL (t) = 1 -Ь е-10,/ sin 103f А.
2. При совместном решении уравнений ис (0 = ис пр(0 I*
2 2
-г 2 4^' и k(0 = knP(0+ 2 для f = 0+
i=l i=l
Л1 + Л2=100; (•)
Bl + B2=0; (2)
Bl = (—1+/).10! *
= (—1 —fl.io«
Решив уравнения (1)—(4), получим-
л2 = —e/»-; Л.= 100%2-e-l“'-, B2=l/(2j); В,—l/(2fr
304
Таким образом,
__ /р/(10*/И 46”) । р/(— 10*1 — 46°) \
ис (t) = 100 К2е-*«’'( -------------------у =
= 100K2e-‘»’'cos(103/4 45°)В;
J1I4 р-/10*1
iL (/) = 1 1------------= l+e-10,'-sinl03/A.
8.30 р. Свободные составляющие напряжения па конденсаторе
и тока в катушке при t = 0+ найдем непосредственно по законам
коммутации.
а) В этом случае
ис св (0+)= ис (^+) испр (®+)= 45 В;
Q«.(0+) = iI(0J-itn,(0+)=9A.
Начальные значения свободны к составляющих токов в осталь-
ных ветвях определим по схеме замещения для свободных токов
при f = 0+ (рис. Р.8.8, а), которую рассчитаем по методу наложе-
Рис. Р.8.8
ния. Результаты расчета частичных свободных токов при / = 0+
указаны непосредственно на схемах рис. Р.8.8, б, в, где значе-
ния токов даны в амперах, а напряжений—в вольтах.
б) Решение аналогично решению п. а):
wccb(0+)= 225 В; i£CB(0+) = 0; i\kb(0J = 7,5A;
G? зев (0+) = — 7.5 A; iR 4СВ (0+) = 15 А;
<есв(0+) = 7,5 А; 1С св (0+) = 15 А.
8.31 р. Выражения для определения напряжения и тока на кон-
денсаторе для случаев а) и б) имеют вид
“с (0 = “с П, (0 + “с св (0 = ис „р sin (al + <рг Пр) +
+ Ае-" sin (м0« + v); ic (f) = С aCUc „ • cos (at + <pc np)—
—6СДе-б/ sin (d)0/ v) + (i)0C • Д e~e/ cos (co0/ + v).
По условию, Q^>1 и поэтому
lc ^CC7c np m cos (at + <pc np) си0СЛе-й* cos (g>0Z 4- v)>
гДе (&CUc Пр m—/пр m\ е)0СД = /св<д.
305
Использовав законы коммутации (0+)= ис(0_) =0;
=ид(0+)=0, получим
пр „ sin фс пр Ч-Л sin v = 0;
&CUc пр т cos Фс пр Ч- ю0СЛ COS V = 0.
0)
(2)
Из уравнений (1) и (2) следует tg фСпр — /г *g v.
COq
По условию, Q> 1 и <о = (йо, поэтому фСпр« v; Л « (/ .
*прл> 'свлг
Таким образом, для заданных условий независимо от началь-
ной фазыэ. д. с. e(t) значение амплитуды свободного тока при
/ = 0+ равно и противоположно по знаку
амплитуде установившегося тока.
Найдем выражение для тока в контуре и
напряжения на конденсаторе при ф=0
(D = CD0. ПрИ (I) = (i)0
w0L=l/(fi>0C); Z„ = R; 6 = /?/(2L);
'С(П = ^-(1-е-")8тШ1,гА;
Рис. Р.8.9
ис (t) = — EQ (1 — е~б/) cos В,
VTic i
где Q— R “rWoc*
Огибающие тока ic и напряжения ис изменяются по одному и
тому же экспоненциальному закону (рис. Р.8.9).
б) При конечном значении 6, но &<^1, после разложения
экспоненты в ряд получим
иС (0 COS ~ —^К>?- t cos СО0/.
При 6 —- 0 (R —► 0) этот ход процесса имеет место для всех /.
8.33р. Характеристическое уравнение имеет вид
г(р)=^(Г1Р + 1)+-^- = 0.
где Т। = RrfLi — R^fТ9~R^C^~R^C^
После преобразований получим
nstf * I 1 А п । _ 1 Г1 । (КзЧ-Яз) (КхЧ-Кз) 1_л
Р Ч" Л Ч- т& ) Р 1- Т1Т8 L1 Т" RJb J -и*
a) с'1; 1/Гэ=6,= 10* с’1.
р,= —1,62-Ю4 с’1; р2 = — 7,38-10* с"1;
^c»=^c^ = “cnp+Лle'’.,+Лe'’^,; “cct= в в BR>--------=10 В:
r‘
А + А, = ис, (0+)—ис „„ (0.) = —10; A,pt + А#, =
Aj=—12,7; Л,=2,7; иС1= 10— 12,7е-*-” *’"+ г.Те-’-» *’*' В>
306
1
б) uC4= 16—2416е-23‘3'1°4/4-8,6е-«’в71°ч В;
аС4 = аС8/4.
8. 35р. а) Ток в цепи после коммутации
i = *пр + =p1_j_^a+A *eF,f •
₽!=* — — 2-104 с’2.
И I и
Использовав обобщенный закон коммутации ф(О+) = ф(О_),
найдем t(0+):
(LIЧ- LJ i (0+) = Llt\ (0_) + ЛЛ (0_);
il(0_) = £/7?1 = 2A; /а(0_) = 0,
откуда i(0+)=lA; A1 = i1(0+)—йпР(0+) = 0,5 А.
Следовательно, i(<) = 0,54-0,5е-2104 А. Напряжение на вы-
ключателе иаЬ(0 — Rai + Lt^-j-= 150 + 50е-210,/ В.
б) Решение аналогично решению п. а)’
При заданных условиях Аа = 0, т. е. процесс устанавливается
мгновенно.
в) Ток *в /у. #t+ Лае^*, где ра = — +'£^2М = — 1,6 • 101 с »
Определим i(0+) из условия непрерывности потокосцепления:
(Lx+ La+ 2М) i(0+) = L,i, (0 J + L2i,(0_) 4- Mi, (0_) + Ah,(0_);
i\(0_) = £/P1 = 2A; ta(O_) = Oj
откуда *(0+)=l A; As = 0,5 A.
Следовательно, i (/) = 0,5 -1- A.
Напряжение на контактах
Ц.»(0 = я.«’+ U-.+ Л1)-£ = 150 + 50е-'« В.
Графики изменения токов во времени для первых двух случаев
приведены на рис. Р.8.10, а, б.
8.42р. а) Применив преобразование Лапласа, найдем
При синусоидальном напряжении на входе, заменив р на /со,
Получим
К (it-Л 7ю 1
А у “ и2. • оГнй “ С/1 1 Ч-а/О'о)’
307
р
Если считать, что а=1/(₽С), то K(fo) = и схема
может быть составлена из /?С-цепи (рис. Р.8.11,а).
б) Для этого случая
/С(» =
а
а-|- /со*
Полагая а = /?/А, определим
К(/Ш)=
К +
В этом случае схему можно составить из ЯЬцепи (рис. Р.8.11,6).
Рис. Р.8.10
Рис. Р.8.11
8.45р. Коэффициент передачи = Ki (р) Ка (р).. .Кд (р) =
с=(Лр+1)...(7’лР+1)‘
Операторное выражение для напряжения на выходе
(у"+* =₽(Г1р+1)(Т^+1)...(Т^+1)-
Применим предельные соотношения [р6п+1(р)]р->ов==14п+1(0л->о+;
[р^п+1(Р)]р-^о=^«я+1(О/-». Отсюда ця+1(0+) = 0; п„+1(оо)-£.
Операторное выражение для напряжения на выходе третьего
звена
U*^~ Р(Т1Р+1)(Г^+1)<Т,р+1) •
Применив формулу разложения, получим
“«(0 = £ [ 1 ~(Т1-Т,)1г,-Т,)e~>ir,~a't-T^(Tt-T^' е""г“"
т8 1
________£*______е-г/т»
(Л“Л)(7'»-Т2)е J’
8.46р. Изображение входного тока
ря_|_с/->4_у
308
Для получения разложения изображения по обратным степе-
ням поделим числитель на знаменатель. В результате получим
учитывая, что 1/р—1; I/ps-^-fa/2!, определим выраже-
ние для тока
\ л
Полученное выражение пригодно для описания переходного
процесса при t ж 1/а. При больших t (t —► оо) i (/) —► 0, так как
[р/ (Р)1л -» о =
8.48р. а) По методу двух узлов
£ > +!^РС
{/С(Р)=?Л--|Р--------.
где ис(0) = Е; /2(р) = £/г(р)/Я3.
Перейдя к оригиналам, получим ис (Q = 50 4- 50е 10о< В; i2 (/) =
== 0,25 4-0,25e“100t А.
U,2(t)
Рис. Р.8.12
б) Применим метод эквивалентного генератора. Найдем напря-
жение на выключателе до коммутации: цХ2 (/) = £. Составим рас-
четную схему с нулевыми начальными условиями (рис. Р.8.12),
из которой получим
/, (Р) = W = 0.25 + 0,25е-“»' А;
uc(t) = E—Е+ Rjzft) [см. п. а)].
8.49р. а) По закону Ома,
4+ь«(0)
(Р) = дтрR,+R, ' (р) ~ (р)'
где i(0)=£//?,= 100 А.
Следовательно, i (/) = 50 4- 50е_< A; uu(/) = 50-|-50е“* А.
б) Для расчета напряжения между контактами, используя
**етод эквивалентного генератора, составим схему замещения с ну-
309
1
левыми начальными условиями (рис. Р.8.13). В этой схеме ток
эквивалентного источника тока jB(t)—E/R2 —100 А. По закону
Ома, в операторном виде после размыкания контакта
и* (р)=/в (р) Z (р) =4-
РАд А1-|-А2~гРЬ
Соответственно Z/ei (p) = t/f2(p)//?1; /2(p) = t/12(p)/(/?34- pL). Следо-
вательно, u12 (0 = 50-h 50е * В; i^2(/) = 50—50е~# А.
Истинный ток через резистор R2 (с учетом тока, протекающего
в цепи до коммутации)
//?знст~ (/) == 50 4-50е“* А.
8.52р. а) Операторные уравнения имеют вид
( Я + pL + /£ (р) - рМ Ц (р) = ;
-рМ/1(р)+ (я+рЯ + ^)/,(р)=0.
Будем искать решение для [Л (р) 4-/я (р)] и [/s (р)—/8(р)].
Сложив и вычтя эти уравнения, получим
[/? + p(L—M) + ±] [/. (р) + /2 (р)] = "я;
[fl + P(L+ М) +±] [/, (р)-/,(р)] = ;
_____J______________t/cptof______.
p2+261p4-co5i -o)1L (1 -fe)[(p 4-60*4-“I] *
J Uco ft>2
P34~262p 4‘^,o3 <1)2^- (14-^) l(p 4_®2)*4~t,521
где k = L/M; 6lt 8 = R/2L (1 т A); 4.02 - 1 /[(AC) (1 =F A)] = cog/ 1 T ft;
co3 =<0*!—6*; (05 — too2—63.
Использовав таблицу изображений и соответствующих ориги-
налов, найдем:
<’1 (0 + U (0=e’tl'sin
«1 sin^:
(0 [^(i-t)6-01' si"^ +Ц^(l1+J^)e~<,^'sin^]:
Ч(0=[ц.ц'-цe-e,'sin“>.<-^(1-^) e-»-'sin.
б) При A 1, Л? 62 = 6, (Qqj 62, (Oof Л? (0{ц = COja
г> w ~ ^•cos 0sin 0 e’";
*« w » Sin (^5^ t) cos f ^4^ 4 e’“
/‘<P) + ^<P)=E^-
/l(p)-/,(p)=r^-.
310
в) При R = 0, 6х = 6а = О
i (0 == sin "Г O2£(J Sin <м] *>
it (О == -f2 [^£(1—fe)sin ~(1>2L(i+&) sin ®zt ]'
В этом случае после коммутации возникают незатухающие ко-
лебания различных частот.
8.58 р. Представим напряжение на входе в виде суммы двух
составляющих и* и и2, сдвинутых во времени (пунктир на
рис. Р-8.14, а—г). В интервале
времени от 0 до действует на-
пряжение ии а при —сумма
+ “г-
Ток в цепи определим по фор-
муле Дюамеля, используя пере-
ходную проводимость g(l), найден-
ную в задаче 8.53 (см. рис. 8.30, в).
Для рис. 8.33, а при 0 tt
‘(О = ^(0 = О»1е-1оЧА;
при
H0=^(0—*0=
=0,le“lo*r—O,le-lo’1<_#P А;
для рис. 8.33,6 при
t
чо=^(О+$“»ГОг(<—
оа
—x)dx = (0,2e_10ч—0,1) A;
при t^ti
t
i (0 — Ug (/) 4- J ut (x) g (t—x) dx + ? ui(x) g (t—x) dx=
° . '*
= 0,2e-10 *—0,le-lo*«-G’ A;
Для рис. 8.33,в при
i (/) = 0,1 (I—e“le*f) А;
пРи
i(0 = 0,l (1—е~10’9—0,1 [I—е-*»1 «-*?] А;
Для рис. 8.33, г при О С t h
i(i) = 0,05/2sin(10’t45°)—0,Обе*‘ А;
“Ри t^tt
i (Z) = 0,05е-«’ «-«.>—О.Обе-*»" ‘ А.
в последнем случае задача решается проще без помощи интеграла
Дюамеля, например классическим методом в сочетании с методом
Наложения.
311
8.59 р. Применим метод эквивалентного генератора. В резуль,
тате получим схему замещения, в которой начальные условия
нулевые, а эквивалентная ЭДС = —Uco (рис. Р.8.15)
v По методу наложения найдем i(t) для слу!
।—V----□□—I чая, когда u(t) задано рис. 8.33, а:
хК 1 при
Т i(0 = ({/-l/co)g(O = O;
Рис. Р.8.15 П₽И
» (0=-l/CTg(«-O=-0,le-“’‘ А.
Если u(t) задано рис. 8.33, в, то:
при 0 t
t
i (0=- Ung (0 + $ u; (т) g (1-т) dr = О, le-”3' + 0,1(1 -е-“3') А;
О
при t ti *
i (/) = — UCQg (/) 4- J u'i СО g(/—т) dx 4- J uj (т) g (t—т) dx =
о Л
= — 0,2е**10* f-|-0,1е-10* А.
8.60 р. Проще всего решить задачу с помощью классического
метода в сочетании с методом наложения. При воздействии им-
пульса, изображенного на рис. 8.34, 6, в интервале времени от 0 до tt
th — Щ пр+ и2 с. = Е+ Ае-“ sin (mot + -v),
где 6=R/(2/.); 1//LC.
Определим А и v из уравнений
£“ + A sinv = u5j(0+) = 0; (I)
— 6А sin v + w0 A cos v —(0+) = = 0. (2)
и»
Отсюда A cos v — — Е « 0, так как, по условию, 6 о\; v л
л 90°; sin v ж 1; А ——Е. Следовательно, и2 (/) = Е (1 —e“l6/ cos (s)stj.
При t— tY
uz (/J = E (1 —e 6Z* coscVJ = E (1 —e-6<i)i
при t^tt
иг (/) = u2 (rj е"6 <*-*»> cos соо (i—= E [e~6 <*-*»)—e_fl/] cos <V-
Для прямоугольного радиоимпульса, изображенного на
рис. 8.34, в, решение аналогично решению задачи 8.31 р:
при 0 t tf
их (t) = — EQ (1 —e~w) cos <oof;
при t^ti
u2 (t) — — EQ (1 —е~вЛ) e~6 cos
Qr 1
~ —R~~^CR'
График u2 — f(t) показан на рис. P.8.16.
312
8.61 р. Пусть для любого k-ro цикла, где А = л+1, ал = 0,
j 2, •••• напряжения пСэ(т) и uCft(x) означают напряжения на
конденсаторе при его заряде и разряде. Время т = /—пТ будем
^считывать от начала &-го цикла (рис. Р.8.17), Обозначим исхо-
де значения напряжений в начале А-го и (fe4- 1)-го циклов через
Цс(п) и нс(п + В-
В случае заряда и разряда конденсатора при 0 т
«сэ(т) = Е + (лс(л) — £‘]e"i,T = £(l—е“в*т)4- ис(л)е-*»т;
при Ъ^х^Т
где 6, = 1/(/?зС); 6,= 1/(/?2С); ис, (t,) = Е(1-е-«.<.) + ис (л)е-«.'-.
По закону коммутации, напряжение на конденсаторе в конце
t
Рис. Р.8.16
fc.ro цикла равно напряжению в начале следующего (k 4- 1)-го цикла,
Т. е. uCJ> (7) = ис (л 4- 1). Отсюда ис(л +
j-|)=[£(1—е-6*^) 4-ис(л)е-б,г']е“в«<г-Г1). иг
Если а = Е (1 — е“6,/>)
Ь=е“б,й e-Ci(r~z,), то выражение для раз- о
костного уравнения, связывающего меж-
ду собой напряжения на конденсаторе
в начале каждого периода, имеет вид
цс[л+1]—Ьцс[л] = с,
где «с [л]—решетчатая функция.
Для его решения воспользуемся дискретным преобразованием
Лапласа или эквивалентным ему Z-преобразованием. Если функ-
ции ис[л] соответствует изображение (7£(г)= 2 2-Пис[п]> т0>
п=0
по теореме сдвига, uc[n41] 4- zU'c(z), так как. по условию,
Uc [0] = 0, a -b az/(z— 1). В результате получим Uc (z) =az/(z— 1) х
Х(г—b). Применив обратное преобразование, найдем
Окончательно получим:
при 0OCG
«сэ(т, л) = £(1— е-«х/) j-aL^e-ctT;
при it
цСр(т, л) = (1 —е“б«#') +
Установившийся периодический режим соответствует л —* оо
и 6—^0. Подставим в полученные выражения числовые значения:
псэ(т, л)= 100+(44,6(1 —0,67я)—100]е~10От В;
ис₽(т,я) = 118 4- 36,5( 1 —0.67я)] е- 2-В.
Изменение напряжения на конденсаторе для первых шести цик-
Ов показано на рис. Р.8.17.
313
Предельные (установившиеся) значения при разряде и заряда
конденсатора: ис («)«.*.« =44,6 В; ис (G)n-* х = 54,5 В. Для оценки
минимального числа циклов nmin, при котором приближенно
стирается установившийся режим, примем Ьп = 0,05. При эТом
^min ~ 8.
8.66р. В качестве переменных состояния цепи выберем вектор
где = x2 = Il- Соответственно dxr'd/ = duc/d/
— ic/C и dxJdt — diJdt — ujL, Вектор внешних воздействий (источ.
ников) [z] = £*1]» г1 = е> z2 = j, вектор выходной переменной
= По условию задачи, У! — и2.
Рис. Р.8.17
Рис. Р.8.18
Уравнения состояния и связи выходных переменных имеют вид
^! = [M][x] + [W][z];
(I)
м=1^и+гаи. И
где [М]=Г"“ "Я; [JV]= Г"11 [Р]=[р11Лг]; [<2]=[?n <?.J-
LTKji nijjJ LH21 «22 J
Элементы матриц можно определить методом наложения при рас-
смотрении эквивалентной схемы, которую получим, если заменим
в послекоммутационной схеме емкостный элемент источником на-
пряжения с ЭДС ис, а индуктивный элемент источником тока
с током iL (рис. Р.8.18). Из уравнений (1) и (2) следует, что
dxi/dt Ж — ic/C
“‘11 — dxifdl ПК — 1 ООО 11 11 « 1 *7 N >? 1 е=о ’ и т. Д. D
"Ч'> - *3 Х( N N It II н ООО »£ и *5 и Д®
Элементы матриц mn, ..., лп, л12, ... можно найтп пр
рассмотрении схемы рис. Р.8.18, полагая в ней все источник
кроме одного, нулевыми. Например, считая е = 0, / = 0, 1
314
домучим 1С — — ис/(Я2 Ч-Я3). Следовательно, mu = —
Полагая е = 0, /=0, пс = 0, получим
. Rz I Rs
tc = R>+R3r’ 'П12 = ‘СЯ7Т
jj результате,
И т. д.
г j 1
С Ri + R*
____1 ₽5
£ /?2~г Ri
(1)
(2)
8.68р. Уравнения
шмеют вид
состояния и связи выходных переменных
воздействие; [#] =
^=[М]И+[ЛПМ;
[</]=[/’] И + [<?] I ч.
—переменные состояния цепи; [г] = [е]—внешнее
гс
—выходные переменные.
(1)
(2)
__g
__ |g
I
1
2
т
___1_
4
2
—3
“О'
[Q] = 0 (см. задачу 8.67).
Решение уравнения (1) запишем в виде
t
[л-]=еГЛ1И[х(0)1 + е^Р J e-^rf/V] [г(т)]dx, (3)
о
ГДе первое слагаемое, определяемое начальным состоянием цепи»—
Реакция цепи при нулевых источниках [z]=0, второе слагаемое,
Характеризуемое действием источников,— реакция цепи при нуле-
вом состоянии [х(0)] = 0; e[Afl*—переходная матрица состояния
Вепи, элементы каждого столбца которой представляют собой соот-
ветствующие реакции на единичное начальное состояние.
315
В данном случае первый столбец е^м]/ реакции—переходу
напряжение uc(t) и ток it(0 при ыс(0)= 1 В, (0) = 0; второй-^,
при цс(0) = 0; it(0)= 1 А. Для определения найдем собст-
венные значения Xf матрицы [М], совпадающие с корнями хара^
герпетического уравнения цепи Р(1) = 0:
₽(*.) = det {X[l]-[M]} = det {л [* ?]~[=3 -1в]|
= det {ГХ + 4 х+%]} = (* + 4) (* + ’8) + 24=0
или
1«4-22X4-96 = 0,
откуда Хх =—6; Х2 =—16.
По формуле Сильвестра, для различных X,
е«И= 2ех‘'[Л(М],
1=1
п
Па**]-*/1»
где [Л(У]=«^ _Д--------------
-дгЦ п (*•-*/>
/=>
При п —2
Переходную функцию e[Af Л с матрицей [Af] порядка п для
различных Xf можно найти, воспользовавшись ее общим вира*
жением
eW^cto [1] 4-ах[Af] 4- ая[М]« + ... 4- ал_х [Лф-\
где [М]8=[М][Л4]; [М]8 = [М]8[М] и т. д.; а,, а,.....
функции времени, подлежащие определению. Учитывая, что е '
= <х01 4- 4- 4- ... 4- а„_Л"-1» и составляя п уравнений ДЛ*
всех X,-, определим Oq, ах, ..., ая_х. При д = 2,1Х = — 6, Х2=
e-ef = a0—6ах; е~ш = а0—16а1(
откуда ав= 1,6е-в*—0,6е“1в/; ах=0,1е~Л—0,1е~ш. Соотв#
316
етвенно
et«J'=а, [ 1 ] а, [М] = (1 ,6е'—0,бе*»') R ° 4
+ (0,1е-«—0,1е->") _ifl =
__Г(1,2е*и—0,2е-1М) (0,8е~"—0,8е'“') ]
L (—0,Зе-" + О,Зе'1") (—О,2е-“ 4-1,2е"‘")J ‘
а) Решения уравнений (1) и (2) при е=О принимают вид*
[х] =^1"1' [х(0)]; = [Р]el"l' (х(0)],
где по законам коммутации
Г «с (0)‘ _
1л (0)J
101
5Г
В результате получим
'с
4
I
4
1
2_
2
£
2
[*(0)] =
ы=
1
X
— 3
2
(1,2е“"—0,2е~18') (0,8е-"—0,8е~ш) 7 Г10
(—0,Зе-" 4- 0,Зе"1") (—0,2е"" + 1,2e-iM) J L 5
Г 2e-" + 3e-1" 7
= — 6e-ef 4 6е~ш .
4е“8*— 24е-1в'_
б) При 61 = 0, ис (0) == 0 и t£(0)=0 имеем нулевые начальные
.условия. Поэтому решение уравнения (1) при е = Е =—20 при-
нимает вид
[х] = $ el"! <'-*[#] [z (т)] dx =
о
Я(1,2е-в<'-”—0,2е-1в<'-^) (0,8е-в<'-г>—0,8е~
(—0,Зе-в+0,Зе~г« <'-*>) (—0,2е~в <'-*>+ 1,2е^1«'~«
t
—120 J (0t8e-«<'-^—0,8e-ie<'-T>dT)
о
t
—120 (—0.2е-«<'-т»4- 1,2е-1в«'-тМт)
о
—10-Ь16е“в<—6e~lef
—5—4e-ef + 9e-1"
* В п. а) и б) напряжения даны в вольтах, токи—в амперах.
3J7
Соответственно найдем решение уравнения (2);
1 Л ”
4 2
I 1 Г—10+ 16e-et—6е“иП
4 2 [_5—4e-et + 9e-i6t J
Г01
0 (—20) —
-__5 + 2е-в‘ + Зе-1в/'
—6е“вЧ бе"10'
4е“а/—24е~1в/
Выражение для переменных состояния л выходных перемен-
ных при постоянных источниках можно получить и иным путем.
Действительно, решение уравнений (1) и (2) при постоянных во
времени источниках (г не зависит от t) и нулевом состоянии цепи
[х(0)] = 0 принимает вид
[Х] = е[мв Je-tMB[N][z]dT = elW(—еЧМ]т)|'[М]-1[М]|/|=:
<[!]_e-[MJ 9[М]"1 [/V][z] = (е^'-[1])[Лф1[/V][z]; (3)
М = И [М]-* [ЛГ| И + [Q] И, (4)
где [М]-1 = —матрица, обратная матрице [/И]; Adj [Л4]<—
присоединенная (взаимная) матрица, которая получается из исход-
ной заменой каждого элемента его алгебраическим дополнением и
последующим транспонированием; det—определитель матрицы
[М]
Для рассматриваемого случая
[z] = [Е] — 20],
ГЛЛ1-1 Г—4 18 —8]
[М] * —[_з _18J — 96 [ 3 — 4j’
Подставив [Л4]~*, [N], [Р], [Q], е^!' и [z] в выражение для вы-
ходных переменных (4), получим тот же результат, что и ранее,
в) В этом случае решение представляет собой сумму решений
п. а) и б). Сложив матрицы, получим
'я
*с
"—5 + 4е~6' + бе-10'
—12е~в, + 12е-1в'
8e~af—48е-1а<
8.73р. При составлении дифференциальных уравнений пепй
можно пользоваться их символической формой, рассматривая опе-
ратор дифференцирования d/dt как алгебраическую величину^
и, обратно, р как d/dt. В этом случае выражению
эквивалентно выражение uL=pbiu а = —'с “ рСи(:- С°*
318
^етственно
гле V(pQ—символические (операторные) индуктивные и ем-
костные сопротивления; рС, 1/(р£)—символические (операторные)
рроводимости.
г Для составления дифференциальных уравнений цепей можно
воспользова гься любым методом расчета на синусоидальном токе,
заменяя в уравнениях для комплексных амплитуд Z(/w) на Z(p),
р на d/dt, р- на d*!d? и т. д.
г Для рис. 8.38, а после коммутации u^=u2 — Z{p)j, где Z(p)=
(R, + pc)₽’ fliRaCp+R.
Следовательно,
[(#1 + Ср + 1 ] и = (RJ^Cp + /?2) /;
(я.+я,)с%+и=ъкгс-£+rj.
Подставив в последнее уравнение числовые значения, получим
•^-+0,5и = 5-10’ + 5-103/.
В нормальной форме = t), где
f(u, t) = — 0,5u + 5-103H 5-103/. (1)
При численном интегрировании уравнения (1) считают, что
время t и переменная u(t) изменяются дискретно с шагом M~h.
Если известны значения tn и и(/я), то по ним могут быть най-
дены значения t„+i=tn-Vh и приближенно после интегрирова-
ния (1) м(/п+1), где n = 0, 1, 2, ... . Проинтегрировав (1), найдем
tn + t
u„+i—u„= J f(u, t)dt.
in
В явном методе Эйлера функция f(u, t) полагается постоянной
®нутри интервала t„—tn+1 и равной ее значению в начале интер-
®зла, в неявном—в конце. В результате для явного метода un+<=
+ /„), а для неявного un+l = un4- hf(un+lt tn+1). Метод
Эйлера обобщается для системы уравнений вида
dr
аг=н*. о.
гДе х= (х, у, г, , ..)—вектор переменных состояния, в качестве —
компонент которого может быть принята искомая величина х,
** первая производная y=dxjdl, вторая производная z=dyjdt
313
и т. д. вплоть до (г—1)-й производной, где г—порядок ура»,
нения.
Для числовых расчетов уравнения (1) воспользуемся преград
мой М2 (см. приложение 4), составленной по неявному метолv
Эйлера, полагая /о = О; й = 0,5; x,) = h(0) = 0; ^ = 0.5; а==о.
р = 0; й = 5103; В = 5103. Здесь шаг й « а начальное
условие = так как ис(0) = 0 по закону коммута-
ции. Результат расчета по программе М2 следующий:
tn, с...0 0.5 1 1,5 2 2,5 3 3,5 4 4,5 5
unt В...0 2 4,6 7,68 11,1 14,9 18,9 23,1 27,5 32 36,6
Глава девя та я
9.4р. Для рис. 9.2, а x(w) = coL; dx/dw = L > 0; для рис. 9.2,6
x(w) =— 1/(<оС); dx/dta — l/(Cw)2 > 0; для рис. 9.2, в x(w) = uiL_
— l/(wC); dx/dto = L+ l/(Cws) > 0; для рис. 9.2, г х (со) = »
dx £ (1+<ог£С) р
dw ~ (1 -(02£С)2 > и-
Сложные схемы, содержащие только реактивные сопротивления,
можно представить как совокупность схем рис. 9.2, а—г. Поэтому
и для них dxfdto > 0.
9.8р. Коэффициент передачи
zz (л __ U ъ 1 ________1_______
U } Ui (М /wC ’ [Я 4- / (<о£ — 1 /<оС] *
Если резонансная частота
R ~ R ~(орЯС» то
ор = 1 ИLC, а добротность Q =
----TTS-TT. “•=-
l-t- jQ (ь) Ь__П шр
(о* /
Q
K(w) = |K(jw)|=
Для Q^> 1 резонансная кривая имеет острый максимум, т. е.
при малом отклонении частоты Aw от резонансной К (ю) меняется
существенно. Это позволяет упростить выражение для K(jw'-
Заменим в области w/wp=I выражение, содержащее частоту, ли-
нейным приближением. Для этого разложим в ряд Тейлора соот-
ношение, данное в круглых скобках. При
К (/<*>)«
14-гё’
где ——обобщенная расстройка контура. Соответствен110
Л(И)»С/Р/Т+Т».
320
g.9p. Для резонансного контура с большой добротностью
(рие. 9.4, с) К ((о)тах = К (top) « Q, так как Q = /Z/C//? = 100 (см.
решение задачи 9.8р).
Найдем обобщенную расстройку контура E=-^-Q, соответст-
уюшую границе полосы пропускания. В результате получим
тода £ = 1; 2Лю = top/Q = R/L — 10 с~*; 2Лоу«р = 1 /Q = 0,01, т. е.
= 0,01©р.
Аналогично решается задача и для цепи рис. 9.4, б:
К (л - __________¥__________________1
А ” U. (/со) ~ (/?2-(оЗ£2) + /За>Л/? “ ш2 о *
1
где &=R/L. Таким образом,
к (<0) = IК (/«>) I = -- 1 ,
гае К (<»)„,„=К(0)=1.
Полоса пропускания лежит между to = 0 и to = toc, где ©с на-
ходится из условия /С(шс)/К (0) = 1/V2.
В результате
(<ос/6)4 + 7 (toc)/6)a 4-1=2; toc = 0.3756 = 3.75 с"1.
9.18р. Для трапецеидального импульса (рис. 9.9, а)
/ со/2 (А \
Q... 4Е I cos 2 “C0S 2 )
S (<o) = 7^77 <---------------) =
sin”
to 1 — t g)
____4
w(G4-
4
4
4
Полагая /2 = 0, получим спектр треугольного импульса (рис. 9.9,6):
. Eti sin®cj/i<‘4
S(“)=-2-^4F-
Для обоих случаев 3(0) равна площади импульса.
Для прямоугольного импульса (рис. 9.9, в) с высокочастотным
^волнением
ее /,
S (/to) = J e (/) dt = JJ E sin w0/e_/<,)/ dt =s
— CO C
= Е j sin (sin to/ — j cos to/) dt,
о
Таким образом,
S (w)=| S (/©) |= К(to) -j- S’ (to).
321
где
ft
Sa (о)) — E J sin &ot sin dt =
о
£*
t= —------(co sino^A cos w/i—<oo cos &att sin to/J;
<1)0 — co2
Sp (co) — E § sin й)0/ cos &t dt =
о
p
= -5------(d)0—CD0 COS (Яй1 COS (D/x —co sin (!)(>/J sin&ti).
COo—<o2
Соответственно
E i г--------------------------------------
S (w) = —5-------V ©о 4 ®0 COS2 + CO2 sin2 Ct)0/t--------►
<do —Ci)s
—*• —2ws cos cd()/1 cosco/j—2(oo(i) sin ©(Л sin co/,.
При co—>coo, раскрывая неопределенность по правилу Лоли-
та ля, получим
S (со0) = V ©o^+sin2 (Vi—ci)04 sin 2(0^.
2соо
По условию задачи, tJT = 2. Поэтому sino0Z1 = sin4uT==
— О, COS CQo? 1 = 1 и
5(ш) = _Л_)/2ы5(* — COSfflrt) = -^-lsin^l| (рис. р.9.1);
<1)0 — 40* <О0—О)*| Z I
S(to0)=Etj2.
9.20р. Для всех трех импульсов Д/\« 1//х. Убедимся в пра-
вильности этого соотношения для прямоугольного импульса. Из
2£2
решения задачи 9.19 следует 52(ш) =-^-(1—cos ©А). Поэтому
о
W (ы) =1 j S« (Й) dSi=^- (<tSi -~“s<a<1),
О
G>ft
с. . « С sinx «
где Sicofi—интегральный синус \ -у-ах.
о
Так как полная энергия прямоугольного импульса W = E-tlt то
W(со) 2 [с. . I—совш/Л
=— ( Si (dt<----------.
Характер изменения энергии иллюстрируется рис. Р.9.2. Прй
построении графика интегральный синус можно представить в виДе
ряда
Si,./ ИЛ8 » (<^>6 1
—3 3! 4- 5 51 -••]•
Из рисунка видно, что при ci)=cd1 W (oj «0,9W,
322
9.21р. Найдем автокорреляционную функцию R (т) для сигна-
лов, соответствующих случаям а) и б):
' о
При таком определении /?(т)
имеет смысл мощности сигнала.
5(Ы}
R,
О 0,5 1 1,5 2
Рис. Р.9.1
а) Для е(0 = £о
о
б) Для е (Z) = Ет cos (со/—<р)
R (с) = Нт
Т —* ос
т
— ^Em cos (со/—<р) Em cos [о) (/ — т)—<p]d/
о
Е*т
= —— COS (ОТ.
Таким образом, автокорреляционная функция гармонического
сигнала не дает никакой информации о его начальной фазе.
в) Для сигналов конечной длительности
ОС 00
Я(т) = $ e(t)e(t—t)dt= $ e(l)e(i + t)dl.
— ® —оо
В этом случае R (т) имеет физический смысл энергии сигнала
ПР*> различных по времени сдвигах сигнала относительно его копии.
Для прямоугольного импульса длительностью 4#(т) =
N) ПРИ Я(т) = 0 при|т|>Л-.
Автокорреляционная функция R(t) пропорциональна заштри-
хованной на рис. Р.9.3, а площади.
г) Если сигнал e{t) дан в виде 6-функции, то и автокорреля-
’У’онную функцию R{%) получим в виде 6-функции. Это следует
•^Посредственно из определения Я (О-
График автокорреляционной функции для всех четырех слу-
показан на рис. Р.9.3, б.
323
9.24р. Для решения задачи используем предельные соотношения
[?(0] = R (0) = 1; НО] = ИЯ(°°) = 0.
со
J R (т) Л
Время корреляции тр = ° .
Интеграл подсчитаем графоаналитическим способом (рис. Р.9.4)
применяя кусочно-линейную аппроксимацию /?(т). В результате
Рис. Р.9.3
получим
С J? Лт т I frO /т -г \ ЛА
\ к (т) ат «--------тг 4 — (т2—TJ = О.Ь.
о
Следовательно, то-^О,6 с и можно считать, что через это время
R Ы ~ 0. Таким образом, сигналы e(t) и е(/н-т) взаимно не-
зависимы.
9.26р. Взаимная корреляционная
функция двух импульсов малой дли-
тельности
СО
............7?e.,.W=$e(0i(<-T)dZ.
-/ 0~Т-1 2 ^3 t °
Рис. Р.9.4 Здесь i (т) имеет размерность энер-
гии.
Для двух прямоугольных импульсов (рис. 9.12, а) решение
аналогично решению задачи 9.21 р:
R.. М = Е1 ± при 0<|т|<-Д-;
1т0 нри
R,. <W = 0 при
324
Для рис. 9.12, б Ret i (т) — J е (/) /6 (i—т) dt=!е (т), что сле-
о
из фильтрующего свойства 6-функции.
Таким образом, взаимная корреляционная функция Ее>/(т)
повторяет форму импульса напряжения.
Аналогичный результат получим и для рис. 9.12, в. Так как
— —/0), то Rgt /-(т) = /^(т4 /0). В этом случае функция
р у(т) также повторяет форму импульса напряжения, но со сме-
щением на /0 влево (рис. Р.9.5, с).
б)
Рис. Р.9.5
Для рис. 9.12, г функция Re* ,(т) имеет вид, показанный на
рис. Р.9.5, б.
9.27р. На выходе четырехполюсника имеем сумму двух сигна-
лов: полезного ц, (0 и шумового иш (0, т. е. щ (0 = и„ (0 4- (t).
В качестве входного сигнала используем сигнал ut(i) = Um cos to/.
Тогда полезный сигнал на выходе и„ (0 = UmK (со) cos [со/ 4 ф (со)].
Для выделения полезного сигнала на фоне помех определим
взаимную корреляционную функцию входного ut (0 и выходного
М0 сигналов. Учтя при этом, что, по условию, помехи и полез-
ный сигнал не кор рели рова ны, получим
г t
в, W = 1пп 4- \ut (0 ца (/ + т) dt = ~ К (со) cos [сот 4- <р* (со)].
Г-»- <с ' V £
О
При т=0 /?и„ Я1(0) = -^-/С(со)со5фл(со), при т=г1==л/(2со)
ва (b) == К (со) sin <pk (со).
Из этих выражений следует, что модуль К (со) и фазу <р*(со)
Коэффициента передачи цепи при любой частоте гармонического
Угнала можно найти по значениям корреляционных функций при
T:fc0 и т = Tj = л/(2со).
325
Действительно,
. 2|/" /?И II (0)4-/?« « (Т|) П J (Т1)
к (»)=---------—г———; fg*M=—-s—(бг-
Um «• М
Заметим, что корреляционные функции /?о,. Пз(0) и И1(т)
можно определить не только расчетом, но и непосредственно ц3
опыта.
9.28р. По определению, энергетический спектр
G(w)= lim -^=М,
Г-»® 1
Т!2
где Sr(/to)= J с(/)е~/ш/ dt.
-
Кроме того, спектр G (со) связан преобразованием Фурье с кор,
реляционной функцией /?(т)—теорема Винера—Хинчина:
00
6 (ш) = R (т) e_/WT de.
— 00
а) Использовав выражение для корреляционной функции R (т)
из решения задачи 9.21р, найдем
00
G(w)= J Ele-iu*dt = £q6(cd) (рис. Р.9.6, о).
— зо
00
То, что интеграл J е_/’штс?т = б(со), где 6(d))—6-функция, еле-
- я>
дует из «физических» соображений. Действительно, указанный
интеграл соответствует комплексному преобразованию Фурье нуле-
Б
Фл» с4е(а*а')
Б
-/у, 0 ы -ty-Zty-bJi 0 су
5) в)
Рис. Р.9.6
О (л)
а)
вой гармоники единичной амплитуды, спектр которой состоит из
одной спектральной линии при о) = О, т. е. определяется 6-функциен-
б) Автокорреляционная функция (см. задачу 9.21р) R(y)^
р*
— cos cofT. Следовательно,
00
Ой
00
Eln
4
[6 (w—wj 4- 6 (со -Ь eh)
(рис. Р.9.6, б).
326
в) Решение для случая, когда e(t) представлена рядом Фурье,
следствие наложения полученных ранее решений, т. е.
= [6(0—(j)ft)4*6(to + (t)ft)] (рис. P.9.6, e).
a=i
DC
9. 29р. Считаем 7? (т) ж Сй6 (т), где GQ= J R (?) dx; 6 (т)—6-функ-
— СО
дня. Следовательно,
G(co) = J 7? (x)e“'WT = G0 J 6 (х) е**^ dx =
— 00 —а
со
coswxdx—j \ 6(x)sinci)Tdx = G0(cosOc—jsinOc)=Go,
— CD
так как 6-функция обладает фильтрующим свойствам, а именно
Рис. Р.9.7
В данном случае то = 0 и интеграл определяется значением
функции при то = 0. Поэтому cosx0=l, sinxo = O. Таким обра-
зом, энергетический спектр белого шума
не зависит от частоты и равен площади
под кривой, являющейся корреляцион-
ной функцией.
9.32р. Для приближенного расчета
напряжения на входе схемы считаем, что
и импульс тока повторяется с периодом
Г (рис. Р.9.7, с). Выберем период пов-
торения Т = 4/1 = 6,28 с, что во много
раз больше постоянной времени цепи.
При таком выборе Т можно использо-
вать данные расчета предыдущей задачи,
точное решение:
«(о—/«,[*(0—<i)L
-А,
где k (П = Re L = e"f.
Графики точного (кривая 7) и приб-
Л1<Женного (кривая 2) решений приведе-
«Ы на рис. Р.9.7, б.
9.33р. Для импульса малой длительности можно приближенно
унтать, что ik(t) wQ06(7), где 6(/)—6-функция. Спектр тока
y(/<o) = Qo, спектр напряжения на входе V (j\o) = J (/со) Z (jw), где
Ч<*М(о)-НЖ
327
Рис. р.9.8
Применив обратное преобразование Фурье, получим
00 «
и (/) = ~ § V (jto) J [# (®)cos tot—X (to) sin to/]
— CD — CD
CD
так как § [Я (to) sin со/ 4- X (®) cos ©/] d© = 0 (как интеграл в беско-
нечных пределах от нечетной функции).
В подынтегральном выражении
для u(t) оба члена представляют
собой четные функции относитель-
но ©; следовательно,
СО
Ц (/) = -^ J [/? (to) COS ©/—
о
— X (to)sintof]d(fl.
Учтем, что ц(/)=-0 при /<0-
Тогда при замене i на—/функция %(©) поменяет знак и
u(t) =-~-^ /? (w) cosco/dto.
о
По условию задачи, ₽(w) имеет вид трапеции. Поэтому
~Ш| (1),
*(0)
©1—W2
Ь),
cin Ыг—1°1 t
= Ю*. R (0) W1------------------
Л ' ' 1 41)2 — 0)!
2
Lo
(w—©J cos ©/dco ~
Подставив числовые значения, получим
и (/) = 100
sin 100f sin 50/
"ЛОО 50Г“
Для построения графика u(t) (рис. Р.9.8) удобно пользоваться
таблицами функций sinx/x.
Примечание. Любую по виду функцию R (со) можно приближен110
заменить несколькими трапециями. Тогда и (/) « где u^t—решение Д'1*
Л-й трапеции.
9.34р. Спектральная плотность напряжения на выходе фильтра
а) При Bl(0=6(O и С/1(/ы) = 1.
<ос
ило=4г $ =-^ --7?’ <рис- р-9-9>а)-
М. <l)g
328
Из решения следует, что выходное напряжение имеет вид
^ульса длительностью 2л/юс и амплитудой й<ос/п. С ростом по-
лосы пропускания фильтра длительность импульса уменьшается,
а амплитуда растет. При сос-+ оо напряжение на выходе
t
б) Единичная функция 1(0® J поэтому при
«*(0—1(0
t
u,(t) f .Ц Sln^jr-f,) dt, = ± Г л Si (/_/)! ( Р 9 9 б)
34 ' J д <ос(г — /3) л | 2 1 сх 3,J vr
— CD
COc(/~/3)
где Sie)c(f—13) = V — интегральный синус. При
gj %
0
tuc—оо напряжение на выходе ► 1 (t—4).
9.37р. Спектр тока в нагрузке
1г / : .\/н (Йэ) _ _1_.
'»'“ Ui (jw) ~ R ~ 2 (1 -Ь /со) *
R У44-w2/?2C2*
Спектр прямоугольного импульса
S-((o) = Efi
| sin (ofj/21
(u/i/2
откуда
s. (w)=Ett !.51п;У
• ' * U><1.4
I
R К4-t ‘
329
По теореме Рейли, энергия, выделяющаяся в нагрузке,
со от
П7 ЯСС2/Ч. R С Е* sin2 tott'2
1,7 =т\ S*<w) dta = — 1-R2 -.2. -X
о 0
1 , £2 f ti л я RC , 1 RC лягЛ
X4-i-(D2/?2C2G Irtfl \ 2 2 24^24 )~~
“4/?
где T — RCt2.
Подставляя числовые значения, получим lF=10_<e~1 Вт.
Рассчитаем энергию, выделяющуюся в нагрузке, при непосред.
с гвенном интегрировании по времени. Найдем ток в нагрузке при
»>(0=Д(>-е-'-г).
где Т = RC,2= 1 с.
При i >
Энергия, выделяющаяся в нагрузке,
IF = $ Ris(t) dt = j Я/’(0<й+ $ Ril= ~ (tt-T + Te'^
OOf]
т. e. получаем тот же результат, что л при использовании тео-
ремы Рейли.
9.38р. Спектральная плотность импульса напряжения
sUi (И = е”'"7 (см. задачу 9.16).
Ц)» 1[
. При <0 = (ор — 2л/Т — л/ti
Спектральная плотность тока
S; (/ш) = У (/ш) SUt (ja),
где Y (/©) =
r|
L \ w /J
Для контура с Q^> 1 (см. задачу 9.8р)
Г 9(га — гл 1 I / , (0—Юр
2(<о—d)pV|
J
где 2Дй)п = top/Q—полоса пропускания.
ззэ
Соответственно
.я
t * \ с /• \ 2£71 Дсопе
Г(/")5С\(/«р)- nPfA^-LJ^-Wp)]
Перейдем к изображению тока по Лапласу:/(р) = 51 (/ад)
Найдем оригинал и возьмем его мнимую часть. В результате по-
дучим
i до да е 1 sin (<V—90').
9.42р. Энергетические спектры тока
соотношением Gt- («) = Y- (ю) Gy (to), где
и напряжения связаны
YW=Y№)Y(-j4
Рис. Р.9.10
Определим комплексные проводимости цепи:
ЯЧ-М ’ я—М ; в ЯЧ-й>*£« •
Отсюда Gi(со) = 60 w-2p (рис. Р.9.10, а).
Корреляционную функцию найдем по теореме Винера—Хин-
чина:
= G(.(w)e^^e‘T,tl
На рис. Р.9.10, б, в показаны корреляционные функции напря-
жения Rfl(x) и тока /?,(т).
Глава десятая
10.2р. Согласно методу Штурма, исследуемую функцию пред-
ставим в виде
7 (п\ = = п» (₽)
М(р) mi(p) + m2(p) ’
ПК п, (р), тг (р)—полиномы с четными степенями р; п3 (р), т, (р) —•
Полиномы с нечетными степенями р. Заменив в уравнении р на
/Ч найдем
Re Z (ко) = ”т (/<й^ т* (цо)
Следовательно» ReZ(/to)^0 при ntmt—плп2=Ра^().
331
Величина Ро является функцией со2 = х; функцию Ро (О):)'Р0(Х)
называют первой функцией Штурма. Предполагается» что фу и к.
цня Ро (х) не имеет кратных и нулевого корней. Производную qj.
Ро по х называют второй функцией Штурма Рх (х) = Р'0(х). Третьей
функцией Штурма является остаток от деления Ро {х)/Рх (х), в3я.
тый со знаком минус. Деление прекращают, когда степень остатка
станет ниже степени делителя на единицу. Четвертой функцией
Штурма Р3(х) называют остаток от деления Р](х)/Р2(х), взятый
со знаком минус. Деление прекращают при том же условии. По-
следующие функции Штурма рассчитывают до тех пор, пока в
результате деления не будет получена вещественная величина.
После нахождения всех функций Штурма определим их знаки
при х = х1 = О и х=х2=оо. Этим значениям х соответствуют ча-
стоты 0 и оо. Составим таблицу знаков функций Штурма при
Xi = 0 и х2 = со (табл. Р.10.1).
Таблица Р.10.1
X Р, 17
Р.(х) РИх) ₽з(х) 1Г
Xt=0 — - 4. 2
Х2 —► оо Ч” —* —» I '
Подсчитаем число изменений знака IT, в первом ряду табли-
цы при xt = 0 и число изменений знака UZ2 во втором ряду таб-
лицы при х2 —* оо. Для рассматриваемого случая Wt=-2, IF2 = 1.
Если разность Wx— 0 (в нашем примере она равна 2— 1 == 1),
то при изменении х от 0 до оо, а следовательно, и изменении ш
от 0 до оо исследуемая функция Ро(х) = л,/П1—п.>тл не меняет
знака. Это означает, что если функция Р0(х) положительна при
х = хг = 0, то она положительна и во всем диапазоне изменений
х от 0 до оо. Если же — 1Г2^0, то при некотором х функ-
ция Р0(х), а следовательно, и ReZ(/<o) изменяют знак. При этом
условие ReZ(/<o)^O не выполняется во всем диапазоне частот.
Руководствуясь изложенным, проверим, выполняется ли условие
ReZ(/oj)>0 для Обозначим п, =
= р4 + 4р*4-1, = р* 4 6р2 -1- 1, л, = р3 + Зр; т2==7р344р.
Первая функция Штурма (заменили р на /<о)Р0(х)=х*—Зх3 +
4 х2 4 2х 4 1, вторая Рх (х) — 4х?—9хг 4 ^х 4 2.
Разделим Ро (х) на Рх (х):
9 П[15 11
Р0(х) 1 3 16**‘8*+8
Рг(х)~4Х 16+ Л(х)
Третья функция Штурма равна остатку от деления Р0(х) на РЛ$’
332
взятому со знаком минус:
15 11
8 Х 8 *
разделим Р1(х) на РДх):
1164 181
Р^с) _ 4Х3-9х24-2x4-2 64 41-16 19-19 * 361
15 II “19Х 19-19 + Ря(х)
16 8 8
Четвертая функция Штурма равна остатку от деления Ря(х) на
рв(х)» взятому со знаком минус:
Р ы = _Л64_х+!81
19*19 361*
Разделим Р*(х) на Ps(x):
19 15 II 30 857
Ря(х) 16* 8* 8_ 19-19-19 29*10-19 16-1164
Р,(х) “ 1164 181” 16*1164 Х+ 16*1164 + Р3(х) •
19-19 * ' 361
Пятая функция Штурма равна остатку от деления (х)/Р, (х),
взятому со знаком минус:
16*1164’
Составим таблицу знаков функций Штурма и числа перемен
знаков (табл. Р.10.2).
Т абл и ца Р.10.2
X Р, W
P.W ЛЮ Р.(х) Рз(х) Рд(х) г
8 ° t м и “Ь 4" 4“ 4“ 2 2
Разность ITj—Wz=2—2 = 0; следовательно, ReZ(/w)^0.
10.4р. В обоих случаях можно, так как нули и полюсы рас-
положены на отрицательной действительной оси и ближайшей к
Началу координат особой точкой является полюс.
10.7р. Является, так как такой двухполюсник не имеет полю-
сов на мнимой оси (нули plt 3 = —0»5^/0,5; полюсы ptt 4 = —1 ± /).
10.9р. Полагая Z (р) = , найдем вычет Z(p) прир = 0
И приравняем его к 10/3: А/1,5 = 10/3. Отсюда k=5.
10.11р. Полагая
7(п\— _*р(р24-1»
(р~г /0,578) (р—/0,578) “ р2 4-1/3 ’
ззз
найдем вычет Z(p) в полюсе р2 = /0,578 и приравняем его к двум.
В результате получим уравнение для определения k: А(1—0,334)/2=^
=2, откуда А = 6.
10.14р. За исходную при составлении непрерывной дроби при,
мем схему рис. Р.10.1, а. В соответствии с этой схемой
Так как Zx — p* то сопротивление Zx представляет собой сопро-
тивление катушки индуктивностью 1 Гн, Y„ = p\ следовательно,
проводимость Yt представляет собой конденсатор емкостью 1 Ф,
Рис. Р.10.1
Zs=l— резистор сопротивлением 1 Ом и т. д. Искомая лестнич-
ная схема изображена на рис. Р.10.1, б.
10.19р. Согласно методу Бруне, в выражении для входного
сопротивления заменим р на /со и выделим действительную и мни-
мую части:
Re Z (/со) = -тр—=-у-;—г ; I m Z (;ы) — -77—3.
м f 16—7о)2-|-(й4 м 1 16—7(j)3-f-iD4
Минимум ReZ(/co), равный нулю, имеет место при <о£ = 2. При
этом 1т2(/й))=^/2/2; р=лФ-, чему соответствует xx=oQLv
где Lx = .vv4 = И2/2 К2 = 0,5. Реализуем Z (р)—pLx =
Р (р2-1-2)(1—р) т—f . „
—-х=-ь Проводимость оставшейся части
2 2(р24-р~}-4) г
^-±2)(1-р) *
На мнимой оси имеются полюсы р = ±/И2. Им соответствует
последовательный колебательный контур индуктивностью Ц
— (l/2)afc и емкостью С2= 1/со£Л3. При этом
at=Resy.(p)=^^|- =1; £, = 0,5 Гн; Сг=1 Ф;
334
Проводимость Y (р) = 2р/(р*Ч- 2). Осталось реализовать Yt(p) =
2d 4
^Ув(р)—~»_р2~ — • Ей соответствуют последовательно соеди-
ненные L3 =—0,25 Гн и /?а — 0,25 Ом. В результате получим
схему рис. Р.10.2, а. Так как отрицательную индуктивность из
одних линейных элементов осуществить нельзя, перейдем к схеме
с идеальным трансформатором (рис. Р. 10.2, 6), для которой Lt =
ssS£1-|-L2=1 Гн; £5 = £24-L3 — 0,25 Гн; Ct— 1 Ф; /?3 = 0,25 Ом;
М===^2 = 0,5 Гн.
Рис. Р.10.2
10.22р. Определим изображения тока 7 (р) = 100/р2 и напря-
женин t'(p)= р1(р'^[00) . Отсюда 2 (Р) =• Схема двухпо-
люсника показана на рис. Р.10.2, в.
10.25р. В соответствии с формулами перехода от Т- к П-схеме
запишем выражения для проводимостей У* и схемы рнс. 10.2, б
через проводимости V2 и У3 схемы рис. 10.2, а:
V— __ okg(k2—k3) . akg , . .
* Yt + Yt+Уз 1 + (*8-*з)2’ 14
у ______Г1Г3 __ ak3 (Л3—k2) . ak3_________
1-МА2_*3)« 1 w
Из формулы (1) следует, что действительная часть У4 отрица-
тельна при k3 > й2, а из формулы (2)—что действительная часть
отрицательна при k2 > k3. Таким образом, при любом соотно-
шении между k2 и k3(k2^k3) нельзя физически из линейных
пассивных элементов осуществить У4 или У5. Формула для не
Дана, так как при осуществлении Fe препятствий не возникает.
10.27р. Сопротивление последовательно-параллельного соеди-
нения на рис. 10.3, а
<7 . Zt (oZj -|- aZ2 -4- Zg) _ gZ^ Z2 (1 g)
1+zz+z; _ гтл *
‘+z;
Сопротивление параллельного соединения на рис. 12.3, б
7 I Cd 7
dZt(bZj + cZ2) _ fe-t-d 1 1 ЬЧ-d 2
(ь+<1)гг-1-С2г- 1+^^z^z •
(1)
(2)
335
Входные сопротивления схем рис. 10.3, а, б должны быть оди.
каковы при всех возможных частотах. Следовательно, должны
быть равны и коэффициенты при соответствующих членах числи-
телей и знаменателей выражений (1) и (2):
bd . . ( cd с __________«
1 ' а~ TFT’ д-н “ Ь
Решим эти уравнения относительно 6, с, d: Ь = о(14-я); с=?
= (1-о)2; d^l-ia.
10.31р. Входная проводимость двухполюсника на рис. 10.4,0
. _________I_______________<»С1
J —/ 1 \ “ /taCj—jb
b= 1—со2!/?*.
Входная проводимость двухполюсника на рис. 10.4, е
b
У’= = •
/Cili-j ‘ Ь
R*
Входная проводимость при параллельном соединении двухполюс-
ников
у _i_ у oC1 W 1 « /<*^1^) j
10.33 р. В соответствии с правилом составления дуальной схе-
мы на рис. 10.5, а в двух контурах ставим точки 1 и 2, авовнеш-
ней области—точку 3. Эти точки будут узлами дуальной схемы.
Проведем линии между точками /, 2, 3 через элементы исходной
схемы, которые заменим на дуальные. Заменив Lx на С2, С] на
А, и Rt на /?2, получим схему рис. Р.10.3, а. Значения С2, Ь.г и
/?а найдем, исходя из того, чю произведение сопротивлений
взаимно дуальных элементов должно быть равно /?2:
Л, = ; /со!, = R1; Lt = CIR1.
Входное сопротивление исходного двухполюсника Zt — jwA +
4- Входная проводимость дуального двухполюсника
относительно узлов 1 и 3
Уд = /ь)С2 4- = -^2 [/wLx + 1+•
Произведение ZtZt = Z1~ = R2.
* Я
336
10.34 р. Проверим» выполняется ли условие ktk2—в
ролюсе р = 0. Вычеты Z„, Zla, Z22 при р = 0 равны 1. Условие
учетов в полюсе р = 0 выполнено, так как Iя—Iя —0. Выясним,
руполняется ли условие Геверца гпгаз—
rn= ReZ11 = Re^±^±'=2;
p~j(£> 1
ra = r„=Re £±1=1; 21-Р > 0.
р= /ш **
Условие Геверца выполняется. Каждое из сопротивлений Zin
Zn=Z£2 удовлетворяет условиям, накладываемым на входные со-
Рис. Р.10.3
противления двухполюсников. Поэтому приведенные выражения
для Zn, Z12, Z22 могут соответствовать некоторому физически осу-
ществимому двухполюснику, схема которого изображена на
рис. Р.10,3 б.
10.37 р. Не является, так как его нули plt 3 = 0,5 ±/0,865
находятся в правой полуплоскости (рис. Р.10.3, в).
10.40 р. Может, так как кроме выполнения общих требований,
Которым должна удовлетворят^ передаточная функция четырех-
полюсника, приведенная в условии задачи функция имеет нули в
левой полуплоскости (рис. Р. 10.3, а).
10.43 р. Для перехода от нормированных параметров (/?„, LH,
С») к ненормированным (/?, L, С) воспользуемся соотношениями
$ = #Н/?О1 £ = Ln . С = CH/(to0/?0). Схема с ненормированными
параметрами изображена на рис. Р. 10.4, а.
337
10.45р. а) Сопротивление
. __ ₽i/(o£i .
* — 4-/«U-i ’ (•)
Возведем (2) в квадрат и запишем его при частотах со2 и су
R’[eI‘““*1—1] = (<1>JLJ)1 ; (3)
R«[e’«I] = (и,^)» 17 1 + e““’’I. (4)
n
Поделим (3) на (4) и определим 1 + :
-л/ «op
/? V 1—а
__/ (О| \2 — 1
\ ш2 / __]
(5)
(6)
Из (5) следует, что решение возможно, если а < 1,
По найденному значению 14- RJR подсчитываем R.
определим £х:
. / e2Q(^>-l
1 1/ 1 I у с«а(ю.) '
Сопротивление
^2 + /(оС2 ~ + /wLi ’ ^2 ” Я W1*. Сг —
6) Сопротивление
(9) 1+4г=
1 -j-jaRiCi
Из (3)
(7)
(8)
(10)
Из соотношения e“ = |l + Z1R,| следует, что
(1+4-У+“>,«?с;
е«в —. X /_________
!.+(0*К1сЛ
(11)
Согласно (П), при ш = 0 находим 14- Rt/R = е°Таки*1
образом,
R1 = [e“<°>— 1]R. (12)
По условию, при некоторой частоте известно затухание
afpt). Подставив эти данные в (11), определим Ct:
е*к°>—e2a(“'’ /|3)
о?/?8 [е« <?>— ip 1] *
1 +/<o/?iCi ’
338
Сопротивление
/?8 “I- jcoL>j:=
R2 R’a+iwRA)
Zi “ Rx
Следовательно,
₽s = /?3/Ri; L^R^
(14)
10.46р. Определим изображение напряжения на выходе:
ю
10
(р 4-26,17) (р 4-3,83) р2-|-30р4 100 *
Изображение входного напряжения U1(p) = }/p. Передаточная
, (/8(р) Юр
функция по напряжению ^-{77(^ = (р+з,83)(р-1 26,П)'
Выберем дополнительный полином Q = p-j-10. Его корень
р——10 находится в промежутке между корнями —3,83 и —26,17.
Числитель и знаменатель Ких разделим на полином р~\- 10. Даль-
нейшую реализацию осуществим так же, как и в задаче 10.41.
В результате получим = (М — N)/Q = р 4-10; Zs = = -ffi-Q *
Полная схема четырехполюсника изображена на рис. Р. 10.4, б.
Глав а одиннадцатая
11.1р. Требуемые величины сведены в табл. Р.11.1, по данным
которой на рис. Р. 11.1, а, б и Р.11.2 построены соответствующие
графики.
Таблица Р.11.1
о, рад'с 0 314 4000 10000
Zo~ Ro4 /ш£с, Ом/км 2 24/0,765 24-/10 24-/25
То=(6о-У /ыС0)- 10 ~в, См/км 0,5 0.54-/1,57 0,54-/20 0,54-/50
ZeV0.10-s, км-1 1 1.088 4-/1,357 1,3984 /14,2 1,64 /35,3/
а-10”3, Нп/км 1 1,088 1,398 1.6
Р-Ю-3, рад/км 0 1,357 14,2 35,37
км/с 0 231.4-Ю3 281.7.103 282,7
X, км 00 4627 442,25 177,5
ZB = V ZOI’YO, Ом 2000 1136е_;2В’5° 713е-/&.«в 707е-;2°
0,606 0,59 0,497 0,449
11.6 р. По известным величинам /?0, Ло, Go, Со определяем по-
стоянную распространения у = аЦ-/|3 для нижней и верхней гар-
монических составляющих передаваемого сигнала. Результаты
расчета сведены в табл. Р.11.2.
Допустимую длину линии, при которой затухание не превы-
шает 3,3 Нп, находим исходя из наибольшего значения коэффи-
циента затухания %ах = 2,94 . 10-8 Hn/км (агоах соответствует верх-
339
Таблица Р.ц g
Л Гц 100 10. КР
ш, рад/с 628 —— 6,28.103
Zo=/?o4-jw£o> Ом/км 2,5-4-/1.193 ьэ СП -F цэ Се
Уо = (Go + /с*)С0)• 10“’, См/км 14-/5.024 14- /502,4
Т=У Zoyo = (a + /₽)d0-®, KM-i 1,906^/2,99 2,944-/245
а-10”а, Нп/км 1,906 2,94
Р-10~3, рад/км 2.99 245
«ф = й)/р.Ю3; км/с 209,4 255
Af = (^тах/^ф)" »0"а. С 5,36 4,4
ней частоте в спектре передаваемого сигнала /,= 10-10s Гц):
аш>Лах = 3,3 Нп; /ю„==3,3/(2,94. lO"8^ 1122 км.
Как видно из табл. Р.П.2, фазовые скорости, а следовательно,
по линии различных гармонических
составляющих сигнала различ-
ны. Поэтому за время распрост-
ранения принимаем наиболь-
шее, соответствующее нижней
частоте — 100 Гц: иф1 = 209,4 х
X Ю3 км/с; A^ = ^max/^i^5,36x
ХЮ’3 с.
и время распространения
ptOjailfa
а-№,Нп/кн
1,5
J5
20
~Ш00 5000 lOOOO ы.рай/с
Рис. Р.11.1 Рис. Р.11.2
Для верхней частоты /2=10 Ю3 Гц: цф2 —255-103 км/с;
Л^=^тВх/Уф2 = 4,4-10-8 с.
Ввиду разницы во временах распространения по линии Раз*
личных гармоник фазовые соотношения между гармоническими
составляющими сигналов на входе и выходе различны, поэтому
форма выходного сигнала отлична от формы входного, т. е. имеет
место искажение сигнала, называемое фазовым искажением.
Кроме того, причиной искажения передаваемого сигнала я®*
ляется зависимость от частоты коэффициента затухания
(см. табл. Р.11.2).
340
В данном случае волновое сопротивление также является функ-
цией частоты, что не позволяет согласовать линию с нагрузкой
go всем рабочем диапазоне частот.
11.7 р. В да ином случае L 4- £доп= /?0С0, G3 = 2,5 • 8 • 10" •/( 1 • 10_<)=
^0,02 Гн; £^ = 0,02—1,910~3= 18,1-10-3 Гн. ___
После включения дополнительной катушки а=|//?0С0 =
1,591 -IO"3 Нп/км (не зависит от частоты);
Р = w l^(L0 ч- £доп) Со = со У0,02-8-10~’=со V160-10-12 рад/км;
= со/р = 79 • 103 км/с.
Фазовая скорость уменьшилась более чем в два раза. Теперь
она не зависит от частоты.
Наибольшая допустимая длина линии, при которой затухание
напряжения (тока) в согласованном режиме не превышает 3,3 Нп
/тач = 3,3/а — 3,3/1,591 • 10-з = 2074 км. До включения 1т9* =
-= 1122 км (см. решение П.бр). Следовательно, дальность передачи
возросла в 1,85 раза. Время распространения сигнала по линии
длиной 2074 км А/=/тах/уф = 2074/(79-10э) = 26.25 -10-3 с.
До включения £1гп время распространения сигнала по линии
такой же длины составило бы
АГ = 2074/(209,4 103) « 10 -10“’ с.
Таким образом, включение дополнительных катушек привело
к значительному снижению фазовой скорости, а следовательно,
к увеличению времени распространения сигнала по линии (более
чем в 2,5 раза).
11.9 р. После включения дополнительных катушек
а = ИЛА=4,012-10-’ Нп/км;
= 1 .'/(*-» + 4<т) со = 4>846 103 к“/с-
Первое условие соблюдается при длине линии
Сах = (а/)тах/а-3,3/(4,012-10-3) = 822 км.
При этом время распространения сигнала по линии
А/, = Cax/v* = 8,22/(4,846 -103) =0,169 с,
т. е. второе условие не удовлетворяется. Исходя из него наиболь-
шая длина линии Сах =А/шахиф = 0,15-4,846 • 103—727 км. Таким
образом, Сах — 727 км.
11.16р. Входные сопротивления линии при коротком замыка-
нии и холостом ходе:
« = U,„/l , = 500ei71e/M"3°' = 500е~<21-5” Ом;
2.XK = t7,„//,„ м = 500е/71е'’8-*"=500е-1« ” Ом;
4 - Г4А. = 500е-яг Ом; th yl = КZ„ Д,, =
= (/" g-/21.bo/e-/e8,S° — 1^/23,6 °.
-г PV*_e-W 1
Так как thTZ = -7—у
341
Рис. P.11.3
Последнее выражение приводим к показательной форме записи
учитывая, что определенному положению вектора на комплексной
плоскости соответствует бесконечное множество комплексных
чисел, отличающихся аргумен-
том на целое число 2л. Поэтому
e2vi — е2а/е/2р/ _. 4,74е/ <e0°+®пп> *
следовательно, 2а/ = 1п 4,74 i
= 1,556; 20/ = 90° 4- 2пл; а/
^0,78; 0/ = 45°Ч-пл.
По условию, длина линии
/ < Х/2. Тогда 0/ < л, т. е. р/ =
= 45° = 0,78 рад, откуда
а — al/l =
₽ 0,78/55,5 1,41 • 10"» Нп/км*
₽=₽/// =
= 0,78/55,5 = 1,41•10"» рад/км.
У = (1.41 +
4 /1,41) -10"» км"1.
Первичные параметры линии:
Яо + /«Т0 = у2в = (1,41 4-/1,41)-10~»-500 е-'«° =
= 2 10~2e'*6’• 500е-/*5’ = 10е'° Ом/км;
/?„ = 10 Ом км; £, = 0; y/Zb = Gb+;<i>Cl)=^^^F- =
= 0,4-10"4е',“° = 40-10_,/См/км; GB = 0; С„ = 40-10"’Ф.
Мгновенные значения напряжения и тока на нагрузке в сог-
ласованном режиме
“s (0 = Sin (at—pZ);
Z, (0=тН-e-a/ sin M—₽Z + 45°).
Учтя, что а/= 0,78; е~а, = 0,459; р/ = 45°, получим
(/) = 229,36 sin (со/—45°) В;
й (/)=0,46 si поз/A.
11.20р. Определяем длину волны: A, = o*// = 250-103/2500=
= 100 км. Относительная длина линии //1=62,5/100 = 5/8. Заме-
ним индуктивное сопротивление нагрузки эквивалентным коротко-
замкнутым отрезком линии с теми же параметрами, что и основ-
ная линия (рис. Р. 11.3,а). Длину эквивалентного отрезка М
находим из уравнения
ZBxB = /zBtg^-AZB = ZB = jZB; tg-^AZB=l;
^AZ,=n/4; AZB = l/8.
342
После такой замены приходим к случаю линии короткозамкну-*
-ЮЙ на конце длиной Г — I4- Д/эк — 5Х/8 -4 Х/8 — ЗХ, 4 (рис.Р. 11.3»а),
р точке, отстоящей от фиктивного кольца линии на расстоянии
у 0-4 Х/8 (у—расстояние от действительной нагрузки), справед-
ливы уравнения для комплексов напряжения и тока
£f(/) = jV»sinPy';|
/(!/-) = 4 COSp/, J ()
а для соответствующих модулей (действующих значений)
I/(/) = ?,/,! sin Р/|; 1
/(/) = /2|cosP/|, f
гдекомплекс тока в точке у'— Согласно (I),
/ „___/ 1 = е'”’.
jzBsinpZ /500sinf sin^S
\ Л 4 у x
Тогда
U (у') = 5001 sin fiy' I = 5001 sin 0 (у-г X/8) |; |
/ (/) = 1.1 cos ft/' I = 1 • I cos ₽ (y 4- X/8) I. J (2)
На рис. P.11.3,6 по выражениям (2) построены эпюры U (у').
I (у'). Часть эпюр, расположенная левее сечения //' = А/ЭК = Х 8
(где сосредоточена действительная индуктивная нагрузка), спра-
ведлива для заданной линии с сосредоточенной нагрузкой.
Напряжение и ток в нагрузке найдем по (2):
и, = 5001 sinР = 500 sin i = 500, /2 В;
/.= l.|cosp|| = ^A.
Ток на входе Л^0.
Согласно рис. Р.11.3, б, ближайшая к нагрузке пучность
напряжения расположена на расстоянии Х/8=1,5км. а ближай-
ший узел—на расстоянии Х/8 4- Х/4 = 37,5 км от нагрузки.
11.25р. Входное сопротивление нагруженного четвертьволно-
вого отрезка линии ZBX = Z|2/ZH; для обеспечения в основной ли-
нии режима бегущей волны должно выполняться равенство ZBX=
a=ZB1=100OM. Следовательно,
= KzZX = = г 100-400 = 200 Ом.
При этом ввиду отсутствия потерь в основной линии дейст-
вующее значение напряжения на входе согласующего отрезка
линии U (Х/4) будет равно напряжению на входе Ц = 100 В. При-
мем начальную фазу комплекса О (Х/4) равной нулю:
L/(Х/4) = 100 е>°°.
343
Этот комплекс связан с комплексом напряжения на нагрузке U
известным соотношением
(J (1/4) = и, cos ₽ 1+jZn sin р 4;
а Л 2л А л
с учетом ₽т=-^-4 =У
U (1/4) = jZ* 4^ sin i = /ZM
Тогда для напряжения на нагрузке получаем
ft _ U (А/4) _ ЮОе7 ___ ;9ЛП*
/ZB£/ZH - 200 “ /2UU’
7 400
U3 = 200 В.
11.26р. Входное сопротивление линии
„ Ui ^памЧ" ^отрх 1 ^отр1/^пал1 __% l-t-Ti
А (^пад1—^отр1)/^8 1 & отр1/^пад1 1 П
14-1 е-'“"
= 400-----i—— 629е-'=«” = 556-/295 Ом.
1 '«-/«•
О
Выразим коэффициент отражения от нагрузки i\ = t/0T₽a/t7naai
через коэффициент отражения на входе линии Гх:
/у 7/
Г — отр* — отр1 — г р2₽*
2₽/=2TL^>- = T! °-
г Л 16 Л
Следовательно,
4 *
Г1 = 4-е'/'5°е‘'"°=4--
О О
Сопротивление нагрузки
ZB = ZBl±h. = Ztl~^ = 2Z. = 800 Ом.
Глава двенадцатая
12.1р. По условию, в момент коммутации / = 0+ напряжен^
на входе линии скачком возрастает на £, т. е. и1(0 = £ -НО-
Возникает падающая волна, расчет которой ведем с помопхы0
эквивалентной схемы рис. Р. 12.1, а. Пока в линии существу61*
волна одного направления, ее входное сопротивление в любом
сечении равно ZB. Поэтому на рис. Р. 12.1, а линия по отнош6'
нию к выходным зажимам заменена на Zp. Учитываем, что 1*1(01=5
344
*)]x=o==£'1 (0-Согласно рис. Р. 12.1,a, i, (Z) = «t(0/ZB=
^пад(С*)1х=о==(ВДв) 40-
В точке, отстоящей от входа на расстоянии х, напряжение и
ток изменяются во времени по тому же закону, что щ (0 и G (0,
Рис. Р.12.1
но с запаздыванием на время t = x/v:
Ц,ад(/, х) = £-1(/-х/и); (I)
*) = £• 4t-x/v). (2)
Независимо от вида нагрузки
режим работы линии от момента
когда падающая волна достигает
конца линии. Дальнейший рас-
чет зависит от значения и ха-
рактера сопротивления нагруз-
ки.
а) В этом случае отражен-
ной волны не возникает; выра-
жения (1) и (2) справедливы и
при Графики iz(0, i (0
при х = //2, х-t построены на
Рис. Р.12.2. В момент / = //и =
300/(300- 10э)=1-10-3 с по
всей линии устанавливается на-
выражения (1) и (2) определяют
коммутации до момента t = l!vt
Рис. Р.12.2
пряжение £ = 500 В, ток i = Е/£ъ — 500/400 = 1,25 А. Переход-
ный процесс заканчивается.
б) Выражения (1) и (2) характеризуют первую падающую
Волну:
«™, (Л X) = Е-1 (t —1)-. inaw (/, ж) = -f--1 (t-±\
\ * / "В \ I* /
Расчет первой отраженной волны. Режим в месте возникно-
вения отраженной волны в общем случае можно рассчитывать
345
по эквивалентной схеме с сосредоточенными параметрами
(рис. Р. 12.1,6), которая при ZB = ©o соответствует рис. 12.11в
Напряжение на выходных зажимах линии 2—2*
= /) = 2Е-1 /) + ио1р1 (/,/).
Тогда
«огр. (Л 0 = «г(0-«„.я /) = 2Е-1 (t-liv)—E- 1 (/-Z.v) =
= Е • 1 (/ - Z/v); (t. /)--(t, /), ZB=
ЛВ
если для foTpl сохраняется положительное направление тока /па.ь
В точке х с учетом запаздывания на время (/—л) и
Расчет второй падающей волны. Определение unaig (/, л), (7, л)
проводим по эквивалентной схеме рис. Р. 12.1, г. Она составлена
с учетом того, что вторая падающая волна возникает за счет
повторного отражения первой отраженной волны от коротко-
замкнутого входа линии:
«палг (Л ОН «отр! (h 0) = 0; «„а-я (/, 0) = — мотр1 (1, 0) —
2/ \ , - <а ЛХ ^ПЗД2^«^) Р 1 { 4
J. <naa2V» 2в — 2В'Ч ?
С учетом запаздывания на время x/v
/ 9/ 1 г \ р /
*) = — £I U— )'• =
\ u / ьв \
Расчет второй отраженной волны. По эквивалентной схеме
рис. Р. 12.l.c?,
«2 (0 — ^«пад5 > 0 ^ПЭД2 0 *Т ^отр2 • 0»
«от (Л /) = «пздг (Л /) = -£ 1 (/-3//U);
C,p2(t Г)----«ОТР.(*. =
(положительные направления zOTp2 и »пад£ считаем одинаковыми)!
346
В интервале (31/и) <i < (4Z/u)
u(t. л) = е[1(/—х/0)+1 («——1х
X(t-^)] ; i(t, = f [ 1 (z—^)-
К моменту t = M/v во всей линии u(t, х)~0, i(t, х) = 0, т. е.
система приходит к первоначальному состоянию, затем процесс
Рис. Р.12.3
повторяется с запаздыванием на время 4Z/U. Графики «(Z), i(t)
при х = / и x=Z/2, построенные по последним выражениям, даны
на рис. Р.12.3.
в) Расчет проводится аналогично предыдущему. Рекомендуется
его сделать самостоятельно. Приводим окончательные выражения
Функций:
Графики «(/), i’(0 ПРИ * = 4'2; х=1 построены на рис. Р.12.4.
12.3р. Время прохождения прямой волной участка линии дли-
347
ной I = 600 м т = l/v = 600/(3 • 108) = 2 •10_< с. В интервале О
от входа линии распространяется падающая волна с прямоуголс
ным фронтом
1 (<-£); <„.а(0=£1 (<-£)•
X v \ V /
В момент т достижения падающей волной сосредоточенной
индуктивности возникают отраженная (распространяется на у част.
Рис. Р.12Л
ке 0 х Z) и преломленная (распространяется на участке х > /)
волны. Для места возникновения отраженной и преломленной
t-1/v
Рис, Р.12’5
волн в течение интервала времени т—Зт справедлива эквивалент'
ная схема с сосредоточенными параметрами (рис. Р. 12.5, a).
чет переходного процесса для рис. Р. 12.5, а дает следукиДО
348
результаты:
2£ Г fr—-)1
'НС=-^[,-е к °J:
и, /
uM = 2E-iL(t)Z.=E+E<i t V »Л (2)
u,(t) = iL(t)Z,=E-Ee > V-»A (3)
Участок линии O^x^Z. Зажимы 2—2' (рис. P. 12.5, а) при-
надлежит рассматриваемому участку линии, поэтому
Чг (0 = ^пад 2 (О “Ь ^отр 2 (О»
^Отр 2 (0 ~ Ut (О ^оа*»(0-
согласно (1), при unan2(Z) = £- Тогда с учетом (2) ыотр1(/)=
= £е L \ °' =uOTp(f, Z). Возникшая отраженная волна рас-
пространяется по линии без потерь без затухания. Мгновенное
значение напряжения отраженной волны в точке х запаздывает
по отношению к функции итр 8 (/) = иотр (/, Z) на время (/—х)/о:
fr-—1 / 1\
Ио,р(Г, х) = Ее М » » М (/-4).
Множитель 1 (/—Z/v) позволяет математически учесть момент воз-
никновения отраженной волны (^t = l/v, при t потр=0) . Пол-
ное напряжение на участке 0—I
u(t, x) = uria(Z, x)4-uotf (/, x) = E-l(Z—x/v)-j-
/ 2/—x\
+ £e L ’ ' •!(/—Z/d) = 400 -1 (Z—x/0)-I-
- 50-10* (
+ 400e V 3 I0’ / •!(/—2-10"’)B. (4)
Участок линии x > l. Этому участку линии принадлежат за-
жимы 3—2' (рис. Р. 12.5, а). Напряжение п3(/) может рассмат-
риваться как мгновенное значение напряжения преломленной
волны при х = 1. Для преломленной волны отсчет расстояния
Удобно вести от места ее возникновения. Обозначим хх = х—Z. Тогда
(Z)=UnP (Z) k=o=HnP U. 0). Мгновенное значение напряжения пре-
ломленной волны в произвольной точке хх запишем с учетом за-
паздывания на время xt/v:
Множитель 1 (/ — 2-10“’) свидетельствует о том, что при /<2х
XlQ~e с unp(Z) = 0 во всех точках линии. По выражениям (4) и
349
(5) на рис. Р. 12.5, б построен график и (х) для момента времени
^.ЭД^З-Ю-'с.
12.5р. После замыкания ключа, когда в линии существует лИщь
падающая
у
волна, входное
\txQ
ЧТ
сопротивление линии в любом сечении
равно ZB. Временная зависимость
напряжения на входе линии (или
на конденсаторе) может быть полу,
чена с помощью эквивалентной схемы
(рис. Р. 12.6. а):
а)
2
о
uz(t)
Uc(t)
Е_
г
"пад(^»
л=с-
О
Рис. Р.12.6
о
2
= ^I-e (6)
А1ад(^» ^) = "пад(^» -^Ь^в* (О
При достижении фронтом волны
разомкнутого конца линии режим на
выходе (зажимы 2—2Г на рис. 12.2)
определяется эквивалентной схемой
которой и2 (0 = 2«пад(Г, /) = ппад(Г,
рис. Р.12.6, б, согласно
О "огр (^» О' Следовательно,
"отр(^» 0 = “"пал (^» 0 "пад(^« 0 "пад(^» 0 1
п
D
В точке х мгновенное
запаздывает на время
значение напряжения отраженной волны
"отр
^ОТр ♦ -^) "отр
(5)
(9)
Е
и
1 — е
е
2
и
в
с
(положительное направление iOTP берем совпадающим с направ-
лением tna3).
По выражениям (6)—(9) на рис. Р.12.7 построены график11
нпад(х), Аыд(*). "отр (-0» <отр(Л’) и результирующие зависимости
"nafllv)-Lt/OTp(x), iпаз (х) -ь Аир (*) для t = l;v\ 1.5//U.
12.8р. Коммутация происходит в цепи с ненулевыми началь-
ными условиями. В исходном состоянии напряжение по всей л11*
нии равно Е, а ток отсутствует, т. е. при / = 0_ и (х) — Е, i (л) = 9т
ис(0_) = Е. При разомкнутом ключе напряжение
= <РЬ = £‘
350
ррлючаем последовательно с разомкнутым ключом два источника
9 д.с. u'K = u* = Et направленные встречно (рис. Р.12.8, а). Это не
рзденит режима работы цепи как до коммутации, так и после
Ь(%?мутации. Пользуясь принципом наложения, разбиваем схему
Рис. Р.12.7
Рис. р. 12.8, а на две (рис. Р.12.8, б, в). Коммутация в первой
с*еме не приводит к возникновению переходного процесса, режим
Дается таким же, как и до коммутации [u(x) = b, i(x) = 0] Во
‘уърой схеме после коммутации возникает переходный процесс
Ри нулевых начальных условиях. Режим работы в месте ком-
351
мутации определяется схемой с сосредоточенными параметрами
(рис. Р.12.8, е). и
Расчет переходного процесса для рис. Р.12.8, е ведем отно-
сительно напряжения на конденсаторе ис (/):
нс(0_) = 0; i/ (0_) = 0;
пр ~
Z (р) = Zp 4 — 0 (характеристическое уравнение),
где
П - 1 4 1 7 1 У 1 - 1
Pl'* 2ZBC V \2ZBC ) LC~ 2.400.1,25-К)-»
_j_ тХ f_____J------у___________!___________i-io®
Г \2-400-1,25-10-®^ 0.8-10-3.1,25-10~6 —
Это случай двух кратных корней:
( «с (0 = “с пр + (А + Л J) е₽‘ = - Е4- (Лх + Л20 е~i°";
t тг=л»е‘10" + (-»0^е-«”;
( кс(0+)=—£4“ЛХ;
352
уравнения для определения постоянных и Д2 получаем, поль-
зуясь начальными условиями
“с (0+) = ис (0.) = 0; iL (0+) = iL (0.) = 0;
i ю 1 1
Ч ic(0J «7((М-Н((М ZD _п
-4T<U+J-—с ~ С ”и-
Таким образом,
-£+Л1 = 0; 1
Д8—10еДг = 0; (
Л = £; Л2=10в£;
ис (/) = -600 + 600(1 + 10*0 е-10,/ = «лад (П L-o,
где расстояние от конца линии.
Для бегущей волны, распространяющейся по схеме рис. Р. 12.6, в,
UnM(/, «/)=—6004-600 |1 + 10* fz— iJle-l’Ml-WW; (1)
//)==^пад(^‘ Р)/^в.
Выражения (1) справедливы для интервала времени M = l/v
после коммутации.
Накладывая режим, рассчитанный для схемы рис. Р.12.8, в„
на режим схемы рис. Р.12.8, б [u(y) = Et t(£/) = 0], получаем
выражение для напряжения и тока в исходной схеме. На участке
линии между ее концом и фронтом падающей волны =
г ( и \ 1 ~10' (1 1
и(1, у) = &Х 1+10'1/ —М е V "'В; 11
L V °' 1О.Л_Л\ 1 (2)
«(/. </) = -!,5+ 1,5 [ 1 + 10“(< —|)]е" }
В момент времени t = 2,5- 10~в с фронт падающей волны до-
стигает середины линии. На рис. Р. 12.8, г, д построены эпюры
распределения мгновенных значений напряжения и тока для
1 = 2,5-10~в с с учетом выражения (2).
12.11р. Основным уравнениям линии без потерь, связывающим
Мгновенные значения напряжения и тока
du(t, х) т di(t,x} \ /1Ч
di с —дГ~ * I
di (/, х) п du (t, х) | /fn
dx dt" ’ J
ПРИ нулевых начальных условиях соответствуют уравнения для
Изображений
—+£^- = Дор/(р, X); | (3)
-^+-=С«Р^(Р. х). J (4)
353
Решения (3) и (4) имеют вид
U(p, x) = ^ie-'“ + 4ev<; (5) !(р, х) = , (6)
где у -- у (р) = р И L0C0 = p/и: ZB (р) = И L0;C0=ZB: г» = 1.
Аг, Л2—функции оператора р, не зависящие от координаты х и
удовлетворяющие двум граничным условиям:
х = 0; U(p, х) = 6г1(р) = Л14-Л2;
». U (р. X) _ и (р. О _ 41е~т/Ч- Д2е?/ 7 i..\ __
А ’ 1 (р, X) - / (Р, I) - Zie-T'_ A*evl * ~
= l±^^ZB(p)==Z1(P),
1 — (Лв/Лж) e“v*
где Ux (р)—изображение напряжения на входе линии.
Из последнего выразим величину
Л 2 рлу/_^2 (Р) ^в (Р) _Т /М
-ZzW+Ztip)-1
(8)
— операторный коэффициент отражения от нагрузки.
Из (7) и (8) получим
л и' ™ А
1 “ 1 + Г(р)е'!« ’ 2 1+Г(₽)е-"-'< ’
Тогда (5), (6) с учетом у=р/у принимают вид
</(р.*)=£Л(р)
х 21-х
е Р ° -4- Г (р) с
-Ъ>~-
1-1-Г(р)е 1*
х 21-х
—р— -р---
цр, ,P-rWe j.
-2р —
! + Г(р)е й
(9)
(Ю)
Рассматривая (9) при х—/, находим искомую передаточную
функцию:
Операторное
х^О;
t
Н(п\ - Ф) _ П-^г(РПе Р v
Пи^~£Л(Р)
14-Г(р)е v
входное сопротивление получаем из (9) и (10) при
Z (о) = ^р-
z«x it (р)
-2р —
|-Г(р>е р
~2р~ *
I —Г(р)е v
а) При согласованной нагрузке
р / _\ (p}—Zb (р) __ л
^-<и(Р}-г2в(р)
354
Тогда в соответствии с (9), (10)
U (р, х) = Ut (р)е’Рv; Л (р,х) = [(/i (p)/ZB] е"₽
Если оригинал изображения Z/t(p) обозначить ия(0 (мгновенное
значение входного напряжения), то по теореме запаздывания для
мгновенных значений напряжения и тока в точке х справедливы
выражения и (х, t) = ut (Z —x/v); i (Z, x) — ur (Z—x/u) . В рассмот-
репном случае ux (Z) = Е • 1 (Z). Следовательно, и (Z, х) = Е• 1 (/—x/v);
б) При ZH = oo Г(р)= 1. Выражения (9) и (10) принимают вид
Е
21-х
-Р —
и =
Р
х 21-х
Е е~Р~-е~Р~
(11) 7(р,х)^.!------Ч—.(12)
14-е“₽ v
if -р-\
Для перехода к оригиналу рассмотрим выражение 1/\14-е v )
как сумму бесконечной убывающей геометрической прогрессии со
21
-р —
знаменателем q — — е и:
f( ~Р—\ -2р — — 4р — -6р —
1/V1 ~Ь е t,/=l—е t 4- е v—е 11 4-«. • •
При этом
-Г х 21-х
l(pt х) = -=-| е Р v — е Р v —е Р
р£,^ L
(На)
(12а)
Оригиналы, соответствующие (Па) и (12а), представляют собой
бесконечные суммы скачков, запаздывающих друг относительно
Друга:
u(t, х) = е[1 (t—-} + 1 (t——1 (i——
-1 + (13)
+10~^)+•••]• .04
355
21 —х
в) При коротком замыкании, согласно (8), Г(р) =
U (р, х) — —-г (е Р ° —е
-2₽4 4
1-е °
(х 21-х
e_pV+e-₽—
-лР —
1-е . u
1(Р. х)=
Рассмотрим выражение
вающей прогрессии со
1/(1—е*2р//г) как сумму бесконечной у бы»
р а/
знаменателем е v :
1/(1—е-= 14- е~2^и4* e-4p//D-Ь... .
Тогда
г) При Z„=2ZB
р f -Л _ (р) (р)___1_
2н(Р) + 2в(р) -3 •
Согласно (9), (10),
356
д) При ZH=l/(Cp) найдем по (8)
Г (I/O?) + Z ” Р+а * где а ~ WCZJ'
£ соответствии с (9)
U(p, х) =
£7р
21
2/—X
р— а -р—р—
Д—— е v
Выражение 1 ‘у 1 — е “
сумму бесконечной убывающей геометрической прогрессии со
меяателем е Р ° (необходимо иметь в виду, что
можно рассматривать
как
зна-
при
2/
2/
о—а -Р-7Г
—;— е v
р—a\s
— 1 е v
X
е Р v
1 :
р—а
—е
>г. х Е I -₽ — р—а -Р
U (р, л)=— е v —— е
v ' р L Р4-сь
2/-t
-Р
V
р—а
— е
V
р—а\з -р—-—
i—-—’) е v
P—<Z у-Р
--1-- 1 С
р—а \з ~р
— е
*1-х
о
) \ F \ /
При x=Z
U(p, 0 = —[е-’’ » —£^
' р L р+а
р—а \2 -Р —
— ) е v
l S1
рч а
,5/1
р—а \« -P-zr |
_ I е v ... I
V
Оригинал изображения вида можно определить по
теореме разложения (случай кратных корней):
1 р а —t , .
Д ( у=1 — 4а/е-
Р \ р+а/ ’
Д(_£^у=:—1+2е-“Ч1—2а/ + 2а!/г) и т. д.
С учетом теоремы запаздывания
357
12.16р. В рассматриваемом случае коммутация происходит
в цепи с ненулевыми начальными условиями, поэтому изображе-
ния напряжения и тока в линии удовлетворяют следующей системе
уравнений:
—** *)-«'(.V, 0)];
"fcl=-C0[pt/(p, х)-и(х, 0)], (])
где Г(х, 0); и(х, 0}—функции распределения тока и напряже-
ния по линии в момент времени, непосредственно предшествую-
щий коммутации. Перепишем систему (1) в виде
dt/(p. X) +ЦрЦрг x) = L„i(x, 0);
^^-+Сор(/(р, x) = C„u(.v, 0). (la)
Выражения (la) представляют собой систему линейных неод-
нородных дифференциальных уравнений, причем в данном случае
(когда до коммутации в линии без потерь имел место установив-
шийся режим постоянного тока) члены, стоящие в правой части,
не зависят от х; действительно,
t(x, 0) = E/(2ZB) = const; u(x, 0) = Е/2 = const.
При этом системе (1а) удовлетворяет частное решение
/(р, х) = £*(х, 0)/р; U(p, x) = u(x, 0)/р, (16)
в чем убеждаемся подстановкой (16) в (1а).
Общее решение системы однородных уравнений, соответствую-
щих (1а), определяется выражениями (5), (6) задачи 12.11р.
Поэтому общее решение (1а) может быть записано так:
1/(р, х) = £^.+л1е-гх+лге»«;
1(р,
Р ^в
(2)
Постоянные Аг и Ай удовлетворяют следующим двум гранич-
ным условиям:
при х = 0
4-/(р, O)Z,=t/(p, 0); ,z,=
Р Р L Р J
=Л<ьа.+ д1 + Л2; £--^А-Д1 + Д!=|-+д,+д,; д =0;
при х=1
I е
Щр. [) z’cj Z, . 2^+ z„ .
Up. I) , I 1 z„Cp+i ’ e . 1 w ~ z.cp+1 ’
, 2
P+ZBC
358
обозначив а = 2/(ZBC), получим А2 —----т— e~v/ —-----— е-₽ *• .
Р~Га Р~г^
'Тогда изображение напряжения в линии, согласно (2),
U(p. *)-£
^/2 с-р
Р+«
/- г
V
*
его оригинал
и (I, х) = 41 (0 -4 е 3 (' ~ ) • 1 (t - .
При х — 1
и2(0=«с(0=4(1-е-о,)1(0;
при х— О
«ио=41<о
В полученных выражениях а=110вс^1; //и —т= 1 • 10’® с.
На рис. Р. 12.9, а, б построены эпюры распределения мгновен-
ных значений напряжения для
/, = 0,5-10-® с, /, = 0,75-10“® с.
12.19р. В момент времени, не-
посредственно предшествующий
коммутации, Цх, 0) = 0, и(х, 0)=
= Е. Изображения для напряже-
ния и тока в линии ищем в виде
£/(р, х)=~ +Ае"₽ и + А& е;
/(р, x)=-J-( Д1е~Р~— Л2е₽”-).
При л = 0
Рис. Р.12.9
при Х—1
Следовательно,
/8(p)Jlp=t/2(p).
£
р
359
u(t, x) = E-1 (0 — E\l—e
12.21р. В исходном состоянии, т. е. при t = и (л, 0) = Gc;
i(x, 0) = 0. Согласно (2) решения задачи 12.16р,
Щр, *)=-у-+ Ае ₽ ° + Ае” р ;
/(р, = (Л1е~Р~— Л2еР~У
Л-В
Уравнения для постоянных Лх и At получим из граничных усло-
вий: при х=0
1(р, 0) = 0; ’ (Л1-Лг) = 0;
при Х = 1
и (Р- D
Ир. 0.
Л,=А.= — Д-е"’"
1 - 2р
Следовательно,
U(p, х) = -^
UM-U(p, x)U=.=-^—^е'₽
Г г
1п (₽) I (Р. х) к=< 2pZ„ 2pZB е V
= * W—«(*“)=5П (0-1 «-2-10-)] A.
Таким образом, в нагрузке возникает прямоугольный импульс
тока амплитудой (7O/(2ZB) = 5 А, длительностью 2//и = 2 - 1СГ0 с
(рис. Р. 12.10» б).
Напряжение на разомкнутом конце линии u^i) др момента
t—ljv сохраняет докоммутационное значение, а при t=l[v= 1 * 10'6с
скачком падает до нуля (рис. Р.12.10, а).
360
12.25р. Решение для каждой линии ищем отдельно. Для пер-
вой линии расстояние отсчитываем от
для второй расстояние отсчитываем
от места коммутации и обозначаем
jt2. В момент времени, непосредстве-
нно предшествующий коммутации:
для первой линии
М-Ч, 0) = Е; 1
1(хп 0) = 0; J
для второй линии
u(x2, 0) = 0Д
t(xs, 0) = 0.j
Изображение напряжения и тока
в линиях:
для первой линии
источника и обозначаем хх,
Рис. Р.12.10
U'[p> -Ч)=-~4-Д1е Р v + Д2е₽ 1 ; 1
** >
/'(Р. = Р v —v )* !
для второй линии
Г/"(Р. х2) = Д3е~₽ v + Д4е₽ 1 ;
Г(Р. ^) = -5-\^эе Р v — Д4е₽“)
Постоянные At—Д4 определим из следующих условий:
при х4=0
0) + /'(Р. 0)ZB = E/p; Е/р-Ь Д4д-Д8~р Дх—Д2 = Е/р; Д4=0;
при х4 = /, х2^0
Ь"(р, /)=ь"Чр» 0);
t
EfpArA9t =Д3Н-Д4;
i
Г(р,1)=Г(р,0)-
при х2 = 1
I I
—р— р —
l"(p,l) = fr, Аяе ~А,е “ =0.
(1)
(2)
(3)
Согласно (2)—(3),
( 3pl п
2р1
А -£- А —
э—2р’ 1— 2р
3*51
Рис. Р.12.11
Для первой линии
1 Е Е Sp'~^~ . Е - I
(A *i) — р 2ре + 2р е ’ I
я - з1~х I
7/ ч Е ~Р~ Е ~ 1
х1)—2pZBe 2pZBe ’ I
для второй линии
х. v-х, \
Г// ХЕ I Е !
(Р» ^г) 2р ® ”Ь 2р £ * |
х, 2/-Х, (
.. . - Е ~р— Е -*-Т“ , J
/(P.^2) — 2pZae 2pZee ,J
362
«(t, X.) = £ [ 1 (0-1 1 («I М
По полученным выражениям на рис. Р.12. И построены зави-
симости п(х), i (х) для различных моментов времени.
Глава тринадцатая
13.1р. Сначала строим ВАХ нелинейного резистивного эле-
мента /7Р9> эквивалентного параллельно соединенным НРг и HPt.
Для этого складываем абсциссы ВАХ НРг и HPt. В результате
получим пунктирную кривую на рис.
Р.13.1. НРа соединен последовательно
с резистором /?, поэтому для получения
результирующей ВАХ складываем ор-
динаты ВАХ НР9 (пунктирная кри-
вая) и резистора сопротивлением R =
— 0,5 Ом (прямая линия). Жирно вы-
черченная кривая представляет собой
входную ВАХ.
13.3р. Ток в схеме рис. 13.2,6 оп-
ределим по точке пересечения ВАХ
туннельного диода с нагрузочной пря-
мой, построенной по уравнению Ул =
~Е—1дР,гдеиа—напряжение на дио-
Рис. Р.13.2
Делим рабочий режим. При возрастании R от 0 до оо нагрузоч-
ная прямая поворачивается против часовой стрелки, меняя поло-
жение от вертикального до горизонтального. При 0 < R < 240Ом
Ток плавно снижается от 5 до 1,5 мА (рис. 13.2. б). При 240 < 7? <
363
< 1000Ом для каждой нагрузочной прямой появляются три точ-
ки пересечения с ВАХ диода, поэтому получаются три участка
на характеристике / = f(R); при R> 1000 Ом образуется одна
точка пересечения нагрузочной прямой с ВАХ диода. Ток при
этом плавно уменьшается от 1 мА до 0.
13.7р. Чтобы цепь рис. 13.4, а работала как стабилизатор
тока, нужно подобрать такое сопротивление 1?, при котором сум-
марная в.а.х. параллельной цепи имеет горизонтальный участок
(/—const). Эго достигается при равенстве сопротивления R ре.
зистора модулю дифференциального сопротивления позистора на
падающем участке ВАХ. Следовательно, на участке 8 ^t/^32 В
(см. рис. 13.4,6) дифференциальное сопротивление позистора /?диф=
= Д///Д/ = —600 Ом. Тогда R — | | = 600 Ом. Ток стабилизации
можно определить аналитически для любого значения напряже-
ния на данном участке, например для U — 8 В: /ст = 1нр~ ~
— 80 + (8/600) 103 — 93,3 мА. Ток стабилизации можно получить
графически, сложив ординаты в.а.х. позистора и резистора.
13.10р. При условии, что сеточный ток равен нулю, сначала
определим ток через делитель напряжения, состоящий из резис-
тора Rt и /?2, а затем напряжение смещения па сетке Г/с, равное
напряжению на R2:
Если построить по уравнению (/а = Еа—/а/?а нагрузочную пря-
мую на рис. 13.6,6 по точкам /а = 0; Ua~ Еа = 250В и £7а = 0;
/а — EjRa — 100 мА, то полу-
чим рабочую точку при Uc =
= 8В; /а = 44мА;Ua= 140В;
^а = £а-1/а=1ЮВ.
13.12р. Методом эквива-
лентного генератора опреде-
лим ток в HP. Исключив из
схемы HP (третья ветвь обор-
вана), найдем параметры эк-
вивалентного генератора Uob*
и РыаЬ. Напряжение Uabx определим методом двух узлов:
/?.х=^-=20м.
Схема эквивалентного генератора показана на рис. Р. 13,3, л-
Рабочий режим HP найдем путем пересечения ВАХ HP (на
рис. 13.7,6 кривая /) с нагрузочной прямой, построенной по
уравнению иНР = иаЬк—13Р9каЬ или U/fP=-8—2/3, где /3—ток
через HP. В результате получим /3 = ЗА; иир=иаЬ — 21&. Ток»
в остальных ветвях определим по закону Ома:
4 — (^а 4" Uab) Ел — 1 з А* •
364
Проверка по первому закону Кирхгофа подтверждает правиль-
ность решения: /,—/-—/8 — J — 0.
13.16р. Для расчета токов в HPt и НР2 воспользуемся ме-
тодом одновременного холостого хода двух ветвей. Для этого
размыкаем в схеме рис. 13.10, а ветви ab и cb. Определим для
этой схемы Uab* и Ucb1. (рис. Р. 13.3, б):
Uab^E^-JRs=\6B;
Ucbx = E—JRt=6B.
Линейную часть схемы по отношению к зажимам ab и cb за-
меним пассивным четырехполюсником. Для этого из исходной
схемы удаляем источники, вместо которых оставим их внутрен-
Рис. Р.13.4
ние сопротивления. Схема, собранная из двух источников, ЭДС
которых соответственно равны Uab* и Ucbx, пассивного четырех-
полюсника и двух ЯР, показана на рис. Р.13.4, а. Эта схема
эквивалентна исходной в отношении режимов работы HPt и HPt.
Методом двух узлов, предварительно заменив последовательно
соединенные HPt и Р3 эквивалентным ЯРя, а последовательно
соединенные ЯР2 и Р2—ЯР4, найдем токи 1аЬ и 1сЬ. ВАХ ЯРа
и ЯР4 показаны на рис. Р. 13.4,6.
Строим ВАХ Iab=I(ЯЬе);/сЬ=Н^);/ьеЧт(РИС. Р. 13.5, о)
на основании уравнений Ube = Uab1( — Ube = Ucb*—U hpJ,
= По первому закону Кирхгофа, 1аЬ 4-7cb = /be.
Складываем кривые Iab = f(Ube) и Icb = f(Ube). Точка пересе-
чения суммарной кривой с характеристикой ^be — f(^be) Дает Ра‘
бочую точку (значения 1Ье и Ube) для схемы рис. Р. 13.4, а. Про-
ведя вертикаль через эту точку, получим значения 1аЬ и 1сЬ в
точках пересечения вертикали с характеристиками Iab = f(Ubt) и
^=/(1/,,); /аЬ = 2,4А; 1сЬ-0,5А (/,. = 0,5А).
Для расчета остальных токов обратимся к исходной схеме
Рис. 13.10, а, в которой теперь известны токи в НРг и ЯР2.
В результате получим Ida = Iab—J = 0,4A: = 1 >9А;
4г ~ 7bd— 1 da = 1 »5 А.
Правильность расчета проверим по второму закону Кирхгофа:
+ IbdRl + IdaRi —
365
Значение Uab определим по ВАХ НРг при / = 2,4А: ^==1,26
Тогда 1,2+1,9-4 + 0,4-3= 10 = £.
13.18р. Произвольно выбираем положительные направления
токов /х и /2 (см. рис. 13.1 1,с). Строим зависимость токов /и J
Рис. Р.13.5
п /2 в функции (/аЬ на основании следующих уравнений:
Рис. Р.13.6
входе двухполюсника / = / + /х—/х. Токи построены в функЮ”1
одной и той же переменной Uab, поэтому строим зависимость
характеристики J = f(Uab) и = складываются
и из полученной суммы вычитается зависимость =
Возможны две схемы эквивалентного двухполюсника: 1) с нс'
точником ЭДС Е* и последовательно с ним соединенным ЕР&
366
(рис. Р. 13.6, а); 2) с источником тока 28 и параллельно ему вклю-
ченным НР23 (рис. Р. 13.6, б).
Для первой эквивалентной схемы запишем уравнение Uab =
E9 + Uhpi3' Значение £э определяется точкой пересечения за-
висимости / = f (Uab) с осью абсцисс (рис. Р. 13.5, б); Еъ = 5 В. ВАХ
получим на основе уравнения UHPl3 = Uab—Е^ сдвигая ха-
рактеристику l = f(Uab) влево на Е3 (рис. Р. 13.6, а).
Для второй эквивалентной схемы запишем уравнение / (Uab)=
с= Iffp (Uab\ 4- Jg. Ток Jg определяется точкой пересечения зависи-
мости I~f(Uab) с осью ординат (рис. Р.13.5,б); 2Э= —1,8 А.
Рис. Р.13. 7
В.а.х.ЯР2э строим по уравнению Il1p (Uab) = I(Uab)—J3,сдвигая
характеристику I = f(Uab) вниз на величину J9. Так как ток
J9=—1.8 А отрицателен, следует характеристику I = f(Uab) под-
пять вверх на 4-1,8А (рис. Р. 13.6, б).
13.21р. Схема содержит узлы а и Ь. По методу двух узлов
строим зависимости /ь /, и J в функции Uab (см. построение в
задаче 13.18р). По первому закону Кирхгофа, = Точка
пересечения суммарной кривой J + It(Uab} с кривой ft = f(Uab)
дает рабочую точку л (см. рис. Р. 13.5, б). Координаты этой точки:
/д = 2,5А; £7аЬ = 5В. Проведя вертикаль через точку л, получим
/.= 1,5 А (или, по первому закону Кирхгофа, 12 = —2=1,5 А).
13.24р. Произвольно зададимся положительным направлением
токов в ветвях (см. рис. 13.13). Рассмотрим два способа решения
задачи.
1-й способ.
эквивалентной,
Для этого по
тику /i = f(L/bJ (кривая /); по уравнению Ubc =— U&P2—харак-
теристик)7 /2 = f(Ubc) (кривая 2). По уравнению /4 = It—вы-
читая из кривой 1 кривую 2, строим характеристику /i = f(^ bc)
(кривая 3).
Заменим ветви, содержащие НР3 и 2, эквивалентной, построив
ее ВАХ 14 = f (Uab) (Рис- Р. 13.7, б) на основании уравнения
!»?= 19—2 (кривая 2). Строим характеристику /< = /((/„) по урав-
нению Uеа — — Е3-^ЦР (прямая 3).
Заменив ветви, содержащие НРг и ЯР2, одной
построим ее ВАХ li = f(Uab) (Рис- Р-13.7, в),
уравнению Ubc = — El-j-Ut1P1 строим характерис-
367
По второму закону Кирхгофа, Ubc-^ Uca-}-Uab = 0. Получен-
ные характеристики (кривая «3 на рис. Р. 13.7, а и кривые 2 и з
на рис. Р.13.7,6) можно рассматривать как зависимости напря.
жений Ubc, Uab и Нса от одной и той же переменной /4. Следо-
вательно, для нахождения рабочей точки нужно сложить абсциссу
трех характеристик (кривая 4) на рис. Р. 13.8, а. Точка пересе-
чения с осью ординат (точка т) дает значение тока /4=1,ЗА.
Рис. Р.13.8
Проведя горизонталь че-
рез рабочую точку, по-
лучим Ubc = — 2,5 В-
<4. = -13,5 В; Uab^
= 16В. Ток /3 = /4ч-
+ J = 2,3A; /2 = 0,5Д
(по ВДХ при инр =
= 2,5 В); /1 = /. 4-/1 =
= 1,8А.
2-й способ. Считаем
всю схему, кроме НР3,
нелинейным активным
двухполюсником, а
НРа~ его нагрузкой.
Точка пересечения ВАХ
этого двухполюсника с
ВАХ НР3 и определит рабочую точку: значения тока /3 и нап-
ряжения Uab на НРЧ.
Для получения в.а.х. двухполюсника произвольно зададимся
значением тока /х. Пусть Д = 0, тогда UHPi = 0; Ucb = El—1/НР1=^
= Е1=10В; /2 = 2А (по ВАХ ИР); Uac =
= Е2-/4£ = ЗОВ; Uab = Uac + Uet = 4№, /3 = /4 Ч- J = -1 А.
В результате получим Uab — 40 В; /3 =—1 А. Задаваясь значениями
тока /j = 0,5; 1; 2А, найдем и другие точки ВАХ двухполюс-
ника. Сведем все значения в табл. Р.13.1.
Таблица Р.13.1
Uab. В /3. А иаЬ, В /3, А
40 — 1 25 1
32,5 0 10 3
Пересечение полученной ВАХ с кривой НРа (см. рис. 13.8,6)
дает рабочую точку л: /3 = 2,ЗА; UHP. = Uab= 16В. Рассчитаем
остальные токи и напряжения:
Л = j = 1.3 A; Uac = Е.-l,R = 13,5 В; Ucb = = 2,5 В;
/2 = 0,5А (по ВАХ HP при (/„р = 2,5В);
Л = ^4-/а=1»8А.
368
13.26р. Найдем токи Л и /2: /х = В ([/х 4- С/2Р; /2 = В ((Д—U^y.
foK через амперметр равен разности этих токов: 1Л = /г—/2= 4В£71£72.
|3.28р. Выберем характерные точки, принадлежащие как па-
оВболе, так и будущей ВАХ: [/=10; 20; ЗОВ и /==0,1; 0,4,
0.9 А.
При 0 < иъх < 10 В диоды Д, и Д2 заперты и ток идет лишь
ро R- I = U/R- По первой характерной точке определим R —
-10/0,1=100 Ом. При
10 В < иък < 20 В диод Д1
открыт, а диод Д2 заперт,
входной ток складывается
из токов первых двух вет-
вей:
I— и ±и~Е1
R + Ri '
Значение Rt получим,
подставив в выражение дли
тока параметры второй ха-
рактерной точки (/ = 0,4 А;
U = 20 В): /?, = 50Ом.
При (/^20 В оба дио-
да открыты. Ток на входе
равен сумме токов всех тр
. и .и —el и —Ez
R + Rt + R2 *
По третьей характерной точке (/ = 0,9 A; U = 30 В) найдем /?, =
= 50Ом. Результирующая в.а.х. построена на рис. Р. 13.9,а.
Пунктиром показаны ВАХ отдельных ветвей, сплошной линией—
результирующая.
13.31р. По закону Ома для участка цепи ab, I = (Uab—Ej/R.
Ток определяется этим выражением при всех значениях Uab в
случае, когда диод открыт (ток источника тока проходит через
Диод). Если ток / достигает значения «/, диод закроется (ток /
проходит не через диод, а через источник ЭДС). Поэтому при
дальнейшем увеличении Uab ток / = </ = const. График / = f (Uab)
показан на рис. Р. 13.9, б.
Глава четырнадцатая
14.4р. Задачу решаем графически на основании второго закона
Кирхгофа для магнитной цепи: /иу = ///ср4 0,8 -103 В -26 = [/М£.
Здесь первое слагаемое определяет падение магнитного напряже-
ния в магнитном материале, второе—падение магнитного напря-
жения в воздушном зазоре. Значение индукции берется в теслах,
Длина зазора—в миллиметрах. Строим вебер-амперную характе-
ристику магнитной цепи—Ф({/Мх). Зависимость потока от паде-
ния магнитного напряжения в стали, построенная на основании
Отношений Ф = В5, Uu = Hlcvt приведена на рис. Р.14.1 (кри-
369
вая /). Зависимость магнитного потока от падения напряжения в
воздушном заЗоре линейна (прямая 2). Кривая 3 является резуль.
тирующей вебер-ампервой характеристикой всей цепи. Таким
образом, наблюдается полная аналогия с нелинейной цепью по-
стоянного тока—замена двух последовательно включенных нели-
нейного и линейного сопротивлений одним эквивалентным нели-
нейным. При /w=200 А Ф = 4,85Ю~4Вб; В=0,97Тл.
14.12р. Особенностью построения вебер-амперной характерис-
тики Ф = Н^мвь) участка цепи является наличие МДС. При на-
правлении магнитного потока от а к b Uuolt— ±/ьу-Н Hlcv 4 Ярб,
где 4- Iw соответствует направлению тока от т к п (кривая 2
на рис. Р.14.2);—Iw—обратному направлению тока (кривая /).
Таким образом, наличие МДС приводит к смещению вебер-ам-
перной характеристики по оси абсцисс на отрезок, по значению
равный МДС. При направлении магнитного потока от 6 к a
= —nlcp—Hbb, что соответствует кривым 3 и 4.
14.14р. Задачу решаем методом двух узлов. Строим вебер-ам-
перную характеристику (рис. Р.14.3) участков цепи для выбран-
ных на рис. 14.9 направлений потоков и МДС; = где
А/А (кривая /); ®s = /(t/Mflb), где £/^ = 7% +Яьб
(кривая 2). Кроме того, проводим вспомогательную кривую
Ф2—0,5-10“* Вб (кривая 3). Графическое решение ищется пз
условия удовлетворения первого закона Кирхгофа
Ф1 = ФаЧ-Ф3 или ФХ = (2Ф2—0,5-10“*)Вб,
что соответствует точке т на рисунке.
Определим Ф1Э Ф2, Фя, Uaab.
Ф, = 3,9• 10-‘Вб; Ф,= 2,210-*Вб; Ф,= 1.7- 10-*Вб; 1/„ь=92А.
Для третьего стержня £/Мо6 = —/аи>,4-ДЛ- При Ф,= М*
X 10-‘ВбЯэ/,= 14 А. откуда = НЛ)/ш,=-О.78А.
т. е. направление тока в обмотке обратно указанному на рисунке-
14.16р. Чтобы перемагнитить । сердечник от —Вг до 4-
в нем необходимо создать напряженность магнитного поля
= 300 А/м. Эта напряженность создается током линейного пр°в^
да: Я = //(2л/?). При /=151А перемагнитится часть сердечник >
370
ограниченная
^l~~2nHc 2-3,14-300“ 0,08 М*
Зависимость B — f(R) приведена на рис. Р. 14.4, а.
При отключении тока магнитное состояние сердечника вновь
изменится: магнитная индукция, равная + Brt сохранится только
р той части сердечника, напряженность магнитного поля которой
151
//тах=500 А/м. Эта область ограничена ^2=2й7/—~2-3 14-500~
= 0,048 м. В остальной части сердечника В = ~ВГ (рис. Р. 14.4, б).
14.18р. Процесс перемагничивания магнитопроводов, выпол-
ненных из материала с ППГ, происходит последовательно начи-
ная с внутренних слоев, имеющих меньшую длину пути перемаг-
ничивания и в которых прежде всего достигается величина Яс.
Индукция в этих слоях изменяется от ~ ВГ до Ч-Вг. Процесс
перемагничивания начинается с тока
min
3-10MC-IQ-2
w 100
0,ЗА,
Рис. Р.14.5
Магнитный поток среднего стержня Ф9 = BrS2 = 0,5 10~4 Вб,
когда перемагнитятся все слои вплоть до контура При
этом /1 = /7c/fllt>1C>jl/tt/ = 0,54 А. Перемагничи-
вание слоев, проходящих по первому и третье-
му стержням, начнется при
Н I
=0,66 А и закончится при /тах = с а*ь^» =
г шад
= 0,9 А. Магнитный поток Ф3 — BrSs —
= 0,5- 10~4Вб, а Ф1 = Фа-|-Ф3. Связь между
током, и магнитным потоком линейная.
Если рассмотреть контур, отстоящий от
внутреннего контура на расстоянии х, то
Магнитный поток, проходящий через сече-
RHe Лх,.Ф=В|Лх, где h—толщина пакета
вода.
листов магнитопро-
371
Для создания этого потока необходим ток
/ = = HfJabcd 1 j . Л. Ф
w w ' Bfhw m *п ' - *
где и k2—коэффициенты пропорциональности. Графики
приведены на рис. Р.14.5.
Глава пятнадцатая
15.2 р. Для случая на рис. 15.1,6 на участке от —0,95 д0
0,95 В-с ф = ^11, где ^ = 0,95/0,05=19. На этом участке dty/dt^z
= cos ю/= 19- 103coswZ. Изменение dty/dt по такому закону
происходит на участке от (о/1до<о/1= arcsinO,05=2°53' (рис. Р. 15.1).
На участке от 0,95 до 1В-с ф = ф0 + &2/, где k2 = 0,05/0,95= 1/19^
Здесь dty/dt = k^alm cos со/ = 52,7 cos о/ В. График изменения dty/dt
для рис. 15.1,в изображен на рис. Р.15.2.
15.5 р. К концу отрицательного полупериода ф =— фЛ и t==0.
В положительный полупериод в уравнении dty/dt + Ri = e(t) сла-
гаемое Ri = 0 в случае, когда изображающая точка перемещается
по вертикальному участку зависимости ф = /(с), т. е. когда про-
исходит перемагничивание индуктивной катушки. В этом интер-
вале времени d$/dt = E; ty^-Et-}-C, где С—постоянная интегри-
рования. При / = 0 ф = — фст, отсюда С = — потокосцепление ф
изменяется по закону ф = Е7—фт до момента времени tl = 2^)m/E^:
= Т/3, когда ф достигает фя. В интервале от 7/3 до Т/2ф=ф|«'
Ri = е (/). Следовательно, i = E/R = 0,1 А. Г рафики требуемы31
величин в функции t показаны на рис. Р.15.3.
15.7 р. К началу положительного полупериода ф =—фя и / -О-
Когда сердечник индуктивной катушки перемагничивается и по-
токосцепление изменяется от —фст и до (т. е. на 2фст),тоК
i = 0 и i\=us. Перемагничивание происходит под действием на-
пряжения
ucd = Ri2 = 10 sin 10* t — dty/di‘t
Ф = J tieddt + C= —103 cos co/4- C,
где C=—фя—постоянная интегрирования. Если —время окон-
372
иания перемагничивания, то 2фад=10~3(1—cos co/J; cos otl=—0,706;
cot^ 135°.
Когда пере.магничивание закончится, ucd спадает до нуля,
/^0, а / = с\. Напряжение uab — uac-^-ucd. Графики искомых
2дичин в функции о/ изображены на рис. Р.15.4.
15.8 р. Напряжение uac = L^ положительно и равно 0,71 В при
dildt^Q и отрицательно и равно —0,71В при di/dt < 0. При
перемагничивании индуктивной катушки от —До (за
время от 0 до tx) ток t, протекающий через нее, равен
л
нулю и i1 = i8. Уравнение для определения tt: \updt = 2tym\
о
= На участке роста тока ц = 4/at!T. На участке спада
тока i\ —/ст( 2—4у j; tx = -g-7\ Графики изменения всех величин
вфункции / даны на рис. Р. 15.5.
15.12 р. Нелинейная индуктивная катушка перемагничивается
в интервале времени отсо/ = 0 до cotx=120° под действием напря-
жения ucd. Это напряжение равно напряжению на нелинейном
Резисторе. За интервал времени от со/ = 0 до со/ = i = 0 и tx = t2.
На начальном участке характеристики нелинейного резистора в
интервале времени от со/ = 0 до cot = 30° и = Rti29 где Rx — 2 Ом.
Напряжение исd = ujj = sin cot достигает 0,2 В. В интер-
вале от cot — 30е до со/, = 120° u}d = UM sin cot—i\R. В этом случае
^OK iх = Za остается неизменным и равным 0,1 А, поэтому иЦ =
sincot—0,3 В. Для определения <о/х служит уравнение
30° ь)С,
$ u]dd(ot+ J иЦ dat = 2софя,
о зос
373
или
©6
—0,4 (cos 30э—cos 0е) — cos со/ —0,3 (со/, —л/6) = 0,948.
30°
2
Отсюда со/,= 120° = у л. В интервале изменений со/, от 120 д0
180° ucrf = 0; i = c\ = ^psinto/ = 0,333sinco/. Графики изменения
всех величин в функции со/ изображены на рис. Р. 15.6,
15.16р. Как и в задаче 15.14, проводящий период начинается
с ©/1 =— 68°20'. Ток имеет в своем составе принужденную и
свободную составляющие. Принужденная составляющая состоит
из постоянной и синусоидальной Компонент, так что
t = ~ 4—л_- Ет —-sin (со/ + 45°—<р) -j- Де М+;
4 = 50 мА; - -£.”__=90,1 мА; tg<p = ^= 1; <р = 45°,
где Д — постоянная интегрирования. В показателе свободной со-
ставляющей добавлено время со/,, указывающее на то, что пере-
ходный процесс начинается не с момента со/ =0, а с момент3
<oG = —68°20' = —1,2 рад; «= 50 +90,1 sinco/+ He‘“’2+"" 731
Постоянную Д найдем из начальных условии, имея в ВИДУ»
что при со/=—68°20' = —1,2 рад ток / = 0:
0 = 50—90,1 sin 68°20' + А; 4 = 33,5.
374
Следовательно, i — 50 4- 90,1 sin coZ 4- 33,5e ” . Г рафики
изменения требуемых величин в функции wZ даны на рис. Р.15.7, а.
15.19р. На рис. Р.15.7,б изображены кривые изменения
ЭДС е, принужденного, свободного и полного токов в функ-
ции tfZ.
Рис. Р.15.7
В первый полу пер иод
irctg^; >л = -.- -т —
Ця) — i (0). Поэтому
откуда
R t
i = lCTsin(<j}Z—ф)4-Ле w£ ; ф —
В силу периодичности процесса
„*_я
[(л—ф)-}-Ле ш£ = — /м5шф4-А
л _ 2ZCTsln<p
Я -A
l-e
(1)
Среднее значение тока за полпериода (среднее за период)
Ср = j [.Ад sin (<oZ—ф) 4- Ае‘ы£ ] dioZ =;
о
__ 2/д cos ср , Л to£ f .
л “* л R v е /•
Подставив в это соотношение выражение (1), получим
/ — Г сос П) _L gin П) —1 — — %ImZ — £т2 2 Ет zqx
'ср- л [СОЗф + ЗШф^ —(2)
Среднее значение тока не зависит от индуктивности катушки,
°Днако от нее зависит степень пульсации тока Z. Формулу (2)
**ожно получить и проще, взяв среднее значение двухполупе-
Риодно выпрямленной синусоиды и считая при этом, что сред-
значение напряжения на индуктивной катушке равно нулю.
15.21р. Графики ЭДС, напряжения на конденсаторе, тока
через конденсатор, тока через резистор R, тока i = Zr4 iR и на-
пряжений на полупроводниковых диодах 1 и 2 в функции ait
375
показаны на рис. Р.15.8 за первый полупериод. Диоды / ц з
в первый полупериод открыты в интервале времени оты/j доц^
При coZi напряжение источника становится равным напряжений
на конденсаторе:
E^sinco/! — Uc (0)е
d Е
При результирующий ток i — С Ет sin w/ -|- ~ sin со/ ста.
новится равным нулю:
аСЕтcos<s>t,+£"м<> = 0,- tg®>/,= —
Так как процесс периодический, то n)~uc{tnt^.
Среднее значение напряжения на нагрузке
<0/1 +Л Г-Ю** Л+Ь)/Х
= — f ucdat = — f sincofdco^-Ь sinwE С e °^л/с dart =
Л J JT J J
ш/i о/,
— [cos 11)4 — COS Co/24-(x)/?/yC sin COE (1 —e-(n+<W»-<&G))J.
Рис. P.15.8
15.22 р. Если uBX < E2, to открыт диод 2 и izBnlX = E2. Прй
Е1>мвх>Еа оба диода закрыты и ивых — ивх. Если ивх> 1
открыт диод 1 и ивих^Е1. Зависимость ивык = [(ивх) изобра#ей
на рис. Р. 15.9, а.
15.24 р. По закону Ома, I = uab/R. Если I > 0, то ток
ходя через диод 2, будет направлен встречно току Д. Как т0-пЬ f
ток / достигает значения диод 2 закрывается и ток J9
376
через источник ЭДС- При этом I — Если напряжение иаЬ
изменит знак, то ток 1 станет отрицательным, т. е. при прохож-
дении через диод 1 он будет направлен встречно току При
I ~ — Ji диод 1 закроется, после чего ток J1 потечет через
источник ЭДС, а ток / = — График I = f(uab) показан на
рис. Р. 15.9, б.
15.26 р. Для входной и выходной цепей составим уравнения
второму закону Кирхгофа:
4” ^д ) 4” ^эб == ^6 ^к^п»
(/?«4“ Яд) 4~ = Ен
В соответствии с этими уравнениями расчет проводим методом
последовательных приближений, взяв в качестве исходного при-
ближения /б = 0,023 А; 1б/?д = 0,23В; iK = 0,168At полученные при
решении задачи 15.25.
Рис. Р.15.10
Проводим пунктирную прямую 1'б = /(ц9б) на рис. 15.15, б и
пунктирную прямую 1к = [(изк) на рис. 15.15, в. По точкам пере-
сечения прямой с кривыми рис. 15.15, в на рис. Р. 15.10, а строим
две зависимости 4 = f(u9K) (кривые 1 и 2). Точка В определит
рабочий режим.
15.30 р. Составим уравнения по методу узловых потенциалов
для схемы рис. 15.17, в:
Кпфг4- ( — Ук)ф2 = — — УбЕу; (1)
4* Е22Ф2 = (2)
где
= Y6 -г Y3 4 Ук; Y22 = YK 4- Уя, (3)
но
= —КзФГ. к = УиФа. (4)
из выражений (1)—(3) найдем
Ф1 ~ ^1э 4* bi^Ey 4* Ь12Фа1 (5)
Ф2 = Ь2Э1Э4-Ь21Ф1, (6)
где
^1э = а/^11> ~ Yfi/У п" Ь^ = Уя/У1Х;
= ot/Vjg, b2i “ b3l = У8-
377
В соответствии с уравнениями (5) и (6) составим граф, изо(у
раженный на рис. Р. 15.10, б. По формуле Мезона,
V С V ^1у^21+ &1у^э1^2э
«н = у яФ« =
15.32 р. В соответствии с методом узловых потенциалов соста.
вим систему уравнений [У] [<₽] = [/]. Решим ее относительно
и <Га:
ф.=^Л+^(-4); Я)
+ (2)
где Л—определитель укороченной матрицы [У]’» Длст—алгебрам,
ческое дополнение с принадлежащим ему знаком: /г = Ф>Ун. Под.
ставим это значение Д в уравнения (1) и (2), выразим /2 через
Г _ I А^дУ Н
^~У1Д + Д22гн'
Найдем входное сопротивление между точками /—0:
1 ./a f * f\ а IV ДцДйЗ — ^12^21
' д- (Д11* 1 — А 21*27 Д11+* Н -Л-
вх /\ Л а+д22гн • - w
Величину A11A2g~^lzAgj обозначают через Д11122 и называют
двойным алгебраическим дополнением; его получают из выраже-
ния для Д, вычеркивая строки 1 и 2 и столбцы 1 и 2 и умно-
жая на (—iji+i+a+a-- 1. Тогда ZBX — An^~^H_A|l-_zg. Коэффициент
A4-A22FH
передачи напряжения
Л„=А=—Ai-—. (4)
и фх All + * нА 11,2а
Коэффициент передачи тока
(5)
Д А -|- Д„Г н
15.40 р. В качестве примера на рис. Р. 15.11, а построена век*
торная диаграмма по первой гармонике при напряжении на па*
раллельной группе (назовем его (72), численно равном 50 В. Т°к
/2 через индуктивную катушку отстает на 90° от (?8 и числен^
равен 50/50 = 1 А. Откладываем его на оси действительных зна-
чений. Ток /3 опережает Ut на 53° и численно равен 1 А.
равен геометрической сумме токов /2 и /s н по модулю пРй
близительно составляет 0,6 А. Геометрически складывая 14» й*е
пряжение на Ru равное 12 В и имеющее одинаковое направлю
378
с током Л* напряжение на конденсаторе (его находим по графику
рис. 15.22, б, оно равно 18 В и по фазе на 90° отстает оттока /3).
Определим (/вх = С/аЬ=^58е'69°. Сдвиг фаз между входным напря-
о) б) *
Рис. Р.15.11
жением и током ф = 69°—7Г40' =—2°40'. Аналогичные построе-
ния позволяют найти угол <р и напряжение Uab при других
значениях Ц. Результаты подсчетов сводим в табл. Р.15.1.
Таблица Р. 15.1
А — <р, град УаЪ. В 4. А — Ф1. град В
0.3 0,8 29 1.0 14.5 98
0.5 2 48 1.2 25 126
0.6 2.7 58 1,4 38 170
0,8 6.5 77
15.45 р. Сумма потерь в сопротивлении R и в стали сердеч-
ника равна полным потерям: PR + Рс — Р. Потери в стали сер-
#чника РС = Р—РР = 1,38 Вт. Сдвиг фаз между напряжением
G на входе и током / найдем из выражения cos ср = P/L//=0,158,
‘Лхуда ф = 8О°5Ю'. Напряжение на зажимах ab (рис. Р. 15.11, б)
i(R + jXs)= 100—0,1е-/80°5°'(20+ /50)= 94,75е-/<° В.
Ток, обусловленный потерями в стали, /с = РсД/лЬ = 0,0146 А.
Сопротивление Рс = £/^/Рс = 6520 Ом. Намагничивающий ток
= 0,0985 А.
15.47 р. Запишем основные соотношения для трансформатора:
+ + (1)
/2 №+ixsJ + =0; (2)
Л^ -F = (3)
^чтем, что при н пряжении питания, сниженном в 10 раз по
сравнению с номинальным, поток в сердечнике также в 10 раз
379
меньше номинального и ток холостого хода /х « 0. В этом случае
/а= —(4j
Подставив выражение (4) в (2) и решив его совместно с урав.
нением (1), найдем
/ =______________________________________________s_.
1 4~(и^/^г)2 4" / [ 4~ Х$2 (tt'i/K'a)”]
Так как, по условию, R2(wl/w2)2= Rlt a XS2(te/1/tt?2)a^X51i То
= Ui/(2Ri 4- /2Х51).
Таким образом,
г=Г(2R,)’+ (2Х\,)2 = Ujl„ cos<P = T^;
2/?! = z cos g;; 2XS1 — zsin<p; X51 = 4-sin<p;
Ri=^ cos <p; /<> = ₽! (uv^i)2; XSs = XS1 (^2/wJ2;
= 302.
15.49 р. Полагаем -ф = фт sin со/. Разность амплитуд напряжений
равна амплитуде воздействующей ЭДС, взятой со знаком плюс
или минус;
. I 3 . в 1 Е?
Плюс соответствует режиму до резонанса, минус—режиму
после резонанса. Имея в виду, что частота о должна быть болы^6
нуля,
Искомая характеристика показана на рис. Р.15.12, а сплошными
линиями.
15.50 р. Частотная характеристика описывается уравнен^
ip -----------
380
jIpH резонансе подкоренное выражение равно нулю, поэтому
^£т/(ЯС) = 2,8. Левая часть уравнения при резонансе дает
(Л)=‘ФСТ- Таким образом, координаты точки резонанса <о = фад = 2,8.
Резонансная кривая показана пунктиром на рис. Р.15.12, а.
15.52 р. Полагая, что потокосцепление ф имеет постоянную не
зависящую от времени составляющую фл и первую гармонику
Фст sin wf, запишем -ф = “фо + фл sin ы/. Из формулы =
= с(Фо + Фта sin «03 найдем
/о/а = фо + J.51M& (1)
/-i Зф5фот. (2)
Можно придать отношению 10/а некоторое фиксированное зна-
чение и по уравнению (1) найти зависимость ф0 — f (фст) при вы-
бранном /0/а. Для /0/а = 6 зависимость фо=НФ/? приведена
в табл. Р.15.2.
Таблица PJ5.2
Флп В-С фо. В-с Ф«. В-с Фо, В-с
0 1.81 2 0.89
0.5 1.75 2,5 0,612
1.0 1,54 3,0 0.437
1,5 1,22
Первая гармоника напряжения на конденсаторе равна
cos tat. Она имеет амплитуду (ф™ + 4ф1фда).
Разность напряжений на нелинейной индуктивной катушке и
«а конденсаторе равна ЭДС, взятой со знаком плюс и минус:
“Фи—(Фт + 4ф5фя) = ± Ет. (3)
По условию, За/(4С) = 1. Решим у равнение (3) относительно
“При £т = 2:
=*= £ ± V
Придавая фя значения 1; 1,5; 2; ... и беря соответствующие
Нм значения ф0 (при /0/д = 6) из табл. Р. 15.2, найдем по два
Учения cd для каждого фл. Радикал возьмем со знаком плюс,
апервоесл гаемое—с двумя знаками. По результатам подсчетов
СтРоим кривую фя — f(ta) на рис. Р. 15.12, б.
15.53 р. Полагаем q — since#. Первая гармоника напряже-
ния на конденсаторе uc = -| a^sinco#. Первая гармоника тока
I — dqldt =± coQm cos tat =а2ф3. Мгновенное значение потокосцепления
t|)=(idQw/q2)V3COsim Амплитуду первой гармоники потоко-
381
сцепления найдем, разложив функцию ф(/) в ряд Фурьез
= — f ф cos со/ dcoZ — — ( У/3 С cos*/3 wt dint.
V1/n л J т л \ c2 J j
о о
Учтем, что
Л.'2
sin4'4-1 <oZ cos2v+1 (oZ dcoZ = »
о
где Г(ц-Ь 1), F(vq- 1) и Г(р 4- v + 2)—гамма-функции.
В рассматриваемом примере 2р-г 1 =0; р = —0,5; 2v-f-1 — 4/3;
v = 1/6. Тогда
Г (u-J-1) Г (v-Г!)_ Г (0.5) Г (7 6) _0 Q.
2Г(р-Н-4-2) “ 2Г(5.3)
Поэтому Ф1т = 4о,91(^а)1/3 = 1.16(^)1/3Qms- Первая гар-
моника напряжения на индуктивной катушке
ф1ст cos (oZ =—1,1 6<о ( у У/3 Q'f’ sin wZ.
Разность амплитуд первых гармоник напряжений на конден-
саторе и индуктивной катушке равна амплитуде ЭДС Emt взя-
той со знаками плюс и минус:
^С.\т' U1Дт ~
*.4^-^“'3<Ж3=±£„. (1)
3
Знак минус в правой части (/) со-
ответствует режиму до резонанса, плюс—
режиму после резонанса.
Уравнение (1) решим относительно
Рис. Р.15.13 частоты ю:
О1 Г Я 1
Считая п1-|-=1, поделим обе части этого уравнения на коэф-
фициент д|/Э/1,16 и обозначим (o*=(ofb^Y'4 , Тогда
Придавая Q различные значения, строим кривую
(рис. Р.15.13). Верхняя часть кривой соответствует знаку минус,
нижняя—знаку плюс в формуле (2). Поскольку предположение
о синусоидальности тока в действительности не выполняется, ан3'
лиз носит приближенный характер.
382
15.55р. Введем следующие обозначения: a — a'f(R-r Rt); b =
gpb'/(R + /?i); I =E;(R + Rd. Дифференциальное уравнение при-
мет вид ^-}-aq + bq* = L Перенеся нелинейный член в правую
пасть уравнения и умножив его на малый параметр р = 1, по-
лучим
dq/dt 4- aq == I—pbq3. (1)
Положим 9 = 9o4-|h7i- Уравнение (1) разобьем на два уравнения;
4г+‘“h(2,
^-+aql = — bq,a. (3)
Из уравнения (2) определим ^0 = -^-(1—е"в?). Решим уравне-
ние (3) операторным методом:
9. (0 = [Цг^~ 3/е’“'+4 (е-" - -
Подставив qOt q3 и р в выражение <? = g04-pQv найдем
«(о = 4+
ЬР
а4
• | а 2а< J
ЗМ3 -int г ЬР -Зя# ЪЪР .
— г _L. — р ЗСГ_______________
а4 е 2а4 е а3 fe *
15.56р. По условию,
х = а'ф4-6'ф8. (1)
Запишем дифференциальное уравнение для послекоммутационпой
схемы:
d^dt + Ri = 0. (2)
Подставим в него выражение (1): d$/dt 4-/?(л'фЧ-6'фг) = О.
Нелинейный член перенесем в правую часть уравнения и ум-
ножим на малый параметр р=1:
d^'dt 4-с'Яф=—£'Яф2р. (3)
Запишем выражение для ф в виде ряда по степеням р:
^ = Фо4-рф14-рЧ4 (4)
В свою очередь,
фг = ф5 4 р2ф0ф1 4- р2 (2ф0фа 4- ф2) 4 р3 2фхф2 4- р*ф1.
Обозначим a'R = at bfR = b и подставим выражение для ф*
ь Уравнение (4):
= — рбфг— рг2дф0фх—рэ5 (2ф01|?2 4 ф!).
383
Составим уравнения с нулевой, первой и второй степенями р;
+ = j (5)
+ = — Ш j* (6)
тг4-офг = — 26iM>i. I (7)
Ш j * '
Величина ф0 = Де“в/. Постоянную А найдем по начальному
условию а' А 4- Ь'А2 = р р :
К] -j- к
А =
а'
2Ь
~\f ( 2L V _L Е
Подставим выражение для у0 в правую часть уравнения (6):
’МР)=^^20): (0=(е'“'-*=“')
Уравнение (7) примет вид
^+a$s
Изображение
Т1)2 (р) = 2bSA3 --:-Г-;—/о ,f—ГТТ «
(p4*a) (р-г2а) (рЧ-Зя)
По формуле разложения,
Ф. (О = (0,5е-“'—е““' Ч- 0,5е-3»').
В соответствии с уравнением (4) при ц== 1
Ч) = (Л-^ + ^)е-+(^-^)е-+^е-.
При t — Q ф = Д.
15.57р. Решим уравнение методом малого параметра с точ-
ностью до первого приближения. В уравнении I x-r-g- 1—
=0 W5 = ap/C. Поделим это уравнение на со^ и перейдем к безраз-
мерному времени = В результате получим
o)2dzx , / , х3
= 0.
6 J
Обозначим = Q2. Тогда последнее уравнение примет в*1-1
d2x . х3
+ (Г
384
Перенесем нелинейный член в правую часть уравнения и вве-
дем малый параметр р(р=1/6):
3-5 4~ х= — их*.
</т2 1 г
Положим й= 1 4- pQj и х= х04- pxt. Тогда Q2« 1 4- 2pQj -Н •
= (x0-!-px1)’!®x|! + l*3x{x1+ ..., 375 = + •
Следовательно,
(1 + 2ЦЙ0 + н +*„ + Н*. = - nxS -g’34x,- • • • • (О
Приравняв коэффициенты при одинаковых степенях р в левой
И правой частях (1), получим два дифференциальных уравнения:
^+а>=0; (2)
££!+*,=_ 2Q^. (3)
АХ® 11 1 ат® '
Пусть хо(О) —Л; Хо(0) = 0. Тогда решение (2) запишем следую-
з 1
шим образом: Хо = Лсозт. Так как Л3cost 4--^- Л3соэЗт,
а ~| =— Л cost, то уравнение (3) переходит в следующее:
= —у Л3cost—Л3созЗс4-2£21Л cost. (4)
Решение уравнения (4) не будет содержать векового члена,
если в его правой части отсутствует вынуждающая сила на еди-
ничной частоте, т.е. должна быть равна нулю амплитуда выра-
жения Л(2Й!—-^ЛИсозт. Приравнивание к нулю амплитуды
этого выражения позволяет найти поправку на угловую частоту
&1=-^Л2. При этом уравнение (4) переходит в
-т-5 4- *1 = —т~ cos Зт. (5)
Полагая решение уравнения (4) в виде x1 = BsinT4-CcosT4-
4~£>sin3T4-£cos3T, найдем коэффициенты В, С, О, Е. Для этого
определим
—Bsinr—С cost—9Osin3T—9Ecos3t (6)
di2 ' *
й подставим значения d2Xj/dT2 и в уравнение (5)*
— В sin т— С cos т—9D sin Зт—9Е cos Зт 4 В sin т 4- С cos т 4-
Д®
4- D sin Зт 4- Е cos 3 с= —г cos Зт.
Отсюда Е = Л3/32 и 0 = 0. Имея в виду, что (0) = 0, получим
С4-Е = о Или С— — Л3/32. Так как хх(0)—0, то В4-30= 0 или
385
В — —3D — 0. Следовательно, cos т 4- cos Зт. Оконча.
тельное решение для первого приближения получим, если в вы-
ражение х = х0-грл'1 подставим найденные значения х0, и
= l/ft, учтем поправку на угловую частоту и перейдем ко
времени f:
х=Д ( 1 —cos( 1 + 4 Д2^ ^ + i-^-cos3f 14
\ и OZ / \ о У о OZ \ О j
» *
15.60р. Площадь статической петли гистерезиса обозначим через
St. По данным условия, St —600 В’А-с/м3. Площадь между
пунктирной и сплошной кривой на рис. 15.28 обозначим через S ;
численно S2 также равна 600 В-А-с/м*. Потери на вихревые токи
при одном перемагничивании на частоте соответствуют площа-
ди S2. Одному перемагничиванию на частоте ft сопутствуют по-
тери на вихревые токи, равные Потери в единице объема
на частоте f2 равны Sj24-j^fl, потери в объеме V равны
+ fAv. Следовательно, Р = (бОО-2О0 + ~ 200!) 10'*=
= 3,6 Вт.
15.64р. Используя первое соотношение теоремы Менли и Роу
с учетом того, что h — f и /0 = 3/, определим
^2,^1 ^4 2 Г 2 2В?! 2W\ 2U74_
2/ + f + 4f 4/ f + f + 4/
Отсюда
«71-й7.+ |»7. = 0. (1)
Применяя второе соотношение теоремы Менли и Роу, получим
Wt , Wt w< ,2iF4_n
/ + 2/ + 3f ~r 4/ + 4/ —U’
w,1+-^-*+v+4wr*=0- (2)
Совместно решив уравнения (1) и (2), найдем
Wt= —(3)
Из соотношений (3) следует, что на частоте 4/ отдается боль-
шая мощность, чем на частоте 2/.
15.66р. Считая ф = ф0 4- sin со/ -|- ф.?|Я s‘n (2со/ 4- 4), запишем
i/a = sh ₽ [(40 4- ф1ст sin со/) 4- sin (2со/ 4- <p)] =
= sh ₽ (40 4* sin art) ch ₽ sin (2<oi 4- <r)] 4- ch (40 4-
+ 4’im sin <of) sh ₽ [42m sin (2<oZ + <p)].
Произведя разложение в- ррд Фурье, ^коэффициенты котороГ°
являются бесселевыми функциями, выделим постоянную состав*
386
льющую правой части и приравняем ее нулю. Пссле преобразо-
ваний получим
21 Mi ОРМ~। я»)И ^2 (/РФад)) nffi
J0 (7₽Ф1ст) 4> (/P4-2CT)
Правую часть уравнения подсчитаем по известным значениям
fl, 4'ict« Ф->ст, Ф. после чего по thfkp0 найдем рфс, а по ₽фс — Фо'
15.70р. По второму закону Кирхгофа, IR 4^нр = ^(0- Полага-
ем, что напряжение на нелинейном резисторе <НР) состоит из
достоянной составляющей, первой и второй гармоник:
«нр = UQ 4- Uim sin (at 4 а) 4 ^2(Я sin (2ю/ 4 ф) = 4 .
Значения L70, l/1CT, Us„, а и ф неизвестны, но
4 = (С«4-<)8 = 1/?4-3№<4 3l/„«t+u3_; (1)
= [^1я sin (ы‘ + «) + sin (2<а.' 4- <р)Р =
t/? (У?
= —[ 1 —cos (2d)/ 4 2а)] -гНр- [1 — cos (4ю/ 4- 2<р)] 4
4 UlmUzm [cos И -г ф—а)—cos (Зю/ Ч ф 4 а)];
и\ = A Uln sin (at -J- а) -г - sin (at 4 а) 4
+ UlJJ^ sin (2о>.‘ 4- ф) + sin (2а- <р) +
+ sin (2ш< 4- ф) 4- -4-" sin (2а— Ф) +
+- т Uta sin (2ю/ 4- ф) 4- UlmUlm sin (ю/ 4 а).
После подстановки и\ в уравнение (1) получим следую-
щие пять уравнений. Для постоянной составляющей
paR 4 По=0, (2)
где
Р = t/H 1,5адл 4- I*5H|rat/04- 0,75(7?га/73га sin (2а-ф).
Для синусной составляющей первой гармоники
[Ran 4 Ulm\ cos a— 3UQUcos (ф —а) = E. ж. (3)
Для косинусной составляющей первой гармоники
[Ran 4- sin а 4- 3U0UimU2tn sin (ф—а) = 0. (4)
Для синусной составляющей второй ] армоники
(Ram 4 USm) cos ф 4 1,5£/0lri1n sin 2а = Eim cos ф. (5)
Для косинусной составляющей второй гармоники
(Ram 4 t/2rt) sin ср — 1,5U0Utm cos 2a = Ein sin ф, (6)
m = 3U>U2m 4- 0,75/7^ 4 1 tbU*mU2a,
ffle n = 3UIU4- 0,75(7?,. 4- J ,5(/?„(71и.
387
Уравнения (5) и (6), так же как и формулы для пит, имеют
симметричную структуру. Решение уравнений (2)—(6) может быть
осуществлено на ЭВМ.
15.73р. Подставим ф—фо + ф^зта»/ в формулу i = ashpty и
определим связь постоянной составляющей тока /0 через обмотку
нелинейной индуктивной катушки с рф0 и рфя. В результате
получим
/,= ashpV,(/₽i|>J. (1)
Первая гармоника тока i через индуктивную катушку
2a ch Рф0 [—/Jx (/Рф„)] sin wf.
По закону электромагнитной индукции, мгновенное значение
напряжения между точками а и b
иаЬ = дф/d/ = <офя cos ©/.
По первому закону Кирхгофа, + или
Z, + sin ю/ cos <р + Ia cos юГ sin ф = юфт G cos со/—
—йгСфжsincof + ashрф0 Je (/рф„) + 2a ch рфв [—jJt (/Рфя)] sin ©t (2)
Из равенства постоянных составляющих (2) следует ранее по-
лученное соотношение (1). В свою очередь, синусные и косинус-
ные составляющие первой гармоники равенства (2) позволяют
записать два следующих уравнения:
—©Ч?фж + 2a ch Рф0 [—/Ji (/РФ.)] = /в cos ф; (3)
(офв6 — 1Я sin ф. (4)
Возведем в квадрат (3) и (4) и сложим их:
{2a ch ₽ф„ [—/Л ь>’С%}* + (иОф.)* = /£,. (5)
Решим (5) относительно сЬРф0:
сЬРф0 =
15.74р. Во время заряда конденсатора ис = Е 4- ДхеР1'; Pi^
s= — 1/(₽С); Л1==иг—Е. При < =
“с=из=£+(«г—^)е
/1=/?cin|E^=KCin£l.
Разряд конденсатора происходит в соответствии со схемой
рис. 15.33,г:
иС — иСП9 + ксСв № -^доо) nfa ^*°п ^*е
388.
Счет времени ведется с момента начала разряда. При /=0
йс = ыэ, поэтому Л1 = и3 + £доя—(Е-Ь Едоп)у~^. При / = /3
11
«с=«г=(£+ £Шп)£«оп+»=е
отсюда
а а+b Гт—(14-т) 1
G= RC----In----1--------.
1 4-a l-f-dlm—(14~т)т*“;—I
Период колебаний
Определим /? и С через заданные 7, ir и Е при о = 3; 6=6;
а= 1/11=0,091; т=1/. = 0,166; сс/(1 + а) = 0,0833:
[к 1
In 4 + 0,0833In 2,415 = ЯС-0,5865;
О J
/?С= 1,717; /? = 8ur/ir=l,33E/ir; С= 1,717//?= 1,2871Г/Е.
15.77р. Составим характеристическое уравнение Z(p) = 0 для
схемы рис. 15.36,в, обозначив г = /?д—/?' <0:
-ZF- Я+pL
Я'+^-+-----------------=0,
г+тг” ргЬСи4-Си/?р4-1
Р^-л
ЙЛН
О.р’ + С1Р*+aj> + а,=0;
a0=₽'C,LCk; at = LCj-^-+CuRR'C^+LCi
о, = ЛС. + Я'СД+4-+/?СД;
о.= — д+<? ; а, > 0, од > 0, а,> 0;
Яа>0 при /?'—>0, если L > (Сж Ч-Q/? |г|.
15.79р. Выберем направление контурных токов в соответствии
с рис. Р.15.14 и составим уравнения по методу контурных токов:
Л [/?з + ^к(1 аЯ'/й>с] ^я^^ = 0;
э^э "Ь 7g (/?$ + /?э + i^^o)—7а/юЛ1 = 0;
+ + jcaL-f-JL) = 0.
389
Оценим слагаемые по порядку малости, имея в виду, чТо
Составим определитель системы:
R6 4- jwLo
— /<йЛ4
I
faC
—/wM
Приравняем к нулю его действительную и мнимую части:
Re Д = RR. (1 -a) R6-~RM (1 -a)«>L0 (<»£—-+ -&+
\ MAh' 1 <JU V*
4-w’M’Rlt (1 — a) — Rs ( R + = 0;
Im A = /?K(1—a) R6(a)L——U)4-/?K(I — a)+
\ uM^ J
t Lq Ю.И2 n /„Г 1 \ f\
^wC2 С toe)-°*
(1)
(2)
Уравнение (2) поделим на /?к(1—а)#6 и, учтя малость члена
М2 . ~
по сравнению с LC и
Члена CR>(l-a)^ "° С₽авне-
нию с (1), определим
aR„I
M
R
Рис. P.15.14
“« 1/ ------, ' Р L\ • (3)
Из выражения (1) получим
уравнение относительно Л4:
(4)
6 =
ЛР—аМ + Ь = 0,
2/?3
где а~~ й>*СЯк(1—а) ’
wC
!-6.
со2 { + <й2С2/?к (I —а)
Решение уравнения (4):
Так как взаимная индуктивность М действительна и положи-
тельна, то между параметрами схемы должны выполняться соот-
ношения и 6 > 0.
15.81р. Обозначения токов примем в соответствии с рис. 15.39-
Потенциал точки 2 <р2= 1„RZ. Так как входной ток ОУ ран#1
нулю, то /, = /3. Потенциал точки 3 <р3 = (ра 4- ЛЯэ! ЧР1 = Фа +
= фг 4-/3^з + Л^и* Так как входное напряжение ОУ <рх—<рг#9,
то Ф1 = ф2 и потому /, = —/3-7^* Входное сопротивление
=^^7! = —RsZ„/R9 соответствует входному сопротивлению кон
вертора отрицательного сопротивления.
390
15.86 р. Воспользуемся обозначениями токов и напряжений на
рис. 15.44. Сопротивление параллельно соединенных Rt и Ск
равно сопротивление параллельно соединенных Rt и С2
R*
составляет i^R2c2p '
Учтем, что 1/х = (Л; U2=I.2Z<>. Входное напряжение ОУ сгре-
мится к нулю, поэтому /XZX -г (/х 4- /) R = 0. Отсюда lxZx =—I2R.
U* /2 Z1
n v Vi
Входное сопротивление схемы ZBX «= 7- = —= —$
ZjZ-i
—Входная проводимость при р = /<о
у«= - z5;=“ [ i - R,Rac ,(>»+/<>> (RA + R2Q]
Если при фиксированной частоте со параметрами Ru R2, Clt С,
распорядиться таким образом, что RxR2CxC,w2= 1, то Увх = /шС,
«еС=-(4л+£с=)-
15.87 р. Потенциалы узлов 7, 2, 3 на рис. 15.45 обозначены
Фп фг. <р8. Токи ветвей Л = —7^ > Л = Л = —^у-
^2^~рС
1,=^; Ц = Так как 1^ = 1,*,. то Л = •
Входной ТОК ln — It /з = Ч>1 —RsRjtbl-RjcJ) Р • При R3R..=
= RjR, входное сопротивление ZEX= фх//вх = R2R4C^.
15.89 р. Пользуемся обозначениями на рис. 15.47. Так как
входное напряжение ОУ стремится к нулю, то /XRX = /4R3 или
/х = /гх/4, (1)
где = R3/Rx. Напряжение между узлами 3 и 2 можно записать так:
1/и=Л(К,+ Л4)=/.-^.
ИЛИ
где
k3 = (R3 + RJCp. (?)
По первому закону Кирхгофа, для узла 2 /х + Л4-/5 = /2. Заме-
ним в последней строке /х и /6 согласно (1) и (2). В результате
Получим
где
= 1/(1 4-+ ^2). (3)
С учетом (1) и (3) входной ток /вх = /х = ^к912. Входное
Спряжение = /XRX 4- /3R, = Л г ?-tf т-т^ > Входное сопротив-
391
ление
Ze=^ = ₽1+^=(₽f+₽.+^) + W^l + ^)p.
Таким образом, входная индуктивность может регулироваться
резистором /?4.
15.90 р. Воспользуемся обозначениями на рис. 15.48. Выразим
потенциал четвертого узла через' потенциал первого узла
<Р1 = ~Ф1ГЬ^- (1)
Знак минус в (1) учитывает инвертирующее включение пер-
вого ОУ.
Потенциал второго узла
Ф.= (<Рж— (2)
Определим токи в ветвях. Ток = . С учетом (1)
I-----(П ^fr+P*
Согласно (2),
Г ф1 1^0 — 1 — рт] — ^0<Р1
afl(l-J-pr)
Ток
/ = Ф* _ Фя
’ Лр + р—Лр р *
Потенциал
Фз = Мр = йф2.
По первому закону Кирхгофа, для узла 1
Ш=о.
(3)
(4)
(5)
(б)
(7)
Подставив (4) и (3) в (6), заменив <р3 на <р4 в соответствии с (5)
и учтя, что и^1, получим
N(p)
Ф1 М{р) “°’
(8)
где N (р)=а р2 +bp -У с\ (9) М (p) = cJ?(l + рт)(1 + ^0-Ьрт); а-
=т2(1-{-а); 4-а)—(1— a)]; c=kkla.
При возникновении автоколебаний <р, является функцией времениh
а изображение Ф1 (0 -=* Ф1 (р)¥=0. Поэтому в соответствии с урав*
нением (8) /V (р) = 0. Чтобы амплитуда автоколебаний не возра‘
стала и не убывала во времени, необходимо, чтобы в уравнений^
коэффициент 6 = 0. При этом корни уравнения (9) будут чисТ°
мнимыми:
Ь — 0 при fe=(l—а)/(1 + а).
392
Частоту автоколебаний определим при b=0t полагая р = /ш0:
„ _ ko i/' ka
wo ~ т I' rzz -
практически 10“3-i- 2- 10~a; (ofl составляет несколько десятков
jpin сотен килогерц.
15.91р. Полная схема замещения, соответствующая рис. 15.49,
изображена на рис. Р. 15.15. В ней два управляемых напряжением
источника напряжения: 7С(р)1/3з и K(p)Ubl. Входное напряжение
Рис. Р. 15.15
ОУЛь выходное К(р)Оь1. Входное напряжение ОУ/Ле» выход-
ное К (р) U3*. В дальнейшем падением напряжения в малых вы-
ходных сопротивлениях ОУ /?вык пренебрежем и будем полагать,
что потенциал второго узла (р) USi и потенциал четвертого
узла Ч>4 = К(р)йь1.
Сопротивление /?в—это входное сопротивление ОУ. У высо-
кокачественных ОУ оно составляет несколько мегаом и много
Больше остальных сопротивлений схемы. Так как входной ток ОУд
стремится к нулю, то <рв ж Ток /. = D р-. Потенциал узла 1
АЗ “Г" Аз
<₽1 = / 1₽з = <Р« » ИЛИ в числах <р, = 0,99<рг. Ток /8 = -
Управляющее напряжение ОУг (761 = <р6—фд = £вх—0,99ф2. Управ-
ляющее напряжение 0У2
^32 = <Рз — «bi Фз = Фз+Л^| =
__ " « ^?4 /* * \ * / 1 Лл \ । ’ /?4
= Я4+ЯБ = 1 — 7?44~/?э) + Ri + Rs
или
‘ 10 • • 0.09 0.09 . ’ • ч ~ ллпт / ' i
Ю•ОЗ Фз “1“ Ф4 ю оу ’ за ~ Ю,090,00882 ((р4^—(р2).
Потенциал узла 4
• • ь
q><=/C(7«>)MB1 = rA-(E1>,-0>99<pJ. (1)
I I
Потенциал узла 2
Ф,« К (М и„ = -^£1— • 0,00892 (ф4 - ф8). (2)
393
Из уравнения (2) определим
0.008926о
• __ • 14- /ют
0,00892*7 ’
‘ 14- /ют
подставив его в уравнение (1), найдем передаточную функцию
фильтра:
Л1_ =
£вх
ко
1 -Г /ют
0,00883*0
О,ОО892Ло
Подсчитаем передаточную функцию при / = 50 кГц:
*0 2.106
т—;—•— — п—i——е 1 л* — 20,68/
14-уют 14-/2л-5«104 г
<f4 — 20.68/
£*ВХ
________________________________________ 7 4^р/7Ь,8Л
0.00883 (—20,68/р___’
4- (—20,68;) 0,00892
Передаточная функция в децибелах 201g17,45 дБ.
£вх
Глава шестнадцатая
16.1р. а) Заменим ВАХ ф(/) двумя отрезками прямых I и II
(рис. Р. 16.1, а). Для обеспечения наилучшего приближения выби-
раем положение наклонной прямой так, чтобы существовало
равенство площадей под прямой и под кривой. После замены
действительной ВАХ кусочно-линейной функцией решение задачи
сводится к рассмотрению двух линейных задач в областях I и II.
В области / (вертикальный участок) при 0 < t < t0
i(I) = G; dty/dt = E; ф(/) — Et-^A0.
При t = Q ф(0) = 0. Поэтому Ло = 0. При t = t9 ф (f0) = Е/о =
откуда г0 = ф0/Е.
В области // при t > i0
Уравнение цепи имеет вид
где Еэ = (ф1т—ф0)//1и.
Решим это уравнение относительно тока:
F Е —Т~ w I —т“ I
*(‘)=т-£е а -'А1-* аА
где Ia = E/R-t Ta^L3/R,
394
Изменение потокосцепления ф (f) при t > определим из урав-
нения 4- •£- ф = Е, где ф/£э = I.
t-ia
Таким образом, ip (/) = ф1я—-(ф1я>—ф0)е т* .
Графики изменения тока и потокосцепления в функции вре-
jieHH приведены на рис. Р.16.1, б.
Рис. Р.16.1
б) Аппроксимация ВАХ показана нз рис. Р. 16.1, в. В об-
ласти / (горизонтальный участок) dtydt = 0, поэтому ток —
устанавливается мгновенно. В области // уравнение цепи при-
мет вид
**+Ri = L,4 + Ri = E,
где Гэ = ip2m/(/ow—/0>. При этом начальное условие для тока
ненулевое, т. е. i (0+) = /0.
Изменение тока и потокосцепления (рис. Р.16.1,г) найдем из
Выражений
i (0 =
Ч’(О = 'Ра»—
где Т9=£,/Я.
в) Аппроксимирующая прямая проходит через начало коор-
динат (рис. Р. 16.1,д). Следовательно.
* (() = (1 — е'//Г’); t(/) (1 — е”Чт,)-,
= L3/R‘t Ls = ipara//3m.
16.2р. Рассмотрим случай аппроксимации ВАХ, приведенный
рис. Р. 16,1,о. Так как Тв<^Т/2, то можно считать, чго в конце
395
первого полупериода ток и потокосцепление достигнут уставе,
вившихся значений: E/R\ = Законы
изменения ф (/) и i (/) при О С * С 772 характеризуются теми
выражениями, что и в п. а) задачи 16.1р.
При расчете тока и потокосцепления во второй полупериод
можно считать, что схема подключается к источнику ЭДС при
ненулевых начальных условиях, а именно: ф(772)==ф .
В результате решение уравнения цепи Ls-^--[-Ri =— Е при-
мет вид
t-T/t
/(/)=—/1ж+2/1яе г» .
Найдем время при котором ток i (fx) = 0. Из последнего
выражения следует, что /х = 772 + Та In 2. При tх < t < tt i (/) = о
Рис. Р.16.
(вертикальный участок ВАХ от ф0 до —*фо)- Время 1г определим
из решения уравнения dty/dt = E. Учтя, что 'ф(*х) = 'Фо» ф(У =
=—ф0> получим /, = /, + 2ф0/Е. При < t < Т
t-t,
i (0 = — Ilm + Га.
Для следующего (третьего) полупериода решение аналогично
решению для второго полупериода с тем различием, что ф(Г)^
——ф1я>; I (Т)=—/Ъя. Графики/ (/) и ф(/) показаны на рис. Р. 16.2, л-
Аналогично решается задача и для случая, когда ВАХ ап-
проксимирована, как показано на рис. Р.16.1,в. Графики
и ip = fs(t) для этого случая даны на рис. Р.16.2,б.
16.10р. а) Запишем уравнение цепи:
396
р1ри a= 1/2
7. (1 —S-) =- uc, где 7. = RtC„.
Для удобства анализа перейдем к относительным единицам:
^==ис/Е; 1* = ЦТ0. Тогда уравнение цепи с начальным условием
(0) = Е или ис (0) = 1 примет вид
du'cldt* = — ис!{ \—Uc\
Уравнение изоклин представим в виде
k = — uc!{\—uc) или «с = — ft),
где ft = tga.
б) Для линейного случая dq/duc = Cf). Уравнение изоклин
имеет вид k = — lie.
Рис.
Р.16.3
Таким образом, в обоих случаях (линейном и нелинейном)
линии равных наклонов—прямые, параллельные оси абсцисс.
Задаваясь в области изменения ис от 1 до 0 различными его
значениями, получим соответствующие значения fe = tga и а
(табл. Р.16.1).
Таблица Р.16.1
ис Л —tga a ис A = tga a
1 — со —90° 0,4 —0,66 —33°30'
0,8 —5 —76° 0,2 —0,25 —14°
0,6 —1,5 —56СЗО' 0 0 0
Для линейного случая (а = 0) решение аналогично. Поле
изоклин и кривые изменения во времени напряжения при разряде
Нелинейного и линейного конденсаторов показаны соответственно
На рис. Р. 16.3, а, 6.
16.11р. а) Уравнение цепи имеет вид
£“'S'+R<>i=£ или
397
где
7*0—£о/7?о» — EfRo*
Начальное условие: i (0)=0. После введения относительных едп-
ниц 1*=1/Лл; t*=t/To получим di*idt*=l—i*.
Уравнение изоклин примет вид А=1—Р или Р=1—k.
Задаваясь значениями токов Р от 0 до 1, найдем соответству-
ющие k и a —arctgft.
б) Уравнение цепи примет вид
di Е—и (О
dl Lq
В установившемся
В установившемся режиме di/dt =0; u = Um = E\ i = lm =_
= (E/a)1/m. Сопротивление R (Im} = Ujlm обозначим Rz.
После введения относительных еди-
ниц Р = £//м, Р = t/T0, где То = Lv/ROt
получим di*/dt*=l—aL где
__ а
а' ~ ад.""'
Уравнение изоклин примет вид
k — 1 —а2 (Р)га.
Задаваясь значениями Р в преде-
лах от 0 до 1, определим k и а —
= arctgA. Характер кривых измене-
ния тока для т = 2; 0,5; 1 (линейный
случай) показан на рис. Р.16.4.
16.15р. По закону Кирхгофа,
ис = Е—(ic + i)Rlt
где ic=C-^; i = А (“с)-
После подстановки значений ic и £ в исходное выражение
получим
'г due_р J 1 Г wc I /1 (ис)
где T1 = RlC.
Введя относительные единицы и*с — ис!Е\ t9 = t/Tlt найдем
^=1-[«г+*/.(«»].
где к — коэффициент, определяемый видом зависимости j\ (исУ
’Обозначим х—и'с\ y — du*ddt*. Тогда уравнение фазовых тра-
екторий примет вид
0 = 1 — [x-l kfx (к)] =f (x).
а) Для линейного резистора i = uc/R0’t i* = ilmt где Im = E/R^
В результате
due * • ( \ ипн .._I_ /1 । Ri \
^=1—^ j или у-l
398
Фазовый портрет изменения и*с показан на рис. Р. 16.5, а. Так
как ^с(0)~0, начальной точкой траектории является точка Л.
б) Фазовый портрет изменения дан на рис. Р. 16.5, б.
в) Решим задачу, используя уравнение
С dt ~ Ri I /?! +M«c)j-
Правую часть уравнения найдем графически. Для этого снав
чала строим суммарную характеристику, соответствующую выра-
жению в квадратных скобках (рис. Р. 16.5, е), а затем нелинейную
зависимость, которая определяется всей правой частью уравнения
Рнс. Р.16.5
(рис. Р. 16.5, г). По полученной кривой найдем фазовую траекто-
рию, считая х=ис; У = С^-- После коммутации рабочая точка
(точка Л) движется по траектории AEBCDEB, образуя предель-
ный цикл. В цепи устанавливается режим релаксационных (неси-
нусоидальных) колебаний.
16.16 р. Запишем уравнение цепи в следующем виде:
duc/dt = f(uc) или y —
Промежуток времени Д/ между любыми двумя соседними точ-
ками фазовой траектории, например точками хд и хд+х, определим
из выражения
Д/ = J <р (х) dxt
хк
где ср (х) = 1/f (х).
По теореме о среднем, Af = <p(£)(xft+X—хд), где хд<£г^хд+{.
Если Д/ мало, то приближенно принимаем Д/«Ах/^ср, где
Дх = хд+Х—хд; i/cP=0,5(z/fe+14-z/J.
Для более точного расчета времени можно применить метод
х
графического интегрирования, используя выражение t = J <p(x)dx,
где х0—начальная точка фазовой траектории. Строим кривую ф(х)
И подсчитываем графически площадь под кривой (рис. Р. 16.6, а).
Качественный характер графика иг(1) показан на рис. Р. 16.6,б.
16.17 р. Если точка равновесия (точка F на рис. Р. 16.5, г)
Устойчива, то любое малое возмущение режима Днс —»• 0 при
399
t—> оо. Полагая
получим
uc = «c0 + Auc, из уравнения задачи 16.15р
^со . п
dt +L dt
Здесь выражение duCD/dt = f(uCc)^O, так как точка равновесия
физически соответствует установившемуся режиму постоянного
тока.
а) б)
Рис. Р.16.6
После разложения правой части уравнения в ряд Тейлора
Найдем С ж f (иса) + f (иСо) &ис. Так как f (исо) = 0, то в ре-
зультате получим уравнение для малых отклонений;
С^с_/'(Uco)AUc = O.
Характеристическое уравнение имеет вид
Ср f (нсо) = О; pi = f (иСа)/С.
Чтобы процесс при малых отклонениях был затухающим, необ-
ходимо соблюсти условие
Pi < 0 или Г <“«)==а| „ < °-
L -1ис—иС0 ***1^=0
Таким образом, необходимым условием устойчивости является
условие отрицательного наклона касательной к фазовой траек-
тории в точках, где она пересекает ось абсцисс. В нашем случае
это условие не выполняется, поэтому равновесие неустойчиво.
16.20 р. Уравнение цепи имеет вид
+ + сё" У * = О»
^ + 260A+<o59 = 0,
где q=^idt\ о>?= 1/(LOCO);
Введем относительные единицы f* = G)0Z; q* = q/q0. Считая
x = q*t y^=dq*ldt*t получим
dy _( 26о
Л* к со0 У Г
400
После деления последнего уравнения на dx!di* = y найдем
2д0
.--------------------------у—X
ау (оо
dx у
Для построения фазовых траекторий на плоскости у, х исполь-
зуем метод изоклин. Полагая k^=dy!dx, где A=tga, определим
уравнение изоклин:
^+-^=х или нац». •
Для качественного построения фазового портрета возможных
движений изображающих точек на плоскости ytx достаточно
построить поле наиболее характерных изоклин, а именно:
]) ^ = 0 (сч = 0); 2) As = oo (а2 = 90°); 3) £3 = + 1 (а3 = 45°);
4) = — 1 (а4 = —45°).
Рис. Р.16.7
Уравнения для этих изоклин имеют вид: 1) у——;
2) «/ = 0; 3) у = — j +2fio/Wo ; 4) у = — 26o/Wo-i *
а) Для заданных параметров схемы 260/w0—1, поэтому урав-
нения изоклин запишем в виде: 1) у — — х; 2) z/ = 0; 3) у —— х/2;
4) у = оо (х=0).
Поле изоклин, построенное по этим уравнениям, и фазовая
траектория, соответствующая х = ха = показаны на
рис. Р. 16.7,а.
Полученная траектория указывает на то, что процесс в цепи
колебательный, затухающий. Точка О — устойчивый фокус.
б) Уравнения наиболее характерных изоклин примут вид:
1) У—°° (*=0); 2) #=0; 3) у = — х\ 4) у=х.
Поле изоклин и фазовая траектория для этого случая пока-
заны на рис. Р. 16.7, б. Траектория в виде замкнутой кривой
(предельный цикл) близка к окружности. Поэтому колебания
в цепи синусоидальные, незатухающие.
16.22р. Уравнение цепи имеет вид
401
• due
или с учетом t — C0-~
Введя обозначения Юо= 1/(£0С0) и /•=<оо£ получим
<Рис 1 ₽ / 1 <*цс \ . „ _
rf/*a 1-/^ у Lo/Cq dt* с
Полагая х=ис, y=duc/dt* = dx/dt\ найдем
После деления этого уравнения на dxidt* = y определим
dy _ х4-Г (у)
dx у
х—[—F(y)l
где F(y) = f(-^==-\—Е.
\Г Lo/Co /
Функция f
является фактически ВАХ
нелинейного
резистора, у которой масштаб тока изменен в КL0/Co раз. Строим
на фазовой плоскости
мость [— F(0]=£—f(
завися*
у \
К Lo/cj ‘
Затем по методу Льенара строим
фазовую траекторию. Для опреде-
ления отрезка фазовой траекто-
рии в любой точке по этому ме-
тоду, например в точке А (рис.
Р.16.8, й), проводим прямые АВ
и ВС и перпендикулярно гипоте-
Рнс. Р.16.8
нузе построенного треугольника
АВС—отрезок АА‘. Аналогичные
построения выполняют для точки
А' и т. д. Отрезок А А' совпада-
ет с направлением касательной к
фазовой траектории в точке А, что
следует из подобия А АВС и
ДПАС.
а) Фазовая траектория пока-
зывает, что переходный процесс
колебательный, затухающий вок-
руг точки равновесия ис(<х) = Е
(устойчивый фокус).
б) Характер переходного про-
цесса зависит от начального
напряжения на конденсаторе. Для начальных напряжений, опре-
деляемых точками Ах, Аа, Аа (рис. Р. 16.8,6), фазовые траектории
402
сжимающиеся спирали (переходный процесс колебательный, зату-
хающий). Для напряжения, определяемого точкой Л41 фазовая
траектория — раскручивающаяся спираль (переходный процесс
расходящийся). Границей между ними является фазовая траекто-
рия в виде неустойчивого предельного цикла (пунктир на рис.
Р.16.8, б).
16.23р. Уравнение цепи имеет вид
7 — О
"Г I Со -V,
или в безразмерных величинах
где q' = q}q0\ cog = 1/(LOCO).
Полагая x = q*, получим
d-x . r f dx\ . 4 л
dt~ 1 ** y"*’’
r. I dx\ оЛ dx
ire F (/.s) = 26„s.
Приближенное решение будем искать в виде
х (/) = а (/) sin со/ 4- b (t) cos со/,
где c(/), b{t)—медленно меняющиеся амплитуды; частота со близка
соо ибо Q^> 1.
В общем случае
F (х, dx'dl) = Fi (a, b) sin со/ 4- F*(a, b) cos со/,
где Fx(at Ь), F2(a, b)—коэффициенты разложения в ряд Фурье
функции F(x, dx,dt).
а) Система автономна, и выбор фазы колебаний произволен.
Поэтому решение можно искать в виде х=а(/) sin со/, положив
Ь = 0. В результате получим
F(x, dxldt) = 26О~ = 26оясо cos со/; Fl(at b) = 0; Fi(ai 6) = 26oaco.
Уравнения для амплитуд примут вид
da/di = — 1 /2со [Г2 (а, Ь) 4- b (cog—со®)J = — 60а; (1)
db/dt =— 1/2(о 1/4 (а, Ь) 4- a (cog—<о2)] = О, так как Ь = 0. (2)
Запишем уравнения для огибающей амплитуд а (/) н частоты со:
da'dt 4- 0; (3)
со = со0. (4)
Решением уравнения (3) является выражение а(/) = Де-Зо/,
где Л=а(0)—начальная амплитуда, определяемая заданным на-
чальным зарядом q(0) = qo.
403
Общее решение имеет вид
х=а (/) sin at или q = goe_6<,r sin о>о/,
т. е. возникает режим затухающих синусоидальных колебаний.
б) При Яо = О 6о=0. Поэтому решение для амплитуд имеет
вид а(/) = А. Общее решение: q = q0sinci>0L Для анализа измене-
ния огибающей амплитуд используем фазовую плоскость yt х,
где x^=a(t); y=dajdt.
При/?о#:О^ = — боХ.При Ро — 0, г/ = 0, х = А — а(0). Фазовые
траектории для случаев а) и б) показаны на рис. Р. 16.9, а, б.
Ряс. Р.16.9 Ряс. Р.16.10
1в.26р. Приведем уравнение цепи к виду
^_Й(1_Х.)* + Л=О,
где k — <о?= 1/(LOC?).
Ищем решение в виде x=nsin(oG полагая 6=0. Тогда
dx/dt = ato cos со/; х* = 0,5а* (1 —cos 2a>t).
Найдем Ft (а, b) и F2(a, b) из уравнения —6(1—хл)~ =
= —k ( 1 —v 4-^- cos 2с£>/ ) a® cos cat — ( — too 4~~т~ cos at —
—^^cos3cof, откуда Fl(at h) = 0; Ft(a, b) = — to>(l—fla/4).
Уравнения, определяющие изменения во времени амплитуд а,
b и частот со, имеют вид
*)+*(««—”И=4 (*-?):
Ч+«(«4-^)1=о.
Отсюда следует, что da/df = ^(l—я*/4); ш = ш0 = 1/ИЬ0Со.
При установившемся режиме (da/dt—O) получим два значения
амплитуд: aiycT = 0; я3 уст = 2 (рис. Р.16.10).
Для анализа изменения амплитуд обратимся к фазовой пло-
скости у, xt где х = а\ y = da/dt. Уравнение фазовой траектории
у=^(1-х»/4).
Устойчивый режим соответствует точке, где a = a2ycT^2, так
как здесь dy/dx < 0 (см. вывод условия устойчивости в малом в
задаче 16.17р).
404
Глава семнадцатая
17.1р. Воспользуемся системой уравнений, составленной по
методу узловых потенциалов при <р4 = 0:
Ф1 (£i + + £6)—Ф*&—Фз£6 «
Ф. (§2 4- ga 4- Я«)—Ф1Я2—ФаЯз = 0;
Фз(£|4-£4 4-£6)—Ф1£6—Ф^з = 0; Л = Фз£4-
Преобразуем эти уравнения в форму, удобную для построения
графа. Для этого первое уравнение запишем в явном виде отно-
сительно <plt второе—относительно <р3, третье—относительно <р8:
Ф1 = Е1П4-Ф8Ь4-Фзс; Ф2 = Ф^4 Ф3/;
Фз = ф1/и4-фгп; /4 = ФаЯ4»
где а — - - *-- b = • * с = ___—-
£14-£а4-£?5 ’ gi4-g»4"£5 ‘ gi4-g»+g5 ’
([ __ ______ f — ___----- • fJl-, g*____ • fl-----g3
gs4*ga4'Se ’ £а4_£з4_£в * gs+gt+gs’’ &з4"₽4+Яв *
Узлами графа являются Et, фх, фа, <ps, /4. Составим граф в
форме причина—следствие, т. е. расположим сначала слева узел
источника, затем узлы потен-
циалов, а крайним справа— ^z***'^*^^\
узел искомой величины /4. Сое- с—> /* о
диним все узлы ветвями с coot- h
ветствующими передачами, ис- ^^*"/^***>^
пользуя последнюю систему рис> р.пд
уравнений (рис. Р.17.1). Найдем
передачи ветвей: a=b=c=d = f — m — n—\/3\ g4=l См.
а) Исключив узел ф4 как простую узловую точку, получим
граф рис. Р. 17.2, а. Заменим параллельные ветви эквивалентными
(рис. Р. 17.2, б) и исключим узел фх (рис. Р. 17.2, в, г). Две петли
заменим одной эквивалентной (рис. Р. 17.2, д). Исключив узел <р„
окончательно упростим граф (рис. Р. 17.2, е,зе). Искомая величина
равна передаче графа (рис. Р. 17.2, ж): Як = /</^1=1/4 См.
2
б) Согласно формуле Мезона, Ян — — » где
личина А-го прямого пути от истока к стоку, равная произведе-
нию передач ветвей вдоль этого пути; А—определитель графа;
Afc—алгебраическое дополнение, равное определителю части графа,
не касающейся А-го пути.
Для схемы рис. Р. 17.1
Л = а/п£4; Ai = l; Ps=adng4, Ая=1;
А = 1 —(db 4- nf -Ь тс 4- mfb 4- cdn).
Передача графа
а__________________amgrl+adngcl I г
®14 1—db—nf—тс—mfb—cdn 4 * *
405
17.7р. а) Узлами графа являются два источника сигнала;
контурная ЭДС £\]t равная £, и ток J, равный контурному
току /88; два неизвестных контурных тока /п и /2,, а также
искомый ток /8, равный разности токов /22 и /83. Граф, соответ-
Рис. Р.17.2
ствующий схеме рис. 17.4, а, показан на рис. Р. 17.3, а. Найдем
передачи ветвей:
111 __^?12_ __ 1 .
= a”~R^~ Ri+Ri+R<~ 3 ’
_ ^*13 Ri _________1 . _ ___Rn________Rt______1 .
lk~ Ru^Ri+Rz+Rr' 3 * ati~R2i Я8Ч-Яз+₽в 2’
f?g3 Rs 1
a2k~ R-2~~ Ri+Rs-rRi 3'
Получен граф с двумя источниками сигнала. Для решения
задачи можно использовать метод наложения (найти передачи от
Рис. Р.17.3
каждого источника к стоку, а затем их сложить) или метой
объединения источников сигнала. Воспользуемся вторым методом.
Предварительно выберем базисное значение сигнала объединенного
406
источника: S = 5. От источника Ег1 к узлу /„ в графе рис. Р. 17.3, а
идет сигнал^ВцДц. Сохраним этот сигнал, изменив значение £IL
на базисное* = S, а значение аи на а\ так, чтобы Enau =
Тогда о Ji=Euau/S— 1. Параметр второго источника равен базисному
значению (J =£)и остается без изменения. Передачи ветвей, идущих
от источника J, не меняются. В результате получим граф с двумя
одинаковыми истоками, что позволяет их объединить (рис. Р.17.3, б).
Передача графа рис. Р. 17.3, б
4
G =—=—_____
S Д’
Определитель графа А=1—а12а21, Искомый ток
_________£ вцС21~4~с1Л°21 ~Т-ДйЛ—(1 — О12°21)
“ 1— о12а21
А.
б) Пусть <р4 = 0. Узлами графа являются неизвестные потен-
циалы узлов схемы <plt ср, и <р3, узловые токи /„ = Egi = 15 А,
/33 = — Egi+J = —Ю А (/22 — 0), а также искомый ток /ь = — Фз£5.
Соединим узлы источников сигнала с соответствующими узлами
потенциалов ветвями с передачей bkft. Узлы потенциалов соединим
между собой ветвями обратной связи с передачами bkp и bplt. Узел
/5 соединим с узлом <р2 ветвью с передачей—g5. Искомый граф
показан на рнс. Р. 17.4, а. Найдем передачи ветвей графа:
Ь^ — = —, — = 0,6; б12 = ^ = —= 0,2;
“ £п £14-£я + £з 12 £и £1 + £24-£э
и ___(fa £i _ n п. _£2i _ £j_________________2 .
Х3 £u £i + £i+£s * ’ 21 £22 £24-£44-£6 7 ’
^23 = |^ = ^74-^+£s = "7 ’ ^3i=£f3i/£3s = gi/(gi-b£4) = 0.5;
h.2=33 = £</(£1-+-£,) = 0,5; 633= l/g33 = = 1,5;
--g5 =—l//?d==—0,5.
407
Объединим источники сигналов. Пусть базисный сигнал S= 15
Определим передачи ветвей от объединенного источника к соот-
ветствующим узлам:
41=^«-и = 6ц = 0,6; &i=^68S=-l.
Граф с объединенным источником показан на рис. Р. 17.4,6.
Для этого графа есть четыре прямых пути от S к /8:
Р\ — ^11^21 ( ёъ)* = = ^11^31^23 ( Йб)»
Лд=1» Рз==Ь3зЬ28( '^ffi)» А3— 1,
Р 4 — ^33^13^21 ( £5)» ^4=1»
Определитель графа
Д = 1 ^23^32’^^31^13“”’^21^32^13 ^12^31^23*
Передача графа G = /6/S — У] PftAft/A, откуда /Б = SG = 1 А.
17.9р. Графы четырехполюсников строим в соответствии с
уравнениями в Л- и //-формах;
U^AUt+BI^ ( +
Ii~CUt-[- DI 2; \ Iг = Иц!
Схемы четырехполюсников с обозначениями токов и напряже-,
ний, а также графы для Л- и Я-параметров даны на рис.
Р.17.5, а—а.
17.11р. Для получения эквивалентного (объединенного) графа
сначала вычертим графы каждого четырехполюсника. Затем узлы,
отражающие один и тот
же тип переменной и
LQ. объединим в один.
Так как /2 = — Г[, узлы
Гл и Гх соединяем ветвью
с передачей, равной — 1.
Исходный граф показан
на рис. Р. 17.6, а. При объ-
единении узлов предъяв-
ляют определенное требо-
вание к форме графа каж-
Рис. Р.17.5 дого четырехполюсника.
Узел стока тока (напряже-
ния) можно объединить лишь с узлом истока тока (напряже-
ния), но нельзя объединить непосредственно с узлом другого
стока тока (напряжения). Это правило соблюдено при каскадном
соединении графов для //-параметров —сток второго графа -'"
объединен с U'2—истоком первого графа). По этой же причине
соединяют узлы /2 и ветвью с передачей —I и стрелкой, на-
правленной к Гг (Г2 является стоком первого графа; следовательно,
для других сигналов стоком быть не может; стоком ветви —*
является /j—узел, являющийся истоком второго графа).
403
правило было бы нарушено при непосредственном объединении
узлов графов, построенных для У- или Z-параметров (см. рис.
0.17.2), например узел Ux является стоком второго Z-графа, а
узел U2—стоком первого Z-графа (подобное объединение привело
бы к ошибочному соотношению U2 = Ux = l[Z21 4- /2Z22 4- IXZ~U -j- /2^12»
полученному из объединенного графа).
Исключая узел /^ получим более простой граф (рис. Р. 17.6, б).
Применяя к нему правило Мезона, т. е. рассматривая попарно
передачи сигнала от /, к U'x и Г2, а также от U2 к V и /2, най-
дем значения //-параметров для эквивалентного графа:
__//»(»4-Ян//;2)-//;^1Я
1 4~//ц/^2! А
ГГ ._Я12Я12, U _____ Я21Я2| __ ^21^21 ,
12 ~ Д ’ 21 “ 14-HL/4- д ’
tj _ Я22 (14- я22яц)—НХ2Н Н”22Н2д х2
22 —
22
А
где Д, = НххН'г—Н{2Н2Х> Д2 = ВД3- fTl2HZc, Д = 1 4- НХХН22.
17.14 р. Существует несколько вариантов построения эквива-
лентного графа. Для построения графа всей схемы воспользуемся
представлением четырехпо-
люсника 1 в У-, а четы-
рехполюсника 2 в //-пара-
метрах (объединить узлы
СД” и можно, так как
—сток, — исток).
Соединяем узлы /‘21’ и /р
ветвью с передачей—/и
стрелкой, направленной к
А2>(^2П —сток, Д4’ —исток).
Четырехполюсник 3 пред-
ставляем в У-параметрах,
что позволяет объединить
(эти узлы являются истоками).
гР/ г fl) t Т(2) н(2) Tfz)
7 y/V J2 ~f Jf h2! *2
и
z»
/2
Рис. Р.17.7
tG)
у (з)
J2
ц№
Lfo
узлы
t/?‘, а также
>1 и
Учитывая, что 1Х — /V’ + /^ и
/в = /£2>4-/‘а8’, построим эквивалентный граф (рис. Р.17.7).
17.15р. Используем S-граф лампы, основанный на характери-
стике триода для низких частот: ia = Suc 4- g,ua\ ic = 0, где ia, ка,
*c> uc—переменные составляющие анодного тока и напряжения,
и //<*’
409
а также сеточного тока и напряжения; S—крутизна характери-
стики лампы; = —проводимость лампы. S-граф изображен
на рис. Р. 17.8, а. Добавив ветви, полученные на основании урав-
Рис. Р.17.8
нений, описывающих эквивалентную схему для малых сигналов
(рис. Р. 17.8, б), найдем
7?с _ _ . р ________
«с «ах > «вых а* «а «вых*
Построенный граф изображен на рис. Р. 17.8,в. Коэффициент уси-
ления по напряжению
С (_р А
, “вых _ /’lAi S= Яг-Г Яс S
и «в.х Д l-bg/Яа (Яг + Яс)/(Я.-гЯа)‘
17.17 р. Граф строим на основе линейных уравнений, связы-
вающих параметры схемы (рис. Р.17.9):
l"al = ^1«с1 4~ £н1«а1» ~ "^2«с2 "Ь
«а 2 = *'н'gn • = аг ^*о» Ц ~ »
«о ~ «cl «as» «С2 = iai/gi» *al ” «сз*
Передача графа (коэффициент усиления по напряжению)
“ «вых^«вх = «аг/«с1 = 2
Прямых путей передачи два:
Pi = g^ Л1=И-(^т/Я1);
Р*2~ Sglgw ^2= !•
Определитель графа
Д — 1 + (Яо/£в) + (giitei) + (git/gn) + (giJgl) [Uo/Ян) + (gfr/gj]-
После подстановки значений Рк, ДЛ и Д в выражение для kB
получим
° (gil + gl) (gd + Sit + go)
17.18 р. Для построения графа (рис. Р. 17.10, а) воспользуемся
системой уравнений, составленной для схемы рис. Р. 17.8, б:
«б = 1з -Г иЭб = 1^3 + 1бЯб» + ujRw U* = «Кб— №•
410
Для упрощения графа и перехода к Я-параметрзм можно вос-
пользоваться двумя способами: 1) последовательным упрощением
графа
ик и i6. что довольно трудоемко);
2) использованием формулы Мезона.
Воспользуемся вторым способом.
(исключением узлов
s2
caf
1л?
аа1 ис2 uaZ
Рис. Р.17.9
Ь
а)
Hl2
1*
J
Ам
6)
Рис. Р.17.10
Передача от 1Ъ к пэб
Я3[1+Л;/Як1 + Яб-аЯб_ р , *б (!-<*) .
1 + Яб/Кк 1-1-К6/Кк *
передача от ииб к и&6
U /?б/^К .
12 1 + Яб/Як ’
передача от iB к i*
ГГ _____________________________ .
41 ~ 1 + Кб/Кк ’
передача от и*6 к 1К
LT __
-2" 1Ч-/?б//?к'
Преобразованный граф показан на рис. Р. 17.10, б.
17.19 р. Проводимость ветвей с источником тока и вольтметром
теоретически равна нулю, поэтому при расчете определителя лю-
бым способом эти ветви следует считать разомкнутыми.
а) Найдем определитель как сумму величин всех возможных
Деревьев. Вычертим сначала все возможные деревья, помня, что
дерево—это совокупность ветвей, касающихся всех узлов схемы,
но не образующих ни одного контура (рис. Р. 17.11).
Величина дерева равна произведению проводимостей его вет-
вей. Тогда определитель исходной схемы
А=abate 4- batef 4- abcdg 4 abdef 4- abdeg 4- abdfg 4- bcdfg 4- bdefg 4-
4- abceg 4- acdef 4- acefg 4- bcefg 4- acdfg 4- abefg 4- adefg.
б) Вычислим определитель, используя разложение по узлу 1.
К узлу 1 присоединены три ветви схемы: 6, с и d. Найдем
А = ЬАь 4- с\с 4- dbd 4- ЬсАЬс 4- bd&bd 4- cdbcd 4- bed bbcd,
где A6—определитель схемы, получающейся при закорачивании
ветви b и размыкании ветвей end (Дс и Д4 находят аналогично);
411
&bc—определитель схемы, получающейся при закорачивании вет-
вей b и с и размыкании ветви d (&bd и Д^ находят аналогично);
Д6с<£—определитель схемы, получающейся при закорачивании всех
трех ветвей, подсоединенных к выбранному узлу.
b d
b d
Рис. Р.17.11
Из рис. Р. 17.12, а—в найдем Д&= Дг = &d = aefg. Из
рис. Р. 17.12, г—е получим Д6е=(а+Л^; &bd = af (e+g)+eg(a+fyt
&ctt~(e+g)af. Из рис. 17.12,ж определим AtCd = (fl+7)(e + g).
а) б) 6) г)
Рис. Р.17.12
Определитель исходной схемы
^ = baefg-]-ca£fg-]-daefg^bc{a^f)eg-]-bd[af(e+g) +<?g(a + f)]+
+ cd(e + g)aZ + &rf(a + O(e + g).
в) Рассчитаем определитель, используя разложение по пути
между узлами 1 и 2 (см. рис. 17.9, а). Возможны три пути между
этими узлами. Величина пути Рк равна произведению проводи-
мостей ветвей А-го пути, отсюда Px = abf; Ря = с; P9=deg, Алге-
браическое дополнение пути ДА представляет собой определитель
цепи, полученной из исходной после того, как все ветви Jfe-ro пути
закорочены. Из рис. Р. 17.13, а найдем k^de+eg+dgi и3
рис. Р. 17.13, б определим Д3~ (ab + bf + aft (de+eg+dg)', из
рис. Р. 17.13, в получим Д3 = 064-6/ 4- af.
412
Таким образом, определитель исходной схемы
з
2 4- РА + Р»Д3«& 4- eg4 dg) 4-
+ c(ab + bf ±af) (de+eg 4- dg) 4- deg (ab+bf+af).
г) Рассчитываем определитель, используя разложение по ветви а:
Д = Д04-дДа,
где До—определитель цепи, полученной из исходной при обрыве
ветви а; Дв—определитель цепи, полученной из исходной при
закорачивании ветви а.
а)
б)
Рис. Р.17.13
Значение Де определим из схемы рис. Р.17.14, а. При подсчете
используем разложение определителя по пути между узлами,
к которым присоединялась ветвь а
исходной схемы: о-* о * о
До = bcf (de+eg 4- dg) 4- bdefg. q |g f
Значение Да найдем из схемы f 2 Я
рис. Р. 17.14, б. При подсчете нс- '
пользуем разложение определителя ₽ис* р-17-14
по путям между узлами 1 и 2:
Дв = bf (de -р eg -|- dg) 4- c (b 4- f) (de 4- eg 4- dg) 4- deg (b 4- f).
Таким образом,
A =bcf (de 4- eg 4- dg) b bdefg + a [bf (de + eg 4- dg) +
+ <4b4-D0te4-eg-Mg)4 deg(b + f)].
17.20р. Для определения передачи графа используем тополо-
гическое уравнение передачи:
2
fe=i
1 ~ J ~ д
где Т—передача графа, равная отношению показания измери-
тельного прибора UM к активному параметру источника J; P‘k —
пути передачи, равные произведению проводимостей ветвей fe-ro
пути, содержащего ветвь измерительного прибора и два зажима
Уточника; Д*—определитель цепи, остающейся после того, как
путь передачи, включая цепи измерительного прибора, будет
Замкнут накоротко.
413
Первый путь передачи содержит ветвь 12 и ветвь вольтметра;
P,l = gi (проводимость измерительного прибора равна единице).
Из рис. Р. 17.15, а, найдем AJ. При закорачивании первого пути
, узлы /, 2 и 4 объединяются в одну точку и
Ж Uy Ai=&+g,+g..
а(л| fa Второй путь передачи содержит ветви
/3,32 и ветвь вольтметра:
3 Л Определитель Д2=1,так как при закора-
о* чивании второго пути все узлы схемы объ-
а1 8} единяются в одну точку. Значение определи-
Рис. Р.17.15 теля всей схемы подсчитаем с учетом того,
что ветви источника тока и вольтметра раз-
мыкаются. По графу рис. Р. 17.15, б найдем Д=^|(§1^а + Оз-г
+g2g3). Таким образом, передача графа
у — — 2 2 Ом
g-i (gig2-i-gig3-|-g2g3) *
Показание вольтметра*. U^ — JT = 11 В.
17.25р. Как известно, комплексный коэффициент усиления
Л = t/BMX/#BX. Воспользуемся схемой замещения анодной цепи для
переменной составляющей (рис. Р. 17.16, а). Представим ее в виде
Ряс. Р.17.16
графа (рис. Р. 17.16,6), каждая ветвь которого характеризуется
своей проводимостью: g£ = 10“4 См; ga = 5 • 10”5 См; gc = 5 • 10-8 См;
= 2л2103-10“в = 1,256-10“- См; соСо = 2л2-103-10“10 =
= 0,1256-10“6 См. Передача графа
т=и^л- iAx)=Ж**
Рассчитаем числитель и знаменатель этого выражения. Пере-
дача имеет только один путь, содержащий ветви /2, 23 и ветвь
вольтметра: Pj = gI7wCe. Так как этот путь закорачивает все узлы
графа, то &{= 1.
Определитель графа найдем, воспользовавшись разложением на
пути между узлами 2 и 4. Ветвь источника э. д. с. при этом за-
корачивается, а ветвь вольтметра разрывается:
Pi^gf, Ai = jcoCcygc-HwCo‘. Aa==JtoCc + ^c+ju)C0;
P3 = /wCcgc; Д3 = 1; Д4 = 1.
Отсюда
у»___________ £» jtOCc
(gi4~ ga) (faCc ~i~gc 4“
После подстановки числовых значений получим Т — 0,593е/71>*3'.
Комплексный коэффициент усиления К = ^вых/^вх = — рТ =
— 11,86 е'’°«3' = 11,86 е-/‘ ’ E°i7'.
Глава восемнадцатая
18.3р. По первому закону Кирхгофа,
1 (О — Ц 4“
(1)
но
1 d
R dt
Подставив выражение для в уравнение (I), найдем
1 (0 = /» + ря( 1 - т?/Jsinm/+ [/и Г1 +
L \ ^А / к J L \ ** J
/2ilc°Sto/ + cos2(of + hi sin3o)/-h
A J А & А
+ -Н- ^7Г-/И COS 3(1)Л
Z а
18.7р. Для цепи рис. 18.2, в справедливо уравнение
rduc,uc_ j
С di + Я “
Для первого интервала времени Uc= рт =—!/(/?/?),
для второго иЦ = JRt 4- Д2е₽«(/-Т); р2 = —1/(/?гС). Составим два
уравнения для определения постоянных интегрирования:
JRX-1 4t;
JRi+ Л1 = /Я2-|-Лел\
где
А - а -
1 1—ер,ге₽«т ' 8 1—е₽*тер«т
<4
15.07
11,87
При заданных значениях параметров i4: = 20 — 18,Зе“*00<В; ис~
= 10-гб.ОУе-1000^-^ В. График ис = [ (/) изображен на рис. Р. 18.1.
18.12р. В общем виде [3] для возни-
кновения параметрических колебаний
малой амплитуды, когда характерис-
тика нелинейного резистора имеет <jx>p-
му квадратичной параболы [в данном
случае R (i) = 2+ 1СЮ/2, т. е. коэффи-
циент 100, 7?О = 2], необходимо вы-.
полнить условие _ ° Отсюда
АС 2 2 ° Г£/С’
г^~ > тип — 0,04. Следовательно; ЛС>“
IvnJ
1
Г It t
Рис. Р.18.1
415
>0,4 мкФ. Квадрат амплитуды тока при <» = 1/|/АЛС0
7-=М 2R°) = зЛоо(100 0-08-2-2) = 2-665 10-*;
1т = 0,1635 А.
18.14р. Мгновенное значение напряжения u = R (i)i=/?ei4-£i\
Положим i = ilm sin at. Подставив это значение в предыдущей
выражение, получим зависимость амплитуды первой гармоники
напряжения на резисторе Ulm от амплитуды первой гармоники
тока:
и1а=яй11т+ълыг1т.
При Лт = 0,1А; /?0 = 2Ом; k~ 100 Ulm= 0,275В. Энергия,
выделяющаяся в виде теплоты в резисторе по первой гармонике,
равна t/1CT/lw/2 = 0,0138 Вт. Такое же количество энергии должно
доставляться в цепь за 1 с при модуляции индуктивности. За одно
изменение индуктивности доставляется энергия, соответствующая
AL/^/2. За 1 с доставляется энергия, равная —^1Л^-~ ; следова-
тельно, ДА = 0,00867 Гн.
18.15р. Чтобы полупроводниковый диод работал в запертом
состоянии, необходимо выполнить условие £с > 1„т (чЛ)2-
Частоту параметрических колебаний сор определяют как соб-
ственную частоту контура (см. рис. 18.5, г) при г3 = 0; сор= 1 LCV
В установившемся режиме работы потери энергии в резисторе
сопротивлением R должны быть равны энергии, вносимой на ча-
стоте накачки ын генератором накачки (генератором тока iH). Если
бы емкость р-п-перехода изменялась во времени скачкообразно
(см. рис. 18.5, д), то за один период 7’р = 2л/ыр в колебательный
контур от генератора накачки доставлялась бы энергия, равная
2-^-^р- (вывод см. [3]), где qm—амплитуда синусоидально изме-
няющегося заряда на емкости С. За 1 с в колебательный контур
доставлялась бы энергия
р <7rn AC I_AC /п
Z 2С С Тр — С С 2л * V
Но
q —CU„=CIm —(2)
Чт т т сор
где 1т—действующее значение синусоидального тока частоты оу
Подставляя в формуле (1) эквивалент qm из уравнения (2)<
найдем энергию, доставляемую генератором накачки за 1 с:
72 АС 1
л С СОрС
Колебания будут незатухающими, если доставляемая в коле-
бательный контур энергия равна тепловым потерям в нем за т0
416
время:
рр , /2АС 1
1 К ~ л С ырС *
или
(3)
р _ 1 АС 1
Л л С ырС '
При выводе формулы (3) предполагалось, что емкость конден-
гора (емкость полупроводникового диода) изменялась во вре-
ни по прямоугольному закону с амплитудой АС (см. рис. 18.5, д).
в параметрическом генераторе рис. 18.5, а емкость модулиро-
на во времени не по прямоугольному, а по синусоидальному
кону с амплитудой АС, (см, рис. 18.5, в) и средним значением С,.
Чтобы в формуле (3) перейти от АС и С к АС, и С„ надлежит
прямоугольную кривую разложить в ряд Фурье и амплитуду
рвой гармоники этого ряда приравнять к амплитуде АС,.
Амплитуда первой гармоники ряда Фурье прямоугольного
4 4
колебания равна АС—. Следовательно, AC — = АС, или АС =
-^ДС,. Подставив в формулу (3) J-АС, вместо АС, С, вместо С
заменив <ор на юн/2, получим
1 АС1 1
2 С, сонС,
(4)
Таким образом, чтобы схема рис. 18.5, а могла работать в
качестве параметрического генератора, необходимо выполнить соот-
ношения (1), (2) и (4). Расчет элементов генератора по заданной
и известной зависимости С = / («J может производиться сле-
ющим образом.
1. По характеристике С = /(нд) определим ЭДС Ео. Берем Ео
примерно соответствующей средней точке участка наибольшей
крутизны характеристики С = /(нл).
2. Задаваясь значением /НлгК/?2Ч-(wHL)2 0.8£о, строим зави-
симость C = f(<oH/) и по ней оцениваем отношение АС,/С,.
3, По формуле (4) найдем сопротивление R.
4. Подсчитаем L = 1/((о2С,).
5. Определим значение + (чЛ2) и амплитуду тока накачки
I ____ 0,8£q
КR!+(<d„L)>
Вычислим комплексную амплитуду тока источника тока:
в,л Вт
18 .16р. В уравнении ^57т + Я^-|-£-=О заменим 1/С на
1
^(14-/ncos2(o/) и вместо переменной i введем т —со/. Получим
417
уравнение
где
-3^ + fM^ + G(r)<7 = 0,
G(t) = 55^(l + mcos2T).
(1)
Считаем, что заряд q в исследуемом на устойчивость режиме
равен q^ (в частном случае ?у = 0). Пусть заряд получил прира.
щение I и q = q? -Ь Составим уравнение относительно прираще-
ния Оно будет в точности повторять уравнение (1):
-£| + F(t)-j| + G(t)6=0. (2)
„ ff(T)rfc -~-т
Введя подстановку £=т|е z J — т|е , от уравнения
перейдем к уравнению
£я + Л(т)П=О,
где Л(т) = 6(т) —~Г(т)—JL[F(t)]’.
В нашем случае
Л W =“577^(1 + ж cos 2т)—4-(5-) .
' ' ii)aLC0' 1 * 4
П I । ( R V m
Положив a— 4 ; Я— i^LCo ’
получим уравнение Матье:
^ + (а+ 16? cos 2т) т| = 0.
18.18р. Исходим из уравнения
i'(0^+K0^+«^+^=O. (1)
Поделим уравнение (1) на £(0:
d*q Я+Г(0 dq ,__4_п
L(t) dt 'CL(t) v‘
Учитывая малость т, заменим тттг=т^1—1
’ Ьо(1—mcosZw*)
-т- (1 + т cos 2©/).
Перейдем от времени t к безразмерному времени т=ю/1
^ + «±^s!n2£(I+mcos2t)^ + 5>(1 + mcos21:)1?==0.
Уравнение для q (и. для приращения Е) имеет вид
^ + FW^+GWJ=0,
418
где F(t) = 2^1 ч-mcos 2т +sin 2т j [слагаемое ш2 sin 4т в F(t)
не учитываем ввиду малости т2 (тг1)]; 6 =/?/(2(о£о); G(t) =
-^(1+mcos2T)-
_ «. —— \ F (т) dr
Введя подстановку t = i]e 2 < , получим уравнение
^2- + Л(г)П==0,
л / \ \ 1 dF (т) 1 г С I—\ТЧ 1 ^F ^"0
где А (т) - G(t) ----т [F(t)]\ - у—^- =
₽2d^msin2T—— cos 2т ; —^-[£(т)]2~—& р +^- + у ("у } 4“
4- 2т cos 2т + sin 2т 1 .
о J
Таким образом, А + + (т^с “
— 2m—2mb2} cos 2т.
Обозначив а = -тг7т—Ь3( 1 + 0,5/и2 4-0,5-^^ ; Ь = -^—\ р=
2—26*^ г придем к уравнению Матье
Ч-(а + 16р cos 2т) 1) = 0.
18.19 р. Потокосцепление ip = §uLdf + А = Ет sinco/dt 4- Л —
——cosw/4-Д, Постоянную А найдем из начального усло-
— т( *
"" 161 ш3£0С
вия ip = 0 при t — 0:
A = ^s--, ф = £г = ^2-(1—coscoZ),
(d * х <oL ' '
Для первого полупериода £ = £04-Д£, для второго L — La—AL.
419
Ток в первом полупериоде t1 = » во вт0Р°м <»
_ —cos сор
со (Lq—&L)
Кривые ф, uLt L и t в функции cot изображены на рис. Р.18.2, а
Среднее значение тока за период 2л/ю
/ - 1 £« Г f l-cosq* t j_ F I - LqEm
7с₽“2л <0 [J £0+AZ. ^J- шЩ_(ДЛ)2р
18.20 р. Заряд q = §idl =—~ cos wt 4- A. Из начальных уело-
вий (при t = 0 q — 0) найдем постоянную Л = /,л/©. Следовательно,
q — ~——-cos tot. Напряжение на конденсаторе в первом полу.
t Q /«>(! — cos»/) ~ и /«(I —cosco/)
периоде ^—5^= мса-ДС) в0 втором = МСГ-ДСГ-
Среднее значение напряжения на конденсаторе
2л
I С л 4 / т^О
“с<р-2п,) “саш/-ш[с=_(4С).] •
Кривые /, q, С, ис в функции cot изображены на рис. Р.18.2, б.
18.21 р. Начальную фазу ф синусоидальной ЭДС положим
равной нулю. Выражение для переменного тока запишем в ваде
< = /OTsin(tot—а). Тогда потокосцепление
ф = L (г 4- /0) = Lo (1 4- т sin ©t) [Zo + Im sin (©t —ос)] = ф0 фо
где
11>„=ДЛ + Ц^соза; (1)
ф1 — £0/0msin(o/4-£(/„, sin (cot—a). (2)
Постоянная составляющая потокосцепления ф0 является функ-
цией не только постоянной составляющей тока /0, но и функцией
амплитуды и фазы первой гармоники тока, а также глубины
модуляции индуктивности. По второму закону Кирхгофа,
но
uiL = -- = (aLQml0 cos cot + uLJ" cos (tot—a);
«i/г = HIm sin (tot—a); u1C§ i dl = — Im cos (wt—a).
Подставив в выражение (3) эквиваленты ult, ulR, uiC, получи4
уравнения для синусных и косинусных составляющих:
(wLo"“7^r)Z«»sina^ HImcosa = Ein;
( ©£0—j Im cos a—Rlm sin a -|- ыЬот!й — 0.
420
Решим их относительно Im cos а:
EmR—toLom/0 f <ot0
/„ cosa =-----------
\mL°—^C J 4
Подставив /mcosa в уравнение (1), найдем
. REm— /0( oL0--—\ wLom
I _ f I I boffl____\_____(OCo/___
TO — 7 "О7 О I 9 / I \ 2 1
me
ф0 = а-ЬЬ/0,
Коэффициент b < 0 при выполнении следующих условий:
йс > 0’ 2")
Я» <|^-о 2~j HJc] •
Возникновение падающего участка на зависимости ф0=/(/0)
можно трактовать как появление отрицательной дифференциаль-
ной индуктивности в линейной электрической цепи с переменным
параметром. Сделаем следующие замечания:
1) при выводе искомых соотношений предположили, что началь-
ные фазы источника ЭДС и модулируемой части индуктивности
одинаковы. Однако качественно тот же результат будет получен,
если начальные фазы вынуждающей ЭДС и модулируемой части
индуктивности различны;
2) как и для любой резонансной цепи с переменными во вре-
мени параметрами, рассмотренный режим работы может быть про-
верен на устойчивость по отношению к малым приращениям путем
сведения уравнений для приращении к уравнению Матье. Анализ
Показывает, что режим работы на падающем участке зависимости
Фо=/(^о) является неустойчивым.
Глава девятнадцатая
19.3р. Напряженность электрического поля точечного заряда
в произвольной точке
£ = <7/(4левЯэ).
(1)
421
q f ‘.___i_Y
4mc \Ra Ri г
(2)
(3)
Напряженность электрического поля в точке с
Ec = q/{4maRl}.
Напряжение между точками а и b
Rb
1/Л= f EdR = ^— f
₽ J 4леа J
На На
Получим выражение для заряда q из уравнения (3) и подста-
вим его в уравнение (2). Так как q > 0, то
£. = £»-----U°!>--- = £"-525 В/м.
UlRa-l/RblR-'
19.6р. Напряженность поля максимальна на поверхности внут-
реннего цилиндра, т. е. в точках r — rv
Е________".
max г. |п ,
(1)
По условию, £тах = £пр/3. Решив уравнение (1) относительно на-
пряжения U с учетом соотношения (2), получим
{/=^/4 In —=12,2 кВ.
*> Г1
19.8р. Для области, находящейся внутри цилиндра, по теореме
Гаусса,
Ex2sirl — -~nr-lt
®0
откуда Fi = pr/(2e0).
Потенциал внутри цилиндра меняется по закону
ч>.=-У ^=-§С+с>-
Так как при г = 0 потенциал <р = 0, то Ci = 0. Таким образом,
<рх = — рг’/(*е0) = —282 • 10*гг В. (1)
Для области, находящейся вне цилиндра,
£«, 2 л г/ = -^-лго/,
60
“* огг
Edr = — 1п г + Сг
Постоянную интегрирования Са найдем из граничного условия:
при г = г0 <Р1==ф2. Тогда
г -^1пг____—
-~2ео Г° 4е0’
Окончательно получим
а — ed? in
е^=1411л——70,5 В.
4е0 г
422
Пользуясь выражением (1), определим <р|г=0—ф|г=го = 70»5 В.
В соответствии с выражением (2) найдем <р|г=Го—Ф |r=ro+a= В-
19.12р. а) Пусть Ну и Н2—расстояния между геометрическими
осями первого и второго цилиндров
и эквипотенциалью <р = 0 (рис. Р. 19.1).
Тогда
Я.=Я + 4=4 =3,25 см;
Н, = Н+-^г =4>75 см-
Расстояние d между эквипотен-
циалью <р = 0 и электрическими осями
определим из уравнения d* = Н?—г;';
d=2,57 см. Найдем расстояние меж-
ду электрическими и геометрически-
ми осями цилиндров: Sl = H1—d=0,68 см; S3 = Ht—d = 2,18 см.
6) Напряжение между цилиндрами
f7 =<₽..-% = 2^
1П^.
Определим расстояния alt blt a2t b2.
al = r1—Sx=1,32cm; bt = 2d—Oi —3,82 cm;
b2 — r3—S2 = 1,82 cm; a2 = 2d—b2 = 3,32 cm.
Напряженность поля в точке tn
Ё„ = Г—+4-')=Г-6290 В/м.
Oi&a
в) Поверхностная плотность заряда в точке т
<L»==DCT = eo£CT = 5,57 10-8 Кл/мя.
г) Емкость между цилиндрами на единицу длины
С = —^!- = 33.3-10~1г Ф/м.
1п^
19.17р. При определении закона изменения потенциала для
области, находящейся внутри цилиндра, воспользуемся уравнением
Пуассона, а для внешней области—уравнением Лапласа.
Так как р зависит только от координаты г, уравнение Пуас-
сона в цилиндрической системе координат принимает вид
I d / X kr
г dr \ dr ) eel ’
(1)
Уравнение Лапласа имеет вид
(2)
г dr \ dr / ' 1
423
Решив дифференциальные уравнения (1) и (2), получим ддя
внутренней области
ч>1=—4'А+С11п'’+С>;
для внешней области фа=Са 1п r-Ь С4.
- Решение должно оставаться конечным на оси, поэтому С1=гО.
Остальные постоянные интегрирования найдем из следующих
условий:
при г=0 <₽1=0;
г» ko? Сз
при r = a Dl = Dt, или ео =——еа ;
• СС л
при г = а <р! = ф2, или —1па-|-С4.
Окончательно получим С2 = 0; С3 = 375 В; С4 = —2016,5 В. Законы
изменения потенциала внутри и вне цилиндра:
ФА = — 0,25-10ег3 В; <р2 = —375 In г—2016,5 В.
Эквипотенциальная поверхность, для которой ф =—2 В, рас-
положена внутри цилиндра и является цилиндрической поверх-
ностью радиусом гт. Радиус гт найдем нз уравнения —2 =
==— 0,25-10»^; rCT—2-10-3 м.
19.28р. Элемент заряженной поверхности dS создает дипольный
момент dp = о/ ds = rj ds, где rj—поверхностная плотность распре-
деления моментов диполей. Потенциал произвольной точки поля
р cos On
диполя <р = ;* а , где 0—угол между моментом диполя р и ра-
диусом-вектором г точки. Потенциал произвольной точки Л1, соз-
данный элементом заряженной поверхности ds,
dyTLS^dS,
v 4ле0 ra *
а суммарный потенциал точки, созданный всей поверхностью S,
(1)
Для двойного слоя, имеющего форму диска, из выражения (l)i
учитывая, что cos0 = г[г и т] = const, получим
___Ф С
Ф 4ле0 j г3 ‘
S
Используя полярные координаты (рис. Р. 19.2, а), найдем
424
Ro
Напряженность поля
F = £ — ^2. = _2L 'хо
я дг . 2е0 (ЯоЧ**)3'2’ * '
Из выражений (2) и (3) следует, что при переходе через двой-
ной заряженный слой функция <р (?) терпит разрыв, а функция
£ (г) непрерывна (рис. Р. 19.2, б).
Рис. Р.19.2
19.31р. Для расчета поля в среде с относительной диэлектри-
ческой проницаемостью ег1 воспользуемся расчетной схемой
рис. Р. 19.3, а. Расчетный заряд ft —Qi£fTT Er?.=: — 0,4 -10“в Кл.
ег1 I ег2
Расстояния от зарядов и Qa до точек а и b обозначим R'at R2,
R'b, R£.
Напряженность поля в точке а
Еа = Е-а + Е-а= + —= 37,8 • 1 №
4nefli(fla£ 4лес1(₽йГ
В/м.
Напряженность поля в точке b (считаем ее принадлежащей
Реде /)
£‘ = Л . = 26’25 •102 В/м.
Wt 4лео1 {ЪЬГ
425
= 1,4-10”* Кл.
в точках
найдем,
Для расчета поля в среде с относительной диэлектрической
проницаемостью воспользуемся схемой рис. Р. 19.3, б. Расчетный
заряд Q3=& е
Напряженность поля
надлежащими среде 2)
fr, с и d (считаем точки при.
пользуясь выражением £
= 2з/(4я6-2Л2)- В результате
получим: Еь= 11,25-102 В/м-
Ес = 7,2-102 В/м; £4=5-102
В/м. По этим данным строим
график E=f(x), который изоб-
ражен на рис. Р. 19.3, в.
19.33р. Задачу решаем
методом зеркальных изобра-
жений.
Расположение расчетных
зарядов определим, осущест-
вив последовательное отра-
жение относительно гранен
угла. В результате получим
систему, состоящую из восьми
зарядов: одного заданного и
семи расчетных. Поверхност-
ная плотность заряда в точ- '
ке а равна модулю вектора
смещения в этой точке. Поль-
зуясь теоремой Гаусса, най-
дем векторы смещения в точ-
ке о, обусловленные каждым
зарядом, и геометрически их сложим (рис. Р. 19.4, а). При этом
8 8
/=1 1=1
О1я + Оап = -2-^- = -31,8-10-* Кл/м2;
D._ -f- D. = 2 тг— cos as = 2 ----------— — 9,9 • 10“® Кл/м2,
,п * 4" 2л.-, 5 2лг8 г» ’
где 1$~аК (рис. Р. 19.4, о).
Аналогично определим:
D6n+Den=-4,43.10”* Кл/м2; D7n+ D8n= 1,32-10”* Кл/м2;
Da = Dan = 25,01 -10”® Кл/ма.
Следовательно, о^=—25,01-10”® Кл/м2.
19.34р. Задачу решим методом зеркальных изображений. Огра*
жения осуществим поочередно относительно граней раздела сред
ММ и NN. Справа и слева от изоляционного слоя получим бес-
конечно большое число зеркально отраженных расчетных зарядов«
расположение которых показано на рис. Р. 19.4, б. Напряженность
426
электрического поля в точке а определим как сумму напряжен-
ностей, обусловленных каждым зарядом. Так как модуль напря-
женности поля резко убывает с увеличением расстояния до заря-
да, ограничимся учетом влияния конечного числа зарядов.
Напряженность поля в точке а от зарядов, находящихся справа,
7* Т ( 1 1 1 1 1 1 \ Г* * Л
Е а—— I •—(--------1-------1-------+— ---- 0,569.
2я£ву Гу 2г у 4гу 5г, 7г, 8г,/ 2я&вг1
Напряженность поля в точке а от зарядов, находящихся слева,
т / 1 1 1 1 1 1 \ -+ t _ _ __
E:=z -—----------+--------+--------]=i --------0,565.
2jua\rj 2г, 4г, 5г, 7rj 8г1?/
Суммарная напряженность поля в точке а £в=Т*-683 В/м.
Модуль вектора смещения De—EaEa—1,82* 10"8 Кл/м2. Поверх-
ностная плотность зарядов аа= —1,82-10~8 Кл/м2.
——
д) ё)
Рис. P.lfi.5
19.36р. Качественно построенная картина поля приведена на
рис. Р. 19.5, а. Используя метод изображения в сфере, определим
расстояние между центром шара и расчетным зарядом —q\ S =
— /?6/d=0,05 м.
Найдем заряд: q = Q-^- = 0,5-10“° Кл.
Расстояние от заряда Q до точки ветвления получим из урав-
нения
А ,а =7—, с.а; h = 0,512 м.
4ле0Ь3 4ле0(Л— d-f-S)2’ ’
Напряженность поля в точке а
Е.=---------,+---------=2700 В/м,
где га—расстояние от точки а до заряда Q.
19.38р. Расчетная схема дана на рис. Р. 19.5, б. Определим
потенциальные коэффициенты:
an==!-In—= 65,2-10’ м/Ф;
2ле0 И
ая=А-1п^ = 90-10’ м/Ф; aI.=ari=s^ln^!=12,2-I0* м/Ф,
где Лг= 15-10~» м; Л2 = 30- 10“2м;а1а=25- 10-2м;1>1а = 49,2 Ю~2м.
427
Воспользуемся первой группой формул Максвелла:
<Pi = + wlst; (1)
+ (2)
Так как т2 —0, то <р1 = т1ап ит^ф^схц = 3,07- 10"®Кл/м. Из урав-
нения (2) найдем <ра = т1а21 = 37,45 В. Напряжение f7n=<p1—Ф2 =
= 162.55 В.
19.43р. Потенциалы точек, лежащих внутри и вне цилиндра,
Ф* =—7-~r5-£<>rcOS0t’ (1)
ьл ~г вге
r)cos“- (2)
Так как точка В находится вне цилиндра, а точка Л—внутри
его, разность потенциалов между ними
Фв—^£о(г5гг)с05а*_ ( — е ‘ £оглсозалу (3)
Подставив числовые значения в уравнение (3) и решив его
относительно Ео, получим Ео=10О0 В/м.
Напряженность поля внут-
ри цилиндра
£/=Г^-£о = 400 В/м.
19.49р. Картина электри-
ческого поля, построенная
графическим методом, приве-
дена на рис. Р.19.6. При этом
число силовых трубок т= 12,
число клеток в трубке п = 6.
Отношение ширины клетки к
ее длине b/а = 2. Емкость меж-
ду цилиндрами на 1 м длины
С = е0 btnl/(an) = 35,4 -10 ~12 Ф/м.
19.52р. Пусть z = x4~ jy—переменная на плоскости z; W =
= U 4- jV—переменная на плоскости W, Тогда
z = 2 sin 0.5W7 = 2 sin 0,5 (U 4- jV) = 2 sin 0,5(/ ch 0,5V 4-
4- /2 cos 0,5(7 sh 0,5 V.
Приравняв вещественные и мнимые части функций z и W, найдем
№ 2 sin 0,5(7 ch 0,5У; (1)
у = 2 cos 0,5(7 sh 0,5V. (2)
Возведя в квадрат и сложив уравнения (1) и (2), получим
х2 у2
4 ch2 0,5V + 4sh»0,5V
428
Возведя в квадрат уравнения (1) и (2) и вычтя из уравне-
ния (1) уравнение (2), определим
х*___________у*
4 sin4 С.51/ 4 cos2 0,51/
(4)
На плоскости г в соответствии с выражением (3) имеем семей-
ство эллипсов, в соответствии с выражением (4)—семейство гипер-
бол.
а) Ь)
Рис. Р.19.7
Полагая U потенциальной функцией, получим картину поля
гиперболических электродов (рис. Р. 19.7, я). Полагая V потенци-
альной функцией, найдем картину поля эллиптических электро-
дов (рис. Р. 19.7,6).
Рис. Р.19.8
19.58р. а) На основании метода вторичных источников соста-
вим расчетную схему рис. Р. 19.8, а. Поверхностная плотность
расчетных зарядов на плоскости S <fP>s=cr-|-aCB, где о, осв—по-
верхностные плотности свободных и связанных зарядов. Для
определения о<р> воспользуемся интегральным уравнением Фред-
429
гольма второго рода:
^(Р)___ едд ( Оц с08\ГдцН / ।
“ 2n(eeI+efl2) Js Гин
«2 9₽ F
. ле0Мл11«
dS
2?о
Искомой функцией является плотность расчетных зарядов
в точке истока off” и точке наблюдения oft”, ядром уравнения —
cos \ гинп / cos ip
2 ~2 »
'ИН 'ИН
в котором гян—расстояние между точками истока и наблюдения;
параметром — ; заданной функцией------—°н —
— е**2^^ 2е0£одн» где он—плотность свободных зарядов; ЕОпн —
нормальная составляющая напряженности внешнего поля в точке
наблюдения.
В данном случае свободных зарядов на поверхности раздела
сред нет и ои = 0. Нормальная составляющая внешнего поля,
т. е. поля, обусловленного зарядом q (рис. Р. 19.8,а),
Р ____ q cos а ___ qh
£очн— 4ле0У?- — 4.1£оЯ3 •
Так как для плоскости cos У = cos ф = cos 90°, то подынтег-
ральное выражение уравнения (1) обращается в нуль и интег-
ральное уравнение вырождается в алгебраическое. Так как при
стн = 0 осв н = <йр> и /? = Ий2 + /Л плотность связанных зарядов
в точке наблюдения
^св в
tjfl ®fll)
Связанный заряд, находящийся на поверхности круга радиу-
сом г.,
Я (&а2 ®а1)
1
Q -О. I -В» 1_ г - I # ->
б) Положив ед2 —► оо в выражениях (2) и (3), получим
qh Г. 1 1
; qs = —q 1
<^св в
Задача может быть решена также методом зеркальных изобра*
жений.
19.60р. а) Используем метод зеркальных изображений. Допол-
ним полуцилиндр до полного цилиндра. Отобразим расчетные
заряды и источник, создающий внешнее равномерное поле. ПлоТ'
430
кость отображенных зарядов равна и противоположна по знаку
Напряженность поля, обусловленная отображенным источни-
ком, £,=£0, а напряженность результирующего поля Ео + Е{ —
“2£0 (рис. Р. 19.8, б).
Определим осв на поверхности цилиндра, воспользовавшись
методом вторичных источников и интегральным уравнением (1)
решения задачи 19.59р. Преобразовав его для случая плоско-
параллельного поля, получим
оу» =—— а„—Г2е0Е0„н + - [ «8* ) Д1
ед2твв* Ва1 । еа2 L п •' гми J,
Z
Так как цилиндр не заряжен, то ая=0. Из рис. Р. 19.8,б
найдем cos(гнип) = cosip = гИ|1/(2а); dl = ad&. После подстановки
в уравнение (1) определим
°У’ = 2е<|-2Е11вн +
•ЙоГ‘Ю
О
Интеграл в правой части полученного уравнения равен нулю
вследствие симметрии в расположении положительных и отрица-
тельных зарядов на поверхности цилиндра. Интегральное урав-
нение (1) в этом случае превращается в алгебраическое. Учиты-
вая, ЧТО <\:вн = он”; £©ли = £<Jcos а> ПОЛуЧИМ
<’«. = 4e0-^=^E0cosa. (2)
При 1 — 1; ег2 = 5 осв н = 2,13 • 10-® cos а Кл/м1.
б) Воспользовавшись выражением (2), определим
<тсви = —2,13-10-ecosa Кл/м1.
в) Положив в соотношении (2) ед2—«-оо, найдем освн = 3,18х
X10-ecosot Кл/м1. Задача может быть решена также методом
разделения переменных.
19.61р. В силу осевой симметрии поля и учитывая, что 2г0<^/,
можно считать заряд распределенным вдоль оси цилиндра с плот-
ностью x(z).
Потенциал, создаваемый элементарным зарядом T(z)dz, в про-
извольной точке М.
т (г) dz
4лЕд£
Потенциал, созданный зарядом всего цилиндра,
i
1 Р т (z) dz
4л£а J Л •
о
431
Поместим точку М на поверхность цилиндра. При фм = <р0
i
__ 1 С т (г) dz
4яеа £ И го-Н*— zH)2
где zH—координата точки наблюдения; z—координата точки
истока; /? — И / о + (г— гн)2.
Уравнение (I) является уравнением Фредгольма первого рода.
Для его решения разобьем цилиндр на п равных участков. Бу-
дем считать плотность заряда каждого участка т, = const. Тогда
интеграл в уравнении (1) можно заменить суммой. Расположив
точку наблюдения в середине участка и обозначив т0 = 4леа<р01
найдем
(2)
где i—номер участка (t = l; л); j—номер точки наблюдения
(/ = 1, л). Помещая точку наблюдения на поверхность каждого
участка, можно составить п алгебраических уравнений. Записав
их в матричной форме, получим
[“J М=[1] ч-
О)
Элементы квадратной матрицы коэффициентов [а,7] рассчиты-
вают по формуле
«//= In
+ у + d- (2i-2/+l) 2
d-1)4-1 ri + I ' (2.-2,-1) 1’
zzi r l zn j
Принимая л = 6 и пользуясь выражением (4), получим мат-
рицу [а,-/], которую преобразуем с учетом равенства зарядов
та = т5, т3 = т4:
•“4,165 1,089 0,51 0,336 0,251 0,200"!
1,089 4,615 1,089 0,51 0,336 0,251
г п 0,510 1,089 4,615 1,089 0,51 0,336
0,336 0,51 1,089 4,615 1,089 0,51 ==
0,251 0,336 0,51 1,089 4,615 1,089
0,200 0,251 0,336 0,51 1,089 4,615_
г4,815 1,340 0,846 т
= 1,34 4,951 1,599 .
0,816 1,599 5,704
Решив матричное уравнение (3), определим т1 = О,153то; т3 =
= 0,122то; т3 = 0,118то. Здесь т0 = 5-10“8 Кл/м. График т = /Й
представлен на рис. Р.19.9,а.
482
Полный заряд цилиндра Q = — (тх + та + т3) = 39,3 10 10 К л,
а его емкость С = 39,3 пФ.
Закон изменения потенциала поля вне цилиндра ф = /(г) при
z = 0,3 м получим, пользуясь соотношением
Lt
п " .
I у* С
J Ггг+(0.3-гГ
где г, z—в м.
График <р = /(г) приведен на рис. Р. 19.9, б.
Глава двадцатая
20.3 р. Разность потенциалов связана с напряженностью элек-
трического поля соотношением
2
Фх— ф„= С Е dr = E^ 2л г = 4г Ег.
J 4 2
1
Учитывая это соотношение, а также используя закон Ома
в дифференциальной форме, выразим модуль плотности тока че-
рез разность потенциалов: 6 — 2у <Flj~^2 • Очевидно, что 6 = 6тах
при r — rlt т. е. 6тах = 2у(ф1 — ф2)/(Зп'Г]). Следовательно, раз-
ность потенциалов фг—ф2 = Злт*! • 6тах/(2у) = 0,0235 В.
20.10 р. Плотность тока утечки в функции расстояния от цен-
тра сферического конденсатора
6 = //(4лЯ2). (1)
Напряжение между электродами
«8 ' R, , ч
и = \EdR = [-dR = -'-( 2------11 (2)
433
Из соотношений (1) и (2) получим
6=-tjl_=д/м..
кг(ъ~ъ) Rt
При R = Ri 6 = 6max = 0,25-10 4 А/м®. Максимальные удельные
тепловые потери ртах — бтах/? = 6,25 В т/м'4. Ток утечки / ==
Рис. Р.20.1
==4n/?®6max = 12,56-10-« А.
20.16р. Применим метод зеркальных изображе-
ний. Дополним электрод его зеркальным изобра-
жением, расположенным над поверхностью земли
(рис. Р.20.1). Воспользуемся аналогией с электро-
статическим полем. При этом приближенно при-
мем линейную плотность заряда цилиндра т —
= const. Найдем емкость цилиндра длиной 21 и
диаметром d, который может рассматриваться
как эллипсоид вращения. Потенциал произволь-
ной точки Р с координатами b и а от элемен-
тарного заряда Tdx, расположенного на расстоянии
г от начала координат, dtp = т dx/(4near), где r = Va*-V(b—х)2.
Полный потенциал точки р, определяемой всем заряженным
цилиндром,
+t _________
___r_f dx Q 1п М-/+Кв®-НН-0*
4лед —л)2 8леа b—I +a® -f- (ft—/)® ’
где t = Q/(2Z).
Потенциал на поверхности провода в его середине (при 6=0;
a = d/2) по отношению к бесконечно удаленной точке
При tp = U ж 1п • Емкость цилиндра С —
~ Tn (7//dj * Проводимость электрода и его зеркального изображе-
ния G= Проводимость заземления Go = - Сопро-
тивление заземления R0=l/G0 = 36,6 Ом.
20.19 р. Для расчета поля в среде с удельной проводимостью
воспользуемся схемой рис. Р. 20.2, а. Пренебрегаем взаимным
влиянием шаров и сдвигом электрических центров относительно
геометрических. Расчетный ток, стекающий со второго электрода
в грунт, /2 = Vi> где ^«=(7!—yJ/tVi+vJ; 0<6i<l. Потен-
циал произвольной точки М.
т _ А 1 .
Ч’А! 4Лу! R *Т
Zjfei 1 .
4лтх (2а —Я)
434
Так как Ct = 0, то для области /?0 < /? < а получим
Л / 1 , kj
4n*yj \ R "J” 2a — R
Для расчета поля' в среде с удельной проводимостью у3 исполь-
зуем схему рис. Р.20.2, б. Расчетный ток /8 = Л2/А, где —
Рис. Р.20.2
= 2Т2/(Т1 + Тг); о < Л2 < 1. При а < /? < оо
_ Vi 1
4л?2 R
20.21 р. Так как плотность тока утечки 6 =//(4л/?2), то на-
пряженность электрического поля Е = //?/(4л/?2у0).
Потенциал между электродами изменяется по закону <р =
= 1П-Б- + С.
4лу0 R 1
Постоянную интегрирования С найдем из условия ф = 0 при
4луо
Закон изменения потенциала между электродами имеет вид
/ 1*1 icnt 5-10-*
<Р = 159 In —5—
т 4лу0 R R
J R
Напряжение между электродами £7 = -^-In-^ —256 В. Полная
проводимость утечки G = //// = 7,82 • 10-4 См.
20.25 р. Выражая напряженность электрического поля через
ток утечки, найдем
£ — С = 7 (И
Т 2лг1уг (2— kry ''
Напряжение между электродами
U = ТТ— 'ПЧ9~»Ы- (2)
4л/у1 д(2—-Л&) ' 7
435
Решив уравнение (2) относительно тока, определим
1----Ж^-=’-1310” А- (3)
Ina(2— kb)
Закон распределения плотности тока:
? Л» Л / Л 1800-10-® *. . ...
6 = г°о — г° к—= г°-----А/см2. (4)
2nrl г ' '
Закон изменения напряженности электрического полях
Закон распределения объемного заряда:
р = div еаЁ = га div Е + Е grad ед. (6)
В данном случае имеем зависимость Е и еа только от коорди-
наты г, поэтому
di vF = — {гЕг) = г(2—0,1г)2;
grad еа = г° — == г°0,5еЛ. (8)
Из выражений (6), (7) и (8) окончательно найдем
_ 3,18.10-®
Р~г(2—0,1г)'
(9)
Глава двадцать первая
21.3р. Магнитное поле внутри и вне цилиндрического про-
вода может быть рассчитано
Рис. Р.21.1
путем наложения двух полей: поля
тока плотностью 6, протекаю-
щего вдоль монолитного цилинд-
рического провода радиусом а
(напряженность И J, и поля то-
ка той же плотности, протекаю-
щего в противоположном направ-
лении вдоль цилиндра радиу-
сом b (напряженность Н2).
Напряженность магнитного
поля в произвольной точке О,
расположенной внутри цилиндрического отверстия,
Но= Hw + 2Яг0 = 4 [?£-?,)],
где Я1О= -[6 Tj/2; Hw=\6 Tj/2.
436
Так как гх—ra^d—j^d (рис. Р.21.1, а),то H = ^[k(—7)d] —
₽ i -H- = t25-102 А/м. Напряженности полей в точке А:
л»
Я1Л = —7^= —125-10* А/м;
Ал = 1тг-^—= 7^^- = 7з,13 1О= А/м,
где г1Л, гаЛ—расстояния от точки А до оси первого и второго
цилиндров. Таким образом, НА = Я1Л ~Ь HiA — —/21,87 • 102 А/м.
Модули напряженностей полей в точке В:
= К/м-,
йв = ^=1.5Ы0’ А/м,
где г1Я и rz3—расстояния от точки В до оси первого и второго
цилиндров.
В векторной форме
Н1В—— /25- 10х А/м;
H2B = iHlBsma + ///a5cosa = (Л,51 sin 14,5° +
Ч- /1,51 cos 14,5°) 102 = (Ю,377 + /l,46) 102 А/м.
Окончательно получим Нв = Н1В 4- HtB — (— /23,54 4- /0,377) х
Х102 А/м.
21.9р. По закону Био—Савара—Лапласа, напряженность
магнитного поля в точке О (рис. Р.21.1, б), обусловленная током
в отрезке провода pqt
= <cos ai—cosai) =
/ cos <Х1
2ла sin *
где cos «j = — cosct2; h~ asinc^.
Из треугольника pqO найдем at=n/2—0/2 = n/2—л/п, так как
P — 2n/n.
Напряженность магнитного поля в точке О, обусловленная то-
ком в рамке,
1 Z л л '\
Inw COS -х--------------------I
Яо=9 -,-/я я\=-2^-^7=143-6 A/M‘
2juj sin I -pr-
\ 2 n /
21.13р. Магнитное напряжение между точками М и N по
пути MLN, обусловленное током левого провода (рис. Р.21.2, с),
C/M1/IiV = /a/360°, где a =18,5°.
Магнитное напряжение между точками М и N по пути MkNt
обусловленное током правого провода, ^/и2Л1.. = — /6/360°, где
0 = 45°.
437
Магнитное напряжение между точками М и N
~ ^ulMN "Г ^мгЛШ ~ 360J (® Р) 2,6о А.
Магнитное напряжение между точками М и Р (рис. Р.21.2, б)
Мцмр — 4- ~ з5о<5 (Pi ai) ~ 12,5 А,
где рг = 243,5°; ах= 116,5°.
21.15р. Так как В—rot А, то модуль вектора магнитной ин-
дукции внутри и вне провода найдем из выражений
Bi = 8Ш = rota А, = — дАп!дг = 12,56г;
B, = Bsa = rotaA2 = —^=25,1 • 10-'l.
Определим модуль напряженности магнитного поля внутри и вне
провода:
/71 = В1/ра1 = 2-105г А/м; (1)
^2 = В2/М<й = 20/ А/м. (2)
Пользуясь выражениями (1) и (2), строим график зависимости
(рис. Р.21.3,а).
438
Так как индукция В — р1)(Н+ J), то модуль вектора намагни-
ченности внутри и вне провода
/1 = ^0—Ях = 9,8- 10V А/м; (3)
J2 = 0. (4)
По уравнениям (3) и (4) строим график зависимости J = f(r)
(рис. Р.21.3, а).
21.17р. Проинтегрировав уравнения Пуассона и Лапласа для
векторного магнитного потенциала и определив постоянные ин-
тегрирования, найдем проекции векторного магнитного потенциала
на ось z внутри и вне шины:
А = —роЛ2/2; Л = — рс26ш/+ °Дха1),
где и рса—абсолютные магнитные проницаемости стали и воз-
духа. Разность векторных магнитных потенциалов между точ-
ками тип
k(Am-A„) = k &фл—
Из этого уравнения определим плотность тока: 6=2,21 • 1(? А/м2.
Ток, протекающий вдоль шины, / = 2ай6 = 3,53 А.
21.25р. Воспользуемся методом зеркальных изображений. Най-
дем расчетный ток /4 (рис. Р.21.3, б):
/ _ / Мг2—Им
а ’Мгй-Рн
=/х=/.
В силу симметрии поля в точке а напряженность На = 0. Напря-
женность магнитного поля в точке b — где
Нх = —/ 2лх^~— А/м; Я, = t//2cosa — jH2sina = ix
x 2n(4’+№0 ----«72—7114 А/м. Окончательно
получим = Hi — iYTZ—/432 А/м.
21.35р. Наивыгоднейшим является случай расположения щели
вдоль силовых линий.
Модуль напряженности магнитного поля внутри сферического
экрана
где ра—абсолютная магнитная проницаемость стали. Сечение
рамки S = л£)2/4 = 28,2« 10“‘ м*. Потокосцепление рамки ф =
= 1,2-10“* Вб.
Отклонение луча баллистического гальванометра при переклю-
чении тока в обмотке возбуждения электромагнита с Н-/ на —/
ct=2ф/Сф = 133M21.
439
21.37р. По закону полного тока, I=(ptHdl. Произведя обход
вдоль замкнутого контура вокруг каждого из токов и используя
значения скалярных магнитных потенциалов, получим: /х = 2-25
= 50 А; /, = 2-5=10 А; /а = 2(25—5) = 40 А. Ток /, направлен
«от нас», токи /2 и /8 направлены «к нам».
Определим магнитную индукцию в точке А, пользуясь карти-
ной поля. Напряженность магнитного поля // = — grad фм; НА
«Дфи/Дл. По картине поля найдем Дфы = 2 А; Дп = 0,225 м;
ВА — pQHA = 111-10~* Тл. Определим магнитную индукцию в точ-
ке А, пользуясь законом полного тока (рис. Р.21.3, в): ВА — В14-
+ где В,=р,^= 110,5-10-’ Тл; Вг=р.^-=в8,4Х
ХЮ*7 Тл; В3 = ц„^ = 26,6-10-’ Тл.
Глава двадцать вторая
22.6р. ЭДС, наводимая переменным магнитным полем в дви-
жущейся рамке, е = ех + е2, где ег — ЭДС, обусловленная измене-
нием магнитного поля во
времени; е2—ЭДС, обус-
ловленная движением рам-
ки.
Применяя закон элект-
ромагнитной индукции,
найдем ех. Напряженность
магнитного поля определим
по закону полного тока:
Н = //2л(х4- а).
Магнитный поток, про-
низывающий рамку,
Ф= С i^Hbdx=^
(а+*)
ЭДС, наводимая в рамке,
‘0Ф и0/„,соЬ . а+сЧ-х .
е = —дГ=In~s+r-cos
ЭДС, обусловленная движением рамки,
е,= $ [t5]d/ = vB16—vB.6=&^ I —Ь-
ж J L 4 1 2 2л |_а~г*
sin со/,
где В1 = р01/[2л(а-Ьх)] — индукция в левой стороне рамки; В2==
— — индукция в правой стороне рамки; / = х/и. Окон-
440
чательно получим е = — Г со In £±£i* cos ю А—v ( —1-
J 2л [ a+* v \ a-|-x
----* . sinco—l . При x—20 см ЭДС e = 6,32 10“e B.
22.8p. Плотность тока
6=z°—/-^r =?Ч0Б А/м2.
По закону Ома в дифференциальной форме, напряженность элек-
трического поля
A = z0Er = z®- = z0-210-s В/м.
По закону полного тока, напряженность магнитного поля на
внешней поверхности
Н == а°Яа = а0 = а°750 А/м.
Нормальная составляющая вектора Пойнтинга (рис. Р.22.1, а)
Пп = — г° Пг = [z°£r• а°Яа] = — г° • 15 Вт/ма.
Тангенс угла <р tg <p = nt/n„= 1,5-102/15= 10, откуда <р = 84°30'.
а) В области 0 < г < rt £=0, Н = 0 и, следовательно, П = 0.
б) В области гг < г < г3
Е = Et = гйЕг = z°6/y; Н=а*На = а0—
Вектор Пойнтинга
8»И-гЭ 10» (.Г»—0,01*) Вт/м,_
в) В области < г < оо
£-/«£,=5* =-4-;
г 2лг£о
Я = а»Я<х=а»51-; П = г°Пг = г” ^4-= ? А-
Для точек, лежащих на внешней поверхности провода, известно,
что П, = П2 = 1,5-102 Вт/м8. Следовательно, постоянную k получим
из уравнения 2а,^0л = 1.5-102, откуда k = 6-10“2 Вт. Таким обра-
зом, вектор Пойнтинга П = г°^^— Вт/м2. График зависимости
модуля вектора Пойнтинга от координаты показан на рис. Р.22.1, б.
Глава двадцать третья
23.3р. Комплекс действующего значения модуля вектора Пойн-
тинга на поверхности плиты
441
где
(|)
Й, = £,/£.; (2)
Za ==Ира<о/уе'«в=8,85- Ю-Ч^Ом. (3)
Подставив числовые значения в выражения (1)—(3), получим
П = = 1130е'«* Вт/м1.
Комплекс действующего значения модуля вектора Пойнтннга
на глубине лс = 0,5 см
Па = = 1130е~ si*-o.oo5e/45° Вт/м»,
где k — Ирвусо/2 = 314 м-1.
Активная мощность, поглощаемая слоем металла толщиной
0,5 мм и площадью s = 1 ма,
Р = (П,—П2) s cos 45° = Пх (1 — е-2^) s cos 45° == 762 Вт.
Глубина проникновения электромагнитной волны в металл
h = 1/Л = 3,18-10“3 м.
Длина волны 1 = 2л/£ = 2 10“* м.
23.5р. Среднее значение магнитной индукции по сечению шины
Д.„ = H-W.thpa =5,06-Тл,
с₽ ра
где р — ИPaW e/4S“ = 1780е/45° м-1; th ра = 0,895- е/31*.
Действующее значение магнитного потока
Ф = Вср2ah = 25,3- 10~8е'31° Вб.
Плотность вихревых токов распределяется по сечению шины
в соответствии с законом
б= pH,4s-. (!)
r а ch ра
О
0,25
0,5
Таблица Р.23.1
z, мм 6-104, А/м2
0
1,44е'“5°
3,18е'121*
442
Подставим числовые значения в выражение (1) и результаты
расчетов, проведенных для различных значений z, запишем
в табл. Р.23.1.
По данным таблицы строим зависимость модуля действующих
значений плотности вихревых токов в функции координаты
(рис. Р.23.1, а).
23.9р. Плотность тока по сечению провода, расположенного
в пазу ротора электрической машины, меняется по закону
Ь = рН0
ch р (д— г)
sh ра *
(1)
а напряженность магнитного поля—по закону
Й = shP<°-;). (2)
° sh ра ' '
Здесь H — ijh—напряженность магнитного поля в точках пло-
скости г = 0.
Значения
вычислим по
аргументов
гиперболических функций комплексных
формулам
sh рх = sh kx cos kx 4- / ch kx sin kx;
ch px = ch kx cos kx 4- / sh kx sin kxt
где х — а~ z; p = k = \p (W2.
Для нашего случая р— 149е'4Б° м~х; k =105 м'1.
Подставляя числовые данные в выражения (1) и (21, опреде-
лим б и Н для различных значений координаты z. Результаты
вычислений сведены в табл. Р.23.2.
Таблица Р.23.2
г-10-8, м Н-10*. А/м 6-10*. А/мг
0 е-/зо° 149е'*6в
1 0,373е~'86’ 49е~Л1°зС'
2 0 Зб.бе-'10’0
По данным таблицы строим графики и =
(рис. Р.23.1, б).
Комплекс сопротивления провода, расположенного в пазу ротора
электрической машины, на 1 м его длины
z=/?+jX-p._L_.
4 -у ft th ра
В нашем случае thpa«l; Z= 13,3-10“V45’ Ом/м.
Активное сопротивление провода R =9,36-10~4 Ом/м. Внутрен-
нее индуктивное сопротивление Хвн — 9,36-10"*1 Ом/м. Сопротив-
ление данного провода при постоянном токе = l/(yS) =
s=4,47-10_| Ом/м.
443
23.13р. Плотность тока на поверхности цилиндрического про-
вода
2nr0Ji (дг0)*
(1)
где J0(qr0)—функция Бесселя первого рода нулевого порядка;
^1(^0)—функция Бесселя первого рода первого порядка. В на-
шем случае
q = К—)2л50-4л10-’- 10г 2- 10е = 282е-'«а м'1.
Аргумент функций является комплексным (qrc~ 1,41 К—/);
следовательно, и функции являются комплексными. Пользуясь
таблицами функций Бесселя, найдем модули и аргументы функ-
ций Бесселя; /0(<?г0) = l,05e/a,e; Jt(qr^ = 0,7е_/31<>.
Подставив числовые значения в уравнение (1) и решив его
относительно /, получим / — 74,5е_ /1а’ А/м.
По закону полного тока, напряженность магнитного поля на
поверхности провода /?го=//(2лго) = 2380е/1ав А/м. Модуль вектора
Пойнтинга на поверхности провода
П,о = £,Д. = Нп = 1190е'13° А/м.
Потери мощности в проводе на 1 м его длины
Р =ЯеП,02яг01 = Re 1190е'13в2л5-10~3 = 36,6 Вт/м.
23.16р. Получим соотношения, характеризующие магнитный
поверхностный эффект в цилиндре бесконечной длины. Из ура в-
нений
rotH = v£;
4 ’ U)
rot Е — — j
найдем
Wi + q'H = 0, (2)
где д =
Так как Я = уравнение (2) запишем в виде
££/ dH\
г dr v /
После преобразований получим уравнение Бесселя!
, 1 dti , „ п
dW^qr d(qr)' n-V-
(3)
Его решение!
(4)
444
Так как ЛГ0(0) = оо, а напряженность магнитного поля на оси
цилиндра /7а=#=оо, то постоянную интегрирования В принимаем
равной 0.
Определим постоянную интегрирования А. Пусть На—напря-
женность магнитного поля на поверхности цилиндра. Тогда при
г~а напряженность На — AJo(qa). Следовательно,
А = (?“)] (5)
Из уравнений (4) и (5) найдем
Н = //„Ж (6)
Напряженность электрического поля
E«=-!-rotH =—а»- (7)
у у дг у ° Jo (qa) v '
Так как ^Edl =— /<оФ, то после преобразований получим
ф = = 2ЭТ°Нд‘/1 М ft
—/Ъ) qJfAqa) °* * '
Из уравнения (6) и (8) определим
в= Р..Н = (7\. (9)
“а 2лаJj ' г
Среднее значение магнитной индукции
В ___а (*7°). /1П1
о<*“лаа — qaJ^qa) ' ' }
Относительная комплексная магнитная проницаемость
^сР fyvAfaa)
(II)
В нашем случае да = 8,85е“/45<>; Jo(ga)=73,O5/33’°; Л(фО —
= 70,2e'S60°. Из уравнения (11) вычислим рг = 2,2е^3’. Подставляя
числовые значения в выражение (9), найдем за-
кон распределения магнитной индукции в функ-
ции расстояния от оси цилиндра. График B — f(r)
приведен на рис. Р.23.2.
23.19р. Запишем первое и второе уравне-
ния Максвелла для плоской волны, распрост-
раняющейся в проводящей среде (рис. Р.23.3, а):
ан, р
&
дЕх „..
дг ~^а~дГ'
Пользуясь операторным методом
(1)
(2)
и учитывая, что в данном
445
случае £ = ЕХ, Н~Ни> найдем
_^ = V£(p); (3)
-^ = И»рН(р). (4)
После преобразований получим
^ = WopH(p). (5)
Решением уравнения (5) являются
Я(р) = Сгег4-Сге-^ (6)
где v = V урвр.
Изображение напряженности электрического поля
Я(р)=>|(С2е-”-Схе'г*). (7)
Волновое сопротивление в операторной форме
Z(p) = v/p = K цар/у.
Из-за отсутствия отраженной волны С^О. При z = 0 Н (t)=Hc
и Н (р) = Hjpt поэтому C2^~Hjp. Тогда изображения напряжен-
но
Рис. р.23.3
ностей магнитного и электрического полей получим в следующем
виде:
Н(р) = !^ e-v р 2 ;
£(/,) = 1Z£s.J^.f.-v^tV:^
(8)
(9)
446
Пользуясь таблицами соответствия, по выражениям (8) и (9)
найдем оригиналы:
Я(О = НоГ1-Ф
(10)
(11)
-- и WaZ*
^-Я=е" “ .
Т У nt
где Ф(j —функции вероятности ошибок.
23.21р. Воспользуемся выражениями (6) и (7) решения зада-
чи 23.19р. Постоянные интегрирования найдем из граничных усло-
вий. При z = а
= Яв(р) = //(2М,
при 2 —— а
После преобразований получим выражения для изображений
напряженностей магнитного и электрического полей:
Н(р}- ' . /]}
По таблицам соответствия определим оригиналы:
® п*п*
г 2 V (—1)" - / ллг \ •
---— 7 J -—— sin ------} е °
а п П \ а J
л= I
®----------------------л,яж
1 , 2 V1 Z пт t
—— X (—l)"cos----------е а
уа 1 уа v 1 а
(3)
(4)
Из выражений (3) и (4) следует, что при / = оо, т. е. в уста-
новившемся режиме, напряженность магнитного поля меняется по
сечению шины согласно закону Н (г) = а напряженность
электрического поля остается постоянной: Е (t) == l/(2hay).
Таблица Р.23.3
с Н (О. А/м, при 2=а
2=0 2=0.Sa 1 2=0.75а
1 0 0,005 0.22 1
2 0 0,033 0.344 1
10 0 0,339 0.634 1
50 0 0,499 0,676 1
00 0 0.5 0,75 1
Подставив в выражения (3) и (4) числовые значения, вычислим
Н и Е в заданных точках сечения шины в различные моменты
времени. Результаты подсчетов сведены в табл. Р.23.3.
На основании данных таблицы построены графики рис.
Р.23.3, б.
Глава двадцать четвертая
24.5р. Комплексная диэлектрическая проницаемость морской
воды
ёо = е,е,-/ ^ = (0.708-/ • I) 10-« Ф/м.
Коэффициент распространения
р= a+//f=l 8,07+J 34,85 м'1.
Напряженность электрического поля на глубине Zi = 0,l м
= В/м.
Напряженность электрического поля на поверхности
Р--------£1ГП _ = 60 97 е71вв,т° В/м
где ₽Z!= 199,7°.
Волновое сопротивление
ZB = ^ЙХ"=32,02 Ом.
Напряженность магнитного поля на поверхности
^о» = Дя./^в=1.9е/1«’«с А/м.
(ДО> VflV в • •
Мгновенное значение вектора Пойнтинга на поверхности
Я,(О«£.(0» Но(0 = 51,56—58,04 cos (2ю<—47,3°) Вт/м«.
24.7р. Так как, по условию задачи, волна полностью прохо-
дит в стекло, то поляризация волны должна быть параллельной
и угол падения равен углу Брюстера: <р=<рБр« Из соотношения
% Фбр =* Vнаходим диэлектрическую проницаемость стекла:
ег2 = 4. Волновое сопротивление стекла ZB2 = Kp-a/Cj = ZB1/2 —
= 188,5 Ом. При полном прохождении электромагнитное поле в
воздухе содержит только падающую волну и не содержит отра-
женной. При этом Н2 — Нх. Вектор Пойнтинга в стекле ПаИ ==
= П2, =£i/ZBi = £;/4Z,, = l,3110-i Вт/м2.
При повороте плоскости поляризации на 90° (перпендикуляр-
ная поляризация) коэффициент прохождения
—, 2 sin 9 cos о п А
т^=-5мёТ^-^0’4’
где в — arc sin (Кerl/tr2 sin ф) — 26°35'.
448
В этом случае на основании граничных условий =
= Е* -\~E~ = Eit где£*\ Е", Еп—напряженности электрического по-
ля падающей, отраженной и прошедшей волн соответственно. Напря-
женность поля в стекле £, — EtT^ = 4 мВ/м, вектор Пойнгинга
П,хE2/ZB2 = O,819-10’’ Вт/м2.
Так как коэффициенты затухания в обеих средах равны нулю,
то коэффициенты распространения
?! = /Р1 = /Ь> I %1Р-Д1 = /2 м~3,
Та = А = /“ И Wei = /4 и’1-
Волновой вектор падающей волны
К — (i° sin <f 4 2® cos <р) /pt = Гjl ,79 4- z°/0,894 м-1.
Волновой вектор прошедшей волны
Кsin 6 2® cos б) /Р2 =u /1,79 4- 2°/3,58 м’1.
24.11р. При sin© = 1 sin<р = sin q?Kp = k £ri/erl. Следовательно,
критический угол полного внутреннего отражения фкр =
= arcsin Иег2,ег1 = 41°30'. По условию, угол падения <р > <ркр.
Поэтому 0—комплексное число. При этом sin 0 = Vtrftn s,n * Я
0 в= л/2 + /0. Используя соотношения sin 6 = sin (л/2 4- /0) = ch 0 и
cos 0 — cos (л/2 4- 0) = —/ sh 0, найдем коэффициенты прохождения
и отражения:
Tj.=-=----2Z,iC°:*1’ u = 1.6 е'8*'*»'.
-1- ZB2cosq> —/ZB1 sh 0 *
Г> _ ^В2 COS ф4~ jZB1 sh 0 __ j р/73°2С'
1 ZBS cos ф— /Z„1 sh 0
Мгновенное значение вектора напряженности электрического
поля поверхностной волны
Еп(.т, 2, 0 = /E^e-cusin(w/~Px).
Амплитуда напряженности поля поверхностной волны Е„ —
2л ‘
Коэффициент затухания а =-г—У sin2 ф— №, где К,—
А1
— c/f Ие,!*» № = Коэффициент фазы р = sin <р. Подставив
AJ
числовые значения в выражение (1), получим
Еп(х, 2, 0 = /8-10~3е”1е,вг51П(2л10^—35,6л)В/м.
Определим фазовые скорости:
^Фп =«/р^ 1,76-108 м/с; =с,'У ег1 = 1,41 10s м/с;
Иф2 = спУег8 — 2,12-10* м/с.
Следовательно, иф1 < офп < ифз.
449
24.16р. а) Составим граф. Падающая волна Е *• попадает в узел /
(рис. Р.24.1, с)*. Передача ветви g= 1. Узел 1 соответствует
точкам, лежащим на поверхности раздела сред. Волна частично
отражается от поверхности, сигнал, соответствующий отраженной
волне, попадает в узел 2, Передача ветви равна /?й. Кроме того,
сигнал из узла 1 проходит в узел 3, что соответствует прохож-
Рис. Р.24.2
дению волны из первой среды во вторую. Передача ветви Т21.
Полученный граф имеет один исток и два стока. Сигнал истока
£+. Найдем сигналы стоков:
= £" = ти£+.
Определим передачи ветвей:
Я„ = фЦ-Ы. -=о,217 у 2г-» - = 0,81
б) Составленный граф изображен на рис. Р.24 Л, 6. Найдем
передачи ветвей графа:
Яя=----₽и-0,217е-/«'; Тц= = l^-W.
^В1 I ^Вй
24Л7р. Граф (рис. Р.24.2) составляют аналогично графам за-
дачи 24.16р. Коэффициент радиопрозрачности Т «= G7l = Еп/Ёт <
где СТ1—передача графа от узла / к узлу 7, которую находим,
применяя формулу Мезона:
с=2рд/д. 0)
1* = А
В данном случае п— 1; Pi = T21T32e^d; Дх= I; Д=1 — /?2tX
X/?23e-2vd. Пользуясь формулой (1), получим
гр /9)
Коэффициент отражения пластины /? = б21~ Е~/£+, где G2I—пе-
редача графа от узла / к узлу 2. Учитывая, что в этом случае
п = 2; ₽, = «„; &!=!—P,=TaTaR^t-^; Д,= И
* Номера узлов даны в кружках.
450
A — 1—#2iR23e 2V<?, в соответствии с формулой (1) определим
р______________4 7'2i7'ia/?32e^8v<*
1-RnRi#-™ ‘ W
Так как вл3 = еи, то из выражения (2) имеем
_ __ Т^Тне-У*1 /л\
1 • V*/
Используя соотношения (3) и (4), получим
/? = /?„ 4 Т/?ие-^. (5)
Вычислим передачи ветвей графа:
21гГТ 2
Ти = 1,26; Та=-==-=0,73;
У ега 4-1 У сгз4“ 1
Ra-----/?Ц=^Е~‘=0,268.
V £Г2 Т 1
Коэффициент распространения волны в диэлектрике
V = / /ё^= /1,36 103 м1.
£
После подстановки числовых значений в выражения (4) и (5)
найдем Т = 0,92е-уз07°; /? = 0,4е^мз°.
Эта задача может быть решена также аналогично расчету7 це-
пей с распределенными параметрами.
24.25р. Воспользуемся решением задачи для электростатиче-
ского поля. Учтем, что в квазистатическом электрическом поле
потенциал и напряженность поля являются функциями коорди-
нат и времени:
<рД0 = Л (/) Я cos 0; (I)
Ф<(П=[-£(0« + 4т1]с<1!’в- <2>
Постоянные интегрирования А (0 и В (0 найдем, используя
граничные условия в квазистатическом электрическом поле. Гра-
ничные условия запишем, применяя операторный адетод. При
R = a
ф,(р)=ч><(р); (3)
(V, + Е«.Р) (Р) = (V. + е«р) (Р)- W
Подставив в уравнение (4) выражения для изображений ра-
диальных составляющих напряженности поля в первой и второй
средах [Ед. (р) и ЕдДс)] и учтя, что Е(р) = Е0/р, получим
р (п\ fl3£o [(Vi 4~cgrP) (Ye4~eaeP)} /г\
p[2(Te + e0rf)4-(w4-^)J ’ * '
пользуясь формулой разложения, определим
SVi+Tj
в (/) - aSE‘ S+аЗЕ' е’ ' • <6)
451
Постоянная интегрирования
Л(/) = -Е(, + -^-. (7)
Подставляя постоянные интегрирования в выражения (1)И (2),
окончательно получим
ФДЯ, в, 0 =
есе_
2вае-|-ев/
фе(К, 9, 0==ЕО
VI—Те
гте+У/
а3 / £af — Еде Yi —Те
У/—Те X ~
2Уе + Ъ'Г
_ О t °Э Т>~
* - /?г2Те-ЬТ(-
2Ve+V/ ‘
_^е 2£ae^oi
COS0.
R cos 9; (8)
(9)
Постоянная ф0 принята равной нулю*
Глава двадцать пятая
25.3р. Скалярный электродинамический потенциал связан с
векторным потенциалом выражением div А= —^2-. В комплекс-
ной форме
di v А = — /цхрт/&*. (1)
Векторный потенциал от элемента
тока в точках, удаленных на расстоя-
ние /?,
j mR
i _ Ho fa u dl
* 4л R
Воспользуемся сферической системой
координат. Тогда векторный потенциал
может быть разложен на две
ляющие (рис. Р.25.1):
/л = ДМл4-0Мо,
(2)
состав'
(3)
где
Л0 = —4Msin0;
^ = Afflcos0*
(4)
(5)
В данном случае
div — № ж (Я2ЛЛ) + я sin е (sin 0 Л о).
(6)
Из выражений (4)—(6) получим
1 X
Ri)
-<i>R
tTl v
V
452
е i v~
Используя выражение (1), найдем скалярный электродинами-
ческий потенциал:
• = cosed/ / О у*
'*т 4л \ R ' /7?2ю
Для точки с координатами Rx и 0Д
’ pn//flCos6id/ (у v \
= v ’
25.7р. 1. Сопротивление излучения для излучающего диполя
2л /2
р__ 7 __
А 3 в X2 *
(1)
В выражении (1) длина излучающего диполя состоит из длины
антенны и длины ее зеркального изображения, т. е. / = 2/п Сопро-
тивление же антенны равно половине сопротивления излучающего
диполя:
р __ R _ 1 2п
«ант- 2^23
2_ 4л у hi
” 3 Zb Ла *
(2)
Длина волны X1 = v/fJ = 300 м.
Подставив числовые значения в выражение (2), найдем сопро-
тивление излучения: —Яант —7 Ом. _____
Мощность излучения Ps— PRs- Отсюда 1 = }^PS/Rs = 25 А.
2. Мощность излучения Psz=J*~^-Z3 = • Следователь-
но, для одной и той же мощности Ps длина антенны и длина
волны связаны уравнением Л2 Лр = Для частоты /2=10 мГц
длина волны Х2 = 30 м, длина антенны hz=hl~--^ 2 м.
Глава двадцать шестая
26.1 р. Для возбуждения волны типа Н10 следует электрический
излучатель (штырь) расположить в середине широкой стороны
сечения (а), напротив его вдоль оси у. Петлю (магнитный излу-
чатель) помещают в середине узкой стороны (Ь) так, чтобы ее
плоскость была параллельна плоскости хоу. Критическая длина
ЬОЛНЫ
2
V <т,а)*±(п/Ь)* ’
Учитывая, что для волны 7/10 т—\, а л = 0, получим Хкр10 =
— 2а =17,28 см. Длина волнц в свободном пространстве X = c/f =
= 10 см, где с—скорость света.
Длина волны в волноводе
Х, = - К =г= 12,25 см.
453
Мощность, передаваемая поперечной электрической волной вдоль
волновода,
р _ 7 ( 2ур V Н2 (п
г — 8 Лвт£ Лв / 1т' ' '
Волновое сопротивление для поперечной электрической волны
Z = т/ -На. —=462 Ом.
"гг У У I-
Пользуясь соотношением (1), найдем Р=ЗЬ5 Вт.
Групповая скорость
VrP ~с К1 —(л/лкр)2 = 2,45-1010 см/с.
Фазовая скорость
о* = г с. .=- = 3,68-1010 см/с.
* /i-(Z/ZKp)2
За один период колебаний энергия переместится на расстоя-
ние, равное энергетической длине волны Хэ =vrp/f=с2/лв = 8,15 см.
Глава двадцать седьмая
27.2р. Считаем поле Е между каждой парой сеток однород-
ным. На рис. Р.27.1,а—г показаны графики потенциалов <р(х),
поля Е(х) =— <?ф/дх, сил F(x)=qE(x) и скоростей с(/) =
t t
Рис. Р.27.1
ствие поля сеток равно нулю).
д < 0 средняя скорость больше.
Отрицательно заряженная
частица преодолеет потен-
циальный барьер при лю-
бой начальной скорости
с0 > 0, положительно за-
ряженная частица—толь-
ко при
9
— >ФР1. (П
Это выражение следует
из закона сохранения
тх2 , mvo
энергии — + 4/<р = -тр•
Если условие (1) выпол-
няется, то на выходе сис-
темы частица независимо
от знака заряда имеет та-
кую же скорость, что и на
входе (суммарное воздей-
Время пролета / = 2d/ucp. При
чем прид>0. (рис. Р.27.1, г).
454
Поэтому время пролета отрицательно заряженной частицы всегда
меньше, чем положительной. Для данного случая -------2d ,
27.8р. Полная энергия частицы в
любой точке траектории (по закону
сохранения энергии)
mv- t . mu*
так как при x=0 <р(0) = 0. По усло-
вию, № < до (± Ь), поэтому частица
совершает в «потенциальной яме» (рис.
Р.27.2) гармонические колебания с пе- Рис. Р.27.2
риодом
T=/2zn Г
-*1
dx
К UZ—
1
2 / 2zzz, (a<?) J =
b F
I
= 2 V 2ni/(aq) arcsinz | = л И 2m, (aq).
о
Движение вдоль оси x неустойчиво. Любое отклонение вдоль
оси у будет нарастать.
27.9р. В центрально-симметричном поле потенциал Ф^^^г.
Скорость о является функцией расстояния между зарядами г и
угла поворота 0:
Использовав законы сохранения момента количества движе-
ния М и полной энергии получим
М =mrs-^ = const; (1)
ТГ — mt’e । _ т 17 dr V _U 1 J^1?2 /9Ч
w~ 2 • 2 “ 2 |Д dl ) "t'm2r2J'r г * W
Исключив из выражений (1) и (2) время найдем
<Ю =-------d' —
г2 1/ 2т w 2™Мг 1
V М3 г
После интегрирования
6=0О 4- arccos — (----
е \ г р
или у = 14- е cos (0—0О) — уравнение конического сечения, где
2UZ/W2
1 4---^-г—эксцентриситет; 0О—произвольная постоянная
455
интегрирования, связанная с начальным положением частицы;
p = Mi/(mqlq2)—параметр конического сечения.
а) Если заряды qt и q2 имеют разные знаки, то W < 0 и дви-
жение происходит по эллипсу.
б) Если заряды qt и qz одного знака, то W > 0 и движение
происходит по гиперболе.
27.11р. 1. Заряженные частицы в однородном магнитном поле
движутся по окружностям (рис. Р.27.3, с), радиусы которых опре-
Рис. Р.27.3
деляются условием равенства цент-
ростремительной силы и силы
Лоренца: mv'/R — quB. Следова-
тельно, R — mu/(qB). Центры ок-
ружности О' для q > 0 и О" для
q < 0 лежат на оси у. Условие
отражения выполняется, если
R<d, т. е. при
2. Условие отражения не зави-
сит от знака заряда (рис. Р.27.3, а),
3. Если V— 10итах, то R = 10d
Угол отклонения (рис. Р.27.3,6)
после пролета частицей «магнит-
ной стенки» определим из выра-
жения a==arcsin(d/R)» 1/Ю рад, так как при малых a sina«a.
27.12р. 1. Движение заряженных частиц можно представить
как суперпозицию двух независимых движений: равномерного
перемещения вдоль силовых линий магнитного поля со скоростью
ои= и cos а и равномерного вращения по окружности радиуса
R—qv±/(rnB) вокруг силовой линии, где v± = usina. (В совокуп-
ности оба движения приводят к перемещению частиц по винто-
вым линиям.)
Так как время одного оборота частицы (период ее вращения)
Т ^2nR/VjL = 2nrn/(qB)t то шаг винтовой линии= и cos a.
2. При малых a cosa« 1—as/2 и, следовательно, все частицы
с одинаковыми q/m и v, испускаемые из точки О под малыми
углами а к силовым линиям, соберутся на той же линии на рас-
стоянии (разброс порядка ~а2/2).
Движение частиц вдоль силовой линии (а = 0) неустойчиво.
После любого малого возмущения, направленного перпендику-
лярно магнитному полю, частица будет двигаться по винтовой
траектории вокруг силовой линии.
27.16р. Уравнение движения частицы в скрещенных полях
Е и В m-^T- = q{E^\yB\) в данном случае разбивается на два
456
уравнения:
mr^-.
(1)
(2)
Перейдя к системе координат, движущейся вдоль оси у с по-
стоянной скоростью v—E{B, т. е. введя новую переменную yt —
— у—vt, из выражений (1) и (2) получим
d2iji _qB dz . /q.
dt2 — m dt ’
_______qBdyj_
dt2____m dt ' 1 '
В уравнениях (3) и (4) отсутствует Е. Это означает, что
в движущейся системе координат на частицу оказывает влияние
только однородное магнитов поле, под действием которого в си-
стеме координат (ylt z) она будет двигаться по окружности.
Результирующее движение частицы есть наложение вращения
в плоскости уОг и поступательного (дрейфового) движения со ско-
ростью v=E/B вдоль оси у. Через время Т, равное одному обо-
роту (период вращения), частица пройдет вдоль оси у расстояние
1—vT и вновь пересечет ось у. Так как скорость дрейфа v= Е/В
и период Т = 2nm/(qB) (см. задачу 27.12р) не зависят от началь-
ной скорости, все частицы с одинаковым отношением q/m попадут
в точку 01( отстоящую от начала координат на расстоянии I =
— 2nmE/(qB2).
Направление дрейфа частиц при q > 0 и q < 0 одно и то же
(ср. с задачей 27.14), так как с изменением знака заряда ме-
няется и направление действия электрической силы.
27Л8р. Характер траектории движения электрона зависит от
соотношения между электрическими и магнитными силами. Если
силовое действие магнитного поля в зоне движения электрона
мало по сравнению с действием электрического поля, то вихре-
вое поле Е заставит электрон двигаться по раскручивающейся
спирали. В противоположном случае электрон будет двигаться по
сжимающийся спирали к центру. Следовательно, при определен-
ных соотношениях между Е и В возможно движение по окруж-
ности. Допустим, что эти соотношения выполняются. Тогда при
круговом движении
mv2!R = qvB и mv=qBR, (1)
где R — радиус окружности.
При движении электрона по окружности изменение импульса
обусловлено электрическими силами: ——дЕ;
где Е =
I
2л/? dt ’
457
Отсюда rndv = ~gd& и, следовательно, /nv(f) =-g^-Ф(0-
По условию, начальная скорость п(0) и поток Ф(0) равны
нулю.
Используя уравнение (I), получим
В (/) = Ф (/)/(2лВ2) = 0,5В(Т),
где В(Г) = Ф(/)/(лВ2)—среднее значение.
Это условие означает, что электрон может вращаться по кру-
говой орбите, если поле В (Z) на орбите в два раза меньше сред-
него поля внутри нее.
Глава двадцать восьмая
28.1р. При у = оо электрическое поле Е* в системе координат,
связанной с движущейся со скоростью v плазмой, должно отсут-
ствовать, т. е. Е* = Е-f-[иВ] = О или Е= — [tB], где Е—поле
в неподвижной системе координат.
Если п = и±-|-п1|, где иц—составляющие, перпендикуляр-
ные и параллельные полю В, то [иВ] = [охВ] и, следовательно,
Е~—[п±В]. Отсюда [ЕВ] =— [[иВ]В] = и±В2. При преобразова-
ниях векторного произведения [[vB] В] использовано известное
тождество [[ДВ] С] = В (СД)—Д (ВС). В результате
= [ЕВ]/В2= [Е ±В]/В2,
где Ej_—составляющая поля Е, перпендикулярная В. Соответ-
ственно |п±| = |Е|/В.
При В — 1 Тл Е±= 1В/м, Uj_— I м/с-
Существенно, что электрическое поле Ех не вызывает электриче-
ского тока, ибо и электроны, и ионы дрейфуют в одну и ту же
сторону и, следовательно, отсутствует их относительное движение.
28.3р. Согласно правилам векторного анализа,
rot [иВ] = [V [vBJ] = (BV) и—(uV)B + v (VB) — В (?w).
Так как divB = (VB] = 0, rot[t’B] = , а -Ц- — —(vV)B, то
(I)
т, - dp
Из уравнения непрерывности сжимаемой жидкости —
=— V(pu), после аналогичных преобразований следует
divo=(Vi')=— (2)
458
(3)
Подставив выражение (2) в (1), найдем
dB В dp л d f В
(/*)о = -5Г--;£ = Р7йА7
Л\Р/ \Р 1
Уравнение (3) показывает, что значение В/p меняется в каж-
дой точке пропорционально растяжению (сжатию) соответствую-
щей «жидкой» трубки. Если р = const (жидкость несжимаема), то
пропорционально растяжению (сжатию) меняется индукция В.
28.7р. 1. В условиях магнитостатики (ц = 0), если силу тя-
жести не учитывать, магнитная сила
F* — [6В] = — [rot ВВ] = grad р.
t-о
Чтобы FM = 0(p = const), необходимо выполнить условие
6 = 0;
rot В = 0,
либо 6 = РВ;
rot В = рВ,
(1)
(2)
где p = const (илн р—скалярная функция координат).
Условие (1) относится, например, к однородному полю, для
которого rot В = 0. Более общее условие (2) физически означае г,
что линии тока совпадают по направлению с магнитными сило-
выми линиями.
Условие (2) можно привести к виду
V2B-bPaB = 0, (3)
если учесть, что rot rot В — grad div В—V2B;divB = 0; р = const.
2. Указанные в задаче поля удовлетворяют условию (2). Дей-
ствительно,
rotaB=^—^ = РВа;
При дифференцировании учтено, что /о(х) =— J\(x);
= Jq (-V) — J} (x).
28.13р. Уравнение движения (без учета сплы тяжести):
р~=—gradp4- [6B] + pvV2tf. (1)
459
Так как внешнее электрическое поле отсутствует, то
6 = у[и£]; [б£] = у[[иВ]В] = у{В(иВ)—vB£] (см. задачу 28.1р).
По условию задачи, v= vxi, где их = пх(г) и ux(±d)~ 0. За
счет растяжения магнитных силовых линий движущейся средой
появляется составляющая поля Вх. Таким образом, суммарное
поле В = V 4 В*. где Вг = Во.
В условиях стационарного течения (dv/dt—O) для составляю-
щих по оси х из (1) следует
(2)
Учтено, что (vB) = vxBx; В% = В*—ВХ. Решение уравнения (2):
их = vx пр 4* -Д ieaz 4- А £е az,
/Др\ 1 , , л z vBo
где ожпр = ( -г)—г: ai.8=±a = ± У —корни характе-
ристического уравнения; Л1<2—постоянные интегрирования, опре-
деляемые из условия их|г=±а = 0.
Таким образом,
сЪЛ14
а
ch Л1
где Л4 = ad= j/
d—число Гартмана.
При М 1 практически во всей области скорость постоянна,
за исключением пристеночного слоя толщиной порядка d/M. При
М 1 скорости распределены по параболическому закону.
28.14р. При р = 0; 6=4-0 £ = р6=0 и rot£ = 0. При этом из
уравнения Максвелла rot£ =— dB^di следует, что дВ,/д/ = 0 и
Bt- = const, но не обязательно В,-=0, где В, — поле внутри СП.
Таким образом, из условия р — 0 следует только «вморожен-
ность» магнитного поля в проводник, а не его отсутствие. По-
этому В, = 0 должно рассматриваться при построении теории как
дополнительное условие.
При этом равенство Bt — 0 относится к толще массивных сверх-
проводников, исключая тонкий слой 10“5 см) у поверхности
(скин-слой). По этой причине это равенство неприменимо для
малых частиц и тонких сверхпроводящих пленок, толщина кото-
рых соизмерима с толщиной скин-слоя (ЛЛ).
28.15р. а) Если бы в односвязном теле в отсутствие внешнего
поля поверхностные токи существовали, то во внешнем простран-
стве они создали бы исчезающее на бесконечности магнитное поле
с потенциалом (рм при граничном условии д^м/дп — 0. Но такая
460
задача имеет решение фм = 0. (^Она аналогична электростатической
Эф Z-. \
задаче о поле, созданном незаряженным телом с о = Efl= 0. )
Таким образом, такого магнитного поля быть не может, а
следовательно, не могут существовать и поверхностные токи.
б) Вторая задача (сверхпроводящее кольцо) имеет электриче-
ский аналог. Это поле, созданное двойным заряженным слоем.
Поэтому в двухсвязном теле поверхностные токи могут существо-
вать в отсутствие внешнего поля.
Ответы
Глава первая
1.2. £/=0,3-91 = 27,3 В. 1.3. По закону Ома. 1= фа ~ = —2,5 А.
Kt-j-Aa
1.4. По закону Ома для участка цепи, /2=^—~i^=12MA. По первому
закону Кирхгофа, 1—12—Л=2 мА. Замена источника ЭДС на источник
Рнс. 0.1.1
тока приводит к схеме рис. 0.1.1, о, где 7= 7,5 мА; 7? = 2 кОм. 1.5. J =
———^i=21 мА. 1.7. /3 =—10мА; <pm = 65B. После замены
источника ЭДС на источник тока получим схему рис. 0.1.1, б\ 7=3 мА;
R — 1.9. 15мА; 74 = 5mA; Ze=0; Z5 =—15 мА; <rfc=20B. 1.10. £ — —I В.
,'»*«+<'+»* '•=2«*
/\4Т’А5Т^е I ^7
/7=—1мА. 1.12. Рис. 0.1.2; ^ = 56: £2=
= 12 В; /?j=5kOm; /?2=6кОм. 1.13. По пер-
вому закону Кирхгофа следует составить во-
семь уравнений, по второму закону—четыре.
Если учесть, что токи через резисторы R-. и
Ri и токи через резисторы /?е и /?б попарно
одинаковы, то по первому закону Кирхгофа
достаточно составить шесть уравнении, а по
второму—четыре. Прн составлении уравнений
по второму закону Кирхгофа контуры следует
выбирать так, чтобы были охвачены все ветви
схемы, кроме ветвей с источниками тока. 1.16.
Рис. 0.1.3, с. 1.17. Рис. 0.1.3, б; ^=10 В;
£2 = 24 В; £3 = 48,75 В; Ц = 1 A; /2=0,25А;
/з=1,25 A; Z?! = 10 Ом; /?2=24 Ом; Rt =
=/?$= Ю Ом; 7?в = 5Ом. 1.20. 1) Zx=1.25—
Рис. 0.1.2
—1,5/4; 2) /1=1— 4/4. 1.21. flfrf=4/3Jr-b 1/3«йб-
1.23. Потенциал точки О не равен потенциалу точки О'. Соединить эти точки
нельзя. 1.24./?ай = /?4+^Ц%^^-. 1.25. Явй = 0,9 Ом. 1.26. Rab = 2O^
"1 ТЛ2ТЛЗ
482
1.27. х=1,5 0м. 1.29. а) Для схемы рис. 1.13,а /?аь = 2 ^-~|—^/? = 1.5/?;
ддя схемы рис. 1.13, б Rab — % /? = ,У'Я; б) для схемы Рпс- ЫЗ, в
/?С6 = 1,5/?; Rcd= 10/13/?; в) <ptf=8,25B; >qpd=3B; ^ = 3,75В; ф7=фя=0.
Рис. 0.1.3
В перемычках de и eh и в аналогичных перемычках нижней части схемы про-
pd pnd 2
.екают токи 7 = 0,25 А. 1.31. 7?.t = 2 4S. 4S j Y
4-4S 1 pd . pnd 4S \2 1 2-|-л/
4S"1- 8S
1.33. gn = 0,261 Cm; gi2 = 0,0719 Cm; g13 = 0,0468 Cm; g2s ~ 0.0937 Cm; g’23 =
— 0,0586 См; £зз = 0.1614См. 1.35. £i = —14,45мВ. 1.36. 1. В первом режи-
ме Zi’isfigii; 4—fiffis, во втором /Р = — E’ng-rf, /2l = — E2g2i (знак минус
поставлен потому, что направление Е2 встречно положительному направлению
тока /2), в третьем /J11- — E[gn—£Zgi2; 4lI = — Ezgn —Figiz- Имея в виду,
что Е[ = ЗЕ'ъ Е2=4Е2. найдем /1" = —3-80— 4-80=—560 мА; Дп=—4-96 —
— 40-3 = —504мА. 2. /Г=—740мА; 4V = 0. /Jv=—840мА. 1.37. gn =
= 0,269 См; Д/2=—0,637 А. 1.39. Uab = 1,6В; /s = 2.2 А; /3= 1,2 А. Источник
тока доставляет мощность 6,6 Вт, источники ЭДС—40 Вт; "S /2/? = 46,6 Вт.
1.40. Число уравнении, которое
следует составить для схемы рис.
1.18,6 по методу узловых потен-
циалов, такое же, что я число
уравнений этой схемы, необходи-
мых для решения методом контур-
ных токов, и равно двум. При со-
ставлении уравнений по методу
узловых потенциалов для узлов b
и с не следует забывать слагаемых
с <ра. В соответствии с обозначе-
ниями на рис. 1.18, б /1=0,15 А;
/я = 1,845 А; /4 = 0,215 А; /ь =
рис. 1.19,0. Полагаем, что токи ветвей имеют те же индексы, что и со-
противления ветвей. Тогда /1 = 0,94 А; /2=’0,54А; /з = 0,06А; /< = 0,16 А;
/5 = 0,4А. 1.43. а) Замена первой и второй ветвей схемы рнс. 1.18, о эквива-
лентной ветвью приводит к схеме рис. 0.1.4, о; б) замена второй и третьей
ветвей схемы рнс. 1.18, а эквивалентной ветвью приводит к схеме рис. О.1 Л, б.
Рис. 0.1.1
1,78 А; /е=1,63А. 1.11. Ответ дандля
463
1.44. a) E=10B; Kv=50Om; 6) J = 0,2А; Я=50Ом. 1.45. £/оЬх=15В;
/?их = 25 0м; /з = 0,5А. 1.46. Для рис. 4.19, а /5= 1,2/(2.44 0.6) = 0,4 А; для
рис. 1.19,6 /6=—0,8/(2,44-0,6)=—0,267 А; для рис. 1.19, в 76=1,2/(2,3934-0,6) %
«0,4 А; для рис. 1.19, г /5 = —0.8/2,993=—0,267 А. 1.49. a) Uab х = 1 В;
.6) ЯвхоЬ=1 Ом; в) 1)= 1/3 при Ян=0,5 Ом; t]=2/3 при Ян=2Ом. 1.50. Э. д.с.
Е = 0,5В и направлена от точки b к точке а. 1.52. т] = 36/57. 1.54. gn =
__ — Д/i • —Д/2 _ Д71 .
(Ь+ы'дм ’ 522 ~ (/2+д/;)д/г ’ Я12“~ (73+д/;)д/? * 3==
— Д/i --. 1.56. х—RK пп I п » У——х‘» бн i укор
/в4-Д/2
1
“ /г 4-/г -Л/? 4-яR»Ri -4- R«R'R* ’’ gH1 ясх
Ra 4-4-(Я14-Яз)+-^~ +
£/4*^2 У~Г^2
= 0»5 g«i укор-
1.58. Уравнения по первому закону Кирхгофа [А) [/в]г=0:
Ветви
7 8
Узлы I
1 г—1
2 0
3 0
4 L 0
2 3 4 5 6
0 0 0 1 0
10 0—1 1
0 1 0 0—1
0 0—1 0 0
О —И
О О
1 О
lW3hhW6]T = ^
—1
и
Уравнения по второму закону Кирхгофа [Кг]1^в1г=0:
Ветви
Контуры 1 2 3 4 5 6 7
5 г 1 I 0 0 10 0
6 0—1 I 0 0 10
7 о 0—1—1001
8 L—1 0 0 1 0 0 0
8
0-|
О
О
1J
[{А«ЛВДЛ(/Б£/6£/7{/в]г= 0.
1.59. В соответствии с формулой [Kr] [Яв] [Кг]г [4*] = [ KJ {[£в~ [#в] 1ЛП
Контуры 1 2
5 г 1 1
6 0—1
7 0 0
8L—1 О
Ветви
3 45678
О 0 1 0 0 0-1
1 00100
—1—10 0 10
О 1 0 0 0 1 J
г 1 1 0 0 1 0 0 0-1
0—1 1 0 0 10 0
о 0—1—10010
L—1 о о 1 о о о 1J
1.60. В соответствии с общей формулой |А] (gBJ [А]г[ф] = [ A] {[J*] — [gB] [EJ}
имеем
Ветви
Узлы I 2 3 4 5 6 7 8
1 г—I 0 0 0 1 0 0 —1-1
2 0 1 0 0 —1 1 0 0
3 0 0 1 0 0 —1 1 0
4 L ооо —1 0 0 —1 1J
61 1 ооо-
62 0 10 0
ёз 0 0 10
0 0 0 —1 \у
1—10 0 X
ёь 0 1—10
£7 0 0 1—1
£eJ —10 0 1
464
1.61.
[Kr] = [Fi /), где
Ю=-[<ЫГ=
О 1 О 0—1-
0—1 10 0
0 0—1 10
—1 О 0—1 1J
Г 1 1
О —I
о о
L—1 о
о О-i
1 о
—1 —1
О 1J
1<?г] = 11- <?2].
Рис. 0.1.5 Рис. 0.1.6
1.62. Граф изображен на рис. 0.1.5,
Трина главных контуров
1.63. Граф показан на рис. 0.1.6. Ма-
О 0 1 0 0 0 0-1
1 001000
О 000100
—1—1 0 0 0 1 0
—1 —1 О О О О 1J
Глава вторая
2.4. L=—^ 1пф=2,75 мГн. 2.5. а) J----2_\=л.ю-*® Гн;
Ki Z \ Ki f
б) = я* 10~10 cos 1000/ Гн. 2.7. е= В. 2.8. Рис. 0.2.1, а. б. 2.9. е =
оО
— wtixibB sin <о/ В. 2.10. a)ej=0,4B; ЭДС направлена по часовой стрелке;
6) е2 =—0,2 В; ЭДС направлена против часовой стрелки. 2.11. а) —~&~ =
1000/ В; б) е = = i =
। dt dt ' dl dt dl
?=—n-10-8 cos 2000/ B. 2.12. Fm = 2-10~6 H. 2.13. а) Провода A С (B, D);
finin=0,33.10~4H; б) провода Д B(C,D). Гтах=1,66-10“4Н. 2.14. F = 0,0t H;
П — 500об/мин; E^Uao. 2.15. Л1 = 7Ъ=5,25.10~5 H-m. 2.16. IT=5.I2.10~s Дж.
2.17. W’M=0.5L1/J+0,5L2/^+AfZ1/a== 1,15Дж. 2.18. 0,5- 10-7Гн;
В d
62=10-’Гн. 2.20. ITM=/cpS J Яг/б^З-Ю-гДж. 2.22. J E dl=Ed^
О 0
2-10*B; 9=еЛ &EdS= eo€r£S = 8f86-10-^-4.2.l0*.200 = 1.42.10“\Кл;
465
it
^idt
C=qlU=taES}Ed=taS;d=7\ пкФ. 2.23. C--£-=5— = =Ю-бф.
U U ivU
h
q=\idt подсчитывается графически. 2.24. /=-^==-^-/С£Л = C^£ ==
<J dt dt dt
о
— 2 cos 1000/ A. 2.25. а) 1ГВ=?2/2С=1,42.10-2 Дж; 6) й’-э=С/Д/2=0,5.10~2 Дж.
2.26. Емкость двух конденсаторов Cz~2W3/U~ — 2- l/10e=2-10“e Ф=2 мкФ-
Cz=qx/U==(CU+CU)/U==2C; C=Cz/2=l мкФ.
Глава третья
3.1. 1т =5К 2 А; <рй = 45°; (о=314с-\ 3.5. L=47.6мГн; / = 2е~'71в30’ А;
U^Ule-'s^'B; Z=/?ujtoL-J^=50+j (150-100) =50К 2е/15°Ом.
3.6. ф=41°. 3.7. С=26,5мкФ; ZRX = (4,ЗД/2,88)Ом; Увх=(0,16—/0,107)См.
3.8. Увк = О,О224е~/вз°зо*См; ZBX=44,6е/вз<>30' Ом; u=63sin (со/4 6,3°30') В:
i\=0,63 sin (<o/-j-63e30') A; i2= 1,26 sin (со/—2G°3G') А. 3.9. 2=7.65-/38.5 Ом;
Л = 3,6e/l£s4<>' А; /в=2,82е-/16° A; g = 2,5- 10~B См; /?=4,32-10“3 См-
466
3.11. А=:3,35е***вА; /З=2,36е'’°° А; /=2,36 A; <^ = 0; <Гс=Фл+ /J₽a=/23,6 В;
^ = <РсЧ-4(—/Хс)= 47,2-/23,6 В; q>c = <h>-r hRi =70,8 В. Рис. 0.3.1.
3.13. /2 = 7 А; /3=5 А. 3.14. ZI=25/43,2 Ом; Z2 = 43,2-f-/25 Ом; Z3 — /50 Ом;
ZBX= 68 4/18,3 Ом. Рис. 0.3.2. 3.15.
3.18. а) С= 120мкФ; б) С = 75мкФ. 3.19.
Увеличить в 1,78 раза. 3.20. /Л = 2А;
7S=1 А; /3=1,73А; ’ (Л = 64-86,5 В;
P=Re f£/J = /§/?=150 Вт; Q=Im [£Л]=
/гХс=86,5 вар. 3.21. Ё] =
= 100 В; £2 = /50В; )3 = 7,07е-/15<’А;
?3 = 7.«5е/71°10'А; Хс = 5Ом; R = 10 Ом.
3.22. P = Re = 630 Вт, где
Clтп ~ /i^i- 3.25. Для а) и б)
Q = Q1Q2/(Q1 + Q2)- 3.27. w0L=I06Om;
R= 2,82 Ом. 3.28. R = 16,5 0м; L =
=26,3 мГн. 3.29. / = 0,0216 A; t//? = 2,6B;
f/c = 3,9B; 6/; = 15,6В. 3.30. /?=100Ом;
L= 10 мГн; С=100пФ. 3.31. <о0 =
Рис. 0.3.4
L= 500 с-1; 3.32. to0=433 с"1. 3.33. /1=3,35е”/2в°30' А; ?.=/1»5А; Хс=13,3 0м;
Х£ = 2,67 0м; R2 = 5,34 0m. 3.34. ыт = 500с-1; wH = 707C-1; Л = 20 А;
23=— 20 А; /я = 40А. 3.36. Рис. 0.33, в для схем рис. 3.22, а, г и рис. 0.3.3, б
Рис. 0.3.5
для схем рис. 3.2.2, б, в. 3.37. Рис. 0.3.4. 3.38. Рис. 0.3.5, а, б. 3.40. «3 =
= /ffico(M31— Af13) cos и/ В. 3.41. Р2=Ю,90м. 3.42. Z=/8O.m; /а = 2 А; /,=7 А;
1/1 = 61,8е/ьв’80'В. 3.44. 2i = /l0,2A; /2 —20—/10,2 А; 7Э= 14—/7.14 А;
Д-6-/3,06 A; Uac= 154-]-/50 В;
Ubr = 504/102 В. 3.45. Рис. 0.3.6.
3.46. а) 6/2=8С В; Р, =0;б) Uz~27В;
Р2=1 32 Вт;/2R2=(/pt/3 cos
+/iX^f/3 cos (/JXX1; 7а), т. е. 296
Вт» 163-}-132 Вт. 3.47. Одноименные
зажимы* *—1—2‘, С—1—3'-, —2‘—3.
3.48. С=1/(о2 (/.^Рз + глу. 3.49.
Х = 0,52. 3.50. С = 4 мкФ; Л =5 А;
/2=2,5 А. 3.54. Условие равновесия схе-
п
мы (после преобразования треугольника в звезду): ,3Р n i =
J -|"/wCq (.Котла)
= /?1рг+ ]• «пчда = [Ло
467
J?x=jyk. 3.SS. /,-12,6е 3.56. Zt=-il20M-, Л=6.72е'»’’А;
?2-=3.25e'1,3°A; ?J=5,62e/”“ A; h = 25,2 e/2‘° A; ?, = 22.6efl2‘“'A;
E= 130е/07вз0' В. 3.57. /t = I6 e“/n3° A; Ja = 11.3e”/tC A; = 14.3e'es°3e' A.
3.58. Ul3~ 3.59. Рис. 0.3.7. 3.60. Рис. 0.3.8,
О
4
Рис. 0.3.7 Рис. 0.3.8
Глава четвертая
43. (71—A^a-pB?3= Aut/a-f-Aii/a
}i~ CUD^—A21Ua-pAgj/j
^*1__Г Вц 1 ^*1 . (6)
Ji J l^31 B,aJ Jl J
4.3. Zu = -/Хс0м; Z13-Z21-—/ХсО.м; Z22--(/?- /Xc)Оу; у^^Т^См;
— Pty
Ги=Ги=-1/ЯСи; F„=I/RCm; Ом; Я,2=-//„=^^;
”H-—Tv—См; 0ц=—гр—См; GjS=—Оц——1; баа=/?0м; Вц—
K—jAc —]ас
= R—Мс . в1а=£ Ом; B*i = —Lf-Cm; Вм=1. 4.4. Для рис. 4.3. а А-па-
—/лс —Мс
раметры: Ац= l-pZi/Za; Лц= Zf-J-Zg-I-у 2 ; Aai=I/Z3; Ац=1-у ZifZ3,
4.3
Z-параметры: Zn-Zi-}-^; Zls= Z2! = Zs: Za2 = Za-|-Zs; W-параметры: 7/ц =
, Z1Z3-PZ1Z2+Z2Z3 „ f, Z8 „ ___________ 1 44^
“------z^z,-----• Я1г=-Ня=5+г.- w"“-?rra- Для рис- ’
Z-параметры: Zn = l4~^; Лц=Х4; Zsi=-i4-=—A-; Z-
"5
rnn^up-mu- 7 ^l^s + ZgZg . _ „ Z5Z, 7 ZjZg-|~ Z5Z6 _
параметры.. Zu—. Zl2~ Zn~ Z^Z6-} ’ Zla~ Z4+Zb+Ze *
468
gj и rj fj if ^4~}~Z^-\-Z^
^-параметры: Hn—H„—ZiZ^ ZiZg
.-, л _K,+iXt_ „ (Ri+jX,)(R,-| )Хг}-аХ„у „ 1 „
*•«• Ли—--=:--, /112 =---------Tv------------I л21 — "Ту— • Лм=
1AM Мм ]*M
S=^+M?> 4A ZK= 10 + /60 Ом; Z2i = —Z1± = /30Om: Z2£=—(8 + /40) Om.
1ЛМ
4.9. Fn = F23=/760 См; Из=^21 - //30 Cm. 4.10. Z-n 1раметры определяют из
основного уравнения четырехполюсника, решенного относительно Ut и U* с уче-
том знака у ^2-^и = Л„/Л21; Zt%~ | Л |/Л21; Z£] = 1/Л21; ^22 ~ Л22/Л21, где
I A| = ЛцЛ22—Лх2Л2| = 1. //-параметры: //ц — Л12/Л2£; //12 = ] A |/Л22; //31 =
— —I/A22; //22= ^21/^22- В-параметры: Ви = Лм/|Л|; Вц— Л1а/|Л|; Вп =
= Л£1/| Л |: Вм = Лп/| Л |. У-параыетры: Fn = А^Ац; У12 = — | А |/Лм;
/Z Z
-------гт'Х'1К7 \ • НЛИ
&2к V^ix — ^1х)
х'" **7—» Л12 — Лц23к: Л£1 = Лп/21Х; Ла£= Л^'^ц. Z-парамсгры:
Z.2X*- ^гк
Zji = Zjx; Z|2— Z2j— "г Z2x (21ж21к); Z22=Z£x. //-параметры: //ц— Zjxt
//j2 = — //2i = V"(Zjk—ZiK)/Z2^; Z/£j = I/Z£v 4.12. Zix =— /1000м; Z1K =
= 50—/50 Ом; Z2x=100—/100 0м; Z2lt= 100Ом. Л-параметры: Лп = 1; AI2 —
= 100 Ом; Л21/0.01 См; 422=1+/; Z-параметры: 2ц =— /100 Ом; ZI£ = Zw =
=—/100 Ом; Z£2= 100—/100 Ом; //-параметры: f/n=50—/50 Ом; //« =
= ~//3| = 0,5—/0,5; Я22 = 0,005 4-/0,005 См. Zfl = 7O.7e“/e7°30' Ом; Zc3 =
-НЭе’/**030'Ом. 4.13. Zlx = Z2x = 54-/5 Ом; Zitl = Z£lt= 10+/100м. Л-пара-
метры: 4U= Л22 = —/; Л1Я= 10—/ЮОм; Л£1 = — 0.1— /0,1 См; Z-параметры:
Zn=Z£2=54-/5Ом; Z12 = Z2l = — 5 + /5Ом. Zc= Юе'**’Ом. £=0,88—/90°.
4.14. Лп = Л22 = 0; 41а=/500Ом; Лм — /0,002 См. 4.15. Для Т-схемы Zt —
= (Л— 1)/С; Zt=(D—l)/C; Z3=l/C; для П-схемы Z^=B\ Z5=B/(D—1);
Ze = B/(4—I). 4.16. Для Т-схемы Zj = Z2 = — /40 Ом; Zs=80Om; для П-схемы
Z4 = — )60Ом; Z5=Z,=/120Ом. 4.17. Z4 = /30Om; Zb= Z.= — / 20 Ом.
4.18. Для Т-схемы Zi==Zu — Z2j; Z£=Z2£—Z2j; Zg^^Z2i; для П-схемы Z^ =
=(ZUZ23—Z2i)/Z£i; Z5= (ZnZ-22—Z2i)/(Z22—Z2i); Ze=(ZnZ22 Z£i)/(Zn—Z£ik
4.1». Zi-/?i + /(Xi— Хл,) = 104-/30Ом; Z£=/?a+/(^3-Xw) = 8-4/ЮОм;
^з-/хМ = /30Ом. 4.20. Zi=—/20Om;Z£ = —/200м; Z3 = /40Om. 4.2L Z1=
= Z£=50Om; Zs = 385Om. 4.23. Для рис. 4.9, a
2+/ 10+/КП Г I 10] Г2+/ЗО+/2О].
/0,2 / J Lo 1J 1/0.2 /3 J’
для рнс. 4.9, б
Г 1 01Г1+/ 10+/201Г1+/ 10+/201
L/o.11J L 0.1 2 J-L/0.1 / J'
4.24. Четырехполюсник на рнс. 4.10,6.
4.2». Zs=—/И/?н₽в = —/1^27.3= —/9Ом; Z1 = Z3= + /9Om, т. е.
в продольные ветви Т-схемы следует включи гь дополнительные индуктивные
сопротивления ^1доп=:8 Ом; -2^£доп=3 Ом. 4.30. 23дол—/ Д) Ом; 2здрп,=—/60 Ом.
Сопротивление /?и определим из равенства Zi=/\Xj—V<i+/?B) (₽я+/?и),
469
откуда /?„ = 67 Ом. 4.32. л =1/6; 2ДОП= — /46 0м. 4.34. Для схемы рис. 4.15,а
для схемы рис. 4.15.6
для схемы рис. 4.15, в
для схемы рис. 4.15, г
20е/‘46
4.36. ZBX = C|Z„/Gb Gx = 2. 4.43. а) /8=
(линейная диаграмма); 6) /2 =
20е'*45’
1 4-Ае-/ыи°
(круговая диаграмма). 4.44.
t^„x=/IOOB; UmMl=0-, ф = —150°;
-200 В. 4.45. 7ХХ= 10е’/46эД; 11к = 31,5е-Лз° A; ф = —90°; Q = 160мкФ;
С2=17,7мкФ. 4.16. /1х=-10А; t/flbx = 200B; /1К = 15,8е-/1Оа’30' д. =
=212е/«° В; Z2bx=10}< 2е/«°Ом; ф= —45°.
Г лава пятая
Б.З. Рис. 5.4, а,б—ФНЧ с <ос = 1/VLC; рис. 5,4, в. г—ФВЧсо)с= l/V^LCi
рис. 5.5, а, б—ППФ; рис. 5.5, s, г—ПЗФ. Для рис. 5.5, а—г частоты среза
определяются выражениями (1) решения 5.2р. 5.4. <0!= l/V^L1Ci = 2,5.104 рад/с;
e>3= VCin-Cg/p^(Li + La) С1Сг= .— • 104 рад/с. Если Lx, C\ н L2, С2 поменять
местами, то полоса «прозрачности будет ограничена частотами С1)г =
=йЙЙ%^Г=Л ’ ,0‘рад/с: ai=vhi=5‘ 10‘рад/с's-8’к ™пу *
не принадлежат схемы рис. 5.2, д, е и 5.6. Для остальных схем k — ^L/C-
5.12. Заданные симметричные фильтры расщепляются на полузвенья, рассмот-
ренные в задаче 5.11р. Поэтому a (w) — 2ах (w). ft (<o)=2fti (<о), где и ftx —
коэффициенты затухания и фазы одного полузвена (см. рис. Р.5.7, Р.5.11, о).
Характеристические сопротивления Т-схем совпадают с характеристическими
сопротивлениями ZT составляющего полузвена, а характеристические сопротив-
ления П-схем—с Zn полузвена (см. рис. Р.5.8, Р.5.11, б). Зависимости Ки(ы) =
— е-а<ш) приведены на рис. 0.5.1, а,б (рис. 0.5.1, а для ФВЧ, рис. 0.5.1,б
470
для ПФ). 5.13. toc—2,34-10* рад^с. 5.14. л^-3. 5.15. д = 5,27 Ни. 5.16. Полоса
прозрачности ограничена частотами <j>i—о2.ь>] — О,5соо (—
со2~0,5(1)0 (4-Vх £2/^1+^-}-4). Ширина полосы прозрачности Aw—ш2—Cui —
1/V ЦСг- ZT(too) = Zn(wo) =A=KM7C2=Kf^Ci. 5.17. £j =20-10~a Гн;
£г=Ь|0-»Гн; Ci =0,4-10~fl Ф: Сг=8-10~вФ. 5.18. ©I = O,5coo(K£1/£e4-4 —
— V £1/£a); <og = 0.5(jo (У£1/£24-44“У<Ь1/£2); Zt M = Zr (©2) = 0; Zi |u=0 =
= Zj !<«)«=« = fe= КLi/Cs; Zn (Oj) = Zn (co2) = 00; Zn|a₽o = Zn|ui-« = k. Харак-
тер Zr в полосе затухания coj—co2: в интервале <O|—©e—индуктивный; в ин-
тервале ©0—(i)3—емкостный. Характер Zn противоположен характеру Zj.
5.19. Полузвенья включены по П-схеме; Ci = 8-10-вФ; £1=Ы0-эГн; Съ =
— 0,4‘Ю-вФ; Z2=20-10~“ Гн.
со, рад/с 0.75-10* 1,1 • 10* соо=1тИ8.Ю* 1,2-10* 1,5-10*
д, Нп 0 5,23 оо 2,06 0
б, град 97,6 4-180 0 — 180 —41
5.22. Схема m-полузвена дана на рис. 0.5.2, а: £]Л=3- 10“3Гн; £2/п=5,33- 10-8Гн;
C3ffl =0,3-10~е Ф. Зависимости Zfkn(w) и Zn (w) представлены на рис. 0.5.2, б.
Рис. 0.5.2
5.23. Зависимости Znm(<o) при т = 0,4; 0,8 даны пунктирными кривыми на
рис. 0.5.2, б, а при т=0,6—сплошной кривой. Для обеспечения меньшей
зависимости Znm^i в полосе прозрачности следует взять т—0,6. 5.25. Схема
/n-полузвена приведена на рис. 0.5.3, д; £iCT = 4,69-10“3 Гн; Ci,n = 0.833-10_® Ф;
^2т = в>33’ 10~8Гн. Зависимости Ztzti(w) и Zt (о) даны на рис. 0.5.3, б.
5.27. Схема фильтра дана на рис. 0.5.4, д, зависимость д (си) = 2д* (со) -f-2om (со)—
471
на рис. Р.5.13 (пунктирная кривая). 5.28. Рнс. 0.5.4, б. 5.29. Схема /л-поду-
звена приведена на рис. 0.5.4, в. При 0,6 Llm = mL — 3-10-3 Гн; Clm = C/m^
= 0,833* Ю-® Ф; L2m = L '-^-=5,28*IO"3 Гн; C2n=C-0,469* 10~*ф.
Рис. 0.5.4
L*m—Llm~8,33* 10-s Гн; CSw=Cm=0,3- 10~e Ф. 5.30. Схема и параметры после-
довательно-производного комбинированного фильтра приведены на рнс. 0.5.5, й,-
схема и параметры параллельно-производного комбинированного фильтра—на
рис. 0.5.5, б. 5.32. Н(— 1 , где — \] (RC);
х. B)q / __ / { /? № / tn
AV
r \ Rh / \ Ш0 / j
wc = (l-|-R/RH)a)o. Прн уменьшении RH частота среза увеличивается. 5.33. <дс=
Рис. 0.5.5
| 7 \
= j • При уменьшении RM от со до 20 кОм полоса задерживания
расширяется от <во=1О3рад/с до 1,5<оо= 1,5*103рад/с. 5.35. QaK = l/(m-f-2);
Дх=т+2. 5.36. Нули передаточной функции фильтра комплексно сопряжены
при т < 1; с уменьшением т они располагаются ближе к мнимой оси.
АЧХ фильтра И (~\=Н (х)= т — достигает мини-
т
X"
472
пума Hmin—-j-qri7(2,n) ПРИ x= 1 где <o0=-—-_. . Для умень-
шения уровня //^(приближения нулей передаточной функции к мнимой оси) зна-
чение т необходимо уменьшать. При т —- 0. //min —►©. однако при этом (в0 —- эо,
что соответствует ФНЧ. Следовательно, неограниченное приближение нулей
передаточной функции данной схемы к мнимой оси невозможно. На рис. 0.5.6
Рис. 0.5.7
£ । 35
приведены АЧХ для ряда значений т. 5.37. //м(р)==—;— ------------——« . где
3(р2-|-3<а0р+(1$
о0 = 1 /(/?С). Нм I — \ = Нк (х) = Д1"**1 -. График Нм (х) дан иа
\<°о 1 у 1-р7х2-4-х4 _
рис. 0.5.7. 5.38. См. ответ к задаче 5.37. 5.40. /С(р)— — 2свор-|-«о
_ P*+F 2<0орЦ-С1>о
где о>о = К 2/(/?Q = 1000 рад/с. График соответствующей АЧХ дан на рис. 0.5.8.
5.45. В качестве четырехполюсника А выбираем двухзвенный ФВЧ по схеме г)
табл. Р. 5.5. Параметры элементов: Ci — Co =2,5-i0~e Ф; ==50рг'2 кОм: рези-
стор /?2 не оказывает влияния на работу схемы и может быть исключен.
[2/(/?Q] Р
p«+li/(RC)j»
5.46. /С (р) =
(полосно-пропускающин фильтр). 5.48. К (р) =
/?4 1
2 1 1 / 1 1 1 1 1 \ '
Р ~^С2\ )Р' RxRiC2C$
Ri t
i> . .5
p--fa(o0p4- <DC
где w0 =
= 500 рад/с; 2, = К fo) — - — (ФНЧ с частотой
V 1 -j- (ю/соо)4
среза (о0 = 500 рад/с, ^оа79Гц). График К (<о) дан иа рис. 0.5.9. 5.49. А (р) =
473
—-------—— ;----[ФВЧ с частотой среза l/(P2PbCsC*)=
Р2_| £1±£1±£4 рj_____!____
р csc4ps P^p2₽acsc4
= 20 рад/с].
Глава шестая
6.1. а) Р, = Ра = 25Вт; б) Pi = 25Bt; Р2=0; в) Рг = Рг = 75Вт.
6.2. а) Л, = 10 А; /,= 17,3 А; иф=220В; Р1== 1900 Вт; Р2= 3800 Вт; б) UAB=
= 220В; UBc = ^са— НО В; IAfj=lQA; Jrc—^ca = ^^ Ia—- Ib=15 A;
/с = 0; Pi = 2850Bt; P2=0; в) Uab — Urc~Uca = 2‘2OP>; /AB— ?ca~ ?b =
= /c=10A; /вс = 0; /Л=17.3А; Px=Pa = 1,9 кВт. 6.3. C= 127 мкФ; Uui> =
= 100B; 6нф=107В. 6.4. а) /л,в, = /вл = 2,72е-рз’М' А; /л = 4,7е-/63Л2&'A;
{/л'В'=183е/ЗО°В; б)/Л5В'=2.72e”/33°“'A; /в-о = 2,72e"'1M°26'A; ic.A, =
= 2,72е/8’036, А; /л = 4,7е^вз°25';/B=4,7e/17ft°34' A; /C = 4,7e/W35'А; /лв=0;
/вс = -/в; /сл = Л; Va'B' = 183е/ЗО° В; UB'C- = 183е"7’°’в; 6/с.л.=
= 183е/1ЬО<,В. 6.6. Р1Ях0,21кВт; Ра=1,59кВт; Р=1,8кВт; (?=2.4квар;
5 = ЗкВ-А. 6.7. 2=11,5е_/30°Ом. 6.9. 6/^ = 220 8; UBC = — /380В; (JCA =
= 440e/lz°°B; /лв=22е^30° А; /Bc=38e“'12O° А; /сл=44е/9°’А; 1А =
= Бве'^70056'А; 7В= 40e",1W°46' А; 7с = 79,2е7ввь* А. 6.11. Глв=0,315е”/вЬ° См;
YBC = 0.236е~'Б2в См; /А = I22,5e'/W’A; /в = 122,5е“'172° А; /с = 122,5 e/w° А.
6.12. /л = 13е/в°м'А; /в = 6,8е“/131° А; 1С= 18е',8в°10' А; 4= Ile“'U6C30' А;
йА.О' = ВОе76*50' В; йв-С' = 68е"'131° В; Uc>O'«180е/вв°10'В; Pu7 = 2kBt.
6.13. a) UО'О= 192 В; /Л=18,2А; /в=20,8А; /С = 39А; б) /л=20А; /д='
= 22А; /С = 36А; /О-О=5,9А. 6.15. /л = 15,4e"j3e’А; 7В= !6,5е“/1вз° А;
1С= 15е/‘7*’30' А; 6.16. /<=—17,3 А; /3=3315е-/75° А; 4=33,5еръ° А; /<=17,ЗА;
4=8,95е-/1в6° А; 7в=8,95е/1“° А; 7л = 0; 7В=— /34А; 7С = /34А; йс<01 =
= 346 В. a) ZOiOt = 17,3 А; б) /010> = 10 А. 6.17. Р = 20 Ом; XL = 5,5 Ом;
Хс = 22,7 0м. 6.19. /л = /л'С'=5,38е"/в,о20'А; 1в = 1в'С' = 6,26е“/1ЬЗЭ1°' А;
7с=В,45е"/6’е81'А; UA-B’ = 131е"/ив40' В; йв'С' = 176е~/10в°,<>' В; йсА' ==
с/
Рис. 0.6.1
= 238е/104О’гВ.6.21./л=10е"/1,8С40' А; /в=9,14е"/ив30'А; )г=16,22 е/0°й45'А;
(/у=48В. 6.23. Круговая диаграмма смещения нейтрали приведена на
рис. 0.6.1, а, а круговая диаграмма тока fA—на рис. 0.6.1, б; СГАО' = 132 е^41° В;
474
йво' = -50 В; и СО- = 180е/106° В; 1А = 4,4е’/"° А. 6.24. 1/О'Ох = 42,7 е/1М В;
i/o'OK = 24,5e-/MeB; iL/OMx= 141е'176° В; (+MK=87e“716T3 В; ZBX=19е“'в0°Ом;
^)= 109°. 6.26. />5=57е_;ББО4Ь'А; 18.9е/12В°30'А; /с = 38.4 е/121°30' А.
6.27. /д = —/34,7А; /С = /34,7А; йА-о- = 140 В; йво- = 203Г'11™' В;
t)co* = 203e/n°eis' В; 6и.в=284е/42’10' В; t/FC=-/380B; bc?v-284 е/137°50' В;
6дд'=120В. 6.29. При 1/л = 100В iA 5«4e“'32OA; 1В-- 5,4 е-'118"А;
lc = 12.51 е/68» Л; /\=9,2 еЛ»° А. 6.31. В0=^-Вт. 6.32. Во=6.10-*Тл;
£
ысетн-
Глава седьмая
7.1. Для рис. 7.1, а:
а)
нечетные
синусоиды;
б) </ = £+,„]/1
4а
Зя
(при а = 0 L' = (/max; при а —п/6 U = 0,882(/max; при а=л/2 (/=0.578(/П)ЗХ);
£/ср=0; в) при а = 0 U = 0,9651/max', при а = л/6 (/ = 0,882 l/max; ПРИ а—л/2
{/=0,578(/шах. Для рнс. 7.1, б; а) постоянная составляющая и нечетные си-
нусоиды; б) (/^t/max/K^; ^cp = (/max/2; в) l/ = 0,682L/niax. Для рис. 7.1, в:
а) постоянная составляющая и косинусоиды; б) L' = 0,5Lmax; t/cp =0,318с'|П1ах;
Рис. 0.7.1
в) {/=0,445(/тах. Для рис. 7.1, г: а) постоянная составляющая и косинусоиды;
б) £7 = 0,707£7max; 1/ср = 0,6361/тзх; в) U = 0,705йП1ах. 7.3. Для рис. 7.2.6
П / ] i \
П—2 —Узх. [ sincof—- sin2tof-|- —sin .. ) (рис. О. 7.1. с); а) для рис.7.2,в
z «5 J
sinco/—- sin2oj/-|—- ‘sin За/—...)(рис. O.7.I, б); для
z о у
sin<o/-}-*o'SIn^+“5‘ sin3ci)/+ • • ) (рис. 0.7.1,в).
О ]
•__ *тах 1 ^тах
2 ‘ л
р
7 л _ _ *-тах *-тэх
•2.ге=—----------—
7.5. а) Для рис. 7.3, с / = 0,632А; для
рис. 7.3,6 / = 0,652А; для рис. 7.3, в
/ = 1,46А; б) для рис. 7.3, а /о = О;
/срм=0,2А; для рис. 7.3.6 /0 —0.15А,
/ср и=0,25А; для рис. 7.3,в/о=О.533А;
/ср м = 0,533А; в) /ср = 0,2А; г) для
рис. 7.3,а йф=3,16; Аа=3,164;для
рис. 7.3,6 £*=2,608; А?а = 3,07; для
рис. 7.3.в = 2,74; Аа=2,74. 7.6.
i (/)= 14,1 sin (103/+45°)+9,7sin (2Х
X103/+ 166°) + 4,7 sin (3.103/—45е) A;
/=12,5 A; uR^ 141 sin (103/ + 45э)+ Рис. 0.7.2
+ 97sin(2-108/ + 166°)+47sin (3- JO3/—
—45°)B; £/p=125B; ut (/) = 71 sin (IO3/+ 135=) + 97sin (2-I03/- 104°) +
+ 71 sin (3-103/+ 45°) B; UL = 98,5 B; (/) = 212 sin (103/ —
475
—45°) + 75 sin (2- IO3/ + 76°) + 23,5 sin (3-IO3/ — 135°) B; (7C = 170 B;
P=1580 Вт; Q —1230 вар; 3 = 2060 B-A. 7.8. uBHX (/)-0,955 sin (106/— 90“)+
+ 0,59 sin (2-10е/—146°20') В; (7ВЫХ=0,794 В. 7.9. iL (/) = 10+ lOsin (co/ —
Pkc. 0.7.3
— 30°)+2,24 sin (2oj/—1I6°35')A; l^= 12,3 А. График Q.= /(co/) показан на
рис. 0.7.2. 7.13. ц (/) = 50+30 sin (1000/—60°)+100 sin (5000/—90°) мА; <2(/)=
= 50 мА; /^1 = 89 мА; 7^2 = 50 мА; Руу= 0,25 Вт. 7.14. ij (/) = 0,562 sin 3000/ +
+ 0,333 sin (9000/—135°) A; i2 {/) = 0,062 sin (3000/ —180°) + 0,333 sin (9000/ +
+ 45°) A; i8 (/) = 0,5 sin 3000/ A; lAl = 0,46 A; /»,= 0,243 A; 7^,=0,354 A;
t/r. = 108B; t/y =35,4 B; Pw= 12,5 Вт. 7.15. uc (/) = 100 К 2 sin (1000/ +
+ 75°)+200 sin (2000/ —135°) B; U v=
= 173 В; PWr=500 Вт. 7.16. umn (/) =
= 42 sin (co/ + 92°44') + 44 sin (2<d/—
-177 24') B; Umn = 43 В;Р^=9Вт.
7.18. (7V=24,2 В; 7Л=1,73 A. 7.19
Рис. 0.7.3, a. 7.21. Рис. 0.7.3,6
7.22. L+, = 50B; L+, = 40 КЗВ. 7.23.
*л<1)=^«ЗА; 7ffl(S)=8,5A. 7.25. iA=
- iCA = 2,42 sin (<0/ + l°10') +
+0,48 sin (5(0/ —1°10') А; ip = ipc =
= 3 sin (со/ — 72°) + 0,77 sin (5о>/+72е)
A; i'c=5,Isin (<0/ +135“)+1,02sin (5o>/—
— 135°) A. 7.26. (7V=14,2 B; iA=
= 8,5 A._7.27. Uv=47,8 B;_ 7Л, = 26,2 A; IAt=J,17 A. 7.28. uEC(t) =
=1001^3 sin (co/—90°)+30)^3 sin (5<o/+45°)+ 20 к 3 sin (7(0/— 30°) B. 7.29.
ip (/) = 30sin (co/+150°)+12sin (ScoZ+SO0) A; 7p = 22,9 A. 7.31. /(/)=
= 0,448 sin (10е/+ 26°30') sin 10е/ A. 7.32. Рис. 0.7.4. 7.33. 7 = 0,075 A;
(7 = 2,14 B.
Г лава восьмая
8.1. nc(0+)=100B; ic (0+) = —0,1 А; ис (/) = 100е“10‘х В; ic(/)=—0,1Х
СО
Xe"10*rA; IF= J Р<2Л = 0,5С«2=0,5л10-в Дж. 8.2. 1. а) «с(/)=100(1 —
о
— е-10,/)В; i(/) = O,2e“10**А; б) нс(/)=100В; «(/) = 0; в) ^с-(/)=100 —
— 200е“10,/В; i(/) = 0,4e“10*x А. 2. a) кс(/)= lOOsin 103/ В; i(/) = 0,2x
Xcos 103/ А; б) «с(/)= 100 sin 103/ + ЮОе-10*' В; if/) = 0,2 cost О3/—0,2е“1оЭ/ А;
в) ыс(/)= lOOsin IO3/— 100е~10,/В; f (/)=0,2 cos 103/+0,2е“1о’/А. 8.3. а) «с(0=
= 100е“100' В; fi = —0,1е-,<,0/ A; i2 = 0,le“100/ А; /8 = —0,2е"1О0/ А; б) ис (/)==
= _ 100+ 200е-1О0/В; it=—0,1—0,2е-1ОО/А; /2=— 0,1+O,2fe"looxА; <8 =
476
= —О,4е~100'А; в) uc(t) =—1004-ЮОе"10°' B; £t=—0,1—O,1e-too/A; t2 =
= — OJ+O.le-100' A; is ——0,2e~*oo/ A. 8.4. a) uc (0 = 75-75e-,o,/ B;
«c(0^0.05e-1B,/A; 6) «C(0=9O—6Oe“’40' B; ic (0=O,O375e_*4,>/A.
8.5. 1) uc(0 = 2O—20e-100/B; in (0 = I — e"100' mA; ic (0 = e“io0'mA;
2) uc (0 = 20 sin (100/—90°) 4-2Oe"100* B; Q?(0= 1 sin (100/—90°)4-e“1<MU mA;
. —— t
(0 = 1 sin 100/—e-loo/mA. 8.6. a) (0 = 20—20e B*8 B; i (0=0,0408X
-—/
Xe e'e A; 6) uc(0=2O—2Oe“100' B; i (0 = 0,04e*100' A. 8.11. a)»(0 =
.. »
« lOe-10*' A; ul{1)=L~=—lOOe-10*' В; №л= J ^£эЛ=£»2(0)/2 = 0,05 Дж;
0
GO
9=С/а/=^^=^^=103 Кл; 6) /(')=—JOe"101'A; «L(0 = lOOe'104 B;
J A A
0
в) i = 0; W7 = 0. 8.12. a) i (0 = 10e“6l°4< A; uL (0 = —500е“ь'гО4 В; иЛ(0 =
= lOOe"610*'В; u/ji (/) = 400e“6‘lOV В; 6) i (/) =— 24- 12e-61°4' A; (0 =
= —600e'6-‘o,/ В; «Л(/) = —204-I20e-6,I°4' В; •мЛ1(0=—804-480е-5'104,/ B;
в) <(/)= —24 2e"61°4' A; uL(t) = — lOOe-410*' B;u/? (/) = —2O4-2Oe“6-104 B;
и/г1(/)=—804-e0e“6”°‘f B. 8.13. a) x£(f)=x (0 = 10— lOe"10*' A; uL (0 =
= 100е-'°д' B; 6) t£{0 = 2O—IOe"lo4/ A; uL (.0 = 100e"™4/ В; в) /£(0=—ЮХ
Хе“104'А; «£(/) = 100е-124/ В; г) /£ (0= 104-Ю К2 sin (104/—45°)-|-10 X
Хе-104 A; uL (/) = 100 2 sin (104/4-45°) — lOOe-104 В. 8.14. a) i£(f) = 10 —
— 13е-10*'мА; пуИ(/) = Л1-^=500е-10*/ мВ; б) /£ (/)= 10 sin (KW4-90°)—
— 10е*10*'мА; им (/) = —500sin 10s/4-500e-10S/ мВ. 8.15. а) <£(/) —3—е_< А;
4(0 = 1,5—е-< А; б) /£ (0=2—е~^3 А; »л (/) = 1 4-2,ЗЗе~//3 "А. 8.18. а) При
0^/^Т i(/)=!— е~104' А; «Бых (0 =L-^-= Ю0е"1О,/В; при /^7/(0 =
= (|_e-lo’r)e-l0*(Z-r> А; ивых (0=—100(|-е-1О’г)е“1О,</" Т} В; б) при
О^/в^Г (?м. ответ для п. а); при t^T i{t)—2—(14-е-10*г)е-101^_Г> А;
«вых (0 = 130(14-е“10,Г)е-10,<,-Г> В; в) при 0<;/<;Т см. ответ для п. а);
при t^T »(0=-14-(2-е-1О’г)е“1О,</"Г)А; нвых(0=-1ОО(2-е"10’г)х
Уе-юЧГ-П в 810> а) При о^/<0 i (Q = ю/з sin(103/—45°)+ Юх
Хе-1®4 А, при /^/j (= 1О,42е~10*А (рис. 0.8.1,а); б) при 0^/^/£
(см. ответ для п. а); при /(/^Ю^З.бе"10*4*-*11 (рис. 0.8.1, б).
8.21. иС1 (0+) = 100В; «С2(0+) = 0; q (0+) = (2 (0+)^=0,1 A; ia(0+)=0;
477
^(O+)=—/l£±L=_iOOO B/c; ^(O+)=i^-=lOOOB/c; -^(0+) =
u* Cj al Cg си
« -2 A/c ; ^(0+)=-3A /с; ^?(O+)=lA/c; «C1=72,56-®-*+27,Se-^B;
uc3=45e-3-®'—45е-2в’2Г В; ir =0.0275e-’-®%0,0725e-=«-* A; Zs= —0,0I7e-3 ®%
4-0,ll7e-2®-s* A; ig=—0.0445e-2«-^ A. 8.22. а) нС1(/) = 10—7,25е-’* —
—2.75е-2б»В; — 2.75е~39<—7,25е"2в« В; i, (Z) = 0,0725e~38* +
4- 0,0275е-8И* A; i2 (/) = 0,0275e-3e#+0,0725e-M2f A; i3 (/) = 0,045е-ЗЙ* —
— 0.045e-M2< A; 6) uCi (0 = 10,5 sin <100/—72е)-f 5,77e“38'4-4,23e‘2e« B;
1з=С—*i=(e—ИС1)/Я; ia=it—t’2; ucz~uci—Rtfs- 8.23. a) uci =
= 100— 40e-M0* В; «Сз=40е-е3-3* B; »j = 0,08e”10D< A; i2=—O.le"83-3* A;
6) wCl=86,5sta (100/—88°)4-36,3e-10W В; uCa=— ЗЗе”83-34 В; h =
= 0,173 cos (100/—88°) —0,0726e*10cf A; i2 = 0,0825e"83,sf A. 8.24. a) i\ =
= 7,25e~38t+2.75e-2e2* A; i2= ll,75e-3*'—1,75е-2Ш A; i3=—4.5e“s®* +
+ 4.5e-2«< A; uli=Lx ; tt£a=L8-^ ; 6) G = 2,75e-®*'+7.25e-2«* A;
i2=4,45e-^—4.45e-2’« A; i3=—l,7e_38/+il,7e“2Mt A; uLV= —10.5x
Хе-з«—[89,5е-2в2* В; u£a= — 17e~®«+ 117е~2В2‘ В; в) G = —4,45e-33*4-
4-4,45e-2<« A; ia=—I .бОе-38^ Il,69e-2e2‘ А; 13=2,76е-8в*+7,24е-М!« A;
«11=^-^: «12=^^-- 8.25. a) B;
6)uet(0=—10e-MootB. 8.26. a) Q=—»c=—0,334e”°,5‘I044-l,334e“2‘l0<< A;
Wc=—66.7e”0'b'10*'4-66>7e“2'10*/ В; uL= 1б.7е"°1Ь*1о4<— 266,7e“a10*';
= — 115,5e“610>/sin5/3 ИО3/ В; в) iL=— ic = (1 — I0‘/)e-lc‘f А; ыс =
= —lO’te”10** B; uL=. 8.28. a) uc (0+)=0; iL (0+)=0; i (0+) = tc (0+) =
= 5A;«£(0+)=50B;^(0+) = 5.103A/c; -^-(0+) = 0; (0+) =-5-10® A/c;
б) и в) «с(°+)г100 в» к(0+) = 10 A; i(0+) = ic(0+) = 5 A; Ul(0+) = 50 В;
-^(0+)=0; ^(0+) = 5.1(Я A/c;^(0+)=-5.I03A/c;r)uc(0+) = 0;»i(0+)=
= 0; ic(0p = 5 А; £(0+)=-10А; ^(0+)=^(0+) = 5И03 А/с; ~-(<М =
= —104 А/с. 8.29. а) Р1=—Ю^*1; ра=—3- lO’c"1; ilce (0+)=0; иСса (0+)=40 В;
б) Pi^-O.S-IO^-1; рв = —5,9-103с-1; »£св(0+)^0: иСс8(0+) = 80 В; в) Pi =
= —1,31 • Ю’с-1; ра=—2,29- 103с~»; 11св (0+) = 0; иСсв (0+)=53,3 В. 8.32. pi,2=
йН V 4^-Й 1 а> ‘i=We— »“-1.07е-“—'А;б)<£ =
=].2e-10^sln(5300/4-56o) А;в)/£~---e’ilic* sln( 1/
V L/C \T LC VnR J
8.34. а) При Z=0_ wci (®-)4“ttC2 (®-)~1~^сз (®—) = wc*(®-)=^b где
Oci(<’-) = K-^-£i=50 В; »c,(0_)=0; пс,(0_) = —£,=50B, При«=
Gj-j-Ca Gj'j-Ga
= 0+, согласно законам сохранения заряда, для узла 1
Ci«ci (®+)—(Р+)=Cluci (0-)—Ctficz (0_);
для узла 2
Ctfics (0+) — Сз«с» (®+) ^2ИСЗ (0-) — ^»исз {0_).
478
По закону Кирхгофа, для емкостного контура
vCi (0+)Ч~^С2 (0+)-1~иса (0+*) == —£• (3)
Из формул (1) —(3) следует, что wpi (0+)-0, пс2(0+) =—в* wcs(0-i) в
= 0. По закону коммутации, i/d (0+)= (0_)—£i—100 В. б) При /=0_
it (0_) = i2 (0_) — 0; is(0j=E;/?s-4 A; t4 (0_) «= E/R> = 4 Л. При /=0+, со-
гласно закону сохранения потокосцепления, для двух контуров
(0+)—t2i2 (0+)= (0_)— I2f2 (0_); (la)
£гЧ (0+) 4“^3*3 (®+) — (0—) (0—). (2а)
По первому закону Кирхгофаг для индуктивного сечения
- Ч (0+) - Ч (0+) + 1з (0+) = /. (За)
Из выражений (1а)—(За) следует, что i2(0+) = 1 A; i2(04)=1 А; 13(0+)=ЗА
и, по закону коммутации, i4 (0+) = i4 (0_) =4 А. 8.36. a) i2 (0= !,5е“1Л^ А;
225е-10‘* В; б) i2 —0,5е~101/ A; ui2=(L2-M) =
= —25e“lo4f В. 8.37.а) 4 = I— О.бе'1®’* —O,5e~3'lo>< A; is= 1—0.5е~103* 4-
+ 0.5e-S IO’f А; б) i1== l-e"1’610*' A; i2=l А; в) h« 1 -О.бе"™* А;
i2=l+0,5e-«°i А. 8.38. а) «с=50— Збе-8*00* В; б) = —50e~S50D/В.
8.39. а) нС1 = 160—120е~2Б0« В; Wc2=404-120e“S5W,t В; б) иС1 =
е=200-160е-20<м,/ В; цС2= 16Ое-*000* В. 8.40. Z(p)=-#4-^; Z(p)=/?4-p£;
pG
= T+pC-
RLp
R-\-pL ’
z(₽)=ira+pLl+£: yW=4+^: YW> =
+4+₽C: rW=-7—4-44------BoT’
P 'г<₽с+4т+та:)+1
дельных RC-t RL-цепях переходные процессы происходят, а в общих —нет.
... ^(Р) R*LP . <МР) R^p
8.41. а) ———----------------------ГТ' б) "7~ ТЛ -----------ПТ •
,(₽) ЯЛ+<Я. + Я.)(р*-+^) 1W +
8.43. а) /(р)= р(р^_ х00> ' 40 = 1—« 1м( А; б) 1 <Р)=(р_|_2О0) (р+100) ’
А; в) /(р)= р8 J”l00y : А:
Г> /^°(р-Х)^+<1^0) = 40 = 1 sin(1(X)/-90") + e—«А.8.44.a) U2 (р)=
«.(П-Юа-^В; б) t/«W = (pq.25(^+-i68)! М') =
с200е~1м|—200е-ио< В; в) ; ».W=-^ X
Xsta(10«+135-)+5e-»«B; г) <7, (,»=__ ; М0=-р^Х
X Sin (100/4-45°)-5e-w°f В. 8.47. Для а) и б) / = V— 5 а) * (0 =
К -\~pL
=e~JM* А;б) i (/)=—Ц 2е“1C0f А; в) /*(р)
£2 (Р) + /^i(0) 200-г-/' (р+ 100)
/? + р£ (р-/100)(р+100) *
<(/) = ! sin 100/4-е“1М# А. 8.60. а) (Ях-|- R2+RJ 1и (р)-^/22 (р)- ₽2/за (р)=
479
= f lp\ —#1/ц (p)-|- f + pL + “7^ Лг(Р)—77' Лзз (p)-- (0);
—Яг/ц (p)—^2~\~^3-i”Z7^\ ^зз(р)~~~—» где Zji (p); Z22(p);
\ P^~* 1 P
E
/33 (p)—токи внутренних контуров; uc (0) = U42 (0) =-5—т*н" ^з! Q (0) =
Кз ~Г/<4
Е
— ~——=-. б) Решение аналогично решению п. а). 8.51. а) £Л2(Р)=
Кз~т “4
pin\ 1 j ‘7(0) ।_____lic (0) । j /_\
- Р' R, гда £w = £/p; /(р) = у/р;
ЯГ"*"рД+Я2"''«з f 1/(₽Q
, _Е_, UL (0) t/c(0) J_ j«.
lL (0) = J; Uc (0) = RJ;6) U„(p) = p(R,+tlpC} ‘ p-fv.
Ri ~^~pE~\~ /?2~1”Яз4- 1/pC
где<£(0)=1п>(Л„); /£я = /яв_р^!«^—Uc(0)=Im(£/c„); £(₽)=
Em .LiL(0) uc(ty .;J
;E •}/„]- #s+p£ P + I/(pO] P
-/j.-'(P)-^^.b)£/12(p)----------—- t t--------
Ri Ri~j~ pL /?з+1/(рС)
где ECT = Eme^£; i/.(0) = J; ис^)~Ег J. 8.53. Для рис. 8.30, a g(t)= ,
= ^e"e/; k(t) = e~6t\ 6=-^; для рнс. 8.30. б g(Z)=^ (1 —е"в/); Л(0 =
= 1— е~б/; 6=/?/£; для рнс. 8.30, в g (i) = ^-е~б/-. A(Z) = I —О.бе"^; б =
zz<
__ I • __________ с On - — /л ___ 1 ft бА. l/д пс ft ЙА е 2/?
для рис.
для рис.
8.30, д g (0—•“£ sin ioof; A(Z) = cos(o0Z; o0 = -^=^-. При Z^0+
8.30, a ka(t) = k' {t)= — 6e~w; для рнс. 8.30, 6 = Be"6f; для
рнс. 8.30, в ka (/) — 0,58e_fi/; для рис. 8.30, г ku{t) = — 0.56е-й<; для
рис. 8.30, д, ku (/) = — (00sino0L 8.54. Для рис. 8.31, а Л/ (/) = ~1=^е-вг;
— e"fiZ; б=₽/Е; для рис. 8.31, б Л,-(/) = /? (l—e"fl/); Л (/)=
«I
= е б/;6=^С; рис- 8-31, ° h (0 = 0,5 (I -е-6');
б=^; для рис. 8.31, г k,(t) = R (1-0,бе"6'); h (/) = 0,5е’д/;
8.55. Д»я рис. 8.3!. aeiaW = ^_+(J--^-)e-»'; 6=^;
для рис. 8.31. е 6=^^-. 8.56. Для
рис. 8.30,а а) н2(/) = — 100е-< В; б) иа= 100е-<*-*.> В; в) и2= 100(1—е~П В;
г) «2 = 200е-2*—ЮОе-* В; д) и« = 200— 200/ — 100е~< В. Для рис. 8.30,6.-
а) «а= -100(1 -е‘Э В; Q м2 = 100[1-е-(,-'*>] В; в) «а= 100/-100(1-е~Э В;
480
г) 100е-* — lOOe-2' В; д) н2 = — 1004-200/— 100/*-]- 100е“* В. 8.57. а) нвх =
=Юе-10М В; i£ = 0,l (1—е-100<) А; б) ывх =20(e“lpw—e-wo*)— 1000/e“lcW В;
I О*
/д= 10/₽-100*4-0,1 (е-«оо*—e loof) А; в) uBX sin (100/4-45°) —5e-loW В;
— -yLsin (100/—45°)4-0,05е“100* А. 8.62. В общем виде выражение для
напряжения на выходе для случаев а) н б) имеет вид: при O^t^/j u(t, п)=
= £4-[«(’О—£]е“бт; при /х^т^Т л(т, л) = [£(1—ей/,) + н(п)е-вг*]х
Хе“б<т~Ч где tzn=aq—а — Е (l — е-в/1) 6 = е“6^е-
т = /—пТ—время, отсчитываемое от начала Л-го периода; k—л4-1 (п =
— О, 1, 2. 3, ...). Установившийся режим соответствует л—► <». При решение
п. в) необходимо учесть н40п—реакцию на скачок £-1 (/). а) При 0е^т«^/1
л(т. л) =100 4 (76,5 (1 —0,67")-100] е~10ОХ В; прн t^x^T и (т, л) =
= [27,34-55.7(1—0,67”)] е"160^-210"*’ В; б) при 0<t^/l и (т, л) =
= 1004-[44.6(1—0,67")—100]е“,вот В; при t^x^T и (т, л) = [184-36,5х
Х(1___0,67”)]e_lв0(т”1‘26'l0~^, В; в) решение есть сумма решения п. б) и
нДоп(т. л)~ 1ОО[1-е"100 tt+2-5 l0*n)] В. 8.63. При О^т^Т /(т, л) =
= 9,8 {sin (2510т 4-Ф—<р)4-51п(ф—Ф) [14-3,3 (1—0,535”.)]е“воох}, где т —
время, отсчитываемое от начала Л-го интервала длительностью Т, А=л4-1;
л=0, 1, 2, 3....Установившийся режим соответствует л= со; <p = arctg^^=
Г\
Т
=78°55'. Среднее значение тока в установившемся режиме /Ср=^* \
о
а) ^=-“^31,8 А; б) /ср=0; в) /ср=^-=6,35 А, где г=К/?2-H<V-)a =
г 31К г к Л2
= 10,2 Ом. 8.64. Для рис. 8.37, а и любого fe-ro интервала времени, когда
k— л4-1; л=0, 1,2, ..при 0^тг^7 ц(х, л) — (л4-1) £44^(«) — («4-1) £|е-йх,
где x — t—пТ—время, отсчитываемое от начала fe-ro интервала; и (п) — напря-
жение в начале Л-го интервала, определяемое из разностного уравнения и [л4-1 ]—
— Ьи [л] = а(л4-1). в котором д=е~йг; а-£(1— е~6т); и |л] —
V о гп~1агг а(п-|-1) а(1—Ь” + 1)
= 2- ------(|_h)> • в Результате получим «(/)=
= Е | (п +1)- Де-бг е
довательность импульсов представим как сумму ступенчатой функции
£
(см. рис. 8.37, а) и напряжения мВх дог =-а суммарную реакцию —как
сумму реакций от ступенчатого и косоугольного воздействий. Реакция на сту-
пенчатую функцию найдена в п. а). Дополнительная реакция пДОп (Л =
= ^0—е-6Г)—Для рис. 8.37, при 0<;т*С.Т н(т, л) = £е-паГ4-
4-[м («)—£е~паГ]е_вт. Разностное уравнение имеет вид и[л+1] — Ьи [л] =
=де-паГ, где й= е“бг; и [л] = У. Res, г —r=a—f——; а=£(1 —е"дг);
(z—о) (г—с) р-—с
n -оА-
. Для рис. 8.37, б заданную после-
с—е 'х,т. Следовательно, н(/)=£<е
е“вг__е~аГ
481
лГ)| 8в5 Для рис 838(О — — с{/?1 +^-ис4-
। К. , Я® . RiRi . av> a &1
+ C(Rt+R^' U*~Ri + RiUc+Rt+Rii' РНС* ,38* 6 dt ~
I RiRz . ( 1 R RiRt . । Rz
L Ri+Rt tL^T Ri+R** Uz~ Ri+R»il^ /W/‘
8.67.
Уравне-
ние состояния цепи имеет вид
Г 1 1
С Ri + Rz
1 r9
L /?2“Ь/?3
1 Rz
С Ri~i~Rt
1 I n , R3R3
fc
Я1+Я3
Rs
R3+R3
Rs
Pi-f- R»
Rs
Rs~i-Ra
R2R3
Rz~i~Rs
8.69. Уравнение состояния цепи имеет вид
Г 1 I Ус
где [*]= j
^=1лщг]-нлпи,
С Ri-^-Rz
1 Rs
I Rs 1
[Af]=
1 Ri
С Rz^R9
( n I R2R3
RzRs
— Г°
~ 2 —2
41 <
. Собственные значе-
L Ri-\-Rs-
иия Ki матрицы [Л1] совпадают с корнями характеристического уравнения P(Z)=0;
PW = det(Ml]-W = det(x[* ®]-[J t£]) = det[(>+2> (^] =
= (X4-2)(A-|-6)4-4=X-s4-8X+16=0. Отсюда KiiZ= — 4. т. e. корни уравнения
кратные. По формуле Сильвестра для кратных корней (s=2),
е(Л1] i-----1 Г
(S-1)!
<
d r<A*Adj(Ml]—Wh
е-« 4/е-« -1
« (1 —2/)e-«J*
2 4
О
I
л
П
!
(2-1)1
482
Переходную матрицу 1 * можно найти и из вира кения е^м = а0 11]+»1 [Л1 ],
где а0, ai определяют из решения уравнений е~**=-а0—4<Xi;
de** I ..
— -te-V-a.!.
at ]?.= - 4
Отсюда cci=/е-4<; a0— (1 + U) е~и- Следовательно, е[Л^ (I -j-4t) e”4*
f[-2 4] [(1+20 e'4' 4/e~4<
Г 1—1 —6 “ -te~*i (l-2/)e-
а) И-е-'^‘х
X e^MJт [АО [г] dr = (er^IJ *— [IJ) [M1 pV] [г}—см. решение задачи 8 68р, слу-
о
чай б). Таким образом,
[1 0Ц±[“е — 41 ГО
[О 1JJ 16 [ 1 —2J [2
t
= е>* [х (0)] +е-* J elM3 т [JV] [z] dx,
с
[Г(1+20е-« 1
|| (1 —20e-**J
15+(-15+200 е-« 1
—2,5+ (2,5+100 J ’ J1 J~
4
—2
где e[AIj * [х (0)} =
10е-«*
8.70,
Г (1 + 20 е~4< 4/е-« 1 Г 10 ‘
[ —/е~« (1 —20е~«] [—5
Просуммировав эту матрицу с матрицей, полученной при решении п. а), получим
г 154-(—5+200 е~« |
: [—2,5+ (—2,5+ ЮО е~‘* J ‘
Г(40е-^—32е~«—2e-w*) 1 .
[ (8е~в*—3e-1B0 J ’
(10е-^~ 4e-ef—1е-18') *
л
L J
0? ’
L«l J
J
10e-‘<-
—lOe-^ .
0
(_ 8е-«+8е-1в*)
_ Г(40е-«—^е-®^
> I_ \ v у
J 20 -в!
L з J
^10е-«~е-«У
= (—10е-^+10е-«0 ;
L зе J
с! Г(40е-«—10e~16i 1
t]“L 15е-«ф
г (Юе-**+ 5е-»<’
= (—10e-4«+10e-Je< ;
_40е -м*
40е-«1
О I ’ С
J J
Решения п. а) и г) указывают на существенное влияние начальных усло-
вий на характер переходных процессов. В случае а) решение содержит при-
нужденную составляющую и обе компоненты свободной. В случаях бу—г) реше-
483
ния вырожденные—отсутствует одна [случаи б), в)[ или обе [случай г)| компо-
ненты свободных составляющих. В последнем случае принужденный режим на-
ступает сразу после коммутации. Кроме того, во всех решениях £/. и не
содержат принужденной составляющей. Это объясняется своеобразным свойст-
вом схемы—контур Я 2/?2С имеет коэффициент затухания 1/(/?2-Ь₽з) С = 4с-1
такой же, как к коэффициент затухания е (О- 8.71. Переходные характеристики
цепи [п. а), б)] для выходных величин вычисляем по формуле [см.
решение задачи 8.68р, случай б)] [у] = [Р] (e^J*—[[]) [ЛГ] [z], где
ГЛЛ1 -Г ® 1 . 1 Г—18 —Г ЛЛ1 Г 0 1
W 1—3 —18J ’ 96 | 3 — 4 J ’
ЯЧ Г Г(0.25-0,1е-»'-0,15е-^) 1
} I “a I L (— 0.2е-* + ка!-«9 J*IW’
m ГО? I Г(0.5-0,!е-«+0,1е-1«) 1
f L“L J ~ I (—0,2е~в<—0.8е-«0 J ’ 1 ь
Импульсные характеристики цепи [см. п. в), г)] для /^0 находим диф-
ференцированием переходных характеристик с учетом того, что ~ 1 (0 = 5(0:
f (t) 6(0 = /(0)6(0- Их можно также определить непосредственно из общего
решения:
t
[х]=е<№* J e-^IAqecO^ef'^l/q.l (0; [у]ЧР]е^И[ЛГ]-1 (04-[Q]5(0-
о
[ iR 1 _ Г (0,6е-**+2,4е-”*).| (0 1
7 I «1 J~L>-6(04-(l,2e-w—19,2e-le<)*l (0 J’
. Г iK 1 Г°,56(О + (0,6е-«— (0 1
П L«£j I—!6(0 + (i.2e“«+12.8e-w<).l(0 J*
Для t > 0 члены, содержащие в решении импульсные функции, отсутствуют
8.72. Уравнение состояния цепи имеет вид
о з-
—3 3
484
Собственные значения Хх матрицы (Л4] определим из выражения
Р (X) = det (X [ 1 ]—[ MJ) = det
“(Х+3)
О
_ V3
О
(Х+3)
1/3
откуда Х1 = —1; Хг=—2;
где [М]2=[/И] [М]=
- (Х4-3) (Х®+ЗХ+2)==0,
-з
О
_-1/3
Хз=—3. Матрица efA,J*= «.[IJ+aHMJ+aHMp,
0 3" -—з 0 3" - 8 —i —О'
—3 3 0 —3 3 —1 8 —9 .
—1/3 0_ —1/3 —1/3 0. 1 1 —2
Находим Oto, осмоса из решения уравнения е 1 =а0*1-Ьа1Х,-Ьа2Х| при 1=1, 2,3.
В результате получим
— 4-е-Ч-е-**—4е- м W- ~ e-q^-lе" (Зе'«-3е29
X а 1 \ л» L !
— 4-е-Ч-е-2/~е"а<У—4-e-f+e'W+4-e"3'V3e"t-3e“s0
-Т'-'+Г”* ) (-уе-‘+4е-«) (2е-<-2е-«)
Решение для а) и б) имеет вид [х]=егЛ11 1 [х (0)]. Для нс (0) =0; иС2 (0)=0;
ȣ(0)=0
для «С1(°)=1; «сг(0)=—1; *7(0)=о
«С1
псз
Jl -
- 1е-3*-
_1е-зе
0
При 1^0 + решение имеет вид [х]=ef A,J<(A7J [(см. ответ задачи 8.71, случаи в) и г)1.
Для е(0 = б(0* / (0 = °
дл я е (/) = 0; / (0 = б (/)
“с.
“са
JL -
"(Зе-* + 6е“Ч “
(_Зе-«4-6е’«)
_(—2е-*Ч-2е-2*)_
В задачах 8.69р—8.72р числовые значения напряжений даны в вольтах,
токов—в амперах.
8.74. Дифференциальное уравнение цепи (/?1Ч-/?з) L-^-^RiRtUa — RzL^-\-
+ RiRsP* нли в числах ^^4-H2==54-3,75e_0*!f.
Напряжение «а(0+) =
Ра+Рз
е(0+) = 5.
485
Программа М! (см. приложение 4). Ввод: /о=0; 6=0,25; хо = 0,25;
х0 —н(0) = 5; 1; а=—0,5; р = 0; А = 3,75; В =5.
Результат счета:
tn. с . . .0 0,25 0,5 0,75 1 1,25 1,5 1,75 2 2,25 2,5
п2, В . . .5 5,75 6,26 6,59 6,79 6,89 6,91 6.88 6,82 6,73 6,63
8.75. Дифференциальное уравнение цепи
(/?,+/?,) IC^f+[Z.+(i?1R,+R2Rs+K,R1)C]^ + (i?i+R2)«c=R^,
или в числах —480; ис (0) = х- ел (0) = 10;
at* at
^£(0+)=^i^=0.
и» 1-*
Программа M4 (приложение 4). Ввод: /0=0; Л=0,01; хо=«с(0)=10;
fo=^(O+)=O; а,=22; о2=96.
Точное решение: пр =—5-[~24e-ef—9е~1в*.
Результат счета по программам М4 (вторая строка таблицы) и Мб (третья строка):
Г„. 10-», с .... 0 1 3 5 7,5 10 15 20 25 30
хп^иСп, В.. . .10 10 9,6 8,85 7,71 6,37 3,7 1.47 —0,26 —1,56
хяр=пСл. В. . . .10 9,93 9,48 8,74 7.59 6,35 3,94 1,86 0.19 —1,1 ;
Примем а и и е: 1) В первых четырех столбцах 6=0,01, в остальных 0,025
2) для сокращения записей часть значений не приведено.
8.76. Дифференциальное уравнение цепи r6i£ = 0.
Начальные условия: х0 = iL (0) =0, (°+) — > где i/д (0+) =
= — «С1 (®+)— uCa(®+)~ I*
Уравнение цепи
d?if dur ,n . *0,(9+) “Ci(°+) «с2(°+)
------с;--------с^=_^сГ+"адГ=3-
Определение корней см. контрольный пример программы М8. Расчет x=q
дан в программе М7. Ввод: fo=0; 6 = 0,1; х0 = 0; Уо=-—1; z© = 3; а=6; 6=11;
с=6; А=0.
Результат счета:
tn, с........ 0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8
хл = »д(/п), А. 0 —0,1 —0,17 —0,217 —0,247 0,262 —0,269 —0,269 —0,263
0,9 1
—0,253 —0,24
8.77. Представим зависимость и (/) дискретными значениями с шагом 6 = 0,1 с
в виде таблицы, где п—номер дискреты; и (/„) — напряжение на входе в мо-
мент времени — —ток в момент времени tn. Результат счета (см.
программу М10):
п....................
tn, С................
«(in): В.............
Xrt — t (/п) А . • .
0 I
0 0.1
0 5
0 0
23456789 10
0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1
10 8 5 2 0.5 0 0 0 0
1,84 4,36 4.55 3,51 2,02 0,93 0,34 0,13 0,046
Начальный ввод: у0 = 0; fo = O’t 6=0,1; х=1с (0)=0; а= 1; ах=—1;а = 10; м0 = 0;
ui = 5. Ввод после первого счета: п2 — Ю (в ячейку памяти П9); ввод после
второго счета: «3=8 (в ячейку памяти D9) и т. д.
486
Глава девятая
в. I. Л(М=7р-^
1
; фаИ =
a)X(w) =
— — arctg о/2; б) К (ш) ~ —г — ; Фа (о) = — arctg to. 9.2. Y (jo) = 1 /₽;
V i-rto2
К (jto) «= joL/(R Jto£). 9.3. Z (jo) = R (to) 4 jx (to) = z (to) cos <pz (to) 4-
+ p«o)sin<M«). 8.3. К0“)=-£^=4тНпЖ: KW=|K(MI=4-:
Ф* (0>)=arctg (—4^)— arctg^=—2arclg^; 6(и)—=
2L/R
9.10. Z (jo) = R (to) 4-/Х (to) = 4
' R^
to
Фз И “5 *3 (<°) do—ot3.
о
g _________Р
+ 'll. '2Т2 • Исключив to в выражениях R (о) и х(о), найдем зависимость
x (to)=f [/? (to)]. В результате получим урав-
нения окружностей, в соответствии с кото-
рыми строим кривые (рнс. 0.9.1). 9.11.
Se(co) = Ле~°'6(Л о)1. Ширина спектра 2//j
обратно пропорциональна ширине импуль-
са 2tx. т. е. короткий импульс имеет широ-
кий спектр, а длинный — узкий, a) Se(a) =
= Л; б) S* (о) == 2лВб (со). 9.12. е (/)=
л=а>
— — У2 Sin 0’5ntD^i c~/0.5mt>t/,(JnB>i/i где
Яп^« п
jXfa»
4?=Z7
-I
&
О 0.5 1 1JS 2 2,53 R(U)
Рис. 0.9.1
4г
5
\ C\
•E
C 2S.22L HL
T tt if
•О 2Я
— , JttUlfVlThrtTr»____ Л.
пш^п^. 0^ & flUfn—
' Н1Ш^ПМПГК
О 2K W пб)гП‘
L ?LiiLiTlni1
HQJfn^ 0 gr to nw?r№o 2Я 41Г
tf tt tf tf
S) 3}
Рис. 0.9.2
ПЫ;*П~£
I , пл ]
2E I2 I 9rr
tof=2n/T. 9.13. a) toi=2jt/T Cn = — -------; при 0 < иа, < ~ q>„ =
Tt n
пл 2л 4л
»= ~2~ i ПРЫ 7^- < ЛС)1 < Фп=о,5пл—л и т. д. (рлс. 0.9.2, о); б) С„=
487
I , лл|
2Е Is 4 - 2л .. 2л 4л
==----!------ ; при 0 < лох < — ф„=лл/4; при — < лац < — ф„ — пл/4 —
ЯП <1 *1 *1
— ли т. д. (рис. 0.9.2,б);в) рис. 0.9.2,в. Спектр становится более плотным, а
амплитуды спектра уменьшаются обратно пропорционально T/(2t]). При Т —- оо
спектр становится сплошным (непрерывным), а его амплитуды стремятся к нулю.
Поэтому вычисление амплитуды каждой отдельной гармоники теряет смысл. 9.14.
а) Рис. 0.9.3, а; решение аналогично решению п. а) задачи 9.13; б) рнс. 0.9.3. б;
в) если а площадь под кривой при этом остается конечной, т. е.
h
^e(t)dt=l [импульс е (/) имеет вид б-фуикции], то получим равномерный
о
амплитудный спектр (рис. 0.9.3, в). 9.15. По определению, средняя мощность
1 Р о2 °°
сигнала е2(/) = у \
о п=»
rt, гдеС_я =
Л— — <ю
+ » +/1/2
= С„. 9.16. S(/co)= ( е (0 е~/“* dt. Для рис. 9.7, а S (/со) = Ее~№ dt =
-« -г,/2
2л л
__ фя(ш) = 0; при
sinco/j/2 х lsinco/j/21
= £/1-TS^2-; 5<“>=£/*-Чп72 :П|
2л 4л . . „
— < со < —- (со) ==я и т. д. Для рис.
Еет№ di = Eixx
о
sin со/1/2 — 1<л#./2 о/ч r-j I sin co/,/21 2zl . . .
X <о^/2 e i 5 (<°) = ; при 0 < co < — ф5 (co)=o)/i/2; при
2л 4л , . ftoti \ - /sincof^X ,
77 < “ < 77 ’'<e) " т* a- Так как 1-777?-,Ur11 TO
S (0)= E (it), t. e. S (0) равна площади импульса. 9.17. Спектр можно опреде-
лить, применяя преобразование Фурье или преобразование Лапласа. Используя
второй метод, для рис. 9.8, а получим 5 (/‘со)=£ (р)р-»/ц= ~ ^2 ~а2—
со® 1
— / “П—5 > 5 (со) = — ; q?$ (со) = arctg (— co/а). Для рис. 9.8, б S (/со) =
. a j _ .о • ’ * • w *
1
, ж . / а .со
= Jim I -—— ) = Iim ( ——-—/—5—
а-+о\/“-Ьа/ а— о\<*>+а2 <о2 +
S (со) = 1 /со; ср5 (со) = л/2;
—оэ
Re [S (/со)] = лб (со), так как С ^&> 2=я; Im [S (/со)] =— 1/со. Для рис. 9.8, в
5(/со) = 1. 9.19. По теореме Рейли, энергия сигнала е (/) W ~ \ e2(t)dt =
— СО
4- CD
— С Sa(co)dco. a) S (со) = 1; Sa(co)=l и, следовательно, 1Г=оо; б) S2 (со) =
о
= -^2"(1 —cosco/i); W=E*tit в) ^(<0)=^^^
Г <оо/2 о0 П
Г) 1Г = — С Idco-f- f 2(1— ^dco =-Дсоо.
nJ J \ coo J 4л °
- 0 toc/2
1 Г cfco 1
л 2a '
0
9.22. R(T)=£o-b
488
p* pa
-I- cos COT 4—32 cos 2tox; e® (i) = R (0) = £0-|-£im/2 + £L/2. 9.23. R(t) =
£2
= -££ cos tor при любой начальной фазе гармонического сигнала. 9.25. Ре ,(т) =
А
г
~ lira \ е(0 i (t 4-т) dt. Для случаев а) н б) /?е,;(т) = 0 ввиду ортогональ-
с
ностн тригонометрических функций, входящих в подынтегральное выражение.
£ 7
в) Яе./(*) = т- cos (tor—(фе—ф;)]. 9.30. Средняя мощность определяется
значением корреляционной функции при т=0 (аналог теоремы Рейли): R (0) =
СО
If 15
= — \ G (to) dto. Подсчитав интеграл графически, получим R (0) = -i- G (0) tox.
nJ л
с
g0
9.31. и (0=4 У
a) и (t) = 1 + 0,9 cos (t — 45°'
4- 0,402 cos (3/ — 72°) -4- 0,25 cos (5t — 78°) В;
+ 0.565 cos (2/—63°) 4-0,286 cos (3t~117i) 4-0,175 cos (5/—33е) B. 9.35. SOi (fo>) =
= К (M SM (/co); SU3 (to) =-|Si”b9V21 t/=; <ps (to) =-£-arctg (-to). 9.36.
CD
По теореме Рейли, R,^} (со) dto. Так как St- (со) задано графически,
о
вычисление интеграла производим также графически, т е. строим кривую
Sa=/(to) и вычисляем площадь под ней. W=--------1 = 3,2 Вт-с. 9.39. По теореме
Л
Котельникова, это время равно’/г/с- 0-40- К = (/<о) =£С 1 *
Используя предельные соотношения, найдем й (0) — К (а>) = 1; й (со) = К (0) = 0.
9.41. tf(/to) =--L_
14~/ —
_________ а
k (о) = У GolGai (to). 9.44. При to < toc Ga> (to) =
= Gfll (to) Ao = Go& Raa(x) —i-
__ G0Ao<oc sin toct
Л tOcT
б)
. 9.43. GUi (о) = GUi (to) fc2(to);
wc
У G0£o cos от do =
0
co
2 3 nZfhtF, Гг
a) T
\ Jj Js
0 i
Глава десятая
ЮЛ. а) Удовлетворяют; б) не удовлетворяют,
так как Re Z (/«» = < 0 а
(18—3ur)2H-(D2 (24—о2)2
области 19,83 > со8 > 4; в) не удовлетворяют, так
как ReZ(/to) < 0 в области 22,7 > to® > 4. Ю.З.
Во всех трех случаях можно, поскольку нули и
полюсы расположены на мнимой осн н чередуются.
10.5. Из R и L. 10.6. /Может, так как нули pt = 0,
Рз — —Ю0, а также полюс р2----10/3 расположены
на действительной оси и чередуются, а ближай-
шей точкой к началу координат является нуль.
10.8. Является. 10.10. Z(p) =^il.
0
1
c
Я23ИИ
о)
coL _
0 1 2 3„2ГЮ3.С-*
пТ *
8)
Рис. 0.9.3
489
4 (пЗ-L П 1
10.(2. Y (p)= -. 10.13. У (p) =-------------------j-------
p{p f 2pJ--------Ц-------
10.15. Рис. 0.10 1, a.
4p 1 5
10.16. а) Рис. 0.10.1,6; б) рис. 0.10.1, в. 10.17. Рис. 0.10.2, а. Для п. б) деление
возможно только при расположении полиномов по возрастающим степеням р.
10.18. 1. Рнс. 0.10.2, б. 2. Рнс. 0.10.2, е. 10.20. а) Рис. 0.10.3, в; б) рис. 0.10.3, б.
Рис. 0.10.1
10.21. а) Рис. 0.10.4, а; б) рнс. 0.10.4,6; в) рис. 0.10.4, в. 10.23. В (со) =
= 4/W4-ш!). 10.24. о>В(И) = №/£. 10.26. z1=—+
Z<Zg akg (k«—^б)
ofee
. Физически
l-H*s-*«)2
Z<-1-Z5-J-Ze 1 + (Л$—Лв)3
Рис. 0.10.2
/
невозможно при Л* > а
реализовать Z; линейными пассивными элементами невозможно при > Л5, а
Z8 при Л5 > ks, так как действительная часть сопротивлений отрицательна.
10.28. 5 = а2/(а+1); с = [а/(а+1)1»; d = а/(а +1)- 10.29. Рис. 0.10.5, а.
10.30. Сопротивление после-
------, М=2 довательно соединенных
двухполюсников (рис. 10.4,
е, е) равно /?. 10.32. Рис.
] 0.10.5,6. 10.35. Выполняют*
ся; рис. 0.10.5, е. 10.36. а)
Соответствуют; рис. 0.10.5, в;
б) соответствуют. 10.38. Мо-
жет, так как у приведенно-
го в условии выражения нет
полюсов в правой полуплос-
а)
№ JL
М=2
/
О------
Рис. 0.10.3
б)
/
кости, нет полюса в нуле
к бесконечности, полюсы простые с мнимыми вычетами при положитель-
ном вещественном р; А^х = 0ч-1. До сокращения на общий множитель
.коэффициенты числителя не превышают соответствующих коэффициентов
знаменателя. Схема четырехполюсника дана на рис. 0.10.5, а. 10.39. Может.
10.41. а) Рнс. 0.10.6, а; б) рнс. 0.10.6.6; в) рис. 0.10.6, в. 10.42. Корня
уравнения; р24-11р-}-1 = 0; —0,1; р4« —10,9. У полинома Q=p~b5
490
Рис. 0.10 4
Рис. 0.10.5
Рис. 0.10.6
нуль находится в промежутке между р2 и В соответствии с решением за -
дачи 10.41 найдем Zi=—; Z2=~= Схема четырехпо-
w Р~г^ Q р-г-5
люсника показана на рис. 0.10.7, а, 10.44. Zi=-----------—----------• =
н (Р т 0.625) (р +1,752) ’ Лз
491
= 1094 * Схема четырехполюсника дана на рис. 0.10.7, б,
10.47. Если входную проводимость со стороны зажимов 1—1 обозначить Yllf
7 I - адъ v - А ,/7д V
то искомое сопротивление у—-—у—; ^и=—2—г у \~2 ) —
10.48. Z,= l/p. 10.49. а=3,01
z z | Zj zaj Zj
и 18,1 дБ. 10Л0. Степень полинома Баттерворса равна 7.
Глава одиннадцатая
11.2. v=(l,339+/i.486).I0-> км-1; ZB=737e-M8° Ом. ц.3. При
/=1 кГц р =6-10-я рад/км; при /=4кГц у = (124-/12)-10_* км-1. 11.4.
= 10 Ом/км; Go=0; Со=4О-К)-» Ф/км; £о=0. 11.5. /=100 км; Г1 = 266 В;
/1=0,532 А; (72=64,5 В; /х=0,129 А; р/« 80°. 11.8. До подключения
£доп Рк— Ю,37 Вт; РПотерь=724 Вт; q=0,014i; после подключения £доп
14,37 Вт; РПОтерь=7,53 Вт; Т) = 0,659. 11.10. Pi = 500 Вт; Рх=183,6Вт;
Т] = 0,368; /?рх = /?в = 2000 Ом. Графики U (х) и / (х) даны на рнс. 0.11.1.
11.11. й (/) = 0,7 sin (со/ + 5,65°) А; цх (/) == 269 sin со/ В; /а (/) =
=0,353 sin {(0/4-5,65°). Графики и(х) см. на рис. O.I1.2, где 1— 1 — 0’ 2—/ =
= л/(4<й), 3—/=л/{2(о), 4-/=л/ы. 11.12. Напряжение ток увели-
с (/, Х/2) =
*пад (/» ^/2)
чиваются в е я =1,362 раза. Мощность Ря увеличивается в е®^= 1,856 раза,
a Pi не изменится, КПД т] возрастает 8 6^=1,856 раза. 11.13. п2(/) =
= 327 sin со/ В; it (<) =0,229 sin (со/ 4- 5,6°) А; и (/. Х/4) = 216 cos со/ В; i (t, 1/4)=
= 0,498 cos (со/4-5,6°) А; и (/, 1/2) =—394.8 sin со/; '
= —0,383 sin (со/ -)-5,6о); Т) = 0,25. В согласованном режиме Лсогл —9,29
11.14. ипая(/, 1/2) = —335 sin со/ В; ногр(/, //2) =—50 sin (о/В;
«= —0,47 sin ((0/4-5.65°) A; iOTp (/, 1/2) = —0.084 sin (со/4-5,65°) А. 11.16. иг (/)=
= 417,4 sin ы/ В; ц (/) = 0,395- sin (и/ 4-6°) А. 11.17. ZH = 4654-/193 Ом;
РНВ1ах = 53,46 Вт. 11.18. a) «2(/) = 500sin (со/—60°); (/)= I sin (<о/ — 60°);
6) ия (/а)= 1000 sin со/; /8 (/) = 0; в) ия (/) = 0; /*(/)=-^=rcos<o/. 11.19. а) При
р 3
изменении частоты амплитуда напряжения на нагрузке не изменится; б) с уве-
личением частоты на 3% амплитуда напряжения в конце линии возрастает в
4 раза. 11.21. 1/и=1673 В; /В=1,93А. 11.22. ZH = — /500/3 Ом.
11.23. a) ZBX=ZB = 250 Ом; б) Zbx=1000 Om; в) ZBX=4004-j300 Ом.
11.24. Ри = 400 Ом; хв = —400 Ом.
492
Глава двенадцатая
12.2. Графики ц(х), i(x) для 1=2.5 (/с даны иа рис. 0.12.1. 12.4. Графи-
зооо ) |В;
кн п (х), 1(х) приведены на рис. 0.12.2.
Рнс. 0.12.1
12.6. щх) = 250 | 1—е
Рнс. 0.12.2
__ /— i/p \
I—e 2bc } • I (t—llv).
График и(х) для Z=8‘i0-e с дан на рис. 0.12.3. 12.9. Переходный процесс
заканчивается в момент / = 2//о=2т.
Графики u(t), I (/) см. на рнс. 0.12.4.
12.10. Результирующее напряжение на
выходе: а) бесконечная последователь-
ность прямоугольных импульсов ампли-
тудой 2Е. длительностью 2т(рис. 0.12.5,
а): б) одни прямоугольный импульс
амплитудой 2Е, в интервале т ч- Зт
(рнс. 0.12.5, б). 12.12. а) и (/, х)=
= 0,5Е-1(/—х/и), i(t, х) = «(Л x)/ZB;
6)u(/,x) = 0,5E-l(Z—x/v)-\-0,5E «1 (/-
0.5Е f 21—х
ZB V v
Л SF
i(/t x) = -~^-.l
.f x\ 0,5£
1(х)=0,5
А. 12.7.
«с
2/—x
о
К97в
600
0 0,41*600"
Ряс. 0.12.3
0.5E
Z*
X \
tl }
. n , 21__x \
— 0.5E-1 t—;
\ о / \ V }
r) u(U)=0.5£x
~’V »J’r з "V о У’ zB ' v vj 3ZB x
X I . 12.18. «2(/)=100e“w'<«-ie^e>.l a—10-»)B; h(/) =
=0,1 [1 (O-H (/—2-10 ’)—2е-10,<*-*-10"в’-1 (/—2-10~*)] А. На рис. 0.12.6 дан
Г » f. i
, 0.5E
' 7
Лв
2/—x
и
график и (x) для t = l,5Z/v= l,5-10~ec. 12.14. (/)=-—[J —e
Г 1 / . I \ 1
. Эпюры напряже*
_____ t
ння даны на рис. 0.12.7. 12.15. ис (Q = l/Oe R&c = lOOe
/—Л/о t— ю~* t-t-10^*
= U&~ rbc ^ЮОе"1’8'10"* B; uat rbc =100e 10“, где Ro=
Xl t
rbc =100e 1’B 10
493
= (2BlZB2)/(ZBf+2B2).12.17. u(t, x)==£-l (/)~
21 —х
v
t--—2
V
x\ E ~L/(2Z >
FT* " X
V
nt. *)=£. j (0-g-. 1 L“^' X
Рис. 0.12.4
Xl «1(0=250-1 (0—250e 10'l0“* .J (t—4-10-®)B. 12.18. iH (0=
E E / 9/ \
= - 1 (04-Ат- - 1 (/-—) = 1,5-1 (0—0,5-1 (/ — 2-10-®) А. График
xZB O£B \ О /
Рис. 0.12.5
iH (0 см. на рис. 0.12.8. 12.20. Графики u(x), i(x) см. на рис. 0.12.9, а, гра-
фик «2(0—на рис. 0.12.9. б. 12.22. В нагрузках возникают прямоугольные
импульсы тока (рнс. 0.12.10) амплитудой ()0/2ZB=-5A, длительностью //« =
= Ы0~вс (амплитуда та же, что и в задаче 12.21 р, длительность в два раза
494
Рнс. 0.12.8 Рве. 0.12.7
495
меньше). Графики и (х), i(x), даны на рис. 0.12.11. 12.23. = • 1(0—
>('—7)+^- • 1 (<-т)=5'* И-10'1 a-10-")+5.|(/-2.10-»)A
__ t__________________________________ / _ t — l[u \
рис. 0.12.12). 12.24. «cW = ^c-l(/)-f7(>e‘’CZB.l(O-l/oV-e С2в Jx
Iх
Рис. 0.12.11
Рис. 0.12.12
7 t \ 7 I- 10* \
х1 (*—1/г)=4-103Ь—е~ ) I (О—4«103\1 — е” 10)•! (/—10~в) В. Гра-
фик uc(t) см. на рис. 0.12.13. 12.26. Для первой линии и (/, xj) =
=£ Г1 (0—1 ( — 1 f t— 3l~X1 Yl; i (/, xj) =-^- [ 1 ( H
I \ v J \ v / J ' 2ZB L \ v i
1 1 1 Л n
-j- 11 /----i; ) ’ где — РасСтоянне» отсчитываемое от входа линии. Для
второй линии и (t, х2)=-^- [ 1 (/—x8/f) —1 f t————^1 ; i (/, xs) =
I \ V J 1
496
с I . I \ . t [ 1 21—хл\ I
==2Z"| 1 V----v * v----------5—J I ’ ГДе X* — Расстоянне> отсчитываемое от
места коммутации. 12.27. Графики и(х), i (г) построены на рис. 0.12.14. Длн-
£
тельность переходного процесса равна l/v. 12.28. а) и (I, jcj)=-^-x
А*
XI (0—=-е" u(/,x2) = -^.l(0—f-e" сг*!г X
*1 (' —V 'I; *9 и<1- =4 1W —7Г1 (‘ —‘-7Г-}: “ ('• =4* <’> - 4 *
\ V J At Q V V 7 ** О
U2
'SSAfS/SSZfSSSSSSSS/SSSS/SSSSSSSSt
i
Ы2ТВ
L/2 I х.
1/2 L X
tzl/J
и
Рис. 0.12.14
х|('- «> «('• ^-41«-4 •,(/--Чг-У<
\ V / At Al V J А
X 1(0-4 •*('—)•
Эпюры и (х) для случаев а)—в) построении на рис. 0.12.15, а—а.
12.29. а) и2(0-£ [1 (0-2-1 —2-1 ...]
(рис. 0.12.16, п); б) и2(/) = £•! (рнс. 0.12.16, 6). В этом случае пере-
ходный процесс по всей линии заканчивается в момент времени t=3llv.
.f . 31 X . 1 , f . 5/ \ 1 , /, 71 \ , 1 <А
X1 [ i--Ц—т" • 1 ( t — -— } —Jr ’ll /-) -j-. - - I • 12.31. Мя (^)
\ о/ 4 \ v/о \ v J ' J
497
Переходный про-
цесс во второй линии заканчивается в момент 2//и, а в первой—в момент
3//Р. 12.32. aa(Z) = £.l(l-l).
12.33. MO=^[1(O+1 (<—)]: u„(O=-^!!-[i(z-|) +
+ 1('-4г)]! “НО—
13.2. /=0,4 А. 13.4, Рис.
0.13.1, а. 13.5. Рис. 0.13.1, 6.
13.6. а) 7?я=18 кОм; /?ст =
= 6 кОм; ₽дИф = —6 кОм; б)
Г7Вых = —15 В; Яст = 11,5 кОм;
/?диф = —7 кОм. 13.8. /? =
—500 Ом; ZCT = 30 мА; 5,5 В<
< и < 13 В. 13.9. /?2=8000м;
Г7СТ=8,8 В; /?х=940 Ом; нап-
ряжение не изменится. 13.11.
Ra 2,5 кОм. 13.13. /нр=4 А;
Р=24 Вт. 13.14. /Нр=1 А;
/?сг=5 Ом; /?диф=! 1 Ом;
Zhp= 4 А; /?ст =2,5Ом; ^?днф=
= 7 Ом. 13.15. а) /нр=2А;
/^=4.5А; /я2=1,5 А; /д3 =
=1 А; //?.=3 А; б) /нр =
= 0,8 А;//а=2А; //?2=0,7А;
//?3 = 0,5 А; /д4=1.3 А. 13.17.
/нР1 = 3,1 А; /я1 = Ъ?з = 4,3 А;
/№=],2 А. 13.19.
498
а) Еэ —20 В
б) Js = 3,5 А
{/, в /, А и, В /, А~
—20 —3,5 —20 —3,5
—10 —0,25 —10 -3,25
0 0 0 0
10 2 10 3,25
20 4 20 3,5
30 4,25 30 5,5
13.20. Еэ —20 В; направлена к точке Ь.
и» В /. А и, в /, А
—20 —6,5 20 0,5
—10 -3,25 40 I
0 0 60 5
13.22. Л-3 А; /а = 5 А; /3 = 2 А. 13.23. Л = 2 А; Л-ЗА. 13.25. /i=0,7A;
/3 = 0,46 A; t/it/z= 10 В. 13.27. 1/выж = 4 BEl/jtA. 13.29. Рис. 0.13.2, а.
13.30. Я = 1,11 кОм; /?1=/?3=186 Ом; /?2 = Я4 = 75 Ом. 13.32. Рнс. 0.13.2,б.
Рнс. 0.13.2
14.1. В=0,1 Тл; 7 = 799,2 А/см; ur= 1000. 14.2. /=1,6 А. 14.3. В =
— 1,1 = 1,38 Тл. 14.5. 6 = 0,09 мм. 14.6. По кривым Ф (£>м), полученным при
S —5; 6; 7 см2, строится зависимость Ф (S) для /а'=200 А, откуда 5=5,7 см3
при Ф=5,5«10~4 Вб; толщина пакета 2,85 см. 14.7. /а?=45 А; Ф2=5,2х
499
X 10-*Вб. 14.8. а)Ф1=7,05*10-®Вб;Ф1 = Ф8=3.53-10-® Вб; б) Фх = 3,96-10“<
Вб; Фв=Фж= 1,98-10-* Вб. 14.9. /ш=2590 А. 14.10. /?м1 = 5,56-10® Гн*1;
Ямх=10® Гн-1; /?м,=4,78-10® Гн"1; l/Mot=382 A; = 6,85-10-® Вб;
Ф»= 14,85* 10~® Вб; Ф8=8*10-б Вб; /2&у2 = 530,5 А. 14.11. /а=56,2 А.
14.13. а) = 4,55* 10“4 Вб; Ф2 = 1,82* 10“® Вб; Ф, = 2,73-10“® Вб; С/м вЬ=78 А;
б) ®i=2,12*10-® Вб; Фа=0,28-10-® Вб; Ф3=2,4*10-® Вб; Uuab = — И А;
в) Ф1 = 4,63-10-® Вб; Фя= 1,8-10-® Вб; Фа = 2,83-10-® Вб; 1/ма6 = 7б А.
14.15. /^ = 88 А. 14.17. а) У сердечников /, 2, 3 В=±ВГ’, у сердечника 4
В = —Вг-, б) у сердечников /, 2 B=-j-Br; у сердечников 3, 4 В — —Вг.
14.19. бДср=0,14. 14.20. 6=1,33 см.
Глава пятнадцатая
15.1. Напряжение на индуктивной катушке —57- = U т cos urf. Отсюда
{/ at
= sin со/ (постоянная составляющая при установившемся режиме в потоко-
сцеплении отсутствует), или ip=sln 1000/. Кривая, получаемая при первом
способе аппроксимации, изображена на рис. 0.15.1, а. В интервале от 0
до orf1=arcsin0,9475 = 7ГЗО', когда поток нарастает от 0 до 0,9475 В-с, ток
пикообразно нарастает, а в интервале от 108°30' до
равен нулю. Затем ток
180° он опять равен нулю. Кривая тока при втором способе аппроксимации
дана на рис. 0.15.1,6, при третьем—на рнс. 0.15.1, а. Амплитуда тока равна
1 А_. 15.3. Для всех трех случаев i- dqldt—
= Im cos со/, отсюда q = sin со/ =
= 10“ ® sin 1000/. В задаче цифры подобраны
так что кривая q = f(a>t) имеет такую же
форму, как и кривая ip=f (со/) на рнс.
О.15.1,а, но ее амплитуда в 10® раз мень-
ше. Кривая 1/с = /(о)О соответствует кривой-
i = этого рисунка, только вместо чис-
ловых значении тока в амперах на кривых
даны числовые значения напряжения в воль-
тах. 15.4. Кривые l = f(co/) для характе-
ристик на рнс. 15.2, бив такие же, как н
кривые u = на рис. 0.15.1, только
вместо напряжения в вольтах следует счи-
тать ток в микроамперах. Так, для кривой
рис. 15.2,6 на участке изменения q от О до
0,95*10“® Кл q=6iu, где Ах= 19-10“®; ii=
= &!<!)Um cos 1000/= 19-103cos 1000/ мкА.
По такому же закону изменяется ток в интер-
вале от —со/ до cirf1=arosin0,05 = 3°53/.
Далее ток изменяется по закону < = 52,7 cos со/ мкА. 15.fi. В уравнении
/?~4-«с=е(0 напряжение ис~ 0. когда заряд изменяется от —qm до
500
В интервале времени от erf = 0 до с
— 2-10~ь(1—cos erf)—10“s; (=2 sin erf. 1
crf=180° q—q„; i=0; uc = 2000 sin erf B.
/=90“ cos «>/)-,„ =
интервале времени от со/—90е до
График изменения е, i, q, ис в функ-
.15.3
ции erf изображен на рис. 0.15.2. 15.9. Амплитуда напряжения на индуктив-
ной катушке (oL/w=10 В. Нелинейный конденсатор перезарядится за интер-
вал времени от 0 до coflt где orf| = 45°. В этом интервале ц — i; ia = 0. Графики
требуемых величин даны на рнс. 0.15.3,0. 15.10. Рис. 0.15.3,6 (ток дан в ам-
перах, напряжение — в вольтах). Переразрядка нелинейного конденсатора про-
исходит за 3/8Г. Условие для нахождения i dq=2qm. 15.11. Рис. 0.15.4.
О
Рнс. 0.15.4 Рис. 0.15.5
15.13. В первом интервале временя о’т wt=0 до й)/ = 1° ток ц = 0,388 sin erf—
— 0,727-10“* A; i0 =—0,097 sin со/ 4-0,18-10-3 А. Во втором интервале времени
от 0)/ = Г до cdf1 = 26oJ0' значение ctrfj найдено из трансцендентного уравнения
cos ь>/1—0,0187(0/! =0,884; ii = io=0, В третьем интервале времени от
до я ток *!= 0,338 sin erf4-0,727-10“« A; i0 = 0,097 sin erf 4-0,181-10“* А. Коэф-
фициент усиления по мощности kp=44,5. 15.14. По второму закону Кирхгофа,
i/?-[-Ид ~е (0 4 -Ео- Ток в цепи проходит с момента времени со/г, когда правая
часть этого уравнения становится равной нулю, т. е. с момента, при котором
sln(<irf14-45j = —50/127=—0,393; (irf1 =—68о20'. Ток в цепи прекращается
при (irfa=158°20' и вновь появляется при (irfe = 29l°40'. Графики t = f(<irf);
изображены на рнс. 0,15.5. 15.15. При х/?4-цд=е(/)— £0, Ci)xt и
501
tot2 найдем из уравнения sin (ы/4-45°) = 50/127; <o/i+45°=23°20'; cof£=—21°40';
ci)/2+45o= 156°40'; (o/s=Hl°40\ Графики i = f(u>t); uD = f(iot) даны на
рис. 0.15.6. 15.17. Рис. 0.15.7; а; амплитуда й равна 0,183 А. 15.18. По вто-
рому закону Кирхгофа, для левого и
правого контуров ид1— ei (О4~£о:
*2^2 4‘“д2=^о~еа(О- Ток »i протекает
по цепи в интервале значении cot от
—30° до 210°, когда ei > 0: ток
f2—в интервале значении Cirf от 72э50' до
287°!0/, когда Ео—е2(/) > 0. Требуемые
кривые построены на рис. 0.15.7, б. 15.20.
Рис. 0.15.8. Полупроводниковый днод
открывается при cot=©/lt когда напря-
жение источника питания становится рав-
ным напряжению на конденсаторе:
пс(0)е ыЕС =Ет sin ait. (1)
При ©f=©/2 ток через диод становится равным нулю, диод закрывается
и напряжение на нем иа=е—ис становится отрицательным. Условие равен-
ства нулю полного тока:
£
©C£ffl cos cof2 4—sin©/2=0.
Следовательно,
tgtirfa=—1/(<йС/?). (2)
В силу периодичности процесса цс(0)=пс (2я) или
(2Я-<а4,)
i/c(0) = £fflsinw/2e wRC t (3)
Уравнения (1) —(3) служат для определения coti, cot2, Uc(0). При задан-
ных числовых значениях R, со, С ю/1 = 24°; ©f2=100°. 15.23. £j = 50 В;
£г =—20 В; R=80 кОм. 15.25. Рабочая то 4 к а соответствует положению
точки А на рнс. 15.15, в; iK л 168 мА; ig а 23 мА. 15.27. гл = (1—Л1г)//122;
^6 = ^i2/(l—Л12); а== — C*2i+^is)/(l—Л12); ra=/iu—Й12/> (I—а). 15.28. За-
502
эемлим узел 2 и составим два уравнения относительно ф£ и фз-
• f 1 . 1 । 1 j . . • [ I \ s
ffil-в . г -И——Ь —-F/toC )+фз(—— =-р~Т7—а/ь
\АгТ'Э 'б ГК / \ Гб / Агт'э
- 7 1 \ । • 7 1 . 1 । I \ £i
’Ч_^}+фз1т+й7+л7+77)=-л+77-
15.89. Л, = (4тг-\ =Э,«.№ Ом; 3=-^-=2мА/В; u=SR, = 18,86.
\ Д|д /uc=-lB _ Дпс
15.31. Невзанмнын активный четырехполюсник, каким является транзистор
Рнс. O.15.S
(схема замещения его изображена на рис 15. 18, а), имеет следующие У-пара-
метры:
Уц=Ув(Уб+Ук)/в; У12=-УаУк/о;
У з!=—У в (У« И- ®Уб)/с;
Уи=Ук(У8+Уб)/а; а=Уб4-Ум+(1-а)Уэ;
Ук = GK+/соСк.
ем 1. SiS34~yo (Удк^-Уа)
’ ’ (r.+r.+rkXr.+yL,)’
15.34. Рис. 0.15.9. 15.35. Рнс. 0.15.10. 15.36. Если для описания вебер-ампер-
ной характеристики воспользоваться формулой 1=аф4~£ф*> то а = 0,5 мА/(В-с); 5=1 мАДВ^с3).
,, , [ а \ .. 0,75,,,з Vi„. В 7i„, mA
Для в. а. х. ] ^iOT+—g-51/vn.
15.37. 1. а=0,13 кВ/(см*мкКл); 5 = 0,078 Q f)
кВ/[см (мкКл)3]- 2- /iol=wQ„, где Qm — ампли- 100 1,25
туда первой гармоники заряда. Амплитуда первой 150 3,29
гармоники напряжения на конденсаторе 200 7
250 13
~ d t aQ т 4“ b yr Qm • \ о J
503
15.38. а) б)
/j, мА l/i. в и, В /, мА и, в 7, мА
0 0 0 0 0 0
0,5 6,65 25,8 0,5 50,4 1
1 17,86 53,3 1.0 101 2
1.5 56,5 94 1,5 160 3
2 181,5 208 2,0 270 4
15.39.
/, А f/c&, в ф, град
0,1 15,7 71.5
0,3 46.5 71,17
0,5 54.2 62,5
0,7 54 49,5
1,0 57,2 29,5
1.3 65 —2.8
1.7 90,5 —20,67
15.41. С — 25,8 мкФ; Я =20,9 Ом. 15.42. Если построенные характеристики
аппроксимировать прямыми линиями, то при холостом ходе илых =
= 107,5 +0,0975 1/вх начиная с t/BX = 78 В; при индуктивной нагрузке
1/вых = 102,5+0,12 UBX начиная с 1/вх я 30 В; при активной нагрузке 7/вых =
= 93+0,26 С/вх начиная с С/Вх = 92 В. 15.43. L1=——|- X
О) Gj, ЫСт
15.44. I. Рис. 0.15.11.
2. С/ал=84У 2. 15.46. Учесть, что для опыта холостого хода, проведенного
при номинальном напряжении, потери в меди первичной обмотки много меньше
потерь в стали сердечника, так как ток
холостого хода много меньше тока нагрузки,
а для опыта короткого замыкания, прове-
денного при сниженном в 10 раз напряже-
нии, потери в стали сердечника ничтожно
малы по сравнению с потерями в меди
обеих обмоток; Ri= Pik/(2/ik) — 0,833 Ом;
/?й = Ri (w2M)2-83.3 Ом; XS1 = 1,445 Ом;
(aW^i)2 = 1 *4,5 Ом; Рс =2,967 Вт.
15.48. Искомую характеристику строим по
уравнению Qm—(o2Qm= ± Ет (рис. 0.15.12).
15.51. Зависимость Q т — f (со) строим по урав-'
нению
(2^-й1£<?я= ± /й. —Rs (и<2пр
ИЛИ
+ Ие,п —(<i>Qra)s.
504
Прн резонансе подкоренное выражение равно нулю: Qfflpes= V Em/R.
Практически резонансная кривая при наличии активного сопротивления заметно
отличается от резонансной кривой при /?=0 только в окрестности точки резо-
нанса. На рис. 0.15.12 пунктиром показаны две резонансные кривые при
Я=0,2; Qffl=:3J6H/? = 0,3; Qpe3 =шрез-2,58. 15.54. ? = ( Д — А дз } е-°Ц-
+ ~ Д3е*
2а
15.59.
а а'//?; b=b4R. 15.58. x = e~a* —-Л-(е е-®<*).
^43 \ । Зшо/ с Cl f
| COS—- —Гт™ COS—- 15.61. fs = 2,dOft.
192 / у ] _ д2/8 *192 /1 _ Д2;8
Eh E
15.62. За время t = 1 с источник доставляет энергию —ms = ~2^Г х
Х(л—йА4-0,5 sin 2to/!), где /1СТ$— амплитуда синусной составляющей тока.
ёг Г-/?Л =
2л J
О
^0: В7- =
При этом в резисторе
R выделится энергия
pi
= -ггъ- (л—4-0.5 sin 2co/t).
15.63.
2/t 1 2/.
= ----57- Если мощность отрицательна, тс на данной частоте она
2/ о
отдается нелинейным элементом. 15.65. Первое соотношение теоремы Менлн и
Роу дает тождество — №4/(2/) — Ws/(3f) — Wrff + Witf -j- Ws/3/—IF2/f-f
4-*^2//+^4/(2/)= 0. Второе соотношение теоремы Менли и Роу тождествен-
ного нуля не дает: 2W\//:4-1^2/(2f)4- ^2//4-^^4/0/)=О. Однако одного этого
уравнения недостаточно для определения двух неизвестных: н ^4.
15.67. ^O.TSbl^l^ Sin <]>,. 15.68. th ₽<?,=- sin 4<p •
(Jpviw) •’о ирч?4га)
где J0, Ji, J4- функции Бесселя от мнимого аргумента. 15 69. /0 =
505
= —s*n Ф- 15.71. При разомкнутом выключателе РВО=2;
РВЯ —4, при замкнутом рВ0 = 2,85; рВт = 3,Я. 15.72. При разомкнутом выклю-
чателе PQo= 1,66; PQffl=2,2. 15.75. Нелинейный резистор имеет N-образную
ВАХ -На схеме замещения для исследования устойчивости положения равно-
весия (рнс. О.15.13,а) он заменен участком схемы, обведенным пунктиром. На
этом участке /?лиф—дифференциальное сопротивление в точке равновесия;
Ri—добавочный резистор; Са — емкость диода. Запишем операторное сопротив-
ление для схемы рис. 0.15.13, а, применив критерий Гурвица. Состояние равно-
весия будет неустойчиво при L > | (Ядиф—J?j) (/?1 + Я) Сд |. При /? = эООм;
£1 = 2 Ом; Ся=0,5.10“® Ф; /?двф= — 710м £>1,9мкГн. 15.76. Первый
восходящий участок ВАХ описываем уравнением и = ш’, второй — уравнением
и=~ий+Ы. Время нарастания тока от G до
L , 11 7+Т
F«,n-—ё-
‘‘“T+R
L b 1 R
Время слада тока от ia до и G=—r^-ln----------• Для ВАХ диодана
fl-f-K . с— По
1 6+К
рис. 15.35 а =10 Ом; 6 = 50 Ом; «=0,5 В; <1 = 0,5 мА; it=5 мА; /? = 40 Ом;
Л—9-10~3 Гн; следовательно, /j = 1,8» 10~41п 2,5=0,165 мс; /а = 10“* In 3,8=
= 0,136 мс. Кривые i(0, «я(/) в «/.(/) изображены на рис. 0.15.13,6.
«с -тс &ис । ( R 'MS \ due ,1 л «е on
,5-78- -лг-+(т—cr)-dF+7c“c=0-|5-80- “=
®1С1СЛ(Лв-Яг)=1,
£Ci—
Глава шестнадцатая
16.3. t=—£ (a-]-26£) In (1 — и}Е}. При и Et -» оо, т. е. установившийся
режим теоретически наступает при / = оо. Если резистор линейный (6=0), то
(_ Ах\
1 —е L ) , где R — Ifa. Качественные гра-
фики « = /(/) для нелинейной (кривая 1) и линейной (кривая 2) задач приве-
Рис. 0.16.1
Рис. 0.16.2
Uc\ f t
) (кривая I рис.
дены на рнс. 0.16.1. 16.4. а)
0.16.2); б) / = — Т01п-~ или
<=-7,1п
£
ис = Ее~ (кривая 2 рис. 0.16.2). 16.5. Строим
ffi и, (i]
зависимость «£ (i) = £— ri—uB (i) (рис. 0.16,3, а). Так как -jr=—у— = f (О»
Qi
то £=J y~-di. Подсчитывая площадь под кривой • 1 If (i) при изменении i от О
о
506
до i (рнс. 0.16.3,6), получим зависимость i (0 (рис. 0.16.3, в). 16.6. Уравнение
цепи после подстановки 1 = имеет вид 4~/?Лф* = £*. Разделив перемен-
ные, получим /=--^-=- ( — In L arctg-^-V где — Y^ .
W&i\4 —ф ' 2 \kRj
Графики ф(0 и i (0 даны на рис. 0.16.4 (кривые / и 2}. 16.7. По методу Во-
лынкина интеграл уравнения цепи представляют приближенной суммой:
я
2 д<>+RHJ (•„+а, 4- 2i, 4-...+i„)=£„ ы.
1
Графическое решение этого уравнения с шагом A/- 2«10_| с приведено
на рис. 0.16.4 (кривая 3). 16.8. Вычисление для л-го интервала производим
Рнс. 0.16.3
по формуле фп = фп_1-]-(Е—Ri)M. Графическое решение этого уравнения
с шагом Af = 2-10~* с показано на рнс. 0.16.4 (кривая 4). 16.9. Аналитиче-
ское решение. Заменяя ВАХ диода в проводящей области линейной зависи-
мостью, что эквивалентно замене диода сопротивлением /?д—35 Ом, получим:
при 0 < со/< 0,907л (проводящий интервал) 1/^(0= 1,3 sin (314/—2Г30')Ч~
4-О,472е-^1’24'10”’ А. Численное решение. По законам Кирхгофа, иа +
f f
+ ^Sicdi?=Emsin(ot‘, ia = ip'T->C' Заменяя интегралы сум-
С J и J
о О
мами и используя ВАХ диода, методом последовательных интервалов вычис-
ляем 0?(0 с шагом А/= 7724 (рис. 0.16.5). 16.12. Решение аналогично приве-
денному в задаче 16.11р. a) i*(O) = i (0)/1 Rn/(R} 4-/?0); б) iB находится гра-
фически нлн аналитически из нелинейного уравнения iJ?i4~ai2 = E. Поле изо-
клин аналогично представленному в задаче 16.Пр, однако построение зависи-
507
мости i* (/*) следует начинать не от 0, а от i*(0). 16.13. Обозначим ис- х;
£ -~у. Для построения фазового портрета определим зависимость 0—/(<).
а) 0=0: х=± Uсо (точки равновесия); б) у=± а при любом х; в) у = 2Ы,
*=Ы\ Исключив t из уравнений для у и х, получим y=2Ybx; г) у =
Si
ei м) з)
Рис. 0,16.6
= ± ote±a<; х=е±аЛ 0= ± ах; д) 0=ае~«*; х=1—е~а'; 0=а(1—х); е) у —
= (t)cosct)f; X— SlncoL После возведения в квадрат найдем 02/<о2-|-х2= I
(уравнение эллипса); ж) 0= Т ae^* slnZ-l-e^®* cos/; x=e^a/sln/. Фазовые
портреты для всех случаев приведены на рис. 0.16.6, а—з. 16.14. а) Уравне-
ние фазовой траектории у = ~ х, где y=duc/dt*;x — uc; uc— nc/^co'’t*~t/7'o>
T0=R0C0; б) 0=—х (1 — х) (рис. 0.16.7,0,6). 16.18. Рис. 0.16.8, п—й.
Рнс. 0.16.7
Точка О на рнс. 0.16.8, о—в—устойчивый узел, на рис. 0.16.8, д— неустой-
чивый узел, а на рнс. 0.16,8, г—центр. Замкнутые кривые на рис. О.16.8хд—
— о —предельные циклы. 16.19. Рнс. 0.16.9, а, б. 16.21. Уравнение изоклин:
0=— * ГДе k=dVldx'- y=&fldt\ /*—<о0/; <о| =
= ; 2бо=/?о/До; C (q) — --с—. Поле изоклин для cti=O; a3 = 90°;
ЬоС iffoi q
аз,«=±45 и фазовые траектории для случаев а) и б) приведены на
рнс. 0.16.10, а, б. На рнс. 0.16.10, в построен график С (0*)=/(<?*). 16.24. Урав-
нение иепн: -^-4-<й§х+₽1х®= О, где x-^qlq^, — „ -; Его
60S
решение имеет вид х—а (/) sin cof. где а(/) = А=^0; ю1=<оо -f-y pja* Таким
образом, имеем незатухающие колебания с амплитудой, зависящей от началь-
ного заряда. Нелинейный эффект проявляется в зависимости частоты колебаний
Рнс. 0.16.10
от амплитуды. 16.25. Уравнение цепи: -^--h<o’x=©osin(i)f, гдех=$/$т; цл—
& C©£„,; <оо — 1 /(Z.0Cc). Его решение имеет вид х — a (t) sin wt 4- b (/) cos (at,
a) a(t)=A — const; b(t)=—<iiQt/2-\-b (0). Амплитуда косинусоидальной состав -
509
ляющей монотонно возрастает, так как при ш—Ь)о в цепи наступает резонанс;
б) Пуст ==: GJ®).
Глава семнадцатая
17.2. а) Граф дан на рис. 0.17.1, с; /З=2,34е 20°32 А; б) граф дан
на рис. 0.17.1,6; /3=3,5е-|5°15' А. 17.3. gii^-0,05 См. 17.4. a) Glt =
________abd (1—/и) 4- abegh____ _ - _______________abg(e~{-df)________
V — bdc)(\—m)—gh(f-\-bce) ’ * 16“ (1— bdc) (1 — m)—gh bee)
Рис. 0.17.1
17.5. £оз = 0,2 Cm. 17.6. У13 = 0,31е“/7<’Cm. 17.8. /a = 0,l A. 17.10. Граф четы-
рехполюсника в Z-форме показан на рис. 0.17.2,0, граф четырехполюсника
в У-форме записи — на рнс. 0.17.2,6. 17.12. Граф эквивалентного четырехпо-
люсника дан на рис. Р. 17.5,6; передачи его ветвей через параметры первого
и второго четырехполюсников: А = Л1Л24-ВгС2; В = C-CiA^-j-
Рис. 0.17.2
~^-DiC2', D = DtDa-J-CjBg- 17.13, Граф дан на рнс. 0.17.2,6; передачи ветвей:
Гц=Уп-ь*и; ИГ+Ш’; 17.16.kttl=
. k л =__________S^K___________ 17 91 См OTRPT
к задаче 17.2.17.22. a) RBX =0,5 Ом; б) /?вх = 1,75 Ом. 17.23. Гц=0,7l5ejM°4-' См;
У18=0,156е“/38°40'> См. 17.24. С/|/=63,3 В.
Глава восемнадцатая
• —
18.1. В соответствии с § 18.2 [1] 1+-^—Ьчг
/\ \ * о
= — j • Пренебрегая в этих выражениях слагаемыми в скоб-
ках со степенями т выше второй, найдем 11т//0 —т/(1 4- 0,5тъ)=0,08/1,0032=
р
=0,0796; т —0,08. При т-~=8-10~5 /?0=1 кОм. 18.2. По первому закону
По второму закону Кирхгофа, [r2L (/)] или 4=ГL (Л~зг+*
Подставив значение i't в уравнение (1), получим L (/)ттт4'*2 I
at I «
510
е L . Из условия задачи iJ^o/i/^T=O,9
= RJ. 18.4. В первом интервале времени с1 =0,5+0,252 woo/; ——50,4е“2ЭДО/;
во втором *11 = 1—0,4073-е~1<х>0</”т> А; и™ = 40,73е 1000 (* т> В. График ul =
=з= /(0 изображен на рис. 0.18.1. 18.5. Ток в первом полупериоде «* =
.г. Е- t / _
“Я,+ -K'tR'x
1 — е
2т
)8.e.p=lJ£,A=|
О
т
-«o»/)d/+J (1—ОЛОТе-100**'-^ (/—т)
о
т
L0
= 67 Вт. 18.8.
2т
А-Р«С(О<«=4-
О
L О
18 9 I
. 18.9. /„------,/13-
Я
Ofi
О,
44
в
Рис. 0.18.2
0,2'
к
0^
= ——SH1L; /2f = y/n—v/i2; /22 = v/ii—Y/и. а = M = ~cosif; N =
а к к
E , . ... E 1+4вг— 0.5c’A! „ a(J+4a*—a’F)
= 1,=т-. a=------------------;₽ =--------- ;
ok Zcfik kLn
y= 1+4д8~ ’ ^о=£сЛ4—^n' *—0,815sln a>/+0,545coscitf—
—0.0464sin2uj/+0.081 cos 2w- А; фо = 8,15.1О-« B-c. 18.11. i=3,53+0,!365x
Xsincof—0,683 cos erf+ 0,697 sin 2<о/+0,0205 cos 2ю/ А; ф0 = 351,4-IO-4 B-c.
18.13. За одно скачкообразное изменение емкости конденсатора в цепь достав-
ляется энергия l±W9=$~r^-. За один период изменения тока происходит
Сд
два скачкообразных изменения емкости; следовательно, энергия, доставляемая
(7^ АС
за один период в цепь, равна . В I с (й/(2п) периодов. За это время
Cg Сд
2
в цепь доставляется энергия (мощность), разная -^-ДС—. Учитывая, чтоп-=я
С5 2л
/ в АС
= получим с ” 0,035 Вт. 18.17. На рис. 0.18.2 заштрихованы
ХДШСд О о
области неустойчивой работы цепи. Если изображающая точка, соответствую-
щая подсчитанным а и tj, попадает в заштрихованную область, то режим ра-
боты окажется неустойчив, если в незаштрихованную—устойчив, а) п г;: 1,
?=0,00313; режим неустойчив, так как изображающая точка находится в эз-
511
штрихованной области; б) fl=2: q=0,0626; режим устойчив, так как изобр>
жающая точка находится в незаштрихованной области. 18.22. Условия задач*
18.21р выполнены; с=0,0405 В-с, Ь=—0,365 В-с/А.
Глава девятнадцатая
19.1. а) хт — 4 см; хп=—12 см; £„ =—1-125 В/м; Ft=—i-2,5-10-8 Н;
б) хт—— 12 см; хп = 4 см; £„=7-1125 В/м; 7j=?-2,5-10*8 Н. 19.2. АаЬ—
=—207-Ю-1® Дж; Л(,с=23-10-1® Дж; Л₽а = 184-10-18 Дж. Перемещение
на участке ab может быть совершено за счет действия внешних сил, а на уча-
стке Ьс—за счет действия сил поля. 19.4. t/m„=H0B. 19.5. т-=1,66-10“* Кл/м.
19.7. Внутри шара ф- 188 В; | grad ф | = 0. Вне шара ф = 9,4'г В; ^абф| —
= 9,4/г2В/м (г—в м); (У12-94 В; С=16,7-10-12 Ф. 19.9. £д=0;
(3—х\г in!
= 7,85 кВ/м; £с=8,45 кВ/м. 19.10. ф(х, у) = 9 in ' _ 2 ;grad(jp=18x
J 7 Г з—x 1 зч-х 1 т 7*Г у u 11
X \ J (3-x)!+j« + P+xJ'+j1 Г ' I (3-X)2+J(« (3+*)=+^ J I x
Х£в=1 -4,32 В/м (x, у—вм). Эквипотенниаль ф = 4-25 В строим по следую-
щим данным: радиус окружности г =1,6 м; координаты центра окружности*.
Х1=—3,4 м; у=0. 19.11. фд = 0,9 В; фЛ = 0,78 В; £д=£°-18 В/м; £В=Я‘Х
Х15,64-0°-4,5 В/м. 19.13. а) Электрическая ось сдвинута влево относительно
геометрической осн первого цилиндра на расстояние 5=0,285 см; б) Ем =
= 49,7 кВ/м; в) С = 3-10-10 Ф/м. 19.14. £ =—г°(3аг24 6/г); div£ = —9аг;
rot£=0; р = —9еваг. 19.15. Q— 5-Ю-8 Кл. 19.16. фх= 1,5-105х3 В; £| =3х
ХЮ®х В/м; ф3 = —15-Ю® (2,5-10s—х) В; £2= 15-10® В/м (х—в м) 19.18. фх=
=—108fl»_|_ 103 В, фа = 9/Я; £1 = 7°-3-Ю”Я2 В/м; £2 = Я°-9/Я2 В/м; UAB =
Ct “* * U л___п -+ “+
=537,5 В. 19.19. а) ф=С/ — ; £=—а°— ; 6)q>=U ——— ; £=а
' ао аог ' л—а0
в) <р=0; £=0. 19.20. q>~ A|2h~: £=_?-------------------------------------
in tge'/2' tg 02/2 я sin e in -
и .
(л—а) г ’
tge,/2 •
tgOa/2
19.21. £2 = 5,88- IO4 В/м; а2 = 58°; £3=22,25-10* В/м; «8=13°. 19.22. ef2 =
= 4,56. 19.23. Для конденсатора без воздушного зазора t/no=90 кВ; £ =
= 7500 кВ/м; D = 28,6-10-* Кл/м2; £ = 21,8-10-* Кл/м2; ф = —75-106х В;
С = 126-Ю-12 Ф. Для конденсатора с воздушным зазором 4/пр = 6,47 кВ;
£пара* = 348 кВ/м; £в=1500 кВ/м; £>=1,33-10-5 Кл/м2; Рпараф = 1.015Х
ХЮ~* Кл/м2; Рв = 0; Осв~Рпараф; фпарзф = —348-103Х В (0< Х< dj; фв =
= —15- 10^x4-5760 В № < х < dx j d2); C = 82,2-IO-12 Ф (х—в м). 19.24. С=
= 17,7-10-12 Ф. 19.25. rt = 2 см; £/Пр=400 кВ; №э = 0,353/г2 Дж/м8; W =
=0,445 Дж (г—в м). 19.26. a) tr2^2,5\ Дл — 4,1 мм; Д2=5,9 мм; С=7,85х
Х10-“ Ф; б) £1тах = 3,6.10* В/м, £imin= 1,8-10* В/м; £2тах 0,9-10* В/м;
£гтш = 0,45-106 В/м; С = 7-10-12 Ф. 19.27. ф = 565(/Ю-а—г2— |г|) В;
г
прн z > 0 £=565( 1
; при г < 0 £=565
z
где г—в м. 19.29. а) £х=20
Яс
; б) £я=г°
X1 Яр . О»—<71
\2ест (/Й+г2)а/‘ 2е„
Gj» j Og~ Oi Г
2евЯ0 2ев [ У1
г—1/2
__। Ga—
2 2е0
г—//2
Т(г-//2)а
г-//2
; в) £s z°x
. 19.30. a) F = 9х
— 1
512
Х10-' H; A=9- io-10 Дж; б)
19132. фЯ-=0,09 В; £-Й®1,8+е°8.95
т Kd<—И!
= _1л ? /с . 19.37. Еа = 2250
2ле0 d К 2
F= 6,43-10-’ Н; Л=6,43-10-10 Дж.
В/м. 19.зв. F=-—к;ф =
2ле0 (d2— гс)
В/м; Еь = 46,7 В/м; ав=—19,9Х
Я
Рнс. 0.19.1
ХЮ"9 Кл/м3; ое=3,03-10-’ Кл/м3. 19.39. Tl = 3,75-10-’ Кл/м;
Х10-’ Кл/м; т3 = 0; Ф1 = 2ОО В; фг = 0; фз = 50 В. 19.40.
Х10-11 Ф/м; С1Х= 1,366.10-u Фи; С22=0,93Ы0-“ Ф/м;
ХЮ"11 Ф/м. 19.41. а) Ср =12,5 кВ; б) (7р =
= 80 кВ. 19.42. а) С = 100 кВ; б) [/р = 200кВ.
19.44. <7СВ=-Н,05х 10-’ Кл/м3. 19.45. Ед =
=138,4 кВ/м; £^=69,2 кВ/м. 19.46. о =
=79,74-10~’-{-53,16-10_’ cos 0; £о = 7-10в В/м.
19.47. Пл = 2,66-10-7 Кл/м2; DB= 1,58-10-’
Кл/ма. 19.48. £1=Ю-108 В/м; £, = 5-103 В/м;
Еа^г.б-Ю3 В/м; Е4=!,1-103 В/м. 19.50.
С-7-10-11 Ф/М. 19.51. а) Ед =28.6.103 В/м;
б) Uar~ 100 В; в) ос=3,55-10-7 Кл,'м2; г)
A/Vf= 106 В м; &Nd= 9,35-10—’® Кл; д) Q =
=1,69-10-» Кл. 19.53. a) U = х/(х2 4 $г2>; К =
= — у/(х® Ц-1/3); рис. 0.19.1, а; .М = i/(x2 + j/®);
tg а=(2xt/)/^/3—х2); б) U = x-j- а2х/(л^ 4 J/2);
V = i/—ач/Дх2-^#2); рис. 0.19.1, б. 19.54. а^
ха+уг=е£/,5'1 i/=f/tgV/10; б) Xs— у2 =
= 100U; xi/=50V; в) х=5Са— у®/(20С2) (эк-
вшютенциалв); х=у3/(20Ка)—51/2 (силовые ли-
нии). 19.55. Ё*=400е_,8,° В/м; ф*=18,5 В;
ат=3,54-10 в Кл/м2. 19.56. а) г = 2№'1/*: б)
г=Г1/3; в) г=Г8/2. 19.57.
_________________(У—Е)_________________
~(Ц7 — А)(Й7— ЛгКГ—D)2K(W7—В) (IF —С),
где Д1, Да, В, С, Dt Е— точки плоскости W, со-
ответствующие заданным точкам плоскости г.
тв = —?,25х
Cia = 0,2Ux
Ср = 0,764X
где х—в м. График
,псо _ 1,2-10-10 1,2Ю-в
19.59. 5.J0-4.J 2d0-2x-|-*v
513
0св=/(•*) приведен на рис. 0.19.2, а. 10.62. а) Каждый электрод разбиваем
на три равных участка. Обозначим линейные плотности зарядов: Т]. Та, т3^г
на участках электрода А; —т4, —т6, —т4—на участках электрода В. (Но-
мера возрастают в направлении увеличения координат г и у.)
Система алгебраических уравнений в матричной форме:
г5,997 1.096 0,51 —0,562 —0,374 —0,276~|
1.096 5,997 1,096 —0,693 —0.405 —0,287
0,51 1,096 5,997 —0,562 —0,374 —0,276
0,553 0,654 0,553 —5,997 —1,096 —0.51
0,37 0,397 0,37 —1,096 —5,997 —1,096
.0,274 0,284 0,274 —0,51 —1,096 —5,997J
"ТГ Т» Г То То — То — То L— ТО •
Решение системы уравнений: Т1=О.158то; т2=0,145то; Та=О,158то; т4 =
= 0.175т0; тб = 0,138то; тв=0,148то; где т0 —4лаофо=1,11-10-® Кл/м. График
зависимости т(г) для электрода А приведен на рис. 0.19.2,6 (кривая 7).
График зависимости т(у) для электрода В дан на рис. 0.19.2, в; Qa —— Qb =
= 1-0,14* 10-10 Кл. б) График зависимости т(г) для электрода А приведен на
рис. 0.19.2,6 (кривая 2); Qa =0,847*10'*’ Кл.
Глава двадцатая
20.1. 7 = 276А. 20.2. 6=—7*2.10-*х+7*2*10-*уА/м*; divЬО; / = 5Х
Х10-вА. 20.4. 6=2,1 -105/г А/м* (г—в м). 20.5. 6тах = 2,88* 10я А/м*; рта, —
= 2,5*10® В т/м3. 20.6. р= 187,5* 10®/г« = Вт/м3 (г—в м); Т=0,37 ч. 20.7. G =
= 1,818-10-*° См; Ui=I81,82 В; Я2=18,18В. 20.8. 17 = 52,5 В. 20.0. 7 =
= 30,21 • 10-*А; = 1,442 А/м*; 6B = r®-2,884 А/м*. 20.11. ^=5 см;
G = 6,28-10-10 См. 20.12. а) 7=9,984*10“® А; б) 7= 10,013-10-° А; и) 7= Юх
ХЮ-’А. 20.13. Я0=193см. 20.14. у= 1,99*10-* См/м. 20.15. Яо = 39,8 Ом.’
20.17. £в=43*10< В/м. 20.18. G= 1,13* Ю"10 См/м; 7= 1,13-Ю"7 А/м; 6в =
= 1,08-10-® А/м®. 20.20. 0 = 6.87*10“’ См; 7=0,0687 А; Р=6,87 кВт.
20.22. Кл/ма; <р = 2,07* 10s In (14-20х> В (х—в м). 20.23. р =
= _2^yifex. 20.24. р(х, у)=0. 20.26. G = 10,65 См/м; С=4,72-10-11 Ф/м;
идв=100В.
21.1.
Н.=0; rotW,=0; А/и. rofg,=?x
X56.7.W* А/м’;
в-ю'*, Тл
А/м; rot Я»=Л* 107.5Х
хК^А/м»; Я4=31,9/г А/м; rot/^=
= 0 (г—в м). 21.2. г2= 11,2-10-» м.
-Ot2 -Q1 О 0,1 0,2 Х,М
Рнс. 0.21.1
Г|<г<„в=.з1Ц102 25>1гТд
(г—в м). 21.4. 6=0,9 см; 4= 1,8 см.
21.5. ?1=72= 7*8,66-10-® Н/м;7а =
= — 717,3* I0-® Н/м; Ва=3- 2,31 • 10-’
Тл; 2£= (i-3,46+/.3). 10-’ Тл.21.6.
Тл («к нам»);
Тл. 21.10.
Рис. 0.21.1. 21.7. В.=6,66.10-»
(«от нас»). 21.8. Во= 6,8*10-5
grad(pM = — a°-i^- А/м (г—в м). 21.11. Яа=а°*31,8 А/м. 21.12. Ямгдс =
Во = 1,1.10-« Тл
фм=—47,8а А;
— —7,5 А; 1/имс=-17>5 А; ЯмЛВ = !0 A; gradg)Mx=—7.100+/.16 А/м,
514
81.14. £ =— a°(2*ir4-b/r);6e=—z°—. 21.16. ПрнО<у<аЛА — —18,84уяВб/м;
при а<у< » Аа=—(6280i/44670)-10“7 Вб/м (у— в м); Ф = 2,16-!0“7 Вб.
21.18. При 0 < г < г0 Л1=—157-10~М Вб/м; при г0 < г < оо Л2=—I256X
X Ю 7 In ”q 02~^~"2") Вб/м; Ф — 160* 10“7 Вб; ^г=0101м—Ал_о_о8м = й-963,5 X
X Ю“7 Вб/м. Эквипотенциальной поверхностью является цилиндрическая
поверхность радиусом г=5 см и с осью, совпадающей с осью провода
21.19. фив—Фмь=—2.83 А. 21.20. А< = —12,56-10“8г2 Вб/м; Л2 = 3,14-10“®х
х( 1 +21пе-1^ Вб/м; А8= — 15,76-10-в-j-12,56 . 10" М—6,28-10-® х
Xln^-^д—25,12-10-81п Вб/м (г-вы). 21.21. А= 10“® In Вб/м
(х—в_м); Ави — 2,2 мГн/км. 21.22. /И=0,965-10“® Гн/км. 21.23. А=^х
IR Г/2 \ 2 1 Л
х / — 11 Л j К ~ I’ гда и & — полные эллиптические интегралы перво-
го я второго рода. Аа 6,8• 10“" Вб/м. Эквипотенциалью является окруж-
ность радиусом г=0,2 м. При г«0; х—0 j4q«=co; £0 = 3-6Д8 10"5 Тл.
21.24, X, СМ Я, А/м £-10“*, Тл
5 37,2 4,68
10 22,5 2,83
15 19,5 2,46
0,246
20 14,3 0,28
25 11,14 0,143
оттолкнуться от поверхности плиты с силой
21.26. £л = *-3,65 Тл. 21.27. £ви = 15,95-10“5 Гн.
Яв = 22,7 А/м; Я&=163 А/м; £О = 3,8-10“* Тл; £о1 =
Провод стремится
F — 0,543-10-3 Н/м.
21.28. Но = 16 А/м;
= 5,43-10“* Тл; Вд2 = 0,285-10“* Тл; В~ь = 2,04-10“* Тл. 21.29. В<> = 0,278 Тл;
1,1-10* Дж/м®. 21.30. //<-7-182 А/м; Д2=Ь238 А/м; Яв-~Ь794 А,м.
21.31. ф=2,22.10“® Вб; Я, = 500 А'м; Ям = 14000 А/м; Яед = 12 100 А/м;
ЯеС=500 А/м. 21.32. А/н=0,203, Яво = 17490 А/м; £*=0,098 Тл; Л* = 0,33;
Яшо = 18 180 А/м; £„„=0,071 Тл. 21.33. а) £^7-25—J-50 А/м; 7?у=—iX
X25 А/м; б) Я,=(/-1000-750) А/м; Я^=7-950 А/м; №м=^4-^1п^- =
= 3.6-10“* Дж/м. 21.34. /=200 А. 21.38. фмд — фиД=—6 А; Яс=220 А'м;
Ф« 8,25-10“’ Вб/м. 21.38. а) /?м= 1,97-10® Гнб) L= 1,34-Ю“2 Гн;
в) М = 8,37-10“® Гн. 21.39. а) ^=9,7-10® Гн“1.
а. град М-10-®. Гн
0 5,7
30 3,9
60 1,4
90 0
Глава двадцать вторая
22.1. ’ /. Гц ^лхпр» А/м1 см> А/М1
0 10 0
300 10 10“1
300-10® 10 10*
22.2. Я=0,132г cos (10®/60е) А/м (г—в м). 22.3. При 0 < г < гл £ =
= a°1125,sln г (ю/.4-90^ А/м; rot Н= z°22,5stn (tot 4-90°) А/м1; при п < г < га
515
Н=а° Г°’45^10~* . SIn (W^9O°)14-63,5rsin (о/ + 45°)- 2,54Ч9~* sta (w/ +
-♦ -♦ 5-10-3
4-45°) А/м; rot H=f -127 sin И4-450) А/м* 22.4. Ex= - ™ sin (art—30°) В/м;
£3=1Ь® sin (о/—45°) В/м; n=6 000 sin (w/ — 36°40')B. 22.5. e=-i^x
"P" *=6 “
22.7. rotE=—z°-3l,4 cos 100/ B/м*; Uz=ll,l B. 22.9.
e 0.167- 10“» B.
J ffdS= JlldS =
>=0.5-10’Вт; Р=10’Вт.
22.11. а) П=Д(х).
—к > > 3
22.10. A=0.3 мы; J HdS = J fid? =2,24 Bt/m.
5ж ^об
б) п=м*)-
X, CM IL 10*. Bt/m* Z, CM ГТ-10*, Bt/m* | 2, CM П-10*, Bt/m*
—99 304-10* —oo 0 i 25 104
—50 215 —100 29 75 49
0 120 —75 49 100 29
50 215 —25 104 oo 0
99 304-10» 0 120
р -> -> р -* -* U 1аг р -» -> Z1 р-»-> п
22.12. 1. \ UdS=U/; \ ndS=^£-. 2. \ ndS=~V; 1 ГЦ5'=-Д-.
J J 2bh J 2айу J Bahy
Si s. s. s4
Глава двадцать третья
23.1. 6=1078sin (<й/4~24°20') А/м*. 23.2. А/о = —4,8 А/м; Hi 1,75 А/м.
23.4. Л = 0.642 мм. 23.6. PL=^ = 6.№.
р9 а2сп2ка1 — со&2одх sd2az8—sin2«a2
ki chpai
JE~~chpaj~l»09, где pi, pt—удельные потери на вихревые токн в первом и
втором магнитопроводах; ki, —значения k для первого и второго магнито-
проводов. 23.7. Д=0,54 мм; Па = 2,1 -104 Вт/м*; Пх —870 Вт/м1, где z=a—Д;
1=1.4 мин. 23.8. Па=—fe l7,5e/8° Bt/ms; Р=1,41 Вт/м; Ф=8,7-10-7х
XSin (w/+77°30') Вб; /?ПОСт= 2,23-10"* Ом/м.
Л Гц R-10*, Om/m L-10-», Гн/м
10» 2,24 5,2
10» 10,5 16,9
23.10. ^=4shpJ;-z); Ё^^.с11Р(а-£)
Л sh 2pa hy sh 2pa
8:10?A/Mz
Рнс. 0.23.1
2, CM
6’10*, А/м*
0
6,8
— a
516
23.11. Z=(l 1,5 4-/22,82)- IO-* Ом/м; при /=5кГц >4 = 4,47 см; 26=0,127 см.
23.12. Рве. 0.23.1; /= 10, 25 А.
А кГц 6о-10», А/ма Я/Яо
0 10,2 1 I
0,1 10,1 1,005 1
1 8,42 1.317 0,83
10 0,354 3,9 0,29
Яи = 2,28104 Ом/м;
23.17. Д=1,7 мм; h= 1,59 мм;
23.15. as=2,69 см; а)
= /?ст = 2,63-10~* Ом/м.
Фи—фп = 65.7 мВ.
/?ст=0,442-10" *Ом/М; б) /?и =
23.18. Р=207 Вт/м;
г, мм 6-10®, А/м®
0 0
в/2 17,8
а 312
г, мм П, Вт'м2
0 0
гл/2 10,1
6050
23.20.
4 у (-1)"
л 2п— 1
п— 1
2л—1 яг'
2 a t
(ЯЛ-1)1 л* _
1 y(_I)»sln?2=l^\e «•-»'
V / 2 а I
п=!
cos
£(/) =
= Я
Глава двадцать четвертая
24.1. а) (/лв=2,67 В; б) С/Лд =0. 24.2. Еа = ~1300 В/м; На=— 3.46 А/м; £ь=1300 В/м; ЯЬ=3.46 А/м. 24.3. П = 6,28-!0-’ Вт/м2, /=600 МГц. 24.4. Ht = 0,81 sin (со/4-14,2°) А/м. 24.6.
/, МГц 400 1000 8500
р, Вт/м3 0,879 0,94 1,69
24.8. Ё- = 1,53е'4»’ В/м; Й~ =0,572-10-V‘5° А/м;1£в=3,2е/«в В/м; Н* =
- 2,4А/м; <р1=фБр =63*35'. 24.9. C/t « 6,8 мкВ. 24.10. е7 = 3,2.
24.12. <ркр=69,63°; ДЯ11о=0,93 мкм. 24.13. £i(0 = 15,3-10-esin(3-10®f 4-
Ф, град 69.63 70 80 90
h, мкм со 1,171 0,214 0,186
4-241°21Э В/м; tf1(Z) = 2,63-lO-8sin(3 IO®f+165°33') А/м. 24.14. £^(0) =
= 2,474е-/°О1Ь' мВ/м; (0) = 0,532е/1 ,®40' мВ/м; Ё" (0)=-2 мВ/м; Л+=
= ? (0,0717 4-/-1,4) м"1; £-=—г°-(0,07174-/ 1,4) м"1; F =7°-(0,487 4-/X
Х2.04) м-1; nt= 1,4-/ 0,0717; л2 = 2,04—/-0,487; ^ = 2,14- 10е м/с; =
= 1,47-10® м/с. 24.15. Я=0,0386еМ41°‘°'; 7’=0,966е/1’®'. 24.18. ег8=9;
21£е„ 2
d=l мм. 24.19. Рис. 0.24.1, о, б. Гц= *_L ; Т^=-Л—
517
..ТиТюТпе-1'Ае-1'А
X т I
где Д= 1 +
-f-^iReiVaae-^e-^^O+^Raa^Rsie-2^--^’.
24.21.
со, с-1
0 6 0
250 3,5 2,5
00 1 0
р—8,86 Вт/м8.
24.22.
(1). с-1 Ё-104, В/м Р-10-», Кл/м8 Й-Ю-’.Кл/м8
0 3,65 1.6 1,93
250 3,65 1,14е-/«в 1,38е-/«в
518
24.23. Уо= (1,274-/.50,73) -10* ™ См/м; Go= 1,27* 10*10 См/м; С0=4,49.10~M Ф/м.
6в= 14,9-Ю~ 8 е/А/м* 24.24.£=6- 10"*(I—еР*)В/м;6np=0,06(!-eF*) А/м<
б€М=0,1 eF* А/м’; а= 2,66-10*» (1—eF*) Кл/м’; Оо=—2,12-10*’(1 — eF*) Кл/м’;
р=—3,76.Ю3 с~\ 24.26. ф, =Ев ( — 2~Ь, eF* V cos а; <ре = £0 ( — г —
\ 1 т ъге 1 \
—-v+~ IX/ «*)«»«; бег=Еоуе( 1—cosa;
а.а=-£.Т.(1+^^|^)81па. W Р------------e,u^ew)-
Глава двадцать пятая
25.1. ф=—25,57sin (3-104—54,6° В). 25.2. Ф= —1г — Г14
x(<-r/pSD]; 4=-?>Jig^in-9-- 25Л- А>— е».5.ю-»цо+5.1о»х
Г
Х(*—2’ 10’»)1 Вб/м; £Л = Й®100-|-6« 25В/М; Дя=(/?°—0<’).5.10-®[10 4-
5* 108 (/—1,41-Ю-*) Вб/м; £ = 14,75+? 14,75 В/м. 25.5. В точке А
Яя = 7,88’10-4 А/м; Ет0=О.347 В/м; Ет^=1,56 В/м; в точке В На—4,17%
ХЮ'7 А/м; Ете = 1»54-10-* В/м; АаВ = 5- 1О’« Вб/м; /в=10-* с. 25.6. 1 =
= 73 sin (art—30°) А; Е1л = 1,375 sin 0 В/м; £Sm = 697* В/м;
рис. 0.25.1, с, б. 25.8. Япа=а°-0,335 e-/W° В/м; Нте = — 6<0,915х
X 10~’е*7 ио° А/м. 25.9. П=^э-5,65.10“И cos* (erf— 115°) Вт/м’; Ps=0,607 мВт.
Глава двадцать шестая
26.2.
Тип волны \р. Тип волны см
Я1б 2.14 Лао 1,07
^01 0,86 | лп 0,43
0,798 ,
619
Так как 1 = 1,5 см, в волноводе может распространяться волна Н^.
26.3. cos 36.4хsin (со/ —51,2г) А/м; Ях=35,4 sin 36,4х cos (со/—51,2г) А/м;
Я„=0; Ev ——1,63-10* sin 36,4х cos (со/—51,2г) В/м; £х — £г=0; бсм» =
= 2,72* 10s sin36,4хsin (со/—51,2г) А/м8; 6СН х ^6смг=0. 26.4. НИ — /. 5;
И—2, 3, 4, 6. 26.5. Поперечная магнитная волна Ей1', XUP1I = 2.86 см.
26.6. £„х = 39.7.103 В.м; EaJ/ = 18.3- 10s В/м; tfmx = 72,5 А/м; HmV= 157.5 А/м;
//mx=0; £=985 Вт. 26.7. р=9.64 Вт/м; а=4,88’10~3 м~1. Штырь следует
расположить в центре сечення, направив вдоль оси г, а петлю—в середине
узкой стороны сечения так, чтобы ее плоскость была параллельна плоско-
сти yOz. 26.8. £етах^°^аМ = 2160 Вт. 26.9. d-10,2 см. 26.10. £„=
= 1,88 мВт.
Глава двадцать седьмая
27.1. y=v J/ Условие пролета: x=d/2. 1. Следовательно, <
< Vo- 27.3. а) < qbxf, где при d < £ разность потенциалов на двой-
q™ 2
цом слое Дф ~ Ed-. Е “ a/Sol б) частица совершает колебания внутри сферы
вдоль радиуса со скоростью tzi и периодом Т к в) iz2=t?£ 1/ 1 —
27.4. oi = oln4“i?1f; vs = v«n+«2b где 4t = v1slna1; v2t=o2sina2 (рис. 0.27.1)
_ sin оцг _
Так как o2f, то о1=о1———. По закону сохранения энергии, т(А'2 =
Ъ1П (Xg
= mv\i2-^qEd и, следовательно, sina2—-------sln q-- - - 27.5. ----—L —
1/1 + ^ 2 2
r mvi
2
= q \ Edl—<?i(<Pi—фз). Если qi=-—q < 0, Uj=O при ф1 = 0, то лк/2/2=4?ф2
I _____
и, следовательно, v— 2^’®’ sin ai/sin a2 =» Фа/фх- 27.7. Траекто-
рия движения электрона q < 0 показана на рис. 0.27.2. При построении яс*
пользован закон преломления: sin af/sin a,-+1 = Ф, j.i/ф/. 27.10. Гиул =
4Se7V?; = таК как Н»=1/(е<»с2):
При qi=qs £кул—силы отталкивания; Ги — силы притяжения. 27.13. Магнит*
ный момент А!*, обусловлен вращательным движением частицы: Mw = iS, где
i=q]T;=qviJ(2aR)—средний ток; S = ji/?2. Учитывая,
mv.
что /?=—(см. за-
520
лиЛ
дачу 27.1 Ip).
2 о
Магнитный момент не зависит от знака заряда и на-
лравлен противоположно внешнему полю. 27.14. В верхней полуплоскости ча-
стица движется по окружности радиусом — в нижней—по окруж-
ности радиусом ₽2“ mv$/(qB^ = Rif2 (рис. 0.27.3). Поэтому средняя скорость
перемещения (дрейфа) частицы вдоль оси х
ifep=₽i/(0»5Ti-|-0.57’aJ. где Т1 — 2лт/(<дВ}};
Тъ=2лт/(дВ2)—время одного оборота в верх-
ней н нижней полулл хжостях. а) оср =
2
Ц) « О,2ио; б) оср « О,О7ио. Из решений
для случаев а) и б) следует, что чем меньше
ДВ/В, тем меньше скорость дрейфа. Направ-
ление скорости дрейфа зависит от знака заряда.
27.15. 1. Под действием поля В частица с заря-
дом q > 0 вращается вокруг силовой линии,
а под действием поля £ равномерно ускоряет-
ся вдоль ,поля. Поэтому траекторией движения
линейно возрастающим шагом. 2. Если поля В и £
чала частица движется по сжимающейся спирали. Достигнув нулевой ско-
является винтовая линия с
антипараллельны, то сна*
рости вдоль оси х, частица начинает двигаться в противоположном направле-
нии по растягивающейся спирали. 27.17. £'=£-|-(иВ]; В' = В—[пЕ].
Глава двадцать восьмая
28.2. Если движущийся проводник пересекает магнитные силовые линии,
то в нем возбуждается, согласно закону электромагнитной индукции, ЭДС
Для идеального проводника (у=оо) это приводило бы к бесконечному току,
что невозможно. Поэтому движение проводника с у-оо в магнитном поле
должно носить особый характер, т. е быть таким, чтобы пересечения линий
поля не было. Это возможно в том случае, если проводник «увлекает» за собой
магнитные силовые линии (поле «вморожено» в проводящую среду). Математи-
чески уравнения «вмороженного» поля следуют из уравнения rot£ = — dB/dt
с учетом того, что £=—(иВ] (см. задачу 28.1р). В результате дВ/dt = го( |iВ].
Это же уравнение можно получить, если положить у—оо в уравнении (28.5) 11 ].
28.4. а) При поперечном сжатии плоского слоя плазмы [В?] и=0, так как
направление сжатия (изменения) перпендикулярно скорости. Следовательно,
В/р = const; В~р-, рм = В2/(2ро) ~ р2- Этим обстоятельством
можно, например, объяснить происхождение сильных магнитных полей в звез-
дах за счет гравитационного сжатия разреженного газа со слабым «вморожен-
ным» полем, б) При продольном сжатии магнитные силовые линии только со-
кращаются в длину, но не сгущаются. Поэтому ни В, нн рм не зависят от р.
в) При сжатии сферического сгустка В ~ 1/I?8; р=^т/п~ 1/Я3; следовательно,
В~р^3, рм~р4'3’ 28.5, а) При и=0 уравнение диффузии для плазменных
сгустков -^-=vMv2B, где vM = 1 /(уро) — коэффициент диффузии (магнитная
вязкость). Считаем, что на границе сгустка поле максимально. Bmax= Во- Тогда
г» 5аВ , д»В , ^В Во дВ Во п
VZB е------1-----J----ж —; ------а —— . Отсюда для сферического сгустка
дх2 dy2 дг2 Rq dt /0
t0 ж ypafto (аналшичный результат см. в (1J). б) Для тороидального сгустка
t9 « |xeY'o* Для процессов, происходящих при / </0, допустимо считать поле
«вмороженным». 2b.6. 1. /0 « 60 с. 2. l0 = 60< U)'6 с ~ 17 млрд, лет (это время
521
сравнимо с возрастом Вселенной, который, по современным оценкам, состав*
ляет ~20 млрд. лет). 28.8. Основное уравнение магнитостатики gradp=—X
Ма
-* -* й» -* В
Xjrot B«BJ=— grad -г-}-(В grad) — В данном случае изменение вектора В
2рв Ра д
происходит только в перпендикулярном к В направлении. Поэтому (В grad) В=0;
/ й® \ в8
grad( р+ тт— |=0; р-Н>—=₽*=const, где />•—суммарное давление, вклю-
\ 2ра / 2рв
чая и магнитное. В данной задаче р—nekT-{-n^ kT—2nkT и, следовательно,
#пяп = К 4р<>пА7' и 2 Тл. 28.9. Для устойчивых конфигураций характерно то,
что магнитные линии обращены выпуклостью к
плазме. В связи с этим конфигурация рис. 28.4, а
устойчива; рнс. 28.4, б—неустойчива; рис. 28.4, в—
безразличная. Устойчивые конфигурации создают-
ся, например, в так называемом антипробкотро-
не—системе из двух катушек со встречными токами
(рис. 0.28.1) и в других системах с минимумом поля
внутри. 28.10. 1. р (г) = Ртах—Ро—a гДе Ртах=
Wo
U
= Ратм+-^ • 2- р (г) = ртах = const. 3. В От-
ЛГо
ношении изгиба при гй ~ Р равновесие устойчиво,
так как при малом радиальном изменении жид-
кого проводника возникает возвращающая сила за
счет бокового распора магнитных силовых линий в
зазоре. Прн г0 < Р такое равновесие может стать
неустойчивым. В отношении «перетяжек» обе конфигурации неустойчивы.
4. «Вморозить» в жидкий проводник достаточно сильное осевое поле, например
с? В* 2
помещая всю систему в поле соленоида. 28.11. a) 2L_d=_2_ я> следовательно,
2
Рис. 0.28.1
В‘ -К) ₽^=₽»V»+_BL : омз«1/ £2Ь-|_Я«.. 28.12. 1. Прн
У PoPfl 2 2 2щ у Ро щ ро
движении слабоионизированного газа в магнитном поле на проводящих стейках
накапливаются заряды (положительные—на .верхней, отрицательные—на ниж-
ней) и образуется разность i
когда электрическая сила
Отсюда наводимая э. д. с.
ток /=(/о/(Кян+Яи), где
потенциалов Uq. Процесс накопления заканчивается,
। FBRiq~~ уравновешивает магнитную Fn —qvB.
U0 = 2dBv. 2. При включении нагрузки /?и пойдет
RBb ~ внутреннее сопротивление МГД-гене-
Y QD
ратора. При /?в=/?вя Wr, где Vr=2da&—активный объем
Р
МГД-генератора. Соответственно ?=2,5 МгВт/м8. 28.16. I. На
поверхности Е<—0; Вп—С. 2. Ht——J sin 0, где J=—Яо/(1—N)—намагни-
ченность; 0—угол между направлением поля Но и внешней нормалью; АГ —
коэффициент размагничивания. Для случая a) ^=l/2; для случая б)Л=0;
для случая в) Л^ = 1/3.28.17.1. М = /Ушв—• -у где Hi=lW10 вдо—
= 3«; 2) М.=^=и,£15л=_мй,_2-Уш;
hi Ji h 1—л
522
xf t 1 • V где V*=n₽Ihi—объем катушки. 28.18. а) Уравнение
1—Af У* /' jig ।
Лондонов v’2='4-3 при B = BA позволяет получитьВ=0.
XL
ch £2
Его решение при условии Вх=±а = Во ныеет вид & (х)~ д“ • Ф В —ВоХ
СЬк
, где J0(rМ—функция
Бесселя.
Список рекомендуемой литературы
Учебники
1. Бессонов JLA. Теоретические основы электротехники: Электрические пели
- - М.: Высшая школа, 1996.
2. Бессонов Л.А. Теологические основы электротехники: Электромагнитное
ноле М<: Гардарики, 2001.
3. Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники. Т 1,2
— Л: Эяергоиздат, 1981.
4. Теоретические основы электротехники/ Под ред. П.А. Ионкнна, Т. 1,2 —
М.1 Высшая школа, 1976.
Учебные пособия
5. Бессонов ЛА. Линейные электрические цепи. — М.: Высшая школа, 1983.
6. Бсссоков Л.А. Нелинейные электрические цепи. — М.: Высшая школа, 1977.
7. Кухаркин Е.С. Инженерная электрофизика. Техническая электродинамика
— М.: Высшая школа, 1982.
8. Матханов П.Н. Основы анализа электрических цепей: Линейные цепи
М.: Высшая школа, 1981.
9. Методы расчета электростатических полей/ Н.Н Миролюбов, М.В. Ко-
стенко, МЛ. Левинштейя, Н.Н. Тиходеев. — М.: Высшая школа, 1963.
10. Основы инженерной электрофизики. Т 2/ П.А. Ионкин, В.Г. Миронов,
А.А. Соколов, Ф.Е. Паушканис — М.: Высшая школа, 1972.
Сборники задач
11. Сборник задач и упражнений по теоретическим основам электротехники^
Под ред П.А. Ионкнна. — M.i Энергоатомиздат, 1982.
12. Задачник по теоретическим основам электротехники. Теория целен/ Под
ред К.М. Поливанова. — М.: Энергия, 1973.
Оглавление
Предисловие................................................. • 3
Глава первая. Линейные электрические цепи постоянного тока....... 5
А. Законы Ома и Кирхгофа. Источники ЭДС и тока. Разность
потенциалов..................................................... 5
Б. Потенциальная диаграмма. Линейные соотношения................ 7
В. Входные сопротивления. Преобразование треугольника в звезду
и звезды в треугольник.......................................... 9
Г. Входные и взаимные проводимости ветвей. Теорема взаимности.
Принцип наложения. Теорема вариаций....................... 1!
Д. Метод контурных токов. Метод узловых потенциалов. Метод двух
узлов. Баланс мощностей. Замена нескольких параллельных вет*
вен эквивалентной.......................................... 13
Е. Активный двухполюсник. Метод эквивалентного генератора . . 14
Ж- Передача мощности от активного двухполюсника нагрузке. Тео*
рема компенсации . .......................................... 15
3. Задачи на различные темы.................................... 16
Глава вторая. Индуктивные я емкостные элементы электрических цепей 19
А. Индуктивность н взаимная индуктивность катушек.............. 19
Б. Индуцированные ЭДС.......................................... 90
В. Механические усилия* в магнитном поле....................... 2!
Г. Энергия магнитного поля................................... 22
Д. Емкость как параметр электрической цепи..................... 23
Глава третья. Электрические цепи однофазного синусоидального тока . 24
А. Мгновенные значения синусоидального тока, напряжения н мощ-
ности. Активные, реактивные, комплексные сопротивления и
проводимости. Символический метод расчета...................... 24
Б. Векторные и топографические диаграммы....................... 25
В. Активная, реактивная и полная мощности в цепи переменного тока 26
Г. Резонансы и частотные характеристики........................ 28
Д. Магнитно-связанные цепи..................................... 30
Е. Задачи на различные темы 32
Глава четвертая. Четырехполюсники и круговые диаграммы............. 34
А. Определение параметров пассивных и активных четырехполюсников 34
Б. Т- и П-схемы замещения четырехполюсника..................... 36
В. Схемы соединений четырехполюсников.......................... 37
Г. Четырехполюсник как согласующее звено между источником
энергии и нагрузкой ......................................... 38
Д. Невзаимные и активные четырехполюсники...................... 39
Е. Круговые диаграммы.......................................... 40
Глава пятая. Электрические фильтры ............................... 42
А Общая методика анализа фильтрующих свойств реактивного че-
тырехугольника .............................................. 42
Б. Фильтры типа &....,........................................ 44
524
В. Фильтры типа ............................................... 46
Г Пассивные ₽С-фильтры....................................... 49
Д. Активные RC фильтры......................................... 51
Глава шестая. Трехфазные цепи...................................... 55
А. Симметричная нагрузка и режимы, возникающие при обрывах
проводов....................................................... 55
Б. Режимы при несимметричном источнике или несимметричной на-
грузке ............................................... , . . . 57
В Цепи с магнитно-связанными ветвями......................... 60
Г. Круговые диаграммы.......................................... 61
Д. Метод симметричных составляющих............................ 61
Е. Вращающееся магнитное поле................................. 62
Глава седьмая. Периодические несинусоидальные режимы в линейных
электрических цепях............................................. 63
А. Разложение несинусоидальных токов и напряжений в ряд Фурье.
Действующие и средние значения. Коэффициенты, характеризую-
щие форму.....................-................................ 63
Б. Применение рядов Фурье для расчета электрических цепей, содер-
жащих несинусондальные источники тока и ЭДС.................... 65
В- Резонансные явления при несинусоидальных токах и напряжени-
ях. Показания измерительных приборов........................... 66
Г. Расчет простейших электрических цепей с иесинусоидальными
источниками тока и ЭДС без разложения в ряд Фурье .... 68
Д. Несинусоидальные токи я напряжения в трехфазных цепях . . 63
Е. Амп л и ту дно-мод ул крова иные колебания.................. 70
Глава восьмая. Переходные процессы в линейных электрических цепях
с сосредоточенными параметрами..............,.................... 70
А. Классический метод.......................................... 70
Б. Операторный метод........................................... 81
В. Метод интеграла Дюамеля..................................* 84
Г. Метод дискретных преобразований............................. 86
Д. Метод переменных состояния ................................. 88
Е. Численные методы ........................................- 89
Глава девятая. Спектральный метод анализа линейных электрических
цепей......................................................... - 90
А. Частотные характеристики цепей.............................. 90
Б. Спектры периодических и апериодических сигналов............. 92
В. Корреляционные функции детерминированных и случайных сиг-
налов и их спектры.............................................. 94
Г. Прохождение периодических, апериодических в случайных сигна*
лов через линейные цепи........................................ 95
Глава десятая. Синтез двухполюсников и четырехполюсников......... 98
А. Возможн >сть реализации двухполюсников по заданному Z (р).
Определение элементов двухполюсника............................ 98
Б. Составление входных сопротивлений двухполюсников.......... 99
В. Реализация Z(p) лестничной схемой, путем последовательного
выделения простейших составляющих и методом Бруне .... 99
Г. Реализация двухполюсника по временному отклику. Связь между
действительной и мнимой частями............................. 100
Д. Некоторые особенности преобразования треугольника в звезду я
звезды в треугольник. Эквивалентные замены, Дополняющие и
взаимно обратные двухполюсники.............................. 101
Е. Проверка возможности реализации четырехполюсника по его па-
раметрам ................................................... 103
Ж. Определение типа четырехполюсника по его передаточной функции 103
3. Реализация четырехполюсника Г-схемой ..................... 104
525
И. Задачи на различные темы..................................... 105
Глава одинадцатая. Установившиеся процессы в электрических цепях,
содержащих линии с распределенными параметрами.................. 106
А. Первичные и вторичные параметры линии ....................... 106
Б. Искажения сигнала, передаваемого по линии. Линн я без искажений 107
В. распределение по линии мгновенных и действующих значений
тока и напряжения.............................................. 108
Г. Линия без потерь............................................ 109
Глава двенадцатая. Переходные процессы в цепях с распределенными
параметрами...................................................... ПО
А. Волновой метод............................................. 110
Б. Операторный метод............................................ Ill
В. Формирование импульсов с помощью заряженного отрезка линии 114
Г. Каскадное, последовательное и параллельное соединения двух линий 115
Глава тринадцатая. Нелинейные электрические цепи постоянного тока . 117
А. Построение характеристик нелинейных цепей. Расчет токов и на
пряжений графическим методом в цепях с одним источником . . 117
Б. Метод эквивалентного генератора. Метод одновременного холо-
стого хода двух ветвей...................................... 120
В. Замена нелинейного активного двухполюсника эквивалентным. Ме-
тод двух узлов. Расчет разветвленной цепи...................... 122
Г. Аналитический расчет нелинейных цепей........................ 123
Д. Цепи с идеальными диодами.................................... 124
Глава четырнадцатая. Магнитные цепи................................. 125
А. Неразветвленные магнитные цепи............................... 125
Б. Разветвленные магнитные цепи................................. 126
В. Магнитные цепи, содержащие ферромагнитные сердечники с пря-
моугольной петлей гистерезиса.................................. 128
Г. Постоянные магниты......................................... 129
Глава пятнадцатая. Нелинейные электрические цепи переменного тока в
установившемся режиме........................................... 129
А. Цепи с неуправляемыми нелинейными индуктивными катушками
и конденсаторами. Расчет по мгновенным значениям величин . . 129
Б. Цепи с неуправляемыми нелинейными резисторами. Расчет по
мгновенным значениям величин............................... 133
В. Цепи с управляемыми нелинейными трехполюсниками. Расчет по
мгновенным значениям и линейным схемам замещения для малых
переменных составляющих токов и напряжений..................... 135
Г. Расчет по первым гармоникам и действующим значениям .... 138
Д. Частотные характеристики................................... 142
Ь. Метод малого параметра..................................... 143
Ж- Некоторые энергетические соотношения....................... 145
3. Появление постоянных составляющих потока, заряда и тока при
отсутствии выпрямителей. Метод гармонического баланса . . , 146
И. Зависимость постоянной составляющей потока (заряда) от пере-
менной составляющей........................................ 147
К. Исследование устойчивости положения равновесия. Автоколебания 148
Л. Электрические цепи с операционными усилителями ............. 151
Глава шестнадцатая. Переходные процессы в нелинейных электрических
цепях.................................................... 154
А. Расчет переходных процессов в цепях первого порядка .... 154
Б. Расчет переходных процессов в цепях второго порядка .... 157
В. Численные методы.......................................... 158
Глава семнадцатая. Анализ линейных электрических цепей методом графов 160
526
А. Направленные графы (линейные графы сигналов)............. 160
Б. Ненаправленные графы...................................... 163
Глава восемнадцатая. Электрические цепи с изменяющимися во времени
параметрами .................................................. 164
А. Установившиеся процессы в цепях с периодически изменяющимися
параметрами при наличии источников электрической энергии . . 164
Б. Параметрические колебания................................. 166
В. Исследование устойчивости режимов работы цепей с периодически
изменяющимися параметрами .................................... 168
Г. Некоторые явления в цепях с периодически изменяющимися па-
раметрами ................................................ 168
Глава девятнадцатая. Электростатическое поле..................... 170
А. Интегральные соотношения между зарядом, напряженн >стью поля
и потенциалом................................................. 170
Б. Дифференциальные соотношения между плотностью заряда, на-
пряженностью поля и потенциалом.......................... 172
В. Граничные условия. Многослойные диэлектрики н конденсаторы 173
Г. Поля простого н двойного заряженного слоев................ 175
Д. Метод изображений......................................... 176
Е. Поле системы заряженных тел. Формулы Максвелла............ 177
Ж. Метод разделения переменных.............................. 1 78
3. Графическое построение картины поля....................... 179
И. Метод конформных преобразований........................... 181
К. Метод интегральных уравнений ............................. 182
Глава двадцатая. Электрическое поле постоянного тока............. 184
А. Законы Ома, Кирхгофа и Джоуля—Ленца в дифференциальной
форме......................................................... 184
Б. Определение проводимостей и токов утечки.............. 185
В. Метод изображении......................................... 186
Г. Расчет постоянного электрического поля в неоднородной прово-
дящей среде................................................. 188
Д. Графический метод построения картины плоскопараллельного
электрического поля......................................... 189
Глава двадцать первая. Магнитное ноле постоянного тока........... 190
А. Закон полного тока ....................................... 190
Б. Закон Био—Савара—Лапласа.................................. 191
В. Скалярный магнитный потенциал и магнитное напряжение . . . 192
Г. Векторный магнитный потенциал........................... 193
Д. Метод изображений ........................................ 196
Е. Метод разделения переменных.............................. 197
Ж. Графическое построение картины магнитного поля и ее исполь-
зование ................................................. 199
Глава двадцать вторая. Основные уравнения переменного электромагнит-
ного поля 201
А. Уравнения Максвелла ...................................... 20!
Б. Теорема Умова—Пойнтинга................................... 203
Глава двадцать третья. Переменное электромагнитное поле в однородной
и изотропной проводящей среде................................. 204
А. Установившиеся процессы при распространении плоской электро-
магнитной волны в проводящем полупространстве............... 204
Б. Поверхностный эффект в плоском теле....................... 204
В. Поверхностный эффект в цилиндрическом теле................ 207
Г. Переходные процессы при распространении плоской электромаг-
нитной волны в проводящей среде ............ . . 208
527
Глава двадцать четвертая. Переменное электромагнитное поле в диэлект-
рике и полупроводящей среде........................................
А. Распространение плоской электромагнитной волны в однородных
и изотропных диэлектрике и полупроводящей среде................
Б. Переход плоской электромагнитной волны из одной среды в
другую...............................,.........................
В. Расчет электромагнитного поля в слоистых средах методом нап-
равленных графов...............................................
Г. Квазистатическое электрическое поле в вязкой среде и несовер-
шенном диэлектрике ............................................
Глава двадцать пятая. Запаздывающие потенциалы переменного электро-
магнитного поля и излучение электромагнитной энергии...............
А. Запаздывающие электродинамические потенциалы................
Б. Излучение электромагнитной энергии .........................
Глава двадцать шестая. Электромагнитные волны в направляющих си-
стемах .....................................................
А, Электромагнитное поле в волноводах..........................
Б. Электромагнитное поле в объемных резонаторах................
Глава двадцать седьмая. Движение заряженных частиц в электрическом
и магнитном полях..................................................
А. Движение заряженных частиц в электрическом поле.............
Б- Движение заряженных частиц в магнитном и скрещенных полях
Глава двадцать восьмая. Основы магнитной гидродинамики. Сверхпрово-
димость ...........................................................
А. Уравнения магнитной гидродинамики, равновесные конфигурации/
волны, течения.................................................
Б. Сверхпроводимость...........................................
Решения............................................................
Ответы ............................................................
Список рекомендуемой литературы ..............- ..................
Учебное издание
Лев Алексеевич Бессонов, Илиада Григорьевна Демидова,
Моисеи Ефимович Зарудд, Валежпиа Пеграма Каменска,
Светлана Александровна Ммлемииа, Светлана Эфраимопва Расавская
СБОРНИК ЗАДАЧ ПО ТЕОРЕТИЧЕСКИМ ОСНОВАМ
ЭЛЕКТРОТЕХНИКИ
Редактор Н. Е Овчеренко. Художественный редактор Ю. Э. Иванова.
Технический редактор Н. В. Быкова.
Лицензия ИД № 06236 от 09.11.2001
Изд. № ВТИ-83. Подл, в печать 05.12.2002. Формат 60x90 */к. Бум. газеты.
Гарнитура литературная. Печать офсетная. Объем: 33,0 усл. печ. л.,
33.0 усл. кр.-отг.. 33.87 уч.-изд. л. Тираж 6000 экз. Заказ № 152
ФГУП «Издательство «Высшая ткана»
127994. Москва, ГСП-4. Неглинная ул.. 29/14
Тел. (095) 200-04-56
E-mail: info@v-shkola ru http://www.v-shkola.ru
Отдел реализации: (095) 200-07-69. 200-59-39.
факс (095) 200-03-01. E-maii: sales@v-shkola.ru
Отдел «Книга-почтой»: (095) 200-33-36
E-mail: bookpost@v-shkola.ru
Отпечатана во ФГУП ИПК «Ульяновский Дом печати»
432980, г. Ульяновск, ул. Гончарова, 14