А. С. ВОЛЬМИР
 ГИБКИЕ ПЛАСТИНКИ И ОБОЛОЧКИ
 ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО ТЕХНИКО-ТЕОРЕТИЧЕСКОЙ ЛИТЕРАТУРЫ МОСКВА 1956

ОГЛАВЛЕНИЕ
 Предисловие 7
 Основные обозначения. 11
 Глава I. Общая теория гибких пластинок 13
 § 1. Классификация пластинок по характеру напряженного состояния.
 Гибкая пластинка 13
 § 2. Деформации срединной поверхности и кривйзны. Уравнение совместности деформаций 16
 § 3. Напряжения в пластинке при больших прогибах. Уравнения равновесия элемента пластинки 26
 § 4. Соотношения между деформациями и напряжениями 33
 § 5. Основные дифференциальные уравнения 35
 § 6. Граничные условия 39
 § 7. Применение принципа возможных перемещений. Вариационное
 уравнение равновесия 44
 § 8. Вычисление энергии системы 51
 § 9. Полное вариационное уравнение 53
 § 10. Приближенные методы, связанные с вариационными уравнениями 58
 §11. Другие приближенные методы 62
 § 12. Анизотропные пластинки 65
 § 13. Трехслойные пластинки 69
 Глава II. Большие прогибы прямоугольных пластинок при поперечной нагрузке 74
 § 14. Удлиненная пластинка, шарнирно опертая по контуру; приближенное решение задачи 74
 § 15. Шарнирно опертая пластинка; точное решение • 79
 § 16. Удлиненная пластинка, защемленная по контуру; приближенное
 решение 86
 § 17. Случай защемленных краев; точное решение 88
 § 18. Влияние начальной погиби на деформацию удлиненной пластинки 92
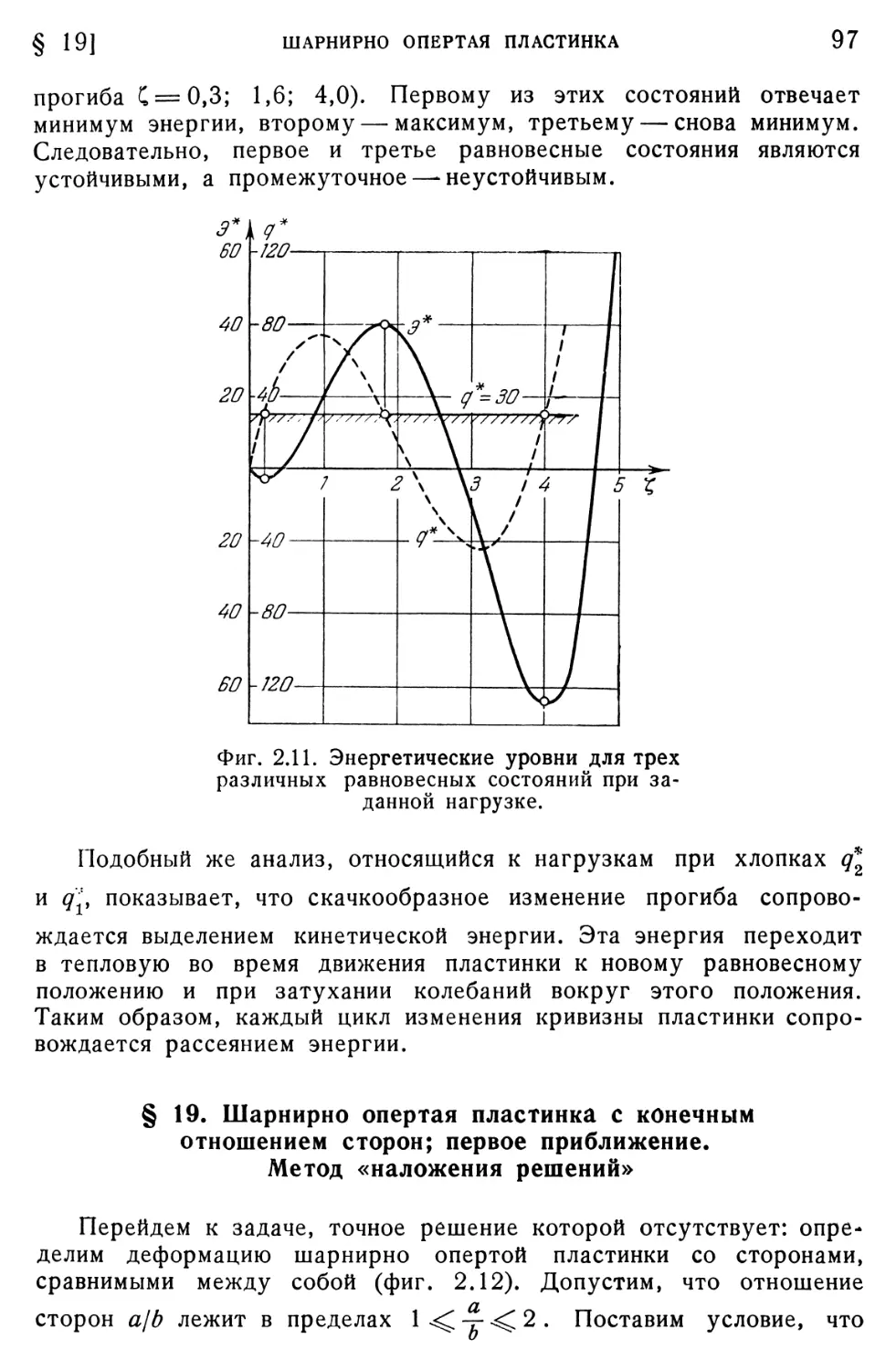
 § 19. Шарнирно опертая пластинка с конечным отношением сторон;
 первое приближение. Метод «наложения решений» 97
 § 20. Уточнение расчета квадратной шарнирно опертой пластинки
 Данные опытов 103
 § 21. Защемленная по краям пластинка с конечным отношением сторон;
 первое приближение 109
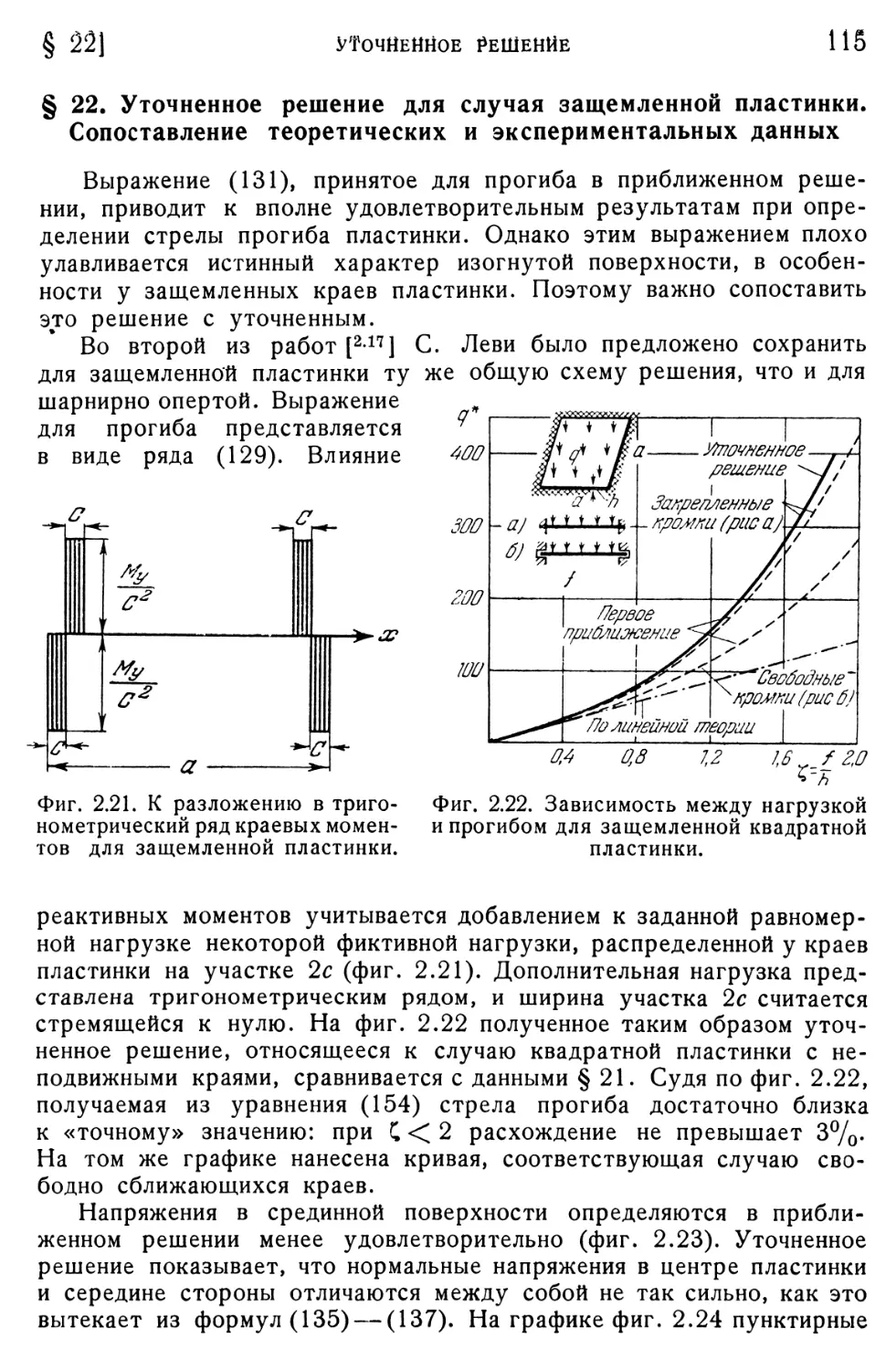
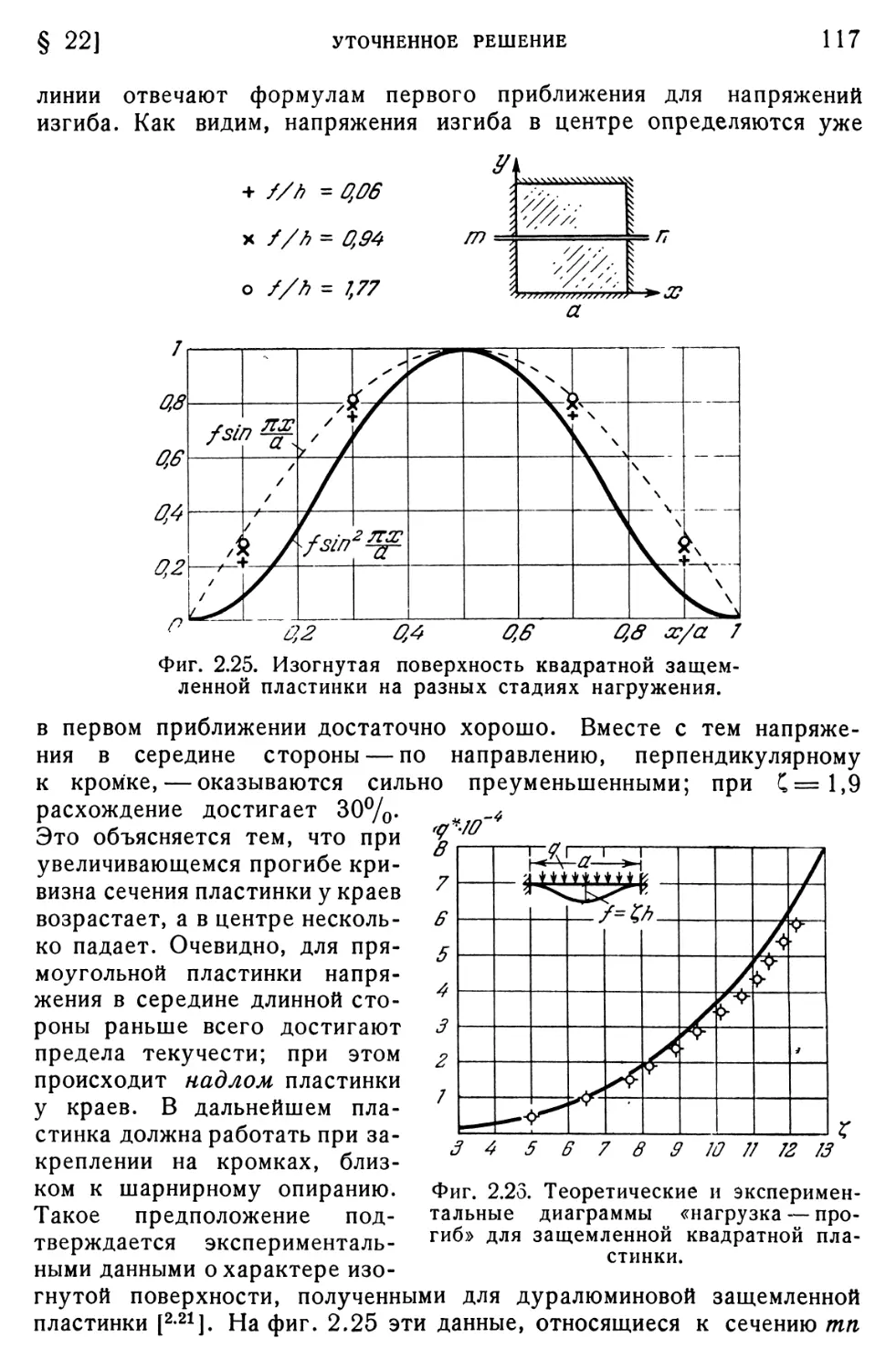
 § 22. Уточненное решение для случая защемленной пластинки. Сопоставление теоретических и экспериментальных данных 115
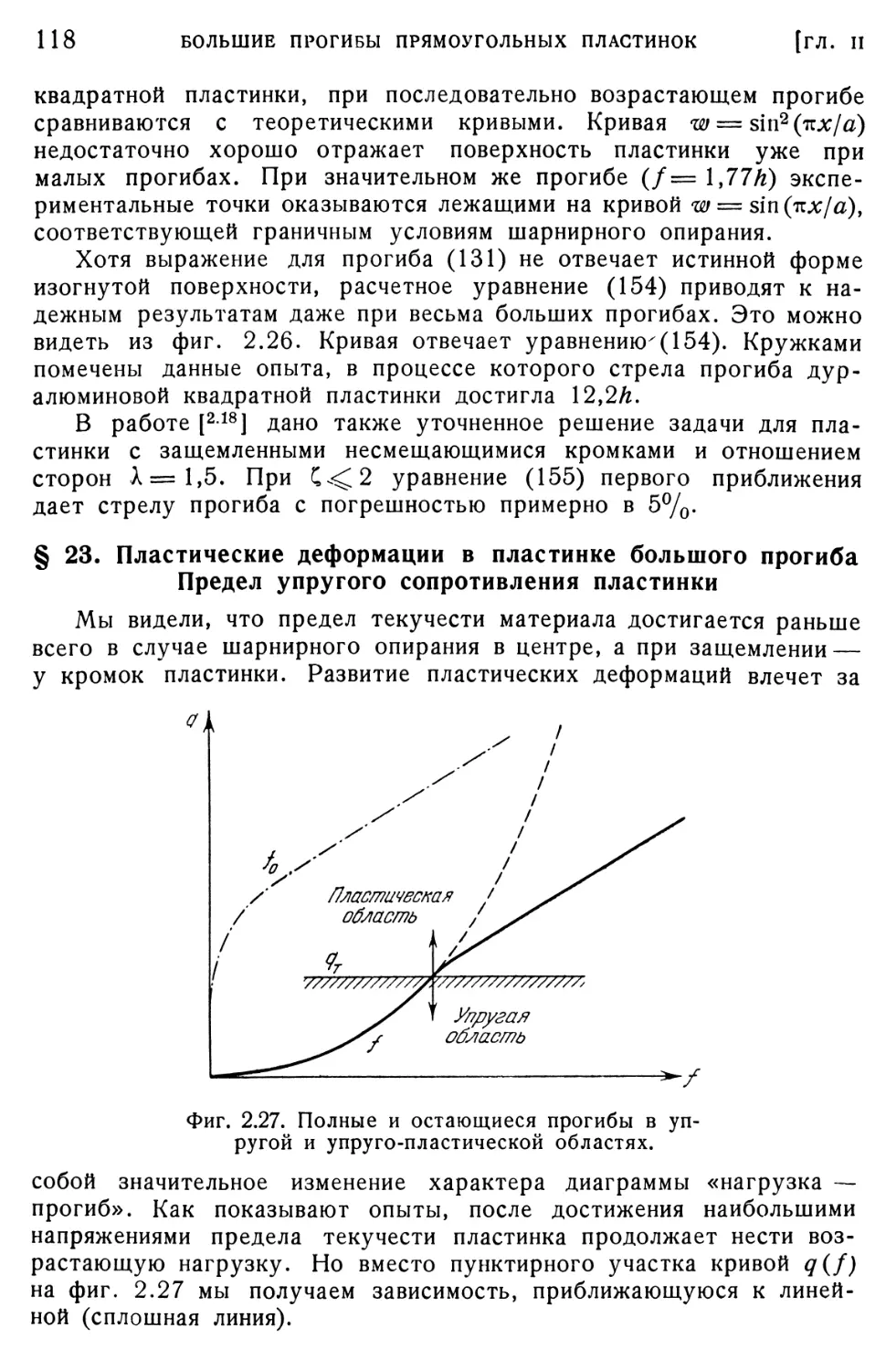
 § 23. Пластические деформации в пластинке большого прогиба. Предел
 упругого сопротивления пластинки 118
 § 24. Мембрана с предварительным натяжением 121

4
 ОГЛАВЛЕНИЕ
 Глава III. Закритическая деформация прямоугольных пластинок 124
 § 25. Сжатие прямоугольной пластинки после потери устойчивости. Понятие редукционного коэффициента 124
 § 26. Пластинка, шарнирно опертая по краям; первое приближение.
 Частные случаи квадратной и удлиненной пластинок 126
 § 27. Уточненные решения для квадратной пластинки 134
 § 28. Квадратная пластинка, защемленная по краям 141
 § 29. Приближенные формулы для редукционного коэффициента.... 143 § 30. Экспериментальное исследование закритической деформации пластинок 145
 § 31. Пластинка, подкрепленная упругими ребрами 151
 § 32. Редукционные коэффициенты при вычислении момента инерции
 сечения панели 155
 § 33. Квадратная пластинка после потери устойчивости от сдвига... 157
 § 34. Удлиненная пластинка при сдвиге 162
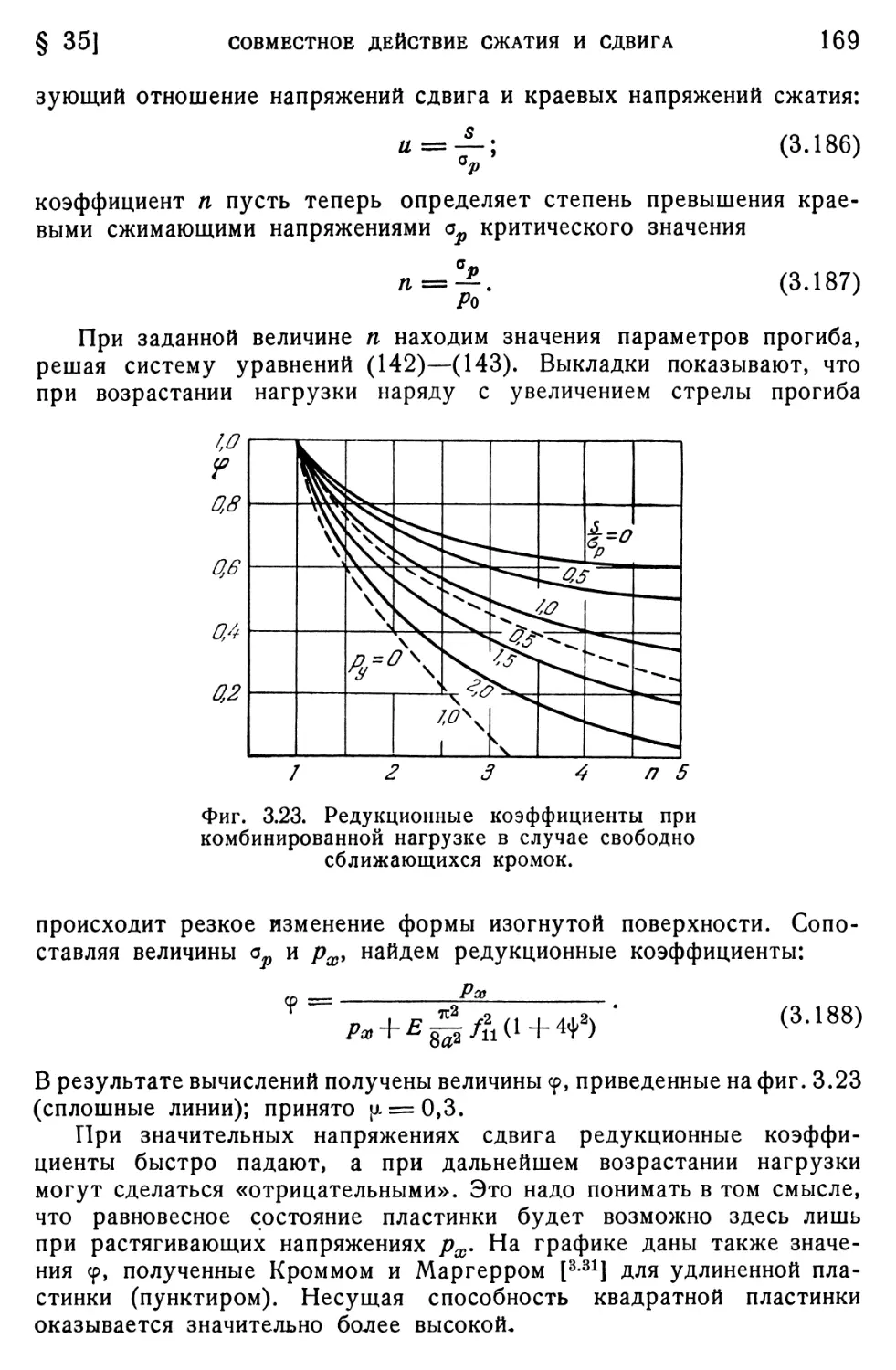
 § 35. Совместное действие сжатия и сдвига 167
 Глава IV. Круглые пластинки 171
 § 36. Осесимметричный изгиб круглой пластинки. Деформации и кри-
 вйзны. Условие совместности деформаций 171
 § 37. Напряжения в срединной поверхности. Изгибающие моменты и
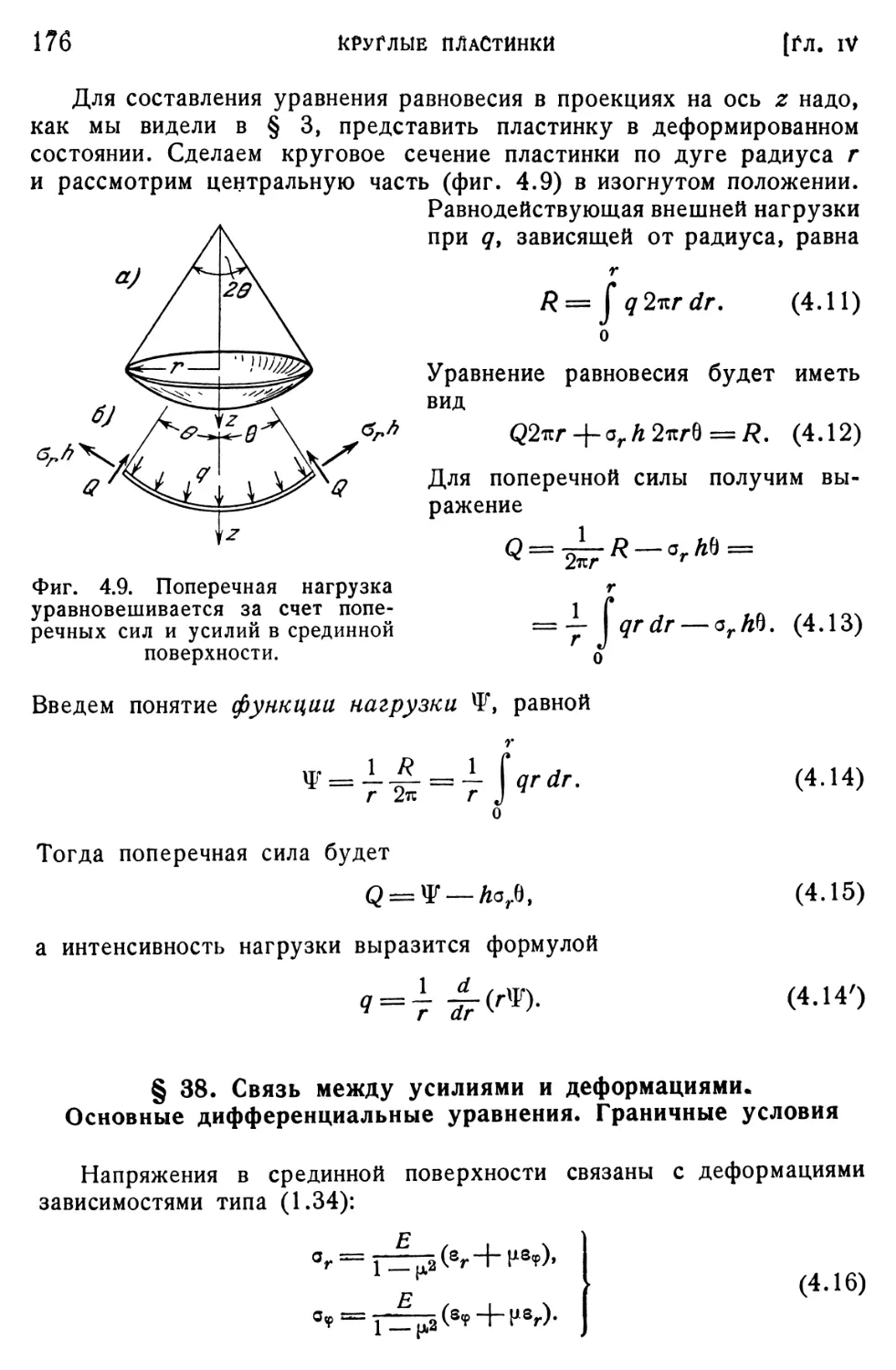
 поперечная сила. Условия равновесия 174
 § 38. Связь между усилиями и деформациями. Основные дифференциальные уравнения. Граничные условия 176
 § 39. Основные уравнения при несимметричной деформации. Случай
 анизотропии 180
 § 40. Применение вариационных методов 183
 § 41. Защемленная по контуру пластинка при равномерной поперечной
 нагрузке 186
 § 42. Шарнирно опертая пластинка при равномерной нагрузке 191
 § 43. Случай сосредоточенной нагрузки 193
 § 44. Уточненное решение по методу возмущения 196
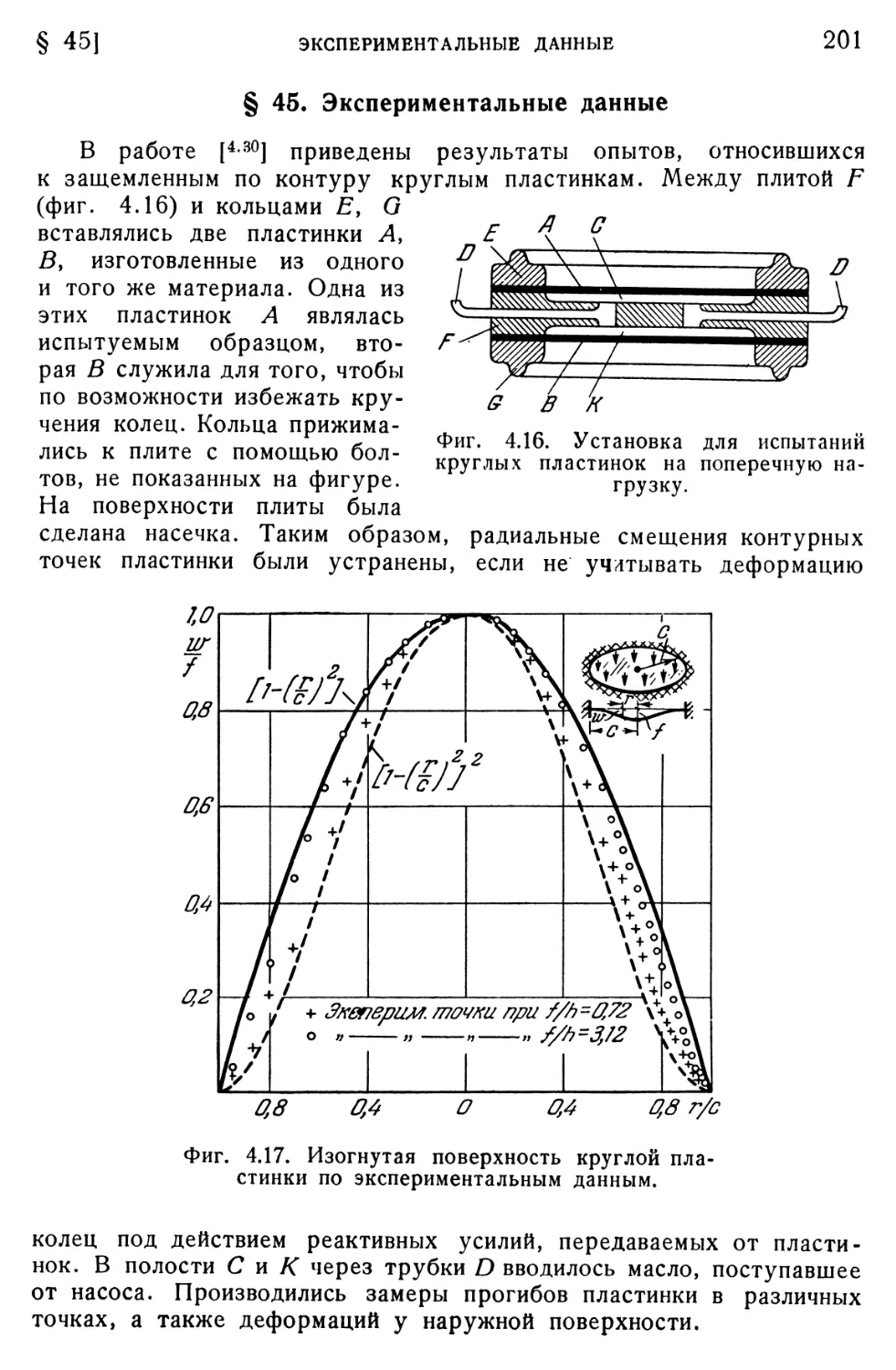
 § 45. Экспериментальные данные 201
 § 46. Предел упругого сопротивления пластинки 203
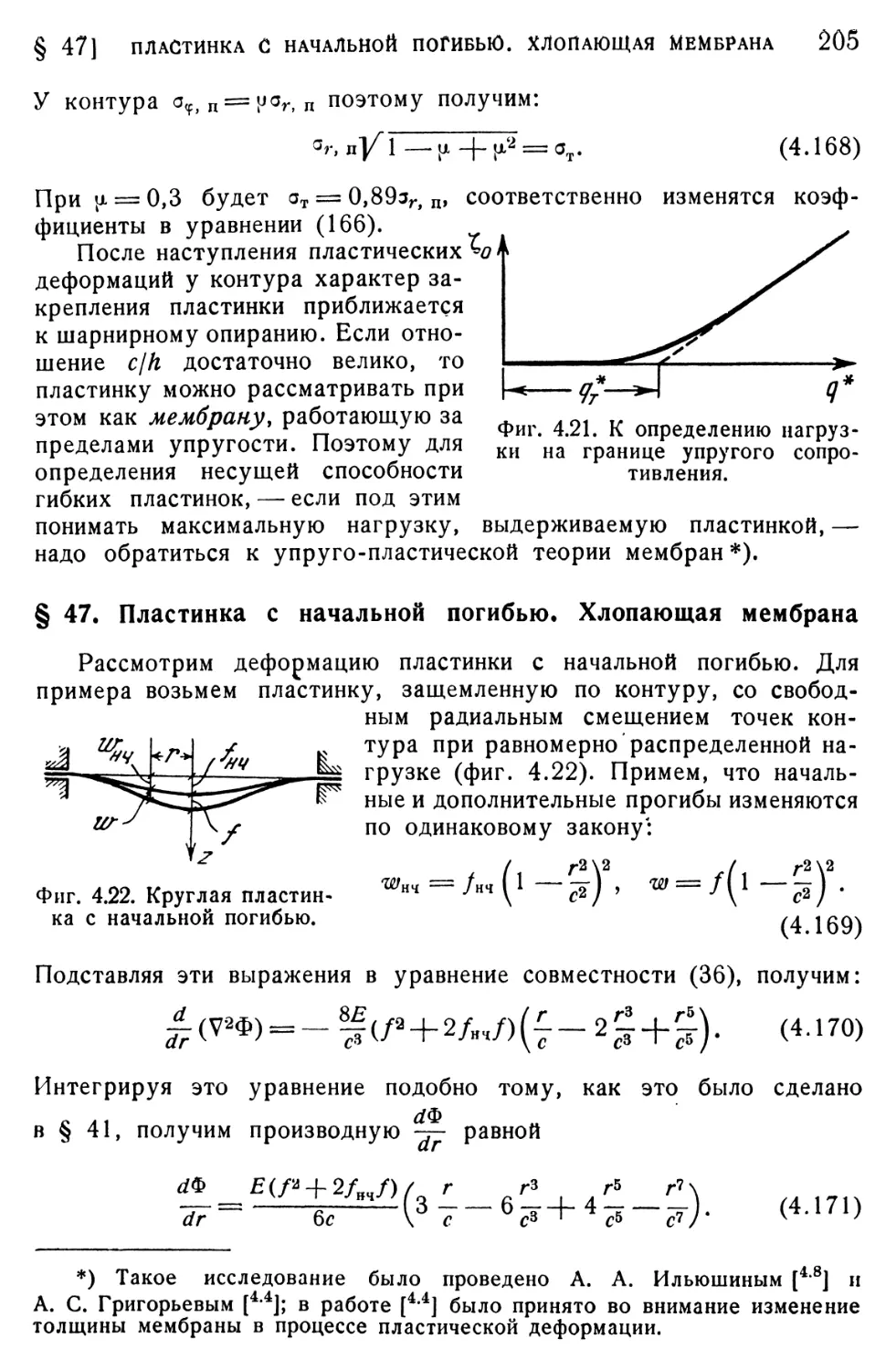
 § 47. Пластинка с начальной погибью. Хлопающая мембрана 205
 § 48. Пологая коническая панель 210
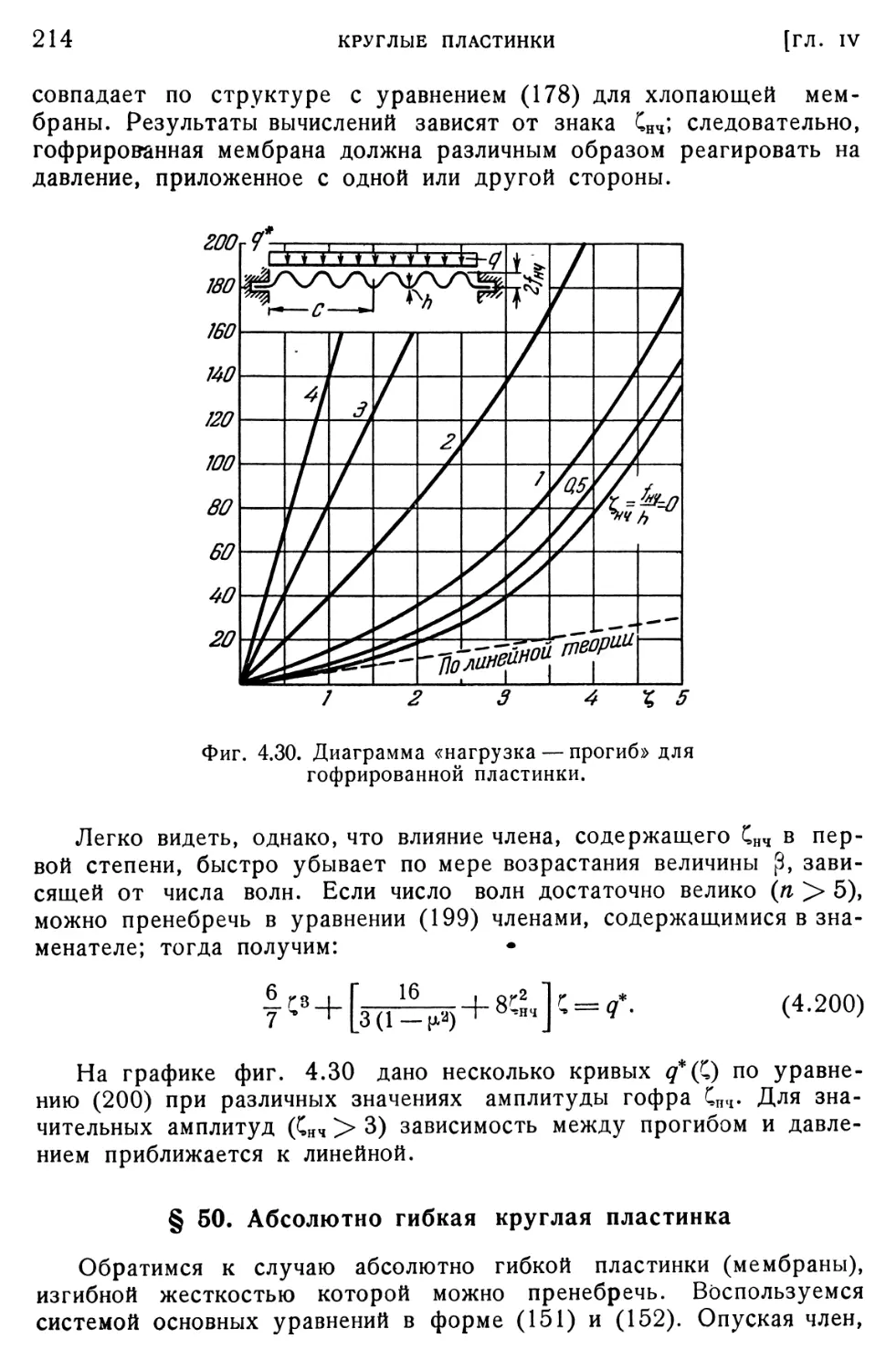
 § 49. Гофрированная пластинка 211
 § 50. Абсолютно гибкая круглая пластинка 214
 § 51. Круглая пластинка после потери устойчивости при радиальных
 сжимающих усилиях. Аналогия с прямоугольной пластинкой... 221
 Тлава V. Общие сведения о гибких оболочках 226
 § 52. Основные определения 226
 § 53. Деформации срединной поверхности и изменения кривизн. Уравнение совместности деформаций 229
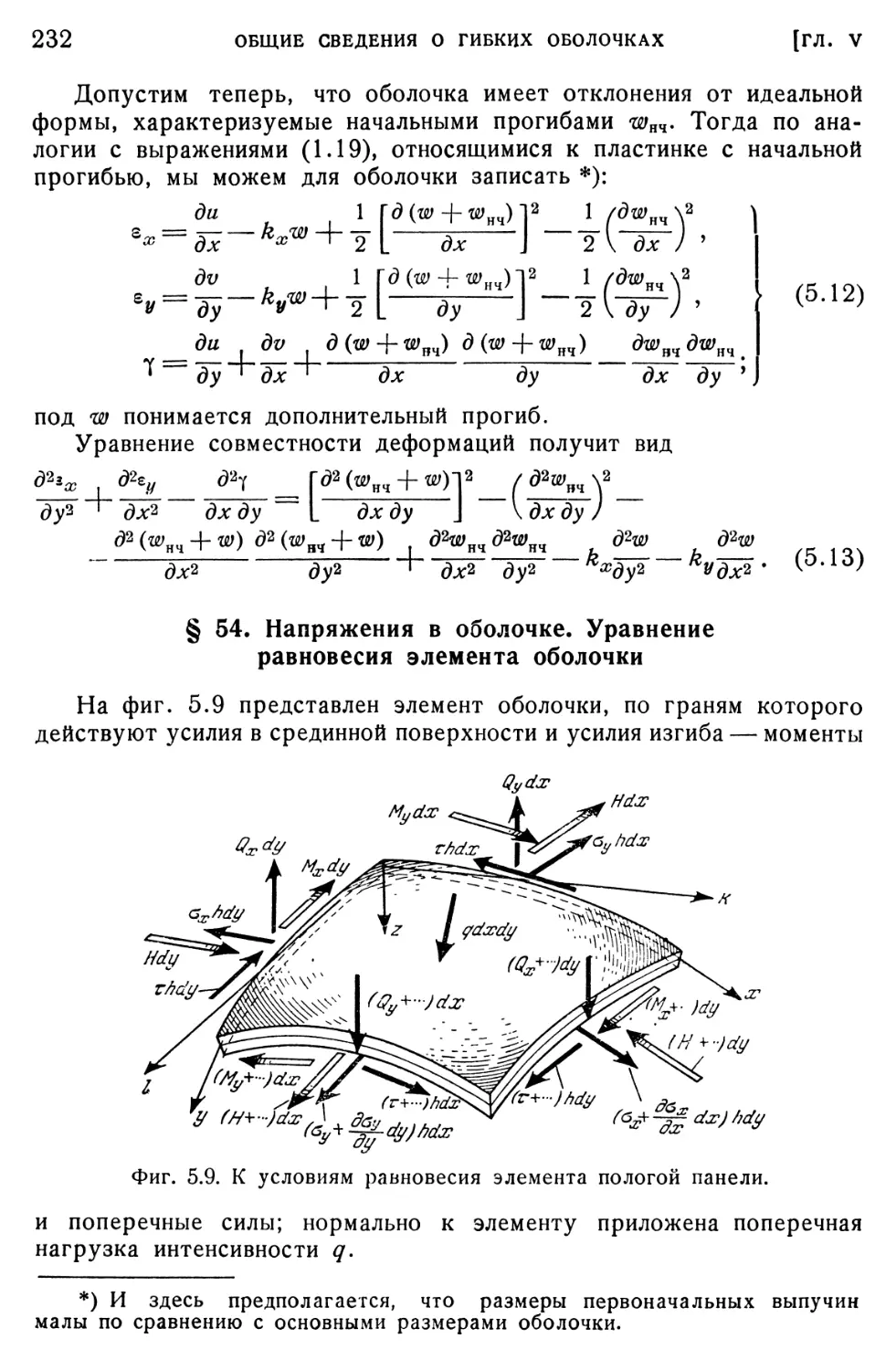
 § 54. Напряжения в оболочке. Уравнения равновесия элемента оболочки 232 § 55. Соотношения между деформациями и напряжениями. Основные
 дифференциальные уравнения •.. 234
 § 56. Вариационные уравнения. Применение приближенных методов.. 238
 Г л а в а VI. Большие прогибы пологих оболочек при поперечной
 нагрузке 240
 § 57. Удлиненная цилиндрическая панель, шарнирно закрепленная по
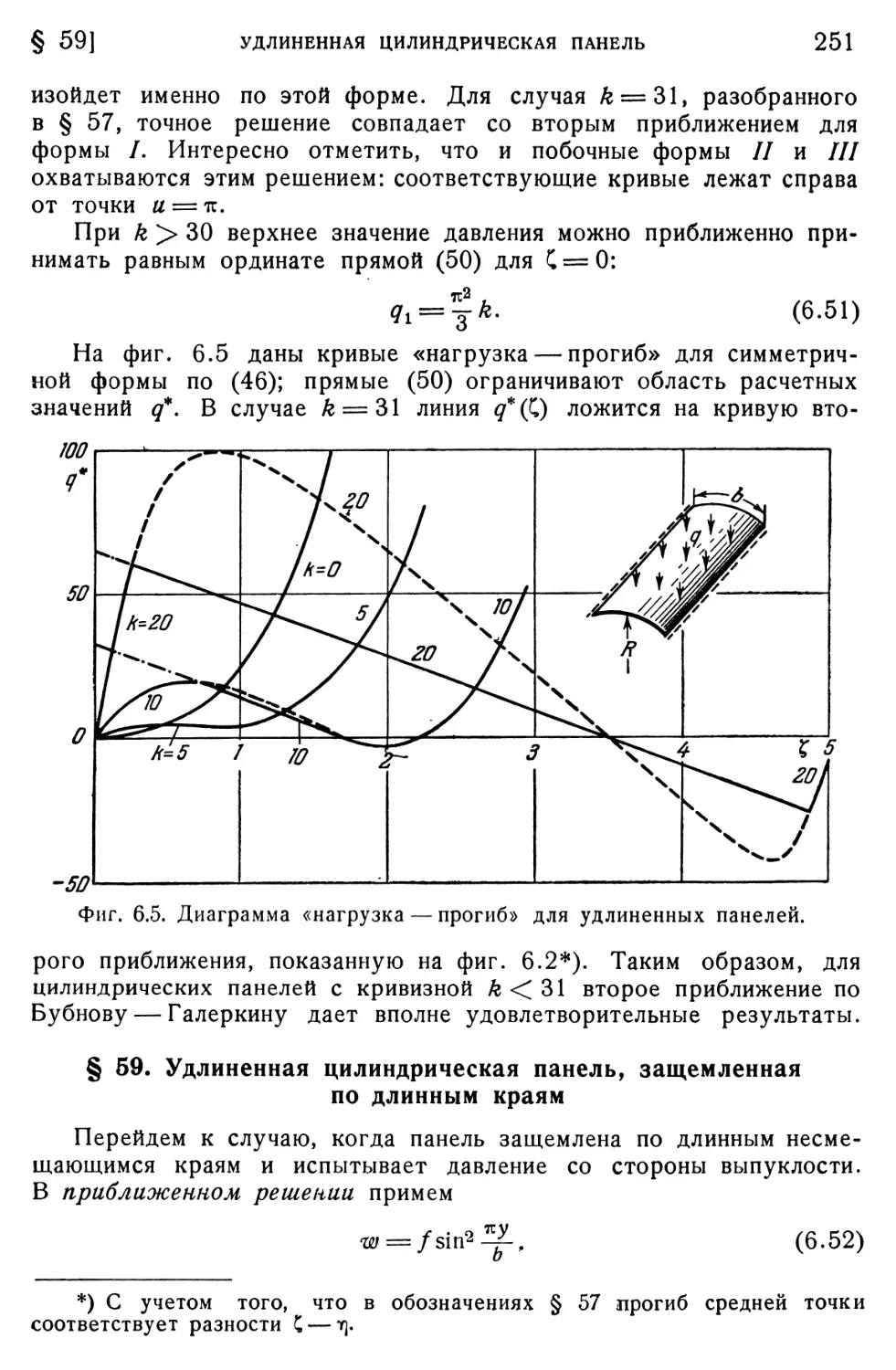
 длинным краям; приближенные решения 240
 § 58. Удлиненная шарнирно закрепленная панель. Точное решение.. 248 § 59. Удлиненная цилиндрическая панель, защемленная по длинным краям 251

ОГЛАВЛЕНИЕ 5
 § 60. Шарнирно опертая пологая панель, прямоугольная в плане; первое приближение 254
 § 61. Шарнирно опертая панель; решение, более полно удовлетворяющее граничным условиям 259
 § 62. Квадратная панель, защемленная по краям 261
 Глава VII. Устойчивость и закритическая деформация цилиндрических панелей 263
 § 63. Устойчивость цилиндрической панели при сжатии вдоль образующей; линейная задача 263
 § 64. Экспериментальные данные о форме волнообразования 266
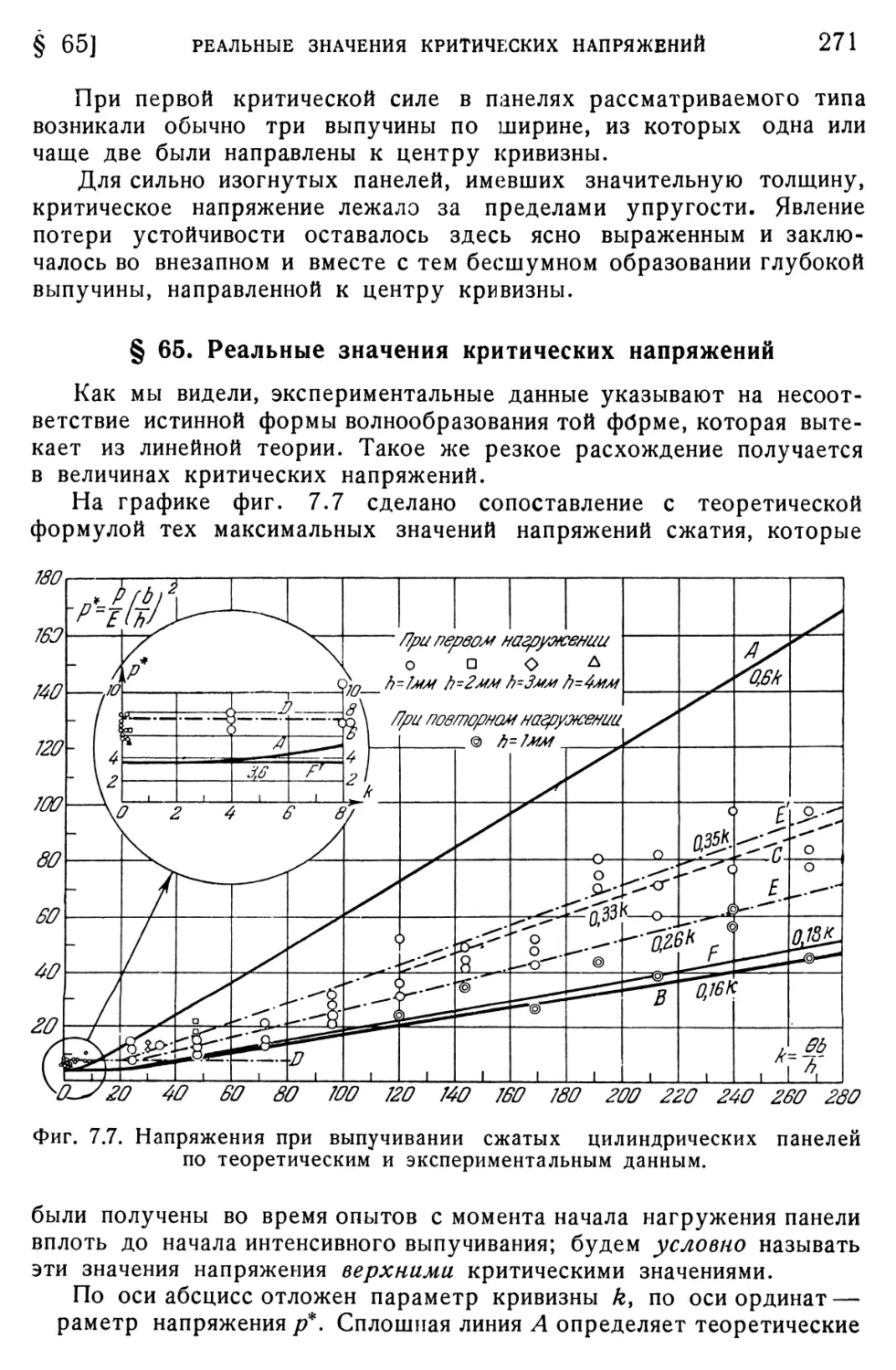
 § 65. Реальные значения критических напряжений 271
 § 66. Большие прогибы шарнирно опертой квадратной пологой панели;
 первое приближение 275
 § 67. Определение энергии системы. Анализ равновесных форм панели 279
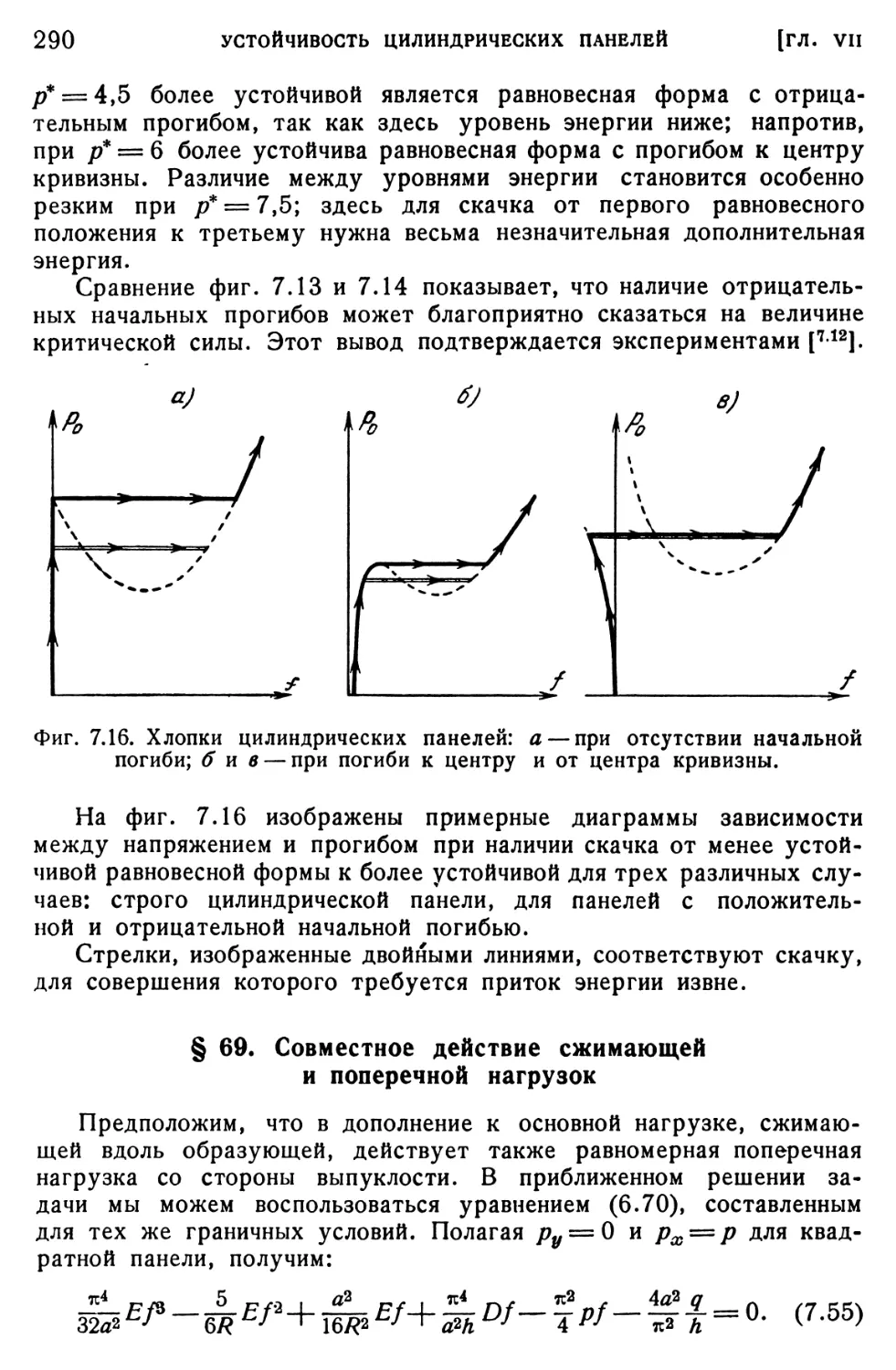
 § 68. Влияние начальной погиби 285
 § 69. Совместное действие сжимающей и поперечной нагрузок.... 290
 § 70. Квадратная панель с защемленными краями 292
 § 71. Собственные колебания панели. Графики на фазовой плоскости.. 294 § 72. Уточненное решение для удлиненной панели произвольной кривизны. Расчетные формулы 296
 § 73. Панель, подкрепленная продольными ребрами 304
 § 74. Устойчивость шарнирно опертой панели при сдвиге. Линейная задача 306
 § 75. Нелинейная задача для квадратной панели 310
 § 76. Панель с произвольным отношением сторон при сдвиге 312
 § 77. Совместное действие сжатия и сдвига 314
 § 78. Анизотропная панель 316
 Глава VIII. Замкнутые цилиндрические оболочки 318
 § 79. Устойчивость круговой цилиндрической оболочки при осевом сжатии. Линейная задача 318
 § 80. Экспериментальные данные. Изучение явления хлопка 320
 § 81. Большие прогибы оболочки после потери устойчивости. Условие
 замкнутости 325
 § 82. Применение метода Ритца. Варьирование по двум параметрам.. 327
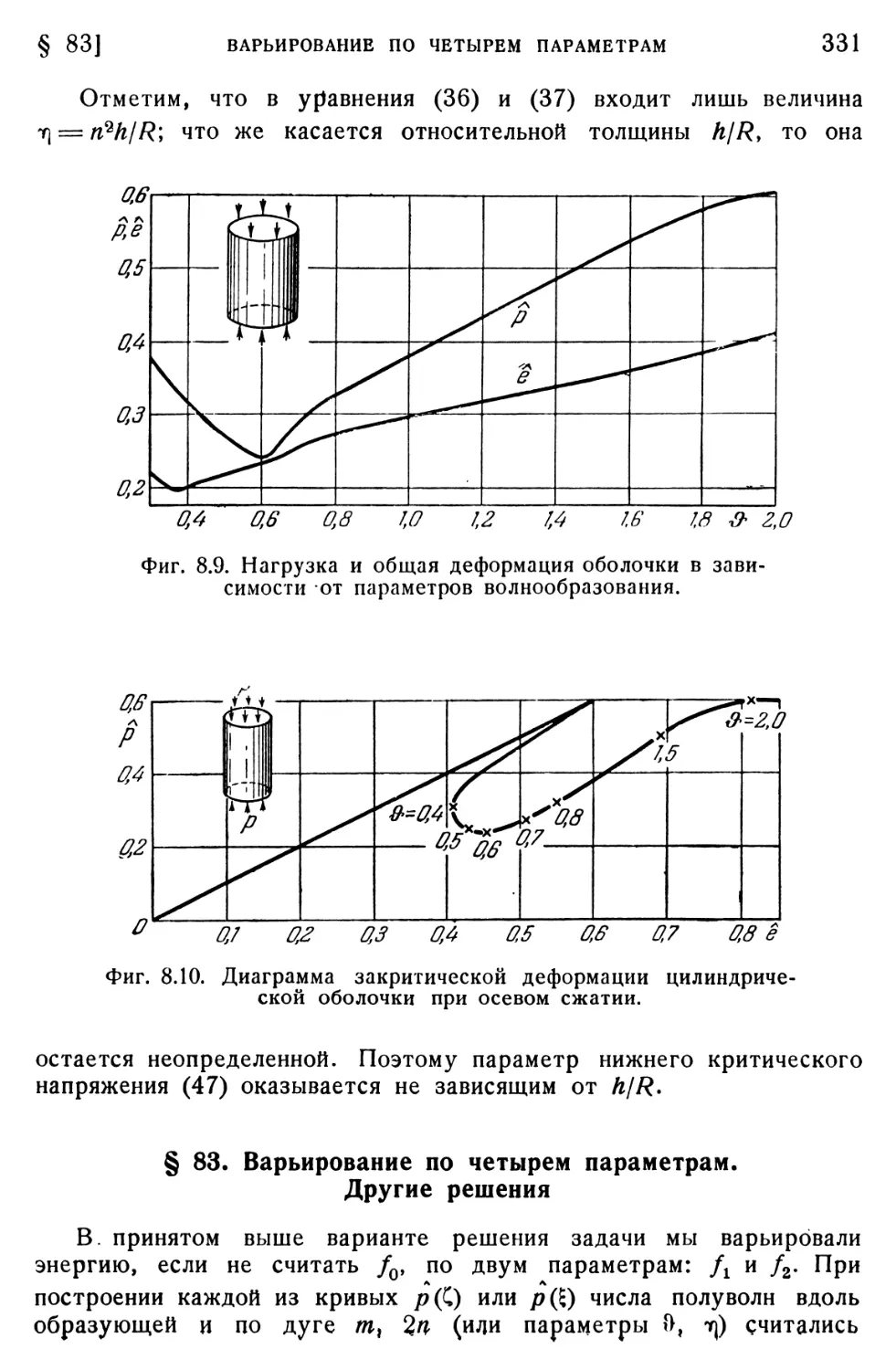
 § 83. Варьирование по четырем параметрам. Другие решения 331
 § 84. Замкнутая оболочка при внешнем давлении 335
 § 85. Совместное действие осевой и поперечной нагрузок 342
 § 86. Кручение оболочки. Одновременное действие сжатия и кручения 345
 § 87. Устойчивость оболочки при изгибе 350
 § 88. Влияние начальной погиби на устойчивость замкнутых оболочек. 352
 Глава IX. Сферические оболочки 357
 § 89. Сферическая оболочка при равномерном внешнем давлении. Линейная задача 357
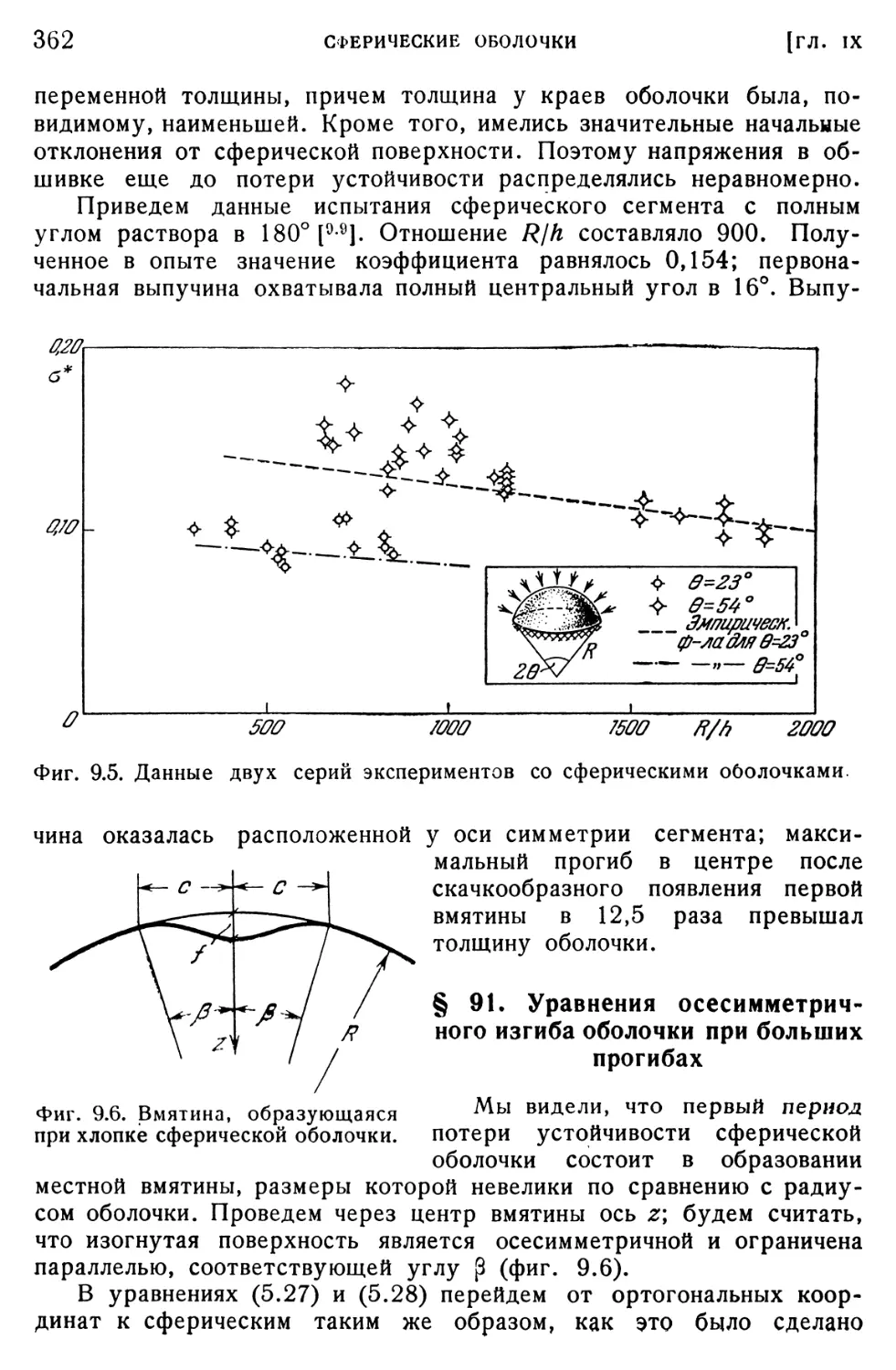
 § 90. Опыты со сферическими оболочками 359
 § 91. Уравнения осесимметричного изгиба оболочки при больших прогибах 362
 § 92. Деформация оболочки после потери устойчивости; решение в первом приближении 364
 § 93. Второе приближение 367
 Глава X, Особенности расчета оболочек на устойчивость.... 370
 § 94. Характерные диаграммы в задачах устойчивости. Некоторые аналогии 370
 § 95. Факторы, ускоряющие или замедляющие наступление хлопка
 оболочки 374

6 ОГЛАВЛЕНИЕ
 § 96. Использование данных нелинейной теории для практических расчетов § 97. «Скелет» оболочки в закритической области § 98. Об особенностях применения вариационных методов к нелинейным задачам § 99. Моделирование оболочек при экспериментальных исследованиях
 Глава XI. Очерк развития теории гибких пластинок и оболочек
 § 100. Сочинение Эйлера по колебаниям мембраны. Общая теория пластинок в трудах Кирхгофа и Сен-Венана § 101. Труды И. Г. Бубнова по теории гибких пластинок. Приложения
 в кораблестроительных расчетах § 102. Нелинейные уравнения А. Феппля и Т. Кармана § 103. Развитие теории гибких пластинок с 1920 по 1940 г. Запросы
 самолетостроения § 104. Уточненные решения 1941—1955 гг. Новые практические приложения § 105. Развитие общей теории гибких оболочек. Труды X. М. Муштари
 и В. 3. Власова, § 106. Исследования устойчивости и закритической деформации оболочек. Работы по пологим оболочкам § 107. Некоторые актуальные задачи Добавление. Основные уравнения в косоугольных координатах
 Литература Именной указатель Предметный указатель.
 376
 378
 380
 383
 386
 386
 387
 389
 390
 392
 395
 396
 399
 400
 403
 414
 417

ПРЕДИСЛОВИЕ
 В настоящей книге рассматриваются тонкие пластинки и оболочки, упругие прогибы которых сравнимы с их толщиной и вместе с тем малы по отношению к основным размерам.
 В курсах теорий упругости излагается, как правило, линейная теория «жестких» пластинок; она может быть использована при исследовании малых прогибов, не превышающих 15-- 14 толщины пластинки. Между тем во многих областях техники находят применение «гибкие» пластинки с прогибами, выходящими за такие пределы. Это относится прежде всего к самолетостроению обшивка крыла, фюзеляжа и оперения, кораблестроению обшивка днища и настил палубы и приборостроению плоские и гофрированные мембраны. Для гибких пластинок связь между прогибом и нагрузкой будет уже нелинейной.
 Важные исследования по гибким пластинкам, тесно связанные с запросами практики, принадлежат известному русскому ученому и инженеру И. Г. Бубнову. В его трудах «Напряжения в обшивке судов от давления воды» 1902 г. и «Строительная механика корабля» 1912—1914 гг. нашли разработку методы расчета обшивки корабля, основанные на нелинейной теории пластинок. И. Г. Бубновым был введен также метод редукционных коэффициентов, позволяющий определять несущую способность тонкостенной конструкции, некоторые из элементов которой испытали потерю устойчивости. Эти идеи И. Г. Бубнова нашли широкое применение в расчетах на прочность металлического корпуса самолета. В курсах строительной механики корабля и самолета нелинейной теории пластинок и ее практическим приложениям уделяется серьезное внимание. Наиболее значительной книгой в этой области является 2-я часть «Строительной механики корабля» П. Ф. Папковича, изданная в 1941 г.
 Теории оболочек посвящены вышедшие в свет в последние годы монографии В. 3. Власова, А. Л. Гольденвейзера, А. И. Лурье,

8
 ПРЕДИСЛОВИЕ
 В. В. Новожилова. В этих книгах рассматриваются по преимуществу линейные задачи. В то же время в ряде сборников и журналов как в СССР, так и за границей были опубликованы работы по нелинейной теории оболочек большого прогиба. Оказалось, чтоименно эта теория дает ключ к объяснению процесса потери устойчивости оболочек, состоящего обычно во внезапном образовании глубоких выпучин. Подобная потеря устойчизости «в большом» приводит нередко к полному разрушению конструкции. Поэтому данные нелинейной теории оболочек имеют большое значение для практических расчетов на устойчивость многих ответственных конструкций в инженерных сооружениях стенки и днища резервуаров, в кораблестроении корпуса и переборки подводных лодок, самолетостроении оболочки реактивных двигателей и т. д.
 Ниже изложены общие сведения по теории гибких пластинок и оболочек и рассмотрены ее важнейшие технические приложения. Сравнительно широко представлены данные экспериментов; они кладутся в основу приближенного решения отдельных задач и служат для оценки полученных результатов.
 В ряде разделов книги приведены теоретические и экспериментальные данные, полученные автором в период с 1941 по 1955 г. Вместе с тем в книге отражены другие исследования, опубликованные в отечественной и иностранной литературе.
 Первые четыре главы посвящены пластинкам большого прогиба; все задачи при этом рассматриваются в нелинейной постановке. В главе I дан вывод основных уравнений общей теории гибких пластинок; значительное место уделено приложению вариационных методов. Следующие главы относятся к прямоугольным пластинкам. В главе II рассмотрен случай, когда пластинка получает большие прогибы под действием, по преимуществу, поперечной нагрузки. В главе III определяется деформация пластинки, нагруженной сжимающими усилиями в срединной плоскости, после потери устойчивости. Здесь основное внимание сосредоточено на определении редукционных коэффициентов. При изучении закритической деформации пластинки, подвергающейся действию сдвига, внешние усилия считаются сравнительно мало превышающими критическое значение, — именно этот случай имеет в настоящее время наибольшее практическое значение. В главе IV изучаются большие прогибы круглых пластинок, в том числе пластинок, имеющих начальную погибь.

ПРЕДИСЛОВИЕ
 9
 Остальная часть книги посвящена гибким оболочкам. В главе V даны основные зависимости теории пологих оболочек при больших перемещениях. Общая теория гибких оболочек в книге не приводится; однако полученные в главе V уравнения могут служить и для исследования устойчивости «в большом» цилиндрических и сферических оболочек значительной кривизны. Глава VI дает обобщение результатов, полученных в главе И, на пологие оболочки с плоским прямоугольным контуром, находящиеся под действием поперечного давления. Главы VII и VIII содержат материал по устойчивости и закритической деформации цилиндрических оболочек как открытого профиля цилиндрические панели, подкрепленные по контуру, так и замкнутых тонкостенные трубы. Глава IX посвящена устойчивости сферических оболочек. Каждый из разделов последних глав начинается с изложения решения соответствующих линейных задач. В главе X приводятся некоторые общие выводы, относящиеся к устойчивости оболочек «в большом»; обсуждаются вопросы о влиянии различных факторов на критические напряжения и об использовании данных нелинейной теории для практических расчетов. Здесь же рассматриваются особенности применения вариационных методов к нелинейным задачам теории оболочек, а также вопросы моделирования оболочек при экспериментальных исследованиях.
 Глава XI содержит краткий исторический очерк развития теории гибких пластинок и оболочек.
 К книге приложен указатель известной автору литературы; он разбит на разделы, соответствующие главам книги. На работы, относящиеся к нескольким главам, сделаны дополнительные ссылки в конце разделов.
 Работы по пластинкам большого прогиба публикуются на протяжении более полувека; некоторые вопросы здесь разработаны уже достаточно подробно. Между тем теория гибких оболочек находится в настоящее время в процессе быстрого развития. Поэтому решение отдельных задач, разобранных в книге, нельзя считать окончательным. Наиболее актуальные вопросы, подлежащие исследованию, перечислены в заключительном разделе книги.
 При подготовке книги автор стремился сделать ее доступной не только для научных работников, но и для инженеров и студентов старших курсов втузов. Тензорный аппарат в книге не используется. Изложение построено «от частного к общему» с неизбежными

10
 ПРЕДИСЛОВИЕ
 в некоторых случаях повторениями выкладок. Во второй части книги, посвященной оболочкам, дано обобщение многих результатов, полученных в первой части для пластинок. Считая, что ознакомление с первыми главами книги дает возможность освоить методы решения задач, автор счел уместным изложить материал последующих разделов болёе сжато.
 Формулы по каждой главе нумеруются отдельно; при ссылках на формулы внутри главы цифра, указывающая номер главы, опускается. В списке литературы также введена нумерация по главам.
 Постоянное внимание к работе автора над рукописью было проявлено А. А. Уманским. С. А. Алексеев и Э. И. Григолюк ознакомились с рукописью и сделали ряд ценных замечаний. Отдельные части книги просмотрели И. И. Ворович, Л. М. Куршин, В. В. Новицкий и Р. Г. Суркин. Помощь автору в подготовке рукописи к печати была оказана И. Н. Землянских. Этим лицам автор приносит свою благодарность.

ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
 h — толщина пластинки или оболочки. а, b — стороны прямоугольной пластинки, с, d — радиус и диаметр круглой пластинки. ky — главные кривизны срединной поверхности оболочки.
 Г — гауссова кривизна срединной поверхности.
 Рх> ?у — главные радиусы кривизны.
 R — радиус срединной поверхности круговой цилиндрической оболочки или сферической оболочки. х, у — координаты точек срединной плоскости прямоугольной пластинки вдоль сторон я, b или срединной поверхности оболочки по главным направлениям, г, <р — полярные координаты в случае круглой пластинки. z — координата, отсчитываемая по нормали к срединной поверхности пластинки или оболочки.
 Рху Ру — интенсивность внешних нормальных усилий, приложенных в срединной поверхности вдоль линий х, у. s — интенсивность внешних касательных усилий. q — интенсивность поперечной нагрузки приложенной по нормали к поверхности. и, v — перемещения точек срединной поверхности пластинки или оболочки вдоль координатных линий х, у. w — прогиб произвольной точки срединной поверхности. — стрела прогиба. weч — начальный прогиб. ах> Qy — нормальные напряжения в срединной поверхности пластинки или оболочки вдоль линий ЛГ, у. z — касательные напряжения в срединной поверхности.
 Ф — функция напряжений в срединной поверхности. гх> еу — деформации удлинения в срединной поверхности вдоль линий х, у.
 у — деформация сдвига срединной поверхности.
 Мх, Му — изгибающие моменты, приходящиеся на единицу длины сечений, нормальных к линиям х и у.
 Н—крутящий момент.
 Qxt Qy — поперечные силы.

12
 ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
 Qx, и» ау, и — нормальные напряжения, соответствующие изгибающим моментам.
 си — касательное напряжение, отвечающее крутящему моменту.
 х> — кривизны изогнутой срединной поверхности пластинки
 или изменения кривизн в случае оболочки.
 X — кручение изогнутой срединной поверхности.
 ЕУ G — модули упругости материала при растяжении сжатии и сдвиге.
 р. — коэффициент Пуассона.
 D E№j2 1 — fx — цилиндрическая жесткость.
 Д., Ая — работа усилий в срединной поверхности и усилий изгиба.
 W—работа внешних сил,
 U„ UR — энергия деформации срединной поверхности и энергия изгиба.
 V — потенциал внешней нагрузки.
 Э — полная энергия системы.

ГЛАВА I
 ОБЩАЯ ТЕОРИЯ ГИБКИХ ПЛАСТИНОК
 § 1. Классификация пластинок по характеру напряженного состояния. Гибкая пластинка
 Пластинкой постоянной толщины называется тело, имеющее форму прямой призмы или прямого цилиндра, высота которых толщина пластинки мала по сравнению с размерами основания.
 Плоскость, делящая пополам толщину пластинки, называется срединной плоскостью; линии пересечения срединной плоскости с боковыми гранями образуют контур пластинки.
 В дальнейшем мы будем рассматривать пластинки, известным образом закрепленные по контуру и испытывающие нагрузку двоякого рода: нагрузку, действующую в срединной плоскости пластинки, и поперечную нагрузку, действующую по нормали к срединной плоскости фиг. 1.1. При этом нас будут интересовать Фиг- Пластинка под действием усилий J J г в срединнои плоскости и поперечной на-
 только такие случаи нагру- грузки.
 жения пластинки, которые
 сопровождаются ее изгибом. При деформации изгиба точки пластинки получают перемещения прогибы, перпендикулярные к срединной плоскости. Поверхность, на которой оказываются лежащими точки срединной плоскости после деформации, называется срединной поверхностью.
 Примем, что прогибы в общем случае сравнимы с толщиной пластинки; условимся вместе с тем считать прогибы малыми по сравнению с основными размерами пластинки, а изогнутую поверхность — пологой.
 По характеру напряженного состояния, образующегося при изгибе пластинки, различают следующие три класса пластинок: 1 жесткие, 2 гибкие, 3 абсолютно гибкие пластинки, или мембраны.
 Пластинку называют жесткой, если можно без заметной погрешности считать срединный слой нейтральным или, иными словами, свободным от напряжений растяжения — сжатия. Подобное допущение характерно для обычной теории изгиба балок.

14
 ОБЩАЯ ТЕОРИЯ ГИБКИХ ПЛАСТИНОК
 ГЛ. I
 Гибкой называется пластинка, при расчете которой в пределах упругости наряду с чисто изгибными напряжениями необходимо учитывать напряжения, равномерно распределенные по толщине пластинки и называемые цепными или мембранными напряжениями. Так как цепные напряжения распространяются и на срединный слой пластинки, то их принято также называть напряжениями в срединной поверхности. Эти напряжения появляются во всех тех случаях,
 когда срединная поверхность пластинки переходит при изгибе в неразвертывающуюся поверхность. Так, например, изогнутая b круглая пластинка, контур которой остается плоским, всегда имеет форму неразвертывающейся поверхности; подобное выпучивание не может произойти без известных удлинений или укорочений волокон срединного слоя.
 Возьмем, для примера, круглую пластинку, изображенную на фиг. 1.2, а. Допустим, что пластинка получила прогиб вверх, как показано на фиг. 1.2, б. Будем считать, что отрезок acb при изгибе пластинки не удлинился, так что длина ду-
 Фиг. 1.2. Срединная плоскость круглой пластинки переходит в неразвертывающуюся поверхность.
 ги а'с Ьг равна первоначальной длине
 отрезка. Точки, расположенные ранее на дуге akb, лежат теперь на дуге a'k'b' меньшего радиуса, при этом длина дуги уменьшится. Иными словами, должно иметь место укорочение кольцевых волокон пластинки.
 Цепные напряжения могут быть вызваны также полным или частичным стеснением взаимного смещения контурных точек пластинки. Допустим, что пластинка опирается на несмещающиеся в ее плоскости ребра. Тогда, очевидно, изгиб пластинки должен сопровождаться удлинениями волокон срединного слоя, приобретающими заметное значение при больших прогибах пластинки.
 Абсолютно гибкой пластинкой, или мембраной, называется пластинка, при исследовании упругой деформации которой можно пренебречь собственно изгибными напряжениями по сравнению с напряжениями в срединной поверхности. Для мембраны характерна, таким образом, равномерность распределения напряжений по толщине.
 Приведенная классификация является условной, так как отнесение пластинки к той или иной категории зависит от принятой
 в качестве допустимой степени погрешности расчета. Одна и та же пластинка, находящаяся под действием возрастающей поперечной нагрузки, может последовательно рассматриваться как жесткая,
 гибкая и абсолютно гибкая. Металлическую пластинку принято считать жесткой, если стрела прогиба ее не превышает приблизительно

КЛАССИФИКАЦИЯ ПЛАСТИНОК
 15
 хб толщины; с другой стороны, при стреле прогиба, превышающей толщину более чем в 5 раз, пластинку можно обычно рассматривать как абсолютно гибкую.
 Если независимо от поперечной нагрузки пластинка подвергается действию значительных усилий в срединной плоскости, то эти усилия должны быть учтены при любых значениях прогиба. Но при малых прогибах усилия в срединной поверхности можно рассматривать как заданные и не зависящие от деформации пластинки. Так поступают при определении критических напряжений для пластинки, подвергающейся сжатию или сдвигу: рассматривая бесконечно близкие к начальному состоянию формы равновесия, учитывают лишь дополнительные напряжения изгиба.
 В случае пластинки малого прогиба напряженное состояние мы считаем чисто изгибным. Это допущение отвечает реальному распределению напряжений лишь для тонких пластинок: относительная толщина их отношение толщины к наименьшему размеру основания не должна превышать б. При большей толщине в расчет должны вводиться уточнения по теории толстых плит.
 Собственно тонкие пластинки можно, в свою очередь, подразделить по их относительной толщине. Для пластинок сравнительно большой толщины наибольшие напряжения достигают предела упругости материала уже при малых прогибах. Лишь пластинки средней и малой толщины могут получить значительные прогибы, деформируясь в пределах упругости. Поэтому гибкие пластинки называют также пластинками средней толщины или средней жесткости, а абсолютно гибкие — весьма тонкими.
 Жесткие пластинки применяются, как известно, во многих областях техники: в инженерных сооружениях фундаментные плиты, безбалочные перекрытия, машиностроении детали поршневых двигателей, плоские днища резервуаров и т. д.
 Широкое применение на практике находят также гибкие пластинки. Так, например, участок плоской обшивки крыла самолета, подкрепленный продольными ребрами стрингерами и поперечными ребрами нервюрами, следует рассматривать как гибкую пластинку. Учет цепных напряжений особенно важен для тонкой обшивки в сжатой зоне крыла, так как здесь обшивка может претерпеть потерю устойчивости и получить большие прогибы уже при эксплуатационной нагрузке. Расчет обшивки осложняется, если наряду с продольными силами приходится учитывать поперечную воздушную нагрузку.
 Пластинки занимают большое место в кораблестроении. Обшивка днища корабля подвергается сжатию, участвуя в общем изгибе
 См., например, Б. Г. Г а л е р к и н, Упругие тонкие плиты, Госстройиздат, 1933, стр. 5. Более строго границы применения теории тонких пластинок должны быть определены с учетом характера нагрузки и условий опирания.

16
 ОБЩАЯ ТЕОРИЯ ГИБКИХ ПЛАСТИНОК
 ГЛ. I
 корпуса, и, вместе с тем, испытывает значительное давление воды; прогибы обшивки, как правило, сравнимы с ее толщиной. В определенных положениях корабля по отношению к гребням волн оказывается сжатой также палуба, причем настил палубы зачастую теряет устойчивость в упругой области; поэтому и здесь необходимо для расчета привлекать теорию гибких пластинок.
 При проектировании балок с высокими тонкими стенками в строительных конструкциях стенку приходится рассчитывать как гибкую пластинку: здесь может произойти потеря устойчивости от сдвига с образованием наклонных выпучин.
 Обшивка затворов в гидротехнических сооружениях воспринимает давление воды также как гибкая пластинка; это надо учитывать при определении несущей способности обшивки.
 Круглые гибкие пластинки часто встречаются в приборостроении. Так, например, упругими чувствительными элементами манометрических приборов являются гофрированные мембраны — пластинки с начальной погибью, получающие значительные прогибы.
 § 2. Деформации срединной поверхности и кривизны. Уравнение совместности деформаций
 Рассмотрим деформацию гибкой прямоугольной пластинки, изве-
 контуру. Обозначим через а, b и h длину большей стороны основания, длину меньшей стороны и толщину пластинки фиг. 1.3.
 Условимся располагать плоскость опорного контура горизонтально. Выберем систему координат таким образом, чтобы плоскость ху совпадала со срединной плоскостью пластинки; начало координат О совместим с одной
 из вершин контура. Ось х будем
 направлять вдоль длинной сторо¬
 ны, ось у — вдоль короткой стороны, ось —по вертикали вниз.
 Перемещения точек срединной плоскости будем обозначать следующим образом: и — перемещение вдоль оси х, v — вдоль оси у, w — вдоль оси z; величины и, vy w являются функциями координат
 точек срединной плоскости х, у.
 Определим деформации срединного слоя пластинки. Деформации удлинения в направлении осей х, у обозначим через гу, деформацию сдвига через у. Каждая из этих величин зависит от перемещений и, v в плоскости срединного слоя и от прогиба w. На
 стным образом закрепленной по
 <2?
 Фиг. 1.3. Оси координат при рассмотрении прямоугольной пластинки.

§ 2 ДЕФОРМАЦИЙ СРЕДИННОЙ ПОВЕРХНОСТИ И КРИВИЗНЫ 17
 фиг. 1.4 изображен элемент срединного слоя со сторонами dx и dy, параллельными координатным осям хну. Пусть точка А с координатами xf у получит перемещения а, v. Для точки В с координатами х --dx, у перемещения будут тогда u dx,
 Фиг. 1.4. К определению деформаций в срединной поверхности.
 точка С с координатами х, y--dy получит перемещения и-- -dy,
 v -J- -0- dy. Новая длина стороны dx будет равна
 dst ЛД --Jj dxj J- dx,
 ИЛИ
 ,й2 l <•
 На фиг. 1.5 сопоставлены стороны dst и dxпричем точки Л и At совмещены.
 Рассматривая выражение в квадратных скобках как величину, малую по сравнению с единицей, разложим выражение а в биноминальный ряд. Ограничиваясь двумя членами ряда, получим:
 .-'■т££У- с»
 Относительное удлинение гх> равное
 dsi — dx лЧ

18
 ОБЩАЯ ТЕОРИЯ ГИБКИХ ПЛАСТИНОК
 оказывается выраженным через перемещения и, v.
 1 ди а 1 dv ' 2 дх “Г 2дх '
 d
 Изучая деформацию гибкой пластинки, мы принимаем, что она получает большие прогибы w в то же время будем считать перемещения и, v в плоскости пластинки величинами малыми. В самом деле, перемещение w совершается в направлении наименьшей жесткости, в то время как перемещения и, v происходят в массиве материала. Такое же допущение сделаем по отношению к произ-
 ди dv dw
 дх и дх ’ считая их малыми в сравнении с величиной-.
 Пренебрегая поэтому в выражении d квадратами производных, получим:
 водным
 в
 k
 Йг
 дха
 t
 < fadx.
 <■ - ал>■ от
 г ди 1 1ч <1Л>
 По аналогии
 Фиг. 1.5. Отрезок dx в смещенном положении.
 dv
 dy'
 1.2
 Деформацию сдвига можно определить по фиг. 1.4 как разность между прямым углом, образованным сторонами dx, dy до деформации, и углом между теми же элементами после деформации. Представим величину улл в виде суммы углов Ti T2 В пРе“ делах той же точности, что и для удлинений, мы можем положить
 -у1 см. также фиг. 1.5, а Тогда найдем:
 ди, dv
 Тил “Г дх •
 1.3
 Перейдем к определению деформаций, обусловленных прогибом w. На фиг. 1.6 изображен элемент пластинки со сторонами dx, dy. Пусть перемещение точки А по направлению оси £ будет w, тогда
 перемещения точек В и С будут соответственно w--dx и w-fdy. Новая длина элемента dx оказывается равной
 '■V Srfx2rf41S1
 ds9
 е
 Раскладывая выражение е в ряд, получим с прежней степенью точности
 rfS2rfia. f

§ 2 ДЕФОРМАЦИИ СРЕДИННОЙ ПОВЕРХНОСТИ И КРИВИЗНЫ 19
 Деформация удлинения в направлении оси х будет равна
 dSb — dx 1 dw3 л,ч
 e-ir-ifc' К4>
 Здесь квадрат производной сохраним, считая, что эта величина имеет тот же порядок малости, что и первая степень производной от перемещений и и v.
 Таким же образом находим составляющую деформации гу
 гг 1 dw2
 е2Ы- L5
 Для определения составляющей деформации сдвига, вызванной прогибом пластинки, обратимся снова к фиг. 1.6. Прямой угол между
 Фиг. 1.6. К определению деформаций в срединной поверхности, связанных с прогибами.
 элементами dx и dy при изгибе пластинки искажается; новое его значение пусть будет. Найти этот угол можно, пользуясь
 соотношением между сторонами треугольника А2В2С2. Квадрат стороны А2В2 ds2 согласно е будет
 ds2a < l Q2. g
 Квадрат стороны А2С2 ds2 равен
 i2. h>
 Определим далее сторону ds3 — В2С2. Сопоставляя длины отрезков В2С2 и ВС у находим:
 W1 dxf dyf rfy _ g dxf. i

20
 ОБЩАЯ ТЕОРИЯ ГИБКИХ ПЛАСТИНОК
 ГЛ. I
 По теореме косинусов
 dsf ds22 ds'2f — 2 ds2 ds'2 cos J — 4. j
 Принимая cosy — ТТ» подставим в соотношение j выражения g, h и i; полагая с точностью до малых высшего порядка dslds2 dxdy, получим:
 dw dw 1
 Т <L6>
 Сопоставляя полученные результаты, находим полные выражения для деформаций удлинения и сдвига срединного слоя:
 да. 1 dw2
 г°° дх 2 дх ’ •
 dv, 1 dw2 п Q4
 еУду 2ду ’,8
 _<dv_,dwdw_. „
 ‘ — ду дх дх ду ' '
 Судя по структуре выражений 7 — 9, деформации срединного слоя гх, еу и должны быть связаны определенной зависимостью: в эти выражения входят одни и те же перемещения иу v, w. Для установления этой зависимости продифференцируем 8 два раза по xt 7 — два раза по у и 9 — последовательно по х и по у. Тогда получим после некоторых преобразований соотношение
 д2гх д2£у d3Y d2w 2 d2w d2w
 ду2 1 дх2, дх ду
 ow 2 ow ow
 дх ду дх2 ду2 О • 10
 Это соотношение носит название уравнения совместности или неразрывности деформаций.
 В правую часть уравнения 10 входят вторые производные от прогиба, каждая из которых имеет определенный геометрический смысл. Сделаем сечение срединной поверхности изогнутой пластинки плоскостью, параллельной плоскости xz фиг. 1.7. Это сечение дает линию abc, аналогичную изогнутой оси балки. По нашему условию
 эта линия является пологой, и производная равна углу между касательной к изогнутой линии и осью х, причем Вто¬
 рая производная будет тогда приближенно определять кривизну
 сечения. Условимся считать кривизну положительной, если выпуклость кривой обращена вниз, тогда
 d2w

§ 2
 ДЕФОРМАЦИИ СРЕДИННОЙ ПОВЕРХНОСТИ И КРИВИЗНЫ
 21
 Для сечения срединной поверхности вдоль оси у аналогично находим кривизну уу
 Ы2
 0 d2w dw
 Величина определяет изменение угла наклона при изменении
 координаты х. Однако угол может, вообще говоря, меняться
 также вдоль линии, параллельной оси у, т. е. при переменном у. Это видно из сопоставления кривых abc и alb1cl фиг. 1.7, плоскости
 Фиг. 1.7. К определению кривизн срединной поверхности.
 которых находятся на расстоянии dy. Если угол наклона касательной для кривой abc будет, то для кривой афхсх этот угол окажется
 dw д dw, 1 dw d2w, лх
 или XdiW3ydy' Изменение
 dw
 дх’
 угла, приходящееся на единицу длины, у дхду
 минус взят здесь в предположении, что при увеличении у угол наклона касательной уменьшается по аналогии со случаем, когда определялись кривизны ух и уу.
 Таким же образом можно убедиться, что в перпендикулярном сечении при переменном х изменение угла характеризуется
 d2w ъ
 той же смешанной производной. Здесь можно провести аналогию со случаем кручения стержня, когда угол поворота поперечного сечения меняется вдоль оси стержня. Принято говорить, что
 d2w производная определяет уже не кривизну изгиба, а «кривизну»
 дх ду, будет -
 d2w
 знак

22
 ОБЩАЯ ТЕОРИЯ ГИБКИХ ПЛАСТИНОК
 ГЛ.
 кручения срединной поверхности Обозначим эту величину через у
 в точке с координатами х, у.
 d2w
 У дх ду 1.13
 Уравнение теперь в виде
 совместности деформаций 1.10 можно переписать д
 дх ду2
 _i__
 ' дх2 дх ду
 : у: — -'-х'-у
 1.14
 Величины
 7 условимся в дальнейшем объединять термином «деформации' срединной поверхности», а величины у.у и
 у—термином «кривйзны срединной поверхности». Зная деформации и кривизны срединной поверхности, можно полностью определить деформированное состояние любого слоя пластинки, параллельного срединной плоскости и удаленного от него на расстояние 2. Полные деформации произвольного слоя гх> п, гУ п, 7п складываются из деформаций
 а
 -g rrrt W
 1
 I
 b
 -,i—н,
 Фиг. 1.8. К определению деформаций изгиба.
 срединного слоя еж, гу1 у и деформаций изгиба, для которых введем обозначения zXi и, е,и,
 Для определения деформаций изгиба воспользуемся гипотезой прямых нормалей: примем, что для тонкой пластинки любая прямая, нормальная к срединной плоскости до деформации, остается после деформации прямой, нормальной к срединной поверхности. Надо отметить, что при наличии поперечной нагрузки в срединном слое и параллельных ему слоях пластинки возникают касательные напряжения, вызывающие деформацию сдвига, т. е. искажение прямого угла между нормалью к срединной плоскости и волокнами срединной изогнутой поверхности; сама нормаль получает искривление. Однако при малой толщине пластинки эти сдвиги оказываются пренебрежимо малыми по сравнению с общим поворотом нормали.
 На фиг. 1.8, а представлен элемент пластинки, рассеченный параллельно плоскости xz. Границы этого элемента составляют две нормали
 См. книгу С. П. Тимошенко 125, стр. 107. Для слоистой пластинки, один из сл ев которой обладает малой жесткостью на сдвиг, от этой гипотезы придется отказаться см. § 13.

§ 2
 ДЕФОРМАЦИИ СРЕДИННОЙ ПОВЕРХНОСТИ И КРИВИЗНЫ
 23
 к срединной плоскости, расстояние между которыми равно dx. При искривлении волокна срединного слоя эти нормали поворачиваются одна относительно другой. Если первая нормаль поворачивается на
 dw dw dhsu. угол, то вторая — на угол — dx x’ таким образом, взаимный угол поворота равен Фиг показано относительное расположение нормалей по- еле деформации, причем первая нормаль условно принята закрепленной.
 Как видно из чертежа, элемент волокна, удаленного от срединного слоя на расстояние 2, получает абсолютное удли-
 .
 нение I — z dxj; соответствующее
 относительное удлинение волокна равно
 1.15
 d2w
 Таким же образом можно установить, что произвольное волокно, параллельное оси у, получает деформацию
 dw
 8У. и — Z 0 Zy'V I®
 Фиг. 1.9. Деформация сдвига при изгибе.
 Для определения деформации сдвига произвольного слоя обратимся к фиг. 1.9. Здесь представлены три нормали к срединной поверхности, проведенные на концах взаимно перпендикулярных отрезков dx и dy фиг. 1.9, а. Допустим, что нормаль ааг повернулась
 dw dw d2w,
 на угол -gy, а нормаль bb'— на угол ———dxjt тогда взаим-
 ный угол поворота будет равен — На фиг. 1.9, б пер-
 вая из нормалей принята закрепленной. Точка b' нормали, имеющая
 координату 2, сместится на отрезок —z dx,
 что отвечает
 dw пл
 углу сдвига f — z • Такое же перемещение получит соответствующая точка нормали с', так что угол сдвига Y'— —
 Таким образом, деформация сдвига оказывается равной ч' Y'> или
 Ти — 2z
 d2w dx dy
 2 z.
 1.17

24
 ОБЩАЯ ТЕОРИЯ ГИБКИХ ПЛАСТИНОК
 ГЛ. I
 Полные деформации произвольного слоя определяем суммированием деформаций срединной поверхности и деформаций от изгиба:
 S£B, П гХb е£С, и> ег, П гу гу, И> Тп Т Ти- 18
 Обратимся теперь к случаю, когда срединная поверхность пластинки имеет начальную погибь, в то время как опорный контур попрежнему лежит в плоскости ху. Начальный прогиб срединной
 поверхности в точке с коор-
 Щп
 J
 w
 'iz
 - da?-
 Ufa
 ur
 дигнк
 dw
 dx
 w
 dr
 динатами x, у обозначим через wa4; величина wH4 является функцией координат х, у. Примем, что начальные прогибы сравнимы с толщиной пластинки.
 Условимся обозначать через w дополнительный упругий прогиб. Полный прогиб wn будет равен wn wa4-- w. Найдем выражения для деформаций срединной поверхности. Легко видеть, что составляющие деформаций, обусловленные перемещениями и и v, будут попрежнему определяться формулами 1 — 3. Изменятся выражения для составляющих, обусловленных перемещением w. На фиг. 1.10 выделен элемент в плоскости xz, проекция которого на ось х равна dx. Начальные прогибы для
 Фиг. 1.10. К определению деформаций в срединной поверхности для пластинки с начальной погибью.
 концов отрезка АВ отрезка АВ равна
 или приближенно
 пусть будут wa4 и
 Ъ-dxV 12,
 dw„
 дх
 -dx. Длина
 Тот же отрезок после деформации имеет длину
 dsi dx ”l -gj 2 -д-
 Относительное удлинение отрезка оказывается равным
 » _dx_ Г_ dWn2 _ _1_ нч2
 Вх ds0 2 дл: 2дху
 или с точностью до малых высшего порядка
 1 dwn2 1 dwu
 1 OWn2 I OWE42
 2 dx 2 dx J •

§ 2 ДЕФОРМАЦИИ СРЕДИННОЙ ПОВЕРХНОСТИ и КРИВИЗНЫ 25
 По аналогии для удлинения в направлении оси у имеем:
 1 dwny 1 dwm 2
 e — 2 ду 2 V ду •
 На фиг. 1.11 изображены элементарные отрезки АС и АВ, лежащие в плоскостях yz и ЛГ2. Угол между отрезками близок к пря-
 к dwB4 dwK
 мому; до деформации он равен —ду ' этом можно
 7 за?
 4
 Фиг. 1.11. Деформация сдвига в срединной поверхности при наличии начальной погиби.
 убедиться путем тех же рассуждений, что и при определении угла сдвига у для плоской пластинки. Угол между теми же отрезками
 те dwn dwn
 после деформации равен дхду' Таким образом, обусло¬
 вленная прогибом w составляющая сдвига ? оказывается равной
 dwn dwn
 dwuv dwu
 дх ду
 дх ду
 Выпишем окончательные выражения для деформаций срединной поверхности, подставляя вместо wn сумму wa--w:
 _ди 1 Гнч2 1 dwH42
 дх' 2 дх J 2 дх 9
 дх
 __dv Гнч 12 1 dw„4y
 ду 2 L ду J 2 ду 9
 дх
 dwn
 да dv ду дх
 ду д w
 ду
 w д яунч w
 dwE4 dwn
 дх
 ду
 дх ду
 1.19
 Выражения для деформаций изгиба произвольного слоя пластинки 15 — 17 остаются без изменения.

26
 ОБЩАЯ ТЕОРИЯ ГИБКИХ ПЛАСТИНОК
 ГЛ. I
 Уравнение совместности деформаций получает для пластинки с начальной погибью вид:
 , Ъу d2Y Г WH4 W-12 нч 2
 ду2 ' дх2 дх ду дх ду J дх ду
 dwmww„4w дЧт №w„4 дх2 ду “I дх2 ду '
 Его легко получить тем же путем, что и уравнение 10.
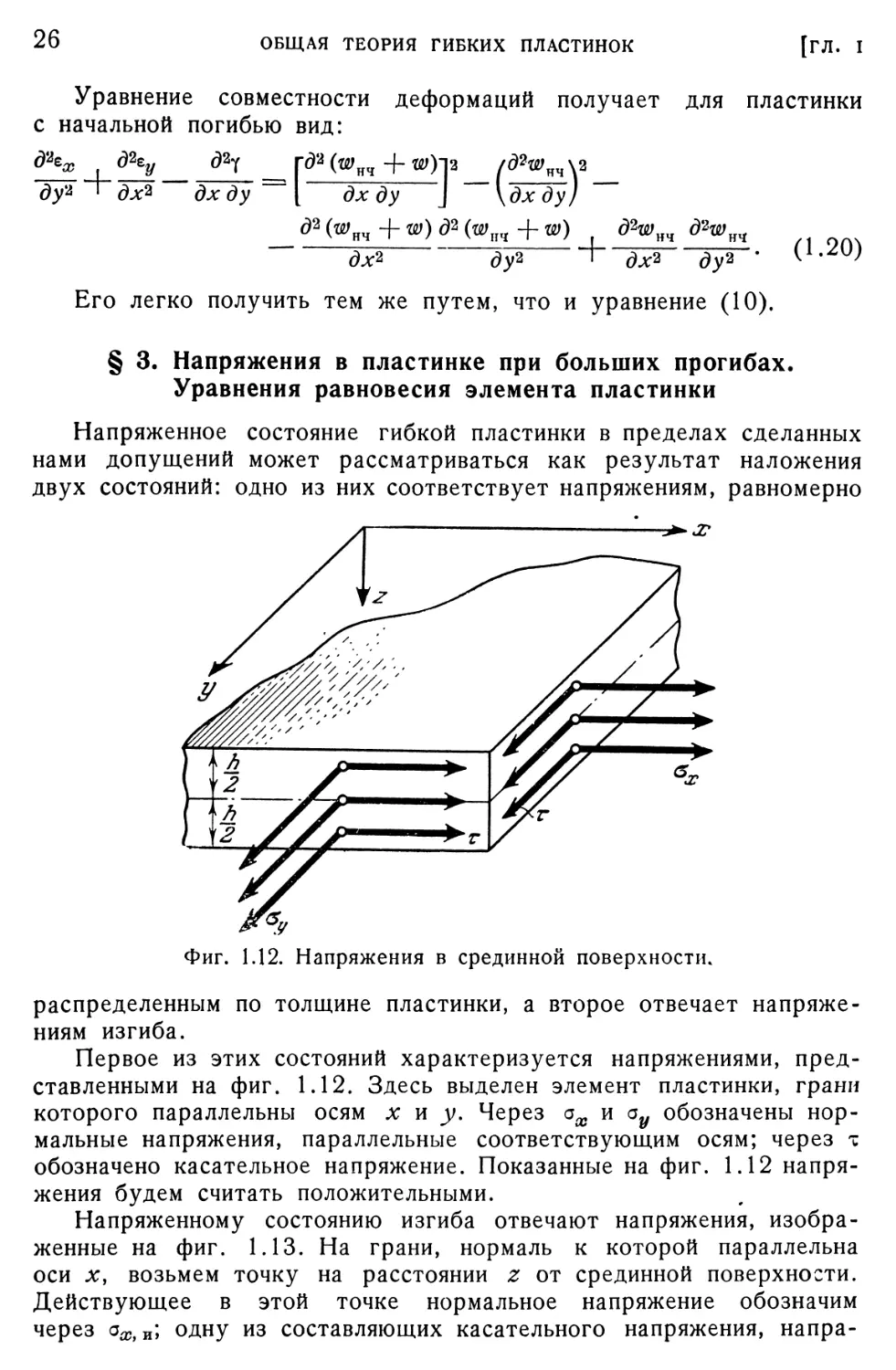
 § 3. Напряжения в пластинке при больших прогибах. Уравнения равновесия элемента пластинки
 Напряженное состояние гибкой пластинки в пределах сделанных нами допущений может рассматриваться как результат наложения двух состояний: одно из них соответствует напряжениям, равномерно
 распределенным по толщине пластинки, а второе отвечает напряжениям изгиба.
 Первое из этих состояний характеризуется напряжениями, представленными на фиг. 1.12. Здесь выделен элемент пластинки, грани которого параллельны осям х и у. Через ах и оу обозначены нормальные напряжения, параллельные соответствующим осям; через т обозначено касательное напряжение. Показанные на фиг. 1.12 напряжения будем считать положительными.
 Напряженному состоянию изгиба отвечают напряжения, изображенные на фиг. 1.13. На грани, нормаль к которой параллельна оси х, возьмем точку на расстоянии z от срединной поверхности. Действующее в этой точке нормальное напряжение обозначим через ох,п> одну из составляющих касательного напряжения, напра¬

НАПРЯЖЕНИЯ В ПЛАСТИНКЕ ПРИ БОЛЬШИХ ПРОГИБАХ
 27
 вленную вдоль контурной линии,—через ти и вторую составляющую, направленную по вертикали, — через zXt и. По грани с нормалью, параллельной оси у, действуют напряжения, которые усло¬
 вимся обозначать, соответственно, через ти и у,и. Напряжения ти на обеих гранях равны по теореме взаимности касательных напряжений; знаки напряжений для той и другой грани будем считать одинаковыми.
 Фиг. 1.14. К определению изгибающих моментов в сечениях пластинки.
 Введем понятие об изгибающем моменте, приходящемся на единицу длины сечения пластинки фиг. 1.14. Для сечения, нормального

28
 ОБЩАЯ ТЕОРИЯ ГИБКИХ ПЛАСТИНОК
 ГЛ. I
 к оси х, изгибающий момент
 h
 2
 1.21
 h
 2
 Для сечения, нормального к оси у,
 2
 1.22
 ь_
 2
 Будем считать положительными моменты, придающие пластинке положительные кривизны. На фиг. 1.14 указаны положительные на¬
 правления Мх и Му, причем моменты представлены также в виде векторов светлые стрелки. При этом мы пользуемся правилом правого винта.
 Усилия, отвечающие касательным напряжениям ти, образуют пары. Векторы этих пар перпендикулярны к соответствующим сечениям фиг. 1.15; момент, приходящийся на единицу длины сечения, назовем крутящим моментом и обозначим через Н:
 Фиг. 1.15. Крутящие моменты.
 2
 1.23
 h_
 ,2

НАПРЯЖЕНИЯ В ПЛАСТИНКЕ ПРИ БОЛЬШИХ ПРОГИБАХ
 29
 Моментам Н отвечает деформация кручения пластинки. Будем считать Н положительным, если направление пар соответствует фиг. 1.15.
 Что касается касательных напряжений хх, и и у, и» им соответствуют поперечные силы, обозначаемые через Qx и Qy.
 h ь_
 Т 2
 Qx J xx>vdz, Qy J Xy,adz. 1.24
 A _ A
 “ 2 2
 Изображенные на фиг. 1.16 поперечные силы будем считать положительными.
 Составим уравнения равновесия элемента пластинки, находящегося под действием внешней поперечной нагрузки и всех перечисленных
 выше внутренних усилий фиг. 1.17. Обозначим через q интенсивность внешней нагрузки, являющуюся, вообще говоря, функцией координат х, у. Приходящаяся на элемент со сторонами dx, dy нагрузка равна qdxdy. Усилия в срединной поверхности будут равны соответствующим напряжениям, умноженным на площадь сечения: oxhdy, Gyhdx и т. д. Эти усилия меняются в зависимости от координат. Поэтому, если в сечении с координатой х действует усилие oxhdy, то в соседнем сечении с координатой x--dx мы
 получим новое значение усилия, равное ах -rdx h dy. Аналогичные приращения получают остальные усилия. Будут меняться также действующие по граням элемента изгибающие и крутящий моменты и поперечные силы.

30 оёЩай Теория гибких пластинок гл. 1
 Элемент пластинки изображен на фиг. 1.17 в недеформированном состоянии. Существенной особенностью задачи о больших прогибах пластинок — как и в других случаях совместного действия усилий в срединном слое и усилий изгиба — является то, что уравнения равновесия должны быть составлены для деформированного состояния пластинки..Однако в случае пологой изогнутой поверхности
 Фиг. 1.17. К выводу условий равновесия элемента пластинки.
 это обстоятельство играет заметную роль лишь при составлении уравнения, выражающего равенство нулю суммы проекций всех сил
 на ось z. Рассмотрим сначала прочие условия равновесия. Прирав¬
 нивая нулю сумму проекций всех сил на ось х, получим:
 ° Ж dx h dy °xh dyJr Т SJdy hdx — ‘hdx °- 0 -25
 После упрощений находим:
 §?°-,-2б>
 Уравнение проекций сил на ось у дает:
 2_0. 1.27
 дх' ду
 Составим, далее, уравнение моментов всех сил относительно линии,

§ 3 НАПРЯЖЕНИЯ В ПЛАСТИНКЕ ПРИ БОЛЬШИХ ПРОГИБАХ 31
 лежащей в плоскости левой грани и параллельной оси у. м1Уу-М»У н d-£dydx-
 — Hdx — qdxdy—dydx- — Qx--dx dydx 0.
 Отбрасывая малые высшего порядка, получим:
 дМх дН дх ду —и
 Аналогично уравнение моментов относительно оси х имеет вид
 1.28
 дН, дМу
 дх ду
 Qy — 0.
 1.29
 >7
 h exdsjdy
 Остается составить уравнение проекций сил на вертикаль, но уже для элемента, находящегося в изогнутом состоянии. Напомним, что углы поворота нормалей к срединной поверхности при деформации мы считаем малыми; при этом косинусы этих углов можно принимать равными единице, а синусы или тангенсы — самим углам.
 На фиг. 1.18 показано сечение деформированной пластинки плоскостью, параллельной оси ; нормаль- Фиг. 1.18. Нормальные усилия и попереч-
 ный элемент слева услов- ные силы в «чениях деформированной J пластинки, параллельных оси х.
 но считается закрепленным,
 а справа — повернутым относительно первого на угол dx. Поперечные силы Qxdx и -f- dx dy, действующие по
 кромкам, дают результирующую проекцию вниз, равную Qdxdy.
 Нормальное усилие в срединном слое слева равно Qxhdy проекция
 его на вертикаль равна нулю. Усилие справа ох dx h dy дает
 проекцию, которую — если отбросить малые высшего порядка —
 д
 можно считать равной Gxh- dx dy.
 Рассматривая фиг. 1.19, находим аналогичные члены для сечения пластинки плоскостью yz: равнодействующую поперечных сил dQy
 —jdxdy и сумму проекций. нормальных усилий в срединной

32
 ОБЩАЯ ТЕОРИЯ ГИБКИХ ПЛАСТИНОК
 ГЛ. I
 плоскости Gyh-pdxdy. По фиг. 1.20 определяем вертикальные проекции касательных усилий в срединном слое, сумма которых равна dxdy. Необходимо, наконец, учесть проекцию поперечной
 2 тг
 d2w
 дхду
 Фиг. 1.19. Усилия в сечениях пластинки, параллельных оси у.
 нагрузки qdxdy. Суммируя все полученные проекции, находим после деления на dxdy:
 dQx dQv d2w d2w dw
 ' y ' • 1 ' ' -1- 0. 1.30
 dx dy a1 dx2 11 dy- l Перейдем к случаю пластинки с начальной погибью. Уравнения равновесия 26 — 27 сохраняют при этом свой вид. Повторяя
 вывод уравнения 30, за¬
 ключаем, что вместо членов
 d2w дх1 '
 ду2 “ w дх ду
 должны быть теперь взяd2wn
 ты произведения oxh
 о yh
 и 2тh
 где
 Фиг. 1.20. Касательные усилия в сечениях деформированной пластинки.
 по-прежнему получим: dQx. dQy д w„4 w
 ■dF57 0'
 ду2 Ik w' дхду 9 под wn понимается полный прогиб после деформации. Заменяя wn суммой
 дх2
 о„г
 д2 wH4 w
 2т h
 ду2 1
 д2 w„, w дх ду
 q 0. 1.31

СООТНОШЕНИЯ МЕЖДУ ДЕФОРМАЦИЯМИ И НАПРЯЖЕНИЯМИ
 33
 § 4. Соотношения между деформациями и напряжениями
 Будем предполагать, что деформации пластинки лежат в пределах упругости: для достаточно тонкой пластинки значительные прогибы могут иметь место и при малых деформациях.
 Примем, далее, гипотезу об отсутствии взаимного давления слоев пластинки, параллельных срединной плоскости: будем считать, что нормальные напряжения о2 в направлении толщины, если и имеют место, то являются пренебрежимо малыми по сравнению с нормальными напряжениями, параллельными срединной поверхности.
 Эти допущения приводят к таким же соотношениям между удлинениями волокон срединной поверхности и напряжениями, как и в случае плоского напряженного состояния:
 где х — коэффициент Пуассона. Находя отсюда напряжения, имеем:
 Соотношение между деформацией сдвига и касательным напряжением имеет вид
 1.33
 1.32
 1.34
 1.35
 v — JL —
 ' G Е
 1.36
 или
 в
 1.37
 Для напряжений и деформаций изгиба в произвольном слое пластинки справедливы аналогичные соотношения

34 ОБЩАЯ ТЕОРИЯ ГИБКИХ пластинок гл. I
 Пользуясь выражениями 15 — 17, получаем:
 1дуа’
 Ez
 d2w
 Х, И 1 — А
 da
 Ez
 fd2w
 2Л и -
 1 — J.2
 дУ
 Ez
 d2w
 си
 1 p. дх ду
 1.41
 1.42
 1.43
 Подставляя выражение 41 для ах>я под знак интеграла 21, находим для момента Мх выражение
 -DS>D’ <ь44>
 где через D обозначена цилиндрическая жесткость пластинки
 dT2Гг о-45
 Таким же образом находим выражения для изгибающего момента Му и крутящего момента Н:
 Му 1х:ху х 1.46
 Я_01-х-г 01-,х. 1.47
 Сопоставляя соотношения 44 — 47, можем кривизны выразить через моменты:
 Мх — 12 х DQ-W М>’ <'-48>
 W-pMJ, 1.49
 L5°
 Уравнения равновесия 28 и 29 дают возможность определить поперечные силы. Подставляя в уравнение 28 выражения 44, 47, получим:
 rdw, dw гл д 70 1 с 1
 -DW5T-DdIV; L51>
 через V2 обозначен двумерный оператор Лапласа:
 V'2
 Аналогично из уравнения 29
 «о d2w, d2w 1 соч
 L52>
 Qy-DVw. 1.53

ОСНОВНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
 35
 Заметим, что величина V'2w может быть определена как сумма кривизн пологой изогнутой поверхности, взятая со знаком минус:
 —х--Yy. С известным приближением эту сумму можно считать независящей от расположения осей х, у и равной удвоенной средней кривизне изогнутой поверхности.
 Из формул типа 41 и 44 вытекают следующие зависимости между напряжениями и моментами:
 12 Mxz __Шуг _12 Hz
 сх, и дз ’ ау, и ” № 04
 Максимальные по толщина пластинки напряжения будут у поверхности:
 Шх 6МУ ен
 °Х, и да > °у, и да > Ти -Д2-. 1.54
 Полные напряжения равны
 П К х, И1 Gy, п : Зу 4“ °У, и» ТдТ--Ти. 1.55
 § 5. Основные дифференциальные уравнения
 . Для установления связи между поперечными силами и прогибом мы воспользовались двумя уравнениями равновесия 28 и 29. Обратимся далее к системе уравнений 26 и 27, содержащих напряжения в срединной поверхности. Представим эти напряжения как производные от некоторой функции Ф:
 дФ дФ дФ ссч
 ду2’ <3Удх' х дхду‘ 1-56
 Подставляя выражения 56 в уравнения 26, 27, мы убеждаемся в том, что эти уравнения будут выполняться автоматически. Функция Ф носит название функции напряжений в срединной поверхности или, короче, функции напряжений.
 Теперь рассмотрим пятое уравнение равновесия 30. Подставив в него выражения 51 и 53 для поперечных сил, получим:
 DV»V« Аоя 4- ■ V1Г-Ш ШГу Ч- 1 -57
 Здесь чгрез V'3V2 обозначен оператор
 VVa - 2 <- У -д-Ы. П58
 ; дх ' дхду ду Уравнение 57 связывает прогиб пластинки с интенсивностью внешней нагрузки; оно, однако, содержит дополнительные неизвестные ах, Оу и т. Решение задачи оказывается невозможным без привлечения уравнения 10, выражающего условие совместности

36
 общая теория Гибких пЛлстиНок
 деформаций. Подставляя в это уравнение вместо деформаций еж, гу и т выражения 32, 33 и 36, получим:
 ду2
 О д2т, д дЪх, 9 д2т, дзу _
 дхду'' дха ду j __р dw у да» дЫЛ п 59ч
 — дхa dy2j- U-ОУ
 Выразим теперь напряжения о, су и с через функцию Ф; тогда уравнения 57 и 59 примут следующий окончательный бид:
 V3v2w —— Ч- —— — 2 —— 4--а Ш
 h ду2 дх2 ' д2 ду2 дхду дхду ' h '
 <>■<»>
 Эти уравнения можно записать в единообразной форме:
 JL V2V2w Lw, Ф -f, 1 -600
 iv2V2<J> — ijLw, «; 1.6Г
 оператор L в применении к функциям w> Ф будет
 г лч d2w 2ф I д2Ф 0 д2до д2Ф х г.оч
 ’ дх2 dy2 ду2 да dxdydjtdy Уравнения 60 и 61 образуют основную систему нелинейных дифференциальных уравнений теории гибких пластинок. В случае пластинки переменной толщины h hxy у и переменной
 жесткости D Dх, у тем же путем приходим к следующим
 уравнениям 2ЛЗ:
 д2 дх2
 р д2® I о д2 р dw I р d2w I
 d2 j dy V дх ду ' ду2 ду2
 . Г <?2 Л o__n й2 лл1_
 1 дх2 dy2 дх 0у дх ду ду дх2 J
 d2F d2w d2F d2w. d2F d2w..
 ду2 дх2 дхду dxdy ' dx2 dy2 ' '
 a2 1 d2F. о d2 1 a27 d2 1 d2
 d2 h dx2 dx dyh dxdy ' dy2 h dy2
 _ Г °2 l d2F 9 d2 l d2F 1 32 l —
 dx2 h dy2 dx dy h dx dy dy2 h dx2 J
 n d2w s d2w d2w.,Л Л1ч
 EUr b61 Эти уравнения были получены Т. Карманом 116.

ОСНОВНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
 37
 здесь принято
 1 dF. _ F. _ 1 Р.
 °х h ду’ °У h дх ’ Z h дхду '
 Исходя из уравнений 60—61, можно получить исходные дифференциальные уравнения для различных частных случаев. Так, для жесткой пластинки, находящейся под действием одной только поперечной нагрузки, срединная поверхность принимается свободной от напряжений. Поэтому в уравнении 60 мы должны положить Ф 0; получим известное линейное уравнение
 DV2V2 q. 1.63
 Если пластинка наряду с поперечной нагрузкой подвергается действию значительных усилий в срединной поверхности, которые можно считать независящими от прогиба, то уравнения 60—61 принимают вид
 h у у ду дх I дх ду» дхду дхду h ’ ■ '
 У2У2Ф 0. 1.65
 Каждое из уравнений 64—65 также оказывается линейным; второе из них используется, как известно, для решения плоской задачи теории упругости.
 В случае абсолютно гибкой пластинки изгибная жесткость D принимается равной нулю, и уравнения 60, 61 получают вид
 , д2Ф dw _, д2Ф d2w, д2Ф d2w п
 ду2 дх2 дх2 ду2 дх ду дх ду '
 <>.б7
 и будут, вообще говоря, нелинейными.
 Уравнение 31 для жесткой пластинки можно переписать в виде
 dQot dQy
 дх ду С другой стороны, уравнение 66 для абсолютно гибкой пластинки
 можно представить следующим образом:
 teyv.y 2гту q. b
 Наконец, для общего случая гибкой пластинки имеем:
 дОм dQy
 — -fo jy- havy 2гг q. с
 Как видим, для элемента жесткой пластинки поперечная нагрузка уравновешивается разностями проекций поперечных сил, действующих по граням элемента. Напротив, в случае абсолютно гибкой пластинки та же нагрузка уравновешивается проекциями на вертикаль усилий

38
 ОБЩАЯ ТЕОРИЯ ГИБКИХ ПЛАСТИНОК
 ГЛ. I
 в срединной поверхности. В общем же случае гибкой пластинки действуют усилия обоих типов. На фиг. 1.21 и 1.22 эти выводы иллюстрируются для элемента искривленной пластинки, размеры которого считаются равными единице. Приращения поперечных сил
 на фиг. 1.21 обозначены через QX и AQy на фиг. 1.22 принято т 0.
 Обратимся к уравнению совместности деформаций 61, соответствующему как гибкой, так и абсолютно гибкой пластинкам. Подставим в правую часть вместо производных от прогиба величины кривизн по формулам 11—13. Тогда получим:
 величину хУу — х? можно с известным приближением считать инвариантом, не зависящим от направления осей х и у и равной гауссовой кривизне поверхности в данной точке см. § 52:
 Если обозначить через и х2 главные кривизны поверхности, — для соответствующих направлений величина равна нулю, — то получим:
 Таким образом, функция напряжений в срединной поверхности пластинки, а вместе с тем и сами напряжения зависят от гауссовой кривизны изогнутой поверхности.
 Фиг. 1.21. Поперечная нагрузка уравновешивается за счет поперечных сил.
 Фиг. 1.22. Поперечная нагрузка уравновешивается за счет усилий в срединной поверхности.
 1.68
 Для пологой изогнутой поверхности
 1.69
 Г 2.
 Уравнению 66 можно придать вид
 1.70
 1 у2У2Ф — — Г.
 Е
 1.71

ГРАНИЧНЫЕ УСЛОВИЯ
 39
 Отметим, что в уравнении Ь для мембраны мы можем вместо кривизн у.х и уу ввести радиусы кривизны рх и рг Положив при этом кривизну кручения равной нулю, получим:
 — — 4- 1-72
 P Ру h
 Это — известное уравнение безмоментной теории оболочек.
 Разберем теперь случай когда гибкая пластинка имеет начальную погибь. Уравнение равновесия 31, выведенное для этого случая, преобразуем таким же путем, как и уравнение 30 для плоской пластинки; следует подставить значения Qx и Qy и ввести функцию напряжений Ф. Что же касается уравнения 20, то здесь необходимо
 выразить еж, и через напряжения по формулам § 4, а затем
 ввести функцию напряжений Ф. Тогда система дифференциальных уравнений для гибкой пластинки с начальной погибью примет вид
 D „OI-ГО WH4 w НЧ w
 - V2V2W •
 h ду2 дх2 ' дх2 ду2
 д2Ф д'
 дх ду
 д2 нч w 12 2 wE4 w д2 до w
 д2ф д2 wH w, 1
 T1- <lra>
 1 Г'
 — v-v3 -
 дх dy J fx‘J ду
 ГдЧгЛ8 diwwl д>н<Л Lдхду ' дх dy J ‘ ' '
 Если воспользоваться оператором L 62, то уравнения примут вид
 R-W2w Lw, Ф 1®нч, -£-, 1.730
 -1 уФ Lw, w — Lww. 1-740
 Уравнение 74 можно также представить в виде
 _l_V-2V — Гп — Г„ч — ДГ; 1.75
 здесь Гп — гауссова кривизна деформированной поверхности пластинки, Гнч — кривизна начальной поверхности, ДГ — «приращение» гауссовой кривизны.
 § 6. Граничные условия
 Интегрирование дифференциальных уравнений изгиба пластинки должно вестись с учетом граничных условий.
 Выясним, какое число граничных условий следует формулировать для каждой точки контура пластинки. В основе теории гибких

40
 ОБЩАЯ ТЕОРИЯ ГИБКИХ ПЛАСТИНОК
 ГЛ. I
 пластинок лежит гипотеза прямых нормалей. Допустим, что нам известны перемещения и, v, w точек контурной линии. Этим определяется положение данной линии в пространстве после деформации. Нормаль, проведенная в любой точке контура, может переместиться поступательно вместе с этой точкой' и повернуться на некоторый угол в плоскости, перпендикулярной к контурной линии. Следовательно, положение нормали после деформации пластинки фиксируется с помощью четырех величин.
 Отсюда можно сделать заключение, что для каждой точки контура должны быть заданы четыре граничных условия. Эти условия могут быть не только геометрическими, относящимися к перемещениям или углам поворота нормалей, но и статическими, т. е. они могут быть связаны как с усилиями в срединной поверхности, так и изгибными.
 Геометрическим условиям, относящимся к перемещениям точек контурной линии в плоскости пластинки, соответствуют статические
 условия для касательных и нормальных усилий. Вместо того чтобы задать угловое перемещение нормали, можно задать изгибающий момент.
 Остается выяснить, какое же статическое условие эквивалентно условию, относящемуся к прогибу точек контурной линии w. Рас¬
 смотренные пока условия не включали крутящего момента и поперечной силы; следовательно, новое граничное условие, связанное с давлением на поддерживающее пластинку ребро, зависит от каждого из них. На фиг. 1.23 показана часть контурной линии х const.
 Так как граничное условие не может быть формулировано для каждой точки по толщине пластинки, то пары, соответствующие напряжениям 7И, необходимо заменить эквивалентными парами. Возьмем две точки, находящиеся на расстоянии A3; 1, и представим крутящий момент Н в виде пары, состоящей из сил, каждая из которых равна Н. Напомним, что размерность момента Н совпадает с размерностью силы. При переходе к следующему участку вдоль
 дН А дН п
 оси у крутящий момент возрастает на величину ку. Поэтому
 При решении частных задач с помощью вариационных методов, связанных с принципом возможных перемещений см. § 10, геометрические граничные условия являются существенными: их необходимо выполнить при выборе апроксимирующих функций. Статические же условия будут тогда естественными: их выполнение — точное или приближенное — обеспечивается в процессе решения задачи.
 М.
 -в
 1_
 4, fcj
 Ду1 Ay-f
 Фиг. 1.23. К определению реактивных усилий, отвечающих крутящим моментам.

ГРАНИЧНЫЕ УСЛОВИЯ
 41
 г,, дН D л
 новая пара состоит из сил В точке А направленные по
 д 11 д
 одной линии силы Н и Дают результирующую напра¬
 вленную по вертикали вниз. Эта результирующая приходится на полоску грани пластинки длиной, равной единице, и должна быть сложена с приходящейся на ту же полоску поперечной силой Qx.
 Отсюда видно, что приходящаяся на единицу длины контура х const сила давления Rx со стороны пластинки на поддерживающее ребро равна
 R Qx Ь •
 Подставляя вместо Qx и И их значения 23 и 24, получим:
 .—■,-76 Для грани у const по аналогии находим:
 я. -°р<2->г5У- <‘-77>
 Отметим, что в каждой точке грани х const одной из сил пары Н соответствовала противоположно направленная сила соседней пары. Однако в месте пересечения двух граней прямоугольной пластинки такой соседней пары уже не находится. Поэтому благодаря действию крутящих моментов, распределенных по грани х const, в углу пластинки создается неуравновешенная сила Ну передающаяся на опорный контур. Такая же по величине и направлению сила появится, если подходить к углу со стороны грани у const. Таким образом, в каждом углу пластинки на опорный контур передается сосредоточенная сила, равная 2. Происхождение этой силы станет ясным, если учесть, что при действии по граням пластинки крутящих моментов два угла пластинки стремятся приподняться по отношению к опорному контуру, а два других угла — опуститься. Препятствие этим смещениям со стороны опорного контура реализуется в виде четырех сил, действующих по линиям пересечения граней фиг. 1.24.
 Фиг. 1.24. Силы в углах пластинки, отвечающие крутящим моментам.

42
 ОБЩАЯ ТЕОРИЯ ГИБКИХ ПЛАСТИНОК
 ГЛ. I
 Перечислим теперь граничные условия, наиболее часто встречающиеся при решении частных задач. Выпишем условия, относящиеся к сторонам а: 0 и х а читатель без труда получит условия для сторон у — О и у Ь, меняя местами х и у.
 1. Край пластинки оперт на ребро, не допускающее прогиба по отношению к плоскости ху. Тогда должно быть
 4. Точки не загруженного края свободно смещаются вдоль оси г. При этом должно быть равно нулю давление на подкрепляющее ребро
 5. Край оперт на упругое ребро, жесткость которого по отношению к изгибу в вертикальной плоскости равна EL Тогда граничное условие запишется в виде дифференциального уравнения изгиба для ребра
 6. Точки не загруженного края свободно смещаются вдоль оси х. В этом случае на границе должно быть равно нулю напряжение, направленное по оси х:
 бФ л 1 004
 w 0.
 1.78
 2. Край защемлен. При этом
 1.79
 3. Край шарнирно оперт. Тогда
 Мх 0.
 Условие это можно переписать в виде d2w. d2w л
 1.80
 1.81
 или
 , 0 ч dw 1
 д2 —
 1.82

ГРАНИЧНЫЕ УСЛОВИЯ
 43
 7. Точки не загруженного края свободно смещаются вдоль оси т. е. по направлению самой грани. Тогда должно быть
 ■с Л- 0. 1.84
 дх ду 4
 8. Края х 0 и х — а закреплены таким образом, что взаимное смещение их точек вдоль оси х невозможно. При этом
 Ux-a 0.
 Для того чтобы выразить это условие через функции f и Ф, воспользуемся формулой 7. Имеем:
 ди 1 dwz
 дхех2дх
 или, если определить гх через напряжения и ввести функцию Ф,
 ди _ 1 дФ fx дФ 1 dwy
 дх Е дуа Е дх3 2 длс Взаимное смещение точек краев х а и х 0 при некотором фик¬
 сированном значении у равно
 а
 Сди.
 ха х-0 — J dx,
 о
 поэтому поставленное условие выразится следующим образом: а
 ЯдФ дФ Е dw 1. л 1 окч
 ду2 дх 2 djc J О
 9. Взаимное смещение краев х — 0 и х а вдоль оси д: имеет фиксированное значение. Введем обозначение ех для относительного сближения краев
 вх Мха х—о•
 Тогда получим:
 а
 1 СдФ дФ Е dwI. t осч
 a J ду 11 дх 2 U-7 J — вх' о
 В зависимости от постановки той или иной частной задачи мы получаем для каждого края, как было сказано, четыре условия. Пусть, например, сторона х — а шарнирно оперта на ребро, не поддающееся изгибу в вертикальной плоскости; в то же время

44
 ОБЩАЯ ТЕОРИЯ ГИБКИХ ПЛАСТИНОК
 ГЛ. I
 перемещения точек контура в плоскости пластинки не стеснены. Тогда получим условия
 1 	w 0, 2МХ 0, 3 0, 4 0.
 Граничные условия получились смешанного типа: первое является геометрическим, а остальные три — статическими.
 § 7. Применение принципа возможных перемещений. Вариационное уравнение равновесия
 Решение частных задач, относящихся к гибким пластинкам, связано с интегрированием системы нелинейных дифференциальных уравнений. Точные методы интегрирования такой системы уравнений почти отсутствуют, все успехи в данной области связаны с применением различных приближенных методов. Наибольшее значение до настоящего времени имели вариационные методы, хорошо разработанные в различных областях математической физики и в применении к задачам теории упругости тесно соприкасающиеся с энергетическими принципами строительной механики.
 Одним из наиболее общих энергетических принципов является начало возможных перемещений, которое для деформируемых систем формулируется следующим образом: реальное равновесное состояние упругой системы характеризуется тем, что сумма работ всех внешних и внутренних сил на любых кинематически возможных перемещениях точек упругой системы равна нулю.
 Под возможными перемещениями понимаются бесконечно малые перемещения точек системы, находящиеся в соответствии с геометрическими граничными условиями и являющиеся непрерывными функциями координат; отвечающие этим перемещениям деформации должны удовлетворять условию совместности.
 Рассмотрим прямоугольную пластинку, находящуюся под действием нормальных усилий рх и ру по граням х 0, а и 0, b и касательных усилий 5 по всем граням фиг. 1.25; под рх, ру и 5 понимаются силы, приходящиеся на единицу площади грани. Сохраним для внешних усилий то же правило знаков, что и для внутренних § 2: показанные на фиг. 1.25 направления будем считать положительными. Кроме того, примем, что пластинка подвергается действию поперечной нагрузки интенсивностью q направление q вниз примем положительным.
 Обозначим через Ъи, fry и dw возможные перемещения точек срединной поверхности, т. е. вариации перемещений этих точек при
 Обзор приближенных методов решения нелинейных задач см., например, в книге Л. Коллатца «Численные методы решения дифференциальных уравнений», ИЛ, 1953.

§ 7 ПРИМЕНЕНИЕ ПРИНЦЙПА ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ 45
 воображаемой деформации пластинки, по направлениям осей, соответственно, х, у и z. Обозначим также Ьгх, Ьгу и 87 вариации деформаций срединной поверхности, т. е. изменения деформаций при возможном перемещении пластинки. Возможные перемещения совершаются по отношению к окончательному деформированному состоянию пластинки, когда внеш-
 Возможность такого разделения вытекает из того, что усилия в срединной поверхности не совершают работы при деформации изгиба, так как срединная поверхность остается при изгибе нейтральной; в то же время усилия изгиба не совершают работы при деформации срединной поверхности.
 Для кубика с размерами, равными единице, работа внутренних сил равна — ЗоМя а2г ТТЬ Определяя полную работу усилий в срединной поверхности 8ЛС для всего объема пластинки, найдем:
 ние и внутренние силы пришли в равновесие, достигнув своей полной величины.
 Работа внутренних сил 8Л на возможном перемещении системы состоит из двух независимых величин: работы усилий в срединной поверхности 8ЛС и работы усилий изгиба 8ЛИ:
 ЪА ЪА0 ЪАЯ. 1.87
 Фиг. 1.25. Внешние усилия по кромкам пластинки и поперечная нагрузка.
 ЪАВ — h eJ>ta,--eybzy--ib‘dxdy, 1.88
 F
 интеграл распространяется на площадь пластинки F. Введем обозначение
 F
 Учитывая формулу 7, получим:
 или
 •' Знак минус объясняется тем, что внутренние силы, действующие со стороны кубика на остальную часть пластинки, направлены противоположно смещению точек их приложения.

46 ОБЩАЯ ТЕОРИЯ ГИБКИХ ПЛАСТИНОК ГЛ. I
 Пользуясь формулой интегрирования по частям, находим:
 ь ъ
 А - h J xbudyJ_ah J dy J д£ъ adx-
 О 0 0
 - h i bw dyx_о h J йУ J Tx 8w dx•
 0 0 0
 Здесь первый и третий интегралы берутся для контурных линий х — а со своим знаком и х 0 с обратным знаком. После некоторых преобразований получим:
 , — а «. s« <о£‘- г» <о£о
 J Jla-wdxdy.
 F F
 Производя аналогичные преобразования других членов, входящих в выражение 88, представим 8ЛС в виде
 Ь а
 2ЛС — h ахи 4“ т у — h J “Ь zyv dx —
 0 0 J
 h JIШ s“> »
 F
 h'Л9
 F
 При определении работы усилий изгиба ЬЛЯ необходимо учесть, что направления и деформации будут переменными по толщине пластинки, поэтому в отличие от выражения 88 получим:
 ъ
 2
 J dz J J ?xt и j Gy, и и f” dx dy. 1.90
 _h F 2

§ 7 ПРИМЕНЕНИЕ ПРИНЦИПА ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ 47
 Выразим напряжения через моменты, а деформации — через кривизны. Тогда выражение 90 получит вид ь
 2
 8Ли — j z1 dz J j МХЪХ МуЪу 2НЬу; dx dy.
 Jh F
 2
 Здесь 8хж, 8уу и 8 — вариации кривизн срединной поверхности. Интегрируя по z, найдем:
 8А, — J J Мх Ьу.х МуЪу 2НЬу dxdy. 1.91
 F
 Подставив вместо кривизн их значения 48 — 50, получим:
 >Аш J I M MAw2m£rkdx,,>’- 1'92
 F
 Представим это выражение в виде
 8ЛИ jdy J МХ±Ъ dx Jrfx J 0 0 0 0
 2 4> н“■
 О 	о
 Пользуясь формулой интегрирования по частям, получим: м„ dy «.W,
 О 0 0
 J M>sdxJ‘<,-dx J e-wk<Wd?
 0 9 о 0
 2 j
 Новое интегрирование по частям дает
 mm®c:msh::-
 <2««»c.“i;:iJ RTf2kMx“y- <>•»

48
 ОБЩАЯ ТЕОРИЯ ГИБКИХ ПЛАСТИНОК
 «2?
 Предпоследний член может быть развернут следующим образом:
 2С.1и‘ 2ЯМа; 6 2Hbw 0 - 2Я8ОТ0. - 2НЩа; 0;
 индексами в правой части здесь служат координаты х и у точек, для которых должны быть вычислены момент Н и вариация прогиба dw.
 Каждая из величин 2Н представляет собой сосредоточенную силу, передающуюся от пластинки опорному контуру в соответствующей угловой точке.
 Вычислим далее работу внешних сил dW на возможном перемещении пластинки. На участок грани х а, длина которого составляет dy, будут приходиться усилия pxhdy и shdy. Определим работу этих сил на возможных перемещениях Ьа и bv в плоскости пластинки; по фиг. 1.26 находим работу равной pxh dyba sh dy §г>; по всей грани получим:
 “Г
 _L
 да 1 Shdy
 Фиг. 1.26. К определению работы внешних усилий на возможных перемещениях.
 J pxhbu -f- shbv dy.
 Для грани а: 0 знак работы будет отрицателен, так как усилия рх
 а?
 Фиг. 1.27. К определению работы внешних усилий, связанной с прогибами.
 и 5 направлены в обратную сторону. Суммируя работу по граням х а и х 0, найдем:
 ъ
 MU — LL
 J.Tt — O
 О
 bwi h J pju -I- qbv ■

§ 7 ПРИМЕНЕНИЕ ПРИНЦИПА ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ 49
 Для двух остальных граней будем иметь:
 1 уь
 oW2
 h J py'jv ?Sa dxy_0 ■
 Перейдем к определению работы усилий в срединной поверхности на возможных перемещениях bw. Здесь нужно считать исходное равновесное положение пластинки изогнутым с учетом больших смещений подобно тому, как это мы делали при составлении уравнения равновесия элемента пластинки 30. На фиг. 1.27 изображен участок грани пластинки х — а в повернутом положении; усилие pjtdy составляет с осью х угол усилие shdy отклонено от оси у на
 угол Вертикальные составляющие этих усилий будут pxhdy
 и sh а их работа на перемещении bw оказывается равной
 pxh dybwdy.
 Для граней л; а и л: 0 окончательно получим:
 SГ3 Л J с
 О
 а для граней у b и у 0
 гг,_й <d
 Наконец, работа поперечной нагрузки будет равна
 bWb J J qbw dx dy. е
 F
 Суммируя выражения а — е, находим элементарную работу внешних сил:
 Ь а
 ZW h f pJ>u-- sbv dy -f-Г h pybv--sbudx
 L J Ja? 0 L j Ji о
 0
 a
 J swdx _ H- J J dxdy. 1.94
 А У tp

50 ОБЩАЯ ТЕОРИЯ ГИБКИХ ПЛАСТЙНОК ГЛ. I
 Согласно принципу возможных перемещений равновесное положение системы характеризуется равенством
 ЗГ8Л 0 1.95
 или
 8 W 8 Лс 4- а Ли О. 1.96
 Подставим сюда выражения 89, 93, 94 и используем вытекающие из формул 44—47 соотношения:
 дШх. _ дН. дШ
 4. ' 2та7V “DV73’ <ь97>
 W 2 -DS<2-rt5 -R-
 «г <>•>
 Тогда уравнение 96 примет вид ъ
 КАг — За,8и « —т1< о
 О
 а
 ,х-а х0
 У Ь У
 а Г s — т8ир„ — оу ог» flfx 1 J 2 0
 J й 40 1 МуЬ HLo
 J — Rx.Px — — hYwdyx 0 J —Ry--s — — °»Лrdxy 0
 2ям::0°о6л JJ ££«£•
 ikdvbwdxdy- J J D™iw-°ih-
 F
 — avh — h-yb‘wdxdy0- О-100
 Нами получено так называемое вариационное уравнение для гибкой пластинки, основанное на принципе возможных перемещений. Как известно, этот принцип является наиболее общим началом статики. Поэтому из вариационного уравнения должны вытекать все

ВЫЧИСЛЕНИЕ ЭНЕРГИИ СИСТЕМЫ
 51
 выведенные ранее в § 3 уравнения равновесия элемента пластинки, а также формулированные в § б статические граничные условия. Отметим, что последние являются, по существу, условиями равновесия элементов пластинки, прилегающих к контуру и находящихся под воздействием внешних и внутренних сил.
 В самом деле, из уравнения 100 мы получаем — если считать вариации координат Ьи, bv> Згепроизвольными и независимыми— следующие равенства, относящиеся к любой точке на контурных линиях х — а и х 0:
 ах Рх 0 > Т —s 0, Мх — 0, Rx 0.
 Эти равенства отвечают статическим граничным услозиям § 6, если предположить, что по свободно смещающимся краям х а и х 0 распределены внешние усилия рх и s. Аналогичные равенства вытекают из уравнения 100 для граней j 0 и у Ь. Кроме того, для углов пластинки получаем условия Н— 0, относящиеся к случаю свободных углов пластинки; при закреплении углов силы 2И уравновешиваются реакциями опорного контура.
 Из рассмотрения двух последних интегралов в уравнении 100 видно, что для каждого элемента пластинки, расположенного внутри контура, должны удовлетворяться полученные нами ранее уравнения 26, 27 и 57. Первые два из них автоматически выполняются при введении функции напряжений Ф. В случае, когда контурные интегралы в 100 обращаются в нуль, вариационное уравнение приводится к виду
 Г Г ®vava«——— — — —
 J J h ду дх дх?ду
 2ШГуШ-,—1ь>ыу0. 1.101
 § 8. Вычисление энергии системы
 Определим полную энергию для изогнутой гибкой пластинки Э как сумму потенциальной энергии деформации U и потенциала внешней нагрузки V:
 Э иУ. 1.102
 Величина U> в свою очередь, может быть вычислена как сумма энергий, соответствующих деформации срединной поверхности и деформации изгиба:
 1.103

52 ОБЩАЯ ТЕОРИЯ ГИБКИХ ПЛАСТИНОК ГЛ. I
 Вариация первой из этих величин WG равна элементарной работе усилий в срединной поверхности 8Л0 88, взятой с обратным знаком:
 bUc —bA0 hjj ож8зж зуЪгу тЗ? dxdy. 1.104
 F
 Пользуясь формулами 32 — 36, находим:
 J- J J К — ГЧ Зг Заг — 1х5за>
 F
 —j— 21 —j— д. т8т dx dy. а
 Произведение охЬах можно представить в виде 8 а2. Преобразуя таким же образом другие члены подинтегрального выражения в а, получаем:
 c 2fM J f °2у — ажаг 21 xdx dy.
 F
 Выражение для энергии UG имеет вид
 Ш J J К«» °,,в —21 — <У- 1.105
 Fr
 Вводя функцию напряжений, получим следующее выражение:
 h С Г 1д2ф. д9ф9 01..ГдФдФ <Э2ф2Ъ
 0 — 2Е I Цдлга2 Ьдхду дхду Jахс1У-
 V' 1.106
 Если воспользоваться оператором L 62, то выражение для UG можно представить также в виде
 Uo lE f J Ку2ф9 —1VLP, Ф1 dxdy. 1.1060
 Вариация энергии изгиба по 92 будет
 Юя — Л„ 5 J Ж Мум„ 2НЬуdxdy. 1.107 ‘f
 Используя формулы 44 — 47, находим:
 Ши D3 J j v.x vyy Sxx 'j Sy2 1— ;а xsXldx аУ- b
 F

ПОЛНОЕ ВАРИАЦИОННОЕ УРАВНЕНИЕ
 53
 Энергия изгиба равна
 Введем значения кривизн И, 13; тогда получим:
 или
 ия f j VM2 — 1— jiL®, wdxdy. 1.109'
 F
 Будем считать, что к пластинке приложены внешние усилия в срединной плоскости рх> pyi s и поперечная нагрузка q. Вариация потенциала этих сил найдется как элементарная работа 8W, взятая с обратным знаком:
 При вычислении потенциала величина нагрузки считается постоянной. Поэтому элементарной работе pxbady будут соответствовать изменение потенциала — pj>u dy и полный потенциал —рхи dy; нулевой уровень энергии при этом отвечает недеформированному положению пластинки.
 Учитывая остальные члены выражения 94, получим:
 Приведенные выражения для составляющих энергии Э будут часто использоваться в дальнейшем.
 В § 7 мы получили вариационное уравнение равновесия, пользуясь принципом возможных перемещений. Зададимся теперь целью составить более полное вариационное уравнение, из которого вытекали бы не только условия равновесия, но и условие совместности деформаций. Для этого придадим выражению для вариации полной энергии 83 системы другую форму.
 Вернемся к выражению 104 для 8£с. Представим произведение как разность 180 — Sas. Тогда 104 можно переписать
 8 — Ш.
 ь
 qxudxdy.
 l.iii
 § 9. Полное вариационное уравнение

54 ОБЩАЯ ТЕОРИЯ ГИБКИХ ПЛАСТИНОК ГЛ. I
 в виде
 ьис AS J J рхгх <зугу -I- Т-f — Ьахгх Ьаугу 7 dx dy.
 F
 Выражение
 оRc h j j sa;aa7 4“ TT dx dy
 F
 представляет собой вариацию так называемой дополнительной энергии.
 Пользуясь законом Гука, мы можем для рассматриваемой задачи представить §R0 в виде
 8с 2Г8 j f — 2:JOa;3tf21 ?■ dxdy.
 F
 Если подставить теперь вместо деформаций гж, гу> у их значения 7 — 9, получим:
 т з ё ЗЗГ —у1° 4 —2:Ja4-2l«rfA:d> 1.112
 Таким же образом можно преобразовать выражение для вариации ШИ 107:
 ьии 5 J Мах Муу„--2Ну -
 е FJ
 — ШМ м2у - 2'<ХММУ 2 1 1 2 dx dy. 1.113
 Для определения вариации потенциала внешних сил oV 110 воспользуемся выражением 94.
 Равновесное состояние деформированной гибкой пластинки можно теперь охарактеризовать, приравнивая нулю первую вариацию полной энергии системы:
 ЪЭ Ш0 Ьия ЬУ 0. 1.114
 Это понятие в применении к нелинейным задачам было введено Энгессером Zeitschr. des Archit. und Ing. Ver. zu Hannover 35, 1889, 7 33—744.

§ 9 ПОЛНОЕ ВАРИАЦИОННОЕ УРАВНЕНИЕ 55
 В итоге получаем следующее вариационное уравнение:
 -• J J К№Мж’«, тгН£1
 F
 . f ди, dv t dw dw дЬю, OL dhs Лъ Ж-М-ШМУ1у-2Н-дуГ
 Y IK 0-20,x o - ta> -
 1 12
 2 b№
 b
 lMx — 21—1 MxMy - Я2 dx dy -
 - j,j,svpxr«-£ «■; v -
 - J««v p»-y »’;■« --
 — j jqwdxdy — 0. 1.115
 e F
 Вводя в это уравнение функцию напряжений в срединной поверхности и считая, что прогиб контурных точек пластинки равен нулю, находим:
 ? и Г Г Iдщ Г ди, 1 dw ai, д?Ф Г dv, 1 dw 21
 оЭЧМ J-жтUrшЫ2-дуJ-
 F
 д2Ф f ди - ди. dw dw d2w. d2w ОИ dw
 dx dy ду dx Tdx dy x dx МУ dy2 dx dy
 1<?2ф <?2ф2 ГЗфЗф <?2ф 21
 2 Wya дх2 Zi _hJXl dx2 dy2 dxdy J
 1 12
 J lMx Myf- — 21—ц Ai — Я-2 dx dy -
 г i® « г -УЬ
 — J i.Pxu svdy— у supvvdx

56 ОБЩАЯ ТЕОРИЯ ГИБКИХ ПЛАСТИНОК ГЛ. I
 Примем далее, что варьируется только функция прогиба wt и найдем частную вариацию 8w3:
 ? о г, Г Г Г 2ф I 2ф д
 A J J Idy5r-3J1F<0W>dP--5jT?y ow_
 F
 д2Ф dw д f<s v д2Ф dw д Л ч д2 ч
 дл: ду ду дх дх ду дх ду а? й<и0
 _ Ж, 8® - 2 8® -18® dx dy.
 Повторяя выкладки § 7, сделанные при выводе формул 89 и 93, и принимая попрежнему на контуре 8<я 0, получим:
 «.а j mj £ j м„ 8 к Л2
 F
 , - Г д2Ф д 0 д2Ф д2до д3Ф д‘>. ? 11 <> » » 11174
 ду2 дх2 дх ду дх ду дх ду2 д -У Приравняем вариацию 8ЮЭ нулю. Учитывая соотношение 97 и отбрасывая контурные интегралы, приходим к вариационному уравнению
 8 Э f 7-2-VV«r—-- 2-— w J J Л ду2 дх2 dx dy dx dy
 F
 д2Ф n
 —эгг-—<1л18>
 оно совпадает с полученным в § 7 уравнением 101.
 Будем теперь варьировать только функцию напряжений Ф. Вычислим, исходя из уравнения 116, частную вариацию 8ФЭ:
 •«-Я£ч4£Я<>
 F
 I Г дк 1 dw 21 ?з 5?д>ч <ц dv dw dw д
 l_dy‘2dyj дх2 L дл: дх ду J дл: ду ШМ>>-2 Д AHI- <1П9

ПОЛНОЕ ВАРИАЦИОННОЕ УРАВНЕНИЕ
 57
 Интегрированием по частям получаем:
 ь
 С другой стороны,
 F
 dw dw
 дх дх ду2
 J 8Ф dx dy.
 Далее,
 F
 Ь
 Произведем такие же операции над остальными членами выражения 119, причем условимся считать контурные интегралы равными нулю. Приравнивая 8Ф3 нулю, после приведения подобных членов получим второе вариационное уравнение
 Так как вариация 8Ф является произвольной, то отсюда мы получаем уравнение совместности деформаций 61. Таким образом удается получить энергетическую формулировку условия совместности деформаций. Если вариационное уравнение 118 связано с принципом возможных перемещений, то уравнение 120 основывается на другом энергетическом принципе — начале возможных изменений напряженного состояния.
 Отметим, что по отношению к каждой из вариаций 8Ш3 и 8ФЭ может быть проведено дополнительное варьирование по второй переменной. Смешанные вариации, полученные при различной
 Идея вывода двух вариационных уравнений типа 118 и 120 была высказана Л. И. Балабухом в докладе на семинаре в Институте механики АН СССР 1951 г.. Близкие по форме зависимости получены также Ху Хай-ченом 1Л0 и Стайпсом 1,24J.
 Об особенностях применения этого принципа к нелинейным задачам см. ниже в § 98.
 F
 d'Hs dw
 дх2 ду2
 ■j — -iV;2VS<rfdy 0. 1.120

58
 ОБЩАЯ ТЕОРИЯ ГИБКИХ ПЛАСТИНОК
 ГЛ. I
 последовательности варьирования, оказываются, как это и следовало ожидать, равными между собой:
 8фи>Э J J 2 8Ф8 dx dy;
 F
 для контура попрежнему принято 8 0 и 8Ф 0.
 Исходному выражению 116 для вариации полной энергии системы может быть при однородных граничных условиях придан более компактный вид
 83 8 J J -—V29 — 1—jxLw, w —
 F
 — 1— 1 —— jJbАФ, Ф1 -ФLw, w — qwdxdy. 1.116'
 Здесь введен оператор L 62.
 § 10. Приближенные методы, связанные с вариационными
 уравнениями
 В теории гибких пластинок с вариационными методами связаны, как было уже сказано, наиболее эффективные пути интегрирования основных дифференциальных уравнений. Чаще всего в литературе применяется следующий способ решения конкретных задач. Функцию прогиба wx, у представляют в виде ряда
 ‘ i1 272 •••• Л 1.121
 г 1
 Здесь через обозначены некоторые наперед заданные и независимые друг от друга функции координат х и у, которые, будучи подставлены вместо w в равенства типа 78 — 86, удовлетворяют всем геометрическим и статическим граничным условиям рассматриваемой задачи; через fx обозначены параметры, подлежащие определению.
 Подставим ряд 121 вместо w в правую часть уравнения совместности деформаций 61 и проинтегрируем его, подчиняя решение заданным граничным условиям для функции Ф. Тогда мы получим выражения для w и Ф, содержащие параметры.
 Далее должны быть определены величины ; при этом возможны различные пути. Остановимся вначале на методе, разработанном И. Г. Бубновым и примененном Б. Г. Галеркиным для решения ряда задач строительной механики. Обратимся к вариационному урав-
 См. И. Г. Бубнов, Отзыв о сочинениях профессора Тимошенко 1913 г. и Строительная механика корабля, ч. 2 1914 г., а также Б. Г. Г а леркин, Стержни и пластинки, «Вестник технологов» 1915 г..

§ 101
 ВАРИАЦИОННЫЕ МЕТОДЫ
 59
 нению 100 и подставим вместо w и Ф найденные выражения. Так как статические граничные условия считаются заранее выполненными,
 то контурные интегралы из уравнения 100 выпадут, а уравне¬
 ние 101 приобретет вид
 Xbwdxdy Q; 1.122
 F
 через X здесь обозначено выражение
 1-123
 Пользуясь выражением 121, выразим 8w через вариации пара-' метров
 00
 i 1
 Подставим ряд а в уравнение 122; тогда получим:
 Но вариации 8 являются произвольными; следовательно, уравнение Ь окажется выполненным, если в отдельности будет удовлетворено каждое из уравнений типа
 J J Xtidxdy 0, 1, 2,..., п. 1.124
 F
 После интегрирования по х и у мы получаем алгебраические уравнения, содержащие искомые параметры г. Число этих уравнений равно п легко показать, что они будут кубическими относительно. Решая полученную систему кубических уравнений, находим параметры fi и тем самым определяем функции f и Ф,
 Уравнения типа 124 мы будем называть уравнениями Бубнова — Галеркина. Напомним, что контурные интегралы в вариационном уравнении 100 выражают работу сил, приложенных к пограничным элементам пластинки на возможных перемещениях, а интегралы по площади — работу сил, приложенных к внутренним элементам.
 Если уравнение 124 переписать в виде
 J J XrijSfidxdy — 0, с
 F
 то стоящий в левой части интеграл можно рассматривать как сумму работ усилий Xdxdy, приложенных к элементам пластинки на возможных перемещениях 8. Но если раньше при составлении уравнения 100 мы считали возможные перемещения совершенно

60
 ОБЩАЯ ТЕОРИЯ ГИБКИХ ПЛАСТИНОК
 ГЛ. I
 произвольными, то в уравнении с фигурирует вполне определенное возможное перемещение пластинки, характеризуемое функцией rit Таким образом, метод Бубнова — Галеркина как бы суживает принцип возможных перемещений, заменяя весь диапазон возможных перемещений несколькими, произвольно выбранными.
 Степень точности полученного таким образом решения зависит от того, насколько удачно выбрано исходное выражение 121 для прогиба. При этом необходимо не только правильно подобрать отдельные функции 7, удовлетворяющие нужным условиям, но и найти их наиболее приемлемое сочетание. Для этого должны быть самым тщательным образом изучены экспериментальные данные, касающиеся •вида изогнутой поверхности пластинки на различных стадиях нагружения. В некоторых случаях удается подобрать функции удовлетворяющие лишь геометрическим граничным условиям задачи. Тогда вариационное уравнение уже не может быть приведено к виду 101: необходимо подставить приближенные выражения для w и Ф в полное вариационное уравнение 100, т. е. учитывать входящие в это уравнение контурные интегралы. Это означает, что при невыполнении статических граничных условий необходимо принимать во внимание работу сил, приложенных к пограничным элементам пластинки. При использовании полного уравнения 100 выкладки значительно усложняются; в таких случаях уместно воспользоваться другим методом, известным в литературе как метод Ритца.
 Обратимся к вариационному уравнению в том виде, как оно было представлено в § 9: 83 0. Определим тем же путем приближенные выражения для прогиба w и функции напряжений Ф, а затем вычислим полную энергию системы Э по 102. Выражение для энергии будет содержать параметры прогиба fp иными словами, энергия системы окажется функцией fi Вариация 8Э может быть представлена в виде суммы вариаций, соответствующих изменениям различных параметров и
 П
 i 1
 Ввиду произвольности вариаций 8 получаем п уравнений, связывающих параметры :
 и 0, 1,2,...,». 1.125
 Ofi
 Уравнения 125 имеют ту же структуру, что и уравнения Бубнова— Галеркина 124. Решая систему уравнений 125, находим.
 W. Ritz, Ueber eine neue Methode zur Losung gewisser Variationsprobleme der math. Physik, J. f. d. reine und angew. Math. 135 1908, 1—61.

§ 101
 ВАРИАЦИОННЫЕ МЕТОДЫ
 61
 Тем самым мы определяем функции w и Ф в зависимости от внешней нагрузки и, следовательно, решаем задачу. При таком выборе функций гг в выражении 121, когда они удовлетворяют всем граничным условиям как геометрическим, так и статическим, результаты вычислений по методам Ритца и Бубнова — Галеркина должны совпадать: имеется в виду, что уравнения Бубнова — Галеркина составлены в соответствии с принципом возможных перемещений.
 Если метод Бубнова — Галеркина применяется к задаче об изгибе пластинки с начальной погибью, то весь ход решения остается тот же, но для X должно быть взято вместо 123 другое выражение:
 XDV2Y2w
 -4
 д2Ф d2wn4--w ду2 дх2
 д2Ф d2wn4 w д2Ф d2wU4 w 1 дх ду дх ду дх2 ду2 J Это следует непосредственно из рассмотрения уравнения 73.
 Мы считали до сих пор, что при решении задачи выбирается приближенное выражение для прогиба а функция напряжений Ф определяется путем интегрирования уравнения совместности деформаций 60. Однако в некоторых случаях оказывается затруднительным удовлетворить заданным граничным условиям для Ф. Тогда может быть выбран другой прием, заключающийся в одновременном назначении функций w и Ф с помощью рядов
 W
 Затем используются оба вариационных уравнения 118 и 120 и составляются уравнения типа:
 J J Xdxdy 0, f f Yfj dx dy — 0; 1.128
 F
 при этом под X попрежнему понимается выражение 123, а функция У для плоской пластинки будет
 Так как в методе Ритца и примыкающем к нему методе Бубнова — Галеркина вариационная задача рассматривается исходя непосредственно из условия экстремума некоторого интеграла выражения для энергии системы, в вариационном исчислении они характеризуются как прямые методы; при пользовании этими методами задача сводится к решению системы алгебраических уравнений.

62
 ОБЩАЯ ТЕОРИЯ ГИБКИХ ПЛАСТИНОК
 ГЛ. I
 а для пластинки с начальной погибью
 уаузф Гд2 «О 1а нч w д w„4 w
 Е L дх ду J дх2 ду2
 При таком методе решения задачи не только дифференциальное уравнение равновесия, но и уравнение совместности деформаций удовлетворяются как бы «в среднем» для всей площади пластинки.
 Наконец, возможен и третий путь применения энергетического метода. Он состоит в приближенном задании всех трех перемещений и, V, w с помощью рядов
 « » w wk; 1.131
 функции uit Vjy wk должны удовлетворять геометрическим граничным условиям. Далее вычисляется энергия системы Э и составляются уравнения типа
 0, 0, - 0, 1.132
 dai dbj дск v 7
 из которых определяются коэффициенты а, bj, ск. После этого могут быть найдены напряжения в произвольной точке пластинки. При этом нет надобности особо заботиться об удовлетворении условия совместности деформаций: перемещения и, v, w задаются как непрерывные функции координат и совместность деформаций обеспечивается автоматически. Недостаток метода состоит в том, что во многих
 случаях трудно уловить характер изменения функций и и w по пло¬
 щади пластинки и подобрать соответствующие им приближенные выражения.
 § 11. Другие приближенные методы
 Наряду с вариационными методами решения задач, относящихся к гибким пластинкам, в последние годы получили распространение некоторые другие методы.
 Значительный интерес представляет прежде всего метод возмущения. Пусть основные уравнения представлены в виде 60'—61'» причем пластинка подвергается действию равномерной поперечной нагрузки q. Введем обозначение для прогиба в избранной точке с координатами х0, у0 в частности, стрелы прогиба и выберем эту величину в качестве основного параметра. Искомые функции w и Ф, а также
 Этот метод может быть также назван методом малого параметра; в теории гибких пластинок он был впервые применен П. Я. ПолубариновойКочиной 3.10.

§ 11
 ДРУГИЕ ПРИБЛИЖЕННЫЕ МЕТОДЫ
 63
 нагрузку q разложим в бесконечные ряды по степеням параметра :
 со со со
 «>2 vnx, уп, ф 2 ?пх, уп, я 2 °nfn‘ ызз
 п— 1 п 1 п - 1
 Подставим эти выражения в левую и правую части уравнений 60'
 и 61' и выделим члены, содержащие одинаковые степени. Тогда получим новые дифференциальные уравнения, содержащие функции vn и срп с последовательно возрастающими индексами. Индексу п 1 будут соответствовать уравнения
 DVaV2 av 1.134
 V2V‘2cPl 0. 1.135
 Для п 2 будет
 VWv2 Lvv ?1«2, 1.136
 Ivcp2-Lvv vty, 1.137
 для п 3
 jW2v3 Lv2, ?2 «з. 1-138
 -i V2V2cp3 — ®i> vJ — ±Lvt, vl-Lvl, v2 1.139
 и т. д. К этим уравнениям надо присоединить граничные условия, отвечающие характеру закрепления пластинки. Кроме того, могут быть введены дополнительные условия, которые позволят определить постоянные av а2» • • • Так, например, можно использовать соотношение wx t Vq. Тогда будет
 <М40>
 <»>», ••• -0- О-141
 Уравнения 134 и 135 являются линейными и, как легко видеть, относятся к задаче об изгибе жесткой пластинки. Если начальные усилия в срединной плоскости отсутствуют, то во втором из этих уравнений функция напряжений может быть принята тождественно равной нулю: cpt 0. Из первого же уравнения с учетом граничных условий и соотношения 140 определяются постоянная <х1 и функция i>iх, у, характеризующая форму изогнутой поверхности пластинки. Далее функция vxx, у подставляется в правую часть уравнений 136
 Целесообразно привести уравнения к безразмерной форме и в качестве параметра взять безразмерную величину Л. Параметрами могут служить и другие величины, характеризующие деформированное состояние пластинки или нагрузку.

64
 ОБЩАЯ ТЕОРИЯ ГИБКИХ ПЛАСТИНОК
 ГЛ. 1
 и 137; в данном случае дополнительный член Lvv cpt обратится в нуль, так что уравнение 136 будет повторять 134. Уравнение же 137 даст возможность определить функцию ср2 л:, у. На третьем этапе подставим vt и ср2 в правую часть уравнений 138 и 139, это даст возможность определить постоянную а3 и функцию v3x, у. После того, как найдены ае> • • •> значение при заданной на¬
 грузке q определяется приближенно из последнего соотношения 133.
 Таким образом, общая идея метода состоит в том, что в основу решения берется хорошо исследованное невозмущенное линейное уравнение теории жестких пластинок. Затем определяются поправки к решению этого уравнения, связанные с нелинейностью задачи. Повидимому, этот метод должен сходиться при достаточно малых отклонениях от линейного решения; однако достоверные границы применения метода пока не определены. Конкретные выкладки в применении к осесимметричному изгибу круглой пластинки будут приведены ниже в § 43.
 Несущественные дополнения позволяют использовать данный метод и в том случае, когда q есть функция х, у.
 При отыскании методом возмущения форм равновесия пластинки, близких к критическим, он должен быть видоизменен. Пример решения такой задачи будет дан в § 27.
 Остановимся, далее, на методе последовательных приближений. На первом этапе применения этого метода уравнения 60' и 61' также приводятся к линейным уравнениям
 DVVwx q, 1.142
 1.143
 На втором этапе функции wt и Ф1 первого приближения подставляются в правую часть уравнений вида
 £vVa»2.«,, >, 1.144
 i 	V2V-<£2 —jL wv Wj. 1.145
 что также близко к 136 и 137. Вообще же уравнения 1 1-го приближения имеют вид
 § V-2V„l Lwn, ф„-ь f-, 1.146
 1 V2„1 —I Lwn, wn. 1.146'
 Отметим, что под wn и Фп здесь понимаются каждый раз полные выражения для прогиба и функции напряжений я-го приближения,

АНИЗОТРОПНЫЕ ПЛАСТИНКИ
 65
 в то время как в методе возмущений речь шла о множителях при п. Однако и здесь задача сводится к последовательному интегрированию линейных уравнений. Сходимость метода для нелинейных задач пока мало исследована.
 Отметим возможность приведения системы уравнений 60'—61' к уравнениям в конечных разностях, после чего снова может быть применен метод последовательных приближений.
 Преимущество описанных здесь методов по отношению к вариационным методам состоит в том, что они не связаны с интуитивным подбором аппроксимирующих функций. Правда, первые приближения обычно не дают существенных поправок к энергетическим решениям, выполнение же последующих приближений затруднено из-за громоздкости выкладок. Применение вычислительных машин должно облегчить получение достаточно точных результатов.
 § 12. Анизотропные пластинки
 Рассмотрим пластинки, обладающие различными упругими свойствами по разным направлениям. Это могут быть пластинки, изго-
 г
 гнг
 Фиг. 1.28. Пластинка с конструктивной анизотропией: случай часто расставленных ребер.
 товленные из анизотропного материала например, из фанеры; кроме такой «естественной анизотропии» может иметь место «конструктивная анизотропия». Допустим, что пластинка подкреплена ребрами, достаточно часто расположенными в одном направлении фиг. 1.28 или в двух взаимно перпендикулярных направлениях. С известным приближением можно считать жесткость ребер равномерно распределенной по сечению пластинки; после такого приведения подкрепленная пластинка может рассматриваться как анизотропная. Модель анизотропной пластинки оказывается также уместной в случае гофрированного листа фиг. 1.29 или листа, подкрепленного гофром фиг. 1.30.
 Фиг. 1.29. Гофрированная пластинка.

66
 ОБЩАЯ ТЕОРИЯ ГИБКИХ ПЛАСТИНОК
 Наибольшее значение для технических применений имеет случай ортотропной пластинки. Будем считать, что упругие свойства
 Фиг. 1.30. Пластинка, подкрепленная гофром.
 подобной пластинки определяются четырьмя независимыми параметрами: модулями упругости Ех и Е2 при растяжении по двум взаимно перпендикулярным главным направлениям х и у, модулем сдвига О
 и коэффициентом Пуассона фиг. 1.31. Величина отвечает поперечной деформации в направлении оси у при растяжении или сжатии вдоль оси х. Поперечная деформация по направлению оси л; при действии усилий вдоль оси у характеризуется коэффициентом 2, эта величина может быть найдена из соотношения
 1-147
 Общая теория изгиба гибкой ортоФиг. 1.31. Пластинка из ани- тропной пластинки может быть построена зотропного материала. таким же образом, как для изотропной
 пластинки; исходной плоскостью пусть будет попрежнему срединная плоскость. Все полученные в § 2 геометрические соотношения, относящиеся к деформациям срединной поверхности и кривизнам, остаются в силе. В частности, оказывается справедливым уравнение совместности деформаций 10. На случай ортотропной пластинки полностью распространяются также статические уравнения 26 — 30, в которые входят напряжения в срединной поверхности, моменты и поперечные силы. Новыми будут здесь «физические» уравнения, связывающие напряжения и деформации:

12 Отсюда
 АНИЗОТРОПНЫЕ пластйНкй
 , -ЕУ— х 1 — №2
 о _ £»
 V 1 — Н-2
 г 0Т.
 e£D I lJ2®t> Н-Лв»
 6?
 1.1480
 Напряжения изгиба в произвольном слое пластинки при этом оказываются
 Gy, и —
 Ez d2w, i dw 1 — x2 dy2 9
 Ez d2w. d2w 1 — jj1j2 dy2 ' dx2 ’
 T —20z
 d2w
 dxdy
 1.149
 Пользуясь выражениями 149, находим изгибающие и крутящий моменты:
 лл г» d2<w I Мх Dx у дх2 i2 J,
 Дуг Г» I d2w f — 2 ду 1X1 ал:2 J >
 H -2Dsd2w
 1.150
 дх ду
 Здесь под Dx и D2 понимаются изгибные жесткости по главным направлениям:
 и1— 12 п _
 Dй
 121-ра>’
 Еф>
 1.151
 '2 12 1 — 2
 Через Дс обозначена крутильная жесткость:
 As Gг8. 1.152
 Исходя из уравнения равновесия 28, находим поперечную силу Qx:
 г гл I d2w I d2w о гл д d2w Qx — Di дх дхг Нг дуъ 2£к дудхду‘ Представим это выражение в виде
 п — L d w 4- D
 “ дхГ1 дх2 rUi
 dy’
 где через Dz обозначена приведенная жесткость:
 Ds О1У2 “t” 2D,.
 Ь
 1.153

68 бЩАЯ ТЕОРИЯ ГИБКИХ ПЛАСТИНОк гл. 1
 Отметим, что в силу соотношения 147 должно быть
 D1 '<2 —D2'lV
 так что выражение 153 можно переписать следующим образом:
 Z>, yZV2 D2XiH-4Dk. 1.154
 Поперечную силу Qy находим равной
 п д n d2w. n d2w ч
 v ду 6 дх2 2 ду2 Пользуясь уравнением равновесия 30, получим:
 _
 и дх4 —
 V д2 дду °У ду2 q'
 Уравнение совместности деформаций 10 приобретает с учетом формул 148 вид
 1 д2ах 1_ d2z 2_ д2°у Н д2зх, 1 d2<jy
 Еt ду2 G дх ду Е2 'ду2 Е Ш ' 'дх2'
 d2w 2 d2w d2w, ч
 дх ду дх2 ду2 'е'
 Уравнения равновесия 26 и 27 будут удовлетворены, как и в случае изотропной пластинки, при введении функции напряжений Ф по формулам 56. Вводя функцию Ф в уравнения d и е, получим :
 £>i d4w j 0 D, d4w j D2 d4w 7TaJ ' h дх2ду2 h ду4 “
 д2Ф d2w д2Ф d2w. д2Ф d2w
 ду2 дх2 дх ду дх ду ‘ дх2 ду2 ’ '
 j4 д4Ф, 0 дФ, дФ d2w 2 d2w д 1 1
 62 'Ш“ 3 дх2 ду2 1 ду4 — V дх ду — д ду2 ' у1'100’
 Здесь приняты обозначения:
 <1Л57> В уравнениях 155 — 156 получили обобщение уравнения 60 — 61, относившиеся к изотропной пластинке. Заметим, что в случае изотропной пластинки будет D2 Ог D, где D — цилиндрическая жесткость, и 8Х 82 1Я.
 Уравнения 155 —156 были получены Г. Г. Ростовцевым 314.

§ 13
 ТРЕХСЛОЙНЫЕ ПЛАСТИНКИ
 69
 При рассмотрении пластинок, подкрепленных ребрами в направлении оси х фиг. 1.28, жесткости вычисляются по формулам
 D,
 Ehз
 El
 Do —
 Eh
 3 “ 12 1 — 2 ’
 1.158
 1.159
 здесь —момент инерции сечения ребра относительно оси, проходящей через центр тяжести сечения, — расстояние между ребрами.
 § 13. Трехслойные пластинки
 Обратимся к пластинкам, составленным из трех слоев: двух одинаковых тонких наружных слоев из материала с высокими механическими характеристиками и склеенного с ними легкого промежуточного слоя заполнителя. Такие пластинки находят все большее распространение в различных конструкциях и особенно в самолетостроении, так как оказываются значительно легче однослойных пластинок,
 имеющих ту же изгибную жесткость.
 Примем, что толщина каждого из наружных слоев t мала по сравнению с общей толщиной пластинки h, условно измеряемой между срединными плоскостями
 этих слоев фиг. 1.32. Будем считать, что крайние слои передают нормальные и касательные усилия в своей
 Фиг. 1.32. Трехслойная пластинка.
 плоскости, причем эти усилия равномерно распределены по их толщине, а средний слой работает только на сдвиг.
 Введем обозначения ив, vB и wB для перемещений точек верхнего слоя, ян, Vя и w™ — для перемещений нижнего слоя. Считая, что средний слой несжимаем, примем wB w™ w. Деформации срединной поверхности верхнего и нижнего слоев будут равны при
 Слоистые пластинки можно сопоставить с балкой двутаврового сечения, имеющей высокую тонкую стенку.
 Для двутавровых балок это равносильно пренебрежению собственным моментом инерции полок по отношению к общему моменту инерции сечения.

70
 ОБЩАЯ ТЕОРИЯ ГИБКИХ ПЛАСТИНОК
 ГЛ. I
 больших прогибах индекс «н», относящийся к нижнему слою, дан в скобках
 вв н.
 дав‘н
 дх
 1 I dw 2 дх ’
 в н dvB н, I dw 2
 гУ — ду т 2 V ду ’
 тВы.вн,,»<■>
 ' ду дх '
 Соответствующие им напряжения будут равны
 Е
 1.160
 0В Н 5
 0В Н : У
 тВ н
 1 —
 Е
 е5иК,н.
 » н •
 1.161
 2i rt
 через Е и jx здесь обозначены модуль упругости и коэффициент Пуассона материала крайних слоев.
 Определим полные напряжения в срединной плоскости трехслойной пластинки, обозначаемые через ож, ау, т. Так как по условию средний слой не воспринимает нормальных усилий в своей плоскости, будем иметь:
 ав 4- ан ав с хв 4- тн
 UX I UX у ' у I
 х 2 ’ у
 Вводя, кроме того, обозначения:
 ив ич
 получим:
 X ■
 1.162
 1.163
 1.164
 Е Г ди. dv. 1 dw2, >dwa
 2lyjJ’
 Е Г dv. ди. I dw у, jj. 31
 0vrlyPdZ2Ydy 2dJF'
 Е I ди. dv. dw dw
 T 21 -f- x dT ' dx dx dy Изгибающие моменты для сечений пластинки в целом, образуемые усилиями в наружных слоях, будут равны
 1.165

§ 13 ТРЕХСЛОЙНЫЕ ПЛАСТИНКИ 71
 Подставляя сюда выражения 161 и пользуясь обозначениями
 « <1Л66
 найдем:
 1.167
 Через D здесь обозначена цилиндрическая жесткость трехслойной пластинки
 1.168
 Так как средний слой передает только сдвигающие напряжения, постоянные по толщине слоя, то прямая линия, нормальная до деформации к срединной плоскости, получит перекос, оставаясь при этом прямой. Для перемещений и° и v° некоторой точки, находящейся на расстоянии z от срединной плоскости, будем иметь:
 мв ан и-и, и —-5 Т—г «4-«г,
 2 h 1.169
 VG — J
 Деформации сдвига в любой точке среднего слоя будут равны по аналогии с выражением 3
 ди
 dw
 — ИГ -7ГГ дг
 dv°
 дх
 dw
 dw dx’
 1.170
 они будут связаны с касательными напряжениями в среднем слое т°,
 соотношениями
 Т° G Y°,
 : О YC, 32
 1.171
 где через G3 обозначен модуль упругости материала заполнителя на сдвиг.
 Поперечные силы в сечениях среднего слоя, а вместе с тем и пластинки в целом выразятся следующим образом:
 Qx — О °зЛ 4-, Qy vh G3h p •
 1.172

72 ОБЩАЯ ТЕОРИЯ ГИБКИХ ПЛАСТИНОК ГЛ. 1
 Введем функцию перемещений F, связанную с разностями перемещений наружных слоев соотношением
 <u73>
 Тогда из уравнений 172 получим:
 Составим далее уравнения равновесия элемента пластинки, составленной из трех слоев. Уравнения равновесия в плоскости ху будут иметь вид, аналогичный 26—27. Эти уравнения будут автоматически удовлетворяться, если ввести функцию напряжений
 дФ дШ дФ л 17,,
 ао>— ду> ау дл:2 ’ х—' дхду' 1.170
 Уравнения моментов напишутся аналогично уравнениям 28—29 Пользуясь выражениями 165 для Мх, Му и, можем записать:
 Qx DV2a, Qy DY23. 1.176
 Наконец, уравнение равновесия в проекциях на нормаль к деформированной срединной поверхности будет иметь вид 30; надо лишь заменить h на суммарную толщину наружных слоев 21. Подставляя в уравнение 30 значения поперечных сил 176, найдем:
 да, д л 0, dw. d2w. 0 d2w,л 177Ч
 DV4- --24°-лР'°2х7 1Л77
 или
 D 1 д'-Ф d2w д2Ф d'w, 0 д2Ф d2w
 2t 2tq Jy дх ду' дхду дхду ’
 Из уравнения 174 и выражений 176 можно, далее, получить
 уравнение сопряжения слоев:
 F — vaw-V37. 1.179
 Кроме того, сопоставляя выражения 160, 161 и 175,, выпишем обычное уравнение совместности деформаций 61:
 <1Л80>
 Мы получили, таким образом, систему трех дифференциальных уравнений относительно функций w, Ф и F. При бесконечно большой жесткости среднего слоя на сдвиг G3 -> оо окажется
 F — T-w, 1.181

§ 13
 ТРЕХСЛОЙНЫЕ ПЛАСТИНКИ
 73
 после чего уравнение 178 перейдет в уравнение типа 60 для
 однослойной пластинки, но с иным значением D.
 Уравнения 178 и 179 легко привести к одному уравнению,
 исключив функцию F. Тогда придем к уравнению
 оператор V2 здесь должен быть применен к выражению, стоящему в скобках.
 Пользуясь оператором L 62, представим полученные уравнения в виде при q const:
 при G0-> оо они переходят в 60' и 61'.
 При более общих предположениях, если считать, что средний слой воспринимает не только сдвигающие, но и нормальные напряжения и что толщина крайних слоев сравнима с толщиной среднего слоя, можно также получить три дифференциальных уравнения относительно функций w, Ф и F более сложной структуры.
 1.182
 1.184
 1.183
 Уравнения 180 и 182 были получены Э. Рейсснером 123.

ГЛАВА II
 БОЛЬШИЕ ПРОГИБЫ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК ПРИ ПОПЕРЕЧНОЙ НАГРУЗКЕ
 § 14. Удлиненная пластинка, шарнирно опертая по контуру; приближенное решение задачи
 Рассмотрим большие прогибы прямоугольной пластинки, находящейся под действием равномерно распределенной поперечной нагрузки, при условии, что один из размеров пластинки значительно превышает
 второй: а>Ь фиг. 2.1. Не будем интересоваться участками пластинки, прилегающими к коротким краям, и примем, что на остальной длине пластинка изгибается по цилиндрической поверхности. Тогда достаточно исследовать изгиб балки-полоски, длина которой равна Ъ, а ширина — единице. Решение такой задачи облегчается тем, что от общих уравнений теории пластинок, содержащих частные производные, здесь можно перейти к обыкновенным дифференциальным уравнениям.
 Будем считать, что длинные края пластинки закреплены шарнирно и что
 взаимное смещение их затруднено благодаря наличию упругих стержней ребер, обладающих одинаковой жесткостью и расставленных параллельно короткой стороне через равные промежутки с, как показано на фиг. 2.1. Условимся, что стержни работают только на сжатие, создавая распорные усилия, но не препятствуя непосредственно изгибу пластинки. Если площадь сечения каждого ребра равна Ft то на выделенную нами балку-полоску будет приходиться площадь F — Fjc.
 Фиг. 2.1. Удлиненная пластинка с подкрепляющими ребрами, параллельными короткой стороне.

§ 14 УДЛИНЕННАЯ ПЛАСТИНКА, ШАРНИРНО ОПЕРТАЯ ПО КОНТУРУ 75
 Начнем с приближенного решения задачи по методу Бубнова — Галеркина. Условия шарнирного опирания будут удовлетворены, если изогнутую линию балки представить с помощью уравнения
 w fsin-,
 2.1
 здесь —стрела прогиба.
 Воспользуемся схемой решения задачи, намеченной в § 10. Уравнение совместности деформаций 1.61 в нашем случае выпадает, так как прогибы зависят лишь от у.
 Напряжения в срединной поверхности оу, вызванные реактивными
 силами со стороны подкрепляющих
 стержней, в § 14—18 будем обозначать а без индекса. Они будут постоянными по всей длине балкиполоски. В этом можно убедиться, рассматривая условия равновесия элемента балки фиг. 2.2. При прогибах, малых по отношению к пролету b, усилия oh, действующие по концам элемента, должны быть равны между собой; проекция
 силы qdy на направление касательной к изогнутой линии прини¬
 мается равной нулю.
 В данном случае уравнение типа 1.124 примет вид
 ъ
 Фиг. 2.2. Усилия в срединной поверхности удлиненной пластинки.
 J X sin j-dy 0,
 2.2
 где под X следует понимать выражение
 Х D
 dw
 • ho
 dw
 2.3
 dy4 dy
 Подставляя взамен w выражение 1 и производя интегрирование, приходим к уравнению
 г> 7:4 Ь г,, к b г 2b п
 D 2 На м т— — Я °,
 № 2
 или
 D-£rf--ho-fq.
 2.4
 2.5
 Далее следует составить уравнение совместности деформаций балкиполоски и соединяющего опоры стержня. Определим взаимное смещение опор, вызванное деформацией балки-полоски. Исходя из уравнения 1.8, находим заменяя частные производные на полные:
 dv 1 dw 2

76 БОЛЬШИЕ ПРОГИБЫ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК гл. II
 Принимая во внимание соотношение 1.35, будем иметь:
 — и-2— >х- 2-6'
 Но рассматриваемая балка-полоска составляет.часть весьма длинной в направлении оси х пластинки. Поэтому деформацию в этом направлении можно считать равной нулю: гх 0. Полное взаимное смещение опор А будет равно величину эту считаем положительной при сближении опор
 2J
 о о
 С другой стороны, величина А определяется как укорочение подкрепляющего ребра
 А — — b, 2.8
 Ер
 где через ар обозначено сжимающее напряжение в ребре, а через Ер — модуль упругости материала ребра. Множитель 1—jx2 введен здесь потому, что самый стержень обычно является тонкостенным профилем. В дальнейшем мы будем считать, что стержень и пластинка изготовлены из одного и того же материала и примем Е Ер. Тогда, сравнивая найденные значения А, получим:
 а а.
 о
 £ 2.9
 О
 Из условия равновесия подвижного края находим:
 oh OpF ед. 2.10
 Таким образом, для напряжения в срединной поверхности будем
 иметь выражение
 ь
 Е 1 1 0 114
 1_ц2 lv 26 Jirfy -У’ о
 или с учетом выражения 1
 ' 2Л2
 через v здесь обозначено отношение

§ 14 УДЛИНЕНИЕ ЙЛАСТЙЙКА, ШРНЙРНО ОПЁРТАЯ ПО КОНТУРУ 77
 Величина v равна нулю, если обе опоры балки-полоски соответствующие длинным сторонам исходной пластинки являются неподвижными; в этом случае следует положить 7ед оо; напротив, при отсутствии стеснения свободно сближающихся длинных сторонах пластинки получим v oo. Рассматривая общий случай, подставим выражение 12 в уравнение 5, получим:
 £161-WtT-t3Dwf<- 2-14
 Вводя выражение для D, будем иметь:
 Кубическое уравнение 15 связывает стрелу прогиба пластинки с интенсивностью нагрузки. Воспользуемся безразмерными параметрами
 'f <2Л6>
 причем под Et будем понимать величину
 £1Г- 2-17
 Вычисляя коэффициенты уравнения 15, приведем его к виду
 19.14 _»_С»--6,38С. 2.18
 Для пластинки, длинные края которой неподвижны 0, получим уравнение
 19,14С3 6,38£ q. 2.19
 Рассмотрим отдельные частные случаи.
 1. Жесткая пластинка. Если прогибы пластинки малы по сравнению с ее толщиной, в уравнении 16 можно пренебречь членом, содержащим С3. Тогда получим:
 2.20
 Это линейное соотношение оказывается не зависящим от степени подвижности опор. Его можно сопоставить с известной формулой для стрелы прогиба, получаемой в обычной теории изгиба балок:
 f-шНт- <2-21>
 Если заменить Е на Ех и положить 1 - Л312, то найдем:
 C i-9. 2-22
 Отклонение величины 20 от 22 не превышает 1°0.

78
 БОЛЬШИЕ ЙРОГЙБЫ ПРЯМОУГОЛЬНЫХ ПЛАСТЙЙОК ГЛ. И
 2. Абсолютно гибкая пластинка мембрана. Считая пластинку абсолютно гибкой, мы пренебрегаем ее изгибной жесткостью. Тогда в уравнении 14 следует принять £ 0. Полагая также v 0, получим: С -у<щ- « 0,37 frq. 2.23
 Таким образом, для мембраны, которая в случае балки-полоски переходит в гибкую нить, стрела прогиба оказывается пропорциональной кубическому корню из интенсивности нагрузки.
 Возвращаясь к общему случаю гибкой пластинки, отметим, что в левой части уравнения 15 второй член определяет интенсивность нагрузки, уравновешиваемой за счет усилий изгиба, а первый — за счет усилий в срединной поверхности. Удельный вес каждого из этих членов меняется в зависимости от прогиба и от степени подвижности опор коэффициента v. Отношение первого члена ко второму составляет 3А’31 v. Следовательно, пренебрегая при расчете жестких пластинок усилиями в срединной поверхности, мы совершаем ошибку, пропорциональную квадрату стрелы прогиба к толщине пластинки. Поэтому при классификации пластинок естественно в качестве критерия выбрать отношение А С.
 Обратимся к определению напряжений, возникающих при изгибе
 пластинки. Для определения напряжений в срединной поверхности
 может служить выражение 12:
 а-2,4ТЕ1Т-2. 2.24
 Пользуясь обозначением
 <2-25>
 найдем:
 о 2,47-г4—С2. 2.26
 1 V
 Напряжения собственно изгиба аи индекс у отбрасываем будут равны по формуле 1.42
 и dw — — dy2.
 Наибольшие напряжения по толщине пластинки будут при z А2
 2-27
 Подставляя выражение 1, найдем, что наибольшее значение напряжения изгиба получат посредине пролета при у — Ь2:
 о 	4.945. 2.28

§ 15j ШАРНИРНО ОПЕРТАЯ ПЛАСТИНКА; ТОЧНОЕ РЕШЕНИЕ 79
 Вводя безразмерный параметр
 °Hir7r’ 2,29
 получим:
 ои 4,94£. 2.30
 Сопоставим это приближенное выражение с формулой, известной
 из теории изгиба балок:
 qb2 6 3 оо1
 °и V Л2 ’ ИЛИ °и4- 2-31
 Учитывая выражение 21 для стрелы прогиба, получим:
 аи 4,8£,
 что отличается от 30 примерно на 3.
 Отметим, что отношение напряжений в срединной поверхности к максимальному напряжению изгиба равно
 4 2.32
 Си 2 1 V
 и, 	следовательно, возрастает пропорционально относительной стреле прогиба С.
 Мы выделили балку-полоску из удлиненной пластинки. В последней наряду с напряжениями оу с возникают напряжения сх вдоль образующей изогнутой цилиндрической поверхности. Принимая во внимание условие гх 0, получим: Расчет гибкой пластинки
 на прочность следует вести по главным напряжениям:
 а1 о, а2 ха, о3 0. 2.33
 § 15. Шарнирно опертая пластинка; точное решение
 Задача об изгибе удлиненной пластинки по цилиндрической поверхности может быть в пределах принятых допущений решена точно. Приведем это решение, полученное впервые И. Г. Бубновым 1Л. Попрежнему будем рассматривать выделенную из пластинки балкуполоску.
 Обратимся к дифференциальному.уравнению
 DJt haw q- 2-34
 Принимая во внимание, что напряжения о постоянны для всей площади полоски, перепишем уравнение 34 в виде
 d4w 1 q d2w q о о

80 БОЛЬШИЕ ПРОГИБЫ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК гл. 11
 где обозначено
 12г- <2-36>
 Соответствующее характеристическое уравнение будет
 s — 2 0;
 корни его равны s1>2 0; sd, 4 ±.
 Общее решение однородного уравнения получит форму
 wt A sh y-- Boh ky--Cy--L.
 Присоединяя к этому выражению частное решение
 W0
 ду _ ду'
 >2
 2 “ 2Dh — Ш ’ окончательно находим:
 w — Asy--Bch у --Cy-- L —. 2.37
 Постоянные интегрирования определим, пользуясь граничными условиями. Для шарнирно опертых краев имеем:
 w — 0 при у 0, Ъ
 сШо л л,
 а 0 при 3' 0,
 Подставляя решение 37, приходим к следующим четырем уравнениям:
 £ L 0,
 ДвИХаДсИ C6--Z.— -£ 0, BA9--£- 0,
 h<s
 2
 Отсюда находим
 ЛХ2 sh Aft ВХ2 ch м — 0.
 4 п л Rh-
 С”ТГВ’ А -В1ЬТ, L В.
 После некоторых преобразований получаем следующее выражение для прогиба:
 Ь

2.41
 § 15 ШАРНИРНО ОПЕРТАЯ ПЛАСТИНКА; ТОЧНОЕ РЕШЕНИЕ 81
 Повторяя вывод соотношения 11, находим напряжение равным
 <2-39
 О
 Подставим под знак интеграла выражение
 £.8,ХтУ, £ П _ 2 40
 dy hak.lb ТЛз2 У'
 с 2
 При интегрировании можно использовать подстановку b2 — y z. Принимая во внимание зависимости
 §zshkzdz± kz ch kz — sh kz,
 J sh2 kzdz c£ sh kz ch kz — kz,.
 получим:
 thkb
 e 2 42
 1 v tiKW 24 4 2M 4l 2 K'
 Введем безразмерный параметр
 Иу. 2.43
 Исходя из выражений 36 и 25, находим также
 « 2.43'
 Пользуясь, кроме того, обозначениями 16, приходим к соотно¬
 шению
 2-44
 О ■- Ш ‘ —1 • 2-«
 Допустим, что опоры являются несмещающимися, так что v 0;
 тогда можно записать:
 '«•“КуУ- 2-46
 Стрела прогиба определится по выражению 38:
 _„Л х - Я I 1 l I О ЛТ

82
 БОЛЬШИЕ ПРОГИБЫ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК
 гл. II
 Пользуясь соотношениями 40, 41 и 16, находим безразмерный параметр стрелы прогиба равным
 <2-48>
 где под понимается функция
 Ь®-Мап;-1- <2-49>
 Напряжение в срединной поверхности определится по 43':
 « • 2.50
 Максимальное напряжение изгиба определится из выражения 27. Находим:
 ©..•—0-гв- 2-5,
 ch-
 Безразмерная величина 29 будет равна
 °Н ??• 2-52
 где
 <2-53>
 Сопоставление полученных формул с уравнениями 22 и 31 показывает, что коэффициенты и срх представляют собой отношения между стрелами прогиба и напряжениями изгиба для гибкой и жесткой пластинок, имеющих одни и те же размеры.
 Величины lgq, и cpt были табулированы И. Г. Бубновым для значений и, лежащих в пределах от 0 до 12. Ниже в таблице I эти данные приводятся в расширенном виде с изменением и от О до 20. Помещенные в таблице I разности между соседними значениями gq могут служить для интерполирования стр. 89.
 Допустим, что заданы размеры пластинки, интенсивность нагрузки и величины Еу х; тогда по формуле 16 находим <7, а из таблицы I определяем соответствующее значение и. При v Ф 0 следует вместо q подставлять величину qV 1 -f- v. Зная и, можно найти стрелу прогиба и расчетные напряжения.
 В случае абсолютно гибкой пластинки величины инк сравнительно велики. Тогда в выражении 38 можно пренебречь первым членом; будем иметь:
 w 4£b—y. 2.54
 В таблице И. Г. Бубнова см. -1, стр. 250 приведены значения не lg q a lg УЩ

§ 15 ШАРНИРНО ОПЕРТАЯ ПЛАСТИНКА; ТОЧНОЕ РЕШЕНИЕ
 83
 Мы получили известное уравнение упругой линии гибкой нити для случая, когда прогибы малы по сравнению с длиной нити. Стрела прогиба определится из выражения
 С-£. 2.55
 При достаточно большом и соотношение 44 переходит в следующее при v 0:
 ±2 _9_
 qJ 8 и
 2.56
 Но тогда для о получаем выражение
 2-57
 Пользуясь 55, получим:
 C J f 247 « 0,36 2.58
 Эту формулу можно сопоставить с полученной ранее приближенной зависимостью 23. При и > 20 для практических расчетов гибких пластинок можно пользоваться соотношениями 57 и 58.
 На фиг. 2.3 представлена зависимость между нагрузкой, напряжением в срединной поверхности и прогибом для общего случая гибкой пластинки с неподвижными краями v 0; шкала по оси ординат логарифмическая. Сплошные кривые относятся к точному решению настоящего параграфа и построены по формулам 46 и 50, а пунктирные — к приближенному решению § 14. Как видим, при С < 2,5 приближенные зависимости практически совпадают с точными, а при 2,5 <С< Ю мало отличаются друг от друга.
 На графике фиг. 2.4 нанесены значения наибольших напряжений изгиба. При С 4 расхождение между точным и приближенным решениями составляет: по стреле прогиба 2,5, по напряжению в срединной поверхности 1,2, по напряжению изгиба 18. Сравнительно хороший результат, полученный уже в первом приближении— при варьировании только одного параметра, объясняется тем, что полуволна синусоиды 1 хорошо отображает изогнутую линию балки-полоски не только при малых прогибах, но и при больших, когда балка переходит в гибкую нить: это можно видеть из сравнения уравнений 1 и 54. Сопоставление зависимостей 26 и 50 показывает, что параметр и приблизительно пропорционален стреле прогиба.
 В заключение приведем численный пример на определение стрелы прогиба и напряжений для гибкой пластинки.

84 БОЛЬШИЕ ПРОГИБЫ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК гл. II
 Допустим, что толщина пластинки составляет h 1 мм, а сторона Ъ 100 мм; нагрузка q — 0,5 кгсм2. Размеры подкрепляющих ребер пусть будут такими, что коэффициент v 0,2. Примем Е 0,75 • 10е кгсм и х 0,316.
 Фиг. 2.3. Зависимость между нагрузкой, напряжениями в срединной поверхности и прогибом для удлиненной пластинки.
 Находим:
 W161»-60-
 Логарифм величины <fl yl-f-v равен
 Ig 1 гЛ lg 1,778 — - • 0,079 1,739.
 KVlv Y 1,2 2

§ 15 шарнирно опертая пластинка; ТОЧНОЕ РЕШЕНИЕ 85
 По таблице I стр. 89 находим с помощью линейного интерполирования И 3,5 0,5 • 1,7390в’689 3,660.
 Соответствующие значения и будут 0,155, <рх 0,142 они также
 Фиг. 2.4. Напряжения изгиба для удлиненной пластинки, найдены интерполированием. Отсюда, по формуле 48
 С <7Ж 4-6°-0-,55 145-
 Стрела прогиба равна СЛ 0,145 см. Далее по уравнению 50
 3 3 ’
 Напряжение в срединной поверхности будет
 Е ла лт 0,75-10» IV».,
 1—нД 4’47, о,9 доо “ «гсм.
 Исходя из формулы 52, имеем:
 °и 4 441 - • 60 • °-142 6-38-
 По графику фиг. 2.4 мы получили бы иную величину С 1,33, относящуюся к случаю v 0. •

86 БОЛЬШИЕ ПРОГИБЫ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК гл. II
 Наибольшее напряжение изгиба
 Е h2 с 00 0,75-106 1 2 аи аи 1 _ р.2 ь ’ 0,9' 100 кгсм ‘
 Наибольшее суммарное напряжение составляет ап 903 кгсм2.
 Сопоставим эти результаты с приближенным решением § 14. Кубическое уравнение 18 принимает вид
 19 14
 -утр С3 6,38С 60.
 Приводя это уравнение к виду
 С 3?С — 2г 0,
 находим 7 0,133, г 1,884. Дискриминант уравнения будет положительным: р3 42>0, так что уравнение имеет один вещественный корень. Для отыскания корня используем решение, содержащее гиперболические функции. Находим величину для которой
 sh <f —Г- ’884 — 38,7.
 pYp 0,1330,133
 По таблице гиперболических функций 4,35. Далее определяем sh ?3 2,014. Параметр стрелы прогиба С равен
 £ 2 YP sh -- 2 УОДЗЗ • 2,014 1,47.
 О
 Далее, по формулам 26 и,30 находим параметры напряжений:
 с 2,47 -4— i2 2,47 • Д: • 1,472 4,44;
 1v 1,2
 а 4,94; 4,94 • 1,47 7,26.
 Заметное отклонение от точного решения получено лишь в величине о.
 В практических расчетах удобнее вместо того, чтобы для каждого q определять С из кубического уравнения- 18 или 19, построить график £.
 § 16. Удлиненная пластинка, защемленная по контуру; приближенное решение
 Обратимся к случаю, когда длинные края пластинки защемлены; попрежнему будем считать, что смещению этих краев препятствуют
 соединяющие их упругие стержни фиг. 2.5. Что касается условий закрепления по коротким краям, то, по нашему предположению, они не сказываются на характере деформации пластинки.
 Фиг. 2.5. Сечение удлиненной пла- Решим сначала задачу прибли-
 стинки с защемленными краями. женно, по методу Бубнова — Га-
 леркина. Граничные условия будут удовлетворены, если выбрать приближенное выражение для прогиба
 В ВИДе 1,2 t»2 «->£ '-£• <2-59>
 » j J i
 < b >■
 'z

§ 16 УДЛИНЕННАЯ ПЛАСТИНКА, ЗАЩЕМЛЕННАЯ ПО КОНТУРУ 87
 По такой именно форме изгибается жесткая балка-полоска, защемленная на опорах.
 Функция X по выражению 3 будет
 D — ай -L 0 _ 6уЬ 6у, - д. 2.60
 Вариационное уравнение
 ХтХ-таУ- 2-61
 о
 принимает форму
 °3-1т fwhofq- <2-62
 Подставляя производную от выражения 59 в формулу 11, найдем:
 Е 1 256 а
 ° — 1— х 1v 105 Ь‘ 2.63
 Уравнение 62 в безразмерных параметрах получит вид
 22,4С332;. 2.64
 Из 63 имеем:
 о 2,43 С2, 2.65
 что мало отличается от выражения 26, полученного для шарнирно опертых краев.
 Напряжения изгиба определим по 27. У краев для верхних волокон
 v Exh dP-w Ehf п
 °h»o— 2 dyyo 1— ца «з > 2.66
 по средней линии, для нижних волокон
 у d2w q Е hf 0 7Ч
 <Ч-4-т-Ы,.8 <2-67>
 Отсюда
 з:,о16 ю,-8С- 2-68
 J 2
 Примем теперь иное исходное выражение для прогиба:
 w sin2-. 2.69
 Идя тем же путем, мы получили бы уравнение 64 в виде 24,3-рр-С3 32,7С 7,

88 БОЛЬШИЕ ПРОГИБЫ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК гл. II
 Напряжение в срединном слое будет определяться из выражения
 о 	2,47 т±7 С2. 2.70
 Напряжения изгиба окажутся по краям и в центре одинаковыми:
 °и 9,87С. 2.71
 Различие по сравнению с первым вариантом оказывается суще¬
 ственным только по отношению к о.
 § 17. Случай защемленных краев; точное решение
 Точное решение задачи об изгибе удлиненной пластинки с защемленными краями найдем, исходя из общего уравнения изогнутой поверхности 37:
 w A sh y-- Bchy-Cy--L— 2.72
 Для граничных условий
 w Q при у 0, by
 dw п,
 — 0 при _у 0, Ь
 получим постоянные интегрирования:
 А — 2Ш> B —Acth-T> С — АХ, L — В.
 Выражение 72 получает вид
 qb
 w —
 2hal th 'Щ-
 ch
 Ы_,
 chx
 Определим о по формуле 39. Имеем:
 dw qb
 dy 2hoX, 1 ho
 Sli72
 Используя формулы 41, найдем:
 Ei g I 1,1
 i-4

§ 17
 СЛУЧАЙ ЗАЩЕМЛЕННЫХ КРАЕВ; ТОЧНОЕ РЕШЕНИЕ
 89
 Таблица I
 Вспомогательные функции для расчета удлиненных пластинок
 Нагрузка
 шарнирн.
 края
 1 gq
 защемлен, края 1 gq
 Стрела прогиба
 шарнирн.
 края
 <Vi
 зашемл.
 края
 Ф.
 Напряжения
 посре¬
 посре¬
 дине;
 дине;
 у зашемл.
 шарн.
 защемл.
 краев
 края
 края
 X
 Vi
 1,000
 1,000
 1,000
 0,905
 0,972
 0,984
 0,704
 0,894
 0,939
 0,511
 0,788
 0,876
 0,367
 0,673
 0.806
 0,268
 0,563
 0,736
 0,200
 0,467
 0,672
 0,153
 0,386
 0,614
 0,120
 0,320
 0,563
 0,097
 0,267
 0,519
 0,079
 0,224
 0,480
 0,066
 0,189
 0,446
 0,055
 0,162
 0,417
 0,047
 0,139
 0,391
 0,041
 0,121
 0,367
 0,036
 0,106
 0,347
 0,031
 0,093
 0,328
 0,028
 0,083
 0,311
 0,025
 0,074
 0,296
 0,022
 0,066
 0,283
 0,0200
 0,0599
 0,270
 0,0166
 0,0496
 0,248
 0,0139
 0,0417
 0,229
 0,0118
 0,0355
 0,213
 0,0102
 0,0306
 0,199
 0,00889
 0,0267
 0,187
 0,00781
 0,0235
 0,176
 0,00692
 0,0208
 0,166
 0,00617
 0,0185
 0,158
 0,00554
 0,0166
 0,150
 0,00500
 0,0150
 0,142
 0
 — оо
 0,5
 0,111
 1,0
 0,517
 1,5
 0,827
 2,0
 1,089
 2,5
 1,316
 3,0
 1,514
 3,5
 1,689
 4,0
 1,845
 4,5
 1,986
 5,0
 2,114
 5,5
 2,232
 6,0
 2,340
 6,5
 2,440
 7,0
 2,533
 7,5
 2,620
 8,0
 2,702
 8,5
 2,779
 9,0
 2,852
 9,5
 2,921
 10
 2,986
 11
 3,108
 12
 3,220
 13
 3,323
 14
 3,419
 15
 3,509
 16
 3,592
 17
 3,670
 18
 3,744
 19
 3,814
 20
 3,881
 Вводя
 параи
 406
 310
 262
 227
 198
 175
 156
 141
 128
 118
 108
 100
 93
 87
 82
 77
 73
 69 65
 122
 119
 103
 96
 90
 83
 78
 74
 70 67
 ОО
 0,783
 1,114
 1,337
 1,519
 1,680
 1,826
 1,960
 2,084
 2,199
 2,306
 2,406
 2,499
 2,587
 2,669
 2,747
 2,821
 2,891
 2,958
 3,021
 3,082
 3,195
 3,300
 3,397
 3,487
 3,572
 3,652
 3,727
 3,798
 3,865
 3,928
 331
 223
 182
 161
 146
 134
 124
 115
 107
 100
 93
 83
 82
 78
 74
 70 67 63 61
 113
 105
 97
 90
 85
 80
 75
 71 67 63
 1,000
 0,908
 0,711
 0,532
 0,380
 0,281
 0,213
 0,166
 0,132
 0,107
 0,088
 0,074
 0,063
 0,054
 0,047
 0,041
 0,036
 0,032
 0,029
 0,026
 0,0235
 0,0195
 0,0164
 0,0140
 0,0121
 0,0106
 0,00930
 0,00825
 0,00736
 0,00661
 0,00597
 1,000
 0,976
 0,909
 0,817
 0,715
 0,617
 0,529
 0,453
 0,388
 0,335
 0,291
 0,254
 0,223
 0,197
 0,175
 0,156
 0,141
 0,127
 0,115
 0,105
 0,0960
 0,0811
 0,0694
 0,0601
 0,0525
 0,0462
 0,0410
 0,0366
 0,0329
 0,0297
 0,0270
 Вводя параметр и 43, приходим к соотношению
 где
 _ _9.,6 3 9 га 8в« ' и2 2shaa 2uthu'
 При v 0 будем иметь:
 2.74
 2.75

90
 БОЛЬШИЕ ПРОГИБЫ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК
 ГЛ. II
 Стрела прогиба оказывается равной
 у j 2Хаг th -g- ch 2
 Безразмерная величина С fjh будет
 32
 где
 Щ‘жгстг-'- 2'78
 Напряжения в срединной поверхности будут попрежнему определяться равенством
 >-у. 2-79
 Далее находим:
 dw q
 dy ha
 1 _
 chxA_y
 2 u b 2
 Напряжения изгиба будут наибольшими у краев; они найдутся йз выражения для верхних волокон пластинки
 1
 где
 2-80
 -'.-тНтпг-1- <2'8’>
 Посредине пролета для нижних волокон пластинки
 <Ч-ЯЪ. 2-82
 причем
 ъ-Ц'-ш- <2-83>
 Величины lg для случая v 0, й2, ?2 и X приведены в таблице I. Последние три величины представляют собой, как и раньше, коэффициенты уменьшения стрелы прогиба и напряжений по отношению к случаю жесткой пластинки.
 На фиг. 2.3 приведены кривые qС и о С по точным зависимостям 77 и 79 и по приближенным формулам § 16 для первого
 варианта решения. В случае малых прогибов значения q сильно зависят от условий закрепления длинных краев пластинки: при защемленных краях они почти в 5 раз больше, чем при шарнирном опирании. По мере возрастания прогиба разница между пластинкой,

§ 17 СЛУЧАЙ ЗАЩЕМЛЕННЫХ КРАЕВ, ТОЧНОЕ РЕШЕНИЕ 91
 защемленной по краям и шарнирно опертой быстро сглаживается. Значения напряжений в срединной поверхности не зависят от условий закрепления краев: кривые о на фиг. 2.3 совпадают.
 Напряжения изгиба представлены на фиг. 2.4. Здесь можно отметить резкое расхождение между точным и приближенным решениями. Напряжения у краев возрастают в действительности гораздо быстрее с увеличением прогиба, а напряжения в центре — медленнее, чем по первому варианту приближенного решения. Расхождение со вторым вариантом оказывается еще более сильным. Все эти результаты легко объяснить, если проследить за изменением формы изогнутой линии балки-полоски.
 На фиг. 2.6 показана форма упругой линии для половины балки-полоски; точное решение при и —> 0 совпадает с уравнением 59 и близко к функции 69. В то же время при значительном прогибе а 30 мы получаем совершенно другую кривую, которую можно аппроксимировать выражениями
 4т1т или sin“F •
 Характерным является быстрое смещение точки перегиба упругой линии к краям, — это обстоятельство будет не раз отмечаться нами в дальнейшем. Быстрое возрастание напряжений у защемленных краев обычно приводит к развитию здесь пластических деформаций; пластинка как бы надламывается у краев и начинает работать как шарнирно закрепленная. Поэтому при и > 20 в случае защемленных краев можно пользоваться расчетными формулами 57 — 58.
 Рассмотрим тот же численный пример, что и в конце § 15, но для случая защемленных краев. На стр. 84 было найдено значение
 lg?11 v 1,739. По таблице I находим, интерполируя, и 2,702. Этому значению и соответствуют 2 0,581, х 0,711, <р2 0,524. Далее получим:
 С 1,14, о 2,43, Зд_о 21,3 а ь 7,86. Отсюда 1,14 мм,
 УТ
 7 	203 к'гсмз, аи 0 1780 кгсм,1 ся ь 655 кгсмз.
 ?У я —
 Фиг. 2.6. Изогнутая поверхность удлиненной пластинки на разных стадиях нагружения.
 Это явление было отмечено И. Г. Бубновым J1,1.

92
 БОЛЬШИЕ ПРОГИБЫ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК
 ГЛ. II
 Воспользуемся теперь приближенным решением § 16. Первый вариант 59 дает а 2,45, а 17,6, а ъ 8,8. По второму варианту 69
 У У2
 мы получили бы С 1,08, а 2,41, с£ 0 ая ъ 10,6.
 Из анализа графиков фиг. 2.4—2.5 и численного примера можно сделать тот вывод, что различные приближенные уравнения изогнутой поверхности приводят к примерно одинаковым значениям стрелы прогиба и напряжений в срединной поверхности, если только общий характер истинной поверхности отображен правильно. В то же время для определения напряжений изгиба этого недостаточно. Здесь приходится дважды дифференцировать выражение для прогиба, так что на первый план выступают местные особенности изогнутой поверхности.
 § 18. Влияние начальной погиби на деформацию удлиненной пластинки
 В реальных конструкциях тонкие пластинки всегда имеют ту или иную начальную погибь. Выясним, как влияет начальная кривизна пластинки на ее деформацию при больших прогибах.
 Будем считать края пластинки шарнирно опертыми; примем уравнение начальной поверхности пластинки в виде
 'Инч — нч sin J
 2.84
 через нч здесь обозначена начальная стрела прогиба.
 Определим изменение стрелы прогиба при возрастающей нагрузке q. Воспользуемся для этого вариационным уравнением 1.124, причем для функции X примем выражение, которое вытекает из
 1.126:
 XD
 dAw
 dx
 ho
 d3 wH w dy2
 Фиг. 2.7. Удлиненная пластинка с начальной погибью.
 Выберем приближенное выражение для дополнительного прогиба попрежнему в виде
 w f sin--; 2.85
 под теперь будет подразумеваться стрела дополнительного прогиба фиг. 2.7. Подставляя выражения 84 и 85, перепишем уравнение 1.124 в форме ъ
 J Df:wsin Xho M sin 4q
 siny- dy 0.

§ 18 ВЛИЯНИЕ НАЧАЛЬНОЙ ПОГИБИ 93
 После интегрирования получим:
 А, ?• 2-86
 Выразим, далее, напряжения в срединной поверхности через стрелу начального и дополнительного прогибов. Пользуясь выражениями 1.19 и 6, получим:
 dV 9 1 Г«®нч1, 1
 Идя тем же путем, что и в § 14, т. е., сопоставляя взаимное смещение краев пластинки и упругую деформацию подкрепляющих ребер, найдем:
 av Л Г dv —г-и-мь--Гуу.
 О
 Отсюда
 о
 Подставляя выражения для w и wa4i будем иметь:
 ‘’ гг»тттда<2- <2'88>
 Уравнение 86 приобретает вид
 Д5 Г2 трг 2-89
 Вводя безразмерные параметры
 ’яч X ’ h' 9 1гт 2-9°
 получим:
 48 1 _ хЗ 1161 — цЗ i-j-v ’ 4 ’ч’2 2'Сич q. 2.91 При jx 0,3 уравнение принимает вид
 7С—— 21 С С„,;24-2:СЯЧ. 2.92
 Мы располагаем, таким образом, кубическим уравнением, связывающим параметр дополнительного прогиба с интенсивностью нагрузки. Проведем анализ этого уравнения применительно к случаю неподвижных краев пластинки у 0. Перепишем его в виде
 21С8 63СнчС2 42СМ1 7С. 2.93

94
 БОЛЬШИЕ ПРОГИБЫ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК
 гл. И
 Характерной особенностью этого уравнения является наличие члена, содержащего квадрат С. Допустим, что начальная кривизна пластинки обращена в сторону нагрузки, так что Снч и Я имеют одинаковый знак. Получающаяся при этом зависимость между Си q представлена на фиг. 2.8; кривые соответствуют различным значениям стрелы начального прогиба СНч 0,5; 1; 1,5; 2. Как видно из графика, каждому значению интенсивности нагрузки отвечает одно, вполне определенное равновесное состояние.
 Фиг. 2.8. Диаграмма «нагрузка — прогиб» для пластинки с начальной погибью, направленной по нагрузке.
 Фиг. 2.9. Диаграмма «нагрузка — прогиб» для пластинки с начальной погибью, направленной против нагрузки.
 Перейдем к другому случаю, когда нагрузка действует в сторону, обратную начальной кривизне пластинки. Тогда значения Снч следует принимать отрицательными. На фиг. 2.9 даны кривые, выражающие зависимость между Си при некоторых значениях СнчХарактер кривых, соответствующих определенным значениям СцЧ начиная с Снч —О» здесь совершенно иной, чемв предыдущем графике. В известном диапазоне нагрузки каждой интенсивности q отвечает не одно, а три различных равновесных положения пластинки. Допустим, что нагрузка возрастает от нуля; при некотором прогибе она достигает максимума, затем снижается и после перехода через минимальное значение снова начинает возрастать. Для того чтобы установить, при каких величинах стрелы прогиба нагрузка получает экстремальные значения, приравняем нулю производную от q по С. Получим:
 gisecLo.
 Решая это уравнение, находим значения С, которым соответствуют

§ 18
 ВЛИЯНИЕ НАЧАЛЬНОЙ ПОГИБИ
 95
 максимум q знак минус перед радикалом и минимум q знак плюс:
 С,,, -5„з4ЗЗП.
 Из последних формул видно, что образование трех различных равновесных состояний, соответствующих одной и той же нагрузке, становится возможным, если стрела начального прогиба составляет
 нч>-г 0,58Л.
 Описанный выше процесс изменения нагрузки мог бы оказаться возможным, если бы он происходил бесконечно медленно, т. е. если бы фактически действующая на пластинку нагрузка увеличивалась или уменьшалась в точном соответствии с изменением несущей способности пластинки.
 Если же нагрузка меняется иначе, например непрерывно увеличивается независимо от деформации пластинки, то, очевидно, пластинка должна скачкообразно изменить направление кривизны с изменением прогиба, показанным на фиг. 2.10 стрелкой. Напротив, при последовательном уменьшении нагрузки должен совершиться скачок, показанный пунктирной стрелкой. Подобное явление скачкообразного изменения прогиба пластинки принято называть хлопкбм.
 Обозначим параметр напряжения, соответствующий наивысшей точке кривой нагрузка — прогиб, через qlt а наинизшей точке —
 через qt; эти напряжения отвечают безразмерным прогибам и С2« Как видим из графика, наличие трех равновесных состояний возможно при qt q <72 Чтобы установить характер каждого из этих состояний, исследуем изменение потенциальной энергии системы при некотором определенном значении q, лежащем в указанных пределах, если стрелу прогиба считать переменной. Потенциальную энергию изгиба, приходящуюся на единицу длины пластинки, вычисляем по формуле типа 1.109:
 ь
 IT D Г dwY,
 Un—r d?-
 о
 Мы учитываем здесь только симметричную относительно середины пролета форму изогнутой поверхности; при известной величине Снч хлопбк может произойти по несимметричной форме см. ниже § 57.
 Фиг. 2.10. Хлопки при нагружении и разгрузке пластинки с начальной погибью.

96 БОЛЬШИЕ ПРОГИБЫ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК гл. и
 Подставляя выражение 85 для w, получим:
 и a —f - » — - я.
 4 № 481 —fx2 mJ
 Энергию деформации в срединной поверхности U0, приходящуюся на единицу длины, определим по формуле
 UG -bh,
 где через е обозначено удлинение вдоль оси у. Принимая во внимание 6', имеем:
 а2
 и0 шЬН.
 •О4„м ■
 и и
 ' J qwdy q j fsin?£dy qf.
 Исходя из соотношения 88, получим при v 0 Работа внешней нагрузки будет
 ь
 W--
 о 	б
 Полная энергия системы оказывается равной
 3 Щ 1T V t,‘W.'.,-?t ■ 2.94
 дЭ
 Составляя уравнение метода Ритца - 0, мы пришли бы к кубическому уравнению 89.
 Найдем безразмерную величину энергии
 а __ о к.
 Э —Э 2 ЕЬ> ’
 будем иметь:
 Э с2 2 3 С2Сяч'Ч _ ЯХ,
 или при а 0,3
 1,75С22 3 С2Сич2 — qX. 2.95
 На фиг. 2.11 представлена зависимость между нагрузкой и прогибом для случая, когда начальная стрела прогиба нч равна удвоенной толщине пластинки Снч 2. Здесь же отложены значения безразмерной энергии Э при фиксированной интенсивности нагрузки q 30. Мы видим, что каждому из трех равновесных состояний пластинки соответствует экстремум энергии при стрелах

§ 19
 ШАРНИРНО ОПЕРТАЯ ПЛАСТИНКА
 97
 прогиба С 0,3; 1,6; 4,0. Первому из этих состояний отвечает минимум энергии, второму — максимум, третьему — снова минимум. Следовательно, первое и третье равновесные состояния являются устойчивыми, а промежуточное—- неустойчивым.
 Фиг. 2.11. Энергетические уровни для трех
 различных равновесных состояний при заданной нагрузке.
 Подобный же анализ, относящийся к нагрузкам при хлопках q2 и q показывает, что скачкообразное изменение прогиба сопровождается выделением кинетической энергии. Эта энергия переходит в тепловую во время движения пластинки к новому равновесному положению и при затухании колебаний вокруг этого положения. Таким образом, каждый цикл изменения кривизны пластинки сопровождается рассеянием энергии.
 §19. Шарнирно опертая пластинка с конечным отношением сторон; первое приближение. Метод «наложения решений»
 Перейдем к задаче, точное решение которой отсутствует: определим деформацию шарнирно опертой пластинки со сторонами, сравнимыми между собой фиг. 2.12. Допустим, что отношение
 сторон ajb лежит в пределах 1 2. Поставим условие, что

98
 БОЛЬШИЕ ПРОГИБЫ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК
 гл. II
 края пластинки остаются во время деформации прямолинейными. Сближение краев пластинки при изгибе пусть будет стеснено упругими стержнями; предположим, что на единицу длины стороны b приходится площадь сечения распорки, равная Fх, а на единицу л длины стороны а — равная
 Введем обозначения
 h
 Т,
 -£- V 2-96
 ГУ
 Граничные условия шарнирного опирания будут выполнены, если выбрать для прогиба выражение
 w sin — sin ; 2.97
 Фиг. 2.12. Пластинка с конечным отношением сторон, подкрепленная ребрами.
 через обозначается стрела прогиба.
 Выпишем уравнение совместности деформаций 1.61
 таиэф — Е Г d2w V — — —1
 V V V— С Далг?у дх2 ду2 j •
 2.98
 Подставляя вместо w выражение 97, получим:
 1 Г70Г70ЛЧ лл 7Г4 о ™ О ку • О • О
 _ vw Р ш cos- — cos--f - sm- - Sin- т,
 или
 1 г7огтол 1 и4 2пх. 27гу
 _ _ЯЖасо — COS
 Частный интеграл уравнения 98 представим в виде лч л 2тгд:, D 2тсу
 Ф Л cos h Б cos г.
 1 а 1 b
 Определяем коэффициенты А и В, вычисляя и сравнивая
 левую и правую части уравнения 98:
 Л — Е — — В — Е — —
 32 Ь2' 32 а2 Таким образом,
 . - £ ’ - Ч01 “• т •
 При аb > 2 приближенное решение настоящего параграфа становится неприемлемым; такую пластинку лучше приближенно рассчитывать как бесконечно длинную см. §§ 14 и 15.

§ 19 ШАРНИРНО ОПЕРТАЯ ПЛАСТИНКА 99
 Выпишем далее решение Ф2 однородного уравнения V2V2 О, принимая во внимание наличие стержней, стесняющих смещение сторон пластинки. Обозначим через рх и ру средние величины усилий, приходящихся на каждую из сторон пластинки со стороны краевых ребер. Тогда
 2 2 ’
 Окончательно решение уравнения 1.61 будет
 4’ ?¥¥• <••«
 Напряжения в срединной поверхности оказываются равными
 <?2Ф,,«а2 2яу. -
 cosГР> дЩ „ 2 V2 2tijc. -
 'дх 8ь C0S «
 0.
 2.100
 дхду
 Определим взаимное смещение краев у 0 и у — Ь. Для произвольного волокна, параллельного оси, найдем величину смещения сближения Ад, равной
 а а
 . С ди. 1 Г Гд2Ф Ф Е dw 21.
 х I дх Е J а 2дх ' 2Л01
 О о
 Подставим найденные нами значения w и Ф; после интегрирования будем иметь:
 2Л02
 Как видим, сближение концов всех волокон, параллельных оси х, оказывается одинаковым — не зависящим от координаты у. Таким образом, решение удовлетворяет условию прямолинейности кромок пластинки. Для взаимного смещения кромок л; 0 и х а аналогичным путем получим:
 bv TT-PjLnfb- <2Л03
 Величины Аж и Ау мы должны приравнять упругим деформациям распорок. Обозначая через aXt р и оУг р напряжения сжатия в распорках, придем к зависимостям
 Дл, 4а, Ь. 2.104

100
 БОЛЬШИЕ ПРОГИБЫ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК
 гл. II
 С другой стороны, условия равновесия узлов, в которых распорки скреплены с пластинкой, дают
 — h —
 аУ> Р Ру 7Г“ уРу •
 Таким образом, приходим к равенствам
 — тс2 А2 — —
 Рх VPy>
 — тt2 f V2 — —
 уРу Г7»’
 для ря, и получаем следующие выражения:
 0»1V„
 Р Е
 ТС?
 Ц.
 а2
 ■А
 в 1 1V-
 №
 -_РЯ IVa1Va’ „
 Ру с т l vel V-a 7“-
 Перейдем к безразмерным параметрам
 - 1 6з » -16 2 а
 а>— Л £ г ’ рурУ Eh ’ Ь‘
 тогда будем иметь:
 4
 7:2
 1Л,
 8 lXlV-
 . г-2
 С2.
 2.105
 2.106
 2.107
 2.108
 8 lHlV-l
 Составим теперь уравнение метода Бубнова — Галеркина
 а Ь
 и
 о о
 Xsin — sin dx dy 0.
 a b
 2.109
 Функцию X определяем по формуле 1.123; пользуясь выражениями 97 и 99, находим:
 Х АА4 2 г Pxhf Pyhf J2
 Etf4 if sin тsi 1 т-q-

§ 19 ШАРНИРНО ОПЕРТАЯ ПЛАСТИНКА 101
 Подставляя это выражение в 109 и производя интегрирование, придем к уравнению
 D7ii'йида?, да
 £тжр--?у°- <2110>
 После перехода к безразмерным параметрам и простых преобразований оно приобретает вид
 710 Л I YV I 714 — Т I
 1921 — J.2 Ч
 '’;¥,;sж••• <2ли>
 Подставляя величины р и ? из выражения 108, получаем:
 71®
 И, 6 А —1
 L128 1 v 1 v„ - а -г-128 1 ve 1 vy - х2 ха ■
 25б1 X 1921—2 I1 Т ’ ' 2-112
 Уравнением 112 устанавливается зависимость между стрелой прогиба и интенсивностью нагрузки. Разберем некоторые частные случаи.
 1. Жесткая пластинка. При рассмотрении малых прогибов жесткой пластинки можно пренебречь членом, содержащим С3. Тогда мы получим независимо от условий смещения краев в плоскости пластинки
 г 1921-2 1
 2.113
 Если сравнить значение коэффициента при q с уточненными решениями теории жестких пластинок, то отклонение составляет для квадратной пластинки 2,5, для пластинки с соотношением сторон А. 2 — около 4,5.
 2. Абсолютно гибкая пластинка. Пренебрегая в уравнении 112 членом, соответствующим изгибной жесткости, придем к соотношению между стрелой прогиба и интенсивностью нагрузки, отвечающему случаю абсолютно гибкой пластинки мембраны. Для квадратной мембраны, имеющей неподвижные края 0, получим:
 1 <2-114
 Б. Г. Галеркин, Прямоугольные пластинки, опертые по краям, Собрание сочинений, т. 2, изд. АН СССР, 1953, стр. 13.

102 БОЛЬШИЕ ПРОГИБЫ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК гл. II
 При а 0,3 будет
 С 0,326. 2.115
 По полученному Г. Генки 214 более точному решению для мембраны коэффициент в формуле 115 равен 0,285.
 3. Гибкая пластинка со свободно смещающимися краями. Полагая v oo, придем к уравнению
 Йб1 бС8 192<Г— I i2c 9’ 2.116
 ИЛИ при А 0,3
 3,751 -—1.с85,51 ±>д 2.117
 Для квадратной пластинки будем иметь:
 7,бС® 22С 9. 2.118
 Напряжения в срединной поверхности ау будут наибольшими по абсолютной величине у кромок х 0, а и по средней линии пластинки л: а2:
 °. ЕЩ'- <2П9>
 Напряжения изгиба равны
 Eh дЧи, дЧ> 0 10т
 аУ'я 21— а Р дх и приобретают максимальное значение для центра пластинки
 °у>н 2 1 — i2Е W О • 1-121
 Наибольшие полные напряжения находятся суммированием этих величин: агу,п ау ал и- Введем безразмерные параметры
 <2-122>
 их значения в центре пластинки будут при jx 0,3
 oj 1,23 С3, «у, и 5,42 l С. 2.123
 4. Гибкая пластинка с неподвижными краями. В этом случае надо положить чх чу 0. Тогда получим следующую зависимость между С и q:
 г 1 22хХ2--—
 3.75 l j С8--5,5 l ± С. 2.124

§ 20 УТОЧНЕНИЕ РАСЧЕТА КВАДРАТНОЙ ПЛАСТИНКИ 103
 Для квадратной пластинки будет
 28,9;822С ?. 2.125
 Наибольшие напряжения в срединной поверхности оказываются равными для центра пластинки
 а»£-тт2- <2Л26>
 Безразмерная величина при х 0,3 будет
 тг 0’3
 1,231-■§,- Jca. 2.127
 Наибольшие напряжения изгиба попрежнему определяются по 121 или 123.
 Сопоставление уравнений 118 и 125 позволяет оценить влияние различных факторов, вызывающих появление напряжений в срединной поверхности. В случае неподвижных краев коэффициент при С3 оказывается примерно в 4 раза больше, чем при свободно смещающихся краях. Из этого можно сделать вывод, что основное влияние на напряжения в срединной поверхности оказывает здесь характер закрепления краев; напряжения же, появляющиеся в результате изменения гауссовой кривизны пластинки, имеют второстепенное значение.
 А. Фепплем был предложен 116 простой метод расчета гибких пластинок, заключающийся в «наложении» решений для жесткой пластинки и абсолютно гибкой пластинки тех же размеров. Рассмотрим случай шарнирно опертой квадратной пластинки с неподвижными краями. Уточненное решение для абсолютно гибкой пластинки 214 дает <7 43,3, а для жесткой q 22,6£. Считая, что в случае гибкой пластинки при заданном прогибе внешняя нагрузка уравновешивается за счет суммарного действия усилий в срединной поверхности и напряжений изгиба, получаем:
 43Р 22,6: ?; 2.128
 по структуре получаем прежнее уравнение 125, однако коэффициенты при С3 расходятся. Таким же образом можно приближенно найти суммарные напряжения.
 § 20. Уточнение расчета квадратной шарнирно опертой пластинки. Данные опытов
 Выражение для прогиба 97, положенное нами в основу приближенного решения задачи, содержало только один неопределенный параметр. Однако уже для малых прогибов это выражение не
 См. сноску на стр. 101,

104
 БОЛЬШИЕ ПРОГИБЫ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК
 ГЛ. II
 вполне отвечает реальной форме изогнутой поверхности пластинки. С увеличением же прогиба характер изогнутой поверхности непрерывно меняется. Для получения уточненного решения следует увеличить число неопределенных параметров. Можно, например, выбрать выражение для прогиба в виде двойного тригонометрического ряда
 J. TZX. TCV - TZX 2тгу. £. 2пХ. 71 у.
 w usin — sin-- 18 sin —sin-- 2t sin — sin--j-... или в более короткой записи
 w И S 2.129
 m 1, 2,... n 1,2,...
 причем под fmn понимаются независимые неопределенные параметры.
 Каждый из членов этого ряда удовлетворяет граничным условиям шарнирного опирания. Решение задачи получается тем более точным, чем больше членов ряда 129 учитывается. Однако получение уточненных результатов сильно осложняется тем, что вместо одного
 кубического уравнения мы получим здесь систему кубических уравнений, число которых равно числу неопределенных параметров. Это приводит к весьма громоздким вычислениям; подробнее процедура решения будет освещена в § 27. Решение задачи несколько облегчается в случае квадратной пластинки, так как ввиду симметрии изогнутой поверхности число уравнений сокращается.
 Приведем данные, полученные
 С. Леви 217 для квадратной пла¬
 стинки.
 1. Квадратная пластинка со свободно смещающимися краями. Как показали вычисления, введение дополнитель¬
 ных параметров по отношению к параметру п, учитывавшемуся в § 19, вносит здесь относительно малую поправку. Наибольший по величине дополнительный коэффициент 13 31 составляет
 при q 500 около 7 от основного коэффициента и, остальные
 коэффициенты не превышают 3. На фиг. 2.13 показано сечение
 изогнутой поверхности для у Ц-. По приближенному решению 97
 прогиб в этом сечении меняется по закону
 Фиг. 2.13. Сечение изогнутой поверхности пластинки по различным вариантам решения.

§ 20 УТОЧНЕНИЕ РАСЧЕТА КВАДРАТНОЙ ПЛАСТИНКИ
 105
 По уточненному решению при q 500 прогиб составляет 3,6 К:
 ‘a,U«2 °40 sin --1-0,046 Sin iH- 0,006 sin 2.130
 Как видно из графика, кривизна изогнутой поверхности в центральной части меньше, чем это предполагалось в первом приближении. По мере возрастания нагрузки кривизна в центральной части постепенно уменьшается.
 Зависимость между стрелой прогиба и нагрузкой изображена на фиг. 2.14. По уточненному решению сплошная кривая интенсив-
 500
 Уточненное решение для прямолинейных промок —Т
 Область эхсперим. значений для искривляющихся кромок
 Фиг. 2.14. Зависимость между нагрузкой и прогибом для квадратной шарнирно опертой пластинки со свободно сближающимися краями.
 ность нагрузки получается несколько большей, чем по приближенному пунктирная кривая. Следует отметить, что оба эти решения относятся к случаю, когда кромки пластинки связаны с жесткими ребрами и остаются прямолинейными. На графике указана также область, в которой лежат экспериментальные точки для одной стальной и четырех дуралюминовых пластинок 215, 221; деформации при испытаниях оставались упругими. Найденные из опытов значения нагрузки лежат значительно ниже теоретических. Расхождение объясняется, повидимому, тем, что кромки испытывавшихся пластинок могли искривляться в плоскости опорного контура. Это подтверждается теоретическим решением Р. Кайзера 215, относящимся к случаю свободно искривляющихся кромок. По методу конечных

106
 БОЛЬШИЕ ПРОГИБЫ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК
 ГЛ. II
 разностей было получено <7 117 при С 2,5; соответствующая точка отмечена на графике кружком.
 б
 30
 20
 О
 faxJc, f
 I Уточненное решение fju0,36
 A
 faxA, C '
 r Первое 'приближение рЦ
 Фиг. 2.15. Напряжения в срединной поверхности квадратной пластинки со свободно сближающимися краями.
 На фиг. 2.15 и 2.16 даны значения напряжений в срединной поверхности и наибольших по толщине напряжений изгиба. Судя по
 формулам § 19, напряжения
 в срединной поверхности достигают наибольшей величины в центре пластинки растяжение по осям х и у и в углу сжатие в обоих направлениях, причем абсолютные значения напряжений в этих точках одинаковы. Как видно из результатов уточненного решения, напряжения в углу возрастают с увеличением стрелы прогиба несколько быстрее, чем в центре. В отношении напряжений изгиба важно отметить, что касательные напряжения ти получают значительные большие значения, чем это следует из формул § 19; в то же время нормальные напряжения в цен-
 30
 20
 о
 У,
 —  а
 7ервое
 приближение
 •
 L
 а
 L1
 kf
 J,
 jiimttj
 'is
 л
 У776
 pet
 иеше
 7
 3X4
 Фиг. 2.16. Напряжения изгиба для квадратной пластинки со свободно сближающимися краями.
 тре возрастают менее интенсивно. Сопоставление графиков на фиг. 2.15 и 2.16 показывает, что опасная зона при малых прогибах располо

§ 20
 УТОЧНЕНИЕ РАСЧЕТА КВАДРАТНОЙ ПЛАСТИНКИ
 107
 жена в центре пластинки, а
 при больших — в углу. Это подтверждается данными эксперимента 2-21, представленными на фиг. 2.17. Отрезки со стрелками пропорциональны деформациям удлинения или укорочения, измеренным по различным направлениям. Особенно велики деформации в угловых точках по направлению перпендикуляра к диагонали. Очевидно, здесь и возникают прежде всего пластические деформации.
 2. Квадратная пластинка с неподвижными краями. На фиг. 2.18 приведен график зависимости между нагрузкой и стрелой прогиба для того случая, когда края пластинки не могут сближаться. Как видим, формула 125, полученная в качестве первого приближения, дляС<1 совпадает с уточненным решением. При С>1 приближенное решение приводит к заниженной величине нагрузки.
 По графикам на фиг. 2.19 и 2.20 можно судить о напряжениях в срединной поверхности и напряжениях изгиба, максимальных по
 Фиг. 2.17. Длины стрелок пропорциональны деформациям удлинения или укорочения, измеренным по соответствующим направлениям.
 0,2 0,4 0,8 0,8 1,2 1,4 16 1,8 2 2,2 2,4
 Фиг. 2.18. Диаграмма «нагрузка — прогиб» для квадратной шарнирно опертой пластинки с несмещающимися кромками.
 толщине пластинки. Судя по фиг. 2.19, формулы первого приближения достаточно точно определяют величину напряжений в срединной

БОЛЬШИЕ ПРОГИБЫ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК
 ОА as
 Уточненное решение -
 Фиг. 2.19. Напряжения в срединной поверхности квадратной пластинки с несмещающимися кромками.
 Фиг. 2.20. Напряжения изгиба для квадратной пластинки с несмещающимися кромками.

§ 21
 ЗАЩЕМЛЕННАЯ ПО КРАЯМ ПЛАСТИНКА
 109
 поверхности, соответствующих центру и углу пластинки. В то же время по отношению к напряжениям изгиба уточненное решение вносит существенные поправки. И здесь при больших прогибах С > 1,7 становятся опасными напряжения в углу пластинки. При некоторой заданной стреле прогиба напряжения в срединной поверхности пластинки с закрепленными краями значительно больше, чем в случае свободных краев.
 § 21. Защемленная по краям пластинка с конечным отношением сторон; первое приближение
 Рассмотрим случай пластинки, защемленной по краям и нагруженной равномерно распределенной нагрузкой q. Примем, что отношение сторон пластинки лежит в пределах ajb 1,5. Смещение краев пластинки предполагается связанным, как и в случае шарнирно опертой пластинки, с деформацией упругих стержней; края должны оставаться прямолинейными.
 Возьмем приближенное выражение для прогиба, удовлетворяющее граничным условиям, в виде
 Уравнение совместности деформаций 1.61 после подстановки в правую часть выражения 131 и простых преобразований примет форму
 cos 4ах cos 2у -f- cos 2ах cos 4у — 2 cos 2ах cos 2fty. 2.133 Выпишем решение этого уравнения
 ф £ li Scos 2otxf cos 2—
 — 512 -§0054ах Y cos 4Ж ьаТрcos4х cos
 w sin2 ах sin2 Зу,
 2.131
 где
 2.132
 узузф iL 2a2j3‘2 cos 2ах cos 2 у — cos 4ах — cos 4 -f-
 a3 -j- 4i2
 Прия£>1,5 решение настоящего параграфа не может считаться удовлетворительным. Как показано в работе ?17, при аЬ> 1,5 пластинку можно приближенно рассматривать как бесконечно длинную см. §§ 16 и 17.

110 БОЛЬШИЕ ПРОГИБЫ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК гл. II
 Через рх и ру попрежнему обозначаются средние значения внешних усилий вдоль кромок.
 Напряжения в срединной поверхности оказываются равными
 C l — E f2a т cos 2'3-у —
 — 1 cos 4,3у £ 1д2 2-2 cos 4аX cos 2?у •
 tt2 44р22 cos2ctxcos 4лу-4а2 22co»2axcos2y рж, 2.135 аУ Ш — Е J C0S 2с,Х S2 C0S 4ах I-
 Т 4Т25 cos 4ах cos 2?У -да _'422 cos 2ot cos 4?у —
 — 42 р22 cos 2<хх cos 2Ь Рг 2.136 Т - -Щ-у - g2 4д2 sin 4ах sin Цу а2--4р2 Sin 2в Si 4?У — а22 Sitl 2аХ Sin 2?У ■ 2‘ 1 37>
 Отметим, что на кромках пластинки касательные напряжения обращаются в нуль.
 Для определения взаимного смещения краев у — 0 и у — Ь воспользуемся выражением
 а
 - J dx 2.138
 О
 положительным считается сближение краев. Найдя величину по выражению 1.7 и произведя интегрирование, получим:
 А- Ж аРа - РХЕ РУ а■ 2-139
 Взаимное смещение краев х 0, а будет равно
 Ау ± ррь — Ру ь. 2.140
 Судя по этим выражениям, условие прямолинейности кромок оказывается выполненным. Сохраняя зависимости 104 между смеще¬
 ниями Дж, А у и напряжениями ох,р> °у,р в упругих распорках, будем иметь:
 Х, р хРх 32' Px V'Pу'
 2.141

§ 21 ЗАЩЕМЛЕННАЯ ПО КРАЯМ ПЛАСТИНКА 111
 Определяя отсюда значения рх и ру и переходя к безразмерным параметрам 107, получим:
 . £1 р« — 32 lHlvJ-ixa <• >
 1
 1 У
 РУ 32 1 чх 1 V„ — J.2
 2.142
 Уравнение, составленное по методу Бубнова — Галеркина, запишется в виде
 а Ъ
 J j Xsin2axsin2ydxdy Q. 2.143
 о 	о
 Определим функцию X по формуле 1.123. После подстановки выражений для w и Ф найдем:
 X £3 — а4 ft4 cos 2ах cos 2j3y -f- cos 2ах cos 4j3y -f-
 Jr C0S 4<ХХ C0S 2?У 8 4а ° зУ C0S 2аХ C0S 4<ХХ C0s _
 — 8а2 422 «4 cos 2а C0S 2.3-У cos 4ЯУ —
 — 2 с.2 V2' C°S2 2“ С0§ 43-У “ 2 4а° ifo C0S 4а COs9 2
 4a2p88 т COS<2 2“ C0S 2
 4а22 4 «4 cos 2«x cos2 2,3у
 -h Y 4 J'pp cos2axcosAcX 2.3-V
 If g8p2» C0S’ 21X C0S 2‘3-У C0S 4‘3>' —
 — 2 J py 0084 2ax COS,J — 2 4a« pay»' Sitl 2<XX Sin 4otA: si2 2 —
 — 2aa4i22 sin'2 2алг sin 2?У sin 4?У 2 „2 p2a sin 2ax sin2 2fty -j- 2pyfafi cos 2ax sin2 ay -f- 2pxf2 cos 2y sin2 y — —
 — 4a4 cos 2ал: -f- 34 cos 2£y — a2 322 cos 2ax cos 2y. 2.144

112 БОЛЬШИЕ ПРОГИБЫ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК гл. и
 Подставим это выражение в 143 и выполним интегрирование; тогда придем к следующему уравнению:
 I 34_1_Ё1 Г I 1 I I
 11024v ' ' 128 4oa f;ayj Т a2_j. 422 J 32 а2_j_ р22 W
 Р> Р„«2 А 3 ««• ? 23 JjLf — ±jq Q. 2.145
 Переходя к безразмерным параметрам, получим:
 256 j '•Ч-'-311 “Nl 16X33 8хг 14 '8_“
 Тйр;г-щг3хг12>?“'''- <2,46
 Используем уравнение 146 для установления зависимости между стрелой прогиба и нагрузкой в различных частных случаях.
 1. Жесткая пластинка. Так как средние значения 142 усилий рх и ру пропорциональны С2, то при малых прогибах влиянием этих усилий можно пренебречь. Ограничиваясь линейным членом уравнения 146, приходим к такому выражению для стрелы прогиба:
 Г_ 121-р.2 1 - •■£
 или при а 0,3
 2.147
 С ?• 2.148
 Коэффициенты при q, найденные по 148, при 1,5 отклоняются от уточненных значений теории жестких пластинок не более чем на 3,5.
 2. Гибкая пластинка со свободно смещающимися краями. При свободно смещающихся краях в уравнении 146 следует принять ?? 0. Рассмотрим сначала случай квадратной пластинки; получим уравнение
 533гз_ 2те<—г;а 2.149
 3200 4 3 1 — ха4 4 ’ '
 или при х 0,3
 16,ЗС3 —— 71,4£. 2.1490
 Если сравнить формулы 118 и 149'» то окажется, что квадратная пластинка с защемленными краями выдерживает при той же
 См. ссылку на стр. 101.

§ 21
 ЗАЩЕМЛЕННАЯ ПО КРАЯМ ПЛАСТИНКА
 113
 стреле прогиба примерно в 3 раза большую нагрузку, чем такая же шарнирно опертая пластинка.
 Для пластинок с отношением сторон к Ф 1 уравнение 146 можно упростить, так как один из членов, заключенных в фигурные скобки, оказывается пренебрежимо малым. Уравнение приобретает вид при х 0,3:
 Напряжения в срединной поверхности определяются выражениями 135 — 137. Для центра пластинки
 Что касается напряжений изгиба, то при выборе изогнутой поверхности в форме 131 они определяются со значительной погрешностью. Лучше воспользоваться формулами теории жестких пластинок, выразив напряжения через стрелу прогиба.
 3. Гибкие пластинки с неподвижными краями. В этом случае следует в 142 положить v 0. Тогда найдем:
 Для определения напряжений в срединной поверхности следует величины а и а, найденные по формулам 151, сложить соответственно с ? и р. Напряжения изгиба также лучше определять по формулам, относящимся к жестким пластинкам.
 6,481, _«_г, 8,98з1 i A;,.. 2.,50
 а
 2.151
 2.152
 Уравнение 146 теперь получит вид
 2.153
 Для квадратной пластинки будем иметь при у 0,3
 35,9С871,4С ?.
 2.154
 При X Ф 1, если пренебречь малыми величинами, получим:
 6,481 	1 2,,8ТП1ТЧ7 7,531 С»
 8,98з1 l 2lc-«. 2.155

114 БОЛЬШИЕ ПРОГИБЫ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК гл. и
 В заключение приведем сводную таблицу расчетных данных
 первого приближения для квадратных пластинок с различными условиями закрепления. Уравнение для определения С представим в виде
 Ж8 ЯС ?, 2.156
 а выражения для напряжений в центре пластинки в виде
 о 	о а:2, о а т;. 2.157
 X IJ 1 х,п у, и V В круглых скобках помещены уточненные значения коэффициентов для жестких, а в квадратных скобках—для абсолютно гибких пластинок 214.
 Таблица II
 Вспомогательные данные для расчета квадратных пластинок
 при ji 0,3
 Условия закрепления кромок
 А
 в
 а
 т
 Шарнирно
 закреплены
 Свободно смещаются в плоскости контура
 7,5
 22
 22,6
 1,23
 7,05
 6,50
 Не смещаются
 28,9
 43
 22
 22,6
 3,00
 3,40
 7,05
 6,50
 Защемлены
 Свободно
 смещаются
 16,3
 71,4
 72,5
 2,16
 9,95
 Не смещаются
 35,9
 71,4
 72,5
 3,48
 9,95
 При расчете пластинок по допускаемым напряжениям используется та или иная теория прочности. Допустим, что найдены полные напряжения по направлениям у и х, являющиеся для данной точки главными: <зг и о2. Если эти напряжения имеют одинаковый знак и ot > о2, то по теории наибольших касательных напряжений должно быть
 По теории октаэдрических напряжений
 Уа — оЛ--о< о.
 См. сноску на стр. 101.

уточненное Решение
 115
 § 22. Уточненное решение для случая защемленной пластинки.
 Сопоставление теоретических и экспериментальных данных
 Выражение 131, принятое для прогиба в приближенном решении, приводит к вполне удовлетворительным результатам при определении стрелы прогиба пластинки. Однако этим выражением плохо улавливается истинный характер изогнутой поверхности, в особенности у защемленных краев пластинки. Поэтому важно сопоставить это решение с уточненным.
 Во второй из работ 217 С. Леви было предложено сохранить для защемленной пластинки ту же общую схему решения, что и для шарнирно опертой. Выражение для прогиба представляется в виде ряда 129. Влияние
 Фиг. 2.21. К разложению в тригонометрический ряд краевых моментов для защемленной пластинки.
 16 г £2,0 ■>
 Фиг. 2.22. Зависимость между нагрузкой и прогибом для защемленной квадратной пластинки.
 реактивных моментов учитывается добавлением к заданной равномерной нагрузке некоторой фиктивной нагрузки, распределенной у краев пластинки на участке 2с фиг. 2.21. Дополнительная нагрузка представлена тригонометрическим рядом, и ширина участка 2с считается стремящейся к нулю. На фиг. 2.22 полученное таким образом уточненное решение, относящееся к случаю квадратной пластинки с неподвижными краями, сравнивается с данными § 21. Судя по фиг. 2.22, получаемая из уравнения 154 стрела прогиба достаточно близка к «точному» значению: при С < 2 расхождение не превышает 3. На том же графике нанесена кривая, соответствующая случаю свободно сближающихся краев.
 Напряжения в срединной поверхности определяются в приближенном решении менее удовлетворительно фиг. 2.23. Уточненное решение показывает, что нормальные напряжения в центре пластинки и середине стороны отличаются между собой не так сильно, как это вытекает из формул 135 — 137. На графике фиг. 2.24 пунктирные

БОЛЬШИЕ ПРОГЙБЫ ПРЯМОУГОЛЬНЫХ ПЛАСТИЙОк
 Фиг. 2.23. Напряжения в срединной поверхности квадратной защемленной пластинки.
 0,4 0,8 7,2 1,6 X 2,0
 Фиг. 2.24. Напряжения изгиба для квадратной защемленной пластинки.

§ 22
 УТОЧНЕННОЕ РЕШЕНИЕ
 117
 линии отвечают формулам первого приближения для напряжений изгиба. Как видим, напряжения изгиба в центре определяются уже
 fh 0,06 х fh 0,94 о fh 7,77
 Фиг. 2.25. Изогнутая поверхность квадратной защемленной пластинки на разных стадиях нагружения.
 в первом приближении достаточно хорошо. Вместе с тем напряжения в середине стороны — по направлению, перпендикулярному к кромке, — оказываются сильно преуменьшенными; при С 1,9
 расхождение достигает 30. Это объясняется тем, что при увеличивающемся прогибе кривизна сечения пластинки у краев возрастает, а в центре несколько падает. Очевидно, для прямоугольной пластинки напряжения в середине длинной стороны раньше всего достигают предела текучести; при этом происходит надлом пластинки у краев. В дальнейшем пластинка должна работать при закреплении на кромках, близком к шарнирному опиранию. Такое предположение подтверждается экспериментальными данными о характере изо-
 <gVO' В
 ТЖгз Л fc
 4
 N
 JХГ к
 А
 7
 Г
 1
 3 4 5 6 7 в 9 Ш 71 72 73
 Фиг. 2.23. Теоретические и экспериментальные диаграммы «нагрузка — прогиб» для защемленной квадратной пластинки.
 гнутой поверхности, полученными для дуралюминовой защемленной пластинки 2-21. На фиг. 2.25 эти данные, относящиеся к сечению тп

118
 БОЛЬШИЕ ПРОГИБЫ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК
 гл. II
 квадратной пластинки, при последовательно возрастающем прогибе сравниваются с теоретическими кривыми. Кривая w sin27tjta недостаточно хорошо отражает поверхность пластинки уже при малых прогибах. При значительном же прогибе 1,77 h экспериментальные точки оказываются лежащими на кривой w sinizxa, соответствующей граничным условиям шарнирного опирания.
 Хотя выражение для прогиба 131 не отвечает истинной форме изогнутой поверхности, расчетное уравнение 154 приводят к надежным результатам даже при весьма больших прогибах. Это можно видеть из фиг. 2.26. Кривая отвечает уравнению 154. Кружками помечены данные опыта, в процессе которого стрела прогиба дуралюминовой квадратной пластинки достигла 12,2г.
 В работе 218 дано также уточненное решение задачи для пластинки с защемленными несмещающимися кромками и отношением сторон X 1,5. При £<2 уравнение 155 первого приближения дает стрелу прогиба с погрешностью примерно в 5.
 § 23. Пластические деформации в пластинке большого прогиба Предел упругого сопротивления пластинки
 Мы видели, что предел текучести материала достигается раньше всего в случае шарнирного опирания в центре, а при защемлении — у кромок пластинки. Развитие пластических деформаций влечет за
 Фиг. 2.27. Полные и остающиеся прогибы в упругой и упруго-пластической областях.
 собой значительное изменение характера диаграммы «нагрузка — прогиб». Как показывают опыты, после достижения наибольшими напряжениями предела текучести пластинка продолжает нести возрастающую нагрузку. Но вместо пунктирного участка кривой qf на фиг. 2.27 мы получаем зависимость, приближающуюся к линейной сплошная линия.

§ 23 ПЛАСТИЧЕСКИЕ ДЕФОРМАЦИИ В ПЛАСТИНКЕ БОЛЬШОГО ПРОГИБА 119
 Допустим, что после придания пластинке известной нагрузки q произведена разгрузка и отмечена величина 0 остаточной, или «пластической», стрелы прогиба. Если на графике фиг. 2.27 нанести зависимости между 0 и q, то получим также прямую, примерно параллельную «пластическому» участку кривой qf. Это показывает, что после достижения нагрузкой величины qT, отвечающей границе упругой области, дополнительный прогиб возникает главным образом за счет пластической деформации.
 Фиг. 2.28. Полные и остающиеся прогибы по экспериментальным данным.
 На фиг. 2.28 приведены экспериментальные данные для защемленной по краям дуралюминовой пластинки с отношением сторон а£ 1,25. Одна из кривых отвечает полной стреле прогиба п, а вторая — стреле остаточного прогиба 0. Результаты испытаний примерно соответствуют графику фиг. 2.27. Пунктирная линия построена по уравнению 155.
 Условимся понимать под пределом упругого сопротивления ту нагрузку qT, при которой наибольшие напряжения достигают величины предела текучести материала от. Надо учитывать, что эта величина может быть значительно меньше максимальной нагрузки,
 Опыты проведены Ю. Б. Горюновым.

120
 БОЛЬШИЕ ПРОГИБЫ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК
 ГЛ. II
 Фиг. 2.29. Нагрузка на границе упругого сопротивления пластинки.
 Фиг. 230. Нагрузка на границе упругого сопротивления np:i малых

§ 24
 МЕМБРАНА С ПРЕДВАРИТЕЛЬНЫМ НАТЯЖЕНИЕМ
 121
 выдерживаемой пластинкой. Однако превышение предела текучести основными напряжениями в элементах реальных конструкций обычно считается недопустимым.
 Для определения предела упругого сопротивления пластинки необходимо установить связь между наибольшими напряжениями и интенсивностью нагрузки. Это легко сделать, если считать деформации упругими на всем участке до предела текучести.
 Рассмотрим случай шарнирно опертой квадратной пластинки с закрепленными краями. Пользуясь данными таблицы II и приравнивая максимальное напряжение пределу текучести материала от, получим при X 1:
 под Сг мы будем понимать безразмерную стрелу прогиба, соответствующую пределу упругого сопротивления. Согласно уравнению 125 этой стреле прогиба отвечает нагрузка
 Сопоставление уравнений 160 и 161 позволяет найти q при заданном а. На фиг. 2.29 и 2.30 изображена зависимость между о и qT для малых и значительных прогибов С. Здесь же даны «предельные» нагрузки, полученные при том же условии для жестких и для абсолютно гибких пластинок. В первом случае находим <7 3,14з, а во втором qT 5,56 о1’5.
 В практических расчетах надо вычислить о по формуле 159 и найти q из графиков фиг. 2.29 или 2.30.
 Для пластинок с другими условиями закрепления предел упругого сопротивления может быть найден аналогичным образом.
 § 24. Мембрана с предварительным натяжением
 Допустим, что пластинка получает до прогиба значительное предварительное натяжение в своей плоскости, причем напряжения во всех направлениях оказываются равными ах оу о фиг. 2.31. Тогда можно пренебречь дополнительными усилиями в срединной поверхности по сравнению с начальными, т. е. считать напряжения неизменными в процессе прогибания. Если, кроме того, пренебречь
 2.158
 Безразмерная величина
 2.159
 будет равна
 2.160
 2.161

122
 БОЛЬШИЕ ПРОГИБЫ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК
 ГЛ. II
 изгибной жесткостью пластинки, то мы получим классическую задачу об изгибе мембраны с предварительным натяжением, рассмотренную еще Эйлером 1ЛЗ. Для прогибов, малых по сравнению с размерами основания, уравнение 1.30 принимает вид
 Так как оно вытекает из условия равновесия элемента мембраны,
 то может быть применено и в том случае, когда напряжение о превышает предел упругости материала.
 Полагая прогиб w равным
 z
 Фиг. 2.31. Пластинка со значительным предварительным натяжением, подвергающаяся поперечной нагрузке.
 w sin ах sin
 2.162
 выпишем уравнение Бубнова — Галеркина:
 F
 Тогда получим:
 “w sin ах sin
 или
 Г 16 1 q • а Ь 2
 ‘-тЫ-

§ 24 МЕМБРАН С ПРЕДВАРИТЕЛЬНЫМ НАТЯЖЕНИЕМ 123
 В случае квадратной мембраны
 С 10,082-Jr. 2.163
 Если вместо 162 взять выражение типа 129 с параметрами
 и» Лз» 31» зз> то Для квадратной мембраны будем иметь:
 C 0,07l£. 2.164
 Таким образом, для мембраны, получившей значительное предварительное натяжение, стрела прогиба связана с нагрузкой линейной зависимостью.

ГЛАВА III
 ЗАКРИТИЧЕСКАЯ ДЕФОРМАЦИЯ ПРЯМОУГОЛЬНЫХ
 ПЛАСТИНОК
 § 25. Сжатие прямоугольной пластинки после потери устойчивости. Понятие редукционного коэффициента
 Рассмотрим панель тонкостенной конструкции, состоящую из прямоугольной пластинки и подкрепляющих ребер и подвергающуюся действию сжимающих усилий в одном направлении. При некотором
 значении сжимающих напряжений, называемом критическим, происходит потеря устойчивости пластинки, выражающаяся в образовании одной или нескольких выпучин фиг. 3.1. Во многих конструкциях жесткость подкрепляющих пластинку ребер настолько велика, что потеря устойчивости пластинки не приводит к сколько-нибудь заметной деформации ребер. Поэтому при продолжающемся сжатии конструкции прилегающие к ребрам полосы пластинки не могут деформироваться свободно; пластинка оказывается способной после возникновения выпучин нести возрастающую нагрузку. Углубление выпучин, возникающих в момент потери устойчивости, ведет к развитию не только напряжений изгиба, но и напряжений в срединной поверхности.
 Допустим, что возникающие при изгибе пластинки напряжения лежат в пределах упругости. Тогда обратный процесс — разгрузка конструкции — приводит к полному восстановлению начальной формы пластинки и исчезновению выпучин. Для достаточно тонких пластинок такое явление вполне возможно даже при образовании значительных выпучин, превышающих толщину пластинки в несколько раз.
 Картина распределения сжимающих напряжений по ширине пластинки после образования выпучин резко меняется. Увеличение.
 Фиг. 3.1. Волнообразование при потере устойчивости удлиненной сжатой пластинки.

§ 25 сжатие прямоугольной пластинки после Потери устойчивости 125
 общей сжимающей нагрузки происходит главным образом за счет продольных подкрепляющих ребер и прилегающих к ним полос пластинки: напряжения в краевых полосах быстро возрастают, в то время как в средней части пластинки они остаются почти неизменными.
 Пусть на панель, состоящую из пластинки и подкрепляющих ребер, действует вдоль оси х сжимающая сила Р. Обозначим через Fр общую площадь сечения двух продольных ребер; при рассмотрении конструкции, состоящей из ряда панелей, под Fv будем понимать площадь сечения ребер, приходящуюся на ширину одной панели фиг. 3.2.
 При расчете тонкостенных конструкций принято относить сжимающую силу Р, воспринимаемую всей панелью, к площади сечения продольных ребер с присоединением к ней редуцированной,
 или приведенному площади сечения пластинки обшивки Fn ybh через ср здесь обозначается редукционный коэффициент. В полученном таким образом редуцированном сечении напряжения считаются распределенными равномерно и равными напряжению в продольном ребре:
 <ЗЛ
 S
 Фиг. 3.2. Пластинка, подкрепленная упругими ребрами стрингерами.
 Ширину полос пластинки, присоединяемых к продольным ребрам, принято называть приведенной шириной; обозначая ее через пр имеем:
 Ьщ> ср Ь. 32
 Обозначим приходящуюся на пластинку часть нагрузки через Рпл; она будет равна Рдл Мсрор. Если теперь ввести понятие среднего напряжения в сечении пластинки pxt то будем иметь РПЛ pxbh. Сравнение последних формул показывает, что под редукционным коэффициентом ср можно понимать отношение среднего напряжения в сечении пластинки к напряжению в продольном ребре:
 ср.. 3.3
 Р
 Отметим, что сжимающее напряжение в прилегающем к продольному ребру волокне пластинки может отличаться от напряжения в ребре; общей для ребра и смежного с ним волокна пластинки

126
 ЗАкРИТИЧЕСКАЯ ДЕФОРМАЦИЯ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК ГЛ. III
 является деформация укорочения. Различие в напряжениях будет иметь место при разных модулях упругости материалов пластинки и ребер, а также в связи с образованием в срединной плоскости пластинки двухосного напряженного состояния.
 Увеличение сжимающей нагрузки, воспринимаемой панелью после потери устойчивости пластинки, имеет определенные границы. Так, явление местной потери устойчивости пластинки может перейти в общую потерю устойчивости всей панели вместе с подкрепляющими ребрами. Тогда панель в целом будет вести себя как сжатый стержень при продольном изгибе. Для изолированной панели такая общая потеря устойчивости равносильна разрушению. Во многих конструкциях, однако, серия смежных панелей связана с еще более жесткими связями, сохраняющими устойчивость и ограничивающими деформацию пластинок и легких продольных ребер. Например, для корпуса корабля такими жесткими связями являются продольные переборки; для крыши цельнометаллического вагона — ее склоны, имеющие значительную кривизну. Тогда площадь сечения легких ребер и обшивки может быть, в свою очередь, редуцирована и присоединена к площади сечения жестких связей.
 Редуцирование площади сечения пластинок, входящих в состав тонкостенной конструкции, является удобным при рассмотрении ее общей прочности. Так, обшивку крыла самолета редуцируют при расчете крыла на изгиб и кручение, обшивку корпуса корабля — при расчете корпуса на изгиб. Расчет ведется путем последовательных приближений. Задаются ориентировочными значениями редукционных коэффициентов и включают приведенные площади сечений пластинок в общее сечение эквивалентного бруса, заменяющего в отношении общей прочности данную конструкцию. Тогда оказывается возможным найти напряжения в любом волокне бруса, в том числе напряжения в продольных ребрах. Зная эти напряжения, находят новые приближенные значения редукционных коэффициентов и т. д.
 § 26. Пластинка, шарнирно опертая по краям; первое приближение.
 Частные случаи квадратной и удлиненной пластинок
 Поставим себе целью выяснить характер деформации сжатой пластинки после потери устойчивости. Допустим, что пластинка по форме близка к квадратной, так что потеря устойчивости происходит в направлении каждой из сторон пластинки по одной полуволне. Края пластинки будем считать шарнирно опертыми на вполне жесткие ребра, остающиеся прямолинейными во все время деформации. Примем вместе с тем, что края пластинки свободно скользят вдоль ребер или, иными словами, что касательные напряжения вдоль всех кромок отсутствуют. Оси координат расположим, как показано на фиг. 3.3.

ПЛАбТИНКА, ШАРНИРНО ОЙЕРТАЯ ПО кРАЙМ
 127
 В качестве первого с помощью уравнения
 приближения представим прогиб пластинки
 -. пх. тсу
 W Sin Slfl —т
 J a b
 отвечающего характеру волнообразования в вости пластинки.
 Подставляя это выражение в уравнение 1.61, получим:
 3.4
 момент потери устойчи-
 <27
 1 У'¥Ф 3
 да-
 COS-
 2тсх
 -cos
 Кромки пластинки х 0 и х а подвергаются действию сжимающих усилий, среднюю величину которых будем обозначать через рх. Кроме того, предположим, что по кромкам у О и у b действуют усилия, средняя интенсивность которых составляет ру они понадобятся нам для удовлетворения граничным условиям по продольным кромкам. Чтобы учесть усилия рх и уравнения в § 19:
 Фиг. 3.3. Шарнирно опертая пластинка, сжатая в одном направлении.
 ру, выпишем решение 5 в той же форме 2.99, какую мы придавали ему
 Ф:
 2 2пх COS-
 РхУ
 Ру2
 а ' а - - b J 2 2’
 в отличие от § 19 усилия рх и ру мы считаем здесь положительными при сжатии.
 Напряжения в срединной поверхности при этом будут д2ф
 дуз дФ дх2
 -Ру>
 д2ф
 о.
 дх ду
 Как видим, условие отсутствия касательных усилий по кромкам пластинки выполняется; эти усилия обращаются в
 вообще для всей площади пластинки. Отметим, что
 3.7
 3.8
 3.9
 всем
 нуль
 остаются постоянными вдоль каждого поперечного волокна.
 Относительное сближение волокна равно
 каждого продольного,
 напряжения оа а
 концов произвольного продольного
 а а
 _ _± Oil и— — Г 1 Г2ф д2ф EdwYn с 1пч
 а дх а в W Ж Т Ыdx' ЗЛ0

128 ЗАКРИТИЧЕСКАЯ ДЕФОРМАЦИЯ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК ГЛ. III
 Подставляя значения ® и Ф, находим:
 Рх V'Py
 е —Е 3.11
 Условие прямолинейности каждой из нагруженных кромок выполняется. Аналогичным образом убеждаемся в том, что относительное сближение концов поперечных волокон не зависит от положения волокна и равно
 Этот результат можно объяснить тем, что, хотя кинематическое сближение концов волокон, вызванное образованием выпучин фиг. 3.4, а, само по себе ведет к искривлению каждой кромки пластинки,
 оно компенсируется действием цепных напряжений; последние вызывают удлинение волокон, расположенных в средней части ширины или длины пластинки, и укорочение волокон, лежащих в крайних частях фиг. 3.4, б. Благодаря этому смещения концов всех волокон выравниваются.
 Снова воспользуемся для решения задачи методом Бубнова — Галеркина. Повторяя выкладки § 19 и полагая q 0, записываем уравнение 2.110 в виде
 Далее следует различать случаи свободных и неподвижных продольных кромок.
 а.
 7
 Фиг. 3.4. а искривление кромок при выпучивании пластинки; б усилия, появляющиеся в случае прямолинейных краев.

§ 26 ПЛАСТИНКА, ШАРНИРНО ОПЕРТАЯ По КРАЯМ 129
 1. Продольные кромки смещаются свободно. При этом надо принять во всех уравнениях ру 0. Считая т0 и вводя обозначение каЬ, определяем рх
 DB5-t Х £т1р'-2та' Х'‘ ЗЛЗ
 Первый член полученного уравнения соответствует критическому напряжению
 АР'тЛ <ЗЛ4>
 , D
 и может быть получен, путем решения линейной задачи об устойчивости пластинки при заданных граничных условиях.
 Зависимость между средним напряжением и стрелой прогибд в послекритической стадии имеет вид
 Рх 0кР £ 2 х2 3.15
 Приращение рх по отношению к критическому значению оказывается пропорциональным квадрату стрелы прогиба.
 Сжимающее напряжение в волокнах, прилегающих к продольным ребрам, при у 0, b будем в дальнейшем условно обозначать через ар, отождествляя эту величину с напряжениями в самих ребрах Считая сжимающие напряжения ар положительными, имеем:
 Ор рх рх Кр 3.16
 Наименьшее напряжение будет равно для центрального волокна
 °тпРх — Рх °К'гр- ЗЛ7>
 Перейдем к определению редукционных коэффициентов. По 16
 Рх — з ха ар з акр 3.18
 Подставляя это выражение в 3, получим:
 _ 1 л4 1 2
 3-fXi3 XV Здесь п — отношение краевого напряжения к критическому:
 3.19
 п. 3.20
 дкр
 В момент потери устойчивости при п 1 будем иметь ср 1. При возрастании сжимающей нагрузки редукционный коэффициент падает, причем интенсивность уменьшения оказывается зависящей от отношения сторон пластинки.

130 ЗАКРИТИЧЕСКАЯ ДЕФОРМАЦИЯ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК гл. III
 Для квадратной пластинки выражения 16 и 17 дают:
 0«,т °кр • 3.21
 Судя по этому результату, напряжение в среднем волокне минимальное по ширине остается во все время деформации постоянным и равным критическому. Эпюра распределения напряжений по ширине
 пластинки показана на фиг. 3.5. Редукционный коэффициент для квадратной пластинки оказывается равным
 <р 0,5 3.22
 Это выражение можно истолковать таким образом, что при определении воспринимаемой пластинкой нагрузки половину сечения пластинки можно непосредственно присоединить к ребрам, а остальную часть редуцировать по соотношению ср 1 я. Редукционный коэффициент получается по 22 более высоким, чем по формуле
 3.23
 предложенной ранее И. Г. Бубновым 1Л по аналогии со случаем сжатого стержня. Таким образом, пластинки обладают в закритической области дополнительным «запасом» сопротивления сжимающей нагрузке.
 При расчете конструкций, состоящих из ряда панелей, целесообразно пользоваться диаграммами зависимости между средним сжимающим напряжением в панели и сближением нагруженных кромок. Такая диаграмма как бы заменяет график «усилие — деформация», получаемый при испытании образца на растяжение или сжатие. Обозначив через ел деформацию в момент потери устойчивости, имеем:
 Пользуясь первым из соотношений 21, найдем:
 Фиг. 3.5. Эпюра распределения сжимающих напряжений по ширине пластинки.
 е еКу — 2 Рх
 3.25

§ 26
 ПЛАСТИНКА, ШАРНИРНО ОПЕРТАЯ ПО КРАЯМ
 131
 Введем понятие касательного модуля £к. ц для пластинки в целом, понимая под этим отношение малых приращений £к. д
 • В нашем случае касательный модуль, равный до потери
 устойчивости модулю упругости Е, падает в момент выпучивания пластинки до значения 0,5 Е и затем остается постоянным фиг. 3.6.
 Обратимся теперь к исходному выражению 19 для редукционного коэффициента, относящемуся к пластинке с произвольным отношением сторон. Судя по этому выражению, в случае вытянутой по направлению стороны b пластинки коэффициент ср несколько уменьшается по сравнению со случаем квадратной пластинки; в самом деле, для широкой пластинки влияние продольных ребер падает. Надо помнить, однако, что в этом случае приближенное выражение для прогиба 4 хуже отображает истинную форму изогнутой поверхности пластинки.
 Будем поирежнему называть пределом упругого сопротивления Ядред такую величину силы Р, при которой напряжения в краевых волокнах достигают предела текучести а,
 Лед через среднее напряжение, получим:
 Рпред Рщ>ъррЬ
 или
 Фиг. 3.6. Изменение сжимающего усилия и касательного модуля, характеризующего общую деформацию пластинки.
 пред
 “В
 Х4
 3 р
 Для квадратной пластинки находим:
 Адод ат “Ь акр;
 j bh.
 Выражая
 3.26
 3.27
 3.28
 величина ?щед оказывается равной полусумме предела текучести и критического напряжения.
 2. Продольные края неподвижны. В этом случае слеИз выражения И тогда получим:
 12
 дует положить еу 0.
 3.29
 Подставляя 29 в 12,
 Рх £>
 придем к следующему выражению для рх
 7 л2 1 JtXa
 162
 3.30
 Эту величину не надо смешивать с касательным модулем в диаграмме «усилие — дефор ация» для материала.

132 ЗАКРИТИЧЕСКАЯ ДЕФОРМАЦИЯ ПРЯМОУГОЛЬНЫХ ПЛАСТИЙОК гЛ. III
 Критическое напряжение будет равно
 3.31
 После простых выкладок находим выражение для редукционного коэффициента
 Касательный модуль определим, найдя относительное сближение кромок ех:
 Полученные зависимости дают решение задачи лишь в первом приближении. В самом деле, они составлены в предположении, что форма изогнутой поверхности 4 сохраняется во все время деформации пластинки; это не соответствует действительности. Однако их можно использовать для случая удлиненной пластинки, теряющей устойчивость с образованием большого числа перемежающихся выпучин; введем вместо а длину полуволны изогнутой поверхности и обозначим через т отношение bjl. Величина т указывает, сколько раз длина полуволны умещается в ширине пластинки. В момент потери устойчивости для удлиненной пластинки можно положить т 1. Как показывают опыты, по мере увеличения нагрузки в закритической области выпучины делаются более короткими. Перепишем теперь выражение для редукционного коэффициента 19, считая
 Если учесть, что при увеличении п должно также расти значение т но гораздо медленнее, чем п, то мы придем к заключению, что редукционный коэффициент падает в пределе до величины ср з» в то время как раньше получалось для квадратной пластинки, что предельное значение ср равно х2• Таким образом, учет изменения
 у 3 М 2 1 ц ха В случае квадратной пластинки
 о>2
 1 21
 3.32
 2
 1 1ji
 3.33
 П 3 -f— А 9
 3.34
 3.35
 при этом
 3.36
 Pv 0:
 3.37

§ 26
 ПЛАСТИНКА, ШАРНИРНО ОПЕРТАЯ ПО КРАЯМ
 133
 формы волнообразования приводит к существенному изменению величины редукционного коэффициента, особенно при значительном превышении критического напряжения.
 Можно попытаться также найти уточненные значения ср для всего процесса деформирования панели, рассматривая для некоторого фиксированного п величину <р как функцию т и находя такое т, которое придает ср минимальное значение. Приравнивая нулю произ-
 . водную, мы при этом найдем следующее уравнение для определения т:
 ЗTt8 —— 4 — 8п2 т2 -f-1 0. 3.38
 Более обоснованный результат можно получить, определяя полную энергию Э пластинки как функцию величин и т условие экстремума энергии приводит к равенствам
 ■»■ Л-°- <3-39>
 Развертывая эти равенства, получаем:
 3 40>
 S.V-1 <3-41>
 Первое из полученных таким образом уравнений совпадает с уравнением 13, полученным с помощью метода Бубнова — Галеркина. Второе уравнение определяет связь между стрелой прогиба и длиной полуволны bт и показывает, что с увеличением стрелы прогиба величина т должна возрастать, а волны становиться более короткими. Пользуясь последними уравнениями, приходим к следующему выражению для редукционного коэффициента
 ф — 3 42
 ‘ Зт — m2-f-2 ко.ы
 Предельное значение ср при т-оо снова оказывается равным х3. Введем безразмерные параметры
 <3<3>
 Тогда уравнение 13 примет для а — Ь вид
 Р < р т'9 <3-44
 при
 в«Р 31 — л.3 3>62- 3.45
 Эти уравнения соответствуют случаю квадратной пластинки и cro бодно сближающихся продольных кроток.

134 ЗАКРИТИЧЕСКАЯ ДЕФОРМАЦИЯ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК ГЛ. III
 § 27. Уточненные решения для квадратной пластинки
 Мы видели, что для послекритической деформации пластинки характерным является сокращение длины выпучины по мере увеличения нагрузки. Постараемся отобразить это в выборе приближенного выражения для прогиба, рассматривая случай квадратной пластинки, шарнирно опертой по краям. В предыдущем параграфе форма волнообразования характеризовалась одним параметром. Выберем теперь новое выражение для прогиба, содержащее два независимых параметра п и 31:
 вычисляя правую часть 1.61, получим это уравнение в виде
 Идя тем же путем, что и в предыдущем параграфе, приходим к следующему выражению для функции напряжений:
 Продольные края пластинки будем считать свободно смещающимися и примем Ру 0.
 Напряжения оказываются равными:
 . TZX. TCV, -
 ™ п sin — sin -j- -f— 31 sin
 3.46
 Ф E кfn cos 1 cos ft, 4 cos S cos 1г
 . £ г Г 1 2ъх. 1 4nx. 1 2kx 2ny
 “Г 11Л1 — COS f- £1 COS H ГБ cos —1- cos —- —
 16 a 1 64 a 1 16 a a
 3.47
 3.48

§ 27 УТОЧНЕННЫЕ РЕШЕНИЯ ДЛЯ КВАДРАТНОЙ ПЛАСТИНКИ 135
 Уравнений Бубнова — Галеркина 1.124 будет теперь два:
 а Ъ а Ь
 j j'.Ysin sin dx dy 0, j j,Ysin sn-dx dy 0. 3.49
 6 6 oo
 Вычисляя выражение 1.123 для X, подставляя его под знак интегралов 49 и интегрируя, получим следующие алгебраические уравнения относительно fn и 31:
 — Pxfn Л Ehщп — giisi §iisi 0, 3.50
 D 25fn-Pxhf31 Eh £ -1 fn щ fnfn bi0. 3.51
 Введем безразмерные параметры
 n Рма2 Г и.,1. fn О КО
 Р — Eh ’ —JT' V— u- <.52
 Уравнению 50 может быть тогда придана форма
 <3'53 мы считаем при этом и Ф 0. Исключая затем величину рх из уравнений 50 и 51, получим уравнение
 3 суip-1НР 0. 3.54
 С помощью этого уравнения можно при заданном значении С определить величину последняя характеризует «удельный вес» вновь введенного во втором приближении коэффициента 31 по отношению к основному коэффициенту и. Затем из уравнения 53 может быть определен параметр нагрузки р. Отсюда находим зависимость между р и С
 При х 0,3 уравнения 53 и 54 получают вид
 > 3,62 1,231 — ибфв.бг, 3.55
 71,4f> — 27-2 0,96 — Цр •> 1 0. 3.56
 Легко видеть, что при 0 получим уравнение 44.
 Допустим, что из уравнений 55 и 56 найдены величины и р для ряда значений С. Тогда могут быть определены соответствующие значения редукционных коэффициентов. Примем в первом из выражений 48 у 0 или у Ь; тогда найдем напряжения в краевых продольных волокнах равными
 gpE -ii §i 4из1 cos щиз1 cos4Рж» 3.57
 причем сжимающие напряжения здесь считаются положительными,

136 ЗАКРИТИЧЕСКАЯ ДЕФОРМАЦИЯ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК ГЛ. Ill
 В отличие от решения предыдущего параграфа напряжения оказываются зависящими от х, т. е. переменными по длине пластинки. Определим среднее по длине напряжение ор с помощью выражения
 а
 аг»,1ед jdx. 3.58
 о
 Находим для нашего случа <
 аг,сред £? 3.59
 Эта величина будет отвечать относительному сближению нагруженных кромок пластинки. В этом можно убедиться, определяя величину ех по выражению 10; она будет равна
 <3-60>
 Введем теперь безразмерный параметр
 <п. пмп Я2
 F’
 будем иметь
 Р вред. и
 аР— F Тъ » о.Ы
 « > 1.23С2 1 9<. 3.62
 Редукционный коэффициент может быть найден по соотношению
 ? 3.63
 СР
 Примем для примера С равным 4. Уравнение 56 примет вид 71,4з _ Щ2 — 4,9 10.
 С помощью подстановки
 »< щч-11117
 приводим это уравнение к виду
 X3 — 0,117 0,0013 0.
 Дискриминант уравнения оказывается отрицательным:
 следовательно, все корни будут вещественными. Определить корни можно таким же образом, что и в § 15, но с заменой гиперболических функций на круговые. Находим:
 ул 0,011, Х2 — 0,347, ’„ 0,336.
 Соответствующие значения ф будут
 0,138, — 0,220, фа 0,463,

§ 27 УТОЧНЕННЫЕ РЕШЕНИЯ ДЛЯ КВАДРАТНОЙ ПЛАСТИНКИ 137
 Первому из этих корней будет отвечать согласно формуле 55 среднее безразмерное напряжение:
 р 3,62 1,23 • 16 1 — 1,5 • 0,138 8,52 • 0,1383 22,42.
 Двум другим корням будут соответствовать большие значения р, которые нас интересовать не будут. По формуле 62 определяем при ф 0,138
 о 22,4 1,23- 161 9 - 0,1382 45,5.
 Таким образом, принятое значение С отвечает моменту сжатия пластинки
 после потери устойчивости, когда краевое напряжение превышает критиче-
 45 5 22 4
 ское в п оо 12,6 раза, а среднее напряжение — в 6,2 раза; кри-
 тическое напряжение определяется ири этом попрежнему выражением 45. Редукционный коэффициент будет равен
 22 4
 45Г5°’49-
 Если решать эту же задачу в первом приближении, получим но формуле 2 2
 <Р °,5 -f щ 0,54.
 Второе приближение даег при С 4 заметное изменение редукционного коэффициента: снижение составляет около 9.
 В таблице III даны значения р, а и ср, найденные для различных С.
 Таблица III
 Редукционные коэффициенты по данным второго приближения
 У
 0
 0,5
 1,0
 1,5
 2,0
 2,5
 3,0
 3,5
 4,0
 4,5
 5,0
 5,5
 6,0
 ф
 0
 0,00269
 0,0108
 0,0240
 0,0425
 0,0646
 0,0885
 0,113
 0,138
 0,162
 0,187
 0,215
 0,261
 р-
 3,62
 3,93
 4,83
 6,30
 8,31
 10,89
 13,92
 17,82
 22,4
 28,1
 35,0
 43,6
 56,2
 3,62
 4,23
 6,06
 9,08
 13,31
 18,89
 25,7
 34,6
 45,5
 58,8
 75,5
 93,6
 127,5
 1
 0,926
 0,796
 0,694
 0,624
 0,576
 0,540
 0,515
 0,492
 0,477
 0,465
 0,464
 0,440
 п
 1
 1,170
 1,675
 2,51
 3,68
 5,22
 7,10
 9,56
 12,57
 16,25
 20,9
 25,6
 34,7
 В исследовании П. А. Соколова 317 было принято следующее приближенное выражение для прогиба, относящееся к квадратной пластинке:
 .. пх. 7iy,,. Зпх. гсу,. тех Зпу 0
 ™ usin--sin-f3xsin — sin--13sin—sin--. 3.64
 Это выражение содержит уже три независимых параметра. Для взятого нами примера при я 12,6 мы получили бы ср 0,48. Если взять в основу решения выражение для w, содержащее четыре

138
 ЗАКРИТИЧЕСКЛЯ ДЕФОРМАЦИЯ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК ГЛ. III
 параметра и> 13, 31, 33 первый индекс соответствует числу полувюлн по оси х, а второй — по у, то при г 12,6 получим новое снижение редукционного коэффициента до ср 0,44, т. е. на 7,5°0. Как было показано С. Леви 217, дополнительное введение новых параметров 1б и б1 не оказывает в пределах п <13,5 сколько-нибудь существенного влияния: значения редукционных
 Фиг. 3.7. Нагрузка и редукционный коэффициент для квадратной сжатой пластинки.
 коэффициентов остаются в пределах трех десятичных знаков неизменными.
 На фиг. 3.7 представлена зависимость между нагрузкой р, основным параметром прогиба С и редукционным коэффициентом ср, полученная исходя из выражения 46.
 Приложим теперь к той же задаче метод возмущения см. § 11. Так как в данном случае пластинка загружается до возникновения прогиба начальными критическими усилиями, то надо дополнить разложение для Ф 1.133 членом <р0лт, у, не зависящим от.
 Примем
 оо оо
 « 2 vnx. yfn> Ф 2 ?». yf. 3.65
 п 1 п—О
 В «нулевом» приближении п 0 получаем уравнение
 V2V'2cp0 0. а
 Решение этого уравнения выпишем в виде

§ 27 УТОЧНЕННЫЕ РЕШЕНИЯ ДЛЯ КВАДРАТНОЙ ПЛАСТИНКИ 139
 Уравнение 1.135 следующего приближения повторяет а, так что
 можно положить cpj 0. Уравнение 1.134 должно быть заменено
 другим:
 »£„ ?0, с
 или по 1.62
 -rV9V4££-о- «о
 Решение этого уравнения, удовлетворяющее граничным условиям, будет
 vx A sin хх sin <ху при а е
 вместе с тем находим критическое напряжение
 . пЮ
 5bp4PT-
 Условимся понимать под не полную стрелу прогиба, а амплитуду, отвечающую первому члену разложения для Ф; тогда t>i а 1- Но при этом и А 1. Функцию v1xi у можно
 ж ? —
 охарактеризовать как первую собственную форму для рассматриваемой краевой задачи.
 Уравнения 1.136 — 1.137 второго приближения получат вид
 4V2VJ Lvv «Pj, 1.V2V2<f>2 -jLV» vj. f
 В первом из этих уравнений правая часть тождественно обращается в нуль, так что надо положить v2 0. Второе же уравнение после подстановки е переходит в следующее:
 -g- V2 V2cp2 cos 2ax cos 2oy. g
 Решение его будет
 <p2 Jjcos2ax cos2«y —2; h
 под p2 здесь понимается то среднее дополнительное усилие, которое воспринимается пластинкой сверх критической нагрузки и отвечает второму члену разложения функции Ф.
 Определить р2 в процессе последовательных приближений нельзя; надо прибегнуть к энергетическим соотношениям. Используем уравнение метода Бубнова— Галеркина 1.124. В выражении для ?
 X--V9Vw — Lwt Ф

140 ЗАКРИТИЧЕСКАЯ ДЕФОРМАЦИЯ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК ГЛ. III
 будем понимать под w и Ф величины
 w vj, Ф <р0<р2а. 0
 Принимая во внимание с, получим окончательно условие для определения ?2 в виде
 § f Lvv yjvxdy 0; k
 F
 j?a2
 отсюда p2 — -g—. Если ограничиться этими результатами, найдем: w sin ах sin ay,
 a V2 DoV 1
 Ф y f2--Ef'2cos2ax cos 2<xy.
 Величина среднего сжимающего напряжения
 Р РгР ’кР £
 будет той же, что и в § 26, по формуле 15. Следовательно, на этом этапе метод возмущения не дал ничего нового.
 Можно, однако, привлечь следующее — третье — приближение.
 Из 1.139 получим <р3 0; уравнение же 1.138 примет вид
 -£-VaV3 Lvv ?2.
 Подставляя е в h, после сокращений получим:
 V2V3 Еа1 sin Sax sin ay-f- sin ax sin Say.
 Отсюда при заданных граничных условиях
 vs —— -2 sin Зал: sin ay -f- sin ал: sin Say. 1
 Выражение прогиба принимает вид
 w — fn sin ал: sin ay -f-3i sin Зал: sin ay --13 sin ax sin Say, m
 где
 f _ f f __ f _31-Я
 .mi > 13 31 400 Д2 •
 Таким образом, нам удалось уточнить форму изогнутой поверхности; по мере возрастания прогибов она все более отличается от собственной формы е. Вновь полученные параметры 13 и и оказываются пропорциональными кубу основного параметра и, причем отношение ф 13и составляет при х 0,3
 h, '

§ 28
 КВАДРАФЙАЯ ПЛАСТИНКА, ЗАЩЕМЛЕННАЯ ЙО КРАЙМ
 141
 Такое соотношение между основным и дополнительными параметрами близко к тому, которое было получено выше. Это можно проследить по таблице III: отношение йС2 остается при С <2,5 почти постоянным и равным 0,01.
 Продолжая выкладки, можно определить функцию ср4 и найти постоянную ?4 из нового уравнения типа к. Так может быть уточнена диаграмма сжатия пластинки.
 § 28. Квадратная пластинка, защемленная по краям
 Рассмотрим деформацию после потери устойчивости квадратной пластинки со стороной а, защемленной по всему контуру. Сохраним при этом условие свободного скольжения кромок вдоль подкрепляющих ребер; продольные кромки будем считать свободно смещающимися. Выберем выражение для прогиба в виде
 w sin2 sin2. 3.66
 Уравнение совместности деформаций примет форму 2.133. Решение этого уравнения представим аналогично 2.134, считая а р--,
 Ра; —Рх и Ру °
 cosi? cos г - 512 fi cos Ч- cos г
 , 1 4ъх 2тсу, 2пх 4пу
 4- 2 COS COS —- -Ь COS COS —- —
 1 800' a a 1 a a
 • <3-67>
 Напряжения в срединной поверхности будут определяться выражениями 2.135 — 2.137 с теми же изменениями. Приведем выражение для ох:
 ц2 2 2гс у. ТС2 2 4 ТС у я2 f2 4кх 2тсу
 о ■S' C0S -QO cos S COS COS —
 x 8 a2 a 1 32 a2 a 200 a? a a
 tc2 2 2nx 4ny. rc2 2 2kx 2ny 0
 - 50cos — cos Тб cos — cos-Г-P- 3-68>
 Касательные напряжения на кромках оказываются равными нулю; условие прямолинейности кромок выполняется.
 Уравнение метода Бубнова — Галеркина получает вид 2.143. Выпишем полученное этим же путем в § 21 окончательное уравнение 2.145. При q 0 для квадратной пластинки будем иметь:
 533 4, q Я 3 712

142 ЗАКРЙТИЧЕСКАЯ ДЕФОРМАЦИЯ ИРЯМОУГОЛЬЙЫХ ПЛАСТИНОК ГЛ. III
 Считая Ф 0, будем иметь:
 „_32п 0 » 5332 А2
 р 3 аШ' 2400 а ‘ 3.70
 Критическое напряжение получается равным
 оК1, 10,670--. 3.71
 Погрешность по отношению к уточненному решению 16
 овр 10,50-- 3.72
 составляет около 1,5°0.
 Полагая
 <3'73>
 представим 70 в виде
 <3-74>
 критическому напряжению будет соответствовать величина при
 х 0,3
 а а2 8тс2
 ’1 -гт -9<ГГ9-6- <375>
 Напряжения в краевых волокнах будут равны сжимающие напряжения считаем попрежнему положительными:
 I с о23 1 4гсл:. 17 2я Q 7ч
 ММзг - 200 cos — 400 cos—; 3' 76
 напряжение ор меняется по длине пластинки. Вычислим «среднюю» величину напряжения по формуле 58; найдем
 P §2EifK <3-77>
 Пользуясь безразмерным параметром 61, перепишем 77 в форме
 <3-78
 Сопоставляя уравнения 74 и 78, находим:
 >0,7о; 0,3о;. 3.79
 Редукционный коэффициент получается равным
 <Р 0.7 - 3-8«
 Судя по этому выражению, в случае защемленных краев пластинки редукционный коэффициент имеет большие значения, чем

§ 29 ПРИБЛИЖЕННЫЕ ФОРМУЛЫ ДЛЯ РЕДУКЦИОННОГО КОЭФФИЦИЕНТА 143
 при шарнирно опертых краях; 0,7 ширины пластинки здесь может быть непосредственно присоединено к подкрепляющим ребрам и лишь 0,3 ширины редуцируется по отношению 1я.
 § 29. Приближенные формулы для редукционного коэффициента
 Мы видели, что по мере повышения нагрузки в закритической области напряжения сжатия значительно возрастают у краев и остаются почти постоянными или даже уменьшаются в средней части пластинки. При достаточно большой нагрузке почти вся сжимающая сила воспринимается полосами пластинки, прилегающими к подкрепляющим элементам. Основываясь на этом, Т. Карман предложил следующий метод определения приведенной ширины пластинки 329.
 Предположим, чго сжимающая нагрузка воспринимается только краевыми полосами, общая ширина которых равна приведенной ширине ЬЩ, и что напряжения ор распределены по этой ширине равномерно. Попытаемся определить напряжения ор как критические напряжения, удерживающие в равновесии «приведенную пластинку»:
 где k — коэффициент, зависящий от условий закрепления. Но истинное критическое напряжение для реальной пластинки равно
 Считаем граничные условия для «приведенной» и реальной пластинок одинаковыми. Сравнивая 81 и 82, получаем:
 a b2
 — 7Г- 3‘83
 акр ЯГ
 Таким образом, отношение краевого напряжения к критическому равно квадрату отношения истинной ширины пластинки к приведенной. Отсюда вытекает формула для редукционного коэффициента
 ¥
 -Т“ 1 <3'84>
 Судя по этой формуле, при весьма большом п редукционный коэффициент приближается к нулю; напомним, что раньше мы получали другие предельные значения для ср, равные 0,5 или 0,33. Полученный здесь результат надо признать более вероятным. Из определения редукционного коэффициента вытекает соотношение <ррар. Поэтому для среднего сжимающего напряжения получаем выражение
 pzY<3vQt, 3.85

144 ЗАкРЙТЙЧЕСКАЙ ДЕФОРМАЦИЯ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК ГЛ. III
 т. е. среднее геометрическое из краевого и критического напряжений вместо среднего арифметического по формуле 21.
 Для определения предела упругого сопротивления пластинки
 краевое напряжение положим равным пределу текучести; тогда
 найдем:
 Рпред • 3.86
 П. Ф. Папкович, анализируя данные решения П. А. Соколова,
 предложил для редукционного коэффициента практическую формулу иной структуры :
 0,56
 ? 0,44 0,56 0,44 —. 3.87
 По сравнению с формулой первого приближения 22 здесь введены
 другие коэффициенты. Нижний предел для ср получается равным 0,44. Повидимому, эта формула должна давать хорошие результаты для сравнительно небольших значений п.
 К. Маргерр ЗЬ7 на основании своей работы, выполненной с помощью энергетического метода, дал формулу
 3.88
 Среднее напряжение оказывается равным
 3-89>
 Предел упругого сопротивления определится выражением
 йм-Tv <3-90>
 Легко видеть, что значения ср и р будут при этом несколько выше,
 чем по формулам 84 и 86.
 Допустим теперь, что напряжения в подкрепляющих ребрах превосходят предел пропорциональности материала. При этом в средней части пластинки напряжения могут попрежнему лежать в упругой области. Приведем приближенный способ определения редукционного коэффициента в предположении, что закон распределения деформаций по ширине панели остается тот же, что в упругой области. На фиг. 3.8 слева от оси симметрии показана эпюра деформаций г. Если бы деформации были упругими, величинам е соответствовали бы напряжения о Ег и мы получили бы аналогичную эпюру для напряжений пунктирная линия 1 справа. Однако за пределами упругости каждому значению е отвечает новое значение а, определяемое по
 См. 16, стр. 914.
 Считаем его равным пределу упругости.
 Этот метод предложен Жераром а-2,<.

ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ
 145
 диаграмме о г для данного материала линия 2. Примем для упрощения, что эпюра напряжений имеет вид линии 3; такое допущение будет давать некоторый дополнительный запас прочности. Но тогда можно, определив по диаграмме ае напряжение в стрингере ар, отвечающее заданному укорочению панели е, воспользоваться обычными формулами для редукционного коэффициента, например применить формулу
 где под о' понимается истинное напряжение в подкрепляющем ребре, превышающее предел пропорциональности материала. Эти рассужде¬
 ния относятся к случаю, когда напряжение о' не достигает предела текучести для материала с ясно выраженной площадкой текучести, так как при этом напряжении должен произойти продольный изгиб ребер независимо от размеров конструкции.
 § 30 Экспериментальное исследование закритической деформации пластинок
 Деформации сжатых пластинок после потери устойчивости был посвящен ряд экспериментальных исследований. Приведем данные опытов автора книги, в которых определялись форма волнообразования, характер распределения напряжений и редукционные коэффициенты для защемленных по краям пластинок.
 Образцы были изготовлены из дуралюминового листа материал Д16Т толщиной h 1 мм; ширина и длина составляли b — 240 мм и а — 480 мм. По продольным кромкам лист приклепывался к мощным
 3.91
 7
 Фиг. 3.8. Эпюры деформаций слева и напряжений справа по ширине пластинки в упругопластической области.

146 ж ЗАКРИТИЧЕСКАЯ ДЕФОРМАЦИЯ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК ГЛ. III
 П-образным профилям, как показано на фиг. 3.9. Общая потеря устойчивости панели вместе с профилями была исключена, так что края пластинки оставались прямолинейными; не наблюдалось и местного
 выпучивания листа или стенки профиля между заклепками. Панели подвергались сжатию между плитами гидравлического пресса.
 Запись деформаций на различных ступенях нагружения велась с помощью электрических проволочных датчиков, наклеенных в про-
 Фиг. 3.10. Установка для исследования деформации пластинки с помощью «отраженной сетки».
 дольном и поперечном направлениях с разных сторон листа. Кроме того, непрерывно передавались на особые электронные приборы показания «парных» датчиков, учитывающих только деформации изгиба; эти датчики служили для определения момента потери устойчивости.

§ 30
 ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ
 147
 Характер волнообразования выяснялся с помощью особого оптического метода. На некотором расстоянии от панели устанавливался экран — лист кальки с нанесенными в шахматном порядке черными и белыми клетками. Сквозь экран на панель падал рассеянный свет от прожектора; в центре экрана имелось отверстие, через которое производилось фотографирование поверхности оболочки с отраженными клетками фиг. 3.10. На панель предварительно наносился слой черной блестящей эмали. При самых незначительных прогибах, сопровождающихся поворотами нормалей к поверхности оболочки, отражение шахматной доски получало искажения: на выпуклых местах
 Фиг. 3.11. «Отраженная сетка» на различных ступенях нагружения
 пластинки.
 клетки размельчались, а на вогнутых — укрупнялись. На фиг. 3.11 приведены три фотографии «отраженной сетки» для пластинки: а — до потери устойчивости, б—после выпучивания при малых прогибах и в — при больших прогибах. Сопоставление подобных фотографий показывает, что реальный процесс деформации пластинки не вполне сходится с теоретическими результатами. В § 24 предполагалось, что форма волнообразования меняется при нагружении пластинки непрерывно. В действительности постепенные изменения прерываются хорошо заметными скачками, сопровождающимися изменением числа волн изогнутой поверхности. На фиг. 3.12 схематически изображен «механизм» такого скачка. Пусть при малой нагрузке выпучина имеет форму, показанную на фиг. 3.12, а внизу изображено поперечное сечение оболочки. Возрастание сжимающей силы приводит к образо¬
 Подобный метод был применен В. И. Блох для решения задач о кручении стержней с помощью мембранной аналогии Труды конференции по оптич, методу, Ленинград, 1936. См. также статью Э. Челлара Melyepitestudimangi Szemle 3, № 2, 1953, 87—93.

148 ЗАКРИТИЧЕСКАЯ ДЕФОРМАЦИЯ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК гл. III
 ванию новых мелких выпучин у краев фиг. 3.12, б; в последующем эти краевые выпучины углубляются и расширяются фиг. 3.12, в. Наконец, происходит скачок к положению, указанному на фиг. 3.12, в пунктиром. Очевидно, величина потенциальной энергии системы, соответствующей новому равновесному положению фиг. 3.12, г, меньше, чем в прежнем: при скачке происходит переход части потенциальной энергии в кинетическую. Это выражается в резких колеба-
 Фиг. 3.12. Волнообразование сжатой пластинки в процессе закритической деформации.
 ниях всей конструкции машины. Такие скачки повторяются при повышении нагрузки несколько раз и приводят к размельчению волн в продольном направлении. При этом, повидимому, скачкообразно должны изменяться и редукционные коэффициенты.
 На фиг. 3.13 показаны эпюры распределения напряжений по ширине одной из панелей на различных ступенях нагружения. Критическое напряжение, равное 523 кгсм?, отвечает нагрузке 10 т; до этой нагрузки напряжения распределялись по сечению равномерно. В дальнейшем напряжения в средней части панели оставались почти постоянными, в то время как в краевых полосах они последовательно возрастали. При максимальной нагрузке на панель 40 т краевые напряжения составляли около 2000 кгсм2, т. е. превышали критическую величину примерно в 4 раза. Штрих-пунктирная кривая построена по приближенному уравнению 7, полученному в качестве первого приближения для шарнирно опертой пластинки.
 Пунктирные линии на фиг. 3.13 указывают уровень средних напряжений по ширине панели при каждой нагрузке. Как видим,
 Теоретическое исследование подобного процесса было проведено Г. Г. Ростовцевым 3.14 и В. П. Белкиным Работа после потери устойчивости элементов палубных перекрытий, Судпромгиз, 1956.

§ 30
 ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ
 149
 среднее напряжение возрастает в течение всего периода нагружения. Пользуясь этими данными, можно установить зависимость между средним и краевым напряжениями. Подобная зависимость представлена на фиг. 3.14. Закон изменения среднего напряжения после потери
 Фиг. 3.13. Распределение напряжений по ширине панели при закри тической деформации.
 устойчивости приближается к линейному; это соответствует теоретически найденному графику фиг. 3.5. Напомним, что краевое напряжение ар пропорционально сближению нагруженных кромок панели е.

250
 Критическое напряжение бкр523кгсм2
 250 500 750 1000 7250 1500 1750 2000
 вр кгсм2
 Фиг. 3.14. Диаграмма «нагрузка — краевое напряжение» для сжатой панели.
 10 Г
 Jiff
 as
 Q7 QS
 0,5
 Q
 as 02
 0,7
 2 4 S 8 Ю 72 74 7o 76 n 20
 Фиг. 3.15. Редукционные коэффициенты для сжатых панелей по теорети ческим и экспериментальным данным.

§31 ПЛАСТИНКА, ПОДКРЕПЛЕННАЯ УПРУГИМИ РЕБРАМИ 151
 Полученные в опытах значения редукционных коэффициентов даны на фиг. 3.15. Здесь же приведены кривые, отвечающие приближенным формулам 22, 84 и 88, уточненным решениям с двумя параметрами см. таблицу III и с шестью параметрами 2Л7, а также формулам Папковича 87 и Бубнова 23. Из графика можно заключить, что экспериментальные значения редукционных коэффициентов лежат ниже величин, найденных в уточненных решениях. Формула же 84 дает при п > 3 преуменьшенные значения ср.
 В практических расчетах можно пользоваться уточненным решением с шестью параметрами или формулой 88, если есть уверенность, что допущения теории выполняются и, в частности, что напряжения в ребрах лежат значительно ниже эйлеровых. В том случае, когда жесткость ребер недостаточно велика, следует пользоваться формулой 84.
 § 31. Пластинка, подкрепленная упругими ребрами
 Несущая способность сжатой пластинки в значительной мере зависит от жесткости подкрепляющих ребер. До сих пор предполагалось, что пластинка связана по кромкам с ребрами, абсолютно жесткими на изгиб и кручение. Примем теперь, что по продольным сторонам а пластинка защемлена, причем подкрепляющие ребра стрингеры податливы по отношению к изгибу в направлении оси г фиг. 3.16, а.
 Что касается нагруженных кромок Ъу то будем считать их прямолинейными и опертыми шарнирно.
 Примем уравнение изогнутой поверхности пластинки в виде
 w i sin2 — sin2
 J1 a b 1
 “bosin a • 3.92 фи g jg Конструкция из пластинки и ребер, податливых по отношению Параметр 0 характеризует к изгибу вдоль оси г.
 изогнутую линию стрингера,
 а х — дополнительный прогиб пластинки; величины 0 и fx равны стрелам прогиба стрингера и пластинки. На фиг. 3.16, б показано сечение тп в смещенном положении после изгиба пластинки.
 К результатам опытов автора книги присоединены данные экспериментов 2.17.

152 ЗАКРИТИЧЕСКАЯ ДЕФОРМАЦИЯ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК гл. III
 Уравнение совместности деформаций в срединной поверхности пластинки 1.61 примет форму
 J. V2V2<I> -i a2p2i cos -j- cos 2y — cos 4y — cos 2<xx cos 2y -f-
 -f- cos 2y — cos 2<xx cos 2y 3.93
 как и прежде,
 Р-f- <3-94>
 Интеграл этого уравнения будет
 i ф т icos 2ахf cos тврcos —
 — ffjpy cos 2ax cos 2?у ш ®W‘ j?cos —
 — аа -j р22'cos 2oar cos 2?у — §?» 3-95
 где через р обозначено среднее сжимающее напряжение в пластинке. Относительное сближение нагруженных кромок равно
 а
 1 	Г Г 1 дф 1 дтЦ.
 в а е дуг V-dtf 2 дх J dX’
 О
 после вычислений получаем:
 е 32 Зi 8о 8oi • 3 • 96
 Отметим, что в приближенном решении выполняется условие прямолинейности нагруженных кромок.
 Воспользуемся методом Ритца. Энергию изгиба пластинки определим, пользуясь выражением 1.109; будем иметь:
 ип ?з 5 8о Wi • 3-97
 Энергия деформации в срединной поверхности UG 1.106 оказывается равной:
 1 wwulhfb
 4-Й-1-ё-Ь2ТЭррт5»Л —<3'98
 Энергию изгиба двух стрингеров вычислим по формуле
 з

§ 31 ПЛАСТИНКА, ПОДКРЕПЛЕННАЯ УПРУГИМИ РЕБРАМИ 153
 где через обозначен момент инерции сечения стрингера относительно центральной оси, параллельной плоскости пластинки. Получим:
 ии,р ±Е1Уа. 3.100
 Работа внешних сил, приложенных к пластинке, будет равна
 Г phea ±phab<fi Щ Щ 80хг ab. 3.101
 Будем считать, что стрингеры несут сжимающие усилия ор. Обозначая через Fp площадь сечения стрингера, найдем работу этих усилий
 равной
 3.102
 о
 или
 с2 1
 W' -Fia — 3.103
 Общая энергия системы равна
 3 IHtcfHfp — W— W'. 3.104
 Равновесному положению системы «пластинка — стрингеры» отвечают уравнения:
 1°> 1°- <зл05>
 Введем обозначения, характеризующие изогнутую поверхность:
 с4 fi' ЗЛ06
 и относительную жесткость стрингера на сжатие и изгиб:
 8М’ 3.107
 Выполняя дифференцирование и полагая А Ф 0, придем после простых преобразований к следующим уравнениям:
 гв I4 2cfj2J 2 s4WJ 3 2а pi» '>’2 31-, 3 1614
 8I24--212i 0; 3.108
 2a2 p2a2't'H“ 1а 3i — p.a 1 Н 2Ф
 Р а2,с,<, о,ч, 16. ®РУл'а

154 ЗАКРИТИЧЕСКАЯ ДЕФОРМАЦИЯ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК гл. III
 Отбрасывая в этих уравнениях нелинейные члены, получим систему уравнений, отвечающих моменту потери устойчивости:
 здесь принято ор р.
 При заданных значениях f и 8 из последних уравнений можно определить критическое напряжение окр и параметр ф. Допустим, что сжимающие усилия приложены только к пластинке; тогда надо положить 8 0. При этом критическое напряжение можно выразить следующим образом:
 Если стрингеры абсолютно жестки на изгиб, следует считать оо. Тогда из уравнений ПО — 111 получим:
 Если, к примеру, отношение сторон пластинки равно 23, будем иметь т 9,72 и К 7,3. Уточненное решение 1>6 дает в этом случае К 7,0.
 Возвратимся к полной системе кубических уравнений 108— 109. Для любого усилия р, превышающего критическое, можно из этгх уравнений найти параметры С и Далее, для каждой ступени нагрузки может быть найден редукционный коэффициент ср как отношение напряжения р к напряжению в краевых волокнах При¬
 водим таблицу IV значений ср, полученных для пластинки с отношением сторон X 93 в предположении, что нагрузка приложена только к пластинке.
 Считается, что края пластинки свободно скользят вдоль стрингеров.
 3.110
 3.112
 причем коэффициент К равен
 К ±т— 1 6тг —.т— 1 6-гЯ — 2отТ-f-т—2; 3.113
 через т обозначено

§ 32
 РЕДУКЦИОННЫЕ КОЭФФИЦИЕНТЫ
 155
 Таблица IV
 Редукционные коэффициенты для панели, скрепленной с упругими ребрами
 1
 2
 3
 4
 5
 оо
 1
 0,69
 0,63
 0,60
 0,58
 20
 1
 0,68
 0,61
 0,57
 0,55
 15
 1
 0,67
 0,60
 0,55
 0,52
 10
 1
 0,66
 0,58
 0,53
 0,48
 5
 1
 0,61
 0,49
 —
 —
 Как видим, с уменьшением изгибной жесткости подкрепляющих ребер редукционные коэффициенты падают.
 § 32. Редукционные коэффициенты при вычислении момента инерции сечения панели
 До сих пор мы говорили о редукционных коэффициентах, определяющих долю участия обшивки или тонкой стенки в воспринятии некоторой сжимающей нагрузки. Предположим теперь, что вслед за местной потерей устойчивости пластинок, входящих в состав конструкции, происходит продольный изгиб конструкции в целом, т. е. «жестких» элементов вместе с «гибкими». Тогда для вычисления критической нагрузки необходимо вычислить момент инерции сечения конструкции. Войдут ли при этом «гибкие» элементы с теми же редукционными коэффициентами, как и при воспринятии статической сжимающей нагрузки? Чтобы ответить на этот вопрос, надо учесть, что в задаче о нахождении эйлеровой силы речь идет об изменениях напряжений при малых приращениях деформаций. Гибкая обшивка может при этом оказаться как на стороне дополнительного сжатия, так и на стороне разгрузки.
 Обратимся к диаграмме зависимости между нагрузкой и сближением краев пластинки или, что то же самое, к диаграмме ре
 фиг. 3.17. Малому изменению величины е на -f-Ae или —Ае соответствует приращение Ар; для малых величин Ае можно принять,
 что отношение Ар к Ае равно производной. Но относительное
 сближение краев е мы считаем пропорциональным напряжению в жестком элементе oF. Поэтому доля гибкого элемента пластинки
 Фиг. 3.17. Диаграмма «нагрузка — общая деформация» для сжатой пластинки.

156 ЗАКРИТИЧЕСКАЯ ДЕФОРМАЦИЯ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК ГЛ. III
 в воспринятии изменяющейся нагрузки будет отвечать не отноше-
 инерции сечения панели мы должны вводить обшивку или тонкую стенку с редукционным коэффициентом
 т. е. здесь нужно пользоваться касательным модулем диаграммы ре вместо секущего модуля.
 Вычислим величину ср, соответствующую различным приближенным значениям ср. Если воспользоваться формулой первого прибли-
 Таким образом, редукционный коэффициент для гибких элементов при вычислении момента инерции сечения панели всегда меньше, чем при определении площади сечения. Однако на практике пользование различными коэффициентами ср и ср сильно осложняет расчеты: надо учесть, что при определении эйлеровой нагрузки для конструкции напряжения ор заранее неизвестны и величины ср и ср можно установить только после нескольких проб. Поэтому обычно принимают коэффициенты ср теми же самыми, что и при определении площади сечения, т. е. считают ср ср, хотя это и несколько преувеличивает несущую способность конструкции.
 По свидетельству JI. Я. Резницкого такое предложение было выдвинуто П, Ф. Папковичем.
 нию рсзр, а величине. Иными словами, при определении момента
 3.115
 жения 21, то получим для ср постоянное значение
 ср 0,5.
 3.116
 Исходя из формулы Папковича 87, будем иметь:
 ср 0,44.
 Пользуясь формулой Кармана 85, найдем:
 3.117
 3.118
 Отсюда вытекает, что коэффициент ср вдвое меньше «обычного» редукционного коэффициента: ср 0,5ср. Наконец, по формуле Маргерра 88
 2
 Здесь коэффициент ср оказывается равным ср --ср.

§ 33 КВАДРАТНАЯ ПЛАСТИНКА ПОСЛЕ ПОТЕРИ УСТОЙЧИВОСТИ 157
 Окончательное заключение можно здесь сделать только после проведения тщательно поставленных опытов, в которых конструкция с гибкими элементами подвергалась бы продольному изгибу.
 Разберем случай квадратной пластинки, шарнирно опертой по краям, подвергающейся действию приложенных ко всем кромкам сдвигающих усилий 5. Введем также сжимающие усилия рх и ру с тем, чтобы распорядиться условиями закрепления краев пластинки фиг. 3.18. Допу-
 где а — сторона пластинки, п и f22 — независимые параметры. Уравнение 1.61 принимает форму
 Определим, далее, сближение краев пластинки по направлениям х и у:
 § 33. Квадратная пластинка после потери устойчивости от сдвига
 стим, что сдвигающие усилия превысили критическое значение и пластинка получила прогибы, сравнимые с ее толщиной.
 Прогиб пластинки будем аппроксимировать в первом приближении двумя членами тригонометрического ряда:
 ь
 Фиг. 3.18. Квадратная пластинка при, 3.120 сдвиге с учетом нормальных усилий по
 кромкам.
 Решению этого уравнения придадим вид

158 ЗАКРЙТИЧЕСКАЯ ДЕФОРМАЦИЯ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК ГЛ. III
 Имеем:
 ди _ 1 дФ дФ 1 dw2 Q 10ч
 дх Едуъ 2 U ’ 3.124
 dv 1 дФ д2Ф 1 dw2 0 1оеч
 ду Едл;2 2ду ‘ 3.125
 Пользуясь выражениями 120 и 122, находим:
 ех Ш “2022 — 3.126
 и по аналогии
 f2 I 712 2 I Ря о 1074
 у 8о2и 2а322“1Г— л,£г• 3.127
 Деформация сдвига в произвольной точке пластинки равна
 т ® _2_1Ф ' ду 1 дх 1 дх ду Е дх ду 4 7
 Отсюда
 ди, dv 21 г г2 л3. 2ъх. 2тт:у
 J ■ 5 и j-5 sin sin — —
 ду 1 Е 1 ;а 4аа а а
 .2 тс2 47тл:. 4теу -. 2. Зкх. Злу. те. теу 0 10ЛЧ
 - 22 згsm — 5111 л 1122 sin —- sm -JL — sin - sin -f • 3.129
 Желая определить перемещения произвольной точки и, находим из выражения 128 величину а из 125 — i
 вели-
 ди д2и п
 чину • Отсюда получаем производную • С другой стороны,
 дифференцированием 124 находим. По этим двум производным определяем с точностью до постоянной Аналогичным образом находим и после подстановки в 129 определяем постоянные. Далее находим функцию и:
 х2 те2 Г. л ч а. 2тел: а. Ъх. 2теу
 и — —lirsUT —po-sin 7S“ sin sin—- —
 J11 8aa _ 14 ‘ ' 2те а 2те a a J
 ,2 Г, 1, a. 4кх a. 4те. 4теу1
 f 22 гГо I —г 1 X — Sin — Sin Sin —- J 2a2 1 v 4те а 4те a a J
 —fit fa m 3 3 — 2ii sin cos1Г — V 2>sin T cos IT
 25 sin cos — у sin cos j — p—W>„§- 0 1.У-
 3.130

§ 33 КВАДРАТНАЯ ПЛАСТИНКА ПОСЛЕ ПОТЕРИ УСТОЙЧИВОСТИ 159
 Вычислим «среднее» смещение и вдоль стороны у — а
 Uya ij “ yadx —f -25Г
 О
 ii22 22fc164-36ii-lxa. 3.131
 Аналогичным путем для стороны 0 найдем:
 “ U; - л ш f £- «»253?1<:164- 36>>- <3-132>
 Определим сдвиг, соответствующий взаимному смещению сторон у а и у 0:
 О'- - Ъ-о 164- 36 -1 г.
 Такой же сдвиг будет соответствовать взаимному смещению двух других сторон пластинки х а и х 0, поэтому общая деформация сдвига пластинки, рассматриваемой как одно целое, будет равна
 e 20' 41-9x 7±s. <ЗЛЗЗ>
 До потери устойчивости соотношение между деформацией сдвига и приложенным усилием характеризуется соотношением
 9 2 1Хs s- 3.134
 После потери устойчивости деформация растет быстрее, чем нагрузка; при jx 0,3 найдем:
 в -£ 2-72V2 2, 3.135
 где
 Введем понятие касательного модуля сдвига Ок. ц для пластинки в целом, как это мы делали в случае закритического сжатия по отношению к модулю Е, и примем
 <3к.ц §. 3.137
 Обозначим далее через п коэффициент, характеризующий степень превышения напряжением 5 критического значения :

160 ЗАКРИТИЧЕСКАЯ ДЕФОРМАЦИЯ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК ГЛ. III
 Тогда из 135 получим:
 Касательный модуль будет равен
 GK. ц О
 3.139
 3.140
 Для определения зависимости параметров прогиба от нагрузки составим уравнения Бубнова — Галеркина:
 j J Xsin ™ sin dx dy 0,
 F
 J J X dx dy 0.
 3.141
 Находя функцию X по выражению 1.123, подставляя ее в уравнения 141 и производя интегрирование, придем к таким кубическим уравнениям относительно параметров и и 22:
 «4 3, 2тс4 f 2 I Э f ТС2 f Я2 - 32 S г п
 Ъ2с 11 ‘ 25л2 •'И-'22“Г2Ж-'11 ePxJ 4£pyJ22 “9 £22 и>
 3.142
 ГС з. 2т:4 2 £> я2 Я2 32 5 а
 2а22 ‘ 25а2'11'22 ‘ a2 Eh 22 Е ЕРу22 9 Е11
 3.143
 Для случая малых прогибов получим линейные уравнения, связывающие параметры flv 22 и усилия:
 тЛ D г 32 S J. ТС2 ТС2 г Л
 Rhhi -QЁ22 TpPxJn TpPyJ22 U>
 16
 a2 Eh тс О
 9 Е-
 32 s
 4Е1 2
 4 Е1
 ТС2
 а2 Eh
 22 g j?11 £pxfl £ Pyf2 ®
 3.144
 Рассмотрим случай, когда рх ру 0. Если п и 22 отличны от нуля, то должно быть
 тс4 D_ a? Eh
 32 s_ ’ 9 Е. Z
 32 1 г.
 9 £ a Eh
 0.
 Отсюда находим критическое напряжение равным
 _ ___9 тс4 Z
 s — •е.р — 8 д2 д.
 3.145
 3.146

§ 33
 КВАДРАТНАЯ ПЛАСТИНКА ПОСЛЕ ПОТЕРИ УСТОЙЧИВОСТИ
 161
 Отклонение от уточненного значения 16
 TBi, 92,2
 составляет около 19. Напомним, что величина 146 была получена нами при задании лишь двух независимых параметров прогиба; для того чтобы получить лучшее приближение, должно быть взято не менее пяти надлежащим образом выбранных параметров.
 Уравнения 142 и 143 дают возможность определить зависимость между параметрами прогиба а и 22 и нагрузкой после потери устойчивости. Вводя параметры
 п-тд'- л-• ЗЛ47
 и пользуясь обозначениями 136, приведем эти уравнения к виду
 г 2 _ г Г Г
 8
 2q
 7:2 3 8гс2 » г
 R “г “9S 12 ' кр 1
 -рА-
 8г-2
 25
 здесь ор отвечает критической нагрузке для пластинки,
 3.148
 сжатой
 в одном направлении:
 ТС2
 JKp •
 31 -ь24
 3,6.
 3.149
 В дальнейшем будем различать два случая закрепления кромок пластинки.
 1. Кромки пластинки сближаются свободно. В этом случае рхру 0. Примем
 4
 Ыг
 3
 г
 2
 ————
 2 2
 “Cl “Л
 3.150
 5 л
 Фиг. 3.19. Параметры прогиба пластинки при сдвиге в зависимости от нагрузки.
 и исключим s из уравнений 148; тогда получим биквадратное уравнение относительно ty:
 W 0. 3.151
 Задаваясь различными значениями Сх, находим отсюда величины ф. Подставляя затем и ф в уравнения 148, определяем s, а затем п по 138; в качестве тр взята приближенная величина 146.
 Таким образом устанавливается соотношение между параметрами прогиба и нагрузкой. Сплошные кривые на фиг. 3.19 дают зависи¬

162 злкритичЕСкАя дёформация Прямоугольных Пластинок гл. m
 мость между С2 и п. Путем графического дифференцирования
 можно далее найти производные и и по 140 определить касательный модуль Ок. ц. Значения отношения г Ок. 4G представлены на фиг. 3.20 сплошная линия. В момент потери устойчивости модульФк.ц снижается до0,820, а в дальнейшем изменяется менее заметно.
 2. Кромки пластинки не сближаются. Величины р
 И
 и ру найдем из условий ех еу 0. Пользуясь выражениями 126—127, получим:
 pl py - 8 11,л Г4 4ф. 3.152
 Подставим эти значения в уравнения 148 и исключим s; тогда получим следующее уравнение относительно
 0,76'У — 0,0625 0,0477 0. 3.153
 Окончательная зависимость между Сх, С2 и п дана на фиг. 3.19 пунктирные линии.
 На фиг. 3.20 представлены соответствующие значения GK. ц также пунктиром. Величина сдвигающих усилий, воспринимаемых пластинкой, значительно возрастает по сравнению со случаем свободно сближающихся кромок.
 § 34. Удлиненная пластинка при сдвиге
 Перейдем к случаю пластинки, сторона которой а значительно превышает сторону b. Допустим, что пластинка шарнирно оперта по всем кромкам и испытывает действие сдвигающих усилий 5 фиг. 3.21. Так же как и для квадратной пластинки, введем дополнительно сжимающие усилия рх и ру.
 Примем, что изогнутая поверхность пластинки при потере устойчивости и во время закритической деформации определяется выражением
 w sin у л: — ky sin ; 3.154
 через k здесь обозначается тангенс угла наклона узловых линий к оси у, через — расстояние между узловыми линиями, через Ъ — ширина пластинки.
 1.0
 V
 0,8
 Фиг. 3.20. Модуль общей деформации сдвига в зависимости от нагрузки.
 1 •

§ 34 удлиненная Пластинка при сдвИГё
 Уравнение совместности 1.61 принимает форму VW cos X - ky cos.
 Решение уравнения 155 представим в виде
 фЕй т 17005 т £005 ¥ -
 163
 3.155
 Напряжения в срединной поверхности будут
 „ я2 Г а 1 2л.. ч 1 2ялЛ
 в® — £ 8 aT°°S1 Х У гZ0 МРх’, 22
 Зу — Е
 1 Е
 1
 8 62 l-f £22 тг2 2 £
 2тс ✓ cos у-л:-
 •ky—Py,
 2тс, cos у л; ■
 Ау-
 S.
 3.156
 3.157
 3.158
 3.159
 8 2 1 £22
 Идя тем же путем, что и в случае квадратной пластинки, опре
 J7
 Фиг. 3.21. Пластинка при совместном действии сжатия и сдвига.
 деляем перемещения и и v произвольной точки пластинки:
 “ ш w<JTW 1 —'cosJsinт<■-W -
 2я£ __ 2fe у 4- sin — 1 Jx — рр9 X 2 1 gy,
 3.160
 - т2 2 т 1 -cos т sin 2х “
 — py — v-py- 3.161

164 ЗаКРИТИЧЕСКаЯ деформация прямоугольных пластинок гл. п
 Сближение кромок пластинки по направлениям осей х и у будет определяться формулами типа 126. В нашем случае
 3.162
 т£д’- <3163
 Вычислим «среднее» смещение и точек кромки у Ь на длине участка :
 “U T 5и1.ъах Щ-1-Я2<Р-Р' ШР18Ь‘
 о
 Аналогично для точек кромки у 0:
 -т «аа
 8
 Вводя понятие деформации сдвига пластинки «в целом» и обозначая ее попрежнему через 6, найдем:
 а 1 ГН “I 1 kf2 I 21 fA
 — b I u w°J — 42 £ s>
 или
 <ЗЛ64>
 здесь С fjh — параметр прогиба.
 Касательный модуль Ок. ц 137 определится из соотношения
 1 1. dc, _L
 <..ц 2 а
 при л sfткр. Отсюда
 °к- 4 0. tfC • 3.165
 2 » А»
 Составим уравнение Бубнова—Галеркина:
 Ш' 6, £й_2_д2ф if«L_DiV2vUy
 ду2 д4 дх2 ду2 дду дхду h J
 о 	о
 X sin х — kysn у 0

§ 34
 УДЛИНЕННАЯ ПЛАСТИНКА ПРИ СДВИГЕ
 165
 Подставим под знак интеграла выражения для производных от w и Ф; после интегрирования получим:
 Мы предполагаем, что до потери устойчивости усилия рх и ру отсутствуют; поэтому критическое напряжение ткр будет равно
 В этом выражении неизвестными остаются величины k и. Определим их из условия минимума ткр, приравнивая нулю производные от ткр по отношению Р№ и па L Тогда получим:
 Таким образом, в момент выпучивания расстояние между узловыми
 узловых линий <х должен составлять около 35°. Критическое напря жение составит при этом
 Ошибка приближенного решения по сравнению с точным значением р46 ткр 5,35т'PDjbh составляет около 5,5°0.
 Перейдем к рассмотрению закритической деформации пластинки; сделаем при этом допущение, что форма волнообразования остается после потери устойчивости неизменной, т. е. оставим в силе
 1 ЩЧ
 1
 i D mk ? ¥26<J
 —swf—pwf—pv тУ 0- ЗЛ66
 Полагая £0, найдем:
 1 2 ь
 1
 ’»те“,25'ж<'Н- 368
 3.169
 Из этих уравнений находим:
 3.170
 линиями в
 11,5 раза превышает ширину пластинки: угол наклона

166 ЗАКРИТИЧЕСКАЯ ДЕФОРМАЦИЯ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК ГЛ. III
 соотношения 170. Тогда выражениям 167, 162 и 163 можно придать вид
 yfPl-h 0.58?. 3.172
 £W- Pl->Pv °>822- 3.173
 fiT Py Wx 1 >64’2- ЗЛ74
 Критическому напряжению ткр будет соответствовать безразмерный параметр
 'Ь
 Ткр
 х о
 “-И» 5Л' <3-175
 Выражение 165 приобретает вид
 Ок. ц G. 3.176
 10,176С
 1 dn
 В дальнейшем будем различать несколько случаев закрепления кромок пластинки.
 1. Продольные и поперечные кромки сближаются свободно; ?? 0. Уравнение 172 дает
 5 	ткр0,58£2; 3.177
 отсюда
 1 	0,114с3; — 4,39
 1 dn
 и
 ц Г0,1'76■ 4,39 ° 0,5640' <3'178>
 Судя по этому результату, касательный модуль GK. ц, характеризующий упругую деформацию пластинки «в целом», получает
 в момент потери устойчивости пластинки резкий скачок, уменьшаясь почти в 2 раза, и затем остается постоянным. Напомним, что примерно такое же соотношение между £к,ц и £ получалось для сжатой пластинки, когда задача решалась в первом приближении.
 Аналогичным образом находим характерные зависимости для других случаев.
 2. Продольные кромки не сближаются, поперечные— сближаются свободно; еу 0, рх 0. При этом
 Ру — 1,64;2, п 1 0,567:2, Ок ц 0,865G. 3.179
 3. Поперечные кромки не сближаются, продольные— сближаются свободно; е„ 0, р— 0. Тогда
 X у
 4 — 0.822С2, я 1 -f- 0.227С;2, Окц 0,7220. 3.180

СОВМЕСТНОЕ ДЕЙСТВИЕ СЖАТИЯ И СДВИГА
 167
 4. Продольные и поперечные кромки не сближаются; ех еу 0. При а 0,3 будет
 Таким образом, характер закрепления кромок пластинки сильно влияет на закритическую деформацию: касательный модуль меняется в зависимости от граничных условий от 0,91G до 0,564G.
 Если воспользоваться моделью пластинки, предложенной полвека тому назад нашими кораблестроителями и нашедшей в дальнейшем известность как модель диагонально растянутого поля, то с качественной стороны результат получится весьма близким. В теории диагонально растянутого поля пренебрегают сжимающими напряжениями в срединной поверхности пластинки и ее изгибной жесткостью и считают, что образовавшиеся после потери устойчивости диагональные складки удерживаются благодаря наличию достаточно жестких продольных ребер и поперечных стоек. Получающиеся при этом значения GK. ц не превышают 0,65G и оказываются меньше величин, найденных с помощью теории гибких пластинок.
 Рассмотрим квадратную пластинку, шарнирно опертую по краям и подвергающуюся одновременно действию сдвигающих усилий s, распределенных равномерно по всем кромкам, и сжимающих усилий рх. Допустим, что преобладающими являются сжимающие усилия, и поставим перед собой задачу оценить влияние сдвига на редукционные коэффициенты пластинки после потери устойчивости. Воспользуемся для этого уравнениями, полученными в § 33 в предположении, что изогнутая поверхность пластинки представлена с помощью выражения 120.
 Будем различать два случая закрепления продольных ненагруженных сжимающими усилиями кромок пластинки.
 1. Продольные кромки сближаются свободно. Критические напряжения найдем из уравнений 144, полагая в них ру — 0. Приравнивая нулю определитель, составленный из коэффициентов при fn и 22:
 § 35. Совместное действие сжатия и сдвига
 3.182
 См. П. Ф. Папкович 1,е, стр. 918.
 Эта теория была разработана Г. Вагнером 3‘47.

168
 ЗАКРИТИЧЕСКАЯ ДЕФОРМАЦИЯ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК ГЛ. III
 получаем следующее соотношение между критическими напряжениями сжатия и сдвига при комбинированной нагрузке:
 3.183
 Здесь через р0 и 0 обозначены критические напряжения простого сжатия и простого сдвига:
 _ А __ 9 пЮ
 Ро 4 am ’ S0 R а2 h •
 3.184
 Выражение для s0 отвечает, как мы видели, первому приближению в решении задачи. На фиг. 3.22 представлена зависимость между
 РхРо и slsо по 183-
 Обращаясь к закритической деформации пластинки, воспользуемся полными уравнениями 142—143, считая в них рх — 0. Принимая
 Фиг. 3.22. Критические напряжения для квадратной пластинки при комбинированной нагрузке.
 во внимание выражение 126 для сближения продольных кромок, находим напряжение в подкрепляющем ребре:
 ср Еех рхЕ Рп 4'У'.
 3.185
 В качестве параметров прогиба возьмем попрежнему величины С fnh и 22и Обозначим через и коэффициент, характери¬

СОВМЕСТНОЕ ДЕЙСТВИЕ СЖАТИЯ И СДВИГА
 169
 зующий отношение напряжений сдвига и краевых напряжений сжатия:
 5
 и —
 3.186
 коэффициент п пусть теперь определяет степень превышения краевыми сжимающими напряжениями ар критического значения
 п —. Ро
 3.187
 При заданной величине п находим значения параметров прогиба, решая систему уравнений 142—143. Выкладки показывают, что при возрастании нагрузки наряду с увеличением стрелы прогиба
 Фиг. 3.23. Редукционные коэффициенты при комбинированной нагрузке в случае свободно сближающихся кромок.
 происходит резкое изменение формы изогнутой поверхности. Сопо-
 найдем редукционные коэффициенты:
 ставляя величины ор и рх,
 Pat
 Tz2
 P Es AiО 3.188
 В результате вычислений получены величины ср, приведенные на фиг. 3.23 сплошные линии; принято а 0,3.
 При значительных напряжениях сдвига редукционные коэффициенты быстро падают, а при дальнейшем возрастании нагрузки могут сделаться «отрицательными». Это надо понимать в том смысле, что равновесное состояние пластинки будет возможно здесь лишь при растягивающих напряжениях рх. На графике даны также значения ср, полученные Кроммом и Маргерром 3-31 для удлиненной пластинки пунктиром. Несущая способность квадратной пластинки оказывается значительно более высокой.

170 ЗАКРИТИЧЕСКАЯ ДЕФОРМАЦИЯ ПРЯМОУГОЛЬНЫХ ПЛАСТИНОК ГЛ. III
 2. Продольные кромки не могут сближаться; еу 0. Из выражения 127 тогда получим:
 7с22
 Ру Рх — Е Ц. 3.189
 Полагая в системе 144 ру ipx, приходим к следующему уравнению для критических напряжений:
 £ I 1 У Ря j _ О ЬУРхЛ _ s 2
 4Ро J 50
 3.190
 При простом сжатии будет
 P i р, Ро 3.191
 в случае простого сдвига остается справедливым вы 2 3 4 п 5 ражение 146. Зависимость
 Фиг. 3.24. Редукционные коэффициенты при межДУ критическими напрянесмещающихся кромках. жениями представлена на
 фиг. 3.22.
 Выражение для ех приобретает форму
 <ЗЛ92
 так что напряжение в продольном ребре следует считать равным
 °р — Рх1 —Iх2О Н“0 Ч“42. 3.193
 Редукционный коэффициент будет
 <Р. 3.194
 Ра, 1- £_ 1 1 4’jj2
 Далее решаем уравнения 142—143, вводя в них ру 189, и находим зависимость между рх, и ф.
 На графике фиг. 3.24 сплошные линии дают окончательные значения редукционных коэффициентов для различных п при х 0,3; пунктирные линии относятся к удлиненной пластинке и построены по данным 3-31. Можно видеть, что при закреплении продольных кромок пластинки редукционные коэффициенты сильно повышаются.

ГЛАВА IV
 КРУГЛЫЕ ПЛАСТИНКИ
 § 36. Осесимметричный изгиб круглой пластинки.
 Деформации и кривизны. Условие совместности деформаций
 Обратимся к изучению круглых пластинок, известным образом закрепленных по контуру. Будем считать, что пластинка является сплошной, радиуса г и толщины h однако все основные зависимости будут относиться и к кольцеобразным пластинкам.
 Вместо прямоугольной системы координат введем теперь цилиндрическую систему. Совместим ось z с осью симметрии пластинки, а основную плоскость системы — со срединной плоскостью фиг. 4.1. Расстояние л г произвольной точки от оси z обозначим через г, полярный угол через ср.
 Рассмотрим случай, когда прогибы симметричны относительно оси z. При этом прогиб, а также все остальные величины, характеризу ющи з напряженное и деформированное состояние, будут функциями только г.
 Возьмем произвольную точку т изогнутой поверхности с координатой г фиг. 4.2. Нормаль п к поверхности, проведенная через т, будет пересекать ось z в некоторой точке А. Обозначим через 6 угол между нормалью и осью 0.
 Проведем через точку т две взаимно перпендикулярные плоскости 5 и 7, содержащие нормаль п пусть одна из плоскостей — меридиональная радиальная—проходит через ось z. Сечения искривленной поверхности плоскостями S w Т образуют кривые, обозна¬
 ченные на чертеже через s и t. Пусть будет и — радиальное перемещение точек срединной поверхности, w—прогиб. Определим деформацию удлинения ег в меридиональной плоскости S. Сечение этой плоскостью срединной поверхности кривая 5 на фиг. 4.2 соответствует сечению изогнутой прямоугольной пластинки
 Фиг. 4.1. Основные обозначения при рассмотрении круглой пластинки.

172
 КРУГЛЫЕ ПЛАСТИНКИ
 ГЛ. IV
 плоскостью xz фиг. 1.7. Рассуждая таким же образом, как в § 2, заключаем, что ег выражается формулой типа 1.7:
 du_, _1_ tdw X2
 dr I 2 dr •
 4.1
 Найдем, далее, деформацию удлинения е9 в плоскости 7 т. е. в направлении, перпендикулярном к радиусу. Вместо деформации
 на бесконечно малом отрезке прямой, касательной к окружности радиуса г, мы можем рассматривать деформацию на бесконечно малой дуге этой окружности. Пусть точки т и е, расположенные в срединной плоскости на дуге радиуса г фиг. 4.3, перемещаются вдоль радиуса на отрезок я. Если начальная дуга те равнялась г dy, то после перемещения длина дуги те будет гяй?ср; следовательно,
 г u dy — г dy
 г Жр
 или
 и
 г
 4.2
 Фиг. 4.2. Нормальные сечения срединной поверхности круглой пластинки.
 77?
 Деформации сдвига при осесимметрическом изгибе пластинки не будет; направления г и ср являются главными.
 Сопоставление выражений 1 и 2 показывает, что каждое из них содержит величину и, так что они не являются независимыми. Подставляя в 1 u rzv находим уравнение совместности деформаций:
 d 1 fdwX2,а оч
 _Г.9_вг -т;. 4.3
 Определим далее кривизны линий s к t9 проходящих через точку т фиг. 4.2. Из фиг. 4.4 заключаем, что тангенс угла наклона касательной к кривой 5 равен
 ± а _4_ dw
 а
 Фиг. 4.3. Радиальные перемещения точек срединной поверхности.
 Положительное направление касательной примем в сторону возрастания г. Заметим, что отсчет угла 0 ведется по часовой стрелке, в то время как вращение от оси г к оси z происходит против часовой стрелки. Поэтому
 От частных производных”по х переходим здесь к полным производным по г.

§ 36
 ОСЕСИММЕТРИЧНЫЙ ИЗГИБ КРУГЛОЙ ПЛАСТЙНКИ
 173
 для равенства а выбираем знак минус:
 . „ ц dw
 tgO -r-
 Считая кривую s пологой, а угол 0 малым, примем:
 й dw
 0 57-
 Кривизна кривой s равна
 db
 r ds'
 где ds — дифференциал дуги. Для пологой кривой
 db
 хг ■ r dr
 или
 b
 4.4
 c
 4.5
 4.6
 Для определения кривизны кривой t обратимся к фиг. 4.5. По известной теореме дифференциальной геометрии кривизна нормаль-
 Фиг. 4.4. К определению кривизны срединной поверхности в радиальном сечении.
 Фиг. 4.5. К определению кривизны в сечении плоскостью Т.
 ного сечения поверхности равна кривизне произвольного сечения, умноженной на косинус угла между-соответствующими плоскостями, при условии, что данные кривые имеют общую касательную. Зная

174
 кРУГЛЫЁ ПЛАСтИНкИ
 гл. IV
 кривизну окружности, равную 1 г, находим:
 4.7
 4.8
 При осесимметричном прогибе кривизна кручения оказывается для любой точки изогнутой поверхности равной нулю, кривизны же 5 и 7 будут главными кривизнами: одна из них минимальна, а другая максимальна по отношению к кривизнам всех линий, являющихся нормальными сечениями поверхности для рассматриваемой точки.
 § 37. Напряжения в срединной поверхности. Изгибающие моменты и поперечная сила. Условия равновесия
 На фиг. 4.6 и 4.7 показаны сечения пластинки, одно из которых— цилиндрическое дуговое — соответствует дуге радиуса г, а второе — плоское—’ проведено вдоль радиуса. Напряжения в срединной поверхности, действующие в этих сечениях, обозначены
 через аг и от; касательные напряжения здесь равны нулю. Для изгибающих моментов введены обозначения Мг и Ж®; двойными стрелками показаны вектор-моменты. Поперечная сила в дуговом сечении обозначается через Q. Крутящие моменты, а также поперечная сила в радиальном сечении отсутствуют.
 Выделим элемент пластинки фиг. 4.8 двумя радиальными сечениями, угол между которыми равен dy, и двумя дуговыми сечениями, одно из которых расположено на окружности радиуса г, а второе — на окружности радиуса r--dr. На фиг. 4.8 изображены усилия
 Фиг. 4.6. Нормальные усилия в срединной поверхности круглой пластинки.
 Фиг. 4.7. Изгибающие моменты и поперечная сила в сечениях пластинки при осесимметричном прогибе.

§ 37
 напряжения в Срединной поверхности
 175
 в срединной поверхности, поперечные силы и векторы пар изгибающих моментов. Действующая на элемент поперечная нагрузка считается равной qrdydr, где q — интенсивность нагрузки.
 Через точку, делящую внешнюю дугу пополам, проведем взаимно перпендикулярные оси по направлению радиуса ось х и вдоль ка¬
 сательной ось у. Составим уравнение равновесия элемента в проекциях на ось х:
 Выпишем теперь уравнение моментов сил, действующих на элемент пластинки, относительно оси у:
 Mr dMr г -drdy — Mrr dy -j- Qr dy dr —
 — 2My dr -- qr dy dr 4 0.
 Отбрасывая малые высшего порядка, получим: dM„ Mr М
 Фиг. 4.8. К выводу условий равновесия элемента круглой пластинки.
 зг -f- dor г dr hdy — or hr dy — 2a<ph dr —- 0.
 Arer-« 0.
 4.9

176
 кРУГЛЫЕ ПЛАСТИНКИ
 tn. iV
 Для составления уравнения равновесия в проекциях на ось z надо, как мы видели в § 3, представить пластинку в деформированном состоянии. Сделаем круговое сечение пластинки по дуге радиуса г и рассмотрим центральную часть фиг. 4.9 в изогнутом положении.
 Равнодействующая внешней нагрузки при q, зависящей от радиуса, равна
 г
 R fq2nrdr. 4.11
 О
 Уравнение равновесия будет иметь вид
 Q2icr-f-arH2nrb R. 4.12
 Для поперечной силы получим выражение
 1
 Фиг. 4.9. Поперечная нагрузка уравновешивается за счет поперечных сил и усилий в срединной поверхности.
 Т
 ifqrdr —
 Введем понятие функции нагрузки равной
 Ч’ т4; 7<>Ыг-
 О
 Тогда поперечная сила будет
 Q W — horbt
 а интенсивность нагрузки выразится формулой
 «“7
 агА9. 4.13
 4.14
 4.15 4.14'
 § 38. Связь между усилиями и деформациями. Основные дифференциальные уравнения. Граничные условия
 Напряжения в срединной поверхности связаны с деформациями зависимостями типа 1.34:
 °Г — fZTjv ®г 118»’
 fZ2 ® “Ь
 4.16

§ 38 СВЯЗЬ МЕЖДУ УСИЛИЯМИ и ДЕФОРМАЦИЯМИ 177
 Выражая изгибающие моменты через кривизны срединной поверхности, воспользуемся формулами вида 1.44:
 Mr Dxr Ixx<p -D- f.
 4.17
 I 7<ГЛ1 Л ЫЛ Л
 AL
 Уравнение равновесия 9, содержащее напряжения в срединной поверхности, будет удовлетворено, если ввести функцию напряжений по формулам:
 1 йФ
 °г г dr ’ 0tp— dr2 • 4-18
 Сопоставляя уравнения 10 и 15, находим: dMr Мг М<р
 _ — ЫгЬ. 4.19
 Воспользуемся выражениями для изгибающих моментов 17 и для кривизн 5 и 7; тогда получим:
 °1£т£-тз-—<4-20>
 Как легко видеть, уравнение 20 может быть записано в виде
 Dwt 4.21
 или после введения функции напряжений
 0¥tfH Ч'т»- <4-22>
 Выразим 0 через прогиб w по формуле 4; тогда будет
 и.23
 Можно показать см. ниже § 39, что выражение, заключенное здесь в квадратных скобках, соответствует оператору V'2, записанному в полярной системе координат при w, не зависящем от полярного угла ср:
 Twrd-v‘w- 4-24>
 Поэтому уравнение равновесия 23 может быть представлено
 в виде:
 i-v d ч ш, h йФ dw А леч
 D¥V W7F. 4.25

i?8
 КРУГЛЫЕ ПЛАСТИНКИ
 гл. IV
 Выразим далее деформации 16 через функцию напряжений:
 Вводя эти выражения в уравнение совместности деформаций 3, придадим ему вид
 Таким образом, основная система дифференциальных уравнений для круглой гибкой пластинки имеет вид
 Уравнения 30 — 31 содержат полные производные третьего порядка, в то время как-система уравнений 1.60—1.61, полученная в главе I для прямоугольных координат, содержала частные производные четвертого порядка. Поэтому интегрирование системы 30—31 представляет собой менее сложную задачу.
 Для жесткой пластинка малого прогиба уравнение 31 отпадает, а уравнение 30 принимает вид
 Напротив, для абсолютно гибкой пластинки можно пренебречь членом в уравнении 30, содержащем D; тогда получим следующую систему уравнений:
 4.26
 №_, аФ_
 dr' г dr2 г2 dr
 4.27
 Пользуясь и здесь оператором V2, найдем:
 4.28
 или
 4.29
 4.30
 4.31
 4.32
 h d dw r dr dr
 — W.
 4.33
 4.34

§ 381
 СВЯЗЬ МЕЖДУ УСИЛИЯМИ И ДЕФОРМАЦИЯМИ
 179
 Повторяя вывод основных уравнений для круглой пластинки, имеющей начальную погибь, получим следующую систему:
 Здесь через wm обозначен начальный прогиб, считающийся некоторой функцией г.
 Двум обыкновенным дифференциальным уравнениям третьего порядка должны соответствовать, вообще говоря, шесть граничных условий. Однако здесь можно ограничиться пятью условиями, так как сама по себе функция Ф нас не интересует: достаточно определить ее первую производную по г.
 Граничные условия для прогиба w будут: при шарнирном опирании по контуру
 В случае пластинки, не имеющей центрального отверстия, к этим условиям может быть добавлено условие отсутствия поворота нормали для центра пластинки:
 Выясним, каковы будут граничные условия для Ф. Допустим, что смещение точек контура в радиальном направлении оказывается невозможным. В этом случае должно быть
 Следовательно, при полном закреплении точек опорного контура по отношению к радиальным смещениям должно быть
 dr v ' г dr dr dr
 d _ Е 1 dw 2 dwn
 dwdw
 4.35
 4.36
 dr dr
 4.37
 4.38
 при защемлении по контуру
 4.39
 4.40
 4.41
 4.42
 Сопоставляя формулы 2 и 26, получим:
 4.43

180 КРУГЛЫЕ ПЛАСТИНКИ гл. IV
 В другом предельном случае, когда радиальное смещение контура ничем не стеснено, должны быть равны нулю на контуре радиальные напряжения ог:
 7§L °- <4'45>
 К условиям 44 или 45 должно быть добавлено условие ограйФ
 ниченности производной для всей площади пластинки, в частности, и при г 0. Величина напряжения сг также является ограниченной; но тогда, как это видно из 18, должно быть
 аФ
 dr г0
 0. 4.46
 § 39. Основные уравнения при несимметричной деформации. Случай анизотропии
 Тот случай, когда нагрузка и изогнутая поверхность круглой пластинки не обладают осевой симметрией, удобнее исследовать с помощью общих соотношений главы I; но при этом надо перейти от прямоугольной системы координат к цилиндрической.
 Прямоугольные координаты точки срединной плоскости х, у связаны с полярными координатами г, ср равенствами фиг. 4.10:
 Г2 X g <р L. 4.47
 Дифференцируя 47, получим:
 Фиг. 4.10. Полярные координаты точек срединной поверхности. r dy — cos ср dy — sin ср dx,
 Ч'ИГ. пиленые и и координаты точек сре- г dr х dx у dy, Считая в равенствах 48 dy 0 или dx 0, находим частные производные по х и у:
 cos ср, - — sin ср. 4.49
 dx т dx г
 sin ср, -—• — cos ср. 4.50
 dy dy г
 Пусть некоторая функция Z зависит от координат г и ср. Частные производные от Z по х и у можно выразить следующим образом:

§ 39 ОСНОВНЫЕ УРАВНЕНИЯ ПРИ НЕСИММЕТРИЧНОЙ ДЕФОРМАЦИИ 181
 Дифференцируя по той же схеме 51, находим вторые производные:
 4.53
 d2Z тт sin ср
 гг-г- U cos ср — К,
 дх2 т г J
 d2Z тт., тг coscp
 U sin ср V -
 где
 -№■
 дх ду
 dZ sin ср ду г2 дг дер г
 d2Z sin ср
 d2Z
 dZ
 ■ч а cos ср — —— sin ср • dr cty т дг т
 d2Z sin ср df2 г
 dZ
 cos ср
 dcp
 4.54
 Перепишем эти выражения, совмещая ось х с направлением радиуса-вектора т. е. принимая ср 0. При таком расположении будем обозначать оси х и у через 5 и Y. Тогда
 d2Z d2Z
 d2Z
 dtdri
 д
 d2Z
 дг2 ’ 1 dZ
 dr dcp r2 dcp
 дг
 4.55
 4.56
 Полагая в первом из выражений 53 ср тс2, найдем вторую производную по yj:
 d2Z 1 dZ_, J_ KZ dt2 r dr r2 dcp2
 Сумма вторых производных по £ и yj отвечает оператору V2:
 _ d2Z 1 dZ 1 d2Z dr2 ' г дг г2 дф ’
 или
 1 д2 Z г2 д?2
 4.57
 4.58
 4.59
 Пользуясь полученными соотношениями, можно выразить в полярных координатах кривизны и напряжения в срединной поверхности по формулам § 2 и § 3 считая оси х и у совпадающими с 5 и к:
 d2w
 дг2 J_ дФ г
 1 dw г дг
 1 d2w
 г2 д2
 х -
 J_
 дг
 — J- jh. л. JL — JL1 дФ
 •• dr ' r2 df2 ’ a<p dr2 ' T dr r d? 4.60
 Для осесимметричной деформации, когда w и Ф не зависят от ср, получим отсюда формулы 6 — 8 и 18.
 Основные дифференциальные уравнения можно теперь представить в общей форме 1.60 — 1.61:
 _ у22ф. Е
 1
 L w, w;
 4.61
 4.62

182 КРУГЛЫЕ ПЛАСТИНКИ гл. IV
 оператор V2 находится по 58 или 59, a L w, Ф выражается следующим образом:
 v ’ ’ дгг дг г д
 . 1 dw. 1 дФ nddФdldw лсо
 “Mr drr dp dr Z drr d4dr7di' 4‘W
 В случае осевой симметрии для каждого из уравнений 61 и 62 может быть легко получен первый интеграл. Вводя в уравнение 61 функцию нагрузки ¥ по 14', найдем:
 <«•>
 После интегрирования будем иметь:
 Dr JL V2W h jL r4r Cl. 4.65
 Уравнение 62 можно переписать в виде
 Htf’' 4М
 отсюда
 '4<'»>--И£’с <467>
 dw
 Но в центре пластинки при г 0 ввиду симметрии должно быть 0;
 поэтому С1 С20. Окончательно получаем систему уравнений третьего порядка 30 — 31, к которой мы раньше пришли другим путем.
 Для пластинки с начальной погибью можно также воспользоваться общими уравнениями § 5. В осесимметричном случае от них можно перейти к уравнениям 35 — 36, выписанным в § 38.
 В случае пластинки с цилирикеской анизотропией основные уравнения могут быть получены по аналогии с прямоугольной пластинкой см. § 12. Допустим, что пластинка ортотропна радиальные плоскости являются плоскостями упругой симметрии. Тогда мы можем сохранить соотношения § 12, введя следующие обозначения:
 _ ЕГНЪ EJ, оп
 121-’ 2 12 1 — ivi ’ -Df 2Dk,
 »-£• 2Ь11-2Ь
 4.68
 индексы г и <р относятся к радиальному и окружному направлениям.
 Учитывая формулы 60, перепишем окончательные уравнения § 12 в виде
 w 2 wfr writ L до, Ф, 4.69
 h ' h 1 h
 8ХФ 253 Ф 52 Ф — -j L w, w. 4.70

§ 40
 ПРИМЕНЕНИЕ ВАРИАЦИОННЫХ МЕТОДОВ
 183
 Здесь введены обозначения:
 dw дг±> д 1
 w“
 wr — -Т Т—
 д д 1
 dr г ду дг г
 dw
 дч
 4.71
 w
 r dr 2 дч2 г dr г2 df2 j’
 оператор Z, определяется по 63.
 § 40. Применение вариационных методов
 Приложим к задаче об осесимметричном изгибе круглой пластинки принцип возможных перемещений. Работа усилий в срединной поверхности на возможном перемещении может быть представлена в виде
 с
 8Ас — h J зг 8«, -- в, Ц 2яг dr. 4.72
 О
 Пользуясь формулами 1 и 2, получим:
 5ЛС - h J зг8 -g- 1 2 з?8 £ 2w rfr. 4.73
 о
 Будем считать, что в точках контура обращаются в нуль перемещения ои 0, либо усилия в срединной поверхности аг 0. Тогда, интегрируя выражение 73 по частям, будем иметь:
 с с
 о А с 2«Л J гзг — оЛ ои dr — 2тгЛ J гзг 8 dr. 4.74
 О о
 Работа усилий изгиба равна
 с
 ЪАи — J Мг 8хгН- М, ах, 2w dr, 4.75
 О
 или
 с
 ЬАи 'жг8- Ж,зг2Лгйг. 4.76
 б
 Положим, что в точках контура равны нулю изгибающий момент Мг 0, либо угол поворота 4г“ 0. Воспользуемся

184 КРУГЛЫЕ ПЛАСТИНКИ гл. IV
 формулами 17; интегрирование по частям выражения 76 дает
 о
 или
 с
 ЬАи V8 2dr. 4.77
 0
 Наконец, работа внешней нагрузки выражается следующим образом:
 с
 bW J qbw2nrdr. 4.78
 О
 Вводя функцию нагрузки по 14', получим:
 с
 № j-£prWbw2itrdr. 4.79
 О
 Считая для точек контура 8 0, приведем выражение 79 к виду
 с
 bw — J г'Г8 2кг dr. 4.80
 о
 Объединяя полученные результаты, приходим к вариационному уравнению:
 с
 J d -Jr СVw - W — Ыг Щ ± bw 2nr dr
 о
 с
 з9 A2ir§Mtfr 0. 4.81
 О
 Если принять, что возможные перемещения 810 и Ьи являются произвольными, то отсюда пол чим дифференциальные уравнения равновесия 10 и 9. Допустим, что выполняется лишь второе из этих уравнений; тогда, вводя функцию напряжений Ф, найдем:
 J О ± Va« - W — h Щ ± bw г dr 0. 4.82
 О

§ 40 ПРИМЕНЕНИЕ ВАРИАЦИОННЫХ МЕТОДОВ 185
 Путем нового интегрирования по частям уравнению 82 можно придать форму
 _ i Л- £ to, 0. 4.83
 О
 При использовании метода Бубнова — Галеркина представляем w в виде ряда
 « 4-84
 i-1
 тогда вариационные уравнения 82 и 83 приведут к системе
 уравнений
 с
 j X г dr 0 4.85
 или
 J Yfirdr 0, 4.86
 О
 где под X и Y понимаются функции
 d i-го i? h йФ dw
 гт-r, 4-87
 yd«-i-tww- <4-88>
 Для пластинки с начальной погибью
 d h dФ dw. dwaxl
 В_.„„_»-_7__ _. 4,89
 Заметим, что уравнение типа 85 можно, формально рассуждая, составить и иначе, например в виде
 с с
 j Xrr dr 0 или J Хщ dr — 0; 4.85'
 о о
 однако такие уравнения уже не будут отвечать принципу возможных перемещений; при прочих равных условиях полученные при этом приближенные результаты должны быть, повидимому, дальше от истинного решения задачи, чем при пользовании уравнением 85.
 Приведем в заключение выражение для потенциальной энергии системы, необходимое при пользовании методом Ритца. Энергия

186 КРУГЛЫЕ ПЛАСТИНКИ гл. IV
 напряжений в срединной поверхности равна
 с
 Eh Г Г<яГ2ф42 1 <фЧ2 2л <2ф-
 U° — J Аж 7 IF - — IF 2lcr dr’ <4-90
 энергия изгиба
 ■•- тШ т wj w 2r dr, 4.9,
 o
 работа внешней нагрузки
 с
 W j qw • 2тиr dr. 4.92
 о
 Полная энергия равна
 3 UQ-- U— W. 4.93
 Допустим, что при решении какой-либо задачи по методу Бубнова — Галеркина выполнены все геометрические и статические граничные условия; результат будет совпадать с решением по методу Ритца лишь в том случае, если уравнения взяты в форме 85 или 86.
 § 41. Защемленная по контуру пластинка при равномерной поперечной нагрузке
 Рассмотрим круглую пластинку радиуса с, защемленную по контуру и подвергающуюся действию равномерно распределенной поперечной нагрузки интенсивностью q фиг. 4.11.
 Выберем приближенное выражение для w в виде
 ™1_52’ 4-94
 отвечающем решению той же задачи в случае пластинки малого прогиба ; здесь —стрела прогиба. Получаем:
 ¥7-5-<4-95>
 Уравнение совместности деформаций 31 после подстановки 95 в правую часть принимает вид
 Ау-2ф _МЯ£_ИУ‘.
 dr К ’ СГ С Ф '
 См. 125, стр. 65.
 Фиг. 4.11. Круглая пластинка при несмещающемся а и свободно смещающемся контуре б.

§ 41 ЗАЩЕМЛЕННАЯ ПО КОНТУРУ ПЛАСТИНКА 187
 Интегрируя, найдем:
 гф1А _, С>
 г dr dr с2 2с2 2с4 ' 6с6 • 1
 Умножая на г и интегрируя повторно, получим:
 . С £. С» 4 96ч
 rfr “ с l2c5 3r52 г •,УЬ'
 Постоянная С2 должна быть равна нулю в силу условия 46. При определении Ct надо учитывать условия закрепления точек контура в его плоскости.
 1. Точки контура смещаются свободно фиг. 4.11, б. Пользуясь условием 45, находим:
 _ Е2. ui — W >
 тогда
 d<b
 dr
 ЕР о г а гз, л г5 г7 Л7Ч
 6с с СЗ4 С5 с?- 4-97
 При q const функция нагрузки 14 будет
 W 4.98
 С другой стороны, следовательно,
 rV. 4.99
 Выпишем уравнение Бубнова — Галеркина 85. Функции X к г равны
 XD
 32г qr h 2 pffK 5 — 3 г
 2 	3 7 1—t '
 с4 2 1 г 3 у 1 — X с
 <41о°>
 ■ч,—l— £. 4.101
 Вводя безразмерную величину
 рт, 4.102

188
 КРУГЛЫЕ ПЛАСТИНКИ
 получим уравнение 85 в виде
 1
 J 32Dp - 1 дрс ЕР р - 6р°
 4Рб — Р7 Р — Р3 Р — Р8 Р dp 0.
 Имеем:
 1
 32Dp р — р8 р rfp -- Df,
 0
 1
 fqpcHp—р8рФ •
 О
 Далее, обозначая I интеграл
 1
 J3p —6р» 4р5 - Р7 Р - Р dp,
 находим:
 L
 - J Зрз — 12рб 1 Эр — 15р9 -f 6р1г — р18 dp
 О
 Окончательно приходим к уравнению
 55£V
 или
 31 — I» где
 ‘-f
 при JJL 0,3 будет
 0,857С3 5,862С. Напряжения в срединной поверхности 18 будут
 ar ff3-6p2V-p6. J
 °? Й3-18р220р4-7р6- J
 Введем параметры
 а_?:ЛМ2
 •— Еh ’ 9 Eh
 гл. IV
 4.103
 a
 b
 c
 к- <d>
 4.104
 4.105
 4.106
 4.107
 4.108
 4.109

§ 411 ЗАЩЕМЛЕННАЯ ПО КОНТУРУ ПЛАСТИНКА 189
 Для центра пластинки будем иметь:
 o;a; it
 у контура
 В полосе пластинки, прилегающей к контуру, напряжения о9 оказываются сжимающими; краевая полоса выполняет здесь как бы функции контурного подкрепляющего ребра. Поэтому при известной нагрузке здесь наступает потеря устойчивости, выражающаяся в образовании складок.
 Изгибающие моменты по формулам 17 будут
 Mr4Dl-3 xp2, М¥ 401у-1 3,ар.
 4.110
 Напряжения изгиба, наибольшие по толщине пластинки, равны
 6МГ 6М9
 °г, и ’ сф, И Д2 4-111
 Вводя обозначения
 найдем для центра пластинки при l 0,3
 У контура
 о 	0 2,86С.
 Г, И <р, и ’
 о;4,4С, о;;1,32С.
 2. Точки контура не смещаются фиг. 4.11, а. По условию 44 постоянная в выражении 96 будет
 с _ ЕР 5 — 3х.
 1 Зс2 1—Л >
 отсюда
 йФ_ dr
 тР-6Р84-4рБ-р. 4.113
 Уравнение Бубнова — Галеркина принимает вид
 з20л-«»‘£»тр-брЧ-
 4р5 — Р7Р — Р8Р — Р8РdP 0. 4.114
 Это явление было исследовано Д. Ю. Пановым и В. И. Феодосье-
 ВЫМ 4.12.

190 КРУГЛЫЕ ПЛАСТИНКИ
 Обозначая через ' интеграл
 гл. IV
 l' I т tit р—6р84рб—pvp—р82 р dp' а
 находим:
 ' § £ ? - '6, р 21, _ р> - I5р»
 250
 200
 150
 100
 50
 у
 ч
 1
 Т Г Т Т Т Т
 Т
 Контур
 . не смещается
 Контур скользи,
 7о rttrrtryf'irtfr тпг
 f
 V
 щи
 ф4
 г иси
 f
 J
 У
 г
 'Zl—
 —
 А
 12 3 4 5
 Фиг. 4.12. Диаграмма «нагрузка — прогиб» для круглой защемленной пластинки.
 Окончательно зависимость <7 С принимает форму
 2 23 — 9
 С3 ■
 16
 ;С <7,
 21 1— А 31 — Д-2
 или при х 0,3
 2,762£3Н 5,862£ q.
 Напряжения в срединной поверхности оказываются равными
 »v;I?tt-,8p520p‘-7c
 4.115
 4.116 по 18:
 4.117

§ 42 ШАРНИРНО ОПЕРТАЯ ПЛАСТИНКА ПРИ РАВНОМЕРНОЙ НАГРУЗКЕ 191 Для центра пластинки будем иметь:
 г <Р 61— х
 у контура
 1
 с2, о;.
 ’ з1— • > — 3i-rt
 Напряжения изгиба будут определяться прежними формулами 111 и 112.
 На фиг. 4.12 представлена зависимость £ для различных случаев закрепления контурных точек по уравнениям 107 и 116. Пунктирная линия отвечает уравнению
 16 £5,86; ?, 4.118
 31 -Ц2
 относящемуся к жесткой пластинке.
 § 42. Шарнирно опертая пластинка при равномерной нагрузке
 В случае шарнирного опирания по контуру теория жестких пла¬
 стинок приводит к следующему выражению для прогиба:
 <49
 Будем исходить из 119 при рассмотрении больших прогибов. Введем обозначения
 ““5Й- 4-sS: <4Л20>
 тогда
 „ «1-25»'4. 4.12
 Подставляя это выражение в уравнение 31, получим:
 Отсюда
 е й 4.122
 __ ЕРаР I
 dr 6с
 Постоянная С2, как и раньше, равна нулю; постоянную Сг находим с учетом условий закрепления.
 См. ссылку на стр. 186.

192 КРУГЛЫЕ ПЛАСТИНКИ гл. IV
 1. Точки контура смещаются свободно. Из условия 46
 Cl4r6-4 -
 Окончательно
 ОФ
 dr
 <6-4276545-- <4-123>
 Составляя уравнение Бубнова — Галеркина и повторяя выкладки § 41, приходим к следующему уравнению:
 DabZ-2bf-q-Z-2b
 232 Eha?p 84 — 168£ 140£2 — 56£3 М 0. 4.124
 В безразмерных параметрах при ja 0,3 уравнение примет вид
 0,376С3 1,436С <7. 4.125
 Напряжения в срединной оказываются равными по 18:
 ЕРаа
 6с3
 61 —Р2 — 41 —р<Н- 621 —Р6,
 О» 61 - Зр2-461 - 5рН-1 -7р6.
 4.126
 И здесь напряжения у контура оказываются сжимающими, что может привести к образованию складок.
 2. Точки контура не смещаются. По 44 имеем:
 С1 з сйt6 3 -11 - Ab <5 - Р ■ 7 — »•
 Зависимость -- здесь будет
 2,66С3 1,436С q. 4.127
 Для жесткой пластинки в обоих случаях получим в соответствии с известным решением:
 16
 3i-w5rtt;5“1'4361'<4,2S>
 В таблице V приведены окончательные расчетные данные для пластинок с различными условиями закрепления. Уравнение для определения стрелы прогиба представим в виде
 ££ ?; 4.129
 напряжения выразим следующим образом:
 О 	рр, о;н оС. 4.130

§ 43
 Случай сосредоточенной нлгрузкй
 193
 Таблица V
 Данные первого приближения для расчета круглых гибких пластинок при равномерной нагрузке 0,3
 Условия закрепления контурных точек
 в
 В центре
 У
 контура
 А
 ар
 т 5
 а
 Р
 Т
 §
 Шарнирное
 закрепле¬
 ние
 Свободно
 смещаются
 0,376
 1,436
 0,295
 1,778
 0
 —0,427
 0
 0,755
 Не смещаются
 2,660
 1,436
 0,905
 1,778
 0,610
 0,183
 0
 0,755
 Защемле¬
 ние
 Свободно
 смещаются
 0,857
 5,862
 0,500
 2,860
 0
 —0,333
 4,400
 1,320
 Не смещаются
 2,762
 5,862
 0,976
 2,860
 0,476
 0,145
 4,400
 1,320
 § 43. Случай сосредоточенной нагрузки
 Обратимся к случаю, когда пластинка подвергается действию поперечной силы Р, сосредоточенной в центре. Рассмотрим различные условия закрепления.
 1. Защемление по контуру; точки контура смещаются свободно фиг. 4.13, 6. По теории защемленных жестких пластинок изогнутая поверхность отвечает уравнению
 w
 1-32Sit- <4ЛЗ>
 Ь'0г
 Л
 Принимая это выражение в качестве исходного, придадим уравнению 31 вид
 '’f- <432
 Фиг. 4.13. Круглая защемленная пластинка под нагрузкой, сосредоточенной в центре.
 При интегрировании здесь и в последующем пользуемся формулой
 Г п С
 J Рмln”Рdp 1-J rlnn-idp. 4.133
 Последовательно интегрируя, находим: d<>
 dr
 AHlJllnL-Z-r±nL_L_Lr± _i_ с £_, C2 4 n4
 с С 8 c с ' 1 2 ' r ' 4-1,i4
 У нижней поверхности — сжатие.
 См. 1 25, стр. 78.

1S4
 кРУГЛЫЁ ПЛАбТЙНКЙ
 гл. IV
 По условиям 46 и 44
 • 0.
 4 са
 Функция нагрузки W 14 равна в данном случае
 Р_
 ' 2кг'
 W
 Имеем, далее,
 dr
 В уравнение Бубнова — Галеркина 85 подставляем:
 Х D4r — Т — Щ т,п3 —— -I т1п3-
 с1г 2кг сз сЗ а 2 с3 с 1
 ,7 г3, г 7 г г, г
 -«■ Ш о— In — Г 1п —,
 '8 с3 с 8 с с с '
 1 г2 I ог? 1 г
 12а1п7
 Окончательно приходим к уравнению
 191 648
 Ehp-- 16D-c2
 При х 0,3 будем иметь:
 0,294С3 1,47С Р; под Р понимается параметр
 р Рс
 nEh
 4.135
 4.136
 4.137
 4.138
 отметим, что при нагрузке P qTzc2t равномерно распределенной по площади пластинки, мы получили бы P q.
 Напряжения в срединной поверхности находим по формулам 18. В центре будем иметь:
 у контура
 о 	о — С2, г <р 8
 Напряжения изгиба, наибольшие по толщине пластинки, вычислим, пользуясь формулами 17:
 '.и Г-Цс 0 1п7 V-1пт'
 ,..-ТТа1П7,П7-
 4.139

§ 43 СЛУЧАЙ СОСРЕДОТОЧЕННОЙ НАГРУЗКИ 195
 Эти выражения приводят к бесконечно большим значениям напряжений в центре пластинки, т. е. у места приложения сосредоточенной нагрузки. Можно показать, однако, что в области, прилегающей к центру, исходные допущения теории должны быть пересмотрены. Для точек контура получим:
 - 	2 2р» «.
 г» и 1 — р.2» <р, и 1—
 2. Защемление по контуру; точки контура не смещаются фиг. 4.13, а. Постоянная Ct в выражении 134 оказывается равной
 Г _ 1
 W — 4 с С2 ТГСтрела прогиба определится из уравнения
 мЛ £V16P. 4.140
 или при х 0,3
 0,651С1,47С Р. 4.141
 3. Шарнирное опирание; точки контура смещаются свободно. Теория жестких пластинок дает здесь
 w fl — £2 lny- 4.142
 Уравнение 31 получает при подобном выражении для прогиба вид
 -У2ф — „У, Г——21.-1п-4-
 dr 3 -f- J.2 с3 _ с v ‘ ' с с 1
 12т1п27. 4143
 После интегрирования находим:
 JF“—<slt ?—2<11?7 —Т?
 l rt''5',T-Sl7 T? c.fT- <4144>
 Граничные условия дают
 С1 з'нР2р1 f1 j -1 rt3. с2 0. Расчетное уравнение будет 0,3
 0,157С3 0,577С Р. 4.145
 См. сноску на стр. 193.

196
 КРУГЛЫЕ ПЛАСТИНКИ
 ГЛ. IV
 4. Шарнирное опирание; точки контура не смещаются. Постоянная Сх в выражении 144 будет
 сх
 3 1
 В итоге получаем:
 3 - rt 5 - ад1±£2 <9 - 7rt.
 0,825'»0,577С Р. 4.146
 В таблице VI приведены окончательные расчетные данные; принято
 Жз вс я, 4.147
 4.148
 Таблица VI
 Данные первого приближения для расчета круглых гибких пластинок при нагрузке, сосредоточенной в центре ji 0,3
 Условия закрепления контурных точек
 А
 В
 в
 центре а — Р
 У контура
 а
 3
 Т
 8
 Шарнирное
 закрепле¬
 ние
 Свободно
 смещаются
 0,157
 0,577
 0,407
 0
 —0,341
 0
 0,606
 Не смещаются
 0,825
 0,577
 0,895
 0,488
 0,147
 0
 0,606
 Защемле¬
 ние
 Свободно
 смещаются
 0,294
 1,47
 0,875
 0
 —0,250
 2,198
 0,659
 Не смещаются
 0,651
 1,47
 1,232
 0,357
 0,107
 2,198
 0,659
 § 44. Уточненное решение по методу возмущения
 Ограничиваясь в §§ 41—43 первым приближением, мы характеризовали изогнутую поверхность пластинки с помощью одного параметра. Поставим себе целью получить уточненное решение с помощью метода возмущения применительно к защемленной пластинке с несмещающимся контуром. Нагрузку примем равномерно распределенной по всей площади.
 Преобразуем предварительно общие уравнения задачи для случая пластинки, загруженной равномерно распределенной нагрузкой.
 У нижней поверхности — сжатие.
 Изложенное ниже решение принадлежит Цянь Вэй-чану 419.

§ 44 УТОЧНЕННОЕ РЕШЕНИЕ ПО МЕТОДУ ВОЗМУЩЕНИЯ 197
 Пользуясь соотношениями 98 и 18, представим уравнение 30 в виде
 °14'5т- <■■«•
 Введем новые переменные:
 1—4.150 Тогда уравнениям 149 и 31 можно придать форму
 -Щ<45>
 Соотношение 9 между напряжениями в срединной поверхности перейдет в следующее:
 d
 < <-21-- 4.153
 Следуя общему ходу решения задачи, намеченному в§ 11, представим величины wy о и q в виде рядов :
 w w.х С С8. • •,
 1_,х2 «1Г азГЗ...1
 4.154
 где С г— безразмерная стрела прогиба. В выражениях для w и q пропущены четные члены, а для а — нечетные; как легко показать см. § 27, эти члены в процессе выкладок выпадают. Подставим 154 в уравнения 151—152 и сравним члены, содержащие С в первой степени, в кубе и т. д. Тогда получим систему дифференциальных уравнений относительно w, wv g2, и т. д.
 Уравнение первого приближения будет
 1 У2 г dwA ТйлЗ1 ХЧх-1”1»
 оно соответствует основному уравнению теории жестких пластинок. Считая прогиб в центре Сдого С, полУчим
 KW1- 4-155
 В отличие от § 11 функции g л: отвечают непосредственно напряжению а.

198 КРУГЛЫЕ ПЛАСТИНКИ гл. IV
 Принимая во внимание также граничные условия, найдем:
 « 1. Ч 1-52- 4-156
 Выражение 156 определяет изогнутую поверхность жесткой защемленной пластинки: оно и было выбрано в качестве исходного в § 41.
 Выпишем далее уравнение второго приближения
 Интегрируя его, будем иметь:
 1— xg2 - Ax B. 4.157
 Так как смещение и для краевых точек должно быть равно нулю, то при х О
 Отсюда вытекает условие
 О—tfft — 21— г 0 при 0. 4.158
 С другой стороны, в центре пластинки, т. е. при jtl, величина напряжения g2 должна оставаться конечной. Пользуясь этими условиями, получаем:
 Л_ 11 в- 1
 61-1»’ 31 — J. ‘
 Приходим к следующему выражению для g2:
 4-159
 Проделанные до сих пор 'операции совпадают с теми, которые мы выполняли в § 41: выражение 159 соответствует функции напряжений 113. Но здесь пути решения задачи расходятся. Вместо того чтобы выписывать вариационное уравнение, прибегаем к уравнению третьего приближения:
 - 	т <11 - ■'• <11 -1 ■-1 11 - Л е, • 4 • I ■S0
 Граничные условия для w будут

§ 441 УТОЧНЕННОЕ РЕШЕНИЕ ПО МЕТОДУ ВОЗМУЩЕНИЯ 199
 Учитывая также 155, мы должны положить:
 w«a,»i0.
 dw6
 Четвертое условие состоит в том, что производная--должна оставаться конечной прид;1. Пользуясь этими условиями, опреде-
 О 0,4 0,6 7,2 7,6 2f0 2А 2,8 Г
 Фиг. 4.14. Напряжения в срединной поверхности и напряжения изгиба для круглой защемленной пластинки.
 ляем постоянные интегрирования и величину qr Окончательно третий этап решения дает:
 1-«3 1173-73, X, j
 j 4Л61
 Далее можно перейти к четвертому этапу и найти функцию g±x.

200
 КРУГЛЫЕ ПЛАСТИНКИ
 ГЛ. IV
 Если ограничиться этими приближениями, то соотношение между стрелой прогиба и нагрузкой будет иметь вид
 ip173 — 73ц С3-f-С 1-рв; 4.162
 при jj. 0,3 будет
 3,19£3 5,86£ q. 4.163
 Коэффициент при С8 мало отличается от найденного в § 41 3,19 вместо 2,76. Иначе обстоит дело при определении расчетных напряжений. На фиг. 4.14 приведены кривые, определяющие радиальные напряжения в пластинке, в зависимости от стрелы прогиба. Наибольшими являются напряжения изгиба и у краев; уточненная теория сплошная линия дает величины, значительно превышающие значения первого приближения пунктирная линия. Уже при С 2 расхождение достигает 60 от уточненного значения. Напротив, напряжение изгиба в центре оказывается ниже приближенного, что вызывается уменьшением кривизны изогнутой поверхности. Метод возмущения приводит здесь к тому результату, что напряжение аг и при С 2,4 делается равным нулю, а затем меняет знак. Это следует из выражения для w, получаемого во втором приближении: кривизна изогнутой поверхности делается отрицательной вблизи центра пластинки фиг. 4.15. Образование подобной выпучины при наличии поперечной нагрузки трудно оправдать; данные экспериментов для С 3,12 см. ниже фиг. 4.17 также не подтверждают этого. Повидимому, закон распределения изгибных напряжений устанавливается во втором приближении недостаточно точно.
 Напряжения в срединной поверхности, полученные в первом приближении и по методу возмущения, лучше сходятся между собой; уточненные значения напряжений у контура оказываются несколько выше, чем по формулам § 41.
 Задача об определении прогибов и напряжений для защемленной гибкой пластинки рассматривалась также с помощью других методов. Уравнение, определяющее стрелу прогиба, обычно имеет тот же вид 129, но коэффициент при С3 в различных вариантах решений сравнительно сильно меняется. На фиг. 4.14 приведены значения расчетных напряжений штрих-пунктирные линии, полученные в уточненном решении Надаи 121. Отметим, что изгибное напряжение в центре получилось у него ниже, чем по формулам § 41, но, тем не менее, оно возрастало с увеличением прогиба.
 Фиг. 4.15. Изогнутая поверхность круглой пластинки, найденная по методу возмущения.

ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ
 201
 § 45. Экспериментальные данные
 В работе 430 приведены результаты опытов, относившихся к защемленным по контуру круглым пластинкам. Между плитой F фиг. 4.16 и кольцами Et G вставлялись две пластинки Л,
 В, изготовленные из одного и того же материала. Одна из этих пластинок Л являлась
 испытуемым образцом, вторая В служила для того, чтобы по возможности избежать кручения колец. Кольца прижимались к плите с помощью болтов, не показанных на фигуре.
 На поверхности плиты была
 сделана насечка. Таким образом, радиальные смещения контурных
 точек пластинки были устранены, если не учитывать деформацию
 10 иг 0,8
 0,6
 0,4
 0,2
 >
 -ffA
 S?

 г
 vO
 1
 J ч ; Г 1
 Vij
 V
 2

 л

 L ;
 Г о

 1 о
 V°A °
 А
 о
 у - -j- Г
 ■1 и
 л
 о
 °
 1
 °
 о— ° i° v°
 О — 1 1
 “IS
 Фиг. 4.16. Установка для испытаний круглых пластинок на поперечную нагрузку.
 0,8 0,4 О 0,4 0,8 гс
 Фиг. 4.17. Изогнутая поверхность круглой пластинки по экспериментальным данным.
 колец под действием реактивных усилий, передаваемых от пластинок. В полости С и К через трубки D вводилось масло, поступавшее от насоса. Производились замеры прогибов пластинки в различных точках, а также деформаций у наружной поверхности.

202
 КРУГЛЫЕ ПЛАСТИНКИ
 ГЛ. IV
 На фиг. 4.17 показаны экспериментальные точки, характеризующие форму изогнутой поверхности пластинки на двух различных стадиях нагружения.
 При прогибах, лежащих в пределах С < 0,72, изогнутая поверхность с известным приближением может быть охарактеризована уравнением 94, положенным выше в основу приближенного решения. Однако при возрастании прогиба вид изогнутой поверхности
 7
 280
 гьо
 200
 160
 120
 80
 40
 1
 - р
 f
 щ
 70
 ■
 Ч
 - «
 i ■
 о
 UxUiGfJUMon U010L
 данные. о Дуралюм. пласт h,67мм _ о п у, 0.76мм
 7
 л-
 Зачерне.г ocmami
 iHbie точки- в области ?чтл деформаций
 , °
 и
 Уточнет решение 1
 ое
 У
 f Первое Ь приближение

 линейной
 L3 j
 теории
 По
 2 3 4 5
 Фиг. 4.18. Зависимость между нагрузкой и прогибом для защемленных круглых пластинок по данным экспериментов.
 сильно меняется. В пределах упругих деформаций имеет место смещение точки перегиба изогнутой линии к краям. Кроме того, при развитии пластических деформаций происходит «надлом» пластинки у края, так что условия опирания приближаются к шарнирному закреплению. При С 3,12 поверхность пластинки можно уже рассматривать как сферическую и приближенно охарактеризовать уравнением 1 —гЛО2
 Зависимость между стрелой прогиба дуралюминовых пластинок и нагрузкой изображена на фиг. 4.18. Уравнение 115, полученное в качестве первого приближения, хорошо сходится с данными опытов при изменении С в весьма широких пределах — до пяти толщин. Уточненные решения несколько отходят от экспериментальных дан-

§ 46
 ПРЕДЕЛ УПРУГОГО СОПРОТИВЛЕНИЯ ПЛАСТИНКИ
 203
 ных. Повидимому, здесь оказывается некоторое скольжение пластинки между кольцом и плитой, проявляющееся при значительных нагрузках. Возрастание прогиба связано также с образованием пластиче¬
 ской зоны у краев пластинки.
 § 46. Предел упругого сопротивления пластинки
 Рассмотрим случай защемленной пластинки с неподвижным контуром. Суммарное напряжение у края равно см. таблицу V, стр. 193:
 Од 4,40Е 0,48Я§. 4.164
 Если воспользоваться теорией наибольших касательных напряжений, то при определении предела упругого сопротивления мы должны ол считать равным пределу текучести ах. Вводя безразмерную величину
 <jm с 2
 < -в т> 4Л65>
 получим:
 4,401 0,48™, 4.166
 где Ст — безразмерная стрела прогиба. Соответствующее давление по табл. V будет
 ?: 5,86Ст2,76С. 4.167
 На графике фиг. 4.19 нанесена пунктирная линия, отвечающая уравнению 166. Если при построении графика выбрать логарифмическую шкалу, то эта линия оказывается очень близкой к прямой. Сплошная кривая получена по уточненному решению 121.
 График фиг. 4.20 определяет зависимость между о и q; шкалы также взяты логарифмическими. Линия, построенная по уравнениям 166 и 167, дана пунктиром. Здесь же отмечены точки, полученные в опытах с пластинками из дуралюмина, магниевого сплава и нержавеющей стали 430. Величина q условно определялась по замерам остаточной стрелы прогиба Со- Если сопоставить величину Со с давлением q, то соотношение между ними при достаточно большом q приближается к линейному фиг. 4.21. Продолжая прямой участок полученной линии до пересечения с осью qt находим значение а.
 т
 По теории октаэдрических напряжений наступление пластических деформаций будет определяться соотношением
 lа2 — а о -I— о2 а.
 г г г <Р I Ср т

204
 КРУГЛЫЕ ПЛАСТИНКИ
 ГЛ. IV
 бт
 100
 80
 60
 50
 40
 30
 20
 О
 8
 6
 5
 4
 3
 0,3 0,4 0,5 0,60,70Щ9 1,0 1,4,8 2,22,63,0 4,0 5,0 Хт
 Фиг. 4.19. Напряжения на границе упругого сопротивления пластинки.
 100г
 80-
 60-
 40-
 L 1.1.. 1,1
 Эксперимент томи -Ф- Дурашмин -Ф- Магниев сплав держав, стам
 линия
 приближение
 ттт
 I
 40 БОвОЮО гоо
 Фиг. 4.20. Нагрузка на границе упругого сопротивления.

§ 47 ПЛАСТИНКА С НАЧАЛЬНОЙ ПОГИБЬЮ. ХЛОПАЮЩАЯ МЕМБРАНА 205 У контура п п поэтому получим:
 ar, n 1
 Iх h Iх
 2 в,.
 4.168
 Фиг. 4.21. К определению нагрузки на границе упругого сопротивления.
 ПриА 0,3 будет от 0,89зг, ш соответственно изменятся коэффициенты в уравнении 166.
 После наступления пластических? деформаций у контура характер закрепления пластинки приближается к шарнирному опиранию. Если отношение cjh достаточно велико, то пластинку можно рассматривать при этом как мембрану, работающую за пределами упругости. Поэтому для определения несущей способности гибких пластинок, — если под этим
 понимать максимальную нагрузку, выдерживаемую пластинкой, — надо обратиться к упруго-пластической теории мембран.
 § 47. Пластинка с начальной погибью. Хлопающая мембрана
 Рассмотрим деформацию пластинки с начальной погибью. Для примера возьмем пластинку, защемленную по контуру, со свободным радиальным смещением точек контура при равномерно распределенной на-
 грузке фиг. 4.22. Примем, что началь-
 ные и дополнительные прогибы изменяются по одинаковому закону:
 У
 у
 Фиг. 4.22. Круглая пластинка с начальной погибью.
 4.169
 Подставляя эти выражения в уравнение совместности 36, получим: у-2ф -f 2H4f-2£ £. 4.170
 d_
 dr
 Интегрируя это уравнение подобно тому, как это было сделано
 d
 в § 41, получим производную -jp равной
 d
 dr
 £Я 2нч 6с
 Г Г3 Г5
 3 6 о —— 4 —г
 с с3 1 с5
 ■сЧ
 4.171
 Такое исследование было проведено А. А. Ильюшиным 48 и
 А. С. Григорьевым 44; в работе 44 было принято во внимание изменение толщины мембраны в процессе пластической деформации.

206 КРУГЛЫЕ ПЛАСТИНКИ гл. IV
 Выпишем выражение для функции X в уравнении Бубнова — Галеркина 85. Первые два члена в выражении 87 уже вычислялись выше § 41. Третий член равен
 h d< dw
 г dr dr dr
 h r r3 i -7у4яч 4r r®
 r 6c С С С5 С7 с с с Объединяя эти результаты, приходим к следующему уравнению при р — гс:
 1
 J 32Р - у - А 4 »■ 32ич 2, X
 О
 X Зр — 6рЗ 4р — рр — рЗ Р — Р8 р dp 0. 4.172
 Учитывая формулы а — d на стр. 188, находим следующую зависимость между и q:
 4 °f - i Eh fS зя„ Vfl, 0. 4.173
 При безразмерном параметре
 4-174
 будем иметь:
 4 <? ЗСНЧС2 20 3 С 9. 4.175
 В случае отсутствия начальной погиби получим прежнее уравнение 105.
 Этот вывод основного уравнения для пластинки с начальной погибью можно легко распространить на все другие случаи закрепления при условии, что форма начальной погиби отвечает принятому приближенному выражению для дополнительного прогиба. Поэтому основное расчетное уравнение можно выписать в такой общей форме:
 А КР 2ВД в' 4 •176
 Коэффициенты А и В могут быть взяты из таблицы V стр. 193. Рассмотрим два различных случая.
 1. Нагрузка действует в сторону начальной погиби. Тогда q будет монотонно возрастающей функцией С. Темп возрастания зависит от стрелы начальной погиби; при £ 0 наклон касательной будет определяться выражением
 Я,гв
 Это было отмечено Г. Нюландером 429.

§ 4? ПЛАбТЙНКА С НАЧАЛЬНОЙ погибью. хлопающая мембрана 207
 На фиг. 4.23 показан график С для пластинки со свободно смещающимся защемленным контуром для различных значений стрелы начальной погиби.
 теории при любом
 FT
 Фиг. 4.23. Диаграмма «нагрузка — прогиб» для круглых защемленных пластинок со свободно смещающимся контуром.
 2. Нагрузка направлена против начальнойпогиби фиг. 4.24. В уравнении 176 надо тогда заменить нч на —нч; получим:
 А С3 - ЗСнчС'2 2С,С ВС q 4.178
 Исследование этого уравнения приводит к тем же выводам, что и в случае прямоугольной пластинки Q
 § 18. Вычислим производные:
 ЛЗС»—6Сн,С2С,--В, а
 6С—Снч.
 fH4 W’uJ
 '’НЧ • Ь
 Приравнивая нулю а, найдем значения С, отвечающие экстремуму q:
 Фиг. 4.24. Поперечная нагрузка действует на пластинку с начальной погибью со стороны выпуклости.
 В случае малой начальной погиби кривая qС не имеет петли; для точки С Снч будем по Ь иметь точку перегиба. В предельном случае £Нч — ВА1 получим точку перегиба с горизонтальной

208
 КРУГЛЫЕ ПЛАСТИНКИ
 ГЛ. IV
 касательной. Соответствующие кривые показаны на фиг. 4.25 для примера, рассмотренного в начале параграфа.
 Если же начальная стрела достаточно велика, то кривая образует петлю. При этом верхнее значение q будет
 ч г>ч 1 - Ф и<к 1 -НО С2Н,в,
 а нижнее значение
 здесь
 ж;,-
 4.179
 4.180
 4.181
 На фиг. 4.26 представлены кривые <7С, относящиеся к нескольким значениям СНч Для защемленной пластинки. На графике фиг. 4.27, б
 дано сопоставление энергетических уровней различных равновесных положений при нагрузках <7 18; 24; 30 для £нч4; по оси ординат отложены величины Э Эс2ЕНЪу где Э—полная энергия системы. На фиг. 4.27, а дана соответствующая кривая С.
 Пластинки, для которых имеет место прямое и обратное выщелкивание при определенных значениях давления теоретически по линиям FP и МА на фиг. 4.27, а, часто называют хлопающими мембранами.
 Для определения напряжений можно использовать таблицу V, представив расчетные формулы в виде
 Фиг. 4.25. Зависимость между нагрузкой и прогибом для круглой пластинки с малой начальной погибью.
 з, а2С„,С,
 а„ рС2 2С„чС:
 4.182
 это легко видеть из сопоставления выражений 97 и 171 для —. Напряжения изгиба определяются прежними формулами 110 и 111.
 Задача о хлопающей мембране была исследована В. И. Феодосьевым 415.

§ 47J ПЛАСТИНКА С НАЧАЛЬНОЙ ПОГИБЬЮ. ХЛОПАЮЩАЯ МЕМБРАНА 209
 к
 Фиг. 4.26. Диаграмма «нагрузка — прогиб» для Фиг. 4.27. Энергетические уровни для круглой пластинки с большой начальной погибью. заданных нагрузок в случае пластинки
 с начальной погибью.

210
 КРУГЛЫЕ ПЛАСТИНКИ
 in. iv
 § 48. Пологая коническая панель
 Замкнутую пологую коническую панель фиг. 4.28 можно рассматривать как круглую пластинку с начальной погибью, для которой
 dw ч
 производная —- постоянна и равна малому углу а наклона образующей конуса:
 dwuu
 Фиг. 4.28. Пологая коническая панель под действием нагрузки, сосредоточенной в вершине.
 dr
 а.
 4.183
 Если не учитывать местных возмущений вблизи вершины конуса, то на подобную панель уместно распространить основные уравнения 35 — 36. Подставляя 183, получим:
 4.184
 4.185
 Разберем случай, когда коническая панель, защемленная по контуру, подвергается действию нагрузки Р, сосредоточенной в вершине. Примем, что точки контура свободно смещаются в его плоскости.
 Пусть упругие прогибы подчиняются зависимости 94. Уравнение 185 принимает вид
 1 	ущ _ гр ' In JL - 4f± In г..
 4.186.
 Е dr 4' ; с4 с с2 с
 Интегрируя с помощью формулы 133, находим:
 -iEH,a7c‘i- 4Л87
 Учитывая граничные условия, будем иметь:
 c>iEr'-rE-i- с-°-
 Далее составляем уравнение Бубнова — Галеркина 85, принимая
 -i7'7-4E«£l7-£ 4>7 7<4>

§ 49
 ГОФРИРОВАННАЯ ПЛАСТИНКА
 211
 и — по выражению 101. Окончательно получаем следующее уравнение для безразмерной стрелы прогиба С при i — 0,3:
 0.294С3 — 0,332 -j- С2 0,160 С ■ 1-.47С Р- 4.189
 Произведение ас равно высоте панели Н и отвечает начальной стреле прогиба пластинки см. § 47. Пользуясь уравнением 189, определяем параметры панели, при которых может иметь место прощелкивание, и соответствующую нагрузку. Аналогичным образом можно исследовать другие виды нагрузки или условия закрепления.
 § 49. Гофрированная пластинка
 Распространенным элементом различных приборов является гофрированная пластинка или, как чаще выражаются, гофрированная мембрана. Последний термин является условным, так как применяется к пластинкам с конечной изгибной жесткостью.
 Пластинка, снабженная концентрическими складками гофром, обладает гораздо большей жесткостью, чем плоская; при одной и
 ;Ч
 V0 н
 Фиг. 4.29. Круглая пластинка с синусоидальным гофром.
 той же интенсивности поперечной нагрузки величина прогиба резко меняется в зависимости от характера гофрировки.
 Разберем случай синусоидального гофра фиг. 4.29; будем считать, что начальные прогибы пластинки определяются уравнением
 -„cos 2;- l. 4.190
 Наибольший начальный прогиб амплитуда гофра характеризуется параметром нч. Угол между нормалью к срединной поверхности и осью z равен
 dwu„ 2 пп 2 ппг
 0НЧ dr “ fH4 с sn с ’ 4.191
 Предположим, что амплитуда гофра нч сравнима по величине с толщиной пластинки, но вместе с тем мала по отношению к радиусу.
 Случай равномерно распределенной нагрузки был рассмотрен Э. И. Григолюком 4.6.
 Теория гофрированных мембран разработана Д. Ю. Пановым 411,
 В. И. Феодосьевым 414 и Л. Е. Андреевой 4.2 и Инж. сб. 21, 1955.

212
 КРУГЛЫЕ ПЛАСТИНКИ
 ГЛ. IV
 Тогда можно воспользоваться уравнениями 35 и 36. Введем обозначение j3 2,im; получим
 4.192
 На контуре при г с величины wH4 и 0НЧ обращаются в нуль. Нагрузку будем считать равномерно распределенной по всей поверхности пластинки. Примем, что дополнительные прогибы пластинки подчинены условию скользящего защемления по контуру. В первом приближении деформацию пластинки можно описать, пользуясь прежним выражением 94 для дополнительного прогиба. При этом имеется в виду отразить лишь общую картину деформации; число складок и их расположение считается неизменным. Уравнение 36 принимает вид
 d 8Е г г3 г5 4£„чВ г2 В г
 _УФ2сТ l--sinL. 4.193
 Интегрируя, находим:
 г dr dr с2 2с2 2с4 ' 6с6
 Отсюда
 d d 8Е2 г3 г_. г7 dr dr с 2с3 2с5 6а7
 -4E-cosT:-Ssinf“ TFcosCir-
 Интегрируя вторично, будем иметь:
 <1Ф 8ЕР г г«. г®
 с 8с3 12с» 48с?
 г
 dr
 , „, ЯЧР Г1 гз. В г 6с2 6 г бег. рг. 3-2 Р г
 • с 5Ш т - -Fcos 7 - F sin с Fcos с т1 cos7тsin ?Ci Г2 'с2-
 Более подробные данные для практических расчетов гофрированных мембран см. в Справочнике машиностроителя, изд. 2, т. 3, Машгиз, 1955.

ГОФРИРОВАННАЯ ПЛАСТИНКА
 § 49
 Условия скользящего защемления дают
 .ff
 2 ’
 213
 С, 40Е-Л'
 ЛчР
 <ф
 Выражение для — принимает следующий вид:
 аф Е-Ь. Eff
 dr
 6я
 7i-
 Ф2.
 где
 1 q г а г3 лгЬ г?
 Vi 3 у —6 7з 47б — 77 >
 4.194
 4.195
 С3
 -т1-соз7 з1п7- <4Л96>
 В уравнение Бубнова — Галеркина 85 надо подставить
 -D?_sBigf-4X¥f-S¥-?-
 При интегрировании используем формулы:
 f rwsin — dr —cos Г г4'1 cos —dr,
 J с p с 1 p J с
 f „ 8r, rwc.8r nc f „ -. 8r.
 w COS — fifr -q— Sin 5- rw-1Sin — dr.
 J с p с p J с
 Получаем следующее уравнение:
 л_2£ 1р£л 1-ЕА 2 240 50 400
 3 U с 24 28 с '6с nj нч р2 р4 “ ре
 icc Л 1,5 1050. 37800.
 с ' 'нч 24р г 4 рв г 4£4.,А5-1-0. 4.198
 4.197
 1814 400
 Р8
 -
 или находим:
 у Р 24 р
 120, 25200
 Р2 Р4
 И
 907 200 г Г9
 55 j ’нч->“ -f-
 з11Л2 8 1 — г™ 4л
 В этом окончательном виде уравнение, определяющее относительную стрелу прогиба С в зависимости от параметра нагрузки д,

214
 КРУГЛЫЕ ПЛАСТИНКИ
 ГЛ. IV
 совпадает по структуре с уравнением 178 для хлопающей мембраны. Результаты вычислений зависят от знака СНч> следовательно, гофрированная мембрана должна различным образом реагировать на давление, приложенное с одной или другой стороны.
 200 °
 180 160 140 120 100 60 60 40 20
 2 3 4 X5
 Фиг. 4.30. Диаграмма «нагрузка — прогиб» для гофрированной пластинки.
 Легко видеть, однако, что влияние члена, содержащего Снч в первой степени, быстро убывает по мере возрастания величины j3, зависящей от числа волн. Если число волн достаточно велико п > 5, можно пренебречь в уравнении 199 членами, содержащимися в знаменателе; тогда получим:
 f '•’япЬ?8:-' г-<4'200
 На графике фиг. 4.30 дано несколько кривых £ по уравнению 200 при различных значениях амплитуды гофра Снч. Для значительных амплитуд Сн, 3 зависимость между прогибом и давлением приближается к линейной.
 § 60. Абсолютно гибкая круглая пластинка
 Обратимся к случаю абсолютно гибкой пластинки мембраны, изгибной жесткостью которой можно пренебречь. Воспользуемся системой основных уравнений в форме 151 и 152. Опуская член,

§ 50
 АЗСОЛЮТНО ГИБКАЯ КРУГЛАЯ ПЛАСТИНКА
 215
 содержащий изгибную жесткость, получим:
 dw °г х
 d2
 dx 2
 i
 v. 1 rfw’ea
 ■ -2 Ы-
 Подставляя
 dw
 из 201 в 202, будем иметь:
 Перейдем к новым переменным: у1-х £,
 32
 dw jLfУ <£_
 z V 2’
 z
 у±
 г2 '
 4.201
 4.202
 4.203
 4.204
 4.205
 4.206
 4.207
 4.208
 дф dr V qcW тогда 201 и 203 перейдут в уравнения:
 dy d2z dy2:
 Напряжения в срединной поверхности окажутся равными
 <-g-77W
 а соответствующие им деформации будут
 с2 l-j-р z dz Гq Л2
 '1Т -2-у-ГауУ т
 с2 uc rdz 1f г,8Аа2
 4 — JThdy 2 у1 2
 Для новой функции напряжений zy могут быть поставлены различные граничное условия.
 1. Радиальные смещения точек контура имеют заданную величину и0; тогда надо принять
 <4'2,0
 4.209
 Предполагается, что мембрана работает только на растяжение, так
 что е;>0 и еХХ

216 КРУГЛЫЕ ПЛАСТИНКИ гл. IV
 В частном случае несмещающегося контура и0 0 получим:
 dZ 1 4- Л £,.0114
 - при у. 4.211
 2. Радиальное натяжение на контуре имеет заданную величину оГ к; тогда
 . °г.к при у 1. 4.212
 В центре мембраны должно быть а и по 208
 j при у 0. 4.213
 При интегрировании уравнения 206 должно быть формулировано также граничное условие для w, например
 w 0 при у1. 4.214
 Таким образом, общее число граничных условий для сплошной мембраны составляет 3, в то время как для гибкой пластинки применительно к уравнениям 30 и 31 их было 5. Условия, относящиеся к углам поворота нормалей или изгибающим моментам, здесь отпадают.
 Судя по уравнениям 206 и 208, прогибы мембраны должны быть пропорциональны дз, а напряжения дз; это отвечает предыдущим приближенным решениям задачи, когда мембрана рассматривалась как предельный случай гибкой пластинки.
 Центральное место в теории мембран занимает интегрирование уравнения 207. При этом можно разложить функцию z в бесконечный ряд по степеням у:
 z ахУ- агУ'Л аъУг • • • 4.215
 Как легко видеть, условие 213 будет выполняться. Подставляя это выражение в 207, будем иметь:
 aiУ а2У2 аъУъ Н” • • 9 22-f- 63у-- 2а4у--... --у2 0.
 Сравнивая коэффициенты при одинаковых степенях у> получаем равенства:
 2tf2 1 » 42“f 6:: 0,...
 Этот метод был предложен Г. Генки 4>28 и развит Д. Прескоттом 122, Е. Швериным 42, П. Ф. Папковичем 16 и С, А. Алексеевым 4Л.

§ 50 АБСОЛЮТНО ГИБКАЯ КРУГЛАЯ ПЛАСТИНКА 217
 Таким образом, все коэффициенты, начиная с а2> можно выразить через ах
 1 1 13 17
 То у Я J
 'Ц' 3“_6< 144а’ б 288“''
 Выражение 215 для z перепишется в виде
 г<,'у-йу,у‘ку‘?у''''' <4'26 Подставляя 216 в уравнение 206, получим:
 dw 1 1
 у a4 Ly L «а Я. у».
 2а 6 л® 144л?
 ft.
 ИЛИ
 —' — — l — V — УЧ—— Уь ■ ■ -v С- 4.217 dy йД 2а31 12аУ 144а1 Г 2
 Интегрируя, будем иметь:
 w c—L.-5-4._®Lу,...liС. 4.218 L ai V 4л® 36а® 576л® _ Г 2
 Постоянные С и находим из граничных условий. По 214, полагая у 1, найдем:
 с -1ЛА—»•••• 4-219>
 «Л 4aJ 36л® 576aj С другой стороны, условие 211 дает
 j 1 1 13_
 а 2л® 36 af 1 Н-
 13
 4.220
 2л® 6а® 144л®
 Отсюда можно определить аи ограничиваясь тем или иным числом членов ряда. Стрела прогиба мембраны будет равна при у 0
 С С £. 4.221
 Отсюда получаем соотношение
 Ж8 ?, где А 4.222

218 КРУГЛЫЕ ПЛАСТИНКИ
 Пользуясь 208, находим напряжения: Напряжения в центре будут
 oale,2,
 гл. IV
 4.223
 у контура
 ■'-ЬО-йНгОт
 1 2аЛ
 2 а 12а®
 4.224
 4.225
 Если решать задачу в первом приближении, то надо принять аО, аг а3 — а4... 0. Тогда из 220 и 219 найдем:
 «-тгЗ. ckf
 4.226
 Соотношение между нагрузкой и стрелой прогиба будет иметь вид
 Ж8 qy где А ;
 для напряжений получим не зависящие от у выражения
 1 т 3 чс>
 °гТу izrato'
 1 3 —Х 4 1 — м.
 С2.
 4.227
 4.228
 Уточненное решение дает несколько другие коэффициенты в формулах 227 и 228. Возвращаясь к обозначениям § 42, представим расчетные формулы в виде
 Ж3 ?, о осО2, о ?С3.
 4.229
 В таблице VII даны значения коэффициентов А, а и 3, полученные при удержании в выражении для z десяти членов ряда.
 Эти данные можно сопоставить с такими же коэффициентами, полученными в первом приближении с помощью метода Бубнова — Галеркина таблица V.
 По решению С. А. Алексеева 4Л. Данные со звездочкой — по Е. Шверину 432; им же получена табл. VIII.

§ 501
 АБСОЛЮТНО ГИБКАЯ КРУГЛАЯ ПЛАСТИНКА
 219
 Таблица VII Данные для расчета круглых мембран
 Коэффициент
 Пуассона
 Н-
 Для стрелы прогиба А
 Для напряжений
 в центре
 у контура
 <Х р
 а
 9
 0,25
 3,39
 0,962
 0,30
 3,58
 1,010
 0,783
 0,285
 V.
 3,73
 1,047
  В случае кольцеобразной мембраны, подвергающейся действию равномерно распределенной нагрузки, метод решения задачи может бьТть сохранен, но должно быть введено граничное условие для внутреннего контура вместо условия, относящегося к центру сплошной пластинки. В таблице VIII помещены расчетные данные для кольцеобразной мембраны с неподвиж-
 Таблица VIII Данные для расчета кольцеобразных мембран с внешним неподвижным контуром при i 0,3
 ным внешним контуром и свободно смещающимся внутренним контуром. Внутренний радиус обозначен через cv Коэффициенты Л и 3 относятся к формулам
 Напряжение ог у внутреннего контура принято равным нулю.
 Если центральное отверстие весьма мало, то коэффициент 3 получает предельное значение 2,02, вдвое превышающее такую же величину для сплошной пластинки.
 Рассмотрим далее случай, когда сплошная мембрана имеет значительное предварительное натяжение, так что напряжения о и з можно считать не зависящими от прогиба:
 Отношение внутреннего радиуса к внешнему ctc
 Для прогиба х по внутреннему контуру
 Для напряжения <j<p у внутреннего контура J
 0,1
 3,59
 1,68
 0,5
 4,74
 2,07
 0,9
 50,9
 5,92
 Тогда уравнение 201 примет вид
 dw _ 1 dx 4
 <f
 Интегрируя, получаем принимая w — 0 при х — 0:
 1 д, '
 _ 1 <7
 , '3
 4.230
 4.231

220
 КРУГЛЫЕ ПЛАСТИНКИ
 ГЛ. IV
 Стрела прогиба равна
 С 4-233
 Отсюда
 fTs3£s'>-m‘2b3’ <4'234>
 где d — диаметр пластинки. Стрела прогиба получается несколько
 меньше, чем для квадратной мембраны: в формуле 2.164 коэффи¬
 циент был равен 0,071 вместо 0,0625.
 Попытаемся теперь приближенно оценить влияние прогиба на напряжения, считая последние постоянными по всей площади мембраны. Определим относительную деформацию некоторого радиального волокна по формуле 1, условно полагая, что радиальные смещения отсутствуют:
 1 dw 0 22 г2
 8 2 dF с РИ W A1--
 Найдем среднюю деформацию е по всему радиусу:
 с
 If, 22 8— с J Zrdr— 3 С2 •
 О
 Считая напряженное состояние однородным, найдем соответствующее напряжение:
 Е - 2 Е 2
 1 — х 31 — р-с2 В безразмерных параметрах
 4.235
 »• 4'236
 Эту величину надо прибавить к «основному» напряжению о в уравнении 233; тогда получим:
 8 1
 3,-3 «>- <4-23Т
 Отсюда можно определить С для некоторой поперечной нагрузки q при заданном предварительном натяжении о. Если допустить, что предварительное натяжение вообще отсутствует, то этот прием приводит при а 0,3 к формуле типа 227 с коэффициентом Л 3,81 вместо уточненного значения 3,58.

§ 51 КРУГЛАЯ ПЛАСТИНКА ПОСЛЕ ПОТЕРИ УСТОЙЧИВОСТИ
 221
 § 51. Круглая пластинка после потери устойчивости при радиальных сжимающих усилиях. Аналогия с прямоугольной пластинкой
 Рассмотрим круглую пластинку, защемленную по контуру и подвергающуюся действию сжимающих радиальных усилий рг, равномерно распределенных вдоль контура фиг. 4.31. При критическом значении внешней нагрузки происходит потеря устойчивости пластинки, сопровождающаяся осесимметричным изгибом. Исследуем большие прогибы пластинки после потери устойчивости.
 Изогнутую поверхность представим, как и при изучении действия поперечной нагрузки, с помощью выражения 94. В дальнейшем мы должны определить функцию напряжений Ф из уравнения 31. Это было уже сделано в § 41, поэтому можно выписать в окончательном виде уравнение 96:
 йФ
 dr
 _ 2ЕР г2
 с 2с3
 3
 12с7
 Фиг. 4.31. Круглая пластинка под действием радиальных сжимающих усилий.
 Из условия 46 находим С2 0. Величина Сх должна быть теперь найдена с учетом того, что при г с
 1 аФ г dr
 —р.
 4.238
 Окончательно находим:
 Уравнение, написанное по методу Бубнова — Галеркина, имеет вид 85. К выражению 100 для X надо теперь прибавить член
 В дополнение к вычислениям § 41 надо найти интеграл
 1
 А - J hP Ц- Р — Р82 <Р — Jphc.
 о

222 КРУГЛЫЕ ПЛАСТИНКИ гл. IV
 Уравнение, определяющее зависимость между стрелой прогиба и усилием р, приобретает форму
 Df±Ehf-Pf0. 4.240
 При малых прогибах можно пренебречь средним членом; тогда получим уравнение
 d_2° 4 241 Отсюда, считая f Ф 0, находим критическое напряжение:
 4.242
 Точное решение задачи в функциях Бесселя приводит к коэффициенту 14,68 вместо 16; ошибка составляет около 9. Введем параметры
 '•-£■’• r-f <4-243> Тогда уравнению 240 можно придать вид
 ><р-3- 4-244>
 При одновременном действии поперечной нагрузки и радиальных усилий уравнение 240 должно быть дополнено членом qcA24 см. § 41. Тогда стрела прогиба будет определяться из уравнения
 ТсзГ-4'Ф «-- <4-245>
 При действии растягивающих усилий знак перед р должен быть изменен на обратный. При относительно большом значении р получим при этом зависимость 4рС <7, совпадающую с 233.
 В опытах с круглыми пластинками, подвергающимися воздействию поперечной нагрузки, закрепление образцов часто связано с приложением начальных напряжений в плоскости пластинки — сжимающих или растягивающих. Для введения поправок к результатам опытов можно использовать уравнение 186.
 При шарнирном закреплении пластинки по контуру изогнутую поверхность можно охарактеризовать уравнением 121:
 w
 “х—<4-246>
 с обозначениями:
 “-5TF- <4'247>
 См. А. Н. Динник 4.7, Избранные труды, стр. 63.

§ 51 КРУГЛАЯ ПЛАСТИНКА ПОСЛЕ ПОТЕРИ УСТОЙЧИВОСТИ 223
 Если учесть новые граничные условия, то выражение 123 для перепишется так:
 4.248
 Уравнение 124 в дополненном виде будет иметь вид при q 0 f Db 3 — 2b —p 6 — 8b ЪР hc'f
 -r Ehaf 84— 1686-f- 14062 — 566s 9 b 0. 4.249
 йФ __ EPa? dr 6c2
 Критическое напряжение акр находим из уравнения 8
 получаем:
 3 Ко № — 8Ь 32 haf
 6 Dab 3 — 2b— —- - 0;
 При j. 0,3
 _ 63-26 D
 6 — 86 362 сШ ' 4.20U
 зВр 4,21 -щ- 0,385£ ff ’ 4-251
 что почти совпадает с точным решением.
 В безразмерных параметрах уравнению 249 можно придать вид при jx 0,3
 pW 0,10. 4.252
 Обозначим через п степень превышения критического напряжения:
 4.253
 Р _ Р‘
 а 0,385
 Тогда из уравнения 252 получим:
 С 1,9бК«— 1. 4.254
 Придадим этому соотношению вид
 1,9бГ31. 4.255
 Если допустить, что пластинка способна в пределах упругих деформаций выдерживать весьма большие усилия р, и условно принять, что изогнутая поверхность не теряет при этом осевой симметрии, то в пределе, при г—> оо, получим Cjл- 1,96.
 См. сноску на стр. 222.

224
 КРУГЛЫЕ ПЛАСТИНКИ
 ГЛ. IV
 На фиг. 4.32 пунктирной линией представлена зависимость 255. Сплошная линия дана по уточненному решению Фридрихса и Стокера 427. Представляя изогнутую поверхность пластинки с помощью
 3 5 7 п 9
 Фиг. 4.32. Диаграмма закритической деформации шарнирно опертой круглой пластинки.
 степенного ряда, они установили, что при значительном превышении критического напряжения центральная часть пластинки делается почти плоской, как показано на фиг. 4.33.
 Если в приближенном решении задачи, относящемся к шарнирно опертой пластинке, не ограничиваться определением стрелы прогиба,
 Фиг. 4.33. Изменение формы изогнутой поверхности круглой пластинки в процессе закритической деформации.
 а попытаться выяснить распределение напряжений, то мы придем к следующим выводам. В момент потери устойчивости по всей площади пластинки радиальные и дуговые напряжения равны критическим: ог аф —зкр. После выпучивания напряжения в центре ог>ц оф, ц падают по абсолютной величине, а затем меняют знак, т. е. становятся растягивающими. Отношение ог, цр равно при этом
 1,15

§51 КРУГЛАЯ ПЛАСТИНКА ПОСЛЕ ПОТЕРИ УСТОЙЧИВОСТИ
 225
 В пределе при оо получим аг, цр->2. Напряжения по радиальным сечениям в центральной части пластинки также становятся растягивающими. Вместе с тем в полосе пластинки, прилегающей к контуру, они остаются сжимающими и при этом быстро возрастают. У самого контура напряжения а<р, к особенно велики; в пределе, при г-оо, получим о<р, кр — — 5,35.
 В работе 4 27 рассмотрен предельный случай п -> оо; с качественной стороны сделанные нами выводы, касающиеся характера напряженного состояния, подтверждает и уточненное решение. Здесь можно сделать сопоставление с прямоугольной пластинкой, сжатой в одном направлении и деформирующейся после потери устойчивости. Если рассмотреть сечения круглой и прямоугольной пластинки, нормальные к контуру, то в обоих случаях сжимающие напряжения концентрируются в пограничной зоне фиг. 4.34.
 Не надо забывать, однако, что при увеличении п сжимающие напряжения по радиальным сечениям быстро возрастают и при п -> оо должны стать бесконечно большими. В действительности такое возрастание сжимающих напряжений при условии, что деформации остаются упругими будет связано с образованием новых мелких выпучин, обозначающих как бы вторичную потерю устойчивости; в дальнейшем, выпучины должны размельчаться. Это явление связано с нарушением осевой симметрии изогнутой поверхности и может быть исследовано с помощью полных уравнений 61 — 62.
 В случае одновременного действия радиального сжатия и поперечной нагрузки стрела прогиба шарнирно опертой пластинки определится из уравнения
 0,376C3-f-l,44 — 3,73? С q. 4.257
 Если усилия р являются растягивающими, перед соответствующим членом в скобках надо поставить знак плюс. При достаточно большой величине р придем к зависимости Ъ,7Ър — q, близкой к 233.
 ниш
 Гр
 es1
 : jJ 1
 к:
 llii: Щ
 iiii:' -nijjj
 ttttttt
 а
 Фиг. 4.34. Напряжения в пограничных зонах прямоугольных и круглых сжатых пластинок.

ГЛАВА V
 ОБЩИЕ СВЕДЕНИЯ О ГИБКИХ ОБОЛОЧКАХ § 52. Основные определения
 Оболочкой называется тело, ограниченное двумя криволинейными поверхностями, расстояние между которыми толщина оболочки мало по сравнению с другими размерами тела. Поверхность, делящая пополам толщину оболочки, носит название срединной поверхности.
 В дальнейшем мы будем рассматривать только оболочки постоянной толщины. В зависимости от формы срединной поверхности различают оболочки сферическую, цилиндрическую, коническую и т. д.
 На фиг. Ъ. 1 изображен отрезок срединной поверхности оболочки, имеющий произвольное очертание. Проведем в некоторой точке т нормаль п к поверхности. Если через нормаль провести ряд плоскостей, то в пересечении с поверхностью они дадут различным образом ориентированные плоские кривые линии — так называемые нормальные сечения. Фиг. 5.1. Нормальные сечения оболочки. Допустим, что плоскость S’ поворачивается вокруг нормали; будем определять кривизны образующихся при этом нормальных сечений 5. Тогда окажется, что для двух кривых ги, лежащих во взаимно перпендикулярных плоскостях R и Т, кривизны имеют экстремальные значения по отношению ко всем другим нормальным сечениям; для одной из этих линий кривизна будет максимальной, а для другой — минимальной. Направления, соответствующие кривым г и, называются главными направлениями для данной точки поверхности, а кривизны по этим направлениям — главными кривизнами. С этими понятиями мы уже встречались в § 36 при рассмотрении изогнутой поверхности круглых пластинок.

§ 52
 ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
 227
 Допустим, что в различных точках поверхности найдены главные направления. Если провести линии, касательные к которым в каждой точке совпадают с этими направлениями, то получим так называемые линии кривизны.
 Положение некоторой точки на поверхности можно определить по ее координатам, отсчитываемым по определенным направлениям. Условимся в качестве координатных линий х и у выбирать линии кривизны недеформированной поверхности. Эти линии будут образовывать на поверхности ортогональную сетку фиг. 5.2.
 Для известной точки поверхности может быть найдена так называемая гауссова кривизна, равная произведению главных кривизн:
 Г kxky. 5.1
 Под средней кривизной поверхности в даннойГ точке подразумевается величина
 K kx ky. 5.2
 Фиг. 5.2. Линии кривизны срединной поверхности оболочки.
 Оболочки могут быть классифицированы по знаку гауссовой кривизны их срединной поверхности. Положительную и вместе с тем постоянную для всех точек гауссову кривизну имеет сферическая
 поверхность. Примером поверхно сти отрицательной гауссовой кри¬
 визны может служить поверхность вращения, изображенная на фиг. 5.3. В некоторой точке т поверхности одно из главных направлений образует меридиональная плоскость S. Нормальное сечение, перпендикулярное к этой плоскости, дает второе главное направление. Для всякой поверхности вращения центр кривизны этого второго сечения лежит в точке Р2 пересечения нормали с осью симметрии. На той же нормали лежит центр кривизны меридиана Pv Так как центры кривизны находятся по разные стороны от точки т, то кривизны kx lRxHky Ry будут иметь разные знаки. На фиг. 5.3 нанесены
 Фиг. 5.3. Оболочка отрицательной гауссовой кривизны.
 В некоторых случаях целесообразно воспользоваться иной системой координатных линий, не являющихся ортогональными. Одна из таких систем рассмотрена в добавлении к книге стр. 400.

228
 ОБЩИЕ СВЕДЕНИЯ О ГИБКИХ ОБОЛОЧКАХ
 ГЛ. V
 также линии кривизны поверхности: в случае поверхности вращения они совпадают с меридианами и параллелями.
 Цилиндрическая и коническая поверхности принадлежат к поверхностям нулевой гауссовой кривизны: одна из главных кривизн здесь обращается в нуль. Существенная особенность поверхностей нулевой гауссовой кривизны состоит в том, что они являются развертывающимися, т. е. могут быть развернуты на плоскость без образования складок или разрывов; длины всех линий на поверхности остаются неизменными.
 Цилиндрическую оболочку, поперечное сечение которой очерчено по окружности, называют круговой. Подобную оболочку будем считать замкнутой, если сечение ее представляет полную окружность, и открытой, если сечение составляет часть окружности.
 Фиг. 5.4. Пологая панель положи- Фиг. 5.5. Поперечная нагрузка вос-
 тельной гауссовой кривизны. принимается за счет усилий в сре¬
 динной поверхности.
 Под пологой оболочкой будем понимать отрезок оболочки произвольного очертания, стрела подъема которого Н мала по сравнению с основными размерами фиг. 5.4.
 Допустим, что к отрезку оболочки приложена поперечная нагрузка. При относительно малых нагрузках в оболочке будут возникать прежде всего цепные напряжения, равномерно распределенные по толщине оболочки. Здесь можно провести аналогию с аркой, воспринимающей поперечную нагрузку по преимуществу за счет осевых усилий фиг. 5.5. Так как изгибные напряжения в оболочке будут сравнительно малы, то оболочку можно назвать безмоментной. В этом состоит существенная особенность оболочки по сравнению с плоской пластинкой: последняя воспринимает поперечную нагрузку при малых прогибах главным образом за счет напряжений собственно изгиба.
 Если оболочка достаточно тонка, то при дальнейшем увеличении нагрузки она может получить упругие прогибы, сравнимые с толщиной. Тогда к напряжениям- в срединной поверхности присоединятся сравнимые с ними по величине напряжения изгиба; напряженное состояние станет уже смешанным или моментным.
 Таким образом, два различных напряженных состояния, имеющих место при малых нагрузках в случаях плоской пластинки и безмоментной оболочки переходят для гибких пластинок и оболочек в единое — смешанное напряженное состояние. Из этого вытекает, что дифференциальные уравнения теории гибких пластинок и оболочек

§ 53 ДЕФОРМАЦИИ СРЕДИННОЙ ПОВЕРХНОСТИ И ИЗМЕНЕНИЯ КРИВИЗН 229
 должны иметь общую структуру. Что касается пологих оболочек, то для них уже при малых нагрузках характерным является смешанное напряженное состояние.
 В задачах устойчивости оболочек обычно можно считать, что в первоначальном равновесном положении оболочка работает как безмоментная. Однако при потере устойчивости сразу же возникают значительные напряжения изгиба. Как мы увидим в дальнейшем, оболочки теряют устойчивость, как правило, с образованием глубоких выпучин. Но при этом оболочку надо рассматривать как гибкую. Поэтому теория гибких оболочек должна найти практическое приложение во всех тех областях техники, для которых важным является расчет оболочек на устойчивость.
 В конструкции самолета на устойчивость должны быть рассчитаны криволинейные панели обшивки крыла и фюзеляжа, а также герметические кабины. При проектировании реактивных двигателей должен быть проведен расчет на устойчивость форсажной камеры, внешнего и внутреннего кожухов камеры сгорания. В корпусе надводного корабля необходимо обеспечить устойчивость криволинейных участков обшивки; в подводных лодках — обшивки корпуса, цилиндрических и сферических переборок.
 Крупные резервуары, применяемые в химической промышленности:, работают в некоторых случаях при избыточном внешнем давлении и также рассчитываются на устойчивость. В инженерных сооружениях находят применение пологие оболочки в виде перекрытий и покрытий; они должны обладать достаточной устойчивостью при статической нагрузке, а в сейсмических районах — и при динамическом нагружении.
 § 53. Деформации срединной поверхности и изменения кривизн.
 Уравнение совместности деформаций
 Выберем координатные линии хну таким образом, чтобы они совпадали с линиями кривизны срединной поверхности. Координату z будем отсчитывать по нормали к поверхности, считая z положительным по направлению к центру кривизны фиг. 5.6. Обозначим перемещения точек срединной поверхности вдоль линий х, у, z соответственно через и, v, w. Для начальных кривизн линий х и у введем обозначения kx и ky.
 Найдем выражения для деформаций срединной поверхности при прогибах оболочки, сравнимых с ее толщиной. Для этого воспользуемся выражениями 1.7 — 1-9, выведенными выше для плоской пластинки. В случае оболочки они должны содержать дополнительные члены. Эго можно видеть из фиг. 5.7, изображающей элемент
 Имеются в виду оболочки положительной или нулевой гауссовой кривизны.

230
 ОБЩИЕ СВЕДЕНИЯ О ГИБКИХ ОБОЛОЧКАХ
 ГЛ. V
 линии х в начальном и смещенном положениях. Радиус кривизны элемента, первоначально равный pxkx, после смещения будет рх — w. Относительная деформация, обусловленная перемещением элемента к центру кривизны, оказывается равной
 w
 Рх
 Рх
 Для линии у по аналогии
 5.3
 5.3'
 Окончательные выражения для деформаций срединной поверхности получают вид
 да и.1 dw2
 — dxkxW 2 w ’
 dv и,1 dw2
 Zv Ty — kvW2dj ’
 да dv dw dw
 dy ' dx ' dx dy
 5.4
 Подобно случаю пластинки, деформации 4 не являются независимыми. По аналогии с 1.10 получаем следующее уравнение совместности деформаций:
 <Э2е,
 dv
 <?2Y
 dy2 1 dx2 dx dy
 d2w 2 d2w d2w d2w d2w
 dx dy dx2 dy2 dy2 У dx2
 Для определения деформаций изгиба воспользуемся, как и в случае пластинки, гипотезой прямых нормалей. Обозначим через и изменения кривизн, которые получат в некоторой точке срединной поверхности координатные ли-
 dx
 Фиг. 5.6. Координатные линии при рассмотрении оболочки.
 Фиг. 5.7. К определению деформаций в срединной поверхности, связанных с прогибами.
 нии х и у; через будем попрежнему обозначать «кривизну» кручения поверхности. В случае плоской пластинки величины ху и у

§ 53 ДЕФОРМАЦИИ СРЕДИННОЙ ПОВЕРХНОСТИ И ИЗМЕНЕНИЯ КРИВИЗН 231
 определялись по формулам:
 d2w d2w d2w
 v'VdyZ’ dxdy■
 Для оболочки формулы 6 не всегда могут быть применены. Из
 фиг. 5.7 заключаем, что кривизна отрезка линии dx получает в связи
 с прогибом w изменение
 А 1 1 W С 7
 Ах т г • 5.7
 Рх Pcc — W PaPx — W v 7
 Примем приближенно Дх ?0р и введем эту величину в выраже-
 d2w w я
 — Т2 2 °'Ь
 дх pz.
 - wp2
 ние для тогда получим:
 По аналогии
 dw w к ЛЧ
 У ду2 р 9
 Определим изменение кривизны круговой цилиндрической оболочки радиуса R в сечении, сделанном вдоль дуги фиг. 5.8 при условии, что зависимость между прогибом w и дуговой координатой у имеет вид
 W -
 sin; 5.10
 для замкнутой оболочки п COOT- ? XV
 ветствует числу волн по окруж- 'г ности. Вычисляя изменение кри- ?
 визны ууу получим: 7
 - я2. пу. пу Фиг. 5.8. Выпучины, располагающиеся
 у — J 7SinR ' вдоль координатной линии у.
 5.11
 Как видим, удельный вес второго члена по сравнению с первым измеряется отношением п2. Опустить второй член можно в том случае, если по окружности образуется достаточно большое число волн, например п 4. В более общей форме это требование можно выразить таким образом, что размеры выпучин, образующиеся при деформации оболочки, должны быть малы по сравнению с радиусами кривизны. В задачах, относящихся к устойчивости оболочек, это условие обычно выполняется. Имея в виду именно этот случай, мы будем в дальнейшем пользоваться для гибких оболочек формулами 6.
 Такое же ограничение относится к формулам 4; в общем случае они имеют более сложный вид,
 Исключение составляют случаи, когда относительно длинные цилиндрические оболочки при длине, значительно превышающей радиус кривизны теряют устойчивость при внешнем давлении или закручивании.

232
 ОБЩИЕ СВЕДЕНИЯ О ГИБКИХ ОБОЛОЧКАХ
 ГЛ. V
 Допустим теперь, что оболочка имеет отклонения от идеальной формы, характеризуемые начальными прогибами wa4. Тогда по аналогии с выражениями 1.19, относящимися к пластинке с начальной прогибью, мы можем для оболочки записать :
 1 dw wH4l2
 ди 1 dw w„42 1 dwn ч2
 dx xW 2 дх 2 дх ’
 1 dw wH4y 1 dwB42 vw 2 L dy J 2 diT ’
 dv
 гУду k
 da. dv
 dy J 2 dy dw wm dw wH4 dwmdw„4
 1 dy'dx ' dx dy dx dy
 под до понимается дополнительный прогиб.
 Уравнение совместности деформаций получит вид
 d2x d4y d2 y
 d dx2
 dx dy
 d2H4 d2 ttfg, w
 Г d2 шнч w2 _ d2te;H4 2 _
 L dxdy J dxdy J
 d2wH, d2wH4
 dx2
 dy2
 dx2 dy2
 d2w
 d2w
 5.12
 5.13
 § 54. Напряжения в оболочке. Уравнение равновесия элемента оболочки
 На фиг. 5.9 представлен элемент оболочки, по граням которого действуют усилия в срединной поверхности и усилия изгиба — моменты
 Qvdx
 У Hdx
 Фиг. 5.9. К условиям равновесия элемента пологой панели.
 и поперечные силы; нормально к элементу приложена поперечная нагрузка интенсивности q.
 И здесь предполагается, что размеры первоначальных выпучин малы по сравнению с основными размерами оболочки.

§ 54
 НАПРЯЖЕНИЯ В ОБОЛОЧКЕ
 233
 Выпишем уравнения равновесия элемента. Начнем с уравнения проекций всех сил на направление касательной k к линии х. Считая, что ввиду малости углов усилия в срединной поверхности проектируются в натуральную величину, получим:
 °® Шах hdy- dy ? y hdx — xhdx 0. 5.14
 В это уравнение не включены проекции поперечных сил. Более подробное исследование показывает, что при образовании сравнительно мелких выпучин эти проекции пренебрежимо малы. После простых преобразований получаем:
 tjcty
 24 0.
 дх 1 ду
 5.15
 Для линии у аналогичным образом найдем:
 дт да у
 Ё — о
 дх ду
 5.16
 Фиг. 5.10. К выводу условий равновесия деформированного элемента оболочки.
 Уравнение моментов всех сил относительно касательной I к линии у будет иметь вид
 Mx d-dxdy-- Mxdy Hd- dy dx —
 —Я dx — qdx ЛуЦ; — Ях--г dx dydx — d-- dydx 0. 5.17 Отбрасывая малые зысшего порядка, находим аналогично 1.28:
 дМл
 дН
 дх ду ®х ° Уравнение моментов относительно k будет
 дН дМу дх ду
 Qy — 0.
 5.18
 5.19
 Составим теперь уравнение проекций всех сил на направление нормали, причем рассмотрим элемент оболочки в деформированном состоянии. Усилия oxh и oyh дадут дополнительные составляющие, равные фиг. 5.10
 kx S dxdy, ayh 4 gJ dxdy.
 Окончательно уравнение равновесия будет иметь вид
 dQx dQy d2w d2w d2w
 dy °xh x аУН dxdy1 0 •20

234
 ОБЩИЕ СВЕДЕНИЯ О ГИБКИХ ОБОЛОЧКАХ
 ГЛ. V
 Для оболочки с начальными отклонениями от идеальной формы будем иметь:
 dQx. dQy Г а Л
 д7 ду Ikx Ш 'Шнч J
 --Oyh ky ta 2ih 0-w-- w„4-- q — 0. 5.21
 § 55. Соотношения между деформациями и напряжениями. Основные дифференциальные уравнения
 Выпишем соотношения между деформациями и напряжениями в срединной поверхности:
 0» rs» J>
 Е
 Х-21 Т-
 5.22
 Зависимости между моментами и изменениями кривизн останутся теми же, что и для плоской пластинки:
 «м d2w, d2w
 — D д2 5х >
 ЛГ №w, d2w
 H —D 1 — i
 d2w дх ду
 5.23
 Для поперечных сил получаем выражения, соответствующие 1.51 и 1.53:
 Qv DTyw-
 5.24
 Уравнения равновесия 15 и 16 автоматически выполняются при введении функции напряжений по формулам 1.56.
 Подставим выражения 23 и 24 в уравнение равновесия 20; тогда придем к следующему уравнению:
 DWw aJt g yh ky- 2hgL q. 5.25

§ 55 СООТНОШЕНИЯ МЕЖДУ ДЕФОРМАЦИЯМИ И НАПРЯЖЕНИЯМИ 235
 Преобразуем теперь уравнение совместности деформаций 5. Выражая деформации ех9 гу> у через напряжения, найдем:
 , t_L2L I ду2 дх ду дх2 ‘А ду- ' дх ду дх'
 Гd2w2 d2w d2w и d2w и №w 0я
 — LVy — э2 дУ2 х дУ2 у дх2 J ‘
 Введем в уравнения 25 и 26 функцию напряжений Ф. Тогда
 основные уравнения теории гибких пологих оболочек примут вид
 Ww Lw, ф 5.27
 VTO -±L«, 5.28
 В частном случае круговой цилиндрической оболочки радиуса R
 получим
 5.V'2V2m — — 4-—— — — 4--- 5 29
 h дх2 ду2 ду2 дх2 дх ду дх dy'R дх2 h ’ ' '
 lvav4 —5 зо Е дхду дх2 ду R дха ‘ wov>
 Если начальные усилия в оболочке отсутствуют, то при рассмотрении малых прогибов нелинейными членами в уравнениях 27 и 28 можно пренебречь; будем иметь:
 T™—k3? b£ i, 5.31
 <5-32>
 Считая кривизны и ky постоянными и применяя к 31 оператор VaVa,e найдем:
 4 V9V9V»V»«r kx ТО ky УУФ 17«Vr.
 Если- подставить сюда V2V‘2 по 32, то можно привести систему
 31 — 32 к одному разрешающему уравнению восьмого порядка
 относительно функции w:
 ж V2V2V2V2™. ж v'2va • <5-33>
 Для круговой цилиндрической оболочки будет
 '’-д£жтя1- <534>
 Эти уравнения применимы и при рассмотрении оболочек произвольного очертания, если деформация «имеет характер местной потери устойчивости, см. 5.1.

236 ОБЩИЕ СВЕДЕНИЯ О ГИБКИХ ОБОЛОЧКАХ ГЛ. V
 Рассмотрим теперь случай, когда надо учесть начальные усилия в срединной поверхности, постоянные по величине, как, например, в задачах устойчивости оболочек:
 д2Ф д2Ф д2Ф
 ич — п ° ич — д ° нч _ С ОКЧ
 <Э_у2 — Рх> дхъ — ру> дхду -S- О.дЬ
 Тогда уравнение 29 примет вид при 0:
 D гтогто d2w d2w 0 д2w, и д2Ф., д2Ф 0ч
 h V'Va’ РхШРу дхду 5-36
 под Ф здесь понимается функция напряжений, зависящих от обстоятельств изгиба. Присоединяя сюда 32, получаем разрешающее уравнение:
 ш v’v w«к-Ш“л к> st£■
 ™1Ь£™1©-«- <5-37>
 В случае круговой цилиндрической оболочки
 т 1Sл.™ IS
 №Дг’.'? £“0- 5'38
 Считая в 25 0, получим известное уравнение теории безмоментных оболочек:
 Х°Х kyGy у
 напомним, что поперечная нагрузка считается положительной по направлению к центру кривизны.
 Если принять в уравнениях 27 и 28 kx ky 0, придем к системе уравнений 1.60—1.61 для плоской пластинки.
 В § 5 было показано, что правая часть уравнения совместности деформаций 1.61 отвечает гауссовой кривизне изогнутой. поверхности пластинки. Правую часть уравнения 28 можно также приближенно представить как приращение гауссовой кривизны срединной поверхности пологой оболочки. Для этого, пользуясь выражениями 6, перепишем 28 в виде
 V2 У2Ф X2 — V-x'y kx'v kv'-xКривизны линий х и у после изгиба равны
 fox Ху foy ky У-у • • 39

§ 55 СООТНОШЕНИЯ МЕЖДУ ДЕФОРМАЦИЯМИ И НАПРЯЖЕНИЯМИ 237
 Линии х и у не будут теперь линиями кривизны; поэтому надо учесть кривизну кручения деформированной поверхности
 k'xy — ■ 5.40
 Новая гауссова кривизна оказывается равной
 Г kxky kxy X I £0 У-хЬу 2> 541
 изменение гауссовой кривизны при этом будет
 ДГ Г' — Г — X2 -Ь ау — kxv — V- 5-42
 Таким образом, уравнению 28 можно придать вид
 узузф — — др. 5.43
 Основные уравнения для оболочки с начальной погибью начальными отклонениями от идеальной формы можно получить по аналогии с системой 1.73—1.74 из условия совместности деформаций 13 и уравнения равновесия 21:
 §V»V»« £««„, Ф 5.44
 ±у2У2Ф — -jLw 2«r,„ w — kjgp — kyd. 5.45
 Обратимся к ортотропной оболочке с главными направлениями, совпадающими с линиями х, у. Пользуясь обозначениями § 12 и вводя в 1.155 и 1.156 дополнительные члены, учитывающие кривизны оболочки, придем к таким основным уравнениям:
 Dtdw, 0Z>3 d4w. D2dw T лч.. д2Ф,, д2Ф. q. а
 Т дх h дх2 ду h ду 00 ду V дх h ’ s дФ, дФ. дФ 1,, ч. d2w, dw с
 2 дх4 8 дх2 ду2 °1 ““ 2 х дуз у дх2 • В случае трехслойной оболочки, отвечающей допущениям § 13, основные уравнения 1.183—1.184, полученные для слоистой пластинки, перейдут в следующие:
 •т. _, _ v i „,•. g 4, » i. 5.48
 5.49
 Для D здесь сохранено выражение 1.168.

238
 ОБЩИЕ СВЕДЕНИЯ О ГИБКИХ ОБОЛОЧКАХ
 ГЛ. V
 § 56. Вариационные уравнения.
 Применение приближенных методов
 В § 7 было составлено вариационное уравнение для пластинки, основанное на принципе возможных перемещений. Таким же образом может быть составлено уравнение для оболочки при однородных граничных условиях
 л Xbwdxdy 0, 5.50
 F
 где
 XDWw-hLw, Ф-hkx-hky-q. 5.51
 Решение конкретных задач, относящихся к гибким оболочкам, может быть построено по той же схеме, что и для пластинок, если кривизны kx и ky постоянны. Для w выбирается приближенное выражение
 •о» 2iu; 5.52
 г 1
 далее определяется функция Ф из уравнения совместности деформаций 28, после чего используется метод Бубнова—Галеркина,
 либо метод Ритца. По первому из этих методов составляются урав¬
 нения типа
 Xiidxdy 09 5.53
 F
 по второму — варьируется по параметрам fi выражение для полной энергии системы Э. Потенциальная энергия изгиба оболочки и энергия деформации срединной поверхности определяются с помощью тех же выражений 1.109 и 1.106, что и в случае пластинки.
 Можно также составить выражение типа 52 для всех трех перемещений иу v, w см. § 10 и варьировать Э по всем параметрам; при этом уравнение совместности деформаций выпадает.
 Для оболочки с начальной погибью выражение для X составляется, исходя из уравнения 44:
 XDWw-hLw wm, Ф — hkx — hkv — q. 5.54
 Для круговой цилиндрической оболочки идеальной формы
 г 72Г7> и d2w д2Ф. d2w д2Ф 0 d2w д2Ф, 1 д2Ф
 hdx дуа ду дха дхду дхду R дх q'
 5.55

§ 56
 ВАРИАЦИОННЫЕ УРАВНЕНИЯ
 239
 а при наличии начальной погиби
 ду2 ду2
 о д2 ДО нч 2ф дх ду дх ду
 Можно идти также по пути, указанному в § 9, составляя выражения для вариаций полной энергии системы Э ив предположении, что в одном случае варьируется прогиб w, а в другом — функция Ф. Тогда получим два вариационных уравнения, одно из которых совпадает с 50, а второе имеет вид
 Уравнение 57 можно использовать для составления второй системы уравнений Бубнова—Галеркина, выражающих условие совместности деформаций. Такой путь наиболее естественен в том случае, если при интегрировании уравнения совместности деформаций не удается удовлетворить граничным условиям задачи. Для оболочек с начальной погибью выражение типа 58 строится исходя из 45.
 Наконец, во всех задачах, относящихся к оболочкам, могут быть применены метод возмущения, метод последовательных приближений или метод конечных разностей см. § И.
 5.57
 F
 где
 5.58
 Этот путь был предложен В. 3. Власовым б4.

ГЛАВА VI
 БОЛЬШИЕ ПРОГИБЫ ПОЛОГИХ ОБОЛОЧЕК ПРИ ПОПЕРЕЧНОЙ НАГРУЗКЕ § 57. Удлиненная цилиндрическая панель, шарнирно закрепленная по длинным краям; приближенные решения
 Рассмотрим простейший случай пологой круговой цилиндрической панели радиуса ?, размер которой по образующей длина значительно превышает размер b вдоль дуги ширину, так что изогнутую
 поверхность можно считать цилиндрической. Примем, что панель шарнирно скреплена с неподвижными ребрами и подвергается действию равномерно распределенной нагрузки фиг. 6.1. Рассуждая таким же образом, как и в случае плоской панели § 14, заключаем, что напряжения в срединной поверхности ау должны быть постоянны для всех точек
 пан и: ел
 оу з c°nst, 6.1
 а ох и т равны нулю.
 Выберем в качестве первого приближения выражение для прогиба в виде
 та sin-—, 6.2
 тем самым предрешая, что изогнутая поверхность симметрична относительно линии у Ь2.
 Уравнение равновесия 5.29 приобретает вид
 D dw dw а
 h dy 6.3
 здесь введены полные производные вместо частных, так как w за¬
 висит только от у. Если нагрузка приложена со стороны выпуклости,
 Фиг. 6.1. Удлиненная пологая цилиндрическая панель под действием поперечной нагрузки.

§ 57 УДЛИНЕННАЯ ЦИЛИНДРИЧЕСКАЯ ПАНЕЛЬ 241
 как показано на фиг. 6.1, то напряжение <з до прощелкивания будет
 сжимающим, так что можно положить
 о —р 6.4
 и переписать 3 в форме
 D dw, d2w, р,а 0ч
 ITlwP-dWR4- 6-3
 Выписываем уравнение Бубнова—Галеркина в виде ъ
 Xsin -dy 0,: 6.5
 О
 где
 I
 v гч dw,, dw. 1,п а
 Х hP-dy-R-q- 6-6
 Подставляя 2 и интегрируя, находим:
 67
 Для определения р следует обратиться к условиям закрепления
 длинных краев панели. Взаимное сближение кромок А должно быть
 равно нулю:
 А Swdyo- б-8
 Выражения 5.4 дают
 dv р, 1 оч 1 dw 2, w.
 £1_i-2W 7?
 из 8 будем иметь:
 о о
 Подставляя 2, найдем:
 Е к22 2 У— 1 _р,а 4 Ь я 7?
 Подставим это выражение в 7 и перейдем к безразмерным параметрам
 c-f «'-Кй'о-л 6.10

242
 БОЛЬШИЕ ПРОГИБЫ ПОЛОГИХ ОБОЛОЧЕК
 гл. VI
 тогда получим следующее уравнение относительно стрелы прогиба:
 Сравним это уравнение первого приближения с уравнением 2.93, относящимся к удлиненной пластинке с начальной погибью в виде полуволны синусоиды. Если учесть соотношение между параметром кривизны панели k и стрелой начального прогиба цилиндрической панели Н см. ниже формулу 7.15 и фиг. 7.2, то можно представить 11' в виДе
 Принимая Н — Си, придем к уравнению 2.93 с несколько другими коэффициентами; надо учесть различие в обозначениях q 2.90 и 10. Зависимость £ будет приблизительно отвечать графику фиг. 2.9, если положить QH4 kS. При параметре кривизны k >4,5 получаем петлеобразную кривую.
 Желая уточнить решение задачи и попрежнему интересуясь симметричной формой изогнутой поверхности, Ттерейдем к функции прогиба второго приближения:
 включающей два независимых параметра. Уравнения Бубнова — Галеркина будут:
 Подставляя 12 в выражение 6 для X и интегрируя, приходим к следующим уравнениям:
 Отметим, что С здесь характеризует не полный прогиб посредине панели, а амплитуду первого члена в 12.
 или
 19,14™ — 7,4 № 6,38 0,64£2С д. 6.11'
 19,14С8 — 59,2 Я С2 6,38 41Я2 С д.
 6.12
 ь
 ь
 6.13
 о
 о
 6.14
 здесь р ъЬ.
 Введем обозначения
 6.15

§ 57 УДЛИНЕННАЯ ЦИЛИНДРИЧЕСКАЯ ПАНЕЛЬ 243
 ф определяет «удельный вес» коэффициента 3 по отношению к fv Из уравнений 14 находим:
 243Dpa — 21 hp 6'16
 Для момента, когда нагружение только начинается, р близко к нулю, и поэтому для оболочек любой кривизны, в том числе и плоской панели, получим равным
 ♦ -ЗВ- 6Л7>
 Напротив, при достаточно больших прогибах можно опустить члены, содержащие изгибную жесткость; тогда
 Ф 6-18
 Пользуясь 9, определяем р:
 Подставляя это выражение в 16, приходим к следующему кубическому уравнению для
 7298 _ 27? 2 kOj f
 4- 81С2 — kr, 24з 4- — 3£2 — § К4- l 0. 6.20
 Допустим, что из уравнения 20 найдены для данного С значения тогда безразмерные параметры усилия р и нагрузки q определяются из равенств:
 Р ? С24-т- 4 6.21
 4 ' 4 л ’ Зл
 7С5 г
 : 48 4
 ХЧ-?рС; 6.22
 полагаем:
 6-23
 Обратимся сначала к случаю плоской панели 0. Уравнение 20 дает при этом один действительный корень, постепенно возрастающий по мере увеличения С от начального значения 17 к предельному 18. На фиг. 6.2, а показано изменение нагрузки q в зависимости от С. Сплошная кривая второго приближения почти совпадает с пунктирной кривой первого приближения. Можно считать, что решение § 14 для плоской панели не нуждается в уточнении.
 Это обстоятельство было отмечено Чжан Фу-фанем 211.

244
 БОЛЬШИЕ ПРОГИБЫ ПОЛОГИХ ОБОЛОЧЕК
 ГЛ. VI
 Примем теперь k — тс3 « 31; это соответствует начальной стреле прогиба нч, равной приблизительно 4h. При С < 0,4 и С > 7,1 и здесь получаем один действительный корень. В промежуточной же области все три корня будут действительными; отвечающие этому случаю формы — III изогнутой поверхности показаны на фиг. 6.2, б
 300
 200
 100
 Плоская панель к- OJ 1-ое прибл.-а 2-ое прибл.
 ,, x 2-ое прибл
 ' 2-ое
 r L
 ? с
 ? 4
 vs.
 О4
 к
 -47
 2-ое прибл Начальная L Форма Л Р°Ра2-оел£. Шфо.
 тбл.
 п tfУ
 ч
 A7U д
 >
 1
 2-ое прибл. I-ое прибл. I форма
 V
 -100-
 -200-
 -300
 -400
 Фиг. 6.2. Диаграмма «нагрузка — прогиб» для удлиненной цилиндрической панели по различным вариантам решения.
 в сопоставлении с формой первого приближения 1. На фиг. 6.2, а приведены кривые для q, полученные из 22 для различных ф. Величины q, отвечающие отрицательному корню форма, сильно расходятся с величинами, найденными в первом приближении. Верхняя граница для q снижается, а нижняя граница повышается. Другим двум корням и формы II и III соответствуют значения qf показанные на фиг. 6.2, а соответственно штрих-пунктирной и

УДЛИНЕННАЯ ЦИЛИНДРИЧЕСКАЯ ПАНЕЛЬ
 245
 пунктирной линиями; они служат продолжением одна другой и образуют «восьмерку».
 При больших прогибах цилиндрической панели в срединной поверхности появляются значительные сжимающие усилия р. Вводя параметр 3 в выражение для прогиба, мы ослабляем наложенные на систему связи; тогда оказываются возможными новые равновесные формы со сниженными значениями р. Это и приводит к резкому изменению q во втором приближении по сравнению с первым.
 «Восьмерка» равновесных форм II и III оказывается замкнутой, так что к этим формам нельзя непосредственно перейти, монотонно изменяя С. Однако их можно получить при хлопке оболочки после преодоления некоторого энергетического барьера.
 Для исследования устойчивости различных равновесных форм определим энергию системы 9:
 ь « ъ DC cPw 2 1 р Г
 9l dp dy2E О—Л— J 4>dy, 6.24
 О о
 первый член отвечает энергии изгиба, второй — энергии срединной поверхности и третий — работе внешней нагрузки. Введем безразмерную величину
 эЖ-' 6-25
 тогда найдем:
 э 	5 С81 V J рУ — я с ч; 6.26
 здесь р можно выразить через С и Сф, исходя из выражения 21.
 Вводя два независимых параметра С и tj, мы рассматриваем оболочку как систему с двумя степенями свободы. Если представить Э геометрически как функцию координат С и т, то получим поверхность, по главным кривизнам у.® и х которой можно судить об устойчивости системы.
 Для примера на фиг. 6.3, а построена поверхность, отвечающая нагрузке q 100 при k тг3. Фиг. 6.3, б повторяет график фиг. 6.2; прямая q 100 дает в пересечении с кривыми q С точки №, М 2,..., № 5, отвечающие различным равновесным положениям панели. Поверхность Э образует «яму», дно которой имеет обращенную кверху выпуклость. На вершине этой выпуклости помещен шарик М 5, соответствующий точке № 3 фиг. 6.3, б и форме III изогнутой линии. Это положение оказывается неустойчивым. Вершина окружена «рвом», содержащим четыре других шарика. Два
 Это отмечено А. Р. Ржаницыным Ю.4, стр. 30.

246
 БОЛЬШИЕ ПРОГИБЫ ПОЛОГИХ ОБОЛОЧЕК
 ГЛ. VI
 из них характеризуют устойчивые равновесные положения № 1 и М 5 по форме : на начальном участке кривой £ и после прощелкивания панели; оба эти участка, судя по фиг. 6.2, являются восходящими: здесь q возрастает. Наконец, шарики № 2 к № 4 отвечают частично неустойчивым положениям панели: одна из главных кривизн поверхности Э здесь положительна по стенкам «рва»,
 а вторая — отрицательна. Эти два положения соответствуют нисходящим участкам кривой £ и формам I и II изогнутой линии.
 Фиг. 6.3, а дает возможность объяснить, почему первое приближение в некоторых случаях приводит к неправильным заключениям об устойчивости системы; пользуясь им, мы располагаем лишь сечением поверхности Э плоскостью т 0.
 В общем случае надо определить знак гауссовой кривизны поверхности энергии
 Г 3 xfxf. 6.27

УДЛИНЕННАЯ ЦИЛИНДРИЧЕСКАЯ ПАНЕЛЬ
 247
 Если Тд > 0 и выпуклость поверхности обращена вниз, то равновесие устойчиво. Судя по формулам § 5, величину Тэ можно выразить через вторые производные от Э по координатам С и tj:
 „о дЭкд23 дЭ дЭ л
 Г — д дг? <?СЭт ’ при с?С дг, 0' 6-28
 Таким образом было установлено, что всем точкам «восьмерки» фиг. 6.2 отвечают неустойчивые равновесные положения, в то время как в первом приближении близкие к ним положения представлялись устойчивыми восходящие участки до Лх и от Bt. Следовательно, надо считать точки Л2 и В2 верхним и нижним пределами для q, определенными во втором приближении, вместо точек At и Вг первого приближения.
 Для панелей, кривизна которых не столь велика, как в разобранном примере, различие между вторым и первым приближениями оказывается меньшим.
 Исследуем далее несимметричные формы изогнутой поверхности панели. Представим w в виде
 ■да Л sin 2 sin. 6.29
 Второй член отвечает здесь изгибу панели по двум полуволнам с неподвижной средней линией у Ь2; первый же член попрежнему характеризует общее смещение панели. Уравнение 9 дает теперь вместо 21
 pj, 6.30
 уравнение же 22 остается без изменений. Подставляя в него 30, получаем:
 '-■»т-4 <6-3>
 Судя по 30, в случае изгиба по форме 29 усилие в срединной поверхности остается неизменным; оно отвечает эйлеровой силе при потере устойчивости сжатой плоской панели по двум полуволнам. Зависимость 31 стрелы прогиба от давления оказывается теперь линейной.
 На фиг. 6.2у а изображена прямая 31 для k отсекающая на оси ординат отрезок тгб3 102. На участке между точками А3 и Вг ординаты прямой дают более низкие по абсолютной величине давления по сравнению с линией симметричной формы. Поэтому изгиб панели должен происходить сначала по симметричной форме на участке ОЛ3, после чего наступит хлопок по прямой AZBZ дальнейшее возрастание давления снова произойдет по симметричной форме на участке ВгЕ. Если определить энергию системы как функцию

248
 БОЛЬШИЕ ПРОГИБЫ ПОЛОГИХ ОБОЛОЧЕК
 ГЛ. VI
 не двух, а трех параметров fv 2, 3, то, очевидно, симметричная форма окажется неустойчивой при нагрузках, лежащих выше ординат прямой 31. Поэтому в конечном счете верхнее и нижнее значения давления определяются точками As и Bs.
 § 58. Удлиненная шарнирно закрепленная панель.
 Точное решение
 Обратимся к точному решению исходного уравнения 3. Полагая сначала, что нагрузка приложена со стороны вогнутости панели- и напряжение о является растягивающим, перепишем 3 в виде
 где
 dw ha. д
 dy4 dy2 TtD
 Повторяя выкладки § 15, находим:
 A sh ky -f- В ch Ху -f- Су L —.
 Граничные условия см. стр. 80 приводят к зависимостям: B--L 0, A sh kb--B ch b--Cb--L—— — 0,
 Я
 ЛаХ2 :
 С Щ-В, L — В.
 Отсюда
 вш1г
 Кроме того, должно быть
 shich£sh 0. При sh л£2 Ф 0 будет
 А — В th
 U 2
 Вместо 34 получаем теперь hew
 W '■
 Ы_,
 . и chT
 6.32
 6.33
 6.34
 6.35
 a
 6.36
 b

§ 58 УДЛИНЕННАЯ ШАРНИРНО ЗАКРЕПЛЕННАЯ ПАНЕЛЬ 249
 При R-00 придем к выражению 2.38. Как легко видеть, изогнутая поверхность панели по 37 симметрична относительно линии у Ь2. Соотношение 9 принимает вид
 f fffidy- J 1у. 6.38
 О 	о
 Подставляя 37 и интегрируя с помощью формул 2.41, найдем:
 4th
 — 	— 6,39 Воспользуемся обозначениями:
 «“ 13?. £•, ■-••: 6.40
 тогда получим следующее уравнение относительно и
 . гг2£2 9 27 5 гг— th и — гг th2 гг
 V IШ Гбгг» —
 л, иЧиЧ 9 27гг — th гг 1 л‘ С11Ч
 —-f—з; -3- да—т —Б»—;—1 °. 6.41
 В частном случае плоской панели k 0 отсюда вытекает разрешающее уравнение 2.46, которым мы пользовались в § 15.
 Полагая в 37 у Ь2, находим безразмерную стрелу прогиба
 6-42
 где под попрежнему подразумевается функция 2.49.
 Допустим теперь, что нагрузка приложена к панели со стороны выпуклости, как показано на фиг. 6.1. Полагая
 о —>, о —jо, u V — 3p ttt, 6.43
 воспользуемся найденным выше решением, заменяя и на iu и переходя от гиперболических функций к тригонометрическим; в полученных таким образом зависимостях значки над и будем опускать. Вместо 41 будем иметь уравнение
 и q _ kgy к д - £ 1 0, 6.44
 Уравнение такого типа было получено И. Г. Бубновым, см. р1, стр. 284. Исследование уравнения с учетом несимметричной формы прогиба дано М. С. Корнишиным и X. М. Муштари 6-7.

250
 БОЛЬШИЕ ПРОГИБЫ ПОЛОГИХ ОБОЛОЧЕК
 ГЛ. VI
 где
 и
 27 5 u — iga--u tg2 и
 V
 4 и6
 8и<> ' 169
 Стрела прогиба 42 будет
 причем здесь
 27 и — tg и
 4 «»
 6.45
 6.46
 6.47
 Это
 решение отвечает симметричной изогнутой поверхности. Но
 теперь оказывается возможным и другое решение, вытекающее из 36:
 sin я 0, 6.48
 откуда
 u iг, 2тг, Зтг,... 6.49
 При наименьшем значении и — ъ будем иметь
 2
 Р з,
 что совпадает с 30. Выражение для прогиба будет тогда
 иметь несимметричный член A sin 2тсу£, которому будет отвечать узловая линия у
 — Ь2. Но прогиб панели при у Ь2 можно попрежнему найти по 46, считая u tz:
 с“»‘4т-'ГЬ<6-50>
 что очень близко к 31.
 На фиг. 6.4 представлена зависимость между нагрузкой и
 параметром сжимающего напряжения в срединной поверхности и для панелей различной кривизны по уравнению 44. Все кривые пересекаются в точке, для которой u tz2 и qk Tzi22. Вертикальная прямая и ‘к отвечает случаю несимметричного прогиба. При А» 10 и k 20 хлопок про¬
 Фиг. 6.4. Зависимость между нагрузкой и параметром усилий в срединной поверхности для удлиненных панелей различной кривизны.
 Амплитуда А несимметричной составляющей остается в пределах данного решения неопределенной.

УДЛИНЕННАЯ ЦИЛИНДРИЧЕСКАЯ ПАНЕЛЬ
 251
 изойдет именно по этой форме. Для случая k 31, разобранного в § 57, точное решение совпадает со вторым приближением для формы. Интересно отметить, что и побочные формы II и III охватываются этим решением: соответствующие кривые лежат справа от точки и тт.
 При k > 30 верхнее значение давления можно приближенно принимать равным ординате прямой 50 для С 0:
 qt jk. 6.51
 На фиг. 6.5 даны кривые «нагрузка — прогиб» для симметричной формы по 46; прямые 50 ограничивают область расчетных значений q. В случае k 31 линия С ложится на кривую вто-
 100
 Ч'
 50
 О
 -50
 Фиг. 6.5. Диаграмма «нагрузка — прогиб» для удлиненных панелей.
 рого приближения, показанную на фиг. 6.2. Таким образом, для цилиндрических панелей с кривизной k < 31 второе приближение по Бубнову — Галеркину дает вполне удовлетворительные результаты.
 § 59. Удлиненная цилиндрическая панель, защемленная по длинным краям
 Перейдем к случаю, когда панель защемлена по длинным несмещающимся краям и испытывает давление со стороны выпуклости. В приближенном решении примем
 ■a sin2-, 6.52
 С учетом того, что в обозначениях § 57 прогиб средней точки соответствует разности С— ?.

252 БОЛЬШИЕ ПРОГИБЫ пологих ОБОЛОЧЕК гл. VI
 Применяя метод Бубнова — Галеркина, находим:
 лг 2яу, г.г2ля 2ку hp п -оч
 XDf-SiC0S-f--phf-wC0s-f — -£ — q. 6.53
 Сжимающие напряжения в срединной поверхности будут по 9 равны
 <6М>
 или при С fjh Уравнение
 j jxsindy 0 6.56
 приводит к зависимости
 24,ЗС3 — 7,4А£2 32,7 0,5 С q. 6.57
 По структуре это уравнение сходно с И. Кривая <7С образует петлю при k > 11,8.
 Обратимся к точному решению задачи, принимая сначала, что нагрузка действует со стороны вогнутости панели. Интегрирование уравнения 32 снова приводит к выражению для прогиба 34. Граничные условия см. стр. 88 дают теперь
 B-£R-“J3'c -“-i В <6б8>
 и, кроме того,
 th-Bth 0. 6.59
 При thX£2£X£2 имеем:
 А — Bth™.
 Окончательно
 -1 » Гса-Ы,
 WJ2Uh« „„и
 ch 2
 2УФ—У- 6-60
 Составляя выражение для а 38, получим вместо 41 следующее уравнение:
 о I u2kY 9 1 27 27 81 V 	3 8ae ‘ 4«8 16tfesh2tf 16и7 th и
 , u2k u2k 9 27 i 27 1 А с сп
 “I Т-Ы-4ТО455-10- 6-61>

§ 59 УДЛИНЕННАЯ ЦИЛИНДРИЧЕСКАЯ ПАНЕЛЬ 253
 Стрела прогиба окажется
 С 3 gg я ■k f 2» 6.62
 где определяется по 2.78.
 Если нагрузка приложена со стороны выпуклости, то, пользуясь приемом § 58, получим разрешающее уравнение для симметричной формы прогиба
 Ui я - х2 - ? ? 1 0 > <663>
 где
 _9_, 27 _
 816 I 4i8
 27
 81
 причем
 V 2L± I IV
 8а6 4а8 16aesin2a 16u7tgu 9 1 4ии2 utgu 3
 6.64
 Стрела прогиба будет равна
 С - I,• - - f «, 6.65
 <4 ЦГ> — -г- —Л1- б«б
 Г и2 L utgu cos и J J v у
 Несимметричная форма определяется по 59 из уравнения
 t gu — и 0;
 иж 4,49; 7,72... р 6,73; 19,9...
 Наименьшие значения и 4,49 и ? 6,73 соответствуют критической силе для сжатой плоской панели с защемленными краями при наличии узловой линии посредине пролета.
 Таблица IX
 Данные для расчета удлиненных цилиндрических панелей
 тогда
 Параметр 1ривизны
 Шарнирное закрепление по длинным кромкам
 Защемление по длинным кромкам
 k
 верхнее значение ♦
 ч
 нижнее значение ч
 верхнее значение ч
 нижнее значение ч
 5
 4,29
 3,94
 Нет петли
 Нет петли
 10
 19,4
 — 2,60
 ъ ъ
 » ъ
 20
 60,6
 — 26,5
 95,0
 47,4
 30
 95,5
 — 44,5
 —
 —
 40
  255
 65,2
 Звездочками отмечены значения qt отвечающие несимметричной форме изогнутой поверхности.

254
 БОЛЬШИЕ ПРОГИБЫ ПОЛОГИХ ОБОЛОЧЕК
 ГЛ. VI
 В таблице IX приведены окончательйые значения верхнего и нижнего критических давлений для панелей различной кривизны и при разных условиях закрепления.
 § 60. Шарнирно опертая пологая панель, прямоугольная в плане; первое приближение
 Рассмотрим пологую панель, имеющую в плане вид прямоугольника со сторонами а> Ъ фиг. 6.6, в предположении, что главные кривизны срединной поверхности kXi ky постоянны для всех ее точек.
 Это может относиться к цилиндрической панели радиуса R, когда
 ь — о Ь J-
 кх ку—
 и к сферической панели при
 k — k — JL
 кх ку ft
 Будем считать, что по краям оболочка шарнирно скреплена с подкрепляющими ребрами, не допускающими смещений контурных точек к центру кривизны. В отношении смещений точек контура в плане условия пока остаются неопределенными.
 Пусть панель подвергается действию равномерно распределенной
 поперечной нагрузки q со стороны выпуклости.
 Примем в качестве первого приближения выражение для прогиба
 w sin ах sin 3у, 6.67
 где
 Подставляя 67 в правую часть уравнения 5.28, получим:
 _L уау-2ф _ f?a2’2 cos2 ах cos2 — sin2 ах sin23y --
 а2 у0 fsn ах sn
 По таблицам М. С. Корнишина и X. М. Муштари 6-7 с некоторыми дополнениями.
 Для пологой оболочки можно считать перемещения точки срединной поверхности в плане в плоскости, проходящей через углы панели равными перемещениям в плоскости, касательной к поверхности в данной точке.
 «27
 Фиг. 6.6. Пологая панель с конечным отношением сторон.

§ 60 ШАРНИРНО ОПЕРТАЯ ПОЛОГАЯ ПАНЕЛЬ 255
 Решение этого уравнения будет
 iфй у2 cos 2а42 cos
 w5f h I 1л>sinsinИ-Ж-Ж : <6-68> U2 2
 под px и py понимаются средние значения распорных усилий, возникающих в результате взаимодействия, оболочки с подкрепляющими ребрами положительных при сжатии. Уравнение Бубнова — Галеркина будет
 J J Xsnaxsnydxdy 6.69
 F
 Составляя выражение 5.51 для X и интегрируя, получим следующее уравнение:
 — Е2— П kx -I ky 1 1 —Е—Р —JL
 п 3 J b' a2 a2b2 2_j_aJa 24у Ь Г a2 “Г
 „К2 Xfkx, ky 1 Я4 тс4 g
 Px Py 7бРЛ.‘
 6.70
 Введем безразмерные параметры, отличающиеся от принятых в § 19:
 • kxa2 kyb2 а о т 1 ч
 > 2 — д> » 6-71
 q сАЬ2, 62 » _Руа
 Я Eh’ Р°° Е Л2 ’ Ру Е № ’ 6.72
 тогда будем иметь:
 -2,
 7Сб
 256
 la Л3 ™ — If Л » iy ’2 й ’2
 Jga; 2 Х2 ’ 16 рх Ь ’“Ь
 х £ж>ш kypy -f- f92iIIji2Г6.73

256 БОЛЬШИЕ ПРОГИБЫ пологих ОБОЛОЧЕК гл. VI
 В частном случае плоской пластинки при kx ky 0 придем к уравнению 2.110 главы И.
 Определим теперь относительное взаимное смещение ех краев панели х 0 и х а положительное при сближении краев:
 а
 '.“-НаИ- <6-74>
 о
 По 5.4 находим:
 да 1 д2Ф д2Ф 1 dw2,, а
 дх Е ду2 дх2 2 д xWt '
 Подставляя 67 и 68, будем иметь:
 :-4Sli7,-V4«to
 wSf p—5 i, па ¥sin №
 2 by
 Величина ex зависит от координаты у, так что в рамках нашего решения края панели не могут считаться прямолинейными. Определим «среднее» смещение краев:
 ь
 оно будет
 Рх — №у. 2
 i 5МЙ-г TTTjvi • <6'77>
 а2 ьу
 По аналогии находим относительное смещение еу краев у 0 и У Ь:
 дагг-т1Т1у-6-78>
 U2 by
 Рассмотрим отдельно случаи свободных и несмещающихся краев панели.

ШАРНИРНО ОПЕРТАЯ ПОЛОГАЯ ПАНЕЛЬ
 257
 1. Края панели свободно смещаются в плане. При этом мы можем воспользоваться уравнением 73, полагая в нем
 р р 0. Рассмотрим случай квадратной панели А 1 со сто¬
 роной Ъ. Обозначим через k величину
 £ 4; 6.79
 тогда уравнение 73 получит вид при х 0,3
 7,5С3 — 2,06;2 0,154А9 22 С q. 6.80
 На фиг. 6.7 построены кривые qС для различных значений k. Для цилиндрической панели радиуса R и ширины Ъ надо принимать
 7 2 3 4 5 6 7
 Фиг. 6.7. Зависимость между нагрузкой со стороны выпуклости и стрелой прогиба пологой оболочки.
 k bqRh, для сферической панели будет k 2bRh; в обоих случаях длину b дуги можно считать равной соответствующему размеру в плане. Образование петли имеет место, начиная с кривизны k 25,3. •
 Определим расчетные напряжения в общем случае прямоугольной панели, исходя из выражения 68 для Ф. Безразмерные напряжения

258
 БОЛЬШИЕ ПРОГИБЫ ПОЛОГИХ ОБОЛОЧЕК
 ГЛ. V
 в срединной поверхности
 Qx Ь 2 °x Hh '
 будут в центре панели равны
 6.81
 6.82
 Первый член этого выражения отвечает растягивающим напряжениям, возникающим в пластинке большого прогиба, второй же относится к сжимающим напряжениям, характерным для искривленных панелей
 при нагрузке со стороны выпуклости. Для квадратной панели
 а о 1,23С2 — 0,25С. 6.83
 Напряжения изгиба в центре определяются теми же выражениями 2.120, что и для плоской пластинки:
 7Г2
 :2l-i С. A2 C
 6.84
 оучп 21
 В случае квадратной панели при J. 0,3
 Фиг. 6.8. Зависимость между нагрузкой со стороны вогнутости и стрелой прогиба пологой оболочки.
 о а 7,1C.
 а?, и у, и 6.85
 При нагрузке, действующей со стороны вогнутости панелиу можно воспользоваться теми же уравнениями 73 или 80, изменив знак при С на обратный. На фиг. 6.8 даны кривые <7С для этого случая применительно к квадратной панели.
 2. Края панели не смещаются: е — еу — 0. Исходя из 77 и 78, найдем безразмерную величину среднего напряжения вдоль краев х — 0 и х — а:
 px — Pfj — — X2 AгIqГ2:2
 -- ', kv 2 f _qia — kx kv 1л
 W
 ; 6.86

§ 61
 ШАРНИРНО ОПЕРТАЯ ПАНЕЛЬ
 259
 Не
 в аналогичном выражении для ргу надо заменить в первом члене 1Д2 <а на 2 а и во втором £eA2-f-pfty на Аа Р®«
 После введения этих выражений в 73, получим расчетное уравнение:
 йрх kypy Jg 1 X» 128IC_-jl2j- 2 i■ x‘2 с3 —
 — т ' I “1 kyX Iх Х5 — T k«> kv 1 1 у
 UXJ
 ¥» 7ГТТХй жk2 1C2
 r
 192Г-Х2“ т X Тб ky? C q' 6'87
 Для квадратной цилиндрической панели будем иметь при jjl 0,3: 28,9С3 — 6,1гС2 0,52 22 С q 6.88
 По аналогии со случаем удлиненной цилиндрической панели § 57 можно утверждать, что первое приближение дает удовлетворительные результаты лишь для панелей малой кривизны. При больших k решения, в которых варьируется несколько параметров прогиба, должно привести, повидимому, к понижению q и повышению ; должны быть приняты во внимание и составляющие, не симметричные по отношению к линиям х а2 и у Ь2.
 § 61. Шарнирно опертая панель; решение, более полно удовлетворяющее граничным условиям
 В решении задачи, изложенном в § 60, удовлетворялись условия шарнирного опирания кромок, цо вместе с тем оставались не вполне определенными граничные условия, касающиеся усилий в срединной поверхности. Как видно из 68, нормальные напряжения в различных точках кромки могут значительно отличаться от средних значений рх и ру, а касательные напряжения также лишь в среднем обращаются в нуль. Можно предложить путь решения задачи, при котором напряжения ох и Оу будут в каждой точке края равны заданным значениям. Рассмотрим, например, случай свободно сближающихся кромок и положим
 °хх 0, а ?уу 0, Ь 0 6.89
 Этим условиям можно удовлетворить, если в первом приближении задаться функцией напряжений в виде
 Ф A sin ах sin jty. 6.90

32
 260 БОЛЬШИЕ ПРОГИБЫ ПОЛОГИХ ОБОЛОЧЕК ГЛ. VI
 Составим уравнение Бубнова—Галеркина типа 5.57, оставив для w выражение 67; тогда получим амплитуду А равной
 16 _ кх, К 1 1
 jrrwf 27Х. IVf' 6,91
 а Ь U2 ЬУ
 Второй член совпадает с коэффициентом при в выражении 68, первый же член оказывается иным. Если теперь подставить 90 в уравнение «обычного типа» 5.53, то найдем:
 D f тсв1, 19 2 и _
 h 16 U2 2 3 — Ч-
 Подставляя сюда 91 и переходя к безразмерным параметрам, придем к уравнению
 322 1 ;C3fe—-2-г.-2--Са
 ЫУ Ы
 5л97_1т» с Т1—V' g- 6-92
 lT> 192l-rf т х
 Здесь k kx-- ky. Для квадратной панели при jjl 0,3 будет
 8,77С8 — 2,46Ы? 0,154> 22 С q 6.93
 Это уравнение отличается от полученного ранее 80 коэффициентами при С3 и С9. Легко видеть, однако, что и это новое решение оставляет неопределенными касательные усилия по кромкам, попрежнему обращающиеся в нуль лишь «в среднем». Поставим себе целью удовлетворить дополнительным условиям
 0,a «Wo, Ь °- 6-94
 Представим функцию напряжений Ф в виде произведения двух функций, каждая из которых зависит только от х или у:
 Ф ЦхУу. 6.95
 Условия 89 и 94 приводят к следующим равенствам для U и V:
 U 0 при л: 0, а; V — 0 при у 0,Ь. 6.96
 Таким образом, для каждого края панели должны обращаться в нуль функция U, либо V и соответствующая первая производная. Но в таком случае мы можем воспользоваться при аппроксимации U
 Уравнение 92 было получено М. А. Колтуновым 6-4.

§ 62
 КВАДРАТНАЯ ПАНЕЛЬ, ЗАЩЕМЛЕННАЯ ПО КРАЯМ
 261
 и V теми функциями, которые используются при рассмотрении прогиба балок или пластинок с защемленными краями. Если обратиться, например, к собственным функциям задачи о свободных колебаниях балки с защемленными краями, то для случая квадратной панели со стороной а можно положить :
 гт. Хх, Хх Хх их па й Т 7’
 „ » I ьМ <6'97
 V sin — — sh — — a cos — — ch —.
 а а а а Здесь X 1,51ir 4,73
 а параметр а равен
 а
 Вместо 91 получим теперь
 4 	-Шо4 Ша“Г- <6-98>
 Окончательное уравнение «нагрузка — прогиб» будет при а 0,3
 7,48С3 — 2,42АСа 0,151 ft ■ 22С q 6.99
 оно очень близко к зависимости 80 § 60. Заметно отличаются лишь члены с квадратом С2, благодаря чему уравнение 99 дает более низкие значения qt и qf чем 80.
 Уравнения 93 и 99 получены при более полном удовлетворении граничных условий, чем уравнение 80, найденное по обычной схеме. Однако уравнение совместности деформаций теперь удовлетворяется лишь «в среднем», в то время как раньше оно выполнялось для всех точек срединной поверхности. Поэтому эти новые решения надо рассматривать не как уточненные по отношению
 к прежним, а скорее как равноправные варианты. Преимущество
 того или иного метода можно выяснить лишь путем сравнения с уточненными решениями при варьировании большего числа параметров.
 § 62. Квадратная панель, защемленная по краям
 Рассмотршм случай квадратной панели со стороной Ь; края панели будем считать защемленными и вместе с тем свободно смещающимися в плане. Приближенное выражение для прогиба примем
 См., например, «Основы современных методов расчета на прочность в машиностроении» под ред. С. Д. Пономарева, т. 2, Машгиз, 1952, стр. 174.
 Уравнение 99 получено М. М. Козаровым 6-5.
 На это обратили внимание X. М, Муштари и И. В. Свирский 6-8.
 •наименьший корень уравнения ch X cos k— 1,
 sh I — sin X 1>018
 ch X — cos X

262
 БОЛЬШИЕ ПРОГИБЫ ПОЛОГИХ ОБОЛОЧЕК
 ГЛ. VI
 в виде
 w sin2 ах sin2 ay; а у. 6.100
 Уравнение 5.28 принимает вид
 1 	Г7 4
 _ vaV2<b 4 Р cos 2ах -f- cos 2ау — cos 4ах — cos 4ay -f-
 -f- cos 4ax cos 2ay -f- cos 2ax cos 4ay — 2 cos 2ax cos 2ay —
 — kxf cos 2XX — cos 2аУ
 kx kyf-fi cos 2ax cos 2ay; 6.101
 отсюда
 Ф f2 cos 2ax - j- cos 2aу — P cos cos 4<y -f-
 щ f'2cos ax cos 2ay cos 2ax cos 4 —
 1 2 b 2
 — 64Z3 cos 2ax cos 2ay — kj cos 2a — jg cos 2«У
 A2
 §42cos2a.x:cos2ay. 6.102
 Находя касательные напряжения т, убеждаемся в том, что по кромкам они обращаются в нуль. Средние напряжения рх и ру также считаем равными нулю.
 Выписываем уравнение Бубнова — Галеркина
 J ХкР ах sin ay dx dy 0; 6.103
 F
 функцию X составляем, пользуясь выражением 5.51 подобно тому, как это было сделано для плоской пластинки в § 19. После интегрирования получаем уравнение
 Ji Efd J2 E а> а? kyf Ef--
 <6'l04>
 или
 16,3C3 — 2,31£C2 -f 0,14£271,4C <f. 6.105
 Если принять k 0, то получим уравнение 2.149, доставленное ранее для плоской пластинки.
 Напряжения в срединной поверхности определяются дифференцированием выражения 102. Напряжения изгиба могут быть найдены по функции прогиба 100, но, как было показано в § 17, эти значения могут сильно отличаться от истинных.

ГЛАВА VII
 УСТОЙЧИВОСТЬ И ЗАКРИТИЧЕСКАЯ ДЕФОРМАЦИЯ
 ЦИЛИНДРИЧЕСКИХ ПАНЕЛЕЙ
 § 63. Устойчивость цилиндрической панели при сжатии вдоль образующей; линейная задача
 Рассмотрим отрезок круговой цилиндрической оболочки, ограниченный двумя образующими и двумя дугами поперечных сечений цилиндрическую панель. Обозначим радиус кривизны срединной поверхности через ?, охватываемый панелью центральный угол через 6, размеры панели через а и Ь.
 Координату х будем отсчитывать вдоль образующей, у— по дуге фиг. 7.1.
 Примем, что панель шарнирно скреплена по краям с ребрами, абсолютно жесткими по отношению к изгибу в радиальной плоскости, и подвергается действию сжимающих усилий рху равномерно распределенных вдоль кромок х — О, х а. Будем считать, что на первых ступенях нагружения поперечная деформация панели осуществляется свободно и оболочка сохраняет чисто цилиндрическую форму. Фиг. 7.1. Цилиндрическая панель,
 При некоторой критической ве- сжатая вдоль образующей, личине рх происходит потеря устойчивости оболочки. Условимся называть верхним критическим напряжением рв ту величину рх> при которой, наряду с начальной формой равновесия оболочки, становится возможной другая — изогнутая— форма, бесконечно близкая к первой. Так как при этом речь идет о весьма малых прогибах, то определение верхнего критического напряжения сводится к решению линейной задачи,
 Эта задача была рассмотрена С, П. Тимощенко 18, стр. 395

264 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКИХ панелей гл. VII
 Воспользуемся уравнением 5.38, считая рх — ръ, py — s 0:
 о V4W. -p. VV0. 7.1
 Решение этого уравнения в соответствии с принятыми граничными условиями представим в виде
 V 	• mTZX • П11У оч
 w2jm»sins,n_T- 7-2
 ш п
 Любой член этого ряда с индексами т, я удовлетворяет уравнению 1 при условии выполнения равенства
 Dm2. г2тс2 2 Е tnTt т2тс2, л2тс22т2тс2 л
 тг—лтзг-р-; -зг °- 73
 Уравнение 3 определяет верхнее критическое напряжение рв в зависимости от индексов m, г:
 т2£, г22 тп2
 D Т Т 2 ЕЫ Ifi 74ч
 Рв h№ m2 Р? тЧ. г2 '
 а2 i а2 6 я2
 Подберем эти индексы т, г таким образом, чтобы величина ?в имела наименьшее возможное значение. Вводя обозначение
 тЧ. г2 а 7
 Х -ЖТт' <7'5>
 перепишем 4 в виде
 D 0 о. Е № а
 Р Ш х“ “I- 2 Щ2 7-®
 и положим
 отсюда
 hb2 - -Т- Д2 22
 3й2 ш —2 4Ц0;
 дл: h№ R2 тс25
 1 '20-Л. 7.7
 Подставляя это значение л; в 6, получим критическое напряжение равным
 -7яЬгв- 78
 При х 0,3 -f- 0,32 можно принять
 р 0,6 Е±. 7.9

§ 63 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКОЙ ПАНЕЛИ ПРИ СЖАТИИ 265
 Чтобы выяснить, применима ли формула 8 к панелям любой кривизны, обратимся к условию 7, которое перепишем в виде
 ГЗ— <7'0>
 Отметим, что из равенства 10 нельзя найти индексы тип порознь. Но эти индексы определяют числа полуволн изогнутой поверхности соответственно вдоль образующей и по дуге. Следовательно, характер волнообразования остается в пределах данного решения невыясненным.
 Однако условие 10 может иметь место лишь при достаточно больших значениях параметра bRh. Наименьшее число полуволн по ширине составляет г 1. Принимая я1 в 5, найдем х 2 при т ajb. Поэтому формулы 8 и 9 справедливы, если >2
 ИЛИ
 7-Н
 т. е. если охватываемый панелью центральный угол 6 отвечает неравенству
 >--- 1 Г. 7-12
 j 12 1 — а2 При меньших значениях угла 0 в случае, если отношение сторон панели ajb является целым числом, критическое напряжение оказывается
 равным
 л tD I 1 „ Ь2 'г 1 о
 Рв Тф' 7-18
 Принимая в формуле 13 R—> оо, получим известную формулу
 Л 4ж» 7ЛЗ'>
 Фиг. 7.2. Стрела начальной погиби цилиндрической панели.
 относящуюся к плоской пластинке.
 Введем безразмерные параметры нагрузки и кривизны панели
 РхЬ 6Ь №_ у 1 А
 Р Eh2’ h Rh Л4
 Для малых углов 0 величина k пропорциональна отношению стрелки панели Н к толщине h фиг. 7.2:
 b 7.15

266
 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКИХ ПАНЕЛЕЙ ГЛ. VII
 Формула 8 после введения безразмерных параметров примет вид
 р. 1 fe, 7.16
 ИЛИ
 £« 0,6ft. 7.17
 Условием применимости формул 16 и 17 будет
 k> 4п2, 7.18
 121-
 или приближенно
 ft>12. 7.19
 Для панели малой кривизны получим по 13
 зтгг5’ 7-20>
 или
 -3‘вшв- <7'21
 Формулы 20 и 21 справедливы при условии, что параметр кривизны ft лежит в пределах 0<ft<;i2.
 При составлении формулы 8 мы ограничились определением наименьшего значения параметра х в предположении, что волнообразование не стеснено размерами панели. Если при заданных размерах нельзя подобрать целочисленных индексов т, п, соответствующих 7, необходимо найти значения индексов, отвечающих минимальной величине р. На фиг. 7.22 изображены кривые, соответствующие формуле 4 для квадратной панели при значениях индексов т п от 1 до 5. Индексы т—п 1 относятся к диапазону 0<Cft<24; при 24 ft <С72 надо положить т п 2 и т. д.
 § 64. Экспериментальные данные о форме волнообразования
 Данные опытов показывают, что формулы линейной теории 17 или 21 не могут быть непосредственно использованы в практических расчетах.
 Ниже приводятся результаты экспериментального исследования цилиндрических панелей различной кривизны. Панели были изготовлены из дуралюмина Д16Т и имели те же размеры, что и плоские панели, описанные в § 30; было принято: h 1--4 мм,
 Описанные в главе VII опыты проведены автором книги.

§ 64 ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ О ФОРМЕ ВОЛНООБРАЗОВАНИЯ 267
 Ь 240 мму а 480 мм. Прямолинейность кромок была обеспечена тем, что лист по продольным кромкам приклепывался к мощным П-образным профилям фиг. 7.3. Для всех панелей, принадлежащих к одной и той же серии, переменным являлся только радиус кривизны; параметр кривизны k изменялся в достаточно широких пределах: от 0 до 268. Методы определения формы волнообразования, прогибов и деформаций были изложены в § 30.
 Испытанные панели можно условно разбить на три группы по величине параметра кривизны k.
 Фиг. 7.3. Сечение панели, подвергавшейся испытаниям.
 1. 	Панели малой кривизны 0 < < 50. Здесь нагружение образцов сопровождалось, как правило, уже с самого начала появлением прогибов и напряжений изгиба. Характер прогиба в первый период нагружения зависел от формы начальной погиби; при приближении к критической силе в одних случаях прогибы резко возрастали, в других — меняли знак.
 Потеря устойчивости при первой критической нагрузке происходит в панелях малой кривизны без ясно выраженного скачка. Однако при дальнейшем нагружении скачки имеют место: они совпадают с моментами резкого изменения числа полуволн по длине панели.
 На фиг. 7.4 даны фотографии, характеризующие изогнутую поверхность одной из таких панелей. Фиг. 7.4, а изображает «отраженную сетку», полученную для ненагруженной панели. Отдельные искажения клеток объясняются тем, что панель подвергалась уже нагружению ранее. На фиг. 7.4, б показано отражение тех же клеток от поверхности листа после потери устойчивости. Хорошо заметна выпучина в нижней половине листа, обращенная к читателю. При «возрастании нагрузки форма волнообразования постепенно менялась

268 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКИХ ПАНЕЛЕЙ гл. VII
 фиг. 7.4, в. В момент, когда нагрузка превзошла в 5,4 раза критическую, произошел скачок; он выразился в резком изменении характера изогнутой поверхности. Фотография, помещенная на фиг. 7.4, г, сделана после скачка. Сравнение фиг. 7.4, виг пока-
 Фиг. 7.4. «Отраженная сетка» для панели малой кривизны.
 зывает, что находившаяся в центре панели выпучина переместилась вниз; общее число полуволн вдоль образующей панели возросло. Судя по фиг. 7.4, г, размеры сторон каждой клетки изменились: сторона, расположенная по длине, вытянулась в средней части

§ 64 ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ О ФОРМЕ ВОЛНООБРАЗОВАНИЯ 269
 панели или сократилась в крайних частях по сравнению с другой стороной, имеющей поперечное направление. Это означает, что выпучины не являются квадратными: при максимальной нагрузке они оказываются вытянутыми вдоль дуги.
 2. Панели средней кривизны 50 < k < 175. Эти панели отличались от предыдущих характером волнообразования уже в самый момент потери устойчивости. Здесь было явно выражено преимущественное направление выпучин к центру кривизны, в то время как по данным линейной теории, изложенным в предыдущем параграфе, выпучины, обращенные к центру кривизны или от центра, имеют равные амплитуды.
 В большинстве случаев при потере устойчивости панелей образовывалось несколько выпучин, как показано на фиг. 7.5, а или б. Чаще осуществлялся вариант фиг. 7.5, а с одной глубокой выпу-
 чиной к центру кривизны и двумя, более мелкими, — от центра. Дальнейшее нагружение панелей сопровождалось расширением основной выпучины и образованием дополнительных выпучин, расположенных в шахматном порядке.
 При испытаниях большинства панелей данной группы были отмечены скачки в момент потери устойчивости, причем стрелка силоизмерительного устройства машины указывала на значительное снижение нагрузки.
 Своеобразным был и процесс разгрузки. Мелкие выпучины исчезали незаметно, но затем наблюдался весьма сильный скачок, во время которого как бы продавливалась основная выпучина. Значение сжимающей силы, которому соответствовал этот обратный скачок, было гораздо ниже критической нагрузки. После полной разгрузки для некоторых панелей были отмечены остаточные деформации.
 Естественно поэтому, что при повторном нагружении критическая сила была заметно ниже первоначального значения. Так, при испытании одной из панелей сжимающая сила возросла до 7900 кг. Затем произошел хлопок, в момент которого сила упала до 7600 кг. В процессе разгрузки наблюдался «обратный хлопок» при силе, равной 4600 кг. Новое нагружение привело к потере устойчивости уже при силе 7500 кг.
 Форма волнообразования, присущая панелям средней кривизны, иллюстрируется фиг. 7.6. Фиг. 7.6, а относится к панели, которая
 -— b
 а I
 Фиг. 7.5. Волнообразование панели средней кривизны.

270
 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКИХ ПАНЕЛЕЙ ГЛ. VII
 подвергалась повторному нагружению. Фотография фиг. 7.6, а сделана для разгруженной панели, фиг. 7.6,6'—после потери устойчивости. Как видим, выпучина захватывает лишь центральную часть ширины. Фиг. 7.6, в и г изображают изогнутую поверхность панели при последующем нагружении. Фиг. 7.6, д хорошо передает своеобразную картину деформации цилиндрической панели. Центральная выпучина,
 Фиг. 7.6. «Отраженная сетка» для панели большой кривизны.
 распространившаяся вдоль дуги, окружена новыми симметрично расположенными выпучинами.
 3. Панели большой кривизны > 175. Эти панели очень слабо реагировали на различные «возмущающие» факторы в первой стадии нагружения. Вплоть до момента потери устойчивости упругие прогибы почти отсутствовали. Вместе с тем переход от цилиндрической к изогнутой равновесной форме здесь сопровождался весьма сильным ударом. Падение нагрузки в момент выпучивания также было более резким. За этим ударом следовали при образовании дополнительных выпучин новые хлопки. Появление каждой из них вызывало падение нагрузки; это явление для панелей прежних типов не наблюдалось.

РЕАЛЬНЫЕ ЗНАЧЕНИЯ КРИТИЧЕСКИХ НАПРЯЖЕНИЙ
 271
 При первой критической силе в панелях рассматриваемого типа возникали обычно три выпучины по ширине, из которых одна или чаще две были направлены к центру кривизны.
 Для сильно изогнутых панелей, имевших значительную толщину, критическое напряжение лежало за пределами упругости. Явление потери устойчивости оставалось здесь ясно выраженным и заключалось во внезапном и вместе с тем бесшумном образовании глубокой выпучины, направленной к центру кривизны.
 § 65. Реальные значения критических напряжений
 Как мы видели, экспериментальные данные указывают на несоответствие истинной формы волнообразования той фбрме, которая вытекает из линейной теории. Такое же резкое расхождение получается в величинах критических напряжений.
 На графике фиг. 7.7 сделано сопоставление с теоретической формулой тех максимальных значений напряжений сжатия, которые
 Фиг. 7.7. Напряжения при выпучивании сжатых цилиндрических панелей по теоретическим и экспериментальным данным.
 были получены во время опытов с момента начала нагружения панели вплоть до начала интенсивного выпучивания; будем условно называть эти значения напряжения верхними критическими значениями.
 По оси абсцисс отложен параметр кривизны, по оси ординат — раметр напряжения ?. Сплошная линия А определяет теоретические

272
 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКИХ ПАНЕЛЕЙ ГЛ. VII
 значения верхнего критического напряжения для случая шарнирно опертой по всем краям оболочки и построена по формулам 16 и 20. Отдельные точки отвечают экспериментальным значениям верхнего критического напряжения; напомним, что в опытах дюралевая оболочка была защемлена по всем краям, причем отношение длины панели к ширине измеренной по дуге равнялось 2. На графике указаны также теоретические значения критического напряжения для плоской пластинки тех же размеров, защемленной по всем краям штрих-пунктирная линия D.
 Как видим, для плоских и слегка изогнутых панелей экспериментальные значения достаточно близки к теоретическим, если учесть защемление кромок. При значительной кривизне влияние защемления кромок в случае достаточно большой длины оболочки делается мало заметным, так что данные опытов можно сравнивать с теоретическими формулами, выведенными для случая шарнирного опирания по всем кромкам.
 При k > 100 средние значения критических напряжений, полученные в опытах, определяются формулой
 р 0,33£ 7.22
 см. пунктирную линию С на фиг. 7.7.
 Некоторые из испытанных панелей были подвергнуты повторному нагружению. Для панелей малой кривизы критические напряжения при первом и втором нагружении почти совпадали. Вместе с тем для панелей значительной кривизны при k > 95 второе нагружение шло совершенно иначе, чем первое, и потеря устойчивости происходила заметно раньше. На графике фиг. 7.7 нанесены соответствующие точки двойные кружки. Как видим, верхние критические напряжения, найденные при повторных испытаниях, гораздо меньше первичных значений.
 Наименьшая величина критического напряжения при первом нагружении линия В на фиг. 7.7 оказалась в данной серии опытов равной
 р o,16ft. 7.23
 Что касается распределения напряжений в срединной поверхности после потери устойчивости, то для панелей различной кривизны получаются качественно различные данные. Остановимся на них подробнее.
 1. Панели малой кривизны. Как только происходила потеря устойчивости панелей этой группы, распределение сжимающих напряжений по ширине переставало быть равномерным. Для слабо искривленных панелей изменение картины напряженного состояния происходило последовательно с увеличением краевых напряжений, как и в случае плоских панелей.
 2. Панели средней кривизны. Резкий скачок, имеющий здесь место при переходе от одной формы равновесия оболочк

§ 65
 РЕАЛЬНЫЕ ЗНАЧЕНИЯ КРИТИЧЕСКИХ НАПРЯЖЕНИЙ
 273
 к другой, почти всегда сопровождается падением среднего напряжения. Поэтому характер изменения среднего напряжения или, иными
 Панель Ь240мм; h-lMM; R 300мм; в—45°; И192
 о -экспериментальные точки
 среднее напряжение
 2900кгсм2 условно
 2300кзсм2 условно
 Р 12,5т до скачка
 кгсм
 Напряжения в срединной поверхности
 Фиг. 7.8. Распределение напряжений при последовательном нагружении цилиндрической панели.
 словами, воспринимаемой панелью нагрузки является здесь совердпенно своеобразным. Напряжение возрастает до верхнего критического значения, а затем во время скачка мгновенно падает.

274
 УСТ0ЙЧИВ0С1Ъ ЦИЛИЙДРЙЧЕСКЙХ ПАЙЕЛЕЙ гл. VII
 Дальнейший процесс может протекать различно. В одних случаях непосредственно после скачка начинается новое возрастание нагрузки; в других — результатом скачка являлось образование малоустойчивой равновесной формы. Это было видно из того, что после некоторого возрастания среднего напряжения происходило снова падение его величины либо постепенно, либо в виде повторного скачка.
 В отличие от панелей плоских или слегка изогнутых в случае панели средней кривизны потеря устойчивости ведет к значительному уменьшению сжимающего напряжения в месте образования выпучины.
 780
 760
 740
 120
 700
 80
 60
 40
 20
 п pbf
 РЕ IhJ
 О До ХЛО
 <? После х о Промежу
 im
 у
 -
 : § 1 1
 ачения и
 Ппптепы
 шряж.
 vunp
 1 напряжен падение Y скачком напряжения
 Hi
 У0
 К268
 Л
 7<792
 о.
 U23
 f
 л
 ,744 —
 I?
 h
 ©
 i
 <
 ' V
 I
 ч
 V-
 В
 3-
 11
 Фиг.
 740 760 780 200 220 240 260 280
 7.9. Напряжения при хлопках цилиндрических панелей.
 В то время как у плоских панелей минимальное напряжение в сечении оставалось после потери устойчивости почти равным критическому, здесь оно оказывалось меньше критического и во многих случаях меняло знак, т. е. становилось растягивающим.
 3. Панели большой кривизны. Эффект скачкообразных изменений нагрузки оказался для этой группы еще более сильным, чем в случае панелей средней кривизны.
 Для одной из подобных панелей R 300 мм на графике фиг. 7.8 дано распределение напряжений в срединной поверхности и напря-j

§ 66 БОЛЬШИЕ ПРОГИБЫ ШАРНИРНО ОПЕРТОЙ ПОЛОГОЙ ПАНЕЛИ 275
 жений изгиба по ширине панели при последовательном увеличении нагрузки. Как видно из фиг. 7.8, а, во время хлопка произошло резкое падение среднего напряжения, примерно до половины верхнего значения. Вместе с тем, судя по фиг. 7.8, б, получили резкий скачок напряжения изгиба, причем величина их превысила предел пропорциональности материала. При испытании другой панели выпучивание произошло при 1250 кгсм2 ПРИ теоретическом значении 2050 кгсм2. В результате трех хлопков среднее напряжение снизилось до 740 кгсм2.
 В связи с тем, что образование глубоких выпучин связано в большинстве случаев с переходом напряжений за пределы упругости, после разгрузки в отдельных точках обнаруживались остаточные деформации. Между тем в случае плоской или слабо изогнутой панели той же толщины деформации оказывались упругими даже при значительном превышении нагрузкой критического значения.
 Мы видели, что скачкообразная потеря устойчивости сопровождается, как правило, уменьшением воспринимаемой панелью нагрузки. На графике фиг. 7.9 даны экспериментальные значения среднего напряжения и указаны размеры уменьшения напряжения в момент хлопка по данным электротензометров. В тех случаях, когда падение нагрузки происходило мгновенно, на графике, нанесены сплошные линии; отмечены также случаи последовательных скачков. Если же падение совершалось постепенно, стрелки даны штрих-пунктирными линиями. Надо считать, что чем более совершенными являются начальная форма листа и условия опыта, тем ближе к теоретической линии лежат точки реальных критических напряжений. Но, как видно из графика, большей оказывается тогда и высота падения напряжения к нижней критической точке.
 На результаты опытов влияла также скорость нагружения. При быстром темпе нагружения рв несколько возрастает, а хлопок в момент потери устойчивости становится более резким. Если же нагружение производится через небольшие ступени, эффект хлопков до некоторой степени сглаживается.
 § 66. Большие прогибы шарнирно опертой квадратной пологой панели; первое приближение
 Из экспериментальных данных вытекает, что процесс потери устойчивости цилиндрической панели можно теоретически описать лишь при исследовании больших прогибов оболочки. Рассмотрим сначала случай шарнирно опертой по краям квадратной цилиндрической панели со стороной а в предположении, что параметр k невелик и лежит в пределах 0 < k < 24. Для таких панелей переход от начальной формы к изогнутой форме с весьма малыми прогибами ооисходит с образованием одной полуволны как вдоль образующей,

276 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКИХ ПАНЕЛЕЙ гл. VII
 так и по дуге. Решая задачу в первом приближении, будем считать, что и при последующем изгибе эта форма выпучивания сохраняется; положим поэтому
 -. 7UT. тиу т сл
 w sin— sin —. 7.24
 J a a v у
 Дальнейшие выкладки при решении нелинейной задачи аналогичны проведенным в § 60. При kx 0, ky— 1?, рх р по 6.68 получим, если ненагруженные кромки сближаются свободно:
 1 л 1,0 2пх, 2гсу, 1.CL2 7ГЛТ. тсу ?у2 осч
 в'W2cos—C0Sr4Rfzsin<7-25
 Напряжения в срединной поверхности будут
 г, г о к2 271 у 1.. tzx. пу
 о 	— Ef2 COS — Е THSin— sin — —?,
 х J 8а a 4RJ а а с, к2 2кх г, 1 -. пх. 7ту
 о„ — £2 COS Е TTssin— sin —,
 J 8а2 a 4RJ а а ’
 1 тех тгу
 т — Е-rf cos — cos —.
 4? а а
 7.26
 И здесь мы можем отметить, что лишь средние значения напряжений у краев панели равны заданным величинам:
 ах — —р, оу 0, х 0.
 Если считать, однако, что по краям панели приложены внешние усилия по закону, отвечающему 26, то мы можем снова воспользоваться уравнением Бубнова — Галеркина 6.69.
 Окончательное уравнение 6.70 в рассматриваемом случае получит вид
 Ш Ef-£k ЕРТШБЖ Df-?Pf °- <7-27>
 Считая, что при начавшемся после потери устойчивости прогибе оболочки Ф0, и вводя безразмерные параметры, найдем:
 » 10 < j ф л ло
 Ш ЫН 31 — 2 Р — 7.28
 Опуская в 28 нелинейные члены, мы получим верхнее критическое напряжение 20. С учетом этой последней формулы имеем:
 I К2 ГО 10 иг оп
 р —рв g С Зтс2 7.29
 Как видим, закон изменения нагрузки после потери устойчивости
 будет различным в зависимости от кривизны панели. Для плоской
 Это решение было предложено автором 72.

§ 66 БОЛЬШИЕ ПРОГИБЫ ШАРНИРНО ОПЕРТОЙ ПОЛОГОЙ ПАНЕЛИ 277
 панели при k 0 придем к формуле 3.15:
 I 7с2
 Р — акр у.
 Наличие дополнительного линейного члена в уравнении 29 указывает на своеобразие в поведении цилиндрической панели по сравнению с плоской пластинкой: после возникновения прогибов нагрузка падает,
 дрической панели в первом приближении.
 достигает известного минимума и лишь затем начинает возрастать. Минимум имеет место при
 откуда
 £1 — -г — J®. k — о
 rfC 4 ’ 32 к — и>
 С >0,146. Зтс4
 Этому прогибу соответствует параметр нагрузки
 Рн
 7.30
 7.31
 На фиг. 7.10 изображена диаграмма рС для 24. Как видимf в пределах между ря и ря каждому значению нагрузки соответствует

278 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКИХ ПАНЕЛЕЙ гл. VII
 не только начальная цилиндрическая, но и изогнутая форма равновесия. Этим задача устойчивости отличается от рассмотренных раньше задач, относящихся к пологим оболочкам или пластинкам с начальной кривизной: там речь шла о тройных значениях нагрузки при однородных изогнутых равновесных формах.
 Величину ря назовем нижним критическим напряжением, понимая под этим то минимальное напряжение, при котором, наряду с начальной равновесной формой, возможна изогнутая равновесная
 Фиг. 7.11. Зависимость между нагрузкой и общей деформацией панели по данным первого приближения.
 форма оболочки. Напомним, что при определении верхнего критического напряжения имелись в виду равновесные формы, бесконечно близкие к первоначальной. Для плоской панели ря сливается с рв, при увеличении же k перепад значений ра и рв возрастает. Найдем, далее, по формуле 6.76 «среднее» взаимное смещение нагруженных кромок панели ех. Введем обозначение
 При С 0 будет е ръ. Возрастание С связано на первых порах с падением е: это отвечает расхождению кромок, т. е. некоторому удлинению первоначально сжатой панели. Такое расхождение торцов
 М л отвлекаемся здесь от реальной картины загружения панели в испытательной машине см. § 95.

§ 67 ОПРЕДЕЛЕНИЕ ЭНЕРГИИ СИСТЕМЫ 279
 объясняется значительной разгрузкой панели. Затем кромки снова начинают сближаться, в то время как нагрузка продолжает падать. Таким образом, нижние значения ?н и ен отвечают различным прогибам фиг. 7.10.
 На фиг. 7.10 представлены также ветви кривых рС и е£, лежащие за верхней критической точкой.
 Сравнение кривых р и е позволяет установить зависимость между нагрузкой и сближением дуговых кромок. Такая диаграмма представлена для k 24 на фиг. 7.11.
 § 67. Определение энергии системы. Анализ равновесных форм панели
 Исследование равновесных форм панели облегчается, если сопоставить соответствующие им значения потенциальной энергии.
 Найдем потенциальную энергию изгиба £и» подставляя 24 в выражение 1.109:»
 UB DP. 7.33
 Потенциальная энергия деформации срединной поверхности по 1.106 будет
 7.34
 Перейдем к определению работы внешних сил. Предварительно надо найти перемещения точек кромок панели вдоль линий х и у.
 По первому из выражений 5.4 при kx 0 имеем:
 ди 1 f ч 1 dw2
 дх Ех 'Х<1У' 2дх'
 Подставляя выражения для ох, оу и w, находим:
 ди 1 о1 ча 27ur 1 хt.. tzx. ну.
 ш ¥ а0 - V cos- 41 - V sm - sm
 №«¥'°Ф-Ъ-if'i- <>
 Найдем смешанную производную
 д2и 1 ТС3 2тглг 27су 11 ч TZ. 1ZX ТС V ч
 3—3— — Т cos COS— TTjO —a — Sin — cos—. b
 дх dy 4 J a3 a a 4RJ K K ; a a a v '
 Производная no 5.4 оказывается равной
 dv ay 1 dw 2. w
 ду Ж 2dyj

280 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКИХ ПАНЕЛЕЙ ГЛ. VII
 ИЛИ
 dv 1 о 1..ч”2. 1 -02 2кх 2ку
 dj 8f V-aC0Sir -8f 7TC0S — C0S1T-
 Отсюда
 . 1 fali_L_ ц, Р. I 3 -ЬН' 4in У гч
 8 ф -г I1 £ - 4 яп — sin л. с
 <fiv 1 ха • 2tzx 2r.y 3-j-txn 7ZX. пу
 WW -TJ?s'nTcosT -f7fcos7sinf <d>
 Для определения других частных производных от и и v, воспользуемся третьим из соотношений 5.4; будем иметь:
 ди - dv 1мО пх тсу 1 ге>т. 2пх. 2тсу.
 5у агe —w cosTcosi-Tf2asm—sinir <е
 и
 д2и I d‘v 1 -f- а к. пх пу 1 лтеЗ.2пх. 2гсу
 ■д- Ч-— ов Tsltl — COS — — тг COS sin —. f
 ox dy 1 ox 2 R a a a 2 J cfi a a w
 Сопоставляя равенства b и f, находим:
 d2v 1.л n 2 пх. 2ny. 3 4-p, n. пх к у. ч
 J-ТГ — -Т- Tcos sin—“4 Trf f— sin — COS—. g
 ox2 4 y a3 a a ' 4R J a a a Vfe
 По выражениям d и g ищем выражение для первой произвол-
 1 dv. ной ;г-: дх
 dv 1 п2. 2пх. 2яу 3 4-а пх пу.. ч
 3- Б-f -о Sin Sin — -г- 4т COS —cos — Ct. h
 дл: 8 J a2 a a 4 R a allv
 Аналогично находим:
 -4-24 sin sin LJi- coscos C2. i
 dy 8 J a2 a a 1 4 R a a 1 w
 Складывая выражения h и i и сравнивая результат с е, убеждаемся в том, что постоянные Ct и С2 могут быть приняты равными нулю. Далее, по выражениям а, i, h и с для первых производных определяем самые перемещения. Будем принимать, что в точке
 лг 0, з 0 перемещения равны нулю. Тогда найдем:
 1.о. 2пх 2пу I jtq1 я • 2пх.
 и sin — cos—- — тс 1 —Ю — sin -
 16у a a a 16у 4 ‘ ’ a a 1
 I f CL, 4 tzx. ny px 1 r.yK2 _ Q-
 71-cos7s,n7-£-85' 7-35
 v Л2 — cos? sin — i3l — a — sin —
 16y a a a Ш' 4 ‘ ' a a
 3 -j- IX. f CL. ПХ Tty, Jxpy 1 -Q7l2
 sin — cos — 4r— -q f — У • 7.36
 4 	R n a a 1 E 8 J a2 v J

§ 67 ОПРЕДЕЛЕНИЕ ЭНЕРГИИ СИСТЕМЫ 281
 Вычислим перемещения и точек кромки х а:
 «и.—F'S5«' 7-37
 Усилия рх> действующие по этой же кромке, равны
 р» х-а — ■ЕР Й C0S1¥ — •Р-
 Зная усилия и перемещения, можем вычислить работу внешних сил. Надо принять во внимание, однако, что составляющая усилий р постоянна по величине, в то время как составляющая
 „ тс2 2тгу
 ШС05
 является переменной. При изменении величины на 8 работа bW будет пропорциональна выражению 28; можно принять 8№833. Поэтому соответствующая величина полной работы должна вычисляться с коэффициентом V3. Окончательно
 О
 о
 После вычислений находим:
 w' и f а 1 2л, г?2а2,, 1 о Ii £3
 Аналогичное выражение для кромки л: 0 будет
 IV а 1 2 11 ту Р
 Wt—ph — 1 J —
 Вычисляя таким же образом работу усилий ру по двум кромкам д 0 и у — а, получим:
 Ер 3 Х
 R 144
 Остается определить работу усилий 5. Судя по выражениям 26, усилия 5 меняются по закону С, в то время как перемещения v 0 — по закону Л2. Соответствующая полная работа должна
 быть взята с коэффициентом 23:
 8Г3 - 8ЛС3.

282 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКИХ ПАНЕЛЕЙ ГЛ. VI
 Для одной кромки
 W» --t-Л-
 R 3 48 ‘ 16 •
 Полная работа усилий s по четырем кромкам будет
 3 R 3 б 2'
 Окончательно работа внешних сил получается равной
 Г ЕНР 7 Зц hp L -1 _ _f_ hpf W. 7.38
 Энергия системы Э, равная
 Э иж и0— W, 7.38
 выразится следующим образом:
 тс4.._ 4 £ АА_ Р-Х- Ehf2-- ph— f-2 1 a C 28cfi1 C 18R 1 32R 2E P 8 7 2cflh UJ
 7.4C
 Вводя безразмерный параметр
 э- эяг <7-41
 и используя формулу 20 для ?, получим:
 3 г _ Jg. ж рр_7-4а
 Величина 4pqn2 соответствует энергии деформации, не связанно
 с изгибом оболочки и не зависящей от параметра С. Обозначи
 через Uв безразмерную величину энергии, накапливаемой в панел до момента потери устойчивости и соответствующей верхнему кри тическому напряжению. Будем иметь:
 7.43
 В дальнейшем условимся отсчитывать энергию от уровня, отва чающего энергии чистого сжатия. Тогда получим:
 э -g- С - JJ->: -г. 7.Ц
 Если пользоваться теорией малых прогибов, то в выражени энергии мы должны отбросить члены, содержащие С в степени выш второй. Тогда получим:•
 Э 	рв— рФ. 7.4Е

§ 67 ОПРЕДЕЛЕНИЕ ЭНЕРГИИ СИСТЕМЫ
 Для плоских пластинок будем иметь:
 Эти выражения могут быть использованы для анализа ных форм оболочки или пластинки.
 Фиг. 7.12. Энергетические уровни различных равновесных состояний цилиндрической панели.
 На фиг. 7.12 показан характер изменения энергии Э при заданных нагрузках р применительно к панели кривизной k 12. На фиг. 7.12,6 дан график зависимости между р и С. На фиг. 7.12, а
 283
 7.46
 равновес-

284
 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКИХ ПАНЕЛЕЙ ГЛ. VII
 по оси абсцисс откладываются те же значения С, а по оси ординат — безразмерная энергия Э.
 Примем, например, р — 3. На фиг. 7.12, б этому значению соответствует линия. Как видно из графика, при С 0 возможна лишь одна равновесная форма. Из фиг. 7.12, а заключаем, что равновесие будет устойчивым: энергия здесь минимальна как
 по отношению к бесконечно близким равновесным формам, так и по сравнению с равновесными формами, отвечающими конечным прогибам.
 Пусть, далее, р 3,8 линия II. При этом возможны уже две равновесные формы, соответствующие: первая — нулевому прогибу £ 0 и вторая — прогибу С 1,65. Первая является устойчивой, вторая — безразличной; линия Э на графике имеет при С 1,65 точку перегиба. Отметим, что уровень энергии для этой точки выше, чем для начальной точки, при С 0. Следовательно, для того чтобы панель перешла из первого равновесного положения ко второму, должен быть преодолен энергетический барьер. Высоту этого барьера можно сопоставить с величиной энергии сжатия, отвечающей верхнему критическому напряжению и вычисляемой по формуле 43. Всем значениям ?, превышающим 3,8, отвечают уже три равновесные формы.
 Так, например, при ? 5,5 линия IV одна из равновесных форм соответствует С 0; форма эта является устойчивой. Равновесие панели имеет место также при С 0,5; однако оно является неустойчивым, так как энергия здесь максимальна по отношению к соседним значениям С. Наконец, третья равновесная форма отвечает прогибу С 2,8; она будет устойчивой, и при этом уровень энергии здесь ниже, чем для С 0. Равным уровням энергии в начальном и изогнутом состояниях соответствует линия, построенная для р — 4,24.
 По мере возрастания р запас устойчивости первоначальной формы равновесия £ 0 уменьшается, и при 7,2 верхнее критическое напряжение первоначальная форма равновесия будет уже безразличной по отношению к соседним бесконечно близким формам.
 Линия VI отвечает параметру нагрузки, превышающему критическое значение: ? 8. Нулевому прогибу отвечает неустойчивое равновесие; две другие равновесные формы будут устойчивыми, причем одна из них соответствует отрицательному прогибу от центра кривизны.
 Мы можем теперь нарисовать вероятную картину потери устойчивости оболочки в реальных конструкциях. Допустим, что величина нагрузки лежит в пределах 0 < р < 3,8. Если какой-либо возмущающий фактор эксцентриситет в приложении нагрузки, небольшое поперечное давление и т. д. вызовет изгиб панели, то по удалении этого фактора равновесная форма, которая является здесь единствен¬

ВЛИЯНИЕ НАЧАЛЬНОЙ ПОГИБИ
 285
 ной, восстановится. Иначе будет вести себя панель при нагрузках 3,8 <р 7,2. Если возмущающий фактор будет в состоянии преодолеть энергетический барьер, панель скачкообразно перейдет в новое устойчивое равновесное положение — изогнутое, минуя при этом промежуточную неустойчивую равновесную форму. Таким образом, потеря устойчивости цилиндрической панели вполне вероятна при нагрузках, соответствующих р > 3,8, и особенно при р > 4,24. Вероятность такого перехода к изогнутой равновесной форме возрастает по мере приближения к значению нагрузки р 7,2, так как энергетический барьер при этом делается более низким.
 Если же возмущающие силы отсутствуют, то при постепенном возрастании нагрузки напряжение должно достигнуть верхней критической величины, а затем может произойти выщелкивание; при этом панель перейдет в новое равновесное положение, характеризуемое прогибом С 3,29. Резкий скачок от одной равновесной формы к другой, более устойчивой, должен, очевидно, сопровождаться значительным изменением потенциальной энергии внешней нагрузки, переходящей частично в кинетическую энергию. Обратный скачок должен произойти при р р.
 § 68. Влияние начальной погиби
 Поставим себе целью в развитие приближенного решения § 66 Изучить влияние начальной погиби оболочки на ее деформацию. Примем, что контур квадратной панели расположен на цилиндрической поверхности и начальный прогиб отвечает уравнению
 -. TZX. гсу
 нч sin — Sin--. 7.47
 Будем придавать стреле начальной погиби нч знак плюс, если погибь обращена к центру кривизны.
 Для дополнительного прогиба воспользуемся попрежнему выражением
 w sin sin —. 7.48
 J а а 4 у
 Подставляя 47 и 48 в правую часть уравнения 5.45, получим: £ m -- 4 2h icOS COS f I « „„ Ц. S>„ S.
 7.49
 Предполагается, что панель имеет возможность изогнуться при постоянной нагрузке, как, например, при непосредственном приложении груза см. § 95.

26 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКИХ ПАНЕЛЕЙ ГЛ. Vll
 Решение его будет
 i Ф I. 2.осо. cos S sin Н Sin 2 _ Жг.
 7.50
 Для функции X получаем выражение 5.54:
 E<2WcoscoSs,n sl„ i
 £ - j- ■М I» « V- :А»3 -«» ■ COS? 3L -
 -Eip VMCO-Ef Sin £1 sin SL-
 , п 1,. ид:. ну if - ч тс2. пх. г,у 7 еп
 -ADTf sin- sin --р „, sin — sin 7.51
 Уравнение типа 6.69 получает вид
 gfir Я 3а„, 2нЧ if я „,
 wfD“x- 0- <7-52>
 При нч 0 придем к уравнению 27. Считая
 С,.., 4 7.53
 и пользуясь обозначениями § 66, будем иметь:
 Р Н“ 8“ “f” H<1 ’ 2 H4J fV ' Судя по 54, приложение сжимающего усилия любой величины приводит к появлению дополнительного прогиба в отличие от случая панели строго цилиндрической формы.
 На фиг. 7.13 и 7.14 даны диаграммы зависимости между параметрами нагрузки р и величиной полного прогиба, характеризуемого параметром Сп С —Снч Фиг. 7.13 относится к предельному случаю плоской панели k 0; кривые построены для следующих отношений стрелы прогиба к толщине пластинки:
 Снч 0; 0,025; 0,05; 0,1; 0,25; 0,5.
 Пусть знак направления дополнительного прогиба совпадает со знаком направлением начального прогиба. Тогда мы получим сплошные кривые первого квадранта диаграммы, изображающие плавное увеличение прогиба при возрастании сжимающего усилия. Для того

ВЛИЯНИЕ НАЧАЛЬНОЙ ПОГЙБЙ
 28 7
 4Тобы получить постепенно возрастающие дополнительные прогибы обратного знака, нужно вначале при Сп > 0 положить усилие растягивающим величина р получает знак минус, см. четвертый квадэант диаграммы. Сплошные кривые второго квадранта соответствуют эавновесным формам пластинки, полный прогиб которой обратен ю знаку начальному прогибу; усилия здесь снова оказываются сжинающими.
 Фиг. 7.14 относится к цилиндрической панели, параметр кривизны соторой равен 12. Серия сплошных кривых соответствует слу4аю, когда начальный прогиб направлен к центру кривизны; пунктирные кривые построены в предположении, что начальные прогибы
 риг. 7.13. Диаграмма «нагрузка — полный прогиб» для плоской пластинки
 с начальной погибью.
 меют обратное направление. Если бы мы нанесли пунктирные линии а фиг. 7.13 для плоской панели, то они были бы расположены овершенно симметрично по отношению к сплошным линиям.
 Деформация цилиндрических панелей, обладающих начальной югибью, имеет существенные особенности по сравнению с плоскими анелями. При достаточно малом положительном начальном прогибе сплошные линии постепенному возрастанию прогиба соответствует начале увеличение сжимающей силы подобно случаю плоской панели. днако кривая рСп имеет максимум, после которого дальнейшее

288
 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКИХ ПАНЕЛЕЙ ГЛ. VII
 возрастание прогиба связано с уменьшением нагрузки. Лишь после достижения некоторого минимального значения сила начинает снова возрастать.
 Рассмотрение фиг. 7.14 позволяет уяснить истинную картину деформации реальной цилиндрической панели. Мы видим, что даже самый незначительный начальный прогиб существенно снижает верхнюю критическую силу по сравнению со случаем идеально цилиндри¬
 ческой панели; это и отражается на результатах экспериментов. С другой стороны, мы находим объяснение тому факту, что сжатие цилиндрических панелей большой кривизны сопровождается хлопками, т. е. резким изменением величины прогиба при некотором значении нагрузки. Эффект скачка должен исчезать при больших начальных прогибах, так как при этом сжимающая сила возрастает постепенно; отметим, что наибольшая интенсивность в увеличении прогиба имеет место при значении силы, близкой к нижней критической силе для строго цилиндрической панели.

§ 68
 ВЛИЯНИЕ НАЧАЛЬНОЙ ПОГИБИ
 289
 Изучение пунктирных кривых показывает, что наличие начальных прогибов от центра кривизны может изменить характер деформации панели. Бесконечно медленный процесс заключается здесь в постепенном увеличении дополнительных прогибов, направленных в сторону начального прогиба. Однако после достижения сжимающим напряжением нижнего критического значения становится вероятным
 Фиг. 7.15. Энергетические уровни равновесных состояний цилиндрически панелей с начальной погибью.
 скачок к другой равновесной форме с выпучиной к центру кривизны.
 Ш графике фиг. 7.15 показано, как изменяется величина энергии системы Э для случая, когда начальная стрела прогиба равна Снч — 0,1; на фиг. 7.15,6' повторена соответствующая пунктирная кривая фиг. 7.14. Параметры нагрузки р приняты для линий, II и III соответственно р 4,5; 6 и 7,5. Как видим, при всех выбранных значениях р из трех равновесных положений два являются устойчивыми, а третье — промежуточное — неустойчивым. При

290
 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКИХ ПАНЕЛЕЙ
 ГЛ. VII
 р 4,5 более устойчивой является равновесная форма с отрицательным прогибом, так как здесь уровень энергии ниже; напротив, при р 6 более устойчива равновесная форма с прогибом к центру кривизны. Различие между уровнями энергии становится особенно резким при р 7,5; здесь для скачка от первого равновесного положения к третьему нужна весьма незначительная дополнительная энергия.
 Сравнение фиг. 7.13 и 7.14 показывает, что наличие отрицательных начальных прогибов может благоприятно сказаться на величине критической силы. Этот вывод подтверждается экспериментами 712.
 Фиг. 7.16. Хлопки цилиндрических панелей: а — при отсутствии начальной погиби; б и в — при погиби к центру и от центра кривизны.
 На фиг. 7.16 изображены примерные диаграммы зависимости между напряжением и прогибом при наличии скачка от менее устойчивой равновесной формы к более устойчивой для трех различных случаев: строго цилиндрической панели, для панелей с положительной и отрицательной начальной погибью.
 Стрелки, изображенные двойными линиями, соответствуют скачку, для совершения которого требуется приток энергии извне.
 Предположим, что в дополнение к основной нагрузке, сжимающей вдоль образующей, действует также равномерная поперечная нагрузка со стороны выпуклости. В приближенном решении задачи мы можем воспользоваться уравнением 6.70, составленным для тех же граничных условий. Полагая ру — 0 и рх р для квадратной панели, получим:
 § 69. Совместное действие сжимающей и поперечной нагрузок

§ 69 СОВМЕСТНОЕ ДЕЙСТВИЕ СЖИМАЮЩЕЙ И ПОПЕРЕЧНОЙ НАГРУЗОК 291 Вводя параметр поперечной нагрузки
 «•-§-'• <7-5<ч
 придем к зависимости
 I КО 10. 16 1 я Гяч
 Р 32С”> 757
 связывающей среднее сжимающее напряжение со стрелой прогиба и интенсивностью поперечной нагрузки.
 Фиг. 7.17. Зависимость между нагрузкой и прогибом для сжатой панели при наличии поперечной нагрузки.
 Допустим, что величина q является заданной; поставим себе целью выяснить характер зависимости рС. График фиг. 7.17 соответствует цилиндрической панели, параметр кривизны которой равен k a2Rh 24. Сплошные линии построены по уравнению 57

292
 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКИХ ПАНЕЛЕЙ ГЛ. VII
 и соответствуют случаю, когда поперечная нагрузка различной интенсивности направлена к центру кривизны q > 0; пунктирные линии отвечают поперечной нагрузке от центра кривизны <q <0.
 Как видим, характер полученных кривых такой же, как и в рассмотренном выше случае панели с начальной погибью. При q > 0 достаточно весьма малой поперечной нагрузки, чтобы значительно снизить верхнее критическое напряжение. Заметим, что параметру q 10 в случае дуралюминовой панели с размерами а 200 мм и А 2 мм отвечает давление q 750 kzms.
 Поперечная нагрузка обратного знака q < 0 имеет место, например, в сжатой зоне крыла самолета. Из рассмотрения фиг. 7.14 заключаем, что наличие этой нагрузки может благоприятно сказаться на величине критического напряжения. Однако возрастание сжимающего напряжения имеет место лишь до некоторого значения, лежащего между «верхним» и «нижним» пределами рв и рн, после чего происходит резкий скачок с образованием выпучины к центру кривизны.
 § 70. Квадратная панель с защемленными краями
 Предположим, что сжатая вдоль образующей квадратная пологая панель жестко защемлена по всему контуру, причем ненагруженные кромки смещаются свободно. Приближенное выражение для прогиба примем в виде
 w sin2 sin2 —. 7.58
 J a a v 7
 Соответствующее выражение для Ф будет иметь вид 6.102, если положить kx 0 и kyR и ввести член —ру22.
 Уравнение Бубнова—Галеркина 6.103 приводит к зависимости
 533 714 гу го 15 £ 9 £ 714 з Я2
 Ш?-64«2648аТ1°-4:0- <7'59>
 Считая 0 и вводя безразмерные параметры, получим:
 Р <? - £ -т А» f ■ 7 • 60
 Полагая С 0, определим верхнее критическое напряжение:
 Для плоской панели отсюда вытекает прежнее выражение 3.75. В таблице X значения р по 61 сравниваются с величинами р для случая шарнирного опирания.
 Как видим, защемление краев оказывает значительное влияние на величину верхнего критического напряжения лишь для плоской

§ 70
 КВАДРАТНАЯ ПАНЕЛЬ С ЗАЩЕМЛЕННЫМИ КРАЯМИ
 293
 панели; по мере увеличения кривизны это влияние становится менее заметным и в случае k 24 приводит к повышению критического напряжения лишь на 14. Для панелей, параметр кривизны которых k превышает 24, решение задачи должно основываться на ином выборе приближенного выражения для прогиба. Однако легко убедиться в том, что для сильно искривленных панелей защемление краев должно в весьма малой степени повышать критическое напряжение.
 Таблица X
 Верхние критические напряжения для квадратной цилиндрической панели
 Параметр кривизны k
 0
 6
 12
 18
 24
 р при шариирно опертых кромках 9,6
 10,3
 12,3
 15,8
 20,6
 р при защемленных кромках 3,6
 4,5
 7,2
 11,8
 18,0
 В самом деле, выпучивание таких панелей сопровождается образованием нескольких волн вдоль образующей и по дуге, но при этом граничные условия на кромках становятся несущественными.
 О 	деформации панели с защемленными кромками после потери устойчивости можно судить по уравнению 60; перепишем его в виде
 р рв 2,26С2 —0,31 С. 7.62
 Это уравнение имеет ту же структуру, что и 29. Величина нижнего критического напряжения, определяемая из 62, приближается к критическому напряжению 3.75 для плоской панели тех же размеров.
 Сопоставляя- результаты, полученные, выше, мы можем сделать следующее заключение. Неблагоприятные факторы, приводящие к уменьшению критического напряжения и преждевременному возрастанию прогибов: начальная погибь и влияние поперечной нагрузки — сказываются в случае цилиндрической панели особенно резко. Они вызывают скачкообразную потерю устойчивости при напряжениях, далеко не достигающих теоретического напряжения, вычисленного для случая идеально гладкой оболочки. В то же время благоприятный фактор — защемление краев панели, дающий значительное увеличение критического напряжения для плоской пластинки, оказывает при сжатии цилиндрической панели незначительное влияние.

294
 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКИХ ПАНЕЛЕЙ ГЛ. VII
 §71. Собственные колебания панели. Графики на фазовой плоскости
 Допустим, что цилиндрическая панель выведена из состояния равновесия и затем предоставлена самой себе. Характер возникающих при этом колебаний панели будет зависеть от интенсивности начального возмущения.
 Примем, что в центре панели сосредоточена некоторая приведенная масса. Сопротивлением движению будем пренебрегать; тогда мы получим консервативную нелинейную систему с одной степенью свободы.
 Интеграл энергии системы можно представить в виде
 Здесь под Э мы попрежнему понимаем полную потенциальную энергию системы; через Т обозначается кинетическая энергия, через С—полный запас энергии, приданный панели в начальный момент времени.
 Обозначая через пг приведенную массу системы, имеем:
 Под v понимается скорость центральной точки панели; при определении запаса энергии С она будет равна
 Пользуясь выражением 65, можно для каждого значения С найти «фазовый портрет» системы, т. е. совокупность кривых на фазовой плоскости, определяющих зависимость между скоростью v и стрелой прогиба. Fla. фиг. 7.18 и 7.19 изображены кривые «равной энергии» на фазовой плоскости для квадратной цилиндрической панели, отвечающие приближенному решению § 66 при k — bRh— 12. В § 67 была применительно к этому случаю найдена безразмерная потенциальная энергия Э. Диаграмма фиг. 7.18 построена в предположении, что сжимающее усилие равно нижней критической нагрузке р 3,8. По осям отложены безразмерные параметры прогиба С и скорости v. Центр А, окруженный рядом замкнутых траекторий, соответствует устойчивому равновесному положению; точка возврата D отвечает точке перегиба d соответствующей кривой Э на фиг. 7.12 с горизонтальной касательной.
 Г3 С.
 7.63
 7.65
 См., например, Б. В. Булгаков, Колебания, Гостехиздат, 1954 или И. М. Капчинский, Методы теории колебаний в радиотехнике, Госэнергоиздат, 1954,

§ 711
 СОБСТВЕННЫЕ КОЛЕБАНИЯ ПАНЕЛИ
 295
 Фиг. 7.19 относится к значению ? 5,5, лежащему в области между нижней и верхней критическими нагрузками. Здесь имеются два центра А, В и, кроме того, седло С, отвечающее неустойчи-
 Фиг. 7.18. График на фазовой плоскости для на грузки, равной нижней критической величине.
 В точке D совмещаются центр и седло.
 вому равновесному положению. В случае панели, имеющей малые начальные прогибы или получающей небольшие скорости, колебания
 Фиг. 7.19. Диаграмма на фазовой плоскости для нагрузки, превышающей нижнюю критическую величину.
 будут совершаться вокруг точки А: изображающая точка на фазовой плоскости будет перемещаться по траекториям, окружающим А. Пусть теперь панели придано большее начальное отклонение, так

296 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКИХ ПАНЕЛЕЙ гл. VII
 что С лежит справа от С, за так называемой разделяющей траекторией аа. Тогда изображающая точка устремится к положению В и панель будет совершать малые колебания вокруг В; иными словами, произойдет хлопок панели. Если же начальный прогиб будет иметь обратный знак и С окажется слева от С, то колебания должны охватывать оба центра устойчивого равновесия. Колебания вокруг обоих центров должны иметь место и в том случае, если панели, не имеющей начальной погиби, придана скорость превышающая отрезок As. Интересно отметить, что хлопок к центру В должен совершиться также в случае, если панели приданы прогиб или скорость в направлении от центра кривизны на диаграмме— влево от А.
 Диаграммы, нанесенные на фазовую плоскость, хорошо передают особенности поведения гибких пластинок и оболочек.
 § 72. Уточненное решение для удлиненной панели произвольной кривизны. Расчетные формулы
 В предыдущих разделах мы рассматривали квадратную пологую панель, выпучивающуюся с образованием одной полуволны вдоль каждой стороны. Перейдем теперь к случаю удлиненной панели произвольной кривизны. Края панели будем попрежнему считать опертыми на абсолютно жесткие ребра и скользящими вдоль них. Решение линейной залачи привело в § 63 к форме изогнутой поверхности 2:
 . ткх. ппу
 wl ft sin sin 7.66
 Для удлиненной оболочки выпучины, обращенные к центру кривизны при wx > 0, должны, судя по 66, чередоваться с выпучинами, направленными от центра кривизны wt < 0; амплитуды первых и вторых выпучин получаются равными. Таким образом, верхнему критическому напряжению соответствует изогнутая поверхность, как бы симметричная по отношению к начальной цилиндрической поверхности.
 Между тем при прогибах, сравнимых с толщиной оболочки, эта симметрия должна нарушиться. Как мы видели, при изгибе пологой квадратной панели по одной полуволне выпучивание всегда происходит по направлению к центру кривизны. Этому направлению при заданной внешней нагрузке отвечает значительно более низкий уровень энергии системы по сравнению с направлением от центра.
 Эксперименты с удлиненными панелями показывают, что форма изогнутой поверхности сильно искривленной цилиндрической панели
 Подобные диаграммы были построены Э. И. Григолюком для пологой панели, находящейся под действием поперечной нагрузки 6•,
 Эта задача была рассмотрена автором в 7.1.

§ 72
 УТОЧНЕННОЕ РЕШЕНИЕ ДЛЯ УДЛИНЕННОЙ ПАНЕЛИ
 297
 отличается от формы изгиба плоской панели; между тем потере устойчивости плоской пластинки как раз соответствует уравнение 66. Судя по данным § 64, выпучивание цилиндрической панели большой кривизны связано с образованием сравнительно глубоких выпучин, обращенных к центру кривизны. При ft > 100 число выпучин по ширине может быть равно двум или трем; образующиеся вдоль дуги и по длине выпучины перемежаются в шахматном порядке. Такая форма прогиба может быть названа несимметричной по отношению к начальной поверхности и приближенно представлена уравнением
 При 2 > 0 прогибы всех точек панели получаются направленными к центру кривизны, а форма выпучин довольно близко подходит к наблюдаемой в опытах. Однако, исследуя бесконечно медленный процесс перехода от цилиндрической формы панели к равновесной форме большого прогиба, мы не можем ограничиться выражением 67, так как верхнему критическому напряжению, т. е. весьма малым прогибам, соответствует изогнутая поверхность 66.
 Надо учесть также, что для слабо искривленных панелей форма волнообразования должна быть промежуточной между случаями плоской пластинки и цилиндрической панели значительной кривизны. Поэтому примем, ограничиваясь двумя независимыми параметрами, смешанное выражение
 Удлиненная плоская пластинка, шарнирно опертая по контуру, выпучивается, как известно, по «квадратным» волнам. Примем и для цилиндрической панели в качестве первого приближения а b и т п, подразумевая под а уже не размер панели, а длину т полуволн вдоль образующей.
 Выражение 68 удовлетворяет условию равенства нулю прогиба по краям панели. В то же время изгибающие моменты на кромках в нуль не обращаются, что противоречит выбранным граничным условиям. Но при большой кривизне панели защемление краев, как мы видели, незначительно изменяет критическое напряжение; при малой кривизне влияние защемления усиливается, однако тогда параметр 2 теряет свое значение по сравнению с х.
 Для того чтобы пояснить метод решения задачи и получаемые результаты, примем сперва более простое выражение для w в виде
 7.67
 Ш у-Л..
 t Sin Sin
 1 а
 пъх. tnzy
 — sin -7
 a b
 7.69
 т. e. допустим, что односторонний прогиб к центру кривизны происходит с образованием выпучин постоянной глубины по всей длине оболочки,

298 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКИХ панелей гл. VII
 Для исследования зависимости между параметрами fv 2 и сжимающим напряжением воспользуемся методом Ритца. Определим энергию Э для отрезка панели длиной 2а, с тем чтобы учесть эффект наложения двух различных видов деформации «симметричной» и «несимметричной». Потенциальная энергия изгиба может быть определена по 1.109:
 U„ Dfi 2fi. 7.70
 Функция напряжений в срединной поверхности определяется из уравнения 5.30. Идя обычным путем, находим:
 £ Ш
 -iAA-i. 7-7.
 Энергия J0 будет равна по 1.106
 Ehb2 7t4jirt4 13 тс4г4 2 2 f 122?2
 Т ”3254 Н Ш W f1?2 Н 82 Щ W If 72
 Для определения работы внешних сил найдем сближение нагру¬
 женных кромок панели. Укорочение А отрезка панели длиной 2а равно
 2 а 2 а
 ‘—is— <7-73
 О о
 Подставляя выражения 69 и 71, получим:
 22 2 Л М tl
 4 42“ 4-- <7.74»
 Работа внешней нагрузки будет
 _2рг r?fn2
 Полная энергия системы
 W-hab ph--. 7.75
 a U,--Uo—W. 7.76
 Уравнения метода Ритца получают вид
 дЭ дЭ л

§ 72
 УТОЧНЕННОЕ РЕШЕНИЕ ДЛЯ УДЛИНЕННОЙ ПАНЕЛИ
 299
 Подставляя значения 70, 72 и 75, найдем уравнения, связывающие параметры прогиба с нагрузкой:
 Отношение ф характеризует как бы удельный вес несимметричной деформации в общем прогибе оболочки. Уравнения 78, 79 принимают форму
 2,57С2 7,23 п • 7.82
 Уравнение 81 по своей структуре аналогично уравнениям 29 или 62, полученным нами ранее для панелей малой кривизны, но выражает сжимающее напряжение уже не через один, а через два параметра С и ф, представляющих различные виды деформаций.
 Соотношение между этими видами деформации определяется простой формулой 82. Мы видим, что в случае плоской пластинки £ 0 параметр равен нулю при любом прогибе; удельный вес односторонней деформации возрастает по мере увеличения параметра k кривизны цилиндрической панели. С другой стороны, при весьма малых прогибах С-»0 величина также близка к нулю независимо от кривизны оболочки. Таким образом, формула 82 отображает своеобразие в характере деформации цилиндрических панелей, наблюдаемое при экспериментах.
 Судя по формуле 82, по мере увеличения прогиба коэффициент возрастает от нуля до некоторого значения отвечающего относительному прогибу С 1,7 и зависящего от кривизны, а затем падает. Иными словами, при значительном прогибе цилиндрическая панель должна приближаться по характеру деформации к плоской панели тех же размеров. Это обстоятельство также подтверждается экспериментами.
 Заменим упрощенное выражение 69 ранее составленной полной формулой 68. Ввиду того, что выкладки при этом значительно усложняются, приводим лишь некоторые важнейшие соотношения.
 Введем обозначения:
 7.80
 31-х2 0,25С

300 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКИХ ПАНЕЛЕЙ гл. VII
 Функция напряжений в срединной поверхности оказывается равной Ф £2 Ef cos cos 2nr A cos 2яа -j- cos 2я,3 —
 — 5l2 cos An<x I cos щ2 cos cos 2«,9 --
 £
 -j- cos 2га cos 4г,3 — — 2 cos 2га cos 2г43 -f-
 3 	1
 2qq 12 sin na sin 3я43 sin 3га sin ф — Efj2 sin га sin t43 —
 — TQEW cos 2ла Й Ef n cos 2«« cos 2ra?
 Tkfi-sinn<xsinn — НГ 7-83
 Здесь а и,3 определяются прежними формулами а тtа, р Энергия системы 3 равна
 9 Bhab ГпЫ 1 -4 1 533 л i 168 2г
 2 i Ь узг-71 12800 •'2 800-'i-'2 т
 1 2 92 5. fdn№ 5_ f2f nW
 8?2 у1 “Г 128?2'2 64У2 £2 16?у1у2 £2
 х Р _3 nVi
 £2 £ 2 62 Е 8 •'а 62 J Г
 ±D24fV 7.84
 Уравнения 77 принимают вид
 1 г22 168 г2тс2..2. 1 №,
 W J2 ' 4Я2 л2 -'1
 -Н..--г. ЖТ?‘“0- 7.85
 533 я2я2 3 168 «22 2 f I 9 62
 3200 62 2 -т- 400 62 ■'2 «222
 <7-86>
 Система уравнений 85 — 86 отвечает различным типам равновесных состояний цилиндрической панели; нас будут интересовать
 те равновесные формы шарнирно опертой панели, которые обра¬
 зуются после потери устойчивости и соответствуют наименьшему возможному значению среднего сжимающего напряжения.
 В работе автора т.1 некоторые коэффициенты в выражении для Э, а затем и в уравнениях 87 и 88 были найдены неправильно.

§ 72
 УТОЧНЕННОЕ РЕШЕНИЕ ДЛЯ УДЛИНЕННОЙ ПАНЕЛИ
 301
 Считая 4 Ф 0 и Ф 0, приведем систему 85 — 86 к виду 3,6я»4 f я90 3,36 С?-0,625:; 7.87
 ,,47«2гчз _ _ з,22я2Са- g 5 4,52л’ ф « 0.
 7.88
 Уравнение 88, определяющее величину соответствует полученному в первом приближении уравнению 82. Один из вновь появившихся при этом корней в интервале, когда все три корня вещественны отвечает прогибу в направлении от центра кривизны. Этот корень меняется по абсолютной величине по закону, приближающемуся к 82, но имеет отрицательный знак.
 Второй корень относится к тому случаю, когда прогиб начинается с чисто односторонней деформации: исследуя этот случай по исходному уравнению 67 при п 1, мы пришли бы к уравнению 59, полученному ранее для защемленной по контуру пластинки. Оба дополнительных корня нас здесь не интересуют, так как дают более высокие значения напряжения.
 Что касается основного корня, то изменение его в зависимости от С происходит по закону, подобному 82. В момент потери устойчивости, т. е. при С—0, получаем попрежнему ->0. Из этого следует, что для определения верхнего критического напряжения выражение для прогиба может быть выбрано в форме 66, как это и делается в классической теории устойчивости оболочек. Однако сразу же по возникновении прогиба начинает возрастать, достигая некоторого максимального значения тах. Как величина йтах, так и отвечающий ей прогиб зависят от кривизны панели и, что весьма важно, при различных параметрах кривизны k соответствуют разному числу полуволн п.
 Уравнение 85 определяет при заданных к и п? сжимающее напряжение как функцию прогиба панели и по своей структуре не отличается от уравнения 81.
 Полагая в 85 прогиб £—>-0, найдем верхнее критическое напряжение
 p:3,6«»w. 7.89
 Это выражение совпадает с решением линейной задачи 4, если принять т п и а — b. Уравнению 87 можно теперь придать вид
 р рв «2 1 4- 3,36фа С3 — 0,625А<£. 7.90
 На фиг. 7.20 приведен график для случая 24. Верхнее
 критическое напряжение равно здесь р18, причем ему отвечает п 2. При С>0 равновесные формы отвечают сначала п — 2,

302
 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКИХ ПАНЕЛЕЙ ГЛ. VII
 но затем оказывается, что при С > 0,4 значения напряжения, соответствующие п 1, лежат ниже первой кривой. Минимум напряжения р 8,4 достигается при п 1. При ft 140 получаем сначала п 3, в то время как нижнему значению р отвечает п — 2 фиг. 7.21.
 Подобные графики могут быть построены для различных параметров ft. На фиг. 7.22 представлен сводный график для верхних и нижних значений критических напряжений с указанием числа п. На графике нанесены также прямые, проведенные через наинизшие точки кривых, отвечающие разным п. Для слабо искривленных паненапряжение может быть
 Фиг. 7.20. Кривые «нагрузка — прогиб» для цилиндрических панелей малой кривизны при квадратных волнах.
 лей при ft < 25 нижнее определено по формуле
 критическое
 ■р — 3>6 ПоПри ft > 25 можно принять
 0,35ft,
 7.91
 7.92
 что соответствует прямой Ег на фиг. 7.7.
 Все эти результаты основаны на предположении, что выпучины являются «квадратными». Действительно, в некоторых экспериментах можно наблюдать образование именно «квадратных» волн. Однако надо иметь в виду, что изучение изогнутой поверхности оболочки производится уже после хлопка, когда имела место значительная пластическая деформация. Поэтому в теоретическом исследовании процесса выщелкивания удлиненной оболочки нельзя ограничивать себя каким-либо заданным значением Ijb. Правильнее считать Ijb произвольным и установить такие значения этого отношения, для которого энергия системы экстремальна, либо при котором будет наименьшим ?. Первый из этих путей дает более обоснованные результаты, но связан с громоздкими вычислениями. Поэтому пойдем по второму пути и повторим все предшествующие выкладки, находя
 Графики фиг. 7.22 и 7.23 получены О. Н. Ленько 73, применившим к исследованию уравнений 87 и 88 метод множителей Лагранжа.

§ 72 УТОЧНЕННОЕ РЕШЕНИЕ ДЛЯ УДЛИНЕННОЙ ПАНЕЛИ 303
 значения £, придающие минимум величине р Окончательные данные показаны на фиг. 7.23. Отношение 1Ь оказывается зависящим от кривизны и меняется от 1 для плоской панели до 1,67 при
 Фиг. 7.21. Кривые «нагрузка — прогиб» для панелей большой кривизны при квадратных волнах.
 некоторых определенных значениях ft. На фиг. 7.23 даны также соответствующие значения нижнего критического напряжения рн при
 Фиг. 7.22. Верхние и нижние критические напряжения для цилиндрических панелей при квадратных волнах.
 разных числах полуволн по ширине панели. Прямая, соединяющая наинизшие точки кривых pft, будет
 р 0,26ft. 7.92'

304 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКИХ ПАНЕЛЕЙ гл. VII
 Такая же прямая нанесена на фиг. 7.7 в сопоставлении с экспериментальными данными линия Е. Как видим, ряд опытов привел к более низким значениям ?. Поэтому для практических расчетов целесообразно пользоваться более низким коэффициентом 0,182, полученным для замкнутых цилиндрических оболочек см. ниже § 83,— это оправдывается тем, что в случае панели большой кривизны размер выпучин невелик по сравнению с шириной.
 Фиг. 7.23. Нижнее критическое напряжение для цилиндрических сжатых панелей при меняющейся форме выпучин.
 Таким образом получаем следующие расчетные формулы для нижнего критического напряжения: для пологой панели k 20
 £ 3,6 7.93
 и для панели большой кривизны k 20
 р 0,18. 7.94
 Этим формулам соответствуют линии F' и F на графике фиг. 7.7. Напомним, что в экспериментах автора была получена несколько более низкая граница 23, соответствующая прямой В.
 § 73. Панель, подкрепленная продольными ребрами
 Рассмотрим случай, когда сжатая вдоль образующей цилиндрическая панель, закрепленная по контуру, подкреплена в пролете сравнительно слабыми продольными ребрами стрингерами. Если кривизна панели мала, то участки ее, расположенные между стрин¬
 С некоторым снижением ? по сравнению с 91.

§ 73 ПАНЕЛЬ, ПОДКРЕПЛЕННАЯ ПРОДОЛЬНЫМИ РЕБРАМИ 305
 герами, могут выдержать нагрузку, лежащую выше критической величины; однако задача об устойчивости стрингеров должна ставиться для закритической стадии по-новому. Взаимодействие между обшивкой и стрингерами развивается здесь аналогично тому, как это было в случае плоской пластинки, подкрепленной упругими ребрами по продольным краям § 31. Это взаимодействие приводит, как правило, к более ранней потере устойчивости стрингера, чем
 при изолированном стрингере: так как криволинейная обшивка склонна выпучиваться к центру кривизны, то участки обшивки, расположенные по разные стороны от стрингера, оказывают на него давление в одну и ту же сторону фиг. 7.24.
 Если обшивка имеет значительную кривизну, то это, с одной стороны, должно благоприятно сказаться на устойчивости стрингера: криволинейная обшивка служит для стрингера как бы упругим основанием. Но, с другой стороны, при местной потере устойчи¬
 вости панели, происходящей обычно с сильным хлопком, обшивка оказывает значительное динамическое давление на стрингеры и заставляет их прогнуться иногда задолго до того момента, когда должен был бы иметь место продольный изгиб изолированного стрингера.
 В испытаниях, проведенных автором, панели различной кривизны подкреплялись одним стрингером, расположенным посередине пролета фиг. 7.25. Жесткость стрингера менялась в широких пределах. Оказалось, что при большой кривизне критические напряжения для
 Фиг. 7.24. Волнообразование цилиндрической панели с упругими стрингерами.
 Фиг. 7.25. Сечение панели со стрингерами, испыты вавшейся на продольное сжатие.

306 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКИХ ПАЙЕЛЕЙ ГЛ. VI
 обшивки мало зависят от расположения и жесткостей подкрепляющих ребер: расстояние между ребрами превышает ширину выпучины. При последующем увеличении сжимающего усилия число выпучин возрастает. Наконец появляется выпучина, включающая стрингер. Это иллюстрируется фиг. 7.26. На фиг. 7.26, а, б показаны первичные выпучины, а на фиг. 7.26, в — глубокая выпучина, захватывающая стрингер и образовавшаяся в процессе весьма резкого
 хлопка. Важно отметить, что стрингер изогнулся в этом примере при напряжении меньшем, чем в случае плоской обшивки тех же размеров.
 При волнообразовании оболочки, происходящем совместно со стрингером, форма выпучин зависит от соотношения между жесткостями стрингера и оболочки. Чем сильнее стрингер, тем волны оказываются более вытянутыми вдоль образующей. Это обстоятельство надо учитывать при исследовании устойчивости ортотропных оболочек или оболочек с часто расположенными ребрами, приводящихся к ортотропным.
 При решении нелинейной задачи о закритической деформации пологой цилиндрической панели с редко расставленными ребрами можно воспользоваться методом Ритца и аппроксимировать изогнутую поверхность панели с помощью выражения
 • о ЪХ • о ТСУ, г. ПЪХ • 1КУ х. ъПКХ. о Ыу
 w — A sin — sin £ 2sin sinb “b3 Sltl sin • 7.95
 Первый член соответствует общему выпучиванию панели вместе со стрингером, второй и третий — выпучиванию между ребрами. В выражение для энергии системы была введена энергия деформации ребер. Анализ результатов решения задачи показывает, что для повышения несущей способности панели следует подкреплять оболочку не часто расставленными слабыми ребрами, а реже расположенными, но более мощными ребрами.
 § 74. Устойчивость шарнирно опертой панели при сдвиге. Линейная задача
 Предположим, что цилиндрическая панель подвергается действию сдвигающих усилий, равномерно распределенных по всему контуру. Допустим, что панель имеет равные размеры по образующей и вдоль дуги а Ь края панели будем считать опертыми шарнирно.
 aj 6J 8J
 Фиг. 7.26. Последовательное изменение волнообразования панели с упругим стрингером.
 Эта задача рассмотрена О. И. Теребушко 77.

§ 74 УСТОЙЧИВОСТЬ ШАРНИРНО опертой панели при сдвиге 307
 При определении верхнего критического напряжения здесь можно дать лишь приближенное решение линейной задачи ; воспользуемся методом Бубнова — Галеркина. Выражение для прогиба представим в виде ряда
 ®SS»sinfsitl'T’ 7,96
 т п
 где т, п — целые числа.
 Уравнение 5.30 принимает вид
 7.97
 т п
 Решение этого уравнения выпишем в форме
 В VI VI т2 л3. тпх. mzy
 ф й 1V» SWsl— sm-T; <7-98
 т п
 здесь через s обозначено среднее касательное напряжение вдоль каждой кромки.
 Определим функцию X 5.55:
 - 2 S'-1 f 5<-’>,£ отг -- ? -
 т п
 n mnrZ nnzx mzy
 — 2s-cos —cos аj 7->
 и составим уравнение
 J Jsin sin dxdy 0. 7.100
 f
 Учитывая, что при нечетной сумме индексов m--i
 а
 С. Ых rmzx. 2a i Т 1ЛП
 Sin COS dx -75 5-, 7.101
 J a a it2 — m2’ 4 7
 о
 при четной сумме m--i
 a
 f. Ых rmzx, A ? 1Л1Л
 sin--cos ——dx — 0t 7.101
 о
 Эта задача была рассмотрена Н. В. Зволинским в трудах ЦАГИ, JSfe 246, 1936, а в дальнейшем—автором книги 72 и В. А. Марьиным.

308 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКИХ ПАНЕЛЕЙ гл. VII
 при т — i
 а
 Г. miix. Ых. а
 I Sin—— sin — dx -g- 7.102
 О
 и при тФ i
 получаем уравнение
 U
 J
 . тпх. inx, л
 sin —— sin dx 0, 7.102  Г D я4 т2 -j- г22, Е т4 а2
 шп Х д2 4 Г 2 т2-_Л22 TJ —
 Т2-2
 5 	7Z2—2 «2 2 0» 7.103
 суммирование по индексам, j распространяется лишь на такие индексы, для которых сочетания m--i и n--j одновременно являются нечетными.
 Вводя обозначение
 <7Л04
 для безразмерного параметра сдвигающей нагрузки и
 я2
 ПЛ 3 1 —л2 '
 3,6 7.105
 для параметра, отвечающего критическому напряжению при сжатии плоской панели, будем иметь:
 т
 m2 -f- г22 j k2 4m4
 °пл mn ' 72 2 __ пРртп
 710б
 г з
 Решая задачу в первом приближении, выберем следующие сочетания индексов при четной сумме т--п:
 т, п
 J
 1, 1
 2, 2
 1, 2
 1, 1
 Тогда мы получим систему двух уравнений, линейных относительно коэффициентов fn и 22. Приравниваем нулю определитель этой

§ 74 УСТОЙЧИВОСТЬ ШАРНИРНО опертой панели ПРИ СДВИГЕ 309
 системы
 4, I
 . 1 128, I
 — 9S2S 16опл4
 0.
 7.107
 Подобное же уравнение мы получали в § 33 для плоской пластинки.
 Параметр s, отвечающий верхнему критическому напряжению сдвига цилиндрической панели, оказывается в первом приближении равным
 о Г1 т w Ь2
 7.108
 ИЛИ
 sb Юl Ч 142“1“ 2272 7.109
 Считая k 0, получим критическое напряжение для плоской
 панели 3.146, найденное в § 33. Как мы видели, ошибка этого
 приближения оказывается довольно значительной и составляет
 около 19°0.
 Исследуем теперь случай, когда сумма индексов т, п является нечетной:
 т,
 п
 1,
 j
 1,
 2
 2,
 1
 2,
 1
 1,
 2
 Тогда получим окончательно:
 s, 15,7 l gjgl ш’
 7.110
 Сопоставление формул 109 и 110 показывает, что первая из них дает меньшие расчетные значения s при k 28, а вторая — При k 28.
 Перейдем теперь ко второму приближению; выберем такие сочетания индексов с четной или нечетной суммой т--п:
 т,
 п
 l> j
 т,
 п
 1. j
 1,
 1
 2, 2
 1,
 2
 2, 1; 2, 3
 2,
 2
 1, 1; 1, г
 ; 3,
 1; з, 3 2,
 1
 1, 2; 3, 2
 1,
 3
 2, 2
 или
 3,
 1
 2, 2
 2,
 3
 1, 2; 3, 2
 3,
 3
 2, 2
 3,
 2
 2, 1; 2, 3

310
 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКИХ ПАНЕЛЕЙ ГЛ. VII
 Приравнивая нулю определитель системы, находим критическое напряжение во втором приближении sBn; в случае четной суммы л я его можно выразить через 109 следующим образом:
 что отличается от известного в литературе более точного результата не более чем на 1. На выражении 111 можно остановиться как на окончательном для цилиндрических панелей, кривизна которых сравнительна мала: £<120. В случае k > 20 расчетные значения s должны находиться уже при нечетной сумме т--п.
 § 75. Нелинейная задача для квадратной панели
 Допустим, что потеря устойчивости шарнирно опертой квадратной панели произошла; поставим себе целью исследовать напряженное состояние оболочки при последующем прогибе.
 Решая задачу в первом приближении, представим выражение для прогиба в виде
 по аналогии с задачей, относящейся к плоской пластинке § 33. В правую часть уравнения 3.121 надо теперь ввести дополнительные члены
 1
 - 2.7.111
 Для плоской пластинки получим:
 8,5,
 Окончательно функция напряжений будет
 См., например, П. Ф. Папкович 16, стр. 849. Эта задача была рассмотрена автором в 72.

§ 75
 НЕЛИНЕЙНАЯ ЗАДАЧА ДЛЯ КВАДРАТНОЙ ПАНЕЛИ
 311
 Составляя уравнения Бубнова дующей системе уравнений :
 ГС4 о. 2 я4 л л 5 f2 2 2 _l
 322 и22 fi?-'11 1ЯЛ>'22”Г'
 ■Галеркина 3.141, придем к сле-
 25 а2
 6 R-
 162
 15?
 °> 7Л14>
 •2221122 •
 ТС4
 2а2
 128 JL f __
 • 45 я 1122 ■-
 й2 2216g22-?-§n 0. 7.115
 16Я2
 9 £
 Полагая
 г и С 2
 Л ’ h 5
 получим в безразмерных параметрах:
 я
 7.116
 ТС2
 8
 J0
 Зи2
 -556 4S
 0LC —Л 0, 7.117;
 ьге
 4е16°“л —
 0,3-
 T.GO 1
 S
 1
 II 1 W
 ои
 ' N. ч
 л
 '40 ч t
 ’ -77
 S'
 у
 JU •.
 о
 Ло
 ли
 r?-..
 72У
 • £
 —’24
 -g °. 7.118
 Решая совместно уравнения 117 и 118, находим о,7 зависимость между сдвигающей нагрузкой и прогибом.
 Введем обозначение SС по величине можно судить о характере изогнутой поверхности оболочки. На графике фиг. 7.27 первая серия кривых определяет
 значения коэффициента ф для плоской панели к 0 и для цилиндрических панелей разной кривизны: 12 и 24. Напомним, что увеличение С связано с общим, односторонним прогибом к центру кривизны, в то время как увеличение £ означает, что выпучивание
 2 3 X 4
 Фиг. 7.27. Зависимость между нагрузкой и параметрами прогиба для квадратной цилиндрической панели при сдвиге.
 В работе автора 72 один из коэффициентов уравнения 115 был выписан неправильно.

312
 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКИХ ПАНЕЛЕЙ
 ГЛ. VII
 оболочки происходит по двум полуволнам и является двусторонним. Как видим из графика, в случае плоской пластинки коэффициент ф, равный 0,25 в момент потери устойчивости, постепенно возрастает при последующем прогибе. Для цилиндрических панелей начальное значение ф, соответствующее верхнему критическому напряжению, выше, чем для плоских: при 612 оно составляет 0,345, а при 6 24 равно 0,5. Однако после потери устойчивости коэффициент падает, что указывает на преобладание одностороннего прогиба. В последующем ф начинает возрастать.
 Вторая серия кривых фиг. 7.27 определяет напряжение s. При
 С 0 получаем верхние критические значения Sb, найденные в § 74.
 Нижнее критическое напряжение 4 составляет при k 12 около 72
 от 4> а при 6 24 около 45°0 от 4.
 Фиг. 7.27 построена по данным первого приближения при варьировании двух параметров. Учитывая снижение верхнего критического напряжения при переходе к уточненному решению, можно впредь до получения более точных результатов предложить следующие расчетные формулы:
 1 для определения верхнего критического напряжения
 при 0<6<5 4 8,5; при 5<6<25 4 6,7 0,366; 7.119
 2 для нижнего критического напряжения
 при 0<6<10 48,5; при 10<6<25 s7,50,l£. 7.120
 § 76. Панель с произвольным отношением сторон при сдвиге
 Метод решения задачи, примененный в случае квадратной панели, можно использовать и для панели с иным отношением сторон X аb. При рассмотрении линейной задачи примем попрежнему w в виде 96. В первом приближении при двух параметрах получаем такие два решения для верхнего критического напряжения:
 Первое из этих выражений относится к случаю четных сумм m--tiy второе — к случаю нечетных сумм т-- п; величины Атп определяются по формуле
 7Са т2222 4тт £2
 3 1 — л-2 тпк2 m2 гЩЬп 9
 7.122
 Приведенное здесь решение принадлежит В. А. Марьину.

§ 76 ПАНЕЛЬ С ПРОИЗВОЛЬНЫМ ОТНОШЕНИЕМ СТОРОН ПРИ СДВИГЕ 313
 Из второго приближения при пяти параметрах получаем следующие выражения:
 г. тг п2 - Г 1122133133 2 ГА12А21А2Ая2 7 10Q4
 «в, и — У28 V Тх ’ в>11 —128 К ц ’,лгл>
 где
 1 iHi3 025 75 тш зИзз 75 f“ gy Аз >
 2 	525 221 Н- gy 2332 75 -1223 Н“ 213э
 На фиг. 7.28 даны окончательные значения в, и для различных k и X, причем сплошные участки соответствуют четным, а штрихпунктирные— нечетным т--п.
 Л3
 Фиг. 7.28. Верхние критические напряжения для цилиндрических панелей при сдвиге.
 Нижнее критическое напряжение определяем из решения нелинейной задачи. Принимая в первом приближении w снова в виде 112, получим для s следующую зависимость от ф 22и :
 <7-124
 где
 р 163X2 Ь2 929X2 12 8Х2_ Г 16 Л
 9X2 12 Х2 -j_ 92 4 15тс2 Х2 _f_ 12 1J К'
 я2М1 2X2-_J6 Лц, X2 16X2 3„2LX212--1J--„2X212« “Г
 I 2 Ха02
 “т- 12 1 —Л-З ха

314
 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКИХ ПАНЕЛЕЙ ГЛ. VII
 Величина определяется по формуле
 фЯ Л 1Л2 R
 ■В;
 7.125
 здесь
 Л
 2 	Т
 причем
 Н 15тг2
 64
 Х2 12
 оо2 92 99Х2-Ь 12 1
 9X3 -f- 12 2 -J_ 93 AJ
 Х22
 42 X2-j-l2
 тс2 Х1
 7г2,2-_12 3 1 — 2
 Х2
 Х2
 С2.
 7
 При С-0 вместо 125 получаем
 — 5?. На фиг. 7.29 дана зависимость С по 124 и 125 для k 12 при х 0,3. При X 1,5 отношение sHsB оказывается несколько бодее высоким, чем для квадратной панели, и равным 75°0; при X 2 оно составляет 80°0.
 § 77. Совместное действие сжатия и сдвига
 Предположим, что цилиндрическая панель малой кривизны к < 25, шарнирно опертая по краям, подвергается одновременному действию сжатия вдоль образующей и сдвига.
 Для квадратной панели аЬ функцию прогиба по аналогии со случаем простого сдвига представим в виде 112. Выражение для функции напряжений Ф должно быть дополнено членом —ру22, где р — среднее напряжение сжатия. Окончательно уравнения 117 и 118 примут форму
 — — 8 k№ -425 'v Зя2 152 п-
 0, 7.126
 Фиг. 7.29. Нижние критические напряжения для цилиндрических панелей при сдвиге.
 156
 150ti2
 -Ь16а-525§-4 0. 7.127

§ 77
 СОВМЕСТНОЕ ДЕЙСТВИЕ СЖАТИЯ И СДВИГА
 315
 При определении верхних значений для критических напряжений сжатия и сдвига в уравнениях 126 и 127 следует оставить лишь линейные члены; получим:
 A к4iC - 4g - 4С О, 164 - Л g- 4р 0.
 Приравниваем нулю определитель этой системы:
 4 	128
 44 5-4
 1 128 1ft
 --9Г5 163п
 -4 р
 0.
 7.128
 7.129
 7.130
 В случае простого сжатия верхнее критическое напряжение, отвечающее потере устойчивости по одной полуволне, равно по 20
 t
 Pi — °пл42,
 а при двух полуволнах по общей формуле 4
 I
 р2 4зпл
 №
 16712-
 7.131
 7.132
 Верхнее критическое напряжение сдвига в первом приближении 109 обозначим через s0. Тогда вместо 130 получим:
 7.133
 •4
 Pl Рг1 NOo'
 Уравнение 133 применимо также при более точных подсчетах второго приближения, когда критическое напряжение простого сдвига определяется по формуле 111.
 Пользуясь уравнением 133, можно в случае комбинированной нагрузки найти одно из критических напряжений сжатия р или сдвига s, если задано второе.
 Исследование деформации панели после потери устойчивости может быть проведено с помощью уравнений 126 и 127 с учетом нелинейных членов. Для ориентировочного определения нижних значений критического напряжения при совместном действии нагрузок сжатия и сдвига можно пользоваться уравнением 133, если переписать его в более простой форме:
 1
 Р«
 7.134
 нижние критические напряжения простого сжатия и сдвига ра и sH определяются по данным § 66 и 75.

316
 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКИХ ПАНЕЛЕЙ ГЛ. VII
 § 78. Анизотропная панель
 Рассмотрим большие прогибы пологой ортотропной панели, шарнирно опертой по краям и сжатой вдоль образующей усилиями ?. Основные уравнения 5.46 и 5.47 для круговой цилиндрической оболочки принимают вид
 D dAw j 0 Z, d4w j D2 dw h dx ' h dx2 ду2 “Г л —
 д2Ф 0 д2Ф d2w j д2Ф 1. d2w 71огч
 ду2 дх2 дх ду дх ду ' дх2 ? 'ду2 ’ ' '
 х дФ - дФ d2w 2 d2w d2w 1 d2w 7 10сч
 2 дх “■ 3 дх2 ду2 1 ду ду дх2 dyRl9 -lob;
 Будем считать в первом приближении
 OT sinsin-. 7.137
 Подставляя это выражение в 136 и интегрируя, находим при
 X аb:
 1 л sq 2пх. 1,Q 2пу.
 £ C0S а 32X25 f cos
 1 а2 г. ъх. у ру2 100Ч
 83 283X2 8 Sln a Sin Ъ 2' 7Л38
 Применяя метод Бубнова — Галеркина и повторяя выкладки § 66, приходим к следующему уравнению:
 64J2 й7 8 f2 3R ь2 253Х2 8 28
 4R4 8а 283Х2 84 4Ш т 4Х,‘ 7Л39
 В частном случае квадратной изотропной панели отсюда вытекает уравнение 27.
 Анализ зависимости 139 показывает, что верхнее критическое
 напряжение для ортотропной панели зависит от отношения сторон,
 а также от параметров упругости при изгибе и кручении; нижний же предел существенным образом зависит только от модулей упругости при растяжении и сдвиге. Эффект хлопка усиливается по сравнению с изотропной панелью, если ось наибольшей жесткости расположена перпендикулярно к образующей, а также при увеличении относи¬
 Это уравнение было получено О. Н. Ленько 73.

АНИЗОТРОПНАЯ ПАНЕЛЬ
 317
 тельной величины модуля сдвига. В том же случае, когда ось наибольшей жесткости параллельна образующей, поведение панели в закритической области оказывается близким к поведению изотропной плоской пластинки.
 Закритическую деформацию трехслойной пологой шарнирно опертой панели, сжатой вдоль образующей, можно исследовать тем же путем, что и в § 66. Пользуясь обозначениями § 13, получим вместо 27:
 Dtc2 тЕ,п 10 Е, Еа2, t а2 7
 7Л40>
 l 2iT-rПГ ' a? G3h
 Анализ выражения 140 показывает, что эффект хлопка в этом случае несколько снижается по сравнению с наблюдаемым в однослойной оболочке той же толщины.
 Это уравнение дано Л. М. Куршиным.

Г Л А:В А VIII ЗАМКНУТЫЕ ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧКИ
 § 79. Устойчивость круговой цилиндрической оболочки при осевом сжатии. Линейная задача
 Определение устойчивости замкнутой цилиндрической оболочки при осевом сжатии представляет собой одну из центральных задач теории оболочек. Расчеты трубчатых конструкций часто встречаются на практике. Для сжатой стойки трубчатое сечение является наиболее экономным по весу конструкции, если рассматривать общую устойчивость продольный изгиб стойки. С другой стороны, явление местной потери устойчивости сжатой замкнутой цилиндрической оболочки особенно ярко свидетельствует о своеобразии задач по устойчивости оболочек; здесь весьма велико различие между данными опытов и расчетными формулами классической теории.
 Допустим, что круговая оболочка радиуса R и толщины h подвергается центральному сжатию вдоль образующей, причем усилие, приходящееся на единицу площади поперечного сечения, равно р фиг. 8.1.
 Длину оболочки обозначим через L примем нагруженные кромки опертыми шарнирно. Поставим себе целью определить критическое напряжение сжатия, ограничиваясь вначале рамками линейных уравнений. Дифференциаль-
 Фиг. 8.1. Замкнутая цилиндрическая оболочка при сжатии вдоль образующей.
 ное уравнение 5.38 принимает вид
 Эта задача рассматривалась впервые Р. Лоренцем Zeitschr. d. Ver. d. Ing. 52, 1908, стр. 1706 и Physik. Z. 13, 1911, стр. 241 и С. П. Тимошенко Z. Math. Physik 58, стр. 378 и Труды Электротехн. ин-та 2, Петербург, 1914.

§ 79 УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКОЙ оволочки ПРИ СЖАТИИ 319 Представим решение в виде ряда
 ™22mresinsin7f- 8-2
 т п
 Здесь т отвечает числу полуволн изогнутой поверхности вдоль образующей, а п — числу полных волн, образующихся в поперечном сечении. Значению п — 1 соответствует смещение сечения в целом без искажения формы; при исследовании местной потери устойчивости мы должны поэтому считать 2.
 Каждый член ряда 2 удовлетворяет уравнению 1; при подстановке получаем зависимость
 D т2 п2 Y j В ттЛ т2к2. п2 2 т2ъ2 Twa--1- ЯУ TRiA Р № Тф W
 Отсюда находим:
 D Iтп2т:2. п2 2 L2. Е т2к2 т2к2. г22
 р nWTrLrWi ' ' '
 Будем пользоваться безразмерным параметром нагрузки
 <8-4>
 Длины полуволн вдоль дуги и по образующей равны, соответственно,
 Ь а— —. 8.5
 2 п 9 m 4
 Отношение длин полуволн, характеризующее форму волнообразования, обозначим через ft:
 а —. 8.6
 a Ln 4 7
 Введем, кроме того, параметр
 tl2fl SQ
 ’Ч -д> 87
 связывающий число волн по окружности п с относительной толщиной оболочки hR. Выражению 3 можно тогда придать вид
 1 1022. О2,я Q4
 121 — а> 02 'fl 1»а2,- v •
 Воспользуемся обозначением
 В § 72 через п обозначены числа полуволн, образующихся по всей ширине панели.

320 замкнутые цилиндрические оболочки гл. VIII
 Желая найти минимальное значение р, составляем условие
 dJL I _L 0-
 dp 12 1 — Д.2 р2
 отсюда
 р 121— 1а. 8.10
 Таким образом, решение линейной задачи приводит к выражению для верхней критической величины р:
 р.. 1. 8.11
 УЗ1-
 При значении у, лежащем в пределах 0,25-0,32, получим:
 рв0,6. 8.12
 Критическое напряжение будет
 1 	-Е-0,6Е. 8.13
 У 31—12 R R
 Форма волнообразования остается неопределенной; можно лишь выписать соотношение 10 в виде
 1 	--2Э У 121 —х2. 8.14
 Если считать, что волны являются квадратными 01, получим значение при 0,3
 0,206. 8.15
 Формулу 13 можно получить также, если исходить из предположения об осесимметричном характере волнообразования.
 § 80. Экспериментальные данные. Изучение явления хлопка
 Судя по формуле 2, при потере устойчивости оболочки должны образовываться волны, направленные в шахматном порядке к центру кривизны и от центра, причем амплитуды тех и других выпучин должны быть равны между собой.
 Однако такая форма волнообразования на практике не осуществляется и обычно выпучивание оболочки происходит в большом, т. е. сопровождается внезапным появлением глубоких выпучин. Эти выпучины обращены преимущественно к центру кривизны, имеют ромбовидный характер и разделяются резко выраженными складками. Вблизи гребней деформации обычно являются пластическими, так что после разгрузки оболочки можно отчетливо различить линии складок даже в том случае, когда выпучины исчезают.

§ 80 ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ ИЗУЧЕНИЕ ЯВЛЕНИЯ ХЛОПКА 321
 Приведем данные экспериментального исследования, относящегося к дуралюминовым оболочкам. Образцы имели толщину от 0,5 до 0,75 мм; отношение радиуса к толщине составляло Rjh 100180 и в отдельных случаях доходило до 360. Нагрузка передавалась на оболочку через утолщенные концевые части, навинчивавшиеся на головки зажимных приспособлений. Отношение длины рабочей части L к радиусу было равно LR 2,4. Места перехода от концевых частей к тонкой оболочке были очерчены по дуге достаточно большого радиуса с целыо устранения концентрации напряжений. Заготовками для образцов служили трубы из материала Д16Т; окончательные размеры придавались обработкой на токарном станке. Нагружение производилось на машине, позволявшей осуществлять не только сжатие, но и кручение образцов, а также создавать внутреннее давление. Специальная установка давала возможность, кроме того, получить вакуум внутри оболочки. Деформации в различных точках оболочки определялись с помощью электротензометров; принимались меры к тому, чтобы нагрузка распределялась равномерно по поперечному сечению.
 На фиг. 8.2 приведена фотография образца, подвергавшегося осевому сжатию; хорошо видны ромбовидные выпучины, образовавшиеся при хлопке. Обычно в момент хлопка появлялось два или три пояса выпучин; в отдельных случаях имелся лишь один пояс или, напротив, выпучины охватывали почти всю рабочую часть образца. Длины волн, измеренные после хлопка вдоль образующей и по дуге, оказывались приблизительно равными между собой, так что выпучины можно было считать «квадратными»; были, однако, случаи, когда волны слегка вытягивались вдоль дуги. При дальнейшем же нагружении образцов размер выпучин вдоль образующей быстро сокращался, как показано на фиг. 8.3.
 Если условно принять 01, то из формулы 15 получим число волн пъ, отвечающее верхнему критическому напряжению при 0,3:
 пв 0,91 YWh- 8.16
 При отношении Rh, меняющемся в пределах от 120 до 180, мы должны были бы получить пъ 10 -г- 12. Отмечаемое после хлопка число выпучин по окружности составляло г 7-т-9.
 Безразмерные критические напряжения р, полученные в данной серии опытов, отмечены на фиг. 8.4. Как видим, в пределах изме¬
 Опыты, описанные здесь и в § 86, — если не сделаны особые ссылки, — выполнены Л. Р. Исправниковым.
 При изготовлении образцов из листового материала трудно избе жать значительной начальной погиби.
 По данным других опытов 814, число выпучин, фиксируемое после хлопка, в ряде случаев составляет половину от пй.

322 Замкнутые цилиндрические оболочки гл. viii
 нения Rh от 90 до 200 величину р можно считать не зависящей от отношения Rh, Средняя величина р оказалась равной
 р 0,364 8.17
 проставила около 60 от верхнего критического значения рв. Напомним, что для панелей большой кривизны было получено почти
 Фиг. 8.2. Оболочка, ежа- Фиг. 8.3. Оболочка, по-
 тая вдоль образующей лучившая дополнитель-
 непосредственно после ную деформацию после
 хлопка. хлопка.
 такое же среднее значение коэффициента 0,33. Вместе с тем надо
 отметить большой разброс экспериментальных точек: величина р колебалась в пределах от 0,23 до 0,42.
 Данные ряда других опытов 814, относящихся к широкому диапазону значений Rh, приведены на фиг. 8.5; здесь очерчены области, внутри которых размещались экспериментальные точки. Можно отметить тенденцию к уменьшению р с возрастанием отношения Rjh
 относительно низкие значения р при весьма малых Rh в опытах Вильсона объясняются, повидимому, тем, что потеря устойчивости происходила при значительных пластических деформациях. Судя по фиг. 8.5, в некоторых случаях были получены совсем низкие значения р, порядка 0,07—0,1. Надо полагать, что в этих опытах образцы

§ 80 ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННОЕ. ИЗУЧЕНИЕ ЯВЛЕНИЯ ХЛОПКА 323
 были весьма несовершенными и не соблюдалась равномерность распределения напряжений по окружности.
 Для исследования динамических явлений при хлопке JI. Р. Исправниковым была осуществлена запись на ленту шлейфового осцил-
 180 Rh 200
 Фиг. 8.4. Верхние и нижние критические напряжения при осевом сжатии.
 лографа изменения нагрузки и одновременно с этим взаимного смещения нагруженных кромок оболочки. Один из шлейфов осцилло-
 и
 ft
 ’еллулоид Флюгге Сталь U
 Ъбертсой
 пь, латунь Бриджет
 1 J
 ,ч
 N.
 -
 'Дуралюмин Лс А wdxeucmj. Сталь fбол ейJ
 1 v
 д Сталь, лату а Сталь Вильсон
 А Доннел 7
 —
  :
 Сталь
 Р
 0,45
 0,30
 0J5
 ООО 2000 Rfj 3000
 Фиг. 8.5. Данные испытаний цилиндрических панелей на осевое сжатие.
 графа отмечал показания датчиков омического сопротивления, наклеенных на трубопровод гидравлической испытательной машины вблизи цилиндра; это давало возможность определить давление масла

324
 ЗАМКНУТЫЕ ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧКИ
 ГЛ. VIII
 в трубопроводе, отвечающее прикладываемой к образцу нагрузке. Для контроля применялся также специальный емкостный датчик,
 Фиг. 8.6. Осциллограмма нагрузки и общей деформации оболочки при хлопке.
 измерявший давление масла непосредственно в цилиндре. Взаимное смещение верхней и нижней траверс машины, к которым присоединялся образец, регистрировалось с помощью специальной мостиковой
 схемы и передавалось на второй
 шлейф осциллографа. Кроме того, имелся отметчик времени.
 Одна из полученных таким образом осциллограмм приведена на фиг. 8.6. Общая продолжительность нестационарного процесса составляла около 0,08 сек. Собственно хлопок, заключавшийся в резком
 падении нагрузки Р, занимал примерно 0,015 сек. При этом деформация е образца также изменяется скачком; возрастание е отвечает взаимному сближению торцов образца. В дальнейшем имеют место затухающие колебания нагрузки Р и деформации е со сдвигом по фазе на 180°. По кривым фиг. 8.6 можно нагрузкой и деформацией образца для всего процесса нагружения оболочки. На фиг. 8.7 по оси ординат
 отложена величина сжимающего напряжения а, отнесенная к Е, по оси
 абсцисс — относительное сближение торцов е. До потери устойчивости
 Фиг. 8.7. Диаграмма хлопка оболочки по экспериментальным данным.
 определить зависимость между

§ 81 БОЛЬШИЕ ПРОГИБЫ ОБОЛОЧКИ ПОСЛЕ ПОТЕРИ УСТОЙЧИВОСТИ 325
 эти величины равны между собой. Затем происходит падение а при одновременном возрастании е. После окончания динамического процесса напряжение слегка возрастает, а затем остается почти постоянным; при этом в местах образования складок имеют место значительные пластические деформации.
 §81. Большие прогибы оболочки после потери устойчивости.
 Условие замкнутости
 Как мы видели, волнообразование замкнутой оболочки после потери устойчивости имеет такую же форму, что и в случае панели большой кривизны. Поэтому, желая исследовать закритическую деформацию оболочки при сжатии, выберем выражение для прогиба в виде, близком к 7.68:
 . тпх. пу, -.о тпх. g пу. 0 л 0
 w sin —sin - г sin2-J- sin3-f 0. 8.18
 Первый член отвечает выражению 2 и относится к волно¬
 образованию оболочки при малых прогибах; второй член должен отобразить выпучивание оболочки после хлопка с образованием ромбовидных выпучин. Параметр 0 отвечает радиальному смещению точек, принадлежащих шпангоутам — кольцевым ребрам, с которыми связаны торцы оболочки. Мы полагаем, что концевые сечения оболочки всегда сохраняют круговую форму, но могут «дышать»
 в радиальном направлении. Для случая чистого сжатия это допущение не является особенно существенным: при длине оболочки, сравнимой с диаметром, по каждому из направлений — вдоль дуги и по образующей — наблюдается значительное число выпучин, так что способ закрепления краев не будет сколько-нибудь сильно влиять на процесс деформации.
 Второй член выражения 18 не удовлетворяет условию шарнирного опирания на кромках, но в случае сжатия это также не должно заметно сказаться на результатах решения задачи. Подставляя 18 в правую часть уравнения 5.28, получим :
 L у2у2ф — 2 jp C0S 2ах -f- cos 2фу —
 — R cos — IT cos ax cos b
 -f- sin ax sin фу -- a92 — ф2 cos 2ax cos 2фу
 -у- f cos 4ax cos 2фу cos 2ax cos 4,3y --
 -- asin Зал: sin фу -f- sin ax sin 343y; 8.19
 Приведенное здесь и в § 82 решение задачи выполнено J3. Л. Агамировым»

326
 ЗАМКНУТЫЕ ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧКИ
 ГЛ. VIII
 здесь введены обозначения:
 8.20
 Напомним, что длины полуволн, соответствующие первому члену выражения 18, определяются равенствами 5; поэтому отношение длин полуволн д, характеризующее форму отдельной выпучины, будет равно Ь Ьа а.
 Решение уравнения 19 выпишем в виде
 Ф gt cos 2ах g2 cos 2fry -f g cos 4ax gA cos 4y
 -f- sin ax sin -f- gQ cos 2<xx cos2,33 -- g4 cos 4ax cos 2,3у -f gs cos 2ax cos 4y -f- g9 sin Зал: sin 3y -f- g-10 sin ax sin 33у —
 Под put здесь подразумеваются сжимающие напряжения в срединной поверхности оболочки, соответственно, вдоль образующей и по дуге. Величина р, очевидно, отвечает внешним усилиям, приложенным к торцам оболочки; между тем параметр t зависит от условий сопряжения оболочки со шпангоутами и пока остается неопределенным. Коэффициенты gv g2t... заменяют выражения
 gn 2 16а2 4р23 > £8 — 2 4а2 -f 1623’
 _ Заар _ 3a2S2
 9 29a2-f р22 12» 10 2a2-f-9p22 •'I'2’
 Исходя из выражения 21, можно найти через параметры, р и t напряжения в срединной поверхности, а затем и перемещения и, v. Надо при этом принять во внимание условие замкнутости оболочки: перемещения должны быть периодическими функциями координаты у. Формулируем это требование по отношению к перемещению v. Очевидно, v не должно получать приращения при возраста-»
 _ Р2 а2 г2
 — 512а272’ 8 512р2 '2’
 8.23
 :2
 2

§ 82 ПРИМЕНЕНИЕ МЕТОДА РИТЦА 327
 нии координаты у на 2nR:
 2itR
 Jgrfy 0. 8.25
 О
 Пользуясь выражением 5.4 для гуу находим:
 dv 1 д2Ф д2Ф 1 dw2 w Q Ооч
 Ту Ё ш-Гф-2 Ы Л • 8-26
 Подставляя значения Ф, -до и интегрируя, приходим к уравнению
 jt ±pp — — Л £-.• 8.27
 Это условие связывает параметры 0 и t.
 § 82. Применение метода Ритца. Варьирование по двум параметрам
 Определим потенциальную энергию системы. Исходя из выражения 1.106 для энергии срединной поверхности, найдем:
 Ue j hRLE gf 2«У gl ДО gf 4a4
 g 4,3 g 2P224 «ft42
 jg'U 16«2 gf 4«2 1 б?
 j g 9«? ?22 j g„ «2 92
 22 J-4bj. 8.28
 Потенциальная энергия изгиба по 1.109 будет
 и.и1у4л«‘1;?
 1-У.У <;. 8-29
 Работу внешних усилий сжатия р находим аналогично тому, как это было сделано для цилиндрической панели:
 L 2 nR
 о 	о
 или
 г 1CW.p2.§•. 8.31
 Полная энергия системы Э определяется выражением 7.76.

328
 ЗАМКНУТЫЕ ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧКИ
 ГЛ. VIII
 Учитывая 27, выпишем уравнения метода Ритца:
 w00' S0> i0- 8>32
 Первое из этих уравнений будет
 ?-жЛ?-Л?Л. 0. 8.33
 Сравнивая 27 и 33, находим:
 t 0. 8.34
 Таким образом, при свободно смещающихся в радиальном направлении шпангоутах среднее напряжение в радиальных сечениях равно нулю. Это можно заключить и непосредственно из условия равновесия части оболочки, отделенной продольным диаметральным сечением. Воспользуемся безразмерными параметрами:
 р Eh' г ’ Д ’ V fi c
 С учетом 34 и 27 остальные два уравнения метода Ритца можно привести к такой системе:
 р вх врвгад, 8.36
 ад-8 - ад» В7 ВР ф Я9с 0. 8.37
 В уравнение 36 введены следующие функции параметров ft и т,:
 о.... «»,, 1 »4..,0 004
 1 121 — j.a»2 yj j _f_ аза » 1603 °-38
 Б Ш■1 f’4 1 W2 1 9Pj» 9WJ’ 8-39
 в — if1 dW’ 8-40
 а в уравнение 37 — функции
 о — 5 11 I V I т I 804 192 L 51 423 5 4 -- 22
 32»4 432» 432» 1»22 5 1 -Ь 9»23 5 9 922 J >
 В,
 8.41
 —<8 42>
 91 2»2 1
 Bl 36 1 —12 6
 <8'43
 в» 0 ‘ 8 ‘ TTTS?TTPji57тУ ’ <8'44
 1 fi 164

§ 82
 ПРИМЕНЕНИЕ МЕТОДА РИТЦА
 329
 Если в уравнении 36 оставить только линейные члены, то придем к выражению 8, определяющему верхнее критическое напряжение рв. Исследование закритической деформации можно провести следующим образом. Задаваясь определенными значениями и f>, определяем из 37 параметр как функцию С; это дает возможность оценить изменение формы волнообразования при возрастающем прогибе. Далее по 36 определяем зависимость между параметрами напряжения р и прогиба С
 Можно также воспользоваться другим способом. Учитывая соотношение 35 и считая С ф 0, из уравнения 37 получим:
 £2 7»
 — В В2
 Выражению 36 можно теперь придать вид
 р В, - В, 8.46
 Здесь р выражается непосредственно через параметр «несимметричной» составляющей прогиба £. Задаваясь значениями и ft, можем
 л. построить графики р и ?£.
 На фиг. 8.8 приведен для примера график рС, соответствующий параметру ft 0,6. График содержит семейство кривых, построенных для т 0,672; 0,356; 0,200; 0,139; 0,089. В случае оболочки, имеющей относительную толщину hR Viso этим значениям т отвечают числа волн по окружности п 11; 8; 5; 4. Находим огибающую кривых р наинизшая точка ее отвечает относительному прогибу С5 и величине 0,723. Такие же графики были построены для других значений П. В результате получаем сводный график фиг. 8.9, определяющий зависимость между
 наинизшими значениями р и параметром ft. Минимальная величина р оказывается равной
 ря 0,234; 8.47
 она соответствует нижнему критическому напряжению данного приближения.
 Определим теперь относительное сближение торцов
 L L
 1 	Сди, 1 Г Г1 дФ дФ 1 дтЦ, с,оч
 е L J дх d L J U дуг дх 2 Ur J 8.48
 о о
 Этот способ указан В. М. Даревским,

330 ЗАМКНУТЫЕ ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧКИ ГЛ. VIII
 Подставляя выражения 18 и 21 и вводя обозначение
 8.49
 найдем:
 е рх1 f СЗ- 8'50
 На фиг. 8.9 приведена диаграмма еС, полученная по уравнению 50, а на фиг. 8.10 — график «нагрузка — сближение торцов»,
 характеризующий общую картину поведения оболочки в закритической области: его можно сопоставить с графиком фиг, 7.11, полученным выше для цилиндрической панели.

§ 83
 ВАРЬИРОВАНИЕ ПО ЧЕТЫРЕМ ПАРАМЕТРАМ
 331
 Отметим, что в уравнения 36 и 37 входит лишь величина yj tihR; что же касается относительной толщины hR, то она
 Фиг. 8.9. Нагрузка и общая деформация оболочки в зависимости от параметров волнообразования.
 0,6
 Л
 р
 0,4
 02
 UL
 £Л
 1 i
 It-
 Р
 ♦ —
 Г 1
 2,0
 0,4
 <5
 С
 '5 Я6 1
 л
 y<QS
 9,7
 0,7 0,2 0,3 0,4 0,5 0,6 0,7 0,8 е
 Фиг. 8.10. Диаграмма закритической деформации цилиндрической оболочки при осевом сжатии.
 остается неопределенной. Поэтому параметр нижнего критического напряжения 47 оказывается не зависящим от hR.
 § 83. Варьирование по четырем параметрам.
 Другие решения
 В. принятом выше варианте решения задачи мы варьировали энергию, если не считать 0, по двум параметрам: fx и 2. При построении каждой из кривых рС или р£ числа полуволн вдоль образующей и по дуге 2п или параметры 0, ч считались

332 ЗАМКНУТЫЕ ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧКИ гл. VIII
 фиксированными; огибающая этих кривых определяла ?„• Но эти данные надо рассматривать лишь как первое приближение по отношению к истинным зависимостям рС или ?. Мы не определяли энергетических уровней, отвечающих различным кривым и не интересовались условиями перескока от одной формы волнообразования к другой. Не исключено, что точки кривых с малыми ординатами отвечающими низким значениям р характеризуются высоким энергетическим уровнем, так что переход к этим равновесным состояниям требует значительного притока энергии извне.
 Уточненное решение задачи можно дать, варьируя энергию не только по параметрам прогиба, но и непосредственно по числам полуволн т, 2п или величинам »>, '. Введем безразмерный параметр полной энергии
 <8J5I>
 его можно представить с помощью выражений 28 — 31 после
 подстановки величин 0 и t в виде
 Э 	— — р 8.52
 где
 D, 	Л АД 4- Atf, D2 АД Atf, Ds Ag'j1 Л7, 1 з 8.53
 DAtAtf, °5 т1Т'Н J
 и в свою очередь Av..., Л10 — некоторые функции параметра Я.
 Составим уравнения метода Ритца, варьируя четыре параметра не
 считая 0:
 дЭ дЭ дЭ дЭ д£ — ’ д'Ъ — ’ дг — дй о.54
 Первые два уравнения примут вид
 рфъ 2D, да - ад D3 ВД, 8.55
 т I дР3, дР4 3 egv
 д<1> ” д<> дб дф д'Ъ ’ о.оо
 Отсюда можно получить систему 36 — 37, которой мы уже поль¬
 зовались в § 82. Остальные уравнения будут
 pDb 21 ftC — D2y£ 2 Dtf, 8.57
 2 'рфь О2-d dw ''I2' 8'58
 Из равенств 55 и 57 находим:
 <8-59>

831
 ВАРЬИРОВАНИЕ ПО ЧЕТЫРЕМ ПАРАМЕТРАМ
 333
 равенства же 56 и 58 приводят к соотношению
 Ki ОФ3—Ы8 °> 8-б0
 причем Kv..С3 — коэффициенты, зависящие от Dv..D и их производных.
 Задаваясь некоторыми значениями 0 и ф, определяем величины Dlf..., а затем t и С из уравнений 59 и 60. Далее добиваемся одновременного выполнения равенств 55 — 58; таким образом устанавливаем минимальные величины р при различных 0. Подобные выкладки привели к значению нижнего критического напряжения
 рп 0,334 8.61
 при параметре формы волны 0 0,59. Сравнение 47 и 61 показывает, что ри во втором приближении получается выше, чем в первом.
 Полученные нами величины ра как в первом, так и во втором приближениях нельзя считать окончательными, так как результат решения задачи в значительной мере зависит от выбора исходного выражения для прогиба. Обратимся к данным других решений, имеющихся в литературе. Выражение 18 для прогиба, принятое нами выше, можно представить в виде
 -, -. ткх. пу,
 o i sin — sin7?
 , 1 - 2tmtx, 2пу, 2тъх пу 0
 -4 Л cos—1 h cos-Ь cos —— cos-j. 8.62
 В работе Кармана и Цзянь Сюэ-шеня 815 было принято выражение, сводящееся к следующему:
 г, г. тпх. пуг I 2ткх, 2пу 0 оч
 w oiSin —sin- 2cos — cos-j. 8.63
 Уравнение 63 относится к достаточно длинной оболочке; граничные условия по нагруженным кромкам не учитываются. Вычисления были проведены этими авторами для Rh 1000 в двух предположениях: а 0 0,5, когда выпучины вытянуты вдоль образующей, б 01, когда волны являются квадратными. В первом случае огибающая семейства кривых, отвечающих различным числам волн, уходила
 в сторону отрицательных р и нижнее критическое напряжение ан не могло быть определено. Во втором случае огибающая имела наинизшую точку, соответствующую а„ 0,194£Уг?.
 В более поздней статье Михилсена 8201 было принято то же выражение 63 для прогиба, но варьирование энергии велось не только по коэффициентам ft и 2, но и по параметрам, определяющим

334
 ЗАМКНУТЫЕ ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧ Й
 ГЛ. Vlll
 число волн по окружности и форму выпучины. Наинизшее значение р оказалось не зависящим от отношения Rjh и равным 0,195; при этом параметр 0 равнялся 0,4. По данным Михилсена после хлопка р возрастает до значения р 0,77, превышающего верхнее критическое значение ?в 0,6; в дальнейшем р снижается.
 Наконец, Кемпнер 816 воспользовался выражением
 .... тъх. пу,, 2тъх,, 2пу ft
 •W о A sin — SinН- 2 COS —J— -1- s cos -щ-; 8.64
 особенность его состоит в том, что члены, содержащие cos 2ткх1Ь и cos2nyR, могут иметь различный удельный вес. Кемпнер принимает в качестве варьируемых уже не четыре, а пять параметров Л» 2» U ® и l Наинизшая величина рн оказалась равной 0,182 и отвечающей параметру формы волны 0 0,36. Этот результат нельзя рассматривать как третье приближение по отношению к вариантам § 82 и 83, так как он относится к несколько иным граничным
 условиям. Пользуясь выражением 18, мы принимали, что торцевые
 сечения остаются круговыми, в то время как выражение 64 этому условию не удовлетворяет.
 Судя по данным фиг. 8.9, согласующимся с выводами Кемпнера, в закритической области параметр 0 должен быстро возрастать:
 если при р ра выпучины вытянуты вдоль образующей, то в последующем они становятся квадратными, а затем сильно вытягиваются вдоль дуги. Как мы видели в § 80, в опытах удается наблюдать лишь вторую стадию этого процесса; выпучины, вытянутые вдоль образующей, зафиксировать удается редко.
 Для сравнения теоретических данных с экспериментальными воспользуемся фиг. 8.4 и 8.5. На первой из них нанесены линии рл по двум'вариантам: первому приближению § 82 и решению Кемпнера.
 Как видим, для тщательно изготовленных оболочек экспериментальные значения напряжений при выпучивании во всех случаях лежат выше значения ра 0,182. Значительная часть экспериментов, отраженных на фиг. 8.5, также привела к величине р> 0,182. Лишь две серии опытов дали более низкие значения р. Вытекающая из графика фиг. 8.5 тенденция к уменьшению р при возрастании Rjh не соответствует теоретическим выводам, касающимся верхнего или нижнего критических напряжений. Надо помнить, что реальные значения напряжений при выпучивании оболочек вовсе не должны совпадать с рл можно лишь утверждать, что при малой начальной погиби эти напряжения должны лежать в области между рв и ра. Надо предположить, что для более тонких оболочек начальная погибь сказывается сильнее и именно поэтому экспериментальные значения р лежат ближе к нижнему пределу.

ЗАМКНУТАЙ ОБОЛОЧкА ПРИ ВНЕШНЕМ ДАВЛЕНИЙ
 335
 В итоге следует считать, что величина
 ? 0,18 8.65
 может быть принята в качестве исходной при расчете на устойчивость замкнутых оболочек, сжатых вдоль оси, но лишь при условии, что обеспечена достаточная тщательность изготовления и сборки конструкции, так что, например, амплитуда начальной погиби не превышает толщины оболочки.
 § 84. Замкнутая оболочка при внешнем давлении
 Рассмотрим задачу об устойчивости замкнутой оболочки при действии равномерно распределенного внешнего давления q. Начальная равновесная форма характеризуется в этом случае сжимающими напряжениями в радиальных сечениях ау qRh, так что линейная задача сводится к интегрированию уравнения
 7Г V WV- 1 0. 8.66
 Для случая шарнирно опертых кромок представим w попрежнему в виде 2; тогда
 D пт, г24. Е тк qR т2тР, л22л2
 R RL Т Z.2 R2 tf2 — °‘ 857
 Оставляя обозначения § 82 и полагая
 q R2 ч — приходим к уравнению
 8-68
 121— 1x2 а221 1 -J-023г, • 8.69
 Оба члена этого выражения возрастают при увеличении ; поэтому при определении критического давления надо выбрать для Ь наименьшее возможное значение и в формуле 6 принять т 1. В дальнейшем будем обозначать
 °S> S 7T- <8'70>
 Число волн п должно быть выбрано таким, чтобы выражение 69 было минимальным.
 Выражение 69 не всегда определяет q с необходимой точностью, так как мы пользуемся теорией пологих оболочек и предполагаем, что число волн п достаточно велико см. § 53. Так, в случае весьма длинной оболочки можно принять 0 —> 0; вместо 69 тогда получим:
 Y n2h
 Я
 12 1 — J.2 121—р.2R'

336
 Замкнутые Цилиндрические оболочки
 ГЛ. VIII
 Как мы видели в § 53, минимальное значение п составляет 2; поэтому найдем верхнее критическое давление равным
 Но точное значение qB дается здесь формулой, относящейся к тонкому кольцу:
 так что ошибка приближенного решения составляет 33.
 Чтобы получить значение 72, надо преобразовать исходное дифференциальное уравнение 66. Если воспользоваться уточненным выражением для кривизны 5.9, то с помощью принципа возможных перемещений можно придти к следующему варианту более полного уравнения:
 Однако для оболочек средней длины обычно получается п 4, и уравнение 69 дает вполне удовлетворительные результаты. При этом удается вывести простую расчетную формулу, если положить
 О 1; тогда будет
 ЩТу 8.74
 Подставляя сюда вместо гу 0 выражения 6, 7 и минимизируя 74 по я, получим :
 Обратимся к данным опытов. На фиг. 8.11 представлена дуралюминовая оболочка, испытавшая потерю устойчивости при внешнем давлении. Подобно случаю осевого сжатия и здесь имеет место
 См. статью С. В. Александровского 8 1, в которой это же выражение для кривизны 5.9 использовано и в нелинейной задаче; но в этом последнем случае целесообразно воспользоваться более общими выражениями для деформаций и кривизн, приведенными В. В. Новожиловым 1б.
 Эту формулу приводят X. М. Муштари и А. В. Саченков 8б. Уточненная формула была пблучена Р. Мизесом Zs. VDI 58, 1914, стр. 750; расчетные графики см. 3,46J, стр. 398.
 Образец испытан Л. Р. Испрпвниковым.
 <7“— 31—R '
 8.71
 <7в 41—2?’
 8.72
 8.75
 или при а дй 0,3
 8.76

§ 84
 ЗАМКНУТАЯ ОБОЛОЧКА ПРИ ВНЕШНЕМ ДАВЛЕНИИ
 337
 продавливание хлопком глубоких выпучин, обращенных внутрь
 оболочки; лишь разделяющие их узкие складки отклоняются во внешнюю сторону. Характерным для испытаний на внешнее давление является то, что каждая выпучина распространяется на всю длину оболочки т 1, что соответствует решению линейной
 задачи.
 На фиг. 8.12 представлены две оболочки, изготовленные из фотопленки и различающиеся только длиной. С помощью насоса скрытого в подставке установки внутри оболочек создавался вакуум. Как видим, число выпучин по 'окружности меняется в зависимости от длины модели.
 Отмечаемые в опытах критические давления значительно лучше согласуются с верхними значениями, чем при осевом сжатии. Чаще всего в опытах кромки оболочки оказываются защемленными; в данной задаче, когда выпучины распространяются на всю длину оболочки, это обстоятельство надо учитывать. При тщательном изготовлении образцов реальные критические давления составляют 65-f-105°0 от верхнего значения, вычисленного для случая шарнирного опирания; при наличии же значительных начальных несовершенств образование глубоких выпучин имеет место уже при нагрузке, составляющей 45-7-65 от верхней критической нагрузки.
 Если внутрь оболочки поместить под некоторым натягом тонкий диск, разделяющий образец на две приблизительно равные части, то для каждой из этих частей один из краев можно считать шарнирно опертым; критические давления оказываются при этом на 20—
 25°0 ниже, чем для аналогичных образцов с жестко защемленными кромками.
 Надо оговориться, что в опытах на внешнее давление образцы находятся, как правило, в условиях всестороннего сжатия. При этом напряжениям в радиальных сечениях qRjh сопутствуют осевые qR2h; однако влияние этих дополнительных усилий на устойчивость оболочки обычно является незначительным.
 Фиг. 8.11. Дуралюминовая оболочка, подвергавшаяся внешнему давлению, после хлопка.
 Установка, сконструированная П. Г. Бурдиным, позволяет также подвергать оболочки кручению и изгибу.
 По данным опытов В. Л. Агамирова см. ниже фиг. 8.15 и П. Г. Бурдина, а также исследований Эбнера, Винденбурга и Триллинга Trans. ASME 56, 1934, 819—825.
 Об этом можно судить по приближенной формуле 97,

338 замкнутые Цилиндрические оболочки гл. viii
 Желая исследовать равновесные формы оболочки при больших прогибах, примем функцию прогиба в виде
 w — f sin sin -j- -f-2 sin2 8.77
 Первый член отвечает решению линейной задачи. Второй в отличие от варианта § 81 не зависит от у и отражает общее перемещение внутрь оболочки точек каждого поперечного сечения. Третий член учитывает радиальные перемещения точек, принадлежащих конце-
 Фиг. 8.12. Оболочки различной длины из фотопленки после хлопка, вызванного внешним давлением.
 вым сечениям. Граничные условия шарнирного опирания не вполне выполняются.
 Для функции напряжений вместо 21 получим теперь выражение
 -1 ф rx cos 2<хх -f- r2 cos 2,3у -- r3 sin ax sin §y -f-
 t x2
 -f- r4 sin 3<xx sin fly—
 здесь
 r —- JL. f2
 — 32a2 Jl'
 8Ra 2
 U
 a2 о
 Гг Wipf1’
 212
 8.79
 p2 -f 9«22
 и a iti, j3 nR. Условие периодичности 25 приобретает форму
 »• 8-80
 Это выражение применили Ф. С. Исанбаева 84 и Наш 8,21J. Приведенное ниже решение принадлежит В. Н. Нагаеву.

ЗАМКНУТАЯ ОБОЛОЧКА ПРИ ВНЕШНЕМ ДАВЛЕНИИ
 339
 Потенциальная энергия срединной поверхности 1.106 будет
 Далее составляем уравнения метода Ритца 32. Первое из них получит вид
 То же значение t получим, рассматривая равновесие части оболочки, отсеченной диаметральной плоскостью, и принимая во внимание условие свободного обжатия торцевых сечений, скрепленных с подкрепляющими кольцами шпангоутами. При других граничных условиях величина t окажется иной. Допустим, например, что шпангоуты являются абсолютно жесткими. Тогда в выражении для прогиба следует принять 0 0; условие замкнутости 80 даст возможность определить t через параметры х, 2 и q. Если же считать, что точки шпангоутов могут свободно получать равномерные радиальные смещения, то мы пришли к тому же результату, полагая с самого начала о 0, t — qRjh и не обращаясь к условию замкнутости; этот путь и избран в последующих разделах.
 После подстановки значений 0 и t безразмерный параметр 51 полной энергии получит вид
 U<; —. 2 тгhRL Q4 1 1 2?4i-j_ 22 Ь i 922J f'f2
 1 _j_ 22 “ 1 922
 Энергия изгиба по 1.109
 Uн RL 341 022i 4?44iJ • 8-82
 Работу внешней нагрузки вычислим следующим образом:
 F
 отсюда
 8.85
 Сравнивая 80 и 85, находим:
 8.86
 1

340 ЗАМКНУТЫЕ ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧКИ ГЛ. VIII
 где под Cv..., С6 понимаются следующие функции 0 и 3:
 _ 1 ■ 1 8.2 1 — 64 0 ’ 2— 4 L122 'l 9»22j0 ’
 r 1х2 1 Г1, 804 I
 S 16 »2 L1 “Г 1 »а2 J
 1
 4 1»22
 714
 481 — н--
 Ь
 Cb 61— J.2
 §•3 I _L Q —. ±_
 ° TQ С6 Л А2
 8.88
 8 ’ « 4 02
 Составим уравнения метода Ритца первого приближения
 0, 0.
 <К di
 8.89
 Первое из них связывает нагрузку с параметрами прогиба
 СвСЧ-С,» —с,6 с4, 8.90
 а второе выражает зависимость между самими параметрами :
 сл; — С.р--Сь1 0. 8.91
 Задаваясь 8 и 3 и пользуясь этими уравнениями, находим кривую
 <7 С или <7. Можно найти, как в § 82, и непосредственную связь
 между q и Ь
 8.90'
 -С3-С£
 На фиг. 8.13 изображены полученные таким образом кривые q С при 3 1260 и различных значениях i. Проводя огибающую этих кривых, находим нижнее критическое давление qH — 0,034, что составляет 56°0 от верхнего значения qB 0,061.
 Перейдем теперь ко второму приближению и будем дополнительно дифференцировать энергию по числу волн п или параметру 1:
 -§0. 8.92
 Тогда придем к уравнению, сходному по структуре с 90:
 дСь
 дЪ
 -я
 дС.
 дСЛ
 дСх
 2
 8.93
 Н. А. Алфутовым 8 3 предложено упростить уравнение 90, отбросив первый член; тогда получится, что стрела «несимметричной» составляющей прогиба пропорциональна квадрату стрелы «симметричной» части С.

§ 84
 ЗАМКНУТАЯ ОБОЛОЧКА ПРИ ВНЕШНЕМ ДАВЛЕНИИ
 341
 На фиг. 8.13 даны кривые 93 для различных 0. Проводя линию через точки пересечения вновь полученных кривых с прежними, определяем нижнее критическое давление второго приближения
 Фиг. 8.13. Кривые «нагрузка — прогиб» для оболочки при внешнем давлении по данным двух приближений.
 qH 0,044, лежащее выше прежнего значения и составляющее уже 73°0 от верхней величины. В таблице XI сравниваются данные двух
 Таблица XI
 Данные для расчета замкнутой оболочки на устойчивость при внешнем давлении в случае Rh 180
 LjR
 0,5
 0,8
 1
 1,2
 1,6
 2,2
 3
 4
 100 qB
 16,5
 9,6
 7,5
 6,1
 4,5
 3,2
 2,3
 1,7
 Отношение
 ЯпГЯъ в
 1-е прибл.
 78 '
 64
 59
 56
 62
 66
 72
 79
 2-е прибл.
 —
 —
 77
 73
 74
 79
 81
 86
 приближений для случая Rh 180 при различной относительной длине оболочки LR.
 Судя по этой таблице, отношение qjqB меняется в зависимости
 от LR. Наибольший перепад между значениями qB и qn имеет место здесь для LR 1,2, в случаях же оболочек большой длины

342
 ЗАМКНУТЫЕ ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧКИ
 ГЛ. VIII
 или, наоборот, коротких нижнее критическое давление приближается к верхнему. Очевидно, при некоторой определенной форме выпучин прощелкивание оболочек осуществляется легче всего; это мы видели уже на примерах цилиндрической панели или замкнутой оболочки, сжатых вдоль оси. Во втором приближении qu получаются более высокими, чем в первом.
 Если теперь проследить изменение qn jqB при фиксированном отношении LR для различных Rh или 8, то получится, что по мере увеличения Rh отношение qH qB падает.
 Приведенные выше теоретические результаты в общем согласуются с данными экспериментов; однако конкретные значения qtt подлежат уточнению путем выбора иных исходных выражения для прогиба и сопоставления с результатами единой серии опытов.
 § 86. Совместное действие осевой и поперечной нагрузок
 В случае одновременного действия на замкнутую оболочку осевой и поперечной нагрузок малые прогибы можно изучить с помощью уравнения, обобщающего 1 и 66:
 Т V«VW» «£ 0. 8.94
 Решение 2 приводит теперь к следующим соотношениям между критическими значениями нагрузок:
 D пъ2 г2. Е m4rJ т2т. 12уЗп2я2
 ТВ ГД2 рит№
 -¥т?5да-° <8'95>
 или между их безразмерными параметрами
 я. 1 а»22, а»
 Р ' О2 “ 121 — р.2 О2 ' 122‘ кр.ъъ
 Судя по 96, верхние критические величины р и q связаны между собой при фиксированных 0 и т линейной зависимостью: поэтому на графике ?в <7„ мы должны получить ломаную линию, отрезки которой отвечают определенным значениям тип или 0 и tj.
 В случае всестороннего сжатия надо положить ? 2; тогда получим :
 а_ 1 Г1»22У, _ 8 97
 Ч в 121 -Х.2 Т- 1»82 YjJ-
 1 2
 Уточненное решение было получено Мизесом, см. з.4б.

§ 85 СОВМЕСТНОЕ ДЕЙСТВИЕ ОСЕВОЙ И ПОПЕРЕЧНОЙ НАГРУЗОК 343
 При совместном действии растяжения и внешнего давления или сжатия и внутреннего давления следует принимать, соответственно,
 величины р или q в уравнении 96 отрицательными.
 Как показывают опыты, при сочетании сжатия и внешнего давления оболочки теряют устойчивость «в большом», причем форма волнообразования существенно меняется по сравнению со случаем простого осевого сжатия: возрастание относительной величины поперечной нагрузки влечет за собой постепенное удлинение выпучин вдоль образующей; число п выпучин по окружности при этом сокращается.
 Когда сжимающая нагрузка сопровождается внутренним давлением, то при малой интенсивности давления выпучины продавливаются попрежнему внутрь, но форма их будет другой: они становятся удлиненными уже в направлении дуги. Если же внутреннее давление сравнительно велико, то потеря устойчивости происходит с образованием сплошных кольцевых выпучин, обращенных наружу оболочки, как показано на фиг. 8.14.
 На фиг. 8.15 приведены данные опытов над выточенными из труб дуралюминовыми оболочками при Rh 180 и LR 2,2.
 В этих опытах оболочки сначала получали определенную поперечную нагрузку, которая удерживалась в дальнейшем постоянной; затем прикладывалась постепенно возрастающая сжимающая сила вплоть до наступления хлопков. Экспериментальные точки на фиг. 8.15 отвечают значениям
 р и q в момент потери устойчивости. Здесь же нанесена сплошная прямая, соответствующая линейному решению 96; для рассматриваемого примера в первом квадранте диаграммы получается только один отрезок ломаной линии. Случаю простого сжатия отвечают пять точек, расположенных на оси ординат; они лежат между значениями 0,186 и 0,38, составляющими от 31 до 63 по отношению к верхнему пределу 0,6. Другому граничному случаю простого внешнего давления соответствуют шесть точек, лежащих на оси абсцисс; здесь экспериментальные значения q состав¬
 Фотография фиг. 8.14 получена Л. Р. Исправниковым. Данные фиг. 8.15 найдены В. Л. Агамировым. Ему же принадлежит приведенное ниже решение нелинейной задачи.
 Фиг. 8.14. Дуралюминовая оболочка, подвергавшаяся совместному действию осевого сжатия и внутреннего давления.

344
 ЗАМКНУТЫЕ ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧКИ
 ГЛ. VIII
 ляют 67—95 от Яв • Надо отметить, что для образцов одной и той же серии мы получаем в случае внешнего давления значительно меньшее рассеяние критических значений нагрузки, чем при сжатии; кроме того, реальные значения критической нагрузки в первом случае лежат, как правило, ближе к верхнему пределу. Очевидно, при внешнем давлении, когда вдоль длины образуется только одна выпучина, влияние начальных неправильностей будет меньшим, чем при осевом сжатии.
 В случае комбинированной нагрузки испытанные образцы можно
 л
 разбить на две группы: для первой q составляло менее половины
 1
 >
 <
 ft
 0
 Y
  ®
 - A
 I
 4
 N
 ft
 4
 4
 N
 4
 4
 4
 -O-
 0,4
 аз
 а?
 Фиг. 8.15. Верхние и нижние критические напряжения для цилиндрической оболочки при действии осевого сжатия и внешнего давления
 от верхней критической нагрузки простого внешнего давления, а для второй — более половины. Можно отметить, что у образцов первой группы критические значения нагрузки лежат дальше от верхнего предела и более разбросаны, чем у второй группы.
 Большие прогибы оболочек при совместном действии сжатия и внешнего давления опишем с помощью такого же выражения для прогиба 18, что и при простом сжатии см. § 81 и 82. Тогда выражение для функции напряжений 21 сохранится. При вычислении работы внешней нагрузки надо учесть в дополнение к 30 работу поперечного давления
 W —q j J wdxdy — q-ttRL j2-f-20. 8.98
 F

§ 86
 КРУЧЕНИЕ ОБОЛОЧКИ
 345
 Первое из уравнений метода Ритца 32 приведет подобно случаю простой поперечной нагрузки § 84 к значению t qRh.
 Составляя следующие два уравнения 32, убеждаемся в том, что одно из них дополнится членом — ?2?Л2, а второе — членом — 32?22. Тогда уравнение 36 примет вид
 р в1 вр В, 8.99
 а уравнение 37 останется без изменений.
 При решении полученной таким образом системы уравнений поступаем следующим образом. Задаемся определенными значениями q и меняем тип или и tj, разыскивая наименьшее значение р. Этот путь наиболее естественен для случая, когда сжатие сопровождается сравнительно небольшой поперечной нагрузкой и можно считать, что по длине оболочки образуется несколько выпучин. Однако выкладки были проведены и для случая простого внешнего давления в качестве второго варианта решения задачи, рассмотренной в § 84. В этом предельном случае нижняя критическая нагрузка при Rh 180 и LR 2,2 составила 68 от верхнего значения ; такой результат близок к полученному выше в первом приближении 65.
 На фиг. 8.15 пунктирной линией даны нижние критические значения р при определенных q и нижнее значение q при простом внешнем давлении для оболочек с этими же параметрами Rh 180 и LR 2,2, найденными по уравнению 99. Почти все экспериментальные точки 21 из 25 оказались в области, лежащей между верхним и нижним пределами. Это не дает, конечно, права считать решение нелинейной задачи окончательным: и здесь должны быть исследованы другие варианты приближенного решения с варьированием большего числа параметров.
 § 86. Кручение оболочки. Одновременное действие сжатия и кручения
 Рассмотрим замкнутую оболочку, подвергающуюся по торцам действию скручивающих пар
 Мк 2 R4st
 где 5 — средняя величина касательного напряжения. Волнообразование при потере устойчивости характеризуется в данном случае выпучинами, идущими от одного торца к другому по винтовым линиям. Задача об устойчивости в линейной постановке сводится
 Примерно такой же результат получил Р. М. Финкельштейн в предположении, что выпучины являются квадратными.

346
 ЗАМКНУТЫЕ ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧКИ
 ГЛ. VIII
 к интегрированию уравнения
 т ЖI?2s w Шт°- <8-100>
 Представим прогиб в виде
 TO sinsin yTJr. 8.101
 По кромкам х 0, L будут тогда удовлетворены условия шарнир-
 Фиг. 8.16. Дуралюминовая оболочка, подвергавшаяся кручению.
 При этом можно установить следующие приближенные формулы для параметров угла наклона узловых линий и формы выпучин:
 1 1,732 y'l, » — 0,722 у'1, 8.104
 причем попрежнему В RhL?.
 Формула такого типа была получена Швериным Zs. ang. Math, und Mech. 5, 1925, стр. 235.
 См. работу Штурма Proceedings ASCE 73, № 4, 1947.
 ного опирания. Прогиб обращается в нуль также по линиям у ух, п раз повторяющимся в каждом поперечном сечении; под у понимается тангенс угла наклона узловой линии к образующей цилиндра.
 Подстановка 101 в уравнение 100 приводит к определению верхнего критического напряжения sB. Для длинной оболочки, принимая п — 2 и минимизируя 5 по к, можно предложить аналогичную 75 приближенную формулу
 8-102
 Безразмерная величина
 '-§ <8-,оз>
 будет при i 0,3
 sB 0,29 j
 Для расчета оболочек произвольной длины могут быть использованы графики, построенные на основании уточненного решения.

§ 86
 КРУЧЕНИЕ ОБОЛОЧКИ
 347
 Опыты над серией дуралюминовых оболочек, подвергавшихся кручению, показывают, что и здесь выпучивание происходит с резко выраженным хлопком; образующиеся при этом выпучины показаны на фиг. 8.16. Судя по показаниям силоизмерителя испытательной машины, крутящий момент падает при хлопке примерно вдвое; быстро уменьшается также угол между осевой линией выпучины и образующей. Реальные значения критических напряжений составляют в среднем 70—75 от значений, вычисленных по линейной теории 812, 819; разброс экспериментальных точек заметно меньше, чем при осевом сжатии. Как видим, эффект нелинейности здесь примерно такой же, как и в задаче об устойчивости оболочек при внешнем давлении, и-далеко не так велик, как при осевом сжатии; это связано с различием в форме выпучин, охватывающих в первых двух случаях всю длину образца.
 Для аппроксимации изогнутой поверхности оболочки при больших прогибах можно избрать следующее выражение:
 Первый член отвечает решению линейной задачи; второй выбран в том же виде, что и в случае внешнего давления § 85. Подставим 105 в правую часть уравнения 5.30; после интегрирования найдем функцию напряжений
 a1ft >, 6 —0, a8 ft3>, bz k — 30. 8.107
 Если положить 6 0, то придем к выражению 78, полученному в § 84.
 w ft sin -
 f2 sin-. 8.105
 ф ___ да 7Г“ 32
 т
 -f-sxy; 8.106
 здесь
 Эта серия опытов на кручение и комбинированную нагрузку сжатие и кручение была проведена Л. Р. Исправниковым.
 Изложенное здесь решение принадлежит Лу 8.19.

348 ЗАМКНУТЫЕ ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧКИ гл. VIII
 Вычислим теперь энергию деформации срединной поверхности
 IJ К Г 1 I _1_1 4 I
 с 8 I Ш L 1 22 04 Jyl f
 U 1 й?2 1 > 1 4? 1 6D2 ?2
 те2 1 г 4л 4£>f 1 I 2
 Т л2- L 1 af 1 ь? a2 J а
 R2 1 Iff 1 ? Л22 I 8Л08
 и энергию изгиба
 t JWiHl «?2l2?16nVi- 8-109
 При £ 0 приходим к прежним выражениям 81 и 82.
 Определим взаимный угол закручивания торцов оболочки. По соотношению 5.4 имеем:
 да. dv 1_ д2Ф _ dw dw
 ду дх G дх ду дх ду ' '
 «Среднее» значение деформации сдвига будет
 1
 Т
 2 tzRL
 <8‘>
 F
 После подстановки выражений 105 и 106 получим:
 8-112
 угол закручивания будет
 0 ТА. 8.113
 Работа внешней нагрузки оказывается равной
 WMk0 2RLh 8-114
 Находя полную энергию системы 3, выписываем уравнения метода Ритца:
 Ш0- Ш<■ <8 П5
 В работе 8Л9 эти уравнения составлены в предположении, что параметры k и 0 определяются по приближенным формулам 104, т. е.

§ 86
 КРУЧЕНИЕ ОБОЛОЧКИ
 349
 являются постоянными в течение всего процесса закритической деформации. Характер изменения 5 при росте угла закручивания оказался зависящим от параметра 8. В случае относительно коротких оболочек Ь 120 нагрузка лишь слегка падает по отношению
 к верхнему критическому напряжению, так что sH составляет 94
 от sB. Если величина 8 равна 200» то sa будет составлять 80 от при
 8 V2000 отношение sHsB будет 87, т. е. снова возрастает. Для весьма длинных оболочек решение не дает удовлетворительных результатов: в пределах
 прогибов, на которые можно распространить данное решение, нижней границы установить не удается.
 Данный вариант решения является лишь первым приближением, но он убедительно показывает, что в случае кручения нижняя граница критических напряжений лежит гораздо ближе к верхней, чем в случае осевого сжатия.
 Совместное действие сжатия вдоль образующей и кручения было экспериментально изучено следующим образом.
 Вначале образец подвергался закручиванию и достигалось определенное значение крутящего момента. Затем к образцу прикладывалась постепенно возрастающая сжимающая нагрузка, в то время как крутящий момент удерживался постоянным. Форма волнообразования получалась здесь смешанной, как показано на фиг. 8.17: выпучины были мелкими, как при сжатии, но располагались они по винтовым линиям. Как показали опыты Л. Р. Исправникова, зависимость между критическими напряжениями сжатия и сдвига может быть выражена формулой
 лШ31, 8Л16
 где под р0 и Sq понимаются экспериментально найденные критические напряжения простого сжатия и простого кручения. Видимо, такое же соотношение можно распространить на теоретически найденные нижние критические напряжения.
 Эта формула была предложена в работе 812.
 Фиг. 8.17. Оболочка, получившая выпучины при действии осевого сжатия и кручения.

350
 ЗАМКНУТЫЕ ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧКИ
 ГЛ. VIII
 § 87. Устойчивость оболочки при изгибе
 Рассмотрим вначале изгиб оболочки парой сил. Допустим, что по торцам оболочки приложены две пары с моментами Ж, лежащие в некоторой диаметральной плоскости. Примем закон распределения нормальных усилий в каждом поперечном сечении до потери устойчивости оболочки в виде
 • У М У О 1 1 7
 Рх — Ро sin -jf cos » 8.117
 где у отсчитывается от точки срединной поверхности, расположенной в плоскости действия пары. Будем считать, что начальные равновесные состояния являотся безмоментными и что поперечные сечения до потери устойчивости оболочки остаются круговыми. Волнообразование при выпучивании оболочки должно, очевидно, распространяться главным образом на сжатую зону. Основное уравнение 5.38 линейной теории принимает вид
 Т w '■o' 4S “s i °' <«'118>
 Представим решение в виде ряда
 оо
 . тъх,. пу о 1 1 а
 w sin—ZT- 2и sin ' 8.119
 П-1
 Подставим 119 в уравнение 118 и приравняем нулю коэффициенты при однородных членах; учитывая соотношение
 . пу у 1. я 1у, 1. п—1 у
 sin-cos- у sm. д 7у sin-v—-д-,
 получим трехчленные уравнения относительно параметров прогиба fn такого типа:
 та2 -W п“р»f а2 '2»-1 » i °> 8-12°
 где а — тъL, nR. Ограничиваясь определенным числом параметров fn и приравнивая нулю определитель системы уравнений типа 120, находим верхнее критическое напряжение.
 Результаты вычислений показывают, что амплитуда сжимающего напряжения р0, в лишь незначительно на несколько процентов превышает величину критического напряжения для центрально сжатой вдоль оси оболочки, т. е. что эффектом неравномерности распределения напряжений рх по сечению в практических расчетах можно пренебречь. Поэтому верхнее критическое напряжение для оболочки,
 Эти результаты получены Ю. Г. Одпноковым Труды Каз. авиац.
 ин-та, 1940 и А. В. Кармишиным.

УСТОЙЧИВОСТЬ ОБОЛОЧКИ ПРИ ИЗГИБЕ
 35 i
 подвергающейся чистому изгибу, можно принять равным
 Ро,в 140-6 <8Л21>
 Судя по опытам над точеными образцами, находящимися в условиях чистого изгиба, реальные критические напряжения составляют 68—75 от рогв и имеют сравнительно слабый разброс. Для оболочек той же серии, подвергавшихся простому сжатию, этот коэффициент составил в среднем 60. При изгибе образцов, изготовленных менее тщательно, критические напряжения составляют 40—70 от ро,в и превышают экспериментально найденные критические напряжения центрального сжатия примерно на 20—40;
 Фиг. 8.18. Цилиндрическая оболочка при поперечном изгибе.
 средняя величина критических напряжений оказывается зависящей от отношения Rh. Надо считать, что вероятность перескока через энергетический барьер у оболочек, подвергающихся изгибу, меньше, чем при центральном сжатии, так как различные случайные факторы начальная погибь, концентрация напряжений оказывают при изгибе различное влияние в зависимости от того, в какой зоне поперечного сечения они имеют место. Поэтому вместо коэффициента 0,18, принятого нами для нижнего критического напряжения для случая центрального сжатия, мы должны здесь взять несколько более высокий коэффициент, например
 Рон 0,22. 8.122
 Перейдем к случаю, когда оболочка, закрепленная по одному торцу, подвергается на другом торце действию поперечной нагрузки Р фиг. 8.18. Характер выпучивания оболочки будет при этом зависеть от относительной длины оболочки LR.
 Если оболочка сравнительно длинная, то потеря устойчивости носит примерно тот же характер, что и при центральном сжатии, но
 Описанные здесь опыты проведены П. Г. Бурдиным.

352
 ЗАМКНУТЫЕ ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧКИ
 ГЛ. VIII
 выпучины сосредоточиваются у корневого сечения вблизи точки А на фиг. 8.18. При потере устойчивости таких оболочек образуется один или два ряда мелких выпучин; амплитуда их уменьшается от наибольшей у точки А до нуля у нейтрального диаметра фиг. 8.19. Реальные значения критических напряжений для длинных оболочек оказываются на 8—10 выше, чем при чистом изгибе, что также можно объяснить сокращением зоны влияния начальных неправильностей.
 Для относительно коротких оболочек главную роль будут уже играть наибольшие касательные напряжения у нейтрального слоя волокно В В на фиг. 8.18, равные z PTzRh. Потеря устойчивости
 р
 Фиг. 8.19. Волнообразование длинной оболочки при поперечном изгибе.
 сопровождается здесь образованием в средней части сечения у нейтрального диаметра наклонных выпучин, характерных для случая кручения оболочки фиг. 8.16. Напряжениям в нейтральном слое т будут соответствовать наибольшие нормальные напряжения p0 zLR• Для дуралюминовых образцов с отношением Rh 170 и длиной, лежащей в пределах между 2R < L < 4R, критические значения р0 оказались примерно пропорциональными I?, чго отвечает постоянной величине т. В действительности критические значения z зависят от LR; с известным приближением их можно принимать равными критическим напряжениям кручения для оболочек тех же размеров.
 Переход от одного вида потери устойчивости в крайних волокнах к другому по нейтральному слою имеет место для испытанных образцов при длине L, составляющей около 4R. В случае, если L близко к 4?, волнообразование имеет смешанный характер.
 § 88. Влияние начальной погиби на устойчивость замкнутых оболочек
 Приведем данные опытов, в которых изучалось влияние начальной погиби на устойчивость замкнутых оболочек при внешнем давлении точнее, при всестороннем сжатии. Оболочка А помещалась
 Эти опыты были проведены В. Е. Минеевым.

ВЛИЯНИЕ НАЧАЛЬНОЙ ПОГИБИ НА УСТОЙЧИВОСТЬ
 353
 в резервуар В, наполняемый водой или маслом; внутренняя полость оболочки оставалась открытой для наблюдателя фиг. 8.20. Избыточное давление в резервуаре создавалось с помощью насоса D, соединенного с электромотором. Дополнительная емкость С содержала «воздушную подушку», с помощью которой поддерживалось давление жидкости в момент внезапного выпучивания оболочки. Деформации в среднем сечении по длине оболочки определялись при помощи проволочных датчиков, наклеиваемых как с внутренней, так и с наружной стороны образца.
 Провода от датчиков, помещавшихся внутри резервуара, выводились через токосъемник Е. Кроме того, внутрь оболочки вставлялся индикатор, который позволял определять прогибы в среднем сечении.
 Опыты с первой группой гладких, выточенных из дуралюминовых труб образцов показали, что потеря устойчивости оболочек при всестороннем внешнем давлении всегда происходит «в большом». Число выпучин по окружности для испытанных образцов при LR 2,2 и отношении Rh, менявшемся в пределах от 90 до 180, составляло всегда 6; каждая выпучина распространялась на всю длину оболочки. Иногда потеря устойчивости происходила в несколько этапов: сначала образовывались две-три выпучины, после чего нагрузка продолжала возрастать; затем возникали дополнительные выпучины.
 Вторая группа образцов подвергалась отжигу, после чего оболочкам придавались выпучины, обращенные к центру кривизны и сходные по форме с вмятинами фиг. 8.12..После новой термической обработки образцы помещались в установку фиг. 8.20 и подвергались постепенно возрастающему внешнему давлению. Третья группа оболочек получала начальную погибь без отжига и последующей термической обработки. Деформация оболочек второй группы протекала примерно таким же образом, как и оболочек третьей группы.
 Как показали испытания, характер деформации оболочки существенным образом зависит от числа и расположения начальных выпучин. Допустим, что. модели придана только одна выпучина, глубина которой равна толщине оболочки. Тогда возрастание внешнего давления
 Фиг. 8.20. Установка для испытаний оболочек на всестороннее сжатие.

354
 .ЗАМКНУТЫЕ ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧКИ
 ГЛ. VIII
 вызывает углубление этой выпучины; вместе е тем в ближайшей части оболочки намечаются волны, быстро затухающие по мере удаления от основной выпучины. Далее наступает хлопок, сопровождающийся образованием двух новых выпучин по обе стороны от первой.
 При дальнейшем увеличении нагрузки происходят новые хлопки; в итоге образуются те же шесть выпучин, что и при потере устойчивости гладкой оболочки.
 Интересно отметить, что при этих последовательных хлопках напряжения в зонах ранее образовавшихся выпучин остаются почти неизменными.
 Если до испытания оболочка получала две или три симметрично расположенные выпучины, возникали два или три «очага» волнообразования такого же типа, как и при одной начальной выпучине. Во всех этих случаях полная потеря устойчивости, характеризующаяся образованием всех шести выпучин до этого момента нагрузка продолжала возрастать, имеет место примерно при одной и той же нагрузке, составляющей около 70 от критической нагрузки для гладких образцов.
 Если же число начальных выпучин равнялось 5 или 7, то окончательная потеря устойчивости также происходила по пяти или семи волнам, и «идеальная» форма волнообразования шесть выпучин не осуществлялась. Критическое давление получалось при этом несколько более высоким, чем при одной, двух, трех или шести начальных выпучинах.
 Наиболее высокая критическая нагрузка, составлявшая 85 -ч- 90 от нагрузки для гладкого образца, была получена при четырех начальных выпучинах; оболочка здесь вынуждена была в процессе деформации «перестраивать» форму волнообразования, причем окончательная изогнутая поверхность характеризовалась здесь пятью или шестью выпучинами.
 Таким образом, влияние начальной погиби оказывается наиболее сильным в том случае, если форма ее соответствует характеру волнообразования гладкой оболочки при потере устойчивости. Поэтому с теоретической стороны должен быть исследован прежде всего именно этот случай; при этом может быть использован тот же метод, что и в § 68.
 Примем, что оболочка, шарнирно закрепленная по торцам, подвергается действию только внешней поперечной нагрузки. Пусть начальные прогибы распределяются по закону
 где а — nL, 3 nR. Примем для дополнительного прогиба выражение
 wK4 — нч sin ах sin фу sin2 ах,
 8.123
 w fx sin ах sin фу sin2 ах.
 8.124

§ 88 ВЛИЯНИЕ НАЧАЛЬНОЙ ПОГИБИ НА УСТОЙЧИВОСТЬ 355
 Подставляя 123 и 124 в правую часть уравнения 5.45, получим функцию напряжений в виде 78:
 -4- Ф г, cos 2ах г г cos 2,3у —— rs sin ах sin у
 Е
 r4 sin Ъах sin где
 r IS Р2 f2 f ф r ft g2 2
 1 — А 32а2 J 1 8У?а2 JM> Г2 — Ъ J v
 Г — — к 44-- - л 8.126
 г3— А а2__£22 1Т“ а2__р22 •'1 I V 7
 r — 2 ф
 Г4 74 р2__9а22'1 Т J
 под С подразумевается коэффициент
 К 14-214-2-. 8.127
 Л •
 Здесь СНч ичЙ1. С ЛА. При нч 0 будет ЛГ 1 и коэффициенты rt,..., г примут вид 79.
 Для полной энергии системы получаем вместо 87 выражение
 Э 1 ССхС 4- С,2 4-C6Ca<.2 — KCPq — fc 8.128
 коэффициенты Cv..., С6 определяются по 88; 5 f2jh. Составляя
 • в первом приближении уравнения метода Ритца
 °. Ц-0’ <8129
 находим зависимость между нагрузкой и параметрами прогиба при некотором заданном значении стрелы начальной погиби Снч или коэффициента К> Получаемые при этом кривые qt> аналогичны линиям, расположенным в первом квадранте диаграммы фиг. 7.14.
 Т а б л и ц а XII
 Верхние и нижние значения сжимающего напряжения для замкнутой оболочки с начальной погибью в процентах от рй для гладкой оболочки
 0
 0,025
 0,05
 0,1
 0,15
 к
 100
 74
 65
 52
 45
 нч
 52
 51
 50
 48
 44

356
 ЗАМКНУТЫЕ ЦИЛИНДРИЧЕСКИЕ ОБОЛОЧКИ
 ГЛ. VIII
 В работе 8Л9 проведены аналогичные выкладки для случаев осевого сжатия и кручения. В таблице XII сопоставлены верхние и нижние значения среднего напряжения, найденные для центрально сжатой оболочки; все эти значения отнесены к верхней критической
 величине рв, принятой за 100. Надо помнить, что приводимые в таблице данные относятся к одному из вариантов исходного выражения для прогиба, не являющегося окончательным. Как видим,
 верхние значения р резко падают уже при стреле начальной погиби, составляющей 0,025 от толщины оболочки, между
 тем нижние значения р мало отличаются друг от друга. Примерно такие же соотношения были получены в § 68 для цилиндрической панели, сжатой вдоль образующей.
 В случае оболочки, подверженной действию кручения или внешнего давления, влияние начальной погиби оказывается не столь значительным.
 L R
 Так, например, для оболочки с параметрами -- 2,2 и 180,
 испытывающей внешнее давление, заметное падение qB имеет место лишь при стреле начального прогиба, достигающей 0,25 и более от толщины оболочки. Различием в эффекте начальнойпогиби объясняются многие особенности поведения реальных оболочек при испытаниях на те или иные нагрузки по характеру хлопков, рассеянию экспериментальных данных и т. д..

ГЛАВА IX
 СФЕРИЧЕСКИЕ ОБОЛОЧКИ
 § 89. Сферическая оболочка при равномерном внешнем давлении.
 Линейная задача
 Рассмотрим задачу об устойчивости сферической оболочки, подвергающейся действию равномерно распределенной поперечной нагрузки q со стороны выпуклости. Как показывают опыты, потеря устойчивости состоит здесь в образовании выпучин, размеры которых малы по сравнению с радиусом оболочки. Поэтому форма
 потери устойчивости и величина критической нагрузки будут одними и теми же для полной сферической оболочки фиг. 9.1 и для сферического сегмента, охватывающего достаточно большой центральный угол 2а фиг. 9.2.
 Фиг. 9.1. Замкнутая сферическая оболочка при действии внешнего давления.
 Фиг. 9.2. Сферическая панель.
 Исследование устойчивости сферической оболочки также является одной из важнейших классических задач теории оболочек. Решение ее имеет практическое значение: оболочки, имеющие форму сферы или близкую к ней, встречаются в строительных конструкциях перекрытия, химическом машиностроении днища резервуаров, авиации
 Эта задача была впервые рассмотрена в линейной постановке Цолли R. Zoelly, Dissertation, Zurich, 1915 и Л. С. Лейбензоном Уч. зап. Юрьевского ун-та, 1917; см. Собр. трудов 1, Изд. АН СССР, 1951, 50—85.

358
 СФЕРИЧЕСКИЕ ОБОЛОЧКИ
 ГЛ. IX
 днища герметических кабин, обтекатели радиолокационных антенн, в кораблестроении переборки подводных лодок и т. д.
 Наряду со случаем сжатой вдоль оси цилиндрической оболочки пример равномерно сжатой сферической оболочки показывает, насколько резко могут расходиться формулы линейной теории и результаты опытов.
 До момента потери устойчивости во всех нормальных сечениях оболочки будут иметь место сжимающие напряжения а, величина которых равна
 через R здесь обозначен радиус оболочки, через h — толщина. Для определения верхнего критического напряжения воспользуемся линейными уравнениями 5.31—5.32; при kx — ky—R они примут вид
 Находим из первого уравнения величину У‘2Ф и подставляем ее во второе; тогда получим следующее уравнение шестого порядка относительно w:
 Следуя В. 3. Власову 54, не будем интересоваться формой вол нообразования оболочки, а воспользуемся зависимостью
 где X2— подлежащий определению параметр. Выражая через X2 таким же образом остальные дифференциальные операторы, представляем уравнение 4 в виде
 9.2
 9.3
 V2V2V2?0 -j- Vaw oV2V2w 0.
 9.4
 V2ot —
 9.5
 9.6
 Отбрасывая решения A 0 и w 0, находим:
 9.7
 Выпишем условие минимума <з:
 da _ 2 DX IE «
 dX h RW
 9.8
 Сама по себе величина q в уравнение не вводится, так как изогнутые состояния сравниваются с равновесной формой оболочки, уже подвергшейся предварительному нагружению.

§ 90J
 ОПЫТЫ СО СФЕРИЧЕСКИМИ ОБОЛОЧКАМИ
 359
 Отсюда
 13 — DRз
 ИЛИ
 а121У- 9-10
 Подставляя это выражение в 7, находим критическое на¬
 пряжение:
 1.:-£• 4-, 9.11
 131 — ЛЗ Я 4
 или при х 0,3
 ОвЯьО.бЕ-. 9.12
 Этому напряжению соответствует давление
 <93>
 при А 0,3 получим:
 ?,«1,2Е 9.14
 Сопоставляя выражение 11 с формулой 8.13, заключаем, что критические напряжения для сжатой вдоль оси цилиндрической
 трубы и подвергающейся внешнему давлению сферической оболочки в точности равны между собой, если толщины и радиусы совпа¬
 дают. Это объясняется особенностью местной потери устойчивости, выражающейся в образовании мелких волн: характер выпучивания остается одним и тем же для оболочек различного очертания.
 § 90. Опыты со сферическими оболочками
 Судя по результатам испытаний сферических оболочек, формулы 11 или 13 не могут служить основанием для практических расчетов
 На фиг. 9.3 представлены данные опытов над сферическими сегментами с углом раствора 0 17°45, защемленными по краю и подвергавшимися действию постепенно возрастающего давления воды со стороны выпуклости 99. Вода была заключена в закрытую камеру, помещавшуюся над образцом; как только начиналось образование выпучины, поступление воды прекращалось. По оси абсцисс графика откладывается отношение Rh, менявшееся в пределах от 700 до 2000. По оси ординат отложены значения коэффициента К в формуле
 9-15

360
 СФЕРИЧЕСКИЕ ОБОЛОЧКИ
 ГЛ, IX
 пунктирная линия соответствует теоретическому значению К — 0,606. Верхние точки определяют максимальное напряжение в срединной поверхности, достигнутое до начала выпучивания; стрелки ведут к точкам, определяющим напряжение после хлопка. Как видим, полученные в опытах верхние критические напряжения в 2—2,5 раза меньше теоретических.
 Другая серия опытов была проведена над защемленными по краю стальными и латунными сегментами, изготовленными механическим способом из листового материала Радиус кривизны и толщина
 44
 Q2
 я
 и
 l.tTtZ1—1 ют теории
 1... 1..J 1
 •Ф-,До дяолка х 7осу?е яяоляа
 Л
 А
 т
 ч
 ч
 у
 <j
 У
 Л
 1
 V
 >
 f
 •
 -f-
 У
 1
 1
 Ч
 500
 7500
 Яh 2000
 Фиг. 9.3. Напряжения при выпучивании сферических оболочек по экспериментальным и теоретическим данным.
 оболочки составляли для одной группы образцов 250 и 0,34 мм, для другой — 520 и 0,45 мм. Отношение Rh было равно, соответственно, 740 и 1155. Образцы подвергались с выпуклой стороны давлению сжатого воздуха. Процесс потери устойчивости начинался с образования небольшой вмятины, обычно прилегавшей к краю сегмента. В некоторых опытах после появления первой вмятины давление тотчас же снижалось до нуля; тогда вмятина полностью исчезала. Если же давление продолжало повышаться, вмятина расширялась, захватывая постепенно центральную часть сегмента. Это можно видеть по кадрам скоростной киносъемки процесса выпучивания, приведенным на фиг. 9.4. В некоторых случаях в дополнение к первой мелкой вмятине возникали дополнительные вмятины, впоследствии соединявшиеся между собой. Заключительная часть деформации оболочки заключалась в полном «выщелкивании» оболочки в обратную сторону. В описанных опытах баллон с воздухом имел достаточно большой объем, так что первоначальная вмятина образовывалась при почти постоянном давлении; при полном же вы-

§ 90 ОПЫТЫ СО СФЕРИЧЕСКИМИ ОБОЛОЧКАМИ 361
 щелкивании оболочки объем баллона значительно возрастал, благодаря чему давление воздуха падало.
 Величины полученных в этих опытах критических напряжений для гладких оболочек приведены на графике фиг. 9.5; они соста-
 Фиг. 9.4. Последовательные положения сферической оболочки при хлопке по данным скоростной киносъемки.
 вляют лишь 20-?-25 от теоретических. Надо отметить, что технология изготовления образцов была весьма несовершенной: вытяжка оболочки j3 листового материала была связана с приданием ей

362
 СФЕРИЧЕСКИЕ ОБОЛОЧКИ
 ГЛ. IX
 переменной толщины, причем толщина у краев оболочки была, повидимому, наименьшей. Кроме того, имелись значительные начальные отклонения от сферической поверхности. Поэтому напряжения в обшивке еще до потери устойчивости распределялись неравномерно.
 Приведем данные испытания сферического сегмента с полным углом раствора в 180° °-9. Отношение Rh составляло 900. Полученное в опыте значение коэффициента равнялось 0,154; первоначальная выпучина охватывала полный центральный угол в 16°. Выпу-
 Ц20 в
 Ф0
 <> е2з°
 ♦ 054°
 Змлирическ.
 ф-ла Зля 923 0 500 АООО WOO flfy 2000
 Фиг. 9.5. Данные двух серий экспериментов со сферическими оболочками.
 чина оказалась расположенной у оси симметрии сегмента; максимальный прогиб в центре после скачкообразного появления первой вмятины в 12,5 раза превышал толщину оболочки.
 § 91. Уравнения осесимметрич¬
 ного изгиба оболочки при больших прогибах
 Фиг. 9.6. Вмятина, образующаяся Мы виДели> чт0 первый период
 при хлопке сферической оболочки, потери устойчивости сферической
 оболочки состоит в образовании местной вмятины, размеры которой невелики по сравнению с радиусом оболочки. Проведем через центр вмятины ось z; будем считать, что изогнутая поверхность является осесимметричной и ограничена параллелью, соответствующей углу 3 фиг. 9.6.
 В уравнениях 5.27 и 5.28 перейдем от ортогональных координат к сферическим таким же образом, как это было сделано

§ 91 УРАВНЕНИЯ ОСЕСИММЕТРИЧНОГО ИЗГИБА ОБОЛОЧКИ 363
 в § 39, но с учетом осевой симметрии задачи. Выражение запишется в виде 4.59:
 _.2 Jd dw dw. d2w
 W r dr dr r dr dr2
 Здесь иод г следует понимать расстояние, измеренное от данной точки до полюса вмятины. Вспоминая соотношения § 39, мы должны
 д2 w d2w d2w 1 d
 производную ' заменить на -, а на аналогичные
 выражения будем иметь для производных от функции Ф. Уравнение 5.27 получит тогда вид
 D I d Г d T7Q Л d<b, d2w, РФ 1. 1 dw. 1
 h г dr dr г dr R dr2 dr2 R r dr h
 или
 Л r tfr _ tfr Rr dr dr ' r dr dr dr ' h 4
 Умножая на г и производя интегрирование, будем иметь:
 0± Н-±£-±- У-, 9.16
 под х¥ здесь понимается выражение 4.14.
 Далее, уравнение 5.28 можно представить в виде
 1 AL Гг А. У2фч1 _ _ Р Г1, _1_ l_ dw_,
 r dr I dr K r dr dr ' R r dr dr2 '
 или
 1 ± r А. у-2ф 1 — E f± AL A. 4. _L A. r
 r dr I dr ' 'J r dr dr2 • Rr dr dr J
 После интегрирования получим:
 гт-£Шт' 7¥' <9л7>
 Если положить в уравнениях 16 и 17 ? со, то придем
 к системе уравнений 4.30‘—4.31 для круглой пластинки. Полученные нами уравнения можно сопоставить также с уравнениями, соответствующими круглой пластинке с начальной погибью; нужно лишь в уравнениях 4.35 и 4.36 принять dwHHdr 1R.
 Пользуясь данными § 37, выпишем выражения для напряжений:
 1 аФ а2Ф d, ч л t оч
 °r 7dF ’ 9-18
 Отметим соотношение
 9.19

364
 СФЕРИЧЕСКИЕ ОБОЛОЧКИ
 ГЛ. IX
 Уравнения метода Бубнова — Галеркина, заменяющие уравнение равновесия 16, будут иметь такой же вид, как и для круглой пластинки см. § 40:
 fjxrdr 0, 9.20
 F
 но под Л здесь следует понимать величину
 D £ <''■«-''-'■-§-1; <9-21>
 для lF остается выражение 4.14.
 § 92. Деформация оболочки после потери устойчивости; решение в первом приближении
 Допустим, что при потере устойчивости оболочки образовалась вмятина радиуса с, охватывающая полный угол 2к3 фиг. 9.6. Будем условно считать, что сопряжение вмятины с остальной частью оболочки соответствует жесткому защемлению: элемент, нормальный к контуру вмятины, не получает смещения и поворота. Граничные условия для‘ функции Ф были для этого случая выписаны в § 38 применительно к случаю круглой пластинки:
 0, — 0. 9.22 ro dr2 г dr г0
 с1Ф
 4F
 Примем такое уравнение изогнутой поверхности в пределах вмятины, какое мы использовали неоднократно в главе IV для защемленных по контуру круглых пластинок:
 « l— -J2- 9-23
 Уравнение 17 примет тогда форму
 В § 41 было уже найдено выражение 4.97 для йФdr, соответствующее первому члену правой части. Производя аналогичные вычисления со вторым членом и учитывая граничные условия, приходим к следующему уравнению:
 ЕР 15 — 3х г а г3, - г5 г1

§ 92 ДЕФОРМАЦИЯ ОБОЛОЧКИ ПОСЛЕ ПОТЕРИ УСТОЙЧИВОСТИ
 365
 Последний член соответствует напряжениям, накопившимся в оболочке до потери устойчивости. Полные напряжения в срединной поверхности будут равны
 _ 1 йФ _ ЕР 5 — 3х fi г2. г г®
 Зг—' г dr 6с2 1 — X D с2 т' с Е Г22 —IX r2 HI qR 2
 L 1 —Х с2 с J 2h '
 w -18 20 7-у-
 -Р£?-»£»£-£-
 Составим теперь уравнение Бубнова — Галеркина 20. Интегрирование будем производить для площади вмйтины, охватывающей круг радиуса с. Из экспериментальных данных мы видели, однако, что в процессе деформации площадь вмятины должна изменяться. Поэтому к полученным результатам нужно будет отнестись с осторожностью.
 Выражение 21 для X получает вид
 -8>
 Принимая для функции ?, входящей в 20, выражение 4.101 и производя интегрирование, придем к следующему алгебраическому уравнению относительно стрелы прогиба :
 г> 3 д ЕР he2 qR - g.
 3UJ 241— л R 12ус1
 _L Ehp 7 fo-,.. ?fJLc4 Q 9 29
 2521 —x cnj 1 —p. 180 R? v-Kv-W
 Введем безразмерные параметры:
 - C2 R2 Л a R qR2 r
 Rh h ' a E h 2Eh ’ Л ' 9.30
 Величина k характеризует кривизну вмятины подобно выражению 7.15, вводившемуся в § 63 для цилиндрической панели. Подставляя в 29, кроме того, выражение для D, получим уравнение
 з — 1 L 7 k I 23 С2 3 г 9 3D
 31-1 301 —р. 421 — р. 41—р. '
 Рассмотрим вначале линейную задачу, предполагая прогибы весьма малыми. Считая С0, найдем выражение для верхнего критического

366
 напряжения:
 Сферические оболочки
 4, 7 — 2х
 :31— А2“т- 301 —X
 гл. IX 9.32
 Определим величину, придающую ав наименьшее значение. Из уравнения йсвйк — 0 находим:
 40
 1Ю7-2л ’ при jx 0,3 5 2,3. Критическое напряжение будет
 3Г--,;2 0 2Л ; при 0,3 ав 1,27.
 Найденная нами величина примерно в 2 раза превышает истинное значение критического напряжения, полученное в § 89. Это объяс-
 5
 1 1 I1
 7,5 10 12,5 15 17,5 20 30 45 ll I 1 ' 1 1 1 11 И 1.
 д у
 1 V J1 1 и 1 1 1 1 11 V
 VI
 1 V 1 1 1 1 i
 1
 I
 1 1
 v
 ягу
 mi
 А •
 И 1
 • М ' 1 1 1
 71
 1 1 1 1
 ft 1 1 1
 10
 ft WU
 7 Л
 ?1 1 20 2,
 5 13
 О 3,
 5 4
 5
 17,5
 20У
 1
 3L
 7 хх
 -40
 45
 ...... J
 44
 <7
 0,2 О -0,2
 -Q4 -0,8 -0,8
 Фиг. 9.7. Данные первого и второго приближений в задаче о хлопке цилиндрической оболочки.
 няется тем, что принятое нами выражение для прогиба 23 достаточно хорошо отражает форму вмятины, развивающейся после хлопка, но вместе с тем не соответствует виду изогнутой поверхности при малых прогибах.

ВТОРОЕ ПРИБЛИЖЕНИЕ
 36?
 Возвратимся к полному уравнению 31 и установим зависимость
 между а и С, придавая размеру вмятины различные значения. На фиг. 9.7 изображены кривые q С для величин 6, изменяющихся от 5 до 45. Судя по этим данным, при увеличении размера вмятины
 величина о и вместе с тем давление q должны падать и даже становиться отрицательными. Иными словами, равновесные положения оболочки при ‘значительных прогибах должны соответствовать давлению со стороны выпуклости фиг. 9.8. Такой результат при сво-
 Фиг. 9.8. Равновесное состояние сферической оболочки по данным первого приближения.
 бодно изменяющейся площади вмятины представляется маловероятным. Поэтому желательно получить уточненное решение задачи. Для этого исп >льзуем энергетический метод, считая варьируемыми два параме pa: I. и k.
 § 93. Второе приближение
 Составим выражение для полной энергии системы. Потенциальная энергия деформации срединной поверхности вычислится, как и для круглой пластинки:
 с
 tcMjV3>2-2l 7:S-2ltrdr- <9-33>
 О
 Величину У2Ф определим с помощью соотношений 26 и 27:
 —<9-34> Подставляя под знак интеграла, кроме того, выражения 26, 27 и производя вычисления, получим:
 .. _23 —9h „ 3 —хл Eh.
 0 126 1 —ri cJ 91—jx R J r
 9.35

368 СФЕРИЧЕСКИЕ ОБОЛОЧКИ гл. IX
 Выражение для энергии изгиба будет
 и«т I V2 2-TW2vrdr- <9-36>
 о
 Интеграл, соответствующий второму числу в квадратных скобках, обращается в нуль. Величина равна
 V -i£l-25. 9 37
 Следовательно,
 9.38
 Перейдем к вычислению работы внешних сил W. Здесь необходимо учесть работу давления q не только на перемещениях изгиба w, но и на смещениях w0, образовавшихся при нагружении оболочки до потери устойчивости. Величину w0 найдем из соотношения
 —gl-F. 9.39
 Таким образом
 с
 W J qw-- w0 2izr dr. 9.40
 о
 Подставляя значения w 23 и w0, будем иметь:
 W 9.41
 Введем параметр полной энергии Э:
 с учетом 30 найдем :
 Ь' _ 23 9а 3 j 4.2 I
 84 1 — -» k 61— х 4 31 — k 4 »
 3oV--kr- - —1 -г1 оЧ- 9AS
 Составим уравнения метода Ритца. Если варьировать стрелу прогиба С, то надо положить
 -g- 0 9.44
 Подобное выражение для энергии получено в статье 911. Дальнейший ход решения в этой статье отличен от приведенного здесь.

ВТОРОЕ ПРИБЛИЖЕНИЕ
 369
 или
 - Г-1 7-2.1Х... ь _j 23.г:91, - гз 3-7.. гз_2аГ 0 f9 45
 31 — ц2£ 15 1 — 21 1 — Ь- 2 1 — л и
 Как легко видеть, это уравнение при С£0 совпадает с уравнением 31, составленным нами ранее по методу Бубнова — Галеркина. Таким образом, меняя только одну величину С, мы придем к тем же результатам, что и в предыдущем параграфе. Желая уточнить решение, будем в дополнение к этому варьировать радиус вмятины или, иначе говоря, величину ft, подобно тому как это было сделано в § 84 для цилиндрических оболочек при внешнем давлении. Тогда
 получим второе уравнение:
 -0 9.46
 ИЛИ
 Г 2-
 5йда ' - ЯГой VWF V 4 <> -Ю ”-»• 9-«
 Считая С¥0, придадим системе уравнений 45—47 вид : А 1 _7 —2 ь —23 —9ц С2 — ■,3,Л. С, 9.48
 3 1 —J.3 А 301—A f 421 — >.k ' 41 — Н-
 • 31-Vafc-84iL'i• <9-49>
 На графике фиг. 9.7 нанесены кривые qС для различных значений ft. Семейство сплошных кривых 48 мы уже получили в предыдущем параграфе. Пунктирные кривые построены по уравнению 49. Через точки пересечения соответствующих кривых проведена новая линия, наинизшая точка которой теперь отвечает положительной величине напряжения
 о 0,155, или о 0,155£--, 9.50
 и стреле прогиба 9,16ft. Напомним, что в одном из проведенных опытов со сферическим сегментом было получено о 0,154. Однако такому совпадению не надо придавать большого значения. Полученное нами теоретическое решение дало скорее возможность осветить вопрос с качественной стороны. Нами было условно принято, что вмятина жестко защемлена по контуру, в то время как в действительности закрепление надо считать упругим. Этот вопрос был подробно разработан в работах X. М. Муштари, Р. Г. Суркина 9-2, 9-4 и В. И. Феодосьева 8-6. Р. Г. Суркиным был найден коэффициент в формуле для нижнего критического напряжения, равный 0,17; при этом энергия варьировалась по трем параметрам.

ГЛАВА X
 ОСОБЕННОСТИ РАСЧЕТА ОБОЛОЧЕК НА УСТОЙЧИВОСТЬ § 94. Характерные диаграммы в задачах устойчивости. Некоторые аналогии
 Сделаем некоторые общие выводы, касающиеся задач устойчивости оболочек. Введем параметры Р и А, из которых первый характеризует нагрузку сжимающую силу, крутящий момент или давление, второй — общую деформацию конструкции сближение нагруженных кромок, угол взаимного поворота торцов или объем вмятины. Кроме того, обозначим через параметр прогиба, предполагая для простоты, что оболочка может быть представлена как система с одной степенью свободы.
 Допустим, что при действии на оболочку той или иной нагрузки в ней возникает безмоментное напряженное состояние. Для оценки устойчивости этого состояния можно сравнивать исходную равновесную форму с бесконечно близкими формами, либо с такими равновесными формами, для перехода к которым оболочка должна получить большие прогибы.
 В первом случае речь идет об устойчивости «в малом», и для определения критической нагрузки Ркр здесь надо идти по тому же пути, что и в теории устойчивости стержней или пластинок. Равновесное состояние системы при критической нагрузке в пределах малых перемещений рассматривается как безразличное: любому значению
 прогиба соответствует одна и та же нагрузка. На фиг. 10.1
 показан получаемый при этом график «нагрузка — прогиб». Он состоит из двух прямых, одна из которых совпадает с осью ординат, а вторая — параллельна оси абсцисс. Точка пересечения этих прямых соответствует критической нагрузке; мы будем интересоваться только
 63 >0
 эо, в эо
 г и
 330, 8?Э0
 >. -<-ч
 н- г-ъ-ВЗО
 33< О
 JS30, дЗгО
 Фиг. 10.1. Диаграмма «нагрузка — прогиб» по линейной теории.

§ 941 ХАРАКТЕРНЫЕ ДИАГРАММЫ В ЗАДАЧАХ УСТОЙЧИВОСТИ
 371
 наименьшей критической силой. Прямые 0 и Р Ркр отвечают равновесным формам оболочки; следовательно, для всех точек этих линий независимо от знака первая вариация полной энергии системы должна обращаться в нуль: 89 0. При нагрузках Р <С РКр равновесная форма устойчива, поэтому на этом участке вторая вариация энергии должна р быть положительна: 823 > 0; при Р Ркр равновесие безразлично и 823 0, наконец, при Р > РКР равновесная форма неустойчива и 8ЧЭ < 0.
 Для точек плоскости Р,, не лежащих на прямых 0 и Р Ркр, мы должны получить 8«Э0. Предположим, что совершается переход от одной неравновесной формы оболочки к другой, соседней фиг 102 Нагру3ка в зави.
 с ней, причем параметр нагрузки является симости от общей деформа-
 заданным. Тогда при удалении от поло- ции по линейной теории,
 жения устойчивого равновесия должно
 быть ЬЭ > 0, а в случае приближения к нему 83 < 0. Для различных квадрантов графика получаем знаки 8<9, указанные на фиг. 10.1. На следующей фиг. 10.2 изображена зависимость между нагрузкой и деформацией. До потери устойчивости нагрузка например, сжимающая сила пропорциональна деформации укорочению оболочки, а при Р Ркр деформация оказывается неопределенной.
 АР
 Фиг. 10.3. Нагрузка, общая деформация и прогиб для плоской пластинки.
 Еще раз отметим, что понятие безразличного равновесия связано с условием малости прогибов по отношению к длине стержня или стороне пластинки.
 Обратимся к равновесным формам тонкостенных конструкций, соответствующим большим прогибам. Напомним, что прогибы считаются сравнимыми с толщиной стенки, но малыми по отношению

372
 0С0БЕНН0С1И РАСЧЕТА ОБОЛОЧЕК НА УСТОЙЧИВОСТЬ ГЛ. X
 к другим размерам конструкции. Поэтому для стержней с массивным сечением интересующий нас тип деформации не является характерным. Между тем для тонких пластинок можно с помощью теории больших прогибов определить равновесные формы в закритической
 области. Графики «нагрузка — прогиб», «деформация — прогиб» и «нагрузка — деформация», харак¬
 терные для пластинок любого очертания, изображены на фиг. 10.3 и 10.4. Отправные равновесные формы являются устойчивыми вплоть до критической нагрузки. В точке Р Ркр получаем 83 0, о2Э 0. При Р > Ркр каждой нагрузке соФиг. 10.4. Диаграмма закритиче- ответствуют три равновесные формы,
 ской деформации плоской пла- из которых две являются устойчи-
 стинки. выми при прогибах и —,
 а одна — неустойчивой при 0. Знаки вариации 8Э для неравновесных изогнутых форм указаны на графике.
 Графики, типичные для оболочек, даны на фиг. 10.5. Характеристики равновесных форм будут различными в зависимости от того, заданы ли на кромках оболочки усилия испытание при задаваемой нагрузке или перемещения испытание при задаваемой деформации.
 Первому случаю соответствует фиг. 10.6, второму— фиг. 10.7. Как мы видели, состояние безразличного равновесия, разделяющее устойчивую и неустойчивую области, будет при этом отвечать разным значениям прогиба fx и 2.
 Интересующие нас диаграммы примут иной вид, если на начальной стадии нагружения напряженное состояние конструкции не является безмоментным. Так, при действии на искривленную панель поперечной нагрузки изгиб будет происходить уже при малых значениях давления. График Р А примет вид, показанный на фиг. 10.8. Разветвления равновесных форм здесь не будет, но попрежнему для некоторой области нагрузок имеют место три различных равновесных формы. Нагрузки Рв и Рн> соответствующие верхней и нижней границам этой области, мы условились называть критическими.
 Фиг. 10.5. Нагрузка, общая деформация и прогиб для оболочки.

§ 94 ХАРАКТЕРНЫЕ ДИАГРАММЫ В ЗАДАЧАХ УСТОЙЧИВОСТИ
 373
 Приведенные выше графики являются характерными для многих нелинейных систем; аналогичные зависимости встречаются не только в теории упругости, но в некоторых других областях механики и физики. Так, явление перескока от одного устойчивого равновесного положения к другому имеет место для арок, подвергающихся действию нагрузки со стороны выпуклости. В отличие от рассматри-
 Фиг. 10.6. Диаграмма закритиче- Фиг. 10.7. Диаграмма закритиче-
 ской деформации для оболочки при ской деформации оболочки при
 задаваемой нагрузке. задаваемой деформации.
 ваемых нами задач перемещения арки — в том случае, когда она не является пологой, — сравнимы с ее размерами. Задачи, относящиеся к подобному перескоку упругого стержня, обсуждались в работах И. Я. Штаермана 10-5 и Е. П. Попова 1и.
 К одному из разделов астрономии — космогонии — относится теория фигур равновесия небесных тел В ней изучается устойчивость вращения жидкой массы вокруг некоторой оси с учетом действующих между частицами сил притяжения, а также центробежных сил. Основы этой теории были заложены А. М. Ляпуновым в диссертации, относящейся к 1884 г., и в ряде последующих трудов.
 В книге П. Аппеля, специально посвященной такого рода задачам, приведены графики фигур равновесия вращающейся жидкости; некоторые из них весьма сходны с диаграммами Pf или РД для оболочки. Место потенциальной энергии упругой системы
 Обзор этих трудов дан в книге Н. Д. Моисеева «Очерки развития теории устойчивости», Гостехиздат, 1949, стр. 553.
 П. Аппель, Фигуры равновесия вращающейся однородной жидкости, ОНТИ, 1936. См. также книги Джинса J. Jeans, Astronomy and Cosmogony, Cambridge, 1928 и В. А. Крата «Фигуры равновесия небесных тел». Гостехиздат, 1950.
 Фиг. 10.8. Закритическая деформация оболочки с начальной погибью, обращенной в сторону вогнутости.

374 ОСОБЕННОСТИ РАСЧЕТА ОБОЛОЧЕК НА УСТОЙЧИВОСТЬ ГЛ. X
 заменяет здесь разность между потенциальной энергией сил притяжения и энергией центробежных сил. Исследование первой вариации энергии при различных значениях параметров массы тела или средней плотности буквально повторено в рассуждениях настоящего параграфа. Точка разветвления двух кривых, отвечающих фигурам равновесия, называется в космогонии точкой бифуркации; точка с вертикальной касательной подобной точке Дн на фиг. 10.7 носит название предельной.
 Аналогичные задачи встречаются также при анализе нелинейных систем в электротехнике и радиотехнике.
 § 96. Факторы, ускоряющие или замедляющие наступление хлопка оболочки
 Допустим, что при нагружении оболочки удается обеспечить полную однородность напряженного состояния благодаря отсутствию начальной погиби, равномерности распределения нагрузки, постоянству толщины оболочки и т. д. Будем называть такие условия нагружения «идеальными». Тогда нагрузка должна достичь верхнего критического значения; на графике РА на фиг. 10.9 ему соответ-
 Фиг. 10.9. Хлопки оболочки при задаваемой нагрузке, задаваемой деформации и в упругой испытательной машине.
 ствует точка А. После этого должна произойти потеря устойчивости «в большом» — перескок к новому устойчивому положению равновесия. При задаваемой нагрузке скачок происходит по горизонтальной прямой Л, при задаваемой деформации — по вертикальной прямой А2у на реальной испытательной машине с некоторой упругой характеристикой — по наклонному участку АЗ.
 Если предположить, что при хлопке не образуются пластические деформации, то обратный процесс разгрузки — «выхлоп» оболочки— должен снова привести к одному из устойчивых состояний на участке О А. Здесь исходными точками для перечисленных вариантов нагружения будут, соответственно, точка В нижнего критического

§ 95 ФАКТОРЫ, УСКОРЯЮЩИЕ ИЛИ ЗАМЕДЛЯЮЩИЕ НАСТУПЛЕНИЕ ХЛОПКА 375
 напряжения, либо точка С нижней критической деформации, либо, наконец, точка D, отвечающая упругой характеристике испытательной машины наклонной линии dd.
 К факторам, ускоряющим наступление хлопка, относятся прежде всего начальная погибь и неравномерность распределения напряжений. Наиболее опасной является, как мы видели в § 88, начальная погибь, форма которой отвечает форме потери устойчивости гладкой оболочки. В зоне концентрации сжимающих напряжений всегда образуются начальные выпучины, а это равносильно появлению начальной погиби.
 На процесс потери устойчивости могут также влиять начальные напряжения. Допустим, что несколько искривленных панелей соединяют путем наложения сварных швов. После охлаждения конструкция получает как пластические, так и упругие деформации. В узкой зоне вблизи шва напряжения являются растягивающими; в остальной части панели возникают сжимающие напряжения. Если под действием внешней нагрузки конструкция подвергается сжатию по направлению шва, то дополнительные напряжения будут складываться с начальными и потеря устойчивости произойдет при относительно низких дополнительных напряжениях.
 Влияние поперечной нагрузки на устойчивость оболочки при наличии основных усилий в срединной поверхности может иметь различный характер. Поперечная нагрузка, действующая к центру кривизны, снижает критические напряжения. При поперечной нагрузке, направленной от центра, критические напряжения в известных пределах повышаются.
 Температурный режим оказывает влияние на критические напряжения прежде всего благодаря изменению механических характеристик материала. Расчет оболочки на устойчивость сводится при этом к определению критической нагрузки в неупругой области с учетом видоизмененной диаграммы «напряжение — деформация». С другой стороны, потеря устойчивости оболочки может быть связана с явлением ползучести; при этом особое значение приобретают величина и форма начальной погиби.
 Надо ли учитывать в расчетах на устойчивость повторность приложения нагрузки? Судя по известным данным о разрушении образцов при повторных растягивающих нагрузках, разрушающее напряжение уменьшается при возрастании числа циклов нагружения. Надо полагать, что и при действии на тонкостенную конструкцию повторных сжимающих нагрузок, лежащих ниже «номинальной» критической величины, должно иметь место постепенное накопление прогибов на определенных ограниченных участках оболочки. В начальной стадии погибь может оказаться почти неуловимой; однако повторение нагрузки повлечет за собой появление остаточных деформаций, особенно вблизи гребней выпучин. В конечном счете должен произойти хлопок, причем, повидимому, критические напряжения могут

376 ОСОБЕННОСТИ РАСЧЕТА ОБОЛОЧЕК НА УСТОЙЧИВОСТЬ ГЛ. X
 лежать заметно ниже напряжений, соответствующих однократному нагружению. Желательно проверить это экспериментально.
 Наконец, скорость нагружения также оказывает существенное влияние на характер выпучивания оболочки. В случае динамического нагружения волнообразование происходит в форме, заметно отличающейся от обычной. Так, например, при подводном взрыве замкнутая цилиндрическая оболочка получает на участке, ближе расположенном к источнику взрывной волны, большее число выпучин по окружности, чем в остальной части. Но повышение числа волн связано с увеличением давления, воспринимаемого оболочкой, так как соответствует высшим формам потери устойчивости. При рассмотрении условий ударного нагружения оболочки можно,. повидимому, непосредственно сравнивать передающуюся оболочке кинетическую энергию с высотой энергетического барьера, соответствующего той или иной форме выпучивания.
 То обстоятельство, что перескок нелинейной упругой системы от одного равновесного состояния к другому обычно связан с преодолением некоторого энергетического барьера, дает основание провести некоторые аналогии с понятиями квантовой механики. Так, например, при исследовании влияния различных факторов на устойчивость оболочки «в большом» можно поставить задачу об определении вероятности прохождения системы через энергетический барьер.
 § 96. Использование данных нелинейной теории для практических расчетов
 Как должен использовать данные нелинейной теории инженер, проектирующий заново тонкостенную конструкцию или производящий поверку устойчивости конструкции, находящейся в эксплуатации? К этому вопросу можно подойти с различных точек зрения.
 1. Можно положить в основу расчета величину верхнего критического напряжения, найденную с учетом возможных неправильностей в форме оболочки. При этом нужно пользоваться диаграммами типа фиг. 7.14, устанавливающими связь между верхними точками диаграммы «напряжение — прогиб», и параметрами, характеризующими начальную погибь. Такой подход обосновывается таким образом, что при статическом приложении нагрузки среднее напряжение должно пройти все точки диаграммы pf> вплоть до ?в, и
 Это было теоретически и экспериментально йоказано М. А. Лаврентьевым и А. Ю. Ишлинским 10-2. В других работах были изучены условия динамического нагружения стержней в испытательных машинах 10Л.
 На это обратил внимание Я. Налешкевич юло.
 Этот путь избран в работах Доннела 813, 8 14 и ряда других авторов.

§ 96
 ИСПОЛЬЗОВАНИЕ ДАННЫХ НЕЛИНЕЙНОЙ ТЕОРИИ
 377
 лишь после этого должен произойти хлопок к новому равновесному положению с большими прогибами. Такой расчет является наиболее естественным, если при проектировании удается установить предельные амплитуды начальных неправильностей и учесть другие обстоятельства, приводящие к прощелкиванию оболочки. Надо признать, однако, что такого рода данные далеко не всегда известны проектировщику.
 2. Другой исходной величиной может явиться напряжение равных энергий p9i для которого полная энергия системы в неизогнутом положении оболочки равна энергии выпученного состояния. Здесь мы уже не интересуемся причинами, непосредственно вызывающими хлопок, и считаем, что упругая конструкция должна занять то равновесное положение, удовлетворяющее условиям закрепления, которое соответствует минимуму полной энергии.
 3. Наконец, в качестве критерия устойчивости оболочки может быть принято нижнее критическое напряжение рн. Это равносильно предположению, что оболочка может совершить хлопок к любому равновесному состоянию независимо от того, какая энергия ему отвечает, так как всегда могут найтись налицо факторы, помогающие оболочке преодолеть соответствующий энергетический барьер. К этому можно прибавить, что верхнее критическое напряжение в сильной степени зависит от различных случайных обстоятельств, в то время как нижняя граница является более стабильной это видно, например, из фиг. 7.14.
 Против такого подхода были выдвинуты некоторые возражения. С одной стороны, указывалось на то, что теоретические выкладки по определению нижней границы могут привести к физически неоправданным результатам, как, например, к отрицательному значению критического давления для сферической оболочки см. § 92. С другой стороны, выдвигается то положение, что в некоторых случаях нижняя граница, так же как и верхняя, резко меняется в зависимости от начальных неправильностей.
 Надо учесть, однако, что к различным «неожиданностям» приводит обычно определение нижнего критического напряжения в первом приближении. Если же, как мы видели на многих примерах в главах VIII и IX, установить величину ра хотя бы во втором приближении с учетом изменения формы волнообразования, то это значение хорошо согласуется с результатами опытов, ограничивая снизу область экспериментальных точек. Вместе с тем возможное изменение нижней границы при учете начальных неправильностей должно идти, повидимому, в сторону повышения этой величины,
 Такой подход рекомендовался в работе Кармана и Цзянь Сюэшеня 8-15.
 Это положение было выдвинуто в статье Цзянь Сюэ-шеня 8ю.
 На это указал В. И. Феодосьев 96.
 См. статью М. С. Корнишина и X. М. Муштари в.т. t

378 ОСОБЕННОСТИ РАСЧЕТА ОБОЛОЧЕК НА УСТОЙЧИВОСТЬ ГЛ. X
 так что расчет по р„, вычисленному для гладкой оболочки, будет производиться в запас прочности.
 В итоге приходится признать, что накопленные до сих пор теоретические и экспериментальные сведения о поведении оболочек при больших прогибах позволяют уверенно вести расчет лишь по нижнему критическому напряжению при условии, что эта величина определена в достаточно высоком приближении. При назначении коэффициента запаса устойчивости надо учитывать, что после хлопка оболочка уже, как правило, не в состоянии нести возрастающую нагрузку.
 «Скелет» оболочки в закритической области
 Изучая деформацию сжатой прямоугольной пластинки в закритической области, мы выяснили, что нагрузка воспринимается ею за счет сравнительно узких краевых полос, связанных с подкрепляющими ребрами. Такая же узкая рабочая полоса образуется вдоль жесткого контура в случае сжатой круглой пластинки. При сдвиге удлиненной прямоугольной пластинки передача нагрузки после потери устойчивости происходит благодаря наличию растянутых наклонных складок, протягивающихся от одного продольного края пластинки
 к другому.
 Представим себе теперь длинную гладкую цилиндрическую оболочку, работающую на сжатие. Здесь нет продольных жестких ребер, вблизи которых могли бы концентрироваться рабочие участки оболочки после потери устойчивости. Поэтому оболочка
 «сама» создает для себя такие подкрепляющие ребра. Напомним, что в процессе
 хлопка вокруг ромбовидных выпучий образуются складки, т. е. узкие сильно искривленные участки оболочки, обладающие сравнительно большой изгибной жесткостью фиг. 10.10.
 Определяя равновесные формы оболочки и выбирая приближенные выражения для прогиба, мы много говорили о форме глубоких вмятин, продавливающихся в процессе хлопка. Однако сами по себе площадки
 вмятин не должны нас интересовать: напряжения в срединной
 поверхности внутри этих площадок пренебрежимо малы, так же как в средней полосе сжатой прямоугольной пластинки. Нагрузка передается от одного конца оболочки к другому через складки,
 Фиг. 10.10. «Скелет» оболочки, сжатой вдоль образующей, после выпучивания.

§ 97
 «СКЕЛЕТ» ОБОЛОЧКИ В ЗАКРИТИЧЕСКОЙ ОБЛАСТИ
 379
 пересекающиеся между собой и образующие как бы «скелет» оболочки, подобно арматуре в железобетонных конструкциях. Окончательное разрушение оболочки, выражающееся в появлении трещин, связано, с одной стороны, со значительным возрастанием суммарных напряжений в волокнах складок и, с другой стороны, с вторичной потерей устойчивости складок как тонкостенных стержней. Как правило, уже в самый момент хлопка вдоль складок развиваются пластические деформации. Очертания «стержневой системы»,
 образованной складками, зависят от интенсивности нагрузки, передающейся оболочкой, и ее общей деформации.
 В том случае, если оболочка испытывает всестороннее сжатие, складки вытягиваются вдоль образующей фиг. 10.11; здесь вторичная потеря устойчивости складок, вызывающая образование трещин и полное разрушение конструкции, выражается особенно четко.
 К изучению формы изогнутой поверхности после потери устойчивости можно подойти и с чисто геометрической точки зрения. Мы говорили о том, что в области выпучины цепные напряжения близки к нулю. Но это означает, что после хлопка эти участки оболочки представляют собой поверхности, развертывающиеся на плоскость. Правда, они не могут быть получены путем непрерывного изгибания начальной цилиндрической поверхности, потому-то они и образуются лишь в процессе хлопка. Но для таких вмятин
 Фиг. 10.11. «Скелет» оболочки, подвергающейся внешнему давлению, после выпучивания.
 Фиг. 10.12. Предельная форма срединной поверхности оболочки при сжатии вдоль образующей.

380
 ОСОБЕННОСТИ РАСЧЕТА ОБОЛОЧЕК НА УСТОЙЧИВОСТЬ ГЛ. X
 характерно то, что они ограничиваются пересекающимися складками; в пределе эти складки можно рассматривать как линии фиг. 10.12. Исходя из такого представления об изогнутой поверхности сжатой оболочки, Кирсте 8Л8 предложил своеобразный метод определения критической нагрузки; элементарный вывод привел к значению коэффициента р в формуле для напряжения о pEhR, равному 0,187. Хотя такое совпадение с более обоснованным результатом см. § 83 и является, видимо, случайным, самый подход к рассмотрению поверхности оболочки после потери устойчивости, как развертывающейся без непрерывного изгибания на первоначальную поверхность, заслуживает внимания.
 § 98. Об особенностях применения вариационых методов к нелинейным задачам
 Рассмотрим диаграмму РА, характеризующую зависимость между нагрузкой и общей деформацией пластинки или оболочки, с энергетической точки зрения.
 Начнем со случая пластинки; пусть на фиг. 10.13 докритической деформации отвечает прямая СМ, а послекритической — кривая АВ. Площадь, заключенная между кривой РА и осью абсцисс на фиг. 10.13, очевидно, соответствует потенциальной энергии деформации пластинки U, складывающейся из U0 и Un. Приращение dU,
 выражающееся площадью заштрихованного участка, равно
 dU Р А й?Д, 10.1 а общая площадь будет
 Фиг. 10.13. К применению теорем Лагранжа и Кастилиано в нелинейных задачах по пластинкам.
 Из равенства 1 вытекает соотношение
 P-dJL
 10.3
 известное как теорема Лагранжа пластинку мы считаем здесь системой с одной степенью свободы. Таким образом, теорема Лагранжа может быть распространена на нелинейные задачи теории пластинок.
 Многогранник, изображенный на фиг. 10.12, легко получить из листа плотной бумаги см. Г. М. М и р а к ь я н, Прямой круговой цилиндр, Гостехиздат, 1955, стр. 35.

§ 98 ОБ ОСОБЕННОСТЯХ ПРИМЕНЕНИЯ ВАРИАЦИОННЫХ МЕТОДОВ
 381
 Иначе обстоит дело с другой теоремой, связанной с именем Кастилиано. Если бы речь шла только о линейном участке диаграммы ОЛ, то можно было бы выписать известные зависимости
 dU А Р dP л dU
 10.4
 10.5
 При нелинейной характеристике процесса равенство 5 уже не будет иметь места. Можно, однако, получить аналогичную зависимость, если воспользоваться понятием полной энергии Э, равной разности между потенциальной энергией U и работой внешней нагрузки 1РА. На графике фиг. 10.13 надо из площади О ABC вычесть площадь прямоугольника ODBC; тогда получим «отрицательную» площадь О DBA, лежащую между линией А Р и осью ординат. Приращение dd равно
 d3 —A PdP, 10.6
 а полная величина
 р
 э—jAPdP. 10.7
 Следовательно, в нелинейных задачах теории гибких пластинок мы не можем пользоваться теоремой Кастилиано в обычной форме; ее заменяет соотношение
 А
 йЭ_
 dP 9
 10.8
 Фиг. 10.14. К применению энергетических теорем в задаче об устойчивости оболочки.
 Все сказанное относится и к нелинейным задачам теории оболочек. На фиг. 10.14 изображена диаграмма РД для оболочки до потери устойчивости отрезок ОА и в послекритической стадии линия АКВ. Некоторой точке кривой отвечает потенциальная энергия деформации У,
 измеряемая площадью О АКВ направление обхода площади указано стрелками. Пусть требуется определить три различных значения нагрузки при заданной деформации А. Мы можем воспользоваться теоремой Лагранжа 3, причем производные должны быть найдены отдельно для различных участков диаграммы. Полная энергия Э отвечает на фиг. 10.14 взятой со знаком минус заштрихованной площади; направление обхода и здесь показано стрелками. Вычисляя производные от Э по Р для различных ветвей диаграммы, мы найдем три различных значения А.

382 ОСОБЕННОСТИ РАСЧЕТА ОБОЛОЧЕК НА УСТОЙЧИВОСТЬ ГЛ. X
 Как известно, теорема Лагранжа связана с принципом возможных перемещений, а теорема Кастилиано — с принципом возможных изменений напряженного состояния. Мы видим, что применение второго из этих принципов в теории гибких пластинок и оболочек имеет свои особенности; это относится также и к другим нелинейным задачам теории упругости и пластичности.
 В нелинейных задачах теории оболочек некоторые новые черты приобретают также вариационные методы Ритца и Бубнова — Галеркина. При изложении метода Ритца обычно указывается 16, что в задачах устойчивости он приводит к завышенному значению критической нагрузки. Задавая изогнутую поверхность оболочки с помощью одного или нескольких параметров, мы учитываем лишь некоторые из возможных изогнутых состояний, превращая оболочку из системы с бесконечно большим числом степеней свободы в систему с одной или несколькими степенями свободы. Этим на систему накладываются лишние связи, благодаря чему она становится как бы менее гибкой; поэтому принято говорить, что метод Ритца дает «верхнюю оценку» для критической нагрузки. Ошибка приближенного решения сводится к нулю, если предполагаемая форма изогнутой поверхности оказывается совпадающей с действительной формой.
 Но все эти рассуждения относятся к верхней критической нагрузке, при которой происходит переход от начальной формы равновесия оболочки к изогнутой. Было бы опрометчиво распространять их на всю диаграмму «нагрузка — прогиб» и, особенно, на ее правую часть, содержащую нижнюю критическую точку. Допустим, что на диаграмме фиг. 10.9 мы движемся по линии 1В сверху вниз — от устойчивых равновесных форм участка 1В к неустойчивым участка ВА. Накладывая в приближенном решении на систему лишние связи, мы и здесь делаем систему более жесткой; но тогда можно предположить, что отброшенные нами формы изогнутой поверхности отвечали бы более раннему переходу от устойчивых состояний к неустойчивым, т. е. более высокому значению Р. Именно такой результат был получен выше для цилиндрической и сферической оболочек § 83 и 93. Надо учесть, правда, что весь участок 1В построен на основании приближенного решения, в то время как начальный участок ОА определенно соответствовал истинным равновесным формам гладкой оболочки. Поэтому в различных вариантах решения мы далеко не всегда получаем закономерное изменение нижней границы.
 Все сказанное о методе Ритца относится и к методу Бубнова — Галеркина, если: а уравнения типа 5.53 соответствуют принципу
 Цзянь Сюэ-шень отмечает, что аналогичные зависимости формулируются в термодинамике между объемом и давлением и двумя потенциалами: теплосодержанием и внутренней энергией ело.
 См. статью X. М. Муштари и И. В. Свирского. G-8.

МОДЕЛИРОВАНИЕ ОБОЛОЧЕК -
 383
 возможных перемещений и б выбранное выражение для прогиба удовлетворяет всем граничным условиям. Напомним, что при этом метод Бубнова — Галеркина должен привести к тем же результатам, что и метод Ритца. Если хотя бы одно из условий не выполнено, то заранее ничего нельзя сказать о знаке ошибки, получаемой при определении как верхнего, так и нижнего критических напряжений. Условие б можно не принимать во внимание лишь в том случае, когда уравнение Бубнова — Галеркина применяется в обобщенном виде, т. е. включает «внеинтегральные» члены.
 § 99. Моделирование оболочек при экспериментальных исследованиях
 Исследования устойчивости оболочек затрудняются тем, что образцы, претерпевшие хотя бы один хлопок, выходят из строя и, как правило, не могут быть испытаны вторично. При изготовлении моделей приходится считаться с особой чувствительностью оболочки к различным возмущающим факторам, в особенности к начальной погиби; это сильно повышает стоимость моделей. Поэтому к определению размеров испытуемых моделей следует подходить с большой осторожностью.
 Чтобы установить критерии подобия для гибких оболочек, надо представить исходные дифференциальные уравнения и граничные условия задачи в безразмерной форме. В применении к случаю круговой цилиндрической панели перепишем систему уравнений 5.29—5.30 в виде
 IS У-f Ij ll j JUtl V- 10.9
 dsdri d;2Rh ‘ dr?'
 Здесь введены обозначения:
 x a
 У_ b ’
 10.10
 Такое преобразование предложено О. И. Теребушко.

384
 ОСОБЕННОСТИ РАСЧЕТА ОБОЛОЧЕК НА УСТОЙЧИВОСТЬ
 ГЛ. X
 под а и b понимаются длина и ширина панели. Пользуясь безразмерными параметрами главы VII, получаем уравнения:
 1 д<, 0 дК, дК_ 121—x2 V4rz ддт2 ГдУ
 Аналогичным образом могут быть представлены в безразмерной форме геометрические и статические граничные условия. Нетрудно заметить, что значение координаты на дуговых кромках панели будет зависеть от параметра к ajby т. е. от отношения сторон панели. Мы приходим к заключению, что при моделировании цилиндрической панели должны быть соблюдены равенства
 А2 а
 const, Л у const 10.12
 и материалы натуры и модели должны удовлетворять равенству
 const; 10.13
 при этом для нагрузок и усилий можно выписать соотношения:
 ят С0П5’ <p9onst и т- д-
 Судя по этим соотношениям, при моделировании гибких оболочек должно быть выполнено условие полного геометрического подобия натуры и модели и, кроме того, соответствия коэффициентов Пуассона материалов. Это последнее условие обычно выдерживается лишь приближенно с учетом того, что х меняется для таких материалов, как дуралюмин, сталь и т. д. в узких пределах и что влияние величины х на искомые величины критических напряжений относительно невелико. Если следовать условию полного геометрического подобия, то при моделировании крупных сооружений приходится выбирать толщину стенки модели сравнительно малой. При
 этом нельзя идти слишком далеко, так как чрезмерное уменьшение
 толщины нарушает условие однородности материала; надо также считаться с особенностями технологии изготовления моделей различной толщины. Следует учесть также и то, что при одной и той же точности изготовления одинаковых допусках влияние начальных неправильностей может быть иным, чем для реальной конструкции
 Здесь имеются в виду однородные граничные условия. О других условиях см. в статье А. А. Курдюмова 10Л.

§ 99
 МОДЕЛИРОВАНИЕ ОБОЛОЧЕК
 385
 например, при другой относительной начальной погиби. Поэтому при изготовлении моделей с малой толщиной стенки надо требовать большей точности изготовления.
 В некоторых случаях теми или иными граничными условиями можно пренебречь. Так, например, для удлиненной цилиндрической панели условия закрепления на дуговых кромках становятся несущественными. Тогда моделирование, естественно, облегчается: вместо двух критериев подобия 12 остается один: k — b2Rh const;
 иными словами, длину модели можно в известных пределах варьировать. Это же относится к случаю сжатия длинных замкнутых цилиндрических оболочек.
 При обработке экспериментальных данных необходимо представлять их в безразмерных данных, пользуясь критериями подобия.

ГЛАВА XI
 ОЧЕРК РАЗВИТИЯ ТЕОРИИ ГИБКИХ ПЛАСТИНОК И ОБОЛОЧЕК
 § 100. Сочинение Эйлера по колебаниям мембран. Общая теория пластинок в трудах Кирхгофа и Сен-Венана
 В трудах Петербургской Академии наук за 1766 г. было опубликовано первое научное исследование по теории абсолютно гибких пластинок мембран; оно принадлежало Л. Эйлеру 1ЛЗ. В этой статье изучались собственные колебания мембран прямоугольного и круглого очертания. Прямоугольная мембрана рассматривалась Эйлером как система взаимно перпендикулярных гибких нитей; им было получено дифференциальное уравнение колебаний
 d dz ddz,.,d dz
 Hfi eedT ffdy-
 В случае произвольной поперечной нагрузки это уравнение переходит в 1.72 в последнем уравнении надо кривизны 1Ра? и уру выразить через прогиб.
 21 октября 1788 г. перед конференцией Петербургской Академии наук выступил ученик Эйлера — молодой академик Я. Бернулли. Он изложил теорию колебаний прямоугольной жесткой пластинки при малых прогибах, представляя пластинку в виде системы взаимно перпендикулярных балок. Выписанное им дифференциальное уравнение для прогиба имело форму
 dz. d4z _ z я дх4 ' ду4 с4
 здесь с — постоянная, зависящая от жесткости пластинки и частоты колебаний. По сравнению с 1.63 в уравнении Бернулли отсутствовал член
 d4z
 2 ду2 ’ отвечающий’ как мы видели, кручению пластинки. Представление
 о пластинке как системе балок содержалось и в позднейшей работе французского математика Софи Жермен; полученное ею в 1811 г. дифференциальное уравнение также было неполным. С. Жермен использовала вариационный метод, примененный до того Лагранжем в его «Аналитической механике к исследованию деформации гибких нитей и балок; однако составленный Жермен функционал не соответствовал потенциальной энергии пластинки. Одним из рецензентов сочинения С. Жермен был Лагранж. Им была исправлена ошибка автора и составлено без подробного вывода полное уравнение изгиба жестких пластинок; запись уравнения была найдена в 1813 г. в бумагах Лагранжа. Впоследствии в трудах ряда ученых и прежде всего
 В транскрипции подлинника: частные производные обозначаются прямыми d; ее и ff—постоянные, соответствующие натяжению мембраны вдоль осей х и у; z — прогиб.

§ 101 ТРУДЫ И. Г. БУБНОВА ПО ТЕОРИИ ГИБКИХ ПЛАСТИНОК 387
 Навье и Кирхгофа были формулированы исходные положения теории жестких пластинок, уточнены граничные условия и решены многие частные задачи, в особенности по круглым пластинкам.
 В «Лекциях по математической физике» Кирхгоф 119 поставил перед собой новую задачу: построить теорию пластинок для того случая, когда перемещения нельзя считать малыми по сравнению с толщиной пластинки. Составив выражение для элементарной работы усилий в срединной поверхности и усилий изгиба, Кирхгоф сопоставил порядок различных членов и установил, что в этом случае нельзя отбрасывать нелинейные члены в формулах для деформаций срединной поверхности. Кирхгофом были приняты для деформаций выражения типа
 __ да, 1 дт2
 “ дх 2 <Г
 дх ’
 совпадающие с 1.7. В то же время для кривизн он счел возможным оста вить линейные выражения типа 1.11. Далее Кирхгоф воспользовался принципом возможных перемещений. Преобразуя вариацию энергии системы, он должен был прийти к дифференциальным уравнениям равновесия и статическим граничным условиям. Им не было выписано уравнение равновесия в окончательном виде, хотя все предварительные выкладки были сделаны.
 В 1881 г. был издан французский перевод книги Клебша «Теория упругости» с многочисленными примечаниями Сен-Венана 112. В оригинальном тексте книги содержалось уравнение изгиба пластинки, подвергающейся равномерному растяжению срединной поверхности усилиями Т:
 DV2V — TV2w fx, у.
 В примечаниях к § 73 Сен-Венан дал подробный обзор предыдущих исследований по теории пластинок и привел полное дифференциальное уравнение изгиба пластинки с учетом усилий в срединной поверхности:
 DW-fix. уТхд 2Тху-Туд.
 Усилия Ту, ТХу считались Сен-Венаном заданными, не зависящими от прогиба. Уравнения этого типа в 1890—1895 гг. были использованы Брайеном при рассмотрении устойчивости пластинки, сжатой в одном или двух направлениях.
 § 101. Труды И. Г. Бубнова по теории гибких пластинок. Приложения в кораблестроительных расчетах
 Как мы видели, во второй половине XIX века были сделаны первые шаги в исследовании гибких пластинок; однако применения для практических расчетов они не находили. Настоятельная необходимость в разработке технической теории гибких пластинок возникла на рубеже XIX и XX веков в связи с развитием металлического кораблестроения. Переход от деревянного парусного флота к металлическим судам с гребными винтами осуществлялся в первый период без коренных изменений в архитектуре корпуса корабля. Толщина обшивки назначалась без обоснованных расчетов. Между тем быстрое увеличение водоизмещения и глубины посадки кораблей приводило к значительному возрастанию нагрузки, испытываемой обшивкой днища; прогибы обшивки были сравнимы с ее толщиной. Разработка метода
 Proceedings London Math. Soc, 22, 1891.

388
 ОЧЕРК РАЗВИТИЯ ТЕОРИИ ГИБКИХ ПЛАСТИНОК
 ГЛ. XI
 расчета панели обшивки, получающей под давлением воды большие прогибы, оказалась одной из самых важных задач. Заслуга постановки этой задачи и ее решения принадлежит выдающемуся ученому и кораблестроителю И. Г. Бубнову. В J902 г. он опубликовал работу «Напряжения в обшивке
 судов от давления воды» 1Л, в которой показал, что напряжения в листах наружной обшивки от статической нагрузки во многих случаях сильно превосходят допускаемую величину. «Практические выводы из этого положения, идущего вразрез с практикой современного судостроения, весьма важны, — писал И. Г. Бубнов, — и всесторонний разбор его и составит предмет настоящей статьи. Вопрос этот усложняется еще и тем обстоятельством, что непосредственное аналитическое решение его еще не найдено, так что приходится подходить к нему окольными путями, в некоторых заключениях довольствоваться не строго точными доказательствами, а аналогиями... Ожидать же строгого и точного решения вопроса, которое появится, может быть, через десятки лет, — значит оставить корабельную архитектуру в том застое, в каком она находится полвека, со времени постройки первых железных судов»...
 И. Г. Бубнов установил классификацию пластинок по характеру напряженного состояния. Под жесткими он предложил понимать пластинки, при деформации которых преобладающими являются напряжения изгиба; если напряжения в срединном слое принимаются равными нулю, то лист называется бесконечно жестким. В случае, если преобладающими являются напряжения срединного слоя, пластинка характеризуется И. Г. Бубновым как гибкая, а в пределе, когда напряжениями собственно изгиба можно пренебречь, как бесконечно гибкая.
 Наибольшее внимание И. Г. Бубнова привлекла задача об определении напряжений и прогибов для гибкой прямоугольной пластинки, имеющей удлиненную форму и изгибающейся по цилиндрической поверхности. При этом напряжения в срединном слое можно считать постоянными по всей площади пластинки. И. Г. Бубнов определил зависимость между усилиями в срединной поверхности и относительным смещением длинных кромок пластинки при условии полного или частичного закрепления кромок. Им были тогда же составлены таблицы функций, с помощью которых можно провести расчет гибкой пластинки по формулам, относящимся к жесткой пластинке тех же размеров. Наряду с этим он рассмотрел случай гибкой круглой пластинки в предположении, что напряжения в срединном слое неизменны для всех точек пластинки. Такое допущение сделало возможным решение задачи в бесселевых функциях. Служащие для практических расчетов вспомогательные функции И. Г. Бубновым были также табулированы.
 При проектировании корпуса линейных кораблей типа «Севастополь» в 1906—1907 гг. И. Г. Бубнов ввел метод последовательных приближений в расчете тонкостенных конструкций. В первом приближении корпус корабля рассчитывается на изгиб как балка, в сечение которой входят полностью сечения всех элементов. При этом определяются напряжения волокон, находящихся на том или ином расстоянии от нейтральной оси. Во втором приближении площади сечения гибких элементов вводятся уже с учетом редукционных коэффициентов. Это прежде всего относилось к пластинкам: обшивка днища и настилу палубы, напряжения в которых часто превосходили эйлерову величину. И. Г. Бубнов считал тогда, что пластинка не может воспринять нагрузку, превышающую критическую, и принимал редукционный коэффициент равным отношению критического напряжения к напряжению в жесткой связи: <р акрар.
 Наиболее полное изложение теории гибких прямоугольных пластинок удлиненной формы было дано И. Г. Бубновым в курсе «Строительная механика корабля» 1912—1914 гг.. Здесь он дает определение гибкой пластинки как такой, в которой «при изгибе от нагрузки рх развиваются настолько

§ 102 НЕЛИНЕЙНЫЕ УРАВНЕНИЯ А. ФЕППЛЯ И Т. КАРМАНА
 389
 значительные напряжения ру и pz, направленные параллельно средней плоскости ее, что обстоятельства изгиба пластины заметно изменяются...» 1Л. Автор курса вводит понятия коэффициента распора, зависящего от продольной жесткости подкрепляющих ребер и коэффициента опорной пары, учитывающего крутильную жесткость контура. И. Г. Бубнов приводит окончательные формулы для расчета гибкой пластинки и подробно анализирует их, останавливаясь на предельных случаях вполне жесткой и вполне гибкой пластинок. Рассматривается и более сложный случай, когда пластинка подвергается действию не только поперечной нагрузки, но и значительных начальных усилий в своей плоскости.
 Большой интерес представляет исследование в «Курсе строительной механики корабля» влияние начальной кривизны пластинки. И. Г. Бубнов показывает, что при поперечной нагрузке, действующей со стороны выпуклости, пластинка, может находиться в неустойчивом равновесии и устанавливает границы области неустойчивости. «Всякое дальнейшее увеличение нагрузки p°z, — говорится в Курсе, — заставит пластину изменить свою кривизну на обратную, так что стрелка с0 станет положительной и равновесие пластины— устойчивым». И. Г. Бубновым была изучена, таким образом, модель «хлопающей мембраны».
 § 102. Нелинейные уравнения А. Феппля и Т. Кармана
 В «Лекциях по технической механике» А. Феппля 1907 г. были составлены уравнения изгиба абсолютно гибких пластинок, при больших перемещениях 114. Оставляя нелинейные выражения Кирхгофа для удлинений срединной поверхности, А. Феппль положил цилиндрическую жесткость пластинки равной нулю. Уравнение равновесия, полученное ранее Сен-Венаном, приняло форму
 d2w, d2w, 0 d2w, q _ n °x Jx ai>dy 2 dxdy ¥
 Сопоставив выражения для деформаций и выразив деформации через напряжения, Феппль получил уравнение совместности деформаций
 д2зх d2z д2зу Г d2w 2 d2w d2wl
 ду2 дх ду дх2 _дх ду дх2 ду2 J
 Далее он выписал уравнения равновесия усилий в срединной поверхности в проекциях на оси х и у и ввел функцию напряжений. Таким образом, им были получены уравнения типа 1.66 и 1.67. Перейдя к цилиндрической системе координат, А. Феппль составил соответствующие уравнения для круглой пластинки.
 Через несколько лет, в 1910 г., Т. Карман дал обзор теоретических
 работ по прочности в машиностроении 1>18. Он изложил результаты исследований И. Г. Бубнова, относящихся к гибким пластинкам, и указал на важное значение их для расчета обшивки корпуса корабля: благодаря усилиям в срединной поверхности реальная пластинка получает значительно большую несущую способность, чем это вытекает из теории жестких плит. Т. Карман дополнил первое из уравнений Феппля членом, содержащим цилиндрическую жесткость, и таким образом придал системе нелинейных дифференциальных
 уравнений окончательную форму 1.60 — 1.61. В этом виде уравнения
 были использованы впоследствии для решения различных частных задач.
 В работе С. П. Тимошенко 413, относящейся к 1915 г., определялась деформация круглой пластинки под действием приложенной по контуру

390
 ОЧЕРК РАЗВИТИЯ ТЕОРИИ ГИБКИХ ПЛАСТИНОК
 ГЛ. XI
 моментной нагрузки. Выражения для перемещений а и v были представлены в виде степенных рядов; был использован метод Ритца, причем потенциальная энергия варьировалась по трем параметрам. Таким путем было получено уточненное значение стрелы прогиба пластинки.
 § 103. Развитие теории гибких пластинок с 1920 по 1940 г. Запросы самолетостроения
 Исследование закритической деформации сжатых прямоугольных пластинок с привлечением аппарата теории упругости было впервые дано П. Ф. Папковичем. В 1920 г. была опубликована в «Морском сборнике» его статья «К вопросу о выпучивании плоских пластин, сжимаемых усилиями,
 превосходящими их эйлерову нагрузку» зл. В этой работе еще не были использованы уравнения 1.60 и 1.61 в полном виде, однако сама по себе постановка задачи имела неоценимое значение.
 В последующий период теории гибких пластинок были посвящены многочисленные труды. Значительное внимание как общетеоретическим вопросам, так и решению конкретных задач было уделено советскими учеными; это объяснялось прежде всего запросами быстро развивающихся в нашей стране областей техники и, в особенности, кораблестроения, самолетостроения и приборостроения. Особенно сильный толчок к разработке теории гибких пластинок был дан в 30-е годы в связи с развитием металлического самолетостроения. Оказалось, что тонкая дуралюминовая обшивка крыла, фюзеляжа и оперения самолета получает подобно обшивке корабля прогибы, сравнимые с ее толщиной. Однако большие перемещения возникали здесь не столько из-за действия поперечной нагрузки, сколько благодаря усилиям сжатия и сдвига в срединной поверхности. Под влиянием этих усилий обшивка теряла устойчивость, часто в пределах нормальной эксплуатационной нагрузки. Панели обшивки, расположенные между подкрепляющими ребрами — стрингерами и нервюрами, получали при этом заметные выпучины; происходило перераспределение внутренних усилий по ширине панели. Однако панель обшивки в целом продолжала нести нагрузку, в некоторых случаях заметно превышающую критическую. Определение несущей способности обшивки явилось одной из наиболее актуальных задач и вызвало ряд теоретических и экспериментальных исследований.
 С нуждами приборостроения оказался связанным расчет круглых гибких пластинок — не только плоских, но и имеющих начальную кривизну, а также гофрированных мембран с различным очертанием гофров.
 Наиболее важными для практических приложений оказались следующие вопросы: а определение прогибов и напряжений в прямоугольных и круглых пластинках, испытывающих большие прогибы под действием поперечной нагрузки; б изучение закритической деформации прямоугольных пластинок после потери устойчивости при сжатии и сдвиге и установление редукционных коэффициентов. Надо было также разработать эффективные методы приближенного интегрирования нелинейных уравнений задачи.
 Одна из ранних попыток решения первой из этих задач была сделана
 А. 	Фепплем. Его решение 116 соединяло результаты, полученные для жесткой пластинки и абсолютно гибкой мембраны. В книге Прескотта 122, относящейся к 1924 г., рассматривались пластинки прямоугольного и
 круглого очертания, шарнирно опертые по контуру, причем было использовано одно из уравнений системы 4.30 — 4.31.
 Ряд работ, посвященных большим прогибам прямоугольных пластинок при поперечной нагрузке, был выполнен в СССР в 1935—1939 гг.; они принадлежали П. М. Варваку 22, В. М. Даревскому 2 3, Б. И. Слепову 2Л1-

§ 103
 РАЗВИТИЕ ТЕОРИИ ГИБКИХ ПЛАСТИНОК
 391
 При этом, как правило, применялся метод Ритца; были рассмотрены случаи шарнирно опертых и защемленных пластинок со свободно перемещающимся или закрепленным в плоскости пластинки контуром. В дальнейшем по инициативе Д. Ю. Панова 49 в теории пластинок большого прогиба начал широко применяться метод Бубнова — Галеркина.
 В 30-х годах под руководством П. Ф. Папковича были поставлены исследования работы сжатых пластинок в закритической области. Один из наиболее важных трудов в этой области, относящийся к шарнирно опертой прямоугольной пластинке, был опубликован в 1932 г. П, А. Соколовым 317. Принятое им выражение для w в случае квадратной пластинки имело вид
 л, КХ ъу Зпх 7ZV 7ZX 3 пу
 W A sin — sin — 4- В sin sin — С sin — sin——,
 a a a a ' a a '
 т. e. содержало три независимых параметра. Задача была решена до конца, с построением графика редукционных коэффициентов. П. А. Соколов получил также практически ценные результаты для пластинок, ширина которых в 2 или 3 раза превышала длину.
 В 1929—1932 гг. Г. Вагнер 347 и Т. Карман 3-29 рассмотрели закритическую деформацию пластинок при сдвиге и сжатии без привлечения аппарата теории гибких пластинок. Ими были выдвинуты допущения, оправдывающиеся для случая значительного превышения нагрузкой критической величины.
 В нескольких работах Маргерра, Кромма и Треффца 1937 г. те же задачи исследовались с помощью энергетического метода. В первой из
 этих работ 3 36 форма волнообразования сжатой пластинки принималась такой же, как и в момент потери устойчивости. Была получена величина «касательного модуля» в диаграмме р е, равная половине начального модуля Е. Во второй статье 337 форма волнообразования задавалась с помощью нескольких параметров; была получена приближенная формула для
 редукционного коэффициента <крзр3- В третьей работе 3-31 рассматривалась удлиненная пластинка, подвергающаяся одновременному действию сжатия и сдвига.
 П. Я. Полубаринова-Кочина дала в 1935 г. решение задачи 31° о закритической деформации сжатой прямоугольной пластинки в предположении, что распределение сжимающих усилий вдоль двух кромок остается равномерным, а кромки пластинки свободно искривляются. Ею был впервые применен в теории гибких пластинок метод возмущения: прогиб, функция напряжений и нагрузка раскладывались в ряд по степеням некоторого параметра и подставлялись в исходные дифференциальные уравнения; затем приравнивались коэффициенты при одинаковых степенях параметра в левых и правых частях уравнений.
 Н. В. Зволинский 3 3 поставил перед собой целью определить верхнюю и нижнюю граничные кривые, между которыми должна лежать истинная диаграмма сжатия пластинки после потери устойчивости. Кромки пластинки принимались прямолинейными. Верхняя граница.находилась с помощью метода Ритца: задавались выражения для перемещений и, v, w, причем каждое из них содержало неизвестный параметр. Для разыскания нижней границы варьировались усилия в срединной поверхности.
 На целесообразность применения этого метода к нелинейным задачам теории упругости указал Г. Генки Zs. angew. Math, und Mech. 7, 1927, 80—81.

392
 ОЧЕРК РАЗВИТИЯ ТЕОРИИ ГИБКИХ ПЛАСТИНОК
 ГЛ. XI
 Особенностью расчета обшивки самолета на устойчивость является необходимость учета касательных усилий, передаваемых обшивкой. В связи
 с этим в работах А. Ю. Ромашевского 312, И. А. Свердлова 318 и
 В. 	М. Стригунова 319 была изучена закритическая деформация пластинок при сдвиге и при совместном действии сжатия и сдвига.
 Подробное экспериментальное исследование несущей способности пластинок при сжатии было проведено в 1938 г. Г. А. Олейниковым 36: им было испытано около 100 плоских панелей с определением формы волнообразования, редукционных коэффициентов и разрушающих нагрузок. Редукционные коэффициенты для обшивки, подвергающейся одновременно сжатию и сдвигу, были экспериментально найдены А. А. Подорожным
 в 1940 г. 39. Отметим также эксперименты над фанерной обшивкой И. И. Фаерберга з.ао.
 Одновременно с решением частных задач развивался и общий аппарат теории гибких пластинок. В 1936 г. Г. Г. Ростовцевым была получена система дифференциальных уравнений 1.155 и 1.156 для анизотропной пластинки 314; с помощью этих уравнений можно рассматривать также изгиб тонкого листа, подкрепленного часто расположенными ребрами.
 Итоги теоретических исследований по гибким пластинкам, выполненным до 1940 г., были подведены П. Ф. Папковичем во второй части его курса
 «Строительная механика корабля» 1в. Изложение теории пластинок открывается в этом курсе подробным выводом исходных дифференциальных уравнений. П. Ф. Папкович указывает, как лучшим образом выбрать приближенное выражение для прогиба; при уточненных решениях задач, относящихся к пластинкам различного очертания и с разными условиями закрепления, им приводится таблица коэффициентов в окончательном выражении для функции напряжений. П. Ф. Папковичем была предложена простая формула для вычисления редукционных коэффициентов, вытекающая из работы П. А. Соколова. В курсе намечаются пути решения отдельных задач в более высоких приближениях.
 § 104. Уточненные решения 1941 —1955 гг. Новые практические приложения
 Во время Великой Отечественной войны и в послевоенный период теория гибких пластинок получила дальнейшее развитие. Был выдвинут ряд новых вопросов; задачи, уже разбиравшиеся ранее, получили уточненное решение. Широкое послевоенное строительство в СССР сопровождалось внедрением научно обоснованных методов расчета в самые различные области техники. Теория гибких пластинок нашла новые приложения в строительстве гидротехнических сооружений проектирование затворов плотин, в вагоностроении расчет набора крыши цельнометаллического вагона, в инженерных сооружениях подбор высоких стенок балок и расчет различных тонкостенных конструкций.
 Г. Г. Ростовцев исследовал более подробно процесс закритической деформации сжатых прямоугольных пластинок — изотропных и ортотропных. Он установил, что при возрастании нагрузки число выпучин по направлению сжатия должно увеличиваться, причем переход от одного числа полуволн к другому должен иметь скачкообразный характер. Г. Г. Ростовцевым было
 также рассмотрено 314 влияние на распределение напряжений условий сопряжения пластинки с подкрепляющими ребрами: до этого обычно прини¬

§ 104
 УТОЧНЕННЫЕ РЕШЕНИЯ 1941 —1944 гг.
 393
 малось, что кромки пластинки свободно скользят вдоль ребер. Далее, им была подробно изучена деформация пластинки с начальной погибью при действии поперечной нагрузки.
 В книге В. И. Петрашеня 38 разработаны методы расчета затвора плотин с учетом больших прогибов обшивки. В связи с этим им было проведено подробное исследование закритической деформации обшивки при одновременном действии усилий в срединной плоскости и поперечной нагрузки. В. И. Петрашень провел анализ изменения потенциальной энергии при переходе от одной формы равновесия к другой. В работе В. И. Петрашеня отмечены также особенности работы обшивки после потери устойчивости при продольной и поперечной системах набора. Он выяснил, что продольная система набора обладает по сравнению с поперечной меньшей чувствительностью к начальной погиби.
 С. 	Н. Никифоров разобрал задачу о выпучивании сжатой прямоугольной пластинки после потери устойчивости при своеобразных граничных условиях, имеющих место в элементах строительных конструкций 35.
 В работах С. Леви 217, относящихся к 1942—1944 гг., было дано уточненное исследование деформации шарнирно опертых защемленных по краям пластинок при одновременном действии сжатая и равномерно распределенной поперечной нагрузка. Для шарнирно опертой пластинки прогиб w представлялся в виде отрезка тригонометрического ряда, причем в случае квадратной пластинки число параметров бралось равным девяти в случае чистого сжатия или семи при поперечной нагрузке и комбинированном действии сил. Функция напряжений находилась обычным методом из уравнения совместности деформаций. Далее раскладывалась в ряд Фурье поперечная нагрузка:
 ,-22мм.f
 Величины w, Ф и q подставлялись в дифференциальное уравнение равновесия; сопоставление членов, отвечающих одним и тем же индексам г и j, приводило к уравнениям, выражающим зависимость между параметрами нагрузки и прогиба. Таким образом были получены значения редукционных коэффициентов для случая чистого сжатия, приведенные на фиг. 3.15. В работе 221 приведены результаты экспериментов над квадратными пластинками с шарнирно опертыми и защемленными краями при действии поперечной нагрузки.
 В. А. Постновым в 1953 г. изучался характер взаимодействия между двумя смежными участками плоской обшивки и подкрепляющим ребром, имеющим тонкую стенку, при условии, что произошла местная потеря устойчивости обшивки и конструкция подвергается сжатию. В частности, определялось влияние крутильной жесткости продольных ребер на величину редукционного коэффициента обшивки 311.
 В книге Б. М. Броуде 3 2 оценивается влияние начальной погиби сжатой пластинки на ее несущую способность применительно к расчету высоких стенок стальных балок.
 Книга С. Бергмана 322, вышедшая в 1948 г., посвящена закритической деформации прямоугольных пластинок при сдвиге. В ней рассмотрены случаи квадратной пластинки с шарнирно опертыми краями, причем подкрепляющие ребра считаются жесткими или податливыми на изгиб в плоскости пластинки. Задача решается методом Ритца; упругая поверхность пластинки задается с помощью двух или трех независимых параметров. Далее исследовано влияние начальной погиби на деформацию пластинки. Особенность решения Бергмана состоит в том, что им учитывается взаимодействие между

394
 ОЧЕРК РАЗВИТИЯ ТЕОРИИ ГИБКИХ ПЛАСТИНОК
 ГЛ. XI
 пластинкой и подкрепляющими ребрами. В книге разобран также случай удлиненной пластинки; теоретические результаты сравниваются с данными некоторых опытов.
 Подобные же задачи изучены были в работе 31 И. И. Ааре 1953 г.. Им исследована деформация прямоугольной пластинки, подвергающейся сдвигу, при различных граничных условиях: а кромки пластинки свободно скользят вдоль ребер; б точки кромок неподвижны; в пластинка и ребра деформируются совместно. Первая из этих задач рассматривается с помощью метода Бубнова — Галеркина; прогиб задается с помощью двух параметров. Вторая задача решена в перемещениях, причем проведены параллельно вычисления по методам Ритца и Бубнова — Галеркина. Решая третью задачу, автор принял в выражении для прогиба пять независимых параметров. И. И. Ааре сравнил полученные им данные с решением Вагнера и показал, что теория гибких пластинок приводит к картине распределения напряжений, значительно отличающихся от «диагонально растянутого поля».
 Пластинкам круглого очертания был посвящен ряд работ Д. Ю. Панова 4Л0, В. И. Феодосьева 4Л6, Федергофера 424 и сл., Рейснера 431, Уэя 4.35. в. И. Феодосьевым в,16 рассмотрен случай защемленной пластинки при поперечной нагрузке с заданием угла поворота нормали в виде 0 С р — р; показатель степени z считается неопределенным. Параметре определяется по методу Бубнова — Г алеркина, а величина z находится из условия минимума работы нагрузки. Задача решалась как осесимметричная; однако при значительных прогибах пластинки, когда стрела прогиба превышает толщину более чем в 10 раз, оказалось необходимым дать более общее решение. Если радиальные перемещения точек контура не ограничены, пластинка теряет устойчивость в области, прилегающей к контуру; в связи с образованием складок упругая поверхность пластинки становится несимметричной. Большое внимание в книге 4Л6 уделено расчету хлопающих мембран, а также гофрированных мембран; изучены мембраны с синусоидальным гофром, имеющие плоский центр и без него, со свободной заделкой или полным защемлением по контуру. Для случая мембраны, не имеющей плоского центра, дано решение задачи во втором приближении с учетом местной потери устойчивости отдельных гофров. Расчету гофрированных
 мембран были посвящены также работы JI. Е. Андреевой 42, рассмотревшей гофр трапецевидного и пилообразного очертаний. Ею предложено вести расчет гофрированной мембраны как анизотропной пластинки Инж. сб. 21, 1955, 127—141.
 Китайский ученый Цянь Вэй-чан в 1947 г. 4Л9 применил к расчету пластинок круглого очертания метод возмущения; в качестве основного параметра была избрана стрела прогиба пластинки. Пользуясь этим методом, Цянь Вэй-чан, Ху Хай-чан и Е Кай-юань рассмотрели в 1953—1954 гг. большие прогибы сплошных и кольцеобразных мембран при разных условиях закрепления для случаев равномерно распределенной и сосредоточенной нагрузок. В предельном случае абсолютно гибкой кольцеобразной пластинки результаты оказались близкими к данным, полученным в 1951 г. С. А. Алексеевым 4Л.
 Круглые гибкие пластинки, находящиеся под действием неравномерно распределенной нагрузки и пар, приложенных по контуру, изучаются в курсе
 теории упругости польского ученого Губера 1Л6.
 Большие прогибы круглых пластинок после потери устойчивости при радиальном сжатии изучались различными методами Фридрихсом и Стокером 4'27, Э. И. Григолюком 46 и И. И. Воровичем 4’3

§ 105
 РАЗВИТИЕ ОБЩЕЙ ТЕОРИИ ГИБКИХ ОБОЛОЧЕК
 395
 § 105. Развитие общей теории гибких оболочек. Труды X. М. Муштари и В. 3. Власова
 В трудах X. М. Муштари, относящихся к 1935—1938 гг., был изучен
 общий случай гибкой оболочки произвольного очертания 5‘8. В качестве координатных линий были избраны линии кривизны поверхности. Изогнутое положение оболочки определялось деформациями срединной поверхности и углами поворота трехгранника, образованного нормалью к поверхности и касательными к линиям кривизн. В отличие от А. Лява, определившего эти величины в предположении малости перемещений, X. М. Муштари получил выражения для деформаций срединной поверхности и углов поворота при перемещениях, сравнимых с толщиной оболочки. Вместе с тем перемещения считались малыми по сравнению с другими размерами оболочки, а деформации — лежащими в пределах действия закона Гука. Далее X. М. Муштари были выписаны приближенные зависимости между усилиями и деформациями для анизотропной оболочки, предложенные ранее в 1925 г. И. Я. Штаерманом. Получив уравнения равновесия элемента оболочки, X. М. Муштари подробно проанализировал их, сопоставляя порядок отдельных членов. Оказалось, что при известных условиях, когда деформация оболочки сопровождается волнообразованием и число волн для ограниченной оболочки сравнительно велико квадрат числа волн велик по сравнению с единицей, эти уравнения могут быть значительно упрощены. X. М. Муштари выписал выражения для потенциальной энергии оболочки при конечных перемещениях. В применении к задачам устойчивости он получил далее линейные уравнения нейтрального равновесия для цилиндрических анизотропных оболочек и рассмотрел ряд конкретных задач. X. М. Муштари показал, что при этом задача сводится к. интегрированию линейного уравнения восьмого порядка в частных производных.
 В. В. Новожилов рассмотрел в 1948 г. гибкие пластинки и оболочки,
 исходя из общих соотношений нелинейной теории упругости 1б. Он отчетливо формулировал условия, которым должны отвечать углы поворота элементов пластинки или оболочки, с тем чтобы деформации срединной поверхности были представлены выражениями типа 5.4.
 В 1949 г. вышла в свет книга В. 3. Власова «Общая теория оболочек» 54. В ней было приведено нелинейное уравнение совместности дефор¬
 маций 5.5:
 д2гу д2у d2w d2w d2w d2w d2w 2
 dy2 dx2 dx dy dx2,r dy2 dx2 dy2 djc dy
 где под надо понимать
 Уравнения равновесия у В. 3. Власова выписаны также в предположении что деформация является местной или, иными словами, что на рассматриваемом участке оболочку можно считать пологой. В. 3. Власов вводит функцию напряжений и получает систему уравнений 5.27—5.28, отвечающих
 См. Zs. f. angew. Math, und Mech. 5, № 6, 1925.

396
 ОЧЕРК РАЗВИТИЯ ТЕОРИИ ГИБКИХ ПЛАСТИНОК
 ГЛ. XI
 большим прогибам оболочки множитель h введен в выражение для Ф:
 г7огто и д2Ф и д2Ф д2Ф д2w, 0 д2Ф d2w д2Ф л
 W у дх2 х ду2 ду2 дх2 дх ду дх ду дх2 ду2 ’
 Лу2У2Ф4- k — -I- __2 0
 Eh У дх2 л ду2 дх2 ду2 А ду
 В. 	3. Власовым был предложен метод интегрирования системы 5.27— 5.28, заключающейся в представлении функций Ф и w в виде
 Ф Аи х V у, w ВХ х Y у
 и применении метода Бубнова — Галеркина одновременно к обоим уравнениям системы. В качестве функций U, V,... он рекомендовал выбирать балочные фундаментальные функции, соответствующие основной частоте колебаний однопролетной балки. В. 3. Власов указывает, что такой метод интегрирования эквивалентен совместному приложению принципа возможных перемещений и принципа возможных изменений напряженного состояния.
 Цянь Вэй-чан, X. М. Муштари, Н. А. Алумяэ и К. 3. Галимов, пользуясь тензорным аппаратом, составили систему дифференциальных уравнений для гибких оболочек в произвольных координатах. Ими был проведен качественный анализ уравнений и показано, для каких случаев деформации оболочки «малые изгибы», «средние изгибы» и т. д. следует пользоваться той или иной системой уравнений; существенную роль играет здесь также форма оболочки до приложения нагрузки «пологая оболочка», либо «оболочка конечной кривизны». Так как уравнения теории оболочек являются приближенными, то все выводы делаются, исходя из избранной точности. Для суждения о порядке малости величин, характеризующих деформированное состояние удлинения и сдвиги срединной поверхности, углы поворота, изменения кривизн, они сравниваются с некоторым «мерилом», в качестве которого избирается величина удлинения при пределе пропорциональности материала.
 В последние годы были опубликованы работы Н. А. Алумяэ, К. 3. Галимова, Т. В. Невской, И. В. Свирского и А. Р. Ржаницына, посвященные применению вариационных принципов к нелинейным задачам теории пластинок и оболочек и обоснованию различных приближенных методов интегрирования системы уравнений 5.27—5.28.
 § 106. Исследования устойчивости и закритической деформации оболочек. Работы по пологим оболочкам
 Расхождение между теоретическими и экспериментальными значениями критических напряжений для оболочек различной формы было замечено прежде всего инженерами самолетчиками и кораблестроителями. Оказалось, например, что при сжатии труб и цилиндрических панелей реальные критические напряжения в несколько раз меньше величин, определяемых по формулам линейной теории. Поэтому в практических расчетах обычно пользовались экспериментальными формулами, приводимыми в курсах строительной механики самолета.
 В 1934 г. Доннелл пытался объяснить это противоречие, исходя из
 нелинейных зависимостей, но не пришел к убедительным выводам 813.
 Т. Карман и Цзянь Сюэ-шень в 1939—1942 гг. подошли к вопросу с иных позиций. Они изучили поведение сжатого стержня, подкрепленного пружиной с нелинейной характеристикой: такой стержень служил моделью для
 полосы, вырезанной вдоль образующей из цилиндрической оболочки 106.

§ 106
 ИССЛЕДОВАНИЯ УСТОЙЧИВОСТИ
 397
 Применение нелинейной теории позволило установить наличие равновесных изогнутых форм стержня при нагрузках, лежащих ниже критической. Карман и Цзянь Сюэ-шень поставили перед собой целью определить подобные равновесные формы для сферической оболочки, подвергающейся равномерному
 давлению 99, и для сжатой цилиндрической оболочки 8Лб. Они назвали нижней критической нагрузкой величину нагрузки, соответствующую нижней границе устойчивых равновесных изогнутых форм. Рассматривая хлопок при потере устойчивости оболочки, они предложили различать случаи «задаваемой нагрузки» и «задаваемой деформации» и выяснили, что случай сжатия образца в реальной испытательной машине является промежуточным.
 Для замкнутой цилиндрической оболочки Карман и Цзянь Сюз-шень приняли выражение для прогиба в виде
 . - Я со, f COS ы
 Вычисления, сделанные в работе 815, не дали вполне удовлетворительных результатов: для цилиндрической оболочки было получено нижнее критическое напряжение при допущении, что волны являются квадратными. Для иной формы выпучины нижнее критическое напряжение не было получено, так как огибающая семейства кривых р С уходила вниз подобно тому, как изображено на фиг. 9.7. В 1941 г. Фридрихе дал новое, более обоснованное решение для сферической оболочки, но и оно не могло считаться
 окончательным f9,8.
 Вопрос об устойчивости открытой цилиндрической оболочки панели был исследован в марте 1941 г. С. А. Кудриным. В результате анализа экспериментальных данных он пришел к выводу, что значительное снижение критических напряжений по отношению к расчетным вызывается влиянием начальной погиби. Им было дано также теоретическое решение задачи; оказалось, что для панели значительной кривизны среднее напряжение после потери устойчивости падает. С. А. Кудрин установил, что защемление краев мало влияет на величину критического напряжения сильно искривленных панелей.
 В 1944 г. автор настоящей книги предложил принимать выражение для прогиба цилиндрической панели при деформации после потери устойчивости
 в виде 7Л
 -. ткх. пъу. тъх Л 0 ппу... оч
 w — ft sin sin —— 4- о sin2 sin2 —г-. 112
 a b a b
 И. А. Свердлов в 1945 г. рассмотрел случай одновременного действия поперечной нагрузки и сжимающих усилий на защемленную по краям цилиндрическую панель 76. Закритической деформации цилиндрических панелей
 посвящены также работы X. М. Муштари 7‘4, Кокса и Прибрема 78.
 В последнее пятилетие 1951—1955 гг. круг исследований по гибким оболочкам значительно расширился. Требование уменьшения веса различного рода конструкций и связанной с этим экономии металла вызвало разработку более обоснованных методов расчета оболочек на устойчивость; с другой стороны, уменьшение толщины оболочек во вновь проектируемых
 . С. А. Кудрин погиб во время Великой Отечественной войны; работа его осталась неопубликованной.

398
 ОЧЕРК РАЗВИТИЯ ТЕОРИИ ГИБКИХ ПЛАСТИНОК ГЛ. XI
 конструкциях приводило к повышению напряжений при эксплуатационной нагрузке или при возможной перегрузке.
 X. М. Муштари и Р. Г. Суркин подвергли критическому анализу предыдущие работы по сферическим оболочкам 92. Ими были определены нижнее критическое напряжение и напряжение «равных энергий» для сферической оболочки с помощью метода Ритца. При этом было обращено особое внимание на условия сопряжения выпучины с остальной частью оболочки; прогиб был представлен в одном из вариантов решения затухающей функцией. В работе Р. Г. Суркина 94 вычисления, относящиеся к сферической оболочке, были уточнены; кроме того, была решена аналогичная задача для эллипсоидальной оболочки вращения. Во второй из статей 95 для исследования устойчивости сферической оболочки применен метод Бубнова—Г алеркина.
 В статье автора книги 72 рассмотрена в первом приближении закритическая деформация шарнирно опертой, пологой цилиндрической панели при сжатии вдоль образующей и при сдвиге; был применен метод Бубнова — Галеркина. В другой работе 1950 г. было охарактеризовано влияние на устойчивость панели начальной погиби и дополнительной поперечной нагрузки, направленной к центру кривизны или от центра, а также приведены результаты экспериментов с панелями различной кривизны. В дальнейшем Т. В. Невская 7б исследовала влияние поперечной нагрузки на устойчивость пологой цилиндрической панели при сдвиге и при совместном действии продольных и сдвигающих сил. Работа О. Н. Ленько 7ф3 посвящена устойчивости при сжатии и сдвиге анизотропной цилиндрической панели. О. И. Теребушко изучил закритическую деформацию сжатой панели, подкрепленной упругими стрингерами 7Л.
 Продолжалось также уточнение решения задачи устойчивости замкнутой цилиндрической оболочки при сжатии. Михилсен 8,2° и Кемпнер 8Л6 приняли форму волнообразования, близкую к 1, но избрали другой метод решения; ими варьировалась потенциальная энергия не по двум, а по четырем или пяти параметрам. При этом было получено значение нижнего критического напряжения 0,182EhR, мало отличающееся от найденного ранее для квадратных волн; однако форма выпучины оказалась иной.
 В работе В. М. Чебанова 8>9 приведены данные опытов с бумажными моделями оболочек. Теоретическое определение критической нагрузки при сжатии анизотропной цилиндрической трубы в сочетании с внешним давлением было проведено С. В. Александровским 8Л.
 Ряд работ, законченных в последние годы, был посвящен большим прогибам пологих оболочек при действии поперечной нагрузки. М. А. Колтунов воспользовался методом, предложенным В. 3. Власовым, и задался выражениями для «;иФ, содержащими фундаментальные балочные функции; при этом был рассмотрен в первом приближении случай панели произвольной гауссовой кривизны 64. М. С. Корнишин и X. М. Муштари подробно исследовали задачу о деформации удлиненной цилиндрической панели 67.
 В диссертации О. Д. Ониашвили 6-9 были исследованы малые колебания пологой оболочки около равновесного состояния, характеризуемого большими прогибами. Э. И. Григолюк получил фазо-частотные характеристики собственных и вынужденных нелинейных колебаний пологой оболочки; при этом удалось описать динамические явления, имеющие место при хлопке 68.
 Это не относится к послевоенному самолетостроению, для которого характерно повышение толщины обшивки в связи с новыми аэродинамическими требованиями.

§ 107 НЕКОТОРЫЕ АКТУАЛЬНЫЕ ЗАДАЧИ 399
 § 107. Некоторые актуальные задачи
 Как мы видели, общие уравнения теории гибких пластинок получили окончательную форму еще в 1910 г., но в связи со сложностью решения конкретных задач накоплено еще недостаточно данных для практических расчетов. Между тем инженеры нуждаются в надежных методах расчета на прочность и жесткость гибких пластинок различного очертания и при разных условиях закрепления, в методах определения редукционных коэффициентов и несущей способности пластинок. Поэтому желательно расширить круг рассматриваемых задач. Так, например, закритическая деформация пластинок изучена достаточно подробно лишь для шарнирно опертых прямоугольных пластинок с определенными соотношениями размеров, опертых на абсолютно жесткие ребра. Надо более подробно рассмотреть взаимодействие в закритической области пластинки и упругих ребер. Слабо еще изучен случай сдвига при малом превышении критического напряжения и комбинированного действия различных нагрузок сжатия и сдвига, поперечной нагрузки и усилий в срединной плоскости. Должны быть поставлены систематические опыты по определению несущей способности подкрепленных панелей.
 Приведенный в главе V вариант уравнения теории гибких оболочек был разработан в период 1935—1950 гг. Из частных задач по устойчивости оболочек здесь сравнительно подробно рассмотрены случаи круговой цилиндрической оболочки, сжатой вдоль образующей, и сферической оболочки, подвергающейся действию внешнего давления. В дальнейшем необходимо получить уточненное решение задач об изгибе пологих оболочек различной формы под действием поперечной нагрузки для разных условий опирания. Должны быть более подробно рассмотрены в нелинейной постановке задачи
 об устойчивости цилиндрической оболочки при кручении и изгибе, а также при совместном действии усилий разного вида. Надо установить, в каких случаях расчеты на устойчивость могут с достаточной точностью вестись с помощью линейной теории. Особенно важно выяснить для нелинейных задач устойчивости, какие из характерных параметров нагрузку, соответствующую «равным уровням энергии», верхнюю или нижнюю критическую нагрузку целесообразно взять за основу при проектировании. Для этого должны быть проведены теоретические и экспериментальные исследования влияния начальных неправильностей в форме оболочки и начальных напряжений на процесс выпучивания с привлечением статистических методов.
 Определение несущей способности гибких пластинок и оболочек и установление критических усилий в оболочках относительно большой толщины должны вестись с учетом пластических свойств материала; наряду с теоретическими решениями, основывающимися на теории пластичности, здесь важно провести систематические опыты.
 Надо возможно более полно изучить влияние скорости нагружения на несущую способность пластинок и оболочек.
 На различных ступенях решения задач, относящихся к гибким пластинкам и оболочкам, необходимо широко использовать большие электронные машины; в связи с этим должны быть развиты метод последовательных приближений, метод конечных разностей, метод возмущений. Должны быть изучены особенности применения этих методов, а также методов Ритца и Бубнова — Галеркина к нелинейным задачам теории пластинок и оболочек и исследована сходимость решения. Это особенно важно при разыскании нижнего критического напряжения в задачах устойчивости оболочек. Надо установить границы применимости исходных дифференциальных уравнений и рассмотреть деформацию оболочек при перемещениях, сравнимых с габаритными размерами оболочки. Желательно более подробно с помощью методов современной дифференциальной геометрии проанализировать форму изогнутой поверхности оболочки при закритической деформации.

ДОБАВЛЕНИЕ ОСНОВНЫЕ УРАВНЕНИЯ В КОСОУГОЛЬНЫХ КООРДИНАТАХ
 Для всех задач, встречавшихся в книге, было удобно пользоваться ортогональной системой координат. Однако в некоторых случаях — например, при рассмотрении косоугольных панелей обшивки стреловидного крыла самолета, — целесообразно перейти к косоугольным координатам. Придадим поэтому основным уравнениям теории гибких пластинок и оболочек более общий вид.
 В случае пластинки введем косоугольные декартовы координаты хi и jc2 индексы 1, 2 обозначают номер координаты для точек срединной плоскости; обозначим угол между осями хх и х2 через <р. Будем считать ось хi совмещенной с осью х ортогональной системы координат ху у. Тогда соотношения между вторыми производными от функции прогиба примут вид:
 ч>,хх 11>,п; w,xy -w,12 — w,ncos<f;
 W'VV 0-22 — 2®,12 COS W,u C0S2 Cf ;
 1
 индексы после запятой обозначают дифференцирование по соответствующим переменным, т. е.
 d2w dw
 ит-дДля оператора Лапласа 1.52 получим выражение
 V2W — 2W-12 C0S t ®-22> • 2 Основные уравнения 1.60' и 1.61' для гибких пластинок
 R V2V I Ю, Ф-,
 -L 72?2ф _ JL L w, W
 Ь 2
 3
 можно теперь сохранить; входящие в них операторы выразим через новые координаты, пользуясь 1 и 2:
 ®,Ш1 да,2232 21 2 C0S2 9 w,im —
 — 4 COS tp W,lm W,1222»; 4
 z. да, Ф sin‘2 да,иФ,22 да-гаФ.и—2да,12Ф.12- 5

ДОБАВЛЕНИЕ
 401
 Выражения для VV2< и L w, w выписываются по аналогии.
 Напряжения в срединной поверхности должны определяться по формулам:
 Здесь аи, а12 — составляющие вдоль осей х1, х2 полного напряжения в сечении пластинки х1 const; <j2i ff22 — составляющие в сечении х2 const. Переход к составляющим напряжения в ортогональной системе координат осуществляется так:
 Перейдем с случаю полсгсй сб<Мсчки. Примем, что квадрат расстояния ds между двумя соседними точками на срединной поверхности выражается через приращения координат с помощью той же формулы, что и на плоскости см. 54, стр. 303:
 Если записать уравнение начальной срединной поверхности оболочки в виде wнч х1, х2, то можно показать, что в формуле 8 мы пре-
 сравнению с 1; это можно видеть из уравнения на стр. 19.
 Судя по выражению 8, коэффициенты первой квадратичной формы срединной поверхности принимаются нами приближение в виде
 Кривизны нормальных сечений срединной поверхности мы характеризовали в главе V, пользуясь главными кривизнами kXy ky. Чтобы применить новые координаты, введем коэффициенты втсрой квадратичной формы исходной срединной поверхности оболочки Ьп, Ь22, Первые две из этих величин
 определяют также приближенно кривизны нормальных сечений вдоль линий х1 и х2:
 Коэффициент Ь12 родственен «кривизне» кручения изогнутой поверхности пластинки см. стр. 22.
 Условимся совмещать координатную линию х1 с одной из линий кривизны поверхности, например с линией л:, так что kx. Кривизну вдоль
 второй координатной линии х2 можно выразить через главные кривизны по формуле Эйлера:
 Известно, кроме того, соотношение между кривизной k любого нормального сечения и коэффициентами Ь
 6
 7
 ds2 dx'Z -f- 2 dx' dx2 COS <f> dx22.
 8
 квадратами углов поворота нормалей по
 вц1; д12 cos <р; «221-
 6 1 Aj 22 2
 10
 отсюда
 2 cos2 tp --ky sin2 'f; 22 11 COS2 Ч ky Sin2 f.
 11
 12
 13

402 ДОБАВЛЕНИЕ
 Здесь ds — длина дуги вдоль интересующего нас сечения. Применяя зависимость 13 к элементу, отложенному по направлению у, найдем:
 ,, cos ф2 nt costp 1,, 1
 кУ - Ьп iitTlp 26,2155TV UP7 14
 Из 12 и 14 вытекает простая зависимость:
 12 bn cos Ь 15
 Предыдущие формулы дают:
 kxW,yy kyW,хх.6ltW,22 22®.11 — 212®, 12 • 16
 Если ввести оператор
 В W tl®.22 22«».U — 212®.12>. 17
 то можно переписать основные уравнения 5.27—5.28, относящиеся к пологим оболочкам, в виде
 R V2V2o, — L W, Ф В Ф -Is И h
 1 1 18
 — У2?2Ф — — L w, w — В w.
 Уравнения 18 развертываются следующим образом:
 Т SinVf №1т 2 1 2 C0s2 Ср W’im,2222 4 C0S ?,Ш2 »1222
 sin2 »11Ф»22гг;»22Ф»11—,12Ф,122-11Ф,22“212Ф,1222Ф»11'> 19
 Sin2 ср 1 2 COs2 ? Ф»И22 Ф>2222 — 4 COS <р Ф,Ш2 Ф>12221
 >122 — 1122 — 11»22 — 212t0, 12 4 22>ll 20
 Рассмотрим, в качестве примера, косоугольную панель, вырезанную из круговой цилиндрической оболочки радиуса R. Совместим линию х1 с образующей; тогда в 18 надо положить:
 12 0» 22 sln2 <Р
 Систему 18 можно получить также, исходя из более общих зависимостей, записанных Н. А. Алумяэ 5Л и распространяющихся на произвольно выбранные координатные линии. Интегрирование уравнений 18 может быть проведено методом, изложенным в § 61.

ЛИТЕРАТУРА
 К главе I
 1.1. И. Г. Бубнов, Напряжения в обшивке судов от давления воды, 1902; Строительная механика корабля, ч. 11, 1914 см. И. Г. Бубнов, Труды по теории пластин, Гостехиздат, Москва, 1953, И—111.
 1.2.' Я. И. К о р о т к и н, А. 3. Л о к ш и н, Н. Л. Сивере, Изгиб и устойчивость пластин и круговых цилиндрических оболочек, Судпромгиз, Ленинград, 1955.
 1.3. Л. Д. Ландау, Е. М. Лившиц, Механика сплошных сред, изд. 2-е, Гостехиздат, Москва, 1954, 701—706.
 1.4. С. Г. Лехницкий, Анизотропные пластинки, Гостехиздат,-Москва, 1947, 152—153.
 1.5. В. В. Н о в о ж и л о в, Основы нелинейной теории упругости, Гостехиздат, Москва, 1948, 170—175.
 1.6. П. Ф. Пап ко вич, Строительная механика корабля, ч. II, Судпромгиз, Ленинград, 1939, 494—527.
 1.7. С. В. С е р е н с е н, Основы технической теории упругости, ОНТИ, Харьков, 1934, 142—147.
 1.8. С. П. Тимошенко, Курс теории упругости, ч. II, Петербург, 1916.
 1.9. Ю. А. Шиманский, Изгиб пластин, ОНТИ, Москва, 1934.
 1.10. Ху Хай-чан, О некоторых вариационных принципах теории упругости, Ули сюэбао на кит. языке 10, № 3 1954, 259—290.
 1.11. J. Bernoulli, Essait theoretique sur les vibrations de plaques elastiques rectangulaires et libres, Nova Acta Acad. Petropolit. 5, 1789, 197—219.
 1.12. A. Clebsch, Theorie de l’elasticite des corps solides, avec des notes etendues de Saint-Venant, 1883, 687—706.
 1.13. L. E u 1 e r, De motu vibratorio tympanorum, Novi commentarii Acad.
 Petropolit. 10 1766, 243—260.
 1.14. A. Foppl, Vorlesungen tiber techn. Mechanik, 1907, т. 5, 132—144.
 1.15. A. F 6 p p 1, L. Foppl, Drang und Zwang, 2 Aufl., Miinchen, 1924 в переводе: А. Феппль, Л. Феппль, Сила и деформация, Гостехиздат, Москва, 1933, 243—251.
 1.16. М. Т. Huber, Teoria sprezystosci, Варшава, 1950, 166—190.
 1.17. R. Карр us, Zur Elastizitatstheorie endlicher Verschiebungen, Zs. fur
 angew. Math, und Mech. 19 1939, 273—285; 344—361.
 1.18. Th. Kerman, Festigkeitsprobleme im Maschinenbau, Encycl. der math. Wiss. IV 4 1910, 348—351.
 1.19. G. Kirchhoff, Vorlesungen iiber math. Physik;- Mechanik, 449—458.
 1.20. K- Marguerre, Zur Theorie der gekrummten Platte grosser Formanderung, Jahrbuch 1939 der deutschen Luftfahrtforschung, 413—418.
 1.21. A. N d d a i, Die elastischen Platten, Berlin, 1925, 284—288.
 1.22. J. Prescott, Applied elasticity, London, 1924, 435—442.
 1.23. E. R e i s s n e r, Finite deflections of sandwich plates, J. Aeron. Sci. 15,
 № 7 1948, 435—440; 17, № 2 1950, 125.
 1.24. M. S t i p p e s, Large deflections of rectangular plates, Proc. of the 1-st

404
 ЛИТЕРАТУРА
 U. S. Nat. Congr. of Appl. Mech., 1952.
 1.25. S. Timoshenko, Theory of plates and shells, New York, 1940, 329—350 в переводе: С. П. Тимошенко, Пластинки и оболочки, Гостехиздат,
 Москва, 1948, 315—334.
 1.26. С. Т. Wang, Principle and application of energy method for thin plates and shells with finite deflections, NACA Techn. Note № 2620, 1952.
 К главе II
 2. 1. В. В. Болотин, Динамическая устойчивость упругих систем, Гостехиздат, Москва, 1956.
 2. 2. П. М. В а р в а к, Приближенный расчет пластинок средней толщины, Сб. тр. Киевского стр. ин-та 3, 1936; Водный трансп. № 1, 1944.
 2. 3. В. М. Д а р е в с к и й, Изгиб прямоугольной пластины средней толщины, Труды ЦАГИ, № 297, 1936.
 2. 4. М. А. Колтунов, Изгиб прямоугольных пластинок с учетом больших прогибов, Инж. сб., 13, 1952.
 2. 5. Я. Д. Лившиц, Изгиб гибких пластин, Автореф.. докт. дисс., Киев, 1955; Прикладная мехашка № 1 1956, 51—66.
 2. 6. И. В. С в и р с к и й, Видоизменение метода Б. Г. Галеркина для решения нелинейной задачи о хлопке искривленной пластины, Инж. сборник, 22, 1955, 42—47.
 2. 7. Б. И. С л е п о в, Применение теории Кармана к изгибу прямоугольных пластин, Сборник теоретических работ ЦНИИ НКСП, Оборонгиз, 1934, 155—196.
 2. 8. Н. С. С о л о м е н к о, В. С. Ч у в и к о в с к и й, Я. В. Шаров, Строительная механика корабля, Машгиз, Ленинград, 1954.
 2. 9. М. Р. Фельдман, Разрахунок гнучких пластин, Доповш АН УРСР, № 5, 1955, 451—457.
 2.10. О. А. Ющенко, Велию прогини прямокутно1 мембрани, Доповш АН УРСР, № 2, 1953, 103—106.
 2.11. Чжан Ф у-ф а н ь, Равномерно нагруженные удлиненные прямоугольные пластйнки, имеющие начальную кривизну, Туму гунчэн сюэбао на китайском языке 2, № 2, 1955, 147—154.
 2.12. D. G. A s h w е 11, A characteristic type of instability in the large deflections of elastic plates, Proc. Roy. Soc. A 214 1952, 98—118.
 2.13. J. F u n g, W. W i t tr i с k, The anticlastic curvature of a strip, J. Applied Mech. 21, № 4 1954, 351—358.
 2.14. H. H e n с k y, Berechnung diinner recteckiger Platten, Zs. d. VDI 65, N® 17 1921, 976—977; Zs. f. angew. Math, und Mech, 1, 1921, стр. 81 и 423.
 2.15. R. Kaiser, Rechnerische und experimentalle Ermittlung der Durchbiegung von quadratischen Platten, Zs. f. angew. Math, und Mech. 16, № 2 1936, 73—98.
 2.16. L. К i r s t e, Elastische Verformung einer dtinnen Platte nach eine abwickelbare Flache, Oesterr. Ing. Archiv 7, № 1—2 1953, 134—139.
 2.17. S. Levy, Bending of rectangular plates with large deflections, NACA Rep. N® 737; NACA T. N. № 846 1942; Square plate with clamped edges under normal pressure producing large deflections, NACA Rep. N° 740; NACA T. N. № 847 1942.
 2.18. S. Levy and S. Greenman, Bending with large deflection of a clamped rectangular plate with length — width ratio of 1,5 under normal pressure, NACA T. N. Я® 853 1942.
 2.19. A. Love, A treatise on the mathematical theory of elasticity, 1927 в переводе: А. Л я в, Математическая теория упругости, ОНТИ, Москва, 1935, 586—591.

ЛИТЕРАТУРА
 405
 2.20. F. М u 11 е г-М a g у а г i, Endliche Deformationen diirtrief Piatteristreifens mit freien Langsrandern, Oesterr. Ing. Archiv 7, № 4 1953, 319—328,
 2.21. M. Ramberg, A. Me Pherson, S. Levy, Normal — pressure tests of rectangular plates, Rep. NACA № 748 1942.
 2.22. Q. Sonntag, Einfluss einer Nachgiebigkeit der Randeinspannung auf die Durchbiegung und Spannungen bei Platten grosser Durchbiegung bzw Membranen, Zs. angew. Math, und Mech. 35, № 9—10 1955, 356—358.
 2.23. F. S. Shaw, N. P e г г о n e, Non-linear deflections of membranes, J. Appl. Mech. 21, № 2 1954, 117—128.
 2.24. S. Timoschenko, Ueber die Biegung von Staben, die eine kleine anfangliche Kriimmung haben, 1924; Buckling of flat curved bars and slightly curved plates, 1935 cm. S. Timoshenko, Collected Papers, New York, 1953.
 2.25. S. W a y, A laterally loaded clamped square plate with large deflection, St. Timoshenko anniv. volume, 1938, 240—256; Proc. 5-th Intern. Congr. Appl. Mech., 1939, 123—128.
 См. также i-i, стр. 218—308; •«, стр. 779—795; 115, стр. 254—260.
 К главе III
 3. 1. И. И. Ааре, Исследование работы опорной панели сплошной стальной балки в послекритической стадии, диссертация, Таллинский политехи, ин-т, 1953; Тр. Тал. полит, ин.-та, № 65 1955 61—75.
 3. 2. Б. М. Б р о у д е, Предельные состояния стальных балок, Стройиздат, 1953, 190—214.
 3. 3. Н. В. 3 в о л и н с к и й, Сжатие прямоугольной пластинки за пределом упругости, Труды ЦАГИ, № 505, 1940.
 3. 4. М. А. Колтунов, Поведение пластинки после потери устойчивости, Вестн. Моск. ун-та, N® 9 1953, 57—62.
 3. 5. С. Н. Никифоров, Сжатая прямоугольная пластинка со свободно искривляющимися в ее плоскости продольными кромками, Уч. записки МГУ, № 117 1946.
 3. 6. Г. А. Олейников, Исследование работы подкрепленных и неподкрепленных обшивок на сжатие, Труды ЦАГИ, № 370 1938.
 3. 7. П. Ф. П а п к о в и ч, К вопросу о выпучивании плоских пластин, сжимаемых усилиями, превосходящими их эйлерову нагрузку, Морск. сборник, № 8—9 1920.
 3. 8. В. И. П е т р а ш е н ь, Расчет стальных конструкций с плоской обшивкой, Стройиздат, 1948.
 3. 9. А. А. Подорожный, Данные для расчета обшивки с гофром на. сжатие и сдвиг, Труды ЦАГИ, № 520 1940.
 3.10. П. Я. П о л у б а р и н о в а-К о ч и н а, К вопросу об устойчивости пла¬
 стинки, Прикл. матем. и мех. 3, № 1 1936.
 3.11. В. А. Пост но в, Поведение после потери устойчивости сжатых пластин, подкрепленных продольными ребрами, диссертация, Ленинград, Кораблестр. ин-т, 1953. Тр. ЛКИ, 16 1955, 21—33.
 3.12. А. Ю. Р о м а ш е в с к и й, Исследование работы балочных систем с тонкой стенкой с непараллельными поясами, Труды ЦАГИ, № 203 1935; Данные для расчета деревянных обшивок, Техн. зам. ЦАГИ, № 194
 1938.
 3.13. А. Ю. Р о м а ш е в с к и й, К расчету на прочность конструкции типа
 фюзеляжа монокок, Труды ЦАГИ, № 531 1940.
 3.14. Г. Г. Ростовцев, Приведенная ширина изотропной и анизотропной плоской пластинки, Труды ЛИИГВФ, № 5 1936; Расчет плоской обшивки, подкрепленной ребрами, Труды ЛИИГВФ, № 20 1940.
 3.15. Г. Г. Ростовцев, Строительная механика самолета, ч. 2, ОНТИ, Москва, 1936, 118—129, 185—202.

406 ЛИТЕРАТУРА
 3.16. Г. Г. Ростовцев, Продольно-поперечный изгиб гибкой прямоугольной пластинки, Инж. сб. 8 1950, 83—104.
 3.17. П. А. С о к о л о в, О напряжениях в сжатой пластинке после потери устойчивости, Труды НИСС, № 7 1932.
 3.18. И. А. Свердлов, О редукционном коэффициенте для пластин, работающих на совместное действие сжатия и сдвига, Техн. возд. флота, № 5 1938.
 3.19. В. М. Стригунов, Расчет металлических фюзеляжей на прочность, Труды ЦАГИ, № 432 1939.
 3.20. И. И. Ф а е р б е р г, Экспериментальное исследование фанерной обшивки, подкрепленной стрингерами при сжатии, Труды ЦАГИ N° 404
 1939.
 3.21. Р. Н. Э э к, Расчет гибких обшивок, диссертация, Ленинград, Политехи, ин-т, 1954.
 3.22. S. Bergman n, Behaviour of buckled rectangular plates under the action of shearing forces along all edges, Stockholm, 1948.
 3.23. P. P. Bijlaard, Determination of the effective width of plates with small deviations from flatness, Proc. of the 1-st U. S. Nat. Congr. Appl. Mech., 1952, 357—361; Compressive buckling due to forces crippling of stiffeners, Preprint NACA № 408 1953.
 3.24. H. L. С о x, Buckling of thin plates in compression, Rep. and Memor. №N® 1553, 1554 1933; Stress analysis of thin metal construction, J. of the R. Aeron. Soc. 44, № 351 1940.
 3.25. N. Dow, R. Anderson, Prediction of ultimate strength of skin-stringer panels, Preprint NACA, N2 431 1954.
 3.26. В. H. Falconer, Post-buckling behaviour of long square boxes under torsion, Engineer 196, № 5105 1953, 690—694; Compressive buckling of stiffened plates, Engineer 195, № 5080, 781—789, № 5081, 822—825 1953.
 3.27. O. Oerard, Effective width of elastically supported flat plates, J. of Aeron. Sci. 10 1946, 518—523.
 3.28. W. L. Howland, P. E. Sandorff, Stress by permanent buckling o thin panels under compression, J. Aeron. Sci. 8, № 7 1941, 261—269.
 3.29. Th. К r m d n, E. E. S e с h 1 e r, L. H. Donnell, The strength of thin plates in compression, Trans. ASME 54 1932, 53—57.
 3.30. R. Kuhn, Investigation on the incompletely developed plane diagonaltension field, NACA Rep., № 697 1940.
 3.31. A. Kromm, K. Marguerre, Verhalten eines von Schub- und Druck-
 kraften beanspruchten Plattenstreifens, Luftfahrtforschung 14 1937,
 627—639; Jahrbuch deutscher Luftfahrtforschung, 1938, 263—275.
 3.32. S. Le v у, K. L. F i e n u p, R. M. Woolley, Analysis of square shear web above buckling load, NACA T. N., № 962 1945.
 3.33. S. Le v y, D. Qoldenberg, G. Z i b r i t о s k y, Simply-supported long rectangular plate under combined axial load and normal pressure, NACA T. N., № 949 1944.
 3.34. S. Le v y, P. Krupen, Large deflection theory for end compession of long rectangular plates rigidly clamped along two edges, NACA T. N., Ms 884 1943.
 3.35. S. Levy, R. M. W о о 1 e y, J. N. С о r r i с k, Analysis of deep rectangular shear web above buckling load, NACA T. N., № 1009, 1946.
 3.36. K. Marguerre, E. Trefftz, Ueber die Tragfahigeit eines Plattenstreifens nach Ueberschreiten der Beullast, Zs. f. angew. Math, und Mech. 17 1937, 85—100.
 3.37. K. Marguerre, Die mittragende Breite des gedriickten Plattenstreifens, Luftfahrtforsch. 14, N2 3 193 перевод в сборнике под ред. А. А. Уманского, Оборонгиз, Москва, 1938.
 3.38. W. Н. Ned der man, Secondary buckling in hollow rectangular column section of steel plates, Jowa State Coll. J. Sci. 27, № 2 1953, 227—228.

ЛИТЕРАТУРА
 407
 3.39. R. A. Needham, The ultimate strength of aluminum-alloy formed structural shapes in compression, J. of the Aeron. Sci 21, № 4 1954, 217—229.
 3.40. A. Pfliiger, Nicht-lineare Beulprobleme, Zs. angew. Math, und Mech. 35, № 9—10 1955, 353—355.
 3.41. H. A. S с h a d e, Larguer effective de toles renforcees travaillant sous Taction de forces de flexion, Bulletin technique du bureau veritas, 1953, 215—227.
 3.42. G. Schnadel, Die Ueberschreitung der Knickgranze bei diinnen Plat-
 ten, Proc. of the 3-d Int. Congr. for Appl. Mech., т. 3, 1930.
 3.43. L. S с h u m a n, G. Back, Strength of rectangular plates under edge
 compression, NACA Rep., № 356 1930.
 3.44. E. E. Sechler, Stress distribution in stiffened plates under compression, J. Aeron. Sci. 4 1937, 520; Progress Report in methods on analysis applicable to monocoque aircraft structures, ARC Rep., № 4313 1942.
 3.45. Т. K. Steele, С. T. Wang, The effect of the torsional rigidity of a
 single stiffener on the buckling characteristic of a panel subjected to
 axial compression with large deflection, J. Aeron. Sci., Jsfe 1 1953, 12—18.
 3.46. S. Timoshenko, Theory of elastic stability, New York, 1936 в переводе: С. П. Тимошенко, Устойчивость упругих систем, Гостехиздат, Москва, 1946 и 1955. В тексте даны стр. по изд. 1946 г.
 3.47. Н. Wagner, Ebene Blechwandtrager mit sehr diinner Stegblech, Zs. f. Flugtechnik und Motorluftschiffahrt, № 8—12 1929 в переводе: Г. О. Вагнер, Балка с весьма тонкой стенкой, Сб. перев. под ред. А. А. Уманского и П. М. Знаменского, изд. ЦАГИ, 1937, 58—117.
 3.48. R. М. Woo ley, J. N. Corrick, S. Levy, Clamped longrectangular plate under combined axial load and normal pressure, NACA T. N., No 1047, 1946.
 См. также f1-6, стр. 891—924, 215.
 К главе IV
 4. 1. С. А. Алексеев, Кольцеобразная упругая мембрана под действием поперечной силы, приложенной к жесткому центрально расположенному диску. Инж. сб. 10 1951, 71—80; Круглая плоская упругая мембрана под равномерной поперечной нагрузкой, Инж. сб. 14 1953, 196—198.
 4. 2. Л. Е. Андреева, К расчету мембранных коробок, «Расчеты на прочность в машиностроении» 11, Машгиз, Москва 1950, 98—115; Расчет мембран с пологой трапецоидальной гофрировкой; Расчет конических и сферических гофрированных мембран, «Расчеты на прочность маш. констр.», Машгиз, 1953, 125—150, Инж. сб. 21 1955, 128—141.
 4. 3. И. И. В о р о в и ч, О поведении круглой плиты после потери устойчивости, Уч. зап. Рост. гос. ун-та 32, № 4 1955, 55—60.
 4. 4. А. С. Григорьев, Исследование работы круглых мембран при больших прогибах за пределами упругости, Инж. сб. 9 1951, 99—112.
 4. 5. Э. И. Г р и г о л ю к, К вопросу о поведении круглых пластинок после
 потери устойчивости, Вестн. инж. и техн., № 3 1949.
 4. 6. Э. И. Г р и г о л ю к, О потере устойчивости при больших прогибах замкнутой слоистой конической оболочки под действием равномерного нормального поверхностного давления, Инж. сб. 22 1955, 111—119.
 4. 7. А. Н. Д и н н и к, Круглая мембрана при произвольной нагрузке, Изв. Киевск. политехи, ин-та, № 4 1910, 563—571; Приложение функций Бесселя к задачам теории упругости, Изв. Донск. политехи, ин-та 2, 1913, 242—256 см. Избранные труды, т. И, Изд. АН УССР, Киев, 1955.
 4. 8. А. А. Ильюшин, Пластичность, Гостехиздат, Москва, 1948.

ЛИТЕРАТУРА
 409
 4.29. Н. Ny 1 a n d er, Die Durchschlaglast von Platten, Oesterr. Ing.-Archiv 9, № 2—3, 1955, 181—196.
 4.30. A. McPherson, W. Ramberg, S. Levy, Normal-pressure tests of circular plates with clamped edges, Rep. NACA, № 744 1942.
 4.31. E. Reissner, A problem of linite bending of circular ring plates, Quart, of Appl. Math. 10, № 2 1952, 167—173; On finite deflections of circular plates, Proc. Symp. Appl. Math. 1 1949, 213—219.
 4.32. E. Schwerin, Ueber Spannungen und Formanderungen kreisrlngfdrmiger Membranen, Zs. f. techn. Phys. 10, № 12 1929, 651—659.
 4.33. M. S t i p p e s, A. H. Hawsrath, Large deflections of circular plates, J. Appl. Mech. 19 1952, 287—292.
 4.34. S. Timoshenko, Deflections of a uniformly loaded circular plate with clamped edges, Collected Papers, New York, 1953, 401—402.
 4.35. S. Way, Bending of circular plates with large deflection, Trans. ASME 56, № 8 1934, 627—633.
 См. также i.i, стр. 42—59; i.e, стр. 704—723; i.ao, стр. 288—308; i.i, стр. 443—474, 2.20.
 К главе V
 5. 1. H. А. А л у м я э, Равновесие тонкостенных упругих оболочек в послекритической стадии, ГИЗ «Научная литература», Тарту, 1948; Труды Таллинского политехи, ин-та, серия А, 1948; Прикл. матем. и мех. 13, № 1 1949.
 5. 2. Н. А. А л у м я з, Применение обобщенного вариационного принципа Кастилиано к исследованию послекритической стадии оболочек, Прикл. матем. и мех. 14, N2 1 1950, 93—98, № 2, 1950.
 5. 3. Н. А. А л у м я э, О представлении основных соотношений нелинейной теории оболочек, Прикл. матем. и мех. 20, № 1 1956, 136—139.
 5. 4. В. 3. Власов, Общая теория оболочек и ее приложения в технике, Гостехиздат, Москва, 1949, 475—478.
 5. 5. И. И. В о р о в и ч, О существовании решений в нелинейной теории оболочек, Изв. АН СССР, сер. мат., 19 1955, 173—186; О некоторых прямых методах в нелинейной теории пологих оболочек, Докл. АН СССР 105, № 1 1955, 42—45.
 5. 6. К. 3. Г а л и м о в, Уравнения равновесия теории упругости при конечных перемещениях и их приложение к теории оболочек, Изв. Каз. ф-ла АН СССР, № 1, 1948, 25—45; Общая теория упругих оболочек при конечных перемещениях, Изв. Каз. ф-ла АН СССР, № 2, 1950, 3—52.
 о. 7. К. 3. Г а л и м о в, К общей теории пластин и оболочек при конечных перемещениях и деформациях, Прикл. мат. и мех. 15, № 6 1951, 723—742; Уч. зап. Каз. гос. ун-та 113, № 10 1953, 155—160.
 5. 8. X. М. М у ш т а р и, Некоторые обобщения теории тонких оболочек с приложением к задаче устойчивости упругого равновесия, Изв. физ.мат. об-ва при Каз. гос. ун-те, 1938, 71—97; Прикл. матем. и мех. 2, N° 4 1939.
 5. 9. X. М. М у ш т а р и, Об определении деформаций срединной поверхности оболочки при произвольных изгибах, Труды Каз. хим. технол. ин-та, № 13, 1948; Прикл. матем. и мех. 13, № 2 1949, 121—134.
 5.10. X. М. М у ш т а р и, Об упругом равновесии тонкой оболочки с начальными неправильностями в форме срединной поверхности, Прикл. матем. и мех. 15, № 6 1951.
 5.11. Ю. Н. Р а б о т н о в, Локальная устойчивость оболочек, Докл. АН СССР 52, № 2, 1946, 111—112.

410
 ЛИТЕРАТУРА
 5.12. Цянь Вэй-чан Weii-zang Chien, The intrinsic theory of thin shells and plates, Quart, of Appl. Math. 1, N2 4 1944, 297—327: 2, N2 1, 43—59, № 2, 120-135 1945.
 5.13. J. L. Synge and W. Z. Chien, The intrinsic theory of elastic shells and plates, Appl. Mech. Th. Кагшйп Annivers. Vol. 1941, 103—120.
 См. также •, стр. 178—185.
 К главе VI
 6. 1. E. Ф. Бурмистров, Расчет пологих ортотропных оболочек с учетом конечных деформаций, Инж. сб. 22, 1955, 83—97.
 6. 2. Г. А. Гениев, Н. С. Ч а у с о в, Некоторые вопросы нелинейной теории устойчивости пологих металлических оболочек, Стройиздат, Москва, 1954.
 6. 3. Э. И. Г р и г о л ю к, Нелинейные колебания и устойчивость пологих стержней и оболочек, Изв. АН СССР, отд. техн. наук, № 3, 1955, 35—68; Прикл. матем. и мех. 19, № 3 1955, 376—382.
 6. 4. М. А. Колтунов, Учет конечных перемещений в задаче об изгибе и устойчивости пластин и пологих оболочек, Вестн. МГУ, № 5, 1952.
 6. 5. М. М. К о з а р о в, Исследование устойчивости пологих оболочек, канд. диссертация, МИСИ, 1955.
 6. 6. М. С. Кор ни шин, Об устойчивости и больших прогибах пологой цилиндрической панели под действием внешнего нормального давления, канд. диссертация, Каз. ф-л АН СССР, 1954.
 6. 7. М. С. К о р н и ш и н, X. М. Муштари, Устойчивость бесконечно длинной пологой цилиндрической панели под действием нормального равномерного давления, Изв. Каз. ф-ла АН СССР 7 1955, 36—50.
 6. 8. X. М. Муштари, И. В. С в и р с к и й, Определение больших прогибов цилиндрической панели, опертой на гибкие нерастяжимые ребра, под действием внешнего нормального давления, Прикл. матем. и мех. 17, № 6 1953, 755—760.
 6. 9. О. Д. Ониашвили, Некоторые динамические задачи теории оболо¬
 чек., докт. диссертация, Изд. АН СССР, 1956.
 См. также 210.
 К главе VII
 7. 1. А. С. В о л ь м и р, О напряжениях в сжатой цилиндрической панели
 после потери устойчивости, Сб. научн. трудов к ХХ-летию ВВА им. Жуковского, т. 11, 1944.
 7. 2. А. С. В о л ь м и р, Теория устойчивости и больших деформаций цилиндрической оболочки при сжатии и сдвиге, «Расчет пространственных конструкций» 1, Машгиз 1950, 285—316, Тр. ВВИА N2 3891950.
 7. 3. О. Н. Ленько, Устойчивость круговой цилиндрической ортотропной оболочки, «Расчет пространств, конструкций» 4, Стройиздат, Москва 1956.
 7. 4. X. М. Муштари, Об упругом равновесии цилиндрической оболочки под действием продольного сжатия в закритической области, Труды Каз. авиац. ин-та 17 1946; Приближенное определение редукционного коэффициента обшивки при осевом сжатии, Изв. Каз. ф-ла АН СССР
 7 1955, 23—35.
 7. 5. Т. В. Невская, Влияние внутреннего давления на устойчивость цилиндрической панели при сдвиге, «Расчет пространств, конструкций»
 3, Стройиздат, Москва 1955, 421—452.
 7. 6. И. А. Свердлов, Определение прогибов обшивки крыла, Техн. зам. ВВИА им. Жуковского, № 7, 1945.

408
 ЛИТЕРАТУРА
 4. 9. Д. Ю. Панов, Применение метода акад. Б. Г. Галеркина для решения некоторых нелинейных задач теории упругости, Прикл. матем. и мех. 3, № 2 1939.
 4.10. Д. Ю. Панов, О больших прогибах круглой пластинки, Труды ЦАГИ, № 450 1939.
 4.11. Д. Ю. Панов, О больших прогибах круглых мембран со слабым гофром, Прикл. матем. и мех. 5, № 2, 1941, 308—318.
 4.12. Д. Ю. Панов и В. И. Феодосьев, О равновесии и потере устойчивости пологих оболочек при больших прогибах, Прикл. матем. и мех. 12, № 4> 1948, 389—406; 13, № 1 1949, 116.
 4.13. С. П. Тимошенко, О больших прогибах круглых пластинок, 1915.
 4.14. В. И. Феодосьев, О больших прогибах и устойчивости круглой мембраны с мелкой гофрировкой, Прикл. матем. и мех. 9, № 5 1945, 389—412; Расчет мембран с мелкой гофрировкой, «Новые методы расчета пружин», Машгиз, Москва, 1946, 102.
 4.15. В. И. Феодосьев, К расчету хлопающей мембраны, Прикл. матем. и мех. 10, № 2 1946, 295—300; Расчет хлопающей мембраны, «Труды кафедры строит, мех. МВТУ», Машгиз, Москва, 1947.
 4.16. В. И. Феодосьев, Упругие элементы точного приборостроения, Оборонгиз, Москва, 1949, 206—337.
 4.17. Е К а й-ю а н ь, Большие прогибы кольцеобразной пластинки, Ули сюэбао на кит. языке 9, № 2 1953, 110—129; Acta Scientia Sinica на кит. языке 2, № 2 1953, 127—144.
 4.18. Ху Ха й-ч а н, О больших прогибах круглых пластинок, Ули сюэбао на кит. языке 10, N° 4 1954, 383—393.
 4.19. Цянь В э й-ч а н, Большие прогибы круглой защемленной пластинки, Chinese J. of Phys. 7, № 2 1947, 102—113; Ули сюэбао на кит. языке 10, № 3 1954, 209—238.
 4.20. Цянь В э й-ч а н, Е Ка й-ю а н ь, К вопросу о расчете круглых пластинок большого прогиба, Цзисе гунчэн сюэбао 3, № 1 1955,
 15—32.
 4.21. Цянь В э й-ч а н, Асимптотическое поведение тонкой защемленной круглой пластинки под равномерной поперечной нагрузкой при весьма больших прогибах, 1948.
 4.22. S. R. Bodner, The post buckling behaviour of a clamped circular plate, Quart. Appl. Math. 12 1955, № 4, 397—401.
 4.23. K Biezeno, R. Gramme 1, Technische Dynamik в переводе: К. Бицено и Р. Граммель, Техническая динамика, т. I, Гостехиздат, Москва, 1950, 860—873.
 4.24. К. Federhofer, Ueber die Berechnung der dunnen Kreisplatte mit grosser Ausbiegung, Eisenbau 9 1918, 152; Zur Berechnung der dunnen Platten mit grosser Ausbiegung, Forsch. aus dem Geb. d. Ing.-wesens 7, № 3 1936, 148—151; 11 1940, 97; Die dunne Kreisplatte mit grosser Ausbiegung, Oesterr. Ing.-Archiv 1 1946, 21—35; Zs. f. angew. Math, und Mech. 24 1944, 189—194.
 4.25. K. Federhofer, Berechnung der dunnen Kreisplatte mit grosser Ausbiegung. Zs. f. Luftfahrtforsch. 21 1944, 1—8; Die Grundgleichungen fur elastischen Platten veranderlicher Dicke und grosser Ausbiegung, Zs. f. angew. Math, und Mech. 2527 1947, 17—21.
 4.26. K. Federhofer, H. Egger, Berechnung der dunnen Kreisplatte mit grosser Ausbiegung, Sitzungsber. der Ac. der Wiss., Wien, mathem., Abt. Ha 155 1946, 15—43.
 4.27. K. Friedrichs, J. Stoker, The non-linear boundary value problem of the buckled plate, Proc. of the Nat. Ac. of Sci. 25 1939, 535—540; Amer. J. Math. 63 1941, 839—888.
 4.28. H. H e n с k y, Ueber den Spannungszustand in kreisrunden Platten, Zs. f. Math, und Phys. 63, № 3 1915, 311—317.

ЛИТЕРАТУРА
 411
 7.7.0. И. Теребушко, Устойчивость подкрепленных цилиндрических, панелей, «Расчет пространств, конструкций» 4, Стройиздат, Москва 1956.
 7. 8. Н. L. Сох, W. I. С 1 a n s h о w, Compression tests on curved plates
 of thin sheet duralumin,.Rep. and Memor., Nfc 1894 1941.
 7. 9. H. L. Cox, E. Pribram, The elements of the buckling of curved
 plates, J. of the R. Aeron. Soc., 1948.
 7.10. D. Legget, The buckling of a long curved panel under axial compression, Rep. and Memor., № 1899 1942; № 1972 1943.
 7.11. E. C. Redshaw, Elastic stability of a curved panel, J. of the Aeron. Soc., № 330 1938.
 7.12. O. Welter, Curved aluminum-alloy sheets in compression, J. Aeron.
 Sci. 12, No 3 1945; 13, № 4, 11 1946.
 7.13. W. W e n z e k, Die mittragende Breite nach dem ausknicken bei krum-
 men Blechen, Luftfahrtforschung 15, № 7 1938.
 К главе VIII
 8. 1. С. В. Александровский, Об устойчивости цилиндрической обо¬
 лочки при больших прогибах, «Расчет пространств, конструкций» 3, Стройиздат 1955, 453—492.
 8. 2. Н. А. Алумяэ, К определению состояний равновесия длинных цилиндрических оболочек при осесимметричной нагрузке, Изв. АН Эст. ССР 3, Я° 1 1954, 89—99.
 8. 3. Н. А. А л фу то в, Устойчивость цилиндрических и конических подкрепленных оболочек, нагруженных внешним давлением, Автореф.
 канд. дисс., МВТУ, Москва, 1956.
 8. 4. Ф. С. И с а н б а е в а, Определение нижней критической нагрузки цилиндрической оболочки при всестороннем сжатии, Изв. Каз. ф-ла АН СССР 7 1955, 51—58.
 8. 5. X. М. М у ш т а р и, А. В. С а ч е н к о в, Об устойчивости цилиндрических и конических оболочек кругового сечения при совместном действии осевого сжатия и внешнего нормального давления, Прикл. матем. и мех. 18, № 6 1954, 667—674.
 8. 6. Л. Ю. Поверус, Устойчивость равновесия упругой оболочки вращения малой положительной кривизны, Автореф. канд. дисс., Таллин, 1955.
 8. 7. Р. К. Р я я м е т, Устойчивость равновесия упругой конической оболочки, Автореф. канд. дисс., Таллин, 1954; Тр. Таллин, пол. ин.-та, 651955.
 8. 8. А. В. С а ч е н к о в, Приближенное определение нижней границы критической нагрузки при продольном сжатии тонкой конической оболочки, Изв. Каз. ф-ла АН СССР 7 1955, 16—22.
 8. 9. В. М. Ч е б а н о в, Исследование устойчивости тонкостенных оболочек при помощи моделей из бумаги, Инж. сб. 22, 1955, 150—159.
 8.10. Ц з я н ь Сю э-ш е н ь Н. S. Т s i е n, A theory for the buckling of thin shells, J. Aeron. Sci. 9 1942, 373.
 8.11. P. Cicala, The effect of initial deformation on the behaviour of a cylindrical shell under axial compression, Quart. Appl. Math. 9, № 3 1951, 273—293.
 8.12. L. H. Donnell, Stability of thin walled tubes under torsion, NACA Rep., JSf?479 1934 см. перевод в сборнике под ред. А. А. Уманского и П. М. Знаменского, Изд. ЦАГИ, Москва, 1937, 29—57.
 8.13. L. Н. D о n n е 11, A new theory for the buckling of thin cylinders under axial compression and bending, Trans. ASME 56, №11 1934, 795—806.
 8.14. L. H. Donnell, С. C. Wan, Effect of imperfections on buckling of thin cylinders, J. Appl. Mech., March 1950, 75—83.
 8.15. Th. Karman and H. S. T s i e n, The butlcling of thin cylindficaljiens under axial compression, J, of the Aeron. Sci. 8, №8 1941, 303—ЗГ?Г

412
 ЛИТЕРАТУРА
 8.16. J. Kempner, Postbuckling behaviour of axially compressed circular cylindrical shells, J. Aeron. Sci. 21, № 5 1954, 329—335, 342 см. перевод в сборнике «Механика», №2, 1955, ИЛ, Москва, 105—116.
 8.17. L. К ir s t е, Abwickelbare Verformung diinnwandiger Kreiszylinder, Oesterr. Ing. Archiv, 8, № 2—3 1954, 149—151.
 8.18. D. M. A. Legget, R. Jones, The behaviour of a cylindrical shell under axial compression when the buckling load has been exceeded, Rep. and Memor., №2190 1942; Pubis Inst. math. Acad, serbe sci. 7 1954.
 8.19. T s u-T a о Loo, Effects of large deflections and imperfections on the elastic buckling of cylinders under torsion and axial compression, Proc. of the 2-nd U. S. Nat. Congr. of Appl. Mech., New York, 1954, 345—357.
 8.20. H. F. Michielsen, The behaviour of thin cylindrical shells after buckling under axial compression, J. Aeron. Sci., № 12 1948, 738—744.
 8.21. W. Nash, Effect of large deflections and initial imperfections on the buckling of cylindrical shells, J. Aeron. Sci., N° 4 1955.
 8.22. Chi-Teh Wang. G. Rao, A study of an analogues model giving the nonlinear characteristics in the buckling theory of sandwich cylinders, J. Aeron. Sci., № 2 1952.
 К главе IX
 9. 1. М. И. Б а б и ч е в а, Об устойчивости сферических оболочек, диссертация, Моск. гос. ун-т, 1950.
 9. 2. X. М. М у ш т а р и и Р. Г. С урки н, О нелинейной теории устойчивости упругого равновесия сферической оболочки при действии равномерного распределенного внешнего давления, Прикл. мат. и мех., 14, № 6 1950, 573.
 9. 3. С. Д. П о н о м а р е в, В. J1. Б и д е р м а н, В. М. М а к у ш и н, Н. А. М алинин, В. И. Феодосьев, Основы современных методов расчета на прочность в машиностроении, Машгиз, Москва, 1952, 733—754.
 9. 4. Р. Г. С у р к и н, К теории устойчивости и прочности сферических и
 эллипсоидальных оболочек, днищ и мембран, диссертация, Казанск. фил. АН СССР, 1952.
 9. 5. Р. Г. С у р к и н, К теории устойчивости вытянутой эллипсоидальной
 оболочки вращения при внешнем равномерном давлении, Изв. Каз.
 ф-ла АН СССР 7, 1955, 3—15; К вопросу о потере устойчивости
 сферической оболочки, Изв. Каз. ф-ла АН СССР 10, 1956.
 9. 6. В. И. Феодосьев, Об устойчивости сферической оболочки, находящейся под давлением внешнего равномерно распределенного отделения, Прикл. матем. и мех. 18, № 1 1954, 35—42.
 9. 7. Ху Хай-чан, О прощелкивании тонкой сферической панели, У ли сюэбао на кит. языке 10, N° 1 1954, 105—136.
 9. 8. К. О. Friedrichs, On the minimum buckling load for spherical
 shells, The Karman anniv. volume, 1941, 258—272.
 9. 9. Th. Karman, H. S. T s i e n, The buckling of spherical shells on
 external pressure, J. Aeron. Sci. 7 1949, 43.
 9.10. K Kleppel, O. Jungbluth, Beitrag zum Durchschlagproblem diinnwandiger Kugelschalen, Stahlbau 22, N° 6 1953, 121—130.
 9.11. U. M a s u j a, J. J о s h i m u r a, The buckling of spherical shells by external pressure, Proc. 2-nd Japan. Nat. Congr. Aj.pl. Mech., 1953, 145—148.
 К главе X
 10.1. А. А. Курдюмов, Об экспериментальном решении задач изгиба
 пластин, Труды ЛКИ 16 1955, 3—10.
 10.2. М. А. Лаврентьев, А. Ю. И ш л и н с к и й, Динамические формы потери устойчивости упругих систем, Докл. АН СССР 64, N° 6 1949, 779—782.

ЛИТЕРАТУРА
 413
 10.3. Е. П. Попов, Явление большого перескока в упругих системах, Инж. сб. 5, 1948.
 10.4. А. Р. Ржаницын, Устойчивость упругих систем, Гостехиздат, Москва,
 1955.
 10.5. И. Я- Ш т а е р м а н, Устойчивость упругих круговых арок под действием сосредоточенной силы, Прикл. матем. и мех. 1, № 3, 1938.
 10.6. Цзянь С ю э-ш е н ь Н. S. Tsien, Buckling of a column with nonlinear supports, J. Aeron. Sci. 9, № 4 1942, 119.
 10.7. Цзянь Сюэ-шень H. S. Tsien, Lower buckling load in the nonlinear buckling theory for thin shells, Quart. Appl. Math. 5, № 2 1947,
 230 237.
 10.8. N. J. Hoff, Buckling and stability, J. R. Aeron. Soc. 58, № 1 1954, 1—52 в переводе: H. Хофф, Продольный изгиб и устойчивость, ИЛ, Москва, 1955.
 10.9. К. Marguerre, Die Durchschlagskraft eines schwach gekrummten Balkes, Sitzungsber. der Berliner Math. Ges. 37 1938, 22—40.
 10.10. J. Naleszkiewicz Я. Налешкевич, Квантовые свойства явлений упругой неустойчивости, Бюлл. Польск. АН 3, № 2 1955, 59—72.
 К главе XI
 11.1. А. С. Вольмир, Очерк жизни и деятельности И. Г. Бубнова в книге: «И. Г. Бубнов, Труды по теории пластин», Гостехиздат, 1953, 311—393; Обзор исследований по теории гибких пластинок и оболочек за период с 1941 по 1955 г., «Расчет пространственных конструкций» 4, Стройиздат,
 1956.
 11.2. Ю. Н. Ра бот но в, Пластинки и оболочки, «Механика в СССР за тридцать лет», Гостехиздат, 1950, 226—239.
 11.3. Цянь В э й-ч а н, Ху Ха й-ч а н, Линь X у н ь-с у н ь, Е. К а й-ю а н ь, Теория круглых упругих тонких пластинок большого прогиба, Сборник матем. ин-та АН Китая на кит. языке, Пекин, 1954.
 11.4. С. В. В i е z е п о, Survey of papers on elasticity published in Holland 1940—1946, Advances in Appl. Mesh. 1 1948 перевод в сборнике «Проблемы механики», ИЛ, Москва, 1955.
 11.5. J. W. Geckeler, Mechanik der elastischer Kdrper, 1928 в переводе: И. В. Геккелер, Статика упругого тела, Гостехиздат, Москва, 1934, 154—161; 263—287.
 11.6. Th. Кйгтйп, The engineer grapples with non-linear problems, Bull. Am. Math. Soc. 46, № 7 1940, 615—683.
 11.7. S. Levy, Large deflection theory for rectangular plates, Proc. Symp. Appl. Math. 1 1949, 197—210.
 11.8. S. P. Timoshenko, History of strength of materials, New York,1953, 254—258; 408—411.

ИМЕННОЙ
 Ааре И. И. 394, 405 Агамиров В. Л. 325, 337, 343 Александровский С. В. 336, 398, 411 Алексеев С. А. 216, 218, 394, 407 Алумяэ Н. А. 396, 402, 409, 411 Алфутов Н. А. 340, 411 Андерсон P. Anderson R. 406 Андреева Л. Е. 211, 394, 407 Аппель П. Appel Р. 373
 Бабичева М. И. 412 Балабух Л. И. 57 Белкин В. П. 148
 Бергман С. Bergmann S. 393, 406 Бернулли Я. Bernoulli J. 386, 403 Бижляр Bijlaard Р. Р. 406 Бицено К. Biezeno К. 408, 413 Блох В. И. 147 Боднер Bodner S. R. 408 Болотин В. В. 404 Брайен Bryan G. Н. 387 Броуде Б. М. 393, 405 Бубнов И. Г. 58, 79, 80, 82, 91, 130, 249, 388, 389, 403 Булгаков Б. В. 294 Бурдин П. Г. 337, 351 Бурмистров Е. Ф. 410 Бэк Baok G. 407
 Вагнер Г. О. Wagner Н. 167, 391, 394, 407
 Ван Wang Chi-Teh 404, 407, 412 Варвак П. М. 390, 404 Вельтер Welter G. 411 Венцек Wenzek W. 411 Винденбург Windenbu>rg D. 337 Власов В. 3. 239, 358, 395, 396, 39в,
 409
 Ворович И. И. 394, 407, 409 Вулей P. Woolley R. М. 406, 407
 Галеркин Б. Г. 15, 58, 101 Галимов К. 3. 396, 409 Геккелер И. В. Geokeler J. W. 413
 УКАЗАТЕЛЬ
 Гениев Г. А. 410
 Генки Г. Henoky Н. 102, 216, 391, 404, 408
 Гольденберг Д. Goldenberg D. 406 Горюнов Ю. Б. 119 Граммель P. Gramme R. 408 Григолюк Э. Й. 211, 296, 394, 398.
 407, 410 Григорьев А. С. 205, 407 Гринмен Greenman S. 404 Губер Huber М. Т. 394, 403
 Даревский В. М. 329, 390, 404 Дау Н. Dow N. 407 Джинс Jeans J. 373 Джонс Jones R. 411 Динник А. Н. 222, 406 Доннелл Л. Donnell L. Н. 376, 396, 406, 411
 Е Кай-юань 394, 408, 413 Ёсимура Joshimura J. 412
 Жерар Gerard G. 144, 406 Жермен С. Germain S. 386
 Зволинский Н. В. 307, 391, 405 Зехлер Э. Sechler Е. Е. 406, 407 Зибритоски Zibriitosky G. 406 Зоннтаг Sonntag G. 405
 Ильюшин А. А. 205, 407 Исанбаева Ф. С. 338, 411 Исправников Л. Р. 321, 323, 336, 343, 347, 349 Ишлинский А. Ю. 376, 412
 Кайзер P. Kaiser R. 105, 404 Каппус P. Kappus R. 403 Капчинский И. М. 294 Карман Т. Karmani Th. 36, 143, 333, 377, 389, 391, 396, 397, 403, 406, 412, 413 Кармишин А. В. 350 Кемпнер Kempner J. 334, 398, 412 Кирсте Л. Kirste L. 380, 404, 412

ИМЕННОЙ УКАЗАТЕЛЬ 415
 Кирхгоф Kirchhoff G. 387, 403 Клебш Clebsch А. 387, 403 Клеппель К. Kloppel К. 412 Клэншоу Clan,show W. I. 411 Козаров М. М. 261, 410 Кокс Сох Н. L. 397, 406, 411 Коллатц Collatz L. 44 Колтунов М. А. 260, 398, 404, 405, 410 Корик Corriok J. N. 406, 407 Корнишин М. С. 249, 377, 398, 410 Короткин Я. И. 403 Крат В. А. 373
 Кромм Kromm А. 169, 391, 406 Крупен Krupen Р. 406 Кудрин С. А. 397 Кун P. Kuhn R. 406 Курдюмов А. А. 384, 412 Куршин Л. М. 317
 Лаврентьев М. А. 376, 412 Лагранж Ж- Lagrange J. 386 Ландау Л. Д. 403
 Леви С. Levy S. 104, 114, 115, 138,
 393, 404, 405, 406, 407, 409, 413 Леге Legget D. 411 Лейбензон Л. С. 357 Ленько О. Н. 302, 316, 398, 410 Лехницкий С. Г. 403 Лившиц Е. М. 403 Лившиц Я. Д. 404,
 Линь Хунь-сунь 413 Локшин А. 3. 403 Лоренц P. Lorenitz R. 318 Лу Loo Tsu-Tao 347, 412 Ляв A. Love А. 395, 404 Ляпунов А. М. 373
 Макферсон McPherson А. 405, 409 Маргерр К- Marguerre К 144, 169, 391, 403, 406, 413 Марьин В. А. 307, 312 Масуя Masuja U. 412 Мизес P. Mises R. 336, 342 Минеев В. Е. 352 Миракьян Г. М. 380 Михилсен Michielsen Н. F. 333, 334, 398, 412 Моисеев Н. Д. 373 Муштари X. М. 249, 261, 336, 369, 377, 382, 395, 396, 397, 398, 409, 411, 412
 Мюллер-Магьяри Miiller-Magyari F. 405
 Навье Navier 387 Нагаев В. А. 338 Надаи Nadai А. 200, 403
 Налешкевич Я. Naleszkiewicz J.
 376, 413 Наш Nash W. 338, 412 Невская Т. В. 396, 398, 410 Недермен Nedderman W. Н. 406 Нидхэм Needham R. А. 407 Никифоров С. Н. 393, 405 Новожилов В. В. 336, 395, 403 Нюландер Г. Nylander Н. 206, 409
 Одиньков Ю. Г. 350 Олейников Г. А. 392, 405 Ониашвили О. Д. 398, 410
 Панов Д. Ю. 189, 211, 391, 394, 407,
 408
 Папкович П. Ф. 144, 156, 167, 216, 310, 390, 391, 392, 403, 405,
 Перрон Perrone N. 405 Петрашень В. И. 393, 405 Поверус Л. Ю. 411 Подорожный А. А. 392, 405 Полубаринова-Кочина П. Я. 62, 405 Пономарев С. Д. 261 Попов Е. П. 373, 413 Постнов В. А. 393, 403 Прибрем Pribram Е. 397, 411 Прескотт Дж. Prescoitt J. 216, 390, 403
 Пфлюгер Pfliiger А. 407
 Работнов Ю. Н. 409, 413
 Pao Rao G. 412
 Резницкий Л. Я. 156
 Рейснер Э. Reissner Е. 73, 304,403,
 409
 Ряямет Р. К. 411 Ржаницын А. Р. 245, 396, 413 Ритц Ritz W. 60 Ромашевский А. Ю. 392, 405 Ростовцев Г. Г. 68, 148, 392,,405, 406 Рэдшоу Redshaw Е. С. 411 Рэмберг Ramberg М. 405, 409
 Саченков А. В. 336, 411 Свердлов И. А. 392, 397, 406, 410 Свирский И. В. 261, 382, 396, 404,
 410
 Сен-Венан Sain;t-Venanit 387
 Сервисен С. В. 403
 Сивере Н. Л. 403
 Синг Synge J. L. 410
 Слепов Б. И. 390, 404
 Соколов П. А. 137, 144, 391, 392, 406
 Соломенко Н. С. 404
 Стайпс Stiippes М. 57, 403, 409
 Стил Steele Т. К. 407

416
 ИМЕННОЙ УКАЗАТЕЛЬ
 Стокер Stoker J. 224, 394, 408 Стригунов В. М. 392, 406 Суркин Р. Г. 369, 398, 412 Сэндорф Sandorff Р. Н. 406
 Теребушко О. И. 306, 383, 398, 411 Тимошенко С. П. 22, 263, 318, 389, 404, 405 407, 409, 413 Треффц Trefftz Е. 391, 406 Триллинг Trilling С. 337
 Уэй Way S. 394, 409 Уэн Wan С. С. 411
 Фаерберг И. И. 392, 406 Федергофер К. Federhofer К. 394, 408
 Фельдман М. Р. 404 Феодосьев В. И. 189, 208, 211, 360, 377, 394, 408, 412 Феппль A. Foppl А. 103, 389, 390 Феппль JI. Foppl L. 403 Финкельштейн Р. М. 345 Финуп Fienup К. L. 406 Фокнер Falconer В. Н. 406 Фридрихе Friedirichs К. 224, 394, 397, 408, 412 Фын Fyng G. 404
 Холенд Howland W. L. 406 Хофф Н. Hoff N. J. 413 Ху Хай-чан 57, 394, 403, 408, 412, 413
 Цзянь Сюэ-шень Tsien Н. S. 333,
 377, 382, 396, 397, 411, 412, 413 Цянь Вэй-чан Chiein Wei-zang 196,
 394, 396, 408, 410, 413 Долли Zoelly R. 356
 Чаусов Н. С. 410 Чебанов В. М. 398, 411 Челлар Э. Csellar 147 Чжан Фу-фань 243, 404 Чикала Cicala Р. 411 Чувиковский В. С. 404
 Шаров Я. В. 404
 Шверин Е. Schwerin Е. 216, 218, 346, 409 Шиманский Ю. А. 403 Шнадель Schnadel G. 407 Шоу Shaw F. S. 405 Штаерман И. Я. 373, 395, 413 Штурм Sturm 346 Шумэн Schuman L. 407
 Эбнер Ebner 337 Эггер Egger Н. 408 Эйлер JI. Euler L. 386, 403 Энгессер Engeaser 54 Эшвелл Ashwell D. G. 404 Ээк Р. Н. 406
 Юнгблут Jungbluth 412 Ющенко О. А. 404

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
 Амплитуда гофра 211 Аналогии в теории устойчивости оболочек 373 Анизотропия естественная 65
 — конструктивная 65
 — цилиндрическая 182
 Барьер энергетический 284, 376 Брус эквивалентный 126
 Влияние на устойчивость оболочек начальной погиби 285, 352, 375
 начальных напряжений
 375
 температурного режима
 375
 Волнообразование при деформации сферической оболочки 360
 цилиндрической панели 266
 и д., 304 и д.
 замкнутой оболочки 320,
 337, 347, 351
 Гипотеза об отсутствии взаимного давления слоев пластинки 33
 — прямых нормалей 22, 40 Гофр синусоидальный 211
 Деформации срединной поверхности 22, 229
 Деформация закритическая оболочек 275 и д., 325 и д., 364 и д.
 круглых пластинок 221 ид.
 прямоугольных пластинок 124
 и д.
 — пластическая в пластинке большого прогиба 118
 Диаграммы характерные в задачах устойчивости оболочек 370
 Жесткость анизотропной пластинки изгибная 67
 крутильная 67
 приведенная 67
 — цилиндрическая 34, 68
 Заполнитель в трехслойной пластинке 69
 Изгиб цилиндрической оболочки парой сил 350 поперечной нагрузкой 351
 Колебания собственные панели 294 Контур пластинки 13 Координаты косоугольные 400 Коэффициент редукционный 125, 143, 150 155
 при вычислении момента инерции сечения панели 155 Коэффициенты второй квадратичной формы 401
 — первой квадратичной формы 401 Кривизна гауссова 38, 227
 нулевая 228
 отрицательная 227
 поверхности энергии 246
 положительная 227
 — главная 38, 174, 226
 — средняя 227
 Кривизны срединной поверхности 22, 229
 Кручение цилиндрической оболочки 345
 Линия кривизны 227, 400
 Мембрана 14, 78, 101, 205, 386
 — гофрированная 16, 211
 — кольцеобразная 218
 — круглая 214 и д.
 — с предварительным натяжением 121
 — хлопающая 208
 Метод Бубнова—Галеркина 58, 185, 238, 383
 — возмущения 62, 138. 196
 — конечных разностей 65
 — малого параметра 62
 — последовательных приближений 64
 — редукционных коэффициентов 126
 — Ритца 60, 185, 238, 382

418
 ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
 Методы приближенные в теории оболочек 238
 — прямые 61
 Моделирование оболочек при экспериментальных исследованиях 383 Модуль для пластинки в целом 131, 159
 Момент изгибающий 28, 174
 — крутящий 28
 Надлом пластинки у края 202 Направление главное 226 Напряжение равных энергий 377
 — критическое верхнее 263, 278, 376
 нижнее 278, 377
 Напряжения изгиба 27, 35, 189
 — полные 35
 — цепные в срединной поверхности, мембранные 14
 Начало изменений напряженного состояния 57 возможных перемещений 44
 Оболочка 226
 — безмоментная 228
 — замкнутая при внешнем давлении 335, 354
 — ортотропная 237
 — пологая 240, 396
 — сферическая 357 и д.
 —■ трехслойная 237
 — цилиндрическая круговая 228, 235
 замкнутая 228, 318 и д.
 открытая 228
 Обшивка корпуса корабля 15, 229
 — крыла самолета 15, 229, 400
 Панель коническая 210
 — пологая при поперечной нагрузке 240 и д.
 — цилиндрическая анизотропная 316 подкрепленная продольными
 ребрами 304
 при сдвиге 806 и д.
 сжатая вдоль образующей 263
 — — удлиненная, шарнирно закрепленная по длинным краям 240 и д., 248 и д.
 , защемленная по длинным
 краям 251 Перемещение возможное 44 Пластинка 13
 — абсолютно гибкая — см. Мембрана
 — анизотропная 65
 — гибкая средней толщины, средней жесткости 14, 102, 112
 Пластинка жесткая 13, 101» 112, 178
 — квадратная 134
 , защемленная по краям 141
 после потери устойчивости от
 сдвига 157, шарнирно опертая 103
 — косоугольная 400
 — круглая 171 и д.
 гофрированная 211
 , защемленная по контуру при
 равномерной поперечной нагрузке 186
 под действием сосредоточенной
 нагрузки 193 и д.
 при несимметричной деформации 180
 — многослойная 69
 — ортотропная 66
 — переменной толщины 36
 —, подкрепленная гофром 66 —, — упругими ребрами 151
 — прямоугольная 74 и д., 124 и д., защемленная по краям с конечным отношением сторон 109 и д.
 удлиненная 74 и д.
 — трехслойная 70 Плоскость срединная 13
 — фазовая 294
 Площадь сечения пластинки редуцированная приведенная 125 Поверхность развертывающаяся 228, 379
 — срединная 13, 226
 Погибь начальная 24, 32, 39, 61, 92, 179, 182, 205, 237, 285, 352, 375 Поле диагонально растянутое 167 «Портрет фазовый» системы 294 Потенциал внешней нагрузки 51 Предел упругого сопротивления 119, 203
 Принцип возможных перемещений 44, 183
 изменений напряженного состояния 57 Прогиб большой 18, 228
 Седло 295
 Сечение нормальное 226
 — редуцированное 125 Сила поперечная 29, 174, 232 Система координат косоугольная 400
 цилиндрическая 171
 «Скелет» оболочки в закритической области 378

И£ёдМе?ный УКАЗАТЕЛЬ
 419
 боотношения между деформациями и напряжениями усилиями 33, 176, 234 Стрингеры 15, 151, 304
 Теорема Кастилиано 381
 — Лагранжа 380 Точка возврата 294
 — изображающая на фазовой плоскости 295
 Траектория разделяющая 296
 Уравнение Бубнова — Галеркина 59
 — вариационное для гибкой пластинки 50
 в теории оболочек 238
 полное 53
 — равновесия элемента оболочки 232 пластинки 26, 175
 — совместности деформацией 26, 172, 230
 — сопряжения слоев 72 Уравнения основные теории гибких
 оболочек 235
 пластинок 36
 Условие граничное 39 и д.
 геометрическое 40
 естественное 40
 статическое 40
 существенное 40
 Условие граничное
 — совместности деформаций 57 Устойчивость круговой цилиндрической оболочки при внешнем давлении 335
 при изгибе 350
 при кручении 345
 при осевом сжатии 318
 — панели цилиндрической при сдвиге 306
 при сжатии вдоль образующей 263
 Функция нагрузки 176
 — напряжений 35
 — перемещений 72
 Хлопок 95, 320 и д., 374 Центр 294
 Ширина приведенная 125 Шпангоуты 339
 Энергия деформации в срединной поверхности 51
 — дополнительная 54
 — изгиба 51
 — полная 51, 381

Вольмир Арнольд Сергеевич. Гибкие пластинки и оболочки. Редактор И. К. Снитко.
 Техн. редактор Н.. Мурашова. Корректор JI. И. Савочкана.
 Сдано в набор 6IV 1956 г. Подписано к печати 16VII 1956 г. Бумага 6JX92je. Физ. печ. л. 261. Условн. печ. л. 26.25. Уч.-изд. л. 26,38. Г04449. Тираж 6U00 экз. Цена книги 15 р. 20 к. Заказ № 1118.
 Государственное издательство техникотеоретической литературы, Москва, В-71, Б. Калужская ул., 15
 Министерство культуры СССР. Главное управление полиграфической промышленности.
 4-я тип. им. Евг. Соколовой. Ленинград. Измайловский пр., 29.

Опечатки
 Стра¬
 ница
 Строка
 Напечатано
 Должно быть
 50
 5 сн.
 d2w
 w
 дхду
 дхду V
 84
 Фиг. 2. 3
 Защемленные
 с; защемленные
 182
 10 сн.
 ортотропна
 ортотропна и
 208
 6 »
 Qr
 аг
 208
 5 з>
 а,Л
 255
 2 св.
 cos 2у
 cos 25у
 255
 3 »
 sin М —
 sin jty —
 255
 8 сн.
 Я
 ' h ’
 II
 259
 5 св.
 . г
 kypy
 ЬуРу
 261
 6 »
 х
 — cos V Л
 х
 — а COS V а
 350
 7 »
 — Ро sin
 — Ро cos £■
 350'
 12 сн.
 -£-а р
 350
 12
 -fa2p2
 2 Р22
 355
 1 »
 нч
 Ри
 400
 3 »
 w> 1122 —
 1122 —
 415
 10 св.
 Одиньков
 Одинокое