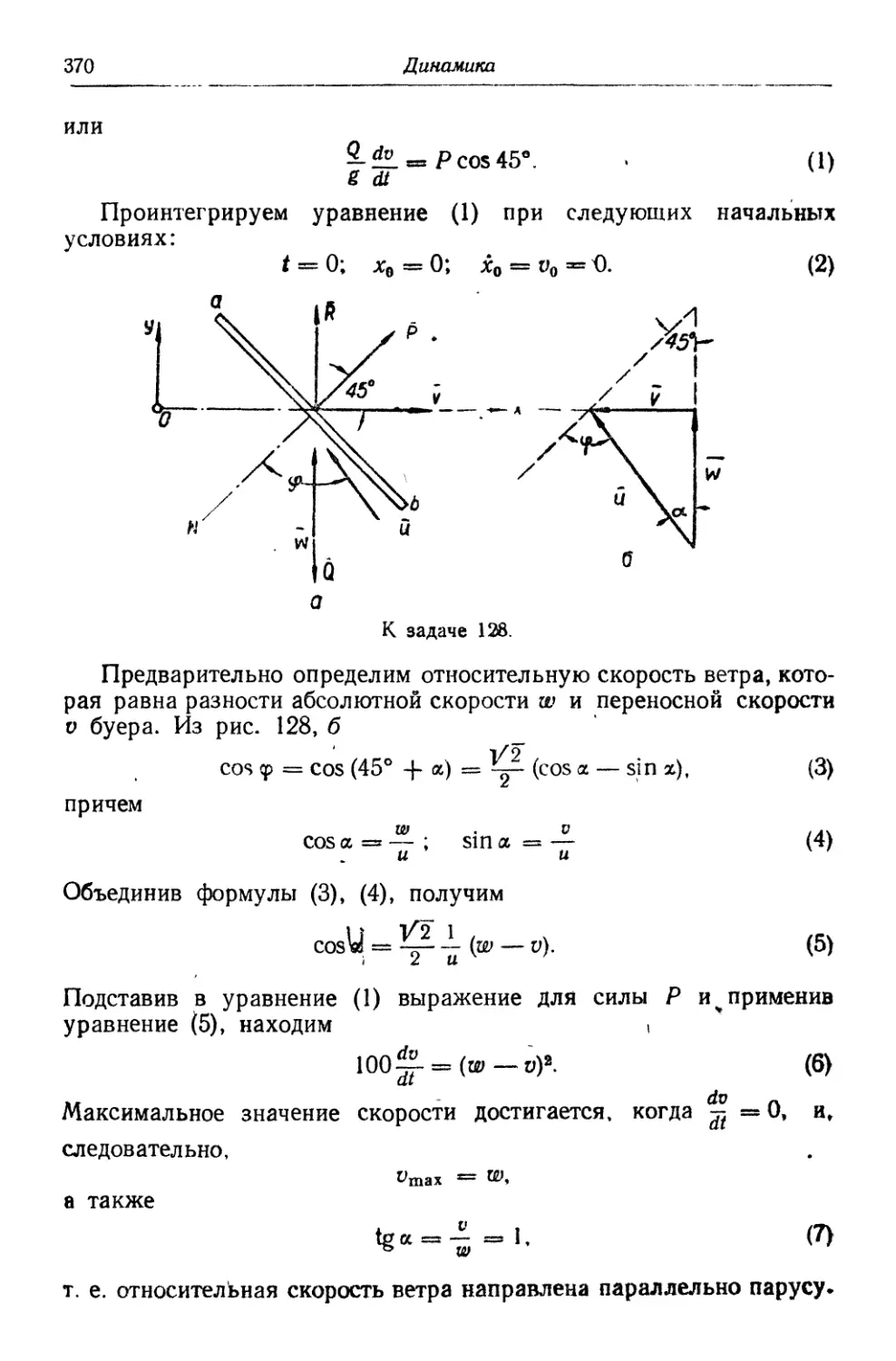
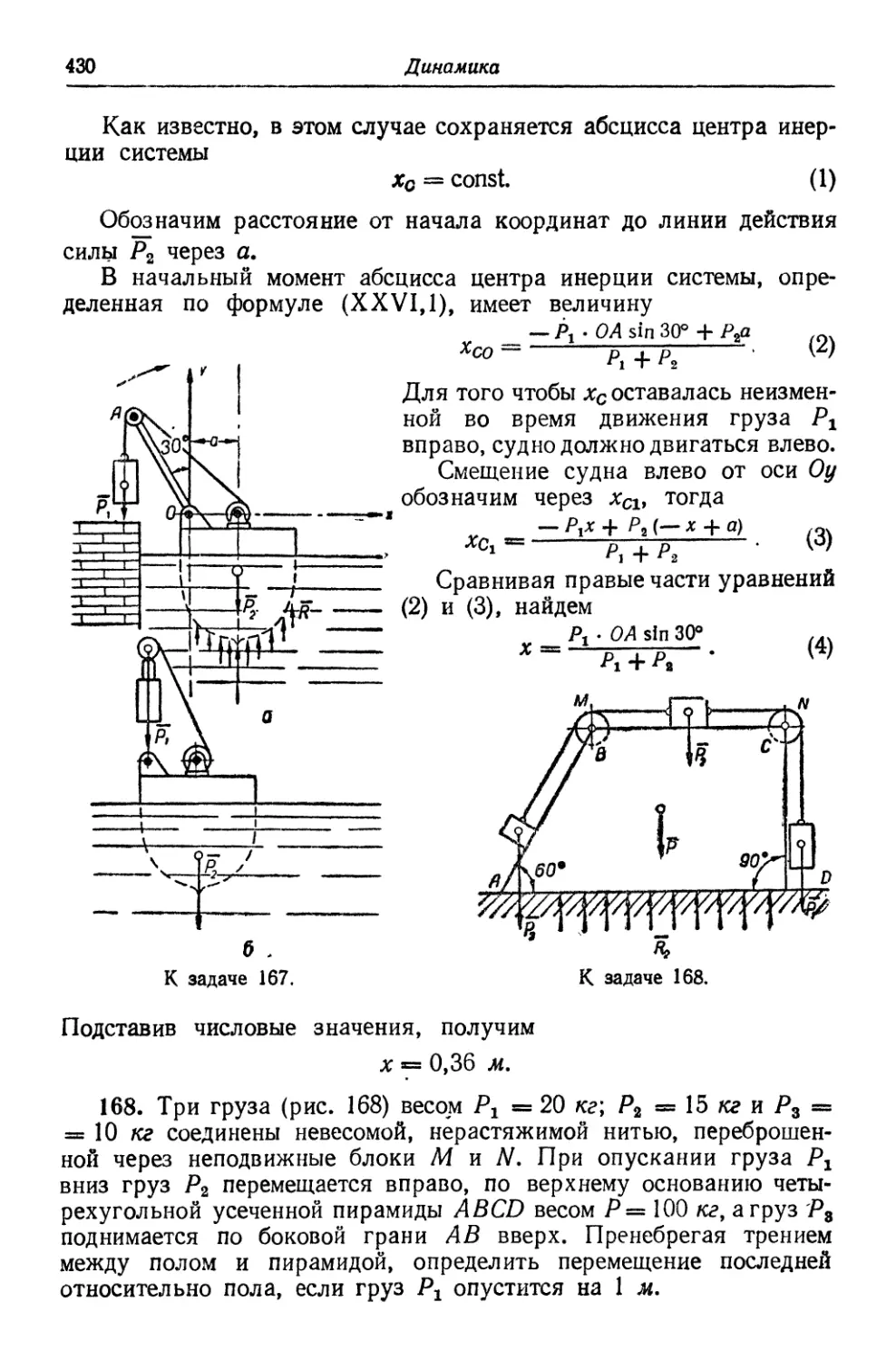
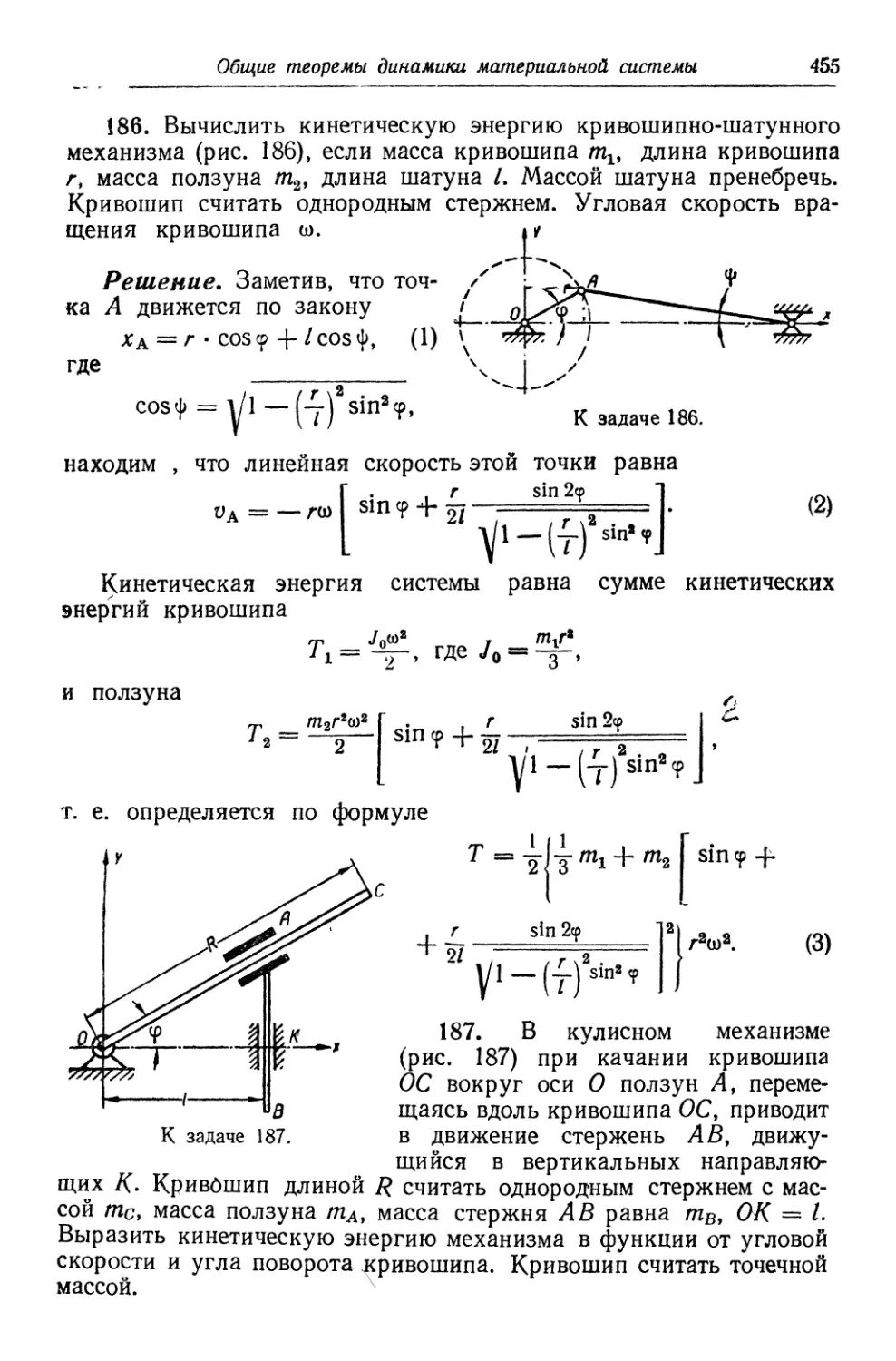
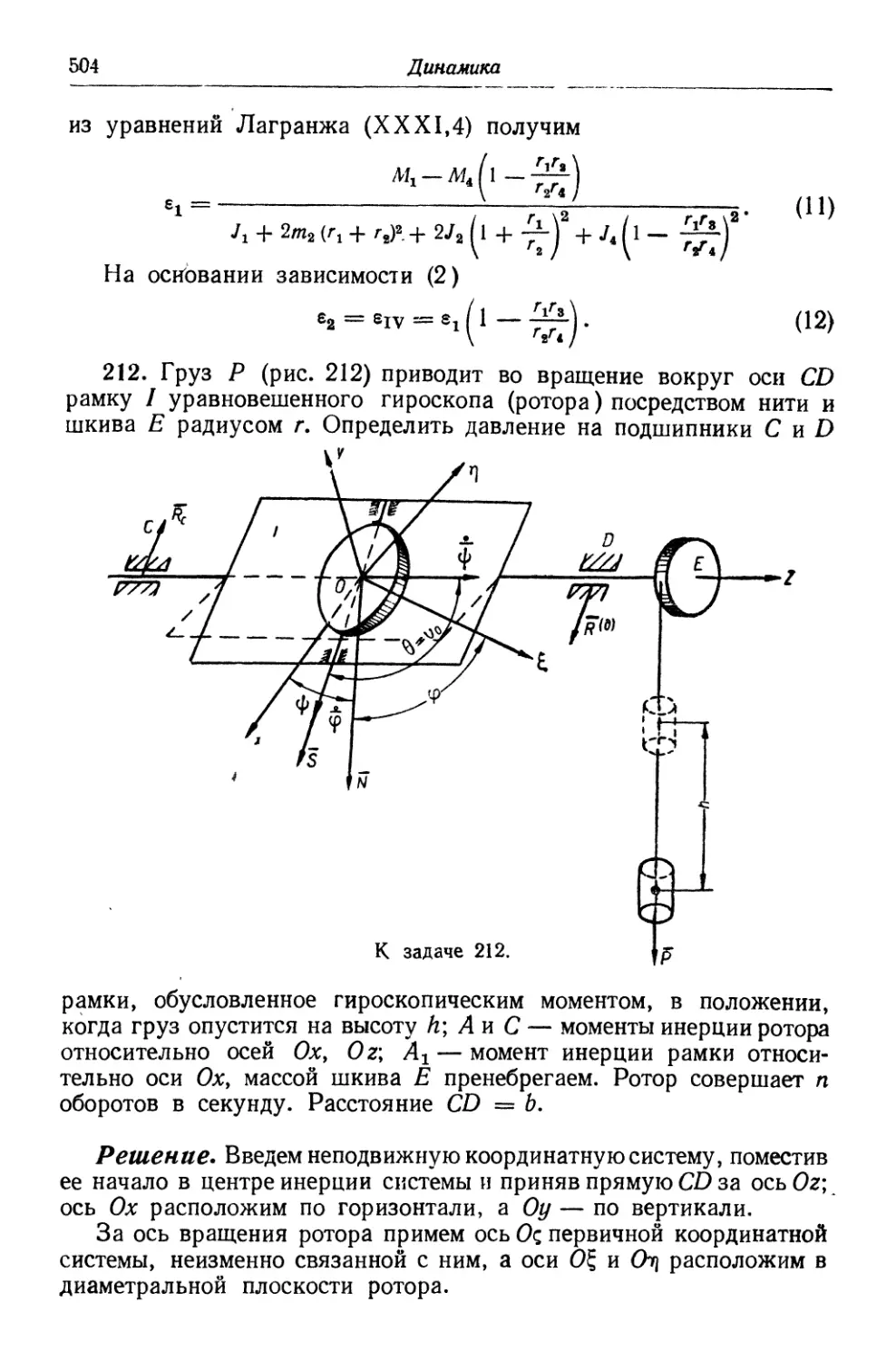
Автор: Кабальский М.М. Кривошей В.Д. Савицкий Н.И. Чайковский Г.Н.
Теги: решение задач теоретическая механика
Год: 1956
Текст
М. М.,КАБАЛЬСКИЙ, В. Д. КРИВОШЕЙ.
Н. И. САВИЦКИЙ. Г. Н. ЧАЙКОВСКИЙ
ТИПОВЫЕ ЗАДАЧИ
ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ
И МЕТОДЫ ИХ РЕШЕНИЯ
Под редакцией докт. техй наук
проф П. М. Варвака
ГОСУДАРСТВЕННОЕ ИЗДАТЕЛЬСТВО
ТЕХНИЧЕСКОЙ ЛИТЕРАТУРЫ УССР
Киев—1956
ОГЛАВЛЕНИЕ
Предисловие 7
Часть первая
Статика твердого тела
РАЗДЕЛ ПЕРВЫЙ
Система сил, действующих в плоскости
Глава L Силы, линии действия которцх пересекаются в одной точке . ДО
§ 1. Силы, действующие по одной прямой A0). § 2. Сложение двух пе-
пересекающихся сил A1). § 3. Разложение сил A1). § 4. Определение
равнодействующей произвольного числа сил A1). § 5. Геометрические
и аналитические условия равновесия плоского пучка сил A2).
§ 6. Условия равновесия трех непараллельных сил A2). § 7. Исследо-
Исследование связей и установление направления их реакций A2). § 8. Выбор
положения координатных осей A5). § 9. Порядок решения задач A5).
§ 10. Задачи A6).
Глава //. Параллельные силы 25
8 1. Сложение параллельных сил B5). § 2. Разложение силы на
две составляющие, ей параллельные B6). § 3. Сложение и условие
равновесия пар B6). § 4. Положение точки опоры стержня, балки B7).
§ о. Условие равновесия сил, приложенных к блокам, рычагам B7).
§ 6. условия равновесия плоской системы параллельных сил B7).
§ 7. Определение опорных реакций балок B7). § 8. Методические ука-
указания к решению задач B8). § 9. Порядок решения задач, рассмотрен-
рассмотренных в § 7 B9). § 10. Задачи C0).
Глава III. Устойчивость одного элемента конструкции (сооружения)
или всей конструкции против опрокидывания 37
§ 1. Методические указания к решению задач C7). § 2. Задачи C7).
Глава IV. Произвольная плоская система сил, не пересекающихся в од-
одной точке ... 42
§ 1. Аналитическое условие равновесия системы сил, приложенных к
рычагу D2). § 2. Аналитические условия равновесия произвольной
плоской системы сил D2). § 3. Исследование связей и установление
направления их реакций D3). § 4. Методические указания к решению
задач D4). § 5. Порядок решения задач D5). § 6. Задачи D6).
Глава V, Аналитическое определение усилий в стержнях статически
определимых ферм Г.З
§ 1. Определение усилий в стержнях ферм методом вырезания узлов
E3). § 2. Определение усилий в стержнях ферм для некоторых частных
случаев E5). § 3. Определение усилий в стержнях ферм методом сквоз-
сквозных сечений E6). § 4. Задачи E7).
Глава VI. Произвольная плоская система сил, приложенных к связан-
связанным между собой телам м»
§ 1. Равновесие системы сил, приложенных к шарнирно-стержневому
многоугольнику F0). § 2. Равновесие системы сил, приложенных к
системе рычагов, шаров и цилиндров F1). § 3. Определение усилий
в элементах механизма F1). § 4. Равновесие системы сил, приложен-
приложенных к шарнирно-консольньш мостам и балкам F1). § 5. Равновесие
системы, сил приложенных к трехшарнирньш аркам. Частные случаи
F2). § 6. Задачи F4).
1*
Оглавление
Глава VII. Силы трения . 86
§ 1. Силы трения при скольжении (86). § 2. Силы трения при ка-
качении (88). § 3. Задачи (89).
Глава VIII. Основы графической статики 122
§ 1. Сложение произвольной плоской системы сил. Частные случаи A22).
§ 2. Разложение одной силы на две составляющие. Частные случаи A25).
§ 3. Определение опорных реакций балок is ферм, имеющих одну по-
подвижную и одну неподвижную шарнирные опоры. Частные случаи A26).
§ 4. Определение опорных реакций трехшарнирных арок. Частные слу-
случаи A32). § 5. Определение усилий в стержнях статически определимых
ферм A36). § 6. Задачи A42).
РАЗДЕЛ ВТОРОЙ
Система сил, действующих в пространстве
Глава IX. Силы, линии действия которых пересекаются в одной точке . 162
§ 1. Определение равнодействующей пространственного пучка сил A52).
§ 2. Разложение одной силы на три взаимно перпендикулярные состав-
составляющие A52). § 3. Аналитические условия равновесия пространствен-
пространственного пучка сил A52). § 4. Методические указания к решению задач A53).
§ 5. Порядок решения задач A53). § 6. Задачи A54).
Глава X. Приведение произвольной пространственной системы сил к
простейшему виду 162
§ 1. Порядок решения задач A62). § 2. Задачи A65).
Глава XI. Произвольная пространственная система сил, не пересекаю-
пересекающихся в одной точке 170
§ 1. Аналитические условия равновесия. Частные случаи A70). § 2. Ис-
Исследование связей и установление направления их реакций A71).
§ 3. Методические указания к решению задач A72). § 4. Порядок реше-
решения задач A73). § 5. Задачи A73).
Глава XII. Определение положения центра тяжести твердых тел .... 187
§ 1. Основные предпосылки к определению положения центра тяжести
тел A87). § 2. Аналитическое определение координат центра тяжести
тел произвольного очертания A88). § 3. Методические указания к опре-
определению положения центра тяжести плоских фигур A94). § 4. Порядок
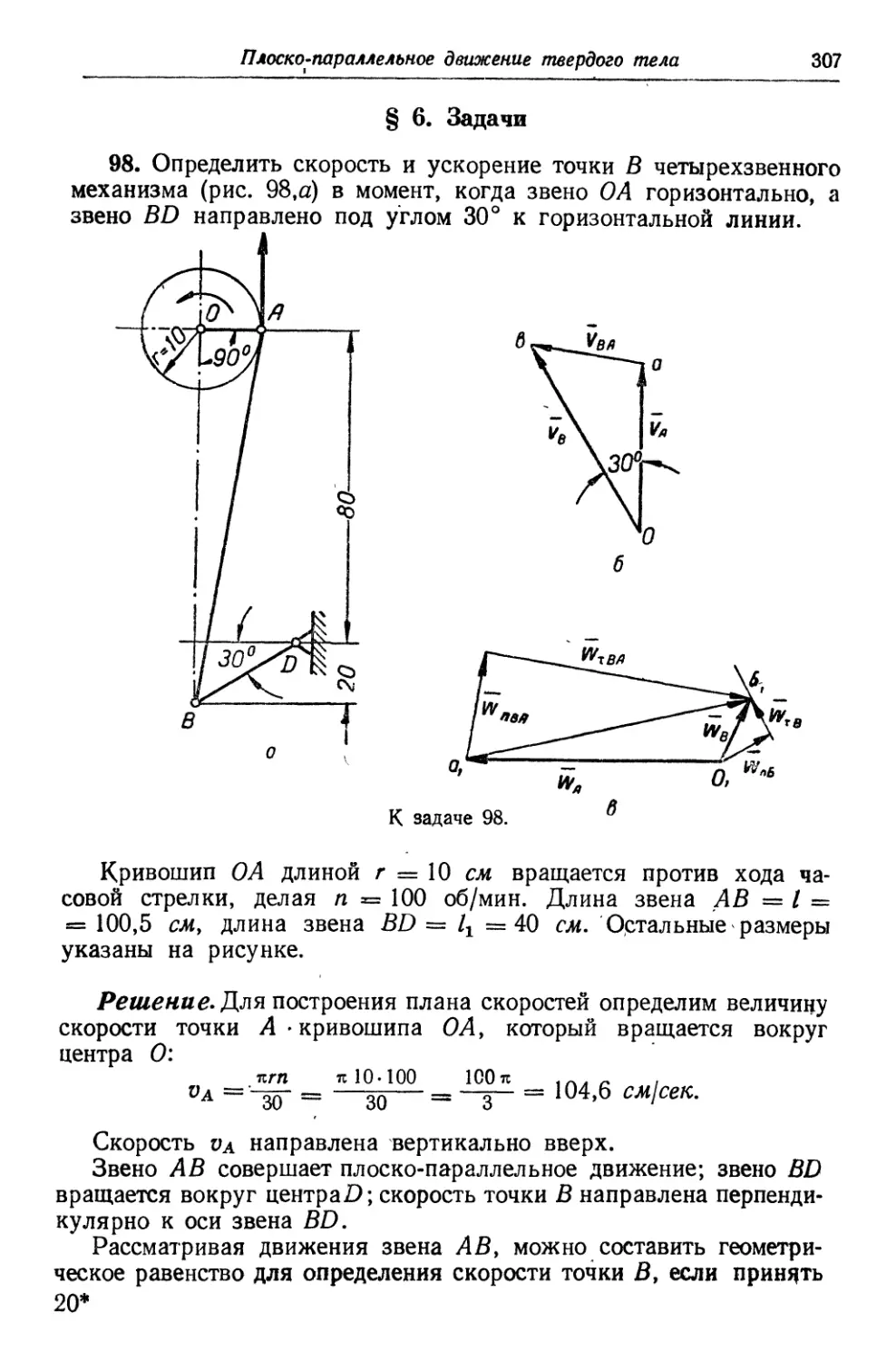
решения задач A96). § 5. Графическое определение положения центра
тяжести тел A97). § 6. Задачи B00).
Часть вторая
Кинематика
РАЗДЕЛ ПЕРВЫЙ
Кинематика точки
Глава XIII. Основные элементы движения точки . . 221»
§ 1. Краткие сведения B21). § 2. Методические указания к решению
вадач B27). § 3. Задачи B29).
РАЗДЕЛ ВТОРОЙ
Основные виды движения твердого тела и сложное движение точки
Глава XIV. Основные виды движения твердого тела 246
§ 1. Поступательное движение B46). § 2. Вращательное движение во-
вокруг неподвижной оси B4,6). § 3. Методические указания к решению
вадач B49). § 4. Задачи B53).
Глава XV. Сложное движение точки 265
§ 1. Абсолютное, относительное и переносное движения. Скорость
и ускорение точки B65). § 2. Методические указания к решению задач
B67). § 3. Задачи B70).
Оглавление
РАЗДЕЛ ТРЕТИЙ
Сложное движение твердого тела
Глава XVI. Плоско-параллельное движение твердого тела 292
§ 1. Общие сведения B92). § 2. Аналитический способ определения ско-
скоростей и ускорений точек тела B93). § 3. Методические указания к ре-
решению задач B96). § 4. Задачи. B96). § 5. Графический способ определе-
определения скоростей и ускорений точек тела и методические указания к
построению планов скоростей и ускорений C03). § 6. Задачи C07).
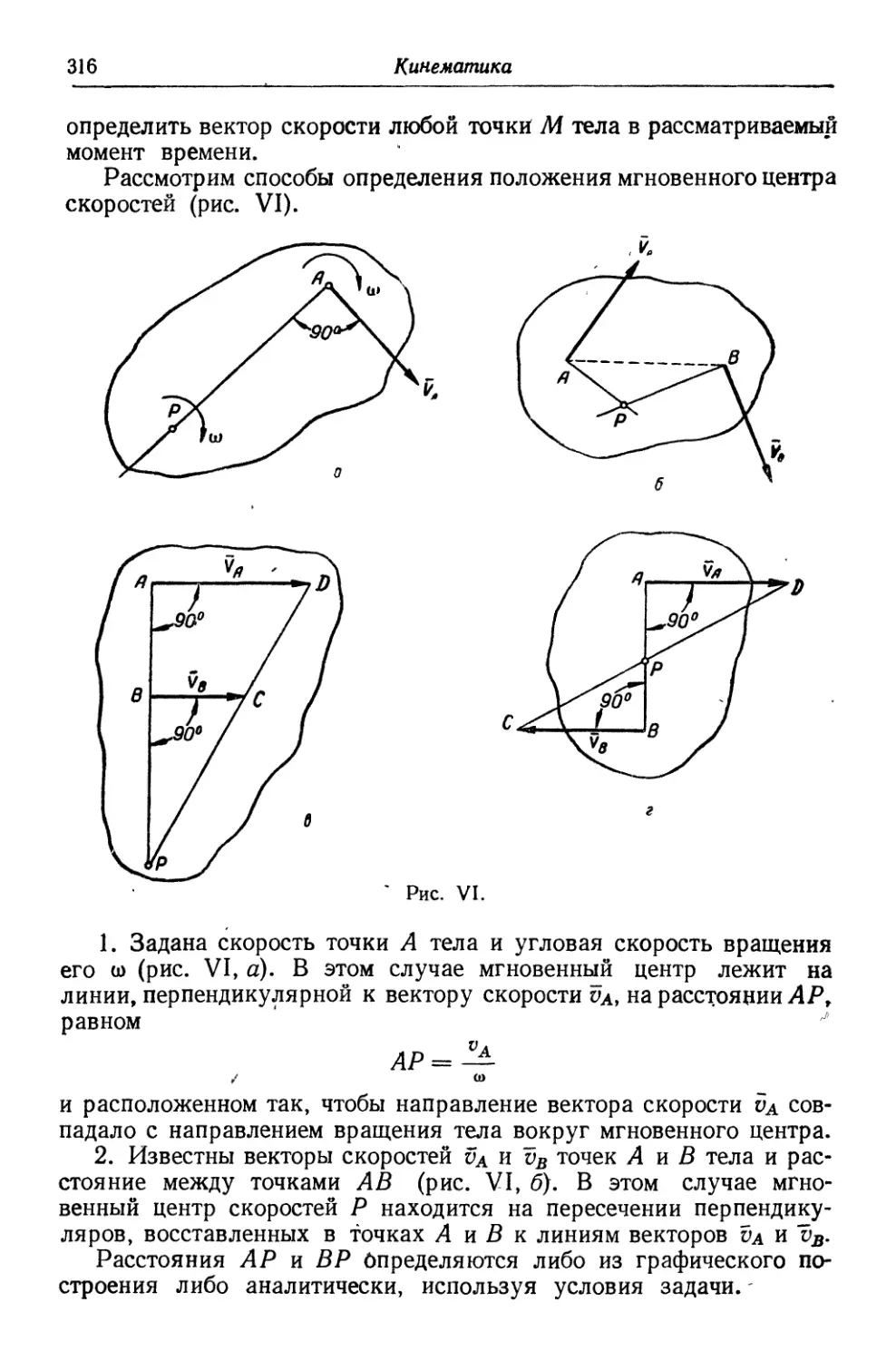
§7. Графоаналитический способ определения скоростей и ускорений
и методические указания к решению задач C11). § 8. Задачи C11).
§ 9. Определение скоростей точек тела при помощи мгновенных центров
скоростей. Центроиды C14). § 10. Методические указания к решению за-
задач C15). §11. Задачи C17). § 12. Определение ускорений точек тела при
помощи мгновенного центра ускорений C28). § 13. Методические указа-
указания к решению задач C28). § 14. Задачи C30).
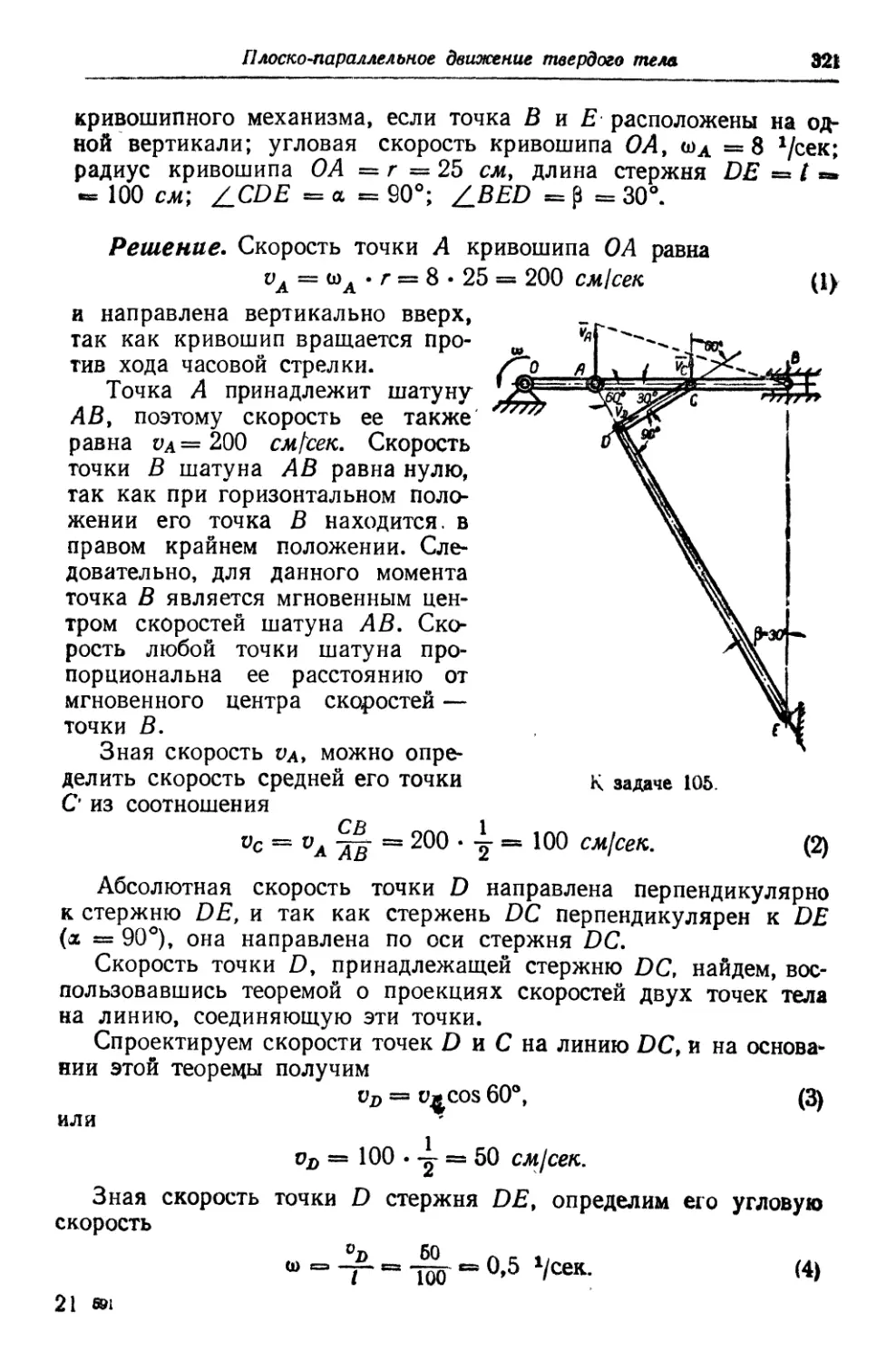
Глава XVII. Кинематика рядовых, планетарных и дифференциальных
зубчатых передач 336
§ 1. Краткие сведения о кинематике зубчатых передач C36). § 2. Мето-
Методические указания к решению задач C37). § 3. Задачи C39).
Глава XVIII. Движение твердого тела вокруг неподвижной точки .... 347
§ 1. Общие сведения C47). § 2. Методические указания к решению за-
задач C50). § 3. Задачи C51).
Часть третья
Динамика
РАЗДЕЛ ПЕРВЫЙ
Динамика материальной точки
Глава XIX. Дифференциальные уравнения движения материальной точки 359
§ 1. Определение сил по заданному закону движения C59). § 2. Задачи C60).
§ 3. Определение закона движения точки по заданной силе и массе C64).
§ 4. Прямолинейное движение C04). § 5. Криволинейное движение по
плоской кривой C65). § 6. Задачи C65).
Глава XX. Общие теоремы динамики материальной точки 372
§ 1. Методика решения задач на теорему об изменении количества движе-
движения C72). § 2. Задачи C73). § 3. Теорема об изменении момента
количества движения C75). 8 4. Задачи C77). § 5. Работа и мощность
C77). § 6. Задачи C80). § 7. Теорема о кинетической энергии материаль-
материальной точки C81). § 8. Задачи C83). § 9. Задачи смешанного типа C85).
Глава XXI. Колебательное движение материальной точки 390
§ 1. Свободные колебания C90). § 2. Затухающие, колебания C91). § 3. Вы-
Вынужденные колебания C92). § 4. Методические указания к решению
задач C94). § 5. Задачи C94).
Глава XXII. Сложное движение материальной точки 403
§ 1. Методические указания к решению задач D03). § 2. Задачи D04).
РАЗДЕЛ ВТОРОЙ
Динамика материальной системы
Глава XXIII. Основы кинетостатики 409
§ 1. Методические указания к решению задач D09). § 2. Задачи D10).
Глава XXIV. Принцип возможных перемещений 414
§ 1. Методические указания к решению задач D14). § 2. Задачи D16).
Глава XXV. Общее уравнение динамики 422
§ 1. Методические указания к решению задач D22). § 2. Задачи D23).
Глава XXVI. Общие теоремы динамики материальной системы 428
§ 1. Теорема о движении центра инерции системы D28). § 2. Задачи D29).
| 3. Изменение количества движения системы D34). § 4. Задачи D35).
§ 5. Теорема об изменении главного момента количества движения
системы. Дифференциальное уравнение врашения твердого тела
вокруг неподвижной оси Элементарная теория гироскопов D38) § 6. За-
Задачи D42). § 7. Теорема об изменении кинетической энергии системы
D52). § 8. Задачи D54).
б Оглавление
Глава XXVII. Плоско-Параллельное движение абсолютно твердого тела . 461
§ 1. Основные формулы теории D61). § 2. Задачи D63).
Глава XXVIII. Давление вращающегося абсолютно твердого тела на ось
вращения 468
§ 1. Методические указания к решению задач D68). § 2. Задачи D70).
Глава XXIX. Задачи смешанного типа 475
§ 1. Методические указания к решению задач D75). § 2. Задачи D76).
Глава XXX. Удар 481
§ 1. Методические указания к решению задач D81). § 2. Задачи D85).
Глава XXXI. Уравнения Лйгранжа II рода 493
§ 1. Методические указания к решению задач D93). § 2. Задачи D96).
ПРЕДИСЛОВИЕ
Для успешного изучения курса теоретической механики необ-
необходимо решить большое количество задач, часть которых решается
студентами в аудитории, значительная же часть должна быть
решена ими самостоятельно.
Предлагаемое учебное пособие содержит типовые задачи по
статике, кинематике, динамике и методы их решения. Предназна-
Предназначается пособие для студентов высших технических учебных заве-
заведений, а также для лиц, самостоятельно изучающих теоретическую
механику.
В каждой главе пособия приводятся основные формулы
из теоретического курса, даются общие методические указа-
указания к решению задач и рекомендуется порядок их решения. Кон-
Конкретные методические указания увязываются с подробным
решением типовых задач и их анализом, а также — в некоторых
случаях — со сравнением различных вариантов решения.
Рассмотренные типовые задачи взяты из наиболее распростра-
распространенного сборника задач И. В. Мещерского, причем приведенные
задачи представляют лишь небольшую часть общего количества
задач указанного сборника. Некоторые задачи предложены авто-
авторами.
Пособие составили: часть первую (Статика твердого тела) —
В. Д. Кривошей; часть вторую (Кинематика) — Н. И. Савицкий;
часть третью (Динамика) —М. М. Кабальский; главу XIII и часть
глав XIX и XX —Г. Н. Чайковский.
Все замечания и пожелания просим направлять по адресу:
Киев, Красноармейская ул., 11, Гостехиздат УССР.
Авторы
ЧАСТЬ ПЕРВАЯ
СТАТИКА ТВЕРДОГО ТЕЛА
Основная задача статики — преобразование системы сил, при-
приложенных к,абсолютно твердому телу, и замена ее другой систег
мой, ей статически эквивалентной. Преобразование системы сил
производится либо путем присоединения или отбрасывания* системы
сил, эквивалентной нулю, либо путем замены двух сил одной,
статически им эквивалентной.
Кроме того, задачей статики является выяснение условий,
которым должна удовлетворять система сил, приложенных к телу,
чтобы оно находилось в состоянии равновесия.
Пользуясь условиями равновесия, мы можем определять неиз-
неизвестные реакции связей.
Решение задач статики основывается на применении ряда
аксиом и их следствий.
Аксиома 1. Изолированная материальная точка находится в
покое или движется прямолинейно и равномерно.
Аксиома 2. Две силы, приложенные к твердому телу, взаимна
уравновешиваются тогда и только тогда, когда они равны по вели-
величине и действуют по одной прямой в противоположные стороны.
Аксиома 3. Присоединение или отбрасывание взаимно уравно-
уравновешивающихся сил не нарушает равновесия твердого тела.
Следствие аксиомы 3. Равновесие твердого тела не нарушается
от перенесения точки приложения силы вдоль ее линии действия
в любую точку тела.
Аксиома 4. Равнодействующая двух пересекающихся сил при-
ложена в точке их пересечения и изображается диагональю паралле-
параллелограмма, построенного на данных силах.
Аксиома 5. Всякому действию соответствует равное и проти-
противоположно направленное противодействие.
Аксиома 6. Равновесие нетвердого тела не нарушается от за-
затвердения данного тела.
Силы, приложенные к нетвердому телу (тросу, проводу и т. д.),
должны удовлетворять условиям равновесия твердого тела и,,
кроме того, добавочным условиям, зависящим от физических свойств
данного тела; например, равновесие нити возможно только при
ее растяжении.
10 Статика твердого тела
Аксиома 7. Состояние твердого тела не изменится, если, ос-
освободив его от связей, заменить их действие на тело соответствую-
соответствующими силами (приложить к нему силы, геометрически равные реак-
реакциям отброшенных связей).
Примечание. В ряде задач, после замены действия связей силами, чтобы
не повторять каждый раз фразу,'что эти силы геометрически равны реакциям
отброшенных связей, в дальнейшем решении эти силы названы реакциями.
РАЗДЕЛ ПЕРВЫЙ .
СИСТЕМА СИЛ, ДЕЙСТВУЮЩИХ В ПЛОСКОСТИ
ГЛАВА I
СИЛЫ, ЛИНИИ ДЕЙСТВИЯ КОТОРЫХ ПЕРЕСЕКАЮТСЯ
В ОДНОЙ ТОЧКЕ
§ 1. Силы, действующие по одной прямой
В частном случае, когда угол между линиями действия сил
равен нулю или 180°, силы располагаются на одной прямой.
В этом случае величина равнодействующей сил, действующих
по одной прямой, равна алгебраической сумме величин данных
сил, взятых с соответствующими знаками, т. е.
« = fi+f2 + f3+...+f^^i. A,1)
Величина силы, уравновешивающей систему заданных сил,
действующих по одной прямой, равна величине равнодействую-
равнодействующей данной системы сил
R' = -R = -YiFi A,2)
и направлена по линии действия сил — в сторону, обратную рав-
равнодействующей.
Силы, действующие по одной прямой, взаимно уравновеши-
уравновешиваются, если алгебраическая сумма их величин равна нулю
Я = ?Л = 0. A,3)
Внутренние (растягивающие или сжимающие) усилия, которые
возникают в различных сечениях стержня, подверженного дей-
действию внешних осевых сил, могут быть определены методом сечений
мысленно рассекая стержень на две части и отбрасывая одну из
них, мы заменяем ее действие, прикладывая к сечению оставшейся
части стержня силу, являющуюся равнодействующей всех сил,
приложенных к отброшенной части стержня; эта сила и является
искомой.
Силы, линии действия которых пересекаются в одной точке
11
§ 2. Сложение двух пересекающихся сил
Согласно аксиоме 4, равнодействующая двух пересекающихся
сил (рис. I) приложена в течке их пересечения и изображается
по величине и направлению диагональю параллелограмма, построен-
построенного на векторах, изображающих эти силы г.
Величина равнодействующей и обра- ?,
зуемые ею с силами углы определяются ^S^\ "\
из уравнений: #^^_/ V
или
R =
+ Q2 + 2PQ cos (Р, Q)
(P,/?) + Qcos(Q,/?)
Q = R
sin (Q, R) sin (Л R) sin (Р, Q)
. (I. 4)
Qcos<Q,R
Рис. I.
§ 3. Разложение сил
Разложение одной силы на две составляющие _может быть про-
произведено при помощи параллелограмма или треугольника сил.
Для этого, кроме раскладываемой силы, должны быть заданы
линии действия обеих составляющих сил, или линия действия
одной и величина другой силы, цли величины обеих составляю-
составляющих сил; в последнем случае может быть два решения. Могут
быть и другие условия разложения силы.
§ 4 Определение равнодействующей произвольного числа сил
Равнодействующая произвольного числа пересекающихся в
одной точке сил может быть найдена последовательным построе-
построением параллелограммов сил или построением силового многоуголь-
многоугольника; величина и направление равнодействующей определяются
замыкающей стороной силового многоугольника (ее стрелка на-
направлена навстречу общему течению 2 стрелок составляющих сил),
а ее линия действия проходит через точку пересечения линий дей-
действия рассматриваемых сил.
Аналитические выражения равнодействующей плоского пучка
сил и косинусов углов, образуемых ею с координатными осями,
имеют вид:
cos (/?, х) =
cos (Rt у) =
El
A,5)
где SXi и HY{ — суммы проекций всех сил на соответствующие
координатные оси.
1 Равнодействующая, а следовательно, н уравновешивающая этих двух сил
меньше их суммы, но больше разности.
2 Общее течение стрелок заданных сил при построении силового многоугольни-
многоугольника получается само собой, так как конец предыдущего вектора является началом
следующего.
12 Статика твердого тела
§ 5. Геометрические и аналитические условия равновесия
плоского пучка сил
Геометрическим условием равновесия рассматриваемой системы
сил является замыкание силового многоугольника; при этом стрелки
всех векторов, изображающих силы, направлены по одному тече-
течению.
Аналитические условия равновесия плоского пучка сил выра-
выражаются уравнениями
и формулируются так: пересекающиеся в одной точке силы взаимно
уравновешиваются, 'если сумма проекций всех сил на каждую из
двух координатных осей равна нулю.
§ 6. Условия равновесия трех непараллельных сил
Случай равновесия трех непараллельных сил широко исполь-
используется как при графическом, так и при геометрическом определе-
определении неизвестных; условием их равновесия является пересечение
линий действия указанных сил в одной точке и замыкание силового
многоугольника. Из этих условий и определяются неизвестные
силы.
§ 7. Исследование связей и установление направления их
реакций
Исследуем связи, наиболее часто встречающиеся в задачах этого
раздела, и установим возможное направление их реакций.
1. Некоторые рассматриваемые в данном разделе конструк-
конструкции представляют собой систему стержней, каждый из которых
прикреплен к двум шарнирам; внешние активные силы приложены
к одному из узлов (шарниров) этой конструкции \
Если вся рассматриваемая конструкция находится в равнове-
равновесии, то, следовательно, и каждый стержень ее также находится
в равновесии. Линии действия реакций связей, приложенных4 к
стержню, мы найдем, рассмотрев его равновесие. Для этого мыс-
мысленно отделяем любой стержень от остальной части конструкции
(отбрасываем связи-шарниры) и, чтобы не нарушилось его равно-
равновесие, прикладываем у обоих концов стержня силы, заменяющие
собою действие на стержень отброшенных связей.
Так как выделенный стержень находится в равновесии под
действием двух сил — реакций шарниров, мы приходим к выводу,
что эти реакции равны друг другу, действуют по одной прямой
(оси стержня) и направлены в противоположные стороны. В зави-
1 Собственным весом стержня — ввиду4его малой величины — пренебрегаем»
Силы, линии действия которых пересекаются в одной точке
13
симости от направления реакции шарниров стержень либо
растягивается (рис. II, а), либо сжимается (рис. II, б). Реакции
шарниров представляют собой осевые усилия, возникшие в рас-
рассматриваемом стержне.
По аналогичным > соображениям в шарнирно закрепленных под-
подвесках также могут возникать только осевые усилия.
При решении ряда задач
встречается необходимость рас-
рассмотреть равновесие какого-либо
узла (шарнира); в этом случае
к нему нужно приложить реак-
реакции соединенных с ним стер-
стержней. Согласно аксиоме 5, реак-
реакция каждого стержня по вели-
величине равна . направленной на
стержень реакции шарнира, но
направлена в противоположную
сторону, т. е. либо к узлу (когда
стержень сжат), либо от узла
(когда стержень растянут).
Иногда при решении задач
необходимо последовательно рас-
рассмотреть равновесие двух узлов
(шарниров) А и В, к которым
прикреплен стержень АВ кон-
конструкции.
В этом случае поступаем еле- Рис. II.
дующим образом: если стержень
растянут, то, применяя при рассмотрении равновесия узла А метод
сечений (рис. II, в), направляем реакцию Sx стержня АВ от
узла А к узлу В1, а при рассмотрении равновесия узла В (рис. Н,г)
ту же реакцию St того же стержня АВ направляем уже от узла В
к узлу А.
Таким образом, в зависимости от того, равновесие какого
узла рассматривается, одна и та же реакция Sx растягивае-
растягиваемого стержня АВ направляется или к узлу В, или к узлу Л, но
в обоих случаях — от узла, равновесие которого рассматривается,
в сторону отброшенной части конструкции.
1 Рассмотрев, аналогично предыдущему, равновесие узлов С и D
(рис. II, д, е), к которым прикреплен стержень CD, и предполо-
предположив, что стержень CD сжат, придем к выводу, что реакцию S2
стержня нужно направлять в обоих случаях к узлу, равновесие
которого рассматривается.
1 На рис. Н, в, г, кроме стержня АВ, показаны и другие примыкающие к
узлам А к В стержни, но реакции их не рассматриваются и поэтому не нанесены
на рисунок.
14
Статика твердого тела
При решении задач растягивающему усилию будем приписы-
приписывать знак плюс, сжимающему — минус.
При геометрическом решений задачи, основой которого являет-
является построение екло&ого многоугольника, характер усилии,-а
следовательно, и $га знак определяется течением стрелок векто»
ров, образующих мййгоугольник (при равновесии стрелки всех
векторов, изображающих силы, направлены по одному течениюI.
При аналитическом решении задачи условимся неизвестные
усилия, возникающие в стержнях конструкции, считать растягиваю-
растягивающими и реакции этих стержней направлять от узла в сторону отбро-
отброшенной части конструкции; при этом условии полученный при
решении знак плюс при неизвестной реакции подтвердит, что
стержень растянут, а знак минус покажет, что он сжат.
2. Неподвижный блок, не изменяя величины силы, изменяет ее
направление (незначительными силами трения в блоке пренебре-
пренебрегаем).
3. Нерастяжимые нити, веревки, канаты, провода, проволоки,
струны, тросы, цепи и т. д. могут испытывать только растягиваю-
растягивающие усилия (натяжения); реакции при этом направлены по их
осям. При криволинейном очертании нитей, веревок и др. реакции
их, следовательно, и натяжения изменяются по их длине как по
величине, так и по направлению; в каждой точке кривой реакция на-
направлена по касательной к кривой; в самой низкой точке кривой
реакция горизонтальна.
Реакции каждой части троса, поддерживающего какой-либо
груз 2 (рис. III, а), одинаковы независимо от уровня закрепления
концов троса (углы, образуемые в положении равновесия обеими
частями троса с вертикалью или горизонталью, между собой равны).
В частях провода или троса, поддерживающих два (рис. III, б)
1 Направлены в одну сторону по обводу многоугольника.
2 Груз при этом занимает на тросе самое низкое из всех возможных положение.
Силы, линии действия которых пересекаются в одной точке 15
или большее число грузов, возникают, как правило, различные
растягивающие усилия.
4. При свободном опирании конца стержня или балки на глад-
гладкую плоскость реакция направлена по нормали к опорной плос-
плоскости.
5. Если шар опирается на гладкую плоскость или сферичес-
сферическую поверхность, то реакция плоскости или поверхности направ-
направлена по нормали к ней * и проходит через центр шара.
6. Рассмотрим случай, когда на балку действует одна сила,
составляющая с двумя реакциями опор три непараллельных силы.
Плоскость под подвижным концом
балки, не препятствуя его переме-
перемещению вдоль самой себя 2, препят-
препятствует перемещению балки только в
перпендикулярном направлении, по-
поэтому реакция такой опоры на-
направлена по нормали к плоскости
(рис. IV, а).
Шарнирная неподвижная опора (рис. IV, б), не препятствуя
повороту конца балки или стержня вокруг своего центра, препят-
препятствует его перемещению в любом ином направлении, следовательно,
реакция такой опоры, проходя через центр шарнира, может иметь
любое направление; положение ее линии действия зависит от по-
положения линий действия заданной силы и реакции плоскости под
подвижным концом балки, так как линии действия всех трех сил
при равновесии балки должны пересечься в одной точке.
§ 8. Выбор положения координатных осей
При аналитическом решении задачи, когда необходимо опреде-
дить две неизвестные силы, координатные оси лучше всего направ-
направлять соответственно перпендикулярно и параллельно одной из
неизвестных сил; тогда проекция силы на перпендикулярную к ней
ось обратится в нуль, а на параллельную — сила спроектируется
в натуральную величину.
§ 9. Порядок решения задач
Большинство задач, рассматриваемых в этой главе, рекомендуем
решать в следующем порядке:
1. Установить, равновесие какого тела (узла, шарнира, стержня,
балки) нужно рассмотреть, чтобы определить неизвестные величины
(усилия, углы), выбирая то тело, к которому приложены внешние
активные силы.
1 Нормаль к поверхности в точке касания — это цориаль к касательной
плоскости, проведенной через данную точку.
2 Силами трения пренебрегаем.
16 Статика твердого тела
2. Установить, какие активные силы приложены к телу; от-
отбросив связи или применив метод сечений, заменить действие
связей силами.
3. При геометрическом решении нужно построить силовой
треугольник (многоугольник) и из подобия этого треугольника и тре-
треугольника из рисунка задачи или при помоги геометрических,
тригонометрических формул устайовить зависимость между неиз-
неизвестными искомыми величинами и данными из условия задачи.
При аналитическом решении задачи необходимо составить схему
действия сил на тело, выбрать положение координатных осей и
составить уравнения равновесия.
4. Определить неизвестные величины из решения уравнений,
причем, если этими неизвестными являются 'силы, то при геометри-
геометрическом решении направление этих сил определить из силового тре-
треугольника (по направлению стрелки соответствующей силы), а при
аналитическом решении — по найденному знаку.
5. Если из уравнений определены реакции связей, а необходимо
найти давления, оказываемые телом на плоскость Поверхность), —
учесть, что, согласно аксиоме 5, эти давления по величине равны
найденным реакциям, но направлены в противоположные им сто-
стороны.
§ 10. Задачи
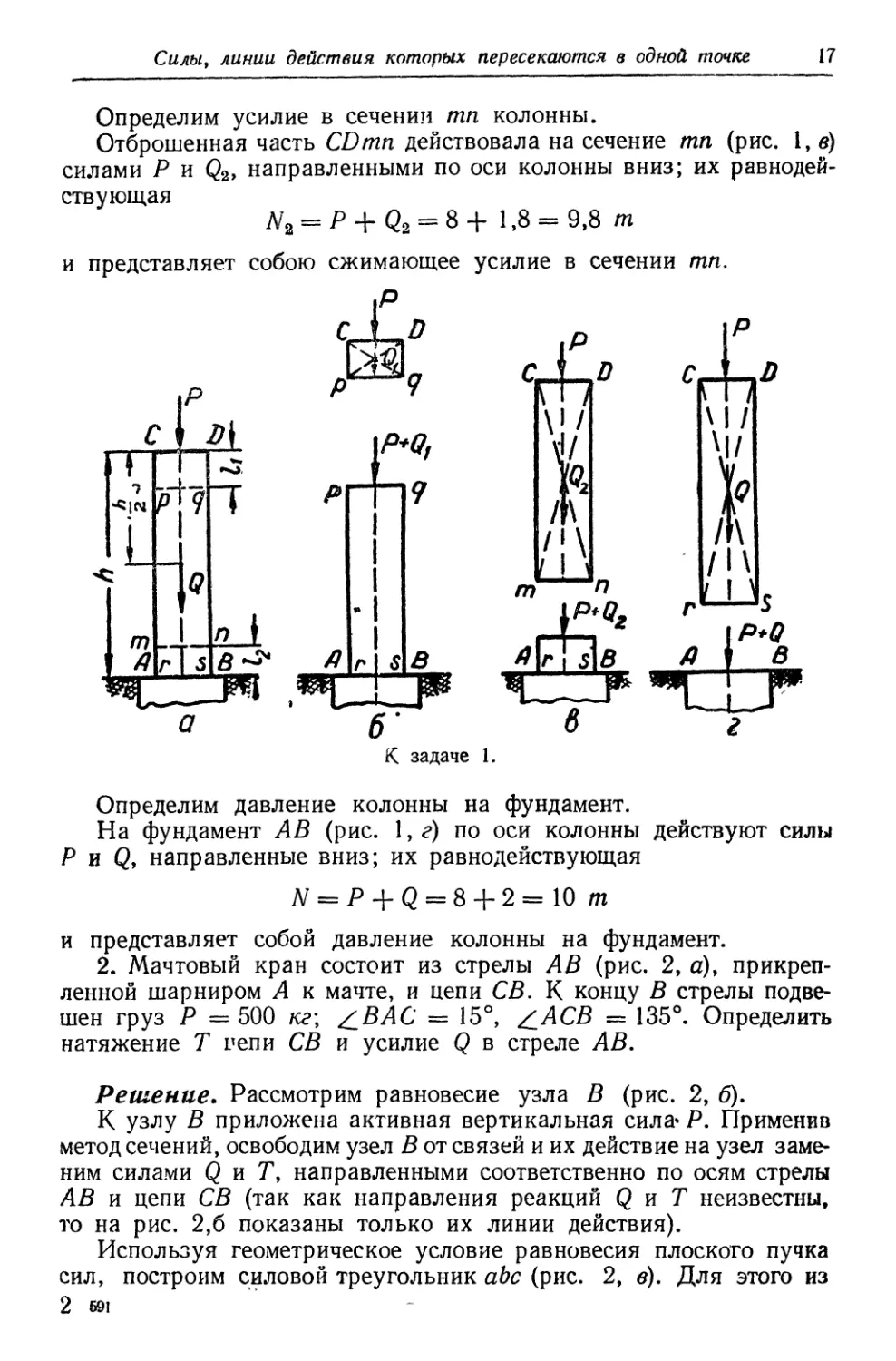
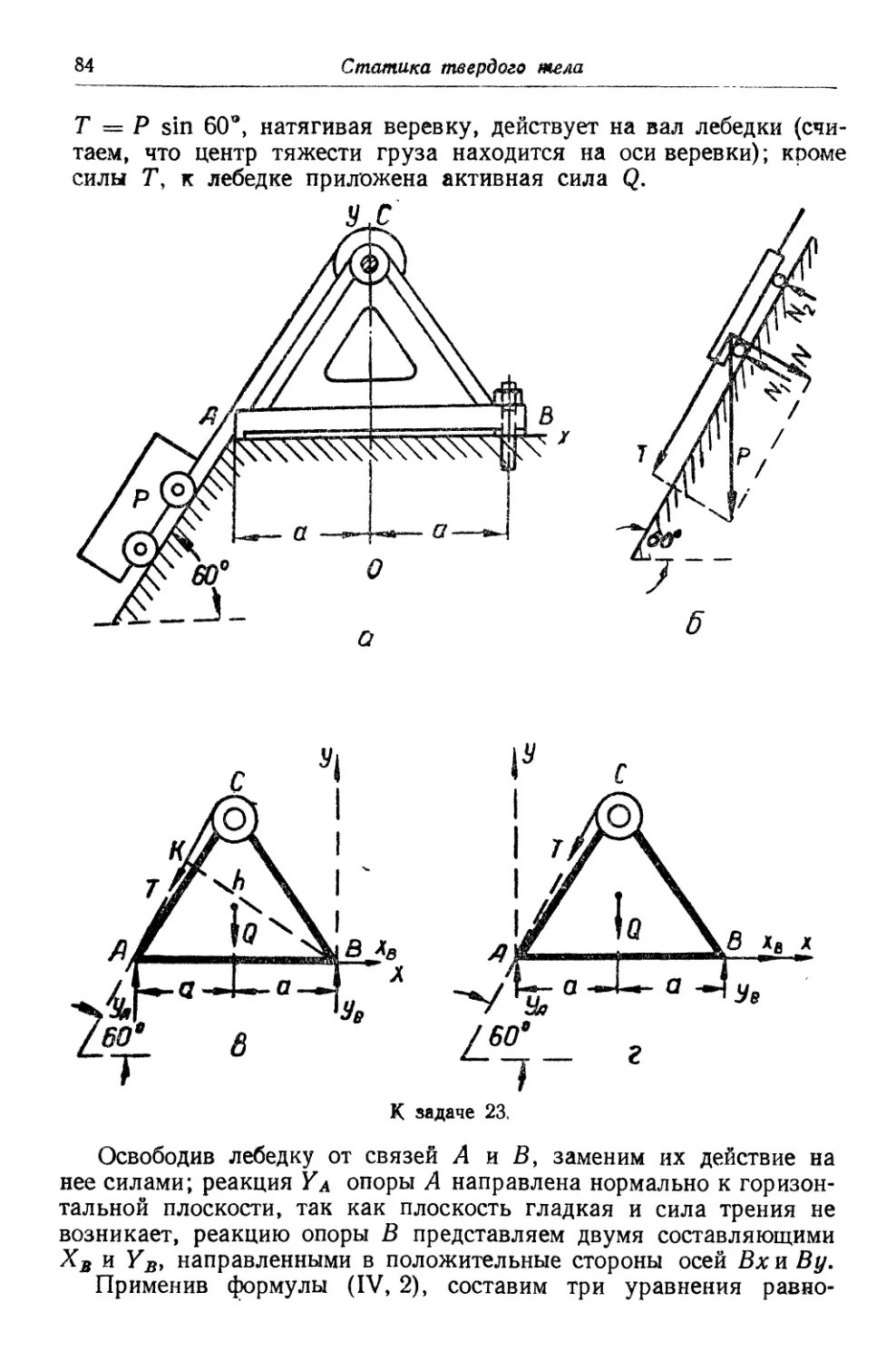
1. Однородная вертикальная колонна (рис. 1,а) высотой h = 5 м
и весом Q = 2 т нагружена вертикальной силой Р = 8т; колонна
опирается на фундамент. Определить сжимающие усилия в сече-
сечениях, находящихся от верхнего и нижнего концов колонны на рас-
расстоянии /х = /2 = 0,5 м, а также давление колонны на фундамент.
Решение. Применив метод сечений, отбросим верхние части CDpq
и CDmn колонны,, а их действие на оставшиеся части ApqB и АтпВ
заменим соответствующими силами, для чего предварительно оц-
ределим веса Q2 и Q2 отброшенных частей колонны:
Определим усилие в сечении pq колонны.
Отброшенная часть CDpq действовала на сечение pq (рис. 1, б)
силами Р и Qx, направленными по оси колонны вниз; их равнодей-
равнодействующая
Nx = Р + Qx = 8 + 0,2 = 8,2 т
и представляет собой сжимающее усилие в сечении pq.
Силы, линии действия которых пересекаются в одной точке
17
Определим усилие в сечении тп колонны.
Отброшенная часть CDmn действовала на сечение тп (рис. 1, в)
силами Р и Q2, направленными по оси колонны вниз; их равнодей-
равнодействующая
N2 = Р + Q2 = 8 + 1,8 = 9,8 m
и представляет собою сжимающее усилие в сечении тп.
о б'
К задаче 1.
Определим давление колонны на фундамент.
На фундамент АВ (рис. 1,г) по оси колонны действуют силы
Р и Q, направленные вниз; их равнодействующая
и представляет собой давление колонны на фундамент.
2. Мачтовый кран состоит из стрелы А В (рис. 2, а), прикреп-
прикрепленной шарниром А к мачте, и цепи СВ. К концу В стрелы подве-
подвешен груз Р == 500 кг\ ^ВАС = 15°, ^АСВ = 135°. Определить
натяжение Т гепи СВ и усилие Q в стреле АВ.
Решение. Рассмотрим равновесие узла В (рис. 2, б).
К узлу В приложена активная вертикальная сила* Р. Применив
метод сечений, освободим узел В от связей и их действие на узел заме-
заменим силами Q и Г, направленными соответственно по осям стрелы
АВ и цепи СВ (так как направления реакций Q и Т неизвестны,
то на рис. 2,6 показаны только их линии действия).
Используя геометрическое условие равновесия плоского пучка
сил, построим силовой треугольник abc (рис. 2, в). Для этого из
2 591
18
Статика твердого тела
произвольной точки а отложим вектор Р и затем проведем из его
начала а и конца в прямые, соответственно параллельные прямым
СВ и АВ до взаимного пересечения в точке с.
Направив стрелки реакций по одному течению со стрелкою силы
Р и нанеся их затем (мысленно) на рис. 2, б, убедимся, что реакция Q
стрелы АВ направлена к узлу Ву следовательно, стрела АВ сжата, а
реакция Т цепи СВ направлена от узла, следовательно, цепь СВ
растянута.
К задаче 2.
Установив углы силового треугольника abc из сопоставления
с рис. 2,а и воспользовавшись теоремой синусов, найдем зависимость
искомых реакций Т и Q от известны* из условия задачи данных
ГР _ т _ Q __ Q
sin 30°, ~~ sin 15° ~~ sin 135° "~ sin 45° '
A)
Из пропорции A) найдем искомые величины:
Р sin 15°
sin 30°
500 • 0,2588
0,5
Р sin 45° 500 -0,7071
sin 30°
0,5
= 258,8 кг;
= 707,1 кг.,
Усилие Т (натяжение цепи), растягивающее цепьСВ, и усилие Q,
сжимающее стрелу АВ, соответственно равные найденным реак-
реакциям, также приложены к узлу В (рис. 2, г), но направлены в
противоположные реакциям стороны.
3* Вес однородного трамбовочного катка равен 4 т, радиус
его 50 см (рис\ 3,а). Определить горизонтальное усилие Р, не-
необходимое для подъема катка на каменную плиту высотой 10 см.
Решение. Рассмотрим равновесие катка при разных его поло-
положениях.
В момент, когда к центру тяжести катка еще не приложена сила
Р (рис. 3, б) и он одновременно касается ребра С каменной плиты
Силы, линии действия которых пересекаются в сдноп точке
19
и опирается на плоскость по линии Е \ каток находится в равнове-
равновесии под действием сил Q и RB (собственного веса и реакции плос-
плоскости), равных друг другу, действующих по одной прямой в про-
противоположные стороны, приложенных к среднему (по длине) се-
сечению катка.
В
К задаче 3.
^ действием силы Р (рис. 3, в) каток отделяется от горизон-
горизонтальной плоскости и, поворачиваясь вокруг ребра С, нажимает
на каменную плиту, встречая с ее стороны реакцию, направленную
по нормали к плоскости, касающейся цилиндрической поверх-
поверхности катка по образующей С. Эта реакция направлена по радиусу
среднего сечения катка, к его центру. В рассматриваемом положе-
положении к центру среднего (по длине) сечения катка в плоскости сече-
сечения приложены активные силы Р и Q и реакция Rc каменной плиты.
Построим силовой треугольник abc (рис. 3, г). Для определения
величины силы Р, необходимой для подъема катка на плиту, пред-
предварительно найдем сторону CD из ДА CD:
CD = ]/(ЛСJ — {ADf = ]/502 —402 = 30 см.
Из подобия Д abc и /\ACD определим силу Р:
R
CD
откуда
P-QCD
1 Ребро С р линия Е перпендикулярны к плоскости рисунка.
20
Статика твердого тела
Примечание. Сила Р такой величины нужна только в начальный мо-
момент; из рис. 3, д видно, что сила Р в дальнейшем уменьшается и в момент,
изображенный на рис. 3, е, равна нулю.
4. Верхний конец А однородного бруса АВ (рис. 4, а), длина
которого 4 Л?, а вес Р = 10 /сг,. упирается в гладкую вертикальную
К задаче 4.
стену, а к нижнему концу В привязана веревка ВС, второй конец
которой закреплен в шарнире С. Найти расстояние АС в момент
равновесия бруса АВ, когда угол BAD = 45°, и определить натя-
натяжение Т веревки и реакцию RA стены.
Решение. Рассмотрим равновесие бруса АВ.
К брусу ЛВ(рис.4,б) на средине (в точке а) приложена активная
сила Р — собственный вес; кроме того, в точке А по нормали к
вертикальной плоскости (плоскость гладкая), т. е. горизонтально,
приложена реакция Ra плоскости и в точке В — реакция Т веревки.
Таким образом, брус АВ находится в равновесии под действием
трех непараллельных сил.
Условиями равновесия сил Р, R и Т являются пересечение
линий действия указанных сил в одной точке (в данном случае
в точке Ь — средине отрезка ВС) и замыкание силового треуголь-
треугольника.
Построим силовой треугольник def (рис. 4, в).
Для определения искомых величин предварительно определим
угол а из рис. 45, б.
Из прямоугольного Д ADB найдем
м.
. Силы, линии действия которых пересекаются в одной точке 21
CD
Так как AD = be, то и BD = be = -у- (to — средняя линия
&BCD).
Из ДВС?
t а = — — ^? — 2
Т
§а~" -SP ""* ЛР *~^»
откуда
2,83 ж,
Из Д cfe/ найдем:
sec а = -~ = Vl + tg»« = VT+T3 = К 5.
б. Балка АВ (ркс. 5, а, б) длиной 8 ^ имеет шарнирную непо-
неподвижную опору в точке А и шарнирную подвижную — в точке В.
К середине балки под углом 45° к ее оси приложена сила Р = 6 т;
собственным весом балки пренебрегаем. Определить реакции опор
для случаев, указанных на рис. 5, а и б.
Решение. Рассмотрим равновесие балки АВ.
Случаи, указанные на рис. 5, а и б, выражают равновесие
тела, находящегося под действием трех непараллельных сил:
Р, Ra и Rb — реакций опор Л и В, причем реакция подвижной
опоры В (трением пренебрегаем), направленная по нормали к
опорной плоскости, вдоль которой может перемещаться конец В
балки, в случае а — вертикальна, а в случае б — наклонна.
В обоих случаях найдем линию действия реакции Ra* соединив
точку А приложения ее с точкой К пересечения силы Р и реакции
RB, а ее направление и величины обеих реакций определим из
соответствующих силовых треугольников (рис. 5, г, ё).
Случай а. Определим углы силового треугольника (рис. 5. г)
из сопоставления с рис. 5, в.
Из Л КВС
ВК =ВС =4 м.
Из Д АВК .
= V W2 + (ВКJ = VS2 + 42 = 4 У 5 м,
ВК 4 I
Sill a = -Т77 = Г=. = -т= I
АК 41/5 1/5
АВ 8 2
ЛЛС л» — _____ «——. __________ —— ,
АК 41/5 1/5
22
Статика твердого тела
Установим зависимость между искомыми величинами Ra и Rb
и известными из условия задачи данными, применив теорему си-
синусов, для чего предварительно определим значение sin D5° — а),
sin D5° — а) = sin 45° cos а — cos 45° sin а =¦
_V~2 _2 Vj _J V~2 ш
~~ 2
У 5
2 VI 2/5'
Я Р
sin 45° ~~ sin D5° — a) ~ sin (90° -f a) ~~ cos a
P P
К задаче 5.
Приравняв первое отношение последнему, определим
Psin45° б~2~~
COS a
2
/5
: 4,74 т.
Приравняв второе отношение последнему, найдем RB:
Я sin D5° — a) 2T/5 _ 31^ 2
cos а
2
2Л2 т.
Силы, линии действия которых пересекаются в одной точке й$
Случай б. Установив углы силового треугольника (рис. 5, е)
из сопоставления с рис. 5, д, определим значения синуса и коси-
косинуса угла р; для этого рассмотрим Л>ВКС, /\CDK, A&DK и А
Из равнобедренного Д В КС получим
Из Д CDK
KD = CD = 2 м.
Из Д ЛО/С
ЛС + CD = 4 + 2 = 6 jw;
б5 = |/б -=2/10 = 6,32 м.
Из Д Л/СС, применив теорему синусов, определим sin p*.
AC AK AK
sinp~" sin 135° ~" sin 45° э
откуда
AVJ
sin в == ЛСз1'п45° « 2 L
P AK в 21^*10"
а затем определим cosp:
5
Из силового треугольника найдем:
==3 m.
Решим оба случая, применив аналитические условия равнове-
равновесия плоского пучка сил.
Случай а. Направим координатные оси согласно рис. 5, в и
составим два уравнения проекций всех сил на эти оси, считая
sin а и cos а известными.
— Pcos45° = 0, * A)
+ flB = 0. B)
Подставив данные из условия задачи и найденные значейия
sin a и cos a. в уравнения A) и B), получим Ra и Rb.
24 Статика твердого тела
Из уравнения A)
= 4,74 /л;
cos о
из уравнения B)
~ q ^», 1 d til .
Знак плюс при реакциях RA и /?Б показывает, что направление
их выбрано нами правильно.
Случай б. Направим ось Ах горизонтально, а ось Ау — верти-
' кально (рис. 5, д) и составим два уравнения проекций всех сил
на эти оси, предварительно определив значения sin а и cos а из
A ADK.
/CD 2 1
sin а = -~ = —— = —==.;
АК 21/10 1/10
AD 6 3
COS а = -г^ = —т= = -т=г ;
АК 21/10 1/10
J] Хг = /?^ cos а — Р cos 45° — RB cos 45° = 0; A')
2 У< = #а sin а — Р cos 45° + /?5 cos 45° = 0. B*)
Получили систему двух уравнений с двумя неизвестными.
Сложив уравнения (Г) и B'), определим Ra'-
RA (sin a + cos а) — 2Р cos 45° = 0,
откуда
R 2PCOS45 д 2 =3^5-6,71 Ш.
л sin о + cos а 1 3 г
1/То т/15
Из уравнения B')
Р cos 45° — RA sin a "^ '
Составление уравнений проекций всех сил на координатные
оси и решение их можно значительно упростить, направив ось
Кух по линии действия силы Р, а ось Кхх по линии действия реак-
реакции RB (рис. 5, д). При таком положении осей из каждого уравне-
уравнения проекций всех сил (на оси Ку\ и Кхг) выпадает одна из сил
(RB или Р), а вторая спроектируется в натуральную величину и,
Параллельные сады
25
кроме того, в одно из уравнений войдет только одна неизвестная
величина.
Составим эти уравнения равновесия.
Решив уравнения A*) и B"), получим:
(Г)
4=
У 5
= = 3 т.
ГЛАВА П
ПАРАЛЛЕЛЬНЫЕ СИЛЫ
§ 1. Сложение параллельных сил
Сложение двух параллельных сил, направленных в одну или
в противоположные стороны, сводится к нахождению их равнодей-
равнодействующей (ее величины, направления и линии действия).
в
в к л
fid" f
Равнодействующая двух параллельных сил, направленных в
одну сторону (рис. I, а, б), равна их сумме, параллельна им и
направлена в ту же сторону; линия ее действия проходит между
линиями действия составляющих сил ближе к линии действия
большей силы и делит расстояние между ними (или прямую.
6 Статика твердого тела
соединяющую точки приложения сил) на части, обратно пропорцио-
пропорциональные силам, т. е.
Равнодействующая двух параллельных сил, направленных
в противоположные стороны (рис. I, в, г), равна их разности,
параллельна им, направлена в сторону большей силы и приложена
за большей силой; линия действия равнодействующей делит
расстояние между линиями действия составляющих сил (или пря-
прямую, соединяющую* точки приложения сил) внешним образом на
части, обратно пропорциональные этим силам, т. е.
(И. 2)
b a а — b
Равнодействующая произвольного числа параллельных сил мо-
может быть найдена путем последовательного применения одной1 или
обеих формул (II, 1) и (II, 2).
§ 2. Разложение силы на две составляющие, ей параллельные
При разложении одной силы на две составляющие, ей параллель-
параллельные, пользуются формулами (II, 1) и (II, 2); для этого, кроме
раскладываемой силы, должны быть заданы линии действия обеих
составляющих сил или величина, направление и точка приложе-
приложения (или линия действия) одной из них. Возможны и другие усло-
условия разложения сил.
§ 3. Сложение и условие равновесия пар
При сложении пар руководствуются следующим.
Система пар может быть заменена эквивалентной ей одной па-
парой, их равнодействующей, момент которой равен алгебраической
сумме моментов составляющих пар, т. е.
М = т1 + т2 + тъ + ... + тп = ]? т^ (II, 3)
В частном случае, когда пары взаимно уравновешиваются,
формула (II, 3) принимает вид
М = тг + щ + тг + ... + тп = ? т{ = О (И, 4)
и формулируется так: пары взаимно уравновешиваются, если ал-
алгебраическая сумма их моментов равна нулю.
Параллельные силы 27
§ 4. Положение точки опоры стержня, балки
Если стержень или балка имеют одну точку опоры, то ее по-
положение (иначе говоря, положение точки приложения равнодей-
равнодействующей всех активных сил) определяется при применении тео-
теоремы Вариньона о моменте равнодействующей системы сил отно-
относительно точки; величина равнодействующей параллельных сил
определяется как алгебраическая сумма всех заданных сил.
§ 5. Условие равновесия сил, приложенных к блокам,
рычагам
Неизвестные силы, действующие как на простой, так и на диф-
дифференциальный блок или рычаг, определяются из одного уравне-
уравнения равновесия: сумма моментов" всех активных сил относительно
точки опоры блока или рычага равна нулю
A1,5)
§ 6. Условия равновесия плоской системы параллельных сил
Аналитические условия равновесия плоской системы параллель-
параллельных сил выражаются двумя уравнениями равновесия:
(И, 6)
и формулируются так: плоская система параллельных сил нахо-
находится в равновесии, если сумма проекций всех сил на любую ось,
не перпендикулярную к ним, и сумма моментов всех сил относи-
относительно любой точки плоскости их действия равны нулю (удобнее
всего проектировать силы на ось, им параллельную).
Иначе, условия равновесия выражаются следующими Двумя
уравнениями равновесия:
(И,7)
и формулируются так: плоская система параллельных сил нахо-
находится в равновесии, если сумма моментов всех сил относительно
каждой из двух точек, расположенных на любой прямой, не парал-
параллельной силам, равна нулю.
§ 7. Определение опорных реакций балок
Почти во всех рассматриваемых в этой главе балках, кагружен-
ных вертикальными силами, опорой шарнирного подвижного конца
ее является горизонтальная плоскость; пренебрегая незначитель-
28 Статика твердого тела
ными силами трения, возникающими между этой плоскостью и
концом балки, считаем, что реакция плоскости направлена по нор-
нормали к ней, т. е. вертикально, следовательно, и реакция плоскости
под шарнирным неподвижным концом балки тоже вертикальна,
иначе равновесие балки было бы невозможным.
Таким образом, действующие на балку активные и реактивные
силы образуют систему параллельных сил; величины реакций
опор балок могут быть определены из уравнений равновесия*этой
системы; в частном случае одна или обе опорные реакции могут
быть равны нулю.
В задачах данной главы, кроме балок, имеющих две опоры,
встречается балка-консоль, имеющая один свободный конец, а
другой заделанный (защемленный) в стену или в какую-либо
массивную часть конструкции, препятствующую повороту и сме-
смещению этого конца в любом направлении. *
В такой заделке, как правило, в результате действия активных
нагрузок возникают сила (реакция) и пара, момент которой назы-
называется реактивным моментом; для их определения пользуются
уравнениями (II, 6).
В частных случаях нагружения консоли в заделке может воз-
возникнуть только сила (реакция) или-только пара; возможен случай,
когда действующие на консоль активные силы взаимно уравнове-
уравновешиваются, не вызывая в заделке ни реакции, ни реактивного мо-
момента (например, когда консоль нагружена двумя противоположно
направленными парами с одинаковым моментом).
Случай приложения нагрузок к балке не непосредственно, а при
помощи какого-либо механизма (крана) рассмотрен в задаче 7.
§ 8. Методические указания к решению задач
При решении задач необходимо помнить следующее:
1. Сумма моментов сил, составляющих пару, относительно
любой точки плоскости их действия является величиной постоянной,
равной моменту пары, поэтому в уравнение моментов всех прило-
приложенных к балке сил относительно какой-либо точки момент пары
(если пара приложена) вписывается с соответствующим знаком,
зависящим от направления вращения пары, без умножения его на
какое либо плечо.
2. Реакции опор балок, нагруженных только одной парой или
несколькими не уравновешивающимися между собой парами, равны
между собой по величине, параллельны, направлены в противопо-
противоположные стороны, т. е. также образуют пару, уравновешивающую
приложенную к балке пару (пары).
3. Момент нагрузки, распределенной на части длины балки или
по всей ее длине (равномерно или по какому-нибудь другому за-
закону), относительно какой-либо точки плоскости ее действия оп-
Параллельные силы ' 29
ределяется по теореме Вариньона как момент ее равнодействую-
равнодействующей, проходящей через центр тяжести соответствующей грузовой
площади, относительно той же точки.
4. Реактивный момент, возникающий в заделке балки-консоли,
равен сумме моментов всех активных сил о1тюсительно центра
моментов, расположенного в заделке. Возникающая в заделке
реакция всегда равна по величине равнодействующей всех актив-
активных сил, приложенных к консоли, но направлена в противо-
противоположную ей сторону.
5. Определяя положение точки опоры балки или стержня,
удобнее всего для применения теоремы Вариньона выбирать за
центр моментов начальную или конечную точку оси балки,
стержня.
6. Неизвестные реакции опор балки лучше определять по урав-
уравнениям (И, 7) с последующей проверкой правильности их опреде-
определения по первому из уравнений (II, 6). Если сумма проекций
всех сил на ось Оуу параллельную силам, равна нулю, реакции
найдены правильно *.
7. При составлении уравнений моментов всех приложенных к
балке сил центр моментов лучше выбирать последовательно
в опорных точках; тогда в каждое из этих уравнений равновесия
войдет только по одной неизвестной реакции.
§ 9. Порядок решения задач, рассмотренных в § 7
При решении этих задач рекомендуем:
1. Установить, равновесие какого тела нужно рассмотреть для
определения неизвестных величин.
2. Установить, какие активные силы действуют на тело; отбро-
отбросить связи и заменить их действие на тело силами, геометрически
равными реакциям связей.
3. Составить уравнения равновесия A1,7), выбрав центр или
центры моментов, а при использовании уравнений (II, 6) выбрать и
направление координатной оси.
4. Решив уравнения равновесия, определить неизвестные силы;
положительный знак при найденном значении реакции (реактивного
момента) подтвердит правильность выбранного направления, а отри-
отрицательный — покажет, что реакция (реактивный момент) направ-
направлена в сторону, противоположную выбранной.
5. Если найдены реакции связей, а необходимо найти давле-
давления, оказываемые телом на те или иные плоскости (поверхности),
1 Отмечаем, что равенство нулю суммы проекций всех сил на параллельную
им есь не является еще гарантией правильности найденных значений реакций;
так, например, ошибка в знаке момента пары, приведя к увеличению одной и
уменьшению другой реакции на одну и ту же величину, не изменит суммы реак-
iP| следовательно, не нарушит указанное выше равенство.
30
Статика твердого тела
то необходимо учесть, что, согласно аксиоме 5, давления равны
реакциям по величине, но направлены в противоположные им
стороны.
§ 10. Задачи
6. Между опорами двухкоисольной горизонтальной балки
(рис. 6, а) приложена пара сил (Р, Р), к левой консоли — равно-
равномерно распределенная нагрузка интенсивностью р, а в точке D
р
\ш\
4,
V,
— а-»-
й В
JL-p **r
D С
Щ
К задаче 6.
правой консоли — вертикальная нагрузка Q. Определить реак-
реакции гопор, если Р = 2 m, Q = 4 т, р = 4 m/ж, а = 2,5 ж.
Решение. Рассмотрим равновесие двухконсольной (имеющей
два сбободных конца) балки CD как свободного твердого тела.
К балке приложена активная нагрузка, состоящая из: пары
(Р, Р) с моментом т, равным Ра, равномерно распределенной
нагрузки интенсивностью р (на каждый метр участка СА действует
вертикально вниз сила, равная 4т), равнодействующая которой
приложена к средине участка СА и равна ра, и силы Q.
Освободив балку от связей А к В (рис. 6, б), заменим их дейст-
действие силами Ra и Rb- Реакция RB подвижной опоры нормальна к
плоскости опоры, т. е. вертикальна, реакция Ra шарнирной непо-
неподвижной опоры А также вертикальна. Таким образом, активные
силы и реакции Rb и Ra вертикальны (действие пары не изменится,
если мы повернем ее в плоскости ее действия, т. е. в плоскости
рисунка, так, чтобы силы Р и Р, входящие в состав пары, стали
вертикальными). Будем считать, что обе реакции направлены
вверх.
Применив формулы (II, 7), составим уравнения равновесия
плоской системы параллельных сил, приняв за центры моментов
точки Л и В.
ра-%
т
A)
B)
Параллельные силы 31
Подставив значение т в уравнения A), B) и решив их, полу-
получим:
Rb = 2 = 2 e 2'5 т'
-> p. 2,5a+ P-Q 4.2,5.2,5+2-4 -
A j. = 2 = 2 = 11,0
т.
Положительные знаки при Ra и #в подтверждают правиль-
правильность выбранного направления их.
Сделаем поверку, спроектировав все силы на вертикальную
ось Су.
При этом необходимо учесть, что в каком бы положении
ни была задана пара (Р, Р), проекции каждой из сил Р,
входящих в состав этой пары, на любую ось равны между собон>
по величине, но направлены в противоположные стороны, поэ-
поэтому сумма обеих проекций всегда равна нулю и в уравнении про-
проекций фигурировать не будет.
%?< = ра + RA+ RB — Q = — 4-2,5 + 11,5 + 2,5-4 = 0,
следовательно, реакции Ra и Rb найдены правильно.
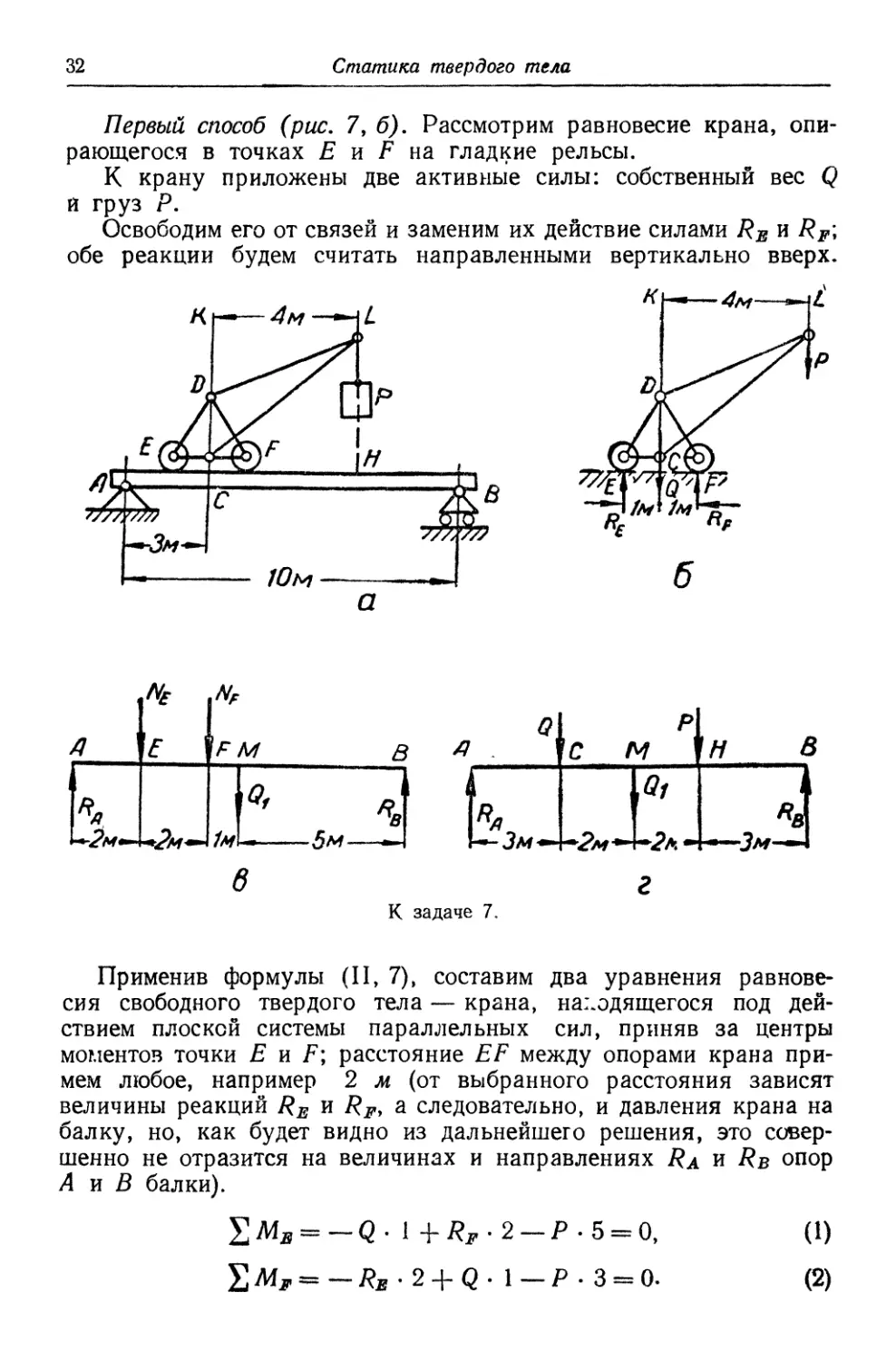
7. На балке АВ длиною 10 м (рис. 7, а) уложен путь для подъем-
подъемного крана. Вес крана равен 4 т, центр тяжести его находится на
оси CD; вес груза Р равен 1,2 т\ вес балки АВ равен 2 т\ вылет
крана KL = 4 м; расстояние АС = 3 м. Найти опорные реакций
в точках А и В для такого положения крана, когда его стрела DL
находится в одной вертикальной плоскости с балкой АВ.
Решение. Решим эту задачу двумя способами:
а) сначала, рассмотрев равновесие крана (рис. 7, б) и приме-
применив аксиому 5, определим давления NB и NF% оказываемые им на
балку АВ (рйс. 7, б, в) в точках Е и F касания, а затем, рассмот-
рассмотрев равновесие балки, определим реакции Ra и Rb опор А и В\
б) рассмотрим равновесие балки (рис. 7, г), считая, что собст-
собственный вес крана Q и груз Р приложены непосредственно
к ней, причем первый — в точке С, а второй — в- точке Н пересе-
пересечения вертикали LP (линии действия груза Р) с балкой АВ. Этим
методом можно пользоваться и в том случае, когда при ином рас-
расположений крана на балке линия действия груза Р выйдет за
опору В, оставаясь в плоскости рисунка; при этом нужно условна
считать, что балка не заканчивается на опоре В, а продолжается
дальше, до вертикали LP в ее новом положении. Такое условное
увеличение длины балки не изменит ее веса и не приведет к измене-
изменению реакций RA и Rb>
32
Статика твердого тела
Первый способ (рис. 7, б). Рассмотрим равновесие крана, опи-
опирающегося в точках Е и F на гладкие рельсы.
К крану приложены две активные силы: собственный вес Q
й груз Р.
Освободим его от связей и заменим их действие силами RE и RF\
обе реакции будем считать направленными вертикально вверх.
Б
F М
1м
В
-5м-
в
К задаче 7,
Применив формулы (II, 7), составим два уравнения равнове-
равновесия свободного твердого тела — крана, находящегося под дей-
действием плоской системы параллельных сил, приняв за центры
моментов точки Е и F\ расстояние EF между опорами крана при-
примем любое, например 2 м (от выбранного расстояния зависят
величины реакций RE и RF, а следовательно, и давления крана на
балку, но, как будет видно из дальнейшего решения, это совер-
совершенно не отразится на величинах и направлениях Ra и Rb опор
А и В балки).
= — Q. i±
.5 = О,
(I)
B)
Параллельные силы 33
Подставив значения Р и Q в уравнения A) и B) , получим:
Давления Л^# и NF крана на балку АВ соответственно равны
по величине реакциям RE и Rp, т. е.
NE = RE = 0,2 т; NF = RF = 5 m,
но направлены в противоположные им стороны.
Переходим к рассмотрению равновесия балки АВ (рис. 7, в).
К балке приложены три вертикальные активные силы: NB9 NF и
собственный вес балки Qv
Освободим ее от связей А и В и заменим их действие силами Ra
и Rb- Реакция Rb подвижной опоры В нормальна к горизонталь-
горизонтальной плоскости опоры, т. е. вертикальна (силой трения пренебре-
пренебрегаем); реакция Ra шарнирной неподвижной опоры А также верти-
вертикальна, так как остальные действующие на балку силы: NE9 NF и
Rb — вертикальны. Направим (условно) обе реакции вверх.
Применив формулы (II, 7), составим два уравнения равновесия
свободного твердого тела — балки АВ, находящейся под действием
плоской системы параллельных сил, приняв за центры моментов
точки А и В:
ZMA = -NE.2 — NF-4 + RB. 10 — Qx - 5 = 0, (Г)
%МВ =ь — RA • 10 + NE • 8 + NF • 6 + Qx • 5 = 0. B')
Подставив найденные значения NE и NF в уравнения (Г) и
B'), получим:
iys + iye + Cb-S
RA = ^ = 4,15 m,
т.
Сделаем поверку, спроектировав все силы на вертикальную
ось Ау,
IiYi-RA-NE — NF-Q1 + ^ = 4,16-0,2 — 5-2 + 3,04 = 0,
следовательно, реакции RA и Rb найдены правильно.
Второй способ (рис. 7, г). Рассмотрим равновесие балки АВ.
К балке в точках С, М и Ц приложены три активные вертикальные
силы: Q, Qt и Р (вес крана, вес балки и вес груза). Освободив
ее от связей Л и Б, заменим их действие силами Ra и Rb\ обе реак-
реакции, по доказанному выше, вертикальны, условно направим их
вверх.
3 591
34 Статика твердого тела
Применив формулы A1,7), составим уравнения равновесия
свободного твердого тела — балки АВ, находящейся под действием
плоской системы параллельных сил, приняв за центры моментов
точки Л и В.
%MA = -Q.3-P.7 + RB. 10 —Qx • 5 = 0, (Г)
%МВ = -Ял . 10 + Q • 7 + Р • 3 + Qi • 5 = 0. B")
Подставив значения Р и Q в уравнения (Г') и B") и решив их,
получим:
Q ^3 Q
Второй способ решения значительно проще, а поэтому в подоб-
подобных случаях рекомендуем решать задачи этим способом.
Примечание. При решении задачи можно было вместо давлений Njs и Njpv
фактически приложенных к точкам Е и F балки, приложить силы Q и Р непосред-
непосредственно к самой балке в точках С и Я, так как эти силы и силы Ne и Мж представ-
представляют собою две статически эквивалентные системы1.
8. Однородная горизонтальная балка АС в точке А (рис. 8,а)
соединена шарниром со стенсй, а в точке В, находящейся на рас-
расстоянии 4 м от .шарнира Л, опирается катками на гладкую горизон-
горизонтальную плоскость. Длина балки равна 6 м, вес Q = 400 кг. На
расстоянии 1 м от шарнира А к точке D прикреплена веревка,
переброшенная через неподвижный блок. К свешивающемуся
концу веревки прикреплен груз Ръ равный 200 кг; на расстоянии
1,5 ж от свободного конца С балки в точке Е приложен груз Р2,
равный 800 кг.
Определить реакции Ra и Rb и величину груза Ру который дол-
должен быть приложен к балке в точке Fy находящейся на расстоянии
3,2 м от шарнира Л, исходя из условия, что при одинаковых и
противоположных направлениях реакций реакция опоры В должна
быть в 10 раз больше реакции опоры Л.
Решение. Рассмотрим равновесие балки АС (рис. 8, б).
К балке приложены четыре активные вертикальные силы:
Р19 направленная вверх (неподвижный блок, не изменяя величины
силы, изменяет ее направление; трением на блоке пренебрегаем),
и Q, Р, Р2, направленные вниз.
1 Силы Р и Q и силы Ne и Njp уравновешиваются одними и теми же реакциями
Re и Rp% следовательно, их равнодействующие геометрически равны, т. е. равны
по величине, действуют по одной прямой (в данном случае — по вертикали) и
направлены в одну сторону, а такие системы статически эквивалентны.
Параллельные силы
35
Освободим балку от связей А
и В9 заменив их действие силами
RA и RB', реакция RB подвижной
опоры В нормальна к плоскости
опоры, т. е. вертикальна (силой
трения пренебрегаем); реакция RA
шарнира А в данном случае также
вертикальна. Будем считать (усло-
(условно), что обе реакции направлены
вверх.
Таким образом, к балке АС
приложена плоская система парал-
параллельных сил.
Применив формулы A1,7), со
ставим два уравнения равновесия
свободного твердого тела — балки
АС, находящейся под действием
плоской системы сил, приняв за
центры моментов точки А и В.
Zj ivia — l\ • а — Ч: • о — г • otz,
В Е
к Ql Л р I
- Ц ; 3 JJ в\ \2 I
я [ " $м -» 1 1 • f,5*A
задаче 8.
. 4-Р2 . 4,5 = 0,
%МВ=— Р2. 0,5 + Р -0,8+ Q. 1 —Рх. 3 — ^.4 =
Решим уравнение A) относительно RB:
р '
4>5 -
Решим уравнение B) относительно RA:
Я — р ' °>8 Ч- Q - 1 ~ Р2 ' 0>5 — Рх - 3
A)
L B)
A')
B')
Для определения величин RA и /?б необходимо найти значение
груза Р. Определим Р при условии, что реакции RA и #в направ-
направлены в противоположные стороны.
Для этого изменим знак любой реакции, например RA (что рав-
равносильно умножению на минус единицу), и Еыразим известную из
условия задачи зависимость4 между реакциями опор А и В:
Q - 3 + Р . 3,2 + Р2 . 4,5 — Рг ¦ 1
4
Р • 0,8 + 0 • 1 — Р2 . 0,5 — Рг • 3
4
Подставив в уравнение C) значения сил Р1? Р2 и Q, получим
3,2 Р + 4600 = — 8 Р + 6000,
откуда
Р = 125 кг.
3*
C)
36 Статика твердого тела
Подставив найденное значение Р в уравнения (Г) и B') и решив
их, определим реакции Rb и Ra:
п 400 . 3 + 125 . 3,2 + 800 . 4,5 — 200-1 1ОСЛ
RB = J = 1250 кг,
D 125 ¦ 0,8 + 400 • 1 — 800 • 0,5 — 200 . 3 __ 1О-
i\A — * 7 — — ^'
Знак плюс при RB показывает, что эта реакция направлена
вверх, а минус при RA — что эта реакция направлена вниз, следо-
следовательно, реакции RA и Rb направлены в противоположные сто-
стороны.
Примем, что обе реакции направлены в одну сторону, тогда
RB=l0RA. '
При этом уравнение C) примет вид
Q. 3 4- Р • 3,2 +/у 4,5 — рг. 1 _ 1Пр. 0,8 + Q. \ — Р2 . 0,5 — Рг . 3. /Q/4
4 ~~ 4 ^ '
Подставив в уравнение (З7) значения сил Р1У Р2 и Q, получим
3, 2Р + 4600 = 8Р — 6000,
откуда
Р = 2208,33 кг.
Подставив найденное значение Р в уравнения (Г) и B7) и ре-
решив их» определим реакции RB и Ra-
п 400 . 3 + 2208,33 • 3,2 + 800 . 4,5 — 200 ¦ 1
Нв — 4
. 2208,33 . 0,8 + 400 . 1,— 800 . 0,5 — 200-3
Н = :
7
4 == ^^,Ъ1 кг,
кг.
Сделаем поверку правильности найденных значений реакций RA
и Rb, спроектировав все приложенные к балке силы на ось Ау.
В первом случае
+ 1250 + 200 — 400 — 125 — 800 = 0.
Во втором случае
+ 2916,67 + 200 — 400 — 2208,33 — 800 = 0.
Следовательно, в обоих случаях реакции найдены правильно.
Устойчивость одного элемента конструкции против опрокидывания 37
глава in
УСТОЙЧИВОСТЬ ОДНОГО ЭЛЕМЕНТА КОНСТРУКЦИИ (СООРУЖЕНИЯ)
ИЛИ ВСЕЙ КОНСТРУКЦИИ ПРОТИВ ОПРОКИДЫВАНИЯ
§ 1. Методические указания к решению задач
Предельные (максимальные или минимальные) значения неиз-
неизвестных величин (нагрузок, некоторых размеров сооружения и
расстояний линий действия нагрузок от определенных осей), при
которых еще возможно равновесие элемента конструкции, опреде-
определяются из условий равновесия этого элемента. Малейшее изменение
неизвестных (в сторону увеличения — для найденного Максимума
или в сторону уменьшения — для найденного минимума) приведет
к нарушению равновесия, к опрокидыванию рассматриваемого
элемента конструкции (сооружения) вокруг некоторой оси, перпен-
перпендикулярной к плоскости рисунка.
Если неизвестна только одна величина, то для ее определения
необходимо и достаточно составить одно уравнение равновесия
рассматриваемого тела: приравнять нулю сумму моментов всех
активных сил относительно возможной точки (центра) опрокиды-
опрокидывания, т. е. точки пересечения оси с плоскостью рисунка.
Характерным для данного типа задач является отсутствие реак-
реакций опор в указанном выше уравнении моментов; когда искомые
величины достигают максимума или минимума, то конструкция
только касается одной из опор (не вызывая ее реакции), опираясь
на вторую, опрокидывание вокруг которой и рассматривается.
В этот момент равнодействующая всех активных сил, приложенных
к рассматриваемому телу, проходит через вторую опору.
Если определяются две неизвестные величины,, то составляются
два уравнения моментов активных сил: по одному относительно
каждой из двух возможных точек опрокидывания конструкции,
в каждое из которых вводится определенная условием задачи часть
активных сил, создающих наибольшую возможность опрокидыва-
опрокидывания.
Из решения системы этих уравнений и определяются неизвест-
неизвестные величины.
Примечание. Таким же способом решаются задачи и в случае, когда
рассматривается устойчивость тела, * подверженного действию произвольной
плоской системы сил.
§ 2. Задачи
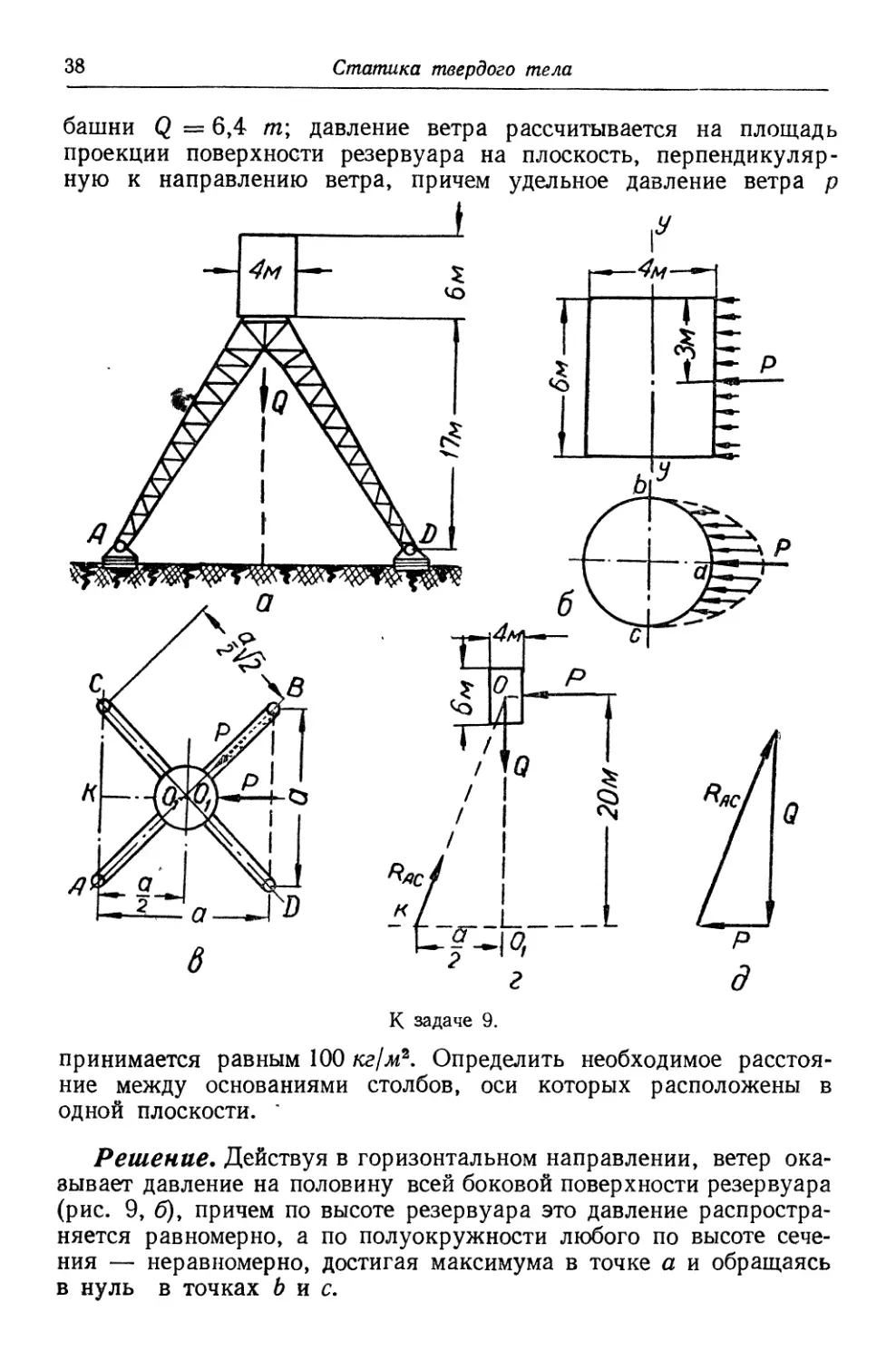
9. Водонапорная башня (рис. 9, а) состоит из цилиндрического
резервуара высотой /г=б м и диаметром d=4 м, укрепленного на четы-
четырех симметрично расположенных столбах, наклонных к горизонту.
Дно резервуара находится на высоте 17 м над уровнем опор; вес
38
Статика твердого тела
башни Q = 6,4 т\ давление ветра рассчитывается на площадь
проекции поверхности резервуара на плоскость, перпендикуляр-
перпендикулярную к направлению ветра, причем удельное давление ветра р
К задаче 9.
принимается равным 100 кг/м2. Определить необходимое расстоя-
расстояние между основаниями столбов, оси которых расположены в
одной плоскости. "
Решение. Действуя в горизонтальном направлении, ветер ока-
оказывает давление на половину всей боковой поверхности резервуара
(рис. 9, б), причем по высоте резервуара это давление распростра-
распространяется равномерно, а по полуокружности любого по высоте сече-
сечения — неравномерно, достигая максимума в точке а и обращаясь
в нуль в точках Ь и с.
Устойчивость одного элемента конструкции против опрокидывания 39
Из условия задачи принимаем удельное давление р ветра, при-
приходящееся на 1 м2 проекции половины боковой поверхности резер-
резервуара на плоскость be, перпендикулярную к направлению ветра
(диаметральное сечение), равным 100 кг. Определим величину
равнодействующей Р сил ветра, находящейся на средине высоты
резервуара в вертикальной плоскости, перпендикулярной к be,
Р = p.h-d = 100 • 6 • 4 = 2400 кг = 2,4 т.
В зависимости от расположения сил ветра (рис. 9,в) их равно-
равнодействующая Р может действовать либо между плоскостями АВ и
CD, либо в одной из них.
Действуя в различных плоскостях, но на одном и том же расстоя-
расстоянии от горизонтальной плоскости, в которой расположены опор-
опорные шарниры столбов башни, сила Р может опрокинуть башню.
Наиболее опасно такое горизонтальное направление сил ветра,
при котором плечо постоянной силы Q, удерживающей башню от
опрокидывания (либо вокруг оси, проходящей через центры двух
опорных шарниров, либо вокруг опорного шарнира одного из
столбов), будет минимальным. Наибольшая опасность опрокиды-
опрокидывания башни наступит при расположении сил ветра в плоскости,
перпендикулярной к одной из сторон квадрата ACBD (рис. 9, в),
в вершинах которого расположены опорные шарниры столбов,
так как при этом плечом силы Q является половина стороны квад-
квадрата, т. е. ~, тогда как при менее опасном направлении сил ветра,
когда Р проходит в плоскости АВ или CD, плечо силы достигает
максимума ~ У2 .
Рассмотрим равновесие башни в наиболее опасном положении,
когда сила Р действует в вертикальной плоскости, перпевдикуляр-
ной к сторонам АС и BD квадрата ACBD (рис. 9, в).
Исследуем действующие на нее силы.
При расстояниях ~ (плечо силы Q относительно оси АС),
больших искомого, устойчивость башни возрастает с увеличением
плеча; при этом равнодействующая активных постоянных сил Q и
Р, проходя в пределах контура ACBD, прижимает столбы башни
к опорам и уравновешивается четырьмя опорными реакциями.
Постепенно сближая основания столбов, т. е. уменьшая стороны
квадрата ACBD, мы можем найти такое (искомое) расстояние между
ними, при котором равнодействующая рассмотренных выше актив-
активных сил пересечет в точке К ось АС, прижимая к опорам только
столбы Л и С и уравновешиваясь уже только равнодействующей
Яас 1 двух равных между собою опорных реакций /?д и Rc (дальней-
(дальнейшее сближение опор привело бы к опрокидыванию башни вокруг
1 Равнодействующая RAC также проходит через точку /С.
40 Статика твердого тела
оси АС, так как равнодействующая вышла бы за пределы контура
ACBD).
В этом случае в вертикальной плоскости ООгК (рис. 9, г) к
центру О резервуара приложены три взаимно уравновешивающиеся
непараллельные силы: Q, Р и Rac (точку приложения силы Q
переносим по ее линии действия в точку О).
Решим эту задачу двумя способами.
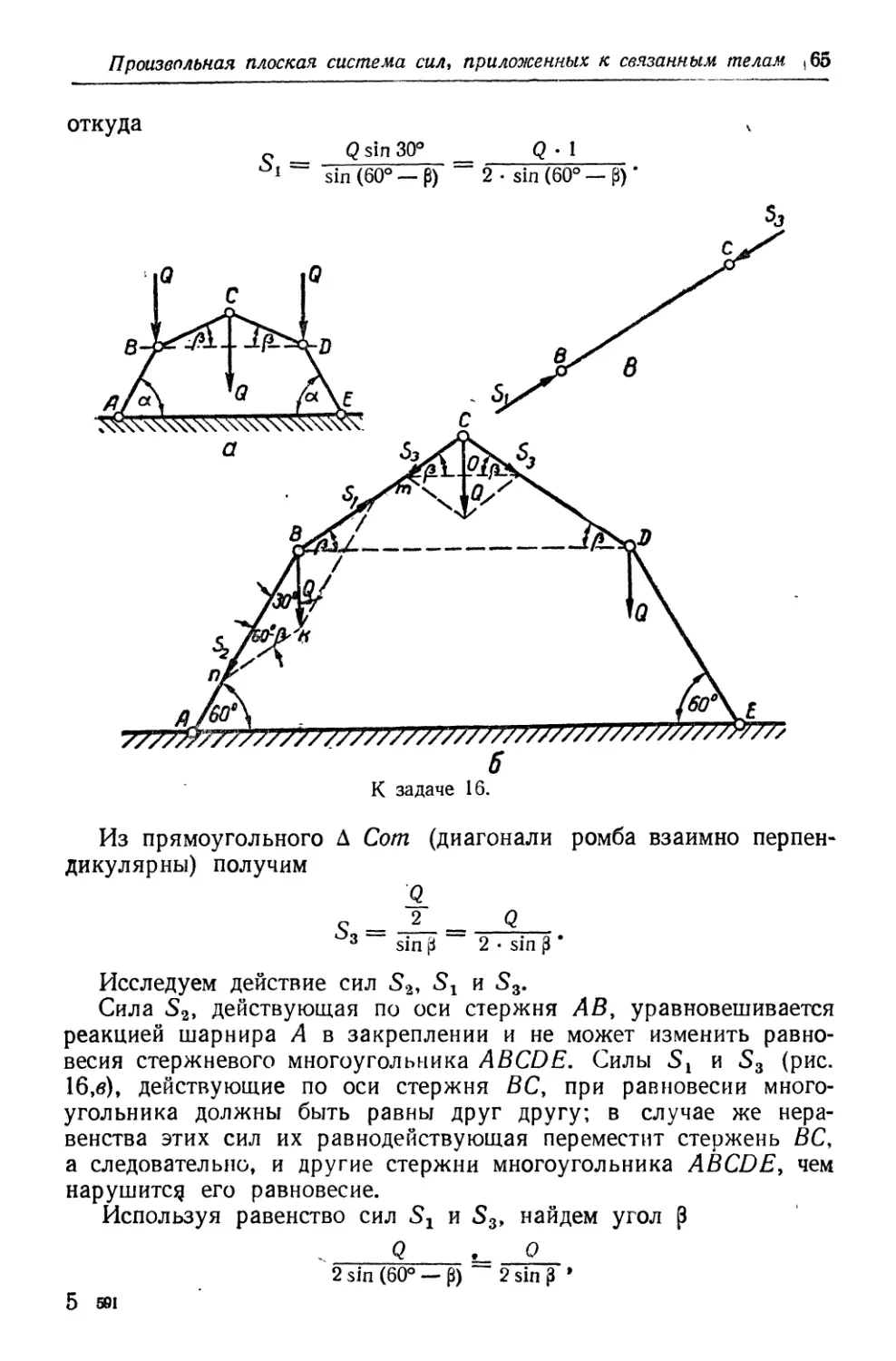
Первый способ. Построим силовой треугольник (рис. 9, д). Из
подобия этого треугольника и ДОС^/С (рис. 9, г) найдем
а
— = Ш
Q ~~20
откуда
__ 40 • 2,4
п~~ 6,4
== 15 М-
Искомое расстояние АВ определим как диагональ квадрата
ACBD
АВ = а]/ = 21,21 м.
Второй способ. Сохраняя прежние рассуждения об устойчи-
устойчивости башни, необходимые размеры можно определить ц^още,
приравняв нулю сумму моментов всех активных сил, приложенных
к башне, относительно оси АС, перпендикулярной к плоскости
рис. 9, г, или (что то же) относительно точки К пересечения этой
оси с плоскостью рисунка.
Решив это уравнение, получим
Й==2^О1= 2-2,4.20 =15м
Расстояние АВ определяется, как и в первом способе.
10. Вес G травеллера (рис. 10, а) без веса Q противовеса ра-
равен 30 т и действует по прямой, расстояние которой от вертикаль-
вертикальной оси сечения правого рельса А равно 1,5 м. Подъемная сила Р
крановой тележки равна 15 т, вылет травеллера — наибольшее
расстояние линии действия груза Р от вертикальной оси сечения
правого рельса Л — равен 10 м. Определить наименьший вес
Qmin и наибольшее расстояние лгтах центра тяжести противовеса от
вертикальной оси сечения левого рельса В, при которых не про-
произойдет опрокидывания крана при любых положениях тележки как
нагруженной, так и ненагруженной. Собственным весом тележки
пренебречь.
Устойчивость одного элемента конструкции против опрокидывания 41
Решение. Рассмотрим равновесие травеллера.
Неблагоприятное положение (рис. 10,а), если говорить о возмож-
возможности опрокидывания травеллера вокруг головки правого рельса Л,
наступит, когда загруженная до максимума A5 т) тележка располо-
расположится в конце вылета (тележка может перемещаться только по*
горизонтали в пределах правой треугольной части фермы).
6
1*0
а
К задаче 10.
Считая положение противовеса фиксированным, найдем мини-
минимальный его вес Q при условии, что вертикальная равнодействую-
равнодействующая всех активных сил проходит через точку Л (рис. 10, б), уравно-
уравновешиваясь реакцией /?л. (Если при том же значении х вес Q будет
больше искомого, то равнодействующая всех активных сил, пере-
переместившись влево, "в сторону расположения силы Q, пройдет между
опорами Л и В и травеллер будет находиться в более устойчивом поло-
положении, уравновешиваясь уже двумя реакциями Ra и Rb\ умень-
уменьшение веса Q при том же значении х приведет к перемещению ли-
линии действия равнодействующей вправо, за вертикаль, проходя-
проходящую через точку Л, что вызовет опрокидывание травеллера
вокруг головки правого рельса.)
В таком случае момент этой равнодействующей относительно
точки Л, равный — согласно теореме Вариньона — сумме моментов
составляющих сил относительно той же точки, обратится в нульг
т. е.
или
^ = Q(x + 3)-G. 1,5 -Р . 10 = 0,
Qx+3Q — G- 1,5 — Р • 10 = 0.
A)
Самое неблагоприятное положение, если говорить о возмож-
возможности опрокидывания травеллера вокруг головки левого рельса fi,
наступит тогда, когда тележка совершенно не будет загружена
(рис. 10, в). Считая вес противовеса фиксированным, найдем макси-
максимальное расстояние #тах центра тяжести противовеса от вертикаль-
42 Статика твердого тела
ной оси сечения левого рельса В при условии, что вертикальная
равнодействующая активных сил G и Q проходит через точку В
(см. объяснение при рассмотрении опрокидывания вокруг головки
правого рельса), уравновешиваясь реакцией RB.
В этом случае момент равнодействующей относительно точки В,
равный сумме моментов составляющих сил относительно той же
точки, обратится в нуль.
Составим это уравнение.
?AfB = Q* —G C+1,5) = 0. B)
Определив Qx из уравнения B) и подставив его значение в урав-
уравнение A), найдем:
Qx = G-4,5,
п P.10 + G-l,5 — Qx p. 10 +G • 1,5 —G-4,5
Q
_
^20 m.
Подставив найденное значение Q в уравнение B) и решив его,
найдем х:
X —— —————— __ и j / О At •
Итак,
Qmin = 20 m; xmax = 6,75 м.
ГЛАВА IV
ПРОИЗВОЛЬНАЯ ПЛОСКАЯ СИСТЕМА СИЛ, НЕ ПЕРЕСЕКАЮЩИХСЯ
В ОДНОЙ ТОЧКЕ
§ 1. Аналитическое условие равновесия системы сил,
приложенных к рычагу
Аналитическое условие равновесия системы сил, приложенных
к рычагу, выражается следующим уравнением равновесия
Мо = 0 * (IV.1)
и формулируется так: система сил, приложенных к рычагу, нахо-
находится в равновесии, если сумма моментов всех активных сил отно-
относительно оси его вращения (или относительно точки пересечения
этой оси с плоскостью действия сил) равна нулю.
§ 2. Аналитические условия равновесия произвольной плоской
системы сил
Аналитические условия равновесия произвольной плоской си-
системы сил выражаются тремя уравнениями равновесия
(IV, 2)
Произвольная плоская система силу не пересекающихся в одной точке 43
и формулируются так: произвольная плоская система сил нахо-
находится в равновесии, если сумма проекций всех сил на каждую из
координатных осей и сумма моментов всех сил относительно любой
точки плоскости их действия равны нулю.
Иначе условия равновесия выражаются следующими тремя
уравнениями равновесия
I! мА = о
(IV, 3)
и формулируются так: произвольная плоская система сил нахо-
находится в равновесии, если сумма моментов всех сил относительно
каждой из трех точек плоскости действия сил, не лежащих на одной
прямой, равна нулю.
Кроме того, условия равновесия могут быть выражены и такими
тремя уравнениями
(IV, 4)
которые формулируются так: произвольная плоская система сил
находится в равновесии, если сумма моментов всех сил относительно
каждой из двух точек плоскости действия их и сумма проекций
всех сил на любую ось, не перпендикулярную к прямой, соединяю-
соединяющей эти точки, равны нулю.
Наличия условий равновесия, выражаемых уравнениями (IV, 2),
(IV, 3) или (IV, 4), достаточно, чтобы убедиться в равновесии тела,
но если нам заранее известно, что тело находится в равновесии,
то для определения неизвестных величин (сил, реакций опор, углов)
можно составить любые три уравнения равновесия (из рассмотрен-
рассмотренных в указанных формулах) при условии, что ни одно из них не
повторяет другого, т. е. что каждое из трех уравнений дает новую
зависимость между входящими в уравнение величинами.
§ 3. Исследование связей и установление направления их
реакций
Исследуем связи, которые еще не рассматривались в предыду-
предыдущих главах (или рассматривались, но при действии определенной
системы сил), и установим возможное направление реакций этих
связей, пренебрегая возникающими в них незначительными силами
трения:
а) если стержень опираетсяi на столб, выступ стены и т. д.
какой-либо промежуточной точкой, то реакция связи направлена
44 Статика твердого тела
по нормали к поверхности стержня в точке касания (для прямоли-
прямолинейного стержня — по нормали к его оси);
б) подшипник (цилиндрический шарнир) — это тип опоры, не
препятствующей перемещению детали конструкции вдоль своей
оси, но препятствующей перемещению ее в перпендикулярном к оси
направлении, поэтому реакция подшипника всегда направлена
перпендикулярно к оси цилиндра;
в) шарнирная неподвижная опора, не препятствуя концу балки
поворачиваться вокруг своего центра, препятствует его перемеще-
перемещению в любом направлении; такой тип рвязи определяет только
точку приложения реакции, тогда как ни ее величина, ни угол,
образуемый ею с каким-либо известным направлением (йапример,
с координатной осью), неизвестны, поэтому такую реакцию пред-
представляют двумя составляющими, направленными в положительные
стороны двух координатных осей;
г) подпятник — это тип шарнирной неподвижной опоры, поэ-
поэтому его реакцию также представляют двумя составляющими,
направленными в положительные стороны двух координатных осей;
д) неподвижный болт препятствует перемещению детали конструк-
конструкции в любом направлении, поэтому его реакцию представляют
двумя составляющими, направленными в положительные стороны
двух координатных осей;
е) при определении реакций ферм последние необходимо рас-
рассматривать как целое твердое тело;
ж) при равномерном прямолинейном движении транспорта (па-
(паровоза, автомобиля) действующие на него силы взаимно уравно-
уравновешиваются, поэтому для определения неизвестных величин нужно
воспользоваться соответствующими уравнениями равновесия про-
произвольной плоской системы сил;
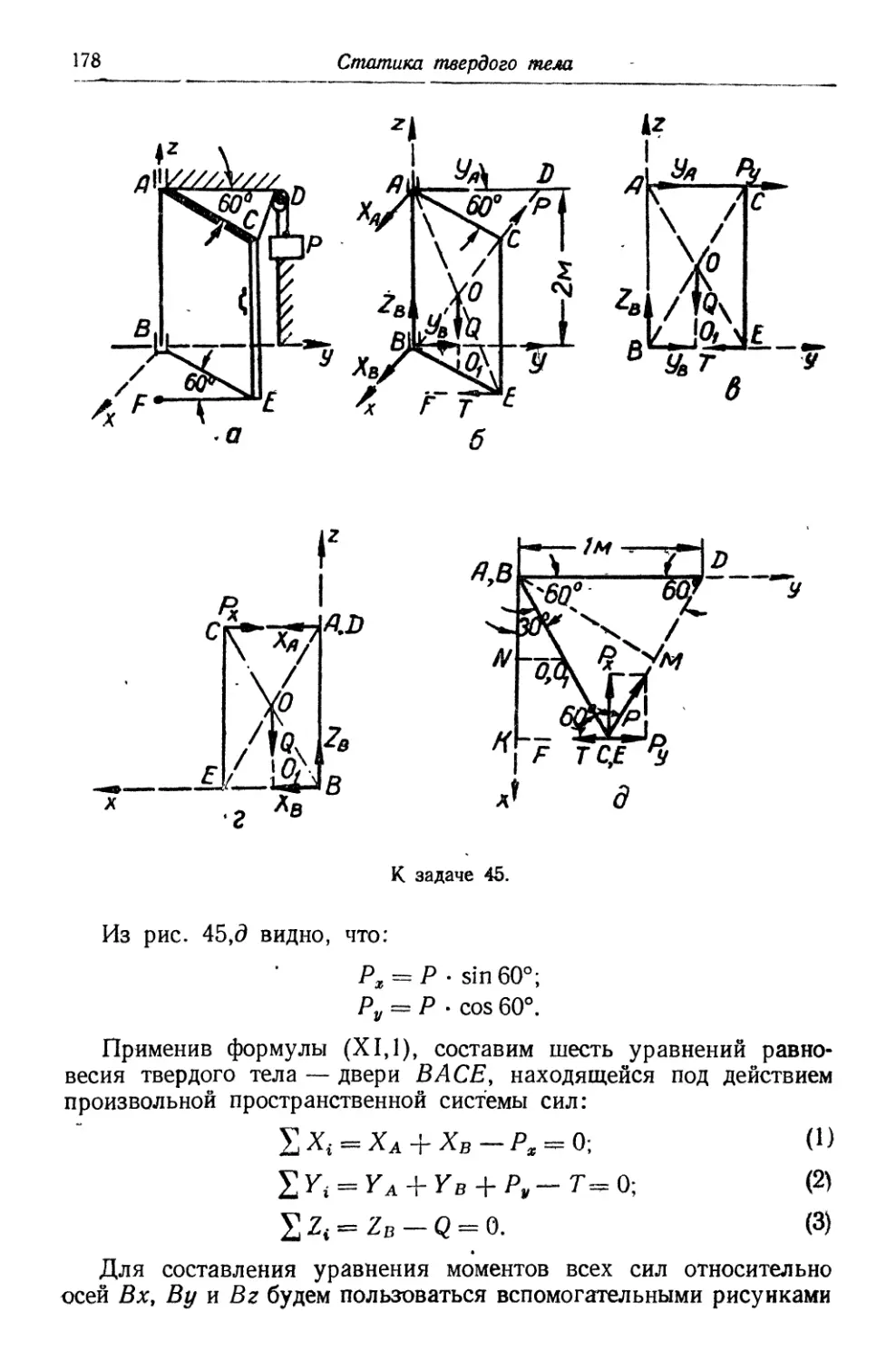
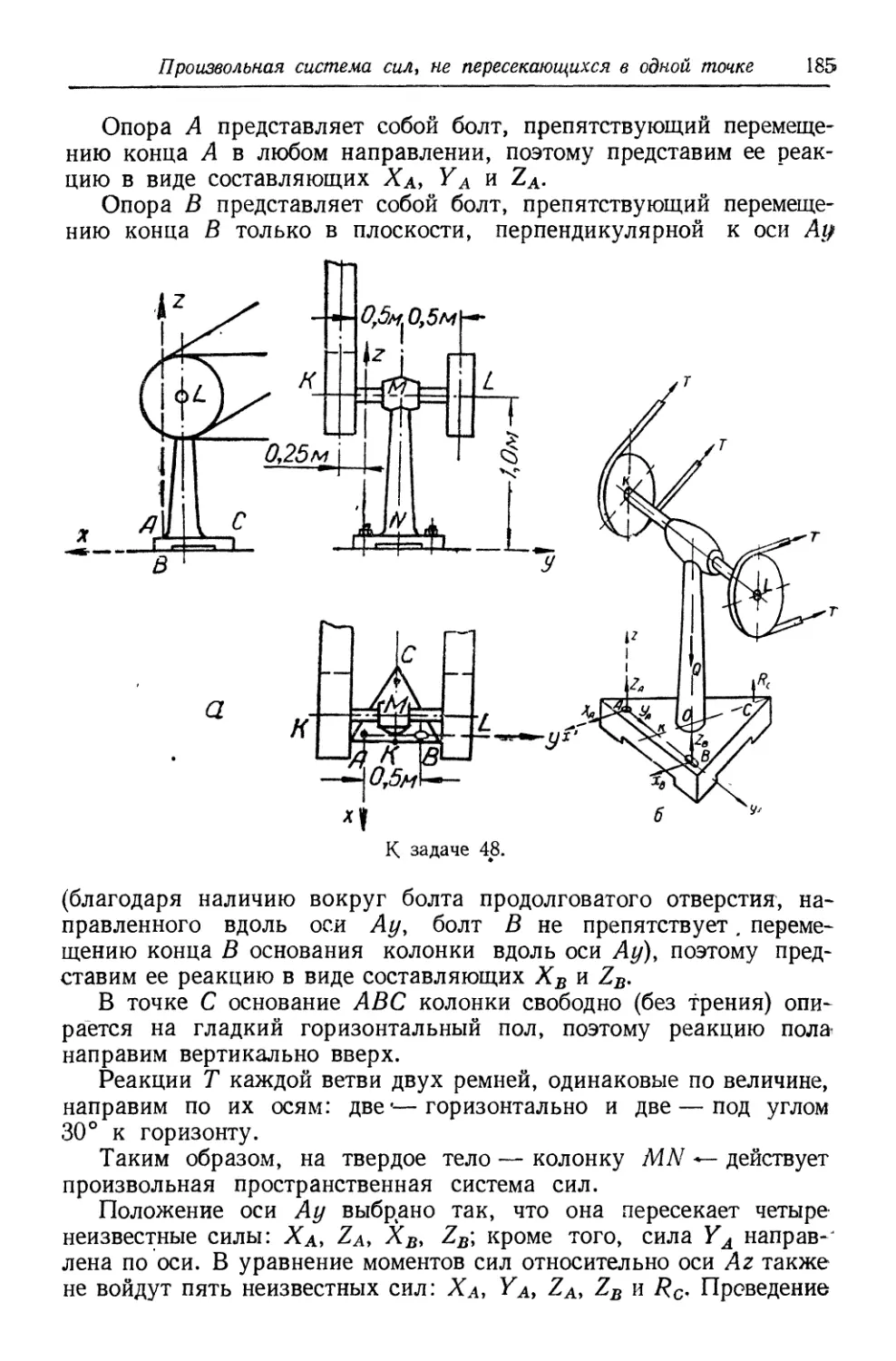
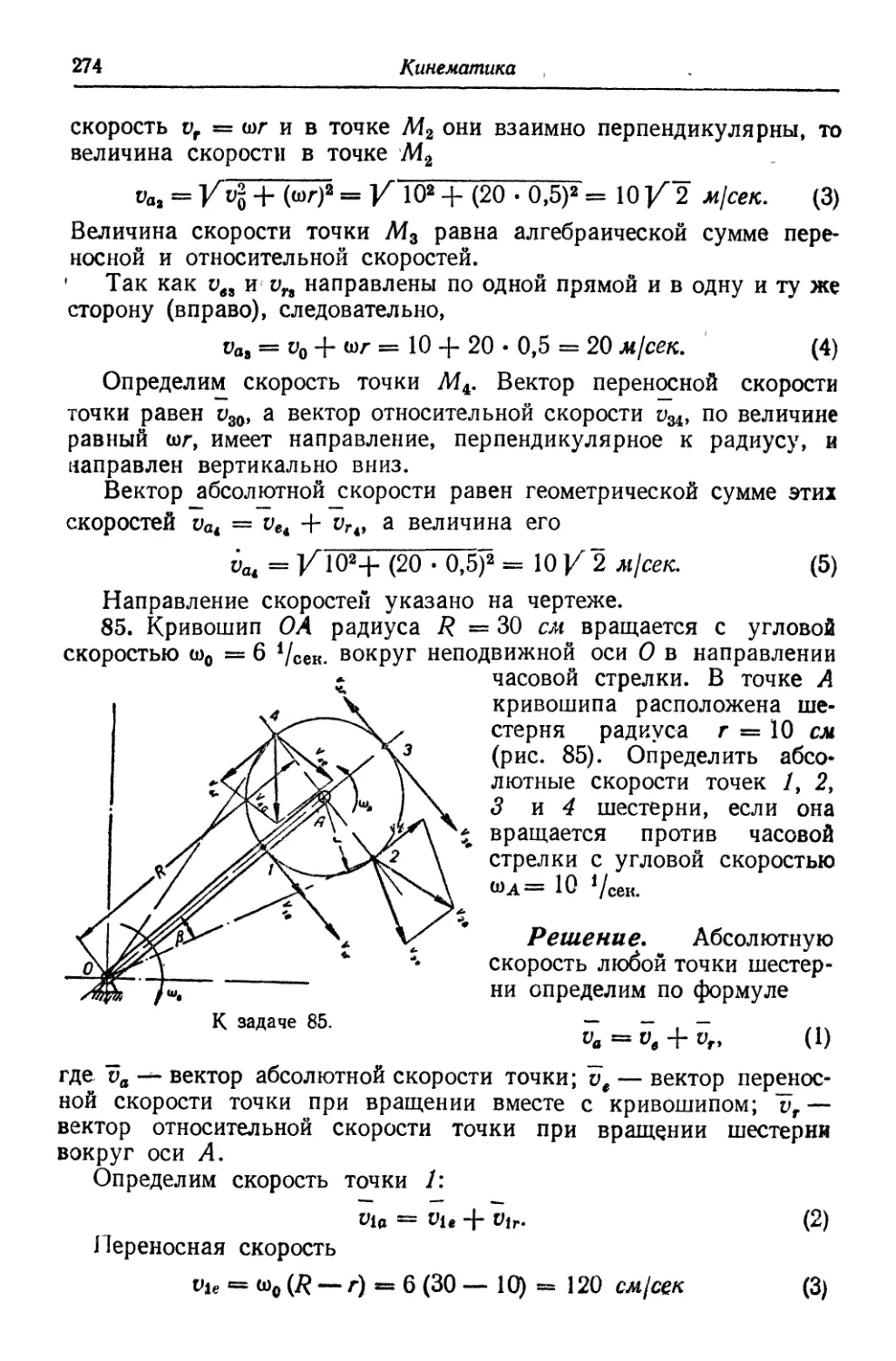
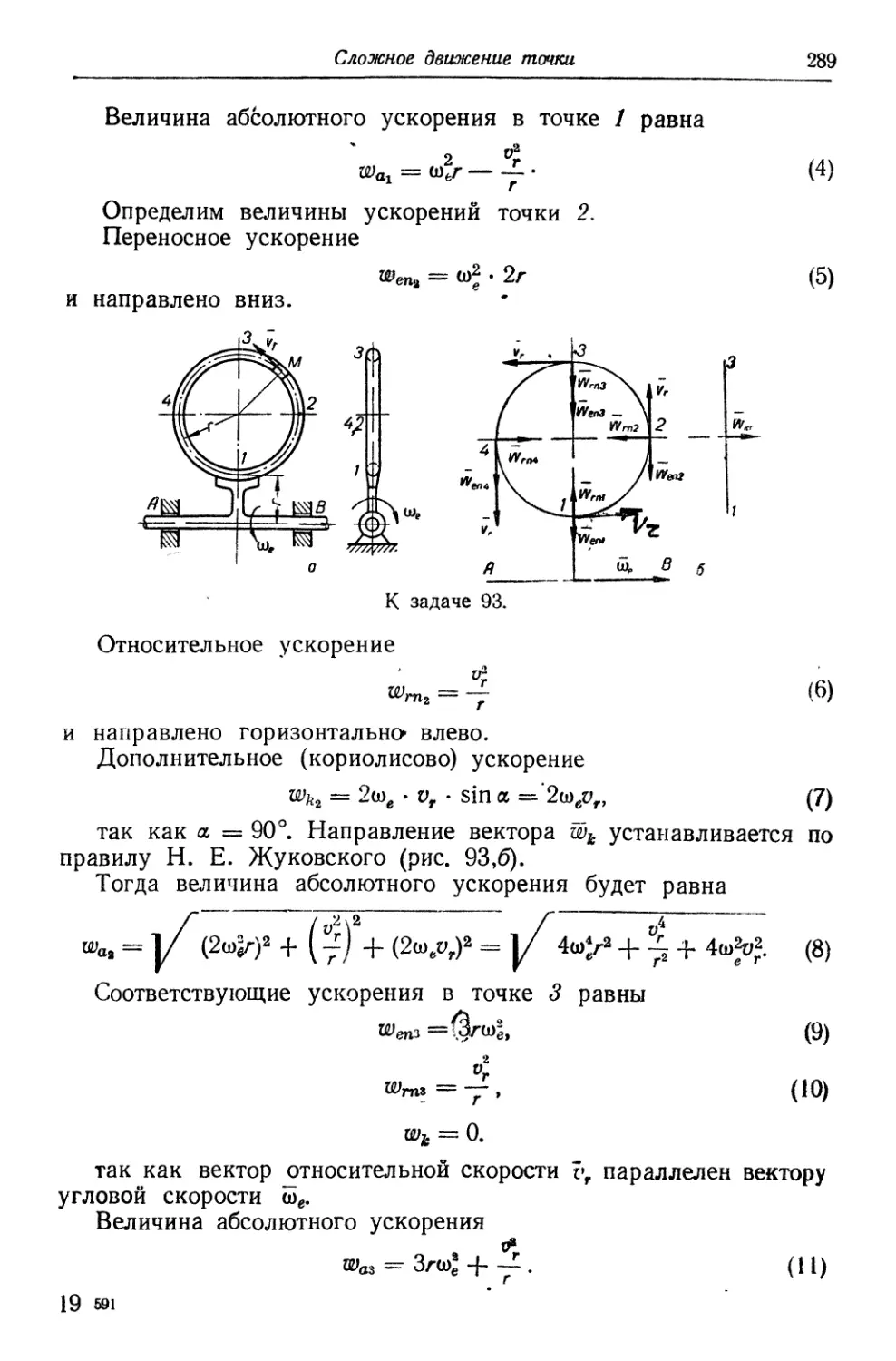
з) для Определения распора — внутреннего растягивающего уси-
усилия затяжки или ригеля (рис. 14, а) симметричной наслонной
стропильной конструкции, возникшего в этом элементе под дей-
действием внешних сил, необходимо рассмотреть равновесие одной из
половин конструкции, отделенной от другой мысленно проведенным
по оси симметрии сквозным сечением, заменив действие на нее
отброшенной части стропил силами; при этом нужно учесть, что
в силу симметрии стропильной конструкции и схемы нагрузки в
верхнем узле одна половина стропил действует на другую гори-
горизонтально направленной силой.
§ 4. Методические указания к решению задач
При решении задач полезно пользоваться следующими указа-
указаниями.
1. Центр моментов рекомендуем выбирать в точке пересечения
двух неизвестных сил; тогда в уравнение моментов всех сил войдет
только одна неизвестная величина (центр моментов удобно выби-
Произвольная плоская система сил, не пересекающихся в одной точке 45
рать на шарнирной неподвижной опоре, если таковая имеется среди
связей).
2. Применение формул (IV,3) зачастую значительно упрощает
решение задачи (см. задачу 12).
3. При выборе положения координатных осей рекомендуем,
как правило, одну ось направлять перпендикулярно к линии дей-
действия одной, а если возможно, то и двух неизвестных сил; при этом
проекция силы на эту ось обратится в нуль, а на ось, ей параллель-
параллельную, сила спроектируется в натуральную величину, что облегчит
решение задачи.
Координатные оси могут быть взяты под произвольным между
собой углом, отличным от 90°, если это облегчает нахождение
неизвестных величин.
4. При решении задачи иногда необходимо самим ввести ка-
какую-либо величину (длину стержня, угол наклона его к какой-
либо прямой, плечо силы и т. д.), не заданную в условии; в таких
случаях введенные величины в ходе решения задач исчезают (см.
решение задачи 12).
5. Для упрощения выводов при составлении уравнений иногда
целесообразно разложить какую-либо силу на две составляющие.
6. Иногда в условии задачи предлагается определить только
одну неизвестную величину из трех имеющихся; при этом нужно
исследовать, какое из трех уравнений равновесия нужно составить,
чтобы из всех неизвестных в него вошла только искомая; чаще всего
таким уравнением является уравнение моментов всех сил либо
относительно шарнирной неподвижной опоры, либо относительно
опоры, реакция которой представляется двумя составляющими, либо
относительно точки пересечения линий действия двух неопределяе-
неопределяемых неизвестных сил (см. решение задачи 11). Аналогично поступают
и тогда, когда из трех неизвестных величин требуется определить
только две: выбирают такие два уравнения равновесия, в которые
не входит третья неизвестная величина (см. решение задачи 14).
§ 5. Порядок решения задач
Большинство задач этого раздела рекомендуем решать в следую-
следующем порядке.
1. Установить, равновесие какого тела нужно рассмотреть,
чтобы определить неизвестные величины.
2. Выбрать центр моментов и положение координатных осей
или только центр (центры) моментов.
3. Установить, какие активные силы действуют на тело; отбро-
отбросив связи или применив метод сечений, заменить их действие на
тело силами, геометрически равными реакциям связей.
4. Составить соответствующие уравнения равновесия.
5. Решив уравнения равновесия, определить неизвестные вели-
48
дтатика твердого тела
чины; найдя знаки неизвестных сил, установить их действительное
направление.
6. В случае, если найдены реакции связей, а необходимо найти
давления, оказываемые телом на те или иные плоскости (поверх-
(поверхности), нужно учесть, что, согласно аксиоме 5, давления равны
найденным реакциям по величине, но направлены в противополож-
противоположные им стороны.
§ 6. Задачи
П. К однородному стрежню А В (рис. 11, а), который может
вращаться вокруг шарнира Л, в точке В подвешена на веревке
гиря С весом 1 /сг. От конца В стержня АВ идет веревка, переки-
перекинутая через блок D и поддерживающая гирю весом 3 кг. Найти
*¦&
К задаче 1i.
величину угла BAD = а, при которой стержень будет находиться
в положении равновесия, зная, что АВ == AD и вес стержня 4 кг.
Трением на блоке пренебречь.
Решение. Рассмотрим равновесие стержня АВ (рис. 11,6). Коор-
Координатные оси направим согласно рисунку.
К стержню АВ в точке В приложены две активные силы: верти-
вертикальная Рг = 1 кг и наклонная Р2, направленная по оси веревки
BD, равная 3 кг (неподвижный блок, изменяя направление силы,
не изменяет ее величины), а на средине его длины приложена ак-
активная вертикальная сила Р3 — 4 кг (собственный вес стержня).
Кроме того, б точке А к стержню приложена реакция шарнира;
не зная ее величины и направления, представим эту реакцию в
виде двух составляющих ХА и YA, направленных в положитель-
положительные стороны соответствующих координатных осей.
При равновесии любой плоской системы сил можно составить
три уравнения равновесия, из которых и определяются неизвест-
неизвестные величины, но так как по условию задачи требуется определить
Произвольная плоская система сил, не пересекающихся в одной точке 47
только одно неизвестное — угол а, то из всех возможных уравне-
уравнений нужно составить одно, в которое не вошли бы неизвестные
величины Ха и Ya.
Таким уравнением является уравнение моментов всех действую^
щих на стержень сил относительно центра шарнира Л.
Для составления этого уравнения предварительно определим
плечо силы Р2 из равнобедренного /\ABD, в котором h является
и высотой и биссектрисой /_BAD:
= Рг- АВ- cos A80° —а) —Р2 •. АВ • cos? +
^ —а)=0. A)
Подставив данные из условия задачи в уравнение A), получим
— 1 • АВ ¦ cos а — 3 • АВ • cos-^- — 4 -у cos а = 0.
Сделав приведение подобных членов и сократив на —ЗАВ,
получим
cosa + cosy = 0. (Г)
Так как
1-V1
cos-- - "-+со"
2
то, возведя в квадрат обе части, найдем значение cos a:
cos а = 2 cos2 у — 1.
После подстановки значения cos a в уравнение (Г) получим
2 cos2| + cos ™— 1=0. B)
Решив уравнение B), получим
^ а1==360°.
cos^ = l; -^=60; a2 = 120°.
Из двух корней квадратного уравнения условию задачи удов-
удовлетворяет второй корень, следовательно,
a = ao=
Примечание. Обращаем внимание на то, что к концу В стержня при-
прикреплены две разные веревки; если бы оба блока огибала одна веревка, то веса
гирь Рг и Р2 были бы равными.
48
Статика твердого тела
Эту задачу можно решить и иначе.
Продлив горизонтальную прямую DA (рис. 11, б) до точки К
пересечения^ с вертикалью ВС, получим прямоугольный ДЛВ/О
Линия действия силы Р3 пересекает катет А К посредине.
Составим уравнение моментов всех сил относительно точки А.
-?з~2 P2h = 0. (Г)
Подставив в уравнение A") зна-
значения сил Р19 Р2 и Р3, определим А:
^ — 3/г =
////7///У/////7///77
а
откуда
Для определения угла а исполь-
используем равенство прямоугольных
треугольников АВК и ABL (гипо-
(гипотенуза АВ у них общая, а катеты
А К и h равны между собой); из
равенства следует, что
поэтому
откуда
a = 120°
К задаче 12.
12. Однородный стержень АВ
iA (рис. 12, а) весом 40 кг опирается
|я одним концом на гладкий гори-
i л зонтальный пол, а другим — на
^? гладкую плоскость, наклоненную
под углом 30° к горизонту. Конец
В стержня поддерживается верев-
веревкой, перекинутой через блок С
и несущей груз Р\ часть веревки ВС параллельна наклонной пло-
плоскости. Определить, пренебрегая трением на блоке, величину груза
Р и давления Na и Nb на пол и на наклонную плоскость.
Решение. Эту задачу решим двумя способами.
Первый способ. Рассмотрим равновесие однородного стержня АВ
<рис. 12, б).
Произвольная плоская система сил, не пересекающихся в одной точке 49
Приняв за центр моментов точку В (точка пересечения двух
неизвестных сил Р и RB), направим координатные оси, как пока-
показано на рисунке.
К стержню приложены две активные силы: в точке В наклон-
наклонная сила Р (неподвижный блок, не изменяя величины силы, изме-
изменяет ее направление) и на средине стержня — вертикальная сила Q
(его собственный вес). Освободим стержень АВ от связей А и В
и заменим их действие на него силами RA и RB\ так как обе плос-
плоскости опоры концов балки гладкие, то каждая из реакций RA и RB
направлена по нормали к соответствующей плоскости.
Применив формулы (IV, 2), составим три уравнения равновесия
свободного твердого тела — стержня АВ, находящегося под дей-
действием произвольной плоской системы сил (углом а обозначен угол
наклона стержня АВ к горизонту).
2 Х< *» — Р cos 30° + RB sin 30° = 0; A)
= P • sin306 + RBcos30° — Q + RA = 0; B)
? ^ 0. C)
Сократив уравнение (З) на ABcos <z и решив его, получим
RA = f- = 20 кг.
Зависимость между RB и Р определим из уравнения A)
Цв = Р\Гз. D)
Подставив значение RB в уравнение B), получим
откуда
Р = 10 кг.
Подставив в уравнение D) значение Р, получим
RB=: 10/3= 17,32 кг.
Давления NA и NB концов стержня АВ на соответствующие
плоскости равны по величине реакциям RA и RB опор А и б, т. е.
NA = RA « 20 кг;
#Л = #я= 17,32 кг,
но направлены в противоположные им стороны.
Второй способ. Начало решения задачи этим способом такое же,
как в первом случае.
Применив формулы (IV, 3), составим три уравнения равновесия
свободного твердого тела — стержня АВ, приняв за центры мо-
моментов точки В, D и Е — (точки пересечения неизвестных сил Р и RB,
4 581
50 *> Статика твердого тела
RB и RA> Р и Ra) (рис. 12, в) и обозначив равные друг другу от-
отрезки BF и FK через а,
VMB=—Qa + RA.2a = 0; (Г)
VMD = Qa — P.BD = 0; B')
VME = Qa — RB-BE = 0. C')
Из прямоугольного /\BDK найдем гипотенузу BD:
Из прямоугольного /\ВКЕ найдем гипотенузу BE:
rf _ 2а - J*L - 4 О
13 ~~ cos 30° ~~ |/"з ~~ 3
Сократив на а и решив каждое из уравнений (Г)* B') и C'),
получим:
RA = 20 кг; Р = 10 кг и RB = 17,32 /сг.
Давления А/а и Л/5 стержня на пол и на наклонную плоскость
определим согласно аксиоме 5:
MA^RA = 20кг; NB = RB= 17,32 кг.
Примечание. Преимущества второго способа решения задачи следую
ющие: в каждое из трех уравнений равновесия вошло по одному неизвестному,
число членов уравнения минимально. Введение ртрезка а, что возможно и при
первом способе, также упрощает решение задачи.
13. Литейный кран ABC (рис. 13, а) имеет вертикальную ось
вращения МЛ/. Даны расстояния: М/г =5 м, АС = 5 м; вес
крана Q = 1 т; вес груза Я, подвешенного в точке С, равен 4 т;
центр тяжести D крана находится на расстоянии ED = 2 м от оси
вращения. Найти реакции подшипника М и подпятника N.
Решение. Рассмотрим равновесие крана ABC (рис. 13, б).
Направим координатные оси, как показано на рисунке, приняв
за центр моментов точку N.
К крану приложены две активные вертикальные силы Q и Р.
Связь М представляет собой подшипник с вертикальной осью;
его реакцию Хм направим в положительную сторону оси Nx. Связь /V
представляет собой подпятник; представим его реакцию в виде двух
составляющих XN и YN, направленных в положительные стороны
'осей Nx и Ny.
Применив формулы (IV, 2), составим три уравнения равновесия
крана ABC, находящегося под действием произвольной плоской
Произвольная плоская система сил, не пересекающихся в одной точке 51
системы сил, приняв за центр моментов точку Af. пересечения неиз-
неизвестных сил Хя и YN
A)
B)
C)
Подставив данные из условия задачи в уравнения B), C), A)
и решив их в соответствующей последовательности, получим
YN = 5m; XM = — 4,4 т и XN = 4,4 т.
Знак минус при Хм показывает, что направление этой составляю-
составляющей выбрано неправильно; в действительности она направлена в
противоположную сторонv.
К задаче 14.
14. Стропила крыши (рис. 14, а) состоят из двух брусьев АС и
ВС одинаковой длины, свободно лежащих нижними концами на
стенах и связанных горизонтальным ригелем ЕК- Наклон крыши
tga = 0,5; АС = ЗСЕ; нагрузка на каждый из брусьев АС и ВС
равна 1 т, вертикальна и приложена к середине бруса.
62 Статика твердого тела
Определить давление на стену в точке А и распор S в ригеле ЕК,
считая крепления в точках С, Е и К шарнирными и пренебрегая
трением.
Решение. Внутреннюю силу S (распор), возникшую в ригеле ?7(,
можно определить, только применив метод сечений, поэтому рас-
рассечем (мысленно) стропильную конструкцию по оси симметрии,
отбросим одну из половин, например правую, и заменим действие
отброшенной половины на оставшуюся соответствующими силами
(рис. 14, б), приложенными в местах разреза; затем отбросим
связь Л, заменим ее действие соответствующей силой и рассмот-
рассмотрим равновесие левой половины ЛЕС стропильной конструкции
как свободного твердого тела, находящегося под действием произ-
произвольной плоской системы сил, Направление осей показано на ри-
рисунке.
На средине стропильной ноги АС приложена активная вертикаль-
вертикальная сила Р = 1 т, в точке С, в силу симметрии стропильной конструк-
конструкции и ее нагрузки, приложена горизонтальная реакция F, по оси
ЕК — реакция5, равная распору ригеля ЕК, и на опоре А — реак-
реакция Ra> направленная вертикально, так как плоскость опоры
конца А стропильной ноги АС горизонтальная, а трением прене-
пренебрегаем.
Так как из трех неизвестных величин по условию задачи необ-
необходимо определить только две (давление на стену в точке А и рас-
распор S в ригеле), то из трех возможных уравнений равновесия сво-
свободного твердого тела составим такие два, в которые не войдет
реакция F; такими уравнениями являются: уравнение проекции
всех сил на вертикальную ось А у и уравнение моментов всех сил
относительно точки D пересечения реакций RA и F.
Составим эти уравнения:
^ ^ 0. B)
Прдставив данные в уравнения A) и B) из условия задачи и
решив их, получим:
RA = Р = 1 т;
ЗЯ 3* 1 о
6 т
Давление Na конца А стропильной ноги Л С на опору А равно
по величине реакции Ra> но противоположно по направлению, т. е.
NA - — RA - - 1 т.
Аналитическое определение усилий в стержнях статич. определ. ферм 53
глава V
АНАЛИТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ УСИЛИЙ В СТЕРЖНЯХ
СТАТИЧЕСКИ ОПРЕДЕЛИМЫХ ФЕРМ
Ферма представляет собой геометрически неизменяемую си-
систему стержней, шарнирно связанных между собою таким образом,
что каждый стержень прикреплен к двум шарнирам (ось каждого
стержня проходит через геометрические центры двух шарниров).
Расположенные внутри контура фермы стержни образуют решетку
фермы. При определении осевых усилий в стержнях фермы счита-
считают шарниры идеально гладкими и поэтому не учитывают возникаю-
возникающие в них незначительные силы трения.
Внешние силы прилагаются к узлам фермы.
В данной главе рассматриваются только Статически опреде-
определимые фермы, у которых опорные реакции и усилия в стержнях
могут быть определены методами статики.
Для таких ферм зависимость между числом стержней (k) и
числом узлов (п) выражается формулой
fe = 2/z —3. (V, 1)
Как правило, приступать к определению внутренних усилий,
возникающих в стержнях фермы под действием внешней нагрузки,
можно только после нахождения опорных реакций фермы. Для
фермы-консоли можно определять возникшие в ее стержнях уси-
усилия, не находя предварительно опорных реакций фермы (аналити-
(аналитически опорные реакции определяются из уравнений равновесия,
рассмотренных в предыдущей главе).
Усилия в стержнях фермы могут быть определены методом вы-
вырезания узлов и методом проведения сквозных сечений.
§ 1. Определение усилий в стержнях ферм методом вырезания
узлов
Мысленно проведенным сечением отделяем от фермы один узел,
к которому примыкают только два стержня, усилия в которых
неизвестны; заменив действие отброшенной части фермы силами,
приложенными к рассеченным стержням, направленными по их
осям (от узла) в сторону отброшенной части фермы (предполагая,
что оба Усилия растягивающие), рассматриваем равновесие узла.
Так как линии действия всех сил пересекаются в одной точке
(центре шарнира), составляем два уравнения равновесия A,6),
из которых и определяем оба неизвестных усилия (при направле-
направлении неизвестных усилий от узла знак плюс перед найденным зна-
значением силы покажет, что стержень растянут, а знак минус — сжат).
Иногда вместо уравнений A,6) пользуются уравнениями
моментов, выбирая за центр моментов центр шарнира узла
54
Статика твердого тела
отброшенной части фермы, к которому примыкает один из рассе-
рассекаемых стержней; в такиз уравнения равновесия входит только
по одному неизвестному усилию.
Усилия в стержнях можно определить и из силового мнйго-
угольника, построенного для взаимно уравновешивающихся в узле
сил (этот метод подробно рассмотрен в главе I).
Для определения усилий во всех стержнях фермы необходимо
в определенной последовательности вырезать узлы (рис. I), каж-
каждый раз выбирая такой узел, к которому, кроме нескольких уже
известных усилий (а в некоторых узлах и внешней силы), прило-
приложено не более двух неизвестных усилий.
Рис. I.
Последовательность вырезания узлов рассматриваемой фермы
определена проставленными у узлов порядковыми номерами.
Двойные номера 14 A5) и 15 A4) при узлах показывают, что, опре-
определив неизвестные усилия в узле 13, можно приступать к рассмот-
рассмотрению равновесия любого из этих узлов, так как в каждом из них
число неизвестных усилий не превышает двух. Из равновесия
последнего из двух узлов 15A4) или 14 A5) определяется только
одно неизвестное усилие. Рассмотрение узла 16 не требуется, так
как в обоих примыкающих к нему стержнях усилия уже найдены
(из рассмотрения равновесия узлов 14 A5) и 15 A4).
Может быть принята и иная последовательность вырезания
узлов. Так, например, после узла 8 можно перейти к рассмотре-
рассмотрению равновесия узлов правой половины фермы, т. е. узлов 16,
15 A4), 14 A5), 13, 12, 11, 10 и 9 или рассматривать равновесие
узлов в такой последовательности: 16, 15 A4), 14 A5), 13, 12,
$1, 10, 8, 9, 7, 6, 5, 4, 3 (или 2) и 2; (или 3); рассмотрение узла 1
(как при первой последовательности — узла 16) не потребуется.
В случае симметрии фермы и схемы нагрузки достаточно рас-
рассмотреть равновесие узлов, входящих в одну из половин фермы,
включая узлы, расположенные на оси симметрии ее, так как в
этом случае усилия в симметрично расположенных стержнях фермы
соответственно равны между собой.
Аналитическое определение усилий в стержнях статич. определ. ферм 55
§ 2. Определение усилий в стержнях ферм для некоторых
частных случаев
Определение усилий в стержнях ферм упрощается, если при
рассмотрении равновесия узлов встречаются следующие случаи:
а) двухстержневой узел фермы не нагружен (рис. II, а). В этом
случае усилие в каждом из стержней равно нулю, так как иначе
равновесие узла было бы невоз-
невозможным;
б) к двухстержневому узлу
фермы по оси одного из стер-
стержней приложена нагрузка Р
(рис. II, б). В этом случае усилие
в этом стержне по величине
равно, а по направлению про-
противоположно нагрузке, а в дру-
другом стержне усилие равно нулю;
в) трехстержневой узел фер-
фермы, в котором оси двух стерж-
стержней направлены по одной пря-
прямой, не нагружен (рис. II, в).
В этом случае усилие в третьем
стержне равно нулю, а в каждом
из двух остальных стержней
либо также равны нулю, либо
равны между собою по величине
и направлены в противополож-
противоположные стороны, т. е. эти стер-
стержни или не испытывают усилий,
или оба сжаты, или растянуты
одинаковыми силами;
г) к трехстержневому узлу рис ц
фермы (рис. II, г), в котором оси
двух стержней направлены по одной прямой, по оси третьего стерж-
стержня приложена нагрузка Р. В этом случае усилие в третьем стержне
по величине равно, а по направлению противоположно нагрузке,
а усилия в каждом из двух остальных стержней либо равны нулю,
либо равны между собою по величине и направлены в противо-
противоположные стороны;
'д) к трехстержневому узлу фермы (рис. II, д) по оси одного
из стержней приложена нагрузка Р, а усилие в одном из двух
остальных стержней равно нулю. В этом случае усилие в стержне,
ось которого совпадает с линией действия нагрузки Р, по величине
равно, а по направлению противоположно нагрузке, а усилие в
третьем стержне, как и во втором, равно нулю;
е) четырехстержневой узел (рис. II, е), в котором оси стержней
56 Статика твердого тела
попарно расположены по одной прямой, не нагружен. В этом
случае усилие в каждом стержне равно нулю, или равны нулю
только усилия в стержнях, расположенных на одной из прямых,
а усилия в двух остальных стержнях равны между собой по вели-
величине и направлены в противоположные стороны, или усилия каж-
каждых двух стержней, расположенных на одной прямой, равны между
собой по величине и направлены в противоположные стороны.
§ 3. Определение усилий в стержнях ферм методом
сквозных сечений
Мысленно проведенным сквозным сечением ферма делится на
две части таким образом, чтобы в разрез попало не больше трех
стержней, усилия в которых неизвестны \ затем одна из частей
фермы отбрасывается, а ее действие на оставшуюся часть заме-
заменяется усилиями, направленными по; осям рассеченных стержней
в сторону отброшенной части (предполагается, что усилия во всех
рассеченных стержнях — растягивающие).
Благодаря этому методу внутренние усилия в стержнях (при
рассмотрении равновесия всей фермы в целом) становятся внеш-
внешними для любой ее части и могут быть определены из уравнений
равновесия всех сил, приложенных к отсеченной части фермы
(рекомендуется рассматривать равновесие той отсеченной части
фермы, к которой приложено меньшее количество внешних сил).
Уравнения равновесия (IV, 2) при пересечении трех стержней при-
приводят к необходимости решать систему трех уравнений с тремя
неизвестными.
Значительное упрощение достигается при применении уравне-
уравнений равновесия (IV, 3); при этом для составления каждого из трех
уравнений моментов всех сил за центр моментов выбирается
точка пересечения двух неизвестных усилий в рассеченных стерж-
стержнях. В случае рассечения двух стержней за центр моментов реко-
рекомендуется выбирать центр шарнира отброшенной части фермы,
к которому примыкает один из рассеченных стержней; таких урав-
уравнений нужно составить два. При таком выборе центра моментов в
каждое уравнение равновесия входит только одно неизвестное
усилие, что упрощает его определение.
Применение этого метода дает возможность определить усилие
в любом стержне фермы без предварительного определения
усилий в каких-либо других стержнях, тогда как определение
усилия (в рассматриваемом стержне) методом вырезания узлов
требует предварительного определения усилий в других стерЖ-
1 При бблынем числе неизвестных задача становится статически неопреде-
неопределимой, так как для определения неизвестных из рассмотрения равновесия любой
части фермы статика дает возможность составить только три независимых урав-
уравнения равновесия.
Аналитическое определение усилий в стержнях статич. определ. ферм Ъ7
нях, т. е. предварительного рассмотрения равновесия ряда узлов
фермы.
В частном случае, при определении усилий в стержнях решетки
фермы с параллельными поясами (разрезы а—а и Ь—Ь фермы,
рис. III), центр моментов — точка пересечения усилий в двух
параллельных стержнях, попав-
попавших в разрез, удаляется в беско-
бесконечность, поэтому вместо урав-
уравнения моментов составляем урав-
уравнение проекций всех сил на ось,
перпендикулярную к параллель-
параллельным усилиям (при таком выборе
оси в уравнение проекций, как Рис. Ш.
и в уравнение моментов, в общем
случае войдет толькб одна неизвестная величина — усилие в рас-
рассматриваемом стержне).
§ 4. Задачи
15. В мостовой ферме (рис. 15, а) узлы С, D и Е загружены оди-
одинаковой вертикальной нагрузкой Р = 20 т. Определить усилия во
всех стержнях фермы.
Решение. Рассмотрим равновесие фермы АВ (рис. 15, б).
К ферме приложены три активные вертикальные силы: Р и
реакции RA и RB опор Л и Б. В силу симметрии вертикальные
реакции RA и Rb равны между собой; каждая из них равна поло-
половине всей нагрузки, т. е.
on
RA = RB = Ц. = 30 m.
Определив все внешние силы, действующие на ферму, перейдем
к нахождению внутренних усилий, возникших в стержнях фермы
(эти усилия будем обозначать буквой S с индексом соответствую-
соответствующего стержня). В силу симметрии фермы и схемы нагрузки опреде-
определим усилия только в стержнях одной половины фермы, например
левой, так как усилия в симметрично расположенных стержнях
равны между собой.
Прежде всего исследуем, в каких стержнях фермы можно опре-
определить усилия на основании частных случаев, рассмотренных
в § 2. Анализ показывает, что узлы А и К аналогичны рассмотрен-
рассмотренным в пунктах б и в. На этом основании устанавливаем величину
и направление усилий, возникающих в стержнях / и 2, примыкаю-
примыкающих к узлу А (рис. 15, в):
S2 = 0; Sj = —- RA = — 30 т (стержень / сжат),
58
Статика твердого тела
а также величину усилия в стержне 9 и зависимость между уси-
усилиями в стержнях 8 и 10, примыкающих к узлу К (рис. 15, г):
S9 = 0; Ss = S10.
Величину и направление усилия в стержне 8 найдем из дальней-
дальнейшего решения.
4 в к ю
1У
С Ss
ж 3
К задаче 15.
Затем мысленно проводим сквозное сечение в — в (рис. 15, д)у
рассекая при этом стержни 4, 3 я 2, заменяем действие отбро-
отброшенной части фермы на оставшуюся силами 54 и S3 E2=0),
направленными по осям соответствующих стержней в сторону отбро-
отброшенной части фермы, и рассматриваем равновесие оставшейся
части (равновесие левой части фермы, к которой приложено мень-
меньшее количество внешних сил).
Для определения усилия 54 составляем уравнение моментов
всех действующих на лезую часть фермы сил относительно точки С
откуда
S4 = — RA = — 30 m.
Аналитическое определение усилий в стержнях спгатич. определ. ферм 59
Для определения усилия S3 составляем уравнение проекций
всех сил на ось Су
откуда
53=^ = 30]/2 = 42,4 т.
Для определения усилий 55 и 5б мысленно проводим сквоз-
сквозное сечение с — с (рис. 15, ё) и рассматриваем равновесие левой
части фермы. .
Усилие S5 находим из уравнения проекций всех сил на ось Су
откуда
S5 = P — RA = 20 — 30 = — 10 т.
Усилие 56 находим из уравнения моментов всех сил относи-
относительно точки пересечения линий действия усилий 54 и S5
откуда
56 = RA == 30 т.
{Сила Р не вошла в уравнение моментов, так как центр моментов
находится на ее линии действия.)
Для определения усилий 58 и S7 мысленно проводим сквозное
сечение d—d (рис. 15, ж) и рассматриваем равновесие левой
части фермы.
Усилие 58 находим из уравнения моментов всех сил относи-
относительно точки D пересечения линий действия усилий SQ и 57
откуда
S8 = — 2RA + P = — 40 m.
Усилие S7 находим из уравнения проекций всех сил на ось Су
V уг = RA — Р — S7 • cos 45° = 0,
откуда
V^.e »Ь20= 14,14 т.
5° j/^2
Сделаем частичную поверку правильности найденных значений
усилий в стержнях фермы.
Рассмотрим, например, равновесие узла С (рис. 15, з). Если
примыкающие к узлу С силы найдены правильно, то сумма проек-
проекций всех действующих на узел С сил (включая и груз JP)
на каждую из осей Сх и Су должна равняться нулю. Направления
60 Статика твердого тела
всех сил указаны на рисунках .в соответствии с их знаками, т. е.
положительные силы направлены от узла, а. отрицательные — к
узлу; сила S2 не указана, так как она равна нулю.
2JX, = S6 — S3 • cos 45° = 30 — 42,4 .ОаО;
%Yi « S3 • cos45° — 55 — P = 42,4 . ^ — 10 — 20 = 0,
следовательно, усилия S2, S3, 55, и 5б найдены правильно.
Аналогичным путем можно было бы сделать поверку и осталь-
остальных найденных усилий.
ГЛАВА VI
ПРОИЗВОЛЬНАЯ ПЛОСКАЯ СИСТЕМА СИЛ, ПРИЛОЖЕННЫХ
К СВЯЗАННЫМ МЕЖДУ СОБОЙ ТЕЛАМ
§ 1. Равновесие системы сил, приложенных
к шарнирно-стержневому многоугольнику
С системой связанных между собой твердых тел мы фактически
ознакомились уже в предыдущих главах.
Так, например, в главе I рассматривалась система твердых тел-
стержней, шарнирно соединенных между собой и с опорами, обра-
образующих геометрически неизменяемую фигуру-треугольник; в гла-
главе V рассматривалась система шарнирно соединенных между
собой стержней — ферма, состоящая из ряда геометрически неизме-
неизменяемых фигур-треугольников.
Равновесие указанных выше конструкций соблюдалось всегда
независимо от величин и направлений при-
приложенных в узлах сил (если говорить о ферме, то и
при отсутствии нагрузки в некоторых узлах), и для определения
усилий, возникших в стержнях этих конструкций, достаточно было
составить соответствующие уравнения равновесия.
Совершенно иное положение с равновесием состоящего из не-
нескольких стержней шарнирно-стержневого многоугольника, два
крайних шарнира которого закреплены, так как такой многоуголь-
многоугольник — фигура геометрически изменяемая и может находиться в
равновесии в заданном положении лишь при наличии опреде-
определенной нагрузки во всех незакрепленных узлах \
В случае равновесия такого многоугольника неизвестные вели-
величины (внешние силы, усилия в стержнях или углы.между некото-
некоторыми его стержнями) могут быть найдены из последовательного рас-
рассмотрения равновесия всех незакрепленных узлов многоугольника.
Фактически определение неизвестных внешних сил или углов
между некоторыми стержнями многоугольника сводится к рас-
1 Более детально этот вопрос рассматривается в строительной механике.
Произвольная плоская система сил, приложенных к связанным телам 61
смотрению равновесия одного или, что встречается реже, двух
не связанных с опорами стержней многоугольника, так как при
их равновесии крайние стержни многоугольника всегда находятся
в равновесии (усилия, возникшие в крайних стержнях, всегда
уравновешиваются соответствующими реакциями опор).
Равновесие каждого стержня обусловливается наличием прило-
приложенных к его концам двух сил, равных между собой и направлен-
направленных по оси стержня в противоположные стороны (см. решение
16).
§ 2. Равновесие системы сил, приложенных к системе рычагов
шаров и цилиндров
При рассмотрении равновесия системы взаимно связанных ры-
рычагов неизвестные величины определяются из уравнений равно-
равновесия (IV, 1), составленных для каждого рычага.
При рассмотрении равновесиг шаров или цилиндров, связан-
связанных между собой и с плоскостью (или плоскостями) отирания,
неизвестные величины определяются из уравнений равновесия
A,6), составленных для каждого шара или цилиндра.
§ 3. Определение усилий в элементах механизма
Для определения усилий, возникающих в элементах механизма,
рассматривается равновесие его узлов. Вначале рассматриваются
узлы, к которым приложены внешние силы, а затем узлы, при рас-
рассмотрении равновесия которых можно составить достаточное (по
числу неизвестных) число уравнений равновесия.
§ 4. Равновесие системы сил, приложенных к шарнирно-
консольным мостам и балкам
Шарнирно-консольные мосты и балки, опирающиеся одна на
другую или соединенные между собой ч шарниром, представляют
систему связанных между собой р р р
твердых тел (рис. I). / ' I * I J 1^
Составление соответствующих '* ./ I—^—I—?—! Я
уравнений равновесия для сил, **> т -т,
приложенных ко всей конструк- рис. 1
ции в целом, не приведет к опреде-
определению неизвестных величин (опорных реакций и реакций, располо-
расположенных между опорами шарниров), так как число неизвестных в
таких конструкциях больше трех (больше возможного числа урав-
уравнений равновесия), а неизвестные — реакции междуопорных шарни-
шарниров— не войдут в уравнения равновесия, как внутренние силы.
Для определенияАнеизвестных величин в таких конструкциях
составляем уравнения равновесий каждого элемента в отдельности,
62
Статика твердого тела
начав с рассмотрения равновесия второстепенного элемента, а
затем основного \ Если общее число уравнений соответствует числу
неизвестных, то задача статически определима.
Для установления, какой из элементов конструкций является
основным, нужно вначале составить схему взаимодействия между
элементами, а затем уже приступить к составлению уравнений
равновесия.
Для определения неизвестных величин в конструкциях, состоя-
состоящих из двух элементов, иногда рационально рассмотреть равно-
равновесие одного из элементов, к которому приложено меньшее коли-
количество внешних сил, и равновесие всей конструкции в целом.
§ 5. Равновесие системы сил, приложенных к трехшарнирным
аркам. Частные случаи
Трехшарнирная арка представляет собой систему двух твер-
твердых тел (частей арки), соединенных между собой ключевым
шарниром и прикрепленных к основанию арки пятовыми шарни-
шарнирами.
vTT?
О
При определении реакций опор и давления в ключевом шарнире
трехшарнирной арки встречаются следующие основные случаи:
а) к одной из частей трехшарнирной арки, допустим к левой
(рис* II, а), приложена только одна активная сила, а другая часть
арки не нагружена2;
б) к одной из частей трехшарнирной арки, допустим к левой,
приложена произвольная плоская система сил, а другая часть
арки не нагружена2;
1 Основной элемент конструкции — та ее часть, без которой невозможно рав-
равновесие остальных (второстепенных) опирающихся на нее частей.
2 Собственный вес обеих частей арки в случаях а) и б) не учитывается.
Произвольная плоская система сил, приложенных к связанным телам 63
в) к обеим частям трехшарнирной арки приложена произволь-
произвольная плоская система сил (в состав этой системы сил может входить
и собственный вес каждой части арки).
Рассматривая равновесие всей трехшарнирной арки как одного
твердого тела, мы в каждом из указанных случаев не сможем
определить реакций опор, так как статика дает возможность со-
составить только три уравнения равновесия свободного твердого
тела, находящегося под действием произвольной плоской системы
сил, а число неизвестных сил — четыре (по две составляющих каж-
каждой опорной реакции), а также не сможем определить возникаю-
возникающего в соединительном (ключевом) шарнире давления, которое,
являясь внутренней силой, не войдет в уравнение равновесия
приложенных к арке внешних сил. Поэтому в каждом из рассмат-
рассматриваемых случаев применяем метод сечений.
В случае а) решение задачи начинаем с рассмотрения равнове-
равновесия части арки, свободной от внешней активной нагрузки, допус-
допустим правой (рис. II, в)у мысленно отделенной от левой части про-
проведенным через ключевой шарнир сечением, находящейся под
действием двух сил: приложенной к ключевому шарниру силы 5,
заменяющей собой действие левой части арки на правую, и реак-
реакции правой опоры арки.
Из условий равновесия придем к выводу, что эти силы равны
между собой, действуют по одной прямой, проходящей через центры
обоих (ключевого и пятового) шарниров, но направлены в противо-
противоположные стороны.
Затем переходим к рассмотрению равновесия левой отсеченной
части арки (рис. II, б), находящейся под действием трех непарал-
непараллельных сил: внешней активной силы Р (величина, направление и
линия действия которой известны), приложенной к ключевому
шарниру, силы5, заменяющей собой действие правой части арки на
левую1, и реакции левой опоры арки.
При равновесии трех непараллельных сил линии действия их
пересекаются в одной точке, следовательно, линия действия левой
опорной реакции пройдет через точку пересечения линий действия
активной силы Р и силы S (или правой опорной реакции).
Построив силовой треугольник (рис. Ii, г), найдем левую опор-
опорную реакцию и силу 5, а следовательно, и равную ей по величине
реакцию правой опоры арки; все неизвестные можно найти и анали-
аналитически, составив уравнения равновесия (I, 6).
Когда сила Р параллельна силе5, реакция левой опоры арки
также параллельна им; в этом случае для аналитического опре-
определения неизвестных необходимо составить уравнения равнове-
равновесия (II, 6) или (II, 7).
1 Так как действие равно прськводействию, то силы воздействия каждой части
арки на другую равны по величине, но направлены в противоположные стороны.
64 Статика твердого тела
Определение опорных реакций системы, состоящей из несколь-
нескольких трехшарнирных арок, при наличии одной активной силы
осуществляется последовательным рассмотрением равновесия эле-
элементов конструкции, отделенных один от другого шарнирами.
В случае б), установив аналогично предыдущему направление
силы Slt найдем ее величину (а следовательно, и величину равной
ей реакции правой опоры арки), а также величину и направление
реакции левой опоры (или две составляющих реакции по выбран-
выбранным направлениям), составив уравнения (IV, 2) или (IV, 3).
В случае в) мысленно отделим одну часть трехшарнирной арки
от другой сечением, проведенным через центр шарнира, и заменим
действие каждой половины арки на другую равными по величине,
но противоположно направленными силами *,
приложенными в местах разреза; отбросив связи и заменив их
действие силами, получим два свободных тела, находящихся в
равновесии.
Составив для каждой из половин арки, или для одной половины
ее 2 и для всей арки в целом, по три уравнения равновесия (IV, 2)
или (IV, 3), получим шесть уравнений для определения шести
неизвестных величин (по две составляющих в каждом из трех шар-
шарниров), решив которые, найдем все неизвестные.
Таким образом, определение реакций всех трех шарниров
трехшарнирной арки — задача статически определимая.
§ 6. Задачи
16. Стержневой шарнирный многоугольник (рис. 16,а) состоит
из четырех равных стержней; концы А и Е закреплены; узлы JS, С
и D нагружена одинаковой вертикальной нагрузкой Q. В поло-
положении равновесия угол наклона крайних стержней к горизонту а =
с= 60°. Определить угол наклона средних стержней к горизонту.
Решение. Разложим каждую из сил Q, приложенных к шар-
шарнирам В и С, по направлениям осей двух стержней, примыкаю-
примыкающих к соответствующему шарниру (рис. 16,6); в силу же симметрии
силу Q, приложенную к точке D, не будем раскладывать на со-
составляющие.
Из А Впк, применив теорему синусов, получим
sin 30° sin F0° —
1 Силы взаимодействия обеих частей арок представляются обычно в виде двух
составляющих, параллельных координатным осям.
2 Лучше рассматривать равновесие той части арки, к которой приложено
^меньшее количество сил.
Произвольная плоская система сил, приложенных к связанным телам ,65
откуда
Q sin 30°
Q . 1
4 sin F0° —Р) 2 • sin F0° — p)'
У//У
К задаче 16.
Из прямоугольного Л Com (диагонали ромба взаимно перпен-
перпендикулярны) получим
sin p
Исследуем действие сил S2, Sx и S3.
Сила^з, действующая по оси стержня АВ, уравновешивается
реакцией шарнира А в закреплении и не может изменить равно-
равновесия стержневого многоугольника ABCDE. Силы Sx и S3 (рис.
16,в), действующие по оси стержня ВС, при равновесии много-
многоугольника должны быть равны друг другу; в случае же нера-
неравенства этих сил их равнодействующая переместит стержень ВС,
а следовательно, и другие стержни многоугольника ABCDE, чем
нарушите^ его равновесие.
Используя равенство сил Sx и 53> найдем угол р
Q . О
5 591
2 sin F0° — р) 2 sin
66
Статика твердого тела
В
следовательно,
sin F0° — р) = sin p,
откуда
60° — р = Р; р = 30°.
17. Однородный стержень ЛЯ
(рис. 17,а) длиной 2 / и весом Р
может вращаться вокруг гори-
горизонтальной оси шарнира, распо-
расположенного на конце А стержня;
он опирается на однородный
стержень CD той же длины, ко-
который может вращаться вокруг
горизонтальной оси, проходящей
через точку Е. Точки А и Е лежат
на одной вертикали АЕ = L
К концу D подвешен груз
Q = 2Р. Определить величину
угла ф, образуемого стержнем
АВ с вертикалью в положении
равновесия, пренебрегая тре-
трением.
К задаче 17.
Решение. Для определения
угла ф проанализируем, равно-
равновесие какого тела нужно рас-
рассмотреть.
Поскольку в задаче требуется
определить только одно неизвест-
неизвестное — угол ф, то, казалось бы,
для решения достаточно соста-
составить одно уравнение равновесия
стержня, но в действительности
обойтись одним уравнением невозможно, так как, кроме угла ф,
в него войдет второе неизвестное — сила Re взаимодействия между
стержнями. Поэтому необходимо рассмотреть равновесие каждого
из стержней ЛВ и CD, как рычагов, имеющих перпендикулярные к
плоскости рисунка неподвижные горизонтальные оси в точках А и Е.
Рассмотрим равновесие рычага АВ (рис. 17,6).
К рычагу приложены: собственный вес Р (в точке К) и реакция
Re опоры С, направленная по нормали к оси рычага АВ (трением
пренебрегаем), представляющая собой действие рычага CD на ры-
рычаг АВ (положение точки С взято нами произвольно — справа
от точки /С; найденное значение угла ф покажет истинное поло-
положение точки С).
Произвольная плоская система сил, приложенных к связанным телам 67
Применив формулу (IV, 1), составим уравнение равновесия
рычага АВ
P-h = 0. A)
Из прямоугольного A AT К определим h:
h = I • sin ср.
Опустив из точки Е на основание АС равнобедренного А АСЕ
перпендикуляр ES — высоту, являющуюся одновременно и медиа-
медианой, найдем АС из прямоугольного A ECS:
CS = SA=^ = /cos ср,
Подставив значения найденных величин в-уравнение A), получим
%МЛ = — Rc • 2/ • coscp + P . / • sincp = 0. (У)
Рассмотрим равновесие рычага CD.
К рычагу приложены: собственный вес Р (в точке Е) и реакция
Rtc опоры С, представляющая собой действие рычага А В на рычаг
CD (так как действие равно противодействию, то Rxc = Rc no
величине и направлена в противоположную сторону).
Применив формулу (IV, 1), составим уравнение равновесия
рычага CD
YiME = RlC'hl-Q^EM = 0. B)
Из прямоугольника OCSE определим ht:
hx == CS = I • cos ср.
Из прямоугольного A DEM найдем
EM = l- sin A80° — 2ср) = / • sin 2cp.
Подставив значения найденных величин и Q в уравнение B),
получим
%MB = R1C-1 • coscp —2 .P./sin2<p = 0. B')
Умножив обе части уравнения B') на 2 и сложив полученное
выражение с уравнением A), найдем
Р • I • sin ср — 4Р • / • sin 2cp = 0
или, после сокращения на Р1У
sin ср — 4 sin 2ср = 0. C)
Заменив в Уравнении C) sin 2cp тригонометрическими функциями
угла <р и сделав преобразования, получим
sin ср — 4 • 2 sin ср • cos ср = 0,
5*
68 Статика твердого тела
ИЛИ
sin ср A —8coscp) = О,
откуда найдем два значения ср, последовательно приравняв
нулю sin ср и 1—8 cos ср:
sincPl = O; cpi = O°.
(Это значение угла ср не удовлетворяет условию задачи.)
cos <р2 == у или ср2 = arc cos -g-; 92 = 82°48/.
18. Между двумя гладкими наклонными плоскостями О А и
ОВ (рис. 18,а) находятся два гладких соприкасающихся между
собой однородных цилиндра: один с центром Сг имеет вес Рг = 5 яг,
и другой с центром С2 и весом Р2 = 15 кг. Центры тяжести цилинд-
цилиндров находятся в плоскости рисунка. Определить угол ср, образуе-
образуемый прямой Сх С2 с горизонтальной осью хОхъ давления N1 и N2
цилиндров на плоскости, а также величину N взаимного давления
цилиндров, если угол АОхг = 60°, а угол ВОхг = 30°.
Решение. Средние (по длине цилиндров) сечения обоих цилин-
цилиндров находятся в плоскости рисунка, касаясь между собой в точке С,
находящейся на линии СгС2 центров сечений.
Рассмотрим отдельно равновесие каждого цилиндра как сво-
свободного твердого тела.
При равновесии цилиндров давление Ыг (рис. 18,6) правого
цилиндра на левый передается по линии С2СХ центров сечений —
от С2 к Clf а давление N2 (рис. 18,г) левого цилиндра на правый
передается по этой же линии СХС2, но от Сх к С2.
Так как действие равно противодействию, то
Кроме того, на каждый цилиндр действуют собственный вес,
приложенный в соответствующем центре тяжести, и реакция плос-
плоскости; так как плоскости гладкие (силы трения не возникает),
то реакции направлены по нормалям к ним и, следовательно,
проходят через центры тяжести соответствующих сечений.
Таким образом, в плоскости рисунка на каждый цилиндр дей-
действует по три силы, пересекающиеся в его центре тяжести.
Решим эту задачу двумя способами: при помощи силовых тре-
треугольников и применив аналитические условия равновесия пло-
плоского пучка сил.
Первый способ, а) Для левого цилиндра.
Построим силовой треугольник (рис. 18,в). Установив его
углы в соответствии с рис. 18,6, найдем зависимость между иско-
Произвольная плоская система сил, приложенных к связанным телам 69
К задаче 18.
мыми силами и данными, известными из условия задачи, восполь-
воспользовавшись теоремой синусов
sin 60° "" sin C0° + <р) sin (90° — ср) '
Приравняв первое отношение второму, получим
Л/ — Л •s!n 60° ^ Л - У^> .
1 ~- sin C0° + <р) "
U)
70 Статика твердого тела
приравняв ч второе отношение последнему, найдем
• р _ /у sin (90°-у) _ Рг • cos ср
*D ~ sin C0° + ср) "~ sin C0° + ср) * W
б) Для правого цилиндра.
Построим силовой треугольник (рис. 18,5). Установив его
углы в соответствии с рис. 18,г, найдем зависимость между иско-
искомыми силами и известными из условия*задачи данными, применив
теорему синусов
N2 __ P2 Я к
sin 30° sin F0° — ср) sin(90° + <p) *
Приравняв первое отношение второму, получим
Л/ - fi2 • sin 30° __ Ра. 1 «
1 2 "" sin F0° — ср) 2 sin F0° — ср) * W
Приравняв второе отношение третьему, найдем
р __ Р2 • sin (90° + ?) _ P8-cosy u.
*Е~- sin F0 — ср) "~ sin F0° — ср) ' ™
Решим совместно уравнения A), B), C) и D).
Так как Nx = N2t то из уравнений A) и C) найдем
Л У __ Р*
2 sin C0° + ср) "" 2 sin F0° — ср)
или
sin F0° — ср) = Р2 . sin C0° + ?).
Подставив значения синусоз разности и суммы, получим
Рх ]/"T(sin 60° . cos ср — cos 60° • sin 9) =
= Я2 (sin 30° • cos cp + cos 30° . sin cp). E)
Разделив обе части равенства E) на cos cp (cp ф 90°), получим
или, после незначительных преобразований,
УЪ(Рг + Р2) • tgcp = ЗРг-Р2 = 3 • 5- 15 = 0. F)
Так как
то, следовательно,
tg ср = 0; ср = 0.
Из уравнения A)
Произвольная плоская система сил, приложенных к связанным телам 71
Из уравнения B)
р Л-созО° _5-1 ш
^""sInC0° + 0°) - — = Ш «•
2
Из уравнения D)
р _ />acos0° _.15- 1 -2 _ 17_
**- зТГГбб^ГО3) ~" ~j7T~ ~ '
Давление Л/# левого цилиндра на плоскость АО и давление
Л/я правого цилиндра на плоскость ВО соответственно равны реак-
реакциям RD и RK по величине, но направлены в противоположные им
стороны, т. е. от Сг к D и от С2 к К-
Примечание. Угол <р равен нулю, т. е. линия Ct C2 центров сечений
расположена горизонтально, потому что правая часть уравнения F) равна нулю,
так как 3 Р1=Р2; при иных.соотношениях сил Рх и Р2 tg уФ0 и, следовательно,
угол ср будет иметь определенное значение, отличное от нуля.
Второй способ, а) Для левого цилиндра (рис. 18,6).
Приняв начало координат в точке С1у направим ось Сгх гори-
горизонтально, а ось Сгу — вертикально. Применив формулы (I, 6),
составим два уравнения равновесия свободного твердого тела —
цилиндра, находящегося под действием плоского пучка сил
0°= о A)
— P1==0. B)
б) Для правого цилиндра (рис. 18,г).
Приняв начало координат в точке С2, направим ось С2х гори-
горизонтально, а ось С2у—вертикально. Применив формулы (I, 6),
составим два уравнения равновесия свободного твердого тела —
цилиндра, находящегося под действием плоского пучка сил
^ х, = — RK • cos 60° + W coscp = 0, C)
VYi = RK • sin 60° — N sin cp — P2 = 0. D)
Решив совместно уравнения A), B), C) и D) и сложив попарно
A) с C) и B) с D), получим:
RD . cos 30° — RK . cos 60° = 0; E)
RD . sin 30° + RK • sin 60° — Рг — P2 = 0. F)
Подставив значения тригонометрических величин в уравнения
E) и F), получим:
^r-/?D-j/?*«0f E')
З^Л-О. F')
Умножив уравнение E') на УЗ и сложив полученное выражение
с уравнением F')> найдем
2RD = Рг + Р2»
72 Статика твердого тела
откуда
RD = ^L+
Из уравнения E')
= ]ЛЗ • 10 = 17,32 кг.
Оставив в левой части уравнений A) и B) соответственно Ncosf
и N sin <f и разделив уравнение B) на уравнение A), получим
0
?СО5 30° '
7?^ cos 30° RD cos 30° -~/?дСО
следовательно,
9 = 0.
Из уравнения A)
#ncos30°i 101Г
;V = -^-^г- = —f- = 8,66 /сг.
cos 0° 1 '
Внешне уравнения A), B), C) и D) второго способа решения
проще, чем аналогичные уравнения первого способа (в них отсут-
отсутствуют тригонометрические величины и разности углов, один из
которых — неизвестный угол ср) но в каждое из четырех уравнений
второго способа решения входит по три неизвестных, в связи с
чем само решение получается громоздким, так что^ оба варианта
сравнительно одинаковы по сложности.
19. Найти величину усилия, сжимающего предмет М в прессе
(рйс. 19,а), при следующих условиях: усилие Р = 50 кг и направ-
направлено перпендикулярно к рычагу ОЛ, имеющему неподвижную-
ось О; в рассматриваемом положении пресса тяж ВС перпенди-
перпендикулярен к ОВ и делит /_ ECD пополам, причем /_ CED =
= arcctg 0,2 = 11°20'; длина ОА = .1 м\ ОВ = 10 см.
Решение. Сначала рассмотрим равновесие рычага О А (рис. 19,6),,
имеющего неподвижную ось О.
К нему приложены: активная сила Р и реакция R тяжа ВС,
направленная по горизонтали от В к С.
Применив формулу (IV, 1), составим уравнение равновесия
рычага
YMo = — Р • О А + R • ОВ = 0.
Решив уравнение, найдем R:
«-P.g -50.^-500».
Произвольная плоская система сил, приложенных к связанным телам 73>
Затем рассмотрим равновесие узла С (рис. 19,в).
К узлу приложены: горизонтальная сила R (при рассмотрении
равновесия узла С она должна быть направлена в сторону, противо-
противоположную ранее найденной) и две реакции RE и RD, в силу сим-
симметрии равные друг другу (ВС делит пополам /_ ECD); считая
стержни СЕ и CD сжатыми, направим RE и RD к узлу С.
К задаче 19.
Составим только одно уравнение равновесия: сумму проекций-
всех сил на ось Сх\ второе уравнение равновесия плоского пучка
сил (EVt = 0) обращается в тождество, так как мы приняли, что-
реакции RE и RD равны друг другу.
? Хг = — RE • sin a — RD
Решив уравнение, найдем
R
2 sin л '
Перейдем к рассмотрению равновесия узла Е нижней плиты
пресса (рис. 19,г).
К нему приложены: реакция /?я, направленная в сторону, про-
противоположную ранее найденной; вертикальная реакция R*M сжи-
сжимаемого предмета М и реакция вертикальной правой стойки, на-
направленная перпендикулярно к ее оси, т. е. горизонтально.
Из уравнения проекций всех сил на вертикальную ось Еу най-
найдем величину реакции RM.
Решив уравнение, получим
sin а
COS а
== 0.
R
2tgc
500
1250/сг,
1 Так как предмет М прижимается к верхней плите пресса, то его реакция фак-
фактически представляет собой реакцию верхней плиты пресса.
74
Статика твердого тела
Вертикальное давление N, прижимающее предмет М к верхней
плите пресса» равно его реакции RM, т. е.
N = RM = 1250 кг.
20. Консольный мост (рис.
АВ и двух боковых С А и BD.
20,а) состоит из главной фермы
Интенсивность собственного веса
фермы АВ (вес, приходящийся
на 1 пог. м) равна 1 т, а ферм
С А и BD — 0,8 т каждая.
Определить реакции опор в тот
момент, когда на правом про-
пролете FD находится поезд, интен-
интенсивность нагрузки которого
q = 4 т/м. Размеры соответ-
соответственно равны: СЛ = 20 м,
АЕ = FB = 16 му EF = 60 м.
Решение. Реакции RE, RF и
RD шарнирно-подвижных or^op
Е, F и D моста вертикальны,
следовательно, при вертикаль-
вертикальных активных нагрузках реак-
реакция Rc также вертикальна, иначе
равновесие моста было бы не-
невозможно.
Составим (рис. 20,6) схему'
взаимодействия, ферм СА, АВ и
BD. Опоры: А (для фермы С А),
Е (дли фермы АВ) и В (для фер-
фермы BD) показаны на схеме
такими, какими они были бы,
«ели" бы каждая ферма не была связана с другими в одно
целое; в действительности же неподвижность всего моста
CAEFBD обеспечивается неподвижностью шарнирной опоры С.
Из схемы видно, что основной, несущей частью моста является
ферма АВ. Рассматривать равновесие фермы АВ можно только
после нахождения (из рассмотрения равновесий боковых ферм СА
и В) давлений NA и NBy передаваемых этими фермами основной
ферме АВ в точках А и В.
Рассмотрим равновесие боковой фермы СА (рис. 20,<?). К ферме
СА приложена одна активная сила — собственный вес интенсив-
интенсивностью р% равномерно распределенный по всей ее длине, и реакции
опор RA и Rc, направленные вертикально вверх.
В силу симметрии вертикальные реакции Rc и RA фермы равны
между собой и каждая из них равна половине всей действующей
К задаче 20.
Произвольная плоская система сил, приложенных к связанным телам 75
на ферму нагрузки, т. е.
Давление Na конца А фермы СА на конец А фермы АВ равно
по величине реакции /?д, но направлено в противоположную сто-
сторону, т. е. вертикально вниз.
Рассмотрим равновесие боковой фермы BD (рис. 20,г). К ней
приложены две активные равномерно распределенные по всей
длине фермы вертикальные нагрузки: собственный вес интенсив-
интенсивностью р и вес поезда интенсивностью q, *а также реакции Rb и
RD, направленные вертикально вверх.
В силу симметрии вертикальные реакции Rb и Rd фермы равны
друг другу и каждая равна половине всей действующей на ферму
нагрузки, т. е.
Давление NB конца В фермы BD на конец В фермы АВ равно
по величине реакции Rb фермы BD, но направлено в противопо-
противоположную сторону, т. е. вертикально вниз.
Рассмотрим равновесие основной несущей части моста — фермы
АВ (рис. 20,C). К ферме приложены четыре активные вертикальные
силы: в точке А — сила Na', в точке В — сила NB\ на правой кон-
консоли (свешивающейся за опорой F части фермы АВ) — равномерно
распределенная нагрузка, интенсивностью q (поезд), и по всей
длине АВ — равномерно распределенная нагрузка интенсив-
интенсивностью /?!, равной 1 т, а также реакции RE и RF опор Е и F фермы,
направленные вертикально вверх.
Применив формулы (II, 7), составим два уравнения равновесия
фермы АВ, находящейся под действием плоской системы параллель-
параллельных сил, выбрав за центры моментов точки Е и F и предварительно
заменив равномерно распределенные нагрузки их равнодействую-
равнодействующими, приложенными на средине соответствующих участков (в дан-
данном случае участок — это часть моста, на всей длине которой
находится одинаковая равномерно распределенная нагрузка).
A)
B)
76
Статика твердого тела
Подставив значения Na и Nb, а также данные из условия за-
задачи в уравнения. A) и B) и решив их, найдем:
•8- 16+1 .92
(^-16^+4. 16^60 + ^) +48 '76
60
= 177,2 т;
8-76+ 1 -92/^ —
16. Y-
16
60
= 34,8 т.
Проверим правильность найденных значений реакций RE и
KFi спроектировав на вертикальную ось Ау все действующие на
ферму А В силы:
-р1. АВ + RF — q- FB — NB=
92 + 177,2—4.16 — 48 = 0. C)
Равенство нулю левой
части уравнения C) пока-
показывает, что реакции RE и
RF найдены правильно.
21. Горизонтальная раз-
разрезная балка АСВ (рис.
21 Уа) концом А заделана
в стену, а концом В опи-
опирается на подвижную опо-
опору; обе части ее АС =4 м
и СВ = 5 м соединены в
точке С шарниром. На
балке расположен кран,
несущий груз Р = 1,2 т.
Вылет крана KL = 4 м,
вес его Q =±= 4 т\ центр
* тяжести крана расположен
? на вертикали CD; рассто-
5» Р яние между опорами Е и
а F крана равно 2 м. Опре-
Определить, пренебрегая весом
балки, опорные реакции в
точках Л и В, когда кран
находится в одной верти-
вертикальной плоскости с* бал-
балкой АВ.
К задаче 21.
Решение. Поскольку балка АВ, состоящая из двух твердых
тел, соединенных шарниром С, разрезная, нельзя силы Q
Произвольная плоская система сил, приложенных к связанным телам 77
и Р считать приложенными к ней непосредственно в точках С и #,
где линии действия сил пересекаются с осью балки. Поэтому, рас-
рассмотрев равновесие крана, найдем сначала давления NE и NFf
оказываемые им на разрезную балку АВ в точках касания Е и Ff
а, затем уже определим реакции опор А и В.
Определение давлений NE и Л/^уже проделано нами в первом
варианте решения задачи 7, поэтому мы используем уже- гото-
готовый результат решения:
NE = 0,2 т\ NF = 5 т.
(Размеры и вес крана, величина и положение груза в задаче 7
те же, что и в рассматриваемой). Составим схему (рис. 21,6) взаимо-
взаимодействия частей АС и СВ разрезной балки АВ. Опора С указана
на схеме такой, какой она была бы, если бы часть СВ балки АВ
существовала самостоятельно, не будучи связанной с частью АС
балки.
Из схемы видно, что основной несущей частью разрезной балки
АВ является АС.
Рассматривать равновесие балки АС можно, только определив
(из рассмотрения равновесия балки СВ) давление Л/с, передавае-
передаваемое балкой СВ основной балке АС в точке С.
Рассмотрим равновесие балки СВ (рис. 21,в). К балке в точке F
приложена одна активная вертикальная сила NF = 5 /п, а в точ-
точках С и В к ней приложены вертикальные реакции Rc и Rb (cm. ре-
решение предыдущей задачи).
Применив формулы (II, 7), составим два уравнения равновесия
балки СВ, находящейся под действием плоской системы параллель-
параллельных сил, приняв за центры моментов точки С и В.
? Л1С =*-#,. 1+РБ.5 = 0, A)
%МВ = -Rc • 5 + NF • 4 = 0. B)
Подставив значение NF в уравнения A) и B) и решив их, найдем:
Рв=^=1 т,
Давление Nc конца С балки СВ на конец С балки АС равно
по величине реакции Rc балки СВ, но направлено в противопо-
противоположную сторону, т. е. вертикально вниз.
Мысленно отделив балку СВ (рис. 21,г) от балки АС сечением,
проведенным через соединительный шарнир С, и заменив действие
балки СВ на шарнир давлением Л^с, рассмотрим балку АС как
консоль, конец С которой свободен от связи, а конец А защемлен
в стене.
78 Статика твердого тела
Для большей ясности упростим условия закрепления конца А К
балки. Будем считать (рис. 21,д), что она опирается на нижнюю
часть стены и касается верхней не по всей длине А /С, а только на
незначительной части ее; пренебрегая размерами опорных площа-
площадок, примем, что балка опирается на нижнюю часть стены в точке
А и касается верхней — в точке /С.
Вертикальные силы NE и Nc оказывают двоякое действие:
прижимают балку к опоре Л, стремясь переместить ее по верти-
вертикали вниз, и одновременно стремятся вывернуть ее конец А К из
стены, повернув его вокруг опоры А по ходу часовой стрелки;
при этом коней К нажимает на верхнюю часть стены, встречая с ее
стороны противодействие в виде направленной вертикально вниз
реакции RK. Перемещению по вертикали препятствует нижняя
часть стены; ее сопротивление выражается направленной верти-
вертикально вверх реакцией Ra\ кроме того, на опоре А возникает еще
реакция R'a* равная по величине давлению /?#, передаваемому
опоре А концом балки, но направленная в. противоположную ей
сторону, т. е. вертикально вверх.
Силы RK и R'a, отмеченные на рисунке штрихом, образуют
пару, момент которой
т = — RK • d,
где d — расстояние между опорами А и /С.
Таким образом, в заделке (рис. 21,г) возникают реакция На
и реактивный момент т, величины и направления которых зависят
от величин, направлений и точек приложения активных сил;
реактивная пара условно изображена на рисунке моментом т,
направленным против хода часовой стрелки, реакция RA принята
вертикальной.'
Для определения неизвестных реактивных величин рассмотрим
равновесие балки К АС, находящейся под действием произвольной
плоской системы сил, направив ось Ах горизонтально, а ось Ау —
вертикально.
Применив формулы (IV, 2), составим два1 уравнения равновесия,
приняв за центр моментов точку Л.
Силы, составляющие реактивную пару, не входят в уравнение
проекций сил на любую ось, так как сумма их проекций на эту
ось всегда равна нулю.
^ 0.
1 Обозначив горизонтальную составляющую реакции опоры А через ХЛ и
составив,третье уравнение равновесия
убедимся, что реакция в заделке вертикальна.
Произвольная плоская система сил, приложенных к связанным телам 7$
Подставив значение NE и Nc в уравнения C) и D), получимг
Ra = Ne + Nc*= 4,2 т.
m = NE-3 + Nc-4= 16,6*m.
Положительные знаки реактивных величин Ra и т показывают,
что выбранные нами направления их правильны.
22. Вдоль мастерской (рис. 22,а), здание которой поддерживается
трехшарнирной аркой, перемещается по рельсам мостовой кран.
Вес поперечной балки, передвигающейся по рельсам, Qx = 1,2 m;
вес крана Q2 =0,8 т (кран не нагружен); линия действия веса
крана отстоит от левого рельса на четвертую часть длины попереч-
поперечной балки. Вес каждой половины арки Q = 6 т и приложен на
расстоянии 2 м от вертикали, прододящей через соответствующую
опору {А или В); опорные рельсы крана расположены на расстоя-
расстоянии 1,8 м от этих вертикалей. Высота здания 12 м, ширина про-
пролета 16 м. Равнодействующая сил давления ветра Р = 1,2 т и на-
направлена параллельно АВ; линия ее действия отстоит от АВ на
5 м.
Определить реакции шарниров Л и Б и давление в ±арнире С.
Решение. Прежде всего необходимо найти давления ND и NE,
оказываемые поперечной балкой DE на кронштейны; для этого
рассмотрим равновесие балки DE (рис. 22,6).
К балке приложены две активные вертикальные силы: на сре-
средине пролета (расстояния между опорами D и Е) — сила Qx и на
расстоянии четверти пролета балки от левой опоры—сила Q2.
Освободив балку от связей D и Е, заменим их действие силами
Rd и Re; обе реакции RD и RE вертикальны.
Применив формулу (II, 7), составим два уравнения равновесия
свободного твердого тела — балки DE, находящейся под действием
плоской системы параллельных сил.
2MI> = -Q1-^-Q1- ™ + RE.DE = 0^ A)
2 МЕ = - RD . DE + Qx • Щ + Q2.1. DE = 0. B>
Подставив данные из условия задачи в уравнения A) и B) и
решив их, найдем:
^ = 0,8 т и RD= 1,2 т.
* Если бы было задано расстояние d между опорами Л и /С, т. е. длина защемлен-
защемленной части балки,то величину реакции RR можно было бы определить; действитель-
действительно, по абсолютному значению
т = RK- d*= 16,6 m,
откуда
__ m 16,6
Статика твердого тела
ЧР- л d
К задаче 22.
Произвольная плоская система сил, приложенных к связанным телам 81
Давления NB и ND концов Е и D балки DE на кронштейны
арки (передающиеся через рельсы) соответственно равны реакциям
Re и Rd опор ?иОпо величине, но направлены в противополож-
противоположные им стороны, т. е. вертикально вниз.
Теперь можно перейти к определению реакций шарниров Л, В
и С трехшарнирной арки.
Первый способ. Сечением, проходящим через соединительный
шарнир С, отделим левую часть арки от правой, отбросим опоры
А я В и, заменив их действие силами, рассмотрим отдельно равно-
равновесие каждой половины арки.
Рассмотрим сначала равновесие левой половины АС арки
(рис. 22,#). Направим координатные оси согласно рисунку.
К левой половине арки приложены три активные силы: Р, Q
и ND и реакции связей Л и С; каждую реакцию представим двумя
составляющими: Ха и Ya, Хс и Yc, направленными в поло-
положительные стороны координатных осей.
Реакция Rc шарнира С в данном случае представляет собой
действие правой половины СВ арки на левую^ АС.
Применив формулы (IV, 2), составим три уравнения равно-
равновесия левой половины АС арки, приняв за центр моментов точку А.
^Х% = ХА + ХС + Р = О; (V)
lYi = YA + Yc-Q-NJ) = 0; B')
"?,МА = — Р. 5 — Хс- 12 — Q. 2 —AV 1,8 +Ус-8 = 0. C')
Затем рассмотрим равновесие правой половины СВ арки
{рис. 22,г). Направим координатные оси согласно рисунку. К пра-
правой половине арки приложены две активные вертикальные силы
Q и NE и реакции связей С и В; реакцию RB шарнира В представим
в виде двух составляющих Хв и YBy направленных в положитель-
положительные стороны осей Ох и Оу.
Реакция Rc шарнира С в данном случае представляет собой
действие левой половины арки на правую; она равна по величине
реакции правой половины арки, но направшена в противополож-
противоположную сторону, поэтому Хс и Yc необходимо направить в отрица-
отрицательные стороны осей х и у.
Применив формулы (IV, 2), составим три уравнения равно-
равновесия правой половины СВ арки, приняв за центр моментов точку В.
VXi = -Xc + X? = Q; (Г)
Гс.8 + Хс. 12 + Q.2 + tfj. 1,8 = 0. (Г)
Подставив найденные значения ND и NE, а также данные из
условия задачи в уравнения C') и 3") и решив эту систему двух
б И1
82 ... Статика твердого тела
уравнений с двумя неизвестными, найдем:
Ус = + 0,42 т\ Хс = —1,4 т.
Подставив найденные значения, а также данные из условия
задачи й уравнения, (Г), B')> (Г') и B") и решив их в указанной
последовательности, найдем:
ХА « + 0,2 т; YA = + 6,78 т\ Хв = — 1,4 т\ YB = + 7,22 m.
Знак минус при неизвестных Хс и Хв показывает, что эти
составляющие направлены в сторону, противоположную выбранной;
следовательно, составляющая Хв направлена влево, Хс направ-
направлена влево только при рассмотрении равновесия левой половины
арки и вправо при рассмотрении равновесия правой половины арки.
Второй способ. Отделив аналогично предыдущему левую часть
арки от правой, рассмотрим равновесие одной из них и всей трех-
шарнирной арки в целом.
Из двух половин арки выбираем ту, к которой приложено
меньшее количество активных сил, т. е. правую СВ (рис. 22,г).
Уравнения (Г'), B") и C") остаются в силе.
Рассмотрим равновесие трехшарнирной арки АСВ (рис. 22,5).
Направим координатные оси согласно рисунку.
К арке АСВ приложены активные силы Р, Q, Q, ND, NE и реак-
реакции связей Л и В, которые соответственно представим в виде состав-
составляющих Ха и Ya, Хв и YBt направленных в положительные сто-
стороны осей Ах и Ау.
Составляющие Хс и Yc реакции Rc шарнира С, направленные
по обе стороны каждой из осек Ах и А у и представляющие собой
действие левой половины арки на правую, и наоборот, взаимно
уравновешиваются и при рассмотрении равновесия всей арки
АСВ в целом фигурировать в уравнениях равновесия не будут,
так как это силы внутренние (для арки в целом), а в уравнения
равновесия входят только внешние силы.
Применив формулы (IV, 2), составим три уравнения равнове-
равновесия трехшарнирной арки АСВ как одного твердого тела, находяще-
находящегося под действием произвольной плоской системы сил, приняв
аа центр моментов точку А или В.
%Х{ = ХЛ + Хв + Р = 0; (Г")
2Yi^YA+YB-2Q-ND-NE^0; (Г')
y?MA*=—P*5 — NI>.l,8 — Q-2 — Q.\4 — NB. 14,2 +
+ УВ. 16-0. C")
Рассматривая равновесие всей арки А СВ, мы могли бы (см. вто-
второй способ решения задачи 7) вместо давлений ND и NE (рис. 22,3)
поперечной балки, передаваемых арке через кронштейн, учитывать
силы Qj и Q2, т. е. считать, что эти силы приложены непосредственно
Произвольная плоская система сил9 приложенных к связанным телам 83
к арке, тогда, составляя уравнение моментов всех сил относительно
точки Л, можно вместо суммы моментов сил Q, Q и Qx взять
момент их равнодействующей, равной 2Q + Q1% проходящей по
оси симметрии.
Уравнение C'") принимает вид
%MA = —P*5-BQ +Qi) -8-<?a-4,9+ Ув. 16 = 0.
Решив уравнения C'"), B'"), B*), C"), A") и (Г") в указанной
последовательности, найдем:
YB = + 7,22 т\ YA = + 6,78 m; Ус = + 0,42 т;
Хс = —1,4 т; Хв = —1,4 т; Х^=+0,2т,
т. е. то, что было уже найдено при первом способе решения.
Вывод. Из сопоставления обоих способов решения видно, что:
а) в первом способе решения нет уравнений с одним неизвестным и для определения
искомых величин нужно сначала решить систему двух уравнений с двумя неиз-
неизвестными; б) во втором — такое уравнение есть — уравнение C); в) в первом спо-
способе при рассмотрении равновесия второй половины арки нужно было менять
направление составляющих Хс и Ус реакции Re шарнира С; г) во втором —
силы Хс и Ус фигурируют только один раз и поэтому менять их направлений
не нужно.
Рекомендуем задачи такого типа решать по второму варианту.
23. Тело весом Р = 500 кг (рис. 23,а) удерживается на гладкой
наклонной плоскости посредством веревки, параллельной пло-
плоскости и намотанной на неподвижный вал лебедки ABC. Угол
наклона плоскости к горизонту равен 60°. Вес лебедки Q = 250 кг
и направлен по прямой СО; лебедка опирается в точке А на глад-
гладкий пол, а в точке В — прикреплена к полу болтом.
Найти опорные реакции, пренебрегая расстоянием веревки от
плоскости.
Решение. Для определения опорных реакций рассмотрим равно-
равновесие лебедки ABC. Координатные оси направим, как показано
на рис. 23,в.
Анализируя действующие на лебедку силы, иногда ошибочно
считают, что на вал лебедки посредством веревки передается весь
груз Р. Чтобы лучше разобраться в этом вопросе, разложим силу Р
(рис. 23,6) на две составляющие: силу N, перпендикулярную к
наклонной плоскости, и силу 7\ параллельную ей, и исследуем
их действие.
Сила N уравновешивается реакциями Nx и N2 плоскости х, воз-
возникшими в точках касания колес подвижного груза Р с плоскостью
(величины N-l и N2 зависят только от положения центра тяжести
груза Р) и на лебедку никакого действия не оказывает, а сила
1 Так как плоскость гладкая, сила трения не возникает и не передается веревкой
валу лебедки*
6*"
84
Статика твердого тела
Т = Р sin 60°, натягивая веревку, действует на вал лебедки (счи-
(считаем, что центр тяжести груза находится на оси веревки); кроме
силы Т, к лебедке приложена активная сила Q.
К задаче 23.
Освободив лебедку от связей Л и В, заменим их действие на
нее силами; реакция Yа опоры А направлена нормально к горизон-
горизонтальной плоскости, так как плоскость гладкая и сила трения не
возникает, реакцию опоры В представляем двумя составляющими
%в и У в* направленными в положительные стороны осей Вх и By.
Применив формулы (IV, 2), составим три уравнения равно-
Произвольная плоская система сил, приложенных к связанным телам 85
весия свободного твердого тела — лебедки АСВУ находящейся
под действием произвольной плоской системы сил, выбрав за центр
моментов точку В.
У] X, = Хв — Т • cos 60° » 0; A)
? У г = У а — т • sin 60° -Q + YB = 0; B)
2 МБ - Q . а - Ул • 2а + Т . h - 0. C)
(По условию задачи расстоянием между веревкой и наклонной
плоскостью пренебрегаем, т. е. считаем, что линия действия Т
совпадает с СА и наклонной плоскостью.)
Определив h из прямоугольного Д Л В К
h = 2a • sin 60°
и подставив данные из условия задачи, решим уравнения.
Из уравнения A)
XB^T.cos60o==Psin60° .cos6(T = 500.^. 1 = 216,5 кг.
Из уравнения C)
Q • а + Т • h __ Q • g -f P sin 6У ¦ 2д ¦ sin 60°
У _
2а ~~ 2а
500.^-2 •
- 500 «г.
Из уравнения B)
YB = Q + Г . sin60° — YA = Q + Р - sin60° . sin 60е — У^ == 250
Положительные знаки перед найденными значениями составляю-
составляющих ХВу Yа и YB показывают, что направления этих сил выбраны
правильно.
Примечание. Решение задачи можно упростить, приняв центр моментов
в точке Л, где пересекаются линии действия трех сил: Т, УА и Хв (рис. 23, г);
тогда уравнение C) примет вид:
откуда
Неизвестные Хв и УА определяются из уравнений A) й B)
86
Статика твердого тела
ГЛАВА VII
СИЛЫ ТРЕНИЯ
§ 1. Силы трения при скольжении
Если рассматриваемое тело находится в покое, не скользит
по поверхности другого тела под действием приложенной к нему
системы сил, равнодействующая которых R (рис. 1,а) не перпен-
перпендикулярна к этой поверхности \ то сила трения Т равна силе Ff
N
7»"? I
_?] _
U77? .
Те по
движется
Г ело в со сто.
грани** -
равно-
Рис. 1.
стремящейся сдвинуть рассматриваемое тело (сила F—это располо-
расположенная в касательной плоскости составляющая силы R)t и на-
направлена в противоположную ей . сторону.
С увеличением силы F возрастает и остающаяся равной ей сила
трения Tt достигающая в момент предельного состояния покоя,
^граничащего с началом движения тела, максимального значения
(рис. 1,6), определяемого по уравнению:
Tmax = /.iV, (VII, 1)
где N — нормальное давление рассматриваемого тела на сопри-
соприкасающуюся с ним поверхность другого тела, а / — коэффициент
пропорциональности, называемый коэффициентом трения покоя,
зависящий от материалов трущихся тел и* состояния их поверх-
поверхностей 2.
Таким образом, пока сила F не сдвинула тела, сила трения
покоя Т определяется формулой
T.<f-N. (VII, 2)
В частном случае, когда соприкасающиеся поверхности тел
идеально гладкие (/ =0), сила трения отсутствует и реакция
связи Rc перпендикулярна к касательной плоскости.
1 Перпендикуляром к поверхности является перпендикуляр к плоскости,
касающейся поверхности в точке соприкасания рассматриваемых тел, иначе, пер*
оендикуляр к касательной плоскости.
8 Для таких материалов как дерево большое значение имеет угол, образуемый
сдвигающей силой с направлением волокон, слоев.
Силы трения 87
При наличии силы трения покоя полная реакция Rc связи
(рис. 1,а, б) равна геометрической сумме нормальной (к поверх-
поверхности связи) составляющей Л' и расположенной в касательной
плоскости второй составляющей — силы трения Т. По величине
она равна также равнодействующей R всех приложенных к телу
сил, но направлена в противоположную ей сторону, отклоняясь
от нормали к поверхности в сторону, противоположную сдвигаю-
сдвигающей силе Fy на угол ос, достигающий максимума, обозначаемого ср,
одновременно с достижением максимума силой трения Т\ при этом
тангенс этого угла <р, называемого углом трения, становится равным
коэффициенту трения, т. е.
A (VII, 3)
Силы трения, входящие в произвольную плоскую систему сил,
как правило, неопределенны *, поэтому уравнения рановесия такой
системы сил, выражающиеся равенствами (IV, 2), становятся
неравенствами. Это объясняется тем, что число положений тела,
находящегося в покое, получается бесконечно большим и из усло-
условий равновесия определяется уже ряд значений неизвестной вели-
величины (силы, угла, длины стержня и т. д.). Задача становится опре-
определенной, если при ее решении рассматриваются не любые значе-
значения сил трения покоя, а их максимальные значения; при этом из
условий равновесия определяются только максимальные или мини-
минимальные значения неизвестных величин. *
Исследование состояния тела (покой, движение) зачастую
упрощается при геометрическом решении вопроса, т. е. при уста-
установлении взаимного расположения линии действия равнодействую-
равнодействующей всех приложенных- к телу активных сил и конической поверх-
поверхности прямого кругового конуса 2, образующие которого отклонены
от нормали к соприкасающейся с телом плоскости на угол трения <р.
При исследовании состояния тела, к которому приложена
плоская система сил (только такие задачи и рассматриваются в
этой главе), необходимо установить взаимное расположение линии
действия равнодействующей и боковой стороны равнобедренного
треугольника трения 3. Если линия действия равнодействующей R
проходит в пределах треугольника трения (рис. 1,в), то тело на-
находится в покое 4; при совпадении ее с боковой стороной треуголь-
треугольника трения наступает предельное состояние покоя и при малей-
1 Они могут иметь значения, заключающиеся между нулем и максимумом,
равным /. N (см. уравнение VII, 2).
2 Конус становится прямым круговым, если величина силы трения Т не за-
зависит от направления сдвигающей силы F в касательной плоскости, т. е. если f —
величина постоянная. %
8 Равнобедренный треугольник трения представляет собой след сечения ука-
указанной выше конической поверхности плоскостью рисунка — плоскостью дей-
действия приложенной к телу системы сил; этот термин вводится автором.
* Состояние тела не зависит от величины равнодействующей активных сил.
Статика твердого тела
шем отклонении ее за пределы этого треугольника начинается
движение тела по плоскости.
Методика определения неизвестных величин приводится в
решении задач.
§ 2. Силы трения при качении
При рассмотрении сопротивления качению тяжелого цилиндри-
цилиндрического тела по плоскости (рис. II) необходимо отойти от представ-
представления о телах, как об абсолютно твердых, не деформирующихся,
и учитывать, что в той или иной мере
и тело и плоскость деформируются, в
связи с. чем тело соприкасается с плос-
плоскостью не по образующей а, а по неко-
торой поверхности. При этом точка при-
* \ л/ \\ / ложения давления тела на эту поверх-
поверхность \ а следовательно, и точка
приложения к телу реакции опоры,незна-
опоры,незначительно смещается в сторону возмож-
возможного перемещения тела. Реакция опоры
представляет собой геометрическую сум-
сумму составляющей А/", нормальной к не-
деформированной плоскости, и касательной составляющей Т — силы
трения качения.
Пока цилиндрическое тело находится в покое, сила трения
качения Т равна силе F, стремящейся вывести его из этого со-
состояния. С увеличением силы F* возрастают остающаяся равной
ей сила Г и указанное выше смещение точки приложения равнодей-
равнодействующей всех приложенных к телу активных сил. Сила трения ка-
качения Ту достигающая максимального значения в момент предель-
предельного состояния покоя, граничащего с началом равномерного
качения цилиндрического тела по плоскости, определяется по
формуле
rmax = |iV, (VII, 4)
где; 8 — выражающийся в единицах длины (в см) коэффициент
трения качения, зависящий от материалов соприкасающихся тел
и состояния их поверхностей и равный максимальному смещению
(по плоскости) точки приложения давления тела от точки касания
сечения цилиндрического тела с недеформированной плоскостью,
1 Иначе говоря, точка пересечения линии действия равнодействующей всех
приложенных к телу активных сил с соприкасающейся с ним поверхностью. В
плоскости рисунка — плоскости действия сил — расположен и центр тяжести
цилиндра.
* При постоянной тотке приложения ее.
Силы трения 89
N — нормальное давление рассматриваемого тела на соприка-
соприкасающуюся с ним плоскость, а г — расстояние силы F от этой пло-
плоскости.
Таким образом, пока не наступило качение тела по плоскости,
сила трения качения Т определяется по формуле
T<y-N. (VII. 5)
Сравнение формул (VII, 1) и (VII, 4) показывает, что макси-
максимальное значение силы трения покоя при качении значительно
меньше максимального значения силы трения покоя при скольже-
скольжении, так как отношение — значительно меньше коэффициента тре-
трения скольжения /.
§ 3. Задачи
24. Тело весом Р (рис. 24,а) лежит на горизонтальной плос-
плоскости. К нему приложена сила Q, образующая с горизонтом угол а.
Какова должна быть величина этой силы, чтобы она могла сдви-
сдвинуть тело, если коэффициент трения между телом и плоскостью
равен /?
Решение. Тело сдвигается с гори-
горизонтальной плоскости силой F (рис.24,6),
совпадающей с этой плоскостью и пред-
представляющей собоц горизонтальную со-
составляющую силы Q. Найдем эту силу. " за аче 24
F =Q -cosa.
Нормальное давление N, оказываемое телом на плоскость, представ-
представляющее собой равнодействующую его веса Р и перпендикуляр-
перпендикулярной к плоскости составляющей силы Q, уравновешивается нор-
нормальной составляющей реакции плоскости. Найдем ее величину.
N = Р —• Q sin a.
Эта формула теряет смысл как при Q - sin a > Р, когда тело от-
отдаляется от плоскости, так и при Q sin а = Р, когда тело только
касается плоскости, не оказывая на нее никакого давления.
Сдвиг тела с занимаемого им на плоскости положения стано-
становится возможным при Q sin а < Р, когда F > Г, т. е. при
Q • cosa>/. N; Q . cosa>/. (P —Qsina).
Решив это неравенство, получим
25. Два груза А в В (рис. 25,а), веса которых соответственно
вны Р и Q, связаны между собой веревкой, переброшенной через
Статика твердого тела
К задаче 25.
Силы трения 91
блок С, и опираются на плоскости, наклоненные к горизонту
р
соответственно на углы аир. Найти отношение ^- при равновесии
грузов, если угол трения между каждым грузом и соответствую-
соответствующей плоскостью равен <р-
Решение. Примем, что центр тяжести каждого груза и ось
прикрепленной к нему веревки расположены на соответствующей
наклонной плоскости. При различных соотношениях между весами
Р и Q один из грузов (Л или В) будет спускаться по наклонной
плоскости, а> Другой — подниматься. Силы трения, возникающие
между грузами и наклонными плоскостями, будут направлены в
стороны, противоположные движению грузов (для спускающегося
груза — вверх по наклонной плоскости, для поднимающегося —
вниз).
Изменяя соотношение между весами Р и Q> можно найти такое
его значение, при котором движение грузов по наклонным пло-
плоскостям прекратится.
Разберем два возможных случая: .
а) остановились спускающийся вниз груз А и поднимающийся
вверх груз В;
б) остановились спускающийся вниз груз В и поднимаю-
поднимающийся вверх груз Л.
Случай а. Исследуем силы, действующие на груз Л, спускаю-
спускающийся по наклонной плоскости CD (рис. 25,6).
К нему приложены: вертикальная сила Р (его вес), реакция
S2 веревки, представляющая собой действие груза В, поднима-
поднимающегося по наклонной плоскости СЕ,и опорная реакция плоскости
CD, которую представим в виде двух составляющих N и Гд,на-
Гд,направленных соответственно по нормали к этой плоскости (N не
показана на рисунке) и по самой плоскости; Та представляет
собой силу трения.
Разложив силу Р (рис. 25,6) на составляющие Na и Fa, направ-
направленные соответственно по нормали к плоскости и по самой пло-
плоскости CD, найдем их значения из прямоугольного треугольника
Acd1
FA = P sin a.
Давление Na уравновешивается равной ему составляющей
N реакции плоскости, следовательно, груз Л движется вниз под
действием равнодействующей 5Х направленных в разные стороны
сил Fa и Та (Та = / • Na) и реакции 52 веревки.
На рпе. 25,6, в грузы А в Б показаны в виде точбк А и В.
92 Статика твердого тела
Определим S :
S1*=FA — T4 = P - sina —/ - NA f
= P sin a — tg cp1 . P cos a.
Исследуем силы, действующие на груз В, поднимающийся
по наклонной плоскости СЕ (рис. 25, б),
К нему приложены: вертикальная сила Q (его вес), реакция
Sx веревки, представляющая собой действие груза Л, спускаю-
спускающегося по наклонной плоскости CD, и опорная реакция плоскости
СЕ, которую мы представим в виде двух составляющих Nt и Тв,
направленных соответственно по нормали к этой плоскости (Nx,
не показана на рисунке) и по самой плоскости; Тв представляет
собой силу трения.
Разложив силу Q (рис. 25,6) на составляющие NB и FB, направ-
направленные соответственно по нормали к плоскости и по самой плоскости
СЕ, найдем их значения из прямоугольного треугольника Bef1.
Давление NB уравновешивается равной ему составляющей Nx
реакции плоскости, следовательно, груз В движется вверх под
действием реакции 5Х веревки и равнодействующей S2 направлен-
направленных в одну сторону сил FB и ТВ(ТВ = / • NB).
Определим 52:
S2 = FB + Тв = Q sin p + / - NB = Q sin p + / - Q cos p «
= Q sin 8 -f tg cp . Q cos p.
При достижении искомого соотношения между весами грузов
А и В St станет равным S2, и движение грузов прекратится; следо-
следовательно,
Р sin a — tg cp . P cos a, = Q sin p -j- tg cp . Q cos p
или, после вынесения сил Р и Q за скобки,
Р (sin a — tg cp . cos a) = Q (sin p + tg 9 - cos p).
Найдем искомое соотношение между весами грузов А и В:
sin a — tg cp • cos a . sin cp
6 T Sin a 1 • COS a
COS ф
sin p • cos ф + sin ф • cos p sin (p + 9)
sin a • cos ф — sin ф • cos
у ледуем силы, действ
щийся по наклонной плоскости CD.
sin a • cos ф — sin ф • cos a sin (a —
Случай б. Исследуем силы, действующие на груз Л, поднимаю-
поднимаюй й CD
1 Напоминаем, что коэффициент трения / равен тангенсу угла трения <р, т. е.
Силы трения 93
В отличие от случая а, в связи с изменением направления
движения груза, силы Fa и Та (рис. 25,#) направлены уже в одну
сторону и груз А движется вверх под действием реакции 54 ве-
веревки, представляющей собой действие груза В, спускающегося
по наклонной плоскости СЕ, и равнодействующей S3 сил FA и 7V
Определим S3:
S3 = Р sin ос -j- tg <p • Р cos а.
Исследуем силы, действующие на груз В, спускающийся по
наклонной плоскости СЕ. В отличие от случая а, в связи с
изменением направления движения груза, силы FB и Тв (рис. 25,в)
направлены уже в разные стороны и груз В движется вниз под
действием их равнодействующей S4 и реакции S3 веревки,
представляющей собой действие груза Л, поднимающегося по на-
наклонной плоскости CD.
Определим S4:
SQip
Аналогично предыдущему, S3 станет равным 54 при дости-
достижении искомого соотношения между весами грузов Л и В, следо-
следовательно,
Р sin а + tg <р • Р cos а = Q sin р — tg ф ; Q cos p,
или, после вынесения сил Р и Q за скобки,
Р (sin a + tg ср • cos а) = Q (sin р — tg <p . cos P).
Найдем искомое сотношение между весами грузов Л и В.
п • о i о sin 3 • cos S
Р sin g — tg «p • cos p ' cos ф l
Q sin a ¦+• tg cp • cos a . sin ф
ь T Sin a -j 1 . COS a
COS cp
__ sin p ¦ cos <p — sin <p • cos § sin (fJ — 9) e
sin a ¦ COS cp -f- Sift cp • COS a sin (a -f- cp) '
Итак, равновесие грузов Л и В возможно, когда соотношетш
между их весами равны:
sin (a — чр) '
26. Клин А (рис. 26,а), уклон которого tga =0,05, забивается
в углубление ВВг усилием Q = 6 т. Определить нормальное
давление N на щеки клина и усилие Р, необходимое для того,
чтобы вытащить клин, если коэффициент трения /=0,1.
Решение* Действующая на клин активная сила Q вызывает
равномерное проникновение его в углубление BBV В этом случае
все приложенные к клину силы взаимно уравновешиваются.
94
Статика твердого тела
в
як
К задаче 26.
Силы трения $5
Исследуем действующие на клин силы (рис. 26,6).
Проникая под действием активной вертикальной силы Q в
углубление ВВЪ боковые плоскости клина нажимают на сопри-
касающиеся с ними боковые плоскости углубления, встречая с их
стороны направленные по нормали противодействия (реакции).
Кроме того, между боковыми плоскостями углубления клина
при перемещении последнего вниз возникают силы трения, на-
направленные вверх по наклонным боковым плоскостям.
Равнодействующая всех параллельных друг другу сил сопро-
сопротивления, нормальных к каждой боковой плоскости (щеке) клина,
представляет собой давление N. Обозначим силу трения, действую-
действующую на каждую щеку, через Т.
T = f-N.
Как силы N> N, так и силы Т, Т приложены в вертикальной
плоскости, проходящей на средине ширины щеки клина. Пусть
эта плоскость и является плоскостью рисунка.
В силу симметрии действующие на левую и правую щеки
клина силы N, N и Г, Г одинаково отклонены от^ верти-
вертикальной оси симметрии, а точки приложения сил N, N на-
находятся, кроме того, в одной горизонтальной плоскости; силы
N,N пересекаются в точке О, а силы Г, Г—в точке О1 оси симметрии.
Силы Г, Т (рис. 26,я) заменим их равнодействующей R> про-
проходящей по оси симметрии ООг вертикально вверх; ее величину
найдем,из равнобедренного силового треугольника аов (рис. 26,г)г
применив формулу (I, 4).
R = 27 • cos а = 2/ • N • cos а.
Анализ всех действующих на клин сил Q, N, N и R показывает,
что все они пересекаются в одной точке О, следовательно, все
неизвестные величины могут быть.найдены из условий равнове-
равновесия плоского пучка сил.
Решим эту задачу двумя способами: при помощи силовых
многоугольников и аналитически.
Рассмотрим равновесие сил, действующих на клин, когда он
забивается в углубление ВВг.
Первый способ. Для определения силы N построим силовой
многоугольник йек1 (рис. 26,5), для чего из произвольной точки d
плоскости действия х:ил отложи вертикальный вектор Q, затем
из его конца е также по вертикали, но в обратную сторону —
вектор /?*, а из точек d и к проведем прямые, параллельные реак-
реакциям N» N до взаимного пересечения в точке /.
* Так как величина R, выраженная через неизвестную силу N9 — неизвестна,
то положение точки к в силовом многоугольнике условию, поэтому использо-
использовать этот многоугольник для графического определения величины силы N нельзя;
условность положения точки к не повлияет на результат определения величины
силы N геометрическим путем.
96 Статика твердого тела
Опустим из точки / перпендикуляр In на сторону dk силового
многоугольника dekl и установим углы Д dkl из сопоставления
с рис. 26,6. Так как Д dkl равнобедренный, то_/л является и медиа-
медианой, следовательно,
ап—т- -j—~.-j — -jt- 2 — f . /vcosa.
Из л dnl
dn = iV sin a,
следовательно,
iV sin a = -| //V cos a;
откуда
iV cos a • (f + tg a) = ~ .
Ввиду малого значения угла а примем, что cos a = 1, тогда
N Q „ = 6_ 0
2 cos a • (/ + tg a) 2 • 1 - @,1 + 0,05)
Второй способ. Приняв точку О за начало координат, напра-
направим координатные оси, как показано на рис. 26,я.
Применив формулы A,6), составим одно из двух уравнений
равновесия плоского пучка сил — уравнение проекций всех сил
на ось Оу (уравнение проекций всех сил на ось Ох обращается
в тождество — в силу симметрии приложенных к клину сил).
V у{ = _ Q -f W sin a -f R = 0.
После подстановки значения R и некоторых преобразований
получим:
2 Y% = — Q + 2/ . N • cos a -f 2N • sin a == 0;
— 6 -f 2Л/ (/ . cos a -f sin a) = 0;
Л^ • COS a • (f + tg a) = 3,
откуда
"@,1 4-0,05) --*uw-
Рассмотрим равновесие сил, действующих на клин, когда он
вытаскивается из углубления ВВг.
Первый способ. Исследуем действующие на клин силы (рис. 26,г).
На забитый в углубление клин действуют: активная верти-
вертикальная сила Р, стремящаяся вытащить его из углубления, и силы
Л/, N и Г, Ту причем силы трения Г, Т теперь уже направлены
вниз по наклонным боковым плоскостям, так как щеки клина под
действием силы Р стремятся перемещаться вверх по наклошмым
боковым плоскостям.
Силы трения
Силы 7\ Г-(рис. 26, а/с) заменим их равнодействующей /?, про-
проходящей по оси симметрии 00х вертикально вниз; построив силовой
треугольник аов (рис. 26,з), аналогично предыдущему, найдем,
что величина равнодействующей
Я = 2/ . JVcosa.
Анализ всех действующих на клин сил: Р, N, N и R показывает,
что все они пересекаются в одной точке О, следовательно, все
неизвестные величины могут быть найдены изч условий равновесия
плоского пучка сил.
Для определения силы Р построим силовой многоугольник
fmpr (рис. 26,и)у для чего из произвольной точки / плоскости дей-
действуя сил отложим вектор /?, затем из его конца т — вектор N,
(давление на левую щеку клина) и из eto конца р — вектор N
(давление на правую щеку клина); при построении убедимся,
что конец г вектора^ попадет на вертикаль /т.
Так как действующие на клин силы взаимно уравновешиваются,
то силовой многоугольник должен быть замкнут. Соединив точки г
и / (эта вертикальная сторона rf многоугольника совпадает с частью
стороны fm), получим вектор Р.
Опустив из точки р перпендикуляр ps на сторону fm силового
многоугольника fmpr и установив углы Д трг в соответствии с
рис. 26,е, найдем, аналогично предыдущему, что
rm = 2N sin a;
следовательно,
— tga) = 2-20 . 1 . @,1— 0,05) =2 т.
Итак, Р = 2 m.
Второй способ. Приняв точку О за начало координат, направим
координатные оси, как показано на рис. 26,ж.
Аналогично предыдущему, составим одно из двух уравнений
равновесия плоскости пучка сил — уравнение проекций всех сил
на ось Оу.
? Yi = Р — 2/ • N • cosa + 2Nsince = 0.
Подставив все известные величины и решив уравнение, найдем
Р = 2N • cos a (f — tg a) = 2 - 20 . 1 @,1 — 0,05) = 2 т.
Примечание. Сопоставив оба способа решения для каждого из двух;
случаев: когда клин забивается в углубление ВВг и когда 0н вытаскивается из
него, приходим к выводу, что аналитическое* решение этой задачи значительно
проще.
27. Ящик весом Р (рис. 27,а) стоит на шероховатой горизон-
горизонтальной плоскости; коэффициент трения между соприкасающимися
поверхностями ,равен /. .Определить, под каким углом р надо
7 591
98
Статика твердого тела
приложить силу Q и величину этой силы при условии: сдвинуть
ящик при наименьшей величине силы Q.
Решение. На грани покоя и сдвига ящика по горизонтальной
плоскости приложенные к нему силы взаимно уравновешиваются.
Рассмотрим равновесие этих сил в ука-
указанный момент времени.
К ящику (рис. 27,6) приложены две
активные силы: Q, направленная под углом
4 р к горизонту, и вертикальная сила Р.
Точка С пересечения этих сил находится
в плоскости АВ. Освободив тело-ящик от
связи (горизонтальной плоскости АВУ на
которую ящик опирается), приложим к
нему нормальную N .(рис. 27,в) и горн-
горняк зонтальную Т составляющие опорной ре-
реакции (Т—предельное значение силы трения
покоя). Таким образом, на ящик действует
плоский пучок сил. Направление коорди-
\ натных осей показано на рисунке. При-
—V менив формулы (I, 6), составим два ура-
уравнения равновесия плоского пучка сил:
Y Хг = Q • cos p — Т = 0; A)
?Кг = — P + Q- sin р + N = 0. B)
Из уравнения B)
N = Р — Q sin p.
Из уравнения A)
/////ТУ//////////
К задаче 27.
Qcosp = Т = / • N = / • (Р — Qsin
откуда
cos p -f- / • sin f
C)
Горизонтальная составляющая наклонной силы Q cos p равна
предельному значению силы трения покоя Т; геометрически
эта зависимость выражается в совпадении линии действия равно-
равнодействующей сил Р и Q с боковой стороной треугольника трения,
расположенного ниже плоскости соприкасания. Такое совпадение
может быть йри различных значениях Q и р, нас же интересует
минимальное значение Q и соотвествующее ему значение угла р.
Для определения искомых значений Q и р исследуем уравнение C).
При постоянном значении / • Р (числителя дроби) минимальное
значение Q соответствует максимальному значению знаменателя
Силы трения * 99
дроби, который обозначим через п, т. е.
п = cosp + / • sin p.
Найдем то значение р, при котором п достигает максимума,
для чего приравняем нулю первую производную от /i по C
ri = — sin р + / • cos р *= О,
откуда
t Р / P
(это значит, что угол р равен углу трения ер, т. е. углу CEL> так
как tgcp также равен /).
Найдем вторую производную от п по р и по ее знаку установим,
максимуму или минимуму п соответствует найденное значение р.
п" = — cosp — /sin p== — (cosp + /sin p) = — п. D)
Выразим cosp и sinp через /:
JL = sec p = VI
откуда
cosp =
VTTi
Подставив найденные значения cosp и sinp в уравнение D), по-
получим
Так как ]fl + /2 число положительное, то величина пп— отри-
отрицательная, следовательно, при найденном значении р знаменатель
п дроби уравнения C) достигает максимума, а сила Q имеет мини-
минимальное значение.
Подставив найденные значения cosp и sinp в уравнение C)
и используя уравнения D) и E), определим ,
п ^ = =
Vmin созfj 4- /sin p n —n" ууЦГр'
28. Вал (рис. 28,а) вращается под действием приложенной к
нему пары сил с моментом М = 80 кем. На валу заклинено тормоз-
тормозное колесо, радиус г которого равен 20 см. Определить, какими
силами Q достаточно прижать к колесу тормозные колодки, чтобы
оно остановилось, если коэффициент трения / между колесом и
каждой колодкой равен 0,2.
Решение. Примем условно, что все действующие на вал силы
расположены в одной плоскости — в плоскости колеса (изучая
7*
100
Статика твердого тела
в дальнейшем равновесие действующих в пространстве пар, мы
узнаем, что от Перенесения пары в плоскость, ей параллельную,
равновесие тела, не нарушается).
Рассмотрим равновесие укрепленного (заклиненного) на валу
тормозного колеса, имеющего неподвижную ось вращения (ось
вала),
К валу приложены (рис. 28,6): пара сил
с моментом М, две равные друг другу силы
Q, действующие по одной горизонтали в про-
противоположные стороны, и две равные друг
другу силы трения 7\ возникшие в двух
противоположных точках горизонтального
диаметра колеса (в центре поверхностей со-
соприкасания колодок с колесом). Силы трения
направлены по касательной к окружности
колеса в сторону, обратную движению вала,
перпендикулярно к линии действия сил Q,
следовательно, они образуют пару сил.
Условием равновесия такого колеса, со-
согласно формуле (IV, 1), является равенство
нулю суммы моментов всех приложенных к
нему сил относительно центра вращения
(точки пересечения оси вала с плоскостью
колеса), но так как силы Q взаимно уравно-
уравновешиваются, то условие равновесия колеса сводится к равенству
нулю суммы моментов приложенных к нему пар, т. е. к уравнению
(II, 4). Составим это уравнение.
Т . 2г — М = 0.
A)
При минимальном значении сил Q, останавливающих вращение
колеса, каждая сила трения Т =/ • Q.
Подставив в уравнение A) значение Т, получим
откуда
80
0,2 • 2 • 0,2
= 1000 кг.
Примечание. Иногда считают, что увеличение сил Q (свыше 1000 кг)
приведет к увеличению сил трения, к превышению момента этих сил над моментом
приложенной пары, в результате чего колесо начнет вращаться в противоположную
прежнему направлению сторону. Такое предположение ошибочно потому, что
момент сил трения — это момент реактивной пары,
который никогда, ни при каких обстоятельствах не
может быть больше активного момента приложенной
пары. Остановка колеса при увеличении сил Q произойдет при тех же силах
трения, но каждая из них в этом случае будет меньше f . Q.
Силы трения
101
29. Для опускания грузов в шахту применяется ворот с тор-
тормозом (рис. 29,а). С барабаном, на который намотана цепь, скреп-
скреплено деревянное колесо, которое тормозят, надавливая на конец А
рычага АВУ соединенного цепью CD с концом D 'тормозного ры-
рычага DE. Диаметр колеса а = 50 см\ диаметр барабана Ъ = 20 см,
длины рычагов и их частей соответственно равны:
DE = 120 см\ FE = 60 см: АВ = 1 м; ВС = 10 см.
Определить минимальное значение силы Р, останавливающей
опускание в шахту груза Q = 2000 кг, подвешенного к подвиж-
подвижному блоку, если коэффициент трения между деревянным колесом
и стальной колодкой / = 0,4; размерами колодки F пренебрегаем.
Решение. Рассмотрим сначала равновесие подвижного блока Ог
(с подвешенным к нему грузом Q) как свободного твердого тела
(рис. 29,6). Для этого мысленно рассечем поддерживающую его
цепь и заменим действие на блок связей силами N и Nly равными
между собой в силу симметрии; весом цепи пренебрегаем. Таким
образом, к блоку Ох приложена плоская система параллельных
сил. Применив одну из формул (II, 6), составим уравнение равно-
равновесия блока О1э приняв за центр моментов точку С.
102 % Статика твердого тела
Решив это уравнение, получим
N -?
По закону действия и равного ему противодействия блок Ох
действует на закрепление в точке К (рис. 29,в) и на неподвижный
блок Ог силами N' n N'it соответственно равными N и Nlt но направ-
направленными в противоположные им стороны, следовательно,
Сила N' уравновешивается связью К и на барабан никакого
действия не оказывает. На барабан, стремясь вращать его по ходу
часовой стрелки, действует только наклонная сила N\, возникаю-
возникающая в цепи, переброшенной через неподвижный блок О2 и намо-
намотанной на барабан (блок О2, не изменяя величины силы А^, изме-
изменяет ее направление; трением на блоке пренебрегаем).
Удержать барабан от вращения, т. е. задержать опускание в
шахту груза Q, может только сила трения Т, возникающая от
действия силы Р* при помощи системы рычагов (рис. 29,г); точкой
приложения силы трения является точка и (центр соприкасаю-
соприкасающихся поверхностей стальной колодки и скрепленного с барабаном
деревянного колеса). Сила Т направлена по касательной к окруж-
окружности колеса горизонтально, влево. Для определения Т необхо-
необходимо рассмотреть взаимодействие всей системы рычагов.
Рассмотрим сначала равновесие рычага АСВ (рис. 29,5).
Под действием любой направленной вниз вертикальной силы Р,
приложенной в точке Л, рычаг АСВ, стремясь вращаться „против
хода часовой стрелки вокруг центра неподвижного шарнира В,
вызывает растягивающее усилие S в цепи CD, соединенной с рыча-
рычагом DE, испытывая в точке С противодействие Sx цепи, равное
усилию S по величине, но противоположно направленное. При-
Применив формулу (II, 5), составим уравнение равновесия рычага
АСВ.
2 Мв = Р • АВ — Sx • ВС = 0. B)
Решив это уравнение, находим:
S рАВ р 10°
Рассмотрим теперь равновесие тормозного рычага DFE (рис.
29,г). Под действием направленной вниз вертикальной силы S,
приложенной в точке D, рычаг DFE, стремясь вращаться против
хода часовой стрелки вокруг центра неподвижного шарнира Е%
* При наличии силы Р и отсутствии силы Q никакой силы трения не возника-
возникает. Сила трения Т может вызываться силой Р (при помощи системы рычагов)
только как противодействие вращению барабана, осуществляемому силой N\
Силы трения 103
нажимает силой S2 (при помощи стальной тормозной колодки)
на скрепленное с барабаном деревянное колесо, испытывая в
точке F противодействие S3, равное силе S2 по величине, но
противоположно направленное.
Аналогично предыдущему, составим уравнение равновесия ры-
рычага DFE.
SZ- FE = Q. C)
Решив уравнение C), получим
Q DE __ ЮР- 120
^3 ~~ ^ ТЕ ~~ 60
следовательно,
с < оор
О2 О3 ~~~ <L\JL %
Рассмотрев равновесие барабана, сможем определить величину
силы Р, уравновешивающей груз Q. К барабану Q3 (рис. 29,г)
приложены три силы: N'v действующая по оси цепи, S2, пере-
пересекающая ось барабана, и сила трения Т\ при минимальном зна-
значении силы Р сила трения Г равна /. S2.
Считая условно, что все силы действуют на барабан в одной
плоскости, составим уравнение равновесия барабана — уравнение
моментов всех сил относительно точки О3 пересечения оси барабана
с плоскостью рисунка.
v~i ' Ь CL
? АТп = ЛЛ • \- Т — = 0 ^4л
^j /У1Оз — *v 1 о * 2 —
Решив уравнение D), получим J
или, подставив значение S2,
откуда найдем минимальное значение силы Р
2а • / . 20 ~~ 2 • 50 . 0,4 • 20 "" ° *'
Очевидно, что при увеличении силы Р перемещение груза Q
будет остановлено силой трения Г прежней величины,
но в этом случае она будет уже меньше / . Q.
v30. Трамвайная дверь (рис. 30,а) отодвигается под действием
горизонтальной силы Р9 приложенной к ручке двери. Ширина
двери / = 1 ж; центр тяжести двери находится на ее вертикальной
оси симметрии; коэффициент трения / равен 0,5 (трение возникает
в нижнем пазу двери). Определить наибольшее расстояние h ручки
двери от дна нижнего паза двери, при котором дверь, отодвигаясь,
еще не опрокидывается.
104
Статика твердого тела
в
-с
о
Решение. При прямолинейном равномерном дви&ениет двери
действующие на нее силы взаимно уравновешиваются. Рассмотрим
равновесие этих сил.
К Двери (рис. 30,6) приложены две активные силы: собственный
вес Q, направленный по оси симметрии, и горизонтальная сила Я,
приложенная к ручке двери. Кроме того, на дверь действуют верти-
вертикальная N и горизонтальная Т составляющие опорной реакции
нижнего паза двери. Гори-
Горизонтальная составляющая
Т (сила трения) направ-
направлена в сторону, противо-
противоположную перемещению
двери, и равна fN.
Неизвестную точку при-
приложения вертикальной со-
составляющей N будем» счи-
считать смещенной от оси сим-
симметрии в сторону движения
двери на некоторое рас-
расстояние 8 (более подробно
это бyдef разобрано при
К задаче 30. дальнейшем решении за-
задачи).
Приняв за начало координат точку О, направим осц Ох и Оу,
как показано на рисунке.
Применив формулы (IV, 2), составим три уравнения равновесия
двери, находящейся под действием произвольной плоской системы
сил, приняв за центр моментов точку пересечения сил Q и Т.
y?iXi = P Т = 0; A)
ЕГ, = ЛГ — Q = 0; B)
?Afo=— Я-А + #.8 = 0. C)
Решив уравнения B) и A), получим:
р = Т = / • N = / . Q.
Полученный результат показывает, что N и Я постоянные
величины, не зависящие от расстояния Л, и что силы Я и Г обра-
образуют пару с плечом А, стремящуюся опрокинуть дверь вокруг точки
D, а силы N и Q образуют пару с плечом 8, стремящуюся удер-
удержать дверь от опрокидывания, поэтому уравнение C) выражает
также условие равновесия действующих в одной плоскости пар.
Из уравнения C) выразим расстояние h через 8:
Л~ Р ""/.(? ~~7'
Силы трения 105
Как видно из этого уравнения, при увеличении h пропорцио-
пропорционально увеличивается 8, следовательно, точка приложения силы Л;,
или, иначе, точка приложения равнодействующей сил Р и Q к
пазу двери приближается к правому концу основания двери, к
точке D (на рис. 30,6, это показано пунктиром).
Так как скольжение двери возможно только при условии,
что точка приложения равнодействующей сил Р и Q не выходит
за пределы ширины двери (в противном случае, повернувшись
вокруг точки D по ходу часовой стрелки, дверь опрокинется),
то максимальному значению h соответствует и максимальное зна-
значение Ь /8тах = -Л щ
поэтому t
l
f ~ / ~ 2 • 0,5
Практически ручка двери прикрепляется на расстоянии h от
паза, меньшем найденного значения Атах»что обеспечивает большую
устойчивость двери против опрокидывания ее вокруг точки D.
Вывод. Так как пара, образуемая силой, сдвигающей тело с плоскости, и
силой трения г, может уравновеситься только парой, образуемой давлением тела
на плоскость и нормальной составляющей реакции плоскости, то точка приложения
реакции плоскости всегда смещается на некоторое расстояние Ь (плечо уравно-
уравновешивающей пары) от точки приложения давления тела на плоскость, в сторону
возможного или фактического движения. " '
31*. Конец цепи (рис. 31,а), поддерживающей цепной мост,
заложен в каменной кладке, имеющей форму прямоугольного .па-
.параллелепипеда. Цепь расположена по диагонали сечения кладки
(среднего по длине параллелепипеда) и образует угой а с горизон-
горизонтом. Натяжение цепи равно F; коэффициент трения между кладкой
и грунтом равен /. Определить вес Р кладки, удерживающей
цепь1 в заданном положении.
Решение. Рассмотрим равновесие кладки.
Приняв за начало координат точку О, направим оси Ох и Оу, как
показано на рисунке.
К кладке (рис. 31,6) приложены две активные силы: собствен-
собственный вес Р, направленный по оси симметри-и, и сила F, направ-
направленная х по диагонали прямоугольного поперечного сечения кла-
кладки.
1 Такая пара образуется тогда, когда точка пересечения линии действия сдви-
сдвигающей силы с линией действия давления тела на плоскость не совпадает с плос-
плоскостью, на которой находится тело.
* Использована задача, рассмотренная в 1-ой части курса теоретической ме-
механики Е. Л. Николаи.
106
Статика твердого тела
Кроме того, к кладке приложены вертикальная N и горизонтальная
Т составляющие опорной реакции грунта.
Все силы приложены к среднему сечению каменной опоры
моста; считаем, что это сечение совпадает с плоскостью рисунка.
Горизонтальная состав-
составляющая Т (сила трения,
возникающая между кла-
кладкой и грунтом) направле-
направлена влево, в сторону, проти-
противоположную направлению
горизонтальной составля-
составляющей силы F, стремя-
стремящейся сдвинуть кладку
вдоль грунта.
Неизвестную точку при-
приложения реакции будем
считать смещенной (см. вы-
х вод в решении задачи 30)
вправо от оси симметрии,
в сторону действия гори-
горизонтальной составляющей
силы F на некоторое рас-
расстояние S.
Применив формулы
(IV, 2), составим три урав-
уравнения равновесия камен-
каменной кладки, находящейся под действием произвольной плоской
системы сил, приняв за центр моментов точку О — точку пересе-
пересечения линий действия сил Р и F.
? = 0; A)
N^O; B)
?M0 = tf.8 —Г.А^о. ' C)
Решив эти уравнения, определим неизвестные величины
N = Р — F sin a;
Т = F cos а;
б
Условия задачи могут быть соблюдены только при следующих
значениях N, Т и Ь:
а) N > 0, ибо реакция грунта может быть направлена только
вверх;
б) Т ^ f . N> так как только при этом значении силы трения
кладка не будет сдвигаться вдоль грунта;
Силы трения 107
в) & <; у, так как только при этом условии не произойдет опроки-
опрокидывания кладки вокруг ребра D каменной опоры моста. Следова-
Следовательно, услови§ задачи могут быть соблюдены, когда:
Р — F sin a > 0;
Fcosa</(P — Fsina);
2N ^ 2 '
Решив эти неравенства относительно Р, получим:
Р> Fsina;
г» ^ г- / • • Л • cos a \
P>/^sina+ 1 J
или, после подстановки значения /z(/i = /tga),
Р > 2F sin a.
Обычно a< 45° и / < 1, поэтому cosa> sin a, значит и ^—-^ боль-
больше sin a.
Проанализировав все три значения Р, придем к выводу, что
все условия задачи будут соблюдены, если определить вес Р камен-
каменной кладки из следующего неравенства:
Примечание. Если принять знак равенства, то найденное из этих усло-
условий значение Р будет минимальным, при котором еще не будет сдвига кладки вдоль
грунта, но малейшее увеличение силы F приведет к сдвигу кладки. Во избежание
этого необходимо определять значение Р из условий неравенства, вводя в виде мно-
множителя в его правую часть поправочный коэффициент, больший единицы.
32. Горизонтальный стержень АВ (рис. 32,а) имеет на конце А
отверстие, которым он надет на вертикальную круглую стойку CD;
длина втулки Ь = 4 см; в точке F, находящейся на расстоянии а
от оси стойки, к стержню подвешен груз Р. Определить, пренебре-
пренебрегая весом стержня АВ, такое расстояние а, при котором под дей-
действием груза Р стержень останется в равновесии, если коэффициент
трения между стержнем и стойкой / = 0,2; определить также реак-
реакции стойки CD.
Решение. Рассмотрим равновесие стержня АВ.
На стержень, кроме активной силы Р, действуют реакции
стойки CD. Чтобы ясней представить характер этих реакций,
108
Статика твердого тела
приложим в произвольной точке оси CD (рис. 32,6) цилиндрического
отверстия стержня АВ силы Р' и Р", равные друг другу, а также
силе Р, параллельные ей, но направленные в противоположные сто-
стороны (согласно аксиоме 3 присоединение взаимно уравновешиваю-
уравновешивающихся сил Р' и Р" не нарушит равновесия стержня АВ).
8
D
Рассмотрим действие сил Р, Рг и Р*. Под действием пары сил,
образованной силами Р и Р", отмеченными на рисунке черточкой,
стержень АВ, поворачиваясь1 в плоскости рисунка по ходу часовой
стрелки, нажимает на стойку CD в точках S и Е (рис. 32,#), встре-
встречая в этих точках противодействие в виде сил NE и Ns, направ-
направленных по нормали к образующим цилиндрической поверхности
стойки CD. Под действием силы Р' стержень- АВ стремится пере-
перемещаться по вертикали вниз, но встречает в точках S и Е сопро-
сопротивление в виде сил трения Ts и ТЕ, возникающих между наруж-
наружной поверхностью стойки CD и внутренней поверхностью цилин-
цилиндрического отверстия расширенной части стержня АВ.
1 Такой поворот возможен благодаря наличию незначительного зазора между
наружной поверхностью стойки CD и внутренней поверхностью цилиндрическо-
го отверстия расширенной части стержня АВ.
Силы трения 109
Уточнив характер возникающих реакций (рис. 32,в) и приняв
точку S за начало координат, направим ось Sx по горизонтали,
а ось Sy — по вертикали.
Применив формулы (IV, 2), составим три уравнения равновесия
свободной плоской системы сил, приняв за центр моментов точку S
(выбор центра моментов в точке Е привёл бы к аналогичному ре-
результату):
Обозначив радиус стойки CD через /¦, составим третье урав-
уравнение равновесия
? М„ = Гл • 2г + iV, • Ь - Р (а ± г) - 0. C)
Решив уравнение A), получим:
следовательно,
Величину Т определим из уравнения B)
Г = —.
Подставив значение Т в уравнение C), получим
Р
2 ' '
откуда
"-Т1- D)
Возникающая в каждой из точек 5 и ? сила трения Г <; / . N,
так как только при этом значении €е стержень АВ не сдвинется
по стойке CD вниз, поэтому
откуда
Подстарив в D) значение а, определим Л/:
" *Ь ** * . 2/' ^ ^ 2/ *
110
Статика твердого тела
Определив составляющие Т и N, найдем величину каждой
реакции:
Г> г> г>
i\S — AjB — А =
Из решения задачи видно, что ни Г, ни N, ни а не зависят от
величины радиуса стойки.
Геометрическое определение реакций Rs и RE дано во втором
способе решения следующей задачи.
33. К ползуну М (рис. 33,а) длиной Ь = 40 лм*, скользящему
по прямолинейному вертикальному стержню CD, эксцентрично
К задаче 33.
(в точке F) приложена вертикальная сила Р (собственным весом
стержня пренебрегаем), направленная вниз; коэффициент трения
f = 0,2. Определить расстояние OF = а, при котором не про-
произойдет защемления ползуна на направляющем стержне CD, a
также найти реакции стержня CD при помощи треугольников
трения.
Силы трения 111
Решение. Сопоставив условия рассматриваемой задачи и преды-
предыдущей, видим, что длины ползуна и втулки, направления линий
действия сил Р и величины коэффициентов трения / одинаковы.
Это дает основание считать, что реакции стержня (стойки) CD в
обеих задачах одинаковы.
Из решения задачи 32 (рис. 32,#) видно, что реакции стойки CD
приложены к расширенной части стержня АВ в точках S и Е,
следовательно, реакции стержня CD (рис. 33,6) приложены к пол-
ползуну М также в точках S и Е и имеют те же направления.
Определим неизвестные величины двумя способами: графи-
графически и геометрически.
Первый способ. Определим графически такое положение точки
^приложения силы Р, при котором не произойдет защемления, т. е.
ползун вместе с присоединенным к нему горизонтальным стержнем
АВ сможет скользить по стержню CD. Для этого, использовав
коэффициент трения /*, построим треугольники трения KSL и
NEV (рис. 33,6) и исследуем возможное взаимное расположение
линий действия реакций Rs и RE и силы Р, разыскивая такое поло-
положение, при котором линии действия указанных трех непараллель-
непараллельных сил не смогут пересечься в одной точке (в про-
противном случае наступит защемление ползуна, его равновесие).
Направления составляющих,NS и TSy NE и ТЕ опорных реакций
Rs и Re пРи заданном направлении силы Р (вертикально вниз)
таковы, что линия действия реакции Rs может находиться только
в нижней части треугольника тренля KSL, ниже линии 551э а ли-
линия действия реакции RE — только в верхней части треуголь-
треугольника трения NEV — выше линии ЕЕЪ следовательно, линии
действия реакций Rs и RE могут пересечься между собой только
в пределах общей части NF^L обоих треугольников трения (эта
часть на рисунке густо заштрихована). Поэтому, пока линия дей-
действия силы Р проходит левее точки Fx (точки пересечения боковых
сторон этих треугольников), защемление ползуна невозможно,
так как линии действия силы Р и реакций Rs и RE не пересекутся
в одной точке. *
Для графического определения искомой величины OF до-
достаточно измерить этот отрезок в принятом для рисунка мас-
масштабе.
Второй способ. Для геометрического определения неизвестных
величин необходимо прежде всего найти положение линий действия
реакций Rs и RE стержня CD и положение точки (F3) пересечения
их с линией действия силы Р, когда последняя приложена, напри-
например, в точке F2 оси стержня АВ.
* Для построения треугольников трения учтем, что / = tg <р, где ср — угол
трения.
112 Статика твердого тела
Из решения задачи 32 видно, что Ns = NB, аГ5 = Тв, следо-
следовательно, реакции Rs и RE равны между собой и образуют с гори-
горизонталями одинаковые углы. При прохождении линии действия
силы Р через точку Fx каждый из этих углов равен ср, а при смеще-
смещении ее линии действия вправо от этой точки угол уменьшается;
обозначим этот угол через а.
Определим расстояние точки F3 от прямой 55Х (отрезок IFZ),
использовав зависимость между сходственными сторонами подоб-
йых прямоугольных треугольников SIFZ и EIXFZ (эти треугольники
имеют одинаковые углы):
I±hEi
SI ~ Eh ~~ Е1Х '
или, обозначив IFZ через х и заменив остальные входящие в это
равенство величины соответственно через at b и г, получим
х ь — х
a + r = а — г •
откуда
2а а
Полученное выражение дает возможность определить положение
точки Fz графически. Для этого из точки с — средины отрезка
SI проводим прямую cF3, параллельную прямой mll9 до пересе-
пересечения в точке F3 с линией действия силы Р. Соединив затем точки
S я Е с точкой F3, найдем соответственно линии действия реакций
Rs и RB-
Для определения величин реакций учтем, что их равнодействую-
равнодействующая должна уравновесить силы Р, т. е. она должна быть равна ей
по величине, но направлена в противоположную сторону. Напра-
Направив соответствующим образом реакции, строим параллелограм
сил; вследствие равенства реакций и одинакового отклонения их
от горизонтали параллелограм сил превращается в ромб с верти-
калвной и горизонтальной диагоналями, разбивающими его на
четыре равных треугольника.
В прямоугольном треугольнике kF2Fz катет F2k представляет
собой горизонтальную составляющую Ns реакции R3, а катет
F%FZ — вертикальную составляющую Ts (силу трения).»Так как
в точке Fj диагонали делятся пополам, то составляющая
Ts = F%FZ = -g-.
Использовав зависимость между сходственными сторонами по-
подобных прямоугольных треугольников kF2Fz и SlFZt найдем состав-
составляющую Ns
FJt SI '
Силы трения ИЗ
или, подставив значения входящих в равенство величин, получим
N6 а + г •
откуда, подставив найденное значение х, получим
2а
Расстояние OF линии действия силы Р от оси стержня CD,
при котором ползун находится на грани покоя и движения, опре-
определим геометрически следующим образом.
Продлив до точки Т прямую NFXE (рис. 33,6) влево, установим,
что горизонталями SSj и dEx и прямыми S /С, SFXL и TEFxNy про-
проведенными под углом ср к горизонту из точек S и ?, находящихся
соответственно на левой и правой образующих цилиндрического
стержня CD t на его оси отсекаются равные между собой отрезки
пт9 те и dft следовательно,
ef = ed -\- df = ed-\- me = md = b.
Из прямоугольного A eF1O1(O1F1 — высота и медиана равно-
равнобедренного A eFJ) найдем
O1F1 = еОг ¦ ctgcp = е1 • -L = А « _i_ = ю ^
следовательно,
a = OF = O1F1= 10 cjw.
После нахождения значения а определим величину составляю-
составляющей'^:
а; р ' а — Р "^ — р
а затем определим величину каждой реакции как гипотенузу пря-
прямоугольного треугольника |
Rs = Яж = Кт|+^|
• Найденное расстояние а удовлетворяет только одному положению
силы Р, при котором не произойдет защемления ползуна на направ-
направляющем стержне CD. Защемление ползуна не будет происходить и
тогда, когда линия действия силы Р пройдет левее вертикали FFl9
следовательно, искомое расстояние
а < 10 см.
8 691
114 Статика твердого тела
Из решения задачи видно, что а не зависит от величины радиуса
стержня CD.
Примечания: 1. Сопоставляя результаты решения данной задачи и
предыдущей, мы видим, что геометрически найденный максимальный размер а =
= IOcjm, удовлетворяющий условиям рассматриваемой задачи, равен аналитически
найденному минимальному размеру а, удовлетворяющему условиям предыдущей
задачи, так как длина втулки ползуна и коэффициента трения / в обеих задачах
одинаковы. Разные направления знака неравенства соответствуют разной по-
постановке вопроса о величине а в обеих задачах.
2. Сопоставление аналитического и геометрического способов определения
реакций R$ и Re и расстояния OF показывает, что треугольниками трения рацио-
рационально пользоватьс-я только для графического решения задачи и что анали-
аналитический расчет значительно проще геометрического.
34. К вертикальной стене (рис. 34,а) приставлена лестница АВУ
опирающаяся нижним- концом на горизонтальный пол. Коэффи-
Коэффициент трения между лестницей и стеной равен fl9 а между лестни-
лестницей и полом — /2. Равнодействующая Р собственного веса лест-
лестницы и веса стоящего на ней человека проходит через точку С,
расстояние которой от точки А равно а и от точки В — равно Ь.
Определить нормальные составляющие реакций стены (Na) и пола
(Л/в), а также угол а, образуемый лестницей со стеной в положении
равновесия.
Решение. Решим эту задачу двумя способами: аналитическим я
графическим (с применением треугольников трения).
Первый способ. Рассмотрим равновесие лестницы АВ. На лест-
лестницу (рис. 34,6) в точке С действует активная сила Р, а в точках А
и В — нормальные составляющие Na и Nb реакций опор и касатель-
касательные составляющие (силы трения) Та и Тв, направленные в сторону,
противоположную возможному перемещению концов лестницы.
Равновесие лестницы возможно при различных значениях
угла а, заключающихся между нулем (когда лестница стоит верти-
вертикально, не оказывая давления на стену, опираясь только в точке В
пола и уравновешиваясь вертикальной реакцией Rb = Nb = Р>
направленной вертикально вверх) и некоторой предельной вели-
величиной, при которой силы трения Та и Тв достигают максимального
значения, т. е. Та = h • NA и Тв =/2- ^в- Следовательно, равно-
равновесие возможно при Та < h • NA и Тв < h • Мв- При угле а,
большем искомой предельной величины, лестница теряет равно-
равновесие: конец ее А перемещается по стене вертикально вниз #до
точки D, а конец В — по полу вправо (перемещение возможно в
плоскости рисунка).
Приняв за начало координат точку Л, направим оси Ах и Ад
по горизонтали и вертикали (такой выбор направления осей удо-
удобен, так как к лестнице приложечы горизонтальные я вертикальные
силы).
Силы трения
115
//////////{/Y/////77/
К задаче 34.
Применив формулы (IV, 2), составим три уравнения равновесия
лестницы АВ% находящейся под действием произвольной плоской
системы сил, выбрав за центр моментов точку А*.
2Х| = Л^-7Л = 0; (I)
lYi = TA-P + NB~0; B)
? МА = —• Р - а . sin а + #Б (а + Ь) sina — Гв (а + ft) cosa = 0. C)
* Количество неизвестных, которые могут войти в уравнение моментов сил
при выборе центра моментов в точках Л, В и Д одинаково.
8*
И 6 Статика твердого тела
Решив уравнения A) и B), найдем:
B, A')
NA. B0
Подставив в неравенство B0 значение NA из (Г), получим:
TA = P-NB<f1.f2.NB. (Г)
Решив неравенство B") относительно Nb, найдем
Подставив найденное значение Nb в неравенство (Г), найдем
Разделив уравнение C) на (а + b) cos a (cos а не равен нулю),
получим
- Р ' 5Т* • *8 а + Nb • tg a - Тв = 0. C0
Преобразовав уравнение C') и использовав неравенство (Г),
получим:
tga[ (a + b) NB-P .a] = TB(a + 6)</2 . NB . (a + 6),
откуда
\*Л —[- V) i» -ry Л - U,
Разделив числитель и знаменатель правой части неравенства
на Nb, получим
tga<; ртъ* ( '
в
Подставив в неравенство C'") значение Л^в из уравнения
B*, получим
*Л « ^ h (fl + *)
или
n
Согласно неравенству B'") Л^в может быть больше 1 . , ; в этом
случае неравенство D) также сохранится, ибо при таком значении
* Пренебрегая знаком неравенства.
Силы трения 117
Nb уменьшится третий член знаменателя неравенства C/7/), увели-
увеличится весь знаменатель, а следовательно, еще меньше станет
правая часть неравенства.
Несколько проще можно найти значение tga, приняв за центр
моментов точку О или Ог (рис. 34,6). Тогда уравнение C) при-
примет следующий вид:
?Мо = — ТА • а • Sina + NB- b • Sina — Тв • (a + b)cosa = 0.
Разделив это уравнение на (a + b) Cosa, получим
- TA -^rb ¦ tg a + NB .Jfr • tg a - TB = 0.
После преобразования его получим
tga • NB(b -Ц^-п\ = TB(a + fe)</2 • NB(a + b),
откуда
tea < k'(a+fe>
tga<. ^-a- D')
Подставив в неравенство D7) значение Га из уравнения
и сократив на Nb> получим окончательное значение tga:
Согласно неравенству B") Га может быть меньше h.fa.NB\
в этом случае неравенства D') и D") сохранятся, так как при таком
значении Та уменьшится второй член знаменателя, увеличится
весь знаменатель, а следовательно, еще меньше станет правая
часть неравенств.
Второй способ. Для графического решения этой задачи исполь-
используем треугольники трения SAE и FBL (рис. 34,в,г), построенные
из опорных точек лестницы А и В (на рисунках принято, что срх > <р2,
т. е. что /х>/2).
Исследуем возможное взаимное расположение линий действия
реакций Ra и Rb и силы Р при различных положениях лестницы,
разыскивая такое положение, при * котором линии действия укд-
занных трех непараллельных сил смогут пересечься в одной точке,
что необходимо для возможности равновесия лестницы.
При равновесии лестницы реакция Ra может находиться только
в пределах треугольника трения SAE> а реакция Rb — треуголь-
треугольника трения FBL. Из общей части треугольников трения только
в площади Orde могут пройти обе реакции (реакция Ra может
быть расположена только выше линии ААЪ а реакция Rb — только
левее линии ВВЪ так как сила трения Та направлена по верти-
118 Статика твердого тела
кали вверх, а Тв — влево по горизонтали BD); следовательно,
равновесие лестницы возможно только при расположении линий
действия силы Р между вертикалями ОС и гВ, ограничивающими
площадь Orde.
Для определения искомых величин построим силовые тре-
треугольники (рис. 34,(9).
Сначала определим неизвестные величины из рассмотрения
силового треугольника, соответствующего максимальному углу
отклонения лестницы от вертикальной стены (рис. 34,в), при
котором равновесие лестницы еще возможно; линия действия
силы Р проходит при этом через точку пересечения боковых
сторон треугольников трения.
В этом случае реакции опор А и В направлены по соответствую-
соответствующим боковым сторонам треугольников трения: Ra no AS и Rb
по BF.
Разложив реакции Rb и Ra соответственно на составляющие
Nb и Тв, Na и Та, найдем:
TA^P-NBt A)
NA = Тв. B)
Установив углы силового треугольника в соответствии с рис. 34,# и
учтя, что tg<pj = fv a tgcp2 = /2, найдем
P-NB ^TA = NA'tg9l = TB^tg?1 =
= Nb
откуда
Определим Na-
NA = TB=NB- tgcp2 = Y~^jt •
Для определения угла amax рассмотрим треугольники BCm,
BOm, ABD, ACn и АОп.
Из ABCm
Bm = b • sin amax.
Из ЬВОт
nm Ь • sin ot _v
Из AABD
AD = run = (a + b) • cos amax,
следовательно,
О/г == От — пт= ' S1" ашах — (a -f b) • cos ашах. C)
h
Силы трения 119,
Из АЛСп
An = а • sin
Из ДЛОл
Ол = An - tg cpi == а • sin ocmax • fv D)
Приравняв равенства C) и D), получим
— (а + b) • cos amax = a • fx - -sin amax.
/2
Разделим на cosamax и освободимся от знаменателя:
b • tgamax — afx • f2 • tgamax == /2 (a + 6),
откуда
Из рис. 34,г видно, что при a<amax линия действия силы Р
проходит в пределах площади Orde и, следовательно, лестница
также находится в равновесии; поэтому значение tga при раз-
различных положениях находящейся в равновесии лестницы опре-
определяется следующей формулой:
Из рис. 34,г, 5 видно, что если лестница находится в равнове-
равновесии при a<amax, то определение jVa, jVb и tga становится
задачей статически неопределимой. Действительно, условия рав-
равновесия могут быть осуществлены только при пересечении линий
действия трех непараллельных сил> Р9 Ra и Rb в одной точке, а
таких точек на линий действия силы Р в пределах общей части
треугольников трения много. Предположив, что линии действия сил
пересекаются в точке Сх или С2, мы из соответствующих силовых
треугольников (рис. 34,(9) определим RAl и RBl, Ra2 и Rb2.
Анализ найденных значений Na, Na» Na2 и Nb, Nbx, Nb2 (Na^
Nav Nbx и Nb% на рисунке не приведены) показывает, что при a < а шах
Ыв1 и Nb2 больше Nb, а Nax и Na2 меньше Na, следовательно, при
различных положениях находящейся в равновесии лестницы состав-
составляющие Nb и Na определяются следующими формулами:
35. Определить силу Р, необходимую для равномерного каче-
качения цилиндрического катка (рис. 35,а) по горизонтальной плос-
120
Статика твердого тела
кости, если диаметр катка 100 см, его вес Q — 1085 кг, коэффициент
трения качения Ь = 0,2 см, а угол а, образуемый силой Р с го-
горизонтальной плоскостью, равен 30°. Определить также реакцию
плоскости.
Решение. Рассмотрим равномерное качение цилиндрического
катка, по горизонтальной плоскости, при котором действующие
на него силы взаимно уравновешиваются.
К задаче 35.
К центру среднего (по длине) сечения катка (рис. 35,6) при-
приложены активные силы: Р и собственный вес Q. Кроме того, со
стороны поверхности ab (на рисунке глубина вдавливания катка
в плоскость Л В для большей* ясности увеличена) на каток дейст-
действуют вертикальная и горизонтальная составляющие опорной реак-
реакции, точка приложения которых с смещена на Ь от оси Оа (коэф-
(коэффициент трения второго рода Ь и есть смещение по горизонтали
точки приложения сил N \\ Т от оси Оа).
Таким образом, к катку приложена произвольная плоская
система сил.
Выбрав точку а за начало координат, направим ось ах по го-
горизонтали, а ось ау — по вертикали.
Применив формулы (IV, 2), составим три уравнения равновесия
данной плоской системы сил, приняв за центр моментов точку а:
-Г = 0; A)
B)
C)
= — Q + Р . sina + N = 0;
Силы трения 121
Сила Т не вошла в уравнение моментов, так как мы пренебре-
пренебрегли незначительным расстоянием между горизонталями, проходя-
проходящими через точки а и с.
Плечо h силы Р определим из прямоугольного ДаОк, обозна-
обозначив радиус катка через г:
h = г • cos a.
Подставив данные из условия задачи и найденное значение А
в уравнение C) , получим
Л/ = ~ • Pcosa. . C0
Подставив найденное значение N в уравнение B), получим
— Q + Psirta+y • Pcosa = 0;
Р (sina 4- ~ . cos a) = Q,
откуда
Р = 5 = "« = 5 кг.
sin a + 4- * cos a 0,5 4- ^к-. 0,866
Решив уравнение. A), определим силу трения качения
Т = Р • cos a = 5 • 0,866 = 4,33 кг.
Решив уравнение C'), определим нормальную составляющую
опорной реакции
N = т^ ¦ 5 . 0,866 = 1082,5 кг.
В ряде задач такого типа требуется определить только вели-
величину силы Р. В этом случае составляется одно уравнение равно-
равновесия — уравнение моментов всех сил' относительно точки при-
приложения реакции плоскости — точки с. При этом для упрощения
определения плеча силы Р эту силу раскладываютх на вер-
вертикальную составляющую Psina и горизонтальную — Р cosa;.
плечо последней, пренебрегая незначительным возвышением точки*
с над точкой а, принимают равным радиусу г катка.
Составим это уравнение.
?jWc = Q • S —Psina • h~Pcosa . /- = 0,
откуда
p = _—_-^ц = ^ = 5 /сг.
Ь • sin a -f- r - COS a . , r
Sin a + T • COS a
1 На рис. 35,6 разложение силы Р на две составляющие не показано.
Л 22 Статика твердого тела
ГЛАВА VIII
ОСНОВЫ ГРАФИЧЕСКОЙ СТАТИКИ
§ 1. Сложение произвольной плоской системы сил.
Частные случаи
Сложение произвольной системы сил производится путем пост-
построения силового многоугольника (для системы параллельных
сил такой многоугольник обращается в линию сил), выбора по-
положения полюса, проведения лучей из полюса к вершинам мно-
гоугбльника и построения многоугольника Вариньона, иначе на-
называемого веревочным.
При этом следует помнить следующее.
1. С изменением последовательности рассмотрения сил изме-
изменяются формы силового и веревочного многоугольников и положе-
положение точек пересечения крайних сторон веревочного многоугольника
(если система приводится к равнодействующей), но все эти точки
располагаются на одной и той же линии действия равнодействующей,
величина и направление которой не изменяются.
На рис. I показано два варианта сложения заданной
системы сил при различной последовательности рассмотрения их.
На рис. I, а сплошными линиями /, 2, 3, 4 показан веревочный
многоугольник, соответствующий показанному сплошными ли-
линиями силовому многоугольнику, при следующей последЬватель-
ности рассмотрения сил: Ръ Р2 и Р3- На рис. 1,6 сплошными ли-
линиями /, 2, 3\ 4 показан веревочный многоугольник при следующей
последовательности рассмотрения сил: Ръ Рг и Р2 (соответствую-
(соответствующий этой последовательности силовой многоугольник показан двумя
сплошными и двумя пунктирными линиями).
Точка пересечения крайних сторон веревочных многоуголь-
многоугольников для случаев а и б останется на своем месте, если первые
стороны их совместить; совмещение показано на рис. 1,а.
2. С изменением положения полюса изменяют свое положение
и точки переселения крайних сторон веревочного многоугольника,
но все эти точки располагаются на одной и той же линии действия
равнодействующей заданной системы сил (на рис. I, в, г показано
два варианта сложения заданной системы сил при двух полюсах).
3. Для получения точки пересечения крайних сторон вере-
веревочного многоугольника необходимо, чтобы они не были параллель-
параллельны между собой, а для этого полюс, положение которого выбирается
произвольно, не должен находиться на замыкающей стороне сило-
силового многоугольника или на ее продолжении.
4. В силовом многоугольнике вектор каждой силы соединен
лучами с полюсом, а параллельные этим лучам стороны веревоч-
веревочного многоугольника пересекаются на линии действия рассматри-
рассматриваемой силы.
Основы графической статики
123
При сложении произвольной системы сил встречаются сле-
следующие основные случаи:
а) Силовой и веревочный многоугольники не замкнулись.
Рис. I.
В этом случае система сил приводится к равнодействующей,
величина и направление которой определяются замыкающей сто-
стороной силозого многоугольника, а линия действия проходит через
тдчку пересечения крайних (первой и последней) сторон веревоч-
веревочного многоугольника.
б) Силовой многоугольник не замкнулся, а веревочный замк-
замкнулся (под замыканием веревочного многоугольника понимается
расположение крайних его сторон на одной прямой).
124
Статика твердого тела
В этом случае система сил также приводится к равнодействую-
равнодействующей. v
Этот случай может иметь место для любой системы непараллель-
непараллельных сил, если определенным образом выбрать положение полюса
и начать построение веревочного многоугольника не с произволь-
произвольной точки. Убедиться в этом можно следующим образом.
Определив обычным путем (рис. II) при произвольно располо-
расположенном полюсе (при этом веревочный многоугольник не замыкает-
замыкается) линию действия равнодействующей рассматриваемой системы
Рис. II.
сил и расположив затем полюс в новом месте на замыкающей сто-
стороне силового многоугольника (между ее крайними точками) или
на ее продолжении, начнем построение веревочного многоуголь-
многоугольника, совместив первую его сторону с ранее найденной линией
действия равнодействующей. Дальнейшее построение (изображен-
(изображенное на рисунке пунктиром) покажет, что последняя сторона вере-
веревочного многоугольника также расположится на линии дей-
действия равнодействующей, т. е., что веревочный многоуголь-
многоугольник замкнется. Этим способом мы заменили заданную систему
сил двумя силами, действующими по одной прямой; эта пря-
прямая и является линией действия равнодействующей заданной
системы сил. .
При таком расположении полюса и таком способе построения
первой стороны веревочного многоугольника каждому новому
положению полюса соответствует свой замыкающий веревочный
многоугольник.
в) "Силовой многоугольник замкнулся, а веревочный не замк-
замкнулся. В этом случае крайние стороны его параллельны между со-
собой, так как они соответственно параллельны первому и послед-
последнему лучам, совпадающим друг с другом при замыкании силового
многоугольника. Такая система сил приводится к паре, момент
которой равен произведению совпадающего луча, измеренного в
масштабе сил, на плечо пары — расстояние между крайними сто-
Основы графической статики
125
ронами веревочного многоугольника, измеренное в линейном мас-
масштабе.
г) Силовой и веревочный- многоугольники замкнулись. В этом
случае система сил находится в равновесии.
§ 2. Разложение одной силы на две составляющие. Частные
случаи
Рассмотрим, как производится разложение одной силы на две
составляющие в ряде случаев.
а) Разложение силы на две не параллельные ей составляющие,
линии действия которых известны, производится путем построения
силового многоугольни-
многоугольника; для возможности
такого разложения точ-
точка пересечения линий
действия составляющих
сил должна находиться
на линии действия за-
заданной силы.
б) Для разложения
одной силы на две, ей
параллельные состав-
составляющие, линии действия
которых известны (рис.
Ш,а), проводим из про-
произвольной точки, нахо-
находящейся на линии дейст-
действия заданной силы,
две произвольные пря-
прямые, пересекающие в
каких-то точках линии
действия искомых сил,
после чего соединяем
эти точки прямой; при
этом произвольные пря- i
мые представляют собой /
крайние стороны, а пря- /9
мая, соединяющая ука-
указанные точки пересече-
пересечения,— среднюю сторону веревочного многоугольника для искомых
сил.
Затем, отложив из произвольной точки (рис. II 1,6) вектор,
геометрически равный заданной силе, и проведя из его концов
(до взаимного пересечения в полюсе) лучи, параллельные край-
крайним сторонам веревочного многоугольника, проводим из полюса
Рис. III.
126 Статика твердого тела
луч, параллельный его средней стороне, до встречи с вектором
заданной силы {если она расположена между искомыми силами,
рис. III,а,б) или с его продолжением (если она расположена по
одну сторону от искомых сил, рис. II 1,<?, г).
Из полученного силового многоугольника, пользуясь ука-
указанием § 1 этой главы, пункт 4, определяют величины искомых соста-
составляющих, а их направления г определяют по общим правилам.
в) Если линия действия одной составляющей не параллельна
заданной силе, а для другой известна только точка ее приложения
(рис. 111,C), то одну из крайних сторон веревочного многоуголь-
многоугольника нужно обязательно провести именно через эту точку, а ос-
остальные стороны его найти, как указано в данном параграфе,
пункт б.
При построении силового многоугольника2 нужно из конца
вектора заданной силы (рис. Ш,е) провести прямую, параллельную
известной линии действия составляющей, до пересечения с про-
проведенным из полюса лучом, параллельным средней стороне вере-
веревочного многоугольника, и полученную точку соединить с нача-
началом вектора силы. В этом случае обе составляющие силы не па-
параллельны заданной силе и пересекаются с ней в одной точке.
Линию действия составляющей силы, для которой известна
только точка ее приложения, можно найти и иначе, соединив
эту точку.с точкой пересечения линий действия заданной силы
и второй ее составляющей 3; величины и направления обеих состав-
составляющих сил определяют из силового многоугольника.
§ 3. Определение опорных реакций балок и ферм, имеющих
одну подвижную и одну неподвижную шарнирные опоры.
Частные случаи
Прежде всего уточним некоторые общие положения:
при установлении линий действия опорных реакций реакция
подвижной опоры принимается направленной по нормали к плос-
плоскости возможного перемещения (незначительными силами трения
пренебрегаем);
устанавливается, следующая последовательность рассмотрения
сил: сначала рассматриваются все активные силы, а затем —
реактивные.
1 Стрелка равнодействующей (заданной силы) направлена навстречу общему
течению стрелок составляющих сил.
2 Последовательность рассмотрения сил такова: сначала рассматривается
заданная сила; затем—искомая составляющая, линия действия которой известна,
а затем — составляющая, для которой известна только точка ее приложения.
3 Так как заданная сила является равнодействующей двух непараллельных
составляющих сил, то точка пересечения последних обязательно должна нахо-
находиться на ее линии действия; этот прием удобно применить, если указанная точка
пересечения не выходит за пределы рисунка.
Основы графической статики 127"
Графически определяя величины и направления опорных реак-
реакций, пользуются двумя способами обозначения сил при построе-
построении силовых многоугольников.
-А. Обозначают каждую силу одной (большой) буквой латин-
латинского алфавита с соответствующим индексом (например, Ръ Р2).
В. Обозначают каждую силу двумя буквами латинского алфавита
(или двумя цифрами), представляющими собой наименования огра-
ограничивающих силу полей (под полем понимается часть плоскости
рисунка, находящаяся между внешними силами и контуром балки)..
I
Ж* *
к
К
к К к
а 6
Рис. IV.
В случае А может быть выбрана любая последовательность
рассмотрения активных сил (сначала Ръ затем Р2 и т. д. или сна-
сначала Р2у затем Рг и т. д.), после чего, при известных линиях дейст-
действия обеих опорных реакций балки, эти реакции рассматриваются
в любой последовательности; если же линия действия реакции
шарнирной неподвижной опоры неизвестна, то необходимо сна-
сначала рассмотреть реакцию шарнирной подвижной опоры, а затем
уже реакцию шарнирной неподвижной опоры. Нужно только
помцить, что при построении силового и веревочного многоуголь-
многоугольников необходимо обязательно придерживаться выбранной после-
последовательности рассмотрения сил.
В случае В последовательность рассмотрения всех приложен-
приложенных к балке внешних сил (как активных, так и реактивных) огра-
ограничена: все силы рассматриваются в последовательности их при-
приложения к наружному контуру балки при обходе этого контура
либо по ходу часовой стрелки, либо против хода. На рис. IV,a
показано неправильное обозначение полей, не дающее возмож-
возможности найти опорные реакции балки, так как активные силы че-
чередуются с реактивными, а на рис. IV,6 показано правильное
обозначение полей, позволяющее после рассмотрения всех активных
сил перейти к рассмотрению реактивных сил, следовательно, поз-
позволяющее найти опорные реакции балки г.
1 Толщиной балки пренебрегаем.
128 Статика твердого тела
Обозначение сил при помощи полей особенно рекомендуется,
когда силовой многоугольник обращается в линию сил (активные
и реактивные силы параллельны между собой, — случай, наибо-
наиболее часто встречающийся на практике).
В случае А лучи и стороны веревочного многоугольника обозна-
обозначаются цифрами, в случае В, если поля обозначены буквами, то
лучи и стороны веревочного многоугольника также обозначаются
цифрами, но если поля обозначены цифрами, то лучи и стороны
веревочного многоугольника обозначаются малыми .буквами ла-
латинского алфавита.
При определении опорных реакций балок встречаются следую-
следующие случаи:
1.}К балке пршюжена система параллельных сил, вызываю-
вызывающих параллельные им опорные реакции, линии действия которых
известны (рис. V, а, г).
Определение опорных реакций балки начинаем с построения
незамыкающегося силового многоугольника (линии сил) для ак-
активных сил (рис. V, б, в, д), затем соединяем его вершины с произ-
произвольно выбранным полюсом О и обычным путем строим для этих
сил веревочный многоугольник (рис. V, а, г). Продолжая край-
крайние его стороны до пересечения с линиями действия опорных реак-
реакций и соединяя эти точки пересечения, получаем замкнутый вере-
веревочный многоугольник для всех действующих на балку сил 1
(активных и реактивных).
Затем, проводя из полюса луч, параллельный найденной пред-
предпоследней стороне веревочного многоугольника, — до пересече-
пересечения с линией сил (когда реакции направлены в одну сторону) или
с ее продолжением (когда реакции направлены в противополож-
противоположные стороны), обычным путем определяем величины и направле-
направления 2 опорных ^реакций балки.
При одной активной силе реакции определяются аналогично
рассмотренному.
2. К балке приложена одна сила; линия действия реакции
шарнирной подвижной опоры и точка приложения реакции шар-
шарнирной неподвижной опоры известны. В этом случае опорные
1 Считая первой ту сторону вереврчного многоугольника, которая направлена
к первой активной силе, и продолжая ее до пересечения с линией действия одной
из опорных реакций, находим точку, через которую проходит последняя сторона
веревочного многоугольника для всей системы сил (при равновесии крайние сто-
стороны веревочного многоугольника располагаются на одной прямой). Недостающую
предпоследнюю его сторону мы нашли, соединив прямой точки, полученные на
линиях действия опорных реакций; веревочный многоугольник (рис. V, а, г)
6-1, 2, 3, 4, 5 соответствует рассмотрению после активных сил—реакций R& и RA,
а веревочный многоугольник 5'-, Г, 2, 3, 4\ 5' (рис. V/a) соответствует рассмотре-
рассмотрению после активных сил—реакций RA и R&
2 При равновесии стрелки всех векторов располагаются по одному течению,
т. е. началом каждого последующего вектора является конец предыдущего.
Основы графической статики
129
реакции можно определить двумя способами —с построением вере-
веревочного многоугольника и без построения его.
Рис. V.
Первый способ. В отличие от разобранного в предыдущем пункте
случая проводим первую сторону веревочного многоугольника
(рис. VI,а) не из произвольной точки, а обязательно из точки при-
приложения реакции шарнирной неподвижной опоры (это единствен-
ная известная нам точка, находящаяся на линии действия этой
реакции), доводя ее до пересечения с заданной силой, а остальные
его стороны проводим так же, как и в предыдущем случае.
Затем (рис. VI,б) из конца вектора заданной силы проводим
в силовом многоугольнике прямую, параллельную линии действия
9 591
130
Статика твердого тела
реакции« шарнирной подвижной опоры, доводя ее до пересечения
с проведенным из полюса лучом, параллельным найденной пред-
предпоследней стороне веревочного многоугольника, и полученную
точку соединяем с началом вектора заданной силы.
Из полученного таким образом силового многоугольника опре-
определяем величины и направления опорных реакций балки.
Рис. VI.
Второй способ. В рассматриваемом случае опорные реакции
можно найти и без построения веревочного многоугольника, поль-
пользуясь тем, что три непараллельные, взаимно уравновешивающиеся
силы обязательно пересекаются в одной точке.
Для этого (рис. VI,а) сначала находим неизвестную линию
действия реакции шарнирной неподвижной опоры, соединяя ее
точку приложения с точкой пересечения линий действия заданной
силы и реакции шарнирной подвижной опоры, а затем обычным
путем (рис. VI,б) строим силовой многоугольник без полюса и
лучей, из которого определяем величины и направления опорных
реакций.
3. К балке приложена произвольная плоская система сил;
линия действия реакции шарнирной подвижной опоры и точка при-
Основы графической статики
131
ложения реакции шарнирной неподвижной опоры известны. В этом
случае опорные реакции можно определить двумя способами.
Первый способ. Построение веревочного многоугольника отли-
отличается от рассмотренного в данном параграфе, пункт 1, только тем,
что первая сторона его проводится обязательно из точки прило-
приложения реакции шарнирной неподвижной опоры (рис. VI,#).
Построение силового многоугольника (рис. У1,г) отличается
от рассмотренного в данном параграфе, пункт 2, тем, что прямую,
параллельную линии действия реакции
шарнирной подвижной опоры, проводят
из конца вектора последней активной
силы, а не из конца вектора един-
единственной приложенной к балке
активной силы.
Второй способ. В рассматриваемом
случае опорные реакции можно найти
и иначе, применив построение верево-
веревочного многоугольника только для нахо-
нахождения линии действия равнодействую-
равнодействующей заданной системы сил, поступая
затем так же, как и в § 3, пункт 2,
во втором способе решения \
4. К балке, имеющей три связи
(рис. VII,а)> приложена одна активная
сила Р; линии действия реакций связей
Ту Ra n Rb* не пересекаются в одной
точке и не параллельны между собой.
В этом случае реакции связей могут
быть найдены без построения верево-
веревочного многоугольника — только при
помощи силовых многоугольников.
Для определения реакций связей
необходимо найти линии действия
равнодействующих каждых двух сил, на которые может быть
разбита система действующих на балку четырех сил. Для этого
найдем точку пересечения линий действия активной силы Р
с линией действия одной из реакций связей — Т или RA (на
рис. VII,a показана точка пересечения линий действия силы Р
и реакции Т) и точку пересечения линий действия остальных двух
сил — реакций RA и RB. Заменив приложенную к балке систему
1 Этот вариант удобен только тогда, когда точка пересечения линии действия
равнодействующей заданной системы сил и известной линии действия опорной
реакции находится в пределах рисунка.
* Rb может быть реакцией гладкого горизонтального пола, 7?д — реакцией
гладкой вертикальной стены, а Т — реакцией веревки.
9*
132 Статика твердого тела
четырех сил двумя равнодействующими, приложенными к точкам
К и М, придем к выводу, что обе равнодействующие равны между
собой и действуют по линии МК (аксиома 2).
Затем обычным путем строим силовой треугольник abc
(рис. VI 1,6) для силы Р, реакции Т и равнодействующей R реак-
реакций Ra и RBt откуда и определяем величины и направления реак-
реакции' Т и равнодействующей R. После этого на том же рисунке
строим второй силовой треугольник acd, из которого определяем
величины и направления реакций Ra и Rb.
Заменив приложенные к балке силы равнодействующими сил
Р и Ra, Т и Rs, приложенными соответственно к точкам Л/и5, и
построив затем силовые треугольники abd и bed, получим те же
результаты.
При определении опорных реакций статически определимых
ферм необходимо рассматривать ферму как одно целое твердое
тело и применять методы, рассмотренные в данном параграфе.
§ 4. Определение опорных реакций трехшарнирных арок.
Частные случаи
При определении реакций опор трехшарнирной арки и дав-
давления в соединительном (ключевом) шарнире встречаются такие
основные случаи:
а) к одной из частей трехшарнирной арки приложена только
одна активная сила, а другая часть арки не нагружена. Этот слу-
случай рассмотрен в главе VI, § 5, пункт а (рис. II, а, б, в, г)\
б) к одной из частей трехшарнирной арки, допустим к левой
(рис. VIII,a), приложена произвольная система сил, а другая
часть ее не нагружена;
в) к обеим частям трехшарнирной арки (рис. IX,а) приложена
произвольная система сил, в состав которой может входить и соб-
собственный вес каждой части арки. х
В случае б), установив аналогично предыдущему(рис. \\,в, к главе
VI, § 5) направление силы5 (а следовательно, и направление правой
опорной реакции В арки), находим при помощи силового и веревоч-
веревочного многоугольниковг линию действия равнодействующей R задан-
заданной системы сил (рис. VIII,a,6) и общую точку пересечения взаимно
уравновешивающихся трех непараллельных сил /?, S и Л, после
чего из первой и последней вершин незамкнутого силового много-
многоугольника (рис. VIII,6) проводим — до взаимного пересечения —
прямые, параллельные реакции А и силе S.
1 При построении силовых многоугольников рекомендуем каждую активную
силу обозначать двумя малыми буквами латинского алфавита; лучи, а также со-
отвегствующие им стороны веревочного многоугольника — арабскими цифрами,
а каждую определяемую силу (составляющую реакции опоры или ключевого
шарнира, а также саму реакцию) — одной большой буквой латинского алфавита
(с соответствующим индексом для составляющих опорной реакции).
Основы графической статики
133
Рис. VIII.
\\
Величины (в принятом масштабе сил) и направления А и 5
E == В) определяются из полученного замкнутого силового много-
многоугольника.
134 Статика твердого тела
В случае В) найдем сначала (рис. 1Х,а, б), аналогично предыду-
предыдущему, составляющую Ал левой опорной реакции и силу Sn (Sn =
= Вл), рассматривая только силы, действующие на левую часть
арки (считая условно, что к правой части арки внешние активные
силы не приложены). Затем таким же образом (рис.IX, а, е) най-
найдем составляющую Вп правой опорной реакции и силу Sn(Sn =
= Лп), рассматривая только силы, действующие на правую часть
арки (считая условно, что к левой части арки внешние активные
силы не приложены). После этого, применяя принцип независимости
действия сил, из соответствующих силовых многоугольников
(рис. IX,г, д, в) найдем окончательные величины и направления
равнодействующих Ал и Лп, Вл и ВПу 5Л и Sn, т. е. опорных реак-
реакций А и В и силы S.
При определении величины и направления силы 5П. л, представ-
представляющей собой передаваемое через шарнир С действие правой части
арки на левую при загружении обеих частей ее, нужно силу 5П
принять направленной в сторону, противоположную ранее най-
найденной, когда рассматривалось действие левой части арки на пра-
правую при действии активных сил только на правой части арки;
геометрическое сложение показано на рис. IX,в.
Аналогично нужно поступать и при определении величины и
направления силы 5Л. п, представляющей собой передаваемое через
шарнир С действие левой части арки на правую при загружении
обеих частей арки.
Примечание. Если заданная сила или равнодействующая системы
заданных сил в случаях а), 6) и в) параллельна силе 5, то их точка пересечения от-
отдаляется в бесконечность, следовательно, все три силы образуют систему парал-
параллельных сил. К этим случаям полностью применимо все, сказанное в § 3 данной
главы, пункт 1.
Для компактности (уменьшения числа силовых многоуголь-
многоугольников и числа лучей) и большей ясности о взаимозависимости
между определяемыми величинами все построение сделаем следую-
следующим образом (рис. Х,а, б).
Рассматривая действующие на всю арку активные силы в по-
порядке их приложения, т. е. одну за другой (слева направо), строим
незамкнутый силовой многоугольник abcde и соединяем лучами
/, 2, 3, 4, 5 его вершины с произвольно взятым полюсом О. Сое-
Соединяя первую а и последнюю с вершины разомкнутого силового
многоугольника для системы активных сил, приложенных
к левой части арки, находим величину и направление равнодейст-
равнодействующей /?л; проведя из этих же вершин до взаимного пересечения
в точке Ох прямые, параллельные силам Ал и 5Л (Вл), находим
величины и направления этих сил.
Таким же путем находим /?п, Вп и Sn.
Затем, перенеся в точку Ог параллельно самому себе вектор
О2с, равный Лп, находим ka — опорную реакцию А как равно-
Основы графической статики ,
135
действующую Л п и Ал; перенеся в точку О2 параллельно самому себе
вектор сОъ равный Вл (фигура Юхс02 — параллелограм), находим
ek — опорную реакцию В как
равнодействующую Вп и Вп.
Для определения вели-
величины и направления силы 5
нужно прежде всего устано-
установить — действие какой части
арки на другую (левой на
правую, или наоборот) мы
хотим найти.
При определении величины >
и направления силы 5П. л воз-
воздействия правой части арки
на левую необходимо рассмо-
рассмотреть равновесие левой части
арки, находящейся под дей-
действием приложенной к ней
системы активных сил, силы
Sn. л и реакции А левой опоры.
В этом случае величина и
направление силы 5П. л опре-
определяются стороной ck сило-
силового многоугольника kabc К
Аналогично из рассмотре-
рассмотрения равновесия правой части
арки, находящейся под дей-
действием приложенной к ней си-
системы активных сил, силы 5Л. п
воздействия левой части арки
на правую и реакции В пра-
правой опоры, найдем, что вели-
величина и направление силы 5Л. п
определяются стороной kc си-
силового многоугольника cdek2.
Проверкой правильности
и точности всех построений
{рис. Х,а) является:
Рис.
1 Одновременно сила Sn л является равнодействующей двух составляющих:
5Л (сОх) и 5П (О, к), представляющих собой действие правой часги арки на левую,
когда активные силы действуют соответственно только на левую часть арки и
только на правую ее часть.
2 Одновременно сила Sn п является равнодействующей двух составляющих:
5Л (кО2) и 5П (О2г), представляющих действие левой части арки на правую, когда
активные силы действуют соответственно только на. левую часть арки и только
шп правую ее часть.
136 Статика твердого тела
а) пересечение в одной точке (D) линий действия сил R^ А и
5п.л, так как иначе невозможно равновесие левой части арки
как свободного твердого тела;
б) пересечение з одной точке (?) линий действия сил Rn, В и
Sn. ш без чего невозможно равновесие правой части арки- как
свободного твердого тела;
в) пересечение в одной точке (К) линий действия сил R> А и В,
без чего невозможно равновесие всей трехшарнирной арки, рас-
рассматриваемой как одно твердое тело.
Здесь R — равнодействующая активных сил, приложенных ко
всей арке, выраженная замыкающей стороной ае силового много*
угольника abcde. Линия действия R проходит через точку L пере-
пересечения крайних A и 5) сторон веревочного многоугольника, пост-
построенного для всех приложенных к арке активных сил {Ръ Р2, Pz
и Р^)> а также через точку М пересечения линий действия равно-
равнодействующих Rn и /?п.
§ 5. Определение усилий в стержнях статически определимых
ферм
Усилия в стержнях статически определимых ферм определяются
двумя методами: путем последовательного вырезания узлов фермы
и путем построения диаграммы Максвелла-Кремоны.
1. Метод последовательного вырезания
узлов фермы
Применение этого метода для определения усилий в стержнях
статически определимых ферм подробно рассмотрено в главе V,
§ 1; измеряя в принятом масштабе сил атороны замкнутых силовых
многоугольников, построенных для каждого узла фермы, находим
усилия в каждом стержне фермы.
Недостатком этого метода является построение большого числа
силовых многоугольников и двойное вычерчивание каждого уси-
усилия, поскольку каждый стержень примыкает к двум узлам фермы;
это уменьшает степень точности полученных результатов.
2. Метод построения диаграммы Макс-
Максвелла-Кремоны. Частные случаи
При помощи этой диаграммы разрозненные силовые многоуголь-
многоугольники объединяются в одну компактную фигуру, в которой каждое
усилие вычерчивается только один раз г.
1 Исключением из этого правила является построение диаграммы Максвелла*
Кремоны для фермы, имеющей пересекающиеся (без соединительного шарнира)^
стержни; об этом более подробно сказано дальше.
Основы графической статики 137
Для построения диаграммы Максвелла-Кремоны необходимо
сначала аналитически или графически определить опорные реакции
фермы !, затем, если реакции определялись аналитически, необ-
необходимо построить силовой многоугольник для всех внешних (актив-
(активных и реактивных) сил, обязательно придерживаясь определенной
последовательности их рассмотрения, а именно, последователь-
последовательности приложения внешних сил при обходе контура фермы в одном
направлении — по ходу или против часовой стрелки (мы будем
определять последовательность приложения сил по х о Д у
часовой стрелки).
При графическом определении опорных реакций фермы необ-
необходимо также придерживаться указанной выше последователь-
последовательности отложения внешних сил при построении силового многоуголь-
многоугольника, чтобы иметь возможность использовать этот многоугольник для
построения диаграммы Максвелла-Кремоны. Если силы на ферме
расположены так, что это условие не может быть выполнено (при
обходе контура фермы после неизвестной реакции встречается
известная сила), то необходимо построить второй силовой много-
многоугольник, рассматривая все внешние силы — активные и уже
найденные реактивные — в необходимой для этого последователь-
последовательности. *
После построения силового многоугольника для внешних сил
необходимо приступить к вырезанию узлов фермы, придерживаясь
последовательности, принятой в главе V, § 1.
Рассмотрение равновесия каждого последующего узла фермы
начинаем с рассмотрения расположенных одна за другой — по
ходу часовой стрелки — всех приложенных к нему известных
сил, уже вошедших в диаграмму Максвелла-Кремоны при построе-
построении силового многоугольника для всех внешних сил и при рассмот-
рассмотрении равновесия предыдущих узлов фермы; затем из конца век-
вектора последней известной силы проводим параллель первой (по
ходу часовой стрелки) из двух неизвестных сил, приложенных к
узлу, до пересечения с параллелью второй неизвестной силе,
проведенной из начала вектора первой из известных сил.
Таким образом, при рассмотрении равновесия каждого после-
последующего узла фермы к диаграмме обычно добавляются два новых
усилия (только при исследовании равновесия последнего или
предпоследнего из рассматриваемых узлов к диаграмме добав-
добавляется лишь одно новое усилие).
Контролем правильности построения диаграммы является ее
замыкание. В связи с некоторой неточностью, возникающей при
проведении большого количества прямых, параллельных осям
1 Для фермы-консоли, имеющей двухстержневой узел, не связанный с
опорой, можно определять возникшие в стержнях усилия, не находя пред-
предварительно опорных реакций фермы (см. задачу 37).
138 Статика твердого тела
стержней фермы, возможна незначительная «невязка», искусствен-
искусственное устранение которой не должно приводить к изменению истин-
истинного значения усилий больше чем на 5%.
Для уменьшения возможной «невязки» — при большом числе
стержней в ферме — рекомендуется (если тип фермы позволяет
это), построив диаграмму примерно для половины возникающих
в стержнях усилий, прервать принятую последовательность рас-
рассмотрения узлов фермы и начать, аналогично предыдущему, постро-
построение диаграммы для усилий в стержнях оставшейся части ее с рас-
рассмотрения равновесия узла, к которому примыкают только два
стержня, доводя построение второй части диаграммы до смыкания
ее с уже построенной первой частью.
В правильности решения можно убедиться и иначе, ррименив
метод сквозных сечений (глава V, § 3) и определив усилия в нес-
нескольких произвольно взятых стержнях фермы аналитическим
путем.
Для построения диаграммы Максвелла-Кремоны рекомендуется
обозначать внешние силы и возникающие в стержнях фермы уси-
усилия * двумя цифрами (или буквами) — по номерам ограничиваю-
ограничивающих их полей (если опорные реакции определяются графически,
то рекомендуем лучи и стороны веревочного многоугольника обоз-
обозначать малыми буквами латинского алфавита).
Обозначение сил двумя цифрами (или буквами) имеет еще и
то преимущество, что при пользовании ими нет необходимости
изображать на диаграмме растягивающие и сжимающие усилия
линиями разной толщины или разного цвета и проставлять стрелки
на векторах усилий; характер возникающего в том или ином стержне
усилия может быть легко определен.
Для этого необходимо мысленно вырезать из фермы любой из
двух узлов, к которому примыкает рассматриваемый стержень, и,
обходя по ходу часовой стрелки приложенные к узлу силы, уста-
установить обозначение этого стержня (например, 7—5); затем нужно
найти направление искомой силы из диаграммы (началом вектора
силы является вершина 7 диаграммы, концом вектора силы —
вершина 8) и мысленно приложить найденный на диаграмме вектор
силы к сечению стержня; если вектор силы окажется направленным
1 Особенно удобно такое обозначение сил для ферм, имеющих ряд узлов на
одном прямолинейном поясе (а таких ферм очень много). При отсутствии в этих
узлах внешних сил усилия во всех стержнях фермы, расположенных по контуру
пояса, т. е. по прямой линии, располагаются в диаграмме также на одной прямой;
пользуясь двочным обозначением сил, искомые усилия легко выделить на этой
прямой.
Левая и правая опорные реакции ферм обозначаются нами буквами А я В,
внешние силы—буквами Р, а усилия в стержнях фермы—буквами S с соответствую-
соответствующими индексами граничащих с ними двух полей, например, A5_v Р2—з> $г—8-
Основы графической статика
139
Рис. XI.
от рассматриваемого узла фермы, то стержень растянут, если к
узлу, — то сжат \
После построения диаграммы
рекомендуем составить сводную
таблицу, отметив в ней величины
и знаки всех усилий, возникших
в стержнях фермы (расстяги-
вающим усилиям приписывается
знак плюс, а сжимающим —
минус).
Рассмотрим наиболее часто
встречающиеся случаи прило-
приложения внешних сил к фермам.
а) Схема сил, приложенных
к одному из поясов (верхнему
или нижнему) или к обоим по-
поясам симметричной фермы, —
симметрична (рис. XII,а, б).
В этом случае нет необходи-
необходимости строить всю диаграмму
Максвелла-Кремоны; достаточно
построить ее только для уси-
усилий, возникающих в стер-
стержнях половины фермы, включая
усилие в стержне, который от-
относится к каждой половине
фермы (если такой стержень
имеется), так как усилия в симметрично расположенных стержнях
равны между собой.
1 Перенос силы по оси-стержня на противоположную от узла сторону недо-
недопустим, так как это приводит к ошибке. На рис. XI, а показан правильный
перенос направления усилий, найденных из диаграммы (усилия приложены в тех
местах, где мысленно проводился разрез стержней), а на рис. XI, б — непра-
неправильный.
140
Статика твердого тела
б) Схема сил, приложенных к симметричной ферме, — несим-
несимметрична (см. решение задачи 36).
В этом случае диаграмму Максвелла-Кремоны необходимо пост-
построите полностью для усилий, возникающих во всех стержнях
фермы, так как из-за несимметричности нагрузки усилия в сим-
симметрично расположенных стержнях фермы различны
D P,
Рис. XIII.
в) Силы приложены к одному из поясоЙ несимметричной фермы
(рис. XII,*), к обоим поясам ее, к одному или нескольким узлам
любого пояса.
В любом из этих случаев также необходимо построить диаграм-
диаграмму Максвелла-Кремоны полностью, т. е. для всех усилий, возни-
возникающих в стержнях фермы.
г) Схема сил, приложенных к обоим (верхнему и нижнему) поя-
поясам симметричной или несимметричной фермы, — несимметрична
(рис. XIII,аI.
При таком расположении нагрузки силовой многоугольник
(рис. XIII,*), построенный для графического ^определения опор-
опорных реакций фермы (рис. XII 1,6), не может служить основой для
построения диаграммы Максвелла-Кремоны, так как при его пост-
построении не соблюдается необходимая для этого последовательность
отложения сил; поэтому необходимо построить второй силовой
многоугольник (рис. Х1Н,г), а затем уже строить диаграмму для
усилий, возникающих во всех стержнях фермы.'
1 Рис. XIII б, г лучше рассматривать пекле ознакомления с решением за-
задачи 36.
Основы графической статики
141
д) Силы приложены к ферме с пересекающимися стержнями
(рис. XlV.a).
При отсутствии шарнира в точке Е пересечения стержней нет
возможности четко разграничить поля? так как часть плоскости,
находящаяся между пересекающимися стержнями и каким-либо
третьим стержнем, может быть отнесена к двум полям. В этом слу-
случае для возможности построения диаграммы Максвелла-Кремоны
прибегают к искусственному приему, не приводящему к изменению
усилий, возникающих в стержнях фермы, а именно, считают,
что в точке Е шарнир есть (рис. XIV,б), и Строят диаграмму обыч-
обычным путем (рис. XIV,e); в этом случае усилия в пересекающихся
стержнях фермы повторяются в диаграмме дважды1.
е) Силы приложены к ферме (рис. XV), при последовательном
вырезании узлрв которой обнаруживается узел с тремя неиз-
неизвестными усилиями, что не дает возможности продолжать построе-
построение диаграммы Максвелла-Кремоны2; так, например, построив
1 Рис. XIV, б, в целесообразно рассматривать после ознакомления с реше-
решением задачи 36.
2 Невозможность построения полной диаграммы Максвелла-Кремоны при»
последовательном вырезании узлов данной фермы зависит только от ее струк-
структуры и не опровергает ее статической определимости (число стержней в ферме
соответствует необходимому, так как к = 2п — 3 = 2 • 15 — 3 = 27).
142
Статика твердого тела
замыкающиеся силовые многоугольники для узлов А, В,л С фермы,
обнаружим, что как к узлу Д так и к узлу Е приложено по три
неизвестных усилия.
В этом случае для возможности дальнейшего построения диа-
диаграммы необходимо применить метод сечений (глава V, § 3) и ана-
аналитическим путем определить одно из трех неизвестных усилий.
Проще всего можно определить усилие ъ стержне ER, рассекая
стержни FL, KL и ER и рассматривая равновесие левой части фер-
фермы, после чего следует рассмотреть равновесие узлов ?, D и т, д.
Р
Рис. XV.
Усилие в стержне ER может быть определено и графически —
путем использования метода Кульмана, при этом опорные реакции
фермы обычно находятся графически г.
§ 6. Задачи
36. К узлам D, F, Ь и N фермы (рис. Зб,а) приложены верти-
вертикальные силы Р, каждая из которых равна 2 т. Определить гра-
графически реакции опор Л и В фермы и усилия, возникающие в ее
стержнях.
Решение. 1. Определяем реакции опор А и В фермы.
Находим линии действия искомых реакций:
а) реакция подвижной опоры В вертикальна, так как она
направлена по нормали к горизонтальной плоскости возможного
перемещения опоры В (незначительной силой трения пренебрегаем).
4 * Веревочный многоугольник, построенный для графического определения
опорных реакций фермы, дает возможность найти линию действия равнодейству-
равнодействующей всех внешних сил (активных и реактивных), приложенных к рассматрива-
рассматриваемой левой части фермы, без чего невозможно применение метода • Кульмана.
Оскосы графической статики
143
б) реакция неподвижной опоры А также вертикальна, так
как, кроме нее, на ферму действуют только вертикальные актив-
активные силы и вертикальная реакция опоры В.
ft '
Щ> ic
***3м * 1 тЗм -*-
&
г/
/
/
?
\
\
Г44
\д
А
^7
ю
К задаче 36.
Обозначаем арабскими цифрами внешние и внутренние поля
фермы (рис. 36,6).
Поле 1 ограничено вертикальными линиями действия сил Л, Рг
и отрезком AD\ поле 2 ограничено линиями действия <:ил Ръ Рй
и отрезком DF; поле 3 ограничено линиями действия сил Ръ Р%
и отрезком FL\ поле 4 ограничено линиями действия сил Pz, P4
и отрезком LN; поле 5 ограничено линиями действия силы Р9 ре-
144 Статика твердого тела
акции В и отрезком NB\ поле 6 ограничено линиями действия реак-
реакций опор В и А фермы и нижним ее поясом АВ.
Каждое из остальных полей (от 7 до 16) ограничено с трех сторон
осями соответствующих стержней фермы.
Строим силовой многоугольник (рис. 36,в).
Из произвольной точки / в выбранном масштабе откладываем
одну за" другой все активные силы в порядке приложения их к
•ферме — при обходе ее по ходу часовой стрелки, т. е. сначала
откладываем вектор силы Pi-2> отделяющей поле / от поля 2,
из его конца откладываем вектор силы Р2-з> затем вектора сил
Р3-4 и Р4—5у после чего соединяем верСыины 1, 2, 3, 4 и 5 силового
многоугольника (линии Сил) с произвольно выбранным полюсом О,
обозначая полученные лучи малыми буквами латинского алфавита.
Затем из произвольной точки /, находящейся на линии действия
реакции А (рис. 36, б), начинаем построение веревочного много-
многоугольника abcde, доводя его сторону е до пересечения с линией
действия реакции В в точке //. Соединив точки II и I прямой —
стороной / веревочного многоугольника — и проведя из полюса
О параллельный ей луч / до пересечения с силовым многоугольни-
многоугольником, найдем реакции опор фермы. Так как при принятом порядке
отложения сил в силовом многоугольнике за силой Р4—$ располо-
расположены реакции В5-6 и Аб-и то точка пересечения луча / с силовым
многоугольником должна быть обозначена цифрой 6,
Последний луч fe, соединяющий с полюсом О конец 1 вектора
А6—1у совпадает с первым лучом а> так как при равновесии первая
и последняя вершины силового многоугольника всегда совпадают,
поэтому первая и последняя стороны веревочного многоугольника
а и k также совпадут.
2. Определяем усилия, возникающие в стержнях фермы (рис. 36,в).
Устанавливаем последовательность вырезания узлов фермы
для последующего построения соответствующих силовых много-
многоугольников равновесий, исходя из того, что в каждом узле не
должно быть больше двух стержней, усилия в которых неизвестны:
сначала вырезываем узел Л, затем узлы C,D, F, ?,* /(, L, N, М, О и Q
(можно было бы сначала рассмотреть равновесие узла Q, а затем
уже равновесие узла О). Рассматривать равновесие узла В не
нужно, так как усилия S6-i6U S16^5 будут уже найдены из рассмот-
рассмотрения равновесия узлов О и Q.
Основой для построения диаграммы Максвелла-Кремоны явля-
является ранее построенный силовой многоугольник /, 2, 5, 4, 5, 6, /,
стороны которогЬ войдут в состав силовых многоугольников
равновесия, построенных для усилий, приложенных к узлам Л, D,
F, L, jV и В (к этим узлам, кроме реакций стержней, приложены
еще внешние — активные или реактивные — силы).
Строим диаграмму Максвелла-Кремоны (рис. 36,в).
Построение силового многоугольника равновесия для при-
Основы графической статики 145
ложенных к узлу А сил начинаем из точки 6 силового многоуголь-
многоугольника /, 2у 3, 4, 5, 5, /, так как из этой точки уже отложена извест-
известная сила — реакция A6—i. Затем из точки / проводим прямую,
параллельную линии действия неизвестного усилия Si-7 (порядок
отложения сил в силовых многоугольниках соответствует после-
последовательности приложения сил к узлам фермы при обходе их по
ходу часовой стрелки, причем сначала откладываются одна за
другой все известные силы); зная, что конец вектора, изобра-
изображающего второе неизвестное усилие S7_6, должен совпасть с точкой
6 (при равновесии силовой многоугольник замыкается), проводим
из этой точки прямую, параллельную линии действия усилия
S7—6у До взаимного пересечения з точке 7 с ранее проведенной пря-
прямой.
Мысленно нанеся найденные направления усилий (направление
усилия определяется порядком его обозначения) на узел Ау при-
приходим к выводу, что стержень /—7 сжат (усилие S^? направлено
к узлу), а стержень 7—6 растянут (усилие S7—6 направлено от
узла).
Построение силового многоугольника равновесия для прило-
приложенных к узлу С сил начинаем с уже отложенного известного
усилия S6—7, из конца которого проводим прямую, параллельную
линии действия усилия S7-8, после чего из точки 6 проводим пря-
прямую, параллельную линии действия усилия S8~6- Так как эта
прямая совпадает с прямой, параллельной линии действия усилия
S6—7, то она пересекает прямую, параллельную линии действия уси-
усилия 57_5 в точке 7. Совпадение точек 8 и 7 показывает, что усилие
S7—8 равно нулю. Направление усилия S8—e показывает, что стер-
стержень 8—6 растянут.
Построение силового многоугольника равновесия для прило-
приложенных к узлу D сил нужно начать с отложения известного уси-
усилия 55_7, за которым должны следовать усилие S7—i и внешняя
сила Р|_2, но они уже отложены раньше — при рассмотрении рав-
равновесия всех сил, приложенных к узлам Л и С, и всех внешних
сил, приложенных к ферме. Поэтому фактически для получения
замкнутого силового многоугольника необходимо только достроить
его, проведя из точки 2 прямую, параллельную линии действия
усилия S2-9> До пересечения в точке 9 с проведенной из точки 8
(начала построения силового многоугольника) г прямой, парал-
параллельной линии действия усилия S<?_s. Направлений найденных
усилий показывают, что стержни 2—9 и 9—8 сжаты.
Достраиваем силовой многоугольник для сил, приложенных
к узлу /\ проводя из точки 3 (усилие S9—2 и сила Р2—з уже отло-
1 Прямая, параллельная линии действия последнего из двух усилий, опреде-
определяемых из рассмотрения равновесия любого узла фермы, обязательно
проводится из точки, являющейся началом построения силового многоугольника
равновесия для всех сил, приложенных к рассматриваемому узлу.
10 591
146 Статика твердого тела
жены ранее) прямую, параллельную линии действия усилия »
до пересечения в точке 10 с проведенной из точки 9 прямой, парал-
параллельной линии действия усилия SJ0-g. Направления найденных
усилий показывают, что стержни 3—10 и 10—9 сжаты.
Затем переходим к рассмотрению равновесия сил, приложен-
приложенных к узлу ?. Так как усилия S6-8y S8-9 и S9-]0 уже отложены рань-
раньше, проводим из точки 10 прямую, параллельную линии действия
усилия Sio-n, до пересечения в точке 11 с проведенной из точки
6 прямой, параллельной линии действия усилия Sn-€- Мысленно
нанеся найденные направления усилий на узел, убедимся, что
стержни 10—И и //—6 растянуты.
Из рассмотрения равновесия приложенных к узлу К сил, при-
приходим к выводу, что усилие Sn-i2 равно нулю, так как при пост-
построении силового многоугольника прямые, параллельные линиям
действия усилий S12—e и S6—n> совпали, а следовательно, совпали и
точки 11 и 12. Направление усилия Sj2—в показывает, что стер-
стержень 12—6 растянут.
Переходим к рассмотрению равновесия сил, приложенных
к узлу L. Так как усилия S12-iu Sn-io, SJ0~3 и сила Р3-4 уже отло-
отложены раньше, проводим из точки 4 прямую, параллельную линии
действия усилия S4~i3, до пересечения в точке 13 с проведенной
из точки 12 прямой, параллельной линии действия усилия Su—12-
Направления найденных усилий показывают, что стержень 4—13
сжат, а стержень 13—12 растянут.
Затем достраиваем силовой многоугольник для сил, приложен-
приложенных к узлу N (усилие SJ3—4 и сила Р4—5 уже отложены раньше),
'Проводя из точки 5 прямую, параллельную линии действия уси-
усилия S6-u, До пересечения в точке 14 с проверенной из точки 13 пря-
прямой, параллельной линии действия усилия Su~i3- Направления
найденных усилий показывают, что стержни 5—14 и 14—13 сжаты.
Из рассмотрения равновесия приложенных к узлу М сил
приходим к выводу, что усилие S]4—i5 равно нулю, так как при
построении силового многоугольника прямая, параллельная уси-
усилию S16-G, отложенная из точки 6> пересекает прямую, параллель-
параллельную линии действия усилия S14-15, в точке 14, т. е. точки 14 и 15
совпадают. Направление усилия S15—e показывает, что стержень
15—6 растянут.
Из рассмотрения равновесия приложенных к узлу О сил при-
приходим к выводу, что усилив Sи—и равно нулю, так как при построе-
построении силового многоугольника прямые, параллельные линиям дейст-
действия усилий S6-i5 nSi6~6, совпали, а следовательно, и точки 15 и 16
совпали. Направление усилия S16-6 показывает, что стержень
16—6 растянут.
Последним рассматриваем равновесие узла Q, к которому при-
примыкает только один стержень 5—16, усилие в котором неизвестно.
Так как усилия Sio-u, SJ5-14 и S^-s отложены раньше, то остается
Основы графической статики
147
только из точки 5 провести прямую, параллельную линии действия
УСИЛИЯ S.5-J6.
Контролем правильности построения всей диаграммы Максвелла-
Кремоны является замыкание силового многоугольника,» пост-
построенного для приложенных к узлу Q сил, для чего необходимо»
чтобы прямая, параллельная линии действия усилия Ss~.i6 (про-
(проведенная из точки 5), прошла через точку 16. В данном случае это
имеет место, следовательно, диаграмма построена нами правильно.
Измерив в принятом масштабе реакции опор А и В фермы, най-
найдем:
А = 4,67 т; В = 3,33 т.
Измерив в том же масштабе возникшие в стержнях фермы уси-
усилия, внесем их значения в таблицу.
Обозначение
усилия
$1-7
$2-9
$3—10
$4—13
$5—14
$5—16
• sr_s
S8-e
$11-6
$12 в
$15—6
$16—6
$7 8
$10—9
$11—12
$14—13
$15—16
$9—8
$10—11
$13—12
« $т—15
Величина
растягивающего (+)
—
—.
__
—
—
9,33
9,33
5,33
5,33
6,67
6,67
—
—
—
—
—
3,60
2,38
—
усилия (в т)
сжимающего (—)
10,45
8,22
8,22
7.45
7,45
7,45
—
—
—
—
—
—
2,0Э
—
2,00
—
2,22
—
—
10*
Н8 Статика твердого тела
Убедимся в правильности ряда найденных усилий, использовав
рассмотренные в главе V, § 2 различные случаи.
Случай Ь)
Узел С. Усилие S7—8 равно нулю; усилие57__б равно усилию5$_<?.
Узел /С. Усилие Su^12 равно нулю; усилие Su-s равно уси-
усилию Si2-6-
Узел О. Усилие Si5~i6 равно нулю; усилие Si5—6 равно усилию
5 is—б-
Узел Q (так как усилие S13-i6 равно нулю, то схема расположе-
расположения стержней также соответствует случаю Ь). Усилие Su—u рарно
нулю; усилие S5-.14 равно усилию S5-16.
Случай г)
Узел F. Усилие Sw-9 равно Р2-з = 2т; усилие S2-g равно уси-
усилию 8,3—10-
Узел N. Усилие S14—i3 равно Р4—5 = 2т; усилие S4—13 равно
усилию Ss—u.
Примечание. Прохождение прямой 2—9 через вершину //, 12 диа-
диаграммы соответствует заданной схеме нагрузки; при другом соотношении между
величинами приложенных к данной ферме сил, ином их количестве или при при-
приложении этих же сил к другим узлам прямая 2—9 ие пройдет уже через вершину
;;, 12.
37. Определить графически опорные реакции и усилия в стерж-
стержнях навесной фермы (рис. 37,а), если P1 = P4t~0,5mf a P2=P3= 1 гп.
Решение. Для рассматриваемой 4)еРмы"консоли» имеющей
двухстержневой узел, не связанный с огьерой, можно определять
возникающие в стержнях усилия, ие находя предварительно опор-
опорных реакций фермы.
Обозначаем поля фермы (рис. 37,6).
Поле 1 ограничено неизвестно.й линией действия реакции опоры
А фермы, линией действия реакции опоры В и отрезком АВ\ поле
2 ограничено линией действия реакции В* опоры и линией дей-
действия силы Рг\ поле 3 ограничено линиями действия сил Рх и Р2 и
отрезком ВС; поле 4 ограничено линиями действия сил Р2 и ^з
и отрезком СЕ; поле 5 ограничено линиями действия сил Р3 и Р*
и отрезком ЕК; поле 6 ограничено линией действия силы Р4, неиз-
неизвестной линией действия реакции опоры А и отрезком Л Л'. Каж-
Каждое из остальных полей (от 7 до 11) ограничено с трех сторон осями
соЬтветствующих стержней фермы.
Устанавливаем последовательность вырезания узлов фермы для
последующего построения соответствующих силовых многоуголь-
многоугольников равновесия: сначала вырезаем узел /С, затем узлы Еу F,
* Линия действия реакции опоры В фермы направлена по оси горизонталь-
горизонтального опорного стержня.
Основы графической статики
149
С, D, В, А (после узла D нельзя рассматривать равновесие узла
А у так как неизвестно направление реакции опоры А фермы).
Строим диаграмму Максвелл а-Кремоны (рис. 37,в).
2 '
К задаче 37.
Из рассмотрения равновесия узла К находим, что стержень
6—11 сжат, а стержень //—5 растянут; из рассмотрения равнове-
равновесия узла Е находим, что стержень //—10 сжат, а стержень 10—4
растянут; из рассмотрения равновесия узла F находим, что стер-
стержень 6—9 сжат, а стержень 9—10 растянут; из рассмотрения рав-
равновесия узла С находим, что стержень 9—8 сжат, а стержень 8—3
растянут; из рассмотрения равновесия узла D находим, что стер-
стержень 6—7 сжат, а стержень 7—8 растянут.
Из рассмотрения равновесия узла В находим величину и направ-
150 Статика твердого тела
ление реакции опоры В фермы и устанавливаем, что стержень
7—1 сжат.
Из рассмотрения равновесия узла А находим величину и на-
направление реакции опоры А фермы, соединив прямой вершины
/ и 6 диаграммы.
Положительным при таком построении диаграммы Масквелла-
Кремоны является то, что реакции предварительно (перед построе-
построением диаграммы) не определяются, а находятся при построении
самой диаграммы, а недостатком является отсутствие контроля
правильности графического определения усилий в стержнях фермы
и ее опорных реакций.
При необходимости контроля правильности получаемых резуль-
результатов поступаем как обычно:
1. Определяем реакции опор А и В фермы.
Устанавливаем линию действия реакции шарнирной опоры В
фермы: как указывалось уже раньше, она горизонтальна; для
реакции А известна только точка ее приложения.
Обозначаем поля фермы.
Задавшись масштабом, строим силовой многоугольник (рис. 37,г),
откладывая за вектором силы Рг векторы сил Р2, Р3» ^4 и соединяя
затем вершины силового многоугольника с произвольно взятым
полюсом О.
Затем из точки А (единственно известной точки), находящейся
на линии действия неизвестной реакции опоры А фермы (рис. 37,6),
проводим первую сторону ка веревочного многоугольника до пере-
пересечения ее с линией действия силы Ръ но так как линия действия
этой силы проходит через точку Л, то 'сторона ка веревочного
многоугольника обращается в точку. Из точки А проводим вторую
сторону b веревочного многоугольника до пересечения ее с линией
действия силы Р2; затем, аналогично предыдущему, проводим сто-
стороны с, d и ?, доводя сторону е до встречи в точке / с известной
линией действия реакции В, после чего полученную точку соеди-
соединяем с точкой А прямой — стороной / веревочного многоугольника.
Проведя из полюса О силового многоугольника прямую, парал-
параллельную стороне / веревочного многоугольника, до пересечения
ее с прямой, параллельной линии действия реакции В, проведен-
проведенной из конца вектора силы Р4, найдем реакцию В\ соединив по-
полученную точку пересечения с начальной точкой построения си-
силового многоугольника, найдем реакцию Л.
2. Определяем усилия, возникающие в стержнях фермы.
Построенный силовой многоугольник не может служить основой
для построения диаграммы Максвелла-Кремоны, так как при его
построении не соблюден основной принцип — отложение всех
внешних сил в порядке приложения их к ферме, при обходе ее
по ходу часовой стрелки (при соблюдении этого принципа после
силы Р4 должна была быть отложена реакция Л, а не В).
Основы графической статики
151
Для построения диаграммы Максвелла-Кремоны строим второй
силовой многоугольник /, 2,3, 4у 5, 6, J (рис. 37,#), рассматривая уже
все внешние силы (активные и реактивные) в необходимой для
этого последовательности, считая реакции опор фермы известными *.
Устанавливаем последовательность вырезания узлов фермы.
Вырезание можно начинать с любого из узлов А и /(. Сохраняя
ранее выбранную последовательность, отметим только, что, зная
реакцию Л, можно после узла D рассматривать равновесие лк*-
бого из узлов А и В.
Строим диаграмму Максвелла-Кремоны (рис. 37,#).
Построив силовые многоугольники равновесия для узлов /С, Е9 F,
С и D, переходим к рассмотрению равновесия узла В, к которому
приложены известные силы В^г, Рг-з и усилия S3-s и S8-7.
Для определения единственного в этом узле неизвестного уси-
усилия S7—j проводим из вершины / прямую, параллельную линии
действия усилия 57_j. Так как эта прямая проходит через вершину
7 диаграммы, следевательно вся она построена правильно.
Измерив в принятом масштабе реакции опор А и В фермы, най-
найдем:
В = 2,7 /я; А = 4,04 /я; (ХА = 2,7 m; YA = 3 /я).
Измерив в том же масштабе возникшие в стержнях усилия,
внесем их значения в таблицу.
Обозначение
усилия
s^
$10-4
$11—5
Se-r
S6-U
$11—10
Sr-s
S9—10
Величина усилия
растягивающего (+)
2,05
1,03
1,03
' —
—
—
—
—
—
1,75
1,35
(в т)
сжимающего (—)
—
—
—
2,70
1,80
0,90
3,00
1,50
1,00
—
1 Можно обойтись без построения второго силового многоугольника, если
ири построении силового многоугольника и диаграммы Максвелла-Кремоны откла-
откладывать все внешние силы в порядке приложения их к ферме, при обходе ее
против хода часовой стрелки.
152 Статика твердого тела
РАЗДЕЛ ВТОРОЙ
СИСТЕМА СИЛ, ДЕЙСТВУЮЩИХ В ПРОСТРАНСТВЕ
ГЛАВА IX
СИЛЫ, ЛИНИИ ДЕЙСТВИЯ КОТОРЫХ ПЕРЕСЕКАЮТСЯ
В ОДНОЙ ТОЧКЕ
§ 1, Определение равнодействующей пространственного
пучка сил
Равнодействующая пространственного пучка сил по величине
и направлению выражается диагональю параллелепипеда, пост-
построенного на векторах, изображающих эти силы; точкой приложе-
приложения равнодействующей является точка приложения пучка сил.
Величина равнодействующей и углы, образуемые ею с коорди-
координатными осями, определяются из формул
cos (/?, a:) =
cos (#, #) =
cos (#, г) = ^
§ 2, Разложение одной силы на три взаимно перпендикулярные
составляющие
Разложение одной силы на три взаимно перпендикулярные сос-
составляющие производится так, чтобы эта сила представляла собой
диагональ параллелепипеда, а его стороны — составляющие
силы; определение величин сил и углов производится по формулам
(IX, 1).
§ 3. Аналитические условия равновесия пространственного
пучка сил
Аналитические условия равновесия пространственного пучка
сил выражаются тремя уравнениями равновесия:
и формулируются так:
Силы, линии действия которых пересекаются в одной точке 153
Пространственная система пересекающихся в одной точке сил
находится в равновесии, если сумма проекций всех сил на каждую
из трех координатных осей равна нулю г.
§ 4. Методические указания к решению задач
1. Рассматриваемые в данной главе конструкции представляют
собой системы стержней, соединенных между собой при помощи
шарниров, поэтому все сказанное в главе I, § 7 относится и к этим
конструкциям.
2. Решение задачи нужно начинать с рассмотрения равновесия
такого узла (шарнира), к которому приложена известная сила.
3. Координатные оси следует располагать так, чтобы углы между
силами и осями были известны или чтобы их легко можно было
найти.
4. Когда известны только углы между силами и координат-
координатными плоскостями (углы между силами и осями неизвестны), то
проектирование сил на ту или иную ось производится в два приема:
сначала силы проектируют на плоскость, в которой расположена
соответствующая ось, а затем уже полученную проекцию проекти-
проектируют на ось.
5. Когда углы между силами и координатными осями или
координатными плоскостями неизвестны, то силы сначала проек-
проектируют на какие-либо определенные прямые линии, углы откло-
отклонения которых от осей известны, а затем уже проектируют полу-
полученные проекции на соответствующие оси.
# 6. Если рассматриваемая схема конструкции и нагрузки сим-
симметрична, то, располагая две координатные оси в плоскости сим-
симметрии, а третью — перпендикулярно к ней и используя условия
симметрии, можно привести число неизвестных к двум (урав-
(уравнение проекций всех сил на ось, перпендикулярную к плоскости
симметрии, обращается в тождество).
7. В некоторых случаях решение задачи можно упростить,
приведя все силы к одной плоскости, если это не связано с гро-
громоздкими геометрическими и тригонометрическими вычислениями.
§ 5. Порядок решения задач
Большинство зад&ч этого раздела рекомендуем решать в сле-
следующем порядке:
1. Установить, равновесие какой части конструкции (узла,
шарнира) нужно рассмотреть, чтобы определить неизвестные ве-
величины.
1 Три расположенные в пространстве силы, линии действия которых пере-
пересекаются в одной точке, не могут быть в равновесии, так как любая из них направ-
направлена под углом к равнодействующей остальных двух сил, расположенных в
какой-либо плоскости. Такая система обязательно приводится к равнодействую-
равнодействующей.
154 Статика твердого тела
2. Установить, какие активные силы приложены к рассмат-
рассматриваемой части конструкции; отбросив связи или применив метод
сечений, заменить действие связей силами.
3. Составить схему действия сил на рассматриваемую часть
конструкции и выбрать направление координатных осей.
4. Составить уравнения равновесия (для этого иногда предва-
предварительно необходимо определить некоторые геометрические или
тригонометрические величины).
5. Решив уравнения равновесия, определить неизвестные; опре-
определив знаки неизвестных сил, установить их фактическое направ-
направление.
§ 6. Задачи
38. Подъемный кран (рис. 38,а) поднимает груз Q весом 2 т\
размеры его следующие: !АВ = АЕ = AF =2м\ угол EAF =>
= 90°; плоскость крана ЛВС делит прямой двугранный угол EABF
пополам. Определить силу Ръ сжимающую вертикальную стойку
АВ, и силы Р2, Р3, Р4, растягивающие струну ВС и тросы BE и В/\
пренебрегая весом частей крана.
Решение. Рассмотрим равновесие узла С, к которому приложе-
приложена активная сила Q (рис. 38, б).
Разложим силу Q на составляющие: Р2, растягивающую струну
ВС, и Р5, сжимающую стрелу Л С. Сила Р5 уравновешивается реак-
реакцией плоскости в точке А и никакого влияния на величины иско-
искомых усилий не оказывает, поэтому определять ее не будем; силу
же Р2 определим из подобия треугольников аЬС и ABC, предва-
предварительно найдя ВС из прямоугольного ДВ/СС.
ЯГ - ск - 5 • 2 - 10 л
DKj -sin60°- j/з"-" j/з
Составив равенство отношений сходственных сторон треуголь-
треугольников аЬС и ABC, найдем Р2:
?>С __ АВ
ah "~~ ВС'
откуда
О Д=
nh-p „ЬС-ВС _ Уд _ Ю _ - д
оь - р2 - —Тё- 2— - 7г '
Так как действующие в пространстве на шарнир В силы могут
быть приведены к одной плоскости, то решим задачу двумя спо-
способами.
Первый способа Рассмотрим равновесие шарнира В, приведя
все действующие на него силы к одной плоскости (рис. 38,в).
Силы, линии действия которых пересекаются в одной точке
155
К шарниру приложена сила Р2> направленная от В к С. При-
Применив метод сечений, отбросим связи Л, Е и F и заменим их дейст-
действие на шарнир В силами Plt Р3и Р4, направленными соответственно
по осям стойки АВ и тросов BE и BF (при выборе направлений
реакций исходим из предположения, что стойка и тросы растянуты).
К задаче 38.
Так как тросы BE и BF расположены симметрично пр отноше-
отношению к плоскости крана CBDAy то возникающие в них растягиваю-
растягивающие усилия равны между собой, т. е.
поэтому их равнодействующая R, разделив угол между ними попо-
пополам, располагается в плоскости крана. Для определения этого угла
рассмотрим прямоугольные при вершине А треугольники ВАЕ$
BAF и EAF.
По условию задачи все катеты указанных выше треугольников
равны между собой, следовательно, равны и их гипотенузы,
156 Статика твердого тела
являющиеся сторонами &FBE; поэтому каждый угол равносто-
равностороннего д FBE равен 60°, а линия BD перпендикулярна к основа-
основанию EF.
Величину R определим по формуле A,4), учитывая, что угол
между R и каждой из сторон BE и BF равен 30°:
R ' = 2Р • cos (RyP) = 2Р • cos 30° = 2Р . -^ = Р|/3" т.
Таким образом, к шарниру В в плоскости CBDA приложены
три силы: Р2, Рг и R.
Приняв точку В за начало координат, направим осъВх по гори-
горизонтали, а ось By — по вертикали.
Для составления уравнений проекций всех сил на эти оси
необходимо предварительно найти углы, образуемые силой R с
осями координат.
Из АВАЕ найдем его гипотенузу
BE = V\AEJ + (ABf = 1/24^2 = 2 уТм.
Из прямоугольного при вершине D &BDE найдем его катет
BD.
BD = B?.cos30° = 2У"~2 . ^-=1/бж.
Из прямоугольного при вершине A &BAD найдем тригономет-
тригонометрические функции /_ABD:
AR 9
cos/_ ABD = sin/_ BDA = ^ = -4„;
sin Z ABD = cos Z ВДЛ = ]/l — cos2/.^?> = ]/1 — ¦§• = ^ .
Применив формулы A,6), составим два уравнения равновесия
плоского пучка сил:
?Хг = Р2 • sin 60° — R • cos Z BDA = 0; A)
X^i = — Pi + P2 • cos 60° — Я • cos Z. ЛВЯ == 0. B)
Подставив в уравнения A) и B) найденные значения Р2, /?,
cos/_BDА и cos /_ ABD, получим:
из уравнения A)
откуда
из уравнения B)
Силы t линии действия которых пересекаются в одной точке 157
Положительные знаки при Р3 и Р4 и отрицательный при Рх
показывают, что тросы ?Е и BF растянуты, а стойка АВ сжата.
Второй способ. Рассмотрим равновесие шарнира б, находящегося
под действием пространственного пучка сил (рис. 38,#).
К шарниру приложены силы Р2, Рг, Р3 и Р4.
Приняв за начало координат точку В (рис. 38,г), направим ось
By горизонтально в плоскости ABC, ось Вх—перпендикулярно к
этой плоскости и параллельно прямой EF, ось Bz — вертикально.
Применив формулы (IX,2), составим два уравнения равновесия
пространственного пучка сил (так как приняли, что Р3 =Р4> то третье
уравнение равновесия — уравнение проекций всех сил на ось Вх
обращается в тождество).
Так как углы между осью By и силами Р, Р неизвестны, то
проекции этих сил на ось By получим путем двукратного проекти-
проектирования: сначала спроектируем их на плоскость^AEF, а затем най-
найденные проекции спроектируем на прямую AD, параллельную оси
~ \ = р2 . sin 60° — 2Р cos 45° • cos 45° = 0; (Г)
= —Рг + Р2 cos 60° — 2Р • cos 45° = 0. B')
Подставив в уравнение (Г) значение Р2, получим
1/3" " 2 2 ' 2 ~ U'
откуда
Р = 5 т.
Из уравнения B')
г^ |/3 2 2
откуда
Pi= — 4,2 т.
Из сопоставления обоих способов решения видно, что в данном
случае значение неизвестных сил проще найти, рассмотрев равно-
равновесие шарнира В9 находящегося под действием пространственного
пучка сил.
39. На гладком полу (рис. 39,а) стоит трехногий штатив; ниж-
нижние концы его ножек связаны веревками так, что ножки и веревки
штатива образуют правильный тетраэдр. К верхней точке шта-
штатива подвешен груз весом Р. Определить реакцию пола в точках
опоры и натяжение Т каждой веревки, выразив искомые величины
через Р.
Решение. Неизвестные Р и Т определим двумя способами:
1. Из рассмотрения равновесия одной из ножек штатива, на-
например АВУ предварительно приведя все действующие на нее силы
к одной плоскости.
158
Статика твердого тела
2. Из рассмотрения равновесия любого из нижних концов но-
ножек штатива, для' чего предварительно необходимо рассмотреть
равновесие узла Л, считая его шарнирным, и определить возни-
возникающее в каждой ножке штатива сжимающее усилие S.
К задаче 39.
Первый способ. Рассмотрим равновесие ножки АВ штатива
(рис. 39,6).
Исследуем сначала силы, действующие на конец А ножки АВ
штатива.
Силы, линии действия которых пересекаются в одной точке 159
На конец А каждой из трех ножек штатива, в том числе и АВ,
Р
действует вертикальная сила -д-> направленная вниз; кроме того,
в точке А конец ножки АВ, как и конец каждой ножки, испыты-
испытывает действие двух других ножек.
Выясним, в чем заключается это действие. Для этого силу
-тг, приложенную к концу А любой из двух других ножек, до-
допустим АС, разложим на две составляющие: S, действующую по
оси ножки Л С, и горизонтальную составляющую Sl9 действую-
действующую в вертикальной плоскости АОС.
Сила S, уравновешиваясь в точке С реакцией пола и реак-
реакциями веревок, никакого действия на ножки АВ и AD штатива
не оказывает, поэтому определять ее не будем; определим только
силу S±.
Обозначив сторону равностороннего A BCD через а, опре-
определим отрезок ОС, представляющий собой радиус окружности, опи-
описанной вокруг этого треугольника, воспользовавшись известной
из геометрии формулой
УЪ
Из прямоугольного при вершине О Д АОС найдем АО:
АО = ]/(ЛС)а-(ОС)* = V^ _ |- = aJ|_
(ЛС — сторона правильного тетраэдра — также равна а).
Из подобия треугольников АОС и Аос найдем:
откуда
Р — АО'
"Г
_Я_, ОС _ J>_ У&_ Р
3 •ДО- 3 ' aVT~ 3/2
р
Поступая аналогично с силой -^, приложенной к концу А ножки*
о
AD, заменим действие этой ножки на конец А ножки АВ горизон-
горизонтальной силой Slf действующей в плоскости AOD.
Таким образом, отделив в шарнире А концы ножек АС и AD
от конца ножки АВ (цис. 39,в), заменим их действие на него двумя
горизонтальными силами Slf равнодействующая Rx которых в силу
160 Статика твердого тела
симметрии делит угол между ними пополам, также горизонтальна,
находится в плоскости АОВ и равна S± г.
Исследуем силы, действующие на конец В ножки АВ штатива.
Конец В ножки АВ опирается на гладкий пол и в плоскости
пола связан веревками с концами С и D ножек АС и AD.
Равные между собой (в силу симметрии) реакции Т веревок
(рис. 39,г) направим по их осям — от В к С и D; их равнодейст-
равнодействующая R2 делит угол между ними пополам, также горизонтальна,
находится в плоскости АОВ и согласно формуле A,4) равна
2 7-cos30°. Реакция R гладкого пола (рис. 39,(9) направлена по
нормали к плоскости BCD, т. е. вертикально.
Итак, на отделенную от штатива ножку АВ действуют только си-
р
лы -^ /?lf R и R2, не пересекающиеся в одной точке, расположен-
о р
ные в плоскости АОВ, причем R || у, a Rt \\ R2 (рис, 39,д).
Приняв точку О за начало координат, направим ось Ох по ОВ,
а ось Оу — по вертикали О А (при таком расположении оси Ох
силы /?х и R2 проектируются на эту ось в натуральную величину).
Поскольку неизвестных величин только две, то, применив
формулы (IV,2), составим два уравнения равновесия твердого
тела — ножки АВ, к которой приложена плоская система сил.
^Xi = R1-R2 = 0; A)
VK4 = #_:?=0. B)
Выразив R± и R2 соответственно через Sx и 7\ получим из урав-
уравнения A)
R2 = 2Г • cos 30 = Rx = Sx = -Д= ,
2 х г 31/2
откуда
3]/2 • 2 соз 30° зг/2". 2 .
Из уравнения B)
Если бы мы составили третье уравнение равновесия — уравне-
уравнение моментов всех сил (рис. 39,д) относительно любой точки
плоскости действия системы сил, например точки О пересечения
р
линий действия сил у и /?2, то оно обязательно повторило бы
одно из двух уже составленных уравнений. Такое положение имеет
1 R\ — диагональ параллелограма, образующая с его сторонами равносто-
равносторонний треугольник.
Силы, линии действия которых пересекаются в одной точке 161
место всегда, когда действующие в одной плоскости взаимно урав-
уравновешивающиеся силы приводятся к двум парам.
Проверим это, составив уравнение моментов относительно точки О.
? Мо = R • ОВ — Rx • О А = 0. C)
Подставив найденные значения ОВ, О А и /?х в уравнение C),
получим:
УЪ 3 у2 УЪ
или, после сокращения на ~,
У'д
/? —-? = 0. C')
Уравнение C') полностью повторило уравнение B).
В силу симметрии в точках В, С и D пола возникают одинако-
одинаковые реакции /?, а в веревках у опор В, С и D — одинаковые натя-
натяжения Т.
Второй способ. Рассмотрим равновесие узла А (рис. 39,#).
К узлу А приложена активная вертикальная сила Р. Применив
метод сечений, отбросим связи В, С, D и их действие на узел за-
заменим силами Sbj Sc и Sb, направленными по осям ножек АВ,
АС и AD к узлу А (считаем, что все ножки сжаты).
В силу симметрии
SB = Sc = ^d = о.
Приняв за начало координат точку Л, направим ось Oz по
вертикали О А,
Составим уравнение проекций всех сил на ось Oz, для чего
предварительно определим cosa из &АОС:
аУ2
АО У Ъ У 2
cos а = -тгъ =4
ЛС
ЛС а
(значения ЛО и ЛС взяты из первого способа решения).
Решив это уравнение, получим
5 =
3 cos a
Знак плюс при S показывает, что направление силы принято пра-
правильно, т. е. что ножки штатива сжаты.
Перейдем к рассмотрению равновесия конца В ножки А В
(рис. 39, ж).
11 591
162 Статика твердого тела
К концу В по оси АВ приложена сжимающая сила S.
Применив метод сечений, отбросим связи и заменим их действие
на конец В двумя равными в силу симметрии силами Т>
направленными по осям веревок, а также вертикально направлен-
направленной силой R.
Приняв за начало координат точку В, направим ось Вх по
ВО, ось By — параллельно CD и ось Bz— вертикально.
Так как неизвестных величин две, то для их определения до-
достаточно составить два из трех уравнений равновесия пространст-
пространственного пучка сил (IX,2), а именно, уравнения проекций всех
сил на оси Вх и Bz (третье — уравнение проекций всех сил на ось
By — обращается в тождество, так как мы приняли, что реакции Т
веревок равны друг другу).
Предварительно определим sin а:
sin а = ]/1 — cos2 а = "V1 — ~ = — ;
2X<a=2r-cos300 —S • sina = 0; 00
ZZ^R — S. cosa^O. B')
Подставив в уравнения A') и B') значения S, sin a и cos a и решив
их, получим:
JL JL
S . sin а у6 "l/З" Р
2 • cos 30° |/з" 31/6" *
1/6
Проанализировав оба способа решения задачи, приходим к выво-
выводу, что второй способ значительно проще первого.
ГЛАВА, X
ПРИВЕДЕНИЕ ПРОИЗВОЛЬНОЙ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ
СИЛ К ПРОСТЕЙШЕМУ ВИДУ
§ 1. Порядок решения задач
В общем случае произвольная пространственная система сил
может быть приведена к одной силе, равной их главному вектору
R и приложенной в произвольной точке О, и к паре, момент которой
равен главному моменту Мд данных сил относительно этой точки.
При решении рассматриваемых в этой главе задач будем придер-
придерживаться следующего порядка:
Приведение произвольной системы сил к простейшему виду
163
1. Принимаем выбранный нами центр приведения за начало
координат и направляем координатные оси так, чтобы можно было
проще определять проекции сил на оси и моменты сил относительно
©тих осей.
2. Определяем проекции главного вектора R и главного мо-
момента Мо на каждую из трех координатных осей и на основе ана-
анализа результатов устанавливаем, к чему приводится заданная сис-
система сил.
3. Если каждая проекция R и Мо окажется равной нулю, то
и R и Мо также равны нулю, т. е. система сил уравновешивается.
4. Если окажется равной нулю каждая проекция R и не рав-
равной нулю хотя бы одна проекция М0У то система сил приводится
к паре, момент которой т равен главному моменту Мо данной
системы сил относительно центра приведения О.
Величина главного момента, и косинусы углов, образуемых им
с координатными осями, определяются по следующим формулам:
м
cos (Mo, x) = ~
о
м
cos (Мо, у) = -т/
о
м.
COS (Мо, 2) = тг
о
где Мд., Муи Мг — проекции Л10 на оси Ох, Оу и Oz, соответственно
равные суммам моментов всех сил относительно соответствующих
осей".
5. Если хотя бы одна из проекций R на координатные оси не
равна нулю, а каждая проекция Мо равна нулю, то система сил
приводится к равнодействующей, равной главному вектору R
системы, приложенной в центре приведения О.
Величина главного вектора R и косинусы углов, образуемых им
С координатными осями, определяются по следующим формулам:
R =
cos (#, х) = %
cos (/?, у) = -
cos (Я, г) = Ь
(Х,2)
где RX7 Ry и Rz—проекции R на оси Ох, Оу и Ог, соответственно рав-
равные суммам проекций всех сил на соответствующие оси.
II*
164 Статика твердого тела
6. Если хотя бы одна из проекций R и хотя бы одна из проекций
Мо не равны нулю, т. е. не равны нулю сами R и Мо, а Мо ока-
окажется перпендикулярным к /?, то система сил приводится к равно-
равнодействующей, равной главному вектору R заданной системы сил,
величина и направление которой определяются формулами (Х,2).
Перпендикулярность главного момента Мо к главному вектору
R устанавливается равенством нулю косинуса угла между ними,
Так как ни Ry ни Мо не равны нулю, то условием приведения
системы сил к равнодействующей является равенство нулю числи-
числителя этой дроби, т. е.
R* • Мх + Ry • Mv + RZ-MZ^O. (X, 3)
Положение точки 0х приложения равнодействующей может
быть определено после установления положения плоскости ROMOi
проходящей через R и Мо. Для этого необходимо сначала опре-
определить положение Мо, применив формулы (Х,1). Затем к этой
плоскости восставляется перпендикуляр ООЪ равный •—, в
такую сторону, чтобы наблюдателю, расположенному по вектору
момента Мо, пара представлялась вращающей свою плоскость против
часовой стрелки.
7. Если главный вектор R и главный момент Мо не равны нулю
и, кроме того, главный момент Мо не перпендикулярен к главному
вектору Ry т. е. если не соблюдается условие (Х,3), то система сил
приводится к динаме, т. е. к силе, равной главному вектору R, и
паре, момент которой Мг параллелен силе R (плоскость действия
пары перпендикулярна к силе R). Линия действия силы R на-
называется центральной винтовой осью данной системы сил.
Величина главного момента М1 динамы определяется проекцией
на главный вектор R главного момента Мо данной системы сил
относительно центра приведения О:
М^М0. cos (Мв, *)= ^^.^±^3. (ХL)
Величина и направление R определены раньше из формул (Х,2).
Координаты х и у точки пересечения центральной винтовой
оси данной системы сил с плоскостью хОу определяются следующими
уравнениями центральной винтовой оси после подстановки в них
г =0:
Mx-(yRz-zRy) Mv-{z-Rx-x-Rz)
_
Приведение произвольной системы сил к простейшему виду
165
Примечание. Рассмотренные в пунктах 3, 4, 5 и 6 системы сил пред-
представляют собой частные случаи общего случая, рассмотренного в пункте 7, когда
система сил приводится к динаме.
§ 2. Задачи
40. К вершинам Л, С, D и F куба ABCDEFKO (рис. 40) со сто-
стороной а = 10 см приложены шесть сил по 5 кг каждая. Привести
эту систему сил к простейшему виду.
Решение. Найдем проекции главного вектора R заданной систе-
системы сил на координатные оси по формулам (Х,2):
Я„=Р4-Р3 = 0;
следовательно, главный вектор
D ЛID^ f С>^ ! D^" П
/\ :== у J\x "Т" ^2/ *Т" ^z ¦— ^»
Найдем величину главного мо-
момента Мо заданной системы сил и
образуемые им с координатными
осями углы по формулам (Х,1):
Му = Р2 • а + Р6 • а = 2Ра;
Л12 = Рх • а + Р4 • а = 2Ра,
следовательно, главный момент
СУ
К задаче 40.
Мо = Ум^ + М^ + Ml = уО + 4Р2 . а2 + 4Р2 . а2 =
= 2Р • а 1/2 = 2 • 5 • 10 • 1,41 = 141 /сг. слг;
cos (Мо, х)=7-2 =
cos
cos(Mo, г)
следовательно,
Z (АГв, х) = 90°; /
2Р • а 1/2
2Р ¦ а
2Р . а V2"
2Р «с
2Р • а 1/2"
У1
2
45° и Z (Afe, г) = 45°,
т. е. главный момент Мо направлен по диагонали ОВ грани АВСО
куба от О к В.
Таким образом, заданная система сил приводится к паре, дей-
действующей в какой-либо плоскости, перпендикулярной к 0В\ мо-
166
Статика твердого тела
мент этой пары равен главному моменту Мо заданной системы сил
относительно центра приведения О.
41. К вершинам O,F,C и Е куба ABCDEFKO (рис. 41) при-
приложены четыре равные силы: Рг = Р2 = Р3 = Р4 = Р. Привести
эту систему сил к простейшему виду.
Решение. Приняв точку О за центр приведения и начало коор-
координат, направим оси Ох, Оу и Ог соответственно по сторонам Of,
i
4
л °
X
К задаче 41
ОС и О4 куба.
Найдем величину главного векто-
вектора R заданной системы сил и обра-
образуемые им с координатными осями
углы по формулам (Х,2).
Rx =, рг . cos 45° — Р2 • cos 45° = 0;
Ry = P1. cos45° + Р2 -cos45° —
— Р3 • cos 45° + Р4 . cos 45° =
И? = РУ2 ;
- cos 45° = 2Р
Р3 - cos 45° + Р4 • cos 45° =
следовательно, главный вектор
r^VRI + RI + Щ-
2~P* = 2P;
R
R.
РУ2
2
следовательно,
Z(/?^)=90°; Z(/?,y) = 45° и Z(tf,z) = 45°,
т. е. главный вектор R направлен по диагонали ОВ грани АВСО
куба от О к В.
Найдем проекции главного момента Мо системы сил на коорди-
координатные оси по формулам (Х,1). Сторону куба примем равной а.
МХ = Р3. cos 45° . a — Pz- cos 45° • а = 0;
My = — Р2 • cos 45° • а — Р4 • cos 45° - а = — 2Р • cos 45° • а =
= —2Р*-^-*а = —Р -
Л1, = Р2. cos45° • а + Р4 • cos45° • а = 2Р . cos 45° . а = Р • а|/ f
следовательно, Мо не равен нулю.
Приведение произвольной системы сил к простейшему виду 167
Проверим, приводится ли система сил к равнодействующей,
т. е. соблюдается ли равенство (Х,3).
— Р • a J/2)
+ Р |/ • Р • а У 2 = 0.
Так как равенство (Х,3) соблюдается, то главный момент Мо
перпендикулярен к главному вектору R и система сил приводится
к равнодействующей, равной главному вектору R системы.
Для определения положения плоскости R0M0 найдем величину
главного момента Мо и углы, образуемые им с координатными
осями, по формулам (Х,1):
Мо = УЩ + Ml + М\ = КО + 2Р2 • а2 + 2Р2- а2 = 2Р . а;
cos (Mo, x)=*jj* = ^р— = 0;
COS
С05<УИ0> 2) = -^ = -gpTT" = Т" '
О
следовательно,
/1 (Л10, jc) = 90°, Z (Л4в, у) = 135° и Z (Af«, 2) = 45°.
Таким образом, главный момент Мо заданной системы сил
расположен в вертикальной плоскости yOz и направлен от точки О
по биссектрисе угла, образованного осью Oz и продолжением
влево оси Оу, перпендикулярно к главному вектору /?.
Определим расстояние ОХО точки приложения (О^ равнодейст-
равнодействующей от точки О.
Мп 2Р - а
ОгО =-$ = -&-= *-
Отложив отрезок ОгО в соответствующую сторону (глава X, § 1,
пункт 6) на перпендикуляре ОЕ к плоскости R0M0 (yOz)% в ко-
которой расположены и главный вектор R и главный момент Мо систе-
системы, найдем, что точка Ог совпадает с точкой Е и что линия дейст-
действия равнодействующей направлена от Я к К по диагонали ЕК
грани EFKD куба.
Решение задачи может быть значительно упрощено, если после
установления перпендикулярности главного %момента Мо к глав-
главному вектору R приступить к определению координат точки пере-
пересечения центральной оси системы (линии действия равнодействую-
равнодействующей), параллельной главному вектору R, с плоскостью хОу.
168
Статика твердого тела
Для этого в формулы (Х,5)
M-{x.R-y.R)
подставим ранее найденные величины, а также 2=0 и получим
два уравнения:
¦ у - Р Т/2 __ — Р - а 1/2 + х . Р Т/2
0 — / '
— Я • а |/2
аУ2—х . /> j/2"
Я Т/2"
A)
B)
Правая часть уравнения A) — число конечное, следовательно,
и левая часть его также число конечное, а это может быть только
при у =0, когда левая часть уравнения A) обращается в неопре-
неопределенность; при любых других значениях у левая часть уравнения
обратилась бы в бесконечность, что противоречило бы правой
части уравнения A).
1г Из уравнения B)
следовательно,
х = а.
Таким образом, координаты точки пе-
ресечения центральной оси заданной си-
системы сил с плоскостью хОу следующие:
х = а\ у = 0.
К задаче 42.
Так как этим координатам соответствует
точка Е, то она и является точкой пере-
пересечения линии действия равнодействующей, направленной по ЕК
параллельно R.
42. По ребрам куба ABCDEFKO, равным а (рис. 42), действуют
двенадцать равных сил Р. Привести эту систему сил к каноничес-
каноническому виду и определить координаты х и у точки пересечения цент-
центральной винтовой оси с плоскостью хОу.
Решение. Найдем величину главного вектора R заданной систе-
системы сил и углы, образуемые им с координатными осями, по форму-
формулам (Х,2).
Я. =
Приведение произвольной системы сил к простейшему виду 169
следовательно, главный вектор
R = УЩТЩТЩ = У4Р* + 4Р*+ 16/32 = 2Р
R 2P
cos (Л, 0 = Tf=»
Найдем проекции главного момента Мо заданной системы
сил на координатные оси по формулам (Х,1):
Мх = Р3 • а + Р4 -а — Р6 • а + Р12 • а - 2Р . а\
М9 = Р6-а — Р7-а — Р9-а — Ръ-а = —2Р.а;
М9 = Рв.а + Р7. а+ Р10 .'а + Ри- а = 4Р - а.
Проверим, перпендикулярен ли главный момент Мо к глав-
главному вектору R, т. е. соблюдается ли равенство (Х,3).
R* • М, + Rv • Му + ^2 . М2 = (-2Р) • 2Р . а +
+ 2Р • (— 2Р • а) + АР - 4Р • а = 8Р2 • а> О,
следовательно, главный момент УИ0 не перпендикулярен к глав-
главному зектору R и заданная система сил приводится к динаме.
Найдем главный момент Мх динамы по формуле (Х,4):
М} - М. • cos (Mo, R} = ^-^ + V^ + ^^. =
Определим координаты хну точки пересечения винтовой оси с
плоскостью хОу по формулам (Х.,5):
Mx-(yR-z ¦ Ry) _ My-(z-Rx-x-Rz) _ Mz - (x ¦ Ry - у ¦ RJ
Подставив ранее найденные величины, а также z = 0, получим
2Я ¦ а —у - АР __ — 2Р . a -f х • 4Я _ 4Я • а — х • 2Я + у • (— 2Р)
1Г2Р — 2Я ~ 4Р
Приравняв последовательно первое отношение второму и третье-
третьему, получим систему двух уравнений с двумя неизвестными:
4у — 2а = 4л: — 2а,
4(/ — 2а = 2а — х — у,^
решив которую, найдем
2
х = у = ~а.
170 Статика твердого тела
ГЛАВА XI
ПРОИЗВОЛЬНАЯ ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ,
НЕ ПЕРЕСЕКАЮЩИХСЯ В ОДНОЙ ТОЧКЕ
§ 1. Аналитические условия равновесия. Частные случаи
Аналитические условия равновесия произвольной пространствен-
пространственной системы сил, приложенных к свободному твердому телу, вы-
выражаются шестью уравнениями равновесия:
0 |
и формулируются так: произвольная пространственная система сил
находится в равновесии, если сумма проекций всех сил на каждую
из трех координатных осей и сумма моментов их относительно
каждой из этих осей равны нулю.
В частном случае, когда все приложенные к телу силы действуют
в параллельных плоскостях, уравнение проекций всех сил на
ось, перпендикулярную к этим плоскостям, допустим у, обращается
в тождество. В этом случае условия равновесия выражаются пятью
уравнениями равновесия:
V.Xi=0; VZt==-0; |
В частном случае, когда в'се силы параллельны между собой,урав-
нение проекций всех сил на каждую из двух осей, перпендикулярных
к силам, и уравнение моментов всех сил относительно, оси, им
параллельной, обращаются в тождество. В этом случае условия
равновесия выражаются тремя уравнениями равновесия:
(XI а
Следует напомнить, что момент относительно оси создает не
вся сила, а только ее составляющая, находящаяся в перпендику-
перпендикулярной к оси плоскости; поэтому момент силы относительно оси
равен моменту проекции силы на плоскость, перпендикулярную
к оси, относительно точки пересечения оси с этой плоскостью.
Не создают момента относительно оси только силы, параллельные
ей или пересекающие ее, т. е. силы, расположенные в одной с нею
плоскости, так как в этом случае проекция силы или плечо проекции
силы обращается в нуль.
Для определения^неизвестных величин, возникающих в системе
связанных между собой твердых тел, находящихся под действие^
пространственной системы сил, необходимо, установив опреде-
определенную последовательность, рассмотреть равновесие каждого из
них в отдельности.
Произвольная система сил, не пересекающихся в одной точке 171
§ 2. Исследование связей и установление направления
их реакций
Исследуем связи, которые еще не рассматривались в предыду-
предыдущих главах (или рассматривались при действии иной системы сил),
и установим возможное направление реакций этих связей, пре-
пренебрегая возникающими в них незначительными силами трения.
Подпятник (рис. 1,а) — это тип опоры, не препятствую-
препятствующий повороту тела или какой-либо его детали вокруг своего центра,
Рис. I.
но препятствующий смещению тела в любом направлении, поэтому
для такого типа опоры неизвестны ни величина реакции, ни обра-
образуемые ею с координатными осями углы, а известна только точка
приложения реакции.
Такую реакцию будем представлять тремя составляющими, на-
направленными в положительные стороны трех координатных осей
(отрицательный знак, полученный при решении уравнения равно-
равновесия, покажет, что в действительности та или иная составляющая
опорной реакции направлена в противоположную выбранному на-
направлению сторону).
В большинстве задач и требуется определить не реакцию, а ее
составляющие; сама реакция может быть найдена как диагональ
прямоугольного параллелепипеда, построенного на составляющих
X, Y> Z как на сторонах, по следующим формулам:
cos (tf, x)=~
Y
COS (R, У) = -jr
cos(/?, г) = ~fr
(XI.4)
172 Статика твердого тела
Болт препятствует смещению тела в любом направлении,
поэтому его реакцию также представляем тремя составляющими,
направленными по координатным осям.
Подшипник (рис. 1,6) — это цилиндрический шарнир,
позволяющий телу или его элементу (например, валу, оси крана,
и т. д.) поворачиваться вокруг своей оси, смещаться вдоль нее,
но не позволяющий ему перемещаться в плоскости, перпендику-
перпендикулярной к его оси, следовательно, реакция подшипника может быть
расположена только в плоскости, перпендикулярной к его оси.
Зная в этой плоскости только точку приложения реакции и не
зная угла, образуемого ею с какой-либо находящейся в этой плос-
плоскости осью, представляем реакцию двумя составляющими, на-
направленными в положительные стороны координатных осей, рас-
расположенных в этой плоскости. Сама реакция R может быть опре-
определена как равнодействующая найденных составляющих X и Y
по формулам:
. ? = ух* + F2,
cos (R, х) = -? ; cos (#, у) = ^ - (Х1> 5)
Реакции петель определяются так же, как и реакции
подшипников.
Примечание. В зависимости от характера действующих сил (их на-
направления по отношению к телу) часть составляющих опорных реакций, рас-
рассмотренных в данном параграфе, может обращаться в нуль.
Реакции опор, расположенных под колесами какого-
либо транспорта или механизма, направлены по нормали к плос-
плоскости перемещения колес (незначительными силами трения пре-
пренебрегаем).
§ 3. Методические указания к решению задач
1. Положение осей рекомендуем выбирать так, чтобы они были
параллельны или перпендикулярны к возможно большему коли-
количеству неизвестных сил, тогда такие неизвестные силы соответст-
соответственно либо проектируются на эти оси в натуральную величину,
либо их проекции равны нулю. Кроме того, желательно так вы-
выбирать начало координат, чтобы оси пересекали возможно большее
количество неизвестных сил, тогда такие силы (параллельные
осям или их пересекающие) не войдут в уравнения моментов.
Примечание. Если это приводит к упрощению, то можно для состав-
составления уравнения прекций сил выбирать одни оси, а для составления уравнения
моментов сил — другие.
2. В случаях, когда активные силы не параллельны ни одной
из координатных осей,, для упрощения составления некоторых
Произвольная система сил, не пересекающихся в одной точке 173
уравнений равновесия иногда лучше предварительно разложить
силы на составляющие, параллельные осям.
3. При составлении уравнения моментов всех сил относительно
какой-либо оси иногда, в связи с отсутствием некоторых размеров
целесообразно вводить в уравнение момент равнодействующей
некоторых сил, что приводит к упрощению решения задачи (см. ре-
решение задачи 48).
4. Так как составление уравнений моментов сил относительно
осей вызывает иногда некоторые затруднения, то рекомендуем для
облегчения составлять вспомогательные рисунки, представляющие
собой проекции рассматриваемой конструкции и приложенных к
ней сил на плоскости, перпендикулярные к тем осям, относительно
которых определяются моменты сил. При составлении каждого
такого рисунка наблюдатель предполагается расположенным в
положительной направлении соответствующей оси.
§ 4. Порядок решения задач
Большинство рассматриваемых в этой главе задач рекомен-
рекомендуем решать в следующем порядке.
1. Установить, равновесие какого тела нужно рассмотреть,
чтобы определить неизвестные величины.
2. Выбрать начало координат и положение координатных осей.
3. Установить, какие активные силы действуют на тело.
4. Отбросив связи или применив метод сечений, заменить дей-
действие связей -силами.
5. Составить соответствующие уравнения равновесия.
6. Решив уравнения равновесия, определить неизвестные ве-
величины (для этого иногда нужно предварительно определить не-
некоторые геометрические или тригонометрические величины). Найдя
знаки неизвестных сил, установить их фактические направления.
7. Если найдены реакции связей, а необходимо найти давле-
давления, оказываемые телом на те или иные плоскости (поверхности), —
учесть, что, согласно аксиоме 5, давления равны реакциям по
величине, но направлены в противоположные им стороны.
§ 5. Задачи
43. Подъемный кран (рис. 43,а) установлен на трехколесной
тележке ABC. Известны размеры крана: AD = DB = 1 м\ CD =
= 1,5 м\ СМ =1 м\ KL = 4 м. Кран уравновешивается проти-
противовесом F. Вес Р крана с противовесом равен 8 т и приложен
в точке G, расположенной в плоскости LMNF на расстоянии GH =
= 1 м от оси крана MN; поднимаемый груз Q весит 4 /п. Найти
давление колес на рельсы для такого положения крана, когда
плоскость его LMF параллельна АВ.
174
Статика твердого тела
Решение. Рассмотрим равновесие трехколесной тележки ABC
с укрепленным на ней подъемным краном (рис. 43,6).
На тележку действуют две активные вертикальные силы: вес
Р крана с противовесом и груз Q. Освободив тележку от связей
Л, В и С, заменим их действие на нее силами RA, RB и Rc, на-
направленными вертикально вверх (трением на опорах пренебре-
пренебрегаем). Таким образом, тележка находится в равновесии под дейст-
действием пространственной системы параллельных сил.
Az
К задаче 43.
Приняв за начало координат точку А, направим ось Ау по
ЛВ, ось Ах— параллельно DC и ось Аг — вертикально.
При таком расположении осей, как это будет видно из даль-
дальнейшего решения, упростится составление уравнений равновесия
заданной системы сил.
Применив формулы (Х1,3), составим три уравнения равновесия
свободного твердого тела — тележки ABC:
SZi^Rt+RB + Rc — P — Q^O; 0>
2Afe = -Q.5 + /?c/ 1+ЯБ.2 = 0 B)
(момент силы Р относительно оси равен нулю, так как линия
действия силы Р пересекает ось; по этой же причине равен нулю
и момент реакции R);
= P.0,5 + Q -0,5 — Rc • 1,5 = 0. C)
Подставив данные из условия задачи в уравнение C), B) и A)
и решив их в указанной последовательности, найдем:
Rc = 4m; RB = 8m и ^ = 0'
(если бы ось Ах направить по DC, то количество неизвестных,
вошедших в уравнение B), не изменилось бы, так как вместо мо-
'Произвольная система сил, не пересекающихся в одной точке 175
мента реакции Rc вошел бы момент реакции RA, а число членов
в уравнении увеличилось бы> так как в уравнение вошел бы еще
момент силы Р).
Давления колес В и С тележки
на рельсы равны по величине, но
направлены в противоположные
реакциям стороны, т. е. верти-
вертикально вниз.
NB = Rb = 8 m;
Nc = Rc = 4 m. ¦
Примечание. Тележка не ока-
вывает давления на опору А при данных,
указанных в условии задачи; измене-
изменение же хотя бы одного из них приведет
к возникновению этого давления,
44. Однородная прямоугольная
крышка (рис. 44,а) весом Р =
= 20 кг удерживается приоткры-
приоткрытой на 60° над горизонтом противо-
противовесом Q. Определить, пренебрегая
трением на блоке Z), вес Q и
реакции петель Л и В, если блок
укреплен на одной вертикали с Л,
a AD = АС.
Решение. Рассмотрим равно-
равновесие крышки (рис. 44,6).
Приняв за начало координат
точку Л, направим координатные
оси согласно рис. 44,6. При таком
выборе начала координат в урав-
уравнение моментов сил относительно
оси Л г не войдет сила Q, пере-
пересекающая эту ось, благодаря чему
число членов в уравнении умень-
уменьшится.
Неподвижный блок D, не изменяя величины груза Q, изме-
изменяет его направление, следовательно, в точке С плоскости ACD
на крышку по направлению CD действует наклонная активная
сила Q, кроме того, в центре тяжести однородной крышки прило-
приложена сила Р — ее вес* а в точках А и В приложены реакции свя-
связей — петель.
Так как обе активные силы действуют в плоскостях, перпен-
176 Статика твердого тела
дикулярных к ребру АВ крышки, то составляющие YA, ZA и YBt ZB
опорных реакций в шарнирах А и В также действуют в плоскостях,
перпендикулярных к этому ребру.
Для составления уравнений равновесия данной системы сил
предварительно определим угол наклона силы Q к горизонту.
Для этого воспользуемся рис. 44,в, представляющим собой
проекцию рассматриваемой крышки — вместе с приложенными к
ней силами — на плоскость уАг.
Использовав условие задачи, устанавливаем, что /JZAD рав-
равнобедренного ДСАО равен 30°, а угль/при его основании CD —
по 75°. Затем, восставив перпендикуляр к оси Az из произвольной
точки S и доведя его до пересечения с линией действия силы
Q в точке О, найдем из прямоугольного AODS угол наклона
гипотенузы OD (а следовательно, и силы Q) к горизонту; этот
угол равен 15°.
Применив формулы (Х1,2), составим пять уравнений равно-
равновесия твердого тела — крышки, находящейся под действием про-
пространственной системы сил, расположенных в перпендикулярных
к ее оси плоскостях (шестое уравнение равновесия — уравнение
проекций всех сил на ось Ах обращается в тождество).
V Yt = YA + YB - Q • cos 15° = 0; 0>
? Z{ = ZA + ZB + Q . sin 15° - P = 0. B)
Для составления уравнений моментов всех сил относительно
оси Ах будем пользоваться вспомогательным рисунком 44,#.
У] Мх = Q . А Е — Р • АК = 0 C)
{составляющие опорных реакций — YAtZA и YBy ZB, пересекаю-
пересекающие ось Ах, не вошли в уравнение моментов всех сил относительно
оси Аху так как момент каждой из этих сил относительно этой оси
равен нулю);
%Mv=-ZB.AB-P.^ = 0 . D)
{силы Q, YА и ZAi находящиеся в одной плоскости с осью Ау, и
сила Yb, параллельная оси Ау, не вошли в уравнение моментов всех
сил относительно этой оси, так как момент каждой из них отно-
относительно оси А у равен нулю);
1]Л1г = — YB • AB = 0 Ef
(силы Q, YA и ZA находятся в одной плоскости с осью Az, а сила
Р параллельна ей, следовательно, момент каждой из этих сил
относительно этой оси равен нулю).
Определим величины АЕ и АК> вошедшие в уравнение C).
Из прямоугольного при вершине Е /\АЕС:
АЕ = АС • cos 15°.
Произвольная система сил, не пересекающихся в одной точке 177
Из прямоугольного при вершине К ?±AFK
AK = AF- cos 60° = Щ • cos 60°.
После подстановки найденных значений уравнение C) примет
следующий вид:
У>МХ= Q. AC -cos 15°— Р-Щ.cos60° = 0. C')
Подставив данные из условия задачи и значения тригономет-
тригонометрических функций углов в уравнения D), C'), B), E) и A) и решив
их в указанной последовательности, найдем:
ZB = 10 кг; Q = 5,18 кг; ZA = 8,66 кг;
YB = 0; YА = 5 'кг.
45. Прямоугольная дверь (рис. 45,а), имеющая вертикальную
ось вращения АВ, открыта на /JCAD =60° и удерживается в
этом положении двумя веревками, из которых одна—CD перекинута
через блок D и натягивается грузом Р =20 кг, а другая — EF при-
привязана в точке F пола. Вес двери равен 40 кг, ее ширина AD = Л С =
= 1 му высота АВ = 2 м. Определить, пренебрегая трением на
блоке, натяжение Т веревки EF, а также реакции цилиндрического
шарнира в точке А и подпятника ё точке В.
Решение. Рассмотрим равновесие двери ВАСЕ (рис. 45,6).
Приняв за начало координат точку В, направим координатные
оси согласно рис. 45,6.
Неподвижный блок D, не изменяя величины груза Р, изменяет
его направление, следовательно, в точке С на дверь действует на-
находящаяся в горизонтальной плоскости ACD активная сила Р,
направленная по оси веревки CD. Кроме того, к точке О — центру
тяжести двери ВАСЕ (геометрическому центру прямоугольника
ВАСЕ) приложена вертикальная сила Q — ее вес, а в точках А и
В к двери приложены реакции связей.
Реакцию цилиндрического шарнира А представим в виде двух
составляющих Ха и Ya; реакцию подпятника В представим в виде
трех составляющих: Хв, У в и ZB; реакцию Т веревки EF, по ве-
величине равную ее натяжению Т, направим по оси веревки otEkF.
Перед составлением уравнений равновесия разложим силу
Р на две составляющие силы, параллельные осям Вх и By (это
облегчит составление уравнений).
Для определения составляющих воспользуемся рис. 45,5, пред-
представляющим собой проекцию двери — вместе с приложенными
к ней силами — на плоскость хВу.
Использовав условие задачи, устанавливаем, что /_ACD =
= Z_ADC = 60° как углы при основании CD равнобедренного
ЛСО, угол при вершине А которого равен 60°..
12 591
178
Статика твердого тела
а
а
/1
2
*в
ЯП
в
К задаче 45.
Из рис. 45,5 видно, что:
Ря — Р • sin 60°;
Ру = Р . cos 60°.
Применив формулы (Х1,1), составим шесть уравнений равно-
равновесия твердого тела — двери ВАСЕ, находящейся под действием
произвольной пространственной системы сил:
у лг __ лг , дг р __ q /JJ
V Z- = Zb Q = 0. C)
Для составления уравнения моментов всех сил относительно
осей Вх, By и Bz будем пользоваться вспомогательными рисунками
Произвольная система сил, не пересекающихся в одной точке Г79
45,в, г, <Э, представляющими собой проекции двери — вместе с при-
приложенными к ней силами — на плоскости yBz, xBz и хВу.
?Mx = -Q-O1N~YA.AB-Py.AB = 0 D)
(силы ХВу Yb иТ находятся в одной плоскости с осью Вху сила ZB
пересекает ее, а силы ХА и Ps— параллельны ей; момент каж-
каждой из указанных выше сил относительно оси Вх равен нулю).
XA - АВ — Рх- ЛВ = 0 E)
(силы Хв, YB и Т находятся в одной плоскости с осью By, сила
ZB пересекает ось By, а силы YA и Ру параллельны оси Ву\ мо-
момент каждой из этих сил относительно' оси By равен нулю).
2 мг = р. am — т. щ = о F)
(силы Хл, Уа, Хв и F^g пересекают ось Вг, сила Z^ направлена
по оси Bz и сила Q параллельна оси Bz; момент каждой из этих
сил относительно оси Bz равен нулю).
Определим вошедшие в уравнения D), E) и F) величины AM,
ВК, OtN и BN.
Из прямоугольного Д АМС:
АМ = АС- sin 60°.
Из прямоугольного Д /(В?:
В/( = ЛС . sin 60°.
Из прямоугольного Д BOXN:
После подстановки найденных значений уравнения A), B),
D), E) и F) примут следующий вид:
V х, == ХА + Хв — Р • sin 60° ^ 0; (Г)
~~ ЛП — YA-AB — P .cos60° • ЛВ = 0; Dл)
^ • sin 60° + ХА • АВ — Р . sin 60° ¦ ЛВ = 0; E')
1г = Р . АС - sin60° — Т • ЛС • sin60° = 0. F0
Подставив данные из условия задачи и значения тригонометри-
тригонометрических функций углов в уравнения C), D'), E'), (Г). F') и B) и
решив их в указанной выше последовательности, найдем:
ZBx= 40 кг; YA = — 15 кг; ХА = 8,66 кг;
Хв = 8,66 кг; Т = 20 кг; YB = 25 /сг.
12*
180 Статика твердого тела
46. Ветряная мельница (рис. 46,а) с горизонтальной осью FC
имеет четыре симметрично расположенных крыла, плоскости
которых (рис. 46,6)* составляют с вертикальной плоскостью, пер-
перпендикулярной к оси FC, углы, равные 30°. На расстоянии 2 м
от оси к каждому крылу приложена нормально к его плоскости
равнодействующая сил давления ветра, равная 90 кг. Ось
мельницы опирается в точке А (рис. 46,а) на подшипник, в
точке С — на подпятник и удерживается в покое вертикальным
давлением Р на зубец колеса В, производимым не показанной на ри-
рисунке шестерней. Радиус колеса В раЬен 0,8 м\ расстояния ВС, АВ
и AF соответственно равны 0,5 м, 1 м и 0,5 м. Определить дав-
давление Р и реакции опор в двух случаях: 1) когда ветер давит
на все четыре крыла и 2) когда крыло D снято, а линия DE
вертикальна.
Решение. Рассмотрим равновесие оси FC мельницы (рис. 46,в).
Приняв за начало координат точку С, направим оси согласно
рисунку.
К каждому крылу мельниЦы, соединенному с осью FC, перпен-
перпендикулярно к его плоскости приложена активная сила Q—сила ветра
(на рис. 46,6 показаны силы Q, приложенные к крыльям Е и D);
в плоскости В на зубец колеса, соединенного с осью FC, действует
активная вертикальная сила Р. Кроме того, к оси FC мельницы
в точках А и С приложены реакции подшипника и подпятника,
которые представим в виде составляющих Ya, Za и Хс, YC) Zc
(все составляющие опорных реакции направим в положительные
стороны соответствующих координатных осей).
Для облегчения составления уравнений равновесия данной
системы сил предварительно разложим каждую силу Q на две
составляющие: 7\ действующую в перпендикулярной к оси Сх
плоскости, проходящей через точку F, и силу S, действующую
параллельно оси Сх в направлении от Л к С. Значение составляющих
определим, воспользовавшись рис. 46,г (как сила Q, так и ее
составляющие расположены в горизонтальной плоскости):
Т = Q • sin 30° = 90 • 0,5 = 45 кг\
S - Q . cos 30° = 9°Jp- = 45 V& ™
Чтобы было ясно, какие именно из одинаковых сил Т и S вошли
в те или иные уравнения равновесия, припишем этим силам индексы,
т. е. будем обозначать их Tl9 Т2, Т3, Т4 и Sl9 S2, S3, S4.
Для составления уравнений моментов всех сил относительно
осей Сх, Су, Cz будем соответственно Пользоваться рис. 46,5, е, ж.
* Чтобы не затемнять рисунка, крылья М и N не показаны.
Произвольная система сил, не пересекающихся в одной точке 18J
D о
Т4-к центру крыла N
Т4 - к центру крыла ?
К задаче 46.
182 Статика твердого тела
Применив формулы (XI,I), составим шесть уравнений равно-
равновесия твердого тела — оси FC мельницы, находящейся под дейст-
действием ' произвольной пространственной системы сил.
Vxi = Xc-S1-S2-S3-54-0; A)
2/4 = /а + Кс-Г1 + Г,«0; B)
У Z, = ZA + Zc -Р- Г2 + Г4 = 0; • C)
?МХ = -Р • 0,8 +j Тг • 2 + Г2 • 2 -f Г8 • 2 + Т4 • 2 =0 D)
(в уравнение D) не вошли силы Sl9 S2, S3 и S4, параллельные оси
Сх, и силы YA, Za, Ус и %с* пересекающие ее);
?My = Р • 0,5 -ZA • 1,5 + Т2 • 2 - Г4 • 2 — Sx • 2 + S3 - 2 = 0 E)
(силы Уд, 7\ и Г3 параллельны оси Су> силы 52, S4 и Zc пересе-
пересекают ось Су, а сила Ус направлена по оси Су, поэтому эти силы
в уравнение E) не входят);
I'M, - YA . 1,5 —Sa • 2 + 54 • 2 — 7\ • 2 + Г8 • 2 = 0 F)
(силы Za, Pt Т2 и Г4 параллельны оси Cz, силы Sx, «S3 Xc и Кс пере-
пересекают ось Cz, а сила Zc направлена по оси Сг, поэтому эти силы
в уравнение F) не входят).
После преобразований эти уравйения примут следующий вид:
= Хс — 4S=0; . (И)
Ya + Yc^O; B0
ZA+Zc-P^0; C0
V Мх = — Р • 0,8 + 4 . Г . 2 - 0; D')
?My-P.0,5-~ZA • 1,5-0; E')
?Мг = ГА- 1,5 = 0. F0
Подставив значения S, 7 и Р в уравнения F'), B'), (Г)» Ю»
E') и C') и решив их в указанной последовательности, найдем:
ч ya=Yc = 0; ХС-311,76 кг; Р = 450 кг;
ZA = 150 кг; Zc = 250 кг.
В случае, когда крыло D снято, принцип решения и количество
уравнений равновесия не изменяются, но сами уравнения полу-
"чают более громоздкий вид из-за отсутствия симметрии дей-
действующих на ось FC сил ветра Q. Составление и решение урав-
уравнений равновесия для этого случая не представляют затруднений.
Пользуясь прежними рисунками, нужно только учесть, что силы
S3 и Г3 отсутствуют.
47. Груз Q равномерно поднимается мотором М при помощи
бесконечной цепи (рис. 47,а). Определить реакции опор А и В
Произвольная система сил, не пересекающихся в одной точке i83
я натяжение цепи, если ветви ее наклонены к горизонту под
углом 30° (ось О^уг параллельна оси By). Известно, что г =
= 15 см, R = 30 см, Q = 2 т и натяжение ведущей части цепи
вдвое больше натяжения ведомой ее части, т. е. Тг = 2 Г2.
Решение. Рассмотрим равновесие вала А В (рис. 47, б).
Так как груз Q поднимается равномерно, то вал АВ вращается
также равномерно, следовательно, приложенные к нему силы
взаимно уравновешиваются.
К задаче 47.
Приняв за начало координат точку В, направим оси согласно
рисунку.
К валу приложена одна активная вертикальная сила — груз Q.
Применив метод сечений, заменим действие мотора М на сое-
соединенное с валом колесо Ог силами TjH Г2, действующими соот-
соответственно по осям ведущей и ведомой частей цепи. Отбросив связи-
подшипники А и В — заменим их действие силами, составляющие
У а, %а и YB, ZB которых направим в положительные стороны
координатных осей.
Применив формулы (Х1,2), составим пять уравнений равновесия
приложенной к валу АВ пространственной системы сил, дейст-
действующих в перпендикулярных к оси вала плоскостях (шестое урав-
уравнение равновесия — уравнение проекций всех сил на ось Вх —
обращается в тождество).
184 Статика твердого тела
Для составления уравнений моментов всех сил относительно
осей Вх, By и Bz будем соответственно пользоваться вспомога-
вспомогательными рисунками 47,#, г, д.
? Г. = YA + YB + Тг. cos30° + T2 ¦ cos30° = 0; A)
]?Z,==Za + Zb —Q+7\-sin 30° —Га - sin 30° = 0; B)
SM^-Q.r + ^.b^.^O; C)
%My = — T1. sin30° -40+ Га. sin30° . 40 + Q . 70 —
_ZA • 100 = 0; D)
?Мг = 7\ • cos30° • 40 -f T2 • cos30° . 40 + KA • 100 - 0. E)
Подставив данные из условия задачи и значения тригономет-
тригонометрических функций угла в уравнения C), E), A), D), B) и решив
их в указанной последовательности, найдем:
Ti = 2m; T2=lm; YA=— 1,04 m;
YB = —2,56 m\ 2A = 1,2 m\
ZB = 0,15 m.
48. Для передачи вращения с одного вала на другой, ему па-
параллельный, установлены (рис. 48,а) два одинаковых вспомога-
вспомогательных шкива, заклиненных на горизонтальной оси КЬ. Ось
может вращаться в подшипнике М, укрепленном на колонке MN.
Равностороннее треугольное основание Колонки прикреплено к
полу двумя болтами А и В и свободно опирается в точке С. Болт
А проходит через круглое отверстие в основании, болт же Б —
через продолговатое отверстие, имеющее направление линии АВ.
Ось колонки проходит через центр Д ABC.
Определить реакции RA, Rb' и Rc> если расстояние оси KL
от пола равно 1 м> расстояния осей шкивов от оси колонки
равны 0,5 м и натяжения всех четырех ветвей ремней принимаются
одинаковыми и равными 60 кг. Ветви правого ремня горизонтальны,
а ветви левого наклонены к горизонту под углом 30°. Вес всей
установки равен 300 кг и приложен к точке, расположенной на
оси колонки; АВ = ВС == СА =50 см.
Решение. Рассмотрим равновесие колонки MN с прикреплен-
прикрепленной к ней осью KL и двумя шкивами (рис. 48,6).
Приняв точку А за начало координат, направим оси согласно
рисунку.
К колонке приложена одна активная вертикальная сила —
ее собственный вес Q.
Исследуем характер связей.
Произвольная система сил*, не пересекающихся в одной точке
185
Опора А представляет собой болт, препятствующий перемеще-
перемещению конца А в любом направлении, поэтому представим ее реак-
реакцию в виде составляющих Ха, У а и Za.
Опора В представляет собой болт, препятствующий перемеще-
перемещению конца В только в плоскости, перпендикулярной к оси Ау
а
(благодаря наличию вокруг болта продолговатого отверстия, на-
направленного вдоль оси Ау, болт В не препятствует. переме-
щению конца В основания колонки вдоль оси Ау), поэтому пред-
представим ее реакцию в виде составляющих Хв и ZB.
В точке С основание ABC колонки свободно (без трения) опи-
опирается на гладкий горизонтальный пол, поэтому реакцию пола
направим вертикально вверх.
Реакции Т каждой ветви двух ремней, одинаковые по величине,
направим по их осям: две'—горизонтально и две — под углом
30° к горизонту.
Таким образом, на твердое тело — колонку MN *— действует
произвольная пространственная система сил.
Положение оси Ау выбрано так, что она пересекает четыре
неизвестные силы: Ха, Za, ХВу Zb\ кроме того, сила YА направо
лена по оси. В уравнение моментов сил относительно оси Az также
не войдут пять неизвестных сил: Ха, Ya> Za, Zb и Rc, Проведение
186 v Статика твердого тела
оси Ах через точку Л# (или В) позволит определить неизвестные
силы ZB и Za, не прибегая к решению системы двух уравнений,
что имело бы место при проведении этой оси, например, через
точку к.
Применив формулы (XI, 1), составим шесть уравнений равно-
равновесия твердого тела — колонки MN, находящейся под. действием
произвольной пространственной системы сил, предварительно опре-
определив расстояния до АВ точек. С и О (О — точка пересечения оси
колонки MN с гopизoнtaльнoй плоскостью ABC).
Так как точка О — точка пересечения медиан (а также высот
и биссектрис) равностороннего ДЛ?С, то
AR
Ск±АВ; Л/с = ™ =25 см.
Зная углы Д ABC, найдем из прямоугольного ДЛС/с:
Ск = АС • sin 60° = ™_V][ = 43,3 см,
тогда
Ок = у Ск = 14,43 см;
7 , Л$ = А^4. "Т" А в "— ^ i ^ i * COS oU = U, \i)
J]Z« = ZA' + ZB + /?c —Q + 2Г . sin 30° = O! C)
Отсутствие размера радиуса шкивов К и L требует введения
произвольного размера его; кроме того, введение в уравнения мо-
моментов момента каждой реакции Т также усложняет решение. Чтобы
избежать этого, введем в уравнения моментов моменты про-
проходящих через центр каждого шкива равнодействующих двух
равных реакций Т ветвей ремня.
Для составления уравнения моментов всех сил относительно
оси Ау, чтобы не усложнять решения задачи определением размера
плеча проекции (на плоскость xAz) равнодействующей сил 7\
приложенных к шкиву /С, раскладываем эту равнодействующую
на две составляющие: 2Г . cos 30° и 2Г • sin 30°, направленные
соответственно параллельно осям Ах и А г; это разложение облег-
облегчает также составление уравнений моментов всех сил относительно
осей Ах и Аг\
= ZB . 50 + Rc • 25 — Q . 25 — 2Т • sin30° ¦ 25 = 0; D)
V,My = — Q- 14,43+ /?c. 43,3 — 25Г. 100 — 2Г . cos30° . 100 +
+ 2Г -sin 30°. 14,43 = 0; ' E)
YMZ == —Xb • 50-2Г • cos 30° . 25 + 2T . 75 = 0. F)
Определение положения центра тяжести твердых тел 187
Подставив данные из условия задачи значения тригонометри-
тригонометрических функций угла и ранее найденные геометрические вели-
величины в уравнения B), E), F), A), D), C) и решив их в указанной
последовательности, найдем:
YA = 0; Rc = 597,3 кг; Хв = 128 кг;
ХА = 95,9 кг; ZB = — 118,6 кг и ZA = — 238,7 кг.
ГЛАВА XII
ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ ЦЕНТРА ТЯЖЕСТИ ТВЕРДЫХ ТЕЛ
§ 1. Основные предпосылки к определению положения
центра тяжести тел
Силы тяжести, приложенные к отдельным частицам тела, можно
считать параллельными, поэтому центр тяжести тела представляет
собой центр этой системы параллельных сил.
Точек приложения равнодействующей системы параллельных
сил много, а центр один. Центр системы параллельных сил — это
точка приложения равнодействующей, не меняющая своего поло-
положения при повороте каждой силы (в одном направлении) г вокруг
своей точки приложения на один и тот же произвольный угол,
сохраняющая свое положение и при изменении — увеличении
или уменьшении в одно и то же число раз каждой из сил, входящих
в систему.
С изменением положения тела в пространстве изменяются и
координаты его центра тяжести по отношению к каким-либо осям,
не связанным с телом, но положение центра тяжести данного тела
по отношению к самому телу, т. е. к взятым в нем осям, остается
постоянным.
Определение положения центра тяжести тела облегчается зна-
знанием следующих положений.
а) Если тело имеет плоскость симметрии, то его центр тяжести
находится в этой плоскости, и для определения его положения до-
достаточно найти две координаты относительно осей, расположенных
в плоскости симметрии.
б) Если тело линейного очертания имеет ось симметрии, или
плоское тело имеет в своей плоскости ось симметрии, *или объем-
объемное тело имеет ряд плоскостей симметрии, пересекающихся
между собой по линии, являющейся осью симметрии тела, то центр
тяжести данного тела находится в одной из точек этой оси симметрии
и для определения его положения достаточно найти одну координа-
координату — расстояние центра тяжести тела от какой-либо точки оси
симметрии, положение которой на этой оси известно (формулы ко-
координат центра тяжести приведены ниже).
1 По ходу часовой стрелки или против. ]
188
Статика твердого тела
в) Если плоское тело имеет две или несколько осей симметрии,
то точка пересечения этих осей и является центром тяжести тела
(например, плоские фигуры, ограниченные прямоугольником, квад-
квадратом, кругом).
г) Если плоская фигура имеет центр симметрии (например,
плоская фигура, ограниченная параллелограммом), то эта точка
и является центром тяжести тела.
д) Если объемное тело имеет ось симметрии и перпендикулярно
к ней расположенную плоскость симметрии, то точка пересечения
оси симметрии тела с его плоскостью симметрии и является центром
тяжести тела (например, цилиндр).
е) Центр fяжecти тела, состоящего из двух элементов (частей),
находится на прямой, соединяющей центры тяжести элементов,
и делит это расстояние на части, обратно пропорциональные весам
(а в однородных телах — объемам, площадям, длинам) этих частей.
ж) Когда положение центра тяжести тела неизвестно, то тело
мысленно разбивается на части (объемы, площади, длины), поло-
положение центров тяжести которых известно, после чего координаты
тела определяются по известным- формулам.
§ 2. Аналитическое определение координат центра тяжести
тел произвольного очертания
1. Определение координат центра тяжести тел,
расположенных в пространстве
Положение центра тяжести твердого тела, расположенного в
пространстве, определяется тремя координатами.
ха = ¦
ЕЛ
Уг
(XII, I)
где Pi — силы тяжести отдельных частиц, a xit yif zt — их коор-
координаты; Р — вес всего тела.
2. Определение координат центра
жести тел линейного очертания
т я-
Когда расположенное в пространстве тело представляет собой
линию постоянного поперечного сечения, т. е. когда размеры по-
перечного сечения тела очень малы по сравнению с его длиной L>
Определение положения центра тяжести твердых тел
189
то координаты его центра тяжести определяются по следующим
формулам:
у
Хц =
- 7, ¦ г,
(ХН,2)
где L$ — длины отдельных частей линии, а ^ — веса единиц длины
отдельных частей \ на которые может быть разбито все тело.
При однородности всего тела эти формулы принимают сле-
следующий вид:
хП =
Уп =
zn =
(XII, 3)
Когда линейное тело плоское, т. е. когда оси всех частей, на
которые оно может быть разбито, расположены в одной плоскости
{например плоская ферма), то, расположив оси координат в этой
плоскости, определяют по формулам (XI 1,2) или (XII,3) только
две координаты центра тяжести тела; третья координата при этом
обращается в нуль.
3. Определение координат центра тяжести
плоских тел, площадей и сечений различ-
различных тел.
Когда твердое тело, имеющее плоскость симметрии, — плоское,
т. е. когда оно ограничено двумя плоскостями, параллельными его
гоюскости симметрии, то его центр тяжести находится в плоскости
симметрии, которая расположена на средине между .ограничиваю-
.ограничивающими тело плоскостями.
Приняв плоскость симметрии за плоскость рисунка, а ограни-
ограниченный плоскостью симметрии контур тела за контур плоской
фигуры (сечения тела) площадью F и проведя в этой плоскости
координатные оси Ох и Оу, найдем координаты центра тяжести
плоского тела как координаты центра v тяжести плоской фигуры
1 Предполагается, что в пределах той или иной части тела 7 — величина по-
постоянная. *
190 ( Статика твердого тела
(площади) по следующим формулам:
¦ ji ¦ _
(XII, 4)
где F{ — площади, а т» — веса единиц площади отдельных частей,
на которые может быть разбито все тело.
При однородности всего тела эти формулы принимают следую-
следующий вид:
Л*
(XII, 5)
где Sy и Sx — статические моменты плоской фигуры относительно
осой у и лс, соответственно равные:
5Ж = 2 F< • Л = F • уц.
При определении статических моментов площадей относительно
осей нужно помнить, что:
а) статический момент площади относительно любой оси, прохо-
проходящей через ее центр тяжести (и, конечно, находящейся в ее плос-
плоскости), равен нулю;
б) статические моменты отдельных площадей, на которые разбита
вся площадь плоской фигуры, относительно какой-либо оси, нахо-
находящейся в ее плоскости, имеют разные знаки (плюс, минус), если
их центры тяжести расположены по разные стороны оси.
В некоторых случаях положение центроз тяжести линейных
и плоских тел может быть определено путем применения теорем
Паппа-^Гюльдена.
Первая теорема. Площадь поверхности тела, полученного при
вращении плоской кривой вокруг оси, находящейся в ее плоскости
и расположенной по одну сторону от нее, равна произведению длины,
этой- кривой на длину окружности, описанной центром тяжести)
этой кривой, т. е.
F = L • 2ти . *ц,.
откуда
, 6)
Применяя эту формулу, можно легко определить координату
центра тяжести симметричного тела линейного очертания с очень
Определение положения центра тяжести твердых тел 19t
малыми размерами сечения, ось * которого — плоская кривая (на-
(например, проволока, изогнутая по окружности), как координату
центра тяжести однородной весомой оси тела. Для этого необхо-
необходимо рассмотреть вращение весомой оси тела вокруг оси, перпен-
перпендикулярной к оси симметрии тела^ находящейся с ней (и с осью тела>
в одной плоскости.
Вторая теорема. Объем тела, полученного от вращения плос-
плоской фигуры вокруг оси, находящейся в ее плоскости и расположен-
расположенной по одну сторону от нее, равен произведению площади этой фигуры
на длину окружности, описанной центром тяжести этой площади, т. е.
V = F • 2тг . лгц,
откуда
Применяя эту формулу, можно легко определить координату
центра тяжести однородного плоского тела, имеющего плоскость
симметрии и в этой плоскости — ось симметрии, если оно частично
или полностью ограничено криволинейной боковой поверхностью-
(например, боковой поверхностью прямого кругового цилиндра)*.
В данном случае центр тяжести тела определяем как координату
центра тяжести однородной площади, частично ограниченной кри-
кривой. Для этого необходимо рассмотреть вращение этой площади
вокруг оси, перпендикулярной к оси симметрии тела, находящейся
с ней в одной плоскости.
Координата центра тяжести плоской фигуры, частично огра-
ограниченной кривой, зависимость между координатами которой из-
известна, определяется ino формуле (XII, 5), причем как сама пло-
площадь фигуры, так и ее статический момент относительно оси опре-
определяются при помощи интегралов 2 (см. задачу 54). N
4. О п р е д е л е ние координат центра тя-
тяжести объемных тел
Координаты центра тяжести твердого тела, расположенного в
пространстве, определяются по следующим формулам:
*ц =
2ц =
• 7,
1 Ось тела линейного очертания — это геометрическое место центров тяжест»
всех его поперечных сечений.
2 Для некоторых частных случаев в справочниках даны формулы площадей*
и координат центров тяжести таких фигур.
192 Статика твердого тёщ
где V{ — объемы, a y< — веса единиц объема отдельных частей, на
которые может быть разбито все тело.
При однородности всего тела эти, формулы принимают следующий
»ид:
2У4 • х.
V
~~ V
"~ V
\ ]
y%
h
Уи-ЦЬ^-^Ч^}. (xii, 9)
еде V — объем всего тела.
5. Формулы координат центра тяжести
некоторых простейших геометрических
•фигур.
а) Центр тяжести дуги окружности расположен на ее оси сим-
симметрии; его расстояние от центра окружности определяется по
^формуле
Хц = *^*9 (XII, 10)
где R — радиус, L — длина дуги, а АВ — длина стягивающей
«ее хорды,
или
Хц = #.5-^, (XII, П)
где R — радиус, а „а — половина центрального угла, ограничен-
ограниченного дугой.
Формулой (XII,10) удобно пользоваться, когда в состав линии,
положение центра тяжести которой определяется, входит несколько
дуг; при этом упрощается числитель формулы (ХП,3), так как
длины дуг сокращаются.
б) Центр тяжести площади кругового сектора расположен
на его оси симметрии; его расстояние от центра окружности опре-
определяется по формуле
*ц 2#.i!E±f (XII, 12)
о о
где R — радиус, а а — половина центрального угла сектора.
В частном случае расстояние центра тяжести полукруга ра-
радиуса R от его геометрического центра определяется по формуле
тс
9 Sin "9 4
jcu=|/?. -^-=^-/? = 0,424Д.
Определение положения центра тяжеапи твердых, тел
193
в) Центр тяжести четверти круга расположен на ее оси симмет-
симметрии; его расстояние от любого из ограничивающих фигуру ра-
радиусов равно расстоянию центра тяжести полукруга от его гео-
геометрического центра, т. е.
Хц= А . # = 0,424/?. (XII, 13')
Такое расположение центра тяжести (рис. 1,а) вытекает из
того, что точки С1у С и С2 находятся на прямой, параллельной
диаметру, ограничивающему полукруг; здесь 01 — ось симметрии
Рис. 1.
четверти круга, Сх и С2 — центры тяжести левой и правой чет-
четвертей круга, ОВ — ось симметрии полукруга.
г) Центр тяжести площади кругового сегмента расположен на
его оси симметрии; его расстояние от центра окружности опре-
определяется по формуле
*«-Т* a-sinot.cosa ' ' tAll,14J
где a — половина центрального угла, ограниченного дугой сег-
сегмента.
д) Центр тяжести площади любого треугольника расположен
в точке пересечения его медиан, на расстоянии одной трети каждой
медианы от соответствующего основания треугольника.
Для определения расстояния центра тяжести площади любого1
треугольника от любой оси, находящейся в его плоскости, поль-
пользуются формулой
*ц=^Ш^-, (XII, 15)
где хъ~ Хъ> х2 — координаты вершин треугольника По отношению
к рассматриваемой оси.
Знаменатель дроби формулы (XII, 15) не изменяется и тогда,
когда координаты одной или двух вершин треугольника равны
нулю.
13 591
194 Статика твердого тела
е) Центр тяжести площади любой трапеции с меньшим осно-
основанием а, большим основанием b и высотой h расположен на пря-
прямой, соединяющей средины оснований. Расстояния hb и ha центра
тяжести площади трапеции от большего и меньшего оснований ее
определяются по формулам
h 2a
пь ~ "з # ~а~
(ХП,16)
ж) Центр тяжести площади прямоугольной трапеции (рис. 1,6)
с меньшим основанием а, большим основанием b и высотой h рас-
расположен на прямой, соединяющей средины оснований.
Расстояние центра тяжести площади этой трапеции от боковой
стороны, перпендикулярной к основаниям аи 6, не зависит от
высоты h и определяется по одной из формул
(XII, 17)
з) Центр тяжести объема прямого кругового конуса расположен
на его оси симметрии; его расстояние от основания конуса опре-
определяется по формуле
гц==~, (XII, 18)
где h — высота конуса.
и) Центр тяжести полушара радиуса г расположен на его оси
симметрии; его расстояние от центра шара определяется по формуле
2ц = 4л (XII, 19)
§ 3. Методические указания к определению положения
центра тяжести плоских фигур
1. Если фигура имеет ось симметрии, то координатную ось
нужно проводить перпендикулярно к ней через одну из точек, по-
положение которых на оси симметрии известно.
2 Для облегчения подсчета статического момента площади фигуры
относительно какой-либо оси нужно разбивать фигуру на минималь-
минимальное число элементов, положение центров тяжести которых известно,
и стремиться к тому, чтобы большее (по возможности) число эле-
элементов совпадало с этой осью — одной из сторон, ограничивающих
элемент.
Определение положения центра тяжести твердых тел
195
Так, например, для определения расстояния центра тяжести
плоской фигуры ABCDEFKL (рис. П,а, б) от оси Ох необходимо
найти статический момент ее площади относительно этой оси,
для чего разбивка по типу б лучше, чем разбивка по типу а.
3) Для уменьшения числа элементов фигуры полезно вводить
так называемые отрицательные площади.
. с »'
д
D
X
F К
\
О
\7xV/l
Рис. 11.
Если дополнить заданную фигуру до какого-либо нового кон-
контура и считать площадь, ограниченную им, положительной, то
несуществующая, дополнительно введенная площадь считается
отрицательной. Например, статический момент заданной площа-
площади (рис. II,б, г) относительно оси хх проще найти как разность
статических моментов всей площади прямоугольника A BCD ЕМ и
площади прямоугольника MLKE относительно той же оси хх;
введение отрицательной площади уменьшит число элементов с трех
при первой разбивке до двух при второй.
Если в плоской фигуре имеются вырезы, то площадь всей фи-
фигуры считается положительной, а площадь вырезов — отрицатель-
отрицательной. Например, статический момент заданной площади (рис. П,д,е)
относительно оси хх проще найти как разность статических
моментов всей площади прямоугольника ABCD и площади прямо-
13*
196 Статика твердого тела
угольника KLME относительно той же оси хх\ введение отрица-
отрицательной площади KLME уменьшило число элементов с четырех
при первой разбивке до двух при второй.
При криволинейныхх очертаниях вырезов в фигуре или при
криволинейных очертаниях части контура только введение отри-
отрицательных площадей позволяет определить положение центра
тяжести фигуры без применения интегрального исчисления. Напри-
Например, в заштрихованной фигуре ABCDEKLNPRS (рис. П,ж) необ-
необходимо считать положительной площадь ABCDK и отрицательной—
площадь полукруга DEK. Для определения статического мо-
момента площади LMN относительно какой-либо оси необходимо
дополнить ее до площади квадрата LCyV/W и считать эту площадь
положительной, введя отрицательную площадь кругового сектора
OXLN.
4. Удачным выбором оси, относительно которой определяется
статический момент данной плоской фигуры, можно также умень-
уменьшить подсчеты. Например, подсчет статического момента той же
фигуры (рис. П,г) еще более упростится, если его определять
относительно оси хгх1у проведенной перпендикулярно к оси сим-
симметрии фигуры (Оу) через центр тяжести О положительной площади,
так как статический момент этой площади относительно оси хххх
обратится в нуль и весь подсчет, таким образом, сведется к на-
нахождению статического момента одной (отрицательной) площади
MLKE относительно этой оси.
5. При определении положения центра тяжести плоской фигу-»
ры, состоящей из большого числа элементов, рекомендуем распо-
располагать оси так, чтобы вся фигура находилась в пределах одного
квадранта, так как при таком расположении осей координаты
центров тяжести элементов будут иметь одинаковые знаки, что
уменьшит возможность появления ошибки.
6. Для определения центра тяжести, фигур с числом элементов
больше двух рекомендуем составлять таблицу, внося в нее номера
элементов, размеры площадей их или длин, координаты центров
тяжести и статические моменты площадей элементов относительно
координатных осей или моменты сил относительно тех же осей
(см. решение задач 53, 55).
§ 4. Порядок решения задач
Рассматриваемые в этой главе задачи рекомендуем решать в
следующем порядке.
1. Установить количество координат, необходимое для опре-
определения положения центра тяжести фигуры (тела), в зависимости
от наличия или отсутствия плоскости (плоскостей) симметрии
или оси симметрии.
1 Кривые представляют собой дуги окружностей.
Определение положения центра тяжести твердых тел 197
2. Разбить фигуру (тело) на минимальное количество частей,
положение центра тяжести которых известно.
3. Выбрать расположение координатных осей и написать фор-
формулу координат центра тяжести фигуры (тела).
4. Определить величины, входящие в формулу координат центра
тяжести фигуры, и, если число частей, на которые она разбита,
больше двух, — внести, найденные величины в таблицу.
5. Определить положение центра тяжести фигуры (тела), при-
применив соответствующие формулы.
Примечание. Порядок решения задач на подбор размеров объемного
тела, исходя из условий его устойчивости, приведен при решении задачи 56.
§ 5. Графическое определение положения центра тяжести тел
1. О п р е д е л е н и е положения центра тяже-
тяжести простейших плоских геометрических
фигур
Центр тяжести площади произвольного треугольника находится
на пересечении его медиан.
Центр тяжести площади любого четырехугольника (рис. III,а),
в том числе и трапеции (рис. II 1,6), находится в точке пересечения
прямых, соединяющих центры тяжести площадей двух треуголь-'
ников, при двух вариантах разбивки четырехугольника на треуголь-
треугольники.
Положение центра тяжести площади трапеции может быть
определено и иначе.
а) центр тяжести находится на пересечении прямой (рис. III, в),
соединяющей средины оснований, с прямой, соединяющей центры
тяжести площадей любых двух треугольликов, на которые может
быть разбита трапеция;
б) центр тяжести (рис. Ш,г) находится на пересечении прямой,
соединяющей средины оснований а и Ь трапеции, с прямой, соеди-
соединяющей концы отложенных на продолжении оснований трапеции
отрезков, равных соответственно противоположным основаниям,
причем если отрезок а отложен на продолжении Ь вправо, то
отрезок Ъ откладывается на продолжении а влево (или наобо-
наоборот);
в) центр тяжести-площади прямоугольной трапеции (рис. П1,г, д)
находится на пересечении прямой, соединяющей средины осно-
оснований, с прямой, параллельной основаниям и проходящей через
точку пересечения прямых, соединяющих вершины острого и, ту-
тупого углов трапеции с ближайшей из точек раздела (на три
равные части) стороны трапеции, перпендикулярной к ее осно-
основаниям.
198
Статика твердого тела
Рис. III.
2. Определение положения центра тяже-
тяжести плоских фигур, состоящих из несколь-
нескольких элементов
Определение положения центра тяжести более сложных плос-
плоских фигур осуществляется при помощи веревочного многоугольника.
При этом различают два случая: 1) когда фигура имеет ось симмет-
симметрии; 2) когда фигура не имеет оси симметрии.
В первом случае фигуру на рисунке обычно располагают так,
чтобы ось симметрии заняла горизонтальное положение. Затем, разбив
Определение положения центра тяжести твердых тел 199
фигуру на такие части, положение центра тяжести которых
известно, прикладывают к этим центрам вертикальные силы
веса этих частей в виде векторов, пропорциональных соответ-
соответствующим площадям частей, и обычным путем находят линию
действия равнодействующей рассматриваемой системы параллель-
параллельных сил.
Точка пересечения этой линии с осью симметрии фигуры
и является ее центром тяжести.
Во втором случае, пользуясь тем, что центр тяжести фигуры
(центр системы параллельных сил — сил веса отдельных частей
фигуры) не меняет своего положения при повороте (в одном на-
направлении) всей системы на какой-либо угол, линию действия рав-
равнодействующей определяем дважды: для вертикального и гори-
горизонтального положения векторов (когда система сил повернута на
90°). Точка пересечения обеих линий действия равнодействующих
и является центром тяжести фигуры.
3. Методические указания к определе-
определению положения центра тяжести тел
1) Для уменьшения числа частей, на которые разбивается
площадь заданной фигуры, полезно вводить отрицательные пло-
площади. В таких случаях векторы, изображающие силы веса этих
частей, направляются в сторону, противоположную направлению
векторов, изображающих силы веса положительных частей пло-
площади фигуры.
2) Для повернутой на 90° систегЛ>1 сил можно обойтись без
построения силового многоугольника; в этом случае стороны ве-
веревочного многоугольника нужно направлять перпендикулярно
к соответствующим сторонам веревочного многоугольника, построен-
построенного для вертикально направленных сил.
3) Указанные выше способы определения положения центра тя-
тяжести плоских фигур применимы ик сечениям однородных
тел. Их можно также применять для нахождения центра тяжести
однородных объемных тел и тел линейного очертания, имеющих
плоскость симметрии, прикладывая к центрам тяжести частей
тела векторы, соответственно пропорциональные объемам или
длинам этих частей.
4) Применяя указанные выше способы к определению положе-
положения центра тяжести неоднородных тел, имеющих плос-
плоскость симметрии, нужно прикладывать к центрам тяжести частей !
тела векторы, пропорциональные произведению объемных весов
этих частей на их объемы, площади или длины.
1 Предполагается, что в пределах той или иной части объемный вес постоянен.
200
Статика твердого тела
§ 6. Задачи
49. Определить расстояние от точки F центра тяжести С стерж-
стержневого контура AFBD (рис. 49), состоящего из дуги ADB четверти
окружности радиуса FD = Rt и из дуги полуокружности AFB,
построенной на хорде АВ как на диаметре,
1) при одинаковых линейных плотностях
стержней и 2) когда плотность дуги AFB
вдвое больше плотности дуги ADB.
I Решение. Определим положение центра
_i *. тяжести С стержневого контура AFBD в пер-
первом случае.
Контур AFBD, состоящий из стержней
ADB и AFB одинаковой линейной плотности,
имеет ось симметрии — ось Fx, следовательно,
его центр тяжести находится на этой оси.
Найдем расстояние хп центра тяжести кон-
контура AFBD от точки F, находящейся на оси'
симметрии.F#, или, что тоже, от оси Fy, перпендикулярной к оси
Fx и проведенной через точку F, применяя формулу (ХП,3).
К задаче 49.
SL.
L, + L2
где Lx и Ь2 — длины стержней ADB и AFB, а хг и х2 — расстояния
по оси Fx их центров тяжести от точки F.
Определим Lx и 1^, для чего предварительно найдем г — радиус
дуги A FB.
1 Из прямоугольного Л AOF найдем:
тогда
L% = т.г =
Определим расстояния хг и х2 центров тяжести дуг ADB и AFB
от точки F, воспользовавшись формулой (XI 1,10):
R.AB
U
; х2 = т —
г.АВ
где АВ — хорда дуги ADB, одновременно являющаяся диамет-
диаметром полуокружности AFB.
Центром окружности для дуги ADB является точка F, а для
дуги AFB — точка О.
Определение положения центра тяжести твердых тел 201
Подставив найденные значения в уравнение A), определим коор-
координату хц\
V2 4+ ic 1/2-21/2 p. Q523J?
-"У" *<l+i/2> -^ —"-523/?.
Во втором случае примем линейную плотность дуги ADB рав-
равной 7, а дуги AFB — равной 2?.
Найдем координату центра тяжести стержневого контура AFBD,
применив формулу (XI 1,2):
Подставив в уравнение (Г) ранее найденные значения длин
дуг и координат их центров тяжести, найдем:
R-AB
+2r(L2—2r)
R *
Сократив на у и сделав соответствующие преобразования, полу*
чим:
х2П = ( ±ъУ --2V2) ^ ^ __ о 424*/?.
тгA +21/2)
50. Определить положение центра тяжести С площади (рис. 50).
ограниченной полуокружностью АОВ радиуса R и двумя прямы-
прямыми AD и DB равной длины, причем OD = 4/?.
Решение. Ограниченная контуром AOBD площадь, состоящая из
двух элементов: площади полукруга АОВ я площади треугольника
ABD, имеет ось симметрии OD, следовательно, ее центр тяжести
находится на этой оси.
Направив ось Оу по оси симметрии OD и применив формулу
(XI 1,5), найдем расстояние уц центра тяжести С площади ApBD
202
Статика твердого тела
от точки О, находящейся на оси симметрии или, что то же, от оси
Ох, перпендикулярной к оси 0уу проведенной через точку О:
A)
где F±n F2 — площади элементов АОВ и ЛбО, а */х и #2 — раЕсстоя-
ния их центров тяжести по оси Оу от той же точки О*
К задаче 50.
Определим значения Fl9 F2 и уъ у%.
Расстояние центра тяжести Е площади полукруга АОВ от
центра 0г круга определим по формуле (X 11,13).
4
Определим значения у иначе, применив формулу (ХП,7).
Тело, образованное при вращении площади АОВ (рис. 50,6)
вокруг оси ЛВ, представляет собой шар, объем которого
Согласно
откуда
формуле
V
(XII.7),
2
У
объем
4
тела
3 ^
Ч
вращения
Определение положения центра тяжести твердых тел
2иЗ
Расстояние уг центра тяжести Е площади полукруга от точки О
равно
Расстояние центра тяжести К площади равнобедренного Д ABD
от его основания А В равно
так как центр тяжести площади любого треугольника находится
на пересечении его медиан.
Расстояние у2 центра тяжести К площади Д ABD от точки О
равно
Подставив в уравнение A) найденные значения и решив его,
получим
Зтс
R +
2R
3*+32
3(л -Ь Ь)
51. Определить положение центра тя-
тяжести однородного диска с круглым отвер-
отверстием (рис. 51), предполагая радиус диска
равным гъ радиус отверстия равным г2
и центр этого отверстия находящимся на
расстоянии ~ от центра диска.
Решение. Рассматриваемая площадь
имеет ось симметрии — ось Ох, следователь-
следовательно, ее центр тяжести находится на этой оси.
Применив метод введения отрицатель-
отрицательных площадей, представим себе рассматри-
рассматриваемую площадь состоящей из положи-
положительной площади круга радиуса гг и
отрицательной площади круга радиуса г2.
Применив формулу (XII,5), определим хц— расстояние центра
тяжести рассматриваемой площади от центра О круга, или, что
то же, от оси Оу, перпендикулярной коси Ох, проходящей через точ-
точку О (при таком выборе положения оси Оу числитель формулы
упростится):
К задаче 51.
=±_2—
У F.
A)
204
Статика твердого тела
Определим значения Fl9 F% и xlt x±\
F2 = — тг/f;
*! = U, X2 = -^ .
Подставив найденные значения в уравнение A), получим
пг\ • О + (— иг?) -^ а
Знак минус при х1Х показывает, что центр тяжести рассматри-
рассматриваемой площади находится на отрицательной части оси Ох, т. е.
влево от точки О (координату х2 мы приняли положительной, так
как она расположена на положительной части оси Ох),
Если положительную часть оси Ох принять направленной от
точки О влево, то
тс • ri — тс • г\
Знак плюс при хц показывает, что центр тяжести рассматриваемой
площади находится на положительной части оси Ох, т. е. вправо
от точки О.
Положение центра тяжести левее
точки О объясняется уменьшением
площади в правой части полукруга
радиуса гг.
52. Провести через вершину D
однородного прямоугольника ABCD
(рис. 52,а) прямую DE так, чтобы
при подвешивании отрезанной по
' этой прямой трапеции ABED за вер-
вершину ^Е сторона /4D, равная а, была
горизонтальна. ,
Решение* Рассматриваемая площадь не имеет осей симметрии,
следовательно, если бы стоял вопрос о нахождении положения
ее центра тяжести, необходимо было бы найти две координаты,
но в условии задачи требуется только определить положение
точки ?, т. е. найти величину СЕ или BE.
Определение положения центра тяжести твердых тел 205
Положение точки Е определится из тех соображений, что гори-
горизонтальность стороны AD будет обеспечена только при располо-
расположении центра тяжести трапеции ABED на прямой EF, перпенди-
перпендикулярной к AD9 а положение EF определится расстоянием этой
прямой от оси Ау.
Таким образом, достаточно определить только одну координату
центра тяжести трапеции, а именно — л;ц.
Применив метод введения отрицательных площадей, представим
себе рассматриваемую площадь состоящей из положительной
площади прямоугольника ABCD и отрицательной площади треуголь-
треугольника ВСЕ.
'От выбора положения оси Оу зависит большая или меньшая
сложность решения заДач. Решим эту задачу двумя способами,
направив сначала ось Оу по стороне АВ, а затем — по стороне
CD прямоугольника ABCD. '
Первый способ. Для определения расстояния хц центра тяжести
площади трапеции ABED (рис. 52,а) от оси Ау, направленной по
АВ, воспользуемся формулой (XI 1,5).
~ A)
где F1 и F2 — площади прямоугольника ABCD и треугольника
DCEf а хг и х2 — расстояния их центров тяжести от оси Ау.
Определим Flf F2 и х1У х2, обозначив АВ = CD через by a BE
через Хц.
Fx = а • Ь\
Центр тяжести площади треугольника DCE находится в точке
К на пересечении медиан, поэтому х2 найдем по формуле (X 11,12):
2 3 3 '
Подставив найденные значения в уравнение A), получим:
.а • Ь 2а + х
fl6(fl) JL
После незначительных преобразований уравнение A) примет
следующий вид:
-?лц -t- za л:ц a — и. <* >
Решив уравнение A"), получим
х1И = — I- • A +|/")= — 1,366a, (
~.(УЪ — 1) = 0,366 а.
206 Статика твердого тела
Так как хп не может быть отрицательным, то условию задачи
удовлетворяет только
Хц = х2п= 0,366 а.
Второй способ. Координата центра тяжести однородной плоской
фигуры (рис. 52,6) определяется по формуле (XII,5).
¦~ц — F -r F ' к '
Обозначив СЕ через хп, определим F2 и х2 (площадь Fx опре-
определена ранее, а координата хг сохраняет свое значение и при новом
положении оси Оу).
F — _ А.
Подставив найденные значения в уравнение B), получим.
и а ь к *«
После незначительных преобразований уравнение B') примет
следующий вид:
2*2—
Решив уравнение B"), получим:
/У = 0,634а.
*2Ц= ~-C + 1^3") = 2,366д. (Л
Так как *ц составляет только часть а, то условию задачи удовлетво-
удовлетворяет
хп = *1П = 0,634 а.
Таким образом, ^определяется значительно проще при направ-
направлении оси Ot/ по стороне CD, т. е. когда эта ось примыкает к отри-
отрицательной площади.
53. Определить положение центра тяжести площади сечения
тела (рис. 53,а), если: АВ =6 см; ZC =9 см; AZ = 12 см;
CD =4 см; DF = 7 слг, ?д = 6 слг, qF = Fn = 4 см; FJ || Gtf ;
FJ = GH = 24 аи; Ga? = 6 ли; J/C = 4 см; KL - беле; OL = OP =
= 0M = 0iV-O1Q = 01/? = 02S= O2L/ = О2Г = г = 4 с^;(УК = 6 см;
ZV = 28 см; ad= 4 см и ab = 6 см.
Определение положения центра тяжести твердых тел
207
Решение. Так как рассматриваемая площадь не имеет ни одной
оси симметрии, то для определения положения ее центра тяжести
необходимо найти две координаты.
I/ х
К задаче 63.
Разобьем рассматриваемую площадь (рис. 53,6) на такие части
(элементы), положение центров тяжести которых или известно,
или может быть легко определено, после чего занумеруем их.
Число элементов сведем к минимуму, введя отрицательные
площади прямоугольника abed, полукруга MNP и четверти круга
208 Статика твердого тела
MOL. Кроме того, для учета площади QWR дополним ее до квад-
квадрату O±QWR и введем отрицательную площадь кругового сектора
O±QR.
Таким образом, вся фигура разбита на двенадцать частей: восемь
положительных и четыре отрицательных.
Координатные оси Ах и Ау необходимо расположить так, чтобы
координаты центра тяжести элементов легко можно было найти.
Учитывая сложность фигуры и необходимость упростить под-
подсчеты, располагаем оси Ах и А у так, чтобы вся фигура находилась
в одном квадранте (при таком выборе осей координаты центров
тяжести всех элементов положительны).
Поскольку число, элементов, на которые разбита вся фигура,
больше двух, то после нахождения площадей Fi9 координату, yi и ста-
статических моментов Sty и Six площадей элементов относительно
осей Ау и Ах вносим полученные результаты (по мере их на-
нахождения) в соответствующие графы таблицы.
Определение почти всех указанных в таблице величин не тре-
требует пояснения. Объясним только, как найдены координаты центров
тяжести элементов 1,2,3, 7, 10, 11 и 12.
Элемент 1 (трапеция ABCZ). Центр тяжести площади трапеции
находится на прямой ef, которая делит каждое из оснований АВ
(а) и CZ (Ь) пополам; найдем координаты х и у центра тяжести
площади — точки к соответственно по формулам (XII, 1*6) и
<ХН, 17):
AZ 2Ь +а 12 2-9+6 а А
Л" 3 а + 6 3 6 + 9 '
1
Элемент 2 (треугольник DEF). Центр тяжести площади треуголь-
треугольника находится в точке / на пересечении медиан. Координаты х и у
центра тяжести площади определим по формуле (XII, 15).
л — 3 — з — ,
,, ZD +ZF + & 13 + 20+%24 ,Q
у = л = — о = 1У см.
Элемент 3 (параллелограм FGHJ). Центр тяжести площади па-
раллелограма находится в точке т на пересечении его.диагоналей
FH и GJ. Координату у центра тяжести площади найдем из ри-
рисунка, а координату х точки т средины прямой FH найдем как
среднюю арифметическую координат ее концов (точки Я,и V распо-
расположены на одной вертикали).
AZ + AV 12 + 40 ос
-у" •—- . ¦ ¦ ' /Г\ Г Ы '
ц = ZF + $?- = 20 4- 4' = 23 см.
Определение положения центра тяжести твердых тел
209
№
эле-
элемента
по
пор.
Положение, форма
элемента и его раз-
размеры, в см
1 I
2
7*
_— -
"г
—
и
р
. — _.
6 28
6
-
4\
F!
__
4
Площадь эле-
элемента, в еж2
12
F + 9) х у =
= 90
^ X 7 X 6 :
= 21
24 х 6 = 144
14 х 14 = 196
10 х 4 = 40
28 X 6 = 168
Координаты
центра тяжес-
тяжести площади
элемента, в см
6,4
10
26
19
31
2 ~ 2
= 25,1
4 х 4 = 16
-Dx6) =
= — 24
10
11
12
26
36
28
18
3,8
19
23
13
18
3
7,7
8
Статический мо-
момент площади эле-
элемента относитель-
относительно осей Ох и Оу, в смг
342
399
3312
2548
720
504
193,3
128
576
210
3744
3724
1240
4368
903,6
448
2
3,14 -42 _ 24,3
" 2
= — 25,1
пг2
~" 4 ""
3,14/ 4а
4
-= — 12,6
3,14 ^42
= —12,6
,. = 625,8
27,7
8,3
16
17,7
8,3
— 216
— 401,6
— 223
— 104,6
= 7201,1
— 432
— 609,9
— 349
— 356,6
«13г466Д
14 591
210 Статика твердого тела
Элемент 7 (площадь полукруга STU). Центр тяжести площади
находится на оси симметрии О2Т в точке Л. Координату х центра
тяжести площади найдем из рисунка, а координату у — по формуле
(XII, 13).
= 40 — 4 = 36 см;
и= UV 4- — • г = 6 -I - .4 — 77 см
у _. uv -f Зя Г ° ' 3-3,14 ~ '
Элемент 10 (площадь полукруга MNP). Центр тяжести пло-
площади находится на оси симметрии ОЫг в точке i; его координаты
х и у найдем соответственно по формуле (XII,13) и из рисунка:
x = AZ+FJ — KL — LO — ±
= 12+ 24— 6 — 4 — -3757^ • 4 = 24»3
= 9+ 4 + 7—4= 16 еж
Элемент 11 (площадь четверти круга M0L). Центр тяжести
площади находится на оси симметрии в точке р. Координаты х
и у центра тяжести площади найдем соответственно из рисунка и
при помощи формулы (XII, 13').
12 + 24 — 6 — 4+ тг^ьг-4==27,7 см:
^ DF — JK + ^ • ОМ =
= 9 + 4 + 7,- 4 + -д^щ • 4 = 17,7 см.
Элемент 12 (площадь кругового сектора OXQR — четверти кру-
круга). Центр тяжести площади находится на оси симметрии Ог?
в точке t.
Координаты х и у центра тяжести площади найдем из рисунка
и при помощи формулы (XII, 13'):
* = AZ + ZV — US — SR — -gL • OjQ =
= 12 + 28 — 8 — 2— зг^ • 4 = 28,3 см;
у - VUi-Щ - ± ¦ RO, = 6 + 4 - -^Ijj • 4 = 8.3 «t.
Определение положения центра тяжести твердых тел
211
Определим координаты хц и уц центра тяжести рассматриваемой
площади, применив формулы (XII, 5).
5..
Ел
13 466,1
625,8
7201,1
625,8
• =21,5 см;
= 11,5 см.
*ц ел ел
Найденные координаты центра тяжести рассматриваемой пло-
площади нанесем на рис. 53,6.
К задаче 54.
54. Определить расстояние от оси А у центра тяжести площади
ABC (рис. 54,а), ограниченной осью Ах, кривой АВ и наклонной
прямой ВС, если уравнение кривой АВ следующее: у = 1,5л: —
— 0,2л:2.
Решение. По условию задачи необходимо найти только
одну координату центра тяжести площади ABC — хц.
Разобьем всю площадь (рис. 54,6) на две части, опустив из
точки В на ось Ах перпендикуляр ВЪ\ обозначим площадь АВЬ
через ?ъ а площадь треугольника ВЬС — через F2.
Расстояние хп площади ЛВС от оси Ау найдем, воспользовавшись
формулой (XI 1,5):
г — Sy — Sw * s*v i\\
Для нахождения статического момента площади треугольника
ВЬС относительно оси Ау определим площадь,треугольника ВЬС
и расстояние х2 ее центра тяжести от оси Ау, для чего предварительно
найдем величину ВЬ, подставив х = 6 в уравнение кривой АВ.
Bh = y=\,5- 6 — 0,2 • 62 = 1,8;
F2 = 1,8.1=1,8;
= 6 + f = б'
14*
212 Статика твердого тела
Так как положение центра тяжести площади АВЬ неизвестно,
то ее статический момент относительно оси Ау найдем интегриро-
интегрированием, выразив статический момент элементарной площадки (у . dx)
относительно оси Ау через у . dx . х.
6
= |A,5х — 0,2х2) -x-dx-
о
J'l.W.<te-Jo,S
о
,2x3 • Лх =
о о
= 1,5^.-0,2.-^-43,2.
Площадь ЛВ6 также найдем интегрированием.
0 * 6 6
Fx = f r/rfx = i (l,5x —0,2х2)Л = j l,5x • dx— f 0,2x2 - dx =
0 0 0 0
= 1,5.-^-0,2. ^-=12,6.
Подставив найденные значения в уравнение A), найдем:
43,2 + 1,8-6,67 Q QQ
Х* = 12,6 + 1.8 e d'bd*
55. Найти координаты центра тяжести плоской фермы (рис. 55,а),
состоящей из семи стержней, длины которых указаны на рисунке,
если вес одного метра каждого стержня одинаков.
Решение. Так как рассматриваемая плоская ферма не имеет
ни одной оси симметрии, то для определения положения ее центра
тяжести необходимо найти две координаты.
Ферма состоит из семи частей — стержней; так как все они
однородны и имеют одинаковую линейную плотность, то силы веса
стержней пропорциональны их длинам и приложены на средине
длины каждого стержня (рис. 55,6).
Направим координатные оси согласно рис. 55,6 и определим
координаты центра тяжести плоской фермы по формулам (ХП,5).
A)
B)
Так как все силы пересекают осьВх и параллельны оси By,
то для определения хц и уп в числители фсфмул необходимо ввести
Определение положения центра тяжести твердых тел
213
суммы моментов всех сил относительно оси Bz, перпендикулярной
к плоскости рисунка, соответственно при вертикальном и горизон-
горизонтальном направлении сил.
*1 '
К
I 1
К задаче 55
Повернув в одном направлении все силы на один и тот же угол -
в данном случае на 90° — мы не изменим положения центра тя-
тяжести плоской фигуры.
Пронумеруем все силы и составим таблицу, куда внесем все
величины, необходимые для получения хц и уп.
{о стерж-
стержня по
порядку
1
2
3
4
5
6
7
—
Длина /^
стержня, в м
3
2,5
2,5
2
1,5
2,5
2
ЪЦ = 16
Координаты
центра
стержня,
h
0
1
1
1
2
3
3
—
в м
Уг
- 1,5
2,25
0,75 ~
0
0,75
0,75
0
—
Моменты
оси Bz при
СИЛ (
этносительно
направлении сил
вертикальном
к h
0
2,5
2,5
2
3
7,5
6
23,5
горизонталь
ном
V Уг
4,5
5,63
1,87
0
1,13
1,87
0
ЪЦ'У1 = 15
Подставив найденные значения в формулу (XI 1,5), получим:
23 5
^ = "ПГ = °'94 м-
214
Статика твердого тела
56. Найти такую высоту h конуса (рис. 56,а), при которой
тело, состоящее из конуса и полушара одинаковой плотности и
одинакового радиуса г, теряет устойчивость в том положении рав-
равновесия, когда оно опирается поверхностью полушара на гладкую
горизонтальную плоскость.
К задаче 56.
Решение. Заданное тело имеет бесчисленное множество плос-
плоскостей симметрии; центр тяжести тела находится на линии пере-
пересечения всех плоскостей симметрии — оси симметрии ОС и для
определения его положения достаточно найти одну координату.
Ось ОС одновременно является осью симметрии и для полушара
и для конуса, поэтому их центры тяжести также находятся на
этой оси.
Предварительно рассмотрим три основных положения центра
тяжести тела.
1. Центр тяжести тела находится ниже центра О шара, допустим,
в точке Сх (рис. 56,6).
Пусть тело какой-то, не показанной на рисунке, силой приве-
приведено в состояние, изображенное на рисунке, после чего сила уда-
удалена. Выясним, останется ли тело в таком положении или воз-
возвратится в первоначальное положение с вертикальной осью ОС.
Обозначим вес тела через Р.
Определение положения центра тяжести твердых тел 215
В точке касания шаровой поверхности с плоскостью приложим
направленные в противоположные стороны две равные друг другу
вертикальные силы Р' и Р", каждая из которых равна силе Р,
отчего равновесие тела не изменится.
Направленная вниз сила Р' уравновешивается не показанной
на рисунке реакцией плоскости, а две приложенные к полушару
равные друг другу параллельные силы Р и Р", направленные в
противоположные стороны, образуют пару сил (с плечом а), пово-
поворачивающую тело против хода часовой стрелки. По мере поворота
плечо а пары уменьшается, и когда ось ОС тела займет вертикаль-
ное положение, плечо а обращается в нуль; в этом положении сила
веса Р проходит через точку касания и уравновешивается реак-
реакцией плоскости.
Таким образом, в рассматриваемом случае тело всегда
возвращается к положению, при котором его ось симметрии ОС
вертикальна, т. е. тело находится в состоянии устойчивого равно-
равновесия.
2. Центр тяжести тела находится в центре О шара (рис. 5б,в).
В указанном на рисунке положении тела, когда его ось симметрии
отклонена от вертикали на произвольный угол, вес Р тела обя-
обязательно1 проходит через точку касания и уравновешивается
реакцией плоскости.
В этом случае тело потеряло устойчивость равновесия с верти-
вертикальной осью ОС и находится в состоянии безразличного равно-
равновесия, не возвращаясь в первоначальное положение.
3. Центр тяжести тела находится выше центра О шара, допу-
допустим, в точке С2 (рис. 56,г).
В этом случае, при отклонении тела от положения равновесия
с вертикальной осью ОС оно не возвращается в первоначальное
положение, так как образовавшаяся пара сил (с плечом а), повора-
поворачивая тело по ходу часовой стрелки, еще более отклоняет его от
первоначального положения, делая невозможным равновесие тела
при взаимном касании поверхности полушара с плоскостью.
Таким образом, потеря устойчивости равновесия тела при верти-
вертикальном расположении оси симметрии ОС наступает при таком
значении /г, когда центр тяжести всего тела совпадает с центром О
шара.
Из этих условий и будем исходить при нахождении значения А
конуса (рис. 56,5).
Приняв точку О за начало координат, направим ось Oz по ОС,
ось Or/ по ОВ и ось Ох перпендикулярно к ним.
Определим объемы Vx и V2 полушара и конуса, из которых
состоит тело, а также найдем расстояния гг и zz их центров тяжести
1 Радиус, по которому направлена вертикальная сила Р, всегда перпендику-
перпендикулярен к касательной.
216 Статика твердого тела
от точки О соответственно по формулам (XII, 19) и (XII, 18).
I/ _ г 2 и * _ 1 и
Повернув в одном направлении (на 90°) систему параллельных
сил — сил веса, пропорциональных (при одинаковой плотности)
объемам цилиндра и конуса, найдем координату центра тяжести
всего тела по формуле (XII, 9).
Зг2 — №
~ 4Bг 4- Щ '
Потеря устойчивости равновесия произойдет при zn = 0,
следовательно,
ИЛИ ^- 4Bг + Л) -
Зг2 — А2 = 0,
откуда
57. Определить графически положение центра тяжести плос-
плоской фигуры (рис. 57,а); размеры на рисунке да'ны в см.
Решение. Рассматриваемая фигура имеет ось симметрии — ось
хх, следовательно, ее центр тяжести находится на этой оси.
Применив метод введения отрицательных площадей, представим
себе рассматриваемую фигуру (рис. 57,6) состоящей из четырех
положительных и одной отрицательной площадей; за положитель-
положительные приняты площади: полукруга ABN (FJ, прямоугольника
BCHN (F2), прямоугольника DEK (F3), треугольника EFK (F^), за
отрицательную — площадь полукруга MRS (F5).
Определим положение центра тяжести каждой части фигуры.
Расстояния центров тяжести одинаковых площадей — полу-
полукругов ABN и MRS — от их геометрических центров найдем по
формуле (XII, 13):
хг = хъ = 0,424 г = 0,424 -41,7 см.
Центр тяжести площади треугольника EFК находится в точке
пересечения его медиан на расстоянии одной трети медианы от
Определение положения центра тяжести твердых тел
217
основания ЕК, т. е.
х4 = — • 12 = 4 см,
следовательно, он совпадает с точкой R.
Центры тяжести прямоугольников BCHN и DEKh находятся
в точках пересечения их диагоналей.
i-JL
К задаче 57.
Определим величины площадей всех частей фигуры.
F2= 10 . 8 = 80
Fs = 8- 12 = 96 см*;
F4 = l. 12- 12 = 72 см2; F5 = — 25,1 см*;
Задавшись масштабом, приложим к соответствующим центрам тя-
тяжести вертикальные векторы, пропорциональные площадям частей
фигуры (для отрицательной площади полукруга MRS этот вектор
направим вверх, а все положительные векторы — вниз). Из про-
произвольной точки а (рис. 57,<?) начинаем строить силовой много-
многоугольник, откладывая в выбранном порядке х один за другим
1 Порядок отложения векторов в силовом многоугольнике принимается про-
произвольный, веревочный же многоугольник строится в соответствии с выбранным
порядком отложения векторов в силовом многоугольнике.
218 Статика твердого тела
векторы Р19 Р2, Р3 и ^4 вниз, затем Ръ вверх и соединяем
вершины а, Ь, с, d, e и f полученного многоугольника с произволь-
произвольным полюсом О. Затем, приняв за начало построения произвольную
точку (рис. 57,6), строим веревочный многоугольник 1,2,3,4,5,6, после
чего находим точку пересечения его крайних — первой и шестой —
сторон.
Проведя через эту точку вертикаль /—/, найдем центр тяжести
рассматриваемой фигуры в точке О пересечения этой вертикали
с осью симметрии фигуры.
58. Определить графически положение центра тяжести плоской
фигуры (рис. 58,а), размеры которой (в см) даны в прилагаемой
таблице.
ах
6
) а \ а
|5|4|
28 !
02
161
ь3
8
10 |
б
\d\
8 |
/г
20
Решение. Так как рассматриваемая фигура не имеет ни одной
оси симметрии, то для определения положения ее центра тяжести
необходимо дважды находить линию действия равнодействующей:
при вертикальном и горизонтальном расположении векторов.
Применив метод введения отрицательных площадей, предста-
представим себе рассматриваемую фигуру (рис. 58,6) состоящей из трех
положительных и одной отрицательной площади; за положитель-
положительные приняты площади прямоугольников ABCD, VEFT, SMNR,
за отрицательную — площадь прямоугольника KLOP.
Определив положение центра тяжести каждой части фигуры,
определим величины площадей всех частей:
F1==5. 16 = 80 сж\
F2 = 4 • 9 = 36 см2;
F3 = 6-28= 168 см\
F4==_6.8 = —48 см\
Задавшись масштабом, приложим к соответствующим центрам
тяжести направленные вертикально вниз векторы, пропорцио-
пропорциональные площадям частей фигуры (для отрицательной площади
прямоугольника KLOP этот вектор направим вверх).
Из произвольной точки а (рис. 58,в) начинаем строить сило-'
вой многоугольник, откладывая в выбранном порядке один за
другим векторы Ръ Р2, Р3> ^4> затем соединяем вершины а, Ъ, с, dne
полученного многоугольника с произвольным полюсом О.
Затем, приняв за начало построения произвольную точку
(рис. 58,6), строим веревочный многоугольник 1,2,3,4,5, после чего
находим точку пересечения его крайних — первой и пятой —
сторон.
Определение положения центра тяжести твердых тел
219
Линия действия равнодействующей должна находиться на
вертикали /—/, проведенной через эту точку.
К задаче 58.
Повернув приложенные к соответствующим центрам тяжести
* вертикальные векторы против хода часовой стрелки на 90° и отло-
отложив их затем один за другим в прежнем порядке от той же точки
а,* соединим вершины а, Ьг, съ dx и ег второго многоугольника
с тем же полюсом 2.
Затем, приняв за начало построения произвольную точку,
строим веревочный многоугольник Г,2',3',5'.
1 Второй силовой многоугольник (для горизонтального расположения век-
векторов) может строиться из любой другой точки плоскости и в любом порядке.
Мы строим его из той же точки а, так как при этом вершины вь сь dx и сх можно
найти поворотом циркуля, одна ножка которого ставится в точку ау а другая со-
соответственно в точки в, с, d n е.
2 Результат не изменится, если выбрать новый полюс.
220 Статика твердого тела
Отсутствие в веревочном многоугольнике стороны 4' объяс-
объясняется тем, что векторы Р4 и Р3 направлены по одной прямой,
так что фактически во втором многоугольнике мы откладываем
их разность сгеъ в связи с чем выпадает луч Odx\ на рис. 58,в век-
вектор exdx и луч Od± показаны пунктиром.
Находим точку пересечения крайних — первой и пятой —
сторон веревочного многоугольника. Линия действия равнодей-
равнодействующей должна находиться на горизонтали //—//, проведенной
через эту точку.
Центр тяжести рассматриваемой фигуры находится в точке п
пересечения вертикали /—/ с горизонталью //—//.
Веревочный многоугольник для горизонтального расположения
векторов можно построить иначе, не строя силового многоугольника
аг Ьг сг dx lv Для этого проводим каждую сторону веревочного много-
многоугольника 1",2",3",5" перпендикулярно к соответствующей стороне
веревочного многоугольника 1,2,3,4,5 (сторона 4"отсутствует по ука-
указанной выше причине). Такое построение второго веревочного
многоугольника равносильно принятию полюса в точке Ох\ это по-
построение показано на рис. 58,в пунктиром.
ЧАСТЬ ВТОРАЯ
КИНЕМАТИКА
РАЗДЕЛ ПЕРВЫЙ
КИНЕМАТИКА ТОЧКИ
ГЛАВА XIII
ОСНОВНЫЕ ЭЛЕМЕНТЫ ДВИЖЕНИЯ ТОЧКИ
§ 1. Краткие сведения
Часть теоретической механики, в которой движение тела изу-
изучается независимо от его массы и воздействия на него окружаю-
окружающей среды (сил), называется кинематикой.
Изучение кинематики начинается с изучения кинематики гео-
геометрической точки, а затем систем этих точек, неизменно связанных
между собой, т. е. кинематики абсолютно твердого тела.
Траекторией точки называется геометрическое место положений
точки в пространстве при ее движении. Положения точки в про-
пространстве определяются по отношению к выбранной системе коорди-
координат. В зависимости от формы траектории (прямая или кривая ли-
линия) движение точки называется прямолинейным или криволинейным.
Движение точки считается изученным, если в любой момент
времени можно указать положение точки по отношению к выбран-
выбранной системе координат, ее скорость и ускорение.
Существует три способа, позволяющих определить движение
точки: 1) натуральный, 2) координатный и 3) векторный.
1. Натуральный способ задания движения
точки
При натуральном способе задания движения точки должны быть
известны: траектория точки, начало отсчета расстояний на траекто-
траектории и закон изменения расстояний точки, измеряемых по траекто-
траектории от начала отсчета. Например, пусть задана траектория точки
(кривая АВУ рис. I); возьмем на ней произвольную точку О и
примем ее за начало отсчета расстояний точки М при ее движении.
Зная расстояние точки М от начала отсчета, измеренное по траек-
траектории, определим положение точки, которая может располагаться
222
Кинематика
по отношению к началу отсчета справа или слева. Обычно при-
принимают расстояние s точки М, расположенной справа от точки О,
за положительное расстояние, а расположенной слева от точки
Расстояние s точки М от начала
отсчета, измеренное по траектории,
можно рассматривать как дуговую
координату точки М.
Так как закон изменения рассто-
расстояний точки в зависимости от времени
при натуральном способе задается
О — за отрицательное.
М
м.
Рис. I.
= f(t),
(XIII,1)
то положение точки на траектории в
любой момент времени может быть определено.
Для этого расстояние s, являющееся дуговой координатой,
вычисляют из уравнения (XIII, 1) для заданного момента времени
и откладывают его fro траектории от начала отсчета.
Величина скорости точки М в любой момент времени равна пер-
первой производной от расстояния s по времени
t>=~. (XIII.2)
Вектор скорости направлен по
касательной к траектории в соот-
соответствующей точке в сторону дви-
движения последней.
Величину и направление пол-
полного ускорения, когда известна
траектория точки, определяют по
ее составляющим на оси есте-
естественного трехгранника. Как из-
известно из дифференциальной гео-
геометрии, в каждой точке кривой
можно построить трехгранник,
по ребрам которого проходят три оси координат: ось "х, направ-
направленная по касательной к траектории _в данной точке, ось 7г, направ-
направленная по главной нормали, и ось Ь, направленная по бинормали
к траектории (рис. II). Плоскость, определяемая касательной и
главной нормалью, называется соприкасающейся плоскостью или
плоскостью кривизны кривой. Плоскость, определяемая нормалью
и бинормалью, называется нормальной плоскостью. Плоскость,
перпендикулярная к первым двум, называется, спрямляющей пло-
плоскостью.
Полное ускорение w точки находится в плоскости кривизны
кривой — траектории — в данной точке и может быть определено по
Рис. II.
Основные элементы движения точки 223
величине и направлению, если известны ее составляющие на каса-
касательную wx и главную нормаль wn.
Величина касательного ускорения
^ = -ЗГ- , (ХШ.З)
Вектор касательного ускорения направлен по касательной к
траектории в ту же сторону, что и вектор скорости vt если уско-
ускорение wx положительно.
Величина нормального ускорения
и>.=-у. (ХШ.4)
где р — радиус кривизны кривой в данной точке; v — скорость
точки в данный момент.
Вектор нормального ускорения направлен по главной нормали
к центру кривизны кривой.
Величина полного ускорения
w =
Направление вектора полного ускорения определим, вычислив
угол |х между вектором полного ускорения w и вектором нормаль-
нормального ускорения wn по формуле:
(ХШ,6>
В зависимости от закона движения точки по ее траектории
движения бывают равномерные и неравномерные. При равномерном
движении скорость точки по величине остается постоянной, поэтому
и касательное ускорение точки равно нулю. При неравномерном —
скорость изменяется по величине с течением времени. Следова-
Следовательно, касательное ускорение не равно нулю и может быть в
общем случае функцией времени, а в частном случае — постоян-
постоянным. Если величина касательного ускорения постоянна и положи-
положительна, то движение точки по траектории равноускоренное, если же
постоянна и отрицательна, то движение точки равнозамедленное.
При решении задач в случаях равномерного, равноускоренного и
равнозамедленных движений можно применять следующие урав-
уравнения.
При равномерном движении, когда скорость v постоянна,
где: s — расстояние точки от начала отсчета в любой момент вре-
времени;
Sq — расстояние точки от начала отсчета в начальный момент
времени (при / = 0); /—время (в сек.).
224
Кинематика
При равноускоренном или равнозамедленном движении закон
движения точки имеет вид
s = so + vot±^f. (ХШ.8)
Скорость точки в любой момент времени
v = vo±wj, (XIII.9)
где v0 — скорость точки в начальный момент времени (при t = 0)
Закон движения и закон изменения скоростей и касательных
ускорений точки можно представить графически.
S.CM
tee*
Рис. III.
Рис. IV.
Графические способы помогают наглядно представить движение
точки и часто облегчают решение сложных задач. Закон изменения
расстояний точки от начала отсчета — закон движения — может быть
представлен в координатах s, t в виде кривой, которая называется
кривой расстояний (рис. III). Как видно из рисунка, по горизон-
горизонтальной оси откладывается время t, а по вертикальной — расстоя-
расстояние s.
Кривая скоростей может быть построена в системе координат
v, t (рис. IV). Определив величины скоростей в соответствующие
моменты времени из формулы, дающей закон изменения скоростей
v =/(/), отложим эти значения в указанной системе координат и
получим кривую скоростей.
Для построения кривой касательных ускорений выбирают
систему координат wx, t и вычисляют значения w% для взятых
моментов времени.
Масштаб времени для всех трех диаграмм берется одинаковым.
Масштабы расстояний, скоростей и ускорений берут, исходя из
требований удобства и точности построения этих диаграмм.
Как известно, величина скорости точки равна первой производ-
производной от расстояния по времени, а величина касательного ускорения
равна первой производной от скорости повремени. Поэтому скороаь
точки пропорциональна тангенсу угла наклона касательной к кри-
кривой расстояний (рис. III) в соответствующей точке, т. е.
v =
Основные элементы движения точки 225
а касательное ускорение пропорционально тангенсу угла наклона
касательной к кривой скоростей в соответствующей точке, т. е.
wz = b2 tg a2
(рис. IV), так как тангенс угла наклона между касательной к кривой
и осью абсцисс равен первой производной от соответствующей
функции.
2. Координатный способ задания
движения точки
При координатном способе задания движения точки должны
быть известны координаты ее в выбранной системе координат, выра-
выраженные в функции от времени t:
*=М0; у = М0; * = МО- (хш, 10)
Эти уравнения называют уравнениями движения в проекциях на
оси координат. С другой стороны, эти уравнения представляют
уравнения траектории точки в параметрической форме. Для полу-
получения их в явном виде нужно исключить параметр — время /.
Зная эти уравнения, можно получить закон изменения проекций
скорости на соответствующие оси координат по формулам:
dx dy dz ,VITT ...
Величина скорости точки, выраженная через ее проекции,
Направление вектора скорости v, определяется по формулам:
cos a =
cos В =
cost =
(XIII, 13)
где a, (J, у — углы между вектором скорости и соответствующими
осями координат.
Проекции ускорения точки на оси координат равны вторым
производным от координат по времени:
?F = W" W = w* W = w* (XIII, 14)
15 591
226
КинемтНика
Величина полного ускорения
01 -
-s
Направление вектора ускорения можно установить, определив
углы al9 px, fi» которые находятся между вектором ускорения и
соответствующими осями координат, по формулам
w
cos x, =
V
(XIII, 16)
V o? -f W2y + i
Связь между координатным и натуральным
способами задания движения точки
Если движение точки задано координатным способом, то для
перехода к натуральному — необходимо определить уравнение
траектории точки, положение точки в начальный момент времени
(координатьы0, уои г0), а также закон движения точки по ее траек^
тории.
Закон движения точки по ее траектории определяется уравне-
уравнением
h
s = J V f? it) + Г22 (t) + ПЧП • dt% (XIII, 17)
где s — дуговая координата (расстояние точки от начала отсчета);
/i @» /<1 @» /з @ — первые производные от координат по вре-
времени.
3. Векторный способ задания движения
точки
При векторном способе задания движения точки положение ее
определяется радиусомгвектором, проведенным из произвольно вы-
выбранного центра. Радиус-вектор (рис. V) есть функция времени
или в проекциях на оси координат
zk.
Рис. V.
(XIII, 19)
Основные элементы движения точки 227
Вектор скорости
*=¦?, (XIII.20)
или в проекциях на оси координат
~~ ах т . dy — . dz -г /yttt oi\
V = -7- / 4" *jy / i ~77" ^ • (Alll,zl)
Вектор полного ускорения
S=*-2f. (XIII,22)
или в проекциях на оси координат
Годографы
Линия, соединяющая концы переменного радиуса-вектора, назы-
называется годографом радиуса-вектора. Линия, соединяющая концы
вектЪров скоростей точки, проведенных из произвольно выбранного
центра, называется годографом скоростей. Линия, соединяющая
концы векторов ускорения точки, проведенных из произвольно
выбранного центра, называется годографом ускорений. Касатель-
Касательная к годографу радиуса-вектора совпадает с линией вектора ско-
скорости точки. Касательная к годографу скорости параллельна линии
полного ускорения в соответствующем положении движущейся
точки. Годографы радиуса-вектора, скоростей и ускорений дают
возможность в удобной графической форме представить законы
изменения этих величин.
Для получения уравнения годографа скорости, при задании
движения точки координатным способом, следует продифференци-
продифференцировать уравнения движения и исключить время / из полученных
уравнений vx и vy и графически интерпретировать полученные
зависимости.
Для получения скорости vx точки, вычерчивающей годограф,
т. е. годографа ускорений, при задании движения точки координат
ным способом нужно продифференцировать выражения vx и vp>
исключив из полученных уравнений время / и графически интер-
интерпретировать полученные зависимости.
§ 2. Методические указания к решению задач
Задачи по кинематике точки в основном можно свести к несколь-
нескольким типам. Рассмотрим некоторые из них и укажем способы их
решения.
1. Движение точки задано натуральным способом. Требуется
15*
228 Кинематика
определить кинематические элементы движения (скорость, касатель-
касательное, нормальное и полное ускорения) в функции от времени или
в требуемые моменты времени. Задача решается путем дифференци-
дифференцирования закона движения точки согласно формулам (XIII, 2);
(XIII, 3); (XIII, 4); (XIII, 5), (XIIf, 6).
В случае, когда известна траектория и требуется определить
закон движения точки по заданной скорости или ускорению, задача
решается путем интегрирования заданной функции. При этом
в условии задачи должны быть данные (начальные или конечные
условия), которые применяются для определения постоянных
интегрирования. Определив закон движения точки, остальные
элементы движений можно определить по вышеуказанным фор-
формулам.
2. Движение точки задано координатным способом. Требуется
определить уравнение траектории точки в заданной системе коорди
нат, затем путем дифференцирования определить проекции ско-
скоростей и ускорений точки на соответствующие оси координат, их
величины и направления по формулам (XIII, 12) и (Х1П, 13).
Сюда же относятся и такие задачи, когда заданы проекции
скорости или ускорения точки и требуется определить закой изме-
изменения координат точки в функции от времени и уравнение траек-
траектории точки. В этом случае на основании равенства (XIII, 11) или
(XIII, 14) интегрируют заданные функции и определяют закон
изменения координат точки в функции от времени. Для определе-
определения постоянных интегрирования используются данные, приведен-
приведенные в условии каждой задачи.
3. Движение точки задано координатным способом. Требуется
определить траекторию и закон движения точки по траектории,
касательное, нормальное, полное ускорение точки и другие кине-
кинематические элементы движения.
В этом случае скорость точки и полное ускорение ее в функции
от времени определяется по формулам (XIII, 12) и (XIII, 15), а
затем по формуле (XIII, 3) — величина касательного ускорения.
Зная величины полного и касательного ускорений, можно из фор-
формулы (XIII, 4) получить величину нормального ускорения. Зная же
нормальное ускорение, из этой же формулы определяют величину
радиуса кривизны для любого требуемого момента времени. Закон
движения точки по траектории определяют по уравнению (XIII, 17).
4. Кроме указанных типов задач, имеются и такие, главной
целью которых является ознакомление со способами составления
уравнений движения. Например: составление уравнения движения
точек при полете тяжелого тела, движение точек обода катящегося
колеса и другие. В этом типе задач движение точки рассматривается
в прямоугольной системе координат и полученный закон движе-
движения точки, выраженный координатным способом, используется
для определения искомых величин.
Основные элементы движения точки 229
§ 3. Задачи
59. Точка движется по дуге окружности радиуса R = 30 см.
Закон ее движения по этой дуге s = 30 sin %t (t — в сек., 4s — в см).
Найти величину и направление скорости и полного ускорения
точки в момент / == 5 сек.
Решение. Пусть движущаяся точка (рис. 59) в начальный мо-
момент времени находится на окружности в положении Л. Движение
точки по окружности по ходу часовой стрелки примем за положи-
положительное направление.
Величина скорости для любого момента времени определяется
по (формуле
/ ds
v~-df>
следовательно,
v = — C0 sin тс/) = ЗОтс • cos тс • t см/сек.
В момент / = 5 сек.
v = 30tccos тс • 5 = — ЗОтс см!сек. _. ^ -п
' К задаче 59.
Знак минус показывает, что скорость точки в
данный момент направлена пробив положительного направления
движения.
Для определения величины полного ускорения необходимо
вычислить касательное и нормальное ускорение. Касательное
ускорение для любого момента времени равно
w, = ~ = -^ (ЗОти cos тс/) = — ЗОти2. sin ти/ см/сек2.
В момент времени / = 5 сек.
wx = — ЗОтс2 sin тс . 5 = 0.
Нормальное ускорение для любого момента времени
V2 C0rcCOSTC02 ол 9 9 j. /о
wn=: ^-^ зо— ^ с см/сек2.
В момент времени / = 5 сек.
Wn = ЗОтс2 COS2 те . 5 = ЗОтс2 с
Нормальное ускорение направлено по радиусу к центру враще-
вращения.
Полное ускорение для любого момента времени
w = j/"ay2 4- w\ = V(— ЗОтс2 sin тс/J + (ЗОтс2 cos2 тс/)г =
= ^О^21/sin2 тс/ + cos4 тс/'
230
Кинематика
В момент / = 5 сек., касательное ускорение равно нулю,
следовательно, полное ускорение по величине и направлению
равно нормальному.
60. Трамвай (рис. 60) движется по прямолинейной траектории и в
период разгона расстояние S увеличивается пропорционально кубу
времени; в течение первой минуты трамвай прошел расстояние
90 м. Найти скорость и ускорение
в моменты / = 0 и / = 5 сек. По-
Построить кривые расстояний, скоро-
скоростей и ускорений.
1 2 J 4
б
Решение. Рассмотрим движение
трамвая как прямолинейное движе-
движение точки по закону
s = at*, A)
где s — расстояние точки от начала
отсчета, а — постоянный коэффициент,
t — время.
Скорость и ускорение точки опре-
определим из уравнений
ds
v =
dt
".-*-¦?•
B)
C)
12 3 4
6
К задаче 60.
Так как движение прямолиней-
прямолинейное, то нормальное ускорение wn = 0,
и полное ускорение равно касатель-
касательному w = wT. Предварительно опре-
определим величину t a> подставив в
уравнение A) s = 90 м.
откуда
90 = a • I3,
a = 90,
Следовательно, закон движения трамвая будет
s = 90/3 м.
Скорость точки в любой момент времени
v _ *L — 270t2
Ускорение точки
*-*-54О*
(У)
(Г)
B0
C0
Основные элементы движения точки 231
Из урайнений B') и C') скорость и ускорение трамвая в на-
начальный момент (/ = 0) равны нулю, т. е. v0 = 0 и w0 = 0.
Через 5 сек. после начала движения
v = 270 | у2) = -^ м\мин.
Ускорение в этот момент
wx = 540 tq = 45 м/мин.
Зная аналитические выражения s, v и а;х, закон их изменения
можно представить графически. Для этого в прямоугольной системе
координат построим кривые расстояний, скоростей и ускорений
(рис. 60,а, б, в), приняв при этом следующие масштабы: для времени
1 см — 0,5 мин.; для расстояний 1 см — 900. ж; для скорости
1 см — 900 м/мин2', для ускорений 1 см — 9С0 м/мин2.
61. По заданным уравнениям движения точки: х = 5 +
-J-3 cos?; у =4sin t. Найти уравнение ее траектории.
Решение. Чтобы исключить время из заданных уравнений,
преобразуем их:
х — 5
Возведем эти уравнения в квадрат и, сложив их, получим
или
(*-5)» , if ,
9 + Тб ~~ Ь
Следовательно, траекторией точки является эллипс
hT6
9 hT6
62. По заданным уравнениям движения точки
х = 3 cos (-?- + ict\ ,
У = 4 sin (т +
иайти уравнение ее траектории.
232 Кинематика
Решение. Чтобы исключить время из заданных уравнений,
преобразуем их следующим образом:
.|- = cos (-?+*/), A)
л I • / К Л Я
= 4[sin[-5- +itf|cos j-
X
Подставив из уравнения A) во B) значение о, получим
или
B)
B')
4cos-
o
Возведя обе части уравнений A) и B)" в квадрат и сложив их,
получим
— +
16 cos» 4
о
откуда
L Тб "" Т О111 "8
хг . у2 ху . тс 2 тс
"о Г "Т«" «" Sin "о" — C0S "о" »
т. е. траектория точки — эллипс.
63. Даны уравнения движения снаряда (рис. 63):
х = 250/; # = 430/ — 4,9/2
(/ — в сек., х, у — в м). Определить время, дальность полета,
траекторию снаряда, а также величины и направления скорости
и.полного ускорения в момент падения снаряда.
Решение. Уравнение траекто-
траектории получим, исключив время из
заданных уравнений движения:
х = 250/, {1)
у = 430/ — 4,9/2. B)
задаче 63. Определив из уравнения A)
время / и подставив его значение в уравнение B), получим
у = 430 =^ — 4,9 -^ = 1,72* — 0,0000784х2, C)
т. ?. траекторией снаряда является парабола (рис. 63).
Основные элементы движения точки 233
Для определения дальности полета L найдем то значение х>
при котором у = 0:
430/ — 4,9/2 = 0.
Отсюда время полета
/ = — = 87,75 сек. D)
Дальность полета
х = L = 250/ - 250 . 87,75 - 21,94 км. E)
Величину скорости определим по ее проекциям на оси коорди-
координат из формулы
или
v = )/2502+ D30 — 9,8/J. F)
При / = 87,75 сек. получим величину скорости в момент падения
снаряда на землю
v = |/502 + D30 — 9,8 • 87,75J = 422 м/сек. (!)
Направление скорости получим из соотношения
'dx
-'— v* dt =1 = о,
К
^,24-№2
что соответствует углу 53° 40' и 306° 20'.
Первое значение угла соответствует моменту вылета снаряда
из дула орудия, а второе — моменту падения на землю.
Величину ускорения определим по ее проекциям на оси коорди-
координат из формулы
Подставив значения проекций ускорения на оси координат
"S*= ° и "ж = ~9'8 М1сек2 в ф°рмулу (8)>
получим
w = 9,8 м/сек2.
Направление вектора полного ускорения определим из формулы
d2x
— r~ W Л/2
C0S(OF,t)=-J1=
1 /7 Л \2
234
Кинематика
т. е. ускорение направлено вертикально вниз и параллельно оси у,
т. к. угол (&, J) = 270°.
64. Длина линейки эллипсографа (рис. 64) АВ = 40 см, длина
кривошипа ОС = 20 еж, ЛС = СВ. Кривошип равномерно вра-
вращается вокруг оси О с угловой скоростью со. Найти уравнения
траектории точки М и годографа ее скорости, если точка М нахо-
находится на расстоянии 10 см от конца А.
К задаче 64.
Решение. Составим уравнение движения точки М, приняв
координатный способ задания движения. Абсцисса точки М равна
х = 30coscp; A)
у = 10 sin ср. B)
Так как кривошип вращается равномерно с постоянной скоростью о>,
то угол <р наклона кривошипа к оси х пропорционален времени и
равен
<Р - со/. C)
Поэтому уравнения движения точки имеют следующий вид:
х = 30 cos о)/; (V)
у = Ю sin о)/. B0
Чтобы получить уравнение траектории, нужно из уравнений
(Г) и B') исключить время t. Для этол) разделим правую и левую
части уравнений соответственно на коэффициенты при косинусе и
синусе и возведем обе части уравнений в квадрат, затем,сложив их,
получим
L _#!_ == 1
I 1ПП 1"
900 п 100
D)
Это уравнение эллипса с полуосями, равными 30 см и 10 ел*.
Чтобы получить уравнение годографа точки М, определим
проекции скорости этой точки на оси координат х и у.
—- =;с = —30a>sin<of; E)
^jf- =у = Юо) cos (о/.
F)
Основные элементы движения точки 235
Уравнение годографа составим в системе координат хОу, где х и
у — проекции скорости на эти оси. Для этого из уравнений E)
и F) исключим время t.
jfe-coe«tf. E")
Возведя обе части уравнений E') и E") в квадрат и сложив их,
получим уравнение годографа скорости в явном виде
2 "» ЮОоJ
900u>
Это уравнение эллипса с полуосями, равными 30а> и 10а>.
65. Найти скорости движения (рис. 65) середины М шатуна
кривошипно-шатунного механизма и
ползуна пру г = / = а и ср = со/,
где со = const.
Решение. Решим эту задачу, при-
применив координатный способ задания oi
движения точки. Примем начало ко- I
ординат в точке О, направив ось Ох к задаче 65.
по горизонтали вправо, а ось Оу —
по вертикали вверх. Обозначим координаты точки М через х и у
и определим из рисунка их величины, а именно:
так как по
Определим
условию
проекции
х = г cos со/ -|- Tj" cos со/;
г/= у sin со/;
г = / = а, то
х = _ а cos со/,
а
У ==: ~7Г Sin (о/.
скорости точки УИ на оси координат
dx 3 . .
ж = —- = — — ао> sin со/,
оу = -^- = у со cos to/.
A)
B)
(Г)
B0
C)
D)
236
Кинематика
Величину полной скорости определим по формуле
E)
Закон движения ползуна В получим, выразив расстояние Хв как
функцию от времени. Из А О А В получим
хв = (г + [) cos w/
или
хв = 2а cos Ы. F)
Величину скорости ползуна В определим по формуле
dx
vB = -~ == — 2асо sin w/.
dt
G)
Знак минус показывает, что скорость точки в данный момент на-
направлена в сторону, обратную положительному направлению
оси Ох.
66. Бомба, сброшенная с самолета (рис. 66,а), движется соглас-
согласно уравнениям:
V —— 71 /• 1/ —— h ——
где х, у — координаты бомбы
для любого момента времейи;
х и0 — начальная скорость бом-
бомбы, направленная горизон-
горизонтально и равная скорости
самолета в момент сбрасы-
сбрасывания бомбы (в м/сек)-у
h—высота падения (,омбы(в м)\
t — время (в сек); g — уско-
ускорение силы тяжести (в м/сек2).
Ось, Ох направлена гори-
горизонтально, а ось Оу — вер-
вертикально вверх (рис. 66).
Найти уравнен! е траектории;
величину и направление скорости бомбы в момент падения ее на
землю; дальность полета; уравнение годографа скорости бомбы и
скорость vr точки, вычерчивающей годограф.
Решение. Исключив время из заданных уравнений движения,
определим уравнение траектории
x = vot; A)
У-П-&-. B)
К задаче 66.
Основные элементы движения точки 237
Определив время t из уравнения (IL и подставив его значение
в уравнение B), получим:
Как показывает уравнение C), траекторией бомбы является
парабола.
Из уравнения B) определим время полета бомбы до ее паде-
падения, т. е. когда у = 0:
0 = Л — ^, B0
откуда
I
Дальность полета хтах = ' можно определить из уравнения A), зная
время t, а именно
Определим скорость бомбы.
Проекции скорости на оси координат:
dx /c.
v* = 37 = °ь; F)
* = $--#¦ С7)
Величина скорости для любого момента времени
Скорость бомбы в момент падения на землю, т. е. при t= \
равна
v = Vv*0 + 2gh. (9)
Направление вектора скорости бомбы в момент ее падения на
землю определим, вычислив косинус угла между направлениями
вектора скорости и осью Ох:
Для получения уравнения годографа скорости бомбы исклю-
исключим t из уравнений F) и G). Тогда уравнение годографа будет
х —V (И)
т. е. уравнение вертикальной прямой (рис. 66,6), отстоящей от
начала координат на v0.
238
Кинематика
Скорость vx точки, вычерчивающей годограф, определим при
дифференцировании из уравнения G), т. е.
% = -g. A2)
67. Определить уравнения движения и траекторию точки М
обода колеса паровоза радиуса R = 1 м, если паровоз движется
по прямолинейному пути с постоянной скоростью 20 м/сек. При-
Принять, что колесо катится без скольжения; за начало координат
взять начальное положение точки на пути, принятом за ось Ох.
Определить также величины и направления скорости и полного
ускорения точки обода колеса в момент ^ = §о сек*
О /V
Решение. Обозначим точку касания колеса с рельсом в началь-
начальный момент через О и примем ее за начало координат, направив
ось Ох вдоль рельса вправо, а ось Оу — вертикально вверх (рис. 67,а).
Так как колесо катится по рельсу без скольжения, то дуга окруж-
окружности РМ равна участку рельса ОР, где Р — точка касания колеса
с рельсом в данный момент времени.
Рассмотрим движение точки М. Пусть ее текущие координаты
будут х, у. Обозначив центральный угол РСМ через <р, получим
х = OP — NP = /?ф — R sin ф, A)
y = NM = /? — /? cos ф. B)
Таким образом, уравнения движения будут
х = R (ф - sin ф), B')
У = /?A—cosy). B").
Дуга окружности РМ равна участку рельса ОР, который равен
расстоянию, пройденному центром колеса С от своего начального
положения Со. Центр колеса С движется равномерно со скоростью
v, следовательно, расстояние
С0С = РМ
Основные элементы движения точки 239
или
vt = /?<р, C)
откуда
Ф=?/ = 20/. D)
Подставив значение ср в уравнения B') и B"), получим:4
х = 20/ — sin 20/, E)
у = 1 — cos 20 /. E')
Кривая, которую описывает точка окружности колеса, катящегося
без скольжения по неподвижной прямой, представляет собой ци-
циклоиду. Определим проекции скорости точки обода на оси коор-
координат х и у:
Vx==^t =20-20 cos 20/, F)
0„ = -| = 20 sin 20/. F')
В момент / = ^ сек. точка будет находиться в положении М1У
определяемом величиной угла <р (рис. 67,6).
Угол срх определим из равенства
Фх = 20/ = 20 • ^ = ~ ти радиан, F")
откуда
<рх= 120°.
Определим проекции скорости в момент / =±= ~ сек. Из уравнений
F') и F") получим:
or, = 20 — 20 - cos 20 ~ = 20 + 20 -i = ЗОм/сек, G)
иу = 20 sin 20 -^ = 20 ^ = 10 У3 м/сек. G')
Величина полной скорости
v = уо2 + V2 = у 302 + A0 J/3J - 20
Направление вектора полной скорости определим, вычислив угол
между направлением вектора скорости и положительным направ-
направлением оси Ох:
— — v зо V^iT
cos (v, i)=-f= ^щ- = ~y радиан, (9).
240 Кинематика
т. е. угол между вектором скорости и осью Ох равен 30°. Опреде-
Определим проекции ускорения точки обода на оси координат.
wx = ^- = 400 sin 20t, A0)
wy = ^ =400 cos 20/. A0')
Величину полного ускорения определяем по формуле
w = Vw\ + ш^ = /D00 sin 2002 + D00 cos 20/J = 400 ж/ce/c2. A1)
Направление вектора полного ускорения определим, вычислив
угол между вектором ускорения и положительным направлением
оси Ох:
/- т wx 400 sin 20* . ог>, /1ОЧ
cos (ш, i) = ^ = 4QQ = sm20/, A2)
или
cos(^, f) = cos (-? — 2
Следовательно,
^ (ш, 0 = у — 20* радиан. A3)
В момент времени t — -^ сек. угол между вектором ускоре-
ускорения w и положительным направлением ори Ох равен
^(ш, 0 =у—20~=—|-радиан,
что соответствует отрицательному углу 30°.
68. Ползун В движется по прямолинейной направляющей
(рис. 68,а) с ускорением wx =—т:2 sin ~ tM/сек2. Найти уравнение
движения ползуна, если его начальная скорость vOx = 2тс м/сек,
а начальное положение совпадает со средним положением пол-
ползуна, принятым за начало координат. Построить кривые расстоя-
расстояний, скоростей и ускорений.
Решение. Движение ползуна прямолинейное неравномерное.
Задан закон изменения ускорений, на основании которого тре-
требуется определить закон изменения скорости и закон движения
ползуна. Эту задачу решаем путем последовательного интегриро-
интегрирования дифференциального уравнения, характеризующего закон
изменения ускорения.
Примем ползун за точку, движущуюся по прямолинейной
траектории. Направим ось координат Ох по траектории вправо.
Основные элементы движения точки
241
Согласно условию задачи
_ d%x — 2 • 2L /
Интегрируя это уравнение, получим
_- = \ — ти2 sin тг tdt = 2тс cos -й- i
dt J ^ ^
Так как проекция скорости на ось Ох
равна
то запишем уравнение B) в таком виде:
^ = 2^cosJ-^ + C1. B0
Постоянную интегрирования Сг опреде-
определим из начальных условий. Так как
при / = 0 скорость vox = 2 пм/сек, то,
подставляя в уравнение B') эти значе-
значения скорости и времени, получим:
следовательно, Сх = 0.
Таким образом, закон изменения ско-
скорости ползуна будет
у __ 2тс cos —-1 C)
Интегрируя уравнение C), получим за-
закон движения ползуна
\
X = 4тс • Sin -х-1 Л
К задаче 68.
(О
B)
t.c*<
D)
Задавшись различными значениями времени и вычислив соот-
соответствующие им значения х, vx и wx, соответственно по формулам
D), C), A), построим кривые расстояний, скоростей и ускорений
(рис. 68,6). Кривая расстояний представляет собой синусоиду,
кривая скоростей — косинусоиду, а кривая ускорений — синусоиду,
но иначе расположенную, чем кривая расстояний, и строится она
в координатах wy t.
69. Палец кривошипа паровой машины в период пуска дви-
движется согласно уравнениям х = 25 cos 4/2, у == 25 sin 4P (х, у —
в сму t — в сек.). Найти скорость, касательное и нормальное
ускорение пальца.
16 591
242 Кинематика
Решение.Закон движения пальца кривошипа задан уравне-
уравнениями в координатной форме:
jc = 25cos4/2, A)
у = 25 sin 4/2, B)
поэтому величину скорости пальца кривошипа v найдем, вычислив
предварительно проекции ее vx и vp на оси координат:
vx = ~ = — 25 • 8/ sin 4/2 = 200/ sin 4/2, A')
Vy = ^ = 25 • 8/ cos 4/2 = 200/ cos At\ B')
или
у = К B001 sin 4/2J + B00/ cos 4/2J = 200 / см/сек. C)
Касательное ускорение пальца кривошипа найдем по формуле
dv
Подставив значение vy получим
w, = ~ B00/) = 200 см/сек2. D)
Нормальное ускорение определяется по формуле
V2
Wn = — .
Р
Как видно из формулы, для определения ускорения, кроме скоросщ
необходимо знать радиус кривизны траектории. Поэтому найдем
уравнение траектории по заданным уравнениям движения. Исклю-
Исключая из уравнений A), B) время, получим:
*2 + / = 252, E)
т. е. палец кривошипа движется по окружности радиуса г = 25 см.
Так как радиус кривизны р в этом случае равен г и постоянен,
то величина нормального ускорения
г
70. Найти величины и направления скорости и ускорения и ра-
радиус кривизны траектории точкЪ колеса (рис. 70), катящегося
по горизонтальной оси Оху если точка описывает циклоиду согласно
уравнениям:
х = 9/ — 0,75 sin 12/,
у = 0,75— 0,75 cos 12/
Основные элементы движения точки
243
(/ — в сек., х, у — в м). Определить также значение радиуса кривиз-
кривизны р при / = 0.
Решение. Заданные уравнения движения точки обода колеса
x = 9t — 0,75 sin 12/, A)
у = 0,75 — 0,75 cos 12/ B)
представляют собой для частного случая уравнение циклоиды в
параметрической форме, которое в общем виде имеет следующий
вид:
л: = г9 — г sin 9» C)
у = г — г cos 9, D)
где г — радиус колеса; ср — угол
поворота колеса, равный произ-
произведению угловой скорости вра-
вращения колеса на время /, т. е.
9 = со/ = 12/.
E)
) х р
К задаче 70.
Сравнивая уравнения A) и B) с уравнениями C) и D), можно
установить, что радиус колеса паровоза г = 0,75 м, а угловая
скорость вращения колеса о> = 12— .
Величину скорости точки обода колеей для любого момента
времени определим по ее проекциям на оси координат
u, = J = 9 — 9cos 12/,
Vy = J =
F)
G)
v = |/V + ц2 = У (9 — 9 cos 12/J + (9 sin 12/J =
= 9 У (I — 2 cos 12/ -f cos212/)'+ sin212/ =
= 9|/4sin26/ = 18 sin 6/ Ml сек.
(8)
Направление вектора скорости получим, определив угол между
направлением вектора скорости и положительным направлением
оси Ох, по формуле
_ __ v 9A _cos 12/) . a.
cos (y, i) = -ж = iflt,iw^ = sin6/,
18 sin 6/
откуда искомый угол равен
--J-6/.
(9)
A0)
244 Кинематика
Величину полного ускорения определяем по ее проекциям на
оси координат:
^ 2ff A1)
a4 2^ A2)
w = Yw\ + ts»l = 1/A08 sin 1202 + (Ю8 cos 12*)* = 108 м/сёк2. A3)
Направление вектора полного ускорения w определим, вычислив
угол между направлением вектора полного ускорения и положи-
положительным направлением оси Ох. Косинус угла между ними равен
Г К w* 108 sin 12* . 1О. /лл.
cos (w, i) = — = —ш§— = sin 12/, A4)
откуда искомый угол равен
?(w, i)=~-\2t. A5)
С вертикальной осью Ох вектор ускорения, следовательно, состав-
составляет угол, равный
? E, /) = 12 *. A6)
Полученный результат показывает, что вектор полного ускорения
всегда направлен по радиусу колеса к его центру. Радиус колеса
составляет с вертикалью угол ср == 12^.
Радиус кривизны в любой точке циклоиды определим из фор-
формулы для нормального ускорения
».-f. A7)
предварительно определив его величину из формулы для полного
ускорения
W =
откуда
— w\
w\. A8)
Следовательно, формулу для определения радиуса кривизны полу-
получим из формул A7) и A8):
Подставив в уравнение A9) найденные значения v, w и w?, опре-
определенные из формул (8), A3) и формулы
wx = jt= 108cos6tM/ceK\
Основные элементы двиоюения точки 245
получим величину радиуса кривизны р циклоиды для любого
положения движущейся точки:
р = <18si^ „ 3 sin Ым. B0)
г 1/Ю82 — A08cos60a
Угол между векторами полного и нормального ускорений най-
найдем по формуле
после подстановки в нее значений wT и
wn = |/"Ю82 — A08 cos б/J = 108 sin
получим
108 cos 6/ , с.
или
откуда
?==^_QL ^ B2)
Из рис. 70 видно, что угол, составленный хордой МР с радиу-
радиусом МС9 также равен -к- — 6?, следовательно, нормальное ускоре-
ускорение точки обода колеса, катящегося по горизонтальной прямой
без скольжения, всегда направлено по хорде МР, соединяющей
движущуюся точку с точкой Р касания колеса с осью Ох.
С другой стороны, нормальное ускорение всегда направлено
по главной нормали к центру кривизны, поэтому линия главной
нормали к циклоиде в любой точке ее совпадает с соответству-
соответствующей хордой МР для каждого положения движущейся точки.
Установим связь между величиной радиусд» кривизны в любой
точке циклоиды и длиной хорды МР для соответствующего поло-
положения точки.
Радиус кривизны р = 3 sin 6 tM>
Из равнобедренного Д МСР
МР = 2r sin 6^ = 1,5 sin 6* м.
Следовательно, радиус кривизны р вдвое больше длины хор-
хорды МР:
Р = 2МР. B3)
При / = 0, т. е. в начальный момент времени радиус кривизны
Ро =0.
246 Кинематика
РАЗДЕЛ ВТОРОЙ
ОСНОВНЫЕ ВИДЫ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА И
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
ГЛАВА XIV
ОСНОВНЫЕ ВИДЫ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
§ 1. Поступательное движение
Поступательным движением твердого тела называется такое
движение, при котором любая прямая линия, связанная с телом,
перемещается параллельно самой себе.
При поступательном движении твердого тела все его точки
описывают одинаковые параллельно расположенные траектории
и в каждый данный момент времени имеют равные по величине и
направлению скорости и ускорения.
Траектории точек тела являются, в общем случае, пространст-
пространственными кривыми. В случае, когда поступательное движение про-
происходит так, что все его точки перемещаются параллельно некото-
некоторой плоскости, траектории его точек представляют собой плоские
кривые, расположенные в параллельных плоскостях.
Чтобы изучить поступательное движение твердого тела, доста-
достаточно изучить движение какой-либо одной его точки, использовав
методы, изложенные в кинематике точки.
§ 2. Вращательное движение вокруг неподвижной оси
Вращательным движением твердого тела называется такое дви-
движение, при котором две точки тела (или с ним связанные) и прямая,
проходящая через эти точки, остаются неподвижными.
Неподвижная прямая, проходящая через эти точки, называется
осью вращения.
При вращательном движении твердого тела вокруг неподвиж-
неподвижной оси все точки его перемещаются в плоскостях, перпендикуляр-
перпендикулярных к оси, по окружностям, радиусы которых равны расстояниям
этих точек до оси вращения. Положение какой-либо точки тела,
ее скорость и ускорекие в любой момент времени можно опреде-
определить, зная расстойние точки от оси вращения и закон изменения
угла поворота тела <р в функции от времени.
Угол поворота ср представляет собой угол между двумя полу-
полуплоскостями, проходящими через неподвижную ось вращения тела.
Одна из этих плоскостей принимается за неподвижную, а другая
вращается вместе с телом.
Все точки тела за один и тот же промежуток времени поворачи-
поворачиваются вокруг оси на одинаковый угол, поэтому закон изменения
угла поворота тела ср в зависимости от времени называется законом
вращательного движения тела
/0 (XIV, 1)
Основные виды движения твердого тела 247
Зная закон вращательного движения тела, можно определить
его угловую скорость и угловое ускорение.
Угловая скорость равна первой производной от угла поворота
тела по времени
со=^ = Чсек. (XIV.2)
Угловое ускорение тела равно первой производной от угловой ско-
скорости по времени или второй производной от угла поворота по
времени
?
Зная угловую скорость и угловое ускорение тела, мо#шо опре-
определить линейную скорость и линейное ускорение любой точки
тела, отстоящей на известном расстоянии г от оси вращения.
Скорость точки тела, отстоящей на расстоянии г от оси враще-
вращения, по величине равна
У=и>л (XIV.4)
и направлена по касательной к траектории в сторону вращения.
Касательное ускорение этой точки по величине равно
wx = -rr == г -jT =(e м сек2 (XIV,5)
at at ** ' y '
и направлено по касательной к траектории в сторону вращения,
если s положительно.
Нормальное ускорение точки по величине равно
шп = — = — = ш2г м/сек2 (XIV,6)
и направлено по радиусу к оси вращения.
Полное ускорение этой точки по величине равно
w = УиР + w\ = г |/е2 + to4 м 1сек2. (X IV.7)
Угол р. между вектором полного ускорения w и вектором нор-
нормального ускорения wn определяется из отношения
tg^=_L = LiI. (XIV.8)
При равномерном вращении тела вокруг неподвижной оси
угловая скорость его постоянна и, следовательно, тело делает
в единицу времени одинаковое число оборотов.
Связь между угловой скоростью и числом оборотов тела в мину-
минуту (п об/мин) выражается формулой
co = 5JVceK. (XIV.9)
Линейная скорость любой точки тела, отстоящей на расстоянии
г от оси вращения, может быть выражена через число оборотов в
248 Кинематика
минуту
v = wr = ^ м/сек. (XIV, 10)
Закон вращательного движения тела при постоянной угловой
скорости его выражается формулой
Ф«Ф0 + со*, (XIV, И)
где <р0 — угол поворота тела в начальный момент времени.
При равнопеременном вращении тела (равноускоренном или
равнозамедленном) постоянной величиной является угловое уско-
ускорение 6, которое берется со знаком плюс, если движение ускоренное,
и со знаком минус, если движение замедленное. В этом случае закон
вращательного движения выражается формулой
Ф = Фо + <оо*±1Г%, (XIV,12)
а закон изменения угловой скорости тела — формулой
o) = aH + e*, (XIV, 13)
где ср0 — начальный угол поворота тела; ш0 — начальная угловая
скорость тела.
Угловая скорость и ускорение тела, скорости и ускорения
его точек могут быть представлены в векторной форме, а именно:
вектор угловой скорости тела
, 14)
где o)^, (Оу и (о, — проекции вектора а> на оси координат х, у, г\ /, /,
k — единичные векторы осей этих координат.
Вектор углового ускорения тела
7шш ej+ ej+ ezk, (XIV, 15)
где ев, гуу ег — проекции вектора е на оси координат ху у, z.
Вектор скорости точки тела, определяемой радиусом-векто-
радиусом-вектором г, равен
о = шхг~ (XIV, 16)
или в проекциях на оси координат
v = v~i + vj+ vzky (XIV, 16')
где vxy vy, vz — проекции вектора скорости Ъ на соответствующие
оси координат.
Вектор касательного ускорения
wx = ^- = ex7. (XIV, 17)
Вектор нормального ускорения
in = со х v. (XIV, 18)
Вектор полного ускорения
w = wz + wn = е х г + w х v. (XIV, 19)
Основные виды движения твердого тела 249
§ 3. Методические указания к решению задач
При изучении вращательного движения тел- решаются задачи
различных типов. Основные из них следующие.
1. По заданному закону вращательного движения тела требуется
определить угловую скорость и угловое ускорение тела.
2. По заданному угловому ускорению вращающегося тела тре-
требуется определить закон вращательного движения тела.
3. Требуется преобразовать вращательное или поступательное
движение одного тела во вращательное или поступательное дви-
движение другого тела.
Задачи первого типа решаются путем последовательного
дифференцирования заданного закона вращательного движения.
Например, если задан закон движения ср = / (t), то, взяв про-
производную по времени t, получим угловую скорость
а взяв вторую производную по времени, получим угловое ускоре-
ускорение
d2y do)
е ~ dF ~"dt '
Иногда закон вращательного движения необходимо составить
исходя из условий задачи. , '
Например, диск из состояния покоя начинает вращаться уско-
ускоренно пропорционально кубу времени. Определить угловое уско-
ускорение диска, если известно, что в момент tt его угловая скорость
равна (Dj.
В этом случае закон движения может быть выражен формулой
Ф = а* A)
где а — неизвестный постоянный коэффициент, подлежащий опре-
определению.
Из этого закона движения определим величину угловой ско-
скорости ю
Зная величину угловой скорости со = щ в момент времени t = tly
определяем коэффициент а:
ш3 = ЗагД C>
откуда
250 Кинематика
Следовательно, закон движения определен, а именно*
9=%- E)
Угловое ускорение в получим, взяв вторую производную от ср
по времени:
Задачи второго типа решаются интегрированием. В этом
случае, кроме заданного закона изменения углового -ускорения,
должны быть заданы условия, которые позволяют определить
постоянные интегрирования.
Например, пусть дано угловое ускорение тела
e = btn + a, A)
где a, b и п — постоянные.
Известно также, что в начальный момент t = 0 угловая ско-
скорость тела равна оH, а угол поворота от начала отсчета равен ср0.
Требуется определить закон вращательного движения тела.
Определяем угловую скорость со из равенства
следовательно,
¦откуда
= Г фгп + a) dt + Съ
Постоянную интегрирования получим, используя заданные на-
начальные tусловия; для этого подставим в уравнение C) значение
/ = 0, а вместо со его значение о>0 в момент t = 0. Тогда получим
поэтому
«V
Закон движения получим после интегрирования уравнения C')
at + wo] Л + Ct = (^п^)^ +
+ | *2 + ш0^ + С2. D)
Постоянную С2 получим, используя начальные условия: при / = 0
<Р = То-
Таким образом, из уравнения D) получим ср0 = С2.
Основные виды движения твердого тела
251
Следовательно,
Ф = Фо +
а
~2
(п
- tn+2.
D')
Задачи третьего типа о преобразовании движений разно-
разнообразны. В частности, для решения задач о преобразовании враща-
вращательного движения одного тела во вращательное движение другого
запишем формулы, применяемые при рассмотрении движений
зубчатых зацеплений и ременных передач.
Рис.
Пусть в зацеплении находятся два зубчатых колеса (рис. 1,а)
с радиусами начальных окружностей гг и г2. Первое колесо 0г —
ведущее, а второе 02 — ведомое.
Скорости точки касания зубцов одинакова для обоих колес
по величине и направлению
01A =V2A =VA- A)
Из равенства A) можно получить соотношение между угловыми ско-
скоростями колес и их радиусами, а именно:
откуда
о>2
'C)
т. е. отношение угловой скорости ведущего колеса к угловой ско-
скорости ведомого равно обратному отношению их радиусов.
Как видно из рис. I, при внешнем зацеплении ведомое колесо
вращается в сторону, противоположную вращению ведущего.
При внутреннем зацеплении (рис. 1,6) колеса вращаются в одном
направлении.
252 Кинематика
Отношение угловых скоростей можно выразить через число зуб-
зубцов колес гг и г* и число оборотов их /г4 и /г2, а именно:
5~t D)
¦2-5- E)
Отношение угловой скорости ведомого колеса к угловой ско-
скорости ведущего — = *i,2 называется передаточным числом.
Передаточное число положительно при внутреннем и отрицатель-
отрицательно при внешнем зацеплении пары зубчатых колес.
На основании формул C, 4, 5) передаточное число
, 20)
Если в зацеплении находятся несколько пар зубчатых колес
(например т пар), соединенных последовательно или параллельно,
то общее передаточное число равно произведению передаточных
чисел всех пар зубчатых колес
11Я = flf2 . /2,з • *з,4... i (п — 1)п. (XIV, 21)
Поэтому можно записать
iln =^L(_i)mf (XIV, 22)
т
где т — число пар с внешним зацеплением.
Общее передаточное число может быть выражено и через отно-
отношение числа зубцов или радиусов колес.
Так, в случае последовательного соединения зубчатых колес
передаточное число равно
/1П =-?-(_ i)w == _5l (_ i)m (XIV, 23)
При параллельном соединении зубчатых колес необходимо учиты-
учитывать число зубцов или радиусы всех пар колес, находящихся в
зацеплении, а именно
hn = (%- • Ц • 4 •.. -4^) (- 0т (XIV, 24)
И
/1П =М . 4-- -^-...4!L->1(— l)m, (XIV,25)
где г2 и г2 — радиусы шестерен, сидящих на одном валу, и
z2 и г^ — число их зубьев.
Основные виды движения твердого тела
253
В случае ременной передачи (рис. II) передаточное число
равно отношению угловой скорости ведущего шкива к угловой
скорости ведомого.
Это отношение прямо пропорционально отношению чисел
оборотов и обратно отношению радиусов колес
/12= 2* = !*.=?. (XIV, 26)
Если ремни передачи не скрещиваются (рис. II,а), то
угловые скорости. ведомого и ведущего шкива имеют одинаковое
Рис. II.
направление и, следовательно, передаточное число положительно.
При скрещивающихся ремнях (рис. 11,6) угловые скорости
имеют противоположное направление и передаточное число отри-
отрицательно.
С методами решения задач о преобразовании вращательного
(или поступательного) движения одного тела в поступательное
движение другого тела проще всего ознакомиться, рассмотрев ряд
предложенных задан.
§ 4. Задачи
Рассмотрим задачи первого типа.
71, Диск паровой турбины в период пуска вращается по закону
Ф = tc/2»5 радиан. Определить угловую скорость и угловое ускоре-
ускорение диска через 4 сек. после пуска турбины, а также скорость if
ускорение точки диска, отстоящей на расстоянии г = 0,5 м от
оси вращения.
Решение. По заданному закону вращательного движений ф =
= тс/2»5 определим закон изменения угловой скорости диска
по формуле
Следовательно,
О) =2,5*/*.* Veen. A')
Закон изменения углового ускорения получим, взяв производную
от угловой скорости по времени, а именно
j.. ~ *
B)
254 Кинематика
Угловая скорость диска в момент / = Ч~сек. рав«а
оз = 2,5*4!'5 = 2(к Vcei* C)
Угловое ускорение диска в этот же момент
s = 3,75TC4°'6=7;57rVceb- D)
Скорость точки диска, отстоящей на расстоянии г = 0,5м от
оси вращения, равна
v = (о/- = 20тс . 0,5 = Ютс м/сек.
Касательное ускорение точки в этот же момент времени
wT = е • г = 7,5тг . 0,5 = 3,75т:
Нормальное ускорение ее
шЛ = wV - B0тгJ0,5 = 2
и полное ускорение
w = Yw\ + wl = V C,75тгJ + B00тг2J = 1973 м/сек*.
72. Определить угловую скорость и угловое ускорение вала,
вращающегося в неподвижных подшипниках, если угол пово-
поворота изменяется по следующему закону:
Ф = 2 + 30/ + ^ радиан. A)
Решение. Угловую скорость вала получим, взяв первую про-
производную от ср по времени:
СО = ^ = 30 + Ы 1/оек. B)
Угловое ускорение вала
г = — = о /сек2. (<3)
Следовательно, вал вращается равноускоренно, т. е. с постоян-
постоянным положительным ускорением е = 5 ^сек*
Рассмотрим задачи второго типа.
73. Маховое колесо начинает вращаться из состояния покоя
равноускоренно; через 10 мин. после начала движения оно имеет
угловую скорость, соответствующую 120 об/мин. Составить закон
вращательного движения и определить, сколько оборотов маховое
колесо сделает за 10 мин.
Решение. Так как маховое колесо вращается равноускоренно,
то его угловое ускорение положительно и остается во время дви-
движения постоянным.
Основные виды движения твердого тела 255
Для определения «закона изменения угла ср в зависимости от
времени напишем равенство
Интегрируя его дважды, получим
Тй^' + Ср B)
ср = ~ + С4 + С2. C)
Для определения произвольных постоянных Сг и С2 используем
начальные условия, заданные в задаче.
Известно, что в момент / = 0 угловая скорость (о0 = 0 и угс'л
поворота »ср0 = 0. Тогда из уравнений B) и C) следует, что Сг = 0
и С2 = 0, следовательно,
(о = ги B')
В уравнениях B') и C') неизвестна величина углового ускоре-
ускорения. Для fce определения заметим, что через 10 мин. угловая ско-
скорость махового колеса соответствует п = 120 об/мин.
Следовательно,
W==-30 ==-30-==4тс /сек. D)
Тогда из уравнения B') определим угловое ускорение е.
Так как при / == 10 мин. w = 4 ^сек., то
^ ~ 600 ~ 150
Полный угол поворота колеса в радианах за 10 мин. определим
из равенства C')
ЕР' 71 A0 - 60J 1ОЛЛ
Ф = у = 150 2 = 12ООя Радиан-
Следовательно, число оборотов 'колеса равно
1200тс СЛЛ ^ .
па = —— = 600 оборотов.
74. С момента выключения мотора пропеллер самолёта, вра-
вращавшийся 9 угловой скоростью, соответствующей п = 1200 об/мин,
сделал до/остановки 80 оборотов. Сколько времени прошло с мо-
момента выключения мотора до его остановки, если считать вращение
пропеллера равнозамедленным.
Решение. Движение пропеллера равнозамедленное, следова-
следовательно, угловое ускорение отрицательно и постоянно по величине,
256 Кинематика
Поэтому можно записать уравнение
3—• <¦>
Интегрируя его, получим
5 = -e* + Clf B)
где
По условию задачи в начальный момент / = 0 угловая скорость
4D соответствовала п = 1200 об/мин, следовательно,
Ktl К • 1200 аг\ Л i /гь\
w = 3o = -^o-=4O7r /««¦ . <3>
Подставив это начальное значение а> в уравнение B), получим
40тг = Cv D)
Следовательно, закон изменения угловой скорости
ю = 40^г — в/. EУ
Закон вращательного движения пропеллера получим, интегрируя
уравнение E).
Так как w = ¦?, то после интегрирования получим
ф = 40^ - у + С2. F)
При / = 0 угол поворота ср0 = 0, следовательно, из уравне-
уравнения F) следует, что С2 = 0.
Поэтому
ф'=4(Ы-?. F0
Для определения величины углового ускорения е и времени
до остановки пропеллера tx используем конечные условия движения.
В момент остановки пропеллера его угловая скорость оI=0,
угол поворота за этот промежуток времени
ср1 = 80 • 2ти = 160тс радиан.
Подставив в уравнение E) конечные условия для ш, получим
0 = 40тс — etv G)
откуда
etx = 40ir. G')
Подставив в уравнение F') конечные условия для ф, получим
40< — -21, (8)
Основные виды движения твердого тела 257
или, подставив из уравнения G') значение ztx в уравнение (8),
получим
/^ (8')
откуда
, 160ft о ,г\\
Ь = ~Ш = 8 СеК' (9)
Угловое замедление пропеллера получим из уравнений G') и (9)
е.8 = 4(к, A0)
откуда
8 = ^ = 5 тс 1/сек2. A1)
75. Маховое колесо радиуса г = 2 м вращается равноускоренно
из состояния покоя, т. е. при / = 0, оH = 0 и ср0 = 0. Через / =
«= 10 сек. точки, находящиеся на ободе, обладают скоростью v =
= 10 м/сек. Найти скорость, нормальное и касательное ускорения
точек обода в момент времени / = 15 сек.
Решение. При равноускоренном вращении колеса его угловое
ускорение положительно и постоянно.
Угловая скорость при равноускоренном вращении тела опре-
определяется по формуле
ш = со0 +et. A)
Так как в начальный момент вал находился в покое, то
соо-0. (Г)
Поэтому
(о = et.
Определим угловую скорость вала через 10 сек. после начала вра-
вращения из формулы
откуда v = tor, B)
v 100 ГА 1 г /o/v
со = - = -у = 50 7сек. B )
Из уравнений (Г).и B7) определим угловое ускорение
е — — — JO — D /сек». (Oj
Следовательно, закон изменения угловой скорости в зависимости
от времени равен
со = 5/ 7сек. D)
Из равенства D) определим угловую скорость в момент
t = 15 сек.
а> = 5. 15 = 75
17 sot
258
Кинематика
Теперь определим касательные и нормальные ускорения точек
обода колеса в момент / = 15 сек.
Касательное ускорение wx = е • г = 5 • 2 = 10 м/сек .
Нормальное ускорение wn = w2' • г = 752 -2 = 11 250 л/сея.
76. Ведущий вал редуктора (рис. 76) делает 1400 об/мин.
Определить число оборотов ведомого вала В и общее передаточное
число /3,1 редуктора, если известно число зубцов цилиндрических
шестерен редуктора: гх = 10; z2 = 60; zs = 12; г4 = 70.
Решение. Определим число оборотов
промежуточного вала С. Отношение чисел
оборотов шестерен обратно отношению
чисел зубцои
следовательно,
10
= пх^ = 1400.^ =
К задаче 76.
700. ^г
= ~у об/мИН.
B)
Зная число оборотов п21 определим число оборотов пг ведомого
вала В.
Из соотношения
получим
ги = п9 —.
3 2 г4
D)
Подставив гц из уравнения B) в уравнение D), получим
я,= 1400^- 4^ = 40 о
Передаточное число редуктора
40
i
1зл ~ пх ~" 1400 ~ 35*
Передаточное число редуктора можно определить и по формуле
* Za Za DU * /О ОО
где т = 2 — число пар с внешним зацеплением.
77. Два эллиптических зубчатых колеса (рис. 77) находятся в
зацеплении. Расстояния между осями вращения Ofi2 = 2 а.
Первое зубчатое колесо вращается с постоянной угловой ско-
скоростью о)х. Вывести законы изменения угловой скорости и углового
Основные виды движения твердого тела 259
ускорения второго колеса. Определить наибольшее и наименьшее
значения угловой скорости второго колеса, если первое делает
пх =240 об/мин; расстояние ОХО2 =2 а =50 см и полуоси, эл-
эллипсов равны: а = 25 см и b = 20 сл*.
Решение. Линейная скорость точки касания для обоих колес
одинакова (vx = v2) и может быть определена из равенств:
с;, =«>! . ОЖ A) Д
4. A JL ' V /
1'2 = о>2 . О2М. B)
Из этих равенств определим угловую
скорость второго колеса
ОХМ
Обозначив ОХМ через гг и О2М через г2,
получим
a>2 = WlA. C0
Определим расстояния гг и г2.
Как известно, сумма расстояний любой точки эллипса до его
фокусов равна постоянной величине 2а, где а — большая полуось
эллипса, т. е.
rL + г2 = 2а, D)
а расстояние между фокусами эллипса
ОгО[ = 2с = Уа* — Ь*. E)
Рассмотрев треугольник СуИО/, величину г2 можно выразить
через гг с и угол фг = со/.
В этом треугольнике сторона ОХ'М равна г2, поэтому
г\ == г? + 4с2" 4cricos Ti- F^
Из уравнения D) следует, что
/*2 ^ ^а —¦— гх.
Подставив это выражение в уравнение F), получим
Bа — ГхJ = r\ -f 4c2 — 4^ cos 9i- G)
Из уравнения G) определим гх:
а2 —с2
1 а — с cos срг
а затем определим г2:
17*
2 а — с cos ср2 ^%'
260
Кинематика
Подставив значения гг и г2 в равенство C'), получим
Наибольшее значение угловой скорости <*>2тахбудет при ц>г = 0°,
так как при этом значении фх знаменатель в формуле A0) будет
наименьшим:
2max а2 2ас + с2 а — с х v * /
Наименьшее значение co2min будет при фх = 180°, так как зна-
знаменатель в формуле A0) будет наибольшим:
(а2 — с2) W, а — с
2min a2 -}- 2ас -f с2 а -\- с 1%
Подставив числовые значения
(ох == ^ = 8тс 7сек.; 2а = 50 см; а = 25 см; с = 15
в уравнения A0') и A0"), получим:
A0")
-s i^L s- 2iC Х/
Угловое ускорение второго колеса е2 получим, взяв производ-
производную от угловой скорости С1>2 по времени:
doi2 2ас (а2 — с2) sin ср 1. ..
78. Ведущий вал / фрикци-
фрикционной передачи (рис. 78), делая
пг = 360 об/мин, на ходу пере-
передвигается так, что расстояние
плоскости диска от оси вращения
ведомого вала // изменяется по
закону х =8 — 0,2 t см. Опре-
Определить угловую скорость и угло-
угловое ускорение ведомого вала в
функции от расстояния х, а так-
также скорость и ускорение точки
В на ободе ведомого диска в
момент, когда х равно радиусу
ведущего диска- Радиус ведомого диска JR = 17 см; ведущего —
г = 5 см.
в
К задаче 78.
Решение. Определим угловую скорость ведущего вала /
0
= 0" ^ !
/сек.
A)
Основные виды движения твердого тела 261
Приняв, что окружная скорость точки касания А ведущего и
ведомого дисков одинаковы, т. е. скольжение в направлении окруж-
окружной скорости отсутствует, определим угловую скорость со2 ведо-
ведомого диска из равенства
откуда
(O^Wjy. (Г)
Подставив в уравнение (Г) выражение для х из условия задачи,
получим
щ . щ .__?__ i/oeiL (П
Подставив числовые значения ыг и г в уравнение A"), получим
Wa ^ 8 — 0,2? г/сек' ^'"^
Угловое ускорение ведомого вала и диска получим, взяв первую
производную от угловой скорости по времени:
— ^2 — 60гс . 0,2 __ 12гс 1; /9.
е^ — dt — 5 (8 — 0,27J — (8~0,202 /сек2' l ^
ИЛИ
Ч = ^'Vcw. B)
Так как по условию
я = 8 — 0,2 /,
то определим время ty через которое расстояние х ведущего диска
будет равно радиусу г (х = г = 5 см), т. е.
5 = 8-^-0,2/
и, следовательно,
i = 6 сек.
В этот момент времени угловая скорость
60л: бОтс __ 250^ 1/ (о\
0J ~ 1Г^~Ш "" 8 — 0,2 - 6 "" 17 /сек' &'
Угловое ускорение из уравнения B) равно
12т:12я 75тс 1; ...
Полное ускорение точки В ведомого диска
+90 000т:2 сл«/сек3.
262
Кинематика
Скорость точки В
vB =
17
17 — 150тг см!сек.
79. Определить число оборотов коленчатого вала соломотряса
молотилки, если он приводится во вращение от вала барабана при
помощи ременной передачи (рис. 79). Число оборотов вала бара-
барабана пх = 1150 об/мин. Диаметр ведущего шкива на валу барабана
dx = 100 мм; диаметр ведомого шкива на валу соломотряса d2 =
500 мм.
К задаче 79.
Решение. Как видно из схемы передачи, направление вращения
ведомого шкива (соломотряса) обратно направлению вращения
шкива барабана.
Число оборотов вала соломотряса получим из соотношения
djL
A)
от куда
n2~nld - ilDU500
230 обIмин.
80. Найти закон движения стержня (рис. 80), скользящего
концом А по контуру кругового эксцентрика при равномерном
вращении его вокруг оси О.
Диаметр эксцентрика 2/-, эксцентриситет ОС = а. Ось Ох
направлена по стержню, начало отсчета — на оси вращения, — = X.
Решение. Выберем в точке О начало координат и проведем оси
Ох и Оу. Ось Оу направим горизонтально влево, а ось Ох — вверх
по оси стержня.
Основные виды движения твердого тела
263
Положение стержня определяется величиной абсциссы х. По-
Поэтому закон его движения будет получен, если установить закон
изменения х в функции от времени. Величина х зависит от размеров
и закона вращения эксцентрика.
Обозначим через <р угол между осью Ох и линией ОС. Пусть
угол ф есть заданная функция времени.
Расстояние ОА, равное х, получим из Д О АС:
х = a cos ср + j/~r2 — a2 sin2 cp,
или
х = a cos ср ¦+• г Y1 + ^2 sin2cp;
это и есть закон движения стержня.
К задаче 80.
К задаче 81.
81. Составить уравнение контура кулака (рис. 81,6), создаю-
создающего равномерное возвратно-поступательное движение стержня АВ.
Уравнение движения стержня:
х = 5/ + 30 (х — Ь см, t — в сек)\
кулак делает 7,5 об/мин.
Решение. В течение первой половины оборота кулака стержень
равномерно движется вверх, а в течение второй половины — вниз.
Поэтому контур кулака состоит из двух кривых, для которых
необходимо найти уравнения.
Примем начало координат в точке О и направим ось Ох вверх
по стержню. Уравнение движения стержня
х = 5/ + 30.
A)
264 Кинематика
Определим время одного оборота Т кулака, который делает
п = 7,5 об/мин,
Т = -=-= = 8 сек.
В начальный момент при / = О, согласно уравлению A), стержень
находится на расстояния х0 = 30 см.
Наибольшее удаление конца стержня от начала координат
т
получим за первый полуоборот кулака, через / = -у == 4 сек.,
= 5 • 4 -J- 30 = 50 см.
За вторую половину оборота стержень равномерно движется
вниз до своего Первоначального положения
х0 = 30 см.
Уравнение движения в этот период будет
х = 50 — Ы. B)
Т
Через t = у = 4 сек. стержень вернется в свое первоначальное
положение. Составим уравнение контура кулака в полярных
координатах рх и 9, где рх — расстояние точки контура от оси вра-
вращения, <р — угол поворота кулака. Так как стержень движется
равномерно, то рг должно изменяться пропорционально времени и,
следовательно, пропорционально углу поворота <р:
Pi = Ро + о>Ъ C)
где р0 — наименьший радиус при t = 0, равный 30 см, а — неиз-
неизвестный коэффициент пропорциональности.
Для первой половины оборота рг = р0 (рис. 81,6), следова-
следователь но,
Pi=* D)
или
30 + щ = 30 + Ы, D0
откуда
За первую половину оборота
т
t с= ~ = 4 сек., угол <р = те,
20
поэтому из уравнения D") получим я = — ^^»
Подставив это значение а в уравнение C), получим уравнение первой
половины контура кулака — архимедову спираль
Pl = 30 + f?. E)
Сложное движение точки 265
Аналогично получим уравнение второй половины контура кулака
P2 = *i, F)
р2 = Ртах — Я?- F')
Так как
Ртах === •^max==: OU CM,
а = ~
те '
ТО
p2 = 50-ff (Т)'
ГЛАВА XV
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
§ 1. Абсолютное, относительное и переносное движения.
Скорость и ускорение точки
Механическое движение точки в пространстве по разному
фиксируется в системах координат, связанных с телами, которые
движутся. Одно и то же механическое движение может иметь раз-
различное аналитическое выражение закона движения в зависимости
от выбранной системы координат.
Главной задачей кинематики относительных движений точки
является определение связи между кинематическими величинами,
характеризующими одно и то же механическое движение точки в
двух различных системах координат, движущихся одна относи-
относительно другой. При этом предполагается, что кинематические харак-
характеристики движущихся систем координат известны.
Обычно оДну из этих систем координат условно называют непо-
неподвижной, а другую, в соответствии с этим, — подвижной.
Движение точки относительно условно неподвижного тела и
сЁязанной с ним условно неподвижной системы координат называют
абсолютным движением.
Движение точки относительно движущегося тела и связанной с
ним движущейся системы координат называется относительньш
движением.
Переносным движением точки называют движение той точки
пространства, связанного с подвижной системой координат, с кото-
которой в данный момент времени совпадает рассматриваемая движу-
движущаяся точка.
Абсолютное движение точки можно рассматривать как сложное,
состоящее из относительного и переносного движений.
В соответствии с основными понятиями кинематики относительно-
относительного движения точки различают: абсолютные, относительные и перенос-
266 Кинематика
ные траектории точки, абсолютные, относительные и перенос-
переносные скорости и ускорения точки.
Если переносное и относительное движения точки прямолиней-
прямолинейны, то и абсолютное движение ее прямолинейно и равно геометри-
геометрической сумме переносного и относительного перемещений:
Sa = Se + Sr. (XV)
При криволинейном движении абсолютное перемещение точки
принимается за бесконечно малый промежуток времени (dt) и равно
геометрической сумме переносного и относительного перемещений:
dSa = dSe + dSr. (XV, Г)
Абсолютная скорость точки равна геометрической сумме перенос-
переносной (ve) и относительной (vr) скорости:
va = ve + vr. (XV, 2)
При определении абсолютного ускорения точки (при сложном
движении) следует различать два случая:
1) когда переносное движение поступательное;
2) когда переносное движение вращательное.
В первом случае абсолютное ускорение точки равно'геометриче-
равно'геометрической сумме ускорений переносного (we) и относительного (wr):
Юа^ЪРвЛ- Wr. (XV, 3)
Во втором случае абсолютное ускорение точки равно геометри-
геометрической сумме трех ускорений: переносного (we), относительного
(wr) и добавочного (кориолисового) (wk):
wa = we + wr + wk. (XV, 4)
Добавочное ускорение, или ускорение Кориолиса:
щ = 2о7е х vr (XV, 5)
и, следовательно, его модуль равен
wk = 2b)evrsin(b)e, vr), (XV, 5')
где we — вектор угловой скорости переносного вращательного дви-
движения; vr — вектор относительной скорости точки.
Направление вектора этого ускорения (щ) определяется из
формулы векторного произведения (XV, 5).
Определение направления вектора кориолисового ускорения
облегчается, если применить правило Н. Е. Жуковского: направ-
направление вектора кориолисового ускорения можно получить, если
вектор относительной скорости (vr) повернуть на угол 90° в сто-
сторону переносного вращательного движения.
Сложное движение точки
267
В том случае, когда вектор относительной скорости не перпен-
перпендикулярен к оси вращения, для определения направления кориоли-
сового ускорения нужно повернуть на 90° в сторону переносного
вращательного движения проекцию вектора относительной ско-
скорости на плоскость, перпендикулярную к оси вращения.
Иногда при решении задач необходимо применять указан-
указанные формулы в ином виде, а именно; в проекциях на оси координат.
Так, для определения расстояний Sa, Se, Sr пользуются алгебраи-
алгебраическими равенствами:
ха = хе -f~ хг
для определения скоростей — равенствами:
для определения ускорений — равенствами:
way = wey +
Waz = Wez +
(XV, 6)
(XV, 7)
(XV, 8)
При наличии дополнительного (кориолисового) ускорения
пользуются равенствами-.
= Wez + ™rz +
(XV, 9)
§ 2. Методические указания к решению задач
Как было указано, абсолютное движение точки можно рас-
рассматривать состоящим из переносного и относительного движений.
В задачах этого раздела требуется определить кинематические
характеристики одного из этих видов движений по заданным кине-
кинематическим характеристикам других видов.
Рассмотрим три основные гругпы задач.
1. Определение закона движения и абсолютной скорости точки.
2. Определение абсолютного ускорения точки, когда переносное
движение поступательное.
3. Определение абсолютного ускорения точки, когда переносное
движение вращательное.
Приступая к решению задачи, необходимо, прежде всего,
установить вид движения точки (абсолютное, переносное и
268
Кинематика
относительное). При этом во многих случаях следует выбрать
положение условно неподвижной и подвижной систем координат.
После этого в соответствии с условием задачи использовать при-
приведенные ранее зависимости между расстояниями, скоростями и
ускорениями.
Например, мостовой электрический кран движется вдоль цеха
из состояния покоя согласно уравнению SKp = 0,б/2; по мосту
крана в поперечном направлении катится тележка согласно уравне-
уравнению St = 2 /.
Определить уравнения дви-
движения и траектории, а также
скорость центра тяжести теле-
тележки по отношению к цеху.
В данном случае движение
л тележки по мосту движущегося
крана является относительным
Рис. I.
Движение моста крана яв-
является переносным (SHP =Se).
Абсолютным движением те-
тележки и ее центра тяжести является движение ее по отношению
к цеху. Выберем условно неподвижную и подвижную системы ко-
координат.
Так как в условии задачи положение моста крана и тележки по
отношению к стенам цеха не задано, расположим начало координат
условной неподвижной системы хОу в начальный момент времен»
в центре тяжести тележки (рис. I).
Начало осей подвижной системы координат хх0луъ связанных
с мостом крана, также поместим в точке моста, совпадающей в
начальный момент с центром тяжести тележки (точка О).
Согласно равенству (XV, 6) запишем
У а = Уе + У г
A)
В нашей задаче хв =SKp = 0,6/3; хг =0, так как относи-
относительное движение перпендикулярно к оси Огхг; уе = 0, так как
оси системы координат хг0^ух в направлении оси Оу не переме-
перемещаются, a yr =Sm = 2 /.
Таким образом, координаты абсолютного движения точки
Уравнение траектории точки получим, исключив время,
Сложное движение точки
269
Величину абсолютной скорости точки va получим, определив
проекции ее на оси системы координат хОу,
va =
= ]/1,44/2 + 4 м/сек.
При решении многих задач можно не пользоваться координат-
ным способом задания движения точки.
Рассмотрим пример определения ускорения точки в том слу-
случае, когда переносное движение вращательное, т. е. когда воз-
возникает дополнительное (кориолисово) ускорение.
Пусть требуется определить ускорение ползуна Л, движуще-
движущегося по качающейся кулисе. При этом заданы: скорость ползуна
относительно кулисы vr% относительное касательное ускорение
ползуна wrx, направленное в сторону, обратную скорости vff
угловая скорость кулисы we и угловое ускорение ев, направленное
в сторону, обратную угловой скорости (рис. II), расстояние /точки А
ползуна от центра качания кулисы и р радиус кривизны в
точке Л.
Пусть в рассматриваемый момент времени скорость ползуна
направлена вертикально вниз, а хорда ОА составляет с горизон-
горизонтальной линией угол а = 60°; радиус кривизны кулисы равен р.
Для решения задачи составим равенство
Wa = we + wr + wk 0)
и вычислим величины, указав направления векторов переносного,
относительного и дополнительного (кориолисоцого)
270 Кинематика
Так как
то равенство A) запишем в ином виде и определим величины и на-
направления всех составляющих векторов:
__ __ х"\
**>а = ®еп + We* + Wrn + Wrz + 2 (o>e X l\),
где ускорение oyen= о>^/ и направлено от точки А к центру
вращения О по хорде Л О;
Wez = е/ и направлено перпендикулярно к ДО в сторону ев;
догп = — и направлено к центру кривизны кулисы по радиусу р в
данной точке;
wfX — задано и направлено по касательной в сторону, обрат-
обратную скорости vr\ величина ускорения Кориолиса равна
__s\_
wk = 2bievr sin (we, vr) = 2а)ег;г.
Направление вектора этого ускорения Wk получим по правилу
Н. Е. Жуковского: повернем вектор относительной скорости vr
на 90° в сторону переносного вращательного движения. Полное
ускорение wa получим, сложив эти векторы геометрически:
Можно также вычислить величину и направление вектора wa
аналитически. Для этого спроектируем все векторы на оси коорди-
координат Ах и Ау и затем сложим два вектора геометрически:
= Wk — wrn — wen cos 60° + wex cos 30°,
§ 3. Задачи
Закон движения точки. Скорость точки
82. Найти уравнение относительного движения ползуна в про-
прорези кулисы поперечно-строгального станка и его скорость в момент
/=0,1 сек. (рис. 82), если известно, что кривошип радиуса
г = 200 мм вращается с постоянной угловой скоростью о> = 4 1/сек.»
а расстояние между осями 0х0 = а = 500 мм. Найти также уравне-
уравнение колебательного движения кулисы ОгВ.
Решение, Ползун совершает прямолинейное поступательное дви-
движение вдоль прорези кулисы. Это движение относительное, так
как последняя движется, вращаясь вокруг неподвижного центра Ог*
Сложное движение точки
271
Выберем неподвижную и подвижную системы координат.
Пусть оси системы хОгу, связанные с фундаментом станка,
образуют неподвижную систему координат. Оси хг0хуъ связанные
с кулисой О3 S, вращаются вокруг центра О1#
Координаты точки А ползуна в подвижной системе координат
равны
хг = 09
Л-ОЛ A)
Выразим уг в функции от угла пово-
поворота кривошипа ср = со/. Из треугольника
ОгАО получим
уг =
2ar cos со/
B)
или, подставив числовые значения, полу-
получим уравнение относительного движения
в таком виде:
B0
Относительная скорость ползуна равна
первой производной от координаты уг по
времени
К задаче 82.
_ аУг __ 10 (— 20о) sin со/) ___ 400тг sin 4nt
r~~dt ~~ 21/29 + 20 cos Ы "" "" j/29 + 20 cos 4Й *
C)
В момент t = 0,1 сек.
— — 400тс sin 0,4л
1>"~ 1/29 + 20 cos 0,4л:
= —202 смIсек = — 2,02 лс/с^/с. D)
Уравнение колебательного движения кулисы получим, опре-
определив угол срх =/(/). Угол фх определим из треугольника OJ5A,
где АВ — перпендикуляр к линии 0ХО, а именно
? *Pi ^ а + г cos аз*# ' '
83. Трамвай движется по прямолинейному горизонтальному
участку пути со скоростью v = 18 км/час (рис. 83), причем кузов
совершает на рессорах колебания амплитудой а =0,8 еж с периодом
Т = 0,5 сек. Найти уравнение траектории центра тяжести С ку-
кузова, если его среднее расстояние от горизонтальной плоскости,
проходящей через оси колес, h = 0,9 м. Радиусы колес R = 0,39 ж.
При / = 0 центр тяжести находится в среднем положении и ско-
скорость колебания направлена вверх.
Решение. Центр тяжести кузова вагона совершает сложное
движение. Он перемещается вместе с тележкой колес в горизон-
272
Кинематика
тальном направлении и совершает колебания по отношению к те-
тележке колес в вертикальном направлении.
Выберем неподвижную систему координат хОу и подвижную
хг0уг.
Пусть ось Ох расположена на уровне рельсов, а вертикальная
ось Оу направлена вверх.
Подвижную систему координат расположим на тележках ва-
вагона и направим ось Огхг вправо на уровне осей колес, а О
вертикально вверх через центр тяжести кузова.
К задаче 83.
Выражение координат центра тяжести кузова в подвижной
системе примет вид
хг = 0, A)
yr = h + a sin Ы. B)
Так как амплитуда а = 0,008 м и частота
2те 2тс л м
то
Уг = 0,9 + 0,008 sin 4*2. B')
Координаты точки Ог (хб и уе) по отношенцю к системе хОу соот-
соответственно равны
xe = vt = 5tM, C)
#, = /? = 0,39 ж. D)
Тогда координаты центра тяжести кузова в неподвижной системе
^координат будут равны согласно формулам (XV, 6);
*• = *.+ хг> E)
Уа = ^ + Уг> E0
Сложное движение точки 273
ИЛИ
хл = 5*. F)
уа = 1,29 + 0,008 sin 4«*. F')
Чтобы получить уравнение траектории, исключим время / из
уравнения F'):
уа = 1,29 + 0,008 sin 0,08icxe. G)
Это уравнение показывает, что траекторией центра тяжести
вагона при его движении является синусоида.
84. Определить скорости точек Мъ М29 М3 и УИ4 диска радиуса
г = 0,5 му катящегося без скольжения по
прямолинейному участку пути (рис. 84).
Скорость центра его постоянна и равна
vo= Юм/сек.
Решение. Движение диска (рис. 84) можно
рассматривать состоящим из поступательного
движения вместе с центром О со скоростью v0
и вращательного движения вокруг центра О
диска. Поступательное движение диска для К задаче 84.
любой точки его является переносным, а вра-
вращательное — относительным. Абсолютная скорость любой точки
диска равна геометрической сумме скоростей переносного v0 = v9
и относительного движений vr:
va = ve + vr. A)
Так как диск катится без скольжения по неподвижному участку
пути, то абсолютная скорость точки касания диска в каждый мо-
момент времени равна нулю. Поэтому для точки Мг касания диска
с рельсом из уравнения A) получим
0 = v. + t;f, B)
vr = -v.. B*)
Вектор переносной скорости ve равен вектору скорости vQ
центра диска О. Следовательно, величина относительной линейной
скорости точки vr равна v0.
Вектор vr направлен в сторону, обратную направлению век-
вектора vQt to, как видно из рисунка, колесо вращается вокруг центра
О по часовой стрелке.
Определим величину угловой скорости диска w из формулы
?>о = «г, B0
откуда
Ю ^ 2
Затем определим абсолютную скорость точки М2- Так как пере-
переносная скорость точки М2 равна скорости vo> а относительная
18 591
274
Кинематика
скорость vr = ш и в точке М2 они взаимно перпендикулярны, то
величина скорости в точке М±
Va2 = Vv20 + (шгJ = V Ю2+ B0.0,5J= 10 К 2" л*/а?/с. C)
Величина скорости точки Мг равна алгебраической сумме пере-
переносной и относительной скоростей.
• Так как ve9 и vr9 направлены по одной прямой и в одну и ту же
сторону (вправо), следовательно,
va, = v0 + (or = 10 + 20 • 0,5 = 20 м/сек. D)
Определим скорость точки Л14. Вектор переносной скорости
точки равен и30, а вектор относительной скорости vu> по величине
равный сог, имеет направление, перпендикулярное к радиусу, и
направлен вертикально вниз.
Вектор абсолютной скорости равен геометрической сумме эти
скоростей v<u = vet + Vrv а величина его
vai = Vl 02+ B0 • 0,5р = 10 V 2 л^/^/с. E)
Направление скоростей указано на чертеже.
85. Кривошип О А радиуса R = 30 см вращается с угловой
скоростью ш0 = 6 7сек. вокруг неподвижной оси О в направлении
часовой стрелки. В точке А
кривошипа расположена ше-
шестерня радиуса г = 10 см
(рис. 85). Определить абсо-
абсолютные скорости точек /, 2,
3 и 4 шестерни, если она
вращается против часовой
стрелки с угловой скоростью
О)Л= Ю '/сек.
Решение. Абсолютную
скорость любой точки шестер-
шестерни определим по формуле
К задаче 85.
vr,
A)
где va -*- вектор абсолютной скорости точки; ve — вектор перенос-
переносной скорости точки при вращении вместе с кривошипом; Т>г —
вектор относительной скорости точки при вращении шестерни
вокруг оси Л.
Определим скорость точки 1:
Via = Vie + 0!r. B)
Переносная скорость
v%e « оH (/? — г) в 6 C0 — Щ « 120 см/сек C)
Сложное движение точки 77Ь
и направлена перпендикулярно к ОА в сторону вращения криво-
кривошипа.
Относительная скорость
Vir = ылг == 10 • 10 = 100 см/сек D)
и направлена перпендикулярно к ОА в сторону относительного
вращения.
Как видно из рисунка, обе эти скорости направлены в одну
сторону, поэтому величина абсолютной скорости точки / равна
va = 120 + 100 = 220 см/сек. , E)
Абсолютная скорость точки 2 определяется также по фор-
формуле A). , _
Переносная скорость v2r направлена перпендикулярно к линии
02 и равна
V2e *=со0 VR1 + /-2 = 6]/302 + 10* = 60 КТО см/сек. F)
Величина относительной скорости v2r, как и для точки У, равна
vir = <*а - г = 10 • 10 = 100 см/сек G)
я направлена перпендикулярно к радиусу г в точке 2.
Абсолютная скорость точки 2 равна их геометрической сумме.
Величину ее определяем по формуле .
V2* - Vvl + v\T + 2v2e • v2r cos (90° + ft , (8)
где p — угол между 01 и 02, который определим из ДОА2, а именно,
Следовательно, р «= 18°30'.
Подставляя в уравнение (8) числовые значения, получим
О2а = ^F0 /К)J + 1002 + 260 J/10 • 100cos (90° + 18°30') «
= 155 смIсек. A0)
Аналогично определяем абсолютные скорости точек 3 и 4.
Величина абсолютной скорости точки 5 равна разности вели-
величин переносной скорости ще и относительной vZr, так как скорости
направлены по одной прямой перпендикулярно к 03, но в проти-
противоположные стороны:
0за = wo (R + г) — ыАг = 6 C0 + 10) — 10 - 10 = 140 см/сек. A1)
Абсолютная ^скорость точки 4 равна геометрической сумме
векторов Ъи и ~г>4Г
+ t>l + 2vto cos (90° + p), A2)
18»
276
Кинематика
где:
: со0 Уф + г2 = 60 У10 см/сек,
V!* = ылг = 10 • 10 = 100 см/сек,
Р = 18°30'.
Отсюда
о* = ^ (бОКГбJ + 1002 • 2 • 60 К10 • 100cos (90°"+ 18°ЗоГ=
= 155 см/сек. A20
86. Механизм с вращающейся кулисой (рис. 86) состоит из двух
параллельных валов О и Olf кривошипа О А и кулисы ОгВ. Конец А
кривошипа ОА соединен с камнем, который
скользит вдоль прорези кулисы ОгВ\ рас-
расстояние между осями валов ООг равно а,
длина кривошипа ОА равна г, причем
г > а. Вал О вращается с постоянной
угловой скоростью о).
Найти угловую скорость кулисы и
относительную скорость камня (точка А)
по отношению к кулисе ОХВУ выразив их
через переменную величину ОХА =S.
К задаче 86.
Решение. Принимаем вращательное
движение кулисы за переносное. Тогда движение камня А в про-
прорези кулисы будет относительным, а вращение кривошипа ОА —
абсолютным.
Вектор абсолютной скорости точки А перпендикулярен к кри-
кривошипу и величина его равна
¦va = ">л A)
Переносная скорость точки А направлена перпендикулярно к
оси кулисы ОА и по величине равна
ve = <»i • ОгА = о)! . S. B)
Линия вектора относительной скорости совпадает с осью прорези
кулисы. Из параллелограмма скоростей (рис. 86) найдем, что пере-
переносная скорость
ve = va cos a, C)
где а = /_ ОАОХ — угол поворота кулисы.
Относительная скорость
?>r=* t>asina. D)
Тогда, сравнивая уравнения B) и C), получим угловую ско-
скорость КуЛИСЫ COjl
(or cos a ,c-v
Сложное движение точки 277
где
S = ОгА.
Из треугольника 0А0г можно получить значение косинуса
угла а
a2==r2 + S2_ 2rScosa, F)
откуда
cos a = —-Ь_ . F')
Подставив его в уравнение E), получим
Относительная скорость
vr = ua sin a (8)
или
•Подставив из уравнения F') выражение косинуса в зависимости
от 5 в это равенство, получим
или после преобразований
vr = ^ )/> + S + а) (г + S -а) (а + r-S)lflTS=7). (8")
Ускорение точки, когда переносное
движение поступательное
87. Кривошип О А = г = 0,4 м приводит в движение прямо-
прямолинейную кулису, которая совершает возвратно-поступательное
движение, и в момент, когда угол ср =60°, имеет угловую скорость
а) =3,14 7сек- и угловое ускорение е = — 2 х/сек2 (рис. 87,а).
Найти ускорение кулисы и относительное ускорение ползуна в
указанный момент.
Решение. Так как в задаче заданы величины угловой скорости и
углового ускорения кривошипа, то абсолютное ускорение wa точки
А ползуна известно. Требуется определить относительное ускоре-
ускорение wr точки А ползуна и переносное ускорение we кулисы.
Относительным движением ползуна является его движение в
прорези кулисы. Это движение прямолинейное и поступательное.
Кулиса также совершает прямолинейное поступательное движение
278
Кинематика
в вертикальном направлении, скользя в своих направляющих.
Для точки А движение кулисы — переносное.
В формуле
Wa=zW9 + Wr A)
заменим вектор абсолютного ускорения суммой его составляющих
wXa и хюМУ тогда получим
Величина касательного ускорения:
w,a = ег = — 2 • 0,4 = — 0,8 MJceK*. B)
Знак минус показывает, что вектор ка-
касательного ускорения в данный момент
времени направлен в сторону, противо-
противоположную направлению вектора абсо-
абсолютной скорости va точки А (рис. 87,а).
Нормальное ускорение wna по вели-
величине равно
и>па = ">•/¦ = 3,142. 0,4 = 3,94 м/сек* C)
и направлено по радиусу к центру вра-
вращения кривошипа О.
Величины и направления переносно-
переносного и относительного ускорений неизве-
неизвестны, известны лишь линии, параллель-
параллельно которым направлено ускорение, а
именно, относительное ускорение направлено горизонтально, пе-
переносное — вертикально.
На основании геометрического равенства (Г) построим много-
многоугольник ускорений, из которого определим направление, а затем
а величины ~foe и Щ (рис. 87,6).
Векторы ускорений и5в и wr должны быть направлены навстречу
вектору Т$л. Как видно из многоугольника, относительное ускорение
wf направлено вправо, а переносное we вверх.
Для определения величин ускорений воспользуемся теоремой
о проекции равнодействующего вектора на какую-либо ось.
Так как проекция замыкающей стороны многоугольника на
какую-либо ось равна алгебраической сумме проекций составляю-
составляющих векторов на ту же ось, то, спроектировав все векторы много-
многоугольника ускорений на вертикаль, получим
VJna
К задаче 87.
или
wM cos <p — wza sin cp = wt D)
a», - 3,94 • cos 60° — 0,8 sin 60° = 1,278 м/сек*. D')
Сложное движение точки
279
Спроектировав векторы ускорений на горизонтальную ось, получим
шш cos 9 + wm s*n 9 = Щ E)
или
wr = 0,8 cos 60° + 3,94 sin 60° = 3,307 м\сек\ E')
88. Велосипедист на некотором участке
горизонтального прямолинейного пути
движется по закону 5 =0,1 t2 <(S — в м\
t — в сек.). Дано: R =,350 мм,
I = 180 мм, гг = 18 зубцов, z2 = 48 зуб-
зубцов. Определить абсолютное ускорение
осей М и N велосипедных педалей (предпо-
(предполагая, что колеса катятся без скольжения)
при / = 10 сек.,- если в этот момент
кривошип расположен вертикально.
К задаче 88.
Решение. Принимаем поступательное движение рамы велоси-
велосипеда за переносное. Вращательное движение кривошипов педалей
по отношению к раме велосипеда будет относительным.
Скорость и ускорение переносного движения можно определить
по формулам:
A)
ds
e = jt = 0,2* м/сек,
B)
Для определения угловой скорости и углового ускорения криво-
кривошипов педалей найдем угловую скорость вращения колеса велоси-
велосипеда. Абсолютная скорость точки А касания колеса с опорной
неподвижной поверхностью вследствие отсутствия скольжения
равна нулю va = 0.
Переносная скорость оси колеса v0 направлена горизонтально
вправо, относительная скорость vrt равная окружной скорости
точки А колеса при вращении его вокруг оси, направлена гори-
горизонтально влево- и равна vr = а^/? = 0,35a>i м/сек.
Применив формулу - сложения скоростей для точки А
ц подставив в нее значения этих скоростей, получим
0 = 0,2/ — 0,35ш1(
откуда
sy* Veen.
C)
C0
C*)
280 Кинематика
Определим угловую скорость о)ц зубчатого колеса, связанного
с кривошипом педалей, из соотношения —Е = —,
откуда
Zi 4.1о ^/i/ м\
В заданный момент времени / = 10 сек.
15 г, ,,,,
О)ц == у //сек. D )
Угловое ускорение зубчатого колеса //
8и = "ЗГ = 14 1/сек2* ®
Определим ускорение точки УИ.
Точка М вращается вокруг оси //. Ее относительное ускорение
состоит из двух составляющих: касательного и нормального.
Вектор касательного ускорения в момент / = 10 сек. направлен
горизонтально вправо и по величине равен
w,r = еп / = ^ 0,18 = ~д м/сек2. F)
Вектор нормального ускорения направлен к центру вращения //
(вниз) и по величине равен
или при ^ = 10 сек.
wnr^%MJceKK (Г)
Составляющие относительного ускорения точки N равны по
величине ускорениям точки М и направлены следующим образом:
касательное ускорение направлено горизонтально влево, а
нормальное — по радиусу к точке // вверх.
Переносное движение кривошипов — поступательное. Абсолют-
Абсолютное ускорение точек М и N равно геометрической сумме ускорений
переносного we и относительного wr.
Сложив переносное ускорение we с касательным ускорением
точки М — wXr алгебраически, так как они лежат на одной гори-
горизонтальной прямой, а затем полученную сумму — геометрически
с относительным нормальным ускорением wnr, получим
Абсолютное ускорение точки Af вычислим аналогично, приняв
во внимание лишь иное направление ускорения wXr
-Щ + (|J= 0,841 м\сек\ (9)
Сложное движение точки 281
89. Зубчатое колесо радиуса R = 0,5 м зажато между двумя
параллельными рейками, скользящими в одну сторону с ускорениями
wx = 1,5 м/сек2 и w2 =2,5 м/сек2 (рис. 89). Найти ускорение w0
центра колеса О и угловое ускорение е. Поступательное движение
осей Охъ Оуг принять за переносное.
Решение. В этой задаче переносным движением является прямо-
прямолинейное движение системы координат, связанной с центром О
зубчатого колеса, относительным — вращательное движение ко-
колеса вокруг центра О. Заданные по отно-
отношению к неподвижной системе координат f
ускорения точек М и N колеса являются I
абсолютными. Требуется по абсолютным уско- "^
рениям w-l и w2 точек М и N колеса опреде-
определить переносное ускорение we центра О и отно-
относительное угловое ускорение колеса ег. Пред-
Предположим, что относительное угловое уско-
ускорение ег направлено против часовой стрелки,
тогда относительные касательные ускорения
в точках М и N будут направлены горизон- К задаче 89.
тально, параллельно оси Охъ причем в точке М
ускорение будет направлено влево, а в точке N вправо. Величины
ускорений wlr и w2r одинаковы и равны
w\r = w2r = Rzr = 0,5 • вг м/сек2. A)
Переносное ускорение точки О — w9 направлено по оси Охг.
Составим два уравнения для определения неизвестных
we = w0 и ef.
Для этого составим геометрические равенства для ускорений
в точках М и N:
wt*=w -f щГч B)
Спроектируем обе части этих геометрических равенств на гори-
горизонтальную ось, тогда получим следующие алгебраические равен-
равенства:
W1 = wo — R • еГУ C)
w% = w0 + R.*r. C0
Решая эти уравнения совместно, получим
JJ15J+L215 о ,
2 -~ 2
, —wt _ 2,5--1,5
2R ~* 2 • 0,5
262
Кинематика
Положительный знак гТ величины углового ускорения показы-/
вает, что предположение о направлений углового ускорения
(против движения часовой стрелки) правильно.
Ускорение точки, когда переносное
движение вращательное
90. Стержень ОА колеблется в вертикальной плоскости вокруг
горизонтальной оси по закону ? = g- sin ~ t. Вдоль стержня скользит
К задаче 90.
ползун My перемещаясь по закону 5= а + b - cos j- / (рис. 90).
Определить абсолютное ускорение ползуна в момент t =» 1 сек,,
если а = 0,5 м> Ь = 0,2 м.
Решение. Движение ползуна вдоль вращающегося стержня
является относительным, вращательное движение стержня для
муфты — переносным.
Так как переносное движение вращательное, то для получения
абсолютного ускорения нужно, кроме ускорений при переносном
и относительном движении ползуна, определить и дополнительное
ускорение. Следовательно, абсолютное ускорение может быть опре-
определено по формуле
Определим величины этих ускорений в момент t
(рис. 90,а). Угловая скорость стержня
tf 9 % к я
SF--8 • TcosJ
A)
1 сек.
B)
Сложное движение точки 283
или при t tm 1 сек.
п
п nV2_ n*V2 ч (t>
е "8* # —2~ —6ЙГ"" I06*' ^ '
Тая как со, положительно, то стержень вращается против часовой
стрелки.
Угловое ускорение стержня
•.-$--¦J'-S^t'V—. C)
или при / = 1 сек.
Относительная скорость муфты направлена в каждый данный
момент по стержню и равна
или при I в* 1 сек..
Зная величины о)е, е^ и vr, можно определить величины уско-
ускорений We И Wr.
Переносное ускорение we состоит из двух составляющих: каса-
касательного и нормального ускорений. Величина касательного ускоре-
ускорения равна
We* = ОМ • ев, E)
где
^lt F)
а при t » 1 сек.
ОМ = 0,5 + 0,2 ?? . 0,541 л*.
Следовательно,
wex « 0,541 • в, =х °>5419с!. 2 ж/селя E')
и направлено перпендикулярно к ОМ в сторону, обратную направ-
направлению скорости v$ (рис. 90,а).
Величина нормального переносного ускорения
е
или при t о» ] сек.
Wen^i^p)* 0,541 л«/сека F')
и направлено к центру вращения О.
284 Кинематика
Величина относительного ускорения
dvm d?s jw2
или при / = 1 сек.
_ 0,2*2
G)
/сек*
и направлено к центру вращения О.
Величина дополнительного ускорения
wk = 2(j)evr sin a, (8)
где а — угол между вектором vr и вектором а>в.
В данном случае а = 90 °, поэтому
а;Л = 2u,vr (80
Подставив в формулу (8') значения (ое и у, при / == 1 сек., по-
получим
ft ~ " 8 4
8 4 2 4 ~2~ ~" 640 ^/^^ • V° /
Направление дополнительного ускорения определяем по пра-
правилу Н. Е. Жуковского. Повернем вектор относительной скорости
щ на 90° в сторону угловой, переносной скорости we. Направление
повернутого вектора vr укажет направление ускорения ад.
Зная величины и направления ускорений, можно построить
многоугольник, в котором замыкающей стороной будет вектор
абсолютного ускорения wa (рис. 90,6).
Так как касательное ускорение weX и ускорение wk направлены
по одной прямой, то получим треугольник.
Величина абсолютного ускорения при / = 1 сек. может быть
получена из равенства
0,541*3)/ 2 тсзу* ( 0,541 TC4. 2 \2 8,54iu»
256 +б40"/ "^ \ 64
\2
91. Кривошип ОЛ радиуса 2 г вращается вокруг оси О с по-
постоянной угловой скоростью (ое. На пальце А свободно надето колесо
радиуса г, вращающееся с угловой скоростью wr против часовой
стрелки (рис. 91). Определить величины и направления ускоре-
ускорений точек М и N колеса, находящихся на концах диаметра,
совпадающего с осью кривошипа.
Решение. Переносным движением является вращательное дви-
движение кривошипа, относительным — вращательное движение ко-
колеса по отношению к кривошипу.
Сложное движение точки
285
Так как переносное движение вращательное, возникает допол-
дополнительное (кориолисово) ускорение, тогда абсолютное ускорение
точки М определим по формуле
wa = we + wr -f wk.
Переносное ускорение равно
we = wen = Kr B)t
и направлено к центру вращения
Кривошипа О, так как угловая
скорость (De — постоянна и каса-
касательное ускорение равно нулю.
Относительное ускорение равно
wt = f)rn *± (o^r C)
и направлено по радиусу г к цент- и>е
ру вращения колеса вследствие
отсутствия касательного ускоре-
ускорения, так как ыг — постоянна.
Дополнительное (кориолисово)
ускорение равно
(I)
wh =
D)
К задаче 91
так как угол между векторами о>е и иг равен 90° и иг = о>г л
Направление йL устанавливаем по правилу Н. Е. Жуковского.
Повернем вектор относительной скорости Ъг на 90° в сторону
переносного вращения. Направление его укажет направление
дополнительного ускорения.
Абсолютное ускорение точки М равно алгебраической сумме
трех ускорений, направленных по одной прямой
W™ = — we + Wr + Wk = r (&r — <»2e
В частном случае, когда we == а>г =- о>,
E)
Абсолютное ускорение точки N определяется аналогично.
Переносное ускорение
Относительное ускорение
Дополнительное ускорение
F)
G)
(8)
286
Кинематика
Абсолютное ускорение точки N равно алгебраической сумме
этих ускорений, направленных по одной прямой:
W + W + W Г (Зо>е + wr + 2<0#0)r). (9)
В частном случае np» a>f
w
6/чЛ
92. По радиусу диска, вращающегося вокруг оси ОХО2 с угло-
угловой скоростью ш=2/ ^сек, движется точка М от центра
к ободу по закону: ОМ = р = 4/2сл*. Радиус составляет
lo,.
К задаче 92.
с осью 0!О2 угол а = 60° (рис. 92). Определить величину абсолют-
абсолютного ускорения точки М *в момент / = 1 сек.
Решение- Переносным движением является вращательное дви-
движение диска, относительным — прямолинейное движение точки по
радиусу. Абсолютное ускорение точки М определим по формуле
фл = ф§ + щ + щ. A)
В момент t «= 1 сек. точка М находится от центра О на рассто-
расстоянии р, равном
р = 4tf2 = 4 • I2 = 4 см. B)
Относительная скорость точки М вдоль радиуса равна
vr = -~ = 8/ см/сек,
а в момент t = 1 сек.
•. Ы = 8 • 1 = 8 см/сек.
Относительное ускорение точки М
C)
D)
E)
Сложное движение точки 387
Ускорение wr постоянно и направлено вдоль радиуса от центра О.
Переносное ускорение точки М состоит из касательного и нор-
нормального.
Угловая скорость переносного движения диска
<*е = 2* 7сен. F)
Угловое ускорение переносного движения диска
*% dBt) i;
Так как ев положительно, то касательное ускорение совпадает
с направлением переносной скорости v$9 которая равна
v$ = MB • ш, = ОМ sin a • w«, (8)
или при / = 1 сек. и а = 60°
ve = 4 sin 60° • 2 • 1 == 4 VlS см/сек. (8')
Вектор скорости ve направлен перпендикулярно к плоскости диска.
Величина касательного ускорения при переносном, движении
w,x = MB • 6 = ОМ • е • sin a (9)
или при / = 1 сек. __
шст == 4 • 2 sin 60° = 4 V 3 см/шЛ (9')
Величина нормального ускорения weni которое направлено по
радиусу MB к оси вращения О^, равна
wtn = ciJ . Mfi = 0J ОУИ sin a
или при / = 1 сек. _
wen = 22 • 4 ~-3 = 8 К сж/се/с2. A0')
Величина дополнительного (кориолисового) ускорения опре-
определяется по формуле
wk = 2о), . vr • sin a A1)
или
wh = 2 • 2/ • 8/ • sin а = 32^ sin а, AК)
а при t =x 1 сек. и а = 60°
аъ == 32 • I2 sin 60° = 16 У~3 см/сек2. A Г)
Направление вектора wk устанавливаем по правилу Н. Е. Жу-
Жуковского. Найдем проекцию вектора относительной скорости vr на
плоскость, нормальную к вектору угловой скорости переносного
движения, и затем повернем ее на 90° в сторону переносного враще-
вращения, в данном случае против часовой стрелки. Это направление и
укажет направление вектора wk.
Абсолютное ускорение точки М получим, если геометрически
сложим все ускорения.
288 Кинематика
Величину абсолютного ускорения проще всего вычислить, если
спроектировать векторы всех ускорений на оси координат Оху
Оу, Oz. Расположим оси в точке О. Суммы проекций на
оси Оху Оу, Oz равны
Wax = wr cos 60° = 8~ = 4 см/сек*, A2)
Way = —Wen + o,f sin60° - — 8 V3 + 8^ = — 4К~3 см/сек\ A3)
waz = wex + wk == 41/ + 16 K~3 = 20 ^ см\сек\ A4)
Величину полного ускорения определим по формуле
wa = VwAax +liCTuL = К 4^4O1^+72^ =
= 35,56 смIсек2.
93. Полое кольцо радиуса г жестко соединено с валом АВ и
притом так, что ось вала расположена в плоскости оси кольца.
Кольцо заполнено жидкостью, движущейся в нем с постоянной
относительной скоростью vr Вал АВ вращается по часовой стрелке,
€сли смотреть по оси от А к В (рис. 93,а).
Угловая скорость вала we постоянна. Определить величины
абсолютных ускорений частиц жидкости, расположенных в точках
/, 2^3, 4.
Решение. Переносным движением является вращательное дви*-
жение кольца, относительным — вращательное движение жидкости
в кольце.
Абсолютное ускорение каждой точки жидкости определяется
по общей формуле
Wa = We + Wr + W&
Определим величины всех ускорений точки / (рис. 93,6).
Величина переносного ускорения
We1=:Weni = W*r. A)
Величина относительного ускорения
wri = Wm = -f • B)
Величина дополнительного (кориолисового) ускорения
wkl = 2C)evr sin a. C)
Так как угол а между векторами дг и toe в точке / равен нулю, то
wkl = 0. C')
Сложное движение точки
289
Величина абсолютного ускорения в точке / равна
Определим величины ускорений точки 2.
Переносное ускорение
^епа = U)f • 2г
и направлено вниз. ' *
щ, 8 б
К задаче 93.
Относительное ускорение
и направлено горизонтально» влево.
Дополнительное (кориолисово) ускорение
D)
E)
F)
wk% = 2we . vt • sin a =2coeor, G)
так как а = 90°. Направление вектора щ устанавливается по
правилу Н. Е. Жуковского (рис. 93,6).
Тогда величина абсолютного ускорения будет равна
*"«* •
BсоЛ)« -
%.
Соответствующие ускорения в точке 3 равны
г '
(8)
(9)
A0)
так как вектор относительной скорости Ъг параллелен вектору
угловой скорости йе.
Величина абсолютного ускорения
^аз-Зго>е9 + 7^. (И)
19 691
290
Кинематика
Величины ускорений точки 4 равны:
= 2/4D*,
A2)
A3)
A4)
A5)
94. Найти абсолютное ускорение шаров центробежного регу-
регулятора (рис. 94), если после изменения нагрузки машины он
wh9t = 2uevr
Величина абсолютного ускорения этой точки равна
К задаче 94.
вращается с угловой скоростью cd = и 1/Сек, причем шары опу-
опускаются в рассматриваемый момент времени со скоростью vr =
= 100 см/сек и ускорением wrx =10 см/сек2. Угол раствора
2а = 60°; длина рукояток шаров / = 50 см\ расстоянием между
их осями привеса можно пренебречь. Шары принять за точки.
Решение. Переносным движением шаров регулятора является
вращение их вместе со стержнями вокруг оси ОС (рис. 94,а), a
относительным — вращение их вокруг точки О (рис. 94,6).
Так как переносное движение вращательное, то возникает до-
добавочное ускорение; абсолютное ускорение шаров определим по
формуле
wa = we + wr + wk. A)
Сложное движение точки 291
Рассмотрим ускорения шара А регулятора при его переносном
й относительном вращениях, а также добавочное ускорение в рас-
рассматриваемый момент времени (рис. 94,6).
Переносное вращение шара вокруг оси ОС происходит с постоян-
постоянной угловой скоростью со, поэтому переносное ускорение точки А
равно
wen = о)МС = to2/ sin a B)
или
wen = 3,142 • 501 = 246,5 см/сек*, BЛ)
где АС — радиус вращения (АС = /). Это ускорение wen направ-
направлено по АС к центру С.
Относительное ускорение шара состоит из касательного уско-
ускорения Wn, величина которого задана, и нормального ускорения
./=^, C)
где одг — угловая скорость относительного вращения стержня с
шаром вокруг точки О.
Следовательно,
Нормальное ускорение wrn направлено от точки А к центру
вращения О.
Дополнительное ускорение
wk = 2о)Я, sin p D)
или
хюь = 2 • 3,14 . 100 ^ = 543,2 см/сек\ D')
так как угол р между линиями вектора to и вектора Dr равен 60°.
Для определения направления wh спроектируем вектор отно-
относительной скорости Иг на плоскость, перпендикулярную к оси
вращения, и повернем эту проекцию на 90° в сторону переносного
вращательного движения, т. е. в данном случае против часовой
стрелки. Как видйо, вектор ускорения wk направлен по каса-
касательной к траектории шара А в сторону, обратную направлению
вектора переносной скорости ve.
Геометрическая сумма всех этих ускорений равна вектору аб-
абсолютного ускорения шара А
п>а = Ww + Wrr + Wrn + Wh. E)
Для упрощения вычислений спроектируем все полученные
ускорения шара А на оси координат Ох, Оу и Oz и затем определим
19*
292 Кинематика
величину доа по формуле:
j т„ = v эд A- zap1 4- w^ FY
a r x i у i z- \^;
Определим сумму проекций ускорений на оси координат:
^ах = Wen + Wrx cos л + wrn sin a, G)
a*.* = ^, (8)
waz = шГЛ cos a — шгт sin a. (9)
Так как угол a = 30°, то
wax = 246,5 + 10^- + 200 i- == 355,1 сж/^к:2, G')
а>в„ = 543,2 слс/^/с2, (8')
waz = 200 ^ — 10 у = 168 с*/сюА (9#)
Величина абсолютного ускорения точки равна
wa = ]/"C55,1J + E43,2J + A68M = 671 см/сюА A0)
РАЗДЕЛ ТРЕТИЙ
СЛОЖНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
ГЛАВА XVI
ПЛОСКО-ПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА
§ 1. Общие сведения
Плоско-параллельным движением твердого тела называется такое
движение, при котором все его точки движутся параллельно неко-
некоторой условно неподвижной плоскости.
Изучение такого движения твердого тела сводится к изучению
движения какого-либо сечения тела плоскостью, параллельной
условно неподвижной плоскости и, следовательно, к изучению
движения плоской фигуры в ее плоскости.
Изучение движения плоской фигуры в ее плоскости основы-
основывается на следующих основных теоремах, которые дают возмож-
возможность установить способы составления уравнений движения и
определения скоростей и ускорений любых точек фигуры и, сле-
следовательно, любых точек твердого тела.
Эти теоремы следующие:
1. Всякое перемещение плоской фигуры в ее плоскости можно
осуществить путем поступательного перемещения ее вместе с про-
произвольно выбранной точкой и вращательного перемещения фигуры
вокруг этой точки.
Плоско-параллельное движение твердого тела
293
2. Всякое непоступательное перемещение плоской фигуры в ее
плоскости можно осуществить путем вращения ее вокруг некото-
некоторого центра вращения.
3. Проекции скоростей двух точек плоской фигуры на прямую
линию, соединяющую эти точки, равны между собой.
§ 2. Аналитический способ определения скоростей и ускорений
точек тела
Аналитический способ определения кинематических характери-
характеристик какой-либо точки плоской фигуры основан на указанной
выше первой теореме.
Пусть условно неподвижная система
координат хОу расположена в плоскости
движения плоской фигуры (рис. I).
Для определения положения этой
плрской фигуры возьмем вторую систему
координат хг0гуъ неизменно связанную
с фигурой и, следовательно, движущу-
движущуюся вместе с ней.
Положение подвижной системы ко-
координат определяется в каждый момент
времени координатами ее начала Ог
(полюса) и углом ср между положительным
направлением оси Огхг и положительным
направлением оси Ох условно неподвижной системы координат
(рис. I).
Координаты точки Ог (х01 и уох) системы Охх\уг при движении
фигуры, а также величина угла поворота ср являются функциями
времени, т. е.
Рис I.
Уох = Ш\ (XVI, 2)
? = М0- • (XVI, 3)
Эти три равенства называются уравнениями движения плоской
фигуры и позволяют определить закон движения любой точки
фигуры, траекторию точки величины и направления ее скорости
и ускорения.
Запишем уравнения движения точки М плоской фигуры, поло-
положение которой определяется координатами хг и уг в подвижной
системе Охх^уг и координатами хиув неподвижной системе,
xx cos ср — уг sin ср,
(XVI, 4)
(XVI, 5)
294 Кинематика
Уравнения (XVI, 4) и (XVI, 5) представляют закон движения
точки М фигуры. Если исключить из этих уравнений время /,
то получим уравнение траектории точки М.
Скорость точки М получим, определив проекции ее на оси
координат Ох и Оу. Для этого возьмем первые производные по
времени от уравнений (XVI, 4) и (XVI, 5),
i!L (^ sin
или, так как
TO
vx = vOxx — w to sin cp + y± cos cp), (XVI, 6)
vy = vOlV + a) to cos cp — yx sin cp), (XVI, 60
или1
(XVI, 7)
(XVI, 7')
Величину полной скорости определим по формуле
Найдем также проекции ускорения точки М на оси координат
Ох и Оу. Взяв производные по времени от проекции скоростей vm
и. vy (уравнения XVI,6 и XVI,6'); получим:
wx = wOlX — e to sin cp +
+ Ух cos cp) — oJ to cos cp — yx sin cp), (XVI, 8)
wy = шо1У + e to cos cp — yx sin cp) —
— o>2 to sin cp + yx cos cp), (XVI, 8')
или
Щ = оу01х — e (f/ — f/Ox) — оJ (д: — xOl), (XVI, 9)
Щ = ^oiy + e (x — xOl) — со2 (y - r/Ol). (XVI, 90
Величину полного ускорения определим по формуле
w = ]/до 4иА
Скорость и ускорение любой точки плоской фигуры при пло-
плоско-параллельном ее движении можно определить и другим спо-
способом.
На основании первой теоремы § 1 движение плоской фигуры
в ее плоскости можно рассматривать состоящим из двух
Плоско-параллельное движение твердого тела 295
движений: поступательного вместе с произвольно выбранной
точкой, называемой полюсом, и вращательного — вокруг полюса.
Поэтому, если известен вектор скорости полюса и закон враща-
вращательного движения фигуры вокруг полюса (<р = /3 @)» то вектор
скорости любой точки фигуры может быть получен как геометри-
геометрическая суммах вектора скорости полюса и вектора скорости рас-
рассматриваемой точки при вращательном движении фигуры вокруг
полюса, т. е.
(XVI, 10)
где точка А — полюс, точка В — рассматриваемая точка фигуры.
Величина скорости точки В при вращательном движении фи-
фигуры вокруг точки Л, как известно, равна
vBA = о) • ВА = & • ВА. (XVI, 11)
Величина скорости точки Л
где
__ dx_ я __ dy
х dt у Vy — ^ .
Диалогично вектор ускорения какой-либо точки плоской фигуры
при ее плоско-параллельном движении равен геометрической
сумме вектора ускорения полюса и вектора полного ускорения
рассматриваемой точки при вращательном движении фигуры во-
вокруг полюса
Wb = Wa + №вау (XVI, 12)
где wB — вектор ускорения точки В, wA — вектор ускорения по-
полюса — точки Л, wba — вектор полного относительного ускорения
точки В при вращении фигуры вокруг полюса Л.
Вектор полного относительного ускорения равен
где wxba — вектор касательного относительного ускорения, whba —
вектор нормального относительного ускорения.
Величина касательного ускорения
WxBA = е.вА = ^.ВА=^.ВА. (XVI, 13)
Величина нормального ускорения
хЮпп^^.ВА-^уВА (XVI, 14)
Как видно из уравнений (XVI, 13) и (XVI, 14), величины каса-
касательного и нормального ускорений могут быть определены, если
296 Кинематика
известен закон вращательного движения плоской фигуры вокруг
полюса <р = /3(/) или величины е и ш для каждого момента
времени.
Вектор ускорения точки В может быть получен как геометри-
геометрическая сумма трех векторов
WB ==^Л +~WtBA + ~WnBA- ' (XVI, 15)
§ 3. Методические указания к решению задач
Решение задач аналитическим способом не представляет затруд-
затруднений, если заданы уравнения движения плоской фигуры.
В случаях, когда требуется составить эти уравнения, необхо-
необходимо прежде всего выбрать положение неподвижной системы
координат Оху, затем начало Ог подвижной системы координат
О1хлу1 и положение этой системы в движущемся теле. За точку
Ог подвижной системы координат выбирается такая, для кото-
которой можно было бы составить уравнение ее движения и уста-
установить координаты рассматриваемой движущейся точки в этой
системе координат.
Скорость и ускорение любой точки плоской фигуры можно
определить, пользуясь уравнениями (XVI,6) и (XVI,8).
Скорость и ускорение точки можно определить и другим
способом, а именно, используя геометрические зависимости, ука-
указанные в формулах (XVI,10) и (XVI, 15).
§ 4. Задачи
Аналитический способ решения
95. Линейка эллипсографа приводится в движение кривоши-
кривошипом ОС у вращающимся с постоянной угловой скоростью
<¦> =! VceK (РИС. 95).
Составить уравнения движения линейки эллипсографа, если
ОС = ОВ = АС = г = 10 см.
Определить также скорость и ускорение точки А линейки в
момент / = 0,5 сек.
Решение. Для решения задачи применим аналитический способ.
Расположим начало координат неподвижной системы хОу в точке О,
на оси вращения 'кривошипа. Ось Ох направим горизонтально
вправо, а ось Оу — вертикально вверх (рис. 95,а).
Начало подвижной системы координат Ог расположим в точке С
Плоско-параллельное движение твердого тела
297
кривошипа, ось 0гхг направим вдоль линейки вправо, а ось 01у1
вверх. Составим уравнения движения линейки, принимая точку
С = 0х за полюс, координаты которого обозначим х01, уОъ и выра-
выразим их в функции угла поворота кривошипа <р:
о)
xOl = /;coscp,
У01 = г sirup.
B)
К задаче 95.
По условию кривошип вращается равномерно, поэтому угол <р
изменяется пропорционально времени по уравнению
<р = Ы. C)
Уравнение C) представляет и уравнение вращательного движе-
движения линейки, так как срх = ср.
Подставив теперь значения ср в формулы A) и B), получим урав-
уравнения движения линейки:
xOl == r cos о)/; D)
yOl = г sin а)/; E)
^ = to/. F)
Для определения скорости и ускорения точки А по отношению
к неподвижной системе координат хОу найдем координаты х, у
298 Кинематика
точки Л, которые в подвижной системе х^щ^ как видно из
рис. 95, равны
*! = —/-, G)
1/1 = 0. (8)
Подставим теперь эти величины в общие уравнения движения,
полученные для любой точки тела при его плоско-параллельном
движении:
х = xOv + хг cos cpx — уг sin <fv (9)
У = Уог + *i sin ?1 + ^ cos ?1, (9')
еде <pi — угол между юсями Ох и Огхг — равен углу поворота ср кри-
кривошипа.
Тогда получим величины х и у:
x = rcosd)t—г cos со/= 0, A0)
у = г sin tat + r sin (о/ = 2г sin to/. A0')
Скорость и ускорение точки Л, движущейся прямолинейно
вдоль оси Оу, как видно из рисунка, получим из уравнения A0)
л A0'):
J A2)
Следовательно, величина полной скорости точки Л
v = Ру = 2о)г cos (d/,
а величина полного ускорения ее
w = Шу = -^ = _ 2со2г sin со/. A3)
В момент t = 0,5 сек. скорость точки Л
о = 2у.Ю cos-j-i- = ЬкУ~2 см/сек
и направлена вверх по оси Оу\ а ускорение
w = —2 (-JJ • Юsin-J-!¦ = — 2,5*2 у~2 CMjceKt
и направлено вниз по оси Оу.
Второй способаналитического решения
Скорость точки Л линейки эллипсографа можно рассматривать
как геометрическую сумму двух скоростей: скорости при поступа-
поступательном движении линейки, которая равна скорости йолюса О19
т. е. Vot, и скорости точки Л при вращательном движении линейки
Плоско-параллельное движение твердого тела 299
вокруг полюса т. е.
va=vOi + vAov A)
Скорость полюса точки 0г направлена перпендикулярно к ра-
радиусу и равна по величине
vOl = cor = -^- • 10 = 5тс см/сек, B)
Скорость точки А при вращательном движении линейки вокруг
полюса Ох направлена перпендикулярна к линейке и равна
vAOi = r-^- = гсо = 10-j- == 5тс си/шс. C)
В момент времени / = 0,5 сек. угол
ср = ы — y • 0,5 = ~ радиан,
поэтому скорости Уо! и VAOi направлены под углом 45° к оси Оу
(рис. 95,6) и геометрическая сумма их равна
lx\Qx сж/се/с. D)
Аналогично ускорение точки А можно определить из геометри-
геометрического равенства
ЪА = wOl + wAOv E)
Так как касательная, составляющая ускорение wxch при рав-
равномерном вращении кривошипа, равна нулю, то ускорение точки Ох
кривоЩипа равно нормальной составляющей ускорения, а именно:
WOi = WnOi = ^ = ^! = 25*2 с/ ()
Ускорение точки А при вращательном движении вокруг по-
полюса равно
2
^АОх = WnAOl = "^ = ЛИП в 2'5ТС2 СЖ/С^2' (?)
так как угловое ускорение е = 0 и, следовательно, шта0! == О.
Ускорения wot и waox направлены под углом 90° друг к другу
(рис. 95,в), поэтому величина ускорения точки А — wA равна
г г = 2f6ic VJcMlceK*. (8)
96. Малая шестерня радиуса г = 10 см, катящаяся по неподвиж-
неподвижной шестерне радиуса R = 15 см, приводится в движение кривоши-
кривошипом О А, вращающимся равноускоренно с угловым ускорением
е = 2 см/сек2.
Найти уравнения движения подвижной шестерни, если в на-
начальный момент t = 0, угловая скорость кривошипа о>0 == 0 й на-
начальный угол ср0 = 0 (рис. 96).
300
Кинематика
Определить также для любого момента времени / скорость точки
М" малой шестерни, лежащей на расстоянии г от оси вращения Л и
совпадающей с осью кривошипа ОА в начальный момент времени.
Решение. Малая шестерня совершает плоско-параллельное слож-
сложное движение. Она вращается вокруг своей оси, проходящей через
точку Л, а также вместе с кривошипом О А вокруг неподвижной
оси, проходящей через точку О
перпендикулярно к плоскости
вращения.
Определим закон вращатель-
вращательного движения кривошипа.
Угловое ускорение криво-
кривошипа е задано, оно постоянно
и равно
м
интегрируя его дважды, получим
dt ' ь
B)
К задаче 96.
C)
Постоянные интегрирования Сг и С2 определяем из заданных
начальных условий при: / = 0; а>0 = -— = 0 и ср0 = 0.
Применив их, получим Сг = 0 и С2 = 0.
Подставив эти значения в уравнения C), получим закон враща-
вращательного движения кривошипа
Для составления уравнений движения малой шестерни выберем
неподвижные оси координат хОу в точке О, а за полюс примем
точку А шестерни.
Координаты полюса А в некоторый момент времени будут
равны
* = (/? +г) cos ft, E)
y = (R + r)sln<fv F)
При повороте кривошипа на угол срх малая шестерня вместе
с кривошипом повернется на этот же угол <рх и вокруг своей оси
относительно кривошипа на угол <рг> т. е. на угол ср == срх + ср2.
Угол поворота малой шестерни <рг можно определить, исполь-
использовав условие перекатывания ее без скольжения по неподвижной
шестерне.
Плоско-параллельное движение твердого тела 301
В начальный момент времени, когда срх = 0, точка М малой
шестерни находилась на оси Ох в точке Во. При повороте криво-
кривошипа на угол срх радиус AM займет положение под углом ср2 к
оси ОА.
Так как длина дуги BQB равна длине дуги ВМ, можно написать
равенство
R • «Pi = '?2> G)
откуда
Угол поворота малой шестерни относительно начала координат
О равен сумме углов срх и ср2> т. е.
Подставив значение угла срх в уравнения E), F) и 8), получим
* = (#+r)cos^, (9)
y = (R + r)sin*{, A0)
?• (И)
Подставив в эти равенства их числовые значения, получим:
х = 25 cos /2, (90
#-25 sin/2, A0')
ср=2,5/2. A1')
Так как скорость точки М равна геометрической сумме ско-
скорости полюса Л и скорости точки М относительно полюса Л, то для
определения абсолютной скорости точки М малой шестерни вос-
воспользуемся формулой
vm = va+ vma- A2)
Величина скорости полюса А
.lU = (# + r)(D=(#+r)^, A3)
где
?i = ~2~>
откуда
vA = (/? + г) . е/ = 25 • 2/ = 50/ сж/се/с. A3х)
Вектор скорости Ул направлен перпендикулярно к радиусу R.
302
Кинематика
Величина скорости vma точки М относительно полюса Л равна
Vma === т • ыма ==: г • ~л • A4)
at ^ *
Из уравнения A1')
? = 2,5/2,
откуда
V&A = г • 5/ = 50/ сж/шс. A4х)
Угол между вектором скорости vA и вектором ЪМа равен
A80°— ср2), где
Поэтому величину скорости то^ки М можно определить по фор-
формуле
{+ v2MA+ 2vavAm cos A80° — ср2) =
= YE0/J + E002 — 2 • 50/ . 50/ • cos lf5t2 =
= 50/ ^2—2 Cos 1,5?. ~ A6)
97. Конхоидограф состоит из линейки АВ (рис. 97), которая
шарнирно соединена в точке А с ползуном, скользящим в прямо-
D 0* й А% линейной прорези DE, и проходит
—^-—k- через поворотную трубочку свободно
вращающуюся около неподвижной
оси NN; расстояние оси NN от оси
Ох прорези равно а.
Найти уравнение кривой, описыва-
описываемой точкой Мх линейки АВ, если
расстояние АМг == а; оси координат
указаны на чертеже.
Решение. Обозначим угол, со-
составляемый осью линейки АВ с осью
К задаче 97. Ох через ср, последний изменяется
при движении ползуна А и, * следо-
следовательно, является функцией времени.
Выразим координаты точкиМхчерез заданный размер аи уголср
х = ОА — acoscp, A)
у = a sin ср. B)
Расстояние О А равно
tg?
C)
Плоско-параллельное движение твердого тела 303
поэтому
B')
Чтобы получить уравнение траектории в явном виде, исключим-
параметр ср.
Преобразуем выражение для абсциссы х
(а — a sin cp) V\ — sin2 cp / уг\
> sin cp
Подставив значение sin cp из уравнения B) в уравнение (Г'),
получим
или, после соответствующих преобразований,
Это уравнение кривой четвертого порядка — конхоиды.
§ 5. Графический способ определения скоростей и
ускорений точек тела и методические указания к
построению планов скоростей и ускорений
Приведенные в предыдущем разделе геометрические равенства
для определения скоростей и ускорений точек тела при его плоско-
плоскопараллельном движении
. A)
B)
дают возможность графически определить скорости и ускорения
точек тела в каждый заданный момент времени.
Рассмотрим графический способ определения скоростей и ускоре-
ускорений.
План скоростей. Пусть плоская фигура (рис. II) совершает
плоско-параллельное движение в плоскости хОу\ задан вектор
скорости дл точки А у которую принимаем за полюс, и вектор Ъва
скорости точки В при вращении тела вокруг полюса Л, т. е. век-
вектор относительной скорости точки В по отношению к Л. Тогда
304
Кинематика
скорость точки В по отношению к неподвижной системе коорди-
координат, т. е. ее абсолютная скорость, равная геометрической сумме
va и Ъва, может быть получена графически, как указано на рис. II.
Эта же скорость может быть получена построением плана ско-
скоростей. Для этого из произвольной точки О полюса (рис. \\\уа,6)
отложим в выбранном масштабе вектор скорости точки А — vA = Оа.
Из конца этого вектора отложим вектор относительной скорости
точки В — Ъва = Дв- Их геометрическая сумма Об равна вектору
vB—абсолютной скорости точки В,
У'в
Рис. III.
Построенная фигура (рис. II 1,6) называется планом скоростей.
При помощи плана скоростей можно определить по величине
и направлению скорости любой точки фигуры.
Возьмем, например, точку С на средине линии АВ. Вектор ско-
скорости этой точки получим из плана скоростей, если разделим
линию ab (рис. III,в) в том же отношении, что и на фигуре (в дан-
данном случае пополам), и соединим эту точку С с полюсом плана ско-
скоростей. _
Вектор Ос и будет вектором скорости точки С фигуры
vc = vA + vCA. C)
Относительная скорость Ъса равна половине скорости Ъва и
направлена перпендикулярно к линии АВУ т. е. равна вектору
ас в плане скоростей. Следовательно, вектор Ос, равный геометриче-
геометрической сумме оа и ас, является вектором скорости точки С.
Чтобы определить скорость точки D, не лежащей на линии АВ,
соединим ее с точками А п В (рис. III,а).
Вектор относительной скорости точки D по отношению к А
vda направлен перпендикулярно к линии DA, а вектор относи-
относительной скорости точки D по отношению к A vdb перпендику-
перпендикулярно к линии DB треугольника ADB.
Проведя в плане скоростей из точки а, а затем из точки Ь ли-
линии, параллельные относительным скоростям, т. е. перпендику-
перпендикулярно к линиям DA и DB &ADB, получим на их пересечении
Плоско-параллельное движение твердого тела 305
точку d, вершину подобного и сходственна расположенного, тре-
треугольника adb.
Соединив полюс плана скоростей с точкой dr получим вектора
абсолютной скорости точки Od = vD и векторы относительных,
скоростей
da = vDA и db = vDb.
Вектор абсолютной скорости можно построить, для любой
точки фигуры; /И; все они будут исходить из полюса плана ско-
скоростей, указывая величину и направление скорости соответствую-*
щей точки.
Во многих случаях величина относительной скорости не за-
задается, а известна лишь линия, по которой она направлена. Тогда,,
чтобы построить план скоростей, необходимо знать линию, по кото-
которой направлена абсолютная скорость искомой тачки В.
Зная вектор скорости точки А — 5а, проводим из конца ещ
линию, параллельную линии вектора относительной скорости, а
из начала линию, параллельную линий вектора абсолютной скот,
роста точки В-
На их пересечении получаем точку Ь плана скоростей.
План ускорений. Ускорение точки В плоской фигуры может
быть определено графически на основании одного из. следующих
геометрических равенств:
WxBA, B>
™пВ + WtB = WA + WnBA + ОУтВА. (З)
Ускорение точки В фигуры (рис. IV,a) может быть графически
определено из равенства A) в том случае, если иавестен вектор
ускорения полюса А—wA и вектор относительного ускорения wBa
точки В по отношению к пооюсу А.
Действительно, приняв произвольную точку О (рис. IV,6) aa
полюс плана ускорений, отложим в выбранном масштабе вектор
ускорения wa, & из конца его — вектор относительного ускорения
wba\ соединив полюс О с концом вектора wba, получим вектор
ускорения точки В, т. е. величину и направление абсолютного
ускорения „этой точки. Полученный треугольник ОЬа называется
планом ускорений фигуры М> так как при помощи его можно
определить ускорение любой точки фигуры.
Равенством B) можно воспользоваться для построения плана
ускорений, если, кроме вектора ускорения wa, известна по величине
и направлению нормальная составляющая вектора относительного
ускорения Wuba, а также линия, по которой направлен вектор
абсолютного ускорения точки В —* wB.
20 591
306
Кинематика
В этом случае план ускорений строим следующим образом
(рис. IV). Из полюса О плана ускорений (рис. W,e) откладываем
вектор wa, затем из конца его проводим вектор шпва — нормаль-
нормальную составляющую относительного ускорения. Вектор ы>пва на-
направлен по линии В А к центру вращения — точке А фигуры.
м
Рис. IV.
Из конца вектора шпва проводим линию,_ параллельную ли-
линии касательной составляющей вектора wxba, которая про-
проходит перпендикулярно к линии вектора шпва-
Наконец, из полюса О плана ускорений проводим линию парал-
параллельно линии полного абсолютного ускорения точки В. Тогда на
пересечении линий касательного относительного ускорениями
абсолютного ускорения получим точку b — конец вектора Ob = wB.
Вектор полного относительного ускорения получим, соединив
точки а и b линией ab, которая и представляет вектор ускоре-
ускорения wba.
В том случае, когда линия абсолютного ускорения точки В
неизвестна (рис. 1У,г), для построения плана ускорений надо
вначале определить по величине и направлению нормальные
составляющие векторов абсолютного и относительного ускорений
и, проведя линии, параллельные линиям касательных ускорений
тр и Wiba, получить точку Ь.
Плоско-параллельное движение твердого тела
307
§ 6. Задачи
98. Определить скорость и ускорение точки В четырехзвенного
механизма (рис. 98,а) в момент, когда звено ОА горизонтально, а
звено BD направлено под углом 30° к горизонтальной линии.
В
О,
Кривошип О А длиной г = 10 см вращается против хода ча-
часовой стрелки, делая п = 100 об/мин. Длина звена АВ = / =
= 100,5 см, длина звена BD = 1г = 40 см. Остальные размеры
указаны на рисунке.
Решение. Для построения плана скоростей определим величину
скорости точки Л-кривошипа О А, который вращается вокруг
центра О:
nrn n 10-100 100тт: 1ГМ а ,
= —х- == 104,6 см/сек.
30
30
Скорость va направлена вертикально вверх.
Звено АВ совершает плоско-параллельное движение; звено BD
вращается вокруг центра!); скорость точки В направлена перпенди-
перпендикулярно к оси звена BD.
Рассматривая движения звена АВ, можно составить геометри-
геометрическое равенство для определения скорости точки В, если принять
20*
308 Кинематика
за полюс точку А звена АВ.
vB = vA + vBA. A)
В этом равенстве вектор скорости точки А известен, вектор
относительной скорости точки В звена АВ, при его вращении во-
вокруг полюса Л, по величине неизвестен, но известна линия, по кото-
которой он направлен, так как вектор ЪВА направлен перпендикулярно
к линии звена АВ.
Известна также линия, по которой направлен вектор скорости
точки В.
Построим план скоростей, выбрав масштаб для скорости точки А
(рис. 98,6).
Отложим вектор скорости точки А — vA из точки О полюса
плана скоростей. Из конца вектора дА проведем линию, параллель-
параллельную вектору относительной скорости vBa9 т. е. перпендикулярно к
звену АВ.
Затем из полюса О проведем линию параллельно вектору абсо-
абсолютной скорости точки В, следовательно, перпендикулярно к звену
BD.
На пересечении этих линий получим точку, которая определяет
конец вектора абсолютной скорости точки В — vB и вектора отно-
относительной скорости vba»
Из построенного плана скоростей определим величины скорости
vb и vba-
vB= 127,4 см/сек,
vba ^ ^4,2 см/сек.
Построим план ускорений.
Для определения ускорения точки В запишем равенство
В этом равенстве вектор ускорения wBa и вектор wB неизвестны
ни по величине ни по направлению, поэтому план ускорений можно
построить, применив лишь равенство C).
Определим предварительно величины нормальных составляю-
составляющих векторов wnBA и wnB:
wnBA = ~Г ^ "ЩГ ^ T55J" = 41>1 см1сек2>
WnB - ^ = i^ji- = 405 см/сек*.
Определим также ускорение wA точки А кривошипа.
Так как кривошип вращается равномерно, то величина полного
ускорения точки А равна нормальному ускорению ее в каждый
Плоско-параллельное движение твердого тела 309
данный момент времени
до = до s -А = —~— = 1094 см/сек2.
А 71А Г IU
Выбрав полюс О и масштаб ускорений, построим план ускоре-
ускорений (рис. 98,в).
Отложим из полюса Ог вектор ускорения точки А — wA =
= 1 094 см/сек. Из его конца проведем линию, параллельную
стержню АВ, и отложим величину вектора относительного нор-
нормального ускорения Wuba, направив его вверх, так как вектор
нормального ускорения направлен от точки В к точке А при отно-
относительном вращении стержня АВ вокруг точки Л.
Вектор касательного ускорения перпендикулярен к нормаль-
нормальному, поэтому из конца вектора wuba проводим перпендикулярно к
нему линию вектора касательного ускорения.
Нормальную составляющую вектора абсолютного ускорения
точки В — wnB откладываем из полюса Ог.
Проведя цз конца вектора wnB линию, параллельную вектору
касательной составляющей дотв, т. е. перпендикулярно к вектору
wnB, найдем точку пересечения этой линии с линией вектора Щва,
проведенной ранее. Эта точка указывает конец вектора абсолют-
абсолютного ускорения wB, проведенного из полюса Ог.
Соединив точку вг с точкой аг плана ускорений, получим вели-
величину и направление вектора полного относительного ускорения
Wba> а также величины касательных составляющих векторов ус-
ускорений wxb и Шхвау .которые могут быть использованы для опре-
определения угловых ускорений соответствующих звеньев механизма.
99. Кривошип ОА длиной г = 20 см вращается равномерно
с угловсй скоростью (о0 == 10 7сек и приводит в движение шатун
АВ длиной / = 100 см; ползун В движется по вертикали (рис. 99).
Найти угловую скорость и угловое ускорение шатуна АВ, а также
скорость и ускорение ползуна в момент, когда кривошип и шатун
взаимно перпендикулярны и образуют с горизонтальной осью
углы а и р = 45°.
Решение. Определим скорость и ускорение ползуна Ву а также
величину относительной скорости vba и величину относительного
касательного ускорения wxba* построив планы скоростей и уско-
ускорений. После этого по известным формулам определим угловую
скорость ьува и угловое ускорение $ва шатуна.
Построим план скоростей.
Скорость точки В равна
vB = vA + дВА. A)
310
Кинематика
Величина скорости точки А равна
vA = rw = 20 • 10 =*= 200 слс/шс
и направлена перпендикулярно к радиусу (рис. 99,а). Абсолютная
скорость точки В направлена по вертикали, а относительная ско-
скорость точки В по отношению к точке Л, которую принимаем за
полюс стержня АВ> направлена перпендикулярно к шатуну АВ.-
Отложим вектор скорости va
(рис. 99,6) из полюса О плана ско-
скоростей, из конца его проводим
линию, параллельную вектору от-
относительной скорости vba, т. е.
перпендикулярно к АВ. Далее из
полюса О проводим линию, парал-
параллельную вектору скорости vB,
т. е. вертикально. На пересечении
этих линий получим точку b—ко-
b—конец вектора vB. ,
^ -V. Из этого плана скоростей и
* p\ получаем величины скорости vba
'\ _ и vB
vBA = 200 см/сек;
vB = 200 V см/сек.
Относительная угловая скорость
"ва
_ ?0° _ <> 1/
-loo '°
К задаче 99.
WA = «'«А Г
Строим план ускорений.
Так как кривошип вращается
равномерно, касательное ускоре-
ускорение точки А (рис. 99,я) равно нулю,
поэтому полное ускорение
= 2000 cMJcetf
и направлено от точки А к оси вращения кривошипа.
Ускорение точки Б, по условию, направлено по вертикальной
линии, поэтому запишем векторное равенство для определения
ускорения wB в виде_ ^
и на основании его построим план ускорений.
Вычислим величину вектора
_ = ^- = 400 см[сек*.
Этот вектор направлен от точки В к точке А.
Плоско-параллельное движение твердого тела 31 h
Отложим из полюса Ох плана ускорений вектор шд и- из его
конца #, перпендикулярно к нему, отложим вектор ускорения
®>пва* Затем из конца этого вектора проведем линию, параллельную
вектору касательной составляющей относительного ускорения wxba>
т.' е. перпендикулярно к wnBA- Из полюса О* проводим линию,
параллельную вектору полного ускорения точки В, т. е. верти-
вертикально. На пересечении линий векторов wxba и wb находим точку
b — конца вектора ускорения wB. Линия сив указывает (в мас-
масштабе плана ускорений) величин^ относительного ускорения
Из плана ускорений получим
wB = 400 уТ=: 565,6 см/сек*,
wxba — 1600 см/сек2.
Относительное угловое ускорение шатуна АВ
wxBA 1600
юо
= 16
§ 7. Графо-аналитичгский способ определения скоростей
и ускорений rf методические указания к решению задач
Графический способ определения скоростей и ускорений точек,
плоской фигуры (звеньев механизма) требует построения планов-
скоростей и ускорений в определенном масштабе, что связано с
известными трудностями.
Однако в ряде случаев решение задач можно осуществить,
определив искомые величины из планов скоростей и ускорений,
построенных не в масштабе, а на основании геометрических и три-
тригонометрических соотношений: из подобия треугольников путем
применения теорем синусов или косинусов или путем проекти-
проектирования геометрических равенств на оси координат.
Определение скоростей точки облегчается применением теоремы
о проекции скоростей двух точек плоской фигуры на соединяю-
соединяющую их линию.
§ 8. Задачи
100. Качающаяся вокруг центра А подвижная щека АВ дро^
билки длиной 60 см приводится в движение кривошипом ОЕ дли-
длиной 10 см, делающим п= 100 об /мин, посредством системы рычагов
ВС, CD и СЕ. Длины рычагов ВС и CD равны 40 см каждый
(рис. 100). Найти угловую скорость щеки АВ при положении»
механизма, указанном на рисунке.
312
Кинематика
Решение* Угловую скорость ш звена АВ можно определить
но формуле
Применив для звена ВС теорему о проекциях скоростей двух точек
тела на линию, их соединяющую, можно определить скорость vB
точки 5.
В данном случае скорость vB направлена вдоль линии ВС, а
скорость точки С — под углом 30°. Поэтому
yB = yccos30°. B)
Так как скорость точки С не задана,
то ее определяют, построив (не в ма-
масштабе) план скоростей для четырех-
звенного механизма OECD.
Предварительно определим скорость
точки Е
пгп тс-10-100
vE--
30 "
% шо
30
см/сек.
C)
Затем определим угол а, образуемый
шатуном СЕ с вертикалью
. __ ОЕ _
lga~~ ОС -
ОЕ
80+ CD sin 30°
10 J
К задаче 100.
D)
Построим план скоростей на основании равенства
Х)г — X)j? ~т~ Vfw.
В полученном треугольнике скоростей (рис. 100,6) углы известны,
поэтому, применив теорему синусов, определим скорость точки С
— sin (90 + «)
V° ~~~ Ve sin F0 — а)'
ИЛИ
COS а 200 %
с л sin 60°-cos а — cos60°-sina з ("|/3 0,.,
Мз уравнения B) определим скорость точки В
о ¦- = —— см Iсек
2 3(/з--0,1)
см/сек.
200 тс
E)
E')
F)
Плоско-параллельное движение твердого тела 315
и, следовательно, угловая скорость звена АВ
vB 100 VT- я , осп i/ ,-v
(о = -А- = т== = 1,852 1/сек. G)
№ 60A/3 — 0,1) v ;
Теперь решим задачу 99, решенную ранее графическим спосо-
способом, графо-аналитическим способом.
101. Кривошип ОА длиной г = 20 см вращается равномерно
с угловой скоростью ш0 = КР/секи приводит в движение шатун АВ
длиной / = 100 см; ползун В движется по вертикали. Найти угло-
угловую скорость и угловое ускорение шатуна В в момент, когда криво-
кривошип и шатун взаимно перпендикулярны и образуют с горизонталь-
горизонтальной осью углы а и [3=45° (рис. 99,а).
Решение. Построим планы скоростей и ускорений заданного
механизма (не в масштабе) и затем аналитически определим тре-
требуемые величины.
Строим план скоростей на основании равенства
°b = Va + Vba- 0>
Отложим из полюса О вектор скорости ЪА и проведем линию,
параллельную абсолютной скорости точки В (рис. 99, б), а из
конца вектора Ъа проведем линию параллельно относительной
скорости г>ва> т. е. перпендикулярно к шатуну АВ.
В полученном прямоугольном треугольнике углы при основа-
основании равны 45°. Следовательно, величина относительной скорости Vba
равна величине скорости va и равна vba = 200 см/сек.
Скорость точки В направлена вертикально вверх и равна по
величине
vB = 200 ]/Т см/сек.
Относительную угловую скорость вращения шатуна определяем
из равенства
Далее на основании векторного равенства
wzBA B)
построим (не в масштабе) план ускорений и аналитически опреде-
определим неизвестные величины wB и wzba (рис. 99, в). Направления
ускорений видны из построенного плана ускорений.
Для определения величины wzba спроектируем обе части этого»
равенства на горизонтальную ось. Тогда получим
0 = wA cos 45° — wnBA cos 45° — wzBA cos 45°
или
откуда
=2000 — 400 = 1600 см/секР.
314
Кинематика
Угловое ускорение вВа шатуна получим из уравнения
16
где / — длина шатуна.
Величину абсолютного ускорения точки В (ползуна) определим,
если спроектируем векторное равенство B) на вертикальную ось»
а именно:
— wB = — wnA cos 45° — wnBA cos 45° + wxba cos 45°»
откуда
™B = Ki + WnBA
« B000 + 400— 1600)
2~ = 565,6 см/сек.
§ 9. Определение скоростей точек' тела при помощи
мгновенных центров скоростей. Центроиды
Согласно второй теореме (глава XVI) всякое перемещение
плоской фигуры можно осуществить вращением ее вокруг
некоторого центра, называемого конеч-
конечным центром вращения* Последний
может быть определен, если известны
два положения тела в начальный tx и
конечный t2 моменты некоторого проме-
промежутка времени (рис. V).
От интервала времени /2 — h зависит
положение тела в конечный момент вре*
мени /2, а следовательно, зависит и по-
положение центра конечного вращения.
Если интервал времени t2 — tx стре-
стремится к нулю, то центр вращения стре-
стремится к некоторому своему предельному
положению, которое называется мгновенным центром вращения
или мгновенным центром скоростей.
Зная положение мгновенного центра скоростей, расстояние ка-
какой-либо точки тела от центра скоростей / и скорость ее, можно
Определить величину мгновенной угловой скорости вращения тела
по формуле
VA
—-г-
Если определена величина и направление мгновенной угловой
скорости тела, то можно определить скорость Любой точки тела,1
расстояние которой от мгновенного центра скоростей задано.
. Вектор скорости любой точки тела направлен в сторону враще-
вращения перпендикулярно к линии, соединяющей мгновенный центр
вращения с данной точкой.
Плоско-параллельное движение твердого тела 315
Неподвижная и подвижная центроиды
Геометрическое место мгновенных центров скоростей фигуры,
связанных с неподвижной плоскостью, в которой перемещается
плоская фигура, называется неподвижной центроидой.
Геометрическое место мгновенных центров скоростей, связан-
связанных с движущейся плоской фигурой, называется подвижной цент-
центроидой.
При движении тела подвижная центроида катится без сколь-
скольжения по неподвижной, следовательно, каждой точке подвижной
центроиды соответствует определенная точка неподвижной. Если
центроиды известны, то движение тела можно осуществить путем
перекатывания без скольжения подвижной центроиды по непод-
неподвижной*
Центроиды могут быть получены графически или аналитически.
Неподвижные центроиды определяются аналитически при помощи
формул, позволяющих определить координаты хР и уР мгновенных
центров скоростей на неподвижной плоскости по отношению к
неподвижной системе координат хОу:
хр = *0, ^~ • (!)
р о1 2 B)
Координаты мгновенных центров скоростей подвижных центроид
по отношению к подвижной системе координат, связанной с плос-
плоскостью движущейся фигуры, определяются по формулам:
^Огхsin cp-oOil/cosy
Xw = - , [6)
В формулах A), B), C), D) x0± и yOl— координаты полюса О1 фигуры,
a<p — угол поворота подвижной системы осей относительно неподвиж-
неподвижной; v01x — проекция скороститочкиОх тела на ось абсцисс; v0l —
проекция скорости точки Ог тела на ось ординат; со =~ — угловая
скорость вращения подвижной системы координат относительно
неподвижной.
§ 10. Методические указания к решению задач
v Определение положения мгновенного центра скоростей Р и
угловой скорости тела со имеет большое значение. Зная положения
мгновенного центра скоростей и мгновенной угловой скорости можно
316
Кинематика
определить вектор скорости любой точки М тела в рассматриваемый
момент времени.
Рассмотрим способы определения положения мгновенного центра
скоростей (рис. VI).
* Рис. VI.
1. Задана скорость точки А тела и угловая скорость вращения
его <о (рис. VI, а). В этом случае мгновенный центр лежит на
линии, перпендикулярной к вектору скорости va, на расстоянии APt
равном -*
и расположенном так, чтобы направление вектора скорости vA сов-
совпадало с направлением вращения тела вокруг мгновенного центра.
2. Известны векторы скоростей vA и vb точек А и В тела и рас-
расстояние между точками АВ (рис. VI, б). В этом случае мгно-
мгновенный центр скоростей Р находится на пересечении перпендику-
перпендикуляров, восставленных в точках А и В к линиям векторов Ъа и Ъв.
Расстояния АР и ВР Определяются либо из графического по-
построения либо аналитически, используя условия задачи. -
Плоско-параллельное движение твердого тела
317
3. В том случае, когда векторы скоростей va и vb параллельны
Друг другу и равны (рис. VI, в, г,), тело движется поступательно.
Угловая скорость равна нулю и скорости всех точек одинаковы.
Если же векторы скоростей Ъа и Ъв по величине не равны, то они
должны быть перпендикулярны
к линии АВ, соединяющей точки
А и В, так как в противном
случае проекции их на эту ли-
нию не будут равны, что про-"
тиворечит известной теореме.
Мгновенный центр скоростей
в этом случае лежит на пере-
пересечении линии — соединяющей
точки А и В и линии, соединя-
соединяющей концы векторов скоростей
va и дв, следовательно, поло-
положение его может быть опреде-
определено из подобия треугольников
PAD и РВС
ВР _ "в
АВ - vA '
§ 11. Задачи
102, Блок А (рис. 102) под-
подвешен на канате, правый конец
которого закреплен, а левый, ему
параллельный, движется со ско-
скоростью v = 10 см/сек. Диа-
Диаметр блока равен 2 г= 25 см. Определить скорость центра О блока
Л, его угловую скорость вращения, а также найти неподвижную и
подвижную центроиды блока. Диаметром каната пренебречь.
Решение. Скорость точки С блока А равна скорости левого
конца каната и направлена вертикально вверх. Скорость правого
конца каната равна нулю, так как этот конец неподвижен, следо-
следовательно, скорость точки Р касания блока и каната в каждый
момент времени равна нулю. Поэтому точка Р является в данный
момент мгновенным центром скоростей блока.
Скорость vc точки С блока известна, поэтому можно опреде-
определить угловую скорость вращения блока вокруг мгновенного цент-
центра Р по формуле
A)
318 Кинематика
откуда угловая скорость
Определив угловую скорость, можно определить скорость лю-
любой точки блока, если будет задано ее расстояние от мгновенного
центра скоростей Р.
В частности скорость центра О блока А
vQ = cor = 0,4 • 12,5 = 5 см/сек. B)
Неподвижной центроидой блока, представляющей геометриче-
геометрическое место мгновенных центров скоростей, связанных с неподвиж-
неподвижной плоскостью (неподвижной системой), является вертикальная
прямая линия, совпадающая с осью правого конца каната.
Подвижная центроида представляет окружность, радиус которой
равен радиусу блока.
103. Определить величину и направление скорости v0 оси блока
(рис. 103), если правый конец каната В Вг перемещается вертикально
вниз со скоростью vB = 8 см/сек, а левый ССг — параллельно
ему вверх со скоростью vc = 20 см/сек. -Радиус блока г = 16 см.
Найти также неподвижную и подвижную центроиды.
Решение. Скорости точек В и С блока направлены параллельно,
но в разные стороны.
Определим положение мгновенного центра вращения блока.
Для этого соединим прямой линией концы векторов скоростей
в точках В и С. Точка Р пересечения этой линии с горизонталь-
горизонтальным диаметром СВ блока является мгновенным центром скоро-
скоростей.
Скорости всех точек прямой СР направлены вверх, скорости
всех точек прямой РВ—вниз (рис. 103, б).
Расстояние ОР центра блока О до мгновенного центра скоростей Р
й угловую скорость блока можно определить из следующих двух
равенств
(ОР)о), A)
vG — (r + OP)o>, B)
vG
где vB — скорость точки В; vc — скорость точки С.
Разделив равенство^) на равенство B) и подставив числовые
значения, получим
vc г + ОР •
или
_8__ 16 — ОР
20 ~ 16 + OP y
откуда ОР =.7 см.
Плоско-параллельное движение твердого тела
Угловую скорость получим из равенства A)
vB = (г — ОР) • ш,
откуда
W а т — ОР = 16 —7 вТ
К задаче 103.
Мгновенный центр скоростей перемещается вертикально вверх
по прямой линии, поэтому неподвижной центроидой является вер*
тикальная прямая, отстоящая от оси О блока на расстояний.
ОР=7 см.
Подвижной центроидой будет окружность радиуса R = ОР ¦»
= 7 см (рис. 103, б).
104. Найти скорость ползуна В кривошипного механизма
(рис. 104) при горизонтальном и вертикальном положениях кри-
кривошипа, если \ последний вращается с угловой скоростьк>
(о=2,51/сек против хода часовой стрелки. Радиус кривошипа
г = 32 см, длина шатуна / = 160 см, размер h = 15 см.
Решение. Для решения этой задачи используем мгновенное
центры скоростей. При горизонтальном положении кривошипа
(рис. 104,6) скорость точки А направлена вертикально вверх и равна
п = шг = 2,5 • 32 « 80 см/сек. A>
320
Кинематика
Скорость ползуна В в этот момент направлена по горизонталь-
горизонтальной прямой вдоль направляющих ползуна. Найдем положение
мгновенного центра скоростей для этого положения шатуна.
Мгновенный цен^гр лежит на пересечении перпендикуляров,
восставленных в точках А и В к линиям векторов скоростей ЪА и
1)в. Как видно из рис. 104, б, положение точки пересечения этих
перпендикуляров Рг может быть определено из прямоугольного
треугольника A^PjB^
К задаче 104.
Расстояние Р1В1=: h = 15 см, а расстояние
рхАг = VI2 — /г2- 1/*1602— 1~52~= 159,3 сдв/сас.
Скорости точек шатуна прямо пропорциональны их расстоя-
расстояниям от мгновенного центра скоростей, поэтому
Скорость ползуна В2 в вертикальном положении кривошипа
<рис. 104, в) параллельна скорости точки Л2 кривошипа. Мгновен-
Мгновенный центр лежит в бесконечности, т. е. в данный момент скорости
всех его точек одинаковы по величине и направлению и равны
vB a= vA == 80 см/сек.
105. Кривошипный механизм связан шарнирно в середине
шатуна со стержнем CDt а последний — со стержнем DEy кото-
который может вращаться вокруг точки Е (рис. 105). Определить угло-
угловую скорость стержня DE в приведенном на рисунке положении
Плоско-параллельное движение твердого тела
кривошипного механизма, если точка В и Е расположены на од-
одной вертикали; угловая скорость кривошипа ОА, ыА = 8 */сек;
радиус кривошипа ОА = г = 25 см, длина стержня DE = / «*
— 100 см; /_CDE = а = 90°; /.#??> = Р = 30°.
Решение. Скорость точки Л кривошипа ОА равна
vA = toA . г = 8 • 25 = 200 см1сек
и направлена вертикально вверх,
так как кривошип вращается про-
против хода часовой стрелки.
Точка А принадлежит шатуну
АВ, поэтому скорость ее также
равна ua=200 см[сек. Скорость
точки В шатуна АВ равна нулю,
так как при горизонтальном поло-
положении его точка В находится, в
правом крайнем положении. Сле-
Следовательно, для данного момента
точка В является мгновенным цен-
центром скоростей шатуна АВ. Ско-
Скорость любой точки шатуна про-
пропорциональна ее расстоянию от
мгновенного центра скоростей —
точки В.
Зная скорость va, можно опре-
определить скорость средней его точки
С из соотношения
К задаче 105.
С R
= *>а 7& а 200
1
см1сек-
B)
Абсолютная скорость точки D направлена перпендикулярно
к стержню DE, и так как стержень DC перпендикулярен к DE
(а = 90°), она направлена по оси стержня DC.
Скорость точки D, принадлежащей стержню DC, найдем, вос-
воспользовавшись теоремой о проекциях скоростей двух точек тела
на линию, соединяющую эти точки.
Спроектируем скорости точек D и С на линию DC, и на основа*
нии этой теоремы получим
60°
или
vD = 100 • ~ =± 50 см/сек.
Зная скорость точки D стержня DE, определим его угловую
скорость
60
Too '
0,5
21
322
Кинематика
Рассмотрим примеры графического и аналитического определе-
определения центроид.
106. Найти геометрическим построением неподвижную и под-
подвижную центроиды шатуна АВ (рис. 106), длина которого равна
длине кривошипа ОА = АВ = л
К задаче 106.
Решение. Скорость точки А направлена перпендикулярно к
радиусу кривошипа ОА. Скорость точки В (рис. 106, а) шатуна
направлена по прямой ОВ, так как ползун В перемещается в гори-
горизонтальной прорези DOB. Мгновенный центр скоростей С лежит
на пересечении перпендикуляров к скоростям в точках А и В.
Обозначив угол поворота кривошипа /_АОВ через ср> видим, что
?АВО также равен ф вследствие равенства АВ *и ОА.
Из/\ЛСов (рис. 106,6), вершиной которого является мгновен-
мгновенный центр скоростей Со, видно, что стороны АС{) и А В равны между
собой (углы при основании равны 90° — <р) и» следовательно, точ-
точка Со находится на расстоянии 2г от центра О вращения криво-
кривошипа ОА.
Расстояния мгновенных центров Со, Съ С2 от неподвижной
точки О. равные 2/\ остаются неизменными, поэтому окруж-
окружность радиуса 2/* представляет геометрическое место неподвиж-
Плоско-параллельное движение твердого тела
323
ных мгновенных центров скоростей шатуна АВ, т. е. неподвиж-
неподвижную центроиду.
Мгновенный центр скоростей в любой момент времени отстоит
от подвижной точки шатуна А на расстоянии АС = г. Следователь-
Следовательно, окружность радиуса г с центром в пальце кривошипа Л, пред-
представляет собой подвижную центроиду.
Для построения ее выберем несколько положений кривошипа и
соответствующих положений шатуна АВ и определим мгновенные
центры скоростей (рис. 106, б). Соединим центры скоростей Сх и С2
с шатуном АВ при помощи треугольников AiC1B1 и А2С2В2 и затем
вернем шатун из положения АгВг и А2В2 в начальное положение
АВ с центрами Сг и С2.
Как видно из рис. 106,#, точки Со, Сг и С2 располагаются
по окружности радиуса гс центром в пальце кривошипа Л.
Вычертив неподвижную и подвижную центроиды (рис. 106, г),
убедимся, что плоское движение шатуна АВ можно, в данном
случае, осуществить путем перекатывания окружности ради-
радиуса /*, с которой связан шатун, по неподвижной окружности ради-
радиуса 2л
107. Стержень АВ движется таким образом, что одна из его
точек% А описывает окружность радиуса г (рис. 107) с центром
в точке О, а стержень скользит во втулке Nl9 которая вращается
вокруг точки В, лежащей на той же окружности. Найти уравне-
уравнения центроиды
!жная
центроида
0 центроида
К задаче 107.
Решение. Воспользовавшись аналитическими формулами, со-
составим уравнения центроид.
.Оси координат неподвижной и подвижной систем направим, как
указано на рисунке A07, а). Угол между осями х и хг обозначим
через <р, он изменяется в функции от времени, <р = со/. Тогда закон
21*
324 Кинематика
изменения координат точки А будет таков:
x0 = rcos2cp; A)
j/0 == г sin 2cp. B)
Проекции скорости точки.Л равны:
^; C)
Координаты мгновенного центра скоростей в неподвижной плос-
плоскости равны:
0 2r cos 2<p . -i
xc=*xQ jJ» =»rcos2<p — щ—-—„—tcosty E)
Ж
. F)
Уравнение неподвижной центроиды найдем, исключив время /
или угол 9 из уравнений E) и F).
Возведя обе части уравнений E) и F) в квадрат и сложив их,
получим
ЛС i^ У С — ' v /
Неподвижной центроидой является окружность радиуса г с
центром в точке О.
Координаты мгновенного центра скоростей относительно подвиж-
подвижной системы хг0х уг получим из формул:
^Охх ^п ?—t;QlV cos cp
Чс = » (о)
to< (8)
Подставляя в формулы (8) и (8') значения из уравнений C) и
D), получим
(— 2r sin 2cp sin <р—2r cos 2<p • cos<p) •
at
dt
— 2г B sina ф cos ср + cos2 ср cos ср — sin2 ср cos ср) == — 2r cos <p; (9)
(—. 2г sin 2<p cos ср + 2г cos 2 <р sin <?) ——
y
ylQ в в
— 2г B sin ср cos2 9 — cos2 9 sin 9 Ф sin2 9 sin 9) = — 2r sin 9. (9*)
Плоско-параллельное движение твердого тела
325
Уравнения подвижной центроиды находим, исключив из урав-
уравнений (9) и (9') угол ср. Возведя обе части этих равенств в квадрат
и сложив их, получим
*?с + Йсв4Л 0°)
Подвижной центроидой является окружность радиуса 2 г с
центром в точке А (рис. 107, б).
108. В грохоте, служащем для сортировки руды, кривошип ОгА
вращается равномерно вокруг осиО1э делая 60 об/мин (рис. 108, а).
К задаче 108.
Посредством вилки АВ он передает движение кривошипу O2Bt
вращающемуся вокруг оси О2. Дано: ОХА = О2В = АВ = 10 см;
QtQz = 4 см.
Определить линейную скорость точки В для трех положений
механизма, когда: 1) точка А занимает положение на продолжен-
продолженной линии центров ОХО2 слева; 2) вилка АВ параллельна линии
центров; 3) точка В находится на продолжении линии центров
справа.
Решение. Задачу можно решить, определив мгновенные центры
скоростей вилки АВ для всех трех положений механизма. В пер-
первом положении (рис. 108, б) мгновенный центр скоростей вилки
(Рх) лежит на пересечении перпендикуляров к векторам скоростей
в точке Л и В, а именно, в точке О2.
Поэтому можно написать отношение
02В
ОгА *
0%В
откуда получим
Так как скорость точки А
%т 3,14.10.60
? 35
A)
B)
* 62,8 м/сеъ
326 Кинематика
то
v1B = 62,8 . — = 44,9 м/сек. C)
Для второго положения механизма (рис. 108, в) мгновенный
центр скоростей вилки АВ (Р2) расположен на одинаковом расстоя-
расстоянии от точек А и Вк поэтому скорость точки В равна скорости точкиД.
v2B = иА = 62,8 м/сек. D)
Для третьего положения механизма мгновенный центр скоро-
скоростей вилки АВ (Р2) совпадает с точкой О1(рис. 108, г).
Скорость точкл В определим из соотношения
откуда
»8В = *А * "§J = 62'8 ' "ГО" = 80
109. Качающаяся вокруг# центра А подвижная щека АВ дро-
дробилки длиной 60 см приводится в движение кривошипом ОЕ 'дли-
'длиной 10 см, делающим п = 100 об/мин., посредством системы
рычагов ВС, CD и СЕ каждый длиной 40 см (рис. 109). Найти угло-
угловую скорость щеки АВ при положении механизма, указанном
на чертеже.
Решение. Для определения угловой скорости звена механизма
щеки АВ определим скорость точек С и В (звена ВС). Зная
скорость точки В (v?), определим угловую скорость звена АВ
по формуле
где 1Ав — длина звена АВ.
Скорость точки С определим, воспользовавшись мгновенным
центром скоростей Рг звена СЕ, который лежит на пересече-
пересечении перпендикуляров к скоростям'в точках С и Е.
Вычислим расстояния РгС и РгЕ точек С и ? от мгновенного
центра скоростей Ръ рассмотрев Д РгОС.
Как видно из треугольника, расстояние ОС равно
ОС = 80 + 40 sin 30° = 100 см.
Расстояние Р?
PC- ос - JC0 -900 см
^lC "- sin 30° — ~О5~ ~ ZUU CM-
Расстояние РгО
РгО = РХС cos 30° = 200 . Щ- = 173 см.
Плоско-параллельное движение твердого тела
327
Расстояние РгЕ получим из равенства
РХЕ = РХО — ЕО = 173 — 10 = 163 см.
Скорость точки Е (vE) получим по формуле
пгп 3,14.10-100 ,пл с ,
"*я Гв яо " = 104'6 см/сек.
Р,
К задаче 109.
Скорость точки С (vc) получим из равенства
vc = vB • Щ = 104,6 • -?§- = 128,6 см/сек.
Найдем мгновенный центр скоростей Р2 звена ВС.
Как видно из рисунка, расстояния Р%С и Р2В могут быть вычис-
вычислены из Д/У2С> а именно:
Р2В = Р2С . cos 30° = 80 • J^jL = 69,2 см.
Скорость точки В (vB) получим из равенства
получим по формуле
Угловую скорость звена А В
1АВ
111,1
60
= 1,852 х/сек.
328 Кинематика
§ 12. Определение ускорений точек тела при помощи
мгновенного центра ускорений
Мгновенным центром ускорений плоской фигуры называется та
точка этой фигуры; ускорение которой в данный момент равно
нулю.
При помощи мгновенного центра ускорений К можно определить
вектор пЪлного ускорения любой точки плоской фигуры в данный
момент времени, если угловая скорость w и угловое ускорение t
фигуры в рассматриваемый момент времени известны.
Так, величина вектора ускорения какой-либо точки А фигуры,
отстоящей на расстоянии Л УС от мгновенного центра ускорений К
(рис. VII), равна
Л (П
а угол \it составляемый вектором wA с линией А К, равен
Следовательно, ускорения любых точек фигуры пропорциональны
расстояниям точек от центра ускорений и составляют одинаковый
угол ц с линией, соединяющей точку с центром ускорений.
§ 13. Методические указания к решению задач
• Определить положение мгновенного центра ускорений можно
различными способами, в зависимости от условий задачи. Эти
условия могут быть следующими.
1. Заданы уравнения движения плоской фигуры: х = f\(t)\
у m*f2(t)\ <p =fz(t)9 тогда проекции вектора ускорения любой ее
точки на оси неподвижной системы координат хОу определяются
из равенств:
*• = w<hx — *(У — У о) —<»2(х — xOi), A)
w« e wolV + « (* — хо) -<»2(у — у0). B)
Ускорение мгновенного центра ускорений равно нулю, следова-
следовательно.
p 0 J
На основании этого можно определить1 из уравнений A) и B)
координаты мгновенного центра ускорений х9 у, которые обозначим
яерез хх и ух:
Плоско-параллельное движение твердого тела
329
2. Заданы: вектор ускорения какой-либо точки фигуры, вели»
чины и направления угловой скорости со и углового ускорения е.
В этом случае, мгновенный центр ускорений лежит на прямой,
проведенной под углом р, к вектору ускорения шд. Угол {* опре-
определяется по формуле
«.—9
9
и откладывается от линии вектора
ускорения е.
Расстояние АК мгновенного
центра ускорений от точки А равно
Л»1
АК- -г-
по направлению углового
Рис. VII.
3. Заданы векторы ускорений
двух точек фигуры wa и wB и
расстояние между ними. В этом
случае, необходимо определить не
только положение мгновенного
центра ускорений, но и величины
и направления угловой скорости
со и углового ускорения г фигуры.
Положение мгновенного центра ускорений можно определить
графическим путем, выбрав соответствующие масштабы для уско-
ускорений и длин. Однако во многих случаях такие задачи решаются
графоаналитическим способом, т. е. графические построения прово-
проводят не в масштабе, а требуемые величины определяют аналитически.
Заданные векторы ускорений связаны между собой равенством
wB = wA + wBA. A)
Если точку А (рис. VII) принять за полюс, тогда вектор
относительного ускорения точки В относительно А будет равен
™ва = ™в+(-™а)' B)
Угол вектора wba и линии АВ зависит лишь от величин
угловой скорости и ускорения фигуры
щ как показывает формула, равен углу, который составляет вектор
ускорения любой точки фигуры с линией, соединяющей ее с мгно-
мгновенным центром ускорений. __
Построив вектор относительной скорости шва, можно определить
этот угол jx. Затем, отложив,от векторов Wa и wb углы ji водном на-
цравлении (против хода часовой стрелки), получим на пересечении ли-
линий, проведенных под этими углами, мгновенный центр ускорений К,
330
Кинематика
§ 14. Задачи
ПО. Линейка эллипсографа АВ длиной 2/= 40 см приво-
приводится в движение кривошипом ОС> вращающимся с постоянной
угловой скоростью со =2,5 11сек\ АС =ВС = / (рис. НО). Найти
мгновенный центр ускорений и ускорения точек А и В линейки
в момент, когда ?АВО = 30°.
Решение. Положение мгновенного центра ускорений определим
аналитически. Выберем неподвижную хОу и подвижную xfi^
системы координат.
Координаты мгновенного цен-
центра ускорений согласно форму-
формулам равны:
К задаче 110.
?2 -j- 0L
B)
Координаты xov Уог начала подвижной системы координат
{точка С) равны:
xOi-/coscp; C)
D)
E)
Ускорение точки С по величине равно
wc = ьуЧ = 2,52. 20 = 125 см/сек
»и направлено по радиусу к центру О.
Проекции этого ускорения на оси Ох и Оу равны:
¦—Wc COScp;
• wc sin ср.
Угловое ускорение з по условию равно нулю
8 = 0.
wolX
wolV =
F)
G)
(8)
После подстановки полученных выражений в уравнения коор-
координат A) и B) получим:
Хь = / COS ср
^ = / sin ср
?— COS ср
QJ/to2-
0,
по-
последовательно, мгновенный центр ускорений находится в точке О.
Плоско-параллельное движение твердого тела
331
Ускорения точек А и В определяем по формуле:
wA =
Следовательно,
wA = 2/ sin 30° ]/0 +оL == /оJ = 20 . 2,52 = 125
, = 2/ cos 30°
+
2/
со2 = 125 ]/3
и направлены к центру О. /
111. Найти мгновенный центр, угловую
скорость и угловое ускорение плоской фи-
фигуры (рис. 111), если для данного момента
времени ускорение точки A (wa) = 15 см/сек2 SO
и ускорение точки В (wB) = 10 см/сек2, при- ~*#
чем векторы ускорений wA и wb перпенди- вА
кулярны к отрезку АВ и направлены в одну
сторону; АВ = / = 10 см.
Решение, Вектор относительного ускоре-
ускорения wba равен
К задаче 111.
или
wb
"ва = 10 — 15 ^ — 5 см/сек, I{V)
т. е. направлен влево и составляет с линией АВ угол [а = 90°-
Следовательно,
tg р, = Ц. = оо • B)
Из этого следует, что угловая скорость плоской фигуры <d=0.
Ускорения wa и wb являются касательными ускорениями и
мгновенный центр К лежит на пересечении линии, проходящей
через концы этих векторов, с продолжением линии АВ.
Из подобия треугольников определяем положение точки К
АК ~~ ~57 ' W
ИЛИ
откуда:
ВК
ав+вк "" иг;
wA
1 —
15
= В/С + / = 30 см.
332
Кинематика
Угловое ускорение е получим из формулы
wA
АК • е,
откуда
112. Квадрат ABCD со стороной а =2 см совершает плоское
движение. В данный момент ускорения его вершин А и В (рис. 112)
соответственно равны: wa = 2 см/сек2; wB = 4]/^2 см/сек*. Найти
мгновенную угловую скорость и мгновенное угловое ускорение
квадрата.
К задаче 112.
Решение. Из условия известны векторы ускорений двух точек
квадрата wa, wb и расстояние между точками А и В (рис. 112, а).
Решим" задачу, применив графо-аналитический способ. Связь
между векторами ускорений выражается равенством
из которого определим относительное ускорение точки В по отноше*
кию к точке Л, принимаемой нами за полюс:
Для определения величины относительного ускорения wba по-
построим параллелограм (рис. 112,6)
Д/ xsfiA ~|~ до n -f- 2до w cos 135° =*
C)
W
BA
2»+Dj/2J—2-2- D ^2)cos45e =2^5 ^
Из /\FBE определим угол (i, составляемый вектором
линией АВ, применив теорему синусов
wB sin (90 н- [л)
sin 45°
D)
Плоско-параллельное движение твердого тела 333
откуда
____^^_. D)
Затем определим расстояния точек В и Л (рис. 112, в) от мгно-
мгновенного центра ускорений /С, который лежит на пересечении ли-
линий А К и ВК, проведенных под углом у. к векторам ускорений.
Из Д Л KB имеем
б/( sin (90 + р.)
ТВГ ет sin 45° - • E>
откуда
Расстояние Л/С определим из условия, что ускорения точек
Л и В пропорциональны расстояниям от мгновенного центра уско-
ускорений К> т. е.
откуда
Определим угловую екорость и угловое ускорение квадрата из
уравнений:
-M-, G)
Ke*+u>*. (8)
Из Д A KB определим тангенс угла [а, использовав теорему
синусов
АК_ _ sinD5-ri /о,
ВК ~ sin (90 + р.) • w
или
2 ^ sin 45° cos ц. — cos 45° sin ^ Q/
4|/" ^ cos {л ' ^'
откуда
1
Зная tg |i9 из уравнения G) получим
ш» « 2«. A0)
334
Кинематика
Подставляя в уравнение (8) значения хюв и fi/Си приняв во вни-
внимание уравнение A0), получим
откуда
Из уравнения A0)
е = 1 1/см.
= 2 х/сек.
(И)
A2)
A3)
1J3. Колесо радиуса R = 0,5 м (рис. 113) катится без сколь-
скольжения по прямолинейному рельсу, имея в данный момент в центре О
скорость v0 = 0,5 м/сек и замедление w0 = 0,5 м]сек2. Найти
К задаче 113.
мгновенный центр ускорения колеса, ускорение wp точки колеса,
совпадающей с мгновенным центром Р скоростей, а также ускоре-
ускорение точки М и радиус кривизны ее траектории, если ОМ = МР =
= 0,5 R.
Решение. Решим эту задачу при помощи мгновенного центра
ускорений. За полюс выберем точку О, ускорение и скорость кото-
которой заданы. Так как мгновенный центр скоростей совпадает с точ-
точкой касания Р колеса g рельсом (рис. 113, а), то углоиую скорость
колеса получим из равенства
__ v0 _ 0,5 ___
со —— —jit" — ^ _, ——
A)
Вектор углового ускорения колеса направлен против направ-
направления вектора угловой скорости, т. к. колесо движется замед-
замедленно.
Величину углового замедления е определим, приняв во вни-
внимание, что при мгновенном вращении колеса вокруг центра Р ус-
ускорение точки О -является касательным.
Плоско-параллельное движение Ъгвер&ого тела 335>
Поэтому
w0 = R • е,
откуда
Определим положение мгновенного центра ускорений, зная
величину и направление ускорения точки О:
Угол наклона |х линии ОК к вектору ш0 равен
tgf = ^r = l. D)
следовательно4,
(д = 45° = ~ радиан
и откладывается от вектора ау0 в сторону углового ускорения е.
Расстояние ОК в данном случае равно по величине проекции
радиуса R на линию ОК, проведенную под углом 45°, а именно,
OK = R cos45° = 2F = i~- ж.
Прямоугольный треугольник ОКР равнобедренный (рис. 113,6),
с углом 45° при основании, поэтому расстояние КР равно КО, т. е.
Соединив точку К с точкой М (срединой радиуса /?), замечаем,
что линия КМ перпендикулярна к радиусу ОР и равна
КМ =^ = ^ = 0,25 м.
Ускорения точек колеса пропорциональны расстояниям точек от
мгновенного центра ускорений и направлены под углом 45° к
соответствующим линиям от центра К до рассматриваемой точки.
Ускорение точки Р
КР
Wp = w0 . iiL. = ot5 • 1 = 0,5 м/сек* E)
и направлено вертикально к центру О.
Ускорение точки М
КМ п - 0,25-4 УТ ласос / а /с\
wM =wo-jtq = 0,5 = —-- = 0,3536 м/сек2. F)
Направления ускорений ш0 и ^ показаны на рис. 113, б.
336 Кинематика
Зная полное ускорение точки М> можно определить радиус
кривизны траектории в этой точке. Для этого выразим ш^ через
его составляющие: касательное и нормальное ускорения
или
¦5,
где wXM — -j • е = ¦—? . 1 = —м/сек*.
Скорость точки М
vM « о> у= 1 • 0,25 = 0,25 л/cefc. (8)
Подставив в уравнение G') числовые значения, определим р
(УТ\* /0,5 • 1\а /0,2У^
откуда
р =. 0,25 ж.
ГЛАВА XVII
КИНЕМАТИКА РЯДОВЫХ, ПЛАНЕТАРНЫХ И ДИФФЕРЕНЦИАЛЬНЫХ
ЗУБЧАТЫХ ПЕРЕДАЧ
§ 1. Краткие сведения о кинематике зубчатых передач
. Соединение зубчатых колес, у которых все валы вращаются в
неподвижных подшипниках, называется рядовым соединением или
рядовой зубчатой передачей. Одно из зубчатых колес такой передачи
является ведущим, а остальные ведомыми.
Всякая рядовая передача характеризуется передаточным числом
i, под которым понимают отношение угловой скорости ведущего
колеса к угловой скорости ведомого:
<in==-^ (XVII, 1)
Передаточное число может быть выражено и через отношение
радиусов ведомого и ведущего колес или через отношение их чи-
чисел зубьев:
«i«-*-?[• V"*7~' (XVII, 2)
или
(XVII, 3)
Иногда пользуются передаточным отношением, представляю-
представляющим отношение угловой скорости ведомого колеса к угловой ско-
Кинематика рядовых, планетарных и дифференциальных зубчатых передач 337
рости ведущего
В этом случае соответственно изменяются отношения радиу-
радиусов и чисел зубьев.
Планетарная зубчатая передача образуется, если одно
зубчатое колесо неподвижно, а остальные, находящиеся в последова-
последовательном зацеплении,приводят-
зацеплении,приводятся во вращательное движение
кривошипом, ось вращения
которого совпадает с осью
неподвижной шестерни (рис.1).
Если в планетарной пере-
передаче сообщить вращательное
движение и неподвижной ше-
шестерне (кроме заданного вра-
вращательного движения кри-
кривошипа), то такая зубчатая пе-
передача образует д и ф ф е р е н-
циальную передачу. Рис1
Таким образом, планетар-
планетарная • зубчатая передача может быть рассмотрена, как частный
случай дифференциальной зубчатой передачи, а именно, когда
ведущее зубчатое колесо неподвижно, т. е. а)г = 0.
Рядовая зубчатая передача также является частным случаем
дифференциальной передачи, а именно, когда кривошип диффе-
дифференциальной передачи неподвижен, т. е. шкр = 0.
§ 2. Методические указания к решению задач
Определение кинематических характеристик для звеньев пла-
планетарных или дифференциальных передач производится следую-
следующими способами.
1. Способ сложения векторов угловых
скоростей вращательных движений: переносного, относи-
относительного, и абсолютного. При данном способе применяется гео-
геометрическое равенство
~~ "" 1 — fYVTT 1\
О) — to -f- CO J-**-Vii, ij
где ь)а — вектор абсолютной угловой скорости; со0 — вектор пе-
переносной угловой скорости; ш,— вектор относительной угловой
скорости.
Если оси вращения валов параллельны, то геометрическое
равенство (XVII ,1) заменяют алгебраическим равенством
со. = со, + со,. (XVII, 2)
22 591
338
Кинематика
Положения вектора абсолютной угловой скорости определя-
определяются по правилам' сложения параллельных векторов. Вектор аб-
абсолютной угловой скорости совпадает с мгновенной осью вращения.
2.Способ использования мгновенного
центра скоростей.В том случае, если положение мгновен-
мгновенного центра скоростей известно или может быть определено из
условий задачи, величину и направление абсолютной угловой ско-
скорости звена можно получить по формуле о>а = —. Величина от-
относительной угловой скорости определяется из равенства (XVII, 2).
3. Способ «остановки» является наиболее удобным
для определения абсолютных и относительных угловых скоростей
элементов дифференциальных и планетарных передач. Послед-
Последний заключается в преобразовании рассматриваемой планетарной
или дифференциальной зубчатой передачи в рядовую зубчатую
передачу и в использовании соответствующих кинематических соот-
соотношений.
Для этого мысленно останавливают кривошип планетарной или
дифференциальной передачи, сообщив всем звеньям передачи угло-
угловую скорость равную угловой скорости кривошипа, но обратно
направленную. Тогда угловая скорость кривошипа будет равна
нулю» а угловые скорости зубчатых колес будут равны разностям
своих начальных угловых скоростей и угловой скорости криво-
кривошипа.
При решении задач данного типа удобно составлять следую-
следующую таблицу угловых скоростей.
Угловая скорость
До остановки
После остановки ...
Криво-
Кривошип
—
—
Зубчатое колесо
1
—
—
2
3
—
—
•
—
—
После мысленной остановки кривошипа отношение угловой ско-
скорости ведущего колеса к угловой скорости п-го зубчатого ведомого
колеса равно соответствующему передаточному числу i\n, получае-
получаемому как и для рядового зубчатого зацепления, а именно
~т~ (Оч —— I -4- со ^ «t?
т. z~=iin\—1) , (XVII, 3)
где шя — искомая по величине и направлению угловая скорость
п-го зубчатого колеса; ±а)г — угловая скорость ведущего зубча-
* Знаки плюс и минус перед в)кр и <at предложено ввести в формулу автором.
Кинематика рядовых, планетарных и дифференциальных зубчатых передач 339
того колеса; +о>1ф — угловая скорость кривошипа; iin —- переда-
передаточное число зубчатой передачи; т — число внешних зацеплений
зубчатых колес. Положительный знак принимается перед угло-
угловыми скоростями при вращении соответствующего звена против
часовой стрелки.
Передаточное число принимается, как и для рядовой передачи,
или
lin == Т ' Т *
г г
'п-\
(-1Г,
сп—\
¦(
(XVII.4)
(XVI 1,5)
где zn — число зубьев соответствующего колеса; гп—радиус ко-
колеса; m — число внешних зацеплений.
Формула (XVII, 3) пригодна для всех видов зубчатых передач,
например:
при ь)г =? 0 и о)кр =^=0 — передача дифференциальная;
о>
)г =я 0 и
Oj =f= 0 и о)кр = 0 —
кр
планетарная;
рядовая.
§ 3. Задачи
114. Кривошип /// соединяет оси Ог и О2 двух зубчатых колее
/ и //,' как указано на рис. 114. Колесо / остается неподвижным, а
кривошип /// вращается с угловой
скоростью <о3 вокруг оси Ог. Зная
радиусы колес гг и г2, вычислить
абсолютную угловую скорбеть оJ
колеса // (по отношению к колесу /)
и относительную угловую скорость
оJ3 колеса // по отношению к кри-
кривошипу.
Решение» Колесо // вращается
вокруг центра Ох с угловой скоро-
скоростью а>з против хода часовой стрелки
и вокруг центра О2 с угловой ско-
скоростью ш23 также против часовой
стрелки. Результирующее абсолютное к задаче 114.
движение колеса // будет враща-
вращательным вокруг мгновенной оси вращения, проходящей через точку
С касания колес. Угловая скорость его равна сумме угловых ско-
скоростей переносного и относительного вращательных движений.
22*
340 Кинематика
В данном случае положение мгновенной оси вращения известно,
оно проходит через точку касания С зубчатых колес, поэтому отно-
относительную угловую скорость определим из отношения
2>3 _ Lk. i\\
откуда
0J,3 -0K^. B)
Абсолютная угловая скорость колеса // при вращении вокруг
мгновенной оси равна сумме угловых скоростей о>3 и о>2,3, так как
вращение происходит в одном направлении.
Следовательно,
ОJ = (D3 -J- <О2,3 = W3 {-L—-J¦ ) . C)
Эту задачу можно решить и другим способом.
Определим линейную скорость точки О2 колеса //
^02 = ('l + ?*) W3 D)
и, зная мгновенный центр вращения этого колеса относительно непод-
неподвижного колеса /, можно получить абсолютную угловую скорость
^-~f- E)
Подставив величину v02 из равенства D) в равенство E), получим
Относительную угловую скорость получим как разность
со2K = oj2 — со3 — ш3 —. G)
Применим к решению этой задачи способ остановки.
Мысленно остановим кривошип, для чего всему механизму, т. е.
всем его звеньям: кривошипу ///, колесам I и II сообщим угловую
скорость, равную угловой скорости кривошипа, но обратно направ-
направленную. В результате этого угловая скорость кривошипа будет
равна нулю, а колеса будут вращаться вокруг своих осей, располо-
расположенных на кривошипе.
Таким образом, планетарное зубчатое зацепление преобразуется
в рядовое зубчатое, для которого можно найти отношения угловых
скоростей зубчатых колес по известным формулам, выразив их
через радиусы, числа зубцов или числа оборотов
где индексы от 1 до п указывают номера зубчатых колес передачи.
Кинематика рядовых, планетарных и дифференциальных зубчатых передач 341
Угловая скорость кривошипа после мысленной остановки его
равна нулю; угловая скорость колеса / равна а>3; колеса // —
(о2 — (о3, где о>2 — абсолютная угловая скорость колеса // до оста-
остановки кривошипа.
Составим таблицу угловых скоростей передачи до и после оста-
остановки кривошипа.
Угловые скорости
До остановки
После остановки
Кривошип
III
Колесо /
Колесо //
Взяв отношение угловой скорости колеса // к угловой ско-
скорости колеса / после, мысленной остановки кривошипа, получим
Знак минус перед отношением — взят потому, что зацепление
внешнее, а угловые скорости зубчатых колес направлены в противо-
противоположные стороны.
Из равенства (9) определим
(Ю)
Относительную угловую скорость оJ,3 колеса // по отношению
к кривошипу получим, как разность
@2 з = 0J — 0K, A1)
A2)
откуда
Г2
115. Зацепление, приводящее в быстрое вращение точильный
камень, устроено следующим образом: стержень IV посредством
особой ручки приводится во вращение вокруг оси Ох (рис. 115) с
угловой скоростью (о4; на конце стержня О2 находится палец, на
который свободно надето колесо // радиуса г2. При вращении ручки
палец заставляет колесо // катиться без скольжения по наруж-
наружному неподвижному кругу /// радиусом г3. При этом, благодаря
трению, колесо // вращает без скольжения колесо / радиусом rlf
свободно насаженное на ось Ох и неизменно связаннее с осью
точила. Зная радиус наружной неподвижной обоймы, найти такое
342
Кинематика
значение rl9 чтобы отношение угловых скоростей было — = 12,
т. е. чтобы точило вращалось в 12 раз быстрее ручки, приводя-
приводящей его в движение.
Решение. Решим задачу, использовав мгновенные центры ско-
скоростей.
Зубчатое колесо // катится без скольжения по неподвижному
колесу ///. Мгновенным центром скоростей колеса // будет в каж-
каждый момент времени точка Р касания его с колесом ///.
Скорость центра 02 колеса //
определим по формуле
а затем определим скорость точки
касания С колеса / и колеса //.
Эта скорость пропорциональна рас-
расстоянию точки С от мгновенного
центра скоростей Р и, следова-
следовательно,- будет в два раза больше
скорости tfo,
т. е.
К задаче 115 vc = 2СО2* B)
или, подставив значения v^ из формулы A), получим
vc = 2щ (гг + r2). B'f
С другой стороны, скорость vc точки С является окружной ско-
скоростью колеса / и поэтому равна
vc - ш/,. C)
Приравняв уравнения B') и C) получим
2<*Ari + r2) =^rv D)
откуда
———• D)
Так как отношение 2* = 12, то из уравнения Dх) после преоб-
преобразований получим
E)
1
И
116. Редук-fop скоростей (рис. 116) состоит из неподвижной
шестерни / радиусом гг = 40 см, двух шестерен 2 и 3 радиусом
г2 = 20 см и г3 = 30 см, спаренных между собой, а также шестерни 4
Кинематика рядовых, планетарных и дифференциальных зубчатых передач 343
с внутренним зацеплением радиусом /*4 = 90 см> сидящей на ведо-
ведомом валу //. Ведущий вал / и кривошип, несущий оси шестерен,
делает пг = 1 800 об/мин. Найти число оборотов в минуту ведо-
ведомого вала //.
Решение. Решим задачу, использовав мгновенные центры ско-
скоростей. Так как шестерня 1 неподвижна, то зубчатая передача
редуктора является планетарной зубчатой
передачей.
Кривошип сообщает оси О2 шестерен
окружную скорость
ТСПт
+ r,) = зо" (ri
A)
или
о,
р
Ш
1
D0+20)=3600 см/сек. (Г)
Шестерня 2 катится по неподвижной
шестерне / без скольжения. Точка касания
этих шестерен Р является мгновенным
центром скоростей для шестерни 2. (Ось, к задаче 116.
проходящая через точку касания парал-
параллельно оси вращения О±О2 представляет мгновенную ось вра-
вращения).
Зная скорость Vq2 точки <92, можно определить абсолютную
угловую скорость вращения ш2 шестерни 2 вокруг мгновенного ценг-
ра Р, а именно,
си 3600
со. = -2l = -gp = 180 х/сек. B)
Шестерня 3 насажена неподвижно на ту же ось ОХО2, что и
шестерня 2, поэтому мгновенной осью вращения для нее является
та же ось, что и для шестерни 2, т. е. ось, проходящая через точку Р
Зная положение мгновенной оси вращения РР и абсолютную
угловую скорость вращения а>2, можно определить линейную ско-
скорость точки касания С шестерен 3 и 4
или
vc = 1 800 B0 + 30) = 9 000 cMJ-сек.
C0
Скорость vc является одновременно и окружной скоростью шестерни
4, поэтому ее угловую скорость можно определить по формуле
vc = «л • г4, D)
344
Кинематика
откуда
vr 9000 тс лл „,
-5 = —9о~ = ЮО те 1/сек.
D0
Число оборотов шестерни 4
Пц ==
ео7/ • 30 100 тс • 30
= 3000 об/мин.
Эту задачу можно решить, применив способ остановки.
Составим таблицу угловых скоростей кривошипа и шестерен до
и после остановки (мысленной) кривошипа.
Угловая скорость
До остановки
После остановки ....
Кривошип
0
0
— @/
Шестерня
ОJ
ОJ— (Dj
О)// СО/
Отношения угловых скоростей шестерен после мысленной оста-
остановки кривошипа записываются как для рядового зубчатого зацеп-
зацепления. Так как зацепление внешнее, отношение берется со знаком
минус:
Перемножив уравнения E) и F), получим
откуда
а)// =
F)
G)
G0
Подставив в уравнение G') числовые значения величин, по-
получим
w// = у со/. G")
Так как угловые скорости пропорциональны числам оборотов щ
и п1Ъ то
/17/ = -л/ = -| • 1800 = 3000 о5/мин- (8>
Кинематика рядовых, планетарных и дифференциальных зубчатых передач 345
Решим эту задачу без составления таблицы, а именно, по формуле
/j-o)—Г" — in *— ' *
где (ох — угловая скорость шестерни 1 (ведущей) дифференциаль-
дифференциальной передачи; <оЛ — угловая скорость рассматриваемой шестерни;
о)кр — угловая скорость кривошипа; iln — передаточное число, рав-
равное отношению угловой скорости ведущего колеса к угловой ско-
скорости ведомого; т — число внешних зацеплений передачи.
В рассматриваемой задаче:
1800 %
Так как
получим:
40 30
= 10(k 7/сек.
пи =
e>//-30- 100*. 30
-3000 об/мин.
117. Найти угловую скорость шц ведо-
ведомого вала // редуктора с дифференциаль-
дифференциальной передачей, если ведущий вал / с кри-
кривошипом (рис. 117), несущим на себе
передаточные шестерни 2 и 5, спаренные
между собой, вращается с угловой ско-
скоростью о>2 = 12(Uf ^сек. Шестерня / вра-
вращается с угловой скоростью W/ =180 х/сек
и имеет число зубцов г2 =80. Передаточ-'
ные шестерни 2 и 3 имеют числа зубцов
г2 = 20, г3 = 40; шестерня, сидящая на
ведомом валу, имеет z4 =60. Шестерня
/ и ведущий вал / вращаются в одном
направлении.
Решение Для решения этой задачи применим способ остановки.
Мысленно дадим всем звеньям редуктора — кривошипу и шестерням
К задаче 117.
546
Кинематика
1, 2, 5, 4 угловую скорость o>i, равную угловой скорости рф
шипа, но направленную в противоположную сторону. Обратив,
таким образом, дифференциальную зубчатую передачу в рядовое
зубчатое зацепление, используем для решения задачи соотношения
угловых скоростей.
Предварительно составим таблицу угловых скоростей криво-
кривошипа и шестерен до и после остановки.
Угловая скорость
До остановки
После остановки • • . .
Кривошип
to/
0
Шестерня
1
0I
0)!—-0O
2,3
Wo
0J — ^
4
о)/г
шп — о);
Угловая скорость кривошипа o)z и шестерни / а^ по направ-
направлению одинаковы, поэтому они взяты с одинаковыми знаками.
Составим отношения угловых скоростей после мысленной оста-
остановки кривошипа, выразив их через заданные числа зубцов.
C02 (
B)
Знак минус перед отношением чисел зубцов взят потому, что
зацепление шестерен внешнее.
Перемножив уравнения A) и B), получим
0)Гг Юг у у
II I Zl ' Z3 /Q\
—— ————— ш I О)
Ш1 — ш/ Ч ' **
Из этого равенства определяем неизвестную угловую скорость о)П:
сои = (!>/ + К + wj) - ^,
22г4
= 120 -f A80 — 120)
= 280 г/сек.
Положительный знак угловой скорости ведомого вала показы-
показывает, что направление вращения ведомого вала // совпадает с
направлением вращения ведущего /.
Значительно проще можно решить эту задачу, применив формулу
D)
Движение твердого тела вокруг неподвижной точки 347
Угловые скорости кривошипа (dz = о)кр и шестерни /—а^ имеют
положительный знак; коэффициент т = 2,
поэтому
г2 г4
(- 1Г
Подставив числовые значения, получим
180 — 120 __ 20 60 (_ П2
(Df/ —120 ~ 80 * 40 ^ ' '
откуда
сол = 120 + 60 • IJLlijj = 280х/сек.
ГЛАВА XVIII
ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ
НЕПОДВИЖНОЙ ТОЧКИ
§ 1. Общие сведения
Закон движения твердого тела вокруг неподвижной точки может
быть получен на основе теоремы Эйлера: любое перемещение твер-
твердого тела вокруг неподвижной точки можно получить тремя по-
последовательными поворотами тела вокруг трех осей, которые
проходят через неподвижную тбчку.
Таким образом, закон движения тела считается заданным, если
заданы углы поворота тела вокруг трех осей, проходящих через
неподвижную точку, — углы Эйлера, заданные в функции от
времени:
ф =/,(*); 6 = /2(О; ? = /з@, (XVIIU)
где ф — угол переносного вращения (угол прецессий); <р — угол
относительного вращения (угол собственного вращения); 6 — угол
отклонения (угол нутации).
При помощи углов Эйлера (рис. I) можно для любого момента
времени определить угловую скорость и угловое ускорение тела,
а также скорость и ускорение любой его точки.
Проекции вектора угловой скорости на оси неподвижной си-
системы координат Ох; Оу\ Ог в зависимости от углов Эйлера
выражаются формулами:
шж = 0 cos ф + <р sin 9> (XVIII, 2)
ыу = в sin (р — ф cos ф sin в, (XVTII, 3)
ыг =ф +?cos0, (XVIII, 4)
где
^^dt ; Ж" и ? ~Ж%
348
Кинематика
Величина вектора полной угловой скорости равна
+ ф2 + 2ФФСО8б. (XVIII, 5)
Направление вектора угловой скорости получим, вычислив
величины косинусов направляющих углов.
Проекции вектора углового ускорения получим, взяв произ-
производные по времени от соответствующих проекций угловой скорости,
а именно:
.*». . _*V 8, = ^. (XVIII, 6)
Величина вектора ускорения
• = У%+%+Ц. (XVIII, 7)
Проекции скорости любой
точки тела с координатами хуг
определяются по формулам
vy = uzx — t»xz \ (XVII 1,8)
j
Величина полной скорости
* = /*» + «» + «* (XVIII, 9)
Направление вектора скорости точки тела определяется после
вычисления косинусов направляющих углов.
Аналогично определяются проекции ускорения любой точки
тела и величина ускорения по формулам
wx = tvx — ezy
(XVIII, 10)
w = Vwl + wl + w\. (XVIII, 11)
Направление вектора ускорений также определяется через ко-
косинусы направляющих углов.
Движение тела вокруг неподвижной точки можно изучить, при-
применив другую теорему Эйлера: любое перемещение твердого тела
вокруг неподвижной точки можно осуществить одним поворотом
вокруг выбранной оси вращения.
На основании этой теоремы движение тела, имеющего непод-
неподвижную точку, можно рассматривать как непрерывный ряд вра-
вращений вокруг оси, проходящей через неподвижную точку и меняю-
Движение твердого тела вокруг неподвижной точки 349
щей свое положение в каждый данный момент, т. е. вокруг мгно-
мгновенной оси вращения.
Геометрическое место положений мгновенных осей вращения,
отнесенных к неподвижной системе координат, называется непод-
неподвижным аксоидом.
Геометрическое место положений мгновенных осей, отнесенных
к подвижной системе координат, неизменно связанной с движу-
движущимся телом, называется подвижным аксоидом.
Если известны неподвижный и подвижный аксиоды, то движе-
движение тела вокруг неподвижной точки можно осуществить путем
перекатывания подвижного аксоида по неподвижному без сколь-
скольжения.
Если в некоторый момент времени известно положение мгновен-
мгновенной оси вращения тела, а также векторы угловой скорости й и угло-
углового ускорения е, то скорость и ускорение точки, определяемой
радиус-вектором 7, определяется по формулам
^=,^х7, (XVIII, 12)
откуда величина скорости v равна
v - со г sin К 7) = шг0, (XVIII, 12')
где г0 — расстояние точки до мгновенной оси вращения; и
w = woc+~wBV, (XVIII, 13)
где w — вектор полного ускорения точки; woc — вектор осестре-
мительного (центростремительного) ускорения точки, направлен-
направленной перпендикулярно к мгновенной оси вращения; ШвР— вектор
вращательного ускорения, направленный перпендикулярно к пло-
плоскости, в которой лежит данная точка и вектор углового ускоре-
ускорения 8.
Вектор осестремительного ускорения равен
woo = uxv (XVIII, 14)
и направлен по перпендикуляру к оси вращения, опущенному
из данной точки на ось. Величина его равна
woc - a>*r sin (ш, v) = w2re, (XVIII, 140
.
(XVIII, 15)
где г0 — расстояние точки до мгновенной оси вращения.
Вектор вращательного ускорения
Величина этого ускорения
оЪр = ег sin (Г, г). (XVIII, 15')
?50 Кинематика
Существует еще один способ определения вектора угловой ско-
скорости тела, скоростей и ускорений его точек. А именно, движе-
движение тела вокруг неподвижной точки рассматривают как слож-
сложное движение, состоящее из двух вращательных движений: отно-
относительного с угловой скоростью w вокруг некоторой движущейся
оси (собственной оси), проходящей через центр вращения тела, и
переносного вместе с осью, движущейся вокруг некоторой непод-
неподвижной оси с угловой скоростью п)в и проходящей через ту же
неподвижную точку.
Вектор абсолютной угловой скорости тела
1,16)
Это равенство позволяет определить один из векторов по задан-
заданным двум другим. _ _
Если известны векторы угловых скоростей па , бе и wrt то век-
вектор абсолютной скорости любой точки тела определяется по
формуле
Ъа =Ъе +ЪГ (XVII, 17)
Для определения ускорений точек тела необходимо знать век-
вектор углового ускорения еа в каждый момент времени.
Вектор абсолютного углового ускорения
ё«-^. (XVII, 18)
В тех случаях, когда величина вектора угловой скорости постоян-
постоянна и ось собственного вращения сохраняет угол наклона к непод-
неподвижной оси вращения постоянным (случай регулярной прецессии),
вектор углового ускорения можно определить по следующим фор-
формулам:
Вектор абсолютного ускорения какой-либо точки тела опреде-
определяется по формуле
wa = w,4-wr + wk. (XVIII, 20)
§ 2. Методические указания к решению задач
Задачи рассматриваемого раздела можно разделить на несколько
групп.
1. Задачи, в которых движение тела вокруг неподвижной
точки задано углами Эйлера, изменяющимися в функции от времени.
В этом случае угловые скорости и ускорения тел, скорости и уско-
ускорения точек тела определяются по формулам (XVIII, 2 — XVIII, 11).
(XVIII, 19)
Движение твердого тела вокруг неподвижной точки 351
2. Задачи, в которых абсолютное вращательное движение тела
разделяется на переносное и относительное вращательные движе-
движения тела вокруг соответствующих осей.
При определении угловых скоростей в этом случае строят
параллелограмм угловых скоростей согласно равенству
из которого определяют искомые величины.
Ускорение точки тела определяется двумя способами: как сум-
сумма векторов вращательного и осестремительного ускорений
или как сумма векторов переносного, относительного и кориоли-
сового ускорений
wa = we + wr + wK.
§ 3. Задачи
118. Тело вращается вокруг неподвижной точки О.
Движение его задано углами Эйлера
9 = 2*; ф = |~2/; 6 = -=-.
Определить скорость и ускорение точки А тела, координаты
которой в момент t = ~ сек. равны: х = 4 см, у =5 см, z =6 ел.
Решение» Определим проекции угловой скорости на оси непод-
неподвижной системы координат Oxyz по формулам:
ш, = |совф + J sin ф sine; A)
о)у = -g sin ф — ^ cos ф sin 6; B)
Подставив значения углов и их производных, получим:
(I')
sin-J = — sin 2^; B')
4 C')
352 Кинематика
В момент / = у сек- эти проекции равны
ю, = — li/сек2; A")
о)у=0; <&)
ь>г = (— 2 — 3) = — 0,27 VceK. C*)
Величина полной угловой скорости
ш = K<of+li^ i/сек.
Зная проекции угловой скорости на оси неподвижной системы
координат Охуг, определяем проекцию скорости точки тела по
формулам:
v*^ <»yZ — (!)z • у, D)
vv = о)гл: — шя • г, E)
Wy • X F)
Подставив значения для ых, ыуу о>2 из уравнений (Iя) B") и
в уравнения D), E) и F), получим:'
Va = 0 — (— 0,27) - 5 = 1,35 см1сек, D')
оу = — 0,27 . 4 — (— 1) - 6 = 4,92 см/сек, EГ)
Vz = (_ 1) . 5 — 0 = — 5 сж/шс. F')
Величина скорости точки А равна
v = ]/"(Т^7ТТ4^92J + (— 5J = 7,14 сл/се/с. G)
Проекции ускорения точки А получим из формул:
w22) — ^2^> (8)
(i)zZ) — (D2y, (9)
й)г z)~^Z. A0)
Определим проекции вектора углового ускорения г%> вуу ег
точки А
^=2cos2*, A2)
dt
Движение твердого тела вокруг неподвижной точки
353
При / = у сек. проекции вектора углового ускорения будут равны
е, = — 2 sin 2 J =0, (ПО
е, = _ 2cos 2 у = 2 VceK2, A2')
^ = о. A3')
Подставив значения координат х, у, г точки А, проекции век-
вектора угловых скоростей и ускорений в формулы (8), (9), A0), полу-
получим:
Wa = 12 + 4 + 1,62 — 1,073 • 4 = 16,33 см/сек\
wv = 4 + 1,62—1,073 • 5 =V0,255 см/сек*,
wt = _8 + 4 + 1.62 = 1,073 • 6 = —8,82 см/сек*.
Величина полного ускорения
w «= 1^A6,33)* + @,255J + (— 8,82J = ]/343,54 = 18,53 см/сек*.
119. Конус А обегает 120 раз в минуту (пв = 120 об/мин) не-
неподвижный конус В (рис. 119). Высота конуса ООг = h = 10 см.
К задаче 119.
Определить переносную угловую скорость конуса б5# вокруг оси
Ог, относительную угловую скорость конуса cof вокруг оси Оу,
направленную по линии ООЪ абсолютную угловую скорость ыл и
абсолютное угловое ускорение еа. Определить также абсолютную
скорость и абсолютное ускорение точки D конуса.
i
Решение. Начало системы координат Oxyz примем в вершинах
конусов в точке О (рис. 119,а).
Пусть конус А обегает конус В без скольжения вокруг
оси Ог по часовой стрелке, тогда вокруг собственной оси Оу
конус будет вращаться против часовой стрелки, если смотреть
против положительных направлений осей Ог и Оу.
23 591
354 Кинематика
Линия соприкосновения конусов ОС совпадает с образующими
конусов и является мгновенной осью вращения.
Абсолютное движение конуса А — это вращательное движение
конуса вокруг мгновенной оси ОС с угловой скоростью ша, вектор
которой направлен по оси ОС, как указано на рисунке.
С другой стороны движение конуса можно рассматривать как
сумму двух вращательных движений: переносного вокруг оси Oz
с угловой скоростью сое и относительного вокруг собственной оси
Оу с угловой скоростью о\. Вектор абсолютной угловой скорости
равен геометрической сумме векторов бЗв и wr
™а = <Ое + GV A)
Величина переносной угловой скорости щ может быть опреде-
определена по формуле
«л «120 , .,
Зкая величину w6, можно из прямоугольника углов'ых скоро-
скоростей определить (рис. 119,а)
= 0^ = 8тс '/сек, C)
<о, = ыа cos 30° = 8тс Ц3- = 4 тс j/З х/сек. D)
Вектор абсолютного углового ускорения определим по формуле
еа = (з)а х оуг; E)
он направлен перпендикулярно к плоскости #Ог вдоль оси Ох.
Величина ва равна
еа = (оаа>г sin 30° = 8тс . 4тс УЗ • 0,5 = 16^г2 КЗ х/сек.2 F)
Прежде чем определить скорость и ускорение точки D конуса Л,
вычислим длину образующей конуса OD == /, радиус основания
конуса От D = /• и перпендикуляр DF = /г1э опущенный из точки D
на ось ОС:
00, Л 10 20
1 "~ cos 30° ~~ cos 30° ~ уъ 1/3"
г =/cos60° = -^L -0,5 =4^ж'
]/3 j/3
А, = /соя 30° « -^= • ^ = 10 см.
Скорость vD точки D может быть определена по формуле
vD = ioahx =. 8тс . 10 = 80тс см/сек G)
Движение твердого тела вокруг неподвижной течки зоо
или как сумма переносной и относительной скорости ve и vr:
ve = we • h = 4тс • 10 = 40тг см/сек, (8)
-^ = 40 тг елс/шс. (9)
J/3
Векторы ve и иг направлены по одной прямой перпендикулярно
к плоскости уОг, следовательно, абсолютная скорость равна ал-
алгебраической сумме
va = ve + ь\ = 40тг + 40тг = 80 <к см/сек. A0)
Ускорение точки D равно геометрической сумме осестремитель-
ного Woe и вращательного швр ускорений
wD = w0G + wBp. (П)
Величины ускорений Woe и wBV равны:
Woe = w2a • /гх = (8тгJ Ах - 64тг2 . 10 = 640тг2 см\сек\ A2)
wBV = ва/ = 16т:2 УТ- -^= = 320 ти2 см/сек*. A3)
Вектор ускорения Wqc направлен по ht перпендикулярно к оси
ОС. Вектор ускорения wBV направлен перпендикулярно к образую-
образующей OD.
Величина полного ускорения точки D
Wjy = i/w2 -j- w'* -f- 2tt^ • ^'Bp • cos 120° =
= l/"F40 тс2J + C20 7r2J — 2 • 640 7z2 • 320 ^"^5 =
= 320 тс2 j/3 см/сек2. A4)
Ускорение ^ можно определить и другим способом.
Движение конуса А состоит из двух вращательных движений:
относительного и переносного. Ускорение wD равно
wD = weJc wr -\- wk,
где we — ускорение точки D при переносном вращательном дви-
движении;
wr — ускорение точки D при относительном вращательном дви-
движении;
й?'к — дополнительное (кориолисово) ускорение.
Направление векторов ускорений указаны на рис. 119,6. Ве-
Величины ускорений равны:
we = (of . h = D тгJ • 10 = 160 ти2 см/сек2; A6)
а>, = ш? • г = D * КЗJ • -^ = 160 тсЯКЗел/сек?; A7)
ш^ =2we oyr sin 90° = 2 • 4 тг • 40 ^ = 320л2 см/сек2. A8)
23*
356
Кинематика
Векторы ускорений we и wK направлены перпендикулярно к
оси Ог, а вектор wr вертикально вниз к оси Оу. *
Величина полного ускорения wD
wD
l/(l60ic»-fc320ic*)» + A6(k2j/J = 320ти2 УЗ см/сек. A9)
120. Дифференциальная передача (рис. 120) состоит из двух
конических зубчатых колес ! и 2 радиуса R =7 см, которые вра-
вращаются в одну сторону с угловыми скоростями ь)г = 5 х/сек и
ш2 = 3 х/сек вокруг той же оси CD и малого зубчатого колеса 3
(сателлита) радиуса г = 2 см, насаженного свободно на криво-
кривошип 4, который может вращаться вокруг неподвижной оси CD.
Определить угловую скорость кривошипа о>4и угловую скорость
сателлита по отношению к кривошипу оK,4.
Решение. Для решения задачи при-
применим способ остановки. Мысленно со-
сообщим кривошипу и колесам 2 угловую
скорость равную угловой скорости кри-
кривошипа, но обратно направленную.
Так как направление вращения кри-
кривошипа не дано, примем его положи-
положительным. Если знак угловой скорости
после решения окажется отрицатель-
отрицательным, то истинное, направление вра-
щения кривоШипа будет противоположно
принятому. Составим отношение угло-
угловых скоростей зубчатых колес после мысленной остановки криво-
кривошипа.
Это отношение равно передаточному числу
К задаче 120.
tt)8 —
A)
Знак минус перед передаточным числом взят потому, что при
неподвижном кривошипе, направление вращения зубчатых колес
/ и 2 будет противоположным.
Подставив в уравнение A) числовые значения, получим
B)
откуда
)„ = 4 1/сек.
B')
Движение твердого тела вокруг неподвижной точки 357
В полученном рядовом зубчатом зацеплении скорости точки
касания сателлита и зубчатого колеса / в точке Е одинаковы:
Щв = Vzb C)
или
откуда определим относительную угловую скорость сателлита
Шм »<""-;«>•* . 5-4 . 7 - 3,5 VceK.
ЧАСТЬ ТРЕТЬЯ
ДИНАМИКА
РАЗДЕЛ ПЕРВЫЙ
ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
Часть теоретической механики, в которой изучается механи-
механическое движение материальных тел, в связи с воздействием окру-
окружающей среды, определяющим это движение, называется динами-
динамикой.
Динамика изучает систему тех основных положений теорети-
теоретической механики, которые -объединяют кинематические свойства
движений со свойствами сил, действием которых они обусловлены.
Динамика делится на две части: динамику материальной точки
и динамику системы материальных точек.
В основе динамики лежат аксиомы, полученные в результате
непосредственных наблюдений над механическими движениями ма-
материальных тел и последовательного абстрагирования наблюдае-
наблюдаемых явлений.
Одним из таких абстрактных понятий в динамике является
понятие об изолированной материальной точке.
Изолированной материальной точкой называется точка, кото-
которая перемещается в пространстве и времени, исключая воздей-
воздействие на нее окружающей среды.
Аксиома 1. Изолированная материальная точка сохраняет со-
состояние равномерного и прямолинейного движения, или находится
в состоянии покоя относительно системы координат, которая сама
движется поступательно, равномерно и прямолинейно.
Из этой аксиомы следует, что изменение скорости движущейся
точки может происходить лишь при воздействии на нее окружаю-
окружающей среды — сил.
Эта аксиома, установленная в результате многочисленных наблю-
наблюдений над механическим движением и анализа особенностей этого
движения, называется также первым основным законом механики
или законом инерции.
Системы координат, в которых имеет место закон инерции, на-
называются инерциальными.
В классической механике основной инерциальной системой
Дифференциальные уравнения движения материальной точки &J
обычно считают гелиоцентрическую систему координат, т. е. си-
систему координат с началом в центре солнца и осями, направленными
к трем звездам.
Аксиома 2. Ускорение, сообщаемое материальной точке прило-
приложенной к ней силой, пропорционально величине силы и имеет направ-
ление силы
(XIX,
где w—вектор ускорения; т — масса точки, F — вектор силы.
Обычно это равенство записывается в виде
m.^ = F (XIX, Г)
и называется иногда вторым законом динамики.
Аксиома 3. Всякому действию всегда соответствует равное
и противоположно направленное противодействие, т. е. действия
двух тел одного на другое всегда равны и направлены по одной
прямой в противоположные стороны.
При решении задач применяются две системы единиц: физи-
физическая (CGS) и техническая (FLT).
В физической системе единиц основными единицами измерения
являются: сантиметр, грамм и секунда.
В технической системе единиц основными единицами измере-
измерения являются: метр, килограмм и секунда.
В разделе «Динамика материальной точки» рассматриваются
задачи двух типов. К первому .типу относятся задачи, в которых
по заданному закону движения материальной точки и ее массе
определяют силу, действующую на точку. Задачи этого типа иначе
называют прямыми задачами динамики.
Ко второму типу относятся задачи, в которых задаются силы,
действующие на материальную точку, и ее масса, а требуется опре-
определить закон движения точки. Задачи этого типа называют обрат-
обратными задачами динамики.
ГЛАВА XIX
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ
МАТЕРИАЛЬНОЙ ТОЧКИ
§ 1. Определение сил по заданному закону движения
Силы по заданному закону движения материальной точки опре-
определяют на основании второго закона динамики (XIX, 1).
Если закон движения точки задан натуральным или координат-
координатным способом, то можно определить величину ускорения w точки,
а затем, применив уравнение (XIX, 1'), определить силу F.
360 Динамика
Проектируя обе части уравнения (XIX,I7) на касательную к
траектории и на нормаль к ней, получим при натуральном способе
задания движения следующие уравнения движения:
-~n = Fn <XIX>2)
ИЛИ
t. " <XIX>2')
p — »'
где /n — масса точки, р — радиус кривизны траектории.
Если закон движения точки задан координатным способом, то,
зная массу точки и определив проекции ускорения на оси коор-
координат, можно на основании второго закона динамики определить
тгроекции силы на соответствующие оси из уравнений:
тх=:Х; (XIX, 3)
my = Y', (XIX, 4)
mz = Z. (XIX, 5)
При рассмотрении движения несвободной материальной точки
связи, наложенные на точку, заменяются силами — реакциями свя-
связей. Для решения задач на несвободное движение точки часто
используют «петербургский принцип», который формулируется
так: при движении материальной точки активные силы, действую-
действующие на точку, реакции связей и силы инерции уравновешиваются.
F + R + F* = 0, (XIX, 6)
где F — вектор равнодействующей активных сил; R — вектор
геометрической суммы реакций; Fn — вектор силы инерции.
Это векторное равенство может быть использовано для реше-
решения задач-как в случае задания движения материальной точки
натуральным способом, так и в случае задания движения коорди-
координатным способом.
Рассмотрим примеры- решения задач первого типа (прямые
задачи динамики).
§ 2. Задачи
121. Автомобиль ГАЗ-51 (рис. Г21) с грузом весит Q = 5400 кг
и движется по выпуклому мосту со скоростью v = 10 м/сек, ра-
радиус кривизны в средине моста р = 50 м. Определить давление
автомобиля на мост в момент прохождения его через средину моста.
Дифференциальные уравнения движеШя материальной точки
361
Решение. Определим силы, действующие на автомобиль.
Нормальная реакция связи R направлена вверх и по величине
равна давлению N автомобиля на мост. Сила веса Q автомобиля
направлена вниз. Мысленно присоединим к автомобилю силу
инерции Fn, направив ее вверх, так как ускорение автомобиля
направлено к центру закругления моста.
Из
следует
Так как
то
уравнения равновесия (XIX,6)
A)
B)
К задаче 121.
Подставив численные значения в уравнение B), получим
5400A—5^) = 4298 кг.
М
122. Кузов трамвайного вагона (рис. 122) вместе
с нагрузкой весит Qt = 10 m; тележка с колесами
весит Q2=l я*. Определить наибольшее и наимень-
наименьшее давление вагона на рельсы горизонтального
прямолинейного участка пути, если вагон на ходу
совершает на рессорах вертикальные гармони-
гармонические колебания по закону х = 2 sin • 10/ см.
Решение. Кузов вместе с тележкой рассматри-
рассматриваем как материальную точку М, движущуюся под
действием сил: собственного веса Qx + Q2; реак-
реакции рельс, направленной по вертикали вверх.
Заметив, что указанная точка М движется с
ускорением
К задаче 122.
W = X
— 200 sin 101
A)
(ось Ох направлена по вертикали вниз), вычислим максимальное-
значение силы инерции
= f И
. 0,0102 • 200 = 2,04 т.
Во время колебательного движения точки М направление век-
вектора ускорения w периодически изменяется, а поэтому силы инер-
инерции имеют направление, указанное на рис. 122, с, б."
362 Динамика
Присоединив мысленно к точке М указанные силы инерции, на
основании «петербургского принципа» (XIX, 6) находим
f* + R + Q! + Qa = о. C)
Исходя из уравнения C), давление на рельсы для случая а равно
N1 = Q1 + Q2 — Fw= 11—2,04-8,96 m, D)
а для случая б
N* = Qi + Q2 + ^и = 13,64 m. E)
123. Шарик массой 1 г (рис. 123) падает под действием
силы тяжести и испытывает при этом сопротивление возду-
KiX xa, так что движение его выражается уравнением х~
= 490 / — 245 A — е~2'), где х — в см, t — в сек.; ось Ох
~- направлена по вертикали вниз. Определить в динах силу
! Р ^ сопротивления воздуха, испытываемого шариком, в
» зависимости от его скорости v> приняв g = 980 см/сек2.
К зада-
задаче 123. Решение. На движущуюся точку М действуют сила
тяжести Р и сила сопротивления среды R\ направле-
направления их указаны на рисунке.
Прямая задача динамики решается на основании уравнения
(XIX, 3), составив которое, получим
mx^P — R. О)
Ускорение движения
i = _980e-2', B)
причем
i = о = 490A +е~\ C)
Из уравнения A)
# = 980A +*-*).
Принимая во внимание уравнение C), выразим силу сопротивле-
сопротивления R через скорость
/? = 2а
124. Точка массой т (рис. 124) движется по эллипсу -j + ~ = 1;
ускорение точки параллельно оси Оу. При t = 0 координаты точки
х == 0; г/ = 6; начальная скорость и0. Определить силу, действу-
действующую на точку в каждой точке траектории.
Решение- Проектируя вектор ускорения движущейся точк^ М
на координатную ось Ох, найдем
х = 0. A)
Дифференциальные уравнения движения материальной точки 363
Интегрируя это дифференциальное уравнение, получим
х — bjf -f- o2, (Z)
где Сх и С2 — постоянные интегрирования.
Принимая во внимание начальные
условия движения:
/ = 0; xo = vo\ xo=0, C)
определим величины Сх и С2:
С! = с0; С2-0, C0
в силу чего
X = Уо/. D) К задаче 124.
Для определения величины ускорения движения точки М
продифференцируем дважды по времени t уравнение траектории
7?+-?-1==0- E)
Дифференцируя первый раз, получим
Дифференцируя второй раз, имеем
2 •• 2 • - , 2 ¦• 2 •
а2 'а2 б2 Ь2 ^ '
или
Принимая во внимание, что на основании уравнений D) и E)
после дифференцирования уравнения G) по времени t получим
t/ = — -т • — *t. (8)
На основании уравнений F), (8) и A) определим искомую ве-
величину
Зная проекцию ускорения у точки можно определить проекцию
силы на ту же ось из соотношения (XIX, 4)
У-_«^. ПО,
a?tp
364 Динамика
§ 3. Определение закона движения точки по
заданной силе и массе
Определение движения точки по заданной силе и массе приво-
приводит к интегрированию система дифференциальных уравнений
Z
(XIX, 7)
При решении задач этого параграфа нужно придерживаться
следующей последовательности.
1. Выбрать систему координатных осей,-введя инерциальную
систему отсчета.
2. Составить схему действующих на точку сил, а в случае
несвободного движения точки предварительно применить прин-
принцип освобождаемости от связей.
3. Установить начальные условия движения, т. е. выразить при
/ =0
*о. Уо> *о> Щх, voy, voz.
4. Составить на основании схемы сил дифференциальные урав-
уравнения движения (XIX, 7).
5. Проинтегрировать полученную систему уравнений, опреде-
определив постоянные интегрирования из начальных условий (XIX, 8).
6. Произвести кинематическое исследование полученного ре-
решения.
§ 4. Прямолинейное движение
Если точка движется по прямой, то эту прямую принимают за
координатную ось Ох.
В случае несвободного движения составляют одно дифферен-
дифференциальное уравнение (XIX, 3)
тх = Х (XIX, 30
и одно уравнение статики
Y =*().
Сила X в общем случае является функцией координаты х точки,
скорости v « х и времени /, т. е.
X = X (/, х, х).
Если *
X = X(t9 v),
Дифференциальные уравнения движения материальной точки 365
то уравнение (XIX, 3') при определении скорости движения точки
преобразуют к виду
m~=X(*, v). (XIX,3")
Уравнение (XIX^*) интегрируют, пользуясь методами тео-
теории дифференциальных уравнений. Если
Х = Х(х, v),
то для определения закона движения уравнению (XIX, 3") придают
вид
mv% = X(x, v).
§ 5. Криволинейное движение по плоской кривой
Задачи этого типа приводят к интегрированию системы диффе-
дифференциальных уравнений
щвХ, my = Y. (XIX,9)
Последовательность решения задачи, указанная выше, пол-
полностью сохраняется.
Криволинейное движение точки в пространстве часто изучают
в натуральной системе координат. Дифференциальные уравнения
движения точки в проекциях на касательную к траектории и на
главную нормаль имеют вид:
m§ = Rx; mVj = Rnf (XIX, 10)
где /?т и Rn — проекции соответственно на касательную и главную
нормаль равнодействующей силы, действующей на точку.
§ 6. Задачи
125. За какое время и на каком расстоянии может быть оста-
остановлен тормозом вагон трамвая, движущийся по горизонтальному
пути со скоростью 36 км/час, если сопротивление движению, раз-
развиваемое при торможении, составляет 300 кг на 1 т веса вагона.
Решение. Будем рассматривать трамвай как материальную
точку (рис. 125), предполагая всю массу его сосредоточенной в
его центре тяжести М* За ось Ох примем прямую, по которой дви-
движется точка М; за начало отсчета примем то положение, в котором
находилась точка М в момент начала торможения.
Исследуем движение трамвая, начиная с момента t = 0.
При / =0 из условий задачи имеем х0 = 0 и д-0= 10 м/сек.
Заметим, что в конце движения скорость трамвая х == 0-
366
Динамика
Составим схему сил, действующих на трамвай во время тормо-
торможения. Во время торможения на трамвай действуют три силы
сила собственного веса Р, реакция рельс Rx и сопротивление тормо-
торможения Г. Считаем эти силы приложенными к точке М.
Составим дифференциальное уравнение движения точки М.
Так как точка движется прямолинейно вдоль оси Ох, уравнение
движения имеет вид
тх = — Г,
где т — масса вагона.
р
К задаче 125.
-~*~Х
По условию задачи
Т с=
поэтому
x = -0,3g.
Проинтегрировав уравнение A), получим
A)
где Сг — постоянная интегрирования. При вторичном интегриро-
интегрировании
C)
2
где С2 — новая постоянная интегрирования.
Мы нашли координату х как функцию времени.
Выражение C) содержит две произвольные постоянные. Для
определения Сг и С2 в уравнениях B) и C) предположим, что t =. -,
где х — время торможения, а их левые части заменим соответству-
соответствующими значениями.
Тогда получим уравнения:
0 = vQ — 0,3 gx; D)
х = уох 2 . \0)
Из уравнения D) определим время торможения
х = -г^— == тг^- = 3,4 сек.
Дифференциальные уравнения движения материальной точки 367
Чтобы найти какой путь пройден трамваем за время торможения,
подставим его значение в уравнение E), тогда
ш о л °>3 • 9>81 • 3,42 ла о
х = 10 • 3,4 ¦ g—-1- = 16,9 л#.
Это и есть искомый путь
128. Корабль движется, преодолевая силу сопротивления воды,
пропорциональную квадрату скорости и равную а =0,12 т при
скорости 1 м/сек.
Сила упора винтов направлена по скорости в сторону движе-
движения
и изменяется по закон/ Т = То {1 —), где Го = 120 пг-
Р
сила упора винтов в момент, когда j
корабль находится в покое; v8 = ~
= const = 33 м/сек. Определить наи- 2- —^
большую скорость, которую может
развить корабль, а также установить
ее закон изменения. К задаче 126.
Решение» Рассмотрим корабль как материальную точку Nt
(рис. 126). Эта точка находится в прямолинейном движении под
действием активно приложенной силы упора винтов Г; силы со-
сопротивления воды R, равной
/? = 0,12t?2 A)
и направленной в сторону, противоположную вектору скорости;
полной подъемной силы воды Ф и силы тяжести Р.
Дифференциальное уравнение движения точки по ее прямоли-
прямолинейной траектории имеет следующий вид:
«Ф. B)
В момент времени, когда скорость максимальная, производная
5?-°- <3>
Поэтому из уравнения B) получим
Ч,а* + Г«^1Г-Го=0. D)
Решив уравнение D) относительно vmSiX> получим
t?max ===
и после подстановки числовых значений- имеем
= ]/"Т2Ж5 — 15,2 « 20 м/сек или 72 км/час.
368 Динамика
На основании уравнения B) можно установить закон измене-
изменения скорости в функции от времени, т. к. оно принадлежит к типу
уравнений с разделяющимися переменными и может быть написано
в виде
Считая, что движение происходит без начальной скорости, из урав-
уравнения F) легко определить
г \1 Ц
- V«r,+— (
» 4.1»
JL±Z^ G)
Из уравнения G) следует, что lim v = umax, где макси-
максимальная скорость достигается ассимптотически.
127. Самолет начинает пикировать без начальной вер-
вертикальной скорости. Сила сопротивления воздуха пропор-
пропорциональна квадрату скорости. Найти зависимость между
вертикальной скоростью в данный момент, пройденным
расстоянием и максимальной скоростью пикирования.
Решение. Рассмотрим самолет как материальную точку.
че Tz7*' Точка движется прямолинейно (рис. 127) вдоль оси у.
Принимаем начало координат в точке, с которой самолет
начинает пикировать.
Движение совершается при начальных условиях:
Точка движется, находясь под действием силы* тяжести Р и
силы сопротивления воздуха
R = *v\ B)
где а — коэффициент пропорциональности.
Дифференциальное уравнение движения точки имеет вид.
L. . f?? — р _ о*
g dt * '
Скорость становится максимальной, когда ~ =0. Из уравне-
уравнения C)
Дифференциальные уравнения движения материальной точки
^ 369
откуда
D')
Введя промежуточный параметр s, преобразуем уравнение C)
к виду
1 dv ds _ . о* ._.
"•^lis-^-1 7^- E)
Произведя разделение переменных, получим
, 1 vdv
ds=
g 1J^
F)
После интегрирования
5 = 2~ In 1 — .-7-Г
Принимая во внимание начальные условия A), получим из уравне-
уравнения G), что С = 0, следовательно
V
1 -в
. (8)
128. Буер (рис. 128), весящий вместе с пассажирами Q =
= 196,2 /сг, движется прямолинейно по гладкой горизонтальной
поверхности льда под действием давления ветра на парус, плос-
плоскость которого аЬ образует угол 45° с направлением движения.
Абсолютная скорость ветра w перпендикулярна к направлению
движения. Величина давления ветра Р выражается формулой
Ньютона: Р = kSu2 cos2 <p, где <р — угол," образуемый относитель-
относительной скоростью ветра и с перпендикуляром Af к плоскости паруса;
S = 5 м2 — величина площади паруса; k =0,113 — опытный коэф-
коэффициент. Давление Р направлено перпендикулярно к плоскости ab.
Пренебрегая трением, найти: 1) какую наибольшую скорость vmhX
может поручить буер; 2) какой угол а составляет при этой скорости
помещенный на мачте флюгер с плоскостью паруса; 3) какой путь
х должен пройти буер для того, чтобы приобрести скорость v =-g- w,
если его начальная скорость равна нулю.
Решение* На буер действуют: сила давления ветра, приложен-
приложенная к парусу, сила его тяжести Q и реакция абсолютно гладкой
опоры.
Направив координатные оси, как указано на рис. 128, а, на
основании уравнения (XIX, 6) получим
24 691
370
Динамика
ИЛИ
Ж
Р cos 45е.
A)
Проинтегрируем уравнение A) при следующих начальных
условиях:
* = 0; хо = О; ioei>e~0. B)
К задаче 128.
Предварительно определим относительную скорость ветра, кото-
которая равна разности абсолютной скорости w и переносной скорости
v буера. Из рис. 128, б
л/2
cos 9 = cos D5° -f a) = ~- (cos а — sin %),
причем
cos а
sin а = —
и
Объединив формулы C), D), получим
» 2 и ^ *'
C)
D)
E)
Подставив в уравнение A) выражение для силы Р и применив
уравнение E), находим ,
100^-= (ш— иJ. F)
Максимальное значение скорости достигается, когда ^ =0, и,
следовательно,
а также
т. е. относительная скорость ветра направлена параллельно парусу*
Дифференциальные уравнения движения материальной точки 871
Если на мачте буера поместить флюгер, то он расположится
по направлению относительной скорости ветра и, следовательно,
между плоскостями флюгера и паруса угол р будет равен нулю
Р = 0. (8)
Чтобы ответить на третий вопрос задачи, введем промежуточный
параметр s и уравнение F) перепишем в виде
ИЛИ
ds= 100 It-2^-* — ]*>. (90
[ (w — v)* w — vj v* '
Интегрируя уравнение (9'), найдем
2 2
j^j 100B«пЗ) A0)
Так как In 3 = 1,0986, то
$ = х = 90 ж.
129. Самолет Л летит над землей на высоте А (рис. 129) с
горизонтальной скоростью vv Из орудия В произведем выстрел
по самолету в тот момент, когда
самолет находится на одной i&
вертикали с орудием. !
Найти: 1) какому условию ^
должна удовлетворять началь- ^^ЗДШКЕЗР* J*
ная скорость v0 снаряда для
того, чтобы он мог попасть в
самолет, и 2) под каким углом а
к горизонту должен быть сделан
выстрел. Сопротивлением возду-
ха пренебрегаем.
Решение, Направим коорди- К задаче 129.
натную ось Оу вдоль вертикали,
на которой находится самолет и орудие, а ось Ох по горизонтали.
Снаряд движется в среде без сопротивления 1олько под дей-
действием силы собственного веса.
Составив дифференциальные уравнения движения (XIX, 9)
в, координатной форме, получим:
0)
ту = — mg '
где т — масса снаряда.
24*
372 Динамика
Требуется определить решение системы уравнений A), удов-
удовлетворяющее начальным условиям:
* = 0; хо = О; 1/0 = 0;
vox = vo cos a; v^ ~ v0 sin а B)
Следовательно,
y^—^ + V(wt. C)
В момент попадания снаряда в самолет, должны быть выпол-
выполнены условия:
Ч = х, y = h, D)
где хх = ухГ — путь, пройденный самолетом за время Т движе-
движения снаряда до попадания.
Первое из соотношений D) дает возможность определить угол
наклона оси орудия
cos a = -1. E)
Из второго соотношения D) следует, что время движения снаряда
определяется по формуле
Т = - (v0 sin a ± ]/"^sin2a — 2gh), F)
значит попадание возможно при условии
vi sin2 a — 2hg > 0. G)
Объединив неравенство G) с соотношением E), получим
(^H, (8)
т. е.
у? > у? + 2/ig.
ГЛАВА XX
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ МАТЕРИАЛЬНОЙ ТОЧКИ
§ 1. Методика решения задач на теорему об изменении
количества движения
Существуют две формулировки теоремы об изменении коли-
количества движения материальной точки:
а) в дифференциальной форме, выражающей, что элементарное
приращение количества движения равно элементарному импульсу
(XX, 1Г
Общие теоремы динамики материальной точки 373
б) в интегральной форме выражающей, что приращение коли-
количества движения материальной точки за конечный промежуток
времени геохметрически равно полному импульсу равнодействую-
равнодействующей силы, действующей на точку
= S, (XX, 2)
to to
где: Ъ—конечная скорость; t—конечное время; v0—началь-
v0—начальная скорость; t0 — начальное время; S — полный импульс сил.
На основании формулы (XX, 2) определяют среднее значение
силы, действующей на точку
т (а — щ) = ?Ср (* - to). (XX, 3)
Задачи данного типа решаются в следующей последовательности:
1) выбирают координатную систему;
2) составляют схему действующих сил, включая и реакции
связей;
3) составляют на основании уравнения (XX, 2) три скаляр-
скалярных уравнения:
t
т(х — х0) = S,,. == \ Xdt
(XX, 4)
*j
to
t
С
m (z — z0) = Sz =
h
4) Из уравнений (XX, 4) или определяют искомые неизвест-
неизвестные, или эту систему уравнений рассматривают как первые инте-
интегралы дифференциальных уравнений движения.
§ 2. Задачи
130. Поезд движется по горизонтальному и прямолинейному
участку пути. При торможении развивается сила сопротивления,
равная 0,1 веса поезда. В момент начала торможения скорость
поезда 72 км/час. Найти время торможения и тормозной путь.
Решение. Схема сил, действующих на поезд, аналогична схеме
к задаче 125. Применив зависимость (XX,2) к прямолинейному
движению и заметив, что сила сопротивления постоянна, получим
mv—mvo = —O,lPt. A)
374 Динамика
Согласно условию задачи конечная скорость v =» 0, а началь-
начальная v9 = 20 м/сек.
Поэтому из уравнения A) определяем время торможения
Заменив в уравнении A) v через ~, после интегрирования
получим
s = v-^8. C)
Подставив значение t из уравнения B) в уравнение C), определим
s - 20 • 20,4 - 0>1 29'81 B0,4J = 204 м.
131. Для определения веса груженого железнодорожного сос-
состава между паровозом и вагонами установили динамометр. Сред-
Среднее показание динамометра за 2 мин. — 100,8 т. За это же время
состав набрал скорость v = 57,6 км/час (в начале состав стоял на
месте). Коэффициент трения k = 0,02. Найти вес состава.
Решение. Считаем, что железнодорожный состав движется пря-
прямолинейно (рис. 131). К вагонам приложены силы: F — сила
натяжения динамометра; Т — сила тре-
f ния; Р — сила тяжести; R — нормаль-
нормальная реакция.
- Так как Уск°Рение вдоль оси у от-
сутствует, то
К задаче 131. 7" = kP. A)
На основании теоремы об изменении количества движения ма-
материальной точки (XX, 2) получим
^(v-vo) = (F-T)t. B)
Учитывая, что v0 = 0 из уравнений A) и B), определим
D Ftg 100,8 • 120 • 9,81 Qnm w ,o.
P - T+S& = 16 4- 0,02 ¦ 9,81 ¦ 120 = 300° Ш' C)
132. Точка равномерно движется по окружности (рис. 132) со
скоростью v е= 20 см/сек, делая полный оборот за время Т = 4 сек.
Найти импульс сил 5, действующих на точку за время одного по-
полупериода, если масса точки m = 5 г и определить среднее значе-
значение силы F.
Решение. Пусть в начальный момент времени движущаяся точка
занимает положение Мъ тогда за время одного полупериода она
займет диаметрально противоположное положение М2-
Общие теоремы динамики материальной точка
375
Согласно уравнению (XX,2) импульс сил
S ев тог — mu2 = 2mvb
так как
t>i = — Щ.
Подставив в уравнение A) значение /я, v1%
получим
|S| = 2 • 5 • 20 = 200 дн.сек. B)
Среднее значение действующей силы из урав-
уравнения (XX, 3) равно
A)
ЮО дн
C)
К задаче 132.
и имеет направление импульса, т. е. направлена по конечной ско-
скорости.
§ 3. Теорема об изменении момента количества движения
Теорема об изменении момента количества движения материаль-
материальной точки в векторной ферме выражается так:
(XX, 5)
где /0 — момент количества движения относительно некоторой
неподвижной точки О; L{0 — момент силы Fi относительно той же
точки, т. е. производная по времени от момента количества движе-
движения относительно какой-нибудь неподвижной точки геометри-
геометрически равна моменту равнодействующей относительно той же точки.
Аналитически момент количества движения определяется по фор-
формулам:
1Х = уг — zy\ lu = zx — xz\ 1г = ху— ух. (XX, 6)
При решении некоторых задач применяется другая формули-
формулировка этой теоремы.
Скорость точки, описывающей годограф вектора момента коли-
количества движения, вычисленного относительно точки, геометрически
равна моменту равнодействующей силы относительно этого же
центра
(XX, 7)
376 Динамика
Решение задач производят на основании теоремы моментов в
скалярной форме:
= ^Ь f^^^ f^^^ (хх>8)
т. е. производная по времени от момента количества движения отно-
относительно некоторой оси (/ж, /„, 4) равна сумме моментов прило-
приложенных сил относительно этой же оси (%Lixf %Ь{у, %Liz).
Необходимо обратить особое внимание на два следствия тео-
теоремы об изменении момента количества движения материальной
точки.
Следствие 1. Если момент действующей силы относительно
какой-либо оси равен нулю, то момент количества движения отно-
относительно этой же оси остается постоянным.
Следствие 2. В случае центральной силы момент количества
движения относительно центра этой силы остается постоянным.
При решении задач, в которых применяется одно из указанных
следствий, пользуются полярными координатами. Если ввести
понятие о секториальной скорости
а = ^7 XV (XX, 9)
и в каждой из координатных плоскостей выбрать систему поляр-
полярных координат (pit ф^), то зависимостям (XX, 6) можно придать
вид:
4 = 2сж; /„ = 2ау; 1Ж = 2а2, (XX, 10)
где
х ~ 2 pll' °у ~ ~2 Р2 dt ' г ~~ 2 р3 dt •
Следствия 1 и 2 приводят к так называемым интегралам пло-
площадей, которым придают форму
2/?кГ= const. (хх> И)
Задачи на применение теорем об изменении момента количе-
количества движения и на движение под действием центральных сил реко-
рекомендуем решать в следующей последовательности.
1. Выбрать координатные оси.
2. Составить схему действующих сил.
3. Вычислить моменты сил относительно координатных осей и
проверить не выполняются ли следствия 1 и 2.
4. Составить уравнение (XX, 8) и определить из них искомые
величины, либо соотношения, вытекающие из следствий 1 и 2,
принять за первые интегралы уравнений движения.
Общие теоремы динамики материальной точки 377
§ 4. Задачи
133. Точка М (рис. 133) движется вокруг неподвижного центра
под действием силы притяжения к этому центру. Найти скорость
v2 в наиболее удаленной от центра точке траектории, если скорость
точки в наиболее близком к нему положении юг = 30 см/сек, а гг
в пять раз больше гг.
Решение. Рассматривая движение точки под действием централь-
центральной силы притяжения, заметим, что в точках траектории наиболее
удаленных и наиболее близких к центру притяжения отсутствует
радиальная составляющая скорости vp = 0, а касательная состав-
составляющая скорости v9 перпендикулярна к радиусу-вектору, т. е.
в указанных точках. В самом деле, за-
задав движение в полярных координатах,
заметим, что полярный радиус-вектор
принимает экстремальное значение в тех
точках, для которых
р = 0. К задаче 133.
На основании закона моментов количества движения приходим
к заключению, что в нашем случае сохраняется момент количества
движения точки
/0 = const B)
на протяжении всего движения, т. е. сохраняется секториальная
скорость движения
Г1 х vl — Г2 х V2- W/
В точках экстремально удаленных от центра притяжения
v2 = г-^~ = 6 см/сек.
§ 5. Работа и мощность
Работу А постоянной силы F на прямолинейном участке пути
определяют как произведение величины \F\ силы на величину
перемещения и и на косинус угла а между ними, т. е.
A = F - и -cosa. (XX, 12)
Элементарная работа силы F на бесконечно малом перемеще-
перемещении dr вычисляется по формуле
VA = F • dr
278
Динамика
или
У А » Fds cos a. (XX, 13)
Если сила и элементарное перемещение заданы в системе прямо-
прямоугольных координат F(X, Y,Z) и dr (dx, dyt dz)t то элементарная
работа определяется по формуле
VA = Xds + Ydu + Zdz.
(XX, 14)
Если мы имеем часть (ограниченную или неограниченную) про-
пространства, в каждой точке которого ня данную материальную точку
действует вполне определенная по величине и направлению сила,
то такая часть пространства называется силовым полем.
Рис. 1.
Рис. II.
Представим силовое поле и поместим в этом поле материаль-
материальную точку М, на которую будет действовать некоторая сила
(рис. I).
Силовое поле называется потенциальным полем, если сила F,
действующая в этом поле, обладает следующими двумя свойствами:
1) величина и направление силы зависит только от положения
точки М\ 2) работа силы на некотором пути Мг М2 (рис. II) точки
М не зависит от кривой, по которой происходит движение точки
между положениями Мг и М2.
Таким образом, сила тяжести, а также любая центральная сила,
зависящая от расстояния точки приложения силы до центра, обла-
обладает указанными двумя свойствами.
Выражение элементарной работы потенциальных сил имеет
вид
(XX, 15)
т. е. равна взятому с обратным знаком полному дифференциалу
потенциальной функции.
Общие теоремы динамики материальной точки 379
Полная работа силы на криволинейном участке пути Мг М*
определяется криволинейным интегралом
j Fdr = Jfdscosa, (XX, 16)
Mi Mi
взятым вдоль дуги кривой от точки Мг до точки М2.
В частных случаях действия потенциальных сил работа не
зависит от формы пути.
Например: а) полная работа силы тяжести материальной точки
Ait2 = P(h — Ч)> (XX, 17)
где Р — вес материальной точки; гх — % — разность высот началь-
начального и конечного положений ее.
Работа? силы тяжести положительна, если конечное положение
ниже начального, и отрицательна в противоположном случае;
б) работа упругой силы при растяжении конца пружины на
длину X из начального состояния определяется по формуле
Л = -^\ (XX, 18)
где с — коэффициент жесткости пружины.
Отношение работы, произведенной силой F, к протекшему про-
промежутку времени называют мощнсхлъю. Обозначив мощность через
N, получим
т. е. мощность равна скалярному произведению вектора силы на
вектор скорости.
Мощность силы, приложенной к телу, находящемуся во враща-
вращательном движении, вычисляется по формуле
N = Lg(F)b>, (XX, 20)
где Lg(F) — момент приложенной силы относительно оси враще-
вращения; а) — угловая скорость вращения.
Крутящий момент вычисляется по формуле
U =.71 620-^ кГсм, (XX,21)
где п — число оборотов в минуту.
Мощность измеряется в лошадиных силах (а. с), кГм/сек,
эрг/сек, джоуль/сек, ваттах, киловаттах. Для перевода одних
единиц мощности в другие пользуются следующей таблицей:
1 ватт = 107 эрг/сек = 1 джоуль/сек= 0,102 кГм/сек;
1 1 киловатт = 103 #m= 1010 эрг/сек = 102 кГм/сек;
1 кГм/сек = 9,81 вт\
I л. с. = 75 кГм/сек = 0,735 кет.
380 Динамика
Отношение полезной работы к фактически выполненной назы-
называется коэффициентом полезного действия (к. п. д.), т. е.
т,= п юо%. (XX, 22)
§ 6, Задачи
134. Для того, чтобы поднять 5000 ж3 воды на высоту 3 м,
поставлен насос с двигателем в 2 л. с. Сколько времени потребу-
потребуется для выполнения этой работы, если коэффициент полезного дей-
действия насоса '0,8?
Решение. Как видно из формул (XX, 12), (XX, 19) и /XX, 22)
для вычисления времени работы насоса, необходимо, в первую оче-
очередь, определить работу, затраченную на поднятие воды,
А = 5000 • 103. 3=15 . 106 кГм (I)
и мощность
yVn = A = 15'f1Qe кГм/сек, B)
причем
Л/п.дв = 2 • 75 • 0,8 кГм/сек. C)
Сравнив формулы B) и C), находим
*= 125 - 103 сек. = 34 час. 43 мин. 20 сек.
135. Как велика мощность в лошадиных силах и киловаттах
машины, поднимающей 84 раза в минуту молот весом 200 кг на
высоту 0,75 м9 если коэффициент полезного действия машины 0,7.
Решение. Работа, затраченная машиной на определение силы
тяжести, вычисляется по формуле (XX, 12), т. е.
А =200 • 0,75 = 150 кг. A)
Мощность машины по^ формуле (XX, 19) равна
Nn = 1-^п^- ===2Ю кГм/сек- B)
Полезная мощность машины определяется на основании урав-
уравнений (XX, 19) и (XX, 22), т. е.
Nn = ^у = 300 кГм/сек. C)
Мощность машины в л. с. равна
300 .
Ь с
Общие теоремы динамики материальной точки 381
а в кет
0,736 . 4 = 2,94 кет.
136. Вычислить работу, которая производится при подъеме
груза в 20 кг по наклонной плоскости (рис. 136) на расстояние
6 му если угол, образуемый плоскостью с горизонтом, равен 30°,
а коэффициент трения равен
0,01.
Решение. На точку УМ, дви-
движущуюся по наклонной плос-
плоскости, действуют сила тяжести
Р, сила трения Т и нормальная
реакция R.
Реакция R работы не произ-
производит, так как она перпенди-
перпендикулярна к направлению дви-
движения.
Сила тяжести Р производит работу, которую можно определить
из формулы (XX, 12)
Лг = Р. s. cos 120° = — 20.6.~ = — 60 кГм. A)
Сила трения Т произведет работу
Л2 = — kNs. B)
Нормальное давление N груза на опору определим из условия
равновесия сил вдоль оси Оу
= Я — Pcos30° = 0,
т/з"
т. е. N = Р ~y кг> поэтому
Л2==_0,01 .20^-6 = — 0,173.6 = — 1,04 кГм. C)
Полная работа приложенных сил
А => Аг + А2 = — 60 — 1,04 = —61,04 кГм.
§ 7. Теорема о кинетической энергии материальной точки
В данном параграфе рассматриваются задачи, в которых иссле-
исследуется действие сил, приложенных к точке массой m на расстоя-
расстоянии s. "^
Эти задачи решаются на основании теоремы об изменении ки-
кинетической энергии, которая формулируется так: приращение
кинетической энергии Т на некотором участке пути s, пройден-
пройденном движущейся точкой массой т, равняется работе равнодей-
382 Динамика
ствующей силы, приложенной к этой точке на указанном уча-
участке пути
Y (of— Ф = Л OCX, 23)
или
где Л — работа равнодействующей силы, приложенной к точке;
?>о> vi — соответственно начальная и конечная скорость движу-
движущейся точки.
В случае движения материальной точки в потенциальном сило-
силовом поле полная механическая энергия ее сохраняет свою величину
7Г + П(х, уу г,)-Л, (XX, 24)
где П *— потенциальная функция; Л —постоянная интеграла
кинетической энергии.
Задачи данного типа необходимо решать в такой последова-
последовательности.
1. Выбрать систему координатных осей.
2. Составить схему сил, действующих на точку. В случае изу-
изучения движения несвободной точки, предварительно освободить, ее
от связей, введя действующие реакции.
3. Установить значение для vx и v0.
4. Составить уравнение (ХХ,23) или (XX, 24), из которого
определить искомые величины.
Для определения давления движущейся точки на неподвижную
поверхность в проекциях на прямоугольные координатные оси
исходят из уравнений:
(XX, 25)
N dj
f{x, у, г) «О, (XX, 26)
где
(
{dxj
(ду) + (дг) :
f(xy y> z) — уравнение наложенной связи; N — проекция ре-
реакции связи на орт нормали к поверхности n; kt— коэффициент
динамического трения.
Общие теоремы динамики материальной точки
383
Уравнения движения точки по неподвижной поверхности в про-
проекциях на касательную к траектории, нормаль к поверхности и пер-
перпендикулярное к ним направление имеют вид:
mv^Fv — k\N\
т — cos (я, \)
т — cos (тс, \)
(XX, 27)
где X — орт главной нормали, % — орт направления перпендику
лярного к плоскости, в которой расположены орты касательной г
и орт нормали к поверхности п.
Величины cos (Л, X); cos (i,, X) определяются на основании вспо-
вспомогательных формул дифференциальной} геометрии \
Из второго уравнения системы (XX,27) находим, что нормаль-
нормальное давление точки на поверхность равно сумме проекций ни нор-
нормаль к поверхности заданной силы и нормальной составляющей
силы инерции
- N
+ (— т —
cos
(XX, 28}
Для определения величин, входящих в состав формулы (XX,28),
чаще всего применяют теорему об изменении кинетической энергии
и «петербургский принцип» механики.
§ 8. Задачи
137. Поезд (рис. 137) движется со скоростью 36 км(час под
уклон, угол которого а = 0,008 радиан. В некоторый момент ма-
машинист начинает тормозить поезд. Сопротивление от торможения
и трения в осях составляет
0,1 веса поезда. Определить,
на каком расстоянии и через
какое время от момента на-
начала торможения поезд оста-
остановится, sin a = а.
Решение. Поезд рассма-
рассматриваем как материальную
точку, сосредоточив всю его
массу в центре тяжести М.
На точку Mt движущуюся по наклонной плоскости, действуют
сила тяжести Р, сопротивление Т и нормальная реакция R.
1Рашевский П. К., Курс дифференциальной геометрии, 1950, стр.
165—169.
К задаче 137.
384 Динамика
По уравнению (XX, 23), учитывая, что на точку действуют
постоянные силы, и принимая во внимание, что v = 0, получим
2
mv0
?- = (Psina — T)s, A)
где v0 = 10 м/сек — начальная скорость; s — искомый путь тор-
торможения.
Заметив, что
m = 4; Pi = Psin а = °'008 Р; Г==1^Р'
на основании A) найдем
S = 2 • 9,81 • 0,092 ^ 55'3* ^2)
Время торможения определим на основании теоремы об измене-
изменении количества движения
_ L. Vq = — р . 0,092 /, C)
т. е.
t== 9,81Ш0,092 -П,06 сек.
138. Сопротивление, встречаемое железнодорожной платфор-
платформой (рис. 138) при движении и происходящее от трения в осях,
равно 15 кг у а вес ее 6 т. Рабочий уперся в покоящуюся платформу,
и покатил ее по горизонтальному и прямолинейному участку пути,
¦О---О
с;
С,
'2
К задаче 138.
производя давление, равное 25 кг. Пройдя 20 м, он предоставил
платформе катиться самой. Вычислить, пренебрегая сопротивле-
сопротивлением воздуха и трением колес о рельсы, наибольшую скорость итах
платформы во время движения, а также путь р, пройденный ею до
остановки.
Решение. Будем рассматривать платформу как материальную
точку (рис. 138), предполагая всю массу ее М сосредоточенной в
«е центре тяжести С. Ось х расположим в направлении движения
вдоль рельсов, за начало отсчета х возьмем то положение Cv в
котором находилась точка С в начале движения. Платформа на-
начала двигаться без начальной скорости v0 = 0 и в конце движения
Общие теоремы динамики материальной точки 385
потеряла свою скорость ух=0, поэтому работа сил на пройденном
пути равна нулю.
Активйо приложенная сила производит работу на пути sx =
=а 20 м, сила же сопротивления действует на всем пути, поэтому
25 • 20 — 15 • s = 0, A)
откуда
s = 33, C) м.
Максимальную скорость. платформы определим на основании
формулы (XX, 23)
B)
т, е.
,ГкАА О (Л О 1
^0,808 м/сек. ^
Т~Т
139. Шахтная клеть (рис. 139) движется вниз со
скоростью Vq— 12 м/сек; вес клети Р = 6 т. Какую силу
трения между клетью и стенами шахты должен развить
предохранительный парашют, чтобы остановить клеть
на протяжении пути s = 10 му если канат, удерживаю- к зада-
щий клеть, оборвался. Силу трения считать постоянной. Че 139.
Решение. Рассматривая шахтную клеть как материальную точку
видим, что она движется под действием собственного веса Р и
силы торможения F.
Конечная скорость vx = 0, поэтому на основании теоремы о
кинетической энергии материальной точки находим
mv\
-— = (P-F)s, A)
откуда
или, переходя к числовым значениям,
F = 10,3 т.
§ 9. Задачи смешанного типа
140. Путь, по которому движется вагонетка, скатываясь с
точки А у образует разомкнутую петлю радиусом г (рис. 140);
г^ВОС == /^BOD = а. Найти, с какой высоты h должна скаты-
скатываться вагонетка без начальной скорости, чтобы она могла пройти
всю петлю, а также то значение угла а, при котором высота h наи-
наименьшая,
25 691
386
Динамика
Решение. На основании теоремы об изменении кинетической
энергии для материальной точки, учитывая, что последняя дви-
движется по идеальной связи, находим
mv2
a)]y A)
К задаче 140.
где v — значение скорости в
точке D.
Первая часть равенства A)
представляет собой работу
потенциальной силы тяжести,
которая равна произведению
силы на разность уровней, на
которых находилась движу-
движущаяся точка.
Пространство CD вагонет-
вагонетка проходит как свободная
материальная точка, двигаясь
под действием силы тяжести. Это движение совершается при на-
начальных условиях:
t == 0; vQx = v0 cos а; uOy = v0 sin a. B)
Вагонетка должна пройти путь по горизонтали CD, равный
# = 2rsina. C)
Уравнения движения, свободно движущейся точки имеют вид
х = vot cos a
у = —^ +
Движущаяся вагонетка достигнет точки С в момент времени,
2t'osin о
?==•
пройдя при этом путь
sin a cos a.
E)
Сравнивая формулы C) и E), приходим к соотношению
rg = vi cos a. . F)
Подставив в уравнение F) значение v% из формулы A), йаходим
G)
Высота h будет минимальной для тех значений а, для которых
да=Я *
Общие теоремы динамики материальной точки
387
т. е.
sin« —
(8)
м
или cos а = -^=» что соответствУет а =45°. Предположив, что
а = 0 из уравнения G), найдем решение для случая, когда
вагонетка движется по замкнутому кругу.
141. Груз М (рис. 141), подвешенный на пружине к верхней
точке А кольца, расположенного в вертикальной плоскости, па-
падает, скользя' по кольцу без трения. Найти, какова должна быть
жесткость пружины для того,
чтобы давление груза на кольцо
в нижней точке В равнялось
нулю при следующих данных:
радиус кольиа 20 см, вес груза
5 кг, в начальном положении
груза расстояние AM равно
20 еж и пружина не удлинена;
начальная скорость груза равна
нулю; весом пружины пренебре-
пренебрегаем.
Решение. На точку М в ниж- °
нем положении (в точке В) _ * задаче 1'*1-
действуют сила упругости пружины F и сила тяжести груза Р.
Если мысленно присоединить к указанным силам силу инер-
ции Jп, то вся система сил будет находиться в равновесии, т. е.
F-Jn-P = 0. A)
Упругая сила F равна сг9 так как удлинение пружины равно г.
Сила инерции Уп равна—, а скорость v определим на основании тео-
теоремы об изменении кинетической энергии. Заметим, что А О AM
равнобедренный. Работа упругой силы и силы тяжести равна
А = _-^1 + РгA + cos 60°).
B)
Применив соотношение (XX, 23), найдем
mv2 = г (— сг + ЗР),
а следовательно,
C)
D)
Принимая во внимание соотношение D), равенство A) приведем
к виду
сг — 2Р = 0, E)
откуда
с s=s 0,5 кг.
25*
388
Динамика
142. Точка массой т (рис. 142) движется по внутренней поверх-
поверхности цилиндра радиуса г.
Начальная скорость точки равна по величине v0 и составляет
угол а с горизонтом. Считая поверхность цилиндра абсолютно глад-
гладкой, а ось его вертикальной и учитывая действие силы тяжести, опре-
определить давление точки на цилиндр. Составить также уравнения
движения точки, если в начальный
момент точка находилась на оси.
-* Решение. Составим уравнения
движения точки по цилиндру. Сила
тяжести Р остается параллельной
оси цилиндра на протяжении всего
движения, а поэтому ее момент
относительно оси Oz равен нулю.
На основании первого следствия
из теоремы о моменте количества
движения следует, что
Л> = с, A)
где ф — угловая скорость вра-
вращательного движения вокруг оси
цилиндра.
Это вращательное движение
примем за переносное движение
точки М.
Так как в начальный момент
вектора скорости на направление, перпенди-
К задаче 142.
времени проекция
кулярное к радиусу цилиндра, равна
то
= v0 cos a,
с = rv0 cos а.
Из соотношений A) и B) находим, что угловая скорость враща-
вращательного движения постоянна и равна по величине
C)
Отсюда заключаем, что угол поворота, отсчитываемый от оси
Ох и прямой От, определяющей положение проекции точки М в
плоскости хОу равен
D)
Общие теоремы динамики материальной точки
Следовательно,
389
| Vn cos a
X = Г COS <р = Г COS ~
. Г v0 cos а ,1
(/= r$m<f = rsin -^— t\
E)
Ha точку М, кроме силы тяжести, действует еще реакция цилиндри-
цилиндрической поверхности. Составляя уравнение
mz = 2Z/,
получим
откуда
z = v0 sin a t -J- ~-. F)
Чтобы определить нормальное давление на поверхность, заметим,
что уравнение связи имеет вид
f = x2 + y2-r2 = 0. G)
На основании зависимости G) находим:
дх ' ду у* '
а поэтому уравнения (XX, 25) приобретают вид:
(8)
(9)
ту = N у
mz = mg
так как движение протекает по гладкой поверхности, коэффициент
трения равен нулю. Возведя в квадрат первое и второе уравнения
системы (9), принимая во внимание G), получим
N = т У х2 + у2.
На основании соотношений E)
а поэтому
N =
mc| cos8 a
A0)
(П)
A2)
390 Динамика
Этот же результат можно получить, исходя из следующих рас-
рассуждений. Разложим вектор скорости v на две составляющие:
трансверсальную v9, направленную по касательной нормального
сечения (окружности параллельной основанию цилиндра) к оси
Oz и иг параллельную оси Oz. Так как силы трения мы не учиты-
учитываем, то составляющая скорости vz не оказывает давления на по-
поверхность.
Принимая во внимание, что
v, = rb A3)
ибо cos (X, п) = 1, приходим к уже полученному результату A2).
ГЛАВА XXI
КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
§ 1. Свободные колебания
Движение точки массой т под действием упругой силы, изме-
изменяющейся по закону
F = - (Тсгх + ]с2у +Ъ3г), (XXI, 1)
где с{ — жесткость упругой среды в направлении трех координат-
1 = 1,2,3
ных осей, определяется решениями дифференциальных уравнений
пгх + сгх = 0
(XXI,2)
mz -f- czz = 0
Уравнения (XXI, 2) определяют свободные малые колебания
материальной точки без притока энергии извне. Составлены они
так, что начало отсчета помещено в точке, соответствующей поло-
положению статического равновесия сил, приложенных к колеблюще-
колеблющемуся телу.
Заменив упругую среду пружиной, введем ее статическое удли-
удлинение по формуле
В случае прямолинейного движения точки вдоль оси Oz, реше-
решение третьего уравнения системы (XXI, 2) представим в виде:
z a=s A sin (со/ + р) или z = a sin ш/ + Ь cos о>/, (ХХ1,4)
Колебательное движение материальной точки 391
где со — круговая частота колебаний, которая определяется по
формуле
а величины Лир находятся из начальных условий. Между Лир
и коэффициентами a, b существует связь:
= -?. (XXI.5)
За начальные условия примем следующие величины:
<==5; х = х09 х = х0. (XXI.6)
Период свободных колебаний находим по формуле
-. (XX 1,7)
Свободные колебания точки в плоскости определяются реше-
решением двух дифференциальных уравнений, входящих в систему
(XXI, 2).
§ 2. Затухающие колебания
Затухающие колебания точки, которые возникают в среде,
оказывающей сопротивление ее движению с силой прямо пропор-
пропорциональной первой степени скорости, определяются дифферен-
дифференциальным уравнением
х + 2пх + k\x =* О, (XX 1,8)
где
т ~~ т *
причем а характеризует сопротивление среды.
Напомним, что энергия точки при наличии затухающих колеба-
колебаний поглощается средой*
Общее решение уравнения (XXI, 8) имеет вид
х = АеГ"* sin (со/ + 8)> (ХХ1,9)
где (о — частота затухающих колебаний, определяемая по фор-
формуле
о, = yk* — п*. (XXI, 10)
Период этих колебаний находим по формуле
Т 2* (ХХ1Л1)
Амплитуду колебаний А и сдвиг фаз 8 определяют на основании
начальных условий.
392 Динамика
Декремент затухания, выражающий отношение амплитуд двух
последовательных размахов колебания, находится по формуле
А , пт
? = -*±L = e—Г . (XXI, 12)
Лп
Для вычислений пользуются логарифмическим декрементом зату-
затухания
--^1. (XXU3)
§ 3. Вынужденные колебания
Вынужденные колебания точки под действием возмущающей
силы, определяются дифференциальным уравнением
(XXI, 14)
где
*¦ = -?-.
пг
В случае периодически изменяющейся силы по закону
Q(f) = H sin {pt + 5), (XXI, 15)
при k Ф р и начальных условиях (XXI, 6) решению уравнения
(XXI, 14) придают вид
х = х0 cos kt + ~ sin kt + k2^_ 2 (sin Ь cos kt -f
+ 4-cos 8 sin kt) + b2 h 8 sin (pt + 8), (XXI, 16)
где
При совпадении частот свободных колебаний й и вынужденных
колебаний р, т. е. когда имеет место резонанс, решение уравне-
уравнения (XXI, 14) представляют в виде
2F (XX1,17)
В случае, когда на точку действует периодическая сила общего
вида
со
QV) = y°o + 2 н*sin W + 8«) (XXI, 18)
Колебательное движение материальной точки 393
решение уравнения (XXI, 14) представляется в форме
х = х0 cos kt + -~- sin kt —
— 2] ^ ^S2P2 (sin 8t cos &/ + ~ cos 8, sin kt j -f
^V sin (s/?/ + *•>• (ХХЫ9>
где
н8
При наличии равенств
k == пр
и п = s имеет место резонанс п-го порядка.
Решение уравнения (XXI, 14) в случае резонанса п-го порядка
определяют в виде
х = х0 cos kt -f -^- sin kt + -7^- cos 8Я sin kt —
~~~Ш * cos ^ + ^ ~ ^J fe2_gs2 2 (sin 8, cos A/ -f
8=1
+ ~- cos8e sin^J -f V __*2 a sin (sp + 8e). (XXI,20)
8=1
В случае какой угодно возмущающей силы решение уравнения
(XXI, 14) определяют в виде
t
х = х0 cos kt + ^ sin kt + A J Q(x) sin kit — x) dx. (XXI,21)
о
Если точка совершает колебания в сопротивляющейся среде
при наличии возмущающей силы вида
Q(t) = Н sin (р/ + 8)»
то ее движение определяется дифференциальным уравнением
х + 2пх + k2x == h sin (pt + 8), (XXI,22)
где
m tn tn
394 Динамика
В случае малого сопротивления решению уравнения (XXI, 22)
при начальных условиях (XXI, 6) придают вид:
х = e~nt
_ е-т ¦ * _. |sin(S — e) cos V& —
sin (p/ + 5 — в). (ХХ1.23)
Коэффициент динамичности.определяем по формуле
J (XXI.24)
§ 4* Методические указания к решению задач
Задачи по теории колебаний решаются в такой последова-
последовательности.
1. Определяем положение статического равновесия, т. е. на-
находим Хст. Начало координат помещаем в точке статического равно-
равновесия сил, и указываем координатные оси.
2. Составляем схему сил и определяем вид колебаний, в кото-
которых находится материальная трчка.
3. Устанавливаем начальные условия. В задачах на определе-
определение вынужденных колебаний нет надобности находить начальные
условия движения.
4. Составляем дифференциальное уравнение движения в форме
(XXI, 2), или (XX 1,8), или (XXI,14), или (XXI, 22) в зависимости
от рода колебаний.
5. Интегрируем полученные уравнения. Решая вопрос о перио-
периоде колебаний можно не интегрировать дифференциальные уравне-
уравнения, а пользоваться соответствующими формулами, указанными
выше. Определяя вынужденные колебания находят частные реше-
решения дифференциальных уравнений, определяющих движение.
§ 5. Задачи
143. При равномерном спуске груза (рис. 143) весом Q =2 т
со скоростью v = 5 м/сек произошла неожиданная задержка верх-
верхнего конца троса, на котором опускали груз, в результате защем-
защемления троса в обойме блока. Пренебрегая весом троса, оцределить
Колебательное движение материальной точки
395
наибольшее натяжение его при последующих колебаниях грузи,
если коэффициент жесткости троса с = 4 т/см.
Решение. Поместим начало координат в точке, соответствующей
положению статического равновесия, для которой
. Q = сХст. A)
Направим координатную ось по вертикали вниз. Начальные
условия движения следующие:
; = 0; *0 = 0; хо = 5. B)
Дифференциальное уравнение движения груза
запищем в форме (XXI, 2)
mx = Q — с(Хст + х). C)
Принимая во внимание уравнение A), получим .-?
Решение уравнения (З) представим в форме
х = A cos V ~ t + В sin у ¦—- L E)
Удовлетворяя начальным условиям, находим
с м Q . л! eg . tfs К задаче 143.
х = о V/ — sin у -Q- Л F)
Для определения максимального натяжения троса применяем
«петербургский принцип», согласно которому
G)
На основании F)
Подставив числовые значения в уравнение (8), получим
Гтах = 2 A + 0,51 . 44,16) « 47,1 т.
144. Груз Mt подвешенный к неподвижной точке А на пружине
(рис. 144), совершает малые гармонические колебания* в верти-
вертикальной плоскости, скользя без трения по дуге окружности, диа-
диаметр которой АВ равен / (натуральная длина пружины а); жесткость
пружины такова, что при действии силы, равной весу груза М,
она получает удлинение, равное Ь. Определить период колебаний
в том случае, когда / = а + Ь\ массой пружины пренебрераем и
считаем, что при колебаниях последняя остается растянутой.
396
Динамика
Решение. Положение пружины определяем углом наклона q> ее
средней линии к вертикали.
Необходимо определить этот угол как функцию от времени.
Удлинение пружины
d = {a + 6)coscp— а = Ь cos9 — 2аsin2 -i . A)
Для упругой силы, имеющей направление, указанное на рисунке,
находим
F = с (b coscp — 2а sin2
B)
К задаче 144
Составим дифференциальное уравнение
движения точки М в проекциях на каса-
касательную, тогда
?.-?=F.sin?-.P.sin2?. C)
Принимая во внимание уравнение B), а
также то, что
v = у 2<р = /<р,
уравнение C) перепишем в виде
pi- ?«=¦—- sin 2<p — 2а с sin2|- sin 9 — Р - sin 2cp. D)
Так как в положении равновесия
Р =cb,
то при малых углах ф на основании выражения D) приходим
к уравнению
Т + -f Т = 0- E)
Решение уравнения E) имеет вид
<р= Asi
и искомый период колебаний определяется по формуле
T = 2*yi. F)
145. Материальная точка весом Р подвешена к концу нера-
нерастянутой пружины с коэффициентом жесткости с г/см и отпущена
с начальной скоростью v0 см/сек, направленной вниз. Определить
уравнение движения и период колебаний точки, если в момент
времени, когда точка находилась в крайнем нижнем положении,
к ней прикладывают силу Q = const, направленную вниз.
Колебательное движение материальной точки 397
Решение. Начало координат выберем в положении статического
равновесия, для которого
сХст = Р, A)
т. е. на расстоянии Хст = — от конца нерастянутой пружины.
с
Начальные условия движения имеют вид:
t = О, х0 = — Хст, х0 = v0. B)
Решение дифференциального уравнения колебаний
x + fx = 0, C)
удовлетворяющее начальным условиям B), определяется в виде
x = -XOTcosYf t+% sm]jft, wek = ^~f D)
ИЛИ
*-/(*r+(W-»(Y?'-'.)-
нричем
tg'i-~. E)
Определим время, затраченное на движение точки от равновес-
равновесного положения до момента приложения возмущающей силы Q.
Крайнему нижнему положению, груза соответствует
X = Лст,
поэтому
^Yf F)
Уравнению F) легко придать форму
Сравнивая зависимости E) и G), видим, что
= tv (8)
Отсчет времени будем вести с момента приложения груза, тогда
J^t — х (9)
и уравнение D') примет вид
Динамика
Движение груза под действием упругой силы и постоянной силы Q
определяется дифференциальным уравнением
x cx + Qt
которое необходимо решить при начальных условиях:
0; *0 = j/(^J+(?
A1)
A2)
Общее решение уравнения A1) имеет, вид
*=..§- +Л cos yff + fislny^f. A3)
Удовлетворив начальным условиям A2) находим
*-¦§¦+
Уравнение A4) показывает, что груз находится в гармонических
колебаниях, период ко1горых
Т = 2* yZ. A5)
146. Цилиндр весом Р радиусом г см и
высотой h см (рис. 146, а) подвешен на
пружине АВ, верхний конец которой В
закреплен; цилиндр погружен в воду.
В начальный момент времени цилиндр был
погружен в воду на 2/з своей высоты и
затем без начальной скорости пришел в
движение по вертикальной прямой; в по-
положении равновесия цилиндр погружается
в воду на половину своей высоты; считая
жесткость пружины, равной с г/см, и пред-
предполагая, что действие воды сводится к до-
бавочной архимедовой силе, определить
движение цилиндра относительно положе-
положения равновесия, если сопротивление воды пропорционально пер-
первой степени скорости и равно av. Принять объемный вес воды
равным 7 г/сум3.
Решение. Выталкивающая сила воды определяется по фор-
формуле
К задаче 14Ь.
i*
б
где х — величина углубления цилиндра в воду из равновесного
положения.
Колебательное движение материальной точки 399
Статическое удлинение пружины найдем из условия равнове-
равновесия упругой силы пружины, силы тяжести цилиндра и выталки-
выталкивающей силы воды при х = О
сХст = Р~ т*г*А. B)
Из условия задачи вытекает, что начальная амплитуда коле-
колебаний равна:
а°~ h \ъ ~ ~2/ e ?"
На движущийся в жидкости цилиндр, кроме упругой силы /\
силы тяжести Р, выталкивающей силы воды Ф, действует сила
сопротивления воды R = ах (рис. 146, б).
Цилиндр движется поступательно, его положение определяется
координатой х? определяемой из дифференциального уравнения
•j х = — ai — с(х + Хст)—Ф(х) + Р, D)
или
х + 2пх + k4 = 0, E)
где
.— = /71; т^~=-п\ fe2 = i (с + чъг2).
g 2т т v ' * '
Составив характеристическое уравнение, видим, что
и движение цилиндра буцет колебательным, если
& — п* = — {с + Тиг2) — 4- (—J>0. F)
Считая, что условие F) выполнено, находим
х = ^-n( (A cosVn2 — ^2 / + В sin /я» —ft2/). G)
Постоянные интегрирования А и В определим, исходя из началь-
начальных условий:
Тогда
Преобразуя постоянные
находим
h k
х = ?;т== e~nisin [V& -пЧ + $\ (9)
400 Динамика
где
tgp= Ук%~п% . (Ю)
Рассматривая движение в среде без сопротивления, т. е. при ус-
условии п = 0, имеем на основании уравнений (9) и A0)
(И)
Z О
147. Тело весом 5 кг подвешено на пружине, коэффициент
жесткости которой равен 2 кг/см. Сопротивление среды пропор-
пропорционально скорости. Амплитуда после четырех колебаний умень-
уменьшилась в 12 раз. Определить период колебаний и логарифмический
декремент затухания.
Решение. На основании известной формулы для амплитуды
затухающих колебаний (XX 1,12) имеем
а8 = aQe A)
Так как
~-=12, то /1-^ = -^- = 0,3106. B)
Обозначим
и исключим Т из формулы для периода затухающих колебаний
о—
Т =
при помощи соотношения C), тогда
Так как
**=f, (б)
формулу D) перепишем в виде
Подставив числовые значения в уравнение D'), получим
п* = 2-°80-«».1(Г' в 378 ^
5(9,86+965-1U) ^87
Согласно формуле C)
^ 6.28 6,28
0,318 сек.
Колебательное движение материальной точки
401
148. На пружине жесткостью с = 20 г/см (рис. 148, а) под-
подвешены магнитный стержень весом 50 г, проходящий через соле-
соленоид, и медная пластинка весом 50 г, проходящая между полюсами
магнита. По соленоиду течет ток i = 20 sin 8тг/ и дает силу взаимо-
взаимодействия с магнитным стержнем F — 16тг 1дн. Сила торможения
медной пластинки вследствие вихревых токов равна kv<P2, где k =
= Ю-4, Ф = 1000 ]/5 единиц CGS и v —- скорость пластинки.
Определить вынужденные колебания пла-
пластинки.
Решение, Обозначим силу тяжести маг-
магнита йерез Pi, а силу тяжести пластинки
через Р2.
Статическое удлинение пружины
Л
5 см.
A)
Сила взаимодействия тока с магнитом вы-
выражена в физических единицах; чтобы пе-
перейти к техническим единицам измерения,
заметим, что
1 г : 981 см/сек = 1 дин.
B)
Пластинка и магнит находятся в поступатель-
поступательном движении. Считая, что центр инерции си-
системы движется прямолинейно, введем ось
Ох, поместив ее начало в положение стати-
статического равновесия и составим схему сил Юадаче 148
(рис. 148, б).
Для сил, приведенных на схеме, введем обозначения:
500 -
!== х;
320 ~ sin
Ft = ex.
C)
В данном случае движение пластинки определяется дифферен-
дифференциальным уравнением
х + Ъх + \96х = 10,048 sin 8itf. D)
Вынужденные колебания не зависят от начальных условий движе-
движения и представляются частным решением уравнения D)
х = а • cos 8тг/ -)- 6 • sin 8nt. |5)
Подставив выражение E) в уравнение D) и сравнив коэффи-
коэффициенты при sin 8?;/ и cos 8ти^, придем к системе линейных алгебраи*
26 591
402 Динамика
ческих уравнений относительно а и Ь.
+ 40тга + A96 — 64*2)& = 10,048 \
A96 — 64 *2)а + 40*6-=0 Г
корни которой
а = 0,006336 и Ь = — 0,022. G)
На основании уравнений (XXI, 5) и G) находим:
A ss-0,022: tg a = ~ = 0;288, (8)
в силу чего уравнение E) принимает вид
XQ*— 0,022 sin (8тс* + 0,09 к) (9)
или
х ^ 0,022 sin (8 Kt — 0,91 тс).
149. Статический прогиб рессор груженого товарного вагона
ДХСТ а= 5 см. Определить критическую скорость движения ва-
вагона, при которой начнется «галопирование» последнего, если на
стыках рельсов вагон испытывает толчки, вызывающие вынужден-
вынужденные колебания вагона на рессорах, длина рельсов / = 12 м.
Решение. Товарный вагон представим материальной точкой.
Статический прогиб рессор
4
где Р — вес груженого поезда. На указанную точку действует
упругая сила рессор
F = c(MCT + x) B)
и периодически изменяющаяся возмущающая сила
Фх = A sin tat, C)
где о = -=г; Т — время, затрачиваемое на одно колебание и рав-
равное
Движение точки определяется дифференциальным уравнением
x + -^-x=^-sinoyt. D)
СТ
Галопирование возникает при совпадении частоты возмущаю-
возмущающей силы и частоты свободных колебаний, т. е.
Таким образом
/ Т" 12.14-3600
= 96 км>час'
Сложное движение материальной точки 403
ГЛАВА XXII
СЛОЖНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
§ 1. Методические указания к решению задач
Задачи на сложное движение материальной точки рекомендуем
решать в следующей последовательности.
1. Выбрать подвижную систему координат О^с.
2. Найти ускорение точки в переносном движении we и пово-
поворотное ускорение
wc = 2ue xvr. (XXII,1)
3. Определить силу инерции в переносном движении
Je = -mwe (XXII,2)
и поворотную силу инерции
7е = — tnwc. (XXII,3)
4. Изучить движение несвободной материальной точки предва-
предварительно освободив ее от связей и заменив их реакциями, после
чего составить схему сил.
5. Установить начальные условия движения.
6. Составить и проинтегрировать систему дифференциальных
уравнений относительного движения;
m^^+J' + J' . (ХХИ,4)
7. Изучая относительное равновесие, исходить из системы урав-
уравнений:
Ft + Л = 0
(XXII.5)
Fc + Л = 0
Заметим, что основные теоремы динамики, установленные для
неподвижной координатной системы,, можно сформулировать' в
прежней форме и для относительного движения, учитывая* наряду
с внешними приложенными силами, дополнительно силы инерции
Iе и 7е. ,
Например, теорема об изменении кинетической энергии в диф-
дифференциальной форме имеет вид: ,
^jdr. - (ХХП,6)
26*
404
Динамика
Второй член правой части уравнения (XXII, 6) определяет
работу сил инерции переносного движения на элементарном пере-
перемещении.
§ 2. Задачи
150. Железнодорожный поезд движется со скоростью 15 м/сек
по рельсам, проложенным по меридиану с юга на север (рис. 150).
Вес поезда 2000 т. Определить боковое
давление поезда на 'рельсы, когда он
движется с севера на юг.
Решенае. В данной системе коорди-
координат вектор угловой скорости о> вращения
Земли направляем по оси вращения
вниз. Поезд находится в сложном дви-
движении. Переносное движение поезда
совершается так, что силы инерции в
этом движении не оказывают боковых
давлений на рельсы. Боковые давления
вызываются поворотными силами инер-
инерции Г, которые существуют благодаря
наличию относительной скорости поезда
v^ направленной нами к северному
полюсу Земли,
уравновешивается реакцией рельс R,
К задаче 150.
Давление на рельсы
т. е.
— Jc
Из соотношения A) находим
0. A)
B)
Направление давления на рельсы находим согласно правилу
для векторного произведения vr x о> и приходим к заключению,
что оно передается на правый восточный рельс, т. е. так, как пока-
показано на рисунке.
Для точки, движущейся с севера на юг, давление
2Р - -
— (ОХИ,
C)
и приложено к правому западному рельсу.
Модуль силы давления
д/ = —- а) • vr sin (to, vr).
Сложное движение материальной точки
405
Подставив численные значения, получим
N
4-1000-6,28-1000
15
^ 384,6 кг.
9,81-24-60-60
151. В вагоне, движущемся по прямому горизонтальному пути,
маятник (рис. 151, а) совершает малые гармонические колебания,
причем среднее его положение остается отклоненным от вертикали
на угол 6°. Определить ускорение w вагона и найти разность перио-
периодов колебаний маятника Т — в случае неподвижного вагона и
и Тг — в данном случае.
<pw 7' Г-
К задаче 151
Решение. В среднем, отклоненном от вертикали положении
маятника существует относительное равновесие сил инерции У,
веса Р и натяжения нити 7\
Треугольник, построенный на этих силах (рис. 151, б), замк-
замкнут. Из треугольника PTJ находим
tg«--i—?¦
(i)
Из уравнения A) определяем ускорение движения вагона
w = 9,81 tg6° = 9,81 • 0,1051 = 103,1 см/сек. B)
Период колебаний математического маятника с покоящейся
точкой привеса равен
Для определения периода колебаний маятника с подвижной
точкой привеса составим дифференциальное уравнение движения в
проекциях на касательную:
Р Р
— fy = — Р sin (a -f (р) -| w cos (а + ср),
C)
406
Динамика
где ф — угол отклонения маятника от равновесного положения
при колебаниях.
Принимая во внимание, что:
sin (а + <р) s sin 6° + ср cos 6° \
cos(oc + cp) ^cos6° — cpsin6° jf
a также зависимость B), приведем уравнение C) к виду
+ / cos 6° <Р = 0-
Т + / cos 6 Р
Значит, период колебания маятника равен
гр о V / • COS6°
1 = g '
Окончательно
D)
E)
Тг — Т = Т A — у cos6°) = Т • 0,0028.
152. Для измерения ускорения поршня паровой машины при-
применяется прибор, состоящий из подвижной тележки А (рис. 152, а)
и равномерно вращающегося
'/////////Ж/////Л'' 4VQs =—rr—% барабана D, жестко скреп-
скрепленного с крейцкопфом. Те-
Тележка весит Q кг и благодаря
особым направляющим совер-
совершает поступательное движе-
движение, при котором конец за-
закрепленного на тележке ка-
карандаша описывает прямую,
параллельную оси штока.
Тележка А связана с крейц-
крейцкопфом пружиной В, жест-
жесткость которой с кг/см. Часовой механизм вращает барабан с
угловой скоростью (о=1/сек, радиус барабана г см. Найти урав-
уравнение кривой, вычерчиваемой карандашом на ленте барабана,
если движение крейцкопфа относительно его направляющих выра-
выражается уравнением
х = а + I cos 2/,
где а—некоторая постоянная, зависящая от выбранного начала
неподвижной системы координат; / — ход поршня, 2 — угловая
скорость махового колеса паровой машины.
К задаче 152.
Решение. Введем подвижную координатную систему О^ по-
поместив ее начало в нейтральном положении крейцкопфа. Перенос-
Переносное пцступательное движение крейцкопфа будем определять коор-
координатой х. К тележке приложена (рис. 152, б) упругая сила пру-
пружины
F = с\
Сложное движение материальной точки 407
и опорные реакции, которые на рисунке не показаны, так как они
не расположены в плоскости ?0*], а величина силы инерции оп-
определяется по формуле
Движение точки барабана D, с которой совпадает штифт С,
определяется на основании дифференциальных уравнений относи-
относительного движения
Первое уравнение системы A) перепишем в развернутом виде так
S+^ii^lQtcosQt. B)
Частное решение уравнения B) будет
C)
Подставив уравнение C) в уравнение B), определим Ах
Принимая во внимание, что решение однородного уравнения
можно представить в виде
где А и В — постоянные, определяемые по начальным данным,
заключаем, что решение уравнения C) выглядит так
D)
Интегрируя второе уравнение системы" A), находим
т)~гг const. E)
Учитывая, что относительная скорость штифта, движущегося
по поверхности барабана D, равна /?о>, найдем
•г; = Rut + const F)
408
Динамит
Считая, что при / = 0 штифт самописца находится на оси О?,
имеем
т] = Ro>L G)
Исключая параметр t из уравнений D), G) , определим уравне-
уравнение траектории описываемой штифтом на поверхности барабана D.
153. Артиллерийский снаряд (рис. 153) движется по настиль-
настильной траектории (т. е. траектории, которую можно приближенно
считать горизонтальной прямой). Горизонтальная скорость снаряда
во время движения vQ = 900 м\сек. Снаряд должен поразить цель,
отстоящую от места выстрела на расстоянии 18 км; стрельба проис-
происходит на северной широте Х = 60°. Опре-
Определить, пренебрегая сопротивлением воз-
воздуха, насколько снаряд отклонится от
цели вследствие вращения Земли.
Решение. Поворотное ускорение,
действующее на снаряд, имеет величину
wc = 2n)Vr sin X A)
и перпендикулярно к меридианной плос-
плоскости, в которой движется снаряд.
Введем подвижную координатную
К задаче 153 систему O?tqC, направив ее оси, как
указано на рисунке, и поместив начало
координат в начальном положении снаряда. Снаряд движется под
действием силы тяжести Р.
На основании дифференциальных уравнений относительного
движения (XXII, 4) после проектирования всех сил. на ось Оч\
найдем
гщ = 2mtDprsinX. B)
Интегрируя уравнение B), получим
C)
Снаряд отклонится вправо (если смотреть на него сверху), пер-
перпендикулярно к скорости, на величину \т\\ независимо от направле-
направления стрельбы (на юг или север, вдоль меридиана).
Пройденный путь вдоль оси О\ равен
а поэтому
hi
О)/2
sinX
2тс.182-10в/3
24-36-9-LM04
\ 22,66 м
Основы кинетостатики 409
РАЗДЕЛ ВТОРОЙ
ДИНАМИКА МАТЕРИАЛЬНОЙ СИСТЕМЫ
ГЛАВА XXIII
ОСНОВЫ КИНЕТОСТАТИКИ
§ 1. Методические указания к решению задач
«Петербургский принцип» для системы материальных точек
формулируется так.
Если мысленно предположить, что система материальных точек
остановлена, и, кроме действующих сил и реакций, к каждой точке
ее приложены силы инерции, то в любой момент времени система-
сил будет уравновешиваться.
Силы инерции определяются по формуле
7, = —т,а>, (XXIII, 1)
/ = 1, 2, ... , п.
где ~Wj — ускорение /-ой точки. В задачах, рассматриваемых ниже,
ускорения точек системы задаются либо непосредственно, либо
находятся по законам движения точек.
Пусть материальная точка массой mj движется под действием
внешних и внутренних сил, равнодействующую которых обозна-
обозначим через Fb и реакции связей /?7, тогда
F, + Я + 7, = 0. (ХХШ,2)
Обозначим проекции силы на направления координатных осей
Охуг через Xjy Yh Z,, а для силы R1 — Rja:, RW4 Rn, тогда уравне-
уравнения (XXIII, 2) эквивалентны системе
Y, + Riy - mjyi = 0
(ХХШ.З)
/=1, 2, .„п.
Если при решении за^ач применяют натуральный способ задания
движения, то система уравнений (XXIII, 2) эквивалентна следую-
следующей системе:
do4
(ХХШ,4>
410
Динамика
где т-орт касательной к траектории /-ой точки; я-орт главной
нормали.
Если материальная система представляет собой абсолютно твер-
твердое тело, то уравнения равновесия перечисленных сил состав-
составляются в форме
/? = 0; L0 = 0, (XXIII.5)
где R — главный вектор внешних приложенных сил, реакций свя-
связей и сил инерции; Lo— их главный момент, вычисленный относи-
относительно произвольной точки.
Задачи этого раздела необходимо решать в такой последова-
последовательности.
1. Определить ускорения всех точек системы.
2. Составить схему всех действующих сил на точки системы.
Если изучается движение несвободной системы, то ее необхо-
необходимо освободить от связей, заменив их реак-
циями #,.
3. Присоединить к перечисленным выше силам,
силы инеРции •V» / =.1.2,...,/г.
4. Составить уравнения равновесия сил в
форме (XXIII, 3) либо (XXIII, 4), (XXIII, 5).
5. Привести составленную систему уравнений
к расчетному виду и определить из нее искомые
величины.
л*
\Q
§ 2. Задачи
154. Для исследования влияния быстро чере-
чередующихся растягивающих и сжимающих сил на
3 металлический брусок Л, последний (рис. 154, а)
прикрепляют верхним концом к ползуну В криво-
б шипного механизма ВСО, а к нижнему — под^
вешивают груз Q. Найти силу, растягивающую
J брусок в том случае, когда кривошип ОС вра-
о щается вокруг оси О с постоянной угловой ско-
К задаче 154. ростью со, и вес груза Q равен Р.
Решение. Освободив груз Q от связи, заменив ее реакцией Т,
а также присоединив к нему силу инерции У, получим фиктив-
фиктивное равновесие сил Р, Г, У. Груз движется вниз замедленно, поэ-
поэтому ускорение движения направлено вверх (рис. 154, б), а сила
инерции по направлению совпадает с силой Р. Составив условие
равновесия сил, получим
T = P + ±w. A)
Основы кинетостатики
411
Ускорение любой точки груза Q равно ускорению точки В,
закон движения которой имеет вид
хв = г cos Ы + / у 1 — rjj sin2 tat. . B)
Разложив 1/ 1 — (~j sin2 ш/ в ряд по степеням у, найдем
C)
w = хв = — гаJ (cos to/ -f у cos2шЛ.
Следовательно, сила, растягивающая брусок, изменяется по
закону
D)
Т = Р + — (cos (о/ + 7 cos 2ut) гоJ.
155. Лебедка, поднимающая груз В весом 2 т, поставлена
яа балке (рис. 155, а), опирающейся на опоры С и D; CD = 3 м,
АС = 3 ж. Груз В поднимается равноускоренно с ускорением
0,5 м/сек2. Найти добавочные давления на опоры С и Dot силы
инерции груза, учитывая массу барабана лебедки, если радиус
барабана г = 50 см,, а момент инерции относительно оси вращения
барабана равен 0,8 кГм . сек2.
К задаче 155.
Решение. На точки системы действует одна активная сила Р~—
вес груза В,
Присоединим к точкам системы силы инерции.
К грузу В приложим силу инерции
7, = ——ад. m
a w' V1/
412 х Динамика
Барабан лебедки можно представить состоящим из однородных
круглых дисков радиуса /?, толщиной, равной единице, и имеющих
р
вес т-, где h — длина барабана.
Как видно из рис. 155, б, касательные силы инерции, прило-
приложенные к элементарному кольцу, выделенному в диске, образуют
пару сил.
Момент пары касательных сил инерции диска является свобод-
свободным вектором, величина которого
о
Момент касательных сил инерции для всего барабана
= JlL9 C)
где J =^j-PR2 — момент инерции барабана; w — ускорение точ-
точки В.
Освободим балку от связей, заменив их действие реакциями
#с и Яд-
Силы инерции реально приложены к опорам С и D.
Дополнительные давления на опоры возникают за счет сил
инерции и для их определения рассмотрим равновесие сил, указан-
указанных на рис. 155, в.
Для равновесия этих сил должны выполняться условия:
0; 2?л(/ч) =0, D)
которые в развернутом виде выглядят так:
j . з — М-/?1)а) -8=0;
. —у. 5— М + 1$Р-8 -0. ( )
Дополнительные давления на опоры равны:
Л/с = -^а); Nry^-Rff F)
и их числовые значения определяются из уравнений E):
156. Маятник центробежного регулятора (рис. 156, а) делает
при установившемся движении 180 об/мин. Вследствие, измене-
изменения нагрузки машины регулятор приведен в действие, и шары разд-
раздвигаются с относительной скоростью и = 0,2 м/сек. Считая вес
Основы кинетостатики
413
каждого шара равным 10 кг и пренебрегая весами ручек, вычислить
дополнительное давление на подшипники Сг и С2, вызываемое ко-
риолисовым ускорением. При этом следует считать угол, образуе-
образуемый ручкой с осью регулятора, равным 45° и число оборотов
не изменившимся; размеры
подвески взять с рисунка.
Решение. Поворотная
сила инерции
2Р
g
Г =
: sin 45°
A)
К задаче 156.
и направлена по перпен-
перпендикуляру к плоскости, в
которой расположены век-
векторы п и п.
Освободим стержень ОА
от связей, стержня ВС и
подшипников Сг и С2, за-
заменив их реакциями.
Введем координатные
оси Ог и Ох, расположив
их в плоскости стержней
ОА и ВС.
Составляя на основании «петербургского принципа» уравнения
равновесия, замечаем, что ни ь одно из них силы R и Jc не входят
одновременно, а это значит, что сила Jc не оказывает влияния на
реакцию R.
Дополнительные давления на подшипники Сг и С2 от силы Jc
найдем, предварительно определив реакции Х(
четырех уравнений равновесия:
ЕХ- = 0* SZ- = 0*
v / п« v г п
Уравнения B) в явном виде выглядят так:
XCl + Хс2 = 0 | .
ZCl + ZCl = U Г
, Лл . iLл , ^/^ ИЗ
B)
- ХСх ~
Jcl sin 45° = 0
C;
Первые два уравнения системы C) показывают, что дополни-
дополнительные реакции образуют пару сил.
414 , Динамика
Из системы уравнений C) вытекает, что
|XCi|=jZCil = |XCi-| = |ZCi|-y-isin46e D)
и, следовательно, дополнительное давление
Т+гГ-У--?- E)
Из формул D) и E) вытекает, что дополнительные давления
направлены вдоль стержня, поэтому эту задачу можно решить,
сведя вопрос к изучению равновесия системы сил, расположенных
в плоскости, содержащей стержень ОА и силу Jc.
Принимая во внимание соотношения A) и E), получим
N = -~uw sin 45°, F)
откуда после подстановки числовых значений определим
„ 2-10-25 о~ c V2 г л о
^ = 20б1Г 542 «*
ГЛАВА XXIV
ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ
§ 1. Методические указания к решению задач
Под возможным перемещением точек системы понимаем их одна
временное элементарное перемещение, допускаемое в данный мо-
момент связями. Если материальная то^ка находится на поверхности
или на кривой, то возможные перемещения лежат в касательной
плоскости к поверхности или на касательной к кривой.
Если твердое тело имеет неподвижную точку, то возможным
перемещением точек Тела будет вращение вокруг мгновенной оси*
Положение точек системы определяется обобщенными координатами,
количество которых равно числу степеней свободы.
s Число степеней свободы определяется наименьшим количеством
дополнительных связей, которые нужно наложить на все точки
системы, для того, чтобы они остались неподвижными по отноше-
отношению к некоторой относительно неподвижной координатной системе.
Число независимых возможных перемещений системы называется
числом ее степеней свободы.
Связи называются идеальными, если сумма работ реакций удер-
удерживающих связей, совершаемых на возможных перемещениях
точек системы, равна нулю. Принцип возможных перемещений
формулируется так.
Для равновесия системы материальных точек, на которую на-
наложены идеальные стационарные удерживающие связи, необхо-
Принцип возможных перемещений 415
димо и достаточно, чтобы сумма элементарных работ всех действую-
действующих на систему активных сил при всяком возможном перемещении
была равна нулю.
п
?i. 4)«0f (XXIV, 1)
где F{ — активно приложенные силы; е^ — вектор бесконечно ма-
малого перемещения точки приложения силы F{.
Если конструктивное оформление связей таково, что точки
системы не могут покинуть их, то эти связи называются удержи-
удерживающими и выражаются уравнен/иями:
fk(xv уь zv х2, у2, г2,..., хп, уП1 zn) = О (XXIV,2)
& = 1, 2,..., т.
М. В. Остроградский распространил этот принцип возможных пере-
перемещений для случая, когда на систему наложены нестационарные и
неудерживающие связи.
Связи называются неудерживающими, когда точки системы
могут их покидать. Эти связи определяются неравенствами вида:
h (*i, Hv zv Ч> Уъ 22> - » *п\ Уп> *)
или
/*(*i. Vv zv х* Уъ> **-> *п> Уп> гЛ)>0. (XXIV,3)
Если среди связей есть односторонние связи, а система находится
в равновесии, то сумма работ, произведенная на возможных переме-
перемещениях, должна быть меньше нуля
ll8si)<0. (XXIV.4)
Задачи этого раздела необходимо решать в такой последователь*
ности.
1. Определить число степеней свободы сцстемы и выбрать обоб-
обобщенные координаты.
2. Составить схему внешних приложенных сил. Если требу-
требуется определить силы, действующие внутри абсолютно твердого
тела, то пользуются методом сечения, с помощью которого бнутрен-
ние силы переводятся в разряд внешних сил.
3. Определить возможные перемещения точек приложения внеш-
внешних сил. Если из условия задачи возможно определить коорди-
координаты точек приложения активных сил, а также найти связи, суще-
существующие между обобщенными координатами, то ими нужно поль-
пользоваться для определения возможных перемещений.
416
Динамика
4. Составить уравнения работ в форме (XXIV, 1) или в виде
' П
^ (Х{Ьх, + КС6#, + л^агу =0. {ХХ\ 1,5)
5. Приравнять нулю коэффициенты в выражении работ при неза-
независимых возможных перемещениях.
6. Из полученной системы уравнений найти искомые величины.
$ 2. Задачи
157. На рис. 157 приведена схема машины для испытания об-
образцов на растяжение. Определить зависимость между усилием X
в образце К и расстоянием х груза Р от его нулевого положения 0,
если при помощи груза Q машина
уравновешена так, что при нуле-
нулевом положении груза Р и отсут-
отсутствии усилия в /С все рычаги гори-
горизонтальны. Даны расстояния 1г
/2 и е.
Решение. Стержень / имеет
одну степень свободы и его поло-
положение определим углом <рг. Стер-
Стержень 2 также имеет одну степень
свободы и его положение зададим
углом ср2.
Нулевое положение груза Р определим расстоянием /н, а
положение груза Q зададим числом /3.
Найдем перемещение точек Л, В, С, О,
''///7/7//////////////
К задаче 157.
?С =
A)
Считая, что все связи идеальные, на основании принципа воз-
возможных перемещений находим
Сдвинем груз Р из положения равновесия на расстояние ху
вследствие чего в образце К появятся усилия X, величина которых
равна реакции стержня 3.
Точки D и Е имеют перемещения:
Sp = ?$<pj_; ?% = (/4 ~f~ *^)^p2 V '
и, следовательно, на основании принципа возможных перемеще-
перемещений
Ро у е Do П / А\
Принцип возможных перемещений
417
Из соотношений A)
а из уравнений B) и D) имеем
'0,
значит
Jjl
^ Рх eL
E)
F)
G)
158. Найти зависимость между весом грузов Л и В, подвешен-
подвешенных при помощи системы блоков (рис. 158); система находится
в равновесии.
Решение. Определим перемеще-
перемещения грузов А и В.
Обозначим скорость центра бло-
блока С через п. Мгновенный центр
для блока С помещается в точке
Р (рис. 158, а).
Следовательно,
vE = 2w. A)
Скорость центра блока D также
равна vEf но противоположно на-
направлена.
Груз В движется поступатель-
поступательно, поэтому схема скоростей точек
блока D выглядит так, как ука-
указано на рис. 158, б
Учитывая, что:
К задаче 158,
B)
находим
А
ТаЮш образом, перемещения грузов равны:
ер = иЫ; 8р = — 5иЫ.
На основании принципа возможных перемещений
[-/
C)
D)
т. е.
27 591
418
Динамика
159. В кулисном механизме (рис. 159) при качении кривошипа
ОС вокруг оси О ползун Л, перемещаясь вдоль кривошипа, приво-
приводит в движение стержень АВ> движущийся в вертикальных направ-
направляющих К- Даны размеры: ОС = R, О К = I- Какую силу Q не-
необходимо приложить перпендикулярно к кривошипу ОС в точке С
для того, чтобы уравновесить силу Р,
направленную вдоль стержня АВ
вверх?
Решение* Определяй перемеще-
перемещение точек С и В.
Придадим углу <р приращение 8<р,
тогда
A)
при-
при8
Учитывая, что у a =/tg<p и
нимая во внимание, что eA= sb*=
находим
К задаче 159.
* /sec2 989.
На основании принципа возможных перемещений
Q . е0 — Р • ев = О,
откуда
п Pl
V e R COS2 cp •
B)
(а)
160. Дифференциальный ворот (рис. 160, а) состоит из двух
жестко связанных валов А и В, приводимых во вращение рукоят-
рукояткой С длиной R. Поднимаемый груз D весом Q прикреплен к под-
подвижному блоку ?, охваченному канатом. При вращении рукоятки С
левая ветвь каната сматывается с вала А радиусом rl9 а правая
ветвь наматывается на вал В радиусом г2 (г2 > гх).
Какую силу Р надо приложить перпендикулярно к концу рукоятки
для того, чтобы уравновесить груз D, если Q = 720 кг, гг =10 см,
г2 *. 12 см и R « 60 см.
Решение. Возможное перемещение барабана обозначим через 8ф.
Левая ветвь каната опустится на Ьи «= гх8$, а правая — подни-
поднимется на bv se/iSqp см (рис. 160, б):
Перемещение точки С равно
A)
B)
Принцип возможных перемещений
419
На основании принципа возможных перемещений
т. е.
а
К задаче 160,
161. Фермы / и //, соединенные шарниром D (рис. 161), прик-
прикреплены стержнями /// и IV с помощью шарнира С к земле; в точ-
точках А и В они имеют опоры на каток. Ферма / нагружена верти-
вертикальной силой Р, приложенной на расстоянии а от опоры А.
Найти реакцию катка J3.
Решение. Определим мгновенный центр скоростей фермы /, для
чего мысленно разрежем стержень IV и дадим возможное переме-
перемещение точкам А и Е.
Вектор скорости ЪЕ перпендикулярен ?С, а ЪА параллелен опор-
опорной горизонтальной плоскости.
Мгновенный центр скоростей лежит на пересечении перпенди-
перпендикуляров, восстановленных из начал векторов vA и ЪЕ.
Скорость точки D направлена перпендикулярно к прямой СД
а скорость точки Е направлена перпендикулярно к прямой CXF.
Скорости точек фермы / распределяются по линейному закону
A)
Найдем мгновенный центр скоростей фермы //, для чего мыс-
мысленно разрежем стержень ///. Скорость точки G направлена по
перпендикуляру к CG. Восставив перпендикуляры из начал
скоростей vD и vG> найдем мгновенный центр С2.
27*
420
Динамика
Заметим, что скорость точки В перпендикулярна к прямой С2В
и, кроме того,
VD VB
DC2 BC2 u
B)
Перемещения точек F и В определяются по формулам:
F F * b В v '
К задаче 161.
Освободим ферму // от связи в точке В, заменив ее реакцией RB.
На основании принципа возможных перемещений
PvF sin a — RBvB cos 3 = 0.
Учитывая, что
D)
(S)
и принимая во внимание соотношения A), B), уравнению D) при-
придадим вид
C-tF a BCa b о а /й\
t^ vr° F)
p..
Из уравнения F)
Принцип возможных перемещений
421
где b — плечо реакции RB относительно мгновенного центра С2.
Реакция имеет направление, перпендикулярное плоскости сколь-
скольжения катка В.
162» Три однородных бруска (рис. 162) AC = а, CD = b,
DB = с соединены между собой шарнирами и концами А и В под-
подвешены на шарнирах к горизонтальной прямой АВ = d. Найти
зависимость между углами а, р, 7 при равновесии.
Решение. В данной задаче необходимо учесть действие сил тя-
тяжести брусков, которые обозначим:
Так как стержни однородные, то силы веса равны:
Рг я ра; Р2 = рб; Р3 = рс, A)
гДе р — вес стержня единичной длины, и приложены в геометри-
геометрических центрах стержней.
Примем координатную си-
систему так, как указано на
рисунке, и определим орди-
ординаты точек приложения сил
тяжести стержней
. B)
yL = a sin a ^ -у sin 7
Величины углов а, C, X связаны зависимостями
a cos а 4? b cos 7 4- с cos В = d )
a sin а + b sin 7 = с sin р | » W
из которых первая ойределяет алгебраическую сумму проекций
замыкающего отрезка АВ, представленного в виде
АВ =ЛС + CD+DB
на направление оси Ах> а вторая зависимость дает проекцию этого
отрезка на ось Ау.
Определим возможные перемещения точек приложения сил тя-
тяжести стержней, сообщив обобщенным координатам возможные
приращений 8<х, Щ, 87» тогда: '
&ук = -? cos a8a
byL
a cos
-f у cos
D)
422 Динамика
Составим выражение суммы элементарных работ рассматривае-
рассматриваемых сил на возможных перемещениях в форме (XXIV, 5)
Рг -~ cos а8а + Pa (a cos aba + у cos 78у) +
— cospSpWo. , E)
Принимая во внимание соотношение A), преобразуем уравне-
уравнение E) к виду
а (т + b)cos aSa + "Г cos т&т + Т cos ^ в 0< ^
Провариировав соотношения C), находим:
a sin aba + b sin 7S7 + с sin psp = 0;
a cos a8a -f- b cos 7S7 — с cos Щ = 0,
откуда
h
(a — -y)
°T — b
Подставив полученные значения для 8a и 87 в уравнение F),
получим искомое уравнение равновесия
sin Ф + Т) cosa + ~ sin(a + P) cost тЬ
тЬ ~ cos p sin (a — f) « 0. (8)
Если размеры стержней принять равными
b = с ¦= 2а,
то уравнение (8) приводится к виду
4tga-3tgp-7tgT»0. (9)
ГЛАВА XXV
ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ
§ 1. Методические указания к решению задач
Объединив принцип возможных перемещений с «петербург-
«петербургским принципом», устанавливаем: если на систему наложены
идеальные удерживающие связи, то сумма работ активных сил и
сил инерции произведенных на возможных перемещениях точек
системы равна нулю
+ 7<f 0*0. (XXV, 1)
Общее уравнение динамики
423
Уравнение (XXV, 1) в координатной форме имеет вид
[ (Xt -
+• (Z,
+ (К« — miy\) by,
i] = 0.
(XXV, 2)
Уравнение (XXV, 1) или (XXV, 2) называется общим уравне-
уравнением динамики.
Если на систему материальных точек наложены односторонние
связи, то
п
\ + 7„ ij < о. (xxv, з)
Задачи этого раздела необходимо решать в такой последователь-
последовательности.
1. Определить число степеней свободы и ввести обобщенные
координаты.
2. Составить схему всех внешних сил, действующих на точки
системы, и присоединить к ним силы инерции. ,
3. Найти возможные перемещения точек при-
приложения действующих сил и сил инерции.
4. Составить общее уравнение динамики
(XXV, 1).
5. Приравнять нулю коэффициенты, входя-
входящие в выражение для работы (XXV, 1) при
независимых обобщенных координатах.
6. Найти из полученной системы уравнений
неизвестные величины.
§ 2. Задачи
163. К нижнему шкиву С подъемника
(рис. 163) приложен вращающий момент М.
Определить ускорение груза А весом Р19 под-
поднимаемого вверх, если вес йротивовеса В равен
Р2, а шкивы С и D радиусом г и весом Q
каждый представляют собой однородные цилин-
цилиндры. Массой ремня пренебрегаем.
К задаче 163.
Решение. Обозначим ускорение точек бесконечного ремня на пря-
прямолинейном участке движения через w.
На точки системы действуют активно приложенные силы Ръ Р2
и вращающий момент М. Присоединим ко всем точкам системы силы
инерции, тогда:
— Р\ — />
' l "* a 2 g %
424
Динамика
а силы инерции шкивов образуют пару сил с моментом
B)
Рассматриваемая система обладает одной степенью свободы,
положение ее точек определяется углом <р поворота нижнего диска.
На точки А и В наложена двусторонняя идеальная связь.
Сообщим точкам системы малое перемещение, определив его
приращением угла поворота 8<р.
Перемещения точек А и В имеют величину
гл = — гЗср;
Элементарная работа сил инерции
г8<р.
C)
D)
а вращающий момент М и силы Pv P2 производят работу
ЬА2 = Л%; 8Л3 = (^2 - Рг) /*Р- E)
О
Составив общее уравнение динамики
и учитывая, что &<р имеет величину,
отличную от нуля, находим
W ==
(Pi
Q)
164. В регуляторе (рис. 164) четы-
четыре груза одинакового веса Р распо-
расположены на концах двух равнопле-
равноплечих рычагов длиной 2/, которые
могут вращаться в плоскости регу-
регулятора вокруг конца шпинделя О и
образуют с осью его переменный
угол <р. В точке Л, находящейся от
точки О на расстоянии О А = а, со
шпинделем шарнирно соединены ры-
I чаги АВ и АС длиной а, которые в
точках В и С, в свою очередь, соеди-
соединены со стержнями BD и CD длиной
а, несущими муфту D. В точках В
и С имеются ползунки, скользящие
вдоль рычагов. Вес муфты равен Q. Регулятор вращается с по-
постоянной угловой скоростью о). Найти связь между углом <р и
угловой скоростью о) в равновесном положении регулятора.
К задаче 164.
Общее уравнение динамики
425
Решение. Грузы регулятора обладают осестремительным уско-
ускорением, величина которого
w00 = / sin ерш2.
A)
Если к силам тяжести грузов Р присоединить силы инерции
Т= - ^Ъ™, B)
то вся система будет находиться в фиктивном равновесии.
Сообщив возможные перемещения грузам и изменив угол <р,
на 8ф, замечаем, что они равны
и перпендикулярны к рычагам. Положение центра тяжести муфты
определяется координатой
z = а + 2а cos 2cp, C)
следовательно, возможное ее перемещение имеет величину
eQ = — 4а sin 2cp8cp. D)
Нетрудно заметить, что сумма работ сил тяжести четырех грузов
равна нулю, действительно
ЬАи 2, з, 4 (Р) = 2Р1„2 \е\ sin <р — 2Р3-4 N sin ср = 0, E)
где индексами 1—2 обозначена работа сил тяжести верхних гру-
8ов, а 3—4 — нижних.
На основании принципа возможных перемещений
4/ |е| cos ф — 4aQ sin 2ф = 0. F)
Подставив в соотношение F) значение величины / и е, получим
(О s-a -_-
т. е. равновесное положение
возможно при наличии угловой
скорости G), независимо от
угла ф.
165. Грузы D и Е, весом Р
каждый (рис. 165), привязаны
к концам нерастяжимой и не-
невесомой нити. Эта нить от гру-
груза D идет через неподвижный
блок Л, охватывает подвижный
блок В, возвращается вверх
К задаче 165.
на неподвижный блок С, соосный с блоком Л, проходит парал-
параллельно гладкой наклонной плоскости, где к концу нити при-
привязан груз Е. Наклонная плоскость образует угол а с гори-
горизонтом. К подвижному блоку В прикреплен груз К весом Q.
426 Динамика
Коэффициент трения скольжения груза Е о горизонтальную плос-
плоскость равен /. Массами блоков пренебрегаем. Установить условие,
при котором груз К будет опускаться и найти ускорение его; в
начальный момент скорости всех грузов равны нулю.
Решение. Связь между точками системы осуществляется при
помощи гибкой нерастяжимой нити, для которой
А + 2/ + /а = const. A)
Возможные перемещения удовлетворяют уравнению связи A)
Ыг + 28/ + Ыш - 0. B)
Из уравнения связи A) также вытекает, что
где w—ускорение груза К; щ, щ — ускорения грузов Е и D.
К активно приложенным силам Р, Q, Р, и к силам реакции
связей R, Rl9 T, где
Г-/Л D)
присоединим силы инерции
l-rj-yaV |72|=~яу, !7,|-|.^ E)
тогда система будет находиться в фиктивном равновесии. Среди
возможных перемещений, удовлетворяющих уравнению B), можно
выбрать такие, что
8/2 = Б/х = 8s; 8/ = —8s. F)
На основании принципа возможных перемещений
— (Т + Л) Ыг + (Q — /8) W — W — Р sina8Z2 . 0. G)
Принимая во внимание соотношения C), D), F), из уравнения
G) получим
Ш==^ Q+2P (8)
и приходим к заключению, что груз К движется вниз при условии
Q>P(/ + sina). (9)
166. Призма А весом Q (рис. 166) скользит по гладкой боко-
боковой грани призмы В весом Р, образующей угол а с горизонтом.
Определить ускорение призмы Б, если в начальный момент система
находится в покое. Трением между призмой В и горизонтальной
плоскостью пренебречь,
Общее уравнение динамика
427
Решение. Призма А находится в сложном движении, ее движе-
движение вместе с призмой В примем за переносное, а движение по боко-
боковой грани В за относительное.
Обозначим ускорение переносного движения через w% а отно-
относительного движения через Тдг. Центр инерции призмы А движется
с ускорением
до2 я W -f- Wv A)
Дадим точкам призмы В возможное
перемещение^, а точкам призмы А— _
8^. Точки призмы А в абсолютном»
движении будут иметь перемещение
К задаче 166.
На призмы действуют активно при-
ложенные силы Р, Q и реакция
опоры R.
Присоединим к этим силам еще силы инерции:
На основании принципа возможных перемещений
или в развернутом виде
— -oySs-lr QsinaSsi — — (w + w^^
0,
C)
D)
E)
Вычислив скалярное произведение, входящее в уравнение E),
находим
~A ^ j)W — |"cosa
4- -5- cosa w — -j w^\ bst
0.
F)
Сбитая в равенстве F) поочередно:
bst = 0 и bs i* 0;
Bs = 0 и Bs! ^ 0,
получим
— (Q Ф Р) w + Qcosa . wt » 0,
Q sin a + ~- cos a •
0.
Исключив из соотношений G) ускорение щ, определим
Q sin 2a
Wsssg 2(P + Qsin 2<*V
428 Динамика
ГЛАВА XXVI
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ МАТЕРИАЛЬНОЙ СИСТЕМЫ
§ 1. Теорема о движении центра инерции системы
Центром инерции системы материальных точек называется центр
параллельных сил инерции, возникающих при поступательном дви-
движении системы, если последнюю представить как геометрически
неизменяемую.
Координаты центра инерции определяются по формулам:
п п п
2 mft ? mjyj ? т^
Хс ss —- ; ус = —-—— ; zc = — . (XXVI, 1)
Центр инерции материальной системы движется как материаль-
материальная точка, имеющая массу равную массе системы, под действием
силы, равной главному вектору внешних сил, приложенных к точ-
точкам системы.
Обозначим массу /-ой точки т^ а массу системы через М, тогда
п
М- !>,. (XXVI, 2)
Обозначим равнодействующую внешнюю силу, приложенную
к точке / через Ff\ тогда главный вектор внешних сил опреде-
определится по формуле:
?(е) - ? F). (XXVI, 3)
На основании теоремы о движении центра инерции находим
Mwc=R(e\ (XXVI, 4)
или в скалярной форме
(XXVI, 4')
Если внешние силы параллельны, одной из координатных осей,
например Ог, то
Общие теоремы динамики материальной системы 429
В этом случае координата г0 изменяется по закону
Zo = Сх + c2t. (XXVI, 5)
Если к тому же при t = 0; zc0 = 0, то
zc = cv (XXVI 6)
т. е. имеет место закон сохранения координаты гс центра инерции.
Положение центра инерции сохраняется при условии
=0. (XXVI, 7)
При сохранении координат центра инерции системы можно
определить движение некоторых точек ее. Если известен главный
вектор внешних сил /с , то интегрированием системы уравнении
(XXVI, 4) находят закон движения центра инерции системы.
Задачи этого раздела необходимо решать в такой последователь-
последовательности.
1. Выбрать относительно неподвижную систему координатных
осей.
2. Составить схему внешних сил, приложенных к точкам си-
системы. Если исследуется движение несвободной системы, то осво-
освободить ее от связей, заменив их реакциями.
3. Установить начальные условия движения центра инерции:
хсо> Усо> zco> xco> Усо> гсо-
4. Для определения движения центра инерции составить диф-
дифференциальные уравнения (XXVI, 4), а затем их проинтегриро-
проинтегрировать,
5. Если имеет место сохранение координаты z центра инерции,
то при помощи формулы (XXVI,1) составить соотношение
zC0^zGlt), (XXVI, 8)
из которого найти отклонение интересующей нас точки системы.
§ 2. Задачи
167. Определить смещение пловучего крана (рис. 167), под-
поднимающего груз весом Рг = 2 т при повороте стрелы крана на 30°
до вертикального положения. Вес крана Р2 = 20 т\ длина стрелы
ОА = 8 м. Сопротивлением воды и весом стрелы пренебречь.
Решение* Введем относительно неподвижную систему коорди-
координатных осей, поместив ее начало в точке О и направив ось Ох парал-
параллельно уровню воды, а Оу по вертикали вверх.
Все внешние силы и реакция воды R параллельны оси Оу, а
начальная скорость всех точек системы в направлении оси Ох от-
отсутствует.
430
Динамика
Как известно, в этом случае сохраняется абсцисса центра инер-
инерции системы
хс = const. A)
Обозначим расстояние от начала координат до линии действия
силы Р2 через а.
В начальный момент абсцисса центра инерции системы, опре-
определенная по формуле (XXVI, 1), имеет величину
— Рг-ОА sin 30° -f P2a 9
%СО — р JL р ' \ '
К 12
Для того чтобы хс оставалась неизмен-
неизменной во время движения груза Рг
вправо, судно должно двигаться влево.
Смещение судна влево от оси Оу
обозначим через хсг, тогда
Сравнивая правые части уравнений
B) и C), найдем
К задаче 167. К задаче 168.
Подставив числовые значения, получим
х = 0,36 м.
168. Три груза (рис. 168) весом Рг = 20 к:г; Р2 = 15 кг и Р3 =
= 10 кг соединены невесомой, нерастяжимой нитью, переброшен-
переброшенной через неподвижные блоки М и N. При опускании груза Рг
вниз груз Р2 перемещается вправо, по верхнему основанию четы-
четырехугольной усеченной пирамиды ABCD весом Я= 100 /сг, а груз Ръ
поднимается по боковой грани АВ вверх. Пренебрегая трением
между полом и пирамидой, определить перемещение последней
относительно пола, если груз Рг опустится на 1 м.
Общие теоремы динамики материальной системы
431
Решение. Освободив усеченную пирамиду от связи, отметим,
что ее реакция R и все внешние приложенные силы Р, Р19 Р2> ^з
перпендикулярны к горизонтальной плоскости и что в начальный
момент все точки системы находились в состоянии покоя. В этом
случае абсцисса центра инерции всей системы материальных точек
сохраняется, т. е.
*с = const. A)
Поместим начало координат в центре инерции системы. Для
того чтобы абсцисса центра инерции оставалась неизменной при
движении грузов вправо, вся призма должна придти в поступа-
поступательное движение противоположного направления, т. е. влево.
Обозначим перемещение пирамиды через х> тогда абсциссы грузов
Р* Ръ Р*> Р* изменятся на следующие величины:
и, следовательно, на основании уравнения A)
Рз ' (*~ т) + р2(^- 1) + Pi* + Рх -0- B)
Из уравнения B)
Подставив числовые значения, получим
*« 13,8 « 14 см.
169. Определить давление на грунт
насоса для откачки воды (рис. 169)
при его работе вхолостую, если вес
корпуса D и фундамента Е равен Pl9
вес кривошипа О А равен Р2> вес ку-
кулисы В и поршня С равен Р3. Криво-
Кривошип ОА я= а, вращающийся, равно-
равномерно с угловой скоростью (о, считать
однородным стержнем.
Решение. Кулиса вместе с пор-
поршнем находится в поступательном
движении,
по закону
уг = a cos wt.
Все их точки движутся
A)
К задаче 169.
Кривошип находится во вращательном движении, причем коор-
координата уол его центра инерции изменяется по уравнению
УоА «4 coso>^ B)
432
Динамика
Освободим насос от связи, заменив ее реакцией /?.
На основании теоремы о движении центра инерции (XXVI,4)
где М — масса подвижных частей насоса, т. е.
АЛ гдг ___ (р «L. Р \ (А\
Учитывая формулу (XXVI, 1) для координаты ус — центра
инерции подвижных масс, после двукратного дифференцирования
по времени получим
Myс = — у0 Н—й у . E)
Подставив в уравнение E) значение уъ
и УоА, получим
My с = - ~ (Р2 + 2Р3) cos Ы. F)
Давление на связь по величине равно
динамической реакции, которая согла-
согласно уравнениям C) и F) имеет вели-
величину
7-V2 + 2P3)cosu)/.
170, Ножницы для резки металла
(рис.170) состоят из кривошипно-шатун-
ного механизма ОАВ, к ползуну В. кЪ-
торого прикреплен подвижный нож.
Неподвижный нож укреплен на фунда-
фундаменте С. Определить давление фунда-
фундамента на грунт, если длина кривошипа
К задаче 170. г, вес кривошипа Pl9 длина шатуна /,
вес ползуна В с подвижным ножом равен
Р2, вес фундамента С и корпуса D равен Р3. Массой шатуна прене*
бречь. Кривошип ОА, равномерно вращающийся с угловой ско-
скоростью со, считать однородным стержнем.
Решение. Введем координатную ось Оуу как указано на рисунке.
Ползун В движется поступательно с ускорением
(о
WB = — ГОJ (COS (tit + -у COS tu't\ .
Центр инерции кривошипа ОА вдоль оси Оу имеет составляю-
составляющую ускорения
уг = — у гаJ cos ш*- B)
Общие теоремы динамики материальной системы
433
Освободив ножницы от связи, заменив ее реакцией /?, а также
приложив активные силы Ръ Р2 и Р8» на основании теоремы о дви-
движении центра инерции напишем
Myc^Pl + P2 + Pz — Ry C)
где М — масса подвижных частей механизма, т. е.
Учитывая, что
м'ус=* -г'уг + -*-
D)
E)
а также приняв во внимание выражения A) и B), из уравнения
C) получим
N = рх + Р2 + Р3 + ~ \(Рг + 2Р2) cos со* + 2P%
3 +
171. Однородный стержень АВ (рис.
171,а) длиной 2 / опирается концом В
на гладкую горизонтальную плоскость
под углом а. Определить уравнение тра-
траектории точки А при падении стержня
на плоскость.
Решение. Освободим стержень от
связи в точке В, заменив ее реакцией R.
Заметив, что силы Р и R направ-
направлены перпендикулярно к оси Ox, a так-
также, что отсутствует скорость вдоль этой
оси в начальный момент, находим
хс = / cos а = const. A)
Зависимость A) показывает, что
центр инерции стержня движется по
одной и той же вертикали.
На рис. 171,6 указано положение стержня при условии
К задаче 171
«>Ф, B)
где ф — угол, определяющей положение стержня, и, как видно
из рисунка,
Исключив параметр <р из уравнений C), приходим к заключе-
заключению, что точка А движется по эллипсу, уравнение которого сле-
следующее:
(х — /cosaJ + -— = I*. D)
28 mi
434
Динамика
§ 3. Изменение количества движения системы
Количеством движения системы называется геометрическая
сумма количеств движения точек, образующих систему
К = Х т,ч. (XXVI, 9)
Количество движения системы равно количеству движения ее
центра инерции
К = Mv& где М = V щ% (XXVI, 10)
5=1
Из уравнений (XXVI,9) и (XXVI, 10) вытекают скалярные уравне-
уравнения:
п п п
5=1
5 = 1
.(XXVI, 11)
(z = MZC
Физическая величина, характеризующая эффект действия силы
во времени,
h
(XXVI, 12)
называется импульсом главного вектора внешних сил, или полным
импульсом.
Sx = J X(e)dt
Sw =
h
(XXVI, 13)
Теорема об изменении количества движения системы формулируется
так.
Приращение количества движения системы за некоторый про-
промежуток времени геометрически равно импульсу главного вектора
внешних сил, действующих на точки системы за этот же промежу-
промежуток времени
Kt-K^J®. (XXVIЛ 4)
Общие теоремы динамики материальной системы 435
или в координатной форме:
гу — Kiy — Jy
(XXVI, 15)
Применив теорему об изменении количества движения к сплош-
сплошной среде, приходим к теореме Эйлера. Главные векторы объемных
и поверхностных сил 7?0о и Л?ПОвИ векторы количеств движения масс
жидкости, входящих и выходящих через два каких-нибудь сечения
в единицу времени, направленные внутрь выделенного объема,
образуют замкнутый многоугольник, т. е. дают в сумме нуль.
Mvx — Mv2 + Rog + RnoB = О, (XXVI, 16)
или
М (Vix — V2x) + Хо0 + Хпов = 0 '
М (viy — v2v) + YoQ + Утв =0 . (XXVI, 17)
Если полный импульс внешних сил равен нулю, то вектор
количества движения системы сохраняется.
Если проекция вектора полного импульса системы на одну из
координатных осей равна нулю, то сохраняется проекция вектора
количества движения^ системы вдоль этой оси. Например, при
JM = 0 имеем
/С* = tfi* (XXVI, 18)
Задачи этого раздела необходимо решать в такой последова-
последовательности.
1. Выбрать систему относительно неподвижных координатных
осей.
2. Составить схему внешних действующих сил. Несвободная
система освобождается от наложенных связей.
3. Найти, на основании формул (XXVI,13) проекции полного
импульса на координатные оси.
4. Составить систему уравнений (XXVI,15) или (XXVI,18)
и из них найти искомые величины. При исследовании движения
сплошной среды применяют теорему Эйлера. Составляя уравнения
(XXVI, 17), вектор количества движения массы, проходящей в еди-
единицу времени через нижнее (по течению) сечение, направляют
всегда внутрь выделенного объема жидкости в трубе.
§ 4. Задачи
172. Ствол орудия (рис. 172) образует угол а =30° с гори-
горизонтом и весит 11 000 кг. Вес снаряда равен 54 кг; скорость сна-
снаряда у дульного среза v0 = 900 м/сек. Определить скорость сво-
свободного отката ствола орудия в момент вылета снаряда.
28*
436
Динамика
Решение. Обозначим силу веса пушки через Р, а веса снаряда
через Р2 и освободим систему от связи, заменив ее реакцией 7f.
Силы Р, Рг и R перпендикулярны к оси 0xt следовательно,
имеет место закон сохранения проекции количества движения
системы на эту ось.
В начальный момент, до выстрела, скорости точек системы
равны нулю. Обозначим скорость пушки в момент вылета снаряда
через v9 а снаряда —170.
На основании уравнения (XXVI,18)
откуда
— — о + — ^о cos 30°
cos 30°.
•0,
A)
B)
К задаче 172.
К задаче 173
Подставив в уравнение B) числовые значения величин, получим
54 . 900 . 1,73
11 000 . 2
3,82 м/сек.
173. Человек весом 50 кг прыгает на ходу на подножку тележки
(рис. 173) весом 240 кг, которая движется прямолинейно со ско-
скоростью 3,6 км/час. Определить скорость тележки вместе с челове-
человеком.
Решение. Силы Р, Рг Rlt R2 перпендикулярны к оси х, следо-
следовательно, имеет место закон сохранения количества движения
системы. До прыжка человека на платформу ее количество дви-
движения равно
|F| 240.3,6 п
|Дх1 === JJ • '*/
Обозначим скорость^ тележки после прыжка человека через и%
тогда
Общие теоремы динамики материальной системы
437
Приравняв левые части уравнений A) и B), получим
24 . 3,6
и =
29.
2,98 км/нас.
174. Паровой котел (рис. 174) весом 10,35 т заполнен водой в
количестве 15 т при давлении на свободную поверхность Ро =
« 10 атм.
В некоторый момент времени
происходит разрыв болтов, кото-
которыми крышка А прикреплена к
патрубку В посредством фланце-
фланцевого соединения; вследствие сры-
срыва крышки горячая вода будет •
вытекать в атмосферу; Н = 1 м,
d = 0,4 ле, относительный удель-
удельный вес горячей воды f = 0,9.
Пренебрегая гидравлическими со-
сопротивлениями, скоростями частиц
воды внутри котла и явлением
парообразования воды по выходе
из патрубка В, вычислить дав-
давление котла на опоры в момент срыва крышки Л. Среднюю ско-
скорость, с которой вода будет вытекать в атмосферу после срыва
К задаче 174.
крышки, вычислить по формуле v
+ ~
Решение. Освободим котел от связей, заменив их реакциями
Считаем, что жидкость вытекает из патрубка, имея скорость и,
поэтому за время dt из котла вытечет масса жидкости
Указанная масса обладает количеством движения
A)
B)
которое направлено, как указано на рисунке.
Учитывая, что в начальный момент количество движения системы
материальных точек (жидкость рассматриваем как вещество, со*
стоящее из капель) равнялось нулю на основании второго уравне-
уравнения системы (XXVI, 15) получим
dK = (P + Q — R)dt9 C)
где
438 Динамика
Из соотношения B) и C)
R = Р + Q — т ~о~у2* (*)
Подставив значение у, получим
-Ро). E)
Если вместо буквенных выражений, входящих в уравне-
уравнение E), подставим их числовые значения, то получим R = 0.
§ 5. Теорема об изменении главного момента количества
движения системы. Дифференциальное уравнение вращения
твердого тела вокруг неподвижной оси. Элементарная
теория гироскопов
Моментом количества движения системы относительно некото-
некоторой точки называется геометрическая сумма моментов количеств
движения всех точек системы, вычисленных относительно этой же
точки
п
Т __ у 7 , fXXVI IQ4
Момент количества движения системы относительно оси равен ал-
алгебраической сумме моментов количества движения точек системы
относительно этой же оси
/. = | I* (XXVI, 20)
Момент количества движения тела, вращающегося вокруг непо-
неподвижной оси Oz, определяется по формуле
/г = /го)э (XXVI, 21)
где Jz = \ (л;2 + у2) dm — момент инерции тела относительно оси
(М)
вращения; со — угловая скорость вращения.
Проекции вектора момента количества движения тела, имеющего
одну неподвижную точку, на подвижные координатные оси, свя-
связанные с телом, вычисляются по формулам:
/;=
(XXVI, 22)
где о,,., coy> o)z — проекции вектора мгновенной угловой скорости
на координатные оси.
Общие теоремы динамики материальной системы
439
Экваториальные, или осевые моменты, инерции вычисляются
по формулам:
(XXVI,
(м)
= J (
(М)
dm
а центробежные моменты равны
(М)
(М)
(Af)
(XXVI, 24)
Момент инерции тела относительно оси, образующей углы
а, р, ^ с координатными осями, вычисляется по формуле
Jt ='JX cos2 a -f Jj, . cos2 p -f- Jz cos2 if — 2JxV cos а . cos p —
— 2/yz • cos fJ • cos 7 — 2/zaJ cos 7 • cos a. (XXVI, 25)
Момент инерции тела относительно оси, проходящей через
центр инерции тела, обозначим через Jct тогда момент инерции
относительно любой оси, параллельной центральной, определяется
по формуле
JM = Jc + McP, (XXVI, 26)
где d — кратчайшее расстояние между осями.
Момент инерции стержня длиной /, с равномерно распределен-
распределенной массой М, относительно оси, проходящей через его конец,
перпендикулярно к стержню, равен
М/8
Jz =-3-.
(XXVI, 27)
Момент инерции цилиндра радиуса г, масса которого М рав-
равномерно распределена относительно оси симметрии, равен
/. = ^. (XXVI, 28)
440 Динамика
Момент инерции цилиндра радиусом г и высотой h относительно
центральной оси, перпендикулярной к продольной оси, равен
(XXVI, 29)
Момент инерции сферы радиусом г и массой М равен
Ja « Jv = Jz = 1 Mr*. (XXVI, 30)
Теорема моментов количества движения системы формулируется
так.
Геометрическая производная, взятая по времени от момента
количества движения системы относительно точки, равна главному
моменту внешних сил, действующих на точки системы, вычислен-
вычисленному относительно той же точки, т. е.
|го = Це), (XXVI, 31)
или в координатной форме
~* = Ue); (XXVI, 32)
Ж e L* ;
Ж*
Теорема моментов имеет и другую формулировку, известную
под названием теоремы Резаля.
Скорость конца вектора главного момента количества движе-
движения системы относительно некоторого центра равна главному мо-
моменту всех внешних сил, приложенных к системе, относительно
того же центра.
Если Lq6) = 0, То сохраняется вектор момента количества дви-
движения системы относительно точки 0, т. е.
70 = const. (XXVI, 33)
Если одна из проекций вектора Lq6) на координатную ось равна
нулю, то сохраняется проекция момента количества движения
системы на эту ось. Например, Lz == 0, то
/, = const. . (XXVI, 34)
Если тело вращается вокруг неподвижной оси Ог, то его вра-
вращательное движение определяется дифференциальным уравнением
/,5-L?, (XXVI, 35)
где ср — урол поворота тела вокруг оси.
Общие теоремы динамики материальной системы 441
Период колебаний физического маятника вычисляется по фор-
формуле
^ (XXVI, 36)
где ОС — расстояние от оси привеса да Центра инерции; М —
масса маятника.
Угловая скорость регулярной прецессии гироскопа с тремя
степенями свободы определяется по формуле
o)e= j-^ , (АЛ VI, 37)
где М — масса гироскопа; /с — момент инерции гироскопа отно-
относительно оси симметрии; со — угловая скорость вращения вокруг
собственной оси; ОС — расстояние от опоры до центра инерции
гироскопа.
Вектор гироскопического момента определяется по формуле
L(r) = /ш х ш#, (XXVI, 38)
а его величина
(L(r)| = Усо • со, sin (w, ig. (XXVI, 39)
Разложив сложное движение системы на составные движения,
главный момент количества движения ее можно вычислить по
формуле
4 = I + rexMvc, (XXVI, 40)
согласно которой он равен геометрической сумме момента коли-
количества движения всей массы системы, мысленно сосредоточенной
в центре инерции и движущейся вместе с ним, и главного момента
количества движения ее относительно центра инерции. При этом
последний должен быть вычислен в относительном движении к си-
системе осей, поступательно движущейся вместе с центром инерции.
Теорема моментов сохраняет свою* формулировку и по отноше-
отношению к системе осей, движущихся поступательно вместе с центром
инерции относительно инерциальной системы отсчета.
§в=1Г. (XXVI, 41>
Задачи этого раздела необходимо решать в такой последова-
последовательности.
1. Выбрать систему неподвижных координатных осей.
2. Составить схему внешних сил. Если система не свободна,
то освободить ее от связей.
3. Вычислить главные моменты (L*\ Ly\ L?*) внешних сил
относительно координатных осей.
442
Динамика
4. Вычислить момент количества движения системы и, если это
требуется, предварительно определить соответствующие моменты
инерции по формулам (XXVI-,23—30).
5. Установить начальные условия движения.
6. Составить уравнения (XXVI.32) или (XXVI.35).
7. Проинтегрировать составленную систему уравнений или
использовать ее первые интегралы, например (XXVI,26).
Период малых колебаний физического маятника можно вычислять
непосредственно по формуле (XXVI,36).
Задачи по приближенной теории гироскопов решаются и&
посредственно по формулам (XXVI,37—39)
§ 6. Задача
175. Круглая горизонтальная платформа (рис. 175) вращается
без трения вокруг вертикальной оси, проходящей через ее центр
тяжести, с постоянной угловой
скоростью ш0, при этом на плат-
платформе стоят четыре человека
одинакового веса: два—на краю
платформы, а два — на рассто-
расстоянии от оси вращения, равного
половине радиуса платформы.
Как изменится угловая скорость
платформы, если все люди,
стоящие на ней, движутся по
окружности в сторону ее вра-
вращения, причем люди, стоящие
К задаче 175. на краю, движутся с относи-
относительной линейной скоростью и,
а люди, стоящие на расстоянии половины радиуса от оси вращения,
движутся по окружности с относительной линейной скоростью 2 и.
Определить также/ чему, должна быть равна относительная
линейная скорость и> чтобы платформа перестала вращаться.
Людей считать точечными массами, а платформу — круглым
однородным диском. Радиус платформы R; масса платформы в
четыре раза больше массы каждого человека и равномерно распре-
распределена по всей ее площади.
Решение. На точки системы действуют активные силы веса
Рц Р^ ^з» Pa* Q и реакции оси Rx и R2>
Алгебраическая сумма моментов указанных сил относительно
оси вращения равна нулю.
Lie} = 0.
(I)
Общие теоремы динамики материальной системы 443
На основании уравнения (XXVI,34) главный момент количе-
количества движения относительно оси Ог остается постоянным
lz = const. B)
Заметив, что абсолютные скорости людей определяются по
формулам:
vc = vD = а) -§ + 2«
vA = vB = о)/? + и
и, пользуясь формулами B), C), находим
'* в 2 ¦? (Ч-f + 2wJ4 +2 f К
где Je — момент инерции однородного диска, имеющий величину
ш0 — начальная угловая скорость; о)! — конечная угловая ско-
скорость.
На основании уравнения B) lZQ = ltv откуда
8 и /fiv
Платформа будет находиться в покое при условии
4i = 0. G)
В данном случае из уравнения F) относительная линейная ско-
скорость точек Л, В, С, D
и = -g- /?оH.
176. Два твердых тела вращаются независимо друг от друга
вокруг одной неподвижной оси с постоянными угловыми скоростями
Wj и а>2. Моменты инерции твердых тел относительно этой оси со-
соответственно равны Jx и /2. С какой угловой скоростью будут вра-
вращаться оба тела, если их во время вращения соединить?
Решение. Считаем, что ось вращения вертикальна и на твердые
тела действуют только силы тяжести, тогда:
Lf-0 A)
и
1Ш = const. B)
444 Динамика
На основании формул (XXVI,20), (XXVI,21) до момента наложе-
наложения дополнительной связи
40 = Л*»! + У2о)а. C)
Наложим дополнительную невесомую связь на вращающиеся тела
так, чтобы они соединились в одно тело, тогда его момент коли-
количества движения относительно оси движения будет
l2l = (Jx + У2) со, D)
где о) — угловая скорость вращения образованого тела.
Из условия /^ = 4, находим
У2О)а
У2 -f У2
177. Вал радиусом г приводится во вращательное движение
вокруг горизонтальной оси АВ гирей М, подвешенной посредством
веревки. Для того чтобы угловая скорость вала через некоторое
время после начала движения имела величину, близкую^ постоян-
постоянной, с валом соединены п одинаковых пластин площадью S; со-
сопротивление воздуха, испытываемое пластиной, приводится к силе,
нормальной к пластинке, приложенной на расстоянии R от оси
вала и пропорциональной квадрату ее угловой скорости, при-
причем коэффициент пропорциональности равен k.
Масса гири т, момент инерции всех вращающихся частей отно-
относительно оси вращения равен J, массой веревки пренебрегаем.
Определить угловую скорость о) вала, предполагая, что в начальный
момент она равна нулю. Трением в опорах пренебречь.
Решение* Согласно условию задачи вращающий момент
Uz = mgr, A)
а тормозящий
Ь22 = — knRia*. B)
Начальные условия движения следующие:
/=0; о>0 = 0. C)
Составим дифференциальное уравнение вращательного движе-
движения вала (XXVI.35)
j/-% = mgr-knR<»\ D)
где Jг — момент инерции вращающихся масс, имеющий величину
Разделив переменные в уравнении D), придем к соотношению
_ Уш ¦ д, _УШ . *. {5)
Vmgr — YknR . со Vmgr + У knR • ю
Общие теоремы динамики материальной системы
445'
где
Интегрируя левую часть уравнения E) по времени в пределах
от нуля до t% а правую — по со от нуля до о>, находим
at = in У^ + УЩ • со ^
Решим уравнение F) относительно со, тогда
Vmgr е — 1 ^7Ч
Заметив, что при достаточно большом значении времени
lim-
1,
(8)
из формулы G) получим, что угловую скорость вращения вала
можно приближенно считать постоянной и равной
О) =
1
fcni? сек'
178. В сейсмографах — приборах для регистрации землетрясе-
землетрясений — применяется физический маятник (рис. 178), ось подвеса
которого образует угол а с вертикалью. Расстояние от оси при-
привеса до центра тяжести маятника
равно а, момент инерции маятника
относительно оси, проходящей через
его центр тяжести параллельно оси
привеса, равен /с, вес маятника
равен Р. Определить период колеба-
колебаний маятника.
Решение. Зададим движение фи-
физического маятника линейным углом
9 между вертикалью и прямой ОС,
указывающей положение его центра
инерции.
Составим дифференциальное уравнение малых колебаний маят-
маятника вокруг оси 0гг.
Из теоремы о моменте инерции относительно параллельных
осей (XXVI.26)
Jzx =^с + — аа. A)
К задаче 178.
446
Динамика
Внешние силы, приложенные к маятнику относительно оси Ozlt
создают момент
L<? (Р)»— Pa. sin a. B)
Следовательно, в нашем случае из уравнения (XXVI,35)
получим
» , Pag sin a ___ п
Решение уравнения C) имеет вид
Pag sin
Pag sin я
C)
D)
а значит, угол поворота <р изменяется по гармоническому закону
с периодом колебаний
Г =
Pag sin a
E)
179. Для определения момента инерции J8
тела Л (рис. 179) относительно вертикальной
оси Oz его прикрепили к упругому вертикаль-
вертикальному стержню OOlf закрутили этот стержень,
повернув тело А вокруг оси Oz на малый угол ф0
и пустили колебаться; колебания были гар-
моиическ-ие, период которых равен 7\, так как
момент силы упругости стержня пропорционален
углу закручивания и равен сер. Для определения
коэффициента с проделали второй опыт: одно-
однородный круглый диск весом Р и радиусом г при-
прикрепили к телу, момент инерции которого требуется определить,
и наблюдали его колебания, период которых оказался равным Г2.
Определить момент инерции тела Jг.
Решение. Дифференциальное уравнение малых крутильных
колебаний стержня в условиях первого опыта имеет вид
К задаче 179.
Учитывая, что момент инерции диска относительно оси Oz
равен JZl = y~ » в условиях второго опыта придем к следующему
дифференциальному уравнению малых колебаний
B)
Общие теоремы динамики материальной системы
447
Уравнению "A) соответствуют гармонические колебания, период
которых
а уравнению B) с периодом
I о =
C)
D)
Г
Исключив из выражений C) и D) величину с, получим уравне-
уравнение для определения Jz:
Г, (/. + ^) = ТУ.. E) \,L
откуда
JgKB 2^ т-|—7f"
180. В вибрографе для записи горизонтальных ко-
колебаний фундаментов машин маятник О А (рис. 180),
состоящий из рычага с грузом на конце, может
качаться вокруг горизонтальной осп О, удержи-
удерживаясь в вертикальном положении устойчивого рав-
равновесия собственным весом и спиральной пружи-
пружиной. Определить период собственных колебаний
маятника при малых углах отклонения, если мак-
максимальный статический момент веса маятника отно-
относительно его оси вращения Qh =4,5 kFjcm; момент
инерции относительно этой же оси J =0,03 кГ»сМ'сек2; коэффици-
коэффициент жесткости пружины, сопротивление которой пропорционально
углу закручивания) с = 0,1 кг-см; при равновесном положении
маятника пружина находится в ненапряженном состоянии. Сопро-
Сопротивлением пренебречь.
Решение. Отклоним маятник от равновесного положения на
угол ф.
Момент внешних сил относительно точки О
Lo = — Сер — Qftcp A>
(отклонения считаем достаточно малыми).
Дифференциальное уравнение малых колебаний маятника имеет
вид
К задаче 180.
448
Динамика
Как видно из уравнения B), маятник находится в,гармоническом
колебательном движении, период которых
Т =. 2*
C)
Подставив числовые значения величин, получим
Т = 6,28 • 0,08 « 0,5 сек.
181. Волчок, имея форму диска диаметром 30 см (рис. 181),
вращается с угловой скоростью 80 — вокруг своей оси симметрии.
Диск насажен на ось длиной 20 см, расположенную вдоль оси
симметрии волчка.
Определить угловую скорость регулярной
прецессии волчка, полагая, что его главный
_ момент количества движения направлен вдоль
* оси симметрии и равен /со.
Решение. Угловая скорости регулярной
прецессии волчка определяется по формуле
(XXVI.37).
Момент инерции волчка относительно оси
симметрии равен
/=^, A)
К задаче 181
поэтому
2gOC
B)
Подставив в уравнение B) числовые значения величин, получим
C)
2.981-20 _ о ,n JL
225 - 80 ~ Z'iO сек"
182. Определить максималь-
максимальные гироскопические давления
на подшипники быстроходной
турбины (рис. 182), установлен-
установленной на корабле. Корабль под-
подвержен килевой качке с ампли-
амплитудой 9° и периодом 15 сек.
вокруг оси, перпендикулярной
к оси ротора турбины, который
весит 200 кг и имеет радиус
инерции 0,8 м и делает 18 000 об /мин; расстояние между подшип-
подшипниками 1 м.
К задаче 182.
Общие теоремы динамики материальной системы
449
C)
Решение. В результате качки, совершающейся вокруг оси Оу по
закону
возникает переносное вращательное движение корабля с угловой
скоростью
"е-ш'^Го1 B)
Главный момент количества движения турбины имеет величину
. __ , __ Р_
X X g
Вектор главного момента количества движения направлен
вдоль оси Ох.
Заметив, что векторы <о и Ве взаимно перпендикулярны, по
формуле (XXVI,39) вычислим максимальный гироскопический мо-
момент
^ = 4«W - g • 0,64 • 600 . 3,14 • Ц™> _ ,615 кг D)
Вектор гироскопического момента направлен перпендикулярно
к плоскости, в которой расположены векторы w и (ов, так, чтобы
поворот от первого вектора ко второму с конца вектора Z(r) совер-
совершался по часовой стрелке в крат-
кратчайшем направлении.
Заменим вектор гиррскопиче-
ского момента такой парой сил,
что
F(г) ¦ О А = L(r), E)
где Яг> — гироскопические давле-
давления на подшипники турбины.
Так как ОА = 1 лс, из уравне-
уравнения E) получим
F{T) = 1615 кг.
183. Определить время Т пол-
полного оборота оси симметрии артил^
лерийского снаряда (рис. 183)
вокруг касательной к траектории
центра тяжести его. Это вращение происходит в результате дей-
действия силы сопротивления воздуха /7=2140 /сг, направленной
параллельно касательной и приложенной к оси снаряда на рас-
расстоянии h = 0,2 м от его центра тяжести. Момент количества дви-
движения снаряда относительно его оси симметрии равен 590 кГм • сек.
29 591
К задаче 183.
450
Динамика
Решение. Сила сопротивления воздуха создает относительно
центра тяжести снаряда вращающий момент
L{q6) (F) = —Fh- sin q>. A)
Так как снаряд не опрокидывается вверх, момент внешней силы
F уравновешивается гироскопическим моментом, величина кото-
которого определяется по формуле
?^г) = Уел) • ше • sin ф. B)
(П, О)
D)
Итак,
и, следовательно,
Благодаря гироскопическому моменту ось симметрии снаряда
приходит в регулярное прецессионное вращательное движение
вокруг касательной т к траектории с периодом:
\\
Т — — —
со ~~
в
fA
E)
Подставив в уравнение
E) числовые значения ве-
величин, получим
Т =
2- 3,14 -590
=8,66 сек.
2140 • 0,2
184. Кольцо АВ тахо-
S^ метра (рис. 184,а) может
5 поворачиваться вокруг оси
Л, совпадающей с одним
из его диаметров и укреп-
укрепленной на оси вращения
тахометра, перпендикуляр-
перпендикулярно к последней; кольцо со-
соединено тягой ВС с тяже-
лой муфтой (соединенной
со стрелкой прибора) и
отжимается спиральной
пружиной к начальному
положению, соответству-
соответствующему углу ф0, образо-
образованному продольной осью кольца и осью вращения тахометра при
напряженной пружине.
Определить зависимость между угловой скоростью со тахометра
и углом ф отклонения оси кольца от оси тахометра при устано-
К задаче 184.
Общие теоремы динамики материальной системы 451
вившемся режиме, зная экваториальный и полярный моменты
инерции А и С кольца, вес муфты Q, расстояние АВ = а, длину
хорды ВС = Ъ и коэффициент жесткости с кг •см пружины, момент
сопротивления которой пропорционален углу ее закручивания;
весом тяги ВС и трением пренебречь. Подсчет вести с точностью
до членов, содержащих ~ в степени не выше первой.
Решение. При установившемся режиме движения угол ф остается
постоянным.
Освободим муфту С и кольцо А от связи СВ, заменив ее реак-
реакцией Г, направленной по хорде СВ. При установившемся режиме
муфта С находится в равновесии.
Обозначим угол наклона линии действия силы Т к оси тахо-
тахометра через ф. Тогда, как это видно из рис. 184,6,
Из Д CAB следует, что
sin ф = -J- cos ф. B)
Принимая во внимание уравнение B), находим
i/2
«1 C)
с точностью до величин, содержащих ~ в степени не выше второй.
Рамка тахометра удерживается в равновесии реактивным момен-
моментом пружины
Lj = с (ф0 — ф) D)
и моментом силы Г, приложенной к рамке,
LAB (Т) = ТК E)
где
h = а • sin (90° — ф — ф) = a (cos ф cos ф — sin ф • sin ф). F)
Принимая во внимание формулы A), B), C), F) из уравнения
E) находим
LAB(T) = Q.a(\ — j sin <p\ cos ф. G)
Присоединим к рамке центробежные силы инерции
dJ = dmaJp sin ф. (8)
Как видно из рис. 184,а, эти силы инерции образуют пару,
момент которой равен
L G) = — to2 sin ф cos ф f p2dm. (9)
29*
452 Динамика
Так как
Г 9Чт = JVi A0)
(м)
где р указано на рис. 184,<з, a Jy = С— Л, из формулы (9) находим:
L (J) = — (С — Л) оJ sin ф . cos ф. A1)
Составим условие равновесия рамки
L G) + Lx + ?Ав СО == 0. A2)
Заменив величины, входящие в формулу A2), их значениями
из D), G), A1) получим искомую зависимость
с (<Ро — <Р) + Qa f1 — -j sJn ? J cos cp
0J в {C-~A)sin<i -coscp * A3)
В процессе изменения угла ф до значения, соответствующего
равновесному положению, возникает угловая скорость относи-
относительного движения
и появляется гироскопический момент (рис. 184,г).
Гироскопический момент вызывает дополнительные давления
tfa подшипники, в которых закреплена ось АВ и не влияет на
угол ф поворота рамки.
§ 7. Теорема об изменении кинетической энергии системы
Кинетическая энергия системы равна сумме кинетических
энергий всех точек системы
п
" (XXVI, 42)
2 '
{=1
где mi — масса «-ой точки системы, a vt — ее скорость. Считая,
что система материальных точек стала геометрически неизменяемой,
определим ее кинетическую энергию
(XXVI, 43)
где М = V т%> vc — скорость центра инерции системы.
Кинетическая энергия тела, вращающегося вокруг неподвиж-
неподвижной оси, вычисляется по формуле
J~' ^ , (XXVI, 44)
Z
Общие теоремы динамики материальной системы 453
где Jt — момент инерции тела относительно оси вращения, ш —
угловая скорость вращения тела.
Кинетическая энергия тела в плоско-параллельном движении
определяется по формуле
Г==-^ + Т- (XXVI, 45)
Кинетическая энергия тела, вращающегося вокруг неподвижной
точки, равна
Т = -^2^, (XXVI, 46)
где •/«, — момент инерции тела относительно мгновенной оси вра-
вращения. В этом случае кинетическая энергия тела может быть вы-
вычислена также по формуле
27\ = Jxay2x + Jytol + J2to2z — 2Jxy(j>xb)y ¦—
— 2Jvzb)y<i)z — 2Jzx<Dz<»Xf (XXVI, 47)
где координатные оси Ох> Оуу Oz связаны с движущимся теЛом.
Если в частном случае за координатные оси Ox, Oy> Oz принять
главные, то
2Тг = J^l + J2<4 + J^l (XXVI, 4S)
где Jlf J2, Js — главные моменты инерции.
В общем случае движения тела это движение разлагают на
поступательное вместе с центром инерции и вращательное вокруг
центра инерции и кинетическую энергию вычисляют но формуле
Г = -1ЛЬ2 + Г3, (XXVI, 49)
где Тг — кинетическая энергия вращательного движения вокруг
центра инерции.
Кинетическая энергия системы материальных точек, находя-
находящейся в сложном движении, определяется по формуле
(XXVI, 50)
где щ — относительная скорость /-ой материальной точки.
Теорема об ^изменении кинетической энергии формулируется
так.
Приращение кинетической энергии системы на конечных участ-
участках пути, пройденных точками системы, равно сумме работ внешних
и внутренних сил, приложенных к ним на этих участках.
2, (XXVI, 51)
454 Динамика
где Л!~2 — сумма работ внешних сил, А[11.2 — сумма работ
внутренних сил.
Задачи этого раздела необходимо решать в такой последова-
последовательности.
1. Составить схему всех действующих (внешних и внутренних)
сил на точки системы. Если изучается движение абсолютного
твердого тела, то во внимание принимаются только внешние силы.
2. Определить пути, пройденные точками приложения сил, и
вычислить сумму работ этих сил.
3. Определить начальные и конечные скорости точек системы.
Если заданы уравнения движения точек системы, то их скорости
вычисляются для любого момента времени.
4. Составить выражение для кинетической энергии системы.
5. Применить теорему об изменении кинетической энергии и
из составленного выражения определить искомую величину.
§ 8. Задачи
185. Вычислить кинетическую энергию гусеницы трактора
(рис. 185 ), движущегося со скоростью v0 . Расстояние между осями
тдес радиусом г равно /, вес одного погонного метра гусеничной
цепи равен ?•
Решение. Прежде всего, опре-
определим массу гусеницы
/71 = — , A)
ё
где
К задаче 185. L« 2 (/+ *г) - B)
длина гусеницы.
Гусеница находится в плоско-параллельном движении, поэтому
ее кинетическая энергия определяется по формуле (XXVI, 45).
Абсолютная скорость элементов гусеницы, касающихся земли,
равна нулю, в силу чего
v0 = vrt C)
где vr — скорость относительного движения. Приняв во внимание
уравнение C), приходим к заключению, что
j a
пост == * отя ==
*¦ пост == * отя == ~ '
На основании равенств B), C) и D) находим
Т = 2^ (/ + */•) 4 E)
Общие теоремы динамики материальной системы
455
186. Вычислить кинетическую энергию кривошипно-шатунного
механизма (рис. 186), если масса кривошипа т1У длина кривошипа
Л масса ползуна т2, длина шатуна /. Массой шатуна пренебречь.
Кривошип считать однородным стержнем. Угловая скорость вра-
вращения кривошипа о). 1 /
Решение. Заметив, что точ- / • ч
ка А движется по закону /
хА = /• • coscp -(- /cos^, A) \
где \ | у
соБф - yi — ^7J Sln ?• К задаче 186.
находим , что линейная скорость этой точки равна
vA = — /-(of sincp + |/—= ЗШ2?а =1- B)
I д/l — (_-.\ sin8 ф I
L у \ / ; J
Кинетическая энергия системы равна сумме кинетических
энергий кривошипа
где
и ползуна
ffc^l
т. е. определяется по формуле
у
+ 2
2 «3
sin2cp
I-
Sin ер -p-
_fi-\sin^
C)
187. В кулисном механизме
(рис. 187) при качании кривошипа
ОС вокруг оси О ползун Л, переме-
перемещаясь вдоль кривошипа ОС, приводит
К задаче 187. в движение стержень АВ, движу-
движущийся в вертикальных направляю-
направляющих /С. Кривбшип длиной R считать однородным стержнем с мас-
массой mCt масса ползуна гаА, масса стержня АВ равна тв, ОК = /.
Выразить кинетическую энергию механизма в функции от угловой
скорости и угла поворота кривошипа. Кривошип считать точечной
массой. х
456
Динамика
Решение. Заметив, что
яаходим скорость движения точки А
vA = / to sec2 ф. (О)
Ползун А и стержень АВ находятся в поступательном движении,
следовательно, их кинетическая энергия равна
/2a)a sec4
C)
Кривошип ОС находится во вращательном движении и имеет кине-
кинетическую энергию
Г.*-^. D)
где
Л> = -§- •
Кинетическая энергия механизма равна сумме кинетических
энергий стержня с ползуном и кривошипа
[mcR* cos* у фг12{тА
E)
К задаче 188.
188. Танк приводится в дви-
движение (рис. 188) двигателем, ко-
который вращает четыре колеса (по
два с каждой стороны) радиусом
г = 50 сму которые выступами
захватывают гусеницу. Расстояние
между осями колеса А и В равно
2 м. Через 10 сек. после начала
движения танк приобретает ско-
скорость 36 км (час. Определить сред-
среднюю мощность двигателя танка, если вес последнего без колес
и гусеницы Рг = 5 т\ вес каждого колеса Р2 = 200 кг; вес каждой
гусеницы Р3 = 500 кг. Колеса считать однородными дисками.
Решение. Вычислим кинетическую энергию танка, обозначив
скорость его поступательного движения через v, тогда
Кинетическую энергию гусениц находим, считая, что они движутся
поступательно, т. е.
Та = ^1. B)
Общие теоремы динамики материальной системы
457
Каждое колесо танка находится в плоско-параллельном движении
и- обладает кинетической энергией
так как
Гз "" 2g + °2 "" 4 ? у2'
-1
2g ¦
C)
Кинетическая энергия всего танка равна
На основании уравнения "(XXVI,51), так как v0 = 0,
Т = Л, E)
где Л — работа всех внешних и внутренних сил. Мощность дви-
двигателя определяем по формуле
Подставив в уравнение F) числовые значения величин, получим
189. Транспортер (рис. 189)
приводится в движение из со-
состояния покоя присоединенным
к шкиву В приводом, который
сообщает этому шкиву постоян-
постоянный вращающий момент М.
Определить скорость ленты тран-
транспортера v в зависимости от ее
перемещения s, если вес под-
поднимаемого груза А равен Р, а
шкивы В и С радиусом г и весом
Q каждый представляют собой
однородные круглые цилиндры.
Лента транспортера, массой ко-
которой пренебрегаем, образует с горизонтом угол а. Скольжение
ленты по шкива^ отсутствует.
Решение. Вычислим кинетическую энергию Т системы матери-
материальных точек, состоящей из поступательно поднимаемого груза Р
и шкива транспортера. Тогда
Т~Тг + 2Т%, A)
К задаче 189.
458 Динамика
где
Р .
кинетическая энергия поступательно движущегося груза Р;
кинетическая энергия шкива транспортера.
Учитывая уравнения B), C), а также, что по = v, находим
т =
Обозначим перемещение груза Р вдоль ленты транспортера через
s, тогда шкив повернется на угол
9=7-- E)
Крутящий момент произведет работу
Аг = М.±, F)
а сила тяжести груза Р
Ла = — Р • 5 • sin a. G)
Так как движение транспортера началось без начальной скорости,
на основании теоремы изменения кинетической энергии для системы
получим
Т = Аг + А2. (8)
Из уравнений D), F), G) и (8)
190. При посадке самолет имел скорость 10 м/сек. Определить
путь, пройденный самолетом до остановки, если сила сопротивле-
сопротивления воздуха F = 60 кг, вес обоих колес Р = 100 кг, радиус колес
равен 0,5 м, вес самолета без колес Q = 1100 кг> коэффициент
трения качения колес о землю 1 см.
Решение. Заметим, что конечная скорость самолета равна Hy,do.
Будем считать, что самолет приземляется на три точки, а по-
поэтому на колеса со стороны его корпуса передается давление
N = |-. 1100 = 733 кг. A)
Давление колес на грунт равно
Nt = N + Р = 833 кг. B)
Общие теоремы динамики материальной системы 459
Благодаря наличию трения качения к колесам приложена пара
сил, тормозящая, их вращение, момент которой
т = kNv C)
Эта пара сил производит работу
A^-mtp^-kN^, D)
где s — тормозной путь самолета; г — радиус колес.
Силы сопротивления воздуха производят работу
Л2=—Fs. E)
Кинетическая энергия самолета
Т=Тг + Тш F)
состоит из:
кинетической энергии поступательно движущихся частей самолета
иГ2 — кинетической энергии колес, находящихся в плос^о-^арал-
лельном движении.
Кинетическую энергию колес определим по формуле (XXVI,45):
при составлении которой предположили, что масса колес равномерно
распределена по его ободу.
На основании теоремы об изменении кинетической энергии для
системы
-(Т1 + Т^^А1 + АШ (9)
и, следовательно,
Подставив в уравнение A0) числовые значения величин, получим
__ 100 ¦ 0,5A100 + 200) ftfi
S ~~ 2 • 9,81 • F0 • 0,5 + 0,01 • 833) ~ Ь Mt
191. Груз А (рис. 191) весом Рг подвешен к однородному не-
нерастяжимому канату длиной L и весом Q. Канат переброшен через
блок В, вращающийся вокруг оси О, и прикреплен к оси катка С,
катящегося без скольжения по неподвижной горизонтальной плос-
плоскости.
Блок В и каток С—однородные круглые диски радиусом г и
весом Р2 каждый. Коэффициент трения качения катка о горизон-
горизонтальную плоскость равен р. В начальный момент система находи-
находилась в покое, с блока В свисала часть каната длиной /. Определить
скорость груза А в зависимости от его вертикального перемещения Л.
460 Динамика
Решение. Кинетическая энергия системы состоит из кинети-
. ческой энергии груза—Т19 блока—Т2, катка—Г3 и каната—Г4.
Т = Тг + Тг+Тг+Т1. A)
Груз А находится в поступательном движении, скорость кото-
которого обозначим v, тогда
Ti-^f. B)
Блок находится во вращательном движении, значит,
Каток движется плоско-парал-
плоско-параллельно, поэтому
Все точки каната движутся со
/3 скоростью vt следовательно,
Подставив в уравнение A) значения Т1§ Т2, Т3 и Г4, на основа-
основании формул B), C), D), E) получим
Когда груз А опустится на высоту Л, то сила Рг произведет
работу
Ах = Рг • К G)
а каток вокруг своего центра повернется на угол
9 = 7"- (8)
При этом силы трения качения выполнят работу
А рР
(9)
Определим силу тяжести каната. Прежде всего заметим, что
единица длины каната весит
Т == х . A0)
а центр тяжести части каната, свисающей с блока до начала дви-
движения, занимает положение
Плоско-параллельное движение абсолютно твердого тела 461
В конце движения центр тяжести каната, расположенного на
оси Оу> находится в точке
Работу силы тяжести каната определим по формуле
А3 = ?[(/ + h) yCi - lyc>] = |. B/ + ft). A3)
Действительно, если в некоторый момент времени в вертикаль-
вертикальное положение перейдет у единиц длины нити, то
A4)
полная работа
А3 - \ydy = -}[(/ + Л)а ~ П A5)
Учитывая, что в начальный момент все точки системы находи-
находились в покое, на основании теоремы об изменении кинетической
энергии получим
Т = Аг + Аг + А3- A6)
Применив формулы F), G), (9), A3), из уравнения A6) находим
V =
ГЛАВА XXVII
ПЛОСКО-ПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ АБСОЛЮТНО ТВЕРДОГО ТЕЛА
§ 1. Основные формулы теории
Уравнения плоского движения в векторной форме имеют вид
(XXVII, 1)
где М — масса тела; Jc — центральный момент инерции относи-
относительно оси, перпендикулярной к основной плоскости; /?<е>—глав-
/?<е>—главный вектор внешних сил, L$ — главный момент внешних сил,
вычисленный относительно, центра инерции; е — вектор углового
ускорения.
462 Динамика
Уравнения (XXVII,1) в скалярной форме имеют вид:
Мхс= V
Мус - 2 *Г
7=1
п
(XXVII, 2)
Если известны все внешние силы, то, интегрируя систему диф-
дифференциальных уравнений (XXVII,2), получим хс> Ус> 9 как Функ-
Функции времени.
Внешние силы при плоском движении определяют по уравне-
уравнениям (XXVII.2).
Если заданы хс> Ус> то обычно определяют две неизвестные
силы и угол поворота <р.
Точка приложения равнодействующей внешних сил является
точкой, через которую проходит ось качаний физического маят-
маятника. Если центр ускорений принять за точку, через которую
проходит ось привеса, то имеет место соотношение
рЬ = СК • QC, (XXV11,3)
где рс — радиус инерции.относительно центра инерции (точка С);
К — точка приложения равнодействующей; Q — мгновенный центр
ускорений.
Радиус инерции — это расстояние, на котором нужно поместить
точку, в которой сосредоточена вся масса тела (системы) от точки
или оси, относительно которой вычислен момент инерции, причем
момент инерции этой сосредоточенной массы должен быть равен
моменту инерции тела.
Задачи этого раздела необходимо решать в такой последова-
последовательности.
1. Выбрать неподвижные координатные оси.
2. Составить схему внешних сил. Несвободное тело освободить
от связей.
3. Вычислить /??>; R^; | L^ (F,).
4. Определить начальные условия движения.
5. Проверить, можно ли непосредственно составить уравнения
сохранения движения центра инерции или количества движения
или нужно применить теорему об изменении кинетической энергии
системы и если это возможно, составить соответствующие урав-
уравнения.
Плоско-параллельное движение абсолютно твердого тела
463
6. Составить систему дифференциальных уравнений (XXVI 1,2).
7. Проинтегрировать составленную систему уравнений и найти
искомые величины.
§ 2. Задачи
192. Ось ведомого колеса автомобиля (рис. 192) движется
горизонтально и прямолинейно. К оси колеса приложена горизон-
горизонтально направленная движущая
сила F. Радиус инерции колеса
относительно оси, проходящей че-
через центр тяжести перпендику-
перпендикулярно к его плоскости, равен р.
Коэффициент трения скольжения
колеса о землю равен /. Радиус
колеса равен г, а вес его равен Р.
Какому условию должна удовле-
удовлетворять сила F, для того чтобы
колесо катилось без скольжения? к задаче 192
Решение. Для того чтобы колесо катилось без скольжения,
сила трения его о рельсы по величине не должна быть больше
максимальной силы трения скольжения
Ti<fN, A)
где Тг — сила трения скольжения, N — сила нормального дав-
давления. _
Внешними силами, приложенными к колесу, будут: сила F;
его вес Р; нормальная реакция рельса R и сила трения Тъ приложен-
приложенная в точке касания колеса с рельсом и направленная в сторону
вращения колеса вдоль рельса. Координатную ось Ох направим
по рельсу, а ось Оу — перпендикулярно к нему.
Центр инерции колеса движется прямолинейно, поэтому
Ус=#. B)
Кинематическое условие качения колеса без скольжения заклю-
заключается в том, что точка К соприкасания колеса с рельсом является
мгновенным центром скоростей.
Обозначим угол поворота колеса вокруг оси, перпендикуляр-
перпендикулярной к плоскости рисунка и проходящей через центр тяжести, через ф,
тогда
хс = #ф. C)
Заметив, что
D)
464
Динамика
уравнения плоско-параллельного движения колеса запишем в виде
E)
Принимая во внимание зависимости B), C), уравнецие E)
преобразуем так
Из уравнений F)
= Tt . r ,
F)
G)
Учитывая второе уравнение системы F) и соотношение A),
получим
Ра "
193. Груз А (рис. 193) весом Р, опускаясь вниз посредством
невесомой нерастяжимой нити, переброшенной через неподвиж-
неподвижный блокД и намотанной на барабан Bi заставляет колесо С катиться
к
К задаче 193.
без скольжения по горизонтальному рельсу. Барабан В радиусом г
жестко связан с колесом С радиусом R; их общий вес равен Q,
а радиус инерции относительно оси О равен р. Найти ускорение
груза А.
Решение. Барабан вместе с колесом находится в плоско-парал-
плоско-параллельном движении. К нему приложены силы: собственный вес Q,
Плоско-параллельное движение абсолютно твердого тела 465
сила трения скольжения Т, нормальное давление N и сила натя-
натяжения нити 7\.
Заметим, что центр инерции барабана движется прямолинейно,
Уо = 0, A)
B)
На основании уравнений B) имеем
тхс = Т1 — Т )
| C)
Исключив из уравнений C) силу трения Г» находим
Если учесть, что вращательное ускорение точки Е барабана равно
ускорению точки А груза, то получим зависимость
(Я + г) ф = шА» E)
на основании которой уравнение D) преобразуем к виду
Из дифференциального уравнения движения груза Л
^.^^Р-Г», G)
учитывая зависимость F), находим
wA =
194. Однородный стержень Л?$ весом Р подвешен в точке О
(рис. 194) на двух нитях равной с ним длины. Определить натяжение
одной из нитей в момент обрыва другой.
Решение. Обозначим угол поворота стержня АВ вокруг точки А
после разрыва нити ОВ через #<р и будем считать его достаточно
малым. ' _
К стержню_приложены внешние силы: собственный вес Р и
реакция нити Т.
30 591
466
Динамика
Заметив, что:
2 Xt = T ¦ cos 60°
2У* =Р — Т . sin60°
Ц/.?С)(^») = Ту sin 60°
ка основании уравнений (XXVI 1,2) находим:
— хс = Т • cos 60°
Lyc==p — T -sin 60°
A)
где
К задаче 194.
1^9 = Г|. sin 60°
«/ /"J —— < л •
B)
Для весьма малого угла поворота можно считать ус = -^ <р,
исключив ф из второго и третьего уравнений системы B), получим
зависимость
I
¦ Т • sin 60°) = Т i- sin 60°,
C)
из которой
К задаче 195.
Т = -±— « 0,29Р.
21/3
195. Два цилиндрических
вала ^рис. 195) весом Рг и Р2
скатываются по наклонным
плоскостям, образующим соот-
соответственно углы а и р с го-
горизонтом. Валы соединены
нерастяжимым канатом, кон-
концы которого намотаны на
валы и прикреплены к ним. Определить натяжение каната и его
ускорение при движении по наклонным плоскостям. Валы счи-
считать однородными круглыми цилиндрами, весом нити пренебречь.
Решение. Обозначим ускорение точек движущегося каната
через w и направим его, как указано на рисунке.
Ось Ох направим в сторону положительного значения вектора w.
Освободим оба цилиндра от связей, заменив их реакциями
Rv ^2» Т, а сложное движение цилиндров разложим на перенос-
Плоско-параллельное движение абсолютно твердого тела
467
ное поступательное вместе с канатом и относительное вращатель*
ное вокруг их центров инерции.
В этом случае
(I)
где фх и ф2 — углы поворота первого и второго цилиндров вокруг
ях центров инерции.
Составим дифференциальные уравнения плоско-параллельного
движения цилиндров:
для первого
Рл '-' ' " v «^sina — T
для второго
B)
C)
P9cos8 =0
При составлении системы уравнений C) учтем, что ось Ох направ-
направлена в сторону движения каната.
Из системы уравнений B) и C)
b^w = p sina — ЗГ
g
А ^ = — Р2 sin р + ЗГ
Сложив уравнения системы D), получим
Рл sin a — j
D)
E)
а исключив из них величину w9 определим натяжение каната
~9 (sin а 4- sin В)
F)
30*
468
Динамика
ГЛАВА XXVIII
ДАВЛЕНИЕ ВРАЩАЮЩЕГОСЯ АБСОЛЮТНО ТВЕРДОГО ТЕЛА
НА ОСЬ ВРАЩЕНИЯ
§ 1. Методические указания к решению задач
Задачи этого раздела рекомендуем решать в такой последова-
последовательности.
1. Выбрать две системы координатных осей: одна неподвижная,
а другая связанная с телом, вращающимся вокруг оси, причем
оси подвижной координатной системы располагаются по главным и
центральным осям инерции.
2. Если необходимо определить статические реакции, то нужно
составить схему внешних сил и найти реакции из системы
уравнений:
Sv!"
(XXVIII,!)
Ось Ог координатной системы является осью вращения.
3. Освободить ось вращения от связей, заменив их динами-
динамическими реакциями.
4. Если вокруг оси вращаются отдельные точечные массы, то
к ним необходимо присоединить силы инерции и для определения
динамических реакций составить уравнения равновесия сил инер-
инерции и реакции связи
Давление вращающегося абсолютно твердого тела на ось вращения 469
n
)] = О
(XXVIII.2)
(шестое уравнение равновесия совпадает с дифференциальным
уравнением вращательного движения тела вокруг оси Oz).
5. Если вокруг оси вращается абсолютно твердое тело, то
динамические реакции определяются по уравнениям
М(—еус-ы2хс) =
(XXVIII.3)
ejvz = -
7^=0
где ауЬ — координаты точек приложения динамических реакций;
начало координат неподвижной координатной системы располо-
расположено на оси вращения.
6. Чтобы составить систему уравнений (XXVI 11,3), предвари-
предварительно находят центробежные моменты Jxg, Ууг,метод их вычисле-
вычисления указан ниже, при решении задач.
7. Если ось вращения центральная и тело вращается равно-
равномерно, то уравнения (XXVI 11,3) принимают вид
(XXVIII.4)
^аУ^ — bYf
т. е. динамические реакции приводятся к паре сил.
470
Динамика
8. Если ось вращения главная, а не центральная, то для точки,
расположенной в плоскости материальной, симметрии, динами-
динамические pea-кции определяются из следующей системы уравнение
(XXVIII.5-»
1V1 { """¦""" С ч Q ^^^ vJ ^C/ '
М(ехс — ы*ус) -:
В этом случае динамические реакции приводятся к равнодей-
равнодействующей.
§ 2. Задачи
196. К вертикальному валу АВ (рис. 196,а), вращающемуся
с постоянной угловой скоростью оз, жестко прикреплены два стержня
Стержень ОЕ образует с валом угол <р; стержень 0D перпендк
кулярен к плоскости, содержащий вал АВ и стержень ОЕ. Известно
К задаче 196.
размеры: ОЕ =0D = /; АВ = 2 а. К концам стержней прикреп-
прикреплены соответственно шары ? иО, массой т каждый. Определить
динамические давления на вал в опорах А и ?. Шары D и Е счи-
считать точечными массами, массами стержней пренебречь.
Решение, Присоединим к вращающимся массам силы инерции:
\JE\ = moJ/ • sin cp
\7D\ = moJ/
Давление вращающегося абсолютно твердого тела на ось вращения 47!
Введем динамические реакции, освободив вал от связей в точкам
1.и В.
Составив уравнения равновесия, найдем
О
B!
J e • i • COS О -f- {Y В — У А ) &
Решив эту систему уравнений относительно неизвестных реак-
реакций, получаем
= Лв =
moo2/-sin со
2а
- (а — / cos cp)
/noJ/-sin i
2а
(а + / cos cp)
Ответы, приведенные в сборнике Задач (И. В ' Мещерский «Сбор-
«Сборник задач по теоретической механике»), не соответствуют указан-
указанному выше условию задачи.
Чтобы получить ответы, данные в сборнике, необходимо изме-
изменить условие задачи, а именно предположить, что стержни укреп-
укреплены на расстоянии j coscp от начала координат (рис. 196,6).
Действительно, составив уравнения равновесия сил инерции
и реакции связей
Yf
(XT - XW)a -JD-i- coscp = 0
— Y(f))a + JE • т • /coscp = 0
и решив их, найдем
maJ/Bа —
— 55
maJ/ Bа + / cos cp)
хД = " й
, г(а> _ /ПоJ/ sin cp C/ cos о — 2а)
VyA- 45
да) ___ woJ/ sin cp C/ cos о -j- 2a)
472
Динамика
197, Однородная прямоугольная пластинка (рис. 197) весом Р
равномерно вращается вокруг диагонали АВ с угловой скоростью (о.
Определить динамические давления пластинки на опоры А и В<
если длины сторон равны а и Ь.
Решение. Освободим ось вращения от связей, заменив их дина-
динамическими реакциями.
Учитывая, что вращение вокруг оси А В совершается с постоян-
постоянной угловой скоростью, а избранная система координатных осей
центральная, из системы уравне-
Y«n ний (XXVI 11,4) находим
.A)
Y(Bd) = 0
— в
k
К задаче 197.
Рассмотрим случай, когда ось
сх направлена по перпендикуляру
к плоскости пластинки и является, таким образом, главной и
центральной осью, т. е. для нее
Jzx = 0.
B)
Для вычисления центробежного момента Jzy введем централь-
центральную и главную координатную систему с%т\? так, чтобы оси сх к
с? совпали, а ось ct, была параллельна стороне прямоугольника
длиной а, а т] к ней перпендикулярно.
Между координатными осями cz и с ? образуется угол а, величина
которого определяется по уравнению
tg«-4- C)
Преобразуем в подынтегральном выражении
Jzv = \ zydm
D)
переменные величины г> у в величины С» "Ч ПРИ помощи формул,
выражающих поворот координатных осей:
г = С sin a + т] cos а
^ «= С cos а — т) sin а
E)
Давление вращающегося абсолютно твердого тела на ось вращения 473
Подставив значение z,y в D), находим
L(ilf) (M) J
cos2a
F)
(ilf) (M) J (M)
Так как координатная система c%-rfc главная, то центробежный
момент
= 0.
G)
(М)
Вычислим аксиальный момент инерции:
а Ь
Т Т
(М)
Аналогично
Следовательно,
I /Л 1 Л
а Ь
На основании формул B), A0) систему уравнений A) приведем
к виду
а* — Ь*
У?
(М)
= 0
0
Из системы уравнений A1)
= 0;
198. Однородный тонкий диск (рис. 198,а) насажен по середине
горизонтального вала с эксцентриситетом Ос = I и под углом
90°—а к оси вала; вес диска Р, радиус г. Определить статические
и динамические реакции опор при равномерном вращении диска и*
вала с угловой скоростью си; расстояние между опорами АВ = 2а,.
474
Динамика
Решение. Для определения статических реакций составим схему
сил, действующих на вал (рис. 198,6). На него действует внешняя
сила тяжести диска Р и реакции опор Rat) и i?BT), которые направ-
направлены по перпендикуляру к опорным поверхностям подшипников.
Нетрудно заметить, что
AD = a — /sina j
DB
7 sin а
A)
Составим уравнение равно-
равновесия сил, приложенных к валу
B)
.C-
D;
тогда:
— R^2a+P{a—l sm a) =0
откуда находим:
"> = Р
a -f / sin a
К задаче 193.
_ р
а — / sin <
Та
Вращение вокруг оси АВ совершается с постоянной угловой
скоростью, поэтому для определения динамических реакций исхо-
исходим из системы уравнений
Ф)
(б)
Ось Оу является главной осью, поэтому
Для вычисления Jzx введем подвижную центральную и главную
системы координатных осей с§т]?.
Переход от старой системы координат к новой осуществляется
при помощи формул
х = (/ + 5) cos а — ? sin а
+ С cos а
Давление вращающегося абсолютно твердого тела на ось вращения 475
Принимая во внимание формулы G), получим
Jzx = J xzdm =
j (I +
ТЧ*"Ч
dm -
(M) L(M)
+ cos 2a J (/ -f- (•) X^dm. (8
(M)
Так как начало координат системы с^цъ помещены в центре
инерции диска» то s
Ыт
(к)
= 0; J'gdm^O,
(М)
и„ следовательно,
I sin 2а
('if)
Для диска с равномерно распределенной массой
поэтому
Т' '
Учитывая, что;
i/c = 0; хс = / cos а,
из системы уравнений E) находим:
, Yf = Yf = 0
Ml cos a . ш3 = — {Xf
D eir> 9-, / ' DS
4 /
откуда:
(9
/12
ГЛАВА ХХ1Х
ЗАДАЧИ СМЕШАННОГО ТИНА
§ 1. Методические указания к решению задач
В этой главе приведено решение задач, в которых одновременно
применяются ранее изложенные теоремы о движении материальной
системы и абсолютно твердого
476 Динамика
Закон движения центра инерции системы (XXIX,4) применяется
при изучении поступательной части движения. Теорема об изме-
изменении количества движения (XXIX,14) применяется при изуче-
изучении эффекта действия сил во времени. Теорема об изменении мо
мента количества движения (XXVI,31) используется при исследо-
исследовании вращательного движения системы или тела. При изучении
эффекта действия сил на отрезках пути, проходимых точками их
приложения, используется теорема об изменении кинетической
энергии системы (XXVI,50). Эта теорема также применяется для
определения внутренних сил, действующих между точками си-
системы.
Задачи этого раздела необходимо решать в такой последова-
последовательности.
1. Выбрать систему отсчета.
2. Выделить тело или точки системы, движения которых изу-
изучаются в первую очередь.
3. Составить схему сил и реакций связей.
4. Исследовать тип движения тела и выбрать теоремы механики,
€ помощью которых можно получить ответ на поставленные во-
вопросы.
5. Применяя ту или иную теорему механики, вычисления сле-
следует проводить в последовательности, указанной выше при реше-
решении задач на непосредственное использование теоремы, о которой
идет речь.
6. На основании теорем механики составить систему дифферен-
дифференциальных уравнений или конечных уравнений, являющихся их
первыми интегралами, из которых определить искомые величины.
§ 2. Задачи
199. Определить период малых колебаний однородного полу-
полукруглого диска радиусом R (рис. 199), находящегося на негладкой
горизонтальной плоскости, по ко-
1 . торой он может катиться без сколь-
скольжения.
Решение. Рассматриваемое те-
тело движется под действием внеш-
внешней силы Р.
Освободим полукруглый диск от
связи, введя вместо нее реакцию
Rx и силу трения скольжения 7\.
Положение диска будем опре-
определять углом ф наклона радиуса
ОХА к вертикали.
Для решения задачи применим теорему об изменении кинети-
кинетической энергии.
Задачи смешанного типа 477
Заметив, что мгновенная ось вращения проходит перпендику-
перпендикулярно к плоскости рисунка через точку К касания диска с пло-
плоскостью, приходим к заключению, что работа сил Тг и Rx равна
нулю, а работу произведет сила тяжести Р, причем
А(Р)=— Р-ОХС( 1— cos <p). A)
Как известно из статики, положение центра тяжести полукруг-
полукруглого диска определяется по формуле
0гС-?, B)
поэтому преобразуем формулу A) к виду
с точностью до величин более высокого порядка малости.
Кинетическую энергию полукруглого диска определим по
формуле
Т =* 2" jp?*> D)
где
Jp = Jc + М . СР2 = Jc + JL {ОгС* + ОгР* — 20гС . ОгР cos ср),
а так как:
ОгР^а; coscp« 1 f ; jc e ^ - ^ ОХЛ E)
то
Предположим, что в начальный момент полудиску сообщили
начальную угловую скорость ф0, тогда на основании теоремы об
изменении кинетической энергии для системы (XXVI,51), а также
уравнений D), E) находим
-Ш (9* - 16) (?а - ip = - ^— та. F)
Продифференцировав по времени левую и правую части урав-
уравнения F), получим дифференциальное уравнение малых колебаний
полудиска
Так как частота колебаний
то период малых колебаний определяется по формуле:
Т = JL |^2^(9tc — 16)/?. (9)
478
Динамика
t 200. На гладкой горизонтальной плоскости помещена тре-
треугольная призма ABC весом Р (рис. 200), которая может скользить
без трения по этой плоскости; по грани АВ катится без скольжения
однородный круглый цилиндр весом Q. Определить движение
призмы.
Решение. На тело действуют внешние силы Р и Q.
Освободим систему от связи,' заменив ее вертикальной распре-
распределенной реакцией R.
Ось Ох направим горизонтально.
На основании леммы о количестве движения центра инерции
системы
?Ст=0 ' A)
К задаче 200.
заключаем, что горизонтальная со-
составляющая вектора скорости центра
инерции сохраняется.
Если считать, что в начальный
момент пРизма и Цилиндр были непо-
движными, то из уравнения A) получим
- ^ = q B)
Обозначим вектор скорости центра инерции цилиндра через г0.'
Так как цилиндр приходит в движение, то для сохранения состав-
составляющей вектора количества движения системы вдоль оси Ох необ-
необходимо, чтобы и призма пришла в движение противоположного
направления.
Обозначим вектор скорости центра инерции поступательно)
движущейся призмы через и.
Призма сообщит цилиндру переносное движение, а поэтому
проекция абсолютной скорости его центра инерции на направление
оси Ох будет равна: -
vOx = v0 cos ос. — и. C)
Составим теперь явное выражение для проекции вектора коли-
количества движения системы на ось Ох:
Л'а. = — Yu+ -f-fao cos а — и). D)
Учитывая 'уравнение B), находим:
Для определения кинематических характеристик движения
призмы .воспользуемся теоремой об изменении кинетической энер-
Задачи смешанного типа 479
гни. Прежде всего составим выражение для кинетической энергии
системы, которая состоит из суммы кинетических энергий призмы—
7\ и цилиндра—Г2.
Призма движется поступательно, поэтому ее кинетическая
энергия
'^ = —иУ F)
Цилиндр находится в плоско-параллельном движении, поэтому
его кинетическая энергия определяется по уравнению (XXVI,45),
для составления которого необходимо учесть, что, кроме горизон-
горизонтальной составляющей скорости C), центр инерции цилиндра
имеет и вертикальную составляющую
vVo = v0 sin ос. G)
Момент инерции' цилиндра относительно его центральной про"
дольной оси равен
'.-?• да
Итак, можем написать
Т* ~- -| [("о cos « - и)*+ v I sin2 a] + ^f-. (9)
Учитывая, что цилиндр катится без скольжения, устанавливаем
дополнительное соотношение
Q cos а
На основании формул F), G), A0) рнаходим окончательное
выражение для кинетической энергии системы:
ИЛИ х
Т = ТЩГ^ '3(Р +Q)- ?Q cos" a] ««. A2)
Работа приложенных сил равна
А = Qrcpsina, A3)
где ф — угол поворота цилиндра вокруг центра инерции.
Теорема об изменении кинетической энергии для системы при-
приводит к соотношению
~ 2B cos2 al = "¦ ^ sin a-
Дифференцируя по времени уравнение (\4) согласно A0), най-
найдем:
, X у cos
2Qg COS2 ос t V T- ^c/ v , X у cos a
480
Динамика
откуда
w = ,
Qg sin 2a
A6)
201. На боковой поверхности круглого цилиндра (рис. 201)
с вертикальной осью, вокруг которой он может вращаться без
трения, вырезан гладкий винтовой желоб с углом подъема а. В на-
начальный момент цилиндр находится в покое; в желоб опускают
тяжелый шарик, который, падая по нему без начальной скорости,
заставляет цилиндр вращаться. Дано: масса
цилиндра М, радиус его R, масса шарика т;
расстояние шарика от оси считаем равным R
и момент инерции цилиндра равным г/2 MR2,
Определить угловую скорость со, которую
цилиндр будет иметь в тот момент, когда шарик
опустится на высоту К
Решение. Введем неподвижную систему
координатных осей Охуг.
На систему действуют внешние силы Р,
Q и реакции опор. Эти силы не создают
момента относительно оси Ог, а поэтому мо-
момент количества движения системы относи-
относительно этой оси остается постоянным
1% = const.
Так как в начальный момент шарик и
цилиндр были неподвижными, то
/, = о A)
Соотношение A) остается справедливым во время движения
шарика по желобу, поэтому цилиндр приходит во вращательное
движение в противоположном направлении по отношению* к на-
направлению движения шарика.
Обозначим угловую скорость вращения цилиндра через1 со, а
угол поворота радиуса вектора точки М, отсчитываемый от оси Ок,
через ф, тогда проекции абсолютной скорости движущегося шарика
на неподвижные оси будут
их = (v cos a — Rb>) sin cp
uy = (v cos a — R(j>) cos <p ¦ • B)
uz = v sin a
Соотношение A) в явном виде выглядит так
К задаче 201.
— tnuJR = 0.
C)
Удар 481
Заменив в формуле C) момент инерции его значением, а также
ия, на основании уравнений B) найдем
(M+2m)Rc* ¦
2m cos а ' к >
Из формул B) вытекает, что квадрат абсолютной скорости дви-
движения шарика равен
и2 = (v cos а — #соJ + v2 sin2 а. E)
На основании формулы D) выражению E) придаем вид
2 _ #2а>2 М2 COS2 а + (М + 2юJ Sin2 a fi
tt ~ 4m2 cos2 а • (Ь>
Кинетическая энергия системы равна сумме кинетических
энергий цилиндра
т MR2 « ,„ч
Tj = -j- (о2 G)
и шарика
Т ^
Учитывая формулу F), кинетическую энергию системы выразим
так
Т = ~- (М + 2т) (М Ч- 2т sin2 a). (9)
Работа, произведенная силой Р, имеет величину
А = mgh. A0)
Теорема об изменении кинетической энергии системы материаль-
материальных точек (XXVI,51) приводит к соотношению
(D2R2(M + 2т) {М + 2т sin2 а) = 8ш2 hg cos2 а, A1)
из которого находим
2m cos a
R \ (М -Ь 2т sin2 а) (М + 2т) *
ГЛАВА XXX
УДАР
§ 1. Методические указания к решению задач
Мгновенной силой называется сила, которая действует в течение
ничтожно малого промежутка времени, но достигает при этом
настолько больших значений, что ее импульс есть величина ко-
конечная.
31 591
482 Динамика
При расчете действия мгновенной силы можно пренебрегать
действием конечных сил, а также перемещением материальной
точки за время действия мгновенной силы.
Результат действия мгновенной силы выражается в изменении
скорости точки, приращение которой определяется формулой
у2_^ = ~, . (ХХХ.1)
где
Т
(ХХХ.2)
4м-
О
импульс мгновенной силы; /\ т — продолжительность удара.
Удар называется центральным при условии, что центры инерции
двух твердых, поступательно движущихся тел располагаются на
одной прямой и общая нормаль в точке касания этих тел лежит на
этой же прямой.
Теорема L Количество движения двух шаров с массами тг и
щ сохраняется при центральном ударе
ттРг + ЩЩ = тхих +/таы2, (ХХХ,3)
где иъ и2 — скорости первого и второго шара до удара, vl9 v2 —
скорости этих шаров после удара.
Если тела после удара движутся как одно целое, то удар назы-
называется пластическим.
Если даны массы тел и их скорости до удара и известно, что
удар пластический, то скорость после удара определяется по
формуле:
П т1Ц1 + m*U2 /YVY Л\
V== т. + т, ' (ХХХ.4)
а импульс имеет величину
17", mlm2{u1 — u2) /vyy с\
|У I = -т, + тг • (ХЛЛ,5)
причем их > и2.
Коэффициент восстановления k вычисляется по формуле
iHSL^jc (XXX,6)
При упругом ударе k изменяется в пределе
0<Л<1; (XXXJ)
при пластическом ударе
fe = 0, (XXX,8)
а для абсолютно упругого удара
&=1. (ХХХ,9)
Удар
483
Скорости шаров после упругого удара определяются по формулам
где v находится по формуле (XXX,4).
Закон количества движения материальной системы, применен-
примененный к движению центра инерции за время удара т, приводит к
соотношению
п
М V — Мп = Jj Ле). <ХХХ,11)
i=i
где М — масса системы.
Уравнение (XXX,И) в координатной форме принимает вид
M{vy-uy) =
(XXX',12)
Уравнения (XXX, 12) применяются при расчете влияния мгно-
мгновенных сил на движение центра инерции системы.
Теорема 2. Геометрическое приращение главного момента коли-
количеству движения системы за время удара равно геометрической
сумме моментов импульсов всех внешних мгновенных сил:
(ХХХЛЗ)
/0 (v) - Ци) = J] L0(J<f)).
Из уравнения (XXX, 13) для вращательного движения находим
ШЩ, . (XXX,14)
где ]ъ — момент инерции тела, а)г — угловая скорость после
удара, о>0 — угловая скорость до удара, SLf(J^)—проекция главного
момента импульсивных сил на ось вращения Oz.
Теорема 3. (Остроградского-Карно). Изменение кинетической
энергии при ударе равно кинетической энергии потерянных скоро-
стей, умноженной на коэффициент-г—т.
1 «J- R
31*
484 Динамика
Потерянными скоростями называется разность скоростей и—v
до удара и после удара
Разделим время удара х на две стадии: первая продолжается
от момента начала удара tx до момента /3» в которой скорости шаров
становятся одинаковыми, и вторая от момента tz до момента окон-
окончания удара L.
Первая стадия удара сопровождается потерей кинетической
энергии ударившихся тел
Г3 — 7> = - ъщкщ-иР (XXX,16)
Во время второй стадии удара происходит частичное восстановление
кинетической энергии
Т т fr2 т\Щ{и1 и%Т * /YYY 17^
12 — 13-Ь 2(щ + mj . (АЛА,17)
Уравнение (XXX, 15) можно представить в виде
Г2 —7\ = —A —A2) ^T^mf' (XXX,18)
Если в результате приложения мгновенной нагрузки в некото-
некоторой точке тела ось привеса этого тела не испытывает дополнитель-
дополнительных динамических (ударных) нагрузок, то эту точку называют
центром удара.
Если тело имеет перпендикулярную к оси вращения плоскость
материальной симметрии Я, которая пересекает ось привеса тела
в точке О, а центр инерции располагается на расстоянии ОС, то
центр удара К находится на прямой, проходящей через точку оси
привеса и центр инерции на расстоянии
OK==M%C^ (XXX, 19)
где «V—момент инерции тела относительно точки привеса,
Л{ — масса тела.
При этом импульс 1 ударной силы должен находиться в пло-
плоскости симметрии П перпендикулярно к прямой ОК.
Таким образом, центр удара совпадает с центром колебаний
физического маятника.
Задачи этого раздела следует решать в такой последовательности.
1. Определить скорости тел в момент их удара иъ щ.
2. Составить уравнения теории удара, позволяющие найти
скорости соударяющихся тел после удара vl9 v2. При составлении
этих уравнений необходимо учитывать, в каком движении находятся
тела. Если тела находятся в поступательном движении, то следует
исходить из уравнений (ХХХ,3), (ХХХ,6), (XXX,12), (XXX, 15),
Удар 485
а при вращательном — из уравнений (XXX,13), (XXX,14),
(XXX,15).
3. При решении задач на косой удар векторы скоростей соуда-
соударяющихся тел нужно разложить на составляющие по направлению
общей нормали в точке касаний и на составляющие, находящиеся
в общей касательной плоскости, изучить характер изменения
этих составляющих на протяжении удара й определить их вели-
величину после удара.
4. Изучить движение тел после удара с помощью теорем меха-
механики методами, изложенными в предыдущих главах.
§ 2. Задачи
202. Груз А (рис. 202) весом Р падает без начальной скорости
с высоты h на плиту В весом р, укрепленную на пружине, которая
имеет коэффициент жесткости с. Найти
величину s сжатия пружины после уда-
удара, предполагая, что коэффициент вос-
восстановления равен нулю.
Решение. Удар груза А о плиту
пластический. После удара груз и плита
движутся как одно тело, скорость дви-
движения их обозначим через ив.
Применив теорему об изменении
кинетической энергии для груза Л, най-
найдем, что в момент удара он обладал /х//
скоростью
vA=V2gh. A) К задаче 202.
Из закона сохранения количества движения во время удара
(ХХХ.З)
1
PC
d
Й
р
.о
т
1
в
со
1
g A g
откуда
Для того чтобы найти отклонение s плиты после удара, при-
применим теорему об изменении кинетической энергии.
Прежде всего заметим, что сила тяжести плиты р уравнове-
уравновешена упругой силой пружины, т. е.
р = с . Хст, C)
где Хст — статическое удлинение пружины, а поэтому она не произ-
производит работы на отклонении s.
486
Динамика
На указанном перемещении s работу производят сила тяжести
груза Р и упругая сила F = сх, поэтому
2
Приращение кинетической энергии равно
i 2 i х — —р _|_ р »
следовательно,
2Р 2Я2.Л
-О
откуда
D)
E)
F)
G)
Знак минус в формуле G) отбрасываем, так как отклонение
не может быть отрицательным.
203. Шар массой т1 (рис. 203), движущийся со скоростью vlt
встречает покоящийся шар массой т2, так что скорость,его обра-
образует при ударе угол а с линией, соединяющей центры шаров. Опре-
Определить: 1) скорость первого шара
после удара, считая удар абсолют-
абсолютно неупругим; 2) скорость каж-
каждого из шаров после удара, пред-
предполагая, что удар упругий с коэф-
коэффициентом восстановления k.
Решение. Разложим вектор ско-
скорости v-i до удара на составляющие:
К задаче 203.
вдоль линии, соединяющей центры, и
Vix = vx sin a
в направлении общей касательной к шарам.
Для второго шара
Vln = Vx COS а
A)
B)
C)
Поверхности шаров считаем абсолютно гладкими, поэтому:
Щх = «it, D)
где uXz — величина касательной, составляющей скорости первого
шара после удара.
Рассматривая пластический удар шаров, на основании теоремы
о сохранении количества движения системы при ударе напишем:
mxvxn = (тх
Удар 487
откуда
Модуль, скорости первого шара после удара
V иЪ + и\п = vx ysin2 + (~q^) * cos* a. G)
Обозначим нормальную составляющую скорости второго шара,
которую он приобретает при упругом ударе, через и2п-
На основании теоремы о сохранении количества движения си-
системы при ударе имеем
(8)
а на основании формулы для коэффициента восстановления (XXX,6)
kvin = U2n — Щп- (9)
Решив совместно уравнения (8) и (9), находим
и1п = -^—; 2- vx cos a
« A0)
Принимая во внимание формулы B), D), A0), а также то, что
«2t = 0, (И)
устанавливаем:
V. «
sin a
— km» 2
A2)
к)
204. Для укрепления грунта под фундамент здания вбивались
копром сваи весом Рг = 50 кг. Боек копра весом Р2 == 450 кг па-
падал без начальной скорости с высоты h = 2 м\ коэффициент вос-
восстановления равен нулю; при последних десяти ударах свая углуби-
углубилась на Ь = 5 см. Определить среднее сопротивление грунта при
вбивании свай.
Решение. Эту задачу можно решить двумя способами.
Первый способ. Учитывая, что скорость сваи до удара равня-
равнялась нулю, а удар пластический, скорость движения копра и сваи
после удара вычислим по формуле
где vx = VBgh — скорость копра в момент удара.
488 Динамика
При п ударах на забивание сваи расходуется кинетическая
энергия
пт\ v\ nm\gh
т == —- = B>
1 2(/и1 -f m2) mi + Щ
Работа внешних сил тяжести (Рх' + Р2) и искомого среднего
сопротивления грунта «S на пути / равна
На основании теоремы об изменении кинетической энергии и в
силу того, что после п ударов система теряет скорость, напишем
_ ^ ™ = (рг + Р2 — 5)/, C)
откуда
Подставив в формулу D) числовые значения величин, получим
L 10 • <450>2 • 2
500 . 0,05
Второй способ. Кинетическая энергия Т2 после удара равна
полезной работе Аи до удара — фактически затраченной, поэтому
согласно формуле (XV,И) коэффициент полезного действия копра
Кинетическая энергия копра до удара
T^^vi^P^h. F)
На основании формулы (XXX, 15) вычислим потерю кинети-
кинетической энергии за время удара
гр гр A — k?) Ш^ТП^ 2 у«х
Из формул E), F) и G)
пг1
для пластического удара
В результате /г ударов копра выделяется энергия
Т2 = т]^ • /г, A0)
т. е. находим выражение B), а ход дальнейших рассуждений
остается неизменным.
Удар
205. В приборе для определения коэффициента восстановления
при ударе (рис. 205) имеется стержень, вращающийся в верти-
вертикальной плоскости вокруг горизонтальной оси О и несущий на
определенном расстоянии от нее вставку из испытуемого материала;
стержень начинает падать из горизонтального положения под
действием собственного веса без начальной скорости и в вертикаль-
вертикальном положении ударяется о препятствие в виде неподвижно закреп-
ленной пластины испытуемого материала Определить коэффициент
восстановления ky если после удара стержень отклонился от верти-
вертикального положения обратно на угол <р, и указать, на каком рас-
расстоянии х от оси вращения стержня следует поместить образец
испытуемого материала, чтобы при
ударе не возникали дополнительные
усилия в подшипнике оси О.
Решение. Обозначим вес стержня
через Ръ а вес испытуемого матери-
материала через ' Р2.
На основании теоремы об изме-
изменении кинетической энергии системы
(XXVI,51) можно написать
= |. (щ/
A)
К задаче 205.
где J = -Q- момент инерции стержня относительно оси, про-
о
ходящей через точку О перпендикулярно к плоскости рисунка;
а) — угловая скорость стержня в момент удара.
В момент удара груз М приобретает скорость
VmJ
-f
а после удара
и = ко.
B)
C)
Стержень иосле удара придет во вращательное движение с
угловой скоростью
ко . л.
«!=-. D)
На основании теоремы об изменении кинетической энергии
напишем
-4-
2
л
л (тЛ -4- 2т2х) /л ч
2 = gV 1 ^ 2 ' • A — COS ф).
E)
Учитывая выражения B), D), из уравнения E) находим
k = V 2 sin i.
490 Динамика
Для того чтобы ось вращения не испытывала дополнительных
усилий, груз М необходимо поместить в центре удара.
Так как координата центра инерции системы определяется
по формуле
m + (Щ + Щ) хс, F)
то согласно (XXX, 19) напишем
Лс — j . {If
Из уравнения G)
К задаче 206. 206. Два шкива (рис. 206) вра-
вращаются в одной плоскости вокруг
своих осей с угловыми скоростями оI0 и оJо- Определить угловые
скорости шкивов шх и оJ после того, как на них будет накинут
ремень, считая шкивы круглыми дисками одинаковой плотности и
радиусами Rx и R2; скольжением и массой ремня пренебречь.
Решение. Эту задачу можно решить двумя способами.
Первый способ. Применив теорему о геометрическом приращении
главного момента количества движения системы за время удара,
которое равно геометрической сумме моментов импульсов всех
внешних мгновенных сил (ударов), для первого шкива, находим
Л К — wio) = SRi> (!)
где S— импульс мгновенной силы натяжения ремня.
Помимо этого импульса, к шкиву приложен импульс мгновенной
реакции оси; его момент относительно оси вращения равен нулю.
Для второго шкива аналогично получим
/ /,Л ... ч ер (о\
Исключим из соотношений A) и B) импульс 5, тогда
Скольжение ремня отсутствует
AI^1 = цJ/?2. D)
Подставив значение о>2 в уравнение D), получим:
wi = ~7^м-у^2(°2° " E)
Так как
Удар
-491
из уравнения E) находим
Формулы D), G) дают возможность определить щ:
G)
(8)
Второй способ. Решение задачи по данному способу основано
на применении теоремы Остроградского — Карно.
Кинетическая энергия, соответствующая потерянным скоростям
при пластическом ударе, выражается так
Но, как известно,
J —
ОJ
(Ю)
A1)
A2)
A3)
Из соотношений (9) и A0) находим'
Учитывая, что
из уравнения A1) получим
J -S)
1 2 R, j - <*>1
т. е. приходим к формуле E).
Дальнейший ход.решения совпа-
совпадает с вышеизложенным.
207. Однородная прямая призма
с квадратным основанием (рис. 207)
стоит на горизонтальной плоскости и
может вращаться вокруг ребра АВ9
расположенного в этой плоскости.
Ребро основания призмы равно а,
высота ее — За, масса — Зт. В середи-
середину с боковой грани, противолежащей
ребру АВУ ударяет шар массой т с
горизонтальной скоростью v.
Предполагая, что удар неупругий
и масса шара сосредоточена в его
центре, который после удара остается в точке с% определить
наименьшую величину скорости v, при которой призма опрокинется.
К задаче 207.
492 Динамика
Решение. Момент импульсивных сил относительно оси
равен нулю, поэтому момент количества движения до удара и
после сохраняется, т. е.
-a-mv^J A)
Вычислим момент инерции системы относительно оси вращения
Огуг, состоящий из суммы моментов инерции шара и призмы отно-
относительно этой оси.
Момент.инерции шара массой т равен
Чтобы вычислить момент инерции призмы J2v, предварительно
вычислим центральный момент инерции относительно оси Оу,
параллельной оси O^x
г*
C)
J
Ш)
где
dm
Так как
а а За
Т Т 2"
(*2
J
Ш)
= ydx
+ z2)
а а
Г Т
dm,
dz.
За
2
= Т (J J \x4x-dy.dz+^ J ^z4x.dy.dz)=^\ D)
а а За а а За
J J \^ J ^
а а За а а За
то на основании теоремы о моменте инерции относительно оси,
параллельной центральной оси (XXVI,26), находим:
Из уравнений B) и E) вытекает, что
JVi =ljma2+ Юта2 = ^ та2. F)
Формулы A) и F) позволяют определить угловую скорость
вращения системы тел вокруг оси О^ух после удара:
W = 53T- <7>
Для определения наименьшей скорости v, при которой призма
опрокинется, применяют теорему об изменении кинетической
энергии
-Jy^ = A, (8)
где А — работа действующих сил тяжести.
Уравнения Лагранжа II рода 493
В начальный момент (в момент удара) центр инерции имеет
координаты
3
ma+Yma g
ы— =?a
3
(9)
и находится на расстоянии
Л/9 , 25 13
от оси вращения.
Для того чтобы призма могла опрокинуться вокруг ребра АВ,
центр инерции системы должен подняться на высоту
h A,625 — 1,5) а = 0,125а. A1)
Следовательно, работа действующих сил тяжести, произведен-
произведенная при вращении призмы вокруг ребра АВ до положения, в кото-
котором центр инерции системы занимает наивысшее положение» равна
А = — Amgh = — 095mga. A2)
На основании соотношений (8) и A2) находим искомую ско-
скорость
ГЛАВА XXXI
УРАВНЕНИЯ ЛАГРАНЖА II РОДА
§ 1. Методические указания к решению задач
Если на систему наложены голономные связи, то число диф-
дифференциальных уравнений, определяющих движение системы,
равно числу степеней свободы.
Введем обобщенные координаты, т. е. систему независимых
параметров ql9 q2, ..., qk9 однозначно определяющих положение
точек системы.
Пусть радиусы-векторы точек системы определяются вектор-
векторными функциями
ri = ъ(и qv q2, ... , qh) (XXXI, 1)
(/ = 1,2,..., n).
Выразим кинетическую энергию системы в обобщенных коорди-
координатах
^ = ^0 + ^ + ^2, (XXXI, 2)
494 Динамика
т вул|^-
где
форма нулевого измерения относительно обобщенлых скоро-
скоростей;
k
форма первого измерения, где
п _ k k
форма второго измерения, где аи = 2jmidq^ ' dq~'
Определим обобщенные силы Q,- по формулам
= 1,Z , . ^, R),
где Х{, Уг, Zt — проекции силы /^ на декартовые оси. Когда
обобщенные силы не потенциальны, уравнениям Лагранжа
II рода придают форму
G=1,2,..., ft).
Если на точки системы наложены кинематические связи вида
Д ciyi,) + di = 0 (XXXI, 5)
(/=1,2,..., О,
то на вариации обобщенных координат налагаются дополнительные
ограничения
XRifri = 0 (XXXI-,6)
\s= 1,2, ...,/).
Обозначив множители Лагранжа через ц, (s = 1,2,..., I), предста-
представим дифференциальные уравнения движения точек системы в форме
(ХХХ1>7)
(/=1,2 1).
Уравнения Лагранжа II рода 495
Если система движется в консервативном силовом поле с потен-
потенциальной силовой функцией /7, то вводят функцию
Ь = Т — Я, (XXXI, 8)
называемую кинетическим потенциалом, и систему уравнений
(XXX 1,4) приводят к виду
-|~ = 0 (XXXI, 9}
(/ = 1,2 k).
Если связи стационарны, то кинетическая энергия является
однородной формой второго порядка относительно обобщенных
координат.
Если не все силы, действующие на систему, потенциальны, то
уравнение Лагранжа II рода составляется в форме
k)—^- = Q, (XXXI, 10)
(/ = 1,2,..., fe),
где Qj — обобщенная неконсервативная сила»
Если система движется в консервативном силовом поле и кине-
кинетический потенциал L не содержит явно время, то система уравне-
уравнений (XXX 1,9) допускает обобщенный интеграл энергии
, —Г0 + /7 = Я. (XXXI, 11)
Если связи стационарны,%то из уравнения (XXXI,И) вытекает
закон сохранения механической энергии системы материальных
точек
T + n=h, (XXXI, 12)
Когда некоторые из обобщенных координат не входят в кинети-
кинетический потенциал, то их называют циклическими координатами.
Если обобщенные координаты qlt q2 ,..., qa—циклические, а
обобщенные силы, соответствующие этим координатам,
Qm(m = 1,2, ..., а)
равны нулю, то существуют первые интегралы системы уравнений
(XXXI, 10) вида
~i = Cj (XXXI, 13)
(/ = 1, 2, ..., а).
Уравнения Лагранжа,* примененные к исследованию движения
тела, имеющего неподвижную точку, приводят к уравнениям
496 Динамика
Эйлера:
= Ln
(XXXI'
где Ji,JvJz — осевые моменты инерции; Ц9 Lv Lc — проекции
главного момента внешних сил на подвижные координатные оси;
<о$, со^, о)С — проекции вектора мгновенной угловой скорости на
подвижные оси.
Методика решения задач динамики с помощью уравнений Лаг-
ранжа II рода такова.
1. Найти количество степеней свободы системы.
2. Выбрать систему обобщенных координат.
3. Составить выражение для работы действующих сил на воз-
возможном перемещении и из него определить обобщенные силы.
4. Установить выражение для кинетической и потенциальной
энергии системы в обобщенных координатах.
5. Вычислить частные производные:
дТ дТ . дП
(/=1,2,..., *),
а затем подставить эти величины в уравнения Лагранжа II рода.
6. Указать начальные условия, при которых начинается дви-
движение точек системы.
7. Проинтегрировать систему дифференциальных уравнений,
удовлетворив начальным условиям.
8. Произвести кинематическое исследование движения системы.
§ 2. Задачи
208. Определить движение груза (рис. 208) весом Р, висящего
на тросе весом Рг и длиной /; трос намотай на барабан радиусом а
и весом Р2\ ось вращения горизонтальна, трением и размерами
барабана по сравнению с длиной свешивающейся части троса
пренебречь: массу барабана считать равномерно распределенной
по его ободу. В начальный момент t = 0 система находилась в
покое; длина свисавшей части троса /0.
Решение. Система обладает одной степенью свободы. Движение
груза Р определяется обобщенной координатой х.
Обозначим угловую скорость вращения барабана через ш,
тогда
асо = х, A)
где х — скорость движения груза.
Уравнения Лагранжа II рода
497
Кинетическая энергия системы равна сумме кинетических энер-
энергий барабана — 7\, каната — Т2 и груза — Г3
Т = Тг + Т2 + 73, B)
где
C)
Работа, совершенная силами тяжести ка-
каната и груза, вычисляется по формуле
А = Я (х-
Принимая во внимание D), находим, что
потенциальная энергия системы
§
/7 = Р (/„-*) + -§-(/g
E)
На основании уравнений B), C) и E) ки-
кинетический потенциал системы определяется К задаче 208.
следующим образом:
Составим уравнение Лагранжа в форме (XXX 1,9)
&\дх) дх
EL — р+ pi + р* '. dL п | pi
Так как
из уравнения G) находим
Рг
Введя обозначение
\
а также заметив, что уравнение (9) имеет частное решение
Р1
32 691
Pi'
F)
G)
(8)
(9)
A0)
(И)
498
Динамика
после замены переменных
Pl
х = —-
приведем это уравнение к виду
Т) —- AT У\ = U.
Уравнение A3) допускает решение
A2)
A3)
(И)
Решение уравнения (9) должно удовлетворять начальным усло-
условиям:
, = [0> *о = О,
A5)
следовательно, для определения постоянных интегрирования А ъ В
получим систему уравнений
A6)
0 = А — В
Из соотношений A0), A3), A4), A6) находим
209. В эпициклическом механизме бегающая шестерня радиу-
радиусом гг (рис. 209,а) насажена на кривошип с противовесом, вращаю-
вращающийся вокруг оси неподвижной
шестерни под действием приложен-
приложенного момента М. Определить угло-
угловое ускорение вращения криво-
кривошипа и окружное усилие S в точке
касания шестерни, если: рассто-
расстояние между осями шестерен равно 1У
момент инерции кривошипа с про-
противовесом относительно оси враще-
вращения- кривошипа равен /0, масса
бегающей шестерни тъ а момент
инерции относительно ее оси Jx\
209 центр тяжести подвижной тестер-
задаче ' ни и кривошипа с противовесом
находится на оси вращения кривощипа; трением пренебречь.
Решение. Положение всей системы определяется углом поворота
кривошипа ОО1у поэтому угол ср примем за обобщенную коорди-
координату.
Уравнения Лагранжа II рода 499
Кинетическая энергия системы Т равна сумме кинетических энер-
энергий кривошипа ООг с противовесом—Тг и подвижной шестерни—Т2
Т = Тг + Г2, A)
где
2 г 2
Л to
01 | * 1
B)
и) — угловая скорость вращения кривошипа вокруг оси О,
fc>i — угловая скорость вращения подвижной шестерни вокруг
оси Ov
Подвижная шестерня катится по неподвижной шестерне без
скольжения, поэтому
/со = гхщ = vv C)
Принимая во внимание уравнения B), C), находим:
. D)
Элементарная работа йары сил с моментом М равна
ЬА = MScp, E)
поэтому обобщенная сила имеет вид
Q,=M. F)
Работа сил тяжеЪти равна нулю, так как центр инерции системы
неподвижен.
Составим уравнение Лагранжа в форме (XXXI,4)
*UJ ^~Q" G)
Так как кинетическая энергия системы не зависит явно от
<р> то
J
Окружное усилие S приложено к подвижной шестерне в точке
касания с неподвижной шестерней. Это усилие вызывает пр отно-
отношению, к кривошипу вращательное движение шестерни, кинети-
кинетическая энергия которой
4
а работа окружного усилия (рис. 209,6) на перемещении имеет
величину
ЬА = Sr1by1. A0)
32*
500
Динамика
Составив уравнение Лагранжа в форме G), находим
5r1==yi8l. ' (И)
Приняв во внимание, что угловое ускорение подвижной шес-
шестерни ег выражается через ускорение кривошипа е зависимостью
A2)
S-. — S,
находим
о
. в.
210. В зацеплении, показанном на рис. 210, шестерня 2, при-
приводимая в движение рукояткой ОгО2, катится без скольжения по
внутренней поверхности неподвижной ше-
шестерни 5 и приводит во вращение вокруг
неподвижной оси Ог шестерню /, причем
последняя вращается в 10 раз быстрее ру-
рукоятки. Считая шестерни однородными
дисками одинаковой толщины и из одного
и того же материала, найти движение си-
системы, предположив, что к шестерне /
приложен постоянный момент сопротивле-
сопротивления Мъ а к рукоятке — постоянный вра-
вращающий момент М\ механизм расположен
в горизонтальной плоскости; массой ру-
К задаче 210. коятки% пренебречь.
Решение» Ведущим звеном механизма является кривошип ОгОг.
За обобщенную координату примем угол поворота кривошипа ср.
Угловую скорость кривошипа обозначим через со.
По условию задачи угловая скорость вращения шестерни /
равна ,
Wl= 10 со. . A)
Обозначим радиусы шестерен 1 и 2 соответственно через гг и г2.
Пользуясь методом мгновенной остановки, определим переда-
передаточное число k = - и угловую скорость о>2 вращения шестерни 2.
Составим таблицу распределения угловых скоростей.
Данные для расчета
Угловая скорость до ос-
остановки
То же, после остановки
Вид зацепления ....
Ведущее
звено
0г02
О)
0
Основание
механизма—
шестерня
3
0
О)
Шестерня
2
аJ — to
Ц1естерня
&i = 10 а)
9 со
Внутреннее Внешнее
Уравнения Лагранжа II рода 501
Тогда
Из уравнений B) находив:
>У= 4гх; C)
5 ш,
Ш2==__ ш = _^_. ,D)
Выразим массу шестерни 2 через массу шестерни /,.учитывая,
что их объемы соответственно равны:
V^icrJB; 72=16тгг^, E)
где 8 — толщина колеса.
Таким образом,
ш2 = 16mr F)
Вычислим момент инерции шестерни 2 относительно ее мгно-
мгновенной оси вращения (проходит через точку Р перпендикулярно к
плоскости рисунка).
На основании теоремы о моменте инерции относительно оси,
параллельной центральной оси (XXVI,26), находим
j I m г2 - —2 г2 П\
Заметив, что момент инерции относительно центральной оси
шестерни / равняется
. # (8)
и приняв во внимание формулы C) и F), находим
У2 = 3. 16*./г (9)
Кинетическая энергия шестерни 2 в ее абсолютном движении
равна
У2со2 3 • 162 • l
Г2 = -Г =
2,82
где Tt == ~2 кинетическая энергия шестерни /.
Полная кинетическая энергия механизма вычисляется по фор-
формуле
T=13T1 = ^(/1cof). A1)
Работа пар сил, приложенных к механизму, равна
&Л = LS<p — L^. A2)
Приняв во внимание A), из уравнения A2) находим
502
Динамика
Учитывая, что J[ = 0; Д- = ^ =
из уравнения Лагранжа (XXX 1,4) находим
A4)
где ех — угловое ускорение шестерни /.
Следовательно, угловое ускорение рукоятки
8 ~~ 1300^ сек2 *
211. Определить угловые ускорения ведущего и ведомого
валов / и IV (рис. 211), соединенных редуктором скоростей, со-
состоящим из неподвижной шестерни / ради-
радиусом гъ двух пар бегающих шестерен 2 и
3 радиусом г2 и г3, спаренных между собой,
и шестерни радиусом гъ сидящей на ведо-
ведомом валу* Момент' инерции масс, связан-
связанных с ведущим валом, относительно оси
IV вала равен Jx\ масса каждой пары бегаю-
бегающих шестерен равна т2, ее момент инер-
инерции бтносительно собственной оси /2;
момент инерции ltoacc, связанных с ведо-
ведомым валом, относительно оси последнего
равен /4; вращающий момент, приложен-
приложенный к ведущему валу, равен Mx; момент
сопротивления, приложенный к ведомому
/ \ валУ» равен М4; трением пренебречь.
//////////////////////////У
' К задаче 211. Решение. Механизм имеет одну степень
свободы. За обобщенную координату при-
примем угрл поворота ведущего в&ла ср.
Применив метод мгновенной остановки, определим угловые
скорости шестерен 2, 3 и 4 и их значения внесем в следующую
таблицу.
Данные для расчета
Угловая скорость до оста-
остановки * .
То же, после остановки . .
Вид зацепления
Ведущее
звено
вал /
О)
0
Шестерня
1
0
—О)
2
ОJ— О)
Внешнее
3
Щ
оJ—О)
4
o)jy—ю
Внешнее
Уравнения Лагранжа II рода 503
Следовательно:
Из соотношений A) находим:
«2 = »(!+¦?¦); »r»=»fl—^-V B)
Кинетическая энергия частей механизма, связанных с ведущим
валом, равна
Тг-*?. C)
Кинетическая энергия подвижных шестерен 2 и 3 определяется
по формуле дли кинетической энергии в плоско-параллельном
движении (XXVI,47):
^?] D)
где vA=-(r^+r2)(D.
Кинетическая энергия частей механизма, связанных с ведомым
валом, равна
Таким образом, кинетическая энергия всего механизма имеет
величину
Элементарная работа крутящего и тормозящего моментов выра-
выражается по формуле
ЬА = Q<p&9 = Afx8qp — M4S<p4. .G>
Из соотношения B) видно, что
а поэтому обобщенная сила
(?) (9)
Учитывая, что
504
Динамика
из уравнений Лагранжа (XXXI,4) получим
2 *
На основании зависимости B)
A1)
A2)
212. Груз Р (рис. 212) приводит во вращение вокруг оси CD
рамку / уравновешенного гироскопа (ротора) посредством нити и
шкива Е радиусом г. Определить давление на подшипники С и D
К задаче 212.
рамки, обусловленное гироскопическим моментом, в положении,
когда груз опустится на высоту h; Ли С — моменты инерции ротора
относительно осей Ох, Ог\ Аг — момент инерции рамки относи-
относительно оси Ох, массой шкива Е пренебрегаем. Ротор совершает п
оборотов в секунду. Расстояние CD = 6.
Решение. Введем неподвижную координатную систему, поместив
ее начало в центре инерции системы и приняв прямую CD за осьОг;
ось Ох расположим по горизонтали, а Оу — по вертикали.
За ось вращения ротора примем ось Ос первичной координатной
системы, неизменно связанной с ним, а оси О? и Ch\ расположим в
диаметральной плоскости ротора.
Уравнения Лагранжа И рода 505
Введем теперь углы Эйлера ft, ф, ср.
В нашем случае
| ± A)
поэтому из кинематических формул Эйлера (XVII 1,2) для проекций
угловой скорости вращения тела на оси подвижной координатной
системы находим
и>$ = ф sin ф
а^ = ф cos ф • B)
О)С = ф
Кинетическая энергия системы, состоящей из ротора, рамки и
груза Р, равна
( ?). с
Положение груза Р определяется координатой
*/Р = -гф, D)
поэтому элементарная работа, совершенная этим грузом, имеет
величину *
ЪА = — РаУр=РЩ. E)
Из формулы D) находим
• Q^Pr, F>
Обозначим моменты опорных реакций оси CD относительно
осей 0? и От] соответственно через Ц и /ц.
Составив уравнение Лагранжа (XXX 1,4)
-Рг G>
н построив его первый интеграл — интеграл энергии (XXX 1,1
находим
Г_ 2Ph
/ Ргг
Составим теперь уравнения Эйлера (XXXI, 14), приняв во вни-
внимание, что
7^ = 7, = Л; УС=С; шс = 0, (9>
а также учитывая соотношения B) и (8).
Тогда получим
А фsift ф + Сфф cos ф = ^ ]
Л ф cos ф — Сфф sin ф == Z^, r A0)
J
506
Динамика
Из формул A0) находим
/ /
+
Рг% *
(И)
Уравнение A1) показывает, что случай регулярной прецессии
возможен лишь при дополнительных предположениях:
а) момент инерции рамки Аг значительно больше момента инер-
инерции ротора А:
А « Аг; A2)
б) груз Р после того как он опустится на высоту А, перестает
действовать на систему, т. е.
ф = 0. A3)
Если считать выполненным одно из перечисленных условий
A2), A3), то
-5Д- A4)
В случае регулярной прецессии Ь находится на линии узлов,
поэтому
213. В дифференциальном регуляторе (рйс. 213) валы Ох и О2,
вращающиеся в противоположные стороны с угловыми скоростями
с*! и (о2, снабжены шестернями
ML и М2 и при помощи двух пар
сателлитов С сцеплены с шестер-
шестерней Д9 играющей роль рукоятки
сателлитов. Если (Oj равно (о2, то
шестерня Д остается неподвижной,
в противном случае она начнет
вращаться и через вал А приведет
в действие не- показанное на ри-
рисунке регулирующее приспособ-
приспособление; последнее создает при этом
передаваемые валам Ох и О2 мо-
моменты, причем опережающий вал
будет тормозиться, а отстающий —
увеличивать свою угловую ско-
скорость. Считая эти моменты про-
пропорциональными угловой скорости шестерни Д (коэффициент про-
пропорциональности обозначается через п) и равными по величине и
обозначая через J приведенный к оси ОХО2 момент инерции си-
системы, найти закон изменения угловых скоростей ьух и (о2, если их
К задаче 213.
Уравнения Лагранжа II рода
507*
начальные угловые скорости ш10 и (о20 не равны друг другу. Моменты
инерции Jx и У2 валов Ог и 02 с шестернями Мх и М2 считаем рав-
равными друг другу; приведенный "к оси вращения шестерни Д момент
инерции этой шестерни и приводимых ею через вал А в движение
частей механизма обозначаем через Jд\ при решении задачи вво-
вводится еще в рассмотрение момент инерции Jc сателлитов относи-'
телыю оси их собственного вращения (эта величина не фигурирует
в окончательном результате). Под приведенным к оси вала моментом
инерции системы понимается сумма J =2J1 + Jд+ 4J'C, где J'c—
момент инерции сателлита относительно оси 0iO2-
Решение. Движение всех частей регулятора зависит от дви-
движения валов Ог и О2, поэтому система обладает двумя степенями
свободы.
За обобщенные координаты выберем угол поворота вала Ог—срх
и вала О2—?2-
Предположим, что w2>0; (o1<0 и, кроме того,
Ы > cv A)
Выразим угловую скорость вращения шестерни Д через а)х и со2,
для чего применим метод мгновенных остановок, остановив мыс-
мысленно эту шестерню.
Составим таблицу распределения угловых скоростей до мгно-
мгновенной остановки и после нее.
Данные для расчета
Угловая скорбеть до ос-
остановки
То же, после остановки .
Вид зацепления ....
Шестерня
Д
(Од
0
Шестерня
щ
Сателлит
@
(о-о>д
Шестерня
м2
@2
ft)a—О)д
Внешнее Внутреннее
Таким образом:
»1-«Д
°Д
"Д
B)
Из соотношений B)
°Д
__ 1
откуда
"J + <йд
- у К —
C)
508 Динамика
Обозначим вращающий момент для первого вала через Ьъ а
для второго—через L2.
Элементарная работа, произведенная парами сил, равна
8Л = L1S9l + L28qp2. D)
Согласно условию задачи обобщенные силы равны:
Qx = Ьг = — пыд; Q2 = L2 = лсод>
а учитывая уравнение C), находим:
Qx = — у К — со2); Q2 == у (Wl — оз2). E>
Составим уравнение для кинетической энергии системы, кото-
которая равна сумме кинетических энергий частей механизма:
Т = Т1 + Т2 + ТД + Гс, F)
где T*i = у А10? — кинетическая энергия вала Ог с шестерней Л4Х;
Т2 = у/1со| —кинетическая энергия вала с шестерней М2; Гд=
= ~ /до)^ — кинетическая энергия шестерни Д\ Тс = -д- 4 /^ со^ —
кинетическая энергия сателлитов.
Составляя выражение для кинетической энергии сателлитов,-
исходим из теоремы о кинетической энергии системы, находящейся
в сложном движении (XXVI,50):
| Тс = у [/с<4 + Л* (гд - гх)Ь&д1
где (гд — гг) — расстояние центра сателлита от вала OjOg.
Учитывая, что сое определяется через а>д, и введя приведенный
момент инерции J'c сателлита относительно оси ОгО2, приходим к
вышеуказанному выражению для кинетической энергии сател-
сателлитов.
Заменив в формуле F) а>д его значением из уравнения C), по-
получим
Заметив, что
( 1 - I /' \ ( 1 Т | 7'\. &?. _ Л
. <8>
Уравнения Лагранжа II рода 509
и составив уравнения Лагранжа (XXX,4), находим дифференциаль-
дифференциальные уравнения движения валов
= 7Г (wl Щ) '
(9)
где
Решим систему уравнений (9).
Складывая первое и второе уравнения этой системы, находим:
w^-ov (Ю)
На основании формулы A0) первое уравнение системы (9) пере-
перепишем в виде
а>г = — -2 К — со2), A1)
где
2(а + Ь)=/; f = ~.
Продифференцируем уравнение A1) по времени
тогда, учитывая выражение A0), находим
^ = _Х^, A3)
откуда
6)х^Се-и. A4)
Подставив значение о)х в уравнение A1), получим
fy \л / \ I \ Р\\
Так как при ?=0, ь)г = ш10, аJ =аJ0, из уравнения A5) находим
постоянную интегрирования
Таким образом,
(^ ___ (CiJ0 —
^= 4@.20 -«Ю)^', 07)
510
Динамика
а после интегрирования
1<о10
получим
или
wi = (°1°A
0J0 A —
A8)
Так как
то после интегрирования получим
A9)
К задаче 214.
214. Приведенная на рис. 214 система отвечает принципиальной
схеме электродинамического датчика, используемого для записи ме-
механических колебаний. Масса якоря—
М, жесткость пружин — с. Коэффици-
Коэффициент самоиндукции катушки изменяет-
изменяется вследствие изменения длин воз-
воздушного зазора в магнитолроводе
L= L (х), где л: — вертикальное смеще-
смещение якоря из положения, когда пру-
пружины не напряжены. К катушке при-
ключена электрическая цепь, состо-
состоящая из элемента с заданной э. д. с,
равной ?, и омического сопротивления R. Составить уравнения
движения системы и определить ее «положение равн©весия».
Решение. Система обладает двумя степенями свободы. За обоб-
обобщенные координаты примем смещение якоря х и заряд q, соответ-
соответствующий току / в цепи// = ^].
Для определения обобщенных сил подсчитаем элементарную
возможную работу при изменении расстояния х и заряда д.
Сила тяжести якоря на перемещении Ьх производит работу
ЬА1 = Mg . Ьх. A)
Упругие силы пружины на этом же перемещении выполняют
работу
&Л2 = — схЬх. B)
Уравнения Лагранжа II рода 511
Работа в цепи, питаемой элементом с э. д. с, равной ?, опреде-
определяется по формуле
ЬАг = iEdt = Ebq. C>
Учтем работу тока, преобразовавшуюся в теплоту, затраченную*
на нагревание проводника:
8Л4 = — PRdt = — qRbq. D)
Таким образом, обобщенные силы имеют вид
Электрокинетическая энергия системы равна
\
М s " • vv
где h — коэффициент самоиндукции.
Полная кинетическая энергия системы определяется по фор-
формуле
G)
Заметим, что
C/i I OL 'л СУ
^ 2 <5лс дх
— =0; -—г- = La
dq dq ч
Составив уравнения Лагранжа (XXXI,4), находим
В «йоложении равновесия» х = х0 и i = q = /0; поэтому иа
уравнения (9) следует
? .. . 1 /dL\ .2 /im
i\ ^ V С/Л I v
\ /
Михаил Михайлович Кабальский
Вениамин Давидович Кривошей
Николай Иоилевич Савицкий
Глеб Николаевич Чайковский
ТИПОВЫЕ ЗАДАЧИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ И МЕТОДЫ ИХ РЕШЕНИЯ
Ведущие редакторы: Е. Касперская, О. Бондаренко
Обложка художника Л. Расинского
Технический редактор М. Вуек Корректоры: М. Чеховой, 3, Скоромная, Я. Радецкая
ВФ 01G17. Сдано в набор 26/VIII 1955 г. Подписано к печати 6.1. 1956 г. Формат бумаги
60X02/w. Объём: 32 физич., лист. 32 условн. лист., 34,75 учетно-иэдат. лист.
Тираж 10.000 экземпл. Цена 11 руб. 90 коп.
Государственное издательство технической литературы УССР
г. Киев, ул. Красноармейская, 11.
Зак. 427. Напечатано с матриц Кн.-журнальной ф-ки в типографии б. школы ФЗУ
Главиздата Министерства культуры УССР. Киев, Золотоворотская, 11.