УДК 53 (075)
ББК22.3
Билеты письменных вступительных экзаменов в МФТИ
(2002 г.): Методические разработки по физике и математике. —
М.: МФТИ, 2002. — 62 с.
Приведены задания, предлагавшиеся на вступительных экзаменах
абитуриентам Московского физико-технического института (государ-
ственного университета) в 2002 году. Все задачи снабжены ответами,
часть — подробными решениями, некоторые — основными указаниями
к решению. На выполнение каждой экзаменационной работы давалось
4,5 часа.
Для абитуриентов МФТИ и других физических вузов, а также пре-
подавателей школ с углубленным изучением физики и математики.
Авторы задач по физике:	доценты Чешев Ю.В., Можаев В.В., Чивилёв В.И., Шеронов А.А.
по математике:	проф. Шабунин М.И., доценты Бунаков А.Э., Трушин В.Б., к.ф.м.н. Балашов М.В., к.ф.м.н. Константинов Р.В. © Московский физико технический институт (государственный университет), 2002 © Коллектив авторов, 2002
ФИЗИКА ♦ ЗАДАЧИ ♦ Билет I
3
ФИЗИКА
БИЛЕТ 1
1.	Шайба массой т скользит со скоростью Vq по гладкой гори-
зонтальной поверхности стола, попадает на покоящийся клин
массой 2т, скользит по нему без тре-
ния и отрыва и покидает клин (см. рис.).
Клин, не отрывавшийся от стола, при-
обретает скорость Vb/4. Найти угол а
наклона к горизонту поверхности верх-
ней части клина. Нижняя часть клина
имеет плавный переход к поверхности стола. Изменением потен-
циальной энергии шайбы в поле тяжести при ее движении по кли-
ну пренебречь. Направления всех движений параллельны плос-
кости рисунка.
2.	На чашке пружинных весов уравновесили сосуд,
в котором находится вода массой тв. Для при-
готовления соленого раствора была использова-
на крупная соль, содержащая нерастворимые в
воде примеси. Соль с примесями в марлевом ме-
шочке была опущена на нити в сосуд, так что ме-
шочек оказался полностью погруженным в воду.
После того как соль полностью растворилась в
воде, показания весов изменились на ДР (ДР >
к задаче 2
> 0) по сравнению с их показаниями до опускания соли в воду.
Плотность соленого раствора была измерена и оказалась рав-
ной р. Найти объем примесей Vn, оставшихся в мешочке после
растворения соли, если он остался висеть на нити целиком по-
груженным в раствор. Плотность чистой соли — рс, воды — рв,
ускорение свободного падения — g.
Указание: Считать раствор однородным с плотностью р =
= (mz + rnB)/(Vc + К), где тв и тс — массы воды и соли, а К и
Vc — их объемы.
3.	На рисунке изображена вольтамперная характеристика двух со-
единенных параллельно элементов, одним из которых является
4
ФИЗИКА ♦ ЗАДАЧИ ♦ Билет I
резистор с сопротивлением R = 100 Ом, а другим — неизвест-
ный элемент Z. Используя заданную вольтамперную характери-
стику, постройте вольтамперную характеристику элемента Z.
О 1 2 3 4 5 V, В
к задаче 3	к задаче 4
4.	Оптическая система, состоящая из собирающей линзы с фокус-
ным расстоянием F = 20 см и плоского зеркала в форме посе-
ребренной с одной стороны плоскопараллельной пластинки тол-
щиной d = 6 см с показателем преломления п = 1,5, создает
действительное изображение точечного источника света S, рас-
положенного на главной оптической оси линзы. Расстояние от
источника S до линзы а = 3F/5, а от изображения Si, даваемого
системой, до линзы b = 3F/2 (см. рис.). Найти расстояние L
от линзы до зеркала. Отражением от передней поверхности пла-
стинки пренебречь.
5.	На горизонтальном непроводящем диске по его диаметру укре-
плен тонкий проводящий стержень АС. Диск находится в
однородном магнитном поле с индукцией
В = 10"2 Тл, перпендикулярной плоско-
сти диска и совершает крутильные гармони-
ческие колебания относительно вертикаль-
ной оси, проходящей через точку О: =
= y?ocos(wt), где t — время. Длина стерж-
ня L = а + Ь, где а = 0,5 м, а Ь — 1м.
Определить максимальную разность потен-
циалов между концами стержня А и С, если у?о = 0,6 рад, а ш =
= 0,2 рад/с.
ФИЗИКА ♦ ЗАДАЧИ ♦ Билет 2
5
БИЛЕТ 2
1.	Горка массой 4т с шайбой массой т покоятся на гладкой го-
ризонтальной поверхности стола (см. рис.). От незначитель-
ного толчка шайба начинает скользить по горке без трения,
не отрываясь от нее, и покида-
ет горку. Горка, не отрывавша-
яся от стола, приобретает ско-
рость и. С какой скоростью
шайба упадет на стол? Ниж-
няя часть поверхности горки
составляет с вертикалью угол
7 = 30° и находится на рассто-
янии Н от стола. Направле-
ния всех движений параллель-
ны плоскости рисунка.
нерастворимых
к задаче 2
2.	Для приготовления раствора сахара был использован сахар-
ный песок, содержащий некоторое количество
в воде примесей. Песок с примесями в марле-
вом мешочке был опущен на нити в сосуд с водой,
стоящий на чашке весов, так что мешочек ока-
зался целиком погруженным в воду (см. рис.).
После того как сахар целиком растворился в во-
де, показания весов изменились на ДР (ДР >
> 0) по сравнению с их показаниями сразу по-
сле опускания мешочка в воду сосуда. Мешочек
с примесями после растворения сахара остался
висеть на нити целиком погруженный в раствор. После этого из-
мерили плотность раствора и объем примесей, которые оказа-
лись равными р и Уп. Найти первоначальный объем воды в со-
суде Ув, если ее плотность — рв. Плотность чистого сахара —
рс, ускорение свободного падения — g. Раствор сахара считать
однородным с плотностью р = (тс + mB)/(Vc + Из), где т- и тв
— массы сахара и воды, а Гс и Гв — их объемы.
3.	На рисунке изображена вольтамперная характеристика двух со-
единенных последовательно элементов, одним из которых явля-
6
ФИЗИКА ♦ ЗАДАЧИ ♦ Билет2
стен резистор с сопротивлением В, = 100 Ом, а вторым — не-
известный элемент Z. Используя заданную вольтамперную ха-
рактеристику, постройтевольтамперную характеристику элемен-
та Z.
0 1 2 3 4 5 У, В
к задаче 3
4.	Оптическая система, состоящая из рассеивающей линзы и плос-
кого зеркала в форме посеребренной с одной стороны плоскопа-
раллельной пластинки толщиной d = 3 см с показателем прело-
мления п = 1,5 создает мнимое изображение (после отражения
от зеркала и прохождения линзы) точечного источника света S,
расположенного на главной оптической оси линзы. Найти фо-
кусное расстояние линзы F, если расстояние от источника света
до линзы а = |F|, а от изображения 51, даваемого системой, до
линзы b — 2F/3 (см. рис.). Расстояние между линзой и зерка-
лом L = 10 см. Отражением от передней поверхности пластинки
пренебречь.
5.	Металлический стержень АС одним концом (точка А) шарнир-
но закреплен на вертикальном диэлектрическом стержне АО.
q Другой конец (точка О) связан с вертикальным
-----—-у стержнем с помощью нерастяжимой непрово-
/ дящей горизонтальной нити ОС длиной В. = 1 м.
I g / Стержень АС вращается вокруг стержня АО в
/ однородном магнитном поле, индукция которо-
го вертикальна и равна В = 10’ ’ Тл. Угловая
к задаче 5 скорость вращения стержня АС ш = 60 рад/с.
Определить разность потенциалов между точками А п С.
ФИЗИКА ♦ ЗАДАЧИ ♦ Билет
7
БИЛЕТ 3
1.	На вершине покоящейся на гладком горизонтальном столе гор-
ки массой 3?n удерживают шайбу массой m (см. рис.). Шайбу
отпускают, и она скользит по горке
без трения и отрыва и покидает гор-
ку. Горка, не отрывавшаяся от сто-
ла, приобретает скорость и. Найти
разность высот Н между вершина-
ми горки. Верхняя часть поверхно-
сти правой вершины горки наклоне-
на к вертикали под углом /3 = 30°.
Направления всех движений парал-
лельны плоскости рисунка.
к задаче !
2.	Сосуд с водой уравновешен на чашке весов. Для
приготовления соленого раствора была исполь-
зована крупная соль, содержащая нераствори-
мые в воде примеси. Соль с примесями в мар-
левом мешочке была опущена на нити в сосуд,
так что мешочек оказался целиком погруженным
в воду (см. рис.). Сразу после этого показа-
ния весов изменились на ДР (ДР > 0). По-
сле того как соль целиком растворилась в во-
де, была измерена плотность раствора р и объем примесей Vn,
оставшихся в мешочке. Найти массу воды тв, находящейся
в сосуде. Пдотность чистой соли — рс, воды — рв. Ускоре-
ние свободного падения — g. После растворения соли раствор
к задаче 2
считать однородным с плотно-
стью р = (тс 4- тв)/(К + VB),
где и гпв — массы соли и во-
ды, а 14 и Ув — их объемы.
3.	На рисунке изображена вольт-
амперная характеристика двух
соединенных параллельно эле-
ментов, одним из которых явля-
ется резистор с сопротивлением
к задаче 3
8
ФИЗИКА ♦ ЗАДАЧИ ♦ Билет 3
R = 200 Ом, а другим — неизвестный элемент Z. Используя за-
данную вольтамперную характеристику, постройте вольтампер-
ную характеристику элемента Z.
4.	Оптическая система, состоящая из собирающей линзы с фокус-
ным расстоянием F = 12 см и плоского зеркала в форме посе-
ребренной с одной стороны плоскопараллельной пластинки тол-
щиной (1 = 9 см создает действительное изображение (после от-
ражения от зеркала и прохождения линзы) точечного источни-
ка света S, расположенного на главной оптической оси линзы
между линзой и зеркалом (см. рис.). Расстояние от источника
до линзы а = 2F/3, а от изображения бД даваемого системой,
до линзы b = 2F. Найти показатель преломления пластинки п.
Расстояние между линзой и зеркалом L = 10 см. Отражением от
передней поверхности пластинки пренебречь.
5.	На горизонтальном непроводящем диске по его диаметру укре-
плен тонкий проводящий стержень АС. Диск находится в одно-
родном магнитном поле с индукцией В = 2 • 10-2 Тл, перпен-
дикулярной плоскости диска и совершает крутильные гармони-
ческие колебания относительно вертикальной оси, проходящей
через точку О: <^(i) = <р0 cos(art), где t — время. Длина стерж-
ня 6 = 1м, расстояние а = 0,5 м. Определить максимальную
разность потенциалов между концами стержня А и С, если ipo =
= 0,8 рад, а ш = 0,3 рад/с.
ФИЗИКА ♦ ЗАДАЧИ ♦ Билет4
9
БИЛЕТ 4
1.	Игрушечная пушка может скользить без трения по рельсам,
укрепленным на горизонтальном полу,
под углом д к горизонту (см. рис.).
Масса пушки без снаряда — М, масса
снаряда — т. Из покоившейся пуш-
ки произведен выстрел. В результа-
те пушка, не отрывавшаяся от рельсов,
получила скорость и. На каком рас-
стоянии от места выстрела снаряд упал
на пол? Высоту пушки не учитывать.
Ствол пушки наклонен
Направления всех движений параллельны плоскости рисунка.
2.	Для приготовления раствора сахара был использован сахарный
песок, содержащий некоторое количество нерастворимых в воде
примесей. Песок в марлевом мешочке был опу-
щен на нити в сосуд с водой, стоящий на чаш-
ке весов, так что мешочек оказался целиком по-
груженным в воду. После того как сахар це-
ликом растворился в воде, а примеси остались
в мешочке, показания весов изменились на ДР
(ДР > 0) по сравнению с их показаниями сразу
после опускания мешочка в сосуд. Найти объем
примесей Уп, если мешочек с ними остался ви-
сеть целиком погруженным в раствор. Плотность раствора ока-
залась равной — р, плотность чистого сахара — рс, воды — рв,
ускорение свободного падения — g. Начальная масса воды в со-
суде — тв. После растворения сахара раствор считать однород-
ным с плотностью р = (тс +mB)/(Vc + VB), где тс и тв — массы
сахара и воды, a Vc и VB — их объемы.
3.	На рисунке изображена вольтамперная характеристика двух со-
единенных последовательно элементов, одним их которых явля-
ется резистор с сопротивлением R — 1 кОм, а вторым — не-
известный элемент Z. Используя заданную вольтамперную ха-
рактеристику, постройте вольтамперную характеристику элемен-
та Z.
10
ФИЗИКА ♦ ЗАДАЧИ ♦ Билет4
0 1 2 3 4 5 V, В
к задаче 3
к задаче 4
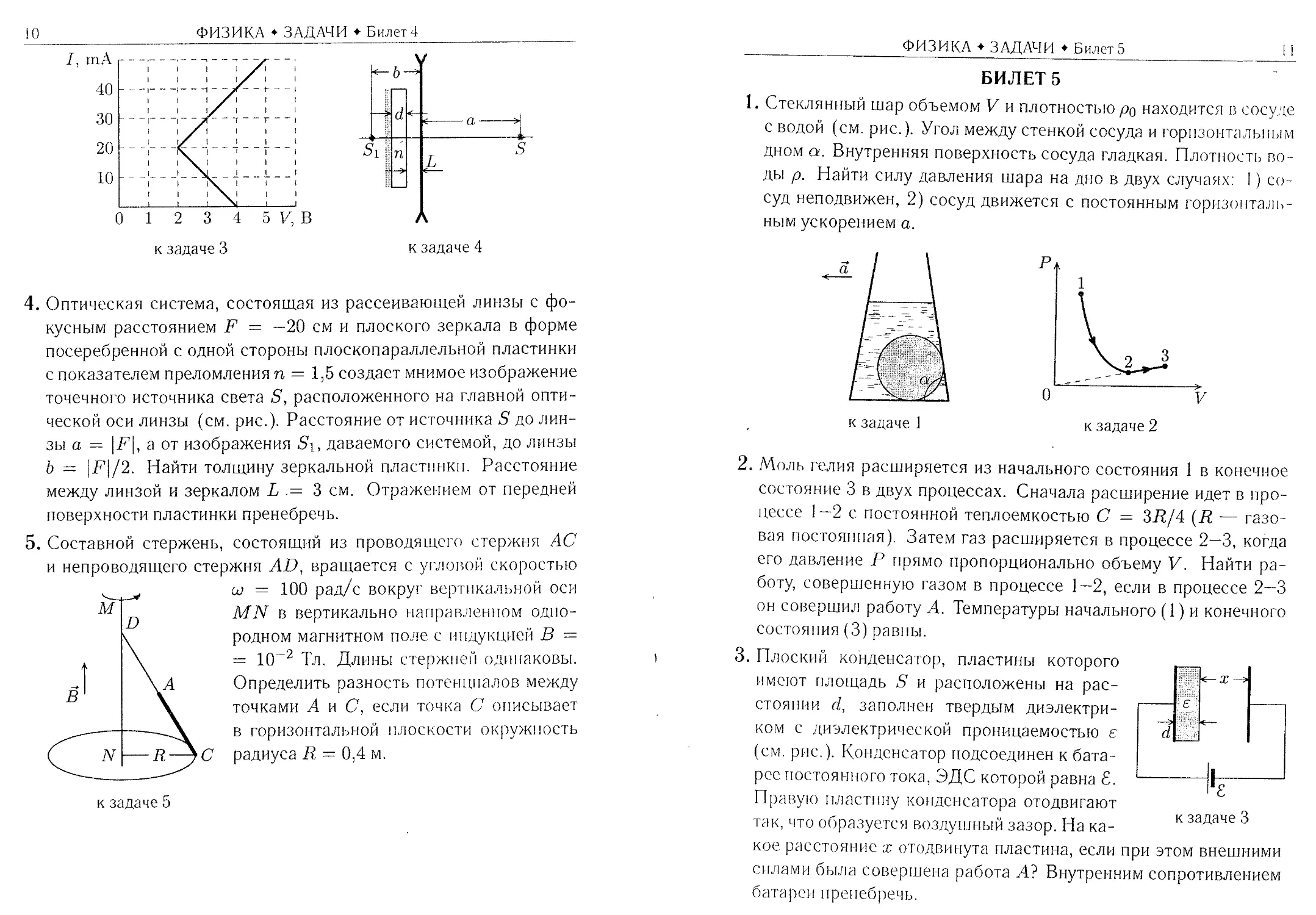
4.	Оптическая система, состоящая из рассеивающей линзы с фо-
кусным расстоянием F = —20 см и плоского зеркала в форме
посеребренной с одной стороны плоскопараллельной пластинки
с показателем преломления п = 1,5 создает мнимое изображение
точечного источника света S, расположенного на главной опти-
ческой оси линзы (см. рис.). Расстояние от источника S до лин-
зы а = \F\, а от изображения Si, даваемого системой, до линзы
b = |F|/2. Найти толщину зеркальной пластинки. Расстояние
между линзой и зеркалом L .= 3 см. Отражением от передней
поверхности пластинки пренебречь.
5.	Составной стержень, состоящий из проводящего стержня АС
и непроводящего стержня AD, вращается с угловой скоростью
к задаче 5
ш = 100 рад/с вокруг вертикальной оси
MN в вертикально направленном одно-
родном магнитном поле с индукцией В —
= 10“2 Тл. Длины стержней одинаковы.
Определить разность потенциалов между
точками А и С, если точка С описывает
в горизонтальной плоскости окружность
радиуса R = 0,4 м.
ФИЗИКА ♦ ЗАДАЧИ ♦ Билет 5
I 1
БИЛЕТ 5
1.	Стеклянный шар объемом V и плотностью р0 находится в сосуде
с водой (см. рис.). Угол между стенкой сосуда и горизонтальным
дном а. Внутренняя поверхность сосуда гладкая. Плотность во-
ды р. Найти силу давления шара на дно в двух случаях: 1) со-
суд неподвижен, 2) сосуд движется с постоянным горизонталь-
ным ускорением а.
к задаче 2
2.	Моль гелия расширяется из начального состояния 1 в конечное
состояние 3 в двух процессах. Сначала расширение идет в про-
цессе 1—2 с постоянной теплоемкостью С = (R — газо-
вая постоянная). Затем газ расширяется в процессе 2—3, когда
его давление Р прямо пропорционально объему V. Найти ра-
боту, совершенную газом в процессе 1—2, если в процессе 2—3
он совершил работу А. Температуры начального (1) и конечного
состояния(3)равны.
3.	Плоский конденсатор, пластины которого
имеют площадь S и расположены на рас-
стоянии d, заполнен твердым диэлектри-
ком с диэлектрической проницаемостью е
(см. рис.). Конденсатор подсоединен к бата-
рее постоянного тока, ЭДС которой равна £.
Правую пластину конденсатора отодвигают
так, что образуется воздушный зазор. На ка-
к задаче 3
кое расстояние х отодвинута пластина, если при этом внешними
силами была совершена работа А? Внутренним сопротивлением
батареи пренебречь.
12 ФИЗИКА ♦ ЗАДАЧИ ♦ Билет6
4.	Муха пересекает главную оптическую ось собирающей линзы на
расстоянии а = 3F, где F — фокусное расстояние линзы, под
малым углом а к оси линзы со ско-
v	ростью V. 1) Под каким углом изо-
£бражение мухи пересекает главную
оптическую ось? 2) Чему равна в
* а ф этот момент скорость изображения
.	мухи?
к задаче 4	J
Указан и е: для малых углов
sin a ~ tga ~ а.
5.	Гамма-излучением называется электромагнитное излучение при
переходах атомных ядер из возбужденных в более низкие энер-
гетические состояния. 7-квант испускается движущимся со
скоростью vq = 63,2 м/с ядром атома олова
119 Sn под углом а = 60° к направлению его дви-
жения с энергией, равной энергии перехода ядра
из возбужденного в основное состояние. Най-
ти энергию 7-кванта. Энергия покоя ядра оло-
ва Wo = тяс2 = 113 ГэВ (1 ГэВ = 103 МэВ =
= 106 КэВ = 109 эВ).
7
к задаче 5
к задаче 1
БИЛЕТ 6
1.	Пробковый шар объемом V привязан ко дну конического
сосуда с водой так, что нить вертикальна, а шар
касается гладкой стенки сосуда (см. рис.). Угол
между горизонтальным дном и стенкой сосуда
7. Плотности воды и пробки р и pi. Найти силу
натяжения нити в двух случаях: 1) сосуд непо-
движен, 2) сосуд движется с постоянным гори-
зонтальным ускорением а.
2.	Моль гелия, расширяясь в процессе 1—2, где его давление Р ме-
няется прямо пропорционально объему V, совершает работу А
(см. рис.). Из состояния 2 гелий расширяется в процессе 2—3, в
котором его теплоемкость С остается постоянной и равной С =
= Д/2 (R — газовая постоянная). Какую работу Л93 совершит
ФИЗИКА ♦ ЗАДАЧИ ♦ Билет 6	13
гелий в процессе 2—3, если его температура в состоянии 3 равна
температуре в состоянии 1 ?
к задаче 2
к задаче 3
3.	Плоский конденсатор с площадью пластин S и расстоянием
между ними d подключен к источнику с постоянной ЭДС £. Ка-
кую минимальную работу необходимо совершить, чтобы в про-
странство между пластинами конденсатора ввести металличе-
скую пластину толщиной L (L < d)? Внутренним сопротивле-
нием батареи пренебречь.
4.	Муравей пересекает главную опти-
ческую ось рассеивающей линзы на
расстоянии а = 4F, где F — фо-
кусное расстояние линзы, под ма-
лым углом а к оси линзы со скоро-
стью?;. 1) Под каким углом изобра-
жение муравья пересекает главную	к задаче 4
оптическую ось? 2) Чему будет равна в этот момент скорость
изображения муравья?
У к а з а н и е: для малых углов sin а « tg а ~ а.
5.	Гамма-излучением называется элек-
тромагнитное излучение при переходах
атомных ядер из возбужденных в более
низкие энергетические состояния.
7-квант испускается свободным покоящимся ядром атома
олова 1195п с энергией Еу = 23,8 КэВ, а затем поглощается
таким же ядром, движущимся навстречу 7-кванту. Какую
скорость v должно иметь ядро, чтобы поглотить испущенный
Н ФИЗИКА ♦ ЗАДАЧИ ♦ 1>11jer7	_
7-квант? Энергия покоя ядра олова И?) = 'тяс2 = 113 ГэВ
(1ГэВ = 103МэВ = 106КэВ = 109эВ). При испускании и
поглощении 7 кванта происходит переход между одними и геми
же энергетическими состояниями ядра.
БИЛЕТ 7
1. В сосуде с водой
находится алюминиевый шар объемом V,
прикрепленный ко дну сосуда нитью .173
(см. рис.). Дно сосуда горизонтальное и
гладкое. Плотности алюминия и воды ро 11
р. Найти силу давления шара на дно со-
суда в двух случаях: 1) сосуд неподвижен,
2) сосуд движется с постоянным горизон-
тальным ускорением а, и нить составляет с
дном угол /3.
2, Моль гелия сжимают из начального состояния 1 в конечное со-
стояние 3 в двух процессах. Сначала сжатие идет в процессе
к задаче 2
1—2, когда давление гелия Р прямо про-
порционально его объему V. Затем из
состояния 2 газ сжимают в процессе 2—3
с постоянной теплоемкостью так, что те-
пло подводится к газу. В конечном состо-
янии 3 температура гелия равна его на-
чальной температуре в состоянии 1. Най-
ти теплоемкость газа в процессе 2-3, ес-
ли в процессе сжатия 1 -2 над газом совершена работа А (А > 0),
а в процессе сжатия 2—3 над газом совершена работа 2Д.
3.	Плоский конденсатор, квадратные пластины которого имеют
к задаче 3
площадь S и расположены на рассто-
янии d, полностью заполнен твердым
диэлектриком с диэлектрической про-
ницаемостью е (см. рис.). Конденса-
тор подсоединен к батарее, ЭДС ко-
торой равна 8. Диэлектрическую пла-
стину выдвигают из конденсатора. На какое расстояние х выдвн-
ФИЗИКА ♦ ЗАДАЧИ ♦ Билет8
15
нута пластина, если при этом внешними силами совершена рабо-
та А? Внутренним сопротивлением батареи пренебречь.
4.	Комар пересекает главную
оптическую ось собирающей
линзы на расстояние а =
= 3F/4, где F — фокусное
расстояние линзы, под ма-
лым углом а к оси линзы со
скоростью V. 1) Под каким
углом изображение комара пересекает главную оптическую ось
линзы? 2) Чему равна в этот момент скорость изображения ко-
мара?
У к а з а н и е: для малых углов sin а и tg а и а.
5.	Электромагнитное гамма-излучение, поглощаясь
атомными ядрами, переводит их в возбужденное
состояние (с основного энергетического уровня на -------
более высокие уровни энергии). 7-квант, испу-
щенный одним из ядер олова, поглощается дви- к задаче 5
жущимся навстречу под углом а = 60° к направлению его дви-
жения ядром олова 119Sn. Найти скорость движения ядра и, ес-
ли энергия 7-кванта равна энергии перехода ядра из основного
в возбужденное состояние Е-, = Eq = 23,8 КэВ. Энергия по-
коя ядра олова W'o = тяс2 = 113 ГэВ (1 ГэВ = 103 МэВ =
= 106 КэВ = 109 эВ). При испускании и поглощении 7 кван-
та происходит переход между одними и теми же энергетическими
состояниями ядра.
БИЛЕТ 8
В коническом сосуде с водой находится деревян-
ный шар объемом V, удерживаемый от всплы-
тия горизонтальной полкой BE, прикрепленной
к стенке сосуда. Поверхность полки и стенки со-
суда гладкие. Угол между полкой и стенкой сосу-
да <д. Плотности воды и дерева р и рг. Найти си-
а
к задаче 1
лу давления шара на полку в двух случаях: 1) сосуд неподвижен,
16	 ФИЗИКА ♦ ЗАДАЧИ ♦ Билет 8
2) сосуд движется с постоянным горизонтальным ускорением о.
2.	Моль гелия из состояния 1 сжимается в процессе с посто-
янной теплоемкостью 12 а затем в процессе 2—3, когда
р	давление газа Р прямо пропорцпопаль-
2	по его объему. В конечном состоянии 3
температура гелия равна начальной тем-
/ \	пературс в состоянии 1. Найти теплоем-
। кость газа в процессе сжатия 1—2, если
/	работа сжатия на участке 1-2 в К =- i .3
О	Г раза больше работы сжатия на участке
к задаче 2	2—3. Известно, что в процессе сжатия
тепло к газу подводится.
3.	В плоском конденсаторе с площадью пластин S и расстоянием
между ними d расположена металлическая пластина толщиной
L[. Конденсатор подключен к источнику с постоянной ЭДС £.
Какую минимальную работу необходимо совершить, чтобы пе-
редвинуть верхнюю обкладку конденсатора на расстояние /?>'
Внутренним сопротивлением батареи пренебречь.
к задаче 3
к задаче 4
4,	Жук пересекает главную оптическую ось рассеивающей линзы
под малым углом а со скоростью v. Поперечное увеличение лин-
зы для данного момента Г = 1/6. 1) Под каким углом изобра-
жение жука пересекает главную оптическую ось линзы? 2) Чему
равна в этот момент скорость изображения жука?
У к а з а н и е: для малых углов sin а и tg а яз а.
5.	Гамма-излучением (поглощением) называется электромагнитное
излучение (поглощение) при переходах атомных ядер из возбуж-
ФИЗИКА ♦ ЗАДАЧИ ♦ Билет9
17
денных в более низкие энергетические состояния и наоборот.
Ядро атома олова il9Sn движется
со скоростью v = 63 м/с и ис-
пускает 7-квант в том же направле-
нии, который затем поглощается не-	к задаче °
подвижным свободным ядром олова. Найти энергию 7-кванта.
Энергия покоя ядра олова Wq = тяс2 = 113 ГэВ (1 ГэВ =
= 103 МэВ = 106 КэВ = 109 эВ). При испускании и поглощении
7 кванта происходит переход между одними и теми же энергети-
ческими состояниями ядра.
БИЛЕТ 9
1.	Толстая однородная веревка массой т
с бруском массой 6т легкой нитью, пере-
кинутой через блок (см. рис.). Коэффи-
циент трения скольжения между бруском
и наклонной плоскостью д = 0,1. Угол
наклона наклонной плоскости к горизон-
ту (3 = 30°. 1) Найти ускорение бруска.
2) Найти силу натяжения веревки в точ-
ке В, для которой BD = AD/^. Массой
блока и трением в его оси пренебречь.
= 0,3 кг соединена
к задаче 1
2.	Подвижный поршень весом mg, подвешенный
на пружине, делит объем вертикально распо-
ложенного откачанного цилиндра на две части
(см. рис.). В положении равновесия высота ниж-
ней части Но, а удлинение пружины равно хо-
В нижнюю часть цилиндра впрыскивается v мо-
лей воды. При медленном нагреве до некоторой
к задаче 2
температуры вся вода испаряется, а поршень пе-
ремещается на величину ад = ажо (а = 1/2).
1) Определить конечную температуру Т.
2)	Найти работу А, совершенную паром.
3.	Частица массой т с положительным зарядом q находится в од-
нородных электрическом и магнитном полях. Напряженность
18
ФИЗИКА ♦ ЗАДАЧИ ♦ Билет 9
электрического поля Е. Линии индукции магнитного поля па-
раллельны силовым линиям электрического поля. В начальный
к задаче 3
момент частице сообщают скорость гд,
направленную под углом а к линиям ин-
дукции (см. рис.). Через некоторое время
частица возвращается в начальную точку.
1) Чему равно это время? 2) Найти ин-
дукцию магнитного поля В, при которой
возвращение частицы в начальную точку
возможно.
к задаче 4
4.	Батарею с ЭДС £ подключают к последовательно соединен-
ным катушке с индуктивностью L и незаряженному конденсатору
емкостью С. В контуре происходят колебания
тока. В тот момент, когда ток в контуре ста-
новится равным нулю, батарею отключают от
схемы и подключают вновь, поменяв местами ее
выводы. Чему будет равен после этого макси-
мальный ток в контуре? Внутренним сопроти-
влением батареи и сопротивлением катушки пренебречь.
5.	Оптическая система состоит из двух линз: собирающей и рас-
сеивающей (см. рис.), главные оптические оси которых па-
раллельны и смещены друг относительно друга на расстояние
.	d — 1 см. Параллель-
__>	ный пучок света, направлен-
V | ный на систему параллель-
	но главным оптическим осям,
* ,	______*	фокусируется системой в точ-
—*____________________ __|  ке F, расположенной на рас-
__v	стоянии а = 10 см от рас-
сеивающей линзы. 1) Найти
расстояние между линзами L.
2) Найти расстояние Ь от фо-
к задаче 5	куса F до главной оптической
оси собирающей линзы. Фокусные расстояния линз Fi = 40 см,
F2 = —40 см.
ФИЗИКА ♦ ЗАДАЧИ ♦ Билет 10
19
БИЛЕТ 10
1.	Однородный канат массой т = 1 кг соединен с бруском мас-
сой 3m,/2 .легкой нитью, перекинутой через блок (см. рис.).
Канат находится на наклоненной под
углом a (cos rv = 0,8) к горизонту по-
верхности. Коэффициент трения сколь-
жения между этой поверхностью и кана-
том д = 0,2. 1) Найта ускорение каната.
2) Найти силу натяжения каната в его се-
редине. Массой блока и трением в его оси
пренебречь.
2.	Подвижный поршень весом mg, подвешенный
на пружине, делит объем вертикально располо-
женного пустого цилиндра на две части. В по-
ложении равновесия высота нижней части ци-
линдра Hq, удлинение пружины х$. В нижнюю
часть цилиндра впускают v молей воздуха. По-
сле установления равновесия пружина оказыва- к задаче 2
ется сжатой. Величина деформации сжатой пру-
жины х\ = axQ (а = 2). После этого воздух медленно охла-
ждают до некоторый температуры, так что в конечном состоянии
деформация сжатой пружины х? = ах0/2. 1) Найти конечную
температуру воздуха. 2) Найти работу, совершенную воздухом в
процессе охлаждения.
3.	Частица массой т с положительным за-	&
рядом q находится в однородных электри- ----Z->
ческом и магнитном полях. Линии индук- ~~mq*-----------
ции магнитного поля параллельны сило- --------3--------В
вым линиям электрического поля. В на- -------->--------
чальный момент частице сообщают ско- к задаче 3
роста до, направленную под углом а к силовым линиям (см. рис.).
Через время г частица оказывается вновь на той же силовой ли-
нии электрического поля, с которой она стартовала, на рассто-
янии L от первоначальной точки. 1) Чему равна напряженность
электрического поля Е? 2) Найти индукцию магнитного поля В.
20
ФИЗИКА ♦ ЗАДАЧИ ♦ Билет 11
4.	В схеме, изображенной на рисунке, при разомкнутом ключе К
к задаче 4
напряжение на конденсаторе емкостью С рав-
но 5£, где £— ЭДС батареи. Какой максималь-
ный ток будет течь через катушку индуктивно-
стью L после замыкания ключа? Внутренним
сопротивлением батареи и сопротивлением ка-
тушки пренебречь.
5.	Оптическая система состоит из рассеивающей линзы Л] и соби-
рающей линзы Лг, расположенных на расстоянии L = 10 см друг
от друга (см. рис.). Главные
/К	оптические оси линз парал-
|	лельны. Параллельный пучок
света, падающий перпендику-
лярно плоскостям линз, фоку-
' сируется системой в точке F,
к задаче 5	расположенной слева от рас-
сеивающей линзы Л1 на расстоянии а = 30 см от нее и на рас-
стоянии b = 1 см от ее оптической оси. 1) Найти фокусное рас-
стояние F2 собирающей линзы Лг. 2) Определить расстояние d
между оптическими осями линз. Фокусное расстояние линзы Л1
F[ = -10 см.
БИЛЕТ 11
1.	Брусок массой т = 0,5 кг соединен с толстой однородной верев-
кой массой 3m легкой нитью, перекинутой через блок (см. рис.).
Коэффициент трения скольжения
между бруском и наклонной плоско-
стью (.1 — 0,4. Угол наклона наклон-
ной плоскости к горизонту /3 — 30°.
1) Найти ускорение веревки. 2) Най-
ти силу натяжения веревки в точке В,
для которой BD = AD/б. Массой
блока и трением в его оси пренебречь.
2.	Подвижный поршень весом mg, подвешенный на пружине, де-
лит объем откачанного вертикально расположенного цилиндра
ФИЗИКА ♦ ЗАДАЧИ ♦ Билет 11
21
на две части (см. рис.). В положении равновесия высота ниж-
ней части цилиндра Но, Удлинение пружины до- В нижнюю часть
цилиндра впрыскивается и молей воды. После того как вся вода
испарилась, поршень переместился на величину = ахо (а =
= 3/2). 1) Найти конечную температуру. 2) Найти работу, совер-
шенную паром.
к задаче 2
к задаче 3
3.	Частица массой т с положительным зарядом q находится в од-
нородных электрическом и магнитном полях. Линии индукции
магнитного поля параллельны силовым линиям электрического
поля. В начальный момент частице сообщают скорость и0, на-
правленную под углом а (а > 90°) к линиям индукции (см. рис.).
Через время г частица возвращается в начальную точку.  1) Чему
равна напряженность электрического поля ®? 2) Найти индук-
цию магнитного поля В.
4.	Незаряженный конденсатор с емкостью С под-
ключают к последовательно соединенным ба--------------—-----
тарее с ЭДС £ и катушке с индуктивностью
L. В контуре происходят колебания тока. В -==-
тот момент, когда ток становится равным нулю,	LJLrxv-',—
конденсатор отключают от схемы и подключают к задаче 4
вновь, поменяв местами его выводы. Какой максимальный ток
будет течь после этого в цепи? Внутренним сопротивлением ба-
тареи и сопротивлением катушки пренебречь.
5.	Оптическая система состоит из собирающей линзы Лi и рассе-
ивающей линзы Лг (см. рис.), главные оптические оси которых
параллельны и смещены друг относительно друга на расстояние
22
ФИЗИКА ♦ ЗАДАЧИ ♦ Билет 12
d = 1 см. На систему со стороны собирающей линзы параллель-
но ее главной оптической оси падает параллельный пучок света.
к задаче 5
Найти положение фокуса F такой
системы: 1) х — расстояние от F
до плоскости линзы Л2, 2) у —
расстояние от F до главной опти-
ческой оси линзы Лг. Расстояние
между линзами а = 30 см, фокус-
ные расстояния линз Лi и Л2 F1 —
= 10 см и F2 = —10 см.
БИЛЕТ 12
к задаче 1
1.	Однородный канат массой т = 3 кг соединен с бруском мас-
сой 2m легкой нитью, перекинутой через блок (см. рис.). Канат
находится на горизонталь-
ной поверхности, а брусок
— на наклоненной по углом
a (sin а = 0,6) к горизон-
ту поверхности. Коэффици-
ент трения скольжения ка-
ната и бруска о соответству-
ющие поверхности у = 0,3. 1) Найти ускорение бруска. 2) Най-
ти силу натяжения каната в точке В, для которой АВ = АС/3.
Массой блока и трением в его оси пренебречь.
2.	Подвижный поршень весом mg, подвешенный на пружине, де-
лит объем вертикально расположенного откачанного цилиндра
на две части (см. рис.). В положении равнове-
сия высота нижней части цилиндра Но, а удли-
нение пружины ж0. В нижнюю часть цилиндра
впускают v молей воздуха. После установления
равновесия удлинение пружины оказалось рав-
ным Xi = ахд (а = 1/4). Затем воздух в цилин-
дре стали медленно охлаждать, так что в конце
к задаче 2 процесса охлаждения удлинение пружины ока-
залось х-2 = Зажо. 1) Найти конечную темпе-
ФИЗИКА ♦ ЗАДАЧИ ♦ Билет 12
23
m,q
Е
к задаче 3
- +68
к задаче 4
клю-
и со-
V
лх
ратуру воздуха в цилиндре. 2) Найти работу, совершенную воз-
духом в процессе охлаждения.
3.	Частица массой т с положительным за-
рядом q находится в однородных элек-
трическом и магнитном полях. Напря-
женность электрического поля Е. Ли-
нии индукции магнитного поля парал-
лельны силовым линиям электрического
поля. В начальный момент частице со-
общают скорость vq, направленную под
углом а к силовым линиям (см. рис.). Через некоторое время
частица оказывается вновь на той же силовой линии электриче-
ского поля,с которой она стартовала, на расстоянии L от перво-
начальной точки. 1) Найти это время. 2) Найти индукцию маг-
нитного поля В.
4.	В схеме, изображенной на рисунке, при разо-
мкнутом ключе К напряжение на конденсато-
ре емкостью С равно 6Е, где Е— ЭДС батареи.
Какой максимальный ток будет течь через ка-
тушку индуктивности L после замыкания
ча? Внутренним сопротивлением батареи
противлением катушки пренебречь.
5.	Оптическая система состоит из рассе-
ивающей линзы Л1 и собирающей лин- “
зы Лг, расположенных на расстоянии
L = 8 см друг от друга (см. рис.). Глав-
ные оптические оси линз параллель- _
ны. Параллельный пучок света, пада- -
ющий на систему параллельно оптиче-
ским осям, фокусируется в точке F, расположенной на расстоя-
нии b = 0,5 см от главной оптической оси линзы Лг- 1) Опреде-
лить расстояние d между оптическими осями линз. 2) Найти рас-
стояние а от фокуса системы F до плоскости собирающей линзы
Л2. Фокусные расстояния линз Л1 и Л2 Fi = —16 см и F> =
= 16 см.

д
к задаче 5
24
МАТЕМАТИКА ♦ ЗАДАЧИ ♦ Билет 2
МАТЕМАТИКА
БИЛЕТ 1
1. Решить уравнение
3 + cos 4ж — 8 cos4 х 1
4(cosa? + sina?) sin х
2. Решить неравенство
х — 8	\
— 2х — 3 у
+ 2^0.
3.	Решить систему уравнений
у/х~+у + у/х + 2у = 10,
у/х +~у + 2х + у = 16.
4.	В равнобедренной трапеции ABCD (ВС || AD) окружность ка-
сается основания ВС, боковых сторон АВ и CD и проходит
через точку пересечения диагоналей АС и BD. Найти радиус
окружности, если AD : ВС = 9 : 7, а площадь трапеции S =
= 8.
5.	Дано число а = 22002 + З2002. Найти последнюю цифру числа а и
остаток отделения числа а на И.
6.	Сторона основания ABCD правильной пирамиды SABCD рав-
на 2. Плоскость а, параллельная прямым SC и AD, пересекает
пирамиду так, что в сечение можно вписать окружность, причем
32
периметр сечения равен Найти: 1) в каком отношении плос-
О
кость аделит ребра пирамиды; 2) отношение объемов частей, на
которые плоскость а разбивает пирамиду; 3) расстояние от цен-
тра описанной около пирамиды сферы до плоскости а.
БИЛЕТ 2
1.	Решить уравнение
3 + cos 4х — 8 sin4 х __ 1
4(sin х + cos ж) cos х
МАТЕМАТИКА ♦ ЗАДАЧИ ♦ Билет3 25
2.	Решить неравенство
( ж \ 1
1“г)3 U J + 3 С °'
3.	Решить систему уравнений
\^Лх - у - у/у - х = 1,
7у/у — х + Qy — 26ж = 3.
4.	В равнобедренной трапеции ABCD (ВС || AD( окружность ка-
сается основания AD, боковых сторон АВ и CD и проходит
через точку пересечения диагоналей АС и BD. Найти радиус
окружности, если AD : ВС = 7 : 5, а площадь трапеции S =
= 4.
5.	Дано число а = З2002 + 72002. Найти последнюю цифру числа а и
остаток отделения числа а на 11.
6.	Сторона основания ABCD правильной пирамиды SABCD рав-
на 2. Плоскость а, параллельная прямым SB и AjD, пересекает
пирамиду так, что в сечение можно вписать окружность, причем
периметр сечения равен Найти: 1) в каком отношении плос-
кость аделит ребра пирамиды; 2) отношение объемов частей, па
которые плоскость а разбивает пирамиду; 3) расстояние от цен-
тра описанной около пирамиды сферы до плоскости а.
БИЛЕТ 3
1.	Решить уравнение
3 + 4 cos 2х — 8 cos4 х 1
sin 2ж — cos 2х sin 2х
2.	Решить неравенство
( х - 10 \
!°й	---3---7 + 3 < 0.
v \х2 — 6х + 5/
3.	Решить систему уравнений
( у/х - 4у - 2у/3у + х = 1,
7y/Зу + х + 22у + 5х = 13.
4.	В равнобедренной трапеции ABCD (ВС || AD) окружность ка-
сается основания ВС, боковых сторон АВ и CD и проходит
26
МАТЕМАТИКА ♦ ЗАДАЧИ ♦ Билет 4
через точку пересечения диагоналей АС и BD. Найти радиус
окружности, если AD : ВС = 5 : 4, а площадь трапеции S =
= 3.
5.	Дано число а = 22002 + 132002. Найти последнюю цифру числа а
и остаток отделения числа а на 11.
6.	Сторона основания ABCD правильной пирамиды SABCD рав-
на 2. Плоскость а, параллельная прямым SB и AD, пересекает
пирамиду так, что в сечение можно вписать окружность радиуса
д/15/5. Найти: 1) в каком отношении плоскость а делит ребра
пирамиды; 2) отношение объемов частей, на которые плоскость
а разбивает пирамиду; 3) расстояние от центра описанной около
пирамиды сферы до плоскости а.
БИЛЕТ 4
1.	Решить уравнение
3 — 4 cos 2х — 8 sin4 х __	1
sin 2х + cos 2х sin 2х
2.	Решить неравенство
( х — 6	\	1
1°g(a;+l)5 I ~2	~ I + - ^ 0.
'	' \xz + 2х — 3/	5
3.	Решить систему уравнений
Зу — у/5х — у = 2,
15л/5ж — у 4- 22х + 4у — 15.
4.	В равнобедренной трапеции ABCD (ВС || AD) окружность ка-
сается основания AD, боковых сторон АВ и CD и проходит
через точку пересечения диагоналей АС и BD. Найти радиус
окружности, если AD : ВС = 5 : 3, а площадь трапеции S =
= 9.
5.	Дано число а = 22002 + 72002. Найти последнюю цифру числа а и
остаток от деления числа а на 11.
6.	Сторона основания ABCD правильной пирамиды SABCD рав-
на 2. Плоскость а, параллельная прямым SC и AD, пересекает
пирамиду так, что в сечение можно вписать окружность радиуса
__________МАТЕМАТИКА ♦ ЗАДАЧИ ♦ Билет 6______27
д/35/7. Найти: 1) в каком отношении плоскость а делит ребра
пирамиды; 2) отношение объемов частей, на которые плоскость
а разбивает пирамиду; 3) расстояние от центра описанной около
пирамиды сферы до плоскости а.
БИЛЕТ 5
1.	Решить уравнение
2х — 1	тг
arctg------1- arcsm х — — .
х	2
2.	Найти действительные решения системы уравнений
j 1 + С + 4 = о.
\ У Х~ X
3.	Решить неравенство
/х2 + 9х - 162	, ,
V	----- > 9 - Ш.
V	х - 2
4.	Один из углов треугольника равен Зтг/4, радиус вписанной в него
окружности равен 4, а периметр треугольника равен 16(6 + д/2).
Найти радиус окружности, описанной около этого треугольника.
5.	Найти все значения а, при которых система
Г log2(3 - х + у) + 3 = log2(25 - 6х + 7у),
[ у + 2 = (ж — 2а)2 + а + 2х.
имеет ровно два решения.
6.	Расстояние от центра О шара радиуса 12, описанного около пра-
вильной четырехугольной пирамиды, до бокового ребра равно
4л/2. Найти: 1) высоту пирамиды; 2) расстояние от точки О до
боковой грани пирамиды; 3) радиус вписанного в пирамиду ша-
ра.
БИЛЕТ 6
1.	Решить уравнение
1 — X	7Г
arcctg —----Ь arccos 2х = — .
Z	z
28
МАТЕМАТИКА ♦ ЗАДАЧИ ♦ Билет 7
2.	Найти действительные решения системы уравнений
{332
У “Ь —т — '—	— 1
У3 х у ’
|+4 + 4 - о.
у X X
3.	Решить неравенство
/500 + ЗОж - 2ж2	, ,
V 2ж +5	i 11
4.	Один из углов треугольника равен тг/4, радиус вписанном в не-
го окружности равен 2(2 — >/2), а радиус описанной вокруг него
окружности равен 3. Найти площадь этого треугольника.
5.	Найти все значения а, при которых система
Г 1о§з(2 ~ ж - у) + 2 = log3(17 - 8ж - 10у),
[ (ж — а)2+ х = у + а + 6
имеет ровно два решения.
6.	Расстояние от центра О шара радиуса 6\/2, описанного около
правильной четырехугольной пирамиды, до боковой грани рав-
но 3. Найти: 1) высоту пирамиды; 2) расстояние от точки О до
бокового ребра пирамиды; 3) радиус вписанного в пирамиду ша-
ра.
БИЛЕТ 7
1. Решить уравнение
1 — X ,	7Г
arctg —----h aresm Зх = — .
Зх	2
2. Найти действительные решения системы уравнений
{X ,	4	1,2
i + х2у2 + 4у2 = 0.
3. Решить неравенство
ж2 + ЗОж - 675	, ,
-------------- > 15 - ж .
ж — 3
4. Один из углов треугольника равен тг/6, радиус описанной окруж-
ности равен 3(2д/3 — 1), а периметр треугольника равен 16\/3.
МАТЕМАТИКА ♦ ЗАДАЧИ ♦ Билет 8
29
Найдите радиус окружности, вписанной в этот треугольник.
5. Найти все значения а, при которых система
Г log2(5z + 7у + 2) = log2(a; + 2у + 1) + 2,
I (у + 2а)2 + у = х + а + 1/2
имеет ровно два решения.
6. Расстояние от центра О шара, описанного около правильной че-
тырехугольной пирамиды до бокового ребра, равно 2у/2, а от О
до боковой грани равно б/х/б. Найти: 1) высоту пирамиды; 2) ра-
диус описанного вокруг пирамиды шара; 3) радиус вписанного в
пирамиду шара.
БИЛЕТ 8
1.	Решить уравнение
Зж — 1	7Г
arcctg-------F arccos х — — .
х	2
2.	Найти действительные решения системы уравнений
{1	з 1
х + -з-д- = X6 у ч-2 ,
х у	ху
+ х3у3 + 10у2 = 0.
3.	Решить неравенство
/243 + 9з; - 2ж2	, ,
V....^ТТз.....
4.	Один из углов треугольника равен 5тг/б, радиус вписанной
окружности равен 1, а площадь треугольника равна 13\/3. Найти
радиус окружности, описанной около этого треугольника.
5.	Найти все значения а, при которых система
Г 1о§з(7ж + 4у - 11) = 10g3(2x + у - 3) + 1,
\(у + а)2 + х + у + а = 7
имеет ровно два решения.
6.	Расстояние от центра О шара радиуса 9, описанного около пра-
вильной четырехугольной пирамиды, до бокового ребра в \/Т0/3
раз больше расстояния от точки О до боковой грани пирамиды.
Найти: 1) высоту пирамиды; 2) расстояние отточки О до боковой
грани пирамиды; 3) радиус вписанного в пирамиду шара.
30 МАТЕМАТИКА ♦ ЗАДАЧИ ♦ Билет 10
БИЛЕТ 9
1.	Решить уравнение
9	9	cos 2т
sm 2х + sin 4х = 1--------.
cos Зх
2.	Решить неравенство
21og23._12 (VaT+T - \/9^~х) < 1.
3.	Окружность с центром на стороне АВ равнобедренного тре-
угольника АВС (АВ = ВС) касается отрезка АС в точке F,
пересекает отрезок ВС в точке G, проходит через точку В и пе-
ресекает отрезок АВ в точке Е, причем АЕ = a, ABFG = д.
Найти радиус окружности.
4.	Сторона основания ABCD правильной пирамиды SABCD рав-
на 8, высота SO равна 3. Точка М — середина ребра SB, точка
К — середина ребра ВС. Найти: 1) объем пирамиды AMSK;
2)	угол между прямыми AM и SK; 3) расстояние между прямы-
ми AM и SK.
5.	Найти все значения параметра а, при которых уравнение
(а + 3 — |т + 2|) (а + х2 + 4х) = 0
имеет: 1) ровно три корня; 2) ровно два корня.
6.	Решить систему уравнений
{х3 + у3 — z3 — xyz + 11 = 0,
х3 — у3 + z3 — xyz — 21 = 0,
у3 + z3 — х3 — xyz — 3 = 0.
БИЛЕТ 10
1. Решить уравнение
2. Решить неравенство
21о?2;с - 8 (VaT + 3 - \/7^~х) < 1.
3. Окружность с центром на стороне АВ равнобедренного тре-
угольника АВС (АВ = ВС) проходит через точку А, пересекает
отрезок АС в точке F, касается отрезка ВС в точке G и Пересе-
____________МАТЕМАТИКА ♦ ЗАДАЧИ ♦ Билет 11______________3£
кает отрезок АВ в точке Е, причем GC/BG = х/3 — 1, FC = а.
Найти радиус окружности.
4.	Сторона основания ABCD правильной пирамиды SABCD рав-
на 4\/2, угол между боковым ребром пирамиды и плоскостью
основания равен arctg Точка М — середина ребра SD, точка
К — середина ребра AD. Найти: 1) объем пирамиды CMSK-,
2) угол между прямыми СМ и SK; 3) расстояние между прямы-
ми СМ и SK.
5.	Найти все значения параметра а, при которых уравнение
(а — 6 + |ж — 1|) (а — ж2 + 2ж) = О
имеет: 1) ровно три корня; 2) ровно два корня.
6.	Решить систему уравнений
{2ж3 — у3 — 2z3 + xyz + 5 = 0,
у3 + 2z3 — ж3 — 2xyz — 2 = 0,
ж3 — у3 — z3 + xyz + 4 = 0.
БИЛЕТ 11
1.	Решить уравнение
cos2 ж + cos2 2ж = 1 + ctg Зж.
2.	Решить неравенство
21og2z-io (х/жТ2 - у/8^~х) < 1.
3.	Окружность с центром на стороне АВ равнобедренного тре-
угольника АВС (АВ = ВС) касается отрезка АС в точке F,
пересекает отрезок ВС в точке G, проходит через точку В и пе-
ресекает отрезок АВ в точке Е, причем GC = a, ABFG = 7.
Найти радиус окружности.
4.	Диагональ основания ABCD правильной пирамиды SABCD
равна 8х/2, угол между боковой гранью и плоскостью основания
равен arctg Точка М — середина ребра SA, точка К — се-
редина ребра АВ. Найти: 1) объем пирамиды DMSK; 2) угол
между прямыми DM и SK; 3) расстояние между прямыми DM
и SK.
32
МАТЕМАТИКА ♦ ЗАДАЧИ ♦ Билет 12
5.	Найти все значения параметра а, при которых уравнение
(а — 2 — \х + 3|) (а + х2 + 6х) = О
имеет: 1) ровно три корня; 2) ровно два корня.
6.	Решить систему уравнений
{х3 + 2у3 + z3 4- 2xyz + 22 = О,
2х3 — 2у3 — z3 + xyz + 2 = 0,
у3 — х3 — z3 + xyz — 13 = 0.
БИЛЕТ 12
1.	Решить уравнение
2 о	cos х
cos х + cos 2х = 1 4------.
cos 2х
2.	Решить неравенство
2 log43._i6 (х/2х - 1 - \/11 - 2ж) < 1.
3.	Окружность с центром на стороне АВ равнобедренного тре-
угольника АВС (АВ = ВС) проходит через точку А, пересекает
отрезок АС в точке F, касается отрезка ВС в точке G и пересе-
кает отрезок АВ в точке Е, причем GC = BG, ЕС = а. Найти
радиус окружности.
4.	Диагональ основания ABCD правильной пирамиды SABCD
равна 8, высота пирамиды SO равна 1. Точка М — середина ре-
бра SC, точка К — середина ребра CD. Найти: 1) объем пира-
миды BMSK-, 2) угол между прямыми ВМ и SK\ 3) расстояние
между прямыми ВМ и SK.
5.	Найти все значения параметра а, при которых уравнение
(а — 3 + |ж + 2|) (а — х2 — 4х) = 0
имеет: 1) ровно три корня; 2) ровно два корня.
6.	Решить систему уравнений
( З.т3 — Зу3 + z3 — xyz — 3 = 0,
< Зу3 — х3 — z3 — xyz + 5 = 0,
[ х3 — у3 + z3 — xyz — 2 = 0.
ФИЗИКА ♦ ОТВЕТЫ И РЕШЕНИЯ ♦ Билет 1
33
ФИЗИКА
БИЛЕТ 1
, 1
1. cos а =
ч/П
Решение. На рисунке изображен момент соскальзыва-
ния шайбы с клина. Обозначим в этот момент скорость шайбы
относительно клина через А0Тц, а ско-	<
рость самого клина через и. Очевид-	/hVam
но, что скорость клина направлена го-	5$.
ризонтально, а относительная скорость
шайбы составляет угол а с горизонтом. :.L>,
Поскольку действующая на систему тел	к задаче 1
«шайба плюс клин» в горизонтальном направлении результиру-
ющая сила равна нулю, то горизонтальная составляющая им-
пульса этой системы остается неизменной:
mvo = 2ти + m(v0TH • cos а + и).	(1)
Поскольку и = vq/4, то уравнение (1) будет иметь вид
vq = 4VQTH • cos а.	(2)
По закону сохранения энергии
mvl _ 2ти2	mv^	, ,
2 “ 2	2	U
В данном уравнении г?ш — скорость шайбы в момент соскальзы-
вания относительно неподвижной системы координат. По теоре-
ме косинусов
= Хги 4" X + 2'Wqth ’ Г4 COS CU.
После подстановки этого соотношения в (3) и с учетом того, что
и = vq/4, получим
13vq = 1бХтн + 8vOTHvo cos а.	(4)
Из совместного решения (2) и (4) относительно cos а получим,
что
1
cos а = ,__
Х1Т
АР _ тв Рс (р - Рв)
Pg Р Рв (ре - р) ’
34 ФИЗИКА ♦ ОТВЕТЫ И РЕШЕНИЯ ♦ Билет 1
Решение. Пружинные весы измеряют вес тела. Первона-
чальные показания весов
Pl = mBg + Mcg.
Здесь Мс — масса сосуда. Массой марлевого мешочка прене-
брегаем. Показания весов после растворения соли в воде
Р = mBg + Mcg + mcg + Vnpg.
Здесь mc — неизвестная масса соли. Изменение показаний ве-
сов
ДР = Р2 ~ А = mcg + Vnpg.	(1)
Плотность солевого раствора
тс + тв
, тв\
V Рс Рв J
Определяя массу соли тс из уравнения (2) и подставляя это вы-
ражение в (I), найдем объем примеси:
пв Рс (р ~ Рв)
Р Рв (рс - р) '
3.	Ответ на графике (см. рис.).
к задаче 3
Решение. На рисунке про-
ведем вольтамперную характе-
ристику резистора с сопроти-
влением R. (прямая 2). По-
скольку неизвестный элемент Z
и резистор соединены парал-
лельно, то падения напряжения
на них всегда равны, а их об-
щий ток равен алгебраической
сумме токов через каждый эле-
мент. Поэтому для построения вольтамперной характеристи-
ки неизвестного элемента Z нужно при фиксированных значе-
ниях напряжения V из заданной вольтамперной характеристи-
ки (прямая 1) вычесть вольтамперную характеристику резистора
R (прямая 2). Полученная таким способом прямая 3 является
вольтамперной характеристикой неизвестного элемента.
ФИЗИКА ♦ ОТВЕТЫ И РЕШЕНИЯ ♦ Билет 1
35
4.	L = 11 см.
Решение. Сначала найдем изображение источника S в линзе
1 1 _ 1
а + bi ~ F '
3	3
При а ~ р- F расстояние от изображения до линзы — - - F.
О	Z
Изображение в линзе S' является мнимым и совпадает с изобра-
жением Si (см. рис.). После прохождения линзы световые лучи
преломляются на передней границе зеркала. Преломленные лу-
чи кажутся исходящими из мнимого источника S". Расстояние
этого источника до передней поверхности зеркала AS" — n(L +
+ b), где п — показатель преломления материала зеркала. Это
соотношение справедливо для параксиальных лучей, то есть для
малых углов падения, которые мы и рассматриваем. После пре-
ломления лучи отражаются от зеркальной поверхности и кажут-
ся исходящими из мнимого источника S'". Расстояние от этого
источника до зеркальной поверхности S'"В = AS" + АВ = d +
+ n(L + 6). Зеркально отразившись, лучи снова преломляются
на передней границе зеркала и кажутся исходящими из мнимого
источника S"". Расстояние AS"" = AS’"/п = 2d/n + L + b. По-
сле преломления лучи проходят линзу и собираются в точке S\.
Расстояние OS"" = AS"" + L — 2d/n + 2L + Ъ. По формуле
36 ФИЗИКА ♦ ОТВЕТЫ И РЕШЕНИЯ ♦ Билет 1
линзы можно записать
1 1 _ 1
2d/n + 2L + b+ b ~ F ’
После подстановки числовых значений получим
1 1 _ 1
38 + 2L + 30 “ 20 ’
Отсюда
L — 11 см.
5.	Аистах = У’оВш	= 4,5.10-4 В.
_	Решение. При вращении стержня
,v .в магнитном поле на свободные элек-
4-1'" _ т _ с 5 —I ч-1 ТРОНЫ стержня будет действовать си-
L-r	/ ла Лоренца (см. рис.). Под действи-
ем этой силы произойдет перераспре-
к задаче 5
деление зарядов, которое приведет к
появлению в стержне электростатического поля, направленного
вдоль стержня. Распределение напряженности электрического
поля по радиусу Е(г) находится из условия равновесия свобод-
ных зарядов
qvB — qE(r).
Поскольку линейная скорость зарядов
v = фг — —<рош sin(wt) • г,
то
£J(r) = —pouBrsm(ut).
Разность потенциалов между концами стержня А и С.
= [ E(r) dr — [ E(r) dr.
Jo	Jo
После подстановки выражений для Е(г) получим
rb	га
АС = — / рдЕшг sin(wt) dr + / роВшг sin(wt) dr =
Jo	Jo
(b2 — a2) .
= — poBu-— ------sm(wt).
Очевидно, что максимальная разность потенциалов между кон-
ФИЗИКА ♦ ОТВЕТЫ И РЕШЕНИЯ ♦ Билет 4
37
цами стержня будет равна
(А2 _ 2\
АрДСтах = роВш---------= 4,5  10~4В.
БИЛЕТ 2
1.	v = >/91zz2 + 2gH.
9	V — f'c p Г АР _ vl
• Vb~ рс-Рв U(p-pb) VnJ
3.	Ответ на графике (см. рис.).
4.	F = l(L + -} = 8 см.
3 \ nJ
5.	и АС =	= 0,3 В.
БИЛЕТ 3
f и _ 2“2	4 \ _ 30w2
g \ tg /?/ s
9т— Рс- F-Р Г AJZ _ у J
р-рв L g ' J
3.	Ответ на графике (см. рис.).
4-	п = 4F/3 - L = 1’5'
5.	иАС =	(2а.Ь + &2) = 4,8 • 10~3
БИЛЕТ4
ч с 2М(М.+ тЗ и2
1.5 = ----—9--— tg (р.
т2	g
9 т/ — АР_______ТПд (рс ~ рв)
п g(.p - Рв) Рв (рс - р) '
3.	Ответ на графике (см. рис.).
4.	d= (F/4 - L)n = 3 см.
5.	Uас = 1вшВ2 = 0,06 В.
О
0 1 2 3 4 5 V, В
к задаче 3
0 1 2 3 4 5 У, В
к задаче 3
к задаче 3
38
ФИЗИКА ♦ ОТВЕТЫ И РЕШЕНИЯ ♦ Билет 5
БИЛЕТ 5
1 - 1) /=20 = (ро - pB)Vg; 2)Р2 = (р0 - PbW(§ + actga).
Решение. На рисунке изображены силы, которые действуют
на шар в случае движения сосуда с постоянным горизонтальным
.	. ускорением a: Fi и F2 — две проекции резуль-
< Q /	\	тирующей силы давления со стороны воды на
L_____\	шар, N — реакция стенки сосуда на шар, Pi
I F2 \	— сила тяжес™ шара, Р2 — сила реакции дна
/ (	сосУда на шаР- В том случае, когда сосуд непо-
I <( „	движен, силы Fi и N равны нулю, а сила Р2 =
/ У= Р2о = Fi-F2 = p0Vg-P!iVg = (po-Pb)V&
р где g — ускорение свободного падения, а рв —
плотность воды. Очевидно, что сила давления
к задаче 1	,,
шара на дно сосуда по величине равна силе г2о
и противоположна ей по направлению. В случае движения сосу-
да с ускорением а, сила Fi = pBVa, а уравнение движения шара
по горизонтали будет иметь вид
poVa = pRVa + TVsina.	(1)
В вертикальном направлении, очевидно, сумма сил равна нулю:
pBVg + Р2 - p0Vg - Ncosa = 0.	(2)
Совместное решение уравнений (1) и (2) позволяет определить
F2:
Р2 = (ро -pB)F(g + actga).
2- Ai2 — | А.
Решение. По закону сохранения полной энергии для про-
цесса 1—2 можно записать
С’(Т2-Т1) = С'У(Т2-Т1)+Л12,
Отсюда работа Л12, совершенная газом в процессе 1—2 , будет
равна
Л12^|в(Т1-Т2).	(1)
Работу, совершенную газом в процессе 2—3, можно выразить
ФИЗИКА ♦ ОТВЕТЫ И РЕШЕНИЯ ♦ Билет 5 39
через площадь под прямой 2—3:
|(Рз + Р2)(^з-К2) = l(P3V3-P2V2) =	(2)
2	2	2
Из совместного решения уравнений (1) и (2) найдем, что
>112 = 2А-
q _ ________d ____
’** Ж	(р. FCp'2	\ ‘
/ еосОС 1 \
е \F>dA J
Решение. Емкость исходного конденсатора
„ eqeS
Емкость конденсатора с отодвинутой пластиной
„ eqeS
= ТЕ---- •
а + ех
Работа, совершенная батареей,
Аб = (g2 - Q1)£ = (С2 - CJS2.
По закону сохранения энергии работа, совершенная внешними
силами, и работа батареи пошли на изменение энергии конден-
сатора:
Аб + А=|с2£2-|С'1£2.
После подстановки работы батареи получим
А =	- С2) =	.
2	2 \d d + sx/ 2d(d + ex)
Отсюда
d
x ~ —7------5’
( EoeSfP , \
£ \j2dT - l)
4.1)	y8 = 2a; 2)u = rsJv.
7'	7 a sin p 4
Решение. По формуле линзы найдем расстояние b от оси
линзы до изображения мухи:
1 1_1
а + b ~ F '
При а = 3F, b = к F. Поскольку а « tga = -, а (3 « tg/З =
А	а
40
ФИЗИКА ♦ ОТВЕТЫ И РЕШЕНИЯ ♦ Билет6
h а а п
= т, то р « т а = 2а.
о’
Обозначим скорость изображения мухи через и.
usin/3	b	b sin а	1
-----= - . Отсюда и = v—;—- яз -V.
v sina	a	asmр	4
5. Е7 = Wo = 23,8 КэВ.
Z.	Решение. Запишем закон сохране-
Е /о\	ния энергии до испускания 7-кванта и по-
—-	xj" еле испускания:
/	р2	р2
/у Ро	^0 + Pq +	= Wq + Е~. + -5- ,
z—1----------*	2тя	2тя
к задаче 5 где Ео — энергия возбужденного состоя-
ния ядра, Е~. — энергия 7-кванта, Ро — импульс ядра до испус-
кания 7-кванта, Ря — импульс ядра после испускания 7-кванта.
По условию Е7 — Eq. Отсюда следует, что Ро = Ря. Закон со-
хранения импульса для системы «7-квант и ядро» в векторном
виде изображен на рисунке. Поскольку Ро = Ря, импульсный
треугольник является равнобедренным, то
Еу
—- — 2Ро  cos а.
с
При а = 60°
Еу = Рос = Ж)~~ = 23,8 КэВ.
с
БИЛЕТ 6
1	• 1)	= (р - Р,)Vg- 2)Т2 = (р- P1)V(g - a etg 7).
2	. Л23 = 2А.
ФИЗИКА ♦ ОТВЕТЫ И РЕШЕНИЯ ♦ Билет 9
41
Q д __ EqSLF3
2d(d — L)'
4. 1) tg /3	= 5 tg а или	/3	« 5а;	2)	и = v —-XX	~ _L v_
' °'	°	'	’	' a sm р 25
5. v = -^2  с = 63,2 м/с.
Мс2
БИЛЕТ 7
1. l)M = (p0-p)Vg; 2)2V2 = (p0-p)V(g + atga).
2. C = R/2.
О _ 2Ad
EoVS(e — 1)£2
4.	l)tg/3 = 4tga; 2)u = v ^sin'/ sa 16v.
' °	4 °	’ a sm /3
5.	v = --X c = 63 м/с.
MP
БИЛЕТ8
1. i) м = (p - pi)V g; 2) N2 = (p - P1)V(g + actg <g).
2. C = 0,7577.
о д _	£qS£2L2
2(4-£0(4-Lj +L2)'
4. l)tg/3 = 6tga; 2)u = v|^«^v.
5. Ey = Me2 - = 23,73 КэВ.
БИЛЕТ 9
1. 1) a =	g « 0,21g = 2,1 м/с2;
2) T2 = mg(3 - pV3) « 0,3mg « 0,89 H.
Zo
Решение. Уравнение движения системы «брусок плюс тол-
стая веревка AD»:
7 та = 6mgsin /3 — Np — mg,
где N = 6mgcos {3. Отсюда ускорение бруска
_ (6 sin /3 - 6g cos /3 — 1)
42 ФИЗИКА <• ОТВЕТЫ И РЕШЕНИЯ ♦ Билет 9
Очевидно, что кусок веревки BD движется с тем же ускорением
а, поэтому уравнение движения этого куска будет иметь вид
1	гт. 1
-та = Т2- -mg.
Отсюда сила натяжения веревки в точке В
Т2 = ~(a + g) =	+ sin/3-/2 cos/3) =
з
= -~-mg(3 — /2\/3) « 0,3mg и 0,89 H.
28

к задаче 2
2.	1)Т= g|(2H0+z0); 2)А=^р.
Решение. Обозначим жесткость пружины через к и запишем
условие равновесия поршня до впрыскивания воды:
mg = kxQ.
Для определения температуры водяного пара воспользуемся
уравнением состояния идеального газа
PV
Т =----
vR ’
где Р и V — давление и объем пара:
mg- Ь?о(1 — a) amg
р =---------------= ___ , у -	+ аж0)5.
О	о
После подстановки Р и V в уравнение состояния получим,
_ amg(HQ + аж0)
vR
Работа, совершенная паром, идет на увеличение потенциаль-
ФИЗИКА ♦ ОТВЕТЫ И РЕШЕНИЯ ♦ Билет9
43
ной энергии поршня и на изменение энергии деформированной
пружины:
кхд __ mgxo
~2~ ~~	8
k{X0 - <Т.'Г())2
А — mgaxQ +
2
ttEN
3.	1)t	2nwocosa	2)
'	qE	'	vo cos, a
Решение. На частицу с зарядом q будут действовать две
силы: сила со стороны электростатического поля F, = qE и си-
ла Лоренца Т'д = qvo sin аВ. Под действием электрической силы
частица движется сначала равнозамедленно, а потом после оста-
новки равноускоренно, и после возвращения в начальную точ-
ку ее скорость вдоль горизонтального направления снова равна
vq cos а:
— vо cos а = г>о cos а-Et\,
тп
где ti — время возврата частицы в начальную точку. Отсюда
2mvo cos а
h = qE ’
В плоскости, перпендикулярной силовым линиям Е и В, под
действием силы Лоренца частица совершает круговые движения.
Найдем период обращения частицы Т по окружности радиуса R.
Уравнение движения по окружности
m(vosina)2 .
----------= qvo sm аВ.
Период обращения
2nR. 27T77Z
T = ----;--- = ---- .
vq sin a qB
Условие возвращения частицы в начальную точку
Е = NT = 27Г-^- , где N = 1,2,3, ...
№
Отсюда набор значений Bn, при которых частица возвращается
в начальную точку:
„ 2-irmN
Bn — —-—
qh
nEN
vq cos a
4.	/max = 3£yf, /тахо-
44
ФИЗИКА ♦ ОТВЕТЫ И РЕШЕНИЯ ♦ Билет9
Решение. Пусть при нулевом токе в цепи заряд на конден-
саторе равен Q. Работа, совершенная батареей, будет равна Q8..
Эта работа равна энергии заряженного конденсатора:
О2
Отсюда Q = 2678, а напряжение на конденсаторе равно 28. По-
сле переполюсовки батареи и при максимальном токе в контуре
напряжение на конденсаторе станет равно ЗС8. Следовательно,
изменение заряда на конденсаторе будет равно ЗОЕ. По закону
сохранения энергии работа батареи при переполюсовке заряда
конденсатора пойдет на энергию, запасенную в катушке, и на из-
менение энергии конденсатора:
2 £4ах СЕ2	4СЕ2
2	2	2
Отсюда максимальный ток в контуре
Алах — 38 у .
Уравнение (1) имеет второе решение: Q = 0. Это означает, что
переполюсовка батареи происходит при напряжении на конден-
саторе, равном нулю. В этом случае закон сохранения энергии
имеет вид
/уе2 _ ^Апахо СЕ2
2	2
Отсюда
Апахо
5. 1) L = Л -	= 32 см; 2) b =	= 0.25 см.
а + д2	5 * 7	F-2
Решение. Поскольку параллельный пучок света фокусиру-
ется справа от рассеивающей линзы, то это означает, что фокус
собирающей линзы больше расстояния L между линзами, и на
рассеивающую линзу падает сходящийся пучок света. По фор-
муле линзы можно записать
1 , 1 1
~ Fl~L+h ~	'
ФИЗИКА ♦ ОТВЕТЫ И РЕШЕНИЯ ♦ Билет 11
4 о
Отсюда
L = Fi -
Для ответа на второй во-
прос рассмотрим ход луча,
проходящего через опти-
ческий центр собирающей
линзы параллельно глав-
ным оптическим осям линз
(см. рис.). Из подобия тре-
угольников АОВ и BFC
следует:
F2 = d
а b
Отсюда
= 0,25 см.
БИЛЕТ 10
1.	1)а = 1,80,3g ^2,9 м/с2;
О
2) Т = mg(l + sin а + ц cos а) « 0,24(2 + p.)mg ~ 5,2 Н.
2.	1)Т= ^(Яо + 2гго); 2)A = -|mgxo.
3.	1)F = |^(F-n0cosQT); 2)В=™^.
4.	Imax = 4£^.
5.	1) F2 = +,L ^4 L) = 40 см; 2)d= b= 1 см.
7 z (a-Fi)	7 (a-Fi)
БИЛЕТ 11
1. 1) a = 5~^V. g ~ 0,54g 5,3 м/с2;
2) T =	(3 + х/Зм) « 0,23mg = 1,1 H.
2.1)Т=в(Я0 + аМ; 2)А=^ = |ад.
46
ФИЗИКА ♦ ОТВЕТЫ И РЕШЕНИЯ ♦ Билет 12
3 1) Е — — v° cos а • 21 В — т
/	q	Т	,	)	~ q	г
4 I
J in ах
Лпахо
5-Di =(^^^5 = 6,7см; 2)9= 4; 1 = о,67см.
БИЛЕТ 12
1. 1) а =	~,-2’6/z g « 0,14g « 1,4 м/с2;
2	2
2)Т = д mg(sino! + //(1 - cos а)) =	(3 + /z)mg « 4,3 Н.
2-1)г = 5яМЯо+?Ч; 2’л"Чга^'
\ Vg cos2 а + 2 ~ L - v0 cos а
3. l)t= v	т
дЕ
т
2) В = = ._..^?-EN -------------.
/2	2 । 2</£' т
В cos2 а + L — v0 cos а
4.Imax = 7£^f.
5. 1) <7 = ~F2f = 0,25 см; 2) а =	= 48 см.
а — Г2	\-Г1 -*/'2 1-^/
МАТЕМАТИКА ♦ ОТВЕТЫ И РЕШЕНИЯ ♦ Билет 1
47
МАТЕМАТИКА
БИЛЕТ 1
1	. X = у + 7ГП, П 6 Z.
Решение. Так как
8 cos4 х = 2(1 + cos 2s)2 =
= 2 (1 + 2 cos 2х +	= 3 + 4 cos 2ж + cos 4s,
то исходное уравнение равносильно уравнению
cos 2s	1	1
sin а; + cos х sins
Используя формулу cos 2х = (cos х + sinх)(cos х — sins) и учи-
тывая, что sin х 0, sin х + cos х 0, преобразуем уравнение (1):
sins — coss = 3 , coss(sins + coss) = 0, откуда coss = 0.
2.	у C x < 2, s > 8.
Решение. Область E допустимых значений неравенства
х — 8	s — 8	. л . ,
определяется условиями —%—5---д = 7—77447—тгчТ > U, s > 1,
X АХ — О	।	о)
х 2, откуда следует, что Е — объединение интервалов 1 < s <
< 2, 2 < s < 3, s > 8. Так как 2 =	— 1) при х > 1, то
исходное неравенство на множестве Е равносильно неравенству
(s - 8)(s - 1)
10g^ (Ж-3)(Ж + 1) « °'	(2>
Рассмотрим два возможных случая: 1<s<2hs>2.
1)	Неравенство (2) равносильно каждой из систем неравенств
' (х ~	~ 1) >i f х ~ V
' iV5V 4 ' ’ is - адлпд«°'
I 1 < s < 2,
11 , о
откуда следует, что -у- < х < 2.
2) Неравенство (2) равносильно каждой из систем неравенств
8)(s — 1) < 1	[
3)(ж+ !)	’	< (5-3)(s + l) °’
I х > 8,
О
откуда получаем, что х > 8.
18
МАТЕМАТИКА ♦ ОТВЕТЫ И РЕШЕНИЯ ♦ Билет 1
3.	х = -4, у = 20.
Р е ш е н и е. Пусть и — /ж + у, v = yjx + 2у, тогда х + у =
= и2, х 4 2у = v2, откуда х = 2и2 — и2, у = v2 — и2. Поэтому
f и + v = 10,	о 2 ,
исходная система примет вид <	9	9 откуда 2и +
I и + 3u“ — v = 16
+ 2Tu —116 = 0, U| = —29/2, U2 = 4. Так как и 0, то и = 4, т.е.
у/х + у = 4, v = у/х + 2у = 6, откуда х + у = 16, х + 2у = 36,
х = —4, у = 20.
4 г _ 7^18
16
Решение. Пусть М — точка пересечения диагоналей тра-
пеции (см. рис. 1), К и L — середины отрезков ВС и AD, О —
центр окружности радиуса В., F — точка касания окружности со
стороной CD, МР || AD, Р G CD. Обозначим а = LD, b =
= КС, тогда LD = bt, где t = 9/7.
Рис. 1
Из подобия треугольников МСР и
ACD, а также треугольников MDP и
BDC следует, что
Так как ОС ± ОР (ОС и ОР — бис-
сектрисы углов, сумма которых равна тг), а
OF ± СР,то OF2 = PF CF = МР-КС
(PF = MP, CF = КС), т.е.
R2 = МР • Ь.	(4)
Из (3) и (4) следует, что
(1 + t)R2 = 2b2t.	(5)
Площадь S трапеции ABCD выражается
формулой S = (KC+LD)(KM+ML), где | = t, откуда
KM + ML = 2R(l+t),
S2 = 4627?2(1 + i)4.	(6)
Из (5) и (6) находим 7?4 = хуДДуз, где S = 8, t = 2, т.е. R =
1 4” t j
- 7/718
16
МАТЕМАТИКА * ОТВЕТЫ И РЕШЕНИЯ ♦ Билет 1
49
5. 3 и 2.
Реше н не. 1) Последние цифры чисел 2к повторяются через 4
(2L = 2, 22 = 4. 23 = 8, 2'4 = 16, 25 = 32, 2° = 64 и т.д.). Поэтому
последняя цифра у числа 22002 такая же, как и у числа 22 (2000
делится на 4). т.е. 4.
Аналогично, последняя цифра у числа З2002 такая же, как и у
числа З2, т.е. 9. Следовательно, последняя цифра числа а такая
же, как у суммы 4 + 9 = 13, т.е. тройка.
2) Остатки от деления на 11 чисел вида 2п повторяются с пе-
риодом 10. Поэтому остаток отделения числа 22002 на 11 равен
остатку отделения на 11 числа 22, т.е. равен 4.
Аналогично, остатки отделения на 11 чисел вида Зк повторя-
ются с периодом 5. Поэтому остаток отделения числа З2002 на 11
равен остатку отделения на 11 числа З2, т.е. равен 9.
Следовательно, остаток отделения на 11 числа а равен остат-
ку от деления на 11 суммы 4 + 9, т.е. равен 2.
6 И3 и2-	26- + 22^
Ь- 5 И 5’ 2 99’
Решение. Плоскость а параллельна плоскости SBC (SC ||
|| «, ВС || AD || ft), а в сечении пирамиды плоскостью а обра-
зуется трапеция AiDiD2A2 (см. рис. 2) такая, что DiD2 || SC,
AjA2 || SB, ArDi || AD, ArA2 = PiA-
Пусть E, Ei и К — середины сторон AD, AiDi и A2D2
соответственно, М — точка касания вписанной в трапецию
AiDiD2A2 окружности со стороной D\D2, г — радиус этой
окружности.
Тогда EiDi = DiM, MD2 = D2K, у = 2EiDi + 2KD2 =
= 2EiDi + 2, откуда EyDi = 3. Кроме того, г = ^D\M  MD2
,	л \	KE1 /з	,
(см. задачу 4), т.е. г =	2 = i/g, а из подобия треугольников
лгр п С Т7 Т А	SD} E\D\ 3 DD}
bhiDi и ЬЕи следует, что	~сгп
D J-J	.lL U	Э О LJ
из подобия треугольников DD\ D2 и DSC находим
DD2
DC
2
F. 1огд;
DD2 DDi 2	4
= ~DS = 5 ’ ”KWa Dlh = 5
2) Плоскость а отсекает от пирамиды клин с основанием
AA2D2D. Проведем через точки А] и Z?i плоскости, параллель-
ные АВ и SE. Эти плоскости разбивают клин на две равные пи-
рамиды с основаниями AA2PiP и DD2Q1Q (см. рис. 2) и прямую
призму с основаниями AjPPi и D1QQ1.
Пусть hwv — высота и объем пирамиды SABCD, hi и гц —
высота и объем пирамиды А| АА2Р1Р, «2 — объем призмы, г?з —
объем клина. Тогда v = h, vj = | АР  PP]h\, где АР = АЕ —
- АЕ, = АЕ - E,D, = I РР, = DD, =	= ?.
т.е. vi = V2 = | PPi • hY  PQ, где PQ = AD - 2АР =
о ' О
6	24 ,	„	п	,	104 ,
—	т.е. V2 =	ту h.	1огда цз	=	2vi	+ V2	=	7—-3 h,	а искомое
'Э	О	 О
л	26
отношение объемов —-— =
V ~ v3 99
3) Пусть F — середина ВС, О — середина EF, Oi — центр
МАТЕМАТИКА ♦ ОТВЕТЫ И РЕШЕНИЯ ♦ Билет2
описанной около пирамиды SABCD сферы, R — радиус этой
сферы, ASFO = /3 (см. рис. 3). Тогда Оу G SO, SOy = R, а
расстояние р от точки Оу до плоскости а равно OyG, где G G
Пусть Т — точка пересече-
ния прямых SO и ЕуК. Так как
ЕуК || 5F(плоскость SEF пе-
ресекает параллельные плос-
кости SBC и а по параллель-
ным прямым), то АЕуКЕ =
= ASFO = /3. Кроме того,
/3 = Z.OKT = AGOyT (углы
с перпендикулярными сторона-
ми).
Из подобия треугольников
ЕуЕК и SEF находим =
£/i А
= где ЕуК = 2r = 2^2 (см. рис. 2), EF — 2, ЕК =
= DD-2 = |. Следовательно, SF = а/15, SO = h =
= x/SF2 - OF2 = Vll, cos/3 = ~ = ^=, tg/3 =
SC - VSO2 + ОС2 = xfiA + 2 = 4.
Так как радиус сферы R равен радиусу окружности, описанной
е D SC2 АС	1
около треугольника SAC, то R — ——, где s =	=
= 2л/7 — площадь треугольника SAC, откуда SOy = R= А1*.
Из Л(?[ GT находим OyG = р = ОуТ• cos /3, где ОуТ = ООу +
+ ОТ = h~R + KO- tg /3, КО = ОЕ ~ ЕК = |.
22л/П
Отсюда находим р =----т=.
Зам 1э
БИЛЕТ 2
1 . X = 7ГП, п G Z.
2. х < -6, 0 < х 3/7.
52
МАТЕМАТИКА ♦ ОТВЕТЫ И РЕШЕНИЯ ♦ Билет 5
3. ж = 1/2, у = 3/2.
5. 8 и 3.
п 1. 5	2
о. I) ? и =
38 .	107/34
305’	119/35
БИЛЕТ3
I	7Г 7ГТ1	— т-р
1. х = 4 + -у, п G Z.
3. х = 13, у = —3.
4-’-=5i/5’
5.3 и 8.
6. 1)|и|; 2)g; 3)^.
’ 5 5’	' 99’	> 35/15
БИЛЕТ4
1	7Г . 7Г71'	Г77
1.	х = j + -у, п € Z.
2.	—3/7 -С х < 0, х > 6.
3.	х = 1/7, у = -58/7.
4.	R =	/3.
16
5.	3 и 9.
6.	2)^; 3)1^.
'7 7	' 305’	' 119У35
БИЛЕТ 5
1. х = 4/5.
Решение. Данное уравнение, ОДЗ которого определяется
условиями |ж| -С 1, х / 0, равносильно уравнению arctgu =
2.7; — 1 л-.	о
= arccoss, где и = —— Отсюда получаем уравнение х =
МАТЕМАТИКА ♦ ОТВЕТЫ И РЕШЕНИЯ ♦ Билет 5 53
= -—j ИЛИ х2 = ----------------^г, х2 + (2.т - I)2 = 1,
1+U	! । <2х-1У
\ х J
5.:г2 - 4х = 0, х = 4/5.
2.	х = 4, у = —2.
Решение. Так как ху 0, то систему можно записать в виде
( у2(х2 + у3) = х(х2 + у3),
[ х2 + у3 = —4у.
Если х2 4- у3 — 0, то из второго уравнения следует, что у = 0.
Если у2 = х, то из второго уравнения системы следует, что у3 4-
4-у24-4 = 0 или (у + 2)(у2 -у + 2) = 0, откуда у = -2 (уравнение
у2 — у 4- 2 = 0 не имеет действительных корней). Итак, у = —2,
х = у2 — 4.
3.	—18 < х < —3, 0 < х < 2, х > 9.
Решение. Так как х2 4- 9х — 162 = (х + 18) (х - 9), то ОДЗ
неравенства — совокупность двух промежутков —18 С х < 2,
х 9.
а)	Если —18 х < — 9 или х > 9, то левая часть исходного не-
равенства неотрицательна, а правая отрицательна. Поэтому ука-
занные значения х являются решениями исходного неравенства.
Число х = — 9 также является решением этого неравенства, а
число х = 9 не есть решение неравенства.
б)	Пусть — 9 < х < 0, тогда исходное неравенство равносиль-
но каждому из неравенств---------> (ж4-9) , ж 4-9х —162 >
> (ж24-18х4-81)(х-2), ж3 4- 15х2 4-Збх > 0, ж(ж4-12)(ж + 3) > 0,
откуда, с учетом условия -9 < х < 0, находим -9 < х < — 3.
в)	Пусть 0 х < 2, тогда исходное неравенство равносильно
[(х~+ 18) (9 — х)	,	[х~+Т8
каждому из неравенств , /--~ > (9 — х), Р 2-х >
> х/9 — х, > 9 — х, х2 - 12.Т < 0, откуда с учетом условия
0 х < 2, получаем 0 < х < 2.
4.	R = 26\/2 + 4.
Р е ш е н и е. Пусть Aly Вь Ci — точки, в которых окружность
с центром О касается сторон треугольника АВС (см. рис. 4).
54
МАТЕМАТИКА ♦ ОТВЕТЫ И РЕШЕНИЯ ♦ Билет 5
АС] = х, ВС] = у, СВ] — z, R — радиус описанной окруж-
ности, тогда АВ]АО = АС]АО = В]А = ,-г, ВА] = у,
Обозначим tg “ = t, тогда tg	— 1, откуда t =
= 1 + \/2, так как t > 0, х = ОС]  ctg	= 4(л/2 - 1).
По условию 2(ж + у + z) = 16(6 + у/2), откуда у + z = 8(6 +
Т ч/2) - х = 52 + 4д/2, R =	= 26^/2 + 4.
5.	— 1 < а < 3.
Решение. Первое уравнение исходной системы равносильно
уравнению 8(3 - х 4-у) = 25 — 6х + 7у или уравнению у = 2х + 1,
если
у 4- 3 — х > О,
откуда следует, что х > -4. Тогда второе уравнение примет вид
2х + 3 = (х — 2а.)2 + а + 2х, или
х2 — 4ах + 4аУ 4- а — 3 ~ О,	(7)
и задача сводится к нахождению тех значений а, при которых
уравнение (7) имеет ровно два корня X] и лд такие, что.тд > —4 и
Х’2 > —4.
Обозначим /(гг) = х2 — 4ах 4- 4о,2 + а, — 3, D — 16а2 - 4(4а2 +
+ а — 3) = 4(3 — а) и воспользуемся тем, что указанные условия
МАТЕМАТИКА ♦ ОТВЕТЫ И РЕШЕНИЯ ♦ Билет 5	55
выполняются тогда и только тогда, когда D > 0, /(—4) > 0, xq >
> —4, где до = 2а — абсцисса вершины параболы у = /(,т).
Итак, D ~ 4(3 —а) > 0, /(—4) = 4а2 + 17а+13 = 4	(а+
+ 1) > 0, 2а > —4, откуда —1 < о < 3.
6.1)^; 2)3^2; 3)| (2д/2-1).
Решение. Пусть ABCD — основание пирамиды, S — се
вершина (см. рис. 5), К и Е — середины соответственно DC и
АС, 01 — центр вписанного в пирамиду шара, г — его радиус,
М и N — основания перпендикуляров, опущенных из точки О
на SK и SC, Р G SK и ОрР ± SK, SE = h. Тогда ОМ =
= ОЕ = г, OS = ОС = 12, ON = 4/2, SN = NC, SN =
= \/OS2 - ON2 = д/144^32 = 4>/7, SC = 8/7. Обозначим
AESK = a, /.ESC = /3. Тогда cos/3 = |^ = sin/5 =
= h = SE = SC  coS/0 = у, ЕС = SCsin/l =
56________МАТЕМАТИКА ♦ ОТВЕТЫ И РЕШЕНИЯ ♦ Билет 8______
р,, ЕС 8у/7 , ЕК 1	/7 .	т/2
ЬЛ = \/2 = ~3~’	= ~SE = COS ° ~ у 8’ smQ' ~ ~Т '
Расстояние от точки О до боковой грани пирамиды равно ОМ,
где ОМ = SO • sin а = Зт/2.
Из треугольника SO\P находим = sin о-, откуда г =
= Лшо = 8(2^_1)
1 + sm а	3 v 7
БИЛЕТ 6
1.	х = 2/5.
2.	х = 4, у = —2.
3.	ГЕ < —10, -5/2 < X < 0, 5/2 < X <25.
4.	S = 20(х/2- 1).
5.	-5 < а < 2-Зх/3/2.
6.	1)—^; 2)4; 3) | (4 - ^2).
БИЛЕТ 7
1.	х = 1/5.
2.	ж = -2, у = 1/4.
3.	—45 < х < —5, 0 < х < 3, х > 15.
4.	г = х/3.
5.	-5/2 < а < -1/4.
6.	1)|; 2)3; 3)^(v/5~2).
БИЛЕТ 8
1.	х = 3/5.
2.	х = —2, у = 1/4.
3.	X < ~9, -3/2<ж<0, 9/2 < X <27/2.
4.	Я = 2(7х/3- 1).
5.	1 < а < 5.
6.1)	2; 2)^; 3)4(v/5-2).
V 5
МАТЕМАТИКА ♦ ОТВЕТЫ И РЕШЕНИЯ ♦ Билет9
57
<	7Г , 7ГП
1.ге= ? + ^-,
Р е ш е н и
уравнений
БИЛЕТ 9
2тгп _ гт,
х = пей.
о
е. Исходное уравнение равносильно каждому из
2
cos 2ге
cos Зх ’
2
cos 4х + cos 8х
2
1 — cos 4ге 1 — cos 8ж _ cos 2x
cos 3x ’
cos 2x
cos 6x cos 2x =----------------------— ,
_____	cos 3x
а при выполнении условия cos Зге 0 равносильно уравнению
cos 2rr(cos Зх  cos 6ге — 1) = 0.
Уравнение cos 2x = 0 имеет корни x = тг/4 + тгп/2, n G Z, a
уравнение cos Зге cos Qx = 1 может иметь корни только в случае,
когда | cos Зж | = 1.
Если | cos Зж| = 1, тогда cos 6х = 2 cos2 Зх — 1 = 1, и поэтому
о	-1	‘11	2тГ72
cos Зх cos 6х = 1 только тогда, когда cos Зх = 1, откуда х = —%-.
2. 6 < ге < у, 7 < ж < 8.
Решение. Область Е допустимых значений неравенства
определяется условиями х 'jt — 1, х 9, \/х + 1 > х/9 — х, 2х —
— 12 > 0, 2ге — 12 7^ 1, откуда следует, что Е — объединение
промежутков 6 < х < 6,5 и 6,5 < х 9. На множестве Е исход-
ное неравенство равносильно неравенству
21оё2_12(7ГП-	< Iog2;r_12(2ж - 12).	(8)
1) Пусть х G 16,	), тогда неравенство (8) равносильно ка-
ждому из неравенств (д/ге + 1 — д/9 — ж)2 > 2(х — 6), 11 — х >
> х/9 + 8ге — ге2, 121 — 22ге + ге2 > 9 + 8ге — х2, х2 — 15ге + 56 =
= (х — 7)(ге — 8) > 0, откуда следует, что значения х из интервала
(б, у) — решения неравенства (8).
/13 1
2) Пусть ге G (у ,9 , тогда неравенство (8) равносильно не-
равенству (ге — 7)(х — 8) < 0, откуда 7 < х < 8.
 (
a sm -г +
3. R =-----V—
1 - sm ( 4 + 2 )
58 МАТЕМАТИКА * ОТВЕТЫ И РЕШЕНИЯ * Ьи.яет 9
Р с ш о н и о. 1 ) Пусть О — центр окружности радиуса /?,
Z.OBG = т? (см. рис. 6), тогда ABOG — 27, 2<р у- 27 = тг, откуда
р = 7 — 7, ZA = 7 — 7 = 7 + 7. Из треугольника OAF находим
Z	Z Z т:	Z
R = (II + a) sin А, откуда R(1 — sin А) = a sin А.
4.1)	8; 2)arccosf; 3)
t)	10
Решение. По условию АВ = а — ?>, SO = h = 3, ВМ =
= MS, В К = КС (см. рис. 7).
1)	Пусть v, vi, V2, Уз — объемы пирамид SABCD, SABK,
АВКМ, SAMK. Тогда v = ~ a2h = 64, vi = 7 v, v2 = 717 =
О	z
1	1 О
= g V, v3 = v2 = g V = 8.
2)	Пусть Kt — середина BK, тогда MKi || SK, MKj ± BK
1	I	/ o \ 2	t-
и MK3 = i SK, где SK = Jh2+ (= 5, MKr = AKy =
= \/a2 + (|)2 =2^17.
Если ip — угол между SK и AM, то AAMKi = <p. По теореме
МАТЕМАТИКА * ОТВЕТЫ И РЕШЕНИЯ * Билет!)59
косинусов
АК] = AM2 + МК2 - 2АМ  MIA cos <р.	(9)
Так как AAI — медиана в треугольнике ABS, в котором BS =
= SA = у )2 + SK2 = л/41, то 4АМ2 + В52 = 2А82 + 2АВ\
13
откуда AM = у. Из равенства (9) находим
гп	169	25	„ 13	5	3
68 =	——I- —--2 • —	• - cos <р, откуда	cos </?	= --
4	4	2	2	5
а искомый угол между прямыми SK и AM (он лежит в пределах
3
от 0 до тг/2) равен arccos = а.
О
3)	Расстояние р между AM и SK находим по формуле
б^з	24
^:ur^r^’OTKyw=i3-
5. 1)а = —3, а = 4; 2)а<—3, а > 4, а —	—-
Р е ш енп е. Пусть t = х + 2, тогда уравнение примет вид
(и + 3 — |t|) (а — 4 + t2) =0.	(10)
60
МАТЕМАТИКА ♦ ОТВЕТЫ И РЕШЕНИЯ ♦ Билет 10
Построим графики функций а = 4 — t2 и а = |/| — 3 (см. рис. 8).
1) Прямые а = 4 и а = —3 имеют ровно три общие точки с
графиком уравнения (10), т.е. с совокупностью графиков а, =
— 4 — t2 и а = \t\ — 3. Это означает, что при а = — 3 и а — 4
уравнение (10) имеет ровно три корня.
2) Если а > 4 и а < —3, то уравнение (10) имеет ровно два
корня. Два корня уравнение (10) имеет и в том случае, когда гра-
фики функций а = 4-12иа = И “ 3 имеют общие точки, т.е.
если 4 — ^о = |Л01 — 3, где to > 0, или 4 — z2 = z — 3 (z = |io|)•
~	729-1	о 729 — 7
Отсюда z =--------> ao = z — 3 =--%---
6. (1-2,2),	(5,2,6).
v
Решение. Складывая уравнения попарно, получим систему
х3 = xyz + 5,
у3 = xyz — 4,
k z3 = xyz + 12,
равносильную исходной системе. Перемножим уравнения этой
системы и обозначим t = xyz, тогда t3 = (t + 5)(£ — 4)(f + 12) =
= t3 + 13t2 — 8t — 240, или 13£2 — 8t — 240 = 0, откуда Д = —4,
,	60
<2 - 13-
Если t = —4, to x3 = 1, y3 — —8, z3 = 8, откуда xi = 1,
У1 = -2, zi = 2.
Если t = 60/13, to x3 = у3 = Д, z3 = откуда ж2 =
id	id	J-O
БИЛЕТ 10
1. ж = 5- + x = 2тгп, neZ.
О о
2. 4 < x <9/2, 5 < x < 6.
О ____ о(73 + 1)
~	2v/2
л м 4	0,	23 о, 8
4.1)^; 2)агссо8зу; 3)
МАТЕМАТИКА ♦ ОТВЕТЫ И РЕШЕНИЯ ♦ Билет 12 61
5.1)	а = 6, а = — 1; 2)а<—1, а > 6; а =
БИЛЕТ И
«	-к , тт	rj,
1.	х = 7 + -5-, n G Z.
6	3
2.	5 < х <11/2, 6 < х < 7.
 (, тА
а sm ( j + ту I
3.	R = тт о \ 
2Sin2 (^L-
Zsm 8	4 J
Ч 24
4.1)8; 2)arccos|; 3)j^.
5.1)	a = 2, a = 9; 2) a <2, a > 9, a =
6. (-2^,-3,2^2), (-2^,-^,-2^.
БИЛЕТ 12
1	. X + 7ГП, x = 2тгп, n E Z.
2	. 4 < x < 17/4, 9/2 < x < 5.
8-я=ж
. .,4	'	23 о. 8
4.1)3; 2)arccoS27; 3)^.
5. 1) a = -4,
6.
a > 3, a = -----------2
3.