Автор: Голованов Н.Н.
Теги: математика геометрия топология математическое моделирование
ISBN: 5-94052-048-0
Год: 2002
Текст
Н. Н-Голованов
ГЕОМЕТРИЧЕСКОЕ
МОпЕПИРОВвНИЕ
Издание с компакт-диском
Москва
Издательство «Физматлит»
2002
ББК 22.151.3
Г 61
УДК 513.7/681.3
ГОЯОВАНОВ Н. Н. Геометрическое моделирование.—М.: Издательство Физико-
математической литературы, 2002.—472 с.—ISBN 5-94052-048-0.
Излагаются методы построения математической модели геометрических объектов с помо-
помощью компьютера. Даны основные сведения из дифференциальной геометрии, топологии, вариа-
вариационного исчисления, численных методов, приведена теория 5-сплайнов. Подробно рассмотрены
методы моделирования различных кривых, поверхностей и тел, а также алгоритмы выполнения
операций над ними и вычисления их геометрических характеристик. Описаны принципы уста-
установления вариационных зависимостей параметров геометрических объектов. Изложены методы
компьютерной графики.
Для прикладных математиков, специалистов по системам автоматизированного проектиро-
проектирования и компьютерной графики. Может быть использована студентами соответствующих специ-
специальностей.
Научное издание
ГОЛОВАНОВ Николай Николаевич
ГЕОМЕТРИЧЕСКОЕ МОДЕЛИРОВАНИЕ
Редактор Л.А. Панюшкина
Компьютерная графика М.В. Ивановского
Компьютерная верстка Г.М. Красниковой
ИД № 01389 от 30.03.2000
Гигиеническое заключение № 77.99.02.953.Д.003724.07.01
от 05.07.2001
Подписано в печать 18.03.2002. Формат 70x100/16.
Бумага офсетная № I. Печать офсетная.
Усл. печ. л. 38,23. Усл. -изд. л. 42,05.
Тираж 1000 экз. Заказ № 5293.
Издательство Физико-математической литературы
117071 Москва В-71, Ленинский проспект, 15
Отпечатано с готовых диапозитивов в типографии
издательства "Экономика и жизнь - Гостиный ряд"
г. Калуга Тел. @842M6-14-96
ISBN 5-94052-048-0
II785940II520481
© Н. Н. Голованов, 2002
© Физматлит, оформление, 2002
ОГЛАВЛЕНИЕ
Предисловие 7
Благодарности 8
Глава 1. Основы геометрического моделирования 9
1.1. Описание геометрических объектов 9
1.2*. Преобразование декартовых прямоугольных координат . . 11
1.3. Модификации векторов и точек 15
1.4." Однородные координаты 20
1.5*. Геометрия кривых линий 22
1.6*. Геометрия двухмерных кривых 29
1.7*. Геометрия поверхностей 32
1.8*. Кривизна линий на поверхности 39
1.9*. Тензоры поверхности 46
1.10*.Криволинейные координаты 54
1.11*.Тензоры в криволинейных координатах 62
1.12*.Ортогональные криволинейные координаты . . 67
1.13. Математическая модель геометрии объектов 70
Глава 2. Моделирование кривых линий 71
2.1. Математическая модель кривых линий 71
2.2. Аналитические линии 72
2.3*. Кривые второго порядка 77
2.4. Сплайны 81
2.5. Кривые Безье . 88
2.6. Представление кривых второго порядка кривыми Безье • • ¦ 93
2.7. Рациональные кривые 100
2.8. 5-сплайны 105
2.9. NURBS кривые 121
2.10. Линии, базирующиеся на линиях 135
2.11. Составные кривые ..........'... 138
2.12. Двухмерные кривые 140
2.13. Способы построения линий 143
4 Оглавление
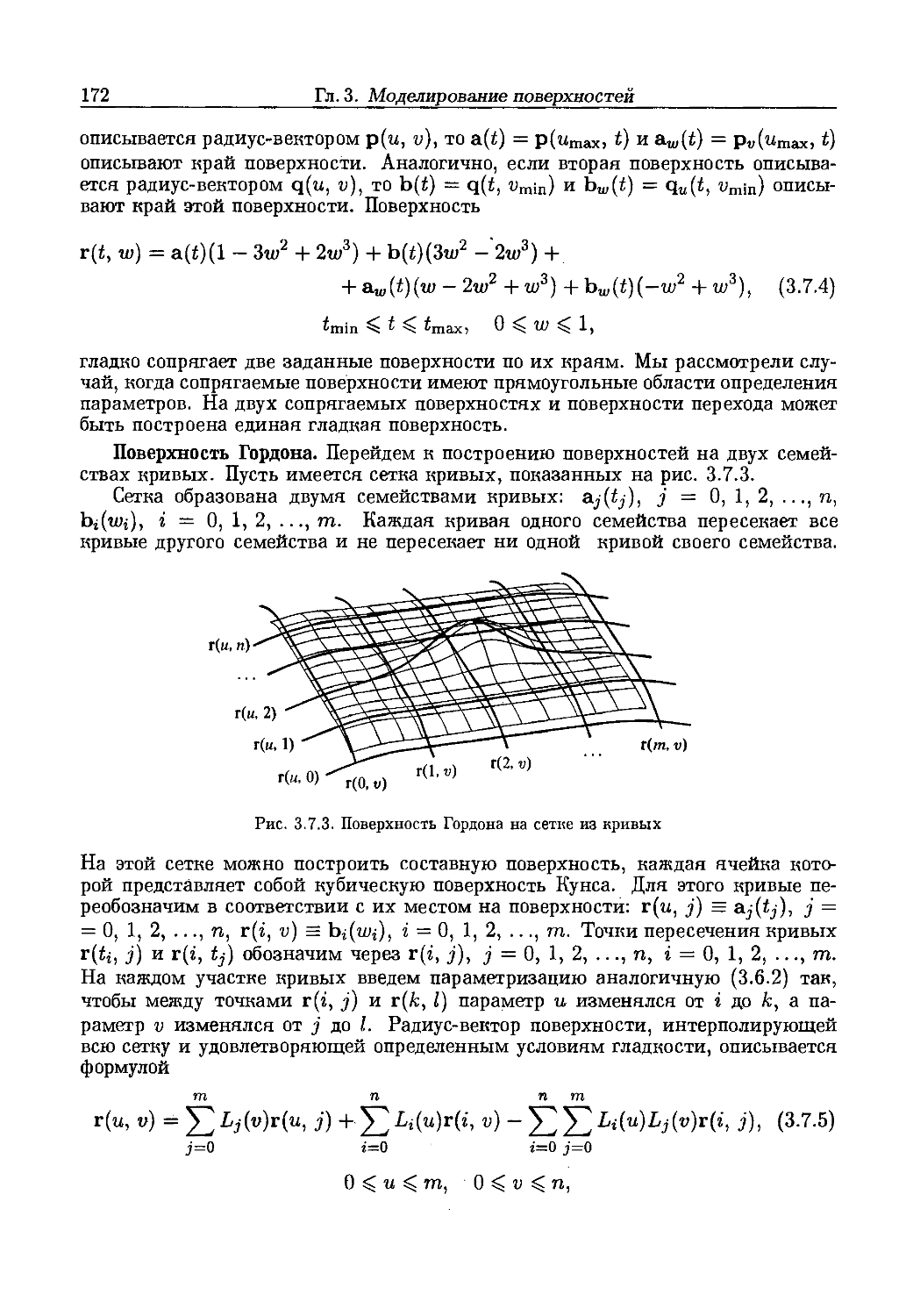
Глава 3. Моделирование поверхностей 145
3.1. Математическая модель поверхностей 145
3.2. Аналитические поверхности 146
3.3*. Поверхности второго порядка 153
3.4. Поверхности движения 158
3.5. Линейчатые поверхности 163
3.6. Поверхности Кунса 165
3.7. Сплайновые поверхности 169
3.8. Поверхности Безье 175
3.9. Рациональные поверхности 176
3.10. NURBS поверхности 179
3.11. Поверхности треугольной формы 184
3.12. Треугольные поверхности Безье 188
3.13. Треугольные сплайновые поверхности 194
3.14. Поверхности, базирующиеся на поверхностях 201
3.15. Ограниченные контурами поверхности 204
3.16. Способы построения поверхностей 207
Глава 4. Операции над кривыми и поверхностями 209
4.1. Выполнение операций 209
4.2. Движение по параметрической области 211
4.3*. Решение системы нелинейных уравнений 215
4.4*. Решение системы линейных уравнений 221
4.5. Проекция точки на линию 232
4.6. Проекция точки на поверхность 234
4.7. Определение точек пересечения линии и поверхности 237
4.8. Определение точек пересечения линий 241
4.9. Построение линий пересечения поверхностей 244
4.10. Поверхность скругления 253
4.11. Поверхность фаски 256
4.12. Определение точек пересечения трех поверхностей 259
4.13. Точность выполнения операций 260
Глава 5. Топология оболочек 262
5.1. Топологические объекты 262
5.2*. Эйлерова характеристика оболочек 262
5.3*. Связность оболочек 267
5.4*. Ориентируемость оболочек 269
5.5. Оболочки для моделирования тел 271
5.6. Поверхностное и твердотельное моделирование 275
Глава 6. Моделирование тел 276
6.1. Математическая модель тел 276
6.2. Простейшие тела 280
Оглавление 5
6.3. Тела, полученные движением плоского контура 287
6.4. Построение тела по плоским сечениям 292
6.5. Тело в форме листа 293
6.6. Булевы операции над телами 294
6.7. Резка тела поверхностью 305
6.8. Построение симметричного тела 307
6.9. Построение эквидистантной оболочки тела 309
6.10. Построение тонкостенного тела 313
6.11. Скругление ребер тела 315
6.12. Построение фасок ребер тела 320
6.13. Некоторые способы построения тел 320
6.14. Последовательность моделирования тел 322
Глава 7. Вариационные связи геометрических объектов 324
7.1. Наложение вариационных связей - 324
7.2. Фиксирующие связи 327
7.3. Вариационные связи точек в пространстве 328
7.4. Вариационные связи точек на кривых и поверхностях 335
7.5. Алгебраические связи 336
7.6. Минимизация изменения параметров 337
7.7*. Условный экстремум функции изменения параметров 340
7.8*. Вариационный метод определения изменений параметров 345
7.9*. Геодезические линии 354
7.10. Вариационные связи двухмерных точек 357
7.11. Вариационные связи двухмерных линий 363
7.12. Формирование и решение системы уравнений связей 372
Глава 8. Вычисление геометрических характеристик 376
8.1. Возможности геометрической модели 376
8.2*. Криволинейные интегралы 377
8.3. Геометрические характеристики плоских сечений 383
8.4. Длина и центр масс кривой линии 388
8.5*. Поверхностные интегралы 389
8.6. Площадь поверхности, объем и центр масс тела 393
8.7. Моменты инерции тела 397
8.8*. Решение кубического уравнения 407
8.9*. Квадратурные формулы 410
8.10*. Кубатурные формулы 417
8.11. Разбиение поверхностей при интегрировании 425
Глава 9. Компьютерная графика 429
9.1. Визуализация геометрических объектов 429
9.2. Параллельные проекции на плоскость 430
Оглавление
9.3. Центральные проекции на плоскость 433
9.4. Полигоны кривых и поверхностей 436
9.5. Линии очерка 439
9.6. Определение видимой части геометрических объектов 443
9.7. Триангуляция поверхностей и тел 446
9.8. Моделирование света 458
9.9. Описание цвета 463
9.10. Формирование реалистических изображений 465
Вместо заключения 470
Список литературы 471
Посвящается Марии —
другу, любимой, жене
ПРЕДИСЛОВИЕ
Предлагаемая книга предназначена для тех, кто изучает, использует в работе
или разрабатывает системы геометрического моделирования. Она посвящена
математическому аппарату этих систем. В основу книги положен опыт работы
автора над математическим ядром CAD системы КОМПАС.
Компьютеры позволяют создавать численные модели различных объектов.
С их помощью можно увидеть еще не существующий объект, получить его гео-
геометрические характеристики, выполнить исследование его физических свойств
путем постановки численных экспериментов, внести необходимые изменения,
подготовить производство и, наконец, изготовить объект. Инструментом для
всего этого служат CAD/CAM/CAE системы. Общим элементом таких систем
является математическая модель геометрии проектируемого объекта.
В работе с системами геометрического моделирования используются раз-
различные области знания. Теоретической основой геометрического моделирова-
моделирования являются дифференциальная и аналитическая геометрии, вариационное
исчисление, топология и разделы вычислительной математики. Геометриче-
Геометрическое моделирование изучает методы построения кривых линий, поверхностей
и твердых тел, методы выполнения над ними различных операций и методы
управления численными моделями.
Глава 1 книги посвящена теоретическим основам геометрического модели-
моделирования. В гл. 2, 3 описаны методы моделирования различных кривых линий
и поверхностей, начиная от элементарных и кончая рациональными кривыми
и поверхностями на основе В-сплайнов (NURBS объектами). Глава 4 посвя-
посвящена методам выполнения операций над кривыми линиями и поверхностями.
В гл. 5, 6 рассмотрены принципы построения твердых тел. Для построения
тел привлекаются топологические понятия. В гл. 7 описан механизм устано-
установления вариационных связей параметров геометрических объектов. Эти связи
представляются в виде нелинейных уравнений относительно зависимых пара-
параметров. В гл. 8 рассмотрены методы расчета геометрических характеристик
моделей. Последняя глава посвящена компьютерной графике.
Для чтения книги требуется знание математического анализа. Необходи-
Необходимые сведения из других разделов математики включены в главы книги. Со-
Соответствующие им параграфы отмечены звездочкой. Подготовленный читатель
отмеченные звездочкой параграфы может пропустить. Книга будет полезна всем
интересующимся геометрическим моделированием.
Список литературы не претендует на полноту перечня работ по рассматри-
рассматриваемой теме. В нем приведены работы, результаты которых использовались в
данной книге.
К книге прилагается компакт-диск с системой КОМПАС-ЗБ LT, которая ис-
использует программную реализацию описанных методов.
БЛАГОДАРНОСТИ
Хочу поблагодарить всех, кто помог мне написать эту книгу.
Благодарю своих учителей и преподавателей МГТУ им. Н.Э.Баумана.
Приношу глубокую благодарность В.И. Мяченкову, вдохновившему меня на
написание книги.
Благодарю Н.Н. Астанина, Е.В. Бахина, О.Г. Волкова, А.В. Голикова, А.В. Го-
ревого, А.П. Духвалова, Д.М. Жамойцина, В.Н.Зорина, В.Н. Комяка, Ю,Г. Лыс-
цева, А.О.Максименко, Э.О.Максименко, В.А.Матюшенкова, В.Б.Москалева,
И.В. Николаеву, В.П. Панченко, Ю.В. Покидова, И.И. Радионюк, А.П. Столярова,
С.Н. Талалу, А.Г. Тимошина, В.Г. Харю, В.И. Шпирько, Т.М. Янкину, всех своих
коллег и друзей за помощь и поддержку во время работы над книгой.
Благодарю сотрудников АСКОН за практическое применение описанных в
книге методов.
Благодарю Л.А.Панюшкину и А.С.Фурсова за полезные советы, позволив-
позволившие улучшить книгу.
Благодарю свою семью и своих родителей за заботу и терпение.
Особую благодарность выражаю издательству, донесшему книгу до чита-
читателей.
Н. Н. Голованов
Глава 1
ОСНОВЫ ГЕОМЕТРИЧЕСКОГО МОДЕЛИРОВАНИЯ
1.1. Описание геометрических объектов
Геометрические объекты. Мы будем интересоваться формой окружающих
предметов, их размерами и взаимным расположением, не вдаваясь в подробно-
подробности физических свойств. Другими словами, мы будем изучать и моделировать
геометрические свойства реальных или воображаемых объектов. Нашей конеч-
конечной целью является построение математических моделей геометрии Этих объек-
объектов. Эти модели нужны для принятия решений, для проведения исследований,
для производства материальных ценностей.
Геометрическое моделирование изучает методы построения математической
модели, описывающей геометрические свойства предметов окружающего мира.
Оно базируется на аналитической и дифференциальной геометрии, ВЫЧИСЛИ-
тр.ттт.ттпй мятемятикр, тчярияттипннпм исчислении, тппп.ттпгии и ряярябятмияет
собственные математические методы моделирования.
Инструментом для геометрического моделирования служат математические
методы решения тех или иных задач. Используемые методы позволят описы-
описывать геометрические свойства предметов, создавать их математические модели
и исследовать их путем проведения различных расчетов и численных экспери-
экспериментов. При необходимости мы сможем редактировать моделируемые объекты
и Строить их графические отображения.
Для описания геометрических свойств окружающих предметов мы будем
строить твердые тела или просто тела. Тела в свою очередь мы будем описывать
точками, линиями и поверхностями. Все они обладают определенными общими
свойствами, поэтому ими можно оперировать как объектами. Точки, линии,
поверхности и тела будем называть геометрическими объектами (рис. 1.1.1).
Рис. 1.1.1
Геометрические объекты будут служить основными элементами математи-
математической модели геометрии реальных или воображаемых объектов. Мы будем
строить их в трехмерном евклидовом пространству считая их неизменными
во времени.
10 Гл.1. Основы геометрического моделирования
В большинстве случаев мы будем использовать декартовы прямоугольные
системы координат. В декартовой системе координат базисные векторы имеют
одинаковую длину и постоянное направление в любом месте пространства. Это
упрощает описание объектов, так как базисные векторы при дифференцирова-
дифференцировании выступают в роли констант. Мы рассмотрим также описание геометриче-
геометрических объектов в криволинейных системах координат.
Обозначения. Для количественных характеристик геометрических объектов
мы будем использовать скалярные величины, векторы, а также тензоры. Ска-
Скалярные величины будем обозначать строчными буквами латинского или грече-
греческого алфавита. Векторы в пространстве будем обозначать строчными буквами
латинского алфавита, выделенными жирным шрифтом. Двухмерные векторы
будем обозначать строчными буквами латинского алфавита, выделенными жир-
жирным курсивом. Точки будем обозначать прописными латинскими буквами. Тен-
Тензоры и матрицы будем обозначать прописными буквами латинского алфавита,
выделенными жирным шрифтом.
Систему координат с началом в точке О и базисными векторами ei, е2, ез
будем обозначать через Ое^ез.
Для векторов в пространстве мы будем использовать записи типа
г = nei + г2е2 +
у,
= [п
где г\, г2, гз — компоненты вектора г. В данной главе нам удобно использовать
обозначения компонент векторов с индексами, равными ее номеру. В других
главах мы будем также использовать обозначения компонент векторов через
х, у, z.
Для описания сложных геометрических объектов нам потребуются векторы
как в трехмерном, так и в двухмерном пространстве, например, на области
параметров поверхности. Для двухмерных векторов мы будем использовать
запись типа
Р =
+ р2е2 = М = [Pi Рг]Т,
LJ
где pi, p2 — компоненты вектора р.
Операцию скалярного произведения векторов будем обозначать точкой: на-
например,
а ¦ b = a\bi + <22&2 + azH-
Символом х будем обозначать операцию векторного произведения векторов:
например,
а х b = (<22&з - G3&2)ei + {а$Ь\ - ai63)e2 + (ai&2 - ^2^1N3.
Запись двух векторов рядом ab будет означать операцию диадного произве-
произведения векторов а и Ь, например,
1.2. Преобразование декартовых прямоугольных координат И
Точка. Геометрическое моделирование мы начнем изучать с простых объек-
объектов, переходя постепенно к более сложным. Точка R пространства в общем слу-
случае описывается координатами и1, и2, иА некоторой системы координат. В де-
декартовой прямоугольной системе координат точку можно описать с помощью
радиус-вектора г = [п тч гз]т. Радиус-вектор определяет преобразование пере-
переноса, переводящее начальную точку декартовой системы координат в заданную
точку пространства. Компоненты радиус-вектора точки равны ее координатам.
Радиус-вектор в отличие от просто вектора связан с началом координат. Эта
разница сказывается на формулах преобразования координат и на формулах
изменения положения в пространстве.
1.2.* Преобразование декартовых прямоугольных координат
Преобразования координат точек в пространстве. Рассмотрим, как изменятся де-
декартовы прямоугольные координаты точки в пространстве при переходе от одной си-
системы координат к другой. Пусть в пространстве заданы две декартовы прямоугольные
системы координат: Oeie2e3 и (ЭЬЫз- Пусть положение некоторой точки R в первой
Рис. 1.2.1
системе описывается координатами г\, гг, гз, которым соответствует вектор г, а во вто-
второй системе положение этой же точки описывается координатами х±, х-2, Хз, которым
соответствует вектор х (рис. 1.2.1).
Заметим, что равенствами
г = г1е1 +Г2е2 + гзгз, A2
X = Xiii -I- X2'l2 + Я3»3
точка R описывается в разных системах координат. Обозначим через
A-2.2)
вектор, направленный из точки О в точку Q. Если к вектору q добавить вектор х, то мы
получим вектор г. Сложение векторов мы выполним в первой системе координат, так
как именно в ней рассматриваемая точка описывается вектором г. Для этого разложим
орты ii, i2, i3 по ортам еь е2, е3:
-I- ,
i2 = o2iei +а22в2 + О2зе3, A.2.3)
Ь -I-
12 Гл.1. Основы геометрического моделирования
где a,ij, i, j — 1, 2, 3 — компоненты ортов ii, i2, i3 в системе координат Oeie2e3-
Сложив векторы q и х, получим равенство
г2е2 + г3е3 = (anXi + 021^2 + 031X3 + gi)ei 4-
0222:2 + a32x3 + q2)e2 + (a13xi + а23х2 4- а33х3 + <?з)ез,
откуда следуют формулы преобразования координат точки при переходе из системы
<5iii2i3 в систему координат Ое\е2ез'-
+О21Х2 + a3iX3 4-gi,
r2 = ai2xi + 022^2 + азгхз + q2, A-2.4)
4- 023^2 + 033X3
В матричном представлении A-2.4) имеет вид
r = AT-x + q, A.2.5)
где Ат — транспонированная матрица поворота:
А =
О21 О22 О23
О31 О32 ОЗЗ
Строки матрицы А составлены из компонент векторов ii, i2, 13- Умножив каждое
из равенств A.2.3) скалярно на ei, e2, ез, получим еще одно выражение для компонент
матрицы А:
an=ii-ei, ai2=ii-e2, ai3 = ii-e3,
a2i=i2-ei, a22 = i2-e2, а2з=12-е3, A.2.6)
o3i = i3 ¦ ei, o32 = i3 ¦ e2, a33 = i3 ¦ e3.
Из A.2.6) видно, что базисные векторы ei, e2, e3 в системе координат с базисными
векторами ii, i2, i3 выражаются через те же коэффициенты, которые присутствуют в
A.2.3):
i 4- a2ii2 + аз^з,
+a22i2 + a32i3, A-2-7)
+ «2312 + a33i3.
Действительно, если каждое и равенств A.2.7) умножить скалярно на ii, i2, i3, то
получим равенства A.2.6).
Обозначим через о = Oiii +O2i2 +Оэ1з вектор, направленный из точки Q в точку О.
Выполнив сложение векторов о и г во второй системе координат, мы получим вектор х.
Приравняв соответствующие компоненты векторов, получим формулы преобразования
координат рассматриваемой точки при переходе из системы Oeie2e3 в систему коор-
координат <3iii2i3:
Xl = ОцГ1 + Oi2r2 + О13Г2 + Ol,
x2 = a2iri + a22r2 + a23r2 + o2, A.2.8)
x3 = a3iri + a32r2 + a33r2 + 03.
Если формулы A.2.8) применить для точки Q, мы получим формулы, выражающие
компоненты 0\, сп, о3 вектора о через компоненты q\, q2, q3 вектора q:
01 = -ongi - oi2g2 -
oi = — a2igi - a22g2 — «гздз,
o3 = —a3igi —03292 -
1.2. Преобразование декартовых прямоугольных координат
13
Подставив последние в A.2.8), получим
gi) + oi2(r2 - g2)
x2 = a,2i{ri - gi) + 022(^2 - дг) + агз(г3 - дз),
- qi) + аз2(г2 - дг) + а3з(г3 - дз)-
В матричном представлении преобразования A.2.8) имеют вид
х = А • г + о = А ¦ (г - q).
A.2.9)
Умножив равенство A.2.9) слева на Ат и прибавив вектор q, в соответствии с
формулой A.2.5) мы должны получить вектор г. Отсюда следует, что
Ат-А =
1
0
0
0
1
0
0"
0
1
= Е,
A.2.10)
АТ=А
-1
Мы видим, что транспонированная матрица поворота равна своей обратной матрице,
т. е. матрица поворота системы координат является ортогональной. Отсюда же следует,
что определитель матрицы А равен единице:
|АТ| = |А| = 1.
A.2.11)
Преобразования компонент векторов в пространстве. Пусть некоторый простран-
пространственный вектор в системе координат Oe\e2^z описывается выражением riei + г2е2 +
+ г3е3, а в системе координат Qhhh этот же вектор описывается выражением
ziii + 2212 + 2:313- С учетом формул A.2.3) и A.2.7) получим, что преобразования
компонент векторов описываются формулами A.2.4) и A.2.8), в которых компоненты
ft 1 42, Чз и oi, O2, оз следует положить равными нулю.
Преобразования координат двухмерных точек. Пусть на плоскости заданы две де-
декартовы прямоугольные системы координат: Ое\ег и Qjij2- Пусть положение неко-
Рис. 1.2.2
торой точки Р в первой системе описывается вектором р = pie\ + Р2^2, а во второй
системе положение этой же точки описывается вектором у = yiji + У2З2 (рис. 1.2.2).
Разложим вектор д, направленный из точки О в точку Q, а также орты j1} j2 no
ортам ei, e2:
g = giei +g2e2, A.2.12)
Ji = auei +ai2e2,
j2 —
A.2.13)
14 Гл.1. Основы геометрического моделирования
Сложив векторы q и у, получим
Piei + р2е2 = (anyi + Я212/2 + gi)ei + (ai2j/i + а222/2 + <?2)е2.
Отсюда следуют формулы преобразования координат точки:
Pi = anyi +O212/2 + ?ь
ь 2
Р2 = О12У1 + Я22У2 + 42.
Матричное представление A.2.14) совпадает с A.2.5): р = Ат -y + q. Так как базисные
векторы j1 и j2 имеют единичную длину, равенствам A.2.13) можно придать вид
j1=cos<pe1+sin<pe2, A2 15)
j2 = - siiK/эв! 4- cosipe2,
если обе координатные системы правые или левые, и
ji = cos i/7 ei + sin </э е2,
j i - cosy?e2,
если одна из координатных систем правая, а другая — левая. Угол <р между векто-
векторами ei и j\ отсчитывается от е\ в сторону вектора е2. Пусть обе системы координат
являются правыми (для систем разной ориентации следует изменить знак o2i и a22
на противоположный). Матрица поворота систем координат, выраженная через угол </?,
имеет вид
_ Г cosy» sinyl
[ siny> cos</jj
Преобразование координат A.2.14) при переходе от системы с базисными векторами
ег и ег к системе координат с базисными векторами j1 и j2 примет вид
Pi =yicosy?-y2siny? + gi, fl 2 16)
q2 \ ¦ ¦ )
Решив систему уравнений A.2.16) относительно у\ и у2, получим обратное преобразо-
преобразование
2/1= {Pi -qi)cos<p + (p2-q2)sm<p, A2 17)
У2 = ~{Pi ~qi) sinip + {p2-q2) cos (p.
Если в A.2.17) положить р\ = 0, p2 = 0, то получим координаты точки О в системе с
базисными векторами jlt j2, выраженные через компоненты q\ и q2:
0\ = -<?i cosip-q2sm(p, A2 18)
о2 = qi sin (p - q2 cos (p.
В системе координат с базисными векторами jlt j2 координаты 0\ и о2 равны ком-
компонентам вектора о, построенного из точки Q в точку О- С учетом формул A.2.18)
преобразование координат точки A.2.17) будет иметь вид
oi = pi cos <p + p2 sin <p +
J/2 = anPi + a22p2 + o2 — -pi simp +p2 cos tp +
Выразим из A.2.18) координаты q\ и g2 через координаты о\ и о2 и подставим их в
A.2.16). В результате получим
Р\ = (yi -Oi)cos<^-(y2-o2)sin<^, A2 19)
Pi = (yi - oi) sin y> + (j/2 - o2) cos yj.
1.3. Модификации векторов и точек
15
Матричные записи преобразований координат точки при переходе от одной декартовой
прямоугольной системы координат к другой в двухмерном пространстве и трехмерном
пространстве совпадают.
Преобразования компонент двухмерных векторов. Пусть некоторый двухмерный
вектор в системе координат Ое\е2 описывается выражением р\е\ + р2е2, а в системе
координат Qjij2 этот же вектор описывается выражением yij1 + y2j2. С учетом формул
A.2.15) получим, что преобразования компонент двухмерных векторов описываются
формулами A.2.16) и A.2.17), в которых компоненты q\, q2 следует положить равными
нулю.
1.3. Модификации векторов и точек
Модификациями будем называть изменения положения и формы геометри-
геометрических объектов. Многие линии, поверхности и тела описываются определен-
определенным образом связанным набором точек, векторов и скаляров. При изменении
положения геометрического объекта в пространстве требуется выполнять соот-
соответствующие модификации радиус-векторов точек и векторов, описывающих
данный объект.
Сдвиг точки в пространстве. Простейшей модификацией точки является ее
сдвиг в пространстве на вектор сдвига t. Положение точки до модификации
будем называть исходным и описывать радиус-вектором го, положение точки
после модификации будем называть новым и описывать радиус-вектором г. По-
Положение точки после модификации будет описываться радиус-вектором, равным
сумме радиус-вектора ее исходного положения го и вектора сдвига t:
г = г0 + t.
A.3.1)
Компоненты вектора г равны сумме соответствующих компонент векторов го и t.
Поворот точки в пространстве вокруг оси. Рассмотрим, как изменится ра-
радиус-вектор точки при ее повороте вокруг некоторой оси. Пусть начальное
положение точки описывается радиус-вектором Го, а ось вращения определяется
Ось вращения
\
Рис. 1.3.1. Поворот точки вокруг оси
точкой Q и ортом v. Пусть q есть радиус-вектор точки Q. Выполним поворот
точки вокруг оси на угол а против часовой стрелки, если взгляд направить
навстречу вектору v (рис. 1.3.1).
16
Гд. 1. Основы геометрического моделирования
Построим вектор р = Го — q. Разложим вектор р на две составляющие:
A.3.2)
р = t + п,
t = (р ¦ v)v, п = р - (р v)v,
где вектор t параллелен вектору v, а вектор п ортогонален вектору v. При
вращении вектор t не изменится, а вектор п повернется на угол а в сторону
вектора
b = vxn = vx(p-(p' v)v) = v x p. A.3.3)
Так как вектор v имеет единичную длину, то вектор b будет иметь длину,
равную длине вектора п. Кроме того, он ортогонален векторам v и п. После
поворота на угол а вектор п станет равным вектору ncosa + bsina. Сле-
Следовательно, после поворота рассматриваемая точка будет определяться радиус-
вектором
г = q + t + n cos a + b sin a =
= q + (p • v)v + (p - (p • v)v)cosa + v X psina, A.3.4)
где p = r0 — q. Преобразуем выражение
(p . V)v =
+ VIV2P2 +
V2VIPI + V2V2P2 + V2V3P3
= (vv) • p.
A.3.5)
V3V1P1 + V3V2P2 + v3v3p3_
С учетом A.3.5) выражение A.3.4) примет вид
г = q + (vv) • р -f cosa(E — vv) ¦ р -f sinav х р = q+• А ¦ (r0 — q). A.3.6)
Матрица поворота определяется равенством
А = A — cosa)vv + cosaE +• sinavx,
где
w =
V3VI
V3VS
1
0
0
0
1
0
0
0
1
vx =
0 — V3 V2
V3 0 -v.
— V2 V\ 0
Матрица А является ортогональной. При транспонировании матрицы А изме-
инхса хольпо onan пород последним ее слагаемым, 4x0 сосггт*ртгтвурт пгтпрпту
точки на угол —а.
Симметрия точки относительно плоскости. Определим координаты точки г,
симметричной точки г0 относительно плоскости. Пусть плоскость симметрии
определяется точкой Q и двумя ортами и и v (рис. 1.3.2).
Пусть q есть радиус-вектор точки Q. Построим вектор р = r0 — q и предста-
представим его в виде суммы трех векторов — проекции на орт и, проекции на орт v
1.3. Модификации векторов и точек
17
и перпендикулярной плоскости составляющей п:
р = (р • u)u + (р • v)v + п,
A.3.7)
где п = р — (р • u)u + (р • v)v. После зеркального отражения вектора р его
нормальная к плоскости составляющая изменит знак на противоположный.
Плоскость
симметрии
Рис. 1.3.2. Симметрия точки относительно плоскости
Положение симметричной точки будет описываться радиус-вектором
г = q + (р ¦ u)u + (р ¦ v)v - (р - (р ¦ u)u - (р ¦ v)v) =
= q + Buu + 2w - E) • p = q + A • (r0 - q), A.3.8)
где матрица А = 2uu + 2vv — E — матрица симметрии, uu и vv — диадные
произведения векторов.
Масштабирование в пространстве. Рассмотрим масштабирование проек-
проекций на координатные оси расстояния до точки го относительно некоторой дру-
другой точки Q, остающейся неподвижной после масштабирования. Пусть q есть
радиус-вектор точки Q. В общем случае при масштабировании проекции на ко-
координатные оси вектора р = го — q могут изменяться в различное число раз,
т. е. масштабирование может быть ортотропным. Пусть проекция вектора р на
орт ei при масштабировании увеличивается в mi раз, проекция вектора р на
орт в2 увеличивается в т,2 раз, проекция вектора р на орт ез увеличивается
в тз раз. Тогда положение рассматриваемой точки после модификации будет
описываться радиус-вектором
0
0
0
ТП2
0
0
0
тя
Pi
Р2
Ра
= q +A- (ro-q),
A.3.9)
где А — матрица масштабирования.
2 — 5293 Голованов
18 Гл. 1. Основы геометрического моделирования
Модификация векторов в пространстве. Формулы модификации свободного
вектора в пространстве получим из формул модификации радиус-вектора, по-
положив в A.3.1) t = 0, а в A.3.6), A.3.8), A.3.9) — q = 0. Вектор в отли-
отличие от радиус-вектора не привязан ни к какой точке пространства и поэтому
модификации вектора можно выполнить в местной системе координат, начало
которой находится в точке Q, а координатные оси параллельны исходным ко-
координатным осям. После переноса начала местной системы координат в точку
Q ее радиус-вектор будет равен нулю. Этим отличаются модификации вектора
и радиус-вектора.
Сдвиг двухмерной точки. Рассмотрим модификации двухмерных точек. Век-
Векторная формула сдвига двухмерной точки на вектор t совпадает с A.3.1)
r = ro + t. A.3.10)
Поворот двухмерной точки вокруг точки. Повороты двухмерной точки выпол-
выполняются вокруг оси, перпендикулярной плоскости, в которой лежит точка. Пусть
начальное положение точки описывается радиус-вектором го, а неподвижная
-J Центр вращения
Рис. 1.3.3. Вращение двухмерной точки
точка Q имеет радиус-вектор q. Выполним поворот точки в плоскости на угол
а против часовой стрелки, если взгляд направить на плоскость (рис. 1.3.3).
Построим вектор р = го — q и вектор Ь, который имеет длину вектора р и
повернут относительно него на прямой угол против часовой стрелки. Вектор Ъ
получен с помощью преобразования
b = N-p, A.3.11)
где двухмерная матрица N имеет вид
Г0 -11 A.3Л2)
После поворота на угол а вектор р станет равным вектору р cos a + b sin а. Сле-
Следовательно, после поворота рассматриваемая точка будет определяться радиус-
вектором
г = q + pcosa + bsina — q + pcosa + N -p sin a = q = A • (ro — q), A.3.13)
где A = cos aE + sin aN— матрица поворота. Матрица А является ортогональ-
ортогональной. При транспонировании матрицы А изменится только знак перед послед-
последним ее слагаемым, что соответствует повороту точки на угол —а.
1.3. Модификации векторов и точек
19
Симметрия двухмерной точки относительно линии. Определим координаты
точки г, симметричной точки го относительно линии. Пусть линия симметрии
определяется точкой Q и ортом г; (рис. 1.3.4).
/
Линия /симметрии
Рис. 1.3.4. Симметрия точки относительно линии
Пусть q есть радиус-вектор точки Q. Построим вектор р = го — q и предста-
представим его в виде суммы двух векторов — проекции на орт v и перпендикулярной
ему составляющей п:
p=(p-v)v + n, A.3.14)
где п = р — (р ¦ v)v. Преобразуем выражение
(p-v)v=\ , \=(vv)-p,
К ' [V2V1P1 + V2V2P2] К '
где w =
/1 о 1 с\
A.3.15)
диадное произведение векторов. После зеркального
[v2v1 v2v2\ v v v
отражения вектора р его нормальная к линии составляющая изменит знак на
противоположный. Положение симметричной точки будет описываться радиус-
вектором
г = q + (р • v)v - (р - (р ¦ v)v) = q+ Bvv - Е)р = q + A-(ro-q), A.3.16)
где матрица А = 2vv — Е — матрица симметрии.
Масштабирование в двухмерном пространстве. Пусть задана неподвижная
точка q и требуется масштабировать относительно нее положения других
точек. Положение точки с радиус-вектором го после масштабирования по коор-
координатным осям относительно неподвижной точки q будет описываться радиус-
вектором
|mi
О
= *+[
A-зл7)
где р\жр2 — компоненты вектора р = tq — q, mi — коэффициент увеличения
компоненты pi, т2 — коэффициент увеличения компоненты р2.
2*
Гл. г. Основы геометрического моделирования
Модификация двухмерных векторов. Модификации свободного двухмерного
вектора получим из модификаций радиус-вектора, положив в A.3.10) t — 0, а
в A.3.14), A.3.16), A.3.17) — q = 0. Вектор в отличие от радиус-вектора не
привязан ни к какой точке двухмерного пространства и поэтому модификации
вектора можно выполнить в местной системе координат, начало которой нахо-
находится в точке Q, а координатные оси параллельны исходным координатным
осям. Этим отличаются модификации вектора и радиус-вектора.
1.4. Однородные координаты
Рассмотренные выше модификации поворота A.3.6), симметрии A.3.8), мас-
масштабирования A.3.9) радиус-вектора точки описываются формулами, имею-
имеющими одинаковый вид:
г = q + А • (г0 - q) = А • r0 + (q - А • q) = А ¦ r0 + t, A-4.1)
где t = q — А ¦ q — преобразованный вектор сдвига. Сдвиг A.3.1) точки описы-
описывается этой же формулой с единичной матрицей А и вектором t, равным вектору
сдвига. Аналогичный вид имеет преобразование координат точки A.2.5). Прео-
Преобразованиям координат и модификациям точки можно придать единый про-
простой вид
R = At-R0. A.4.2)
Для этого нужно увеличить размерность векторов и матриц на единицу. Вектор,
дополненный еще одной компонентой, называется расширенным вектором.
Компоненты расширенного вектора называются однородными координатами.
' Представим каждый радиус-вектор в расширенном виде
Г2 Г2
A.4.3)
Матрица А( представляет собой матрицу А, окаймленную снизу нулями, а
справа — вектором сдвига t в расширенном виде
A.4.4)
Индекс матрицы А( говорит о том, что она является расширенной, и включает
вектор сдвига t. Для преобразований A.4.1) будем использовать запись
а21
аз1
0
0.22
«32
0
агз
азз
0
h
«2
«3
1
R = Q + Ао ¦ (Но - Q) = At ¦ Ц„,
A.4.5)
считая, что расширенная матрица At включает преобразование по матрице А
и сдвиг по вектору t = q — А • q. Расширенный вектор Q описывает точку,
остающуюся неподвижной при преобразовании.
В некоторых случаях, например для построения рациональных кривых и
поверхностей, наряду с координатами для точек необходим дополнительный
параметр — так называемый вес (значимость) точки. Этот параметр точки в
1.4. Однородные координаты
21
вычислениях преобразуется так же, как и координаты, поэтому его считают до-
дополнительной координатой. При наличии у точки дополнительной координаты
w запись ее радиус-вектора в однородных координатах имеет вид
R =
#2
Дз
#4
wr{
гог2
гог3
го
= М =[wr w]T . A.4.6)
[го J L J ч '
При использовании однородных координат вычисления производятся для
однородных компонент Ri, г — 1, 2, 3, 4 без выделения декартовых координат.
Декартовы координаты точки получают на конечном этапе вычислений делением
П = —, Г2 = —, гз = —.
Следует заметить, что векторы R и кЛ. в однородных координатах предста-
представляют одну и ту же точку. Для точек, имеющих вес, сдвиг, поворот, симметрия,
масштабирование и другие модификации описываются общей формулой A.4.2).
С помощью однородных координат и расширенных матриц удобно описы-
описывать преобразования координат. Например, переход из системы координат
вместо равенств A.2.4) может быть описан матрич-
в систему
ным равенством
>1
7*2
rz
1
'аи
«12
«13
0
«21
О22
«23
0
«31
аз2
«зз
0
<?i
Я.2
<?3
1
XI
= А0
хг
A.4.7)
Обратное преобразование A.2.8) может быть описано матричным равенством
'х{
A.4.8)
1
«21 «22 «23 °2
«31 «32 «33 03
0 0 0 1
= А0
Компоненты о\, ог, оз связаны с компонентами q\, q2, дз соотношениями
02 = -
03 = —
- «1393,
- 0,2242 ~ «23^3,
— аз2<72 —
A.4.9)
Матрицы преобразований A.4.7) и A.4.8) удовлетворяют равенству Ао • А9Т =
= А/ • Ао = Е.
Двухмерное пространство. Двухмерные точки в однородных координатах
имеют аналогичный вид
Р =
Р{
р2
Pz
=
wp{
WP2
W
A.4.10)
22
Гл. 1. Основы геометрического моделирования
Pi
P2
1_
ие
У\
У2
1
—
cosy?
sin у?
0
— smy?
cosy?
0
A.2.17) может быть
=
cosy?
— siny?
0
smtp
cosy?
0
Qi
1_
*
V\
У2
1
описано
o{
1
Pi
P2
Преобразования двухмерных расширенных векторов аналогичны преобразо-
преобразованиям пространственных расширенных векторов. Например, преобразование
координат A.2.16) может быть описано матричным равенством
A.4.11)
A.4.12)
где компоненты o\, oi связаны с компонентами qi, qi соотношениями A.2.18).
Использование однородных координат оказывается полезным и там, где до-
дополнительная компонента точки отсутствует. В этом случае ее полагают равной
единице.
1.5.* Геометрия кривых линий
Кривой линией или просто кривой будем называть геометрическое место точек,
координаты которых описываются непрерывными и однозначными функциями ri(t),
r2(t), т"з(?) параметра t, принимающего значения на отрезке tmm ^ t ^ tmax. В декарто-
декартовой прямоугольной системе координат Оехвгез кривую можно описать радиус-вектором
A.5.1)
Представление кривой в виде A.5.1) называется параметрическим. Далее будем пред-
предполагать, что координатные функции г$(?) имеют непрерывные производные до любого
порядка, который нам потребуется. Точку кривой r(t) будем называть обыкновенной,
если в этой точке не обращается в нуль длина вектора первой производной по параметру
г' = dr/dt. В противном случае точку кривой будем называть особой.
Положение точки кривой зависит от параметра t, который является ее внутренней
координатой. Параметр t своими значениями однозначно определяет точки кривой.
Но так как геометрически он ничем не связан с кривой, то для нее можно использо-
использовать другую параметризацию. Для этого достаточно ввести новый параметр v, который
связан с параметром t функциональной зависимостью
t = t{v), v
A.5.2)
где tmin = t(vmm), tmax = t(wmax). Будем предполагать при этом, что функция t(v)
является взаимно однозначной и монотонно возрастающей. Когда параметр v пробегает
свою область изменения от wmin до vmax, параметр t пробегает свою область изменения
от tmin до tmax. Кривая A.5.1), выраженная через параметр v, будет иметь вид
r(v) = r(v(t)), vmin < v ^ wmax.
При этом форма кривой останется прежней. Как параметр t, так и параметр v одинаково
годятся, чтобы характеризовать точки рассматриваемой кривой, и выбор параметра за-
зависит от нас. Мы будем пользоваться этим свойством кривых, чтобы согласовать пара-
параметрические длины кривых. Пусть имеются две кривые: первая a(t), tm;n sj t ^ tmax,
1.5. Геометрия кривых линий 23
вторая с(г>), wm;n ^ v ^ г>тах, и нам нужно, чтобы параметрические длины кривых
были одинаковыми. Изменим параметризацию второй кривой так, чтобы пределы
изменения ее параметров совпадали с пределами первой кривой. Для этого у второй
кривой введем параметр t, связанный параметром v зависимостью
v{t) =vmin- —-— +г>тах- ——. A.5.3)
^тах ^min ^max *min
Вторая кривая теперь будет иметь вид с = c(t) = с(г>(?)), tm\n ^ t ^ tmax. В частном
случае параметром кривой может служить длина ее дуги, отсчитываемая от начальной
точки. В общем случае параметр t, как любая координатная система, может быть
определен удобным для нас способом.
Для векторной функции, как и для скалярной, определяются производные. Произ-
Производные векторной функции также представляют собой векторы. Для любых векторных
функций a(t) и c(t) и любой скалярной функции X(t) справедливы правила дифферен-
дифференцирования
d(a + с) _ da rfc
ей ~ dt + dt'
d(Aa)
dt
d(a • c)
dt
d(a x c)
dt
- a
da
dt
dX
¦dl +
da
dt '
x с -
da
XdV
dc
a dt'
dc
*"aX dt
В декартовой прямоугольной системе координат производные векторной функции п-го
порядка по ее параметру имеют простой вид
В криволинейной системе координат базисные векторы изменяют свою длину и напра-
направление при переходе от одной точки к другой и формулы для производных имеют более
сложный вид.
Если координатные функции кривой в некоторой точке достаточное число раз диф-
дифференцируемы, то векторную функцию кривой в окрестности этой точки можно разло-
разложить в ряд Тейлора
^ ^^^, A.5.5)
где qn = V -—тгЩ- Производные ——— вычислены при некоторых значениях па-
i=1 dtn+L at"
раметра t ^ U ^ t + At. Вектор qn представляет собой остаточный член ряда Тейлора.
Из свойств рядов Тейлора координатной функции ri(t) следует, что длина вектора qn
не превосходит некоторое положительное число, постоянное для всех t из его области
изменения для кривой, и что предел длины остаточного вектора стремится к нулю при
увеличении числа членов усеченного ряда
lira |qn| = 0.
n->oo
24 Гл. 1. Основы геометрического моделирования
При изменении параметризации кривой г(?), t(v) производные по новому параметру
выражаются через производные по старому параметру следующим образом:
dr dr dt
dv dt dv'
<Pt _ Лг /dtV2 dr <Pt_
dv2 ~ dt2 \dv) + dtdv2'
) rPr dt rPt dr d3t
+ dl?dvdu2+~didv3'
Исследуем поведение кривой на бесконечно малом участке вблизи обыкновенной
точки. Если существуют производные по параметру координатных функций, то кривая
также имеет производные по параметру соответствующего порядка. Рассмотрим геоме-
геометрический смысл производной векторной функции. Пусть при каком-либо значении па-
параметра t радиус-вектор г(?) указывает на некоторую
точку R. Перейдем к другому параметру ti = t + At,
при котором векторная функция r(t + At) указывает
на некоторую другую точку R\. Разность этих двух
значений векторной функции Дг = r(t + At) - r(t)
описывает хорду .R-Ri (рис. 1.5.1).
Вектор
t = —- A.5.6)
Рис. 1.5.1 параллелен хорде RRi, но в общем случае не равен ей
по длине. Устремим At к нулю, тогда точка Ri будет
приближаться к точке R, вектор A.5.6) будет стремиться к касательной к кривой в
точке R. Предел отношения A.5.6) при At -> 0 является первой производной векторной
функции
3 3
i=l ~* г=1
Таким образом, производная r'(t) кривой r(t) есть вектор, направленный по касатель-
касательной к кривой в точке, определяемой параметром t. Заметим, что производная всегда на-
направлена в сторону возрастания параметра. Зная первую производную радиус-вектора
кривой, можно вычислить длину кривой. Длина кривой равна пределу, к которому
стремится длина ломаной, вписанной в кривую. Таким образом, длина кривой равна
интегралу
A.5.8)
Натуральная параметризация кривой. Длина вектора производной зависит от спо-
способа параметризации кривой. Существует способ параметризации, при котором длина
вектора производной равна единице. Для этого используется параметризация, геоме-
геометрически связанная с кривой, а именно: за параметр принимается длина дуги кривой,
отсчитываемая от некоторой ее точки (например, начальной). Действительно, в этом
случае длина хорды RRi стремится к длине дуги Д?, а длина вектора г' стремится к
единице, когда At стремится к нулю. Векторная зависимость
г = г(в), A.5.9)
1.5. Геометрия кривых линий
25
где s ¦— длина дуги, называется уравнением кривой с натуральной параметризацией.
Натуральная параметризация удобна в теоретических исследованиях, так как она упро-
упрощает формулы. С практической точки зрения она не всегда удобна, так как требует
знание длины дуги.
Сопровождающий трехгранник. В каждой точке кривой можно построить плос-
плоскость, перпендикулярную ее первой производной. Такая плоскость называется нор-
нормальной плоскостью кривой. Плоскость, в которой лежат и первая производная кри-
кривой и ее вторая производная, называется соприкасающейся плоскостью. Если вторая
производная кривой параллельна первой производной или ее длина равна нулю, то в
качестве соприкасающейся плоскости можно взять любую плоскость, в которой лежит
первая производная кривой. Точка кривой, в которой векторы первой и второй произ-
производных кривой коллинеарны, называется точкой распрямления. Точки распрямления
не зависят от способа параметризации кривой. Название соприкасающейся плоскости
обусловлено тем, что она проходит через заданную точку кривой с наивысшим поряд-
порядком касания, и ее можно определить как предельное положение плоскости, построенной
Соприкасающаяся
плоскость
U. Нормальная
I *"] плоскость
Ч
Спрямляющая
плоскость
Рис. 1.5.2. Сопровождающий трехгранник кривой
по трем бесконечно близким точкам кривой. Плоскость, перпендикулярная нормальной
и соприкасающейся плоскостям, называется спрямляющей плоскостью (рис. 1.5.2).
Единичный вектор, направленный вдоль первой производной кривой, называется
касательным вектором кривой в данной точке. Единичный вектор, направленный
вдоль линии пересечения нормальной и соприкасающейся плоскостей и направленный
в сторону второй производной (в сторону вогнутости кривой), называется главной
нормалью кривой в данной точке. Единичный вектор, направленный вдоль линии
пересечения нормальной спрямляющей плоскостей и образующий с касательным и нор-
нормальным вектором правую тройку векторов, называется бинормалью кривой в данной
точке.
Таким образом, с каждой точкой кривой связаны три взаимно перпендикулярные
плоскости: нормальная, соприкасающаяся и спрямляющая, а также три взаимно орто-
ортогональных вектора единичной длины: касательный t, нормаль п и бинормаль b — txn.
Совокупность трех перечисленных плоскостей и трех векторов t, n, b называется
сопровождающим трехгранником кривой.
Тройка векторов t, n, b выражается через производные векторной функции кривой.
Они помогут нам в исследовании строения кривой в бесконечно малой окрестности
каждой ее точки. Тройка единичных векторов связана соотношениями
= txn, t = nxb,
= bxt.
A.5.10)
26 Гл.1. Основы геометрического моделирования
Формулы Френе-Серре. Предположим, что нам известно уравнение кривой с нату-
натуральной параметризацией A.5.9). В этом случае
Из того, что длина первой производной равна единице и не меняется вдоль кривой,
следует
^ = 2t 2t
ds ds
т. е. векторы первой и второй производной ортогональны. Следовательно, вторая про-
производная кривой с натуральной параметризацией направлена по главной нормали:
"Г = 71 = *п. A.5.13)
ds ds2
Коэффициент к называется кривизной кривой линии. Ниже мы покажем, что обратная
ей величина равна радиусу окружности, соприкасающейся с кривой в рассматриваемой
точке. Бинормаль по определению ортогональна касательному вектору и главной нор-
нормали. Из этого следует, что
d(b-t) dh , «ft dh ,, db
v , ' = t • — + b • — = t • — + M> • n = t • — = 0,
ds ds ds ds ds i-, к-\л\
=2b = 0.
ds ds
Таким образом, вектор dh/ds ортогонален векторам t и b и, следовательно, он парал-
параллелен главной нормали. Это принято записывать в виде
ts = -*"• A'5Л5)
Коэффициент х называется кручением кривой линии. Равенства A.5.13) и A.5.15)
определяют производные ортов t и b по длине дуги. Найдем производную нормали по
длине дуги
?b d(bxt) = At ь х* _xnxt + )fcbxn = Xb-*t. A.5.16)
ds ds ds ds
Нами получены дифференциальные зависимости для векторов t, n и Ь:
dt dn db
k hkt
A-5Л7)
которые известны как формулы Френе-Серре. Они выражают производные векторов
сопровождающего трехгранника в виде разложения по самим этим векторам. Используя
A.5.10), A.5.11) и формулы Френе-Серре, выразим векторы t, n, b, кривизну и кру-
кручение кривой через производные радиус-вектора кривой по ее длине дуги следующим
образом:
dr ^ P
_ dr
ds'
* =
ds2
X k2 \ds ^ ds2)' ds3'
1.5. Геометрия кривых линий
27
Соприкасающаяся окружность. Поясним, почему коэффициент к называют кри-
кривизной кривой. Построим окружность радиусом равным некоторой величине р. Ее
уравнение с натуральной параметризацией в некоторой местной системе координат с
ортами ii, i2 и i3 имеет вид
r(s) = о cos I - lii + о sin I - )i2.
\pj \PJ
Нормаль к окружности и производные радиус-вектора окружности равны
П = — COS I — 111 —
dr
ds
ds2
= - — cos
• fA- {A-
— Sin - li -I- OCOS - 12,
\pj \pj
s\. . fs\. \ n
- li -yOSin - h2 I = -.
p) \pj J p
Очевидно, что коэффициент пропорциональности к для окружности в формуле A.5.13)
равен 1/р. Таким образом, если мы построим для кривой соприкасающуюся с ней
окружность (с таким же d2r/ds2, как у кривой), то радиус этой окружности будет
равен р (рис. 1.5.3).
Величина р = 1/fc называется радиусом кривизны кривой. Для произвольной кри-
кривой ее кривизна к и кручение х являются функциями параметра t.
Поясним, почему коэффициент х называют кручением кривой. Построим в некото-
некоторой точке кривой сопровождающий трехгранник и посмотрим, как он будет себя вести
при движении вдоль кривой. Из A.5.17) получим, что при увеличении параметра на
Рис. 1.5.3. Соприкасающаяся с кривой окружность
Рис.1.5.4. Вектор Дарбу
небольшую величину At касательный вектор t повернется в сторону главной нормали п
на угол к, а бинормаль b повернется в сторону, противоположную главной нормали п,
на угол х (Рис- 1-5.4).
Если наблюдать этот процесс, «сидя на кончике вектора t», то мы увидим, что глав-
главная нормаль п и соприкасающаяся плоскость повернулись в сторону бинормали b на
угол х- Теперь представим, что точка движется по кривой, проходя единицу длины ее
дуги за единицу времени. В этом случае угловая скорость вращения сопровождающего
трехгранника вокруг касательного вектора будет равна кручению кривой х- Если кру-
кручение х = 0, то кривая является плоской. Справедливо и обратное утверждение. Если
кручение кривой равно нулю, то соприкасающаяся плоскость во всех точках кривой
одна и та же, все бинормали параллельны друг другу, а кривая является плоской.
28 Гл. 1. Основы геометрического моделирования
Полный вектор угловой скорости вращения сопровождающего трехгранника по от-
отношению к пути, проходимому по кривой, называется вектором Дарбу. Он равен
u} = kb + Xt. A.5.19)
Вектор Дарбу придает механический смысл формулам Френе-Серре A.5.17), с исполь-
использованием которого последние имеют вид
dt dn db
—- = о; х t, —=a>xn, —- = и x b.
as as as
Натуральные уравнения кривой. Кривизна и кручение полностью характеризуют
форму кривой, если не считать ее положение и ориентацию в пространстве. Они также
являются определенными функциями длины дуги как параметра
k = k(s)>0, X = x(s). A.5.20)
Так как длина дуги, кривизна и кручение не зависят от способа параметризации и от
выбора координат в пространстве, то и функции fc(s) и x(s) также от этого выбора не
зависят. Уравнения A.5.20) называются натуральными уравнениями кривой. Если
две кривые имеют одинаковые натуральные уравнения, то они идентичны и отличаются
только положением и ориентацией в пространстве. Функции s(t), k(t) и \(t) однозначно
определяют кривую с точностью до положения и ориентации в пространстве.
Как правило, параметризация кривой не является натуральной. Определим орты
t, п, b и коэффициенты к и х Для произвольной параметризации. Производные по
параметру будем обозначать штрихами. Первую, вторую и третью производные радиус-
вектора кривой по ее параметру представим следующим образом:
dr dr ds
dt2 ds \dtj
dt2 dt dt2 ds \j
(fr d(s"t + s'2kn) d3s OI dscPs fdsVdk /ds\3
= (s'"-k2s'3)t+Cks"sl+ s'3~]n + kXs'3b, A.5.23)
где s', s" и s"' — первая, вторая и третья производные длины дуги по параметру кривой.
Из A.5.21) получим формулу для вычисления производной длины дуги по параметру и
формулу для вычисления касательного вектора t:
A.5.24)
Mb
dv/dt _ dr/dt _r^
ds/dt~ s>- A 'J
Умножив A.5.21) векторно на A.5.22), получим формулу для определения кривизны
кривой и направления бинормали
г' х г"
кЪ = /3 . A.5.26)
1.6. Геометрия двухмерных кривых 29
Умножив A.5.26) векторно на A.5.25) и используя равенство для двойного векторного
произведения (г' х г") х t = (t • г')г" — (t • г")г', получим формулу для вычисления
направления вектора главной нормали
(г'хг")хг' г" г'-г"
fcn- g/4 -g/2 gD r. A.5.27)
Из правой части равенства A.5.27) видно, что вектор fcn является составляющей век-
вектора r"/(s'J, перпендикулярной к касательному вектору t (составляющая, параллель-
параллельная t, вычитается). Кривизна кривой равна длине вектора, стоящего в правой части
A.5.26),
1г' х г
_ |Г X Г |
К — . [L.O. Ж)
Соответственно, при |г' х г"| ф 0 радиус соприкасающейся окружности определится
формулой
Умножив A.5.26) скалярно на A.5.23), получим формулу для определения кручения
кривой
(г'хг'О-г"' (г'хг")т"'
Х- кЪ'6 = |r'xr'f • (L5-29)
Если кривизна кривой в данной точке не равна нулю, то, поделив обе части равенств
A.5.26) и A.5.27) на кривизну A.5.28), получим бинормаль и нормаль:
г' х г"
Ь = |^|j, A.5-30)
Если известна векторная функция линии A.5.1), то формулы A.5.24)—A.5.31) позво-
позволяют получить всю геометрическую информацию о кривой линии.
Из формул A.5.28) и A.5.29) видно, что кривизна всегда неотрицательна (в чи-
числителе и знаменателе стоят квадратные корни), а кручение может иметь любой знак.
Если кривизна равна нулю, то направление главной нормали, бинормали и кручение не
определены. Если кривизна равна нулю в каждой точке кривой, то она является прямой
линией. Вектор главной нормали в этом случае может иметь произвольное направление
в нормальной плоскости. Если векторы г', г" и г'" коллинеарны, то кручение кривой
равно нулю и кривая является плоской.
1.6*Геометрия двухмерных кривых
Кроме пространственных линий, для нас практическое значение будут иметь двух-
двухмерные кривые на плоскости. В частности, двухмерным пространством будет служить
область параметров поверхностей.
Рассмотрим случай двухмерной кривой. Пусть на плоскости определена декартова
прямоугольная система координат с началом в точке О и базисными векторами е\
и e-i. Компоненты двухмерных векторов будем обозначать через х и у. Большинство
30
Гл. 1. Основы геометрического моделирования
формул для двухмерных кривых можно получить из соответствующих формул для про-
пространственных кривых, положив в них третью координату равной нулю и опустив ее и
все векторы, ортогональные плоскости кривой (в их числе бинормаль). Радиус-вектор
двухмерной кривой r(t) = [x(t) y(t)] будет описываться выражением
r(t)=x(t)e1+y(t)e2.
Для двухмерной кривой r(s) формулы Френе-Серре имеют вид
dt dn
— = kn, — = -kt,
ds ds
A.6.1)
A.6.2)
где t = dr/ds — касательный вектор кривой, s — длина дуги кривой. Кривизна двух-
двухмерной кривой определяется равенством
к =
d2r
ds2
A.6.3)
Натуральное уравнение двухмерной кривой выражает ее кривизну как функцию дуги
вдоль кривой и имеет вид
к = k(s).
Чтобы сохранить справедливость всех приведенных выше формул, следует пере-
переопределить операцию векторного произведения для двухмерных векторов. Результатом
векторного произведения двухмерных векторов гх = [xi t/i]T и r2 = [х? t/г]7 будем
считать скалярную величину, равную
х г2 =
2/2
A.6.4)
Выразим через координаты х и у производную длины дуги и кривизну двухмерной
кривой, используя формулы A.5.24) и A.5.26),
s' = \r'\ = vV • r' =
. r' x r"
у"х' - х"у'
./I3
A.6.5)
A.6.6)
Эволюта и эвольвента. Для каждой обыкновенной точки кривой можно указать
центр кривизны. Геометрическое место центров кривизны всех точек данной кривой
называется эволютой этой кривой. Выражение для радиус-вектора эволюты a(t) по-
получим, добавив к радиус-вектору кривой r(t) вектор нормали, деленный на кривизну
кривой:
o(t)=r(t) + |n(t)=r+ig. A.6.7)
При произвольной параметризации кривой нормаль выразим с помощью равенства
A.5.27) и получим
1.6. Геометрия двухмерных кривых 31
Для двухмерной кривой r(t) = [x(t) y(t)] запишем векторное равенство A.6.8) от-
отдельно для каждой координаты эволюты a(t) = [xa(t) ya(t)] :
В точках распрямления радиус-вектор соответствующей точки эволюты стремится к
бесконечности. Если точка распрямления является точкой перегиба, то эволюта терпит
в соответствующей точке разрыв. Эволюта в каждой своей точке касается нормали к
исходной кривой в соответствующей точке. Эволюту можно определить как огибающую
семейства нормалей.
Исходная кривая по отношению к своей эволюте является эвольвентой (разверт-
(разверткой). Для кривой a(s) эвольвента описывается радиус-вектором
r(s) =a- (s- so)~j~ =a — (s- so)t, A.6.10)
as
где s — длина дуги кривой a(s), sq = const, t — касательная к кривой. Для заданной
плоской кривой можно построить множество эвольвент, в зависимости от so (или от
того, в какой точке кривой принять длину дуги равную нулю). На рис. 1.6.1 показана
кривая a(s) и ее эвольвента.
Эвольвента строится следующим образом. Положим, что длина дуги кривой a(s)
отсчитывается от точки Со- Для получения точки М эвольвенты, соответствующей
некоторой точке С* исходной кривой, построим в точке С, касательную и отложим на
м
Эвольвента
м
Рис. 1.6.1. Эволюта и эвольвента
ней с учетом знака отрезок длиной, равной длине дуги CjCo, взятой с отрицательным
знаком, если значение параметра в точке С, больше значения параметра в точке Со, и
взятой с положительным знаком в противном случае. Можно сказать, что эвольвента
представляет собой развертку исходной кривой.
Для доказательства равенства A.6.10) покажем, что эволюта кривой r(s) есть кри-
кривая a(s). Заметим, что параметр s является длиной дуги кривой a(s), но не является
длиной дуги для эвольвенты r(s), поэтому радиус-вектора эволюты выразится правой
частью формулы A.6.8). Подставим в формулу эволюты A.6.8) значения векторной
функции г и ее производных, выраженные через векторную функцию а и ее производ-
производные по параметру s:
г = о - (з - so)t,
г' ~ t — (s — so)kn — t = —(s — so)kn,
r" = (s - so)kH - kn,
r' x r" = I - (s - so)kn x ((s - so)k2t - kn)\ = (s - soJfc3,
32 Гл. 1. Основы геометрического моделирования
где s — длина дуги кривой a(s), к — ее кривизна, п — главная нормаль и t —
касательная кривой a(s). В результате получим
г"(г' -г') - г'(г' ¦ г")
г + ( У* V ¦r') = a-(s- so)t+
г' х г"|2
((s — so)k2t — kn)(s — soJk2 + (s — so)kn(s — so)k2
что и требовалось доказать.
1.7*Геометрия поверхностей
Поверхностью будем называть геометрическое место точек, координаты которых
описываются непрерывными и однозначными функциями rx(u, v), r%{u, v), гз(и, v)
двух параметров и и и, принадлежащих непрерывной и связной двухмерной области ?1.
В декартовой прямоугольной системе координат Ое^гвз поверхность можно описать
радиус-вектором
з
г(«, v) = J^ n(u, v)et, u,v?u. A.7.1)
i=l
Представление поверхности в виде A.7.1) называется параметрическим. В общем случае
область изменения параметров представляет собой часть двухмерной плоскости. В про-
простейшем случае область изменения параметров поверхности представляет собой прямо-
прямоугольник, который можно описать четырьмя числами umin, wmax, t>min, vmAX. Область
изменения параметров для простейшего случая определяется неравенствами
Такую область изменения параметров могут иметь очень многие поверхности, но для
построения математической модели детали сложной формы необходимы, поверхности
общего вида. Два параметра и и v определяют точку поверхности. Если эти пара-
параметры сами являются функциями двух других параметров uq и Vq, и = u(uq, Vq),
v = ь(щ, Vo), то поверхность будет описываться радиус-вектором
Г(ыо, Vq) = г(«(м0, V0), v(u0, Vq)) , Uq, Vq ? fi0,
зависящим от параметров uq и Vq. Новые параметры uq и vq имеют свою область опре-
определения По- Форма поверхности не зависит от способа ее параметризации и мы имеем
возможность использовать удобную для нас параметризацию и область изменения па-
параметров. Параметры поверхности являются координатами внутренней двухмерной
системы координат, в качестве которой для простоты мы будем выбирать декартову
прямоугольную систему координат на плоскости.
Частные производные радиус-вектора поверхности r(u, v) по параметрам uiav пред-
представляют собой векторы. Будем обозначать частные производные радиус-вектора по-
поверхности численными нижними индексами, соответствующими номеру параметра, по
которому выполнено дифференцирование
ru =
dr
~ du
d2r
''du^'
d2r
r2 =
Г22 =
dr
dv'
d2r
dv2'
d2v
A.7.2)
aw ov
d2r d2r
Г12 = -7.—T" = r21 = a a ¦
du dv dv du
1.7. Геометрия поверхностей 33
Далее будем предполагать, что координатные функции ri(u, v) имеют непрерывные
производные по каждому параметру любого порядка, который нам потребуется. В даль-
дальнейшем ограничимся рассмотрением поверхностей, для которых векторы ri и гг не
коллинеарны и не обращаются в нуль. Такую точку поверхности т(и, v) будем назы-
называть обыкновенной. В противном случае точку поверхности будем называть особой.
В обыкновенной точке существует единственная касательная к поверхности плоскость.
Параметры и и v можно рассматривать как координаты двухмерной точки в плоскости
параметров, тогда радиус-вектор поверхности можно рассматривать как функцию точки
плоскости параметров.
При изменении параметризации поверхности r(u, v), где u = и(щ,Уо), v = v(uq, Vq),
производные ее радиус-вектора по новым параметрам выражаются через производные
по старым параметрам следующим образом:
дт дт ди дт dv du dv
duo du duo dv дщ дщ дщ'
дт дт ди дт dv ди dv
dvo ди dvo dv dvo dvo dvo'
d2r ( duV n du dv ( dv V d2u d2v
TT = rll "я +2г12 о Ь Г22 д + Гх ^-^ + Г2 "^—о ,
duf, \ ои0) ои0 duo \ cm0 / du? дщ
d2r (du\2 du dv fdv\2 d2u d2v
~П = Г11 — "*¦ ^r12—~5 •" Г22 — +Г17Т+Г2ТТ,
\dvo/ dvodvo \dvoj dvfi
d2r du du du dv
•
БЪ• ri2^^1
duo dv0 du0 dv0
du dv dv dv d2u d2v
Д+ Г22 ДQЬ Г1 1 Г2 ДX•
дщ дщ dvo дщ dvo дщ dvo
Если зафиксировать один из параметров, а другой изменять в некоторых пре-
пределах, то мы получим кривую линию, которая лежит на поверхности. Такие кри-
кривые называются координатными линиями поверхности. Будем называть и-линиями
поверхностные кривые, вдоль которых меняется только параметр и, а v-линиями —
поверхностные кривые, вдоль которых меняется только параметр v. Производные ri
и гг радиус-вектора поверхности представляют собой векторы, касательные к соответ-
соответствующим координатным линиям. Для поверхности можно построить семейство
Рис. 1.7.1. Координатная сетка поверхности
u-кривых при различных значениях и, и семейство u-кривых при различных значе-
значениях и. Два таких семейства кривых образуют координатную сетку на поверхности
(рис. 1.7.1). На координатной сетке поверхности можно построить криволинейную
систему координат в пространстве.
3 — 5293 Голованов
34 Гл. 1. Основы геометрического моделирования
Произвольную линию на поверхности можно построить, если ввести зависимость
параметров поверхности «ииот некоторого общего для них параметра t
и - u(t), v = v(t). A.7.3)
Радиус-вектор линии на поверхности будет описываться зависимостью
r(t)=r{u(t),v(t)). A.7.4)
Через каждую точку поверхности можно провести множество различных кривых A.7.4).
Найдем дифференциал радиус-вектора A-7.4) вдоль некоторой кривой на поверхности:
dv = ri(u, v)du + r2{u, v)dv, A.7.5)
где du = v! dt, dv = v' dt. В дальнейшем будем считать, что и' и v' не обращаются в
нуль одновременно, так как в противном случае точка перестает быть обыкновенной.
Вектор производной A.7.4)
dr du dv , . ,ч „ „.
*=ri^+r2^riW+r2U <L7-6>
лежит в плоскости, определяемой векторами ri и гг- Если зафиксировать точку на
поверхности и провести через нее всевозможные кривые, изменяя зависимости A.7.3),
то производные всех этих кривых в рассматриваемой точке будут лежать в плоскости,
определяемой векторами ri и г2- Эта плоскость называется касательной плоскостью
Рис. 1.7.2. Касательная плоскость и производные радиус-вектора поверхности
поверхности в данной точке (рис. 1.7.2). Дифференциал A.7.5) имеет то же направле-
направление, что и производная A.7.6). Из A.7.5) видно, что направление дифференциала и
производной A.7.6) зависят от отношения du.dv = и':v'.
Пространственной кривой A.7.4) соответствует двухмерная кривая
на параметрической плоскости поверхности.
Первая квадратичная форма поверхности. Метрические свойства поверхности выра-
выражаются через метрические свойства кривых на них. Мы будем исследовать геометрию
поверхности в малой окрестности некоторой ее точки R, определяемой параметрами и
и v. Сместимся из точки R по какой-нибудь кривой на поверхности A.7.3) в бесконечно
близкую ей точку .Ri, определяемую параметрами u + du, v + dv и вычислим длину дуги
RRi. С точностью до слагаемых, линейно зависящих от бесконечно малых величин,
длина дуги RRi равна длине дифференциала A.7.5)
ds = |rj du + гг dv\.
1.7. Геометрия поверхностей 35
Квадрат длины бесконечно малой дуги равен
ds2 = (г! du + r2 dv) ¦ (г! du + r2 dv) =ri ri du2 + 2ri • r2 du dv + г2 • г2 dv2. A.7.7)
Скалярные произведения векторов ri и г2, как и сами векторы, зависят только от вы-
выбора точки R и являются некоторой характеристикой поверхности в этой точке. Введем
обозначения
ёп =ri -гь
#12 =?21 =Г1 Т2 =Г2-ГЬ A.7.8)
g22 = г2 • г2.
Тогда квадрат длины бесконечно малой дуги кривой на поверхности будет определяться
формулой
ds2 = gn du2 + 2g12 dudu + g22 dv2. A.7.9)
Выражение в правой части A.7.9) является квадратичной формой дифференциалов du
и dv. Оно называется первой основной квадратичной формой поверхности. Первая
основная квадратичная форма является метрической характеристикой поверхности и
служит для бесконечно малых измерений вдоль поверхности. Выражение A.7.9) можно
записать в матричном виде
ds2 = [du dv] ¦ G ¦ [du dv]T, A.7.10)
где G = n 12 — матрица первой квадратичной формы.
[?21 ?22J
С помощью первой квадратичной формы можно вычислить длину дуги кривой на
поверхности. Пусть задан участок кривой на поверхности и = u(t), v = v(t), t0 ^ t ^
sj ti. Интегрируя дифференциал длины дуги ds в пределах от to до t\, получим длину
соответствующего участка кривой
«1
« = VSuu'u' + 2g12u'u' + g22v'v' dt. A.7.11)
to
Первая квадратичная форма поверхности позволяет вычислять углы между кри-
кривыми на поверхности. Пусть имеются две кривые на поверхности, проходящие через
общую точку М. Обозначим через du и dv дифференциалы параметров поверхности,
соответствующие бесконечно малому смещению вдоль первой кривой на поверхности, а
через 8и и Sv — дифференциалы параметров поверхности, соответствующие бесконечно
малому смещению вдоль второй кривой. Эти бесконечно малые смещения определятся
векторами
dr = Г! du + г2 dv, Sr = ri6u + r26v.
Данные дифференциалы направлены по касательным к кривым и к поверхности и
поэтому угол между кривыми равен углу между векторами дифференциалов. Найдем
косинус угла между кривыми на поверхности как скалярное произведение касательных
к ним векторов, деленное на произведение длин этих векторов:
cos {dv <5r) =
\dr\\6r\
ёи duSu + g12 duSv + g21 dvSu + g22 dvSv 7
dudu + 2g12 du dv + g22 dv dv)(gn6u6u + 2g126u6v + g225v8v)
3*
36 Гл. 1. Основы геометрического моделирования
Выражение A.7.12) позволяет найти угол ц> между координатной u-линией и v-линией
в некоторой точке поверхности, если мы положим в ней du ф О, dv = 0, Su = О, Sv ф 0:
-7==. A.7.13)
Знак косинуса угла мы взяли совпадающим со знаком g12, следовательно, исходя из
обозначения A.7.8), угол у мы измеряем между положительными направлениями коор-
координатных u-линии и v-линии в рассматриваемой точке. Если g12 = 0, то координатные
линии в данной точке ортогональны.
Первая квадратичная форма используется и для вычисления площади поверхности
или ее части. Пусть нам требуется вычислить площадь части поверхности, которая на
параметрической плоскости имеет область П. Разобьем область Cl конечным числом
u + du,v+dv
__ ___ и + du, v
U, V '
Рис. 1.7.3. Бесконечно малый элемент поверхности
координатных u-линий и v-линий. Рассматриваемая часть поверхности разобьется на
конечное число так называемых криволинейных четырехугольников. Один из таких
четырехугольников показан на рис. 1.7.3.
Пусть стороны этого четырехугольника равны du и dv. В первом приближении
площадь четырехугольника равна
dS = \r\ du x r2 dv\ = |ri x r2| du dv.
Представим квадрат длины вектора ri x г2 следующим образом:
|ri х г2|2 = |ri|2|r2|2sin2(/? =
Таким образом, площадь четырехугольника в первом приближении определится фор-
формулой
dS = \Zgng22 ~ gi22 dudv. A.7.15)
Будем теперь измельчать разбиение, увеличивая число координатных линий, та-
таким образом, чтобы наибольшие из значений du и dv стремились к нулю. За искомую
площадь примем предел, к которому стремится сумма площадей криволинейных четы-
четырехугольников при бесконечном измельчении координатной сетки. Из теории кратных
интегралов известно, что если функция g11g22 — ?Ti22 непрерывна по и и v, то пре-
предел указанной суммы существует, не зависит от способа разбиения и равен двойному
интегралу от указанной функции по области О, изменения переменных и и v
5 = JJVgng22-gi22dudv. A.7.16)
1.7. Геометрия поверхностей 37
Заметим, что так как первая квадратичная форма в A.7.9) определяет квадрат длины
дуги, который в обыкновенной точке больше нуля при всех du и dv, одновременно не
равных нулю, то определитель матрицы G положителен:
g=\G\=gng22-gl22>0. A.7.17)
Первая квадратичная форма поверхности используется для вычислений длин кри-
кривых на поверхности, углов между ними, площади поверхности. Те геометрические свой-
свойства поверхности, которые можно установить из знания первой квадратичной формы,
называются внутренней геометрией поверхности.
Вторая квадратичная форма поверхности. Найдем нормаль к поверхности. Так
как векторы ri и г2 лежат в касательной к поверхности плоскости, то их векторное
произведение перпендикулярно к касательной плоскости. Поделив вектор ri x г2 на его
длину, определяемую выражением A.7.14), получим формулу для единичной нормали
к поверхности в рассматриваемой точке
ГХГ2 . A.7.18)
VSllg22 ~ Sl2
Продолжим исследование поверхности вблизи некоторой ее точки R путем исследо-
исследования кривых на ней. Рассмотрим некоторую кривую на поверхности и — u(t), v = v(t).
Вычислим приращение радиус-вектора кривой, которое он получит при бесконечно
малом приращении ее параметра dt. Для этого используем разложение радиус-вектора
в ряд Тейлора A.5.5). Приращение радиус-вектора кривой Дг с точностью до второго
порядка малости относительно dt равно
Найдем проекцию приращения радиус-вектора кривой Дг на нормаль к поверхности в
данной точке. Для этого используем производные радиус-вектора кривой
2 A7 20)
' + tiu" + t2v"
Вектор г' ортогонален вектору нормали, поэтому основную роль в проекции на нормаль
приращения радиус-вектора Дг будет играть вторая производная. Проекция вектора г"
на нормаль к поверхности m характеризует искривление поверхности (именно поверх-
поверхности, а не кривой). Если мы имеем кривую на плоскости, то как бы она искривлена
ни была, проекция вектора г" на нормаль к плоскости будет равна нулю. Умножив
скалярно A.7.19) на нормаль к поверхности, получим
Дг • m = -г" • mdt2 = -(гц • ти'и1 + 2ri2 • mu'v' + г22 • vav'v') dt2.
Скалярные произведения векторов Гц • m, V\2 ¦ т и г22 • т зависят только от выбора
точки на поверхности и являются некоторой ее характеристикой в этой точке. Введем
обозначения
Ьп = Гц • т,
Ъ\г = &2i = ri2 • т = r2i • т, A.7.21)
Ъ22 = г22 • т.
Тогда для главной части отклонения кривой на поверхности от касательной плоскости
получим значение
Дг • m = hbn du2 + 26i2 dudv + b22 dv2). A.7.22)
38 Гл. 1. Основы геометрического моделирования
В A.7.22) использовались обозначения A.7.21). Выражение в скобках правой части
A.7.22) является квадратичной формой от дифференциалов du и dv. Оно называется
второй основной квадратичной формой поверхности. Также как и первая квадра-
квадратичная форма, вторая квадратичная форма является характеристикой поверхности и
служит для определения искривленности поверхности. Выражение A.7.22) можно за-
записать в матричном виде
2Дг • m = [du dv]-B- [du dv)T, A.7.23)
где В = ,n , 2 — матрица второй квадратичной формы.
[«21 022j
Компоненты второй квадратичной формы можно выразить несколько иначе. Ис-
Используем тот факт, что вектор нормали m всегда ортогонален векторам Г\ и г2. Диф-
Дифференцируя равенства m • ri = 0 и m • г2 = 0 по и и v, получим
mi -Гх -t-m-гц = О,
т2 • Г! + т • г12 = О,
rti! -г2 + тг21 = О,
т2 • г2 + т ¦ г22 = О,
где mi и т2 — частные производные вектора нормали по параметрам и и и. Подставим
в эти равенства обозначения A.7.21):
Ьц = -mi • ri,
J12 = -m2-ri' A.7.24)
Ь21 = -П11-Г2) V >
?>22 = —Ш2 • Гг.
Далее вычислим дифференциалы
dv — v\du-\- r2 dv,
dm = nix du + m2 dv
и перемножим их скалярно. В результате придем к равенству
dr • dm = nil • ri du2 + (m2 • r1 + mi • r2) du dv + m2 • r2 dv2 =
= -Fц du2 + 2bn du dv + b22 dv2). A.7.25)
Дифференциалы dr и <fm берутся в одной и той же точке поверхности при одних и тех
же du и dv.
Деривационные формулы Вейнгартена. Для построения эквидистантных поверхно-
поверхностей нам необходимо будет уметь определять производные вектора нормали. Вектор m
характерен тем, что он всегда имеет единичную длину, и поэтому его производные по
параметрам и и v не содержат составляющих, параллельных т, т. е. его производные
лежат в касательной плоскости. Действительно,
д(т-т) d(m-m)
—*-— = 2nii • m = 0, —Ц = 2m2 • m = 0.
ди dv
Используя это, представим производные нормали в виде
mi = -bi1ri - b!2r2,
, i ,2 A.7.26)
Ш2 = —02 Г1 — 02 Гг,
1.8. Кривизна линий на поверхности 39
где &11, Ь\2, 621, Ь22 — пока неизвестные коэффициенты разложения. Знак минус
выбран из соображений удобства в дальнейшем. Для определения этих коэффициентов
умножим каждое из равенств A.7.26) скалярно на гх и г2. Используя A.7.8), получим
две системы уравнений
hi = b^gn +h g12,
bi2 =bi1g2i +h2g22, A7 27)
hi =h1gu + h2gl2,
hi = h1gn + ^2 g22-
Решая эти уравнения относительно искомых коэффициентов, получим
, 1 bng22 - fri2g12
&1 _
, 1 &
b2 =
; 1 j
(\ 7 2Я1
i2 b22gn - b2lgn
h =
где g = gng22 - g12gn =
g g
11 012 _ |q| — определитель матрицы G. Формулы
g2i к
A.7.26) с учетом A.7.28) называются деривационными формулами Вейнгартена. Они
выражают частные производные нормали к поверхности через коэффициенты первой
и второй квадратичных форм в рассматриваемой точке. Запишем эти формулы в ма-
матричном виде
Ы rv ь,2] гГ11 „, rrii
где В' — матрица коэффициентов A.7.28).
Деривационные формулы Вейнгартена можно записать более кратко, если исполь-
использовать матрицу, обратную матрице G. Для компонент матрицы, обратной матрице G,
введем следующие обозначения:
g; Д A.7.30,
где
Матрица В' с учетом A.7.30) равна В' = В • G, а деривационные формулы Вейнгар-
Вейнгартена примут вид
1.8.* Кривизна линий на поверхности
Теорема Менье. Продолжим исследование поведения кривых на поверхности с по-
помощью второй квадратичной формы. Установим зависимость кривизны кривой на
поверхности от ориентации ее касательного вектора на соприкасающейся плоскости.
Рассмотрим равенство
г" • m = гп • пш'2 + 2ri2 • mu'v' + r22 • mu'2 = bnu'2 + 2h2u'v' + b22v'2. A.8.1)
40
Гл. 1. Основы геометрического моделирования
Вторая производная радиус-вектора кривой на поверхности согласно A.5.22) равна
dt2
ds
„
s"t
s' kn,
A.8.2)
где n — главная нормаль кривой на поверхности. Касательный вектор t кривой лежит
в касательной плоскости и ортогонален нормали поверхности т, поэтому равенство
A.8.1) перепишем в следующем виде
ds2kn ¦ m = Ьц du2
dudv + 622 dv2.
A.8.3)
Квадрат дифференциала длины дуги кривой определяется равенством A.7.9). Обозна-
Обозначим угол между нормалью к поверхности и нормалью к кривой на этой поверхности че-
через ш. Разделим последнее равенство на квадрат дифференциала длины дуги и получим
выражение, связывающее кривизну кривой, угол между нормалями ю и коэффициенты
первой и второй квадратичных форм поверхности:
k cos и =
Ъц du2 + 2&12 du dv + 622 dv2
gn du2 + 2gn du dv + 522 dv2 '
A.8.4)
Для уяснения геометрического смысла последнего соотношения рассмотрим
рис. 1.8.1, где показаны некоторая кривая на поверхности и соответствующее ей нор-
нормальное сечение поверхности, проходящее через точку М кривой. Нормальное сече-
сечение поверхности есть кривая пересечения поверхности и плоскости, проходящей че-
через нормаль к поверхности и касающейся кривой в точке М. Так как нормальное
сечение лежит как на поверхности, так и на
секущей плоскости, то нормаль к нему также
лежит в этой плоскости и, следовательно, для
него | cosw| = 1. Коэффициенты первой и вто-
второй квадратичных форм зависят только от по-
положения точки М. А вот дифференциалы du
и dv зависят от направления кривой на по-
верхности, поэтому величина kcosto зависит
как от положения точки, так и от направле-
направления кривой на поверхности, определяемого от-
отношением du.dv. Любая другая кривая на по-
поверхности, проходящая через ту же точку М и
имеющая общую касательную с рассматривае-
рассматриваемым нормальным сечением, будет иметь одно
и то же значение к cos и), несмотря на то, что у нее другая кривизна. Кривизна такой
кривой будет не меньше кривизны нормального сечения, так как нормальное сечение
имеет максимальное значение | cosu;|. Обозначим кривизну нормального сечения через
\i. Таким образом, кривизна нормального сечения определяется равенством
Рис. 1.8.1. Нормальное сечение поверх-
поверхности
_ Ьц du2 + 2b12 du dv + b21 dv2
1 ~ gn du2 + 2gl2 du dv + g22 dv2
A.8.5)
Угол ш есть угол между нормалью к поверхности и нормалью к кривой, он же ра-
равен углу между нормальной к поверхности плоскостью и соприкасающейся плоскостью
кривой. Таким образом, нормальное сечение имеет минимальную кривизну из всех
кривых, проходящих через заданную точку в заданном направлении, и его кривизна
является некоторой характеристикой поверхности. Кривизна нормального сечения на-
называется нормальной кривизной поверхности в заданной точке и в заданном напра-
направлении. Если известна кривизна нормального сечения, то можно определить кривизну
линии на поверхности, касательной к этому нормальному сечению, при условии, что
известен угол между нормалью поверхности и главной нормалью кривой. Этот факт
констатирует
1.8. Кривизна линий на поверхности 41
Теорема Менье. Радиус кривизны р = 1/k в заданной точке кривой на по-
поверхности равен произведению радиуса кривизны рт = 1//л соответствующего нор-
нормального сечения в этой точке на косинус угла между нормалью к поверхности и
главной нормалью кривой:
— = — cosw = — п • т. A.8.6)
К /i /i
В заданной точке поверхности можно построить бесчисленное множество нормаль-
нормальных сечений, которые отличаются направлением, определяемым отношением dv. : dv.
Направление нормального сечения, для которого кривизна нормального сечения равна
нулю, называется асимптотическим направлением в рассматриваемой точке. В каж-
каждой точке поверхности существует не более двух асимптотических направлений, если
не считать те случаи, когда в точке все коэффициенты второй квадратичной формы
равны нулю.
Мы рассмотрели проекцию вектора кривизны А;п произвольной кривой на поверх-
поверхности на нормаль к поверхности т. Теперь рассмотрим оставшуюся часть вектора
кривизны — его проекцию на касательную плоскость, равную
h = A;n — m(A;n • m).
Длина этого вектора равна Aisinw и называется геодезической кривизной линии на
поверхности. Вектор h совпадает с вектором кривизны кривой, являющейся ортого-
ортогональной проекцией на касательную плоскость рассматриваемой кривой на поверхно-
поверхности. Геодезическая кривизна нормального сечения равна нулю. Нормальная кривизна
является характеристикой поверхности, а геодезическая кривизна является характери-
характеристикой линии на ней.
К поверхностям применяют такой термин, как изгибание. Изгибание — это измене-
изменение формы поверхности, не вызывающее ее деформации. При изгибаниях поверхности
ее первая квадратичная форма не меняется, т.е. изгибания не меняют внутреннюю
геометрию поверхности. Пусть мы нарисовали некоторую линию на поверхности. При
изгибаниях поверхности в общем случае изменяется кривизна этой линии и нормаль-
нормальная кривизна поверхности вдоль линии. Геодезическая кривизна линий на поверх-
поверхности при изгибаниях остается неизменной. Геодезической линией на поверхности
называется кривая на поверхности, геодезическая кривизна которой в каждой точке
равна нулю. Длина дуги геодезической линии, проходящей через две заданные точки,
меньше длины дуги любой другой кривой на поверхности, соединяющей эти точки.
Рассмотрим случаи, когда кривизна нормального сечения не равна нулю. Если
нормальное сечение касательно к координатной ы-линии, то dv = О и
ёп
где через /iu обозначена нормальная кривизна поверхности в u-направлении. Анало-
Аналогично нормальная кривизна поверхности fiv в v-направлении равна
#22
Главные кривизны поверхности. В заданной точке поверхности кривизна нормаль-
нормального сечения зависит от выбранного направления на ней. Выражение A.8.5) перепишем
в другом виде (используя равенство A.7.25))
fi(dr ¦ dr) = -(dr ¦ dm), A.8.7)
Обратим внимание на то, что кривизна нормального сечения зависит от направлений
векторов dr и <im относительно друг друга. Зададимся целью найти такое направление
движения по поверхности, при котором векторы dr и <im были бы кол линеарными.
42 Гл. 1. Основы геометрического моделирования
Другими словами, попробуем найти направление на поверхности, определяемое отно-
отношением du:dv, для которого выполняется равенство
dm = — Xdr
или
ri du + r2dv — —-(mi du + m2dv) = --(bi1ri + 6i2r2) du + -rib^ri + 6г2гг) dv =
Л Л Л
= ^-(bi1 du + Ьг1 dv)T! + \{Ьг2 du + b22 dv)r2, A.8.8)
Л Л
где А — неизвестный пока коэффициент. Мы можем считать ri и гг базисными векто-
векторами, по которым разложены векторы dv и dm. Для их коллинеарности нужно, чтобы
коэффициенты при ri и г2 в правой и левой частях A.8.8) были равны. Это равенство
выразится следующим образом:
1 01 [du] _ 1 [V b21] \du
0 jHk Jk
или
Sii ?12] . \du\ _ 1 Гбц 6i2
[dul
[dv\ ¦
Для перехода к последнему равенству мы использовали соотношение В' = В • G 1.
Итак, для определения искомого направления мы пришли к системе линейных алге-
алгебраических уравнений для du и dv
(B-AG)[^]=0. A.8.9)
Данная система является однородной и имеет ненулевое решение, если определитель
ее матрицы равен нулю. Раскрыв определитель, придем к квадратному уравнению
относительно А, откуда в общем случае найдем два корня: Ai и А2. Подставив каждый
из корней в любое из уравнений A.8.9), получим два направления на поверхности,
определяемые отношениями dui :dvi и dui :dv-i-
Направления движения на поверхности, для которых векторы dv и <im колли-
неарны, называются главными направлениями поверхности. Сравним соотношения
A.8.7) и A.8-8) и увидим, что Ai и Аг равны кривизне нормальных сечений в глав-
главных направлениях, которые обозначим через Ц\ и ц2. Нормальные сечения в данной
точке поверхности, касательные к которым идут по главным направлениям, называ-
называются главными сечениями, а их кривизны назьшаются главными кривизнами в данной
точке поверхности. Запишем квадратное уравнение, из которого определяются главные
кривизны
feii&2 - &22)А2 - (Ьп&2 + b22gn - 2b12g12)\ + (ЬцЬ22 - Ь122) = 0. A.8.10)
Из A.8.10) легко получить сумму и произведение корней уравнения, т.е. сумму и
произведение главных кривизн:
bllg22 + b22gn ~ 2Ь12&2 па
, A.0.1
ЬцЬ22 - 612621
A.8.12)
1.8. Кривизна линий на поверхности 43
Полусумма главных кривизн называется средней кривизной поверхности в данной
точке, а произведение главных кривизн называется гауссовой кривизной поверхности
в данной точке.
Обозначим через ti и t2 касательные векторы главных сечений. Покажем, что
главные направления поверхности ортогональны друг другу. Выразим главные напра-
направления через производные радиус-вектора
ti = i"i dui + r2 dvi,
t2 = I"i du2 + T2 dv2.
Их скалярное произведение равно
ti • t2 = [dux dvx] ¦ G • [du2 dv2]T¦ A.8.13)
Покажем, что оно в общем случае равно нулю. Для этого систему двух уравнений A.8.9)
запишем для первого главного направления, первое из этих уравнений умножим на du2,
второе уравнение умножим на dv2 и сложим с первым, в результате получим равенство
[du2 dv2] ¦ (В - ihG) ¦ [dux dVl]T = 0.
Аналогично получим второе равенство, поменяв местами главные направления,
[dux dvx] • (В - /i2G) • [du2 dv2]T = 0.
Вычтем последние два равенства одно из другого и получим равенство:
[dUl dvx) ¦ ((/i2 - Mi)G) • [du2 dv2]T = 0, A.8.14)
из которого следует, что если главные кривизны различны, то выражение A.8.13)
равно нулю и главные направления ортогональны. Если главные кривизны поверх-
поверхности равны, то за главные могут быть выбраны любые два ортогональных направле-
направления (такую ситуацию мы имеем на сфере и плоскости). Точка, в которой fi2 = fix,
называется точкой закругления.
Так как главные направления в общем случае ортогональны, то производные ра-
радиус-вектора поверхности и ее нормали в любом направлении можно разложить по
единичным векторам ti и t2 главных направлений:
— = ti COS (f + t2 Sin If,
ds
dm
—Г— = —/ilti COS Ф — U2t2 Sill Ф,
ds
где угол ip отсчитывается в касательной плоскости от первого главного направления
ко второму. Кривизна нормального сечения в произвольно выбранном направлении с
учетом последних равенств и формул A.7.25) и A.8.4) определится равенством
dv dm , .о ,., „ _ч
// = —-—• -г- = их cos w + u2 sm ip. A.8.15)
ds ds
Формула A.8.15) называется формулой Эйлера. Она выражает кривизну произволь-
произвольного нормального сечения в точке через главные кривизны и угол между нормальным
сечением и первым главным направлением. Из этого равенства мы видим, что главные
кривизны поверхности Цх и fi2 являются максимальной и минимальной кривизнами
44
Гл. 1. Основы геометрического моделирования
соответственно. За определение главных направлений поверхности можно принять сле-
следующее: направления, для которых кривизна нормального сечения принимает макси-
максимальное и минимальное значение, называются главными направлениями поверхности.
Гауссова кривизна поверхности A.8.12) может быть использована для определения
поведения поверхности в некоторой ее точке М. Так как знаменатель в A.8.12) больше
нуля, то знак гауссовой кривизны зависит от знака числителя, т. е. от знака опреде-
определителя матрицы В. Если |В| > 0, то точка М называется эллиптической. Поведение
поверхности в эллиптической точке показано на рис. 1.8.2.
При движении от точки М в любом направлении поверхность изгибается или в
сторону нормали или в противоположную сторону в зависимости от знаков главных
Рис. 1.8.2. Эллиптическая точка поверхности
Рис.1.8.3. Гиперболическая точка поверхности
кривизн. Если |В| < 0, то точка М называется гиперболической. Поведение поверх-
поверхности в гиперболической точке показано на рис. 1.8.3. Так как в такой точке главные
кривизны имеют разные знаки, то согласно A.8.15) существуют такие нормальные
сечения, для которых выполняется равенство
Hi cos2 tp + Ц2 sin2 tp = 0.
Касательные к нормальным сечениям под углами
A.8.16)
tp = ±arctg J
A.8.17)
расположены в касательной плоскости симметрично относительно главных направле-
направлений и определяют асимптотические направления в точке М. Если в точке М |В| = 0, то
такая точка называется параболической. Поведе-
Поведение поверхности в параболической точке показано
на рис. 1.8.4.
В случае ц\ = Hi = 0 каждое из направлений
является асимптотическим. В противном случае
главным направлением является асимптотическое
направление, для которого кривизна равна нулю.
Соответствующее нормальное сечение в точке М
имеет точку распрямления.
Кривая на поверхности называется линией
кривизны, если касательная в каждой точке к ней
параллельна одному из главных направлений в
этой точке поверхности. Линиями кривизны часто являются координатные линии.
Пусть координатные u-линии и v-линии являются линиями кривизны. В этом случае
в каждой точке поверхности выполняются равенства
Рис. 1.8.3. Параболическая точка по-
поверхности
= &1 = &12 = &21 = 0
A.8.18)
1.8. Кривизна линий на поверхности 45
в силу ортогональности главных направлений. Справедливо и обратное утверждение:
если в каждой точке поверхности выполняются равенства A.8.18), то координатные
линии являются линиями кривизны. Действительно, в этом случае согласно A.7.28)
коэффициенты Ь\2 и &21 в разложении A.7.26) равны нулю и, следовательно, вдоль ко-
координатных линий производные нормалей коллинеарны производным радиус-вектора.
Третья квадратичная форма поверхности. Нормаль к поверхности, как и ее радиус-
вектор, есть функция параметров uuv. Модуль дифференциала нормали к поверхности
равен углу между нормалями в двух бесконечно близких точках, связанных параметри-
параметрическим смещением du и dv. Квадрат этого угла определяется равенством
dd2 — dm ¦ dm = mx ¦ mx du2 + 2m2 • mi dudv + m2 ¦ 1112 dv2. A.8.19)
Введем обозначения
/u = mi • mi,
/12 = /21 =mi-m2 = m2-m1, A.8.20)
/22 = П12 • Ш2-
Равенство A.8.19) примет вид
dm ¦ dm = fn du2 + 2/i2 du dv + /22 dv2. A.8.21)
В правой части A.8.21) мы получили квадратичную форму от du и dv. Эта квадратич-
квадратичная форма называется третьей основной квадратичной формой поверхности. Так
же как первая и вторая квадратичные формы она является характеристикой поверхно-
поверхности в заданной точке. Выражение A.8.21) можно записать в матричном виде
dm • dm = [du dv] ¦ F ¦ [du dv]T,
где F = , , — матрица третьей квадратичной формы.
[/21 J22J
Производные вектора нормали по параметрам поверхности ортогональны вектору
нормали. Дифференцируя равенства m • mi = 0 и m • Н12 = 0 по параметрам, получим
еще одно выражение для коэффициентов третьей квадратичной формы поверхности
m • mn — —mi • mi = —/11,
mm12 = -им m2 = -fn, ,1йТО
m-m2i =-m2-mi =-/21,
m • m.22 = -Ш2 ¦ m2 = —/22-
Таким образом, коэффициенты третьей квадратичной формы отражают проекции на
нормаль вторых производных вектора нормали.
Полученные нами три квадратичные формы связаны друг с другом уравнением.
Получим его. Для этого выразим производные радиус-вектора и нормали по. длине дуги
в произвольном направлении, определяемом в касательной плоскости углом if отно-
относительно первого главного направления, через касательные векторы главных сечений
ti и t2:
dr
— = ti COS If + t2 Sin If,
ds
dm .
—— = -|Xlti COS If — |X2t2 Sin ip.
ds
46 Гл. 1. Основы геометрического моделирования
Векторы
dm dr .
—г- + Й1Т" = (А*1 - №)Ь2 sm tp,
dm dr
1Г + М2 d~ = ^ ~ C°Sif>
коллинеарны главным направлениям, и, следовательно, ортогональны. Перемножив
скалярно эти векторы, получим уравнение, связывающее квадратичные формы поверх-
поверхности
dm • dm + (/xi + /i2) dm. ¦ dr + ц\Цъ dr • dr — 0
или
[du dv] ¦ (F +-(mi + Мг)В + /ii/i2G) • [du dv]r = 0. A.8.23)
Так как du и du в общем случае не равны нулю, то для выполнения соотношения A.8.23)
должно выполняться матричное равенство
F+ (/л +/i2)B + /ii|x2G = 0. A.8.24)
Это и есть уравнение, связывающее коэффициенты трех квадратичных форм поверхно-
поверхности. Из A.8.24) следует, что коэффициенты третьей квадратичной формы поверхности
выражаются через коэффициенты первой и второй квадратичных форм поверхности
соотношением
A.8.25)
1.9.* Тензоры поверхности
Далее мы рассмотрим уже известные нам квадратичные формы поверхности не-
несколько с другой точки зрения, а также получим новые связывающие их уравнения.
Квадратичные формы являются характеристикой поверхности в некоторой ее точке.
Если изменить параметризацию поверхности не изменяя поверхность, то изменятся
коэффициенты квадратичных форм, но останутся неизменными формулы определения
площади, главных направлений, главных кривизн, других характеристик поверхности
и уравнения, связывающие коэффициенты квадратичных форм. При изменении пара-
параметризации квадратичные формы ведут себя аналогично тому, как ведут себя векторы
при изменении пространственной системы координат, т. е. меняются описывающие их
числа, но не меняются связывающие их соотношения. По аналогии с векторами можно
считать, что коэффициенты квадратичных форм являются характеристиками некото-
некоторых объектов, связанных с поверхностью. Объекты, математические свойства которых
могут быть описаны упорядоченной совокупностью чисел, преобразующихся по опре-
определенному закону при переходе от одной координатной системы к другой, называются
тензорами. Операции над тензорами не зависят от системы координат, поэтому тен-
тензоры называют инвариантными геометрическими объектами. Они описываются сво-
своими компонентами, которых может быть довольно много, поэтому прежде чем уточнить
определение тензора, мы договоримся о символике записи сумм компонентов объектов.
Соглашение о суммировании по повторяющимся индексам. Многие из приведен-
приведенных выше формул примут компактный вид, если мы будем использовать соглашение
о суммировании по повторяющимся индексам. Для этого наряду с нижними ин-
индексами для некоторых величин будем использовать верхние индексы и смешанные
индексы. Так нижние индексы использовались нами для обозначения производных
радиус-вектора поверхности и коэффициентов основных квадратичных форм в выра-
выражениях A.7.9), A.7.22), A.8.21); верхние индексы использовались для обозначения
компонент матрицы G в A.7.30); смешанные индексы использовались в формулах
A.7.28).
1.9. Тензоры поверхности 47
Соглашение о суммировании заключается в том, что в выражениях выполняется
суммирование по повторяющемуся один раз снизу и один раз сверху индексу, при
котором индекс пробегает значения от единицы до размерности пространства.
Например,
з зз
i=l г=1 k=l
Индексы, по которым производится суммирование, называют немыми, а остальные ин-
индексы называют свободными. Немые индексы отсутствуют в одной из частей равенства.
Свободные индексы могут принимать значение номера одного из измерений простран-
пространства. Чтобы не путаться в индексах при большом их количестве, следует помнить о
трех правилах:
• свободные индексы по обе стороны знака равенства занимают одинаковые
позиции;
• индексы, по которым производится суммирование, встречаются один раз
вверху и один раз внизу и только в одной части равенства;
• индекс параметра, по которому выполняется дифференцирование, является
нижним.
Тензоры. Далее параметры поверхности и и v будем обозначать с помощью верх-
верхних индексов через и1 и и2, а их дифференциалы — через du1 и du2 соответственно.
Использование верхних или нижних индексов для компонент некоторого объекта отра-
отражает зависимости, по которым изменяются компоненты этого объекта при переходе от
одной системы координат к другой. Так при переходе от параметров и1 и и2 к пара-
параметрам и1' = «1'(и1, и2) пи2 = и2 (и1, и2) производные радиус-вектора поверхности
по новым параметрам будут связаны с производными радиус-вектора поверхности по
старым параметрам соотношениями
г=1
тогда как бесконечно малые приращения параметров будут связаны соотношениями
г=1 .
Закон преобразования компонент объекта при изменении системы координат и обусла-
обуславливает место написания его индексов. Обозначим коэффициенты матриц преобразо-
преобразования параметров через
А\. = ^г, A.9.3)
Ак' = — A9 4)
и запишем равенства A.9.1) и A.9.2), опустив знак суммы и используя вместо него
соглашение о суммировании
ге = А* к.ги A.9.5)
duk' - Ак'idu\ A.9.6)
где к' и i принимают значения 1 и 2.
Якобиан матриц преобразования A.9.3) и A.9.4) должен быть отличен от нуля.
Матрицы с компонентами A.9.3) и A.9.4) описывают однородные линейные преобра-
преобразования. При переходе к другой параметризации поверхности компоненты матриц G,
48
Гл. 1. Основы геометрического моделирования
В и G 1 изменяются по формулам
;k,n, =Aik'Ajn'gij,
A.9.7)
Ьк.п.=А'к.А*п.Ьц, A.9.8)
g*'"' =Ak'iAn'jgi>. A.9.9)
Тензорами называются объекты, компоненты которых при изменении системы коорди-
координат подвергаются линейным однородным преобразованиям, причем матрица преобра-
преобразования для каждого нижнего индекса составлена из производных A.9.3), а матрица
преобразования для каждого верхнего индекса составлена из производных A.9.4). Ко-
Коэффициенты первой основной квадратичной формы играют особую роль — они явля-
являются компонентами метрического тензора двухмерного пространства поверхности.
Этот метрический тензор может быть представлен своими ковариантными компонен-
компонентами в виде матрицы G A.7.10) или своими контравариантными компонентами в
виде матрицы G A.7.30). Тензор, представленный своими ковариантными ком-
компонентами, называется ковариантным тензором. Ковариантные компоненты имеют
нижние индексы. Тензор, представленный своими контравариантными компонентами,
называется контравариантным тензором. Контравариантные компоненты имеют верх-
верхние индексы. По количеству индексов у компонент тензору приписывают ранг. Так
метрический тензор является тензором второго ранга.
С помощью коэффициентов метрического тензора производится «поднятие» и «опус-
«опускание» индексов компонент других объектов этого пространства, что уже осуществля-
осуществлялось равенствами A.7.28) и A.7.27), связывающим коэффициенты Ък и 6^:
bik=bijg>k, A.9.10)
Ьц = bikgjk. A.9.11)
¦ В первом равенстве суммирование производится по индексу j, и объект выражается
через смешанные компоненты Ь, , которые получаются из 6у заменой индекса j на
индекс, стоящий рядом с индексом j в компоненте метрического тензора gik. Во втором
равенстве мы получили ковариантные компоненты bij объекта через его смешанные
компоненты bt , а суммирование выполняется по индексу к.
Верхние и нижние индексы являются равноправными. Векторы г^ггит образуют
местный базис в заданной точке поверхности, по которому можно разложить любой
другой вектор в этой точке. Базис ri, Г2, m называется касательным, так как его
Касательная
плоскость
Рис. 1.9.1. Касательный и взаимный базисы поверхности в точке
первые два вектора направлены по касательным к координатным линиям поверхности.
Введем еще один базис, по которому также можно разложить любой другой вектор в
этой точке. Этот базис представлен векторами г1, г2 и т. Он называется взаимным
1.9. Тензоры поверхности 49
упомянутому базису, и определяется равенствами
г1г1 = 1, г1т2=0, г1-т = О,
г2-Г1=0, г2-г2 = 1, г2-т = 0.
Векторы г1 и г2 лежат в касательной плоскости, их ориентация показана на рис. 1.9.1.
Векторы г1 и г2 определим равенствами
г
1 _
г2 х (гг х г2) _ (г2 •г2)г1 - (г2 -ri)r2
y/g ~ g g
2 _ Г1 Х m _ rt X (rt X Г2) _ (Г1 -Г2)Г1 -
sfg К ~ ё
Эти равенства можно получить другим способом: разложить векторы г1 и г2 по векторам
Г1 и гг аналогично тому, как были разложены производные нормали mi и т2 в A.7.26),
и найти коэффициенты разложения, что в результате даст
r*=g«r«.
Умножив скалярно векторы взаимного базиса, получим выражение для контравариант-
ных компонент метрического тензора поверхности
g**=r*TV A.9.13)
Формулы Гаусса и Петерсона-Кодацци. Найдем разложение вторых производных
радиус-вектора поверхности г у по местному базису поверхности в этой же точке, пред-
представленному векторами ri, г2 и т. Для этого запишем их в виде
тц = Гу*г* + bijtn, A.9.14)
где Гц — неизвестные пока коэффициенты разложения векторов гч- по векторам г*.
Коэффициенты разложения векторов Гц- по вектору m равны коэффициентам второй
квадратичной формы Ьц, так как при скалярном умножении A.9.14) на m мы должны
получить равенства A.7.21). Умножим A.9.14) скалярно на Г] и гг и получим систему
уравнений для Гц*
Гу gii + Гц- g12 = Гц, 1,
г 1„ , г 2 r (l.y.lSj
J-У g2l + АЧ #22 = Mj1^,
где введено обозначение Гц, i = гц- -ri и Гц-,2 = гу- -Гг. Коэффициенты Гц-д могут быть
выражены через производные коэффициентов первой основной квадратичной формы.
Для этого выпишем известные равенства
Ij • rfc = gjk, rk-Ii= gki, Tt • Tj = gy-.
4 — 5293 Голованов
50 Гл. 1. Основы геометрического моделирования
Эти равенства выражают одно и то же, просто в них циклически переставляются ин-
индексы г, j, k, которые могут принимать значения от единицы до размерности простран-
пространства. Продифференцируем первое равенство по мг, второе — по vj, третье — по и* и
получим
т^тк +TrTkt = , Гкг + Гк.Т1 = , rk.r+r.rk
Если сложим первые два равенства и вычтем из них третье, то получим формулу для
определения коэффициентов Г^д
1 (dgkj dgik dgiA
Гу,* - о ~я~Г + 1ГТ ~~ 7ГТ • A.9.16)
2 \ oul оы,з оик)
Теперь решим систему уравнений A.9.15) относительно Г у- и получим равенства
V УI у, 2
о о
г 2 _ Slip Й1Г _ _12р , _22г
l.j — iij,2 lij.l — В l»i,l +ёГ 1 ij, 2 -
О О
С использованием соглашения о суммировании последние равенства и равенства A.9.15)
примут вид
ryn = gn*ri>>fc, A.9.17)
Г«,„=а„Г«*. A.9.18)
Подставим в последние равенства значения A.9.16) и получим окончательное выраже-
выражение для коэффициентов в разложении A.9.14)
Ы1 dui
Коэффициенты Tijtk называются символами Кристоффеля 1-го рода, а коэффици-
коэффициенты Tijk — символами Кристоффеля 2-го рода. Они выражаются через коэффици-
коэффициенты первой основной квадратичной формы поверхности и их частные производные по
параметрам. Символы Кристоффеля не являются компонентами тензора.
В A.9.14) мы выразили производные векторов Гх и г2 по параметрам. Формулы
A.9.14) называются деривационными формулами Гаусса. Совместно с деривацион-
деривационными формулами Вейнгартена A.7.26) они представляют собой деривационные фор-
формулы для локального базиса г\, гг, m на поверхности. Перепишем их в виде
1 1 2
7J—т = Гц Ti + Тц Г2 + Oijin,
Р-. = 1УГ1 + Г2Д2 + b2im, A.9.20)
аи1
dm _ j 2
ди1
Эти формулы аналогичны формулам Френе-Серре A.5.17) для кривых. Они выражают
производные векторов локального базиса ri, r2, m в виде разложения по самим этим
векторам. Дифференцируя формулы A.8.9) еще раз и пользуясь имеющимися разложе-
1.9. Тензоры поверхности 51
ниями первых производных, можно получить вторые производные локального базиса,
а за ними — третьи производные и так далее. Например, вторые производные вектора
нормали равны
r bkr
rk - bikbkjnx. A.9.21)
Найдем разложение производных векторов г1 и г2 по взаимному базису поверхности
в этой же точке, представленному векторами г1, г2 и т, дифференцированием формул
A.9.12)
дг1 1 1 1 dg
—-г = r2i x т— + r2 x mi— - r2 x m=
dul y/g уД
= ^r2ifcrfc x m - -=Ь{кт2 x rfc - rlrkik =
= -Ги'г2 + T2i2rl + bi'm - tHTu1 + T2i2) = -Гц1^ - Гз^г2 + Ь^т,
дт2 111 dg
^-т = -гн x m—r - n x m.i— + n x m-—p^-7 -
dul y/g y/g 2gy/gdul
= 7ГГ1Д* x m+ —bikn x г* -T2Tkik =
уД уД
= Tu1*2 ~ Tu'r1 + 6,2т - ^(Гг,1 + T2i2) = -Г^т1 - T2i2r2 + 6,2т,
где использовались деривационные формулы A.9.20) и равенство
^U]V+]V = rfcA A.9.24)
Равенство A.9.24) следует из соотношения
= 2grn • (g11^ + ^2г2) + 2gr2i • (g22^ + g21^) = 2grji ¦ rfcg« = 2grfcifc. A.9.25)
Мы получили деривационные формулы для взаимного базиса г1, г2, m на поверхности,
выражающего производные векторов взаимного базиса г1, г2, m в виде разложения по
самим этим векторам
4
^! = _rli2r1-r2i2r2 + 6i2m, A-9.26)
oul
dm , 2
— = -&iiri-6i2r2.
Функции gij(ux, u2) и bij{ul, u2) однозначно определяют поверхность с точностью
до положения и ориентации в пространстве, аналогично тому, как функции s(t), k(t) и
X(t) определяют кривую. Функции g^u1, u2) и ^(и1, и2) не являются независимыми,
4*
52 Гл. 1. Основы геометрического моделирования
они связаны между собой уравнениями, которые мы получим ниже. Дифференцируя
равенство A.9.14) по одному из параметров, получим вторую производную вектора ri
k
«Tkn
T + Гу'Гь,™ - bljbn-j rm+(^+ Гц'Ььп j m. A.9.27)
Изменим последовательность дифференцирования вектора rj в A.9.27), что приведет к
смене мест индексов п и j:
d2n dvink k dbin
Wd^ = ~^TTk + Tin Tkj + s^m+binmj =
(яр m \ / ai \
„ . +1 in 1 *j — Oin&j I rm + I -x-j + 1 in bkj I m. (l.y.zej
Левые части равенств A.9.27) и A.9.28) равны, следовательно, должны быть равны и
правые их части. Вычитая A.9.28) из A.9.27), получим равенство
яр m a-p
=0- (L9-29)
Так как в обыкновенной точке векторы ri, гг, m некомпланарны, то для выполнения
векторного равенства A.9.29) должны выполняться следующие соотношения
яр "» яр. m
~~q% Q 3 ij kn ~ in kj = °4°n ~ "inbj , A.9..3O)
Эти уравнения связывают между собой коэффициенты первой и второй основных
квадратичных форм поверхности. Уравнение A.9.30) называется уравнением Гаусса.
Уравнения A.9.31) называются уравнениями Петперсона-Кодацци. Правая часть ра-
равенства A.9.30) является тензором, следовательно, и его левая часть также представляет
собой тензор. Этот тензор называется тензором кривизны или тензором Римана и
обозначается
яр. т яр. го
и го _ ui- г] UL т -р т-р к р гор к /¦> Q oo\
HJi ^^ Ш~ + 1к i ~1^' li A.9.32)
Умножим обе части уравнения Гаусса на gmi и, произведя суммирование, опустим в
нем верхний индекс
Ч ^ + Тк^Тчк ~ ГшГгп" - ЪцЬщ - binbji. A.9.33)
Аналогично получим ковариантные компоненты тензора кривизны
1.9. Тензоры поверхности 53
В силу симметрии символов Кристоффеля по первым двум индексам тензор кривизны
A.9.34) обладает определенной симметрией, он кососимметричен по первой паре индек-
индексов и по второй паре индексов: Rjnu = Rujn — —RnjU = —Rjnii- Для поверхностей
равенство A.9.34) эквивалентно одному равенству
о* 11,2 _ Я*- 12,2 р _fc__ pfc_ h h —h h — A9 Vti
du2 du1 ' ' 1 >22
Мы использовали равенство A.8.12) для гауссовой кривизны поверхности. Таким обра-
образом, гауссова кривизна поверхности может быть определена через коэффициенты пер-
первой квадратичной формы и их производные. Уравнения Петерсона-Кодацци A.9.31)
сводятся к двум уравнениям
як як
-Ги*Ьи> A.9.36)
г fc, дЪ21 к . .
- Г21 frfc2 = — - Г22 Ьк1. A.9.37)
Если над тензором кривизны A.9.32) выполнить операцию свертки по индексам п
и т, то мы получим ковариантные компоненты тензора Риччи
Rji = RjUl + Rj2i2 = Rjnin = bijbnn - binbjn = (bijbnk - binbjk)tfn. A.9.38)
Операция свертывания заключается в том, у тензора выбираются два индекса, один
верхний, другой нижний, и выполняется суммирование всех компонент тензора, в ко-
которых два выбранных индекса имеют одинаковые значения. Так как для поверхностей
индексы принимают значения 1 и 2, то ковариантные компоненты тензора Риччи по-
поверхности равны
Найдем уравнения, которым должна удовлетворять геодезическая кривая на по-
поверхности и1 = u1(s), и2 = u2(s), где s — длина дуги кривой. По определению,
проекция вектора кривизны геодезической кривой кп на касательную плоскость к по-
поверхности должна быть равна нулю. Найдем вектор кривизны произвольной кривой
на поверхности
г f du \ „ du du I du \ du du
fcn = -r-r =
=гц [j\ +2n2jг+г22 Ij I +ri7T+r2 ,2
ds2 \ ds ) ds ds \ ds } ds2 ds2
dul duj d2uk „ fc dul duj &ик , du%
+ Г Ь
= Tii1—T + Тк^ГТ = г*Гу —T~ + Тк^ГТ + тЬч1~1Г- С1-9-39)
J ds ds ds2 ds ds ds2 ds ds
По определению, вектор геодезической кривизны равен проекции вектора кривизны
кривой на касательную плоскость к поверхности, т.е. он равен вектору
kdudu^\
ds as J
d2uk
ds2 ds as
откуда следует, что координатные функции ul(s), i = 1, 2, геодезической кривой долж-
должны удовлетворять уравнениям
?? V^=0. A.9.40)
ds ds
54 Гл. 1. Основы геометрического моделирования
Сама геодезическая кривизна линии на поверхности равна длине вектора геодезической
кривизны q, приведенного выше.
Для моделируемых нами поверхностей будет известна их векторная функция. От
нас будет требоваться умение получить всю необходимую информацию о поверхности
по ее радиус-вектору. Выпишем полученные выше равенства, выразив все величины
через радиус-вектор поверхности и его производные. Итак, задана векторная функция
г двух параметров iiv и и*, принимающих ¦аниченин ¦на свканой. cfovacra С1*.
r = r(u1,u2), и1, и2 G П.
По ее производным найдем вектор нормали, взаимный базис и коэффициенты квадра-
квадратичных форм:
дт
_ ri хг2 ! _ г2хш 2 m х п A.9.41)
т— — , г — р—, г — ——,
у/ё VS уД
^ = -т; • г-»'
г-».
По вторым и третьим производным найдем символы Кристоффеля и деривационные
формулы базисов поверхности в заданной точке
Tik ~
bikm' rik = ^ = ~TkjirJ
A.9.42)
В равенствах A.9.41) и A.9.42) верхние и нижние индексы принимают значения
от 1 до 2. Вся необходимая информация о поверхности может быть получена на основе
равенств A.9.41) и A.9.42) при известной векторной функции A.7.1). Из них мы
видим, что для описания поверхности требуются производные ее радиус-вектора до
третьего порядка включительно.
1.10.* Криволинейные координаты
Наряду с декартовыми прямоугольными системами координат можно использовать
и другие в общем случае криволинейные координатные системы. Такие координатные
системы нужны также в неевклидовых пространствах. В криволинейной системе коор-
координат при дифференцировании векторных функций приходится учитывать изменение
базисных векторов системы, что значительно усложняет описание геометрических объ-
объектов. Но в определенных случаях криволинейные координаты удобнее, чем декартовы.
Мы уже сталкивались с двухмерной криволинейной системой координат, которая стро-
строилась по параметрическим линиям на поверхности. Мы вынуждены были ими поль-
пользоваться, так как в общем случае на криволинейной поверхности невозможно постро-
построить единую двухмерную декартову прямоугольную систему координат. Мы рассмотрим
1.10. Криволинейные координаты
55
криволинейные системы координат, чтобы знать, какие трудности нас ожидают при
их использовании и чтобы уметь эти трудности преодолевать. Так как геометрические
объекты не зависят от системы координат, то для их описания можно построить и
использовать математический аппарат, инвариантный по отношению к системе коор-
координат.
Пусть мы имеем в распоряжении эталон единицы длины и инструмент для измере-
измерения углов. С их помощью в той точке пространства, в которой мы находимся, можно
построить декартову прямоугольную систему координат с началом в этой точке и ба-
базисом ei, ег, ез. Координаты точек в ней обозначим через х1, х2, х3. Пусть имеются
непрерывные дифференцируемые и однозначные функции
u1=ul(xl,x2,x3), u2 = u2{x\x2,x3), u3 = u3(x\x2,x3), A.10.1)
такие, что обратные им функции
х1 =xl(u1,u2,u3), x2=x2(u\u2,u3), x3 =x3{ul,u2,u3)
A.10.2)
также являются непрерывными дифференцируемыми и однозначными. Потребуем,
чтобы определитель матрицы Якоби системы A.10.2) был отличен от нуля:
A.10.3)
дх1
ди1
дх2
ди1
дх3
ди1
дх1
ди2
дх2
ди2
дх3
ди2
дх1
ди3
дх2
ди3
дх3
ди3
Если один из параметров в A.10.2) зафиксировать (иг = const), то мы получим некото-
некоторую поверхность в пространстве, которую назовем поверхностью г-й группы. Функции
A.10.2) должны быть такими, чтобы поверхности одной группы не пересекались друг
с другом. В этом случае параметры и1, и2, и3 могут служить координатами точек в
рассматриваемом пространстве. Поверхность г-й группы называют i-й координатной
поверхностью, а линии пересечения координатных поверхностей разных групп назы-
называют координатными линиями.
Метрический тензор. В каждой точке Щи1, и2, и3) пространства можно построить
локальную систему координат с началом в данной точке и базисными функциями п,
гг, г3, определенными следующим образом:
,. R{u1+Su1,u2,u3)-R{u1,u2,u3)
ri = lim —: ,
Su1-*!) OU1
.. R{u1,u2 + 8u2,u3)-R{u1,u2,u3)
Г2 = iim —
A.10.4)
= lim
Rju1, u2, u3+Su3) - R(u\ и2, и3)
Su3
В силу A.10.3) векторы ri, Г2, гз некомпланарны и могут быть использованы в качестве
базиса для разложения по нему любого другого вектора в этой точке пространства. Этот
базис будем называть касательным базисом. Базисные векторы п, г2, г3 в каждой
точке различны, и поэтому по ним можно производить разложение только тех векторов,
которые вычислены в этой же точке пространства. Базисный вектор г* направлен
по касательной к k-й координатной линии в данной точке, его длина в общем случае
56 Гл. 1. Основы геометрического моделирования
отлична от единицы. Квадрат длины бесконечно малого отрезка, заданного бесконечно
малыми приращениями координат du1, du2, du3, равен
ds2 = Ti ¦ Tj du1 dui = дц du1 duj.
Коэф фициенты
gij=gij(u1,v2,u3)=ri-ri, t, .7 = 1,2,3 A.10.5)
являются коеариантными компонентами метрического тензора в точке Щи1 ,и2,и3).
При переходе к другой криволинейной системе координат и1 , и2 , и3 ковариантные
компоненты метрического тензора д/.п' в новой системе координат связаны с компонен-
компонентами gij соотношениями
. gk,n, = А*к>А>п.^,
где
Аг _ Я"*
А к' ~
Аналогичными соотношениями связаны и базисные векторы криволинейных систем
rfc*=AW A.10.6)
Матрицу, составленную из ковариантных компонент метрического тензора, будем обо-
обозначать через G, как и матрицу коэффициентов первой квадратичной формы поверх-
поверхности. Обратную ей матрицу будем обозначать через G.
Для касательного базиса ri, гг, гз в каждой точке можно построить взаимный базис
г1, г2, г3 по правилу
г4-г* = *,-«, A.10.7)
где 6ik — символы Кронекера, они принимают значения 6th = 1 при i = к и 6ik = О
при г ф к. Для нахождения векторов взаимного базиса представим их в виде разложе-
разложения по касательному базису с неизвестными коэффициентами. Из приведенных выше
условий получим систему линейных алгебраических уравнений относительно искомых
коэффициентов. После ее решения получим коэффициенты разложения векторов вза-
взаимного базиса по векторам касательного базиса
rfc = g*'ri, A.10.8)
где g*1 — коэффициенты матрицы G. Коэффициенты g*1 = rfc • гг называются кон-
травариантными компонентами метрического тензора, заданного в системе коор-
координат и1, и2, и3. При переходе к другой криволинейной системе координат и1 , и2 , и3
контравариантные компоненты метрического тензора g"J в новой системе координат
связаны с компонентами g*1 соотношениями
где
Л * ~ ди* •
Аналогичными соотношениями связаны и векторы взаимных базисов криволинейных
систем
г*' = Аг'кгк. A.10.9)
Так как G является обратной матрицей G, то их произведение равно единичной
матрице, откуда следует, что смешанные компоненты метрического тензора равны
функции 8ih
д.. Jk _ к _ rfc
6ij6 — bi — °i ¦
1.10. Криволинейные координаты 57
Векторы взаимного базиса и касательного базиса связаны соотношениями
1 _ Г2 ХГ3 2 _ Г3 ХП з _ Г1
/ ' / '
y/g ' y/g ' y/g ' A.10.10)
, г2=г3хг11Д, r3=r1xr2v/g,
где g равен определителю матрицы G. Последние соотношения можно записать в виде
i X Г
7f
¦ г, Ti X Tj ¦
— е , ц - ец/.г х ,
или
Ti x Tj =
y/g
где используются символы Леей- Чивитпа еч* и e^k ¦ Величины еч* и e^k равны 0, если
в среди индексов встречаются одинаковые; равны 1 для последовательности индексов
1, 2, 3 и получающейся из нее круговой перестановкой последовательностей 2, 3, 1 и
3, 1, 2; равны —1 при нарушении этого порядка (для последовательности индексов 3, 2,1
и получающейся из нее круговой перестановкой последовательностей 2, 1, 3 и 1, 3, 2).
В криволинейной системе координат произвольный вектор а может быть разложен
по касательному или взаимному базису и представлен в виде
а = aJTj = (цг*.
Результатом операции скалярного произведения векторов а и b является число, которое
в зависимости от представления векторов равно
a b = (JVg^ = aibjgi = а% = аф\ A.10.11)
Их векторное произведение может быть представлено в виде
а х b = а1Ъ>eiiky/gTk = aibjei:>k?jz, A.10.12)
где использовались равенства
eijk— = (т1 хт*)-тк, eijky/g= (т{ xr;)-rfc.
Величины
еЦк _ еИк— = (г< х jJ). rfc, eijk = eijky/g= (Г< х г,-) • rfc
y/g
являются соответственно контравариантными и ковариантными компонентами тен-
тензора Леви-Чивита.
Символы Еристоффеля. Найдем изменение векторов касательного базиса при перехо-
переходе из точки Щи1 ,и2, и3) в бесконечно близкую к ней точку R\(ul +5и1 ,и2+8и2, и3+6и3).
С точностью до линейных слагаемых относительно Sul, i — 1, 2, 3 изменение базисных
векторов можно представить в виде
Дг, = 0^ = TijSu* = Гцкгк6и\ A.10.13)
58 Гл. 1. Основы геометрического моделирования
где Tij —неизвестные пока коэффициенты разложения производных Гц касательного
базиса по самому базису ri, г2, гз. Умножив равенство
скалярно на ri, гг и гз, получим систему уравнений для Гц
Гц^21 + Tij2gm + rij3g23 = Гу,2 = Tij ¦ Г2, A.10.15)
^i/Ssi + Pi/?32 + Гц g33 = Гц, 3 = Гц • Г3.
Коэффициенты Fijt k = Гц • rjt могут быть выражены через производные ковариантных
компонент метрического тензора. Для этого выпишем известные равенства
rj ' rfc = gjfc. rjfcTi=gfci, Ti-Tj=gij,
в которых циклически переставляются индексы i, j, k; индексы могут принимать зна-
значения от единицы до размерности пространства. Продифференцируем первое равенство
по иг, второе — по и-7, третье — по ик и получим
Tji-Tk+Tj-Tki = -^ Гу1\ + ГТу = -^ Tik-Tj+Ti-Tjk = -^
Если сложим первые два равенства и вычтем из них третье, то получим формулу для
определения коэффициентов Гц-д
Skj ,dgik dgiA (тты)
+ ) (L1016)
Теперь решим систему уравнений A.10.15) относительно Гц и получим равенства
Г«п = «"%¦,*. A.10.17)
Саму систему A.10.15) перепишем в виде
rij,n=gnkrijk. A.10.18)
Подставим в A.10.17) равенства A.10.16) и получим окончательное выражение для
коэффициентов в разложении A.10.13)
~2^ \dv> + Bui ди*)- ( °
Коэффициенты Гц-jt называются символами Кристоффеля 1-го рода, а коэффициенты
Гу* называются символами Кристоффеля 2-го рода. Они выражаются через компо-
компоненты метрического тензора и их частные производные по криволинейным координа-
координатам. Символы Кристоффеля не являются компонентами тензора. Как можно заме-
заметить, соотношения A.10.15)—A.10.19) идентичны соотношениям A.9.15)—A.9.19) для
оболочек с той лишь разницей, что размерность пространства параметров оболочки на
1.10. Криволинейные координаты 59
единицу меньше. Мы использовали те же обозначения для компонент метрического
тензора, символов Кристоффеля, касательного и взаимного базиса. Все полученные
для них соотношения справедливы для пространства любой размерности.
Векторная функция. В декартовой прямоугольной системе координат компоненты
радиус-вектора точки равны координатам этой точки пространства. В криволинейной
системе понятие; радиус-вектора как преобразования, переводящего начальную точку
координатной системы в заданную точку пространства, теряет смысл.
Линию в криволинейной системе координат можно описать как совокупность функ-
функций u1 = ux(i), u2 = u2(t), u3 — u3(t) параметра t. Пусть приращению St параметра
кривой соответствуют приращения координатных функций Su1, Su2, Su3. Тогда вектор
TiSu1 + гг<5и2 + гзби3 будет направлен по касательной к кривой. Если поделить его на
St и устремить St к нулю, то в пределе мы получим вектор производной кривой
^ = а*(«)г<. A.10.20)
Производная кривой представляет собой векторную функцию параметра t.
Поверхность в криволинейной системе координат может быть описана как совокуп-
совокупность функций и1 — и1 (и, w), и2 = u2(v, w), и3 — u3(v, w) двух параметров v я w.
Касательные к «-линиям и ui-линиям поверхности векторы обозначим через v и w.
Эти векторы определяются равенствами
du%{v, w) .
v{v, W) = ? Г, = V%{V, W)Vi,
av
dul(v, w) i
w(u, w) = —-^ r, = w%{v, w)Ti,
и представляют собой векторные функции параметров поверхности. Свойства поверх-
поверхности могут быть определены с помощью кривых на ней, поэтому далее мы будем
исследовать некоторую векторную функцию а(?) параметра t.
При вычислении производной векторной функции нужно учитывать то, что базис-
базисные векторы в каждой точке пространства в общем случае различные. В декартовой
системе координат базисные векторы во всех точках пространства одинаковы по вели-
величине и направлению, поэтому при дифференцировании они выступают в роли констант.
Пусть изменению параметра St кривой соответствует приращение координат Su1, Su2,
Su3. Найдем приращение векторной функции а(?), связанной с этой кривой. Потре-
Потребуем, чтобы максимальная из величин Su1 стремилась к нулю при St —> 0. Приращение
векторной функции в местном базисе точки uL(i), u2(t), u3(t) равно
Ja = a(t + St) - a(t) = аг(* + St){n + Srt) - а*(*)г4 = a*{t + St){n + Ti:ikrkSuj) - аг(г)г*.
Поделив это равенство на St и устремив St к нулю, получим формулу для производной
векторной функции
Вьфажение
4
называется абсолютной или ковариантной производной контравариантных компо-
компонент векторной функции в направлении кривой ux(f), u2(t), u3(t).
60 Гл. 1. Основы геометрического моделирования
Касательный базис и взаимный базис в некоторой точке пространства равноправны,
поэтому вектор a.(t) кривой может быть разложен также по взаимному базису в точке
кривой
a(i) = aiTj, A.10.23)
где a,i — ковариантные компоненты вектора а. Для вывода производной а(?) в данном
представлении нужно знать, как меняются векторы взаимного базиса при переходе из
точки Щи1, и2, и3) в бесконечно близкую к ней точку /?i(u1 + SU1, и2 + 8и2, и3 +5и3).
Дифференцируя равенства A.10.7), получим
- -— -г* - -Г--Пг . г*--Г--* П 10941
> ~ du* 1ц г„ г - 1Ч , A.10.24)
откуда следует, что — Гу* являются коэффициентами разложения производных drk
по взаимному базису
Я-fc
Г*' = h= ~Fijkri- A10-25)
Действительно, если мы скалярно умножим равенство A.10.25) на г^, то получим ра-
равенства A.10.24). Таким образом, с точностью до линейных слагаемых относительно
6и3 изменение векторов взаимного базиса равно
6rk = ^-jSuj = -Гу V^'. A.10.26)
Используя покомпонентное представление A.10.23), получим формулу для производной
векторной функции кривой
{ dui _ dm , tdu^ _ (dot псЫ\ { .
~aiTki Tk~dT ~ ~dTT ~anTij r dt -\dt~anTij dt)T- {1Ж27)
da
Выражение
dt dt n lJ dt
называют абсолютной или ковариантной производной ковариантных компонент век-
векторной функции в направлении кривой и1 (?), u2(t), u3(t).
Как можно видеть, производная векторной функции представляет собой также век-
векторную функцию. Дифференцируя представления
da Dai „¦ da Da1
dt dt dt dt
и, используя формулы A.10.21) и A.10.27), можно получить для векторной функции
а(?) производные более высокого порядка.
Параметр t кривой определяет некоторую точку пространства, поэтому компоненты
векторной функции зависят от координат точек, через которые проходит кривая. Пред-
Представим, что в каждой точки пространства задана векторная функция а(их, и2, и3). Та-
Такая векторная функция определяет в пространстве векторное поле.
Ковариантные производные. Найдем изменение векторного поля при переходе из
точки Щи1, и2, и3) в бесконечно близкую к ней точку вдоль одной из координатных
линий. Пусть этому переходу соответствует изменение координаты и-7 на бесконечно
1.10. Криволинейные координаты 61
малую величину Su^. Приращение векторного поля в представлении через контрава-
риантные компоненты а(и1, и2, и3) = aVj с точностью до линейных по 6и^ членов
равно
х da% ¦ i dvi -
6a = ^—Su^Ti + аг—6и3.
Поделив обе части этого равенства на 8и3 и устремив 5и3 к нулю, получим формулу для
производной векторного поля в представлении через контравариантные компоненты
да _ da* t k _ f да*
Выражение
Vjo} = —^-7 + апТп/ A.10.30)
называется ковариантпной производной контравариантных компонент векторного поля.
Приращение векторного поля в представлении через ковариантные компоненты
а(и1, и2, и3) = п{Г* с точностью до линейных по 5и3 членов равно
дть , ,
Отсюда получим формулу для производной векторного поля в представлении через ко-
ковариантные компоненты
Выражение
Vjui = аЭ ~anTljn A.Ю.32)
называют ковариантпной производной ковариантных компонент векторного поля.
Итак, нами получены формулы A.10.22) и A.10.28) для вычисления производных
вектора кривой а(?) по параметру t в произвольной криволинейной системе координат.
Формулы A.10.22), A.10.28), A.10.30), A.10.32) представляют собой аппарат абсо-
абсолютного дифференцирования, который дает формулы вычисления производных век-
векторных функций в любой системе координат. Ценой универсальности этого аппарата
является необходимость вычисления производных базисных векторов по координатам
выбранной системы координат. Для вычисления производной вектора нужно знать его
разложение по касательному или взаимному базису точки, в которой он задан.
Покажем, что компоненты метрического тензора можно выносить из-под знака ко-
вариантной производной Vj. Дифференцируя равенства gki = rk • г^ и g*s = г* • гг и
используя A.10.14) и A.10.25), получим выражения для производных компонент ме-
метрического тензора
d8ki = ^JV + g^iV, (i-ю.зз)
= -в*пГп,-'-8пТ„/. A.10.34)
auJ
62 Гл. 1. Основы геометрического моделирования
Подставив в равенство A.10.30) соотношения a1 = ^kak и A.10.34), получим
. A.10.35)
Во время преобразований мы меняли обозначение немых индексов. Это вполне до-
допустимо, так как немой индекс не входит в результат и, следовательно, может быть
обозначен любой буквой. Аналогично подставив в равенство A.10.32) соотношения
ai = Sikak и A-Ю.33), получим
= Sikib + ""sniTki11 = &*?? + a"r«/ = a*vJ° • AЛ0-36)
Из равенств A.10.35) и A.10.36 ) следует вывод о том, что компоненты метрического
тензора можно выносить из-под знака ковариантной производной.
1.11.* Тензоры в криволинейных координатах
В криволинейных координатах мы рассмотрим понятие тензора — объекта, опера-
операций над которым не зависят от координатной системы. Одним из тензоров является
метрический тензор. Компоненты первой квадратичной формы поверхности являются
компонентами метрического тензора параметрического пространства поверхности. При-
Примерами тензоров могут служить тензор деформации и тензор напряжений сплошной
среды, тензор инерции твердого тела, тензор кривизны пространства. Тензоры, за-
заданные для каждой точки некоторой области пространства, образуют тензорное поле.
Тензоры описываются своими компонентами.
Криволинейная поверхность представляет собой двухмерный аналог искривленного
пространства. Продолжим аналогию между трехмерным пространством и поверхно-
поверхностью — представителем двухмерных пространств. Если нам известны компоненты
метрического тензора как функции используемой системы координат, то мы можем
по ним выполнить исследование некоторых свойствах самого пространства, в частно-
частности его кривизны. Выше мы рассмотрели тензор кривизны поверхности. Компоненты
аналогичного тензора можно вычислить и для трехмерного пространства.
Тензор кривизны. В искривленных пространствах последовательность дифферен-
дифференцирования по координатам в общем случае играет роль. При изменении последова-
последовательности дифференцирования появляются дополнительные слагаемые. Пусть дана
некоторая векторная функция а = щ{и1, и2, и3)г\ Рассмотрим некоторую поверхность
й1 = ul(t, w), i = 1, 2, 3 в пространстве. Всегда можно выбрать поверхность так,
чтобы она проходила через любую заданную точку или линию. Вычислим абсолютный
дифференциал ?>^а векторной функции при бесконечно малом смещении из точки и1,
2 ч 1 dul ., 2 9и2 , . 8и3 ,
и , и° в точку и Н——— at, и Н—^— at, и Н—^— at вдоль поверхности в направлении
от at at
первого ее параметра
I1 - а"г'
1.11. Тензоры в криволинейных координатах 63
Аналогично вычислим абсолютный дифференциал Dwa векторной функции при беско-
19ч 1 du1 , 9 2
нечно малом смещении из той же точки и , иА, и в точку и + —— dw, и
dw
з 0«3 .,
и3 + —— dw вдоль поверхности в направлении второго ее параметра
dw
Полученные дифференциалы можно также рассматривать как векторные функции тех
же параметров в той же точке. Вычислим теперь дифференциал векторной функции
Dta. вдоль поверхности в направлении второго ее параметра и дифференциал векторной
функции Dwa вдоль поверхности в направлении первого ее параметра
f d2aj дап пди) dTjj11 ди* „
~ \dtdw dw ij dt пп dw at a" ij
f
\dtdw dw ij dt пп dw at a" ij dtdw
дап пдиг
n dt dw unlij
\dwdt dt li dw n dt dw unlij dwdt
dan ndW mdui Ж\;
" dw Tir ~m + amTni ~b~w~Tir dt )r dwdt
Полученные выражения отличаются тем, что в них переставлены местами производные
по t и по w. Первые и четвертые слагаемые обоих выражений равны. Второе слагаемое
первого выражения равно пятому слагаемому второго выражения (если немой индекс г
переобозначить через j). Вычтем из первого выражения второе и получим (используя
возможность переобозначения немых индексов)
rldwdt =
Ц±1% + агоГп,^1
dw dt dt
ijn du* _ mdu?_ ndur
dt dw dw dt
u*dW fdTirn
- ГкгпГу* ) ^-^-апг{ dwdt =
in-lhlba™dwdtvi> A-11-1)
64 Гл. 1. Основы геометрического моделирования
где введено обозначение
яг. п ЯГ-™
--^T+rkj Tir -Vkr Tij . A.11.2)
Коэффициенты Rrjin являются компонентами тензора кривизны пространства. Тен-
Тензор кривизны называют тензором Римана. Он зависит лишь от точки пространства,
в которой вычислен.
Если в качестве поверхности иг = ul(t, w) взять одну из координатных поверхно-
поверхностей и1 = их(и2, и3), и2 = и2(и3, и1), и3 = u3(ux, и2), проходящую через рассматри-
рассматриваемую точку, то выражение A.11.1) примет вид
DrDjsi - DjDra = Rrj^anT1 dur duj, A.11.3)
так как dw = dur и dt = duK Левая часть A.11.3) называется вторым альтернативным
дифференциалом векторной функции. Если векторную функцию взять в виде разло-
разложения по касательному базису а = аг(и1, и2, u3)rj, то проведя аналогичный вывод,
получим следующее выражение для второго альтернативного дифференциала вектор-
векторной функции
DrDjBL - DjDrb = -Rrjina'rn dur duj. A.11.4)
Из формулы A.11.3) видно, что тензор кривизны кососимметричен по первым двум
индексам
Rrjin = -Rjri1- A-11.5)
Компоненты тензора кривизны A.11.2) являются трижды ковариантными и один
раз контравариантными. С помощью компонент метрического тензора можно получить
полностью ковариантные компоненты тензора кривизны
Rrjik = gnkRjri"-
Если над тензором кривизны выполнить операцию свертки по индексам п и г, то
мы получим тензор Риччи, ковариантные компоненты которого равны
Rn = Rjnin- A.П.6)
В евклидовом пространстве все компоненты тензора кривизны равны нулю:
ЯГ п ЯГ ¦ п
г, п ul ir U1JJ_ | -p n-i-i к -pi пт к п
Rrji = ~ы э^~+ Tkj Tir " Tkr Tij = °-
Двухмерное пространство на некоторой поверхности в общем случае не является евкли-
евклидовым и имеет ненулевой тензор кривизны. Плоская поверхность представляет собой
пример евклидова двухмерного пространства. Хотя координатные линии на плоскости
могут быть кривыми, все компоненты тензора кривизны плоского пространства равны
нулю. Пространства, для которых компоненты тензора кривизны везде равны нулю, по
аналогии с поверхностями называются плоскими. Изучением пространств с ненулевым
тензором кривизны занимается риманова геометрия.
Ковариантные производные компонент тензора. Метрический тензор является тен-
тензором второго ранга, а векторы являются тензорами первого ранга. По аналогии с
записью векторов в виде а = a^r' = aVj можно записать тензор второго ранга, напри-
например, метрический в виде суммы диад базисных векторов
G = gifcr''r* = fpriTb. A.11.7)
1.11. Тензоры в криволинейных координатах 65
Дифференцируя тензор в данном представлении по правилу дифференцирования суммы
и произведения функций, получим выражение для ковариантных производных компо-
компонент тензора второго ранга
= rV + gkr +g,r =
= ||W - &,rn/r"rfc - g,trTn/r" =
,iV, A.11.8)
Г„ =
^ ^ Л = У^*гЛ, A.11.9)
где
^ A.11.10)
„/ + g*Tn/ A.11.11)
— ковариантные производные компонент метрического тензрра. Как и следовало ожи-
ожидать, из соотношений A.10.33) и A.10.34) ковариантные производные компонент ме-
метрического тензора равны нулю. Равенства A.11.10) и A.11.11) представляют собой
определения ковариантных производных ковариантных и контравариантных компо-
компонент тензоров второго ранга (вместо компонент метрического тензора могут быть
подставлены компоненты любого другого тензора второго ранга, так как при выводе
никакие свойства компонент не использовались).
Аналогично записи векторов в виде а = щтг = агГг можно записать тензор произ-
произвольного ранга в виде суммы произведений его компонент на соответствующие базисные
векторы, например, Т = ^г/^г^г. Каждому верхнему индексу компоненты тензора
соответствует вектор касательного базиса rj, а каждому нижнему индексу — вектор
взаимного базиса г\ Используя аналогию с векторами, можно получить формулы для
ковариантных производных компонент тензора произвольного ранга. Например, диф-
дифференцируя правую часть выражения Т = ^г^ГгГт по правилам дифференцирования
суммы и произведения функций
fifki
— Z~SLr, r.rm Л- tkiV, nr rrra 4-fkiV-nv,v vm — tkiV mr, rrn —
— Quj k % +cmifcj гпûà T Iml у Г?ГПГ I1 nj Tk*i* —
Btki
m
/ flfki
— \ +lLnj
i _ ifcip n 1 r-rm — V ffcir, т- т
5 — 5293 Голованов
66 Гл. 1. Основы геометрического моделирования
и взяв компоненты при одинаковых триадах базисных векторов результата, получим
выражения для ковариантных производных смешанных компонент тензора третьего
ранга
ftfki
3 m ~dvJ m j m j ~ n j ' A.11.12)
Из полученного результата можно сформулировать общее правило вычисления кова-
риантной производной компонент тензора произвольного ранга. Кроме частной про-
производной данной компоненты тензора 9t***/9uJ (индексы заменены точками) в кова-
риантной производной добавляются еще несколько сумм, каждая сумма соответствует
одному из индексов. Так каждому нижнему индексу соответствует сумма вида
—?*?*r»j-n, а каждому верхнему индексу соответствует сумма вида +?»™*rnj*, где зна-
значение соответствующего индекса (обозначенного точкой) переходит от компоненты к
символам Кристоффеля, а по индексу п производится суммирование. В символической
записи это выглядит так:
fit***
Оператор Гамильтона. Ковариантные производные компонент тензора в свою оче-
очередь являются компонентами некоторого нового тензора Т = S/jt^r^ri-riT. Символ V
обозначает набла-onepamop или оператор Гамильтона, формальная запись которого
представляется в виде
Оператору Гамильтона приписывают атрибуты вектора: он может действовать на
тензоры тензорно (результатом является тензор, ранг которого на единицу выше ранга
исходного тензора), скалярно (при этом ранг результата на единицу меньше ранга ис-
исходного тензора) и векторно (при этом ранг результата равен рангу исходного тензора):
Va = r»0 = rV (~^ - апТ^ = V^rV = grada, A.11.14)
v"а = lJг" ^ = rJ'ri @ "anTijn) = VjaJ = diva' (L1L15)
Vxa = r^x^=iJxr< (J^r - апГ<А = ^rtVjO, = rota. A.11.16)
Например, в результате действия его на скаляр / (тензор нулевого ранга) получим
градиент скаляра
Для тензора Т = 4^г^г^гт результат действия оператора Гамильтона имеет вид
VT = г* J^j = 4&т*тктрт = gradT,
= rot Т.
V • Т = г' • 0 = V^rjr™ = divT,
ЯПГ рЗЧП ejkn
= __йвул-«*ггпгёгто = —
1.12. Ортогональные криволинейные координаты 67
Оператор Гамильтона может воздействовать несколько раз на один и тот же объект.
Так скалярное произведение операторов Гамильтона называется оператором Лапласа
Например, действие оператора Лапласа на скаляр записывается в виде
V-V/ = V2/ = divgrad/.
В декартовой прямоугольной системе координат оператор Лапласа имеет вид
д2 д2 д2
v2 + +
Оператор Гамильтона используется при описании тензорных (в частом случае ска-
скалярных или векторных) полей. Приведенные формулы позволяют записывать уравне-
уравнения для математических объектов безотносительно к какой-либо системе координат.
Если некоторый вектор а = а(и1, и2, и3) является функцией своего положения в про-
пространстве, то дифференциал этого вектора da. с использованием оператора Гамильтона
можно выразить следующим образом:
da= ~ duj = dunvn ¦ г> -^r = dv ¦ Va = (Va)T • dv, A.11.19)
ou3 аи3
где мы использовали обозначение dr = dunrn.
Формулы для векторных функций. Итак, мы получили формулы для работы с геоме-
геометрическими объектами в криволинейной системе координат. Для моделируемых нами
кривых и поверхностей всегда будем считать известными определяющие их коорди-
координатные функции. Умея вычислять производные векторных функций в криволинейной
системе координат, мы сможем получить всю геометрическую информацию об объекте.
Для этого необходимо знать зависимости A.10.2), которые по формулам A.10.4)
позволят вычислить касательный базис. Всю остальную геометрическую информацию
можно описать в терминах криволинейной системы координат. Полученные выше фор-
формулы позволяют представлять векторные функции и их производные в виде разложения
их по касательному или взаимному базису с помощью соотношений
= Tik ¦ Tj + Г{ ¦ Tjk,
¦ =
1.12.* Ортогональные криволинейные координаты
Описание геометрии объектов в криволинейных координатах является достаточно
сложным. На практике в большинстве случаев используются ортогональные криволи-
криволинейные координаты. В ортогональной системе координат координатные линии раз-
различного семейства взаимно ортогональны. Взаимно ортогональны и векторы ri, гг, гз
касательного базиса, так как они направлены по касательным к соответствующим
координатным линиям. В ортогональной криволинейной системе координат векторы
68
Гл. 1. Основы геометрического моделирования
i"i> 1*2, гз касательного базиса и соответствующие им векторы г1, г2, г3 взаимного
базиса совпадают по направлению, но длина их в общем случае различна; недиагональ-
недиагональные компоненты метрического тензора равны нулю: т. е. gtj = 0 и g*J = О при i ф j,
a g" = —тт. Часть символов Кристоффеля в ортогональной криволинейной системе
координат равна нулю и, следовательно, многие формулы упрощаются.
Цилиндрическая система координат. В качестве примера рассмотрим цилиндриче-
цилиндрическую систему координат. Параметрами цилиндрической системы являются полярный
радиус и1 = г, полярный угол и2 = (р и вертикальная ось u3 = z. Цилиндрические
координаты г, ip, z связаны с декартовыми координатами а;1, х2, х3 равенствами
г =
2x2
x2x
х3
= arctg—, z — x
X
Обратные зависимости имеют вид
х1 = г cos tp, x2 = г sin tp,
х = z.
Матрица Якоби перехода от декартовой прямоугольной системы координат к цилиндри-
цилиндрической системе координат равна:
"«Эх1
ди1
дх2
ди1
дх3
¦ ди1
дх1
дй1
дх2
ди2
дх3
ди2
дх1
дп3
дх2
ди3
дх3
ди3
cosy
sin у
0
—r sin у
r cosy
0
0
0
1
Компоненты метрического тензора в новой системе координат определяются по формуле
dxi
8и
&i
&1
«12
&2
832
Sis'
&3
&3.
=
0
0
0
г2
0
0"
0
1
, G-^
V1
g21
J31
g12
g22
g32
g13!
g23
g33.
=
l
0
0
0
—
Г
0
0
0
1
дип "J '
где 6jl — символы Кронекера A.10.7). Цилиндрическая система координат является
ортогональной, компоненты метрического тензора и отличные от нуля символы Кри-
стоффеля в ней равны
G =
^12,2 = Г21,2 = Г, Гг2,1 = -Г,
Fl2 = Г21 = ~, Г22 = -Г.
Как можно заметить, в цилиндрических координатах длины первого и третьего век-
векторов касательного базиса равны единице, а длина второго вектора, соответствующего
полярному углу, равна г.
Векторные функции в цилиндрической системе координат будем выражать с помо-
помощью векторов касательного и взаимного базисов следующим образом:
a. — arer-\-a<peipJrazez — arer + aipeip + azez. A.12.1)
1.12. Opтогональные криволинейные координаты 69
Частные производные векторов касательного базиса A.10.14) по цилиндрическим
координатам равны
der der I der
or dip r dz
dr r ?" d(p r' dz
^6z — n ^6z — n ^6z — n
dr ' dtp ' dz
Частные производные векторов взаимного базиса A.10.25) по цилиндрическим коорди-
координатам равны
der „ der ,я der „
-U* -V 0
dr ~ г ' dtp ~ г ' dz ~ '
de* де* де*
~dV = 0' s^ = 0' a^ = 0-
Мы видим, что некоторые векторы касательного и взаимного базисов цилиндрической
системы координат изменяются при переходе от одной точки пространства к другой.
Все это в общем случае усложняет описание геометрических объектов, но в некото-
некоторых частных случаях использование криволинейных систем является оправданным.
Формула A.10.21) для производной векторной функции в цилиндрической системе
координат имеет вид
da (dar wd<p\ fda* a? dr ar d<p\ daz . noo,
Пример кривой. Рассмотрим векторную функцию, описывающую один виток ци-
цилиндрической спирали в цилиндрической системе координат. Пусть ось спирали па-
параллельна ег и проходит через начало координат, ее радиус равен р, а шаг равен h.
Опишем спираль функциями координат:
r{t)=p, <p{t) = t, z{t) = h^-, 0s$t^27r.
Касательная спирали в соответствии с A.10.20) описывается векторной функцией
a(t) =ev + —ez.
Производная векторной функции спирали в соответствии с формулой A.12.3) равна
da.
В каждой точке спирали она направлена к ее оси и имеет длину р.
В дальнейшем при построении кривых линий и поверхностей мы будем исполь-
использовать декартову прямоугольную систему координат, как наиболее удобную для вычи-
вычисления производных векторных функций в евклидовом пространстве. При этом будем
использовать нижние индексы, так как в декартовой прямоугольной системе координат
ковариантные и контравариантные компоненты равны.
70 Гл. 1. Основы геометрического моделирования
1.13. Математическая модель геометрии объектов
Моделирование реального или воображаемого объекта представляет собой со-
совокупность действий, которые позволяют создавать его математическую модель,
редактировать ее, изменять ее положение и ориентацию в пространстве и обес-
обеспечивают взаимодействие с другими моделями. Взаимодействием мы называем
выполнение различных операций над моделями: установление зависимости па-
параметров одной модели от параметров других моделей, определение взаимного
положения моделей. Для выполнения этих действий необходима информация
об объекте. Геометрическая информация об объекте может храниться в виде
структуры данных или может вычисляться. Определим математическую мо-
модель реального или воображаемого объекта как совокупность данных и функ-
функций, позволяющих получить необходимую информацию об объекте и изменять
Хранимая структура даных
Набор выполняемых функций
Рис. 1.13.1. Математическая модель
его модель требуемым образом (рис. 1.13.1). Программную реализацию струк-
структуры данных и функций называют классом.
Геометрические объекты будут иметь свои данные и свои функции.
' Для построения точки в структуре ее данных достаточно хранить три коор-
координаты и иметь функции выполнения операций над радиус-векторами.
Для построения произвольной линии нужно знать зависимость ее радиус-
вектора r(t) от параметра, область изменения параметра и иметь функции
вычисления производных радиус-вектора.
Для построения поверхности нужно знать зависимость ее радиус-вектора
r(u, v) от параметров, область изменения параметров и иметь функции вычи-
вычисления частных производных радиус-вектора.
Тело мы будем описывать совокупностью ограничивающих его поверхно-
поверхностей, дополненной информацией об их связях друг с другом.
С математической точки зрения все геометрические объекты равноправны.
Для них существует ряд общих выполняемых функций. Все геометрические
объекты могут быть подвержены модификациям сдвига, поворота, масштабиро-
масштабирования, симметрии, поэтому они должны иметь функции, соответствующие этим
действиям. Кроме того, для работы с геометрическим объектом нужны функ-
функции создания объекта (конструкторы), удаления объекта (деструктор), функция
создания копии объекта, функции доступа к данным объекта, функции редак-
редактирования данных объекта. Математическая модель должна быть дополнена
функциями, обеспечивающими взаимодействие объектов и выполнение над
ними различных операций.
Мы рассмотрели теоретические основы геометрического моделирования.
Дальнейшее изложение будет посвящено конкретным моделям и методам их
построения.
Глава 2
МОДЕЛИРОВАНИЕ КРИВЫХ ЛИНИЙ
2.1. Математическая модель кривых линий
В данной главе мы рассмотрим способы построения линий. Линиями можно
описать отдельные геометрические свойства предметов, с помощью линий можно
представить характерные черты воображаемых объектов. Кривые линии будут
служить нам в качестве строительного материала для создания поверхностей и
тел. В свою очередь, линии мы будем описывать с помощью скалярных вели-
величин, векторов, точек и других линий. Линии могут быть пространственными
и двухмерными. Они имеют много общего. Сначала мы рассмотрим простран-
пространственные линии, а затем остановимся на отличиях двухмерных линий от них.
Пусть в пространстве задана некоторая глобальная декартова прямоугольная
система координат с базисными векторами ei, е2, ез. Мы будем описывать
пространственную линию векторной функцией
(<)ei B.1.1)
г=1
скалярного аргумента t, изменяющегося в пределах tm;n ^ t ^ ?тах- Компо-
Компоненты ri(t), гг(?); гз@ радиус-вектора точки кривой r(t) являются однознач-
однозначными непрерывными функциями параметра t. Такое описание линий назы-
называется параметрическим. Область изменения параметра кривой представляет
собой отрезок <mjn ^ t ^ tmax в одномерном пространстве. Кривые могут быть
замкнутыми или разомкнутыми. Для замкнутой кривой r(?±(?max—imin)) =r(t).
Двухмерную линию мы будем описывать векторной функцией
r(t) = x{t)h + y(t)i2, tmin ^ t < *max. B.1.2)
Двухмерные векторы ti, i2 являются базисными векторами некоторой декарто-
декартовой системы координат двухмерного пространства. Во многих случаях двух-
двухмерные линии аналогичны пространственным линиям.
В общем случае линию можно представить в виде системы двух уравнений,
которым удовлетворяют координаты радиус-вектора точек линии. Каждое из
этих уравнений можно считать уравнением поверхности, тогда система этих
уравнений представит собой линию пересечения поверхностей. Если линия
является плоской, то одним из уравнений может служить уравнение плоскости,
а вторым — уравнение, связывающее двухмерные координаты радиус-вектора
точек линии в этой плоскости. Если уравнение плоскости опустить, то мы при-
придем к двухмерной линии, которая описывается одним уравнением. Такое опи-
описание двухмерной линии называется неявным. Описание линий уравнениями
относительно ее координат в отличие от параметрического описания не всегда
72 Гл. 2. Моделирование кривых линий
однозначно. Оно также не является инвариантным относительно преобразо-
преобразования координат, т. е. при переходе в другую систему координат изменяются
описывающие кривую линию уравнения. Неявное описание линий используется
в теоретических исследованиях. При моделировании кривых линий мы будем
использовать их параметрическое представление.
Для построения математической модели кривой линии нужно знать зави-
зависимость ее радиус-вектора r(t) от параметра и область изменения параметра t.
Каждому типу кривой соответствует свой набор данных и свой алгоритм вы-
вычисления по ним радиус-вектора, а также своя область определения параметра
кривой. При известной функциональной зависимости радиус-вектора от параме-
параметра кривой определяется вся геометрическая информация кривой. Для кривой
всегда можно выполнить замену параметра и области его изменения.
Общение с математической моделью кривой происходит следующим обра-
образом. Мы обращаемся к функциям кривой с некоторым значением параметра
и в качестве ответа получаем геометрическую информацию о кривой в точке,
соответствующей заданному значению параметра. Различные функции кри-
кривой выдают различную информацию. Для одних функций значение параметра
должно принадлежать области его определения, для других — может выходить
за области определения. Если функция допускает выход значения параметра за
область определения, то она должна выдавать геометрическую информацию для
продолжения кривой.
2.2. Аналитические линии
Рассмотрим линии, координаты радиус-вектора которых могут быть пред-
представлены как аналитические функции некоторого параметра t. Простейшими
из них являются конические сечения, спирали и некоторые другие линии, по-
полученные как траектории движения точек механизмов. Многие кривые, описы-
описываемые аналитическими функциями, являются или замкнутыми или неогра-
неограниченными. Для замкнутых кривых областью определения параметра будем
считать отрезок параметрической оси, в пределах которого кривая проходит
один цикл. Неограниченные кривые мы будем усекать, вводя минимальный и
максимальный параметры.
Прямая линия. Одной из простейших линий является прямая линия. Она
может быть описана точкой р и вектором а. Радиус-вектор прямой линии опре-
определим зависимостью
r(t) = p + ta, -оо < t < oo. B-2.1)
Длина вектора а в общем случае может быть произвольной (но отличной от
нуля). Теоретически областью изменения параметра прямой является вся чи-
числовая ось, но на практике удобно ввести ограничения для предельных значений
параметра. В последнем случае мы получим отрезок прямой линии.
Отрезок. Другой простейшей линией является отрезок прямой. Он может
быть представлен через начальную pi и конечную рг точки:
г(*) = A-«)Р1+Ф2, 0<<<1. B.2.2)
Введем обозначение v = A — t), тогда радиус-вектор отрезка будет описываться
формулой
()
2.2. Аналитические линии 73
Величины v и t, на которые умножаются координаты точек pi и р2, являются
барицентрическими координатами. С использованием барицентрических
координат точек pi и Р2 формула отрезка приобретает симметричный вид.
Плоские кривые. Описанию плоских кривых в пространстве можно придать
следующий вид:
, B.2.4)
где р — некоторая точка привязки характерной точки кривой, ix и iy — не
коллинеарные векторы, x(t) и y(t) — скалярные функции. Аналогичный вид
r(t) = р + x(t)ix + y(t)iy имеет описание этих кривых в двухмерном простран-
пространстве. Разница заключается в том, что в двухмерном пространстве линии опи-
описываются точками и векторами, имеющими две компоненты, а в трехмерном
пространстве — имеющими три компоненты. Точка р и векторы ix и iy вы-
выбраны так, что скалярные функции x(t) и y(t) имеют канонический вид. Ка-
Канонический вид примет и соотношение, связывающее эти скалярные функции.
Векторы ix и iy вместе с вектором iz = ix х iy являются базисом местной декар-
декартовой системы координат, в которой кривая имеет канонический вид. Их всегда
можно представить в виде разложения A.2.3) по базису ei, е2, ез глобальной
декартовой системы координат:
ix = апех + а12е2 + а13е3,
iy = п2\ег + а22е2 + а23е3, B.2.5)
iz = a3iei + аз2в2 + а33е3.
Точка р является началом этой местной декартовой системы координат. Она
также может быть представлена в виде разложения по базису ei, e2, е3 глобаль-
глобальной декартовой системы координат:
p = pxei+р2е2+р3е3. B.2.6)
Таким образом, структура данных аналитических линий содержит описание
местной системы в виде начальной точки и трех ортов. При изменении поло-
положения и ориентации подобным образом описанной плоской кривой изменяются
компоненты точки р и векторов ix и iy, а скалярные функции x(t) и y(t) оста-
остаются неизменными, сохраняя канонический вид.
Окружность. Окружность можно описать, задав ее радиус г, положение
центра р и два взаимно ортогональных вектора единичной длины ix, iy, опре-
определяющих положение плоскости окружности:
r(t) =p + rcostix + rsmtiy, 0 < ? < 27г. B.2.7)
Окружность является плоской кривой. Окружность представляет собой геоме-
геометрическое место точек на плоскости, равноудаленных от центра р. Ее неявное
описание с помощью координатных функций x(t) = r-cost, y(t) = r-sint на
плоскости имеет вид
х2 + у2 = г2.
Эллипс. Эллипс в изложенной концепции может быть описан радиус-век-
радиус-вектором
r(t) = p + acostix+bsintiy, 0 < t < 2тг, B.2.8)
74
Гл. 2. Моделирование кривых линий
где а и 6 — полуоси эллипса. Скалярные функции x(t) — a • cost, y(t) = b-sint
эллипса связаны уравнением
Эллипс представляет собой геометрическое место точек на плоскости, для ко-
которых сумма расстояний до двух фиксированных точек fi и f2 этой плоскости,
Рис. 2.2.1. Эллипс
называемых фокусами, есть постоянная величина, равная max Bа, 26). Пусть
a > b, тогда радиус-векторы фокусов равны
f 1 = р — V а2 — Ь2 ix, f2 = р + у а2 — Ъ2 \х.
Эллипс показан на рис. 2.2.1. Окружность и эллипс являются замкнутыми
линиями.
Гипербола. Гипербола может быть описана радиус-вектором
= р + achtix + bshti
y,
t ^ t
max.
B.2.9)
Радиус-вектор B.2.9) описывает только одну ветвь гиперболы. Вторая ветвь
гиперболы может быть описана радиус-вектором
r(t) = р — achtix+bshtiy, t
Скалярные функции x(t) = acht, y(t) = bsht гиперболы связаны уравнением
(§)'-(?)' = '¦
Данному уравнению удовлетворяют и функции x(t) = ±acht, y(t) = ±6shi.
У гиперболы мы будем использовать только одну ветвь. Гипербола представляет
собой геометрическое место точек на плоскости, для которых абсолютная вели-
величина разности расстояний до двух фиксированных точек fi и f2 этой плоскости,
называемых фокусами, есть постоянная величина, равная 2а. Радиус-векторы
фокусов равны
fi = р - у/а2 + b2 ix, f2 = P +
2.2. Аналитические линии
75
Ветвь гиперболы, описываемая функцией B.2.9), показана на рис. 2.2.2.
Рис. 2.2.2. Ветвь гиперболы
Парабола. Парабола может быть описана радиус-вектором
1 2.
г{4 = PP* l+РЩ t
t
B.2.10)
1 ,2
Скалярные функции x(t) = -pt2, y(t) = pt параболы связаны уравнением
2px - у2 = 0.
Парабола представляет собой геометрическое место точек на плоскости, для ко-
которых расстояние до фиксированной точки f этой плоскости, называемой фоку-
Рис. 2.2.3. Парабола
сом, равно расстоянию до некоторой фиксированной прямой d(tu), называемой
директрисой. Радиус-вектор фокуса и директрисы равны
р р
f = Р + gi*» d(w) = Р - 2ix + wiv
Величину / = р/2 называют фокусным расстоянием. Парабола показана на
рис. 2.2.3.
76
Гл. 2. Моделирование кривых линий
Дуга. Дугу окружности можно описать, задав ее радиус г, положение цен-
центра р, два взаимно ортогональных вектора единичной длины ix, i,,, определяю-
определяющих местную систему координат, начальный угол ско, угол дуги а и направле-
направление движения sign:
r(f) = p + rcos(a0 + t sign) ix + г sin (a0 + t sign) iy, 0 < t ^ a, B.2.11)
где sign = +1, если точка перемещается по дуге против часовой стрелки при
взгляде навстречу вектору iz = ix х i^, и sign = —1, если точка перемещается по
дуге по часовой стрелке при взгляде навстречу вектору iz = ix x iy (в двухмерном
случае при взгляде на плоскость).
Аналогичной формулой может быть описана дуга эллипса:
r(t) = р + a cos (а0 + tsign) ix + &sin(ao + ?sign)iy, 0 < t < a, B.2.12)
где а и b — полуоси эллипса.
Спираль. Цилиндрическая спираль также является аналитической кривой,
но не является плоской. Она может быть описана положением начала оси спи-
спирали р, тремя взаимно ортогональными векторами единичной длины ix, iy, iz,
радиусом г, шагом h и параметрической длиной tma.x'-
—iz, 0
27Г
t ^ t
B.2.13)
Цилиндрическая спираль показана на рис. 2.2.4. Левую спираль можно получить
путем присвоения отрицательного значения h.
Производные аналитических линий можно найти дифференцированием ком-
компонент радиус-вектора по параметру. Рассмотренные линии могут быть заданы
Рис. 2.2.4. Цилиндрическая спираль
и несколько иным образом. Например, радиус может быть заменен длиной век-
вектора (уже не единичной), но в определенных случаях удобнее иметь данные о
направлении и длине отдельно.
Можно построить большое количество других плоских и пространственных
кривых, координаты радиус-вектора которых описываются аналитическими
функциями. Мы не будем их рассматривать по той причине, что на практике
они применяются редко.
2.3. Кривые второго порядка
77
2.3.* Кривые второго порядка
Эллипс, параболу и гиперболу называют коническими сечениями, так как они мо-
могут быть получены в результате пересечения конической поверхности с плоскостью, при
условии, что плоскость не проходит через вершину конуса. Если угол плоскости с осью
конуса больше угла образующей конуса с его осью, то получим эллипс. Если угол плос-
плоскости с осью конуса меньше угла образующей конуса с его осью, то получим гиперболу.
Если указанные углы равны, то получим параболу. Конические сечения являются кри-
кривыми второго порядка. Выше мы рассмотрели параметрическое представление кониче-
конических сечений. В некоторых случаях, например, при обмене данными, приходится иметь
дело с координатными уравнениями для этих кривых. Поэтому требуется выполнять
преобразование из неявного представления в параметрическое и обратно.
Декартовы координаты х и у на плоскости кривых второго порядка связаны урав-
уравнением второй степени
сих2 + с22у2 + 2с12ху + 2с13х + 2с23у
= О,
B.3.1)
где en, C22, сзз, Ci2, С13, С23 — коэффициенты, определяющие тип кривой, ее положе-
положение и ориентацию на плоскости (хотя бы один из коэффициентов ец, с22, с\2 должен
быть отличен от нуля). При перемещении или повороте кривой второго порядка ко-
коэффициенты сц, С22, Сзз, Ci2, Ci3, C23 не остаются неизменными. Путем поворота и
перемещения начала системы координат уравнение B.3.1) можно преобразовать к наи-
наиболее простому виду, называемому каноническим. Величины
= Сц + С22, h = СЦС22 - С\2С\2,
Cl2 C22
Cl3 C23
C23
C33
B.3.2)
являются инвариантами линии второго порядка B.3.1) относительно преобразований
декартовой системы координат. Это можно доказать, рассмотрев преобразование пере-
переноса начала системы координат в точку агоУо и поворота на угол <р
х = х' cos tp — у' sin (p + х0,
у = х' sin tp + у' cos (/3 + 2/0-
B.3.3)
Тип линии второго порядка и ее положение в пространстве определяются значениями
инвариантов Д, 12, 13-
В расширенной матричной записи уравнение кривой второго порядка B.3.1)
имеет вид
Rr -Cc R = О,
где использованы расширенный вектор A.4.3)
и расширенная матрица
Сс =
C23
Сзз
C12 C22
.C13 C23
В расширенной матричной записи преобразование координат B.3.3) имеет вид
Я = Аот R',
78
Гл. 2. Моделирование кривых линий
где Ао — расширенная матрица:
cos <p sin <p О
— sin ip cos ip 0
xo 2/o 1
Заметим, что определитель матрицы Aq равен единице. После перехода к новым коор-
координатам х', у' получим уравнение кривой второго порядка
Л'Т ¦Ао-Сс-Аот R' = 0 или R'T • С/ ¦ R' = 0, где Сс' = Ао ¦ Сс ¦ Аот,
откуда следует, что /з есть инвариант относительно преобразования B.3.3). Действи-
Действительно,
h' = \СС'\ = \А0 ¦ Сс ¦ Аот\ = |А>||Сс||Дот| = \СС\ = h.
Доказательство инвариантности величин Д, 12 может быть выполнено путем замены
координат B.3.3) в B.3.1) и вычислении величин B.3.2) аналогично доказательству
инвариантности /3.
Информация о типе линии и ее параметрах содержится в характеристической ква-
квадратичной форме, составленной из квадратичных членов относительно координат.
Предположим, что найдена система координат О'х'у', в которой уравнение кривой вто-
второго порядка имеет канонический вид
/2 /2
Aia; + X2y +1 = 0.
В силу свойства инвариантов будем иметь равенства Д = Ai + Аг, I2 = A1A2, /з =
= А1А2Д откуда следует, что свободный член в каноническом уравнении равен / =
= -/з/(АхА2) = 1з/12- Кривая второго порядка может быть приведена к указанному
каноническому виду, если 12 ф 0. Кривые такого вида называются центральными.
Для определения остальных канонических коэффициентов центральной кривой второго
порядка составим квадратный многочлен
(А - АХ)(А - А2) = А2 - (Ai + А2)А + АХА2 = А2 - ДА + Д.,
корнями которого являются канонические коэффициенты. Так как Д и 12 в любой
системе координат имеют одни и те же значения, то следует вывод, что канонические
коэффициенты Ai, A2 кривой второго порядка являются корнями уравнения
которое называется характеристическим уравнением. В матричной записи характе-
характеристическое уравнение имеет вид
11 — А с\2
с\2 с22 - А
= 0.
Таким образом, канонические коэффициенты являются собственными значениями ма-
матрицы характеристической квадратичной формы кривой второго порядка. Корни Ai, A2
характеристического уравнения являются действительными, так как матрица характе-
характеристической квадратичной формы симметричная.
Если /г = 0, то один из корней характеристического уравнения равен нулю. Пусть
это будет первый по счету корень, и пусть /3 ф 0. Тогда кривая второго порядка может
быть приведена к виду
2 Jx' + Х2у'2 = 0.
2.3. Кривые второго порядка 79
В силу свойства инвариантов для данного уравнения будем иметь равенства h = Л2,
h = 0, h — -A2J2. Отсюда следует, что J2 = -13/Х2 = —h/h- Такая кривая не
является центральной и имеет действительные точки при I3/h < 0.
Приведем классификацию линий второго порядка. Тип линии определяется знаком
инварианта 12:
• эллиптический тип, если 12 > О,
• параболический тип, если 12 = О,
• гиперболический тип, если 12 < 0.
Для того чтобы линии второго порядка не вырождались в прямые, необходимо,
чтобы 13 Ф 0. Если линия имеет эллиптический тип и (h/h) > 0, то уравнению
B.3.1) не удовлетворяет ни одна точка плоскости, а уравнение называют уравнением
мнимого эллипса. Мы получим эллипс при 12 > 0, 13 ф 0 и (h/h) < 0, гиперболу —
при 12 < 0 и 13 ф 0, параболу — при 12 — 0 и 13 ф 0.
Каждая кривая второго порядка B.3.1) в некоторой системе координат принимает
канонический вид. Эту систему называют главной центральной (если линия имеет
центр) системой координат. Кривая имеет центр, если 12 ф 0. Двухмерные коор-
координаты хо, г/о центра системы координат, в которой кривая второго порядка примет
канонический вид, находятся из системы уравнений
B.3.4)
«-12^0 "Г «-22У0 "Г «--23 — и
и равны
B.3.5)
С23 V '
Угол поворота ц> главной системы координат относительно исходной удовлетворяет
системе уравнений
(сц - Л) cos (/з + ci2 sin (/з = 0, ,„„.
B.3.6)
С12 COS (/3 + (С22 — A) Sin If — 0,
где Л — корни характеристического уравнения. Если корни характеристического урав-
уравнения различны, то система B.3.6) имеет одно независимое уравнение. Исключим Л
из уравнений B.3.6) и получим
= ci2 ctg (/з + с22. B.3.7)
СцХ0
с12х0
С13
С23
+ с
122/0
+ с22у0
С12
С22
4-
4-
2/о
си
С23
= 0,
= 0
1
~h
Если с12 ф 0 или сц ф с22, то мы можем найти угол поворота (р главной системы
координат. Он определяется равенством
^^. B.3.8)
После преобразования координат в новой системе уравнение кривой B.3.1) при-
примет вид
у2 +
+ Х2у2 + т = °>
если h ф 0 и, следовательно, оба корня характеристического уравнения отличны от
нуля и
80 Гл. 2. Моделирование кривых линий
если /г = 0 и, следовательно, один из корней характеристического уравнения равен
нулю (штрих около новых координат опущен). Если 12 Ф 0, то каноническое урав-
уравнение кривой имеет симметричный вид и у кривой'есть центральная точка (эллипс и
гипербола). В противном случае кривая не имеет центра (парабола).
При переходе к главной центральной системе координат уравнение кривой второго
порядка приобретает канонический вид:
(X \ ^ / V \ ^
— ] + (т) =1 для эллипса,
/Х\2 /V\2
1-1 — ( т ) =1 Для гиперболы,
2рх — у=0 для параболы.
Перенумеруем корни характеристического уравнения так, чтобы Ai ^ Аг- Полуоси
эллипса можно найти по формулам
Р=-т-\—г, А1=О>А
а = \/-т-т-, Ь=\—Г^> Ai>A2>0, B.3.9)
V А2./2 V A1Y2
действительную и мнимую полуоси гиперболы — по формулам
А2, B.3.10)
У Л2^2
параметр параболы — по формуле
1 / гГ
B.3.11)
Приведенные формулы позволяют построить параметрические зависимости для
кривых второго порядка по их координатным уравнениям. Для перехода от параметри-
параметрического представления к координатным уравнениям нужно знать каноническое урав-
уравнение f(x, у) = 0, которым связаны координатные функции x(t), y(t) кривой. Пусть на
плоскости, в которой лежит кривая, заданы местная двухмерная декартова прямоуголь-
прямоугольная система координат и некоторая глобальная двухмерная декартова прямоугольная
система координат. Пусть положение местной декартовой системы координат описыва-
описывается центром в точке q и ортами jx и j2, заданными в глобальной двухмерной системе
координат выражениями
3\ = cos</3ei +sin</je2, B.3.12)
j2 = — sin ipei + cos ip e2,
где ex, e2 — базис глобальной двухмерной системы координат. Местные координаты
х, у связаны с глобальными двухмерными координатами рх, Рг уравнениями A.2.17),
которые в принятых здесь обозначениях имеют вид
х= (рх -qi)cosip+(p2 -q2)sinip, B 3 13)
у =-{pi-qi)sinip + (p2-q2)costp.
Для получения уравнения F(px, P2) = 0, связывающего глобальные координаты, под-
подставим в уравнение f[x, у) = 0 выражения B.3.13) для канонических координат.
2.4. Сплайны
81
2.4. Сплайны
Во многих практических задачах аналитическая формула линии не известна,
но требуется, например, чтобы кривая проходила через заданные точки, имела
определенную степень гладкости или в определенных точках имела заданные
производные. Рассмотрим такие кривые.
Довольно большой класс линий можно построить по совокупности точек.
Такие линии можно назвать точечно-заданными. Это ломаная линия и различ-
различные сплайны. Мы рассмотрим кубический сплайн, сплайн в форме Лагранжа,
сплайн в форме Ньютона и сплайны Эрмита. Задача ставится следующим
образом: имеется совокупность точек в пространстве, радиус-векторы которых
равны pi, где г = 0, 1,2, ...,п — номера точек; требуется построить линию,
радиус-вектор которой при значениях параметра ti, i = 0, 1, 2, ..., п был бы
равен pj. Другими словами, необходимо построить интерполяционную кривую.
Точки р^ которые определяют линию и являются ее внутренними данными,
будем называть характеристическими точками кривой, точки ti на числовой
оси будем называть узлами, а значения параметра t{ будем называть узловыми.
Ломаная линия. Простейшей точечно-заданной линией является ломаная
линия. Она состоит из отрезков, последовательно соединяющих заданные точки.
Значение параметра в каждой последующей точке должно быть больше значения
параметра в предыдущей точке ti < ij+i- Радиус-вектор ломаной определяется
равенством
() ()
w =
-*,-'
«0
B-4.1)
где ti ^t ^ ti+\. Параметр w будем называть местным параметром на участке
кривой между точками pj и Рг+ь Первая производная ломаной линии в точ-
точках pi терпит разрыв по длине и по направлению. Параметр ломаной линии
изменяется в одномерном пространстве. В этом пространстве для определения
Рис. 2.4.1. Ломаная линия
параметра t мы вправе использовать любую систему координат. Для параме-
параметра можно использовать систему координат, где его значение в точке pi равно
номеру точки: ti — i. Такая параметризация называется равномерной, а па-
параметрическая длина ломаной в таком случае равна числу точек минус один.
Ломаная линия приведена на рис. 2.4.1.
Ломаная может быть замкнутой, в этом случае первая характеристическая
точка одновременно является и последней. Параметрическая длина замкнутой
ломаной линии равна числу точек, на которых она задана. Ломаная обладает
6 — 5293 Голованов
82 Гл. 2. Моделирование кривых линий
рядом полезных свойств: ее точки легко вычисляются, ее легко можно редак-
редактировать (вставить новую точку, удалить или сдвинуть имеющуюся), ее легко
можно разрезать на части, каждая из которых также будет являться ломаной
линией.
Сплайн Эрмита. Во многих практических задачах требуется построить плав-
плавную кривую линию, проходящую через заданные точки. Для этих целей стро-
строятся сплайны. Термин «сплайн» для кривых линий заимствован у названия
чертежного инструмента — упругой гибкой линейки, которая может изгибаться
так, чтобы проходить через заданные точки.
Если задана последовательность т + 1 точек, через которую должна пройти
кривая, и производные ее радиус-вектора в этих точках, то по этим данным
можно построить сплайн, описываемый полиномом степени 2т + 1 и носящий
имя Эрмита. Мы рассмотрим частный случай сплайна Эрмита для т — 1.
Ломаную линию можно рассматривать в качестве составной кривой, постро-
построенной из отрезков прямой линии. По аналогии можно построить составную
кубическую кривую, состоящую из сплайнов Эрмита третьей степени, гладко
стыкующихся между собой. Построим составной сплайн Эрмита, проходящий
через заданную последовательность точек и имеющий в этих точках заданные
производные. Пусть радиус-векторы этих точек равны pj, векторы производных
кривой в этих точках равны qj, а значение параметра в этих точках равны t{
(U < U+i), где г = 0, 1, 2, ..., п — номера точек. На участке между точками р;
и pi+i составной сплайн Эрмита является полиномом третьей степени местного
параметра w
ri(w) = а0 + ецчи + &2W2 + азго3,
t - tt B.4.2)
w =
U+i — U
Местный параметр w изменяется от 0 до 1. Векторы а^, j = 0, 1, 2, 3 найдем
из условий на границе участка кривой
Г;@) = pi, Г;A) = Рй_ь
r/@) = qb r/(l)
После решения этой системы уравнений и подстановки искомых значений в
B.4.2), получим зависимость радиус-вектора для сплайна Эрмита
r(t) = Pi(l-3w2 +2w3) +
+ P;+iCu;2 -2w3) + <n(w - 2w2 + w3) + <n+i(-w2 + w3) =
)<li+i, B.4.3)
w = -, to^t ^ tn,
ч
где t{ ^.t ^ ti+\. В B.4.3) введены обозначения для функций
ao(w) = 1 - 3w2 + 2w3, ati(w) = Зги2 - 2w3,
„.. Л О Q ,,/ч О О I Л. 4.4 )
/Зо(гу) = w — 2tt;J + ги , /3i(«;) == — ^ + ги.
2.4. Сплайны
83
удовлетворяющих равенствам:
ао(О) = 1,
ао'(О) = О,
ai@) = 0,
ai'(O) = 0,
аоA) = 0,
ао'A) = О,
/9Ь'(О) = 1, А/A)=О, А'(О)=О,
ai(l) = 1,
ai'(l) = О,
где штрих означает дифференцирование по го. Если точки pj расположены рав-
равномерно, то можно принять значения параметра в точках pj равные номерам
точек: U = г. При неравномерном расположении точек pj параметрическое
расстояние ij+i ~ ti можно положить пропорциональным расстоянию между
соответствующими точками |pi+i — Рг|- Составной сплайн Эрмита может быть
замкнутым.
Мы рассмотрели случай, когда для кривой заданы производные в точках.
Если производные qi неизвестны, то их можно вычислить по одной из схем.
В первом случае их можно положить равными
Рг+1-Рг-1
При неравномерном расположении точек данный способ определения производ-
производных qj может привести к появлению нежелательных петель. Для предотвраще-
Рис. 2.4.2. Ломаная линия и составной сплайн Эрмита
ния появления петель нужно использовать другую схему определения производ-
производных qj. Например, их можно положить равными
Pi ~ Рг-1 Рг+1 ~ Рг
Si + Si+i
Si +
где Si = \pi — pi_i|, Sj_|_i = |pi+i — Pi| — расстояния между соседними точками.
По третьей схеме меняются местами вклады расстояний между соседними точ-
точками:
о._ Рг -Рг-1 , . Рг+1-Рг
Чг — si~
Si +
Si + Si+1
На рис. 2.4.2 приведены ломаная линия и составной сплайн Эрмита, постро-
построенный данным способом — по характеристическим точкам ломаной.
6*
84 Гл. 2. Моделирование кривых линий
При неравномерном расположении точек данный способ определения произ-
производных qj, как и первый способ, может привести к появлению петель.
Предложенные схемы не позволяют получить производные радиус-вектора
кривой на ее краях, если она не замкнута. Производные на краях можно полу-
получить исходя из целей, которые преследуются при построении кривой. Найдем
производные в крайних точках составной кривой из условия, что в этих точках
обращаются в нуль третьи производные радиус-вектора. Для этого вычислим
по B.4.3) производные для соответствующих участков и подставим в них соот-
соответствующие значения параметра, в результате получим
q0 = 2{px -po) -qb
Я.п = 2(pn — Pn-i) — Qn-i-
Аналогично можно найти производные в крайних точках составной кривой из
других условий. Такими условиями могут служить: равенство нулю вторых про-
производных на концах кривой; равенство производных радиус-вектора на концах
заданным значениям. Составной сплайн Эрмита дает приемлемую аппроксима-
аппроксимацию при большой плотности точек. Вторые производные в характеристических
точках составном сплайне Эрмита не сохраняют непрерывность.
Кубический сплайн. Построим на заданной совокупности характеристиче-
характеристических точек сплайн, который бы имел непрерывными первые и вторые произ-
производные радиус-вектора. На каждом участке между соседними характеристичес-
характеристическими точками будем описывать радиус-вектор кривой кубическим полиномом
типа B.4.2). Введем обозначения для вторых производных в характеристи-
характеристических точках r"(ti) = Sj. Вторая производная радиус-вектора на участке
ti ^t ^ ij+i является линейной функцией параметра t
dt2 '
После двукратного интегрирования получим
r^ = Si+1" + Sil 'tl
b(t,+i — ti) b(ti+i — ti)
Постоянные интегрирования Ci и С2 определим из условий на концах участка
r{U) — Pi и r(^i+i) = Pi+i- После вычислений получим
i+l-ti 6
-ы BА6)
Выражение B.4.6) описывает кубический полином на отрезке t% ^ t ^ ti+\ и
содержит две неизвестные величины Sj и Sj+i. Для их определения приравняем
первую производную сплайна на правом конце отрезка ti-\ ^ t ^ ti первой
2.4. Сплайны
85
производной сплайна на левом конце отрезка U ^ t
рования B.4.6) и подстановки t — t{ получим
. После дифференци-
дифференциdr
(ft
BSj +Si+i)(ti+i -tj) | Рг+1-Рг
6 * *
B 4 7)
После замены в B.4.6) г на г — 1, дифференцирования и подстановки t = t{
получим
dr BSj+Sj_1)(tj-tj_1) Pi - Рг-l @ я.
Приравняв правые части последних двух выражений, получим следующее урав-
уравнение:
~ U
ti ~ U-l
Таких уравнений можно составить для п — 1 характеристических точек (в слу-
случае, незамкнутого сплайна). Подлежат определению п + 1 неизвестных векто-
векторов Sj. Два недостающих уравнения для определения всех неизвестных соста-
составим, исходя из условий на концах кривой. Например, если аналогично сплайну
(линейке-инструменту) считать концы кривой свободными, то можно положить
s0 = sra = 0. В некоторых случаях можно принять So = Si, sra = sn_i, тогда на
концевых отрезках сплайн будет иметь постоянную кривизну. Дополнительные
условия зависят от физических или геометрических условий в каждом конкрет-
конкретном случае. Если требуется построить замкнутую кривую, то мы будем иметь
Рис. 2.4.3. Кубический сплайн A), сплайн Эрмита B)
равное число неизвестных и уравнений. Таким образом, неизвестные век-
векторы вторых производных Sj в характеристических точках найдем из системы
линейных уравнений. Матрица этой системы линейных уравнений трехдиа-
гональная, что значительно упрощает решение системы. После вычисления
86
Гл. 2. Моделирование кривых линий
векторов Sj сплайн будет описываться формулой
r(t) = A - w)pi + topi+i +
+ ((-2w + 3w2 - w3)si + (-w +
~ Uf
B.4.10)
где w =
t-U
— U
t
Полученная кривая называется кубическим сплайном. В отличие от состав-
составного сплайна Эрмита для кубического сплайна изменение положения одной из
характеристических точек приводит к перевычислению сплайна. На рис. 2.4.3
приведены кубический сплайн и составной сплайн Эрмита, построенные по
одним и тем же восьми точкам.
Если положить, что значения параметра в характеристических точках равно
их номерам (t{ = i), то уравнение B.4.9) упростится и примет вид
Такая параметризация является равномерной. Кубические сплайны широко ис-
используются в задачах интерполяции. Равномерная параметризация при постро-
построении интерполяционного сплайна, проходящего через заданные точки, может
привести к необоснованным изгибам кривой, если точки расположены неравно-
неравномерно. Для избежания необоснованных изгибов кубического сплайна нужно ис-
использовать параметризацию, пропорциональную расстоянию между соседними
точками. То есть параметризация должна соответствовать выражению
— U
Н Н— 1
По аналогии с кубическим сплайном могут быть построены сплайны более
высокой степени, когда производные радиус-вектора третьего и более высокого
порядка непрерывны в характеристических точках. Максимально возможный
Рис. 2.4.4. Кубический сплайн A), сплайн Эрмита B), сплайн Лагранжа C)
порядок производных радиус-вектора, для которых можно сохранить непрерыв-
непрерывность, равен п при п+1 характеристических точках. Это можно сделать, постро-
построив интерполяционный полином Лагранжа или Ньютона. Интерполяционные
2.4. Сплайны 87
формулы Лагранжа и Ньютона дают один и тот же полином при разных спосо-
способах его вычисления. В обоих случаях ищется векторный многочлен степени п
вида
r(i) = а0 + ait + a2t2 + ... + antn, B.4.12)
который при заданных значениях параметра U принимает заданные значения
Pi, i — О, 1, 2, ..., п. Для определения векторов а, получим систему линейных
уравнений, определитель которой отличен от нуля, если среди точек нет совпа-
совпадающих друг с другом. Сформулированная задача имеет единственное решение.
Сплайн Лагранжа. Интерполяционная формула Лагранжа представляет
собой решение задачи построения кривой по заданным точкам в виде
B.4.13)
г=0
где функции Li(t) равны 1 при t — t{ и равны 0 в остальных узлах tj, j ф i.
Функции Li(t) будем искать в виде многочленов степени п, а именно:
Li(t) = Xi(t - to)(t -tx)...{t- ti-i)(t - ti+i) ...(t- tn).
Из условия Li(t{) = 1 находим — — (ti — to)(ti — ti)... (t{ — fj_i)(tj — ii+i)...
... (ti — tn) и, соответственно, получим формулы для коэффициентов Лагранжа
п
Li(t) = ^~ . B.4.14)
П (ti-tj)
3=0, Зфг
Итак, интерполяционный полином Лагранжа имеет вид
„ п («-у
1^2*1 p., to<t<tn. B.4.15;
i=o П (U-tj)
j=O,jjti
Часто интерполяционный полином Лагранжа записывают в другом виде
где
Wo,n(t) = (t- to){t - h)(t -t2)...(t- tn-i)(t - in),
dW0>n
w,,;w>- л
= (U - tO)(ti — *!)...(* — ti-l)(t - ti+l) ...(U- tn).
На рис. 2.4.4 приведены кубический сплайн, составной сплайн Эрмита и сплайн
Лагранжа, построенные по одним и тем же восьми точкам. На рисунке видно,
что кривые ведут себя по-разному.
Гл. 2. Моделирование кривых линий
Сплайн Ньютона. Интерполяционный многочлен Ньютона, проходящий че-
через заданные точки, ищется в форме
r(i) = а0 + ai(i - t0) + SL2(t - to){t - h) + ...
- tO)(t -«!>...(*- *n_2)(i - *„_!). B.4.17)
Векторы а, будем определять из условия прохождения векторной функции r(t)
через точки pj при значениях параметра U, i = О, 1, 2, ..., п:
Ро = а0,
Р! = ao + ai(ii -t0),
р2 = а0 + ai(*2 - t0) + SL2(t2 - to)(t2 - h),
B.4.18)
pn = a0 + &i(tn - t0) + a.2(tn - to)(tn -ti) + ...
... + &n(tn - to){tn -h)... (tn - tn-2)(tn ~ tn-\)-
Матрица этой системы уравнений является треугольной и система решается за
один прямой проход. Первое уравнение системы B.4.18) дает ао. Подставляя
этот результат во второе уравнение, получим ai. Из третьего уравнения найдем
а2 и так далее до ага. Ниже будет показано, что Зц могут быть получены как
разделенные разности соответствующего порядка, вычисленные по характери-
характеристическим точкам. Заметим, что вставляя дополнительную точку рп+ъ мы уве-
увеличиваем систему B.4.18) на еще одно уравнение, а все остальные уравнения
остаются неизменными. Это является преимуществом формулы Ньютона по
сравнению с формулой Лагранжа при построении кривых с увеличивающимся
числом точек.
Рассмотренные способы позволяют строить кривые определенной степени
гладкости, проходящие через заданную совокупность точек в пространстве. Для
моделирования геометрических объектов кроме рассмотренных сплайнов на
практике применяются еще более удобные с конструкторской точки зрения
кривые.
2.5. Кривые Безье
Координаты сплайнов являются полиномами параметра кривой. В общем
случае сегменты таких кривых описываются векторными функциями вида
B.5.1)
Смысл векторов а^ заключается только в том, что их компоненты являются ко-
коэффициентами полиномов для компонент результирующего вектора. Другими
словами, векторы а^ не несут геометрической информации каждый по отдель-
отдельности. Но если перегруппировать правую часть B.5.1), то можно получить
выражение, в котором векторные величины имеют определенный геометриче-
геометрический смысл. Это можно наблюдать на примере интерполяционной формулы
Лагранжа, где радиус вектор кривой представлен в виде
B.5.2)
г=0
2.5. Кривые Безье 89
векторные коэффициенты р^ являлись радиус-векторами характеристических
точек кривой, а зависимость кривой от параметра сосредотачивалась в скаляр-
скалярных функциях Li(t), индивидуальных для каждой характеристической точки р^.
Де Кастелье и независимо от него Безье предложили аналогичный B.5.2)
подход для построения кривых. Эти кривые получили название кривых Безье.
Кривая Безье описывается формулой
г=0 ' г=0
где pj — радиус-векторы точек, an — число этих точек минус единица. Сово-
Совокупность функций
Впт = г]{™[г)/A - г)п~< = C\t\l - *)"-' B.5.4)
называется базисом Бернштейна. Можно сказать, что кривая Безье является
полиномом Бернштейна с векторными коэффициентами. Сначала Де Кастелье
и Безье использовали частные случаи кривой B.5.3) и только позже Форрест
установил связь коэффициентов кривой с полиномами Бернштейна. Коэффици-
п!
енты при tl{\ — t)n~l в B.5.4) равны коэффициентам Сгп — — — бинома
г\\п — ъ)\
п
Ньютона: (а + 6)" = ^2 Сгпап~гЬг. Из этого следует, что базис Бернштейна
г=0
представляет собой разложение единицы (сумма всех коэффициентов при лю-
любом t равна единице)
j^B\{t) = (t + {l-t))n = ln = l. B.5.5)
г'=0
Функции Бернштейна удовлетворяют рекуррентному соотношению
Это соотношение доказывается непосредственной подстановкой:
±г>п—1 , /1 ±\г>п—1 г Пш Л i п * п
Л/л j.\n—i i п * п- ti.M 4.\n—i г>п
ni\{n — i)\ n г!(п — г)!
Используя это рекуррентное соотношение, можно вычислить все функции Берн-
Бернштейна. Вычисление начинается с функции
Далее получим Blx{t) = t, B1qA) — 1 — t. Все функции, один из индексов
которых равен отрицательному числу, считаются равными нулю. Продолжив
вычисления, получим все функции Бернштейна.
90 Гл. 2. Моделирование кривых линий
Алгоритм Де Кастелье. Подставим рекуррентное соотношение в выражение
B.5.3), выделив крайние точки и учитывая, что Впо = A — ?)", Впп = ?",
получим
п-\
r(i) = роA - t)n + pntn + J^itB71'1^ + A - t)Bn-\)Vi =
г=0 г=0
где
п-1 п-1
i=0 i=0
Продолжив описанный процессразложения для го^""^ и г^"), в конце придем
к равенствам
о
° = Pi, i = 0, 1, . . . , П.
Обозначив г(?) через ro^"^(i), a pj — через r/°), получим рекуррентное соотно-
соотношение для вычисления точки кривой Безье
ri« = (l-t)ri(fc-1)+*ri+1(fc-1), i + k^n. B.5.6)
Алгоритм, описываемый соотношением B.5.6), называется алгоритмом Де Ка-
Кастелье. Алгоритм Де Кастелье позволяет вычислить любую точку кривой Безье
по характеристическим точкам, ничего не зная о функциях Бернштейна. Вели-
Величины A — t) и t, на которые умножаются координаты точек r^k~1^ и rj+i^),
являются барицентрическими координатами. Кривую Безье можно определить
как линию, точки которой определяются рекуррентным соотношением B.5.6).
Свойства кривых Безье. На рис. 2.5.1 и 2.5.2 приведены полиномы Берн-
Бернштейна третьей и четвертой степени соответственно.
Из полиномов Бернштейна только нулевой и последний принимают макси-
максимально возможные значения Впо(О) = 1, Впп{\) = 1, поэтому кривая Безье
проходит только через начальную ро и конечную р„ точки. Касательные к кри-
кривой Безье в начальной и конечной точках совпадают с направлением векторов
pi — Ро и р„ — р„_1
г@) = ро,
гA) =Рп,
г'@) =n(pi -ро),
г'A) =n(pn-Pn-i)-
2.5. Кривые Безье
91
По вершинам pi строится характеристическая ломаная кривой Безье, которая
касается кривой в крайних точках. Кривая Безье как бы сглаживает углы своей
характеристической ломаной.
Рис. 2.5.1. Полиномы Бернштейна
Рис. 2.5.2. Полиномы Бернштейна
Достаточно гибкой и в то же время достаточно простой для практического
применения является кубическая кривая Безье, радиус-вектор которой описы-
описывается зависимостью
г(*) = A -
- tJPl
- t)p2 + t3p3.
Вид кубической кривой Безье и ее характеристической ломаной показаны на
рис. 2.5.3 и 2.5.4.
Рис. 2.5.3. Кривая Везье
Рис. 2.5.4. Кривая Везье
Коэффициенты aj этой же кривой в форме полинома B.5.1) связаны с вер-
вершинами pi соотношениями
а0 = ро,
г = 3(pi - ро), а2 = 3(р2 -
а3 = Рз-Зр2 + Зр! -р0.
р0),
На примере кубической кривой Безье видно, что ее модификация путем пере-
перемещения точек р^ нагляднее, чем модификация путем изменения векторных
коэффициентов а^, так как в последнем случае трудно предугадать результат.
Из-за того, что кривая не проходит через внутренние вершины своей характе-
характеристической ломаной, довольно сложно задать ей точное положение. Кривые в
92
Гл. 2. Моделирование кривых линий
форме Безье более удобны там, где важна форма линий, например, при проек-
проектировании конструкций типа кузова автомобиля. Чем больше точек участвуют
Рис. 2.5.5. Кривая Безье шестой степени
в построении кривой, тем она более гладкая. На рис. 2.5.5 приведена кривая
Безье, построенная по 7 точкам.
Для построения кривой, проходящей через заданные точки, можно исполь-
использовать составные кривые Безье. Кривая Безье всегда касается своей характе-
характеристической ломаной на концах. Если мы хотим,
чтобы составная кривая была гладкой, необходимо
следить за тем, чтобы в точках стыковки касатель-
касательные к частям кривых совпадали. Но в общем случае
в точках сочленения первая производная будет скач-
скачком менять свою длину, а все высшие производные
будут претерпевать разрыв. Для непрерывности пер-
первой производной составной кривой Безье требуется
касание и равенство длин крайних участков харак-
характеристических ломаных в месте стыковки. Пара-
Параметрическая длина составной кривой Безье равна
сумме параметрических длин частей, т. е. числу
этих частей.
Если вершины кривой Безье лежат на одной пря-
прямой, кривая обращается в отрезок прямой. Отрезком прямой линии является и
кривая Безье первой степени
r(«) = (l-t)po + tpi. B.5.7)
Радиус-вектор кривой Безье второй степени описывается зависимостью
г(<) = A - *Jро + 2<A - *)Pi + *2Р2- B.5.8)
Точка с произвольным параметром t квадратичной кривой Безье обладает тем
свойством, что касательная в ней делит векторы pi — Ро и рг — pi в отношении
t:(l — t). Это можно заметить, если записать равенство B.5.8) в виде
Г(<) = A - t)(Pi + (РО - Pl)(l - t)) + t(pi + (рг - Pi)*)-
В этом же отношении точкой кривой делится и часть касательной, заключенная
внутри характеристической ломаной (рис. 2.5.6).
Рис. 2.5.6. Алгоритм Касте-
лье для квадратичной кри-
кривой Безье
2.6. Представление кривых второго порядка кривыми Безье 93
Рисунок 2.5.6 иллюстрирует алгоритм Кастелье. Точка А имеет радиус-
вектор iv1', точка В имеет радиус-вектор iv1', точка С имеет радиус-вектор
roB)=r(t).
Мы продолжим исследовать кривую Безье второй степени, и это приведет
нас к новым линиям, обладающим весьма полезными свойствами.
2.6. Представление кривых второго порядка
кривыми Безье
Квадратичная кривая Безье B.5.8) является плоской линией и представляет
собой полином второй степени параметра. Конические сечения (эллипс, пара-
парабола, гипербола) записываются в виде функции второй степени координат (но
не параметра). Возникает вопрос: можно ли некоторую часть конического
сечения описать кривой Безье второй степени? Попытаемся найти ответ на
этот вопрос.
В декартовой системе координат на некоторой плоскости Оху коническое
сечение описывается уравнением второй степени B.3.1)
спх2 + 2спху + С22У2 + 2с13ж + 2с2зу + езз = 0.
Для нахождения коэффициентов сц, ci2, С22, С13, С23, С33 необходимо задать
пять независимых условий. Воспользуемся методом построения конических
сечений, который использовал Лайминг для проектирования поперечных сече-
сечений фюзеляжа самолета. Если обозначить через 1\ = 0 и 1^ = 0 уравнения двух
прямых, записанных в виде а\х-\-Ь\у + С\ = 0 и а2? + &2У + с2 = 0, то уравнение
1\1ъ = 0 будет уравнением второго порядка и, следовательно, оно описывает не-
некоторое коническое сечение. Возьмем еще одну пару прямых а^х+Ь^у+сз = 0 и
щх + Ь^у + С4 = 0, записанных в виде уравнений /3 = 0 и Ц — 0, пересекающих
прямые первой пары, и составим уравнение
A — Л)г1Ь + лг3г4 = о, B.6.1)
где Л — некоторый параметр. Это уравнение также является уравнением вто-
второго-порядка и при определенном значении параметра Л описывает некоторое
коническое сечение. При любом значении параметра Л коническое сечение про-
проходит через точки пересечения прямой 1\ с прямыми 1% и Ц и через точки пере-
пересечения прямой l<i с прямыми 1% и 1±. В этих точках удовлетворяется уравнение
B.6.1) при любом Л. Уравнение B.6.1) описывает семейство (или пучок) кони-
конических сечений, проходящих через четыре точки пересечения двух пар линий
(рис. 2.6.1). Выбрать нужное коническое сечение из данного семейства можно,
определив его пятую точку, не совпадающую с имеющимися точками, и тем
самым определится параметр Л.
Используя уравнение B.6.1), можно получить уравнение семейства кониче-
конических сечений, имеющих в двух заданных точках заданные касательные.
На рис. 2.6.1 видно, что по мере приближения прямой ^з к Ц точка А прибли-
приближается к точке В, точка С приближается к точке D, хорда АВ и CD стремятся
к касательным линиям конических сечений семейства. Когда прямые линии 1$
и Ц совпадут, уравнение B.6.1) примет вид
A - \)hh + \lj = 0, - B.6.2)
94 Гл. 2. Моделирование кривых линий
и будет представлять семейство конических сечений, касающихся линий 1\ и li
в точках их пересечения с линией 1з (рис. 2.6.2). Если задать еще одну точку R,
не совпадающую с точками А ж С, то мы определим коническое сечение и пара-
параметр Л в B.6.2). Коническое сечение в данном случае определяется четырьмя
Рис. 2.6.1 Рис. 2.6.2
точками: А, С, R и точкой Е пересечения прямых линий li и /г- Если точка R
лежит внутри треугольника АЕС, то коническое сечение будет иметь непрерыв-
непрерывный участок, лежащий внутри этого треугольника. Можно показать, что если
точка R делит пополам отрезок, соединяющий середины отрезков АЕ и СЕ, то
коническое сечение является параболой, если точка R находится между упомя-
упомянутой параболой и отрезком АС, то коническое сечение является эллипсом, в
остальных случаях коническое сечение является гиперболой.
Уточним поставленный выше вопрос: можно ли описать часть конического
сечения, лежащую внутри треугольника АЕС, квадратичной кривой Безье, по-
построенной по характеристической ломаной с вершинами в точках А, Е и С.
Пусть радиус-векторы точек А, Е, С равны соответственно ро, pi, P2- Введем
косоугольную систему координат на плоскости, начало которой лежит в точке
Pi, а координатным базисом являются векторы Ро — Pi и рг — Pi- Координаты
этой системы обозначим через и и v. В косоугольной системе uv вектор ро
имеет координаты и = 1, v = 0, вектор pi имеет координаты и = 0, v = О,
вектор р2 имеет координаты и = 0, v = 1. Произвольная точка R будет иметь
радиус-вектор
г(«, v) = рх + и(р0 - Pi) + и(Р2 - Pi)- B.6.3)
В косоугольной системе прямые линии h, fo, h описываются уравнениями
v = 0, и = 0, и + v = 1, соответственно. Подставим их в B.6.2) и получим
уравнение
S{u, v) = A - X)uv + \{и + v - IJ = 0, B.6.4)
которое описывает семейство конических сечений в косоугольной системе коор-
координат.
Предположим, что мы выбрали из семейства B.6.4) некоторое коническое
сечение, т. е. нам известен в B.6.4) параметр Л. Возьмем некоторую точку г
на коническом сечении внутри треугольника с вершинами в точках р0, pi, рг
(рис. 2.6.3).
2.6. Представление кривых второго порядка кривыми Безье
95
Пусть ее координаты равны О<ыо<1иО<г;о<1. Квадратичная кри-
кривая Безье описывается уравнением B.5.8) как векторная функция параметра t.
Попытаемся записать в аналогичном виде коническое сечение. В общем случае
«¦("о- "о)
«К- "о)
Pi "о Po "
Рис. 2.6.3. Коническое сечение
«1 Ро
Рис. 2.6.4
можно считать, что оно описывается функцией B.6.3), в которой параметры и
и v связаны соотношением B.6.4). Запишем радиус-вектор конического сече-
сечения в виде функции одного параметра, в свою очередь являющегося функцией
и ж v. Для этого нам потребуется касательная к коническому сечению в точке
г(ыо, vo) и точки пересечения этой касательной с осями косоугольной системы
координат.
Касательная линия к коническому сечению B.6.4), записанному в виде
S(u, v) = 0, в точке с координатами и = щ, v = vq описывается уравнением
95
ди
uo,vo
-
{v - vq) = 0.
B.6.5)
Uq,Vq
Производные dS/du и dS/dv в точке т(щ, г>о) с учетом того, что щ, г>о удовле-
удовлетворяют уравнению B.6.4), равны
ди
dv
= A - Л)и0 + 2Л(и0 + vo - 1) = Л
(и0 + v0- l)(u0 -
U0,VQ
= A - X)uo + 2Х(щ +vo-l) = X-
+vq-
- Щ
Uq,Vq
Таким образом, уравнение касательной к коническому сечению в точке г(щ,
имеет вид
(щ — vo + l)vo(u - щ) + (vo -щ +
Она пересекает координатные оси и и и в точках
o — Щ + 1 2uq
Щ = Щ +
VQ
Uo-Vq + 1
uq-vq + 1
vo — uo + 1
щ - v0 + Г
- vo) — 0.
«i=0,
B.6.6)
— uq + 1'
что показано на рис. 2.6.4.
96 Гл. 2. Моделирование кривых линий
Обозначим отношения длин отрезков, на которые касательная к кониче-
коническому сечению делит векторы ро — Pi и pj — рг, через
* =-^ = —^ г, = ,J»_ = **__. B.6.7)
1-Щ 1 - Щ - V0 1 - V2 I — Uq — Vq
Точку r(uo, vq) конического сечения можно характеризовать координатами
щ, vo, или координатами щ, v-i-, или отношениями z\, Z2- Остановимся на
последнем способе. Выразим щ и vq через Z\ и Z2, используя соотношения
B.6.7)
Zl v0 = • B.6.8)
2 + Z+z У '
2 + zx + z2
Подставив B.6.8) в B.6.3), получим зависимость радиус-вектора конического
сечения как функцию параметров z\ и zi
Координаты щ и vq связаны уравнением B.6.4), а параметры Z\ vi Z2 — более
простым соотношением
4Л „ .
B.6.10
A - и0 - VoJ I - Л
т. е. произведение zi^ = const для заданного конического сечения. Фактически
радиус-вектор конического сечения зависит от одного параметра.
Введем параметр t для конического сечения, от которого будут зависеть ко-
координаты щ и vo и, следовательно, параметры z\ и z-i- В соответствии с кривой
Безье для точки ро параметр t = 0, а для точки р2 параметр t = 1. При движе-
движении по коническому сечению от точки ро к точке рг координата ио изменяется
от 1 до 0, координата vq изменяется от 0 до 1, а параметр t должен изменяться
от 0 до 1. Обратим внимание на выражения B.6.7). Заметим, что из B.6.4)
следует ^_________
Iuqvq{\- 1)
А
Подставим это равенство в B.6.7) и получим
zi=kJ — , z2 = k.—, B.6.11)
где А; = \ = — постоянный коэффициент. В качестве пара-
VA-11-uo-Vo
метра t конического сечения примем величину
B.6-12)
тогда равенства B.6.11) примут вид
Zl=k^, Z2 = k-^- B.6.13)
2.6. Представление кривых второго порядка кривыми Безье 97
Подставим последние равенства в B.6.9) и получим зависимость радиус-
вектора конического сечения B.6.3) как функцию одного параметра t
ЛA - *J + 2*A -t) + kt2
Более удобно для использования последнего равенства ввести параметр
' ЛA - *J + 2*A -t) + kt2
вания последнего равенства ввести параметр
/ХТТ ^«о-^о 1 B.бл4)
4A
который называется весом точки pj. При использовании веса w формула B.6.9)
примет вид
B.6.15)
Сравним выражение для радиус-вектора кривой Безье второй степени B.5.8)
и выражение для радиус-вектора конического сечения B.6.15). Они совпадают
в случае, когда w — 1, что справедливо для одной из кривых семейства кониче-
конических сечений, которой соответствует Л = —1/3. Коническое сечение B.6.4) при
А = —1/3 описывается уравнением
u2 - 2uv + v2 - 1u - 2v + 1 = О,
которое является параболой, так как равен нулю его второй инвариант I2, соста-
составленный из коэффициентов при старших членах переменных и и v. Действи-
Действительно, если ввести новые переменные х = и — v, у = 2и + 2v — 1, то они будут
связаны параболическим уравнением у — х2. Будем рассматривать выражение
Рис. 2.6.5. Построение дуги окружности
B.6.15) как обобщение квадратичной параметрической кривой, позволяющее в
частных случаях получить как кривую Безье второй степени (при w = 1), так
и коническое сечение.
Теперь мы можем ответить на поставленный выше вопрос: кривой Безье
второй степени в общем случае нельзя описать часть конического сечения,
но его можно описать как частный случай кривой B.6.15). Кривая Безье
второй степени также может быть описана как частный случай кривой B.6.15).
Построим с помощью формулы B.6.15) дугу окружности радиуса р и углом
раствора а, показанную на рис. 2.6.5. Через ро и р2 обозначены радиус-векторы
крайних точек дуги, а через pi обозначена точка пересечения касательных
линий к дуге, построенных в крайних ее точках.
7 - 5293 Голованов
98 Гл.2. Моделирование кривых линий
Дуга симметрична относительно линии ОС и имеет симметричную харак-
характеристическую ломаную. Воспользуемся симметрией и найдем коэффициент к
по одной из формул B.6.13) через отношения z\ и Z2, в которых касательная к
дуге в точке В делит отрезки характеристической ломаной. В точке В параметр
t = 1/2 и, следовательно, к = z\ = z^. Из подобия треугольников следует, что
и ВС
Длина отрезков ВС и АВ вычисляются через радиус р и угол раствора дуги а
АВ = р(\- cos |) ,
= СО-ВО = f !™Ш
cos (а/2) И И cos (а/2)
Тогда
1 АВ а
II) = — = = РОЯ —
к ВС 2'
Таким образом, дуга окружности радиуса р с углом раствора а, может быть
построена как квадратичная кривая B.6.15), заданная точками ро, рг и pi с
весом средней точки w = cos (a/2). Радиус-вектор дуги описывается функцией
- t) cos (a/2)Pl + t2p2 r9fi1fi,
0<t<1 B6Л6)
где точки связаны соотношениями
|Ро - Pil = |P2 - Pi| = Ptg (a/2),
(po - Pi) • (P2 - Pi) = |po - P1IIP2 - Pill cosa|.
Параметрическая длина дуги равна единице. Формула B.6.16) справедлива в
диапазоне углов 0 < a < 2тг. На рис. 2.6.6 приведена дуга окружности с углом
120°, а на рис. 2.6.7 приведена дуга окружности с углом 240°. Обе дуги имеют
о-
Рис. 2.6.6. Положительный вес точки pi Рис. 2.6.7. Отрицательный вес точки pi
одни и те же характеристические точки, но в первом случае вес средней точки
равен 1/2, а во втором случае вес средней точки равен —1/2. Можно разбить
дугу на несколько частей и представить в виде составной кривой, тогда параме-
параметрическая длина дуги будет равна числу составных частей.
2.6. Представление кривых второго порядка кривыми Безье
99
Построим с помощью формулы B.6.15) четверть эллипса по трем вершинам
ро, Pi и рг, образующим прямой угол: (ро — pi) • (рг — Pi) = 0, как показано
на рис. 2.6.8.
Полуоси эллипса определяются длинами векторов: а = |ро — pi|, b =
— [рг—Pi|- Для полного определения эллипса остается найти вес точки pj. В ко-
косоугольных координатах ии«, приведенных на рис. 2.6.4, уравнение эллипса
имеет вид (и — IJ + (г; — IJ = 1, которому в
B.6.4) соответствует Л = — 1. В соответствии
с B.6.14) вес средней вершины
ч/2
т. е. такой же, как и у дуги в четверть окруж-
окружности. В косоугольных координатах уравне-
уравнение эллипса имеет вид уравнения окружно-
окружности, поэтому описание дуг эллипса похоже на Рис. 2.6.8. Дуга эллипса
описание дуг окружности.
Рассмотрим общий случай построения конического сечения, чем дуга окруж-
окружности. Пусть известны три вершины характеристической ломаной кривой ро,
Рис. 2.6.9. Коническое сечеиие, построенное по четырем точкам
Pi, P2 и четвертая точка р, лежащая на кривой. Точка р должна лежать в од-
одной плоскости с точками ро, рь рг строго внутри угла, построенного по этим
точкам с вершиной в pi. Построим коническое сечение в виде
- tJPo + 2t(l -
A - tJ + 2«A - t)w(p) + t2
B.6.17)
где w — w(p) — вес вершины pi, который определяется положением четвер-
четвертой точки р относительно первых трех. Точки ро, pi, рг и р на рис. 2.6.9
обозначены через Ро, Р\, Pi и Р.
Из B.6.14) следует, что вес
w =
\-Uq-Vq
B.6.18)
7*
100 Гл. 2. Моделирование кривых линий
Косоугольные координаты щ, г>о точки Р, через которые вычисляется вес в
B.6.18), равны отношениям длин отрезков VP/ Р\Р$ и UP/P1P2, соответствен-
соответственно. Обозначим через L\ длину отрезка P\Pq, через Li — длину отрезка P\Pi,
через 1\ — длину отрезка VP, через ^ — длину отрезка UP, через Si —
площадь треугольника Р\РоР, через S? — площадь треугольника Р1Р2Р, через
S — площадь треугольника P\PqP2, через a — угол PqP\P2- Тогда
, Ь2=
up
Li~ S" V°~ P1P2 ~ L2 ~ S'
В принятых обозначениях вес средней точки выразится через площади тре-
треугольников
Вес w вершины pi можно найти, если S1S2 ф 0, т.е. если точка р не лежит
на линиях PiPo и Р\Рч (точка р должна лежать внутри угла P^P\P>i). В общем
случае вес может быть как положительным, так и отрицательным. Как видно
из рис. 2.6.6 и 2.6.7, если точка Р лежит внутри треугольника PqP\Pi, to вес
точки Р\ положителен, если же точка Р лежит вне треугольника PqP\Pi, to вес
точки Р\ отрицателен.
Если мы вычислили вес w средней вершины, то в соответствии с B.6.14)
вычислим параметр Л = —г конического сечения и конкретный вид урав-
уравнения B.6.4) сечения
u2 + v2 + 2A - 2w2)uv - 2u - 2v + 1 = 0.
Второй инвариант данного конического сечения равен: /г = 4w2(l — w2). В за-
зависимости от знака инварианта /г конические сечения делятся на три типа:
эллиптический тип, если /г > 0; гиперболический, если 7г < 0; параболиче-
параболический, если 7г — 0. Значение инварианта и соответствующий тип конического
не зависят от того, в какой системе координат вычислен инвариант. Таким
образом, если |ю| < 1, то кривая B.6.17) описывает эллипс, если |ю| > 1, то
кривая описывает гиперболу, если |ти| = 1, то кривая описывает параболу.
Возможности кривой B.6.15) можно существенно расширить, если для ка-
каждой из вершин ввести вес.
2.7. Рациональные кривые
В формуле B.6.15) средняя точка pi имеет коэффициент го, называемый
весом. Для полного равноправия точек ро, pi, P2 в этой формуле припишем
каждой из них свой вес wq, w\, W2- В результате правая часть равенства B.6.15)
примет вид
2
(Л _ A *)woPo + 2tA *)WlPl + fw2P2 _ ^° A7
{Х> A - t)*wo + 2t(l - t)wx + Pw2 2 ' У ¦'¦
i=0
2.7. Рациональные кривые 101
Три коэффициента гоо, wi, гог придают правой части выражения B.7.1) симме-
симметричный вид — каждой вершине pj соответствует свой коэффициент W{. Будем
рассматривать выражение B.7.1) как обобщение квадратичной параметриче-
параметрической кривой, позволяющее в частных случаях получить как кривую Безье второй
степени (при wq = w\ = 102), так и коническое сечение (при wq = w<x = kwi).
Коническое сечение можно описать с помощью кривой более высокой сте-
степени, чем это было сделано в B.6.15). Пусть коническое сечение описывается
равенством B.7.1). Умножим числитель и знаменатель правой части равен-
равенства B.7.1) на равное единице число t + A — ?), перегруппируем слагаемые по
степеням произведений t и A — t) и, в результате, придем к выражению
'(*) =
= A - t)zwopo + t(l - tJ{2wipi + wopo) + t2{\ -
Придадим правой части этого равенства форму кубической кривой Безье. Для
этого введем обозначения для весов и вершин в правой части последнего выра-
выражения:
. , 2ioi + wo . 2w\ + w2 ,
W0 = WQ, Wi' = , W2 = , Wz = W2,
о о
2wipi +wopo , \P\ 2P2 ,
po=:po' Pl = 3^? ' P2= ^v ' P3=P2'
Теперь квадратичная кривая B.7.1) примет форму кубической кривой (опустим
штрих у вершин и их весов)
О
- tJwlPl + 3f2(l - t)w2p2 + t3w3pz = hb lWlPl
t:iw3 3
/ , -D iU>i
i=0
Полученная кубическая кривая полностью совпадает с исходной квадратичной
кривой, но внутренние вершины ее характеристической ломаной и их веса стали
другими. Умножив числитель и знаменатель правой части последнего равенства
на неравное нулю число t+(l — t), перейдем к кривой четвертой степени, которая
описывает все то же коническое сечение. Этот процесс можно продолжать и
дальше.
Рациональные кривые Безье. Используем полученный результат для обобще-
обобщения параметрической кривой Безье произвольной степени. Аналогично зависи-
зависимости B.7.1) запишем формулу для вычисления радиус-вектора кривой Безье,
построенной по произвольному числу п вершин, в виде
? Bni{t)wiPi
т(г) = Щ , 0<*<1, B.7.2)
?(K
г=0
где Bni(t) — базисные функции Бернштейна. В общем случае каждая вершина
Pi кривой B.7.2) имеет свой коэффициент W{. Коэффициент W{ называется ве-
весом (значимостью) вершины р{. Кривые, характеристические точки которых
102
Гл. 2. Моделирование кривых линий
обладают весами, называются рациональными. Рациональные кривые широко
применяются в проектировании благодаря Кунсу. Одним из важных свойств
рациональных кривых является то, что описанные ими конические сечения
сохраняют свою природу (остаются рациональными кривыми) при любом про-
проективном преобразовании. Кривая B.7.2), построенная на основе базиса Берн-
штейна, представляет собой рациональную кривую Безье степени го. Если веса
всех вершин равны, то в силу свойства полиномов Бернштейна B.5.5) рацио-
рациональная кривая Безье B.7.2.) становится равной обычной кривой Безье B.5.3).
В общем случае мы всегда можем перейти от рациональной кривой Безье степени
п к рациональной кривой Безье степени п +1, как это было продемонстрировано
выше.
Рациональные кривые дают дополнительные возможности при моделирова-
моделировании линий. Изменяя веса точек, мы изменяем форму кривой. На рис. 2.7.1
приведены рациональные кривые Безье пятой степени, построенные по одним
Рис. 2.7.1. Рациональные кривые Безье с различным весом точки рз
и тем же характеристическим точкам. Веса всех точек, кроме рз, равны еди-
единице, а вес w% точки рз приведен на рисунке. Из рисунка видно, что чем больше
вес точки, тем ближе она к этой точке. Если вес точки отрицательный, то точка
как бы отталкивает кривую от себя.
Если считать, что в знаменателе правой части B.7.2) стоит вес w(t) радиус-
вектора кривой r(t), то его можно считать дополнительной координатой, так как
формула его вычисления через веса вершин совпадает с формулой вычисления
координат радиус-вектора через координаты вершин. При работе с точками,
имеющими вес, удобно пользоваться однородными координатами A.4.6)
"wr{
wrz
w
B.7.3)
где n, Г2, гз — координаты точки г, го — вес точки. В терминах однородных
координат радиус-вектор B.7.3) рациональной параметрической кривой Безье
2.7. Рациональные кривые 103
описывается равенством, по форме совпадающим с равенством для кривой Безье
B.5.3)
п
B.(t) = ^2Bni(t)Pu 0<*<1. B.7.4)
г=0
Мы видим, что вес точки подвергается тем же преобразованиям, что и ее де-
декартовы координаты, поэтому с однородными компонентами Ri радиус-вектора
можно работать без выделения декартовых координат. Декартовы координаты
любой вершины и радиус-вектора точки рациональной кривой получим из од-
однородных координат делением их на последнюю (дополнительную) координату
= R1 =Ba =Rs
Л4 Л4 1щ
В однородных координатах рациональные кривые имеют более компактную
запись, а ее точки могут быть подвержены расширенному матричному преобра-
преобразованию A.4.2), обобщающему все преобразования простой точки.
С помощью кривых Безье можно строить линии произвольной формы на
любом числе точек. Но, если мы хотим построить кривую на п точках, так
чтобы она была заданной степени т < п — 1, то нам не удастся обойтись од-
одной кривой. Если к тому же п не кратно т, то не все составные части будут
кривыми заданной степени. Если совместить первую и последнюю вершины
характеристической ломаной, то получим замкнутую кривую, но в точке замы-
замыкания в общем случае кривая будет иметь излом. Кривые Безье не обладают
достаточной гибкостью в том смысле, что на п точках можно построить кривую
только степени п — 1.
Обобщение рациональных кривых. Рассмотрим формулу для рациональной
кривой Безье B.7.2) в более широком смысле, а именно, подставим в нее вместо
функций Bni(t) некоторые произвольные базисные функции, которые обозначим
через N{(t), и запишем в общем виде формулу для радиус-вектора рациональной
кривой, построенной на п вершинах,
g
? Ni(t)wi
г=1
B.7.5)
где п — число вершин, р, — радиус-вектор г-й вершины характеристической
ломаной кривой, W{ — вес г-й вершины, Ni(t) — функция параметра кривой,
дающая вклад г-й вершины в общую сумму при данном t.
Функции Ni(t) должны позволять интерполировать произвольную функцию
f(t) на некотором заданном отрезке t\ ^ t ^ tn, т.е. для любой функции /(?)
должна существовать линейная комбинация
tp{t) = cxNx{t) + c2N2{t) + ... + cnNn{t),
удовлетворяющая равенствам tp(ti) = f{U), г = 1, 2, ..., n, где *i < t2 < ...
... <tn — последовательность узлов, c\, c2, ¦ ¦., Cn — числовые коэффициенты.
Потребуем, чтобы базисные функции N{(t) обладали свойством функций
Bf(t), а именно, чтобы при любом t они представляли бы собой разложение
104 Гл.2. Моделирование кривых линий
единицы, т.е. удовлетворять равенству
п
?>(*) = 1. B.7.6)
г=1
Это требование выдвинуто для того, чтобы в случае равных весов всех вершин
рациональная кривая B.7.5) превращалась в обычную параметрическую кривую
вида
п
^ *т1п ^ * < *max, B.7.7)
которая в частном случае (в зависимости от функций N{(t)) может быть равна
или кривой Безье, или векторному полиному Лагранжа B.4.13), или ломаной
линии B.4.1). Таким образом, рациональную параметрическую кривую B.7.5)
можно было бы считать наиболее общей формой записи параметрической линии,
которая в качестве частных случаев содержит в себе почти все рассмотренные
выше линии.
Для удобства в кривой B.7.5) нумерация вершин начинается с 1, а не с 0,
как это было у кривых Безье. Заметим, что формула B.7.5) отличается от B.7.2)
еще и тем, что порядок функции Ni(t) не связан с количества вершин п. Един-
Единственная косвенная связь порядка кривой и числа вершин заключается в том,
что порядок кривой не может превосходить число вершин. Мы хотим получить
более универсальную кривую, чем все рассмотренные выше. Область измене-
изменения параметра t кривой B.7.5) в общем случае может быть выбрана удобной
для нас.
В терминах однородных координат радиус-вектор рациональной параме-
параметрической кривой B.7.5) описывается равенством
п
tmin ^ t ^ tmax, B.7.8)
по форме совпадающим с равенством B.7.7).
Радиус-вектор рациональной кривой вычисляется как частное от деления
двух функций параметра кривой ?, поэтому при вычислении производной раци-
рациональной кривой правую часть B.7.5) следует рассматривать как сложную функ-
WY
цию. Если условно обозначим радиус-вектор рациональной кривой как г = —,
W
то производные радиус-вектора рациональной кривой определятся формулами
dr I d{wr) wr dw
dt~w dt w2 dt' [ >
d2r 1 сР(гог) 2 d(wr) dw wr d?w 2гиг /dw\
d3r 1 d?(wr) 3 d2(wr) dw 3 d(wr) Sw wr d3w
~ = ^ ~ ~~?+
г fdw\
dt) ' ( '
dt2 ~dt ~ ^ dt dt2
6 d(wr) fdw\2 6wrd2wdw бгиг
2.8. В-сплайны
105
Ниже мы найдем непрерывные дифференцируемые функции Ni(t), при-
принимающие ненулевые значения на отрезке U ^. t ^ U+m, равные нулю на
остальной части параметрической области кривой и удовлетворяющие равен-
равенству B.7.6). Такими функциями являются фундаментальные сплайны или
.В-сплайны. .
2.8. В-сплайны
Поставим перед собой цель найти некоторую непрерывную то — 1 раз диффе-
дифференцируемую функцию Sm(t), принимающую ненулевые значения только вну-
внутри отрезка to ^ t ^ tm и имеющую равные нулю производные от 0-го до
(то — 2)-го порядка включительно на его концах. Производной нулевого порядка
будем называть значение функции в заданной точке.
Покажем, что теоретически можно построить на отрезке to ^ t ^ tm кусочно-
полиномиальную функцию, удовлетворяющую поставленным условиям. Для
этого разобьем отрезок to ^ t ^ tm оси параметра t на т произвольных участ-
участков. Точки разбиения обозначим через t\, ?г> *3v • •> *m-i> и построим на каждом
1 2
отрезке ij_i ^ t
г = 1, 2, ..., то, полиномы степени то — 1, гладко стыкуя
( )
р ji ^ ^ ^, , , , , , у
их между собой по производным от 0-го до G71 — 2)-го порядка включительно.
Вид искомой функции показан на рис. 2.8.1.
Каждый полином имеет то коэффициентов, всего полиномов то. Для их опре-
определения можно составить то — 1 уравнений в точках стыковки полиномов и т — 1
уравнений на каждом из краев. Всего мы получим G71 — 1)(то + 1) = то2 — 1
уравнений для т2 коэффициентов. Недостающее уравнение может нормиро-
нормировать величину прогиба кусочно-полиномиальной линии, например, путем нор-
нормирования площади под ней, что дает возможность удовлетворить требованию
sm(t)
Рис. 2.8.1. Составной полиномиальный сплайн
B.7.6). Если какие-либо два значения узла совпадают, например t{ =
то полином на этом участке пропадает, а с ним пропадают то неизвестных и
т — 1 уравнений стыковки. Для сохранения равенства числа неизвестных и
числа уравнений откажемся от непрерывности наивысшей производной в крат-
кратном узле. Аналогично поступим при совпадении трех и более узлов. Таким
образом, предъявленные к функции Sm(t) требования не являются противоре-
противоречивыми и могут быть выполнены.
Рассмотренные теоретически возможные кусочно-полиномиальные функции,
а также базисные функции Бернштейна, являются частными случаями .В-сплай-
нов. Основу теории .В-сплайнов заложили Фергюсон, Шёнберг, Уитни и Карри.
Гордон и Розенфельд установили связь между кривыми Безье и 5-сплайнами и
показали, что .В-сплайны являются мощным обобщением функций Бернштейна.
Теория .В-сплайнов базируется на разделенных разностях.
106 Гл. 2. Моделирование кривых линий
Разделенные разности. Приведем необходимые сведения о разделенных раз-
разностях. Пусть имеется некоторая функция /(?) и пусть нам известны значения
функции для некоторых значений параметра /j = f(U), г = 0, 1,2, ..., т. Раз-
Разделенными разностями первого порядка называются отношения
ГГ. , 1 ___ f(U+l) - f(U) ,ЛЙП
f[ti, ti+i\ = . B.8.1)
Ч+l ~ Ч
Точки ti на параметрической оси называются узлами. Будем считать, что разде-
разделенные разности составлены по узлам с соседними номерами. Пока не оговорено
противное, нумерация узлов может быть произвольной, и необязательно, чтобы
узлы были пронумерованы в порядке возрастания значений. По разделенным
разностям первого порядка вычисляются разделенные разности второго порядка
f[U, U+l, 4+21 = " : • B.8.2)
ti+2 - Ч
Следуя данному алгоритму, вычисляются разделенные разности более высоких
порядков. Например, если известны разделенные разности (к — 1)-го порядка,
то разделенная разность А;-го порядка определяется как отношение
.1 f[U+l,U+2,--;U+k] - f[ti,U+l,--;ti+k-l] ,0 о п\
• • •, Ц+к\ = • B.8.6)
Ч+к - Ч
Разделенные разности будем обозначать символами функции, по которой они
вычислены, с квадратными скобками, в которых перечислены значения узлов.
Порядок разделенной разности на единицу меньше числа узлов в квадратных
скобках. Разделенными разностями нулевого порядка являются значения функ-
функций в узлах f[ti] = f(U). Если функция /(?) есть полином степени к, то как
будет показано ниже, разделенная разность А;-го порядка, построенная по этому
полиному, равна коэффициенту при tk полинома.
Если в разделенной разности первого порядка значения узлов совпадают, то
она равна пределу отношения B.8.1), т.е. производной функции в данной точке
?
lim
= f'(U). B.8.4)
Аналогично находятся разделенные разности более высокого порядка, постро-
построенные на совпадающих узлах. Так разделенная разность к-то порядка, соста-
составленная на к + 1 равных узлах, равна к-й производной функции, вычисленной
в данном узле, деленной на к\
1 dkf -J у"г) B.8.5)
k\
(/с! в знаменателе правой части является следствием того, что в знаменателе
разделенной разности стоит длина нескольких участков ti — t). Узлы, значения
которых совпадают, называются кратными узлами. Так, если ij+i = ti+2 — • ¦ •
... = ti+k, то говорят, что эти узлы имеют кратность к.
2.8. В-сплайны 107
Разделенная разность к-ro порядка следующим образом выражается через
значения функции /(?) в узлах:
f[U, U+i, • • м U+k] —
=
- tj+k)
где Witk'(tj) — производная функции W{tk(t) = (t — U){t — U+i)(t ~ U+2)---
...(? — ti+k-i){t ~ U+к)) вычисленная при t = tj. Индексы i и к в обозначе-
обозначении функции VFj?fc(i) говорят об индексе начального узла и о количестве узлов.
Равенство B.8.6) докажем методом индукции. Для разделенной разности пер-
первого порядка формула B.8.6) совпадает с B.8.1), т.е. для к = 1 равенство B.8.6)
справедливо. Предположим, что равенство B.8.6) справедливо для разделенных
разностей (к— 1)-го порядка и убедимся, что из этого предположения следует его
верность для разделенных разностей к-то порядка. Для этого вычтем равенства
и
j[H, H+l, ¦¦¦¦> H+k-l} —
аналогичные B.8.6), для разделенных разностей на порядок ниже, у которых
соответствующие слагаемые приведены к общему знаменателю. В результате
получим равенство
l-i h+2, • • •> U+k] — f[tii ti+l, ¦ • •> ti+k-l] =
= (tj+k-U)f(fi) ^ (<j-<i)/(<j)-(<j-<i+fc)/(<j)
+Д W'it)
(tj+k — U)f(U+k)
из которого после деления на (ij+fc — U) на основании B.8.3) следует B.8.6).
Из равенства B.8.6) видно, что разделенная разность не зависит от порядка, в
котором следуют узлы ?j, U+i, ..., ti+k в списке аргументов.
Разделенные разности полиномов. Если p(t) является полиномом m-й сте-
степени параметра t и нам известны значения полинома p(ti) в точках U, г =
= 0, 1, 2, ..., т, то разделенная разность первого порядка
p(tQ)-p(t)
p[t, щ = —:—:—
to — t
108 Гл. 2. Моделирование кривых линий
является полиномом (т —1)-й степени. В самом деле, функцияp(to)—p(t) имеет
корень to и, следовательно, согласно теореме Безу долится без остатка на to ~~ t-
Разделенная разность второго порядка
г, , , ! Ж), <1].-P[<, to]
p[t, t0, iij = _
является полиномом (m — 2)-й степени. Действительно, функция p[to, t\] —
- p[t, t0] = p[t\, tQ] - p[t, t0] имеет корень ii (p[t\, t0] - p[t\, t0] — 0) и, сле-
следовательно, согласно теореме Безу делится без остатка на t\ — t. С помощью
аналогичных рассуждений приходим к тому, что разделенная разность т-го
порядка есть полином нулевой степени
p[t, t0, h, ..., tm-\] = const, B.8.7)
а разделенная разность (m + 1)-го порядка полинома степени т равна нулю:
p[t, to,tu .... im] = 0. B.8.8)
Пусть теперь p(t) является интерполяционным полиномом функции /(?), со-
совпадающим с ней в т+1 узлах ij, p(ti) = f(ti), i = 0, 1, 2, ..., т. Разделенные
разности, построенные по узлам ij, для функций p(t) и /(?) будут равны. Из
определения разделенной разности для функции p(t), построенной на последо-
последовательности узлов t, to, ii, ¦ ¦., tfc-i, ifc,
¦ u + i + л ff[frb h, h, ¦•¦» tk] -p[t, t0, h, ..., tk-i]
p[t, to, h, t2, ..., tfcj = ¦¦ B.8.9)
и равенств разделенных разностей p\to, ti, ¦ ¦., tk] — f[to, h, ..., ifc] следуют
равенства:
p[t, to, h, ..., tm-{] —
= f[to, h, ¦.., tm] + (t — tm)p[t, to, h, ..., tm] ¦= f[t0, h, ..., tm],
p[t, to, h, ..., tm-2] = /fob *ii ¦ ¦ •) tm-i] + (t - tm-i)p[t, to, ti, ..., im_i],
p[t, h] = f[t0, h] + {t- ti)p[t, to, h],
Так как p(t) = p[t], то подставляя последовательно эти равенства каждое по-
последующее в предыдущее, начиная с последнего, получим интерполяционную
формулу Ньютона B.4.17) для скалярной функции /(?)
P(t) = f[to] + /[to, h]{t - t0) + /[io, h, t2]{t - tQ){t -h) + ...
¦ ¦¦ + f[to, h,..., tk]{t - to){t - h). ..(t- ifc-i) + ...
• • ¦ + f[to, h, ..., tm]{t - to){t - h).. .(t - tm-i). B.8.10)
Таким образом, коэффициенты в полиноме Ньютона являются соответствую-
соответствующими разделенными разностями интерполируемой функции. Если интерполя-
интерполяцию B.8.10) выполнить на совокупности т+1 совпадающих узлов to = t\ =
2.8. В-сплаины 109
= ^2 = • ¦ ¦ = tm-i = tm, то в соответствии с B.8.5) разделенные разности про-
пропорциональны производным соответствующего порядка интерполируемой функ-
функции, и мы получим усеченный ряд Тейлора.
Вычислим с помощью B.8.10) разделенную разность m-го порядка для т
совпадающих узлов to = ii = . • • = tm-\ и одного отличного от остальных
tm-i Ф tm. Все разделенные разности более низкого порядка в соответствии с
B.8.5) будут пропорциональны производным соответствующего порядка функ-
функции /(?), a p{tm) = f{tm). Искомая разделенная разность определяется фор-
формулой
f[to, ^1) • • •) tm] = f\to, to, to, ¦ ¦ ¦, to, tm] =
f(tm)
{tm-tO)
B.8.11)
где f^'(to) ¦— производная j'-го порядка в точке to (производной нулевого по-
порядка мы называем значение функции).
Свойства разделенных разностей. Известно, что по заданной совокупности
значений функции f(U) в узлах ?,-, % — 0, 1, 2, ..., т, можно построить един-
единственный полином степени т, совпадающий в узлах U с заданной функцией.
Из интерполяционной формулы Ньютона B.8.9) видим, что разделенная раз-
разность /[^0) t\, ..., tm] m-ro порядка на заданной последовательности т + 1
узлов равна коэффициенту при наивысшей степени аргумента tm полинома сте-
степени т, значения которого в заданных узлах согласуются с функцией f(t). Это
свойство может быть принято в качестве определения разделенной разности.
Свойство 1. Если f{t) = ао + ait + a,2t2 + ... + amt
f[to, h, ¦ ¦ •> tm, tm+l] = 0
m то
для любого дополнительного узла
Свойство 2. В силу единственности такого полинома, а также в силу
B.8.6), любая разделенная разность является симметричной функцией своих
аргументов, т.е. значение f[to, h, ..., tm] не зависит от порядка, в котором
следуют узлы to, ii, ¦ ¦., tm в списке аргументов
/[?(), <1, *2, • • •, tm] ~ /[<i, to, t2, ¦ ¦ ., tm) = . . . = f[tk, U, . . ., tj], B.8.13)
где tk, ti, ..., tj есть последовательность узлов to, *i, ..., tm, записанных в про-
произвольном порядке. Разделенная разность выражается через значения функ-
функции /(?) в узлах с помощью формулы B.8.6). Если некоторые узлы являются
кратными, то разделенная разность выражается через значения функции f(t)
в простых узлах и ее производные в кратных узлах.
Свойство 3. Если f(t) = kgg(t) + khh(t), то
f[t0, h, ..., tm] = kgg[t0, h, ..., tm] + khh[to, h, ..., tm]. B.8.14)
Это равенство следует из единственности интерполяционного полинома.
110 Гл.2. Моделирование кривых линий
Свойство 4. Если f(t) = g{t)h(t), то
f[to, *i, ..., tm] = ^2g[to, h, ¦ • ¦, tk]h[tk, tk+i, ..., tm]. B.8.15)
fc=0
Для доказательства этой формулы аппроксимируем каждую из функций g(t)
и h(t) полиномом B.8.10) и перемножим их. Коэффициент при наивысшей
степени tm результирующего полинома будет равен правой части B.8.15), что и
требовалось доказать. Равенство B.8.15) носит имя формулы Лейбница.
Свойство 5. Если для функции /(<) построен полином pm-i(t) степени
т — 1 на последовательности узлов to, t\, ..., tm-i, то
f(t)=pm-1(t) +
+ /[*0, *1, • ¦ ¦, *m-l, t]{t - tO)(t - h). . .{t - tm-2){t - tm-l)- B.8.16)
Это равенство получим, рассматривая t как дополнительный узел tm в последо-
последовательности узлов и рассматривая равенство как необходимое условие в допол-
дополнительном узле для полинома степени т.
Усеченная степенная функция. Рассмотрим усеченную степенную функцию
со смещенным началом, которую обозначим через
am(z) = (z- t)m+ = (max @, z - t))m. B.8.17)
Эта функция равна 0 при г^и равна (z — t)m в противном случае. Функция
am{z) — кусочно-монотонная, непрерывная при т > 0; при т = 0 она имеет
скачок в точке z = t, равный единице. Функция am(z) имеет непрерывные
производные до (т — 1)-го порядка включительно. Производная т-то порядка
имеет разрыв в точке z = t, равный ml. Функция B.8.17) примечательна тем,
что ее производные являются аналогичными функциями, только на порядок
ниже. Нам понадобятся как производные по z, так и производные по t:
= m(z — i)m-1+ = mcrm_i,
dz
= — m(z — tI71 , = —mcrm_i,
dcrm
dt
i
г-к _
dkam m! , .4rn_t m!
dzk (m — k)\ +
{ifm\ k _
{-ifm\
k = 0, 1, ..., m.
Графики функций am(z) приведены на рис. 2.8.2. Чем выше порядок функции
crm(z), тем она более гладкая в точке z = t.
Рассмотрим, свойства вычисленных по значениям функции am-i(z) =
= (z — t)m~1+ в узлах to, ti, ..., tm разделенных разностей m-ro порядка
M(t) = crm_i[?0, h, ..., tm]. ¦¦ Разделенная разность вычисляется при фикси-
2.8. В-сплаины
111
рованном параметре t, но является функцией параметра t. Если все U < t,
i = О, 1, ..., m, то все om-\{ti) = 0 и разделенная разность am-i[to, t\, ..., tm]
также равна нулю. Если все U > t, i = 0, 1, ..., m, то разделенная разность
т-то порядка равна нулю, так как все узлы находятся на участке, где функция
представляет собой полином степени, меньшей т.
Предположим, что последовательность узлов является возрастающей, т. е.
ij < ij+i для всех i = 0, 1, ..., т — 1. Тогда по указанным выше причинам
разделенная разность crTO-i[io> *ъ • • •> tm] и ее производные по t при t = to и
0 t z
Рис. 2.8.2. Усеченная степенная функция со смещенным началом
t = tm равны нулю. Разделенная разность am-i[to, t\, ..., tm] как функция
параметра t является непрерывной функцией, отличной от нуля только на ин-
интервале to < t < tm. В соответствии с B.8.6) она выражается через значения
усеченной степенной функции в узлах
i, ..., tm] =
(tj - t)
m-l
(tj - t)
m-l
где Wo,m'(tj) — производная функции Wo,m(t) = (t - to)(t - t\)(t - <г)---
.. .(t — tm-i)(t — tm), вычисленная при t = tj. Производные разделенной разно-
разности no t до (m — 2)-го порядка
dtk
(m-l-А)!
tm] =
B.8.20)
также являются непрерывными функциями параметра t.
Таким образом, разделенная разность M(t) = crm_i[io, t\, ..., tm\ как функ-
функция параметра t удовлетворяет всем требованиям кроме требования B.7.6),
предъявленным к базисным функциям Ni(t) в формуле B.7.5), и имеет вид,
112 Гл. 2. Моделирование кривых линий
приведенный на рис. 2.8.1. Набор функций M(t) является претендентом на роль
базисных функций в формуле B.7.5). Для удовлетворения требованию B.7.6)
функции M(t) можно нормировать, умножив их на некоторый коэффициент.
В-сплайн (фундаментальный сплайн). В литературе используется несколько
различных определений и обозначений 5-сплайна. Вводятся определения не-
ненормированного 5-сплайна и нормированного 5-сплайна. В общем случае эти
определения звучат так. Ненормированный В-сплайн для неубывающей после-
последовательности т узлов есть разделенная разность т-го порядка усеченной
степенной функции со смещенным началом am-i(z) = [z — l)m-1+. Нор-
Нормированный В-сплайн для неубывающей последовательности т узлов есть
разделенная разность т-го порядка усеченной степенной функции со сме-
смещенным началом <7m_i(z) = (z — t)m~l+, умноженная на разность значений
последнего и первого узла. Ненормированный и нормированный 5-сплайны
связаны между собой только коэффициентом и с точностью до множителя их
определения одинаковы. Далее, если не будет указано конкретно, термин
«.В-сплайн» мы будем использовать для обоих указанных сплайнов.
В зависимости от того, к какому узлу заданной последовательности (пер-
(первому или последнему) привязывается обозначение 5-сплайна, и от того, какой
порядок (равный порядку разделенной разности или равный степени усечен-
усеченной степенной функции) приписывается 5-сплайну, в литературе встречается
четыре определения 5-сплайна. Приведем их все. Начнем с нормированных
5-сплайнов, так как именно они представляют для нас наибольший интерес.
Определение 1. Нормированный г-й 5-сплайн m-го порядка Nijin(t) для
неубывающей последовательности узлов ?г-, i,-+i, ij+2> • • •> U+m есть разделенная
разность m-ro порядка усеченной степенной функции am-i(z) = [z — t)m~l+,
умноженная на (ij+m ~ U)'-
Ni,m(t) = {ti+m - ti)am-i[U, ti+u ..., ti+m]. B.8.21.1)
Определение 2. Нормированный г'-й 5-сплайн m-ro порядка Nm:i(t)
для неубывающей последовательности узлов ij-m, U~m+i, ••¦¦> U-i, U есть
разделенная разность m-ro порядка усеченной степенной функции am-i(z) =
= (z — t)m~1+, умноженная на (?,¦ — ij-m):
Nm,i(t) = (U - U-m)<rm-l[U-m, U-m+U ¦ ¦ ; <•]• B.8.21.2)
Определение 3. Нормированный i-й 5-сплайн (m — 1)-го порядка
JVtm-1(<) для неубывающей последовательности узлов ?,-, ij+ь ^г+2) ¦ • •, ti+m есть
разделенная разность m-ro порядка усеченной степенной функции am-i(z) =
= (z — t)m~1 + , умноженная на (U+m — U):
Ni'1^) = (ti+m - U)am-i[U, ti+u ¦ ¦ -, U+m). B.8.21.3)
Определение 4. Нормированный i-й 5-сплайн (m — 1)-го порядка
Nrn~1i(t) для неубывающей последовательности узлов ?j_m, ij_m+i, ..., tt-i,
t{ есть разделенная разность m-ro порядка усеченной степенной функции
(jm_i(z) = (z - t)m~1 + , умноженная на (f,- - U-m)-
Nm~li{t) = (ti - ti-m)om-l[ti-m, ti.m+U . • ., U]. B.8.21.4)
2.8. В-сплайны 113
Аналогично звучат определения для соответствующих ненормированных
В-сплайнов, которые мы рассмотрим ниже. Для приведенных определений
мы ввели различные обозначения В-сплайнов, чтобы не возникла путаница.
В первом определении В-сплайн привязан к первому узлу (наследует его ин-
индекс) и этот индекс стоит перед индексом т порядка В-сплайна. Во втором
определении 'В-сплайн привязан к последнему узлу (наследует его индекс) и
этот индекс стоит после индекса т порядка -В-сплайна. Третье определение
аналогично первому, только В-сплайну приписывается порядок, равный степени
усеченной функции, который оказывается на единицу меньше порядка разделен-
разделенной разности. Для обращения внимания на это отличие мы обозначили поря-
порядок .В-сплайна верхним индексом. Четвертое определение аналогично второму,
только В-сплайну приписывается порядок, равный степени усеченной функции,
который на единицу меньше порядка разделенной разности. Как и в третьем
определении, мы обозначили порядок В-сплайна верхним индексом. В третьем
определении В-сплайн привязан к первому узлу, а в четвертом определении
В-сплайн привязан к последнему узлу (наследует его индекс). Соответственно,
в третьем определении индекс узла привязки стоит перед индексом, обозначаю-
обозначающим порядок .В-сплайна, а в четвертом определении индекс узла привязки стоит
после индекса порядка В-сплайна. Все четыре определения равноправны и при-
приводят к одному и тому же рекуррентному соотношению для В-сплайнов, но
форма записи этих рекуррентных соотношений различна.
Дадим пояснения к определениям В-сплайна на примере первого определе-
определения. Последовательность узлов <;, U+i, ..., U+m должна быть неубывающей, т. е.
должно выполняться неравенство tj ^ tj+i для всех j = г, i + 1, ..., i + m — 1.
В остальном же значения узлов последовательности не оговариваются и в об-
общем случае могут быть произвольными, в том числе и совпадающими. То, что
.В-сплайн Nitm(t) называется г-м, подчеркивает, что разделенная разность по-
построена на последовательности узлов, начинающейся с узла Ц и кончающейся
на узле ti+m. Разделенная разность am_i[?j, ?,-+i, ..., ti+m] вычислена по функ-
функции сгт_](;г) = [z — t)m~1+ при фиксированном значении t, при рассмотрении
ее как функции только аргумента z. Значение разделенной разности, есте-
естественно, зависит от выбранного параметра t, о чем говорит аргумент Nitm(t).
В-сплайн Niiin(t) нормирован коэффициентом (ti+m —ti ), на который умножена
разделенная разность.
При втором определении В-сплайна последовательность узлов Ц-т,
U-m+i, •••> ti также должна быть неубывающей. То, что В-сплайн Nm^{t)
называется г-м, подчеркивает, что разделенная разность построена на последо-
последовательности узлов, начинающейся с узла ti-m и кончающейся на узле t{. Раз-
Разделенная разность crm_i[ij_m, tj_m+i, ..., ti] вычислена по функции am-i(z) =
= (z — t)m~l+ при фиксированном значении t, рассмотренная как функция
только аргумента z. Значение разделенной разности зависит от выбранного
параметра t, о чем говорит аргумент Nmii(t). В-сплайн Nmji(t) нормирован
коэффициентом (ti — U-m), на который умножена разделенная разность.
Далее мы будем строить кривые r(t) на базе точек р^, в которых индекс узла
привязки В-сплайна будет соответствовать (равен) индексу точки pj. Так как
индексация точек обычно начинается с нуля или единицы, то при использова-
использовании второго или четвертого определений В-сплайна индексацию узлов последо-
последовательности придется начинать с отрицательных значений так, чтобы индекс
8 — 5293 Голованов
114 Гл.2. Моделирование кривых линий
m-го по порядку узла был равен нулю, тогда индекс первого по порядку узла
будет равен —т.
Гладкость 5-сплайнов характеризуется порядком, который в первом и вто-
втором определениях равен порядку разделенной разности. В первых двух опреде-
определениях приходится различать степень полиномов и порядок сплайнов. Порядок
сплайна, как и степень полинома, характеризует непрерывность ее производ-
производных. Для сплайна порядка m должна существовать и быть отличной от нуля
(за исключением отдельных точек) производная (т — 1)-го порядка, а произ-
производная т-го порядка должна быть равна нулю. В первых двух определениях
В-сплайны порядка тп представляют собой кусочно-полиномиальные функции,
построенные на полиномах степени m — 1, поэтому их порядок на единицу
больше наивысшей степени полинома. В третьем и четвертом определениях
В-сплайны порядка m представляют собой кусочно-полиномиальные функции,
построенные на полиномах той же степени т, поэтому их порядок равен наи-
наивысшей степени полинома.
Дальнейшие выкладки вьшолним одновременно для первого и второго опре-
определений нормированного В-сплайна. Для третьего и четвертого определений
все формулы могут быть получены аналогично.
Пусть В-сплайн m-го порядка построен на неубывающей последовательно-
последовательности m + 1 узлов ta, ta+i, • • ч tb-ii hi где ij, = ta+m. В-сплайн отличен от нуля
на небольшой области, т. е. Na<m(t) = 0 и ЛГт,ь(*) = 0 при t < ta и при t ^ %.
Действительно, как только t < ta, то между точками ta и % усеченная функ-
функция примет вид am-\(z) = (z — i) и в силу того, что (z — t)'1 является
полиномом степени меньшей т, любая разделенная разность m-го порядка, по-
построенная по этому полиному, равна нулю. Как только t ^ Ц, то разделенная
разность равна нулю в силу того, что между точками ta и t;, am-\{z) — 0.
Только на участке ta ^ t < t\, функция am-\(z) представляет собой отрезок го-
горизонтальной прямой, сопряженный с отрезком смещенной степенной функции,
и поэтому ее разделенная разность am-\[ta, ta+\, ..., tb] отлична от нуля.
Если воспользоваться определением разделенной разности B.8.4), то
В-сплайн можно записать в виде
— (Tm-l[ta+l, ta+2i ¦ ¦ -i Ч] — O"m-l[<o, о+Ь > 6l]>
B.8.22)
= &m-l[ta+l, ta+2, ¦ ¦ ¦, h] — am-l[ta, * 4]
Для любого tj ^ t < ij+i, в силу локальности отличны от нуля только m
В-сплайнов, а именно, Nj-m+ijm(t), Nj-m+2,m{t), •••, Nj-hm(t), Njim(t) и
^ro,i+i(*), Nm>j+2(t), ..., Nm>j+m-.i(t), Nm>j+m(t). Используя равенство
B.8.22), найдем сумму всех В-сплайнов для tj < < < tj+i:
i=j—m+l i—j—m+1
j 3
= 2_j am-l[U+l, U+2, ¦••) ti+m] ~ 2_> am-\[U, U+l, • ¦ м U+m-l] —
i=j—m+1 j=j—m+1
jjm+1
— Vm-l[tj-m+l, tj-m+2, • • •, tj] =1 — 0 =1. B.8.
.23)
2.8. В-сплаины 115
В B.8.23) использовалось то, что am-i[tj+i, ij+2) • • • > tj+m] = 1 как коэффици-
коэффициент при наивысшей степени аргумента полинома (z — t)m~1, которым оцисыва-
ется усеченная степенная функция на открытом интервале i/+i < z <ij+m. При
этом на интервале tj-m+\ < z < tj усеченная степенная функция равна нулю,
следовательно, am-i[tj-m+i, ?j_m+2> ¦ ¦ ¦, tj] = 0. Так как участок tj ^ t < tj+\
был выбран произвольно, то аналогичное равенство выполняется для любого
другого участка. Таким образом, при любом t для суммы всех 5-сплайнов
справедливо равенство
Z> X>m,i(i) = l- B-8-24)
Именно ради свойства B.8.24) нормируются разделенные разности в опреде-
определении нормированного ??-сплайна. Функции iVj>m(i) и Nmti(t) представляют
собой разложение единицы.
Вычисление нормированных ??-сплайнов производится через ненормирован-
ненормированные ??-сплайны, являющиеся обычными разделенными разностями. Обра-
Обратимся к ненормированным 5-сплайнам. Введем четыре различных опреде-
определения ненормированного 5-сплайна. Они соответствуют приведенным выше
четырем определениям нормированного 5-сплайна.
Определение 1. Ненормированный г-й 5-сплайн m-го порядка MijTn(t)
для последовательности узлов ij, ij+ii if+25 • • ¦> ij+m есть разделенная разность
m-ro порядка усеченной степенной функции am-i(z) = (z — t)m~1,:
Mi>m(t) = am-i[U, ti+i, ..., ti+m]. B.8.25.1)
Определение 2. Ненормированный г-й 5-сплайн m-го порядка Mmti(t)
для последовательности узлов ti-m, ij-m+b •••) U-i, U есть разделенная раз-
раз1
ность m-го порядка усеченной степенной функции am-i(z) = (z — i)m-1 ,:
Mm,i(t) = am-i[U-m, U-rn+i, ¦ ¦ •, Ul B.8.25.2)
Определение 3. Ненормированный г-й 5-сплайн (m — l)-ro порядка
Mim~1(t) для последовательности узлов ij, ij+i, ij+2> • • •) ^г+m есть разделенная
l
разность m-ro порядка усеченной степенной функции am-i(z) = (z — t)m~l+:
Mim-l{t) = am-i[U, ti+u ..., ti+m]. B.8.25.3)
Определение 4. Ненормированный г-й 5-сплайн (m — l)-ro порядка
Mm~li{t) для последовательности узлов ij_m, ij-m+b • • ч U-i, ij есть разделен-
разделенная разность m-го порядка усеченной степенной функции crm-\ (z) = (z — i)m-1+:
Mm-\{t) = <rm_i[ii_m, U-m+u ¦ ¦ -, til B.8.25.4)
Индексные обозначения ненормированного 5-сплайна соответствуют ин-
индексным обозначениям нормированного 5-сплайна. Все определения ненор-
ненормированного 5-сплайна равноценны. Рассмотрим свойства ненормированного
.В-сплайна.
8*
116 Гл.2. Моделирование кривых линий
Ненормированный 5-сплайн первого порядка для первых двух определений
и ненормированный 5-сплайн нулевого порядка для последних двух определе-
определений равен разделенной разности первого порядка для функции <jq(z) = (z — t)°+:
-, если ti^t < ij+i,
B.8.2b.
О, если t < ti или t ^ ij+i,
• -T'
о,'
l
о,
1
i Ч—1
о,
-, если
если
если
если
t<
t <
t<
< t < ti,
ti-.\ ИЛИ
ti ИЛИ t i
^. t <C tj,
ti-l ИЛИ
1
t;
>t,
t~i
zti,
iti.
MM(i) = <*<-*,-_!' ——*-—" B.8.26.2)
B.8.26.3)
Формула Кокса-Де Бура. Пусть имеется неубывающая последовательность
т + \ узлов ta = tb-m, ta+\, ...,tb-i, h = ta+m. Используем формулу Лейбница
B.8.15) для вычисления В-сплайна B.8.21), представив функцию am-i(z) =
= {z — t)m~1+ в виде произведения am-i(z) = g(z) ¦ (Tm_2(z), где <jm_2(^) =
= (z — t)m~2+ и g(z) — {z — t). Тогда при ta < ? < Ц разделенная разность
2, ..., ib] + 0+... + 0-
= (*a — i)o"m-2^a) *a+l, ¦ • ч *б] + O"m-2^a+l, *a+2) • • ч 4]- B.8.27)
Подставим в B.8.27) определение разделенной разности B.8.3) для
г 1 Cm-2L^a+l) ^a+2) ¦ • ч ^6J &m—2\ta.) ^a+lj ¦ • ч *Ь— 1 j
&т—2l^aj ^a+lj ¦ • ч ^6J — 7 7
?b — *a
и получим
-t
'" -'*¦¦+¦- +-J-CTm_2lia, *o+li ¦••» "o-ijy '
i ta+2i • • ч ^6J r=
m-2[ a, a+ ,¦•¦, b-U B.8.28)
~" ta
2.8. В-сплаины 117
Перепишем равенство B.8.28) с использованием определений ненормированного
.В-сплайна B.8.25.1)-B.8.25.4) и получим формулы
{tb-t)Ma+l™-\t)
h-
ta
+ (t-ta)Ma^(t)
7-ta)M^b_l{t)
Ma m(t) = ^t)Ma+hm_l{t) + {tta)Ma,m_l{t)^
h - ta
мт 'b(t) = C*-^ii*W + ('-^m-i№ B>8-29>2)
B.8.29.3)
4 — ta
M-\(t) = С.')«-У^('')«"-'.С)
*b — *a
Рекуррентные соотношения B.8.29.1)-B.8.29.4) были получены независимо
Мэнсфилдом, Коксом и Де Буром и носят имя формул Кокса-Де Бура. Эти со-
соотношения занимают центральное место в теории 5-сплайнов. Они побуждают
забыть о разделенных разностях и определить Б-сплайн m-го или (т — 1)-го
порядка для неубывающей последовательности т + 1 узлов ta = tb-i, ia+i> i • ¦ ¦
..., ift-i, ti, = ta+m как функцию, вычисляемую по одному из рекуррентных
соотношений B.8.29.1)-B.8.29.4) при соответствующем начальном значении
B.8.26.1)—B.8.26.4). Все рекуррентные формулы равноценны.
Обратим внимание на то, что в формулах B.8.29.1) и B.8.29.2) В-сплайн
m-го порядка для неубывающей последовательности т + 1 узлов вычисляется
через два Б-сплайна (т — 1)-го порядка, определенных на последовательно-
последовательностях т узлов, лежащих внутри заданной последовательности. Один из двух
Б-сплайнов (т — 1)-го порядка примыкает к началу вычисляемого .В-сплайна,
а другой — к концу вычисляемого .В-сплайна (рис. 2.8.3). Каждый из двух
Рис. 2.8.3. Иллюстрация рекуррентного соотношения Кокса-Де Бура
5-сплайнов (т — 1)-го порядка берется с коэффициентом, пропорциональным
расстоянию параметра t от крайнего узла заданной последовательности, к ко-
которому .В-сплайнов (т — 1)-го порядка примыкает. Сумма этих двух коэффи-
коэффициентов равна единице.
Отвлечемся в формулах B.8.29.1)-B.8.29.4) от индексации и рассмотрим их
с использованием барицентрических координат. Пусть дана произвольная по-
последовательность т + 1 узлов to, ii, •.., tm, хотя бы два из которых имели
отличные друг от друга значения. Вспомним, что разделенная разность не за-
зависит от порядка следования узлов в списке аргументов. Из последовательности
т + 1 узлов выберем два произвольных несовпадающих узла ta и tb- На базе
118 Гл. 2. Моделирование кривых линий
этих двух узлов введем барицентрические координаты
/ ,\ *Ь * >/,ч ta *
Введем следующие обозначения. Последовательность т + 1 узлов to, h, ..., tm
обозначим через Т. Последовательность т узлов, полученную из Т удалением
узла ta, обозначим через Т\а. Последовательность m узлов, полученную из
Т удалением узла Ц, обозначим через Т\Ь. Разделенную разность т-го по-
порядка усеченной степенной функции (z — t)m~1 + на последовательности узлов
Т обозначим через MT(t). Разделенную разность (т — 1)-го порядка усеченной
степенной функции (z — t)m~2 , на последовательности узлов Т\а обозначим
через MT\a(t). Разделенную разность (т — 1)-го порядка усеченной степен-
степенной функции (z — t)m~2+ на последовательности узлов Т\Ь обозначим через
MT^b(t). Тогда формулы Кокса-Де Бура B.8.29.1)-B.8.29.4) для вычисления
ненормированного .В-сплайна на последовательности узлов Т можно заменить
рекуррентным соотношением
MT(t) = A^!mtV(*) + ±±Z±MT\b(t) = a{t)MT\a(t) + b(t)MT\b{t). B.8.30)
Так как в силу свойства 2 разделенная разность является симметричной функ-
функцией своих аргументов, то последнее рекуррентное соотношение не зависит от
выбора узлов ta и Ц- Рекуррентное соотношение B.8.30) начинается с последо-
последовательности, состоящей из двух узлов ta и tb%.
если min(ia, tb) ^ t < max(ia, ij,),
= { \tb-ta
О в остальных случаях.
Последовательность узлов Т в общем случае может быть произвольной. Мы
рассматриваем неубывающую последовательность узлов, так как нас интересует
не отдельно взятый 5-сплайн, а совокупность отличных от нуля В-сплайнов при
заданном параметре t.
Рекуррентные соотношения B.8.29.1)-B.8.29.4) показывают, что если
M0+i,m-i(*)> 0 и M0>m_i(i) ^ 0, то и Ma,m(t) ^ 0, и что если Mm-\,b{t) > 0
и Mm_iib_i(<) > 0, то и Mm,b(t) > 0. Так как в B.8.26.1) Ми(<) Hи
в B.8.26.2) Miti(t) ^ 0, то можно сделать вывод, что .В-сплайны при любых
значениях параметра неотрицательные:
Нормированный В-сплайн связан с ненормированным В-сплайном соответ-
соответствующим соотношением:
Na,m{t) = (ta+m - ta)Ma,m{t), B.8.31.1)
Nm,b{t) = (tb ~ tb-m)Mm,b(t), B.8.31.2)
Na'1® - (ta+m - ta)Mam-l(t), B.8.31.3)
Nm-\(t) = (tb - tb-m)Mm-\(t). B.8.31.4)
2.8. В-сплайны 119
Тогда для нормированного 5-сплайна формула Кокса-Де Бура примет вид
hV -l@ + /~Ч JVa,m-l(*), B.8.32.1)
*а Nm-ltb-i{t), B.8.32.2)
^V^-111^). B-8.32.3)
Nm-2b(t) + *\ ЛГ-2Ь-1@. B.8.32.4)
где индексы а и b связаны равенством b — a + т или a = b — т. Вычисления
начинаются с 5-сплайна наименьшего порядка:
0, если t < ti или t
eCJmtr1^t<t\^, B.8.33.2)
0, если t < U-i или < ^ ij, v ;
^<41;* B-8-33-3)
t <U или t ^ ij+i, v ;
^USM B-8.33.4)
0,
Если формально представить схему вычисления 5-сплайна определения 1,
хо она выглядит следующим образом (порядок 5-сплайна возрастает сверху
вниз, а номера узлов возрастают слева направо):
Niti{t) Ni+ltl(t) ... Ni+m-3,i(t) Ni+m-2,i{t) Ni+m-ltl{t)
Ni,2(t) Ni+i,2(t) ... Ni+m-3t2{t) Ni+m-2i2{t)
... iVi+TO_3K(i)
Ni,m(t)
Среди 5-сплайнов первого порядка B.8.26.1) только один отличен от нуля при
данном параметре t, а для вычисления точки кривой B.7.5) требуются все
В-сплайны, отличные от нуля при данном параметре t. Поэтому для параметра
t{ ^ t < ij+i вычисление всех т отличных от нуля 5-сплайнов m-го порядка
удобнее производить по схеме
Niti(t)
Ni-i,2(t) Nil2(t)
Ni-2fi(t) iVi_1K(i) Nit3(t)
Ni-m+2,m-l(t) ••• Ni^2,m-l(t) JV,-_i>m_i(i) JVi>m_i(
Ni-m+ltm(t) Ni-.m+2im{t) ... ATi_2,m(i) Ni-ijtn(t) Ni>m(t)
120 Гл. 2. Моделирование кривых линий
Эту треугольную таблицу можно вычислять построчно, полагая неупомянутые
крайние соседние 5-сплайны равными нулю. Вычислительные затраты мо-
могут быть меньше, если работать с ненормированными 5-сплайнами Mjim(i),
нормируя их в последней строке.
Схема вычисления ??-сплайна определения 2 выглядит следующим образом
(порядок 5-сплайна возрастает сверху вниз", а номера узлов возрастают слева
направо):
) Nhi.m+2(t) ... Nlti-.2(t) JVi,i_i(t) JVi.i(t)
N2,i-m+2(t) ... N2^2{t) N2*-i(t) N2ti(t)
Nm-2,i~l(t) JVTO-2,i(t)
Среди 5-сплайнов первого порядка B.8.26.2) только один отличен от нуля при
данном параметре t. Поэтому для параметра ij_i ^ t < t{ вычисление всех т
отличных от нуля 5-сплайнов m-го порядка при данном параметре t удобнее
производить по схеме
N2',i{t) N2ti+1(t)
Nm-2)i(t) ^m-2,i+l(*) ¦•¦ Nt
N ¦(+} N iff) N
Эту треугольную таблицу можно также вычислять построчно, полагая неупомя-
неупомянутые крайние соседние 5-сплайны равными нулю. Вычисления проще выпол-
выполнять для ненормированных 5-сплайнов МШ)$(?), а нормированные 5-сплайны
вычислить в последней строке.
Таким образом, мы нашли непрерывные т — 1 раз дифференцируемые функ-
функции Na,m(t) и Nmjb(t), принимающие ненулевые значения только внутри от-
отрезка ta ^ t ^ tb и имеющие равные нулю значения функций и их производных
до (т — 2)-.го порядка включительно на его концах. Мы не имеем аналитиче-
аналитического выражения этих функций, но имеем рекуррентные формулы для вычи-
вычисления значений функций в любой заданной точке. Значения функций зависят
от значений (т — Г)-го внутреннего узла, принадлежащих отрезку ta $C t ^ %.
Действительно, значения последовательности узлов, на которой вычисляются
.В-сплайны, при выводе всех формул ничем не ограничивались. Единственное
требование, предъявляемое к значениям узлов, заключается в том, чтобы они
не убывали. Это дает огромные возможности при построении кривых и поверх-
поверхностей с использованием .В-сплайнов.
Дифференцируя выражение для 5-сплайна, получим формулу для вычисле-
вычисления его производных требуемого порядка. Производные 5-сплайна также вычи-
вычисляются по рекуррентным соотношениям. Их вычисление может выполняться
одновременно с вычислением значений самих 5-сплайнов.
В дальнейшем мы будем пользоваться первым определением 5-сплайна
(если не оговорено противное), хотя все сказанное будет справедливо и при
других определениях 5-сплайна.
2.9. NURBS кривые 121
2.9. NURBS кривые
В-сплайны используют для построения рациональных кривых линий в фор-
форме B.7.5). Формула для вычисления радиус-вектора рациональной параметри-
параметрической кривой на основе 5-сплайнов NitTn(t), построенной по вершинам р,,
г — 1, 2, ..., та (n ^ т), обладающим весами wi, имеет вид
B.9.1)
Радиус-вектор кривой равен частному от деления некоторого вектора на вес
кривой в данной точке. Каждый из 5-сплайнов m-порядка iVj>m(t) построен
на последовательности из т + 1 узлов U, <i+i> ti+2, ¦¦¦, U+m- Значения уз-
узлов должны образовывать неубывающую последовательность, а в остальном на
них не накладывается никаких ограничений. Кривые линии, построенные на
множестве не равноотстоящих узлов, называются неоднородными. Параметри-
Параметрическое расстояние между соседними узлами у неоднородных кривых меняется
при переходе от узла к узлу. Кривая B.9.1) в общем случае является неоднород-
неоднородной и рациональной. Кривая B.9.1) носит имя NURBS кривой, составленное
из первых букв ее названия — Non-Uniform Rational В-Spline (неоднородный
рациональный фундаментальный сплайн).
Когда все вершины NURBS кривой имеют равные веса, то формула B.9.1)
для вычисления радиус-вектора кривой на основе В-сплайнов примет вид
г=1
Эта кривая также может быть использована в моделировании, так как она обла-
обладает определенным порядком гладкости, достаточно легко вычисляется и легко
управляется своими вершинами.
В формуле B.9.1) для построения совокупности из п 5-сплайнов m-ro по-
порядка требуется п + т узлов в случае незамкнутой кривой и п + 2т узлов
в случае замкнутой кривой. Число узлов всегда больше числа вершин, по-
поэтому множество узлов называется расширенным. Воспользуемся той свободой,
которую предоставляет нам выбор значений узлов при вычислении 5-сплай-
нов. Пусть вершины сплайна B.9.1) пронумерованы от 1 до п. Пронумеруем
узлы, на которых построены 5-сплайны, от 1 до п + т. Чтобы незамкну-
незамкнутая NURBS кривая проходила через первую и последнюю вершину, первый
В-сплайн должен иметь кратными первые т узлов (из т + 1 узлов, на ко-
которых он строится), а последний В-сплайн должен иметь кратными послед-
последние т узлов (из т + 1 узлов, на которых он строится). Для построения
незамкнутой (т — 2)-раз дифференцируемой NURBS кривой первые т узлов
должны иметь равные значения: tf! = tf2 = • • ¦ = tm, следующие п — т уз-
узлов должны образовывать возрастающую последовательность: tm+i < ?m_|_j_|_i
(i — 1, 2, ..., n — m), оставшиеся т узлов должны принимать равные зна-
значения: tn+i = tn+2 = ... = tn+m. Для построения замкнутой (т — 2)-раз
дифференцируемой NURBS кривой последовательность узлов должна отражать
122 Гл. 2. Моделирование кривых линий
замкнутость: значения первых п + т узлов должны образовывать возрастаю-
возрастающую последовательность: t{ < t{+i (i — 1, 2, ..., n + m), следующие т узлов
должны идти через интервалы, повторяющие первые т интервалов между уз-
узлами: ti+n+m = tn+m + t{ (i = 1, 2, ..., m). В общем случае параметр NURBS
кривой изменяется от значения узла tm\n = tm до значения узла tmax = tn+m.
Построенная на таких последовательностях узлов кривая будет иметь непрерыв-
непрерывные производные до (т — 2)-го порядка включительно на всей области определе-
определения. Если среди узлов будут кратные, кроме вышеуказанных, то непрерывность
соответствующих производных кривой будет нарушена.
Вычисление радиус-вектора кривой. Для вычисления радиус-вектора NURBS
кривой используется следующая схема. По значению параметра t из условия
Ц ^ t < ti+i определяется номер г отличного от нуля В-сплайна первого порядка
и вычисляется его значение, исходя из определения:
- J 7Г' еСЛИ tj < t <ii+i, (ПйО\
— \ ti+i -U B.9.2)
0, если t < t{ или t ^ U+\.
Далее, используя рекуррентное соотношение Кокса-Де Бура
последовательно вычисляются все отличные от нуля при данном параметре t
5-сплайны до m-го порядка включительно: Mj_m+i m(t), М^_т+2 m(t), •••
M(t):
Mitl(t)
Mi>2{t)
Mi-m+2,m-l(t) ¦¦¦ Mi-2,m-l{t) M<_i,m_i(i) Mj>m_i(i)
Mi-m+l,m(t) Mi-m+2,m(t) ... Mi-2,m{t) Mi_i,m(i) M^m(t)
Данная треугольная таблица вычисляется построчно, поскольку из B.9.2) из-
известен элемент первой строки, а каждый элемент следующей строки можно по-
построить по двум соседним элементам в предыдущей строке с помощью B.9.3).
При вычислении крайних элементов каждой строки используется тот факт, что
один из элементов в предыдущей строке равен нулю. Далее В-сплайны т-го
порядка нормируются
Nj, m(t) = {tj+m - tj)Mjt m(t), j = i - m + 1, г - m + 2, ..., i,
и подставляются в формулу B.9.1), которая примет вид
г
Е
r(t) = J у . B.9.4)
j-l-m+l
2.9. NURBS кривые 123
Одновременно с вычислением 5-сплайнов может проводиться вычисление их
производных. Формулы B.9.2) и B.9.3) можно считать определением 5-сплайна.
5-сплайны являются локальными функциями (имеют малый носитель).
Свойства кривой. Каждый В-сплайн отличен от нуля только на части области
изменения параметра кривой, поэтому при изменении радиус-вектора одной из
вершин подлежит пересчету не вся кривая, а только ее часть. 5-сплайны явля-
являются неотрицательными функциями. Сумма значений всех нормированных
5-сплайнов при любом параметре t NURBS кривой в соответствии со свойством
B.8.24) равна единице: Y^,Nijm(t) = 1, а площадь под любым ненормирован-
г
ным 5-сплайном удовлетворяет равенству
+00 U+m
J Mi>m(t)dt= [ Mi,m(t)dt = ^. B.9.5)
—oo U
Это равенство получим, переставив операции интегрирования и вычисления
разделенной разности. Проинтегрируем усеченную степенную функцию B.8.17)
в указанных пределах
U+m
z — t) ,at——(z — ц) , (z — ti+m) ,.
U
Вычислим разделенную разность полученной функции на последовательности
узлов 5-сплайна. Второе слагаемое правой части на области t% ^ t ^ U+m равно
нулю, а первое слагаемое равно полиному т-й степени (z — ti)m/m, разделен-
разделенная разность m-го порядка которого в соответствии со свойством B.8.12) равна
коэффициенту при zm, т.е. равна 1/т, что доказывает равенство B.9.5).
Из B.9.5) следуют равенства:
+ ОО
ti+m ~~ ti
Nitm(t) dt = (ti+m - U) f Miim(t) dt = ^
m '
— OO ti
+ ОО
]T(t^^.-i
NURBS кривая B.9.1) обладает достаточной гибкостью. Ее можно легко
редактировать путем изменения положения вершин. Например, легко можно
модифицировать имеющуюся NURBS кривую так, чтобы она проходила через
указанную точку или чтобы она касалась указанной кривой в заданной точке.
124 Гл. 2. Моделирование кривых линий
Производные радиус-вектора кривой. Используя определение В-сплайна и
тот факт, что первая производная усеченной степенной функции по параметру t
равна
вычислим первую производную 5-сплайна, переставляя дифференцирование и
вычисление разделенных разностей
5 • • •, Ч+т\ ~ &m-l[H> Ч+Ъ • • -, Ч+m-lJJ ~
dt dtyln~L"^L
= - m~! iVi+i,m-i + .m~\t ^t,m-i- B.9.6)
4+m 4+1 ^i+m—1 4
Продифференцируем числитель выражения B.9.1) с учетом B.9.6) и получим
j+m-l
г=1 7 ч i=j ' i=j
j+m—1 j+m-l
Ч+m—1 Ч ^= ¦ Ч+m 4+1
j+m-l
„_ , гг+т-1
j+m-l
^г'+т—1 4
j+m—1 j+m—1
r. A) /oo-7\
,m-lW ', B.9.7)
где j, j + 1, j + 2, ..., j + m — 1 — индексы отличных от нуля В-сплайнов
m-ro порядка при заданном параметре ?j+m-i < t < tj+m. В равенстве B.9.7)
использовались свойства Nj>m-i(t) = 0 и iVj+mim_i(f) = 0. Действительно, для
заданной последовательности узлов и при любом параметре t, принадлежащем
области определения кривой, среди 5-сплайнов m-го порядка отличны от нуля
только m 5-сплайнов (пусть их индексы равны j, j + 1, j + 2, ..., j' + m — 1),
а среди 5-сплайнов (m — 1)-го порядка отличны от нуля m — 1 5-сплайнов (их
индексы, соответственно, равны j' + 1, j' + 2, ..., j + m — 1). Мы видим, что
первая производная сплайн-функции m-го порядка представляет собой анало-
аналогичную сплайн-функцию, порядок и число вершин которой на единицу меньше.
Вершины р^ ' вычисляются по формуле
р^ = (т-1)ЩР;-Щ-1Р;-\ i = 2,3,...,n. B.9.8)
Ч+m—I H
2.9. NURBS кривые 125
Продолжая дифференцирование, можно найти производную требуемого порядка
для числителя выражения B.9.1):
' г=1+А:
т>() г» Л)
где р^ = (т-к) — ^-± } jfc = 1, 2, ..., m-1, t = 1+А;, 2+к, ..., п,
t—k ~~ H
Для производных знаменателя B.9.1) получим выражение, аналогичное
B.9.9),
dkw _ dk f-^
dtk = dt
где ш/й) = (?тг—к)— , к = 1, 2, ..., m—1, г = 1+А;, 2+А;, ..., п,
Н-\-т—к ^г
Радиус-вектор NURBS кривой B.9.1) вычисляется как частное от деления
двух функций параметра кривой t, поэтому при вычислении производной
NURBS кривой правую часть B.9.1) следует рассматривать как сложную функ-
функцию. Первая производная радиус-вектора NURBS кривой равна
dr d /u;r(f)\ 1 d(wr) wr dw
) У ¦ ¦ )
dt~dt\ w(t) ) ~ w dt w2 dt'
где
n
wr = Y2 NitTnWiPi — числитель правой части равенства B.9.1),
г=\
п
w = Y^ NijTnWi — знаменатель правой части равенства B.9.1),
d(w г) п WiPi — ICj iPi 1
—jr- = (m - 1) XJ Ni,m-i—r : производная,
"ь г=2 Н+т-1 ~~ Н
— = (т — 1) 5D -Wi.m-i— — производная веса.
Аналогично вычисляются производные NURBS кривой более высокого порядка
dr d^ fwr(t)
dt dt(k) V w(t) ) '
Производные второго и третьего порядка определены равенствами B.7.10),
B.7.11). Можно заметить, что радиус-вектор точки и ее вес (wr или WiPi) в
формулах NURBS кривой выступают как единое целое.
126 Гд. 2. Моделирование кривых линий
Алгоритм Де Бура. Преобразуем числитель выражения B.9.1), используя
формулу B.8.32.1), следующим образом:
n j+m-1
i=l г—j
i+m-1
•_ • V'-i+m ~ ьг+1 ьг+т—1 Ч
j+m-1 _
wiPi =
—1 ^J+"*
*Г* ii+m_i—<j '
j+m-1
= 2^ ^.m-il: -w*-iPi-i + ; r^iPi
i^r11 \h+m-l — H H+m-1 — 4 J
i+m-1
Wi,m-i(*)riA), B.9.11)
где i, i + 1, i + 2, ..., j + m — 1 — индексы отличных от нуля В-сплайнов т-то
порядка при заданном параметре ij+m_i ^ t < tj+m. В преобразовании B.9.11),
как и при выводе равенства B.9.7), использовались свойства Nj>m-i(t) = 0 и
-/Vj+m,m-i(?) = 0 при заданном параметре t. Мы свели сумму m слагаемых
к сумме m — 1 слагаемых и понизили на единицу порядок В-сплайнов в этой
сумме. Величины г^1) вычисляются по формуле
m H+m-1 ~t . t — ti
? ' = ЩP + WP
?i Щ-iPi-i + .WiPi,
H+m—l M H+m—1 H
*" = j + l, i + 2, ..., j + m-l.
Продолжим упрощение числителя выражения B.9.1) аналогичным образом и
получим
п j+m—l j+m—l
i-j
r4-i + , r
i_,-, 2 \bi+m-2 ~ Ч Ч+Ш-2 — H
j'+m~l j+m-1
E ^,т_2(«)г/2) = ...= J3- iViil(Ori(m-1) = rJ+m_1(—1). B.9.12)
i=j+2 i=j+m-l
2.9. NURBS кривые 127
Для знаменателя выражения B.9.1) получим аналогичное выражение
п j+m—l j+m—l
w = YiNiim(t)wi= Y, Ni>m(t)wi= Y, ^,т-1(«)«чA) =
г=1 i=j i=j+l
j+m—l ' j+m—l
= Y, Nitm-2(t)wiW = ... = ]T Nitl(t)Wl(m-V = Wj+m^m~l\ B.9.13)
i=j+2 i=j+m—l
Мы пришли к выводу, что положение точки NURBS кривой B.9.1) для за-
заданного параметра tj+m-\ ^ t < tj+m может быть определено по формуле
= «иф » Г^1 B.9.14)
' W(t) tW^-1) V '
с помощью рекуррентных соотношений
(к) ti+rn-k — t (k-1) , t — ti (k-1)
ч = -. ГТгг--1 + 7 ZTri '
bi+m—k H •'i+m—к Ц
(fc) _ ti+m-k ~ t (k-1) t-tj (k-1) B.9.15)
i j. д i—1 j. л i '
li+m—к ~ H H+m—k H
к = 1, 2, ..., m - 1, i = j + k, j + к + 1, ..., j + m — 1,
которые начинаются со значений г/°) = WiPi, w^ = W{, i = j, j + 1,
j + 2, ..., j + m — 1. Эти соотношения являются обобщением алгоритма Де Ка-
стелье и называются алгоритмом Де Бура. Алгоритм вычисления радиус-
вектора точки NURBS кривой для параметра fJ+m_i ^ t < tj+m иллюстрирует
рис. 2.9.1:
г.@) г. @) 'м 'пЛ '^ ""
I ... rj+m_2w Г
„. „(m-2) r. Лт-2)
Lj+m—2 L j+m—l
Рис. 2.9.1. Алгоритм Де Бура
Вставка узлов. У заданной NURBS кривой m-го порядка можно увеличить
число характеристических точек, сохранив неизменной ее форму и параметри-
параметрическую длину. Для этого применяется вставка дополнительных узлов. Вставим
дополнительный узел t* в последовательность узлов t\, t2, ¦ ¦., tn. Пусть значе-
значение t* расположено между значениями узлов fj+m-i и tj+m, т.е. удовлетворяет
неравенствам fJ+m_i ^ t* < tj+m. Используя алгоритм Де Бура, можно показать,
что кривая не изменится, если величины rj+i'°\ rj+2^, ..., rj+m-2^ заменить
на величины rj+1A), tj+2^\ • • •» rj+m-l^ (CM- Рис 2.9.1). Таким образом,
128
Гл. 2, Моделирование кривых линии
вместе с вставкой узла tj+m-i S
ристические точки Pj+i, Pj+2, ¦•
на вершины с радиус-векторами
t* < tj+m мы должны заменить характе-
, Pj+m_2 с весами wj+i, Wj+2,
Л1)
и весами
(к)
..., Wj+m-i^ >. Новых вершин на одну больше, чем старых,
поэтому номера узлов и вершин начиная с j + m нужно увеличить на единицу.
Узел t* может быть вставлен многократно (максимальная кратность равна
т — 1). Если узел t* вставляется к раз, то величины Tj+i^, Tj+2^°\ ¦¦¦
I нужно заменить на величины г3+11^, Tj+2y ', ..., Tj+^^,
г- -, (*0 г- Л^) г- Л2) т-¦ Л1) (r\u mxr 9Q11
"j+m-l j "j+m-14 j • • •, "j+m-V , Yj+m-1 V.CM. рис. Z.\).l).
По их значениям можно определить новые вершины и их веса. Новых вершин
будет на к больше, чем старых, поэтому номера узлов и вершин начиная с j + m
нужно увеличить на к.
Примеры. Для незамкнутой NURBS кривой мы будем использовать следую-
следующие значения узлов. Пусть первые т узлов имеют значения, равные нулю:
ti — ?2 = • ¦ ¦ = tm — 0, следующие п — т узлов принимают целочисленные
0 1 2 3 4 5 6t
Рис. 2.9.2. Набор В-сплайнов 4-го порядка для незамкнутой NURBS кривой
значения от 1 до п — т: tm+i = г, г'¦ = 1, 2, ..., п — т, оставшиеся т узлов
принимают значение п — т + 1: tn+\ = tn+2 — ¦ ¦ ¦ — tn+m = п — т + 1. Для
замкнутой NURBS кривой мы будем использовать равноотстоящие значения
О 1 2 3 4 5 6 t
Рис. 2.9.3. Набор В-сплайнов 4-го порядка для замкнутой NURBS кривой
узлов: ti = г — т, i = 1, 2, ..., п + 2т. Параметр NURBS кривой изменяется в
пределах: tm ^t ^ tn+m, что для незамкнутой кривой есть O^f^n — m + 1,
а для замкнутой кривой есть 0 ^ t ^ п. Параметризация с равноотстоящими
2.9. NURBS кривые
129
значениями узлов называется равномерной. Сплайны с равномерной параме-
параметризацией Шёнберг назвал кардинальными.
На рис. 2.9.2 показан полный набор В-сплайнов 4-го порядка (кубических)
для 9 вершин, построенных на расширенном множестве узлов О, О, О, О, 1, 2, 3,
Рис. 2.9.4. NURBS кривые и их характеристические ломаные линии
4, 5, 6, 6, 6, 6. Параметр t сплайна B.9.1), построенного на данном множестве
узлов, принимает значения на отрезке 0 ^ t ^ 6.
Рис. 2.9.5. Влияние порядка на форму NURBS кривой
Для замкнутой NURBS кривой используется последовательность равноот-
равноотстоящих узлов: U = i — m, г = 1, 2, ..., п + 2т. На рис. 2.9.3 показан полный
Рис. 2.9.6. Влияние веса точки ps на форму NURBS кривой
набор В-сплайнов 4-го порядка для 6 вершин, построенных на расширенном
множестве узлов —3, -2, -1, О, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
Все В-сплайны для замкнутой кривой похожи друг на друга. Параметр t
сплайна B.9.1), построенного на данном множестве узлов, принимает значения
на отрезке 0 ^ t ^ 6.
9 - 5293 Голованов
130
Гл. 2. Моделирование кривых линий
На рис. 2.9.4 показаны незамкнутый и замкнутый сплайны и их характе-
характеристические ломаные, построенные по описанным выше последовательностям
узлов. У незамкнутой кривой крайние точки совпадают. Как и кривая Безье,
NURBS кривая не проходит через свои вершины за исключением крайних точек
для незамкнутой кривой.
На рис. 2.9.5 по одним и тем же восьми вершинам построены NURBS кривые
2-го, 4-го, 6-го и 8-го порядка. На рисунке мы наблюдаем, что чем выше порядок
кривой, тем она более гладкая. NURBS кривая второго порядка совпадает со
своей характеристической ломаной линией.
На рис. 2.9.6 показано влияние веса вершины ps на форму кривой 6-го по-
порядка. Чем больше вес вершины, тем ближе к ней проходит NURBS кривая.
В общем случае вес вершины может быть нулевым и даже отрицательным.
NURBS представление ломаной линии. Если построить NURBS кривую
B.9.1) по п вершинам на последовательности узлов t\ ¦= ti = О, to, = 1,
t\ = 2, ..., ti = i — 2, ..., tn = n — 2, tn+i = tn+2 = n - 1 на базе В-сплайнов
второго порядка Ni^it), то она совпадет с ломаной линией B.4.1). Область изме-
изменения параметра NURBS кривой в этом случае равна 0 ^ t ^ п— 1. В-сплайны
второго порядка iVj,2(?) пропорциональны разделенным разностям второго по-
порядка, вычисленным на последовательности узлов ti, <t+i> ti+2 для функции
() — {z — !)+• -В-сплайны второго порядка определяются равенством
если
t <
U+2 —
О,
-, если fj+i ^ t < ti
i
если t < U или t
B.9.16)
Мы видим, что Nit2{t) представляют собой кусочно-линейные функции, прини-
принимающие значения Nit2(ti+i) = 1 и Njt2{ti+i) = 0, j Ф *• -В-сплайны B.9.16)
для шести вершин показаны на рис. 2.9.7.
6,2
12 3 4
Рис. 2.9.7. В-сплайны второго порядка
Замкнутую ломаную линию как частный случай NURBS кривой B.9.1)
можно построить на последовательности узлов t\ = — 1, <2 = 0, <з = 1» •••
..., U = i - 2, ..., tn = n - 2, tn+i = n - 1, tn+2 = п. Область изменения
параметра NURBS кривой в этом случае равна 0 ^ t < п.
2.9. NURBS кривые
Ш
NURBS представление отрезка прямой. Отрезок прямой может быть пред-
представлен в виде NURBS кривой B.9.1)
= 1
по двум вершинам pi и р2 на последовательности узлов t\ = 22 = 0, Ц —
и на базе S-сплайнов второго порядка Nit2(t) B.9.16):
гз — *2 *з ~ *2
Кривая Безье как частный случай NURBS кривой. Нормированные 5-сплай-
ны Nni(t) определения 4 (см. §2.8) в частном случае последовательности узлов
t-i-n — t-n = t\-n = ... = t-\ —0, to = t\ = ... — tn = 1 совпадают с
базисными функциями Бернштейна Bf(t), a NURBS кривая B.9.1), записанная
в виде
Nni(t)wiPi
B-9.17)
i=0
совпадает с рациональной кривой Безье B.7.2). Это происходит, когда число
вершин на единицу больше порядка S-сплайна Nni(t). Область изменения па-
параметра NURBS кривой в этом случае равна 0 ^ t ^ 1.
Равенство S-сплайнов Nni(t) определения B.8.21.4), построенных на после-
последовательности узлов ?_i_n = t-n = ti-n = ... = t-i — 0, to = ti = ... = tn = 1,
о l t
Рис. 2.9.8. Функции Вернштейна — частный случай S-сплайнов
и коэффициентов Бернштейна Bni{t) можно доказать следующим образом.
Вспомним, что коэффициенты Бернштейна связаны рекуррентным соотноше-
соотношением
Bni(t) = tB-ViW + A - t)Bn-li(t), i = 0, 1, 2, ..., п.
Мы получим все коэффициенты Бернштейна, начав вычисления с B°o(t) = 1.
S-сплайны Nni(t) связаны рекуррентным соотношением
4 ~ <>i—n
H—n—1
t = 0, 1, 2, .... n, B.9.18)
9*
132
Гл. 2. Моделирование кривых линий
где только N°o(t) = 1, а остальные .В-сплайны нулевого порядка равны нулю.
Из приведенных формул видно, что коэффициенты Бернштейна Bni(t) и
S-сплайны Nni(t) вычисляются совершенно одинаково, что доказывает их ра-
равенство. Из сказанного следует, что нормированные 5-сплайны iVj, п(?) опре-
определения 1 в частном случае последовательности узлов t\ = ti = ... = tn = О,
in+i = tn+2 = ... = t2n — 1 совпадают с базисными функциями Бернштейна
Bn~1i-i(t). Этим доказывается, что кривые Безье являются частным случаем
NURBS кривой. 5-сплайны B.9.17) 5-го порядка на последовательности узлов
ti = *2 = ¦ • • = Ц = 0) <б = *7 = • • • = *ю = 1 показаны на рис. 2.9.8.
NURBS представление кривой второго порядка. Выше мы показали, что
кривые второго порядка могут быть представлены в виде рациональных кривых
Безье. NURBS кривые являются обобщением рациональных кривых Безье,
Р4 Рз Р2
Рис. 2.9.9. Эллиптическая NURBS кривая
поэтому некоторая часть любой кривой второго порядка может быть предста-
представлена в виде NURBS кривой по трем вершинам на последовательности узлов
t\ — ^2 — ^з = 0) t^ — tc, — t^ — 1 на базе 5-сплайнов третьего порядка iVj з(?).
Полностью кривую второго порядка можно представить в виде NURBS кри-
кривой, если использовать кратные узлы. На рис. 2.9.9 приведена эллиптическая
NURBS кривая 3-го порядка и ее характеристическая ломаная.
Она построена по точкам pi, рг, Рз, Р4, Р5> Рб> Р7, Ре- Ее характеристиче-
характеристическая ломаная представляет собой прямоугольник, описанный около эллиптиче-
Рис. 2.9.10. NURBS кривая с кратными узлами
ской кривой. Веса характеристических точек равны: wi = w^ — w^ = wj = I,
W2 = Wi — wq = w% = cos Gг/4). Последовательность узлов имеет вид t\ = *2 =
— ^з == 0) ^4 =: ^5 = 1) ^6 == ty = 2, is := ^э = 3, t\Q = tn = ^12 =: 4. Если мы
хотим, чтобы параметрическая длина кривой, показанной на рис. 2.9.9, была
2.9. NURBS кривые 133
равна 27г, то вместо указанной выше последовательности узлов можно исполь-
использовать последовательность: ?1 = t2 = ?3 = 0, ?4 = ?5 = тг/2, ?б = ?7 = я",
?8 = t9 = Зтт/2, ho — t\\ = ?12 = 27Г. NURBS кривая может иметь изломы в
точках с кратными узлами. Изломы возникают, когда соответствующие сосед-
соседние вершины.не расположены на одной прямой. На рис. 2.9.10 приведена та же
эллиптическая NURBS кривая, но с измененными положениями точек рз, Р4.
NURBS кривая B.9.1) обобщает все рассмотренные выше кривые — отрезок
прямой, ломаная линия, кривая Безье, конические сечения могут быть описаны
в виде NURBS кривой. По своей природе NURBS кривая представляет собой
линейную комбинацию кусочно-полиномиальных функций заданной степени,
она позволяет строить кривые заданного порядка гладкости.
NURBS представление кубического сплайна. Пусть построен незамкнутый
кубический сплайн B.4.10) а(х), проходящий через точки а^ при значениях
га+2
параметра Xj, j — 1, 2, ..., п. Построим NURBS кривую r(?) = 5Z -^mWPj
г=1
четвертого порядка (т = 4) на последовательности узлов t\ — t2 = ?3 = ?4 — х\,
h — х2, h = хз, •¦•, tn+rn-i = ?n+m = tn+m+i = tn+m+2 = xn. Для этого
найдем n + 2 вершины pj, i — 1, 2, ..., n + 2 из условий:
= a'i,
da
' dx
*(xj) = &j, j = 2, 3, ..., n-1,
da
da; „.
Веса вершины pj равны единице. Кубический сплайн а.(х) и NURBS кривая
г(?) будут полностью совпадать, так как они состоят из гладко стыкующихся (до
второй производной включительно) участков кривых третьей степени. Таким
образом, вершины pj, i = 1, 2, ..., п+2 мы найдем из системы п+2 уравнений:
ЧАТ ^„ \P2 "Pi , оаг / \ РЗ ~ P2 , ,oAT t NP"+2Pn+l _ _/
3iV2KB;i)- — + 3^3,3(a;i)- — + ... + ?>Nn+i,,b\x\)- = a 1,
*5 — ?2 ?б — ?з tn+5 — tn+2
i + Nn+2ti(x2)pn+2 = a2,
, а„_1,
P2~Pl , пЛГ г чРЗ~Р2 , , „лг f NPn+2 -Pn+1 /
- — + 3JV3>3(a;n)- — + ... + ЪЫп+2^{хп)- = a'n,
*5 — ?2 H — '3 t t
B.9.19)
134
Гл. 2. Моделирование кривых линий
Используя формулы B.9.2) и B.9.3), определим, что для каждого значения па-
параметра t — ti, г = 4, 5, ..., п + т — 1, отличны от нуля только три jB-сплайна
четвертого порядка:
B.9.20)
U+l ~ ^г-2 ^i+1 — ij-1
U — U-i ti+2 ~~ U ^г+l ~ U U — ij_2
ij-f-2 ~ U-\ ^г+1 ~ U-\
~~ ti-2
H+2 — U-\
и два jB-сплайна третьего порядка:
U+i — U-
После подстановки B.9.20) и B.9.21) в B.9.19) система уравнений для
ления вершин примет вид
1 0 0 0 0 ...
-6 6 0 0 0 ...
B.9.21)
опреде-
0
0
0
0
0
0
0
«32
0
0
0
0
0
0
«33
О43
0
0
0
0
0
«34
аи
Й54
0
0
0
0
0
СЦ5
аъъ
0
0
0
0
О
о
о
о
о
о
о
о
о
о
о
о
о
о
О
О
a-n-in О О
апп апп+1 О
О -СС
О 0 1
•
Pi
Р2
Рз
Р4
Р5
Рп-1
Рп
Рп+1
Рп+2.
=
ai
а'!
а2
а3
гц
ап-2
an-i
а'„
. а„ .
B.9.22)
где
Ь =
с =
акк-1 =
— XI Хп — Хп-1
- Xk-l Хк - Хк-1
O-kk =
Xk+l - Xk-2
akk+l —
1
Xk - Xk-2
xk-l — Xk-2
k — Xk-2
Xk - Xk-i xk-i - Хк-г
Xk - Хк-г Хк - Xk-2
k-l — Xk-2
- Xk-2
— Xk-2
Матрица системы уравнений B.9.22) является трехдиагональной.
Для замкнутого кубического сплайна система уравнений B.9.19) упроща-
упрощается, так как в ней исчезнут второе и предпоследнее уравнения, определяющие
производные кривой на краях. Число вершин pj, г = 1, 2, ..., n, NURBS кривой
будет равно числу заданных точек а^, i = 1, 2, ..., п. Последовательность узлов
будет иметь вид ti = Xi-2, г = 1, 2, ..., п (плюс циклическое расширение).
2.10. Линии, базирующиеся на линиях 135
Интерполяция. Совокупность jB-сплайнов порядка m представляет собой
базу, на основе которой можно построить интерполяционные кривые. Пусть
требуется построить кривую г(?) m-го порядка гладкости, проходящую через
точки ai, а2, ..., Щг. Сначала построим NURBS кривую m-порядка с верши-
вершинами в точках .ai, а2, ..., ап на произвольной неубывающей последовательности
узлов t\, t2, • • ¦) tn+m. Затем найдем параметры xi, х2, ¦.., хп проекций точек
ai, &2i • ¦¦> &п> соответственно, на эту кривую. Переместим вершины NURBS
кривой так, чтобы она проходила через точки а^ при t = Х{. Положим веса вер-
вершин кривой равными 1. Новые положения вершин рг- NURBS кривой найдем
из системы уравнений
+ N2>m(x1)p2 + ... + iVn]m(:ci)pn = аь
Ni,m{xn)pi + iV2)mB;n)p2 + ... + Nnjm{xn)pn = an.
Для того чтобы эта система имела единственное решение, необходимо и доста-
достаточно, чтобы определитель ее матрицы был отличен от нуля. Можно доказать
что определитель матрицы
М =
Ni,m(x2) N2i7n(x2)
;n) N2t7n(xn)
B.9.24)
составленной из значений jB-сплайнов, вычисленных в точках Xi, не равен
нулю, если среди точек х^ нет совпадающих. Ни одна из строк матрицы B.9.24)
не является нулевой, так как при любом значении параметра Х{ хотя бы один
из S-сплайнов не равен нулю. Ни одна из строк матрицы B.9.24) не является
линейной комбинацией остальных строк матрицы. Совокупность jB-сплайнов
любого порядка представляет собой чебышевскую систему на их совокупной
области определения.
Пользоваться описанным способом вычисления вершин р^ NURBS кривой
необходимо очень осторожно, так как кривая может иметь необоснованные из-
изгибы на концах. Для устранения необоснованных изгибов кривой нужно увели-
увеличить число узлов путем добавления уравнений, описывающих поведение кривой
на ее концах. Примером может служить рассмотренное выше представление ку-
кубического сплайна.
2.10. Линии, базирующиеся на линиях
Некоторые линии могут быть построены на базе других линий. Мы рассмо-
рассмотрим параметрически усеченную, эквидистантную, ссылочную и продолженную
кривые. Кривую, на основе которой строится новая кривая, будем называть
базовой кривой. Базовая кривая будет определена в структуре данных рассмо-
рассмотренных ниже кривых.
Усеченная кривая. Параметрически усеченная кривая представляет собой
некоторую часть любой другой кривой. Усечение производится путем измене-
изменения области определения параметра базовой кривой. Пусть параметр базовой
136
Гл. 2. Моделирование кривых линий
кривой t изменяется в пределах tm\n ^ t ^ tmax. Усеченную кривую опреде-
определим как часть базовой кривой, начинающейся при параметре tbegin и оканчи-
оканчивающейся при параметре tend, где tm\n < ibegin ^ *max и tmm < tend ^ tmax.
Направление усеченной кривой может совпадать с направлением базовой кри-
кривой или быть ему противоположным, например, при ien(j < ibegin- Если кривая
замкнута, то движение от точки ibegin к точке ?end можно выполнить двумя спо-
способами: в положительном направлении базовой кривой и в противоположном
направлении. Чтобы преодолеть эту неоднозначность для замкнутых кривых,
в данные усеченной кривой вводится параметр sign, характеризующий совпаде-
совпадение ее направления с направлением базовой кривой и принимающий значения
+1 или — 1. Параметру базой кривой tbegin соответствует параметр усеченной
кривой wmin = 0, параметру базовой кривой tend соответствует параметр усе-
усеченной кривой wmax — s, где s = s(?begin> *end) — параметрическое расстояние
между tend и ibegin с учетом замкнутости кривой. Если кривая не замкнута, то
s = l^end ~ ?begin|- Радиус-вектор усеченной кривой описывается формулой
Г(ю) = rb(fbegin + W ¦ sign), 0 < W < s(fbegin, tend),
B.10.1)
где Tb(t), tmin ^ t < imax, — базовая кривая, s(fbegin, *end) — расстояние между
параметрами усечения fbegin> ^end базовой кривой.
Эквидистантная кривая. Эквидистантная линия описывается радиус-век-
радиус-вектором
Г(«) = rb(t) + а X tb(t), tmin ^ t < «max, B.10.2)
где Tb{t) — базовая кривая, tj,(i) =
единичный касательный вектор
/Ч' ¦ Ч'
к базовой кривой в данной точке, а — заданный вектор. Область изменения па-
параметра эквидистантной кривой совпадает с областью изменения параметра ба-
базовой кривой. Эквидистантная кривая оправдывает свое название, если r^(i) —
плоская кривая, а вектор а ортогонален плоскости базовой кривой. В этом случае
Рис. 2.10.1. Эквидистантная кривая
второе слагаемое в правой части B.10.2) есть вектор, который лежит в плоско-
плоскости базовой кривой, ортогонален ей и имеет длину вектора а. В результате
получим кривую, каждая точка которой отстоит по нормали от соответствующей
точки базовой кривой на одинаковом расстоянии (рис. 2.10.1).
2,10, Линии, базирующиеся на линиях 137
Производные эквидистантной линии описываются вектором
r'(?) = rb'(t) + а х tb'(t),
где tb = —- — rb—~— — производная касательного вектора базовой кривой,
s' s'
s' = vV • г' — производная длины дуги.
Ссылочная кривая. Ссылочная кривая представляет собой линию, каждая
точка которой получена путем некоторого преобразования соответствующей
точки базовой кривой. Ссылочная кривая описывается радиус-вектором
Г(«) = Mt • ГЬ(«), *min ^ t ^ «max, B.10.3)
где rb(t) — базовая кривая, М( — расширенная матрица преобразования A.4.5)
базовой кривой. Область изменения параметра ссылочной кривой совпадает с
областью изменения параметра базовой кривой.
Репараметризованная кривая. К линиям, построенным на базе линий, мож-
можно отнести кривую с измененной областью параметра. Пусть требуется, чтобы
кривая rb(t), ?m;n ^ t ^ tmax, имела область определения параметра гит;п ^
^ w ^ готах. В этом случае можно построить репараметризованную кривую
г(го) =rb(t(w)), wmin ^ w ^ готах, B.10.4)
где
W - W
min
i
— Wm\n
которая полностью совпадает с кривой Vb{t), но имеет другую область опре-
определения параметра. Линия с измененной длиной параметра применяется для
согласования областей изменения параметра двух кривых, лежащих в основе
кривой пересечения при построении ребер тел.
Продолженная кривая. Произвольную линию можно не только усекать, но
и продлевать требуемым образом. Любая кривая может быть продолжена (или
усечена) на заданное параметрическое расстояние. Пусть требуется продолжить
кривую !¦;,(?), tm\n ^ t ^ ?max путем расширения области определения параме-
параметров до a + ?mjn ^ t ^ tmax + b. При а < 0 и b > 0 кривая продляется за свои
пределы, при а > 0 и b < 0 кривая усекается. Если кривая является замкну-
замкнутой, то при выходе параметра за границу области определения выполним его
циклический пересчет
{гь(< + ?д), если t < tmin,
rb{t), если imin ^ t ^ tmax, B.10.5)
rb(t - tA), если tmhx < t,
где ?д = tmax — tm-m. Если же кривая не является замкнутой, а ее параметр
вышел за границу области определения, то продолжим кривую по касательной,
которую она имела на соответствующем конце, и вычислим по продленной кри-
кривой необходимые геометрические характеристики. Радиус-вектор продолженной
)
)
(max
если
если
если
t <t
'max
mi
<
<
* ^ *maxi
t.
138 Гл. 2. Моделирование кривых линий
кривой вычислим по формуле
dt
B.10.6)
dt
Дифференцируя формулы B.10.5) и B.10.6), получим производные радиус-век-
радиус-вектора продолженной кривой. По формулам B.10.5) или B.10.6) может вычи-
вычисляться геометрическая информация соответственно замкнутой или незамкну-
незамкнутой кривой при выходе ее параметра за область определения.
Общее правило. Все кривые, в данных которых лежит другая кривая, не
должны допускать многократного наследования своего же типа. Например, в
качестве базовой кривой для параметрически усеченной кривой не должна быть
использована другая параметрически усеченная кривая, а должна быть исполь-
использована базовая кривая последней с соответствующим пересчетом параметров
усечения. Аналогичные правила должны действовать и для других базирую-
базирующихся кривых. Если нужно построить эквидистантную линию на базе другой
эквидистантной кривой r'(t) = г&(?) + а' х t{,(?), то в качестве базовой линии
должна быть использована базовая кривая последней Гь(?), а вектор эквиди-
станты должен быть равен а + а'. Если требуется построить ссылочную кривую
на баде другой ссылочной кривой r'(t) = М/-гь(?), то в качестве базовой линии
должна быть использована базовая кривая последней, а матрицу преобразова-
преобразования получим как произведение матриц М( ¦ М/.
2.11. Составные кривые
Из нескольких кривых можно построить составную кривую — наиболее
общий тип кривой. Составные кривые мы уже строили выше. Они характерны
тем, что первая производная радиус-вектора в точках стыковки терпит разрыв
или по длине или по длине и направлению. Рассмотренные выше сплайно-
вые составные кривые формировались из кривых одного типа, и в них в об-
общем случае первая производная радиус-вектора терпела разрыв по длине. Но
составные кривые можно формировать и из кривых разной природы. Кривые,
образующие составную кривую, будем называть сегментами. При построении
составной кривой должны быть выполнены определенные условия: начало каж-
каждого последующего сегмента должно совпадать с концом предыдущего сегмента.
Если сегменты составной кривой стыкуются не гладко, то составная кривая
будет иметь изломы. В общем случае в местах стыка сегментов производные
составной кривой терпят разрыв по длине и направлению. Составная кривая
приведена на рис. 2.11.1.
Замкнутую составную кривую будем называть контуром. Для контура на-
начало первого сегмента должно совпадать с концом последнего сегмента.
Пусть составная кривая содержит п сегментов
ri{wi), wimin < Wi < wimax, г = 1, 2, ..., п. B.11.1)
2.11. Составные кривые 139
Начальное значение параметра t составной кривой положим равным нулю. Па-
Параметрическую длину составной кривой положим равной сумме параметриче-
параметрических длин составляющих его кривых
п
*min = U, *max = /
При вычислении радиус-вектора составной кривой сначала необходимо опреде-
определить тот сегмент, на который попадем, двигаясь по параметру. Затем нужно
определить соответствующее значение собственного параметра этого сегмента
Рис. 2.11.1. Составная кривая
и с помощью его значения вычислить радиус-вектор сегмента или его произ-
производные. Пусть для параметра t составной кривой найден номер сегмента к, для
которого выполняется соотношение
fc-i к
Тогда в соответствии со сказанным радиус-вектор составной кривой определя-
определяется равенством
j 0 ^ t ^ *max, B.11.2)
где параметр к-то сегмента равен
fc-i
B.11.3)
Как можно заметить, подход к вычислению радиус-вектора составной кривой
аналогичен подходу к вычислению радиус-вектора ломаной линии.
Общее правило. Составная кривая является линией, базирующейся на дру-
других линиях. Для нее должно выполняться требование о недопустимости много-
многократного наследования своего же типа, предъявленное к кривым в предыдущем
параграфе. В качестве сегментов составной кривой не должны использоваться
другие составные кривые, но это не означает, что нельзя построить составную
кривую из набора составных кривых. Если составную кривую нужно построить
на основе других составных кривых, то последние должны рассматриваться
140 Гл. 2. Моделирование кривых линий
как совокупность кривых, а не как единые линии. Задача построения состав-
составной кривой из набора составных кривых должна решаться путем формирования
кривой составляющими сегментами.
2.12. Двухмерные, кривые
Все рассмотренные в этой главе кривые (за исключением цилиндрической
спирали), могут строиться как в трехмерном пространстве, так и в двухмер-
двухмерном (на плоскости). В последнем случае их радиус-вектор имеет две коорди-
координаты и преобразуется по двухмерным матрицам. Выражения для вычисления
радиус-вектора двухмерных кривых полностью совпадают с соответствующими
выражениями для трехмерных кривых. Для построения двухмерных кривых
единственное, что нужно сделать, это заменить трехмерные векторы г(?) =
— [t*i(?) т*2(t) 7*з(?)] на двухмерные векторы r(t) — \x{t) y(t)] . Например,
аналитические двухмерные кривые описываются выражениями вида
c(t) = р + x(t)h + y(t)i2, B.12.1)
где р — начало двухмерной декартовой прямоугольной системы координат, i\
и %2 — орты этой системы.
Другой пример — двухмерные NURBS кривые описываются формулой, по-
подобной B.9.1):
Ё Ni,m{t)WiPi
r(f) - !=1 + . < + < ^
где пространственные точки характеристической ломаной заменены на двух-
двухмерные точки pi- Подобным образом строятся и другие двухмерные аналоги
пространственных кривых вплоть до эквидистантных, усеченных, продолжен-
продолженных и составных кривых.
Двухмерные кривые будут использоваться для нескольких целей: для по-
построения плоских пространственных кривых, для построения кривых на по-
поверхностях, для построения линий (кривых) пересечения поверхностей и для
описания области определения параметров поверхности.
Плоские пространственные кривые. Плоские пространственные кривые
будем представлять в виде совокупности плоскости т(х, у) = р + х\х + у\у и
двухмерной кривой c(t) = [x(t) y(t)] . Трехмерные векторы ix и \у являются
базисными векторами некоторой местной системы координат. Плоская кривая
является пространственной кривой и описывается радиус-вектором
c(t) = р + x(t)\x + y(t)iy. B.12.2)
Данный способ уже использовался для описания кривых второго порядка и дру-
других аналитических кривых. Теперь распространим его на сплайновые кривые,
кривые Безье, NURBS кривые и другие. В качестве кривых c(t) могут исполь-
использоваться и составные кривые.
Кривые на поверхности. Кривые на поверхности r(u, v) будем описывать со-
совокупностью двухмерной кривой cuv(t) = [u(t) v(t)] и поверхности. Двухмер-
Двухмерная кривая и поверхность входят в структуру данных кривой на поверхности.
2.12. Двухмерные кривые 141
Для записи кривых на поверхности будем использовать выражения вида
cUv{t)= [u{t)v{t)]T, cuv{t)?r(u,v), tmin ^ t ^ tmax. B.12.3)
Кривая на поверхности является пространственной кривой и описывается ра-
радиус-вектором с(?) = r[u(t), v(t)). В B.12.3) функции u(t) и v(t) заданы явно.
Во многих случаях двухмерные кривые на поверхностях могут быть описаны в
некоторой местной системе координат, например, эллипс на параметрической
области поверхности имеет канонический вид в системе координат, связанной
с его осями. Такие кривые на поверхностях описываются выражениями вида
cUv{t)=P + x{t)i1+y(t)i2, cuv(t) G r(u{x, y), v{x, у)), B.12.4)
где р — некоторая двухмерная точка привязки характерной точки кривой, ъ\
тл.%2 — двухмерные взаимно ортогональные векторы единичной длины. Точка
р и векторы i\ и *2 определяют ориентацию местной двухмерной декартовой
системы координат относительно глобальной двухмерной системы координат.
Для кривой на поверхности r(u, v) глобальной двухмерной системой координат
для двухмерных кривых на них служит система, связанная с параметрами по-
поверхности. Начало глобальной системы находится в точке р0 = [0 0]т (и = О,
v = 0), а орты г\ и %ч определяются равенствами ъ\ = [1 0]т, %ч = [0 1]т.
Линии пересечения поверхностей. Линии пересечения поверхностей г(u, v)
и s(o, b) представим в виде совокупности двух кривых на поверхностях:
cuvit) = [u(t) v(t)]T, cuv{t) e r(u, v), B.12.5)
eab{t) = [a(t) b{t)]T, cab{t) e s(a, 6), B.12.6)
*
min
Эти кривые совпадают в пространстве, но одна из них построена на поверх-
поверхности r(u, v), а другая построена на поверхности s(a, 6). Обе кривые имеют
одинаковую область определения параметра (общий параметр) и соответствую-
соответствующие точки на поверхностях совпадают в пространстве. В структуру данных
кривой пересечения входят две кривые на поверхности.
Двухмерные составные кривые. Двухмерные составные кривые описыва-
описываются выражениями B.11.2) с соответствующей заменой трехмерных векторов
на двухмерные векторы. Двухмерные составные кривые построены из двухмер-
двухмерных кривых, которые будем называть сегментами. Начало каждого последую-
последующего сегмента должно совпадать с концом предыдущего сегмента. Если начало
первого сегмента совпадает с концом последнего, то кривая является замкну-
замкнутой. Пусть составная кривая содержит п сегментов cj(iUi), Щ'т[п ^Щ К Щта.х1
г = 1, 2, ..., п. Начальное значение параметра t составная кривая положим
равным нулю. Параметрическую длину кривой положим равной сумме пара-
параметрических длин составляющих ее кривых. Радиус-вектор составной кривой
определяется как радиус-вектор некоторого сегмента
O^Ktmax, B.12.7)
/
142
Гл. 2. Моделирование кривых линий
где номер сегмента к и его параметр w^ определяются из условия
fc-l к
г=1
fc-l
B.12.8)
B.12.9)
Двухмерная составная кривая является линией, базирующейся на других
линиях. Для нее должно выполняться требование о недопустимости многократ-
многократного наследования своего же типа, предъявленное к пространственным кривым.
В качестве сегментов составной кривой не должны использоваться другие со-
составные кривые. Если составную кривую нужно построить на основе других
составных кривых, то последние должны рассматриваться как совокупность
кривых, а не как единые линии.
Двухмерные контуры. Замкнутую составную кривую будем называть двух-
двухмерным контуром. Многие геометрические модели могут быть построены,
отталкиваясь от плоского контура — двухмерного контура на некоторой плоско-
плоскости в пространстве. Двухмерные контуры мы будем использовать для описания
области определения параметров поверхности.
Составные кривые являются наиболее общими кривыми. На базе составной
кривой можно строить другую составную кривую, например, усеченную, продол-
продолженную, эквидистантную. На рис. 2.12.1 приведены эквидистантные контуры,
Рис. 2.12.1. Эквидистантные контуры
один из которых построен вне базового контура, а другой — внутри базового
контура.
Если требуется, чтобы эквидистантный контур имел такое же количество
сегментов, как и базовый контур, то некоторые сегменты должны быть продол-
продолженными кривыми, которые в свою очередь являются эквидистантными кри-
кривыми. Для таких сегментов можно ввести новый тип линии, который включает
в себя одновременно свойства эквидистантной и продолженной кривых.
Для отдельной двухмерной кривой сь(го) = \x(w) y(w)] эквидистантная
линия описывается формулой
C(w) = Cb{w) + an(w), Wmin ^ W < U7max,
B.12.10)
2.13. Способы построения линий
143
где n(w) = N- tb{w) — нормаль базовой кривой Cb(w), tb{w) — единичный ка-
сальный вектор базовой кривой, JV = I? "Ц , . - заданное ранние от
[1 0J
базовой кривой. Если к каждой кривой контура построить эквидистантную ли-
линию, то эквидистантные линии в общем случае не образуют контура. В каких-то
местах они будут пересекать друг друга, а в каких-то — претерпевать разрыв.
Их требуется скорректировать. Там, где эквидистанты пересекаются, их нужно
обрезать по точкам пересечения. Там, где эквидистанты не доходят друг до
друга, их следует продлить до пересечения. В последнем случае нужно постро-
построить продолженные кривые. Пусть плоская кривая c{w) имеет область определе-
определения параметра wmm ^ w ^ гутах. Радиус-вектор продолженной по касательной
кривой определяется формулой
{e(wmin) + (w- wmm)c'(wmin), если w < wmin,
C(w), еСЛИ Wmin S$ W < U7max, B.12.11)
e(u>max) + {w- wmax)c'(wmax), если w > wmax,
где с' — производная радиус-вектора c(w) по параметру. Дифференцируя эти
формулы, получим производные радиус-вектора продолженной кривой. Область
определения параметра продолженной кривой определяется точками пересече-
пересечения с соседними эквидистантными кривыми контура.
2.13. Способы построения линий
Все рассмотренные кривые можно поделить на две большие группы: про-
пространственные кривые и двухмерные кривые. Это деление основывается на
том, что пространственные кривые и двухмерные кривые имеют разное число
измерений.
На рис. 2.13.1 приведены способы построения двухмерных линий.
Конические сечения
Прямая линия
Окружность и ее дуга
Эллипс иего дуга
Отрезок параболы
Отрезок гиперболы
Линии на базе точек
Отрезок прямой
Ломаная линия
Сплайн Эрмита
Кубический сплайн
Кривая Безье
NURBS кривая
Линии на базе линий
Усеченная кривая
Эквидистантная и
продолженная кривая
Репараметризованная
кривая
i
h
Сост
крив
1
1вная
1Я
Рис. 2.13.1. Способы построения двухмерных линий
На базе любой двухмерной кривой может быть построена пространственная
кривая. Если двухмерная кривая построена на плоскости, то для этого нужно
знать положение и ориентацию в пространстве этой плоскости. В общем случае
двухмерные кривые могут располагаться на произвольной поверхности. В этом
случае для вычисления точки кривой необходимо знать поверхность.
144
Гл. 2. Моделирование кривых линий
На рис. 2.13.2 приведены способы построения пространственных линий.
Как можно видеть, двухмерные кривые и часть пространственных кривых по-
построены аналогично, только первые построены по двухмерным объектам, а вто-
вторые — по трехмерным. Пространственные кривые на базе двухмерных кривых
по форме могут совпадать со своими трехмерными аналогами, но имеют отлич-
отличную от последних структуру данных и часть "выполняемых функций.
Линии на базе двумерных линий
Двумерная линия
в плоскости хОу
некоторой местной
системы координат
Аналитические линии
Прямая линия
Окружность и ее дуга
Эллипс иего дуга
Отрезок параболы
Отрезок гиперболы
Линии на базе точек
Отрезок прямой
Ломаная линия
Сплайн Эрмита
Кубический сплайн
Кривая Безье
NURBS кривая
Линии на базе линий
Усеченная кривая
Эквидистантная и
продолженная кривая
Репараметризованная
кривая
Линии на базе поверхностей
Кривая на поверхности
Кривая пересечения
поверхностей
Составная кривая
на поверхности
Рис. 2.13.2. Способы построения пространственных линий
Рисунок 2.13.2 отражает процесс построения линий при чтении его слева
направо. Сначала кривые линии могут быть построены по местной системе
координат и скалярным параметрам или по характерным точкам. Далее эти
кривые могут быть продлены или усечены. На базе нескольких кривых можно
построить наиболее общую линию — составную кривую.
Все кривые имеют различные структуры данных, но должны выполнять
одни и те же функции. Последнее свойство обеспечивает равноправие всех кри-
кривых линий. К общим функциям произвольного геометрического объекта для
кривых линий следует добавить функции вычисления радиус-вектора кривой,
производных радиус-вектора по параметру, касательного вектора, нормали и би-
бинормали кривой, функции предоставления информации об области определения
параметра кривой (начального параметра, конечного параметра, замкнутости),
функции модификации формы кривой. Математическая модель кривой не огра-
ограничивается перечисленными функциями. Она должна быть дополнена функ-
функциями, обеспечивающими взаимодействие кривой с другими геометрическими
объектами и выполнение над ней различных операций.
Глава 3
МОДЕЛИРОВАНИЕ ПОВЕРХНОСТЕЙ
3.1. Математическая модель поверхностей
Поверхности, как и линии, являются математическими абстракциями, да-
дающие представление об отдельных свойствах предметов. Так же, как и кривые
линии, поверхности будут служить нам строительным материалом для создания
тел. В свою очередь, поверхности мы будем описывать с помощью скалярных
величин, векторов, линий и других поверхностей. В данной главе мы рассмо-
рассмотрим способы построения различных поверхностей.
Пусть в пространстве задана некоторая глобальная декартова прямоугольная
система координат с базисными векторами ei, ег, ез- Мы будем представлять
поверхность векторной функцией
C.1.1)
двух скалярных аргументов и и v. Будем считать, что компоненты n(u, v),
Г2(и, v), гз(и, v) радиус-вектора точки поверхности r(u, v) являются однознач-
однозначными непрерывными функциями параметров и и v. Такое описание поверхно-
поверхностей называется параметрическим.
Область изменения параметров поверхности О в общем случае представляет
собой произвольную связную двухмерную область на плоскости и v, ограничен-
ограниченB127) () < г 1 2
ру у уру
ную двухмерными контурами B.12.7) Ci(U), ii
П
U
max,
р
г = 1, 2,
п.
у ур ур () (), , , , ,
Параметры поверхности являются координатами некоторой двухмерной точки
р=[и v]T на параметрической плоскости, принадлежащей области П. Область
«min
"min "max «
Рис. 3.1.1. Область определения поверхности П на плоскости параметров
определения параметров поверхности имеет внешнюю границу и может иметь
вырезы внутри, но она должна быть связной, так чтобы из каждой точки обла-
области можно было попасть в любую другую точку, не пересекая границы области.
10 - 5293 Голованов
146 Гл. 3. Моделирование поверхностей
В частном случае область определения параметров поверхности может предста-
представлять собой прямоугольник, когда параметры принимают значения в пределах
umin ^ u ^ ^maxi ^min ^ v ^ vmax. Прямоугольные области определения пара-
параметров удобны для практического применения и часто используются, так как
их математическая модель достаточно проста. Прямоугольные области опреде-
определения параметров имеют исходные или базовые поверхности, которые служат
заготовками для более сложных поверхностей. Пример области параметров по-
поверхности приведен на рис. 3.1.1.
Поверхности могут быть замкнутыми или разомкнутыми. Замкнутые по-
поверхности будут иметь прямоугольные области определения параметров. Для
замкнутой по u-линии поверхности r(u ± (umax — um;n), v) = r(u, v); для за-
замкнутой по и-линии поверхности г(u, v ± (umax — ит,п)) = r(u, v). Поверхность
может быть замкнута по обеим координатным линиям.
Некоторые поверхности можно описать с помощью уравнения F(ri, т^, гз) =
= 0, которому удовлетворяют компоненты радиус-вектора ее точек. Такое опи-
описание поверхности называется неявным. В обыкновенной точке уравнение по-
поверхности можно переписать в виде, разрешенном относительно одной из коор-
координат, например гз = /з(гь гг). Неявное описание поверхности в отличие от
параметрического описания не всегда однозначно, что вызывает определенные
трудности. Кроме того, при переходе в другую систему координат описывающее
поверхность уравнение изменяется. Для моделирования поверхностей мы будем
использовать их параметрическое представление.
Математическая модель поверхности включает в себя функциональную за-
зависимость радиус-вектора г(u, v) от параметров и двухмерную область Q, изме-
изменения параметров и и v. Таким образом, математическая модель поверхности в
общем случае должна содержать и математическую модель области определения
своих параметров.
Общение с математической моделью поверхности происходит аналогично
общению с кривой. Мы обращаемся к функциям поверхности с некоторыми
значениями двух ее параметров и в качестве ответа получаем геометрическую
информацию о поверхности в точке, соответствующей данным значениям пара-
параметров. Если некоторая функция поверхности допускает выход значений пара-
параметров за область определения, то данная функция должна выдавать геометри-
геометрическую информацию для продолжения поверхности.
3.2. Аналитические поверхности
Координаты радиус-вектора некоторых поверхностей могут быть предста-
представлены аналитическими функциями двух параметров. Такие поверхности мы
будем называть аналитическими. К ним относятся плоскость, поверхность
тора, поверхности второго порядка и другие поверхности. Мы рассмотрим их
параметрическое представление, а также приведем неявное описание с помощью
уравнений для координат их радиус-вектора.
Описание аналитических поверхностей удобно представлять в виде
r(u, v) = р + х(и, v)ix + y(u, v)iy + z(u, v)iz,
где р — некоторая точка привязки характерной точки поверхности, ix, i^ и iz —
взаимно ортогональные векторы единичной длины, х(и, v), у (и, v) и z(u, v) —
координатные функции. Точка р и векторы ix, i^, i^ представляют местную
3.2. Аналитические поверхности 147
декартову систему координат, а функции x(u, v), y(u, v) и z(u, v) можно рас-
рассматривать как координаты радиус-вектора поверхности в местной системе
координат. Орты ix, i^, i^ могут быть представлены в виде разложения A.2.3)
по базису ei, ег, ез глобальной декартовой системы координат
\х = onei + oi2e2 +
iz =
Точка р также может быть представлена в виде разложения по базису
глобальной декартовой системы координат
Положение и ориентация местной декартовой системы координат составляют
часть структуры данных аналитических поверхностей. Преобразования из
местной системы координат в глобальную систему координат и обратно описы-
описываются формулами A.2.4) и A.2.8). Для описания аналитических поверхностей
будем использовать параметрические зависимости, дающие однозначные функ-
функции радиус-вектора. Все их будем описывать с помощью местной декартовой
системы координат, в которой запись имеет наиболее простой вид, называемый
каноническим.
Плоскость. Простейшей поверхностью является плоскость. Она может быть
описана точкой р и двумя неколлинеарными векторами ix, i2. Радиус-вектор
плоскости описывается зависимостью
r(u, v) = p + uii + ш2, — оо < и < оо, — оо < v < оо. C.2.1)
Длина векторов ii и i2 и их взаимная ориентация в общем случае может быть
произвольной. Параметры и и v являются координатами местной декартовой
системы координат, связанной с плоскостью. Плоскость может быть предста-
представлена как одна из координатных плоскостей некоторой местной декартовой си-
системы координат. Она используется в качестве конструктивной плоскости для
построения двухмерных (плоских) геометрических объектов. В качестве кон-
конструктивного элемента плоскость используется в совокупности с двухмерными
контурами, описывающими область О определения ее параметров и, v. Такую
плоскую поверхность будем называть ограниченной контурами плоскостью.
Радиус-вектор ограниченной контурами плоскости описывается зависимостью
r(u, v) = p + uij +vi2, и, veil, C.2.2)
где область определения параметров Q состоит из совокупности двухмерных
контуров.
Сфера. Сферическую поверхность или сферу можно описать, задав ее ра-
радиус г, положение центра р и три взаимно ортогональных вектора единичной
длины ix, iy, iz, определяющих положение и ориентацию местной декартовой
системы координат. Радиус-вектор сферы определяется равенством
г (и, v) = р + rcosvcosuix + rcosvs'muiy + rs'mviz,
ю*
148
Гл. 3. Моделирование поверхностей
Сфера замкнута по параметру и, но не замкнута по параметру v, хотя имеет
видимость замкнутой со всех сторон поверхности. Замкнутость по параметру и
характеризуется тем, что г (u ± (umax — ит\п), v) = г (и ± 27Г, v) = г (и, v). Для
параметра v это не справедливо. Скалярные функции х(и, v) = г cos и cos u,
у(и, v) = rcoswsinu, z(u, v) = rs'mv сферьгсвязаны уравнением
9 9
xl + y
= г
Точка р является центром сферы. Все точки сферы удалены от центра на оди-
одинаковое расстояние, равное г.
Эллипсоид. Эллипсоид может быть описан формулой
r(u, v) = p + a cos «cos u i^ + bcosvsinuij, + csinvi2,
7Г 7Г C.2.4)
где а, 6, с — полуоси эллипсоида. Эллипсоид C.2.4), как и сфера, является
замкнутой по и и не замкнутой по v поверхностью. Сечения эллипсоида плос-
плоскостями, ортогональными векторам ix, iy, i2, являются эллипсами. Скалярные
Рис. 3.2.1. Эллипсоид
функции х(и, v) = acosucosu, y(u, v) = 6cosvsinu, z(u, v) — csinv эллипсо-
эллипсоида связаны уравнением
422
C.2.6)
Эллипсоид показан на рис. 3.2.1.
Однополостный гиперболоид. Радиус-вектор однополостного гиперболоида
может быть описан формулой
r(u, v) = p + achucosuiz + bchvs'mu'iy + cshviz,
О < и < 2тг, i;min < v < vmax,
где а, Ь, с — полуоси гиперболоида. Однополостный гиперболоид C.2.6) явля-
является замкнутой по и и не замкнутой по v поверхностью. Скалярные функ-
функции х(и, v) =¦ achucosu, y(u, v) = bchvs'mu, z(u, v) = cshv однополостного
гиперболоида связаны уравнением
B)% " "
3.2. Аналитические поверхности
149
Сечения однополо стного гиперболоида плоскостями, ортогональными векторам
ix, iy, являются гиперболами, а сечения однополостного гиперболоида плоско-
Рис. 3.2.2. Однополостный гиперболоид
стями, ортогональными вектору i2, являются эллипсами. Однополостный ги-
гиперболоид показан на рис. 3.2.2.
Двуполостный гиперболоид. Радиус-вектор одной из двух частей двупо-
двуполостного гиперболоида может быть опи-
описан формулой
r(u, v) = р + ashvcosuix +
bshvs'mu\y + cchviz, C.2.8)
0
u
2тг, 0
umax,
где a, b, с — полуоси гиперболоида. Вто-
Вторая часть гиперболоида описывается этим
же выражением, но орт iz должен иметь
противоположное направление или должен
быть изменен знак с на противополож-
противоположный. Двуполостный гиперболоид C.2.8)
является замкнутой по и и не замкнутой
по v поверхностью. Скалярные функции
х(и, v) = ashvcosu, y(u, v) = 6shusinu,
z(u, v) = cchv двуполостного гиперболо-
гиперболоида связаны уравнением
Рис. 3.2.3. Двуполостный гиперболоид
Сечения двуполостного гиперболоида плос-
плоскостями, ортогональными векторам \х, L,
являются гиперболами, а сечения гиперболоида плоскостями, ортогональными
вектору i2, являются эллипсами. Двуполостный гиперболоид показан на
рис. 3.2.3.
150
Гл. 3. Моделирование поверхностей
Эллиптический параболоид. Эллиптический параболоид может быть опи-
описан векторной функцией
r(u, v) = р + av cos и ix + bv sin и iy + v2iz, ,,oim
0<u^2tt, 0 < у ^ vmax,
где a, b — полуоси эллипса, получающегося как координатные линии v = const
поверхности. Эллиптический параболоид C.2.10) является замкнутой по и и не
замкнутой по v поверхностью. Скалярные функции х(и, v) — av cos и, у(и, v) —
= bvsinu, z(u, v) = v2 эллиптического параболоида связаны уравнением
(§)'+(f)' = .. (з.2.п,
Сечения параболоида плоскостями, проходящими через ось iz, являются па-
параболами, а сечения параболоида плоскостями, ортогональными вектору iz,
являются эллипсами. Эллиптический параболоид C.2.10) показан на рис. 3.2.4.
Рис. 3.2.4. Эллиптический параболоид Рис. 3.2.5. Эллиптический параболоид
Одну и ту же поверхность можно параметризовать различными способами.
Эллиптический параболоид может быть описан другой векторной функцией
г(«, v) = р + auix + bviy + {и2 + v2)iz, ,g 2 12>
umin ^ и *s "max, "mm *% и *% wmaxi
Эллиптический параболоид C.2.12) является не замкнутой по обоим параметрам
поверхностью. Эллиптический параболоид C.2.12) и его сечения плоскостями,
ортогональными вектору iz, приведены на рис. 3.2.5.
Гиперболический параболоид. Гиперболический параболоид может быть
описан векторной функцией
г{щ v) = р + аи\х + bviy + {и2 - v2)iz, .g 2 ig.
где а, Ъ — полуоси гиперболы. Гиперболический параболоид C.2.13) является
не замкнутой по обоим параметрам поверхностью. Если гиперболический па-
параболоид по аналогии с эллиптическим параболоидом представить векторной
3.2. Аналитические поверхности
151
функцией
u
ГЗ 2 141
то она будет описывать только часть поверхности.
Скалярные функции x(u, v), y(u, v), z(u, v) обоих представлений гипербо-
гиперболического параболоида связаны уравнением
Сечения параболоида плоскостями, ортогональными векторам \х и iy, являются
параболами, сечения параболоида плоскостями, ортогональными вектору iz,
Рис. 3.2.6. Гиперболический параболоид
являются гиперболами. Сечение гиперболического параболоида плоскостью, ор-
ортогональной вектору iz и проходящей через точку р, представляет собой две
Рис. 3.2.7. Часть гиперболического параболоида
прямые линии. Гиперболический параболоид C.2.13) и его сечения плоско-
плоскостями, ортогональными вектору iz, показаны на рис. 3.2.6. Гиперболический
параболоид C.2.14) показан на рис. 3.2.7.
152
Гл. 3. Моделирование поверхностей
Формулы C.2.6)—C.2.13) описывают ограниченные гиперболоиды и парабо-
параболоиды, усеченные параметрами vm-m и vmax или ит;п и итах. Если в формулах
C.2.4), C.2.6) и C.2.8) а = Ь, то мы получим соответствующие поверхности вра-
вращения вокруг местной оси iz. Частными случаями поверхности второго порядка
являются цилиндрическая и коническая поверхности.
Цилиндр. Эллиптический цилиндр может быть описан формулой
г(u, v) = р + acosuix + bs'muiy + hviz,
О ^ и ^ 2тг, 0 < и < 1,
C.2.16)
где а и Ь — полуоси эллипса, являющегося поперечным сечением цилиндриче-
цилиндрической поверхности, h — длина цилиндра. Если a = b, то мы получим круговой
цилиндр. Цилиндрическая поверхность C.2.16) является замкнутой по параме-
параметру и и усеченной по параметру v.
Конус. Круговая коническая поверхность может быть описана формулой
г(u, v) = р + (г + hv tg 7) (cos и ix + sin и iy) + hviz,
О ^ и ^ 2тг, 0 ^ v ^ 1,
C.2.17)
где r — радиус одного из оснований конуса, h — длина конуса, 7 — угол между
образующей и осью конуса. Коническая поверхность C.2.17), как и цилин-
\^"
4 ,--'
\ ?*
1 \ 1 \ 1 \ 1 \ \
¦ —
^-—э
4
—--
.—••
-^^
-^\
' \
Рис. 3.2.8. Цилиндрическая поверхность
Рис. 3.2.9. Коническая поверхность
дрическая, является замкнутой по параметру и и усеченной по параметру v.
Круговой цилиндр и круговой конус показаны на рис. 3.2.8 и 3.2.9.
Тор. Поверхность тора может быть описана положением центра р, тремя
взаимно ортогональными векторами единичной длины ix, iy, iz, определяю-
определяющими положение и ориентацию местной декартовой системы координат, глав-
главным радиусом R и малым радиусом г
г (u, v) = р + (R + г cos v) cos и ix + (R + r cos v) sin и iy
0 ^ и ^ 2тг, —7Г ^ v ^ тт.
" C.2.18)
3.3. Поверхности второго порядка
153
Тороидальная поверхность C.2.18) является замкнутой по параметру и и по
параметру v. Скалярные функции х(u, v) = (R + г cos v) cos и, у(и, v) =
= (R + rcosv) cosu, z(u, v) — rs'mv тора связаны уравнением
Область изменения параметра v тороидальной поверхности C.2.18) записана в
предположении, что г < R. Если г > R, то для того, чтобы тор не пересекал сам
себя, нужно уменьшить область изменения параметра v: —тг + vo ^ v ^ тг — г>о,
где vq = arccos (R/r). При R = 0 получим г>о = тг/2 и тор превратится в
Рис. 3.2.10. Открытый тор
Рис. 3.2.11. Закрытый тор
сферу радиуса г. Тороидальная поверхность называется открытой, если г < R,
и называется закрытой, если г > R. Открытый и закрытый торы показаны на
рис. 3.2.10 и 3.2.11.
Существуют еще ряд поверхностей, которые можно описать аналитическими
параметрическими зависимостями. Производные радиус-вектора аналитиче-
аналитических поверхностей можно найти дифференцированием компонент радиус-век-
радиус-вектора по параметрам.
3.3* Поверхности второго порядка
Эллипсоид, параболоиды, гиперболоиды, цилиндр и конус являются представите-
представителями поверхностей второго порядка. Выше приведены параметрические зависимости
для их радиус-вектора. В некоторых случаях, например, при обмене данными, при-
приходится иметь дело с неявным описанием поверхностей. Возникает необходимость из
неявного представления поверхности получить параметрическое представление и на-
наоборот. Аналитические поверхности можно представить в виде уравнения, которому
удовлетворяют координаты х, у, z радиус-вектора г(х, у, z) — xix +yiv + ziz поверхно-
поверхности. Поверхности второго порядка в декартовой системе координат Oxyz описываются
уравнением второй степени
сих2
= 0, C.3.1)
где Си, с22, Сзз, С44, Ci2, С13, С2з, Си, с24, с34 — коэффициенты, определяющие тип
поверхности, ее положение и ориентацию в пространстве (считается, что хотя бы один
из коэффициентов Сц, сгг, Сзз, С\2, С\$, Сгз отличен от нуля). В отличие от пара-
параметрического такое описание поверхности не всегда однозначно, а также не является
инвариантным относительно преобразования координат. При перемещении или пово-
повороте в пространстве поверхности второго порядка коэффициенты Сц, С22, сзз, С44, С\2,
Ci3i C23i C14, с24, С34 не остаются неизменными, причем трудно сразу сказать, изменена
ли поверхность или только ее положение.
154
Гл. 3. Моделирование поверхностей
В расширенной матричной записи уравнение поверхности второго порядка C.3.1)
имеет вид
RT Сс ¦ R = 0, C.3.2)
где использованы расширенный вектор A.4.3)
Cll Ci2
Cl2 C22
X
У
Z
1
C13
(
^23
Си
C24
и расширенная матрица Сс:
cc =
Ci4 C24 C34 C44_
Для уравнения C.3.1) поверхности второго порядка величины
C.3.3)
h =
С22 + С33,
г, —
12 —
СП
С12
С12
С22
С22 с2з
С23 Сзз
сзз
С13
С13
си
СИ
С12
С13
С12
С22
С23
С13
С23
СЗЗ
, и =
СП С12 С13 Cl4
Cl2 C22 C23 C24
Cl3 C23 C33 C34
Cl4 C24 C34 C44
C.3.4)
являются инвариантами относительно преобразований A.2.5) параллельного переноса
и поворота осей декартовой системы координат. Эти преобразования координат описы-
описываются формулами
х = anx' +a2i2/' + a3iz' +x0,
у - а12х' + О.22У1 + a23z' + у0, C.3.5)
z = а\гх' + а2зу' + азз-г7 + z0.
В расширенной матричной записи преобразование координат C.3.5) имеет вид
где Ао — расширенная матрица:
R = Ао • R ,
"оц ai2 013 О'
a21 a22 a23 0
031 азг а33 О
Хо Уо zo 1.
C.3.6)
Заметим, что определитель матрицы Ао равен единице. После перехода к координатам
х', у', z' получим уравнение поверхности второго порядка
R'T-Ao-Cc-AoT-R' = 0 или R'T • Сс' • R = 0, где Сс'= Ао • СС • Аот,
откуда следует, что 1± есть инвариант относительно преобразования C.3.5). Действи-
Действительно,
V = |СС'| = |А0 • Сс • Аот| = |Ао||Сс||АоТ| = |СС| = I*.
__ 3.3. Поверхности второго порядка 155
Доказательство инвариантности величин h, I2, h может быть выполнено путем замены
координат C.3.5) в C.3.1) и вычисления величин C.3.4) аналогично доказательству
инвариантности 1ц. Тип поверхности второго порядка и ее положение в пространстве
определяются значениями инвариантов Ix, 12, 1з, !*¦
Информация о типе поверхности и ее параметрах содержится в характеристической
квадратичной форме Сцх2 + с22у2 + C33Z2 + 1с\2ху + 2c23yz + 1c\zxz. Предположим, что
найдена система координат O'x'y'z', в которой уравнение поверхности второго порядка
имеет канонический (простейший) вид
Xix'2 + Х2у'2 + X3z'2 +1 = 0. C.3.7)
В силу свойства инвариантов будем иметь равенства
7i = Ai + Аг + A3, 12 = А1А2 + А2Аз + А3А1, h = A1A2A3, h = А1А2А3/.
Отсюда следует, что свободный член в каноническом уравнении равен /= = —
А1А2А3 /з
Поверхность второго порядка может быть приведена к указанному каноническому виду,
если 13 ф 0. Поверхности такого вида называются центральными. Для определения
остальных канонических коэффициентов центральной поверхности второго порядка
составим кубический полином
(A-Ai)(A-A2)(A-A3) =
= А3 - (Ai + А2 + А3)А2 + (AiA2 + А2А3 + A3Ai)A - AiA2A3 = A3 - hX2 + I2X - J3,
корнями которого являются канонические коэффициенты Х%, Х2, Аз- Так Д, 12, 1з,
Ц в любой системе координат имеют одни и те же значения, то следует вывод, что
канонические коэффициенты Ai, A2, A3 поверхности второго порядка являются корнями
уравнения
A3-/iA2 + /2A-/3 = 0, C.3.8)
которое называется характеристическим уравнением. В матричной записи характе-
характеристическое уравнение C.3.8) имеет вид
Сц — А С\2 С\з
си с22 - А с23
Ci3 с2з сзз - А
= 0. C.3.9)
Таким образом, канонические коэффициенты являются собственными значениями ма-
матрицы характеристической квадратичной формы поверхности второго порядка. Корни
^ь -^2; Хз характеристического уравнения C.3.8) являются действительными, так как
матрица характеристической квадратичной формы симметричная. Метод решения
кубического уравнения приведен в гл. 8.
Если /з = 0, то один из корней характеристического уравнения равен нулю. Пусть
это будет третий по счету корень, и пусть Д ф 0. Тогда поверхность второго порядка
может быть приведена к виду
Ххх'2 + Х2у'2 - 2Jz' = 0.
В силу свойства инвариантов для данного уравнения будем иметь равенства
I1 = X1 + X2, I2 = X1X2, h = 0, h = -XxX2J2.
Отсюда следует, что J2 = — = —-jr. Такая поверхность не является центральной
AA /
2
и имеет действительные точки, если — < 0.
h
156
Гл. 3. Моделирование поверхностей
Если /з = 0 и /4 = О, то поверхность второго порядка может быть приведена к
одному из видов:
2 + Х2у'2 = 1, если h Ф О,
\хх'2 + 2у' = О, если h = 0.
Поверхность в этих случаях представляет собой цилиндрические поверхности, сечения
z — const которых представляют кривые второго порядка.
Приведем классификацию поверхностей второго порядка. Пусть 1ц ф 0, тогда по-
поверхность второго порядка не вырождена и представляет собой:
• эллипсоид,
• однополостный гиперболоид,
• двуполостный гиперболоид,
• эллиптический параболоид,
• гиперболический параболоид,
если
если
или
если
или
если
если
hh
hh
hh
hh
hh
h =
h =
>
<
>
<
>
o,
o,
o,
0,
o,
o,
o,
и
и
h
h
h
h
h
[ <
[ >
>
>
<
>
<
o,
0.
o,
o,
0,
o,
o,
I3
h
h
h
h
Ф
Ф
Ф
Ф
ф
o,
o,
o,
o,
o,
h
h
h
h
h
<
>
>
<
<
0
0
0
0
о
При Iil3 > 0, I2 > 0, h ф О, Ц > 0 уравнению C;3.1) не удовлетворяет ни одна точка
пространства и оно описывает мнимый эллипсоид. Если Ц = 0, то уравнение C.3.1)
описывает:
• коническую поверхность, если
или
• эллиптический цилиндр, если
• гиперболический цилиндр, если
• параболический цилиндр, если
при условии, что
Ji/3<0, /2>0: 13ф0
hh >0, h<0, 13ф0,
h > 0, 13 = 0,
h < 0, h = 0,
С22
С23
С24
С23
сзз
С34
С24
С34
С44
+
Си
С13
Си
си
сзз
С34
Си
С34
С44
+
Cll C12 C14
С12 С22 С24
Си С24 С44
Если последнее условие не выполняется, то цилиндры вырождаются в плоскости.
Если поверхность второго порядка привести к главной центральной системе коор-
координат, то ее уравнение в ней примет канонический вид. Уравнения, которым удовле-
удовлетворяют координатные функции х(и, v), y(u, v), z(u, v) поверхностей C.2.4)-C.2.13),
имеют канонический вид. Координаты хо, уо, zq центральной точки р поверхности
определяются из системы уравнений
СцХо + Ci2?/o + C31-Zo + Ci4 = 0,
C12Z0 + С222/О + С23^0 + С24 - 0,
C.3.10)
Отсюда
С14
С24
С34
С12
С22
С23
С13
С23
сзз
С13Ж0
, Уо
+
С232/О
1
1з
+ с3
си
С12
С13
3-^0 +
Cl4
С24
С34
С34
С13
C23
СЗЗ
= 0.
> *o = -7-
3
Cll
C12
C13
C12
C22
C23
C14
C24
C34
h
Каждая поверхность второго порядка имеет три главные плоскости, как минимум две из
которых являются плоскостями симметрии. Все они проходят через центральную точку
Р = [хо, 2/о, zq\t¦ Коэффициенты ац, г, j = 1, 2, 3, преобразования C.3.5) уравнения
C.3.1) в главную центральную систему координат являются компонентами векторов
3.3. Поверхности второго порядка
157
ii = [ац ai2 а!з]т, i2 = [an 022 а2з]т, i3 = [031 азг азз]т> ортогональных главным
плоскостям. Векторы ii, i2, i3 называются собственными векторами. Каждый из них
соответствует одному из корней характеристического уравнения.
Пусть Ai ф А2 ф Аз (корни характеристического уравнения различные). В этом
случае базисные векторы главной центральной системы координат могут быть найдены
следующим образом. Для каждого \ составим систему уравнений
(сп -
= О,
(с22 - Aj)ai2 + c23ai3 = 0,
c23ai2 + (C33 - Aj)aj3 = 0.
C.3.11)
Среди уравнений C.3.11) одно является линейной комбинацией двух других, так как
определитель C.3.9) системы равен нулю. Далее вычислим определители
с22 — А,-
С23
с2з
сзз - А,-
с13
- А*
А* =
сц -
с12
C12
с22 -
По крайней мере, один из них будет отличен от нуля. Пусть Аз ф 0. Тогда компоненты
соответствующего главного вектора найдем из системы уравнений
= 0,
= 0,
(с22 - Xi)ai2
22
ai22
ai32 =
Для ее решения из первых двух уравнений выразим ац и щ2 через а*з и подставим
их в третье уравнение. В результате получим ai3. Далее из первых двух уравнений
найдем ац и aj2. Вектор ij = [ац ai2 агз]Т соответствует Aj.
Пусть два из трех корней характеристического уравнения равны между собой, на-
например, Ai = А2 ф Аз. В этом случае базисный вектор i3 = [031 а^2 азз]г может быть
найден описанным выше способом. Другими базисными векторами могут служить
любые два ортогональные друг другу и вектору i3 орта, так как поверхность второго
порядка будет поверхностью вращения.
Если Ai = А2 = A3, то поверхность второго порядка будет являться сферой (или
мнимой сферой). Базисными векторами ее главной центральной системы координат
могут служить любые три взаимно ортогональные орта.
В главной центральной системе координат уравнение поверхности C.3.1) примет вид
^ =0,
C.3.12)
если /з ф 0 и, следовательно, все корни характеристического уравнения отличны от
нуля, или
0, C.3.13)
если /з = 0, следовательно, хотя бы один из корней характеристического уравнения
равен нулю (штрих около новых координат опущен). Если /з ф 0, то каноническое
уравнение поверхности имеет симметричный вид и у поверхности есть центральная
точка (эллипсоид и гиперболоиды). В противном случае поверхность не имеет центра
(параболоиды).
Перенумеруем корни характеристического уравнения так, чтобы Ai ^ А2 ^ A3. По
корням характеристического уравнения определяются параметры поверхностей второго
порядка. Если Ai ^ А2 ^ Аз > 0, то, сравнив C.3.12) с C.2.5), найдем полуоси
158
Гл. З. Моделирование поверхностей
эллипсоида C.2.4) по формулам
Если Ai ^ Аг > 0 > Аз, то, сравнив C.3.12) с C.2.7), найдем действительные и мнимую
полуоси однополостного гиперболоида C.2.6) по формулам
h
Vw Vw Vw C-ЗЛ5)
Если Ai > 0 > Аг ^ Аз, то сравнив C.3.12) с C.2.9), найдем действительную и мнимые
полуоси двуполостного гиперболоида C.2.8) по формулам
Если Ai ^ Аг > Аз = 0, то, сравнив C.3.13) с C.2.11), найдем полуоси эллиптического
параболоида C.2.10) по формулам
a =
к
v
C.3.17)
Если Ai > А2 = 0 > Аз, то, сравнив C.3.13) с C.2.15), найдем действительную и
мнимую полуоси гиперболического параболоида C.2.13) по формулам
C.3.18)
Если 0 > Ai ^ Аг ^ Аз, то уравнение C.3.1) описывает мнимый эллипсоид.
Коническая поверхность является вырожденным случаем гиперболоида. Она пред-
представляет собой предельный случай, к которому стремятся однополостный и двупо-
лостный гиперболоиды. Цилиндрическая поверхность является вырожденным случаем
эллиптического и гиперболического параболоидов. Характеристики вырожденных слу-
случаев поверхностей можно найти по общим формулам.
Приведенные формулы позволяют строить параметрические зависимости для по-
поверхностей второго порядка по их координатным уравнениям. Для перехода от пара-
параметрического описания к неявному описанию нужно знать каноническое уравнение
f(x, у, z) = 0, которым связаны координатные функции х(и, v), y(u, v), z(u, v) по-
поверхности. Местные координаты х, у, z связаны с глобальными координатами ri, r2,
гз уравнениями A.2.8), которые в принятых здесь обозначениях имеют вид
х =
C.3.19)
-Pi) +ai2(r2 -p2) +an(r3 ~Рз),
у - a2i(ri -pi) +a22(r2 -p2) +а2з(г3 -рз),
z = a3i(n -pi) +аъ2{г2 -р2) +а3з(г3 -рз)-
Для получения уравнения F(r\, r2, гз) = 0, связывающего глобальные координаты,
подставим в уравнение /(ж, у, z) = 0 выражения C.3.19) для канонических координат,
3.4. Поверхности движения
Поверхность можно получить путем движения кривой по заданной траек-
траектории. Такие поверхности называются поверхностями движения. Область из-
изменения параметров таких поверхностей представляет собой прямоугольник.
Кривая, движением которой получается поверхность, называется образующей,
3.4. Поверхности движения
159
а траектория движения некоторой ее точки называется направляющей. Поверх-
Поверхность движения в качестве данных содержит образующую кривую и в том или
ином виде направляющую линию. В общем случае направляющей может быть
произвольная кривая. Среди всевозможных направляющих выделяют две наи-
наиболее простые — отрезок прямой линии и дугу окружности. Если направляю-
направляющей служит отрезок прямой, то поверхность называется поверхностью выдавли-
выдавливания. Если направляющей служит дуга окружности или вся окружность, то
поверхность называется поверхностью вращения. Во всех остальных случаях
поверхность будем называть кинематической поверхностью. Для построения
тел мы не будем использовать поверхности, пересекающие сами себя.
Поверхность выдавливания. Поверхность выдавливания, полученная дви-
движением кривой с(<), <mjn ^ t ^ <max) вдоль вектора d, описывается радиус-
вектором
r(u, v) = с(и) + vd, tmiTi < и ^ tmax, 0 < и < 1. C.4.1)
Длина поверхности выдавливания определяется длиной вектора d. В зависи-
зависимости от замкнутости кривой с(?) поверхность выдавливания может быть за-
замкнутой или нет по параметру и. Направляющий вектор d = id может быть
представлен в виде произведения вектора единичной длины на скаляр. Поверх-
Поверхность выдавливания приведена на рис. 3.4.1.
Рис. 3.4.1. Поверхность выдавливания
Рис. 3.4.2. Поверхность вращения
Поверхность вращения. Поверхность, полученная вращением кривой c(t),
?min ^ t ^ <max, на угол а вокруг оси, заданной единичным вектором i и
точкой р, описывается радиус-вектором
r(u, v) = р + ((c(u) — р) • i)i + (c(u) - р - ((c(u) - р) • i)i) cos v +
+ i x (c(u) — p)smu = p + гз(и) + i"i(u) cos v + r2(u) sin v, C.4.2)
<min < и < imax, 0 ^ v < a,
где гз(и) = ((c(u) — p) ¦ i)i — составляющая вектора c(u) — p, параллельная
оси вращения, ri(u) = c(u) — p — гз(и) — составляющая вектора c(u) — p,
перпендикулярная оси вращения, Г2(и) = ix(c(u)—p) — ортогональный первым
двум векторам вектор, длина которого равна длине вектора ri(u). Замкнутость
поверхности вращения по параметру и совпадает с замкнутостью образующей
160
Гл. 3. Моделирование поверхностей
кривой c(t). Если угол вращения a = 2тг, то поверхность C.4.2) замкнута по
параметру v, если a < 2тг, то поверхность вращения не замкнута по параметру v.
Будем строить поверхности вращения, у которых угол вращения не превосходит
2тг. Поверхность вращения приведена на рис. 3.4.2.
Кинематические поверхности. Рассмотрим кинематическую поверхность, ко-
которая является общим случаем поверхности движения. Пусть образующая опи-
описывается кривой c(t), tm[n ^ t ^ <maxj а направляющей является кривая g(v),
^min ^ v ^ vmax. Пусть при построении кинематической поверхности параметр
и совпадает с параметром образующей кривой с (и), а параметр v совпадает с па-
параметром направляющей кривой g(v). При движении образующей кривой вдоль
направляющей кривой ориентация первой относительно второй может меняться
или может оставаться неизменной. Если образующая выполняет плоскопарал-
плоскопараллельное движение, т. е. остается «параллельной» своему начальному положе-
положению, то такую поверхность будем называть поверхностью сдвига, в противном
случае поверхность будем называть поверхностью заметания.
Поверхность сдвига. Поверхность сдвига проще поверхности заметания.
Радиус-вектор поверхности сдвига определяется формулой
г (it, v) = g{v) + (c(u) - g(umin) - h),
&min ^ ^ ^ 'maxi ^min ^ ^ ^ "maxi
C.4.3)
где h — вектор привязки образующей к направляющей. Вектор h сдвигает
кривую с (и) на некоторую величину из ее начального положения относительно
направляющей и сохраняет этот сдвиг во время движения. Если h = 0, то
сохраняется исходное положение образующей кривой относительно начальной
точки направляющей кривой. Радиус-вектор поверхности сдвига строится как
сумма двух векторов: вектора точки на направляющей кривой g(u) и вектора
положения точки образующей относительно начальной точки направляющей со
сдвигом с(и) — g(i)min) — h. Поверхность сдвига приведена на рис. 3.4.3.
Рис. 3.4.3. Поверхность сдвига
Рис. 3.4.4. Поверхность заметания
Поверхность заметания. Для построения кинематической поверхности заме-
заметания (рис. 3.4.4) будем использовать подвижный касательный базис, связан-
связанный с направляющей кривой g(v). Подвижный касательный базис представляет
3.4. Поверхности движения 161
собой местную декартову прямоугольную систему координат. Ее начало нахо-
находится в текущей точке направляющей кривой и определяется радиус-вектором
Ро = g{v)- Первый базисный орт ii = g'/lg'l местной системы координат совпа-
совпадает с касательной к направляющей кривой, второй базисный орт i2 ортогонален
первому, а третий i3 = ii x i2 образует с первым и вторым правую тройку век-
векторов. Из сказанного не ясно, в какую сторону направлен вектор i2. На первый
взгляд, его можно было бы направить по вектору главной нормали к напра-
направляющей, но в точках распрямления кривой нормаль не определена, а в точках
перегиба ее направление может резко поменяться на противоположное. Поэтому
вектор i2 будем строить следующим образом: пусть d есть некоторый не изме-
изменяющийся вектор, который не коллинеарен касательной к направляющей g(v)
ни в одной ее точке. Тогда вектор i2 примем параллельным вектору
d2 = d-(ii-d)ii. C.4.4)
Вектор d2 представляет собой составляющую вектора d, перпендикулярную орту
ii (касательной к направляющей в данной точке). Составляющая d2 никогда не
равна нулю, так как мы предполагаем, что d никогда не коллинеарен ij. Будем
считать, что для любой кривой существует такой вектор d, который никогда
не коллинеарен касательной к кривой. Подвижный касательный базис связан с
кривой g(v) и поэтому является функцией параметра v
Ро(«) = g(t/), C.4.5)
g' d2
il^ = is7!' i2^ = пи' i3^ = 'n xi2'
где d2 определяется равенством C.4.4), a g' = —.
dv
Запомним положение образующей кривой c(u) в подвижном касательном ба-
базисе в начале направляющей (при начальном значении параметра v = ит;п) и
будем сохранять его при движении вдоль направляющей. При движении вдоль
направляющей подвижный касательный базис меняет свое положение и ори-
ориентацию в пространстве и увлекает за собой жестко связанную с ним обра-
образующую кривую. Таким образом, в данных кинематической поверхности на-
находятся две кривые линии, вектор d и положение касательного базиса C.4.5)
в начале направляющей: g(vmin), iifamin), bfamin), 1з(г>тт)- В общем слу-
случае можно запомнить положение образующей кривой относительно начальной
точки направляющей, сдвинув первую на некоторый вектор h (например, чтобы
по направляющей двигался центр тяжести образующей), и сохранить его при
движении вдоль направляющей. Если h = 0, то сохраняется исходное положе-
положение образующей кривой относительно начальной точки направляющей кривой и
касательной к ней. Радиус-вектор поверхности для произвольных параметров и
и v получим следующим способом. Вычислим положение точки на образующей
кривой в местной системе координат при v = vm\n по формуле A.2.9)
= A(umin) • (c(tt) - g(umin) - h),
где через A(vm\n) обозначена матрица, вычисленная по матричной функции
A(v) при начальном параметре v. Матричная функция А(«) является матри-
матрицей преобразования A.2.6) координат радиус-вектора точки при переходе из
глобальной в местную систему координат, ее строки составлены из компонент
11 ~ 5293 Голованов
162
Гл. 3. Моделирование поверхностей
базисных ортов местной системы координат
A(v) =
C.4.6)
Вектор x(u, vmm) выражает положение точки образующей относительно точки
на направляющей кривой в подвижном касательном базисе, которое сохраняется
для произвольного параметра v. Переходя из местной системы координат в
глобальную систему координат уже при текущем параметре v в соответствии с
A.2.5), получим радиус-вектор точки на поверхности
r(u, v) = g(w) + Ar(v) ¦ x.(u, vmin).
Таким образом, радиус-вектор кинематической поверхности заметания описы-
описывается формулой
r(u, v) = g(v) + M(v) • (c(u) - g(vmin) - h),
f ¦ < II < f 1) ¦ < 1) < 1) (О.Ч.1)
lmm ^ " =5; <-maX7 "mm <% " <% "таю
где М(и) —- матричная функция, дающая матрицу поворота текущего подвиж-
подвижного касательного базиса относительно его начального положения. Эта матрица
вычисляется по формуле
т
М(и) = Ат(v) ¦ A(vmin) =
C.4.8)
В начале направляющей кривой матрица M(umjn) равна единичной матрице,
так как Ат = А.
Для вычисления производных радиус-вектора кинематической поверхности
заметания нужно вычислять производные матрицы M.(v), что в свою очередь
сводится к вычислению производных ортов ii(v), i2{v), h(v)- Рассмотрим вы-
вычисление производных векторов единичной длины на примере вычисления про-
производных орта ii. Этот орт получен нормированием вектора g(v). Вычислим
первую, вторую и третью производные этого вектора — g', g" и g'". По этим про-
производным сам орт ij и его первая и вторая производные (ii' и Ц") определятся
по формулам:
i -
C.4.9)
dv2
2 ii-^т Рт1- ii • fe + ^
dv
dv
где вторая и третья формулы получены путем дифференцирования первой с уче-
ds
том того, что длина первой производной направляющей кривой g = — —
dv
= Ve' " &'• Аналогично получим производные остальных ортов. Орт 12 получен
3.5. Линейчатые поверхности 163
нормированием вектора d2 = d — (ii • d)ii, а орт i3 получен нормированием
вектора d3 = g' x d2- Вычислив первые, вторые и третьи производные d2 и
Aз по C.4.9), получим производные соответствующих ортов. Далее вычислим
производные матричных функций A(v) и M.(v), что позволит вычислить про-
производные радиус-вектора поверхности C.4.7).
Замкнутость кинематической поверхности по параметру и совпадает с за-
замкнутостью образующей кривой с(и), а замкнутость поверхности по параметру
Рис. 3.4.5. Кинематическая поверхность
v совпадает с замкнутостью направляющей кривой g(v). На рис. 3.4.5 показана
кинематическая поверхность, полученная движением эллипса вдоль спиральной
линии.
При неудачном сочетании параметров кривых кинематическая поверхность
может пересекать сама себя. Мы не будем рассматривать самопересекающиеся
поверхности.
Из C.4.9) следует, что для вычисления частных производных второго по-
порядка радиус-вектора поверхности требуются производные радиус-вектора кри-
кривой третьего порядка. Для получения всей геометрической информации о
кривой достаточно знать векторную функцию ее радиус-вектора и ее первую и
вторую производные, но для построения некоторых поверхностей требуется тре-
третья производная кривой. Кинематическая поверхность является одной из них.
3.5. Линейчатые поверхности
Линейчатая поверхность представляет собой геометрическое место отрез-
отрезков прямых, соединяющих соответствующие точки заданных двух линий. Ее
можно получить путем движения прямой линии по двум направляющим кривым
линиям, при этом каждой точке одной кривой должна соответствовать вполне
определенная точка другой кривой. Пусть заданы две направляющие кривые
а(?) и d(w), где параметры кривых t и w изменяются в пределах im;n ^ t ^ ?гаах
и гут;п ^ w ^ iumax. Радиус-вектор линейчатой поверхности определяется фор-
формулой
r(u, v) = A - v)a(t) + vd(w),
t = *min(l - u) + *maxW, W = Wmin(l - u) + WmaxU, C.5.1)
0<u< 1, 0<u < 1.
Для направляющих кривых неявно производится репараметризация — приве-
приведение области изменения параметров к отрезку от 0 до 1. Можно было бы репа-
раметризовать только одну кривую — привести область изменения одной из них
к другой. Если параметризация кривых а(и) и d(u) совпадает, то радиус-вектор
и*
164 Гл. 3. Моделирование поверхностей
линейчатой поверхности может быть описан функцией
r(u, v) = A - v)a(u) + vd{u), umin ^ u < umax, 0 ^ v ^ 1.
На рис. 3.5.1 приведен пример линейчатой поверхности.
Если обе направляющие замкнуты, то линейчатая поверхность замкнута
по параметру и. По другому параметру линейчатая поверхность всегда не
замкнута.
Если направляющими линиями являются отрезки прямых линий, то по-
поверхность является линейчатой по обоим параметрам и для ее построения
Рис. 3.5.1. Линейчатая поверхность
достаточно знать радиус-векторы концевых точек отрезков. Пусть один напра-
направляющий отрезок в форме B.2.3) проведен из точки pi в точку Р2, а другой
направляющий отрезок проведен из точки рз в точку р4- Тогда линейчатая по
двум параметрам поверхность определится векторной функцией
Г(и, V) = A-U)
, C.5.2)
Такая поверхность называется билинейной. Она всегда не замкнута. Если все
четыре точки лежат в одной плоскости, то поверхность представляет собой часть
плоскости. В некоторых случаях удобно описывать плоскость по четырем точ-
точкам, лежащим в углах квадрата, в виде зависимости C.5.2). Описанная таким
образом плоскость отличается от C.2.1) тем, что ее параметрические размеры
не зависят от размеров самой плоскости. При выполнении пересечений и дру-
других операций над поверхностями желательно, чтобы у поверхностей области
определения параметров не зависели от размеров поверхностей. Если точки pj
и рз или р2 и р4 совпадают, то мы получим треугольную поверхность, которая
всегда плоская.
Частным случаем линейчатой поверхности является секториальная поверх-
поверхность. Она получается из линейчатой поверхности C.5.1), если одну из кривых,
например d(w), заменить точкой р. Радиус-вектор секториальной поверхности
описывается формулой
г(м, v) = A - и)а(м) + up, imin ^ и ^ imax, 0 sC v < 1. C.5.3)
Если направляющая a(i) замкнута, то секториальная поверхность также за-
замкнута по параметру и. По другому параметру секториальная поверхность все-
всегда не замкнута.
3.6. Поверхности Кунса,
165
Треугольная и секториальная поверхности имеют точку, в которой одна
из частных производных ее радиус-вектора равна нулю. Аналогичные точки
имеют сферическая и коническая поверхности. Эти точки не являются особыми,
так как другая частная производная радиус-вектора поверхности не равна нулю.
Если рассматривать кривые на поверхностях, то в таких точках находятся
отрезки двухмерных координатных линий.
С помощью линейчатой поверхности можно моделировать детали с уклоном
и фаски деталей. Направляющими кривыми поверхности-фаски служат кривые
на поверхностях, отстоящие от ребра на заданном расстоянии.
3.6. Поверхности Кунса
Возьмем векторную функцию линейчатой поверхности C.5.1), прибавим к
ней и вычтем из нее векторную функцию билинейной поверхности C.5.2), где pi
и р2 — концевые точки направляющей кривой а(?), а рз и Р4 — концевые точки
направляющей кривой d(w). В результате этих действий векторная функция не
изменится, но будет иметь вид
r(u, v) = A - v)a.(u) + vd(u) + A - u)(pi(l - v)
+ «(P2(l ~V)+ PiV) - A - «)A - U)pi - U(l - v)p2 -
— A — u)vps — uvp4 = A — v)a(u) + vd(u) + A — u)b(v) + uc(v) —
- A - «)A - U)pi - «A - W)p2 - A - U)vp3 - UVp4, C.6.1)
0<«<l, 0< v < 1.
В обозначениях функций а(«) и d(u) мы использовали их реальный аргу-
аргумент и, а также ввели обозначения для отрезков прямых b(v) = Pi(l — v) +Рз^)
c(v) = ргA — v) + p^v, соединяющих концы кривых а(и) и d(u). Если допу-
допустить, что в качестве Ь(и) и c(v) могут использоваться произвольные кривые,
Рис. 3.6.1. Поверхность Кунса
начинающиеся и оканчивающиеся в тех же точках, то получим вариант поверх-
поверхности Кунса. Поверхность Кунса строится по четырем равноправным кривым.
Рассмотрим четыре кривые a(ia), d(td), b(i(,), c(tc), попарно пересекающи-
пересекающиеся в точках pi, рз, Р2, Р4, как показано на рис. 3.6.1.
166 Гл. 3. Моделирование поверхностей
Построим поверхность внутри «четырехугольника», образованного кривыми.
Пусть точкам pi и рг на кривой а(?а) соответствуют параметры ?amin и tam&x,
точкам pi и рз на кривой Ь(?ь) соответствуют параметры *ьгшп и ?ьтах> точкам
Рз и р4 на кривой d(td) соответствуют параметры tdmin и *dmax> точкам рг
и р4 на кривой c(tc) соответствуют параметры ?crain и tcmax. Поверхность,
построенную по данным четырем кривым, можно описать радиус-вектором
r(u, v) = A - v)(a(te) - A - «)Pi) +
+ A - u)(b(tb) - vp3) + v(d(td) - up4) + u(c(tc) - A - u)p2) =
= A - v)a{ta) + A - u)b(tb) + vd(td) + uc{tc) - A - u)(l - v)pi -
- u(l - v)p2 ~ A - u)vp3 - vup4, C.6.2)
ta = *amin(l ~ u) + tam&xU, tb = tbmin(l - v) + tbmaxV,
td = *drain(l ~u)+ ^max«, *c = *crain(l — v) + tcm&xv,
O^u^l, 0 ^ и ^ 1.
Легко проверить, что вектор r(u, 0) описывает участок кривой а(?а), вектор
r(u, 1) описывает участок кривой d(td), вектор r@, v) описывает участок кри-
кривой b(i(,), вектор гA, v) описывает участок кривой c(tc). Совсем не обязательно,
чтобы ifcmin было меньше i^max» к = о, 6, с, d.
Для того чтобы формула C.6.2) легче воспринималась, переобозначим кри-
кривые и точки, входящие в структуру данных описываемой ею поверхности: кри-
кривую а(?а) обозначим через r(u, 0), кривую d(i^) обозначим через r(u, 1), кривую
ЬD) обозначим через r@, v), кривую c(tc) обозначим через гA, v), точку pi
обозначим через г@, 0), точку р2 обозначим через гA, 0), точку рз обозначим
через г@, 1), точку р4 обозначим через гA, 1), и будем считать, что для кривых
вьгаолнен переход к параметрам ииив соответствии с C.6.2). Для коэффици-
коэффициентов, с которыми граничные кривые входят в C.6.2), введем обозначение
ao(«) = l-u, ai(«)=u,
= 1 — v, cxi(v) = v. '
В результате векторная функция C.6.1) примет вид
r(u, v) = ao(u)r(u, 0) + ao(u)r(O, v) +
+ ai(v)r(u, 1) + ai(u)r(l, v) - ao(u)ao(v)r(O, 0) -
- ai(u)ao(v)r(l, 0) - aQ(u)ai(v)r@, 1) - ai(u)ai(v)r(l, 1) =
1 11
i{u)r{i, v) + ]Гсу(и)г(и, j) + J2^2ai(u)aj{v)r{i, j), C.6.4)
i=0 j=0 i=0 j=0
O^u^l, 0< v ^ 1.
3.6. Поверхности Куяса 167
Поверхность C.6.4) построена на четырех граничных кривых, коэффициенты
при которых являются линейными функциями параметров и и и. Такое линей-
линейное объединение четырех кривых называется линейной поверхностью Кунса.
Функции ai(u) и aj(v) называются функциями смещения. Если граничные ли-
линии являются, отрезками прямых линий, то формула C.6.4) даст билинейную
поверхность C.5.2).
Подобной поверхностью можно описать произвольную часть плоскости, гра-
границу которой можно представить в виде четырех попарно пересекающихся
линий на ней. Например, часть плоскости, лежащей внутри эллипса, можно
описать поверхностью
r(u, v) = р +
/ 2u(l — cosw — sinw) 2v(l — cosu — sinu)
+ о cos и + cos v - H H
V 7Г 7Г
, / . 2u(l — cosw — sinw) 2u(l — cosu — sinu)\ . . „.
+ 6 sinu-sinu - - + —- L)i2, C.6.5)
У 7Г 7Г /
где р — радиус-вектор центра, а и Ь — полуоси эллипса, ii, i2 — орты, лежащие
в плоскости эллипса (рис. 3.6.2).
Формула C.6.5) получена как частный случай формулы C.6.4) путем под-
подстановки в нее конкретных линий и точек. Поверхность C.6.5) построена по
четырем дугам эллипса. Данная поверхность отличается от своего аналога в
Рис. 3.6.2. Частный случай поверхности Кунса
виде плоскости с областью изменения параметров, ограниченной эллипсом, тем,
что имеет прямоугольную область изменения параметров. Следует заметить, что
поверхность C.6.5) имеет особенности в угловых точках: производная по пер-
первому параметру коллинеарна производной по второму параметру. Дуги эллипса
в C.6.5) представлены в явном виде. Для удобства верхние границы области
изменения параметров заменены с 1 на тг/2. Поверхность C.6.5) имеет четыре
особые точки, в которых частные производные радиус-вектора по параметрам и
и v коллинеарны. Это точки стыковки дуг эллипса.
Из поверхностей C.6.4) можно сконструировать составную поверхность, сты-
стыкуя их по граничным кривым (делая граничные кривые общими). Если поверх-
поверхность C.6.4) стыкуется по своим краям с другой такой же поверхностью, то на
границе производная в трансверсальном направлении будет претерпевать излом.
Для того чтобы на граничных кривых производные радиус-вектора поверхно-
поверхности в трансверсальном к граничным кривым направлении являлись заданными
168
Гл. 3. Моделирование поверхностей
функциями, добавим их к ее описанию. То есть добавим к описанию поверхно-
поверхности ее производные вдоль граничных кривых ru(i, v), г„(и, j) и производные
в углах поверхности ги(г, j), rv(i, j), ruv(i, j), с коэффициентами /%(и), /3j(v),
где i = 0, 1, j = О, 1. Линейные функции смещения C.6.3) заменим кубиче-
кубическими функциями B.5.4). Построенная таким образом поверхность описывается
векторной функцией
r(u, v) = [ao(u) ai(u)
[ao(v) ai(v)
f3\{u)}
¦r(O,t;)
r(l, v)
ru@, v)
¦ru(l, V).
r(u,0)
r(u, 1)
rv(u, 0)
~[ao{u) ai(u) /3o(u)
¦r@, 0) r@, 1) rw@,0) rw@, 1
r(l, 0) r(l, 1) г„A, 0) г„A, 1
Ги@, 0) г„@, 1) rtte@, 0) ги„@, 1
г„A, 0) ru(l, 1) rttW(l, 0) rttW(l, 1
0^и<1, 0^г><1,
где кубические функции смещения определяются формулами
, C.6.6)
ao(w) = 1 - Згу2 + 2го3, ai(tw) = Зго2 - 2го3,
/?о(го) = го — 2го2 + го3, /3i(w) = —го2 + го3.
C-6.7).
Поверхность C.6.6) называется кубической поверхностью Кунса. Формула
C.6.6) описывает поверхность Кунса, построенную на тех же четырех кривых,
показанных на рис. 3.6.1, что и поверхность C.6.4). Но в отличие от послед-
последней она имеет заданные производные в трансверсальном направлении вдоль
граничных кривых.
Форрест предложил обобщить поверхности C.6.4) и C.6.6) и использовать
вместо линейных или кубических функций смещения некоторые обобщенные
функции смещения otk,i{u). Индекс к указывает на то, что обобщенная функция
смещения умножается на векторную функцию, представляющую собой произ-
производную fc-го порядка от граничной кривой. Производной нулевого порядка функ-
функции будем называть саму функция. Для граничных кривых к = 0, для каса-
касательных векторов к = 1 или, другими словами, ao,i(u) = аг(и), ai,i(w) = /%(u),
i = 0, 1. Обобщенные функции смещения должны удовлетворять равенствам
1 К
u=j
!> если i=j и к = п,
0, если г ф j или к ф п,
C.6.8)
3.7. Онлайновые поверхности 169
которые являются обобщением условий, которым удовлетворяют линейные и ку-
кубические функции смещения. Радиус-вектор обобщенной поверхности Кунса
определяется формулой
I m
i=0 fe=0 j=0 (=0
1 1 n m
i=0 j=0 fc=0 (=0
0 <u< 1, 0<v < 1,
где используются заданные значения производных на краях поверхности
i = о,
и заданные значения производных в угловых точках параметрической области
поверхности
' i>j = °' L
v=j
dukdvl
В качестве обобщенных функций смещения могут быть использованы по-
полиномы. Обобщенные поверхности Кунса имеют заданные производные &-го
порядка радиус-вектора по параметру и вдоль граничных кривых и = const и
заданные производные Z-ro порядка радиус-вектора по параметру v вдоль гра-
граничных кривых v = const.
3.7. Сплайновые поверхности
Корпуса судов, фюзеляжи и крылья самолетов часто проектируются с помо-
помощью поперечных или продольных сечений, проходящих в заданных местах.
Эти сечения соединяются плавными кривыми, в результате чего получается
единая трехмерная форма. Это выполнялось в натуральную величину, для чего
использовались плазы. По традиции процесс построения поверхности по ее сече-
сечениям называется плазированием, а поверхности, построенные таким способом,
называются сплайновыми поверхностями. Рассмотрим некоторые сплайновые
поверхности.
Поверхность Эрмита. Пусть имеется семейство кривых Tj(tj), j = 0,1,
2, ..., п, показанных на рис. 3.7.1. Кривые семейства не должны пересекать
друг друга. На этом семействе можно построить гладкую поверхность, имею-
имеющую непрерывные производные по всем направлениям. Приведем все кривые
к одной параметрической длине, так чтобы область изменения параметра была
170
Гл. 3. Моделирование поверхностей
[«^ umax. Кривые переобозначим в соответствии с их местом на поверх-
поверхности: r(u, j) = *j(tj), j = 0, 1, 2, ..., п. Пусть параметр поверхности v между
кривыми r(u, г) и r(u, к) изменяется от г до к.
Радиус-вектор сглаживающей поверхности, построенной по семейству сече-
сечений, являющейся аналогом составного сплайна Эрмита B.4.3), описывается
формулой
ГС", 3)
г (и, v) = [ao(w) ati(w) fio(w) fii(w)]- ' ..
.г„(«, j + 1).
= r(u, j){l - Зги2 + 2ги3) + r(u, j + l)Cw2 - 2w3) -
+ i * \ t o2i 3\t ( ' i 1 \ t 2
T* I 11 Oil 111 —— /til —t- 111 I I У* I 11 0 ~+~ I 1 I til —¦
W = w(v) =V-j, Umm ^U^ Umax, 0 ^ V ^ П,
C.7.1)
где j равно целой части параметра v и номеру кривой, п + 1 — число кри-
кривых. Данная поверхность является кубической по v направлению. Параметр w
является местным параметром данной части поверхности в v направлении, он
г(и, и)
г(и. 2)
г(и,
г(и, 0)
Рис. 3.7.1. Поверхность на семействе кривых
изменяется от 0 до 1. Производные на линиях сетки rv(u, j) могут быть вычи-
вычислены по соседним линиям, аналогично тому, как вычисляются производные в
характеристических точках составного сплайна Эрмита, например,
Г«(«, Я =
для внутренних линий и
- г(ц, j -
г„(и,'О) = 2г(«, 1) - 2г(и, 0) - г„(и, 1),
rv{u, n) = 2r(u, n) — 2r(u, n — 1) — г„(«
п —
для крайних линий.
Эти зависимости обеспечивают равенство нулю третьих производных на
крайних кривых поверхности в трансверсальных к краю направлениях. Если
все кривые семейства являются замкнутыми, то поверхность C.7.1) получается
3.7. Онлайновые поверхности 1П
замкнутой в соответствующем направлении. Поверхность может быть замкну-
замкнутой и в другом параметрическом направлении. Производные rv(u, j) могут
Рис. 3.7.2. Поверхность Эрмита на семействе кривых
быть вычислены и по иным формулам, приведенным для сплайна Эрмита. По-
Поверхность Эрмита, построенная на семействе NURBS кривых, приведена на
рис. 3.7.2.
Поверхность Лагранжа. По семейству кривых, показанных на рис. 3.7.1,
можно построить поверхность, являющуюся аналогом кривой Лагранжа B.4.13).
Радиус-вектор такой поверхности, построенной по семейству сечений r(u, г) =
= Vi(U), i = О, 1, 2, ..., п, описывается формулой
Li(v)r{u,i), umin ^ u ^ umax, O^v^n, C.7.2)
г=0
где Li(v) — коэффициенты Лагранжа B.4.14) при Ц = у.
Ш = ?^ • (з.7.з)
П (i-J)
Каждая w-линия такой поверхности представляет собой кривую Лагранжа, по-
построенную по точкам r(u, г), г = 0, 1, ..., n, u = const. Существуют и другие
способы построения сглаживающей поверхности по семейству кривых.
Поверхность перехода. Поверхность типа C.7.1) может служить поверхно-
поверхностью перехода от одной поверхности к другой. Пусть, например, требуется
плавно сопрячь край одной поверхности с краем другой. Обозначим сопрягае-
сопрягаемый край первой поверхности через а(?), а край второй поверхности — через
Ь(?), где t — некоторый общий параметр. Через a.w(t) обозначим частную про-
производную первой из сопрягаемых поверхностей в трансверсальном к ее краю на-
направлении, а через bw(t) обозначим частную производную второй поверхности
в трансверсальном к ее краю направлении. Под параметрически трансверсаль-
ным направлением будем иметь в виду следующее. Если первая поверхность
172 Гл. 3. Моделирование поверхностей
описывается радиус-вектором p(u, v), то a.(t) = p(umax, t) и a«,(?) = pv(wmax, t)
описывают край поверхности. Аналогично, если вторая поверхность описыва-
описывается радиус-вектором q(u, v), то b(f) = q(t, vm[n) и bw(t) = qu(t, vmin) описы-
описывают край этой поверхности. Поверхность
r(f, w) = a(f)(l - Зги2 + 2w3) + h(t)Cw2 -2w3) +
+ aV){t)(w - 2w2 + w3) + hw(t)(-w2 + w3), C.7.4)
tmin < * ^ imax, 0 ^ гУ ^ 1,
гладко сопрягает две заданные поверхности по их краям. Мы рассмотрели слу-
случай, когда сопрягаемые поверхности имеют прямоугольные области определения
параметров. На двух сопрягаемых поверхностях и поверхности перехода может
быть построена единая гладкая поверхность.
Поверхность Гордона. Перейдем к построению поверхностей на двух семей-
семействах кривых. Пусть имеется сетка кривых, показанных на рис. 3.7.3.
Сетка образована двумя семействами кривых: &j(tj), j = 0, 1, 2, ..., п,
hi(wi), i = 0, 1, 2, ..., m. Каждая кривая одного семейства пересекает все
кривые другого семейства и не пересекает ни одной кривой своего семейства.
Г(и, п)
t(m, v)
r(O.u)
Рис. З.7.З. Поверхность Гордона на сетке из кривых
На этой сетке можно построить составную поверхность, каждая ячейка кото-
которой представляет собой кубическую поверхность Кунса. Для этого кривые пе-
переобозначим в соответствии с их местом на поверхности: r(u, j) = &j(tj), j =
= 0, 1, 2, ..., n, г(г, v) = bi(wi), i = 0, 1, 2, ..., m. Точки пересечения кривых
r(tj, j) и г(г, tj) обозначим через г(г, j), j = 0, 1, 2, ..., n, i = 0, 1, 2, ..., m.
На каждом участке кривых введем параметризацию аналогичную C.6.2) так,
чтобы между точками г(г, j) и г(/г, I) параметр и изменялся от г до к, а па-
параметр v изменялся от j до I. Радиус-вектор поверхности, интерполирующей
всю сетку и удовлетворяющей определенным условиям гладкости, описывается
формулой
r(u, v) = ^Ь,(ь)т(щ j) +.?>(u)r(z\ v) - ???,-(«)ЗДг(г\ j), C.7.5)
j=0 г=0 г=0 j=0
O^us^m, 0 ^v ^ n,
3.7. Сплайновые поверхности
173
где Lj(v) и Li{u) — коэффициенты Лагранжа C.7.3). Эта формула аналогична
C.7.2), только интерполяция выполняется по двум направлениям. В формулах
C.7.2) и C.7.5) вместо коэффициентов Лагранжа могут использоваться произ-
произвольные дифференцируемые функции ak{w), удовлетворяющие равенству
L, если w = к,
), если w фк.
В качестве функций смещения a^{w) могут использоваться кубические сплайны.
Поверхность C.7.5) называется поверхностью Гордона. Гладкость такой по-
поверхности зависит от гладкости функций смещения.
Для построения поверхности на сетке, образованной двумя семействами кри-
кривых, могут быть использованы поверхности Кунса C.6.6) в виде ее порций. Так
как в этом случае образуется поверхность, составленная из нескольких поверх-
поверхностей, то она называется составной. Наличие в составе данных поверхности
C.6.6) производных на стыках отдельных порций позволяет получить гладкую
составную поверхность. При использовании в качестве каждой порции поверх-
поверхность C.6.6) составная поверхность будет гладкой на заданной сетке кривых.
Ее радиус-вектор описывается формулой
r(u, v) =
v(u, j + 1)
r«(u, j)
г„(«, j + 1).
[ao(t) ai(t) (k(t) fh(t)]
г(г, v)
г(* +1, v)
vv{i, v)
„(г + 1, v).
r(», j + 1) г„(г, j) rv(i, j + 1)
-[ao(t) ai(t)
r(t + 1, j) г(г + 1, .
Г( n n \ v* A О
r (j _i_ i .л r a _i_ i
vuv(i, j)
ruv(i + l,
: +1, i + i)J
t = u — i, w = v — j, 0
u ^ m,
Pi(t)]x
'ao(w)
ai(w)
C.7.6)
где i равно целой части параметра u, j равно целой части параметра v,m + l —
число кривых ^-направления, п + 1 — число кривых u-направления. Кубиче-
Кубические функции смещения определяются формулами C.6.7). Фактически формула
C.7.6) описывает одну порцию составной поверхности, находящуюся между
кривыми r(u, j), r(u, j + 1), г(г, v), г(г + 1, v), i = 0, 1, ..., m - 1, j =
= 0, 1, ..., n — 1. Параметры t и w являются местными параметрами дан-
данной порции составной поверхности, они изменяются от 0 до 1. Если т = 1 и
п — 1, то формула C.7.5) описывает одну порцию кубической поверхности Кунса
C.6.6), построенной на четырех кривых, показанных на рис. 3.6.1. Производ-
Производные на линиях сетки могут быть вычислены по соседним линиям аналогично
174 Гл. 3. Моделирование поверхностей
тому, как по соседним точкам вычисляются производные составного сплайна
Эрмита B.4.3) в опорных точках
г(г + 1, у) -г(г- 1, у)
ru(i, v) = ^ ,
Ма, Л _ r(u, ,- + !)¦-ГС,,--В <3"»
для внутренних линий и
ги@, у) = 2гA, у) - 2г@, и) - гиA, и),
ru(m, v) = 2r(m, и) - 2r(m - 1, и) - ги(и, п - 1),
г„(и, 0) = 2г(и, 1) - 2г(и, 0) - г„(и, 1), { ' ' '
rv(u, n) = 2r(u, n) — 2r(u, n — 1) — г„(и, п — 1)
для крайних линий. Равенства C.7.8) обеспечивают равенство нулю третьих
производных на краях поверхности в трансверсальных к краю направлениях.
Если все кривые какого-либо семейства являются замкнутыми, то поверхность
C.7.6) получается замкнутой в соответствующем направлении. Заметим, что
поверхность C.7.6) в точках пересечения линий г(г, j) может иметь уплощения.
Предположим, что в формуле C.7.5) сегменты кривых сетки между точками
их пересечения г (г, j) представляют собой кубические сплайны Эрмита B.4.3),
т. е. определяются зависимостями:
г(г, у) = aQ(w)r(i, j) + ai(w)r(i, j + 1) + (k(w)rv(i, j) + Ci(w)rv(i, j + 1),
r(u, j) = ao(t)r(i, j) + ai(t)r(t + 1, j) + Po{t)ru{i, j) + /?i(i)rM(i + 1, j),
ru(i, v) =ao(w)ru{i, j) + ai(w)ru(i, j +1) +/30{w)rvu(i, j) + Pi(w)rvu(i, j +1),
rv(u, j) = ao(t)rv{i, j) + ai(t)rv(i + 1, j) + Po{t)ruv(i, j) + Pi{t)ruv(i + 1, j),
где i равно целой части параметра и, j равно целой части параметра v, t —
= и-— г, w = v — j. После подстановки этих зависимостей в C.7.5) получим три
одинаковых матричных члена, два из них со знаком плюс и один со знаком
минус. В результате формула C.7.5) примет вид
r(u, v) = [ao(t) ai{t)
Гао(гп)'
r«(i, j) ru(i, j + 1) ruv{i, j) ruv(i, j + 1)
ru(i + Г, j) ru{i + 1, j + 1) ruv{i + 1, j) ruv(i + 1, j + 1).
i = u — г, w = v — j, O^u^m, O^w^n, C.7.9)
где г равно целой части параметра u, j равно целой части параметра у. Поверх-
Поверхность C.7.9) полностью определяется точками г(г, j) и значением в них про-
производных поверхности г„(г, j), rv(i, j) и г„„(г, j). Данную поверхность можно
считать составной, так как она состоит из порций кубических поверхностей
3.8. Поверхности Безье 175
Эрмита, которые гладко стыкуются между собой, так как имеют общие произ-
производные на границах. Поверхность C.7.9) еще называют поверхностью тензор-
тензорного произведения. Фактически данная поверхность строится на сетке точек с
заданными производными, а не на сетке кривых.
3.8. Поверхности Безье
Рассмотренные выше кривые Безье B.5.3) характерны тем, что их радиус-
вектор представлен в виде суммы радиус-векторов точек в пространстве, умно-
умноженных на некоторые коэффициенты, являющиеся скалярными функциями
параметра кривой. Скалярными функциями являются функции Бернштейна.
Аналогичным образом строятся поверхности Безье, радиус-вектор которых
представляется в виде суммы радиус-векторов точек в пространстве, умножен-
умноженных на коэффициенты, являющиеся функциями Бернштейна параметров по-
поверхности. Рассмотрим поверхности Безье подробнее.
Пусть имеется совокупность точек р^-, образующих сетку, т.е. условно рас-
расположенных в виде п + 1 рядов по m + 1 точек в каждом ряду. Индексы точки
Pij означают, что данная точка расположена j-й по счету в г-м ряду (первый
индекс равен номеру ряда, второй — номеру точки в ряду). Нумеровать ряды
будем от 0 до п, а точки в них будем нумеровать от 0 до т. Поверхность Безье,
построенная на совокупности точек Ру, определяется радиус-вектором
п тп п m
r(u, v) ^^^(ul^Mftj = ???птпч(«. «)Pv> ,„ я u
г=0 j=0 г=0 j=0 C.8.1)
О <U < 1, О О ^ 1,
где Bnmij(v, u) = Bni(v)Bmj(u) — функции базиса Бернштейна:
C-8>2)
ТП'
Напомним, что коэффициенты Бернштейна удовлетворяют равенству B.5.5), в
соответствии с которым функции Bnmij(v, и) удовлетворяют равенству
Bnm^,u) = l. C.8.4)
i=0 j=0
Будем говорить, что вдоль «-направления поверхность имеет степень т, а вдоль
^-направления поверхность имеет степень п.
11 Если представить, что на каждых четырех соседних точках р^, Pij+i, Pi+ij,
pj+xj+i построена билинейная поверхность, то мы получим многогранник,
йОторый будем называть характеристическим. Точки р^ будем называть
вершинами характеристического многогранника. Поверхность Безье вместе
Со'своим характеристическим многогранником показана на рис. 3.8.1. Так как
из коэффициентов Бернштейна только нулевой и последний принимают мак-
максимально возможные значения, то поверхность Безье проходит только через
176 Гл. 3. Моделирование поверхностей
угловые вершины сетки: poo, Pom, РпО, Рпт- Сечения поверхности C.8.1) по
линиям u = const или v = const представляют собой кривые Безье. Харак-
Характеристический многогранник дает общее представление о поверхности Безье,
а сама поверхность как бы сглаживает углы этого многогранника. Чем выше
порядок поверхности C.8.1), тем она более гладкая. Порядок поверхности в
u-направлении жестко связан с количеством вершин в ряду, а порядок поверх-
поверхности в ^-направлении жестко связан с количеством рядов вершин. Область
изменения параметров поверхности представляет собой квадрат со стороной,
равной 1.
Степень поверхности Безье, а соответственно и ее гладкость, жестко связаны
с количеством вершин, по которым она построена. Это может создать некоторые
неудобства при использовании поверхностей Безье. Преодолеть эти неудобства
Рис. 3.8.1. Поверхность Безье и ее характеристический многогранник
могут помочь составные поверхности. Составная поверхность Безье получается
в результате стыковки отдельных поверхностей Безье, имеющих вдоль сты-
стыкуемых краев одинаковые степени. В общем случае для того, чтобы порции
поверхности Безье гладко стыковались друг с другом, нужно чтобы ребра, при-
прилегающие к углам стыкуемых порций поверхности, лежали в одной плоскости.
3.9. Рациональные поверхности
В предыдущей главе было показано, что кривую Безье можно обобщить так,
чтобы она могла описывать заданное коническое сечение. Рассуждая аналогич-
аналогичным образом, придем к тому, что поверхность Безье можно обобщить так, чтобы
она могла описать требуемую часть поверхности второго порядка — эллипсоида,
гиперболоида, параболоида или их частных случаев.
Наделим каждую вершину кривой C.8.1) р^ весом гиц и будем описывать по-
поверхность в однородных координатах. Поверхности, характеристические точки
которых обладают весами, называются рациональными. Сам радиус-вектор
такой поверхности тоже приобретает вес. Вес радиус-вектора вычисляется по
точно таким же формулам, что и его координаты, поэтому вес принято считать
дополнительной координатой точки. Рациональные поверхности Безье можно
получить подобно тому, как строились рациональные кривые Безье. Расши-
Расширенный радиус-вектор A.4.6) рациональной поверхности Безье описывается
формулой, по виду совпадающей с C.8.1), в которой обычные векторы r(u, v)
и р^ заменены соответствующими расширенными векторами R(u, v) и Р^.
3.9. Рациональные поверхности 177
Обычный трехмерный радиус-вектор рациональной поверхности Безье опреде-
определяется формулой
C.9.1)
? J3ni(«)J3m;(«)t%
Как и у рациональных кривых, у рациональной поверхности играют роль не
абсолютные значения весов вершин, а ах относительные значения. Чем больше
вес некоторой вершины по отношению к весам других вершин, тем ближе к этой
вершине проходит поверхность.
С помощью поверхности C.9.1) может быть построена часть поверхности
второго порядка или часть поверхности тора так же, как с помощью рациональ-
рациональной кривой Безье B.7.2) может быть построена некоторая часть конического
сечения. Для этого проще всего использовать рациональную поверхность Безье
второй степени, построенную по девяти вершинам:
[(I-,J
2u(l
-v)
v2}.
" POO Wu
ги„рю wvw
. P20 Wu
P01 P02
«Pll W«P12
P21 P22
' A -ь
2u{l-
u2
) '
u)
m
C 9 2)
0 <u< 1, 0<u < 1. У '
В C.9.2) веса угловых вершин положены равными единице, а для остальных
вершин введены веса wu и wv, имеющие индексы параметрических направле-
направлений поверхности. Тип поверхности, получаемой по формуле C.9.2), зависит от
положения вершин и от весов wu и wv. Так, например, для того чтобы полу-
получить часть поверхности тора C.2.18) с углами раствора au и av, нужно, чтобы
вершины рог, Рн, Р2г и Pio, Pib Рг2, где i = 0, 1, 2, располагались друг относи-
относительно друга аналогично тому, как было показано на рис. 2.6.5, а веса вершин
имели значения wu — cos (au/2) и wv — cos (av/2).
С помощью составной рациональной поверхности Безье может быть постро-
построена полностью любая поверхность второго порядка. Для этого нужно исполь-
использовать несколько поверхностей C.9.2), гладко стыкующихся между собой, как
было описано выше.
Поверхность скругления. Рациональной поверхностью можно описать по-
поверхность округления ребра детали. Сечение поверхности скругления в одном
из параметрических направлений должно представлять собой дугу окружности.
Эту дугу мы опишем с помощью рациональной кривой Безье B.6.16), в которой
вершины Ро, Рь Р2 и угол дуги а будем считать функциями одного из параме-
параметров поверхности скругления. Радиус-вектор поверхности скругления выразится
формулой
A - tJp0(u) + 2f(l - t)w(u)Pl(u) + t2p2(u)
Г{Щ ' (l-tJ + 2t(l-t)w(u) + t2 ' C.9.3)
"min < U ^ Umax, 0 < < < 1,
12 - 5293 Голованов
178 Гл. 3. Моделирование поверхностей
где w(u) = cos (a(u)/2) — вес линии Pi(u), вычисленный по углу дуги в данном
месте. Метод построения кривых po(w), pi(u), рг(^) по радиусу скругления
Рис. 3.9.1. Поверхность скругления — пример рациональной поверхности
(возможно переменному) будет приведен в следующей главе. Простейший ва-
вариант поверхности скругления C.9.3), построенной между двумя плоскостями,
приведен на рис. 3.9.1.
Будем рассматривать формулу C.9.1) в более широком смысле, а именно,
будем считать, что в них вместо функций Вптц могут стоять некоторые про-
произвольные базисные функции, которые обозначим через F{j. В общем виде
радиус-вектор рациональной параметрической поверхности, построенной на тп
вершинах, определяется формулой
п т
Е 1С Fij(v, ^WijPij
'Г(Щ V) = l~ ra?~m , Umin < U ^ Umax, ^min < V < Wmax, C.9.4)
t=ij=i
где p^ — радиус-векторы j-Vi вершины, расположенной в г-м ряду, характери-
характеристического многогранника поверхности, Wij — вес соответствующей вершины,
Fij(v, и) — функция j-й вершины в j-м ряду, п — число рядов вершин, т —
число вершин в каждом ряду. В отличие от формулы C.9.1) суммирование в
формуле C.9.4) начинается с 1, а не с 0. Это не имеет принципиального зна-
значения, просто для поверхностей Безье удобно было нумеровать, начиная с 0,
а в других случаях удобнее проводить нумерацию, начиная с 1. Параметр и
изменяется вдоль вершин, стоящих в некотором ряду, а параметр v изменяется
вдоль рядов вершин, имеющих одинаковый номер в ряду.
В терминах однородных координат расширенный радиус-вектор A.4.6)
рациональной поверхности определяется формулой
п т
Щи, V) = ]Р ]Т Fij(v, u)Pij, Umin < U ^ Umax, *W < V < Vmax, C.9.5)
t=l j=l
где Pij = [wijPij W{j]T — расширенные векторы вершин поверхности.
Радиус-вектор рациональной поверхности вычисляется как частное от де-
деления двух функций параметров «и«, поэтому при вычислении производных
рациональной поверхности правую часть C.9.5) следует рассматривать как
3.10. NURBS поверхности 179
сложную функцию. Если условно обозначим радиус-вектор рациональной по-
верхности как г = —, то производные радиус-вектора рациональной поверхно-
поверхности определятся формулами
дг _ 1 d(wr) wr dw
аи w аи w* аи
дг _ 1 d(wr) wr dw
~я~ ~ a O~E~i (о.У.1)
OV W OV UT OV
d2r Id2(wr) 2 d(wr)dw wrd2w 2wr (dw\2
ди2 w ди2 w1 ди ди w2 ди2 w3 \ди J '
д2г _ 1 d2(wr) 2 d(wr)dw wrd2w 2wr fdw\2
dv2 w dv2 w2 dv dv w2 dv2 w3 \ dv J '
d2r 1 d2(wr) 1 d(wr) dw 1 d(wr) dw
dudv w dudv w2 ди dv w2 dv ди
wr d2w 2wr dw dw . .
w* ou ov wu аи dv
Производные более высокого порядка вычисляются аналогично.
3.10. NURBS поверхности
В качестве функций Fij(v, и) в формуле C.9.4) будем использовать произве-
произведения 5-сплайнов, один из которых зависит от параметра и, а другой зависит от
параметра v. В результате получим неоднородную рациональную поверхность,
определяемую 5-сплайнами B.8.21), которая приобрела название NURBS по-
поверхности (Non-Uniform Rational B-Spline surface). NURBS поверхность, как
и поверхность Безье, строится на сетке вершин — совокупности точек pij,
условно расположенных в виде п рядов по т точек в каждом ряду. Индексы
вершины Pij означают то, что данная точка расположена j-Vs. по счету в i-м ряду
(первый индекс равен номеру ряда, второй — номеру точки в ряду). В данном
случае нумеровать ряды удобнее от 1 до п, а точки в них — от 1 до т. Пусть
вес вершины ру равен Wij. Пусть 5-сплайны Nj^k(u) u-направления имеют
порядок к, а 5-сплайны Ni>q(v) ^-направления имеют порядок q. Радиус-вектор
NURBS поверхности определяется равенством
n m
V У
n m n m
V* Y^ ЛГ- tiAJV- l.(ii\id- V V ЛГ-¦ i (?j iA?/) ¦•
i=\j=\ i=\j=\
umin ^ u ^ "
maxi
где Nijtqh(v, u) = Nitq(v)Njtk(u) ¦— базисные функции, n — число рядов, вер-
вершин, m — число вершин в каждом ряду. Производные радиус-вектора NURBS
поверхности определяются равенствами C.9.6)—C.9.10).
12*
180 Гл. 3. Моделирование поверхностей
Каждый из Б-сплайнов к-то порядка Njtk(u) построен на последовательно-
последовательности из к + 1 узлов Uj, Uj+i, Uj+2, ¦ ¦., Uj+k't всего для построения совокупности m
Б-сплайнов к-то порядка требуется т + к узлов Uj в случае незамкнутой кривой
ит + 2к узлов в случае замкнутой кривой. Каждый из Б-сплайнов q-ro порядка
Nijq(v) построен на последовательности из q;+ 1 узлов V{, Vi+i, V{+2, ¦ ¦., Щ+д,
всего для построения совокупности п Б-сплайнов q-ro порядка требуется n + q
узлов ы в случае незамкнутой кривой и n + 2q узлов в случае замкнутой кривой.
Как следует из C.10.1), NURBS поверхность имеет две последовательности уз-
узлов, одну — в u-направлении, а другую — в «-направлении. Значения узлов
должны образовывать неубывающие последовательности. Будем называть их
u-последовательностью узлов и ^-последовательностью узлов. Пронумеруем
узлы каждой последовательности, начав нумерацию с 1.
Для незамкнутой NURBS поверхности используются следующие последова-
последовательности узлов. Первые к узлов ^-последовательности имеют значения, равные
нулю: щ = щ = ¦ ¦ • = Uk = 0; следующие т — к узлов принимают целочислен-
целочисленные значения от 1 до т — к: tk+j = j (j = 1, 2, ..., m — к); оставшиеся к узлов
принимают значение т — к + 1: tm+\ = ?m-|-2 = • • • = tm+k — тп — к + 1.
Первые q узлов «-последовательности имеют значения, равные нулю: v\ —
= г>2 — • ¦ • = vq = 0; следующие n — q узлов принимают целочисленные значе-
значения от 1 до п — q: tq+i = i (г = 1, 2, ..., n — q); оставшиеся q узлов принимают
значение п — q + 1: tn+\ = tn+2 = ... = tn+q = n — q + 1.
Для замкнутой NURBS поверхности используются равномерные последова-
последовательности узлов с единичным шагом: Uj = j—m, j = 1, 2, ..., m+2k, V{ = i—n,
i = l, 2, ...,n + 2q.
.Приведенные примеры узловых последовательностей не являются един-
единственно возможными. Как и для любой поверхности, внутренняя параметриза-
параметризация NURBS поверхности может быть произвольной.
Область изменения параметров NURBS поверхности представляет собой пря-
прямоугольник: Uk ^ u ^ um+k, Vq ^ v ^ vn+q. Для указанных последо-
последовательностей узлов параметры NURBS поверхности изменяются в пределах:
0 ^ u ^ (m — к + 1), 0 ^ v ^ (п — (? + 1) для незамкнутой поверхности и
O^u^m, O^v^n для замкнутой поверхности.
Для вычисления радиус-вектора NURBS поверхности используем формулы
B.9.2)-B.9.4). По значению параметра и из условия Uj ^ и < uj+i определим
номер j единственного отличного от нуля Б-сплайна первого порядка
- Uj
Далее, используя рекуррентное соотношение
_ {ur+k - u)Mr+i|fc-i(u) + (u - ur)Mr<k-i{u)
иг+к - иг
r = j-k + l,j-k + 2,...,j,
последовательно вычислим все отличные от нуля при данном и Б-сплайны до
к-го порядка включительно: М?_д;+1)д;(и), Mj-k+2,k(u), ¦¦¦¦> Щ,к(и)- Далее
Б-сплайны к-го порядка нормируем в соответствии с B.9.4)
Nr,k{u) = (иг+к - ur)Mrik(u), r = j-k + l,j-k + 2,...,j.
3.10. NURBS поверхности 181
Аналогично по значению параметра v из условия Vi ^ v < vi+i определим номер
i отличного от нуля В-сплайна первого порядка
MiA(v)
Vi+l ~ Щ
Используя рекуррентное соотношение
. > _ (Уг+д ~ У)Мг+г>д^1(у) + (V- Vr)Mr,q-\{v)
lVlr q\V) — : ,
vr+q - vr
r = i~q + l, i-q + 2, ..., i,
последовательно вычислим все отличные от нуля при данном v -В-сплайны до
q-ro порядка включительно: Mj_g+ij9(u), Mj_9+2,g(u)) • • ¦¦> Mitq(v), и затем нор-
нормируем их
Nr,q{v) = (vr+q ~ Уг)Мг>д(у), г = % - q + 1, % - q + 2, ..., i.
Напомним, что порядок NURBS поверхности в том или ином параметри-
параметрическом направлении равен порядку соответствующих В-сплайнов, а порядок
5-сплайна на единицу больше степени полиномов, из которых он построен.
Рис. 3.10.1. NURBS поверхность
На рис. 3.10.1 показана NURBS поверхность 4-го порядка по обоим параме-
параметрическим направлениям, построенная на сетке, состоящей из 7 х 7 вершин.
Все вершины, кроме центральной, лежат в одной плоскости. Веса всех вершин
равны 1.
Если на каждых четырех соседних характеристических точках построить
билинейные поверхности, то мы получим некоторый многогранник, который
называется характеристическим. Характеристический многогранник поверх-
поверхности, приведенной на рис. 3.10.1, показан на рис. 3.10.2.
В терминах однородных координат расширенный радиус-вектор A.4.6)
NURBS поверхности определяется формулой
u'min ^г u ^ "maxi ^rnin ^ V
где T?ij = [wijPij Wij]T — расширенные векторы вершин поверхности.
182
Гл. 3. Моделирование поверхностей
Когда все вершины NURBS поверхности имеют равные веса, то формула
C.10.1) в силу свойства В-сплайнов B.8.24) примет вид
Г(и, V) =
t=l j=l
^ "maxi
C.10.3)
Эта поверхность называется В-сплайн поверхностью. Она также может быть
использована в проектировании, так как обладает определенной гладкостью, и
для вычисления ее производных не требуется пользоваться формулами C.9.6)-
C.9.10).
Если построить NURBS поверхность C.10.3) на базе В-сплайнов второго по-
порядка, то она совпадает со своим характеристическим многогранником и пред-
представляет собой совокупность билинейных поверхностей.
Рис. 3.10.2. Характеристический многогранник NURBS поверхности
Если n = q и т = к, т. е. если число рядов вершин п равно порядку q
.В-сплайнов ^-направления, число вершин в ряду т равно порядку к В-сплайнов
u-направления, узлы ^-последовательности
имеют значения щ = U2 = • • • = ит = 0,
ит+г = ит+2 = ... = и2т = 1, узлы
«-последовательности имеют значения v\ =
= V2 = ¦ ¦ ¦ - Vn = 0, Vn+l = Vn+2 = . • .
• • • = V2n = 1 > T0 NURBS поверхность
C.10.1) совпадает с рациональной поверх-
поверхностью Безье C.9.1). Это следует из того,
что функции Бернштейна являются част-
частными случаями В-сплайнов. Область из-
изменения параметров NURBS поверхности в
этом случае представляет собой квадрат со
стороной, равной 1.
С помощью поверхности C.10.1) может
быть построена любая поверхность второго порядка. На рис. 3.10.3 приведена
цилиндрическая NURBS поверхность и ее характеристический многогранник.
Рис. 3.10.3. Цилиндрическая NURBS
поверхность
3.10. NURBS поверхности 183
На рис. 3.10.4 приведена тороидальная NURBS поверхность и ее характеристи-
характеристический многогранник. Обе поверхности имеют кратные узлы.
По своему внешнему виду NURBS поверхности и поверхности Безье похожи.
Но в отличие от последних порядок NURBS поверхности не связан жестко с
Рис. 3.10.4. Тороидальная NURBS поверхность
количеством вершин и предоставляет возможность строить поверхности невы-
невысокого порядка C-го или 4-го порядка) на большом числе вершин. Эта воз-
возможность придает поверхности большую гибкость, так как поверхности Безье,
построенные на большом числе вершин, имеют высокий порядок и являются
слишком гладкими.
NURBS поверхность является обобщением большинства рассмотренных
выше поверхностей: многогранной билинейной поверхности, поверхности Бе-
Безье, поверхностей второго порядка, рациональных поверхностей.
Каждая линия u = const или v = const на поверхности C.10.1) является
NURBS кривой B.9.1). Но можно построить рациональные неоднородные по-
поверхности на основе В-сплайнов, которые необязательно давали бы NURBS кри-
кривые в качестве всех своих параметрических и-линий или v-линий. Например,
Рис. 3.10.5. NURBS поверхности на семействе кривых
можно получить поверхность, если в формуле B.9.1) вместо вершин характе-
характеристической ломаной подставить кривые р* = Pi(u), г — 1, 2, ..., п, обла-
обладающие весами u>i = u>i(и), и имеющие одинаковые параметрические длины
184 Гл. 3. Моделирование поверхностей
Umia ^ u ^ umax. В результате, получим поверхность, описываемую формулой
п
х^ \т. • л,л„.,.л,л C.10.4)
Только параметрические линии и — const на поверхности C.10.4) являются
NURBS кривыми. Такую поверхность можно назвать плазовой NURBS поверх-
поверхностью. На рис. 3.10.5. показана плазовая NURBS поверхность и пять кривых,
по которым она построена. Частным случаем этой поверхности является по-
поверхность скругления C.9.3).
3.11. Поверхности треугольной формы
Существует много способов построения поверхностей треугольной формы.
Сейчас мы остановимся на поверхностях, которые при треугольной форме имеют
треугольную область определения параметров. Для треугольных областей в
двухмерном дространстве удобно использовать барицентрические координаты.
Барицентрические координаты на плоскости. Пусть в области определения
параметров и и v некоторой поверхности задана двухмерная декартова система
координат. Пусть в этой области заданы три точки А, В, С, не лежащие на
и
Рис. 3.11.1. Точки на параметрической плоскости
одной прямой. Радиус-векторы точек А, В и С обозначим соответственно через
Pa = [«a Va]T, Vb = [Щ Ч]Т И рс = [ис VC]T (рис. 3.11.1).
Положение любой другой точки р = [и v]T можно описать с помощью точек
Ра> Рб) Рс равенством
V = apa + Ьрь + сРс, C.11.1)
где коэффициенты а, Ь, с определены с точностью до множителя. Для полной
определенности потребуем, чтобы их сумма была равна единице:
a + b + c=l. C.11.2)
Значения коэффициентов а, Ь, с, соответствующие декартовым координатам и
и v, мы найдем из системы уравнений
aua + 1шь + сис = и, C.11.3)
ava + Ьуь + cvc = v.
3.11. Поверхности треугольной формы
185
Коэффициенты а, Ь, с определяются равенствами
. 1 1 1
а =
Ь =
А
абс
С =
АаЬс
АаЬс
U Щ Uc
V - Vb Vc
1 1 1
ua u uc
Va V Vc
1 1 1
Ua Щ U
va vb v
(uvb + ubvc + ucv - vub - vbuc - vcu),
АаЬс
(uav + uvc + ucva — vau — vuc — vciia), C.11.4)
UVa - VaUb - VbU - VUa),
где определитель системы уравнений C.11.3)
1 1 1
АаЬс
Ua Щ Uc
va Щ vc
= uavb + ubvc + ucva - vaub - vbuc - vcua
C.11.5)
равен удвоенной площади треугольника ABC (Aabc = 25аьс).
Во многих случаях для описания положения точки в двухмерном простран-
пространстве удобно перейти от координат и и v к трем барицентрическим координа-
координатам, которыми являются коэффициенты а, Ь, с. Барицентрические координаты
произвольной точки р = [и v]T равны отношению площади треугольника, по-
полученного из треугольника ABC заменой соответствующей вершины точкой р,
к площади треугольника ABC. Барицентрические координаты а, Ь, с точки
р = [и v]T вычислены относительно точек ра, рь, рс и являются функциями
точки р.
Отметим свойства барицентрических координат. Они подчинены равенству
C.11.2). Если точка р лежит внутри треугольника ABC, то ее барицентриче-
барицентрические координаты неотрицательные. Если точка р совпадает с вершиной тре-
треугольника ABC, то две ее барицентрические координаты равны нулю. Если
точка р принадлежит стороне треугольника ABC или лежит на ее продолже-
продолжении, то одна барицентрическая координата точки равна нулю. Если точка р
лежит вне треугольника ABC, то, по крайней мере, одна барицентрическая
координата точки отрицательна.
Любой двухмерный вектор d — [и v]T можно описать с помощью точек ра,
РЬу Рс равенством
d = ара + /Зрь + 7РС- C.11.6)
Коэффициенты а, /3, -у называт барицентрическими компонентами вектора.
Двухмерный вектор го можно представить в виде разности радиус-векторов двух
точек, например, рх = а\ра + bipb + с\рс и р0 = аора + ЬоРь + соРс- Так как
ai + W + с\ — 1 и ао + Ьо + со = 1, то барицентрические компоненты а, /3, j
двухмерного вектора связаны равенством
= 0.
C.11.7)
186
Гл. 3. Моделирование поверхностей
Значения барицентрицеских компонент а, /3, 7, соответствующие декартовым
компонентам и и v вектора d, мы найдем из системы уравнений
aua + рщ + 7uc = и,
ava + Evb + jvc — v.
Компоненты а, C, 7 определяются равенствами
x 0 1 1
a = и щ ис
V Vb Vc
C.11.8)
1
ucv — ущ — vcu),
1 0 1
Ua U Uc
Va V Vc
1
(uav + uvc - vau - vuc),
C.11.9)
1 =
1 1 0
Ua Щ U
Va Vb V
UVa
- VUa),
где определитель АаЬс вычисляется по формуле C.11.5).
Билинейная треугольная поверхность. Одной из простейших треугольных
поверхностей является плоская треугольная поверхность, построенная по трем
точкам pi, p2, рз- Эта поверхность представляет собой треугольный аналог би-
билинейной поверхности C.5.2). Пусть область определения параметров поверх-
поверхности ограничена треугольником с вершинами в точках ра, рь, рс (рис. 3.11.1).
Введем барицентрические координаты а, Ь, с
C.11.4). Радиус-вектор г плоской треугольной
поверхности, построенной по трем вершинам pi,
р2, рз, опишем векторной функцией трех пара-
параметров а, Ь, с
г(а, Ь, с) =
а < 1, 0
+ Ьр2 + ср3,
< 1, 0 < с<
1.
C.11.10)
Рис. 3.11.2. Плоская треугольная
поверхность
Если мы соединим произвольную точку г по-
поверхности C.11.10) отрезками прямых линий
с вершинами pi, рг, рз, то этим мы разобьем
площадь треугольной поверхности на три части
(рис. 3.11.2). Отношение площади части тре-
треугольной поверхности к полной площади поверхности равно соответствующей
барицентрической координате точки г.
Фактически радиус-вектор C.11.10) зависит от двух параметров, так как три
параметра а, Ь, с связаны равенством C.11.2). Можно переписать зависимость
C.11.10) как функцию двух параметров х иу, например: а(х, у) = х, Ь(ж, у) =
= у, с(х, у) = 1 — х — у, где х и у принимают значения на треугольной области.
Можно переписать зависимость C.11.10) как функцию тех же двух параметров
3.11. Поверхности треугольной формы 187
а; и у, принимающих значения на обычной квадратной области 0 ^ х ^ 1,
О < у < 1, например: а = х, Ь — уA — х), с = 1 — х — у + ху или: а = хA — у),
Ь = у, с=1-х-у + ху.
Треугольная поверхность на трех кривых. Еще одну треугольную поверх-
поверхность построим, на трех попарно пересекающихся кривых. Ее можно использо-
использовать для скругления пространственного угла, в котором сходятся три скруглен-
скругленных ребра моделируемой детали. Рассмотрим три кривые qi(ii), 42(^2I Чз(?з)>
попарно пересекающиеся в точках рг, р2, рз, как показано на рис. 3.11.3.
Построим поверхность внутри «треугольника», образованного кривыми. Пре-
Преобразуем с помощью A.5.3) параметризацию кривых так, чтобы точкам рз и рг
на кривой qi(ti) соответствовали параметры 0 и 1, точкам pi и рз на кривой
Рис. 3.11.3. Треугольная поверхность на трех кривых
() соответствовали параметры 0 и 1, точкам р2 и pi на кривой Яз(*з) со-
соответствовали параметры 0 и 1. Радиус-вектор поверхности, построенной по
данным трем кривым, опишем векторной функцией трех барицентрических
координат а, 6, с
г(а, 6, с) = a(q3(l - 6) + q2(c) - рх) +
+ 6(qi(l - с) + оз(о) - Р2) + с(огA - а) + ох(Ь) - Рз), C.11.11)
О < о < 1, 0<6<1, 0<с<1, а + Ь + с = 1.
Фактически радиус-вектор C.11.11) зависит от двух параметров, так как три
параметра а, Ь, с связаны уравнением C.11.2). Края поверхности C.11.11)
совпадают с кривыми, по которым она построена. При с = 0, 6=1 — а вектор
r(a, 1 - a, 0) = a(q3(a) + q2@) - px) + A - a)(oi(l) + Яз(а) - P2) = Оз(а)
описывает участок кривой Оз(<з) между точками р2 и pi. При а = 0, с = 1 — Ь
вектор
г@, 6, 1 - 6) = 6@1 (Ь) + q3@) - Р2) + A - b)(q2(l) + qiF) - Рз) = qiF)
описывает участок кривой qi(ti) между точками рз и р2. При 6 = 0, а = 1 — с
вектор "~
гA - с, 0, с) = c(q2(c) + qx@) - р3) + A - c)(q3(l) + q2(c) - pi) = q2(c)
188
Гл. 3. Моделирование поверхностей
описывает участок кривой Яг(^2) между точками pi и рз. Приведенные формулы
можно получить путем циклической перестановки индексов 1, 2, 3 или 3, 2, 1.
Правая часть C.11.11) симметрична относительно циклической перестановки
индексов. Поверхность C.11.11) является треугольным аналогом линейной по-
поверхности Кунса C.6.4).
На рис. 3.11.4 приведена треугольная поверхность, построенная на трех оди-
одинаковых дугах окружностей. Плоскости окружностей ортогональны плоскости,
Рис. 3.11.4. Треугольная поверхность на трех дугах окружности
Рис. 3.11.5. Треугольная поверхность на трех дугах окружности
в которой лежат точки Р\, Р%, Рз- Каждая дуга содержит четверть окружности.
На рис. 3.11.5 приведена та ?ке треугольная поверхность под другим ракурсом.
Рис. 3.11.6. Поверхность на трех ортогональных дугах в четверть окружности
Рис. 3.11.7. Поверхность на трех ортогональных дугах в четверть окружности
Если плоскости дуг окружностей сделать взаимно ортогональными, то тре-
треугольная поверхность будет описывать часть сферической поверхности. Такая
поверхность приведена на рис. 3.11.6 и 3.11.7.
3.12. Треугольные поверхности Безье
Рассмотрим треугольные аналоги поверхности Безье. Пусть имеется сово-
совокупность некоторых характеристических точек Pijk, образующих треугольную
сетку. На рис. 3.12.1 показана треугольная сетка, вдоль каждой стороны ко-
которой расположены 6 характеристических точек. Точки расположены в виде
треугольника, причем вдоль каждой стороны треугольника расположено оди-
одинаковое число точек. Пусть это число равно п + 1. В нашем случае п = 5.
Общее число характеристических точек равно (п + 1)(п + 2)/2. Каждый из трех
3.12. Треугольные поверхности Безье 189
индексов точки соответствует своей вершине треугольника. Точка, лежащая в
вершине треугольника, имеет значение индекса, соответствующего этой вер-
вершине, равное п (максимальной значение), а значения других индексов равно
нулю. Точки, принадлежащие ряду вдоль одной из трех сторон треугольника,
вершина
третьего индекса (к)
Р005
РЮ4 Р014
Р203 РИЗ Р023
Р302 Р212 Р122 Р032
Р401 РЗП Р221 Р131 Р041
Р500 Р410 Р320 Р230 Pl40 P050
вершина вершина
первого индекса (г) второго индекса (j)
Рис. 3.12.1. Нумерация точек
имеют нулевой индекс, соответствующий противолежащей вершине. Чем ближе
ряд, в котором лежат точки, к вершине, тем большее значение имеет индекс этой
вершины.
Индексы точки р^ означают целочисленное расстояние от нее до соответ-
соответствующей стороны треугольника, измеренное количеством отделяющих рядов.
Сумма индексов характеристической точки р^ имеет постоянное значение
i + j + k = n. C.12.1)
Треугольную поверхность Безье опишем с помощью барицентрических коорди-
координат а, Ь, с. Будем считать, что поверхность Безье имеет ту же область опре-
определения параметров, что и поверхность C.11.10). Радиус-вектор треугольной
поверхности Безье, построенной по характеристическим точкам Pijk, описыва-
описывается формулой
П П |
Т\а, О, С) — / j D ijk\at "i c)Pijk — / J ., ,,,.fl О' С Pijki {O.LZ.4)
i,j,k=O, i,j,k=O,
i+j+k=n i+j+k=n
Суммирование в C.12.2) выполняется по всем характеристическим точкам, а
трехиндексные функции Бернштейна имеют вид
Bnijk(a, Ь, с) = Y^aWc1*, C.12.4)
где должно выполняться равенство C.12.1).
190
Гл. 3. Моделирование поверхностей
Треугольная поверхность Безье, построенная по 7 точкам вдоль каждой сто-
стороны, показана на рис. 3.12.2. Характеристический многогранник треугольной
поверхности Безье приведен на рис. 3.12.3.
Рис. 3.12.2. Треугольная поверхность Безье
Рис. 3.12.3. Характеристический многогранник треугольной поверхности Безье
Крайние линии поверхности C.12.2) описываются векторами г(а, 1 — а, 0),
г@, Ь, 1 — 6), гA —с, 0, с) и представляют собой кривые Безье B.5.3). Покажем
это на примере крайней кривой г (а, 1 — а, 0). Для неес = 0, А; = 0 и функции
C.12.4) примут вид
7371 / N * % L7 _ ^ / 1 \ТЪ~т% t'о Л с\ с \
, -D ij0\Oi \ — ,, ., Сь \j — . ". ^77 v ^/ ) (O.-LZ.0)
что совпадает с B.5.4).
Покажем, что трехиндексные функции Бернштейна удовлетворяют ра-
равенству
Bnijk(a, 6, с) = 1.
C.12.6)
i,j,k=O,
i+j+k=n
Суммирование C.12.6) выполним по строчкам третьего индекса к — 0, 1, 2, ...
..., п. В А;-й строке третьего индекса содержится m = n—к характеристических
точек.
Bnijk(a, b, с) =
i+j+k=n
п
= W
i,j,k=O,
i+j+k=n
n!
П!
n-k
-k)\
i,n
= E C "c
A;=0 i=0
что и требовалось доказать.
= Е С*„с*(а + 6)"-fc = (а + 6 + с)" = 1,
А;=0
3.12. Треугольные поверхности Безье
191
Алгоритм Де Кастелье. Трехиндексные функции Бернштейна удовлетворяют
рекуррентному соотношению
Bnijk = aBn-\_ljk + bBn-\j_lk + cBn-lijk_v C.12.7)
Это соотношение доказывается непосредственной подстановкой:
aBn-li-ljk{a, Ъ, с) + ЬВп-\^1к(а, Ь, с)+cBn-1ijk.l(a, Ъ, с) =
— 1)!
1)!
(г —
¦_, и
+ 6f7ТГ7Г,а
i\{j — ly.kl
t ¦ k j n! t ¦ k к n\
n%\y.k\ n%\y.k\ ni\j\k\
(П — 1)!
i\j\{k — 1)!
к_л
n\
, k
n
что и требовалось доказать.
Начнем вычисление с функции B°qqq(u, b, с) = 1.
Далее получим В1юо(а, Ь, с) = а, В1ою{а, Ь, с) = b, B1ooi(a, b, с) = с.
Функция Бернштейна, один из индексов которой равен отрицательному чи-
числу, считается равной нулю. Подставим рекуррентное соотношение C.12.7)
в выражение C.12.2), выделив крайние точки и учитывая, что Вппоо — ап,
Впо„о = Ьп, ВпООп = с", BnOjk = Vck, BniOk = а'ск, Bnij0 = а{Ъ>, получим
аналогично выводу B.5.6)
г(о, Ь, с) = ^ BnijkPijk =
n-l
= a J2 B
i,j,h=O,
jkl
+c
где введены обозначения:
.^к +
cBn-\jk_x)Vljk =
n-l
i,j,k=O,
jk
n-l
i,j,k=O,
jk
1 ^
ijkPi+ljk,
i,j,k=O,
jk
(n-l)
(n-l)
ijkPij+lk,
i,j,k=O,
jk=n-
n
1 ^
WPijk+1-
i,j,k=O,
j
192 Гл. 3. Моделирование поверхностей
Выполнив описанные действия для ri+ijk^n~l\ nj+i^™) и ?ф+1^п~1\ в конце
придем к равенствам
vijkr' = B°QQo{a, b, c)pijk = pijk.
Обозначим r(a, b, с) через гооо ^ В результате получим рекуррентное соотно-
соотношение для вычисления точки треугольной поверхности Безье
rijkW = ari+lj-ktm-V +brij+lk(m-V +crijk+1(m-l\ C.12.8)
где i + j + к = n-m (i, j, к > 0), г„А:@) = Pijk, rOoo(n) = r(a, b, с). Алгоритм,
описываемый соотношением C.12.8), называется алгоритмом Де Кастелъе.
Точки VijiSm\ получаемые в процессе вычисления, называются точками Де Ка-
Кастелье. Алгоритм Де Кастелье позволяет вычислить любую точку треуголь-
треугольной поверхности Безье по характеристическим точкам, ничего не зная о функ-
функциях Бернштейна. Коэффициенты a, b и с при координатах точек ri+ijk(m~l\
rij+ik ~1^ и rijk+i ~^ являются барицентрическими координатами. Тре-
Треугольную поверхность Безье можно определить как поверхность, точки которой
определяются рекуррентным соотношением C.12.8) по совокупности характе-
характеристических точек.
Увеличение числа характеристических точек. От треугольной поверхности
Безье n-й степени можно перейти к треугольной поверхности (п + 1)-й степени
аналогично тому, как это было сделано для кривых Безье. Для этого умножим
правую часть равенства C.12.2) на сумму а + b + с, равную 1, и получим
п п ,
r(a, Ь,с)= Yl Bn Y i
ij,k=O,
i+j+k=n
n .
V ai+
i,j,k=Q,
i+j+k=n
n .
\—ч П: -• ,• jL.,t
т / ......a " t- I
iijJfe=O,
A (n+1)! i 7+1_fc
^ i\j\k\
ij,k=O,
i+j+k-n+1
"+1 ( , 1M
^ Z^i %\j\k\
i,j,k=Q,
i+j+k=n+l
i+i+fc=n
In fc V~^ П\ ifj+l к
Pijk + / > t'l'jk'0 C ^
i,j,k=O,
i+j+k=n
n /n i 1\|
lJk / j (г + l)'7'fc'
э J+1 1 V (n + 1)! a«ftj-*-
i,j,fc=O,
i+j+k=n
n+1 ( , 1M
?lPi-ljk ST* \n + l.'¦aiuic
n+1 2—i i\j\k\
i,j,k=O,
i+j+k=n+l
h n+l
7 к Pijk—l V~^ dtj+1 *
^ -"" / *-* iikP
i,j,k=O,
i+j+k=n+l
1 ~*~ i
+ 1 fc+l
tjfcn+l
Jk3Pij-lk .
' n+1
: /Q 1 О
3.12. Треугольные поверхности Безье
193
где р ij/. —
JPij-lk
—
— новые характеристические точки.
То | X
Новых характеристических точек на один ряд вдоль каждой из трех сторон
треугольника стало больше. Точки в вершинах треугольника остались преж-
прежние Р*п+юо = Рпоо, Р*оп+ю = PonO, P*oon+i = Рооп- Выражение C.12.9)
описывает ту же поверхность, что и выражение C.12.2), только через другие
характеристические точки.
Треугольная рациональная поверхность Безье. Пусть треугольная поверх-
поверхность Безье построена на совокупности характеристических точек Pijh, образую-
образующих треугольную сетку, показанную на рис. 3.12.1. Припишем каждой точке
Pyfc вес i«ijfc. Построим треугольную рациональную поверхность Безье. Ее
радиус-вектор описывается формулой
nijk{a,, b,
i,j,fc=0,
jk
r(a, b, с) =
Bnijk(a,
, 0 < c< 1,
C.12.10)
i+j+k=n
где суммирование выполняется по всем характеристическим точкам. В силу
свойства C.12.6), поверхность Безье C.12.2) является частным случаем рацио-
цальной поверхности C.12.10) приоди-
йаковых весах точек. Чем больше вес
точки, тем ближе к ней проходит по-
поверхность. Напомним, что роль играет
не абсолютное значение веса каждой
точки, а отношения весов точек друг к
другу. Если веса всех характерных то-
точек одинаковы, то мы придем к обыч-
обычной поверхности Безье C.12.2).
В терминах однородных координат
расширенный радиус-вектор A.4.6)
треугольной поверхности Безье опре- Рис. 3.12.4. Треугольная рациональная
деляется формулой поверхность Безье.
Ща, Ь, с) =
Bnijk(a, b, c)wijk?ijk,
i,j,k=o,
i+j+k=n
C.12.11)
у jjk wijk]T ~ расширенные радиус-векторы вершин поверх-
поверхности. Иа рис. 3.12.4 показана треугольная поверхность Безье, аналогичная
приведенной иа рис. 3.12.2 поверхности, с весом средней точки, равным 5.
13 — 5293 Голованов
194 Гл. 3. Моделирование поверхностей
3.13. Треугольные сплайновые поверхности
Рассмотрим поверхности, которые можно считать обобщением треугольной
поверхности Безье. Они строятся в виде взвешенной суммы некоторых ха-
характеристических точек. Каждая характеристическая точка входит в сумму с
коэффициентом, который является функцией координат двухмерной точки на
области определения параметров поверхности. Каждая такая функция отлична
от нуля на некоторой ограниченной двухмерной области. Базисные функции
координат и и v двухмерных точек, отличные от нуля на ограниченных двух-
двухмерных областях простой формы, называют двухмерными В-сплайнами или
симплексными сплайнами. Они представляют собой аналоги рассмотренных
выше В-сплайнов и имеют с ними много общего.
Рассмотрим аналогию между В-сплайнами и симплексными сплайнами.
Каждый В-сплайн строится на последовательности узлов. Узлами последова-
последовательности можно разделить область определения В-сплайна на полуоткрытые
подобласти. При этом каждое значение параметра В-сплайна может принад-
принадлежать только одной подобласти. Область определения симплексного сплайна
можно разбить на несколько подобластей. Каждая точка р = [и v]T области
определения может принадлежать только одной подобласти. Нужно условиться,
какой из двух подобластей принадлежат точки разделяющей их линии. Для
этого вводится понятие полуоткрытой выпуклой области.
Полуоткрытая выпуклая область. Через [V] обозначим выпуклую область,
которую покрывает некоторый выпуклый многоугольник V, а через [V) обозна-
обозначим полуоткрытую выпуклую область мно-
многоугольника V. Не все граничные точки вы-
выпуклой области [V] принадлежат полуоткрытой
выпуклой области [V). Точка р — [и v]T при-
принадлежит полуоткрытой выпуклой области [V),
если существуют такие е > 0 и г) > 0, при ко-
которых точки р — [и v]T, pi = [и + е v]T и
р2 = [и + е v + rj]T принадлежат [V].
На рис. 3.13.1 приведена полуоткрытая вы-
выпуклая область. Для области, показанной на
рис. 3.13.1, внутренние точки многоугольника
Рис. 3.13.1. Полуоткрытая вы- и точки сплошных линий принадлежат [V), а
пуклая область точки пунктирных линий и точки их стыковки
со сплошными линиями не принадлежат [V).
Симплексный сплайн. Симплексные сплайны являются аналогами ненорми-
ненормированных iJ-сплайнов. Они представляют собой кусочно-полиномиальные функ-
функции точек двухмерного пространства. Каждый симплексный сплайн больше
нуля внутри своей полуоткрытой выпуклой области и равен нулю вне области.
Пусть задана последовательность двухмерных точек pj, p2, ..., рт, хотя
бы три из которых не совпадают друг с другом и не лежат на одной пря-
прямой. Для такой последовательности можно построить выпуклый многоугольник
V — {pi, p2, ..., рт} с вершинами в точках последовательности, так чтобы все
точки заданной последовательности принадлежали [V]. В общем случае часть
точек заданной последовательности будет лежать в вершинах многоугольника V,
часть — на его сторонах и остальная часть — внутри многоугольника V. Неко-
Некоторые точки последовательности могут совпадать. Точки рг, р2, ..., рп
3.13. Треугольные сплайновые поверхно&Щи 195
довательности называют узлами. На базе узлов рх, р2) • • ч Р^ЩШ^ЯО постро-
построить симплексный сплайн Mv(p) n-го порядка, где п = т — 3. П^рфу
вьшуклую область [V) многоугольника V называют носителем симплвасного
сплайна или его областью определения. Все узлы симплексного сплайна'рав-
сплайна'равноправны. Симплексный сплайн является функцией точки р = [и и]т. Введем
еще одно обозначение: через Му\к{р) обозначим симплексный сплайн (п—1)-го
порядка, построенный на последовательности узлов, полученной из заданной
последовательности путем исключения из нее вершины рк.
Симплексный сплайн n-го порядка определяется рекурсивно как взвешенная
сумма трех симплексных сплайнов (п — 1)-го порядка. Используя равноправие
узлов последовательности рх, р2, ¦.., рт, выберем из нее произвольную тройку
не лежащих на одной прямой узлов ра, pj, pc. Будем считать, что при обходе
точек ра, рь, рс мы будем двигаться против часовой стрелки. По формулам
C.11.4) вычислим барицентрические координаты а, Ь, с точки р относительно
точек ра, pj, pc. Симплексный сплайн n-го порядка определяется формулой
Му(р) = аМу\а{р) + ЪМль{р) + сМу\с(р), C.13.1)
где Му\а(р), Му\ь(р), Му\с(р) — симплексные сплайны (п — 1)-го порядка,
построенные на последовательностях узлов, полученных из последовательно-
последовательности Pi, р2, .. -, рт путем исключения из нее соответственно вершины ра, рь, рс.
Результат формулы C.13.1) не зависит от выбранной тройки узлов ра, рь, рс.
Вычисление значения симплексного сплайна n-го порядка начинается с вы-
вычисления значений симплексных сплайнов нулевого порядка на треугольных
областях. Пусть вершинами некоторого треугольника Г являются точки pj =
= [щ Vi]T, Pj = [uj Vj]T, pk = [щ Vk]T¦ Значение симплексного сплайна
нулевого порядка на невырожденной треугольной области Г определяется фор-
формулой
где Aijk =
1
щ
щ
1
Uj
Vi
1
Uk
Vk
О, если
Симплексный сплайн нулевого порядка является раз-
рывной константной функцией положения точки р. Симплексный сплайн
первого порядка является непрерывной функцией с разрывными первыми про-
производными.
Симплексный сплайн Му(р) всегда неотрицателен. Он отличен от нуля вну-
внутри своей полуоткрытой выпуклой области [V) и равен нулю вне ее.
В общем случае симплексный сплайн n-го порядка является кусочно-полино-
кусочно-полиномиальной функцией степени п, имеющей непрерывные производные до (п—1)-го
порядка включительно. В используемых нами обозначениях порядок симплекс-
симплексного сплайна совпадает с наивысшей степенью полиномов, описывающих его.
Обратим внимание на аналогию формулы Кокса-Де Бура B.8.30) и фор-
формулы C.13.1). Обе формулы описывают рекуррентное соотношение для сплайна
(т — А)-го порядка (порядок равен степени соответствующей кусочно-полиноми-
13*
196
Гл. 3. Моделирование поверхностей
альной функции), построенного на последовательности m узлов, где А — чи-
число барицентрических координат. В обоих случаях вычисления начинаются со
сплайнов нулевого порядка для А несовпадающих узлов. Эту аналогию можно
продолжить для пространств большей размерности.
Для симплексного сплайна можно вычислить производную в направлении
любого вектора на плоскости параметров. Пусть дан двухмерный вектор t —
= [u v]T. По формулам C.11.9) этот вектор можно описать с помощью барицен-
барицентрических компонент а, /3, 7 относительно точек ра, pj, рс равенством
* =
+ Ррь + ТРс-
Производная симплексного сплайна C.13.1) в направлении вектора t вычисля-
вычисляется по формуле
ЭМ'
dt
C.13.3)
Производные симплексных сплайнов n-го порядка определяются через сим-
симплексные сплайны (п — 1)-го порядка. В качестве точек ра, р^, рс могут быть
взяты любые три не лежащие на одной прямой узла дифференцируемого сим-
симплексного сплайна.
На рис. 3.13.2 приведен симплексный сплайн первого порядка, построенный
на прямоугольной области (значение симплексного сплайна откладывается в
Рис. 3.13.2. Симплексный сплайн первого порядка
направлении, перпендикулярном плоскости параметров сплайна).
На рис. 3.13.3 приведен симплексный сплайн третьего порядка, построенный
на шести несовпадающих узлах.
Рис. 3.13.3. Симплексный сплайн третьего порядка
Рис. 3.13.4. Симплексный сплайн пятого порядка с кратными узлами
Последовательность узлов iJ-сплайна может содержать кратные узлы. Необ-
Необходимо только, чтобы в последовательности нашлись хотя бы два не лежащих
3.13. Треугольные сплайновые поверхности
197
на одной прямой узла. Узлы рх, p2i •••> Pm симплексного сплайна также мо-
могут быть кратными. Для построения симплексного сплайна необходимо только,
чтобы среди узлов р1; р2, ..., рт нашлись хотя бы три не лежащих на одной
прямой узла. В кратных узлах высшие производные симплексного сплайна те-
теряют гладкость. На рис. 3.13.4 приведен симплексный сплайн пятого порядка,
построенный на восьми узлах, образующих четырехугольную область. В ка-
каждой вершине четырехугольной области находится по два совпадающих узла.
Некоторые узлы симплексного сплайна могут лежать внутри его выпуклого
многоугольника. На рис. 3.13.5 приведен симплексный сплайн третьего по-
порядка, построенный на шести узлах, три из которых лежат в вершинах тре-
треугольной области, а остальные три узла совпадают и лежат в центре этой
треугольной области. Все производные в центре такого сплайна теряют не-
непрерывность.
Некоторые узлы симплексного сплайна могут лежать на границе его вы-
выпуклого многоугольника. На рис. 3.13.6 приведен симплексный сплайн второго
Рис. 3.13.5. Симплексный сплайн третьего порядка с тремя кратными узлами в центре
Рис. 3.13.6. Симплексный сплайн второго порядка
порядка, построенный на пяти узлах, четыре из которых лежат вдоль стороны
треугольника. На этой стороне производные сплайна и сам симплексный сплайн
терпят разрыв.
В местах концентрации узлов значение симплексного сплайна заметно боль-
больше, чем в остальных местах. Если все узлы симплексного сплайна расположены
Рис. 3.13.7. Симплексный сплайн седьмого порядка
в вершинах его выпуклого многоугольника, то чем больше порядок сплайна,
тем меньше центральная существенно отличная от нуля часть сплайна. На
рис. 3.13.7 приведен симплексный сплайн, узлы которого лежат в вершинах
правильного десятиугольника.
Трехиндексные функции Бернштейна C.12.4) являются частными случаями
симплексных сплайнов. Функция Бернштейна
Ь, с) =
n!
198 Гл. 3. Моделирование поверхностей
с точностью до множителя равна симплексному сплайну n-го порядка, постро-
построенному на последовательности (n + З) узлов, из которых (г + 1) узлов совпадают
с точкой pa, (j + 1) узлов совпадают с точкой ръ и (к + 1) узлов совпадают
с точкой рс. Пусть точки ра, рь, рс являются вершинами треугольника Т. На
(n + l)(n + 2)
:= —
плексных сплайнов n-го порядка. Эти симплексные сплайны и соответствующие
им функции Бернштейна связаны равенством
т ni (n + 2)\ (n + l)(n + 2)
треугольной области 1 можно построить С„+2 = ———:— = — сим-
сим<злз-4)
где р = apa + bpb + cpc, Дабс — удвоенная площадь треугольника Т. Симплекс-
Симплексный сплайн Mijk(p) построен на последовательности узлов: ра — кратности
(г + 1), рь — кратности (j + 1), рс — кратности (к + 1).
DMS поверхности. NURBS кривые мы строим на семействе Б-сплайнов,
которые имеют общие узлы. Носители (области определения) .В-сплайнов пере-
перекрываются. Это позволяет стоить гладкие кривые. .В-сплайны NURBS кривых
нормированы, их сумма для каждого значения параметра равна единице, что
позволяет вводить для характеристических точек веса. При построении поверх-
поверхностей на семействе симплексных сплайнов нужно, чтобы сплайны семейства
имели общие узлы, а их полуоткрытые выпуклые области перекрывались. В про-
противном случае сплайновая поверхность не будет гладкой. Кроме того, если сумма
симплексных сплайнов для каждой двухмерной точки параметрической области
.поверхности будет равна единице, то это позволит нам строить рациональные
поверхности, в которых характеристические точки могут иметь веса.
Дамен (Dahmen), Микели (Micchelli) и Зайдель (Seidel) предложили один
из способов построения поверхностей на базе симплексных сплайнов. Этот спо-
способ имеет много общего со способом построения треугольных поверхностей
Рис. 3.13.8. Триангуляция в качестве области определения DMS поверхности
Безье. .Поверхнс^ти, построенные этим способом, называют DMS сплайнами
или D.MS поверхностями. Рассмотрим построение DMS поверхности на базе
симплексных сплайнов порядка п.
Областью определения DMS поверхности служит правильная триангуляция
О некоторой двухмерной области. Триангуляция считается правильной, если
она состоит из невырожденных не перекрывающих друг друга треугольников,
стыкующихся по общим ребрам. Пример правильной триангуляции приведен
на рис. 3.13.8.
3.13. Треугольные сплайновые поверхности
199
Пусть вершины триангуляции описываются двухмерными радиус-векто-
радиус-векторами р{. С каждой вершиной некоторым образом свяжем п + 1 узлов: р{ 0,
Pi,i> • • •> Pi,n- За узел piQ примем вершину pt: piQ = рь остальные узлы мо-
могут не совпадать с вершиной. Совокупность узлов piQ, pib ..., pin называют
узловым облаком. Узловые облака нам понадобятся в качестве узлов симплекс-
симплексных сплайнов.
Рассмотрим некоторый треугольник Ts из области определения DMS по-
поверхности О (рис. 3.13.9). Пусть его вершинами являются точки ра, рь, рс.
Pel
Рис. 3.13.9. Узловые облака вершин треугольника для п — 3
Совокупность всех узлов в вершинах рассматриваемого треугольника ра 0,
Ра,ь •••, Ра,п, Рь,о, Рь,ъ ¦ ¦ •> Рь,™ Рс,о> Рс, 1. • • •> Рс,п называют сеткой
узлов. Для треугольника Ts мы можем получить (п + 1)(п + 2)/2 различ-
различных последовательностей узлов: рО]0, р0>1, ..., pa>i, рь>0, рм, ..., p6j, pc0)
Рс,1> • • ч Pc,ki гДе * ^ 0) i ^ 0) & ^ 0 и * + j + k = п. С каждым треугольником
Ts свяжем (п + 1)(п + 2)/2 характеристических пространственных точек rsijk,
где г ^ 0, J'^ 0, к ^ 0 и г + j + к = п. Количество точек rsjj^ равно количеству
возможных последовательностей узлов для рассматриваемого треугольника. На
характеристические точки никаких ограничений не накладывается. Их положе-
положение в пространстве определяет форму DMS поверхности. Пусть треугольники,
образованные узлами pai, pbj, рск, 0 < г < п, 0 < j < n, 0 < к < п, являются
невырожденными, и при обходе их вершин мы будем двигаться против часовой
стрелки.
На каждой последовательности узлов найдем выпуклую область Sijk =
= {Ра,О, Ра,Ъ ¦••¦, Ра,Ь Pb.Oi Pb,l, • • •> Pb,j, Рс,0. Рс,Ъ • • ¦¦> Рс,к}, построим СИМ-
плексный сплайн Msijk(p). Вычислим нормированный симплексный сплайн
= \Asijk\Msijk(p),
0, к > 0, г + j + к = п,
где |Asjjfc| — удвоенная площадь треугольника, образованного узлами paji, Pbj,
рс к. С каждым нормированным симплексным сплайном Nsijk(p) свяжем со-
соответствующую характеристическую точку rsijk. Радиус-вектор r(p) DMS по-
поверхности определяется как сумма по всем треугольникам области определения
поверхности всех характеристических точек rsijk, умноженных на значения
200 Гл. 3. Моделирование поверхностей
соответствующих нормированных симплексных сплайнов NSijk(p):
Е N
ij,k=o,
i+j+h=n
Ё
C.13.6)
p = [и v]T e o.
Внешнее суммирование выполняется по всем треугольникам области определе-
определения поверхности О. Внутреннее суммирование в формуле C.13.6) выполняется
по всем возможным последовательностям узлов треугольника Г5. Таких после-
последовательностей (п + 1)(п + 2)/2, где п — порядок симплексных сплайнов.
В общем случае DMS поверхность является кусочно-полиномиальной функ-
функцией степени п. Она обладает большой гибкостью. Для одной и той же области
определения О можно построить множество различных DMS поверхностей, ва-
варьируя узлами Piti, Pj,2) • • •) Vi,n B каждой вершине pj = pi 0 триангуляции и
пространственным положением характеристических точек т8цк треугольников.
В работе [39] показано, что сумма всех отличных от нуля в заданной точке
р = [и v]T нормированных симплексных сплайнов C.13.5) равна единице. То
есть для правильной триангуляции выполняется равенство
W J2 \&sm\Msijk(p))=i. C.13.7)
п Ч ij,fc=o, '
jh
i+j+h=n
Это свойство позволяет строить рациональные поверхности. Каждой характери-
характеристической точке rsijk треугольников припишем вес wsijk. Мы можем построить
рациональную DMS поверхность с радиус-вектором
Е( Е \&Sijk\Msijk(p)wsijkr°ijk)
*1JK—и)
i j k=0
. C.13.8)
Е I*
i+j+k-n
Никаких ограничений на расположение узлов в узловых облаках мы не на-
накладывали, за исключением того, что треугольники, образованные узлами ра j,
Pb,ji Pc,ki должны быть невырожденными и одинаково ориентированными. Если
все узлы узловых облаков положить равными соответствующей вершине (Рг,о =
¦= Pt,i = • • • = Р» n — Pi)i T0 нормированные симплексные сплайны C.13.5) бу-
будут равны соответствующим трехиндексным функциям Бернштейна, а каждая
внутренняя сумма в C.13.6) будет описывать отдельную треугольную поверх-
поверхность Безье.
3.14. Поверхности, базирующиеся на поверхностях 201
3.14. Поверхности, базирующиеся на поверхностях
На базе поверхности можно построить другую поверхность. Рассмотрим
эквидистантную, ссылочную и продолженную поверхности. Поверхность, на
основе которой строится новая поверхность, будем называть базовой поверхно-
поверхностью. Базовая поверхность будет лежать в структуре данных рассмотренных
ниже поверхностей.
Эквидистантная поверхность. Для любой поверхности может быть построена
эквидистантная поверхность. Каждая точка эквидистантной поверхности от-
отстоит от соответствующей точки базовой поверхности на заданном расстоянии h
по нормали к ней. Радиус-вектор эквидистантной поверхности описывается фор-
МУЛ°И r(u, v) = b(u, v) + hm{u, v), u, v e п, C.14.1)
где b(u, v), u, v € п — базовая поверхность, п — область определения пара-
параметров базовой поверхности, m(u, v) — нормаль к базовой поверхности.
Нормаль имеет единичную длину и направление вектора h>i x Ьг- Область
изменения параметров эквидистантной поверхности совпадает с областью
Рис. 3.14.1. Эквидистантная поверхность
изменения параметров базовой поверхности. Эквидистантная и базовая поверх-
поверхности показаны на рис. 3.14.1. Производные ri(u, v) и гг(и, v) эквидистантной
поверхности по параметрам и и v описываются векторами
ri(u, v) = bi(u, v) + hmi(u, v), C.14.2)
r2(u, v) = b2(u, v) + ftm2(u, v), C.14.3)
где производные нормали mi(u, v) и тг(и, v) по параметрам определяются с
помощью деривационных формул Вейнгартена A.7.26).
В общем случае можно построить эквидистантную поверхность, у которой
расстояние h = h(u, v) зависит от параметров поверхности.
Ссылочная поверхность. Ссылочная поверхность представляет собой поверх-
поверхность, каждая точка которой получена путем некоторого преобразования соот-
соответствующей точки базовой поверхности. Ссылочная поверхность описывается
радиус-вектором . (о л л л\
r(u, v) = Mt- b(u, v), и, « ? й, C.14.4)
где b(u, v), u, v E ?2 — базовая поверхность, О, — область определения параме-
параметров базовой поверхности, М( — расширенная матрица преобразования A.4.5)
202 Гл. 3. Моделирование поверхностей
базовой поверхности. Область изменения параметра ссылочной поверхности
совпадает с областью изменения параметра базовой поверхности. Ссылочная
поверхность может быть использована при проективных преобразованиях.
Репараметризованная поверхность. Для любой поверхности может быть про-
произведена линейная репараметризация. Пусть область определения параметров
поверхности r(u, г;) описывается неравенствами umjn ^ u ^ um3iX, vm[n ^ v ^
^ ^тах- Пусть требуется, чтобы каждый из параметров изменялся бы в пределах
от ж до у. Будем считать, что u v зависят от новых параметров р и q:
qj an f} Q*
u(p) = umin + umax , C.14.5)
у — x у — x
v(q) = vmin^^- + vmaj^- C.14.6)
y-x y-x
Тогда радиус-вектор поверхности будет описываться функцией
( х^р^у, x^q^y. C.14.7)
После перехода к новым параметрам сама поверхность не изменится, но области
определения ее параметров будет представлять собой квадрат со стороной у — х.
Изменение области определения параметров можно считать одним из способов
построения поверхности на базе другой поверхности.
Продолженная поверхность. Любая поверхность может быть продолжена на
заданное параметрическое расстояние. Пусть требуется продолжить поверх-
поверхность b(u, и), щ ^ и ^ иг, V\ ^ v ^ V2 путем расширения области определения
параметров до аи + щ ^ и ^ иг + bu, av + v\ ^v ^v2 + by. Если аи ^ 0, av ^ 0,
bu ^ 0, bv ^ 0, то поверхность будет продолжена за свои пределы. Если аи > 0,
av > 0, Ьи < 0, bv < 0, то поверхность будет усечена. Если поверхность за-
замкнута по какому-либо из параметров, то при выходе замкнутого параметра
за границу области определения выполним его циклический пересчет. Если
поверхность b(u, v) замкнута по параметру и, тогда
' Ь(и -|- ид, v), если и < щ, V\ ^ v ^ v2,
b(u, г;), если щ ^ u ^ u2, v\ ^ v ^ v2,
г(и, г;) = < Ь(и — ид, г;), если и > иг, v\ ^ г; ^ V2,
b(u, V\) + (v — i?i)b2(u, v\), если щ ^ u ^ u2, v < v\,
. b(u, v2) + (v — г;2)Ьг(и, v2), если щ ^ u ^ u2, v > v2,
C.14.8)
где ид = иг — u\. Если поверхность b(u, v) замкнута по параметру v, тогда
b(u, г; + г;д), если щ < u < u2, v <v\,
b(u, г;), если щ ^ u ^ иг, v\ ^ v ^ v2,
r(u, v) = ^ b(u, г; - г;д), если щ ^ и ^ U2, v> «2,
b(ui, v) + (u —ui)bi(ui, г;), если и <щ, v\ ^v ^v2,
b(u2, v) + (г* — u2)bi(u2, v), если u > иг, V\ ^ г; < г;2,
C.14.9)
где «д = г;2 — vi. Если же поверхность не является замкнутой, а один из
параметров или оба вышли за границу области определения, то продолжим по-
3.14. Поверхности, базирующиеся на поверхностях
203
верхность по касательной на ближайшей границе, и вычислим по продленной
поверхности необходимые геометрические характеристики. Радиус-вектор про-
продолженной поверхности вычислим по формуле
Ъ(и, v), если щ ^ u ^ щ, v\ ^ v ^ V2,
Ъ(щ, v) + (и — ui)bi(u\, v), если и < щ, v\ ^ г; ^ V2,
b(ii2, v) + (и — «2)bi(u2, w), если u > 112, v\ ^ и ^ г>2,
Ъ(и, v\) + (v — i?i)b2(u, ui), если «i < и < иг, г; < wi,
b(u, «2) + (w — W2)b2(u, «2), если щ ^ u < иг, г; > г;2,
r(u, v) =
+ {u —ui)(v — vi)bi2(ui, vi), если u < щ, v<v\,
vi) + (u - u2)bi(u2, wi) + (v - vi)b2(u2, vi)+
+ (u — U2)(v — vi)bi2(v,2, vi), если и > иг, v<t>i,
b(ui, w2) + (u - «i)bi(ui, u2) + {v - v2)b2(ui, w2)+
+ (u — иг)(и — «2)bi2(ui, «2), если u<ui, и > w2,
, v2)
+ (u —
, V2), если
v > V2,
C.14.10)
где bi(u, w) и Ьг(и, w) — частные производные радиус-вектора b(u, г;) по
параметрам и и и, соответственно, bi2(u, и) — смешанная производная ра-
радиус-вектора Ъ(и, v) по параметрам и и и. Дифференцируя формулы C.14.8)-
C.14.10), получим производные
радиус-вектора продолженной
поверхности. На рис. 3.14.2 при-
приведена поверхность, на основе
которой построена продолжен-
продолженная поверхность. Продолжен-
Продолженная поверхность приведена на
рис. 3.14.3.
Рис. 3.14.2. Исходная поверхность
Рис. 3.14.3. Продолженная поверхность
Формулы C.14.8)-C.14.10) могут быть использованы для вычисления ради-
радиус-вектора поверхности и его производных при выходе параметров поверхности
за область их определения.
204 Гл. 3. Моделирование поверхностей
Общее правило. Все поверхности, в структуре данных которых лежит дру-
другая поверхность, не должны допускать многократного наследования своего же
типа. Например, в качестве базовой поверхности для эквидистантной поверхно-
поверхности не должна быть использована другая эквидистантная поверхность, а должна
быть использована базовая поверхность последней с соответствующим пересче-
пересчетом длины эквидистанты. То есть, если нужно построить эквидистантную по-
поверхность на расстоянии /i2 от другой эквидистантной поверхности ri(u, v) =
= b(u, г;) + him(t), то в качестве базовой поверхности должна быть использо-
использована поверхность b(u, v), а длина эквидистанты должна быть равна h = /12+/11.
Если требуется построить ссылочную поверхность с матрицей преобразования
М< на базе другой ссылочной поверхности r\(u, v) = N< • b(u, г;), то в качестве
базовой поверхности должна быть использована поверхность Ъ(и, v), а матрицу
преобразования получим как произведение матриц М< • N^. Аналогичные пра-
правила должны действовать и для других базирующихся поверхностей.
3.15. Ограниченные контурами поверхности
Рассмотрим поверхности, которые выделяются среди всех остальных поверх-
поверхностей и создаются «над ними» (на их основе).
Все приведенные выше поверхности имеют «природные» прямоугольные или
треугольные области определения параметров. Прямоугольные или треугольные
области удобны в использовании из-за их простоты. Прямоугольная область
параметров определяется неравенствами umjn ^ u ^ «max, vm-m ^ v ^ г?тах,
и для любой пары параметров можно сразу сказать, лежит ли она вне обла-
области, внутри области или на границе области. Рассмотренные выше поверхности
дают широкие возможности для моделирования. Неограниченные возможно-
возможности для моделирования мы получим, если границы поверхностей смогут иметь
произвольный вид. Это можно сделать с помощью двухмерных кривых линий
ri{U) = \u(U) v(U)] , ijmin ^ ti ^ timax, i = 1, 2, ..., п, на поверхности, кото-
которые описываются в пространстве параметров и и v поверхности. Эти двухмер-
двухмерные кривые собраны в контуры и разделяют используемую часть поверхности
от остальных частей.
Такая поверхность с произвольной границей представляет собой наиболее
общий тип поверхности. Будем называть ее ограниченной контурами поверх-
поверхностью. Ограниченную контурами поверхность можно построить на основе
любой поверхности с прямоугольной или треугольной областью путем изме-
изменения области определения ее параметров. Именно эта поверхность лежит в
основе моделирования тел. Ее параметрам разрешается принимать значения
только внутри области, ограниченной заданными на ней контурами. Границы
поверхности представляют собой отображение в трехмерное пространство гра-
границ двухмерной связной области.
Исходную поверхность с прямоугольной или треугольной областью опреде-
определения параметров будем называть базовой поверхностью. Пусть Ъ(и, v) есть
радиус-вектор ее точек. Радиус-вектор ограниченной контурами поверхности
описывается тем же выражением, что и базовая поверхность, но имеет другую
область определения параметров
r(u, v) = Ъ(и, v), u,v ей, C.15.1)
где О, — область определения параметров, которая представляет собой ограни-
ограниченную замкнутыми кривыми часть плоскости, из каждой точки которой можно
3.15. Ограниченные контурами поверхности
205
попасть в любую другую ее часть, не пересекая границ. Область определения
параметров определяется двухмерными контурами (замкнутыми составными
кривыми). Двухмерный контур c(t) = [u(t) v(t)] , tm-m ^ t ^ tmax, состоит
из нескольких двухмерных кривых, стыкующихся между собой. Радиус-вектор
контура определяется функцией B.12.7). Таких контуров может быть несколько.
Совокупность контуров ограничивает двухмерную область параметров и придает
границам поверхности заданную форму.
Область определения параметров ограниченной контурами поверхности
представляет собой связную часть двухмерного пространства и описывается
набором непересекающихся двухмерных контуров, один из которых является
внешним, а остальные лежат внутри него и являются внутренними. Внутрен-
Внутренние контуры не могут быть вложены друг в друга. Для того чтобы легче было
определить, принадлежит ли некоторая двухмерная точка р = [u v]T обла-
области определения параметров поверхности, контуры ориентируют определенным
образом. Пусть внешний контур ориентирован так, что обход по нему в поло-
положительном направлении осуществлялся против часовой стрелки, если смотреть
на поверхность навстречу ее нормали. Внутренние контуры должны быть ори-
ориентированы в противоположном направлении.
Принадлежность точки области определения параметров. Пусть требуется
ответить на вопрос, принадлежит ли двухмерная точка р = [и v]T простран-
пространства параметров области определения поверхности — классифицировать точку
относительно области. Для областей прямоугольной формы ответить на него
просто — для этого нужно проверить, удовлетворяют ли параметры и и v не-
неравенствам umin ^ и ^ umax, vmin ^ v ^ vm&x. Для ограниченной контурами
поверхности, это сделать несколько сложней.
Пусть требуется классифицировать точку р = [и v]T в параметрической обла-
области поверхности, ограниченной тремя контурами: одним внешним и двумя вну-
внутренними, как показано на рис. 3.15.1.
В общем случае для того чтобы установить принадлежность точки р неко-
некоторой двухмерной области, можно найти все точки пересечения любой двух-
двухмерной прямой линии (проще горизонтальной или вертикальной), проходящей
Рис. 3.15.1. Определение положения точки относительно области
через эту точку, с границами области. Таких точек пересечения должно быть
четное число - каждой точке входа прямой в область должна соответствовать
точка выхода из области. Но в некоторых случаях, как показано на рис. 3.15.1,
их может быть нечетное число из-за касания или прохождения прямой через
угол граничного контура. Если точек пересечения получено нечетное число, то
206
Гл. 3. Моделирование поверхностей
можно пересечь границу области другой двухмерной прямой, проходящей через
проверяемую точку и составляющую небольшой угол с уже построенной прямой.
Далее легко определить принадлежность рассматриваемой точки заданной обла-
области. Если точка р находится между точкой входа прямой в область и соответ-
соответствующей ей точкой выхода из области, то рассматриваемая точка принадлежит
данной области. В противном случае или в случае отсутствия точек пересечения
прямой с границей области рассматриваемая точка лежит вне данной области.
Если известно, что внешний граничный контур области параметров поверх-
поверхности ориентирован против часовой стрелки, а внутренние контуры ориентиро-
ориентированы по часовой стрелке, если смотреть на поверхность навстречу ее нормали,
то классифицировать точку р = [и и]т в параметрической области поверхности
можно следующим образом. Найдем ближайшую к точке р точку р0 на границе
области. Построим двухмерный вектор w из найденной точки р0 в точку р.
w
Рис. 3.15.2. Определение положения точки относительно области определения параметров поверх-
поверхности.
Вычислим нормаль те к граничному контуру в точке р0. Нормаль те в правой
системе координат всегда направлена влево, если смотреть вдоль направления
контура. Если точка р0 является точкой излома граничного контура, то в каче-
качестве нормали возьмем среднюю нормаль к границе в этой точке. Если теги ^ 0,
то точка р принадлежит области определения поверхности. В противном слу-
случае — нет. Это отражено на рис. 3.15.2.
Примеры. На рис. 3.15.3 приведена NURBS поверхность, имеющая прямо-
прямоугольную область определения параметров, и линии на ней. На рис. 3.15.4
Рис. 3.15.3. NURBS поверхность и линии на ней
Рис. 3.15.4. Ограниченная контурами поверхность
приведена NURBS поверхность, ограниченная кривыми на ней. На рис. 3.15.5
приведена ограниченная контурами поверхность вращения.
При создании тонкостенного тела требуется строить ограниченные конту-
контурами поверхности, базирующиеся на продолженной поверхности, которая явля-
является эквидистантной поверхностью. Для таких поверхностей в качестве базовой
3.16. Способы построения поверхностей
удобно ввести новый тип поверхности, который включает в себя одновременно
свойства эквидистантной и продолженной поверхностей.
В общем случае область определения параметров Q ограниченной контурами
поверхности г(«, v) может выходить за область определения параметров базо-
Рис. 3.15.5. Ограниченная контурами поверхность
вой поверхности b(u, v) при условии, что определено поведение поверхности
Ъ(и, v) за границами ее области определения. Это можно сделать, например, с
помощью формул C.14.8)-C.14.10).
Общее правило. Ограниченные контурами поверхности не должны допускать
многократного наследования своего же типа. В качестве базовой поверхности
для поверхности, ограниченной контурами, не должна использоваться другая
ограниченная контурами поверхность, а должна быть взята базовая поверх-
поверхность последней. Ограниченные контурами поверхности должны создаваться
в последнюю очередь. Например, если требуется построить эквидистантную
поверхность на базе ограниченной контурами поверхности C.15.1), то сначала
должна быть построена эквидистантная поверхность на основе базовой поверх-
поверхности b(u, v), а потом на базе эквидистантной должна быть создана ограничен-
ограниченная контурами поверхность.
3.16. Способы построения поверхностей
На рис. 3.16.1 приведены способы построения поверхностей. Здесь отра-
отражены лишь наиболее распространенные способы. В авиастроении широко ис-
используются различные поверхности сопряжения. Кроме того, можно построить
поверхности с характерными особенностями — фичерсные поверхности (fea-
(feature surface). Способы их построения могут быть различными и зависят от
специфики области применения.
Рисунок 3.16.1 отражает процесс построения поверхностей при чтении его
слева направо. Изначально поверхности могут быть построены или по местной
системе координат и скалярным параметрам, или по характерным точкам, или
на основе линий. Далее эти поверхности могут быть продлены или усечены,
на их основе могут быть получены эквидистантные поверхности. Все упомяну-
упомянутые поверхности имеют прямоугольную или треугольную область определения
параметров. На базе поверхностей с прямоугольной или треугольной областью
определения параметров можно построить ограниченные контурами поверхно-
поверхности произвольной формы.
208
Гл.З. Моделирование поверхностей
Все поверхности являются равноправными по отношению к выполняемым
ими функциям и выполняемым над ними операциям. Кроме общих функций
произвольного геометрического объекта поверхности должны выполнять функ-
функции вычисления радиус-вектора поверхности, частных производных радиус-
вектора по параметрам, нормали поверхности и ее частных производных,
Аналитические .поверхности
Плоскость
Сфера
Эллипсоид
Однопол остный
гиперболоид
Двуполостный
гиперболоид
Эллиптический
параболоид
Гиперболический
параболоид
Цилиндрическая
поверхность
Коническая поверхность
Тороидальная поверхность
Поверхности на базе точек
Четырехугольная
поверхность
Поверхность Безье
NURBS поверхность
Треугольная поверхность
Треугольная
поверхность Безье
Поверхности на базе линий
Поверхность
выдавливания
Поверхность вращения
Поверхность сдвига
Поверхность заметания
Линейчатая поверхность
Поверхность Кунса
Поверхность Эрмита
Поверхность Лагранжа
Поверхность Гордона
Поверхности на базе поверхностей
Эквидистантная
и продолженная
поверхность
Ссылочная
поверхность
Ч
Ограниченная
контурами
поверхность
Поверхность скругления
Поверхность фаски
Рис. 3.16.1. Способы построения поверхностей
коэффициентов первой и второй квадратичных форм поверхности, функции
предоставления информации об области определения параметров поверхности
(замкнутости, граничных контурах), функции определения принадлежности
заданных параметров области определения поверхности, функции изменения
положения и ориентации в пространстве, функции модификации формы поверх-
поверхности,
Математическая модель поверхности должна быть дополнена функциями,
обеспечивающими взаимодействие поверхности с другими геометрическими объ-
объектами и выполнение над ними различных операций, В следующей главе мы
рассмотрим операции над кривыми и поверхностями.
Глава 4
ОПЕРАЦИИ НАД КРИВЫМИ И ПОВЕРХНОСТЯМИ
4.1. Выполнение операций
В предыдущих главах были рассмотрены методы построения различных
кривых линий и поверхностей. Этих методов не достаточно, чтобы модели-
моделировать сложные геометрические объекты, например, поверхности, ограничен-
ограниченные контурами. В большинстве случаев сложные геометрические объекты по-
появляются как результат некоторой операции над более простыми объектами.
В данной главе мы рассмотрим методы выполнения операций. Операцией будем
называть совокупность действий над одним или несколькими исходными объек-
объектами, которая приводит к рождению нового геометрического объекта. Действия,
которые изменяют объект, не изменяя его природы, будем называть модифика-
модификацией или редактированием.
Редактирование объекта сводится к изменению значений его данных при
неизменной их структуре. Все геометрические объекты в итоге описываются
скалярными величинами и векторами. Редактирование объектов приводит к
изменению этих скаляров и компонент векторов. Редактированием можно мас-
масштабировать, зеркально отразить, переместить, повернуть в пространстве гео-
геометрический объект или изменить его форму. Преобразования трансформации
по матрице, перемещение, поворот в пространстве геометрического объекта сво-
сводятся к соответствующим преобразованиям радиус-векторов, лежащих в струк-
структуре данных объекта.
К операциям мы будем относить построение проекций точек на кривые и
поверхности пе-нермали к ним, построение проекций точек на поверхности
по заданному направлению, построение точек пересечения кривых, построение
точек пересечения кривых и поверхностей, построение линий пересечения по-
поверхностей, построение поверхностей скругления и поверхностей фасок, а также
решение других задач. Операция пересечения двухмерных кривых и операция
пересечения поверхностей являются основополагающими, так как они присут-
присутствуют в большинстве других операций, выполняемых над геометрическими
объектами.
Используемые нами математические модели линий и поверхностей постро-
построены так, что они выдают геометрическую информацию, если мы обратимся к
ним с некоторыми параметрами. Если геометрический объект рассматривать
как «черный ящик», то параметры подаются на его вход, а на выходе мы по-
получим геометрическую информацию, например, радиус-вектор точки объекта,
соответствующий введенным параметрам. В обратном направлении подобный
«черный ящик» сигнал не пропускает. То есть, если мы возьмем некоторую
точку в пространстве и захотим узнать, далеко ли она находится от данного
геометрического объекта или какие параметры объекта ей соответствуют, то
построенная нами математическая модель окажется в затруднительном поло-
положении. Подобные задачи возникают часто и математическая модель должна с
14 — 5293 Голованов
210 Гл. 4. Операции над кривыми и поверхностями
ними справляться. Математика располагает методами решения таких задач,
но эти методы являются итерационными и для того, чтобы получить искомое
решение, необходимо указать некоторое нулевое (начальное) приближение ис-
искомого решения.
В качестве примера возьмем задачу определения точки пересечения поверх-
поверхности s(u, v) и кривой линии c(t). В точке их пересечения радиус-векторы
кривой и поверхности имеют одинаковые значения: s(u, v) = c(t). Это век-
векторное равенство представляет собой систему трех скалярных уравнений, иско-
искомыми величинами которых являются параметры и, v и t. Решив эту систему
уравнений, получим параметры и, v и t, по которым при необходимости можно
вычислить точку на поверхности или на кривой. Система уравнений в общем
случае является нелинейной и решается итерационными методами. Точек пе-
пересечения может быть несколько и от того, с какого приближения параметров
начнется итерационный процесс решения, зависит, к каким параметрам сой-
сойдется решение. Из данного примера видно, что для решения задачи нужно
уметь делать две вещи: находить нулевое приближение для каждого решения и
решать системы нелинейных уравнений. Что касается решения системы урав-
уравнений, то существует много методов, которые приводят к искомым решениям,
если корректно задано его нулевое приближение. Мы рассмотрим эти методы
чуть позже.
Для нахождения нулевого приближения каждого решения используем ме-
метод проб и ошибок. Нулевое приближение может быть найдено довольно грубо,
важно только, чтобы оно лежало в области сходимости решения системы урав-
уравнений к одному из точных решений. Важно также, чтобы каждому решению
было найдено свое нулевое приближение. Для поиска нулевых приближений
будем проверять некоторое событие в выбранных точках геометрических объ-
объектов. В упомянутом примере пересечения кривой и поверхности возьмем не-
некоторые значения и^°\ гД°) и № параметров поверхности и кривой и заменим
поверхность частью касательной к ней плоскости в выбранной точке, а кри-
кривую заменим частью касательной прямой линии в выбранной точке. Найдем
точку пересечения касательной прямой и касательной плоскости и оценим, да-
далеко ли от точек касания находится точка пересечения. Если точка пересечения
находится недалеко от точек, в которых построены касательная прямая и ка-
касательная плоскость, то параметры и(°\ гД°) и t(°> можно принять в качестве
начального приближения для дальнейшего определения параметров точки пере-
пересечения. Если же точка пресечения находится далеко от точек, в которых по-
построены касательная прямая и касательная плоскость, то возьмем другие точки
на кривой и поверхности и выполним в них те же действия.
В данной схеме проверок остается неясным, какие точки можно считать
близкими и какие точки следует выбрать для проверки следующими. Для кри-
кривых и поверхностей эти величины удобнее измерять в параметрических еди-
единицах. Расстояние близости и длина перемещения для следующей проверки в
соседнюю точку являются связанными величинами. Действительно, если близ-
близким считать некоторое параметрическое расстояние А, то следующий поиск
следует выполнять на параметрическом расстоянии А от данной точки. Длину
параметрического шага будем связывать с искривленностью геометрического
объекта. Приращения параметров А будем называть параметрическими ша-
шагами. Шаги перемещения по параметрической области кривой через кривизну
связаны с допустимым углом отклонения касательной к ней. Шаги перемеще-
4.2. Движение по параметрической области 211
ния по параметрической области поверхности через соответствующую кривизну
связаны с допустимым углом отклонения нормали поверхности. Максимально
допустимую величину угла отклонения касательной или нормали обозначим Да.
Шагать по параметрической области нужно достаточно часто, чтобы не про-
пропустить решение, и в то же время достаточно редко, чтобы потратить меньше
времени. Это регулируется выбором угла Да, при этом шаг по параметру не
зависит от абсолютных размеров геометрического объекта. Подобная схема вы-
выбора нулевых приближений применима при выполнении всех операций над кри-
кривыми и поверхностями.
Из предложенной схемы видно, что для выполнения операций нужно уметь
корректно перемещаться по параметрическим областям кривых и поверхностей
в поиске нулевых приближений решения, уметь находить нулевые приближения
и уметь находить точное решение, отталкиваясь от некоторого приближения.
Далее мы рассмотрим вычисление шага по параметрам для кривых и поверх-
поверхностей, а также методы решения систем уравнений при известных нулевых
приближениях решений и уравнения, описывающие ту или иную операцию.
4.2. Движение по параметрической области
Для определения нулевого приближения решения системы уравнений будем
двигаться с некоторым шагом по параметрической области и в дискретных точ-
точках проверять выполнение некоторого условия, характерного для данной опе-
операции. Эти дискретные точки должны быть выбраны таким образом, чтобы
было найдено нулевое приближение для каждого решения. Характерным усло-
условием для операции, как правило, является смена знака невязки уравнений рас-
рассматриваемой операции или уменьшение невязки уравнений ниже известного
уровня.
Движение по кривой. Движение по параметрической области некоторой кри-
кривой c(t) будем начинать с минимального значения ее параметра tmin. Двигаться
будем в направлении возрастания параметра до достижения его максимального
значения tmax с некоторым вычисляемым шагом At по параметру. Шаг At
мы будем вычислять, исходя из условия, что при переходе от точки к точке
касательная кривой отклонялась бы на угол, не превышающий некоторую ве-
величину Аа. Приращение параметра или параметрический шаг At меняется
от точки к точке. В каждой точке будет проверяться выполнение некоторого
условия, по которому должно быть принято решение о дальнейших действиях.
Рис. 4.2.1. Заменяющие отрезки касательных кривой при поиске начальных приближений пара-
параметра
В некоторых операциях условие будет проверяться на отрезке касательной пря-
прямой, построенной в данной точке. Фактически будет выполнена замена кривой
отрезками прямых линий, касательных к кривой. На рис. 4.2.1 показана кривая
14*
212 Гл. 4. Операции над кривыми и поверхностями
и заменяющие ее отрезки на начальной стадии операции. Направление отрез-
отрезков совпадает с касательными кривой в точках касания. Касательные строятся
в точках вычисления очередного шага. Дины отрезков и точки, в которых вычи-
вычисляются касательные, зависят от кривизны кривой и определяются следующим
образом.
Пусть в процессе движения мы находимся в некоторой точке кривой, описы-
описываемой параметром t = to- Следующее значение параметра t = to + At должно
быть таким, чтобы касательный вектор в новой точке отклонился бы от каса-
касательного вектора кривой в предыдущей точке на угол, не превышающий Да.
Значение предельного угла отклонения будем считать заданным. Для вычисле-
вычисления нулевых приближений параметров при выполнении операций можно при-
принять тг/10 ^ Да ^ тг/20. Таким образом, нам нужно предвидеть искривление
линии в некоторой окрестности точки t = to и в соответствии с этим выбрать
следующую точку. Если предположить, что кривизна кривой сохраняется по-
постоянной в окрестности точки t = to, то кривая отклонится на угол Да, если
точка сместится по дуге на расстояние
А, = f, D.2.1)
где к — кривизна кривой в данной точке. Если еще предположить, что и длина
производной радиус-вектора кривой сохранится постоянной в окрестности рас-
рассматриваемой точки, то смещению As по дуге будет соответствовать приращение
параметра
где с' — производная радиус-вектора кривой по параметру. Подставив в по-
последнее равенство выражение A.5.28) для кривизны кривой, получим шаг по
параметру
Ы-?Щ-.. D.2.3)
|с' х с"|
Описанным способом пройдем по всей линии и проверим в каждой точке
выполнение некоторого условия, по которому можно судить о близости того или
иного события. В каждой точке остановки мы построим отрезок прямой линии
длиной |с'|Д?, касающийся своей серединой кривой в рассматриваемой точке.
Все рассуждения базируются на том, что рассматриваемую окрестность кри-
кривой мы аппроксимируем дугой окружности конечного радиуса. При стремле-
стремлении кривизны в рассматриваемой точке к нулю длина параметрического шага
стремится к бесконечности. Кривизна кривой в рассматриваемой точке мо-
может быть очень малой или вовсе равной нулю, хотя в достаточно близкой к
рассматриваемой точке области кривизна может иметь гораздо большее значе-
значение. В таком случае мы шагнем слишком далеко. Для учета подобных ситуаций
можно ввести ограничение максимального параметрического шага или сделать
небольшой шаг по параметру и повторить вычисления в новой точке. Если в
рассматриваемой точке длина первой производной радиус-вектора стремится к
нулю, то длина параметрического шага тоже стремится к нулю. Длина пер-
первой производной радиус-вектора кривой в рассматриваемой точке может быть
очень малой или вовсе равной нулю, хотя в достаточно близкой к рассматривав-
4.2. Движение по параметрической области 213
мой точке области длина производной может иметь гораздо большее значение.
В таком случае приращение параметра будет неоправданно малым или вовсе
равным нулю. Для учета подобных ситуаций введем ограничение минималь-
минимального параметрического шага. Для разных кривых это ограничение может быть
различным.
Параметрические шаги допускается определять приближенно, так как мы
ничего не вычисляем окончательно, а лишь находим нулевые приближения для
дальнейшего уточнения. Для некоторых кривых нет необходимости прибегать к
вычислениям для определения шага At. Например, для окружности или ее дуги
At = Aa, если параметром является центральный угол, для отрезка прямой
можно положить At — imax — ?mjn-
Движение по поверхности. Движение по параметрической области некоторой
поверхности s(u, v) будем выполнять аналогично движению по кривой. Поло-
Положим один из параметров постоянным, и будем двигаться вдоль другого пара-
параметра описанным выше способом. При движении будем заодно вычислять и
шаг по параметру, который в данный момент считаем фиксированным с таким
расчетом, чтобы в конце вычислить среднее значение шага и по неподвижному
параметру. Для вычисления шага по параметрам поверхности в правую часть
D.2.2) подставим кривизны A.8.5) вдоль координатных линий поверхности.
При v = const и u = const кривизны линий соответственно равны ци = Ьц/gu
и Цу = &22/ё22> гДе Sn и &22 — коэффициенты первой основной квадратич-
квадратичной формы поверхности A.7.8), 6ц и 622 —¦ коэффициенты второй основной
квадратичной формы поверхности A.7.21). В результате шаг по параметрам
поверхности вычислим по формулам
Au = ^L = ^li, D.2.4)
D.2.5)
022 m • S22
где m — нормаль поверхности, si —производная радиус-вектора поверхности
по параметру и (по первому параметру), S2 — производная радиус-вектора по-
поверхности по параметру v (по второму параметру).
Начинать движение по параметрической области поверхности будем с ми-
минимальных значений параметров umjn и um;n. Двигаться будем в направлении
возрастания одного из параметров до его максимального значения, одновре-
одновременно вычисляя среднее значение шага вдоль другого параметра. Затем сде-
сделаем усредненный шаг по другому параметру поверхности и повторим проход
по первому параметру от его минимального значения до максимального. Так
рядами пройдем всю параметрическую область поверхности. Если поверхность
построена на базе кривых линий, то для вычисления шага по параметру по-
поверхности можно привлекать соответствующий шаг по параметру кривой. Для
аналитических поверхностей нет необходимости прибегать к вычислениям по
формулам D.2.4) и D.2.5), так как шаг можно определить по аналитическим
формулам поверхности.
Так же как для кривых, все рассуждения для поверхностей базируются на
том, что рассматриваемая окрестность точки поверхности сохраняет постоянной
нормальную кривизну вдоль параметрических направлений. Если же одна из
214 Гл. 4. Операции над кривыми и поверхностями
нормальных кривизн в рассматриваемой точке стремится к нулю, то длина соот-
соответствующего параметрического шага стремится к бесконечности. Нормальная
кривизна поверхности в рассматриваемой точке может быть очень малой или
вовсе равной нулю, хотя в достаточно близкой к рассматриваемой точке области
кривизна может быть большой. Для того чтобы не перешагнуть через резкое
изменение формы поверхности, можно ввести ограничение максимального шага
по каждому из параметров или сделать небольшой шаг по соответствующему па-
параметру и повторить вычисления в новой точке. Если же в рассматриваемой
точке длина частной производной радиус-вектора стремится к нулю, то длина
соответствующего параметрического шага тоже стремится к нулю. Чтобы пара-
параметрический шаг не мог стать как угодно малым, можно ввести ограничение
минимального параметрического шага по параметрам поверхности. Для разных
поверхностей это ограничение может быть различным.
Используя описанную схему движения по параметрической области, можно
пройти по отдельным точкам поверхности и проверить в каждой точке выполне-
выполнение некоторого условия, по которому можно судить о наличии решения вблизи
точки. Можно получить разбиение параметрической области поверхности на
прямоугольники со сторонами Аи и Av внутри каждого такого прямоуголь-
прямоугольника поверхность аппроксимировать четырехугольной частью плоскости D.1.2),
которая в средней точке касается рассматриваемой поверхности. Другими сло-
словами, при необходимости можно покрыть поверхность плоскими четырехуголь-
четырехугольниками (рис. 4.2.2), со сторонами Аи и Av (при этом они могут частично пере-
перекрывать друг друга и частично выходить за область определения параметров)
и проверить на каждом четырехугольнике выполнение некоторого условия.
Рис. 4.2.2. Заменяющие поверхность касательные четырехугольники
Результаты этой проверки будут меняться от четырехугольника к четырехуголь-
четырехугольнику и примерно будут равны результатам аналогичной проверки этого же усло-
условия для самой поверхности. По результатам проверки некоторого условия можно
определить нулевое приближение каждого решения.
Описанный способ движения по кривой или поверхности не зависит от раз-
размеров последних. Он преследует цель отследить близость некоторого события
для геометрического объекта и используется в операциях над геометрическими
объектами. Для других целей (например, визуализации объекта) используются
другие способы вычисления параметрического шага и перемещения по параме-
параметрической области.
4.3. Решение системы нелинейных уравнений 215
4.3*Решение системы нелинейных уравнений
Каждая операция содержит свои уравнения, которые отражают ее геометрический
смысл. Уравнений может быть одно или несколько, они могут быть скалярными или
векторными. Векторное уравнение является удобной записью нескольких скалярных
уравнений для соответствующих компонент векторов. В общем случае выполнение опе-
операции сводится к решению некоторой системы скалярных нелинейных уравнений от-
относительно параметров кривых и поверхностей. Задача определения корней системы
нелинейных уравнений решается с помощью некоторого итерационного процесса, ко-
который шаг за шагом уточняет корни уравнения. Итерационный процесс предполагает,
что и на первой итерации известно некоторое приближенное значение корней системы.
Будем считать, что начальное приближение решения нам известно и что оно находится
в области сходимости.
Метод Ньютона-Рафсона. Пусть требуется найти значения п неизвестных х\,
Х2, ..., хп, удовлетворяющих п алгебраическим уравнениям:
fi(xi, х2, ..., хп) = О,
/2A1, ?2> • ¦ -1 хп) = 0, D 3.1)
fn(xi, х2, ..., хп) = О,
где /i, /2, ..., /п — непрерывно дифференцируемые в некоторой окрестности началь-
начального приближения функции. Одним из наиболее часто используемых методов решения
систем нелинейных уравнений является метод Ньютона-Рафсона. Предположим, что
после г итераций нам известно г-е приближение решения x^r\ х2(г\ ¦ ¦., хп^г\ которое
отличается от точного решения х\*, х2*, ¦ ¦., хп* на величины Axi, г = 1, 2, ..., п
х{*=х^ + Ахи « = 1, 2, ..., п.
Погрешности Axi неизвестны и подлежат определению. Введем обозначения: х^ =
= {xi*~r\ Х2*-г\ ¦ ¦-, хп(г)} — для совокупности неизвестных на г-м приближении,
/i(a;W) = Мх^г\ x2(r\ ..., XjS^), i = 1, 2, ..., n — для функций на г-м прибли-
приближении, dfi(x^)/dxj, i, j = 1, 2, ..., п — для частных производных функций на г-м
приближении. Разложим левую часть каждого уравнения системы D.3.1) в ряд Тейлора
по степеням Ах, в окрестности г-го приближения
* = 1, 2, ..., п.
Левую часть D.3.2) заменим нулем, так как fi(x\*, х2*, ¦ ¦.. х„*) = 0, а в правой части
отбросим величины второго порядка малости и выше по Да:*, г = 1, 2, ..., п. Тогда
система D.3.1) заменится системой уравнений
^+A, + ... +
216
Гл. 4. Операции над кривыми и поверхностями
являющейся линейной системой относительно погрешностей Axi, i = 1, 2, ..., п. Ре-
Решив систему линейных алгебраических уравнений D.3.3), вычислим следующее при-
приближение для искомого решения:
+ Ахи г = 1,2,..., п.
D.3.4)
Каждое приближение будет отличаться от точного решения, так как мы линеаризовали
систему уравнений. Погрешности Axi на каждом приближении будут становиться все
меньше и меньше. Мы не будем останавливаться на условиях и скорости сходимости
метода Ньютона-Рафсона. Скажем только, что если начальное приближение выбрано
достаточно хорошо и матрица системы линейных уравнений D.3.3) на каждой итерации
хорошо обусловлена и имеет обратную матрицу, то метод Ньютона-Рафсона сходится
к единственному в данной окрестности решению
lim
1—ЮО
= xf, г = 1, 2, ..., п.
Метод Ньютона-Рафсона имеет квадратичную сходимость
\х^г+^-х{*\ ^М\х^ -Xi*\2, i = l,2,...,n,
где М определяется матрицей системы D.3.3) и удовлетворяет неравенству
D.3.5)
Это сравнительно быстрая сходимость — после очередной итерации погрешность ка-
каждой неизвестной уменьшается примерно на один или два порядка. Итерационный
процесс решения системы нелинейных уравнений D.3.1) заканчивается, когда на оче-
очередной итерации погрешности всех неизвестных становятся меньше заданной вели-
величины е:
|Дж»| < е для всех i = 1, 2, ..., п.
Запишем систему линейных уравнений D.3.3) в матричном виде
D.3.6)
где
dfi
dxi
dh
dxi
dfn
dxi
dfi
dX2
df2
dx2 '"
dfn
dx2 '"
dfr
dxn
df2
dxn
dfn
dxn.
(r)
f(x'r») =
F'(x^) — матрица Якоби, которая одновременно является матрицей системы линей-
линейных уравнений D.3.3), f(a;M) = [fi(x^) h{x{r)) ... fn(x^)]T — матрица-столбец
значений функций D.3.1), х'7") = [х^ х2^ ¦¦¦ xnW]T — матрица-столбец неизвест-
неизвестных на г-м приближении. Запись системы D.3.3) в матричной форме D.3.6) похожа
на запись
4.3. Решение системы нелинейных уравнений 217
метода Ньютона для одного нелинейного уравнения. Рекуррентное соотношение для
одного нелинейного алгебраического уравнения f(x) = 0 имеет вид
df(x('))/dx'
Рекуррентное соотношение D.3.4) для системы уравнений D.3.3) в матричной форме
имеет вид
Модифицированный метод Ньютона. В некоторых случаях для решения системы
D.3.1) применяется модифицированный метод Ньютона, который имеет вид
F'(T(°h(x(r+1) — x(r)i — — f МГЛ (А Ч 71
Модифицированный метод Ньютона отличается тем, что при решении системы линей-
линейных уравнений матрица F' не вычисляется на каждой итерации заново, а использу-
используется матрица, вычисленная на первой итерации F'(a;@)). Модифицированный метод
Ньютона обладает линейной сходимостью, поэтому для получения той же точности он
требует больше итераций, чем метод Ньютона. Но общие вычислительные затраты мо-
модифицированного метода Ньютона за счет расчета по готовой матрице могут оказаться
меньшими, чем у метода Ньютона. Модифицированный метод Ньютона является пред-
представителем стационарных методов решения нелинейных систем уравнений в силу того,
что матрица F'(x(°)) не зависит от номера итерации.
Если система D.3.1) имеет большую размерность, то хорошие результаты дает ком-
комбинация метода Ньютона и модифицированного метода Ньютона, когда после очередной
итерации метода Ньютона выполняется несколько итераций модифицированного метода
Ньютона.
Метод Ньютона D.3.6) допускает еще одно видоизменение, которое называется
методом Ньютона с параметром и имеет вид
F'(r^) • (x(r+1) - x<rh — —r(r)f Cr(rh (A 3 81
где т(г) — изменяющийся на каждой итерации параметр. Параметр как бы коррек-
корректирует правую часть системы D.3.3), «улучшая» решение на итераций. Для исполь-
использования метода Ньютона с параметром нужно иметь способ вычислять или оценивать
параметр т^. Оценку параметра можно выполнять по приращениям неизвестных на
итерационном шаге. Параметр обычно имеет значения 1 ^ т^ ^ 2. Метод Ньютона с
параметром обладает линейной сходимостью.
Метод простой итерации. Рассмотренные методы Ньютона являются представите-
представителями неявных методов решения нелинейных систем уравнений в силу того, что ма-
матрица F'(x(r)) не является единичной. К явным методам относится метод простой
итерации, который получим из D.3.8) заменой F'(x^) на единичную матрицу
x(H-i) _ ХМ _ T(r)f(x(r)\ D.3.9)
Если в D.3.9) т"(г) = г = const не зависит от итерации, то получим метод релаксации.
Метод простой итерации сходится, если ||Е — t^F'(x^)\\ < 1. Метод простой итера-
итерации не требует решения системы линейных алгебраических уравнений, но сходится
медленнее других рассмотренных методов (в определенных случаях он не сходится).
Метод Якоби. Рассмотренные до сих пор методы являлись линейными относительно
новой итерации x^r\ i — 1, 2, ..., п. Существуют и нелинейные методы, когда для
вычисления х^ приходится решать нелинейные уравнения. Одним из нелинейных
218 Гл. 4. Операции над кривыми и поверхностями
методов является метод Якоби, в котором решаются п нелинейных уравнений
i\x2W,...,xn(r))=0,
Wp+1),...,*n(p)) = 0> D.3.10)
В каждом уравнении неизвестной считается только одна величина. Любое уравнение
fi(xi^r\ X2^rK . ¦., Xi-\(r\ x^r+1\ xi+i^r\ ..., xn^) = 0 может быть решено отдельно
от других одним из описанных методов применительно к одному уравнению.
Метод Зейделя. Другим нелинейным методом является метод Зейделя, в котором
решаются п нелинейных уравнений
;W)=V, D.3.11)
fn{x&+l\ x2(r+V, ..., zn(r+1>) =0,
в г-м уравнении неизвестной считается величина х^г+1\ Уравнения D.3.11) решаются
последовательно, так что в г-м уравнении все Xj(r+l\ j = 1, 2, ..., г — 1 известны
из решения предыдущих уравнений. Нелинейные методы сходятся гораздо медленнее
метода Ньютона. В нелинейных методах не требуется строить матрицу системы урав-
уравнений. Решение каждого уравнения D.3.10) или D.3.11) выполняется независимо от
других уравнений системы. Решение каждого уравнения в свою очередь выполняется
итерационно. Эти итерации называются внутренними, а итерации для всей системы
нелинейных уравнений называются внешними.
• Большое распространение получили гибридные методы, когда внешние итерации
осуществляются одним методом, а внутренние итерации — другим. Например, внеш-
внешние итерации можно выполнять методом Ньютона, а внутренние (итерационное реше-
решение системы линейных уравнений) — методом Зейделя. При этом внутренние итера-
итерации необязательно выполнять до тех пор, пока решение будет удовлетворять заданной
точности, а можно ограничиться некоторым заданным числом итераций.
Метод градиента. В методе скорейшего спуска или методе градиента решение
системы D.3.1) сводится к задаче отыскания минимумов функции U(xi, х%, ..., хп),
которую можно построить различными способами, например,
,x2,...,xn)J = fT-f D.3.12)
t=i
или
п п
U(xi, х2, ..., хп) = y^y^e»j/i(si, х2, ..., xn)fj(xi, х2, ..., хп) = fT-Af, D.3.13)
где a.ij — элементы некоторой положительно определенной матрицы A, f T= [/i /2 ... /„]
и f = [/i /2 ... fn]T — матрица-строка и матрица-столбец, элементами которых явля-
являются правые части уравнений системы D.3.1). Функцию D.3.12) будем считать част-
частным случаем функции D.3.13). Если х\*, х2*, ..., хп* есть некоторое решение си-
системы D.3.1), то U(xi*, х2*, ..., хп*) = 0. В других точках U(xi, х2, ..., хп) > 0 в
силу положительной определенности матрицы А. Таким образом, решение системы
D.3.1) сводится к поиску нулевых минимумов функции U(x\, x2, ¦ ¦., хп). Будем рас-
рассматривать функцию U(x\, Х2, ¦ ¦ •, хп) как некоторую скалярную функцию п-мерного
4.3. Решение системы нелинейных уравнений 219
векторного пространства и будем обозначать ее еще и как С/(х), где искомые величины
считаются компонентами п-мерного вектора х = [х\ xi ... хп]т. Производные dU/dxj,
j = 1, 2, ..., п в этом пространстве являются компонентами вектора
,тт \dU dU dU]T ,ЛП л.
Vt/ = gradt/ = — —- ... — , 4.3.14
[dxi дх2 дхп\
для функции D.3.12):
— -V2f.fr, т, dfj(x1,x2,...,xn)
их-, i=i их-,
В матричной записи на r-й итерации градиент D.3.14) для функции D.3.12) имеет вид
Vf/ = 2F'T(xW) ¦ f(x(r)), D.3.15)
где F' (x^7")) — транспонированная матрица Якоби F'(x(r)), которая определена в
D.3.6). Вектор Vf/ как градиент скалярной функции, вычисленный при некоторых
значениях х^г\ Х2^г\ ..-, хп(г\ ортогонален поверхности уровня, для которой
U(xi, x2, ¦ ¦., х„) = U{x^r\ X2^r\ ¦.., х„^) = const, и направлен в сторону возраста-
возрастания функции U(xi, Х2, • • ¦, х„) в данной точке n-мерного пространства. Таким образом,
итерационная зависимость для определения экстремума функции U(xi, Х2, ...,хп)
имеет вид
x(r+i) _ x(r) _ A(r)vf/(x(r>) = x(r> - A(rJF'T(xW) • f(xM). D.3.16)
Остается определить множитель А^. Для этого подставим новое приближение D.3.16)
в исследуемую функцию U(xi, x2, . ¦., х„) и рассмотрим ее как функцию параметра А
п
U(X) = f/(xw - AVf/(xW)) = Y,(fi{x{r) ~ AVf/(xW))J.
Параметр А должен иметь такой знак, чтобы от итерации к итерации функция f/(A)
уменьшалась, а величина параметра А должна позволять при данном векторе УЩх^)
как можно ближе продвинуться к минимуму функции С/(А). Параметр А приближенно
можно найти следующим образом. Считая параметр А малой величиной, разложим
функцию С/(А) в ряд Тейлора по степеням А в окрестности нуля с точностью до слагае-
слагаемых второй степени. В результате получим
( (C))T WJ D.3.17)
t=i
fft 5ft ...M
_dxi дх2 дхп\ |xW
Функция f/(A) дает изменение значения функции t/(x(r)) вдоль нормали Vf/(x(r)) к
поверхности уровня в точке х(г), поэтому значение параметра получим из условия ми-
минимума функции U(X) как корень уравнения С/'(А) = 0. Возьмем производную С/(А)
220 Гл. 4. Операции над кривыми и поверхностями
по Л, приравняем ее нулю и получим уравнение для определения Л
= 0.
Отсюда получим параметр
П -г-
л(г) _ i=l + (t -t -t)-t
где мы использовали равенство D.3.15) и для краткости обозначили F' = F'(x(r)),
f = f(x(r)). Таким образом, для принятых упрощений равенство D.3.16) примет вид
= х(г)
г'Т
T
f) • (F' • F'T • f)T
F'T(x«) • f(x^). D.3.18)
В процессе решения следует следить за поведением параметра Л^г'. Он не должен
возрастать от итерации к итерации и должен изменяться плавно. Существует много
разновидностей метода градиента на основе управления этим параметром. Для дважды
дифференцируемых функций fi(x\, Х2, ¦ ¦., xn), i — 1, 2, ..., п, можно получить более
точные формулы для параметра А^.
Если начальное приближение выбрано удачно и в окрестности искомого нулевого
минимума функции U(xi, X2, ¦ ¦., хп) нет других минимумов, то метод градиента до-
довольно быстро даст искомое решение с заданной точностью. Если в окрестности иско-
искомого решения функция U(x\, X2, ¦ ¦., хп) имеет другие минимумы, то итерационный
процесс D.3.16) сойдется, но не обязательно даст решение исходной системы уравнений
D.3.1).
Сжимающий оператор. Все рассмотренные методы решения системы нелинейных
уравнений можно записать в виде
M(zM)(x(r+1> - х^) = -rfr'b(i(r»), D.3.19)
где М(а;(г)) — квадратная матрица размерности n, b(a;(r)) — матрица-столбец, т^ —
скалярный параметр, х(г) — n-мерный вектор некоторого линейного нормированного
пространства, компонентами которого являются искомые величины на г-й итерации
решения. Для всех методов в искомой точке х* = [xi* X2* ... хп*]т выполняется
равенство Ь(х*) = 0. Если условно решить уравнение D.3.19) относительно х(г+1\ то
получим
x(r+i) _ х(г) _ T(r)M-i(x(r)j. Цх^) = S(xW), D.3.20)
где S(x(r') будем называть оператором, отображающим n-мерное пространство само
на себя. Точка х* является неподвижной точкой оператора, так как для нее выпол-
выполняется равенство х* = S(x*). Оператор называется сжимающим в некоторой области
n-мерного линейного нормированного пространства, если существует число 0 < q < 1
такое, что для любых х^г+1^ и xf-r\ принадлежащих этой области, выполняется нера-
неравенство
4.4. Решение системы линейных уравнений 221
Величина q называется коэффициентом сжатия. Существует доказательство того, что
если оператор S(x) является сжимающим на всем конечномерном линейном нормиро-
нормированном пространстве, то он имеет единственную неподвижную точку х* и итерацион-
итерационный процесс D.3.20) сходится к этой неподвижной точке при любом начальном х(°).
Для погрешности решения на r-й итерации справедлива оценка
||х(г) — х*|| < лг11х(°) - v*ll
IIх х II ^ Ч IIх х II-
Операторы, соответствующие рассмотренным итерационным процессам, являются сжи-
сжимающими только в некоторых окрестностях решений, но если в процессе вычислений
мы не выходим из окрестности, где оператор является сжимающим, то итерационный
процесс сойдется к единственному в этой окрестности решению.
4.4.* Решение системы линейных уравнений
В процессе решения системы нелинейных уравнений D.3.1) на каждой итерации
требуется решать систему линейных алгебраических уравнений
Gi I Xi + О12Ж2 + 013X3 + •••+ ainXn = Ь\,
0,22X2 + CI23X3 + .. . + п2пХп = &2,
0,32X2 + аззжз + ... + a3nxn = Ь3, D-4.1)
апзхз + ... + аппхп = Ьп
для неизвестных величин Xi, г = 1, 2, ..., п. Если вернуться к системе уравнений
D.3.3), то из нее система D.4.1) получена путем обозначения Axi через хс, —¦? —
OXj
через aij\ —fi(x^) — через bj. Для удобства записи системы уравнений коэффици-
коэффициенты aij представим в виде квадратной матрицы А, неизвестные х^ и правые части bj
представим в виде матриц-столбцов х = [xi х2 ¦ ¦ ¦ хп]т и b = [61 62 • ¦ • bn]T. В матрич-
матричной записи система линейных уравнений D.4.1) имеет вид
А ¦ х = Ь. D.4.2)
Система D.4.1) имеет единственное решение, если определитель матрицы А отли-
отличен от нуля. Существует много методов решения системы уравнений D.4.1). Некоторые
методы рассчитаны на матрицы А специального вида (трехдиагональные, симметрич-
симметричные, разреженные). При выполнении операций над геометрическими объектами ма-
матрица А имеет общий вид. Все методы решения систем линейных алгебраических
уравнений условно можно разделить на две группы: прямые методы и итерационные
методы. В прямых методах решение находится за конечное число арифметических
действий. В итерационных методах решение находится как предел последовательных
приближений искомых функций х^г\ г = 1, 2, ..., п. Как правило, прямые методы
быстрее и с большей надежностью дают решение системы, но итерационные методы
требуют во много раз меньше памяти во время вычислений. Эти обстоятельства играют
главную роль при выборе метода решения.
Метод исключения Гаусса. Одним из наиболее часто применяемых прямых методов
решения системы линейных уравнений является метод исключения Гаусса. Заме-
Заметим, что решение системы уравнений D.4.1) не зависит от порядка, в котором запи-
записаны составляющие систему уравнения, поэтому строки системы можно безболезненно
переставлять местами, если это будет необходимо. Среди коэффициентов аи, a,2i, ...
..., ani найдем максимальный по абсолютной величине коэффициент. Пусть это будет
222 Гл. 4. Операции над кривыми и поверхностями
коэффициент aki- Переставим местами 1-е и k-е уравнение. Тем самым мы избежим
ситуацию, когда коэффициент при первом неизвестном равен нулю: ак\ не может быть
равен нулю, иначе был бы равен нулю определитель матрицы А. В матричной записи
перестановка 1-й и к-й строк уравнения осуществляется умножением уравнения D.4.2)
на элементарную матрицу перестановки Рщ
Pifc-A x = Plfc b,
которая получена из единичной матрицы Е перестановкой в ней 1-й и k-ft строк. В про-
процессе решения системы уравнений будут меняться местами строки матрицы. В конце
процесса исключения неизвестных матрица А будет п раз умножена на элементар-
элементарные матрицы перестановки, т. е. фактически мы будем работать не с матрицей А, а с
матрицей Р • А, где Р — произведение элементарных матриц перестановки. У ма-
матриц перестановки в каждой строке и каждом столбце только один элемент отличен от
нуля и равен единице. Элементарные матрицы перестановки определяются в процессе
исключения неизвестных. Для упрощения записи через ау в дальнейшем будем обо-
обозначать коэффициенты матрицы Р • А, а через А в дальнейшем будем обозначать
матрицу Р • А. Другими словами, будем считать, что нам заранее известен способ
перестановки уравнений системы D.4.1), позволяющий избежать появление нулевых
элементов на диагонали матрицы в процессе исключения неизвестных. Умножение
произвольной матрицы на элементарную матрицу перестановки изменяет знак опреде-
определителя матрицы, сохраняя значение определителя.
От перестановки уравнений решение системы не изменится. Решение системы
линейных уравнений не изменится, если любое уравнение поделить или умножить на
произвольное не равное нулю число, а также, если к правой и левой частям любого
уравнения прибавить любое число или линейную комбинацию остальных уравнений
системы. Используем эти свойства для того, чтобы обратить в нуль коэффициенты ад
при первой неизвестной кроме аи (бывший aki). Для этого поделим первое уравнение
на аи и получим его в виде
xi+ui2x2+...+ulnxn = yi, D.4.3)
где
щ j~—-, j=2, 3, ..., n, yi~—.
ац ац
Из остальных уравнений вычтем уравнение D.4.3), умноженное на ак\, соответственно
для к-то уравнения. В результате каждое к-е уравнение примет вид
D.4.4)
где
akj{1) =aki -ajfei^1, j = 2,3, ...,n,
bk{l) =bk-akl^-, 4 = 2,3,..,».
ац
Таким образом, от системы D.4.1) мы перейдем к эквивалентной ей системе уравнений
Х\ + Щ2Х2
4.4. Решение системы линейных уравнений 223
в которой только первое уравнение содержит неизвестную х\. Если бы из остальных
уравнений удалось найти х2, хз,..., хп, то неизвестная х\ определилась бы равенством
xi = yi — U12X2 — «хз^з — ... — щпхп. Матрицу системы уравнений D.4.5) обозначим
через А^1). Рассмотрим систему уравнений D.4.5) без первого уравнения. Она анало-
аналогична системе D.4.1), только содержит на одно уравнение меньше и меньше на одну
неизвестную величину
а3зA)жз + • • • + а3пA)а;„ = 63A), D.4.6)
С системой D.4.6) поступим аналогично тому, как мы от системы D.4.1) перешли к
системе D.4.5). В результате придем к системе уравнений
Х\ + Ui2X2 + U13Z3 + M14Z4 + • . . + ЩпХп = ух,
«24^4 + • • • + U2nXn = J/2,
2)z4 + ... + а3„B)а;п = 63<2),
2)а;4 + • • • + а4„B)а;„ = 64B),
ЯпЗB)а;з + ап4B)а;4 + ... + о„пB>:гп = bj2),
где
U2j =
," = 3, 4, .... n,
Из уравнений D.4.7) можно выделить систему, содержащую еще на одну неизвестную
величину меньше. Матрицу системы уравнений D.4.7) обозначим через А*2). Продол-
Продолжая этот процесс далее, придем к системе линейных уравнений треугольного вида
... + uln-xxn-i + Щпхп = ух,
U23X3 + • . . + «2n-lZn-l + U2nXn = J/2,
Х3 + ... + U3n-ixn-i +U3n.xn = уз,
D 4 8)
Xn_x + «n-ln^n = J/n-1,
%n — Уп>
которая эквивалентна исходной системе D.4.1). Таким образом, мы перешли от си-
системы уравнений D.4.2) к системе
U • х = у. D.4.9)
Матрица U системы D.4.8) содержит нули под главной диагональю и поэтому называ-
называется верхней треугольной матрицей. На главной диагонали этой матрицы стоят еди-
224
Гл. 4. Операции над кривыми и поверхностями
ницы. Коэффициенты матрицы вычисляются строка за строкой
u =
0
0
0
1 .
0 .
0 .
• • Wln-1
1
0
Win
U2n
Un-ln
1
0
0
0
aa
1 ...
0 ...
0 ...
an
a2n-x^
/n
Q,oo ^ ¦*
l
0
an
O2J»
О22*1)
an-in("-2)
1
Алгоритм вычисления коэффициентов матрицы U по коэффициентам матрицы А вы-
выражается формулами
_@)__ к — ~\ 0 г>
J =
D.4.10)
n,
к которым нужно добавить поиск максимального коэффициента ai^, г = к + 1,
& + 2, ..., п и перестановку уравнений. Будем считать, что перестановка уравнений на
каждом шаге выполняется описанным выше способом. Алгоритм вычисления правой
части у по коэффициентам матрицы А и b выражается формулами
= bk, k = 1, 2, ..., n, j/fc =
D.4.11)
Процесс перехода от системы D.4.1) к системе D.4.8) называется прямым ходом
метода Гаусса. Обратным ходом метода Гаусса называется процесс определения неиз-
неизвестных xn, xn-i, •••, %2, х\ из системы D.4.8). Зто легко сделать, определяя хп,
a;n_i, ..., Х2, X} последовательно, начиная с последнего неизвестного и используя со-
соотношение
i = n — 1, n — 2, ..., 2, 1.
D.4.12)
j=t+l
Описанный метод решения системы линейных уравнений называется методом Гаус-
Гаусса с выбором главного элемента по столбцу, так как в процессе прямого хода мы искали
уравнение с максимальным коэффициентом при «первом» неизвестном соответствую-
соответствующей системы уравнений.
В методе Гаусса можно искать главный элемент по строке. В этом случае меняются
местами не уравнения, а неизвестные во всех уравнениях. Например, пусть требуется
решить систему уравнений D.4.1). Среди коэффициентов an, ai2, • •., а\п, найдем мак-
максимальный по абсолютной величине коэффициент. Пусть это будет коэффициент ац..
4.4. Решение системы линейных уравнений 225
Перепишем систему, переставив местами 1-е и к-е неизвестное во всех уравнениях:
+ 012^2 + . • • + aik-iXk-i + anXi + aik+iXk+i + ... + a\nxn = b\,
+ «22^2 + • • • + CL2k-lXk-l + 021^1 + &2k+\Xk+l + ¦ ¦ • + 0,2nXn = b2,
... + a3na;n = 63, D.4.13)
ank-\Xk-i + aniX\ + ank+iXk+i + ... + annxn — bn
Тем самым мы избежим ситуацию, когда коэффициент при первом неизвестном равен
нулю. От перестановки местами слагаемых в уравнениях решение системы не изме-
изменится. Далее перенумеруем неизвестные и выполним описанные в D.4.3) и D.4.4)
действия. В результате придем к системе D.4.5), в которой рассмотрим последние
п — 1 уравнений. Далее найдем максимальный коэффициент среди агг^, агз^> ...
..., п2п^ и повтйоим вышеописанные преобразования для системы размерности на
единицу меньше. Метод Гаусса с выбором главного элемента по строке аналогичен ме-
методу Гаусса с выборок! главного элемента по столбцу, с той разницей, что при выборе
главного элемента по строке выполняется перенумерация неизвестных.
Можно испо ль зовать\ метод Гаусса с выбором главного элемента по всей матрице, в
котором переставляются местами уравнения, и производится перенумерация неизвест-
неизвестных на каждом шаге.
Метод разложения матрицы- Систему линейных алгебраических уравнений D.4.1)
можно решить методом разложения матрицы А в произведение верхней треуголь-
треугольной матрицы U и нижней треугольной матрицы L. Предположим, что имеет место
разложение
А = L U, D.4.14)
тогда система D.4.2) примет вид
L U х = b D.4.15)
и ее можно заменить двумя уравнениями
L • у = Ь, D.4.16)
U • х = у. D.4.17)
Из уравнения D.4.16) с нижней треугольной матрицей L прямой подстановкой, начи-
начиная с первого элемента, легко находится матрица-столбец у, а из уравнения D.4.17) с
верхней треугольной матрицей U подстановкой, начиная с последнего элемента, легко
находится матрица-столбец неизвестных х. Вычисления выполняются по формулам
1 / п
х =
, ( (j/i У2 ijj), » = n-l, n-2, ..., 2, 1. D.4.19)
Остается только получить разложение D.4.14).
Фактически при выполнении исключения неизвестных в методе Гаусса неявно вы-
выполняется разложение матрицы А в произведение нижней треугольной матрицы L и
верхней треугольной матрицы U. Матрицу U мы получаем в явном виде с помощью
15 - 5293 Голованов
226
Гл. 4. Операции над кривыми и поверхностями
формул D.4.10); из этих же формул можно в явном виде получить матрицу L. Пере-
Переход от системы уравнений D.4.1) к эквивалентной ее системе D.4.5) в матричном виде
можно представить как умножение уравнения D.4.2) слева на матрицу Si:
Si Ax = Si b,
где матрица Si имеет коэффициенты
D.4.20)
au
Q21
an
Q31
an
0
1
0
0 ..
0 ..
1 ..
. 0
. 0
. 0
«и
0 0
1
Переход от системы уравнений D.4.5) к эквивалентной ее системе D.4.7) в матричном
виде можно представить как умножение уравнения D.4.20) слева на матрицу S2:
S2 Si • Ax = S2 Si b,
где матрица S2 имеет коэффициенты
Г1 0 0 ... О'
О -Лтг 0 ... О
D.4.21)
S2 =
о -
a22d)
1
О
0 -
0
На k-м шаге исключения метода Гаусса система уравнений, полученная на предыдущем
шаге, умножается на матрицу
D.4.22)
В результате прямого хода метода исключения Гаусса придем к системе уравнений
D.4.8), которую можно представить в виде
SAx= Sb,
D.4.23)
4.4. Решение системы линейных уравнений
227
где
S = Sn-Sn_i-...-S2-Si. D.4.24)
Таким образом, мы получили, что U = Sn • Sn_i •... • S2 • Si • А, откуда следует, что
А = (Sn ¦ Sn_i ¦... ¦ S2 ¦ Si) • U. D.4.25)
Матрица типа D.4.22) называется элементарной нижней треугольной матрицей.
Обратная к D.4.22) матрица также является элементарной нижней треугольной матри-
матрицей и имеет вид
D.4.26)
Произведение элементарных нижних треугольных матриц D.4.26) и есть нижняя тре-
треугольная матрица, которая присутствует в разложении D.4.14):
(Sn ¦ Sn_i • ... • S2 • Si) = Si ¦ S2 •... • Sn-i ¦ Sn =
О anfc(fc-D 0 ... 1.
= L =
"an
a2i
a3i
.ani
0
a22A)
a32«
аП2^
0
0
азз<2> ...
an3B) _ _ (
0
0
0
Inn("-1)
D.4.27)
Докажем, что любую квадратную матрицу А, все угловые миноры которой отличны
от нуля, можно разложить в произведение нижней треугольной матрицы L и верх-
верхней треугольной матрицы U с единицами на главной диагонали. Будем называть г-м
угловым минором Mi матрицы А определитель, составленный из первых i элементов
первых i строк этой матрицы:
D.4.28)
Доказательство проведем методом индукции. Для матрицы второго порядка это разло-
разложение имеет вид
fan a12l = рп 01 Г1 ul2\
\а.2\ a22j [/21 '22J [О 1
an
О21
a3i
an
012
О22
032
а*2
а13 ...
а2з •••
азз •¦•
сцз ...
аи
a2i
азг
аи
где /и = оц,
= a2i, /22 =
Qi'\'\Qi22 —
• По условию
О,
аи аи
— a2iai2 Ф 0, следовательно, 1ц ф 0, /22 ф 0. Пусть существует разложение
15*
228
Гл. 4. Операции над кривыми и поверхностями
D.4.14) матриц (к — 1)-го порядка; докажем, что аналогичное разложение существует
для матриц fc-ro порядка. Для этого представим матрицу fc-ro порядка в виде
аи
ЙЦ-1
Ofc-12
OjtJt-1
Ъ*1
где через A*_i обозначена матрица (к — 1)-го порядка, afc = [a^i ak2 ... akk-i], bfc =
= [au O2fc ••• a*;-u]T- Согласно предположению индукции А*_1 = Ljt-i • U^-i, где
Lfc_i — нижняя треугольная матрица (к — 1)-го порядка, Ufc_i — верхняя треугольная
матрица (к—1)-го порядка с единичной диагональю. Будем искать разложение матрицы
А* в виде
j
J
0
где lfc = [Zfci Z*2 ••¦ /fcfc-i], Ufc = [uik U2k ••¦ Uk-ik]T — неизвестные пока матрицы.
Выполнив умножение в D.4.29), придем к уравнениям
первое из которых выполняется из предположения индукции, а из остальных трех
определятся 1*, и* и hk- Так как матрицы \5k-i и Lfc_i треугольные, то вычисления
выполняются последовательной подстановкой
i-l
'fci = afci -
i = 2, 3, ..., к — 1,
D.4.30)
3=1
= 7^, и** = т-(а**-51'««>¦*)> * = 2, 3, ...,*-1, D.4.31)
HI Hi \ ^J /
D.4.32)
fc-1
hk — a,kk -
Равенство D.4.32) представляет собой продолжение равенств D.4.30) для г = к. Так
как значение к не было определено, то формулы D.4.30)-D.4.32) являются формулами
для вычисления элементов нижней треугольной матрицы L и верхней треугольной
матрицы U разложения квадратной матрицы. Метод решения системы линейных ал-
алгебраических уравнений путем разложения матрицы системы на нижнюю треугольную
и верхнюю треугольную матрицы часто называют методом Холесского. Коэффициент
Ikk не может быть равен нулю. Это следует из того, что det Ak ф 0 и
|Afc| = \U-i\lkk\Uk-i\ = lkk\U-i\ Ф 0.
Определитель треугольной матрицы (верхней или нижней) равен произведению ее
диагональных элементов, поэтому detU^-i = 1, так как на главной диагонали тре-
треугольной матрицы Ufc_i стоят единицы. Таким образом, Ikk ф 0.
4.4. Решение системы линейных уравнений
229
Формулы D.4.29)-D.4.32) доказывают, что любую квадратную матрицу А, все угло-
угловые миноры которой отличны от нуля, можно разложить в произведение нижней тре-
треугольной матрицы L и верхней треугольной матрицы U с единицами на главной диа-
диагонали. Такое разложение единственно. Единственность разложения можно доказать
методом от противного.
Метод Якоби. Одним из итерационных методов решения системы линейных алге-
алгебраических уравнений D.4.1) является метод Якоби. Выразим из каждого уравнения
системы одну из неизвестных величин х^, i = 1, 2, ..., п. Например, из г-го уравнения
выразим г-ю неизвестную и перепишем систему в виде
г-1
Xi =
2S. >-*•* "¦
D.4.33)
j=t+i
В D.4.33) предполагается, что все пц не равны нулю. Этого всегда можно достичь
с помощью перестановок уравнений местами, что приводит к перестановке строк ма-
матрицы. Через х^Т\ Х2^Т\ ¦ ¦., хп^ обозначим значения неизвестных на r-й итерации
решения системы уравнений D.4.1). Метод Якоби определяет неизвестные на (г + 1)-м
приближении через неизвестные на r-м приближении с помощью равенства
.(r+1) _
h
г-1
^ж-(Г) г-1 2 п
D.4.34)
Начальные приближения х\^, х2^, • • •, Хп^ могут быть выбраны любыми, при пол-
полной неопределенности их можно положить равными нулю. Итерации выполняются до
тех пор, пока на очередной итерации погрешности всех неизвестных не станут меньше
заданной величины е > О
< е для всех i = 1, 2,
п.
D.4.35)
Для n-мерного вектора, компонентами которого являются неизвестные на r-м при-
приближении, введем обозначение х(г' = [х^ х2^ ¦ ¦. хп^]т. Через D обозначим диа-
диагональную матрицу, ненулевые элементы которой равны диагональным элементам ма-
матрицы А. Через С обозначим нижнюю треугольную матрицу, ненулевые элементы
которой равны элементам матрицы А, стоящим под главной диагональю матрицы А.
Через R обозначим верхнюю треугольную матрицу, ненулевые элементы которой равны
элементам матрицы А, стоящим над главной диагональю матрицы А. Эти матрицы
имеют вид
0 0
a21 0
an_u an_12
am an2
0
0
0
... ann
*
¦o
0
0
0
-i
a12
0
0
0
o-
0
0
0.
... ain_]
.. a2n-]
0
0
"an
0
0
. 0
a
0
a22
0
0
ain '
a27l
n—1?»
0
0
0
¦ • • an_ln_!
0
0
0
0
Через b обозначим вектор правой части: b = [6i b2 ... bn]T. В принятых обозначе-
обозначениях уравнение D.4.2) будет записано следующим образом:
230 Гл. 4. Операции над кривыми и поверхностями
В методе Якоби это уравнение заменяется уравнением D • х^г+1) + (С + R) • х(г) = Ь.
Итерационный процесс метода Якоби в матричной записи с использованием принятых
обозначений имеет вид
x(r+i) = D-i . (ъ _ (С + R) ¦ х<г)). D.4.36)
Итерационный процесс метода Якоби сходится, если норма матрицы D ¦ (С + R)
меньше единицы
Это соответствует требованию преобладания диагональных элементов матрицы А
п
\ац\> ]_>__ |ау|, для всех i = 1, 2, ..., п. D.4.37)
Метод Зейделя. Другим итерационным методом решения системы линейных алге-
алгебраических уравнений D.4.1) является метод Зейделя. Метод Зейделя представляет
собой некоторую модификацию метода Якоби, которая состоит в том, что при вычисле-
вычислении на (г + 1)-м приближении неизвестной Xi учитываются уже вычисленные (г + 1)-е
приближения неизвестных Х\, х%, ¦ ¦., Щ—\, а остальные неизвестные ajj+i, Xi+2, ...
..., хп берутся для r-го приближения
«-I
^-x^r\ t = l, 2, ..., п. D.4.38)
Уравнения D.4.38) решаются последовательно, начиная с первого. К моменту вычи-
вычисления из г-го уравнения (г + 1)-го приближения г-й неизвестной х^г+х^ (г + 1)-е при-
приближения неизвестных a;i(r+1), x2(-r+1\ ..., Xj_i(r+1) уже вычислены из предыдущих
уравнений. Развернутая запись уравнений системы имеет вид
(г+1) _ ^1 _ a12 (r) _ Q13 (Г) _ Q_4 (r) _ _ Qln (r)
Оц an an «и an
022 a22 О22 Я22 a22
азз азз азз азз азз
Начальные приближения х\(°\ ж2'°\ •••, хп^ могут быть выбраны произвольными.
Итерации выполняются до тех пор, пока на очередной итерации погрешности всех
неизвестных не станут меньше заданной величины е > 0.
В методе Зейделя уравнение D.4.2) заменяется уравнением (С + D) • x^r+1) +
-t-R • х(г) = b. В матричной записи итерационный процесс метода Зейделя имеет вид
x(r+i) = (с + D) • (Ь - R х<г>). D.4.39)
Итерационный процесс метода Зейделя сходится, если норма матрицы (С + D) • R
меньше единицы
4.4. Решение системы линейных уравнений 231
Это неравенство также приводит к требованию преобладания диагональных элементов
в матрице А, т. е. методы Якоби и Зейделя для сходимости предъявляют одинаковые
требования к коэффициентам системы уравнений
\a*j\, для всех i — 1, 2, ..., п.
Обычно метод Зейделя сходится лучше, чем метод Якоби, хотя это происходит не всегда.
Процесс Зейделя может сходиться, когда метод Якоби расходится, хотя известны и
обратные случаи.
Метод релаксации. Иногда перестановка местами уравнений или перенумерация
неизвестных улучшают сходимость метода Зейделя. Можно использовать еще один
способ для улучшения сходимости. Этот способ приводит к методу релаксации. На
r-м приближении каждое уравнение системы D.4.1) удовлетворяется неточно и дает
некоторую невязку
((r) + ^ + ai3x3{r) + ... + ainxjr) -bt), i = 1, 2, ..., п. D.4.40)
Следующее приближение первой неизвестной х^1"^1 найдем из равенства нулю макси-
максимальной невязки, т. е. из уравнения
) + • • • + aknxn^ - bk = О,
где А; — номер уравнения с максимальной по модулю невязкой. Затем вычислим не-
невязки при полученной неизвестной ^^
П = — (auzi(r+
+ <Wr)
и найдем следующее приближение второй неизвестной жг^г+1^ из равенства нулю мак-
максимальной невязки
amixi(r+l) + am2z2<r+1) + am3z3<r) + ¦ ¦ • + amnxn^ - bm = 0,
где m — номер уравнения с максимальной по модулю невязкой. Продолжим такие
действия и дальше пока не используем все п уравнений, из которых уточним все п
неизвестных величин. После этого аналогичным образом найдем следующее прибли-
приближение решения системы. Итерационный процесс заканчивается, когда на очередной
итерации погрешности всех неизвестных не станут меньше заданной величины е > 0.
Начальные приближения х\^°\ Х2^°\ ..., хп(°"> могут быть выбраны произвольным
образом. Критерии сходимости метода релаксации аналогичны критериям сходимости
методов Якоби и Зейделя. Метод релаксации в отличие от методов Якоби и Зейделя
является нестационарным методом.
Метод невязов. Рассмотрим еще один итерационный метод решения систем линей-
линейных алгебраических уравнений. Он относится к итерационным нелинейным методам.
В этом методе новое приближение искомых функций жх(г+1), х2(-г+1\ ¦ ¦ ¦, хп(-г+1^ свя-
связывается с предыдущим приближением искомых функций х\(Т\ Х2^г\ ¦ ¦., хп^ рекур-
рекуррентным соотношением
хр+Ъ=х№-\{-г)р№1 * = 1, 2, ..., п, D.4.41)
где р^ — некоторые коррекции неизвестных, А^г^ — скалярный множитель. В ма-
матричной записи с использованием обозначений х'7") = [х^ Х2^ ¦¦¦ ¦ х„(гЦт и р(г) =
= [pi(r) P2^ ¦ ¦ ¦ Рп^]т для неизвестных и коррекцией на r-й итерации соотношение
232 Гл. 4. Операции над кривыми и поверхностями
D.4.41) имеет вид
x(r+i)=x(r)_A(r)p(r)_ D.4.42)
Рассмотрим матрицу-столбец невязок уравнений системы D.4.1) q'r) = А • х^г^ — Ь,
с компонентами q^ — пцх^ + а^г^ + счзхз^ + ¦ ¦ ¦ + а*па:п(г) - Ь,. Невязки
уравнений системы на соседних итерациях связаны соотношением
q(r+i) _ А . x(r+i) _ ь = А • х<г) - А<г> А • р<г> - Ь = q<r> - AW А • р<г>. D.4.43)
Будем рассматривать неизвестные х'г), коррекции рМ и невязки уравнений q(r) как
векторы n-мерного пространства. Скалярный множитель А(г) найдем из условия ми-
минимума длины вектора невязки D.4.43). Для этого умножим n-мерный вектор q(r+1)
скалярно на себя, продифференцируем это произведение по А'г) и приравняем произ-
производную нулю, в результате получим
q(r)T . А . р(г) _ Л(г)р(г)Т . АТ . А . p(r) = 0.
Отсюда
Выбор вектора коррекции р(г) определяет ту или иную расчетную схему. Если положить
p(r) = q(r), то тогда
qT . AT . а • qM
и мы получим метод минимальных невязок. Метод минимальных невязок сходится к
точному решению примерно со скоростью метода Якоби. Если начальное приближение
находится далеко от искомого решения, то метод минимальных невязок на начальной
стадии может сходиться очень медленно.
4.5. Проекция точки на линию
Проекция точки на прямую линию. Проекция точки на прямую линию на-
находится достаточно просто и при выполнении некоторых операций нулевое при-
приближение вычисляется как проекция точки на касательную прямую. Рассмо-
Рассмотрим этот частный случай общей задачи.
Пусть дана прямая
l(f) = с0 + tw D.5.1)
и точка р. Будем считать, что вектор прямой w имеет произвольную длину.
Прямая линия проходит через точку Со, в которой параметр t равен нулю,
и имеет направление вектора w. Требуется
р_с ^^^ip найти проекцию точки р на прямую линию
Щ). Эта задача имеет единственное реше-
решение. Построим вектор из точки прямой со
в точку р и вычислим скалярное произведе-
Cq w p, 1@ ние этого вектора и вектора прямой w. На
Рис. 4.5.1. Проекция точки р на пря- Рис" 4-5Л "оказаны направляющий вектор
мую линию Щ) прямой w, ее начальная точка Со и проек-
проекция pi заданной точки. Если разделим это
скалярное произведение на длину вектора w, то получим длину проекции век-
вектора р — со на прямую линию. Если же разделим это скалярное произведение
4.5. Проекция точки на линию 233
на квадрат длины вектора w, то получим длину проекции вектора р — со на
прямую в единицах длины вектора w, т.е. получим параметр f для проекции
точки р на прямую линию.
Таким образом, параметр fp проекции точки р на прямую линию и радиус-
вектор проекции р; вычисляются по формулам
(р - с0) • w
Р ~ Н2 ' D-5-2)
рг = 1(*р) = с0 + ipw. D.5.3)
Если длина вектора w равна единице, то в D.5.2) не требуется выполнять де-
деление на |w|2. Расстояние от точки до ее проекции на кривую в общем случае
вычисляется как длина вектора р; — р. Расстояние от точки до ее проекции на
прямую линию можно определить, не вычисляя проекцию точки, а воспользо-
воспользовавшись формулой
lp = I(p-*]XW|. D.5.4)
Частные случаи. Проекция точки на аналитические кривые также может
быть найдена без привлечения численных методов. Например, чтобы найти
проекцию точки на коническое сечение, нужно перевести проецируемую точку
в местную систему координат конического сечения, спроецировать эту точку на
плоскость конического сечения и найти параметр двухмерной проекции задан-
заданной точки.
Общий случай. Пусть требуется найти все проекции точки р на кривую
линию c(t). Каждая искомая точка кривой с(?) удовлетворяет уравнению
Не
(р - с(*)) • Tt = 0. D.5.5)
Это уравнение содержит одну неизвестную величину — параметр t. Как было
уже сказано, решение этой задачи разобьем на два этапа. На первом этапе
определим нулевые приближения параметров проекций точки на кривую, а на
втором этапе найдем точные значения параметров кривой, определяющие про-
проекции заданной точки р на кривую линию c(t).
Здесь и в дальнейшем будем считать заданным значение предельного утла
отклонения Да кривой. С шагом At, определяемым по формуле D.2.3), прой-
пройдем вдоль кривой описанным выше способом и в каждой точке U вычислим
скалярные произведения векторов
dc dc
Щ = (р - c(U - At)) ¦ —, bi = (р - c(U + At)) ¦ —. D.5.6)
Если искомое решение лежит на параметрическом расстоянии At от параме-
параметра fj, то щ и bi будут иметь разные знаки. Смена знака скалярных произ-
произведений D.5.6) и является тем событием, которое сигнализирует о том, что
рядом находится искомое решение. Примем за нулевое приближение решения
параметр f(°) = f j и одним из методов решения нелинейных уравнений найдем
решение с заданной точностью. Например, с помощью метода Ньютона (г + 1)-е
234 Гл. 4. Операции над кривыми и поверхностями
приближение параметра проекции точки на кривую вычисляется по формуле
Дг+1) _ Лг) , (С - р) ¦ (dc/dt)
(р - с) • (d?c/dt2) - {dc/dt) ¦ {dc/dt)
D.5.7)
Процесс уточнения параметра закончим, когда на очередной итерации \t(r+1)— f (г)|
станет меньше заданной величины е. Таким же образом найдем все остальные
корни уравнения D.5.5).
4.6. Проекция точки на поверхность
Проекция точки на плоскость. Проекция точки на плоскость является част-
частным случаем общей задачи нахождения проекции точки на поверхность. В силу
простоты вычисления проекции точки на касательную к поверхности плоскость
используется в качестве нулевого приближения при решении общей задачи.
Рассмотрим задачу проецирования точки р на плоскость, заданную радиус-
вектором
S{u, v) = So + USi + VS2- D.6.1)
Будем считать, что векторы si и S2 не коллинеарные. Допустим, что в общем
случае векторы sj и S2 не ортогональны и имеют не единичную длину. Плос-
Плоскость проходит через точку so, в которой параметры равны нулю, а векторы
Si и S2 определяют параметрические направления. Заданная точка р имеет
единственную проекцию на плоскость D.6.1).
/ Построим единичную нормаль к плоскости
у'-:->- т=Ш- D-б-2)
Вычислим радиус-вектор ps проекции точки на
плоскость как разность радиус-вектора проеци-
s J" „ ~1 руемой точки и составляющей вектора р — so,
01 ''1 параллельной нормали к плоскости,
Рис. 4.6.1. Проекция ps точки . .
р на плоскость s(u, v) ps = р — m((p — So) • m). D.6.3)
Далее найдем параметры uv и vp, соответствующие проекции точки на плос-
плоскость. Для вычисления параметров проекции точки найдем длины проекций
вектора р — so на векторы s\ и S2, которые обозначим через р\ и р^:
(р-so) -si
pi = —m—' D-6-4)
IS2|
На рис. 4.6.1 показаны векторы плоскости si и S2, ее начальная точка so и
проекция ps заданной точки.
Параметры ир и vp и длины проекций р\ и р2 связаны уравнениями
Pi =«p|si| +up|s
4.6. Проекция точки на поверхность 235
где cosy? = (si • S2)/([si[[в21) —- косинус угла между векторами Si и S2 опре-
определяется по формуле A.7.13). Из системы этих уравнений найдем параметры
проекции точки на плоскость
_ pi -p2COS(p _ g22sl ' (Ра ~ so) ~
Р A - COS2 <p)\si\ gng22
(pe " S0) + g1^ • (pe " So), D.6.6)
_ P2 ~ pi COS <f _ guS2 • (ps ~ Sp) - g12Si • (ps - Sp) _
P ~ A - COSV)|S2| gng22 ~ &12
= S^si • (p, - so) + i2s2 ¦ (p, - so), D.6.7)
где gn = Si • Si, g22 = s2 • s2, gu = Si • s2 — коэффициенты первой основ-
основной квадратичной формы плоскости A.7.8), они же ковариантные компоненты
метрического тензора поверхности, g11, g22, g12, g21 — контравариантные компо-
компоненты метрического тензора поверхности. Если векторы Si и s2 ортогональные,
то gi2 — g21 =Ои формулы D.6.6) и D.6.7) примут вид
_ (р ~ sQ) • si _ (р - sp) • s2
Zip — , Vj) —
Sl • Si p S2 • S2
Расстояние от точки до ее проекции на плоскость в общем случае вычисля-
вычисляется как длина вектора р« —р. Расстояние от точки до ее проекции на плоскость
можно определить, не вычисляя проекцию точки, а вычислив проекцию вектора
р — so на нормаль к плоскости
ls = (р - s0) • m. D.6.8)
Частные случаи. Проекции точки на некоторые аналитические поверхности
могут быть найдены без привлечения численных методов. Например, чтобы
найти проекции точки на поверхность кругового цилиндра, конуса, сферы или
тора, нужно перевести проецируемую точку в местную систему координат по-
поверхности, где легко найти параметры проекций. Аналогично могут быть най-
найдены проекции на поверхности выдавливания и вращения. В некоторых част-
частных случаях положения проецируемой точки ее проекции могут быть легко
найдены и на другие поверхности.
Общий случай. Рассмотрим задачу проецирования точки на поверхность в
общем случае. Пусть требуется найти все проекции точки р на поверхность
s(u, v). Каждая искомая точка поверхности s(u, v) удовлетворяет системе двух
уравнений
ds ds
(р - s(u, v)) ¦ ^ = 0, (р - 8(«, v)) ¦ ^ = 0. D.6.9)
Система уравнений D.6.9) содержит две неизвестные величины — параметры и
и v. Эта задача решается так же, как и задача нахождения проекций заданной
точки на кривую. На первом этапе определим нулевые приближения параметров
236 Гл. 4. Операции над кривыми и поверхностями
поверхности для проекций точки, а на втором этапе найдем точные значения
параметров, определяющие проекции заданной точки р на поверхность s(u, v).
Пройдем по поверхности с шагами Аи и Аи, вычисляемыми по формулам
D.2.4) и D.2.5), описанным выше способом движения по параметрической обла-
области. Обозначим параметры точек, через которые мы пройдем, через щ и Vj.
В каждой точке будем вычислять скалярные произведения векторов
оц = (Р ~ s(«i - Аи, Vj)) • —, bij = (p - s{Ui + Аи, Vj)) • —, D.6.10)
ey = (p-s(«i, Uj-Ди))-—, dij = (p - s{uu Vj + Av)) ¦ —. D.6.11)
Если искомое решение лежит вблизи точки с параметрами щ, vj, то ац и bij
будут иметь разные знаки, а также с^ и dy будут иметь разные знаки. Смена
знаков скалярных произведений (aijbij ^ 0 и Cijdij ^ 0) говорит о том, что ря-
рядом находится искомое решение. За нулевое приближение параметров примем
значения и^ = щ, г/°) = Vj. Начиная с нулевого приближения параметров,
одним из методов решения нелинейных уравнений найдем решение задачи с
заданной точностью. Например, в методе Ньютона на r-й итерации приращения
параметров Аи^т> и Av^r' проекции найдутся из системы линейных уравнений
((р - s) • 8ц - si • si) Ди(г) + ((p - s) • S12 - s2 • si) Ди(г) = (s - p) • si,
((p - S) • S21 - Si • S2)Au(r) + ((p - S) • S22 - S2 • S2)Au(r) = (s - p) • S2,
ds ds d2s 92s 92s
где si = —, s2 = —, sn = -r-r, S12 = s2i = я , s22 = -д-^ — частные
аи av оиг oudv ov2
С
аи av ои oudv ov
производные радиус-вектора по параметрам. Следующее приближение параме-
параметров проекции точки равны г/г+1) = и^ +Аи^г\ г»^г+1^ — v^ + Av(r\ Процесс
уточнения параметров закончим, когда на очередной итерации выполнятся не-
неравенства |u(r+1) — г/г)| < е и |?/г+1) — v(r)\ < е, где е — заданная погрешность.
Таким же образом найдем все остальные корни системы уравнений D.6.9).
Если требуется найти только ближайшую проекцию заданной точки на по-
поверхность, то можно пройти по тем же точкам геометрического объекта и вы-
выбрать из них ближайшую к заданной точке. Параметры ближайшей точки и
следует выбрать в качестве нулевого приближения решения задачи.
Проекция точки на поверхность в заданном направлении. В определенных
случаях возникает задача определения проекции точки р на поверхность не по
нормали к ней, а вдоль заданного направления. Пусть направление проециро-
проецирования задано вектором единичной длины q. Построим прямую линию
l(t)=p + *q, D.6.12)
проходящую через заданную точку и имеющую направление заданного вектора.
Проекции точки на поверхность в заданном направлении определим как точки
пересечения поверхности с прямой D.6.12), проходящей через заданную точку
в заданном направлении.
4.7. Определение точек пересечения линии и поверхности 237
4.7. Определение точек пересечения линии и поверхности
Простейшим представителем кривых является прямая линия, а простейшим
представителем поверхности является плоскость. Точка их пересечения может
быть найдена аналитически. Для определения нулевого приближения каждой
точки пересечения кривой и поверхности будет решаться задача пересечения ка-
касательной линии кривой и касательной плоскости поверхности, поэтому сначала
рассмотрим задачу определения точки пересечения прямой и плоскости.
Пересечение прямой и плоскости. Пусть радиус-векторы прямой линии и
плоскости описываются зависимостями
ф) = с0 + zc', D.7.1)
s(x, у) = s0 + zsi + ys2. D.7.2)
Найдем их точку пересечения. Такая точка существует и является единствен-
единственной, если прямая не параллельна плоскости, т. е. если c'-(si xsi) ф 0. Построим
единичную нормаль m к плоскости по формуле D.6.2) и вычислим значение па-
параметра прямой, соответствующее точке пересечения плоскости и прямой
= m.(sQ-4
m • t:' ;
На рис. 4.7.1 показаны прямая и плоскость при взгляде параллельно плоско-
плоскости. В числителе правой части D.7.3) стоит расстояние от начальной точки со
m
Рис. 4.7.1. Пересечение прямой и плоскости
прямой до плоскости, а в знаменателе стоит нормальная к плоскости составляю-
составляющая производной прямой: отношение этих величин даст параметр пересечения
прямой с плоско*стью. Подставим D.7.3) в D.7.1) и получим радиус-вектор ps
тачки пересечения плоскости и прямой
Далее, по формулам D.6.6) и D.6.7) вычислим параметры плоскости xq и уо,
соответствующие точке пересечения
zo = g^si • {ps - s0) + /282 • {Ps - so), D.7.5)
Уо = g^si • (pe - s0) + ^82 • (pe - s0). D.7.6)
Общий случай. Пусть требуется найти все точки пересечения поверхности,
радиус-вектор которой описывается векторной функцией s(u, г;), и кривой, ради-
радиус-вектор которой описывается векторной функцией с(?). Для каждой точки
238 Гл. 4. Операции над кривыми и поверхностями
пересечения должно удовлетворяться векторное уравнение
s(«, v) - с(«) = 0, D.7.7)
которое, будучи записанным покоординатно, представляет собой систему трех
скалярных уравнений
si(u, v) -ci(t) = 0, s2(u, v) -c2{t) = 0, s3(it, v) -c3(i) = 0,
где s(u, v) = [si(u, v) s2(it, и) вз(и, и)] , с(<) = [ci(<) c2{t) c3(t)] . В каче-
качестве неизвестных выступают три параметра — u, v и t. Решив эту систему
уравнений, получим параметры и, v и t, по которым при необходимости можно
вычислить точки на поверхности и на кривой. Система уравнений в общем
случае является нелинейной и решается итерационными методами. Точек пе-
пересечения может быть несколько и от того, с какого приближения параметров
начнется итерационный процесс решения, зависит то, к какой тройке параме-
параметров сойдется решение.
Для нахождения нулевого приближения каждого решения будем двигаться
описанным выше способом по поверхности и кривой, т. е. будем переходить
от точки к точке с вычисляемыми по формулам D.2.4) и D.2.5) шагами Аи
и Av поверхности и вычисляемым но формуле D.2.3) шагом At кривой. При
каждом сочетании точек выполним следующую проверку. Пусть в некоторой
точке поверхности значения параметров равны щ и vq, а в некоторой точке
кривой значение параметра равно tQ. Построим касательную плоскость D.7.2)
в данной точке поверхности и касательную прямую D.7.1) в данной точке кри-
кривой. Начальными точками плоскости и прямой являются точки so = s(ito5 щ)
и Со = с(?о)- Векторами плоскости si и s2 являются частные производные
радиус-вектора поверхности по ее параметрам Si = ds/du, s2 = ds/dv в данной
точке. Вектором с' прямой является производная радиус-вектора кривой по ее
параметру с' = dc/dt в данной точке. По формулам D.7.3)-D.7.6) найдем пара-
параметры точки пересечения касательной плоскости и касательной прямой линии.
Рис. 4.7.2. Поиск пересечений кривой и поверхности начинается с пересечения касательной линии
кривой и касательной плоскости поверхности
Точка пересечения может быть найдена, если выбранные точки поверхности и
кривой являются обыкновенными и если касательная прямая не параллельна
касательной плоскости. Вблизи точки пересечения параметры хо и уо прибли-
приблизительно соответствуют приращениям параметров поверхности, а параметр zq
приблизительно соответствует приращению параметра кривой. На рис. 4.7.2 по-
показаны поверхность, касательная к ней плоскость, кривая и касательная к ней
линия.
4.7. Определение точек пересечения линии и поверхности 239
Далее предстоит решить, можно ли принять значения параметров щ + х0,
^о + УО) to + Zo ъ качестве нулевого приближения при решении системы урав-
уравнений или нельзя. Для этого нужно знать, каких размеров часть поверхности
можно приближенно аппроксимировать частью касательной к ней плоскостью и
какого размера участок кривой можно аппроксимировать частью касательной к
кривой линией так, чтобы при этом не перешагнуть через соседнюю точку пе-
пересечения. Эти размеры определяются шагами параметров Аи, Аи и At. Если
будут выполнены условия
—Аи < хо < Аи, —Av ^ уо < Av, —At < zq < At,
то параметры
и(°) =uo + х0, и@) = v0 + уо, *@) = to + z0 D.7.8)
могут быть приняты в качестве начального приближения при решении системы
уравнений D.7.7) определения точки пересечения поверхности s(u, v) и кривой
линии c(t).
Далее, начиная с нулевого приближения параметров, одним из методов реше-
решения нелинейных уравнений найдем решение с заданной точностью. Например,
в методе Ньютона на r-й итерации приращения параметров Au^r\ Av^ и ^
точки пересечения найдутся из системы линейных уравнений
at
А^г; = с2 - s2,
Ди +
du ov
ди dv dt
где Si, S2, S3 — компоненты радиус-вектора поверхности s, c\, ci, сз — компо-
компоненты радиус-вектора кривой с. Следующее приближение параметров точки пе-
пересечения равны и(г+1> = u^ + AuW, „(r+i) = V^ + Av^, f(r+1) = &) + A&\
Процесс уточнения параметров закончим, когда на очередной итерации выпол-
выполнятся неравенства |u(r+1) - и^\ < е, |г>(г+1) - v^\ < е и \&+l^ - fW| < e, где
е — заданная погрешность.
После этого продолжим поиск других точек пересечения. Сделаем шаг Аи
или Аи по одному из параметров поверхности или шаг Д? по параметру кривой
и повторим аппроксимацию поверхности касательной плоскостью, аппроксима-
аппроксимацию кривой касательной прямой, поиск пересечения плоскости и прямой, на-
нахождение приближенных параметров пересечения и принятие решения, но уже
для других точек кривой и поверхности. Так мы должны дискретно пройти всю
поверхность и всю кривую в поиске нулевых приближений параметров точек
пересечения. Возможны случаи, когда, начав итерационный процесс с различ-
различными нулевыми приближениями, мы придем к одному и тому же решению.
Поэтому все полученные решения необходимо проверить на совпадение. Реше-
Решения и*, v*, t* и и**, v**, t** будем считать одинаковыми, если выполняются
одновременно три неравенства: \и* — и**\ < ?, \v* — v**\ < ?, \t* — t**\ < ?, где
? > e. О величине ? мы расскажем в конце главы.
240 Гл. 4. Операции над кривыми и поверхностями
Если в некоторой точке кривая касается поверхности, то определитель ма-
матрицы системы уравнений D.7.7) на некоторой итерации станет недопустимо
малым или равным нулю и мы не сможем из этой системы найти точку каса-
касания. В этом случае вместо векторного уравнения D.7.7) можно решать систему
трех скалярных уравнений
(s(«, «) - c(t)) • Yu = о,
(s(«, v) - c(t)) ~ = 0, D.7.9)
дс
(s(u, v) - c(t)) ¦ -^ = 0,
определитель которой не равен нулю в точке касания. Но системе D.7.9) удо-
удовлетворяют не только точки касания, а еще и другие точки, в которых каса-
касательная прямая параллельна касательной плоскости и отрезок, соединяющий
точки касания, ортогонален касательной прямой и касательной плоскости. По-
Поэтому после решения системы уравнений D.7.9) следует проверить, являются
ли полученные точки являются точками касания.
Итерационный процесс решения системы D.7.9) закончим, когда на оче-
очередной итерации приращение каждого из параметров станет меньше некоторой
заданной величины е. Предположим, что максимальное отклонение полученных
в результате решения параметров от их точных решений u*, v*, t* составляет
±е, тогда максимальное отклонение радиус-вектора полученной точки пересе-
пересечения от его истинного значения будет равно произведению максимальной по
модулю производной радиус-вектора объекта на погрешность параметра
Ар = emax(|si|, |s21, |с'|). D.7.10)
Величина Ар есть радиус сферы погрешности: если ее центром сделать полу-
полученную в результате решения точку кривой или поверхности, то любая другая
точка геометрического объекта внутри сферы будет считаться неразличимой с
центральной точкой сферы. Значение Ар примем за критерий для ответа на
вопрос, является ли найденное решение системы уравнений D.7.9) точкой ка-
касания или нет. Если расстояние между найденными точками на кривой и по-
поверхности меньше Ар, то решение дало точку касания, в противном случае
решение не является ни точкой касания, ни точкой пересечения и должно быть
опущено. Для различных геометрических объектов и даже различных точек
одного и того же объекта радиусы сфер погрешности будут разными в разных
точках, тем не менее, они удобны для оценки точности решения. Нам не тре-
требуется знать истинные размеры объектов и масштабы расстояний между ними,
требуется знать только погрешность определения параметров при выполнении
операции, а радиус сферы погрешности в любой точке объекта мы всегда най-
найдем. Данная оценка близости точек не зависит от размеров геометрических
объектов, так как размеры области определения параметров не зависят от ре-
реальных размеров геометрического объекта. В дальнейшем будет важно знать,
с какой точностью решена та или иная задача.
Задача определения пересечения поверхности и прямой линии, а также при-
приводимая к ней задача проекции точки на поверхность в заданном направле-
направлении, решаются описанным методом при неподвижной пробной точке на прямой
линии.
4.8. Определение точек пересечения линий
241
4.8. Определение точек пересечения линий
Сначала рассмотрим задачу определения точек пересечения двухмерных кри-
кривых, а далее перейдем к задаче пересечения пространственных кривых. При
решении задачи пересечения двухмерных кривых для определения нулевого
приближения будет решаться задача определения точек пересечения прямых
линий.
Пересечение двухмерных прямых линий. Точка пересечения двухмерных
прямых линий может быть найдена аналитически. Пусть даны двухмерные
прямые
= p1+w1c1', D.8.1)
= р2 + w2c2'. D.8.2)
Прямые имеют точку пересечения, если их направляющие векторы не кол-
линеарны. Через п\ и п2 обозначим единичные нормали к прямым lx(wi)
и /2(го2). Если касательный вектор с' =
= [х у]т кривой имеет координаты ж и у, то
ортогональный ему вектор п имеет коорди-
координаты —ку и кх, где к = —. На
/ 9 i 9
V х2 + у2
рис. 4.8.1 показаны прямые D.8.1) и D.8.2),
нормали к ним и точка пересечения р. Из
рисунка видно, что, например, параметр
второй прямой для точки пересечения мо-
может быть найден как отношение проекции
вектора pj — p2 на нормаль первой прямой
к проекции вектора с2 на ту же нормаль.
Аналогично найдем параметры точки пересечения для первой прямой:
Р\
Рис. 4.8.1. Пересечение прямых
п2 ¦ (Р2-Р1)
П2 • С\'
щ -(pi -р2)
тн ¦ с2' '
D.8.3)
D.8.4)
Радиус-вектор точки пересечения найдем, подставив в D.8.1) или D.8.2) соот-
соответствующий параметр,
та2- (Рг-Pi) /
c
п2 •
= Р2
- р2) ,
щ •
D.8.5)
Пересечение двухмерных отрезков прямых. Аналитически можно найти
точку пересечения отрезков прямых. Пусть даны два отрезка прямых
T
I2{t2) = A - t2)p2 + t2q2,
построенных по точкам pj = [x\ yi]T, p2 = [x2 y2]T, q\ = [a\ bi]
= [a2 Ь2]т. Параметры их точки пересечения найдем из векторного уравнения
) = A - t2)p2 + t2q2,
и g2 —
16 — 5293 Голованов
242 Гл. 4. Операции над кривыми и поверхностями
которое представляет собой систему двух скалярных уравнений
- (х2 - а2)<2 = xi- х2,
= У\~ У2-
Если {х2 — а2){у\ — Ъ\) — {х\—а\){у2 — Ъ2) ф О, то по формуле Крамера параметры
точки пересечения равны
t _ (жг - а2)(щ ~ Ы - (xi - х2)(у2 - Ь2)
t _
(х2 - a2){yi - h) - (xi - а\)(у2 - b2)'
(xi - x2)(yi - h) - (xi - ax)(yi - y2)
(x2-a2)(yi-b1)-(xi-a1)(y2-b2)'
Отрезки пересеканется, если 0^<1^1и0^<2^1|В противном случае
пересеканется продолжения отрезков.
Частные с^чаи. Аналитически могут быть найдены точки пересечения пря-
прямой с кривыми второго порядка, точки пересечения кривых второго порядка
между собой и точки пересечения других кривых, для которых известно ана-
аналитическое описание. В указанных случаях задача решается в координатном
представлении и сводится к вычислению корней многочленов. В общем случае
можно найти корни многочлена, степень которого не превосходит 4. Напри-
Например, задача нахождения точек пересечения двух эллипсов приводит к решению
уравнения четвертой степени. Если аналитическая формула кривой неизвестна
или степень разрешающего уравнения превосходит 4, то задачу пересечения
кривых следует решать численно.
Общий случай пересечения двухмерных кривых. Пусть требуется найти все
точки пересечения двух двухмерных кривых, радиус-векторы которых описы-
описываются функциями ci(ii) и С2(?г)- Для каждой точки пересечения должно удо-
удовлетворяться векторное уравнение
ci(h)-c2(t2) = 0, D.8.6)
которое, будучи записанным покоординатно, представляет собой систему двух
скалярных уравнений
zi(*i)-a:2(i2) = 0, yi(«i)-Jtt(<2) = 0. D.8.7)
Неизвестными являются параметры кривых ti и t2. Система уравнений в об-
общем случае является нелинейной и решается итерационными методами. Точек
пересечения может быть несколько и от того, с какого приближения параме-
параметров начнется итерационный процесс решения, зависит, к какой точке сой-
сойдется решение. Итерационный процесс определения параметров точки пересе-
пересечения закончим, когда на очередной итерации не только параметры кривых
удовлетворят заданным условиям, но и координаты точек удовлетворят задан-
заданным условиям точности. Процесс уточнения решения закончим, когда выпол-
выполнятся неравенства |<i(r+1> - <j(r)| < е, |<2(г+1) - <2(r)| < e, |si(r+1> - xi<r>| < e,
|yi(r+i) _ yi(r)| < ?) |a;2(r+i) _ Ж2(г)| < ?) |№(г+1) _ j^W] < е. Это связано с
тем, что координаты двухмерных кривых сами служат параметрами поверхно-
поверхностей. Для нахождения нулевого приближения каждой точки пересечения будем
4.8. Определение точек пересечения линий 243
двигаться с вычисляемыми по формуле D.2.3) шагами Ati и At2 по кривым, в
каждом сочетании точек строить касательные линии D.8.1) и D.8.2) к кривым
и определять параметры W\ и w2 точки их пересечения. Для этого в D.8.1)
и D.8.2) подставим значения: рх = ci(<i), р2 = ^2(^2) — точки на кривых,
с\ — dci/dti, с2 = d,C2/dt2 -— производные кривых в этих точках. Параметры
касательных прямых в точке их пересечения определим по формулам D.8.3) и
D.8.4). Вблизи точки пересечения параметры w\ и w2 приблизительно соответ-
соответствуют приращениям параметров кривых, поэтому величины
^(°) =ti+ wu t2{0) = t2+w2 D.8.8)
могут быть приняты в качестве нулевого приближения при решении системы
уравнений D.8.6), если удовлетворяются условия
-Д<1 < wi < Ati, -At2 < w2 < At2.
Шаги по параметрам At 1 и At2 вычислены исходя из условия, что касательная
к каждой кривой при данном шаге отклонится на угол, не превышающий за-
заданную величину Да. Шаги определяют, какого размера участок кривой можно
аппроксимировать частью касательной к кривой прямой линией так, чтобы при
этом не перешагнуть через соседнюю точку пересечения.
После этого продолжим поиск других точек пересечения. Сделаем шаг Ati
или At2 по параметру одной из кривых и повторим аппроксимацию кривой ка-
касательной прямой, поиск пересечения прямых, нахождение приближенных па-
параметров пересечения и принятие решения о поиске точного решения. Таким
образом, мы должны дискретно пройти обе кривые в поиске нулевых приближе-
приближений параметров точек пересечения.
Полученные решения необходимо проверить на совпадение. Решения ti*,
t2* и <i**, t2** будем считать одинаковыми, если выполняются одновременно
неравенства: \t\* — t\**\ < ?, \t2* — t2**\ < ?, где ? < e. Величину ? мы
рассмотрим в конце главы.
Если заданные кривые имеют точку касания, то уравнения системы D.8.7)
являются линейно зависимыми и на некоторой итерации определитель системы
станет недопустимо малым или равным нулю, и мы не сможем найти точку
касания. В этом случае вместо векторного уравнения D.8.6) можно решать
систему скалярных уравнений
(ci(ti) - ea(fc)) • ^ = 0, (c2(t2) - «aft» • g = 0, D.8.9)
определитель которой не равен нулю в точке касания. Но системе D.8.9) удовле-
удовлетворяют не только точки касания, а еще и точки, в которых касательные пря-
прямые параллельны друг другу и ортогональны вектору, соединяющему точки,
в которых построены касательные прямые. Поэтому после решения системы
уравнений D.8.9) следует проверить тот факт, что полученные точки являются
точками касания.
Проверку выполним аналогично тому, как это было сделано при определении
точек касания кривой и поверхности. Итерационный процесс решения системы
нелинейных уравнений D.8.9) будет закончен, когда на очередной итерации
приращение каждого из параметров станет меньше некоторой заданной вели-
величины е. Предположим, что максимальное отклонение полученных в результате
16*
244 Гл. 4. Операции над кривыми и поверхностями
решения параметров от их точных решений составляет ±е, тогда максимальное
отклонение радиус-вектора полученной точки пересечения от его истинного зна-
значения будет равно произведению максимальной по модулю производной радиус-
вектора объекта на погрешность параметра
Ap = emax(|Cl'Uc2'|). D.8.10)
Если расстояние между найденными точками кривых и поверхности меньше
Ар, то решение дало точку касания, в противном случае решение не является
ни точкой касания, ни точкой пересечения и должно быть опущено.
Общий случай пересечения пространственных кривых. С помощью системы
уравнений D.8.9) можно найти точки пересечения или касания пространствен-
пространственных кривых Ci(^i) и С2(?г)- Системе уравнений
- c2(t2)) • f[ = 0, (c2(t2) - dfr)) • f^ = 0 D.8.11)
удовлетворяют точки пересечения пространственных кривых, точки касания
пространственных кривых, а также точки, в которых касательные к кривым
прямые ортогональны вектору, соединяющему точки построения касательных
прямых. Система уравнений D.8.11) получена из системы уравнений D.8.9)
путем замены в ней двухмерных кривых ci(ti) и С2(?г) на трехмерные кривые
Ci(ii) и Сг(<2)- После решения системы уравнений D.8.11) следует проверить
полученные точки на близость по формуле D.8.10). Проверкой коллинеарности
производных радиус-векторов кривых можно выделить среди полученных то-
точек точки касания. Метод определения близости найденных точек с помощью
радиуса погрешности D.8.10) инвариантен по отношению к геометрическим
размерам объектов и к единицам измерения координатной системы.
4.9. Построение линий пересечения поверхностей
Пересечение плоскостей. Линия пересечения двух плоскостей
г(u, v) = го + uri + vr2, s(a, b) = So + asi + 6s2,
с единичными нормалями гз и S3 находится достаточно просто. Ее направле-
направление определяется вектором z = Г3 х S3. Если длина вектора z отлична от нуля,
то плоскости пересекаются, в противном случае они параллельны или совпа-
совпадают. Если плоскости пересекаются, то теперь нужно найти точку на линии
пересечения. Построим вектор w = Го — So и вычислим его составляющую,
параллельную плоскости s(a, b): w' = w — S3(w • S3). Далее по формуле D.7.4)
определим точку р пересечения линии, проходящей через точку So в направле-
направлении вектора w', с плоскостью r(u, v)
р 80 +
Гз • W'
Плоскости пересекаются по линии
p + fz. D.9.1)
4.9. Построение линии пересечения поверхностей 245
Параметры плоскостей, соответствующие точки р, определим по формулам
_ Г1 • (р - Гр) _ Г2 • (р - Го)
Up — , Vp — ,
Г1 ¦ Г1 y Г2 • Г2
_ si • (p - s0) _ s2 • (p - s0)
Si • Si У S2 • S2
при условии ортогональности пар векторов ri, r2 и Si, s2, или по формулам
D.6.6) и D.6 7) в противном случае. Аналогичным образом можно найти па-
параметры для еще одной точки линии пересечения q = 1A) = р + z. Пусть
параметры uq и vq соответствуют точке q на плоскости г(u, v), а параметры ач
и bq соответствуют этой же точке на плоскости s(a, b). Построим на плоскостях
двухмерные линии
luv(t)=[u{t) v(t)]T = [Up(l - t) + Uqt Vp{l - t) + Vqt]T, luv(t) ? r(u, v),
lab(t)=[a{t) b{t)]T = [ap(l - t) + aqt bp{l - t) + bqt]T, lab(t) e s(a, b).
D.9.2)
Эти линии при каждом параметре t совпадают в пространстве друг с другом и с
линией l(t). Линию пересечения плоскостей будем строить в виде совокупности
двух двухмерных линий на двух пересекаемых плоскостях. Аналогично линию
пересечения поверхностей будем строить в виде совокупности двух двухмерных
линий на них.
Частные случаи. Во многих частных случаях задачу пересечения поверхно-
поверхностей можно решить достаточно просто. Пусть поверхность C.5.1) получена вы-
выдавливанием кривой на плоскости. Если плоская кривая задана координатными
функциями c(t) = [x(t) y(t)] , 10^^<1,и плоскостью s(x, у) = p + xix + yiy,
то поверхность выдавливания будет описываться радиус-вектором
г(u, v) - р + x{u)'\x + y(u)iy + vd, to^.u^ti.
При пересечении этой поверхности плоскостью w(a, b) = q + ajx + bjy, па-
параллельной плоскости s(x, у), линию пересечения построим из трансформи-
трансформированной копии кривой c(t) на плоскости w(a, b) и отрезка прямой линии
luv{t) — \t v]r на поверхности r(u, v). Трансформированную копию кривой
c(t) на плоскости w(a, b) обозначим через cab(t). Кривая саь{к) должна быть
повернута и перемещена на плоскости w(a, b) в соответствии с взаимной ори-
ориентацией базисных векторов и начальных точек плоскостей w(a, b) и s(x, у).
Отрезок прямой lUv{t) представляет собой координатную линию v = const на
поверхности r(u, v). Необходимо, чтобы отрезок прямой lUv{t) и кривая cab(t),
расположенные на разных поверхностях, имели одинаковую параметрическую
длину t0 < t < t\.
Аналогично можно получить линию пересечения поверхности, полученной
вращением кривой на плоскости вокруг оси, принадлежащей этой плоскости, и
плоскости, проходящей через ось вращения. Кривую пересечения поверхности
вращения плоскостью, ортогональной оси вращения, построим из окружности
на плоскости и линии u = const на поверхности. При построении линии пересе^
246 Гл. 4. Операции над кривыми и поверхностями
чения такими способами следует соблюдать одно правило: линии на пересекае-
пересекаемых поверхностях должны иметь одинаковые области определения параметра и
их соответствующие точки на поверхностях должны совпадать в пространстве.
Общий случай пересечения поверхностей. Обратимся к общему случаю пере-
пересечения поверхностей. Пусть требуется найти линию пересечения поверхностей,
описываемых радиус-векторами г(u, v) и s(a, 6). Каждая точка линии пересе-
пересечения поверхностей должна удовлетворять векторному уравнению
r(u, v) - s(a, b) = 0. D.9.3)
Это векторное уравнение содержит три скалярных уравнения для компонент
радиус-векторов поверхностей:
гг(и, v) -si(a, Ь) = 0,
r2(u, v) - s2{a, b) = 0, D.9.4)
r3(u, v) - s3 (a, b) = 0;
и четыре искомых параметра: и, v, a, b. Данная задача отличается от рассмо-
рассмотренных тем, что из трех уравнений нужно найти четыре неизвестные вели-
величины. Если определить один из четырех параметров, то остальные три можно
найти из системы уравнений D.9.4), т.е. один из параметров может в то же
Рис. 4.9.1. Линии пересечения цилиндрической поверхности и NURBS поверхности
время служить параметром решения или являться однозначной функцией от
него. Таким образом, три параметра являются функциями четвертого параме-
параметра. Чтобы все четыре параметра были равноправными, представим их все в
виде функции некоторого общего параметра t:
u = u(«), v = v(t), a = a(t), b = b(t), D.9.5)
и придем к тому, что результатом решения системы уравнений D.9.4) являются
две двухмерные линии
luv(t) = [u(t) v(t)]T, luv(t) в Г(и, V), g
lab{t) = [a(t) b(t)]T, lab(t)es(a,b).
Эти линии связаны друг с другом общим параметром и определяют одну и ту
же линию в пространстве — линию пересечения поверхностей. На рис. 4.9.1
приведен пример пересечения поверхностей.
4.9. Построение линий пересечения поверхностей 247
В общем случае невозможно оперировать линией пересечения отдельно от
породивших ее поверхностей. Но всегда можно построить линию, которая при
любом заданном параметре t давала бы точку пересечения поверхностей. Эту
линию мы представим в виде совокупности отдельных точек линии пересе-
пересечения поверхностей в порядке расположения их на ней.
Имея упорядоченные точки линии пересечения, всегда можно найти любую
другую точку линии. Пусть параметры щ, v\, а\, Ь\ и параметры иг, г>2, аг, fa
поверхностей соответствуют соседним точкам pi и рг упорядоченной совокуп-
совокупности точек линии пересечения. Пусть первой точке соответствует параметр t\
Рис. 4.9.2. Вычисление точки линии пересечения поверхностей по ранее определенным точкам
линии пересечения, а второй точке соответствует параметр t<i линии пересече-
пересечения поверхностей r(u, v) и s(a, b). Требуется найти точку линии пересечения
с параметром t, где t\ <t < ?2- Построим плоскость
q(x, y) = p + xqi+ yq2 D.9.7)
с началом в точке
«2 -1 t-ti
Р = 7 ГР1 + 7 ГР2
ортогональную отрезку, проведенному из точки pi в точку рг (рис. 4.9.2).
Примем за начальные приближения параметры
h \ (п) h \
*2 ~ *1 *2 ~ *1 *2 ~ *1 *2 ~ 'I
h — t . * — *1 ,(o) ^2~t t — H ,
+ —a2, b^> = -bx + -fa
* * * * * *
a ai + a2, b bx +
*2 ~ *1 *2 ~ *1 *2 ~ *\ *2 ~ *1
поверхностей и найдем точку пересечения поверхностей и плоскости из системы
шести уравнений, которые в векторной записи имеют вид
r(u, v) - q(x, у) = 0, s(a, Ь) - q(x, у) = 0. D.9.8)
Эта точка и будет искомой точкой линии пересечения. Далее можно определить
любую другую геометрическую информацию линии пересечения поверхностей.
Таким образом, совокупность отдельных точек линии пересечения поверх-
поверхностей служит как бы нулевым приближением этой линии, по которому одним
из численных методов всегда можно найти точное решение.
248 Гл. 4. Операции над кривыми и поверхностями
Алгоритм построения линий пересечения. Две поверхности могут пересе-
пересекаться по нескольким линиям. Мы ставим своей целью построить все линии
пересечения, принадлежащие области определения обеих поверхностей. Алго-
Алгоритм построения линий пересечения поверхностей разобьем на два этапа.
На первом этапе, шагая по поверхностям и исследуя их близость, най-
найдем отдельные точки кривых пересечения. Под точками в данном случае будем
иметь в виду пары параметров u, v и a, b на параметрических плоскостях по-
поверхностей. Точки из полученного на первом этапе набора никак не связаны
друг с другом и могут принадлежать различным кривым пересечения. Важно
только, чтобы от каждой кривой пересечения в наборе присутствовала хотя бы
одна точка.
На втором этапе берем любую точку из имеющегося набора и, двигаясь от
нее с некоторым шагом сначала в одну сторону затем в другую, найдем точку за
точкой искомую совокупность точек линии пересечения. Направление движения
дает векторное произведение нормалей к поверхностям. Шаг движения вычи-
вычислим в соответствии с кривизнами поверхностей в текущей точке. Движение по
кривой пересечения закончим, когда дойдем до края одной из поверхностей или
когда линия замкнется (новая точка окажется на расстоянии текущего шага от
точки старта). В процессе движения будем проверять, не лежат ли вблизи пути
следования точки из набора, полученного на первом этапе. Для этого по пути
следования будем вычислять расстояние от текущей точки кривой пересечения
до каждой точки из набора, полученного на первом этапе. Если вычисленное рас-
расстояние до какой-либо точки набора соизмеримо с текущим шагом движения,
то эту точку удалим из набора как более ненужную. Так получим совокупность
отдельных точек щ, Vi и Oj, Ьг, г = 0, 1, 2, ..., п, одной кривой пересечения.
При этом в наборе точек, полученном на первом этапе, не будет содержаться ни
одной точки данной кривой пересечения. Если в наборе останутся еще точки,
то данные поверхности имеют, по крайней мере, еще одну линию пересечения.
Совокупность ее точек найдем, взяв любую точку из набора и повторив все ска-
сказанное о втором этапе построения. Построение линий закончим, когда в наборе
не останется ни одной точки.
Рассмотрим подробнее отдельные элементы алгоритма построения линий
пересечения двух поверхностей.
Для определения начальных точек пересечения на первом этапе решим за-
задачу пересечения линий r(n, const) и r(const, v) поверхности r(u, v) с поверх-
поверхностью s(a, b). He изменяющемуся параметру будем сообщать последовательно
значения const = vm\n+Av (при этом он проходит с некоторым шагом значения
от vm-m до г>тах), а затем — const = nmin + Аи (при этом он проходит с некото-
некоторым шагом значения от ит-т до nmax). При одном неподвижном параметре из
системы уравнений D.9.4) можно найти остальные три параметра. Далее поме-
поменяем поверхности ролями и найдем точки пересечения координатных линий
s(a, const) и s(const, b) поверхности s(a, b) с поверхностью r(n, v). Таким обра-
образом, мы получим набор некоторых точек, принадлежащих в общем случае раз-
различным линиям пересечения заданных поверхностей. В этом наборе нам пона-
понадобится по одной точке для построения каждой линии пересечения. Эти точки
не должны быть точками касания поверхностей. Если известна некоторая точка
линии пересечения, то по ней можно построить и другие точки этой линии.
Возьмем из полученного набора произвольную точку пересечения поверхно-
поверхностей. Пусть ее параметры на первой поверхности равны Uk, г>&, а на второй
поверхности равны а&, 6*. Построим нормали к поверхностям тг(зд, г>&) и
4.9. Построение линий пересечения поверхностей
249
bk). Линия пересечения в каждой точке ортогональна нормалям обеих
поверхностей, поэтому направление линии пересечения коллинеарно вектор-
векторному произведению нормалей к поверхностям
t =
, vk) x ms(ak, bk).
D.9.9)
Выберем в качестве направления движения к следующей точке линии пересече-
пересечения положительное направление вектора t. Далее, по формулам D.2.4) и D.2.5)
определим возможный шаг смещения по каждому из четырех параметров Аи,
Av, Аа, Ab. Если одному из параметров дать приращение и сделать его не-
неподвижным, то из системы уравнений D.9.4) можно найти остальные параме-
параметры. Важно только, чтобы изменение каждого из параметров по модулю не пре-
превышало найденные возможные шаги. В качестве фиксированного параметра,
которому будет дано приращение, выберем тот, направление движения вдоль
которого ближе к направлению кривой пересечения, т. е. составляет меньший
угол с вектором t. Для этого вычислим частные производные радиус-векторов
поверхностей по параметрам
ди
дг
ds
ov да
ds
D.9.10)
которые и дают направления движения вдоль параметров.
На рис. 4.9.3 показаны отправная точка рк = v(uk, vk) = s(ak, bk), век-
векторы производных ri, Г2, si, S2 и сфера смещения, внутри которой приращения
всех параметров не превышают, соответственно, An, Av, Aa, Ab. Следующая
Рис. 4.9.3. Определение неподвижного параметра и начальных приближений для следующей
точки линии пересечения поверхностей
точка линии пересечения не должна выйти за сферу смещения. Радиус сферы
смещения го возьмем равным наименьшей по абсолютной величине проекции
векторов Д«п, Дг>Г2, Aasi, Abs2 на вектор касательной t:
= min(|Auri-t|, |Aw2-t|,
|, |A6s2-t|)|-.
D.9.11)
250 Гл. 4. Операции над кривыми и поверхностями
Для следующей точки линии пересечения в качестве нулевых приближений при-
примем значения параметров:
Тот параметр, производная по которому составляет меньший угол (по абсолют-
абсолютной величине) с направлением линии пересечения, сделаем неподвижным. Да-
Далее, решив систему уравнений D.9.4), в которой неподвижный параметр будет
считаться известным и неизменным, получим остальные три параметра. Таким
образом, найдем параметры щ+х, Vk+i на первой поверхности и параметры a,k+i,
bfc+i на второй поверхности для следующей точки линии пересечения. Продол-
Продолжим этот процесс и дальше пока не дойдем до края одной из поверхностей или
не окажемся вблизи точки отправления.
Если в процессе движения мы оказались вблизи точки отправления, это озна-
означает, что кривая пересечения является замкнутой. Близость точек определяется
с помощью тех же шагов по параметрам, которые используются в процессе дви-
движения. Кривая пересечения должна замкнуться, если на очередном шаге пара-
параметры отличаются не более, чем на величины А«, Av, Да, АЬ соответственно.
Если в процессе движения мы оказались вблизи границы одной из поверхно-
поверхностей и движемся в ее направлении (имеется в виду прямоугольная граница), то
в качестве неподвижного параметра следует выбрать тот, который находится ря-
рядом со своей границей. Важно, чтобы были найдены параметры, соответствую-
соответствующие крайним точкам линии пересечения. Для этого функции поверхностей,
определяющие векторы точек и их производных, должны корректировать пара-
параметры, если они вышли за область определения.
После определения крайней точки линии пересечения поверхностей продол-
продолжим движение и поиск параметров линии пересечения в другом направлении
от точки старта (в противоположном вектору t направлении). Такая линия не
может быть замкнутой, поэтому движение будем продолжать до тех пор, пока
не будут найдены параметры другого края линии пересечения поверхностей.
Если одна из поверхностей или обе имеют не прямоугольную область опре-
определения параметров, а ограниченную контурами область на параметрической
плоскости, то при поиске параметров линии пересечения в качестве границы
можно использовать габаритный прямоугольник внешнего контура области. По-
После построения линий пересечения их следует проверить на пересечение с гра-
граничными контурами и усечь этими контурами, сохранив только те части ли-
линий пересечения, которые лежат внутри областей определения параметров обеих
поверхностей.
Если на некотором участке пересекаемые поверхности имеют близкие (по-
(почти коллинеарные) нормали, то кривая пересечения в этом месте может сильно
менять свое направление. Шаг по фиксированному параметру в этой области
должен быть уменьшен.
Если линии пересечения поверхностей проходят через точку касания, то в
этой точке поверхности имеют коллинеарные нормали. Матрица линеаризован-
линеаризованной системы уравнений D.9.4) в этой точке будет иметь нулевой определитель
4.9. Построение линий пересеченая поверхностей 251
и из этой системы уравнений нельзя найти параметры точки касания поверхно-
поверхностей. В этом случае вместо системы уравнений D.9.4) можно решать систему
четырех скалярных уравнений
fir
(r(u,t,)-s(a, &))• — = О,
D9Л4)
(В(а, 6) - г(«, v)) ¦ — = О,
{s(a,b)-r(u,v))-fb=O,
определитель которой не равен нулю в точке касания. Но системе D.9.14) удо-
удовлетворяют не только точки касания, а еще и другие точки, в которых каса-
касательные к поверхностям плоскости параллельны друг другу и ортогональны
отрезку, соединяющему точки касания. Поэтому после решения системы урав-
уравнений D.9.14) следует проверить то, что полученные точки являются точками
касания. Для этого будем использовать тот же критерий, что применяется в
задаче пересечения кривой и поверхности.
Итерационный процесс решения системы D.9.14) закончим, когда на оче-
очередной итерации приращение каждого из параметров станет меньше некоторой
заданной величины е. Отклонению ±е полученных в результате решения пара-
параметров от их точных значений соответствует максимальное отклонение радиус-
вектора полученной точки от его истинного значения. Это отклонение равно
произведению погрешности параметров и длины максимальной по модулю про-
производной радиус-векторов:
Ap = emax(|ri|, |r2|, |si|, |s2|). D.9.15)
Если расстояние между найденными точками на поверхностях меньше Ар, то
будем считать эти точки неразличимыми и что решение дало точку касания.
В противном случае решение не является ни точкой касания, ни точкой пересе-
пересечения и должно быть опущено.
Итак, в общем случае описанным выше способом каждую линию пересече-
пересечения двух поверхностей будем представлять упорядоченной совокупностью па-
параметров щ, Vi и щ, 6j, % = 0, 1, 2, ..., п, или упорядоченной совокупностью
координат двухмерных точек на параметрических плоскостях. Оформим эти
совокупности в виде двух ломаных B.4.1) линий luv(t) = [u(t) v(t)] и lab{t) =
= [a(t) b(t)] на соответствующих поверхностях. Эти ломаные имеют общий
параметр, при целочисленных значениях параметра они совпадают с линией пе-
пересечения, при других значениях параметра они проходят вблизи линии пере-
пересечения, их концы совпадают с концами линии пересечения поверхностей. Для
любого значения параметра ломаных могут быть получены параметры точки
пересечения поверхностей с любой заданной точностью из решения системы
D.9.8). Кривая пересечения поверхностей в данном представлении ничем не
отличается от любой другой кривой или сплайна. При обращении к кривой пе-
пересечения с некоторым параметром она может выдать любую геометрическую
информацию о себе.
252 Гл. 4. Операции над кривыми и поверхностями
Пусть мы имеем для линии пересечения поверхностей г(и, v) и s(a, b) точ-
точные параметрические зависимости D.9.5). Тогда радиус-вектор 1(?) линии пере-
пересечения поверхностей вычислим как среднее арифметическое радиус-векторов
точек на пересекаемых поверхностях
Производные радиус-вектора линии пересечения поверхностей вычислим как
среднее арифметическое производных кривых на поверхностях по формулам
<п 1 (dx ds\
{) <4'9Л7>
d2\ 1 (Sr d2s
dT2 = 2 [dfi + dfi) '
Производные радиус-векторов кривых на поверхностях вычисляются по форму-
формулам A.7.20)
dr du dv
+
dt
d2r
d3r
dt3 ~~
i 9*.
+0Г1
ds
1dt
= rm
+ r2
'd«>
Vdf
d2^ efat
da
dV
2
) +'
/¦
db
du
, /
Jrii2 ^
cPudv
dt2dt
dv
fdu
vdi
\2d«
У dt
d2t) ditN
'd«\2
dt)
+ 3r12
d2u
du /"^\2
12 dt \dt)
d2v dv
22 M2 ^ + Г
Г Г222 1
d3U
(It
(dvX*
{*) '
dzv
D.9.20)
D.9.21)
D.9.22)
dadb (db\2 d2a d2b ,лппл*
da\3 n fda\2db o dafdb\2 fdb\3
J+ UJ +3UJ +U
UJ +S222U
d3a d3b
+
4.10. Поверхность округленна
253
Если параметрические зависимости D.9.5) не являются точными и дают
точки линий пересечения при целочисленных значениях параметра t (при дру-
других значениях параметра проходят вблизи линии пересечения), то формулы
D.9.16)-D.9.19) будут верны только приближенно. Точные значения радиус-
вектора линии пересечения поверхностей и ее производных можно получить из
системы уравнений D.9.8).
4.10. Поверхность скругления
Многие моделируемые детали имеют скругления, поэтому при построении
тел требуется выполнять операцию скругления ребер тела. Рассмотрим постро-
построение поверхности, которая в дальнейшем будет использоваться для скругления
ребер тел. Пока будем строить поверхности скругления, не связывая их с те-
телами.
Пусть имеются две пересекающиеся поверхности, описываемые радиус-век-
радиус-векторами r(u, v) и s(a, b). Вблизи линии пересечения пространство делится
поверхностями на четыре сектора.
Сектор 1: перпендикуляры, восстановленные от поверхностей к точкам пер-
первого сектора, имеют направление, совпадающее с нормалями обеих поверхно-
поверхностей.
Сектор 2: перпендикуляр, восстановленный от первой поверхности к точкам
второго сектора, совпадает по направлению с нормалью первой поверхности, а
перпендикуляр, восстановленный от второй поверхности к точкам второго сек-
сектора, противоположен по направлению нормали второй поверхности.
Сектор 3: перпендикуляры, восстановленные от поверхностей к точкам тре-
третьего сектора, противоположны по направлению нормалям обеих поверхностей.
Сектор 4: перпендикуляр, восстановленный от первой поверхности к точкам
четвертого сектора, противоположен по направлению нормали первой поверхно-
поверхности, а перпендикуляр, восстановленный от второй поверхности к точкам четвер-
четвертого сектора, совпадает по направлению с нормалью ко второй поверхности.
Построим поверхность скругления, представляющую собой след от качения
сферы радиуса р, касающейся одновременно двух поверхностей. Сфера будет
Ma,b)
Сектор 2
г(и, v)-
Сектор 1
Сектор 3
Сектор 4
Рис. 4.10.1. Скругление плоских граней
двигаться около линии пересечения поверхностей в одном из четырех упомяну-
упомянутых секторов. На рис. 4.10.1 показано сечение поверхностей и сферы.
Частные случаи. Если скругляемыми поверхностями являются плоскости, то
угол а между поверхностями остается постоянным при движении вдоль линии
их пересечения. Пусть радиус скругления остается постоянным и равным р.
В этом случае линии перехода с поверхности скругления на сопрягаемые плос-
плоскости можно получить как эквидистантные линии к линии пересечения. Имея
254 Гл. 4. Операции над кривыми и поверхностями
согласованные по параметру линии перехода lr(?), ls(i) и линию пересечения
плоскостей l(t), поверхность скругления можно представить в виде C.10.3)
_ A - zLr{t) + 2A - z)z cos (a/2)l(t) + z4s(t)
;" A - zY + 2A -z)z cos (a/2) + z2 ' U ^ * *
Линии перехода lr{t), ls(t) построим в виде линий на поверхностях. Ка-
Каждая из них представляет собой двухмерную линию и поверхность (в данном
случае — плоскость). Двухмерные линии могут быть получены как эквиди-
эквидистантные линии к линии пересечения плоскостей 1(?), отстоящие от нее на
расстоянии d = ±ptg (a/2). Знак d зависит от ориентации линии пересечения
и от сектора, в котором строится поверхность скругления. Область определения
параметра t поверхности скругления зависит от дальнейшего ее использования.
Полученная поверхность скругления по форме совпадает с частью цилиндриче-
цилиндрической поверхности. Как правило, в рассмотренном случае строится именно часть
цилиндрической поверхности. Аналогичным образом в качестве поверхности
скругления между цилиндрической поверхностью и ортогональной ее оси плос-
плоскостью может быть использована часть поверхности тора.
Общий случай. Рассмотрим построение поверхности скругления в общем слу-
случае. Построим точки касания катящейся сферы радиуса р с поверхностями.
Продолжение нормалей к поверхностям в точках касания пересекутся в центре
катящейся сферы. Обозначим нормали A.7.18) поверхностей r(u, v) и s(a, Ь)
через mr(u, v) и ms(a, 6), а проекции на эти нормали векторов из точек касания
до центра сферы — через рт и ps соответственно. Величины рг и р3 по модулю
равны радиусу сферы р, но имеют знак, характеризующий упомянутый сектор.
Параметры точек касания сферы связаны уравнением
r(u, v) + prmr(u, v) = s(a, b) + psms(a, b). D.10.1)
Это векторное уравнение содержит три скалярных уравнения для компонент
нормалей поверхностей и четыре искомых параметра u, v, a, b. Построение по-
поверхности скругления по уравнению D.10.1) сходно с задачей построения линии
пересечения поверхностей. В обоих случаях результатом решения являются две
двухмерные линии на соответствующих поверхностях.
Переменный радиус скругления. Пусть требуется построить поверхность
скругления переменного радиуса. Для этого нам потребуется кривая пересе-
пересечения поверхностей. Величины радиуса скругления pr = pr{s) и ps = ps(s)
будем считать функциями длины дуги s линии пересечения c(s) скругляемых
поверхностей. В данном случае катящаяся сфера будет иметь переменный ра-
радиус. Кроме того, положение центра катящейся сферы связано с точкой на ли-
линии пересечения. Расположим центр катящейся сферы в нормальной плоскости
кривой пересечения. Нормальная плоскость ортогональна касательному вектору
кривой. Вместо векторного уравнения D.10.1) параметры точек касания сферы
свяжем уравнениями
т(и, v) + pr{s)mr(u, v) = s(a, b) + ps{s)ms(a, b), D.10.2)
- 2(r("> u) +Pr{s)mr(u, v) + s(a, b) + ps(s)ms(a, b))j ¦ — = 0.
D.10.3)
4.10. Поверхность скругления 255
Эти уравнения содержат четыре скалярных уравнения относительно четырех
искомых параметров u, v, а, Ь. Параметр s линии пересечения является извест-
известной величиной. По текущему параметру s мы вычислим радиусы pr{s) и ps{s),
точку c(s) и касательный вектор кривой в ней c'(s). Решив систему уравнений
D.10.2) и D.10.3), получим параметры и, v, а, 6, касания катящейся сферы и
поверхностей.
Система уравнений D.10.2), D.10.3) может быть использована вместо си-
системы уравнений D.10.1) для построения поверхности скругления постоянного
радиуса. В этом случае необязательно в качестве параметра кривой пересечения
использовать длину ее дуги.
Результатом решения системы уравнений D.10.1) или системы уравнений
D.10.2) и D.10.3) являются две двухмерные линии на поверхностях
I (f\ _ Г«,(/\ v(f\] 1 (f\ (Z v(n, „\
it D10-4)
lab(t) = [a(t) b(t)\ , lab(t) 6 s(a, b),
на соответствующих поверхностях. В общем случае линии lUv(t) и lab(t) могут
быть получены как сплайны, проходящие через заданные точки. Простран-
Пространственные линии, построенные по этим линиям на поверхностях, обозначим
соответственно через
lr{t) = r(u(t),v{t)), D.10.5)
ls(t)=s(a(t),b(t)). D.10.6)
Они определяют края поверхности скругления, полученной качением сферы
одновременно по двум поверхностям.
По двум кривым на поверхностях D.10.5) и D.10.6), являющимися следами
касания катящейся сферы, построим поверхность скругления. Первый параметр
поверхности скругления совместим с параметром t граничных кривых D.10.5)
и D.10.6). При движении вдоль второго параметра поверхности скругления при
фиксированном первом параметре должна быть описана дуга окружности. По-
Построим эту дугу окружности в виде рациональной кривой Безье B.6.16). Для
этого при каждом значении параметра кривых на поверхности нужно знать
радиус-вектор средней точки и ее вес. Вес средней точки рациональной кривой
Безье B.6.16) равен косинусу половины угла между векторами prmr и psms.
Косинус угла между этими векторами равен их скалярному произведению, де-
prmr ¦ msPs Тт .
ленному на произведение длин векторов: cos а = ^ . Используя фор-
Р
мулу 2 cos2 (а/2) = 1 + cos а, вычислим вес средней точки
D.10.7)
На рис. 2.6.5 видно, что радиус-вектор средней точки, который обозначим через
1(?), можно вычислить по формуле
= liW +pr™r(t) + h(t) +psms(t)) - ^Pr^r(t)+psrns(t)^ D1O8)
256 Гл. 4. Операции над кривыми и поверхностями
Радиус-вектор средней точки D.10.8) и ее вес D.10.7) являются функциями
параметра t кривых на поверхности D.10.5) и D.10.6), так как от параметра t
зависят lr, \s и нормали к поверхностям
mr(t) = mr(u{t), v(t)), D.10.9)
ms(t) = ms(a{t),b(t)). D.10.10)
Таким образом, радиус-вектор поверхности скругления при постоянном или
переменном радиусе описывается выражением
где вес w(t) и радиус-вектор l(t) определяются равенствами D.10.7) и D.10.8),
а через z обозначен второй параметр поверхности. Рассмотренная поверхность
скругления не имеет четких границ в направлении первого параметра. Эти
границы будут определены при дальнейшем использовании поверхности для
скругления ребер тел. На рис. 4.10.2 приведен пример поверхности скругления.
В зависимости от замкнутости скругляемых поверхностей и линий D.10.5) и
D.10.6) поверхность скругления может быть замкнутой или незамкнутой.
При решении системы уравнений D.10.1) и D.10.2) требуется вычислять
производные нормалей поверхностей по параметрам. Эти производные дают
Рис. 4.10.2. Поверхность скругления
формулы Вейнгартена A.7.26). Радиус-вектор точки поверхности за ее преде-
пределами может быть вычислен по одной из формул C.14.8)—C.14.10) в зависимости
от замкнутости поверхности. Эти же формулы позволяют определить нормали
поверхности и их производные за пределами поверхности.
4.11. Поверхность фаски
Наряду со скруглениями ребер тела требуется выполнять снятие фасок вдоль
его ребер. Построение поверхности фаски имеет много общего с построением
поверхности скругления. Поверхность фаски несколько проще поверхности
скругления. Остановимся на том, что их отличает.
4.11. Поверхность фаски
257
Пусть имеются две пересекающиеся поверхности, описываемые радиус-век-
радиус-векторами r(u, v) и s(a, Ь). Радиус-вектор поверхности фаски представим в форме
линейчатой поверхности
0<*<1, D.11.1)
D.11.2)
D.11.3)
, z) = A - z)lr(t) + zla(t), 0<г
построенной по двум линиям на заданных поверхностях
lr(t) = r{u(t),v(t)),
ls(t) = s(a{t),b(t)),
проходящим вдоль их линии пересечения. Эти двухмерные линии определяют
края поверхности фаски D.11.1). Линии D.11.2) и D.11.3) должны иметь об-
общий параметр t. Первый параметр поверхности фаски совместим с параметром
кривых, на которых она построена. Границы поверхности фаски по первому
параметру будут определены при дальнейшем использовании поверхности.
Если известна линия пересечения поверхностей (например, при снятии фас-
фаски на ребре тела) и угол а между поверхностями остается постоянным при
движении вдоль линии пересечения, то линии lr(?), ls(t) можно построить как
эквидистантные линии к линии пересечения. Рассмотрим построение поверх-
поверхности фаски в общем виде.
Общий случай. Вблизи линии пересечения пространство будем делить
поверхностями на четыре сектора таким же образом, как и при построении
поверхности скругления. Это нужно для того, чтобы определить, с какой сто-
стороны от линии пересечения проходят линии D.11.2) и D.11.3). Через mr(u, v)
и ms(a, Ь) обозначим нормали A.7.18) поверхностей r(u, v) и s(x, у), а через
tr{u, v) =
ts(a, Ь) =
mr x (mr x ms)
|mr x ms| '
ms x (ms x mr)
\ms x mr|
D.11.4)
D.11.5)
обозначим единичные векторы трансверсалей, которые лежат в касательных к
поверхностям плоскостях и ортогональны линиям 1Г(?) и ls(t) соответственно.
На рис. 4.11.1 приведены нормали и трансверсали D.11.4) и D.11.5).
s(a, Ь)
тг
г(и, v)
Рис. 4.11.1
Задача построения поверхности фаски сходна с задачей построения поверх-
поверхности скругления. Параметры u(t), v(t), a(t), b(t), определяющие линии D.11.2)
и D.11.3) и являющиеся координатами точек на поверхностях, связаны вектор-
17 - 5293 Голованов
258
Гл. 4. Операции над кривыми и поверхностями
ным уравнением
r(u, v) + drtr(u, v) = s(a, Ь) + dsts{a, Ь).
D.11.6)
Величины dT и ds определяют расстояние от линий D.11.2) и D.11.3), соот-
соответственно, до точки пересечения трансверсалей. Знаки величин dr и ds опре-
определяют, с какой стороны от линии пересечения проходят линии lr(t) и \s(t),
т.е. определяют сектор, в котором лежит поверхность фаски. Если в области
пересечения поверхности плоские и ортогональны друг другу, то абсолютные
величины dr и ds равны катетам фаски.
Фаска с переменными катетами. Поверхность фаски можно связать с линией
пересечения поверхностей c(s), а величины dr и ds можно поставить в зависи-
зависимость от длины дуги s этой линии. В этом случае параметры u(t), v(t), a(t),
b(t), определяющие линии D.11.2) и D.11.3), связаны уравнениями
r(u, v) + dr(s)tr{u, v) = s(a, b) + ds(s)ts(a, b),
D.11.7)
(ф) - i(r(u, v) + rfrtr(u, v) + s(a, b) + d.ts(a, b)) V ? = 0. D.11.8)
Данная система содержит четыре уравнения относительно четырех параметров:
u, v, a, 6.
При решении системы уравнений D.11.7) и D.11.8) требуется вычислять
производные нормалей поверхностей по параметрам. Эти производные опреде-
определяют формулы Вейнгартена A.7.26). Радиус-вектор точки поверхности за ее
Рис. 4.11.2. Поверхность фаски
пределами может быть вычислен по одной из формул C-14.8)—C.14.10) в зави-
зависимости от замкнутости поверхности. Эти же формулы позволяют определить
нормали и векторы D.11.4) и D.11.5) поверхности и их производные за преде-
пределами поверхности.
На рис. 4.11.2 приведен пример поверхности фаски.
В зависимости от замкнутости поверхностей и линий D.11.2) и D.11.3) по-
поверхность фаски может быть замкнутой или незамкнутой.
4.12. Определение точек пересечения трех поверхностей 259
4.12. Определение точек пересечения трех поверхностей
В некоторых случаях требуется найти точку (точки) пересечения трех по-
поверхностей. Рассмотрим сначала частный случай — пересечение трех плос-
плоскостей.
Пересечение трех плоскостей. Пусть даны три плоскости
Г(и, v) — Г0
s(o, 6) = so + asi + 6s2, D.12.1)
ф, y) = q0 + zqi + y^a
с единичными нормалями mr, ms, mq соответственно. Плоскости имеют един-
единственную точку пересечения, если смешанное произведение нормалей отлично
от нуля: (mr x ms) ¦ mq ф 0. Пусть искомая точка имеет радиус-вектор р.
Тогда вектор р — Го коллинеарен плоскости г(u, v), вектор р — So колинеарен
плоскости s(a, b), вектор р —qo коллинеарен плоскости ц(х, у). Следовательно,
должны выполняться равенства
(р - г0) • mr = 0,
(p-so)-me = O, D.12.2)
(р - q0) ¦ m, = 0.
Обозначим через р\, р2, Рз координаты точки р, через mi, m2, гпз — ком-
компоненты вектора нормали mr, через щ, П2, пз — компоненты вектора нор-
нормали ms, через l\, h, h — компоненты вектора нормали mg. Тогда система
уравнений D.12.2) примет вид
+ m2p2 + т3рз = г0 • тг,
+ п2р2 + пзРз = So ¦ ms, D.12.3)
^iPi + I2P2 + hP3 = Qo ¦ mg.
Решив систему линейных алгебраических уравнений D.12.3) относительно р\,
Р2-, Рз, найдем общую точку трех плоскостей. Параметры этой точки для каждой
из плоскостей найдем по формулам
_ Г1 ¦ (р - Гр) _ Г2 ¦ (р - Г0)
Р Г1 • Г1 Р Г2 ¦ Г2
Si ¦ (р ~ Sp) S2 • (р - Sp) (ллчл\
ар = , Ьр = , D.12.4)
р si • si р s2 ¦ s2
_
Xp~
(р - go) _ 02 • (p - go)
gi-gi ' Vp g2-g2 '
если ортогональны пары векторов r*i, r2; Si, s2; qi, q2, или по формулам D.6.6)
и D.6.7) в противном случае.
Общий случай. В общем случае пересечения трех поверхностей г (и, v),
s(a, Ь) и с±(х, у) каждая точка пересечения должна удовлетворять векторным
уравнениям
г(«, v) - ф, у) = 0, ,,.»>
17* в(а,Ь)-ф,у) = 0. [ Ь)
260 Гл. 4. Операции над кривыми и поверхностями
Эти векторные уравнения содержит шесть скалярных нелинейных уравнений
относительно шести параметров u, v, о, Ь, х, у поверхностей. Если в точках пе-
пересечения смешанное произведение нормалей поверхностей отлично от нуля, то
система может быть решена одним из описанных численных методов. Как пра-
правило, мы будем обращаться к решению этой задачи с известным начальным
приближением. Например, нам будут известны линии пересечения поверхно-
поверхностей q(a;, у) и r(u, v), q(a;, у) и s(o, 6), и будет требоваться найти пересечение
этих линий. Начальное приближение может быть найдено из решения задачи
пересечения соответствующих двухмерных линий на поверхности <l(x, у).
Пусть нам известно начальное приближение параметров трех поверхностей
в районе их общей точки пересечения. Тогда в методе Ньютона на r-й ите-
итерации приращения параметров Au^r\ Av^r\ Aa^r\ Ab^r\ Ax^r\ Ay^r> точки
пересечения будем искать из системы линейных уравнений
= qi - n,
ду(г) = й _ Г2,
= qi - в1>
^ДЬ fW |
до дх ду
- ^Ау(г) = й - Я2>
ду
^Аа(г) + ^ Дй(г) - %Дж(г) _ |з (г)
аа аЬ аж ау
где п, ^2) ^з "— компоненты радиус-вектора поверхности r(u^r', v^r'), si, S2,
S3 — компоненты радиус-вектора поверхности s(a^r\ b^), qi, q2, Яз — компо-
компоненты радиус-вектора поверхности q(x^r', y^r>). Следующее приближение пара-
параметров точки пересечения равны и^г+1^ = и^ + Au^r\ i;(r+1) = v^ + Av^r\
а(г+1) = о(г) + до(г)) Ь(г+1) = 6(г) + Д6(г); ж(г+1) = x(r) + да;(г)) у(г+1) = у(т) +
+ Ау(г\ Процесс уточнения параметров закончим, когда на очередной итерации
выполнятся неравенства |^г+1^ — и^гЦ < е, |i/r+1) — и^| < е, |о^г+1^ — а^\ < е,
) )
4.13. Точность вьшолнения операций
Для описания кривых линий и поверхностей мы используем параметриче-
параметрическое представление. Геометрические объекты построены так, что они выдают
необходимую геометрическую информацию для заданных параметров. Поэтому
поиск некоторого решения заключается в поиске соответствующих ему параме-
параметров. Если известны параметры, то можно считать, что известно все остальное.
Параметры решения не изменяются при одновременном перемещении, повороте
или трансформировании взаимодействующих геометрических объектов.
4.13. Точность выполнения операций 261
В итерационных методах вьшолнения операций параметры геометрических
объектов мы находим с некоторой точностью е. Мы заканчиваем процесс уточне-
уточнения параметров, когда на очередной итерации изменение каждого параметра по
абсолютной величине становится меньше е: (|a;(fe+1)— х^\ < е). На самом деле,
точность решения ниже величины е. В близи точек касания решение сходится
очень медленно, а в самих точках касания решение может расходиться. Значе-
Значение некоторого параметра х^к+1^ на последней итерации отличается от искомого
точного значения х* на величину ? « |x(fc+1) — x*\, которая в несколько десят-
десятков или сотен раз может быть больше величины е. В то же время, величина е
не должна превосходить 10~п, где п — число точных чисел в мантиссе пред-
представления параметров. Общее количество m > n значащих цифр в мантиссе
представления действительных чисел в памяти компьютера является отправ-
отправной точкой для определения максимальной точности, которую можно достичь
численными методами.
Пусть мы определились с величиной ?, которую назовем заданной точно-
точностью. Две точки геометрического объекта мы будем считать совпадающими,
если соответствующие им параметры отличаются меньше, чем на величину ?.
Кроме величины ? нам потребуется точностью выполнения операций — вели-
величина е, которая связана с величиной ? и должна быть меньше нее (е < ?).
Там, где это возможно, операции следует выполнять без привлечения числен-
численных методов. В этих случаях точность выполнения операций будет зависеть от
точности диагностики частных случаев. Например, при пересечении цилиндри-
цилиндрической поверхности с ортогональной ее оси плоскостью точность построения
линии пересечения будет определяться точностью, при которой вектор нормали
плоскости и ось цилиндра считаются параллельными. Два вектора можно счи-
считать параллельными, если длина их векторного произведения меньше некото-
некоторой величины. Если по результатам проверки векторов на параллельность мы
будем выполнять операцию, то проверка должна выполняться с участием точ-
точности выполнения операций е. Если проверка выполняется для других целей,
то она должна выполняться с участием точности ?.
Возникает вопрос, каким образом с помощью величин ? и е, связанных с
параметрами, оценить близость точек или векторов в пространстве? Для отве-
ответа на этот вопрос нам придется привлечь некоторый геометрический размер
модели. В качестве такого геометрического размера можно взять диагональ d
габаритного куба модели. Предположим, что параметрическая длина некоторой
кривой или поверхности модели не меньше единицы (<тах — *min ^ 1) и Раз-
меры соизмеримы с диагональю d. Тогда две точки геометрического объекта,
находящиеся на параметрическом расстоянии ? или е, в пространстве будут
находиться на расстоянии, не превышающем ?d или ed соответственно. Если
нам известно значение параметра точки г геометрического объекта, в которой
параметр определен с точностью е, то в пространстве эта точка будет опреде-
определена с точностью ег'. Точно так же отклонение вектора длиной d на угол ?
или е даст перемещение в пространстве, примерно равное ?d или ed соответ-
соответственно. Через габаритный размер d геометрические погрешности связаны с
параметрическими и угловыми погрешностями ? и е.
При выполнении операций важно знать, с какой точностью они были вы-
выполнены. Мы будем пользоваться двумя величинами: ? и е. С точностью е мы
будем выполнять операции, а с точностью ? мы будем проверять величины на
равенство.
Глава 5
ТОПОЛОГИЯ ОБОЛОЧЕК
5.1. Топологические объекты
Моделирование окружающих нас предметов требует привлечения более слож-
сложных геометрических объектов, чем точки, кривые и поверхности. Одной поверх-
поверхностью в общем случае невозможно описать геометрическую форму некоторого
заданного предмета, но это можно сделать с помощью нескольких поверхностей,
связав их определенным образом. То, каким образом поверхности будут связаны
друг с другом, составляет дополнительную информацию, которой мы снабдим
новые объекты, построенные на основе уже рассмотренных геометрических объ-
объектов. Нашей целью является получение геометрической модели окружающих
предметов. Все эти предметы занимают некоторую часть пространства, или,
другими словами, занимают конечный объем пространства. Для их модели-
моделирования нужно описать совокупность поверхностей, отделяющих внутренний
объем предмета от остальной части пространства. Для этого потребуется набор
определенным образом построенных и обрезанных поверхностей и информа-
информация о взаимной связи этих поверхностей — как одна поверхность переходит в
другую.
Оболочки. Поверхности могут быть замкнутыми по одному или двум параме-
параметрическим направлениям или незамкнутыми. Незамкнутые поверхности имеют
границу. Границей будем назвать линию на поверхности, соответствующую
движению ее параметров по границе их области определения. Линию на за-
замкнутой поверхности, по которой она замыкается сама на себя, будем называть
швом. Поверхности могут стыковаться друг с другом по границам. Можно ска-
сказать, что по шву замкнутая поверхность стыкуется сама с собой. Совокупность
стыкующихся по границам поверхностей будем называть оболочкой. Оболочка
может состоять из одной поверхности или нескольких поверхностей. Также как
и отдельная поверхность, оболочка может быть замкнутой и незамкнутой. За-
Замкнутая оболочка не имеет границы. Незамкнутая оболочка имеет одну или
несколько границ.
В предыдущих главах мы исследовали геометрические свойства кривых и
поверхностей путем определения их количественных характеристик (длин и
углов). В данной главе нас будут интересовать свойства геометрических объек-
объектов, не зависящие от количественных характеристик. Мы будем рассматривать
непрерывную связь между точками геометрических объектов. Предположим,
что оболочка выполнена из эластичного неразрываемого и не склеиваемого мате-
материала. Исследуем свойства этой оболочки, которые сохраняются при всевозмож-
всевозможных ее деформациях. Деформацией будем называть изменение формы оболочки
путем растяжения, сжатия, сдвига или изгиба ее поверхности, не приводящее
к разрывам и не требующее склеивания поверхностей оболочки. Эластичная
оболочка в виде куба может быть деформирована в сферу, или эллипсоид, или
5.1. Топологические объекты 263
оболочку в виде тетраэдра, но не может быть деформирована в тороидальную
оболочку. Сфера, эллипсоид, оболочка в виде тетраэдра или куба могут быть
преобразованы друг в друга путем непрерывных и обратимых отображений.
Свойства геометрических объектов, сохраняющиеся при непрерывных и обра-
обратимых отображениях одного пространства в другое, изучает топология. С то-
топологической точки зрения сфера, эллипсоид, оболочка в виде тетраэдра или
куба эквивалентны. Свойства, характеризующие непрерывность точек некото-
некоторой оболочки, являются топологическими свойствами. Несмотря на кажущуюся
неопределенность, топологические свойства геометрических объектов связаны с
фундаментальными математическими понятиями.
Топология изучает общий случай оболочек, которые могут самопересекаться,
иметь или не иметь границы, уходить в бесконечность. Топология оперирует
своими объектами, которые несут информацию о их взаимной связи друг с дру-
другом, и устанавливает между ними соотношения. При моделировании окружаю-
окружающих нас объектов мы будем строить оболочки из топологических объектов.
Они будут нести и количественную геометрическую информацию и топологи-
топологическую информацию. Количественная геометрическая информация топологи-
топологического объекта содержится в его геометрическом носителе, которым может
являться точка, кривая или поверхность. В данной главе мы сосредоточим
внимание на топологических свойствах моделируемых объектов.
Вершины, ребра, циклы, грани. Рассмотрим оболочки, построенные на осно-
основе поверхностей в трехмерном евклидовом пространстве. Для отслеживания
связей составляющих оболочку поверхностей дополним поверхности информа-
информацией об этих связях и введем топологические объекты. Топологические объекты
будут нести одновременно метрическую и топологическую информацию. Одним
Рис. 5.1.1. Топологические объекты
из топологических объектов является оболочка. При построении оболочки бу-
будем использовать такие топологические объекты, как грани, ребра, вершины
и циклы (рис. 5.1.1). Все топологические объекты имеют общие принципы по-
построения.
Гранью будем называть топологический объект, построенный на основе по-
поверхности. Фактически грань представляет собой поверхность плюс информа-
информация о том, какая сторона поверхности является наружной стороной грани, и
информация об ее положении в оболочке, т. е. информация об ее соседях. Ин-
Информация о соседних гранях оформляется в виде циклов.
Цикл — это топологический объект, который описывает одну из границ
грани, и содержит информацию о том, где и как к данной грани примыкают
соседние грани. Так как вдоль одного цикла к данной грани могут примыкать
несколько соседних граней, то цикл состоит из нескольких участков. Каждый
участок цикла опирается на некоторое ребро.
264
Гл. 5. Топология оболочек
Ребром будем называть топологический объект, построенный на основе ли-
линии стыковки соседних граней или на основе граничной линии оболочки. Грани
стыкуются только по ребрам. Таким образом, каждая грань со всех сторон
окружена ребрами. Вершиной будем называть топологический объект, постро-
построенный на основе точки, в которой стыкуются ребра. Вершины могут лежать
только на краях ребер. Каждое ребро начинается и оканчивается в вершине.
Если ребро замкнуто, то оно начинается и оканчивается в одной и той же вер-
вершине. Цикл состоит из ребер, образующих замкнутую линию вдоль одной из
границ грани. Цикл всегда замкнут и ему приписывается определенное напра-
направление. Грань может содержать несколько циклов, причем один из них является
внешним, а остальные — внутренними и целиком лежащими внутри внешнего
цикла. За положительное направление цикла примем направление движения
вдоль цикла, при котором грань всегда находится слева, если смотреть с наруж-
наружной стороны грани. Таким образом, внешний цикл грани ориентирован против
Рис. 5.1.2. Ориентация внешнего и внутренних циклов грани
часовой стрелки, а внутренние циклы ориентированы по часовой стрелке, если
смотреть с наружной стороны грани. Каждый цикл проходит по одной из границ
поверхности. На рис. 5.1.2 приведен пример грани с ее циклами.
Грани, ребра и вершины строятся на базе известных геометрических объ-
объектов (точек, кривых и поверхностей) добавлением к ним информации о своих
соседях и о взаимной ориентации. В результате геометрические объекты при-
приобретают новое качество, чем и обусловлено введение топологических объектов.
5.2.* Эйлерова характеристика оболочек
Топологические свойства оболочки могут быть выражены через количество ее гра-
граней, ребер, вершин и циклов. Пусть оболочка содержит F граней, Е ребер, V вершин
и L циклов. Число вершин, ребер, граней и циклов оболочки связаны между собой
соотношением
F - Е + V + (F - L) = Я,
E.2.1)
где величина Н называется эйлеровой характеристикой оболочки. Формула E.2.1) но-
носит имя формулы Эйлера. Если каждая грань оболочки имеет один цикл, то F — L = О
и слагаемое в скобках в левой части E.2.1) может быть опущено. Одну и ту же обо-
оболочку можно построить из различного набора граней. Например, сферическую оболочку
можно построить из двух полусфер или из нескольких сферических сегментов подобно
футбольному мячу. Как будет видно далее, эйлерова характеристика оболочки не зави-
зависит от числа и формы составляющих ее граней, но зависит от природных характери-
характеристик оболочки, которые изучает топология.
5.2. Эйлерова характеристика оболочек
265
Рассмотрим, как изменяется эйлерова характеристика оболочки при изменении
составляющих ее элементов. Для этого будем изменять состав граней, ребер и вер-
вершин некоторого фрагмента оболочки, не изменяя состава остальной части оболочки.
Рис. 5.2.1. Эйлерова характеристика не изменяется при ликвидации ребра оболочки
При желании оболочкой можно считать только показанный на рисунках фрагмент. На
рис. 5.2.1 показан фрагмент оболочки, у которого ликвидируется одно ребро. Из рисунка
видно, что при ликвидации одного ребра число граней, число ребер и число циклов
уменьшается на единицу, а эйлерова характеристика оболочки не изменяется.
Если объединить два ребра, ликвидировав общую для них вершину, то число ре-
ребер и вершин оболочки уменьшатся на единицу. Если разрезать ребро на две части,
вставив вершину, то число ребер и вершин оболочки увеличится на единицу. Эйлерова
характеристика оболочки в обоих случаях не изменится. При введении одного дополни-
дополнительного ребра между существующими вершинами число граней, число циклов и число
Рис. 5.2.2. Эйлерова характеристика не изменяется при добавлении ребра в оболочку
ребер увеличится на единицу. При введении дополнительного ребра с добавлением двух
новых вершин на его концах число граней и циклов увеличивается на единицу, число
ребер увеличивается на три из-за деления двух существующих ребер на две части и
добавления нового ребра, а эйлерова характеристика оболочки не изменяется, что пока-
показано на рис. 5.2.2.
Эйлерова характеристика оболочки не изменяется и при введении одного дополни-
дополнительного ребра, соединяющего существующую вершину и новую вершину, делящую
существующее ребро на два ребра.
В приведенных примерах все грани не изменяли число ограничивающих их циклов,
а все новые грани имели один цикл. В общем случае грань может иметь вырезы внутри.
Грань с вырезами с топологической точки зрения отличается от грани без вырезов, так
как первую нельзя преобразовать во вторую путем деформирования. Число вырезов
Рис. 5.2.3. Добавление грани и двух циклов в оболочку
в грани также играет существенную роль. Топологически эквивалентными являются
грани, которые путем деформирования могут быть преобразованы одна в другую. Для
этого грани должны иметь одинаковое число вырезов или одинаковое число циклов.
На рис. 5.2.3 показано добавление новой грани в оболочку путем введения замкнутого
ребра, целиком лежащего внутри существующей грани.
266 Гл. 5. Топология оболочек
Число граней, ребер и вершин при этом увеличится на единицу, а число циклов
увеличится на два (цикл на добавленном замкнутом ребре должен быть посчитан два-
дважды: один раз в одной грани, второй раз — в другой грани). Эйлерова характеристика
оболочки при этом также не изменится. Эйлерова характеристика оболочки не изме-
изменится, если мы преобразуем грань с двумя циклами в грань с одним циклом, что
Рис. 5.2.4. Добавление ребра и ликвидация внутреннего цикла грани
приведено на рис. 5.2.4. Покажем это. Пусть новое ребро начинается и оканчивается в
уже существующих вершинах, тогда число ребер увеличится на единицу, число циклов
уменьшится на единицу, а эйлерова характеристика не изменится.
Все перечисленные модификации оболочки не изменяют ее эйлеровой характери-
характеристики. Это иллюстрирует то, что эйлерова характеристика не зависит от способа раз-
разбиения оболочки на грани, а зависит только от природы оболочки.
Рассмотрим еще один пример, показывающий, что эйлерова характеристика зави-
зависит от топологии оболочки, и не зависит от способа раскроя ее на грани. Возьмем
Рис. 5.2.5. Эйлерова характеристика оболочек различна
оболочку в форме четырехугольной призмы и превратим ее в оболочку в форме четы-
четырехугольной призмы с четырехугольным отверстием, что показано на рис. 5.2.5.
Исходная оболочки имела следующие числа граней, циклов, ребер и вершин: F = 6,
L — 6, Е = 12, V = 8, и ее эйлерова характеристика равна Н = 2. Результирующая
оболочки имеет: граней F — 10, циклов L = 12, ребер Е — 24, вершин V = 16, а
ее эйлерова характеристика равна Н = 0. В двух гранях увеличилось число ци-
Рис. 5.2.6
клов (было по одному циклу, а стало по два). Эйлерова характеристика новой оболочки
уменьшилась на две единицы. Повторим переход от той же призматической оболочки
к призматической оболочке с вырезом, только верхнюю и нижнюю грань исходной
оболочки представим в виде совокупности девяти граней, как показано на рис. 5.2.6.
5.3. Связность оболочек 267
Исходная оболочки имела следующие числа граней, циклов, ребер и вершин: F = 22,
L — 22, Е = 52, V = 32, и ее эйлерова характеристика равна Н = 2. Результирующая
оболочки имеет: граней F = 24, циклов L = 24, ребер Е = 56, вершин V = 32, а ее
эйлерова характеристика равна Я = 0. Все грани в исходной и результирующей обо-
оболочках имеют по одному циклу. Эйлерова характеристика результирующей оболочки,
как и предыдущем примере, уменьшилась на две единицы.
Это произошло в результате того, что мы получили оболочку, которая топологиче-
топологически неэквивалентна исходной оболочке. Действительно, представив, что обе оболочки,
показанные на рис. 5.2.5, выполнены из легко деформируемого материала, скруглив
Рис. 5.2.7. Сфера и тор имеют различную топологию
углы, из первой оболочки получим сферу, а из второй — тор (рис. 5.2.7). Никакими
деформациями невозможно из сферы получить тор — они имеют разную топологию.
Эйлерова характеристика оболочки отражает ее природные свойства, связанные с
возможностью деформировать одну оболочку в другую или, другими словами, устано-
установить между ними взаимно однозначное соответствие. Для описания топологических
свойств оболочек и их граней используется понятие связности. Оболочки одинаковой
связности могут быть деформированы одна в другую при условии, что они имеют равное
число границ и одинаковую ориентируемость.
5.3.* Связность оболочек
Исследуем топологические свойства оболочек. Эти свойства не зависят от коли-
количественных характеристик (объема, площади поверхности и т.п.). Не будем обращать
внимания на ребра и вершины, а будем воспринимать оболочку как единое целое. Пред-
Представим, что оболочка выполнена из легко деформируемого неразрываемого и не склеива-
склеиваемого материала. Мы можем изменить форму оболочки, но до определенных пределов.
Например, если оболочка имеет форму шара, то ей можно придать ему форму куба
или тарелки, но нельзя придать ему форму тора или кувшина с ручкой. Данный факт
является отражением того, что упомянутые шар, куб и тарелка имеют одинаковую то-
топологию, которая отличается от топологии тора и кувшина с ручкой. Топологической
характеристикой описанного свойства оболочек является связность. В приведенном при-
примере оболочки с формой шара, куба или тарелки, имеют одну и ту же связность, которая
отлична от связности оболочки с формой тора или кувшина с ручкой. Так как тополо-
топология характеризует непрерывную связь точек объектов, то для определения топологиче-
топологических свойств следует изучить поведение топологических объектов при разделении их на
части.
Связность — это топологическое понятие, характеризующее целостность некото-
некоторого объекта. С другой стороны связность отражает возможность разделить некото-
некоторый топологический объект на отдельные части. Простейшей является незамкнутая
оболочка с одной границей (одним циклом) топологически эквивалентная кругу. Если
представить, что оболочки выполнены из легко деформируемого материала, то простей-
простейшей является оболочка, которой путем деформирования можно придать плоскую форму
с границей в виде окружности. Прямоугольная, эллиптическая, любая плоская оболочка
268
Гл. 5. Топология оболочек
с одной границей является простейшей. Рассмотрим вопрос: какое минимальное число
линий можно провести на поверхности оболочки, чтобы по этим линиям ее можно было
бы разрезать на две простейшие? Простейшая оболочка делится на две отдельные части
любой линией, проведенной от одной точки границы до другой. Простейшей оболочке
приписывается связность равная единице. Ее называют односвязной.
Рассмотрим незамкнутые оболочки, имеющие конечное число циклов (границ), ко-
которые путем деформирования без склеивания и наложений можно сделать плоскими.
На рис. 5.3.1 приведены примеры плоских оболочек с различным числом циклов. Если
Рис. 5.3.1. Плоские оболочки различной связности
плоская оболочка имеет L циклов (один внешний и L — 1 внутренних), то на ней можно
провести L — 1 линий, не разрезающих оболочку на две отдельные части (например, от
внешнего цикла к каждому внутреннему циклу). Любая следующая линия, начинаю-
начинающаяся и оканчивающаяся на границе оболочки, разрежет ее на две части. Плоская
оболочка с вырезами обладает дополнительными связями, которые мы режем, а обо-
оболочка не теряет свою целостность. Целостность оболочки заключается в том, что из
некоторой ее точки, двигаясь по ее поверхности, можно попасть в любую другую ее
точку. Плоской оболочке с L циклами припишем связность равную L.
Связность оболочки определим минимальным числом линий, по которым ее можно
разрезать на две простейшие оболочки (на две отдельные части). Если связность обо-
оболочки равна h, то h — 1 разрезов достаточно, чтобы ими раскроить оболочку, превратив
ее в простейшую. Связность обозначим через h.
Рассмотрим замкнутые оболочки. На оболочке как на поверхности можно свободно
строить кривые линии. Предположим, что мы можем резать оболочку по кривым на
ней. Если оболочка имеет топологию сферы, то по любой замкнутой кривой на ее по-
поверхности оболочку можно разрезать на две отдельные части, представляющие собой
односвязные оболочки. Если оболочка имеет топологию тора, то для раскроя ее в од-
носвязную грань, потребуется, как минимум, две замкнутые кривые на ней. Способ
раскроя тороидальной оболочки показан на рис. 5.3.2.
Используя определение, получим, что связность сферы равна единице, а связность
тора равна трем.
На замкнутой оболочке связности h можно построить h — 1 замкнутых кривых,
которые не нарушают ее целостности (которые не разрезают ее на отдельные части),
но нельзя построить h таких кривых, для того, чтобы замкнутую оболочку связности
Рис. 5.3.2. lVi.nuft 1ч1>'Ж1..иы1чй оболочки
Рис. 5.3.3. Раскрой цилиндрической оболочки
h раскроить в односвязную оболочку, ее нужно разрезать по h — 1 замкнутым линиям.
Эти линии не разрезают оболочку на две отдельные части, но любая совокупность,
состоящая из h замкнутых кривых на оболочке, обязательно разрезает оболочку на две
части.
5.4. Ориентируемость оболочек 269
Рассмотренные замкнутые оболочки имеют нечетную связность. Существуют обо-
оболочки четной связности. Четную связность могут иметь незамкнутые оболочки. На-
Например, цилиндрическая оболочка конечной длины имеет связность равную двум.
Действительно, линия, проходящая от одной границы до другой, не разрезает ци-
цилиндрическую оболочку на отдельные части, а только раскраивает ее в односвязную
оболочку (рис 5.3.3). Любая другая линия, проходящая от одной границы до другой,
разрежет цилиндрическую оболочку на части.
На рис. 5.3.4 показаны незамкнутые оболочки, полученные из замкнутых оболочек,
если в последних сделать отверстия. Если в замкнутой оболочке связности h выполнить
одно отверстие с одной замкнутой границей, то связность полученной незамкнутой обо-
оболочки будет равна связности исходной замкнутой оболочки. Каждое последующее отвер-
отверстие с одной замкнутой границей будет увеличивать связность полученной оболочки на
единицу. Связность приведенных на рис. 5.3.4 незамкнутых оболочек соответственно
Рис. 5.3.4. Незамкнутые оболочки
равна 1, 4, 3, 6. Система разрезов на этих оболочках строится аналогично системе
разрезов на соответствующей замкнутой оболочке, только часть линий проводится от
одной границы к другой границе.
Связность не является единственной характеристикой оболочки. Две оболочки могут
иметь одинаковую связность, но быть топологически различными. Кроме связности
оболочка характеризуются ориентируемостью.
5.4.* Ориентируемость оболочек
Для многих замкнутых оболочек одну из сторон можно определить как внутреннюю,
а другую — как наружную. Для точек оболочек вводится такое топологическое понятие
как ориентируемость. Представим, что вокруг всякой точки оболочки проведена окруж-
окружность достаточно малого радиуса, расположенная на поверхности оболочки. Для каждой
окружности определим такое направление обхода, что достаточно близкие точки всегда
будут обходиться в одном и том же направлении. Если для некоторой оболочки это
можно сделать, то такая оболочка называется ориентируемой. Существуют оболочки,
для которых нельзя ввести единое направление обхода для окружностей близких точек.
Такие оболочки называются неориентируемыми.
Лист Мёбиуса. Примером неориентируемой оболочки является лист Мёбиуса,
показанный на рис. 5.4.1. Лист Мёбиуса можно получить, взяв бумажную полосу и
склеив дальние края, повернув предварительно их друг относительно друга на 180°. До
склеивания краев полосы ее стороны можно покрасить двумя разными цветами. Если
покраску проводить после склеивания, то окажется, что мы окрасим одним цветом обе
стороны. При движении по листу Мёбиуса мы пройдем по обеим его сторонам.
Для точек листа Мёбиуса нельзя определить ориентацию. Действительно, задав для
малой окружности некоторой точки ориентацию и двигаясь по оболочке, мы попадем в
исходную точку, но с противоположным направлением. Результатом этого является не-
невозможность окрасить разные стороны оболочки в разные цвета. У оболочки всего одна
сторона. Лист Мёбиуса является односторонней оболочкой. Если оболочка является
односторонней, то она не ориентируема. Справедливо и утверждение, что если оболочка
является двусторонней, то она ориентируема.
270
Гл. 5. Топология оболочек
Оболочка тогда и только тогда неориентируема, когда на ней можно построить такую
замкнутую кривую s, что при движении вдоль этой кривой достаточно малой ориентиро-
ориентированной окружности она придет в исходную точку ориентированной в противоположном
Рис. 5.4.1. Лист Мёбиуса — односторонняя незамкнутая оболочка
Рис. 5.4.2. Ориентируемая самопересекающаяся незамкнутая оболочка
направлении. Если двигаться вдоль кривой s на односторонней оболочке по одну сто-
сторону от этой кривой, то можно оказаться по другую сторону кривой, хотя при движении
кривая не пересекалась.
Лист Мёбиуса является незамкнутой оболочкой. Существуют замкнутые односто-
односторонние оболочки. Односторонняя оболочка не может разбить пространство на внутрен-
внутреннюю и внешнюю части, поэтому односторонняя замкнутая оболочка всегда пересекает
сама себя. Однако не всякая самопересекающаяся оболочка является односторонней.
Оболочка, показанная на рис. 5.4.2, самопересекающаяся, но не односторонняя.
Бутылка Елейна. Примером замкнутой односторонней оболочки является бутылка
Клейна, которая показана на рис. 5.4.3. Бутылка Клейна имеет одну замкнутую линию
Рис. 5.4.3. Бутылка Клейна — односторонняя замкнутая оболочка
самопересечения. Она не может служить сосудом. Связность бутылки Клейна равна
трем. Система линии, разрезающих бутылку Клейна на две односвязные части, анало-
аналогична системе линий тора.
Если бутылку Клейна разрезать плоскостью ее симметрии, то получим две не-
незамкнутые самопересекающиеся оболочки, из которых путем деформирования можно
получить два листа Мёбиуса.
Гептаэдр. Еще одной односторонней оболочкой является гептаэдр. Его можно по-
получить из октаэдра. Для этого удалим четыре грани из восьми: на верхней части
октаэдра — левую переднюю и правую заднюю, а на нижней части — правую перед-
переднюю и левую заднюю грани, и добавим три квадратные взаимно ортогональные грани,
построенные на диагоналях октаэдра. Грани гептаэдра по отдельности приведены на
рис. 5.4.4. Оболочка гептаэдра состоит из семи граней. Ребра и вершины гептаэдра
совпадают с ребрами и вершинами октаэдра (диагонали не считаются ребрами, а явля-
являются линиями самопересечения оболочки). В каждом ребре гептаэдра стыкуются только
две грани. Гептаэдр является замкнутой односторонней оболочкой четной связности.
Он показан на рис. 5.4.5.
Если мы начнем движение по поверхности гептаэдра из точки А, то, двигаясь по
указанной на рис. 5.4.5 траектории, попадем в точку В, расположенную на другой сто-
стороне поверхности.
5.5. Оболочки для моделирования тел
271
Таким образом, кроме связности оболочки характеризуются еще и ориентируемо-
ориентируемостью. Тор и бутылка Клейна обладают одинаковой связностью, обе замкнутые оболочки,
а б
Рис. 5.4.4. Четыре грани октаэдра (а), грани на диагоналях октаэдра (б)
но тор является ориентируемой оболочкой, а бутылка Клейна — неориентируемой. Из-
Известно еще несколько неориентируемых оболочек. Замкнутые неориентируемые обо-
оболочки пересекают сами себя, и поэтому не могут быть использованы для моделирования
Рис. 5.4.5. Гептаэдр (семигранник) — самопересекающаяся односторонняя оболочка
деталей. Оболочки, с которыми мы сталкиваемся в реальности, являются ориентируе-
ориентируемыми. Тем не менее, неориентируемые оболочки с математической точки зрения рав-
равноправны с ориентируемыми оболочками.
5.5. Оболочки для моделирования тел
Рассмотрим взаимно однозначное и непрерывное отображение одной обо-
оболочки на другую. При этом отображении соседние точки остаются соседними.
Такое отображение может искажать оболочку, но при этом связанные части оста-
останутся связанными. Одним из видов отображения является деформация. При де-
деформации топологический объект как целое непрерывно переходит сам в себя.
Движение оболочки в пространстве является частным случаем деформации, то-
тогда как зеркальное отражение оболочки относительно плоскости не является
деформацией. При зеркальном отражении изменяется на обратное направление
обхода всякой замкнутой кривой на оболочке, тогда как деформация сохраняет
направление обхода неизменным.
272 Гл. 5. Топология оболочек
Все многообразие оболочек можно классифицировать с топологической точки
зрения. К одному и тому же типу относятся оболочки, которые топологически
могут быть непрерывно и взаимно однозначно отображены одна на другую. Для
этого должны быть выполнены следующие три условия:
1) оболочки должны иметь одинаковую связность;
2) оболочки должны быть либо ориентируемы, либо неориентируемъц
3) оболочки должны быть либо замкнуты, либо должны иметь одинако-
одинаковое число границ.
Эти три необходимых условия непрерьюного и взаимно однозначного ото-
отображения двух оболочек также являются и достаточными условиями.
Естественно, что оболочки, имеющие разное число границ, не могут быть
отображены одна на другую.
Связность обусловливает существование системы разрезов оболочки, кото-
которая при топологическом отображении переходит в систему разрезов такой же
структуры на другой оболочке. Следовательно, оболочки различной связности
не могут быть отображены одна на другую.
Можно доказать, что всякая оболочка, которая может быть отображена на
ориентируемую оболочку, также является ориентируемой. Это определяет третье
условие принадлежности оболочек к одному типу.
Оболочки, имеющие одинаковую связность, ориентируемость и число гра-
границ, являются топологически эквивалентными.
Формула Эйлера-Пуанкаре. Замкнутые, ориентируемые и не пересекающие
сами себя оболочки имеют нечетную связность. Для таких оболочек эйлерова
характеристика Н связана с ее связностью h соотношением
H = S-h. E.5.1)
ней F,
стью h:
F-E + V + {F-L) = 3-h. E.5.2)
Данная запись формулы Эйлера справедлива для замкнутых оболочек.
Связность не достаточно удобна для характеристики замкнутой оболочки.
Введем еще одно понятие, которым можно заменить связность. Из тора путем
его деформирования можно получить оболочку, по
форме напоминающую гирю, которую будем назы-
называть сферой с ручкой. В общем случае любой за-
замкнутой оболочке путем деформирования можно при-
придать форму сферы с G ручками. Так, если взять
толстую плиту, пробить в ней G отверстий и скруг-
скруглить все ребра, то получим объект, оболочка кото-
которого топологически эквивалентна сфере с G ручками.
На оболочке, топологически эквивалентной сфере с
G ручками, можно провести 2G замкнутых кривых
Рис 5 5 1 С<Ье а с че- линий, по которым она раскраивается в простейшую
тырьмя ручками оболочку. Любая следующая замкнутая линия разре-
разрежет оболочку на две простейшие оболочки. Сфера с
G ручками имеет связность h = 2G + 1. Оболочка реальной детали топологи-
топологически эквивалентна сфере с некоторым числом ручек. На рис. 5.5.1 приведена
сфера с четырьмя ручками.
Используя это соотношение, получим формулу, связывающую число граней F,
число циклов L, число ребер Е и число вершин V оболочки с ее связностью h:
5.5. Оболочки для моделирования тел 273
Более наглядной, чем связность, характеристикой топологии оболочки может
служить число ручек G сферы, к которой путем деформирования можно приве-
привести замкнутую оболочку. Примем во внимание, что сфера с G ручками имеет
связность h = 2G + 1, и получим формулу, связывающую число граней F, ре-
ребер Е, вершин V и циклов L с характерной величиной G,
F-E + V + {F-L)-2{l-G) = 0. E.5.3)
Данная формула называется формулой Эйлера-Пуанкаре. Величина G (genus)
характеризует топологический тип оболочки. Формула Эйлера-Пуанкаре по-
позволяет определить топологический тип оболочки, если известно число ее гра-
граней, ребер, вершин и циклов:
G = l-F+E + L2-V. E.5.4)
Реальные объекты могут иметь внутри пустоты. В этом случае объекты
будут описываться несколькими оболочками. Одна из этих оболочек является
внешней, остальные оболочки лежат внутри нее. Если моделируемый объект
имеет т пустот, то он будет описываться S = т + 1 оболочками. Потребуем,
чтобы внутренние оболочки не пересекали друг друга и внешнюю оболочку. Для
каждой оболочки справедлива формула E.5.3), а для объекта с S замкнутыми
оболочками формула Эйлера-Пуанкаре E.5.3) примет вид
F-E + V + (F-L)-2(S-G) = 0, E.5.5)
где F — общее число граней модели, Е — общее число ребер модели, V —
общее число вершин модели, L — общее число циклов модели, S — общее
число оболочек моделируемого объекта, G — топологический тип моделируемого
объекта, равный общему числу ручек всех описывающих его оболочек. Таким
образом, топологически эквивалентными объектами будут являться два объекта,
у которых равно число описывающих их оболочек и соответствующие внешние
и внутренние оболочки имеют одинаковый топологический тип.
Если оболочка не является замкнутой, то говорить о ее топологическом
типе G не имеет смысла. Для незамкнутой ориентируемой оболочки формула
Эйлера имеет вид
F-E + V + (F-L) + h = 2. E.5.6)
Однородные оболочки. Для моделирования деталей подходят замкнутые дву-
двусторонние не пересекающие сами себя оболочки. К ним относятся оболочки,
топологически эквивалентные сфере с G ручками. Именно такие замкнутые
оболочки мы и будем использовать для геометрического моделирования. К вер-
вершинам, ребрам, циклам и граням предъявим следующие требования. Грани не
должны пересекать сами себя. Грани стыкуются только по ребрам, причем в
каждом ребре стыкуются только две грани. Оболочка, приведенная на рис. 5.5.2,
некорректна, так как в ребре АВ стыкуются четыре грани.
Такая оболочка топологически должна быть представлена одним из спосо-
способов, приведенных на рис. 5.5.3 и 5.5.4. Ребра стыкуются только в вершинах.
В каждой вершине может стыковаться любое конечное число ребер. Каждую
вершину можно обойти по поверхности оболочки, но при этом мы должны пере-
18 - 5293 Голованов
274
Гл. 5. Топология оболочек
сечь все стыкующиеся в вершине ребра и посетить все примыкающие к вершине
грани. Такие вершины будем называть простыми. Оболочка, приведенная на
Рис. 5.5.2. В каждом ребре должны пересекаться только две грани
рис. 5.5.5, также некорректна, так как вершину А можно обойти по поверх-
поверхностям граней, не пересекая всех стыкующихся в ней ребер. Такая оболочка
топологически должна быть представлена способом, приведенным на рис. 5.5.6.
Рис. 5.5.3. Корректная оболочка
Рис. 5.5.4. Корректная оболочка
Таким образом, для моделирования мы будем использовать оболочки, вер-
вершины которых являются простыми, грани пересекаются по ребрам, причем
Рис. 5.5.5. Некорректная оболочка Рис. 5.5.6. Корректная оболочка
в каждом ребре стыкуются только две грани. Такие оболочки будем называть
однородными. У однородных оболочек все топологические элементы построены
по единым правилам.
5.6. Поверхностное и твердотельное моделирование 275
5.6. Поверхностное и твердотельное моделирование
В геометрическом моделировании используются термины «поверхностное
моделирование» (моделирование поверхностей) и «твердотельное моделирова-
моделирование» (моделирование твердых тел). В обоих случаях результатом моделирова-
моделирования является некоторая оболочка (или несколько оболочек), описывающая по-
поверхность моделируемого объекта. Но процесс моделирования в первом случае
отличается от процесса моделирования во втором случае.
В поверхностном моделировании сначала создаются и модифицируются тре-
требуемым образом поверхности, описывающие отдельные элементы моделируе-
моделируемого объекта. Эти поверхности обрезают по линиям пересечения, сопрягают
друг с другом поверхностями скругления или перехода, а также выполняют
над ними другие операции. Затем из полученных поверхностей собирают обо-
оболочку. В поверхностном моделировании результирующая оболочка не обяза-
обязательно должна быть замкнутой. Она может отражать лишь часть (главную
часть) моделируемого объекта. Поверхностное моделирование позволяет сосре-
сосредоточить усилия на сложных формах объекта и широко применяется для про-
проектирования кузовов автомобилей и планеров самолетов.
В твердотельном моделировании с самого начала работа идет с оболочками
тел, а не с отдельными поверхностями. Оболочки полностью описывают поверх-
поверхности моделируемых объектов, отделяющие их внутренний объем от осталь-
остальной части пространства. Процесс построения оболочки тела в данном случае
аналогичен процессу изготовления моделируемого объекта. Сначала создается
оболочка некоторой заготовки простой формы. Далее оболочка заготовки из-
изменяется необходимым образом. Для этого используются булевы операции над
телами, операция построения тонкостенного тела из заготовки, операция скруг-
скругления ребер, операция построения ребер жесткости и другие операции. С помо-
помощью операций оболочке тела придается требуемая форма.
Два подхода к моделированию имеют много общего и отличаются техноло-
технологией создания модели. В обоих случаях выполняются аналогичные действия,
но в разной последовательности. В следующей главе мы рассмотрим моделиро-
моделирование твердых тел, так как оно включает в себя все элементы поверхностного
моделирования.
18*
Глава б
МОДЕЛИРОВАНИЕ ТЕЛ
6.1. Математическая модель тел
Точки, линии и поверхности являются математическими абстракциями.
У них хотя бы один размер полагается равным нулю. Реальные объекты имеют
все размеры, отличные от нуля, и занимают некоторый конечный объем в про-
пространстве. Для геометрического моделирования предметов, занимающих конеч-
конечный объем, в математике используются объекты, называемые твердыми телами
или просто телами. Способ их описания отличается от способа описания кри-
кривых и поверхностей. При моделировании тел строятся поверхности, отделяю-
отделяющие занимаемую ими часть пространства от остальной части пространства.
Существует несколько подходов к описанию тел.
Многие предметы можно смоделировать, используя только плоские поверх-
поверхности. Такое представление тел называется плоскогранным (Faceted represen-
representation или Faceted). Для описания криволинейных поверхностей плоскогранное
представление может аппроксимировать их некоторым количеством пластин
треугольной или четырехугольной формы. Использование плоских поверхно-
поверхностей значительно упрощает выполнение операций над телами. Плоскогранное
представление широко применяется в строительстве и компьютерной графике
для получения тоновых изображений.
Некоторые поверхности можно описать уравнениями в координатной форме
(представить поверхности неявно). К ним относятся поверхности второго по-
порядка, поверхность тора и другие. Используя для моделирования тел такие
поверхности, мы придем к конструктивной твердотельной геометрии (Con-
(Constructive Solid Geometry или CSG). Конструктивная твердотельная геометрия
оперирует примитивами, к которым, как правило, относят прямоугольную
призму, треугольную призму, сферу, цилиндр, конус и тор. Над примитивами и
полученными из них телами можно выполнять различные операции (в первую
очередь булевы операции). Используемые конструктивной твердотельной гео-
геометрией поверхности (сферическая, цилиндрическая, коническая, поверхность
тора и плоскость) делят пространство на две части и для них можно указать, с
какой стороны поверхности находится внутренний объем тела. Неявное пред-
представление поверхностей дает возможность получить линии их пересечения в
аналитической форме. Конструктивная твердотельная геометрия позволяет мо-
моделировать большинство промышленных деталей.
Наиболее общий подход к описанию тел состоит в представлении тела со-
совокупностью ограничивающих его объем оболочек, грани и ребра которых за-
заданы параметрически. Каждая оболочка строится из набора стыкующихся друг
с другом поверхностей произвольной формы, содержащих полную информацию
о своих границах и связях с соседями. Такое описание тел называется пред-
представлением с помощью границ (Bounded representation или В-rep). Оно дает
6.1. Математическая модель тел 277
возможность выполнять над телами множество операций, сохраняя при этом
единый способ их «внутреннего устройства». Представление тел с помощью
границ позволяет моделировать объекты произвольной формы и сложности.
Все перечисленные подходы к описанию тел используют топологические объ-
объекты и удовлетворяют условиям связности, ориентируемости и замкнутости.
Мы будем рассматривать представление тел с помощью границ, опираясь на та-
такие топологические объекты, как вершина, ребро, грань и оболочка. Оболочки
тела должны быть однородными, т. е. должны быть описаны по единым прави-
правилам. Оболочки состоят из набора граней. Каждая грань базируется на некото-
некоторой поверхности. Грань отличается от поверхности тем, что кроме поверхности
она в структуре своих данных несет информацию о связях с соседними гранями
и об ориентации по отношению к внутреннему объему тела. Там, где это не бу-
будет создавать путаницы, грани будем обозначать так же, как и поверхности, на
которых они базируются.
Если взять любую деталь, то можно заметить, что ограничивающие ее по-
поверхности делят пространство на две части: одну часть пространства занимает
деталь и она находится внутри (вне) ограничивающих оболочек, а другая часть
пространства лежит вне (внутри) детали. Перейти из одной части пространства
в другую часть пространства, не пересекая ограничивающие оболочки, нельзя.
Ограничивающие оболочки как бы изолируют одну часть пространства от дру-
другой. Тело может иметь одну или несколько оболочек. Если тело имеет пустоты,
то его объем ограничен несколькими оболочками. Одна из этих оболочек явля-
является внешней, а остальные оболочки — внутренними. Внутренние оболочки
ограничивают пустоты и целиком лежат внутри внешней оболочки. Оболочки
тела не должны пересекать друг друга и сами себя. Для описания тел под-
подходят двусторонние (ориентируемые) оболочки. Одной своей стороной каждая
оболочка обращена внутрь тела, а другой — наружу. Для того чтобы отли-
отличать сторону оболочки, направленную наружу тела, от стороны, направленной
внутрь тела, каждой точке оболочки приписывается нормаль, которая считается
направленной наружу тела. Нормаль внешней оболочки тела направлена вне
ограничиваемой ею части пространства, а нормаль внутренней оболочки тела
направлена внутрь ограничиваемой ею части пространства. Таким образом,
внутренние оболочки тела как бы вывернуты наизнанку.
С математической точки зрения одна внешняя оболочка и, возможно, не-
несколько внутренних оболочек описывают тело. Другими словами, для созда-
создания математической модели тела достаточно смоделировать совокупность обо-
оболочек, ограничивающих его объем. Но для редактирования тела необходима
Оболочки тела
Дерево построения
Рис. 6.1.1. Математическая модель тепа
информация о последовательности и способах его построения, поэтому в мо-
модель тела включают еще и дерево построения (или протокол построения) тела
(рис. 6.1.1).
В большинстве случаев оболочки, описывающие тело, являются замкну-
замкнутыми, но тело можно описать и незамкнутой оболочкой, если ее края стянуты в
точку. Привлечение топологии при моделировании тел необходимо для коррект-
278 Гл. 6. Моделирование тел
ного выполнения операций над ними. Топологические объекты были введены
в предыдущей главе. Здесь мы остановимся на структуре данных этих объек-
объектов. Структура данных должна быть такой, чтобы при желании можно было
найти всех соседей любого топологического объекта. Для этого они должны не-
нести информацию о взаимной связи друг с другом. Будем строить оболочки тел
из топологических объектов, которые будут нести и количественную геометри-
геометрическую информацию, и топологическую информацию.
Оболочка тела состоит из набора граней. Грань строится на основе по-
поверхности, которая входит в структуру данных грани. Поверхность является
геометрическим носителем грани. Одна сторона грани направлена наружу обо-
оболочки, другая внутрь. Грань должна содержать признак ориентации нормали по-
поверхности наружу или внутрь грани. Пусть признак принимает положительное
значение, если нормаль поверхности направлена наружу грани, отрицательное
значение — в противном случае.
Грани стыкуются между собой по ребрам, лежащим на линиях пересечения
граней. Топологический объект ребро строится на основе линии пересечения
поверхностей, стыкующихся в ребре граней. Пусть в ребре стыкуются грани,
построенные на поверхностях r(«, v) и s(a, Ъ). Линия пересечения граней опи-
описывается двумя поверхностями и двумя двухмерными линиями — каждая в
пространстве параметров соответствующей поверхности. На грани, базирую-
базирующейся на поверхности г(«, «), двухмерную линию обозначим векторной функ-
функцией lUv{t) — [u(t) v(t)] , а на грани, базирующейся на поверхности s(o, b),
двухмерную линию обозначим векторной функцией lab(t) = [aW &(*)] • Та-
Таким образом, линию пересечения граней, на которой базируется ребро, будем
записывать в виде
luv{t) =
lab(t) = ["['}] = [a(t) b(t)]T, lab(t) € s(a, b), FЛЛ)
Ребро может иметь совпадающее со своей линией направление или ей противо-
противоположное. Для этого в структуре данных ребра должен быть соответствующий
признак. Пусть этот признак принимает положительное значение, если ребро
направлено по кривой, и отрицательное значение — в противном случае.
Ребра, ограничивающие грань, входят в структуру данных грани в виде ци-
циклов. Цикл •— это топологический объект, характеризующий границу грани.
Цикл всегда замкнут и имеет определенное направление. Он состоит из списка
ребер и их ориентации в цикле. Ориентацию ребра в цикле грани будем описы-
описывать признаком, который назовем флагом. Пусть ребру, направление которого
совпадает с направлением цикла, приписывается положительный флаг, а ребру,
направление которого не совпадает с направлением цикла, приписывается отри-
отрицательный флаг. Таким образом, цикл состоит из списка ребер в порядке их
следования и списка соответствующих им флагов.
Грань может содержать несколько циклов, причем один из циклов является
внешним, а остальные циклы — внутренними. Внутренние циклы должны
целиком лежать внутри внешнего цикла. Цикл будем считать направленным
6.1. Математическая модель тел
279
так, чтобы при движении вдоль него грань всегда находилась бы слева, если
смотреть с наружной стороны грани. Таким образом, внешний цикл грани
ориентирован против часовой стрелки, а внутренние циклы ориентированы по
Рис. 6.1.2. Грань и ее структура данных: поверхность, ее ориентация и список циклов
часовой стрелке, если смотреть навстречу нормали грани. По каждому циклу
можно построить контур на поверхности, который описывает границу грани. На
рис. 6.1.2 приведен пример плоской грани с указанием направлении ее циклов.
Ребро, разделяющее две грани, входит в два цикла: в одном цикле напра-
направление ребра совпадает с направлением цикла, а в другом — противоположно
направлению цикла. Ребро входит в цикл грани слева от него с положительным
флагом, а в цикл грани справа от него с отрицательным флагом.
Ребро начинается и оканчивается в вершинах. Каждая вершина базируется
на точке в пространстве и содержит информацию о ребрах, стыкующихся в ней.
В каждой вершине могут стыковаться несколько ребер. Если ребро замкнутое,
то оно начинается и оканчивается в одной и той же вершине. Ребро должно
Конечная вершина
В
Грань
слева
Грань
справа
А
Начальная
вершина
Рис. 6.1.3. Ребро АВ и его структура данных
содержать информацию о том, какая грань находится слева, а какая — справа
от ребра, если смотреть с внешней стороны оболочки вдоль направления ребра,
и какая вершина находится в начале ребра и какая — в конце. На рис. 6.1.3
показано ребро, начинающееся в вершине А и оканчивающееся в вершине В.
Описанная структура данных топологических объектов содержит двунапра-
двунаправленную связь между ними. Оказавшись на одном из топологических объектов,
можно последовательно пройти всю оболочку, в которую входит этот объект.
Таким образом, математическая модель тела содержит количественную гео-
геометрическую информацию в виде поверхностей, линий и точек их стыковки,
топологическую информацию в виде связей точек поверхности тела между со-
собой и информацию о последовательности и способах построения в виде дерева
построения.
280
Гл. 6. Моделирование тел
6.2. Простейшие тела
Способы моделирования деталей часто повторяют технологический процесс
их производства. Один из способов моделирования тел заключается в том, что
берется некоторая заготовка тела и Затем путем удаления и добавления в опреде-
определенных местах дополнительного объема (материала) получают тело требуемой
формы. В качестве заготовок могут браться тела простейшей формы: прямо-
прямоугольная призма, цилиндр, конус, шар, тор и другие. Простейшие тела состоят
из одной оболочки, построенной по общим правилам. Рассмотрим построение
оболочки некоторых простейших тел.
Для каждого простейшего тела нам потребуется местная декартова прямо-
прямоугольная система координат, радиус-вектор начала которой обозначим через р,
а базисные орты обозначим через ix, iy, i2.
Прямоугольная призма. Начало местной системы координат поместим в одну
из вершин призмы, а ее орты направим по ребрам, стыкующимся в этой вер-
вершине. Пусть в направлении орта ix тело имеет длину, равную х, в направлении
орта iy — длину, равную у, а в направлении орта iz — длину, равную z. Пря-
Прямоугольная призма состоит из шести граней.
Каждая грань представляет собой часть плос-
плоскости, ограниченную прямоугольным контуром
на ней, с признаком ориентации нормали плос-
плоскости наружу тела и одним циклом. Контуры
состоят из отрезков прямых B.2.3). Прямо-
Прямоугольная призма имеет 12 ребер. Каждое ребро
состоит из линии пересечения поверхностей со-
соседних граней и признака совпадения направле-
направления ребра с направлением линии пересечения.
Каждая линия пересечения состоит из двух ли-
линий на поверхности: одна на поверхности одной
грани, другая на поверхности второй грани. Обе
линии на поверхности имеют одинаковую гео-
геометрическую и параметрическую длину и полностью совпадают в пространстве.
Каждая линия на поверхности представляет собой совокупность поверхности и
двухмерной линии на ней. Прямоугольная призма с ориентацией циклов граней
показана на рис. 6.2.1.
Грани тела будут описываться поверхностями:
Рис. 6.2.1. Ориентация циклов
граней призматического тела
r2(u2, v2) = р + u2iy + v2iz,
= p
z\z
ж,
, «б) = p + yiy
0
0
0
0
z,
y,
z,
z.
F.2.1)
У третьей, четвертой и пятой граней нормаль поверхности направлена наружу
тела, а у первой, второй и шестой — внутрь тела. Эта информация содержится
в грани в виде признака совпадения нормалей.
Приведем описание одного из ребер. Например, ребро между первой и вто-
второй гранями описывается линией пересечения этих граней, состоящей из двух
6.2. Простейшие тела
281
двухмерных отрезков:
luvl(t)= [«l(t)
T = [0 yt]T,
1,
F.2.2)
и двух поверхностей. Выражение lUvi(t) € i"i("i> v\) означает, что отрезок
luvi{t) лежит на поверхности ri(ui, v\), а выражение lUV2{t) ? Гг(и2, ^2) озна-
означает, что отрезок lUv2{t) лежит на поверхности Г2(«2, «г)- Пусть направление
ребра совпадает с направлением кривой F.2.2), что зафиксируем в признаке со-
совпадения направлений. Признак совпадения направления ребра с направлением
цикла грани мы назвали флагом. Флаг может принимать два значения: положи-
положительное и отрицательное. Ребро входит в цикл первой грани с положительным
флагом, а в цикл второй грани — с отрицательным флагом. Если смотреть
вдоль направления ребра снаружи тела, то слева от ребра лежит первая грань,
а справа от ребра лежит вторая грань.
Для построения граней тела достаточно знать местную систему координат
р, ix, iy, iz и стороны х, у, z призмы.
Цилиндрическое тело. Другой заготовкой может служить цилиндрическое
тело (рис. 6.2.2). Начало местной системы координат р поместим в центр одного
из торцев цилиндра, а орт iz направим вдоль его оси. Пусть в цилиндр имеет
радиус г и длину h.
Цилиндрическое тело имеет три грани. Торцевые грани состоят из ча-
частей плоскости, ограниченных окружностями на них, граничного цикла и при-
признака ориентации нормали плоскости грани наружу
тела. Цикл каждой торцевой грани состоит из одного
замкнутого ребра. Геометрическим носителем такого
ребра является линия пересечения, состоящая из двух
кривых на поверхности. Одна кривая является окруж-
окружностью на плоскости, а вторая — линией v = vmjn или
и — ^тах на цилиндрической поверхности. Напомним,
что обе линии на поверхности, составляющие линию
пересечения, должны иметь одинаковую параметриче-
параметрическую длину.
Боковая грань тела базируется на цилиндрической
поверхности
14(«1, vi) =
+ hv\ iz
= р + rcosuiix + y
0 ^ «1 ^ 27Г, 0 Oi ^ 1.
F.2.3)
Нормали поверхности F.2.3) и ее грани совпадают по
направлению. Эта грань имеет один цикл. Цилиндри-
Цилиндрическая поверхность боковой грани является замкнутой по одному из параметров.
Грани основания базируются на ограниченных окружностями плоскостях
Рис. 6.2.2. Ориентация
циклов граней цилин-
цилиндрического тела
v2) = р + u2ix
v3) = р
hiz
F.2.4)
F.2.5)
282 Гл. 6. Моделирование тел
где параметры и2, Щ лежат внутри окружности lUv2(t) — [гcost rsint]T,
О ^ t ^ 27г, на плоскости Г2(и2, v2), а параметры из, v3 лежат внутри окруж-
окружности lUv3{t) = [rcosi rsini]T, 0 ^ t ^ 2ж, на плоскости гз(«з, ^з). Нормали
поверхности F.2.4) и ее грани противоположны по направлению, а нормали
поверхности F.2.5) и ее грани совпадают.
Ребро, построенное на линии замыкания оболочки, является швом. Шов,
так же как и любое другое ребро, базируется на линии пересечения. В данном
случае линия пересечения описывается двухмерными кривыми
= [«i(*) «i(*)]T = [о м]т, inMt) e ri(ub Vl), 2
ы{ь)]т = [2тг ht]r, inMt) e п(«ь «О,
являющимися линиями u = «min и « = umax на цилиндрической поверхности.
Ребро между боковой гранью и основанием F.2.4) описывается линией пере-
пересечения этих граней, состоящей из двух двухмерных кривых (отрезка и окруж-
окружности)
т = [t o]T, iuvl(t) e ri(u Wl),
т F.2.7)
=[rcosi ]1" Ы^Ф^
О < t < 2тг.
Отрезок lUvi{t) лежит на поверхности ri(«i, vi), окружность lUv2(t) лежит на
поверхности Г2(г*2, «г). Пусть направление ребра совпадает с направлением кри-
кривой F.2.7), что отметим соответствующим признаком совпадения направлений.
Это ребро входит в цикл первой грани с положительным флагом, а в цикл вто-
второй грани — с отрицательным флагом. Если смотреть вдоль направления ребра
снаружи тела, то слева от. ребра лежит первая грань, а справа от ребра лежит
вторая грань.
Ребро между боковой гранью и основанием F.2.5) описывается линией пере-
пересечения этих граней, состоящей из двух двухмерных кривых (отрезка и окруж-
окружности)
luvllt) = [«i(i) Vx(f)]T = [t h]T, luvl{t) € n(«i, Vi),
(D.^.oj
luvz(t) = [u3(t) v3(t)] =[rcost rsinf]T, lUv3{t) G г3(«з, v3),
0 ^ t ^ 2?r.
Отрезок lUvi(t) лежит на поверхности ri(iti, vi), окружность lUv3{t) лежит на
поверхности гз(«з, v3). Пусть направление ребра совпадает с направлением кри-
кривой F.2.8), что отметим соответствующим признаком совпадения направлений.
Это ребро входит в цикл первой грани с отрицательным флагом, а в цикл тре-
третьей грани — с положительным флагом. Если смотреть вдоль направления
ребра снаружи тела, то слева от ребра лежит третья грань, а справа — первая
грань.
6.2. Простейшие тела 283
Циклы граней основания содержат всего одно ребро. Цикл боковой грани
состоит из списка ребер с соответствующими флагами:
ребро на базе кривой F.2.7) — флаг положительный,
ребро на базе кривой F.2.6) — флаг положительный,
ребро на базе кривой F.2.8) — флаг отрицательный,
ребро на базе кривой F.2.6) — флаг отрицательный.
Цилиндрическое тело и ориентация циклов его граней показаны на рис. 6.2.2.
Для построения граней тела достаточно знать местную систему координат
р, ix, iy, iz, радиус г и высоту h цилиндра.
Коническое тело. Тело в форме усеченного конуса строится аналогично ци-
цилиндрическому телу с той лишь разницей, что в качестве поверхности боковой
грани вместо цилиндрической используется коническая поверхность C.2.10)
ri(ui, vi) =p + (r + /ivitg7)(cosuiia: + sin«iij/) + hvxiz,
(b.2.9)
0 < ui < 2тг, 0 < «i < 1.
Грани основания базируются на ограниченных окружностями поверхностях
Г2(«2, ^2) = Р + U2\x + ЩЦ, F.2.10)
гз(«з, ^з) = Р + из1х + ЩЦ + h\z, F.2.11)
где параметры «2, Щ лежат внутри окружности
Iuv2{l) = [rcost rsin?]T, 0 < t < 27Г,
а параметры щ, v^ лежат внутри окружности
(r + /itg7)sini]T, 0 < t < 2тг.
Ребро, построенное на боковой грани, будет являться швом. В общем слу-
случае коническое тело имеет три грани. Если конус не усеченный, то одна из
торцевых граней стянута в точку. Стянутую в точку грань можно исключить
из модели тела, тогда оболочка тела с топологической точки зрения будет неза-
незамкнутой, хотя диаметр отверстия в ней равен нулю.
Для построения граней тела достаточно знать местную систему координат
р, \х, iy, iz, радиус г одного из оснований конуса, высоту h и угол конусности j.
Сферическое тело. Сферическая поверхность C.2.3) может служить оболоч-
оболочкой сферического тела, но эта оболочка не является замкнутой, так как имеет
два отверстия нулевого радиуса в полюсах. Начало местной системы коорди-
координат р для сферического тела поместим в центр сферы. Оболочка, описываемая
сферической поверхностью
r(u, v) = р + г cos v cos и ix + г cos v sin и iy + rs'mviz,
284 Гл. 6. Моделирование тел
топологически эквивалентна цилиндрической поверхности. Ребра в полюсах
стянуты в точку, но двухмерные кривые на сферической поверхности в полюсах
имеют ненулевую длину. Цикл грани сферического тела составляют три ребра,
одно из которых является швом
luvi{t) = [u{t) v{t)]T = [0 t]T, luvl{t) ? r{u, v),
Iuv2(t) = [u{t) V{t)]T = [27Г t]T, luv2{t) ? v{u, V),
7Г 7Г
~ ?'
а два других описываются линиями на полюсах сферы:
,т
lu«0l(*) = [«(*) v{t)]T =\t - ^J , luvOl{t) ? t(u, V),
luvQ2(t) = [u(t) v(t)]T =\t Jl T , luv02(t) ? V(U, V),
0 < t < 2тг.
Линии пересечения в полюсах состоят из двух одинаковых линий на сфере.
Шов входит в список ребер цикла дважды, один раз с положительным флагом,
второй раз — с отрицательным флагом. Сферическое тело показано на рис. 6.2.3.
Рис. 6.2.3. Ориентация цикла грани сферического тела
Рис. 6.2.4. Построение сферического тела по двум полусферам
Сферическое тело можно построить из двух полусфер, описываемых вектор-
векторными функциями
(u, v) = p + xix + yiy + \Jr2 - x2 — y2iz, F.2.12)
r2(«, v) = p + xix + y'\y - л/г2 -x2-y2iz, F.2.13)
6.2. Простейшие тела 285
где
/ 2u(l — cosv — sinv) 2v(l — cosu — sinu)
x = x(u, v) = r[cosu + cosv — 1 4 +
\ 7Г 7Г
/ . . 2u(l — cosv — sinv) 2v(l — cosu — sinu)
\ 7Г 7Г
r —- радиус сферы, р — радиус-вектор центра, ix, iy, i2 — орты, определяю-
определяющие ориентацию сферы. Поверхность F.2.12) описывает верхнюю полусферу,
а поверхность F.2.13) описывает нижнюю полусферу. Эти поверхности анало-
аналогичны поверхности C.6.5). Нормали верхней поверхности и ее грани совпадают
по направлению, а нормали нижней поверхности и ее грани противоположны
по направлению. Оболочка сферического тела, состоящая из двух полусфер,
является замкнутой. Ее полусферы стыкуются по четырем ребрам:
UiW = [«(*) v(t)]r = \j 0] , iuvU(t) e ri(u, v),
Iuv2l(t) = [u(t) v{t)]T = |y 0|
|
[2 2 J
^u«22(t) = [u(t) v(t)]T - - у , /ut,22(i) G r2(«, w),
0 ^ i ^ 1;
> 'uui3@ € rj(u, v),
, ^ut»23(*) € Г2(и, v),
J
1;
Iuv24{t) = ["(*) V(t)] = 0
L
0<i< 1.
Поверхности F.2.12) и F.2.13) для построения сферического тела приведены
на рис. 6.2.4.
Для построения граней тела достаточно знать местную систему координат
р, ix, iy, i2 и радиус г сферы.
286
Гл. 6. Моделирование тел
Тороидальное тело. Начало местной системы координат р для тороидального
тела поместим в его центр, а орт iz направим по оси симметрии тела. Пусть
больший радиус тора равен R, а малый радиус тора равен г. Тороидальное тело
имеет одну грань, описываемую тороидальной поверхностью
r(u, v) = р + (R + г cos v) cos иix + (R + r cos v) sinuiy + r sinv iz
О
U
два ребра
27Г, -7Г
7Г,
v(t)]T = [*
(<)]
= [* тг]
F.2.14)
F.2.15)
< 27Г,
7Г
7Г,
и одну вершину в точке пересечения ребер р + (R — r)ix- Нормаль поверхности
и грани тороидального тела совпадают по направлению. Грань тела имеет один
цикл. Цикл грани состоит из списка ребер с соответствующими флагами:
ребро на базе кривой F.2.15) — флаг положительный,
ребро на базе кривой F.2.16) — флаг положительный,
ребро на базе кривой F.2.15) — флаг отрицательный,
ребро на базе кривой F.2.16) — флаг отрицательный.
Тороидальная поверхность грани является замкнутой по обоим параметрам, по-
поэтому оба ребра оболочки тела замкнуты и являются швами. Тороидальное
тело, его ребра и цикл грани показаны на рис. 6.2.5.
Рис. 6.2.5. Ориентация цикла грани тороидального тела
Для построения граней тела достаточно знать местную систему координат
р, ix, iy, iz, больший радиус R и меньший радиус г.
Принцип построения тел. Рассмотренные тела иллюстрируют принцип по-
построения математической модели тел. Эти тела называют твердотельными при-
примитивами. К ним могут быть отнесены еще некоторые тела простой формы,
например, треугольная призма (клин). Все тела построены по такому же прин-
принципу, что и твердотельные примитивы.
6.3. Тела, полученные движением плоского контура 287
Может возникнуть вопрос: для чего требуется так усложнять модель тела,
в частности, для чего требуется строить ребра на кривых пересечения поверх-
поверхностей? Действительно, тела можно было бы описать набором поверхностей, не
используя ни грани, ни ребра, ни вершины. У реальных деталей эти поверхно-
поверхности могут иметь очень сложную форму, как в смысле кривизны, так и в смысле
границ, и эти поверхности каким-то образом нужно построить. Одним из удоб-
удобных способов построения поверхностей, описывающих тело, является способ
одновременного построения всех требуемых поверхностей с помощью операций
над телами. Для этого берется одно из простых тел, и далее в определенных
местах к нему добавляется объем или от него отнимается объем. Например, для
того чтобы просверлить отверстие в некотором теле, выполняется булева опера-
операция вычитания из этого тела цилиндрического тела, играющего роль сверла.
Аналогично выполняются пазы и вырезы. Для того чтобы сварить модели двух
деталей, выполняется булева операция объединения тел. Использование топо-
топологических объектов необходимо для корректного выполнения этих операций.
Пусть требуется отрезать от одного из описанных выше простейших тел не-
некоторую часть и пусть резка производится плоскостью. Тогда мы вынуждены
найти линии пересечения поверхностей тела с этой плоскостью и по этим ли-
линиям обрезать поверхности тела и саму плоскость. Кроме того, нужно найти
место стыковки обрезанной плоскости с частью исходного тела. Для плоскости
нужно определить, какая ее сторона будет смотреть наружу тела, а какая —
внутрь. Все это приводит к тому, что нужно знать топологию исходного тела и
строить его по общим правилам.
При проектировании приходится рассматривать несколько вариантов дета-
деталей и сборочных единиц. Различные варианты одной и той же детали можно
получить путем изменения требуемых параметров ее исходного варианта. Для
этого в математической модели детали необходимо иметь информацию о пути
и способах ее построения. Таким образом, геометрическая модель детали или
сборочной единицы должна быть дополнена еще некоторой информацией о по-
последовательности ее построения.
6.3. Тела, полученные движением плоского контура
Многие тела или заготовки для них можно получить путем движения плос-
плоского контура по заданной траектории. Пусть траектория движения описывается
кривой g(v), которую мы будем называть направляющей. Плоский контур будем
называть образующей кривой. Пусть дана ограниченная плоскость
г(ж, у) =р + xix + yiy, х,у?п, F.3.1)
где Q -— область на плоскости параметров, ограниченная двухмерным контуром
c(t) = [x(t) y(t)] . Контур c{t) состоит из набора стыкующихся друг с другом
двухмерных кривых а{и) = [xi(u) yi(u)] , uimin < и < uimax, i = 1, 2, ..., п.
Радиус-вектор контура описывается формулой B.12.7). Каждая кривая контура
в пространстве описывается радиус-вектором
" < Uimax. F.3.2)
Контур не должен иметь точек самопересечения. Если направляющая кривая
g(v) движения контура не замкнута, то оболочка тела имеет торцевые грани.
Торцевые грани тел движения представляют собой плоскости, ограниченные
288
Гл. 6. Моделирование тел
заданным контуром. Они описываются радиус-вектором C.15.1). Если на-
направляющая кривая движения контура замкнута, то оболочка тела не имеет
торцевых граней. Боковые грани оболочки тела базируются на поверхностях
движения. Число боковых граней равно числу кривых в контуре. Каждая бо-
боковая поверхность в качестве образующей содержит пространственный аналог
соответствующей кривой контура. В зависимости от типа траектории движения
g(v) можно построить несколько типов тел.
Тело выдавливания. Если направляющей движения контура служит отрезок
прямой g(v) = р + vhd, 0 ^ v ^ 1, то мы получим тело выдавливания. Одна
из его торцевых граней будет описываться ограниченной плоскостью F.3.1).
Другая его торцевая грань будет описываться аналогичной плоскостью, только
с началом в точке р' = p+/id. Боковая грань тела выдавливания, соответствую-
соответствующая кривой контура Cj(m), описываются поверхностями
ri(u, v) = p + Xi(u)ix + yi{u)'\y + vhd = с*(it) + vhd,
^ U ^ Щтах, 0 ^ V ^ 1.
F.3.3)
Тело выдавливания, построенное по замкнутому контуру, приведено на
рис. 6.3.1. Для контура можно построить эквидистантный контур. По задан-
заданному контуру и эквидистантному к нему контуру может быть построено тело
:ШЪ ::|&;3; ^ШЙЗ ;¦$!¦!!¦:
V1(
№ 'Л
Рис. 6.3.1. Тело выдавливания
||i i;g Ш}' i||j|
Рис. 6.3.2. Тело выдавливания с уклоном
выдавливания с уклоном. Угол уклона определяется эквидистантой и длиной
выдавливания. Тело выдавливания с уклоном приведено на рис. 6.3.2. Выда-
Выдавливание выполнено в обе стороны от плоскости F.3.1). Боковые грани тела с
уклоном построены на линейчатых поверхностях.
Рис. 6.3.3. Тонкостенное тело выдавливания Рис. 6.3.4. Тонкостенное тело выдавливания
6.3. Тела, полученные движением плоского контура 289
Тонкостенное тело выдавливания может быть построено по замкнутой или
незамкнутой составной плоской кривой. Для его построения также исполь-
используются эквидистантные составные кривые. Тонкостенные тела выдавливания
приведены на рис. 6.3.3 и 6.3.4.
Рис. 6.3.5. Замкнутая (а) и незамкнутая (б) составная кривая
Замкнутая составная кривая и незамкнутая составная кривая, по которым
построены приведенные выше тела, показаны на рис. 6.3.5.
Тело вращения. Если направляющей кривой движения контура служит
окружность или ее дуга, то мы получим тело вращения. Пусть ось вращения
проходит через точку ро, а ее направление характеризуется единичным векто-
вектором i. Тогда боковая грань тела вращения, соответствующая кривой Cj (u), будет
описываться поверхностью
г* (и, v) = ро + r3i (и) + cos vru {и) + sin v r2i («),
(D.O.4)
где гзг(«) = ((cj(«) — ро) 'i)i — составляющая вектора Cj(«) — ро, параллельная
оси вращения, гц(и) = Cj(«) — ро — гзг(«) — составляющая вектора Cj(«) — ро,
перпендикулярная оси вращения, Г2г(и) = i x (cj(u) — ро) — ортогональный пер-
первым двум векторам вектор, длина которого равна длине вектора гц(и). Кривая
Ci(u) описывается радиус-вектором F.3.2).
Ось вращения не должна пересекать боковые грани. Определим положи-
положительное направление оси вращения. Пусть мы находимся с той стороны плос-
плоскости контура, откуда движение вдоль контура в положительном направлении
выглядит против часовой стрелки. За положительное направление оси враще-
вращения примем направление, при взгляде вдоль которого контур находится слева.
Если угол вращения а равен 2п, то оболочка тела имеет топологию тора, в
противном случае — топологию призмы. В первом случае оболочка не имеет
торцевых граней. Тело вращения с топологией призмы, построенное по за-
замкнутому контуру, приведено на рис. 6.3.6. Тело вращения с топологией тора,
построенное по замкнутому контуру, приведено на рис. 6.3.7.
По замкнутой или незамкнутой составной плоской кривой может быть по-
построено тонкостенное тело вращения. Для его построения используются экви-
эквидистантные контуры или составные кривые. Тонкостенные тела вращения
приведены на рис. 6.3.8 и 6.3.9.
19 — 5293 Голованов
290
Гл. 6. Моделирование тел
Рис. 6.3.6. Тело вращения
Рис. 6.3.7. Тело вращения с топологией тора
Рис. 6.3.8. Тонкостенное тело вращения
Рис. 6.3.9. Тонкостенное тело вращения
Рис. 6.3.10. Сфероид
Рис. 6.3.11. Тонкостенный сфероид
По незамкнутой составной плоской кривой могут быть построены тела вра-
вращения, приведенные на рис. 3.6.10 и 3.6.11. Из концов образующей на ось
вращения опущены перпендикуляры, по которым построены соответствующие
грани. Для построения тонкостенного тела используется эквидистантная со-
составная кривая. В отличие от предыдущих примеров тела, приведенные на
рис. 3.6.10 и 3.6.11, касаются оси вращения. Такие тела будем называть сфе-
сфероидами.
6.3. Тела, полученные движением плоского контура 291
Кинематическое тело. При всех других случаях формы направляющей кри-
кривой мы получим кинематическое тело. При движении плоского контура вдоль
направляющей кривой ориентация контура относительно направляющей может
меняться или может оставаться неизменной.
Если ориентация образующей в пространстве не меняется, то контур выпол-
выполняет плоскопараллельное движение, оставаясь параллельным своему началь-
начальному положению, и мы получим тело сдвига. Боковые грани тела сдвига стро-
строятся для каждой кривой F.3.2) и описываются поверхностью C.4.3)
Гг{и, V) = g{v) + {Ci{U) - g{vmin) - h),
(о.о.о)
Щппп ^ и ^ ^imaxi umin ^ V ^ f
где h — вектор привязки образующей к направляющей. Вектор h смещает
кривую Cj (it) на некоторую величину из ее начального положения относительно
направляющей и сохраняет это смещение во время движения. Если h = 0, то
сохраняется исходное положение образующей кривой относительно начальной
точки направляющей кривой. Тело сдвига всегда имеет торцевые грани.
Если ориентация контура в пространстве при движении меняется, сохраняя
некоторый заданный угол между плоскости контура и касательцой к направляю-
направляющей кривой, то мы получим тело заметания. Боковые грани тела заметания
строятся для каждой кривой F.3.2) и описываются поверхностью C.4.7)
Гг{и, v) = g{v) + M{v) • (Ci{u) - g{vmin) - h),
(o.o.o)
uimin ^ u ^ uimaxi umin ^ v ^ u
где M(v) — матричная функция, определяемая формулой C.4.8).
Если направляющая кривая замкнута, то получим кинематическое тело с
топологией тора. Если направляющая кривая не замкнута, то получим кине-
кинематическое тело с топологией призмы. Боковые грани кинематического тела
Рис. 6.3.12. Тело сдвига Рис. 6.3.13. Тело заметания
(тела сдвига или тела заметания) не должны пересекать сами себя. Это требо-
требование приводит к тому, что направляющая кривая тела сдвига не может быть
замкнутой. Тело сдвига приведено на рис. 6.3.12. Тело заметания приведено на
рис. 6.3.13.
19*
292
Гл. 6. Моделирование тел
На рис. 6.3.14 приведено тонкостенное кинематическое тело, построенное по
незамкнутой образующей и замкнутой направляющей.
Рис. 6.3.14. Тонкостенное тело заметания
Для построения граней рассмотренных тел нужно знать двухмерный контур
c(t), местную его плоскость р, ix, iy, направляющую кривую g(v) и другие необ-
необходимые параметры (толщину стенки для тонкостенного тела, способ движения
контура — плоскопараллельный или ортогональный).
6.4. Построение тела по плоским сечениям
Многие детали можно построить по их плоским сечениям в определенных
местах. Пусть имеется несколько плоских контуров Cj(?), i — О, 1, 2, ..., п,
одинаково ориентированных, расположенных на некотором расстоянии друг от
друга и состоящих из одинакового числа кривых. Построим тело, сечения ко-
которого ограничены данными контурами. Тело имеет две торцевые грани, по-
построенные на крайних контурах. Торцевые грани тела представляют собой
плоскости, ограниченные одним из крайних контуров. Боковыми гранями обо-
оболочки тела могут служить сглаживающие поверхности C.7.1) или поверхности
C.7.2). Их количество равно количеству кривых в контуре. В каждой боковой
Рис. 6.4.1. Тело, построенное по плоским сечениям
грани участвует по одной кривой каждого контура. Эти кривые будем назы-
называть соответствующими. Между кривыми в контурах должно быть установлено
соответствие, например, по порядковому номеру кривой в контуре. Тело, по-
построенное по плоским сечениям, приведено на рис. 6.4.1.
6.5. Тело в форме листа
293
В общем случае все контуры, за исключением торцевых контуров, могут быть
не плоскими. Тело, построенное по плоским сечениям, может быть замкнутым
Рис. 6.4.2. Тело, построенное по плоским сечениям
и иметь топологию тора. Тело, построенное по сечениям, описываемым неза-
незамкнутыми линиями, приведено на рис. 6.4.2. По незамкнутым линиям в лю-
любом случае строятся замкнутые контуры, в которых участвуют эквидистантные
кривые.
6.5. Тело в форме листа
На основе поверхности произвольной формы можно построить тело в форме
листа конечной толщины. Пусть дана поверхность Ъ(и, v). Выбрав толщину
листа h, построим эквидистантную к ней поверхность
r(u, v) = Ъ(и, v) + hm(u, v),
F.5.1)
где m(u, и) — нормаль к поверхности Ъ(и, и). На этих поверхностях построим
две основные грани листового тела. Остальные (боковые) грани построим на
линейчатых поверхностях C.5.1), одной базовой линией которых является гра-
граничная линия на поверхности b(u, и), а второй — соответствующая ей линия на
Рис. 6.5.1. Тело в форме листа
Рис. 6.5.2. Тело в форме листа
поверхности r(u, v). Если область определения параметров поверхности b(u, и)
имеет прямоугольную форму, то листовое тело будет иметь четыре боковые
грани. В общем случае листовое тело будет иметь столько боковых граней,
294
Гл. 6. Моделирование тел
сколько линий содержат двухмерные контуры, описывающие область опреде-
определения параметров поверхности Ъ(и, и). Направление нормалей основных гра-
граней противоположно друг другу в соответствующих точках. Если поверхность
Ъ(и, v) является замкнутой по одному из параметров, то листовое тело будет
иметь форму трубы и топологию тора. Если поверхность замкнута по обоим
параметрическим направлениям, то мы получим тело с пустотой внутри. Такое
тело будет иметь внешнюю оболочку на основе поверхности r(u, v) и внутрен-
внутреннюю оболочку на основе поверхности Ъ(и, v).
Векторное изображение тела в форме листа, построенного по ограниченной
контурами NURBS поверхности, приведено на рис. 6.5.1, а его тоновое изобра-
изображение — на рис. 6.5.2.
С помощью тел в форме листа можно моделировать детали кузова автомо-
автомобиля и планера самолета. В структуре данных тела достаточно иметь базовую
поверхность Ъ(и, v) и толщину тела h. Тело, построенное по сечениям, и тело
в форме листа, так же как все рассмотренные выше тела, служат заготовками
для моделей деталей. Дальнейшее моделирование деталей связано операциями
над телами.
6.6. Булевы операции над телами
Над телами, как и над другими геометрическими объектами, можно выпол-
выполнять операции — совокупность действий над одним или несколькими исход-
исходными телами, которая приводит к рождению нового тела. Одними из основных
операций для двух тел являются булевы операции.
Булевыми операциями называют операции объединения, пересечения и вы-
вычитания тел, так как они выполняют одноименные операции над внутренними
объемами тел (над множествами точек пространства, находящимися внутри
тел). Булеву операцию объединения тел будем обозначать формулой S = S1US2,
где Si и S2 — исходные тела, S — результирующее тело. Булеву операцию
пересечения тел будем обозначать формулой S = Si П S2- Булеву операцию вы-
вычитания тел будем обозначать формулой S = Si — S2. В порядке следования
тел-операндов будем называть их первым телом и вторым телом. Результатом
Рис. 6.6.1. Два исходных тела
Рис. 6.6.2. Объединение тел
операции объединения двух тел является тело, которое содержит точки, при-
принадлежащие внутреннему объему или первого, или второго тела. Результатом
операции пересечения двух тел является тело, которое содержит точки, при-
принадлежащие внутреннему объему как первого, так и второго тела. Результатом
6.6. Булевы операции над телами
295
операции вычитания двух тел является тело, которое содержит точки, при-
принадлежащие внутреннему объему первого, но не принадлежащие внутреннему
объему второго тела.
На рис. 6.6.1 приведены исходные для булевой операции тела. На рис. 6.6.2
приведен результат операции объединения тел, на рис. 6.6.3 приведен результат
операции пересечения, на рис. 6.6.4 и 6.6.5 приведены результаты операции
вычитания тел.
Операцию вычитания тел можно свести к операции пересечения тел; для
этого нужно вывернуть второе тело наизнанку и найти точки его объема, одно-
одновременно принадлежащие и объему первого тела. Вывернутое наизнанку тело S
будем обозначать S~. При выворачивании тела наизнанку внутренние стороны
Рис. 6.6.3. Пересечение тел
Рис. 6.6.4. Разность тел
Рис. 6.6.5. Разность тел
граней становятся наружными сторонами, а наружные — внутренними и изме-
изменяются направления циклов на противоположные, в результате чего внутренним
объемом тела становится та часть пространства, которая до этого находилась
снаружи тела. Математически операция вычитания сводится к операции пересе-
пересечения тел S = Si — S2 = Si l~lS2~. Конструктор при проектировании использует
операции объединения и вычитания (они могут называться по-другому, напри-
например, операции сварки и сверления), а математический аппарат выполняет соот-
соответственно операции объединения и пересечения. Все булевы операции содержат
много общего и выполняются по единому алгоритму.
Объединение тел. Рассмотрим булеву операцию объединения тел. Кратко
суть операции можно описать следующим образом: нужно найти линии пересе-
пересечения граней тел, удалить ту часть первого тела, которая попала внутрь второго
тела и ту часть второго тела, которая попала внутрь первого тела, а из всего
остального построить новое тело. Операцию условно разобьем на три этапа.
На первом этапе построим линии пересечения поверхностей граней и на их
базе — новые ребра. Построенные новые ребра будем называть ребрами пе-
пересечения, а ребра тел будем называть старыми ребрами. На втором этапе
определим точки пересечения новых ребер со старыми ребрами и в этих точ-
точках разрежем старые ребра на несколько ребер. На третьем этапе операции
перестроим циклы пересекшихся граней. После этого добавим к пересекшимся
граням тел грани, топологически связанные ними. Рассмотрим этапы построе-
построения тела более подробно.
Первый этап операции объединения тел начнем с того, что построим линии
пересечения каждой грани первого тела с каждой гранью второго тела, если
таковые имеются. Для этого используем алгоритм пересечения поверхностей
296
Гл. 6. Моделирование тел
граней. Пусть грани первого тела описываются поверхностями
п{щ, u»), « = 1, 2, ..., m,
а грани второго тела описываются поверхностями
Sj{aj,bj), j = l, 2, ..., п.
На базе линий пересечения граней первого и второго тел
luv{t) = [Ui(t) Vi{t)] , luv{t) e Ti(Ui, Vi),
lab(t) = [aj(t) bj(t))T, lab(t) G Sj(aj, bj),
F.6.1)
F.6.2)
F.6.3)
построим ребра пересечения. При этом ребрам пересечения дадим направление
векторного произведения нормали грани первого тела с нормалью грани второго
тела: tedge = mr x ms. Направление ребра определяется признаком совпаде-
совпадения направления производной линии пересе-
пересечения с требуемым направлением ребра. За
положительное направление нормали грани
примем направление наружу тела. Нормаль
грани может совпадать с нормалью ее по-
поверхности или иметь противоположное на-
направление в зависимости от признака их
совпадения. На рис. 6.6.6 показаны напра-
направления ребер пересечения грани первого тела
с двумя гранями второго тела.
Ребра пересечения должны быть построе-
построены так, чтобы они полностью лежали внутри
циклов граней исходных тел. Ребра пере-
пересечения могут подходить к границам грани
только своими концами. В точках А, В и С (рис. 6.6.6) старые ребра граней
должны быть разбиты каждое на два ребра, так как в результирующее тело
войдет только часть исходной грани.
На втором этапе разрежем старые ребра тела, к которым подходят ребра
пересечения. Резка старого ребра осуществляется путем рассечения кривой, на
которой базируется ребро. Из одной кривой получим две кривые, в совокуп-
совокупности заменяющие исходную кривую ребра. Одна из этих кривых останется
геометрическим носителем разрезаемого ребра, а на базе второй построим но-
новое ребро, которое получит от исходного ребра всю необходимую информацию.
Как было сказано, каждое ребро строится на базе кривой пересечения поверх-
поверхностей F.1.1). Кривую пересечения поверхностей составляют две поверхности
и две соответствующие им двухмерных кривые. Рассечению подлежат именно
двухмерные кривые на двух разных поверхностях. Как до, так и после рассече-
рассечения эти кривые должны иметь одинаковые области определения параметров и
соответствие точек при всех значениях параметра.
Точки пересечения нового ребра со старым ребром грани ищутся как точки
пересечения двухмерных кривых, заданных на общей для них плоскости пара-
параметров. От каждого ребра в формуле D.8.6) точек пересечения линий участвует
Рис. 6.6.6. Направление ребер пере-
пересечения граней тел
б.б. Булевы операции над телами
297
по одной двухмерной кривой, входящей в линию пересечения. Параметры то-
точек пересечения ребер и сами координаты кривых, являющиеся параметрами
поверхности, должны быть определены с заданной точностью.
Если разрезаемое ребро базируется на кривой пересечения, заданной от-
отдельными точками (двухмерные линии являются ломаными и точно совпадают
в пространстве только в характеристических точках), то прежде чем разрезать
такую кривую, нужно в обе линии вставить дополнительные точки, соответ-
соответствующие точки пересечения трех поверхностей — двух поверхностей, лежа-
лежащих по обе стороны разрезаемого ребра, и поверхности грани другого исход-
исходного тела. Например, если режется линия пересечения поверхностей Гг(щ, Vi),
rn{un, vn) поверхностью Sj(a,j, bj), то в линии luv(q) = [ui(q) Vi(q)] и luv(q) =
= [un(q) vn(q)] нужно вставить дополнительные двухмерные характеристи-
характеристические точки, соответствующие пересечению поверхностей ri(itj, Vi), Tn(un, vn),
Sj(a.j, bj). Задача пересечения трех поверхностей сводится к решению системы
шести скалярных уравнений D.12.5) относительно шести параметров щ, Vi, un,
vn, a,j, bj. Начальное приближение решения известно достаточно точно.
Так как каждое ребро исходных тел входит в циклы двух смежных граней,
то после резки ребер исходных тел необходимо произвести корректировку этих
циклов с учетом разрезанных ребер.
После первых двух этапов мы получили совокупность ребер пересечения,
ориентированных определенным образом, стыкующихся друг с другом и с ре-
ребрами исходных тел только в вершинах. Далее необходимо перестроить циклы
пересекшихся граней.
Третий этап завершает булеву операцию. Для того чтобы каждую из пока-
показанных на рис. 6.6.6 граней разрезать на части, нужно перестроить ее циклы и
в соответствии с циклами изменить контуры, описывающие область определе-
определения параметров поверхности грани. На рис. 6.6.7 показаны две пересекшиеся
грани (тонкими линиями со стрелками показано направление циклов граней
исходных тел) и ребро пересечения. На рис. 6.6.8 показаны те части граней,
m
Рис. 6.6.7. Исходные грани тела
Рис. 6.6.8. Обрезанные грани
которые войдут в объединение тел. Стрелками показано направление перестро-
перестроенных циклов граней тел. Каждый цикл представляет собой список ребер в
порядке их следования и список флагов ориентации этих ребер в цикле.
Из рисунка видно, что при принятой ориентации ребер пересечения (tedge =
= mr x ms) в циклы граней первого тела они войдут с отрицательным флагом, а
в циклы граней второго тела они войдут с положительным флагом. Старые ребра
298 Гл. 6. Моделирование тел
исходных тел, которые сохранятся в результирующем теле, войдут в перестро-
перестроенные циклы, сохранив свои флаги. При перестройке циклов пересекшихся
граней будем использовать следующий алгоритм.
Рассмотрим одну из двух пересекшихся граней, принадлежащих первому
телу. Берем любое ребро пересечения рассматриваемой грани и начинаем с
него составлять список ребер цикла. Ребро пересечения должно войти в
цикл грани первого тела с отрицательным флагом, следовательно, цикл будет
иметь направление, противоположное первому ребру. Для продолжения цикла
среди ребер пересечения и среди старых ребер грани ищем все ребра, стыкую-
стыкующиеся с данным ребром в его начальной вершине. Среди найденных ребер
выберем то, которое лежит слева от остальных (заворачивает влево на боль-
больший угол по сравнению с другими найденными ребрами, если смотреть вдоль
цикла с наружной стороны грани). Выбранное ребро ставим в список цикла.
Если выбранное ребро является старым, то оно сохраняет свой флаг в цикле.
Если выбранное ребро есть ребро пересечения, то оно получит отрицательный
флаг. Ребра пересечения обладают преимущественным правом по отношению
к старым ребрам быть выбранными. То есть, если левее других оказались два
совпадающих ребра, одно из которых является старым, а другое — ребром пе-
пересечения, то для продолжения цикла должно быть выбрано ребро пересечения.
Процесс перестроения цикла грани будем продолжать до тех пор, пока цикл
не замкнется. На этом построение очередного цикла заканчивается. Если у рас-
рассматриваемой грани при построении цикла использованы не
все ребра пересечения, то с любого из оставшихся ребер пе-
пересечения начинаем строить еще один цикл грани. Циклы
перестраиваем до тех пор, пока не используем все ребра пе-
пересечения. Таким способом мы построим в общем случае не-
несколько новых циклов рассматриваемой грани первого тела.
Поиск стыкующихся ребер и определение угла поворота в
точке стыка удобно выполнять по двухмерным кривым ребер
грани. При этом можно работать даже с такими ребрами,
которые в пространстве стянуты в точку (например, ребро в
вершине конуса или полюсе сферы). На рис. 6.6.9 показано,
ис' ' ' что с новым ребром В А в точке А стыкуются несколько ребер.
В данном случае для продолжения цикла, начатого с ребра пересечения ВА,
следует выбрать ребро АС.
Вновь построенные циклы рассортируем по группам, каждая из которых со-
состоит из внешнего цикла и входящих в него внутренних циклов. У рассматри-
рассматриваемой грани могут остаться нетронутыми один или несколько старых циклов.
Нетронутыми мы будем называть старые циклы грани, ни одно ребро которых
не вошло в перестроенные циклы. Среди старых нетронутых циклов отберем
те, которые необходимо включить в состав описания перестроенной грани. Ими
являются старые внутренние циклы грани, лежащие внутри новых внешних ци-
циклов. Еще нужно определить, не потребуется ли включить в результат старый
внешний цикл грани, если он остался нетронутым. Это необходимо сделать,
если для некоторых новых внутренних циклов не найден новый внешний цикл
и они лежат внутри старого внешнего цикла. Сортировку циклов удобно выпол-
выполнять с помощью двухмерных контуров, соответствующих каждому циклу.
Если в результате сортировки внешних циклов получилось больше одного,
то это означает, что из исходной грани в результате операции образовалось не-
несколько граней. На рис. 6.6.10о-6.6.13а приведены варианты исходных граней
6.6. Булевы операции над телами
299
первого тела. На рис. 6.6.106-6.6.136 приведены грани с добавлением ребер пе-
пересечения (ребра пересечения выделены). На рис. 6.6.10в-6.6.13в приведены
грани, которые получились в результате операции.
Рис. 6.6.10. Исходная грань (а), грань с. добавлением ребер пересечения
ции (б)
результат опера-
Рис. 6.6.11. Исходная грань (а), грань с добавлением ребер пересечения (б), результат опера-
операции (в)
Рис. 6.6.12. Исходная грань (а), грань с добавлением ребер пересечения {б), результат опера-
операции (в)
Рис. 6.6.13. Исходная грань (а), грань с добавлением ребер пересечения (б), результат опера-
операции (в)
300
Гл. 6. Моделирование тел
На рис. 6.6.10 грань с двумя циклами была разрезана и получилась одна
грань с одним циклом. На рис. 6.6.11 грань с двумя циклами дала две грани.
В примере, приведенном на рис. 6.6.12, потребовалось использовать старый
внешний и внутренний циклы. На рис. 6.6.13 из одной грани получено две
грани, причем для одной из них потребовалось использовать старый внешний
цикл.
Описанное перестроение циклов выполняется для каждой пересекшейся
грани первого тела.
С пересекшимися гранями второго тела поступим аналогично тому, как мы
поступили с гранями первого тела, но с одной небольшой разницей. Ребра
пересечения должны войти в перестроенные циклы граней второго тела
с положительным флагом (в перестроенные циклы граней первого тела они
вошли с отрицательным флагом). В этом состоит отличие перестроения циклов
граней второго тела. Все остальные действия над гранями первого и второго
объединяемых тел одинаковы.
Мы перестроили пересекшиеся грани объединяемых тел. Все их включим в
оболочку результирующего тела. Для получения результирующего тела остается
к этим граням в оболочку тела добавить не пересекшиеся в операции грани, ко-
которые топологически связаны с пересекшимися гранями. Для этого будем брать
последовательно ребра, входящие в оболочку нового тела, и включать в оболочку
смежные грани ребер (если они там отсутствуют). Продолжив эти действия для
ребер всех добавленных граней, получим оболочку результирующего тела.
Пересечение тел. Коротко суть булевой операции пересечения тел можно опи-
описать следующим образом: нужно найти линии пересечения тел, удалить ту
часть первого тела, которая не попала внутрь второго, и ту часть второго тела,
которая не попала внутрь первого, а из всего остального построить новое тело.
Эта операция имеет много общего с операцией объединения тел. Вернемся к
рис. 6.6.6. На нем приведены пересекающиеся грани: одна грань первого тела
и две грани второго тела. Грани режут друг друга, так что в результирующую
оболочку войдут только части этих граней.
В пересечение тел войдет часть грани первого тела, лежащая внутри второго
тела, и часть грани второго тела, лежащая внутри первого тела (рис. 6.6.14)
Рис. 6.6.14. Исходные грани Рис. 6.6.15. Перестроенные грани пересечения тел
(в объединение тел вошла часть грани первого тела, лежащая вне второго тела, и
часть грани второго тела, лежащая вне первого тела). В этом и состоит основное
отличие операций объединения и пересечения тел.
Операцию разобьем на три этапа. Первый и второй этапы операции пере-
пересечения тел полностью совпадают с соответствующими этапами операции объ-
объединения тел.
6.6. Булевы операции над телами
301
Третий этап операции пересечения тел выполняется аналогично третьему
этапу операции объединения тел, но имеет одно отличие в том, с каким флагом
входят в циклы ребра пересечения. Ребра пересечения входят в перестроен-
перестроенные циклы граней первого тела с положительным флагом, а в перестроен-
перестроенные циклы граней второго тела — с отрицательным флагом (в объединении
тел флаги ребер пересечения в циклах имеют противоположное значение). Все
остальные действия над гранями обоих тел в обеих операциях одинаковы.
Разность тел. Коротко суть булевой операции вычитания тел можно описать
следующим образом: нужно найти линии пересечения тел, удалить ту часть
первого тела, которая попала внутрь второго, и ту часть второго тела, которая
не попала внутрь первого, а из всего остального построить новое тело.
Булева операция вычитания тел сводится к булевой операции пересечения
уменьшаемого тела и вывернутого наизнанку вычитаемого тела. Вывернутое
наизнанку тело мы получим из исходного тела путем переориентации напра-
направлений нормалей граней и направлений циклов граней. Переориентация напра-
направления нормали грани производится изменением признака совпадения нормали
поверхности и нормали ее грани. Переориентация направления цикла грани
производится перестроением списка ребер (изменением на обратный порядок
следования ребер в списке) и заменой на противоположные флагов ребер в спис-
списках. Для вывернутого тела внутренним объемом является часть пространства,
находящаяся вне его оболочки. Поэтому при пересечении уменьшаемого тела и
вывернутого наизнанку вычитаемого тела результирующая оболочка будет со-
содержать ту часть объема уменьшаемого тела, которая лежит вне вычитаемого
тела.
Пересекающиеся ребра. Наиболее трудоемким и требующим определенной
точности в процессе выполнения булевых операций является построение ребер
пересечения. Ребра пересечения не должны иметь выступающих за пределы
грани частей, они должны обязательно стыко-
стыковаться или друг с другом или со старыми ре-
ребрами граней. При корректном выполнении
операции пересечения поверхностей эти усло-
условия обеспечиваются. Ребра пересечения не дол-
должны пересекать друг друга вне крайних точек.
В большинстве случаев новые ребра не пересе-
пересекают друг друга, но в некоторых частных слу-
случаях это возможно. На рис. 6.6.16 показаны
два цилиндрических тела одинакового диаме-
диаметра, оси которых пересекаются — крест из ци-
цилиндров. При булевом объединении этих тел
возможна ситуация, когда будут построены все-
всего два замкнутых ребра пересечения. Такие ре-
ребра имеют две точки пересечения: А и В, по
крайней мере, одна из которых не будет совпа-
совпадать с вершинами ребер, а будет лежать где-то на ребре. Точки пересечения
ребер лежат в точках касания цилиндров. Эти ребра должны быть разрезаны в
точках А и В и у их частей должна быть уточнена ориентация, так как при про-
прохождении точки касания поверхностей в данном случае векторное произведение
нормалей к ним, по которому ориентируются новые ребра, меняет свое напра-
направление на противоположное. Обнаружить пересечение новых ребер можно по
пересечению кривых на поверхностях, из которых состоит линия пересечения.
Рис. 6.6.16. В точках А и В нор-
нормали граней совпадают
302
Гл. 6. Моделирование тел
Совпадающие ребра. Описанный алгоритм выполнения булевых операций
работает корректно, если ребра пересечения не совпадают с ребрами исходных
тел. В противном случае он нуждается в уточнении. Рассмотрим примеры.
В булевых операциях возможен случай,
когда какая-либо грань одного тела пере-
пересекает другое тело по его ребру. Возможен
также случай, когда при построении ребер
пересечения граней одного тела с гранями
другого тела мы получим два новых ребра,
совпадающих в пространстве друг с другом
и с ребром одного из тел. Все ребра являются
разными, так как в них стыкуются разные
грани. На рис. 6.6.17 приведены два тела,
при выполнении булевой операции над кото-
которыми, ребра пересечения совпадут с ребрами
меньшего тела. Следуя общему алгоритму,
мы в данном случае получим восемь ребер пересечения, половина из которых
должна быть опущена (или не должна быть построена).
Правило для ребер пересечения. При наличии ребер пересечения, совпадаю-
совпадающих с ребрами граней исходных тел, и в некоторых других случаях будем
выполнять следующую проверку. Построим в плоскости каждой из двух пересе-
пересекаемых граней по два вектора, ортогональные ребру пересечения. На рис. 6.6.18
это векторы ai и bi для грани с нормалью mi и векторы аг и Ьг для грани
с нормалью тг. Векторы ai и аг поворачивают влево от ребра пересечения в
соответствующих плоскостях, а векторы bi и Ьг поворачивают вправо от ребра
пересечения в соответствующих плоскостях. Бели грань не имеет продолже-
Рис. 6.6.17. Совпадение ребер пере-
пересечения с ребрами меньшего тела
Рис. 6.6.18. Пересечение граней
Рис. 6.6.19. Пересечение граней по ребру
ния за ребро пересечения (ребро пересечения частично или полностью совпадает
с ребром тела), то соответствующий вектор положим равным нулю (рис. 6.6.19).
Используя векторы ai, аг, bi, Ьг и нормали mi, тг, мы можем определить,
будет ли данное ребро пересечения использовано в операции или оно должно
быть опущено. Обратим внимание на следующее обстоятельство.
В операции объединения тел грань первого тела мы сможем перестро-
перестроить, если, она имеет продолжение справа от ребра пересечения вне второго
тела, а грань второго тела мы сможем перестроить, если она имеет про-
продолжение слева от ребра пересечения вне первого тела. Таким образом, в
булевой операции объединения тел для ребра пересечения должны быть вьшол-
6.6. Булевы операции над телами
303
нены условия
mi
> 0
и
bi > 0. F.6.7)
В противном случае рассматриваемое ребро пересечения в булевой операции объ-
объединения тел строить не следует (если оно построено, то должно быть опущено).
В булевой операции пересечения тел грань первого тела мы сможем
перестроить, если она имеет продолокение слева от ребра пересечения
внутрь второго тела, а грань второго тела мы сможем перестроить, если
она имеет продолокение справа от ребра пересечения внутрь первого тела.
Таким образом, в булевой операции пересечения тел для ребра пересечения
должны быть выполнены условия
mi • b2 < 0 и т2 • ах < 0. F.6.8)
В противном случае рассматриваемое ребро пересечения в булевой операции пе-
пересечения тел строить не следует (если оно построено, то должно быть опущено).
Как уже было сказано, ребра пересечения обладают преимущественным пра-
правом по отношению к старым ребрам тела быть включенными в перестраиваемый
цикл.
Так как булева операция вычитания тел сводится к операции пересечения
тел, то для нее должно выполнятся правило F.6.8) для вывернутой наизнанку
оболочки тела.
Принадлежность точки пространству внутри тела. Для ответа на вопрос,
внутрь или вне тела продолжается от ребра пересечения грань другого тела,
нужно уметь определять, принадлежит ли некоторая точка р пространству вну-
внутри тела — классифицировать точку относительно тела. Нам известно, что нор-
нормаль каждой грани направлена вне объема тела. Для точки р найдем ближай-
ближайшую точку ро на ближайшей грани. Построим вектор п из найденной точки р0
в точку р. Вычислим нормаль m тела в точке ро. Если точка ро лежит на гра-
границе граней (является точкой ребра или вершины), то в качестве нормали m
тела возьмем среднюю нормаль граничащих граней. Если mn ^ 0, то точка р
принадлежит внутреннему пространству тела. В противном случае — нет.
Перекрывающиеся грани. В булевых операциях довольно часто можно встре-
встретить случаи частичного совпадения некоторых граней двух исходных тел. На
рис. 6.6.20 приведены два тела, некоторые грани которых частично перекрывают
Рис. 6.6.20. Совпадающие грани тел
Рис. 6.6.21. Объединение тел
друг друга. В данном случае не все ребра пересечения граней войдут в булев
результат; некоторые ребра должны быть опущены (или не должны строиться).
Результат объединения тел приведен на рис. 6.6.21.
304 Гл. 6. Моделирование тел
Аналогичная ситуация возникает при выполнении булевой операции над
двумя соосными цилиндрами одинакового радиуса и еще во многих случаях.
Грани могут перекрываться полностью, частично или всего лишь по одной
линии.. Нормали mi и гп2 частично перекрывающихся граней должны быть
одинаково направлены в общих точках. Перекрывающимися являются грани,
которые можно перенести на одну общую поверхность. Таких граней может
быть больше двух. При наличии у тел-операндов перекрывающихся граней все
ребра пересечения этих граней должны быть проверены на предмет присутствия
их в булевом результате. В операции объединения тел нам потребуются
только те ребра пересечения перекрывающихся граней, смежные грани ко-
которых имеют продолжение вне одного из тел. В операции пересечения тел
нам потребуются только те ребра пересечения перекрывающихся граней,
смежные грани которых имеют продолжение внутрь одного из тел.
Циклы перекрывающихся граней тел должны быть перестроены по несколь-
несколько иному алгоритму, чем для остальных граней. Прежде всего, все ребра этих
граней должны быть приведены к одному общему носителю (к поверхности
одной из перекрывающихся граней). В операции объединения тел старые ребра
перекрывающихся граней первого тела, лежащие внутри второго тела, и старые
ребра перекрывающихся граней второго тела, лежащие внутри первого тела,
не войдут в результирующее тело. В операции пресечения тел старые ребра
перекрывающихся граней первого тела, лежащие вне второго тела, и старые
ребра перекрывающихся граней второго тела, лежащие вне первого тела, также
не войдут в результирующее тело.
Построение некоторого цикла перекрывающихся граней начнем с ребра, ко-
которое точно должно войти в результат. Для продолжения цикла среди ребер
пересечения и среди старых оставшихся ребер грани найдем все ребра, стыкую-
стыкующиеся с данным ребром в его соответствующей вершине. Среди найденных
ребер выберем то, которое лежит справа от остальных (заворачивает вправо на
больший угол по сравнению с другими найденными ребрами, если смотреть
вдоль цикла с наружной стороны грани). Выбранное ребро ставим в список
цикла. Отличие алгоритма состоит в том, что при продолжении цикла мы вы-
выбираем самое правое (а не самое левое) ребро.
Тела с несколькими оболочками. Если какое-либо из тел-операндов имеет пу-
пустоты и, соответственно, описывается несколькими оболочками, то нетронутые
операцией внутренние (внешние) оболочки должны быть проверены на вхожде-
вхождение в оболочку булева результата. В общем случае результирующее тело также
может иметь несколько оболочек.
Дерево построения тел. Булевы операции над телами показывают необходи-
необходимость привлечения топологических понятий для построения тел.
Рассмотренные в предыдущих параграфах тела будем называть простыми,
в отличие от тел, полученных в результате операции, которые будем называть
сложными. Структура данных простых тел содержит минимум информации,
по которой могут быть построены все грани тела. В структуре данных тела,
полученного в результате булевой операции, положим структуры данных исход-
исходных тел и тип булевой операции. Оболочки тела всегда могут быть построены
по этой информации. Таким образом, структура данных тела, полученного в
результате многократного выполнения булевых операций, будет содержать де-
дерево построения. Результирующее тело находится в корне дерева, а его ветви
6.7. Резка тела поверхностью 305
начинаются в простых телах. Пример дерева приведен на рис. 6.6.22. В узлах
дерева находятся тела. Дерево имеет несколько ярусов. Операции между те-
телами обозначены соответствующими знаками. Операции выполняются между
телами одного яруса.
Рис. 6.6.22. Дерево построения тела
Структура данных тела в виде дерева построения может быть использована
для всех тел — как для тел, полученных в результате некоторой операции, так
и для простых тел.
6.7. Резка тела поверхностью
Если поверхность полностью пересекает тело, то тело можно разрезать этой
поверхность на две части. Результатом такой операции является новое тело,
представляющее собой часть исходного тела, лежащую по одну или другую сто-
сторону режущей поверхности. Положительной стороной будем называть сторону
поверхности, в которую направлены нормаль к ней (если мы смотрим на по-
положительную сторону поверхности, то нормаль направлена на нас). Другую
сторону поверхности будем называть отрицательной.
Операцию резки тела поверхностью мы сведем к одной из булевых опера-
операций. На базе поверхности построим оболочку. Эта оболочка будет состоять из
одной грани. Нормаль этой грани пусть совпадает с нормалью поверхности.
Построенную незамкнутую оболочку мы будем рассматривать как некоторое
незаконченное тело.
Пусть требуется построить ту часть тела, которая лежит с положительной
стороны режущей поверхности. В этом случае выполним булеву операцию вы-
вычитания из этого тела незаконченного тела, построенного на основе режущей
поверхности.
Пусть требуется построить ту часть тела, которая лежит с отрицательной
стороны режущей поверхности. В этом случае выполним булеву операцию пе-
пересечения этого тела с незаконченным телом, построенным на основе режущей
поверхности.
20 - 5293 Голованов
306
Гл. 6. Моделирование тел
На рис. 6.7.1 показаны тело, режущая поверхность, ее нормаль и ребра пе-
пересечения граней тела с поверхностью. При резке тела поверхностью мы вы-
выполняем операцию пересечения тела с частью пространства, лежащей по ту или
иную сторону поверхности.
m
Рис. 6.7.1. Направление ребер пересечения Рис. 6.7.2. Исходное тело и режущая поверхность
В частном случае тело можно разрезать плоскостью. На рис. 6.7.2 приве-
приведены исходное тело и режущая плоскость. На рис. 6.7.3 приведено разрезанное
плоскостью тело.
. С помощью рассматриваемой операции можно получить сложный разрез
тела. Для этого оболочка незаконченного тела должна состоять из нескольких
стыкующихся между собой граней. Для получения сложного разреза возьмем
Рис. 6.7.2. Разрезанное тело
Рис. 6.7.4. Сложный разрез тела
составную кривую на плоскости и построим по ней незаконченное тело выда-
выдавливания так, чтобы оно пересекало заданное тело требуемым образом. Далее
выполним булеву операцию над заданным телом и незаконченным телом. Ре-
Результат сложного разреза тела показан на рис. 6.7.4.
6.8. Построение симметричного тела 307
6.8. Построение симметричного тела
Пусть имеется тело и плоскость. Построим тело, симметричное данному
телу относительно данной плоскости. Исходное тело будем называть базовым.
Симметричное тело будет зеркальной копией данного тела. Геометрия тела опи-
описывается точками, кривыми и поверхностями, которые в конечном итоге опи-
описываются точками векторами и скалярами. Поэтому построение симметричного
тела в конечном итоге сводится к преобразованию симметрии радиус-векторов
точек, свободных векторов и скаляров. Скалярные величины при преобразова-
преобразовании симметрии не изменяются, свободные векторы меняют свое направление,
а точки — свое положение.
Пусть плоскость симметрии описывается формулой
р(х, у) = ро + a;ii + yh,
где ii и \2 — ортогональные векторы единичной длины. Тогда матрица пре-
преобразования симметрии A.3.8) тела относительно этой плоскости определяется
формулой
А = 2iiii + 2i2i2 - Е, F.8.1)
где iiii и i2i2 — диадные произведения векторов. Свободный вектор vo по-
после преобразования симметрии относительно этой плоскости будет описываться
радиус-вектором
v = А ¦ v0. F.8.2)
Произвольная точка г0 после преобразования симметрии относительно этой
плоскости будет описываться радиус-вектором
г = ро + А • (г0 - Ро). F.8.3)
После преобразования симметрии все точки и линии на поверхностях оста-
останутся неизменными. А вот нормали поверхностей изменят свое направление
на противоположное. Там, где нормаль грани и нормаль ее поверхности в ис-
исходном теле совпадали по направлению, в зеркальной копии будут иметь про-
противоположное направление, и наоборот: там, где нормаль грани и нормаль ее
поверхности в исходном теле не совпадали по направлению, в зеркальной копии
будут иметь одинаковое направление. Кроме того, циклы граней зеркальной
копии будут иметь направление, противоположное своим оригиналам. Поэтому
в гранях зеркальной копии нужно произвести изменение признаков совпадения
нормали поверхности и нормали ее грани на противоположные значения и пере-
переориентировать циклы. Переориентация направления цикла грани производится
перестроением списка ребер (порядок следования ребер в списке обратный) и
заменой флагов ребер в списках на противоположные флаги. Такая же переори-
переориентация производилась и при выворачивании тела наизнанку. Если выполнить
только преобразование геометрических данных тела по матрице F.8.1), то по-
получим зеркальное отражение тела, вывернутое наизнанку. Таким образом, по-
построение симметричного тела сводится к преобразованию его копии по матрице
F.8.1) и выворачивании ее наизнанку (переориентации его граней).
Симметрия части тела. Пусть плоскость симметрии пересекает тело. Пред-
Представим, что оболочка тела разрезана плоскостью, одна из отрезанных частей
удалена, по другой части выполнена зеркальная копия и склеена с ней. Мы по-
получим тело, симметричное относительно плоскости, состоящее из двух полови-
половинок, одна из которых совпадает с частью исходного тела. Плоскостью симметрии
20*
308 Гл. 6. Моделирование тел
может служить плоская грань исходного тела. Построение такого симметрич-
симметричного тела имеет много общих моментов с резкой тела на части и операцией
объединения тел.
Не теряя общности, будем строить симметричное тело по его части, находя-
находящейся с положительной стороны плоскости — с той стороны, в которую напра-
направлена нормаль плоскости. Операцию условно разобьем на три этапа.
На первом этапе построим линии пересечения поверхностей граней тела
с плоскостью. Пусть пересеченные плоскостью грани тела описываются по-
поверхностями гг(ыг, Vi), г = 1, 2, ..., п. Тогда каждая линия пересечения будет
состоять из пары двухмерных кривых
luv{t) = [Ui{t) Vi(t)] , luv{t) e Ъ(Щ, Vi),
( )
ixy(t) = [x(t) y(t)]T, ixy{t) e р(ж, у),
имеющих общий параметр t. Первая кривая лежит на поверхности Гг(щ, Vi), a
вторая — на плоскости симметрии. На базе линий пересечения построим новые
ребра (ребра пересечения). С помощью признака совпадения направления ребра
и его кривой пересечения ребрам пересечения дадим направление векторного
произведения нормали грани тела с нормалью к плоскости: tedge = mr x mP.
На втором этапе определим точки пересечения новых и старых ребер тела,
в этих точках построим вершины и этими вершинами разрежем старые ребра
на несколько ребер. Резка ребер описана в булевых операциях над телами.
Далее построим симметричную относительно плоскости копию части обо-
оболочки тела, лежащей над плоскостью. Для этого построим копию части оболоч-
оболочки,, преобразуем ее по матрице F.8.1) и вывернем ее наизнанку. При вывора-
выворачивании оболочки нужно произвести изменение признаков совпадения нормали
поверхности и нормали ее грани на противоположные значения и переориенти-
переориентировать циклы.
Остается сшить симметричные половинки тела по ребрам пересечения тела
с плоскостью симметрии. Но прежде выполним замену линий на плоскости,
входящих в кривые пересечения построенных ребер, на линии на симметричной
оболочке. Для этого вместо кривых F.8.4) в ребра положим кривые
luv{t) = [ui(t) Vi{t)] , luv(t) ЕГг(щ, ы),
F.8.5)
U{t) = [Ui{t) Vi(t)] , U{t) e п'(щ, v^.
Первую двухмерную кривую lUv{t) кривой пересечения сохраним нетронутой, а
вместо второй возьмем двухмерную кривую /UI/(?), являющуюся точной копией
luv{t) и лежащую на симметричной копии поверхности Гг(щ, Vi). Теперь каж-
каждое ребро пересечения будет базироваться на двух симметричных половинках
искомого тела.
На третьем этапе перестроим циклы пересеченных плоскостью граней
тела. Перестроение циклов грани подробно описано в булевой операции объ-
объединения тел. Каждое ребро пересечения должно войти в цикл исходной грани
с отрицательным флагом, а цикл ее симметричной части — с положительным
флагом.
К пересеченным граням тела добавим непересеченные грани, которые топо-
топологически связаны с первыми, и соответствующие симметричные копии. Так
мы получим оболочку симметричного тела.
6.9. Построение эквидистантной оболочки тела
309
При построении симметричной оболочки следует учитывать все случаи со-
совпадения ребер пересечения и старых ребер тала и частичное перекрытие гра-
граней, описанные в булевых операциях над телами. Кроме того, следует учесть
наличие нескольких оболочек у исходного тела.
Рис. 6.8.1. Тело и плоскость симметрии
Рис. 6.8.2. Симметричное тело
На рис. 6.8.1 приведено исходное тело и плоскость симметрии. На рис. 6.8.2
приведен результат построения симметричного тела.
6.9. Построение эквидистантной оболочки тела
По данному телу можно построить тело с эквидистантной оболочкой. Обо-
Оболочка нового тела расположена на заданном расстоянии по нормали от оболочки
исходного тела. Это расстояние будем называть параметром эквидистанты и
обозначим через h. Тело, по которому строится тело с эквидистантной оболоч-
оболочкой, будем называть базовым, а новое тело будем называть эквидистантным.
Параметр эквидистанты этой операции может принимать как положительные,
так и отрицательные значения. Если h > 0, то базовое тело располагается вну-
внутри эквидистантного тела. Если h < 0, то эквидистантное тело располагается
внутри базового тела. Недопустимыми значениями параметра являются такие,
при которых оболочка нового тела получается самопересекающейся или выро-
вырожденной. Процесс построения оболочки эквидистантного тела условно разобьем
на четыре этапа.
На первом этапе для каждой грани базового тела построим эквидистантную
грань. Эквидистантная грань базируется на поверхности, эквидистантной к
соответствующей поверхности базового тела. На рис. 6.9.1 приведены три грани
базового тела, имеющие общую вершину А, и эквидистантные им поверхности.
310
Гл. 6. Моделирование тел
Каждая эквидистантная поверхность должна быть продолжена до пересече-
пересечения с соседними эквидистантными поверхностями. Радиус-вектор эквидистант-
эквидистантной поверхности определяется формулой C.14.1). На продолжении эквидистант-
эквидистантной поверхности за пределы области определения параметров ее радиус-вектор
Рис. 6.9.1. Эквидистантные поверхности
будем вычислять по одной из формул C.14.8)—C.14.10) в зависимости от за-
замкнутости базовой поверхности. Для построения эквидистантного тела нам
остается построить его вершины и ребра. Для этого необходимо найти линии
пересечения эквидистантных поверхностей. Каждая линия пересечения должна
начинаться и оканчиваться в вершине тела.
¦ На втором этапе построим вершины эквидистантной оболочки. Рассмо-
Рассмотрим последовательно вершины базового тела. В каждой вершине стыкуется
несколько ребер. Нам нужно знать, какие ребра и какие грани базового тела
стыкуются в данной вершине. Вершине базового тела будут соответствовать
Рис. 6.9.2. Вершины эквидистантного тела
одна или несколько вершин эквидистантного тела. В каждой вершине экви-
эквидистантного тела будут также стыковаться несколько ребер. Вершина эквиди-
эквидистантного тела базируется на точке пересечения эквидистантных поверхностей.
6.9. Построение эквидистантной оболочки тела
311
Вычислив эту точку, мы найдем параметры эквидистантных поверхностей, ко-
которые будут служить нам в качестве начальных и конечных точек линий пере-
пересечения поверхностей.
На рис. 6.9.2 приведены точки пересечения продолженных эквидистантных
поверхностей, на которых будут базироваться вершины.
На третьем этапе построим ребра эквидистантной оболочки. Рассмотрим
последовательно ребра базового тела. Для каждого ребра построим соответствую-
соответствующее ребро эквидистантной оболочки тела. Ребро будет базироваться на линии
Рис. 6.9.3. Линии пересечения эквидистантных поверхностей
пересечения эквидистантных поверхностей. Начальные и конечные точки ребер
нам известны из второго этапа. На рис. 6.9.3 приведены линии пересечения
продолженных эквидистантных поверхностей, на которых будут базироваться
ребра.
Рис. 6.9.4. Эквидистантные грани
На последнем, четвертом этапе построим циклы эквидистантных граней
(рис. 6.9.4). Этот процесс аналогичен процессу перестроения циклов граней в
булевых операциях.
Таким образом, мы получим оболочку эквидистантного тела.
312
Гл. 6. Моделирование тел
Пример построения эквидистантного тела приведен на рис. 6.9.5 (исходное
тело показано внутри тонкими линиями).
Заметим, что топология эквидистантного тела (количество вершин, ребер,
граней и их взаимосвязь) не всегда совпадает с топологией базового тела. Если
Рис. 6.9.5. Эквидистантное тело
в вершине базового тела стыкуется более трех ребер (не являющихся швами),
то в эквидистантном теле этой вершине будет соответствовать несколько вер-
вершин и новых ребер. На рис. 6.9.6 приведена пирамида и эквидистантное пи-
пирамиде тело с отрицательным параметром эквидистанты, а на рис. 6.9.7 приве-
приведена аналогичная пирамида и эквидистантное пирамиде тело с положительным
А
Рис. 6.9.6. Эквидистантная пирамида (h < 0)
Рис. 6.9.7. Эквидистантная пирамида (h > 0)
параметром эквидистанты. В вершине А пирамиды стыкуется четыре ребра.
В эквидистантном теле данной вершине соответствует две вершины В и С и
одно дополнительное ребро ВС, что мы и наблюдаем на рис. 6.9.6 и 6.9.7.
Возможна и другая ситуация, когда некоторой вершине или некоторому ре-
ребру базового тела в эквидистантной оболочке не будет аналога. В таких случаях
топология эквидистантного тела будет отличаться от топологии базового тела.
Для обработки подобных ситуаций следует проанализировать расположение со-
соседних вершин и ребер.
6.10. Построение тонкостенного тела 313
6.10. Построение тонкостенного тела
Рассмотрим построение тонкостенных тел двух типов. Тела обоих типов
будут строиться по некоторому базовому телу. Тело первого типа будет иметь
замкнутую полость внутри. Оно имеет две оболочки, делящие пространство
на три части: одна из них лежит вне тела, вторую занимает тело, а третья
является внутренней полостью тела. Тело второго типа будет представлять со-
собой открытое тонкостенное тело, имеющее одну оболочку. Тело первого типа
будем называть закрытым тонкостенным телом, а тело второго типа — откры-
открытым тонкостенным телом. Закрытое тонкостенное тело можно считать частным
случаем открытого тонкостенного тела.
Закрытое тело. Закрытое тонкостенное тело с толщиной стенки h получим
следующим образом. Построим эквидистантную оболочке базового тела обо-
оболочку. Процесс построения эквидистантной оболочки был описан при построе-
построении эквидистантного тела. Далее вывернем наизнанку одну из этих оболочек.
Если h > 0, то вывернем наизнанку оболочку базового тела, если h < 0, то вы-
вывернем наизнанку эквидистантную оболочку. Эти две оболочки и создадут тон-
тонкостенное тело. Закрытое тонкостенное тело можно представить по рис. 6.9.5.
Данное тонкостенное тело является в отличие от других рассмотренных тел
телом с пустотами. В общем случае тело с пустотами имеет несколько оболочек.
Одна из них является внешней, а остальные — внутренними и лежат внутри
внешней оболочки. Все оболочки не должны пересекать друг друга. Вектор нор-
нормали к внешней оболочке направлен вне объема оболочки, а векторы нормалей
к внутренним оболочкам направлены внутрь объема, ограниченного ими.
Открытое тело. Открытое тонкостенное тело строится на базе некоторого
тела путем удаления одной или нескольких граней последнего и «придания
оставшимся граням конечной толщины». Конечно, грань не может иметь тол-
толщину, поэтому к оставшейся после удаления некоторых граней открытой обо-
оболочке строится эквидистантная открытая оболочка, а затем эти оболочки замы-
замыкаются частями удаляемых граней. В результате получается одна замкнутая
Рис. 6.10.1. Исходное тело Рис. 6.10.2. Тонкостенное тело
оболочка. На рис. 6.10.2 приведен пример открытого тонкостенного тела (h > 0),
построенного путем вскрытия одной грани тела, показанного на рис. 6.10.1.
Рассмотрим процесс построения оболочки открытого тонкостенного тела.
Прежде всего, рассортируем грани базового тела на две группы: к первой группе
отнесем вскрываемые грани базового тела, а ко второй группе отнесем осталь-
остальные грани базового тела, которые будем называть сохраняемыми. Сгруппи-
Сгруппируем ребра базового тела: к первой группе отнесем ребра, по которым пересека-
пересекаются между собой вскрываемые грани базового тела, а ко второй группе отнесем
314
Гл. 6. Моделирование тел
ребра сохраняемых граней базового тела. Процесс построения оболочки откры-
открытого тонкостенного тела имеет много общего с процессом построения эквиди-
эквидистантного тела.
Для каждой сохраняемой грани базового тела построим эквидистантную
грань. Поверхность каждой эквидистантной грани и каждой вскрываемой грани
должна иметь возможность быть продолженной до пересечения с поверхностями
соседних граней. Радиус-вектор эквидистантной поверхности определяется фор-
формулой C.14.1). На продолжении эквидистантной поверхности за пределы обла-
области определения параметров ее радиус-вектор будем вычислять по одной из
формул C.14.8)—C.14.10) в зависимости от замкнутости базовой поверхности.
Далее рассмотрим вершины сохраняемых граней базового тела. Каждой
рассматриваемой вершине будут соответствовать одна или несколько вершин
тонкостенного тела. В каждой вершине тонкостенного тела будут стыковаться
несколько ребер. Вершина тонкостенного
тела базируется на точке пересечения экви-
эквидистантных поверхностей или на точке пе-
пересечения эквидистантных поверхностей с
поверхностями вскрываемых граней. Вычи-
Вычислив эти точки, мы найдем параметры пе-
пересекающихся поверхностей, которые будут
служить нам в качестве начальных и конеч-
конечных точек линий пересечения поверхностей.
Рассмотрим последовательно ребра со-
сохраняемых граней базового тела (ребра вто-
второй группы). Для каждого ребра построим
соответствующее ребро тонкостенного тела.
Для этого найдем линии пересечения экви-
эквидистантных поверхностей между собой и с поверхностями вскрываемых граней.
Начальные и конечные точки ребер нам известны.
По построенным вершинам перестроим ребра пересечения вскрываемых
граней (ребра первой группы).
Далее вывернем наизнанку часть граней. Если h > 0, то изменим на про-
противоположные направления циклов и нормалей сохраняемых граней базового
Рис. 6.10.3. Вазовое тело
Рис. 6.10.4. Тонкостенное тело, построенное внутрь от базового тела
Рис. 6.10.5. Тонкостенное тело, построенное наружу от базового тела
тела и направления циклов вскрываемых граней базового тела. Если h < 0, то
изменим на противоположные направления нормалей эквидистантных граней
(циклов они еще не имеют).
6.11. Скругление ребер тела
315
На последнем этапе построим циклы эквидистантных граней и перестроим
циклы вскрываемых граней. Таким образом, оболочка открытого тонкостенного
тела будет составлена из сохраняемых граней, эквидистантных к ним граней и
частей вскрываемых граней.
Открытое тонкостенное тело может быть построено как наружу (h > 0), так
и внутрь (h < 0) от базового тела. На рис. 6.10.4 приведено открытое тонко-
тонкостенное тело, построенное внутрь от базового тела путем вскрытия трех граней.
Базовое тело приведено на рис. 6.10.3. На рис. 6.10.5 приведено открытое тон-
тонкостенное тело, построенное на основе этого же базового тела наружу от него
тела путем вскрытия тех же трех граней (с большей толщиной стенки).
Операция построения тонкостенного тела наряду с булевыми операциями
является мощным средством для построения тел сложной формы. На рис. 6.10.6
приведено открытое тонкостенное тело, построенное на базе тела, показанного
Рис. 6.10.6. Тонкостенное тело на базе тонкостенного тела
Рис. 6.10.7. Разрез тонкостенного тела
на рис. 6.10.5, путем вскрытия двух граней. На рис. 6.10.7 приведен разрез
двумя плоскостями этого тонкостенного тела, на котором видны внутренние
полости тела.
Тонкостенное тело принадлежит к сложным телам. В его дерево построения
положим структуру данных исходного тела, толщину стенки и список удаляе-
удаляемых граней.
6.11. Скругление ребер тела
Операция скругления ребер тела позволяет построить плавный переход от
одной грани к другой. На рис. 6.11.1-6.11.4 приведены примеры скругления
ребер тел. На рис. 6.11.1, 6.11.2 скруглены выпуклые ребра.
Рис. 6.11.1. Призма со скругленным ребром Рис. 6.11.2. Призма со скругленными ребрами
316 Гл. 6. Моделирование тел
На рис. 6.11.3, 6.11.4 скруглены вогнутые ребра.
Рассмотрим общий случай скругления произвольного криволинейного ребра.
Пусть грань, лежащая справа от скругляемого ребра (если смотреть снаружи
тела вдоль ребра), базируется на поверхности r(u, v), а грань, лежащая слева от
Рис. 6.11.3. Скругление ребра Рис. 6.11.4. Вариант скругления ребер
скругляемого ребра, базируется на поверхности s(a, b). Эти грани будем назы-
называть сопрягаемыми. Пусть скругляемое ребро базируется на линии пересечения
c(s) поверхностей г(ы, и) и s(a, b). По кривой c(s) построим поверхность скруг-
скругления q(?, z), которая определяется формулой D.10.11). Краями поверхности
скругления являются линии D.10.5) и D.10.6), совпадающие с двухмерными
линиями D.10.4)
luv(t) = [«(*) v(t)]T, luv(t) 6 r(u, V), ^
lab{t)= [o@ b(t)]T, lab{t) e s(a, b)
на сопрягаемых поверхностях. Построим два ребра вдоль краев поверхности
скругления на базе линий пересечения
luv(t) = [«(*) v(t)]T, luv(t) 6 г(«, v), n
kz{t) = [t 0]т, ltz{t)eq{t,z),
lab(t) = [a(t) b(t)]T, lab(t) 6 S(O, b), (g ^ g)
ltz(t) = [t 1]T,
Эти ребра будем называть продольными, так как они направлены вдоль скруг-
скругляемого ребра и имеют ту же ориентацию.
Если скругляемое ребро замкнуто, то поверхность скругления также будет
замкнутой по параметру t. Тогда на базе линии пересечения
hzi{w) E q(i, z),
) E q(t, Z), F.11.4)
построим ребро, которое будет являться швом.
6.11. Скругление ребер тела
317
Если скругляемое ребро не замкнуто, то найдем все грани (за исключением
сопрягаемых), пересекающиеся с поверхностью скругления (большая их часть
стыкуется в начальной и конечной вершинах скругляемого ребра), и построим
линии их пересечения с поверхностью скругления. На базе этих линий пересе-
пересечения создадим ребра, которые будем называть поперечными.
На базе поверхности q(i, z) построим грань скругления. Цикл этой грани
будет состоять из продольных и поперечных ребер (или шва). Для грани скруг-
скругления определим признак совпадения ее нормали с направлением нормали по-
поверхности. Нормаль грани скругления должна быть направлена наружу тела
(нормаль поверхности скругления может совпадать с ней или быть ей противо-
противоположной) .
После этого перестроим сопрягаемые поверхности г(ы, и) и s(a, b) и ци-
циклы граней на них. Для этого найдем пересечение линий F.11.2) и F.11.3)
с ребрами сопрягаемых граней или их про-
продолжениями и изменим эти ребра. В одних
случаях упомянутые ребра нужно обрезать
(рис. 6.11.1), в других случаях их нужно про-
продлить (рис. 6.11.3). Вместо скругляемого ребра
в цикл грани г(ы, и) поставим ребро на базе
линии пересечения F.11.2), а в цикл грани
s(a, Ь) поставим ребро на базе линии пересе-
пересечения F.11.3) (рис. 6.11.5).
Далее перестроим циклы остальных гра-
граней, пересекшихся с поверхностью скругления
q(t, z). В циклы этих граней войдут попереч-
поперечные ребра. Перестроение циклов производится проверкой последовательности
стыковки ребер между собой и составлением списка ребер цикла в порядке их
следования. Поперечные ребра определят область изменения параметра t по-
поверхности скругления q(?, z).
Скругление сопряженных ребер. Будем называть стыкующиеся ребра со-
сопряженными, если в точках стыковки они имеют общую касательную. Если
в точках стыковки ребра претерпевают излом, то такие ребра будем называть
Рис. 6.11.5. Перестроение циклов
граней при скруглении ребра
Рис. 6.11.6. Исходное тело Рис. 6.11.7. Тело со скруглением нескольких ребер
несопряженными. Если скругляются сразу несколько несопряженных ребер те-
тела, то выполним их скругление последовательно одно за другим. Скругление ре-
ребер тел, приведенных на рис. 6.11.2, 6.11.4, 6.11.7, выполнено последовательно.
318
Гл.6. Моделирование тел
В случаях скругления нескольких сопряженных ребер различные стадии
операции скругления каждого ребра следует выполнять параллельно — одно-
одновременно для нескольких ребер. Перед началом операции скругления следует
составить группы гладко стыкующихся ребер и далее работать с этими груп-
группами как с отдельным ребром описанным выше образом. Случай скругления
Рис. 6.11.8. Исходное тело
Рис. 6.11.9. Тело со скруглением цепочек ребер
нескольких сопряженных ребер приведен на рис. 6.11.9. Исходное тело, пока-
показанное на рис. 6.11.8, получено скруглением двух ребер тела, приведенного на
рис. 6.11.6.
Для группы сопряженных ребер необходимо сначала построить все поверхно-
поверхности скругления, усечь этими поверхностями ребра тела, построить все продоль-
продольные и поперечные ребра пересечения поверхностей скругления и граней тела,
и только после этого построить грани скругления и произвести перестроение
циклов граней тела.
На рис. 6.11.11 приведено тело со скруглением сопряженных ребер, у ко-
которых на концах продольные ребра грани скругления сходятся в одну точку
Рис. 6.11.10. Исходное тело
Рис. 6.11.11. Тело со скруглением цепочек ребер
(рис. 6.11.10). В данном примере между сопряженными гранями поперечные
ребра стянуты в точку, а поверхности скругления в них вырождаются.
6.11. Скругление ребер тела
319
Продольные ребра могут не полностью лежать в области сопрягаемых гра-
граней. В этом случае участки продольных ребер, выходящие за область определе-
определения сопрягаемых граней должны быть заменены на ребра пересечения грани
скругления и соседних с сопрягаемой гранью граней.
Скругление вершин. Если скруглить три ребра, стыкующиеся в одной вер-
вершине, то в вершине получим картину, приведенную па рис. 6.11.12. Как пра-
правило, такую вершину скругляют. Скруглить вершину можно описанным выше
способом: ребро пересечения двух граней
скругления сопряжено с третьим ребром и
может быть скруглено вместе с ним.
Существует еще один способ скругления
вершины. Для этого построим по одной
линии на каждой поверхности скругления,
используя то, что каждая из трех поверхно-
поверхностей скругления пересекается с двумя дру-
другими.
Рассмотрим построение упомянутой ли-
линии на одной из поверхностей скругления
типа q(?, z). Пусть продольная линия lr(t)
этой поверхности скругления пересекается
Рис. 6.11.12. Подлежащая скруглению
вершина
с продольной линией другой поверхности скругления в точке с параметром tr,
а продольная линия ls(t) рассматриваемой поверхности скругления пересека-
пересекается с продольной линией третьей поверхности скругления в точке с параме-
параметром ts. Построим на рассматриваемой поверхности скругления двухмерный
отрезок прямой из точки [tt 0]т в точку [ts 1]T:
= [{l-z)tr zts]T, ltz{z)?q{t,z),
F.11.5)
По отрезку и поверхности построим пространственную линию lq(z). Линии
F.11.5) построим на каждой из трех поверхностей скругления, имеющих общую
точку пересечения. Отрежем и опустим ту часть каждой грани скругления,
которая лежит за построенной линией F.11.5) (со стороны общей вершины).
По трем линиям F.11.5) построим поверхность C.11.11), а на ее базе построим
грань скругления вершины.
Рис. 6.11.13. Скругление ребер и вершин тела
На рис. 6.11.13 приведен пример скругления ребер и вершин призмы опи-
описанным способом.
Аналогично можно скруглить вершину, в которой стыкуются четыре скруг-
скругляемых ребра. Для этого следует использовать поверхность C.6.1), построен-
построенную по четырем кривым.
320
Гл. б. Моделирование тел
6.12. Построение фасок ребер тела
Фаски ребер тела строятся аналогично скруглению ребер с той лишь раз-
разницей, что поверхности скругления заменяются поверхностями фасок. Фаска
описывается линейчатой поверхностью D.11.1), построенной по двум линиям
D.11.2) и D.11.3) на пересекающихся по ребру поверхностях.
Рис. 6.12.1. Исходное тело
Рис. 6.12.2. Тело с фасками ребер
Результат построения фасок ребер тела, показанного на рис. 6.12.1, приведен
на рис. 6.12.2.
Фаска вершин. Если поверхности фасок строятся для трех ребер, стыкую-
стыкующихся в одной вершине, то общую вершину, как правило, срезают. Срез вер-
вершины выполним аналогично скруглению вершины. Для этого найдем три
Рис. 6.12.3. Тело с фасками ребер и вершин
линии пересечения поверхностей фасок и построим по ним треугольную по-
поверхность. На базе трех линий пересечения построим три ребра, а на базе
треугольной поверхности построим грань. Результат среза вершины, в которой
стыкуются три ребра, приведен на рис. 6.12.3.
6.13. Некоторые способы построения тел
Описанный выше метод выполнения булевых операций применим в случае
полной определенности оболочек операндов. На практике часто требуется вы-
выполнить булеву операцию, когда оболочка одного из операндов определена не
полностью и должна быть достроена в процессе операции. Например, к задан-
заданному телу нужно добавить часть тела, полученного выдавливанием заданного
плоского контура, лежащую со стороны контура (рис. 6.13.1).
6.13. Некоторые способы построения тел
321
Результат такой операции приведен на рис. 6.13.2.
В данном случае требовалось «выдавить» заданный контур до ближайших
к нему граней заданного тела. В разных местах контура ближайшими могут
оказаться разные грани, поэтому точки контура должны быть «выдавлены» на
различные расстояния.
Рис. 6.13.1. Исходное тело и плоский контур
Выполнить данную операцию можно следующим образом. По заданному
контуру построим тело выдавливания достаточной глубины для пересечения с
заданным телом. Далее из тела выдавливания вычтем заданное тело. В резуль-
результате операции мы в общем случае получим несколько оболочек. Выберем из
Рис. 6.13.2. Выдавливание контура до ближайшей поверхности тела
них ближайшую к заданному контуру. Тело с выбранной оболочкой объединим
с заданным телом. При выполнении данных действий достаточно строить ребра
пересечения только один раз. Во второй части операции (объединение тела с вы-
выбранной оболочкой) следует использовать только те ребра, которые принадлежат
телу с выбранной оболочкой.
Другим примером может служить операция «вырезки» ближайших граней
заданного тела заданным контуром (рис. 6.13.3).
В данном примере контуром вырезаются ближайшие стенки тела и не тро-
трогаются грани, лежащие за ними. В разных местах контура его точки «выда-
«выдавливаются» на различные расстояния.
Вырезать ближайшие грани заданного тела заданным контуром можно сле-
следующим образом. По заданному контуру построим тело выдавливания доста-
достаточной глубины для пересечения с заданным телом. Далее найдем пересечение
21 — 5293 Голованов
322
Гл. 6. Моделирование тел
тела выдавливания с заданным телом. В результате операции мы в общем слу-
случае получим несколько оболочек. Выберем из них ближайшую к заданному
контуру. Тело с выбранной оболочкой вычтем из заданного тела. При выполне-
выполнении данных действий достаточно строить ребра пересечения только один раз.
Рис. 6.13.3. Вырез контуром ближайших поверхностей тела
Во многих конструкциях используются ребра жесткости. Операция построе-
построения ребер жесткости выполняется по той же схеме, что и операция «выдавли-
«выдавливания» контура до ближайших к нему граней тела. Тело с ребрами жесткости
приведено на рис. 6.13.4.
Рис. 6.13.4. Тело с ребрами жесткости
Когда оболочка одного из тел-операндов должна быть построена в процессе
выполнения операции, после выполнения операций следует проверить оболочку
результирующего тела на замкнутость.
6.14. Последовательность моделирования тел
Моделирование некоторого объекта может включать построение одного тела
или построение нескольких тел — сборки тел.
Создание одиночного тела начинается с построения или одного из простых
тел, или тела на базе линий, или тела на базе поверхности. Эти способы по-
построения тел приведены в левой части рис. 6.14.1. Если исходное тело создается
на базе плоских линий, то для их построения используются конструктивные
6.14. Последовательность моделирования тел
323
плоскости. Перед построением тела на базе поверхности нужно сначала создать
исходную поверхность. Во многих случаях при построении поверхности также
используются конструктивные плоскости. Далее путем выполнения операций,
приведенных в правой части рис. 6.14.1, из исходного тела можно получить
тело с более сложной оболочкой. Операции над телом могут выполняться мно-
многократно и в произвольной последовательности, что отражено на рис. 6.14.1.
Простые тела
Прямоугольная призма
Сферическое тело
Цилиндрическое тело
Коническое тело
Тороидальное тело
Тела на базе линий
Тело выдавливания
Тело вращения
Тело сдвига
Тело заметания
Тело на основе
плоских сечений
Тело на базе поверхностей
Тело в форме листа
Операции над телами
Булево объединение тел
Булево пересечение тел
Булева разность тел
Резка тела поверхностями
Построение симметричного тела
Построение эквидистантного тела
Построение тонкостенного тела
Скругление ребер тела
Фаски ребер тела
Построение ребер жесткости
Построение тела с пустотами
—
Рис. 6.14.1. Способы построения тел
Процесс построения оболочки сложного тела близок к процессу изготовле-
изготовления моделируемого объекта. С помощью булевой операции объединения к телу
можно добавить требуемый объем. Для этого нужно построить еще одно тело
и объединить исходное тело с ним. Аналогично с помощью булевых операций
пересечения или вычитания из тела можно убрать требуемый объем. От тела
может быть отрезана лишняя часть объема. Ребра тела могут быть скруглены
или с них могут быть сняты фаски. Из тела можно получить тонкостенное тело
путем «вскрытия» одной или нескольких граней и «придания оставшимся гра-
граням конечной толщины». Для симметричных тел можно построить только одну
половину тела, а затем получить требуемое тело с помощью операции создания
симметричного тела. К телу могут быть добавлены ребра жесткости.
Из нескольких тел можно получить сборку тел. В сборке все тела равно-
равноправны. Для взаимного расположения и ориентации тел сборки можно исполь-
использовать преобразования сдвига, поворота, масштабирования или симметрии.
Построение отдельных тел и сборок должно сопровождаться протоколом по-
построения, который называют деревом построения. Дерево построения позво-
позволяет выполнять редактирование тел и их сборок, создавать наборы однотипных
моделей и управлять ими.
Наряду с деревом построения для редактирования кривых линий, поверх-
поверхностей, тел, сборок тел и управления ими может использоваться механизм ва-
вариационных связей. Этому механизму посвящена следующая глава.
21*
Глава 7
ВАРИАЦИОННЫЕ СВЯЗИ ГЕОМЕТРИЧЕСКИХ ОБЪЕКТОВ
7.1. Наложение вариационных связей
В данной главе мы рассмотрим один из эффективных способов управле-
управления геометрическими объектами. Каждый геометрический объект имеет свою
структуру данных. Структура данных вместе с набором необходимых объекту
функций представляет собой численную модель геометрического объекта. Ска-
Скалярные величины, компоненты векторов, координаты точек, лежащие в струк-
структуре данных геометрического объекта, которые подлежат редактированию, бу-
будем называть параметрами этого объекта. Именно через эти параметры мы и
будем осуществлять управление геометрическими объектами.
До сих пор геометрические объекты строились и существовали независимо
друг от друга, т. е. редактирование одного из объектов не сказывалось на осталь-
остальных объектах. Редактирование объекта сводится к изменению численных зна-
значений его параметров. Независимость геометрических объектов отражает тот
факт, что значения параметров одного объекта не зависят от значений параме-
параметров других объектов. С практической точки зрения наложение зависимостей
= 11,0
rf-18,0
D-k*d
a = d/2+A
b-D/2+A
с-50
Л-2,0
Л =1,8
Рис. 7.1.1. Вариационные связи геометрических объектов
на параметры геометрических объектов является очень полезным. На рис. 7.1.1
приведен пример наложения зависимостей на две окружности и замкнутую ло-
ломаную линию на плоскости. Зависимость геометрических объектов заключа-
заключается в том, что окружности должны касаться друг друга, ломаная должна пред-
7.1. Наложение вариационных связей
325
ставлять собой прямоугольник, диаметры dn D окружностей связаны заданным
коэффициентом к, центры окружностей должны отстоять на заданных рассто-
расстояниях а и 6 от сторон прямоугольника, размер горизонтальной стороны прямо-
прямоугольника должен быть равен с. Перечисленные связи представлены размерами
и алгебраическими уравнениями, приведенными на рис. 7.1.1. Эскиз автомати-
автоматически перестраивается при изменении одной или нескольких зависимостей. На
рис. 7.1.2 приведены те же геометрические объекты при другом отношении диа-
диаметров окружностей. Изменение коэффициента отношения диаметров к привело
а = 1 1,0
(/=18,0
D = k*d
а = <//2 + Д
b = D/2+A
с = 50
Д = 2,0
к = 2,5
Рис. 7.1.2. Результат изменения одной из связей геометрических объектов
к изменению размера вертикальной стороны прямоугольника, изменению диа-
диаметра и положения центра большей окружности. Все заданные уравнения при
новом коэффициенте к также выполняются. Аналогично могут быть изменены
и другие размеры и уравнения, что приведет к автоматическому перестроению
геометрических объектов.
Наложение связей облегчает труд при проектировании нескольких однотип-
однотипных деталей и при сборке различных деталей. Достигается это путем установле-
установления определенных зависимостей между параметрами геометрических объектов.
Эти зависимости представляют собой некоторые уравнения
х2,
., хп) = 0,
., хп) = 0,
G.1.1)
x2,
., хп) - 0,
326 Гл. 7. Вариационные связи геометрических объектов
относительно параметров х\, Х2, ..., хп объектов. Будем называть связываю-
связывающие параметры уравнения вариационными связями. Кроме координат точек,
компонент векторов, скалярных величин из структуры данных геометрических
объектов параметрами могут служить дополнительные скалярные величины и
координаты точек. Они могут существовать отдельно или могут быть введены
в структуру данных геометрических объектов для удобства управления объек-
объектами посредством вариационных связей. Для наложения вариационных свя-
связей нужно, чтобы геометрические объекты предоставляли свои параметры «во
внешнее пользование» и перестраивались по измененным параметрам. Ва-
Вариационными связями в общем случае могут служить любые алгебраические
уравнения. Естественно, что каждой геометрической задаче соответствует опре-
определенное уравнение (или несколько уравнений) для определенных параметров.
Управление геометрическими объектами с помощью вариационных связей
осуществляется следующим образом. Пусть задан набор вариационных связей.
Каждая связь накладывает одно или несколько уравнений на определенные па-
параметры геометрических объектов. Связями формируется система уравнений
относительно участвующих в связях параметров. Пусть в исходном состоя-
состоянии параметры удовлетворяют этой системе уравнений. Предположим, что мы
изменили некоторую константу в уравнении связи (например, изменили зна-
значение размера) или изменили некоторые параметры геометрического объекта
(например, переместили объект) и зафиксировали их. Чтобы после этого си-
система уравнений связей удовлетворялась, необходимо изменить остальные па-
параметры. Для этого мы должны решить систему уравнений связей и опреде-
определить новые значения параметров. О результатах решения следует сообщить
геометрическим объектам. Они должны перестроиться в соответствии с этим
решением (в соответствии с новыми значениями своих данных). Так как урав-
уравнения в общем случае являются нелинейными, то их решение осуществляется
итерационным методом. Объекты должны перестраиваться на каждой итера-
итерации решения, так как одни параметры объекта могут влиять на другие пара-
параметры этого же геометрического объекта. Уравнения будут изменять значения
параметров, а объекты — перестраиваться в соответствии с новыми значения-
значениями параметров. Когда все уравнения системы будут удовлетворены с требуе-
требуемой точностью, объекты будут перестроены соответствующим образом. Если
систему уравнений удовлетворить нельзя, то всем параметрам присваиваются
первоначальные значения. На практике часто приходится иметь дело с систе-
системой уравнений, содержащей большее число параметров, чем число уравнений.
В последнем случае мы воспользуемся некоторым критерием, определяющим
поведение всей системы параметров, и с помощью этого критерия сформируем
систему уравнений для определения всех параметров.
Дополним вариационные связи информацией связываемых ими геометриче-
геометрических объектах, а также функциями общения с объектами и системой уравне-
уравнений. В результате вариационные связи можно будет называть вариационными
объектами. Они несут и обрабатывают геометрическую информацию. Как и
геометрические объекты, вариационные объекты имеют свою структуру данных
и свой набор функций. Состав структуры данных и функций определяется вы-
выполняемыми связями задачами. Каждый вариационный объект отвечает за то,
чтобы заданные параметры удовлетворяли заданным уравнениям. В структуре
данных вариационного объекта должны находиться: информация о связывае-
связываемых им варьируемых параметрах, исходные значения параметров, информация
об уравнениях связи (одном или нескольких). В набор функций вариационных
7.2. Фиксирующие связи 327
объектов должны войти функции, предоставляющие и изменяющие необходи-
необходимую информацию о варьируемых параметрах, функции, предоставляющие ин-
информацию об уравнениях связей, функции, изменяющие параметры в процессе
решения и после удовлетворения уравнений всех связей, функции восстановле-
восстановления исходного состояния параметров в Случае неудачи в процессе решения.
Сначала мы рассмотрим отдельные вариационные связи и их уравнения.
Далее введем критерий поведения геометрических объектов, позволяющий
сформировать систему уравнений, в которой варьируемые параметры обладают
равноправием при любом их числе. Этот критерий в общем случае требует при-
привлечение методов вариационного исчисления. На примере использования кри-
критерия поведения геометрических объектов мы рассмотрим вариационные связи
двухмерных объектов.
7.2. Фиксирующие связи
Простейшей связью является фиксирующая связь. Она описывается одним
уравнением, содержащим один параметр. Если параметр обозначить через q, то
уравнение имеет вид
q = g(°) = const, G.2.1)
где g(°) — заданное значение параметра, которое должно быть сохранено в даль-
дальнейшем. Фиксирующая связь используется тогда, когда требуется, чтобы неко-
некоторый параметр не изменялся в процессе решения системы уравнений связей.
Если некоторый параметр неизменен, то он может быть удален из списка пе-
переменных системы уравнений связей. Иногда удобнее сохранить неизменный
параметр, но при этом следует ввести для него фиксирующее уравнение G.2.1).
Примером фиксирующей связи может служить вариационная зависимость,
называемая закреплением точки. Она содержит три уравнения типа G.2.1) и
фиксирует три координаты точки р = [х у z]T. Закрепление точки описывается
одним векторным уравнением
р = р(°), G.2.2)
состоящим из трех скалярных уравнений
х = х<°\ у = у^\ z = z®\ G.2.3)
где р(°) = [ж(°) у(°) z(°)]T — заданное положение точки. Координаты за-
закрепленных точек остаются неизменными, поэтому частные производные всех
других уравнений системы по закрепленным параметрам равны нулю.
Уравнение G.2.1) может использоваться для любого параметра геометриче-
геометрического объекта — скалярной величины, компоненты вектора или координаты
точки.
Фиксирующие связи занимают особое место среди вариационных связей.
Количество параметров в фиксирующих связях всегда равно количеству урав-
уравнений, сами параметры остаются неизменными, поэтому фиксирующие связи
могут быть выделены из общей системы связей в самостоятельную группу. Си-
Система уравнений фиксирующих связей и система уравнений остальных связей
не зависят друг от друга и могут быть решены отдельно.
328
Гл. 7. Вариационные связи геометрических объектов
7.3. Вариационные связи точек в пространстве
Наиболее простыми являются вариационные связи, накладываемые на ко-
координаты радиус-векторов точек. Эти связи могут быть наложены на две или
несколько точек. При этом число уравнений связей может быть меньше числа
участвующих в связях параметров. В этом случае можно составить дополни-
дополнительные уравнения, необходимые для решения задачи. Мы рассмотрим при-
пример, построения вариационной связи, фиксирующей расстояние между двумя
точками в пространстве. В этом примере мы составим дополнительные урав-
уравнения исходя из симметрии поведения геометрических объектов. Дополнитель-
Дополнительные уравнения нам потребуются, чтобы проиллюстрировать процесс решения
системы уравнений связи.
Линейный размер. Пусть имеются две точки pi = [х\ у\ zi]T и рг =
= [х2 з/2 ^г]Т- Наложим на точки вариационную связь, называемую линейным
размером. Она описывается уравнением
|p2-pi|-d = 0,
G.3.1)
где d — требуемый размер. В координатном представлении уравнение связи
имеет вид
V(X2 ~ ZlJ + (У2 - У1J + Ы ~ ZXf -d = 0.
Линейный размер приведен на рис. 7.3.1. Точка pi лежит в структуре данных
тора и определяет положение центра его местной системы координат. Точка рг
лежит в структуре данных сферы и определяет положение ее центра. В общем
Рис. 7.3.1. Линейный размер между точками центров тора и сферы
случае это могут быть любые точки из структуры данных геометрических объ-
объектов. Мы имеем одно уравнение G.3.1), связывающее в общем случае шесть
параметров: х\, у\, zi, X2, J/2, ^2- В уравнении G.3.1) величину d будем счи-
считать константой. В общем случае величина d также может быть варьируемым
параметром.
7.3. Вариационные связи точек в пространстве
329
Рассмотрим принцип решения поставленной задачи. В данном случае для
того, чтобы найти все параметры, необходимы шесть уравнений. Существует
несколько способов получить систему уравнений с числом варьируемых пара-
параметров (неизвестных) равным числу уравнений. В данном случае мы составим
некоторые дополнительные уравнения, связывающие те же параметры. Набор
дополнительных уравнений может быть различным, но от этих дополнитель-
дополнительных уравнений будет зависеть поведение точек. Потребуем, например, чтобы
при изменении размера точки перемещались симметрично, т. е. точки переме-
перемещались бы вдоль соединяющей их линии, а центр тяжести точек оставался бы
неподвижным. Эти условия описываются уравнениями
(У2 ~
= (У2 ~
Х2 + XI = Я2@) + Х^°\
У2 + У1 =У2@)+У1@),
G.3.2)
G.3.3)
G.3.4)
G.3.5)
G.3.6)
где pi<°) = [xi<°) yi@) г1@)]Т и р2@) = [Х2@) у2@) гз@)]Т _ ИСХОДНОе положе-
положение точек, которое в общем случае не удовлетворяет уравнению G.3.1). Добавив
G.3.2)-G.3.6) к G.3.1), получим системы шести уравнений относительно шести
параметров. Перепишем все уравнения, придав им вид fi(x\, y\, z\, Х2, У2, ^г) =
= 0, г = 1, 2, ..., 6. Первое уравнение является нелинейным.
Решим систему уравнений методом Ньютона, описанным в гл. 4. Органи-
Организуем итерационный процесс
G.3.7)
г = 1,2,
где г — номер итерации. Приращения координат Axi, Ду^, Azi, i = 1, 2, на
каждой итерации определим из системы линейных алгебраических уравнений
а\\ а\2 ai3 «14 «15
Й21 Я22 О О24 «25
О аз2 «зз 0 «35
10 0 10
0 10 0 1
0 0 10 0
0
«36
0
0
1.
Ду!
Ах2
Дуг
Az2.
ь2
h
64
h
G.3.8)
330 Гл. 7. Вариационные связи геометрических объектов
где
^1 — х2 у\ - У2 z\ — z2
«11 = -«14 = ,/r)—, «12 = -«15 = ,(rj , «13 = -«16 = ,,ч "',
«21 = -«24 = У1@) ~ У2@), «22 = -Я25 = X2^ -X^°\
«32 = -«35 = Zi^> - Z2(°\ ЯЗЗ = -«36 = У2@) ~ У1@),
62 =
63 =
= У2@)+У1@)-у2(г)-У1(г),
- yi(r)J + (г2(г) _ г1(г)J.
Система уравнений G.3.8) в матричной записи имеет вид
А • Дх = Ь. G.3.9)
Эта система имеет единственное решение, если определитель |А| ф 0. На ка-
каждой итерации матрица А вычисляется заново, так как точки перемещаются в
пространстве, и может случиться так, что определитель матрицы А на очеред-
очередной итерации окажется равным нулю. Тогда точки следует вернуть в исходное
положение, а размер положить равным расстоянию между ними. Каждая строка
матрицы А соответствует определенному уравнению. Для г-го уравнения
fi(x\, yi, 2i, х2, У2, z2) = 0 в системе G.3.8) коэффициенты г-й строки ма-
матрицы А определяются по формулам
dfi д/i d/i an an an
t4l — д—i «t2 = 7;—) «i3 = 7;—> «i4 = 7;—, «i5 = 7;—? fli6 = ¦?—,
ox\ dy\ oz\ dx2 oy2 oz2
Итерационный процесс G.3.7) закончим, когда приращения координат на оче-
очередной итерации станут меньше заданной величины.
Возможны и другие варианты дополнительных уравнений. Например, если
требуется сохранить точку pi в заданном положении, то в качестве дополни-
дополнительных уравнений можно использовать уравнения G.3.2), G.3.3) и
Р1 = Р@),
где р(°) — заданное положение точки. В дальнейшем для решения системы
уравнений связей мы не будем использовать дополнительные уравнения, так
как они нарушают равноправие варьируемых параметров.
Размер вдоль координаты. Более простой, чем линейный размер, вариаци-
вариационной связью двух точек является размер вдоль одной координаты. Она свя-
связывает две соответствующие координаты двух точек и описывается одним из
7.3. Вариационные связи точек в пространстве 331
уравнений
x2-xi = dx, G.3.10.1)
У2~У1= dy, G.3.10.2)
z2-zi = dz, G.3.10.3)
где dx, dy, dz — требуемые размеры. Уравнения G.3.10), примененные к коор-
координатам точек отрезка г(?) = A — i)pi + tp2, могут сделать отрезок параллель-
параллельным соответствующей координатной плоскости. Два уравнения G.3.10) могут
сделать отрезок параллельным одной из координатных осей.
Размер вдоль направления. Еще одной вариационной связью двух точек
является размер вдоль заданного направления. Она описывается уравнением
|(p2-Pi)-m|=d, G.3.11)
где m = [mx my mz]T — задающий направление вектор единичной длины, d —
требуемый размер. Уравнение G.3.11) устанавливает, что проекция вектора
Р2 ~ Рь построенного между заданными точками, на направление вектора m
по абсолютной величине равна d. В координатной записи уравнение G.3.11)
имеет вид
\{х2 - х\)тх + (у2 - yi)my + (z2 - zi)mz\ = d. G.3.12)
Уравнение G.3.12) связывает шесть параметров. Если m = [mx my mz]T, 1 =
= [lx ly lz]T, n = [nx ny nz]T — три линейно независимых вектора единичной
длины, то можно задать относительное положение двух точек р2 и pi сразу
тремя размерами вдоль трех некомпланарных направлений т, 1, п:
|(Р2 -
|(Р2 -Pi) -I| = of/, G.3.13)
|(P2~Pi) -n| = dn.
В координатной записи уравнения G.3.13) имеют вид
\(х2 - xi)mx + (у2 - у\)гпу + {z2 - zi)mz\ = dm,
\(х2 - хгIх + (у2 - yi)ly + (z2 - zi)lz\ = dh
\{x2 - x\)nx + (y2 - y\)ny + {z2 - zi)nz\= dn.
Совмещение точек. Можно установить вариационную связь, которая сливает
две точки в одну. Эта связь совмещения точек. Она приравнивает координаты
двух заданных точек и описывается векторным уравнением
Р2 = Р1- G-3.14)
Данная вариационная связь содержит три скалярных уравнения
S2-:ci = 0, G.3.15)
И8-У1 = 0, G.3.16)
z2-*i=0. G.3.17)
332
Гл. 7. Вариационные связи геометрических объектов
Симметрия точек относительно плоскости. Рассмотрим вариационную связь
симметрии точек р2 и pi относительно плоскости
г (ж, у) =
yi2.
G.3.18)
Плоскость будем считать неподвижной, поэтому ее параметры варьироваться не
будут.
Симметрия точек относительно плоскости описывается тремя уравнениями
(Pi — Р) ¦ ii = (Рг-Р) -ii,
(Pi -P) -12 = (Р2-Р) '12,
(Pi - Р) • k + (Р2 ~ Р) • 13 = О,
G.3.19)
G.3.20)
G.3.21)
где 1з = ii х i2- Три уравнения G.3.19)—G.3.21) связывают шесть параметров.
Симметрия точек показана на рис. 7.3.2.
Плоскость /¦
симметрии /
у
А
у
Рис. 7.3.2. Симметрия точек относительно плоскости
Рис. 7.3.3. Угловой размер между тремя точками NURBS кривой
Угловой размер. Для трех точек можно установить угловую зависимость.
Пусть имеется три точки pi = \х\ у\ zi]T, p2 = [х2 у2 z2]T и р3 = [х3 у3 ^з]Т-
На три точки можно наложить вариационную связь, определяющую угловой
размер между отрезками pi — р2, Рз — Рг- На рис. 7.3.3 точками, на которые
наложена вариационная связь, являются характеристические точки рациональ-
рациональной кривой. В общем случае это могут быть любые точки из структуры данных
геометрических объектов.
Уравнение, описывающее угловой размер между тремя точками, имеет вид
arctg - = а,
с
G.3.22)
где
с = (pi — Рг) • (Рз - Рг) =
= (si - х2)(х3 - х2)
-Р2)х(рз-р2)|, G.3.23)
- Уг) + («1 - z2){z3 - z2), G.3.24)
7.3. Вариационные связи точек в пространстве 333
a — заданный угол. Величина s равна произведению длин векторов pi — р2
и рз — Р2 на sin а. Величина с равна произведению длин векторов pi — рг и
Рз ~ Рг на cos а. Квадрат s определяется формулой
s2 = ((У1 - УгН^з - z2) - (zi - z2)(y3 - У2)J +
+ {{z\ - z2)(x3 - x2) - (xi - x2){zs - z2)J +
+ ((si - x2)(y3 - y2) - (yi - y2){x3 - x2)f. G.3.25)
Уравнение G.3.22) связывает девять параметров.
Другой вариационной связью трех точек pi, р2 и рз является угловой раз-
размер в плоскости. Эта связь устанавливает угловой размер между проекциями
векторов pi — рг и рз — Рг на плоскость, ортогональную единичному вектору т,
и описывается уравнением вида G.3.22), где
s = ±|qi X qal, G.3.26)
с = qi • qs, G.3.27)
qi = Pi - Р2 - m((pi - p2) ¦ m),
q2 = Рз - P2 - m((p3 - p2) • m).
Векторы qi и q3 являются составляющими векторов pi — рг и рз — р2, орто-
ортогональными единичному вектору т. Знак плюс в G.3.26) выбирается в случае
совпадения направления векторов qi x q3 и т, знак минус — в противном
случае.
Угол между векторами. Пусть имеется четыре точки pi = [х\ у\ z\]T, p2 =
= [х2 у2 z2]T, рз = [жз Уз •гз]Т и р4 = [х? У4 ^4]т. По четырем точкам можно
построить два вектора. Построим векторы на точках pi, рг и рз, Р4- Будем
считать, что эти векторы не коллинеарны. Два вектора определяют семейство
плоскостей, параллельных одновременно им обоим. Каждая плоскость семей-
семейства будет ортогональна вектору n = (pi — р2) х (рз — Р4).
На четыре точки можно наложить вариационную связь, определяющую угол
между векторами pi — рг, рз'— Р4- Эта связь аналогична угловому размеру
G.3.22). Уравнение, описывающее угол между четырьмя точками, имеет тот же
вид, что и уравнение G.3.22):
arctg - = а, G.3.28)
с
где
в = |(Р1-Р2)х(р3-р4)|, G.3.29)
с= (pi -Рг)- (Рз-Р4) =
= (xi - х2){х3 - х^) .+ (yi - у2)(уз - Уа) + {z\ - z2){z3 - z4), G.3.30)
а — заданный угол. Величина s равна произведению длин векторов pi — р2
и рз — Р4 на sin а. Величина с равна произведению длин векторов Pi — р2 и
334 Гл. 7. Вариационные связи геометрических объектов
Рз — Р4 на cos a. Квадрат s определяется формулой
2 = ((у1 y2){z3 Z4) ~ (Zi - Z2){y3 ~ У4)J
- z2)(x3 - x4) - (xi -
Уравнение G.3.28) связывает двенадцать параметров.
Потребуем, чтобы при изменении угла между векторами точки перемещались
ортогонально вектору п. Для нахождения точек скрещения построим две линии
G.3.
G.3.
и гз на
G.3.
G.3.
31)
32)
ли-
33)
34)
гз(*з) = A -
Точками скрещения пространственных линий являются точки
ниях ri(ii) и Гз(*з)) для которых выполняются равенства
(Pi - Рз) ¦ (ri - гз) = 0,
(Рз - Р4) ¦ (ri - гз) = 0.
Вектор, построенный по точкам скрещения, ортогонален обеим прямым. Па-
Параметры t\ и ?з прямых, соответствующие точкам скрещения, определим из
системы уравнений
(Pi " Рз)" (A - *i)pi + <1Рз " A - *з)рз - *зр4) = 0, G.3.35)
(Рз - Р4) ¦ (A - *i)pi + <1Р2 - A - *з)рз - *зР4) = 0 G.3.36)
или
(Pi - Рг) ¦ (Р2 - Pi)*i + (Pi - Р2) • (рз - Р4)^з = (pi - Р2) • (рз - Pi),
(РЗ - Р4) ¦ (Р2 - Pl)*l + (РЗ - Р4) ' (РЗ - Р4)*3 = (РЗ - Р4) ' (РЗ - Pi)-
По найденным параметрам найдем точки скрещения.
Ортогональность векторов. Частным случаем вариационной связи G.3.28)
является ортогональность векторов, построенных по точкам pi, Рг и рз, Р4-
Данная вариационная связь определяется уравнением
(Pi - Рз) • (Рз - Р4) = 0. G.3.37)
Если на точках построены отрезки прямых G.3.31) и G.3.32), то уравнение
G.3.37) делает эти отрезки ортогональными.
Параллельность векторов. Вариационная связь, делающая векторы pi — р2
и рз — Р4 параллельными, определяется векторным уравнением
(Р1-Рз)х(рз-р4) = О. G.3.38)
Связь G.3.38) будем называть параллельностью векторов. Уравнение G.3.38)
содержит три скалярных уравнения
- 24) = 0, (^i - г2)(х3 - х4) = 0, (xi - х2)(уз ~ У4) = 0.
7.4. Вариационные связи точек на кривых и поверхностях 335
7.4. Вариационные связи точек на кривых и поверхностях
Выше мы рассмотрели связи, накладываемые на существующие в струк-
структурах данных геометрических объектов параметры. Если требуется наложить
вариационные связи на некоторые значения, которые отсутствуют в структуре
данных геометрических объектов, то можно ввести в структуру данных допол-
дополнительные параметры. Например, для описания дуги окружности B.2.11) в
структуре данных не нужны крайние ее точки, но их можно туда ввести, если
необходимо накладывать на них вариационные связи. При этом остальные па-
параметры должны пере считывать ся в зависимости от положения крайних точек.
Вариационные связи можно накладывать на точки кривых и поверхностей,
которые отсутствуют в их структурах данных. Например, мы хотим задать ли-
линейный размер между определенной точкой кривой а(?) и определенной точкой
кривой Ь(ги). Пусть для простоты кривыми являются отрезки
-На2,
а в качестве точек на них мы возьмем середины отрезков. Середины отрезков
определяются параметрами t — to — 1/2, w = wq — 1/2. Будем считать, что to
и wo есть постоянные величины, если не будет объявлено, что они также явля-
являются варьируемыми параметрами уравнения. Линейный размер описывается
уравнением G.3.1), в котором теперь pi = а(?0), рг = Ь(го0)- Координаты свя-
связываемых точек pi = [х\ yi zi]T ирг = [x2 г/2 2г]Т являются функциями коор-
координат точек кривых ai = [xai yai za\]T, а2 = [xa2 ya2 za2]T, bi = [xbi уы zbi]T,
i>2 = [хь2 УЬ2 Zb2]T¦ Число варьируемых параметров в данном случае будет
равно 12. Ими являются координаты xai, yai, zai, xa2, Уа2, Za2, %, УЫ, *ы,
ХЬ2, УЬ2-, Zb2- В общем случае варьируемыми параметрами будут являться пара-
параметры из структур данных связываемых кривых, которыми описываются точки
pi =а(?0) ир2 = b(u?o).
Аналогично можно установить размер по одной из координат G.3.10) или
размер вдоль заданного направления G.3.12) между определенной точкой кри-
кривой а(?) и определенной точкой кривой Ъ(ги). Можно связать определенные
точки кривых вариационной зависимостью G.3.14). Можно установить угловой
размер G.3.28) между заданными точками трех геометрических объектов.
Все сказанное остается в силе, если вместо точек кривых связать опреде-
определенные точки поверхностей. Например, описанным образом можно установить
линейный размер между определенной точкой поверхности а(и, v) и определен-
определенной точкой поверхности b(t, w) или установить угловой размер между опреде-
определенными точками поверхностей а(и, v), b(f, w) и s(x, у).
Между точкой р и произвольным геометрическим объектом S можно уста-
установить вариационную связь, «усаживающую» точку на геометрический объект.
Эта связь описывается уравнением
p = sp, G.4.1)
где sp — проекция точки на геометрический объект. Векторное уравнение
G.4.1) содержит три скалярных уравнения относительно трех параметров —
координат точки р. Геометрический объект в процессе решения уравнений
связей можно считать или неподвижным, или подвижным, но единым целым.
336 Гл. 7. Вариационные связи геометрических объектов
Если требуется, чтобы геометрический объект после установления вариаци-
вариационных связей не изменял свою форму, то его параметры нужно считать неиз-
неизменными или к уравнениям связи следует добавить уравнения, сохраняющие
неизменными параметры, определяющие его геометрию.
7.5. Алгебраические связи
В уравнения связей G.3.1), G.3.12), G.3.22), G.3.28) входят величины d
и а, которые до сих пор читались константами. На рис. 7.1.1 размеры свя-
связаны друг с другом алгебраическими уравнениями. Для того, чтобы величины
d и а, могли изменяться, они должны также являться варьируемыми параме-
параметрами. Эти параметры не принадлежат ни какому-либо геометрическому объ-
объекту, ни какой-либо вариационной связи. Будем называть их свободными па-
параметрами. Алгебраические уравнения, связывающие свободные параметры,
будем называть алгебраическими связями. В частном случае алгебраические
связи используются, чтобы сделать равными несколько параметров различных
геометрических объектов. Для этого вводится свободный параметр и совокуп-
совокупность уравнений, приравнивающих требуемые параметры геометрических объ-
объектов введенному свободному параметру.
В качестве примера использования алгебраических связей рассмотрим два
линейных размера, один из которых связывает точки pi = [х\ у\ zi]T и рг =
= [х2 2/2 %2]Т, а другой связывает точки рз = [хз уз ?з]Т и Р4 = [Х4 2/4 ?4]Т-
Пусть линейные размеры описываются уравнениями
|p2-Pi| = o, G.5.1)
|рз - Р4| = Ь. G.5.2)
Пусть значения размеров а и Ь связаны некоторыми алгебраическими уравне-
уравнениями
9(а, Ь) = О, G.5.3)
h(a, Ъ) = 0. G.5.4)
Уравнения G.5.1) и G.5.2) отличаются от уравнения G.3.1) тем, что в послед-
последнем размер d не варьируется, а в уравнениях G.5.1) и G.5.2) параметры а и b
являются варьируемыми. На (г + 1)-й итерации решения системы уравнений
изменяются как координаты точек, так и значения размеров:
о(г+1) = о(г) + дО) Ь(г+1) = Ь{т) + дЬ>
г = 1, 2, 3, 4.
Свободными могут быть любые параметры уравнений связей, не являющие-
являющиеся параметрами геометрических объектов. В общем случае алгебраические урав-
уравнения нельзя выделить из общей системы уравнений связей и решить отдельно,
так как они могут быть связаны друг с другом через уравнения для параметров
геометрических объектов.
Наряду с алгебраическими уравнениями вариационные связи могут стро-
строиться на неравенствах. Например, вместо уравнения G.5.3) алгебраическая
связь может определяться неравенством
а > Ь. G.5.5)
7.6. Минимизация изменения параметров 337
На каждой итерации решения системы уравнений неравенство заменяется со-
соответствующим уравнением. Неравенство G.5.5) на каждой итерации должно
быть заменено уравнением
а - Ь = е, G.5.6)
где
e = a^-b(r\ если а« > бМ,
е = 0, если а<г) < b^r\
Если на очередной итерации неравенство выполняется, то оно заменяется то-
тождественным равенством, если неравенство не выполняется, то оно заменяется
строгим равенством. Аналогичным образом в процессе численного решения
системы уравнений и другие неравенства заменяются соответствующими ра-
равенствами. Связи, построенные на неравенствах, будем называть нестрогими
алгебраическими связями.
7.6. Минимизация изменения параметров
Идеальным является случай, когда число уравнений связей равно числу
варьируемых параметров. Этот идеальный случай реализуется, когда на задан-
заданную группу параметров наложено максимально возможное число связей. Если
делается попытка наложить связей больше, чем это возможно, то система урав-
уравнений будет переопределена и отвергнет лишние связи. Если число уравнений
связей меньше числа параметров, то необходимо найти способ дополнить си-
систему связей уравнениями. Один из способов — составление дополнительных
уравнений.
На примере линейного размера между двумя точками показано использова-
использование дополнительных уравнений. Возможны ситуации, когда одна и та же группа
параметров участвует в нескольких связях (например, на одну и ту же группу
точек наложено несколько размерных зависимостей). Набор дополнительных
уравнений может быть различным и существенным образом влияет на поведе-
поведение геометрических объектов. Использование дополнительных уравнений нару-
нарушает равноправие варьируемых параметров и может привести к нежелательным
последствиям в поведении геометрических объектов.
Мы откажемся от использования дополнительных уравнений. Необходимую
систему уравнений для удовлетворения всех вариационных связей мы полу-
получим, наложив некоторое общее для всей совокупности геометрических объектов
условие поведения. Поведение системы параметров мы будем определять неко-
некоторым критерием, описываемым функцией или функционалом. Уравнения для
определения параметров мы получим из требования минимума или максимума
функции или функционала данного критерия.
При наложении вариационных связей будем использовать метод миними-
минимизации суммы квадратов изменений параметров. Рассмотрим его применение
на примере линейного размера между двумя точками, описываемого уравнением
G.3.1). Если ввести дополнительные уравнения G.3.2)-G.3.6), то поведение
связанных точек будет симметричным, но сама система уравнений имеет не-
несимметричный вид. Кроме того, если рассматриваемые точки участвуют еще
в каких-нибудь связях, то возникает вопрос, какие из дополнительных урав-
уравнений следует оставить, а какие опустить. В большинстве случаев поведение
такой системы связей теряет симметрию.
22 - 5293 Голованов
338 Гл. 7. Вариационные связи геометрических объектов
Обратим внимание на то, что в варианте дополнительных уравнений G.3.2)-
G.3.6) суммарное перемещение связанных линейным размером точек является
минимальным из возможных. Используем это свойство для составления си-
системы уравнений. Квадрат суммарного перемещения связанных точек описы-
описывается функцией
В координатном представлении эта функция имеет вид
i - *i@)J + (yi - yi@)J + (*i - *i@)J+
+ (Х2 - Ж2(°)J + (у2 ~ У2@)J + (*2 - *2@)J) • G.6.1)
Эта функция пропорциональна сумме квадратов изменений всех связанных па-
параметров. Аргументами этой функции являются те же шесть параметров: х±,
j/i, zi, ж2, J/2) #2- Потребуем, чтобы сумма квадратов изменений параметров
была минимальной. При этом необходимо, чтобы координаты точек удовлетво-
удовлетворяли уравнению связи G.3.1). Используем метод неопределенных множителей
Лагранжа для отыскания минимума функции G.6.1) при условии G.3.1). Необ-
Необходимым условием минимума функции G.6.1) при условии G.3.1) является ра-
равенство нулю частных производных по параметрам функции
F = Ф + А/ = \ (|Р1 - Р1(°)|2 + |р2 - Р2(°)|2) + А(|р2 - pi| - d) =
\ (Ы - Х^J+ (W - У1(°)J+ (*х - г1(°)J+ (Х2 - Х2^)Ч (У2 - и,«»)а +
\
+(z2 - z2MJ) + A (Vfo - a:iJ + (у2 - УгJ + (z2 - ^iJ - d) , G.6.2)
где / = |p2 — pi | — d, A — подлежащий определению множитель. Искомые
координаты точек и множитель А найдем из системы уравнений
~ У1J + {Z2-ZXJ-d = О,
7.6. Минимизация изменения параметров 339
Данная система уравнений имеет решение
GЛЗ'4)
А —
где d(°) = v/(a;2@) - zi(°)J + (У2(о) _ yi(o)J + (Z2(o) _ Zl(o)J. Можно доказать,
что найденное решение является точкой минимума функции G.6.2). Точки пе-
переместятся вдоль прямой, проходящей через точки pi^ и рг^, на одинаковое
расстояние. В данной постановке задачи точки являются равноправными, а
уравнения и решение системы уравнений являются симметричными.
Мы считали, что обе точки могут перемещаться. Если одна из точек закреп-
закреплена, то на нее наложена связь G.2.2) и ее координаты не варьируются. Пусть
точка pi закреплена. Тогда функция G.6.2) будет иметь вид
\ ((Х2 - Ж2(°)J + (и, ~
+А (J{x2 - Х1Щ* + (у2 - У1(°)J + (z2 - г1@)J - d\ . G.6.5)
Координаты закрепленной точки в функцию G.6.5) не входят. Функция G.6.5)
достигает минимума при
Gбб)
22*
340 Гл. 7. Вариационные связи геометрических объектов
И в решении G.6.4), и в решении G.6.6) свободные точки перемещаются
вдоль прямой, проходящей через точки pi и р2. Требование минимума суммы
квадратов варьируемых параметров автоматически создает симметрию в пове-
поведении системы. Симметрия присутствует и в системе уравнений. Это свойство
особенно ценно для сложных связей, в которых много параметров и все они
имеют различный геометрический смысл. На данном примере проиллюстри-
проиллюстрирован критерий, который мы будем использовать для удовлетворения произ-
произвольных вариационных связей.
Сумма квадратов изменений варьируемых параметров отражает реакцию
геометрических объектов с наложенными вариационными связями, на изме-
изменение констант в уравнениях связей или на изменения самих объектов. Кри-
Критерий изменения параметров сформулируем следующим образом. Реакция гео-
геометрических объектов с наложенными на них вариационными связями на
любое возмущение должна быть такой, чтобы сумма квадратов изменений
варьируемых параметров была бы минимальной. Данный критерий ставит все
варьируемые параметры в равные условия. Критерий можно сформулировать
в виде задачи минимизации некоторой функции или (в общем случае) в виде
задачи минимизации функционала. Ниже мы рассмотрим обе формулировки
критерия поведения геометрических объектов с наложенными вариационными
связями.
7.7.* Условный экстремум функции изменения параметров
Пусть имеется некоторая совокупность вариационных связей, наложенных на п
параметров xi, х2, •¦•, хп геометрических объектов. Пусть эта совокупность связей
накладывает т уравнений
fi(xi, х2, ..., хп) = 0,
, х2, ..., хп) — 0, G.7.1)
/m(zi, Х2, ..., Хп) = 0,
на параметры объектов. Связи фиксации здесь учитывать не будем. Фиксированные па-
параметры в процессе решения не изменяются, поэтому в других уравнениях связей они
не варьируются и считаются константами. Если т = п, то все параметры могут быть
найдены путем решения системы уравнений вариационных связей. Если т < п, то для
определения параметров нужно составить систему уравнений, в которой число опреде-
определяемых параметров было бы равно числу уравнений, и среди уравнений содержались
бы уравнения G.7.1). Систему уравнений получим из требования экстремума некото-
некоторой функции параметров, несущей определенный геометрический смысл. Это требо-
требование является критерием поведения параметров связей. Для вариационных связей,
управляющих координатами точек и размерными параметрами, критерием поведения
нам будет служить требование минимума суммы квадратов изменений варьируемых
параметров, т. е. минимума функции
где Х{(°1 — исходные значения варьируемых параметров.
На примере линейного размера выше было показано применение этого критерия
совместно с методом неопределенных множителей Лагранжа. Рассмотрим теоретиче-
7.7. Условный экстремум функции изменения параметров 341
ские основы использованного выше метода неопределенных множителей Лагранжа для
нахождения условного минимума или максимума действительной функции нескольких
переменных параметров.
Экстремум функции. Пусть некоторое требование, предъявленное к варьируемым
параметрам Xi, i = 1, 2, ..., п, определяется экстремумом функции
ip = ip{xl,x2,...,xn). G.7.2)
По определению действительная функция G.7.2) в точке ж, = a,, i = 1, 2, ..., п (кон-
(конкретную совокупность параметров будем называть точкой) имеет минимум (максимум),
если существует такое положительное число S, что при любых Axi, Ах2, ..., Ахп, удо-
удовлетворяющих неравенствам
О < \JAxy2 + Ах22 + ... + Ахп2 < S,
приращение функции
¦- ф + (сц + Д^!, а2 + Ах2, ..., ап + Ахп) — ф(сч, а2, ..., ап) G.7.3)
соответственно больше (меньше) нуля. Будем считать, что функция ф в окрестно-
окрестности экстремума имеет непрерывные частные производные до второго порядка включи-
включительно. Разложим в ряд Тейлора в окрестности точки ж, = a,, i = 1, 2, ..., п первое
слагаемое правой части G.7.3) и получим
± ±
= ± Цд*' + j ± ±
t=l i=l j=
где о{Ах3) — слагаемые третьего порядка относительно Ах,. Слагаемые первого и вто-
второго порядка относительно Axi в G.7.4) составляют первый dip и второй cPip диффе-
дифференциалы функции ip. Дифференцируемая функция ip(xi, х2, ..., хп) в точке Xi = a,,
i — 1, 2, ..., п имеет минимум или максимум лишь в том случае, когда ее первый
дифференциал обращается в этой точке в нуль
dip = Р- сЬц + |^ dx2 + ... + Р^ dxn = 0. G.7.5)
axi ax2 axn
Для этого необходимо выполнение равенств
дф dip dip ,77й1
=° =° =° G76)
при х\ = ai, х2 = а2, ..., хп — ап- Выполнение равенств G.7.6) является необходимым
условием экстремума. Достаточным условием экстремума функции ip(xi, x2, ¦ ¦., х„)
является знакоопределенность второго дифференциала
при xi = ai, x2 = а2, ..., хп = ап- Если второй дифференциал G.7.7) представляет со-
собой положительно определенную квадратичную форму, то функция в рассматриваемой
точке имеет локальный минимум. Если второй дифференциал G.7.7) есть отрицательно
342 Гл. 7. Вариационные связи геометрических объектов
определенная квадратичная форма, то функция в рассматриваемой точке имеет локаль-
локальный максимум. Если второй дифференциал G.7.7) не является знакоопределенной
квадратичной формой, то функция в рассматриваемой точке не достигает экстремума.
Условный экстремум функции. Все сказанное об экстремуме функции G.7.2) спра-
справедливо при отсутствии условий G.7.1). Нас интересует минимум функции G.7.2),
аргументы которой удовлетворяют уравнениям связей G-7.1). Будем говорить, что дей-
действительная функция G.7.2) в точке Xi = bi, i = 1, 2, ..., п имеет условный минимум
(условный максимум), если существует такая окрестность этой точки, в пределах кото-
которой значение функции в точке Xi = bi, i = 1, 2, ..., п является наименьшим (наиболь-
(наибольшим) среди ее значений во всех точках окрестности, удовлетворяющих уравнениям
связей G.7.1).
Если уравнения G.7.1) позволяют выразить любые m параметров через остальные
п — m в виде функций, например,
xi =gi(xm+i, xm+2, ¦ ¦•, хп),
Х2 = g2(xm+l, Xm+2, ¦ ¦ ¦, Хп), G.7-8)
Xm = gm(xm+i, Xm+2> . . ., Xn),
то задача об условном экстремуме сведется к задача об обычном экстремуме функ-
функции. Для этого подставим равенства G.7.8) в G.7.2) и найдем безусловный экстремум
функции
Ф = Ф(д1 {Xm+l, Xm+2, • •-, Хп), g2(xm+i, Xm+2, . . ., Хп), ...
¦ ¦ ; gm(xm+l, Xm+2, ¦ ¦ -, Xn), Xm+i, Xm+2, ¦ ¦ -, Xn), G.7.9)
зависящей от параметров xn-m+i, xn-m+2, ¦ ¦ -, xn.
Установим необходимые условия существования условного экстремума функции ф,
когда невозможно получить выражения G.7.8). В точке условного экстремума должен
быть равен нулю первый дифференциал функции G.7.5). Но при наличии условий
G.7.1) не все дифференциалы параметров являются независимыми. Дифференциалы
параметров в точке условного экстремума связаны уравнениями
dx2 + _+
ox2 axn
Действительно, если точки xt — bi и Xi = bi + Axi, i = 1, 2, ..., n удовлетворяют урав-
уравнениям связей, то в пределе Да;» -> 0, i = 1, 2, ..., п разность уравнений G.7.1) для
этих точек даст уравнения G.7.10). Из системы то уравнений G.7.10) найдем любые
m дифференциалов, пусть это будут dx\, dx2, ¦.., dxm. Для этого необходимо, чтобы
якобиан системы уравнений связей был отличен от нуля. Найденные дифференциалы
подставим в первый дифференциал функции G.7.5) и получим
# = Hm+1 dxm+1 + Нт+2 dxm+2 + ...+Hndxn = 0, G.7.11)
7.7. Условный экстремум функции изменения параметров 343
где через Hm+i, Hm+2, ¦ ¦., Н„ обозначены рациональные функции частных производ-
производных ф, Д, f2, ..., /го в точке условного минимума. Дифференциалы dxm+\, dxm+2,. ¦ ¦
..., dxn являются независимыми переменными выражения G.7.11), поэтому равенство
нулю первого дифференциала G.7.11) возможно, когда выполняются равенства
Ят+1 = 0, Ят+2 = 0, ..., Я„ = 0. G.7.12)
Уравнения G.7.12) совместно с уравнениями связей G.7.1) представляют собой необ-
необходимое условие условного экстремума функции G.7.2).
Метод множителей Лагранжа. В описанном выше методе отыскания условного экс-
экстремума функции параметры х\, х2, ¦ ¦., хп не являлись равноправными. Часть из них
мы должны были выразить через остальные параметры. В результате система урав-
уравнений для определения условного экстремума являлась несимметричной относительно
параметров. Лагранжем предложен метод, который делает параметры равноправными,
а уравнения симметричными относительно параметров. Умножим равенства G.7.10)
на неопределенные пока постоянные множители Ai, A2, ..., Аго и добавим к равенству
G.7.5). В результате получим равенство
где
F = F(xu x2, ...,хп) = ф + Ai/i + А2/2 + ... + \mfm. G.7.14)
Функция F называется функцией Лагранжа. Так как параметры х\, х2, ..., хп свя-
связаны уравнениями связей, то их дифференциалы в G.7.13) не являются независимыми.
Будем считать, что первые m параметров зависят через уравнения связей от осталь-
остальных n — m параметров. Параметры хт+1, хт+2, ..., хп будем считать независимыми.
Множители Ai, Аг, ..., Аго выберем так, чтобы выполнялись равенства
Это можно сделать, решив систему уравнений
, dh df2 д/т
df
h df2 df
1-А2h + A
fir fir 8r Fir
oxm oxm oxm oxm
относительно множителей Ai, Аг, • •., Aro. Как уже было сказано, определитель матрицы
этой системы линейных алгебраических уравнений должен быть отличен от нуля. При
выполнении равенств G.7.15) для выполнения равенства G.7.13) требуется, чтобы
- = 0, -т = 0, ..., -— = 0. G.7.17)
Охт+1 ОХт+2 ОХп
344 Гл. 7. Вариационные связи геометрических объектов
Объединив равенства G.7.15), G.7.17) и уравнения связи G.7.1), придем к тому, что в
точке условного экстремума функции G.7.2) должны выполняться п + тп равенств
г Л1 — h A2 -5 h • • . + Am — — U,
axi axi axi axi
Б— + Л1 г Л2 h • • • + Am — — U,
ОЖ ОЖ ОЖ С*Ж
я+ А13 М2 7h--. + Amr
дхп охп дхп охп
fl(Xl, X2, ..., Хп) = 0,
i, Х2, -.., Хп) = 0,
- П
—0,
fmiXi, X2, •••, Хп) =0.
Эта система уравнений позволяет определить параметры условного экстремума функ-
функции -ф и множители Лагранжа. Мы видим, что поиск условного экстремума функции ф
привел к уравнениям безусловного экстремума функции Лагранжа F. Практически
метод Лагранжа реализуется следующим образом. Составляется функция Лагранжа
G.7.14) и для нее находят возможные точки безусловного экстремума. Для исключе-
исключения множителей Аь Аг, ..., Ат привлекаются уравнения связей.
Найденное из системы уравнений G.7.18) решение может не являться точкой экс-
экстремума. В точке условного минимума (условного максимума) функции яр должны
выполняться достаточные условия. При наличии связей экстремумы функций яр и F
совпадают. Тогда из вышеизложенного следует, что для получения достаточного усло-
условия условного экстремума функции яр к уравнениям G.7.18) нужно добавить требование
знакоопределенности d?F:
В функции Лагранжа все параметры хг, Х2, ¦ ¦ •, хп можно рассматривать как незави-
независимые, если считать, что множители Aj, A2, ..., Am определены из уравнений G.7.16).
В методе Лагранжа все параметры равноправны, а система уравнений G.7.18) явля-
является симметричной относительно параметров. Кроме того, все необходимые уравнения
получены из единого требования к поведению параметров. Платой за эту симметрию
является увеличение числа неизвестных из-за введения неопределенных множителей.
Функция яр(хг, Х2,, • •., хп) формулирует критерий поведения варьируемых параме-
параметров х\, Х2, ¦ ¦., хп при их переходе из начального состояния в конечное состояние, если
изменены константы уравнений связей или сами уравнения. Принятый нами критерий
в форме минимума функции
Х2, ...,ХП) = \ ?>; - ^<°>J, G.7.20)
1
где х,(°^ — начальные значения варьируемых параметров, предъявляет требование
наименьшего суммарного изменения параметров, участвующих в связях. Конечные
значения параметров Х\, Х2, ¦•-, хп должны быть найдены из системы уравнений
7.8. Вариационный метод определения изменений параметров 345
G.7.18). Система уравнений G.7.18) при использовании критерия G.7.20) примет вид
dx2 dx2 dx2
\d^j_\d^^_ j_\ df™ n G.7.21)
ldx-+X2dx- + --- + Xmdx^=°>
fi(xi, x2, ..., xn) = 0,
h{xi, x2, ..., xn) - 0,
fm(Xi, X2, ..., Xn) = 0.
Критерий G.7.20) будем использовать при наложении вариационных связей на коорди-
координаты точек и на любые другие параметры геометрических объектов.
7.8.* Вариационный метод определения изменений параметров
Требование минимума суммарного изменения параметров связей приводит к задаче
поиска условного экстремума некоторой функции. Покажем, что в более общей поста-
постановке эта задача является вариационной и сводится к поиску экстремума некоторого
функционала.
Функционал. Рассмотрим точку, координаты которой участвуют в некоторых урав-
уравнениях вариационных связей. Представим, что мы изменили или сами вариационные
уравнения, или некоторые их параметры. В результате координаты точки в общем
случае должны измениться. Пусть координаты рассматриваемой точки в начальном
положении равны х^, у(°\ z(°\ а в конечном положении равны х, у, z. В декарто-
декартовой системе координат квадрат расстояния между начальным и конечным положением
точки равен
Для минимизации перемещения точки в декартовой системе координат можно потре-
потребовать условного минимума функции ф. В результате мы придем к системе уравнений
G.7.21), из которой определим координаты рассматриваемой точки в конечном поло-
положении.
В криволинейной системе координат квадрат расстояния между бесконечно близ-
близкими положениями рассматриваемой точки определяется формулой
{dsf = gu(dxJ + g22(dyJ + g33(dzJ + 2g12 dxdy + 2g23 dy dz + 2g13 dxdz.
rflegy = gij(x, y, z) — ковариантные компоненты A.10.5) метрического тензора. Пусть
каждая координата является функцией некоторого параметра t. Тогда функции x(t),
y(t), z(t) будут описывать кривую, вдоль которой осуществляется перемещение точки.
Величина
/ds\ /dx\ (dy\ (dz\ dx dy dy dz dx dz
\jt) =ft4*J+g22 UJ +gU +2g+2g+2g
346 Гл. 7. Вариационные связи геометрических объектов
равна квадрату первой производной этой кривой. Рассмотрим интеграл
где t — параметр траектории перемещения точки. Для минимизации перемещения
точки в криволинейной системе координат потребуем минимума интеграла Ф. В этом
интеграле координаты точки считаются функциями некоторого параметра t. Для на-
начального значения параметра координаты принимают начальные значения: a;(imin) =
= я'°\ y(tmin) = y(°\ z(tmin) = z^. Конечные значения координат x(tmax) = х,
y(tmax) = у, z(tmax) = z являются искомыми. Они должны удовлетворять уравнениям
вариационных связей. Значение интеграла Ф зависит от функций x(t), y(t), z(t). По-
Подобные интегралы называются функционалами. Таким образом, требование минимума
суммы квадратов изменения параметров в более общей постановке сводится к поиску
минимума некоторого функционала. Если варьируемым точкам приписать некоторую
массу а параметр t считать временем, то принцип минимума суммы квадратов измене-
изменения параметров будет аналогичен принципу наименьшего действия в форме Гамильтона
для движения механической системы.
В декартовой прямоугольной системе координат интеграл Ф для одной точки опре-
определяется формулой
Функционал представляет собой переменную величину, значение которой зависит
от выбора одной или нескольких варьируемых функций. Параметры связей в этом
функционале выступают в роли варьируемых функций. Начальные значения этих
функций известны, а конечные значения должны удовлетворять уравнениям связей.
Переход параметров из начального состояния в конечное состояние должен минимизи-
минимизировать некоторый функционал, выступающий в роли критерия такого перехода. На-
Например, требование минимума суммы квадратов перемещения точек G.6.1) заменим
общим требованием минимума функционала
dxl\2 (dyA2 (dzA2 (dx2\2 fdy2\2 (dz2
где Xi, yi, z\, X2, J/2> zi — координаты точек pi и рг, соответственно. Функцио-
Функционал записан в декартовой прямоугольной системе координат. Координаты точек мы
представили как функции параметра t, которому можно приписать смысл параметра
траекторий перехода точек из исходного состояния в новое состояние при изменении
констант уравнений связей. Начальное tm-m и конечное ?тах значения параметра t бу-
будем считать известными. Для определенности положим tm-m = 0, tmax = 1- Отличие
вариационной постановки G.8.1) данной задачи от задачи в постановке G.6.1) заключа-
заключается в следующем. Функция G.6.1) предполагает, что точки перемещаются по прямой
линии, а в функционале G.8.1) такое предположение отсутствует, и перемещение точек
может быть произвольным. Функция G.6.1) не зависит от пути изменения параметров,
тогда как функционал G.8.1) зависит от траектории перехода параметров из начального
состояния в конечное состояние. Начальное положение точек нам известно. В своем
7.8. Вариационный метод определения изменений параметров 347
конечном положении координаты точек должны удовлетворять уравнениям связи. Ва-
Вариационная постановка дает больше свободы в выборе критерия перехода параметров
из начального состояния в конечное состояние. Мы увидим, что в декартовой системе
координат условный экстремум функции G.6.1) и условный экстремум функционала
G.8.1) приводят к одной и той же системе уравнений. В криволинейной системе коор-
координат это не так. Рассмотрим метод вариаций в общем случае.
Вариация функционала. Пусть некоторое требование, предъявленное к варьируемым
функциям х\(?), x-x{t), ..., xn(t), определяется экстремумом функционала вида
G.8.2,
Функцию h(t, х\,х-х, ..., х„, х\ , Х21, ¦ ¦., х„') будем считать дифференцируемой необ-
необходимое число раз по t, по каждой функции x\{t), X2(t), ..., xn(t), и по каждой первой
производной xi'(t), X2'(t), ..., xn'(t) каждой функции по параметру t. В функцио-
функционале G.8.2) xi, X2, •-., хп выступают в роли варьируемых функций некоторого па-
параметра t. Параметром t может служить общий параметр траекторий, описывающих
изменение функций х\, Х2, ¦ ¦., хп. Областью изменения параметра t нами выбран от-
отрезок 0 ^ t ^ 1. Значение функционала Ф зависит от функций xi(t), Жг(*)> • ¦ •> хп(Р)-
Предположим, что экстремум функционала достигается на дважды дифференцируемых
функциях xi(t), x2(t), ..., xn(t).
Возьмем совокупность близких к ним функций Xi(t) + Sxi(t), i = 1, 2, ..., п и
представим их в виде
Xi(t, a) -Xi(t)+aSxi(t), 0 < a < 1, i = 1, 2, ..., п. G.8.3)
Величины Sxi(t) называются вариациями соответствующих функций. Эти функции
можно дифференцировать по параметру t:
5х5(
dt ~ дХг = 4 dt ) ' dt*
dtk -dx^'=6{dt
Подставим G.8.3) в G.8.2) и получим новое значение функционала Ф(а). По пред-
предположению эта функция достигает экстремума при a — 0. Необходимым условием
экстремума функции Ф(а) является равенство нулю ее первой производной Ф'@) = 0.
Величина Ф'@) называется вариацией функционала и обозначается через <$Ф. Найдем
производную функции Ф(а) по а как производную сложной функции и положим в ней
a = 0. В результате получим
а=О
da
l
-... 4- hn8xn -f hi/uSxi' + 112A)8x2' + • • • + hnn-jSxn') dt, G.8.4)
= /
348
Гл. 7. Вариационные связи геометрических объектов
где
/ц =
dh(t, xi, х2, ¦ ¦., хп, хх', х2, ¦ ¦ ¦, хп')
fthft T, Гл Т Та' Гп* Г М
. Uiiyb) xjj X2) • • •) Xrij ¦A'l ) ¦А'2 т • • •» ^п /
_ dh(t, xi, x2, ..., хп, xi , х2', ..., хп')
дхп
dh(t, Xi, x2, ..., хп, х\ , х2\ ..., хп')
1A) = ЩхТЩ '
_ dh(t, xi, x2, ..., хп, xi', x2', ..., хп')
2A) ~ d{dx2/dt) '
_ 8h(t, Xi, X2, ¦ ¦ ; Хп, Xi'~, X2, ¦ ¦ ., Хп')
nA) ~ d{dxn/dt)
Таким образом, необходимым условием экстремума функционала является равенство
нулю его вариации, что выражается формулой
1
/ {hiSxi + h28x2 + ... + hn6xn + /ii(i)<5a;i' + h2^Sx2 + ... + hn(i)Sxn ) dt = 0. G.8.5)
о
Проинтегрируем по частям вторую половину слагаемых в G.8.5)
11 1
/f d(8xi) f (d\hu\\oXi) dhi(\\ \
hm\0Xi dt = I /ijM\ dt = I I ^ oxi I dt =
K ' J v ' dt J \ dt dt J
oo о
l
U X I1 f dh'(l) JC A4. • 1 О
= n,i(\)OXi\Q- I ¦ dXi dt, г = 1, 2, ..., п.
J at
о
В результате получим, что необходимое условие экстремума функционала G.8.2) выра-
выражается равенством
о i=l V Ч
г) dt = 0.
G.8.6)
Уравнения Эйлера. Если функции Х\, х2, • • •, хп при вариации не изменяют свои
значения в начальных и конечных точках, т. е. если 5xi(tm\n) = 5х,@) = 0 и Sxi(tmaiX) =
= 5xi(l) = 0, то все слагаемые
г=1
= 0, t = l, 2, ..., п.
G.8.7)
7.8. Вариационный метод определения изменений параметров 349
Это означает, что функции x\{i), X2(t), ..., xn(t) и все их вариации проходят через
фиксированные граничные точки. При этих условиях для выполнения равенства G.8.6)
необходимо выполнение равенств
dt
h2 ~ -JP = 0, G.8.8)
так как вариации Sxt произвольны и в общем случае не равны нулю. Дифференциаль-
Дифференциальные уравнения G.8.8) называются уравнениями Эйлера. После дифференцирования
по параметру t как сложной функции каждое из равенств G.8.8) примет вид
3 = 1 3 3=1 3
или
dh d2h A d2h dx< A d2h d2x
n.
j _
dxi'dt Z^dxjdxi' dt ^ qxjqxi dt2
i- 1, 2, ..., n.
_
>
Проинтегрировав систему G.8.8), получим общее решение для экстремалей, каждая
из которых содержит по две константы. Константы могут быть найдены из гранич-
граничных условий <5rCj|0= 0. Заметим, что система G.8.8) не всегда имеет решение, а если
решение существует, то оно может быть не единственным или не удовлетворять до-
достаточным условиям экстремума. Для функционала G.8.1) уравнения G.8.9) примут
более простой вид:
f^fin ,--i2 G яш
°' l -1; 2- G-8ло)
dt2 - °' dt* - °' dt2 - °'
Решением системы G.8.10) являются линейные функции Xi(t) = CoXi + Cixit, yi(t) —
- COyi + Ciyit, Zi(t) = CoZi + CiZit. Константы CoXi, Clxi, Coyi, Ciyi, Cozi и C\zi
должны быть найдены из краевых условий G.8.7).
В функционале G.8.2) функция h зависит от xi, х2, ..., хп, и их первых производ-
производных Xi', х2', ¦.., Xn no t. В общем случае функция h может зависеть от производных
более высокого порядка. Рассмотрим функционал вида
1
= [
, G.8.11)
350
Гл. 7. Вариационные связи геометрических объектов
где Xi^k\ х2^, ¦ •., xnW — производныеk-roпорядка варьируемых функций Xi,X2, •••
..., хп по параметру t. Подставим вариации G.8.3) функций и их производные в
G.8.11), найдем производную Ф'(а) при а = 0 и приравняем ее нулю. В результате
получим, что необходимое условие экстремума функционала G.8.11) выражается равен-
равенством
/
i=l
= 0.
G.8.12)
где
dh(t, Xi, X2, ¦ ¦., xn,
dh(t, xit x2, ..., xn,
, . . ., XnW, ¦ ¦ ¦, XX (*>, g2W, ¦ ¦ ., Яя(*))
г(т> d(dmxi/dtm)
г = 1, 2, ..., n, m = 1, 2, ..., k.
Проинтегрируем к раз по частям слагаемые, в которые входят к-е производные вариа-
вариаций Sx^
d?hm
n dt2
idf, г = 1, 2, ..., n. G.8.13)
В результате получим, что необходимое условие экстремума функционала G.8.11) вы-
выражается равенством
• • • +
, (k-2)
Sxi '
+
¦...H-(-l)*-1-
г = 1, 2, ..., п.
7.8. Вариационный метод определения изменений параметров
351
Если функции xi, x2, ..., хп и их производные до (к — 1)-го порядка включительно при
вариации не изменяют свои значения в начальных и конечных точках, то
4{mHXi
dt2
= 0, m = l, 2, ..., fc, i = 1, 2, ..., n. G.8.15)
При этих условиях экстремали функционала G.8.11) должны удовлетворять уравне-
уравнениям
h2-
dt
dh2{i) d2h2B) ukdkh2(k)
+ ••• + (-1) ~Пк~
dt
+
dt2
= 0,
G.8.16)
dt dt2
так как вариации 5xi произвольны и в общем случае не равны нулю. Дифференциаль-
Дифференциальные уравнения системы G.8.16) имеют порядок 2к и называются уравнениями Эйлера-
Пуассона. Общее решение для каждой варьируемой функции, если оно существует,
содержит 2fc произвольных постоянных, которые могут быть определены из условий на
границах функций
=0,
= 0, ...,
= 0, i = l, 2, .... п.
Подвижные границы. При выводе уравнений Эйлера предполагалось, что значения
функций xi(t), X2(t), ..., xn(t) в крайних точках не изменяются при варьировании этих
функций. В решаемых нами задачах известны только значения функций на одной гра-
границе — значения xi(t), x2(t), ..., xn(t) при t = *т;п = 0. Значения функций ?i(i),
X2(t), ..., xn(t) при t = imax = 1 являются искомыми. Рассмотрим задачу определе-
определения экстремума функционала G.8.2) при заданных начальных значениях варьируемых
функций и при условии, что конечные значения варьируемых функций х1; хг, ..., х„
удовлетворяют т уравнениям связей
х2, ..
x2, ..
., xn)\t=1=0,
., xn)|t=1=0,
G.8.17)
x2, ¦.., a;n)|t=1= 0.
Данная задача называется задачей с подвижными граничными точками. В такой
постановке варьируемые функции получают большую свободу, чем в предыдущей поста-
постановке. Если на какой-либо совокупности функций достигается экстремум в задаче с по-
подвижными граничными точками, то экстремум должен достигаться и по отношению к
классу функций, имеющих те же граничные точки. Следовательно, функции, реализую-
реализующие экстремум функционала с подвижными границами, должны являться решением
системы дифференциальных уравнений Эйлера G.8.8). Общее решение уравнений Эй-
Эйлера содержат 2п произвольных постоянных. Произвольные постоянные выбираются
352
Гл. 7. Вариационные связи геометрических объектов
такими, чтобы обеспечить выполнение равенств G.8.7). Половина из них может быть
определена из условия, что при t = О вариации искомых функций равны нулю:
i\t=o-0 ИЛИ ?j@)=?j(O), i = 1, 2, ..., П.
G.8.18)
С учетом равенств G.8.18) и уравнений Эйлера G.8.8) необходимое условие G.8.6) экс-
экстремума функционала G.8.2) сведется к равенству
1= 0.
G.8.19)
Если все вариации искомых функций в конечной точке являются независимыми и,
соответственно, могут быть отличны от нуля, то для выполнения необходимого условия
экстремума функционала должны быть справедливы равенства
dh
d(dxi/dt)
= 0, i = 1, 2, ..., п.
G.8.20)
t=i
Эти условия называются естественными граничными условиями. Их принимают в
отсутствие уравнений связей. При наличии уравнений связей G.8.17) не все вариации
функции Sxi, 6x2, ¦ ¦ ¦, $хп при t = 1 являются независимыми, так как они связаны
уравнениями
G.8.21)
-6хп = О,
вытекающими из уравнений связи G.8.17). Действительно, если точки Xi = bi и
Xi = bi + aExi), i = 1, 2, ..., n, удовлетворяют уравнениям связей, то в пределе a -> 0,
i = 1, 2, ..., п, разность уравнений G.8.17) для этих точек даст уравнения G.8.21).
Независимыми являются только п — m вариаций Sxi. Можно найти m вариаций бх^,
i = 1, 2, ..., m из системы уравнений G.8.21), подставить их в G.8.19) и приравнять
нулю коэффициенты при остальных вариациях Sxi, i — m + 1, m + 2, ..., п. Но можно
использовать метод неопределенных коэффициентов Лагранжа, который делает варьи-
варьируемые функции равноправными. Умножим равенства G.8.21) на неопределенные пока
постоянные множители Ai, Аг, ..., Ат соответственно и добавим их к равенству G.8.19).
В результате получим, что для выполнения равенства G.8.6) требуется выполнение ра-
равенств
dh
d{dxi/dt)
L^+Ao
г = 1, 2, ..., n, G.8.22)
t=i
в конечном состоянии варьируемых функпий. Эти равенства называются общими
условиями трансверсальности. Совместно с уравнениями связей G.8.17) уравнения
G.8.22) представляют систему п + тп уравнений относительно а^|<=1, г = 1, 2, ..., п, и
Ai, A2, ..., Am. Они позволяют найти вторую половину произвольных постоянных в
общем решении уравнений Эйлера.
7.8. Вариационный метод определения изменений параметров
353
В результате мы получили, что необходимое условие экстремума функционала
G.8.2) с условиями G.8.17) на границе, требует выполнения уравнений Эйлера G.8.8),
равенств нулю вариаций начального положения G.8.18), выполнения условий транс-
трансверсальности G.8.22) и уравнений связей G.8.17) в конечном состоянии варьируемых
функций (при t = 1). Другими словами, при известных начальных условиях и извест-
известных уравнениях связей для конечных значений варьируемых функций необходимое
условие экстремума функционала Ф(Л) на функциях xi(t), x2(t), • • •> xn(t), удовлетво-
удовлетворяющих уравнениям Эйлера, сводится к выполнению системы уравнений
/ dh dfi df2
8
dh
d(dX2/dt)
,,dhdf2 dfm\
+Xldx+X2dx~+--+Xmdj
= О,
= o,
( dh
\d(dxn/dt)
/]
h
dh
dxn
{XI,
x2, ..
x2, ••
9/2
5xn "¦ '
Am
0,
0,
G.8.23)
fm(xi,x2, ¦¦¦,xn)\t=1=0.
Эта система и ее решение симметричны относительно искомых функций. Функционал
Ф(Л) формулирует критерий поведения варьируемых функций xi(t), x2(t), ..., xn(t)
при их переходе из начального состояния в состояние, удовлетворяющее наложенным
на них вариационным связям G.8.17).
Связь с экстремумом функции. Для принятого нами критерия поведения функций
xi(t), x2(t), ..., xn\t) потребуем наименьшей суммы квадратов изменений функций,
которую мы опишем интегралом
G-8.24)
Подинтегральная функция в данном случае равна половине суммы квадратов произ-
производных
В соответствии с G.8.9) и G.8.18) общее решение системы уравнений Эйлера для функ-
функции G.8.25) имеет линейный вид
я,
G.8.26)
где Х{(°) — а;*@) — начальные значения функций, Xi = Xi(l) —- искомые конечные зна-
значения варьируемых функций. Пусть функции xi(t), x2(t), ..., xn(t) при t¦= 1 должны
удовлетворять уравнениям связей G.8.17). Конечные значения функций должны быть
найдены из системы уравнений G.8.23), которая после подстановки G.8.26) в функцию
23 — 5293 Голованов
354 Гл. 7. Вариационные связи геометрических объектов
G.8.25) примет вид
ОХ2
Хп _Яя(о,
, ..., хп) = О,
, ..., хп) = 0,
fm{xi,X2, ...,!„) = 0.
Эта система совпадает с системой G.7.21). Таким образом, критерии G.7.20) и G.8.24)
эквивалентны, так как при одних и тех же уравнениях связей приводят к одинаковому
необходимому условию экстремума.
Вариационная постановка задачи учитывает не только изменение варьируемых
функций, но и способ этого изменения. Это играет роль в криволинейных координа-
координатах. Вариационная постановка задача позволяет получить критерий минимума суммы
квадратов изменений варьируемых функций в криволинейных координатах. Для двух-
двухмерных точек на криволинейной поверхности, когда координаты точек являются пара-
параметрами поверхности, необходимо использовать вариационную постановку задачи, так
как в общем случае на поверхности невозможно построить двухмерную прямоугольную
декартову систему координат для ее параметров.
7.9*Геодезические линии
В прямоугольной декартовой системе координат кратчайшая линия, соединяющая
две точки пространства, описывается линейной функцией. Если используется криволи-
криволинейная система координат, то кратчайшая линия, соединяющая две точки простран-
пространства, будет в общем случае описываться нелинейной функцией. Если пространство не
является евклидовым, то эта линия не является прямой. Кратчайшая линия, соеди-
соединяющая две точки пространства, называется геодезической линией. На геодезической
линии величина f ds, где ds — дифференциал длины дуги геодезической, принимает
экстремальное значение. Уравнения геодезической линии можно найти из равенства
нулю вариации S (/ ds) ее длины дуги. Мы получим уравнения геодезической линии
из равенства нулю вариации функционала
1
Ф = т I [~
Пусть и1, и2, и3 — криволинейные координаты в трехмерном пространстве. Криволи-
Криволинейные координаты в силу их поведения при преобразованиях координат должны иметь
верхний индекс. Рассмотрим поведение точки, координаты которой являются варьи-
варьируемыми параметрами связей, в криволинейной системе координат. Пусть в исходном
состоянии рассматриваемая точка имела координаты и1 = иг(°\ г = 1, 2, 3. После
изменения уравнений связей или констант в уравнениях связей она займет новое по-
положение в пространстве. Проведем произвольную линию «*(?) из исходного положения
рассматриваемой точки в ее новое положение. Пусть при t = 0 линия проходит через
7.9. Геодезические линии 355
исходную точку с координатами и1 — иг^°\ а при t = 1 линия проходит через новое
положение точки. Найдем уравнения линии, для которой функционал G.9.1) прини-
принимает минимальное значение. В декартовой прямоугольной системе координат и1 = х,
и2 =у, и3 = z, а функционал G.9.1) имеет вид
dxV fdy\2 fdz\2\J
В криволинейной системе координат и1, и2, и3 аналогичный функционал получим,
подставив A.10.5) в G.9.1),
} 2\2 fdu3\2
]
x\2 (du2\2 fdu3
) +e22{-dT) +g33Ur
duldu2 n du2duz du1duz
где gtj — ковариантные компоненты метрического тензора. В G.9.2) используется со-
соглашение о суммировании по повторяющимся верхним и нижним индексам. Пусть
функции w1(i), u2(t), u3(t) дифференцируемы требуемое число раз. Возьмем совокуп-
совокупность близких к ним функций ul(t) + Sul(t), i — 1, 2, 3, где величины Sul(t) называ-
называются вариациями соответствующих функций. Эти функции можно дифференцировать
по параметру t
dt
Символ 6 обозначает переход из какой-нибудь точки искомой линии в точку некоторой
другой кривой, которой соответствует то же значение параметра t. Вариация функцио-
функционала G.9.1) выражается формулой
где использовалась симметрия метрического тензора g^ = g^. Проинтегрируем по
частям вторую половину слагаемых в G.9.3) и получим
о
d{gij{dui/dt))
—^t—Su dt=
о
du
23* °
356 Гл. 7. Вариационные связи геометрических объектов
В силу равенства нулю вари |0
G.9.1) выразится формулой
о
В силу равенства нулю вариаций <JttJ |0= 0 в концевых точках вариация функционала
dV
Необходимое условие экстремума функционала выражается равенством нулю его ва-
вариации. Отсюда в силу произвольности выбора Suk следует, что функционал G.9.1)
достигает экстремума на кривых ul(?), * = 1, 2, 3, удовлетворяющих дифференциаль-
дифференциальным уравнениям
dgikduUu
~2gik
dT
Изменим обозначения индексов (индексы, по которым выполняется суммирование, мы
имеем право обозначать любыми буквами) и преобразуем первое и второе слагаемые в
левой части равенства G.9.6) следующим образом:
_ 2
duk dt dt dum dt dt
~ duk dt dt dum dt dt ~ dum dt dt ~
_ dgtj dul duj dgik dul duj dgjk duj du1 _
= ~F ~ J ~T~ ~T~T ~
dt dt ди* dt dt du{ dt dt
Vduk ~ dui ~ dv* ) ~dt ~dt ~ ~ ij'k~dt"dt'
где Fj, k = - I —-4- + —A— -^r I — символы Кристоффеля 1-го рода A.10.16).
2 \ auJ au* ouK J
С учетом полученного вариация функционала G.9.1) будет равна нулю при выполне-
выполнении равенства
d?um dtSduJ п ,ппп.
Smk^^ + rijik-—^0. G.9.7)
Умножив равенства G.9.7) на g7"*, выполнив суммирование и используя свойство
SrkSmk — &m', где Skr — символы Кронекера A.10.7), получим
где Tif — символы Кристоффеля 2-го рода A.10.19). Таким образом, геодезические
линии должны удовлетворять уравнениям G.9.8). Эти уравнения представляют собой
уравнения Эйлера G.8.8) для частного случая функционала G.9.1), но в общем случае
криволинейных координат. Геодезические линии являются кротчайшими линиями,
соединяющими две заданные точки. В евклидовом пространстве кротчайшей линией
являемся прямая линия. Если в евклидовом пространстве мы построим криволинейную
систему координат^ то прямые линии в этой системе координат будут описываться
уравнениями G.9.8).
7.10. Вариационные связи двухмерных точек 357
В частном случае декартовых прямоугольных координат Гуг = 0 и уравнениями
геодезических линий являются интегралы уравнений d?ur/dt2 = 0, которые совпа-
совпадают с линейными функциями G.8.26). Таким образом, если мы описываем геоме-
геометрические объекты в криволинейной системе координат, то мы должны пользоваться
вариационным критерием их поведения. Например, мы строим вариационные связи
для двухмерных точек на поверхности, координатами которых являются параметры
и и v поверхности. В этом случае для координат двухмерных точек р^ = [щ Vi]T,
i = 1, 2, ..., п, следует использовать вариационный критерий минимума функционала
1 2
du% du% „ dui dvi dvi dvi\ , ,_ „ „.
^ж+^лг+*»1г *-) dt G99)
с подвижными границами, удовлетворяющими уравнениям связей
, «1, «2, V2, . . ., И„, Vn) = 0,
, vi, u2, v2, ¦ ¦., un, vn) -0,
fm(ui, Vi, U2, V2, . . ., Un, Vn) = 0,
при t — 1. Необходимыми условиями минимума функционала G.9.9) является вы-
выполнение уравнений G.9.8) для координат точек. Точки на поверхности при измене-
изменении параметров вариационных связей будут двигаться по геодезическим линиям по-
поверхности.
7.10. Вариационные связи двухмерных точек
Применим метод минимизации изменений связанных параметров для ва-
вариационных связей двухмерных геометрических объектов в декартовой пря-
прямоугольной системе координат. Применение метода минимизации изменений
связанных параметров для вариационных связей трехмерных геометрических
объектов аналогично тому, что будет изложено ниже. Уравнения связей для
трехмерных геометрических объектов приведены выше и мы не будем повто-
повторяться. Варьируемые параметры трехмерных геометрических объектов посред-
посредством свободных параметров могут быть связаны с двухмерными геометриче-
геометрическими объектами.
Двухмерные геометрические объекты используются для построения про-
пространственных геометрических объектов. Многие тела строятся на основе плос-
плоских контуров путем выдавливания, вращения, движения вдоль заданной линии,
плавного соединения нескольких плоских контуров. Плоские кривые и контуры
строятся на двухмерных линиях. Для того чтобы перестроить пространствен-
пространственный объект, требуется перестроить двухмерный объект. Большие возможности
в этом случае дают вариационные связи, делающие зависимыми параметры из
структур данных геометрических объектов.
Для двухмерных объектов многие уравнения вариационных связей имеют
тот же векторный вид, что и для пространственных объектов. Отличие от вы-
вышеизложенного состоит в том, что двухмерные точки и векторы имеют в<;его
две координаты и, соответственно, каждая вариационная связь будет содержать
меньшее число параметров. Рассмотрим некоторые двухмерные вариационные
связи.
358 Гл. 7. Вариационные связи геометрических объектов
Для фиксации скалярных параметров, например, радиуса окружности или
угла дуги окружности, используются фиксирующие связи типа G.2.1). Для
закрепления двухмерной точки применяется векторное уравнение G.2.2), со-
состоящее из двух скалярных уравнений G.2.3).
Размер вдоль координаты. Размер вдоль одной координаты между двухмер-
двухмерными точками pi = [xi yi]T и р2 = [жг 2/2]T описывается одним из уравнений
Х2 - xi - d = 0, или У2 - У1 - d = 0, G.10.1)
где d — требуемый размер. Пусть до постановки размера положение точек опи-
описывалось радиус-векторами рх^ = [xi^ у\^]Т и р2(°) = [^2^ 2/2^]Т- Для
того, чтобы поведение точек при установки размера было симметричным, по-
потребуем, чтобы сумма квадратов перемещений связанных точек
= \ ((*1 - *1@)J + B/1 - 2/!(О)J + (*2 - *2@)J + (У2 - 2/2@)J) G.10.2)
была минимальной. Для определенности будем считать, что размер поставлен
вдоль координат х. Необходимым условием минимума функции G.10.2) при
условии G.10.1) является равенство нулю частных производных по параметрам
xi, J/1, х2, г/2, А функции
F - Ф + а/ = \ {{Х1 - Ж1(°)J + (г/! - г/1@)J + Ы - *2@)J + (г/2 - г/2@)J) +
+ Х(х2 -xi- d). G.10.3)
Искомые координаты точек и параметр А найдем из системы уравнений
Х2 — Х\ = d,
si-si(°)-A = 0, г/1-2/1(О) =0, G.10.4)
х2 - х2^ + А = 0, г/2 - г/2@) = 0.
Данная система уравнений имеет решение
G.10.5)
Можно доказать, что найденное решение является точкой минимума функции
G.10.2). Перемещение точек производится вдоль координаты х. В данной поста-
постановке задачи точки являются равноправными. Уравнения системы и ее реше-
решение являются симметричными без использования каких-либо дополнительных
ограничений относительно поведения системы точек.
7.10. Вариационные связи двухмерных точек 359
Если одна из точек закреплена, то на нее наложена связь G.2.2) и ее коор-
координаты не варьируются. Пусть точка р2 закреплена. Тогда система будет иметь
решение
G.10.о)
\ = x2W-XlW-d. V '
Размер вдоль направления. Размер вдоль заданного направления между
двухмерными точками р1 = [х\ ух]т ир2 = [х2 у2]т описывается уравнением
G.3.12) , которое в координатной записи имеет вид
{х2 - хх)тх + (?/2 - у\)гпу - d = 0, G.10.7)
где га = [тх ту]Т — задающий направление двухмерный вектор единичной
длины. Найдем положение точек из условия минимума их суммарного переме-
перемещения G.10.2). В соответствии с методом Лагранжа составим функцию
f = \ (Ы - Ж1(°)J + (л - ш@)J + {Х2 - *2@)J + (г/2 - г/2@)J) +
+ \({х2 - xi)mx + (г/2 - y\)my - d). G.10.8)
Искомые координаты точек и параметр А найдем из равенство нулю частных
производных этой функции по параметрам х\, у\, х2, У2, А:
(х2 - xi)mx + (г/2 - y\)mv - d = 0,
xi -XI®) -Хтх = 0, г/i -J/i(O) -\гпу = 0, G.10.9)
х2 - ж2@) + Атх = 0, г/2 - г/2@) + Ату = 0.
Данная система уравнений имеет решение
Х1 = Я1@) + ^((Ж2(°) - х^))тх + (w«0 - w(«»))mv - d),
ш = j/i@) + ^((*2<°> - х^))тх + (у2(°) - j/i@))my - d),
Х2 = x2W - ^((Ж2(°) - х^))тх + (г/2(°) - г/1@))тг/ - d), G.10.10)
У2 = »W - ^((^W - х^))тх + (w@) - y^0))^^, - d),
А = | ((^W - Ж1(°))тх + (ЙС) - wW)m, - d) .
Перемещение точек производится вдоль вектора т на одинаковое расстояние
от исходного положения точек. Решение системы уравнений G.10.9) является
симметричным.
Линейный размер. Линейный размер на плоскости между двумя точками
Pi = [Х1 yi]T ир2 = [х2 у2]Т описывается уравнением G.3.1), которое в коор-
координатной записи имеет вид
/ = у (х2 — х{J + (г/2 — у\J — d — 0. G.10.11)
360 Гл. 7. Вариационные связи геометрических объектов
Для симметричного поведения точек при установки размера потребуем, чтобы
суммарное перемещение связанных точек было минимальным. Необходимым
условием минимума функции G.10.2) при условии G.10.11) является равенство
нулю частных производных по параметрам функции
-Рг\ -d) =
(х2 - Ж2(°>J + (у2 - у2<°>J) +
+А (у{х2 - xtf + (у2 - yiJ - d) . G.10.12)
Система уравнений, из которой найдется искомое положение точек, аналогична
системе G.6.3). Решение такой системы уравнений имеет вид
где d(°) = y/(x2^ — xi@)J + (j/2^ — J/i^J- Перемещение точек производится
вдоль прямой линии, проходящей через точки р^0) и р2^°\ на одинаковое рас-
расстояние.
Если точки pj и р2 входят в структуру данных отрезка, то с помощью связей
Х2 = Х1, ИЛИ У2 = ?/Ь
отрезок можно сделать параллельным одной из координатных осей. Пусть тре-
требуется, чтобы отрезок был параллельным оси у. Тогда из равенства нулю част-
частных производных функции
\ (to @)J ( @)J) 4x2 ~ х,) G.10.14)
F \
получим систему уравнений
хх -a?i(°)- А = 0, х2 - ж2@) + А = 0,
ж2 — Ж1 = 0.
Ее решение равно
хг = 1Ы°)+х2Ю), Х2 = 1(я:2@) +а.1@)))
2 2 G.10.15)
7.10. Вариационные связи двухмерных точек 361
Симметрия двух точек. Рассмотрим симметрию точек рг = [х\ yi]T ИР2 —
= [х% 2/2]T относительно прямой линии
l(t)=p + ti, G.10.16)
что показано на рис. 7.10.1. Прямую будем считать неподвижной, поэтому ее
параметры варьироваться не будут.
р
Рис. 7.10.1. Симметрия двухмерных точек относительно прямой
Симметрия точек относительно прямой линии описывается двумя уравне-
уравнениями
(Pl-P)-i = (P2-p)-i,
(Pi - Р) • 3 + (Р2 - Р) • 3 = 0,
где вектор j = [—6 a]T ортогонален вектору i = [а Ь]т. Пусть точка р имеет
координаты х и у. Составим функцию
F = \ ((х! - х^J + (У1 - У1(°)J + (х2 - аг2(°)J + (у2 -
+ Хг ((ял - х2)а + {уг - у2)Ь) + А2((ш +у2- 2у)а - {хх +х2- 2х)Ь). G.10.18)
Систему уравнений для определения положения точек получим из равенства
нулю частных производных функции G.10.18)
xi -si(°) +\\a- А2Ь = О,
Х2 _ Х2@) _ хга - Х2Ь = 0,
У2 ~ У2{0) - Aib + A2a = 0,
(xi - х2)а + (yi - у2)Ь = 0,
(?Л +У2- 2у)а - (xi +х2- 2х)Ь = 0.
Решение этой системы определит новое положение точек.
Если мы хотим, чтобы точка рг осталась неподвижной, то введем уравнение
Р1=Р1@> G.10.19)
362 Гл. 7. Вариационные связи геометрических объектов
или в G.10.18) ее координаты будем считать константами. Если мы хотим,
чтобы точка р2 осталась неподвижной, а точка р\ стала ей симметрична, то
введем уравнение
Р2=Р2@) G.10.20)
или в G.10.18) ее координаты будем считать неварьируемыми константами.
При закреплении одной из точек решение системы уравнений G.10.18) опреде-
определит положение другой точки.
Угловой размер между тремя точками на плоскости. Угловой размер на
плоскости между тремя точками pi = [х\ у\\ , р2 = [Х2 2/г]Т ир3 = [хз Уз]Т
описывается уравнением G.3.28), где
s = (xi- х2){уз - у2) - (У1 - У2)(хз - х2), G.10.21)
с = (xi - х2)(х3 - х2) + (yi - у2)(Уз - У2)- G.10.22)
Величина s равна произведению длин векторов pi — р2 и Рз ~ Р2 на sin а. Ве-
Величина с равна произведению длин векторов Pi — р2 и Рз ~Р2 на cos a- Угловой
размер на плоскости связывает шесть параметров. Составим функцию
^-«), G.10.23)
где.Р1(°) = [Я1(°) У!(°)]т, р2(°) = [х2№ у2(°).]Т и р3(°) = [ ]
исходные положения точек. Систему уравнении для определения параметров
получим из равенства нулю частных производных функции G.10.23)
_ @, + ЛФЗ-У2)-ФЗ-Х2) =
s2 Л-с1
х2 - о**») + xcbnv*)«**ъ**) = о,
S2 +С2
S2 +С2
у2
=
и,
* а.
(si -х2){хз -x2) + {yi -
Решение этой системы определит положение точек при заданном угле а.
7.11. Вариационные связи двухмерных линий 363
7.11. Вариационные связи двухмерных линий
Вариационные связи для нескольких двумерных точек рассмотрим в виде
связей точек двухмерных кривых. С помощью вариационных связей легко
управлять кривыми. Например, отрезки можно сделать ортогональными, па-
параллельными друг другу или осям координат, окружности и сплайны можно
делать сделать касательными отрезкам или друг другу.
Пусть даны два отрезка прямых
G.11.1)
G-11.2)
построенных по точкам рг — [х\ у\]т, р2 — [жг у2]Т, Рз = [хз Уз]Т и р4 =
= [^4 У а] ¦ На данные четыре точки можно наложить вариационную связь,
определяющую угол между отрезками T\{t\) и гз(?з)- Эта связь аналогична
угловому размеру и описывается тем же уравнением
arctg- = a, G.11.3)
С
где а — заданный угол. Синус и косинус угла пропорциональны величинам:
s = (x2- х\){у4 - Уз) - (?/2 - yi){x4 - ж3), G.11.4)
с = (ж2 - х1){х4 - ж3) + (у2 - У1)(У4 - Уз)- G.11.5)
Уравнение G.11.3) связывает восемь параметров.
Ортогональность отрезков. Как частный случай связи G.11.3) может рассма-
рассматриваться вариационная связь устанавливающая ортогональность отрезков.
Данная вариационная связь описывается уравнением
(Р2 - Pi) • (Р4 - Рз) = (Х2 - Xi){x4 - Ж3) + (У2 - У1)(У4 ~ Уз) = 0. G.11.6)
Систему уравнений для определения положения точек получим из равенства
нулю частных производных функции
Л((ж2-Ж1)(ж4-жз) + (уг-У1)(У4 -Уз)), G.11.7)
[ ] — исходные положения точек, в общем случае не удовлетворяю-
удовлетворяющие уравнению G.11.6).
Параллельность отрезков. Другим частным случаем связи G.11.3) является
вариационная связь, устанавливающая параллельность отрезков. Она опре-
определяется уравнением
- Уз) - (У2 - Vi){x4 ~ ж3) = 0. G.11.8)
364 Гл. 7. Вариационные связи геометрических объектов
Пусть в исходном состоянии координаты точек р^ [ ]
= [Х2{О) У2{0)]Т, Рз@) = [*з@) Уз@)]Т и р4@) = Ы0) У4@)]Т не удовлетворяют
уравнению G.11.7). Применим метод минимизации суммарного изменения па-
параметров. Систему уравнений для определения положения точек получим из
равенства нулю частных производных функции
\((х2 - xi)(y4 -уз)- (У2-У1)(х4~хз)). G.11.9)
Для простоты предположим, что точки р2, Рз и Ра зафиксированы и, следо-
следовательно, не изменяют своего положения. Параллельность отрезков G.11.1) и
G.11.2) будет достигнута перемещением точки р\. Система уравнений будет
иметь вид
O, G.11.10)
(х2 - xi)(y4 - уз) - (у2 ~ У\)(Х4 - х3) = 0.
Эта система имеет решение
)^, G.11.11)
где d(°) = |Р4(») - р3@)|2,
х(х4^ — Хз^)- Перемещение точки pi происходит по нормали к отрезку, про-
проходящему через точки р^ — Рз^ (рис. 7.11.1).
Рис. 7.11.1. Параллельность отрезков прямой линии
В описанном случае параллельности отрезков первый зависит от второго и
подстраивается под него. Рассмотрим, как будет себя вести зависимый отрезок
при вращении другого отрезка. Пусть в исходном состоянии точки р2 и Pi
7.11. Вариационные связи двухмерных линий
365
закреплены, отрезки параллельны и их точки имеют координаты
Будем вращать точку р3 вокруг точки р4 так, чтобы их координаты изменялись
по закону
Giii
уз @) =у4@) + a sin (р.
В соответствии с решением G.11.11) точка рг будет двигаться вокруг точки
так, что ее координаты будут изменяться по закону
Х\ —
У\ —
+ b sin <р cosy =
6COS2 (p = X2^ +
^ + b cos ip sin <р =
+ г sin ip,
где г — b cos ср. Из формул видно, что точка р\ будет двигаться вокруг точки p<i
по окружности, но с удвоенной частотой по сравнению с частотой вращения
точки р3 вокруг точки р4- При изменении угла ip от 0 до тг точка Рз сделает
Рис. 7.11.2. Траектории движения отрезка PiP2, параллельно зависимого от отрезка р3р4, при
закрепленных точках р2 и рА
половину оборота по окружности вокруг точки р4> а точка р\ сделает полный
оборот по окружности вокруг точки pi- Траектории движения точек р\ и р3 п0~
казаны на рис. 7.11.2. Точка р3 движется по окружности Сз, а точка р\ движется
по окружности С\.
366
Гл. 7. Вариационные связи геометрических объектов
Касание сплайнов. Рассмотрим вариационные связи касания линий друг
друга. Пусть даны две NURBS кривые. Одна из них описывается функцией
rP(t) = Чг
%iin ^ * ^ Imaxj
G.11.13)
и построена на точках pi, i = 1, 2, ..., п с весами wi, а другая описывается
функцией
к
rq(u) =
3=1
к
Umax,
G.11.14)
и построена на точках qj, j = 1, 2, ..., к с весами Zj. Найдем две наиболее
близкие друг к другу точки rp(to) и гд(щ) на этих кривых, одна — на первой,
Рис. 7.11.3. NURBS кривые будут касаться ближайшими точками
другая — на второй, касательные в которых параллельны. Эти точки должны
удовлетворять уравнениям D.8.9), в данном случае имеющим вид
drp
drn
Пусть этим точкам соответствуют параметры to и щ (рис. 7.11.3).
Точки на кривых выражаются в виде сумм
п
Гр{к) = PlPi + Р2Р2 + ¦ ¦ • + РпРп =
t=l
fc
rq{u0) = Qiq1 + Q2q2 + ¦•¦+ QkQk =
G.11.15)
G.11.16)
G.11.17)
7.11. Вариационные связи двухмерных линий
367
где
_ Njti(u0)zj
г=1
г=1
Пусть точки имеют координаты р^ = [ж* Уг]Т, г = 1, 2, ..., n, <7j = [aj bj]T,
j = 1, 2, ..., к. Если бы точки rp(to) и г9(г*о) совпали, то являлись бы решением
задачи касания кривых G.11.13) и G.11.14). Поэтому в качестве уравнения
связи возьмем уравнение
Ы*о) -гя(и0)\ = \(Р1Р1 + Р2Р2 + ... + РпРп) - (Qm + Q2q2 + ¦¦¦ + QkQk)\ =
\
г=1
з=1
=0-
Составим функцию суммарного перемещения точек касающихся кривых со-
совместно с уравнением связи G.11.18). Эта функция имеет вид
+ A|rp(to)-r,(«o)|. G.11.19)
Систему уравнений для определения положения точек получим из равенства
нулю частных производных функции G.11.19)
Xpjtp) - aQ{u0)
y{xp(to) - aq(u0)J + {yP{t0) -
{xp(to)-aq(uo)J + {yp(to)-l ' чч2
to) \^ xp(t0) — aq(uo)
M ~ M^o)) + (%»(<o) - '
\J(xp(to) - aq(u0)J + (yp(t0) - bg(u0))'
= 0, i = l,2,...,n,
-0, *=1, 2, ...,n,
: = 0, j = l, 2, ..., A;,
= 0, j = l,2, ...,k,
(yP(to) - bq{u0)J = 0,
G.11.20)
368 Гл. 7. Вариационные связи геометрических объектов
где
п
Xp{t0) = P\Xl + Р2Х2 + ... + РпХп = ^
г=1
п
yP{to) = Piyi + Р2У2 + ¦¦¦ + РпУп =
aq(u0) = Qiai + Q2a2 + ... +
3=1
k
bq{uo) — Qibi + Q2b2 + ... + Qkbk =
Система уравнений G.11.20) на (г + 1)-й итерации метода Ньютона дает при-
приращения искомых функций, равные:
/ п к \
К I ST^ о х (г) _ V^ Q а (г) \ г = 1 2 ... П
XTTl^l /7i:= 1
P / n k \
Xr+1) _ _?± I ST^ p (r) _ \p q . (r) \ i-l 2 n
\ro=l ro=l /
Да/г+^ = ^ I 2J Ртх™ ~ L, Qmam(r> I , j = 1, 2, ..., к,
\го=1 го=1 /
ДЬ.(г+1) = Qi(f] РтУт{г) ~ У) Qmbm(r) | , j = 1, 2, . . ., А.
\m=l ro=l
G.11.21)
Значение коэффициента Л на текущей итерации равно
Л
n к ч2
=1 i=l '
s
= -J{xp(to) - aq(u0)J + (ур(<о) - Ьд(щ)J, G.11.22)
где s = ^ Р{ + ^2 Qj . Пока решение не найдено, коэффициент Л остается не
t=i j=i
равным нулю.
Перемещение всех точек на каждой итерации происходит параллельно ка-
касательным к кривым, проходящим через точки rp(to) и rq(uo), на расстояние,
пропорциональное их вкладу (коэффициенту Pi или Qj) в точки касания. Перед
началом новой итерации необходимо заново вычислить параметры to и щ для
наиболее близких друг к другу точек на рассматриваемых кривых и коэффици-
коэффициенты Pi и Qj для новых ближайших точек rp(to) и гя(щ).
7.11. Вариационные связи двухмерных линий 369
Следует заметить, что в искомой точке выполняется равенство G.11.18),
что обращает в нуль числители и знаменатели последних слагаемых ура-
уравнений системы G.11.20). Если на очередной т*-й итерации выполнилось ра-
Рис. 7.11.4. Модификация NURBS кривых при наложении связи касания
венство G.11.18), а решение системы нелинейных уравнений еще не закон-
закончено, то следует использовать \rp(to) — Гд^о)]^^, (xp(to) — хд(щ)) ',
(?/р(^о) ~ Уд{ио)) ) вычисленные на предыдущей итерации. Поведение кри-
кривых приведено на рис. 7.11.4.
Касание отрезка и окружности. Решим задачу касания в частных случаях.
Касание отрезка ri(t) и окружности ro(u),
r1(t) = {l-t)Pl + tp2, G.11.23)
ro(u) = Pq + ixr cos u + iyr sin u,
описывается уравнением
|(l-to)Pi+*oP2-Po|=r, G.11.24)
где pi = [xi y\]T, P2 = [X2 Уг]Т — начальная и конечная точки от-
отрезка, г — радиус окружности, р0 = [xq yo]T — центр окружности,
(Pa ~ Pi) ' {Р2 ~ Pi)
to = -, :—; г — значение параметра отрезка, соответствующее про-
(PP)(PP)
Bl)B)
екции центра окружности на отрезок. В данном случае радиус окружности также
является варьируемым параметром. Параметр to, соответствующий проекции
центра окружности на отрезок, мы будем вычислять на каждой итерации. Си-
Систему уравнений для определения параметров связи получим, приравняв нулю
частные производные по параметрам функции
+ А(|A - <o)Pi + hP2 - Pol - г), G.11.25)
где Pi^°\ Р2^°\ Ро^ — исходные положения точек ръ р2, Ро, г^ — исходное
значение радиуса окружности. Система уравнений для определения положения
24 - 5293 Голованов
370
Гл. 7. Вариационные связи геометрических объектов
точек имеет вид
Уо - Уо(О) - А
= 0,
у (A - *О)Ж1 + *0Ж2 - Ж0J + (A - *о)У1 + *0У2 - :
A — ?о)ж1
v^
(A -
У1 -
v^
(A - *о)У1
- Уо)'
= 0,
= 0,
= 0,
- тЛ°)
+
V((i-
(A - <о)У1
-Уо)'
У2-
y/iO^
Ж0) + (A -
Г - г@) _ Л = О,
= 0,
= 0,
У ((l-tQ)xi +^оЖ2-жоJ+ (A-*о)У1 + *оУ2-УоJ -г = 0.
G.11.26)
Система уравнений G.11.26) решается итерационно. Перед началом но-
новой итерации необходимо заново вычислить параметр ?0- Поведение отрезка
и окружности приведено на рис. 7-11.5.
Рис. 7.11.5. Поведение окружности и отрезка при касании
Касание окружностей. Касание двух окружностей
ri(ti) =gi +ixncosti + iyrismti, G.11.27)
^2(^2) = 92 + ixr2cost2 + iyr2smt2, G.11.28)
описывается уравнением
|9i-g2| = |n±r2|. G.11.29)
В данном случае радиусы окружностей также являются варьируемыми параме-
параметрами. Уравнение G.11.29) связывает шесть параметров. Систему уравнений
для определения параметров связи получим, приравняв нулю частные производ-
7.11. Вариационные связи двухмерных линий 371
ные по параметрам функции
F = \ (\Яг ~ 9i@)|2 + \Я2 ~ «Л2 + (ri -J^J + (r2 - г2(°)J) +
+ А(|в1-д2|-|г1±г2|), G.11.30)
где q^0\ g2^ — исходные положения центров, г^0) и Г2^ — исходное зна-
значение радиусов окружностей. Знак ± должен быть раскрыт в зависимости от
положения ближайших точек окружностей. Эти точки лежат на линии, соеди-
соединяющей их центры. Пусть окружности расположены вне друг друга. Тогда
система уравнений для определения положения центров окружностей и их ра-
радиусов имеет вид
Ж1 _ Ж1(О + Л^ = 0> ш _ yi(o) + ХУ1^_У1 = 0>
Х2 _ Ж2(о) _ х^1 = 0) у2 _ (о) _ xyjLZVl = 0 G.11.31)
a a
П-г1(°)-А = 0, г2 - r2(°) - Л = 0, \qi - Я2\ - (ri + г2) = 0у
где d = \qi — g2|. Эта система имеет решение
У2
G.11.32)
A = ia(
где d<°) = |Ql(°) - g2(°)|, a(°) = |ei(°) - q2{0)| - (n@) - r2(°)). Из решения сле-
следует, что радиусы изменяются на одинаковую величину, равную перемещению
Рис. 7.11.6. Касание окружностей
центров окружностей. Поведение окружностей приведено на рис. 7.11.6. При
расположении окружностей одна внутри другой в уравнениях G.11.31) изменя-
изменяется знак перед одним из радиусов.
24*
372
Гл. 7. Вариационные связи геометрических объектов
7.12. Формирование и решение системы уравнений связей
Вариационные связи являются мощным средством управления геометриче-
геометрическими объектами. Они позволяют редактировать геометрические объекты со-
совместно, когда изменение параметра одного из объектов влечет за собой соответ-
соответствующие изменения параметров других объектов. Параметром может служить
любая величина из структуры данных геометрического объекта или специально
введенная переменная. Специально введенные переменные используются для
удобства редактирования геометрических объектов с помощью вариационных
связей.
С помощью вариационных связей осуществляется управление сразу всеми
связанными объектами. Как правило, на одни и те же параметры наложено
несколько вариационных связей. Каждая связь представляет собой некоторый
вариационный объект, который изменяет параметры геометрических объектов.
Различные типы вариационных связей геометрических объектов приведены на
рис. 7.12.1. Каждая связь имеет одно или несколько уравнений и перечень
параметров, участвующих в каждом уравнении.
Фиксирующие связи
Значение скалярного параметра
Значения координат
Закрепление точки
Алгебраические ,
Размерные связи
Линейный размер
Линейный размер в плоскости
Линейный размер по направлению
Угловой размер
Угловой размер в плоскости
, связи
Алгебраическое уравнение
Алгебраическое неравенство
Связи положения объектов
Равенство скалярных параметров
Равенство координаты
Равенство всех координат точек
Симметрия точек
Касание плоских кривых
Сопряжение кривых
Параллельность отрезков
Ортогональность отрезков
Положение точки на кривой
Положение точки на поверхности
Положение точки иа плоскости
Параллельность векторов
Параллельность плоскостей
Ортогональность векторов
Ортогональность плоскостей
Рис. 7.12.1. Типы вариационных связей
Нормальным состоянием для вариационных связей является состояние, ко-
когда их уравнения выполняются. Будем называть это состояние равновесным.
В процессе моделирования приходится модифицировать геометрические объек-
объекты или их взаимное положение. Таким образом, вариационные связи выводятся
7.12. Формирование и решение системы уравнений связей 373
из состояния равновесия. В результате все или часть уравнений вариационных
связей перестает выполняться. Далее следует найти новые значения варьируе-
варьируемых параметров, чтобы уравнения связей опять выполнялись. Для того чтобы
связанные параметры удовлетворяли уравнениям связей, требуется сформиро-
сформировать систему уравнении и решить ее. В процессе решения этой системы уравне-
уравнений необходимо модифицировать все геометрические объекты, параметры кото-
которых изменились. Рассмотрим, каким образом удовлетворяются вариационные
связи.
Пусть задан набор вариационных связей, приводящий к системе m урав-
уравнений
fi(xi, х2, ..., хп) =0,
/2(жь ж2, ..., ж„) = 0,
G.12.1)
/то(ж1, ж2, ..., ж„) = 0,
для п ^ m изменяемых параметров х\, Ж2, ..., хп геометрических объектов.
Число уравнений связей, как правило, меньше числа связанных параметров.
Для того, чтобы решить систему уравнений связей, требуется сформулировать
критерий поведения связанных геометрических объектов, который бы позволил
решить систему уравнений связей. Простым и эффективным критерием пове-
поведения параметров является требование минимума суммы квадратов изменений
параметров. Этот критерий выражается минимумом функции
ф(Х1, Ж2, . . ., Хп) = \ ((*! - ЖхО)J + (Ж2 - Ж2(°)J + . . . + (Хп - жЛ2) .
G.12.2)
Поиск минимума функции G.12.2) при условии выполнения связей G.12.1) при-
приводит к задаче нахождения минимума функции
ж2, ...,хп)=1- (fo - Ж1(°)J + (ж2 - ж2(°)J + ... + (хп- яЛ
+ Ai/i(aJi, х2, ¦ ¦., хп) + А2/2(ж1, ж2, ..., хп) + ... + Ат/т(жь ж2, ..., хп).
G.12.3)
Для выполнения необходимого условия минимума указанной функции требуется
наряду с G.12.1) выполнение уравнений
ж2 - ж2^ + Ai— + А2-— + . •. + Ат-— = 0,
дх2 дх2 дх
где Ai, А2, ..., Ат —- подлежащие определению совместно с параметрами aji,
ж2, ..., хп коэффициенты. В конечном итоге мы пришли к системе п + тп
уравнений G.12.1) и G.12.4) для п + тп неизвестных жх, ж2, ..., ж„, Ai, А2, ...
..., Ат. В общем случае эта система решается одним из итерационных методов,
374 Гл. 7. Вариационные связи геометрических объектов
описанных в гл. 4. Если на какие-либо из параметров наложены фиксирующие
связи G.2.1), то их можно исключить из функции G.12.2) и при решении общей
системы уравнений считать константами.
В большинстве случаев управление данными происходит следующим обра-
образом. На некотором этапе система уравнений связей G.12.1) выполняется. Да-
Далее одному или нескольким параметрам присваивается новое значение, и эти
параметры фиксируются. Например, мы переместили некоторую точку геоме-
геометрического объекта и хотим узнать, как это повлияет на другие варьируемые
параметры. Управление данными геометрических объектов может происходить
путем изменения констант уравнений, что также выведет систему уравнений
связей из состояния равновесия. Например, мы изменили значение некоторого
размера. В результате для исходных значений параметров некоторые уравне-
уравнения связей перестанут выполняться. Необходимо найти новые значения пара-
параметров, удовлетворяющие системе уравнений связей, и перестроить геометри-
геометрические объекты. Система вариационных связей выходят из равновесия также
при добавлении к ней новых связей. Например, мы хотим, чтобы некоторые две
плоскости геометрической модели были параллельными. При этом рождается
новая вариационная связь, которая добавляет в систему уравнений свои уравне-
уравнения. Нужно решить систему уравнений связей и перестроить геометрические
объекты.
На практике решение системы уравнений является самой сложной и тон-
тонкой проблемой при наложении вариационных связей. В разных случаях для
решения системы уравнений используются разные подходы: аналитический,
конструктивный, численный.
Аналитический подход используется для двухмерных вариационных свя-
связей, когда искомое положение двухмерных геометрических объектов можно
найти с помощью «линейки и компаса». В некоторых простых случаях ана-
аналитический подход применим и для трехмерных объектов.
При наложении вариационных связей на положения твердых тел относи-
относительно друг друга эффективным является конструктивный подход. Конструк-
Конструктивный подход привлекает теорию графов. Для системы уравнений вариацион-
вариационных связей строится граф. Узлами графа являются геометрические объекты,
а ребрами графа являются уравнения связей. На основе графа геометриче-
геометрические объекты и вариационные связи делятся на кластеры (группы). Кластер в
модели ведет себя, как нечто жесткое целое. В результате задача сводится к
задаче позиционирования геометрических объектов кластеров. Сначала опреде-
определяется удовлетворяющее вариационным связям положение геометрических объ-
объектов для каждого кластера в отдельности, а затем кластеры последовательно
стыкуются между собой. Размещение геометрических объектов внутри одного
кластера осуществляется путем решения соответствующей системы уравнений.
Стыковка кластеров между собой выполняется на основе анализа степеней сво-
свободы. Стыковка кластеров производится последовательно. Будем считать, что
положение геометрических объектов некоторого кластера задано. Расположим
геометрические объекты соседнего кластера так, чтобы удовлетворялись связы-
связывающие их уравнения. Тем самым мы состыкуем два кластера. Продолжим
стыковку кластеров до тех пор, пока не будут выполняться все уравнения свя-
связей. В процессе стыковки кластеров возможно потребуется перебирать различ-
различные варианты и численно решать систему уравнений связей нескольких кла-
кластеров. Конструктивный подход уменьшает размерность системы уравнений,
но его можно использовать для строго определенного набора геометрических
объектов и вариационных связей.
7.12. Формирование и решение системы уравнений связей 375
Численный подход заключается в решении системы уравнений вариацион-
вариационных связей численными итерационными методами. При использовании этого
подхода следует помнить, что вариационные связи могут иметь несколько реше-
решений. Численный метод позволяет найти одно из этих решений, и оно может не
совпадать с искомым. Найденное решение зависит от начального приближения,
с которого начинается итерационный процесс. Чтобы начальное приближение
находилось в области сходимости к искомому решению, следует не допускать
сильных отклонений вариационных связей от их равновесных состояний. На-
Например, если вариационные связи выведены из состояния равновесия путем
перемещения некоторой точки геометрического объекта, то решение следует ис-
искать не для окончательного положения точки, а для нескольких промежуточных
ее положений, постепенно сдвигая точку от исходного положения к конечному.
Аналогично, при изменении значения некоторого размера следует последова-
последовательно искать решения для нескольких промежуточных значений этого раз-
размера, постепенно переходя от старого к новому значению. Численный подход
чаще используется для решения двухмерных задач.
При использовании численного подхода желательно, чтобы ненулевые прира-
приращения параметров были одного порядка. Например, если одна часть варьируе-
варьируемых параметров является угловыми величинами, другая часть —¦ компонентами
векторов, а третья часть параметров — координатами точек, то желательно,
чтобы их значения лежали в одних и тех же пределах. Для достижения этого
используется нормирование варьируемых параметров.
Численное решение системы уравнений связей может производиться не-
несколько иначе. Используемый критерий поведения геометрических объектов
стремится сохранить параметры геометрических объектов ближе к их исход-
исходному состоянию. Воспользуемся этим свойством для уменьшения размерно-
размерности системы уравнений. Попытаемся решить систему уравнений, зафиксировав
еще некоторые из варьируемых параметров, кроме тех, которые зафиксированы
уравнениями связей. Если нам это удастся, то мы будем придерживаться пра-
правила, которое заключается в сохранении объектов как модно ближе к их ис-
исходному состоянию, и уменьшим число неизвестных и уравнений в G.12.4).
Остается выяснить, какие из параметров можно дополнительно зафиксировать.
Некоторые из уравнений связей могут быть удовлетворены при исходных зна-
значениях параметров. Определим эти уравнения и составим список варьируемых
параметров, участвующих в них. Попробуем решить полную систему уравне-
уравнений, считая параметры этого списка фиксированными. Если это удается, по-
попробуем расширить этот список, если нет, то будем сужать этот список до тех
пор, пока не удастся решить полную систему уравнений. Таким образом, нам,
возможно, удастся найти новые значения параметров, сохранив некоторым из
них исходные значения. Если даже при отсутствии дополнительной фиксации
параметров систему уравнений G.12.1) и G.12.4) решить не удастся, то сле-
следует вернуться к исходному равновесному состоянию геометрических объектов
и констант уравнений, при которых уравнения связей удовлетворяются.
В процессе решения уравнения связей изменяют значения параметров и тем
самым перестраивают геометрические объекты в соответствии с новыми значе-
значениями параметров. Объекты будут перестроены в соответствии с наложенными
связями, когда все уравнения полной системы будут удовлетворены с требуемой
точностью.
Глава 8
ВЫЧИСЛЕНИЕ ГЕОМЕТРИЧЕСКИХ ХАРАКТЕРИСТИК
8.1. Возможности геометрической модели
Результатом геометрического моделирования некоторого объекта является
математическая модель его геометрии. Математическая модель позволяет гра-
графически отобразить моделируемый объект, получить его геометрические ха-
характеристики, выполнить исследование многих физических свойств объекта
путем постановки численных экспериментов, подготовить производство и,
наконец, изготовить объект.
Для того чтобы увидеть, как выглядит объект, нужно смоделировать поток
падающих и возвращающихся от его поверхностей лучей света. При этом гра-
граням модели можно придать необходимый цвет, прозрачность, фактуру и другие
физические свойства. Модель можно осветить с разных сторон светом различ-
различного цвета и интенсивности.
Геометрическая модель позволяет определить массово-центровочные и инер-
инерционные характеристики проектируемого объекта, выполнить измерения длин
и углов его элементов. Она дает возможность произвести расчет размерных
цепей и определить собираемость проектируемого объекта. Если объект пред-
представляет собой механизм, то на модели можно проверить его работоспособность
и выполнить расчет кинематических характеристик.
Используя геометрическую модель, можно поставить численный экспери-
эксперимент по определению напряженно-деформированного состояния, частот и форм
собственных колебаний, устойчивости элементов конструкции, тепловых, опти-
оптических и других свойств объекта. Для этого нужно дополнить геометрическую
модель физическими свойствами, смоделировать внешние условия ее работы и,
используя физические законы, выполнить соответствующий расчет.
По геометрической модели можно вычислить траекторию режущего инстру-
инструмента для механической обработки объекта. При выбранной технологии изго-
изготовления объекта геометрическая модель позволяет спроектировать оснастку и
выполнить подготовку производства, а также проверить саму возможность изго-
изготовления объекта данным способом и качество этого изготовления. Кроме того,
возможна графическая имитация процесса изготовления. Но для того, чтобы
изготовить объект, кроме геометрической информации нужна информация о
технологическом процессе, производственном оборудовании и многом другом,
связанном с производством.
Многие из перечисленных проблем образуют самостоятельные разделы при-
прикладной науки и по своей сложности не уступают, а в большинстве случаев и
превосходят проблему создания геометрической модели. Геометрическая мо-
модель является отправной точкой для дальнейших действий. При построении
геометрической модели мы не использовали физические законы, радиус-вектор
каждой точки границы раздела внешней и внутренней частей моделируемого
объекта является известным, поэтому при построении геометрической модели
8.2. Криволинейные интегралы 377
нам приходится составлять и решать алгебраические уравнения. Задачи, в
которых используются физические законы, приводят к дифференциальным и
интегральным уравнениям, решение которых сложнее решения алгебраических
уравнений.
В данной главе остановимся на выполнении расчетов, не связанных с фи-
физическими процессами. Мы рассмотрим вычисление чисто геометрических ха-
характеристик тел и их плоских сечений: площади поверхности, объема, центра
масс, моментов инерции и ориентации главных осей инерции. Эти расчеты не
требуют привлечения дополнительной информации. Кроме этого, мы рассмо-
рассмотрим проблемы численного интегрирования, которые приходится решать при
определении геометрических характеристик.
Определение площади, центра масс и моментов инерции плоского сечения
тела приводит к вычислению интегралов по площади сечения. Для плоских
сечений мы располагаем информацией об их границах. Интегралы по площади
плоского сечения мы сведем к криволинейным интегралам, которые в свою оче-
очередь сводятся к определенным интегралам. Определение площади поверхности,
объема, центра масс, моментов инерции тела приводит к вычислению поверх-
поверхностных и объемных интегралов. Мы будем опираться на представление тела
с помощью границ (В-rep), т.е. на описание тела совокупностью ограничиваю-
ограничивающих его поверхностей и топологическую информацию о взаимном соседстве этих
поверхностей. Мы сведем интегралы по объему тела к поверхностным интегра-
интегралам по поверхностям граней тела, которые в свою очередь сводятся к двойным
интегралам. В общем случае область интегрирования представляет собой связ-
связную двухмерную область. Вычисление двойных интегралов численными мето-
методами можно выполнить для областей простых типов — четырехугольной или
треугольной формы. В связи с этим в конце главы рассмотрены методы вычи-
вычисления определенных интегралов и двойных интегралов по четырехугольным
и треугольным областям. Методы разбивки областей определения параметров
поверхностей на совокупности треугольных подобластей рассмотрены в следую-
следующей главе.
В начале главы рассмотрим сведение интегралов по площади к криволиней-
криволинейным интегралам и сведение объемных интегралов к поверхностным интегра-
интегралам. На этом будут базироваться вычисления геометрических характеристик
моделей.
8.2.* Криволинейные интегралы
Определение геометрических характеристик кривых линий и плоских сечений при-
приводит к вычислению криволинейных интегралов, так как всю геометрическую инфор-
информацию о кривой несет функция ее радиус-вектора от некоторого внутреннего параметра.
Криволинейными интегралами первого рода называются интегралы вида
f(r)ds, (8.2.1)
где /(г) — некоторая заданная на кривой L функция ее точки r(t). Интегрирование
в (8.2.1) выполняется по длине кривой s. Криволинейный интеграл (8.2.1) сводится к
обыкновенному определенному интегралу
J
f(r)ds = J f(r)\!^-^dt. (8.2.2)
*min
378 Гл. 8. Вычисление геометрических характеристик
Область, на которой задана функция точки, является областью изменения параметра
кривой.
Криволинейными интегралами второго рода называются интегралы вида
t • F(r) ds, (8.2.3)
L
где t = dr/ds = r'/lr'l — касательный вектор кривой, F(r) — векторная функция
точки кривой r(t). Криволинейный интеграл (8.2.3) сводится к обыкновенному опре-
определенному интегралу
'max
t-F(r)ds = I j--F(r(t))dt. (8.2.4)
|
При изменении направления кривой на противоположное направление криволинейный
интеграл второго рода меняет знак на противоположный.
Так как координаты радиус-вектора r(t) = [x(t) y(t) z{t)\ кривой являются
функциями параметра кривой, то мы можем преобразовать величину t ds к следующему
виду:
tds = ^-dt = i^-dt+j^-dt + k^dt = idx+jdy + kdz. (8.2.5)
at at at at
Пусть в пространстве задана векторная функция
F(r) = iFx{x, у, z) +jFv(x, у, z) + kFz(x, у, z).
Тогда, используя преобразование (8.2.5), получим
/ t • F(r) ds = Fxdx + Fvdy + Fz dz, (8.2.6)
L L
где координаты х, у, z принадлежат кривой.
Формула Стокса. Пусть кривая r(t) замкнутая и построена на некоторой гладкой
поверхности 5, и пусть в пространстве задано векторное поле F(r). Пусть при^цвиже-
нии вдоль кривой в положительном направлении ее обход происходит против часовой
стрелки, если смотреть навстречу нормали поверхности т. Рассмотрим поверхностный
интеграл
II
m • (V x F(r)) dS =
s
где V — набла-оператор или оператор Гамильтона A.11.13). Предположим, что нам
известно явное уравнение поверхности 5 и кривой г(?) на ней. Возьмем, например,
уравнение поверхности в виде z = Z(x, у), а уравнение кривой на ней в виде двух
уравнений, одним из которых является уравнение поверхности z = Z(x, у), а вто-
вторым — уравнение цилиндрической поверхности С(х, у) = 0 с образующей параллель-
параллельной орту к. Пусть линию пересечения цилиндрической поверхности С(х, у) = 0 с
8.2. Криволинейные интегралы
379
координатной плоскостью Оху можно описать двумя двухмерными кривыми у = Y\(x)
и у = Y2(x), изменяющимися от х\ до Х2, что показано на рис. 8.2.1. Кривые у = Ух(х)
и у = Уг(а;) в совокупности описывают проекцию заданной пространственной кривой
S r@ 1
Рис. 8.2.1. Проекция замкнутой кривой г(<) на поверхности г = Z(x, у) на плоскость жу
на плоскость Оху, только направление кривой у = Yi(x) совпадает с направлением
пространственной кривой г(?), а направление кривой у = Уг(^) противоположно напра-
направлению пространственной кривой.
Преобразуем часть интеграла (8.2.7), используя (8.2.5), следующим образом
Найдем значение (in • j)/(m ¦ к) для поверхности, которую можно описать уравнением
z = Z(x, у). Если за внутренние параметры поверхности принять координаты х и у, то
для радиус-вектора и его частных производных по параметрам х иу получим значения
г = [х у Z(x, у)]Т, Г1 = [1 0 dZ/8x]T, г2 = [0 1 dZ/dy]T.
Используя эти соотношения, получим
m
m • k
xr2)-j
x г2) • k
8Z
ду '
Подставим последнее равенство в (8.2.8) и продолжим далее его преобразование, приняв
координаты х и у в качестве независимых параметров интегрирования:
,
dy dz
dxdy.
От поверхностного интеграла мы перешли к двойному интегралу по проекции п поверх-
поверхности 5 на плоскость Оху. Сведем этот интеграл к повторному интегралу по области на
плоскости Оху, ограниченной кривыми у = У\(х) и у = Уъ{х), изменяющимися от х\
380 Гл. 8. Вычисление геометрических характеристик
BF F)F F)Z
до Х2 (рис. 8.2.1). Величину -г-5- + -т-^-^—> стоящую под интегралом, можно рассма-
ду dz dy
dFx 8FX 8FX8Z м _ _, t .
тривать как полную производную —— = — 1- —^—— функции Fx = Fx(const, у, z)
dy dy dz dy
(параметр х при интегрировании по параметру у считается неизменным). Тогда
Х2 У2(Х)
dFx dFx dZ
dZ\,, Г Г fdFx 8FX dZ
^)dxdy = -J J {-ay- + ^^
ЛУз(х) \ X2 X2
^dy\dx = - j'Fx{x,Y2{x),z)dx + jFx(x,Y1(x),z)dx. (8.2.9)
Yi(x) x\ xi
От повторного интеграла мы перешли к двум обычным определенным интегралам.
Функция Fx принимает значения на пространственной кривой r(t). В первом интеграле
правой части (8.2.9) переставим местами пределы интегрирования х\ и х^-, в результате
чего интеграл изменит знак на противоположный. После такой замены интегрирова-
интегрирование в правой части (8.2.9) будет выполняться по замкнутому контуру, являющемуся
проекцией заданной пространственной кривой на плоскость Оху, и мы можем перейти
от двух обыкновенных интегралов к криволинейному интегралу. Таким образом, мы
выполнили преобразование
Х\ Х2
= I Fx(x, Y2(x), z)dx + I Fx(x, Уф), z)dx= I Fx(x, y, z) dx = JF ¦ \dx.
X2 Xi О О
Обозначение области определения криволинейного интеграла означает, что кривая, по
которой выполняется интегрирование, является замкнутой. С помощью аналогичных
рассуждений и преобразований получим еще два равенства
II (^f(m • к) - ^f(m ¦ i)J dS = j Fy(x, у, z) dy = IF ¦ j dy,
^-(m-i) -^-(ш-^ dS = I Fz(x, у, z)dz =
s о о
Сложив три последние равенства, получим формулу Стпокса
ffffdFz dFy\ . (8FX dFA .^fdFy 0Fx
s
= I Fx(x, y, z) dx + Fy(x, y, z) dy + Fz(x, y, z) dz = 11 • F(r) da. (8.2.10)
о о
8.2. Криволинейные интегралы 381
Можно показать, что формула Стокса справедлива и в случае, когда поверхность явля-
является многосвязной, т. е. ограниченной одной внешней замкнутой кривой на ней и не-
несколькими внутренними замкнутыми кривыми, лежащими внутри внешней кривой.
В последнем случае внутренние кривые должны иметь ориентацию, противоположную
ориентации внешней кривой. То есть внешняя кривая должна быть связана с норма-
нормалью поверхности правилом правого винта, а внутренние кривые должны быть связаны
с нормалью поверхности правилом левого винта. При соблюдении этих правил поверх-
поверхность всегда будет находиться слева, если двигаться вдоль ее границы с положительной
стороны по отношению к нормали. При многоконтурной границе в правой части ра-
равенства (8.2.10) должна стоять сумма криволинейных интегралов по всем замкнутым
кривым, ограничивающим поверхность.
Если кривая ограничивает на поверхности 5 связную область, является замкнутой и
регулярной, а функция F(r) является однозначной, непрерывной и имеет непрерывные
частные производные на заданной области поверхности, то поверхностный интеграл
(8.2.7) связан с криволинейным интегралом (8.2.6) равенством
11 • F(r) ds = ± Иm ¦ (V х F(r)) dS. (8.2.11)
s
Знак плюс соответствует случаю, когда ориентация замкнутой кривой и нормали к
поверхности согласованы правилом правого винта, в противном случае в (8.2.11) должен
стоять знак минус. Эта формула выражает теорему Стокса, утверждающую, что
криволинейный интеграл от векторной функции F(r) по замкнутому контуру равен
потоку ротора этой функции через поверхность, натянутую на контур. Для замкнутых
кривых, построенных на поверхности S, справедливы следующие равенства:
i
tx F(r) ds = ± If(m x V) x F(r) dS, (8.2.12)
s
& </>(r)t ds = ± И m x Vvp(r) dS, (8.2.13)
где ip(r) — скалярная функция точки пространства. Знак в (8.2.12) и (8.2.13), как
и в (8.2.11), зависит от ориентации положительного обхода по кривой относительно
нормали поверхности. Знак плюс берется тогда, когда обход по замкнутой кривой в
положительном направлении при взгляде навстречу m осуществляется против часовой
стрелки.
Формула Грина. Для двухмерных кривых r(t) = [x(t) y(t)] криволинейные ин-
интегралы первого и второго рода определяются аналогично криволинейным интегралам
для пространственных кривых
где t =
t ¦ F{r) ds= / — • F(r(t)) dt = / Fxdx + Fy dy, (8.2.15)
L tmin *min
dv v1 -\ т
t = — = у—-: — касательный вектор кривой, f(r) = [fx(x, у) fy(x> y)\ —
as \i I
двухмерная скалярная функция, F\r) = [Fx(a;, у) Fy(x, у)] — двухмерная вектор-
векторная функция точек кривой. Для двухмерных замкнутых кривых существует формула,
382
Гл. 8. Вычисление геометрических характеристик
являющаяся аналогом формулы Стокса. Эта формула называется формулой Грина и
связывает интеграл по некоторой двухмерной (плоской) области с криволинейным ин-
интегралом второго рода (8.2.15) по границе этой области.
Пусть дана некоторая плоская область п,
ограниченная двухмерной кривой L, и двух-
двухмерная векторная функция Щг) на ней. Пусть
r(t) есть радиус-вектор граничной кривой, ко-
которая является замкнутой и направлена так,
что обход области п осуществляется против ча-
часовой стрелки. Пусть границу области П можно
описать двумя кривыми у = Уг(х) и у = Y2(x),
изменяющимися от х\ до х2, что показано на
рис. 8.2.2. Кривые у — Y\{x) и у = Y2(x) в
совокупности описывают границу L заданной
х\
Рис. 8.2.2. Разбиение границы плоской
области
плоской области, только направление кривой у = Y\ (x) совпадает с направлением кри-
кривой r(t), а направление кривой у = Y2(x) противоположно направлению кривой.
Рассмотрим интеграл по области
dFx
dS-
Представим часть этого интеграла в виде двукратного интеграла
x {x, Y2(x)) dx + j Fx (x, yt (я)) dx =
XI X2
= f Fx(x, Y2{x)) dx+ IFx(x, Yi(z)) dx = jFx(x, y)dx.
Xl
Мы перешли от интеграла по области к криволинейному интегралу по границе этой
области. Аналогично получим равенство
Сложив два последних равенства, получим формулу Грина
t
lit
) dS =
'y) dx
)ds- (8-2Л6)
Можно показать, что формула Грина справедлива и в случае, когда область ?1 явля-
является многосвязной. При этом в левой части равенства (8.2.16) должна стоять сумма
криволинейных интегралов по всем замкнутым кривым, а обход по ограничивающим
область кривым должен осуществляться таким образом, чтобы область всегда находи-
находилась слева. Формулу Грина можно получить как частный случай формулы Стокса, по-
положив в (8.2.10) F = [Fx(x, у) Fy(x, у) 0]т, а за поверхность принять плоскость Оху.
8.3. Геометрические характеристики плоских сечений 383
Рассмотрим преобразование векторной функции F(r) с помощью матрицы N, по-
поворачивающей вектор F на прямой угол против часовой стрелки и равной
-J]. (8.2.17)
После такого преобразования получим функцию
1 [№:
1 •[*№:]•
После двойного преобразования получим ту же функцию, но с противоположным знаком
С помощью данного преобразования формула Грина примет вид
it-F{r)ds = - 11 ¦ (N ¦ (N ¦ F(r))) ds =
L L
= - //
V • (N. Fir)) iS-JUg-tg) «& (8.2.20)
n n
где V — двухмерный набла-оператор. Приведенные формулы позволяют свести поверх-
поверхностные интегралы к криволинейным интегралам. Заменим в равенстве
- it- (N ¦ (N ¦ Цг))) ds = - П V- {N-F\r))dS
L П
N- F(r) на F(r) и получим формулу Грина в следующем виде:
V • -Fir) dS= ? t ¦ (N ¦ F(r)) ds = <f^-{N' -Pt7")) dt- (8.2.21)
Q L L
Эта формула будет использоваться при вычислении геометрических характеристик
плоских сечений.
8.3. Геометрические характеристики плоских сечений
При решении некоторых задач, например, расчете напряжений в сечении
балки, требуется оперировать геометрическими характеристиками сечений тел.
Сечения тел описываются двухмерными контурами B.12.7). Плоские контуры
представляют собой двухмерные составные замкнутые кривые. Пусть дан не-
некоторый контур в декартовой прямоугольной системе координат на плоскости,
который описывается двухмерным радиус-вектором r(t) = [x(t) y(t)] . За по-
положительное направление контура примем такое направление его обхода, при
котором сечение остается слева.
384
Гл. 8. Вычисление геометрических характеристик
Периметр сечения. Периметр плоского сечения равен длине ограничиваю-
ограничивающего сечение контура и определяется интегралом
-14
dx\ fdy\ ,
В общем случае периметр можно вычислить как сумму длин сегментов контура.
Площадь и центр масс сечения. Площадь и статические моменты сечения
относительно осей координат определяется формулами
F =
(8.3.1)
Sx=ffydF, Sy=ffxdF,
F F
(8.3.2)
где х и у — текущие координаты бесконечно малой площади dF, а интегрирова-
интегрирование ведется по площади сечения. При параллельном переносе осей координат на
Рис. 8.3.1. Параллельный перенос осей координат
вектор q = [xq yq]T (рис. 8.3.1), статические моменты в новой системе координат
связаны со статическими моментами инерции в исходной системе следующими
равенствами:
Sx> = SX- yqF, Sy> = Sy- xqF. (8.3.3)
Точка, при переносе в которую начала координат статические моменты се-
сечения становятся равными нулю, является центром масс сечения. Координаты
центра масс сечения определяются формулами
(8.3.4)
Ось координат, относительно которой статический момент сечения равен нулю,
называется центральной.
8.3. Геометрические характеристики плоских сечений 385
Моменты инерции сечения. Осевые и центробежный моменты инерции се-
сечения определяются интегралами
Jx = JJy2dF, Jy=[Jx2dF, Jxy=ffxydF. (8.3.5)
F F F
Осевые моменты инерции всегда положительны, а центробежный момент инер-
инерции может быть как положительным, так и отрицательным, в зависимости от
расположения осей относительно сечения. Моменты инерции сечения в системе
координат Оху и системе О'х'у', сдвинутой относительно первой на вектор
q = [xq yq]T, связаны равенствами
Jx> = JJ(y ~ УдJ dF = Jx- 2yqSx + yq2F, (8.3.6)
F
Jy> = jj{x - xqf dF = Jy- 2xqSy + xq2F, (8.3.7)
F
Jxy' = (x - xq)(y - yq) dF = Jxy - xqSx - ygSy + xqyqF. (8.3.8)
F
При переходе от системы координат Оху к системе координат О'х'у1, повер-
повернутой относительно первой на угол (р (рис. 8.3.2), радиус-вектор г = [х у]т
преобразуется по формулам
х' = х cos ip + у sin ip, у' — — xsimp + у cos ip. (8.3.9)
Моменты инерции сечения в системе координат Оху и системе О'х'у', по-
повернутой относительно первой на угол if, связаны равенствами
Jx' = Jx cos2 tp — Jxy sin Ър + Jy sin2 у?, (8.3.10)
Jy' — Jx sin2 V + Jxy sm 2<P + Jy cos2 ?>> (8.3.11)
Jxy' = Jxy cos 2ip + Jx~Jy Sin2^. (8.3.12)
Заметим, что величина Jp = Jx + Jy = Jx< + Jy> одинакова в обеих системах
координат. Эта величина называется полярным моментом инерции сечения.
С изменением угла поворота ip осевые моменты инерции меняются, а их
сумма остается неизменной. Следовательно, существует такой угол (р, при кото-
котором один из моментов инерции сечения достигает своего максимального значе-
значения, в то время как другой момент инерции принимает минимальное значение.
Дифференцируя выражение для Jx> no ip и приравнивая производную нулю,
находим
tg2V=-^Sr. (8.3.13)
Jy JX
25 — 5293 Голованов
386
Гл. 8. Вычисление геометрических характеристик
В соответствии с формулой (8.3.12) центробежный момент инерции при данном
угле равен нулю. Система координат, в которой центробежный момент инер-
инерции равен нулю, называется главной системой координат. Если к тому же
Рис. 8.3.2. Поворот осей координат
эта система является центральной, то она называется главной центральной си-
системой координат. Если сечение имеет ось симметрии, то эта ось всегда будет
главной. Осевые моменты инерции относительно главной системы координат
называются главными моментами инерции. Для их определения перепишем
(8.3.10) и (8.3.11) в вике
/
7
J
7
Учитывая, что
. ' Jx
. Jx
+
2
2
Jy
Jy
1
1
Jy
Jy
—
2
2
*J X
Jx
cos 2</? — J^ sin2</?,
cos 2<p + Jxy sin 2y>.
cos 2ip =
sin2</? =
tg2(f
исключим при помощи (8.3.13) угол <р и получим
Jx
xy
(8.3.14)
(8.3.15)
(8.3.16)
(8.3.17)
(8.3.18)
Вычисление моментов инерции сечения. Так же как и все кривые, контур
описан в параметрической форме и не имеет своих явных уравнений, связы-
связывающих координаты его радиус-вектора. Без явных уравнений мы Не можем
воспользоваться непосредственно формулами (8.3.1), (8.3.2), (8.3.5) для опре-
определения геометрических характеристик сечения. Всю геометрическую инфор-
информацию о контуре несет функция его радиус-вектора от некоторого внутреннего
параметра. Для вычисления геометрических характеристик воспользуемся фор-
формулой Грина (8.2.20), позволяющей свести поверхностный интеграл к криволи-
криволинейному интегралу.
8.3. Геометрические характеристики плоских сечений 387
Положим в (8.2.20) последовательно: F(r) = r, F(r) = xr, F(r) = yr, F(r) =
= x2r, F(r) — y2r, F(r) = xyr, где r — [x y]T — радиус-вектор точки сечения.
Тогда V • (г) = 2, V • (xr) = Ъх, V ¦ (уг) = Зу, V • (х2г) = Ах2, V • (у2г) = Ау2,
V- (xyr) = Axy. Для каждого случая вычислим правую часть равенства (8.2.20):
ff V • rdF = ff2dF = 2F,
F F
ff V • (xr) dF = ff Sx dF = SSy,
F
V-(yr)dF= fUydF = ZSx,
F
ff V • (x2r) dF = ff Ax2 dF = AJ,
Jy,
F F
V • (y2r) dF = II Ay2 dF = Ux,
F F
V ¦ (xyr) dF = II 4xy dF = AJxy.
F F
Подставим вычисленные значения в формулу Грина (8.2.20) и получим формулы
для определения площади, статических моментов и моментов инерции плоского
сечения через криволинейные интегралы по ограничивающим его контурам:
- If (-»'!+*s!
«¦ - i/s • <"• <*»* - If (-»'!+*s!) *•
(M-22>
(8.3.23)
(8.3.24)
25*
388 Гл. 8. Вычисление геометрических характеристик
Если плоское сечение ограничено одним внешним контуром, то криволинейный
интеграл должен быть взят при обходе контура против часовой стрелки. Если
сечение кроме внешнего контура ограничено еще и внутренними контурами,
то к интегралу по внешнему контуру должны быть добавлены интегралы по
внутренним контурам, вычисленные при их обходе по часовой стрелке. Таким
образом, в формулах (8.3.19)—(8.3.24) стоят суммы интегралов по всем кон-
контурам, ограничивающим плоское сечение и имеющим соответствующую ори-
ориентацию. Будем считать, что интегрирование выполняется по всем границам
плоского сечения, и опустим знак суммы. Полученные определенные интегралы
могут быть вычислены с помощью квадратурных формул, которые мы рассмо-
рассмотрим ниже.
8.4. Длина и центр масс кривой линии
Длина кривой. Длина кривой определяется интегралом
t •
Для двухмерной кривой координату z радиус-вектора кривой следует опустить
(положить равной нулю). Если для кривой определить функцию распределенной
по ней плотности p(t), то интеграл
C.4,,
определит массу кривой.
Центр масс кривой. Пусть на кривой определена функция распределенной по
ней плотности р = p(t). Тогда интегралы
(8.4.3)
(8.4.4)
(8.4.5)
8.5. Поверхностные интегралы 389
определяют статические моменты кривой относительно осей координат. Ста-
Статические моменты являются компонентами некоторого вектора, так как при
преобразовании координат они изменяются так же, как компоненты вектора.
При переносе начала координат в точку qc = [хс ус zc]T статические моменты
инерции в новой системе координат будут равны
Sxi = Sx - хсМ, Sy> = Sy- ycM, Sz> - Sz - zcM.
Точка, при переносе в которую начала координат статические моменты стано-
становятся равными нулю, является центром масс кривой. Таким образом, коорди-
координаты центра масс кривой определяются формулами
Q Q Q
хс = —, Ус = —, zc = Т7- (8.4.6)
Для кривой, так же как и для тела, можно определить моменты инерции.
Формулы для их вычисления аналогичны формулам для вычисления моментов
инерции тел, с той лишь разницей, что интегрирование ведется не по объему,
а по кривой линии. Вычисление моментов инерции мы рассмотрим ниже.
8.5.* Поверхностные интегралы
Определение геометрических характеристик тел приводит к вычислению поверх-
поверхностных и объемных интегралов. Так как всю геометрическую информацию о теле
несут его грани, которые описываются поверхностями в параметрическом виде, то объ-
объемные интегралы мы сведем к поверхностным интегралам. Пусть дано некоторое тело
в декартовой прямоугольной системе координат Oxyz. Орты этой системы координат
обозначим через i, j, k. Пусть в этой системе координат задана некоторая скалярная
/(г) или векторная F(r) функция точки г = [ж у z]T. Для точек, принадлежащих гра-
граням тела, эти функции являются функциями параметров поверхностей граней и и v,
так как ж = х(и, v), у = у(и, v), z = z(u, v).
Поверхностными интегралами первого рода называются интегралы вида
f(v)dS, (8.5.1)
где /(г) = /(ж, у, z) — заданная скалярная функция точки поверхности тела г, а
интегрирование выполняется по всей поверхности 5 тела. Воспользуемся равенством
A.7.15) для бесконечно малого участка площади поверхности и перейдем от поверхност-
поверхностного интеграла (8.5.1) к двойному интегралу
jj /(r) dS = jj /(«, v) Vgllg22 - g122 du dv, (8.5.2)
где gn, g22, g12 — коэффициенты первой квадратичной формы поверхности A.7.8), П —
область, на которой задана функция точки, является областью изменения параметров
и и v поверхности, /(и, и) = f(r(u, v)) — функция параметров поверхности.
Поверхностными интегралами второго рода называются интегралы вида
/7m-F(r)dS, И mxF(r) dS, /7V(r)mdS, (8.5.3)
390
Гл. 8. Вычисление геометрических характеристик
где m — нормаль поверхности тела, F(r) = F(a;, у, z) — заданная векторная функ-
функция точки поверхности тела г, <р(г) — заданная скалярная функция точки поверхности
тела г. Интегрирование выполняется по всей поверхности S тела. Подставим в инте-
интегралы (8.5.3) выражение для нормали поверхности A.7.18) и выражение A.7.15) для
бесконечно малого участка площади и перейдем к двойным интегралам по области па-
параметров граней тела
//(ri xr2) -F(«, v)dudv,
п
/ / (ri х г2) х F(u, v) du dv,
п
j j ip(u, v){vx x r2)dudv,
(8.5.4)
где
dv
dr
= —, Г2 = — частные производные радиус-вектора поверхности по параме-
ou dv
o d
трам поверхности, F(«, v) = F(r(«, v)) — векторная функция параметров поверхности.
Запишем интегралы (8.5.4) в несколько ином виде. Рассмотрим величину idydz +
+ j dz dx + kdx dy для точек поверхности. Координаты радиус-вектора г = [х у z]T
поверхности являются функциями параметров поверхности х = x(u, v), у — y(u, v),
z = z(u, v). Используя равенства
dydz =
dy
du
dz
du
dy
dv
dz
dv
du dv, dz dx =
dz
du
dx
du~
dz
dv
dx
dv
du dv, dx dy =
dx
~du~
dy
du
dx
~dv
dy
dv
dudv.
перейдем в величине i dy dz + j dz dx + k dx dy к параметрам поверхности
i dy dz + j dz dx + k dx dy =
_. (dy_dz__dy_dz\ . f dz_dx^
~\dudv dvdu) U V+3\dudv
_ dz_dx\ ,
dvdu) U V
fdxdy dxdy ,
к I — -^--5- I dudv =
dv du .
_ /&e. dy_. dz_
~ \du'1+du'3+du'
\dudv
dz
.dx. dy. dz
dux I —i + —j + — k
dv dv dv
dv =
= (ri x r2) dudv = ray/g11g22 - g12g2i du dv = mdS. (8,5.5)
Мы получили величину, стоящую в поверхностных интегралах второго рода (8.5.4)
или (8.5.3). При переходе от переменных интегрирования х, у, z к переменным ин-
интегрирования u, v предполагалось, что отображения (у, z) —t (u, v), (z, x) —> (u, v),
Сх, у) -> (u, v) взаимно однозначны, непрерывны и имеют отличный от нуля якобиан.
Пусть в пространстве задана векторная функция
F(r) = iFx(x, у, z) +iFy{x, у, z) + kFz(x, y, z).
(8.5.6)
8.5. Поверхностные интегралы
391
Тогда, используя преобразование (8.5.5), получим
II m ¦ F(r) dS = II Fx dy dz + Fy dz dx + Fz dx dy, (8.5.7)
s s
/YmxF(r)d5 =
i(Fz dx dz - Fy dx dy) + j(Fx dy dx - Fz dy dz) + k(Fy dz dy - Fx dz dx), (8.5.8)
/ / if(r)m dS = tpidydz + tpj dz dx + tpk dx dy, (8.5.9)
s s
где координаты х, у, z принадлежат поверхности. Найдем связь поверхностных инте-
интегралов второго рода с объемными интегралами.
Формула Остроградского-Гаусса. Оболочка тела ограничивает односвязную область
пространства. Рассмотрим объемный интеграл от дивергенции векторной функции
(8.5.6)
где V — набла-оператор или оператор Гамильтона A.11.13), который в принятых обо-
обозначениях данной системы координат имеет вид
v, 9 • 9 • д ,
V = — 1 + — j + ^-k.
ох оу az
(8.5.11)
Предположим, что нам известно явное уравнение поверхности оболочки в любом из ви-
видов: х — Xi(y, z), у = Yi(z, x), z = Zi(x, у). Индекс i явных уравнений говорит о
том, что замкнутая оболочка в общем случае описывается несколькими поверхностями.
Рис. 8.5.1. Разбиение замкнутой оболочки на три характерные части
Например, каждая прямая, проходящая через тело, пересекает его четное число раз,
сколько раз входя в него, столько раз и выходя из него. Кроме того, могут существо-
существовать участки поверхности тела, касающиеся указанных прямых. Пусть m есть нормаль
392 Гл. 8. Вычисление геометрических характеристик
тела. Предположим, что в одном из вариантов поверхность тела можно описать тремя
уравнениями х = Х0(у, z), х = Х\(у, z), х = Х2(у, z). Пусть уравнение х = Х\(у, z)
описывает часть Si поверхности тела, нормаль которой образует тупой угол с ортом i
(m ¦ i < 0), уравнение х = Х2(у, z) описывает часть S2 поверхности тела, нормаль
которой образует острый угол с ортом i (m ¦ i > 0), уравнением = Хо{у, z) описывает
цилиндрическую часть So поверхности тела, нормаль которой ортогональна орту i
(m ¦ i = 0). Поверхности х = Х0{у, z), х = Xi(y, z), x = Х2(у, z) приведены на
рис. 8.5.1.
Тогда для части объемного интеграла (8.5.11) можно выполнить следующие пре-
преобразования
х dx \dydz =
= II Fx{X2{y, z), у, z)dydz - II F^X^y, z), у, z)dydz.
Нормаль поверхности х = X2(y, z) совпадает с нормалью оболочки тела, а нормаль
поверхности х = Х\(у, z) направлена против нормали оболочки тела, поэтому при
переходе от интегрирования по перечисленным поверхностям к интегрированию по
поверхности тела, следует изменить знак перед вторым интегралом в правой части
последнего равенства. Добавим к интегралам по поверхностям S\ и S2 интеграл по ча-
части поверхности So х = Х0{у, z), который равен нулю. Таким образом, имеет место
равенство
"хОя» V-i г)'" mdS.
Интегрирование в правой части последнего равенства выполняется по всей поверхности
оболочки. Нетрудно доказать, что данное равенство справедливо при любой форме тела
и любом представлении его поверхности. Аналогично получим еще два равенства
v
dFz
= II Fz{x,y,z)kmdS.
dz
V S
Сложив три последние равенства, получим формулу Остроградского-Гаусса
III (ж
V
dV - lliF-{+щ+F-k)'mdS' (85Л2)
S
Поверхностные интегралы (8.5.8) и (8.5.9) также можно связать с интегралами по объ-
объему. Формулы, связывающие поверхностные интегралы (8.5.8) и (8.5.9) с интегралами
по объему, приведем без вывода.
Если объем тела V является ограниченным и пространственно односвязным,
поверхность тела 5 — замкнутой и регулярной, а функции F(r) и <р(т) — однознач-
однозначными, непрерывными и имеющими непрерывные частные производные внутри обо-
оболочки тела и на ее поверхности, то поверхностные интегралы (8.5.4) связаны с инте-
интегралами по объему тела соответственно теоремой Остпроградского-Гаусса (теоремой
8.6. Площадь поверхности, объем и центр масс тела 393
о дивергенции), теоремой о роторе и теоремой о градиенте:
m • F(r) dS = HI V • F(r) dV, (8.5.13)
П
rax F(r) dS = HI V x F(r) dV, (8.5.14)
S V
ip(r)mdS = HI V<p(r) dV, (8.5.15)
S V
Если тело описывается несколькими гранями, то в формулах подразумевается сумми-
суммирование по граням тела. Заметим, что m есть нормаль грани тела, а не поверхности
этой грани. Нормаль грани всегда направлена наружу тела, а нормаль поверхности,
на которой базируется грань, может совпадать с нормалью грани или может иметь
противоположное направление. При выводе формулы Остроградского-Гаусса мы опира-
опирались на то, что система координат является декартовой. Равенства (8.5.14) и (8.5.15)
справедливы в евклидовых пространствах.
Теорема Остроградского-Гаусса гласит, что интеграл от дивергенции векторного
поля по некоторому объему равен потоку поля через поверхность, ограничивающую этот
объем. Векторная функция F(r) в (8.5.13) сама может быть получена с участием набла-
оператора, например, F(r) = V<p(r), F(r) = ¦0V(/?(r) или F(r) = ip\7tp(r) — ip\7ip(r).
Для приведенных функций теорема Остроградского-Гаусса имеет вид
111
V(r) dV = II m • VV(r) dS, (8.5.16)
v s
r) + V(r)VVW) dV = II V»(r)m • Vy>(r) dS, (8.5.17)
V S
(V^(r)VV(r)-v»(r)V2V(r)) dV = It'т-{ф(т)Ч<р(т)-<р(т)Щ(т)) dS. (8.5.18)
V S
Теорема Остроградского-Гаусса позволит нам при вычислении геометрических харак-
характеристик перейти от интегралов по объему тела к интегралам по его поверхности.
8.6. Площадь поверхности, объем и центр масс тела
Площадь поверхности тела. Площадь поверхности тела слагается из площа-
площадей поверхности его граней. Площадь S каждой поверхности определяется ин-
интегралом
(8.6.1)
5 П
Площадь поверхности тела равна сумме площадей граней
S = Е // dS = Е // vW22-ft22d"i dvu (8.6.2)
* Si i fii
где щ, Vi — параметры поверхности i-Vi грани тела, fli — область определения
параметров поверхности г-й грани тела. В дальнейших формулах геометриче-
394 Гл. 8. Вычисление геометрических характеристик
ских характеристик тела мы опустим знак суммирования и индексы граней,
считая, что суммирование, естественно, выполняется.
Объем тела. Положим в (8.5.13) F(r) = г. Тогда V • (г) = 3 и из теоремы
Остроградского-Гаусса получим
S V
Таким образом, объем тела определится формулой
i-ry/gng22-gi22dudv. (8.6.3)
5 П
Пусть плотность тела р постоянна по всему его объему. Тогда масса тела опре-
определится формулой
М = pV — - // m ¦ rdS — - / / m ¦ гуёпйг ~ Sii2 dudv. (8.6.4)
3 J J 3 J J
S п
Если плотность тела не является постоянной, то нам не удастся перейти от ин-
интеграла по объему к интегралу по поверхности тела при вычислении его массы.
В формулах (8.6.3) и (8.6.4) подразумевается суммирование по граням тела.
Заметим, что m есть нормаль грани тела, а не поверхности этой грани. Нор-
Нормаль грани всегда направлена наружу тела, а нормаль поверхности, на которой
базируется грань, может совпадать с нормалью грани или может иметь про-
противоположное нормали грани, направление. В общем случае тело может иметь
пустоты внутри. Тогда оно описывается несколькими замкнутыми оболочками,
одна из которых является внешней, а остальные вну-
внутренними и полностью лежат внутри внешней обо-
оболочки. Нормаль к любой оболочке направлена вне
объема тела. Интегрирование в (8.6.3) и (8.6.4) вы-
выполняется по всем оболочкам, как внешней оболочке,
так и внутренним оболочкам.
Формулу (8.6.3) можно получить и другим спосо-
способом. Рассмотрим бесконечно малый участок dS по-
поверхности некоторой грани тела. Построим элемен-
Рис. 8.6.1. Пирамида с беско- тарную пирамиду на базе бесконечно малого участка
нечно малым основанием dS dS с вершиной в начале координат и прямолиней-
прямолинейными образующими. Такая элементарная пирамида
приведена на рис. 8.6.1. Основанием пирамиды является рассматриваемый бес-
бесконечно малый участок dS поверхности.
Пусть поверхность рассматриваемой грани описывается векторной функцией
г = г(u, v). Рассмотрим выражение
mrdS, (8.6.5)
где m — единичный вектор нормали рассматриваемой поверхности.
Абсолютная величина выражения m • г dS равна объему элементарной пи-
пирамиды, построенной на участке поверхности dS, так как модуль m • г предста-
представляет собой высоту, опущенную из вершины пирамиды на ее основание. Знак
8.6. Площадь поверхности, объем и центр масс тела 395
mrdS зависит от ориентации нормали поверхности и ее радиус-вектора. Если
вычислить интеграл от выражения (8.6.5) по всем граням тела, то в силу того,
что оболочка тела всегда является замкнутой и ориентируемой, получим объем
этого тела.
Статические моменты тела. Центр масс тела определяется с помощью ста-
статических моментов. Статические моменты тела относительно координатных
плоскостей соответственно равны объемным интегралам
= fffpxdV, (8.6.6)
v
ry = JJJpydV, (8.6.7)
v
= JJJpzdV, (8.6.8)
Мх
v
j
v
v
где р — плотность тела. Интегрирование выполняется по объему тела. Пусть
плотность тела постоянна по всему его объему (р = const). Это позволит нам
при вычислении геометрических характеристик тела перейти от интегрирова-
интегрирования по объему к интегрированию по поверхности тела. Для вычисления стати-
статических моментов тела положим в (8.5.13) последовательно F(r) = xr, F(r) = уг,
P(r) = zv. Тогда V • (хг) = Ах, V • (уг) = 4у, V • (яг) = 4г и из теоремы о
дивергенции получим
Ц m • (xr) dS = Ш V • (xr) dV = 4 Iff x dV,
S V V
jj m • (yv) dS = JIJ V • (yr) dV = 4 jjj у dV,
S V . V
jf m • (*r) dS = jf IV ¦ (zr) dV = 4 [И z dV.
V V
Таким образом, статические моменты тела можно вычислить с помощью по-
поверхностных интегралов по формулам
. (xr) vW22 - gi22 du dv, (8.6.9)
(yr)dS = ijf™- (yr) VW22 - gi22 du dv, (8.6.10)
П
Mz = ?jJm-(zr)dS = ijj™- (*r) VW22 " Si22 du dv. (8.6.11)
396
Гл. 8. Вычисление геометрических характеристик
В формулах (8.6.9)-(8.6.11) подразумевается суммирование по граням тела. Так
же как и в (8.6.6) m — нормаль граней тела. Полученные двойные интегралы
могут быть вычислены с помощью кубатурных формул.
Статические моменты представляют собой компоненты вектора, так как при
преобразованиях координат ведут себя аналогично компонентам вектора. Век-
Вектор М = [Мх Му Mz]r можно получить, положив в (8.5.13) P(r) = (l/4)rr, где
гг — диадное произведение векторов. Тогда
4 \_дх ду dz
хх ху xz
ух уу yz
zx zy zz
д{хх) д{ху) d{xz)
~i ^ г
дх
ду
dz
д(ух) д{уу) d{yz)
дх ду dz
d{zx) d{zy) d{zz)
дх
ду
= г
и, используя теорему о дивергенции, получим
= р fffrdV = ? fffv-{rr)dV = ? ffm- (rr) dS =
V V S
r(xn-r)dS = ^JJ r(xn-r)Vgng22- gn2dudv. (8.6.12)
5 П
Формулу (8.6.12) можно получить, рассмотрев элементарную пирамиду, при-
приведенную на рис. 8.6.1. Центр масс элементарной пирамиды, показанной на
рис. 8.6.1, определяется радиус-вектором C/4)г. Произведение массы на радиус-
вектор центра масс элементарной пирамиды определяет статический момент
элементарной пирамиды. Предел суммы статических моментов всех элемен-
элементарных пирамид тела равен статическому моменту этого тела. При этом объем
элементарной пирамиды должен быть взят со знаком, соответствующим знаку
скалярного произведения m ¦ г. В результате мы придем к формуле (8.6.12).
Центр масс тела. Рассмотрим, как изменятся статические моменты при па-
параллельном переносе начала декартовой прямоугольной системы координат.
Пусть начало декартовой прямоугольной системы координат Oxyz перемещено
на вектор q, имеющий в данной системе компоненты q = [xq yq zq]T. В новой
системе координат O'x'y'z' радиус-вектор точки тела равен г' = г — q, а вектор
статического момента будет равен
М' = [ГГ pt? dV = ГГГ р{г - q) dV = M -
(8.6.13)
8.7. Моменты инерции тела
397
Если мы перенесем начало координат Oxyz на вектор
_ М_ _ М
Чс ~ ~pV ~ М1
(8.6.14)
то статический момент в новой системе координат будет равен нулю. Точка,
при параллельном переносе в которую начала координат статические моменты
тела становятся равными нулю, называется центром масс тела. Таким обра-
образом, формула (8.6.14) определяет радиус-вектор центра масс тела. Координаты
центра масс вычисляются формулами
хг =
pV
Pv
(8.6.15)
Система координат, в которой статические моменты тела равны нулю, называ-
называется центральной системой координат.
При преобразовании координат г' = А • г, где
«11 О\2 «13
«21 022 023
«31 «32 «33.
вектор статического момента и его компоненты преобразуются по формулам
М' = HI pr' dV = HI pA ¦ г dV = А • М (8.6.16)
v
или
Mx' = y
My' = a2iMx + Я22-Ц/ +
Из формул преобразования следует, что в центральной системе координат ста-
статические моменты тела всегда равны нулю независимо от ориентации коорди-
координатных осей.
8.7. Моменты инерции тела
Моменты инерции тела определяются объемными интегралами
Jt.t, —
уу —
(8.7.1)
V
J,,= p(x2 + y2)dV,
J J J
V
398 Гл. 8. Вычисление геометрических характеристик
а также
Jxy = Jyx = ~ I pxydV,
V
Jyz - Jzy = - 111 pyzdV, (8.7.2)
v
Jzx = Jxz = - /// pxzdV,
V
где x, у, z — компоненты радиус-вектора г. Величины Jxx, Jyy, Jzz называ-
называются моментами инерции тела относительно соответствующих координатных
осей, а величины —Jxy, —Jyz, —Jzx называются центробежными моментами
инерции тела. Интегрирование в (8.7.1)-(8.7.2) выполняется по объему тела.
Пусть плотность тела постоянна по всему его объему, это позволит вычислить
объемные интегралы через поверхностные интегралы.
Тензор инерции. Моменты инерции вводятся при рассмотрении движения
(вращения) твердого тела, имеющего неподвижную точку. Поместим начало
координат в неподвижную точку, тогда скорость некоторой точки тела опреде-
определяется соотношением v = ш х г, где ш — вектор мгновенной угловой скорости
тела. Вектор момента количества движения тела равен
L = fffrx (ш х r)pdV = [[[{г2" - (г • u))r)pdV. (8.7.3)
V V
Проекции вектора момента количества движения тела на оси декартовой си-
системы координат равны
Р(У2 + z2) dV - uy [и pxy dV - uz (и pxz dV =
Lx = ujx
V V
Jxy
Ly = -ujx fff pyx dV + uy (И p(z2 +x2)dV-ujz fff pyz dV =
V V V
= iOxJyX + LOyJyy + iOzJyZ,
Lx = -ux / / / pzxdV - uy In pzydV + uz 111 p{x2 + y2) dV =
V V V
— UXJZX + MyJzy + U!ZJZZ,
где шх, ujy, wz — компоненты вектора угловой скорости. В результате вектор
момента количества движения тела можно определить формулой
L = J-w, (8.7.4)
8.7. Моменты инерции тела 399
где величина J определяется матрицей, элементами которой являются осевые
моменты инерции (8.7.1) и центробежные моменты инерции (8.7.2), взятые с
противоположным знаком:
J =
¦'и ^ху <Jxz
Jyx Jyy Jyz
у zx Jzy "zz
(8.7.5)
Так как ш и L являются аксиальными векторами (аксиальный вектор или псев-
псевдовектор изменяет свое направление на противоположное при переходе от пра-
правой системы координат к левой), то величина J должна представлять собой
тензор второго ранга. Действительно, при преобразовании координат, описы-
описываемых некоторой матрицей А, величины ш и L преобразуются по форму-
формулам ш' = А • ш (или ш' = —А ¦ ш) и L' = А ¦ L (или I/ = —А • L), тогда
L' = ±А L = ±А- Зш = ±А- J- Ат- А-ш = A- J- AT-o/ = J' • ш' и величина
J должна преобразовываться по формуле
J' = AJAT. (8.7.6)
Таким образом, моменты инерции тела (с точностью до знака) являются ком-
компонентами тензора J, который называется тензором инерции. Компоненты
тензора инерции зависят от ориентации системы координат, но тензор инерции
представляет собой физический объект, не зависящий от ориентации системы
координат. Тензор инерции характеризует инертность тела при его вращении
вокруг некоторой неподвижной точки и является аналогом массы, которая ха-
характеризует инертность тела при поступательном движении. Тензор инерции
имеет различные значения в различных точках тела (является функцией непо-
неподвижной точки тела). Он образует тензорное поле.
Собственные значения матрицы инерции. В формуле (8.7.4) вектор количе-
количества движения L в общем случае не совпадает по направлению с вектором угло-
угловой скорости ш. Это приводит к тому, что при вращении тела вокруг заданной
оси, в точках крепления тела возникают зависящие от модуля угловой скорости
реакции. Такое вращение является динамически неуравновешенным. Выяс-
Выясним, существуют ли для данного тензора инерции J такие направления, при
которых вектор количества движения L совпадает по направлению с вектором
угловой скорости ш. Пусть это направление определяется единичным вектором
е = [х у z]T, тогда вектор J ¦ е, должен быть пропорционален вектору е.
Запишем это условие в виде равенства
J • е - Ле = (J - ЛЕ) • е = 0, (8.7.7)
где А — пока неизвестный скаляр, Е — тензорная единица ранга тензора J.
Проецируя это равенство на оси координат, получим три равенства
{JXx — А)ж + Jxyy + Jxzz = 0,
Jxyx + {Jyy - \)у + Jyzz = 0, (8.7.8)
JxzX + JyzV + [Jzz ~ A)Z = 0,
400
Гл. 8. Вычисление геометрических характеристик
которые будем рассматривать как однородную систему линейных алгебраиче-
алгебраических уравнений относительно х, у, z. Тривиальное решение нам не подходит,
так как необходимо найти вектор, для которого
x2 + y2 + z2 = 1. (8.7.9)
Система (8.7.8) имеет нетривиальные решения, когда определитель системы
равен нулю:
т
XX A JXy
Jyx
Jzx
Jyy ~ ^
Jzy
Oyz
Jzz-X
= 0.
Это равенство выполняется, когда скаляр А удовлетворяет уравнению
(8.7.10)
(8.7.11)
где
— Jxx т «Л/и "г
Jxx
Jyx
Jxy
Jyy
+
Jyy Jyz
Jzy Jzz
+
Jzz
Jxz
Jzx
Jxx
Jxx
Jyx
Jzx
>xy
'yy
'zy
J
yz
Уравнение (8.7.11) называется характеристическим уравнением тензора
инерции. Корни Ai, A2, A3 характеристического уравнения (8.7.11) являются
действительными, так как матрица тензора инерции является симметричной.
Скаляры Aj, г = 1, 2, 3 являются собственными значениями матрицы момен-
моментов инерции. Каждому Аг- соответствует собственный вектор е^.
Главные оси инерции. Предположим, что собственные значения матрицы
инерции Ai и Аг различны. Покажем, что соответствующие им собственные
векторы ei и ег ортогональны. Действительно, для данных собственных зна-
значений выполняются равенства
=0, J • е2 -
= 0.
Умножим первое равенство скалярно на е2, а второе — на ei и вычтем второе
из первого. Используя симметрию тензора инерции, получим
— ei ¦ J
+
= 0
или
(A2 - Ai)ei -e2 = 0.
Из последнего равенства в силу предположения А2 ф Ai следует, что ei • е2 = 0
и собственные векторы ei и е2 ортогональны. Аналогично доказывается ортого-
ортогональность других собственных векторов. Будем говорить, что собственный век-
вектор определяет главное направление тензора инерции в пространстве. Если два
8.7. Моменты инерции тела
401
из трех собственных значения матрицы инерции равны, то мы сможем опреде-
определить только одно из главных направлений, а другими главными направлениями
могут быть любые направления, ортогональные найденному направлению. Если
все три собственных значения матрицы инерции равны между собой, то глав-
главными направлениями могут быть любые направления в пространстве. В любом
случае можно получить три взаимно ортогональных главных направления.
Три взаимно ортогональных главных направления, соответствующих соб-
собственным векторам ei, в2, ез определяют главные оси инерции тела и являются
базисными векторами главной системы координат. Если орты новой декартовой
прямоугольной системы координат ориентировать вдоль главных направлений,
то осевые моменты инерции тела будут равны собственным значениям матрицы
инерции, а центробежные моменты инерции будут равны нулю, т.е. J\\ = Ai,
J22 — А2, J33 — A3, 3\i — 0, J23 = 0, Ji3 = 0. Докажем это. Для главных
направлений выполняются равенства
J ¦ ei =
Тогда
г = 1, 2, 3.
= \i6ki,
(8.7.12)
что доказывает высказанное утверждение. Матрица тензора инерции в главной
системе координат имеет вид
J =
Ai
0
0
0
A2
0
0
0
Аз
—
Ju
0
0
0
«^22
0
0
0
«^33
(8.7.13)
Система координат, в которой все центробежные моменты инерции тела равны
нулю, называется главной системой координат. Моменты инерции «7ц, J22,
J33 в главной системе координат называются главными моментами инерции.
Главные направления тензора инерции зависят от неподвижной точки тела (от
выбора начала координат). Система координат, в которой статические моменты
и все центробежные моменты инерции тела равны нулю, называется главной
центральной системой координат. Моменты инерции в главной центральной
системе координат называются главными центральными моментами инерции.
Направления главных осей инерции тела лежат в плоскостях симметрии тела.
Начало главной центральной системы координат находится в центре масс тела.
Найдем направления главных осей инерции. Пусть главному моменту инер-
инерции Aj соответствует главное направление, определяемое ортом ei — [xi щ Zi]T.
Возможны три случая соотношений между корнями характеристического урав-
уравнения. Первый случай — все корни характеристического уравнения различны,
второй случай -— два из трех корней характеристического уравнения равны и
отличны от третьего корня, третий случай — все три иорня характеристического
уравнения равны между собой
Пусть Ai ф Аг Ф Аз (корни характеристического уравнения различные).
Для каждого \{ составим систему уравнений (8.7.8)
(Ju - \)хг + JvzVi + JnZi = 0,
hi^i + (J22 - \)Vi + hb*i = 0,
JuXi + J23Vi + (J33 - K)*i = 0.
26 — 5293 Голованов
402
Гл. 8. Вычисление геометрических характеристик
Среди данных трех уравнений одно является линейной комбинацией двух дру-
других, так как определитель системы (8.7.10) равен нулю. Нам нужно выяснить,
какие два из трех уравнений являются линейно независимыми. Для этого вы-
вычислим определители
J22 — Aj J23
«^23 «^33 ~ Aj
J33 — Ai J\Z
J13 Jn —
J\2 J22 — Ai
По крайней мере, один из них должен быть отличен от нуля. Пусть -Аг Ф 0.
Тогда компоненты соответствующего главного вектора найдем из системы урав-
уравнений
J\2Vi
i = 0,
= 0,
Для ее решения из первых двух уравнений выразим Х{ и Z{ через j/i и подставим
их в третье уравнение. В результате получим у{. Далее из первых двух урав-
уравнений найдем Х{ и z\. Так мы можем определить все три собственных вектора.
Вектор ei = \x{ у{ zi\T соответствует А*.
Пусть два из трех корней характеристического уравнения равны между со-
собой, например, Ai = A2 ф Хз- В этом случае базисный вектор ез = [х3 уз ^з]Т
может быть найден описанным выше способом. Двумя другими базисными век-
векторами могут служить любые ортогональные друг другу и вектору ез орта.
Если Ai = A2 = A3, то собственными векторами могут служить любые три
взаимно ортогональные орта, a Ai = Д/З.
Эллипсоид инерции. Рассмотрим поведение компонент тензора инерции при
произвольном повороте осей координатной системы. Пусть мы переходим от
исходной системы координат к новой системы координат с тем же центром и с
ортами ii, i2, 13- Радиус-вектор произвольной точки в новой системе координат
будет равен г' = А • г, где
Х\ у\ Z\
Х2 У2 Z2
хз Уз z3
Компоненты матрицы преобразования А являются координатами ортов ii,
i3 новой системы координат: ii = [х\ yi jzi]t, i2 = [х2 2/2 Z2]T, 13 = [#3 Уз z3
Соотношение (8.7.6) в развернутой записи имеет вид
J21
Jsi
J12
J22
J32
J13
J23
J33
=
У\
У2
Уз
Zl
Z2
Z3
•
Jxx
Jyx
Jzx
Jxy
Jyy
Jzy
lyz
X\ X2 X3
У\ У-i Уъ
Z\ Z2 Z3
8.7. Моменты инерции тела 403
Компоненты тензора инерции при переходе к новой системе координат пре-
преобразуются по формулам
J\\ = Х\ JXx + У\ Jyy + z\ Jzz + 2Х\У\JXy + 2y\Z\JyZ + 2z\X\JZXi
J22 = X2 JXx + У2 Jyy + Z2 Jzz + 2xiy2Jxy + 2у2^2«Л/г + 2z2X2Jzx,
2
J33 = x32 Jxx + Уз2 Jyy + Z32JZZ + 2ж3у3 Jxy + 2y3z3Jyz + 2z3x3Jzx,
J\2 = Ji\ = XiX2JXx + y\yiJyy + Z\Z2JZZ +
+ (Ж1У2 + x2yi)JXy + {y\z2 + yiZ\)Jyz + {z\x2 + z2xx) Jzx, (8.7.14)
J23 = J32 = X2X3JXX + У2УЗ^г/г/ + z2Z3Jzz +
J31 = J\3 = x3xxjxx + y3y\Jyy + z3z\ Jzz +
+ (ЖЗУ1 + Xiy3)Jxy + (Уз^1 + y\Z3)Jyz + {Z3XI + ZXX3)JZX.
Можно показать, что величины Ii, I2, I3 не изменяются при повороте системы
координат. Они являются инвариантами относительно преобразования коор-
координат, сохраняющего начало. Неизменность главных направлений, главных
моментов инерции Jn, J22, J33 и величин Д, /2, 13 при изменении направле-
направления координатных осей является проявлением независимости тензора инерции
от ориентации системы координат. Любая из первых трех формул (8.7.14) мо-
может считаться формулой для определения осевого момента инерции тела от-
относительно произвольной оси, заданной своими проекциями на оси исходной
системы координат. Пусть некоторая ось проходит через начало координат и
имеет компоненты 1 = [xi yi z{\ . Тогда осевой момент инерции тела относи-
относительно этой оси равен
Jll = xfJxx + У? Jyy + zi2Jzz + ZxiyiJxy + 2yiztJyz + 2ztXiJzx.
Разделим компоненты оси на осевой момент инерции Ju, введем обозначения
х = xi/\/Ja, у = yi/y/Ju, z = zi/y/Ju и получим равенство
x2Jxx + У2 Jyy + z2Jzz + 2xyJxy + 2yzJyz + 2zxJzx = 1. (8.7.15)
Равенство (8.7.15) можно рассматривать как уравнение поверхности второго
порядка. Длина вектора, проведенного из начала координат к любой точке по-
поверхности (8.7.15), обратно пропорциональна квадратному корню из момента
инерции тела относительно оси, совпадающей с данным вектором по направле-
направлению. Момент инерции тела относительно любой оси есть величина положитель-
положительная (все собственные значения матрицы инерции положительные), поэтому по-
поверхность (8.7.15) представляет собой эллипсоид. В главной системе координат
уравнение эллипсоида инерции имеет канонический вид
x2Jn +y2J22 + z2J33 = 1. (8.7.16)
Если два из трех главных момента инерции равны, то эллипсоид инерции явля-
является эллипсоидом вращения. Если все три главных момента инерции равны,
то эллипсоид инерции превращается в сферу.
26*
404 Гл. 8. Вычисление геометрических характеристик
Тензорное поле. При параллельном переносе начала декартовой прямоуголь-
прямоугольной системы координат изменяются не только компоненты тензора инерции
тела, но и сам тензор инерции. Пусть начало декартовой прямоугольной си-
системы координат Oxyz перемещено на вектор q, имеющий в данной системе
компоненты q = [xq yq zq] . В новой системе координат O'x'y'z' радиус-вектор
точки тела равен г' = г — q, а компоненты тензора инерции будут равны
Jxx> = [[[(У2 + Z<2- 2УУЧ - 2zZQ + Щ2 + Zq
V
= Jxx - 2УдМу - 2zqMz + {yq2 + Zq2)M,
Jyyi = / / / (Z2 + X2 - 2ZZQ - 2xXq + Zq2 + Xq2)pdV =
V
= Jyy - 2zqMz - 2xqMx + (Zq2 + Xq2)M,
Jzz> = [(x2 + У2 - 2ххя ~ 2УУя + хя2 + y
V
= Jzz - 2xqMx - 2yqMy + {Xq2 + Уд2)М,
Jyz> = - / / / (yz ~ yzq - zyq + yqZq)pdV = Jyz + ZqMy + yqMz - yqZqM,
V
- ZXq - XZq + ZqXq)pdV = Jzx + XqMz + ZqMx - ZqXqM,
= — {
V
= - (ХУ - хУя ~ УХЯ + xqyq)pdV = JXy + УЯМХ + XqMy - XqyqM.
V
Jxy1
V
Пусть система координат Oxyz является главной центральной системой коор-
координат тела. Тогда в ней Мх = Му = Mz = 0, Jxy = Jyz = Jzx — 0. При
перемещении вдоль главной центральной оси две из трех компонент вектора
сдвига равны нулю и, следовательно, главные направления сохраняются. В но-
новой системе координат в общем случае центробежные моменты инерции будут
отличны от нуля и, следовательно, она не будет являться ни центральной, ни
главной. Это говорит о том, что тензор инерции является функцией положения
неподвижной точки тела, образуя в теле тензорное поле.
Вычисление моментов инерции тела. Не имея явных уравнений граней тела,
мы не можем непосредственно вычислить объемные интегралы (8.7.1) и (8.7.2).
В нашем распоряжении есть параметрическое представление граней тела. Грани
тела образуют одну или несколько замкнутых оболочек, поэтому объемный ин-
интеграл для каждой замкнутой оболочки мы сведем к поверхностному инте-
интегралу. Для вычисления компонент тензора инерции положим в (8.5.13) по-
последовательно F(r) = ж2г, F(r) = y2r, F(r) = z2r, F(r) = yzr, F(r) = zxr,
F(r) = xyv. Тогда V • (x2r) - 5x2, V • (y2rMy2, V • (z2r) - 5z2, V • {yzr) = 5yz,
V • (zxr) = 5zx, V • (xyr) = Ьху и из теоремы Остроградского-Гаусса (8.5.13)
8.7. Моменты инерции тела 405
получим
И m • {x2r) dS = b HI х2 dV,
V
S V
m • (z2r) dS = 5 HI z2 dV,
S V
m • (xyr) dS = 5 Iff xy dV,
S V
m • (yzr) dS = 5 Iff yz dV,
S V
m • {zxr) dS = 5 HI zx dV.
S V
Таким образом, компоненты тензора инерции тела определятся формулами
Jxx = ^JJ(y2 + z2)m-rdS= ^JJ(y2+z2)m-rVgngv -gn2dudv, (8.7.17)
s n
Jyy = ^ Л(z2 + x2)m-rdS = ^ Jl(z2 + x2)m-rVgug22 - gn2dudv, (8.7.18)
s n
-gn2dudv, (8.7.19)
Jxy = -g // xym-rdS - -- // xym ¦ ry/gng22 - gn2 du dv, (8.7.20)
s n
Jyz = -7 / / yzm ¦ rdS = -- / / yzm ¦ ry/gug22 -gn2dudv, (8.7.21)
s n
Jxz = -7 // z-zm-rdS1 = -- // юш ¦ r\Zgiig22 - Яи2 с?" du. (8.7.22)
s n
В формулах (8.7.17)-(8.7.22) подразумевается суммирование по граням тела.
Так же как и в (8.6.12), m есть нормаль граней тела. Формулы (8.7.17)-(8.7.22)
позволяют вычислить моменты инерции в той системе координат, в которой
задано тело.
406 Гл. 8. Вычисление геометрических характеристик
Часто тело описывается в некоторой глобальной системе координат, начало
которой не совпадает с центром масс тела, а моменты инерции требуется опре-
определить в центральной системе координат. В этом случае можно поступить сле-
следующим образом. Пусть центр масс имеет координаты хс, ус, zc. Вычислим
интегралы
Nxx = Р I / (х - хсJ dV = ?¦ /1 m • rx2 dS - 2xcMx + xc2pV,
V
Nzz = p?jjj{z - zcJ dV = ?[fm- vz2 dS - 2zcMz + zc2pV,
S
Nxy = p / / (x - xc){y - yc) dV = - / / m • rxydS - xcMy - ycMx + xcycpV,
v s
Nyz = P / / / (У'- Vc)(z - zc) dV = - / / m • xyz dS - ycMz - zcMy + yczcpV,
V S
Nzx = p / / / (z - zc)(x — xc) dV = - / / m • rzx dS — zcMx - xcMz + zcxcpV.
V S
С учетом формул (8.6.15) получим
Nxx = - //m • rx2 dS - x2pV -7 x2m ¦ r\Zgng22 - g\\2 du dv - xc2pV,
// y2mr^SeE2 du dv y2
Nyy =5jlm' ry2 dS ~ y°2pV = 5 // y2m' r^Sue22-En2 du dv - yc2pV,
п
Nzz = I / / m • rz2 dS - zc2pV = | / / z2m ¦ rs/gllg22 - gn2 du dv - z2pV,
S п
Nxy = - //m • rxydS -xcycpV = - xym • ry/gng22 - gn2dudv -xcycpV,
s n
Nyz = - m ¦ xyz dS -yczcpV = - yzm ¦ ry/gng22 - gn2 du dv -yczcpV,
s n
Nzx = - //m ¦ rzx dS -zcxcpV = - zxm ¦ ry/gng22 - gn2 dudv -zcxcpV.
8.8. Решение кубического уравнения 407
Компоненты тензора инерции тела относительно центральной системы коорди-
координат определятся формулами
Jxx = Nyy+Nzz, (8.7.23)
Jyy=Nzz + Nxx, (8.7.24)
JZZ = NXX+Nyy, (8.7.25)
Jxy = ~Nxy, (8.7.26)
Jyz = ~Nyz, (8.7.27)
Jzx = -Nzx. (8.7.28)
По этим компонентам могут быть вычислены главные моменты инерции тела и
направления осей главной центральной системы координат.
Полученные двойные интегралы могут быть вычислены с помощью кубатур-
ных формул, которые мы рассмотрим ниже.
8.8.* Решение кубического уравнения
Для определения канонических коэффициентов поверхности второго порядка и соб-
собственных значений матрицы инерции нужно решить кубическое уравнение C.3.8) и
(8.7.11):
A3-/iA2+/2A-/3 = 0.
Это уравнение может быть решено аналитически. Заменим в уравнении (8.7.11) неиз-
неизвестную А новой неизвестной х, связанной с А равенством
А = * + у- (8.8.1)
После подстановки (8.8.1) в (8.7.11) получим неполное кубическое уравнение относи-
относительно х, не содержащее квадрата новой неизвестной:
х3 +px + q = 0, (8.8.2)
где введены обозначения
р=-±11* + 12, (8.8.3)
g = -^/i3 + |/i/2-/3- (8.8.4)
В соответствии с основной теоремой алгебры уравнение (8.8.2) имеет три корня, в
общем случае комплексных. Пусть Х{ есть один из этих корней. Рассмотрим многочлен
f(y) = У2 ~ ЪУ - jjP
некоторой вспомогательной неизвестной у. Этот многочлен обладает двумя корнями у\
и г/2, удовлетворяющими формулам Виета
У1+2/2= я*, (8.8.5)
У№ = -дР- (8.8.6)
408 Гл. 8. Вычисление геометрических характеристик
Подставим (8.8.5) в (8.8.2) и получим («д + у2K +р{у\ + у2) + <7 = 0 или
2/13 + У2 3 + C2/12/2 +р) B/1 +2/г)+9 = 0.
С учетом (8.8.6) последнее равенство примет вид
2/13+2/23 = -<7- (8.8.7)
С другой стороны, из (8.8.6) следует, что
2/1V = -^Р3. (8.8.8)
Равенства (8.8.7)и (8.8.8) свидетельствуют, что числа yi3 и у23 являются корнями
квадратного уравнения
z2+qz-^P3 = 0. (8.8.9)
Решив это уравнение, получим его корни
В соответствии с (8.8.5) сумма кубических корней z\ и Z2 является решением неполного
кубического уравнения (8.8.2):
Формула (8.8.11) называется формулой Кардано.
Так как кубический радикал на множестве комплексных чисел имеет три значения,
то z\ даст три значения для yi} a z2 даст три значения для у^. В формуле (8.8.11)
должны быть суммированы кубические радикалы (значения у\ и j/2), удовлетворяющие
условию (8.8.6). Пусть j/i — любое из трех значений кубического радикала z\ и j/2 —
удовлетворяющее равенству (8.8.6) значение кубического радикала z2- Тогда корнями
неполного кубического уравнения (8.8.2) будут
xi =2/i+J/2, х2 = eyi + е2у2, х3 = e2yi +еу2, (8.8.12)
где е = cos Bтг/3) + i sin Bтг/3) = -1/2 + г\/3/2 — кубический корень из единицы, а
е2 = cosDtt/3) + isinD7r/3) = —1/2 — i\fZ/2 — квадрат этого кубического корня из
единицы.
Формула Кардано позволяет найти три корня, в общем случае комплексных, ку-
кубического уравнения. Коэффициенты кубического уравнения в общем случае могут
быть комплексными. В случае вычисления главных моментов инерции коэффициенты
(8.8.3) и (8.8.4) неполного кубического уравнения, так же как и инварианты /ь I2, h,
являются действительными числами. В формуле Кадано величина
8.8. Решение кубического уравнения 409
называется дискриминантом неполного кубического уравнения (8.8.2). Если коэффи-
коэффициенты р и q являются действительными числами, то дискриминант также является
действительным числом и может принимать значения: D — 0, D < 0, D > 0.
Пусть D = 0. Тогда 2/1=2/2 = y/—q/2, а е + е2 = — 1. Подставив данные значения
в (8.8.12), получим решение
(8.8.13)
Таким образом, если D = 0, то кубическое уравнение с действительными коэффициен-
коэффициентами имеет три действительных корня, два из которых равны между собой, а третий
равен сумме первых двух, взятой с противоположным знаком.
Пусть D < 0. В этом случае под знаком каждого из квадратных радикалов стоит
положительное действительное число, и, следовательно, под знаком каждого из кубиче-
кубических радикалов стоят действительные числа. Кубический корень из действительного
числа имеет одно действительное и два комплексных сопряженных значения. Пусть
действительными значениями этих кубических радикалов являются 2/i и j/2- Подставив
данные значения в (8.8.12), получим
Xi = 2/i +2/2,
_ 2/1 +2/2 ¦ /g 2/1 ~ 2/2
2 2 (8.8.14)
хз = -
2/1 +2/2 _ гУз^1 ~^2
Таким образом, если D < 0, то кубическое уравнение с действительными коэффициен-
коэффициентами имеет один действительный корень и два сопряженных комплексных корня.
Пусть D > 0. В этом случае под знаком каждого из квадратных радикалов стоит
отрицательное действительное число, и, следовательно, под знаками кубических ради-
радикалов стоят сопряженные комплексные числа. Кубические корни из комплексных чисел
в общем случае также являются комплексными числами. Но среди корней кубического
уравнения с действительными коэффициентами обязательно один из корней должен
быть действительным числом. Пусть действительным корнем кубического уравнения
является число х\ = 2/1 + 2/2- В соответствии с (8.8.5) и (8.8.6) сумма и произведе-
произведение комплексных чисел 2/1 и j/2 равны действительным числам, следовательно, 2/1 и 2/2
являются сопряженными комплексными числами как корни квадратного уравнения с
действительными коэффициентами. Введем обозначение 2/i = а + ib, 2/2 = а, — ib и
подставим данные значения в (8.8.12). В результате получим
xi = 2а, х2 = -а - Ь%/3, х3 = -а + b\/b. (8.8.15)
Таким образом, если D > 0, то кубическое уравнение с действительными коэффициен-
коэффициентами имеет три действительных корня.
Можно показать, что все корни Ai, Л2 и Аз характеристического кубического уравне-
уравнения (8.7.11) являются действительными числами, поэтому рассмотрим подробнее этот
а2 р3
случай. Итак, величина — + — является отрицательной. Тогда
2/13 = -^+ч/-Ш -(?) =-r3(cos7+?:sin7),
410 Гл. 8. Вычисление геометрических характеристик
где
r=MV3' 7 = arccosi^- (8-8Л6)
Знак г должен совпадать со знаком q. После подстановки данных формул в (8.8.11)
получим a = —г cos G/З), Ь — —г sin G/З) и
/ 7 . . 7\ / 7 • . 7\
У1 = -г ^cos - + г sin - J , 2/2 = -г ^cos ^ - г sin - j .
Тогда три действительных корня неполного кубического уравнения выразятся через
его коэффициенты формулами
^ (8.8.17)
О
х2 = г (cos 2 + ^sin ^) = 2r cos (| - J), (8.8.18)
ж3 = г (cos ^ - -^sin |) = 2r cos f ^ + ^) • (8.8.19)
Разыскание корней кубического уравнения с действительными коэффициентами по
формуле Кардано требует извлечение кубических корней из комплексных чисел, что
можно делать путем перехода к тригонометрической записи комплексных чисел. Запись
корней (8.8.11) с помощью радикалов следует рассматривать именно с таких позиций.
Корни характеристического уравнения C.3.8) и (8.7.11) определятся формулами
^ (8.8.20)
(^^) (8.8.21)
Аз = j + 2rcos(| + J), (8.8.22)
где
Возможны частные случаи.
Случай 1: р = 0, тогда Ai = А2 = А3 = —.
Случай 2: D = 0, тогда Ах = у - 2«|, А2 = А3 = у + Л |.
8.9.* Квадратурные формулы
Выше мы показали, как с помощью криволинейных интегралов вычисляются гео-
геометрические характеристики линий и плоских сечений. Рассмотрим некоторые методы
приближенного вычисления определенных интегралов.
Квадратурная формула Гаусса. Пусть требуется приближенно вычислить определен-
определенный интеграл от некоторой функции /(?). Если эта функция однозначна и непрерывна
на интервале интегрирования, тогда по теореме Вейерштрасса для любого положитель-
положительного достаточно малого е существует такой полином p(t), что \f(t) — p(t)\ < s всюду на
8.9. Квадратурные формулы 411
заданном интервале. Если бы нам была известна формула точного вычисления опреде-
определенного интеграла от полинома p(t), то мы могли бы с известной точностью принять
интеграл от полинома за приближенное значение интеграла от заданной функции f(t).
Поставим задачу найти значения аргументов ti, t2, ¦••) tn и весовые множители wi,
w2, ¦ ¦., wn, чтобы формула
J
/(*) Л w у p{t) dt = J2 тр{и) (8.9.1)
была бы точной для всех полиномов p(t) степени 2п — 1. Полином степени 2п - 1
содержит 2п коэффициентов, по которым можно найти п аргументов ti, t2, ¦ ¦ ¦, tn и п
весовых множителей wi, w2, ¦¦¦, wn. К пределам интегрирования от —1 до 1 всегда
можно свести любые пределы путем линейной замены аргумента.
Пусть
p{t) = С0 + Cyt + C2t2 + ... + C2n-ittn~1- (8-9.2)
В соответствии с формулой (8.9.1) должны выполняться равенства
Г ^
tmdt = 2_^Witim, тп = 0, 1, ..., 2п-1. (8.9.3)
В то же время
1
2
tm dt = -, если т четное, и 0, если т нечетное. (8.9.4)
т + 1
-1
Подставим (8.9.2) в (8.9.1) и получим
1
Со
ill 1
I dt + d f tdt + C2 f t2 dt + ... + Can-i f t2" dt =
-l -l -l -l
n n n
Приравняем выражения при Ci, г = 0, 1. 2, ..., In — 1 в правой и левой частях равен-
равенства (8.9.5) и, учитывая равенства (8.9.4), получим систему 2п уравнений
и>1 + ги2 + ... + wn = 2,
+ ... + wntn = О,
+ ... + Wntn2 = ~,
Л (8.9.6)
-2 + W-2 + . . . + Wntn2n~2 = Г-^-Г,
2n — 1
^iti2"-1 + ^ta*1 + • • ¦ + Wntn2"-1 = 0.
412 Гл. 8. Вычисление геометрических характеристик
Из этой системы уравнений могут быть найдены значения аргументов ti, ?2, •¦•, tn
и весовые множители wi, u>2, ¦ •., wn. Система является нелинейной и может быть
решена численным методом.
Если в качестве полинома вместо (8.9.2) взять полиномы
p(t) = tmPn(t), m = 0, I, 2, ..., n-1, (8.9.7)
где Pn(t) — полиномы Лежандра, то окажется, что в качестве значений t\, ?2, • • •) tn
достаточно взять решения уравнения Pn(t) = 0. Полиномы Лежандра определяются
формулой Родрига
или формулой
„m_i v1 (~1ГBп-2т)! 2т
W~2" ^ т!(п - т)!(п - 2т)!
где [п/2] = п/2 для четных п и [п/2] = (п — 1)/2 для нечетных гг. Первые восемь
полиномов Лежандра имеют вид
Po(t) = l, Pl(t)=t, ^^ ^Jl
+3 „ , . 63t5 - 70t3 + 15*
PW
. 231i6 - 315t4 + 105*2 - 5
P7(t) = A
16
5 + 315*3 - 35t
16
Полиномы Лежандра удовлетворяют уравнению Лежандра
которое появляется при решении уравнения Лапласа в сферических координатах мето-
методом разделения переменных.
Полиномы Лежандра обладают следующими свойствами.
Pn(-t) = (-l)»Pn(t), Р„A) = 1, Р„(-1) = (-1)",
(п + l)Pn+i(t) = Bп + l)tPn(t) - nPn-i(t),
Pn+l'{t) - Pn-i(t) = Bn + l)Pn(t),
1
Jpn(t)p(t)dt = O (8.9.9)
1
8.9. Квадратурные формулы
413
для любых полиномов p(t) степени m = 0, 1, ..., п — 1. Полином Лежандра Pn(t) имеет
п различных действительных корней t\, t2, ..., tn, которые расположены на интервале
от -1 до 1.
Полиномы (8.9.7) имеют степень, не превышающую 2п-1, поэтому для них должно
выполняться равенство (8.9.1), т.е.
1
1
tmPn(t)dt =
(8.9.10)
В силу свойства (8.9.9) полиномов Лежандра равенство (8.9.10) примет вид
= о,
(8.9.11)
Эти равенства будут выполнены при любых Wi, г = 1, 2, ..., п, если положить
Pn(ti) = 0, i = 1, 2, ..., п. (8.9.12)
То есть в качестве аргументов t\, t2, ¦.., tn могут быть взяты нули соответствующего
полинома Лежандра. Эти нули действительны, различны и расположены в интервале
-1 ^ ti ^ 1. По известным аргументам t%, t2, •-., tn из первых п уравнений (8.9.6)
могут быть найдены весовые множители w\, w2, • • •, wn. Эта система уравнений ли-
линейная относительно весовых множителей и ее определитель является определителем
Вандермонда
1
h
l
*2
*2П
1
... tn
t П
который в силу различности корней полинома Лежандра не равен нулю. Формула
(8.9.1), где t\, t-ii ¦ ¦ -, tn — нули полиномов Лежандра, называется квадратурной фор-
формулой Гаусса.
Рассмотрим квадратурные формулы Гаусса для интеграла
о
= Jf(x)dx.
(8.9.13)
Путем замены переменной х = (a + b)/2 + t(b — а)/2 придем к интегралу по переменной
t с пределами интегрирования от -1 до 1, для которого применим формулу Гаусса
= J f(x) dx = \{Ъ - a)Jf(x(t)) A « i(b - а) 5></(*0,
а -1 !=1
(8-9.14)
где Х{ = (а + Ь)/2 + ti(b — а)/2 и ti, г = 1, 2, ..., п — корни полинома Лежандра Pn(t).
Путем разложения в ряд интегрируемой функции можно показать, что погрешность
414
Гл. 8. Вычисление геометрических характеристик
квадратурной формулы Гаусса равна
_ (b-aJn+1(n\)id2nf(Q/dx2n
(Bn)!KBn + l)
где a
< b.
(8.9.15)
В табл. 8.9.1 приведены значения аргументов t\, t2, ..., tnn весовые множители
i, W2, ¦ ¦., wn для квадратурных формул Гаусса на интервале -1 ^ t ^ 1.
Таблица 8.9.1
п
1
2
3
4
5
6
U
0
±0,57735026918962576450
0
±0,77459666924148337703
±0,33998104358485626480
±0,86113631159405257522
0
±0,53846931010568309103
±0,90617984593866399279
±0,23861918608319690863
±0,66120938646626451366
±0,93246951420315202781
Wi
2
1
8/9
5/9
0,65214515486254614262
0,34785484513745385737
0,56888888888888888889
0,47862867049936646804
0,23692688505618908751
0,46791393457269104738
0,36076157304813860756
0,17132449237917034504
о
±0,40584515137739716690
±0,74153118559939443986
±0,94910791234275852452
0,41795918367346938775
0,38183005050511894495
0,27970539148927666790
0,12948496616886969327
±0,18343464249564980493
±0,52553240991632898581
±0,79666647741362673959
±0,96028985649753623168
0,36268378337836198296
0,31370664587788728733
0,22238103445337447054
0,10122853629037625915
Квадратурные формулы Ньютона-Котеса. Если, на участке интегрирования функ-
функция может быть аппроксимирована полиномом, то за приближенное значение инте-
интеграла может быть принят интеграл от этого полинома. В некоторых случаях точки
аппроксимации отстоят друг от друга на равном расстоянии по параметру, а в качестве
интерполяционного полинома используется полином Лагранжа B.4.15).
Пусть требуется вычислить интеграл
¦/'<*>
dt.
(8.9.16)
Разобьем отрезок интегрирования равноотстоящими точками
t0 = a, U =*% + ihT! i — 1, 2, ..., n - 1, tn = b
8.9. Квадратурные формулы 415
на п равных участков, где Л = F - а)/п. Заменим функцию f(t) интерполяционным
полиномом Лагранжа
, (8.9.17)
где
(t - to)(t - h)... (t - VQft - ti+1) ...(t-tn)
- to){u - h)... (и - и-1)(и - ti+1) ...(h- tn) ¦
=
тт й *-*O *-*O tt
При введении обозначения q = n- = —-— полином Лагранжа примет вид
о — а п
(8.9.18)
i=o *ч"~ х;чч ~ ч
За приближенное значение интеграла (8.9.16) примем интеграл от интерполяционного
полинома Лагранжа
"г V" А
/ = / f(t)dt& An{t)dt = y a,if{ti), (8.9.19)
to i=0
где введено обозначение
(Ч-п) м_{-1)п~ЧЬ-а) fq(q-l)...(q-n)
_ Г {-\)п-Ы(Ч ~ 1) • • • (Я ~ п) (-1)п-*(Ъ - a) fq(ql)...(qn)
ai~J i\(n-l)\(q-i) M~ t!(n-l)!n J q-i Я'
to 0
(8.9.20)
Обычно полагают ai = F — a)Hi, где постоянные величины
Hi = ,) ' 4, / ™ '"'}4 ' dq, (8.9.21)
il(n — l)!n J q — г
о
называются коэффициентами Котеса.
Полученные таким образом формулы вычисления определенных интегралов назы-
называются квадратурными формулами Ньютона-Котеса и имеют вид
I f(t) dtm(b-aJ2 Hifik), (8.9.22)
/о i=0
.b — a
где ti = а + г .
n
Частные случаи формул Ньютона-Котеса. Положим в формуле (8.9.22) п = 1 и
получим формулу трапеций для приближенного вычисления определенного интеграла
ь
№dt*^(f{o) + f{b)). (8.9.23)
416 Гл. 8. Вычисление геометрических характеристик
Можно показать, что погрешность формулы трапеций равна
r«e «<?<*>• (8-9.24)
Если на участке интегрирования d2 f /dx2 > 0, формула трапеций дает значение инте-
интеграла и избытком, а если на участке интегрирования d2 f /dx2 < О, формула трапеций
дает значение интеграла с недостатком. Для более точного вычисления область инте-
интегрирования разбивают на несколько участков и на каждом из них применяется формула
трапеций. Это равносильно аппроксимации кривой, описываемой данной функцией,
ломаной линией, и вычислению интеграла от этой ломаной.
Квадратурная формула, в которой интегрируемая функция заменяется параболой,
называется формулой Симпсона. Формула Симпсона может быть получена как частный
случай формулы (8.9.22) при п = 2. Из формулы (8.9.22) при п = 2 получим Hq = 1/6,
#! = 2/3, #2 = 1/6 и
/(t) dt « —г^(/(*о) + 4/(ti) + /(*-,)), (8-9.25)
b- a
где ti — to + i—-—, г = 0, 1, 2. Можно показать, что погрешность формулы Симпсона
равна
^?p где «<?<*>• (8-9.26)
Формула Симпсона является точной для полиномов не только второй, но и третьей
степени.
Из формулы (8.9.22) при п ~ 3 получим квадратурную формулу Ньютона
ь
j f(t) dt и ^ (ДМ + 3/(ti) + 3/(t2) + /(t3)), (8.9.27)
а
где?* = to+i—-—, i — 0, 1, 2, 3. Можно показать, что погрешность формулы Ньютона
равна
^^^ где a<i<b. (8.9.28)
Формула Ньютона при одинаковом шаге h — (b — а)/п менее точна, чем формула Сим-
Симпсона. С точки зрения точности формулы Ньютона-Котеса с четным п являются более
эффективными.
В общем случае область интегрирования может разбиваться на несколько участков
и на каждом участке использоваться интегрирование одним из описанных методов.
Полученные таким способом формулы называются обобщенными формулами Ньютона-
Котеса и обобщенными формулами Симпсона.
Рассмотренные квадратурные формулы используются для вычисления геометриче-
геометрических характеристик кривых линий и плоских областей, ограниченных линиями на
плоскости. Из всех приведенных формул при одном и том же числе точек п квадра-
квадратурная формула Гаусса имеет наименьшую погрешность при тех же вычислительных
затратах.
8.10. Кубатурные формулы
417
8.10.* Кубатурные формулы
При вычислении геометрических характеристик тел мы свели объемные интегралы
к поверхностным интегралам. Рассмотрим методы приближенного вычисления двой-
двойных интегралов по параметрическим областям поверхностей. В некоторых случаях
двойной интеграл можно вычислить сразу по всей области, но в большинстве случаев
области определения поверхности мы будем разбивать на совокупность небольших под-
подобластей четырехугольной или треугольной формы и вычислять поверхностный инте-
интеграл как сумму интегралов по областям простейших форм. Формулы приближенного
вычисления двойных интегралов называются кубатурными формулами.
Кубахурная формула Гаусса. Пусть требуется приближенно вычислить двойной ин-
интеграл от некоторой непрерывной и однозначной функции /(w, v) на области п
I — I f (u, v) du dv.
п
(8.10.1)
Пусть область интегрирования можно ограничить двумя непрерывными и однознач-
однозначными кривыми
v =
а ^ и
как показано на рис. 8.10.1.
a b и
Рис. 8.10.1. Область интегрирования
Двойной интеграл (8.10.1) можно свести к повторному интегралу:
Лф(и) . 6
Г }{u, v)dv)du= IF[u)du, (8.10.2)
п
a >(u)
где
F(u) = 7 f(u, v) dv.
tp(u)
Применим к последнему интегралу квадратурную формулу и получим
/ = / / /(w, v)dudv « y^Oi^^t),
(8.10.3)
(8.10.4)
27 — 5293 Голованов
418
Гл. 8. Вычисление геометрических характеристик
где «Zj — весовые множители используемой квадратурной формулы. В свою очередь
значения F(ui) так же могут быть найдены с помощью квадратурных формул
F(Ui) = J f(uh v)
dv
Таким образом, двойной интеграл (8.10.15) приближенно определится формулой
m п го п
y?jaiy?jbjf(ui,Vj) = Ylyll'w4f(ui>vi)' (8.10.5)
(/ i=i j=\ i=\ j=i
где u>ij — dibj — постоянные коэффициенты, вычисленные по весовым множите-
множителям. В случае использования квадратурных формул Гаусса (8.9.14) кубатурная формула
(8.10.5) примет вид
. -
= \I f{u,v)du
= Jj /(u, v)dudv = Jl j /(u, v) dv\
du да
«
i-а
^/(»<. ">)> (8-10-6)
где
a + b b — a
j, i — 1, 2, ..., m —
2 ' - 2 ' ~3 2 ' " 2
параметры корней полинома Лежандра Рт(х), w\, W2, ¦ ¦ •, wm — соответствующие
им весовые множители, yj, j = 1, 2, ..., п — параметры корней полинома Лежандра
Рп(у), zi, z2, ..., zn — соответствующие им весовые множители.
Кубатурная формула Гаусса на четырехугольной области. Пусть при интегрирова-
интегрировании по поверхности общего вида мы разбили ее область определения параметров на
выпуклые четырехугольники. Рассмотрим вычисление двойного интеграла на четы-
четырехугольной области с использованием квадратурных формул Гаусса. Пусть вершинам
Рис. 8.10.2. Четырехугольная область интегрирования
четырехугольника соответствуют параметры ua, va, иь, ьь, ис, vc, Ud, Vd, которые объ-
объединим в точки ра = [иа va]T, рь = [щ vb]T, рс = [ис vc]T, pd — [ud vd]T на плоскости
параметров (рис. 8.10.2).
Пусть требуется вычислить определенный интеграл
= / / f(u, v)dudv
(8.10.7)
8.10. Кубатурные формулы
419
на данной четырехугольной области. Если область интегрирования представляет собой
квадрат со стороной 2, то кубагпурнол формула Гаусса (8.10.6) примет вид
1 1
I = J jf{u,v)dvdu*l
где ui, иг, • •., um — корни полинома Лежандра Pm(u), w\, W2, ¦ ¦ -, wm — соответствую-
соответствующие им весовые множители, ы, v2, ..., vn — корни полинома Лежандра Pn(v), z\,
Z2, ¦ ¦ ¦, zn — соответствующие им весовые множители. Заменим переменные в двойном
интеграле (8.10.7). Для произвольной выпуклой четырехугольной области введем новые
параметры х и у, связанные с параметрами и и v соотношениями
и{х,у) = иа
1-х-у + ху
1-х-у + ху
1 + х-у-ху 1 + х + у + ху 1-х + у-ху
+ ис + ud -,
1 + х-у-ху 1 + х + у + ху 1-х + у-ху
+VC +Vd
ди
дх
dv
Ъ1с
ди
ду
dv
Ъ~у
Ф,У) =Va^+Vb+VC+Vd.
(8.10.9)
Точкам ра, рь, pc, pd соответствуют параметры жа = — 1, j/o = — 1; хь = 1, уь = — 1;
хс = 1, ус = 1; хв. — —1, yd = 1- Функции (8.10.9) являются непрерывными, имеют
непрерывные частные производные первого порядка и отображают квадрат с вершинами
в точках х = ±1, у = ±1на заданную четырехугольную область интегрирования. Это
отображение взаимно однозначно и имеет отличный от нуля якобиан
J(x, у) =
(
= Q (("с - Ua)(Vd ~ Vb) + (Щ - Ua)(vc - Vd)x + (uc ~ Ub)(vd ~ Va)y -
О
- (ud - Ub)(vc ~ va) - (ыс - Ud){vb - va)x - (ud - ua)(vc - vb)y). (8.10.10)
После замены параметров в интеграле (8.10.7) получим
1 1
I f(u, v)dudv =11 f{u(x, у), v(x, y))J(x, y)dxdy&
-l-i
). (8.10.11)
j=lJ=l
где xi,X2, ..., xm — корни полинома Лежандра Pm(x), wi, u>2, ¦ ¦ •, wm — соответствую-
соответствующие им весовые множители, j/i, 3/2, ¦¦•> Уп — корни полинома Лежандра Рп(у), z\,
Z2, ¦ ¦., zn — соответствующие им весовые множители.
27*
420
Гл. 8. Вычисление геометрических характеристик
Кубатурные формулы на треугольной области. Пусть мы разбили область определе-
определения параметров поверхности на треугольники. Покрытие некоторой области треуголь-
треугольниками называется триангуляцией. Рассмотрим вычисление интеграла (8.10.7) по
треугольной области параметров поверхности и и v для одного такого треугольника.
«а. %
Рис. 8.10.3. Треугольная область интегрирования
Пусть его вершинам соответствуют параметры иа, va, иь, ьь, ис, vc, которые объеди-
объединим в точки ра = [иа va]T, рь = [щ Уь]Т, рс = [ис vc]T на плоскости параметров
(рис. 8.10.3).
Площадь 5 треугольника раРьРс равна половине определителя C.11.5)
1
Wo
Va
1
Щ
Vb
1
Uc
Vc
1
0
UcVa —
— VcUa)-
Для треугольных областей удобно перейти от координат и и v к трем барицентриче-
барицентрическим координатам а, Ь, с, определяемых равенствами C.11.4). Барицентрические ко-
координаты произвольной точки р = [и v]T равны площади треугольника, полученного
113 Ра Рь Рс заменой соответствующей вершины точкой р, деленной на площадь 5.
Барицентрические координаты в сумме равны единице. Обратный переход от барицен-
барицентрических координат треугольника к параметрам и и v осуществляется по формулам
и = аиа + Ьиь + cuc,
v = ava+ bvb + cvc.
(8.10.12)
Таким образом, интегрируемую функцию f(u, v) можно представить в виде функции
барицентрических координат /(а, Ь, с) = f(u(a, b, с), v(a, b, с)).
Поставим задачу найти значения барицентрических координат a*, bi, ci и весовые
множители u>i, i = 1, 3, 4, ..., Згг, Зп + 1, чтобы формула
I = JJ /(u, v)dudv =
h, Ci),v(ai, bit a))
(8.10.13)
была бы точной для некоторых полиномов p{u(a, b, с), v(a, b, с)) на треугольной обла-
области. Из трех барицентрических координат только две являются независимыми. В ка-
качестве независимых параметров, не теряя общности, выберем первые две барицентри-
барицентрические координаты. Третья координата связана с двумя другими равенством C.11.2).
Используя равенства (8.10.12) в форме
(8.10.14)
U = а(иа - Ue) + Ь(щ - Uc) + Uc,
v = a(va - vc) + b(vb - vc) + vc
8.10. Кубатурные формулы
421
перепишем интеграл (8.9.15) в виде
/ / f(u, v)dudv = / / f(u(a, b, c), v(a, b, c))j(a, b, c)dadb =
A A
1 , 1-a v
= [[ f /(«(a. b), v(a, b))J{a, b)db)da, (8.10.15)
где интегрирование проводится по треугольной области, а J(a, b)
зования координат
якобиан преобра-
преобраJ(a, Ъ) =
ди
la'
dv
Ъ~а
ди
~дь
dv
ua —ис щ — ис
Va —Vc Vb ~ Vc
= (uo - uc)(vb - vc) - (va - vc)(ub - uc) -
= UaVb
UcVa —
— VcUa = 25.
Потребуем, чтобы барицентрические координаты a,, bi, c\ в (8.10.13) обладали неко-
некоторой треугольной симметрией, например, чтобы две из трех координат были бы равны
между собой. При такой симметрии число точек, по которым производится суммирова-
суммирование, должно быть кратно трем. Для определения параметров трех симметрично распо-
расположенных точек в сумме (8.10.13) нужно знать одну из барицентрических координат.
Все три барицентрические координаты трех точек будут определены, если найдена одна
из них. Пусть одна из барицентрических координат в правой части (8.10.13) равна z,
тогда три симметрично расположенные точки будут иметь координаты
= Z,
1-z
1-z
2 '
a2 =
a3 -
2 '
1-z
2 '
fa = z,
fa = —
c2 =
1-z
2 '
1-z
2 '
(8.10.16)
2 '
c3 = z.
В силу симметрии все три точки должны иметь одинаковые весовые множители w\ =
= u>2 = и>з- В случае, если z = 1/3, три точки сливаются в одну. Таким образом, на
треугольнике в правой части (8.10.13) могут быть использованы следующие количества
точек: 1, 4, ..., 3(п — 1) + 1 или 3, б, ..., Зп. Для определения барицентрических
координат и весовых множителей требуется соответствующее число уравнений: 1,3,...
..., 2п — 1 или 2, 4, ..., 2п. Потребуем, чтобы выполнялось равенство (8.10.13) для всех
функций вида
/(«(о, Ь, с), v{a, Ь, с)) =
+ Bmbm + Cmcm),
(8.10.17)
m=l
где Am, Bm, Cm — коэффициенты полиномиального представления заданной функ-
функции, и найдем независимые барицентрические координаты и весовые множители. При
п > 2 функция вида (8.10.17) не представляет собой полную функцию степени п двух
переменных и и v, но обладает треугольной симметричной на заданной области. Для
функций f(u, v) = f(u(a, b, c), v(a, b, с)) = f(a, b) вида
f(a,b) = am, f(a,b) =
m = 1, 2, .. , n,
422 Гл. 8. Вычисление геометрических характеристик
в соответствии с формулой (8.10.13) и (8.10.15) должны выполняться равенства
\ ( *7а \ k
о \ о / i=i
или
1 , 1-а ч k
1I f amdb)da=^J2wiaim, m = 1,2, ..., п, (8.10.18)
\ / ' 1
О ч О
1-а \ , к
ldb\da= -^Wib™, m=l, 2, ..., n, (8.10.19)
0 \ 0 / »=i
Jl J cmdb\da=^j^v)icim, m = l,2>...,n, (8.10.20)
n V n / 1=1
о ч о
3 3
где к = — (тг — 1) + 1 при нечетных п и к = -п при четных п.
В то же время путем интегрирования по треугольной области получим
1 , 1-а х
/[ f amdb)da= -^ -г, (8.10.21)
о^о '
1 , 1-а ч
/( [bmdb)da=- ~ -, (8.10.22)
J \ J I (m+l)(m + 2)
п \ о '
1-а v
I cmdb\da- -у =¦. (8.10.23)
О v О
1 / 1-а
о ч о
Подставим (8.10.18)-(8.10.20) в (8.10.13) и получим
ff{Aia + Bib + Cic) dadb + ff (A2a2 + B2b2 + C2c2) dadb + ...
л л
к к
...+ f[(Anan + ВпЬп + Спсп) dadb=\
12 Wiai"+B»Y,Wibin+c»fl
i-l i=l i=l
\ (An 12 Wiai"+B»Y,Wibin+c»flWiCi") • (8-10-24)
8.10. Кубатурные формулы 423
Для нахождения барицентрических и весовых множителей приравняем выражения при
Ai, Bi, Ci, г = 1, 2, ..., п в правой и левой частях равенства (8.10.24). В силу треуголь-
треугольной симметрии это достаточно сделать для набора коэффициентов при одной из бари-
барицентрических координат. Например, из равенства выражений при Ai, i = 1, 2, ..., п в
правой и левой частях равенства (8.10.24) с учетом равенств (8.10.21)-(8.10.23) получим
систему п уравнений
1
+ w2a2 + w3a3 + .. ¦ + wkak = -,
-f- W2(L2 -f- W3(L3 -f- . . . -f" Wkdk — —
6
+ uJa23 + W3CI33 + • ¦ • + wkak3 = —,
3 3
где k = -(n — 1) + 1 при п нечетном и k = —n при п четном. При п нечетном бари-
барицентрические координаты одной из точек известны, так как она совпадает с центром
треугольника. При п = 1 получим одно уравнение для веса центральной точки и будем
иметь:
1 и 1 1
ао = д' "° = з' °° = V w° =
При п = 2 будем иметь два уравнения
1-z l-z 1
+
WZ 1 u/ -1 - ^ — ,
_ 2
WZ 1 u/ 1 n 1 1 uy 1 - 1 ,
о
из которых с учетом (8.10.16) получим три симметрично расположенные точки на тре-
треугольной области:
_2 1-z _ 1 1-z 1 _ _1
1-z 1 , 2 1-z 1 1
»2 = Z = -,
= , b=z=-, <» = — = -, w2=w = -,
1-z 1 , 1-z 1 2 1
или три равноценные им точки
, 1-z 1 1-z 1 1
ai=z =
1-z 1 1-z 1 1
0-2 = .—^— = 2» 62 = z = 0, c2 = —^ = -, w2 = w = -,
1-z 1 , 1-z 1 1
аз = Т = Г Ьз = ~Г = Г C3 = z = 0' t"s = to = -.
424 Гл. 8. Вычисление геометрических характеристик
При п = 3 будем иметь три уравнения
1-z 1-2 1 1
+ + +
2 2 3
WZ*
wz3
из которых с учетом (8.10.16) получим вес wo для центральной точки и координаты z,
A - z) /2, A — z)/2 и веса w еще для трех симметрично расположенных точек на
треугольной области. При п = 4 будем иметь уравнения для шести точек и их весовых
коэффициентов:
_ 1
3'
2 A-гхП / а A - г2)
A-^)^ .... Лз , A-*2K\ 1
10'
, , (l-^L^ / 4 A-22LN 1
8 У ' -' V ' 8 ) 15
При п = 5 и будем иметь уравнения для весового коэффициента центральной точки и
шести точек и их весовых коэффициентов:
1 1
Wl +W2 +Wo~ = ~,
1
1
21'
В табл. 8.10.1 приведены значения барицентрических координат и весовые множи-
множители для кубатурных формул по треугольной области при п — 1, 2, 3, 4, 5. При п > 5
система уравнений для определения барицентрических координат не имеет решения.
Для более точного вычисления двойных интегралов можно разбить треугольную область
ш^ретрирования на несколько треугольных подобластей.
8.11. Разбиение поверхностей при интегрировании
425
к
1
3
ai
1/3
2/3
1/6
1/6
bi
1/3
1/6
2/3
1/6
a
1/3
1/6
1/6
2/3
Таблица 8.10.1
Wi
1
CO CO CO
1—1 1—1 1—1
где
где
где
где
где
1/3
a
b
b
a = 0,6
1/3
6
a
6
1/3
b
b
a
= 0,2
-0,5625
0,5208333333333333
0,5208333333333333
0,5208333333333333
ai
6i
bi
O2
62
62
6l
ai
62
a2
b2
61
b2
a2
ai = 0,8168475729804581
a2 = 0,1081030181680702
0,1099517436553224
0,1099517436553224
0,1099517436553224
0,2233815896780112
0,2233815896780112
0,2233815896780112
61 = 0,0915762135097711
b2 = 0,4459484909159648
1/3
a\
61
61
a2
62
62
1/3
61
61
b2
a2
62
1/3
61
61
ai
62
b2
a2
ai = 0,7974269853530880
a2 = 0,0597158717897742
0,225
0,1259391805448265
0,1259391805448265
0,1259391805448265
0,1323941527885112
0,1323941527885112
0,1323941527885112
bi = 0,1012865073234560
b2 = 0,4701420641051129
Погрешность кубатурных формул для треугольных областей имеет порядок
5 • max(dn+1f/dun+1, dn+1f/dvn+1) и при тех же вычислительных затратах она
больше погрешности соответствующих кубатурных формул Гаусса.
Рассмотренные кубатурные формулы применяются для вычисления геометриче-
геометрических характеристик тел.
8.11. Разбиение поверхностей при интегрировании
При численном интегрировании по поверхности требуется разбить область
определения ее параметров на небольшие четырехугольные или треугольные
подобласти. Размер каждой подобласти определим условием: угловое изменение
нормали поверхности в подобласти не должно превышать некоторую заданную
величину Да. В соответствии с формулами D.2.4) и D.2.5) изменение параме-
426 Гл. 8. Вычисление геометрических характеристик
тров поверхности в каждой подобласти не должны превосходить величин
(8.11.1)
Av = *?^ (8Л1.2)
где gn и g22 — коэффициенты первой основной квадратичной формы поверх-
поверхности A.7.8), 6ц и &22 — коэффициенты второй основной квадратичной формы
поверхности A.7.21). Таким образом, мы заменим двухмерную область опреде-
определения параметров совокупностью стыкующихся между собой четырехугольни-
четырехугольников и треугольников.
Рассмотрим разбиение поверхности, показанной на рис. 8.11.1.
Поверхность получена путем усечения контурами NURBS поверхности.
Разобьем прямоугольную область umin ^ u ^ umax, ит;п ^ v ^ vma,x, где
^mim ^maxj ^minj ^max определяют габаритный прямоугольник внешнего гранич-
граничного контура, на прямоугольные подобласти двухмерными линиями щ = const
Рис. 8.11.1. Поверхность для численного интегрирования
и Vj = const, i = 1, 2, ..., m, j = 1, 2, ..., п. Параметрические расстояния
Ащ = щ+i — iij между соседними линиями щ = const в соответствии с форму-
формулой (8.11.1) возьмем равными
для всех vm\n ^ v < umax. (8.11.3)
Параметрические расстояния Avj = uj+j — Vj между соседними линиями Vj =
= const в соответствии с формулой (8.11.2) возьмем равными
Avi = min —г^т^—Y-^- для всех umin < и < umax. (8.11.4)
^ b22[U, Vj) J
На рис. 8.11.2 приведено разбиение области ит{п ^ и ^ итах, vm-m ^ v ^ vmax
базовой NURBS поверхности описанным способом.
Область определения параметров поверхности разбита на прямоугольники,
ноТВ=згг искривленности поверхности каждая подобласть представляет собой
криволинейный четырехугольник.
8.11. Разбиение поверхностей при интегрировании
427
Далее определим те прямоугольники, которые целиком лежат внутри огра-
ограничивающих поверхность контуров (рис. 8.11.3).
Не вошедшую в прямоугольные подобласти часть поверхности r(u, v) разо-
разобьем на треугольные подобласти (рис. 8.11.4).
Рис. 8.11.2. Разбиение прямоугольной области определения параметров поверхности
Рис. 8.11.3. Незаконченное разбиение поверхности
ч,
ч.
\
4,
^5=
4
Г 1 1 1
»^-
>
\
^2
^?
Рис. 8.11.4. Разбиение поверхности при численном интегрировании
428 Гл. 8. Вычисление геометрических характеристик
В результате разбиения двухмерные граничные контуры будут заменены ло-
ломаными линиями. Угол между касательными к участкам этих ломаных линий
не должен превосходить заданную величину Да. Вершины ломаной лежат на
граничных контурах. Параметрическое расстояние At между вершинами будем
вычислять в соответствии с D.2.3) по формуле
Aa\dc/dt\2
At > (8Л1-5)
At ~ \dc/dt х
где c(t) = r(u(t), v(t)) — кривая граничного контура поверхности r(u, v). Вер-
Вершинами треугольных подобластей являются вершины ломаных и вершины
четырехугольных подобластей. Построение треугольников по заданным вер-
вершинам можно выполнить с помощью алгоритма триангуляции Делоне.
Методы разбивки области определения параметров поверхности на треуголь-
треугольные подобласти (методы триангуляции поверхности) мы рассмотрим в следую-
следующей главе.
Глава 9
КОМПЬЮТЕРНАЯ ГРАФИКА
9.1. Визуализация геометрических объектов
Одним из наиболее ярких применений геометрического моделирования
является компьютерная графика. Исходная информация для получения изо-
изображения некоторого объекта на экране компьютера поставляется геометриче-
геометрической моделью этого объекта. На практике используются различные способы
визуализации геометрических объектов. Наиболее простой из них — отобра-
отображение линиями. Он позволяет получить общее представление об объекте, его
размерах и форме. С помощью компьютера можно получить изображение мо-
моделируемого объекта, близкое к его фотографии. Геометрической модели или
ее частям можно придать любой цвет и освещенность. Кроме того, объект на
экране можно заставить двигаться в реальном времени и тем самым получить
видеофильм.
Для того чтобы увидеть, как выглядит объект, нужно смоделировать пове-
поведение потока лучей света, идущего от источников к модели и от поверхности
модели к наблюдателю. При этом граням модели можно придать необходи-
необходимый цвет, зеркальность, прозрачность, излучение, фактуру и другие физиче-
физические свойства взаимодействия со световыми потоками. Модель можно осветить
с разных сторон светом различного цвета и интенсивности. Реалистические
отображения объектов строятся из отдельных точек определенного цвета и яр-
яркости, причем точки должны быть сравнительно небольшой величины и распо-
располагаться достаточно близко друг к другу (расстояние между точками не должно
превосходить размеры точек).
Изображения геометрических объектов линиями называются векторными,
а изображения геометрических объектов точками называются растровыми.
Примеры векторного и растрового изображений приведены на рис. 9.1.1 и 9.1.2.
Растровая графика более информативна, чем векторная, так как позволяет
получать тоновые изображения, но требует больше ресурсов и склонна к искаже-
искажению при редактировании. В обоих случаях мы видим проекции геометрических
объектов на выбранную плоскость.
Проекции могут быть построены с помощью линий, перпендикулярных про-
проекционной плоскости, или с помощью линий, проходящих через общую точку.
Первые называются параллельными проекциями (рис. 9.1.3), вторые — цен-
центральными проекциями или перспективными изображениями (рис. 9.1.4).
Центральные проекции могут быть созданы на плоскости или криволинейной
поверхности. Мы рассмотрим центральные проекции на плоскости.
Центральные проекции геометрических объектов ближе к тому изображе-
изображению, которое возникает на сетчатке глаза, поэтому они дают более реалистиче-
реалистические картины. Хотя центральные проекции ближе к тому, что можно наблюдать
430
Гл. 9. Компьютерная графика
в реальности, размеры отдельных частей объекта на центральных проекциях
зависят от их расстояния до точки наблюдения, поэтому в качестве конструк-
конструкторской документации чаще используются параллельные проекции..
Рис. 9.1.1. Векторное изображение
Рис. 9.1.2. Растровое изображение
Рис. 9.1.3. Параллельная проекция
Рис. 9.1.4. Центральная проекция
Растровая и векторная графика, а также параллельные и центральные про-
проекции не являются альтернативами. Они дополняют друг друга. В данной главе
мы рассмотрим методы визуализации геометрических объектов с помощью ком-
компьютера или методы компьютерной графики.
9.2. Параллельные проекции на плоскость
Параллельные проекции геометрических объектов используются для получе-
получения чертежей, схем и других документов, где требуется сохранить определенную
геометрическую точность относительных размеров и взаимного расположения
отдельных частей объектов.
Пусть требуется построить параллельную проекцию геометрических объек-
объектов на плоскость, которая определяется точкой q и двумя взаимно ортогональ-
ортогональными векторами единичной длины i^ и iy. Проекционная плоскость может быть
связана с чертежом, экраном компьютера или каким-либо другим устройством
9.2. Параллельные проекции на плоскость
431
вывода. Систему координат, в которой описаны отображаемые объекты, будем
называть глобальной системой координат. Свяжем с проекционной плоско-
плоскостью местную систему координат Qxyz. Пусть начальная точка q местной
системы координат в глобальной системе координат описывается радиус-век-
радиус-вектором q = [gi q2 Яг]7, а орты ix, iy, i2 = ±ix x iy местной системы коорди-
координат в глобальной системе координат описываются векторами i^ = [х\ х2 хз]Т,
iy = [У1 У2 Уз]Т! iz = [zi Z2 ?з]Т- Местная система координат может быть как
правой (iz = \х х iy), так и левой (iz = —ix x i^). На рис. 9.2.1 приведен пример
Рис. 9.2.1. Проекционная плоскость
Рис. 9.2.2. Проекция объекта
построения местной системы координат и параллельных проекций ребер пря-
прямого параллелепипеда на плоскости, определяемой радиус-вектором точки q и
ортами ij;, iy, iz. На рис. 9.2.2 приведены параллельные проекции ребер прямого
параллелепипеда на плоскости.
Проекция точки. Рассмотрим произвольную точку г = [п гг ^з]Т- Опреде-
Определить двухмерную точку р = [х у]г, являющуюся ее проекцией на проекционной
плоскости
p{x,y) = q + xix + yiy. (9.2.1)
Параллельную проекцию произвольной точки г отображаемых объектов полу-
получим, опустив из нее перпендикуляр на проекционную плоскость. Пусть точка
г = [г\ 7~2 1~з]Т в местной системе координат имеет координаты х, у, z. Коорди-
Координаты связаны соотношениями A.2.8), которые в данном случае имеют вид
+ x2r2 + Х3Г3 + ох,
+ + + Оу, (9.2.2)
х = xi{n - qi) + x2{r2 - Я2) + хз{гз - ?з) =
У - yi(n - <?i) + У2{г2 - Ы + Уз{гз - 9з) =
z = zi{n- qi) + z2{r2 - 92) + 23G-3 - <7з) =
+ У2Г2 +
+ z2r2
o
z,
где
ox = -xiqi - x2q2
oy = -yiqi - y2q2
- z2q2
432
Гл. 9. Компьютерная графика
В однородных координатах преобразование (9.2.2) описывается равенством
A.4.8)
X
У
z
Л.
Xl
L О
2/2
22
О
УЗ
О
Ox
Оу
Ог
1.
тг
.1.
= А0
Ti"
Г2
Г3
. 1.
(9.2.3)
Коэффициенты расширенной матрицы преобразования выражаются через ком-
компоненты векторов, определяющих положение проекционной плоскости.
Проекция точки на плоскость (9.2.1) описывается первыми двумя коорди-
координатами вектора (9.2.3). Таким образом, первые две координаты расширенного
радиус-вектора, полученного по формуле (9.2.3), являются координатами иско-
искомой параллельной проекцией г = [х у]т рассматриваемой точки.
Масштаб проекции. С помощью преобразования (9.2.3) может быть полу-
получена проекция точек линий в масштабе 1:1, если единица измерения длины
для устройства вывода равны единице измерения пространства, в котором по-
построена геометрическая модель. Вывод на экран компьютера производится в
экранных единицах — пикселах. Пусть при построении геометрической мо-
модели использовалась единица длины — миллиметр. Если размер пиксела не
равен миллиметру, то для получения на экране изображения геометрического
объекта в масштабе 1:1 радиус-вектор каждой точки проекции следует умно-
умножить на масштабную единицу устройства вывода, равную количеству пикселей
в одном миллиметре. Масштабная единица может быть различной для коорди-
координаты х и координаты у. В последнем случае радиус-вектор г = [х
проекции необходимо умножить на матрицу
О
IT
точки
М =
тх
О т.
(9.2.4)
Если требуется получить изображение объекта в масштабе т: 1, то радиус-
вектор двухмерной точки проекции следует преобразовать по формуле A.3.17).
Таким образом, координаты х' и у' проекции некоторой точки г геометрического
объекта с учетом масштаба равны
т
+ т
п
Г2
гз
. 1 .
[Уо
(9.2.5)
где Хо и уо —-координаты точки, которая при масштабировании должна остаться
неподвижной. Вместо матрицы Ао в (9.2.5) используется матрица, содержащая
ее первые две строки.
Мы видим, что для получения координат х' и у' плоской проекции некоторой
точки г = [?"i Г2 гз]Т достаточно знать положение проекционной плоскости в
пространстве (орты плоскости проекции ix = [х\ Х2 хз]Т, iy = [у\ У2 Уз]Т>
iz = ±ixxiy, положение центра плоскости q = [gi дг <7з]Т), масштабные единицы
тх и ту устройства вывода и масштаб отображения т.
9.3. Центральные проекции на плоскость
433
9.3. Центральные проекции на плоскость
В параллельной проекции на плоскость каждая точка геометрического объ-
объекта проецируется на заданную плоскость вдоль одного и того же направления
независимо от положения точки в пространстве. Если размеры объекта соиз-
соизмеримы с расстоянием до объекта, то параллельная проекция объекта будет
отличаться его фотоизображения. Вид также будет отличаться и от фотогра-
фотографии объекта. Это происходит потому, что изображение на сетчатке глаза и на
фотографии получено не с помощью параллельной проекции. Реальное изобра-
изображение близко к центральной проекции объекта на плоскость. Центральные
проекции называют также перспективными изображениями. При графиче-
графическом отображении геометрической модели центральные проекции дают более
реалистичную картину, чем параллельные проекции. Центральная проекция
представляет собой выполненную по определенным правилам проекцию модели
объекта на плоскость и также как и параллельная проекция является плоским
объектом и строится с помощью двухмерных линий.
Пусть требуется построить центральную проекцию геометрических объек-
объектов на плоскость, которая определяется точкой q и двумя взаимно ортогональ-
ортогональными векторами единичной длины ix и iy. Свяжем с проекционной плоско-
плоскостью местную систему координат Qxyz. Пусть начальная точка q местной
системы координат в глобальной системе координат описывается радиус-век-
радиус-вектором q = \q\ qi <7з]Т> а орты ix, iy, iz = ±ix X ij, местной системы коорди-
координат в глобальной системе координат описываются векторами ix = [х\ Х2 хз]Т,
hi = fa/i У2 Уз]Т, iz = [zi z2 z3]T.
Для построения центральной проекции на плоскость требуется знать еще
точку пространства, из которой ведется наблюдение. Эту точку будем называть
точкой наблюдения (точка наблюдения для параллельной проекции находится
в бесконечности в положительном направлении нормали к проекционной плос-
плоскости). Пусть точкой наблюдения является точка W. Проекцию точки W на
проекционную плоскость обозначим через F. На рис. 9.3.1 приведены местная
F
Рис. 9.3.1. Построение центральной проекции Рис. 9.3.2. Центральная проекция объекта
система координат, точка наблюдения и центральные проекции ребер прямого
параллелепипеда. На рис. 9.3.2 приведены центральные проекции ребер пря-
прямого параллелепипеда на плоскости. Если провести плоскость через точку на-
наблюдения, параллельную плоскости проекции, то проецируемый объект должен
полностью лежать в той же части пространства, что и плоскость проекции.
28 - 5293 Голованов
434
Гл. 9. Компьютерная графика
Проекция точки. Рассмотрим построение центральной проекции одной из
вершин прямого параллелепипеда на плоскость (9.2.1). На рис. 9.3.3 рассма-
рассматриваемая точка обозначена через R, а ее центральная проекция обозначена
через Р. Центральная проекция произвольной
точки R строится следующим образом. Пост-
Построим прямую линию, проходящую через точку
наблюдения W и проецируемую точку R. Точ-
Точка Р, в которой эта прямая или ее продолжение
пересекают проекционную плоскость, и явля-
является центральной проекцией точки R.
Радиус-вектор точки R обозначим через г,
/Т^^'л^'Т ~~~~~~^~Л а РаДиУс"вект0Р ее центральной проекции —
У^ через р. Пусть проецируемая точка в глобаль-
глобальной прямоугольной декартовой системе коорди-
координат описывается радиус-вектором с координа-
координатами г = [п Г2 гз]т, а в системе координат
Qxyz, связанной с проекционной плоскостью,
эта точка имеет координаты х, у, z. Коорди-
Координаты точки г в этих координатных системах
связаны соотношением (9.2.3). Обозначим ра-
радиус-вектор точки наблюдения через w. Пусть в местной системе координат
он имеет координаты xw, yw, zw. Расстояние от точки наблюдения W до ее
проекции на плоскость F равно zw. Построим отрезок RA, параллельный от-
отрезку PF. Длина отрезка WA равна zw — z.
Рассмотрим на рис. 9.3.3 два подобных треугольника: WFP и WAR. Из
подобия треугольников следует, что PW/FW = RW/AW. Запишем последнее
равенство в векторном виде:
w
Рис. 9.3.3. Построение цент-
ральной проекции точки R
р — w
г — w
(9.3.1)
Используя это равенство, найдем радиус-вектор р центральной проекции точки г
р = w + (г — w)-
Z-w
= г-
— W-
zw - z
zw - z
zw - z
(9.3.2)
Чтобы получить координаты точки р в проекционной плоскости, нужно с по-
помощью равенства (9.2.3) перевести вектор г ив глобальной системы координат
в местную систему координат. Первые две координаты вектора р в проекци-
проекционной системе координат и будут координатами центральной проекции точки г
на плоскости (9.2.1). Запишем равенство (9.3.2) в местной системе координат:
хр
УР
Z
Z
zw ~~
Z
yw
М
w
xzw — zx
yzw - zyw
0
(9.3.3)
Таким образом, декартовы координаты двухмерной точки р = [хр ур]т, являю-
являющейся центральной проекцией рассматриваемой точки г в пространстве, на
9.3. Центральные проекции на плоскость
435
плоскости (9.2.1) равны
zm - z
yzw - zyw
Zw-Z
(9.3.4)
Если удалить точку наблюдения на бесконечное расстояние от проекционной
плоскости, то zw —> оо и хр —> х, ур —> у.
В расширенном матричном виде с учетом (9.2.3) равенство (9.3.3) можно
записать следующим образом:
p
yPd
Zpd
zw 0
0 zw
0 0
0 0
-xw
-Уы
0
-1
0"
0
0
zw
х~
У
z
1
\zw 0
0 zw
0 0
0 0
Xw
-yw
0
-1
Х\ Х2 Х3 Ох
У\ У1 Уз оу
Z\ Z2 Zz Oz
0 0 0 1
(9.3.5)
Напомним, что пространственные координаты вектора равны первым трем
компонентам расширенного вектора, деленным на его четвертую компоненту.
В силу предположения, что проекционная плоскость и рассматриваемая точка
расположены с одной стороны от точки наблюдения, величина d = zw — z всегда
положительна. Формула (9.3.5) описывает преобразование координат из гло-
глобальной системы координат в двухмерную систему координат на проекционной
плоскости. Это является искусственным преобразованием, так как третья ко-
координата центральной проекции им не определяется (положена равной нулю).
Оно не имеет обратного преобразования, так как определитель одой из матриц
равен нулю.
Матрица преобразования. Центральную проекцию объекта можно получить
с помощью его преобразования по матрице
Xl
X2
xz
0
У1
У2
Уз
0
Z\
22
23
0
Qx
Qy
Qz
1
Zw
0
0
0
и
2*
0
0
~Xyj
-yw
1
-1
0
0
0
zw
Xl %2 X$ Oj;
У\ У2 УЗ Oj,
21 22 Z3 OZ
0 0 0 1
(9.3.6)
После такого преобразования объект исказится так, что его параллельная проек-
проекция на плоскость (9.2.1) будет совпадать с его центральной проекцией на эту же
плоскость. Определитель матрицы Aw не равен нулю, и преобразование (9.3.6)
обратимо.
Для того, чтобы учесть масштабные единицы устройства вывода и масштаб
проекции, двухмерный радиус-вектор р = [хр ур]т нужно умножить на матрицу
(9.2.4) и масштаб изображения.
На рис. 9.3.4 и 9.3.5 приведены перспективные изображения геометриче-
геометрического объекта. Для обоих рисунков использовалась одна и та же проекционная
436
Гл. 9. Компьютерная графика
плоскость, но на рис. 9.3.4 проекция точки наблюдения лежит слева и выше цен-
центра рисунка, а на рис. 9.3.5 проекция точки наблюдения лежит правее центра
п
_ 1
V
Рис. 9.3.4. Центральная проекция объекта
Рис. 9.3.5. Центральная проекция объекта
рисунка. Чем дальше от точки наблюдения находится объект, тем меньше его
перспективное изображение.
9.4. Полигоны кривых и поверхностей
Проекция на плоскость пространственного отрезка является отрезком на
плоскости, а параллельная проекция на плоскость пространственной ломаной
линии является ломаной линией на плоскости. Для того, чтобы получить изо-
изображение кривой линии, мы будем использовать проекцию полигона кривой.
Для каждой кривой линии мы построим набор точек р^, принадлежащих
кривой и следующих в порядке возрастания параметра. Соединив эти точки от-
отрезками, получим ломаную линию, аппроксимирующую заданную кривую ли-
линию. Набор точек для построения аппроксимирующей ломаной будем называть
полигоном кривой. Точки полигона будем вычислять достаточно близко друг
от друга, чтобы линии изображения казались плавными.
Определение шага кривой. Рассмотрим вычисление шага аппроксимации
кривой линии. Пусть задана кривая r(t) и пусть мы находимся в некоторой
ее точке io, являющейся точкой полигона. Требуется найти параметр t\ сле-
следующей точки полигона, так чтобы отклонение кривой от ее полигона не пре-
превышало заданную величину 5. Предположим, что в ближайшей окрестности
кривая близка к своей соприкасающейся в этой точке окружности (рис. 9.4.1).
Радиус р соприкасающейся окружности равен радиусу кривизны кривой и
определяется формулой
|г/|3
Р= 71ГТ377- (9-4-1)
х
По теореме Пифагора квадрат половины длины хорды равен р2 — (р — S) —
— 6Bр — S). Длина всей хорды будет равна
= 2y/5{2p-5).
(9.4.2)
9.4. Полигоны кривых и поверхностей
437
Если кривая близка к дуге соприкасающейся окружности и угол дуги достаточно
мал, то можно считать, что длина хорды примерно равна длине дуги кривой и
приращение параметра At на длине дуги кривой можно принять равным
(9.4.3)
'о.
Таким образом, параметр следующей точки полигона может быть принят рав-
равным t\ = to + At. При резком изменении направления или длины второй
производной в точке t\ по сравнению с предыдущей точкой формула (9.4.3)
дает ошибку, т. е. прогиб может оказаться
значительно больше 5. В этом случае шаг
должен быть уточнен путем определения
среднего радиуса кривизны кривой на рас-
рассматриваемом участке.
Формула вычисления параметрического
шага между точками полигона (9.4.3) по-
позволяет построить полигон кривой, отстоя-
отстоящий от самой кривой на величину, не пре-
превышающую 5. Проекция этого полигона
будет отстоять от проекции кривой также
на величину, не превышающую 5, при мас-
масштабе отображения 1:1 (т = 1). Вели-
Величину 5 будем называть точностью отображения. Для произвольного мас-
масштаба отображения т:\ проекция полигона кривой будет отстоять от проекции
кривой на величину, не превышающую т5. Таким образом, если мы хотим
получить проекцию кривой в масштабе т : 1 с точностью отображения 5, то
мы должны построить полигон, точки которого находятся на параметрической
расстоянии, не превышающем
Рис. 9.4.1. Вычисление шага по пара-
параметру кривой по заданному прогибу 6
At
<у/E/т)BР-5/т)
(9.4.4)
Шаг по параметру кривой мы вычисляли при выполнении операций. Шаг
D.2.3) определяется углом отклонения кривой и не зависит от ее размеров и
масштаба отображения. Шаг (9.4.4) определяется точностью отображения и
зависит от размеров кривой и масштаба отображения.
Определение шага кривой на поверхности. Шаг для полигона кривой ли-
линии на поверхности вычислим аналогично вычислению шага полигона кривой.
Пусть точка некоторого полигона поверхности г(щ, vo) определяется параме-
параметрами щ и vq. Найдем параметры и\ и v\ следующей точки поверхности так,
чтобы пространственный отрезок из точки г(«о, ^о) в точку r(ui, V\) отстоял
от поверхности на расстоянии, не превышающем заданной величины 8. Для
этого вычислим радиус кривизны линии на поверхности, имеющей направле-
направление du : dv. Кривизна линии на поверхности определяется формулой A.8.5), а
ее радиус кривизны определится равенством
_
g\\du2 + 2g12 du dv + g22 dv2
&n du2 + 2&i2 du dv + 622 dv2'
(9.4.5)
438
Гл. 9. Компьютерная графика
Подставим (9.4.5) в (9.4.4) и получим приращения для параметров соседней
точки полигона
y/E/m)Bp-5/m)
\ri + r2(dv/du)\ '
у/E/т)Bр-5/т)
\ri(du/dv) + r2\
(9.4.6)
где ri = дг/du и Гг = дг/dv, т — масштаб отображения. В частных слу-
случаях для и-полигонов получим ри = gu/Ьц, а для и-полигонов — pv = g22/b22.
Соответственно ненулевые шаги вдоль координатных «-линий и и-линий по-
поверхности равны
д,_„,
Аи = 0, Av и 2
V(S/m)B(g22/b22)-S/m)
\dr/dv\
(9.4.7)
(9.4.8)
где glb g12, g2i, g22> Ьц, 6i2, 621, 622 — коэффициенты первой A.7.8) и второй
A.7.21) основных квадратичных форм поверхности. Как можно заметить, шаги
вычисляются приближенно. Это делается с целью уменьшения вычислительных
затрат. При необходимости шаги могут уточняться.
Величина прогиба 8 выбирается достаточно малой, чтобы не было заметно
изломов проекции в точках полигонов. Она составляет доли миллиметра. Рас-
Расстояние между точками полигона зависит от кривизны линии и может быть
достаточно большим.
Сетки полигонов. С помощью полигонов можно отобразить кривые линии,
поверхности или тела. Для удобства полигоны, принадлежащие одному гео-
геометрическому объекту, объединяют в сетки. Сетка представляет собой сово-
совокупность полигонов для векторного отобра-
отображения некоторого геометрического объекта.
Так сетка кривой состоит из одного поли-
полигона. Сетка поверхности состоит из поли-
полигонов ее границ и нескольких полигонов ее
u-линий и и-линий. Сетка тела состоит из
полигонов поверхностей его граней. Ото-
Отображение геометрических объектов полиго-
полигонами обладает универсальностью и просто-
простотой. Для получения параллельной проекции
полигона достаточно вычислить проекции
его точек и соединить их отрезками. На
рис. 9.4.2 приведен пример отображения
сетки поверхности, построенной по коорди-
координатным «-линиям и и-линиям.
В некоторых случаях для векторного ото-
отображения поверхности или тела граничных и координатных линий недоста-
недостаточно. Для большей информативности отображения кривых поверхностей и
граней к проекциям координатных линий добавляют проекции линий очерка.
Рис. 9.4.2. Проекции сетки полиго-
полигонов поверхности
9.5. Линии очерка 439
9.5. Линии очерка
Каждая поверхность одной из своих сторон может быть направлена к на-
наблюдателю и тогда эта сторона будет видимой. В противном случае сторона
поверхности будет не видна из точки наблюдения. Может случиться так, что
только часть стороны поверхности будет видимой. В этом случае на поверхности
можно построить линию, разделяющую видимую и невидимую чисти поверх-
поверхности. Линией очерка будем называть линию на поверхности, отделяющую
Рис. 9.5.1. Проекции линий очерка поверхности
Рис. 9.5.2. Проекции сетки полигонов и линий очерка
видимую часть поверхности или грани от невидимой ее части. На рис. 9.5.1
приведены линии очерка поверхности. На рис. 9.5.2 показаны линии очерка
совместно с сеткой поверхности.
При переходе через линию очерка нормаль поверхности меняет направление
по отношению к линии взгляда. В точках линии очерка нормаль поверхности
ортогональна линии взгляда. В общем случае у поверхности линий очерка может
быть несколько. Каждая линия очерка является пространственной кривой. Она
или замкнута, или оканчивается на краях поверхности. Для разных направле-
направлений взгляда существует своя совокупность линий очерка, поэтому при повороте
поверхности линии очерка необходимо строить заново.
Параллельные проекции. Для некоторых поверхностей, например, сферы,
цилиндра, конуса, линии очерка строятся достаточно просто. Рассмотрим об-
общий случай построения линий очерка поверхности.
Пусть требуется найти линии очерка поверхности, описываемой радиус-век-
радиус-вектором r(u, v). Каждая точка линии очерка для параллельной проекции на плос-
плоскость (9.2.1) должна удовлетворять уравнению
i*-m = 0, (9.5.1)
где m = m(u, v) — нормаль к поверхности, для которой строится линия очерка.
Для поверхности, описываемой радиус-вектором r(u, v), нормаль m(u, v) также
является функцией параметров и и v. Скалярное уравнение (9.5.1) содержит
два искомых параметра и, у. Если задать один из параметров, то другой можно
найти из уравнения (9-5.1), т.е. один из параметров является функцией от
другого. Для равноправия параметров их можно представить в виде функций
некоторого общего параметра t:
u = u(t), v = v(t). (9.5.2)
440 Гл. 9. Компьютерная графика
Результатом решения уравнения (9.5.1) является двухмерная линия
luv(t)=[u(t) v(t)]T, luv{t) E г(м, v) (9.5.3)
на поверхности г(u, v). Эта линия и есть линия очерка поверхности.
Мы построим линию очерка по упорядоченной совокупности точек, удовле-
удовлетворяющих уравнению (9.5.1). Точками мы называем пару параметров щ и
щ поверхности, являющихся координатами двухмерных точек на параметриче-
параметрической плоскости. Имея отдельные точки линии очерка, расположенные в порядке
их следования и на определенном расстоянии друг от друга, всегда можно найти
любую другую точку линии. Например, для нахождения точки, лежащей между
двумя заданными соседними точками линии очерка, проведем плоскость пер-
перпендикулярно соединяющему соседние точки отрезку и найдем общую точку
для поверхности и плоскости, решив три скалярных уравнения пересечения со-
совместно с уравнением (9.5.1). Положение плоскости на отрезке можно задать
параметром линии. По крайним точкам отрезка определяется нулевое прибли-
приближение для искомой точки. Таким образом, совокупность отдельных двухмер-
двухмерных точек линии очерка поверхности служит как бы нулевым приближением
этой линии, по которому одним из численных методов всегда можно найти точ-
точное положение точки. Алгоритм построения линий очерка поверхности можно
разбить на два этапа.
На первом этапе найдем хотя бы по одной точке на каждой линии очерка.
Для этого, шагая по поверхности и исследуя знак скалярного произведения m'iz
в соседних точках, найдем пары точек поверхности, в которых т-Ц меняет знак.
Взяв в качестве нулевого приближения средние значения параметров этих точек,
одним из численных методов найдем параметры и, v точки линии очерка. Пусть,
например, при переходе из точки [и\ ui]T в близкую к ней точку [u2 г»г]т m • iz
меняет знак. Тогда, положив и^°> = («i + иг)/2, у(°> = (vi + г>г)/2, с помощью
итерационного процесса метода Ньютона
(Ч ( "'Ь У** (9.5.4)
-(dm/dv)
или итерационного процесса
vW (9.5.5)
найдем параметры одной из точек линии очерка. Производные нормали mi и
1П2 определяются формулами Вейнгартена A.7.26), A.7.28). Таким способом
получим набор точек линий очерка. Точки из полученного на первом этапе на-
набора никак не связаны друг с другом и могут принадлежать различным линиям
очерка. Важно только, чтобы от каждой линии очерка в наборе присутствовала
хотя бы одна точка.
На втором этапе берем любую точку из имеющегося набора и, двигаясь от
нее с некоторым шагом сначала в одну сторону потом в другую, находим точку
за точкой искомую совокупность точек линии очерка. Направление движения
дает вектор
9.5. Линии очерка
441
где mi и ni2 — частные производные нормали m(u, v), ri и Г2 —¦ частные про-
производные радиус-вектора r(u, v) поверхности по параметрам и и v. Знак перед
слагаемым (mj x m)/|rj|, г = 1, 2 совпадает со знаком скалярного произведения
mj • iz. Шаг движения вычислим в соответствии с кривизнами поверхностей в
текущей точке по формуле (9.4.7) или по формуле (9.4.8). Если
ri
М'
то по формуле (9.4.7) дадим приращение параметру и и по формуле (9.5.4) най-
найдем соответствующий ему параметр v поверхности. В противном случае по фор-
формуле (9.4.8) дадим приращение параметру и и по формуле (9.5.5) найдем со-
соответствующий ему параметр и поверхности. Движение по кривой закончим,
когда дойдем до края одной из поверхностей или когда линия замкнется (новая
точка окажется на расстоянии текущего шага от точки старта).
В процессе движения будем проверять, не лежат ли вблизи пути следова-
следования точки из набора, полученного на первом этапе. Для этого по пути следо-
следования будем вычислять расстояние от текущей точки кривой очерка до каждой
точки из набора, полученного на первом этапе. Если вычисленное расстояние до
какой-либо точки набора соизмеримо с текущим шагом движения, то эту точку
удалим из набора как более ненужную. Так получим совокупность отдельных
точек [щ Vi]T, i = О, 1, 2, ..., п одной линии очерка. При этом в наборе то-
точек, полученном на первом этапе, не будет содержаться ни одной точки данной
линии. Если в наборе останутся еще точки, то данная поверхность имеет, по
крайней мере, еще одну линию очерка. Совокупность ее точек найдем, взяв
Рис. 9.5.3. Линии очерка тела
Рис. 9.5.4. Тело вращения
любую точку из набора и повторив второй этап построения. Построение линий
закончим, когда в наборе не останется ни одной точки. Описанным способом
построим линии очерка всех граней модели.
Линии очерка граней являются линиями очерка их поверхностей. Линия
очерка тела будет видимой, если она не закрыта гранью, лежащей ближе к точке
наблюдения. На рис. 9.5.3 приведена линия очерка тела вращения, показанного
на рис. 9.5.4. Проекция линии очерка может иметь изломы и точки возврата,
29 - 5293 Голованов
442 Гл. 9. Компьютерная графика
но сама линия очерка является гладкой. Точки излома у проекции возникают
там, где касательная линия очерка коллинеарна вектору iz.
Для построения проекции линии очерка будем строить ее полигон, проекцию
которого и возьмем в качестве проекции линии очерка.
Центральные проекции. Линии очерка в центральных проекциях удовлетво-
удовлетворяют уравнению
m-(r-w)=0, (9.5.7)
где m = m(u, v) — нормаль поверхности г = r(u, v), w — радиус-вектор
точки наблюдения. Линия очерка для центральной проекции отличается от ли-
линии очерка для параллельной проекции, хотя алгоритмы их построения ана-
аналогичны. Вместо постоянного вектора iz в (9.5.7) присутствует вектор г — w,
направление которого зависит от проецируемой точки. Линия очерка для цен-
центральной проекции также представляет собой некоторую кривую на поверхно-
поверхности, описываемую зависимостями (9.5.3), и является пространственной кривой.
Эта линия должна быть спроецирована на плоскость по правилам построения
центральной проекции пространственной линии.
На рис. 9.5.5 приведена параллельная проекция линий очерка тора, а на
рис. 9.5.6 для сравнения приведена центральная проекция линий очерка тора.
Как можно видеть, эти проекции отличаются.
Рис. 9.5.5. Параллельная проекция линий очерка тора
Рис. 9.5.6. Центральная проекция линий очерка тора
Алгоритм построения линий очерка для центральной проекции поверхности,
описываемой радиус-вектором г(u, v), отличается от алгоритма построения ли-
линий очерка для параллельной проекции этой поверхности тем, что на первом
этапе будем искать точки поверхности, в которых меняет знак скалярное произ-
произведение m- (r —w). Для определения этих точек вместо формул (9.5.4) и (9.5.5)
следует использовать формулы
_ „(*) (*+i) (*) (m" (r ~ w)^ k
и формулы
m • (г - w) ^{k) „(fc+1) =
()
(9.5.9)
соответственно. В остальном алгоритм построения линий очерка для централь-
центральной проекции поверхности не отличается от алгоритма построения линий очерка
для параллельной проекции.
9.6. Определение видимой части геометрических объектов 443
9.6. Определение видимой части геометрических объектов
Векторная графика. При построении векторных изображений определение
видимой части геометрических объектов сводится к задаче удаления невидимых
линий. Сетки полигонов строятся для всех поверхностей тел. Часть полиго-
полигонов может оказаться закрытой от взгляда
наблюдателя. При удалении невидимых
линий векторные проекции приобретают
более реалистический вид. На рис. 9.6.1
приведена проекция поверхности, показан-
показанной на рис. 9.4.2, без невидимых линий.
Линия очерка будет видимой, если она
не закрыта другой гранью или частью
своей же грани.
Рассмотрим один из алгоритмов удале-
удаления невидимых линий. Сначала построим
пространственные полигоны геометриче-
геометрического объекта, включая полигоны линий
очерка. Совокупность пространственных Рис. 961 Проекция поверхности с
линий Cj(ij), i = 1, 2, ..., п, соответ- удалением невидимых линий
ствующих всем полигонам объекта, будем
называть каркасной моделью. Далее построим проекцию (параллельную или
центральную) каркасной модели на заданную плоскость. Эта проекция бу-
будет состоять из двухмерных линий Cj(ti), i = 1, 2, ..., п. Каждой простран-
пространственной кривой ci(ti) соответствует двухмерная кривая Cj(ti). Каждой точке
г = Ci(t) пространственной кривой соответствует точка г = Ci(t) двухмерной
кривой. Среди линий проекции выделим те, которые являются проекциями
линий очерка, ребер тел и границ поверхностей. Обозначим их через lj(tj),
j = 1, 2, ..., m. Определим, какие части проекции каркасной модели являются
видимыми, а какие нет. Для этого найдем все точки пересечения и самопере-
самопересечения двухмерных кривых lj(tj), j = 1, 2, ..., m между собой и со всеми
кривыми Ci(ti), i — 1, 2, ..., п и разрежем этими точками линии на части.
Соответствующим образом разрежем пространственные линии. Остается поме-
пометить и удалить невидимые части проекции. Теперь каждая часть линии будет
или полностью видима или полностью невидима.
Рассмотрим алгоритм определения видимости линий проекции. Построим
контур на плоскости проекции, охватывающий все двухмерные кривые. Все
линии контура будут видимыми. Для определения видимости остальных ли-
линий возьмем произвольную точку г на двухмерной кривой. Найдем соответ-
соответствующую ей точку г на соответствующей пространственной линии. Построим
прямую линию \{t) = r+ii, проходящую через точку г и точку наблюдения и на-
направленную от точки наблюдения. Для параллельной проекции вектор i = — iz,
для центральной проекции вектор i = (г — w)/|r — w|. Найдем все точки пере-
пересечения этой прямой с поверхностями геометрического объекта. Если значения
параметра t прямой для всех точек пересечения неотрицательные, то кривая
является видимой. Если среди значений параметра t для точек пересечения
найдется хотя бы одно отрицательное, то кривая является невидимой, так как
ее закрывает одна из поверхностей модели, находящаяся ближе к наблюдателю,
чем точка г. Проделаем эту процедуру со всеми двухмерными кривыми и удалим
те части проекции, которые окажутся невидимыми.
444
Гл. 9. Компьютерная графика
Для полигонов тел рассматриваемый алгоритм удаления невидимых линий
проекции можно упростить. Проекция полигона (или его части) грани тела бу-
будет невидима, если нормаль грани в точках соответствующего трехмерного по-
полигона направлена от точки наблюдения. Проекции ребер тела, нормали обеих
смежных граней которых направлены от точки наблюдения, также являются
Рис. 9.6.2. Проекция детали с удалением невидимых линий
невидимыми. На рис. 9.6.2 приведено изображение детали с линиями очерка
и удаленными невидимыми линиями. На рис. 9.6.3 приведено изображение
детали, где невидимые линии имеют меньшую толщину, чем видимые.
Рис. 9.6.3. Проекция детали с утонением невидимых линий
Описанный алгоритм является универсальным, но требует больших затрат
времени. Для геометрических объектов, описываемых плоскими гранями, су-
существует ряд быстрых алгоритмов удаления невидимых линий. В алгоритме
Галимберти и Монтанари каждое ребро геометрического объекта сопоставля-
сопоставляется с плоскостью каждой грани объекта. Каждая плоскость грани делит все
пространство на два полупространства. Если при сопоставлении ребро всегда
располагается в одном полупространстве с точкой наблюдения или лежит на
9.6. Определение видимой части геометрических объектов 445
плоскости, частью которого является грань, то ребро видимо. Если для какой-
то плоскости ребро располагается не в том полупространстве, где лежит точка
наблюдения, то следует проверить, не закрыто ли ребро гранью, на которой по-
построена плоскость. Для этого достаточно проверить положение проекции ребра
относительно проекции контура грани и определить, располагается ли первая
полностью вне второй, полностью внутри второй или частично внутри второй.
Если при сопоставлении ребра и плоскости некоторой грани ребро попадает в
оба полупространства, то его делят на две части и каждую часть рассматривают
отдельно описанным способом. После каждой проверки от рассматриваемого
ребра оставляют только видимую часть.
Растровая графика. Растровое изображение формируется из отдельных то-
точек. При построении растровых изображений возникает необходимость опре-
определять видимую часть геометрических объектов. Уоткинс предложил алгоритм
построения видимой части изображения, имеющий сходство с построчной раз-
разверткой изображения. Проецируемый объект пересекают параллельными плос-
плоскостями, ортогональными плоскости проекции. Эти плоскости называют плос-
плоскостями развертки. Каждая плоскость пересекает геометрический объект по
некоторым плоским кривым. Положение этих кривых анализируется на пред-
предмет удаленности от наблюдателя. На проекции должны быть построены только
ближайшие к наблюдателю линии или их части. Таким образом, на линии раз-
развертки достаточно отобразить части отрезков, видимые из точки наблюдения.
Изображение формируется из строк развертки. Алгоритм Уоткинса применим
для построения параллельных проекций растровой графики.
Поверхности граней тел пересекаются только по своим краям. Если опре-
определить положение граней относительно друг друга и их удаленность от точки
наблюдения, то для получения правильного изображения достаточно вывести
на экран грани в порядке их удаления от точки наблюдения. Первыми следует
вывести наиболее удаленные грани. Этот метод применим, если есть возмож-
возможность изменять изображение в процессе его построения. Если позже выводимые
грани проецируются на ранее выведенные грани, то последующие грани будут
либо закрывать собой предыдущие (если грани непрозрачные), либо их цвет
можно комбинировать с уже имеющимся цветом (если грани частично прозрач-
прозрачные). Этот алгоритм был предложен Ньюэллом и Санча. Основная трудность
алгоритма заключается в определении порядка расположения граней.
При формировании растровых изображений требуется не только определять
видимую часть геометрических объектов, но еще цвет и яркость каждой точки
изображения. Если геометрические объекты не прозрачны, то цвет точки за-
зависит от цвета ближайшей к наблюдателю грани в этой точке, а яркость точки
зависит от освещенности объекта, оптических свойств его поверхности и от ори-
ориентации нормали поверхности по отношению к лучам падающего света и к ли-
линии визирования, соединяющей рассматриваемую точку и точку наблюдения.
Если геометрические объекты прозрачные, то цвет точек изображения зави-
зависит от цвета всех граней, пересекаемых линией визирования, их оптических
свойств и от ориентации их нормалей. Рассмотрим геометрические аспекты
данной задачи.
В общем случае для каждой точки растрового изображения следует построить
линию, проходящую через точку наблюдения для центральной проекции, или
линию, перпендикулярную плоскости проекции для параллельной проекции, и
найти все точки пересечения этой линии с отображаемыми объектами. В точках
446
Гл. 9. Компьютерная графика
пересечения потребуется вычислить нормаль к поверхности объекта для того,
чтобы определить яркость точки растрового изображения. На рис. 9.6.4 приве-
приведено растровое изображение детали, построенное данным способом.
Рис. 9.6.4. Растровое изображение с определением яркости видимых точек
Для криволинейных поверхностей перечисленные действия требуют боль-
больших вычислительных затрат. Если поверхности геометрических объектов
плоские, то задача существенно упрощается. Для уменьшения времени фор-
формирования растрового изображения все поверхности отображаемых объектов
аппроксимируют треугольными пластинами.
9.7. Триангуляция поверхностей и тел
Триангуляция представляет собой аппроксимацию поверхности моделируе-
моделируемого объекта треугольными пластинами, отстоящими от нее на расстоянии, не
превышающем некоторой заданной величины S. Все треугольные пластины
должны стыковаться между собой. Их вершины лежат на поверхности. С на-
набором треугольных пластин легче работать, чем с поверхностью общего вида.
Треугольные пластины будем называть треугольниками. Для треугольника
достаточно быстро вычисляются расстояние до заданной точки или точка пере-
пересечения с заданной прямой в пространстве. Триангуляция граней выполняется
для визуального восприятия геометрической модели, поэтому стороны треуголь-
треугольников выбираются, такими, чтобы глаз не мог заметить изломы.
При отображении геометрических объектов по треугольникам на параме-
параметрических плоскостях поверхностей должна быть построена пространственная
триангуляция граней тела путем вычисления массива точек в пространстве
Рг(ыг> щ) и массива нормалей гп.г{щ, Vi) к граням тела в этих точках по мас-
массиву двухмерных точек pt = [щ Vi]T. Для быстрого отображения тел их грани
аппроксимируют треугольными пластинами, построенными на точках р$. Нор-
Нормали требуются для определения поведения световых лучей, взаимодействую-
взаимодействующих с гранями тела. Тоновые рисунки в предыдущих главах и в данной главе
выполнены с использованием триангуляции.
9.7. Триангуляция поверхностей и тел
447
Результатом триангуляции поверхности мы хотим иметь массив двухмер-
двухмерных точек р^ = [щ Vi]T на параметрической плоскости и массив троек целых
чисел, являющихся номерами точек в первом упомянутом массиве. Таким обра-
образом, каждый треугольник будет представлен тремя номерами его вершин в мас-
массиве параметров. По каждой двухмерной точке параметрической области могут
быть вычислены пространственная точка pt(ui, Vi) на поверхности и нормаль
тДгц, V{) поверхности-в ней. Пространственные точки и нормали могут хра-
храниться в массивах, аналогичных массиву двухмерных точек.
Остановимся на некоторых способах триангуляции. Для плоских поверхно-
поверхностей существуют экономичные методы триангуляции, в которых треугольники
строятся на граничных точках поверхности и не требуется искать точки внутри
параметрической области.
Триангуляция Делоне. Рассмотрим некоторую область на плоскости. Область
будем называть выпуклой, если при движении вдоль ее границы приходится
поворачивать только в одну сторону (только влево или только вправо). Для три-
триангуляции выпуклых плоских областей можно , . .
использовать алгоритм Делоне. Мы не сможем
напрямую применить этот алгоритм для триан-
триангуляции поверхностей произвольной формы, но
мы будем использовать его метод построения тре-
треугольников.
Пусть даны некоторая выпуклая двухмерная
область, ограниченная замкнутой ломаной лини-
линией, и набор точек внутри этой области (рис. 9.7.1).
Требуется разбить указанную область на тре-
треугольники, вершинами которых являются задан-
заданные точки внутри области и вершины ограничивающей ее ломаной линии. Тре-
Треугольники не должны накрывать друг друга, а их стороны могут пересекаться
только в вершинах.
Можно построить несколько различных наборов треугольников, заполняю-
заполняющих указанную область. Во всех случаях число треугольников равно К + 1 — 2,
где К — число вершин ограничивающей ломаной, / — число заданных то-
точек внутри области. Триангуляция области будет триангуляцией Делоне,
Рис. 9.7.1.Выпуклая область с
заданными точками внутри
Рис. 9.7.2. Выбор третьей точки алгоритма Делоне
если внутри описанной вокруг каокдого треугольника окружности отсут-
отсутствуют вершины других треугольников. Триангуляция Делоне строит тре-
треугольники по возможности близкие к равноугольным (не допускает построение
448
Гл. 9. Компьютерная графика
неоправданно вытянутых треугольников). Ее можно назвать сбалансирован-
сбалансированной. Триангуляция Делоне будет уникальной, если никакие четыре вершины
не лежат на одной окружности.
Рассмотрим триангуляцию Делоне. Вершины ограничивающей область ло-
ломаной и заданные точки внутри области будем называть вершинами триан-
триангуляции. Стороны треугольников будем называть ребрами. Среди ребер выде-
выделим отрезки ограничивающей ломаной, которые будем называть граничными
ребрами. Сориентируем все граничные ребра так, чтобы выпуклая область ле-
лежала слева от каждого ребра. Пусть требуется построить треугольник, стороной
которого является граничное ребро АВ, показанное на рис. 9.7.2.
Через вершины А, В и любую, не лежащую с ними на одной прямой, вер-
вершину можно провести окружность. В качестве третьей вершины треугольника
выберем вершину V, соответствующая которой окружность, не содержит других
вершин с той же стороны относительно отрезка АВ, с которой лежит точка V.
Для граничного ребра в общем случае можно найти одну такую вершину. Бу-
Будем называть ее ближайшей. Центр окружности, проходящей через точки А,
В и V, лежит на пересечении перпендикуляров к серединам отрезков АВ, BV
и VA. Положение центра окружности будем характеризовать параметром t от-
отрезка MN, перпендикулярного ребру АВ, равного с ним по длине и проходящего
Рис. 9.7.3. Процесс триангуляции Делоне
через середину ребра АВ. Для всех вершин, лежащих слева от отрезка АВ, бли-
ближайшая вершина имеет наименьший параметр t. Соответствующая ближайшей
вершине окружность не содержит других вершин слева от отрезка АВ. Пусть
вершины А, В и V описываются двухмерными радиус-векторами а = [ха уа]т,
Ь = [хь уь]Т, v = [xv yv]T соответственно. Радиус-векторы середин отрезков АВ
и BV будут равны
= [xm ут] =
Я =
Уд]Т =
-(xv +хь)
1
-2(
ь + Уь)
9.7. Триангуляция поверхностей и тел
449
Значение параметра t прямой MN = A — t)m+tn, соответствующее положению
на ней центра окружности, проходящей через точки А, В иУ, равно
t =
(xv - ХЬ)(хд - xm) + (yv - Уь){Уд ~ Ут)
{Уь ~ УЬ){ХЬ ~ Хп) - (Ху - ХЬ)(уь ~ Уа)
(9.7.1)
Для ближайшей слева к отрезку АВ вершины параметр t имеет минимальное
значение.
Сориентируем все граничные ребра так, чтобы подлежащая триангуляции
область лежала слева от каждого из них. Построение треугольников начнем с
любого граничного ребра. Найдем для него ближайшую вершину, соответствую-
соответствующая окружность которой не содержит других
вершин. Пусть для граничного ребра АВ най-
найдена ближайшая вершина V. Тогда построим
треугольник ABV и переведем ребро АВ в раз-
разряд неактивных. Неактивными будем назы-
называть ребра и вершины, которые не участвуют в
алгоритме триангуляции. Если среди гранич-
граничных ребер отсутствует ребро BV, то на отрезке
VB построим новое граничное ребро. Если же
среди граничных ребер есть ребро BV, то пе-
переведем его и вершину В в разряд неактив-
неактивных. Если среди граничных ребер отсутствует
ребро VA, то на отрезке AV построим новое граничное ребро. Если же среди
граничных ребер есть ребро VA, то переведем его и вершину А в разряд неак-
неактивных. Процесс триангуляции показан на рис. 9.7.3.
Триангуляцию закончим, когда все вершины и ребра станут неактивными.
Результат триангуляции заданной области приведен на рис. 9.7.4.
Триангуляция методом коррекции. Рассмотрим триангуляцию некоторой по-
поверхности r(u, v) с прямоугольной областью определения параметров ит,п ^
< и < «max) umjn < v < vma.x- Разобьем область определения параметров
поверхности на прямоугольные ячейки двухмерными линиями щ = const и
Vj — const, % = 1, 2, ..., m, j = 1, 2, ..., п. Эти линии образуют прямоуголь-
прямоугольную сетку. Параметрические расстояния Ащ — щ+\ — щ между соседними
линиями щ — const в соответствии с формулой (9.4.7) возьмем равными
Рис. 9.7.4. Триангуляция Де-
Делоне
i, v)) - 5/m)
Ли, = min 2
для всех umin ^ v ^ umax. (9.7.2)
Параметрические расстояния Avj = Vj+\ — Vj между соседними линиями Vj =
= const в соответствии с формулой (9.4.8) возьмем равными
= min
ДЛЯ BCeX U
(9.7.3)
450 Гл. 9. Компьютерная графика
Построив диагонали во всех прямоугольных ячейках, мы получим триангу-
триангуляцию поверхности (получим набор треугольников, удовлетворяющий предъ-
предъявленным требованиям). На рис. 9.7.5 приведена триангуляция поверхности
вращения описанным способом.
Рассмотрим триангуляцию поверхности r(u, v) с произвольной границей.
Метод триангуляции построим на коррекции граничными контурами описанной
Рис. 9.7.5. Триангуляция поверхности с прямоугольной областью определения параметров
выше триангуляции поверхности с прямоугольной областью определения пара-
параметров. Пусть граница поверхности в области определения параметров описыва-
описывается несколькими непересекающимися двухмерными контурами B.12.7). Один
из контуров является внешним и содержит остальные контуры. За положитель-
положительное направление для каждого контура примем направление, при движении вдоль
которого область определения поверхности находится всегда слева от контура,
если смотреть навстречу нормали поверхности. Построим полигоны в положи-
положительном направлении граничных контуров области определения поверхности.
Для построения граничных полигонов нужно пройти по граничным контурам
поверхности с некоторым переменным шагом и заполнить массив двухмерных
точек, координатами которых являются параметры поверхности. Полигон будем
строить из точек на параметрической плоскости, но шаг при переходе от одной
точке к другой будем определять из пространственной геометрии, а именно, из
условия, чтобы прогиб дуги кривой между соседними точками был бы не более
заданной величины 8. Параметрические шаги At построения полигона для кри-
кривой r(t) = r[u(t), v(t)) ^граничного контура поверхности вычислим по формуле
(9.4.4).
Каждый полигон состоит из упорядоченного набора двухмерных точек р^ =
= [щ Vi]T. Каждый участок полигона можно рассматривать как отрезок двух-
двухмерной прямой линии, построенный на двух соседних точках. Будем использо-
использовать такие участки в качестве граничных ребер, а точки полигонов, на которых
базируются ребра, будем использовать в качестве вершин триангуляции. Так
как область определения параметров поверхности лежит слева от граничных
полигонов, то при построении треугольников для каждого граничного ребра
триангуляции следует искать третью вершину треугольника слева от ребра.
Далее построим прямоугольную сетку для области ttmjn ^ u ^ ttmax, um;n ^
^ v ^ umax, где ttmjn, «max, vm\n, umax определяют габаритный прямоугольник
внешнего граничного контура. Узлы сетки мы также будем использовать в каче-
качестве вершин триангуляции. Определим, какие узлы лежат внутри граничных
9.7. Триангуляция поверхностей и тел 451_
полигонов, а какие лежат на границе или вне области определения поверхно-
поверхности. Используя эту информацию, рассортируем прямоугольные ячейки сетки
на две группы. К первой группе отнесем ячейки, целиком лежащие внутри
области определения параметров поверхности (ячейки не должны касаться гра-
граничных полигонов). Ко второй группе отнесем остальные ячейки (лежащие вне
области определения поверхности или пересекаемые граничными полигонами).
Рис. 9.7.6. Незаконченная триангуляция поверхности
Внутри каждой ячейки первой группы с помощью диагонали построим два тре-
треугольника. Тем самым мы получим незаконченную триангуляцию. Пример
построения треугольников в ячейках первой группы для ограниченной конту-
контурами поверхности вращения приведен на рис. 9.7.6.
На непересеченных сторонах ячеек второй группы построим граничные ре-
ребра и направим их так, чтобы соответствующая ячейка находилась слева от
ребра. Вокруг ячеек первой группы построим замкнутую ломаную линию (воз-
(возможно несколько замкнутых линий) так, чтобы при движении по ней не раз-
разбитая на треугольники часть области лежала слева, если смотреть навстречу
нормали поверхности. Прямолинейные участки этой ломаной линии также бу-
будем использовать в качестве граничных ребер. Мы будем считать все ребра
равноправными. Для завершения триангуляции нам необходимо построить
треугольники между граничными ребрами. Для каждого ребра будем искать
вершину, которая лежит слева от него и может быть использована для построе-
построения треугольника. Поиск вершины будем осуществлять только среди тех вер-
вершин, которые лежат в одной ячейке с ребром. Для выбора вершины используем
метод Делоне, описанный выше, и проиллюстрированный на рис. 9.7.2. Если
такая вершина найдена, то следует проверить, не пересекаются ли два новых
ребра треугольника с каким-либо граничным ребром. Пусть для граничного
ребра АВ найдена ближайшая вершина V и проверено, что отрезки BV и VA
не пересекают другие граничные ребра. Тогда построим треугольник ABV и
переведем ребро АВ в разряд неактивных. Если среди граничных ребер отсут-
отсутствует ребро BV, то на отрезке VB построим новое граничное ребро, если же
среди граничных ребер есть ребро BV, то переведем его и вершину В в разряд
неактивных. Если среди граничных ребер отсутствует ребро VA, то на отрезке
AV построим новое граничное ребро, если же среди граничных ребер есть ре-
ребро VA, то переведем его и вершину А в разряд неактивных. Если отрезок BV
452
Гл. 9. Компьютерная графика
или VА пересекает другие граничные ребра, то перейдем к поиску ближайшей
вершины для другого граничного ребра. Триангуляция будет закончена после
перевода всех ребер и вершин в разряд неактивных.
Рис. 9.7.7. Триангуляция методом коррекции
На рис. 9.7.7 приведена триангуляция поверхности методом коррекции тре-
треугольников в ячейках, пересеченных граничными контурами. На рис 9.7.8 с
помощью полученной триангуляции отображена сама поверхность.
Рис. 9.7.8
Если граничные полигоны и поверхность обладают некоторой симметрией,
то триангуляция методом коррекции будет обладать аналогичной симметрией.
Триангуляция методом поглощения. Рассмотрим еще один метод триангуля-
триангуляции. По скорости он уступает триангуляции Делоне и ее модификациям. Для
начала процедуры триангуляции необходимо представить границу поверхности
в виде замкнутых полигонов. В процессе триангуляции нам потребуется опре-
определять шаги по параметрам поверхности Аи и Av. При известном направлении
движения эти шаги определяются формулами (9.4.6). Приближенно шаги по па-
параметрам поверхности Аи и Av можно найти следующим образом. Определим
область на плоскости параметров вокруг некоторой точки [щ vq]t таким обра-
образом, чтобы любой пространственный отрезок из точки [щ Vq]t в точку [г*1 vi]T
9.7. Триангуляция поверхностей и тел 453
этой области отстоял бы от поверхности не дальше заданной величины 5. Для
этого вычислим допустимые приращения параметров вдоль координатных
линий
y/F/m)B(gn/bu)-6/m) _ n V(S/m)B(g22/b22) - S/m)
(9.7.4)
где gu, g22, Ьц, b22 — коэффициенты первой и второй квадратичных форм
поверхности в точке [щ vq]t. За границу искомой области примем эллипс с
центром в точке [щ vq] и полуосями Аи и Дг;. Этот эллипс имеет уравнение
U — Uo\ fv — Vo\ /ппг\
-~а + ~и— = 1- (9.7.5)
Аи ) \ Av ) у '
Если требуется на плоскости найти точку рядом с точкой [щ vq] в направлении,
заданном углом ip с осью к, то ее параметрами будут
u\ = Щ + Аи cos if, v\ = vq + Avsinip. (9.7.6)
Сначала рассмотрим более простой случай, когда область параметров по-
поверхности ограничена одним внешним контуром. Аппроксимируем границу по-
поверхности замкнутым полигоном на параметрической области. При построении
триангуляции будем использовать рабочий полигон, за который в данном случае
примем полигон внешнего контура. Точки полигона занесем в результирующий
массив двухмерных точек. Треугольники будем строить от края рабочего поли-
полигона, сужая его до тех пор, пока в рабочем полигоне не останется всего три
точки.
Найдем в рабочем полигоне вершину, в которой он поворачивает внутрь обла-
области. Такая точка всегда существует и угол поворота в ней меньше -к. Обозначим
эту точку через О, а ее параметры — через щ и vq. Около этой точки построим
один или два треугольника в зависимости от угла поворота. Если угол меньше
7г/2, то построим один треугольник на этих трех точках (рис. 9.7.9). В против-
противном случае построим два треугольника на данной, двух соседних и одной новой
точках (рис. 9.7.11). Новая точка обозначена через Р. Точку Р будем искать
на диагонали параллелограмма ВОСР. Если вершина параллелограмма лежит
внутри эллипса (рис. 9.7.10), то примем ее за точку Р. В противном случае за
точку Р примем пересечение эллипса и диагонали параллелограмма. В послед-
последнем случае совсем не обязательно искать пересечение эллипса и отрезка.
Координаты ир и vp точки Р определяются через координаты точек ОВС
Up = иь + ис —- uq, Vp = Vf) + vc — ¦uo- (9.7.7)
Угол отрезка ОР с горизонталью определяется равенством
(9.7.8)
ир -щ
Эти данные позволяют определить положение точки Р относительна эллипса
(9.7.5).
454
Гл. 9. Компьютерная графика
В случае, показанном на рис. 9.7.9, построим треугольник (запомним номера
его вершин) и в рабочем полигоне удалим точку О. В случае, показанном на
рис. 9.7.11, построим два треугольника и в рабочем полигоне точку О заменим
точкой Р и поместим последнюю в результирующий массив точек. На рис. 9.7.12
приведен полигон, полученный после построения двух треугольников и ликви-
ликвидации точки О. В обоих случаях точка О будет удалена из рабочего полигона
и рабочий полигон сузится. Заметим, что треугольники можно строить только
тогда, когда рабочий полигон после сужения не будет сам себя пересекать.
Рис. 9.7.9. Построение треугольника
Рис. 9.7.10. Результирующий полигон
Рис. 9.7.11. Построение двух треугольников
Рис. 9.7.12. Результирующий полигон
Такие ситуации показаны на рис. 9.7.13. Они могут возникнуть, когда сто-
стороны построенных треугольников пересекут несмежные с ними стороны ра-
рабочего полигона. Перед построением нового треугольника как в случае, пока-
показанном на рис. 9.7.9, так и в случае, показанном на рис. 9.7.11, должна быть
выполнена проверка на отсутствие самопересечения результирующего полигона.
Более того, при определении положения точки Р важно, чтобы она находи-
находилась на достаточном расстоянии от других точек рабочего полигона и не подхо-
подходила близко к отрезкам, соединяющим точки полигона. Иначе могут возникнуть
трудности в дальнейшем при построении треугольников. Поэтому прежде, чем
сузить рабочий полигон, следует проверить на самопересечение результирую-
результирующий полигон. Если около точки О нельзя построить треугольник (треуголь-
(треугольники), то вместо нее следует найти другую точку, в которой полигон более, чем
в других, заворачивает внутрь контура, и выполнить в ней описанные действия.
9.7. Триангуляция поверхностей и тел
455
Далее с измененным рабочим полигоном выполним те же действия, кото-
которые мы только что описали. Найдем в рабочем полигоне точку, в которой он
более, чем в других, точках поворачивает внутрь области, выполним проверку
на возможность сужения в ней полигона путем построения одного или двух
U U
Рис. 9.7.13. В данном углу строить треугольники нельзя
треугольников и сузим полигон. Продолжая этот процесс, мы будем расширять
массив двухмерных точек и массив треугольников, и одновременно мы будем су-
сужать рабочий полигон, уменьшая охватываемую им площадь и число его точек.
На некотором этапе этих действий мы получим рабочий полигон, состоящий
из трех точек. Построим на этих точках последний треугольник, ликвидируем
рабочий полигон и закончим триангуляцию. В описываемом способе триангу-
триангуляции область, ограниченная рабочим полигоном, как бы ликвидируется путем
отрезания от нее треугольников.
Рассмотрим общий случай, когда область параметров поверхности ограни-
ограничена одним внешним контуром и несколькими внутренними контурами, цели-
целиком лежащими внутри внешнего контура. Аппроксимируем границу поверхно-
поверхности замкнутыми полигонами на параметрической области. Для каждого контура
построим свой полигон. Так же как и для контуров, для полигонов, построен-
построенных на них, должно быть выполнено правило их взаимной ориентации. Ориен-
Ориентация внутренних полигонов должна быть противоположной ориентации внеш-
внешнего полигона. Построение триангуляции начнем с полигона внешнего контура.
Положим его точки в результирующий массив двухмерных точек, а сам полигон
сделаем рабочим.
Построение треугольников выполним так же, как и в случае односвязной
области. Найдем в рабочем полигоне точку О, выполним проверку на воз-
возможность сужения в ней рабочего полигона и сузим полигон. При наличии
внутренних контуров усложняется проверка возможности сужения рабочего по-
полигона в выбранной точке. Кроме описанных проверок на пересечение сторон
треугольников со сторонами рабочего полигона нужно выполнить проверку на
пересечение сторон треугольников со сторонами всех внутренних полигонов.
Пусть мы проверяем возможность построения двух треугольников в точке О
(рис. 9.7.11), и обнаружили, что новая точка Р, будучи построенной, попадет
внутрь одного из внутренних полигонов или окажется в недопустимой близо-
близости от его отрезков. В этом случае мы не будем строить точку Р, а вместо
этого включим в рабочий полигон данный внутренний полигон, построив два
треугольника, показанных на рис. 9.7.14.
Для того чтобы точки одного из внутренних полигонов включить в рабо-
рабочий полигон, найдем среди точек внутреннего полигона точку, ближайшую к
точке С (смежную с точкой О) рабочего полигона. Построим треугольники на
456
Гл. 9. Компьютерная графика
точках OCF и CEF и между точками О и С рабочего полигона вставим точки
внутреннего полигона, начиная с точки F и кончая точкой Е. Тем самым мы
разорвем рабочий полигон на отрезке ОС, разорвем внутренний полигон на
в
с
Рис. 9.7.14. Построение двух треугольников
Рис. 9.7.15. Слияние внешнего и внутреннего полигонов
отрезке EF и объединим их отрезками OF и ЕС. Результат слияния приведен
на рис. 9.7.15. Конечно, перед объединением внешнего и внутреннего полигонов
должны быть выполнены проверки на корректность этой операции.
Далее будем продолжать сужать рабочий полигон описанным способом до
тех пор, пока не окажемся в непосредственной близости с другим внутренним
полигоном и не включим его в рабочий полигон. В итоге, все внутренние поли-
полигоны будут включены в рабочий полигон,
который должен быть сужен до последних
трех точек. В результате, вся многосвязная
область определения параметров поверхно-
поверхности будет покрыта треугольниками.
Возможны ситуации, когда нельзя по-
построить ни одного треугольника на задан-
заданных полигонах. На рис. 9.7.16 приведена
область ограниченная двумя полигонами,
каждый из которых состоит из четырех от-
отрезков. Для внешнего полигона мы не мо-
можем продолжить триангуляцию, так как ме-
мешает внутренний полигон. В такой случае найдем две соседние точки В и С
полигона, для которых можно построить треугольник ВС Р. Точка Р проециру-
проецируется на середину стороны ВС и находится на таком расстоянии от нее, чтобы
новый треугольник не пересекал полигоны.
Далее продолжим триангуляцию описанным выше способом.
Другие способы триангуляции. Существуют и другие способы триангуляции.
Например, после построения полигонов внешнего и внутренних контуров обла-
области определения поверхности может быть выбрана иная стратегия построения
треугольников. В другом варианте можно перед началом триангуляции объеди-
объединить внешний и внутренние полигоны в один полигон. Можно внутри области
определения параметров по определенному алгоритму «набросать» точки и по
ним и точкам полигонов граничных контуров выполнить триангуляцию Делоне.
Существуют алгоритмы, строящие сначала крупные треугольники, а затем де-
делящие их до приемлемых размеров.
Рис. 9.7.16. В данном углу строить
треугольники нельзя
9.7. Триангуляция поверхностей и тел
457
Триангуляция тела. Триангуляция тела представляет собой совокупность
треугольников, полученных путем триангуляции поверхностей его граней. Три-
Триангуляция отдельных поверхностей отличается от триангуляции граней тела
тем, что в последнем случае должны быть согласованы граничные полигоны
Рис. 9.7.17. Согласованность граничных полигонов граней тела
для смежных граней (рис. 9.7.17). Участки полигонов смежных граней, про-
проходящие по общим ребрам, будут согласованными, если их точки совпадают в
пространстве.
Применение триангуляции. Построенные в результате триангуляции тре-
треугольники используются для получения тоновых изображений. На рис. 9.7.18
и 9.7.19 приведены триангуляции грани листового тела, тоновое изображение
которого показано на рис. 6.5.1.
Рис. 9.7.18. Триангуляция грани тела методом коррекции
Разбиение области определения параметров поверхности на треугольники
может быть использовано в интегралах (8.6.2), (8.6.3), (8.6.12), (8.7.17)-(8.7.22)
при вычислении геометрических характеристик тел. При численном интегри-
интегрировании параметрический шаг At для кривых следует вычислять по формуле
30 - 5293 Голованов
458
Гл.9. Компьютерная графика
Рис. 9.7.19. Триангуляция грани тела методом поглощения
(8.11.5), а для поверхностей параметрические шаги Аи и Av следует вычи-
вычислять по формулам (8.11.1) и (8.11.2). Приближенно интеграл для треугольной
области поверхности вычисляется по кубатурной формуле (8.10.13).
9.8. Моделирование света
Изображение окружающих нас предметов формируется на сетчатке глаза по-
потоками света, пришедшими от этих предметов. Пришедший свет является отра-
отраженным или излученным поверхностями окружающих предметов. Если неко-
некоторое тело полностью поглощает падающий на него свет, то оно называется
абсолютно черным телом. Если тело полностью пропускает падающий на него
свет, то оно называется абсолютно прозрачным телом. Реальные предметы не-
некоторую часть падающего света поглощают, превращая его в тепло, некоторую
часть света пропускают и некоторую часть — отражают. Будем считать, что для
моделируемых объектов доля излученного и поглощенного света незначительна
по сравнению с долей пропущенного и отраженного света.
Поглощенная часть, пропущенная часть и отраженная часть падающего света
зависят от длины его волны. Цвет предмета зависит и от длины волны падаю-
падающего света и от областей спектра, которые поверхность предмета отражает в
большей степени. В этом параграфе мы не будем останавливаться на цвете тел,
а рассмотрим взаимодействие тел с потоком света некоторой длины волны. Све-
Световой поток мы будем характеризовать интенсивностью света — плотностью
потока энергии световой волны.
Тоновое изображение зависит от положения точки наблюдения, положения
источников света относительно геометрической модели и от оптических свойств
ее поверхностей. Поверхность объекта частично поглощает падающий свет, ча-
частично — пропускает, а частично — отражает. При моделировании отражен-
отраженного света его условно делят на две части: диффузно отраженный и зеркально
отраженный. Это деление связано с законами, по которым описывается напра-
направление лучей отраженного света. Соответственно поверхностям приписываются
свойства диффузного и зеркального отражения. Если большую часть отражен-
отраженного поверхностью света можно описать законом диффузного отражения, то
поверхность называют матовой, если же большую часть отраженного поверхно-
поверхностью света можно описать законом зеркального отражения, то ее называют зер-
зеркальной. Объекты, поверхности которых способны пропускать большую часть
9.8. Моделирование света 459
падающего на них света вглубь, называют прозрачными. Пропущенный через
поверхность свет также условно делят на две части: диффузно пропущенный
и направленно пропущенный. Направленно пропущенный свет претерпевает
преломление. Пропущенный свет может быть отражен от других поверхностей.
Падающий на поверхность свет можно условно разделить на направленный
и рассеянный. Направленным является свет солнца или некоторого другого то-
точечного источника. Рассеянный свет возникает в результате дифракции некото-
некоторого направленного света на мелких оптических неоднородностях окружающей
среды (например, воздуха) из-за флуктуации плотности (небольших отклонений
плотности от ее среднего значения в пределах малых объемов). Рассеянный
свет характеризуется равномерным распределением его интенсивности по всем
направлениям. В отсутствие рассеянного света предметы выглядят контраст-
контрастными. Так выглядят предметы, помещенные в темную комнату и освещенные
направленным на них прожектором. При отсутствии воздуха части предметов,
находящиеся в тени, могут быть совсем не видны. В большинстве реальных
ситуаций рассеянный свет присутствует.
Приходящий в точку наблюдения свет разделим на четыре составляющие
части:
• рассеянный свет,
• диффузно отраженный свет,
• зеркально отраженный свет,
• пропущенный свет.
Рассеянный свет. Рассеянный свет, как и направленный, подвержен диф-
диффузному и зеркальному отражению, но в силу одинаковой интенсивности во
всех направлениях в точку наблюдения от каждой точки поверхности приходит
одинаковое количество рассеянного света. Обозначим через 1а интенсивность
рассеянного света. При наличии только рассеянного света в точку наблюдения
от каждой точки объекта независимо от ориентации в ней поверхности придет
свет интенсивности
/ = kja, (9.8.1)
где ка — коэффициент, определяющий отраженную долю рассеянного света.
Диффузно отраженный свет. Матовая поверхность большую часть падаю-
падающего света отражает диффузно. Для диффузного отражения справедлив закон
косинусов Ламберта, устанавливающий соответствие между количеством отра-
отраженного света и косинусом угла в между направлением на точечный источник
света интенсивности 1Р и нормалью к поверхности. Интенсивность диффузно
отраженного света определяется формулой
h = kdlp cos в, l (9.8.2)
где kd — коэффициент диффузного отражения, зависящий от материала по-
поверхности. Количество диффузно отраженного света не зависит от положения
наблюдателя. Матовые поверхности отражают одинаковое количество световой
энергии во всех направлениях, но это количество пропорционально cos в.
Зеркально отраженный свет. Зеркальные поверхности отражают свет нео-
неодинаково по разным направлениям. Вследствие этого на гладких криволиней-
криволинейных поверхностях можно наблюдать световой блик. От зеркальной поверхности
большая часть падающего света отражается в направлении, угол с нормалью ко-
которого равен углу падения и лежащем в одной плоскости с падающим светом
460 Гл. 9. Компьютерная графика
и нормалью в точке падения. Это направление называется направлением от-
отраженного света (рис. 9.8.1). При отклонении на некоторый угол а от этого
направления интенсивность отраженного света резко уменьшается. Изменение
интенсивности зеркально отраженного света около направления отраженного
света Фонг предложил описывать функцией cos" a, где п может зависеть от
свойств поверхности и лежит в диапазоне от 1 до 200.
Направление , Направление
падающего света\ ^ отраженного света
¦ К точке наблюдения
Рис. 9.8.1. Зеркальное отражение света
Количество отраженного света зависит также и от угла падения 9. При моде-
моделировании света зависимость отраженного света от угла падения заменяют кон-
константой fF) — ks, которую выбирают опытным путем так, чтобы результаты
были приемлемы с эстетической точки зрения. Если интенсивность источника
света равна 1Р, то интенсивность зеркально отраженного света определим фор-
формулой Фонга
Is = kslpcosna, (9.8.3)
где ks будем называть коэффициентом зеркального отражения, а п будем назы-
называть коэффициентом блеска. Чем больше п, тем ярче и уже световой блик.
Пропущенный свет. Если отображаемый объект является прозрачным, то от
точки его поверхности в точку наблюдения придет не только отраженный свет,
но и свет, пропущенный поверхностью из глубины объекта. Пропущенный по-
поверхностью свет может прийти в результате отражения от другой поверхности
или от источника света через прозрачный объект. В обоих случаях свет пойдет
через вещество и будет им частично поглощен. Интенсивность света при про-
прохождении через вещество убывает по экспоненциальному закону и описывается
законом Бугера
I = he-*, (9.8.4)
где It — интенсивность света на входе в поглощающее вещество, I — прой-
пройденное расстояние, ц — коэффициент поглощения света данным веществом.
При / = 1/ц интенсивность пропущенного света уменьшается в е раз. Это
равенство можно рассматривать, как определение коэффициента поглощения.
Интенсивность It является одной из составляющих частей падающего света.
Поверхность как граница двух сред характеризуется коэффициентом отражения
к = ks + kd и коэффициентом пропускания kt- Если пренебречь поглощением
света, то интенсивность отраженного и пропущенного света в сумме должны
давать интенсивность падающего света
1Р = Id + Id + It = kdlp + kslp + ktlp. (9.8.5)
Как было упомянуто выше, пропущенный свет условно делят на диффузно про-
пропущенный и направленно пропущенный. Для простоты будем считать, что доля
диффузно пропущенного света мала по сравнению с долей направленно пропу-
пропущенного света, и опустим из рассмотрения диффузно пропущенный свет. На-
9.8. Моделирование света
461
правленно пропущенный свет претерпевает преломление на поверхности раздела
двух сред. Преломленный луч лежит в одной плоскости с падающим лучом и
нормалью в точке падения (рис. 9.8.2).
Направление
преломленного света
Направление
падающего света
Направление
отраженного света
Рис. 9.8.2. Преломление света
Его направление составляет угол в' с нормалью и описывается законом пре-
преломления
п0 sin 0 = ri sin в1, (9.8.6)
где по — показатель преломления среды со стороны падающего света, п' —
показатель преломления среды с другой стороны поверхности раздела. Для
интенсивности направленно пропущенного света примем закон изменения от
направления аналогичный закону (9.8.3) для направленно отраженного света
It = ktlp cosn /3,
(9.8.7)
где /3 — угол отклонения направления пропущенного света от направления в
точку наблюдения.
Пришедший к наблюдателю пропущенный свет проходит четное число гра-
границ сред и претерпевает столько же раз преломление.
Интенсивность наблюдаемого света. Реальные поверхности обладают свой-
свойствами и диффузного и зеркального отражения, а также могут быть частично
прозрачными. В реальных ситуациях присутствует и направленный и рассеян-
рассеянный свет. Рассмотрим вычисление интенсивности света, пришедшего в то точку
наблюдения, от непрозрачной поверхности. Она определится суммой трех со-
составляющих
I = kja + Ipkd cos в + Ipks cos" a. (9.8.8)
Результаты закраски, полученные с помощью формулы (9.8.8), обладают боль-
большой реалистичностью, но они имеют существенный недостаток. Если две плос-
плоские поверхности одного цвета параллельны друг другу и их проекции перекры-
перекрываются, то поверхности будут закрашены одинаково и их изображения сольются
независимо от их расстояния до точки наблюдения. Для устранения этого эф-
эффекта интенсивность пришедшего от поверхности света будем считать зависи-
зависимой от расстояния и запишем формулу вычисления интенсивности света в виде
+А;г(г-г0)
+ Ip(kd cos в + ks cosn a),
(9.8.9)
462 Гл. 9. Компьютерная графика
где г — расстояние от точки наблюдения до точки поверхности, го — расстояние
от точки наблюдения до ближайшей точки объекта, kr — коэффициент влия-
влияния удаленности точки объекта на интенсивность пришедшего от нее света.
При kr = 0 мы получим формулу (9.8.8). Интенсивность света от ближайшей
точки также будет совпадать с (9.8.8). Расстояние го введено из-за того, что
для параллельных проекций точка наблюдения находится на бесконечности.
Для центральных проекций можно положить го = 0, тогда при удалении всего
объекта от точки наблюдения будет наблюдаться уменьшение его яркости.
Формулу (9.8.9) стоит рассматривать как эмпирическую формулу, приемле-
приемлемую с эстетической точки зрения и достаточно простую. В некоторых случаях
вместо этой формулы используется формула
A;dcos0 + A:acos"a 1ПОЛП\
I = kja + Ip —, (9.8.10)
l + kr{r~r0)
Она также позволяет получать достаточно реалистичные изображения.
m
Направление преломленного
света
'Кточке наблюдения
Направление / /^
падающего света ^^ //l^ Направление
отраженного света
Направление падающего
пропущенного света
Рис. 9.8.3
Рассмотрим вычисление интенсивности света, пришедшего в точку наблюде-
наблюдения, от прозрачного объекта, показанного на рис. 9.8.3. Для построения реали-
реалистических изображений интенсивность пришедшего от некоторой точки объекта
света опишем формулой
/ = т~- г + Ip(kd cos в + ks cos" a) + Iwkt cos" 0 =
i + Kr(r — ro)
k I
= - Г7-2 г + Ip(kd cos0 + ks cos" a) + Iokt2e~^ cos" /3. (9.8.11)
1 4" kr[r — ro)
Последнее слагаемое получено следующим образом. После прохождения лучом
света интенсивности Iq первой поверхности интенсивность пропущенного света
равна ktlo, по достижении второй поверхности его интенсивность будет равна
1р> = ktloe~>j'1 и, наконец, после прохождения второй поверхности его интенсив-
интенсивность станет равной k2loe~'xl. Свет интенсивности Iq может прийти от другого
источника или может являться направленно отраженной частью света интен-
интенсивности Тр, но отраженной от некоторой другой поверхности.
9.9. Описание цвета 463
При наличии нескольких источников света каждый из них даст свой вклад
в интенсивность пришедшего в точку наблюдения света. Для нескольких ис-
источников света, с интенсивностью каждого /pj, формула (9.8.9) примет вид
Y« facos %+**cos" <**)• (9-8-12)
1 = 1 л. iYт
X ¦+¦ КГ[Г — Tq) ^
Аналогичным образом изменится формула (9.8.11) вычисления интенсивности
света, пришедшего от прозрачной поверхности. Она примет вид
1 = 1 + kra(ra~r0) + ?Ipi {kd C°S 9i + ks C°S ai) + ?
где /pj' — интенсивность ji-го пропущенного луча света (проникающего с другой
стороны поверхности).
Торрэнс и Спэрроу создали теоретически обоснованную модель отражающей
поверхности. В этой модели предполагается, что поверхность представляет со-
собой совокупность микроскопических идеально отражающих плоскостей. Ориен-
Ориентация граней задается функцией распределения вероятностей Гаусса. Свойства
микроскопических плоскостей и их ориентация относительно направления па-
падающего света определяют распределение интенсивности отраженного света по
различным направлениям. Модель Торрэнса и Спэрроу хорошо согласуется с
опытами, но является более сложной, чем рассмотренная выше модель.
9.9. Описание цвета
Свет и его восприятие человеком представляют собой сложные явления, кото-
которые изучены пока не полностью. Из экспериментальных исследований известно,
что свет с длиной волны из определенной части спектра воспринимаются глазом
в виде света, определенного цвета. Воспринимаемый цвет зависит от источника
света, от свойств поверхности объекта и от зрительной системы человека. Так,
Рис. 9.9.1
если объект освещен красным светом, а его поверхность отражает только синий
свет, то объект будет казаться черным. Зависимость воспринимаемой глазом
интенсивности света от зрительной системы человека показана на рис. 9.9.1.
Яркость круглых областей внутри двух квадратов одинакова, но круг на све-
светлом фоне кажется более темным, чем такой же круг на темном фоне. Это явле-
явление называется одновременным контрастом. Подобное явление существует
464 Гл. 9. Компьютерная графика
и при восприятии цветных изображений. В зависимости от цвета и яркости
окружения цветные области могут иметь разный оттенок (казаться меняющими
цвет). Кроме того, границы областей постоянной интенсивности кажутся более
яркими, чем центральная часть областей. Это явление называется эффектом
полос Маха.
Для получения цветных изображений используется представление света в
виде трех компонент. Это представление основано на физиологической трех-
компонентной теории цвета, в соответствии с которой в сетчатке глаза
имеется три типа колбочек и пик чувствительности каждого из этих типов при-
приходится либо на красный, либо на зеленый, либо на синий цвета. Чувстви-
Чувствительность глаза не одинакова к разным цветам: наибольшая она для зеленого
цвета, наименьшая — для синего цвета. Кроме того, глаз воспринимает не
абсолютное значение интенсивности того или иного цвета, а ее относительное
значение. Следовательно, линейное распределение уровней интенсивности при-
приходящего света в зрительной системе человека становится логарифмическим.
Все сказанное показывает, что в результате моделирования иногда можно полу-
получить не ту цветовую гамму, которая ожидалась.
Интенсивность падающего света будем представлять в виде красной, зеле-
зеленой и синей компоненты. Положим, что в белом цвете все три компоненты
имеют равные интенсивности (хотя области красного, зеленого и синего цвета
видимой части спектра не являются равными). Такая цветовая модель явля-
является аддитивной системой смешивания цветов и называется RGB моделью (Red,
Green, Blue). Перечисленные цвета являются основными цветами данной мо-
модели. Соответствующими дополнительными цветами являются бирюзовый
(Cyan), розовый (Magenta) и желтый (Yellow). Если основной цвет сложить в
равной пропорции с его дополнительным цветом, то получим белый цвет. Таким
образом, бирюзовый цвет можно представить в виде суммы зеленого и синего
цветов, розовый цвет можно представить в виде суммы синего и красного цве-
цветов, желтый цвет можно представить в виде суммы красного и зеленого цветов.
Остальные оттенки получаются в виде смешения основных цветов в различных
(неравных) пропорциях. Эта модель не единственная, но она наиболее рас-
распространена, так как представление света в виде взвешенной суммы красного,
зеленого и синего цветов согласуется с экспериментальными данными и легко
реализуема.
В соответствии с RGB моделью интенсивность падающего и отраженного
объектом света должна быть представлена в виде суммы интенсивностей крас-
красного, зеленого и синего цветов
I = IR + IG + IB. (9.9.1)
Интенсивность каждого цвета определяется по одной из приведенных формул,
в которой каждая цветовая компонента описывается своими коэффициентами,
например,
\ + kr(r — го)
*° = i—ГГ1 T
1 + Kr{r — го)
Iв =
+ Тр(к** cos в + ksR cosH a) + TPktR cos" ft
¦+ ^kdG cos в + к'о cos" a) + Vfcto cos" ft (9-9-2)
a^ г + Ip(kdB cos в + ksB cosn a) + IpktB cos" /3.
kr(r го)
9.10. Формирование реалистических изображений
465
Значения интенсивностей должны быть нормированы при г = tq. Варьируя
направлением падающего света и значениями коэффициентов диффузного от-
отражения, зеркального отражения и пропускания для разных компонент света,
можно подобрать желаемое изображение объекта. Если источников света не-
несколько, то каждый из них должен быть учтен в формулах (9.9.2) соответствую-
соответствующими слагаемыми.
Существуют другие физиологические теории зрения, например, теория до-
дополнительных цветов, а также другие цветовые модели, например, модель CMY,
где основными цветами являются бирюзовый, розовый и желтый, а красный,
зеленый и синий цвета являются дополнительными. Такая модель является
субтрактивной системой смешивания основных цветов.
9.10. Формирование реалистических изображений
Реалистическое растровое изображение геометрического объекта формиру-
формируется путем определения цвета и яркости его точек при некоторой модели света.
Для ускорения этого процесса используется триангуляция поверхностей объ-
объекта. В результате задача сводится к закраске триангуляционной сетки объекта
(аппроксимирующих треугольников).
В большинстве случаев выполняется построчное сканирование изображения.
Для определения отражающей свет точки объекта выполняется пересечение его
триангуляционной сетки со сканирующей линией визирования. Эта линия стро-
строится из точки изображения перпендикулярно проекционной плоскости (как для
параллельной проекции, так и для центральной проекции). Поиск точек пе-
пересечения линии и треугольников упрощается, если его выполнять в местной
системе координат, связанной с проекционной плоскостью. Для этого перед
сканированием аппроксимирующие геометрический объект треугольники пере-
переводятся в местную систему координат. Координаты вершин треугольников пре-
преобразуются по формуле (9.2.3). Компоненты векторов нормалей преобразуются
по формуле
Уг,
Х\
У\
0
Х2
Уг
0
хъ
Уг
0
0
0
0
1
¦
7711
7712
т3
1
= А0-
7711
7712
т3
1
(9.10.1)
где mi, 1^2, "3 — компоненты нормали в глобальной системе координат, хт,
Ут-i %т — компоненты нормали в местной системе координат проекционной
плоскости. Первые три строки матрицы Ао образованы компонентами ортов
ix, iy, i2 местной системы координат. При построении перспективного изобра-
изображения триангуляционная сетка подвергается дополнительному преобразованию:
координаты х и у точек треугольников заменяются, соответственно, координа-
координатами хр и ур, вычисленными по формулам (9.3.5), а координата z остается без
изменений. Аналогичным образом уточним и нормали m в вершинах треуголь-
треугольников: они должны быть повернуты на угол
V = arccos (-
г — w
вокруг вектора
V = —
(г - w) х iz
|(r-w)xiz|'
(9.10.2)
(9.10.3)
466 Гл. 9. Компьютерная графика
где w — радиус-вектор точки наблюдения, г радиус-вектор точки поверхности, в
которой вычислена нормаль, \z — нормаль к проекционной плоскости. Поворот
вектора m описывается формулой
nip = (vv) • m + cos 77(E — vv)m + sin 77 v x m. (9.10.4)
Сканирующая линия визирования ортогональна проекционной плоскости и в
местной системе координат поиск ее пересечения с триангуляционной сеткой
сводится к определению треугольника, в проекции которого лежит проекция
точки. Последняя задача является двухмерной, что уменьшает объем вычисле-
вычислений. Для уменьшения количества просмотров проекции треугольников можно
сгруппировать по отдельным областям.
На практике используются три основных способа закраски: однотонная,
основанная на интерполяции значений интенсивности (метод Гуро) и осно-
основанная на интерполяции нормалей (метод Фонга). Для каждой из них мо-
может применяться любая модель света. Тоновое изображение при любом способе
закраски формируется одинаковым образом: для каждой точки изображения
определяется точка объекта (или несколько точек, если объект прозрачен), от
которой приходит отраженный свет, и по интенсивности света и по оптиче-
оптическим свойствам отражающей поверхности определяются цвет точки изображе-
изображения. Цвет вычисляется по интенсивно стям цветовых компонент модели света.
Однотонная закраска. При однотонной закраске для каждого треугольника
вычисляется уровень интенсивности отраженного света, который используется
для закраски всего треугольника. При этом
для простоты полагается, что в и а явля-
являются постоянными в пределах своего тре-
треугольника. Фактически получается, что
триангуляционная сетка является реальной
моделируемой поверхностью, а не аппрок-
аппроксимацией последней. Однотонная закраска
дает граненое изображение кривых поверх-
поверхностей (рис. 9.10.1).
Рис. 9.10.1. Однотонная закраска Интенсивность отраженного света при
переходе от одного треугольника к другому
меняется скачком. Различие в цвете соседних треугольников хорошо заметно
вследствие полос Маха.
Метод Гуро. Способ закраски, основанный на интерполяции в пределах ка-
каждого треугольника значений интенсивности, был предложен Гуро. В методе
Гуро по значениям нормалей в вершинах каждого треугольника определяются
интенсивности отраженного света в его углах. По интенсивности света 1а, 1ь
и 1С в вершинах а, Ь и с некоторого треугольника интенсивность отраженного
света от любой его внутренней точки определяется формулой
1{а, Ь, с) = ala + Ыь + clc, (9.10.5)
где а, Ь, с — барицентрические координаты произвольной точки треугольника
на параметрической плоскости, которые вычисляются по формулам C.11.4). Ме-
Метод Гуро хотя и сглаживает перепады интенсивности на границах треугольни-
треугольников, но не позволяет их полностью устранить. Методом Гуро трудно получить
четкие блики, особенно, если они небольших размеров.
9.10. Формирование реалистических изображений 467
Метод Фонга. Метод закраски, предложенный Фонгом, основан на интер-
интерполяции в пределах каждого треугольника значений нормалей к поверхности.
В каждой вершине треугольника р{(щ, Vj) должна быть вычислена нормаль
mj(uj, vi) к поверхности отображаемого объекта. Нормали в вершинах имеют
свое истинное направление, а в пределах каждого треугольника принимается
линейный закон их изменения от вершины к вершине. Пусть в вершинах
Pa(ua, va), рь(щ, щ), Рс(^с! vc) некоторого треугольника нормали равны
хПаЫа, va), ть(щ, Vb), mc(uc, vc), тогда нормали на поверхности треугольника
припишем направление вектора
т(а, Ь, с) = ата + Ьть + стс, (9.10.6)
где а, Ь, с — барицентрические координаты произвольной точки р = [u v]T
треугольника на параметрической плоскости, которые вычисляются по форму-
формулам C.11.4). Несмотря на то, что векторы та, гщ, тс нормированы, век-
вектор т(а, Ь, с), в общем случае, не имеет еди-
единичной длины и его следует нормировать. На
рис. 9.10.2 приведен треугольник и нормали в
его вершинах. та
Значение радиус-вектора точки треугольни-
треугольника определяется формулой
р(а, Ь, с) = ара + Ьрь + срс- (9.10.7) рис g 10 2. Направление нор-
Барицентрические координаты а, Ь и с связаны мале тРеУгольника
равенством C.11.2) и в пределах треугольника принимают неотрицательные
значения. Если хотя бы одна из барицентрических координат отрицательна, то
это означает, что точка лежит за пределами треугольника. При аппроксимации
(9.10.6) нормали плавно меняют свое направление при переходе от одного тре-
треугольника к другому, поэтому на тоновых изображениях поверхность выглядит
Рис. 9.10.3. Закраска методом Фонга
гладкой. Метод Фонга полностью устраняет полосы Маха, однако, значительно
увеличивает объем вычислений. На рис. 9.10.3 приведено изображение детали,
полученное методом Фонга.
Детализация поверхностей. Не все поверхности обладают достаточной глад-
гладкостью, например, поверхность апельсина. Некоторые поверхности имеют ри-
рисунок, например, поверхность деревянных досок.
Для создания регулярных неровностей на поверхностях в методе закраски
Фонга могут использоваться регулярные отклонения нормали. Для создания
468
Гл. 9. Компьютерная графика
нерегулярных неровностей могут использоваться случайные отклонения нор-
нормали. На рис. 9.10.4 и 9.10.5 приведены тела, нормалям поверхностей которых
сообщены случайные отклонения. На рис. 9.10.4 случайные отклонения нор-
нормали от исходного положения достигают 10°, а на рис. 9.10.5 эти отклонения
достигают 60°.
Рис. 9.10.4. Неровности на поверхности тора Рис. 9.10.5. Неровности на поверхности сферы
На поверхность моделируемого объекта может быть нанесен рисунок, подоб-
подобный рисунку на стенных обоях. Рисунок выполняется цветом, описываемым на
параметрической плоскости поверхности. Описание может быть аналитическим
или может быть выполнено путем наложения некоторого рисунка на плоскость
параметров поверхности. Рисунок в свою очередь может быть растровым изо-
изображением. Растровый рисунок будем рассматривать как набор цветных точек
на целочисленной плоскости. Для нанесения рисунка на поверхность остается
установить функциональную зависимость между целочисленной плоскостью и
плоскостью параметров поверхности. Детализация поверхности выполняется
методом Фонга.
Тени. В рассмотренных способах закраски мы считали, что на точки по-
поверхности падает рассеянный свет интенсивности Ia и направленный свет
Рис. 9.10.6. Объекты и их тени
интенсивности источника 1Р. Это всегда справедливо, когда точка наблюде-
наблюдения совпадает с положением источника света. В общем случае некоторая часть
9.10. Формирование реалистических изображений
469
поверхности объекта будет закрыта от источника, т.е. будет находиться в тени.
Алгоритм определения затенения точек аналогичен алгоритму определения ви-
видимости точек. Если точка поверхности «видна» из точки источника света, то
она освещена. Те точки поверхности объекта, которые видны из точки наблю-
наблюдения и из источника, освещены рассеянным и направленным светом. Точки
поверхности объекта, которые видны из точки наблюдения, но не видны из ис-
источника света, находятся в тени и освещены только рассеянным светом. Это
же справедливо и для нескольких источников света. Естественно, что при по-
построении теней объем вычислений увеличивается. На рис. 9.10.6 приведено
изображение объектов с тенями.
Четкие тени дают точечные источники света. При освещении объекта рас-
распределенными источниками света возникают области полутеней. Полутени воз-
возникают в тех точках объекта, из которых видна только часть распределенного
источника.
Прозрачность. Для прозрачных моделей в точку наблюдения приходит свет,
отраженный не только от ближайшей поверхности, но и от других поверхно-
поверхностей, которые видны сквозь нее. Если не учитывать преломление света, то в
точку наблюдения придет свет от всех треугольников, с которыми пересекается
линия визирования. На рис. 9.10.7 и 9.10.8 приведены изображения одного
Рис. 9.10.7. Непрозрачный объект
Рис. 9.10.8. Прозрачный объект
и того же объекта с различной прозрачностью материала. Материал объекта,
приведенного на рис. 9.10.7, непрозрачный. Материал объекта, приведенного
на рис. 9.10.8, отражает 40% падающего света, а пропускает 60% (преломление
света не учитывалось).
При моделировании преломления света линия визирования для заслоненных
треугольников должна быть смещена. Интенсивность света, пришедшего от ка-
каждой поверхности, будет ослаблена из-за поглощения света веществом. Чтобы
определить, какие из световых лучей попадают в точку зрения, используют ме-
метод трассировки лучей.
Трассирование начинается из точки наблюдения, и лучи света отслежива-
отслеживаются в обратном направлении к каждому источнику света. Луч света, падающий
на поверхность, разделяется на несколько основных частей: диффузно пропу-
пропущенный свет, пропущенный преломленный свет, диффузно отраженный свет и
470 Гл. 9. Компьютерная графика
зеркально отраженный свет. Аналогично луч света, исходящий от поверхности
объекта, является суммой двух отраженных составляющих света и двух соста-
составляющих света, пришедших из-за поверхности. Таким образом, каждый раз,
когда трассируемый из точки наблюдения луч подходит к поверхности отобража-
отображаемого объекта, возможно появление нескольких новых лучей, т. е. трассируемый
луч расщепляется на несколько составляющих. Диффузно отраженный свет и
диффузно пропущенный свет могут прийти в общем случае из бесконечного чи-
числа направлений, поэтому обычно трассируют только лучи света, появляющиеся
в результате зеркального отражения и преломления. В результате, при под-
подходе трассируемого луча к поверхности прозрачного объекта он расщепляется
на две части. Рассеянный свет и диффузно отраженный свет можно получить
от ближайшей к точке наблюдения поверхности. Для каждого трассируемого
луча нужно получить его пересечение со всеми поверхностями объекта. В точ-
точках пересечения по свойствам поверхности определяется, нужно ли расщеплять
световой луч.
Как можно видеть, построение реалистических изображений геометриче-
геометрических моделей требует больших вычислительных затрат. Геометрическое мо-
моделирование имеет огромные возможности. Через компьютерную графику оно
позволяет увидеть и исследовать то, что раньше могло существовать только в
воображении.
Вместо заключения
Мы рассмотрели моделирование геометрических свойств окружающих нас
и воображаемых объектов, связанные с моделированием математические про-
проблемы и методы их решения. Чтобы создать систему моделирования, нужно
обеспечить взаимодействие с создаваемой геометрической моделью. Это при-
призвана обеспечить внутренняя организация модели и ее окружения — редактор
системы. Проблема организации внутренней жизни геометрической модели и
взаимодействия с ней человека представляет собой отдельную задачу, способы
решения которой тесно связаны с программированием.
Программная реализация рассмотренных в книге математических проблем
составляет математическое ядро системы моделирования. В объектном подходе
к созданию математического ядра точки, кривые линии, поверхности, тела,
топологические объекты, операции, вариационные связи, геометрические ха-
характеристики, полигоны, триангуляции и другие объекты реализуются в виде
классов.
Геометрическое моделирование позволяет существенно сократить время и
материальные затраты на производство проектируемых объектов и повысить
их качество. Геометрическое моделирование автоматизирует труд дизайнеров,
конструкторов, архитекторов, технологов, позволяет им уйти от рутины и со-
сосредоточиться на творчестве.
СПИСОК ЛИТЕРАТУРЫ
1. Алберг Дж., Нильсон Э., Уолш Дж. Теория сплайнов и ее приложения.—М •
Мир, 1972(Ahlberg J.H., Nilson E.N., Walsh J.L. The Theory of Splines
and their Applications.—New York: Academic Press, 1967).
2. Березин И.С, Жидков Н.П. Методы вычислений. Т. 1,2.—М.: Наука, 1962,
1966.
3. Будак Б.М., Фомин СВ. Кратные интегралы и ряды.—М.: Наука, 1967.
4. ГарданИ., Люка М. Машинная графика и автоматизация конструирования.—
М.: Мир, 1987 (Techniques Graphiques Interactives et C.A.O./par Michel
Lucas et Yvon Gar dan.—Prance: Hermes Publishing, 1983).
5. Гильберт Д., Кон-Фоссен С. Наглядная геометрия.—М.: Наука, 1981
(Hilbert D., Cohn-Vossen S. Anschauliche Geometric—Berlin: 1932).
6. Д е Б о р К. Практическое руководство по сплайнам.—М.: Радио и связь, 1985 (D е
Boor С. A Practical Guide to Splines.—Berlin: Springer, 1879).
7. Демидович Б.П., Марая И.А. Основы вычислительной математики.—М.:
Наука, 1970.
8. Дубровин Б.А., Новиков СП., Фоменко А.Т. Современная геометрия.—
М.: Наука, 1986.
9. Ильин В. А., Позняк Э.Г. Аналитическая геометрия.—М.: Наука, 1981.
10. Ильин В. А., Позняк Э.Г. Линейная алгебра.—М.: Наука, 1984.
11. Калиткин Н.Н. Численные методы.—М.: Наука, 1978.
12. Курош А. Г. Курс высшей алгебры.—М.: Наука, 1971.
13. Лаврентьев М. А., Шабат Б.В. Методы теории функций комплексного пере-
переменного.—М.: Наука, 1987.
14. Ласло М. Вычислительная геометрия и компьютерная графика на C++.—М.:
Бином, 1997 (Laszlo M. J. Computational Geometry and Computer Graphics
in C++.—Prentice Hall, 1996).
15. Лойцянский Л.Г., Лурье А.И. Курс теоретической механики. Т. 1,2.—М.:
Наука, 1982, 1983.
16. Препарата Ф., Шеймос М. Вычислительная геометрия.—М.: Мир, 1989
(Preparata F.P., Shamos M. Computational Geometry: An Introduction.—
New York, Berlin, Tokyo: Springer-Verlag, 1985).
17. Рашевский П. К. Курс дифференциальной геометрии.—М-Л.: Физматгиз, 1950.
18. Рашевский П.К. Риманова геометрия и тензорный анализ.—М.: Наука, 1967.
19. Роджерс Д., Адаме Дж. Математические'основы машинной графики.—М.:
Машиностроение, 1980 (Rogers D.F., Adams J. A. Mathematical Elements for
Computer Graphics.—McGrow-Hill, 1976).
20. Розенфельд А. Распознавание и обработка изображений с помощью вычисли-
вычислительных машин.—М.: Мир, 1972.
21. Самарский А. А., Гулин А.В. Численные методы.—М.: Наука, 1989.
22. Сокольников И. С. Тензорный анализ.—М.: Наука, 1971.
23. Стечкин С.Б., Субботин Ю.Н. Сплайны в вычислительной математике.—М.:
Наука, 1976.
24. Тихомиров Ю. Программирование трехмерной графики.—СПб.: BHV-Санкт-
Петербург, 1998.
25. Фаворин М.В. Моменты инерции тел.—М.: Машиностроение, 1977.
472 Список литературы
26. Феодосьев В. И. Сопротивление материалов.—М.: Наука, 1972.
27. Фокс А., Пратт М. Вычислительная геометрия.—М.: Мир, 1982 (Faux I.E.,
Pratt М. J. Computational Geometry for Design and Manufacture.—Ellis Hor-
wood, Chichester, 1979).
28. Фоли Дж., Вен Дем А. Основы интерактивной машинной графики. Т. 1,2.—
М.: Мир, 1985 (James D. Foley, Andries Van Dam. Fundamentals Inter-
Interactive Computer Graphics.—Massachusetts, Menlo Park, California, London, Ams-
Amsterdam, Don Mills, Ontario, Sydney: Addison-Wesley Publishing Company Reading,
1982).
29. Фоменко А.Т. Наглядная геометрия и топология. Математические образы в
реальном мире.—М.: Изд-во Моск. ун-та, Изд-во ЧеРо, 1998.
30. Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление.—
М.: Наука, 1969.
31. Bezier P. Numerical control: Mathematics and application.—N.Y.: Wiley, 1972.
32. Barnhill E.R., Bohm W. Surfaces in CAGD.—Amsterdam: North-Holland,
1983.
33. Bohm W. A. Survey of Curve and Surface Methods in CAGD.—Computer Aided
Geometric Design.—Amsterdam: North-Holland, July 1984. V. 1, № 1.
34. Christoph M. Hoffman. Geometric and Solid Modeling.—San Ateo (Califor-
(California): Morgan Kaufmann Publishers Inc., 1989.
35. Coons S. A. Modification of the Shape of Piecewiese Curves /Computer Aided
Design. 1977. 9, 3. P. 178-180.
36. Coons S. A. Surfaces for Computer Aided Design of Space Form /Report MAC-
TR-41, Project MAC, M.I.T., 1967.
37. Cox M. G. An Algorithm for Spline Interpolation / J. Inst. Math-Applies. 1975.15.
38. Cox M.G. The Numerical Evaluation of a Spline from its B-spline Represen-
Representation.—Middlesex, 1976.
39. D ah men W., Micchelli С A., Seidel H-P. Blossoming Begests B-splines Built
Better by B-patches // Mathematics of Computation. July, 1992. 59A99). P. 97-115.
40. De Boor С On Calculating with B-splines / J. Approx. Theory. 1972. 6.
41. De Boor C. Package for Calculating with B-splines /SLAM J. Number. Anal.
1977. 14, 3.
42. D e С as t el j au F. Outillage methodes calcul.—Paris: Andre Citroen Automobiles
SA, 1959.
43. De Casteljau F. Courbes et surfaces a poles.—Paris: Andre Citroen Automo-
Automobiles SA, 1963.
44. Gordon W. J., Riesenfeld R. F. B-spline Curves and Surfaces /Computer
Aided Geometric Design.—Academic Press, 1974.
45. Ferguson J. С Multivariate Curve Interpolation /Journal ACM. 1964. II, 2.
P. 221-228.
46. Forrest A.R. Mathematical Principles for Curve and Surface Representation.
Curved Surfaces in Engineering.—IPC Science and Technology Press Ltd.
47. Liming R. A. Practical Analitical Geometry with Applications to Aircraft.—New
York: Macmillan, 1944.
48. Richard H. Bartels, John C. Beatty, Brian A. Barsky.An Introduc-
Introduction to Splines for use in Computer Graphics and Geometric Modeling.—San Mateo,
California: Morgan Kaufmann Publishers Inc., 1987.
49. Schoenberg I. J. Cardinal Spline Interpolation.—Philadelphia: SIAM, 1973.