Ж. Сетубал, Ж. Мейданис
^/«sgw/F

СЕРИЯ «БИОИНФОРМАТИКА И МОЛЕКУЛЯРНАЯ БИОЛОГИЯ»
Вышли в свет:
Дурбин Р., Эдди Ш.. Крог А., Митчисон Г.
Анализ биологических последовательностей
Игнасимуту С.
Основы биоинформагики
Эвери Дж.
Теория информации и эволюция
Готовится к публикации:
Бородовский М., Екишева С.
Анализ биологических последовательностей.
Задачи и решения
СЕРИЯ «БИОИНФОРМАТИКА И МОЛЕКУЛЯРНАЯ БИОЛОГИЯ»
Главные редакторы:
Садовничий В. А. (МГУ им. М. В. Ломоносова) Скулачев В. П. (факультет биоинженерии и биоинформатики МГУ им. М. В. Ломоносова)
Редакционная коллегия:
Богданов А. А. (Институт физико-химической биологии им. А. Н. Белозерского МГУ)
Гельфанд М.С. (Институт проблем передачи информации им. А. А. Харкевича РАН)
Есипова Н. Г. (Институт молекулярной биологии им. В. А. Энгельгардта РАН)
Кирпичников М.11, (биологический факультет МГУ им. М. В. Ломоносова) Колчанов Н. А. (Институт цитологии и генетики СО РАН) Миронов А. А. (факультет биоинженерии и биоинформатики МГУ им. М. В. Ломоносова)
Ризниченко Г. Ю. (биологический факультет МГУ им. М. В. Ломоносова) Ройтбсрг М. А. (Институт математических проблем биологии РАН) Рубин А. Б. (биологический факультет МГУ им. М. В. Ломоносова) Финкельштейн А. В. (Институт белка ПНЦ РАН)
Шайтан К. В. (биологический факультет МГУ им. М. В. Ломоносова)
Жуан Сетубал и Жуан Меиданис
ВВЕДЕНИЕ В ВЫЧИСЛИТЕЛЬНУЮ МОЛЕКУЛЯРНУЮ БИОЛОГИЮ
Перевод с англ. А. А. Чумичкина Под ред д. б. н., проф. А. А. Миронова
Москва ♦ Ижевск
2007
INTRODUCTION TO COMPUTATIONAL MOLECULAR BIOLOGY
JOAO SETUBAL and ЮАО MEIDANIS
University of Campinas, Brazil
PWS PUBLISHING COMPANY
I(T)P
An International Thomson Publishing Company
BOSTON • ALBANY • BONN • CINCINNATI • DETROIT • LONDON MELBOURNE • MEXICO CITY • NEW YORK • PACIFIC GROVE • PARIS SAN FRANCISCO • SINGAPORE • TOKYO • TORONTO
УДК 577:004.383
ББК 28.070с51
С334
И нтернет-магазин
http://shop.rcd.ru
•	физика
•	математика
•биология
•	нефтегазовые гехноло!ин
Сезубал Ж., Мейлаиис Ж.
Введение в вычислительную молекулярную биологию. — Москва Ижевск: НИЦ «Регулярная и хаотическая динамика», Институт компьютерных исследований, 2007. — 420 с.
Настоящая книга представляет собой введение в вычислительную молекулярную биологию, описывает наиболее типичные ее задачи и предлагает эффективные алгоритмы их решения. Книга начинается с обзора фундаментальных понятий молекулярной биологии (в том числе структура и функции белков и нуклеиновых кислот, механизмы молекулярной генетики), далее вводятся важнейшие математические объекты, такие как графы и строки, и приводятся общие сведения об алгоритмах. Все это подготавливает почву для понимания дальнейших разделов книги-сравнение последовательностей (и поиск в базе данных), сборка фратментов ДНК, составление физических карт ДНК, филогенетические деревья, перестройка генов, предсказание структуры макромолекулы и вычисления с помощью ДНК. Каждый из этих разделов содержит обсуждение биологических предпосылок, определения ключевых терминов, полное описание применяемых математических или компьютерных моделей, а также примеры реализации алгоритмов.
Книга предназначена для программистов, математиков и биологов, стремящихся расширить свои познания в этой новой захватывающей области науки, где еще так много нерешенных задач.
ISBN 978-5-93972-623-8	ББК 28.070с51
© 1997 by Brooks/Cole Publishing Company,
a division of International Thomson Publishing Inc.
© Перевод на русский язык:
НИЦ «Регулярная и хаотическая динамика», 2007.
http://shop.rcd.ru
http://ics.org.ru
Оглавление
ПРЕДИСЛОВИЕ . .	12
Глава 1 ОСНОВНЫЕ ПОНЯТИЯ МОЛЕКУЛЯРНОЙ БИОЛО-
ГИИ	............................ 20
1.1.	ЖИЗНЬ................................. 20
1.2.	БЕЛКИ................................. 21
1.3.	НУКЛЕИНОВЫЕ КИСЛОТЫ	26
1.3.1.	ДНК............................. 26
1.3.2.	РНК............................. 30
14	МЕХАНИЗМЫ МОЛЕКУЛЯРНОЙ ГЕНЕТИКИ ...	30
1.4.1.	ГЕНЫ И ГЕНЕТИЧЕСКИЙ КОД	...	  30
1.4.2.	ТРАНСКРИПЦИЯ, ТРАНСЛЯЦИЯ И СИНТЕЗ БЕЛКА 32
1.4.3.	ИЗБЫТОЧНАЯ ДНК И РАМКИ СЧИТЫВАНИЯ ... 36
1.4.4.	ХРОМОСОМЫ ...................... 37
1.4.5.	ПОДОБЕН ЛИ ГЕНОМ КОМПЬЮТЕРНОЙ ПРОГРАММЕ? ............................... 39
1 5. МЕТОДЫ ИЗУЧЕНИЯ ГЕНОМА................ 40
1.5.1. КАРТЫ И ПОСЛЕДОВАТЕЛЬНОСТИ	40
1.5.2. СПЕЦИАЛЬНЫЕ МЕТОДЫ ............. 43
1.6. ПРОЕКТ «ГЕНОМ ЧЕЛОВЕКА»............... 49
1.7. БАНКИ ПОСЛЕДОВАТЕЛЬНОСТЕЙ НУКЛЕОТИДОВ	51
УПРАЖНЕНИЯ .	  59
БИБЛИОГРАФИЧЕСКИЕ ПРИМЕЧАНИЯ	59
Глава 2. СТРОКИ, ГРАФЫ И АЛГОРИТМЫ............61
2.1. СТРОКИ..............................   61
2.2. ГРАФЫ..................................63
2 3 АЛГОРИТМЫ ..............................68
УПРАЖНЕНИЯ................................  76
БИБЛИОГРАФИЧЕСКИЕ ПРИМЕЧАНИЯ............... 78
8
Оглавление
Глава 3. СРАВНЕНИЕ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И ПОИСК В
БАЗАХ ДАННЫХ............................... 80
3.1.	БИОЛОГИЧЕСКИЕ ОСНОВЫ СРАВНЕНИЯ ПОСЛЕДОВАТЕЛЬНОСТЕЙ ................................ 80
3.2.	СРАВНЕНИЕ ДВУХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ ... 83
3.2.1.	ГЛОБАЛЬНОЕ СРАВНЕНИЕ - ОСНОВНОЙ АЛГОРИТМ ................................... 83
3.2.2.	ЛОКАЛЬНОЕ СРАВНЕНИЕ..............91
3.2.3.	ПОЛУГЛОБАЛЬНОЕ СРАВНЕНИЕ.........92
3.3.	РАСШИРЕНИЯ К ОСНОВНЫМ АЛГОРИТМАМ......	95
3.3.1.	ЭКОНОМИЯ ПРОСТРАНСТВА........... 96
3.3.2.	ОБЩИЕ ФУНКЦИИ ШТРАФОВ ЗА ПРОПУСКИ ... 100
3.3.3.	ЛИНЕЙНЫЕ ФУНКЦИИ ШТРАФОВ ЗА ПРОПУСКИ 104
3.3.4.	СРАВНЕНИЕ ПОДОБНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ ...................................107
3.4.	МНОЖЕСТВЕННОЕ СРАВНЕНИЕ ПОСЛЕДОВАТЕЛЬНОСТЕЙ ..................................... III
3.4.1.	МЕРА ПАРНЫХ СУММ................112
3.4.2.	ВЫРАВНИВАНИЕ ЗВЕЗДЫ............ 122
3.4.3.	ВЫРАВНИВАНИЕ ПО ДЕРЕВУ .... ... 125
3.5.	ПОИСК В БАЗАХ ДАННЫХ	.127
3.5.1.	МАТРИЦЫ ПТМ ..................  128
3.5.2.	BLAST...........................133
3.5.3.	FAST............................138
3.6.	РАССТОЯНИЕ, СОПОСТАВЛЕНИЕ СТРОК И ТОЧНОЕ СРАВНЕНИЕ ПОСЛЕДОВАТЕЛЬНОСТЕЙ..............141
3.6.1.	* ПОДОБИЕ И РАССТОЯНИЕ......... 142
3.6.2.	ВЫБОР ПАРАМЕТРОВ ПРИ СРАВНЕНИИ ПОСЛЕДОВАТЕЛЬНОСТЕЙ .........................151
3.6.3.	СОПОСТАВЛЕНИЕ СТРОК И ТОЧНОЕ СРАВНЕНИЕ ПОСЛЕДОВАТЕЛЬНОСТЕЙ.................155
РЕЗЮМЕ.....................................157
УПРАЖНЕНИЯ ................................158
БИБЛИОГРАФИЧЕСКИЕ ПРИМЕЧАНИЯ ..............161
ГЛАВА 4. СБОРКА ФРАГМЕНТОВ ДНК...............165
4.1.	БИОЛОГИЧЕСКИЙ АППАРАТ СЕКВЕНИРОВАНИЯ	.165
4.1.1.	ИДЕАЛЬНЫЙ СЛУЧАЙ................167
4.1.2.	ТРУДНОСТИ.......................168
Оглавление
9
4.1.3.	АЛЬТЕРНАТИВНЫЕ МЕТОДЫ СЕКВЕНИРОВАНИЯ ДНК	.	...............176
4.2.	МОДЕЛИ	.	............ 178
4.2.1.	КРАТЧАЙШАЯ ОБЩАЯ НАДСТРОКА........178
4.2.2.	ВОССТАНОВЛЕНИЕ	 180
4.2.3.	МУЛЬТИКОНТИГИ ....................182
4.3.	* АЛГОРИТМЫ.............................184
4.3.1.	ПРЕДСТАВЛЕНИЕ ПЕРЕКРЫТИЙ..........185
4.3.2.	ПУТИ, ПОРОЖДАЮЩИЕ НАДСТРОКИ ......186
4.3	3 КРАТЧАЙШИЕ НАДСТРОКИ В КАЧЕСТВЕ ПУТЕЙ . 189
4.3	4 ЖАДНЫЙ АЛГОРИТМ .	  .192
4.3.5.	АЦИКЛИЧЕСКИЕ ПОДГРАФЫ.............195
4.4.	ЭВРИСТИКИ ..............................202
4.4 1 ОБНАРУЖЕНИЕ ПЕРЕКРЫТИЙ.............205
4.4.2. УПОРЯДОЧЕНИЕ ФРАГМЕНТОВ...........206
4.4.3. ВЫРАВНИВАНИЕ И КОНСЕНСУС..........209
РЕЗЮМЕ.......................................211
УПРАЖНЕНИЯ .	 212
БИБЛИОГРАФИЧЕСКИЕ ПРИМЕЧАНИЯ.................214
Глава 5. СОСТАВЛЕНИЕ ФИЗИЧЕСКИХ КАРТ ДНК	217
5.1.	БИОЛОГИЧЕСКИЕ ОСНОВЫ КАРТИРОВАНИЯ.......217
5.1.1.	СОСТАВЛЕНИЕ РЕСТРИКЦИОННЫХ КАРТ.219
5.1.2.	СОСТАВЛЕНИЕ КАРТ ГИБРИДИЗАЦИИ ...	221
5.2.	МОДЕЛИ..................................223
5.2.1. МОДЕЛИ УЧАСТКА РЕСТРИКЦИИ.........223
5.2 2 МОДЕЛЬ В ВИДЕ ИНТЕРВАЛЬНОГО ГРАФА .225
5.2.3 СВОЙСТВО ПОСЛЕДОВАТЕЛЬНЫХ ЕДИНИЦ . ..227
5.2 4 СВОЙСТВА «ИДЕАЛЬНОГО» АЛГОРИТМА КАРТИРОВАНИЯ .........................229
5.3.	АЛГОРИТМ ДЛЯ ЗАДАЧИ СПЕ ................231
5.4.	ПРИБЛИЖЁННОЕ СОСТАВЛЕНИЕ КАРТ ГИБРИДИЗАЦИИ 240
5.4.1.	ГРАФОВАЯ МОДЕЛЬ...................241
5 4.2.	ГАРАНТИЯ..........................244
5 4 3	ПРАКТИКА ВЫЧИСЛЕНИЙ................247
5.5.	ЭВРИСТИКИ ДЛЯ СОСТАВЛЕНИЯ КАРТ ГИБРИДИЗАЦИИ25О 5.5.1	ОТСЕВ ХИМЕРНЫХ КЛОНОВ.............251
5.5.2.	ПОЛУЧЕНИЕ ХОРОШЕГО ПОРЯДКА ЗОНДОВ 252
РЕЗЮМЕ.....................................  254
УПРАЖНЕНИЯ ..................................254
10
Оглавление
БИБЛИОГРАФИЧЕСКИЕ ПРИМЕЧАНИЯ . .	.........257
ГЛАВА 6. ФИЛОГЕНЕТИЧЕСКИЕ ДЕРЕВЬЯ............260
6.1.	СОСТОЯНИЯ ПРИЗНАКОВ И ЗАДАЧА О СОВЕРШЕННОЙ ФИЛОГЕНИИ............................ 263
6.2.	СОСТОЯНИЯ БИНАРНЫХ ПРИЗНАКОВ..........269
6.3.	ДВА ПРИЗНАКА..........................275
6.4.	ЭКОНОМИЧНОСТЬ И СОВМЕСТИМОСТЬ ФИЛОГЕНЕТИЧЕСКИХ ДЕРЕВЬЕВ.........................280
6.5.	АЛГОРИТМЫ ДЛЯ МАТРИЦ РАССТОЯНИЙ...... 284
6.5.1.	ВОССТАНОВЛЕНИЕ АДДИТИВНЫХ ДЕРЕВЬЕВ . . 284
6.5.2.	* ВОССТАНОВЛЕНИЕ УЛЬТРАМЕТРИЧЕСКИX ДЕРЕВЬЕВ ................................290
6.6.	СОГЛАСИЕ ФИЛОГЕНЕТИЧЕСКИХ ДЕРЕВЬЕВ..... 299
РЕЗЮМЕ.................................... 305
УПРАЖНЕНИЯ .............................   306
БИБЛИОГРАФИЧЕСКИЕ ПРИМЕЧАНИЯ...............309
ГЛАВА 7. ПЕРЕСТРОЙКИ ГЕНОМА.............. ...	312
7.1.	БИОЛОГИЧЕСКИЕ ОСНОВЫ................. 312
7.2.	ОРИЕНТИРОВАННЫЕ БЛОКИ................ 315
7.2.1.	ОПРЕДЕЛЕНИЯ.....................317
7.2.2.	ТОЧКИ РАЗРЫВА...................320
7.2.3.	ДИАГРАММА ЖЕЛАЕМОГО И ДЕЙСТВИТЕЛБНОГО321
7.2.4.	ГРАФ ПЕРЕМЕЖЕНИЙ................329
7.2.5.	ПЛОХИЕ КОМПОНЕНТЫ.............. 333
7.2.6.	АЛГОРИТМ....................... 336
7.3.	НЕОРИЕНТИРОВАННЫЕ БЛОКИ.............. 340
7.3.1.	ПОЛОСЫ......................... 342
7.3.2.	АЛГОРИТМ....................... 345
РЕЗЮМЕ.....................................347
УПРАЖНЕНИЯ................................ 348
БИБЛИОГРАФИЧЕСКИЕ ПРИМЕЧАНИЯ...............350
ГЛАВА 8. ПРЕДСКАЗАНИЕ СТРУКТУРЫ МАКРОМОЛЕКУЛ 352
8.1.	ПРЕДСКАЗАНИЕ ВТОРИЧНОЙ СТРУКТУРЫ РНК...353
8.2.	СВЕРТЫВАНИЕ БЕЛКОВЫХ МОЛЕКУЛ..........362
8.3.	ПРОТЯГИВАНИЕ БЕЛКОВ .	 365
РЕЗЮМЕ.....................................372
Оглавление	11
ГЛАВА 9. ЭПИЛОГ: ВЫЧИСЛЕНИЯ С ПОМОЩЬЮ ДНК . ... 375
9.1.	ЗАДАЧА О ГАМИЛЬТОНОВОМ ПУТИ .........375
9.2.	ЗАДАЧА ВЫПОЛНИМОСТИ................379
9.3.	ПРОБЛЕМЫ И ПЕРСПЕКТИВЫ........... ...	383
УПРАЖНЕНИЯ .............................385
БИБЛИОГРАФИЧЕСКИЕ ПРИМЕЧАНИЯ И ДРУГИЕ ИСТОЧНИКИ ................................385
ОТВЕТЫ К ИЗБРАННЫМ УПРАЖНЕНИЯМ........... 388
ЛИТЕРАТУРА................................395
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ......................410
ПРЕДИСЛОВИЕ
Биология запросто посэавиг увлекательные задачи, над которыми нам придется поработать лет этак 500.
— Дональд Э Кнут
С того времени, когда в 1953 году была открыта структура двойной цепи ДНК, в развитии молекулярной биологии произошел гигантский скачок. По мере того как мы учились манипулировать последовательностями макромолекул, количество получаемых данных увеличивалось с огромной скоростью. Необходимость обработки информации, изливающейся из открытых по всему миру лабораторий, с тем чтобы она могла быть использована в дальнейшем научном прогрессе, породила качественно новые, междисциплинарные по своей природе задачи. Ученые-биологи являются производителями и в то же время конечными пользователями этих данных. Однако, вследствие гигантского объема и сложности информации, на пути от ее получения к использованию требуется помощь специалистов по многим другим дисциплинам - в частности, из области математических и вычислительных наук. Эта потребность привела к созданию новой научной отрасли, известной под общим названием вычислительной молекулярной биологии.
Название «вычислительная молекулярная биология» в самом широком смысле означает науку, занимающуюся разработкой и применением методов теории вычислительных систем и математики, которые могут помочь в решении задач молекулярной биологии. Несколько примеров пояснят вышесказанное.
Банки последовательностей и базы данных необходимы для хранения всей производимой информации. К настоящему времени уже создано несколько международных банков последовательностей, но ученые признали необходимость построения новых моделей баз данных, учитывающих специфические требования молекулярной биологии. Например, такие базы данных должны предоставлять ученым возможность вносить изменения в сведения о молекулярных последовательностях по мере их изучения; известные на сегодняшний день модели непригодны для этой цели. Исследование макромолекулярных последовательностей в свою очередь требу
ПРЕДИСЛОВИЕ
13
ет новых, усовершенствованных методов распознавания структуры, которые разрабатываются специалистами в области искусственного интеллекта С функцией поиска информации в базах данных связано появление новых и сложных статистических задач, для решения которых необходим постоянный поиск новых, специальных программных средств.
Однако существует особый класс задач, решение которых невозможно без построения эффективных алгоритмов. Попросту говоря, алгоритм это разбитая на последовательные шаги процедура решения определенной, хорошо структурированной задачи за ограниченный отрезок времени. Для того чтобы быть эффективным, алгоритм нс должен «чересчур долго» решать поставленную задачу, даже очень большую. Классический пример алгоритмически разрешимой задачи молекулярной биологии — задача сравнения последовательностей. Допустим, мы имеем две последовательности биополимеров и хотим знать, насколько эти последовательности подобны. Такую задачу приходится ежедневно решать тысячи раз, так что было бы весьма желательно иметь под рукой какой-нибудь особенно эффективный алгоритм.
Цель этой книги состоит в том, чтобы представить читателю типичные примеры вычислительных задач молекулярной биологии, а также некоторые эффективные алгоритмы, которые были предложены для их решения. Многие из этих задач были хорошо изучены, а некоторые из алгоритмов их решения известны уже много лет. Остальные задачи более сложны, и пока что не удалось найти никакого удовлетворительного алгоритмического подхода к их решению. В таких случаях мы сфокусировали наше внимание на объяснении некоторых математических моделей, которые могут быть использованы в качестве основы для построения необходимых алгоритмов в будущем
Читатель должен сознавать, что всякий алгоритм решения задач молекулярной биологии — любопытный инструмент. Он должен нравиться сразу двум мастерам: молекулярному биологу, который хочет, чтобы алгоритм был надежным, то есть решал задачу несмотря на все ошибки и неопре деленности, появляющиеся на практике, и программисту, который прежде всего заинтересован в гарантии того, что алгоритм решает хорошо структурированную задачу эффективно, и который обычно готов пожертвовать надежностью в пользу эффективности. Мы попытались найти некое равновесие между этими нередко противоречивыми требованиями, но в большинстве случаев мы принимали сторону программистов. В конце концов, это специальность авторов книги. Тем не менее, мы надеемся, что наше произведение будет в равной стеггени полезно как молекуггярным биологам, так и программистам.
14
ПРЕДИСЛОВИЕ
Настоящая книга является вводным курсом. Это означает, что один из наших руководящих принципов — познакомить читателя только с теми алгоритмами, которые мы сочли простыми, хотя это и не всегда было возможно. Для решения некоторых из представленных в книге задач существуют более эффективные и, как правило, более сложные алгоритмы; ссылки на некоторые из таких алгоритмов приведены в разделе библиографических примечаний в конце каждой главы.
Несмотря на нашу основную цель, некоторые из представленных нами алгоритмов или моделей нельзя счесть простыми. Как правило, это обусловлено сложностью соответствующей темы. Наиболее трудные места мы старались отмстить знаком звезды «*» в соответствующих заголовках или же дать необходимые пояснения в тексте. Кроме того, вводный характер книги означает, что некоторые темы предназначены в качестве отправной точки для непосвященных читателей. Весьма вероятно, а в некоторых случаях и факт, что этим темам можно было бы посвятить целые книги.
Основная аудитория предполагаемых адресатов учебника — студен гы специальностей из области математических и вычислительных наук. Мы нс предполагаем никакого дополнительного образования в сфере молекулярной биологии выше уровня средней школы и специально приводим главу, в которой кратко разъясняем основные понятия, встречающиеся в тексте. Читателей, не знакомых с молекулярной биологией, мы побуждаем выйти за рамки представленного в книге обзора и расширить свои познания, опираясь на куда более серьезные литературные источники, упомянутые в конце первой главы.
Хочется верить, что наша книга будет в некоторой мере полезна и для студентов-биологов. Мы предполагаем, что наш читатель знаком с дискретной математикой и теорией алгоритмов по крайней мерс на уровне колледжа. С целью помочь читателю, совершенно незнакомому с этими предметами, мы написали главу, содержашую краткий обзор всех основных понятий, употребляемых в настоящей книге.
Вычислительная молекулярная биология развивается очень быстро. Постоянно разрабатываются все более совершенные алгоритмы, а новейшие разделы этой дисциплины, очевидно, успеют возникнуть даже прежде, чем мы допишем это предисловие. В пределах упомянутых выше ограничений мы старались охватить, как мы считали, достаточно полную выборку тем и мы верим, что большая часть представленного здесь материала не потеряет свою значимость с течением времени.
Читателя, стремящегося к научным далям, мы снабдили указателями на некоторые источники информации; особенно много ссылок дано в библиографических примечаниях к последней главе (включая адреса интересных
ПРЕДИСЛОВИЕ
15
веб-страниц). Однако эти примечания не следует считать исчерпывающими. Кроме того, при всем нашем желании мы не можем гарантировать точность адресов страниц всемирной паутины. Мы их неоднократно проверяли, но, в силу динамической природы сети, к моменту выпуска книги они могли измениться.
ОБЗОР СОДЕРЖАНИЯ КНИГИ
Глава 1 знакомит читателя с фундаментальными понятиями молекулярной биологии В ней мы описываем основные структуры и функции белков и нуклеиновых кислот, механизмы молекулярной генетики, наиболее важные лабораторные методы изучения генома организмов, а также приводим краткий обзор существующих баз данных и банков последовательностей.
В главе 2 мы рассказываем о строках и графах — важнейших математических объектах, используемых в настоящей книге, а также сообщаем общие сведения об алгоритмах, проводим их анализ и поясняем основные определения из теории ПП-полноты.
Следующие главы посвящены специальным задачам молекулярной биологии. В главе 3 изложена методика сравнения последовательностей, изучена типичная задача сравнения пары последовательностей и представлен классический алгоритм метода динамического программирования. Далее рассмотрены расширения этого алгоритма, разработанные для решения специальных задач данного класса. Задаче множественного сравнения последовательностей посвящен отдельный раздел. В последующих разделах этой главы рассмотрены программы, используемые для поиска в базах данных, а также некоторые другие вопросы.
Глава 4 представляет задачу сборки фрагментов. Подобная задача возникает, когда последовательность ДНК разрезается на маленькие фрагменты, которые затем должны быть сшиты, с тем чтобы воссоздать последовательность исходной молекулы Данная методика широко применяется при крупномасштабном секвенировании (расшифровке последовательностей хромосом и даже целых геномов) — например, в проекте «Геном человека». Мы приводим примеры различных затруднений, возникающих при решении этой задачи. Далее мы представляем некоторые модели упрощенных вариантов задачи. В последующих разделах главы рассмотрены алгоритмы и эвристики, основанные на этих моделях.
В главе 5 представлена задача составления физических карт. Ее можно представить как задачу сборки фрагментов в большем, по сравнению с описанным в главе 4, масштабе. Здесь фрагменты макромолекул намного длиннее, и по этой причине методы сборки должны сильно отличаться
16
ПРЕДИСЛОВИЕ
от применяемых в предыдущем случае Цель составления физических карт заключается в том, чтобы определить местоположение специфических маркеров в исследуемой молекуле ДНК. Приведен также краткий обзор методов и моделей картирования. Далее мы описываем алгоритм для решения задачи с последовательными единицами; в составлении физических карт эта абстрактная задача играет ключевую роль. Глава заканчивается разделами, посвященными алгоритмам аппроксимации и эвристикам, разработанным для решения варианта задачи составления физических карт.
Так же, как и целые организмы, белки и нуклеиновые кислоты изменяются в процессе смены поколений, и важным инструментом в понимании путей их эволюции является филогенетическое дерево объектов. Помимо этого, филогенетические деревья помогают лучше понять функции белков В главе 6 описаны некоторые математические задачи, связанные с восстановлением филогенетических деревьев, а также простые алгоритмы, разработанные для некоторых частных случаев.
Совсем недавно в вычислительной биологии появилась новая важная область, занимающаяся исследованиями перестроек генома. Было обнаружено, что у некоторых организмов генетические различия на уровне после довательностей нуклеотидов практически незаметны, однако проявляются на уровне длинных фрагментов ДНК. Для изучения различий данного типа были разработаны интересные математические модели, представленные в главе 7.
Понимание биологических функций макромолекул является, по сути, основой большинства задач вычислительной биологии. Поскольку эти молекулы свертываются в трехмерном пространстве, а их функции зависят от их специфической конформации, открытие трехмерной структуры биомолекул и, в частности, строения РНК и белков, вызывало первостепенный интерес ученых в течение нескольких последних десятилетий.
Это событие стимулировало развитие методов предсказания сложной структуры макромолекул на основании их первичной структуры, то есть последовательности мономеров. В главе 8 мы описываем алгоритмы метода динамического программирования, разработанные для предсказания струк туры РНК, приводим краткий обзор затруднений, связанных с прсдсказани ем структуры белка, и представляем очень важный недавно разработанный метод, называемый протягиванием белка, которое заключается в выравнивании последовательности исследуемого белка с моделью уже известной белковой структуры.
Глава 9 завершает книгу, представляя описание новой захватывающей области — вычислений с помощью ДНК. В этой главе мы описываем основной эксперимент, показавший возможность использования молекул ДНК
ПРЕДИСЛОВИЕ
17
для решения одной трудной алгоритмической задачи, а также теоретические основы алгоритма решения другой трудной задачи.
Оговорим некоторые обозначения, принятые в этой книге. Как уже было упомянуто, разделы, заголовки которых отмечены знаком звезды «*», содержат материал, который авторы считают наиболее трудным. Условимся, что полужирным шрифтом мы будем выделять важные термины, относящиеся ко всему материалу книги. Все остальные термины будут выделены курсивом. Многие из разработанных нами алгоритмов сначала описаны в виде простых предложений, а затем в форме псевдокодов (язык псевдокодов описан в разделе 2.3). В некоторых случаях псевдокод обеспечивает уровень детализации, необходимый читателям, заинтересованным в практической реализации алгоритмов.
Изложение материала наиболее длинных глав сопровождается кратким резюме.
УПРАЖНЕНИЯ
В конце каждой главы даны упражнения. Упражнения, отмеченные одной звездой «*» трудны, но выполнимы менее чем за день. Для этого могут потребоваться методы программирования, не представленные в данной книге. Задачи, отмеченные двумя звездами «**», в свое время были исследованы и решены, а их решения можно найти в специальной литературе (соответствующие ссылки находятся в библиографических примечаниях в конце глав). Наконец, упражнения, отмеченные знаком алмаза «о», содержат сложные задачи, которые, насколько известно авторам, так и нс были решены.
В конце книги мы приводим ответы и подсказки к избранным упражнениям.
ОШИБКИ
Несмотря на кропотливый труд авторов, в этой книге наверняка присутствуют некоторые ошибки. Мы будем рады получать ваши замечания и предложения по усовершенствованию нашего учебника. Сообщения об ошибках или любые другие комментарии отправляйте по адресу: bio@dcc.unicamp.br или
J. Meidanis / J. С. Sctubal
Institute de ComputaQao, С. P. 6176
UNICAMP
18
ПРЕДИСЛОВИЕ
Campinas, SP 13083-970
Brazil.
(С авторами можно непосредственно связаться по адресам электронной почты meidanis@dcc.unicamp.br и setubal@dcc.unicamp.br.) Заранее благодарим всех читателей, желающих оказать нам помощь в улучшении этой книги. По мере обнаружения ошибок мы будем сообщать о них на следующей веб-странице:
http: //www. dec. unicamp. br/~bio/ICMB. html
БЛАГОДАРНОСТИ
Эта книга — преемник другой, намного более краткой книги по тому же предмету, написанной авторами в Португалии и изданной в 1994 году в Бразилии. Изданию той первой книги во многом способствовала проводимая каждые два года Бразильская конференция по информатике, названная «Эскола ди компутасан». Мы полагаем, что без участия в конференции подобного уровня мы не писали бы сейчас это предисловие, и благодарны за такую возможность.
Настоящая книга начала свою жизнь во многом благодаря Майку Шу-гермену, Бонни Бергер и Тому Литону. Они оказали нам большую поддержку, а также дали некоторые полезные советы. Особенно ценной помощью оказались копии конспектов лекций Бонни, любезно предоставленные нам в начале работы над книгой.
К счастью, нам удалось получить финансовые гранты от FAPESP и CNPq (бразильские научно-исследовательские учреждения); их помощь была многоплановой. Гранты от FAPESP были предоставлены в рамках проекта «Лаборатории алгоритмов и комбинаторики» и обеспечили нам покупку компьютерного оборудования. Гранты от CNPq были предоставлены в форме индивидуальных стипендий на проведение научно-исследовательских работ, а также, в рамках программы PROTEM и проектов PROCOMB и ТСРАС, были направлены на финансирование научных командировок.
Мы благодарим наших студентов, которые помогали нам при чюнии корректуры рукописи. Особую благодарность выражаем Налву Франку ди Алмейде младшему и Марии Эмилии Машаду Телльз Уолтер. Налву, кроме того, сделал много рисунков и дал несколько полезных комментариев.
Беседы с нашим коллегой Жоржи Стольфи были весьма полезны, и, кроме того, он оказал нам значительную помощь в вопросах, связанных
ПРЕДИСЛОВИЕ
19
с набором текста. Фернанду Рейнаш и Жилсон Паулу Манфиу помогли нам при написании главы 1. Назначение и задачи книги, а также прочие вопросы общего плана мы обсуждали с Джимом Орлином. Мартин Фарах и Сампат Каннан, а с ними еще несколько рецензентов, внесли много полезных предложений и замечаний, некоторые из которых были включены в текст учебника. Наши коллеги в «Институте вычислений в UNICAMP» оказывали нам искреннюю поддержку и создавали рабочую обстановку, способствовавшую продуктивной творческой деятельности.
Следует поблагодарить многих коллег, любезно присылавших нам научные статьи: Фарида Ализаде, Альберто Капрару, Мартина Фараха, Дэвида Гринберга, Дэна Гасфильда, Сридара Ханненхалли, Вэнь-Лянь Сю, Сяоцю Хуана, Тао Цзяна, Джона Кецециоглу, Лукаса Кнехта, Рика Лэтропа, Джина Майерса, Алехандро Шеффера, Рона Шамира, Мартина Вингрона (который, ко всему прочему, прислал конспекты своих лекций), Тодда Уэрхема и Тенди Уорноу. При работе над некоторыми разделами книги мы широко использовали материал некоторых из этих статей.
Большое спасибо мы говорим Эрику Бриссону, Эйлин Салливан, Брюсу Дейлу, Карлусу Эдуарду Феррейре и Томасу Русу, которые всячески помогали нам в работе.
Ж. К. С. хочет поблагодарить своих близких: жену Сильвию (Теку) и детей Клаудию, Томаса и Каю за оказанную ими поддержку, без которой эта книга, возможно, не была бы написана.
При наборе текста авторы использовали систему Лесли Лэмпорта IAlgX2e, работающую на ТрХ-системе Дона Кнута. Это поистине изумительные программы!
Цитату Дона Кнута, приведенную в качестве эпиграфа к предисловию, мы взяли из интервью, данного им «Компьютер литераси букшопс, инк.» 7 декабря 1993 года.
Жуан Kap.iyc Ссгубал
Жуан Мсйдаиис
Глава 1
ОСНОВНЫЕ ПОНЯТИЯ МОЛЕКУЛЯРНОЙ БИОЛОГИИ
В згой главе мы представляем основные понятия молекулярной биологии. Ваша цель здесь состоит в том, чтобы дать нашим читателям надежные ориентиры и они могли бы свободно лавировать не только в биологическом контексте этой книги, но и в море остальной литературы по вычислительной молекулярной биологии. Читатели, ранее специализировавшиеся в точных науках, должны с самого начала быть готовы к тому, что в молекулярной биологии ничто не будет действительно точным на 100 %. К каждому правилу всегда найдется свое исключение. Мы попытались указать некоторые из наиболее примечательных исключений к общим правилам, в остальных же случаях опускали такое упоминание, с тем чтобы не превращать эту главу в самостоятельный учебник по молекулярной биологии.
1.1.	ЖИЗНЬ
В природе мы встречаем как живые, так и неживые объекты. Живые природные объекты способны передвигаться, воспроизводить себе подобных, расти, питаться, и т. д. — словом, они принимают активное участие в процессах окружающей среды, в отличие от неживых форм. Однако результаты исследований за последние столетия показывают, что оба вида материи состоят из одних и тех же атомов и подчиняются одним и тем же физическим и химическим законам. Но в чем же тогда заключается различие между ними?
В течение длительного периода человеческой истории люди думали, что некоторый вид «сверхматерии» даровал живым существам их активные характеристики, — что они «одушевлялись» этой особой субстанцией. Но до сих пор ничего подобного так и не удалось обнаружить. Напротив, наши современные представления свидетельствуют о том, что живые сушества организованы именно так, как они есть, а не иначе, в силу множества происходящих в них сложнейших химических реакций. Эти реакции никогда не
1.2. БЕЛКИ
21
прекращаются. Часто продукты одной реакции сразу же включаются в следующую, и такой принцип поддерживает непрерывное функционирование системы (организма) в целом. Кроме того, живой организм постоянно обменивается с окружающей средой материей и энергией. Напротив, что-либо, находящееся в равновесии с окружающей средой, можно, как правило, считать мертвым. (Некоторые известные исключения — вегетативные формы жизни наподобие семян и вирусов, которые могут быть абсолютно неактивными в течение длительных периодов времени, и несмотря на это нельзя сказать, что они мертвы.)
Современная наука показала, что жизнь зародилась приблизительно 3,5 миллиарда лет назад, вскоре (в геологических сроках) после того, как была сформирована и сама планета Земля Первые формы жизни были весьма примитивны, но непрерывно действующий процесс, названный эволюцией, который в течение миллиардов лет заставлял их развиваться и изменяться, привел к тому, что сегодня мы можем встретить как очень сложные организмы, так и совсем простые.
И сложные и простые организмы имеют сходную молекулярную химию, или биохимию. Главные актеры в химии жизни — молекулы белков и нуклеиновых кислот. Описывая их функции в общих чертах, можно сказать, что белки определяют специфическую организацию и физиологические функции живых организмов. (Выдающийся ученый Расселл Дулиттл однажды сказал: «Мы — это наши белки».) Нуклеиновые кислоты, с своей стороны, кодируют информацию, необходимую для производства белков, и отвечают за передачу этого «рецепта» последующим поколениям.
Молекулярная биология, в основном, занимается исследованием структуры и функций белков и нуклеиновых кислот. Поэтому эти молекулы являются фундаментальными объектами настоящей книги, и мы продолжаем наш рассказ вводным и кратким описанием современного представления о них
1.2.	БЕЛКИ
Большая часть веществ, из которых состоят наши тела, — белки самых разнообразных форм и функций Структурные белки являются строительным материалом тканей, тогда как белки другого класса, называемые ферментами, - действую! как катализаторы химических реакций. Катализаторами называют вещества, ускоряющие химические реакции. Если бы многие биохимические реакции протекали самопроизвольно, то для их завершения потребовалось бы слишком много времени, или они не заверши
22
Глава 1
лись бы вовсе, а потому были бы совершенно бесполезны для отправления жизненных функций. Фермент может увеличить скорость протекания реакции на несколько порядков, таким образом делая жизнь возможной. Ферменты чрезвычайно специфичны: как правило, отдельный фермент может воздействовать на биохимическую реакцию только определенного типа. Если представить себе количество реакций, протекание которых необходимо для поддержания жизни, то становится очевидным, что организм нуждается в большом числе разнообразных ферментов. Другими примерами функций белка являются перенос кислорода и антителогенез. Но что же на самом деле представляют собой белки? Как они устроены? И как они выполняют свои функции? В данном разделе мы попытаемся кратко ответить на все эти вопросы.
Макромолекула белка устроена в виде цепи более простых молекул, называемых аминокислотами. Примеры структурных формул аминокислот приведены на рие. 1.1. Каждая аминокислота содержит один центральный углеродный атом, который получил название «альфа-углерод» и был обозначен CQ. С атомом CQ соединены водородный атом, аминогруппа (NH2), карбоксильная группа (СООН) и боковая цепь. Именно боковая цепь отличает одну аминокислоту от другой. Боковые цепи могут быть совершенно простыми и состоять лишь из одного водородного атома (аминокислота глицин) или сложными и содержать в себе, например, два углеродных кольца (триптофан). Всего в природе обнаружено 20 различных аминокислот, названия и обозначения которых приведены в таблице 1.1. Эти 20 аминокислот являются наиболее общими компонентами всех белков; иногда в их состав могут входить лишь несколько нестандартных аминокислот.
НО	СН3
СН3	СН
H2N — Са — СООН	H2N — са — СООН
Н	Н
Рис. 1.1. Аминокслоты: аланин (слева) и треонин (справа)
В белковых макромолекулах аминокислоты соединены посредством пептидных связей, в результате чего они образуют полипептидные цепи.
1.2. БЕЛКИ
23
Таблица 1.1. Двадцать «популярных» аминокислот1
Однобуквенный		Трехбуквенный код		Название
	код			
1	А	Ala	Ала	аланин
2	С	Cys	Цис	цистеин
3	D	Asp	Acn	аспарагиновая кислота
4	Е	Glu	Глу	глутаминовая кислота
5	F	Phe	Фен	фенилаланин
6	G	Gly	Гли	глицин
7	Н	His	Гис	гистидин
8	I	He	Иле	изолейцин
9	К	Lys	Лиз	лизин
10	L	Leu	Лей	лейцин
И	М	Met	Мет	метионин
12	N	Asn	Асн	аспарагин
13	Р	Pro	Про	пролин
14	Q	Gin	Глн	глутамин
15	R	Arg	Apr	аргинин
16	S	Ser	Сер	серин
17	Т	Thr	Тре	треонин
18	V	Vai	Вал	валин
19	W	Trp	Трп	триптофан
20	Y	Tyr	Тир	тирозин
В пептидной связи углеродный атом, принадлежащий карбоксильной группе аминокислоты А,, соединен с атомом азота, входящим в аминогруппу аминокислоты А,+з. При образовании такой связи высвобождается молекула воды, поскольку кислород и водород карбоксигруппы присоединяются к одному водородному атому аминогруппы. Следовательно, в качестве звеньев цепи полипептида в действительности выступают остатки исходных аминокислот. Таким образом, о некотором белке мы можем сказать, что он состоит, например, из 100 остатков, а нс из 100 аминокислот. Обычные белки содержат около 300 остатков, но известны также белки, содержащие всего 100 или целых 5 000 аминокислотных остатков.
’Для обозначения аминокислот используют одно- и трехбуквенный код. Трехбуквенные обозначения более удобны для чтения, а однобуквенные для компьютерного анализа* 2. Прим. ред.
2 Для отличия однобуквенных обозначений нуклеотидов и аминокислот первые принято (однако не все авторы соблюдают это условие сравните обозначения нуклеотидов в тексте кни! и
24
Глава 1
Пептидная связь обусловливает наличие в каждой белковой молекуле основной цепи, образованной повторными структурными звеньями вида N С„(СО). Каждому атому Со соответствует боковая цепь (см рис. 1.2) Поскольку на одном конце основной цепи находится ами ногруппа, а на другом — карбоксигруппа, мы можем различать оба конца полипептидной цепи и придать ей условное направление. Принято считать, что полипептиды начинаются аминогруппой (N-конец) и оканчиваются карбоксигруппой (С-конец).
Рис. 1.2. Полипсптидиая цепь. Боковые цени R, определяют входящие в состав белка аминокислоты. Атомы внутри каждой четырехугольной рамки лежат в олной плоскости, которая может вращаться на у1лы ф и ф
Однако большая часть белков представляют собой не простые линейные последовательности аминокислотных остатков (такая последовательность называется первичной структурой белка), а свертываются в трех измерениях, образуя вторичную, третичную и четвертичную структу ры. Вторичная структура белка формируется посредством взаимодействия только между атомами основной цепи и проявляется в виде «локальных» структур например спиралей. Третичные структуры — результат вторичной укладки белковой структуры на более высоком уровне Следующий уровень укладки, то есть четвертичную структуру, образует группа различных белков, собранных в одну сложную макромолекулу. Эти структуры схематично изображены на рис. 1.3.
Белки могут свертываться в трех измерениях, поскольку плоскость связи между атомом Со и атомом азота может вращаться, так же, как и плоскость между атомом Са и другим углеродным атомом. Эги углы вращения
и в примерах записей баз .чанных) набирают строчными буквами, а вторые — прописными. Таким образом, запись «atg» обозначает последовательность нуклеотидов аденин тимин- гуанин, а запись «ATG» - последовательность остатков аминокислот Ала Тре-Гли. Прим перев.
1.2. БЕЛКИ
25
Рис. 1 3 Первичная, вторичная, третичная и четвертичная структуры белка [28]
обозначаются, соответственно, греческими буквами ф и Ф (см. рис. 1.2). Боковые цепи также способны вращаться, но это уже вторичное вращение по отношению к вращению основной цепи. Таким образом, если мы определим значения всех пар углов ф-ф в молекуле белка, то мы узнаем точную конформацию основной цепи.
Определение рабочей конформации, или трехмерной структуры белка является одной из главных областей исследования в молекулярной биологии по трем причинам. Во-первых, трехмерная структура белка непосредственно определяет его функции. Во вторых, клеточный механизм, который составляет белковую молекулу из набора аминокислот 20 различных видов, делает конечную трехмерную структуру во многих случаях очень сложной и асимметричной. В-третьих, не известно ни одного простого и точного метода определения трехмерной структуры белка. Эти причины побудили нас к написанию главы 8, где мы рассматриваем некоторые методы предсказания сложной структуры молекул по последовательностям входящих в их состав мономеров.
Трехмерная структура белка определяет его функцию следующим образом. Свернутый белок имеет неправильную форму. Это означает, что в его молекуле есть различные бороздки и выступы, и эти особенности формы позволяют белку входить в тесный контакт, или связываться, с некоторыми другими специфическими молекулами. Виды молекул, с которыми может связываться белок, зависят от его формы. Например, форма белка может быть такой, что он способен связываться с несколькими идентичными копиями самого себя, выстраивая, скажем, нить волоса Или же его форма может быть такой, что молекулы вида 4 и В связываются с ним и начинают обмениваться атомами между собой. Другими словами, между веществами А и В происходит реакция, а белок выступает в роли катализатора.
26
Глава 1
Но каким образом организм получает необходимые ему белки? Белки производятся в клеточных структурах, называемых рибосомами. В рибосоме аминокислоты, входящие в состав белка, собираются одна за другой в полипептидную цепь благодаря информации, содержащейся в очень важной молекуле информационной рибонуклеиновой кислоты. Прежде чем объяснить механизм этих процессов, мы должны рассказать о нуклеиновых кислотах.
1.3.	НУКЛЕИНОВЫЕ КИСЛОТЫ
Живые организмы содержат два вида нуклеиновых кислот: рибонуклеиновую кислоту (РНК) и дезоксирибонуклеиновую кислоту (ДНК). Сначала опишем ДНК.
1.3.1.	ДНК
Подобно белкам, молекулы ДНК построены в виде цепи более простых молекул Фактически это двойная цепь, но сначала рассмотрим структуру простой одинарной цепи, называемой нитью. Несущая структура нити представлена основной цепью, состоящей из одинаковых повторных звеньев. Мономерное звено образовано молекулой сахара, а именно 2'-дезоксирибозой, с которой соединен фосфатный остаток. В молекулу сахара входит пять углеродных атомов, обозначаемых, соответственно, цифрами с 1' по 5' (см. рис. 1.4).
Связи, образующие основную цепь, находятся между З'-углеродным атомом одного звена и остатком фосфата, а также между этим остатком
Н
НО-5'-Н
Н
Н0-5'-Н
I I
НО ОН
рибоза	2'дезоксирибоза
Рис. 1.4 Сахара, входящие в состав нуклеиновых кислот Цифры с 1' по 5' обозна чают углеротиые азомы. Единственная разница между двумя сахарами заключается в наличии или отсутствии атома кислорода при углеродном атоме 2'. Рибоза входит в состав РНК, а 2'-дсзоксирибоза — в состав ДНК
1.3. НУКЛЕИНОВЫЕ КИСЛОТЫ
27
Рис. 1.5. Азотистые основания, входящие в состав ДНК. Точечными линиями отмечены связи, которые могут образовывать аденин с тимином или зуанип с ни го (ином
и 5'-углеродным атомом следующего звена. По этой причине молекулы ДНК имеют условную ориентацию; также принято считать б'-конец началом нити, а З'-консц — се окончанием. Когда мы видим изображение последовательности нуклеотидов одинарной цепи ДНК на технической бумаге, в книге или файле базы данных последовательностей, она всегда записана в этом каноническом направлении 5' —> 3', если не оговорено противное.
К l'-углсродному атому каждого звена основной цепи присоединены другие молекулы, называемые основаниями3. В природных биополимерах встречаются азотистые основания четырех видов: аденин (А), гуанин (G), цитозин (С) и тимин (Т). На рис. 1.5 представлены структурные формулы молекул этих оснований, а на рис. 1.6 изображено схематичное представление одной нити ДНК, которую мы только что рассмотрели. Основания А и G входят в группу веществ, названных пуринами, тогда как основания С и Т относятся к пиримидинам.
Когда мы рассматриваем фрагмент молекулы ДНК, состоящий из моносахарида, фосфата и азотистого основания, в качестве мономерного звена, мы называем его нуклеотидом. Таким образом, хотя основания и нуклеотиды — не одно и то же, мы можем говорить, что молекула ДНК содержит,
’Здесь и далее азотистые основания. — Прим, перев.
28
Глава 1
Рис. 1.6. Схематическое представление одной нити ДНК: Ф — фосфат; М — моносахарид; G. А, С, Т соответственно, гуанин, аденин, цитозин и тимин
например, 200 оснований или 200 нуклеотидов. Молекулу ДНК, включающую в себя несколько (десятки) нуклеотидов, называют олигонуклеотидом. Природные молекулы ДНК очень длинные - намного длиннее молекул-полипептидов. В клетках человека находятся молекулы ДНК, состоящие из сотен миллионов нуклеотидов.
Как было упомянуто выше, молекулы ДНК образованы двумя нитями. Две нити связаны вместе и закручены в виде спиральной структуры — знаменитой двойной спирали, открытой Джеймсом Уотсоном и Фрэнсисом Криком в 1953 году. Но каким образом две нити удерживаются вместе? Такая связь возможна благодаря тому, что каждое азотистое основание, расположенное в одной нити, образует пару (связывается) с некоторым основанием другой нити. Основание А всегда взаимодействует с основанием Т, а основание С — только с G, как показано на рис. 1.5 и 1.7. Говорят, что основания А и Т являются комплементами друг друга и образуют пару комплементарных оснований. В свою очередь, С и G — другая пара комплементарных оснований. Данные пары известны как пары оснований Уотсона-Крика. Пара оснований (сокращенно — по) является единицей длины, наиболее удобной при обозначении длины молекул ДНК. Так что мы говорим, что длина фрагмента ДНК равна, например, 100000 по или 100 кпо4.
В этой книге мы будем, в основном, рассматривать последовательность ДНК как строку знаков, где каждый знак обозначает соответствующее основание. На рис. 1.8 показано такое «строчное представление» двойной цепи ДНК, при котором одна строка помещается над другой. Обратите внимание на парность оснований. Даже при том, что обе нити связаны между собой,
4Очевидио, что в каждой молекуле ДНК число пар азотистых оснований равно числу пар нуклеотидов. Английская единица Ьр (по) подчеркивает; что пары образуют именно комплементарные основания; напротив, принятая в российской научной литературе единица п. н. показывает, что общая длина полинуклеотида складывается из сумм его мономерных звеньев нуклеотидов.
Таким образом, Ьр = п. и.; kbp = т. п. н.: mbp = м. п. н. - Прим, перев.
1.3. НУКЛЕИНОВЫЕ КИСЛОТЫ
29
каждая сохраняет свою собственную ориентацию и эти ориентации взаимно противоположны. Этот факт проиллюстрирован на рис. 1.8., где хорошо видно, что З'-конец одной нити соответствует б'-концу другой нити. Это свойство получило название антипаралчельности нитей. Фундаментальное следствие подобной структуры заключается в том, что, определив последовательность одной нити, возможно восстановить последовательность другой. Действие, которое позволяет нам сделать это, называют обратной комплементацией.
Например, задана последовательность s  AGACGT в каноническом направлении, и мы получаем ее обратный комплемент следующим образом. Сначала мы записываем последовательность s в обратном порядке, получая обратную последовательность s' = TGCAGA, а затем заменяем каждое основание его комплементом и получаем обратную комплементарную последовательность s = ACGTCT. (Для обозначения обратного комплемента последовательности s мы используем знак черточки над s.) Именно эти действия выполняет клеточный механизм, обеспечивающий репликацию ДНК в клетке, что позволяет организму, начавшему жизнь с одной-единственной клетки, последовательно превратиться в систему, насчитывающую миллиар-
5'	— TACTGAA — 3'
3'	— ATGACTT — 5'
Рис. 1.8. Строчное представление двойной цепи ДНК
30
Глава 1
ды клеток, где каждая клетка содержит копии молекул ДНК первоначальной клетки.
В организмах, построенных из безъядерных клеток ДНК свободно плавает в цитоплазме. У высших организмов ДНК находится в клеточном ядре, а также в особых органеллах клетки — митохондриях (животные и растения) и хпоропластах (только растения).
1.3.2.	РНК
Молекулы РНК во многом подобны молекулам ДНК, но имеют некоторые отличия состава и структуры:
•	В РНК моносахарид представлен рибозой вместо 2'-дезоксирибозы (см. рис 1.4).
•	В РНК вместо тимина (Т) присутствует урацил (U). Подобно тимину, урацил связывается с аденином.
•	РНК не образует двойную спираль. Иногда мы наблюдаем гибридные ДНК-РНК спирали; кроме того, благодаря комплсментарности оснований отдельные части молекулы РНК могут связываться с другими частями той же молекулы. Трехмерная структура РНК представлена гораздо большим числом форм, чем таковая у ДНК.
Еще одно различие между ДНК и РНК заключается в том, что по существу ДНК выполняет лишь одну функцию (кодирование информации), тогда как, как мы вскоре увидим, в клетке имеются различные виды РНК, выполняющие разнообразные функции.
1.4.	МЕХАНИЗМЫ МОЛЕКУЛЯРНОЙ ГЕНЕТИКИ
Значение молекул ДНК состоит в том, что в них закодирована информация, необходимая для построения всех молекул белков или РНК, функционирующих в организме. По этой причине ДНК иногда называют «матрицей жизни»5. В этом разделе мы опишем механизмы кодирования информации и построения белка с помощью ДНК (процесс синтеза белка). Мы также увидим, каким образом заложенная в ДНК генетическая информация передается от родителей к потомству.
1.4.1.	ГЕНЫ И ГЕНЕТИЧЕСКИЙ КОД
В каждой клетке организма находится несколько очень длинных молекул ДНК. Эти молекулы называют хромосомами. Позже мы сможем по-
5 Другое название — «молекула жизни». — Прим, перев.
1.4. МЕХАНИЗМЫ МОЛЕКУЛЯРНОЙ ГЕНЕТИКИ
31
Таблица 1.2. Универсальный генетический код6
Первая позиция	Вторая позиция				Третья ПОЗИЦИЯ
	G	A	С	U	
	Gly	Glu	Ala	Vai	G
G	Gly	Glu	Ala	Vai	A
	Gly	Asp	Ala	Vai	C
	Gly	Asp	Ala	Vai	U
	Arg	Lys	Thr	Met	G
А	Arg	Lys	Thr	He	A
	Ser	Asn	Thr	He	C
	Ser	Asn	Thr	He	U
	Arg	Gin	Pro	Leu	G
С	Arg	Gin	Pro	Leu	A
	Arg	His	Pro	Leu	C
	Arg	His	Pro	Leu	U
	Trp	СТОП	Ser	Leu	G
и	СТОП	стоп	Ser	Leu	A
	Cys	Туг	Ser	Phe	C
	Cys	Туг	Ser	Phe	U
дробнее рассказать о хромосомах, а в данный момент рассмотрим принципы кодирования генетической информации на примере одной очень длинной молекулы ДНК, которую мы просто будем называть «ДНК». Первая важная вещь, о которой следует упомянуть, — то, что цепь ДНК состоит из смежных участков, либо кодирующих, либо не кодирующих информацию, используемую в синтезе белков. Вторая важная вещь — то, что каждому конкретному виду белка в организме обычно соответствует один и только один участок ДНК. Этот участок получил название ген. Поскольку некоторые гены кодируют РНК, более корректно определять ген как непрерывный участок ДНК, содержащий информацию, необходимую для построения белка или молекулы РНК. Длины генов варьируют; гены человека могут иметь длину приблизительно 10000 п. н. Определенные клеточные механизмы способны точно распознавать в последовательности ДНК точки начала и конца каждого гена6 7.
6Редкая аминокислота селеноцистеин обозначается буквой и и трехбуквенным кодом Sec (Сец). Стоп-кодон обозначается буквой X. При.», перев.
7В современной молекулярной биологии понятие «ген» стало гораздо более расплывчатым и трудно определимым. Прим. ред.
32
Глава 1
Белок, как было показано выше, представляет собой цепь аминокислотных остатков. Поэтому все, что необходимо для того, чтобы «определить» белок, — это определить каждую аминокислоту, входящую в его состав. Именно эту операцию и выполняет молекула ДНК, используя триплеты нуклеотидов для кодирования всех аминокислот. Нуклеотидный триплет называют кодоном. Таблица соответствия всех возможных триплетов аминокислотам и есть так называемый генетический код (см. табл. 1.2). В таблице, как это видно, триплеты нуклеотидов приведены с учетом состава последовательности РНК, а не ДНК. Это связано с тем, что именно молекулы РНК обеспечивают связь между ДНК и непосредственным синтезом белка в процессе, который мы вскоре покажем в деталях. А пока что подробнее рассмотрим генетический код.
Интересно отметить, что существует 64 возможных триплета нуклеотидов, но всего только 20 аминокислот, которые нужно кодировать. Оказывается, одной и той же аминокислоте может соответствовать несколько триплетов. Например, кодоны AAG и ААА кодируют лизин. Напротив, три кодона в таблице не кодируют никакую аминокислоту, а служат сигналом окончания гена. Эти специальные, терминирующие кодоны обозначены в таблице 1.2 словом «стоп». Наконец, следует упомянуть, что генетический код, приведенный в таблице, используется подавляющим большинством живых организмов, однако некоторые организмы используют несколько видоизмененный код.
1.4.2.	ТРАНСКРИПЦИЯ, ТРАНСЛЯЦИЯ И СИНТЕЗ БЕЛКА
Теперь немного подробнее опишем процессы, посредством которых зашифрованная в молекуле ДНК генетическая информация реализуется в белках. Клеточный механизм распознает начало отдельного гена или целой группы генов благодаря промотору. Промотор — это участок ДНК, расположенный перед каждым геном и указывающий клеточному механизму, что непосредственно за ним начинается ген. Кодон AUG (кодирующий метионин) также сигнализирует начало гена8. После распознавания начала гена или группы генов, на молекуле РНК синтезируется копия этого гена. В результате образуется информационная РНК, или, сокращенно, иРНК, которая имеет точно такую же последовательность нуклеотидов, как одна из нитей участка ДНК, содержащего копируемый ген. но с заменой основания Т на U. Данный процесс называют транскрипцией. После этого синтезированная
83десь существенная неточность. Промотор указывает место, с которого надо начинать синтез РНК, тогда как кодон AUG указывает на начало кодирующей области РНК, причем таким указателем служит далеко не каждый триплет AUG. — Прим. ред.
1.4. МЕХАНИЗМЫ МОЛЕКУЛЯРНОЙ ГЕНЕТИКИ
33
цепь иРНК участвует в процессе синтеза белка, происходящего в клеточных структурах, называемых рибосомами9.
Поскольку РНК является одинарной, а ДНК — двойной цепью, последовательность произведенной иРНК идентична одной нити гена и комплементарна другой его нити (с учетом замены основания Т на U). Нить, идентичную синтезированной иРНК, называют смысловой или кодирующей нитью, а другую — антисмысловой, или антикодирующей, или же, иначе, матричной нитью. Фактически транскрибируется именно матричная нить, так как цепь иРНК состоит из рибонуклеотидов, комплементарных этой нити. В процессе транскрипции наращивание цепи иРНК всегда ведется от б'-конца к З'-концу, тогда как матричная нить считывается в направлении 3' —> 5'.
Также необходимо помнить, что матричная нить для разных генов не всегда одна и та же: например, матричная нить для некоторого гена А может быть первой из двух нитей, а матричная нить для гена В может быть второй нитью. Клеточный механизм распознает матричную нить для каждого конкретного гена благодаря промотору. Даже при том, что в другой нити находится обратный комплемент промотора гена, этот обратный комплемент не является его промотором и, следовательно, не будет распознан в качестве такового.
Одно важное следствие из этого факта — то, что гены в хромосомах имеют ориентацию друг относительно друга. Если какие-либо два гена находятся в одной и той же нити, то они имеют одинаковую ориентацию; в противном случае их ориентация будет встречной. Фундаментальное значение этого факта мы раскроем в главе 7. Наконец, обращаем ваше внимание, что для указания расположения какого-либо участка в молекуле ДНК относительно ориентации кодирующей нити, используют термины выше и ниже', например, промоторы всегда расположены выше своих генов.
Описанный вариант транскрипции относится к организмам, принадлежащим к надцарству доядерных, или прокариотов. ДНК данных организмов свободно плавает в цитоплазме клетки, поскольку у них отсутствует ядерная мембрана. Известные примеры доядерных организмов — бактерии и синие морские водоросли.
Организмы, относящиеся к ядерным, или эукариотам, имеют оформленное ядро, отделенное от остальной среды клетки ядерной мембраной, так что их ДНК постоянно находится в ядре. В этих организмах процессы генетической транскрипции намного сложнее. Многие гены ядерных организмов составлены из чередующихся частей, названных интронами
’Этот процесс называется трансляцией. — Прим. ред.
34
Глава 1
и экзонами. По завершении этапа транскрипции интроны вырезаются из последовательности иРНК. Это означает, что интроны - участки гена, не используемые в сингезе белка. Распределение интронов и экзонов покажем на примере гена (1082 п. н.) белка натрийуретрического фактора бычьего предсердия: экзоны расположены в позициях 1120, 219-545 и 1071-1082; интроны занимают позиции 121-218 и 546-1070. Таким образом, участки, кодирующие иРНК, содержат только 459 нуклеотидов, и соответствующий белок состоит из 153 остатков. После того как интроны вырезаны, укороченная иРНК, включающая в себя только копии экзонов и регуляторные участки в начале и конце, покидает ядро, поскольку рибосомы находятся в окружающей его цитоплазме10.
Феномен интрона-экзона обусловливает различные названия для обозначения исходной последовательности генов, находящейся в хромосоме, и укороченной последовательности, состоящей только из экзонов. Первую называют геномной ДНК, последнюю комплементарной ДНК или кДНК11. Ученые могут получить кДНК, не зная ее геномную копию. Сначала они захватывают иРНК, вышедшую из ядра и продвигающуюся к рибосомам. Затем, в процессе так называемой обратной транскрипции. они производят молекулы ДНК, используя иРНК в качестве матрицы. Поскольку иРНК содержит только экзоны, проводят также дополнительную сборку синтезированной ДНК. Таким образом, возможно получать молекулы кДНК, не используя генетический материал хромосом.
Как транскрипция, так и обратная транскрипция — сложные процессы, нуждающиеся в участии ферментов. Транскриптаза и обратная транскриптаза, или ревертаза, ферменты, катализирующие эти процессы в клетке. Известен также феномен альтернативного сращивания. Он наблюдается, когда, вследствие выборочного сочетания интронов и экзонов, одна и та же геномная ДНК может произвести две или более различных молекул зрелой иРНК. С них в свою очередь синтезируются различные белки.
Теперь возвратимся к синтезу белка и иРНК. В этом процессе очень важные роли играют молекулы РНК двух других видов. Как уже было упомянуто, процесс синтеза белка протекает в клеточных структурах, называс мых рибосомами. Рибосомы построены из белков, прикрепленных к каркасу из специфического вида РНК, получившей название рибосомной РНК, или рРНК12. Рибосома функционирует подобно сборочной линии, на «вход»
10Этот процесс называется сращиванием, или сплайсингом. Прим. ред.
11 Эта молекула называется зрелой иРНК, в отличие от пред-иРНК (иРНК-пре тшест-венннка), которая была транскрибирована, но не сплайсирована. При», ред.
12Скорее, рибосомы построены из РНК и сравнительно небольшого количества белка. — Прим. ред.
1.4. МЕХАНИЗМЫ МОЛЕКУЛЯРНОЙ ГЕНЕТИКИ
35
которой подается молекула иРНК, а также молекулы РНК другого вида (транспортной РНК, или тРНК), а с «выхода» снимается готовая полипеп-тидная цепь.
Репликация
Обратная транскрипция
Рис. 1.9. Передача генетической информации в клетке: так называемая «Центральная догма молекулярной биологии»
Именно молекулы транспортной РНК фактически включают генетический код в процесс, называемый трансляцией. Они обеспечивают связь между кодоном и кодируемой им определенной аминокислотой. На одной стороне каждой молекулы тРНК находится структура, имеющая высокую степень сродства с определенным кодоном, а на другой стороне - структура, которая легко связывается с соответствующей аминокислотой13. Когда информационная РНК продвигается через внутреннюю часть рибосомы, тРНК распознает текущий кодон — кодон в иРНК, находящийся в данное время внутри рибосомы,  комплементарно связывается с ним. принося с собой соответствующую аминокислоту («вблизи» активной рибосомы всегда имеется богатый запас аминокислот). В этот момент трехмерное положение всех этих молекул таково, что, как только тРНК связывается со своим кодоном, прикрепленная к ней аминокислота оказывается в непосредственной близости с предыдущей аминокислотой в формируемой полипептидной цепи. Тогда специальный фермент катализирует присоединение новой аминокислоты к белковой цепи и освобождает се от тРНК14. В ходе данного процесса полипептидная цепь последовательно наращивается остаток за остатком. Когда появляется стоп-кодон, ему не соответствует никакая тРНК н синтез прекращается. Информационная РНК освобождается и расщепляется клеточными механизмами до рибонуклеотидов, которые в свое время будут повторно использованы для синтеза новой молекулы РНК.
1 *Э1 о делают специальные белки аминоацил-тРИК-синтетаэы. Именно они устанавливают еоо1вететвие антикодон«-*аминокислота. Прим. ред.
’’Удивительно, но роль этого фермента исполняет рРНК, а не белок! Прим. ред.
36
ГЛАВА 1
На первый взгляд может показаться, что существует столько же видов молекул тРНК, сколько кодонов, но это не верно. Фактическое число молекул тРНК варьирует у разных видов организмов. Например, бактерия Е. coli имеет приблизительно 40 видов тРНК. Некоторые кодоны не представлены молекулами тРНК, а некоторые виды тРНК могут связывать более одного кодона.
На рис. 1.9 только что описанные нами процессы показаны в виде блок-схемы. Как правило, выражение «Центральная догма» используется для обозначения нашего современного, синтетического представления о передаче генетической информации в клетках.
1.4.3.	ИЗБЫТОЧНАЯ ДНК И РАМКИ СЧИТЫВАНИЯ
Здесь мы осветим некоторые дополнительные детали процессов, описанных в предыдущих разделах.
Ранее было сказано, что гены — это определенные непрерывные и смежные участки хромосомы; однако они не покрывают всю молекулу целиком. Каждый отдельный ген (или же группа сцепленных генов) с обеих сторон окружен регуляторными участками, роль которых заключается в управлении транскрипцией гена и другими связанными с ней процессами, тогда как функции всех прочих межгенных участков до сих пор не известны. Их называют избыточной или некодирующей ДНК, потому что они, по-видимому, находятся там без какой-либо конкретной цели. Более того, эти участки накапливают мутации, поскольку изменение, не затрагивающее гены или их регуляторные участки, часто оказывается не смертельным и поэтому передается потомству.
Однако недавние исследования показали, что избыточная ДНК имеет больше информационного содержания, чем полагали ранее. Количество избыточной ДНК варьирует у разных видов. Прокариоты, как правило, имеют совсем немного таких участков — их хромосомы почти полностью покрыты генами. Напротив, у эукариотов много избыточной ДНК. Хромосомы человека, по оценкам специалистов, на 90 % состоят из некодирующей ДНК.
Еще одна деталь, относящаяся к процессу транскрипции, которую следует знать, — понятие рамки считывания. Рамка считывания — это один из трех возможных способов группировки оснований при формировании кодонов в последовательности РНК или ДНК. Например, рассмотрим последовательность
TAATCGAATGGGC.
1.4. МЕХАНИЗМЫ МОЛЕКУЛЯРНОЙ ГЕНЕТИКИ	37
Одна рамка считывания может быть представлена кодонами ТАА, TCG, ААТ и GGG, не включая последнее основание С. Другая рамка считывания игнорирует первое основание Т и формирует кодоны ААТ, CGA, ATG и GGC. Еще одна рамка считывания дала бы кодоны АТС, GAA и TGG, не учитывая два основания в начале (ТА) и два основания в конце (GC).
Заметим, что эти три рамки считывания начинаются, соответственно, в позициях 1, 2 и 3 данной последовательности. Если бы мы должны были рассмотреть рамку считывания, начинающуюся в позиции 4, то полученные кодоны были бы поднабором кодонов для стартовой позиции 1, так что мы бы получили фактически ту же самую рамку считывания, но только начинающуюся с другой позиции. Вообще, если мы выбираем стартовые позиции г и j, где разница j i кратна трем, то мы фактически рассматриваем одну и ту же рамку считывания.
Иногда мы говорим не о трех, а о шести различных рамках считывания в последовательности. В этом случае мы рассматриваем последовательность ДНК и притом учитываем обе нити. Тогда получается: три рамки считывания в одной нити и другие три — в комплементарной нити, что дает общее количество шесть рамок. Обычно так поступают, когда исследуют недавно расшифрованную молекулу ДНК и хотят сравнить се с последовательностью белка из базы данных. Сначала нужно транслировать последовательность ДНК в последовательность белка, но для этого существует шесть способов, в каждом из которых необходимо выбрать новую рамку считывания. Тот факт, что мы теряем одно или два основания на концах последовательности, не важен; эти последовательности достаточно длинные, чтобы обеспечить достоверное сравнение, невзирая на несколько отсутствующих остатков.
Открытой рамкой считывания, или ОРС последовательности ДНК называют непрерывный участок этой последовательности, начинающийся в стартовом кодоне и включающий в себя целое число кодонов (его длина кратна трем), причем ни один из его кодонов не является стоп-кодоном. Дополнительные регулирующие участки, расположенные выше стартового кодона, также используются, чтобы характеризовать ОРС.
1.4.4.	ХРОМОСОМЫ
В этом разделе мы кратко опишем процесс передачи генетической информации на уровне хромосом. Сначала мы отметим, что полный набор хромосом в клетке называют геномом. Число хромосом в геноме организма характеризует его принадлежность к определенному виду. Например, каждая клетка человека содержит 46 хромосом, тогда как у мышей это чис
38
ГЛАВА 1
ло равно 40. В табл. 1.3 приведены наборы хромосом и размеры генома некоторых характерных видов.
Таблица 1.3. Размер генома определенных видов. Не говоря уже о человеке, пред ставленные здесь организмы чрезвычайно важны для исследований в области молекулярной биологии и генетики
Вид организма	Число хромосом (диплоид)	Размер генома (п. н.)
Бактериофаг А (вирус)	“ 1Т5—	5-Ю4
Escherichia coli (бактерия)	I15	5  106
Saccharomyces cerevisiae (дрожжи)	32	1- 107
Caenorhahditis elegans (червь)	12	1  108
Drosophila melanogaster (плодовая мушка)	8	2 - 108
Homo sapiens (человек)	46	3- 109
Прокариоты, как правило, имеют только одну хромосому, которая иногда представляет собой молекулу кольцевой ДНК. Напротив, в клетках эукариотов хромосомы присутствуют в парном виде (по этой причине такие клетки называют диплоидными). Например, геном человека состоит из 23 пар хромосом. Каждый член пары наследуется от каждого родителя. Две хромосомы, формирующие пару, называют гомологичными, и гены в одном члене пары соответствует генам в другом.
Некоторые гены абсолютно идентичны в отцовском и материнском членах пары — например, ген, кодирующий гемоглобин (белок, осуществляющий перенос кислорода в крови). Другие гены могут присутствовать в альтернативных формах, получивших название аллели. Типичный пример данного явления (аллслизма) — ген, кодирующий группу крови людей. Этот ген встречается в трех формах: А, В и О. Как известно, если человек унаследует, скажем, аллель А от матери и аллель В от отца, то он будет иметь группу крови АВ.
Клетки, содержащие только по одному члену из каждой пары хромосом, называют гаплоидны ми. Эти клетки участвуют в половом размножении организмов. Когда гаплоидная клетка матери сливается с гаплоидной клеткой отца, образуется яйцеклетка16, которая снова является диплоидной. Гаплоидные клетки формируются в процессе мейоза, при котором клетка
,5Эти организмы имеют одинарный набор хромосом. Прим, ред
,бЯйцеклеткой называется материнская половая клетка (гаплоидная), а после ее слияния с отцовской половой клеткой образуется оплодотворенная яйцеклетка17. Прим. ред.
1.4. МЕХАНИЗМЫ МОЛЕКУЛЯРНОЙ ГЕНЕТИКИ
39
делится на две и каждая дочерняя клетка получает по одному члену из каждой пары хромосом.
Интересно отметить, что, несмотря на тот факт, что во всех клетках организма присутствует полный набор генов, лишь только малая часть генома обычно используется, или, если употребить биологический термин, экспрессируется любой отдельной клеткой. Например, клетки печени экспрессируют набор генов, отличный от того, который экспрессируют клетки кожи. Механизмы, посредством которых клетки организма дифференцируются на клетки печени, клетки кожи и т.д., все еще во многом не ясны
1.4.5.	ПОДОБЕН ЛИ ГЕНОМ КОМПЬЮТЕРНОЙ ПРОГРАММЕ?
После краткого обзора основных механизмов синтеза белка возникает соблазн рассмотреть их в свете так называемой «метафоры генетической программы». Согласно этой метафоре геном организма — это компьютерная программа, полностью определяющая характеристики организма, клеточные механизмы — простые интерпретаторы этой программы, а биологические функции белков — лишь результат механического выполнения команд >той «программы».
Безусловно, метафора выглядит чрезмерно упрощенной, особенно если принять во внимание следующие два факта:
•	В реальном процессе транскрипции и трансляции «программа ДНК» подвергается изменениям, так что невозможно узнать, какой белок соответствует данному гену, непосредственно применив генетический код к участку ДНК, кодирующему этот ген
•	Экспрессия гена — сложнейший процесс, который может зависеть как от пространственного, так и от временного контекста. Например, нс все гены, присутствующие в геноме, экспрессируются в течение жизни организма, тогда как другие экспрессируются снова и снова; некоторые гены экспрессируются только тогда, когда организм подвергается определенным внешним воздействиям например вирусной инфекции и т. п. Иногда можно наблюдать обратное явление гены, которые экспрессируются в нормальных условиях, могут подавляться под воздействием определенных внешних фак-1оров. Известно, что экспрессия некоторых генов в значительной степени безотносительна, и именно благодаря этому свойству развитие биотехнологии становится возможным. Но это свойство ни в коем случае не верно для всех юнев. Если мы рассматриваем экспрессию гена в клетке как «вычислительный процесс», мы можем сказать, что в случае генома человека
1 Оплодотворенная яйцеклетка (диплоидная) образуется в результате слияния мужской и женской гамет (гаплоидных) и называется зиготой. Прим перев
40
ГЛАВА 1
существует более 1018 таких процессов, происходящих и взаимодействующих одновременно.
Ввиду этих наблюдений, представляется более верным рассматривать организм нс как биологическую систему, абсолютно обусловленную своим геномом, а, скорее, как продукт очень сложной сети одновременных взаимодействий, в которых набор генов является лишь одним из нескольких составляющих факторов.
1.5.	МЕТОДЫ ИЗУЧЕНИЯ ГЕНОМА
Первое, на что следует обратить внимание при научном исследовании генома, различный порядок величин, с которыми придется иметь дело. В качестве примера будем рассматривать геном человека. Основная информация, которую мы хотим извлечь из любой части ДНК - послсдо вательность пар нуклеотидов. Процесс получения этой информации называют секвенированием. Человеческая хромосома содержит около 108 п. н. С другой стороны, длина наибольших фрагментов ДНК. которые могут быть секвенированы в лаборатории, составляет всего 700 п. н. Это означает, что между масштабами длин фрагментов, которые мы можем фактически сскве-нировать, и длиной хромосомы существует разрыв приблизительно в 105 порядков. Этот разрыв лежит в основе многих проблем и задач вычислительной биологии; некоторые из них будут рассмотрены в главах 4 (сборка фрагментов) и 5 (составление физических карт). В этом разделе мы кратко опишем несколько лабораторных методов, применение которых сопряжено с трудностями, обусловленными этими проблемами.
1.5.1.	КАРТЫ И ПОСЛЕДОВАТЕЛЬНОСТИ
Расположение генов в хромосомах — особенно важный момент, требующий отдельного рассмотрения. Термин локус используют для обозначения местоположения гена в хромосоме (иногда — как синоним слова ген). Самый простой вопрос, возникающий в этом контексте: если рассматривать два гена, — принадлежат ли они одной или разным гомологичным парам? На него можно ответить, не обращаясь к молекулярным методам, поскольку в данном вопросе подразумеваются гены, затрагивающие видимые признаки организма, — например, цвет глаз или форма крыльев. Требуется всего лишь проверить, наследуются ли эти признаки совместно или независимо. Мы скажем, что они наследуются или, более профессионально, — что они распределяются, или расщепляются независимо, если вероятность того, что потомство унаследует от одного родителя оба признака, прибли
1.5. МЕТОДЫ ИЗУЧЕНИЯ ГЕНОМА
41
жённо равна 50 %. Если признаки распределяются независимо, то вполне возможно, что соответствующие гены не сцеплены, то есть скорее всего они принадлежат разным хромосомам. Два гена, принадлежащих одной гомологичной паре, должны распределяться совместно, и тогда потомство, вероятно, унаследует от одного родителя оба признака.
Как это обычно имеет место в биологии, веши не настолько четки: 100 %-е или 50 %-е расщепление признаков встречается далеко не часто. На практике можно наблюдать любой процент распределения генов вследствие кроссинговера. В процессе особого клеточного деления, ведущего к образованию половых клеток, могут появляться новые последовательности генов. В таком случае мы говорим, что происходит рекомбинация генов. Рекомбинация становится возможной, поскольку гомологичные хромосомы перед расхождением могут «перекрещиваться» и обмениваться концевыми фрагментами.
Число возможных вариантов рекомбинации огромно, и на практике мы видим, что частота рекомбинации варьирует в значительной степени. Эти частоты в свою очередь дают информацию о том, как далеко друг от друга в хромосоме расположены исследуемые гены. Если эти гены находятся близко друг к другу, то шанс на расщепление при кроссинговере весьма мал. Если же они отстоят далеко друг от друга, то возможность расщепления возрастает и гены распределяются независимо.
Для составления первых генетических карт изучали последовательные поколения организмов и анализировали наблюдаемые процентные часто-1Ы расщепления исследуемых признаков. Карта сцепления генетических признаков хромосомы представляет собой составленную с использованием подобной информации схему, показывающую порядок и относительное расстояние между генами. Генетические карты полученные на основании частот рекомбинации, безусловно важны, но они имеют два существенных недостатка:
1)	они не показывают фактические длины участков хромосомы в парах нуклеотидов или в других линейных единицах;
2)	если гены расположены очень близко друг к другу, то нельзя определить их порядок, поскольку при этом вероятность расщепления настолько мала, что наблюдаемые частоты рекомбинации равны нулю.
Карты, которые отражают фактические длины участков в парах нуклео-|идов, называют физическими картами. Для составления физических карт необходимо использовать совершенно иные методы. В частности, мы должны работать с фрагментами ДНК намного меньшей протяженности, чем длина хромосомы, но все еще слишком большими для их непосредственной расшифровки. Физическая карта может указать положение маркеров,
42
Глава 1
которые представляют собой точно известные короткие последовательности длиной до 104 п. н. или около того. Вычислительные задачи, связанные с составлением физических карт, представлены в главе 5.
Хромосома
Карта сцепления генетических признаков (уровень 10 10 пн)
Клоны
Физическая карта 5	6
(уровень 10—10 п.н.)
Секвенирование
(уровень 10 —10 п.н.)
/ CGGACACCGACGTCATTCTCATGTGCTTCTCGGCACA X
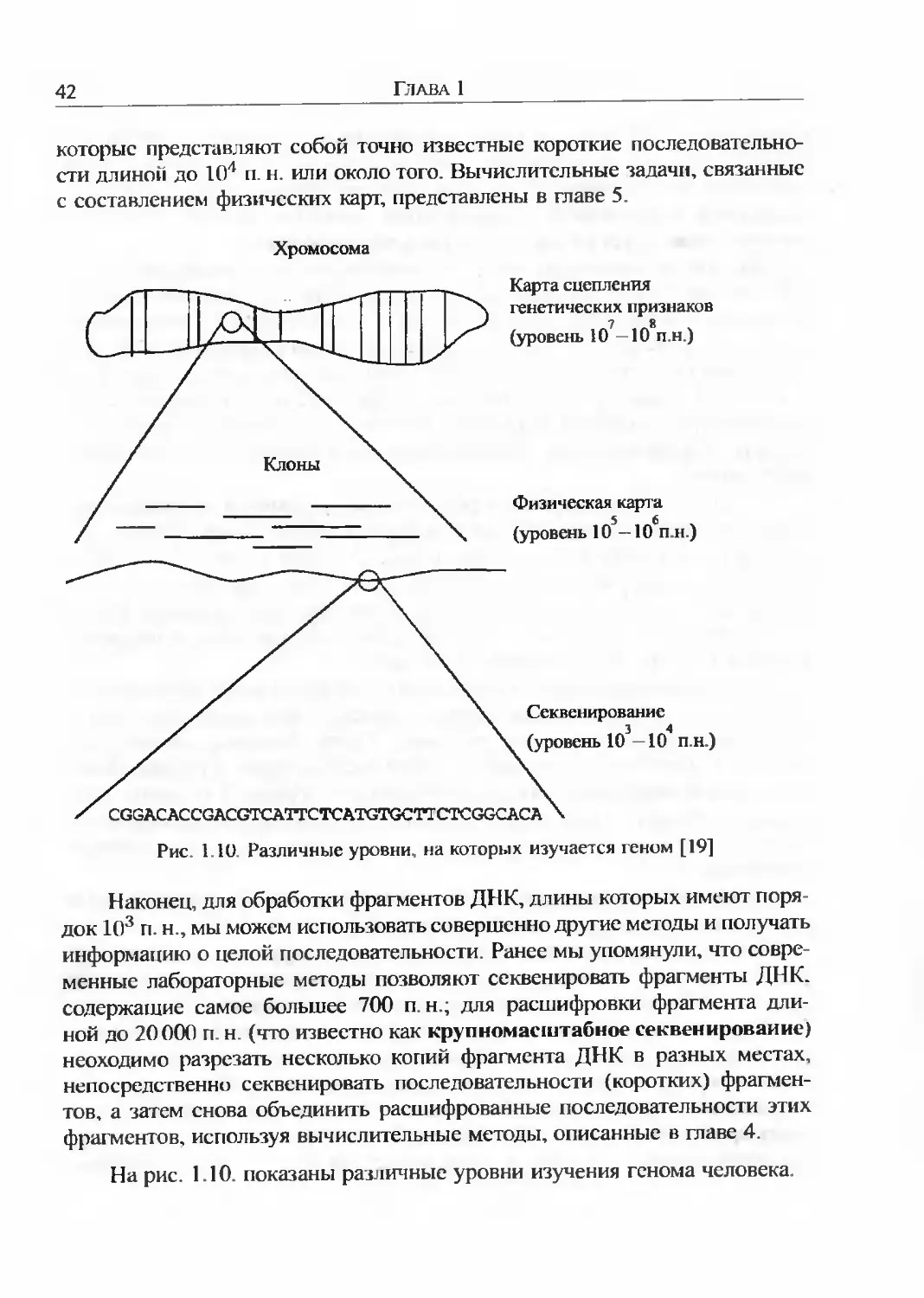
Рис 1.10. Различные уровни, на которых изучается геном [19]
Наконец, для обработки фрагментов ДНК, длины которых имеют порядок 103 п.н., мы можем использовать совершенно другие методы и получать информацию о целой последовательности. Ранее мы упомянули, что современные лабораторные методы позволяют секвенировать фрагменты ДНК. содержащие самое большее 700 п н.; для расшифровки фрагмента длиной до 20000 п. н (что известно как крупномасштабное секвенирование) неоходимо разрезать несколько копий фрагмента ДНК в разных местах, непосредственно секвенировать последовательности (коротких) фрагментов, а затем снова объединить расшифрованные последовательности этих фрагментов, используя вычислительные методы, описанные в главе 4.
На рис. 1.10. показаны различные уровни изучения генома человека.
1.5 МЕТОДЫ ИЗУЧЕНИЯ ГЕНОМА
43
1.5.2.	СПЕЦИАЛЬНЫЕ МЕТОДЫ
При составлении физических карт и расшифровке последовательностей необходимо использовать некоторые специальные лабораторные методы. В ном разделе мы приводим краткий обзор таких методов.
Важно понять, что в молекулярной биологии лабораторные меюды почти что всегда производят данные, содержащие ошибки. По этой причине большая часть алгоритмов, разработанных для решения задач вычислительной биологии, применима только в пределах, в которых они могут контролировать ошибки. Данная проблема будет неоднократно подниматься в этой книге.
Вирусы и бактерии
Мы начнем с краткого описания тех организмов, которых наиболее часто используют в генетических исследованиях, то есть с вирусов и бак тсрий.
Вирусы — это паразиты на молекулярном уровне. Едва ли их можно счесть формой жизни, хотя они и могут воспроизводиться при инфицировании подходящих клеток, называемых хозяева ми. Вирусы не проявляют никакого метаболизма: в них не происходят никакие биохимические реакции Вместо этого, для собственной репликации вирусы всецело полагаются на метаболизм хозяина, и именно это их свойство используют в лабораторных экспериментах.
Большинство вирусов состоит из белковой оболочки (капсида), внутри которой содержится генетический материал (ДНК либо РНК) Вирусная ДНК намного меньше ДНК хромосом и поэтому намного больше подходит для всевозможных манипуляций. Когда вирусы заражают клетку, их генетический материал вводится в цитоплазму. Клеточный механизм по ошибке интерпретирует ДНК вируса как свою собственную, и по этой причине клетка начинает производить кодируемые вирусом белки как если бы они были собственными белками клетки. Эти белки активизируют репликацию ви русной ДНК и формирование новых капсидов, так что в зараженной клетке скапливается большое количество вирусных частиц. Затем другие вирусные белки разрушают мембрану клетки и выпускают новые вирусные частицы в окружающую среду, где они могут атаковать следующие клетки.
Некоторые вирусы не убивают хозяев сразу. Вместо этого вирусная ДНК встраивается в геном хозяина и может оставаться там в течение длительного промежутка времени без какого-либо заметного изменения в жизни клетки. При некоторых условиях дремлющий вирус может активизиро
44
Глава 1
ваться, после чего он отделяется от генома хозяина и начинает реплицироваться.
Вирусы чрезвычайно избирательны; они способны инфицировать клетки только определенного вида. Так, например, вирус Т2 заражает только бактерию Е. coli; ВИЧ, вирус иммунодефицита человека, заражает только клетки иммунной системы человека; ВТМ, вирус табачной мозаики, заражает только листья табака. Бактериофаги, или просто фаги, являются вирусами, атакующими бактерии.
Бактерия одноклеточный организм, имеющий только одну хромосому18. Бактерии могут размножаться путем простой репликации ДНК, причем этот процесс можег осуществляться за очень короткий период времени, что делает бактерии очень полезными для генетических исследований. Бактерия, наиболее часто используемая в лабораториях, — уже упомянутая нами Escherichia coli, которая способна делиться всего за 20 минут. Бла> о-даря малым размерам и высокой скорости воспроизводства, в лабораторных условиях можно легко получать и использовать миллионы бактерий.
Разрезание и расщепление ДНК
Поскольку молекула ДНК чрезвычайно длинна, необходимо иметь специальный инструмент для ее разрезания в определенных местах (подобно ножницам) или же расщепления ее на части каким-либо иным способом. Рассмотрим основные методы осуществления этих процессов.
«Ножницы» представлены рестриктазами. Это белки, катализирующие гидролиз ДНК (расщепление молекулы с присоединением воды) в некоторых определенных местах, названных участками рестрикции, которые определяются специфической последовательностью оснований. Другими словами, они разрезают молекулы ДНК во всех местах, где появляется определенная последовательность. Например, £coRJ - рестриктаза, которая разрезает ДНК везде, где появляется последовательность GAATTC. Интересно, что эта последовательность является своим собственным обратным комплементом, то есть GAATTC = GAATTC. Последовательности, тождественные своим обратным комплементам, называют перевертнями или палиндромами. Так, каждый раз, когда такая последовательность появляется в одной нити, она обязательно появляется также и в другой нити. Разрезы делаются в обеих нитях между основанием G и первым А. Поэтому оставшиеся фрагменты ДНК будут иметь «липкие» концы, то есть их 5'-концы в точке отреза будут на четыре основания короче З'-концов (см. рис. 1.11). Это способствует взаимной гибридизации фрагментов ДНК,
18Бактерия холерного эмбриона имеет две негомологичные хромосомы. — Прим. ред.
1.5. МЕТОДЫ ИЗУЧЕНИЯ ГЕНОМА
45
разрезанных одним и тем же ферментом, и обеспечивает своего рода методику «вырезания встраивания ДНК», очень полезную в генной инженерии для производства рекомбинантной ДНК.
   ATCCAgJaATTCTCGGA.......ATCCAG AATTCTCGGA. . .
. . .TAGGTCTTAaJgAGCCT. . .	. . .TAGGTCTTAA	GAGCCT. . .
ДНК до разрезания	ДНК после разрезания
Рис. 1.11. Фрагменты ДНК с «липкими» концами после обработки рестриктазой
К обычным типам рсстриктаз относятся: 4-, 6- и 8-рсстриктазы. Нечетные рестриктазы встречаются сравнительно редко, так как последовательности нечетной длины не могут быть палиндромами. Рестриктазы называют также эндонуклеазами, поскольку они расщепляют Д1IK в какой-либо внутренней точке. Экзонуклеазы ферменты, разрушающие ДНК в направлении от концов внутрь.
В бактериях рестриктазы выступают в роли защитников от вирусных атак. Эти ферменты способны разрезать вирусную ДНК прежде, чем она успеет вызвать какие-либо повреждения. Бактериальная ДНК, с своей стороны, защищена от рестриктаз посредством метилирования оснований в участках рестрикции.
Молекулы ДНК могут быть разорваны методом дробовика, который иногда используют при секвенировании. Раствор, содержащий очищенную ДНК — большое количество идентичных молекул - подвергается некоторому разрушающему процессу например вибрации высокого уровня. Каждая отдельная молекула ДНК рвется в нескольких случайных местах, и затем некоторые из фрагментов фильтруются и отбираются для дальнейшей обработки — в частности, для копирования или клонирования (см. ниже). В результате мы получаем набор отдельных клонированных фрагментов, которые соотвстшвуюг случайным смежным фрагментам очищенной последовательности ДНК. Секвенирование этих фрагментов и дальнейшая сборка полученных последовательностей стандартный способ определения последовательности очищенной ДНК. Кроме того, этот метод может быть использован при составлении клонотек — коллекций клонов, покрывающих определенную длинную молекулу ДНК.
копирование ДНК
Другой очень важный метод, необходимый в исследованиях молекулярной биологии, — процесс копирования ДНК (называемый также размно-
46
Глава 1
жснием, или амплификацией ДНК). Здесь мы имеем дело с молекулами, представляющими собой микроскопические объекты. Чем больше копий молекулы мы получим тем легче будет ее изучать. К счастью, для этой цели было разработано несколько методов.
Клонирование ДНК. Для проведения любого эксперимента с ДНК в лабораторных условиях, необходимо иметь хотя бы минимально необходимое количество материала; одной молекулы явно не достаточно. Тем не менее, иногда в распоряжении исследователя имеется всего-навсего единственная молекула ДНК. Кроме того, материал должен быть сохранен некоторым способом, который давал бы возможность по существу неограниченного производства нового материала для повторения старого эксперимента или же проведения новых, если это необходимо Клонирование ДНК — название обшей технологии, способствующей достижению этих целей.
Один из способов получения копий фрагментов ДНК состоит в использовании самой природы. Мы встраиваем исходный фрагмент в геном организма-хозяина, или вектора, и затем позволяем этому организму размножаться. Посредством размножения хозяина встроенный фрагмент (встроика1С>) амплифицируется наряду с его собственной ДНК. После чего мы можем убить хозяина и избавиться от его генома, сохраняя только встройки в желаемом количестве. Производимую этим способом ДНК называют рекомбинантной. В число популярных векторов входят: плазмиды, космиды, фаги и дрожжевые искусственные хромосомы.
Плазмида — это кольцевая молекула ДНК, присутствующая в клетках бактерий20. Она намного меньше бактериальной хромосомы и не зависима от нее Тем не менее, плазмида также реплицируется в процессе деления клетки, и каждая дочерняя клетка содержит одну (или много) копию плазмиды Плазмиды являются хорошими векторами, но налагают ограничение на размер встройки: приблизительно 15 т. п. н. Встройки, намного превышающие этот предел, значительно увеличивают размер плазмиды, а большие плазмиды в ходе репликации обычно укорачиваются.
”В нашей литературе в данном контексте употребляются термины ве|авка и ветровка Хотя с точки зрения русского языка более правильным в этом случае является слово «вставка> встраивание предполагает более тесную связь нового объекта с основой, чем вставление. Таким образом, если мы говорим, что фрагменты клонируемой ДНК встраивают, например, в плазмиду, то естественнее называть такие встроенные фрагменты встройками. Кроме того, это позволит не путать данные объекты со вставками пробелов в последовательности при их выравнивании, со вставками знаков при выполнении редактирующих операций и с мутациями типа вставок. Прим, персе.
20В одной клетке часто находится много (десятки или сотни) одинаковых плазмид (мулыи-копнйные плазмиды). Прим. ред.
1.5. МЕТОДЫ ИЗУЧЕНИЯ ГЕНОМА
47
Фаги тоже довольно часто используют в качестве векторов. Наиболее известный пример — фаг А, который заражает бактерии Е. coli. Встройки в ДНК фага реплицируются, когда этот вирус заражает колонию хозяина. Длина ДНК фага А обычно составляет 48 т. п. н., и эти молекулы, как правило, хорошо переносят встройки до 25 т. п. н. Превышение этого предела недопустимо, поскольку в таком случае образованная ДНК просто не войдет в белковую капсулу фага. Однако если ДНК фага целиком заменить на встройку плюс некоторый минимум репликативного аппарата, то можно получить допустимые встройки длиной до 50 т. п. н. Такие встройки называют космидами.
Для очень больших встроек (порядка миллиона пар нуклеотидов) в качестве вектора может быть использована ДИХ (дрожжевая искусственная хромосома). ДИХ — дополнительная, искусственно полученная хромосома, которая может быть построена путем добавления регуляторных участков дрожжевой хромосомы ко встройке, в результате чего репликативный механизм дрожжей воспринимает ес как собственную дополнительную хромосому.
Полимеразная цепная реакция (ПЦР) — способ производства множества копий молекулы ДНК без необходимости ее клонирования. Вначале исходную молекулу ДНК прогревают, чтобы разрушить водородные связи, и получают две одинарные матричные нити. Затем реакционную смесь охлаждают в присутствии двух коротких фрагментов (праймеров), каждый из которых связывается с комплементарным участком в начале соответствующей матричной нити ДНК и задает точку начала синтеза новой нити. Удлинение комплементарных нитей на матричных ДНК катализируется ДНК-полимеразой. К растущим нитям присоединяются нуклеотиды, пока длина синтезированных нитей не станет равной длине матричных нитей и не сформируются две новые двойные цепи ДНК.
ПЦР, в основном, состоит из чередующегося повторения двух стадий: стадия разделения двунитсвой ДНК на две отдельных нити под воздействием температуры и стадии, в которую каждая отдельная нить прсобра-|уется в двойную путем присоединения праймера и действия полимеразы. При каждом повторении этих стадий число молекул удваивается. Благодаря экспоненциальному закону роста числа молекул в ходе этой процедуры удвоения, после требуемого числа повторений количество произведенного материала становится достаточным для проведения дальнейших экспериментов.
Любопытно отметить, что Кэри Б. Муллис, изобретатель ПЦР (1983), осознал, что эта, посетившая его, идея, хороша, потому что «проводил уй
48
Глава 1
му времени за написанием компьютерных программ» и таким образом быт знаком с итерационными функциями а, следовательно, и с процессами экспоненциального роста.
Измерение и считывание ДНК
Каким же образом мы непосредственно «считываем» пары оснований в последовательности ДНК? Считывание осуществляется с помощью методики, известной как гель-электрофорез, которая основана на разделении молекул по размеру. В процессе разделения участвует гелевая среда и сильное электрическое поле. Молекулы ДНК или РНК заряжаются в водном растворе и движутся в определенном направлении под действием электрического поля. Свойства гелевой среды определяют специфический характер их движения — медленного, совершаемого со скоростью, обратно пропорциональной размеру молекул. Первоначально все молекулы погружают в гель вблизи одного края емкости и помещают ее в постоянное электрическое поле. В течение нескольких часов молекулы меньшего размера постепенно мигрируют к противоположному краю емкости, тогда как более крупные молекулы отстают и остаются позади, около стартового места. Тогда с помощью метода интерполяции можно с достаточно хорошим приближением рассчитать относительные размеры молекул.
В подобных экспериментах молекулы ДНК могут быть помечены радиоактивными изотопами, с тем чтобы гель можно было сфотографировать и получить графический отпечаток положений молекул в конце пробега. Этот процесс используют при секвенировании ДНК, определении длин ре-стриктов и т. п. Альтернативный вариант — вместо радиоактивных изотопов использовать флуоресцентные красители. Лазерный луч может сканировать гель, отслеживать красители и посылать информацию о местоположении молекул непосредственно компьютеру, полностью избегая фотографического процесса. Так, на основании этой методики были созданы автосеквенаторы.
Следующая технология, в которой используют этот процесс, позволяет считывать основания ДНК или РНК. Например, имея некоторую молекулу ДНК, можно получить все ее фрагменты, которые оканчиваются в каждой точке, где появляется основание А. Подобно этому, могут быть получены все фрагменты, оканчивающиеся основаниями Т, G или С. Таким образом мы получаем четыре различные пробирки — по одной для каждого основания. Фрагменты в каждой пробирке будут иметь различную длину. Например, предположим, что мы исследуем следующий фрагмент ДНК:
GACTTAGATCAGGAAACT.
16 ПРОЕКТ «ГЕНОМ ЧЕЛОВЕКА»
49
Рис. 1.12. Схематичный эскиз пленки, полученной при гсль-электрофорезе. Отдельные основания ДНК могут быть идентифицированы на каждой из четырех дорожек. Метки более коротких фра! ментов находятся вблизи вершины, более длинных — вблизи основания пленки
Тогда оканчивающиеся основанием Т фрагменты ДНК GACT, GACTT и GACTTAGAT, а также и сама последовательность в целом. Таким образом, если мы разделим такие фрагменты по размеру (и сделаем это одновременно, но отдельно для всех четырех пробирок), то мы определим все позиции соответствующих оснований, то есть точный состав исходной последовательности ДНК. Процесс показан на рис. 1.12.
При чтении гелевой пленки могут появляться ошибки, поскольку иногда метки расплываются, особенно около границ пленки. Еще одно ограничение состоит в том, что размер фрагментов ДНК, которые могут быть определены этим способом, не должен превышать 700 п. н.
1.6. ПРОЕКТ «ГЕНОМ ЧЕЛОВЕКА»
Проект «Геном человека» — международная программа, начатая в 1988 году, цель которой состоит в том, чтобы полностью расшифровать последовательность человеческой ДНК и составить полную физическую карту всех хромосом человека. Как часть этого проекта, изучаются также геномы таких организмов, как бактерии, дрожжи, мухи и мыши.
50
Глава 1
Это нелегкая задача, так как геном человека является чрезвычайно большим. К настоящему времени уже полностью расшифрованы геномы мно1их вирусов, но их размеры, как правило, находятся в пределах 110 т.п.н. Первый свободно живущий организм, который был полностью секвенирован, — бактерия Haemophilus influenzae, содержащая геном длиной 1800 т. п. н. В 1996 году была успешно определена целая последовательность генома дрожжей — последовательность длиной 10 м. п. н. Это событие можно считать важной вехой в осуществлении проекта, если учесть, что дрожжи являются свободно живущими эукариотами. Картирование генома человека все еще кажется отдаленной мечтой, поскольку его размер в 100 раз превышает наибольший геном, который удалось расшифровать к настоящему времени21.
Одна из причин, по которой в проект вошли другие организмы, — совершенствование методов секвенирования, с тем чтобы в дальнейшем их можно было бы применять к геному человека. Можно ожидать, что благодаря появлению новой, усовершенствованной технологии стоимость расшифровки понизится. Другая причина заключается в непосредственной пользе расшифровки геномов этих организмов, поскольку, как уже было отмечено, все вовлеченные в проект виды организмов широко используются в генетических и молекулярных исследованиях.
Кроме того, в ходе работы над проектом были усвоены некоторые уроки. Осуществление крупных проектов, подобных этому, нельзя возлагать на одну лабораторию. Скорее, более эффективный путь (а, возможно, и единственный) доведения работы до конца  консорциум совместно работающих первоклассных лабораторий. Одна только координация всех этих задач уже сама по себе является вызовом нашим ученым. Что же касается вычислительной техники, то должны поддерживаться банки последователь ностей и базы данных с обновляемой, унифицированной и согласованной информацией, а также с возможностью быстрого доступа к данным. Главным образом обеспокоенность вызвана возможностью присутствия ошибок во вносимых в базу последовательностях. Основная задача для решения этой проблемы состоит в получении последовательностей ДНК, содержащих не более одной ошибки на каждые 10 000 нуклеотидов.
Другая проблема — отыскать и принять за основу некий «усредненный геном». Как известно, различные индивиды имеют различные геномы (именно благодаря этому становится возможной ДНК-дактилоскопия}.
21В настоящее время секвеиированы геномы нескольких сотен видов бактерий, нескольких видов мух, комара, червя, человека, мыши, крысы, шимпанзе, собаки, арабидопси-са22(растение), риса и многие другие. Прим. ред.
22Arabidopsis lhaliana однолетнее цветковое растение резушка Таля. - При.», перев.
1.7 БАНКИ ПОСЛЕДОВАТЕЛЬНОСТЕЙНУКЛЕОТИДОВ
51
В пределах одной популяции ген может быть представлен множеством аллелей, а последовательность межгенных участков (которые нс кодируют белки) у разных людей может варьировать. Известно, что геномы двух случайно отобранных человек отличаются в среднем на один из каждых 500 нуклеотидов. В связи с этим возникает резонный вопрос: чей же геном должен быть расшифрован9 Даже если один индивидуум каким-либо образом выбран и ее или его ДНК принята за стандарт, то все равно остается неразрешенной проблема транспозиции локусов23. Совсем недавно стало известно, что определенные части генома продолжают перемещаться из одних участков хромосом в другие, так что в лучшем случае после секвенирования мы получим лишь «моментальный снимок» генома.
Как только полная последовательность ДНК будет расшифрована, мы столкнемся с трудной задачей се анализа. Мы должны будем распознать гены и определить функцию кодируемых ими белков. Однако методика распознавания генов находится еще в фазе младенчества, а определение функций белков — пока что очень трудоемкая процедура. До лечения генетических болезней на основании данных, полученных в проекте «Геном человека», все еще очень далеко, хотя бурно развивающаяся передовая стратегия уже дала определенные ободряющие результаты.
1.7. БАНКИ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
НУКЛЕОТИДОВ
Частично благодаря методикам, описанным в предыдущих разделах, за последние десятилетия было определено большое число последоватсльно-с1ей ДНК, РНК и белков. Были учреждены некоторые институциональные папки последовательностей, призванные вместить в себя как сами секвени-рованные последовательности, так и прочие сопутствующие данные. Скорость, с которой новые последовательности ганосятся в банки, экспоненциальна. Для осуществления быстрого поиска в базах данных были разработаны специальные вычислительные методы (некоторые из них описаны и главе 3). Ниже мы приводим краткое описание нескольких крупнейших банков последовательностей нуклеотидов.
«Геибанк» (GenBank): Поддерживается «Национальным центром био-ехпологичсской информации» («НЦБИ»), США, и содержит сотни тысяч
'При тгом надо понимать, что геном человека динлонд и ратные хромосомы не идентичны. хоть и гомологичны. Прим ред.
52
Глава 1
LOCUS DEFINITION ACCESSION KEYWORDS SOURCE ORGANISM	HUMRHOA	539 bp mRNA	PRI	04-AUG-1986 Human ras-related rho mRNA (clone 6), partial cds. M12174 c-rayc proto-oncogene; ras oncogene; rho gene. Human peripheral T-cell, eDNA to mRNA, clone 6. Homo sapiens Eukaryota; Animalia; Chordata; Vert ebrat a.- Mammalia; Theria; Eutheria; Primates; Haplorhini; Catarrhini; Kominidae.
REFERENCE AUTHORS JOURNAL	1 (bases 1 to 539) Madaule,P. Unpublished (1985) Columbia U, 701 W 168th St, New York, NY 10032
REFERENCE AUTHORS TITLE JOURNAL MEDLINE COMMENT	2 (bases 1 to 539) Madaule,P. and Axel.R. A novel ras-related gene family Cell 41, 31 40 (1985) 85201682 [2] has found and sequenced a family of highly evolutionarily conserved genes with homology to the ras family (И-ras, K-ras. N-ras) of oncogenes. [2] named this family rho (for ras homology). In humans at least three distinct rho genes are present. A draft entry and computer-readable copy of this sequence were kindly provided by P.Madaule (07-OCT-1985). NCBI gi: 337392
FEATURES	Location/Qualifiers
source	1..539 /organism-“Homo sapiens"
CDS	<1..509 /note="rho protein; NCBI gi: 337393" /codon_starts=2
BASE COUNT ORIGIN	105 a	180 c	172 g	82 t 185 bp upstream of Hinfl site.
1 cgagttcccc	gaggtgtacg	tgc	....	tatgtggccg	acattgaggt
61 ggacggcaag	caggtggagc	tgg	....	ggccaggagg	actacgaccg
121 cctgcggccg	ctctcctacc	egg	. . . .	atgtgettet	cggtggacag
181 cccggactcg	ctggagaaca	tee	gaggtgaagc	acttctgtcc
421 egaggtette	gagacggcca	ege	....	cgctacggct	cccagaacgg
481 ctgcatcaac	tgetgeaagg	tgc	....	cgcgcctgcc	cctgccggc
//
Рис. 1.13. Типичная запись «Генбанка». Файл записи был отредактирован, чтобы он мог уместиться на странице. В реальной записи каждая строка последовательности состоит из 60 символов, с возможным исключением для последней строки
1 7. БАНКИ ПОСЛЕДОВАТЕЛЬНОСТЕЙ НУКЛЕОТИДОВ
53
ID ECTRGA standard; RNA; PRO; 75 BP.
M24860;
24-APR-1990 <Rel. 23, Created) 31-MAR-1992 (Rel. 31, Last updated. Version 3)
E.coli Gly-tRNA.
transfer RNA-Gly.
Escherichia coli prokaryote; Bacteria; Gracilicutes; Scotobacteria; Facultatively anaerobic rods: Enterobacteriaceae; Escherichia.
[1] 1-75 Carbon J., Chang S-, Kirk L.L.; "Clustered tRNA genes in Escherichia coli: Transcription and processing";
Brookhaven Symp Biol. 26:26-36(1975).
Key	Location/Quallf lers
tRNA	1..75
/note»"Gly-tRNA"
SQ Sequence 75 BP; 13 A; 24 C; 19 G; 19 T; 0 other; gcgggcatcg tataatggct attacctcag _________ tgatgatgcg ogttcgattc
ccgctgcccg ctcca //
Рис I 14. Типичная запись «ЕЛМБ», отредактированная к размеру страницы. В рс Ильной записи в поле «Последова1ельность» строки по 60 символов, с возможным исключением для последней строки

54
Глава 1
PIR1:CCHP cytochrome с - hippopotamus
Species: Hippopotamus amphlbius (hippopotamus)
Date; 19-Feb-1984 lsequence_revision 19-Feb-1984 «text_change 05-Aug-1994
Accession: AO0008
Thompson, R.B.; Borden, D.; Tarr, G.E.; Nargoliash, E. J. Biol. Chera. 253, 8957-8961, 1978 Title: Heterogeneity of amino acid sequence in hippopotamus cytochrome c.
Reference number; A00008; MUID;79067782
Accession: A00008 Molecule type: protein Residues: 1-104 <THO> Note: 3-1le was also found
Superfamily: cytochrome c; cytochrome c homology
Keywords: acetylated amino end; electron transfer; heme; mitochondrion; oxidative	phosphorylation;	respiratory chain
Residues	Feature
1	Modified	site: acetylated	amino end	(Gly)
♦status predicted
14,17	Binding	site: heme (Cys)	(covalent)	Istatus
predicted
18,80	Binding site: heme iron (His, Net) (axial
ligands) «status predicted
	Composition
6 Ala А	4 Gin Q	6 У eu L	2 Ser S
2 Arg	R	8	Glu	E 5 Asn	N	14	Gly	G 3 Asp	D	3	Hie	H 2 Cys	C	6	lie	I Mol. wt. unjnod. chain » 11,530 5	10	IS 1GDVEKGKKIFVQKCA 31NLHGLPGRKTGQSPG 61EETLMEYLENPKKYI	17 Lys	К	8	Thr	T 2 Net	N	1	Trp	W 4 Phe	F	4	Tyr	Y 4 Pro	P	3	Vai	V Number of residues » 104 20	25	30 QCHTVEKGGKHKTGP FSYTDANKNKGITWG PGTKMIFAGIKKKGE
Рис. 1.15. Типичная запись «РИБ», подо! манная к размеру страницы
1.7. БАНКИ ПОСЛЕДОВАГЕЛЬНОСТЕЙ НУКЛЕОТИДОВ
55
HEADER	MYOGLOBIN (CARBONMONOXY)		19-JUL-95	1MCY
TITLE		SPERM WHALE MYOGLOBIN (MUTANT	WITH INITIATOR MET	AND
TITLE	2	WITH HIS 64 REPLACED BY GLN,	LEU 29 REPLACED BY	PHE
COMPND	MOL_ID: 1;			
COMPND	2	MOLECULE: MYOGLOBIN (CARBONMONOXY) I		
COMPND	3	CHAIN: NULL;		
COMPND	4	ENGINEERED: YES;		
COMPND	5	MUTATION: INS(MET 0), F29L, Q64H, N122D		
SOURCE	MOL_ID: 1;			
SOURCE	2	SYNTHETIC: SYNTHETIC GENE;		
SOURCE	a	ORGANISM-SCIENTIFIC: PHYSETER CATODON;		
SOURCE	4	ORGANISM—COMMON: SPERM WHALE,		
SOURCE	5	EXPRESSION-SYSTEM: ESCHERICHIA COLI		
KEYWDS	1	HEME, OXYGEN TRANSPORT, RESPIRATORY PROTEIN		
EXPDTA		X-RAY DIFFRACTION		
AUTHOR		Г.LI,G.N.PHILLIPS JUNIOR		
REVDAT	1	07-DEC-95 1MCY	0		
JRNL		AUTH	X. ZHAO, K.VYAS.B.D. NGUYEN, K. RAJ ARATHNAM,		
JRNL		AUTH 2 G.N.LAMAR,T.LI,G.N. PHILLIPS JUNIOR,R.EICH,		
JRNL		AUTH 3 J.S.OLSON.J.LING,D.F.	.BOCIAN	
JRNL		TITL A DOUBLE MUTANT OF SPERM WHALE MYOGLOBIN		
JRNL		TITL 2 MIMICS THE STRUCTURE	AND FUNCTION OF	
JRNL		TITL 3 ELEPHANT MYOGLOBIN		
JRNL		REF	J.BIOL.CHEM.	V. 270 20763	1995
JRNL REMARK	1	REFN ASTM JBCHA3 US ISSN	0021-9258	0071
REMARK	2			
REMARK	2	RESOLUTION. 1.7 ANGSTROMS.		
REMARK	3			
REMARK	3	REFINEMENT.		
REMARK	3	PROGRAM	X-PLOR	
REMARK	3	AUTHORS	BRUNGER	
REMARK	3	R VALUE	0.182	
REMARK	3	RMSD BOND DISTANCES	0.020 ANGSTROMS	
REMARK	3	RMSD BOND ANGLES	1.82 DEGREES	
REMARK	3			
REMARK	3	NUMBER OF REFLECTIONS	23187	
REMARK	3	RESOLUTION RANGE	5.0	- 1.7 ANGSTROMS	
REMARK	3	DATA CUTOFF	0.0	SIGMA(F)	
REMARK	3			
REMARK	3	DATA COLLECTION.		
REMARK	3	NUMBER OF UNIQUE REFLECTIONS	25787		
REMARK	3	RESOLUTION RANGE INFINITY	-1.7 ANGSTROMS	
REMARK	3	COMPLETENESS OF DATA	95.8	%	
Рис. 1.16. Типичная запись «БДБ», неполный заголовок. Последние столбцы с символами 1MCY г, 1де г — номер строки, были опущены. Также произведены другие тмеиения, чтобы размер записи соответствовал странице
56
Глава 1
АТОМ	1	N	МЕТ	0	24.486	8.308	-9.406	1.00	37.00
АТОМ	2	СА	МЕТ	0	24.542	9.777	-9.621	1.00	36.40
АТОМ	3	С	МЕТ	0	25.882	10.156	-10.209	1.00	34.30
АТОМ	4	О	МЕТ	0	26.833	9.391	-10.078	1.00	34.80
АТОМ	5	св	МЕТ	0	24.399	10.484	-8.303	1.00	39.00
АТОМ	6	CG	МЕТ	0	24.756	9.581	-7.138	1.00	41.80
АТОМ	7	SD	МЕТ	0	24.017	10.289	-5.719	1.00	44.80
АТОМ	8	СЕ	МЕТ	0	24.761	12.009	-5.824	1.00	41.00
АТОМ	9	N	VAL	1	25.951	11.334	-10.816	1.00	31.10
АТОМ	10	СА	VAL	1	27.185	11.834	-11.382	1.00	28.40
АТОМ	11	С	VAL	1	27.330	13.341	-11.124	1.00	26.30
АТОМ	12	О	VAL	1	26.444	14.135	-11.452	1.00	26.60
АТОМ	13	СВ	VAL	1	27.270	11.547	-12.912	1.00	29.30
АТОМ	14	CG1	VAL	1	28.532	12.207	-13.526	1.00	28.60
АТОМ	15	CG2	VAL	1	27.275	10.038	-13.163	1.00	29.70
АТОМ	16	N	LEU	2	28.435	13.739	-10.500	1.00	23.00
АТОМ	17	СА	LEU	2	28.691	15.142	-10.318	1.00	20.80
АТОМ	18	С	LEU	2	29.289	15.737	-11.599	1.00	20.10
АТОМ	19	О	LEU	2	30.129	15.110	-12.276	1.00	19.50
АТОМ	20	св	LEU	2	29.661	15.356	-9.134	1.00	20.90
АТОМ	21	CG	LEU	2	29.036	15.387	-7.726	1.00	20.40
АТОМ	22	CD1	LEU	2	28.556	13.983	-7.402	1.00	19.60
АТОМ	23	СО2	LEU	2	30.058	15.904	-6.689	1.00	19.50
АТОМ	24	N	SER	3	28.996	17.003	-11.826	1.00	18.80
АТОМ	25	СА	SER	3	29.696	17.733	-12.852	1.00	19.40
АТОМ	26	С	SER	3	31.096	18.141	-12.385	1.00	19.50
АТОМ	27	О	SER	3	31.397	18.121	-11.174	1.00	19.10
АТОМ	28	СВ	SER	3	28.861	18.954	-13.223	1.00	20.60
АТОМ	29	OG	SER	3	29.019	19.969	-12.261	1.00	22.10
АТОМ	30	N	GLU	4	31.947	18.561	-13.310	1.00	18.40
АТОМ	31	СА	GLU	4	33.293	18.956	-12.937	1.00	19.00
АТОМ	32	С	GLU	4	33.173	20.215	-12.047	1.00	19.20
АТОМ	33	О	GLU	4	34.026	20.457	-11.206	1.00	19.10
АТОМ	34	СВ	GLU	4	34.135	19.270	-14.198	1.00	19.60
АТОМ	35	CG	GLU	4	35.491	19.937	-13.932	1.00	21.10
АТОМ	36	CD	GLU	4	36.537	19.020	-13.295	1.00	22.60
АТОМ	37	ОЕ1	GLU	4	36.355	17.787	-13.230	1.00	23.90
АТОМ	38	ОЕ2	GLU	4	37.569	19.550	-12.840	1.00	24.60
АТОМ	39	N	GLY	5	32.182	21.062	-12.313	1.00	18.30
АТОМ	40	СА	GLY	5	32.039	22.287	-11.532	1.00	19.10
АТОМ	41	С	GLY	5	31.669	22.025	-10.056	1.00	18.20
АТОМ	42	О	GLY	5	32.251	22.638	-9.140	1.00	18.60
Рис. 1.17. Типичная запись «БДБ», пространственные координаты атомов. Последние столбцы, содержащие символы 1MCY г, где г — номер строки, были опущены. В каждой строке были удалены по несколько символов пробела
1.7. БАНКИ ПОСЛЕДОВАТЕЛЬНОСТЕЙ НУКЛЕОТИДОВ
57
последовательностей ДНК. «Генбанк» разделен на несколько секций по по-24 следоватсльностям, сгруппированным согласно видам, включая :
•	PLN: растения
•	PRI: приматы
•	ROD: грызуны
•	МАМ: прочие млекопитающие
•	VRT: прочие позвоночные
•	INV: беспозвоночные
•	ВСТ: бактерии
•	PHG: фаги
•	VRL: прочие вирусы
•	SYN: синтетические последовательности
•	L'NA: нсаннотированные последовательности
•	РАТ: патентованные последовательности
•	NEW: новые последовательности
Поиск может вестись по ключевым словам или же непосредственно по последовательностям. Типичная запись «Генбанка» показана на рис. 1.13. Запись разделена на поля, и каждое поле состоит из идентификатора поля — слова, описывающего содержание поля, и информации как таковой. Записи представляют собой обычный текст. Важное поле — помер доступа, который является уникальным кодом записи и может быть использован для более быстрого доступа к ней. В приведенном примере номер доступа равен М12174. Некоторые записи имеют несколько номеров доступа как результат объединения нескольких связанных между собой, но все же немного отличных записей в одну общую запись. Другие поля большей частью говорят сами за себя.
«Генбанк» — часть исследовательского проекта международного сотрудничества, куда входят также «ЯБД» «Японский банк ДНК» (DDBJ) и «Европейская лаборатория молекулярной биологии» («ЕЛМБ»). Записи «Генбанка» доступны по следующему веб-адресу:
24К настоящему времени в «Генбанке» произошли следующие изменения: 1. В секцию PI N входят не только растения, но также и грибы с водорослями. 2. Появились новые секции: RNA структурная РНК; EST — ярлыки экспрессируемых постелователыюсгей (ЯЭПы); STS — меченые участки последовательностей (МУПы); GSS характеризующие геном последовательности (ХГП); HTG — последовательности высокопроизводительной геномики (Bill) Прим, перев.
58
ГЛАВА 1
http://www.ncbi.nlm.nih.gov/
«ЕЛМБ» (FMBL): «Европейская лаборатория молекулярной биологии» — учреждение, которое обслуживает несколько хранилищ последовательностей. включая банк ДНК, или «Банк последовательностей нуклеотидов». Организация «ЕЛМБ» подобна организации «Генбанка», а записи имеют примерно те же поля. В банке данных «ЕЛМБ» записи идентифицированы по двубуквенным кодам (см. рис. 1.14). Номер доступа, например, определяется по буквам АС. Код XX указывает на пустые строки. Как «Ген-банк», так и «ЕЛМБ» разделяют последовательности на блоки по десять букв, с шестью блоками в строке. Такая схема облегчает поиск определенных позиций в пределах последовательности. Записи «ЕЛМБ» можно найти по следующему веб-адресу:
http://www.embl-heidelberg.de/
«РИБ» (PIR): «Ресурс идентификации белка» — банк последовательностей белка, совместно обслуживаемый и развиваемый тремя учреждениями: «НФБИ» — «Национальным фондом биомедицинских исследований» (США), «Мартинсридским институтом последовательностей белка» (Европа) и «ЯМИББ» (JIPID) — «Японской международной информационной базой (данных) белка» (Япония). Типичная запись «РИБ» показана на рис. 1.15.С этим банком данных обеспечивают связь несколько веб-страниц, включая следующие:
http://www.gdb.org/ http://www.mips.biochem.mpg.de/
«БДБ» (PDB): «Банк данных белка» хранилище трехмерных структур белков. Для каждого представленного здесь белка имеется заголовок с общей информацией, сопровождаемый списком всех атомов, присутствующих в структуре, с тремя пространственными координатами для каждого атома, которые указывают их положение с точностью до трех десятичных знаков. Пример записи «БДБ» приведен на рисунках 1.16 и 1.17. Это хранилище обслуживается в Брукхейвене, США. Доступ к нему может быть осуществлен по веб-адресу:
http://www.pdb.bnl.gov/
Прочие банки данных: Для хранения данных молекулярной биологии были созданы многие другие банки, кроме упомянутых выше. Среди них
УПРАЖНЕНИЯ
59
стоит упомянуть ACEDB, мощный банк данных, подготовленный для проекта расшифровки генома червя С. elegans, но легко адаптируемый к подобным проектам; «Флайбейс» (Flybase) — банк последовательностей генома мух; кроме того — банки данных рестрпктаз, предпочтительного использования кодонов и т. д.
УПРАЖНЕНИЯ
1.	Рассмотрите последовательность TAATCGAATGGGC. Транслируйте с нее шесть возможных последовательностей белка.
2.	Имея воображаемый «ген», представленный ниже, найдите:
а)	последовательность соответствующей нРНК;
б)	последовательность синтезируемого белка (используйте стандартный генетический код).
ATGATACCGACGTACGGCATTTAA
TACTATGGCTGCATGCCGTAAATT
3.	Сколько последовательностей ДНК могли произвести последовательность белка LMK? Подсказка: Одна из них — CTGATGAAG.
4.	Приведите примеры рестриктов, полученных в результате обработки рестриктазами 5ашН1 и
5.	Предположим, что мы имеем молекулу ДНК длиной 40000 п. н. и гидролизируем ее 4-рестриктазой. Если допустить случайное распределение оснований в молекуле, то сколько фрагментов мы можем надеяться получить?
6.	Просмотрите вирусную секцию последовательностей «Генбанка» и найдите любой болезнетворный агент, о котором вы прежде никогда не слышали.
БИБЛИОГРАФИЧЕСКИЕ ПРИМЕЧАНИЯ
Читателям, впервые знакомящимся с молекулярной биологией, возможно, будет интересно заглянуть во вводную «книжку комиксов» Розенфельда, Зиффа и Ван Луна [165]. Желающим выйти за рамки нашего краткого обзора стоит ознакомиться с известными книгами по молекулярной биологии, в том числе:
60
Глава 1
•	Уотсон, Хопкинс, Робертс, Стейц и Уэйнер [203; 204].
•	Альберте, Брей, Льюис, Рафф, Робертс и Уотсон [7],
•	Левин [124].
Следует иметь в виду, что вследствие быстрого прогресса исследований в молекулярной биологии такие книги постоянно обновляются.
Другие учебники, которые мы нашли полезными в ходе подготовки этой главы, следующие: По биохимии — Мэтьюз и ван Холд [131], по генетике Тамарин [183], по белковым структурам - Бранден и Туз [28].
Цитата Р. Ф Дулиттла, приведенная на странице 13, взята из журна ла [50], который содержит достаточно хороший для «любителей-самоучек» обзор белков и выходит под специальной рубрикой, посвященной «молекулам жизни». Интересное описание открытия Муллисом ПЦР можно прочи тать в [141]. Цитата на странице 37 была взята из той же статьи.
Роббинс [162] и Френкель [66] в своих статьях обсуждают трудности проекта «Геном человека» с точки зрения информатики. Роббинс подчеркнул важность научного взгляда на организм как на результат сложного взаимодействия многих «клеточных процессов». Левонтин [125] приводит отрезвляющий критический анализ проекта «Геном человека»
Проблемы, связанные с «метафорой генетической программы», были освещены многими специалистами; нашим источником была работа Атла-иа и Коппела [17]. С другой стороны, заинтересованный читатель может заглянуть в книгу Гофштадтера [96], в который содержится интересное обсуждение параллелей между молекулярной биологией и математической логикой
Глава 2
СТРОКИ, ГРАФЫ И АЛГОРИТМЫ
Эта глава представляет символику, условные обозначения и краткий обзор главных понятий математики и информатики, используемых в этой книге, однако же не является введением в рассматриваемые предметы. Читателю, не знакомому с этими темами, мы предлагаем несколько книг в биб-лиографичсских примечаниях
2.1. СТРОКИ
Сгроки — основной тип данных, с которыми мы будем работать в этой книге Сз рока предс гавляет собой упорядоченную последовательное гь знаков, или символов, взятых из конечного набора — алфавита. Термин последовательность употребляют как синоним термина «строка». В большинстве наших примеров мы используем либо алфавит нуклеотидов ДНК {А, С, G, Т}, либо 20-значный алфавит аминокислот (см. главу 1). Но все же мы хотим подчеркнуть, что некоторые из представленных в книге результатов имеют смысл и являются общезначимыми для любого алфавита В частное ги, определения, которые мы даем в этом разделе, действительны во всех случаях.
В строках могут встречаться повторные знаки, например, в строке s AATGCA знак А появляется три раза. Длина строки 8, обозначаемая s|, равна числу знаков в строке. В данном примере |.s| = 6 Знак, занимающий г-ю позицию в строке з, обозначают «[г]. Индексы знаков — цифры от 1 до |в|. Снова обращаясь к тому же примеру, мы имеем: s[l] = A, s[2] = A, s[3j = Т и т.д. Существует также строка нулевой длины, называемая пустой строкой Пустую строку обозначают специальным символом е.
Несмотря на то, что термины строка и последовательность имеют тождественное значение, термины подстрока и подпоследовательность выражают различные понятия. Подпоследовательностью строки s называют последовательность, которая может быть получена путем удаления некоторых знаков из строки в. Например, последовательность ТТТ является
62
Глава 2
подпоследовательностью строки АТАТАТ, а последовательность ТААА — не является Пустую строку можно считать подпоследовательностью любой строки. Если строка t является подпоследовательностью строки s, то говорят, что s — надпоследовательность строки t.
В отличие от понятия подпоследовательности, подстрока последовательности s — это строка, образованная последовательными знаками строки я, стоящими в том же порядке, в котором они расположены в самой строке s. Например, подстрокой последовательности AGTACA можно считать строку ТАС, но не TTGAC. Быть подстрокой некоторой строки также означает быть подпоследовательностью но не все подпоследовательности можно считать подстроками. Если последовательность t является подстрокой последовательности s, то говорят, что s — надет рока последовательности t.
Иногда подстрока w появляется в строке и несколько раз, например, когда w = ТТ, а и = CTTTAGCATTAA. Иногда требуется различать такие случаи, и для этого существует понятие интервала. Интервал строки s — это такой набор последовательных индексов г .. .у], что 1 г j + 1 С |s| +1. Интервал включает в себя все индексы между г и j, включая и сами индексы г и j. Для интервала г. .у] строки s, запись вида ,ч|г... j] обозначает подстроку s[i]s[i + 1]... s[j| строки s при г С j, и пустую строку — при г = j + 1 Поэтому для любой подстроки I строки s существует по крайней мерс один интервал г... j] строки s, где t = s[i.. .j].
Сцепление двух строк s и t обозначают st и образуют присоединением всех знаков строки t к концу строки s в порядке их появления в t. Например, если s = GGCTA и t СААС, то st - GGCTACAAC. Длина сцепления st равна |s|+|t|. Сцепление нескольких копий одной и той же строки я обозначают возведением я в соответствующую степень — например, я = sss.
Префиксом строки s называют любую подстроку s вида s[l...j], где 0 С j $ |s|. Мы допускаем j = 0 и определяем подстроку s[l . О как пустую строку, которая вместе с тем является префиксом строки s. Обратите внимание, что строка t является префиксом строки s тогда и только тогда, когда существует некоторая строка и, такая, что s = tu. Иногда необходимо обратиться к префиксу строки s, содержащему точно к знаков, где О /с |s|, тогда для этой подстроки мы используем обозначение prefix(s, к).
Аналогично суффикс строки s подстрока вила ,s|z... [s|] для некоторого г, где 1 г |s| + 1. Мы допускаем i = |s| + 1, и в данном случае s[|s| + 1 .. |s|] обозначает пустую строку. Сзрока t является суффиксом строки s тогда и только тогда, когда существует некоторая строка и.
2.2. ГРАФЫ
63
такая, что s = ut. Выражение .suffix(.s, к) обозначает уникальный суффикс строки S, содержащий точно к знаков, где О С к |s|.
Облитератор. Все строки s удовлетворяют условию |s|	0. Чтобы
упростить некоторые аргументы, мы постулируем существование специ альной строки к, такой, что

Эта строка действует как курсор, стирающий знаки, с которыми он соприкасается при сцеплении, и таким образом укорачивает строку. Например,
KGCTAGT = CTAGT.
Интересно отметить, что полученный результаз — суффикс первоначальной строки. Вообще, сцепление с облитсразором к, стоящим в какой-либо степени, может быть использовано в качестве альтернативной формы обозначения префиксов, суффиксов, а также подстрок в целом:
prefix(s, к) = fc, suffixes, к) = к'®' fc.s,
Однако в использовании облитератора есть один недостаток в при сутствии к сцепление теряет свойство сочетательности. Например,
(ATCk)GTC = ATGTC.
тогда как
ATC(kGTC) = АТСТС.
Следовательно, значение выражения aTCkGTC без скобок не является однозначно определенным. Однако следующее равенство по-прежнему верно
|st| = |s| + |t|,
где s и t — общие выражения для строк, в которых допустимо присутствие облитератора к.
2.2. ГРАФЫ
Граф может быть описан при помощи двух множеств. Одно из них — V, множество узлов, или вершин графа; другое Е, множество его ребер,
64
Глава 2
Рис. 2.1. Примеры графов: а — неориентированный граф; б — орграф
которое является также множеством различных пар вершин. Графы обозначают записью вида G = (V,E), его вершины — буквами и, v или ш, а ребра — буквой е или парами вершин в круглых скобках, например (u, v). Граф может быть неориентированным, тогда его ребра представляют собой неупорядоченные пары вершин ((u, v) = (v, и)), или ориентированным, и тогда его ребра — упорядоченные пары вершин {(u,v) ф (у, и)). Когда мы упоминаем графы в остальных разделах этой книги без указания дополнительных характеристик, мы подразумеваем неориентированный граф; в этом разделе термин «граф» означает, что утверждение касается как ориентированных, так и неориентированных графов. Хотя графы — нс более чем абстрактные математические объекты, их обычно представляют в виде топологических схем (см. пример на рис. 2.1). Если нс оговорено противное, то все графы в этой книге — простые графы, а это значит, что они не содержат петель (то есть ребер вида (и, и)) и также кратных ребер между одной парой вершин (здесь следует обратить внимание на то, что в ориентированном графе ребра (u, v) и (у, и) не являются кратными). Число вершин графа мы обозначаем как |V| или п, а число ребер — как |Е?| или т.
Говорят, что точки и и v ребра (u, и) — его конечные точки. Также говорят, что точки и и v инцидентны ребру (y,v), а ребро (и, и) инцидентно точкам и и V. Если (и, и) — ориентированное ребро, то точка и — хвост этого ребра, a v — его голова. Если и и v — конечные точки неориентированного ребра, то говорят, что они смежные. Степенью вершины v неориентированного графа считают число смежных с ней вершин. В случае ориентированных графов (орграфов) вершина v имеет полустепень исхода, которая показывает число ребер вида (у, х), и полустепень захода, которая равна числу ребер вида (т, г). Например, степень вершины Т’з на рис. 2.1 равна трем, а степень вершины vg — единице. Полустепень захода вершины из равна единице, а ее же полустепень исхода — двум.
Во взвешенном графе к каждому ребру приписано некоторое вещественное число. В разных литературных источниках и в зависимости от
2.2. ГРАФЫ
65
контекста, вес ребра (u. v) называют его стоимостью, расстоянием между точками и и v или же просто весом.
Рассматривая графы G = (V, Е) и G' = (V, Е'), мы говорим, что граф G' является подграфом G, если V' С V и Е' С Е. Если граф G' является подграфом G, но G' G, то мы говорим, что G' является собственным подграфом графа G. Если G' является подграфом G и при этом V = V, то мы говорим, что граф G' является остовным подграфом G. Если V — множество всех вершин, инцидентных некоторому ребру данного графа Е', то мы говорим, что граф G' индуцирован графом Е'. Наоборот, если Е' является множеством ребер, обе конечные точки которых принадлежат данному множеству V, то мы говорим, что граф G' индуцирован графом V.
Путь в графе представляет собой список различных вершин (vj, v%,  ., Vk), таких, что при 1 г < к каждая пара соединенных между собой вершин (ц,, является ребром этого графа. Цикл в орграфе — это путь, для которого к > 1 и V] = iy. Цикл в неориентированном графе — такой путь, что г>1 = Vk и никакое ребро не повторяется. Если не оговорено противное, то все упоминаемые в данной книге циклы простые; это означает, что все вершины цикла, кроме первой и последней, различны. Пример (простого) цикла в неориентированном графе — цикл (vi,U2,^3,^i) на рис. 2.1. Если между вершинами и и v существует путь, то говорят, что вершина v достижима из вершины и. Вес пути во взвешенных графах — это сумма весов входящих в него ребер.
Если каждая вершина неориентированного графа G достижима из любой другой вершины, то говорят, что граф связный. Когда граф не связен, мы можем найти его связные компоненты. Понятие связного компонента интуитивно. Например, на рис. 2.1, а показан неориентированный граф с двумя связными компонентами. Можно дать и более формальное определение: множество связных компонентов графа G является таким множеством всех связных подграфов G, что никакой элемент множества не является подграфом другого элемента этого множества. В случае орграфов мы говорим, что граф может быть сильно связным, слабо связным или несвязным. В сильно связном графе каждая вершина может быть достижима из любой другой вершины. В слабо связном графе это условие выполнимо, только если мы игнорируем направления ребер (таким образом, основной неориентированный граф связен); пример такого орграфа см. на рис. 2.1, б. Если ни одно из этих двух условий не выполняется, граф несвязен.
Теория графов подразделяет все графы на классы согласно некоторым свойствам. Вот несколько важных примеров:
•	ациклический граф — граф без циклов.
66
Глава 2
•	полный граф граф, где для каждой пары вершин v и и> справедливо выражение (v, w) е Е (и также выражение (w. v) е Е в случае орграфов).
•	двудольный граф — граф, вершины которого разделены на такие два нсперссекающихся подмножества U и V, что одна из конечных точек любого ребра принадлежит подмножеству U, а другая — подмножеству V.
•	дерево — ациклический и связный граф. Граф, связные компоненты которого в свою очередь являются деревьями, называют 1есом.
Деревья образуют важный класс графов, для которого разработана особая терминология. Каждый узел дерева, имеюший степень 1, называют листом. Все остальные узлы дерева — его внутренние уллы. Дерево может быть корневым, что означает, что один из его узлов выделяют и называют корнем (обозначают г). Если мы рассматриваем некоторый узел и и произвольный узел V, находящийся на пути от и к корню г, то мы говорим, что v — предок узла и, а и — потомок узла ц; если узлы и и v смежны, то i' называют родителем узла и, а и — сыном узла v. Листья не имеют сыновей, а корень не имеет родителя. Число ребер на пути от узла v к корню г называют глубиной узла v. Наинилший общий предок узлов и и v — это самый глубокий узел, который является общим предком этих узлов.
Другой важный класс графов в вычислительной биологии — класс графов интервалов, или интервальных графов. Интервальный граф G = (V, Е) представляет собой неориентированный граф, образованный множеством интервалов С на вещественной оси. Каждому интервалу множества С соответствует вершина графа G; при этом ребро между вершинами и и г мы проводим тогда и только тогда, когда их интервалы имеют непустое пересечение.
Ниже мы приводим несколько важных задач с графами, которые особенно важны для предмета этой книги:
1.	В заданном ориентированном или неориентированном графе необходимо найти цикл, который включал бы в себя вес ребра графа, но чтобы каждое ребро графа входило в него только один раз (вершины могут повторяться). Графы, в которых можно найти такой цикл, называют Эйлеровыми. В другом варианте этой задачи требуется найти путь в графе, соблюдая то же условие (в таком случае говорят, что граф содержит Эйлеров путь).
2.	Имея ориентированный или неориентированный граф, нужно найти в нем такой цикл, чтобы каждая вершина графа принадлежала этому циклу, но входила в него только один раз (кроме первой и последней вершины). Графы, для которых это условие выполнимо, называют Гамильтоновыми. В другом варианте этой задачи требуется найти путь, пролегающий через
2.2. ГРАФЫ
67
все вершины графа, но так, чтобы каждая вершина появлялась в этом пути только один раз (говорят, что такой граф содержит Гамильтонов путь). Еще один вариант этой задачи определен на взвешенных графах: необходимо найти Гамильтонов цикл минимального веса. Эта задача известна также как задача коммивояжера, поскольку города могут быть представлены вершинами, дороги - ребрами графа, а коммивояжеры, будем надеяться, заинтересованы в сокращении расстояния, которое они проходят при посещении множества городов.
3.	В неориентированном взвешенном связном графе желательно найти такое остовнос дерево, чтобы сумма весов его ребер была минимальной среди всех возможных остовных деревьев. Эта задача получила название «задача о минимальном остовном дереве».
4.	Требуется найти минимальное число красок, необходимых для получения раскраски заданного неориентированного графа. Раскрашивание вершин (или просто раскраска) графа представляет собой функцию, которая приписывает целые числа (краски) к вершинам так, чтобы никакие две смежные вершины не были окрашены в одинаковый цвет.
5.	Имея неориентированный граф, надлежит найти для него паросо-четание максимальной мощности. Паросочетанис — такое подмножество ребер Л/, что никакие два ребра в М не имеют общую конечную точку. Вариант этой задачи для взвешенных графов требует найти паросочетанис с максимальным суммарным весом.
В компьютерных программах графы могут быть представлены множеством способов. Один из наиболее известных — представление с помощью матрицы смежности. Для матрицы Л/, содержащей п х п элементов, принимаем Л/у = 1, если (i,j) е Е; в противном случае Л/у = 0. Если граф взвешен, то мы заменяем единицы в матрице весом каждого соответствующего ребра. Для такого представления используется порядка п2 ячеек памяти. Другой способ представления графов — описание с помощью списка смежных вершин. В данном случае мы храним все вершины в форме списка и для каждой вершины в списке мы создаем дополнительный список, содержащий смежные с ней вершины. В случае орграфов необходимо иметь дна списка на вершину и: один для выходящих из г1 ребер, и другой — для ребер, входящих в v. При таком представлении необходимо использовать порядка п + тп ячеек памяти. Когда число ребер в графе относительно мало, списки смежных вершин имеют преимущество по сравнению с матрицами смежности, состоящее в использовании меньшего объема памяти. Такие 1 рафы называют разреженными. Когда число ребер т намного превышает число вершин н, мы говорим, что граф насыщен.
68
ГЛАВА 2
2.3. АЛГОРИТМЫ
В общем смысле слово «алгоритм» означает вполне определенную конечную последовательность шагов, предназначенную для решения хорошо структурированной задачи. Простейший пример алгоритма — последовательность шагов при умножении двух целых чисел. Алгоритмы предназначены для выполнения людьми или машинами. Важно определить заранее, кто или что будет выполнять разрабатываемый алгоритм, потому что именно это придаст алгоритму качество «вполне определенного». В этой книге мы прежде всего интересуемся алгоритмами, понятными для людей, но которые могли бы (с дополнительными деталями) быть выполнены машинами. Под «машиной» мы подразумеваем не какую-либо конкретную модель ЭВМ, а абстракцию, которую назовем моделью машины с произвольным доступом (МПД). Скажем вкратце, что такая машина содержит следующие компоненты: один процессор, рассчитанный на пошаговое выполнение операций; конечную памя гь (набор слов); и конечный набор регистров (еще один набор слов). В каждом слове может храниться отдельное целое или вещественное число. Процессор выполняет шаги программы, то есть алгоритма, закодированного с помощью машинных команд. Нередко мы злоупотребляем термином машинная команда и допускаем неформальные команды, которые предназначены для людей, но требуют значительного расширения (детального формального описания) прежде, чем они могут быть выполнены на настоящем компьютере.
В этой книге алгоритмы описаны в виде обычных предложений и (затем) на языке псевдокодов. Одна из целей представления такого псевдокода состоит в том, чтобы помочь читателям, желающим применить описанные здесь алгоритмы на практике. Мы не даем формального описания этого кода, а просто объясняем его со ссылкой на известные языки программирования, такие как «Си» или «Паскаль». Ниже приведены условные обозначения, принятые в этой книге:
1.	Ключевое слово Algorithm стоит в начале псевдокодов описания алгоритмов.
2.	Ключевые слова input: и output: использованы для обозначения, соответственно, входа и выхода алгоритма.
3.	Ключевые слова набраны в полужирном начертании.
4.	Имена переменных, процедур и функций набраны курсивом.
5.	Константы набраны капителью.
6.	Комментарии начинаются с символа И, продолжаются до конца строки и набраны наклонным шрифтом.
2.3. АЛГОРИТМЫ
69
7.	Неформальные операторы и условия набраны обычным шрифтом.
8.	Как правило, различные операторы находятся в разных строках; точки с запятой используются только в качестве разделителя операторов, находящихся в одной строке Если неформальный оператор занимает более одной строки, то следующая строка начинается абзацным отступом
9.	Блочные структуры выделяются отступом, без ключевых слов begin и end. Иногда мы используем комментарии, чтобы сигнализировать конец длинного блока.
10.	Массивы обозначены квадратными скобками (например, И[г]), а записи — точкой (например, R.field).
11	Параметры в обращении к процедуре или функции заключены в круглые скобки и отделены запятыми.
Ниже мы описываем формальные операторы, которые мы используем в наших алгоритмах. Большинство из них подобно тем, которые встречаются в любом современном процедурноориентированном компьютерном языке.
1.	Оператор присвоения «—, например: а <— а + 1.
2.	Оператор организации цикла for, например: for г <— 1 to п do. Его разновидности включают ключевое слово dowiito и выражают, если употребить неформальный термин, повторение какой-либо операции (например: for (для) каждого элемента множества S do (выполнить))
3.	Оператор условия if <условие> then... else....
4.	Оператор цикла while <условие> do....
5.	Оператор цикла repeat... until <условие>.
6.	Оператор выхода из цикла break, который останавливает выполнение оператора окружения самого внутреннего цикла.
7.	Оператор возврата return, который останавливает выполнение процедуры в том месте, где он появляется, и возвращает текущий ответ.
Условие> в представленных здесь операторах может быть задано как формально, так и неформально.
Алгоритмы предназначены для решения всех вариантов задач, для которых они были разработаны; если алгоритм отвечает данному требованию, го он считается правильным. Следовательно, для любого алгоритма в первую очередь имеет значение гарантия его правильности. Другой важной характеристикой алгоритмов является время счета. За время счета алгоритма принято число машинных команд, которые он выполняет при решении
70
Глава 2
определенной задачи. Таким образом, предмет анализа алгоритма включает в себя две составляющие: предоставление гарантии, или доказательство его правильности, и оценку времени счета.
Вместо подсчета точного числа машинных команд мы оцениваем время счета алгоритма. Это связано с тем, что мы хотим иметь представление относительно поведения алгоритма при решении любого варианта задачи. Чтобы получить такую информацию, необходимо следовать двум правилам. Первое - время счета алгоритма следует определять для наихудшего варианта задачи. Второе время счета должно зависеть от объема решаемого варианта задачи. Таким образом, вместо числа мы получаем функцию времени счета. Например, мы можем сказать, что время счета алгоритма А равно 5п2 + Зп + 72, где переменная п отражает объем задачи. Функции времени счета упрощают, опуская все константы и члены более низкого порядка. В приведенном выше примере Зп и 72 члены более низкого порядка по сравнению с величиной т?. Следовательно, время счета алгоритма А можно считать равным О(п2), где буква О (от слова overall — общее, или полное время счета) означает то, что мы не учитываем константы и члены более низкого порядка. Благодаря этому мы сможем сравнивать алгоритмы только на основе их асимптотического поведения. Таким образом, алгоритм О(п2) может быть быстрее алгоритма О(п) при малых значениях п; однако мы знаем, что при достаточно больших значениях п быстрее будет алгоритм О(п). Между прочим, алгоритмы, время счета которых равно О(п), называют линейными; если же их время счета равно О(п2), то они квадратичны.
Из сказанного в предыдущем параграфе ясно, что для сравнения времени счета алгоритмов, выраженного через функцию О, мы должны уметь сравнивать скорость роста функций, то есть, рассматривая две функции, действительные для всех целых вещественных чисел, отвечать на вопрос: Какая из этих функций растет быстрее? Мы предполагаем, что читатель без труда справится с задачей сравнения простых функций, пользуясь следующими формальными определениями. Сравнивая две функции /(п) и </(п), действительные для всех целых вещественных чисел, мы говорим, что д(п) = О(/(п)), если существуют такие константы с и по, что для всех п > по справедливо неравенство д(п) с/(п). Другими словами, если g(n) =	то мы знаем, что функция д(п) растет не быстрее, чем
функция f(n); функция f является верхним пределом функции д. Например, д(п) = logn, а /(п) = у/п. Учитывая, что мы отбрасываем константы, основание логарифмов (если оно постоянно) для функции О становится несущественным, в силу того, что, когда а и Ь постоянны, функции loga п и log6 п связаны через постоянный множитель.
2.3. АЛГОРИТМЫ
71
Иногда желательно описать функцию д(п) как растущую по крайней мере с такой же скоростью, как некоторая другая функция /(п). В этом случае мы принимаем д(п) = Q(/(n)). Формально это означает, что существуют такие константы с и по, что для всех п > по выполняется неравенство д(п) cf(n). Функция f представляет собой нижний предел функции д. Когда функция д(п) одновременно равна О(/(п)) и П(/(п)), мы говорим, что g(ri) = 0(/(п)).
В этой книге мы прежде всего рассматриваем эффективные алгоритмы. Алгоритм эффективен для решения задачи объемом п, если его время счета ограничено многочленом р(п). Алгоритм, время счета которого равно П(2П), считают неэффективным, так как функция 2П растет быстрее любого многочлена степени п.
Одна из главных проблем, волнующих специалистов в области теоретического программирования, заключается в том, чтобы классифицировать задачи на два класса: задачи, для решения которых существуют эффективные алгоритмы (класс П) и задачи, для которых такие алгоритмы нс существуют, — то есть провести так называемый анализ сложности задач. Однако существует очень важный класс задач, для которых проблема классификации до сих пор так и не была решена. Пока что никому нс удалось найти эффективные алгоритмы для их решения, но также не было показано, что подобных алгоритмов не существует. Это НП-полные задачи1. Они принадлежат к классу НП - классу задач, решение которых, после того как его нашли, может быть проверено методом полиномиальной оценки временных затрат. Этот класс включает в себя класс П в качестве подкласса. В очень строгом смысле, НП-полные задачи - самые трудные задачи в классе НП. Это означает, что любой вариант любой задачи класса НП может быть преобразован за полиномиальное время к варианту НП-полной задачи. Частный случай этого утверждения гласит, что при полиномиальных преобразованиях все НП-полные задачи равносильны друг другу. А это, в свою очередь, означает, что если для решения какой-либо одной НП-полной задачи найден алгоритм с полиномиальным временем счета, то все НП-полные задачи могут быть решены за полиномиальное время.
Упомянутая выше нерешенная проблема известна как задача П = НП. )то выражение означает вопрос: Могут ли все задачи класса НП быть решены за полиномиальное время? Если П = НП, то существуют эффективные алгоритмы для каждой задачи класса НП и, в частности, для НП-полных
'Аббревиатура НП образована оз названия «недетерминированный полиномиальный» и означает, что задачи класса НП могут быть решены на недетерминированной машине Тьюринга за время, определяемое полиномиальной функцией, аргументом которой является размер входа задачи. — Прим, перев.
72
Глава 2
задач; если П НП, то все НП-полные задачи являются трудными для вычислений, а П - собственный подкласс НП. Большинство специалистов по теории алгоритмов полагают, что последнее утверждение верно.
НП-полные задачи встречаются в этой книге довольно часто. Еще один термин из этой области — НП-трудная задача. Чтобы объяснить различие между задачами этих двух классов, мы должны несколько уточнить наши утверждения о классах задач, высказанные чуть выше. Строго говоря, классы П и НП включают в себя только задачи принятия решений', ответ должен быть либо «да», либо «нет». Типичный пример -- задача, в которой требуется решить, является ли заданный граф Гамильтоновым. Однако большинство задач, которые мы встретим в этой книге, представляют собой задачи оптимизации — это означает, что есть некоторая функция, соотнесенная с задачей, и мы хотим найти решение, которое минимизирует или максимизирует значение этой функции. Типичный пример задачи оптимизации — задача коммивояжера, упомянутая в разделе 2.2. Задача оптимизации может быть преобразована в задачу принятия решений путем включения в ее условие параметра К и постановки вопроса о том, существует ли решение, значение которого К (в случае задач минимизации) или К (в случае задач максимизации). Этот прием позволяет нам говорить о варианте с принятием решений для каждой задачи оптимизации и, следовательно, пытаться классифицировать эту задачу как принадлежащую либо к классу П, либо к классу НП. Таким образом можно показать, что вариант с принятием решений для задачи коммивояжера — НП-полная задача. Но что можно сказать о самой задаче коммивояжера? Она не принадлежит к классу НП, так как не является задачей принятия решений; но совершенно очевидно, что она по крайней мере столь же трудна, как и ее вариант с принятием решений. Задачи, которые являются по крайней мере столь же трудными, как НП-полная задача, но которые не принадлежат к классу НП, называют НП-трудными. Все задачи оптимизации, варианты с принятием решений которых НП-полные, сами являются НП-трудными.
Для задач, описанных в разделе 2.2, известно следующее. Задача, в которой требуется решить, является ли заданный граф Эйлеровым, принадлежит к классу П, учитывая, что она может быть задана в виде варианта со временем счета О(п + т). Задача, в которой требуется решить, является ли граф Гамильтоновым, является НП-полной. Как уже было упомянуто выше, задача коммивояжера — НП-трудная задача. Минимальное остовное дерево может быть найдено за время О(п2), и, следовательно, (ее вариант с принятием решений) принадлежит к классу П. Раскрашивание вершин — еще одна НП-трудная задача. Наконец, задачи о совпадении могут быть решены за полиномиальное время.
2 3. АЛГОРИТМЫ
73
Когда мы впервые сталкиваемся с задачей X неизвестной сложности, мы имеем два варианта выбора: мы можем попытаться найти алгоритм, который решает задачу X эффективно (то есть доказать, что эта задача принадлежит к классу П), или же мы можем попытаться доказать, что задача X является НП-полной. Ниже приведены краткие рекомендации относительно того, как нужно поступать при решении подобной проблемы. Сначала мы должны доказать, что задача принадлежит к классу НП (то есть, что найденное для нее решение может быть проверено методом полиномиальной оценки временных затрат). Затем мы должны доказать, что решение какой-либо известной НП-полной задачи Y может быть сведено к решению задачи X. Для этого нужно показать, что если мы действительно имеем полиномиальный алгоритм решения задачи X, то мы могли бы его использовать и для решения задачи Y также за полиномиальное время. Как правило, самая трудная часть в доказательствах НП-полноты отыскание НП-полной задачи Y, наиболее легко сводимой к задаче X. Тот факт, что уже более тысячи задач были классифицированы как НП-полные, свидетельствует о том, что эта проблема стала теперь значительно легче.
Что мы должны делать, когда сталкиваемся с НП-полной или НП-труд-ной задачей? Вот несколько вариантов действий:
1.	Проверить, действительно ли варианты задачи, которые необходимо решить, являются общими. В некоторых случаях решение НП-трудной задачи с ограниченным классом условий может быть найдено за полиномиальное время. Раскрашивание графа — классический пример такой задачи. Отыскание минимальной раскраски для графов общего вида НП-трудная задача, но если по условию исходные графы могут быть только двудольными, то она может быть решена за полиномиальное время (любой двудольный граф может быть раскрашен самое большее двумя красками).
2.	Изобрести исчерпывающий алгоритм поиска (то есть алгоритм метода перебора всех возможных решений и выбора лучшего). Как правило, на практике такие алгоритмы применимы только для маленьких задач, поскольку их время счета растет экспоненциально.
3.	Изобрести алгоритм аппроксимации с полиномиальным временем счета. Такой алгоритм находит решение, гарантированно близкое к оптимальному, но не обязательно оптимальное. Гарантия может быть выражена в форме отношения между решением, найденным алгоритмом, и оптимальным решением. Например, для одного варианта задачи коммивояжера существует алгоритм аппроксимации, который гарантированно выдает решение, вес которого не более чем в 1,5 раза превышает оптимальное значение. Эта
74
Глава 2
гарантия может иметь, либо не иметь практического значения — в зависимости от самой гарантии и решаемой задачи.
4.	Изобрести различные эвристики Под эвристиками мы понимаем полиномиальные алгоритмы без какой бы то ни было гарантии касательно точности решения. Во многих случаях эвристики имеют удовлетворительные характеристики и широко используемы на практике.
Оставим НП-полные задачи и опишем несколько других важных задач, для решения которых были найдены эффективные алгоритмы. В первой из них требуется проверить неориентированный граф на связность Эту задачу можно решить, используя хорошо известные методы обхода графов. Один из них — метод поиска в глубину, начав обход с произвольной вершины v, нужно посетить сначала ее, затем зайти в одну из еще не пройденных смежных с нею вершин. Мы повторяем этот процесс до тех пор, пока все вершины не будут пройдены или пока не застрянем (то есть когда все достижимые вершины уже пройдены, но в графе остались еще не пройденные вершины). В первом случае граф связен, во втором нет. Другой известный метод обхода — метод поиска в ширину, в котором для обработки вершин мы используем очередь. Мы обходим все соседние с первой вершины в порядке очереди, после чего помещаем их все в очередь для дальнейшего исследования Затем мы выбираем следующую вершину из очереди, и так далее. Время счета обоих алгоритмов равно О(п + т). Эти же методы могут быть использованы для решения многих других задач теории графов; с помощью метода поиска в глубину, в частности, можно проверять графы на ацикличность. Используя один из рассмотренных методов, можно, кроме того, совершать обход деревьев. Связность дерева не вызывает сомнений, однако эти методы обеспечивают систематический и удобный способ обхода его узлов.
Задача о минимальном остовном дереве (МОД) также может быть решена эффективно, хотя и при помощи методов, намного более сложных, чем простой обход вершин. В графе на п вершинах мы можем найти МОД с помощью простого алгоритма за время О(п2). Идея заключается в том, чтобы начинать обход с произвольной вершины и выращивать из нее дерево, добавляя ребра с наименьшим весом, соединяющие вершины дерева с вершинами, еще не принадлежащими дереву. Удивительно, что такая простая идея работает, ведь мы выбираем ребра, основываясь лишь на том, что кажется «локально» наилучшим выбором. Алгоритмы, в основу которых заложены подобные методы, называют жадны ни.
Еще одна задача класса П гадача сортировки. Для заданного вектора, содержащего п различных чисел, необходимо сортировать их в порядке
2.3. АЛГОРИТМЫ
75
возрастания или убывания. Можно показать, что при произвольном выборе чисел сортировка потребует время ©(nlogn). Если числа ограничены некоторой постоянной или даже многочленом постоянной степени (например, д3), то задача может быть решена за линейное время.
Мы завершаем этот раздел, упоминая несколько идей и методов, касающихся построения алгоритмов. Индукция один из таких методов. Если толковать этот термин широко, то идея данного метода заключается в следующем. Рассматривая задачу, варианты которой имеют размер п, мы начинаем с поиска способа решения очень маленьких вариантов задачи (например сортировки числа 1), предполагая при этом, что способ решения вариантов размером п — 1 заранее известен. Тогда мы видим, что необходимо сделать для того, чтобы расширить решение вариантов размером п - 1 к вариантам размером п. Во многих случаях такое расширение осуществить достаточно просто, и путем математической индукции можно показать, что мы решили задачу в целом. При построении алгоритмов по данной методике результат часто выражается в рекурсивном виде. В языках программирования рекурсивной считается функция, которая обращается сама к себе (прямо или косвенно). На рис. 2.2. приведен пример рекурсивного алгоритма.
Algorithm RSort1
input: массив А с п различными элементами output: массив А, сортированный по возрастанию if /г - 1 then
return А
else
х <— mm(A) // mm возвращает наименьший элемент
Remove х from А
RSort(A) И рекурсивное обращение
return х : А // сцепление х с началом А
Рис. 2.2. Рекурсивный алгоритм сортировки массива из п элементов
Методика построения алгоритмов, известная как динамическое программирование, особенно важна для этой книги. Суть методики заключается в том, что мы находим решение задачи, постепенно решая многие меньшие и подобные ей подзадачи. Эту методику можно рассматривать как частный случай метода индукции. Конкретные примеры приведены в главе 3 Обратите внимание, что нет никакой связи между этой методикой и компьютерным программированием в современном смысле этого слова Она получила свое название по историческим причинам.
’Рекурсивная сортировка. Прим иерее
76
Глава 2
Использование структур данных — другая идея, применяемая в построении алгоритмов. Это структуры, предназначенные для хранения данных и эффективного выполнения некоторых операций наподобие операций поиска или ввода данных. Обычно на эти операции затрачивается постоянное время или время O(logn), где п — число хранимых элементов данных. Типы используемых структур данных меняются в зависимости от задачи.
К самым известным структурам данных относятся специальные виды списков, называемые стеками и очередями, хэш-таблицами и деревьями дихотомического поиска. Читатели, незнакомые с этими структурами, могут обратиться к книгам, приведенным в библиографических примечаниях.
Одна из часто упоминаемых в этой книге структур, хотя и не столь известная, как указанные выше, — структура данных, получившая название леса непересекающихся множеств. Она поддерживает действия с динамическим семейством непересекающихся множеств, в результате которых первоначально каждый элемент данных находится в отдельном множестве, а по мере выполнения алгоритма множества постепенно объединяются друг с другом. Эта структура данных поддерживает три основных операции: MakeSet(a), которая помещает элемент а в отдельное множество; FindSedp.), которая возвращает множество, которому в настоящее время принадлежит элемент а; и Union(S, Т), которая объединяет множества S и Т (по этой причине структуры данных, поддерживающие такие операции, также называют структурами объединения-поиска данных). Если мы имеем в сумме п элементов, то лес непересекающихся множеств вместе с двумя другими методами позволяет выполнить ряд т > п операций FindSet и/или Union за время О(та{т,п)), где а(т, п) — функция, которая растет настолько медленно, что для всех практических целей ее можно счесть постоянной.
УПРАЖНЕНИЯ
1.	Сколько различных подстрок содержится в строке АСТАС? А сколько различных подпоследовательностей и интервалов?
2.	Постройте и проанализируйте алгоритм проверки того, является ли строка р подстрокой данной строки t. Можете ли вы построить алгоритм, время счета которого равно О(|р| + |t|)?
3.	Используя любимый язык программирования, напишите компьютерную программу, которая принимает на вход последовательность ДНК любого размера и возвращает ее обратный комплемент.
4.	Сколько ребер содержит полный орграф на п вершинах? А сколько, если этот граф неориентирован? Сколько ребер имеет дерево с п узлами?
УПРАЖНЕНИЯ
77
5.	Покажите, что в неориентированном графе G = (V,E) полная степень 'И1') = где степень вершины v.
6.	Опишите графы, изображенные на рис. 2.I., с помощью матрицы смежности и списка смежных вершин.
7	Объясните, каким образом при малых значениях п алгоритм О(п2) может быть быстрее алгоритма О(п)
8.	Допустим, что для решения одной задачи, размер которой определяется параметром п, вы построили два алгоритма: ,4| и Л2. Если время счета алгоритма Ai равно О(п/ logn), а время счета алгоритма А> равно то который из этих двух алгоритмов асимптотически быстрее?
9.	Леонард Эйлер показал, что существует такой связный граф (Эйлеров), что все его вершины имеют четную степень. Основываясь на этом наблюдении, предложите алгоритм, который находит в заданном графе Эйлеров цикл, если таковой существует.
10	Покажите, что во взвешенном неориентированном графе, где стоимости всех ребер различны, минимальное остовное дерево уникально
11.	На основании информации, приведенной в разделах 2.9 и 2.10, постройте эффективный алгоритм решения задачи о минимальном остовном дереве. Проанализируйте свой алгоритм.
12	Топологическое упорядочение вершин орграфа G является таким, что на всех ребрах (и, v) вершина и появляется прежде вершины v. Топологическое упорядочение является вполне определенным только для ориентированных ациклических графов. Постройте и проанализируйте алгоритм топологического упорядочения ациклического орграфа G.
13	Допустим, что вы имеете структуру данных в виде леса нспсрссе-кающихся множеств. Используйте ее для построения алгоритма, определяющего связные компоненты неориентированного графа G. Сравните свой алгоритм с каким-либо другим, основанным на методе поиска в ширину или в глубину.
14	Предположим, что вам задали задачу X неизвестной сложности, но вам удалось свести ее к известной НП-полной задаче. Что вы можете сказать о сложности задачи X?
15.	Задача покрытия веришн определена для неориентированного графа G = (V,E), и в ней требуется найти такое минимальное множество вершин И С V, чтобы по крайней мере одна из конечных точек любого ребра < € Е принадлежала множеству И’. Для этой задачи напишите собственный вариант с принятием решений.
78
Глава 2
16.	Кчитй в графе G называют полный подграф графа G. Задача о клике определена для неориентированного графа G = (V, Е) и требует найти такое максимальное множество вершин С С V. чюбы множество С было кликой. Учитывая, что задача покрытия вершин, определенная в предыдущем упражнении, является НП-полной, покажите, что задача о клике также НП-полная.
17.	Учитывая, что задача о Гамильтоновом цикле НП-полная, покажите, что задача о Гамильтоновом пути между двумя произвольными вершинами и и г - также НП-полная.
18.	Алгоритм аппроксимации для задачи покрытия вершин (описанной в упражнении 15) следующий. Начинаем с пустого покрытия множества И . Возводим покрытие вершин, выбирая любое ребро (и, V) и добавляя ко множеству 1Г вершины и и V. Затем удаляем пит из графа G (то есть удаляем любые другие инцидентные к ним ребра) и повторяем эти шаги до тех пор, пока все ребра графа не будут покрыты. Покажите, что этот алгоритм находит такое покрытие вершин, размер которого превышает минимальное покрытие вершин не более чем вдвое.
19.	Постройте и проанализируйте исчерпывающий алгоритм поиска для задачи о Гамильтоновом цикле.
20.	Задача о ранце формулируется следующим образом. Задано множество объектов п, где объект I имеет вес wz, и положительное целое К (вместимость ранца); требуется определить, существует ли подмножество объектов, суммарный все которых в точности равен К. Это типичная НП-полная задача, но для се решения возможно построить алгоритм со временем счета О(пК). В этом нет никакого противоречия, потому что величина К может быть произвольно большой (например. 2П). и. следовательно, этот алгоритм не строго полиномиален. Постройте такой алгоритм, используя вышеописанный метод динамического программирования.
БИБЛИОГРАФИЧЕСКИЕ ПРИМЕЧАНИЯ
Книги Стивена [180], а также Крошемора и Риттера [39] посвящены исключительно алгоритмам обработки строк. Ахо [6] дает полезный обзор. Новая книга Гасфилда [85] должна быть особенно полезна для изучения вычислительной биологии.
Читателям, незнакомым с теорией графов, было бы желательно прочитать главу по этому предмету в учебнике по дискретной математике хотя бы на уровне колледжа. К этой категории можно отнести книгу Розена [163];
БИБЛИОГРАФИЧЕСКИЕ ПРИМЕЧАНИЯ
79
кроме того, она содержит ссылки на другие источники, посвященные теории графов Принятая нами система обозначений и описание теории графов во многом основаны на первой главе книги Тарджана [184].
Еще две превосходные книги по теории алгоритмов написали Ман-бср [ 129], а также Кормен, Лейсерсон и Ривест [37]. Манбер ставит акцент на описании метода индукции при построении алгоритмов, тогда как Кормен [37] обеспечивает более энциклопедический охват материала. В книгах Седгсвика [170], а также Тонне и Баеза-Ятеса [76] приведены удобные примеры алгоритмов для решения множества разнообразных задач.
Классическое описание НП-полных задач и общей теории НП-полноты можно найти у Гэри и Джонсона [68]. Более современная книга Пападимит-риу [151] охватывает общие вопросы сложности вычислений.
Глава 3
СРАВНЕНИЕ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И ПОИСК В БАЗАХ ДАННЫХ
В этой главе мы представляем некоторые из самых известных и наиболее часто используемых на практике методов сравнения последовательностей и поиска в базах данных. Сравнение последовательностей, несомненно, есть самая основная операция в вычислительной биологии. Именно к ней мы будем прямо или косвенно обращаться во всех последующих главах этой книги. Кроме того, эта операция в различных вариантах встречается в других разделах информатики.
3.1.	БИОЛОГИЧЕСКИЕ ОСНОВЫ СРАВНЕНИЯ
ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Для чего же нужно сравнивать последовательности? И зачем для этого использовать компьютер? Каким образом можно сравнивать последователь ности с помощью компьютера? Это главные вопросы, которые мы будем рассматривать в этой главе. На первые два мы ответим в этом разделе, а последнему посвятим остальную часть настоящей тлавы.
Сравнение последовательностей — наиболее важная элементарная операция вычислительной биологии, служащая основанием для многих других, более сложных, манипуляций. Попросту говоря, эта операция состоит из поиска схожих и отличающихся частей последовательностей. Однако за этим, на первый взгляд простым, понятием скрывается большое число весьма разнообразных задач с многоликой формализацией, для эффективного решения которых иногда требуются особые структуры данных и специальные алгоритмы.
В качестве примеров мы приводим задачи, часто встречающиеся в вы числительной биологии В этих примерах мы используем два понятия, точные определения которых будут даны в последующих разделах. Первое —
3.1. БИОЛОГИЧЕСКИЕ ОСНОВЫ
81
понятие подобия двух последовательностей, определяющее меру того, насколько рассматриваемые последовательности подобны. Второе понятие — выравнивание двух последовательностей, выражающее способ, согласно которому одну из сравниваемых последовательностей помещают над другой, чтобы определить меру их соответствия, пропорциональную числу одинаковых знаков или подстрок в соответствующих позициях этих последовательностей. Кроме того, в приведенных ниже примерах задач (и во всей главе) используются сформулированные в разделе 2.1 основные понятия, касающиеся строк.
1.	Даны две последовательное i и знаков, взятых из одного алфавита; обе примерно одной длины (десятки тысяч знаков). Мы знаем, что эти последовательности почти тождественны и имеют лишь несколько одиночных различий типа вставок, удалений и замен знаков. Средняя частота таких различий низка - например, одно на каждую сотню знаков. Необходимо найти все позиции, в которых появляются эти различия.
2.	Мы имеем две последовательности знаков из одного алфавита, содержащие несколько сотен знаков каждая. Требуется ответить на вопрос, существует ли в первой последовательности некоторый префикс, который подобен суффиксу второй. Если ответ положительный, то такие префикс и суффикс должны быть воспроизведены в ответе.
3.	Условие задачи аналогично пункту 2, но теперь мы имеем несколько сотен последовательностей, которые необходимо сравнить (каждую со всеми остальными). Кроме того, мы знаем, что большая часть пар последовательностей нс связаны между собой генетически, то есть они нс будут иметь требуемой степени подобия.
4.	Рассматриваем две последовательности знаков из одного алфавита, состоящие из нескольких сот знаков каждая, и хотим знать, существуют ли две подстроки (каждая из своей последовательности), которые являются взаимно подобными.
5.	Задача аналогична п. 4, но вместо двух нам задана одна последовательность, которую мы будем сравнивать с тысячами других.
Задачи, подобные п. 1, встречаются, когда, например, один и тот же ген был секвенирован двумя разными лабораториями и нужно сравнить полученные результаты; или же когда какая-нибудь длинная последовательность дважды введена в компьютер и мы ищем возможные опечатки. Задачи, подобные п.
2 и п. 3, решают в контексте сборки фрагментов в программах, участвующих в расшифровке длинных последовательностей ДНК. Задачи, подобные п. 4
82
Глава 3
и п. 5, встречаются при поиске локальных подобий при помощи мощных баз данных последовательностей.
Далее в этой главе мы увидим, что для решения всех перечисленных выше задач может быть достаточно одной-единственной основной идеи, воплощенной в универсальном алгоритме. Однако это решение может оказаться не самым эффективным. Иногда для решения каждой конкретной задачи лучше подходят менее универсальные, но зато более быстрые методы.
Применение компьютеров едва ли требует обоснований, когда мы имеем дело с большим количеством данных, как, например, при поиске в крупных базах данных. И даже в тех случаях, когда сравнения возможно проводить «вручную», использование компьютеров безопаснее и удобнее, как показывают следующие примеры, взятые из статьи Смита [176].
Симс с группой сотрудников исследовал подобные области ДНК двух бактериофагов. В статье [173] они представили выравнивание между областями Н-гена фагов St-1 и G4, содержащее 11 совпадений (то есть 11 столбцов, в которых знаки обеих последовательностей совпадают). Процедура, которую они использовали для получения хороших выравниваний, была описана как «вставка случайных пробелов с целью максимизации гомологии [числа тождеств]». Однако Смит вместе с коллегами [176] отмстил выравнивание с 12-ю случаями совпадения, найденное с помощью компьютера, и которое, несомненно, было пропущено первой группой исследователей.
В статье [164] Розенберг и Корт описали результаты своих экспериментов по выравниванию 46-ти последовательностей промоторов различных организмов. Авторы построили множественное выравнивание путем выравнивания определенных областей, по предположению относительно инвариантных, и последующего расширения этого «затравочного» выравнивания в обоих направлениях без введения в него пробелов. Хотя построенное выравнивание было хорошо в целом, полученные из него попарные выравнивания были относительно плохими. При множественном выравнивании это случается довольно часто, но в данном случае Смит с группой коллег с помощью компьютера нашли выравнивание между двумя подстроками этих последовательностей, содержащее 44 одинаковых знака при общем количестве 45 знаков. Это, конечно, удивительно хорошее локальное выравнивание, и тот факт, что оно не было упомянуто Розенбергом и Кортом, опять-таки должен означать, что они не смогли найти его вручную.
Эги два примера показывают, что использование компьютеров позволяет обнаружить интересные подобия, которые могли бы остаться незамеченными.
3.2. СРАВНЕНИЕ ДВУХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ 83
3.2.	СРАВНЕНИЕ ДВУХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
В этом разделе мы изучим основные методы сравнения двух последовательностей. А именно, мы интересуемся отысканием оптимальных выравниваний между двумя последовательностями. На практике встречается несколько вариантов этой задачи, в зависимости от того, ищем ли мы выравнивания целых последовательностей или только их подстрок. Это ведет к определению понятий глобального и локального сравнения. Известен также третий вид сравнения где мы строим выравнивание не произвольных подстрок, а только префиксов и суффиксов данных последовательностей. Этот третий вид сравнения мы называем полуглобальным сравнением. Далее мы увидим, что все упомянутые здесь задачи могут быть решены эффективно методом динамического программирования.
3.2.1.	ГЛОБАЛЬНОЕ СРАВНЕНИЕ - ОСНОВНОЙ АЛГОРИТМ
Рассмотрим последовательности GACGGATTAG и GATCGGAATAG. Трудно не заметить, что фактически они выглядят очень подобными, и это становится более заметно, когда мы выравниваем их, поместив одну над другой следующим образом:
GA-CGGATTAG
(3.1) GATCGGAATAG.
Единственные отличия второй последовательности — дополнительный знак Т в третьей позиции слева, а также замена Т на А в четвертой позиции справа. Обратите внимание, что в первую последовательность мы вставили пробел (обозначенный черточкой), чтобы основания до и после него расположились точно над соответствующими основаниями второй после-ловательности.
Наша цель в этом разделе состоит в том, чтобы представить эффек-|ивный алгоритм, который оценивает две последовательности и определяет оп1имальное выравнивание между ними, как мы сделали в приведенном выше примере. Конечно, прежде чем подойти к решению самой задачи выравнивания, мы должны дать определение «оптимального» выравнивания. Чтобы упростить рассуждения, мы примем простой формализм; позже мы ладим возможные обобщения.
Начнем с точного определения того, что мы подразумеваем под выравниванием двух последовательностей. Исследуемые последовательности moi ут иметь различные размеры. Как было показано в последнем примере, выравнивания могут содержать пробелы в любой из последовательностей.
84
ГЛАВА 3
Таким образом, мы определяем выравнивание как вставку пробелов в произвольных позициях последовательности, с тем чтобы в результате длина этих последовательностей совпала. Удлиненные до одного размера последовательности могут быть расположены одна над другой, образуя соответствие между знаками или пробелами первой последовательности и знаками или пробелами второй последовательности. При этом никакой пробел в одной последовательности не должен быть сопоставлен с пробелом в другой. Пробелы могут быть вставлены даже в начале или в конце обеих последовательностей.
Построив выравнивание между двумя последовательностями, мы можем назначить ему счет следующим образом. Каждому столбцу выравнивания в зависимости от его содержания мы присваиваем некоторую величину (очко), и тогда полный счет выравнивания будет равен сумме очков, назначенных его столбцам. Если столбец содержит два одинаковых знака, то ему будет назначено +1 очко (совпадение). Различные знаки дадут —1 очко (несовпадение). Наконец, пробел в столбце понижает его счет до —2. Оптимальным будет считаться выравнивание с максимальным полным счетом. Этот максимальный счет будем называть подобием между этими двумя последовательностями и обозначать как функцию sim(s, t), где suf — выравниваемые последовательности. Как правило, может быть найдено множество выравниваний с максимальным счетом.
В качестве примера практического применения этих понятий вычислим счет выравнивания (3.1). Оно содержит девять столбцов с одинаковыми знаками, один столбец с разными знаками и один столбец с пробелом, что дает полный счет
9-1 + 1 (-1)4-1 (-2) = 6.
Почему же для назначения счета мы выбрали именно величины (+1, — 1 и —2)? Такая система очков часто используется на практике. Мы награждаем совпадения и штрафуем несовпадения и пробелы. В разделе 3.6.2 мы обсудим выбор этих параметров подробнее.
Один из подходов к вычислению подобия между двумя последовательностями состоит в том, чтобы построить все возможные выравнивания и затем выбрать из них оптимальное. Однако число выравниваний между двумя последовательностями экспоненциально, и такой подход привел бы к недопустимо медленному алгоритму. К счастью, существует намного более быстрый алгоритм, который мы сейчас опишем.
В основу этого алгоритма заложен метод так называемого динамического программирования. Этот метод главным образом состоит из разбиения задачи на подзадачи и последовательного решения основной задачи, ис
3.2. СРАВНЕНИЕ ДВУХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
85
пользуя решения промежуточных, более легких подзадач. Итак, имея две последовательности s и t, вместо того, чтобы определять подобие между целыми последовательностями s и t, мы выстраиваем решение, определяя все подобия между произвольными префиксами этих двух последовательностей. Мы начинаем с более коротких префиксов и затем используем результаты предыдущих вычислений для решения задачи с более длинными префиксами.
Пусть т — длина последовательности .s, ап — длина последовательности t. Тогда существует т Ч 1 возможных префиксов последовательности s и п + 1 префиксов последовательности t, включая пустую строку. Таким образом, мы можем организовать наши вычисления в виде массива размером (т + 1) х (n + 1), где элемент (г, j) содержит подобие между префиксами s[l... г] и f[l. . j].
На рис. 3.1 показан массив, соответствующий последовательностям s АААС и t AGC. Для более удобного индексирования префиксов мы расположили знаки последовательности s по левому краю, а знаки последовательности t — по верхнему краю массива. Обратите внимание, что элементы первой строки и первого столбца массива инициализированы значениями, кратными штрафу за пробел ( -2 в нашем случае). Это связано с тем, что если одна из последовательностей пуста, то существует только одно возможное выравнивание. Нужно всего лишь добавить столько же пробелов в пустую последовательность, сколько знаков содержит другая последовательность. Счет этого выравнивания равен 2/с, где к — длина непустой последовательности. Следовательно, заполнение первых строк и столбцов массива не представляет никакой сложности.
Теперь сосредоточим наше внимание на остальных элементах массива. Ключевой принцип состоит в том, что мы можем вычислить значение элемента (г, j), оценивая всего только три предшествующих элемента: (г — 1, j), (г - 1,J — 1) и (i,J — 1). Это связано с тем, что есть только три способа получить выравнивание между префиксами в[1...г] и	и
в каждом способе необходимо использовать один из этих предшествующих ыементов. Фактически, мы имеем следующие три возможности построения выравнивания между префиксами s[l... г и f[l... j]:
•	выровнять si... г] с t[l... j — 1] и сопоставить пробел с t[J];
•	выровнять s[l... г — 1] с 1[1... j — 1] и сопоставить s[i] с t[j];
•	выровнять s[l... г — 1] с t 1... j] и сопоставить в[г] с пробелом.
Эти возможное 1 и являются исчерпывающими, поскольку в последнем столбце выравнивания не должно быть пары из двух пробелов. Если мы
86
ГЛАВА 3
А
G
С
Рис. 3.1. Двумерный массив для вычисления выравниваний. Цифра в левом верхнем углу ячейки (г, j) показывает, равны ли знаки я[г] и t[j]. Индексы строк и столбцов начинаются нулем
выберем подходящий порядок вычисления элементов массива, то в нем автоматически сохраняются счета оптимальных выравниваний между меньшими префиксами, вследствие чего искомое подобие может быть найдено
3.2. СРАВНЕНИЕ ДВУХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
87
Algorithm Similarity1
input: последовательности .s и t
output: подобие между s и t
т <— |s|
И
for г «— 0 to т do
n[t,0] <-гд
for 3 «— 0 to n do
<- 39
for г <— 1 to m do
for j <— 1 to n do
a[i, j] «- max(o[i - 1, j] + <?, o[i-l.J-l]+p(i,j), a[t,j-l]+p)
return a[m, n]
Рис. 3.2. Основной алгоритм метода динамического программирования для сравнения двух последовательностей
по формуле
sim(s(l.. .z], t[l ..j — 1]) - 2
sim(s[l... г], t[l •.. j]) - max < sim(s[l.. .г — 1], t[l... j — 1]) + p(i, j) sim(s[l.. .i — l],t[l. . j]) — 2,
(3.2) где p(i,j) = +1 при s[i] = t[j] и p(i,j) = —1 при s[t] t[j]. Значения записаны в верхних левых углах ячеек массива на рис. 3.1. Если мы обозначим массив буквой а, то это уравнение может быть переписано в следующем виде:
а(г, j) = max
a(i,j - 1) - 2
a(i - l.j - 1) + p(z, j) а(г - l,j) - 2
(3 3)
Как было упомянуто выше, необходимо соблюдать подходящий порядок вычислений. Это требование легко выполнимо Для этого достаточно заполнять массив строку за строкой, слева направо каждую, или столбец за столбцом, сверху вниз. Вообще, для заполнения массива подходит любой порядок, в котором при вычислении значения элемента обеспечен доступ к величинам a[i,j 1], а[г — 1,j 1] и а[г — 1, j].
1 Подобие. Прим персе.
88
ГЛАВА 3
Мы провели стрелки на рис. 3.1, чтобы указать, откуда максимальные значения берутся согласно уравнению (3.3). Например, значение а[1.2] было выбрано как максимальное среди следующих чисел:
а[1,1] - 2 = -1 а[0,1] - 1 = -3 а[0,2| — 2 = —6.
Поэтому есть только один способ получить это максимальное значение выбрать его из элемента (1,1), и именно этот порядок и показывают стрелки.
На рис. 3.2 представлен алгоритм заполнения массива указанным способом. Этот алгоритм вычисляет элементы массива строку за строкой. Он зависит от параметра д, который определяет штраф за пробел (обычно д < 0), и от функции парных счетов р (счетов пар знаков). При индексировании массива на рис. 3.1 мы использовали следующую систему очков: д 2, р(а. b) = 1 при а = b и р(а. b) = 1 при а / 6.
Оптимальное выравнивание
Итак, мы узнали, как надлежит вычислять подобие между двумя после-довагсльностями. Здесь мы научимся строить оптимальное выравнивание между ними. Стрелки на рис. 3.1 будут полезны также и в этом отношении. Все, что мы должны сделать — начать построение с элемента массива (ш, п) и следовать за стрелками, пока не дойдем до элемента (0,0). Каждая пройденная стрелка даст нам один столбец выравнивания. Например, рассмотрим стрелку, выходящую из элемента Если эта стрелка горизонтальна, то она соответствует столбцу с пробелом в последовательности s, сопоставленным со знаком t[j|; если же она вертикальна, то она соответствует знаку в[г], сопоставленному с пробелом в последовательности t, наконец, диагональная стрелка означает сопоставление знаков s[i] и f[j|. Заметим, что первую последовательность, s, всегда помещают вертикально. Таким образом, оптимальное выравнивание может быть легко построено справа налево, если мы имеем массив а, вычисленный основным алгоритмом (рис. 3.2). Нет необходимости задавать направление явно (стрелками) — простая проверка может помочь выбрать каждый последующий элемент пути.
На рис. 3.3 показан рекурсивный алгоритм для определения оптимального выравнивания; для этого на входе необходимо иметь матрицу а и последовательности s и t. Процедура Align(m, п, 1еп) строит оптимальное выравнивание. Ответ будет выдан в паре векторов align-s и align-t, содержащих
3.2. СРАВНЕНИЕ ДВУХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
89
Algorithm Align2
input: индексы i и j, массив а из Similarity output: векторы выравнивания align-s и align-t, длина выравнивания len
if г = 0 and j = 0 then
len «— 0
else if i > 0 and a[i, j] = a[i — 1, j] + д then
Align(i — l,j, len)
len *— len + 1
align s[len] «— s[z]
align-t[len] <--
else if z > ( and j > 0 and <i[z.j] = a[i l,j — 1] + p(z,j) then
Align(i — 1, j — 1, len)
len «— len +1
aligns[len\ «— s[i]
align-t[len] <- t[j]
else // должно быть j> 0 и а[г, j] = a[i,j — 1] + д
Align(i,j 1, len)
len — len +1
align-s[len] <--
align t[len] <- t [j]
Рис. 3 3. Рекурсивный алгоритм оптимального выравнивания
в позициях 1... len выровненные знаки, которые могут быть пробелами или символами из мданных последовательностей. Переменные aligns и align-t программа рассматривает как глобальные. Длину выравнивания алгоритм возвращает в переменной len Здесь max(|s|, |t|) len ^тп + п.
Как было сказано ранее, для одной пары последовательностей может быть найдено множество оптимальных выравниваний. Алгоритм на рис. 3.3 возвращает только одно из них, отдавая максимальное предпочтение направлениям (стрелкам), выходящим из элемента (г, у) вертикально (см. рис. 3 4). В результате оптимальное выравнивание, возвращенное этим алгоритмом, имеет следующую общую характеристику: когда есть возможность выбора, столбец с пробелом в последовательности I имеет приоритет над столбцом с двумя символами (и предшествует ему), который, в свою очередь, имеет приоритет над столбцом с пробелом в последовательности s. Например, при выравнивании последовательностей s = АТАТ и t = ТАТА, мы, скорее
2 Выравнивание. При», перев.
90
Глава 3
максимальное предпочтение
Рис. 3.4. Предпочтительные направления построения оптимального выравнивания
всего, получим выравнивание
-АТАТ
ТАТА-,
а не
АТАТ—
-ТАТА,
представляющее собой альтернативный вариант оптимального выравнивания этих последовательностей. Проше говоря, при выравнивании последовательностей s = АА и t = АААА мы получаем выравнивание
—АА
АААА,
хотя существует еще пять других оптимальных выравниваний. Это выравнивание иногда упоминают как наивысшее выравнивание, потому что оно всегда использует стрелки матрицы, направленные вверх. Чтобы изменить порядок предшествования столбцов на противоположный, мы должны изменить условие операторов if в программе алгоритма и получить в таком случае наинизшее выравнивание. Столбец, появляющийся как в наивысшем, так и в наинизшем выравниваниях, будет присутствовать во всех оптимальных выравниваниях между двумя рассматриваемыми последовательностями.
Данный алгоритм возможно преобразовать таким образом, чтобы он производил все оптимальные выравнивания между последовательностями s
3.2. СРАВНЕНИЕ ДВУХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
91
и t. Мы должны оставлять в стеке адреса элементов массива, в которых есть варианты путей, чтобы возвращаться к ним и исследовать все возможности достижения элемента (0,0). Однако число оптимальных выравниваний может быть очень большим. В этих случаях желательно сохранять в некотором усеченном виде все или часть этих выравниваний — например, наивысшее и наинизшее.
Теперь определим сложность алгоритмов, описанных в этом разделе. Основной алгоритм на рис. 3.2 имеет четыре цикла. Первые два выполняют инициализацию и затрачивают, соответственно, время О(т) и О(п). Последние два цикла вложены и заполняют остальную часть матрицы. Число выполняемых операций главным образом зависит от числа элементов, которые должны быть вычислены, то есть от размера матрицы Таким образом, в этой части программы мы затрачиваем время O(mri), и это главный член в формуле временной сложности алгоритма. Используемое пространство памяти также пропорционально размеру матрицы. Следовательно, сложность основного алгоритма равна О(тп) как в отношении времени, так и пространства. Если последовательности имеют одинаковую или почти одинаковую длину (например, п), то мы получаем пространственно-временную сложность О(тг2). Именно поэтому мы говорим, что сложность таких алгоритмов квадратична
Построение выравнивания — при уже заполненной матрице — требует время О(1еп) (где 1еп — размер возвращенного алгоритмом выравнивания), то есть О(т + п).
3.2.2. ЛОКАЛЬНОЕ СРАВНЕНИЕ
Локальное выравнивание последовательностей s и t представляет собой выравнивание между подстроками последовательностей s и t В этом разделе мы представляем алгоритм поиска оптимальных локальных выравниваний между двумя последовательностями.
Этот алгоритм является разновидностью основного алгоритма, приведенного на рис. 3.3. Как и прежде, основная структура данных — массив размером (m+1) х (zi+1). Только на сей раз интерпретация значений элементов массива будет иной. Теперь каждый элемент (г, у) хранит максимальный счет выравнивания между суффиксами подстрок s[l... г] и t[l... у]. Первая строка и первый столбец массива инициализируются нулями.
Для любого элемента (i,j) всегда существует выравнивание между пустыми суффиксами подстрок .ч[1 . .г] и t[l.. .j], которое имеет нулевой счет; поэтому значения всех элементов данного массива больше или равны нулю. Это частично объясняет принятую здесь систему инициализации.
92
Глава 3
= шах •
Следуя данной инициализации, массив может быть заполнен обычным способом, где величина а\г, J] зависит от значений грех ранее вычисленных элементов. В результате получаем заполнение в виде
о[г,> - 1] + д a[i~l,j- 1] +р(г, а[г- l,j] +д О,
то есть то же самое, что и в основном алгоритме, за исключением того, что теперь мы имеем четвертую возможность (пустого выравнивания), недоступную в случае глобального выравнивания.
Итак, достаточно найти максимальный элеменг массива. Его значение равно счету оптимального локального выравнивания. Чтобы построить такое выравнивание, в качестве отправной точки может быть выбран лю бой элемент с максимальным значением Остальная часть выравнивания выстраивается обычным прохождением элементов в обратном порядке, но здесь мы должны остановиться, как только достиг нем элемента, из которого не выходит ни одна стрелка, или же элемента с нулевым значением.
Вообще, при выполнении локального сравнения мы интересуемся нс только оптимальными выравниваниями, но также и близкими к оптимальному, счет которых превышает некоторый порог. Ссылки на методы поиска выравниваний, близких к оптимальному, даны в библиографических примечаниях.
3.2.3. ПОЛУГЛОВАЯЬНОЕ СРАВНЕНИЕ
При полуглобальном сравнении мы назначаем счет выравниваниям, игнорируя некоторые крайние пробелы* в последовательностях. Интересная характеристика основного алгоритма динамического программирования то, что посредством очень простых преобразований первоначально выбранной системы очков мы можем управлять штрафом за крайние пробелы
Начнем с точного определения понятия крайних пробелов и ответа на вопрос, почему в некоторых ситуациях может быть более выгодно вставлять их без назначения штрафных санкций. Крайние пробелы расположены перед первым или после последнего знака последовательности. Например, все пробелы во второй последовательности изображенного ниже выравни вания - крайние, а единственный пробел в первой последовательности —
3Крайиие пробелы в свою очередь подразделяются на начальные (стоящие в начале строки) и конечные (стоящие в конце строки). - Прим. перев.
3.2. СРАВНЕНИЕ ДВУХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
93
не крайний
CAGCA-CTTGGATTCTCGG
(3.4) ---CAGCGTGG---------
Интересно отметить, что длины этих двух последовательностей отличаются значительно. Первая имеет длину 18, вторая — 8 знаков. В подобных случаях в любом выравнивании будет присутствовать много пробелов, вносящих большой отрицательный вклад в общий счет Тем не менее, если мы игнорируем крайние пробелы то получаем довольно хорошее выравнивание: 6 совпадений, 1 несовпадение и 1 пробел.
Заметим, что это далеко нс оптимальное выравнивание между данными последовательностями. Ниже представлен другой вариант выравнивания с более высоким счетом (—12 против —19 у предыдущего), соответствующий применяемой системе очков.
CAGCACTTGGATTCTCGG
CAGC------G-T-----GG	(
Несмотря на то. что мы получили более высокий счет и все знаки второй последовательности совпадают с идентичными знаками первой, >то выравнивание нс столь интересно с точки зрения поиска подобных областей в последовательностях нуклеотидов. В таком случае только ради полного совпадения оснований вторую последовательность пришлось бы попросту жестоко разорвать на отдельные фрагменты. Если мы ищем области более длинной последовательности, приближённо подобные более короткой последовательности. то для этого случая, несомненно, первое выравнивание (3.4) подходит гораздо больше второго (3.5). Это отражено в счете, получаемом, когда мы игнорируем (то есть нс штрафуем) крайние пробелы: выравнивание (3.4) получает 3 очка в отличие от - 12 у выравнивания (3.5).
Теперь опишем разновидность основного алгоритма, который будет игнорировать крайние пробелы Рассмотрим вначале случай, где мы не штрафуем конечные пробелы в последовательности s, и найдем для него оптимальное выравнивание. Пробелы в конце s сопоставляются с суффиксом последовательности Если мы удаляем эту конечную часть выравнивания, то остается выравнивание между последовательностью s и префиксом последовательности t, с таким же счетом, как в выравнивании целых последовательностей. Поэтому, чтобы вычислить счет оптимального выравнивания между последовательностями я и t без штрафа за пробелы в конце я, все, что мы должны сделать, это найти наилучшее подобие между последовательностью s и префиксом последовательности t Но из раздела 3.2.1 мы знаем, что элемент (i,j) матрицы а содержит подобие между префикса
94
Глава 3
ми ,s[l... г] и t[l... j]. Следовательно, для отыскания подобия достаточно выбрать максимальное значение в последней строке матрицы а, то есть
sim(s,t) = maxa[m,j].
>=1
Учтите, что в этом разделе мы изменили определение функции sim(s, t), так что теперь она обозначает подобие, игнорирующее конечные пробелы в последовательности .ч. Это выражение дает счет оптимального выравнивания. Чтобы построить само выравнивание, мы выполняем действия, как и в основном алгоритме, но начинаем с элемента (тп, к), где к выбирается так, чтобы выполнялось равенство bini(s,t) = а[т, fc].
Аналогичный способ применяется и тогда, когда мы нс штрафуем конечные пробелы в последовательности t. В этом случае мы выбираем максимум в последнем столбце матрицы а. Мы можем даже объединить эти два способа и искать оптимальное выравнивание без штрафов за конечные пробелы в обеих последовательностях. Ответ будет найден, если выбрать максимальный элемент в последней строке и последнем столбце матрицы. В любом случае, чтобы построить оптимальное выравнивание, мы начинаем с элемента, который содержит значение подобия, и следуем за стрелками, пока ие достигнем элемента (0,0). Как и в случае основного алгоритма, каждая стрелка лает один столбец выравнивания.
Теперь обратим наше внимание на начальные пробелы. Предположим, что мы хотим построить оптимальное выравнивание, не штрафуя начальные пробелы в последовательности s. Оно эквивалентно оптимальному выравниванию между я и суффиксом последовательности t. Чтобы получить желаемый результат, мы, так же, как и в основном алгоритме, используем массив размером (тд + 1) х (п + 1), но с небольшим отличием. Теперь каждый элемент (i,j) содержит максимальное подобие между префиксом .ч[1... i и суффиксом некоторого префикса, например, суффиксом префикса t[l... j].
Ясно, что при этом результатом будет величина а[т, п]. Что менее ясно, но тем нс меиее верно, — так это то, что данный массив может быть заполнен с использованием той же формулы, что и в основном алгоритме, то есть уравнения (3.3)! Однако инициализация будет отличаться. Первая строка должна быть инициализирована нулями вместо значений, кратных штрафу за пробел, что связано с иным назначением элементов. Мы предоставляем читателю возможность убедиться в том, что и в этом случае уравнение (3.3) истинно.
Мы можем применить тот же прием и инициализировать первый столбец нулями, игнорируя при этом пробелы в начале последовательности t.
3.3. РАСШИРЕНИЯ К ОСНОВНЫМ АЛГОРИТМАМ
95
Если же мы инициализируем нулями и первую строку и первый столбец, а затем применим уравнение (3.3) для остальных элементов, то в каждом элементе мы вычислим максимальное подобие между соответствующими суффиксами последовательностей s и t. Чтобы найти оптимальное выравнивание, начиная от элемента с максимальным значением мы следуем за стрелками, пока нс достигнем одной из границ, инициализированных нулями, после чего возвращаемся по этой границе к началу массива.
В таблицу 3.1 сведены все рассмотренные нами случаи. Существует четыре позиции, в которых мы можем не штрафовать пробелы: начало или конец последовательности s и начало или конец последовательности t. Мы можем независимо комбинировать эти условия любым способом и использовать описанные выше примеры, чтобы найти подобие. Единственные озличия — это инициализация и позиция, в которой нужно искать максимальное значение. Прощение начальных пробелов преобразуется в инициализацию определенных позиций нулями. Прощение конечных пробелов означает поиск максимума в определенных позициях. Но заполнение массива - всегда один и тот же процесс, основанный на уравнении (3.3).
Таблица 3.1. Действия, заменяющие штрафы за крайние пробелы
Позиция прощения	Эквивалентное действие
Начало первой посл-ти Конец первой посл-ти Начало второй посл-ти Конец второй посл-ти	Инициализ-ть первую строку нулями Искать максимум в последней строке Инициализ-ть первый столбец нулями Искать максимум в последнем столбце
3.3.	РАСШИРЕНИЯ К ОСНОВНЫМ АЛГОРИТМАМ
Алгоритмы, представленные в разделе 3.2, в общем случае адекватны для решения большинства задач сравнения последовательностей. Однако иногда мы имеем особую ситуацию и нуждаемся в лучшем алгоритме. В этом разделе мы рассмотрим несколько методов, которые могут быть использованы в некоторых из таких ситуаций.
Один вид усовершенствований связан с вычислительной сложностью задачи. Мы покажем, что за счет увеличения времени вычислений приблизительно в два раза пространственную сложность алгоритмов возможно уменьшить от квадратичной (тпп) до линейной (m + n). С другой стороны, мы также покажем способ сокращения временной сложности, но он
96
Глава 3
работает только в случае сравнения подобных последовательностей и при использовании определенной системы очков.
Другое усовершенствование имеет отношение к биологической интерпретации выравниваний. С биологической точки зрения, более реалистично рассматривать непрерывный ряд последовательных пробелов вместо отдельных, разрозненных пробелов. Мы представим версии основных алгоритмов, адаптированные к этому варианту задачи сравнения.
3.3.1.	ЭКОНОМИЯ ПРОСТРАНСТВА
Квадратичная сложность основных алгоритмов делает их неприменимыми в некоторых практических приложениях для работы с очень длинными последовательностями или для повторного сравнения нескольких последовательностей. Нс известен никакой алгоритм, который затрачивал бы асимптотически меньшее время и сохранял бы при этом ту же универсальность, хотя существуют более быстрые алгоритмы с ограниченной возможностью выбора параметров.
Algorithm BestScore*
input: последовательности я и t
output: вектор a
rn«— |.s|
|t|
for j t— 0 to n do
a[j] >~j-S
for i«— I to in do
old <— a[0]
a[0] <- г • g
for J <— 1 to n do
temp <- a[j]
a[j] «- max(a[j] + g, old + p(i,j), a[J - 1] old <— temp
Рис. 3.5. Алгоритм поиска подобия в линейном пространстве. На выходе элемент a[n] содержит значение функции sim(s,t)
Максимальный счет. Прим. перев.
3.3. РАС ШИРЕНИЯ К ОСНОВНЫМ АЛГОРИТМАМ
97
Однако пространственную сложность алгоритма возможно уменьшить ог квадратичной до линейной без снижения его универсальности. 11ена, которую нужно за это заплатить, — приблизительное удвоение времени счета. Тем не менее, асимптотическая временная сложность остается неизменной, а во многих случаях именно пространство, а не время является ограничивающим фактором, так что такое преобразование имеет большую практическую ценность. В этом разделе мы опишем этот изящный прием экономии пространства.
Начнем с того, что вычисление функции sim(s, t) может быть легко выполнено в линейном пространстве. Каждая строка матрицы зависит только от предыдущей строки, поэтому возможно проводить вычисления, сохраняя в памяти только один вектор, в котором будет храниться часть строки, вычисляемой в данный момент, и часть предыдущей строки. Этот метод отражен в алгоритме на рис. 3.5. Ясно, что то же самое верно и для столбцов, и если т < п, то, используя этот же прием со столбцами, мы занимаем еще меньше пространства памяти. Заметим, что каждый раз после выполнения операций цикла с переменной г в алгоритме на рис. 3.5, вектор а содержит подобия между префиксом s[l ...г] и всеми префиксами последовательности t. К этому факту мы возвратимся чуть позже.
Самос трудное заключается в построении оптимального выравнивания в линейном пространстве. Для работы алгоритма на рис 3.3 нужна целая матрица элементов. Чтобы устранить эту трудность, мы используем стратегию по принципу разделяй и властвуй, то есть мы делим задачу на две меньшие подзадачи, а затем объединяем их решения и получаем решение целой задачи.
Ключевая идея заключается в следующем. Находим одно оптимальное выравнивание, выбираем позицию г в последовательности s и оцениваем, что можно сопоставить символу s[i] в этом выравнивании. Есть только два возможных случая:
1.	Символ s[i] совпадет с символом t[j] для некоторого j в интервале 1... п.
2.	С символом s[i] совпадет пробел между символами ф] и t[j 4-1] для некоторого j в интервале 0 .. п.
Во втором случае индекс j изменяется между 0 и п, потому что в последовательности всегда существует одна дополнительная позиция для пробелов, но не для символов. Мы также нарушили принятую систему понятий, допустив j = 0 и j — п. В этих случаях мы подразумеваем то, что пробел будет стоять, соответственно, в позициях перед t 1] или после t[n].
98
Глава 3
Пусть функция
обозначает оптимальное выравнивание между хну. Любое выравнивание между последовательностями s и t соответствует случаю I или 2 независимо от того, оптимально оно или нет. В частности, наше оптимальное выравнивание также должно относиться к одному из них. Если оно соответствует случаю 1, то для построения всех оптимальных выравниваний мы должны произвести следующее сцепление:
л ,/s[l.. .г — 1]\ s[i] _ . .(s[i + 1.. .
Optimall ,	) +	1 + Optimall	1,	(3.6)
если же оно соответствует второму случаю, то мы производим сцепление следующего вида:
„	/я[1 . . .1 — 1]\ s[l] „ .	,/s[l+ 1...7n]\
Optimall	-i)+ J + Optimall	.	(3.7)
Эти соображения дают нам рекурсивный метод вычисления оптимального выравнивания, до тех пор пока мы можем определить, для данной позиции г, какой из случаев (1 или 2) рассматривается и каково соответствующее значение позиции j.
Вычисления выполняют следующим образом. Согласно уравнениям (3.6) и (3.7), для определенной позиции i мы должны найти подобия между префиксом s[l ...г — 1] и произвольным префиксом последовательности t, а также подобия между суффиксом ,s[i + 1... т] и произвольным суффиксом последовательности t. Если мы знаем эти величины, то мы можем в явном виде вычислить счета j выравниваний по уравнению (3.6) и j +1 выравнивания по уравнению (3.7). Выбирая оптимальное среди них, мы получаем информацию, необходимую для следующего шага рекурсии.
Как было показано ранее, наилучшис счета выравниваний между некоторым префиксом последовательности s и всеми префиксами последовательности t возможно вычислить в линейном пространстве (см. рис. 3.5). Подобный алгоритм существует и для суффиксов. Следовательно, наша задача почти решена. Остается только решить, какое значение г следует использовать в каждом рекурсивном обращении. Лучший вариант — выбирать г как можно ближе к середине последовательности. Полный алгоритм показан на рис. 3.6. В этом алгоритме обращение
BestScore(s[a... г — 1], t[с... d], pref-sim)
3.3. РАСШИРЕНИЯ К ОСНОВНЫМ АЛГОРИТМАМ
99
Algorithm Align5
input: последовательности suf, индексы а, Ь, с и d,
стартовая позиция start
output: оптимальное выравнивание между s[a.. .6] и t[c.. .d], помещенное в векпоры align-s и align-t, начинающиеся в позиции start и оканчивающиеся в позиции end
if s[a... 6] пуста or t [с... d] пуста then
// Основной случай: s[a... 6] пуста или t[c... d] пуста Выровнять непустую последовательность вставкой пробелов end *- start + max(|s|, |£|)
else
И Общий случай
i-L(« + 6)/2J
Bes/5core(s[a... (i — 1)], t[с... d], pref-sim)
BestScoreRev(s[(i + 1)... 6], t[c... d], suff-sim)
posmax •— c — 1
typemax •— space
vmax «— pref-sim\c — 1] + д + suff-sim[c — 1]
for j *— c to d do
if pref-sim[j — 1] + p(i, j) + sujf-simfj] > vmax then posmax«— j
typemax •— SYMBOL
vmax •— pref-sim[j — 1] + p(i, j) + sujfsim[j]
if prefsim[j] + д + suff-simUj > vmax then
posmax«— j
typemax<— SPACE
vmax *— pref-sim[j] + д + suff-simlj]
if tvpemax = SPACE then
Align(a, i — 1, c, posmax, start, middle)
align-s[middle]«— s[i]
align-t[middle]«— SPACE
Alignfi + 1, 6, posmax +1, d, middle +1, end)
else // typemax = symbol
Align(a, г - 1, c, posmax -1, start, middle)
align-s[middle]«— s[t]
align-t[middle]«— t[posmax]
Align(i + 1, b, posmax +1, d, middle +1, end)
I’nc. 3.6. Алгоритм построения оптимального выравнивания в линейном пространстве
нощращает в переменной pref-sim подобия между префиксами s[a... г — 1] и t|c... J] для всех j в интервале с — 1.. .</. Аналогично, обращение
'Выравнивание. — Прим, перев.
100
Глава 3
BestScoreRev(s[i + 1... 6], t[c... d], suffsim) возвращает в переменной suffsim подобия между суффиксами s[i + 1... 6 и t [j + 1 ... d] для всех j в интервале с — 1... d. Наконец, обращение
Align(\, т, 1,п, 1,1еп)
возвращает оптимальное выравнивание в глобальных переменных align-s и align-t, а также размер этого выравнивания в переменной 1еп
Остается неразрешенным только один вопрос: Может ли благодаря этим дополнительным вычислениям время обработки возрасти слишком сильно? Может, но не намного. Как мы покажем ниже, время приблизительно удваивается.
Пусть Т(т,п) — количество вычислений максимума во внутреннем цикле BestScore или BestScoreRev в результате обращения Align(a, b, с, d, start, end), где m = 6 — а +1 и п = с — d +1. Легко увидеть, что общее время обработки будет пропорционально выражению, содержащему член Т(ш, п) плюс дополнительные линейные члены, связанные с управлением программой и инициализацией элементов. Мы утверждаем, что Т(тп, и) 2r,in.
Доказательство этого утверждения может быть построено методом индукции на тп. При m = 1 не произойдет никаких вычислений максимума, так что, безусловно, Т(1, п) 2п. При m > 1 мы будем иметь обращение к процедуре BestScore (самое большее тпп/2 вычислений максимума) плюс такое же число операций для BestScoreRev и, кроме того, два рекурсивных обращения к процедуре Align (самое большее T(m/2,j) и Т(т/2,п — j) вычислений максимума). Складывая это все, мы получаем
Т(т,	+	T(m/2,j) + Т(т/2, п-3)
тп + mj + т(п — j)
= 2тп,
что доказывает наше утверждение.
3.3.2.	ОБЩИЕ ФУНКЦИИ ШТРАФОВ ЗА ПРОПУСКИ
Определим пропуск как группу последовательных пробелов количеством к > 1. Известно, что, когда в последовательности аминокислотных остатков происходят мутации, появление пропуска из к пробелов более вероятно, чем появление к отдельных пробелов. Это связано с тем, что пропуск может появиться из-за единственного мутационного события, которое удалило целый участок аминокислотных остатков, тогда как отделенные
3.3. РАСШИРЕНИЯ К ОСНОВНЫМ АЛГОРИТМАМ
101
пробелы появляются скорее всего вследствие независимых музационных событий, а появление одного события, несомненно, более вероятно, чем появление целой группы событий.
До сих пор мы не проводили никакого различия между сгруппированными или отдельными пробелами. Это означает, что штрафы за пропуски мы налагаем посредством линейных функций. Обозначая штраф за пропуск из к пробелов через w(k), где к 1, мы получаем
w(k) = bk,
где b - абсолютное значение счета, назначенного пробелу.
В этом разделе мы представляем алгоритм, который вычисляет подобия по общим функциям штрафов за пропуски w. Этот алгоритм имеет временную сложность О(п3) для последовательностей длиной п и поэтому работает медленнее, чем основной алгоритм. Однако между этими двумя алгоритмами есть много общего. Главное отличие нового алгоритма состоит в том, что схема назначения счета не аддитивна, в том смысле, что мы не можем разделить выравнивание на две части и ожидать, что полный счет будет равен сумме счетов частей общего выравнивания. В частности, мы не можем отделить последний столбец выравнивания и ожидать, что счет выравнивания будет суммой счета этого последнего столбца и счета остальной части (префикса) выравнивания. Однако аддитивность счета сохраняется, если мы разделяем выравнивание на блоки. Каждое выравнивание может быть уникальным образом разделено на группу последовательных блоков. Ниже перечислены три типа блоков:
1.	Два выровненных знака из алфавита Е.
2.	Максимальный ряд последовательных знаков строки t, выровненных с пробелами строки s.
3.	Максимальный ряд последовательных знаков строки s, выровненных с пробелами строки t.
Термин максимальный означает, что ряд не может быть продолжен. На рис. 3.7 показано выравнивание и его блоки. Блоки первого типа получают счет р(я, 6), где а и Ь — два выровненных знака. Блоки 2-го и 3-го типов получают счет — w(k), где к длина пропуска.
Как видно, теперь назначение счета выравнивания проводится не на уровне столбцов, а на уровне блоков. Соответственно, мы можем ожидать, что аддитивность счета сохранится только в том случае, если мы разделим выравнивание на блоки. Это в свою очередь подразумевает, что для вычисления подобия по общей функции штрафов за пропуски, в алгоритме
102
Глава 3
Si	AAC---AATTCCGACTAC
s2	ACTACCT------CGC--
«I
$2
AAC---
ACTACC
Рис. 3.7. Выравнивание и его блоки
динамического программирования необходимо произвести некоторые существенные изменения. Вместо того, чтобы рассматривать последний столбец выравнивания, мы должны рассматривать последний блок. Кроме того, блоки не могут следовать друг за другом в произвольном порядке. Блок 2-го или 3-го типа не может следовать за блоком того же типа. Из этого следует, что для каждой пары (i,j) мы должны сохранять не наилучший счет выравнивания между префиксами s[l... г] и t[l... j], а наилучший счет этих префиксов, которые, кроме того, должны заканчиваться в блоке определенного типа.
Для того чтобы сравнить последовательность s длиной т с последовательностью t длиной п, мы используем три массива размером (т + + 1)х(п+1) — по одному для каждого типа конечного блока. Массив а используем для выравниваний, заканчивающихся в блоках типа знак-знак; массив b используем для выравниваний, заканчивающихся пробелами в последовательности s; массив с используем для выравниваний, заканчивающихся пробелами в последовательности t.
Инициализация первой строки и первого столбца проводится следующим образом, согласно назначению массивов:
«[0,0] =0 Ь[о, J] = -w(j) с[г.О] = —го (г).
Все остальные значения в начальных строках и столбцах должны быть установлены в -оо, чтобы сделать их безопасными для вычислений максимума, в которых они используются.
Теперь зададим естественный вопрос: Блоком какого типа заканчивается наше оптимальное выравнивание? Ответ на него определяет, который массив, а, b или с, будет обновлен. Рекурсивные соотношения для этой операции следующие:
а[г, j] = р(г, j) + max <
a[i — 1, j — 1] Ыг- 1,7-1] с[г - 1, j - 1]
3.3. РАСШИРЕНИЯ К ОСНОВНЫМ АЛГОРИТМАМ
103
6[г, J] = max	[ я[г, j — /с] — w(k), 1 с[г, j — fc] — w(k),	при при
с[г, j] = max <	[ я[г — k,j] — w(k), 1 Ь[г — к, J] — w(k),	при при
1 < к < j 1 < к < j
1 < к < г 1 < к < г.
Как обычно, p(i,j) показывает счет совпадения знаков а[г] и t[j].
Обратите внимание, что элементы массивов бис зависят от более чем одного предыдущего значения, потому что последний блок может иметь переменную длину. Кроме того, при вычислении элемента массива b мы не смотрим на предыдущие элементы Ь, потому что блоки 2-го типа не могут следовать сразу же за блоками типа 2. Аналогично, элементы массива с не зависят непосредственно от предшествующих элементов того же массива с. Чтобы получить окончательный ответ, то есть значение функции sini(s, t), мы выбираем максимум среди значений n[m, n], 6[т, п] и с[т, п].
Временная сложность этого алгоритма равна О(тп? + ?n2n). Чтобы понять смысл этого выражения, с помощью известных формул подсчитаем число обращений к некоторому элементу любого массива Это главный член выражения для временной сложности. Легко видеть, что для вычисления значений a[i,j], 6[г, J] и с[г, J] мы должны выполни хь
3 + 2j + 2г
обращений к предыдущим элементам массива, что в сумме даст
m п
££(з + 2Н2«)
г=1 э=1
обращений к массивам в целом. Эта сумма может быть вычислена в конечном виде следующим образом:
У^(2г + 2j + 3) = 2ni + п(п + 1) + Зп = 2m + п2 + 4п, 7=1
т
У^(2ш + т? + 4п) = пт(т + 1) + тп2 + 4тп = т2п + 5тп + тп2. i=l
11остроение оптимального выравнивания не вызывает затруднений. Достаточно руководствоваться теми же принципами, что и в предыдущих алгоритмах. В массивах мы проходим в обратном порядке те элементы, которые
104
ГЛАВА 3
мы выбирали для вычислений максимумов, и при этом отмечаем, которому из массивов эти элементы принадлежат.
Таким образом, мы видим, что в принципе возможно использовать любую функцию штрафов за пропуски. Однако цена за такую универсальность • значительное увеличение времени вычислений и пространства памяти (три вспомогательных массива). Это обстоятельство может быть критическим, когда алгоритм сравнения последовательностей методом динамического программирования является «узким местом» более крупного алгоритма.
3.3.3.	ЛИНЕЙНЫЕ ФУНКЦИИ ШТРАФОВ ЗА ПРОПУСКИ
Мы узнали, что время счета основного алгоритма с линейной функцией штрафов равно О(п2), где п — длина последовательностей; мы увидели также, что применение общих штрафных функций приводит к возрастанию времени счета до О(п3). Однако если мы используем менее общую функцию штрафов за пропуски, но такую, которая по-прежнему назначает меньший штраф за пропуск с к пробелами, чем за к отдельных пробелов, то можем ли мы все еще получить алгоритм со временем счета О(п2)? В этом разделе мы покажем, что это действительно возможно.
Если мы хотим поддержать идею о том, что появление к последовательных пробелов более вероятно, чем появление к отдельных пробелов (или по крайней мере столь же вероятно), то следующее уравнение должно быть верным:
w(k) С А:ш(1)
или, в общем виде,
w(ki + к-2 4--1- кп) w(ki) + w(k2) Ч---1- w(kn). (3.8)
Функцию w, удовлетворяющую уравнению (3.8), называют субаддитивной функцией. Линейная функция — функция w вида w(k) = h + gk, где k 1, причем ш(0) = 0. Она будет субаддитивной при h > 0 и g > 0.
Другой способ задания функции w как субаддитивной заключается в назначении первому пробелу пропуска стоимости h + g, а всем остальным пробелам стоимости д. Эта стоимость основывается на разнице Дщ(А') = = w(k) — w(k — 1) штрафов за к — 1 и к пробелов.
Теперь опишем алгоритм метода динамического программирования для этого случая. Главное различие между основным алгоритмом и этим состоит в том, что здесь мы должны штрафовать первый пробел пропуска и все остальные пробелы этого пропуска по-разному. Это достигается при
3 3. РАСШИРЕНИЯ К ОСНОВНЫМ АЛГОРИТМАМ
105
помощи трех массивов, а, b и с, как и в случае общей функции штрафов. Элементы каждого из этих массивов имеют следующее назначение;
•	a[i,j] = максимальному счету выравнивания между префиксами s]l ..г и	оканчивающегося символом s[z , сопоставленным
с ф].
•	Ь[г, j] = максимальному счету выравнивания между префиксами s[l.. .г] и t[l.. .j], оканчивающегося пробелом, сопоставленным с ф].
•	c[z,J] = максимальному счету выравнивания между префиксами s[l...i] и t[l...J], оканчивающегося символом s[i], сопоставленным с пробелом.
Элементы (г, j) этих массивов зависят от предшествующих элементов согласно следующим формулам, действительным при	и 1 С jC п:
{«[г - 1 J - !] 6[г — 1, j — 1] с[г — 1, j — 1]
6[г, j] = max <
—(/г + р) 4- «[г, j — 1]
~(h + g)+c[i,j - 1]
f-(/i+p)+a[i-1,J] с[г, J] = max < — (h + g) + 6[i — 1, J] (-p + c[i - l,j].
Как и прежде, значение р(г, j) показывает счет совпадения между соответствующими знаками .ч[г] и ф].
Попробуем понять смысл этих формул. Формула для вычисления «[г, j] включает в себя член р(г, j), который является счетом последнего столбца, и наилучший счет выравнивания между префиксами s[l.. ,г—1] иф . .	1].
Что касается величины 6[г j], то мы знаем, что последний столбец будет содержать пробел Однако мы должны проверить, является ли он первым или последующим пробелом пропуска, с тем чтобы мы могли оштрафовать его правильно. Кроме того, мы должны прочитать из массивов значения наилучших счетов для проверяемых префиксов, то есть префиксов si .г Ht[l...j — 1] Именно поэтому в формулах для b\z,j мы всегда оцениваем элементы (г, j — 1). Выравнивания, соответствующие величинам a[i,j — 1] и с[г, j — 1), не оканчиваются пробелом в последовательности s, и, следовательно, конечный пробел должен быть оштрафован как первый в пропуске,
106
Глава 3
то есть вычшанием величины h + g. Выравнивания, соответствующие величине b\i,j — 1], уже имеют в конце пробел, принадлежащий последовательное ги s, так чго пробел, сопоставленный со знаком t[y], должен быть оштрафован как последующий пробел, то есть вычитанием величины д. Эти три возможности являются исчерпывающими, так что, выбирая максимум среди них, мы находим точное значение. Подобное же рассуждение объясняет формулу для величины с[г, у].
Инициализация этих массивов требует некоторого внимания. По-прежнему она будет зависеть от того, хотим ли мы штрафовать начальные пробелы. Чтобы рассуждать более конкретно, допустим, что мы будем штрафовать вес пробелы, а возможность адаптации алгоритма к другим случаям мы предоставим читателю.
Инициализировать необходимо элементы с индексами вида (г,0) для 0 г тп или вида (0,у) для 0 уп. Инициализацию следует проводить согласно содержанию каждого массива, как показано в определении этих массивов. Таким образом, для массива Ь. например, мы имеем:
6[г, 0] = —оо при 0 С г С m и Ь[0, j] = - (h + gj) при 1	ji	п.
Для того, чтобы определение оставалось непротиворечивым, величине b[г, 0] мы присваиваем значение оо, потому что между префиксами .ч[1...г] и /[!...()] (пустая последовательность) нс существует никакого выравнивания, в котором пробелу соответствует знак t 0, так как нс существует самого знака t[0|. Следовательно, если нет никаких выравниваний, то максимальное значение должно быть равно —оо, что равносильно вычислениям максимума. С другой стороны, существует ровно одно выравнивание, оканчивающееся пробелом в последовательности .ч — выравнивание между префиксом ,ч[1 ... 0] (тоже пустая последовательность) и префиксом t[l...у], — и счет этого выравнивания равен —(/г + gj).
Подобным же образом мы инициализируем массив с:
с[г, 0] = - (Л + gj) при 1 г тп и с[0,у] = — со при О^у^п,
и, в конечном счете, массив а:
я[0,0] = 0, а[г, 0] = —оо при 1 С г С тп и «[0, у] = —оо при 1 С у п.
3.3. РАСШИРЕНИЯ К ОСНОВНЫМ АЛГОРИТМАМ
107
При инициализации массива а мы использовали выравнивания, которые не оканчиваются пробелами, в общем смысле данного определения. Чтобы получить окончательный результат, то есть подобие, достаточно выбрать максимальную величину из n[m, n|, 6[m,n] и с[гп,п], учитывая, что эти величины охватывают все возможности выбора.
Мы можем построить оптимальное выравнивание способом, аналогичным применяемому в случае общих штрафных функций. Для этого требуется всего лиш1. пройти обратный путь от конечной позиции (т, п) через элементы, значения которых выбирались как максимумы в процессе заполнения массивов, пока не будет достигнута начальная позиция — элемент массива (0 0). В течение этого процесса необходимо запоминать нс только текущий элемент, ио также и то, которому из массивов (я, b или с) ои принадлежит.
Возможность доказательства утверждения, что временная сложность этого алгоршма действительно равна О(тп), мы предоставляем читателю. Только что описанный вариант алгоритма тоже имеет пространственную сложность, равную О(тп); известны также варианты этою алгоритма с линейным пространством решения (см. библиографические примечания).
3.3.4,	( РАВНЕНИЕ ПОДОБНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Две последовательности считают подобными, если они «выглядят похожими» в некотором смысле. Мы уже развили наше представление о подобии и формализовали его через понятия выравнивания и счета. Таким образом, две последовательности подобны, когда счета оптимальных выравниваний между ними очень близки к возможно максимальному (позже термин «возможно максимальный» будет уточнен). Этот раздел посвящен более быстрым алгоритмам поиска хороших выравниваний для подобных последовательностей. Здесь мы анализируем только глобальные выравнивания.
Сначала разберем случай, где две интересующие иас последовательности s и t имеют одинаковую длину п. Это допущение справедливо в силу того, что здесь мы рассматриваем подобные последовательности. Если последовательности я и t имеют одинаковую длину, то матрица динамического программирования является квадратной, а ее главная диагональ проходит от элемента (0,0) к элементу (п, п). Путь по этой диагонали соответствует уникальному выравниванию последовательностей s и t, без включения в него пробелов. Если это выравнивание не оптимально, то мы должны вставить некоторые пробелы в последовательности, чтобы получить более высокий счет. Учтите, что пробелы всегда будут парными: один в s, другой — в t.
108
Глава 3
По мере того как мы вставляем эти пары пробелов, выравнивание отходит от главной диагонали. Рассмотрим слсдуюшие две последовательности:
s=GCGCATGGATTGAGCGA t = TGCGCCATGGATGAGCA.
Оптимальные выравнивания соответствуют путям, которые идут по диагоналям, не более чем на две позиции отошедшим от главной, как показано на рис. 3.8. Оптимальные выравнивания содержат две пары пробелов. В данном случае число пар пробелов равно числу позиций отступа выравнивания от главной диагонали, но эго не всегда так. Определенно известно, что число пар пробелов больше или равно максимальному отступу от главной диагонали.
-GCGC-ATGGATTGAGCGA
TGCGCGATGGAT-GAGC-A
мического программирования. Линия проведена через главную диагональ матрицы
Тогда основная идея выравнивания выглядит следующим образом. Если последовательности подобны, то пути оптимальных выравниваний проходят вблизи главной диагонали матрицы. Чтобы вычислить оптимальный
3.3.	РАСШИРЕНИЯ К ОСНОВНЫМ АЛГОРИТМАМ
109
Algorithm к-ВапсР
input: последовательности s и t равной длины п, целое число к output: наилучший счет выравнивания, отходящего самое большее на к диагоналей от главной диагонали матрицы п — |s|
for i <— 0 to к do
а[г, 0] «— г • д
for j «— 0 to к do
я[°Л J -9
for i *— 1 to n do
for d «--к to A do
j «- г + d if 1 j n then // вычисляем максимум среди И предшествующих элементов «[ij] <- e[t - 1J - 1] +p(i,j) if InsideStrip(i — 1 j, k) then «[i.j] «— max(a[i,j].n[i - l,j] + </) if InsideStrip(i,j — 1, A’) then
«- max(a[t,j],e|i, j - 1] +p)
return n[n,n]
Рис. 3.9. Алгоритм заполнения матрицы динамического программирования в пределах A-полосы вокруг главной диагонали
счет и построить выравнивания, нет необходимости заполнять всю матрицу целиком. Достаточно заполнить тишь узкую полосу вокруг главной диагонали.
Представленный на рис. 3.9 алгоритм k-Bandосуществляет заполнение матрицы вблизи главной диагонали в пределах полосы с горизонтальной (или вертикальной) шириной 2А + 1. В конце работы алгоритма величина о[п, л] содержит наивысший счет выравнивания, ограниченного этой полосой. Время счета этого алгоритма равно О(кп), что является большой победой над обычной функцией О(п2), если к мало по сравнению с и.
Заметим, что мы никак нс используем элементы вне A-полосы. Мы нс инициализируем их и не обращаемся к ним при вычислении максимумов. Чтобы проверить, находится ли некоторая позиция (?, j) в А-полосс, мы используем следующий критерий:
InsideStrip(i.j,k) — (—к	г — j А).
6А-11олоса Прим, перев.
но
Глава 3
Как и в других алгоритмах метода динамического программирования, каждый элемент «[г, j] зависит от элементов а[г — 1,у], «[г — 1, j — 1] и п[г, j — 1]. Программа алгоритма устроена таким образом, что проверять элемент (г — — 1, j — 1) не обязательно, поскольку он находится на той же диагонали, что и элемент (г, j), так что он всегда будет внутри полосы. Проверке должны подвергаться элементы (г — l,j) и (i,j — 1), которые могут выходить за границы полосы, при том что элемент (г, j) находится внутри нее.
Как мы используем алгоритм k-Bandl Мы выбираем значение к и запускаем алгоритм. Если величина а[п, п] больше или равна возможно лучшему счету выравнивания с к + 1 или более парами пробелов, то нам крупно повезло: мы нашли оптимальное выравнивание всего за О(кп) шагов. Учитывая, что мы имеем по крайней мерс к+1 пар пробелов, возможно лучший счет равен
М(п — к — 1) + 2(к + 1)<?
(3.9)
и при этом вычисляется с допущением, что в выравнивании находится точно к + 1 пара пробелов и что все остальные пары дают совпадения. Здесь М — счет совпадения и штраф д налагается за каждый пробел. Примем А/ > 0 и д 0.
Если значение «[п, п] оказывается меньше найденного из (3.9), то мы удваиваем к и снова запускаем алгоритм. Если начальное значение к равно 1, то последующие значения будут степенями двойки. Условие остановки алгоритма принимает вид
М(п — к — 1) + 2(к + 1)д,
что эквивалентно
Мп - од[п, п]
К этому моменту мы уже запускали алгоритм много раз, и каждый раз с большим значением к, так что при допущении о том, что значения к равны степеням двойки, полная сложность равна
п + 2п + 4n -I--+ кп 2кп.
Чтобы ограничить эту полную сложность, нам нужен верхний предел к. Пока что мы не останавливали алгоритм, поэтому
Мп — щ./2|п,ц]
2 < А/ - 2д
3.4. МНОЖЕСТВЕННОЕ СРАВНЕНИЕ ПОСЛЕДОВАТЕЛЬНОСТЕЙ 111
Если я/;[п, n] = fifc/2[n, п], то это оптимальный счет функции sim(s, t) и тогда наш предел равен
к < 2
Л/п — sim(s, t) М-2д
Если a*[n, п] >	,2[п, п], то оптимальное выравнивание имеет более
чем к/2 пар пробелов и, следовательно,
sim(s. t) М
+ 2
S-
что даст
к С 2
Мп — sim(s,t)
М - 2д 1
то есть почти тот же самый предел, что и полученный выше.
Обратите внимание что значение разницы Л/ — 2д остается постоянным Тогда временная сложность алгоритма равна O(dn), где d — разница между возможно максимальным счетом Л/zi (счетом двух идентичных последовательностей) и оптимальным счетом. Таким образом, чем выше счет подобия, тем быстрее мы получаем ответ.
Не вызывает затруднений расширить этот метод на общие последовательности, причем не обязательно одинаковой длины Также могут быть легко получены варианты с экономией пространства.
3.4.	МНОЖЕСТВЕННОЕ СРАВНЕНИЕ
ПОСЛЕДОВАТЕЛЬНОСТЕЙ
До сих пор мы обсуждали сравнение пары последовательностей. Однако часто нам дают несколько последовательностей, которые мы должны выровнять между собой возможно лучшим способом. Например, такая ситуация возникает, когда мы исследуем последовательности некоторых белков с похожими функциями, встречающихся у организмов различных видов. Тогда необходимо определить, какие части этих последовательностей подобны, а какие — различны. Чтобы получить эту информацию, мы должны построить множественное выравнивание этих последовательностей, и именно этой задаче и посвящен настоящий раздел.
112
ГЛАВА 3
MQPILLL MLR-LL— MK-ILLL MPPVLIL
Рис. 3.10. Множественное выравнивание четырех последовательностей аминокислот
Множественное выравнивание представляет собой естественное обобщение выравнивания двух последовательностей. Пусть	— мно-
жество последовательностей знаков, взятых из одного алфавита. Множественное выравнивание последовательностей sj,... ,Sfc выстраивают путем вставки пробелов в эти последовательности таким образом, шобы привести их длины к одному значению. Обычной практикой является помещение удлиненных последовательностей в вертикальный список так, чтобы столбцы были образованы знаками (или пробелами), стоящими в соответствующих (номерам столбцов) позициях. В дополнение к этим условиям мы требуем, чтобы никакой столбец не был составлен исключительно из пробелов На рис. 3.10 показано множественное выравнивание четырех коротких последовательностей аминокислот. (Более обычны множественные выравнивания белков, так что в некоторых из наших примеров в этом разделе мы используем последовательности аминокислот.)
Одна важная проблема, требующая разрешения во множественном выравнивании, — >то точное определение качества выравнивания. Далее мы изучим один способ вычисления счета множественного выравнивания, основанный па попарных выравниваниях. Кроме того, ученые иногда оценивают множественные выравнивания, выращивая из последовательностей деревья, вместо того, чтобы складывать из них поленницы. Это ведет к нескольким различным мерам качества, которые мы рассмотрим в последующих разделах.
3.4.1.	МЕРА ПАРНЫХ СУММ
Вычисление счета множественного выравнивания более сложно, чем его определение у попарного аналога. Здесь мы ограничимся строго аддитивными функциями; то есть счет выравнивания будет равен сумме счетов столбцов. Поэтому мы нуждаемся в некотором способе, посредством которого можно было бы назначить счет каждому столбцу, а затем просуммировать эти счета и таким образом получить полный счет выравнивания.
Однако для вычисления счета столбца требуется определить функцию с к аргументами, где к — число последовательностей. Каждый из этих
3.4. МНОЖЕСТВЕННОЕ СРАВНЕНИЕ IЮСЛЕДОВАТЕЛЬНОСТЕЙ 113 аргументов — знак или пробел Один известный способ — организовать (--мерный массив, который мог бы быть индексирован этими аргументами и возвратить искомое значение. 11роблсма такого подхода связана с тем, что необходимо установить точное значение для каждой возможной комбинации аргументов, тогда как число таких комбинаций может быть равно 2к — 1. Типичное значение к равно 10, и тогда получается более чем 1000 возможных комбинаций. Отсюда видно, что для определения этой функции необходимо разработать более продуктивные методы.
Такие методы могут быть получены путем определения «разумных» свойств искомой функции. Во-первых, функция должна быть независима от порядка следования аргументов. Например, если один столбец содержит знаки I, -, I, V, а другой — знаки V, I, I, -, то оба столбца должны получить одинаковый счет Во-вторых, это должна быть функция, которая награждает присутствие многих подобных или генетически связанных аминокислотных остатков и штрафует несвязанные остатки и пробелы. Решение, которое удовлетворяет этим свойствам — так называемая функция парных сумм (ПС). Она определяется как сумма парных счетов всех пар символов в столбце. Например, счет столбца с вышеупомянутым содержанием вычисляется как
SP-score(I, -, I, V) = p(I, -) + p(I, I) + p(I, V) + + р(-, I) + p(-,V) + p(I,V),
где р(а.Ь) — парный счет символов а и 6. Заметим, что функция ПС может включать штрафы за пробелы, если знак а или Ь — пробел. Это очень удобная система очков, поскольку она полагается на парные счета, подобные тем, которые мы используем при сравнении двух последовательностей. Систему очков ПС используют довольно часто благодаря ее простоте и эффективности.
Чтобы завершить определение, осталось обратиться к маленькой, но очень важной детали. Хотя никакой столбец не может быть составлен исключительно из пробелов, допустимо иметь два или более пробела в одном столбце При вычислении счета ПС необходимо определить значение р(—, —). Данное значение не устанавливают при сравнении двух последовательностей, потому что в этом случае появление такой пары невозможно по определению. Однако для множественного сравнения, основанного на функции ПС, это необходимо. Обычная практика — принять р(—,—) — 0. Это может показаться странным, если учесть, что пробелы, как правило, штрафуют (то есть всегда, когда в парс присутствует пробел, парный счет отрицателен), так что пара с двумя пробелами тем более должна быть отрицательна. Тем не менее, есть серьезные основания, чтобы установить
114
Глава 3
для р(—, —) нулевое значение. Одно из них опя1Ь же связано с попарными выравниваниями. Часто выводы о множественном выравнивании мы делаем на основании оценки попарных выравниваний, которые оно индуцирует. Действительно, в любом множественном выравнивании возможно выбрать две произвольные последовательности и оценить способ, которым они выровнены друг с другом, безотносительно всех остальных последовательностей. Не трудно увидеть, что такая политика приводит к попарному выравниванию, за исключением того, что здесь мы допускаем столбцы с двумя пробелами. Но тогда мы просто удаляем эги столбцы и строим истинное попарное выравнивание. Пример этой процедуры представлен на рис. 3.11. Это то, что мы называем индуцированным попарным выравниванием или проекцией множественного выравнивания.
Очень полезное свойство, верное только при р(—, —) = 0, описывает следующая формула для определения счета ПС множественного выравнивания а:
SP- score(a) — score(&ij).	(3.10)
Здесь — попарное выравнивание пары последоваюлыюсюй st и индуцированное множественным выравниванием а. Это свойство верно, поскольку оно отражает два встречных способа определения одной величины. Мы можем вычислить счет каждого столбца и затем сложить счета всех столбцов, или же вычислить счет каждого индуцированного попарного выравнивания и затем просуммировать эти счета В любом случае, для каждого столбца с и для каждой пары (i,j) мы находим суммарный счет p(s<[c],Sj[c]), где s' обозначает удлиненную последовательность (со вставленными пробелами). Но выражение (3.10) верно юлько при р(—, —) = 0, потому что эти величины присутствуют только в первом вычислении.
Динамическое программирование
Выбрав меру, или счет, для определения качества множественного выравнивания, мы хотели бы вычислить выравнивания с максимальным счетом для заданного множества последовательностей, то есть оптимальные выравнивания.
Как и в случае двух последовательностей, для решения этой задачи возможно использовать метод динамического программирования. Для простоты предположим, что мы имеем к последовательностей, все одинаковой длины п. Для хранения оптимальных счетов множественных
3.4. МНОЖЕСТВЕННОЕ СРАВНЕНИЕ ПОСЛЕДОВАТЕЛЬНОСТЕЙ 115
Множественное выравнивание:
1	PEAALYGRFT---IKSDVW
2	PEAALYGRFT--IKSDVW
3	PESLAYNKF---SIKSDVW
4	PEALNYGRY---SSESDVW
5	PEALNYGWY---SSESDVW
6	PEVIRMQDDNPFttQSDVY
Выбираем только 2-ю и 4-ю последовательности: PEAALYGRFT---------------IKSDVW
PEALNYGRY-----SSESDVW
Удаляем столбцы с двумя пробелами:
PEAALYGRFT-IKSDVW PEALNYGRY-SSESDVW
Рис. 3.11 Индуцированное попарное выравнивание (проекция множественного выравнивания)
выравниваний префиксов этих последовательностей мы используем к-мерный массив а длиной п + 1 в каждом измерении. Таким образом, массив а[й,..., ifc] хранит счет оптимального выравнивания между префиксами sj [1.. .й),..., sfc[l.. .ifc].
После инициализации по схеме а[0,..., 0] <— 0 мы должны заполнить этот массив до конца. Только для его хранения требуется пространство О(пк). Это также нижний предел времени счета, поскольку мы должны вычислить значение каждого элемента массива. Тем нс менее, действительная временная сложность выше по ряду причин. Во-первых, каждый элемент массива зависит от 2*' — 1 ранее вычисленных элементов - по одному для каждого возможного состава текущего столбца выравнивания. В каждой позиции (ярусе) каждого столбца может находиться либо некоторый знак, либо пробел из расположенной на данном ярусе последовательности. Поскольку мы имеем к последовательностей, число возможных комбинаций составов равно 2к. Удаляя запрещенный состав (когда все знаки — пробелы), мы получаем заключительное число составов 2fc - 1. В него входит множитель 2fc экспоненциальной временной сложности.
Тогда возникает вопрос о доступе к данным массива. Лишь малая часть языков программирования и, определенно, ни один из самых популярных языков не дает пользователям возможность определения массива с числом
116
Глава 3
измерений к и приемлемым временем обработки. Альтернатива — применить наши собственные программы доступа. В любом случае, имея или не имея языковую поддержку, мы ожидаем О(к) шагов на один доступ.
Другая проблема — вычисление счетов столбцов. Метод ПС требует О(к2) шагов на каждый столбец, поскольку необходимо просуммировать к (к — 1)/2 парных счетов. Более простые схемы — например, подсчет только числа значащих символов (не пробелов) — требуют по крайней мере О(к) шагов, так как они предполагают просмотр всех аргументов.
Наконец, остается возможность вычисления значения afij,...,ifc], которое включает в себя операцию определения максимума. Используя полужирные буквы для обозначения fc-кортежей, команду, которую мы должны выполнить, запишем в виде
a[i] <— max{a[i — Ь] + SP-sc.ore(Cmo.46ey(s. г. Ь))}, 6^0
где Ъ изменяется в пределах всех ненулевых бинарных векюров к элементов, и
Столбец(з, i,b) = (Cy-JicfCfc,
где
если Ьз = ] i |	, если bj = 0.
Таким образом, оценка полного времени счета для этого первого плана применения алгоритма равна О(к22кпк) при использовании ПС, или О(к2кпк), если счета столбцов могут быть вычислены за время О(к). Если к постоянно, то для заполнения массива достаточно использовать к вложенных for-циклов. Оптимальные выравнивания могут быть восстановлены из этого массива в соответствии с процедурой обратного отхода, аналогичной применяемой в случае попарного выравнивания (раздел 3.2.1). Прямые расширения алгоритма дают подобные методы для случая, где последовательности нс обязательно должны быть одинаковой длины. В любом случае, сложность этого алгоритма экспоненциально зависит от числа входных последовательностей, а существование полиномиального алгоритма кажется маловероятным: было показано, что задача множественного выравнивания с ПС-мерой является НП-полной (см. библиографические примечания)
Экономия времени
Экспоненциальная сложность алгоритма метода динамического программирования делает его непригодным для решения широкого круга задач.
3.4. МНОЖЕСТВЕННОЕ СРАВНЕНИЕ ПОСЛЕДОВАТЕЛЬНОС1 ЕЙ 117
Главную проблему создает размер массива. Для трех последовательностей мы уже имеем кубическое пространство из О(п3) ячеек, и по мере того как число последовательностей к растет, мы имеем все большие и большие «объемы», которые необходимо заполнять. Ясно, что если бы мы могли как-нибудь уменьшить количество ячеек, которые нужно вычислять, го это привело бы к прямому сокращению времени обработки.
В этом разделе мы описываем эвристику, которая позволит нам достичь именно этой цели. Мы покажем, как встроить ее в алгоритм динамического программирования, чтобы ускорить его вычисления. Но это всего лишь эвристика, потому что в наихудшем случае придется вычислять все ячейки; однако на практике мы можем ожидать хорошее ускорение счета. Эвристика основана на взаимосвязи между множественным выравниванием и его проекциями на массивы с двумя последовательностями, и, в частности, она использует уравнение (3.10), связывающее счета ПС с парными счетами. Таким образом, метод, который мы собираемся ввести в употребление, работает только для ПС-мсры.
Общая структура метода состоит в следующем. Мы имеем к последовательностей с длинами пг, где 1 г к, и хотим вычислить оптимальные выравнивания согласно ПС-мере. Здесь мы будем использовать опять же метод динамического программирования, но обрабатывать не все ячейки Мы выбираем только тс ячейки, которые для оптимальных выравниваний «важны» в некотором смысле. Но какие именно ячейки мы будем считать важными, и почему?
Ответ на этот вопрос нужно искать в попарных проекциях ячейки На стадии предварительной обработки мы определяем условия, которые позволят нам провести анализ важности произвольных ячеек. Чтобы извлечь пользу из этого анализа и сократить число ячеек, к которым мы должны обращаться, мы должны изменить также и порядок заполнения массива.
Анализ важности ячеек
Пусть а — оптимальное выравнивание множества последовательностей s(,. ..,Sfc. В первую очередь необходимо знать, что даже при том, что выравнивание а оптимально, его проекции нс обязательно будут оптимальны для данной пары последовательностей На рис. 3.12 показан случай, в котором проекция оказывается неоптимальной. К несчастью, такие случаи возможны. Если бы этого не происходило, то мы могли бы легко провести анализ важности ячеек по следующему условию: ячейка важна, если каждая из сс попарных проекций является частью оптимального выравнивания двух последовательностей, соответствующих этой проекции.
118
Глава 3
AT А— -Т АТ АТ Оптимальное множ, выравнивание
А-
-Т
Неоптимальная проекция
Рис. 3.12. Оптимальное выравнивание с нсоптимальной проекцией
Прежде чем мы продолжим, позвольте нам подчеркнуть, что рассмотренные нами алгоритмы сравнения удобно применять в случае двух последовательностей s и t, для того чтобы произвести матрицу, в которой каждый элемент (i,j) содержит наивысший счет выравнивания, которое включает сечение (i.j)- Попарное выравнивание о содержит сечснис (г, j), когда п может быть разделено на два подвыравнивания: одно выравнивание между префиксами s[l... г] и t[l... j] и другое — между оставшейся частью последовательности я и остатком последовательности t.
Чтобы получить искомые величины, мы добавляем две матрицы динамического программирования а и Ь со следующими значениями элементов:
a[i,j] = sim(s[l... г], t[l... j]) t>[i, j] = sim(s[i + 1.. .п],ф' + 1.. .m]),
где n = |s| и m = |i|. Матрица a — обычная матрица, которую мы использовали все это время. Матрица Ь может быть вычислена точно так же, как матрица а, но только в обратном порядке. Мы инициализируем последнюю строку и столбец и продвигаемся назад, пока не достигнем элемента Ь[0,0]. Мы делали это в разделе 3.3.1, когда обсуждали применение линейного пространства в алгоритмах метода динамического программирования. Тогда процедура BestScoreRev выполняла как раз те операции, которые мы должны сейчас выполнить в матрице Ъ. Итак, сумма с = а + 6 содержит точное значение наивысшего счета выравнивания, усеченного в элементе (i, j). Матрицу с мы называем матрицей полных счетов, тогда как матрицы я и 6 — соответственно, матрицами префиксных и суффиксных счетов.
Матрица с намного удобнее для визуального анализа, чем матрицы а и Ь. Для быстрого определения оптимальных выравниваний требуется всего лишь взглянуть на элементы матрицы с — простой трюк, который значительно труднее продслагь с матрицами а или Ь. Объясним это на следующем примере. На рис. 3.13 мы видим матрицы о и с для некоторой пары последовательностей и некоторой системы очков. Сможете ли вы точно определить,
3.4. МНОЖЕСТВЕННОЕ СРАВНЕНИЕ ПОСЛЕДОВАТЕЛЬНОСТЕЙ 119
G А Т Г С
0	-2	-4	-6	8	-10
-2	-1	-1	3	-5	-7
—4	-3	-2	0	-2	—4
-6	-5	—4	-1	1	-1
-8	-7	-6	3	-1	-2
10	-7	-8	-5	3	0
- 12	-9	-8	-7	-5	-2
G А Г Т С
—2	—2	-7	12	-17	-22
-7	—4	2	-7	-12	-17
-10	-7	5	-2	-7	-12
13	-10	7	-5	-2	-7
14	-13	10	-5	—4	-2
-17	-14	-13	-8	—4	-2
-22	-17	-14	-11	-7	-2
Рис. 3.13. Maiptiubi динамического программирования' префиксных счетов (слева) и полных счетов (справа)
где находятся оптимальные выравнивания, по матрице а? Их намного легче опрелелить по матрице с, потому что для этого достаточно просто следовать за ячейками с наивысшим счетом.
Хотя проекции оптимальных выравниваний могут нс быть оптимальны сами по себе, мы можем установить нижний предел для счетов проекций, так же как мы имеем нижний предел для оптимального счета. Этот принцип сформулирован в следующей теореме.
Теорема 3.1. Пусть а оптимальное выравнивание множества по-следовательностей .si....Sk- Ест SP-score(n) L, то
score(ctij) Ltj,
где
Lij = L— У' (simfSa:, Sy)).
(я- !/)/(* j)
Доказательство. Последовательно получаем:
SP- score (а) L, score(axy) L, х<у
(score(axy)) > L — scone(a,j),
У2 (sim(sx, sy)) L — score(atj), sc<V
ч го доказывает теорему.
120
Глава 3
Теперь мы имеем возможность проверить, является ли ячейка с индексом г = (ij,..., ifc) важной для оптимальных выравниваний относительно нижнего предела L. Проще говоря, эта ячейка важна, если все ее проекции удовлетворяют условиям предыдущей теоремы. Другими словами, ячейка i важна, когда
Cxylix, гу] Lxy
для всех х и у при 1 Si х < у С к, где сху — матрица полных счетов для пары последовательностей sx и sy. Согласно этой теореме, в оптимальных выравниваниях могут участвовать только важные ячейки, хотя не все важные ячейки будут участвовать в оптимальных выравниваниях. Тем не менее, это предполагает сокращение числа ячеек, которые являются потенциальными кандидатами на оптимальное выравнивание. По мере приближения L к истинному оптимальному счету это сокращение становится более существенным.
Чтобы определить подходящий нижний предел L, достаточно выбрать произвольное множественное выравнивание, включающее в себя вес последовательности, и принять его счет за нижний предел L. Этот предел действительно нижний, поскольку оптимальные выравнивания имеют возможно максимальный счет. Если мы уже имеем достаточно хорошее выравнивание, то мы можем использовать его счет и улучшить это выравнивание, чтобы построить оптимальное только что описанным способом. Альтернативный нижний предел может быть найден с помощью результатов, полученных в разделе 3.4.2.
Применение эвристики
Описанную в этом разделе эвристику следует применять с некоторой осторожностью. Отнюдь не достаточно проверить все ячейки на важность и затем использовать только важные. Это не даст никакого заметного сокращения времени, потому что мы по-прежнему просматриваем все ячейки, чтобы оценить их важность. Мы нуждаемся в способе практически полного отбрасывания неважных ячеек, чтобы к ним вообще не нужно было бы обращаться.
Вот одна из возможных стратегий. Мы начинаем с исходной ячейки 0 = (0,0,..., 0), которая является всегда важной, и распространяем ее влияние на зависимые от нее важные ячейки. Каждая из них в свою очередь распространит свое влияние на следующие ячейки, и так далее, пока мы не достигнем конечной угловой ячейки (гц,.... nt). В результате этих действий будут проанализированы только важные ячейки.
3.4, МНОЖЕСТВЕННОЕ СРАВНЕНИЕ ПОСЛЕДОВАТЕЛЬНОСТЕЙ 121
Чтобы лучше объяснить эту стратегию, нужно определить несколько новых понятий. Ячейка г влияет на другую ячейку j, если г — одна из ячеек, используемых в вычислении максимума при определении значения a[j]. В этом случае мы также говорим, что ячейка j зависит от ячейки i. Другая характеристика этого факта состоит в том, что элемент b = j — г является вектором, каждый компонент которого равен 0 или 1, причем i j. Так, каждая ячейка зависит от самое большее 2fc — 1 других ячеек и влияет на самое большее 2к — 1 других. Мы говорим «самое большее», потому что краевые ячейки могут влиять или зависеть от менее чем 2fc — 1 других ячеек.
Algorithm Multiple-Sequence Alignment1
input: множество s = (si,..., Sk), нижний предел L
output: Значение оптимального выравнивания
// Вычисляем Lxy, 1 х < у к
for всех х и у, 1 х < у к do
Вычисляем сху — массив полных счетов для sx и sy
for всех х и у, l^rc<7/^fcdo
<— L — 52(pjQ)yt(a:ijZ)Sim(Sp,sg)
// Вычисляем массив а
pooh—{0}
while pool не пустой do
г <— лексикографически наименьшая ячейка в pool pool «— pool {г}
if cXy[ix,iy] Lxy,X/x,y, 1 x < у k, then // Анализ важности for всех j зависимых от i do
if j	pool then
pool <— poolU{j}
a[J] <— a[i] + SP-score(Cmon5eq(s, i,j — «)) else
a[J] <— max(a[j],a[i] + SP-score(Cmo.i5eq(s. i.j — «))) return a[ni....rife]
Рис. 3.14. Алгоритм метода динамического программирования с эвристикой экономии времени для множественного выравнивания последовательностей
Мы поддерживаем пул ячеек, которые необходимо исследовать. Первоначально в пуле находится только ячейка 0. Пул всегда содержит только важные ячейки. Когда ячейку г заносят в пул, ее значение а[г] инициализируется. В течение пребывания ячейки в пуле ее значение обновляется
’Множественное выравнивание последовательностей. — Прим, перев.
122
Глава 3
Когда ячейку удаляют из пула, текущее значение а[г] принимают за истинное значение этой ячейки и используют в pacnpociранении на все важные ячейки, зависимые от г.
Значение ячейки распространяется следующим образом. Пусть ячейка j — важная и зависит от ячейки г. Если ячейка j не находится в пуле, то мы помещаем ее туда и инициализируем ее значение командой
o[j] «— а[г] + SP-score(Cmoi6ei{(s, г. Ь)).
Если ячейка j уже находится в пуле, то мы условно обновляем ее значение командой
о [у] <— max(o[j], а[г] + SP-score(Cmo.i6eii(s, i, Ь))).
Важно удостовериться, что каждый раз некоторая ячейка должна быть удалена из пула, при этом выбирается лексикографически меньшая Это гарантирует, что данная ячейка уже подверглась влиянию других важных ячеек и се значение нс нуждается в последующих обновлениях. Процесс останавливается, когда мы достигаем ячейки (гц,... пт), которая непременно является последней исследованной ячейкой; ее значение — искомый счет ПС. Алгоритм вычисления этого счета показан на рис. 3.14. Чтобы построить огпимальныс выравнивания, мы должны каким-либо образом отслеживать обновления. Один путь состоит в построении графа зависимостей, где важные ячейки будут представлены узлами, а зависимости, которые обеспечили максимальное значение, - ребрами. Временная и пространственная сложность этого алгоритма пропорциональны числу важных ячеек.
3.4.2.	ВЫРАВНИВАНИЕ ЗВЕЗДЫ
Вычисление оптимальных множественных выравниваний может занять долгое время, если мы используем стандартный подход динамического программирования, даже с методами экономии времени, кратко описанными в предыдущем разделе; однако были разработаны совершенно иные методы. Эти альтернативные методы часто являются эвристическими — в том смысле, что они не дают никакой гарантии качества найденного выравнивания. Это всего лишь более быстрые способы получения ответа, который во многих случаях оказывается достаточно точным.
Один из таких методов ~ так называемое выравнивание звезды. Он состоит в построении множественного выравнивания, основанного на попарных выравниваниях между фиксированной последовательностью из множества входов и всеми остальными последовательностями множества Эта фиксированная последовательность образует центр звезды. Построенное
3.4.	МНОЖЕСТВЕННОЕ СРАВНЕНИЕ ПОСЛЕДОВАТЕЛЬНОСТЕЙ 123 выравнивание о — такое, что его проекции aLj являются оптимальными, где г или j индекс центральной последовательности.
Пусть Sj,..., sk — множество к последовательностей, которые мы хотим выровнять. Чтобы построить выравнивание звезды, мы должны сначала выбрать одну из последовательностей в качестве центра. Мы отложим обсуждение методики этого выбора. В данный момент мы просто допустим, что центральная последовательность уже выбрана и ее индекс — некоторое число с в интервале 1... к. Затем для каждого индекса г с мы должны построить оптимальное выравнивание пары последовательностей яг и вс. Оно может быть получено с помощью стандартного метода динамического программирования, так что эта стадия процесса занимает время О(кп2), если допустить, что длина всех последовательностей равна О(п).
Затем мы объединяем все попарные выравнивания, используя методику, известную как «один пропуск — всегда пропуск», и применяем ее к центральной последовательности sc. Построение начинается с одного из попарных выравниваний (например, между последовательностями S] и sc) и продолжается добавлением каждого попарного выравнивания к фигуре. В ходе этого процесса мы последовательно увеличиваем пропуски в цен-зральной последовательности вс, чтобы они удовлетворяли последующим выравниваниям, и никогда нс удаляем пропуски, уже присутствующие в sc: один пропуск в sc — всегда пропуск.
Каждое последующее попарное выравнивание добавляется ко звезде, используя выбранную в качестве ее центра последовательность sc как ориентир. Мы имеем множественное выравнивание последовательности .sc с некоторыми другими последовательностями с одной стороны, и попарное выравнивание между sr и новой последовательностью с другой. Мы добавляем в оба выравнивания столько пропусков, сколько необходимо для того, чтобы все удлиненные копии sc пришли в соответствие. После этого достаточно только включить новую удлиненную последовательность в фигуру, поскольку теперь она имеет такую же длину, что и остальные удлиненные последовательности.
Временная сложность такой операции присоединения зависит от структуры данных, используемой для представления этих выравниваний, но она не должна быть выше О(к1) при использовании подходящих структур, где I верхний предел длины выравниваний. Поскольку число добавляемых в фигуру последовательностей равно О (к), постольку временная сложность стадии присоединения составляет О(к21), а полная временная сложность всего алгоритма — О(кп2 + к2Г). Если мы дополнительно вычисляем общий счет выравнивания, то сложность возрастет на величину О(к21), но асимптотическая сложность при этом остается той же самой.
124
Глава 3
Пришло время обсудит ь вопрос о том, каким образом мы должны выбирать центра тьную последовательность. Один путь выбора состоит в том, чтобы просто оценить их все и затем выбрать наилучший окончательный счет. Другой путь позволяет нам вычислить все O(fc2) оптимальных попарных выравниваний и выбрать в качестве центральной ту последовательность, которая максимизирует сумму парных счетов подобий между ней и входными последовательностями8:
57sim(s,,sc).	(3.11)
Пример 3.1. Рассмотрим следующие пять последовательностей ДНК Начнем с составления таблицы попарных подобий между этими последовательностями (см. рис. 3.15). Используемая система очков та же самая, что и в разделе 3.2.1, где мы рассматривали основной алгоритм.
Si = ATTGCCATT S2=ATGGCCATT 83 = АТССААТТТТ S4—АТСТТСТТ ss = ACTGACC
	«1	S2	S3	S4	SS
Si		7	-2	0	-3
«2	7		-2	0	—4
вз	-2	-2		0	-7
S4	0	0	0		-3
S5	-3	—4	-7	-3	
Рис. 3.15. Парные счета для последовательностей из примера 3.1
Из этой таблицы мы видим, что именно первая последовательность, Sj, является той, которая максимизирует выражение (3.11). Наш следующий шаг — выбрать оптимальные выравнивания между последовательностью S]
^Формула (3.11) исключает счет самоподобия центральной последовательности (уело-вне i с). При использовании меры подобия для этого нет никаких оснований; при использовании меры расстояния, конечно, главная диагональ таблицы на рис. 3.15 всегда была бы нулевой. — Доп. авт.
3.4. МНОЖЕСТВЕННОЕ СРАВНЕНИЕ ПОСЛЕДОВАТЕЛЬНОСТЕЙ 125
и всеми остальными последовательностями из таблицы. Предположим, что мы выбрали следующие оптимальные выравнивания:
ATTGCCATT
ATGGCCATT
ATTGCCATT—
АТС-СААТТТТ
ATTGCCATT
АТСТТС-ТТ
ATTGCCATT
ACTGACC
В этом примере единственными пробелами, представленными в центральной последовательности Si, причем во всех ее выравниваниях, являются два пробела в конце S], вставленные для построения выравнивания с последовательностью S3. Поэтому в окончательном множественном выравнивании последовательность S] будет содержать только эти два пробела. Другие последовательности выравнивают с Si, как показано в этом примере. Итоговое выравнивание звезды представлено ниже:
ATTGCCATT—
ATGGCCATT—
АТС-СААТТТТ
АТСТТС-ТТ—
ACTGACC----
3.4.3.	ВЫРАВНИВАНИЕ ПО ДЕРЕВУ
В этом разделе обсуждается альтернативный метод множественного сравнения последовательностей — выравнивание по дереву9. Причина появления и предпосылка к применению этого подхода связана с тем, что иногда нам известно эволюционное дерево изучаемых последовательностей
’Этот метод часто называют прогрессивным выравниванием. — Прим. pet).
126
Глава 3
(эволюционные деревья предмет главы 6). В таком случае мы можем вычислить обшее подобие, основанное на попарных выравниваниях по ребрам дерева. Сравните это с ПС мерой, которая учитывает все попарные подобия.
Предположим, что нам дано к последовательностей и дерево с к листьями и взаимно однозначным соответствием между листьями и последовательностями. Если мы припишем заданные последовательности к внутренним узлам дерева, то мы сможем вычислить вес каждого ребра, который отражает подобие между двумя последовательностями в узлах, инцидентных этому ребру. Сумма всех этих весов счет дерева для данного варианта приписывания последовательностей к внутренним узлам. Отыскание такого приписывания последовательностей, которое максимизирует счет, представляет собой так называемую задачу выравнивания дерева. Выравнивания звезд можно рассматривать как частные случаи выравниваний деревьев, в которых дерево является звездой10.
Пример 3.2. Рассмотрим вход задачи, показанный на рис. 3.16. Приписывая последовательность СТ к вершине .г, а последовательность CG — к вершине у, мы получаем счет 6. Используемая система очков: р(а, —) = —1; р(а, b) = 1, если о - 6; р(а. 6) = 0, если а Ь. 
Рис. 3.16. Вход задачи выравнивания дерена
Задача выравнивания дерева является НП-т рудной. Су шествует алгоритм, который находит оптимальное решение, но он экспоненциально зависит от числа последовательностей. Используя идеи, развитые в разделе 3,4.1, возможно улучшить пространственные и временные требования на практике. Алгоритмы аппроксимации с хорошими гарантиями эффективности были разработаны для случая, когда веса ребер определены в единицах расстояния, а не подобия (см. раздел 3.6 1) В этом случае мы ищем та
10Как было показано в предыдущем разделе, центральная последовательность может быть выбрана нз множества входных последовательностей, либо та центр может быть принята последовательность, вычисленная по формуле (3.11). Именно в этом случае выравнивания звезд можно рассматривать как частные случаи выравниваний деревьев, в которых дерево является звездой. Доп. авт.
3.5. ПОИСК В БАЗАХ ДАННЫХ
127
кое приписывание последовательностей, которое минимизирует суммарное расстояние. В библиографических примечаниях даны ссылки на источники, в которых рассмотрены эти алгоритмы11 *
3.5.	ПОИСК В БАЗАХ ДАННЫХ
С появлением быстрой и падежной технологии секвенирования последовательностей нуклеиновых кислот и белков, были созданы централизованные базы данных, способные хранить большое количество информации о последовательностях, производимых лабораториями во всем мире. Это вызвало потребность в использовании эффективных программ для обработки запросов в этих базах данных. Типичная задача поиска - сравнить запрашиваемую последовательность со всеми уже имеющимися в базе данных и найти локальные подобия, что означает сотни тысяч операций сравнения последовательностей.
Квадратичная сложность рассмотренных нами методов для вычисления подобий и оптимальных выравниваний между двумя последовательностями делает эти методы непригодными для поиска в больших базах данных. С целью ускорения поиска были развиты новые и более быстрые методы. Как правило, эти методы основаны на эвристиках, и поэтому трудно теоретически установить их временную и пространственную сложность1’ Тем не менее, основанные на них программы стали очень важными средствами поиска, и потому эти методы заслуживают внимательного изучения.
В этом разделе мы сконцентрируем наше внимание на двух из самых популярных программ поиска в базах данных. Ни одна из них нс использует метод динамического программирования в чистом виде, хотя одна из них использует вариант этою метода для улучшения выравниваний, полученных с помощью других методов.
Прежде чем мы начнем описание этих программ, мы сделаем небольшое отступление, чтобы объяснить назначение некоторых матриц счетов для сопоставления аминокислот, поскольку эти матрицы являются очень
нМетол прогрессивного выравнивания в настоящее время является наиболее популярным. Основная идея алгоритма попарным выравниванием последовательностей можно определить расстояния. Затем с использованием расстояний строится бинарное кластерное дерево («путеводное дерево»). В каждом узле дерева строится множественное выравнивание (стопка) как попарное выравнивание выровненных стопок последовательностей в дочерних узлах. Здесь на каждом шаге используется алгоритм попарного выравнивания обобщенных последовательностей (стопок). Прим. ped.
Ьеда в том, что не всегда удается сформулировать математическую задачу, которую решают эти алгоритмы Они не ищут оптимального выравнивания! — Прим ред.
128
Глава 3
важными для поиска в базах данных, а также для сравнения белковых последовательностей в целом.
3.5.1.	МАТРИЦЫ ПТМ
При сравнении белковых последовательностей простые системы очков (как. например, +1 за совпадение, 0 за несовпадение и —1 за пробел) не достаточны. Биохимические свойства аминокислотных остатков, из которых состоят белковые последовательности, влияют на их относительную взаи-мозамснимость в ходе эволюции. Например, гораздо более вероятно, что друг друга заменят аминокислоты сходных размеров, чем таковые со значительно отличающимися размерами. Другие свойства (например, тенденция связываться с молекулами воды) также влияют на вероятность взаимной замены остатков. Поскольку сравнения белков часто проводятся в эволюционном контексте, важно использовать такую систему очков, которая могла бы отражать эти вероятности настолько, насколько это возможно.
Факторы, влияющие на вероятность взаимной замены остатков аминокислот, настолько многочисленны и разнообразны, что лучшим способом определения счета подобия для пар остатков часто оказывается прямое наблюдение фактических частот замен. Стандартная процедура, предназначенная для этих целей, основана на важном семействе матриц счетов — так называемых матриц ПТМ, очень популярных среди практиков в этой области. Аббревиатура ПТМ13 обозначает понятие принятых точечных му таций и процента точечных мутаций и освещает тот факт, что основная матрица ПТМ-1 отражает количество эволюции, производящее в среднем одну мутацию на сотню аминокислот. В этом разделе мы кратко опишем, как вычисляются матрицы ПТМ и каково их назначение.
Наше описание немного отходит от вопроса первоначального получения этих матриц, но оно выдвигает на первый план роль, которую частоты появления и мутабильность (способность к изменению) аминокислот играют в определении счета. В частности, определение мутабильности может отличаться в различных источниках.
Прежде всего, пользователь должен выбрать эволюционное расстояние, на котором он будет сравнивать последовательности. Матрицы ПТМ являются функциями этого расстояния. Например, матрица ПТМ-250 подходит для сравнения последовательностей, отстоящих на 250 единиц эволюции. Сначала мы организуем матрицу, соответствующую ПТМ-1, а затем из этой
13Здесь авторы восхищаются языковыми способностями Маргарет Дейхофф, язык которой отчеканил сей универсальный триплет, кодирующий сразу три сущности: оба представленных выше понятия, а также название изобретенных ею матриц. - Прим, перев.
3.5. ПОИСК В БАЗАХ ДАННЫХ
129
матрицы получим матрицы для других расстояний. Здесь мы рассматриваем мутации только на аминокислотном уровне, но никак не на уровне ДНК.
Для каждого эволюционного расстояния мы строим вероятностную матрицу переходов Л/ и матрицу счетов S. Матрица счетов получается из вероятностной матрицы, так что наше описание мы начнем именно с матрицы переходов Л/. Необходимые компоненты для построения матрицы М ПТМ-1 следующие:
•	список принятых мутации;
•	вероятности появления ра каждой аминокислоты а.
Принятая мутация — мутация, благополучно прошедшая процесс естественного отбора, то есть она не привела к гибели организма и была принята (допущена) окружающей средой. Один из способов выявления принятых мутаций состоит в выравнивании двух гомологичных белков из организмов разных видов (например, цепи а-гемоглобина человека и орангутанга). Каждая позиция, в которой последовательности отличаются, даст нам принятую мутацию. Принятые мутации мы рассматриваем как ненаправленные собы тия; то есть, определив пару а-Ь выровненных аминокислот, мы не знаем наверняка, какая из них является мутантной, а какая — дикой. Какая бы из них ни присутствовала в этой позиции в последовательности предка — она очевидно мутировала в другую, но мы не знаем, какая из них принадлежит организму-предку, а какая — потомку. Возможно даже, что последовательность предка содержала какую-либо третью аминокислоту, которая мутировала в обе существующие, но вероятность этого минимизируется, когда берут очень тесно связанные последовательности. Важно, чтобы в основной матрице ПТМ-1 мы рассматривали непосредственные мутации а —> Ь, а не опосредствованные например я —> с —> 6.
Вероятности возникновения мутаций могут быть оценены путем простого вычисления относительной частоты появления аминокислот в пределах большого, достаточно разнообразного множества последовательностей белка. Значения вероятностей удовлетворяют выражению
L
а
Из списка принятых мутаций мы можем вычислить частоты /аь, показывающие число появлений мутации а <-> b Вспомним, что здесь мы имеем дело с ненаправленными мутациями, так что /аь — fba- Помимо этого нам
130
Глава 3
понадобится сумма
показывающая общее количество мутаций аминокислоты а, и сумма
/ = £/-
дающая общее число появлений аминокислоты, участвующей в мутации. Число f равно удвоенному общему количеству мутаций.
Частоты fab и вероятности ра — все, что необходимо для построения вс роятностной матрицы переходов А/ ПТМ-1. Это матрица размером 20 х 20, где элемент Маь — вероятность замены аминокислоты а на аминокислоту Ь. Обрати ге внимание, что остатки а и Ь могут быть одним и тем же веществом, и в таком случае мы имеем вероятность сохранения аминокислоты а неизменной в течение данного эволюционного периода. В случае матриц ПТМ вычисление вероятности Afaa проводится на основании относительной мутабильности аминокислоты а, определяемой как
Мутабильность аминокислоты — мера ее изменчивости, то есть вероятность того, что данная аминокислота изменится в течение данного эволюционного периода. Следовательно, вероятность сохранения аминокислоты а неизменной равна дополнительной вероятности
ATqq -- 1 Шг; .
С другой стороны, вероятность замены аминокислоты а на Ь может быть вычислена как произведение условной вероятности замены а на Ь при условии, что аминокислота а изменилась, на вероятность изменения аминокислоты а. Условную вероятность мы оцениваем как отношение между мутациями вида а «-> Ь и общим количеством мутаций аминокислоты а. Поэтому
Mab = Рг(а —> Ь) =
= Pr(a —> Ь | а изм.) = Рг(а изм.)
Обратите внимание, что мы вычисляем эти вероятности, используя упрощенную модель эволюции белка. Например, здесь мы допускаем, что
3.5. ПОИСК В БАЗАХ ДАННЫХ
131
аминокислота мутирует независимо от предшествующих мутационных событий, что в силу природы генетического кода далеко не всегда верно. Кроме того, мы игнорируем влияние, которое другие аминокислоты в той же самой последовательности могут оказывать на мутацию данного аминокислотного остатка. В частности, независимость от предыстории ведет к эволюционной модели типа марковской, которая имеет хорошие математические свойства; некоторые из них будут упомянуты в дальнейшем.
Легко убедиться, что вероятностная матрица переходов А/ обладает следующими свойствами;
^МаЬ=1,	(3.13)
ь
^РаМ^ 0,99.	(3.14)
а
Уравнение (3.13) просто показывает, что, складывая вероятность того, что аминокислота а останется неизменной, с вероятностями ее замен на каждую другую аминокислоту из матрицы, мы получаем 1. Таким образом, мы вполне оправданно называем эги величины «вероятностями». Вспомним, что эти вероятности относятся к единице эволюционной изменчивости. Возникает соблазн думать об единице эволюции как о временной единице, однако хорошо известно, что в общем ходе эволюции различные объекты изменяются с разными скоростями, так что в общепринятом смысле время и количество эволюции нс являются прямо пропорциональными величинами.
Единица эволюции, используемая в этой модели, отражает количество эволюции (число эволюционных событий, или периодов), которое приводит к изменению в среднем одной из 100 аминокислот. Далее мы упоминаем эту единицу как эволюционное расстояние ПТМ-1. Чтобы отразить этот факт, вероятностная матрица переходов была нормализована, как видно из уравнения (3.14). Эта нормализация осуществлена делением уравнения (3.12) на 100. Если бы в этом уравнении вместо 100 мы бы использовали другое число, например, 50. то мы бы получили матрицу с точно такими же свойствами, за исключением лишь того, что уравнение (3.14) отражало бы одну из 50-ти средних замен, что составляет вероятность 0,98 того, что никакая замена не произойдет. Таким образом, единица эволюции отражала бы в среднем одну мутацию на 50 аминокислог.
Как только мы определили основную матрицу А/, мы можем найти вероятности переходов для больших количеств эволюции. Например, чему равна вероятность того, что аминокислота а изменится в b за две эволюцион
132
Глава 3
ные единицы ПТМ? Итак, в первый эволюционный период аминокислота а с вероятностью Мас заменяется на любую аминокислоту с, возможно даже на саму себя (то есть сохранится), и затем во второй эволюционный период аминокислота с заменяется на Ь с вероятностью к!сь- Складывая эти вероятности, мы заключаем, что итоговое число — не что иное как то есть возведенный в квадрат элемент матрицы Л/. Тогда Мк — вероятностная матрица переходов за период в к единиц эволюции.
Одно интересное свойство (которое смелый читатель с легкостью сможет доказать) заключается в том, что когда к становится очень большим, скажем, порядка тысяч, вероятностная матрица Мк сходится к матрице с идентичными строками. Каждая строка такой матрицы будет содержать относительную частоту рь в столбце Ь. То есть, независимо от того, какую аминокислоту мы выбираем за исходную, в результате длительного периода эволюции эта аминокислота с вероятностью рь изменится в аминокислоту Ь.
Теперь мы готовы дать определение матрицы счетов. Элементы этой матрицы содержат отношения между двумя вероятностями: вероятностью того, что данная пара аминокислот является мутацией, и противоположной вероятностью того, что ее появление — случайное событие. Это отношение называют отношением правдоподобия или отношением шансов.
Вычислим это отношение для двух аминокислот а и Ь. Предположим, что в данном выравнивании мы сопоставили аминокислоты а и b и рассматриваем их как пару. Если за исходную, или дикую, принять аминокислоту а, то вероятность того, что аминокислота Ь находится в другой последовательности именно из-за мутации, будет равна ЛГа(,. С другой стороны, есть шанс рь случайного появления аминокислоты Ь. Тогда отношение шансов записывают в виде:
Mgb РЬ ’
То же рассуждение остается верным, даже если аминокислоты а и b тождественны. Фактический счет равен десяти логарифмам этого отношения, поскольку при выравнивании нескольких пар сумма отдельных счетов будет соответствовать произведению этих отношений. На практике значения частот округляют до ближайшего целого, чтобы ускорить вычисления. Логарифм умножается на 10, чтобы уменьшить несоответствие между точным значением и целочисленной аппроксимацией.
Предшествующее обсуждение относится к ПТМ-1. Но мы можем использовать точно такую же схему и для произвольного эволюционного расстояния. Матрица счетов для расстояния ПТМ-Л’ определяется следующим
3.5. ПОИСК В БАЗАХ ДАННЫХ
133
образом:
scorek(a,b) — 101g-аЬ
На первый взгляд это не очевидно, но данная матрица факпгчески симмет-рична. Матрицы счетов должны быть симметричными, чтобы давать счет сравнения, независимый от порядка выборки последовательностей. Легко проверить симметричность для k = 1, поскольку
Mab	faWa.   fab
Рь	faPb	WOfPaPb'
Можно показать, что при больших к симметричность также сохраняется (см. упражнение 15). Это свойство обусловлено тем фактом, что рассматриваемые здесь принятые мутации являются ненаправленными, так что при вычислении вероятностей замены а на b и b на а используются одинаковые частоты fab = fba.
Несмотря на то, что матрицы счетов заполняют только на основании наблюдаемых принятых мутаций и общих частот появления аминокислот, в итоге они отражают несколько важных химических и физических свойств аминокислот: например, их сродство к воде и размер молекулы. Как правило, остатки с взаимно подобными свойствами обычно имеют высокие парные счета, а счета сильно отличающихся остатков сравнительно ниже. Этот факт не должен казаться странным, поскольку в результате принятых мутаций аминокислоты гораздо чаще заменяются на подобные чем на отличные. Предпочтение подобных остатков при заменах говорит о стремлении природы сохранить большинство свойств эволюционирующего белка.
Как было упомянуто ранее, для того чтобы выбрать соответствующую матрицу счетов и провести сравнения, мы должны установить расстояние ПТМ. Но иногда мы имеем две последовательности и совершенно никакой информации об их истинном эволюционном расстоянии В этом случае рекомендуется сравнивать последовательности, используя две или три матрицы. охватывающие широкий диапазон расстояний, например' ПТМ-40, ПТМ-120 и ПТМ-250. Как правило, низкие числа ПТМ хороши для поиска близких, сильных локальных подобий, тогда как высокие числа ПТМ позволяют обнаружить дальние, слабые подобия.
3.5.2.	BLAST
В этом разделе мы приводим краткое описание BLAST — семейства программных средств поиска подобия последовательностей. Программы пакета BLAST — одни из наиболее часто используемых средств поиска в базах
134
Глава 3
данных последовательностей во всем мире. BLAST — аббревиатура названия «Basic Local Alignment Search Tool» (основное программное средство поиска локальных выравниваний).
Важно заметить, что в данном контексте термин база данных обозначает обычно большой набор последовательностей, организованных в форме каталога. Это не подразумевает никаких дополнительных функций быстрого доступа, совместного использования данных и т. д., обычно предусмотренных в стандартных системах управления базами данных. Поэтому для нас «база данных» — простая коллекция последовательностей, хотя данные о самих последовательностях сопровождаются дополнительной информацией об источниках данных, библиографическими ссылками, сведениями о функциях последовательностей (если известны) и т. п.
BLAST возвращает список пар сегментов с высоким счетом между запрашиваемой последовательностью и последовательностями в базе данных. Прежде чем мы объясним, что это означает и как BLAST получает эти результаты, мы вкратце представим некоторую терминологию касательно пар сегментов, чтобы наше описание было согласованным с оригинальной документацией семейства BLAST.
Сегментом называют подстроку последовательности. Пара сегментов между двумя последовательностями — это пара сегментов одинаковой длины, взятых из обеих последовательностей. Поскольку подстроки в парс сегментов имею! одинаковую длину, на них мы можем построить выравнивание без пропусков. Этому выравниванию с помощью матрицы счетов замен может быть назначен счет. При этом не нужны никакие функции штрафов за пропуски, так как здесь нет никаких пропусков. По определению, полученный таким образом счет равен счету пары сегментов. На рис. 3.17 показан пример пары сегментов со счетом, назначенным с помощью матрицы замен ПТМ-120. Как правило, пары сегментов представляют собой локальные выравнивания без пропусков.
К A L М	R
V А К	N	S
—4 3 —4 —3 —1 —> Итого: —9
Рис. 3.17. Пара сегментов и ее счет согласно ма>рице ПТМ-120
Теперь мы владеем всей информацией, необходимой для точного описания принципа работы BLAST. Получив на вход запрашиваемую последовательность, BLAST возвращает все пары сегментов между запросом и последовательностями базы данных со счетами выше некоторого порога S.
3.5. ПОИСК В БАЗАХ ДАННЫХ
13*
Параметр S может быть задан пользователем, хотя в большинстве серверов доступа к программе его значение задано по умолчанию. Мы упомянули, что отличительная характеристика возвращаемых программой выравниваний — отсутствие пропусков. По существу, это главная причина высокой скорости BLAST, поскольку поиск хороших выравниваний с пропусками является намного более затратным по времени.
Максимальная пара сегментов (МПС) между двумя последовательностями — это пара сегментов с максимальным счетом. Этот счет является мерой подобия последовательностей и может быть точно вычислен с помощью метода динамического программирования. Однако BI AST оценивает это число намного быстрее, чем любой известный алгоритм метода динамического программирования. Программа также возвращает юкально максимальные пары сегментов, то есть те, счет которых больше не может быть улучшен путем их продолжения или укорачивания.
Принцип работы BLAST
Подход BLAST к вычислению пар сегментов с высоким счетом заключается в следующем. Программа находит некоторые «затравки», представляющие собой очень короткие пары сегментов из последовательности запроса и последовательностей в базе данных. Затем эти затравки без включения в них пропусков наращиваются в обоих направлениях, пока не будет достигнут возможно максимальный счет для продолжений данной затравки. При этом оцениваются нс все продолжения. Программа имеет критерий остановки продолжения затравок, когда их счет падает ниже тщательно вычисленного предела. При этом остается небольшой шанс на то, что правильное продолжение не будет найдено из-за подобного способа оптимизации времени счета, но на практике такой компромисс вполне приемлем.
Программу BLAST можно представив в виде трехступенчатой алгоритмической процедуры, выполняющей следующие задачи:
I.	Составление списка строк (или слов, в терминологии BLASI ) с высоким счетом.
2.	Поиск совпадений — каждое дает затравку.
3.	Продолжение затравок.
Каждый шаг алгоритма зависит от типа сравниваемых последовательностей: ДНК или белка. Далее мы рассматриваем каждый случай подробно.
В случае сравнения последовательностей белка, список слов с высоким счетом состоит из всех w-значных слов базы данных (названных ш-мсрами), причем счет сравнения этих слов с некоторым w-мсром запроса
136
ГЛАВА 3
равен по крайней мере Т; для вычисления счета используют матрицу ПТМ. Здесь w и Т — параметры программы. Обратите внимание, что этот список может содержать далеко не все w-меры запроса! Если w-мср запроса состоит из очень часто встречающихся аминокислот, то он может быть отброшен. поскольку даже счет его сравнения с самим собой может упасть ниже порога Т. Однако в программе предусмотрена специальная опция, вызывающая включение в список всех ш-меров запроса. Для поиска белковых последовательностей рекомендуется устанавливать длину затравки w, 14 равную четырем14.
На следующем этапе программа просматривает базу данных двумя методами поиска совпадений в списке, составленном на предыдущем шаге. Согласно первому методу, из слов списка составляется хэш-таблица. Затем, для каждого слова размером w, взятого из базы данных, по таблице легко определить его индекс и сравнить со словами в списке.
Второй метод поиска совпадений основан на использовании детерминированного конечного автомата. Это устройство характеризуется наличием состояний и переходов и работает подобно вычислительной машине. Автомат начинает работу в установленном начальном состоянии, и для каждого знака в базе данных происходит переход в другое состояние. Слово из списка распознается на основании оценки текущего состояния и предыдущего перехода автомата. Автомат строят только один раз, он использует в качестве входа список слов с высоким счетом и представляет собой компактный способ хранения всех этих слов. Поиск осуществляется быстро, поскольку для распознавания одного знака требуется только один переход автомата в другое состояние.
Заключительный этап — продолжение затравок — не вызывает трудностей. Как мы упоминали, с целью экономии времени алгоритм останавливается, когда при некоторой степени удлинения затравки счет падает ниже наилучшего, полученного для самых коротких продолжений. Удлинение затравок производится в обоих направлениях, и пара сегментов с высоким счетом, полученная из этой затравки, сохраняется в памяти. При этом существует небольшая вероятность потери хороших продолжений, но она пренебрежимо мала.
При сравнении последовательностей ДНК начальный список содержит только w-мсры запроса. Поскольку система очков для последовательностей ДНК более проста, этого достаточно для всех практических целей. Стратегия просмотра радикально отличается от случая белков. Используя преимущества малого размера алфавита (4 знака), база данных сначала сжимается
14 В настоящее время используют длину слова 3. Прим. ред.
3.5. ПОИСК В БАЗАХ ДАННЫХ
137
так, чтобы каждый нуклеотид был представлен двумя битами (тогда четыре нуклеотида умещаются всего в один байт) Теперь, помимо экономии пространства памяти, поиск может быть проведен намного быстрее, потому что каждый раз необходимо сравниваеть только один байт. Дополнительный inai фильтрации удаляет из исходного списка очень частые слова базы данных, чтобы избежать большого количества неинформативных совпадений.
Продолжение затравок осуществляется тем же способом, что и при сравнении белковых последовательностей. В обоих случаях продолжение основано на адаптированной статистике, которая дает точное распределение счета локального максимума для случайных последовательностей без пропусков и очень точное вычисление вероятности того, что найденная пара сегментов появилась в результате случайного события. Чем меньше эта вероятность, тем более значимо совпадение данной пары сегментов.
Теперь мы вкратце опишем наиболее важные моменты статистики. Распределение счега МПС (определение см. выше) для случайных последовательностей -ч и t с соответствующими длинами тип может быть найдено методом точного приближения, описанным ниже. Это приближение улучшается по мере увеличения длин тип.
Имея матрицу счетов замен для пар знаков из некоторого алфавита и вероятность р, появления каждого отдельного знака в сравниваемых последовательностях, сначала мы вычисляем значение Л, решая уравнение
= 1.
Параметр А — единственное положи гельное решение этого уравнения; оно может быть найдено методом Ньютона. Когда значение А известно, ожидаемое число различных пар сегментов между последовательностями s и t со счетом выше порога S равно15
Kmne~xs,
где К — вычислимая постоянная. Фактически, распределение числа пар сегментов со счетом выше порога S — это распределение Пуассона со средним арифметическим, определяемым по предыдущей формуле. Из формулы для числа пар сегментов легко получить выражения и для других интересующих нас величин: среднего счета, интервалов, в пределах которых счет будет падать в течение 90 % времени, и т. д.
15Эта величина называется e-vahie. Прим. ред.
138
Глава 3
3.5.3.	FAST
FAST — другое семейство программ для поиска в банках последовательностей. Основная программа пакета — FASTP — первая общедоступная программа поиска в базах данных последовательностей, предназначенная для поиска подобий запрашиваемой последовательности. Основной алгоритм, используемый FASTP, по очереди сравнивает каждую строку базы данных с последовательностью запроса и выдает строки, оказавшиеся существенно подобными ей, наряду с выравниваниями и другой полезной информацией. Поэтому скорость FASTP обусловлена главным образом се способностью очень быстрого сравнения пары последовательностей. Соответственно, наше внимание в этом разделе будет сосредоточено на том, как именно FASTP выполняет этот основной шаг алгоритма.
Обозначим две сравниваемые последовательности буквами я и t и допустим для данного случая, что это белковые последовательности. Их длины обозначим m = |s| и п = t|. Сравнение начинается с определения к-кортежей, общих в обеих последовательностях, где к равно 1 или 2. В программе значение к задано параметром ktup. Смещение общего fc-кортсжа — еще один важный параметр алгоритма и представляет собой величину между —п + 1 и т — 1, которая определяет относительный сдвиг двух последовательностей. Болес точно, если общий /г-кортеж начинается в позициях л [г] и Z[j], то мы говорим, что смещение этого кортежа равно г — j.
Необходимы следующие структуры данных: 1) таблица соответствия и 2) вектор, индексированный смещениями и инициализированный нулями. Вначале программа просматривает последовательность я и заполняет таблицу соответствия значениями всех позиций данного /г-кортежа в последовательности я (см. рис. 3.18). Затем программа просматривает последовательность t и ищет в таблице соответствие каждому fc-кортежу этой последовательности. При каждом совпадении программа прирагцает векторный элемент соответствующего смещения. На рис. 3.18 показано итоговое содержание вектора смещения и таблицы соответствия для последовательностей я = HARFYAAQIVL и t = VDMAAQIA. Заметим, что при смещении +2 значение векторного элемента максимально; это означает, что при данном смещении было найдено достаточно много совпадений. Этот метод называют диагональным, потому что смещение можно рассматривать как диагональ в матрице динамического программирования. Одно возможное использование максимального смещения — свести область работы алгоритма динамического программирования к некоторой полосе вокруг диагонали, соответствующей этому смещению.
3.5. ПОИСК В БАЗАХ ДАННЫХ
139
123456	789 10 11
s = Н A R FYAAQIVL
А F Н
I
L
Q R
V Y прочие
-7-6-5-4-3 2-1 0+1+2-3|4~5+-6+7--8т9т1(1
	1			1	2	1		1	4	1|						1	
Рис. 3.18. Таблица соошстстния и вектор смещения для сравнения последовательностей программой FASTP. Значение ktup равно 1
Но FASTP проводит более детальный анализ общих А-кортежсй и объединяет два или более таких А-кортсжей, когда они находятся на одной диагонали и вместе с тем не очень далеко друг от друга. Кри герии анализа являются эвристическими. Сцепленные Ажортежи формируют так называемую область. Область можно рассматривать как пару сегментов, в терминологии BLAST, или, иначе, как локальное выравнивание без пропусков. Областям назначается некоторый счет в зависимости от числа содержащихся в них пар совпадающих и не совпадающих знаков. Важно помнить, что области нс имеют пропусков.
Следующий шат про, рам мы состоит в переназначении счетов пяти наилучших областей, полученных на предыдущем этапе с помощью матриц ПТМ, чаще всего ПТМ-120 или ПТМ-250. Наилучший из этих новых счетов является первой мерой подобия между последовательностями s и t и назван начальным счетом16. Начальный счет вычисляется для каждого сравнения запроса с последовательностью базы данных. Эти значения выдаются в виде гистограммы счетов наряду со средним значением счета. Начальный счет используется также для ранжирования всех последовательностей базы данных. Для наивысшего ранжирования таких последовательностей вычисляется оптимизированный счет с помощью алгоритма динамического
16В других источниках эту величину (iniln, то есть initial number) называют начальным числом (НЧ). Прим перев.
140
Глава 3
программирования, ограниченного полосой вокруг начального выравнивания того, которое произвело начальный счет. Эта процедура имеет много общего с методом, представленным в разделе 3.3.4. На практике, когда последовательности на самом деле генетически связаны, оптимизированный счет обычно значительно выше начального. Это свойство часто помогает отличать случайно появившиеся хорошие выравнивания от действительно связанных.
Величина ktup влияет на работу алгоритма через его главные параметры: чувствительность и избирательность. Чувствительность — способность средства поиска распознавать отдаленно связанные последовательности. Избирательность — способность средства отбрасывать ложные совпадения — совпадения между генетически несвязанными последовательностями. Вообще, чувствительность и избирательность взаимно противоположные параметры. При использовании FASTP и других программ этого семейства, низкие значения ktup увеличивают чувствительность, а высокие повышают избирательность.
Помимо средств поиска семейство FAST включает в себя программу, полезную при оценке статистической значимости счета. Это средство работает, перемешивая одну из последовательностей, например t, (при этом сохраняя состав аминокислот неизменным, но изменяя их порядок), и запуская алгоритм метода динамического программирования для сравнения перемешанной последовательности t с исходной последовательностью в. Этот процесс повторяется много раз, так чтобы могли быть вычислены среднее значение и среднеквадратическое отклонение счета. Далее по этим значениям определяют значение z-параметра по формуле
счет усредненный счет z ~ среднеквадратическое отклонение счета ‘
Однако, поскольку статистическое распределение счетов подобий для случайных последовательностей не подчиняется закону нормального распределения, эти z-параметры имеют ограниченную пригодность.
Усовершенствование FASTP привело к созданию программы FASTA. Одна из ее новых функций — способность обрабатывать последовательности ДНК, а не только белковые последовательности. В этом отношении программу FASTA можно рассматривать как комбинацию FASTP с FASTN — программой, специально разработанной для работы с последовательностями нуклеотидов. Еще одна программа семейства — TFASTA — предназначена для сравнения запрашиваемой белковой последовательности с последовательностями из базы данных ДНК (выполняет операции трансляции одновременно с процессом поиска).
3.6. РАССТОЯНИЕ, СОПОСТАВЛЕНИЕ СТРОК
141
Другое дополнение связано с вычислением начальных счетов После того как наилучшие области были отобраны, FASTA производит дополнительный шаг и пробует объединять близлежащие области, даже если они не лежат на одной диагонали. При этом начальные счета значительно улучшаются для генетически связанных последовательностей и становятся ближе к улучшенным счетам («оптимизированные счета» на языке FASTA). Кроме того, в FASTA сохраняются десять наилучших областей — против пяти наилучших в FASTP. В пакет входят также другие программы, использующие те же самые методы. Например, LFASTA — средство поиска локальных подобий, в том смысле, что для сравниваемой пары последовательностей эта программа выдает более одного хорошего выравнивания
Средство оценки стагисгической значимости также было улучшено. Его наиболее выдающаяся функция возможность выполнения локальной перетасовки последовательностей. Было замечено, что очень часто биологически невыразительное выравнивание получало высокое значение г-парамстра, потому что перетасовка разрушала неравномерное распределение остатков в последовательности. Локальная перетасовка в некоторой степени устраняет эту проблему. Перетасовка проводится блоками по 10-20 остатков, таким образом давая перетасованные последовательности со случайным распределением в целом, но неизменным локальным составом исходной последовательности. Тогда, если высокие счета были вызваны действительно измененным локальным составом, то это затронет средний счет локально перетасованных последовательностей. Другие усовершенствования этого средства включают в себя высокую гибкость в выборе матрицы счетов и вычисление большего количества счетов для каждой перетасованной последовательности.
3.6.	РАССТОЯНИЕ, СОПОСТАВЛЕНИЕ СТРОК
И ТОЧНОЕ СРАВНЕНИЕ
ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Настало время рассмотреть некоторые дополнительные вопросы, связанные со сравнением последовательностей Первый вопрос имеет отношение к понятию расстояния между последовательностями и его взаимосвязи с подобием. Второй вопрос связан с правилами выбора параметров при сравнении последовательностей. Наконец, мы кратко обсудим методы сопоставления строк и точного сравнения последовательностей.
142
Глава 3
3.6.1.	* ПОДОБИЕ И РАССТОЯНИЕ
Подобие и расстояние обусловливают два различных, взаимно противоположных подхода к сравнению строк символов. При поиске подобия мы интересуемся наилучшим выравниванием между двумя строками, и счет такого выравнивания дает нам меру того, насколько эти строки похожи. При определении расстояния мы присваиваем стоимости элементарным редактирующим операциям и ищем наименее дорогой их набор, который преобразует одну строку в другую. Таким образом, расстояние — мера различия строк. В обоих случаях мы ищем численную величину, которая измеряет степень того, насколько последовательности подобны или различны.
Если раньше мы акцентировали наше внимание в основном на вычислении подобия, то в этом разделе мы вводим понятие расстояния и связываем его с подобием. Мы покажем, что во многих случаях эти две меры могут быть связаны с помощью простой формулы, так что мы можем легко получить одну меру из другой.
Мы должны особо подчеркнуть, что наше описание расстояний ограничено глобальным сравнением. Мера расстояния не подходит для локальных сравнений. Это ограничение — одна из причин, по которым мы посвятили эту главу главным образом мере подобия. В таблицу 3.2 сведены основные различия между подобием и расстоянием. Некоторые термины могут быть неясны читателю, но суть их будет раскрыта в дальнейшем.
Таблица 3.2 Отличительные свойства подобия и расстояния
Свойства	Подобие	Расстояние
Аксиома треугольника? Локальное сравнение? Возможность р(а, а) р(Ь, Ь)	нет да да	да нет нет
Начнем с точного определения понятий подобия и расстояния. Пусть s и t — две последовательности знаков, взятых из алфавита £. Этот алфавит может состоять из азотистых оснований ДНК или аминокислотных остатков, но представленные здесь результаты применимы также и для общих случаев. Вспомним, что мы ищем численную величину, которая показывает меру того, насколько строки подобны или различны. Как и прежде, подобие мы обозначаем функцией sim(s. t), а расстояние — функцией dist(s, f).
Подобие
Мера подобия всегда основывается на выравниваниях. Вспомним и пересмотрим точное определение понятия выравнивания. Выравниванием по
3.6. РАССТОЯНИЕ, СОПОСТАВЛЕНИЕ СТРОК
143
следовательностей s и t будем называть пару последовательностей (s',£z), полученных, соответственно, из последовательностей s и t путем вставки в них знаков пробелов. Выравнивание а = (s'.f) должно удовлетворять следующим условиям:
1-И = И-
2.	Удаление всех пробелов из последовательности s' даст последовательность s.
3.	Удаление всех пробелов из последовательности t’ дает последовательность t.
4.	В любой позиции г выравнивания должен стоять по крайней мере один значащий символ: s'[г] либо Г[г].
Выравнивание образует связь между символами s'[г] и t'[i], занимающими одинаковую позицию г в каждой последовательности. Говорят, что символы s'[г] и 4'[г] выровнены по а.
Подобие — наивысший счет любого выравнивания. Здесь мы делаем допущение об аддитивности системы очков. Теперь вспомним и уточним понятие системы очков. Система очков состоит из пары (р. д), где р — функция вида р : £ х S н» Я, используемая для назначения счета парам выровненных знаков, и д штраф за пробелы. Обычно принимают д < О, но мы не требуем этого. С такой системой очков мы способны назначить численное значение, или счет, каждому возможному выравниванию. Мы прибавляем р(а, Ь) каждый раз, когда знаки а и b совпадают в выравнивании а, и налагаем штраф д каждый раз, когда знак а оказывается в паре с символом пробела. Полная сумма - счет выравнивания <т, обозначаемый как score(n). Тогда, согласно принятой системе очков, подобие между двумя последовательностями s и t равно
sim(s,t) = max score(a), aeA(s,t)
где _4(s, t) — множество всех выравниваний между последовательностями s и t. Такую систему очков называют аддитивной, так как, если мы разделим любое выравнивание на два последовательных блока, то счет полного выравнивания будет равен сумме счетов его блоков.
Расстояние
Расстояние на множестве строк Е может быть выражено функцией d: Е х Е R, удовлетворяющей следующим условиям:
144
ГЛАВА 3
1.	d(x, х) = 0 для всех х G Е и й(ж, у) > О для всех х у
2.	d(x, у) = d(p, х) для всех х G Е и у G Е (d симметричная)
3.	d(x, у) С d(x, z) + d(y, z~) для всех х G Е, уСЕигсЕ.
Третье условие известно как аксиома треугольника. Это условие очень полезно во многих контекстах, и многие алгоритмы полагаются на его обоснованность. В случае выравнивания строк возможно определить расстояние на множестве всех строк из алфавита S, основанное на количестве операций, необходимых для преобразования одной строки в другую.
Последовательным применением ряда допустимых операций, любая строка из множества может быть преобразована в любую другую. Если мы назначим стоимость каждой допустимой операции, то мы сможем определить расстояние между двумя строками как минимальную полную стоимость преобразования одной строки в другую. Допустимые операции следующие:
1	Замена знака а знаком Ь.
2	. Вставка или удаление произвольного знака.
Чтобы назначить счет этим операциям, мы используем меру стоимости {с, h), где с функция стоимости вида с : Гх Г н Ли вещественное число. Тогда замена знака b на а стоит с(а, Ь), а вставка или удаление знака стоит h. Стоимость ряда операции а равна сумме стоимостей отдельных операций и обозначается функцией cost(a').
Итак, согласно мере стоимости расстояние между двумя последовательностями s и t равно:
dist(s, t) = mm cost(a),
„(SlsJ'l
где S(s. t) — множество всех рядов операции, выполненных для преобразования последовательности s в последовательность I.
Для того чтобы это определение было достаточно обоснованным, необходимо ввести некоторые ограничения на меру стоимости (с, h). Во-первых, мы имеем дело только с неотрицательными значениями стоимости, иначе минимум этой функции не имел бы смысла. Мы также допускаем, что функция стоимости с является симметрической, иначе расстояние нс было бы необходимо симметричным Этот минимальный набор требований гарантирует, что функция dist(s, t) является симметрической и удовлетворяет аксиоме треугольника. Чтобы удостовериться в том, что эта функция действительно выражает расстояние, мы нуждаемся в дополнительном
3.6. РАССТОЯНИЕ, СОПОСТАВЛЕНИЕ СТРОК
145
условии: с(а, Ь) > 0 при а b, h > 0. Это необходимо, чтобы избежать случаев, когда две последовательности s и t не равны между собой, но функция dist(s,Z) оказывается равной нулю. Мы хотим, чтобы расстояние было нулевым только когда последовательности идентичны.
Также мы сделаем допущение, что функция стоимости с удовлетворяет аксиоме треугольника, то есть
с(х, у) с(х, z) + с(у, z)	(3.15)
для всех х, у и z из алфавита S. Причина введения этого последнего допущения состоит в том, что, даже если мы начинаем выполнение операций с пары (с, h). не удовлетворяющей аксиоме треугольника, у нас всегда будет возможность определить новую пару (с', Л), которая действительно удовлетворяет ей и позволяет определить ту же самую функцию расстояния. Например, если три знака х, у и z — такие, что с(г, у) > с(х, z) + c(z, у), то каждый раз, когда мы должны заменять х на у, мы не будем делать этого непосредственно, а вначале заменим д’ на г, а уже затем z на у, получая тот же самый результат, но уже с более низкой стоимостью. Во всех случаях ответ выглядит так, как если бы эффективная стоимость замены т на у была бы равна с(х, z) + c(z, у), а не с(х, у), поскольку первое выражение - это суммарная стоимость операций замены. Используя выражение (3.15), мы можем избежать подобных ситуаций.
Пример 3.3. Принимая
с(з.,.)==10 пРи Х = У '	1 при х у
и h = 1, мы получаем так называемое редактирующее расстояние между двумя последовательностями, и<вестное также как расстояние Левенштей-на.	
Вычисление расстояния
Имея меру стоимости (с, h) и постоянную М, мы можем определить систему очков (р, д) следующим образом:
р(а, b) = М — с(а, 6),
(3.16)
(3-17)
146
Глава 3
Если мы имеем выравнивание а между двумя последовательностями s и I, то возможно определить такой ряд операций <т, что
score(a) + cost(a) =	+ n)i	(3.18)
где т = |я| и n = t. Чтобы найти ряд операций <т, достаточно разбить выравнивание а на столбцы, как мы делали ранее при вычислении счета. Столбцы непосредственно соответствуют допустимым операциям. Совпадения знаков соответствуют заменам. Пробелы соответствуют вставкам или удалениям знаков. Эти операции могут быть применены в любом порядке, потому чго они действуют на непересекающиеся области выравнивания и не мешают друг другу.
Ряд <т будем называть рядом допустимых операций, выполненных слева направо. Теперь вычислим счет выравнивания а и стоимость ряда <т. Предположим, что в выравнивании а есть точно I совпадений знаков, где каждое г-е совпадение — совпадение знака сц последовательности s и знака bi последовательности t. Предположим далее, что в выравнивании а есть точно г пробелов. Считая эти предположения верными, мы получаем следующее выражение для счета выравнивания а:
1
score(a) = У^р(аг,Ьг) + гд.
«=]
С другой стороны, стоимость ряда а равна
1
cost{<j) =	с(а,, bi) + rh.
2=1
Почленное сложение этих двух уравнений и отношений (3.16) и (3.17) дает
score(a) + costfcr) = IM +	(3.19)
Заметим, что величины I и г не являются независимыми. Они должны удовлетворять соотношению, включающему в себя также общее количество знаков в этих двух последовательностях. Действительно, на каждое совпадение нужно учитывать два знака, тогда как пробел соответствует только одному знаку. Поэтому общее число знаков т + п должно быть равно
т + п — 21 + г.
(3-20)
3.6. РАССТОЯНИЕ, СОПОСТАВЛЕНИЕ СТРОК
147
Теперь мы можем видеть, что уравнение (3.19) может быть переписано в виде
score(a) + costfa) = — (т + n),
что представляет собой уравнение (3.18).
Это верно для любого выравнивания. В частности, если а есть оптимальное выравнивание, то мы имеем
sim(s, t) + cost(a) = ^(т + n)i
где <т — ряд операций, произведенных в выравнивании а. Поскольку расстояние между последовательностями в и t равно минимальной стоимости любого ряда операций, мы окончательно получаем
л#
sim(s, t) + dist(s, t) (m + n).
Теперь резюмируем полученный выше результат в виде теоремы, на которую будем ссылаться в дальнейшем.
Теорема 3.2. При заданной мере стоимости (с, /г), соответствующей системе очков и некоторой постоянной М, для каждой пары строк s и t мы имеем:
dist(s,/.) + sim(s,t) < ^(|s| + HD-
Теорема 3.2 дает нам верхний предел значения функции dist(s, t). Мы хотим показать, что это также нижний предел и что расстояние может фактически быть получено из подобия прямым способом.
Теорема 3.3. При условиях теоремы 3.2 следующее неравенство верно:
sim(s. t) 4- dist(s. t) 4^-(|s| + |t|).
ДОКАЗАТЕЛЬСТВО. Последовательно рассмотрим теорему 3.2. Во-первых, имея ряд допустимых операций <т, мы строим выравнивание а со следующим свойством:
score(a) + cost (с) > 4r(m + n).
(3-21)
148
Глава 3
Следуet подчеркнуть, что здесь мы не можем получить равенство в общем виде, как мы делали в предыдущем дока таз ельстве. Этот случай немного отличен, потому что ряд может состоять из противоположных операций, и тогда соответствующее выравнивание покажет только суммарный эффект выполнения этих операций. Например, если ряд <7 в некоторый момент вставляет знак а где-нибудь и затем немедленно удаляет его, то суммарный результат этого ряда операций будет пустым, хотя мы назначили им счет. Предыдущее уравнение должно вычислять все ряды операций вне зависимости от их эффективности, и именно поэтому оно представляет собой неравенство вместо равенства.
Докажем соотношение (3.21) методом индукции на числе операций ряда <7. Если <т| = 0, то это значит, что никакая операция не была выполнена, так что .ч = t. Выравнивание (s.s) имеет счет Мт Мп = М(т + п)/2, и в этом случае соотношение верно.
В случае, когда ряд <т состоит из по крайней мере одной операции, необходимо рассмотреть последнюю операцию отдельно. Запишем ряд операций в виде <7 = а'и, где и — эта последняя операция, так что
д' .1 «	.
s —> t —> t,
то есть t' — строка, полученная из последовательности s посредством всех операций ряда, кроме последней, а строка f получена из последовательности t' в результате применения операции и.
Сделаем индуктивное предположение, что мы имеем такое выравнивание а' между последовательностями s и t', чго
score(ct) + со st {а')	+ п')-
где п' = |t'|. Поскольку cost(a) = cost(<r') + cost(u), достаточно всего лишь найти выравнивание о между последовательностями s и t и получить следующее неравенство:
scorefa) score(ct) +	— п') ~~ costfu).	(3.22)
Почленное сложение этих двух неравенств даст нам желаемый результат. Согласно типу последней операции и можно pacCMOtpeib три следующих случая: замена, вставка, удаление.
Случай 1: и — операция замены.
3.6. РАССТОЯНИЕ, СОПОСТАВЛЕНИЕ СТРОК
149
В этом случае cost(u) = c(a,b), п = п' и строка t отличается от строкиЕ./' только в одной позиции, как показано ниже:
s	.. .х...
t'	.. .а...
t	...Ъ...
Мы можем построить выравнивание о простой заменой знака а на b в выравнивании а', что на вышеприведенной схеме соответствует игнорированию средней линии. Если символ х в строке s значащий, то
score(ct) = score(a') — р(а,х) + p(b,x)
= score (а') — А/ + с(а, х.) + А/ — с(Ь, х)
= score(a') + с(а, х) — с(Ь, х) score(a') —c(a,b),
где последний шаг — следствие аксиомы треугольника для функции стоимости с. Таким образом, мы пришли к желаемому результату.
Если х - знак пробела, то счета выравниваний о и п' равны и, следовательно, score(a) = score(a') scorefa') — с(а, b),
поскольку в соответствии с индуктивным предположением с(а, Ь) 0.
Случай 2: и — операция вставки.
В этом случае cost(u) h и п' = п — 1. Чтобы операция вставки знака стала возможной, выравнивание а' должно быть «открытым» в некоторой позиции, как показано ниже:
s
t'
|...
|...
t ...|а|...
В последовательность s вставлен дополнительный пробел. Тогда разница в счете между выравниваниями о и а' обусловлена этим дополнительным пробелом в выравнивании о:
score[a)=score(a') + д = =score(a') — h +
Это доказывает верность соотношения (3.22) в случае, когда и является операцией вставки.
Случай 3: и — операция удаления.
150
Глава 3
В этом случае снова cost(u) = h, но п' = п+1. Получается следующая картина:
S	. . .X...
t'	.. .а...
t	.......
Здесь мы выделяем два подслучая, согласно тому, является ли знак х пробелом или нет. Если х — значащий символ, то
score(a) = score(a') —р(а,х) + д
= score(a') — А/ + с(а, х) — h + 4/-= score(a') — h —	+ с(а. х)
scorefa') — h—
что и требовалось, поскольку с(а, х) 0. Если же х — знак пробела, то score(a)=score(a’) — д
=score(a') -h + ~-^scorefa') — h —
поскольку h > 0.
Этот случай завершает индуктивное доказательство и показывает, что соотношение (3.21) верно. В частности, оно верно для минимальной стоимости ряда операций <т, и поэтому
score(a) + dist(.s,£)	+ п),
или же, принимая во внимание, что sim(s,t) — возможно максимальный счет выравнивания между последовательностями в и t,
А/ sim(s,t) + dist(.s,t) — (m + n), что доказывает теорему.	
Объединяя теоремы 3.2 и 3.3, мы можем записать соотношение
sim(.s,£) + dist(s,t) = ^-(тп + п),	(3.23)
3.6. РАССТОЯНИЕ, СОПОСТАВЛЕНИЕ СТРОК
151
которое показывает нам, как надобно вычислять расстояние через подобие. Таким образом, вычисление расстояния может быть сведено к вычислению подобия. Чтобы вычислить расстояние, все, что мы должны сделать, — это выбрать подходящую постоянную М. определить параметры системы очков р и д, как в выражениях (3.16) и (3.17), и применить один из алгоритмов глобального сравнения, которые мы уже рассмотрели. После чего найденное подобие преобразуется в расстояние вышеприведенной формулой.
Например, в случае редактирующего расстояния мы можем выбрать М = 0 и запустить алгоритм подобия со следующими параметрами системы очков: совпадение = 0, несовпадение = — 1, пробел = — 1. Или же мы можем выбрать А/ = 2 и принять: совпадение = 2, несовпадение = 1 и пробел = 0. Обе системы очков дают одни и те же оптимальные выравнивания, хотя и с различными счетами. Но после применения формулы (3.23) расстояние получается одинаковым.
Прежде чем мы закончим этот раздел, надлежит сделать комментарий относительно постоянной М. Может показаться странным, что для теоремы 3.2 подходит любое значение М. Если М — большое положительное число, то в результате система очков может дать отрицательные значения штрафов за пробелы w'(k) для многих, а возможно и всех, значений к. Это противоречит нашей интуиции, учитывая, что пробелы должно штрафовать, а никак не награждать. То же самое происходит при отрицательном, но очень большом по абсолютной величине значении М. Функция р на сей раз будет отрицательной, что снова противоречит здравому смыслу. Причина этой очевидной аномалии связана с тем фактом, что здесь мы рассматриваем только глобальные сравнения. Когда мы изменяем значение Л/, счет всех выравниваний возрастает или убывает взаимно пропорционально, так что оптимальные выравнивания всегда остаются теми же самыми. Для локальных выравниваний уравнение (3.20) не действительно, и, варьируя параметр М, мы можем отдать предпочтение более длинным или более коротким локальным выравниваниям.
3.6.2.	ВЫБОР ПАРАМЕТРОВ ПРИ СРАВНЕНИИ
ПОСЛЕДОВАТЕЛЬНОСТЕЙ
В этом разделе мы приводим некоторые соображения относительно выбора параметров системы очков и выбора алгоритма для каждого конкретного случая сравнения последовательностей.
При выборе системы очков должны быть учтены многие факторы. Эта система включает, в простейшем виде, очки за совпадения (М), несовпадения (тп) и пробелы (д < 0).
152
Глава 3
Выбирая ту или иную систему очков, важно убедиться в том, что совпадение стоит больше несовпадения, с тем чтобы мы поощряли выравнивания идентичных знаков. Другое общеизвестное правило состоит в том, чтобы убедиться, что несовпадение мы всегда предпочитаем паре пробелов. Например, следующее левое выравнивание должно иметь более высокий счет, чем столь же возможное правое:
А	-А
С	С-.
Вышеприведенные правила записывают в виде неравенства параметров системы очков:
2д < т < Л/.
Обратите внимание, что, если мы умножим все веса на некоторую положительную постоянную, то оптимальные выравнивания останутся теми же самыми. Это свойство может быть использовано для округления значений всех весов до целых чисел, которые большинством современных компьютеров обрабатываются значительно быстрее чисел с плавающей запятой.
Рассмотрим транспозиции знаков. Если мы имеем, например, последовательности АТ и ТА, то для них можно построить по существу два выравнивания, соревнующихся за лучший счет:
АТ	-АТ
ТА	ТА-.
(Есть еще третье выравнивание с таким же счетом, как у второго, но в нем пару совпадения образуют символы Т.) Счета этих двух выравниваний равны, соответственно. 2т и Л/ + 2д. Таким образом, если т равно среднему арифметическому значений Л/ и 2д, то два предыдущих выравнивания эквивалентны в значении счета. Чтобы отдать предпочтение одному из них, мы должны выбрать значение т ближе к одной из конечных точек интервала [2д, М].
Рассуждая подобным же образом, возможно представить другие примеры пар коротких последовательностей и в каждом случае постулировать, какое выравнивание является наиболее предпочтительным. Это дает нам дополнительные неравенства параметров т, М и д. Например, при сравнении последовательностей ATCG и TCGA мы можем предпочесть первое из двух следующих выравниваний:
ATCG-	ATCG
-TCGA	TCGA.
3.6. РАССТОЯНИЕ, СОПОСТАВЛЕНИЕ СТРОК
153
Это предпочтение будет отражено в счете при выполнении нсравенова 4т < 4М + 2д. Помимо некоторых других причин, значения параметров, используемые в разделе 3.2.1, были выбраны именно на основании этих критериев.
Иа практике часто необходимы более сложные системы очков, чем простая система параметров А/, т и д. Обычно предпочитают субаддитивные функции штрафов за пробелы, упомянутые в разделе 3.3.3. Среди них очень популярны линейные функции благодаря квадратичному времени счета в противоположность кубическому для общих функций. Другое важное свойство, особенно для сравнения белковых последовательностей, — способность дифференцированной оценки совпадений аминокислот. Так, совпадение аминокислот с подобными химическими или физическими характеристиками (размер, заряд, гидрофобность и т. д.) должно получать больше очков, чем совпадение между незначительно подобными. Отсюда следует, что системы очков, основанные только на идентичности, как правило, недостаточны. При сравнении белков общепринятым является использование матриц ПТМ.
Тем не менее, простой метод идентичности/нсидснтичности достаточно универсален, чтобы включить в себя в качестве частных случаев несколько известных задач сравнения последовательностей. Одна из этих задач состоит в том, чтобы найти длиннейшую общую подпоследовательность (ДОП) пары последовательностей. Это равносильно использованию основного алгоритма при А/ = 1 и т = g = 0. Таким образом, при заданных последовательностях длиной т и п мы можем решить эту задачу в пространстве O(min(m, п)) за время О(тп). Эта задача получила большое внимание, и для се частных случаев были описаны несколько более быстрых алгоритмов17.
Теперь обсудим выбор алгоритмов18. Решение о том, стоит ли штрафовать крайние пробелы, а также выбор локальных или глобальных методов во многом зависит от области применения и вида желаемых результатов. Если мы хотим сравнись относительно подобные последовательности приблизительно одинаковой длины, то, вероятно, более уместным будет метод глобального сравнения со штрафами за все пробелы. Например, сюда можно включить случай двух молекул тРНК различных организмов, или же двух тРНК одного организма, но специфичных к разным аминокислотам.
^Существенно, что для этого случая есть точные оценки статистической значимости вы-равни вания. — Прим. ред.
11а самом деле шесь имеются в виду не разные алгоритмы решения одной математической задачи, а разные математические задачи. Прим. ред.
154
Глава 3
Если, напротив, одна из последовательностей коротка, а другая намного длиннее то наиболее желательно штрафовать только крайние пробелы в более короткой последовательности. Это позволит нам с заданной точностью найти все появления короткой последовательности в длинной. Такой поиск полезен при попытке определить в недавно расшифрованной молекуле ДНК местонахождение сравнительно сильно консервативных структур.
Локальное сравнение следует использовать при сравнении двух относительно длинных последовательностей, которые могут содержать области высокого подобия. Типичный случай последовательности белка с подобными функциями, принадлежащие организмам, в действительности далеко отстоящим в единицах эволюционного расстояния. Так как исследуемые в данном случае белки выполняют подобные функции, то весьма вероятно, что в их последовательностях существуют некоторые области высокого подобия (активные центры, мотивы, функционально тождественные структуры и т. д ), разделенные избыточными несвязанными областями, которые накопили мутации и не оказывают заметного влияния на их функции.
Если сравнение последовательностей проводят с целью проверки гипотезы об их общем происхождении, то интерпретации результатов необходимо уделять особое внимание. Как правило, случайные оптимальные выравнивания являются наименее вероятными, однако всегда желательно сравнивать полученный счет с тем, что ожидалось в среднем от генетически несвязанных последовательностей с теми же самыми характеристиками, как у этих двух сравниваемых последовательностей. Если оптимальный счет получается намного выше среднего, то это служит хорошим показателем тою, что подобие между сравниваемыми последовательностями не случайно. Но даже в таком случае этот результат сам по себе не подразумевает гомологию или любой другой признак общего происхождения последовательностей. Как правило, с целью подтверждения или опровержения гипотезы об общем предке проводят дополнительные эксперименты, основанные на информации, полученной из этого выравнивания. С другой стороны, если подобие почти равно ожидаемому среднему, то вполне вероятно, что данные последовательности не связаны. Однако в биологии не существует правил без исключений и известны случаи гомологичных белков без каких-либо следов подобия на уровне последовательностей. Для подтверждения гомологичности в этих случаях были использованы другие виды данных — “	T9
например, результаты анализа трехмерной структуры молекулы .
,9При выборе способа формализации задачи и при подборе параметров, а также при оценке качества используют «золотой стандарт», для которого известен ответ. В частности, для оптимизации методов и параметров выравнивания используют выровненные пространственные структуры белков. - Прим. ред.
3.6. РАССТОЯНИЕ, СОПОСТАВЛЕНИЕ СТРОК
155
3.6.3.	СОПОСТАВЛЕНИЕ СТРОК И ТОЧНОЕ СРАВНЕНИЕ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Две другие задачи, имеющие важное значение для вычислительной молекулярной биологии, — это задачи сопоставления строк и точного сравнения последовательностей. При сопоставлении строк мы выбираем строки s и f, где |s| = п и |t| = т, и хотим найти все появления строки t в строке s Другими словами, ответить на вопрос, является ли строка t подстрокой последовательности s. Если да, то в каких именно позициях строки s мы можем найти строку t? Это классическая задача информатики, и она может быть решена эффективно. Так, разработаны алгоритмы, которые могут решить эту задачу за время О(п + т), что намного быстрее по сравнению с квадратичной сложностью основного алгоритма сравнения двух последовательностей. Мы не будем описывать такие алгоритмы, ибо их можно найти в любом хорошем учебнике по теории алгоритмов; некоторые из них мы упоминаем в библиографических примечаниях главы 2. Обратим наше внимание на го, что эффективные алгоритмы были развиты также для задачи о приближённом совпадении строк, где мы допускаем появление некоторого числа ошибок при поиске совпадения. Такие алгоритмы, конечно, тоже важны для молекулярной биологии. Ссылки на них даны в библиографических примечаниях.
Большую часть этой главы мы посвятили методам сравнения последовательностей, допускающих появление ошибок. Несомненно, такое допущение справедливо для большинства случаев сравнения последовательностей в реальной жизни, но в некоторых ситуациях мы нуждаемся в точных сравнениях. Многие задачи точного сравнения последовательностей могут быть решены с помощью очень полезной и универсальной структуры, известной как суффиксное дерево. Ниже приведены примеры задач этого класса.
•	В главе 4 будет показано, что присутствие повторных подстрок (повторений) в последовательностях — одна из главных проблем, возникающих при крупномасштабном секвенировании ДНК. Естественно, в данном случае задача состоит в том, чтобы найти самую длинную повторную подстроку последовательности.
•	При использовании ПЦР (см. раздел 1.5.2) мы должны найти короткий фрагмент ДНК, называемый праймером, причем сам он не должен появляться в молекуле ДНК, предназначенной для клонирования. Эта задача может быть формализована следующим образом. Даны строки А (длинная) и В (короткая) и для каждой позиции i строки В требуется найти такую кратчайшую подстроку, которая начинается в строке В с позиции i и притом не появляется ни в одной позиции строки А.
156
Глава 3
Рис. 3.19. Пример суффиксного дерева для строки GTATCTAGG. Знак доллара ($) обозначает конец строки
•	В разделе 1.5.2 было показано, что участки рестрикции для рестрик-таз представляют собой перевертни равной длины. Задача состоит в том, чтобы найти все максимальные палиндромы данной последовательности ДНК.
Теперь мы объясним, что такое суффиксное дерево. Как правило, оно содержит все суффиксы строки s, причем общие префиксы вынесены за скобки в максимально возможной для данной структуры дерева степени. Формальное определение звучит следующим образом: суффиксное дерево строки s = Si, S2,. -., sn — это корневое дерево Т с п + 1 листьями, обладающее перечисленными ниже свойствами:
•	Ребра дерева Т ориентированы в направлении от корня, и каждое ребро помечено подстрокой последовательности s.
РЕЗЮМЕ
157
•	Ребра, выходящие из данной вершины, несут различные метки, а все такие метки имеют различные префиксы (не считая пустых префиксов).
•	Каждому листу дерева соответствует суффикс последовательности s, и этот суффикс образован сцеплением меток всех ребер, принадлежащих пути от корня к данному листу
На рис. 3.19 показан пример суффиксного дерева. Чтобы избежать проблем с пустым суффиксом, к концу последовательности s мы обычно добавляем дополнительный знак $, нс встречающийся где-либо еще в этой строке. Суффиксные деревья могут быть построены с помощью одного хорошего алгоритма (не будем его описывать), время счета которого при постоянном объеме алфавита равно О (и). Как только суффиксное дерево построено, большинство задач, рассчитанных на его применение, могут быть решены за время О(п) Это относится к только что описанным задачам. Задача поиска праймера может быть решена за время О(|В|) Мы предоставляем читателю возможность самолично найти варианты применения суффиксных деревьев для решения описанных выше задач.
Относящаяся сюда же структура, называемая массивом суффиксов, также можез быть использована для решения задачи точного сравнения последовательностей Эта структура состоит в основном из всех лексикографически сортированных суффиксов последовательности s.
РЕЗЮМЕ
Мы начали главу с рассмотрения способов сравнения пары последовательностей. Для этой цели может быть успешно применена методика построения алгоритмов, называемая динамическим программированием, которая дает точные и эффективные алгоритмы. Затем мы изучили несколько расширений к основным алгоритмам метода динамического программы рования Некоторые из этих расширений позволяют экономить время или пространство, что в некоторых случаях особенно необходимо. Другие расширения нацелены на решение более общих вариантов задачи сравнения последовательностей, разработанных для некоторых специальных случаев.
Вспомним различные способы сравнения и области их применения’
•	Глобальное сравнение целых последовательностей;
•	Локальное поиск подобных участков последовательностей;
•	Полуглобальное — определение степени подобия суффиксов, префиксов или внутренних областей последовательностей.
158
Глава 3
Алгоритмы, построенные для решения этих задач, имеют квадратичную сложность как в отношении времени, так и пространшва. Однако для всех этих алгоритмов были разработаны версии, экономящие пространство. Эти версии используют линейное пространство, но при этом могут удваивать время счета.
В приведенную ниже таблицу сведены обобщенные характеристики алгоритмов по типу используемой ими функции штрафов за пропуски.
Тип функции	Уравнение	Сложность	Пространство
линейная	w(fc)= ак		один массив
линейная	w(k) = ак + b		три массива
общая	любое w(k)	O(n3)	три массива
Далее мы рассмотрели проблемы множественного выравнивания последовательностей. В данном случае метод динамического программирования привел к неэффективному алгоритму, так что возникла необходимость выбора других методов; мы описали ряд альтернативных методов. Другая ситуация, в которой алгоритмы, основанные на методе динамического программирования, работают недостаточно быстро, возникает при поиске некоторой последовательности или структуры в базе данных. Мы изучили эту задачу в разделе 3.5, исследуя эвристики, используемые в системах программного обеспечения, специально разработанных для поиска в базах данных.
Большая часть материала этой главы основана на понятии подобия, однако это не единственный подход к сравнению последовательностей. Понятие расстояния, используемое в качестве меры отличия двух последовательностей, также является важным. В разделе 3.6.1 мы рассмотрели соотношение между этими двумя понятиями. Глава завершается кратким обсуждением выбора методов сравнения и параметров при решении задач сравнения последовательностей.
УПРАЖНЕНИЯ
1.	Найдите соответствие между перечисленными ниже алгоритмами и задачами (описание задач см. в разделе 3.1):
полуглобальное сравнение;
полуглобальное сравнение после предварительной фильтрации;
k-Band',
УПРАЖНЕНИЯ
159
поиск в базах данных;
локальное сравнение.
2.	Определите счет выравнивания (3.1) на стр. 49 согласно следующей системе очков: д = — 1, р(а, b) = 1 при а = b и р(а, Ь) = 0 при а Ь.
3.	Найдите все возможные оптимальные выравнивания между последовательностями AAAG и ACG, используя систему очков из раздела 3.2.1.
4.	Обычно наинизшсс и наивысшее выравнивания (см. определения в конце раздела 3.2.1) включают в себя все оптимальные выравнивания между двумя сравниваемыми последовательностями. Приведите пример выравнивания, опровергающий это утверждение.
5.	Рассмотрите системы очков из упр. 2 и из раздела 3.2.1. Найдите две последовательности, оптимальные выравнивания которых различны для этих двух систем.
6.	Преобразуйте алгоритм Align на рис. 3.3 так, чтобы он находил оп-|имальное полу глобальное выравнивание последовательностей s и t и при этом не штрафовал пропуски на обоих концах одной из последовательностей: s либо t. Сделайте допущение о том, что массив а заполнен способом, подходящим для этого метода сравнения.
7.	Найдите иаилучшее локальное выравнивание между последовательностями ATACTACGGAGGG и GAACGTAGGCGTAT. Используйте любую систему очков на ваше усмотрение.
8.	Какая величина является большей при оценке любых двух последовательностей: их локальное подобие или их глобальное подобие? Почему? Какова взаимосвязь полуглобального подобия с другими двумя величинами?
* 9. Разработайте алгоритмы с линейным пространством для решения задач поиска локального и полуглобального подобия, включая построение оптимального выравнивания.
10.	Решите вопрос о том, верно ли следующее утверждение или ложно, и обоснуйте ответ. Два оптимальных выравнивания между последовательностями s и t всегда могут быть разбиты на одинаковое число блоков (определение понятия блока выравнивания см. в разделе 3.3.2).
11.	Вспомните понятия из раздела 3.3.4. Найдите такую пару последовательностей, чтобы наилучший счет при к = 0 был бы равен наилучшему счету при к = 1, но был бы значительно ниже при к = 2. Для этой задачи примите М =1ит = д = —1.
160
Глава 3
12.	Преобразуйте алгоритм k-Band (рис. 3.9) так, чтобы он мог обрабатывать последовательности неравной длины. Какова его полная временная сложность?
13.	Найдите все оптимальные множественные выравнивания между последовательностями АТС, CAGC и CGC, используя меру ПС, где р(а, b) = 1, если знаки а и Ъ значашие и а = Ь; р(а, Ь) — 0. если знаки а и b значащие и а Ь; р(а, —) = —1.
14.	Сколько пространства памяти занимает алгоритм Multiple-Seq-uence Alignment на рис. 3.14 помимо пространства пула важных ячеек?
15.	Докажите, что матрица счетов ПТМ-/с симметрична для всех к.
16.	Было показано, что матрица ПТМ-1 соответствует мутациям примерно 1 % аминокислот. Можем ли мы на этом основании утверждать, что матрица ПТМ-2 соответствует в среднем 2 % мутаций?
17.	Используя программный пакет BLAST, запросите последовательность GAATTCCAATAGA в «Генбанке». Какие последовательности, идентичные этой, были найдены в результате поиска?
1	К. Функция штрафов за пропуски w является вогнутой, если Д w(Jc) Д|/ (/с4 1). Докажите, что вогнутая функция, для которой w(0) = 0, является также субаддитивной. (Определение функции &w(k) см. на стр. 64.)
* 19. Определите, верно ли следующее утверждение: Субаддитивная неубывающая функция штрафов за пропуски ш является также необходимо вогнутой функцией.
20.	Рассмотрите выравнивание длиной I между последовательностями s и t. Разделите это выравнивание на две части, одна от столбца 1 до столбца к, и другая — от столбца fc+1 до столбца I. Какие свойства системы очков гарантируют, что при любых значениях к счет целого выравнивания будет равен сумме счетов его частей?
21.	Являс ся ли представленная в примере 3.2 схема приписывания последовательностей оптимальной?
22.	Согласно рассмотренному в разделе 3.6.1 соотношению между подобием и расстоянием, разработайте одну возможную систему очков, соответствующую редактирующему расстоянию.
о 23. Имея две случайные последовательности ДНК с длинами тп и п, найдите распределение глобального подобия между ними. Приближается ли оно к любому известному закону распределения по мере возрастания п и т?
БИБЛИОГРАФИЧЕСКИЕ ПРИМЕЧАНИЯ
161
24. Постройте алгоритм поиска кратчайшей общей надпоследовательности любых двух последовательностей. Подсказка: это может быть сделано простой адаптацией основного алгоритма сравнения последовательностей.
25. Покажите, каким образом можно использовать суффиксные деревья для решения задач, упомянутых в разделе 3.6.3.
БИБЛИОГРАФИЧЕСКИЕ ПРИМЕЧАНИЯ
Книгу Санкова и Крускала [168] можно по праву считать классическим трудом о сравнении последовательностей. Работа Уотермсна [196] представляет собой хороший обзор методов оптимального выравнивания, поиска подобия, расстояния, а также построенных на этих методах алгоритмов. Довольно полный обзор Пирсона и Миллера [156] посвящен методам динамического программирования. Другим полезным источником сведений о сравнении последовательностей можно назвать книгу Хейнс [191].
Известную работу Нидлмена и Вунша [146] обычно рассматривают как первый важный вклад в сравнение последовательностей с точки зрения биологов, хотя С. Улам еще в 1950-х гг. оценивал расстояния на пробелах последовательности. Описанный Нидлменом и Вуншем алгоритм имеет фиксированный штраф за пропуск, не зависящий от его длины. В этой работе нс было представлено никакого анализа сложности. Болес поздний анализ показал, что в представленном в статье виде алгоритм имеет кубическое время счета. Теперь мы знаем, как выполнить то же самое вычисление за квадратичное время, используя алгоритм с линейными функциями штрафов за пробелы, который дополнительно использует и постоянные функции. В любом случае, название «алгоритм Нидлмена-Вунша» часто используют для обозначения любого вида алгоритма (глобального выравнивания), основанного на методе динамического программирования.
Подобное же явление произошло и с методом локального выравнивания последовательностей. Плодотворная статья Смита и Уотермсна [175] оказала большое влияние на развитие соответствующей научной области и предоставила имена своих авторов в качестве наименования почти что любого алгоритма метода динамического программирования для локального выравнивания. Сама работа очень коротка (всего три страницы) и приводит только формулу для заполнения массива, но не содержит никакого анализа сложности В примере, представленном в этой статье, авторы использовали линейную функцию штрафов за пробелы. Позже, Хуан с коллегами разработали версии этого алгоритма с квадратичным временем счета и линей
162
Глава 3
ным пространством [100]. Уотермсн [197] описал версии этого алгоритма, предназначенные для эффективного восстановления выравниваний, близких к оптимальному.
Не известно, когда основной алгоритм, представленный в разделе 3.2.1, был разработан впервые. Вероятно, его много раз псрсоткрывали для решения различных классов задач [172]. Благодаря Хиршбергу [94] появился полезный алгоритм, позволяющий экономить пространство памяти. Позже он был включен в большинство важных версий алгоритмов метода динамического программирования для сравнения последовательностей [100; 145].
Большое внимание в специальной литературе было уделено также вогнутым функциям штрафов за пробелы [140]. Частично это связано с тем, что они хорошо моделируют систему очков, в которой за отдельные пробелы назначаются более крупные штрафы — так же, как при использовании субаддитивных функций. В общем случае вогнутость и субаддитивность несравнимы, хотя вогнутость плюс дополнительное условие 2w(l)	ш(2)
подразумевает субаддитивность (см. упражнение 18).
Наш раздел, посвященный сравнению подобных последовательностей, главным образом основан на работе Фикетта [63]. Укконен [188], Майерс [142], а также Чан и Лолер [34] создали более эффективные алгоритмы для систем очков с некоторыми специальными свойствами.
Матрицы ПТМ были представлены в работе Маргарет Дейхофф и ее колле! [45]. В [70] приведено достаточно хорошее их описание. Альт-шуль [10] описывает полный анализ, согласно которому для каждого конкретного сравнения следует выбирать расстояния ПТМ. Этот анализ во многом зависит от оценки статистической значимости, проведенной Карлином и Альтшулем [109], а также Карлином, Дембо и Кавабатой [110]. Многочисленные вопросы, связанные с поиском в базах данных рассмотрены в работе Альтшуля и др. [11]. Супруги Стивен и Перья Хеникофф [93] предложили матрицы БЛОЗАМ20 (BLOSUM) — альтернативу матрицам ПТМ.
Были найдены также способы вычисления оптимальных выравниваний одновременно для многих систем очков. Подобные методы рассмотрены Уотерменом [198].
Применение программного пакета FAST описано в статьях Липмена и Пирсона [127], Пирсона и Липмена [155], а также Пирсона [153]. Полное сравнение между методом, заложенным в программу FASTA, и классическим методом динамического программирования было проведено Пирсоном [154]. Программа BLAST описана в работе Альтшуля и др. [12]. Интересный вариант метода рекурсии — использование общих окон (которые могут быть найдены очень быстро) с целью построения больших вырав
20Сложноусеченное слово БЛОЗАМ означает «блочные гамены». — Прим, перев.
БИБЛИОГРАФИЧЕСКИЕ ПРИМЕЧАНИЯ
163
ниваний. Среди различных описаний приложений этого нового метода мы приводим работу Чао, Чзана, Остела и Миллера [36], посвященную локальному сравнению чрезвычайно длинных последовательностей См. также следующие работы Чао и Миллер [35], Иозеф, Мейданис и Тивари [104].
В ряде работ обсуждается взаимосвязь между расстоянием и подобием. Стандартное преобразование, использованное нами в разделе 3.6.1, уже было рассмотрено ранее в статье Смита, Уотермсна и Фитча [176]. Обзорная глава из книги Уотсрмена [197] посвящает этой теме один раздел. В [134] описан алгоритм выравниваний, который допускает совпадения типа пробел пробел
Каррилло и Липмсном [32] был разработан метод проекций, позволяющий экономить время при построении множественного выравнивания. Аль-тшуль и Липмен [13] обобщили этот метод к методу выравнивания звезд. Гасфилд [83] также рассматривал методы выравнивания звезд и доказал надежность характеристик меры расстояния парных сумм. Гупта, Кецсциоглу и Шефер [81 ] описывают разработанную ими на основе алгоритма Каррилло и Липмена программу Multiple Sequence Alignment (MSA). Кецециоглу [113] формализовал понятие «множественного выравнивания, которое является настолько близким, насколько возможно к множеству попарных выравниваний», и назвал его задачей о следе с максимальным весом Он доказал, что эта задача является НП-трудной и разработал для се решения алгоритм метода ветвей и границ. Описание альтернативного, эвристического метода выравнивания последовательностей, основанного на понятии следа, дано в [137]. Ван и Цзян [193] показали НП-трудность задач множественного выравнивания, меры ПС и задачи выравнивания дерева. Алгоритм с экспоненциальным временем счета для выравнивания дерева описан в [166]. Алгоритмы аппроксимации для выравнивания дерева на основе расстояния описаны Ваном и Гасфилдом [192], которые улучшили прежний результат Цзяна, Лолера и Вана [102]. Несколько эвристик для множественного выравнивания призваны решить задачу выравнивания множества выравниваний. Две ссылки на эту тему: Миллер [139] и Гото [77]. Обзор методов множественного сравнения последовательностей приведен в статье Чаня, Вона и Чиу [33].
Поскольку на практике известные методы построения оптимальных выравниваний иногда оказываются недопустимо медленными, объединение компьютеров в сеть для параллельной работы часто расценивают как способ ускорить процесс вычислений. Одна такая попытка описана в статье Джонса и др. [103].
Суффиксные деревья и многие алгоритмы обработки строк описаны в книге Стивена [180], а также Крошемора и Риттера [39]. Массивы суф
164
Глава 3
фиксов впервые были упомянуты в статье Манбера и Майерса [130]. О применении суффиксных деревьев к задаче поиска праймера и к задаче поиска палиндрома (см. раздел 3.6.3) мы узнали из разговора с Дэном Гасфилдом. Недавно Гасфилд выпустил новую книгу, в которой достаточно подробно описаны различные алгоритмы обработки строк и варианты их применения в вычислительной биологии [85].
Глава 4
СБОРКА ФРАГМЕНТОВ ДНК
В главе 1 мы рассматривали пространственные структуры, химическое строение и методы секвенирования молекул ДНК. В этой главе мы обсудим вычислительную задачу секвенирования — гак называемую задачу сборки фрагментов. Разработка математических моделей и алгоритмов решения этой задачи связана с тем, что с помощью современных технологий возможно непосредственно секвенировать1 фрагменты нуклеотидных последовательностей длиной не более нескольких сот нуклеотидов. С другой стороны, в арсенале ученых имеется технология, позволяющая нарезать длинную молекулу ДНК на случайные фрагменты и производить достаточно много копий этих фрагментов для последующего секвенирования Таким образом, типичный подход к расшифровке длинных молекул ДНК фрагментация и последующее секвенирование полученных фрагментов. Олнако в таком случае остается нерешенной задача сборки фрагментов, анализу которой мы и посвятим эту главу. Кроме того, мы представляем формальные модели этой задачи и алгоритмы ее решения.
4.1.	БИОЛОГИЧЕСКИЙ АППАРАТ СЕКВЕНИРОВАНИЯ
Секвенировать ДНК - шачит расшифровать последовательность азотистых оснований этой молекулы. При крупномасштабном секвенирова нии молекул ДНК мы пытаемся разгадать шифр, закодированный в очень длинной целевой последовательности ДНК (тысячи2 пар нуклеотидов) Мы можем представить эту задачу как головоломку, в которой перед нами лежит двойной ряд карт, повернутых тыльной стороной вверх, как показано на рис. 4. ]. Мы не знаем, какая буква из алфавита {А, С, G, Т} написана на каждой карге, но зато мы точно знаем, что карты в одинаковых позициях обоих
’Секвенировать — определять последовательность оснований в молекуле ДНК или после-донагельность аминокислот в белке. Прим. ред.
' Миллионы и миллиарды. — Прим. ред.
166
Глава 4
5'	... □□□□□□□...	3'
3'	... □□□□□□□...	5'
Рис. 4.1. Неизвестная последовательность ДНК — цель секвенирования
рядов формируют комплементарные пары. Наша цель состоит в том, чтобы определить буквы, используя некоторые подсказки, в качестве которых мы можем использовать (приближённые) подстроки этих рядов. Длинную последовательность, которую необходимо восстановить, называю! целью.
В биологическом варианте этой задачи нам известна приближённая длина целевой последовательности с точностью до 10 % или около этого. Невозможно секвенировать целую молекулу непосредственно. Однако вместо этого мы можем получить некоторый отрезок молекулы, начинающийся в случайной позиции в одной из нитей и секвенирвать этот отрезок в каноническом направлении (5' —» 3') в пределах некоторой длины. Каждый такой отрезок называют фрагментом. Фрагмент соответствует подстроке одной из нитей целевой молекулы, но мы не знаем, к которой из нитей он относится, не известна также его позиция относительно начала нити, и, кроме того, он может содержать ошибки. Используя метод дробовика (см. раздел 1.5.2), мы получаем большое количество фрагментов и затем на основании анализа их взаимного перекрытия пытаемся восстановить после-довагельноегь целевой молекулы. В зависимости от особенностей эксперимента, допустимая длина фрагмента может находиться в пределах от 200 до 700 п. н. Типичные задачи молекулярной биологии ставят целью расшифровку последовательностей длиной от 30000 до 100 0003 п. н., что означает секвенирование 500-20004 фрагментов.
Таким образом, наша задача состоит в том, чтобы восстановить всю последовательность целевой молекулы ДНК. Поскольку для этого необходимо соединить множество фрагментов, ее называют задачей сборки фрагментов. Мы обращаем внимание, что так как последовательность второй нити может быть легко восстановлена по правилу комплементарное™ пар, то достаточно определить код одной из нитей исходной молекулы.
Далее в этом разделе мы осветим дополнительные детали биологического плана, важные для построения алгоритмов сборки фрагментов.
3В настоящее время секвенирование одной бактериальной хромосомы несколько миллионов пар оснований - занимает около недели работы хороню оснащенной лаборатории. Прим ред.
4Поскольку секвеннруются случайные фрагменты, некоторая часть целевой последовательности будет покрыта многими фрагментами. В то время как другая часть может н не быть покрыта прочитанными фра1ментамн вовсе. Суммарная длина прочитанных фрагментов, отнесенная к длине целевой последовательности (она может быть определена экспериментально без чтения), называется покрытием. — Прим ред.
4.1. БИОЛОГИЧЕСКИЙ АППАРАТ СЕКВЕНИРОВАНИЯ
167
4.1.1.	ИДЕАЛЬНЫЙ СЛУЧАЙ
Как известно, лучший способ изучения любою материала — использование наыядного примера. Однако следует сделать оговорку относительно того, что реальные задачи молекулярной биологии намного сложнее абстрактных примеров, которые мы приводим в учебнике. Предположим, что вход задачи представлен четырьмя последовательностями:
ACCGT CGTGC ТТАС TACCGT
и мы знаем, что ответ (целевая последовательность) содержит приблизительно 10 оснований. Один из возможных способов сборки множества этих последовательностей следующий:
—ACCGT—
----CGTGC
ТТАС-----
-TACCGT—
TTACCGTGC
Обратите внимание, что мы выровняли входное множество, игнорируя крайние пробелы. Мы стараемся всего лишь переместить строки выравнивания таким образом, чтобы каждый столбец содержал одинаковые основания. Единственным руководством на сборку, кроме приближённого размера цели, являются перекрытия фрагментов. Здесь под перекрытием мы подразумеваем подобие между конечными частями одних фрагментов и начальными частями других (как у первой и второй, а также у третьей и четвертой последовательностей в приведенном примере). Расположив фрагменты так, чтобы они хорошо выровнялись друг с другом, мы получаем так называемую компоновку, которую можно рассматривать как разновидность множественного выравнивания фрагментов.
Последовательность под горизонтальной чертой внизу компоновки, которую называют согласованной последовательностью или просто консенсусом, и есть ответ на нашу задачу. Консенсус определяют простым подсчетом большинства голосов среди всех оснований в каждом столбце. В данном примере все столбцы единогласны (содержат основания одного типа), так что вычисление консенсуса не вызывает трудностей. В данном примере согласованная последовательность содержит девять оснований, что
168
Глава 4
близко к заданной целевой длине, равной 10 основаниям, причем каждый фрагмент является точной подстрокой консенсуса. Однако на практике, как будет показано далее, фрагменты редко соответствуют точным подстрокам согласованной последовательности.
4.1.2.	ТРУДНОСТИ
Как было упомянуто выше, реальные примеры задачи сборки фрагментов очень сложны. Помимо этого факта существует еще несколько осложне ний, которые делают эту задачу намного труднее, чем только что рассмотренный упрощенный пример. Основные факторы, дополнительно усложняющие задачу, — это ошибки, неизвестная ориентация, повторные области и неполное покрытие. Опишем каждый из этих факторов последовательно.
Ошибки
Простейшие ошибки называют ошибками обращения к основанию, к которым относят замены, вставки и удаления оснований во фрагментах. Примеры ошибок каждого типа приведены, соответственно, на рис. 4.2, 4.3 и 4.4. Еще одной распространенной ошибкой является транспозиция оснований, но мы можем рассматривать ее как сочетание вставки и удаления или двух замен знаков.
Вход:	Ответ:
ACCGT	—ACCGT—
CGTGC	----CGTGC
ТТАС	ТТАС------
TGCCGT	-TGCCGT—
TTACCGTGC
Рис. 4.2. В этом примере произошла ошибка типа замены во второй позиции последнею фрагмента, где основание А было заменено на G. Консенсус остается верным вследствие большинства голосов
На практике ошибки обращения к основанию появляются с частотой от 1 до 5 ошибок на каждые 100 знаков5. Их распределение по последовательности неравномерное, так как они имеют тенденцию концентрироваться ближе к З'-концу фрагмента. Как видно из примеров, правильный консенсус возможно восстановить даже в присутствии ошибок, но компьютерная программа должна быть подготовлена к обработке возможных ошибок, и это
Современные машины допускают значительно меньше ошибок. Прим. ред.
4.1. БИОЛОГИЧЕСКИЙ АППАРАТ СЕКВЕНИРОВАНИЯ
169
Вход:
ACCGT CAGTGC
ТТАС
TACCGT
Ответ:
—ACC-GT— ----CAGTGC ТТАС------ -TACCGT— TTACC-GTGC
Рис 4.3. В этом примере произошла ошибка типа вставки во второй позиции июрого фрагмента: появилось лишнее основание А. Консенсус все равно верен благодаря вставке пробелов во множественное выравнивание и большинству голосов. Учтите, что при выдаче ответа пробел в консенсусе будет отброшен
Вход:
ACCGT CGTGC ТТАС
TACGT
Ответ:
—ACCGT—
---CGTGC
ТТАС----
-TAC-GT—
TTACCGTGC
Рис 4.4. В этом примере произошла ошибка типа удаления втретьей (или четвертой) позиции в последнем фрагменте. Консенсус верен благодаря пробелам в выравни вании и большинству голосов
обычно означает построение алгорит мов, которые требуют большего количества времени и пространства. Например, если нет никаких ошибок, то оптимальные выравнивания между двумя последовательностями возможно найти за линейное время, тогда как для обработки последовательностей с пропусками необходимы квадратичные алгоритмы (см. главу 3).
Помимо ошибочных обращений к основаниям, сборку могут испортить ошибки других двух типов: присутствие химерных фрагментов и загрязнение материалом ДНК хозяина или вектора. Далее мы объясним оба вида ошибок.
Химерные фрагменты, или химеры, появляются, когда два правильных фрагмента из различных частей целевой молекулы присоединяются встык и формируют фрагмент, который не является непрерывным участком цели Пример химерного фрагмента показан на рис. 4.5. Эти ложные фрагмен ты должны быть распознаны в качестве таковых и удалены из множества фрагментов еще на стадии предварительной обработки выравнивания.
Иногда во входном множестве присутствуют фрагменты или их части, которые не имеют никакого отношения к целевой молекуле. Это происхо-
170
Глава 4
Вход:
ACCGT CGTGC ТТАС TACCGT TTATGC
Ответ
—ACCGT—
----CGTGC
ТТАС----
-TACCGT— TTACCGTGC
TTA---TGC
Рис. 4.5. Последний фрагмент в этом входном множестве — химера. Единственный способ оперировать с химерами распознавать и удалять их из входного множества прежде чем начинать сборку
ди г вследствие загрязнения клонов материалом ДНК хозяина или вектора. Как было показано в разделе 1.5.2, процесс репликации фрагмента состоит из встройки его в геном вектора, то есть организма, который будет воспроизводить и переносить в себе копии встроенного фрагмента. В конце репликации фрагмент должен быть очишен от векторной ДНК, и если эта очистка неполная, то загрязнение происходит именно на этом этапе. Когда в качестве вектора используется вирус инфицированная клетка как правило, бактериальная клетка — также может внести некоторый генетический материал во фрагмент.
Загрязнение — довольно обычное явление в практкс секвенирования. Свидетель этому — значительное количество векторной ДНК в банках данных. Иногда ученые оказываются не в состоянии отсеять векторные последовательности до начала сборки и вносят в банки данных загрязненные консенсусы.
Как и в борьбе с химерами, средство от этой проблемы проверка данных перед началом сборки. Последовательности векторов, обычно используемых в секвенировании ДНК, хорошо известны, так что нс трудно проверить все фрагменты на содержание этих последовательностей и определить, присутствует ли некоторая часть их в любом фрагменте. Обнаружение химерных фрагментов ведет к интересным алгоритмическим тадачам, но мы нс будем описывать их в этой книге. Соответствующие ссылки даны в библиографических примечаниях.
Неизвестная ориентация
Фрагменты могут быть взяты из любой нити ДНК, и мы, в общем то, не знаем, к какой именно нити принадлежит данный фрагмент. Но зато
4.1. БИОЛОГИЧЕСКИЙ АППАРАТ СЕКВЕНИРОВАНИЯ
171
мы точно знаем, что, независимо от принадлежности к той или иной нити, считывание последовательности происходит в направлении 5' —» 3'. Вследствие комплементарное™ и противоположной ориентации нитей, тот факт, что фрагмент является подстрокой одной нити, равносилен факту, что его обратный комплемент является подстрокой другой нити. В результате мы можем допустить, что все входные фрагменты являются приближенными подстроками искомой согласованной последовательности либо в исходном состоянии, либо в виде обратного комплемента. На рис. 4.6 показана задача сборки свободных от ошибок фрагментов в обеих ориентациях, первоначально неизвестных. На практике, к сожалению, приходится иметь дело как с ошибками, так и с неизвестной ориентацией фрагментов.
Вход:
CACGT
ACGT ACTACG GTACT
ACTGA CTGA
Ответ:
-> CACGT---------
-» -ACGT---------
<- —CGTAGT-------
<- -----AGTAC----
-> --------ACTGA
-> --------CTGA
CACGTAGTACTGA
Рис. 4.6. Сборка фрагментов с неизвестной ориентацией. Каждый фрагмент может быть использован в прямой или обратной ориентации. В решении мы обозначаем стрелкой выбранное направление: —» означает фрагмент в исходной ориентации. «— означает его обратный комплемент
Поскольку ориентация фрагментов не известна, в принципе мы должны перепробовать все возможные комбинации, число которых равно 2" для множества из п фрагментов. Конечно, этот метод неприемлем и поэтому его не используют в программах сборки, но он указывает на высокую сложность задач с неизвестной ориентацией.
Повторные области
Повторные области, или повторения6, — это последовательности, которые появляются в целевой молекуле два или более раз. На рис. 4.7 показан пример таких ошибок. Короткие повторения, то есть повторения, которые
6На профессиональном жаргоне часто употребляется термин «повтор», однако с точки зрения русского языка повторные области, как и вообще побые повторяющиес места или фрагменты, правильно называть повторениями. — Прим, перев.
172
Глава 4
Рис. 4.7. Повторные области. Блоки Xj и Хг представляют собой примерно одинаковые последовательности
могут быть полностью покрыты одним фрагментом, абсолютно безвредны. Настоящие проблемы вызывают более длинные повторения Кроме того, сборку могут нарушить не только идентичные копии одного повторения. Если степень подобия между двумя копиями некоторого повторения достаточно высока, то различия могут быть приняты за ошибки обращения к основаниям. При построении сборки фрагментов следует учитывать возможность появления ошибок, так что в обнаружении перекрытий обычно устанавливают некоторую степень допуска.
Проблемы, вызываемые повторениями, являются двоякими Во-первых, если какой-либо фрагмент целиком содержится в некотором повторении, то в конечном выравнивании мы можем поместить его в несколько мест, поскольку данный фрагмент может достаточно хорошо соответствовать нескольким копиям этого повторения. Можно было бы возразить, что не имеет значения, куда мы помещаем его, так как при выборе любой копии одного и того же повторения консенсус будет приблизительно тем же самым. Но все дело в том, что когда такие копии нс полностью тождественны, мы можем ослабить консенсус, поместив фрагмент не в ту копию.
Во-вторых, повторения могут быть расположены таким образом, что сборка становится существенно неопределенной; то есть две или более компоновки совместимы со входными фрагментами и приближённой длиной цели с равной степенью соответствия. Примеры обеих ситуаций представлены, соответственно, на рис. 4.8 и 4.9. Первый показывает три копии одного повторения, а второй изображает две перемежающиеся копии различных повторений. Общее свойство этих двух случаев присутствие двух различных областей, по обе стороны которых находятся одинаковые повторения. В первом примере области В и С окружены повторениями вида X. Во втором примере области В и D находятся между повторениями X и У'.
До сих пор мы обсуждали только прямые повторения, то есть повторные копии в одной и той же нити. Однако инвертированные повторения, которые являются повторными областями во встречных нитях, также могут появиться и потенциально более опасны. Всего лишь двух копий длинного инвертированного повторения достаточно, чтобы сборка стала неопределенной. Пример такой ситуации представлен на рис. 4.10.
4.1. БИОЛОГИЧЕСКИЙ АППАРАТ СЕКВЕНИРОВАНИЯ
173
А X С X В X D
Рис. 4 8 Целевая последовательность, ведущая к неопределенной сборке вследствие повторений вида XXX
А X D Y С X В	Y Е
Рис. 4.9. Целевая последовательность, ведущая к неопределенной сборке вследствие повторений вида А'У'ХИ
Неполное покрытие
Другая проблема — неполное покрытие. Покрытие в позиции I цели мы определяем как число фрагментов, покрывающих эту позицию. Покрытие — вполне определенное понятие, но его невозможно вычислить, потому что мы не знаем действительные позиции фрагментов в цели. Даже после сборки мы имеем лишь гипотетическое предположение об этих позициях. Тем нс менее мы можем вычислить среднее покрытие, складывая длины всех фрагментов и деля эту сумму на приблизительную длину цели.
Если для одной или более позиций покрытие равно нулю, то это значит, что во множестве фрагментов имеется недостаточно информации для полного восстановления цели. На рис. 4.11 показан пример цели с непо-
174
Глава 4
X поворот 180° X
Рис. 4.10. Целевая последовательность с инвертированным повторением. Область X обратный комплемент области X
крытой областью. В таких случаях лучшее, на что мы можем надеяться, компоновка для каждой отдельно взятой непрерывно покрытой области, или контига7. Например, на рис. 4.11 можно определить два контига.
Целевая ДНК
Фрагменты
Непокрытая область
Рис. 4.11. Пример неполного покрытия
Неполное покрытие возникает в силу по существу случайного характера процесса отбора фрагментов; поэтому возможно, что некоторые области окажутся не полностью покрытыми или не покрытыми вовсе. Вообще, желательно, чтобы не только один, но несколько различных фрагментов покрывали каждый отдельный участок целевой молекулы. Чем больше фраг
7Варваризм «контиг» есть калька с английского термина contig, образованного сокращением слова contiguous, которое характеризует цельные объекты, состоящие из плотно, без зазоров, пригнанных (смежных) частей. По сути в данном случае имеется в виду непрерывно покрытая область (НПО). - Прим, персе.
4.1. БИОЛОГИЧЕСКИЙ АППАРАТ СЕКВЕНИРОВАНИЯ
175
ментов мы имеем, тем более надежна наша оценка консенсуса, основанная на голосовании. Также желательно, чтобы каждая область была покрыта фрагментами из обеих нитей, поскольку, как было замечено на практике, появление серий ошибок некоторого вида возможно только в одной нити.
Обычно неполного покрытия можно избежать, отбирая больше фрагментов, но мы должны быть осторожны с этим подходом. Если целевая последовательность покрыта почти полностью, кроме отдельных непокрытых участков, то случайный отбор фрагментов может оказаться весьма неэффективным способом покрытия этих зазоров. В подобном случае может быть использован подход, называемый прямым секвенированием или обходом (см. раздел 4.1.3). Чтобы избежать формирования таких небольших зазоров, некоторые исследователи рекомендуют получать выборку фрагментов с очень высокой степенью покрытия посредством отбора фрагментов, общая длина которых достаточна для как минимум восьмикратного покрытия целевой молекулы.
Важно знать, сколько фрагментов мы должны произвести, чтобы получить необходимое покрытие. Конечно же, ответ не может быть абсолютен, так как отбор фрагментов — случайный процесс, но разумные границы могут быть определены. Здесь мы приводим важную формулу, которая при некоторых упрощающих допущениях становится общезначимой.
Обозначим длину целевой молекулы буквой Т. Допустим, что все фраг-мсп гы имеют примерно одинаковую длину I и что мы можем безошибочно распознать перекрытия по крайней мере t оснований. Если мы произвели случайный отбор п фрагментов, то ожидаемое число р кажущихся контигов определяется по следующей формуле:
р = пе-п(‘-^/т.	(4.1)
Термин «кажущийся контиг» связан с принятым допущением о том, что мы способны распознать перекрытия, только если они имеют размер по крайней мере t оснований. Таким образом, некоторые контиги, которые на самом деле представляют собой части более длинного истинного контига, могут перекрываться фрагментами меньше, чем на t оснований, и «казаться» нам двумя отдельными контигами.
Обратите внимание, что по мере возрастания числа фрагментов п величина р приближается к нулю, хотя это и кажется странным, поскольку мы знаем, что всегда существует по крайней мере один кажущийся контиг. Это происходит потому, что формула (4.1) приближённая. Она может быть использована также в контексте картирования ДПК, где число контигов является намного большим, так что разница в один или два пренебрежимо
176
Глава 4
мала. Формула полезна в том смысле, что она обеспечивает область приближённой оценки для самых разных ситуаций.
Известна также формула для определения покрытой фрагментами долн целевой молекулы. При тех же обозначениях область, покрытая точно к фрагментами, определяется как
гк =	(4.2)
к!
где с = nl/T — среднее покрытие.
4.1.3.	АЛЬТЕРНАТИВНЫЕ МЕТОДЫ СЕКВЕНИРОВАНИЯ ДНК
Думаем, что стоит упомянуть также несколько альтернативных подходов к секвенированию ДНК. Мы начнем с прямого секвенирования - метода, который может быть использован для покрытия маленьких зазоров, остающихся при получении фрагментов методом дробовика. В прямом секвенировании из последовательности около конца контига производят специальный праймер, чтобы в ходе ПЦР генерировались фрагменты, перекрывающие этот контиг, включая конец этого контига и продолжение его в целевой последовательности. Затем эти новые фрагменты секвенируют и определяют последовательность, примыкающую к контигу, таким образом наращивая его. Повторяя этот процесс, мы можем постепенно покрыть зазор, простирающийся до следующего контига. Проблема этого подхода, в основном, связана с очень высокой стоимостью получения специальных праймеров. Кроме того, каждый последующий шаг может быть выполнен только после окончания предыдущего, так что процесс по большей части последователен, а нс параллелен (но может быть осуществлен параллельно для всех зазоров).
Другую методику, которая недавно стала очень популярной, называют секвенированием с двух концов или встречным секвенированием. Методом дробовика несколько копий целевой молекулы ДНК разрывают в случайных позициях, и короткие фрагменты молекулы отбирают для клонирования и последующего секвенирования. Вспомним из раздела 1.5.2, что эти фрагменты называют встройками, потому что для амплификации их встраивают в вектор. Размер встроек варьирует в пределах от 1 до 5 т. п. н., но только приблизительно 200-700 оснований могут быть непосредственно считаны с одного конца встройки и дать секвенированный фрагмент последовательности. Однако если мы имеем подходящий праймер, то возможно в то же самое время считывать и другой конец встройки. Два фрагмента, полученные таким образом, принадлежат встречным нитям и в конечном
4.1. БИОЛОГИЧЕСКИЙ АППАРАТ СЕКВЕНИРОВАНИЯ
177
выравнивании должны быть выделены по приближённому выражению: размер встройки минус размер фрагмента. Такая дополнительная информация чрезвычайно полезна — например, при покрытии зазоров. Иногда секвенирование проводят с двух концов только в том случае, когда необходимо покрыть зазор. Стоит отметить, что метод встречного секвенирования основан на том факте, что длина встроек обычно превышает длину считываемой с них области.
Недавно был предложен подход, совершенно отличный от метода дробовика и названный секвенированием посредством гибридизации (СПГ). Этот подход состоит из сборки целевой молекулы на основании данных, полученных в результате многих реакций гибридизации участков молекулы с очень короткими, фиксированной длины, мечеными фрагментами, или зондами. Гибридизация просто показывает, связывается ли зонд (благодаря свойству комплементарности) с молекулой ДНК. Идея состоит в том, чтобы спроектировать чип ДНК, который выполняет все необходимые реакции гибридизации одновременно и выдает список всех строк длиной w, то есть w-меров, присутствующих в цели. Современная технология позволяет строить такие чипы для зондов длиной до восьми оснований. Большие размеры зондов кажутся на данный момент все еще недопустимыми8.
С методом СПГ связаны следующие важные проблемы. Ясно, что не все целевые молекулы могут быть восстановлены с помощью зондов размером всего лишь восемь оснований (см. упражнение 10). В связи с этим возникает несколько серьезных проблем. Во-первых, необходимо охарактеризовать молекулы, которые действительно могут быть восстановлены с помощью зондов такого размера. Во-вторых, реакции гибридизации не дают информации о числе появлений w-мсров в цели, а только показывают, присутствует ли такой-то w-мер в молекуле или нет. Ясно, что было бы хорошо иметь дополнительные данные о том, сколько копий фрагментов появляется в действительности. Наконец, нужно заняться проблемой погрешности экспериментов гибридизации, а также проблемой неизвестной ориентации фрагментов. Была предложена стратегия, рекомендующая сводить метод дробовика к методу гибридизации, просто используя все ш-мсры полученных фрагментов молекулы вместо самих фрагментов и представляя, что они были генерированы реакциями гибридизации. Однако эта стратегия отбрасывает некоторую информацию, потому что, как правило, невозможно восстановить фрагменты из w-меров, тогда как сами w-меры возможно генерировать из фрагментов. В этой книге мы нс рассматриваем алгорит
8Современные гибридизационные чипы могут содержать многие сотни тысяч типов зон-дов. Прим. ред.
178
Глава 4
мы решения задачи СНГ, а лишь приводим некоторые интересные ссылки в библиографических примечаниях в конце этой главы9.
4.2.	МОДЕЛИ
Вспомнив биологические основы задачи сборки фрагментов, мы готовы построить ее математические модели. В этом разделе мы представим три модели: КРАТЧАЙШАЯ ОБЩАЯ НАДСТРОКА (КОН), BOCCTAHOR4FHHF И МУЛЬТИКОНТИГ. Каждая модель освещает различные стороны вычислительной задачи, хотя ее биологические основы по-прежнему остаются в тени. Все три модели принимают допущение о том, что выборка фрагментов свободна от загрязнения инородным генетическим материалом и избегает химер.
4.2.1.	КРАТЧАЙШАЯ ОБЩАЯ НАДО РОКА
Одной из первых попыток формализовать задачу сборки фра! ментов была задача поиска кратчайшей надстроки заданного множества строк. Соответственно, ее назвали задачей поиска кратчайшей общей надстроки, или КОН. Хотя эта математическая модель имеет серьезные недостатки в формальном описании задачи сборки фрагментов (например, она не нс объясняет ошибки), методы, используемые для эффективного решения конечной вычислительной задачи, находят применение также и в других моделях. Поэтому изучение этих методов заслуживает пристального внимания. Задача поиска кратчайшей обшей надстроки может быть формализована следующим образом:
Задача: Кратчайшая общая надстрока (КОН).
Вход: Множество строк у.
Выход: Возможно кратчайшая строка S, являющаяся надстрокой всех строк f G у.
Пример 4.1. Пусть у = {ACT, СТА, AGT}. Тогда последовательность S = ACTAGT — кратчайшая общая надстрока множества Очевидно, что все фрагменты из у являются се собственными подстроками. Чтобы доказать, что она является кратчайшей, мы покажем, что любая строка S', которая содержи! строки и = ACT и и  AGT в качестве собс гвенных подстрок, должна иметь длину по крайней мере 6. Более того, при длине |S"| =6 мы
9В настоящее время идея секвенирования на гибридизационных чипах не популярна, однако эта технология привела к появлению высокоэффективных диагностических тестов и к многим другим приложениям. — Прим. ред.
4.2. МОДЕЛИ
179
имеем только сцепления uv и vu. Но строка СТА является подстрокой только для сцепления uv = S.	
В контексте сборки фрагментов множество строк соответствует множеству фрагментов, каждый из которых определен своей последовательностью в правильной ориентации, а строка S — последовательности целевой молекулы ДНК.
Заметим, что вычислительная задача предполагает, что строка S должна быть совершенной, а не приближенной надстрокой каждого фрагмента, так что она не допускает ошибок во фрагментах. Кроме того, должна быть известна ориентация всех фрагментов, что редко возможно Наконец, даже в проекте совершенной сборки, в котором все эти факторы можно так или иначе контролировать, кратчайшая обшая надстрока можег нс быть реальным биологическим решением из-за присутствия повторных областей в целевой последовательности ДНК, как показывает следующий пример
Пример 4.2. Предположим, что целевая молекула содержит две копии точного повторения и что фрагменты отобраны, как показано на рис. 4.12. Обратите внимание, что копии повторений длинны и включают в себя много фрагментов. В этом случае, даже если фрагменты являются точными подстроками консенсуса, и даже если мы знаем их правильную ориентацию, поиск кратчайшей общей надстроки может дать непредсказуемый результат.
Действительно, на рис. 4.13 изображена альтернативная сборка с более коротким консенсусом для того же самого множества фрагментов. Поскольку копии повторений идентичны, надстрока может содержать только одну копию, то есть все фрагменты, целиком содержащиеся в любой из этих копий. Другая копия может быть короче, поскольку она должна содержат!. только фрагменты, которые пересекают границу между повторением Д' и примыкающими к нему областями. На этом рисунке укороченная версия повторения X обозначена X'.
Рис. 4.12. Целевая последовательность с длинным повторением, содержащим много фрагментов. Этот пример показывает, что даже без ошибок и при известной ориеп-1 ации формулировка задачи поиска КОН теряет смысл в присутствии повторений
180
Глава 4
Рис. 4.13 Альтернативная сборка множен на фратмсшов, изображенною иа пре «идущем рисунке. Эта сборка даст более короткий консенсус, поскольку все фраг-мешы, целиком содержащиеся в правой копии (обозначенные илриховои линией), были перенесены в левую копию что и вызвало сокращение длины правой копии
Очевидно, что, хотя эта альтернативная сборка короче, она хуже как в отношении покрытия, так и сцепления. Покрытие неравномерное: повторение X покрыто гораздо большим числом фра! ментов, чем повторная область Сцепление плохое, потому что никакой фрагмент не связывает левый край повторения X' с его правым краем. Фактически, этот консенсус представляет собой сцепление двух несвязанных частей и и г>, где часть и простирается от начала сборки до приблизительно середины X', а часть т от середины X' до конца сборки. Поскольку мы ищем кратчайшие налегро-ки, сцепление vu было бы вполне равнозначным консенсусом.	
Задача поиска КОН является НП-трудной, но для се решения существуют алгоритмы аппроксимации. Однако, учитывая все недостатки этой модели по отношению к реальной биологической задаче, такие алгоритмы вызывают главным образом теоретический интерес.
4.2.2.	ВОССТАНОВЛЕНИЕ
Эта модель учитывает и ошибки и неизвестную ориентацию. Прежде чем говорить об ошибках, необходимо дать несколько новых определений. Вспомним из главы 3, что мы можем преобразовать основной алгоритм (метода динамического программирования) сравнения последовательностей таким образом, чтобы он удовлетворял многим различным потребностям. Здесь мы будем использовать меру расстояния, а нс подобия, и версию алгоритма, которая штрафует только крайние пропуски во второй последовательности. Система очков — редактирующее расстояние; то есть одна единица расстояния назначается за каждую операцию вставки, удаления или замены знака, кроме удалений в крайних позициях второй последовательности, которые являются «бесплатными». Вычисленное таким образом расстояние будем называть редактирующим расстоянием подстроки, чтобы
4.2. МОДЕЛИ
181
отличать его от классического редактирующего расстояния, которое штрафует крайние удаления в обеих строках. Мы обозначим его ds и формально опишем его выражением
dB(a,b) = min d(a,s), s£S(b)
где S(b) обозначает множество всех подстрок строки b, a d — классическое редактирующее расстояние. Следует помнить, что редактирующее расстояние подстроки — асимметрическая функция, то есть в общем случае dB(a, b) dB(b, а).
Пример 4.3. Если а = GCGATAG и b - CAGTCGCTGATCGTACG, то оптимальное выравнивание соответствует представленному на рис. 4.14, а редактирующее расстояние dB(a, b) =2.	
------GC-GATAG-------
CAGTCGCTGATCGTACG
Рис. 4.14. Оптимальное выравнивание с таким редактирующим расстоянием подстроки при котором не штрафуются крайние пропуски в первой строке
Пусть е — вещественное число между 0 и 1. Тогда строка / является приближённой подстрокой строки S с частотой появления ошибок г. когда
dB(f,S)^e\f\,
где |/| — длина строки /. Это означает, что мы допускаем появление в среднем 6 ошибок на одно основание в приближённой подстроке /. Например, если 6 = 0,05, то мы допускаем пять ошибок на сотню оснований. Теперь мы в силах формально описать задачу сборки фрагментов с помощью модели ВОССТАНОВЛЕНИЕ.
Задача: Восстановление.
ВХОД: Множество строк и допустимый коэффициент ошибок е со значением от 0 до 1.
ВЫХОД: Возможно кратчайшая строка S. причем для каждой строки / С У мы имеем неравенство
min(ds(/,S),ds(/,S))O|/|,
где / — обратный комплемент строки /.
182
Глава 4
Идея данной модели заключается в отыскании таков возможно кратчайшей строки S, чтобы строка f (либо ее обратный комплемент /) была приближённой подстрокой строки S при частоте появления ошибок е. Данная формулировка корректна для всех примеров, приведенных в разделе 4.1, кроме одного — с химерным фрагментом. Однако обшая задача по-прежнему НП-трудная. В обшем, это не удивительно, поскольку она включает в себя задачу КОН в качестве частного случая с е = 0 (см. упражнение 18).
Итак, модель ВОССТАНОВЛЕНИЕ учитывает ошибки и ориентацию, но заю не учи1ывает повторения, неполное покрытие и размер цели.
4.2.3.	МУЛЬТИКОНТИГИ
Модель МУЛЬТИКОНТИГ учитывает фактор сцепления. Предыдущие модели нс заботятся о внутреннем сцеплении фрагментов в компоновке важен только окончательный ответ. Таким образом, модель выдает ответы, сформированные несколькими контигами, и по этой причине их называют «мультиконтнгами»10.
Сначала мы даднм определение версии модели МУЛЬТИКОНТИГ, основанной на допушенин об отсутствии ошибок. Имея на входе множество фрагментов J7, мы строим множественное выравнивание, или компоновку. Компоновка должна быть такой, чтобы каждый столбец содержал основания только одного типа. Именно это требование и отражено в гипотезе об отсутствии ошибок. Кроме того, для учета ориентации фрагментов мы требуем, чтобы в выравнивании находились либо фрагмент, либо его обратный комплемент, но никак не оба.
Компоновку, отвечающую этим требованиям, обозначим буквой £. Мы нумеруем столбцы цифрами от 1 до | £ | - длины компоновки. Согласно этой нумерации, каждый фрагмент f имеет левую конечную точку 1(f) и правую конечную точку r(f), так что |/| = r(f) — 1(f) + 1. Тогда, если целочисленные интервалы [1(f).. -r(f)] и [1(g) ...г(§)] пересекаются, то мы говорим, что фрагменты I и д перекрываются в этой компоновке. Непустое пересечение [1(f)    г(/)] П [1(g)    г(</)] называют перекрытием между фрагментами f и д. Таким образом, размер перекрытия фрагментов равен размеру пересечения соответствующих интервалов. Поскольку мы используем целочисленные интервалы, все множества конечны.
Из всех перекрытий между фрагментами мы интересуемся только самыми важными — теми, которые обеспечивают сцепление. Мы говорим,
|0По сути, это multiple contigs, то есть множественные непрерывно покрытые области (МНПО). Прим. перев.
4.2. МОДЕЛИ
183
что перекрытие [х.. .у] — не связь, если во множестве Т существует фрагмент, который полностью содержит перекрытие с обеих сторон, то есть если фрагмент содержит интервал [(а; — 1)... (у + 1)]. Если никакой фрагмент не обладает таким свойством, то перекрытие — связь. Слабейшая связь в компоновке — любая связь наименьшего размера. Наконец, мы говорим, что компоновка представляет собой t-контиг, если размер се слабейшей связи равен по крайней мере t. Если из фрагментов множества Т возможно построить t-кон гиг, то мы говорим, что множество Т допускает /-контиг.
Теперь мы можем формализовать задачу сборки фрагментов с помощью модели МУЛЬТИКОНТИГ. Имея множество фрагментов F и целое число t, мы хотим разбить множество F на минимальное число подмножеств Ci, где 1 гк, с тем чтобы каждое подмножество Сг допускало t-контиг.
Пример 4,4. Пусть F = {GTAC, TAATG, TGTAA}. Мы хотим разбить множество F на минимальное число t-контигов. Если t = 3, то это число равно двум:
—TAATG	GTAC
TGTAA—
Нс существует никакого способа покрыть один отдельный контиг всеми тремя фрагментами, так что возможный в этом случае минимум — два контига. Интересно отметить, что строка GTAC — собственный обратный комплемент.
Если t = 2, то же самое решение — разбиение на 2-контиги, так как каждый 3-контиг равен 2-контигу. Однако существует и другое решение:
TAATG---- GTAC
---TGTAA
Здесь снова невозможно собрать множество F в один t-контиг.
Наконец, сели t = 1, то мы видим, что сушсствуст решение с одним t-контигом:
TGTAA------
—TAATG-----
-------GTAC

Версия модели, учитывающая ошибки, может быть определена следующим образом. Компоновка не обязательно должна быть свободна от
184
Глава 4
ошибок, но с каждым выравниванием мы должны ассоциировать согласованную последовательность S одинаковой длины, возможно содержащую знаки пробелов (-). Числа 1(f) и г(/) по-прежнему определяются как крайний левый и крайний правый столбцы фрагмента f в выравнивании, но теперь мы допускаем |/| r(f) — 1(f) + 1. Подстроку S[l(f).. .г(/)] мы называем образом выровненного фрагмента f в консенсусе. Задавшись допустимым коэффициентом ошибок 6, мы говорим, что если редактирующее расстояние между каждым выровненным фрагментом / и его образом в консенсусе равно самое большее б|/|, то строка S — е-консенсус данного контига. Теперь мы готовы к формальному определению.
Задача: мультиконтиг.
ВХОД: Множество строк J7, целое число t J 0 и допустимый коэффициент ошибок 6, со значением от 0 до 1.
ВЫХОД: Разбиение множества Т7 на минимальное число подмножеств Ci, где 1 г к, с тем чтобы каждое подмножество Ci допускало ^-контиг с е-консснсусом.
Обратите внимание, что в модели восстановление фрагмент просто обязан быть приближённой подстрокой последовательности S, но конкретная позиция его выравнивания в S не важна. Напротив, в формулировке задачи МУЛЬТИКОНТИГ мы должны явно указать позицию каждого фрагмента.
Даже в простейшем случае (без ошибок и с известной ориентацией) формальное описание сборки фрагментов с помощью модели МУЛЬТИКОП-ТИ1 представляет собой НП-трудную задачу. В качестве частного случая математическая модель мультиконтиг включает в себя задачу о Гамильтоновом пути в графах строго определенного класса.
Эта модель учитывает ошибки, ориентацию и неполное покрытие, но не предоставляет никакой возможности использования данных о приближённом размере целевой молекулы. Кроме того, она частично моделирует повторения в том смысле, что она может удовлетворительно решать некоторые варианты задачи с повторениями, хотя и не все из них. Например, она может правильно восстановить согласованную последовательность, представленную на рис. 4.12.
4.3.	* АЛГОРИТМЫ
В этом разделе мы представляем два алгоритма сборки фрагментов, свободных от ошибок и с известной ориентацией. Первый известен как
4.3. * АЛГОРИТМЫ
1X5
жадный алгоритм; многие практические системы были созданы на основе той же самой идеи, но с дополнениями, которые позволяют учитывать ошибки и неизвестную ориентацию. Второй алгоритм основан на модели МУЛЬТИКОНТИГ и полезен, когда, отбрасывая ребра с малым весом, мы можем получить ациклический граф перекрытий. Следует упомянуть, что из-за ограничивающей гипотезы, на базе которой они построены, сами алго-ригмы имеют небольшую практическую ценность. Тем не менее, заложенные в них идеи могут быть полезны при построении алгоритмов решения прикладных вариантов этой задачи.
4.3.1.	ПРЕДСТАВЛЕНИЕ ПЕРЕКРЫТИЙ
Общие надстроки соответствуют путям в некоторой топологической структуре, построенной на множестве J7. Мы можем наделить пути свойствами соответствующих им надстрок. Поскольку к настоящему времени теория графов разработана достаточно хорошо, многие задачи возможно (а часто и очень удобно) описывать при помощи графов.
Мультиграф перекрытий ОЛДУ) множества у — это ориентированный взвешенный мультиграф, определяемый следующим образом Множество узлов V графа представлено множеством строк у. Ориентированное ребро с весом t 0, идущее от фрагмента a G у к другому фрагменту b € У, существует, если суффикс фрагмента о, содержащий t знаков, является префиксом фрагмента Ь. В символьной записи это утверждение принимает вид:
suffix(a, t) = prefix(b, t),
или
ИЛИ
(як‘)6 = а(к‘Ь),
где к — облитератор (определение см. в разделе 2.1). Обратите внимание, что это ребро существует только при |а| t и |b| t. Учтите также, что между фрагментами а и b может существовать множество ребер, соответствующих различным значениям t. Именно поэтому данную топологическую структуру называют мультиграфом, а не просто графом. Следует отмстить, что мы запрещаем петли, то есть ребра, выходящие из узла и входящие обратно в себя же, но допускаем ребра с нулевым весом.
186
Глава 4
Скажем несколько слов о весах ребер. Реберные веса представляют перекрытия между фрагментами, и мы используем перекрытия, чтобы объединять фрагменты в более длинные строки посредством перекрытия общих частей. Такое объединение означает, что мы допускаем, что два объединяемых фрагмента принадлежат одной и той же области в целевой ДНК. Но это допущение должно быть как-то обосновано. В нашем случае обоснованием служит размер перекрытия. Короткое перекрытие обеспечивает слабое обоснование, тогда как длинное перекрытие дает прочное обоснование. Когда обрабатывают сотни фрагментов, каждый длиной несколько сотен знаков, было бы безрассудно допускать, что два фрагмента имеют общие концы, основываясь на перекрытии, скажем, трех знаков. По этой причине мы иногда устанавливаем минимально допустимое количество перекрытия и отбрасываем все ребра с весом ниже этого порога. Но, в принципе, мы будем сохранять все ребра в мультиграфе, включая ребра с нулевым весом. Существует всего п(п—1) таких ребер, потому что любые две строки имеют условное перекрытие из нулевых знаков.
4.3.2.	ПУТИ, ПОРОЖДАЮЩИЕ НАДСТРОКИ
Мультиграф перекрытий важен, потому что ориентированные пути в нем дают множественное выравнивание последовательностей, которые принадлежат этому пути. Путем построения общей надстроки множества последовательностей из этого выравнивания может быть получена согласованная последовательность. Рассмотрим этот процесс подробнее.
Имея ориентированный путь Р в мультиграфе перекрытий ОМ(р), мы можем следующим образом построить множественное выравнивание последовательностей, составляющих путь Р. Каждое ребро е = (f, д) этого пути имеет некоторый вес t, и это означает, что t конечных оснований в хвосте / ребра с составляют префикс головы д ребра е. Таким образом, хвост f и голова д могут быть выровнены, причем голова д должна быть расположена на I позиций раньше конца хвоста /.
Пример мультиграфа перекрытий приведен на рис. 4.15. Изображены только ребра со строго положительным весом. Здесь множество р множество строк {а, Ь, с, rf}, где
а = TACGA, b = АССС, с = CTAAAG, d = GACA.
4.3. * АЛГОРИТМЫ
187
TACGA
Рис. 4.15. Мультиграф перекрытий; ребра с нулевым весом не показаны
Обычно мы описываем пути при помощи списка: вершина, ребро, вершина, ребро, ..., вершина, где каждое ребро соединяет две вершины, соседние с ним в списке. Однако в этом примере нет параллельных ребер, так что для простоты мы будем описывать пути только списком принадлежащих им вершин. Путь Pi = dbc дает следующее выравнивание:
GACA--------
------АССС-- ------------CTAAAG
тогда как путь Рг = abed порождает другое выравнивание:
TACGA- ------------АССС-------- ----------------CTAAAG---------- ----------------GACA
В общем случае, пусть Р — путь в мультиграфе перекрытий С?Л4(Р) и А — множество фрагментов, принадлежащих пути Р. По определению, вершины в путях не могут повторяться, так что путь Р содержит точно |Л| — 1 ребро. Общую надстроку, порождаемую путем Р, обозначим S(P)
Соотношение между общей длиной фрагментов А, весом пути и длиной надстроки описывает уравнение вида
||Л||=ш(Р) + |5(Р)|,
(4.3)
188
Глава 4
где ||Д|| =	|а| — сумма длин всех последовательностей во множе-
стве Л; w(P) — вес пути Р. Верно ли это соотношение? Проверим его на нескольких простых примерах.
Начнем с пути, содержащего единственный фрагмент f и ни одного ребра. Тогда А = {/}, ||Л|| = |/| и w(P) = 0, поскольку путь Р не имеет ребер. Кроме того, общая надстрока S(P) состоит из единственного фрагмента /. Легко видеть, что уравнение (4.3) в этом случае верно. Попробуем увеличить дистанцию. Предположим, что путь Р = /161/262.../< и что формула для него верна. Что случится, если мы введем в этот путь дополнительное ребро? Тогда при w(ej+i) = к мы имеем Р' = PtT+i/i+i и
w(P') = w(P) + w(el+i) = w(P) + к.
С другой стороны, S(P') = S(P)suffix(fi+i,\fi+i\ к), потому что первые к «наков фрагмента /;+1 уже присутствуют в общей надстроке S(P). Мы должны прицепить только оставшийся суффикс фрагмента fi+i. Тогда
|S(P')|=|S(P)| + |/1+1| - к =
=||Л|| - w(P) + |/1+1| -к = =||Л'|| - ш(Р’)
и формула по-прежнему верна. Мы только что доказали уравнение (4.3) методом индукции.
Другой способ его записи — с помощью облитератора. Если путь Р = = /161/262 • • - /ь то
S(P) =
В этом случае правая часть формулы не является неопределенной, поскольку, согласно определению веса ребра,
(/*кю(е<))/*+1 = /.(Kw(ei)/.+i)-
Тогда длина обшей надстроки
|£(Л1=1/11 - w(fii) + I/2I - w(e2) +---w(ef_i) + |/f| =
= Е l/.|- Ew(ei) =
=||А|| - w(P).
Итак, каждый путь порождает общую надстроку составляющих его фрагментов. Это особенно важно, когда мы имеем путь, который обходит все
4.3. * АЛГОРИТМЫ
189
вершины. Такие пути называют Гамильтоновыми (см. раздел 2.2). Если мы провели Гамильтонов путь, то мы имеем общую надстроку множества А = р. В этом случае уравнение (4.3) преобразуется к виду
|S(P)| = ||^||-w(P)	(4 4)
и, поскольку — постоянная величина, то есть не зависит от выбора Гамильтонова пути, постольку мы видим, что минимизация |S(P)| равносильна максимизации »'(Р).
4.3.3.	КРАТЧАЙШИЕ НАДСГРОКИ В КАЧЕСТВЕ ПУТЕЙ
В предыдущем разделе мы выяснили, что каждый путь соответствует надстроке. Верно ли обратное? Не всегда, как показывает следующий пример Для множества фра!мснтов, породившего граф на рис 4.15. надстрока
GTATACGACCCAAACTAAAGACAGGG
нс соответствует никакому пути, и легко увидеть почему Надстроки могут содержать лишние знаки, которые нс встречаются ни в одном из фрагментов множества
Но крат чайшие падстроки не могут содержать избыточные знаки. Итак, всегда ли кратчайшие надстроки соответствуют путям? Ответ является утвердительным, и далее мы докажем это утверждение Мы сначала покажем, что это верно для гак называемых не содержащих подстрок множеств и затем распространим наше доказательство на любые множества.
Говорят, что множество У7 нс содержит подстрок, если в нем нет никаких двух различных строк а и Ь, таких, что а является подстрокой Ь. Преимущество нс содержащих подстрок множеств состоит в том, что в них легче доказать частичную обратимость построения типа путь надстрока
Теорема 4.1. Пусть р — не содержащее подстрок множество. Тогда для каждой общей падстроки S множества р в мультиграфе перекрытий ОМ{р) существует такой Гамильтонов путь Р, что общая надстрока S(P) является подпоследоватегьностью общей надстроки S
ДОКАЗАТЕЛЬСТВО. Строка S — общая надстрока множссзва р, так что для каждого фрагмента f G р существует такой интервал [/(/)... r(f)] строки S, что S[l(f).. . г(/)] = /. Для некоторых фрагментов может существовать множество позиций, в которых их можно прикрепить. Это нс имеет значения Выберем и запомним одну из них.
190
ГЛАВА 4
Никакой интервал вила [/(/).. .г(/)] не содержится в другом таком интервале, потому что множество У не содержит подстрок. Эти интервалы обладают следующим важным свойством. Все левые крайние точки различны и все правые крайние точки различны, хотя могут существовать левые крайние точки, равные правым крайним точкам. Более того, если мы сортируем фрагменты по возрастанию левых крайних точек, то правые крайние точки также образуют порядок возрастания. Действительно, если из множества р мы выберем две строки fug, где 1(f)	1(g) и r(f) т(д), то
интервал строки д будет содержаться в интервале строки /, что является невозможным. Итак, мы получили интервалы, сортированные по возрастанию начальных, а также конечных точек. Пусть (fi)i=i,...,m — такое упорядочение. Фрагменты в этом порядке составляют требуемый путь.
Рассмотрим соотношение между фрагментами ft и /,+] для всех г, где 1	— 1. Если Z(/l+i) r(fi) + 1, то в ОМ(Р) существует ребро
с весом r(fi) + 1 - /(/i+i). Если Z(/i+i) > r(ff) + 1, то мы выбираем ребро с нулевым весом, идущее от узла fi к узлу /,+j. Знаки S[J] для r(fi) + + 1 Sj j Sj l(fi+i) — 1 будут отброшены, потому что они не принадлежат никакому интервалу и. следовательно, являются избыточными, поскольку мы ищем именно общую надстроку. Эти знаки находятся в надстроке S, но не в S(P), которая поэтому представляет собой подпоследовательность общей надстроки S.	
Следствие 4.1. Пусть р — не содержащее подстрок множество. Если S — кратчайшая общая надстрока множества р, то существует такой Гамильтонов путь Р, что S = S(P).
Доказательство. Согласно предыдущей теореме, такой путь существует, причем строка S(P) является подпоследовательностью кратчайшей обшей надстроки S. Но строка S(P) также является общей надстрокой, потому что путь Р является Гамильтоновым. Поскольку S — кратчайшая общая надстрока, мы имеем |S(P)|	|S| и поэтому S = 8(Р).	
Теперь мы обобщим это доказательство для любых множеств. Сначала введем несколько новых определений. Множество фрагментов р доминирует над другим множеством Q, когда каждый фрагмент g Е Q является подстрокой некоторого фрагмента f 6 _Р. Например, если Q С р, то р доминирует над Q. Говорят, что два множества р и Q эквивалентны (обозначается Р = Q), когда р доминирует над Q, и Q также доминирует над р. Эквивалентные множества имеют одинаковые надстроки, так что для нас это понятие очень важно.
4.3. * АЛГОРИТМЫ
191
Лемма 4.1. Два эквивалентных не содержащих подстрок множества являются тождественными
Доказательство. Если д = Q и множество Д не содержит подстрок, то Д С (J. Чтобы показать это, рассмотрим фрагмент f 6 Д. Поскольку множество Q доминирует над Д, то должен существовать такой фрагмент g е Q, чтобы фрагмент f был подстрокой фрагмента д. Но множество Д также доминирует над (?, так что во множестве Д существует надстрока h фрагмента д. По свойству транзитивности фрагмент f является подстрокой фрагмента h. Но множество Д не содержит подстрок, так что f = h, и, поскольку фрагмент д находится «между» ними, f = д = h. Из этого следует, что f = д е б Поскольку выбор фрагмента f произволен, мы заключаем, что Д б То же самое рассуждение при обратном порядке множеств Д и б показывает, что б С Д. Следовательно, Д = б-	
Следующая теорема помогает нам понять, как получить не содержащее подстрок множество из множества произвольно отобранных фрагментов.
Теорема 4.2. Пусть Д — множество строк. Тогда существует однозначно определенное не содержащее подстрок множество б. эквивалентное множеству Д.
Доказательство. Однозначную определенность множества гарантирует предыдущая лемма. Докажем его существование. Мы хотим показать, что для каждого множества Д существует не содержащее подстрок множество б, эквивалентное множеству Д. Мы сделаем это индукцией на числе строк во множестве Д.
При | Д | = 0 множество Д само по себе не содержит подстрок и теорема доказана. При Д |	1 множество Д может либо содержать, либо
не содержать подстрок. Если не содержит, то мы снова считаем теорему доказанной. Если содержит, то во множестве Д существуют такие строки а и Ь, что строка а является подстрокой Ь. Удалим строку а из множества Д и получим меньшее множество Д' = Д {а}. Согласно индуктивному предположению, множеству Д’ соответствует эквивалентное не содержащее подстрок множество б- Но легко убедиться, что Д = Д'. Ясно, что Д доминирует над Д', поскольку Д' является подмножеством множества Д. С другой стороны, единственная строка, принадлежащая множеству Д, но при этом не принадлежащая его подмножеству Д', строка а, которая является частью строки Ь е Д'. Следовательно, множество б также эквивалентно множеству Д и теорема полностью доказана.	
Данная теорема свидетельствует о том, что, если мы ищем общие надстроки, то, пожалуй, мы могли бы ограничиться не содержащими подстрок
192
Глава 4
множествами, потому что для любого множества существует эквивалентное ему не содержащее подстрок множество, то есть имеющее те же самые общие надстроки. Кстати, доказательство теоремы 4.2 также дает нам способ получить однозначно определенное не содержащее подстрок множество, эквивалентное данному множеству J7. Для этого достаточно всего лишь удалить из множества У все строки, которые являются подстроками каких-либо компонентов множества у.
4.3.4.	ЖАДНЫЙ АЛГОРИТМ
Теперь мы знаем, что поиск кратчайших общих надстрок равносилен поиску Гамильтоновых путей с максимальным весом в ориентированном мультиграфс. Болес того, поскольку наша цель состоит в максимизации веса, мы можем упростить мультиграф и рассматривать только самые тяжелые ребра между каждой парой узлов, отбрасывая другие, параллельные ребра меньшего веса. Любой путь, который не использует самое тяжелое ребро между парой узлов, может быть улучшен, и, следовательно, он не является путем с максимальным весом. Назовем этот новый граф графом перекры тии множества Т7 и обозначим его	На практике мы не строили бы
эти ребра одно за другим Используя суффиксные деревья (см. раздел 3 6 3) мы можем строить ребра одновременно, экономя и пространство памяти и время счета компьютера (см. библиографические примечания). Подобные структуры могут помочь в обнаружении фрагментов, являющихся подстроками каких-либо других фрагментов множества и поэтому могущих быть не включенными в граф
Следующий алгоритм «жадная» попытка вычисления самого тяжелого пути. Основная идея, заложенная в нем непрерывно добавлять к пути самое тяжелое ребро, не нарушающее при этом текущий Гамильтонов путь, построенный на ранее выбранных ребрах. Поскольку этот граф полный, то есть в нем есть ребра между каждой парой узлов, этот процесс останавливается только тогда, когда будет сформирован путь, содержащий все вершины
В Гамильтоновом или практически в любом пути для этой задачи мы не должны иметь двух ребер, выходящих из одного и того же узла, или двух ребер, входящих в один и тот же узел. Кроме того, мы должны предотвратить формирование циклов. Итак, мы имеем три условия, которые мы должны проверять перед принятием каждого нового ребра в Гамильтонов пуль. Ребра обрабатываются в порядке невозрастания веса, и процедура заканчивается, когда мы имеем точно п — 1 ребро, то есть когда принятые ребра индуцируют связный подграф.
4.3 * АЛГОРИТМЫ
193
На рис. 4.16 показан алгоритм. Для каждого узла мы сохраняем текущие значения его полустепсни захода и полустепени исхода относительно принятых ребер. Эта информация используется для проверки того, имеет ли предыдущее выбранное ребро тот же самый хвост или голову, как исследуемое в данный момент ребро. Кроме того, мы сохраняем непересекающиеся множества, которые формируют связные компоненты графа, индуцируемые принятыми ребрами. Легко видеть, что новое ребро формирует цикл тогда и только тогда, когда его хвост и голова находятся в одном и том же компоненте. Поэтому эту структуру необходимо проверять на наличие циклов. Непересекающиеся множества поддерживаются структурой данных типа леса непсрссскающихся множеств (см. раздел 2.3).
\lgorithm Greedy'1
input: взвешенный орграф OG(F) на п вершинах
output: Гамильтонов путь в графе OQ(F)
И Инициализация
tor г <— 1 to п do
/и [г] <— 0 // сколько выбранных ребер входят в г
ouf[i] <— О И сколько выбранных ребер выходят из г
MakeSet(i)
И Обработка
Сортировать ребра по убыванию веса
for каждого ребра (/, д) в данном порядке do
И проверка ребра на приемлемость
if tn[p] — 0 and out /] = 0 and FindSet(f) ^FindSet(g) выбрать (f,g) '«If/1 ч- 1 ow/[/] «- 1
Union(FindSet(f), FindSet(g))
if получен только один компонент
break
return выбранные ребра
Рис. 4.16. Жадный алгоритм построения Гамильтонова пути
Мы описали жадный алгоритм для задачи на графах, но он может быть применен с непосредственным использованием самих фрагментов Алгоритм соответствует следующей процедуре, непрерывно применяемой ко множеству фрагментов, до тех пор, пока не останется только один фрагмент. Выбираем пару (f,g) фрагментов с наибольшим перекрытием к, удаляем
"Жадный При.» перев
194
Глава 4
эти два фрагмента из множества Т7 и добавляем кон гиг /ккд ко множеству J:. Мы основываемся на допущении, что множество У нс содержит подстрок.
Однако, как показывает следующий пример, эта жадная стратегия не всегда производи! наилучший результат.
Пример 4.5. Предположим, что мы имеем множество
F - {GCC, ATGC, TGCAT}.
Граф перекрытий показан на рис. 4.17, где мы опустили ребра с нулевым весом, чтобы избежать загромождения рисунка.
Рис. 4.17. Граф, в котором жадный алгоритм дает сбой
В этом графе ребро с весом 3 — первое, которое будет исследовано и, очевидно, принято, потому что первое ребро всегда принимается. Однако при этом два ребра с весом 2 автоматически признаются непригодными, так что для завершения Гамильтонова пути алгоритм вынужден выбрать ребро с нулевым весом. И это при том, го два отброшенных ребра формируют пут ь с общим весом 4, то есть самый тяжелый путь в данном примере. 
Этот пример показывает, что жадный алгоритм не всегда возвращет кратчайшую надстроку. Существует ли алгоритм, который надежно работает во всех случаях? По-видимому, нет. Мы пытаемся решить задачу поиска КОН с помощью задачи о Гамильтоновом пути; но, как мы видели в разделе 2.3, задача о Гамильтоновом пути является НП-полной. Возможно, мы могли бы получить лучшие результаты, применив другой подход к решению задачи поиска КОН. К сожалению, по всей вероятности, это тоже не выход, поскольку, как уже было упомянуто, можно показать, что задача поиска КОН является НП-трудной.
4.3. * АЛГОРИТМЫ
195
4.3.5.	АЦИКЛИЧЕСКИЕ ПОДГРАФЫ
Выводы о трудности, которые мы упоминали в предыдущем разделе, относятся к произвольной выборке фрагментов. В этом разделе мы рассмотрим задачу сборки фрагментов без ошибок и с известной ориентацией, допуская, что эти фрагменты были взяты из «хорошей выборки» целевой ДНК. Как будет показано далее, это допущение позволяет нам построить алгоритмы, которые дают верное и особенно эффективное решение.
Что мы подразумеваем под «хорошей выборкой»? Как правило, мы хотим, чтобы фрагменты полностью покрывали целевую молекулу, и чтобы множество в целом показывало сцепление, достаточное для гарантии надежности сборки. Вспомним определение t-контига из раздела 4.2.3. В этом разделе все определения основаны на подобных понятиях.
Предположим, что S — строка знаков из алфавита {А, С, G, Т}. Согласно определению из раздела 2.1, интервал строки S это такой целочисленный интервал [i.. .j], что 1 С i С j + 1 С |S| + 1. Выборкой строки S называют множество Д интервалов строки S. Выборка А покрывает строку S, если для любого г. такого, что 1 С Д |S'|, мы имеем по крайней мерс один интервал [j ... к] & А, где г С [j ... /с].
Мы говорим, что два интервала а и /3 сцеплены на уровне t, если |<э С (3\ t. Полная выборка А, как говорят, связна на уровне t, если для каждых двух интервалов п и р из выборки А существует такой ряд интервалов аг (где 0 С i /), что а = ао> Р = а/ и интервал оц сцеплен с <тг+1 на уровне t при 0 С г С I — 1. Обратите внимание, что мы используем параметр t в качестве меры того, насколько сцепление сильное. Выборка А считается хорошей, если она связна на уровне t.
Наша цель состоит в том, чтобы изучить множества фрагментов, получаемые из связных на уровне t выборок, покрывающих некоторую строку S. Обычно в практических приложениях значение t примерно равно 10, но в нашем примере мы не будем его фиксировать. Все же мы сделаем допущение, что t - неотрицательное целое число.
Множество фрагментов, порожденное выборкой А, равно
£ = [Д1 = -№] I о ед}.
Мы говорим, что выборка Д не содержит подынтервалов, если в ней не существует никаких двух интервалов [г... j] и [/с... /], таких, что [г ... j] С С [А-... I]. Следующее свойство не содержащих подынтервалов выборок мы будем упоминать часто. В нс содержащей подынтервалов выборке никакие два интервала нс могут иметь одинаковую левую крайнюю точку. Иными словами, какой бы интервал ни имел большую (из двух) левую крайнюю
196
Глава 4
точку, он обязательно будет включать в себя и другую. Аналогичное рассуждение справедливо и для правых крайних точек.
Графы перекрытий могут быть преобразованы следующим образом. Имея множество J7, неотрицательное целое число t и мультиграф перекрытий ОЛ4.(У), мы получаем граф ОМ(^Л), сохраняя в OM(F) только ребра с весом, равным по крайней мере t. Подобное же построение определяет граф OQ(^,t). Такое преобразование позволяет уменьшить общее число ребер и сохранить лишь более тяжелые.
Мы будем использовать символ [] для обозначения ряда соотношений: |а| w, |/3| w и l(/3) + w— 1 = г(п). Точно так же f д означает, что в графе ОМ^) существует ребро с весом ш, идущее от вершины / к вершине д.
Предположим теперь, что мы имеем такое множество Т и хотели бы восстановить надстроку S. Как мы можем сделать это? Каковы хорошие алгоритмы для такой задачи? Оказывается, ответ однозначно зависит от структуры повторений в надстроке S. Если S не содержит никаких повторений размером t или больше, то ее восстановление не составляет труда. Но если S содержит такие повторения, то задача становится более сложной, и в некоторых случаях надстрока S не может быть восстановлена без присутствия неопределенности.
Существование Гамильтонова пути в графе	t) нс зависит от
структуры повторений в надстроке S. Перед тем, как приступить к анализу структуры повторений в надстроке S, мы сформулируем и докажем это основное свойство. Сначала докажем вспомогательную лемму.
Лемма 4.2. Пусть S — строка знаков из алфавита {А, С, G, Т} и А — не содержащая подынтервалов связная на уровне t выборка строки S, при некотором t 0. Если а — интервал выборки Д, такой, что в А существует другой интервал, /3, причем 1(a) < 1((3), то интервал /3 может быть выбран так, чтобы удовлетворялось неравенство
r(a) + 1 - l(/3) I.
Доказательство. Мы знаем, что выборка А связна на уровне t, поэтому в выборке А существует такая последовательность интервалов что л = Од. /3 = at и |<kt П ol+i| t при 0 г I — 1.
Пусть г — наименьший индекс, при котором 1(a) < l(at). Поскольку равенство /3 = at удовлетворяет этому условию, мы знаем что г I. С другой стороны, г > 0, потому что равенство а = аи нс удовлетворяет этому условию. Поскольку г — наименьший индекс, то, согласно условию,
4 3 * АЛГОРИТМЫ
197
мы имеем Z(a4_j) < 1(a) < 1(аг). Из этого следует, что r(a4_i) < г(а) < < т(а,), поскольку выборка А не содержит подынтервалов Граф изображен на рис. 4.18.
Рис 4.18. Три взаимно перекрывающихся интервала
Мы также знаем, что |a4_j Па4| > t. Но |оСаг| 5г |«i-i Г)а4| > t (см.
рис 4 18), так что аг является интервалом в выборке Л, таким, что
г(о) + 1 — 1(аг) t.
Теперь докажем теорему о существовании Гамильтонова пути.
Теорема 4.3. Пусть S — строка знаков из алфавита {А, С, G, Т} и Л — не содержащая подынтервалов связная на уровне t выборка строки S, для некоторого t 0. Тогда мультиграф OM(Jr,t), где ? - множество фрагментов, порожденное выборкой Л, допускает Гамильтонов путь Р Кроме того, если выборка Л покрывает строку S, то путь Р может быть выбран так, чтобы S(P) — S
Доказательство. Пусть	— последовательность всех интер-
валов из выборки Л, сортированных по левой крайней точке. Поскольку выборка Л нс содержит подынтервалов, эта последовательность оказывается сортированной также и по правой конечной точке. Пусть фрагмент /4 = к
= S[a4] при 1 i п. Мы утверждаем, что /4 Л fi+i для некоторого kt t, так что узел /г в вышеупомянутом порядке формирует Гамильтонов путь.
Пусть аг — любой интервал, кроме последнего. Согласно предыдущей лемме, существует другой интервал в € Л, такой, что Z(a4) < 1(0) и г(а4) + + 1-1(0) t. Последовательность (a4)i^4^n сортирована по левой крайней точке, так что Z(o4) < 1(ацл) 1(0). (Интервалы a4+i и 0 могут оказаться одним и тем же интервалом.) Следовательно,
кг = |а4Па4+1| = |[Z(o4+i).. г(а4)]| =
= г(а4) - Z(ft4+i) + 1 > r(a4) + 1 - 1(0) t.
198
Г1АВА4
Это соотношение показывает, что в графе ОЛ4(р. t) действительно существует ребро /г —> f,+i, и завершает доказательство первой части теоремы.
Доказательство второй части, которая гласит, что S(P) = S, построим на следующем свойстве. Каждый раз, когда верно а 0, мы имеем также S[o] Д[Д] и тогда Д[а]к“Д[Д] = Д[л U Д].	
Присутствие повторных областей, или повторных элементов, в целевой строке S зависит от существования циклов в графе перекрытий. В этом и последующих разделах мы покажем эту взаимосвязь в более явном виде.
Повторный элемент, или повторение, появляется в строке S, когда два различных интервала строки S дают начало одинаковым подстрокам Другими словами, существуют два интервала а Д, таких, что S а] = 5[Д]. Ример этого повторения равен (S а] и точно так же равен |Д[Д]|. Повторение является самоперекрывающимся, когда п П Д 0, в противном случае мы имеем несовместные появления этого повторения.
Следующая теорема показывает, что циклы в графе перекрытий всегда вызваны (индуцированы) повторениями в строке S. Обратное утверждение нс обязагсльно верно; то есть мы можем иметь повторения, но по-прежнему ациклический граф перекрытий. И снова, прежде чем мы сможем доказать саму теорему, необходимо доказать несколько промежуточных утверждений.
Лемма 4.3. Если а —> Д. то 1(a)	1(0) и г(а) г(Д).
Доказательство. Из|о| w мы находим/(a)+w—1 г(о) Изо Д мы получаем 1(0) + w — 1 = г(о) Посему 1(a) + w — 1	1(0) + w — 1, то
есть 1(a)	1(0). Точно так же, согласно предыдущим уравнениям, |Д| w
подразумевает, что 1(0) + w — 1 г(Д) и г(а) $ г(Д).	
И вновь мы не можем продолжить, пока не выучим несколько новых определений. Ложное перекрытие на уровне t такая пара интервалов а и Д, что верны условия w t и S[o] Д[Д], но а ™ 0 не верно. Название связано с допущением о том, что повторения S[a] и Д[Д] выбраны из пересекающихся областей в целевой молекуле, потому что их последовательности перекрываются, но дело обстоит не так. Они выглядят перекрывающимися, но на самом деле не перекрываются, так что они образуют ложное перекрытие
Лемма 4.4. Существование ложного перекрытия на уровне t подразумевает существование повторения размером по крайней мере t.
Доказательство. Из Д[а] Д[Д] мы имеем |а| w и |Д| > w. Если 1(0) = г(а) — w + 1, то а —> 0, поскольку в соответствии с гипотезой а Д. Следовательно, 1(0) r(a) — w + 1.
4.3. * АЛГОРИТМЫ
199
Кроме того, соотношение S[n] S[/3] подразумевает, что S[c/] = = S,[/7], где а' последние w элементов интервала п. а 0' - первые w элементов интервала 0. Поскольку 1(0) 5^ r(a) — w + 1, интервалы о' и 0' являются различными и дают начало одной и той же подстроке; то есть мы имеем повторение размером w > Е	
Теорема 4.4. Пусть р—множество порождаемое выборкой А строки S. Если граф OQ(p, t) содержит ориентированный цикл, то в строке S существует повторение размером по крайней мере t.
Доказательство. Пусть ft —» /2 —» •  • -+ fi —► /1 — ориентированный цикл в графе OQ(P t). Рассмотрим интервалы ai....,Oj, такие, что 5[ог] = /г при 1 г Sj I. Мы покажем, что по крайней мерс одна из пар (o,,oi+j), включая (п(,П[), является ложным перекрытием, что, согласно лемме 4.4, подразумевает существование повторения в строке S.
Предположим, что все пары - истинные перекрытия. Тогда вер но сц —> П;+1 при 1 г < I и верном сц —> од. Из этого следует, что /(<>])	1(а2)	l(ai) 1(<*1)- Так что вес 1(сц) равны. Анало-
гичное рассуждение справедливо и для г(пг). Но тогда пт = о2 = • • - = п;, что является невозможным, поскольку в соответствии с гипотезой ребра Д различны. Следовательно, существует по крайней мерс одно ложное перекрытие и теорема доказана.	
Все эти соображения ведут к удовлетворительному решению задачи сборки фрагментов, когда целевая строка S нс содержит повторений.
Теорема 4.5. Пусть S — строка знаков из алфавита {А, С, G, Т}, А — не содержащая подынтервалов связная на уровне t выборка строки S. покрывающая S, и пусть Р = 5’[Д]. Если строка S не содержит никаких повторений размером t или больше, то граф OQ(p, t) имеет единственный Гамильтонов путь Р, a S(P) = S.
Доказательство. Мы показали, что граф OQ(P, t) является ациклическим (теорема 4.4) и что граф OM(p,t) содержит Гамильтонов путь Р, причем S(P) = S.
Для начала заметим, что если строка S не имеет никаких повторений размером t или больше, то OM(p,t) = OQ(P,t). Это следует из отсутствия ложных перекрытий. Ясно, что множества вершин графов OM(p,t) и OQ(p,t) являются эквивалентными. Также ясно, что каждое ребро графа OQ(P, t) принадлежит также графу ОМ(Р, t). Итак, осталось лишь убедиться, что все ребра графа ОМ(Р, t) принадлежат также графу OQ(P, t).
Пусть f g — ребро графа OM(p,t). Тогда w > t. Если это ребро не находится в графе OQ(P,t.), то это происходит из-за существования
200
Глава 4
другого ребра f Л д с весом х > ш. Пусть а и (3 — интервалы выборки Л, где S[ct] = f и S[/3] = д. Так как нет никаких ложных перекрытий, мы должны иметь как а /3, так и а /3, что невозможно. Вес этого ребра однозначно определяется выражением w = r(a) — l(/3) + 1.
Итак, OCfT7,0 — ациклический граф, содержащий Гамильтонов путь. Оказывается, что каждый раз, когда ациклический граф имеет Гамильтонов путь, этот путь единственный. Чтобы показать, почему это утверждение верно, рассмотрим узлы в графе, которые имеют нулевую степень захода (истоки). Поскольку рассматриваемый граф является ациклическим, он должен содержать по крайней мере один исток. Но, включая в себя Гамильтонов путь, он может иметь самое большее один исток — начальную точку этого пути. Все другие вершины имеют по крайней мерс одно входящее ребро. Исходя из этого, мы заключаем, что в таком графе должен быть единственный исток и что этот исток должен быть начальной точкой Гамильтонова пути.
Теперь, если мы удалим этот исток из графа, то оставшийся граф по-прежнему будет ациклическим и содержать Гамильтонов путь, потому что вершина, которую мы удалили, — крайняя точка первоначального Гамильтонова пути. Продолжая действовать по той же схеме, мы видим, что Гамильтонов путь единственный, и мы знаем, как его определить: для этого необходимо последовательно удалять истоки из графа.	
Только что описанный алгоритм широко известен в информатике (см. упражнение 12 главы 2). Его называют топологи ческой сортировкой и в более общем виде используют для поиска упорядочений узлов, совместимых с ациклическим множеством ребер в следующем смысле. Во всех ребрах вида f —у д узел f появляется в упорядочении перед узлом д. Если ациклический граф кроме того содержи'! Гамильтонов путь, то, как мы только что показали, это упорядочение однозначно.
Мы завершаем этот раздел примером, где алгоритм Greedy не работает, но существует ациклический подграф для подходящего порога t, так что алгоритм топологической сортировки найдет правильный путь. Когда мы говорим, что алгоритм Greedy не работает, мьг подразумеваем, что он нс обеспечивает правильную сборку, хотя он дает хорошие результаты поиска кратчайшей общей надстроки. В этом примере фрагменты берутся из целевой последовательности, действительно содержащей повторения размером больше /. Покажем, что отсутствие длинных повторений не является необходимым для получения ациклического графа. Выражаясь математическим языком, оно всего лишь достаточно.
4.3. * АЛГОРИТМЫ
201
Рис. 4.19. Граф перекрытий для данного множества из пяти фрагментов
AGTATTGGCAATC---AATCGATG---- ------------------------------------ATGCAAACCT-------------------------- ------------------------------------TTGGCAATCACT-CCTTTTGG AGTATTGGCAATCACTAATCGATGCAAACCTTTTGG
Рис. 4.20. Плохое решение задачи сборки, с множественным выравниванием, консенсус которого есть кратчайшая общая нале t рока. Это решение имеет длину 36 и генерировано жадным алгоритмом. Однако его слабейшая связь равна нулю
AGTATTGGCAATC-CCTTTTGG--------------- -------------------------------------AATCGATG-----------------------------TTGGCAATCACT -------------------------------------ATGCAAACT- AGTATTGGCAATCGATGCAAACCTTTTGGCAATCACT
Рис. 4.21. Решение, полученное с помощью единственного Гамильтонова пути. Это решение имеет длину 37, но показывает лучшее сцепление. Его слабейшая связь равна трем
Пример 4.6. Рассмотрим следующую целевую строку S и фрагменты w, z, и, х и у:
S=AGTATTGGCAATCGATGCAAACCTTTTGGCAATCACT w=AGTATTGGCAATC z=AATCGATG
U=ATGCAAACCT z=CCTTTTGG у“TTGGCAATCACT
Выбрав порог t = 3, мы получаем граф перекрытий, изображенный на рис. 4.19. Сборка, построенная алгоритмом Greedy, даст кратчайшую общую надстроку, сформированную сцеплением контига wk9 у с конти-
202
Глава 4
гом zk3uk3x в любом порядке, как показано на рис. 4.20 и 4.21. Это решение имеет длину 36, то есть на один знак короче, чем целевая последовательность, хотя оно также является надстрокой. Однако, решение, найденное при помощи Гамильтонова пути, имеет лучшее сцепление.	
4.4.	ЭВРИСТИКИ
Мы видели, что ни одна из формальных моделей, предложенных для сборки фрагментов, не адекватна полностью, так что на практике часто приходится обращаться к эвристическим методам. В этом разделе мы рассмотрим некоторые из них, начиная с указания важных свойств компоновки для хорошей сборки фрагментов.
Сборку фрагментов можно рассматривать как задачу множественного выравнивания с некоторыми дополнительными особенностями. Наиболее поразительная из таких особенностей — это, возможно, тот факт, что каждый фрагмент может участвовать в выравнивании как в прямом виде, так и в виде обратного комплемента. Вторая специфическая особенность — то, что сами последовательности обычно намного короче общего выравнивания. Это побуждает нас по-разному штрафовать внутренние и внешние пропуски во фрагментах гак, чтобы за внутренние пропуски налагался бы более значительный штраф. Если бы мы за оба вида пропусков налагали одинаковый или почти одинаковый штраф, то не было бы никакого стимула оставлять знаки фрагмента вместе, а наоборот, мы бы, в принципе, заставляли их рассеиваться по всей протяженности выравнивания. Более того, тот факт, что фрагменты короче самого выравнивания, вынуждает нас при оценке качества выравнивания учитывать помимо счета некоторые другие критерии. К последним относятся покрытие и сцепление. Критерий сцепления является мерой того, как сильно последовательности связаны, или сцеплены (по степени их перекрытия), как было показано в разделах 4.2.3 и 4.3.5. Обсудим эти критерии подробнее.
Счет: В каждом столбце множественного выравнивания мы имеем некоторое покрытие (определение см. в разделе 4.1.2). Идеальная ситуация возникает тогда, когда все последовательности, покрывающие некоторый столбец, входят в него одинаковым знаком. Обычно в столбце наблюдается хорошая однородность и плохая изменчивость знаков.
Это свойство дает возможность использовать понятие энтропии для измерения качества столбца. Энтропия - величина, определяемая на группе относительных частот, и она низка, когда одна из этих частот значительно выделяется среди других, и высока, когда все частоты более или менее
4.4. ЭВРИСТИКИ
203
равны. Ясно, что при оценке качеова столбца, чем ниже энтропия, тем лучше. Частоты, которые мы используем при оценке качества, — это частоты появления каждого знака, где знак может быть основанием А, С, G и Т или внутренним пробелом.
Предположим, что мы имеем п последовательностей, покрывающих некоторый столбец, и знаем относительные частоты рд, pq, pq, р^ и РПробел появления каждого знака. Тогда энтропия этого распределения определяется как
Е = -£pclogpc.
С
Если для некоторого знака с частота рс = 1, а все остальные частоты равны нулю, то мы имеем (допуская OlogO = U):
Е = 0.
Если, напротив, все частоты равны, то мы получаем рс = 1/5 для всех знаков с и тогда
Е = -5- |log| =log5, О о
что есть возможно максимальное значение для пяти частот.
Вспомним из раздела 3.4, что при анализе множественных выравниваний мы использовали схему счета парных сумм. Эта схема объединяет в одном показателе и покрытие и однородность столбца. Если однородность столбца высока, то чем больше покрытие, тем выше счет парных сумм. Аналогично, при фиксированном покрытии счет парных сумм возрастает вместе с однородностью. Напротив, энтропия независима от покрытия. Она измеряет только однородность. В зависимости от ситуации ученый может использовать комбинированную оценку — счет парных сумм — или покрытие и энтропию по отдельности.
Покрытие: В разделе 4.1.2 мы определили покрытие множества фрагментов относительно цели, из которой они были получены. Здесь мы определяем аналогичное понятие — покрытие компоновки. Фрагмент покрывает столбец г, если он входит в этот столбец либо некоторым принадлежащим ему знаком, либо внутренним пробелом. Пусть 1(f) и г(/) — соответственно, крайняя левая и крайняя правая позиции знака фрагмента f (или его обратного комплемента) в компоновке. Предыдущее определение означает, что фрагмент f покрывает столбец г, если 1(f) г r(f).
Дав определение покрытия отдельных столбцов, мы можем говорить о минимальном, максимальном и среднем покрытии компоновки. Значения
204
Глава 4
этих определений понимаются буквально. Если покрытие достигает нулевого значения в столбце г, то мы нс можем получить сцепленной компоновки. Действительно, никакой образ фрагмента не перекрывает столбец г, так что части компоновки слева и справа от столбца г являются в некотором смысле независимыми. Например, возможно поменять правую и левую части компоновки местами и получить альтернативную компоновку, столь же хорошую, как и первоначальная.
Это означает, что, если мы имеем много столбцов с нулевым покрытием, то любая перестановка промежуточных областей становится приемлема. Каждая из таких областей соответствует тому, что мы называли контигом. Покрытие важно также для определения доверительной оценки согласованной последовательности. Если существует несколько фрагментов, покрывающих столбец, то мы имеем больше информации относительно обращения к каждому отдельному основанию этого столбца. Наконец, в компоновке важно иметь достаточно много фрагментов из обеих нитей.
Сцепление: Кроме счета и покрытия известен другой показатель качества компоновки — сцепление отдельных фрагментов компоновки. Например, рассмотрим компоновку на рис. 4.22. Покрытие очень хорошее, но нег никаких реальных связей между фрагментами. Каждый блок состоит из многих почти точных копий некоторой последовательности, но сами блоки выглядят абсолютно нс сцепленными. Чтобы показать некоторые признаки сцепления, образы фрагментов должны иметь перекрывающиеся концы.
------АСТТТТ------ TCCGAG------------ACGGAC ------------------АСТТТТ------------ TCCGAG------------ACGGAC ------------------АСТТТТ- TCCGAG------------ACGGAC TCCGAGACTTTTACGGAC
Рис. 4.22. Хорошее покрытие, но плохое перекрытие: отсутствует сцепление
Сборка на практике
Хорошая программа сборки должна разумно сочетать эти требования и найти все решения, которые удовлетворяют им достаточно хорошо. Эта задача сама по себе весьма нелегка, и, более того, известно, что никакой
4.4. ЭВРИСТИКИ
205
совершенной формальной модели нс существует; в связи с этим построение алгоритма является очень трудным В результате, на практике часто целую задачу делят на три стадии и для решения каждой последующей стадии используют результаты, полученные на предыдущих. Типичное разделение включает в себя следующие три стадии:
•	Обнаружение перекрытий;
•	Построение компоновки;
•	Вычисление консенсуса.
При таком разделении задача становится более управляемой, потому что каждую стадию можно выполнять как отдельную задачу, более или менее независимо от других Однако при этом становится труднее понять взаимосвязь между начальным входом и конечным выходом задачи. Методы, используемые в этих промежуточных задачах, часто являются эвристическими. и потому нельзя дать никаких ясных гарантий относительно качества решения. Однако многие из существующих алгоритмов показывают на практике хорошие результаты и потому некоторые из используемых в них методов заслуживают нашего внимания.
4.4.1.	ОБНАРУЖЕНИЕ ПЕРЕКРЫТИЙ
Первый шаг в любой про|рамме сборки — обнаружение перекрытий фрагментов. Мы должны перебрать все пары фрагментов и их обратных комплементов и определить такие префиксы фрагментов, которые хорошо совпадают с суффиксами других фрагментов. Как правило, нам понадобятся все такие пары. Кроме того, мы интересуемся фрагментами, полностью содержащимися в других фрагментах. Все эти сравнения проводят в пределах допустимой частоты появления ошибок.
Мы упоминаем здесь способ сравнения двух фрагментов с целью обнаружения таких перекрытий. В практической задаче мы могли бы применить этот метод ко всем парам, включая обратные комплементы, но так поступают редко, иначе потребовалось бы слишком много времени, поскольку этот метод основан на квадратичном алгоритме. И все же это один из наиболее надежных методов оценки перекрытия.
Метод сравнения состоит в применении алгоритма метода динамического программирования, описанного в разделе 3.2.3, а именно, версии основного алгоритма Similarity. Эта версия не штрафует крайние пробелы: ни начальные, ни конечные. На рис. 4.23 представлен результат применения такого алгоритма для обработки двух фрагментов. Система очков, используемая в этом сравнении; 1 для совпадений, 1 для несовпадений
206
Глава 4
AGGAGAAGAATTCACCGCTAT----------
----------ТТССССТ-ТАТТСААТТСТАА
фикс-суффиксных выравниваний или выравниваний целых фрагменюв, пригодных
для сборки
и —2 для пробелов. Следует подчеркнуть, что для того, чтобы можно было найти префикс-суффиксное подобие, этот алгоритм не штрафует пробелы после первой или перед второй последовательностью. Тот же самый алгоритм может быть использован для поиска приближённого подобия целых фрагментов.
4.4.2.	УПОРЯДОЧЕНИЕ ФРАГМЕНТОВ
В эзом разделе мы кратко обсудим один вопрос, связанный с построением компоновки в реальной задаче сборки, а именно, проблему поиска хо
4.4. ЭВРИСТИКИ
207
рошего упорядочения фрагментов в контиге Получив такое упорядочение и зная, что каждый фрагмент перекрывается с последующим, мы можем построить компоновку, прибс1нув к методам, изложенным в следующем разделе. К сожалению, не известны алгоритмы, которые были бы одновременно простыми и достаточно универсальными; такое не под силу даже алгоритмам, опирающимся на различные эвристики. Поэтому, вместо того, чтобы представить такой алгоритм, мы приводим важные соображения, которые должны быть приняты во внимание при попытке построить хорошие упорядочения фрагментов.
В реальной задаче нам приходится иметь дело с обратными комплементами, так что необходимо расширить входное множество У за счет добавления к каждому фрагменту его обратного комплемента. Принимаем
Т = {! | /еЛ
и
VF = FUF-
Кроме того, мы должны учитывать и ошибки, а это означает поиск прибли жённого совпадения Мы будем использовать обозначение f —» д в немного отличном смысле от введенного ранее. Теперь оно означает, что конец фрагмента f приблизительно равен началу фрагмента д. Мы также предполагаем, что всякий раз, когда верно выражение f —» д, верно и выражение д —> f, потому что разумно ожидать, что, независимо от используемого критерия оценки подобия между двумя последовательностями, этот же критерий равносилен и в случае оценки их обратных комплементов.
Это можно показать следующим образом. Если f —» д верно, то f = = uv, д = wx и фрагменты v и w подобны. Это подразумевает, что д = х ш, f = vu и что обратные комплементы w и V тоже подобны, что эквивалентно записи д —» /. Мы будем использовать обозначение f С д, означающее, что фрагмент f является приближённой подстрокой фрагмента д. Рассуждение, аналогичное предыдущему, показывает, что f С д => f Сд.
Тогда граф, который мы будем строить, — граф перекрытий OQt'DF'}, причем его ребра показывают приближённое перекрытие. Кроме того, важно знать, какие фрагменты являются приближёнными подстроками других.
Поиск хорошего упорядочения перекрывающихся фрагментов по существу равносилен поиску ориентированных путей в графе OQ(T>J-). Эти пути порождают контиги. Необходимо помнить, что для любого пути
/1 —»/2 —»•••—> А
208
Глава 4
в этом графе существует соответствующий ему «комплементарный» путь
fk —» fk-1 —» • • • —» fi,
дающий начало контигу с согласованной строкой, которая является обратным комплементом консенсуса. Это означает, что обе нити целевой ДНК расшифровываются одновременно. В идеале мы бы хотели получить такую пару комплементарных путей, чтобы каждый отдельный фрагмент принадлежал точно одному пути в паре. Вложенные фрагменты (то есть покрывающие внутренние участки некоторой области консенсуса и поэтому не дающие никакой информации о сцеплении) могут быть размещены в упорядочении позже, так что их присутствие в путях не существенно. Фактически, их принудительное присутствие может повредить формированию пути (см. упражнение 14). Вложенные фрагменты могут обеспечить важную связь лишь в редких случаях, так что при построении пути мы рассматриваем их в качестве необязательных компонентов.
На пути к идеальной цели построения пары путей, покрывающих все отдельные фрагменты, две проблемы могут стать серьезными препятствиями: неполное покрытие и присутствие повторений. Несвязный граф перекрытий — обычно признак неполного покрытия. Повторения вызывают появление циклов в графе перекрытий, если покрытие хорошее, или же могут проявиться в виде ребер f —+ д и f —> h, хотя фрагменты g и h не сцеплены (д и h не сцеплены, если д -£> h, h, -£> д, д h и h д). Это случается, когда f — фрагмент около конца повторения X, а д и h — фрагменты, идущие от X к различным окружающим это повторение областям цели. Цикл, включающий в себя как сам фрагмент /, так и его обратный комплемент /, свидетельствует о присутствии инвертированного повторения.
Другой признак повторных областей — необычно высокая степень покрытия (см. рис. 4.13). Все фрагменты из всех копий данного повторения размещаются точно друг над другом, приводя к увеличению покрытия до величины, равной произведению приближённого среднего значения и числа копий повторения (если допустить приблизительно равномерное распределение фрагментов по цели).
В завершение приводим четыре правила, которые необходимо учитывать при построении путей. 1. Каждому пути соответствует комплементарный ему путь. 2. Не обязательно (а иногда просто нежелательно) включать в путь вложенные фрагменты. 3. Циклы обычно указывают на присутствие повторений. 4. Пиковые значения покрытия также могут быть вызваны повторениями.
4.4. ЭВРИСТИКИ
209
4.4.3.	ВЫРАВНИВАНИЕ И КОНСЕНСУС
В этом разделе мы кратко обсудим задачу построения компоновки с помощью пути в графе перекрытий. Если перекрытия точные, то это легко, но приближённые перекрытия требуют от нас особого внимания. Мы представляем два метода, относящихся к построению выравниваний. Первый метод помогает в построении хорошей компоновки с помощью пути, возможно содержащего ошибки. Второй призван обеспечить локальное улучшение уже построенной компоновки. Чтобы представить первый метод, мы приводим следующий пример.
Пример 4.7. Предположим, что мы имеем путь f —> д —» Л. где
/=CATAGTC g=TAACTAT h=AGACTATCC
Два оптимальных полуглобальных выравнивания между последовательностями (фрагментами) fug выглядят следующим образом:
CATAGTC-- CATAGTC-----
—ТАА-СТАТ	—ТА-АСТАТ
Мы не имеем никакой причины предпочесть одно из них другому, так как их счет одинаков. Однако, когда в компоновку входит последовательность h. становится ясно, что второе оптимальное выравнивание (где второй знак А фрагмента д сопоставлен с Т во фрагменте /), лучше:
CATAGTC------ —ТА-АСТАТ— -------------AGACTATCC CATAGACTATCC
Согласованная строка S удовлетворяет условиям ds(f, S) = 1, ds(g, S) = = 1 и ds(h, S) = 0. Если бы мы выровняли знак А со знаком G, то голосование в столбце 6 было бы неопределенным, где знаки Т, А и пробел дали бы равенство голосов за счет однократного появления каждого знака В согласованной последовательности любой другой выбор, кроме знака А в этом столбце, привел бы к худшему результату — в том смысле, что сумма ds(f, S) + ds(g, S) + ds(h, S) была бы больше, чем в первом случае. 
210
Глава 4
Чтобы избежать таких проблем, мы используем схематичную структуру, которая представляет выравнивания и проводит различие между основаниями, действительно совпадающими с некоторым другим основанием, и основаниями, которые являются «свободными» (то есть не нашедшими себе пару), как это имеет место у второго основания А последовательности д в вышеупомянутом примере. Эту идею мы можем осуществить следующим образом. Каждую последовательность представляем связным списком оснований. Когда некоторое выравнивание сформировано, совпадающие основания объединяются и становятся одним узлом в общей структуре. Если мы не уверены в совпадении некоторого основания, то мы можем оставить его свободным, как мы сделали на рис. 4.24 для последовательностей fug в примере 4.7. Тогда по мере добавления новых последовательностей некоторые из свободных оснований будут объединяться согласно подходящим выравниваниям. Структура может быть представлена в виде ациклического графа, и его обход в топологическом порядке даст компоновку. Применяя эту методику к примеру 4.7, мы получаем оптимальную компоновку. При добавлении последовательности h будет добавлена стрелка от узла G к узлу А, расположенному сразу под ним, и также добавлены дополни(ельные основания, принадлежашие последовательности h.
Рис. 4.24. Связная сгрукгура для приближённых перекрытии
ACT-GG
ACTTGG
AC-TGG
ACT-GG
AC-TGG
ACTTGG
ACT-GG
ACTTGG
ACT-GG
ACT-GG
ACT-GG
ACT-GG
Рис. 4.25. Дне компоновки для одинаковых миожссзв последовательное гей. Правая компоновка лучше, но вследствие неопределенности попарных выравниваний программа сборки может произвести левую
РЕЗЮМЕ
211
Второй метод применяют для улучшения уже построенной компоновки. Одну из типичных задач, встречающихся на практике, рассмотрим на следующем примере.
Пример 4.8. На рис. 4.25 показаны две компоновки для одного и того же множества последовательностей. В левой компоновке согласованная последовательность содержит два последовательных знака Т в силу голосе вания путем простого большинства, но четыре из пяти последовательностей содержат всего один знак Т. Правая компоновка лучше, поскольку ее консенсус находится в согласии с большинством последовательностей. 
Один из методов решения таких задач заключается в выполнении множественного выравнивания на локальном уровне. Мы выбираем короткий блок последовательных столбцов, который нуждается в исправлении извлекаем из каждого фрагмента его часть, содержащуюся в этих столбцах, и выравниваем эти блоки. При умеренных значениях локального покрытия и длины блоков алгоритм множественного выравнивания, несмотря на свою экспоненциальную сложность, будет затрачивать разумное количество времени. Схема счетов парных сумм кажется здесь адекватной. Если принять p(ci, b) = 1 при а b,p(a.b) = 0 при а Ь,р(а, —) = — 1 ир( —) = 0, то правая компоновка в примере 4.8 максимизирует счет парных сумм.
РЕЗЮМЕ
В этой главе мы рассмотрели задачу сборки фрагментов, решаемую при крупномасштабном секвенировании молекул ДНК. Как правило, эта задача состоит из сборки в правильном порядке и ориентации множества фрагментов, получаемых из неизвестной длинной последовательности ДНК.
Мы начали с обзора биологических основ этой задачи и биологических же факторов, влияющих на ее вход. Затем мы представили варианты математических моделей, формально описывающих эту задачу, было показано, что предложенные модели не способны учитывать все необходимые факторы В частности, трудно обрабатывать фрагменты с повторными областями и учитывать информацию о размере целевой последовательности. Кроме того, все модели основаны на допущении о том, что множество фрагментов свободно от химер и загрязнения генетическим материалом вектора. Также были представлены алгоритмы, построенные на этих моделях.
Сборка фрагментов предполагает построение множественного выравнивания особого вида, называемого компоновкой, в которой мы постоянно должны беспокоиться о правильной ориентации, полном покрытии и на
212
Глава 4
лежком сцеплении фрагментов, но зато при вычислении счета этого выравнивания нам не приходиться штрафовать крайние пробелы.
Из-за трудностей, связанных с поиском точной формулировки задачи сборки фрагментов, на практике часто используют эвристические методы. Задачу обычно разбивают на три стадии: обнаружение перекрытий между фрагментами, построение компоновки и вычисления консенсуса. Программы, основанные на этом подходе, хорошо работают в практических приложениях этой задачи, если последовательности нс содержат повторений Мы представили крат кий обзор таких эвристик.
Новые методы например секвенирования посредством гибридизации могут радикально изменить способ, посредством которого осуществляется крупномасштабное секвенирование молекул ДНК. Если это произойдет, то ученые будут озадачены поиском новых алгоритмов.
УПРАЖНЕНИЯ
1 Предположим, что мы отобрали фрагменты
/1 :ATCCGTTGAAGCCGCGGGC
/2 :TTAACTCGAGG
/з :TTAAGTACTGCCCG
f4 :ATCTGTGTCGGG
/5 :CGACTCCCGACACA
/б:CACAGATCCGTTGAAGCCGCGGG
/7 :CTCGAGTTAAGTA
/8 = CGCGGGCAGTACTT
и знаем, что полная длина целевой молекулы приблизительно равна 55 п. н. Осуществите сборку этих фрагментов и получите согласованную последо-ватетьность. Будьте готовы к возможным ошибкам. Вам, вероятно, придется использовать также обратные комплементы некоторых фрагментов
2.	Каково минимальное, максимальное и среднее покрытие компоновки на странице 106?
3.	Каково наименьшее значение е, при котором ответ на рис. 4.2 является верным согласно модели восстановление?
4.	Повторите упражнение 3, на сей раз для компоновок на рис. 4.3 и 4.4.
5	На основании рис. 4 8 предположите, что существует фрагмент, состоящий из конца области В, копии X и начала области D. Как этот фрагмент повлиял бы на общую сборку?
УПРАЖНЕНИЯ
213
6.	Постройте граф перекрытий для следующего множества фрагментов: Т - {AAA, ТТА, АТА}. Определите кратчайшую общую надстроку этого множества.
7.	Найдите последовательности, которые дают начало следующему графу перекрытий (показаны только ребра с положительными весами). Численные значения весов, которые вы находите, не важны, поскольку известно, что они строго положительны.
8.	Опишите алгоритм поиска наибольшего точного перекрытия между двумя строками длиной т и п; время счета этого алгоритма должно быть равно О{т + п).
★ 9. Изобретите способ поиска приближённых повторений в последовательности ДНК.
10.	Приведите пример последовательности ДНК, которая не может быть однозначно восстановлена из множества собственных 8-меров.
11.	Покажите, что формулировка задачи поиска КОН неприменима для примеров в разделе 4.1. Какова кратчайшая общая надстрока в каждом случае?
12.	Пусть = {АТС, TCG, AACG}. Постройте оптимальную компоновку для этого множества согласно модели восстановление при г = 0.1 и е = 0,25. Убедитесь, что были рассмотрены также и обратные комплементы.
13.	Пусть = {ТСССТАСТТ, AATCCGGTT, GACATCGGT}. С помощью модели мультиконтиг найдите для множества Т оптимальное множество контигов при е = 0,3 и t = 5.
14.	Приведите пример такого множества что кратчайшая надстрока не соответствует пути в графе перекрытий OQ^T')-
15.	Для каждого т > U найдите такое не содержащее подстрок множество чтобы жадный алгоритм возвращал надстроку по крайней мере на т знаков длиннее возможно кратчайшей для Ут.
214
Глава 4
16.	Пусть Л, В, С, D, E,X,Y и Z — блоки в целевой последовательности ДНК. Предположите, что размер этих блоков превышает длину любого фрагмента, который может быть отобран из целевой молекулы. Заполните пропуски в изображенной ниже последовательности буквами А', I' или Z так, чтобы эта последовательность стала существенно неопределенной для сборки.
цель =4 А В ... С Y D ... Е Z
17.	Как бы вы использовали BLAST или другую программу поиска в базах данных, чтобы проверить фрагменты на загрязнение вектором?
18.	Постройте алгоритм с полиномиальным временем счета для решения задачи поиска КОН согласно модели ВОССТА1ЮИ.П Н11Е.
★ 19. Предположим, что некоторая последовательность имеет перекрывающееся повторение S. Покажите, что для некоторых непустых блоков А' и 1 и некоторого к 2 повторение S имеет форму либо А А А, либо X{YX)k.
о 20. Постройте алгоритм, который получает на вход множество последовательностей ДНК и строит общую надстроку длиной нс более чем вдвое превышающей минимально возможную.
БИБЛИОГРАФИЧЕСКИЕ ПРИМЕЧАНИЯ
Задачу поиска КОН исследовали многие специалисты. Тёрнер [187] описал несколько алгоритмов ее решения, включая жадный метод, и представил гарантию точности вычисления суммы перекрытий. Ли [126] дал первую гарантию точности вычисления фактической длины надстроки с верхним пределом O(nlogn), где п — оптимальная длина. Затем Блюм, Цзян, Ли, Тромп и Яинакакис [24] улучшили эту гарантию до Зм и показали, что жадный алгоритм дает надстроки длиной до 4п. Это вызвало целую серию статей, в которых авторы описывали все более и более изощренные методы и, соответственно, все лучшие и лучшие отношения. Работая в этом же направлении, Тен и Яо [185] доказали отношение 2 + 8/9; Чумай, Га-сенсц, Петров и Риттер [41] доказали отношение 2 + 5/6; Косараху, Парк и Штейн [118] доказали отношение 2 + 50/63; и наконец, Армен и Штейн доказали отношения 2 + 3/4 [15] и 2 + 2/3 [16]. Большая часть этих алгоритмов затрачивают па вычисления время O(|S| + п3), где |S| — длина падстроки, ап — число фрагментов (см., например, статью Гасфилда [84]). Используя метод из работы Гасфилда, Ландау и Шибера [86], с помощью суффиксных деревьев можно построить граф перекрытий OG(X) за время О(|| ,А|| +п2).
БИБЛИОГРАФИЧЕСКИЕ ПРИМЕЧАНИЯ
215
Модель восстановление была представлена в статье Пслтолы, Зёдср-лунда, Гарио и Укконена [157]. Диссертационная работа Ксцециоглу [114] и статья Ксцециоглу и Майерса [115], написанная на основании этой диссертации, в основном посвящены этой модели. Этими авторами была разработана также формальная модель МУЛЬТИКОНТИГ. Майерс [144] предложил метод, основанный на распределении конечных точек фрагментов в компоновке, в качестве перспективной формальной модели сборки фрагментов, особенно хорошей в случае присутствия повторений. Майерс также предложил алгоритм, основанный на графе специального вида, отличного от представленных в этой книге. Рис. 4.12 основан на примере из этой статьи.
Несколько групп ученых успешно применяли прикладные программы построения сборки фрагментов ДНК. Ранние системы описаны в [71; 138]. Изыскательские работы по воплощению обоснованного математического формализма в прикладных методах были выполнены Пелтолой, Зёдерлун-дом и Укконеном [158]. Хуан [98] описал хорошую программу сборки фрагментов, позже улучшенную до возможностей обработки повторений, обнаружения химерных фрагментов и автоматического редактирования полученной компоновки [99]. Кецсциоглу и Майерс [115] разделили полный процесс на три стадии, обеспечив точные формальные модели, а также точные и приближенные алгоритмы для каждой стадии. Штадсн [178; 46], начиная с конца 1970-х годов, поддерживает систему обработки последовательностей с неплохими возможностями сборки фрагментов. Очень популярная во многих лабораториях компьютерная система GCG [47] также обеспечивает возможность сборки. Цели проектирования систем сборки фрагментов были в общих чертах перечислены Майерсом [143]. Книга под ред. Адамса, Филдса и Вентсра [1] — приводит хороший общий обзор по автоматизированной обработке ДНК. Подробное описание метода, рассмотренного нами в разделе 4.4.3, можно найти в статье Мсйданиса и Сетубала [137].
Ингл и Бурке [53; 54] описали ряд программных средств для генерации искусственных примеров задачи сборки фрагментов. Сото, Куп и Худ [171] представили данные, полученные в настоящем проекте секвенирования, в качестве испытательного примера для компьютеризированных методов сборки. Уравнения (4.1) и (4.2), формально описывающие метод дробовика, взяты из книги Уотермена [199], раздел 7.1.5. Предшествующая работа на эту тему была проведена Пендером и Уотерменом [120].
Уотсрмсн [199], раздел 7.3, представляет алгоритм СПГ и дает также ссылку на более подробную статью.
Сборка фрагментов была одной из тем прикладного симпозиума (при поддержке «Национального научного фонда США») в «Центре дискретной математики и теоретической информатики» (DIMACS) в 1995 году. Был
216	Глава 4
опубликован сборник избранных тезисов этого симпозиума. Дополнительная информация по симпозиуму находится по адресу
http://dimacs.rutgers.edu/SpecialYears/
19 94_1995/chailenge.html
Глава 5
СОСТАВЛЕНИЕ ФИЗИЧЕСКИХ КАРТ ДНК
Из первой главы мы узнали, что хромосома человека это молекула ДНК, состоящая приблизительно из 108 пар нуклеотидов. Рассмотренные нами методы позволяют секвенировать фрагменты ДНК длиной до десятков тысяч пар нуклеотидов. Это означает, что всякий раз, когда мы секвенируем такой фрагмент, мы расшифровываем чрезвычайно маленькую часть хромосомы. Это как если бы мы рассматривали Землю с Луны посредством телескопа, позволяющего нам видеть особенности рельефа, которые отстоят дру1 от друга на пару дюймов (основание ДНК), но при этом обладающего полем зрения не более мили (фрагмент ДНК длиной 15000 п.н., см. рис. 1.10) Такой телескоп не был бы хорошим инструментом для изучения крупномасштабных структур например горных цепей, континентов и островов. Чтобы обозреть такие структуры целиком, нам понадобился бы другой прибор. Аналогично, молекулярные биологи используют специальные методы секвенирования молекул ДНК, размеры которых сопоставимы с длиной хромосомы. Эти методы позволяют им составлять карты целых хромосом или хотя бы их существенных долей. В этой главе мы исследуем вычислительные методы, которые могут помочь биологам в составлении физических карт ДНК, то есть в картировании1.
5.1.	БИОЛОГИЧЕСКИЕ ОСНОВЫ КАРТИРОВАНИЯ
Физическая карта молекулы ДНК сообщает нам местоположение некоторых маркеров в молекуле. Обычно маркеры представляют собой маленькие, но точно известные последовательности. Такая карта помогает молекулярным биологам глубже исследовать геном. Например, предположим,
1 Иногда в специальной литературе этот процесс называют картированием, хотя составление всеразличных карт и всевозможных картограмм это, конечно же, картографирование. Прим. перев.
218
Глава 5
что некоторая область ДНК была полностью расшифрована и нам известна последовательность ее оснований S. Тогда, если мы знаем к какой именно хромосоме относится область S и если мы имеем физическую карту этой хромосомы то мы могли бы попытаться найти в последовательности S один из маркеров карты. Если нам это удается, то это значит, что мы определили местонахождение области S в хромосоме. См. иллюстрацию на рис. 5.1.
Рис 5.1. Эскиз фтичсской карты. На этом рисунке очень длинная молекула ДНК (например хромосомы) изображена в виде сплошной кривой. Маркеры вдоль молекулы отмечены знаком алмаза «о». Каждый маркер уникален и обозначен соответствующей ему буквой Отрезок S представляет расшифрованный фрагмент ДНК. содержащий, например, некоторый ген С помощью физической карты может быть определено местоположение области S в хромосоме
За вопросом о назначении карт следует естественный вопрос о методах их составления. Первый шаг состоит в получении нескольких копий молекулы ДНК, которую мы хотим картировать, то есть целевой ДНК. Затем каждая копия должна быть разбита на несколько фрагментов с помощью ферментов рестрикции. (Фрагментация ДНК рестриктазами описана в разделе 1.5.2.) Картирование осуществляют путем тщательного сравнения полученных фрагментов между собой — в частности, посредством оценки их перекрытия. Следует подчеркнуть, что каждый такой фрагмент все еще слишком длинная для ссквенированния часть ДНК, так что мы не можем определить перекрытие путем секвенирования и сравнения фрагментов, как это делают при сборке фрагментов (глава 4). Вместо этого информацию о перекрытии мы получаем, анализируя специфические отличительные признаки, или индикаторы фрагментов Индикатор некоторого фрагмента должен описывать часть информации, содержащейся в этом фрагменте, некоторым уникальным способом, подобно тому, как отпечатки пальцев служат для идентификации личности. Два популярных способа получения индикаторов — анализ участков рестрикции и гибризизация.
5.1 БИОЛОГИЧЕСКИЕ ОСНОВЫ КАРТИРОВАНИЯ
219
При составлении рестрикционных карт наша задача состоит в определении местонахождения участков рестрикции данного фермента на целевой ДНК. Таким образом, участки рестрикции являются упомянутыми выше маркерами. Метод, используемый для определения местоположения участков рестрикции, основан на измерении длин фрагментов; в данном случае индикатором является длина фрагмента. При составлении карт гибридизации мы проверяем, связываются ли определенные маленькие последовательности с фрагментами; в результате индикатором некоторого фрагмента становится подмножество таких маленьких последовательностей, которые связываются с ним Кроме того, индикатор фрагмента может быть получен как его гибридизацией, так и измерением его длины, но в этой главе для ясности описания мы рассматриваем каждый способ отдельно. В любом случае, сравнивая индикаторы, мы стараемся определить, перекрываются ли фрагменты, и таким образом определить их относительный порядок (который был потерян в ходе фрагментации молекулы).
Так же, как и в других задачах молекулярной биологии, возможный недостаток информации и присутствие многочисленных экспериментальных ошибок значительно усложняет задачу составления физических карг В частности, может оказаться невозможно получить одну непрерывную фи зическую карту для множества фрагментов. Например, это может случиться потому, что процесс фрагментации не произвел фрагменты, покрывающие некоторые области целевой ДНК. В подобных случаях области физической карты называют контигами (то же самое название используют при сборке фрагментов). Эта особенность свойственна всем процессам составления физических карт. Теперь мы подробнее обсудим каждый из упомянутых выше методов.
5.1.1.	СОСТАВЛЕНИЕ РЕСТРИКЦИОННЫХ КАР!
В этом разделе мы кратко представляем два возможных метода картирования, основанных на измерении длин фрат ментов между участками рестрикции^.
Один из способов получения фрагментов самых разных размеров состоит в том, чтобы для расщепления целевой ДНК использовать не одну а две рсстриктазы Мы объясним этот способ на следующем примере. Пред положим, что мы имеем две рсстриктазы; 4 и В, и каждая специфична к строго определенной последовательности (участку рестрикции). Обрабатывая одну копию целевой ДНК рестриктазой А, мы получаем фрагменты
2Этот раздел представляет интересную математическую задачу, однако на практике теперь уже не используют подобную технику.  Прим. ред.
220
Глава 5
длиной 3, 6, 8 и 10 единиц (например, т. п. н.). Обрабатывая другую копию целевой ДНК рестриктазой В, мы получаем фрагменты длиной 4, 5, 7 и 11 единиц. И наконец, применяя обе рестриктазы к третьей копии целевой ДНК, мы получаем фрагменты длиной 1, 2, 3, 3, 5, 6 и 7 единиц. Теперь необходимо расположить эти фрагменты таким образом, чтобы полученный в третьем случае порядок соответствовал экспериментальным результатам, определенным при действии каждой из рестриктаз в отдельности. Это так называемая задача с двойным перевариванием, потому что процесс расщепления молекулы ферментом называют перевариванием. Решение данного примера задачи показано на рис. 5.2.
1 3 1		8	1 6		1 ю	1	
1 4 1	5	1	11		—7	1
1 3 |1|	5	1 2 |	6	1 3	7	1
Рис. 5.2. Решение задачи с двойным перевариванием
Частичное переваривание3 — вариант способа двойного переваривания. Здесь мы обрабатываем целевую ДНК только одной рестриктазой, но проводим реакции с набором копий ДНК, изменяя время, в течение которого фермент воздействует на каждую копию. Участвуя в реакции более или менее продолжительное время, фермент распознает больше или меньше участков рестрикции, и мы таким образом получаем фрагменты разной длины. В идеале такие реакции должны обеспечить нас по крайней мере одним фрагментом для каждой пары участков рестрикции. Затем, анализируя длины полученных фрагментов, мы пытаемся с очень высокой точностью определить местоположение участков рестрикции. Например, на рис. 5.2 фермент Л распознал три участка рестрикции. Реакция частичного переваривания этим ферментом дала бы фрагменты следующих размеров: 3, 11, 17 и 27 (фрагменты между крайней левой точкой и всеми остальными участками); 8, 14 и 24 (фрагменты между первым участком рестрикции и всеми, стоящими справа от него); 6 и 16 (фрагменты между вторым участком рестрикции и всеми справа от него); и 10 (последний фрагмент).
В ходе реакций переваривания могут появляться ошибки нескольких видов. Во-первых, погрешность измерения длины. Длину фрагментов определяют с помощью электрофореза в агарозном геле (см. раздел 1.5.2), где допустима погрешность измерений до 5 %. Во-вторых, если фрагменты
3На самом деле это совершенно разные техники и характер данных. — Прим. ред.
5 1 БИОЛОГИИ ЕСКИ Е ОСНОВЫ КАРТИ РОВАН ИЯ
221
слишком малы, то измерение их длин становится вообще невозможным. В-трстьих, некоторые фрагменты могут быть потеряны в процессе переваривания, что приводит к появлению зазоров в покрытии молекулы ДНК Как можно ожидать, все эти ошибки вносят осложнения в процесс картирования. Позже мы увидим, что лаже в отсутствие ошибок соответствующие вычислительные задачи оказываются очень трудными.
5.1.2.	СОСТАВЛЕНИЕ КАРТ ГИБРИДИЗАЦИИ
Вспомним, что при составлении карт гибридизации информация о перекрытии между фрагментами основана на данных о составе каждого фрагмента. Прежде чем объяснить, что это за данные, следует отмстить, что в данном контексте фрагменты называют клонами и получают методом так называемого клонирования (см. раздел 1.5.2). После того как все копии целевой ДНК были фрагментированы (различными способами) и после того как каждый полученный фрагмент был клонирован, мы получаем набор из многих тысяч клонов (клонотеку), где каждый клон обычно имеет длину несколько тысяч пар нуклеотидов4.
Информацию о клоне получают в ходе реакций гибридизации. С помощью этих реакций мы пытаемся определить, связывается ли (или гибридизируется) маленькая последовательность (зонд) с клоном. Если связывание происходит, то это означает, что клон содержит в себе последовательность, комплементарную последовательности зонда. Мы можем провести эту реакцию с одним и тем же клоном, используя несколько разных зондов, и тогда набор зондов, которые были успешно гибридизированы клоном, будет индикатором этого клона. При этом весьма вероятно, что два клона, которые гибридизируют некоторую общую часть набора соответствующих им индикаторов, получены из перекрывающихся областей целевой ДНК. Например, если мы знаем, что клон А связывает зонды х, у и z, а клон В связывает зонды х, w и z, то мы имеем серьезное основание полагать, что клоны А и В перекрываются друг с другом, например, как показано на рис. 5.3 (если при этом нет повторений', подробнее об этом будет сказано позже). Здесь следует подчеркнуть, что, располагая подобной информацией, мы, как правило, не сможем определить местоположение зондов в целевой ДНК, а
4Есть несколько масштабов:
1. Клонирование в дрожжевых искусственных хромосомах (ДИХ) и бактериальных искусственных хромосомах (БИХ) сотни тысяч или миллионы п.н.
2. Космиды и фазмиды — десятки тысяч п. н.
3 Плазмиды и фаги от сотен до тысяч пн— Прим, ред
222
Глава 5
вычислим только их относительный порядок. Чуть позже мы возвратимся к этому важному пункту.
Рис. 5.3. Пример ни о, как четыре зонда могут бьпь гибридизированы двумя клонами
Различные ошибки могут появиться также при протекании реакций гибридизации. Во-первых, зонд может нс связаться с клоном там, где он должен; это создает ложное несовпадение. Во-вторых, зонд может связаться с участком, где он не должен связываться; это создает ложное совпадение. Иногда в опытах присутствует субъективная погрешность исследователя неправильное чтение результатов эксперимента, — также приводящая к появлению ложных результатов. Ошибки могут появиться даже до начала гибридизации. В ходе процесса клонирования две отдельные части целевой ДНК могут соединиться и затем реплицироваться, как будто первоначально они были одним клоном. Такие клоны называют химерами, и из-за их присутствия может быть сделан ложный вывод об относительном порядке расположения зондов. Химеры возникают часто и, таким образом, являются одной из самых серьезных проблем в составлении карт гибридизации. По некоторым оценкам, во многих клонотеках от 40 % до 60 % всех клонов химеры. Другой тип ошибок в процессе клонирования удаление, когда внутренняя часть клона теряется, и таким образом снова объединяются два фрагмента, которые не были смежны в целевой ДНК.
И еще две ситуации могут причинить вред в составлении карт гибридизации. Первая возникает, когда зонды не строго специфичны и, следовательно, зонд может быть связан несколькими участками целевой ДНК; такие участки называют повторениями. Методика, называемая меченый участок последовательности (МУП), позволяет избежать этой проблемы за счет производства зондов, которые гибридизируются строго определенными участками целевой ДНК. Вторая проблематичная ситуация — простой недостаток данных, поскольку иногда невозможно осуществить все необ
5.2, МОДЕЛИ
223
ходимые реакции гибридизации. Для решения этой проблемы были разработаны методы с использованием пулов.
5.2.	МОДЕЛИ
Ознакомившись с различными стратегиями картирования, рассмотрим некоторые из соответствующих им математических моделей. Наша цель состоит в том. чтобы оценить вычислительную сложность задач картирования, основанных на этих моделях Как мы увидим, задача картирования оказывается алгоритмически грудной, но ее описание затрагивает также несколько интересных моментов построения алгоритмов, которые мы обсудим в конце этого раздела.
5.2.1.	МОДЕЛИ УЧАСТКА РЕСТРИКЦИИ
Сначала мы рассмотрим модель задачи с двойным перевариванием, которую мы обозначим аббревиатурой ЗДП. В этой модели мы полагаем, что каждый фрагмент будет представлен собственной длиной. Мы сделаем допущение об идеальном процессе переваривания, что означает, что измерения длин фрагментов безошибочны и ни один из фрагментов не может быть потерян Это очевидно нереально, но, как мы увидим вскоре, даже с этими чрезмерными упрощениями конечная вычислительная задача оказывается очень трудной.
Представив результаты эксперимента с помощью математической модели, мы получаем множество длин (положительные целые числа) для каждой реакции. Переваривание целевой ДНК первым ферментом даст нам множество А — {aj.a2,... .ап}. Некоторые из этих фрагментов могут иметь одинаковую длину, что означает, что это множество — фактически мультимножество Точно так же после применения второго фермента мы получаем множество В = {bi .Ъ?,  .  Ь7П}. Наконец, после совместного переваривания ферментами А и В мы получаем мультимножество О — = {oi,o2,...,ok}.
Какую именно информацию мы хотим извлечь из этих мультимножеств? А хотим мы найти перестановку тгд элементов множества А и перестановку тгв элементов множества В, с тем чтобы можно было достичь следующих результатов. Мы отмечаем на линии значения длин элементов множества А согласно порядку, определяемому перестановкой тгд. Точно так же мы отмечаем длины элементов множества В согласно перестановке тгв, но мы делаем это поверх предыдущей схемы. Благодаря перекрытию элементов возможно получить несколько новых подынтервалов. Теперь мы,
224
Глава 5
вероятно, можем установить взаимно однозначное соответствие между каждым полученным подынтервалом и каждым элементом множества О Если это действительно может быть сделано, то мы называем перестановки тгд и тгв решениями ЗДП.
Докажем, что поиск этих перестановок — НП-полная задача. Во-первых, не трудно увидеть, что, зная решение ЗДП, легко проверить, является ли оно истинным. Все, что для этого необходимо сделать, - сортировать множество О и нанесенные на карту подынтервалы и определить, получаем ли мы тождественные результаты Чтобы завершить доказательство, мы обращаем внимание, что, как было отмечено, ЗДП представляет собой простое обобщение задачи о разбиении множества — широко известной НП-полной задачи.
В задаче о разбиении множества мы имеем заданное множество целых чисел X = {а:], х?,..., X/} и хотим знать, можем ли мы разбить множество V на множества А'[ и А'г так, чтобы сумма всех элементов множества Xi была равна сумме элементов множества Х%. Это соответствует задаче с двойным перевариванием, где А = X, В = {А'/2, А/2} и О = А, при А’ =	ДРУГИМИ словами, задача о разбиении множества рав-
носильна ЗДП, в которой один из двух ферментов производит только два фрагмента, причем оба одинаковой длины.
Учитывая, что мы всегда ищем истинное решение ЗДП, с этой задачей связан еще один вопрос, который значительно усложняет этот поиск. Число решений можег быть экспоненциальным. Чтобы показать это, рассмотрим случай, где между двумя участками рестрикции фермента А находятся три участка 61, 62 и 63, расщепляемых только ферментом В. В этом случае мы нс сможем определить порядок фрагментов [61,62] и [62,63]. Как правило, на к участков рестрикции одного фермента мы имеем (к — 1)! решений. Фактически, ситуация еще хуже, чем эта, из-за так называемых совпадении. Совпадение возникает, когда участок рестрикции фермента А расположен очень близко к участку рестрикции фермента В (они не могут совпасть полностью; почему?). Когда мы имеем последовательные совпадения, то соответствующие фрагменты, определенные реакциями переваривания ферментами А и В, окажутся одинаковой длины (из-за погрешности измерений). Поэтому ряд из п последовательных совпадений также даст п! возможных решений. Продолжая подобное рассуждение, можно показать, что число решений возрастает экспоненциально по мере увеличения длины целевой ДНК (см библиографические примечания).
Таким образом, мы видим, что даже очень простая модель двойного переваривания ведет к серьезным вычислительным проблемам. НП-полнота частичного переваривания не была доказана, и, кроме того, эта задача кажет-
5.2. МОДЕЛИ
225
ся легче разрешимой по следующей причине. При картировании способом частичного переваривания определяется п участков рестрикции (включая крайние точки) и в результате реакции мы получаем по крайней мере один фрагмент для каждой пары участков, то есть Q) фрагментов. Будучи измерены, эти фрагменты дают мультимножество расстояний. Задача состоит в определении такого местоположения участков на линии, чтобы множество расстояний между их позициями было эквивалентно множеству длин, полученных реакциями переваривания. Задачу частичного переваривания можно считать более легкой, так как было показано, что максимальное число ее решений сравнительно мало, и, следовательно, с комбинаторной точки зрения эта задача является хорошей альтернативой задачи с двойным перевариванием.
5.2.2.	МОДЕЛЬ В ВИДЕ ИНТЕРВАЛЬНОГО ГРАФА
Мы можем бросить первый взгляд на вычислительную сложность картирования посредством гибридизации (или, в более общем виде, картирования индикаторов), используя простые модели, построенные на графах интервалов, или интервальных графах (см. раздел 2.2). Эти модели далеко отбрасывают многие трудности процесса картирования; и все же, при всей своей простоте, опи также дают начало НП-трудным задачам, как и в случае рассмотренной выше задачи с двойным перевариванием.
В этих моделях мы строим графы, вершины которых представляют клоны, а ребра отражают информацию о перекрытии соответствующих клонов. Если бы мы располагали полной и правильной информацией о перекрытии клонов, то конечный граф был бы графом интервалов; это ключевое свойство таких моделей.
а
b
с d	е
Рис. 5.4. Пример диаграммы перекрьпия клонов
В первой модели мы создаем два графа. Первый граф Gr = (V,Er). Если ребро (i,j) G Ег, то это означает, что мы точно знаем, что клоны г и j перекрываются. Второй граф Gt = (V, Et), где множество Et отражает известную плюс неизвестную информацию о перекрытии клонов (таким
226
Глава 5
образом, Ег С Et). Граф С< не обязательно полный, потому что мы можем знать наверняка, что некоторые пары клонов не перекрываются, и, следовательно, соответствующие им ребра изъяты из множества Et. Тогда задача, которую мы должны решить, может быть сформулирована следующим образом: Существует ли такой интервальный граф Gs (Г'-£?8), что Ег С Еа С Et‘! Заметим, что графы Gr и Gt не всегда являются интервальными (тогда решение было бы тривиально). См. пример на рис. 5.4, 5.5 и 5.6.
и d
Рис. 5.5. Интервальный граф, соответствующий рис. 5.4
-О а
G,
Рис. 5.6. Возможные графы Gr и Gt для примера на рис. 5.4. Ни один из них не является интервальным
Во второй модели мы не допускаем, что известная нам информация о перекрытии фрагментов надежна. Тем не менее, на основании этой информации мы строим граф G — (V, Е). Тогда в решении нашей задачи мы ищем ответ на вопрос, существует ли такой интервальный граф G' = = (V. Е'), что Е' С Е и l-E'l - максимально. Требование Е' С Е означает, что для решения этой задачи нам, возможно, придется отбросить некоторые ребра графа С, которые могут быть интерпретированы как ложные совпадения. Тогда искомое решение — это такая интерпретация графа, в которой присутствует минимальное число ложных совпадений.
5.2. МОДЕЛИ
227
В третьей модели мы используем информацию о перекрытии наряду с информацией об источнике каждого клона следующим образом. Поскольку клоны отбирают из различных копий одной и той же молекулы, разумная идея — пометить каждый клон для идентификации той копии молекулы, из которой он был взят. Допустим, что мы имеем к копий целевой молекулы ДНК и что для расщепления каждой копии был использован отдельный фермент рестрикции. Тогда, на основании известной информации о перекрытии между клонами мы строим граф G = (V, Е). Поскольку клоны помечены, мы можем представить, что соответствующие им вершины графа раскрашены к красками (одна краска для каждой копии молекулы). Построенный граф не будет иметь ребер между вершинами одного цвета, потому что такие вершины соответствуют клонам, взятым из одной и той же копии молекулы, и, следовательно, которые не могут перекрываться. В таком случае мы говорим. что граф имеет правильную раскраску. Теперь мы ломаем голову над вопросом: Существует ли такой интервальный граф G' = (V, Е'), что выражение ЕСЕ1 верно и раскраска графа G правильна также и для графа G'? Другими словами, можем ли мы добавить ребра к графу G и преобразовать его в интервальный граф, не нарушив при этом его раскраску?
Только что мы описали три различные модели картирования посредством гибридизации, причем все из них относительно просты. Однако оказывается, что все три формальные задачи НП-трудныс. Мы нс будем давать доказательств: их можно найти в ссылках, приведенных в конце главы. Опишем модели, разработанные для специальных случаев.
5.2.3.	СВОЙСТВО ПОСЛЕДОВАТЕЛЬНЫХ ЕДИНИЦ
Модели, представленные в предыдущем разделе, предназначены для формального описания картирования посредством гибридизации, но в принципе они могут быть использованы в любой ситуации, где для каждого фрагмента мы можем получить уникальный индикатор какого-либо вида. Здесь мы представим модель, использующую в качестве индикатора клона набор связывающихся с ним зондов. В этой модели мы делаем следующие допущения:
•	Обратный комплемент последовательности каждого зонда появляется в целевой ДНК только один раз («уникальность зондов»).
•	Эксперименты свободны от ошибок.
•	Были проведены все необходимые реакции гибридизации типа «клон х зонд».
228
ГЛАВА 5
Читатель может испугаться, что здесь его подстерегает очередная НП-трудная задача. К счастью, на сей раз дело обстоит не так. Как мы увидим, конечная задача разрешима за полиномиальное время, хотя некоторые из ее обобщений действительно НП-трудные.
Допуская, что в экспериментах участвует п клонов и тп зондов, мы можем построить бинарную матрицу М размером п х т, где элемент А/ц содержит информацию о том, гибридизируется ли зонд j клоном i (MtJ = = 1) или нет (А/у = 0). Составление физической карты на основании этой матрицы представляет собой задачу поиска такой перестановки столбцов (зондов), чтобы все 1-цы в каждой строке (клоне) были последовательными. Говорят, что строки бинарной матрицы, для которой такая перестановка может быть найдена, обладают свойством последовательных единиц (СПЕ). Далее мы мы будем использовать термины перестановка СПЕ и задача СПЕ, значение которых очевидно.
Проверка матрицы на СПЕ и последующий поиск правильной перестановки известная задача, для решения которой существуют полиномиальные алгоритмы. Один из таких алгоритмов мы представляем в разделе 5.3. Ясно, что такая модель слишком проста. Если в экспериментах присутствуют ошибки, то в некоторых строках даже правильной перестановки, возможно, не все единицы будут стоять в последовательных позициях. Но зачем тогда об этом беспокоиться? Проверка матрицы на СПЕ необходима, так как анализ свободного от ошибок случая помогает нам получить информацию, полезную при построении алгоритмов обработки данных с ошибками. В частности, мы можем использовать следующее важное допущение. Во многих лабораториях исследователи стараются минимизировать число ошибок в экспериментах. Если бы эксперименты были совершенны, то конечная матрица гибридизации безусловно обладала бы СПЕ. Это означает, что любой алгоритм поиска истинной или приближённой перестановки столбцов должен дать решения, которые минимизируют число ситуаций, объяснимых погрешностью эксперимента. Следовательно, такие алгоритмы должны быть способны найти перестановку СПЕ, если таковая возможна.
Обратите внимание, что даже если перестановка СПЕ существует, то мы не можем утверждать, что именно она - правильная перестановка. С одной стороны, для одной матрицы входов может существовать несколько таких перестановок. Возможно ли определить, которая из них является правильной? В большинстве случаев нет. Мы можем лишь утверждать, что все перестановки, в которых все 1-цы последовательны, представляют собой возможные варианты правильной перестановки. По этой причине алгоритм для задачи СПЕ должен давать нам не одно, а все возможные решения. Кроме того, учитывая, что ошибки действительно существуют, может
5.2. МОДЕЛИ
229
случиться и так, что лаже если будет найдена только одна перестановка, то перестановка СПЕ не будет искомой правильной перестановкой.
С другой стороны, возникает вопрос: Каким обазом мы можем усовершенствовать модель, с тем чтобы она могла учитывать ошибки? Для этого есть много возможностей. Вместо того, чтобы требовать присутствие строго одного блока последовательных 1-ц в каждой строке, мы можем стараться найти такую перестановку столбцов, чтобы в каждой строке было самое большее к блоков последовательных 1 -ц, где значение к может быть 2 или 3. Или же мы можем пытаться минимизировать общее количество блоков последовательных 1-ц в матрице. В таком случае мы можем ожидать, что большинство строк будет иметь только один блок последовательных 1-ц, тогда как случайная строка могла бы иметь четыре или пять. К сожалению, как мы уже намекнули выше, эти обобщения приводят к НП-трулным задачам (см. упражнение 16). Даже если при полном отсутствии ошибок мы ослабим допущение об обязательной уникальности зондов, задача опять-таки становится НП-трудной (см. библиографические примечания).
5.2,4.	СВОЙСТВА «ИДЕАЛЬНО! О» АЛГОРИТМА КАРТИРОВАНИЯ
Перед описанием алгоритмических методов составления физических карт, мы хотели бы рассмотреть некоторые ограничения, связанные с трудностью данной задачи. Эти соображения представляют в несколько ином свете то, что мы подразумеваем под «решением» задачи с помощью алгоритма, и поэтому должны быть интересны также вне контекста составления физических карт.
Первое соображение заключается в гом, что на самом деле мы пытаемся решить реальную практическую задачу, а нс абстрактный математический формализм. В реальной задаче мы хотим определить истинный порядок клонов в целевой ДНК. В комбинаторной задаче мы пытаемся найти истинное упорядочение из конечного множества возможных
Мы будем стараться найти это истинное упорядочение посредством абстрактных моделей, которые дают начало задачам оптимизации. Сами по себе эти задачи могут быть очень трудными, вопреки тому факту, что они являются абстракциями еще более трудной задачи. Например, оптимизационные варианты всех задач, представленных в разделе 5.2 2, НП-трудные В общем случае мы не сможем найти оптимальные решения этих задач быстро; и даже в том случае, если мы действительно решим одну из них оптимально в пределах разумного времени, мы не получим никакой га
230
Глава 5
рантии того, что найденное решение соответствует истинному. Итак, мы с ужасом понимаем, чго перед нами просто безвыходная ситуация.
Однако картина не столь уж безрадостна, как кажется на первый взгляд. Во-первых, поскольку мы не имеем никакой гарантии, что любое оптимальное решение является истинным, хорошие приближённые решения могут практически полностью отвечать нашим целям. Во-вторых, мы должны помнить, что алгоритмы в молекулярной биологии часто приходится использовать многократно. Ученый получает экспериментальные данные и «скармливает» их алгоритму. Основываясь на одном или нескольких решениях, выданных алгоритмом, ученый может провести большее число экспериментов и получить больше данных, после чего запустить алгоритм снова. На каждом этапе мы можем ожидать, что будут найдены «лучшие» (или «более близкие к истинному») решения.
Эти наблюдения предлагают желательные свойства алгоритма картирования, которые мы перечисляем ниже:
•	Алгоритм должен работать лучше с большим количеством данных, если при этом частота появления ошибок остается неизменной.
•	Алгоритм должен возвращать решение вместе с дополнительной информацией, показывающей, как именно это решение было получено, и выделять «хорошие» части решения (группы клонов, для которых найденное упорядочение может быть обосновано) на фоне «нс столь хороших» частей. Это значительно облегчает дальнейшие эксперименты.
•	Если критериям оптимизации соответствует несколько вариантов решения, то должны быть выданы все из них. Если получено слишком много решений, то это значит, что критерии оптимизации слишком слабы (или входные данные содержат слишком много ошибок). Наоборот, если не было найдено ни одного решения, то, возможно, следует ослабить критерии оптими зации.
Кроме того, мы хотели бы иметь некоторую гарантию того, что истинное решение находится среди найденного алгоритмом множества приближённых (оптимальных) решений. Как правило, это невозможно. Вместо этого мы пытаемся получить несколько различных функций оптимизации и соответствующие им алгоритмы, оптимальные решения которых имеют свойства истинного решения. При этом мы надеемся, что истинное решение с высокой вероятностью будет лежать на пересечении множеств решений, найденных каждым алгоритмом. Пример подобной гарантии мы приводим в разделе 5.4.2.
Интересно отметить, что вместо того, чтобы использовать несколько алгоритмов, как было предложено, мы можем попытаться построить алго
5.3. АЛГОРИТМ ДЛЯ ЗАДАЧИ СПЕ
231
ритм, который может оптимизировать многоцелевые функции. Это очень важная специальная область исследования.
5.3.	АЛГОРИТМ ДЛЯ ЗАДАЧИ СПЕ
В этом разделе мы представляем простой алгоритм, который определяет, обладают ли СПЕ строки бинарной матрицы М размером п х т. Цель алгоритма состоит в отыскании такой перестановки столбцов матрицы, чтобы в каждой сс строке все 1-цы были последовательны. Для простоты мы допустим, что все строки различны (то есть индикаторы всех клонов уникальны) и что никакая строка нс состоит полностью из нулей (то есть каждый клон гибридизировал по крайней мере один зонд).
Объяснение принципа работы алгоритма требует, чтобы мы сначала разобрали способ, которым строки могут взаимно зависеть друг от друга. Для этого, как известно, мы должны дать очередное новое определение.
Определение 5.1. Для каждой строки i матрицы А/, пусть S, - множество столбцов к, где Mlrk — 1-
Тспсрь, на основании этого определения мы способны определить взаимосвязь строк матрицы. Рассматривая две строки i и j, можно представить три возможные ситуации:
1.	StC\Sj = 0.
2.	S, С Sj либо Sj С 8г.
3.	St О S} 0 0, и ни одно из них нс является подмножеством другого.
Ясно, что в первой из этих ситуаций мы можем обрабатывать строки отдельно, так как перестановка столбцов, соответствующих элементам множества строк 8г, нс будет затрагивать элементы множества строк Sj. В таком случае мы можем поместить строки г и j в различные компоненты и обрабатывать каждый компонент отдельно. Но как быть со строками, которые имеют непустое пересечение? (Здесь мы немного злоупотребляем понятиями и говорим о строках вместо соответствующих им множеств S.) Должны ли все они быть в одном компоненте? Рассмотрим этот случай подробнее.
Сначала объединим в один компонент все строки с непустым пересечением. Предположим, что в этом компоненте существует такая строка к, что множество Sk является либо подмножеством множества Si, либо непе-рссскающимся с Si множеством, для всех г 0 к в этом компоненте. Ясно, что во время обработки этого компонента мы можем не учитывать строку к
232
Глава 5
Рис. 5.7. Граф (?с. соответствующий матрице из табл. 5.1. Связные компоненты обозначены греческими буквами
(и любые другие с тем же свойством). Таким образом, строка k будет находиться в своем собственном компоненте, возможно, вместе с некоторыми другими строками. Объясним, что это за «некоторые другие» строки.
Таблица 5.1. Бинарная матрица
	C| C2 C3 C4 C5 C6 c7 C8 Cg
h h 1з «4 ^5 I? <8	110 110 10 1 0 11111111 0 10110101 0 0 1 0 0 0 0 1 0 0 0 1 0 0 1 0 0 0 0 0 0 1 0 0 1 0 0 0 1 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0 1
Руководствуясь только что представленными свойствами матрицы, дадим формальный способ определения принадлежности пары строк к одному компоненту. На элементах матрицы М мы строим граф Gc- Естественно, каждая вершина графа Gc соответствует строке матрицы Л/. Если S2r\Sj 0 0 и если ни одно из них не является подмножеством другого, то в графе Gc существует неориентированное ребро, соединяющее вершины г и j. Компоненты матрицы, которые мы хотим получить, будут представле
5.3. АЛГОРИТМ ДЛЯ ЗАДАЧИ СПЕ
233
ны связными компонентами графа Ge- Например, на рис. 5.7 изображен граф Ge, соответствующий матрице из таблицы 5.1.
Опишем основные шаги алгоритма: 1) разделить строки матрицы на компоненты, 2) переставить столбцы каждого компонента и 3) некоторым образом объединить компоненты. Первый шаг алгоритм выполняет согласно приведенному выше правилу, остальные два сформулируем в виде отдельных подзадач 1) найти правильную перестановку для каждого компонента и 2) объединить компоненты. Сперва произведем перестановку столбцов в компоненте.
Перестановка столбцов в компоненте
Чтобы объяснить эту часть алгоритма, мы используем в качестве примера матрицу из табл. 5.2 (допуская, что это только ссченис некоторой матрицы имеющей более грех строк).
Сначала отдельно рассмотрим строку Ц. Если бы она была единственной строкой в этом компоненте, зо все, что мы должны были бы сделать, переставить столбцы так, чтобы все 1-цы стали последовательными. Обратите внимание, чго, если в этой строке существует к 1 -ц, го мы получим к\/2 возможных перестановок. При этом мы нс учитываем инверсии в качестве отдельных решений, поскольку они дают точно такую же последовательность 1-ц. В случае строки Zi, 1-цы находятся в столбцах 2, 7 и 8. Тогда множество возможных перестановок равно 2, 7, 8, или 7, 2, 8, или же 2, 8, 7. Мы можем кодировать все эти решения, приписывая множество возможных столбцов к каждому элементу данной строки, равному 1-це (мы назовем эти множества множествами столбцов). Для компонента, состоящего только из одной строки, этим множеством столбцов является множество S, определенное выше, и мы описываем конечную конфигурацию следующим образом:
{2,7,8} {2,7,8} {2,7,8}
Zi -» ... О 1	1	1	0 ...
Теперь взглянем на следующую строку, Iz- Поскольку эта строка на ходится в том же компоненте, что и строка Zj, то очевидно, что некоторые
Таблица 5.2. Сечение бинарной матрицы
	С1	С2	сз	с4	с5	св	с?	С8
Z1	0	1	0	0	0	0	1	1
h	0	1	0	0	1	0	1	0
1з	1	0	0	1	0	0	1	1
234
Глава 5
столбцы компонента состоят из двух 1-ц, принадлежащих, соответственно, строкам /1 и I2, а некоторые — из 1-цы одной последовательности и нуля другой. Теперь мы должны расположить строку I2 относительно строки Zi так, чтобы значения столбцов были взаимно согласованными. Мы имеем возможность выбора из двух вариантов такого размещения: поместить 1-цы строки I2 слева либо справа от 1-ц строки Ц. Это означает размещение столбца 5 слева либо справа от столбцов 2 и 7. Предположим, что мы поместили столбец 5 слева. Тогда возможные решения, закодированные множествами над каждым столбцом, принимают вид:
{5} {2,7} {2,7} {8}
Z, — ... О О	1	1	10...
12 -» ... О 1	1	1	0 0...
Если бы строки I] и I2 были единственными двумя строками в этом компоненте, то мы имели бы две возможные перестановки столбцов: 5, 2, 7, 8 и 5, 7, 2, 8. Если бы мы выбрали размещение столбца 5 справа, то мы бы получили инверсию этих двух перестановок. Это означает, что выбор направления для размещения второй строки не имеет значения, и это — важное свойство.
Теперь рассмотрим третью строку, I3. Поскольку она находится в том же компоненте, что и другие две, мы знаем, что в графе G< мы должны найти ребро (Z3, lj), или ребро (Z3,I2), или же оба. В нашем примере присутствуют оба ребра. Найдем расположение строки /3 относительно строки I2. Очевидно, что мы снова можем выбирать между размещением 1-ц строки 1% слева или справа от 1-ц строки I2. Но теперь мы должны учитывать также взаимосвязь между строками /3 и Zj. Это можно сделать, рассматривая число элементов в пересечениях между множествами Si, S2 и S3. Пусть для любых двух множеств х и у равенство х • у = |ST П SjJ верно (скалярное произведение строк х и у). Если Zi -Z3 < min(Zi - Z2, ^2^3), то строка 1з должна быть помещена в компонент в том же направлении, в котором строка I2 была расположена относительно строки 1г. Если Zi -Z3 > inin(Zj -/2, (2^3),то мы должны поместить строку Z3 во встречном направлении тому, в котором мы расположили строку I2 относительно строки Zi (здесь нс должно быть равенства; почему?). В любом случае, если компонент обладает СПЕ, то это значит, что строки Zi и Z3 расположены правильно: и наоборот, сели строки Zi и Z3 расположены неправильно, то компонент не обладает СПЕ. Эта особенность связана с тем, что единственный случай выбора, который мы делали до сих пор, касался расположения строки I2 относительно строки Zb и мы знаем, что обе возможности (левое или правое расположение единиц) дадут тождественные решения, включая инверсии.
5.3. АЛГОРИТМ ДЛЯ ЗАДАЧИ СПЕ
235
Algorithm Place'’
input: и, v и w — вершины графа Gc = (V, Е), где (и, v) & Е и (у, w) G Е.
И вершины v и w могут иметь значение nil output: Возможное расположение строки и if v = nil and w = nil then
Расположить все 1-пы строки и последовательно else if w nil then
Расположить 1-цы строки и слева или справа относительно
1 -ц строки v
Запомнить направление расположения
else
if и  v < min (и  v.v • w) then
Расположить и относительно V, используя то же направление, что и при расположении vотносительно w
Запомнить направление расположения else
Расположить и относительно V, используя встречное направление тому, которое использовалось при расположении v относительно w
Запомнить направление расположения
Проверить множества столбцов на непротиворечивость.
Рис. 5.8. Процедура расположения строки в компоненте по отношению к двум другим строкам
В нашем примере S3 = {1,4,7.8}. Тогда 1-3 = 2, 1-2 = 2и 3-2 = 1, что означает, что мы должны поместить 1-цы строки 13 справа от 1-ц строки I?, как показано ниже:
		{5}	{2} {7}	{8} {1,4} {1,4}
G	—*	... 0	0	1 1	1	0	0	0 ...
<2 —»	... 0	1	1 1	0	0	0	0 ...
h —»	... 0	0	0	1	1	1	1	0 ...
Теперь мы знаем,		ЧТО 1	правильная	перестановка столбцов 2, 5, 7 и 8
равна 5, 2, 7, 8. Перестановки, содержащие также и остальные столбцы, могут быть определены, когда мы рассмотрим больше строк. Но каким образом мы должны располагать последующие строки? Как мы видели, при
Расположение. — Прим, перев.
236
Глава 5
размещении третьей строки мы не имели никакой альтернативы. То же самое верно для всех последующих строк в том же компоненте. Все, что мы должны сделать для новой строки к, — это найти две предварительно помешенные строки г и j, которым в графе Gc соответствуют ребра (к, г) и (i,j), и продолжать действия, как мы делали в компоненте с тремя строками. Интересно отметить, как именно алгоритм сохраняет возможные перестановки компонента во множествах над каждым столбцом. Полагая, что после размещения первых двух строк нет альтернатив размещения последующих, мы видим, что этот алгоритм даст нам все возможные перестановки столбцов компонента, обладающего СПЕ, вплоть до инверсии. Если бы компонент в приведенном выше примере имел только три строки, то две возможные перестановки были бы 5, 2, 7, 8, 1,4 и 5, 2, 7, 8,4, 1. Как мы уже упомянули, отслеживание всех возможных решений — желательная функция алгоритма в случае картирования ДНК.
Реализация вышеописанного алгоритма проста. 11собходимо построить граф Gc и совершить обход его вершин, используя метод поиска в глубину. При посещении каждой вершины вызывать процедуру Place, представленную на рис. 5.8. Чтобы выяснить, нашел ли алгоритм перестановку СПЕ, мы можем проверять множества столбцов на непротиворечивость, когда мы анализируем очередной вариант размещения, как обозначено в последней строке процедуры Place. Если мы пытаемся расположить строку и узнаем, что один из ее столбцов должен идти, скажем, направо, а существующее размещение говорит нам, что он должен идти налево, то компонент и, следовательно. матрица не обладают СПЕ.
Оценим время счета этой процедуры. На построение графа Gc требуется время О(пт). Затем, чтобы проверить множества столбцов на непротиворечивость. мы обрабатываем п строк, затрачивая время О(т) на строку. Таким образом, полное время счета равно О(пт).
Объединение компонентов
Займемся теперь второй частью алгоритма — процедурой объединения компонентов. Организуем информацию о взаимном соответствии компонентов в виде графа Gm. Каждый компонент исходной матрицы Л/ будет соответствовать вершине графа Gm- Соединим вершины а и (3 ориентированным ребром, если множества S, для всех i е (3 содержатся по крайней мере в одном множестве S} компонента а (здесь мы не делаем никакого различия между строкой j и соответствующим ему множеством S}) Граф Gm, соответствующий компонентам матрицы из таблицы 5.1, показан на рис. 5.9.
В начале этого раздела было показано, что соотношения пребываний между множеством компонента В и множествами компонента <т те же самые
5.3. АЛГОРИТМ ДЛЯ ЗАДАЧИ СИЕ
237
Рис 5.9. Граф Сд/. соответствующий компонентам матрицы из таблицы 5.1
для всех множеств компонента fl. Покажем это более ясно. Предположим, что множество 8г, принадлежащее компоненту /?, содержится во множестве Sj, принадлежащем компоненту п. Поскольку строки г и j находятся в различных компонентах, то в компоненте п не существует строки к, такой, что множество S, не содержится во множестве и 5г П Sfc / 0. Другими словами, множество Sz содержится в некоторых множествах компонента и нс пересекается с остальными множествами этого компонента. Мы утверждаем, что точно те же соотношения пребываний и непересекаемости верны для всех множеств компонента В. Предположим обратное и проанализируем одно из таких исключений. Предположим, что г, I G (3, St Pi Si £ 0, j G а и Si С Sj, но Si <£ S3 В этом случае единственная возможность, чтобы строка I нс принадлежала компоненту о — Si CI.S’j = 0. Но это невозможно, поскольку множества S, и Si имеют по крайней мерс один общий элемент и множество Si содержится во множестве Sj. Возможность анализа других случаев мы предоставляем читателю.
Объединение компонентов зависит от соотношений пребываний множеств одних компонентов во множествах других. Ясно, что в первую очередь мы должны обрабатывать компоненты, множества которых нс содержатся где-нибудь еще. Поскольку пребывание множеств определяется направлением соответствующих рсбер, мы должны обрабатывать граф Gm в топологическом порядке (Это возможно только в том случае, если граф Gm является ациклическим. Это действительно так? Да, и это нетрудно доказать.)
Осуществив правильную перестановку столбцов во всех компонентах, мы отбираем из графа Gm все вершины без входящих в них ребер и оконча
238
Глава 5
тельно фиксируем соответствующие им столбцы. Затем мы выбираем следующую в топологическом порядке вершину. Предположим, что мы следуем за ребром Это означает, что мы должны найти в компоненте а так называемый «опорный столбец», который укажет нам, как следует разместить строки компонента /3. Выберем из /3 строку I, которая имеет крайнюю левую 1-цу. и столбец, где находится эта 1-ца, назовем сд. Мы знаем, что множество Si содержится в некоторых множествах St компонента а и нс содержится в других. Найдем все строки из компонента а, которые содержат множество Si, и найдем крайний левый столбец, в который все такие строки входят 1-ми (и назовем этот столбец cQ). Это и есть искомый опорный столбец, так как мы теперь можем объединить столбцы са и ср в один столбец.
Иллюстрируем этот процесс с помощью матрицы из таблицы 5.1 и графа на рис. 5.9 и будем рассматривать его вершины в топологическом порядке. Один возможный порядок — компоненты а, (3, 6 и 7. Переставим столбцы компонента а так, чтобы 1-цы в его строках были последовательны:
	{1}	{2,4,5,7,9}	{3,6,8}
11 —> .	. 1	11111	ООО
h —» .	. 0	11111	1 1 1
Присоединим следующий компонент, [3, состоящий из одной строки: I {2,4.5, 7,9}	|
... L 1 1 1 1
Для этого нам нужно присоединить строку 13 к строкам из компонента а,
без производства каких-либо перестановок:			
	{1} 1	{2,4,5,7,9}	I {3,6,8}
/] —>	... 0	11111	ООО
<2 —>	... 0	11111	111
7з —»	...	0	11111	ООО
Далее следует компонент <5. Вот его строки с последовательными 1-ми:
	 {9,5}	{4}	{7}	{2}
fe —» -.	.00	1	1	0
/7 —» ..	.00	0	1	1
/в —> ..	.. 1 1	1	0	0
Мы можем видеть, что в компоненте <5 именно строка имеет крайнюю левую 1-цу (в столбце 5 или 9) В компоненте а обе строки /1 и /2 содержат
5.3. АЛГОРИТМ ДЛЯ ЗАДАЧИ СПЕ
239
строку 1g, и именно второй столбец (представляющий группу возможных столбцов) состоит исключительно из 1-ц. Поэтому второй столбец должен совпасть со столбцами 9 или 5 компонента <5. Вот результат:
{1} «1 - ... 1 — ... о /з— ••• 0 /6-> --- о h -> ... 0 /8— ... 0	{9, 1 1 1 0 0 1	5} 1 1 1 0 0 1	{4} 1 1 1 1 0 1	{7} 1 1 1 1 1 0	{2} 1 1 1 0 1 0	{3,6,8} 0 0 0 ... 1 1 1 ... 0 0 0 ... 0 0 0 ... 0 0 0 ... 0 0 0 ...
Подключаем компонент 7:						
.. <5 —► . .			{6} 0 1	{3} 1 1	{8} 1 0	
В конечном счете мы получаем матрицу, где все						1 -цы последовательны:
h —»	{1} 1	{9.5} 1 1		{4} 1	{7} 1	{2} 1	{С} 0	{3} 0	{8} 0
ь —»	0	1	1	1	1	1	1	1	L
/з^	0	1	1	1	1	1	0	0	0
—»	0	0	0	1	1	0	0	0	0
1? —»	0	0	0	0	1	1	0	0	0
<8^	0	1	1	1	0	0	0	0	0
	0	0	0	0	0	0	0	1	1
—»	0	0	0	0	0	0	1	1	0
Заметим, что одно		из	множеств		столбцов		; НС	является однозначным,	
что указывает на то, что мы нашли два решения. В этом конкретном случае причина состоит в гом, что столбцы 5 и 9 являются идентичными. Но в общем случае могут быть неоднозначные решения, обусловленные нс только перестановкой идентичных столбцов. Например, 1, 2, 7, 4, 9, 5, 8, 3, 6 альтернативное решение для гой же самой матрицы. Крагныс решения могут существовать, потому что граф Gд/ допускает различные топологические порядки, и эта причина дополняется следующими двумя фактами. Во-первых, каждый компонент может иметь несколько решений; во-вторых, каждое из них может быть использовано двумя способами (найденная перестановка и ее инверсия).
240
Глава 5
Определим время счета алгоритма. Топологическая сортировка графа Gm занимает время О(п 4- т). Возможно предварительно обработать элементы матрицы М таким образом, чтобы запросы, необходимые при обходе вершин графа Gm, занимали фиксированное время. Например, мы можем сохранять для каждой строки столбец, в котором находится ее крайняя левая 1-ца. Такая предварительная обработка расходует самое большее время О(пт). Поэтому данная функция показывает также время, необходимое для объединения компонентов. Полное время обработки каждого компонента, как было показано, также равно O(nni), так что это полное время счета всего алгоритма.
Существует другой алгоритм, который может найти СПЕ за время О(п 4- т 4- г), где г — общее число 1 -ц в матрице. Кроме того, этот алгоритм компактным способом кодирует все возможные решения. Однако этот алгоритм значительно сложнее алгоритма, представленного в этом разделе. Соответствующие ссылки даны в библиографических примечаниях.
5.4.	ПРИБЛИЖЁННОЕ СОСТАВЛЕНИЕ КАРТ
ГИБРИДИЗАЦИИ
В предыдущем разделе мы изучили алгоритм решения задачи СПЕ. Мы увидели, что такая задача — хорошая модель составления карт гибридизации, когда эксперименты свободны от ошибок и когда зонды уникальны. Если ошибки присутствуют, то необходим иной подход, который и составит предмет настоящего раздела
Вначале рассмотрим эффект воздействия ошибок на бинарную матрицу А/ размером п х т. Предположим, что перестановка столбцов матрицы А/ правильна. Тогда, если нет никаких ошибок, то в каждой строке все 1 цы будут последовательными. Если строка соответствует химерному клону, где были соединены два фрагмента, то мы увидим два блока 1-ц, разделенных некоторым числом нулей (если допустить, что в этой строке не присутствуют никакие другие ошибки). Последовательный блок нулей, ограниченный 1-ми, мы будем называть промежутком. Учтите, что этот термин отличается от термина пропуск, употребляемого в других главах этой книги. Таким образом, мы можем сказать, что промежуток в этой строке образован химерным фрагментом. Если в другой строке есть ложное несовпадение, то соответствующий 0 может разделить два блока 1-ц, создавая еще один промежуток, как показано ниже
0 110 11110 0
Т
ложное несовпадение
5.4. ПРИБЛИЖЁННОЕ СОСТАВЛЕНИЕ КАРТ ГИБРИДИЗАЦИИ
241
Этот промежуток не был бы создан, если бы зонд был крайним левым или крайним правым в соответствующем клоне. Наконец, ложное совпадение может расщепить нулевой блок на два, таким образом создавая еще один промежуток. Таким образом, мы видим, что существует тесная взаимосвязь между ошибками во фрагментах и промежутками в матрице. Если принять основное допущение о том, что мы в максимально возможной степени хотим избежать объяснения промежутков погрешностью экспериментов, то разумный подход будет заключаться в том, чтобы стараться найти перестановку с минимальным общим числом промежутков в матрице. Такой подход основан на свойстве, согласно которому если перестановка СПЕ возможна, то именно она будет иметь минимальное число промежутков. Другими словами, минимизацию промежутков можно рассматривать как обобщение задачи с последовательными единицами. В разделе 5.2.3 мы упомянули, что некоторые расширения к задаче СПЕ являются НП-трудными. Это же относится и к только что описанной задаче минимизации промежутков. Однако, как мы покажем далее, для того чтобы получить приближенные решения этой частной НП-трудной задачи, мы можем использовать различные специальные методы, которые, предположительно, дают достаточно хорошее решение.
5.4.1.	ГРАФОВАЯ МОДЕЛЬ
Оказывается, что минимизация промежутков равносильна решению известной задачи из теории графов. Это так называемая задача коммивояжера, описанная в разделе 2.2.
Таблица 5 3 Матрица п х тп с дополнительным столбцом pj
	Pl	Р2	Рз	Р4	Р5	Рб
С1	1	1	1	0	0	0
С-2	0	1	1	1	0	0
сз	1	0	0	1	1	0
С4	1	1	1	1	0	0
Вход этого варианта задачи коммивояжера полный неориентированный взвешенный граф G. Вершины графа G соответствуют столбцам бинарной матрицы М размером п х тп, то есть зондам. По причинам, которые скоро станут ясными, мы также должны ввести в матрицу 1/ дополнительный столбец, заполненный нулями, и соответствующую этому столбцу вершину — в граф G. Вес каждого ребра графа G — число строк, в кото
242
Глава 5
рых два соответствующих столбца отличаются (так называемое Хеммингово расстояние между строками). Например, в таблице 5.3 мы видим пример бинарной матрицы, а на рис. 5.10 — соответствующий ей граф. Покажем, что цикл с минимальным весом в графе G соответствует перестановке столбцов с наименьшим числом промежутков в матрице Л/.
Рис. 5.10. Граф чадачи коммивояжера, соответствующий матрице чгч табл. 5.3
Для этого заметим, что при такой перестановке столбцов промежуток в строке означает, что в некоторой точке мы имеем переход от 1-цы к нулю, и далее — переход от нуля к 1-це. Таким образом, на каждый промежуток мы имеем два перехода, и каждый промежуток вносит точно 2 единицы в вес цикла, соответствующего данной перестановке столбцов. Однако веса ребер могут быть увеличены и за счет экстремальных переходов, то есть переходов между элементами в экстремальных (1 или т) столбцах, и они не соответствуют промежуткам. Чтобы гарантировать, что каждая строка имеет пару экстремальных переходов, мы включаем дополнительный нулевой столбец с индексом т +1. Без такого столбца циклы в графе соответствуют перестановкам, где возможен последовательный переход единиц из строки в строку, чего мы не должны допускать. Тогда взаимосвязь между циклами и перестановками дает следующее выражение
вес цикла - число переходов в промежутках + 2п.
Это ошачасг, что при постоянном п уменьшение веса цикла равносильно уменьшению числа промежутков.
5.4. ПРИБЛИЖЁННОЕ СОСТАВЛЕНИЕ КАРТ ГИБРИДИЗАЦИИ
243
Итак, мы только что показали, как задача минимизации промежутков может быть сведена к задаче коммивояжера6. Как мы знаем, задача коммивояжера является НП-трудной, так что в принципе мы достигли немногого. Однако известно большое множество методов точного или приближённого решения различных вариантов задачи коммивояжера, и эти методы мы можем использовать в нашем случае. Существование таких методов само по себе нс достаточно, чтобы уверить нас в том, чзо решение задач данного класса даст нам истинную перестановку зондов. Мы нуждаемся в гарантии того, что такие решения, в некотором смысле, будут близки к истинному решению. Одну такую гарантию мы покажем в разделе 5.4.2.
Перед этим возвратимся к задаче минимизации промежутков и представим пример идей, очерченных в конце раздела 5.2.4. Выше мы определили функцию, возвращающую общее число промежутков в матрице входов. Далее мы показали, что перестановка с минимальным значением этой функции (или приблизительно минимальным) помогает нам найти истинную перестановку столбцов. Так как мы не имеем гарантии, что истинная перестановка будет среди найденных нами решений, мы должны искать другие функции, которые также могли бы быть полезны. Идея заключается в том, что, тщательно определив несколько таких функций оптимизации и разработав для них алгоритмы, мы увеличим степень правдоподобия достижения истинного решения. В частности, разумно ожидать, что истинное решение будет находиться в пересечении всех множеств решений. Однако эго возможно только в том случае, если каждая функция отражает одно из известных или предполагаемых свойств истинных решений.
Приведем пример другой функции оптимизации. Один возможный недостаток минимизации промежутков состоит в том, что в перестановке с минимальным значением этой функции одна или несколько строк могут содержать много промежутков, а другие — ни одного. Наличие многих промежутков в одной строке нежелательно, так как это означало бы, что один клон был подвергнут намного большему числу экспериментальных ошибок, чем другие клоны, что противоречит лабораторной практике. Полому следует пытаться минимизировать число промежутков в строке. В качестве упражнения 15 мы предоставляем возможность показать, что предыдущая графовая модель может быть использована также и для этой функции оптимизации. Конечная задача на графе известна как задача коммивояжера на v/кие места и является НП-трудной.
6То, что наша задача сводится к НП-полной задаче, — не беда, поскольку это означает, что наша галача не сложнее НП-полной задачи. Хуже, если НП-полная задача сводится к нашей. Н/WK. pt4>.
244
Глава 5
5.4.2.	ГАРАНТИЯ
В этом разделе мы приводим формальное доказательство того, что подход с использованием задачи коммивояжера, очерченный в предыдущем разделе, даст нам, с высокой вероятностью, правильную перестановку. Доказательство, которое мы представляем, опирается на два основных допущения: 1) число зондов достаточно велико; 2) процесс картирования подчиняется некоторой математической модели. Предположительно, эта модель достаточно точно описывает крупные проекты картирования. Опишем эту модель чуть позже.
Сначала мы сделаем допущение, что молекула ДНК, с которой мы имеем дело, настолько длинна, что мы можем думать о ней как об интервале на вещественной оси, простирающемся от 0 до N. Тогда клоны представлены подынтервалами этого длинного интервала, и мы допускаем, что все они имеют одинаковую длину; для удобства примем каждый клон за единицу длины. Чтобы упростить концепцию модели, мы будем говорить о перестановках клонов, а нс о перестановках зондов. Допущение о единице длины, равной клону, делает эти перестановки равносильными. Это означает, что теперь мы будем искать последовательные 1-цы в столбцах, а не в строках, и что каждая вершина в соответствующем графе задачи коммивояжера будет соответствовать клону. Мы используем левую конечную точку каждого клона в качестве его локатора. Мы, конечно, не знаем точного положения каждого клона в молекуле; и поскольку мы имеем дело с гибридизацией, все, что мы сможем определить, — это относительный порядок клонов.
Главная особенность этой модели — распределение клонов вдоль целевой ДНК. Мы сделаем допущение, что позиция каждого клона представлена независимой случайной переменной, что локаторы клона распределены равномерно в интервале [0. N — 1] и что клоны покрывают интервал [0. Л’] (то есть для каждого подынтервала I в интервале [0. ЛГ] всегда существует по крайней мере один клон С, такой, что С П1 ф 0)-
Другой важный параметр модели — распределение зондов. Мы не будем делать допущение об уникальности всех зондов; вместо этого мы допустим, что в целевой ДНК каждый зонд появляется редко. Более формально мы скажем, что появление данного зонда подчиняется распределению Пуассона со степенью Л. К тому же, закон распределения каждого отдельного зонда не зависит от распределения остальных зондов. Эта часть модели позволяет нам немедленно получить выражение для вероятности гибридизации клоном специфичного зонда:
, \к
Рг{данный зонд появляется к раз в данном клоне} = е -уг- (5-1)
5.4. ПРИБЛИЖЁННОЕ СОСТАВЛЕНИЕ КАРТ ГИБРИДИЗАЦИИ
245
Это выражение может быть получено из любой формулы, описывающей распределение Пуассона, так как наши клоны являются интервалами единичной длины.
На этом мы завершаем описание модели. Теперь мы покажем, что для данной бинарной матрицы п х т перестановка строк, найденная решением соответствующего варианта задачи коммивояжера, даст хорошее приближение к правильной перестановке. Это свойство отражено в следующем утверждении: По мере увеличения числа зондов вероятность того, что обе перестановки являются тождественными, стремится к 1-це. Обратите внимание, что для каждого отдельного варианта задачи число зондов фиксировано. Мы лишь утверждаем, что в больших варианзах задачи (размер задачи мы измеряем числом зондов) перестановка в задаче коммивояжера будет с более высокой вероятностью тождественна правильной перестановке.
Чтобы доказать это утверждение, мы должны опираться на веса ребер графа, то есть на расстояния между клонами. Как мы упоминали, вес каждого ребра в графе, соотнесенном с матрицей входов Л/, называют Хем-минговым расстоянием между двумя конечными точками этого ребра (клонами). Обозначим величиной Хеммингово расстояние между клонами г и j. Кроме того, мы можем ввести понятие истинного расстояния между клонами. Обозначив координаты клона буквами I (левая) и г (правая), мы можем определить это расстояние как
= IG - М + lrj ~ = 2IG “	(5.2)
учитывая, что все клоны имеют одинаковый размер.
Предположим теперь, что мы знаем все истинные расстояния. Тогда становится ясно, что наибольшее истинное расстояние дало бы нам клоны, которые являются самыми отдаленными, то есть клоны, которые появляются на противоположных концах интервала [О, 7V], Следующее (в порядке убывания) наибольшее расстояние дает нам другую пару клонов, которые находятся между предыдущими двумя клонами, и так далее. Это означает, что, зная истинное расстояние, мы способны получить правильную перестановку клонов (что не удивительно). Однако на самом деле мы определяем Хсмминговы расстояния а не истинные расстояния (у. Но именно потому, что мы пытаемся получить лишь правильный относительный порядок клонов, будет достаточно, если мы могли бы сказать, что для данных любых четырех клонов г, j, г и я неравенства htj < hrs и ty < tra равносильны. Эго связано с тем, что некоторое понятие порядка расстояний между клонами было всем, чго нам нужно для расположения клонов друг относительно друга на основании истинных расстояний. Если мы докажем, что по мере
246
Глава 5
увеличения числа зондов вероятность htJ < hrS <=> t,j < trs стремится к единице, то мы получим искомый результат.
Рассмотрим некоторую пару клонов г и j и определим вероятность того, что некоторый зонд р вносит вклад в Хемминтово расстояние между клонами этой пары. Это случится, если зонд р гибридизирует клон г и при этом не гибридизирует клон j; или наоборот. Обращаясь к уравнению (5.1), мы видим, что вероятность того, что зонд р не появляется в клоне j, равна е~\ поскольку к = 0. С другой стороны, вероятность появления зонда р по крайней мере однажды в клоне г тождественна дополнительной вероятности того, что зонд р не появляется в той области клона г, которая не перекрывается с клоном j. Если это перекрытие обозначить zy, то мы получаем следующее выражение:
Рг{зонд р гибр. клон i и не гибр. клон j, или наоборот} =
= ру = 2е-А(1 -	(5’3)
По существу это выражение означает, что существует вполне определенная вероятность наступления такого события. Теперь мы можем учитывать все зонды, и каждый из них будет иметь некоторую вероятность гибридизации клонами г и j. Допустим, что мы имеем т зондов и рассмотрим отношение h-^/m. Оно отражает средний вклад каждого зонда в Хеммингово расстояние между клонами i и j (вклад зонда в Хсммингово расстояние всегда равен 0 либо 1). Если число зондов достаточно велико, то мы можем обратиться к закону больших чисел и сказать, что отношение hijlm приближается к вероятности ру. Или, для любого постоянного малого положительного вещественного числа е, что
при т —> оо. Здесь следует подчеркнуть, что так как все клоны имеют единичную длину, истинное расстояние между двумя перекрывающимися клонами i и j с мерой перекрытия zy определяется выражением ty = 2 — — 2zy (см. уравнение (5.2)). Это позволяет нам подставить ty вместо zy в уравнение (5.3) и показать, что фактически tv > trs тогда и только тогда, когда ру > ргв, для пар клонов i,j иг, s. Но если дело обстоит так, то мы можем сказать, что
Pr{|ty - Лу| > е} —» 0.
Это в свою очередь подразумевает hij < hr8 <=>	< tr8, что и требова-
лось доказать.
5.4. ПРИБЛИЖЁННОЕ СОСТАВЛЕНИЕ КАРТ ГИБРИДИЗАЦИИ
247
5.4.3.	ПРАКТИКА ВЫЧИСЛЕНИЙ
В этом разделе мы представляем некоторые важные результаты вычислительных испытаний алгоритмов для решения задачи составления карт гибридизации. Однако прежде чем представить эти результаты мы должны привесги соображения относительно возможного способа интерпретации результатов таких испытаний. Некоторые из этих соображений общезначимы для многих задач вычислительной биологии.
Вначале мы оценим входные данные, используя другой граф. После этой оценки станет более ясно, что мы можем ожидать от любого алгоритма поиска правильной перестановки зондов. Этот граф будет использован также и в следующем разделе.
Граф гибридизации Н мы определим как двудольный граф ((7. V. Е), который строится на основании информации из матрицы гибридизации: клоны — вершины доли U, а зонды — вершины доли V. Если некоторый зонд гибридизирует специфичный ему клон, то между соответствующими вершинами графа существует ребро. На рис. 5.11 изображен двудольный граф Н, который был построен на матрице М из табл. 5.3 за исключением нулевого столбца.
Рис. 5.11. Граф гибридизации Н, соответствующий матрице гибридизации (табл. 5.3) без нулевого столбца
Первое, на что можно обратить внимание, — что даже если все элементы матрицы гибридизации правильны, граф Н может не быть связным Если дело обстоит именно так, то независимо от того, насколько хорош наш алгоритм, мы не сможем определить относительный порядок зондов, принадлежащих различным связным компонентам графа: просто необходимая для этого информация не присутствует в матрице гибридизации. Связный
248
Глава 5
компонент графа может быть очень прост и состоять из одной вершины, — представляя зонд, который не был гибридизирован никаким клоном, либо клон, который не был гибридизирован ни одним зондом.
Второе наблюдение состоит в том, что зонды могут быть избыточными, то есть гибридизировать одно и то же множество клонов. Это может случиться, если различные зонды гибридизируются участками целевой ДНК, расположенными близко друг к другу. Кроме того, это возможно в том случае, если некоторые клоны, соответствующие данной области ДНК, отсутствуют, оставляя некоторые зонды без положительных результатов гибридизации.
Связные компоненты графа Н появляются, когда мы решаем соответствующую задачу с последовательными единицами. Избыточные зонды могут быть легко обнаружены также путем анализа элементов матрицы гибридизации. Это столбцы, которые имеют одинаковую перестановку нулей и единиц. Но если в матрице присутствуют ошибки, то мы можем получить неверную информацию относительно числа и структуры связных компонентов графа Н, а также об избыточности пар зондов. В таком случае мы говорим, что ошибки маскируют эти свойства. Так что в присутствии ошибок возникает довольно трудная ситуация: матрица входов, не содержащая ошибок, может иметь недостаточно информации, необходимой для отыскания правильной перестановки (например, не содержащий ошибок граф Н состоит из нескольких компонентов), и даже в распознавании такого недостатка информации мы можем испытывать большие затруднения (потому что граф Н с ошибками состоит только из одного компонента). Если допустить, что матрица из табл. 5.3 свободна от ошибок, то зонды р? и рз очевидно избыточны, но если бы между клоном сз и зондом рз был ложный признак гибридизации, то мы были бы неспособны распознать их избыточность.
Исходя из возможности возникновения такой ситуации, становится ясно, что оценка алгоритма картирования является трудной задачей (в дополнение к самому картированию!). Взглянем теперь на то, как мы можем оценить такие алгоритмы при допущении, что мы так или иначе знаем правильный ответ на любую задачу картирования. Например, это возможно, если мы используем компьютерную программу, генерирующую искусственные варианты картирования и моделирующую при этом различные ошибки. Если такие задачи правильно описывают реальные задачи, то из предыдущих рассуждений должно быть ясно, что матрица входов может содержать недостаточно информации для того, чтобы алгоритм мог определить правильный порядок зондов. Поэтому мы должны пытаться оценить, насколько решение, найденное алгоритмом данного варианта задачи картирования,
5.4. ПРИБЛИЖЁННОЕ СОСТАВЛЕНИЕ КАРТ ГИБРИДИЗАЦИИ
240
«приближено» к истинному порядку зондов. В связи с этим возникает естественный вопрос: Что мы понимаем под «приближением» в данном случае? В настоящее время не существует четкого определения. Однако, чтобы дать некоторое представление о принципах работы известных алгоритмов картирования на практике, мы приведем в качестве примера одно из недавно появившихся в литературе определений. Это удобное и хорошо обоснованное определение, но даже если оно станет общепринятым, оно всегда может быть дополнено или уточнено в будущем.
Мы будем оценивать алгоритм картирования долей сильных смежностей от общего числа решений. Сильные смежности определяются числом Ь блоков последовательных единиц, присутствующих в матрице гибридизации с данной перестановкой зондов тг = р\ ,р2,... -Рт- Мы анализируем эффект транслокаций, то есть операций, инвертирующих порядок множества последовательных зондов Мы говорим, что два смежных зонда рг и рг+ [ имеют сильную смежность, сели обособление этих зондов при любой транслокации увеличивает число блоков b в каждой строке. Когда такое увеличение имеет место, мы имеем некоторое доказательство (хотя и нс неопровержимое), что зонды рг и 1 должны остаться смежными во всех решениях.
Взяв за основу это понятие, мы можем определить стоимость сильной смежности для данной перестановки. Она определяется формулой
где 5, = 1, если зонды рг и p2+i имеют сильную смежность в правильной перестановке, но при этом не смежны в предложенной перестановке; в противном случае 5г = 0. Обратите внимание, что стоимость определена в процентах. Хорошие перестановки должны иметь низкую стоимость сильной смежности.
Опираясь на это определение, мы, наконец, можем дать читателю представление относительно принципа работы алгоритма. Таблица 5.4 представляет стоимость сильной смежности для двух алгоритмов. Один из них «случаен»: выбирает решение из множества случайных перестановок зондов. Другой основан на решении задачи коммивояжера; принцип его работы следующий. Алгоритм строит цикл в графе задачи коммивояжера, выбирая пары вершин и делая их смежными в пути. Пара (u, v), выбираемая на каждом шаге алгоритма, должна удовлетворять следующим условиям: 1) если обе вершины и и v уже принадлежат некоторым путям и эти пути различны, то эти пути могут быть объединены, только если вершины и и v являются
250
Глава 5
конечными точками соответствующих им путей (то есть каждая из них имеет только одну соседнюю точку); 2) эти вершины должны быть ближайшими среди всех оцениваемых пар вершин. После того как все вершины будут принадлежать одному пути, алгоритм замыкает этот путь, формируя цикл. Затем это решение предоставляется другому алгоритму, который пытается улучшить его, применяя другую эвристику.
Таблица 5.4. Стоимости сильной смежности для двух алгоритмов на матрицах с разным типом ошибок. Частоты появления ошибок показаны над каждым столбцом (в каждом столбце ошибки только одного типа). По-крыше во всех случаях равно 10 (здесь покрытие — отношение между общей длиной всех клонов и длиной целевой ДНК)
	СПЕ 0	Химеризм 0,5	Л. совп. 0,04	Л. несовп. 0,32
Жадн. коммив.	1,9	0,9	16,0	28,3
Случайный	86,4	89,7	94,4	94,9
Из табл. 5.4 мы можем видеть, что алгоритм, основанный на решении задачи коммивояжера (названный «жадным»), имеет довольно хорошие, по сравнению со «случайным», показатели. Статья, из которой были взяты эти данные, представляет характеристики трех других, намного более сложных алгоритмов, и результаты, подобные показанным выше для «жадного коммивояжера». Эти результаты можно рассматривать как очко в пользу алгоритма коммивояжера, но, в некотором смысле, это всего лишь еще один показатель того, насколько трудна задача картирования. Таблица также показывает, что в присутствии ложных несовпадений решение «жадного коммивояжера» оказалось довольно неудовлетворительным. Справедливо допустить, что результаты были бы еще хуже, если бы в одной задаче совместно присутствовали ошибки всех видов. Эти выводы закладывают основу следующего раздела, в котором мы представляем эвристику, оказавшуюся устойчивой в присутствии ложных несовпадений.
5.5.	ЭВРИСТИКИ ДЛЯ СОСТАВЛЕНИЯ КАРТ ГИБРИДИЗАЦИИ
Как было показано в предыдущих разделах, картирование — грудная задача, и никакие универсальные и хорошие алгоритмы для нее не были найдены. Как следствие, на практике исследователи обращаются к различным эвристикам, в надежде найти искомое решение. В этом разделе мы
5.5. ЭВРИСТИКИ ДЛЯ СОСТАВЛЕНИЯ КАРГ ГИБРИДИЗАЦИИ 251
представляем две такие эвристики, показавшие неплохие результаты в про ектах составления карт гибридизации
5.5.1.	ОТСЕВ ХИМЕРНЫХ КЛОНОВ
Как мы о I метили выше, химерные клоны появляются в клопозеках с высокой частотой и их присутствие приносит серьезные проблемы любому алгоритму картирования. В этом разделе мы представляем простую эвристику, призванную расщеплять химерные клоны на отдельные фрагменты. Такая эвристика очень полезна в качестве процедуры отсева, которая может быть использована па этапе предварительной обработки перед применением более сложных методов.
Зонды
Клоны
Рис. 5.12. Над горизонтальной линией мы видим граф гибридизации //, построенный для некоторой матрицы п х т. Слева под этой линией построен граф 11ь для клона Ь. Этот клоп, вероятно, не химерный, поскольку граф Нь связен. Справа показав граф Нс, соответствующий клопу е. Этот клоп, возможно, химерный, поскольку |раф Не несвязен
Идея очень проста: если клон является химерным (сделаем допущение о том, что он состоит только из двух фрагментов), то зонды, которые гибридизируются одним из его фрагментов, не должны быть связаны с зондами, гибридизирующими другой фрагмент этого клона. Ключ здесь — конечно, понятие «связанности» зондов. Поясним его на следующем примере
Возьмем клон i и множество Р, зондов, которые гибридизируют этот клон. Для каждого клона i мы создаем граф Н, =	Мы проводим
252
Глава 5
ребро между двумя зондами из множества Рг, если они гибридизируются каким-либо отличным от г клоном. Если построенный граф связен то мы говорим, что клон г не химерный. Если граф состоит из более чем одного компонента, то мы говорим, что клон г является химерным и заменяем его новыми «искусственными» клонами, где каждый новый клон определяется связным компонентом графа Ht. Этот метод может быть улучшен путем наложения дополнительного требования, которое состоит в том, что между зондами р и q в графе Нг ребро существует только в том случае, если зонды р и q гибридизируют по крайней мере к других клонов, где к — параметр, зависящий от конкретного варианта задачи. См. пример на рис. 5.12.
На практике эта эвристика показала хорошие результаты. С другой стороны, опа может счесть клон химерным, когда фактически он не является таковым. Поэтому, было бы полезно на стадии заключительной обработки применять эвристику, объединяющую два клона, которые на самом деле являются одним клоном, но на предшествующем этапе обработки были ошибочно приняты за химеру и разделены. (См. упражнение 22.)
5.5.2.	ПОЛУЧЕНИЕ ХОРОШЕГО ПОРЯДКА ЗОНДОВ
Представленная здесь эвристика более претенциозна, чем рассмотренная в предыдущем разделе. Эта эвристика по существу стремился именно решит ь задачу, то есть найти правильную перестановку зовдов путем оценки с помощью графа гибридизации Н (см. раздел 5.4.3) числа зондов слева и справа от каждого зонда р. Затем на основании этой оценки мы можем сортировать зонды и таким образом получить одну «хорошую» перестановку.
Выбрав некоторый зонд, мы сможем сосчитать число зондов слева и справа от него, если нам удастся так или иначе расщепить остальные зонды на два отдельных компонента: один левый и один правый компонент. Зонды около концов целевой ДНК не могут расщепить другие зонды пополам; поэтому те зонды, с помощью которых мы можем получить два компонента, будут называться расщепителями. Метод обнаружения расщепителей описан ниже.
Для данного зонда р строят множество вершин Sp (элементы которого — клоны и зонды), включая в Sp зонд р и каждый следующий зонд, имеющий общий клон с зондом р. Во множество Sp включают все клоны, инцидентные любому зонду в Sp. Затем из графа Н удаляют все вершины, принадлежащие множеству Sp. Мы скажем, что зонд р — расщепитель, если итоговый граф состоит точно из двух компонентов. Использующая этот метод эвристика поиска хорошего порядка зондов представлена на рис. 5.13.
5 5 ЭВРИСТИКИ ДЛЯ СОСТАВЛЕНИЯ КАРТ ГИБРИДИЗАЦИИ 253
Algorithm Probe Permutation Heuristic1 input: матрица гибридизации n x m output: «хороший» порядок зондов Распознать расщепителей, как описано в тексте for каждого расщепителя i do Определить компоненты Аг и Bt for каждого зонда р do Инициализировать 1р и гр нулями Выбрать произвольную пару (Л*, Bk) for каждого зонда р do
for каждой пары компонентов (А,,Вг) do
if р € Аг then
if |А, П А*| > |А, П Bk| then
Прирастить 1Р
else
Прирастить rp
else if р € Bt then
if |B, О ^4^1 > |Bt П Bk\ then Прирасзшь lp else
Прирастить rp
Сортировать зонды в порядке убывания разницы lp — гр.
Рис. 5.13. Эвристика «хорошего» упорядочения зондов
Для каждого зонда р алгоритм поддерживает два счетчика 1Р и гр, соответственно, для записи числа левых и правых областей, содержащих зонд р. Эти счетчики инициализируются нулями и приращаются с помощью зондов-расщепителей. Не совсем ясно, каким образом это может быть сделано, потому что, хотя мы знаем два компонента А, и BL расщепителя i, мы не можем сказать, который из них является левым, а который правым компонентом. Чтобы разрешить эту трудность, мы полагаемся на фиксированный произвольный зонд к, который мы используем в качестве опорного. Мы допускаем, что компонент Ад. лежит слева от компонента Вд. Тогда для другого расщепителя i компонент X зонда г (А, либо Вг) будет крайним левым при [X П Afc| > |Х П В*|. Как только мы получаем заключительную оценку, мы сортируем зонды так, чтобы сначала шли зонды с более высоким сдвигом влево, определяемым разницей счетчиков 1р — тр. Простое усовершенствование этой эвристики заключается в выборе расщепителя к. Чем более «центральным» будет этот зонд, тем лучше должны быть результаты.
Как и в случае эвристики из предыдущего раздела, практические испытания свидетельствуют, что данная эвристика имеет высокие показатели
7Эвристика упорядочения зондов. — Прим, перев.
254
Глава 5
точности и эффективности. В частности, она относительно устойчива к ложным несовпадениям. Кроме того, можно предусмотреть использование этой эвристики также в качестве поставщика результатов другим алгоритмам или эвристикам, которые могли бы пытаться улучшить найденное решение.
РЕЗЮМЕ
В этой главе мы изучили два метода, лежащие в основе картирования ДНК: переваривание рсстриктазами и реакции гибридизации. Один из способов использования данных рестрикции заключается в измерении и сравнении соответствующих длин фрагментов. Это ведет к задачам с двойным или частичным перевариванием. Мы показали, что задача с двойным перевариванием НП-трудная. Данные о фрагментах могут быть использованы также для того, чтобы характеризовать индикатор некоторого фрагмента. В этом случае порядок фрагментов может быть восстановлен путем определения перекрытий между фрагментами с помощью индикаторов. Этот способ может быть смоделирован посредством интервальных графов, но большинство моделей можно описать только НП-полными задачами.
При составлении карт гибридизации мы используем в качестве первичных данных матрицу гибридизации размером п х т. Если к этой матрице мы предъявим строгие требования (уникальность зондов и отсутствие ошибок), то конечная задача может быть решена за полиномиальное время. Все, что мы должны сделать, — это определить, обладает ли матрица свойством последовательных единиц. Мы представили один алгоритм решения этой задачи. Когда появляются ошибки, мы вынуждены обращаться к приближениям, и мы показали, как задача составления карт гибридизации может быть сведена к варианту задачи коммивояжера. Это сведение, вкупе с другой моделью процесса гибридизации, обеспечивает гарантию того, что решение задачи коммивояжера будет достаточно хорошо приближено к решению задачи картирования. Алгоритмические трудности картирования побуждают к поиску критериев оценки алгоритма. Мы представили один из таких критериев и показали, что, согласно этому критерию, основанный на задаче коммивояжера алгоритм имеет высокие показатели по сравнению с другими, более сложными алгоритмами. В конце этой главы мы представили две эвристики для отсева ошибок и восстановления хорошего порядка зондов.
УПРАЖНЕНИЯ
1.	Найдите альтернативное решение задачи, показанной на рис. 5.2.
2.	Используя следующие результаты, попытайтесь найти решение задачи с двойным перевариванием:
УПРАЖНЕНИЯ
255
Фермент Л: 4, 5, 7, 8, 12.
Фермент В: 3, 4, 4, 6, 9, 10.
Ферменты А + В'. 1, 2, 3, 3, 4, 4, 4, 4, 5, 6.
3.	На основании следующих результатов попытайтесь найти решение задачи с частичным перевариванием:
2, 3, 7, 8, 9, 10, 11, 12, 17, 18, 19, 21, 26, 29.
4.	Постройте исчерпывающий алгоритм поиска для решения задачи с двойным перевариванием.
5.	Объясните, почему два участка рестрикции двух различных рестрик-таз нс могут совпасть.
* 6. Необходимое условие интсрвальности графа G заключается в гом, чтобы любой цикл в графе G, содержащий четыре и более вершин, имел хорду, то есть ребро соединяющее две непоследовательные вершипы, принадлежащие этому циклу. Докажите, что это условие верно.
7.	Покажите, что условие в упражнении 6 не является достаточным.
8.	Докажите, что интервальный граф, в котором никакой интервал полностью нс содержится в любом другом интервале этого графа, тождествен интервальному графу, в котором все интервалы имеют одинаковую длину.
9.	Выполните алгоритм СПЕ из раздела 5.3 на матрице входов из табл. 5.5 и получите такую перестановку столбцов, чтобы в каждой строке все единицы были последовательными.
Таблица 5.5. Бинарная матрица входов для упражнения 9
	12 3 4	5 6	7 8 9	10
1	0 10 0	0 0	0 0 0	0
2	110 1	0 1	I 1 I	1
3	10 0 0	0 0	0 1 0	0
4	0 10 0	0 I	0 0 1	0
5	0 0 0 1	0 1	I 0 1	0
6	0 10 1	0 1	1 0 1	0
7	10 0 1	1 0	1 1 0	1
8	10 10	1 0	0 0 0	0
9	0 10 1	0 1	1 0 I	0
10	0 10 0	0 0	0 0 1	0
10.	Охарактеризуйте бинарные матрицы, обладающие СПЕ как для строк, гак и для столбцов.
256
Глава 5
**11. Охарактеризуйте интервальные графы, опираясь на СПЕ. То сеть, имея граф G, предложите такую бинарную матрицу М, соответствующую графу G, чтобы граф G был интервальным графом тогда и только тогда, когда матрица М обладает СПЕ.
* 12. Используя ответ к упражнению 11, постройте эффективный алгоритм распознавания интервальных графов.
13.	Докажите, что в алгоритме СПЕ из раздела 5.3 соотношения пребываний между множеством компонента /3 и множествами компонента а остаются теми же самыми для всех множеств компонента /3. Это разовое доказательство; доказательство для одного примера было дано в тексте.
14.	Докажите, что граф Сд/, определенный в разделе 5.3, является ациклическим.
15.	Постройте модель минимизации промежутков в строках, краткое описание которой приведено в конце раздела 5.4.1.
16.	Докажите НП-полноту варианта с принятием решений для задачи получения такой перестановки столбцов в бинарной матрице, при которой общее число блоков последовательных единиц было бы минимальным. Подсказка: Выведите этот вариант из задачи о Гамильтоновом пути.
17.	Для решения задачи на графе, изображенном на рис. 5.10, постройте алгоритм жадного коммивояжера, принцип работы которого кратко изложен в конце раздела 5.4.3.
18.	Теоретические и практические исследования показывают, что задачу коммивояжера решать немного легче, когда расстояния подчиняются ограничениям, приведенным в разделе 3.6.1. Подчиняется ли этим ограничениям Хеммингово расстояние?
о 19. Реакции гибридизации иногда дают неопределенный результат: данный зонд может гибридизироваться либо не гибридизироваться специфичным клоном. Сделайте допущение, что результат каждой реакции представлен вещественным числом между 0 и I, которое показывает степень достоверности положительного результата гибридизации. Предложите алгоритм поиска правильной перестановки зондов, использующий эти данные в качестве входа.
** 20. Предложите алгоритм составления карт гибридизации, основанный на эвристике метода решения задачи коммивояжера путем поиска минимального остовного дерева. Описание этой эвристики см., например, в [152].
21.	Иногда при составлении карт гибридизации мы имеем информацию, что некоторые зонды гибридизируются в концах клонов, и мы знаем
БИБЛИОГРАФИЧЕСКИЕ ПРИМЕЧАНИЯ
257
которых именно Какая матрица следует из этой информации9 Как бы вы переформулировали задачу картирования9 Облегчает ли подобная информация решение этой задачи?
22.	Предложите эвристику для объединения клонов которые были неправильно отделены эвристикой отсева химер, описанной в разделе 5.5.1. Предположим, что вашу эвристику будут использовать на стадии заключительной обработки; то есть на ее вход будет поступать возможный порядок зондов, полученный на предыдущем этапе.
23.	В эвристике поиска хорошего порядка зондов, представленной в разделе 5.5 2, покажите, каким образом выбор плохого центрального расщепителя приводит к помещению другого расщепителя в неправильную позицию в упорядочении.
24.	Сборка фрагментов и составление карт гибридизации — однотипные задачи. Любой ли из методов главы 4 применим к составлению карт гибридизации?
25.	Одна из главных организаций, работающих над составлением физической карты генома человека, — «Уайтхедовский институт биомедицинских исследований» при поддержке «Массачусетского технологического института». Посетите его страницу по веб-адрссу http://www-genonie.wi.niit.edu/ и узнайте о текущем состоянии проекта «Геном человека»8.
БИБЛИОГРАФИЧЕСКИЕ ПРИМЕЧАНИЯ
Карп [111] приводит хороший краткий обзор проблем картирования. Неплохой обзор составления рестрикционных карт был представлен Лсн-дером [119] В той же статье Лендер описал алгоритмы составления карт сцепления генетических признаков, которые используют данные, основанные на важных генетических маркерах, известных как полиморфизмы длин рестриктов (ПДР); эту тему мы не включили в материал книги.
Помимо других ученых, картирование с двойным перевариванием изучали Голдштейн и Уотермен [73], а также Шмитт и Уотермсн [169]. Доказательство НП-полноты задачи с двойным перевариванием взято из [73]. В [169] показано, что число решений этой задачи может увеличиваться в экспоненциальной зависимости от длины целевой ДНК В этой статье небольшие надежды возлагаются на общую методику, основанную на классах эквивалентности фрагментов, но эта надежда, к сожалению, не оправ
8 Проект завершен. Прим ред.
258
Глава 5
далась в ходе масштабного исследования, проведенного Певзнером [160], который в конечном итоге пришел к выводу, что предпочтение следует отдавать подходу с множественным перевариванием. Задача с частичным перевариванием была изучена Скиеной и Сандарамом [174], предложившими для ее решения алгоритм метода ветвей и границ. Кроме того, авторы приводят многообещающие экспериментальные результаты применения этого алгоритма.
Уотермен и Григгс [200] представляют алгоритм для следующей задачи из класса задач составления рестрикционных карт. Целевую ДНК независимо переваривают двумя ферментами. Затем получают информацию о перекрытии между фрагментами каждого переваривания. Задача состоит в том, чтобы с помощью этой информации определить порядок участков рестрикции.
Анализ вычислительной сложности задач составления физических карт представлен в [72; 59; 75]. На этих статьях основан раздел 5.2.2, и, кроме того, они содержат доказательства НП-полноты, на которые мы ссылаемся в том же разделе. Каплан, Шамир и Тарджан [ 108] представляют алгоритм для следующей задачи, связанной с составлением физических карт. Необходимо преобразовать входной граф в собственный интервальный граф, добавляя в него как можно меньше ребер. Собственный интервальный граф — это граф, в котором никакой интервал полностью не содержит другой (то есть граф, в котором все интервалы имеют равную длину). Авторы представляют алгоритм с линейным временем счета, если максимальное число ребер, которые будут добавлены, фиксировано и равно k.
Алгоритм для задачи с последовательными единицами, представленный в разделе 5.3, взят из работы Фулкерсона и Гросса [67]. Бутом и Лю-эксром [27] был представлен намного более сложный алгоритм. Его время счета равно О(п + т + г) (где г — общее число единиц в матрице) и он компактным способом кодирует все возможные решения. Однако этот алгоритм оказался довольно громоздким и поэтому были сделаны попытки найти лучшие альтернативы. См., например, работы Сю [97], а также Мсй-даниса и Мунуеры [136].
Картирование посредством гибридизации уникальными зондами было изучено Гринбергом и Истрейлом [78; 79], а также Ализаде и corp. [9]. Статья [79] содержит превосходное описание многих вопросов, касающихся этой задачи, и нескольких алгоритмов ее решения. Материал раздела 5.4.3 был взят из этой статьи, и раздел 5.2.4 также во многом основан на ней Множество других методов описано в [9], и эвристики из раздела 5.5 были взяты из этой статьи. Григорьев, Мотт и Лерах [80] также описывают эвристику для обнаружения химерных клонов. Ализаде и сотр. [8] изучал кар
БИБЛИОГРАФИЧЕСКИЕ ПРИМЕЧАНИЯ	259
тирование посредством гибридизации нсуникальными зондами; раздел 5.4 основан главным образом на этой статье. Модель Пуассоновского распределения клонов была взята из статьи Лендера и Уотермена [120]; та же самая модель была представлена в разделе 4.1.2 при описании темы покрытия. Эту модель используют также в проектах картирования для определения числа клонов, необходимого для получения желаемого покрытия.
Зёдерлунд и Бурке [177] описывают пакет программ с развитым графическим интерфейсом, разработанный для составления физических карт, и в той же статье упоминают программное обеспечение для автоматической генерации контрольных задач.
Глава 6
ФИЛОГЕНЕТИЧЕСКИЕ ДЕРЕВЬЯ
В этой главе мы описываем задачу восстановления филогенетических деревьев. Это общая задача биологии. Например, в молекулярной биологии она помогает понять эволюционные связи между белками. Здесь мы представляем модели и алгоритмы для двух основных типов входных данных: признаков и расстояний.
Современная наука показала, что все виды организмов, живущих на земле, подвергаются медленному процессу изменения с течением времени, измеримом в геологических периодах. Мы называем этот процесс эволюцией. Одна из важнейших задач биологии состоит в том, чтобы объяснить эволюционную историю современных видов и, в частности, то, как живущие сегодня виды связаны друг с другом через общих предков. Обычно это делают путем построения деревьев, листья которых представляют современные виды, а внутренние узлы — их гипотетических предков. Такие деревья называют филогенетическими. Пример филогенетического дерева показан на рис. 6.1. Согласно этому дереву человек и шимпанзе генетически ближе друг к другу, чем ко всем остальным приматам, представленным в дереве Это означает, что у них есть общий предок, который нс является предком остальных приматов. Данное дерево показывает подобную родственную связь также между гиббонами и сиамангами (черными гиббонами).
Проблема построения филогенетического дерева заключается в том, что мы, как правило, не располагаем достаточными данными об отдаленных предках современных видов; и даже если бы мы обладали такой информацией, то все равно мы не могли бы быть уверены на 100 %, ч го данная окаменелость принадлежит виду, который действительно является предком двух или более современных видов. Поэтому эволюционную историю современных организмов мы должны вывести посредством умозакчючений и восстановить их филогенетическое дерево, обычно используя в качестве исходных данных сравнения между современными видами. По этой причине дерево, показанное на рис. 6.1, не обязательно истинное филогенетическое дерево приматов, а всего лишь гипотеза.
ФИЛОГЕНЕТИЧЕСКИЕ ДЕРЕВЬЯ
261
Филогенетические деревья, или филогении, были предложены еще в XIX веке для всех чипов групп организмов. Методы, используемые вплоть до 1950-х гг., как правило, были основаны лишь на опыте и интуиции ученых. Постепенно разрабатывались математические модели и их включали в численные методы восстановления филогенетической истории видов. К сегодняшнему дню образовался целый «культурный слой» литературы по математике и теории алгоритмов, описывающей различные методы восстановления филогений. Созданы также пакеты программ, предлагающие ученым различные средства алгоритмического построения филогенетических деревьев.
сиаманг
гиббон орангутанг горилла
человек шимпанзе
Рис. 6.1. Филогенетическое дерево некоторых приматов
Цель этой главы никоим образом не заключается в описании вычислительных методов восстановления филогений; для этого потребовалась бы целая книга. Наша цель, скорее, состоит в изучении некоторых задач из этой области, поддающихся алгоритмическому решению. Читатель должен знать, что это очень узкая и тенденциозная методика, учитывая объем и разнообразие литературы по этой теме. Указатели на более общие труды даны в библиографических примечаниях в конце этой главы.
В эволюционной биологии мы можем строить филогенетические деревья для видов, популяций, родов или других таксономических категорий. (Таксономия «наука о классификации». Термин численная таксономия употребляют при описании совокупности численных методов, используе
262
Глава 6
мых для классификации любого вида. Тему этой главы можно рассматривать как подобласть численной таксономии.) Поскольку нуклеиновые кислоты и белки тоже эволюционируют, мы можем так же строить филогении и для них, что объясняет, почему молекулярные биологи тоже интересуются методами восстановления филогенетических деревьев. Чтобы ограничить представленный здесь материал рамками общего, насколько это возможно, описания, для обозначения молекул или организмов, филогению которых мы восстанавливаем, мы будем употреблять термин объект.
Вспомним определение деревьев из раздела 2.2. Дерево это неориентированный ациклический связный граф. Мы проводим различие между его внешними узлами, или листьями, и внутренними умами. Листья имеют степень один, тогда как степень внутренних узлов всегда больше единицы. К листьям мы приписываем исследуемые объекты и таким образом можем сказать, что лист помечен объектом или множеством объектов.
Ученых интересуют два главных вопроса касательно филогенетических деревьев. Первый вопрос — их топология, то есть структура связей внутренних узлов между собой и с листьями. (Некоторые авторы используют термин схема ветвления.') Другой важный вопрос — расстояние между парами узлов, которое может быть определено путем взвешивания ребер дерева. Это расстояние — оценка эволюционного расстояния между узлами. В зависимости от многих допущений, которые мы нс будем обсуждать, расстояние между внутренним узлом (предковый объект) и листом (современный объект) может быть интерпретировано как оценка времени, потребовавшегося для эволюции объекта-предка в современный объект. Но читатель должен знать, что в общем случае эволюционное расстояние нс эквивалентно времени, затраченному на соответствующее эволюционное событие.
Еще одна важная характеристика филогенетическою дерева наличие или отсутствие корня. Корневое дерево подразумевает родственные связи между внутренними узлами. Однако во многих задачах, которые нам предстоит изучить, входные данные содержат недостаточно информации для определения корня; в подобных случаях восстановленное дерево будет некорневым.
Мы упомянули, что филогении восстанавливают на основании сравнений между современными объектами. Входные данные для восстановления филогений мы можем классифицировать на две основные категории:
1. Дискретные признаки например формы клюва, числа пальцев, присутствия или отсутствия в молекуле участка рестрикции и т. п. Каждый признак может иметь конечное число состояний. Данные относительно этих
6.1. СОСТОЯНИЯ ПРИЗНАКОВ
263
признаков помещают в матрицу размером п х т (где п — объекты, т — признаки), которую мы называем матрицей состояний признаков.
2. Численные данные сравнений, или расстояния между объектами. Полученную матрицу называют матрицей расстояний.
Обе категории данных ведут к различным методам восстановления филогенетических деревьев. Одно существенное различие между этими двумя категориями состоит в том, что матрицы состояний признаков, как правило, не квадратные, так как число объектов не обязательно должно быть равно числу признаков. С другой стороны, матрицы расстояний представляют собой треугольные матрицы, потому что мы учитываем расстояние каждой пары объектов, а эти расстояния являются симметричными. В последующих разделах мы представляем типичные алгоритмы, разработанные для некоторых из этих методов. Известна также третья категория, непрерывных признаков, но ее мы не будем рассматривать.
6.1.	СОСТОЯНИЯ ПРИЗНАКОВ И ЗАДАЧА
О СОВЕРШЕННОЙ ФИЛОГЕНИИ
Мы начинаем этот раздел с некоторых общих замечаний касательно допущений о признаках, а также с объяснения смысла приписывания состояний к внутренним узлам дерева.
Основное допущение относительно признаков — несколько очевидное: мы допускаем что рассматриваемые признаки «значимы» для восстановления филогенетических деревьев. Задача определения значимых признаков и проверки того, что выбранные признаки действительно являются значимыми согласно выбранному критерию, в значительной степени возложена на ученого, или «пользователя) этого дерева. Тем нс менее, мы кратко упоминаем два допущения, которые лежат в основе всех методов восстановления филогенетических деревьев по признакам объектов.
Во-первых, мы допускаем, что признаки могут наследоваться независимо друг от друга; это ключевое допущение для всех алгоритмов, которые мы рассмотрим в этой главе. Во-вторых, мы примем допущение о том, что все наблюдаемые состояния данного признака должны были развиться из одного «дикого состояния» ближайшего общего предка изучаемых объектов. Признаки, которые подчиняются этому допущению, называют гомологичными. Оно так же важно, когда в качестве объектов мы рассматриваем биологические последовательности. В подобных случаях признаком будет позиция в последовательности, а его состояниями, при исследовании ДНК,
264
Глава 6
будут основания А, Т, С и G. Если мы сравниваем позицию, скажем, 132 в последовательности s с позицией 722 в последовательности I, то мы должны удостовериться в том, что эти две позиции наследовали свое теперешнее состояние из той же самой позиции в последовательности предка.
Вспомним, что внутренними узлами дерева представлены гипотетические предковые объекты. Описываемые нами алгоритмы присваивают определенные состояния этим узлам, но множество состояний внутреннего узла не обязательно имеет биологическое значение. Под этим мы подразумеваем, что интерпретация состояний внутренних узлов не должна восприниматься как обратное предсказание особенностей предковых объектов; главная цель всегда состоит в классификации современных объектов на группы, а восстановление предковых объектов — лишь средство, необходимое для достижения этой цели. Тем не менее, присваивая состояния внутренним узлам, мы должны быть внимательны, чтобы получить как можно лучшее приближение к истинному дереву.
Сделав эти вводные замечания, мы переходим к формальному определению матрицы состояний признаков. Матрицу состояний признаков мы определяем как матрицу Men строками (объекты) и т столбцами (признаки). Таким образом, элемент Л/г) обозначает состояние признака j объекта i матрицы. Один признак может иметь самое большее г состояний, и состояния обозначают неотрицательными целыми числами. Строки этой матрицы представляют собой векторы состояний объектов. Поскольку мы будем присваивать состояния также и внутренним узлам дерева, мы скажем также, что внутренним узлам присвоены векторы состояний. Пример матрицы состояний признаков представлен в табл. 6.1.
При попытке восстановить филогению из матрицы состояний признаков мы сталкиваемся с некоторыми трудностями. Первая трудность возникает, когда два или более объектов имеют одинаковое состояние для того же самого признака. Почти все методы восстановления филогений основаны на допущении о том, что объекты, которые имеют некоторое общее состояние,
Таблица 6.1. Матрица состояний признаков
	Признак
Объект	Cl С2 Сз С4 С5
А	110 0 0
В	0 0 10 1
С	110 0 1
D	0 1110
Е	110 0 1
6.1. СОСТОЯНИЯ ПРИЗНАКОВ
265
расположены генетически ближе друг к другу, чем объекты, не обладающие таким свойством. Однако существует возможность того, что два объекта будут иметь общее состояние, не будучи генетически близкими. Пример данного явления — наличие крыльев у летучих мышей и птиц. Такие явления называют схождением (конвергенцией) или параллельной эволюцией. В природе такие случаи весьма редки; поэтому при формулировании задач восстановления филогенетических деревьев это препятствие мы будем обходить следующим образом: будем считать, что события схождения вовсе не должны случиться, или же их число минимально.
Вторая трудность имеет отношение к взаимосвязи различных состояний одного признака. Иллюстрируем эту проблему на примере матрицы из табл. 6.1.11редположим, что объекты А и В эволюционировали от предка X. Какое состояние признака су мы должны присвоить объекту X? Известно, что у объекта A ci = 1, а у объекта В с± = 0. Если мы присваиваем состояние ci = 0 объекту X, то мы говорим, что 0 — унаследованное состояние, а 1 — приобретенное состояние признака. Допустим, что мы сделали такой выбор, и далее предположим, что объекты С и D имеют предковый объект Y 0 X. Далее допустим, что мы приняли состояние признака С] объекта Y равным 1. В этом случае объект D показывает возврат признака С] к дикому состоянию 0. Поскольку в данном случае признаки являются бинарными, мы могли бы интерпретировать эту ситуацию как приобретение и потерю признака. То есть объект А приобрел новый (относительно своего предка X) признак, тогда как объект D погерял признак своего предка Y. Так же, как и схождение, возврат в природе встречается весьма редко. Поэтому проблему возврата мы будем решать таким же образом, как и трудности, связанные с событиями схождения: мы потребуем, чтобы события возврата не происходили или чтобы их число было минимально. Интересно, что иногда заранее не известно, какое состояние является унаследованным, а какое — приобретенным. Если мы не знаем этого, то мы должны будем самостоятельно классифицировать состояния и затем придерживаться этого выбора, чтобы игнорировать или минимизировать события возврата.
В предыдущем примере мы рассматривали бинарные признаки, однако в принципе один признак может иметь г состояний, поэтому отношения между признаками намного сложнее. В зависимости от того, как много нам известно об этих отношениях, признаки могут быть классифицированы на упорядоченные и неупорядоченные. Для неупорядоченного признака мы не делаем никаких допущений о способе изменения его состояний; то есть каждое состояние может перейти в любое другое. В случае упорядоченных признаков известна дополнительная информация. Например, данный признак может иметь следующий линейный порядок взаимного перехода
266
Глава 6
четырех состояний: 3 «-» 1 «-» 4 «-» 2. Это означает, кроме всего прочего, что в восстановленном дереве состояние 3 никоим образом не должно изменяться непосредственно в состояние 4; состояние 1 должно всегда быть промежуточным между ними. Другими словами, если существует узел с состоянием 3 у данного признака, то не должно быть ни одного ребра, связывающего его с другим узлом с состоянием 4. Признаки могут быть также частично упорядоченными, когда известно дерево вывода, которое показывает, каким образом состояния переходят из одного в другое. Обратите внимание, что даже в случае упорядоченных признаков мы ничего не знаем о направлении изменения состояний; признаки, для которых известно направление изменения состояний, называют ориентированными. В литературе можно встретить также термины качественные признаки (неупорядоченные) и кладистические признаки (упорядоченные). Ориентированные признаки называют также полярными. Интуиция подсказывает нам, что ориентированные признаки несут в себе намного больше информации о порядке построения филогении, и эти соображения будут полезны в понимании некоторых выводов о вычислительной сложности приведенных ниже задач.
Если мы хотим избежать как схождения, так и возврата признаков, то, согласно приведенному выше анализу, искомое дерево Т должно обладать следующим свойством: для каждого состояния s каждого признака с множество всех узлов и (листья и внутренние узлы), для которых признак с имеет состояние s, должно формировать поддерево в дереве Т (то есть связный подграф дерева Т). Это означает, что ребро е, ведущее к лому поддереву, однозначно ассоциировано с переходом от некоторого состояния w к состоянию s. Филогения, обладающая этим свойством, есть совершенная филогения. Теперь мы готовы сформулировать основную задачу восстановления филогении по матрицам состояний признаков. Эта задача известна как задача о совершенной филогении'.
Задача: Совершенная филогения
ПРИМЕР: Множество О, содержащее п объектов, множество С из m признаков, где каждый признак имеет самое большее г состояний (п, m и г — положительные целые числа).
ВОПРОС: Допускает ли множество О совершенную филогению?
Если для матрицы из табл. 6.1 принять 0 за унаследованное, а 1 — за приобретенное состояние признаков, то совершенная филогения для них не существует, как будет показано в следующем разделе. Для матрицы из табл. 6.2 совершенная филогения существует и представлена на рис. 6.2. Признак, помечающий ребро дерева, показывает, что переход от состояния 0 к состоянию 1 проходит именно по этому ребру, так что поддерево,
6.1. СОСТОЯНИЯ ПРИЗНАКОВ
267
растущее из этого ребра, содержит все (и никакие другие) объекты, у которых состояние этого признака равно 1.
Таблица 6.2. Матрица состояний признаков
	Признак
Объект	Cl С2 Сз С4 С5 Сб
А	0 0 0 1	10
В	1	10 0 0 0
С	0 0 0 1	1	1
D	10 10 0 0
Е	0 0 0 10 0
Всякий раз, когда множество объектов, определенных матрицей состояний признаков, допускает совершенную филогению, мы говорим, что определяющие признаки совместимы. Позже данное понятие совместимости будет уточнено для частных случаев задачи о совершенной филогении.
Рис. 6.2. Филогения, восстановленная по матрице из табл. 6.2. Ребра, отражающие переходы состояний, помечены соответствующими признаками
268
Глава 6
Сформулировав задачу, мы хотели бы задать следующий вопрос: Имеется ли эффективный алгоритм для ее решения? Через мгновение мы ответим на него, но сначала получим некоторое представление относительно того, сколько различных деревьев мы можем построить для п объектов. Предположим, что мы строим только некорневые бинарные деревья. Вспомним, что листья наших деревьев представляют объекты; следовательно, важно точно знать, который объект соответствует какому листу. Для трех объектов возможно построить только одно дерево, представленное на рис. 6.3. Для четырех объектов существует три возможных дерева, как видно на рис. 6.4. Можно показать (см. упражнение 2), что для п объектов существует И’,' з(2г — 5) возможных деревьев. Эта функция растет быстрее п!, что исключает любой алгоритм, основанный на методе поиска совершенной филогении из множества возможных деревьев. Для этой задачи мы хотели бы построить такой алгоритм, чтобы время его счета было пропорционально многочлену с аргументами п, т и г.
Рис. 6.3. Единственное дерево для трех объектов
Рис. 6.4. Три возможных дерева для четырех объектов
Оказывается, что вычислительная трудность задачи о совершенной филогении зависит от характера самих признаков. Если они неориентированные, то мы имеем плохие новости: задача НП-полная. Но когда признаки
6.2 СОСТОЯНИЯ БИНАРНЫХ ПРИЗНАКОВ
269
упорядочены, эта задача может быть решена эффективно. Опираясь на эти два факта, мы продолжаем изучать, уже подробнее, некоторые частные варианты задачи, которые представляют серию алгоритмических решений, использующих матрицы состояний признаков.
6.2.	СОСТОЯНИЯ БИНАРНЫХ ПРИЗНАКОВ
Сначала мы исследуем частный случай задачи о совершенной филогении, в котором признаки являются бинарными (например, признаки из табл. 6.1 и 6.2). Заметим, что в данном случае различие между упорядоченными и неупорядоченными признаками зависит от того, ориентированы эти признаки или нет. Это означает, что если мы зиаем, что состояние 0 данного признака унаследовано, а 1 - приобретено (или наоборот), то этот признак упорядоченный; в противном случае он неупорядоченный. Как мы увидим, задача о совершенной филогении бинарных признаков (упорядоченных или неупорядоченных) может быть решена эффективно; в этом разделе мы описываем алгоритм, который находит решение за время О(пт)
Упомянутый алгоритм мы представляем в виде двух отдельных частей-стадий. (На практике эти части могут быть объединены, но для большей наглядности такое разделение удобнее.) На первой стадии алгоритм решает, допускает ли матрица входов Л/ совершенную филогению. Если ответ положителен, го на второй стадии алгоритм строит одну возможную филогению.
В представленном здесь алгори1ме мы принимаем состояние 0 за унаследованное, а состояние 1 — за приобретенное. Позже мы увидим, как можно опустить это ограничение Учтите, что поскольку мы имеем дело с ориентированными бинарными признаками, корневое дерево Т, которое является совершенной филогенией для матрицы входов Л/, будет обладать следующим свойством, упомянутым в предыдущем разделе; каждому признаку в матрице входов Л/ соответствует ребро в дереве Т, и это ребро означает переход этого признака из состояния 0 в состояние 1. Такие ребра будут помечены соответствующими им признаками. К корню всегда приписан вектор состояний признаков (0.0,... ,0). Это означает, что когда мы проходим путь от объекта г в некотором листе к корню дерева, метки ребер, пройденных на этом пути, соответствуют признакам, которые у объекта г имеют состояние 1. (См. рис. 6 2)
В рассмотренном нами частном случае есть очень простое необходимое и достаточное условие, которое позволяет нам сказать, допускает ли данная матрица М совершенную филогению. Прежде чем сформулировать это условие, необходимо дать несколько новых определений
270
Глава 6
Каждый столбец j матрицы М - признак. Таким образом, мы используем без каких-либо смысловых различий термины столбец и признак. Каждая строка i матрицы Л/ — объект, так что мы считаем термины строка и объект равнозначными.
Определение 6.1. Для каждого столбца j матрицы Л/, iiycib Oj — множество объектов, у которых состояние признака j равно 1. Пусть Oj — множество объектов, у которых состояние признака j равно 0.
Теперь сформулируем вышеупомянутое «простое условие»:
Лемма 6.1. Бинарная матрица М допускает совершенную филогению тогда и только тогда, когда для каждой пары признаков i и j множества Ог и Oj не пересекаются или одно из них содержит в себе другое.
Доказательство. Допустим, что матрица М допускает совершенную филогению. Поскольку матрица М является бинарной, мы знаем, что с каждым признаком г мы можем однозначно ассоциировать ребро (и, о) в дереве. Болес того, поддерево с корнем v (при допущении, что он глубочайший из узлов пары u,v) содержит все узлы, имеющие состояние 1 у признака г; а все узлы, имеющие состояние 0 у признака г. не принадлежат этому поддереву. Предположим теперь, что существуют такие три объекта А, В и С, что А.В е С Ог и В, С е Oj, А Oj. Это означает, что, судя по признаку г объекты А и В принадлежат одному и тому же поддереву, а объект С ему не принадлежит. Однако, согласно признаку j, объекты В и С принадлежат одному поддереву, что является противоречием.
Теперь предположим, что все пары столбцов матрицы Л/ удовлетворяют условию леммы. Покажем индуктивно, как строить совершенное корневое филогенетическое дерево. Предположим, что мы имеем только один признак, например 1. Этот признак разбивает объекты на два множества: А = О\ и В = 01. Создадим корень дерева и затем узел а для множества А и узел Ь для множества В. Соединим узел а с корнем посредством ребра, помеченного признаком 1. Соединим узел Ь с корнем с помощью ребра без метки. Наконец, в качестве заключительного шага мы расщепляем каждого сына корня на столько листьев, сколько к этому сыну приписано объектов. Ясно, что созданное таким образом дерево представляет собой совершенную филогению; это наш основной случай. Теперь предположим, что мы построили дерево Т для к признаков, но нс выполнили заключительный шаг (то есть на дереве нет листьев; узлы по-прежнему содержат множества объектов) и хотим обработать признак k + 1. Этот признак также индуцирует разбиение множества объектов, благодаря чему мы должны суметь получить дерево Т' из дерева Т. И мы, очевидно, сумеем, поскольку
6.2. СОСТОЯНИЯ БИНАРНЫХ ПРИЗНАКОВ
271
разбиение, индуцированное признаком к + 1, разделяет объекты, принадлежащие одному узлу; в противном случае мы были бы вынуждены пометить два ребра признаком к + 1 и конечная филогения не была бы совершенной. Но такая ситуация невозможна. Предположим обратное: признак к + 1 разделяет объекты, принадлежащие узлам а и Ъ. Поскольку эти узлы различные, то должен существовать некоторый признак г, который развел бы их по разным узлам. Это происходит при О, П Ok+i 0, потому что множеству Ог принадлежат либо объекты узла а, либо объекты узла Ь. Но при этом О, £ O*:+i и Ог, поскольку либо объекты узла а, либо объекты узла Ь не содержатся во множестве О,. Но это противоречило бы нашему индуктивному предположению, и, значит, лемма доказана.	
Из этой леммы легко видеть, почему матрица состояний признаков из табл. 6.1 не допускает совершенную филогению: столбцы (признаки) ci и eg нс удовлетворяют условию леммы. Мы говорим, что такие признаки не совместимы. Здесь понятие совместимости признаков может быть уточнено и оно выражает всего лишь альтернативную формулировку леммы 6 I множество бинарных ориентированных признаков совместимо тогда и только тогда, когда они попарно совместимы. В формулировке леммы попарная совместимость признаков определена взаимосвязью множеств объектов.
Было упомянуто, что мы представим алгоритм для бинарных признаков, разделенный на две стадии. На первой стадии алгоритм решает, допускает ли матрица совершенную филогению, а на второй строит ее, если это возможно Лемма 6.1 уже дает нам алгоритм для стадии решения: нсобходи мо последовательно оценивать каждый столбец матрицы переходов и проверять, совместим ли он со всеми остальными столбцами матрицы. Каждая такая проверка занимает время О(п), а число таких проверок равно О(т2), что даст алгоритм с временем счета О(пт2). Из доказательства леммы также возможно развить алгоритм для стадии построения дерева, с теми же границами времени. Наша цель, однако, состоит в том, чтобы представить алгоритм с временем счета O(nm).
Но как достичь этой цели9 На стадии решения описанный выше алгоритм при проверке каждого нового столбца просматривает все остальные столбцы матрицы. Чтобы получить ожидаемую эффективность, мы должны просматривать каждый столбец однократно, возможно налагая некоторый порядок проверки столбцов. Каким должен быть этот порядок? Например, алгоритм может обрабатывать в первую очередь признаки, для которых максимальное число объектов имеет состояние 1. Очевидно, что как только мы обработали этот признак, мы можем «забыть» о нем, поскольку все остальные признаки являются или подмножествами этого признака, или
272
Глава 6
Algorithm Perfect Binary Phylogeny Decision1 input: бинарная матрица А/ output: истина, если А/ допускает совершенную филогению, иначе ЛОЖЬ
// Допускаем, что все столбцы различные Сортировать столбцы по числу единиц, используя поразрядную сортировку
(столбцы с большим числом единиц идут вперед) И Инициализируем вспомогательную матрицу L for каждого Ly do
i'ij 4 О
И Вычисляем матрицу L
for i t— 1 to n do
fc — 1
for j <— 1 to m do
if Ml} = 1 then
f'ij 4 k
// k самый левый столбец слева от j, такой, что
И = 1 Если не существует ни одного // такого столбца, то к — —1 к *- j
И проверяем столбцы матрицы L for каждого столбца j матрицы L do
if LtJ f Lij для некоторой пары i, I and элементы и Lij не нулевые then return ложь
return истина
Рис. 6.5. Алгоритм принятия решения о том, допускает ли множество состояний ориентированных бинарных признаков совершенную филогению
непересскающимися с ним множествами. И именно так мы и поступаем. Соответствующий алгоритм показан на рис. 6.5.
Теперь покажем, что этот алгоритм правильный. Сначала заметим, что если Oj С Ок, то столбец к находится слева от столбца j в матрице А/, то есть к < j. Предположим, что матрица М допускает совершенную филогению, но алгоритм говорит нам противное. То есть в матрице М существует такой столбец j, что Ll3 - к и Lij = к' < к. Это означает (проверяем
'Решение о совершенной филогении. Прим. перев.
6.2. СОСТОЯНИЯ БИНАРНЫХ ПРИЗНАКОВ
273
столбец к), что элемент Mik равен нулю, а элемент М^ равен единице. Таким образом, Ok A Oj ф 0. С другой стороны, никакое множество нс является подмножеством другого: О} Ok, потому что элемент Мц: равен нулю, а элемент равен единице; и также верно утверждение Ok Oj, поскольку столбец к расположен слева от столбца j. Поэтому столбцы к и j не удовлетворяют лемме 6.1, и в этом состоит противоречие.
Теперь мы докажем, что положительный ответ алгоритма о существовании совершенной филогении всегда верен. Мы покажем, что все пары столбцов матрицы М удовлетворяют лемме 6.1. Рассмотрим произвольный столбец j и такой столбец к слева от него, что Oj С Ok и к максимально (то есть к - общее ненулевое значение столбца у матрицы £). Согласно этому определению, любой столбец р между к и j обладает свойством Ор A Oj = = 0. Если к > 0, то мы можем рассуждать подобным же образом и показать, что пересечение множества Oj со всеми столбцами q, стоящими между кик' (где к' — общее ненулевое значение столбца к матрицы L), также пустое. Таким образом, мы показали, что для произвольного столбца j соответствующее множество Oj содержится в некоторых множествах, приписанных к столбцам, стоящим слева от него, и имеет пустое пересечение с остальными множествами, что и требовалось доказать.
Время счета этого алгоритма равно О(пт), потому что почленная сортировка матрицы М занимает время О(пт) (О(п') на столбец), а остальные шаги алгоритма легко могут быть выполнены за то же самое время.
Стадия построения
Ключевая идея построения — последовательно обрабатывать объекты и по мерс продвижения строить дерево. Мы начинаем с дерева с единственным узлом-корнем. Проверяя каждый объект, мы смотрим на те из его признаков, состояние которых равно единице. Всякий раз, когда мы видим, что в уже построенном дереве не существует ни одного ребра, помеченного этим признаком, мы создаем новый узел и соединяем его с текущим узлом посредством ребра, помеченного этим признаком. Новый узел становится текущим узлом. Если ребро, помеченное этим признаком, уже существует в дереве, то мы просто переходим к следующему признаку, оставляя текущий узел в качестве конечной точки этого ребра. Формальное описание этого алгоритма представлено на рис. 6.6. Интересно отметить, что получаемое дерево является корневым, но мы можем сделать его некорневым, просто удалив корень и соединив сыновей этого корня ребром. Теперь покажем, что дерево, построенное этим алгоритмом, представляет собой совершенную филогению объектов матрицы М и что время счета этого алгоритма равно О(пт).
274
Глава 6
Algorithm Perfect Binary Phylogeny Construction-input: бинарная матрица А/, столбцы которой сортированы в невозрастающем порядке по числу единиц output: совершенная филогения для матрицы А/ Создать корень for каждого объекта г do
curNode <— root
for j <— 1 to m do
if Afy = 1 then
if уже существует ребро curNode, и, помеченное j then curNode t— и
else
Создать узел и
Создать ребро curNode, и, помеченное j curNode <— и
Поместить г в curNode
for каждого узла и кроме root do
Создать столько листьев, связанных с и, сколько объектов содержится в и
Рис. 6.6. Алгоритм построения совершенной филогении объектов с ориенiирован-ными бинарными признаками
Вспомним сначала, что каждый признак в матрице М должен соответствовать одному и только одному ребру дерева, и именно такое дерево строит алгоритм. Кроме того, на пути от корня к листу (объекту) г мы должны пройти только ребра, соответствующие признакам, которые у объекта г имеют состояние 1, и никакие другие, и опять же, именно такую топологию восстанавливает алгоритм. Поскольку к каждому элементу матрицы А/ мы обращаемся только один раз и на каждый элемент мы тратим фиксированное время, полное время счета алгоритма равно О(пт). Подав на вход этого алгоритма матрицу признаков из табл. 6.2, мы получим филогению, представленную на рис. 6.2.
Мы упомянули, что вариант задачи с неупорядоченными признаками также может быть решен эффективно. Фактически, может быть использован тот же самый алгоритм, если выполнить простое преобразование. Когда признаки неупорядочены, их состояния следует обозначать буквами а и Ь. Преобразование алгоритма заключается в следующем: для каждого признака необходимо определить состояние, которое появляется наиболее часто.
Построение совершенной филогении. — Прим, перев.
6.3. ДВА ПРИЗНАКА
275
Мажоритарному состоянию присваивается значение 0, а другому I. Если оба состояния появляются с равной частотой, то мы можем одно из них принять за 0, а альтернативное — за 1. Теперь мы можем использовать наш алгоритм. Причину необходимости его работы при таком преобразовании объясняет следующий факт:
Факт: Для множества объектов, характеризуемых двумя бинарными неупорядоченными признаками г и j, совершенная филогения существует (то есть эти два признака совместимы) тогда и только тогда, когда пара множеств Ог,О} или Ог,О} подчиняется условиям, сформулированным в лемме 6.1.
В качестве упражнения мы предоставляем читателю возможность показать, что рассмотренное выше преобразование сохраняет совместимость между неупорядоченными признаками, как этого требует факт.
Мы заканчиваем этот раздел двумя наблюдениями. Во-первых, простое рассуждение показывает, что описанный здесь алгоритм самый быстрый из всех возможных алгоритмов этого класса. Должно быть ясно, что любой решающий эту задачу алгоритм должен по крайней мерс однократно обращаться к каждому элементу матрицы, что дает нам нижний предел времени счета, равный Г2(пш). Это означает, что представленный выше алгоритм оптимален. Однако если вход задачи организован в виде списка признаков каждого объекта, то специальные алгоритмы решают се эффективно и при этом затрачивают время, пропорциональное полной длине такого списка, то есть О(п + т). Во-вторых, в случае неупорядоченных признаков известны полиномиальные алгоритмы только для фиксированного числа состояний. Ссылки на работы с подробным анализом o6oitx наблюдений даны в библиографических примечаниях в конце этой главы.
6.3.	ДВА ПРИЗНАКА
Здесь мы изучаем другой частный случай задачи о совершенной филогении. Мы допускаем более общие ситуации, где признаки могут быть неупорядоченными и иметь произвольное число состояний. Однако на сей раз мы налагаем о!раничение на максимальное число признаков', в частности, мы рассматриваем случай, когда объект может иметь только два признака.
Мы увидим, что допущение об объектах с двумя признаками, так же как и допущение о признаках с двумя состояниями, делает задачу о совершенной филогении в вычислительном отношении легкой. Далее мы представим
276
Глава 6
очень простой алгоритм решения этой задачи (хотя он использует нетривиальные следствия из теории графов). Начнем с некоторых определений.
Определение 6.2. Триангулированным графом называют неориентированный граф, в котором любой цикл с четырьмя или более вершинами имеет хорду, то есть ребро, соединяющее две несмежные вершины этого цикла.
Вспомним, что поддерево — это связный подграф дерева и что множество узлов дерева, которые имеют одинаковое состояние у данного признака, образует поддерево в совершенной филогении. Связь между триангулированными графами и задачей о совершенной филогении определяет следующая теорема:
Теорема 6.1. Каждому множеству поддеревьев {Ti,Tz,... ,Т}} дерева Т соответствует триангулированный граф; и наоборот.
Мы не будем доказывать эту теорему, но опишем граф, который должен соответствовать данному множеству поддеревьев. Этот граф оказался очень удобным инструментом проверки множества признаков на совместимость (то есть ответа на вопрос о том, существует ли совершенная филогения для соответствующих объектов). Как будет показано далее, мы можем утверждать, что множество признаков совместимо тогда и только тогда, когда граф, построенный согласно теореме, может быть триангулирован. Для того чтобы понять, что это за граф, мы нуждаемся в некоторых определениях.
Определение 6.3. Граф пересечений для множества множеств С  это граф G, который мы получаем путем отображения каждого множества, принадлежащего множеству С, на соответствующую вершину графа G, и соединения двух вершин в графе G ребром, если соответствующие этим вершинам множества имеют непустое пересечение.
Граф, упомянутый в «доказательстве» теоремы 6.1, — граф пересечений. Прежде чем описать его, мы представим другой граф, который мы называем графом пересечений состояний или ГПС, и который представляет промежуточный шаг построения. Имея матрицу состояний признаков, мы строим ее собственный ГПС следующим образом. Для каждого состояния каждого признака мы создаем вершину в ГПС. Следует помнить, что каждому состоянию, или вершине, соответствует некоторое множество множество объектов, у которых данный признак имеет данное состояние. Затем мы создаем ребро между вершинами и и г в ГПС, тогда и только тогда, когда соответствующие им множества имеют непустое пересечение.
6.3. ДВА ПРИЗНАКА
277
Рис. 6.7. Граф пересечений состояний, соответствующий матрице из табл. 6.3. Индекс метки каждой вершины обозначает цвет зюй вершины
Вот почему мы называем такой граф графом пересечений состояний На рис. 6.7 представлен ГПС, построенный для матрицы из табл. 6.3.
Таблица 6.3. Матрица состояний признаков
	Признак
Объект	Cl С2 с3
А	У] Х2 Z3
В	Х1 2/2 Уз
С	2/1	2/2	2/3
D	2/1 Z2 гз
Обратите внимание, что граф, упомянутый в теореме 6.1, построен на множестве поддеревьев. Граф, который мы описали в предыдущем параграфе, построен на множестве объектов, которые являются листьями филогении. Чтобы получить граф, упомянутый в теореме, мы должны расширить ГПС (добавляя новые ребра), чтобы можно было учитывать также его внутренние узлы. Именно этот расширенный граф мы будем проверять на свойство триангуляции. Фактически, мы будем стараться добавлять ребра в ГПС с надеждой превращения его в триангулированный граф. Однако мы не можем добавлять ребра по желанию; для каждого признака мы должны учитывать связи между объектами. Для объяснения этого условия мы нуждаемся в следующем определении.
278
ГЛАВА 6
Определение 6.4. Дан граф G = (V, Е) с раскраской с множества вершин V. Мы говорим, что граф G может быть с-триангулирован, если существует такой триангулированный граф Н = (V, Е'), что Е С Е', а раскраска с является правильной также и для графа Н. Другими словами, любое ребро, присутствующее во множестве Е', но не принадлежащее множеству Е, должно связывать две вершины с различными цветами.
Здесь мы заметим, что множество признаков в матрице состояний признаков определяет раскраску ГПС, поскольку никакой объект не может иметь два различных состояния у одного и того же признака. Таким образом, мы получили новую формулировку теоремы 6.1, объясняющую связь между ГПС и филогенией.
Теорема 6.2. Матрица состояний признаков М, где множество признаков определяет раскраску с, допускает совершенную филогению тогда и только тогда, когда соответствующий ГПС может быть е-триангулирован.
В примере на рис. 6.7 цвет каждой вершины определяется признаком, который является частью метки вершины. Чтобы триангулировать этот граф, все, что мы должны сделать — создать ребро между вершинами у? и Z3; это возможно благодаря тому, что эти две вершины имеют различные цвета (но мы не были бы способны создать ребро (яд, гд), потому что они имеют одинаковый цвет). Это означает, что матрица из табл. 6.3 допускает совершенную филогению.
Обратите внимание на общий характер теоремы 6.2: ничто не сказано о фиксированном числе признаков. Если вспомнить, что задача о совершенной филогении для неупорядоченных признаков является в общем случае НП-полной, то неудивительным становится и тот факт, что с-триангуляция графов... также НП-полная задача. Однако если матрица А/ содержит только два признака, то ГПС будет раскрашен только двумя красками, что дает нам следующую теорему.
Теорема 6.3. Матрица М состояний двух признаков допускает совершенную филогению тогда и только тогда, когда соответствующий ей ГПС является ациклическим.
Доказательство. Сначала отметим, что если ГПС является ациклическим, то он уже с-триангулирован, и, следовательно, согласно теореме 6.2, матрица М допускает совершенную филогению. Чтобы доказать условие необходимости («только тогда»), достаточно использовать классическое следствие из теории графов, которое гласит, что граф может быть раскрашен
6.3. ДВА ПРИЗНАКА
279
двумя красками тогда и только тогда, когда все его циклы имеют четную длину. Из теоремы 6.2 мы знаем, что ГПС может быть 2-триангулирован, и это означает, что он может быть раскрашен двумя красками. Отсюда следует, что ГПС не может иметь циклов нечетной длины. Как известно, треугольник — цикл нечетной длины. Следовательно, единственное условие, при котором ГПС будет удовлетворять условию 2-триангуляции, — его ацикличность.	
Рис. 6.8. Дерево, восстановленное по данным табл. 6.4
Опираясь на теорему 6.3, мы можем построить простой и эффективный алгоритм проверки того, допускает ли матрица состояний с двумя признаками совершенную филогению, так как проверка графа с | V| вершинами и |E,| ребрами на ацикличность занимает время О(|V| + |£|). В нашем случае число вершин равно О{п) (поскольку объект характеризуется только двумя признаками, может быть самое большее 2п состояний) и число ребер также равно О(п). Следовательно, алгоритм находит решение за линейное время. Восстановление совершенной филогении Т, если она существует, осуществляется следующим образом. Создаем вспомогательный граф G = (V, Е) такой, что каждому ребру в ГПС соответствует вершина во множестве V. Таким образом, вершине v G V, соответствующей ребру (ж, у), в ГПС соответствует также множество объектов Lv: пересечение между множеством х и множеством у (вспомним, что вершина в ГПС соответствует множеству объектов). В графе G создаем ребро между двумя вершинами и, v G V, если Lu П Lv 0. Искомое дерево — любое остовное дерево в графе G (это означает, что дерево может быть не единственным), причем объекты множества Lv добавляются в качестве листьев к каждому узлу v. Конечное дерево некорневое и может быть построено за время О(п). Такое построение применимо только в случае с двумя признаками. Если объекты имеют большее число признаков, то узлы в дереве должны соответствовать максимальным
280
ГЛАВА 6
Таблица 6.4. Матрица состояний двух признаков
	Признак	
Объект	С1	С2
А		а?2
В	У1	У2
С		Х2
D	У1	У2
Е	ич	Х2
F	Х1	Х2
G	Z1	У2
Н	Xi	1/2
полным под! рафам (то есть максимальным тикам) в триангулированном П1С. Это условие опирается на доказательство теоремы 6.1, которое мы опустили, и которое также объясняет, как нужно соединять узлы, таким образом полученные, чтобы построить дерево.
Пример построения дерева для двух признаков из матрицы в табл. 6.4 представлен на рис 6.8. Для того чтобы убедиться, что это дерево является совершенной филогенией, необходимо сначала пометить все внутренние узлы v объектами из множества L, и затем проверить, что все узлы, содержащие объекты с одинаковым состоянием данного признака, формируют поддерево. Например, у всех объектов из ряда .4, С, F и Н признак щ имеет состояние xt, и эти объекты действительно формируют поддерево. Напротив, объекты Е и G не формируют поддерево. См. также упражнение 9.
Представленные здесь положения закладывают основу для намного более общего алгоритма - алгоритма, который за полиномиальное время находит решение для любого фиксированного значения т (другими словами, т показатель степени в функции времени счета) Описание этого алгоритма лежит за пределами наших возможностей, и поэтому мы ограничились лишь ссылкой в библиографических примечаниях.
6.4.	ЭКОНОМИЧНОСТЬ И СОВМЕСТИМОСТЬ
ФИЛОГЕНЕТИЧЕСКИХ ДЕРЕВЬЕВ
Мы увидели в предыдущих разделах, что даже при том, что задача о совершенной филогении объектов с неупорядоченными признака ми НП-полная, ее частные случаи с фиксированными параметрами разреши
6.4. ЭКОНОМИЧНОСТЬ ФИЛОГЕНЕТИЧЕСКИХ ДЕРЕВЬЕВ
281
мы за полиномиальное время. Алгоритмы для таких упрощенных вариантов могли бы казаться удачной находкой для практических целей, но проблема состоит в том, что реальные матрицы состояний признаков вряд ли допустят совершенную филогению. Причина этого двоякая: в биологии всегда присутствуют экспериментальные ошибки и иногда нарушаются допущения, принятые в упомянутых алгоритмах (отсутствует возврат и схождение). По этим причинам необходимо разработать иные подходы к восстановлению филогенетических деревьев.
Известны два очевидных подхода, игнорирующих ошибки, но принимающих допущения. Первый — допускать события возврата и схождения, но пытаться минимизировать число их появлений Этот принцип известен как критерий экономичности. Второй подход — настойчиво избегать возврата и схождения, вплоть до исключения признаков, которые вызывают такие «проблемы». Стараться исключить как можно меньше признаков -несомненно, хорошая идея. Это означает, что в данном подходе мы стараемся найти максимальное множество таких признаков, для которых мы можем найти совершенную филогению (или, другими словами, максимальное множество совместимых признаков). Этот принцип известен как критерий совмести мости.
Оба критерия приводят к задачам оптимизации. Такие задачи обычно более трудны, чем задачи принятия решений — например задачи о совершенной филогении, рассмотренной в разделе 6 1 Поскольку мы знаем, что задача о совершенной филогении для неупорядоченных признаков Н11-полная, то и только что обрисованные задачи должны быть по крайней мере столь же трудны, так оно и есть. Но нам бы гораздо больше повезло в случае упорядоченных признаков, поскольку, как было отмечено в разделе 6.1, для них задача о совершенной филогении действительно разрешима за полиномиальное время. К сожалению, госпожа Удача вновь отвернулась от нас, и оба критерия, упомянутые выше, приводят к НП-трудным задачам также и для упорядоченных признаков. Обсудим эти задачи подробнее.
Как уже было упомянуто, руководствуясь критерием экономичности, мы пытаемся минимизировать число событий возврата и (или) схождения. В общем случае это означает, что мы стараемся минимизировать число переходов состояний (то есть ребер) в восстановленной филогении. Если мы допускаем события возврата, но запрещаем схождение, то мы получаем так называемый критерий экономичности Долю. Если, напротив, мы запрещаем события возврата, но при этом минимизируем число событий схождения, то мы получаем критерий экономичности Камина Сокола. Оба критерия приводят к НП трудным задачам. Доказательства основаны на задаче о дереве Штейнера классической задаче оптимизации в теории графов
282
Глава 6
В литературе понятие экономичности появляется также в связи с еще одной задачей. Имея множество объектов и дерево, посредством которого они связаны, требуется присвоить состояния внутренним узлам, так чтобы число переходов состояний от узла к узлу было минимальным. Известно, что эффективные алгоритмы могут быть построены только для некоторых частных формулировок этой задачи. Мы не будем описывать такие алгоритмы, а ограничимся ссылками в конце этой главы.
Теперь обратим наше внимание на критерий совместимости и представим доказательство НП-полиоты основанной на нем задачи принятия решений. Доказательство опирается на задачу о клике, которая, как известно, является НП-полной. Фактически, мы показываем, что задача о клике и задача на совместимость однотипны. Это означает, что алгоритмы метода перебора для задачи о клике могут быть использованы и для решения задачи на совместимость; с учетом этого свойства были разработаны пакеты программ для построения филогенетических деревьев. Конечно, с помощью этого подхода возможно решить задачи строго ограниченного размера, но, тем не менее, он кажется достаточно полезным
НП-полноту мы будем доказывать для следующего варианта задачи на совместимость:
Задача: Совместимость
ПРИМЕР: Матрица состояний признаков Л/, содержащая п объектов и т ориентированных бинарных признаков, и положительное целое число В тп
ВОПРОС: Существует ли подмножество признаков L, которое удовлетворяет лемме 6.1 при В?
Следует учесть, что здесь мы рассматриваем сильно упрощенный вариант задачи (бинарные и ориентированные признаки). В связи с такими ограничениями, понятие совместимости в точности соответствует приведенному в лемме 6.1. Как было упомянуто, доказательство НП полноты опирается на задачу о клике, которая может быть формально описана следующим образом:
Задача: Клика
ПРИМЕР: Граф G = (V, Е) и положительное целое число К С |У|.
ВОПРОС: Содержит ли граф G подмножество V С V, где |V'| А" и каждая пара вершин подмножества V' соединена ребром, принадлежащим множеству В?
6.4. ЭКОНОМИЧНОСТЬ ФИЛОГЕНЕТИЧЕСКИХ ДЕРЕВЬЕВ
283
Как мы уже говорили, мы хотим показать, что СОВМЕСТИМОСТЬ является НП-полной задачей и что она равносильна задаче КЛИКА. Как было описано в разделе 2.3, для этого необходимо показать, что обе задачи принадлежат к классу НП, и что каждая может быть преобразована за полиномиальное время в другую. НП-полноту задачи КЛИКА мы считаем уже доказанной, так что она очевидно относится к классу НП. Другие части доказательства сформулированы в следующих теоремах.
Теорема 6.4. СОВМЕСТИМОСТЬ — НП-полная задача.
Доказательство. Рассматривая решение задачи совместимость, мы можем легко убедиться в том, что оно фактически представляет собой решение, полученное с помощью полиномиального алгоритма, описанного в разделе 6.2. Таким образом мы видим, что СОВМЕСТИМОСТЬ принадлежит к классу НП. Теперь мы покажем, как за полиномиальное время задачу КЛИКА можно преобразовать в СОВМЕСТИМОСТЬ .
Для графа G = (V,E) из примера задачи клика мы следующим образом строим матрицу состояний признаков Л/ из примера задачи СОВМЕСТИМОСТЬ. Принимаем т = |V\, то есть для каждой вершины ц, G V мы создаем признак г в матрице М. Число объектов (строк) в матрице М определяется как п = 3m(m - 1)/2; то есть мы создаем три объекта для каждой возможной пары признаков. Теперь мы должны заполнить матрицу Л/. Для каждой пары вершин (г,, Vj), которой не соответствует никакое ребро из множества Е, мы создаем три объекта г, s и t в матрице М со следующими значениями соответствующих элементов: Mri = О, Л/в1 = 1 и Mti = 1; Mrj = 1, MS] = 1 и Mtj = 0. Легко видеть, что при таких значениях признаки г и j не будут совместимы (см. лемму 6.1). Остальные элементы матрицы Л/ должны быть нулями. Очевидно, что такое преобразование может быть проведено за полиномиальное время.
Теперь нам осталось показать, что граф G содержит клику V', причем | V'| К тогда и только тогда, когда матрица М имеет совместимое подмножество признаков L, где |L| К. Сначала допустим, что такая клика действительно существует. Тогда каждому ребру этой клики соответствует такая пара признаков в матрице Л/, что когда бы у некоторого объекта состояние одного из них ни было равно 1, состояние другого было бы равно 0 (или оба равны 0) у того же объекта. Поэтому все такие пары удовлетворяют лемме 6.1 и, следовательно, совместимы. Теперь допустим, что подмножество L существует и |L| К. Тогда каждой паре признаков подмножества L соответствует пара вершин множества V, соединенных ребром. Все эти пары, взятые вместе, формируют клику размером К. 
284
Глава 6
Теорема 6.5. Совместимость может быть преобразована в задачу КЛИКА за полиномиальное время.
Доказательство. Имея матрицу М из приведенного выше примера задачи совместимость, построим граф G = (V,E) из примера задачи КЛИКА следующим образом. Для каждого признака матрицы М создаем вершину во множестве V. Соединяем две вершины vt и Vj тогда и только тогда, когда признаки г и j совместимы. Проверка на совместимость между парами признаков может быть легко проведена за полиномиальное время. Лемма 6.1 гарантирует, что граф G содержит клику размером Б тогда и только тогда, когда матрица А/ содержит подмножество совместимых признаков, размер которых также больше или равен В.	
6.5.	АЛГОРИТМЫ ДЛЯ МАТРИЦ РАССТОЯНИЙ
В этом разделе мы рассмотрим задачу восстановления деревьев на основании численных данных сравнения п объектов. Основной вход задачи матрица hl размером п х п, где элемент Mtj — неотрицательное вещественное число, которое мы называем расстоянием между объектами ? и j. Такне расстояния определяют путем сравнения объектов. Например, если объекты - последовательности ДНК, то мы могли бы использовать понятие расстояния между последовательностями, описанное в разделе 3.6.1.
Первая задача, которую мы рассмотрим, может быть неформально описана следующим образом. Имея матрицу расстояний ЛД мы хотели бы построить такое реберно взвешенное дерево, где каждый лиш соответствует только одному объекту матрицы М и расстояния, измеренные на дереве между листьями i и j, точно соответствуют значению элемента Мг]. Когда такое дерево может быть построено, мы говорим, что расстояния матрицы Л/ аддитивны.
Мы увидим, что на практике матрицы расстояний редко аддитивны и что попытка минимизировать отклонение от аддитивности ведет к НП-трудным задачам. Это привело к постановке второй задачи построения дерева, в которой на вход идут две матрицы вместо одной. Эти матрицы дают нам верхний и нижний пределы парных расстояний между объектами, и задача состоит в том, чтобы найти дерево, которое помещается «между» этими пределами.
6.5.1.	ВОССТАНОВЛЕНИЕ АДДИТИВНЫХ ДЕРЕВЬЕВ
При обсуждении рассюяний мы нуждаемся в понятии метрического пространства. Мы уже встречались с этим понятием в разделе 3.6.1, где
6.5. АЛГОРИТМЫ ДЛЯ МАГРИЦ РАССТОЯНИИ
285
называли его расстоянием. Здесь мы еще раз повторим это определение. Метрическое пространство — это такое множество объектов О, что каждой паре i,j € О мы ставим в соответствие неотрицательное вещественное число dtj со следующими свойствами
> 0	при г 7^ j,	(6.1)
dtj	= 0	при г = J,	(6 2)
dtj = djt	при	любых i	и j,	(6 3)
dtj dzk + d^ при любых i.j, к (аксиома треугольника). (6.4)
Потребуем, чтобы наша матрица входов М была метрическим пространством. В частности, это означает, что она будет симметричной (свойство 6.3). Теперь мы должны точно определить, что мы подразумеваем под построением дерева по матрице Л/.
Поскольку Л/ квадратная матрица размером п х п, наше дерево должно иметь п листьев. Листья узлы со степенью один, все остальные узлы должны иметь степень три, поэтому такое дерево некорневое. Все ребра дерева имеют неотрицательный вес. (Это требование вместе с требованием о степенях означает, что каждый внутренний узел со степенью четыре мы расщепляем на два узла со степенью три и соединяем их условным ребром нулевой длины ) Вес пути между узлами дерева и и v равен сумме весов ребер, образующих данный пул ь. Последнее требование состоит в том, что вес пути между любыми двумя листьями г и у должен быть равен Мг}. Если такое дерево Т может быть найдено, то мы говорим, что матрица Л/ и дерево Т аддитивны.
Ознакомившись с данной системой требований, мы нс можем не задать следующие вопросы: Если известно, что некоторая матрица Л/ является метрическим местом, то является ли она также аддитивной? И если да, то как мы будем строить соответствующее аддитивное дерево? Ответ на первый вопрос сформулирован в виде следующей леммы:
Лемма 6.2. Метрическое пространство О аддитивно тогда и только тогда, когда мы можем пометить любые четыре объекта пространства О буквами i, j, к и I, так. чтобы
dij -I- d^i — dt^ + dji dti -Г d^ic-
Мы нс будем представлять доказательство этой изящной леммы, известной как условие четырех точек (см. библиографические примечания). Вместо этого мы сосредоточимся на ответе на второй вопрос, то есть на
286
Глава 6
алгоритме построения аддитивных деревьев. Это алгоритм с полиномиальным временем счета, и лучший способ понять его (или построить) — все тот же метод индукции.
Будем считать, что матрица М удовлетворяет условию леммы 6.2. Предположим теперь, что число объектов п равно 2 (назовем их х и у). Тогда легко построить дерево: это простое ребро с весом Мху, соединяющее узлы хну. Теперь предположим, что мы добавили третий объект z. Как мы должны включить его в дерево? Ясно, что мы должны получить дерево, подобное изображенному на рис. 6.9. Задача состоит в том, чтобы определить, где именно между узлами х и у должен быть расположен центральный узел (назовем его с); или, другими словами, каковы должны быть длины ребер (z,c), (х, с) и (у, с). Обозначая длину ребра (i, j) через переменную мы можем записать следующие уравнения:
— ^хс + d-zc	(6.5)
= dye + dzc	(6.6)
С другой стороны, мы знаем, что
dye — dxc.
Если мы сейчас вычтем уравнение (6.6) из (6.5) и подставим в него dyc из (6.7), то мы получим:
, _ Мху + Mxz — Myz
dXc —	2	*	(6-8)
Обратите внимание, что благодаря аксиоме треугольника (6.4), значение dxc 0. Мы можем продолжить ход решения для двух других неизвестных и получить:
_ Мху + Myz — Mxz
dye —	2	(6-9)
Mxz + Myz — Mxy dzc =----------2---------•	(6.10)
Итак, мы построили аддитивное дерево, соответствующее трем объектам. Заметим, что это дерево единственно возможное, так же, как и в случае с двумя объектами. Теперь добавим четвертый объект, w. (Причина того, что мы рассматриваем так много последовательных шагов индукции, состоит в том, что позже мы будем использовать эти примеры, чтобы показать,
6.5. АЛГОРИТМЫ ДЛЯ МАТРИЦ РАССТОЯНИЙ
287
что аддитивное дерево единственно возможное для любого числа объектов.) Объект и создаст другой внутренний узел, который мы назовем с2. Задача теперь состоит в том, чтобы решить, какое ребро должен расщепить узел г2: (х, с), (у, о) или (z, с). Выбираем любые два узла дерева, например х и у, и применяем уравнения (6.8), (6.9) и (6.10) с подстановкой w вместо г. Если мы находим, что узел с2 должен расщепить ребро (х, с) либо (у, с), то задача решена. Но если мы видим, что узел с2 совпадает с узлом с, то это означает, что должно быть расщеплено ребро (г, с) и мы должны применить те же самые уравнения снова, на сей раз оставляя г и подставляя w вместо х (или у). Нельзя ли для четырех объектов построить два аддитивных дерева? Допустим, что можно. В таком случае мы имеем выбор размещения с2 на два различных ребра, например, (х, с) и (z,c). Но это в свою очередь означает, что есть два различных дерева для трех объектов х, z и w, а это противоречит нашему доказательству, что для любых трех объектов всегда существует только одно дерево. Исходя из этого мы заключаем, что для
Рис. 6.9. Аддитивное дерево для трех объектов
Допустим теперь, что мы построили дерево для к объектов. Процесс добавления объекта к + 1 к дереву подобен тому, что мы делали для четвертого объекта. Мы выбираем на дереве любые два объекта х и у, а затем вычисляем положение нового внутреннего узла. Если этот новый узел не совпадает ни с каким существующим узлом дерева, то задача решена. То есть, мы точно знаем ребро, которое должно быть расщеплено при добавлении к дереву объекта к + 1. В противном случае место расщепления попадает на существующий узел, например, и. Поскольку и — внутренний узел дерева, мы наверное знаем, что из него растет некоторое поддерево (это может быть поддерево с единственным листом). Тогда мы выбираем любой объект, принадлежащий этому поддереву, например, объект г, и применяем уравнения (6.8), (6.9) и (6.10) с аргументами х (или у), г и Л+1. Мы повторяем этот процесс до тех пор, пока правильное место расщепления не будет найдено.
288
Глава 6
Таблица 6.5. Матрица входов М из примера 6.1
	В	С	D	Е	F	G
А	63	94	111	67	23	107
В		79	96	16	58	92
С			47	83	89	43
D				100	106	20
Е					62	96
F						102
Ясно, что этот алгоритм строит действительно аддитивное дерево, если таковое существует. При добавлении к дереву каждого нового объекта, нам, вероятно, придется проверять все другие, уже растущие на дереве объекты, тратя фиксированное время на каждую такую проверку. Это означает, что в худшем случае время счета этого алгоритма будет равно О(п2).
Пример 6.1. Восстановим аддитивное дерево для объектов из табл. 6.5. Мы начинаем построение, создавая ребро (А, В) длиной в 63 единицы. Затем мы добавляем объект С. Применяя уравнения (6.8), (6.9) и (6.10), мы находим, что новый узел Xi должен быть создан на расстоянии 39 единиц от объекта А и 24 единицы от объекта В. Тогда мы добавляем новое ребро (xi, С) длиной 55 единиц. Теперь рассмотрим новый объект, Е. Если мы применим уравнения, используя объекты А и С в качестве старых узлов дерева, то мы находим, что объект Е должен войти в то же поддерево, где уже находится объект В. Поэтому мы должны применить уравнения к объектам Е, В и (например) А. Выполняя это, мы находим положение нового узла, х?: 18 единиц длины от узла xj и 6 единиц длины от объекта В. Продолжая построение подобным же образом, мы получаем конечное дерево, показанное на рис. 6.10.	
Рис. 6.10. Аддитивное дерево из примера 6.1. Цифры указывают длины ребер
6.5. АЛГОРИТМЫ ДЛЯ МАТРИЦ РАССТОЯНИЙ
289
Мы завершаем доказательство уникальности аддитивного дерева, показывая, что при п > 4 как топология, так и длины ребер аддитивного дерева определяются однозначно. Взглянем сначала на его топологию. Любые три листа однозначно определяют один внутренний узел дерева, и этот узел в свою очередь однозначно определяет разбиение {РьРг.^з} всех листьев. Если существуют две различные топологии, то должно быть и множество из трех листьев (например, х, у и z), которое определяет разбиение {Pi, Рг, Рз} в первом дереве и разбиение {Qi,Q2,Qs} во втором, причем эти два разбиения являются различными. Тогда один из листьев, скажем х, должен принадлежать множествам и Q2, но при этом Ру Q2-Это в свою очередь означает, что должен существовать некоторый другой объект, например ш, который принадлежит множеству Ру, но не принадлежит множеству Q2. Но это равносильно высказыванию, что для четырех объектов х, у, z и w существуют два различных дерева, а оно, как мы знаем, не верно.
Теперь мы докажем, что длины ребер также являются однозначно определенными. Любые ребра, ведущие к листу х, должны иметь уникальную длину, потому что дерево, определяемое листом х и любыми двумя другими объектами этого же дерева, единственно возможное. Внутренние ребра также определены однозначно, так как они разбивают листья на множества Ру, Р2, Рз и Р4. Выбирая лист из каждого множества, мы получаем четыре объекта, и снова мы знаем, что с ними мы можем построить только о^но дерево; следовательно, длины внутренних ребер должны быть однозначно определенными.
Мы представили простой и хороший алгоритм восстановления аддитивных деревьев. Однако он нашел ограниченное практическое применение, потому что реальные матрицы расстояний редко бывают аддитивными. Эта ситуация возникает нс обязательно из-за погрешности измерения расстояний. Возможно привести примеры биологических последовательностей, связанных посредством дерева, где предковые последовательности подвергаются многократным изменениям в одном и том же участке (например, некоторое основание ДНК могло бы измениться с А на С и затем на G). Другими словами, последующие изменения разрушают следы предыдущих. Кроме того, эволюция может сходиться. Допущение о возможности таких ситуаций может дать в результате неаддитивные парные расстояния. Такой сценарий особенно вероятен в случае последовательностей белков.
Эти факты ведут нас к обобщению задачи об аддитивном дереве. Формулировка одного из возможных вариантов звучит так: требуется построить дерево, возможно ближайшее к аддитивному. К сожалению, было показано, что при нескольких альтернативных понятиях «близости» деревьев конеч-
290
Глава 6
ныс задачи были НП-трудными. Однако известен другой вариант задачи, который поддается решению', это тема следующего раздела.
6.5.2.	* ВОССТАНОВЛЕНИЕ УЛЬТРАМЕТРИЧЕСКИХ ДЕРЕВЬЕВ
Измерения парных расстояний иногда несут в себе неопределенность. Предположим, что эта неопределенность может быть определена количественно так, чтобы каждое измерение было выражено интервалом. Этот интервал определяет нижний и верхний пределы истинного расстояния. На основании таких данных мы можем получить две матрицы расстояний и Mh, содержащие, соответственно, нижние и верхние пределы парных расстояний. Теперь задача состоит в том, чтобы восстановить такое эволюционное дерево, чтобы расстояния, измеренные на этом дереве, помещались «между» этими двумя матрицами входов. Другими словами, пусть — расстояние, измеренное на дереве между объектами i и j. Тогда следующее неравенство должно быть верно:
(6.11)
Уравнение (6.11) мы называем ограничениями сандвича. В этом разделе мы покажем, что задача может быть решена эффективно, если на искомое дерево наложить одно дополнительное требование. Согласно этому требованию дерево должно быть ультраметрическим. Дерево является ультраметриче-ским, когда оно аддитивно и может быть укоренено таким образом, чтобы длины путей от корня ко всем листьям были равны. Биологический смысл этого требования состоит в допущении о том, что изучаемые объекты эволюционировали от общего предка с равной скоростью.
Поскольку свойство ультраметричности — частный случай свойства аддитивности, реальные матрицы расстояний также редко бывают ультра-метрическими. С другой стороны, при единственном требовании, чтобы дерево росло «между» матрицами М1 и Mh, задача становится более реалистичной; и как мы увидим, алгоритм ее решения весьма интересен. Болес того, это также наиболее запутанный из представленных в этой главе алгоритмов. По этой причине описание алгоритма будет следовать следующей схеме: сначала мы представим несколько новых принципов, определений и понятий; затем мы представим сам алгоритм, но только «в общих чертах»; после чего мы рассмотрим алгоритм подробнее, объясняя принцип работы его частей, и представим анализ времени счета; и, наконец, мы докажем, что построенный нами алгоритм все-таки работает.
Первый необходимый принцип — интерпретация матрицы расстояний в качестве неориентированного реберно взвешенного графа. Имея матрицу
6.5. АЛГОРИТМЫ ДЛЯ МАТРИЦ РАССТОЯНИЙ
291
расстояний Л/ размером п х п, мы можем интерпретировать ее как полный граф на п вершинах, где вес ребра (i,j) определяется элементом М 3. Далее мы будем часто обращаться к такой интерпретации. Мы допускаем, что элемент Mi3 определен для каждой пары вершин г, j, так что соответствующий граф всегда связен. Мы принимаем Мц = 0 для всех г. В связи с этой интерпретацией мы будем говорить о графах G1 и Gh, которые соответствуют матрицам М1 и Mh. Мы описываем веса ребер функцией ру, например: УУ(е) или ру(«, fc), где е и («, Ь) - альтернативные обозначения ребер.
Другое важное понятие — понятие минимального остовного дерева (МОД). Это понятие описано в разделе 2.3. Здесь читатель должен быть очень внимателен и не путать взращиваемое нами дерево (филогенетическое ультраметрическое дерево) с минимальным остовным деревом, которое является всего лишь инструментом в наших руках. Мы различаем эти деревья и всегда обозначаем ультраметрическое дерево буквой U, а МОД -буквой Т.
МОД Т определяют на графе Gh. Мы вычисляем МОД Т, потому что его ребра указывают способ построения дерева U. В частности, ребро старшего веса в уникальном пути между любыми двумя узлами а и b в дереве Т называют связью узлов а и b и обозначают («, b)max. Связь используют в следующем определении ключевой функции на ребрах дерева Т:
Определение 6.5. Вес сечения ребра е минимального остовного дерева графа Gh определяется как
CIV(e) = тах{Л/дЬ|е = (a, fe)rnax}-
Раскроем значение этого определения. Имея матрицу Л/71, мы можем вычислить минимальное оетовное дерево Т соответствующего графа Gh. Каждое ребро е = (a, Ь) Е Т является связью по крайней мере одной пары вершин дерева Т (а именно, вершин а и fc); оно может быть связью большего числа пар. Теперь выберем все пары вершин, для которых ребро е является связью; и выберем среди этих пар максимальный элемент другой матрицы (то есть, матрицы М1). В результате получим вес сечения ребра е.
Догадка о роли весов сечений помогает в понимании принципа работы алгоритма. Рассмотрим такие листья а и b на дереве U, что их расстояние с1.аь равно наибольшему расстоянию между листьями дерева U. Ясно, что расстояние dab должно быть больше, чем максимальный элемент матрицы Л/(, который мы обозначаем max'. Но с другой стороны, расстояние dab пс должно быть больше, чем та.'?. Следовательно, dab — max' и листья а
292
ГЛАВА 6
и Ь принадлежат разным поддеревьям, растущим из корня. Теперь с помощью МОД Т определим разбиение остальных узлов между этими двумя поддеревьями. Свойства дерева Т и определение весов сечений гарантируют, что Mlxy dxy М*у для всех объектов х и у, принадлежащих разным поддеревьям, и что конечное дерево является ультрамстричсскпм. Все это будет показано в доказательствах леммы 6.4 и теоремы 6.6. Итак, мы готовы набросать первый структурный план алгоритма:
1.	Вычислить МОД Т графа Gh;
2.	Для каждого ребра е G Т вычислить CHi(e);
3.	Построить ультрамстрическое дерево U.
Первый шаг прост, так как мы можем применить хорошо известные алгоритмы и затратить время О(п2). Другие два шага более запутанные, поэтому разберем каждый отдельно.
Вычисление весов сечений
Основная информация, необходимая для вычисления весов сечений, связь («, fc)max каждой пары вершин а и Ь. Мы находим такие ребра, строя еще одно дерево, которое мы обозначаем R. Это корневое бинарное дерево, к листьям которого приписаны объекты. В каждом внутреннем узле дерева R мы храним ребро дерева Т. Наша цель заключается в том, чтобы внутренний узел дерева R, который является наиншшии общим предком узлов а и Ь, содержал связь («, Ь)И1ах каждой пары объектов а и Ь. Например, в корне дерева R мы храним ребро старшего веса дерева Т. Это обусловлено тем, что для каждой пары объектов а и Ь, таких, что они находятся на противоположных сторонах дерева Т относительно ребра старшего веса, именно это ребро является связью (a,fc)max. Мы могли бы использовать это свойство, чтобы построить алгоритм, который работает нисходящим способом. Сначала мы создаем корень дерева R и помещаем в него ребро старшего веса е; затем выполняем ту же операцию рекурсивно, сначала рассматривая узлы с одной стороны от ребра е (корень этого поддерева будет левым сыном общего корня), а затем рассматривая узлы с другой стороны от ребра с (корень этого поддерева будет правым сыном общего корня). Однако намного эффективнее строить дерево R восходящим способом (соответствующий алгоритм показан на рис. 6.11).
Этот алгоритм использует структуру данных, известную как лес непе-ресекающихся множеств (см. раздел 2.3), и представлен процедурами MakeSet, FindSet и Union. Анализ времени счета следующий. Сортировка ребер занимает время O(nlogn). На построение дерева R уходит вре-
6.5. АЛГОРИТМЫ ДЛЯ МАТРИЦ РАССТОЯНИЙ 293
Algorithm Construction of 7?3
input: минимальное остовное дерево Т графа Gh
output: дерево 7?
for каждого объекта г do
MakeSet(i)
Создать дерево с одним узлом для объекта i
Сортировать ребра дерева Т в неубывающем порядке весов
for каждого ребра е = (а,6) е Т в этом порядке do
А <— FindSet(a)
В <— FindSedb)
if А В then
// объединение деревьев
га «— дерево, содержащее а
гь «— дерево, содержащее Ь
построить дерево R
R.edge <— е
R.leftChild *— га
R.rightChild<— rj,
UnionfA. В)
return дерево R
Рис. 6.11. Построена дерева R с помощью леса непересекаюшихся множеств
Algorithm Cut-weight Computation*
input: матрица M1, деревья Т и R
output: массив весов сечений С Ил
Предварительно обработать дерево R для операций
поиска наинизшего общего предка (НОП)
for каждого ребра е € Т do
CW[e] <- О
for каждой пары объектов а и b do
е*—НОП( R.a,b)
if Л/^ > CIV[e] then
СНЧе] - Л/'ь
return СИ
Рис. 6.12. Вычисление весов сечений
мя О(па(п,п)) (вследствие свойств леса непсресекающихся множеств).
Следовательно, полное время счета алгоритма равно O(nlogn).
’Построение дерева Я. — Прим, перев.
4Вычислеиие весов сечений. Прим, перев.
294
Глава 6
Algorithm Construction ofU5
input: деревья R и T, массив СИ
output: дерево U
for каждого объекта i do
MakeSet(i)
Создать дерево с одним узлом для объекта i
heighl[t] «—О И вспомогательный массив
Сортировать ребра МОД Т в неубывающем порядке весов сечений
for каждого ребра е = («, Ь) G Т в этом порядке do
А г— FindSet{a)
В FindSet(b)
if А В then
// объединение деревьев
ua «— дерево, содержащее a
щ, «— дерево, содержащее b построить дерево U U. leftChild <- ua U.rightChild<— щ height[U\ <- СИ'[е]/2 W(ua,U) «- height[U] - height[ua] W(ub, U) <— height[U] height^] Union(A. B)
return дерево U
Рис. 6.13. Построение ультраметрического дерева U
Построив дерево R, легко вычислить веса сечений. Основная операция, которую мы должны применить для этого, - поиск наинизшего общего предка любых двух листьев. Это классическая задача информатики, и существуют алгоритмы, которые могут предварительно обработать дерево с п листьями за время О(п), чтобы последующие операции поиска наинизшего общего предка занимали фиксированное время. Конечный алгоритм вычисления весов сечений представлен на рис. 6.12. Так как на обработку каждой пары объектов алгоритм затрачивает фиксированное время, его полное время счета равно О(п2).
Построение ультраметрического дерева
Здесь мы представляем заключительную часть алгоритма стадию построения ультраметрического дерева U. Как мы увидим, процесс по-
5Построение дерева U. — Прим, перев.
6.5. АЛГОРИТМЫ ДЛЯ МАТРИЦ РАССТОЯНИЙ
295
строения во многом сходен с тем, который мы применяли для построения дерева /?, но вместо того, чтобы использовать веса ребер, мы используем веса их сечений. Сначала с помощью весов сечений мы сортируем ребра МОД Т и затем, когда мы строим дерево U из меньших деревьев, мы с их же помощью определяем веса ребер ультрамстрического дерева U. Алгоритм показан на рис. 6.13.
Таблица 6.6. Матрицы входов Л/1 и Мк из примера 6.2
М‘	
	В С D Е
А В С D	3 2 4 3 4 1 1 3 3 1
Mh В С D Е 7 3 6 5 11) 4 8 8 5 7
В настоящий момент читателю может показаться, что этот алгоритм непостижим для простого смертного. Через мгновение мы представим строжайшую аттестацию его рабочих характеристик, которая скрывает в себе также и часть описания принципа его работы. Прежде этого, однако, завершим анализ времени счета. Время, затраченное на построение дерева U, эквивалентно времени построения дерева R и равно О(п log п). Следовательно, полное время счета алгоритма складывается из следующих величин: О(п2) (вычисление МОД), О(п2) (вычисление весов сечений) и O(nlogn) (построение ультрамстрического дерева U). Очевидно,
Рис. 6.14. Граф Gh и МОД Т из примера 6.2
296
ГЛАВА 6
Рис. 6.16. Построенное в примере 6.2 ультрамстрическое дерево V Цифры показывают расстояния между узлами
что в этом выражении доминирует член О(п2), и, следовательно, он же и определяет полное время счета алгоритма.
Пример 6.2. Восстановим дерево по матрицам входов М1 и Л/л из табл. 6.6. Граф Gh и одно из его минимальных остовных деревьев Т показаны на рпс. 6.14. Дерево R изображено на рис. 6.15. Веса сечений, которые
6.5. АЛГОРИТМЫ ДЛЯ МАТРИЦ РАССТОЯНИЙ
297
мы можем определить из дерева R, равны
СН'[В, Г>] = 1, С1К[А С] = 2.
СИ'[Д £] = 3, СИ [А, D] = 4.
Построенное ультрамстрическое дерево показано на рис. 6.16.	
Аттестация алгоритма
Для последовательного доказательства правильности представленного здесь алгоритма мы должны чуть больше знать об ультрамстрических расстояниях Мы упомянули, чю в ультраметричсском дереве расстояние от листа до корня одинаково для всех листьев. Хотя усвоить это понятие достаточно легко, мы все же нуждаемся в альтернативной характеристике ультраметричсских расстояний; представим ее в виде следующей леммы:
Лемма 6.3. Аддитивная матрица А/ является улыпраметрическои тогда и только тогда, когда в соответствующем полном взвешенном графе G ребро старшего веса в любом цикле не уникально
Пытлнвый читатель может самостоятельно доказать эту лемму и тогда автоматически будет освобожден от выполнения упражнения 19. А мы тем временем переходим к первому доказательству правильности алгоритма.
Лемма 6.4. Построенное алгоритмом Construction of U дерево U является улыпраметрическим
Доказательство. Создадим граф G из дерева U: Это простой полный граф, имеющий в качестве вершин п объектов, а в качестве весов ребер — расстояния, назначенные алгоритмом для всех пар объектов. Теперь рассмотрим цикл С в этом графе и ребро старшего веса (а, Ь) в этом цикле. Вес этого ребра по умолчанию равен весу сечения некоторого ребра е е Т (задано программой алгоритма). Когда алгоритм обрабатывает ребро е, возможна одна из двух ситуаций: Либо узлы а и Ь уже принадлежат одному поддереву (и, следовательно, соответствующие им поддеревья были соединены до этого), либо они принадлежат разным поддеревьям. В первом случае, поскольку узлы уже принадлежат одному и тому же поддереву, расстояние между ними в дереве U уже установлено; следовательно, в цикле С должно быть другое ребро равного с ребром е веса, которое было выбрано раньше ребра е. Это удовлетворяет лемме 6.3. Во втором случае, очевидно, при обработке ребра е алгоритм впервые соединил узлы а и Ь. И поскольку с ребро старшего веса в цикле С, никакая другая пара вершин, принадлежащих циклу С, безусловно, не была соединена после обработки ребра е. Но
298
Глава 6
в этом случае ясно, что некоторая другая пара вершин х и у из цикла С также была соединена впервые. Иначе узлы а и b были бы листьями дерева U и расстояния от них до других вершин цикла С остались бы неустановленными, что, как мы знаем, не имеет места быть. Поэтому вес ребра (х,у) в цикле С равен СТГ(е)> и это снова удовлетворяет лемме 6.3.	
Мы все еще должны доказать, что расстояния подчиняются ограничениям сандвича. Выразим его через теорему, которая фактически составляет основу алгоритма.
Теорема 6.6. Ультра метрическое дерево U, которое находится между матрицами М1 и Mh, существует тогда и только тогда, когда для каждой пары объектов а и b неравенство М^ь W((a, b)rnilx) верно.
ДОКАЗАТЕЛЬСТВО. Предположим, что дерево и является ультраметри-чсским и подчиняется ограничениям сандвича, но существует некоторая пара объектов а, Ь, которая не удовлетворяет неравенству W((a, b)max). Тогда верно неравенство М^ь> TV((«, Ь)тах)- Но по определению («, 6)тах — ребро старшего веса на пути от вершины а к вершине b в МОД Т. Следовательно, для любого ребра (х, у) на пути от вершины а к вершине Ь в МОД Т, мы получаем следующую строку неравенств:
МаЬ > С МаЬ > W((«, Ь)тах) >	> dUxy > М1ху.
Теперь рассмотрим цикл, созданный в МОД Т включением в него ребра («, Ь). (Ребро (а, Ь) нс может принадлежать МОД Т, потому что в таком случае («.fc)max = (а,6) и М1аЬ > W((<i. 6)тах) = а это невозможно.) Это цикл, где (а, Ь) — единственное ребро старшего веса (из строгого неравенства > W((«, Ь)тв.х)), что является очевидным противоречием.
Обратная теорема была уже частично доказана в лемме 6.4. Остается только показать, что расстояния, вычисляемые алгоритмом, подчиняются ограничениям сандвича. Сначала рассмотрим матрицу нижних пределов М1. Пусть а,Ь — произвольная пара вершин, а е е Г ребро, посредством которого вершины а и b впервые были присоединены к дереву U. Здесь возможны два случая. Предположим, что е = (a, fc)max. Тогда по определению весов сечений расстояние между вершинами а и b в дереве U равно СПДе) ЛТ'Ь. Если е («, b)max, то СИ’((«, fc)max) С1Е(е) и (a, b)max — ребро, еще не обработанное алгоритмом. Но легко показать, что, когда алгоритм соединяет пару u, v в дереве U, все ребра на единственном путн от вершины и к вершине v в дереве Т (включая ребро е) уже были рассмотрены, что является противоречием.
Теперь докажем, что соблюдаются также верхние пределы. Снова рассмотрим произвольную пару вершин о, b и ребро е G Т, которое первое
6.6. СОГЛАСИЕ ФИЛОГЕНЕТИЧЕСКИХ ДЕРЕВЬЕВ
299
соединило вершины « и 6 в дереве U. Теперь выберем такую пару p,q, что (p.q)max = е и С'1Г(<) = M?Q То есть p,q — пара, которая была использована для определения значения функции СИ7(е) Пара р, q удовлетворяет условию теоремы, то есть Мр9 W((p, <?)max ). Но W((p,<j)max) — = С ^аь- Последнее неравенство верно, потому что Т — минимальное остовное дерево, и ребро е находится на единственном пути от вершины а к вершине Ь в МОД Т.	
На этом доказательстве мы завершаем наше обсуждение алгоритмов для матриц расстояний. Мы обращаем внимание, что представленные в этом разделе алгоритмы все еще витают в области теоретического интереса; частично это связано с тем, что они требуют слишком много допущений о входных данных Практики обычно полагаются на различные эвристики для того, чтобы восстанавливать деревья расстояний, и один пример такого подхода приведен в упражнении 14.
6.6. СОГЛАСИЕ ФИЛОГЕНЕТИЧЕСКИХ ДЕРЕВЬЕВ
В предыдущих разделах мы описали несколько альтернативных методов восстановления филогенетических деревьев; в специальной литературе можно найти множество других. На практике весьма часто случается, что два дерева, построенные на одних и тех же данных (или по крайней мерс для одного множества объектов), но двумя разными методами, отличаются друг от друга (в топологическом смысле). Иногда даже один метод даез различные деревья для тех же самых данных (но организованных по-другому). Так какое же дерево должен выбрать исследователь в таком случае? Это трудный и довольно спорный вопрос Мы вводим читателя в данную область, разбирая пример простой алгоритмической задачи и ее решения.
Задача состоит в следующем: предположим, что для одного и того же множества из л объектов мы построили два различных корневых дерева Т\ и 7г, таких, что каждый внутренний узел имеет точно двух сыновей (кроме корня, который может иметь только одного сына). Мы хотели бы знать, согласны ли деревья Т) и 7г, где понятие согласия сформулировано в следующем определении
Определение 6.6. Мы говорим, что дерево Тг уточняет дерево Ть всякий раз, когда Тг может быть преобразовано в Ts путем удаления некоторых ребер из Тг. Два дерева Т) и Т2 согласны, если существует некоторое дерево Тз, которое уточняет оба.
В литературе встречается также термин совместимость деревьев. Мы
300
Глава 6
выбрали термин согласие, чтобы избежать путаницы с понятием совместимости, употребляемым в предыдущих разделах. Из определения видно: понятие согласия означает, что любая информация, содержащаяся в дереве 71 и не содержащаяся в дереве 7г, может быть добавлена к дереву Т2. не вызывая противоречия, и наоборот. Примеры согласных деревьев показаны на рис. 6.17 и 6.18; дерево, которое уточняет оба, показано на рис. 6.19. Два несогласных дерева показаны на рис. 6.20. Эти примеры настолько наглядны, что простой визуальный осмотр может сказать нам, согласны ли изображенные деревья; конечно, эта задача становится неимоверно трудной, когда на деревьях растут десятки или даже сотни листьев
В предыдущих примерах входные деревья имеют листья, содержащие несколько объектов. Это общий случай, но на первом таге разберем сначала пример, где каждый лист (содержит) помечен только одним объектом. В данном случае мы проверяем деревья Т\ и Т2 на изоморфизм. Деревья 7j и Т2 изоморфны, если между их узлами существует такое однозначное соответствие, что для каждой пары и, v соответствующих узлов и е Т\ и v Е Т2, объекты, содержащиеся в листьях, растущих ниже листа и, являются геми же самыми, что и объекты, помечающие листья ниже листа v.
Хотя проверка графов на изоморфизм трудная задача, изоморфизм бинарных деревьев может быть найден простым алгоритмом. Основная идея алгоритма заключается в сравнении обоих деревьев при спуске снизу вверх и удалении узлов по мерс их прохождения. Как только мы обнаружили, что две пары братских листьев (одна пара в дереве Tj, вторая — в дереве Т2) изоморфны, мы можем удалить их и пометить родителей этих пар новым,
6.6. СОГЛАСИЕ ФИЛОГЕНЕТИЧЕСКИХ ДЕРЕВЬЕВ
301
А, В, С	D, Е	А, В	С, D, Е
Рис. 6.20. Два несогласных дерева
«искусственным» объектом. После удаления всех листьев их родители сами становятся листьями, и мы повторяем этот ряд операций с начала, пока
302
Глава 6
Algorithm Binary Tree Isomorphism6
input: деревья T\ и 7г
output: ИСТИНА, если 7j и 7г изоморфны, иначе — ЛОЖЬ
// Инициализация массивов
к <— п И к — счетчик числа исходных
// плюс «искусственных» объектов
Методом поиска в глубину в дереве 7i do
if узел и является листом then £i [object (u)] «— u if sib(u) является листом then add{S, u)
Методом поиска в глубину в дереве 7г do if узел и является листом then £2[object(w)[ <— u
// Основной цикл
while S 0 do
u t— remove(S)
j «- object(u)
v «- £2[j]
у <— slb{u)
w «— sib(v)
if w не является листом or object(w) object(y) then return ЛОЖЬ
Pi «— parent(u)
P2 <— parent (v)
Удалить листья u, v, w и у из соответствующих деревьев
Маркировать узлы pi и р2 как листья к <- к + 1 £i[fc] <-pi £2[£] <— Р2
// узлы pi и р2 теперь содержат «искусственный» объект к
if sib(pi) является листом then add(S, pi)
И конец основного цикла
return ИСТИНА
Рис. 6.21. Проверка корневых бинарных деревьев на изоморфизм
мы не обработаем все узлы или не обнаружим, что данные деревья не изоморфны. Алгоритм полагается на следующие структуры данных и функции:
^Изоморфизм бинарных деревьев. — Прим. перев.
6.6. СОГЛАСИЕ ФИЛОГЕНЕТИЧЕСКИХДЕРЕВЫ В
303
1) множество S, из которого мы можем добавлять и удалять специфические элементы (объекты) и проверять его на пустоту; 2) функция object{u), возвращающая объект, приписанный к узлу и; 3) функция sib (и), которая возвращает брата узла и; 4) функция parent(u), возвращающая родителя узла и; 5 маркировка узлов, показывающая, является ли данный узел листом; 6) индексированный объектами массив 7ц, который дает нам помеченный объектом i лист дерева Tj, 7) аналогичный массив £2. Алгоритм представлен на рис 6.21.
Алгоритм можно рассматривать как процедуру тщательного сравнения входных деревьев Т1 и Т>, узел за узлом, и, следовательно, его правильность очевидна. Время счета равно О(п), поскольку все, что мы делаем, — обход деревьев с О(п) узлами установленное количество раз при фиксированном времени обработки каждого узла.
Рассмотрим общий случай, где листья на входных деревьях могут содержать несколько объектов. Идея алгоритма подобна принципу представ ленного выше алюритма поиска изоморфизма: Тщательное сравнение деревьев узел за узлом. Однако вместо того, чтобы удалять узлы из деревьев, мы осматриваем дерево Т\ относительно дерева Тг и, возможно, измсня ем топологию дерева Tj, используя дополнительную информацию, обнаруженную в дереве Тг- Например, рассмотрим помеченный объектами А и В лист дерева Tj, изображенного на рис. 6 17. Быстрый взгляд на дерево Т2 на рис. 6.18 говорит нам, что объекты Л и В в действительности должны быть расщеплены на два отдельных узла, и мы соответственно изменяем тополо! ию дерева Т Мы пытаемся выполнять подобные преобразования, учитывая вес узлы дерева 7"i, и затем мы так же обрабатываем дерево Т2 Алгоритм сохраняет число объектов каждого поддерева, что позволяет нам быстро определить, не являются ли два поддерева изоморфными. Если число объектов в деревьях Т\ и Т2 равно, то мы продолжаем сравнивать объекты в каждом дереве. После того как оба дерева были при необходимости изменены, мы применяем процедуру поиска изоморфизма к (возможно) измененному дереву Ti и (возможно) измененному дереву 7г. Эта процедура по сути равноценна алгоритму на рис 6 21. Детальное представление алгоритма поиска согласия дано на рис 6 22
Анализ времени счета этого алгоритма следующий. На инициализацию мы тратим время O(?i), обходя деревья установленное число раз. Обратите внимание, что как только в основном цикле узлы объявлены неактивными, они остаются таковыми для остальной части алгоритма, а каждый активный узел исследуется самое большее один раз Проверка узлов на содержание одинаковых объектов также требует только однократного обхода частей каждого дерева. Следовательно, до этого момента мы затратили время О(п).
304
Глава 6
Algorithm Rooted Binary Tree Agreement1 input: Деревья u T2 output: истина если и 7г согласны, иначе — ЛОЖЬ Методом поиска в тубину в дереве 7i do if если узел и является листом then for каждого объекта г в листе и do
Ej [г] ♦— и
Ai[u] ♦— число объектов в листе и else Ji [и] ♦— число объектов на этом поддереве
Методом поиска в глубину в дереве 7г do if узел и является листом then
Гог каждого объекта i в листе и do
£/2 И
А'гЙ число объектов в листе и else «7г[тт] <— число объектов на этом поддеревс Гог каждого объекта ? do activeft] <— истина
// Основной цикл
// проверяем Т-2 онюсительно '1\ и, возможно, изменяем Т\ for каждого объекта ?' do
if ac7ire(t] and > ATaf?] then
// Т2 содержит больше информации об объекте г w ♦— Егр] repeat
w <— parent(w) //продвигаемся вверх по дереву
until 7г(ад] > А\[г]
// мы достигли корня w поддерева дерева Т?, который
// содержит в себе по крайней мере столько же объектов,
// сколько лист объекта i в дереве Ti
if J2M А’1[?] then return ложь
Обойти поддерево дерева Тг, растущее из корня w, проверяя что каждый объект массива E>i[i] принадлежит соответствующему листу этого потдерева if результат проверки отрицательный then return ложь Заменить узел L\ [г] в 1\ на поддерево дерева Т2, растущее нз корня w
Гог каждого объект а j в узле Li [г] do
Обновить Ei[j] actfve[j] +- ЛОЖЬ // Конец основного цикла for // здесь мы должны повторить программу, // но уже для проверки дерева Ti /I относительно Тъ и возможного изменения Т2 /I (код аналогичен)
Запустить алгоритм Binary Tree Isomorphism для 7 '[ и Т2 return истина если деревья изоморфны, иначе - ЛОЖЬ.
Рис. 6.22. Алгоритм проверки двух корневых бинарных деревьев на согласие
РЕЗЮМЕ
305
Наконец, проводится проверка деревьев на изоморфизм. Мы должны изменить представленный ранее алгоритм поиска изоморфизма, потому что теперь листья во входных деревьях могут содержать более одного объекта. Во-первых, функция object (и) должна возвращать все объекты, содержащиеся в листе и (см. инициализирующую часть алгоритма на рис. 6.21). Во-вторых, в основном цикле алгоритма операции проверки того, помечены ли два узла одним и тем же объектом, должны быть изменены, чтобы проверять равенство множеств объектов. Мы оставляем выполнение этих модификаций (чтобы в итоге полное время проверки было равно О(п)) в качестве упражнения 18. Таким образом, полное время счета алгоритма равно О(п).
На этом наше краткое введение в предмет согласия филогенетических деревьев подходит к концу; хотя, конечно, можно дать и более сложные формулировки этой задачи. Некоторые ссылки для работы в этой области представлены в библиографических примечаниях.
РЕЗЮМЕ
Филогенетические деревья — важнейший инструмент в понимании родственных связей между объектами, эволюционирующими с течением времени, и, в частности, — между молекулярными последовательностями. Построение дерева основано на сравнении объектов по двум основным критериям. Первый критерий сравнения - использование дискретных признаков, из которых мы отбираем множество признаков и для каждого объекта составляем список состояний всех его признаков. Из этих списков, составленных для исследуемой группы объектов, формируют матрицу состояний признаков, по которой может быть построено дерево. Идея такого построения состоит в том, что объекты с большим числом одинаковых состояний соответствующих признаков должны быть ближе в филогенетическом дереве. Второй критерий — расстояние между объектами, где понятие расстояния зависит от природы сравниваемых объектов. И снова идея сравнения заключается в том, что объекты с меньшими взаимными расстояниями должны быть соответственно ближе в филогенетическом дереве.
Если данные сравнений организованы в матрицу состояний признаков и если мы налагаем некоторые ограничения на искомое дерево, то его восстановление может быть представлено в форме задачи о совершенной филогении. В зависимости от характера признаков эта задача может быть НП-полной. Мы представили алгоритмы для некоторых ее частных случаев, которые допускают эффективное решение. Первый алгоритм построен для
7Согласие корневых бинарных деревьев. — Прим, перев.
306
Глава 6
бинарных признаков, а второй разработан для объектов, характеризуемых парой признаков. В этом последнем случае мы увидели, что понятия из теории графов значительно облегчают построение алгори тма и дают основание для более общих случаев.
Экспериментальные данные почти никогда не допускают совершенную филогению. Следовательно, мы должны ослабить ограничения, налагаемые на искомое дерево, и это ведет нас к задачам оптимизации например поиска наиболее экономичного дерева или максимального множества совместимых признаков. Мы видели, что эти задачи НП-трудныс, и это означает, что алгоритмы их решения либо используют метод полного перебора, либо пытаются так или иначе аппроксимировать истинное решение.
Когда объекты сравнивают с помощью расстояний, мы можем потребовать, чтобы наблюдаемое расстояние было равно расстоянию, измеренному на восстановленном дереве. Это задача об аддитивном дереве, и мы представили простой алгоритм ес решения. Но и тут оказывается, что реальные данные редко допускают совокупные деревья. Альтернативное решение — строить дерево, в котором расстояния подчиняются нижнему и верхнему пределам. Когда мы налагаем дополнительное ограничение, состоящее в том, чтобы это дерево было ультраметричсским (то есть, чтобы все пути от корня к листьям имели одинаковую длину), становится возможно построить эффективный алгоритм (см. рис 6 13).
Поскольку в распоряжении биолога имеется уйма всеразличных методов построения филогений, желательно иметь некоторый алгоритм, обладающий функциями сравнительного анализа деревьев, восстановленных для одного и того же множества объектов. Мы представили простой алгоритм, который определяет новое дерево, имея два других, объединяя в нем информацию из обоих входных деревьев Алгоритм производит согласное дерево, если два входных дерева согласны даже в самых мельчайших деталях.
УПРАЖНЕНИЯ
1.	Известно множество вариантов применения филогенетических деревьев Например, с их помощью осуществляют классификацию языков и средневековых рукописей. Попытайтесь применить к этим объектам поня тия упорядоченных и неупорядоченных признаков, а также понятие расстояния.
2.	Покажите, что число помеченных некорневых бинарных деревьев равно ПГ — 5). (Подсказка: Начните с определения числа внутренних узлов и внутренних ребер такого дерева. Затем используйте метод индукции,
УПРАЖНЕНИЯ
307
анализируя дерево, когда вы путем ответвления от любого существующего ребра добавляете к дереву каждый новый объект.)
3.	Предложите форму линейного представления корневого филогене-тичсского дерева. Например, такое представление (в виде списка) может бьпь использовано на выходе компьютерной программы построения филогенетических деревьев.
4.	Алгоритм на рис. 6.5 предполагает, что все столбцы матрицы состояний признаков различны. Как бы вы изменили этот алгоритм, чтобы он мог обрабатывать тождественные столбцы?
5.	Алгоритм для бинарных признаков (раздел 6.5) был представлен в двух стадиях. Объедините все операции в одну стадию.
6.	Обратите внимание на подобие между леммой 6.1 (раздел 6.2) и условиями, используемыми в алгоритме решения задачи с последовательными единицами (раздел 5.3). Покажите, что столбцы матриц бинарных признаков, допускающих совершенную филогению, обладают СПЕ. Можете ли вы разработать алгоритм, который найдет перестановку строк, которая сделает единицы последовательными, и который, таким образом, с выгодой использует специфические свойства этой матрицы.
7.	Покажите, что преобразование, упомянутое в конце раздела 6.2 (замена неупорядоченных бинарных признаков на упорядоченные), работает; используйте факт, упомянутый там же.
8.	Предположим, что мы имеем следующую матрицу состояний признаков:
ст с2 .4	0	1
В	1	1
С	1	0
Согласно свойствам бинарных признаков (раздел 6.2) эта матрица входов не юпускает совершенную филогению, так как признаки Гт и е2 не совместимы. Однако согласно свойствам объектов, характеризуемых парой признаков (раздел 6.3), эта матрица допускает совершенную филогению, поскольку 1 11С является ациклическим. Какая же интерпретация верна?
9.	Если филогения, построенная по матрице состояний признаков, является совершенной, то мы должны быть способны приписать к каждому из ее ребер переход между состояниями соответствующего признака. Припишите такие переходы к ребрам дерева на рис. 6.8.
308
Глава 6
*	* 10. Постройте алгоритм решения задачи о совершенной филогении для случая, когда число состояний каждого признака равно самое большее трем.
*	*11. Разработайте алгоритм решения задачи о совершенной филогении, когда объект характеризует самое большее три признака.
*	12. Разработайте алгоритм решения задачи о совершенной филогении, если максимальное число признаков равно трем и при ипо.и каждый признак имеет не более трех состояний.
13.	Предположим, что мы имеем алгоритм поиска максимальных клик в графах и хотим применить его для решения общей задачи на совместимость состояний признаков. Под «общностью» мы подразумеваем, что состояния признаков — нс обязательно бинарны. Доказательство теоремы 6.5 показывает, как сделать это для случая бинарных признаков. Что нужно изменить для общего случая состояний признаков?
14.	Широко известная эвристика построения филогенетических деревьев по известным расстояниям заключается в следующем. Выбираем пару объектов, наиболее близких друг к другу, например, А и В. Делаем их сыновьями нового объекта О и устанавливаем длину каждого ребра равной d(A. В)/2. Теперь удаляем объекты А и В из матрицы расстояний и добавляем в нее объект О, устанавливая расстояние между О и всеми объектами матрицы г, равным (d(A,i) + d(B, г))/2. Находим следующую пару ближайших объектов и повторяем процесс до тех пор, пока все объекты нс будут находиться в дереве. (Связывая два объекта через новый внутренний узел, мы должны учитывать длины ребер, которые могут уже существовать под соединяемыми объектами.) Примените эту эвристику к матрице из табл. 6.5. Можно ли с помощью этой эвристики строить аддитивные деревья?
15.	При описании алгоритма построения аддитивных деревьев, мы допускали, что матрица входов АГ аддитивна. Предположим, что нам это нс известно. Как мы должны поступить?
** 16. Допустим, что в задаче об аддитивном дереве мы знаем, что его внутренние узлы имеют ограниченную степень. Покажите, что в этом случае возможно построить алгоритм со временем счета О(п log п).
17.	Докажите, что ультраметрические расстояния могут быть охарактеризованы следующим образом. Для любых трех объектов i, j и к мы имеем неравенство A/y Sj max{AAjjt, Af^}.
БИБЛИОГРАФИЧЕСКИЕ ПРИМЕЧАНИЯ
309
18.	Измените алгоритм проверки деревьев на изоморфизм (см. рис. 6.21) так, чтобы он считал вероятность того, что листья могут содержать более одного объекта.
19.	Докажите лемму 6.3.
БИБЛИОГРАФИЧЕСКИЕ ПРИМЕЧАНИЯ
Как было упомянуто в начале этой главы, мы представили лишь небольшую часть необъятного множества алгоритмов построения филогенетических деревьев. В частности, мы нс рассматривали алгоритмы, основанные на методах статистического анализа задачи и обычно известные как методы максимального правдоподобия. Ниже мы приводим некоторые ссылки для заинтересованного читателя.
Хорошей отправной точкой для более глубокого изучения методов восстановления филогенетических деревьев на основании молекулярных признаков является превосходная обзорная статья Своффорда и Ольсена [182]. Другая хорошая, но более старая работа, — Фсльзенштейн [60]. В книге о молекулярной эволюции Нея [147] глава 11 посвяшена полезному обзору этой темы. Пенни, Хснди и Стил [159] приводят краткий обзор материала по дачному предмету.
НН-полнота задачи о совершенной филогении для неупорядоченных признаков (раздел 6.1) была доказана Бодландером, Феллоусом и Уор-ноу [25] и, независимо,— Стилом [179]. Алгоритм, представленный в разделе 6.2, разработан Гасфилдом [82] и упрощен Уотерменом [199]. Макморрис [133] изложил принцип преобразования неупорядоченных бинарных признаков в ориентированные бинарные признаки.
Как мы уже упоминали ранее, всякий раз, когда число признаков фиксировано, задача о совершенной филогении может быть решена за полиномиальное время. Это открытие было совершено Агарвалой и Ферпандес-Бакой [4]; время счета разработанного ими алгоритма описывается функцией О(23г(пт3 + т1)).
Были предложены также алгоритмы для установленных значений г При г = 3 существует два алгоритма: алгоритм Дресса и Стила [52] (время счета равно O(nni2)) и алгоритм Каннана и Уорноу [107] (время счета равно О(п2т)). Алгоритм Каннана и Уорноу годится также для случая с г = 4. Это важный алгоритм, потому что он может быть применен к последовательностям ДНК, выровненным без пропусков. В этом случае каждую позицию в выравнивании мы можем интерпретировать как признак, который может иметь одно из четырех состояний: А, С, G или Т.
310
Глава 6
Агарвала, Фернандес-Бака и Слуцкий [5], а также Меиданис и Муну-эра [135] преподносят нам алгоритмы восстановления бинарной филогении, когда вход задан в виде отдельных, не объединенных в матрицу, списков признаков исследуемых объектов.
Раздел 6.3 во многом опирается на статью Уорноу [194]. Теорема 6.1 была сформулирована Бунеманом [29]; таблица 6.3 и рисунок 6.7 были взяты оттуда же и немного переработаны. Макморрис, Уорноу и Уимер [133] описали алгоритм восстановления филогении для установленного числа признаков; его время счета равно О(ггп+1тпт+А + птп2). Три статьи, описывающие алгоритмы для случая тп = 3: Бодландера и Клокса [26], Каннана и Уорноу [106], а также Идури и Шеффера [101].
Доказательство НП-полноты задачи, основанной на критерии экономичности, приведено в работе Дея, Джонсона и Санкова [43]; авторы использовали важный результат, связывающий филогении с задачей о дереве Штейнера, представленный Фоулдсом и Грэмом [64]. Упомянутая выше «превосходная обзорная статья» Своффорда и Ольсена содержит больше ссылок на литературу по экономичности деревьев. Своффорд и Мсдди-сон [181] разработали алгоритм присвоения состояний предковых признаков согласно так называемому критерию экономичности Вагнера. Доказательство НП-полноты критерия совместимости, представленного в разделе 6.4, было дано Деем и Санковым [44].
Условие четырех точек (см. раздел 6.5.1) было доказано Бунеманом (как сообщается в [202]) и, независимо, Добсоном [49]. Алгоритм восстановления аддитивных деревьев, представленный в разделе 6.5.1, описан в работе Уотсрмена, Смита, Сингха и Бейера [202]. Кулберсон и Рудницкий [40], а также Хейн [90] представляют более быстрые алгоритмы для случая, когда известно, что внутренние узлы имеют ограниченную степень. Дей [42] доказал НП-полноту задачи восстановления дерева, как можно лучше аппроксимирующего аддитивное дерево при различных метриках. Алгоритм построения ультраметрических деревьев, удовлетворяющих ограничениям сандвича, описывают Фарах, Каннан и Уорноу [56]. В гой же статье авторы показывают, что требование, согласно которому дерево должно быть ультраметрическим, является необходимым, потому что поиск аддитивного дерева, удовлетворяющего ограничениям сандвича, представляет собой НП-полную задачу. Они представляют также некоторые другие оценки сложности восстановления аддитивных и ультраметрических деревьев. Агарвала и сотр. [3] использовали результат для ультраметрических деревьев, чтобы представить алгоритм аппроксимации для задачи об аддитивном дереве с гарантированными характеристиками. Кроме того, авторы показали, что получение приближений выше некоторого порога — НП-трудная задача.
БИБЛИОГРАФИЧЕСКИЕ ПРИМЕЧАНИЯ
311
Представленные в разделе 6.6 алгоритмы появились на свет благодаря Гасфилду [82]. Уорноу [195] представила более общий алгоритм восстановления деревьев, где признаки не обязательно бинарны. Она также показала, как этот алгоритм мог бы быть использован в алгоритме метода ветвей и границ для задачи о совершенной филогении с неупорядоченными признаками. Недавние наработки Эмира и Кесельмана [14] по согласию деревьев показали, что задача построения поддерева, согласного с к входными деревьями (при максимизации числа объектов, содержащихся в этом поддереве), становится НП-трудной, начиная с к = 3. Авторы представили алгоритм с полиномиальным временем счета для случая, когда одно из деревьев имеет ограниченную степень; позже их результат был улучшен Фарахом, Пшитицкой и Торупом [57].
Когда исследуемые объекты представлены молекулярными Поспелова тельностями, принято начинать восстановление филогении, используя в качестве входа множественное выравнивание этих последовательностей. С другой стороны, при их выравнивании очень полезно уже знать филогенетические связи последовательностей. Эта ситуация побудила многих ученых предложить алгоритмы, выполняющие обе задачи одновременно. Один вариант такого подхода известен как «выравнивание дерева» (см. раздел 3.4.3). Некоторые ссылки по этой теме даны в библиографических примечаниях главы 3. Дополнительные работы по эвристическим решениям объединенных задач множественного выравнивания и восстановления филогений — Хейн [89; 91; 92], а также Вишрон и фон Хеселср [190].
Два популярных пакета программ восстановления филогений — PHYLIP (пакет выведения филогении), Фельзенштейн [61], и PAUP (филогенетический анализ на основании критерия экономичности), Своффорд (ссылка на этот пакет дается в [182]). Оба пакета прдоставляют множество способов построения филогений.
Глава 7
ПЕРЕСТРОЙКИ ГЕНОМА
В предыдущих главах мы показали, каким образом различия в генах на уровне последовательности нуклеотидов могут быть использованы для восстановления эволюционных связей родственных видов организмов. Однако известны также случаи, когда сравнения соответствующих генов у двух или более видов дают меньше информации, чем сравнения более крупных частей их геномов или даже полных геномов. Сравнение этих больших частей проводят на более высоком уровне. Вместо сравнения последовательностей мы сопоставляем позиции нескольких сцепленных генов и пробуем определить операции перестановки генов, которые преобразуют один геном в другой. Для моделирования этих ситуаций была развита богатая математическая теория, и настоящая глава представляет собой вводный курс этой теории.
7.1. БИОЛОГИЧЕСКИЕ ОСНОВЫ
При сравнении полных геномов различных организмов мы хотим вычислив некое расстояние между ними, используя набор основных редактирующих операций, отличных от рассмотренных в главе 3. Теперь нас интересуют не точечные мутации типа замен, удалений и вставок, а мутации большего масштаба. Участки хромосом могут обмениваться различными способами; причем области обмена участками занимают существенную часть хромосомы. Любой участок может быть скопирован или перемещен в другую позицию, или же покинуть одну хромосому и приземлиться в другой. Изменения такого вида называют перестройками генома.
В некоторых случаях (например, при изучении генома хлоропластов или митохондрий) перестройки одного вида — инверсии оказываются почти что единственным способом проявления эволюционных изменений. Тогда эволюционное расстояние между двумя организмами имеет смысл измерять числом инверсий, необходимых для преобразования генома одного из них в геном другого.
7.1. БИОЛОГ ИЧЕСКИЕ ОСНОВЫ
313
В качестве примера рассмотрим геномы хлоропластов люцерны и гороха — растений двух родственных видов (см. рис. 7.1). На этом рисунке помеченные цифрами стрелки обозначают блоки. Блок здесь означает участок генома, возможно, содержащий более одного гена и представляющий собой единицу транскрипции. Стрелки показывают ориентацию блоков, зависящую от их принадлежности к той или иной нити ДНК, то есть от направления их транскрипции (см. раздел 1.4.2). Два блока из различных геномов несут одинаковую цифровую метку, если они гомологичны, то есть если содержат гены, отвечающие за формирование сходных признаков. И, наконец, расстояния между генами в обоих геномах не всегда равны.
Люцерна
Рис. 7.1. Связь между геномами хлоропластов люцерны и гороха. (Взято из [150].)
Операция инверсии ориентированных блоков может быть определена следующим образом. Она затрагивает группу смежных блоков, изменяет их порядок на противоположный и обращает их ориентацию. В связи с данным определением нас волнует следующий вопрос: Каково минимальное число инверсий, необходимое для преобразования одного генома в другой? Одно возможное решение дано на рис. 7.2. Первая строка представляет геном люцерны, последняя — геном гороха, причем каждая строка (кроме первой) получена из предыдущей путем инверсии подчеркнутых блоков. Но откуда мы знаем, что требуемого преобразования нельзя достичь с помощью более короткого ряда инверсий? Быстрый ответ на оба вопроса может дать полиномиальный алгоритм, построению которого мы и посвятим эту главу.
Причина поиска именно возможно кратчайшего ряда инверсий - тот же критерий экономичности, упомянутый при описании задачи минимизации в предыдущих разделах этой книги. Мы допускаем, что Природа всегда находит пути преобразований, требующие минимум энергетических затрат и структурных изменений, и поэтому, если мы хотим знать, каким образом люцерна могла превратиться в горох или наоборот, то мы должны стараться
314
Глава 7
*8 <— 8	т	б" б-	5" 5"	Т 4“	4— 3 Г	tsjf К>Т	<— 1 <— 1	U п	10 10	*9 *9
	—>		—>	—>	—>	—>				
8	2	3	4	5	6	7	1	11	10	9
<—	—>		—>	—>	—>					
8	2	3	4	5	1	7	6	11	1U	9
			—>	—>	—>					
4	3	2	8	5	1	7	6	11	10	9
		<—	—>							
4	3	2	8	7	1	5	6	11	10	9
		<—	—>	—>			Z						ж.	
4	3	2	8	7	1	5	6	11	10	9
			—>	—*									
4	3	2	8	7	1	5	6	11	10	9
Рис. 7.2. Схема решения задачи на рис. 7.1
найти именно минимальный ряд инверсий, достаточный для выполнения этой задачи.
Так, может быть задумана задача перестройки генома без учета ориентации блоков. Иногда информация о генах недостаточна для точного установления их относительной ориентации, но позволяет определить их относительный порядок. В этом случае мы искали бы кратчайший ряд инверсий, который преобразует один порядок блоков в другой, безотносительно к их ориентации. Например, предположим, что ориентация блоков на рис. 7.1 не известна. В этом случае для решения задачи было бы достаточно ряда из трех инверсий (см. рис. 7.3).
8	7	6	5	4	3	2	1	11	10	9
8	7	1	2	3	4	5	6	11	10	9
4	3	2	1	7	8	5	6	11	10	9
43287156	11	10	9
Рис. 7.3. Решение задачи на рис. 7.1 при неизвестной ориентации блоков
7.2. ОРИЕНТИРОВАННЫЕ БЛОКИ
315
В следующих разделах мы исследуем оба варианта 1ак называемой задачи сортировки инверсиями. Интересно отметить, что хотя в случае с ориентированными блоками существует полиномиальный алгоритм поиска минимального ряда инверсий, было доказано, что вариант с неизвестной ориентацией блоков является НП-трудным.
7.2. ОРИЕНТИРОВАННЫЕ БЛОКИ
Начнем изучение варианта задачи с ориентированными блоками на одном примере. Предположим, что мы имеем два генома, разделенных на гомологичные блоки, как показано на рис. 7.4. Каждый из этих блоков представляет непрерывный участок, сильно консервативный в обоих геномах. В этом примере для преобразования одного генома в другой достаточно ряда из трех инверсий — возможно кратчайшего ряда, как мы покажем далее. Безусловно, можно найти много других равносильных рядов инверсий, но все они будут состоять из трех и более операций.
На рис. 7.5 показано одно возможное решение; метки на блоках показывают действие инверсий; стрелки над метками указывают ориентацию гомологичных блоков. Поскольку метки произвольны, мы используем цифры от 1 до п (п = 5 в этом примере) и расставляем их в естественном порядке по блокам верхнего генома. Тогда метки в нижнем геноме определены однозначно. Каждый блок получает тот же номер, что и гомологичный ему блок, а стрелки отражают действительную ориентацию блоков. Линиями подчеркнуты группы инвертируемых блоков. Исходная перестановка шаг за шагом приближается к конечному порядку блоков.
Как мы можем убедиться в том, что для достижения требуемого преобразования не существует никакого более короткого ряда инверсий? Можно
Рис. 7.4. Два генома с гомологичными блоками. Стрелки изображают блоки. Гомологичные блоки соединены линиями. Кружки на линиях между блоками обозначают противоположную ориентацию этих блоков в исследуемых геномах
316
Глава 7
1	2	3	4	5
--►	4--	4-	"—
1	2	5	4 3
—>	4—	4—	4 —	4—
1	2	5	3	4
—♦	—>	4—	4—	4—-
5	2	13	4
Рис. 7.5. Решение к задаче па рис. 7.4. Каждая строка получается из предыдущей за счет инверсии подчеркнутых элементов
легко доказать, что для решения этого частного варианта задачи ряда, содержащего менее трех инверсий, недостаточно. Доказательство построено на понятии точки разрыва. Точка разрыва это точка между последовательными метками в начальной перестановке, которые обязательно должны быть отделены по крайней мере одной инверсией, чтобы достичь целевой перестановки. Другими словами, эти две последовательные метки не будут последовательны в цели, или, даже если и будут, то их относительная ориентация обязательно изменится. Кроме того, точка разрыва стоит перед первой меткой, если эта метка не будет первой меткой с той же самой ориентацией в цели. На рис. 7.6 показаны точки разрыва для нашей исходной перестановки относительно цели, изображенной на рис. 7.4. Каждая точка разрыва обозначена жирной точкой «•». Например, в позиции между метками 2 и 3 находится точка разрыва, потому что в цели блоки 2 и 3 нс последовательны. Если никакая инверсия не разделяет данные метки, то они будут оставаться вместе до конца и окажутся в неправильном поряд---------------------> 4—
ке. Напротив, пара 1 , 2 не является точкой разрыва, потому что именно в таком порядке (и ориентации) эти два блока расположены в цели. Таким образом, наша начальная перестановка имеет четыре точки разрыва.
—> 4— 4-4—	—♦
• 1 2*3 4*5»
Рис. 7.6. Каждый знак • обозначав г точку разрыва
Инверсия может удалить самое большее две точки разрыва, потому что она разрезает перестановку именно в двух позициях. Целевая перестановка имеет нулевые точки разрыва, и это единственная перестановка, обладающая таким свойством. Следовательно, для закрепления (склеивания, или устранения) четырех точек разрыва в нашем примере мы нуждаемся по
7.2. ОРИЕНТИРОВАННЫЕ БЛОКИ
317
крайней мере в двух инверсиях. Однако более тщательный анализ показывает, что никакая отдельная инверсия не может удалить две точки разрыва из нашей начальной перестановки. Действительно, чтобы удалить первую ------------------------------------------------->
точку разрыва, расположенную в позиции перед меткой 1, мы бы должны были переместить метку 5 в первую позицию, но лаже этого недостаточно ------------------------------------------------>
Единственная инверсия, которая может перенести метку 5 в это место, также переворачивает ее стрелку, и конечная перестановка по-прежнему имеет точку разрыва перед первой позицией. Метка 5 находится в правильной позиции, но ее ориентация обратна правильной.
Подобные же доводы убеждают нас, что последнюю точку разрыва так же невозможно удалить с помощью одной инверсии. Наша единственная надежда на одновременное удаление двух точек разрыва полагается на две центральные точки. Однако единственная инверсия, затрагивающая эти две пошции. нс удаляет ни одной точки разрыва! Итак, мы знаем, что первая инверсия сократит число точек разрыва самое большее на I. После чего в перестановке останется по крайней мере три точки разрыва, а для удаления трех точек разрыва необходимы по крайней мере еще две инверсии. Это показывает, что решение, представленное ранее, действительно оптимально.
7.2.1.	ОПРЕДЕЛЕНИЯ
Перестройка генома — гема, требующая точных определений и связной системы ПОНЯ1ИЙ. Сначала определим, что есть ориен!ированная перестановка. Известно конечное множество £°, содержащее ориентированные .метки из множества неориентированных меток £, где
r° =	“)•
Множество С° содержит вдвое больше элементов, чем множество £. Пусть |т| — элемент множества £, полученный в результате удаления стрелки с элемента х Е £°. Таким образом, | сГ| = |а| = а для всех а Е £ Пусть п — число элементов множества £ Ориентированная перестановка множества £ — такое отображение а : [1.. .n] i—» £°, что для любой метки a G £ существует точно один индекс i Е [1... п], где |а(г)| = °- Другими словами, перестановка «выбирает» для каждого индекса г ориентированную метку *а либо о* из множества £°, но если для некоторого индекса была выбрана метка *а, то метка ~а уже не может быть выбрана ни для какоз о другого индекса; и наоборот. Число индексов п = | £ | гарантирует, что для
318
Глава 7
каждой неориентированной метки а Е £ ориентированная метка либо а будет выбрана только один раз.
Перестановку а мы представляем в виде следующего списка элементов: а(1), а(2),..., а(п). Обычно мы только перечисляем элементы, отделяя их пробелами, как в предыдущем разделе, но иногда мы используем запятые и круглые скобки, чтобы избежать неопределенности. В большинстве случаев множество £ будет содержать только первые п положительных целых чисел: 1,2,..., п. Так, например, при п = 6 примером перестановки £ = — {1,2,..., 6} будет следующее выражение:
а = (*2, З’.Т.б', 5", 4").	(7.1)
Следовательно, в настоящем примере а(1) = 2, а(2)	3 и так далее.
Тождественной перестановкой называют перестановку /, где /(г) = г для всех г в интервале 1... п.
Инверсия - операция преобразования одной перестановки в другую путем изменения порядка 1руппы последовательных элементов на противоположный и обращения ориентации самих элементов. Пусть ? и j — два индекса, где 1 $ г и j п. Инверсию, затрагивающую элементы а(г) через a(J), обозначают [г, j]. Инверсия [г. j] фактически представляет собой отображение множества {1,2,...,п} на само себя; она может быть комбинирована с некоторой ориентированной перестановкой а и дать другое отображение {1,2,..., п] на множество £°, то есть другую перестановку. Комбинация отображений аир, обозначаемая ар, является отображением вида:
(ap)(fc) = a(p(fc)).
Например, применяя инверсию [2,4] к перестановке а из уравнения (7.1), получаем
В общем случае инверсия р = [г, j] преобразует перестановку а в комбинацию ор:
П₽И
[a(fc)	в противном случае,
где I — обращенная метка I. В перестановке, состоящей из п блоков, существует н(н + 1)/2 различных инверсий. Сюда входят также унитарные инверсии [г, г], которые лишь изменяют ориентацию элемента а(г) на противоположную.
7.2. ОРИЕНТИРОВАННЫЕ БЛОКИ
319
Наш главный интерес в этом разделе сосредоточен на задаче сортировки инверсиями. Имея две ориентированные перестановки о и /3 из одного множества меток £, мы ищем минимальное число инверсий, необходимое для преобразования о в fl. Другими словами, прибегая к только что введенным понятиям, мы ищем такой минимальный ряд инверсий р\,рь, - - , Pi, что
ap\P2-Pt fl-
Величину / называют инверсионным расстоянием а от fl и обозначают функцией с!д(а). Ориентированную перестановку а называют начальной перестановкой, а конечную перестановку fl - целью. Этот процесс называют сортировкой а по (относительно) fl.
Заметим, что хотя величина t = d@(a) фиксирована для данной пары a, fl, фактический ряд инверсий, сортирующих а, обычно нс уникален. Как правило, мы будем заняты поиском инверсии р, которая «продвигается» в сторону fl. Такую инверсию называют сортировочной инверсией а относительно fl, и для нее характерно следующее свойство:
dp(ap) < de(a), что равносильно
dp(ap) = d0(a) - 1
Оно обусловлено тем, что инверсионные расстояния перестановок а и ар нс могут отличаться больше чем на единицу.
Важно заметить, что инверсионное расстояние симметрично, то есть d0(a) da(fl), поскольку любая инверсия не имеет никакого суммарного эффекта, будучи применена дважды. Другими словами, для каждой инверсии р инверсия рр дает нулевой эффект. Поэтому, если
ПР1Р2 ...pt= fl,
то, последовательно комбинируя обе части этого уравнения с инверсия 1pi, мы получаем
а = flptPt-1 -Pi-
Мы заключаем, что эти же инверсии преобразуют перестановку fl в а, но тогда они должны быть применены в обратном порядке. Таким образом, сортировочные инверсии перестановки в относительно о не обязательно будут теми же самыми, что и сортировочные инверсии перестановки а относительно fl.
Когда цель в ясна из контекста, мы будем сокращать обозначение dg(a) до d(a). Аналогично, при разговоре о сортировочных инверсиях, точках разрыва и т. д. мы будем опускать букву fl.
320
Глава 7
7.2.2.	ТОЧКИ РАЗРЫВА
Формализуем понятие точки разрыва. Имея перестановку а, первое, что мы должны сделать для определения точки разрыва, рассмотреть продолженную перестановку а, которая получается из а путем добавления новых, искусственных меток: L (левая) перед первой действительной меткой ст( 1) и R (правая) после последней метки п(п). Таким образом, относительно перестановки а из уравнения (7.1), продолженная перестановка выглядит следующим образом:
(£,‘2/з , 1’, 6 , 5~, 4 ,/?).	(7.2)
Точка разрыва в перестановке а относительно — такая пара элемен тов х,у из множества £°, что пара ху появляется в продолженной перестановке ст, но ни сама пара ху, ни обратная ей пара у х не появляются в продолженной перестановке /3. Например, если а — перестановка (7.2), а /3 — тождество, то точками разрыва будут пары: £ 2, 23, 31, 16, 6 5 и 4 R. Пара 5 4 не является точкой разрыва, потому что обратная ей пара 4 5 появляется в перестановке /3.
Число точек разрыва в перестановке ст обозначается функцией 1>д(ст) или просто Ь(а), если цель /3 ясна из контекста. В нашем примере Ь(а) = 6.
Заметим, что искусственные метки £ и R никогда не перемещаются. Таким образом, метка £ примыкает к точке разрыва, только если первые метки в перестановках ст и (3 различны или же равны, но имеют противоположную ориентацию. Аналогичное наблюдение справедливо и для метки R
Нижний предел
Пусть /3 — фиксированная перестановка. Как мы упоминали ранее, одна инверсия может удалить самое большее две точки разрыва. То есть, согласно принятым обозначениям,
Ь(а) - Ь(ар) 2	(7.3)
для любой перестановки ст и любой инверсии р. Это неравенство непосредственно даст нижний предел инверсионного расстояния следующим образом. Пусть Pi,P2, --,Pt — ряд инверсий (не обязательно оптимальный), преобразующий перестановку ст в /3. Тотда
np\p-2---Pt = /3,
7.2. ОРИЕНТИРОВАННЫЕ БЛОКИ
321
так что
Ъ(арлр2 ...pt) = Ь(/3) = 0.	(7.4)
Обратите внимание, что перестановка [3 относительно самой себя имеет нулевую точку разрыва. Однако из уравнения (7.3) следует, что
6(a) — b(ctpi) si 2, b(api) - blapip?) 2.
6(opi.. -pt-i) - bfapt ...pt) ^2.
Складывая эти неравенства и учитывая при этом уравнение (7.4), мы получаем
6(a) < 2t.
Это неравенство верно для любой сортировки перестановки а. Если мы теперь применим его к кратчайшим рядам, то получим t = d(a), и, следовательно.
6(«) ,
— < а(а).
Это нижний предел расстояния rf(a), то есть величина, определяющая минимальное значение, при котором мы можем быть уверены что функция rf(a) остается истинной. Если мы нашли ряд инверсий со значением расстояния rf(a), равным нижнему пределу для данной перестановки а, то мы можем быть уверены, что этот ряд — искомое решение. Однако этот нижний предел не всегда достижим. Например, в начале раздела 7.2 мы видели пару перестановок а и (3, где Ьр{а) = 4 и, следовательно, нижний предел равен 2, но dp(a) = 3.
Интересно отметить, что существуют такие инверсии, которые удаляют две точки разрыва, но нс являются сортировочными инверсиями, то есть оии ведут нас неправильным путем и нс дают сортировку а относительно /3 (см. упражнение 5).
7.2.3.	ДИАГРАММА ЖЕЛАЕМОГО И ДЕЙСТВИТЕЛЬНОГО
Нижний предел rf(a) is 6(а)/2 не очень строгий. При большом числе перестановок он далек от равенства. В этом разделе мы выводим формулу лучшего нижнего предела, основанного на структуре, называемой диаграммой желаемого и действительного одной перестановки относительно другой.
322
Глава 7
Прежде чем объяснить назначение этой структуры, попытаемся определить механизм удаления точек разрыва из гипотетической перестановки п. Общая ситуация изображена ниже, где инверсия обозначена двумя вертикальными линиями:
х \	у		z	\	w  .
В результате отмеченной операции мы получаем последовательность
х	z		у	w
где так же, как и раньше, I означает метку I с обращенной ориентацией Допуская, что точка разрыва ху была удалена, мы видим, что в перестановке /3 находится либо пара xz, либо пара zx. Однако пара ху изначально была точкой разрыва, так что пары ху и у х не появляются в цели Д, хотя пара ху присутствует в перестановке а.
Итак, всякая точка разрыва образована двумя метками, которые в перестановке о являются смежными, но вовсе «не желают» быть таковыми в цели. Они стремятся примкнуть к каким-либо другим меткам перестановки. Таким образом, мы наблюдаем расхождение между действительным соседством меток в перестановке а и желаемым соседством этих меток в перестановке Д. Поскольку метки суть ориентированные вещественные объекты, то нет ничего удивительного в том, что они имеют определенное «желание» на каждом из своих концов. Ориентированную метку можно рассматривать как гальванический элемент с противоположными зарядами на полюсах, обозначенными, соответственно, знаками «плюс» и «минус» (см. рис. 7.7).
Рис. 7.7. Ориентированная метка-батарейка. Положительный полюс всетда соответствует голове стрелки, отрицательный — ее хвосту
Теперь проанализируем типичную ситуацию расхождения действительного и желаемого в приведенном выше примере. Изобразим каждую метку в виде прямоугольника. Кроме того, проведем линии «действитель ного», связывающие полюсы меток, находяшиеся в контакте в текущей перестановке, а также линии «желаемого», связывающие концы меток, которые будут в контакте в целевой перестановке. В результате получаем схему,
7.2. ОРИЕНТИРОВАННЫЕ БЛОКИ
323
подобную изображенной на рис. 7.8. Заметим, что удаление точки разрыва отражено линией желаемого, связывающей смежные полюсы; то есть благодаря этой инверсии желаемое воплотилось в действительное. В данном случае мы не знаем, какие полюсы являются положительными, а какие — отрицательными, но это и не самый удачный пример.
Рис. 7.8. Линии желаемого и действительного в точках разрыва
Вышеупомянутые соображения побуждают нас построить диа1рамму желаемого и действительного перестановки а относительно fl, обозначаемую RD@(a). Каждая метка представлена двумя узлами, благодаря чему мы можем отслеживать текущую ориентацию меток. Для каждой метки I G £ мы создаем два узла I и I в диаграмме RD(a). Узел I представляет —>
хвост стрелки, а I - голову. Кроме того, для регистрации действительного и желаемого крайних меток мы включаем в диаграмму два дополнительных узла L и R. Такой принцип построения верен для любых перестановок.
Диаграмма RD(a) имеет два типа линий, или ребер: ребра действительного и желаемого. Ребра действительного соединяют полюсы последовательных меток в перестановке а, а также узел L с первым полюсом и узел R - с последним. Ребра желаемого соединяют полюсы меток согласно перестановке Д. Наконец, мы выстраиваем все полюсные узлы на окружности: метки L и R всегда занимают две верхние позиции, L слева от R, а остальные узлы — против часовой стрелки, в порядке перестановки а. На рис. 7.9 показаны этапы построения диаграммы желаемого —+ 4— 4-------------------------------4—
и действительного перестановки 3 2 1 4 5 относительно тождества.
На рис. 7.10 показана диаграмма в форме круга. Ребра действительного лежат на окружности; ребра желаемого — хорды. Заметим, что иногда между
324
ГЛАВА 7
Продолжаем a L 3
2	1	4	5
Заменяем метки	•	*	*	*	*	*	*
полюсами:	L	— 3	+3	+2 —2	+1	— 1
—4 +4
+5 -5
Проводим ребра ,_____,	,_______,	,_____,	,_____,	,____, л,
действительного L	_3	+3	+2 _2	+1 _j	_4 +4	+5 _5	R
Проводим ребра желаемого
Рис. 7.9. Построение диаграммы желаемого и действительного
R
одной и той же парой вершин существует два параллельных ребра ребро действительного и ребро желаемого. Это происходит только в тех точках, которые не являются точками разрыва, поскольку их желаемое совпадает с действительным. С другой стороны, в диаграмме нс образуется петель.
Диаграмму желаемого и действительного иногда называют графом .желаемого и действительного. Мы предпочитаем употреблять термин диаграмма, чтобы подчеркнуть тот факт, что мы рисуем ее в частном виде, для конкретной перестановки. Граф может быть построен любым из многих способов, если вершины правильно помечены и ребра обеспечивают правильные связи. Но наша диаграмма RD(a) должна быть начерчена таким образом, чтобы следовать порядку меток в перестановке а. Это будет особенно важно при обсуждении свойств пересекающихся ребер желаемого в некоторых из последующих разделов Несмотря на это, для описания диаграмм мы все же позаимствуем у теории графов стандартную терминологию.
Важное для нас свойство состоит в том, что все узлы диаграммы RD(a) имеют степень 2. Это связано с тем, что как А (множество ребер действительного), так и В (множество ребер желаемого) являются сочетаниями в RD(a). Это означает, что каждый узел инцидентен одному ребру из множества А и одному ребру пз множества В. Объединение A U В формирует определенное число связных компонентов, где каждый компонент — цикл с ребрами, принадлежащими попеременно множествам Л и В. Более того, каждый такой цикл содержит четное число ребер, причем половина из
7.2. ОРИЕНТИРОВАННЫЕ БЛОКИ
325
Рис. 7.10 Диаграмма желаемого и действительного
них — ребра действительного и половина ребра желаемого. Число циклов диаграммы RD(a) обозначают ср(п) или просто с(«), если цель ft подразумевается. Следует помнить, что с/з(/3) — п+1, потому что перестановка ft не имеет точек разрыва, так что все ее циклы образованы двумя параллельными ребрами между парами узлов Поскольку в цели существует всего 2п + 2 узлов, мы имеем п + 1 циклов Кроме того, это единственная перестановка, для которой С/з(<т) = п + 1.
Так, в некотором роде, мы можем рассматривать процесс сортировки перестановки как процесс преобразования диаграммы RD(ct) в граф с возможно максимальным числом циклов. Но это не обязательно означает, что каждая инверсия, увеличивающая число циклов, хороша (см. упражнение 6). Однако в этом контексте возникает естественный вопрос Как именно в результате инверсии преобразуются циклы диаграммы /?/?(<>)? Следующая теорема дает нам естественный ответ. Сначала заметим, что инверсия характеризуется двумя точками, в которых она «разрезает» текущую перестановку, причем пары таких точек соответствуют ребрам действительного.
Теорема 7.1. Пусть (s.t) и (u,v) — два ребра действительного, характеризующих инверсию р, причем в перестановке п ребро (s. t) пред
326
Глава 7
шествует ребру (u,v). Тогда диаграмма RD(ap) отличается от RD(a) следующим образом.
1.	Ребра действительного (s, t) и (w, v) заменены на (s, и) и (t, v).
2.	Ребра желаемого остались неизменными.
3.	Сектор круга между узлами t и и включительно, описываемый против часовой стрелки, инвертирован.
Доказательство. Преобразование на ребрах действительного равнозначно описанному на странице 222; единственное отличие — использование полюсов вместо меток. В любом случае, никакие другие ребра действительною не затронуты. Ребра желаемого не изменены, потому что они зависят только от целевой перестановки. Наконец, инверсия полюсов прямое следствие инверсии меток. Рис. 7.11 и 7.12 показывают диаграмму до и после инверсии.
Рис. 7.11. Диаграмма желаемого и действительного до инверсии, обозначенной двумя жирными линиями

Следующая теорема показывает, каким образом инверсия влияет на число циклов. Перед тем как привести ее формулировку и доказательство, мы нуждаемся в новом важном определении. Пусть ей/ — два ребра действительного, принадлежащие одному и тому же циклу диаграммы RD(a).
7.2. ОРИЕНТИРОВАННЫЕ БЛОКИ
327
Рис. 7.12. Диаграмма желаемого и действительного, полученная инверсией указанного сектора диаграммы на рис. 7.11
Представим на мгновение, что ребра ей/ ориентированы против часовой стрелки. Каждое из них индуцирует ориентацию их общего цикла. Если ориентации, индуцируемые ребрами ей/, совпадают, то мы говорим, что эти ребра являются сходящимися и что они сходятся; иначе мы говорим, что они являются расходящимися и расходятся.
Каждый раз, когда мы должны учитывать ориентацию ребер действительного, мы записываем их в виде упорядоченной пары. Первый элемент пары — хвост, а второй — голова ребра. Как будет показано, ориентация ребер действительного важна для определения хороших циклов.
Теорема 7.2. Пусть р — инверсия, затрагивающая два ребра дей-ствитечьного е и f диаграммы RD(a). Тогда:
1.	Если ребра е и f принадлежат разным циклам диаграммы, то с(ар) = с(а) — 1.
2.	Если ребра е и f принадлежат одному циклу и сходятся, то с(ар) = = с(о).
3.	Если ребра е и / принадлежат одному циклу и расходятся, то с(ар) = с(о) + 1.
ДОКАЗАТЕЛЬСТВО. Рисунок 7.13 поможет разъяснить доказательство. Новые ребра в диаграмме RD(ap) обозначены штриховыми стрелками. Ре-
328
Глава 7
бра ей f ориентированы, как описано выше. Заметим, что мы не нарисовали циклы как часть диаграммы RD(ci), а представили их отдельно, потому что сейчас нас интересует лишь ориентация ребер ей f.
Рис. 7.13. Действие инверсии в циклах графа желаемого и действительною: а — ребра из разных циклов; б — сходящиеся ребра; в - расходящиеся ребра
Как было упомянуто ранее, если рассматривается группа циклов, то могут быть изменены только циклы, содержащие ребра ей/. Другие циклы будут оставаться связными компонентами. Обсудим каждый случай отдельно.
Если ребра ей/ принадлежат разным циклам, то эти циклы объединяются и формируют новый цикл (см. рис. 7.13, а). Таким образом, число циклов уменьшается на один. Если ребра ей/ сходятся, то новые ребра гакие, что цикл остается связным (см. рис. 7.13, б). Таким образом, число циклов остается неизменным. Если же ребра ей/ расходятся, то цикл разрывается на две части, вызывая увеличение числа циклов на один (см. рис. 7.13, в).	
Теорема 7.2 имеет важное следствие: с каждой инверсией число циклов изменяется самое большее на один. Отсюда можно вывести другой нижний предел инверсионного расстояния.
Предположим, что ряд инверсий pi, р2,   , Pt изменяет перестановку о в Д, то есть
apiP2--.pt = /?•
Вычисляя число циклов, мы находим:
c(opiP2 - - - pt) = с(Д) = п + 1.
(7-5)
7.2. ОРИЕНТИРОВАННЫЕ БЛОКИ
329
С другой стороны, из теоремы 7.2 мы имеем.
c(npi)-c(a) c(nptp2)-c(api}
с(ар, ... pt)--c(api .
Складывая эти неравенства и сокращая члены, получаем
п + 1 — с(а) t.
Если ряд р\. р?,..., pt есть оптимальная сортировка, то t = d(a) и
п + 1 — с(<т)	d(o).
(7 6)
Этот нижний предел намного точнее выведенного в разделе 7.2.2. Для большинства ориентированных перестановок он дает очень хорошее приближение к истинному расстоянию. Причину, по которой он нс всегда работает, мы объясним в следующих разделах.
7.2.4.	ГРАФ ПЕРЕМЕЖЕНИЙ
Опираясь на теорему 7.2, мы можем классифицировать циклы диаграммы 7?О(а) на хорошие и плохие по следующим признакам. Цикл хорош, если он содержит два расходящихся ребра действительного; иначе его считают плохим. Хорошие циклы могут быть определены по диаграмме желаемого и действительного, потому что они имеют по крайней мере два пересекающихся ребра желаемою. Однако здесь мы должны быть внимательны, потому что не все циклы с пересекающимися ребрами желаемого хороши. Присутствие пересекающихся ребер всего лишь признак того, что цикл может оказаться хорошим. Когда нас терзают сомненья, мы должны непосредственно проверить цикл на соответствие определению, то есть попытаться найти в нем расходящиеся ребра действительного. Характеристика по признаку пересекающихся ребер полагается строго на расположение диаграммы в виде круга. Если бы нам было позволено рисовать граф в произвольном виде, то мы бы могли пересекать или нс пересекать ребра по желанию. Но в круговых диаграммах ребра желаемого должны быть хордами, и хотя иногда мы рисуем их немного криволинейно (иначе они проходили бы слишком близко к окружности), все их пересечения с остальными хордами сохраняются Эта классификация нс применима к циклам
330
Глава 7
с единственным ребром действительного. Такие циклы не отображают точки разрыва и никогда не должны быть затронуты операциями сортировки. Циклы, содержашие по крайней мере четыре ребра, будем называть правильными.
Оказывается, что если в перестановке а мы имеем только хорошие циклы, то выражение для нижнего предела (7.6) фактически становится равенством, и мы можем сортировать а, увеличивая число циклов на единицу с каждой инверсией. Конечно, мы по-прежнему должны быть внимательны с выбором инверсий (возвратимся к этому вопросу позже).
Даже когда в диаграмме есть плохие циклы (в которых все ребра действительного индуцируют одинаковую ориентацию), иногда возможно проводить сортировку со скоростью один цикл на инверсию. Это связано с тем, что инверсия может закрутить плохой цикл, преобразуя его в хороший. Таким образом, разрывая один цикл, мы можем в то же время закручивать другой, так что после каждой инверсии мы всегла оставляем пару расходящихся ребер, чтобы можно было сделать следующий шаг, пока мы не достигнем целевой перестановки. Однако, закручивать один цикл при разрыве другого возможно только тогда, когда какое-либо ребро желаемого одного из этих циклов пересекает любое из ребер желаемого другого цикла. В таком случае мы говорим, что два цикла перемежаются. Заметим, что в этом определении мы снова полагаемся на факт, что ребра желаемого являются хордами в круговой диаграмме.
Поэтому важно проверить, какие именно циклы в диаграмме Ш)(а) перемежается между собой. Мы строим граф 1р(а), называемый графам перемежения перестановки а относительно (3, выбирая в качестве узлов правильные циклы диаграммы RD(a) и делая два узла смежными тогда и только тогда, когда соответствующие им циклы перемежаются. Кроме построения топологической структуры графа, мы помечаем каждый цикл как хороший или плохой. Связные компоненты графа 1/з(а) классифицируют на основании оценки содержащихся в них циклов следующим образом. Если компонент полностью состоит из плохих циклов, то его называют плохим. В противном случае он хороший. Таким образом, компонент, содержащий по крайней мере один хороший цикл, является хорошим.
Ниже приведены примеры хороших и плохих циклов и компонентов. Диаграмма на рис. 7.14 показывает перестановку с шестью циклами, каждый из которых содержит два ребра действительного и два — желаемого Циклы С и F хороши, а все остальные плохи. Хорошие циклы помечены серым цветом. Там же показан граф перемежений этой перестановки. Он состоит из двух хороших и одного плохого компонента. Единственный плохой компонент графа содержит плохие циклы А и Е.
7.2. ОРИЕНТИРОВАННЫЕ БЛОКИ
331
Рис. 7.14. Диаграмма желаемою и действительного для некоторой перестановки. Циклы помечены буквами от Л до F. Граф псремсжсиий этой перестановки изображен справа, и хорошие циклы помечены серым цветом
Рис. 7.15. Диаграмма без хороших циклов
332
Глава 7
На рис 7.15 изображена диаграмма с двумя перемежающимися плохими циклами Нет ни одного хорошего цикла, и это означает, что в этом случае никакая инверсия нс приводит к увеличению числа циклов. Из этого следует, что здесь инверсионное расстояние строго больше нижнего предела п + 1 — с(о). Фактически, этот довод применим к любой диаграмме с плохим компонентом. Поскольку инверсии, которые действуют на данный цикл А, могут закрутить только перемежающиеся с ним циклы, плохой компонент останется плохим, поскольку инверсии работают с циклами других компонентов. Единственный путь сортировать плохой компонент использовать инверсию которая не увеличивает число циклов. Таким образом, нижний предел п + 1 с(а) не будет crpoi им для перестановок с плохими компонентами
Другой пример представлен на рис 7.16. Здесь мы имеем два правильных цикла В и С, где В — плохой цикл, а С — хороший.
Рис. 7.16 Диа1рамма с тремя циклами. Следует помнить, что только правильные циклы участвуют в построении графа перемежеиии
Используем этот пример для иллюстрации сортировки хорошего компонента. Вспомним, что для определения инверсии, увеличивающей число циклов, мы должны выбрать два расходящихся ребра, принадлежащих одному циклу. На рис. 7.16 единственный хороший цикл имеет следующие
7.2. ОРИЕНТИРОВАННЫЕ БЛОКИ
333
три ребра действительного: е = (L,+3), / = (—3, -4) и у = (—1,4-2). Рсбра f и д сходятся, так что эта пара не годится. Ребра е и д расходятся, и определяемая пми инверсия производит два хороших компонента, каждый из которых содержит единственный цикл. Ребра ей/ тоже расходятся и производят единственный хороший компонент с двумя циклами. В обоих случаях мы не создаем плохие компоненты. Таким образом, в этом примере существуют две сортировочные инверсии.
Мы заканчиваем этот раздел следующей теоремой — общим итогом всех наших выводов. Ее доказательство — простое повторение доводов, которые мы приводили в графических примерах.
Теорема 7.3. Инверсия, характеризуемая двумя расходящимися ребрами одного цикла, является сортировочной тогда и только то<.да, когда ее применение не ведет к созданию плохих компонентов.
Эта теорема характеризует сортировочные инверсии частного вида, но она ничего не говорит об их существовании. Следствие теоремы гласит, что, пока мы имеем хороший цикл, всегда будет существовать сортировочная инверсия, увеличивающая число циклов, но доказательство этого следствия мы опустим.
7.2.5.	ПЛОХИЕ КОМПОНЕНТЫ
Научившись сортровагь хорошие компоненты по методам, изложенным в разделе 7.2.4, обратим наше внимание к плохим. Теперь наша цель состоит в том, чтобы классифицировать плохие компоненты по иерархическому принципу и, основываясь на этой классификации, представить читателю точную формулу инверсионного расстояния перестановки относительно цели.
Схема классификации плохих компонентов представлена на рис. 7.17. Сначала мы обозначим различия между стенами и миражами. Среди стен мы отличаем преграды от простых стен. Определения всем этим понятиям мы дадим ниже.
Мы говорим, что компонент В отделяет компоненты А и С, если все хорды диаграммы RD(ct), которые связывают какой-либо полюс компонента Л с некоторым полюсом компонента С, пересекают ребро желаемого, принадлежащее компоненту В. Ребра желаемого также можно рассматривать как хорды, так что в данном случае применимо обычное определение пересечения хорд. Рис. 7.18 иллюстрирует это понятие. Буквы от А до F указывают компоненты; все компоненты плохие. В этом примере компонент В отделяет компоненты А и С. Другие примеры отделения следующие:
334
Глава 7
Рис. 7.17. Классификация плохих компонентов компонент Е отделяет компоненты F и С, компонент В отделяет компоненты F и D. Вее отделяемые и отделяющие компоненты этой диаграммы можно найти, выполнив упражнение 10.
Отделение — важное понятие, в котором инверсия через ребра действительного в различных компонентах А и С приводит к закручиванию некоторого компонента В, отделяющего А от С. В результате закручивания плохой компонент всегда становится хорошим, но хороший компонент может или остаться хорошим, или же стать плохим. Чтобы избежать осложнений, мы прибегаем к закручиванию только тогда, когда поиск хороших компонентов оказывается безрезультатным.
Стена это плохой компонент, который не отделяет никакие другие два плохих компонента, иначе это мираж. Число стен в перестановке о мы обозначаем й(а).
Мы говорим, что стена А защищает (ограждает) мираж В, когда удаление стены А заставило бы мираж В стать стеной. Другими словами, мираж В защищен стеной А, если каждый раз, когда он отделяет два плохих компонента, одним из них является компонент А. В примере на рис. 7.18 компонент F защищает компонент Е, и это единственный случай защиты на этой диаграмме.
Стену А называют преградой, если она защищает некоторый мираж В. Иначе ее называют простой стеной. Известно, что стена может защитить
7.2. ОРИЕНТИРОВАННЫЕ БЛОКИ
335
Рис. 7.18. Диаграмма без хороших циклов. Одни плохие компоненты, взаимно отделяющие друг друга
только один мираж. На рис. 7.18 единственная преграда — компонент F Все остальные стены простые.
Перестановку о называют крепостью, когда ее диаграмма желаемого и действительного содержит нечетное число стен, и все из них — преграды. Как мы увидим ниже, крепости — это такие перестановки, для сортировки которых, в силу их специфической структуры, необходима одна дополнительная инверсия. Крепость должна иметь по крайней мере 24 метки, учитывая, что на образование правильного цикла нужны по крайней мере две метки, плохой компонент требует четыре метки, преграда и защищенный ею мираж восемь меток, а чтобы возвести крепость, нужно выстроить три такие преграды и соответствующие им миражи. Рисунок 7.19 показывает диаграмму такой минимальной крепости
Теперь мы готовы написать точную формулу инверсионного расстояния для ориентированных перестановок:
d(a) = п + 1 - с(о) + Л(а) + /(о),	(7.7)
где с(а) число циклов (включая правильные и неправильные), h(a) — число стен; f(a) = 1, если а крепость и /(а) = 0, если а не крепость.
Член п + 1 с(а) учитывает хорошие компоненты и любые компоненты, которые изначально являются плохими, но в процессе сортировки ста-
336
Глава 7
Рис. 7.19. Минимальная крепость
новятся хорошими. Член /г(а) необходим, потому что иногда нужны дополнительные инверсии, чтобы обернуть плохие компоненты хорошими. Нет необходимости учитывать миражи, поскольку они всегда будут закручены. Наконец, дополнительная инверсия необходима для крепостей (/(а) = 1). потому что в некоторый момент процесса сортировки мираж становится стеной.
7.2.6.	АЛГОРИТМ
В этом разделе мы описываем алгоритм сортировки произвольно ориентированной перестановки, использующий формулу инверсионного расстояния, представленную выше. Алгоритм на каждом шаге выбирает сортировочную инверсию и таким образом гарантирует, что мы достигаем целевой перестановки посредством минимального числа инверсий.
Позже мы подробно проанализируем сложность этого алгоритма. Сейчас же мы просто убедимся, что это действительно правильная процедура. Перед объяснением принципа работы алгоритма, мы определим инверсии специальных видов, используемые в процедуре сортировки.
Как мы увидели, когда в диаграмме нет хороших циклов, мы вынуждены использовать или инверсию на двух сходящихся ребрах, или инверсию на ребрах из разных циклов. В первом случае число циклов остается постоянным, тогда как во втором случае число циклов уменьшается на один
7.2. ОРИЕНТИРОВАННЫЕ БЛОКИ
337
Инверсию на сходящихся ребрах лучше осуществлять в стене, нежели в мираже. Причина состоит в том, что эта операция преобразует плохой компонент в хороший, не изменяя число циклов. Если мы избавляемся от миража, то мы не изменяем число стен и статус крепости текущей перестановки, так что, согласно формуле (7.7), инверсионное расстояние останется неизменным. Также нс стоит выполнять операцию инверсии в преграде, потому что тогда мираж, находящийся под защитой данной претрады, станет стеной и число стен h(a) останется постоянным. Таким образом, каждый раз, когда мы должны использовать инверсию на сходящихся ребрах, мы будем применять ее к простой стене. Не имеет значения, какой цикл в простой степе мы выбрали: для этой цели все они равнозначны. Инверсию на ребрах действительного из одного и того же цикла стены мы называем разрезанием стены.
Разрезание стены не изменяет число циклов с(а) и уменьшает число стен /г(о), если разрезаемая стена простая, но мы должны быть внимательны, иначе может увеличиться число дополнительных инверсий /(а). Чтобы устранить эту возможность, мы будем использовать разрезание стен только когда их число нечетно. Тогда число стен после инверсии остается нечетным и мы можем быть уверенными, что конечная перестановка не будет крепостью. Поэтому разрезание стены является сортировочной инверсией только в том случае, когда стена простая и величина h(a) нечетная.
Другая возможность состоит в том, чтобы использовать инверсию на ребрах из разных циклов. Такая операция уменьшит число циклов, то есть увеличит член п + 1 — с(а) в формуле инверсионного расстояния, но мы можем добиться успеха, если при этом сумеем уменьшить число стен /?(<т) на два. Единственный способ сделать это — выбрать ребра, образующие разные стены. Инверсию на ребрах действительного из разных стен называют слиянием стен. Эффект ее состоит в том, что эти две стены становятся хорошими компонентами, так же, как любой отделяющий их мираж.
Существует опасность, что слияние стен может преобразовать некоторый мираж в стену (см. рис. 7.20). Это случается, когда две слияемыс стены «защищают» такой мираж так же, как преграды защищают миражи. Чтобы решить эту проблему, мы нуждаемся в дополнительном определении. Стены А и В мы называем противоположными, если при прохождении кругового пути против часовой стрелки от стены Ак В мы встречаем столько же стен, сколько мы находим, идя в том же направлении от стены В к А. Заметим, что противоположные стены существуют, только если общее число стен /;(а) четное. Выбор противоположных стен Ан В обеспечивает безопасность, поскольку он i арантирует, что при слиянии стен А и В мы не создаем новые стены и. следовательно, значение функции n + 1 — c(a) + h(a) уменьшается на единицу.
338
Глава 7
Тем не менее, мы все еще должны следить за поведением функции /(а). Если число стен h(a) четное, то беспокоиться не о чем, так как слияние противоположных стен уменьшит величину Л(а) точно на два, сохраняя ее значение четным. Если /г(а) нечетно и есть простая стена, то противоположных стен не существует, но мы применяем сортировочное разрезание стены и снова получаем нечетное значение h(a). Если h(a) нечетно и нет ни одной простой стены, то это значит, что мы сидим в крепости и, следовательно, значение /(а) уже равно 1 и более не может увеличиться. Мы заключаем, что всякий раз, когда мы выбираем для слияния две противоположные стены, операция слияния стен становится сортировочной инверсией.
Рис. 7.20. Слияние стен Аи В преобразует мираж С в стену. Сортировочная инверсия должна привесш к слиянию стены А либо В с некоторой стеной, отделенной от них миражом С
Все эти выкладки мы суммируем в процедуре Sorting Reversal, представленной на рис. 7.21. Эта процедура находит сортировочную инверсию для заданной ориентированной перестановки а. Полный алгоритм сортировки инверсиями состоит из одного цикла, в котором мы периодически вызываем эту процедуру и применяем возвращенную ею инверсию, пока не достигнем целевой перестановки.
7.2. ОРИЕНТИРОВАННЫЕ БЛОКИ
339
Algorithm Sorting Reversal'
input: различные перестановки а и fl
output: сортировочная инверсия а относительно fl if в диаграмме RDp(a) имеется хороший компонент then выбрать в этом компоненте два расходящихся ребра е и f убедившись, чго соответствующая инверсия не создает плохие компоненты
return инверсию на ребрах ей/ else
if число h(a) четное then
return слияние двух противоположных стен else
if h{a) нечетное и существует простая стена then return инверсию, разрезающую эту стену else
// крепость return слияние любых двух стен
Рис. 7 21 Процедура поиска сортировочной инверсии а относительно цели fl, если о /3
Теперь дадим приближённую оценку времени счета в единицах размера перестановки п. Начнем с анализа построения всех структур, определенных в этом разделе и важных для алгоритма. Построение диаграммы RDp(a) занимает линейное время, так как для этого требуется всего-навсего определить ребра желаемого и действительного. Поиск циклов в этой диаграмме также занимает время О(п) Для каждого цикла мы должны определить, хорош ли он или плох, и для этого на один цикл затрачивается время О(п), а на все циклы время О(п2) Затем мы должны определить взаимные псреме-жения циклов. Это может быть сделано за время О(п2) путем исследования каждой пары ребер желаемого и сохранения графа перемежений в виде матрицы смежности. Подсчет общего числа хороших и плохих компонентов, миражей, простых стен и преград может быть выполнен за линейное время, если мы располагаем информацией относительно хороших и плохих циклов (см. упражнение 11) Поэтому полное время счета, необходимое на построение всех необходимых структур, равно О(п2).
В процедуре Sorting Reversal наиболее затратная по времени часть — обработка хороших компонентов. Мы должны перепробовать несколько инверсий и посмотреть, обладают ли структуры конечной перестановки
‘Сортировочная инверсия. Прим перев
340
Глава 7
после применения очередной инверсии — некоторым свойством. Так как инверсия определяется парой ребер, мы должны перепробовать самое большее О(п2) инверсий. Для каждой должно быть затрачено время О(п2) на проверку конечной перестановки. Следовательно, оценка времени счета процедуры Sorting Reversal в наихудшем случае составляет О(п4). Для сортировки перестановки а по Д мы должны обратиться к этой процедуре с!/з(а) раз, так что конечное время счета равно О(п5). Ссылки на более быстрые алгоритмы см. в библиографических примечаниях.
7.3. НЕОРИЕНТИРОВАННЫЕ БЛОКИ
В этом варианте задачи ориентация блоков в сравниваемых геномах неизвестна. Все, что мы знаем — их относительный порядок. Для этого случая мы можем развить теорию, подобную изложенной в разделе 7.2, и даже получить некоторые аналогичные выводы, но все же эта новая теория будет иметь много отличий. Одно очень важное отличие факт, что вариант задачи с неориентированными элементами НП-трудный, тогда как при известной ориентации элементов задача может быть решена за полиномиальное время.
Начнем с нескольких новых определений, большинство которых походит на определения из раздела 7.2. Неориентированная перестановка о — отображение {1,2,...,п} на множество £, содержащее п меток. Обычно множество £ равно области определения перестановки о. Инверсия определяется так же, как и в случае ориентированных перестановок, за исключением того, что она нс обращает ориентацию меток, поскольку таковая попросту не учитывается. Инверсия всего лишь изменяет порядок группы последовательных меток на противоположный. Заметим, что здесь унитарная инверсия теряет смысл, так как она никак не влияет на перестановку п.
Наша цель снова состоит в том, чтобы получить возможно кратчайший ряд инверсий, преобразующих перестановку а в 0. Если ряд инверсий pi, рг, • - - ,Pt кратчайший и
apiP2 ...pt= 0,
то t — инверсионное расстояние п от 0, обозначаемое как dp(a). Сортировочные инверсии определяются соответственно. Те же рассуждения, что имели место в случае ориентированных перестановок, остаются верны, в результате чего можно показать, что dp(a) = da(0). Если цель ясна из контекста, то мы опускаем явное указание на нее. Тождество в данном
7.3. НЕОРИЕНТИРОВАННЫЕ БЛОКИ
341
Рис. 7.22. Две хромосомы с гомологичными блоками
2	1	3	7	5	4	8	6
1	2	3	7	5	4	8	6
1	2	3	4	5	7	8	6
1	2	3	4	5	7	6	8
1	2	3	4	5	6	7	8
Рис. 7.23. Сортировка перестановки 21375486
случае — перестановка, определяемая как 7(г) = г для всех г в интервале 1... п. Следующий пример должен пояснить игру старых понятий в их новых ролях.
Пример 7.1. На рис. 7.22 показаны две хромосомы с гомологичными блоками, соединенными линиями. Мы ставим метки с 1 по 8 на блоки нижней хромосомы и затем переносим метки на верхнюю, дублируя цифры по линиям. Таким образом мы получаем начальную перестановку в верхней хромосоме, и наша цель состоит в том, чтобы сортировать ее до получения нижней, то есть тождества Ряд четырех инверсий, сортирующих эту перестановку, приведен на рис. 7.23.	
Можем ли мы получить более короткий ряд инверсий? В данном случае — нет. Чтобы убедиться в том, что необходимы как минимум четыре инверсии, мы, как и в случае ориентированных меток, анализируем точки разрыва. Для простоты мы допускаем, что цель — тождественная перестановка.
Точка разрыва неориентированной перестановки о — пара меток, смежных в п, но не смежных в цели, или, что равнозначно, пара смежных меток,
342
Глава?
£•2 1.3«7»5 4»о»6»7?
Рис. 7.24. Точки разрыва в неориентированной перестановке, обозначенные знаком •
но с измененным порядком следования. Точки разрыва нужно рассмагри-вать в продолженной перестановке а, которая включает дополнительный левый (£) и правый (7?) элементы. Величина Ь(а) обозначает число точек разрыва в а. Перестановка в нашем примере имеет семь точек разрыва, как показано на рис. 7.24. Единственные пары, нс являющиеся точками разрыва — пары 2,1 и 5,4.
Так же, как и в ориентированных перестановках, инверсия может удалить самое большее две точки разрыва. Следовательно, здесь может быть применен тот же самый нижний предел, что мы имели ранее для ориентированных перестановок, то есть
d(Q)	(7.8)
Теперь нам становится ясно, почему нельзя сортировав перестановку п на рис. 7.24, применяя менее четырех инверсий. Из уравнения (7.8) мы видим, что rf(ft) 3,5, но, поскольку <£(ст) — целое число, это означает d(n) 4. Итак, наше решение с четырьмя инверсиями является оптимальным.
7.3.1.	ПОЛОСЫ
Рассмотрим перестановку а в ее продолженной форме (точки разрыва отмечены жирными точками):
£•4 5»3 2 !•/?
Обратите внимание, что между двумя последовательными точками разрыва мы наблюдаем последовательность смежных меток, возрастающую либо убывающую. Несложное размышление убеждает нас, что это фактически общее явление. Действительно, если мы имеем две смежные метки, которые не образуют точку разрыва, то они должны иметь следующий вид:
• • -х(х + 1)   
либо
• • • х(х — 1) •  
73 НЕОРИЕНТИРОВАННЫЕ БЛОКИ
343
В первом случае, если метка х + 1 не примыкает к точке разрыва, то справа от нее должна быть метка х + 2, потому что другая смежная с ней метка, х, уже была использована. Таким образом, возрастающая последовательность меток продолжается вправо вплоть до следующей точки разрыва или же до конца перестановки. Подобное рассуждение может быть применено для последовательности, идущей влево от метки х, а также для пары меток из второго случая.
Последовательность смежных меток, окруженная точками разрыва, но без внутренних точек разрыва, называют полосой. Очевидно, что мы имеем два вида полос: возрастающие и убывающие. Отдельная метка, окруженная точками разрыва, также является полосой, и в этом случае она является возрастающей и в то же время убывающей полосой. Исключения к этому правилу — метки L и R, которые всегда считают частью возрастающей полосы, даже если они обе принадлежат одной полосе. Фактически, ради определения полос мы рассматриваем эти крайние элементы как единый элемент. Так, например, если метка 0 входит в более длинную возрастающую полосу 0,1,... и метка п -I- 1 — также часть более длинной полосы ..., п, п + 1, то мы рассматриваем эти две последовательности как одну полосу. Они связаны общим элементом L = В.
Пример 7.2. Здесь мы наблюдаем пять полос две возрастающие (L R, 1 2 и 5,6), одна убывающая (8,7) и две полосы, которые и возрастают и убывают (3 и 4).
L 1 2.8 7.3»5 6»4« R

Визуальный анализ полос может помочь нам удалять точки разрыва, как показывают следующие теоремы.
Теорема 7.4. Если метка к принадлежит убывающей полосе, a item ка к — 1 принадлежит возрастающей полосе, то существует инверсия, которая удаляет по крайней мере одну точку разрыва.
Доказательство. Метки к — 1 и к не могут принадлежать одной и той же полосе, потому что единственные полосы, одновременно возрастающие и убывающие, состоят из одного элемента. Следовательно, эти метки принадлежат разным полосам. Это в свою очередь подразумевает, что каждая из этих меток является последним элементом своей полосы, то есть непосредственно предшествует точке разрыва, как показано на рис. 7.25.
Этот рисунок представляет два возможных порядка. Полоса метки к 1 может либо следовать, либо предшествовать полосе метки к в этой
344
Глава 7
персе i ановкс. В обоих случаях, в результате инверсии, которая разрезает две точки разрыва, непосредственно следующие за метками к — 1 и к. эти две метки становятся смежными, и таким образом число точек разрыва сокращается по крайней мере на одну.	
- • - (fc — 1)»	  • к •
к •
Рис. 7.25. Две возможные перестановки полос, содержащих метки к и к — 1
Мы знаем, что все перестановки включают в себя по крайней мерс одну возрастающую полосу, — содержащую метку L или R. Напротив, перестановка может не иметь ни одной убывающей полосы. Однако если некоторая перестановка все же содержит убывающую полосу, то мы можем обернуться к предыдущей теореме и с ее помощью заключить, что существует инверсия, удаляющая точку разрыва. Это возможно благодаря тому, что если в перестановке присутствуют и возрастающая и убывающая полосы, то они должны где-нибудь «встретиться» — в смысле их порядка в тождественной перестановке. Другой способ показать это - выбрать наименьшую метку принадлежащую убывающей полосе, и назвать ее к. Ясно, что метка к - 1 принадлежит возрастающей полосе, иначе метка к нс была бы минимальной. Подобное суждение верно при подстановке к +1 вместо к — 1 в формулировке теоремы 7.4, как показывает теорема 7.5.
Теорема 7.5. Если метка к принадлежит убывающей полосе, а метка к + 1 — возрастающей полосе, то существует инверсия, удаляющая по крайней мере одну точку разрыва.
ДОКАЗАТЕЛЬСТВО. Так же. как в предыдущей теореме, метки к и А'-|-1 не могут принадлежать одной полосе. Таким образом, обе являются первыми элементами своих полос и непосредственно следуют за точками разрыва. Инверсия на этих двух точках разрыва уменьшает общее количество точек разрыва, поскольку метки к и к + 1 в результате оказываются смежными.

Обе эги теоремы означают, что всякий раз, когда мы имеем убывающие полосы, мы всегда можем уменьшить число точек разрыва. Заметим, что это применимо также к одноэлементным полосам. Однако иногда мы не имеем убывающей полосы. Следующая теорема обеспечивает компенсацию этого досадного факта, применимую в том случае, когда в процессе сортировки требуется создать перестановку без убывающих полос.
7.3. НЕОРИЕНТИРОВАННЫЕ БЛОКИ
345
а)	 (к-1)»	 к •
б)	• I	»(1+ !)
Рис. 7.26. Перестановки без инверсий, оставляющих убывающую полосу
Теорема 7.6. Пусть а — перестановка с убывающей полосой. Ес-1н все инверсии, которые удаляют из перестановки а точки разрыва, не оставляют никаких убывающих полос, то существует инверсия, которая удаляет из перестановки а две точки разрыва.
Доказательство. Предположим, что к - наименьшая метка в убывающей полосе. Из доказательства теоремы 7 4 следусч, что существует инверсия р, которая объединяет метки к и к — 1. Если метка к — 1 находится справа о г к, го инверсия р оставляет убывающую полосу, что противоречит нашему предположению. Следовательно, метка к — 1 должна быть расположена слева от к (см. рис. 7.26, а).
Пусть I — наибольшая метка в убывающей полосе. Согласно теореме 7.5, существует инверсия а, объединяющая метки I и I + 1 Если метка 1+1 расположена слева от I, то инверсия а оставляет убывающую полосу, так что метка I + 1 должна быть справа от / (см. рис. 7.26, б). Заметим, что метка к должна находиться в интервале, инвертированном <т, иначе инверсия о оставила бы убывающую полосу метки к нетронутой. Аналогично, метка I должна принадлежать интервалу инверсии р
Мы утверждаем, что эти два интервала тождественны, то есть инверсия р = о. В самом деле, если это утверждение не верно, то должна существовать некоторая полоса, которая принадлежит интервалу только одной из этих инверсий. Предположим, что эта полоса принадлежит интервалу инверсии р. Если эта полоса возрастает, то инверсия р обратила бы ес в убывающую полосу. Если же эта полоса убывает, то она сохранилась бы в перестановке ент, потому что инверсия ст может лишь удлинить ес. Итак, ни один из этих случаев не возможен. Подобный же вывод может быть получен, если предположить, что эта полоса принадлежит интервалу инверсии о. Таким образом, утверждение верно. Но в таком случае эта инверсия удаляет две точки разрыва, потому что она соединяет метку к — 1 с к и метку I с I + 1.	
7.3.2. АЛГОРИТМ
Теперь мы готовы представить алгоритм, который сортирует перестановку, используя число инверсий, не более чем вдвое превышающее воз
346
I ЛАВА 7
можный минимум d(a). Поэтому это алгоритм аппроксимации. Он полагается на только что рассмотренные нами теоремы. Идея его проста. Организован основной цикл, в котором мы, следуя некоторым критериям, оцениваем текущую перестановку и выбираем для нее возможно лучшую инверсию. Затем мы обновляем текущую перестановку и сообщаем об инверсии, к ней примененной. Цикл останавливается, когда текущая перестановка становится искомым тождеством.
Критерии, на которые мы опираемся при выборе инверсии, основаны на предыдущих теоремах. Если текущая перестановка имеет убывающую полосу, то мы ищем инверсию, которая уменьшает число точек разрыва и притом оставляет убывающую полосу. Хорошие кандидаты на выборы представлены инверсиями, выдвинутыми в ходе доказательств теорем 7.4, 7.5 и 7.6. Даже если никакой такой инверсии не существует, то мы знаем, что есть некоторая инверсия, которая вовлекает все убывающие полосы и удаляет две точки разрыва. Наконец, если текущая перестановка совершенно свободна от убывающих полос, то мы выбираем инверсию, которая удаляет две точки разрыва. Мы знаем, что в текущей перестановке осталось по крайней мере две точки разрыва, иначе она уже была бы тождеством. Никакая перестановка не может иметь только одну точку разрыва, так что все перестановки, отличные от тождества, содержат по крайней мере две точки разрыва. Кроме того, инверсия, которая разрезает перестановку в двух точках разрыва, гарантирует, что общее количество точек разрыва не увеличится. Конечный алгоритм показан на рис. 7.27.
Мы точно знаем, что этот алгоритм имеет точку останова, потому что число точек разрыва уменьшается при каждом повторении цикла, кроме случаев, когда мы сталкиваемся с перестановками без убывающих полос. Но эта ситуация не может произойти дважды в одной строке. Так что мы можем определенно сказать, что число точек разрыва уменьшается по крайней мере на одну за каждые два прогона цикла. На самом деле, как показывает следующая теорема, среднее число точек разрыва, удаляемых алгоритмом за один проход цикла, несколько больше.
Теорема 7.7. Число пригонок алгоритма «Sorting Unoriented Permutation» (см. рис. 7.27) меньше или равно числу точек разрыва начальной перестановки.
Доказательство. Мы хотим доказать, что, в среднем, при каждом прогоне алгоритм удаляет по крайней мерс одну точку разрыва. Единственная трудность связана с выбором инверсий при отсутствии убывающих полос.
2Сортировка неориентированной перестановки. — Прим, перев.
РЕЗЮМЕ
347
Algorithm Sotting Unoriented Permutation2
input: перестановка a
output: ряд инверсий для сортировки а
list«— пустой
while о I do
if о имеет убывающую полосу then
к <— наименьшая метка в убывающей полосе
р ♦— инверсия, режущая в точках после к и после к 1 if ар нс имеет убывающей полосы then
I «— наибольшая метка в убывающей полосе
р <— инверсия, режущая в точках перед I и перед I + 1 else
р «— инверсия, разрезающая в первых двух точках разрыва а ♦— ар
list «— list +р
return list
Рис. 7.27. Алгоритм сортировки неориентированной перестановки с гарантией: число инверсий превышает минимально возможное не более чем вдвое
Но каждый раз, когда мы достигаем этой ситуации, предыдущее повторение, только что удалившее две точки разрыва, поддерживает среднее число равным по крайней мерс одной точке разрыва на прогон. Этот аргумент бессилен при первом прогоне, если нам «посчастливилось» получить начальную перестановку без убывающей полосы. Но тогда на самом последнем прогоне, в котором алгоритм производит тождество, он удаляет две точки разрыва и дает компенсацию за первый «неудачный» прогон.	
РЕЗЮМЕ
Генетический материал организмов изменяется в ходе эволюции. В этой главе мы рассматривали крупные преобразования, происходящие на уровне генома, в противоположность точечным мутациям, появляющимся на уровне последовательности. Мы сфокусировали наше внимание на одном особенно типичном и распространенном преобразовании - инверсии. Сравнивая два генома, мы ищем минимальное число инверсий, достаточное для преобразования одного из них в другой. Это число мы называем инверсионным расстоянием между геномами, и оно представляет наиболее экономичную модель изменений в качестве объяснения их отличий.
348
Глава 7
В зависимости от наличия или отсутствия информации относительно ориентации генов, мы имеем два варианта этой задачи: для ориентированной и неориентированной перестановки. Примечательным фактом является то, что, тогда как в первом варианте инверсионное расстояние может быть вычислено за полиномиальное время, во втором варианте задача становится НП-трудной.
Мы представили изящную теорию, положенную в основу полиномиального алгоритма решения задачи с ориентированными блоками. Эта теория опирается как на простые понятия типа точек разрыва и диаграммы желаемого и действительного, так и на более сложные например стен и крепостей.
Для задачи с неизвестной ориентацией блоков мы развили множество средств, которые предоставляют важную информацию относительно фактического расстояния между сравниваемыми объектами, после чего представили алгоритм аппроксимации, который находит ряд инверсий не боле чем в два раза длиннее оптимального.
УПРАЖНЕНИЯ
1.	Пусть задан следующий фрагмент ДНК:
5'    CCTCACTAGCGACCAGACTATAAATTACGTGACCTGT • • • 3'
3' - •  GGAGTGATCGCTGGTCTGATATTTAATGCACTGGACA • • • 5'
и «гены» а = GGTCA, b = ААТТАС, с = AGTCTGG и d = CACTAG. Определите местоположение этих генов в представленном фрагменте ДНК и запишите перестановку генов {а, 6, с, d}, описывающую их позиции и ориентацию.
___>______
2.	Найдите точки разрыва в перестановке a b с d е относительно _______>—>_►—>_► цели a b с d е .
3.	Даны две перестановки: п —	• □□ и Д = • • □[ •
Преподаватель стер метки, оставив только точки разрыва а относительно Д и точки разрыва Д относительно с Можете ли вы восстановить ориентированные метки в пустых квадратиках так, чтобы точки разрыва соответствовали изображенным?
4.	Восстановите перестановки а и Д, если известны следующие ребра диаграммы RDe(a):
Ребра действительного: (£, —3), (—1, —2), (R, +1), (+2, +3).
Ребра желаемого: (£, —1), (—2. +1), (R, +3), (—3, +2).
УПРАЖНЕНИЯ
349
5.	Рассмотрите ориентированные перестановки. Покажите инверсию, которая удаляет две точки разрыва, но вместе с тем не является сортировочной.
6.	Рассмотрите ориентированные перестановки Покажите инверсию, которая увеличивает число циклов диаграммы RD(a), но не является сортировочной.
7.	Докажите следующее утверждение: ориентированная перестановка допускает инверсию, увеличивающую число циклов, тогда и только тогда, когда она содержит по крайней мере одну метку со стрелкой, направленной справа налево. Допустите, что цель — тождественная перестановка.
8.	Покажите, что каждое ребро желаемого, которое не совпадает с ребром действительного, должно пересечь некоторое другое ребро желаемого на диаграмме желаемого и действительного.
9.	Докажите, что неравенство 6^(а)/2 n+1 — С/?(й) верно для любой ориентированной перестановки о и цели Д.
10.	На диаграмме рис 7.18 найдите все возможные триплеты XYZ плохих компонентов (компонент Y отделяет компоненты X и Z)
11.	Покажите, каким образом за время О(п) можно вычислить число миражей, простых стен и преград в графе персмежсний, имея информацию о хороших и плохих циклах.
12.	Можете ли вы найти все сортировочные инверсии для любой заданной ориентированной перестановки и цели?
13.	Докажите, что любая неориентированная перестановка п элементов может быть сортирована самое большее п — 1 инверсией.
14	Сортируйте инверсиями все 24 возможные неориентированные перестановки цифр {1,2,3,4}. Для сортировки скольки перестановок потребуется три инверсии?
15.	Найдите неориентированную перестановку, которая не может быть оптимально сортирована исключительно инверсиями, разрезающими точки разрыва.
16.	Узлом неориентированной перестановки ст элементов из интервала 1... п] называют такой интервал [г... j' , что г j и г си(к) j для всех к 6 [г...у]. Обратите внимание, что интервал [1 ... п] — узел каждой такой перестановки. Докажите, что если интервал 1... г] является узлом а для некоторого г < п, то d(a) п — 2.
17.	Голанова перестановка интервала 1... п — это такая перестановка а, что интервал [1.. .п] — ес единственный узел и |а(г) — г| 2 для всех г е [1... п].
350
Глава 7
а.	Покажите, что инверсия Голановой перестановки дает Голанову же перестановку.
б.	Покажите, что для каждого п 3 существует только две Голановы перестановки интервала [1... п], причем одна является инверсией другой.
в.	Покажите, что если а — Голанова перестановка и п 4, то 6(a) = = п + 1.
** 18. Докажите, что Голанова перестановка а для интервала ... п] удовлетворяет равенству d(a) = п — 1.
** 19. Докажите, что Голановы перестановки интервала [1... п] — единственные перестановки с инверсионным расстоянием п — 1.
БИБЛИОГРАФИЧЕСКИЕ ПРИМЕЧАНИЯ
Большая часть материала этой главы опирается на работы Бафны и Певзнера [18], Ханненхалли и Певзнера [87], а также Кецециоглу и Санко-ва [116]. По сравнению с оригинальным содержанием этих статей, в нашем описании читатель заметит некоторые отличия в системе обозначений (в частности, использование стрелок вместо знаков «плюс» и «минус»), а также отсутствие наиболее пикантных вкусовых добавок (критерий экономичности). Кроме того, при классификации перестановок мы употребляем термины неориентированный и ориентированный вместо неполярный и по-ырный.
Берман и Ханненхалли [23] дали более эффективную версию алгоритма Sorting Reversal, изображенного на рис. 7.21. Ханненхалли и Певзнер [88] представили полиномиальный алгоритм для задачи перестройки генома, вовлекающей целые наборы хромосом. Феррети, Надо и Санков [62] исследовали проблему восстановления последовательности эволюционных событий на основании информации о присутствии определенных генов в тех или иных хромосомах.
Анализ эволюции генома приведен в статье Санкова [167]. Уоттерсон, Юэне и Холл [205] исследовали проблему сортировки циклических перестановок и изложили множество интересных догадок.
Статьи биологического плана, в которых описанию перестроек генома отведены как главные, так и второстепенные роли, включают работу Кунина и Долджы по изучению РНК вирусов [117]; статьи Палмера [148], а также Палмера, Осорио и Томпсона [150], посвященные изучению ДНК хлоропластов; сравнение геномов митохондрий кукурузы, описанное Фауропом
БИБЛИОГРАФИЧЕСКИЕ ПРИМЕЧАНИЯ	351
и Хавликом [58]; изложение проведенного Палмером и Эрбоном [149] сравнительного анализа геномов митохондрий репы (Brassica гара) и капусты огородной (Brassica oleracea), принадлежащих к роду капуста (Brassica); исследование митохондриальной ДНК моллюска, проведенное Гоффманом, Буром и Брауном [95].
Капрара, Лансия и Нг [31] предложили алгоритм сортировки неориентированных перестановок, показавший на практике неплохие рабочие характеристики. Совсем недавно Капрара [30] показал, что эта задача НП-трудная. Гейтс (известности главы «Майкрософт») и Пападимитриу [69] работали над родственной задачей, в которой сортировка осуществляется только посредством префиксных инверсий.
Глава 8
ПРЕДСКАЗАНИЕ СТРУКТУРЫ МАКРОМОЛЕКУЛ
До сих пор мы изучали биомолекулы лишь на уровне их линейной, первичной структуры. Но, как мы увидели в главе 1, макромолекула РНК или белка фактически представляет собой трехмерный объект. Определение точной пространственной структуры биомолекулы — одна из главнейших целей молекулярной биологии, поскольку именно эта структура и определяет функцию молекулы. Однако определение трехмерных сгруктур белков и РНК с помощью рентгеноструктурного анализа или метода ядерного магнитного резонанса оказывается трудным, дорогостоящим и нс всегда выполнимым. Это представляет резкий контраст той легкости, с которой возможно определить первичную структуру (последовательность мономеров) этих молекул (основания в случае РНК и остатки аминокислот в случае белков). В силу этих причин в настоящее время существует разрыв между числом белков с известной последовательностью (тысячи) и числом белков, у которых была определена также трехмерная струкгура (сотни)1; с каждым годом этот разрыв увеличивается. Такая ситуация привела к интенсивному попеку методов предсказания структуры — методов, могущих на основании анализа первичной структуры молекулы предсказать ее трехмерную структуру. В эту группу входят различные методы от моделирования динамики молекул до программ для нейронных сетей. Однако здесь мы интересуемся прежде всего алгоритмическими методами. В общем случае такие методы, очевидно, еще нс применимы к предсказанию структуры молекул, так как они должны полагаться на довольно точные модели процесса свертывания молекулы; но такие общие модели пока еще нс существуют. Тем не менее, для некоторых специальных случаев алгоритмическая формулировка может быть найдена, и ученые уже в течение ряда лет применяют ее результаты на практике. Это относится к предсказанию структуры РНК, чем мы и займемся в следующем разделе. Затем мы обсудим задачу свертывания белка,
1В настоящее время известны последовательности сотен тысяч, если не миллионов белков, а трехмерная структура определена для десятков тысяч белков Прим. ред.
8.1. ПРЕДСКАЗАНИЕ ВТОРИЧНОЙ СТРУКТУРЫ РНК
353
решение которой — своего рода < Святая Чаша»2 молекулярной биологии. Мы описываем саму задачу и представляем один алгоритмический подход к се решению, показавший большую перспективность.
8.1.	ПРЕДСКАЗАНИЕ ВТОРИЧНОЙ СТРУКТУРЫ РНК
Вспомним из главы I, что молекула РНК представляет собой одинарную цепь нуклеотидов А, С, G и U. Тот факт, что цепь РНК состоит из единственной ниги, составляет главное ее отличие от последовательности ДНК: нуклеотид одного участка молекулы образует пару с комплементарным нуклеотидом некоторого другого участка и таким образом молекула свертывается. Кроме того, последовательность нуклеотидов однозначно определяет механизм свертывания молекулы, и именно благодаря этому мы можем попытаться предсказать структуру РНК на основе анализа структуры ес последовательности. Однако даже в этом случае реальная трехмерная структура слишком сложна для известных на сегодняшний день методов предсказания; вместо нее мы займемся предсказанием вторичной структуры, то есть просто попытаемся определить, какие основания образуют пары.
Представим молекулу РНК в виде состоящей из п знаков строки R = = Г1Г2 . -. гп, где i’i 6 [А, С, G, U}. Обычно число знаков п измеряется сотнями, но может иметь и порядок тысяч. Вторичная структура молекулы - множество S пар оснований (rt, rj), таких, что выполняется неравенство 1 г < j п. Если пара (гг,гу) G S, то, в принципе, мы должны требовать, чтобы знаки были комплементами знаков г3 и чтобы j — i > i, где t - некоторый порог (потому что известно, что молекула РНК нс свертывается слишком острыми углами). Однако используемый метод предсказания основан на вычислении конформаций с минимальной свободной энергией; таким образом, мы можем избежать вышеупомянутых ситуаций, попросту допуская большие значения свободной энергии соответствующих конформаций.
Существует естественная структура, которую мы не будем учитывать, - гак называемый узел. Узел появляется, когда (г,, zy) € S, (rk,ri) G S иг < k < j < l. Без узлов множество S становится плоским графом. В действительности узлы присутствуют в молекулах РНК, но их исключение упрощает задачу. Наиболее весомая причина для исключения узлов состоит
2В том смысле, что это предмет неустанного поиска, как, например, философский камень для алхимиков, и что нашедшему даруется вечная жизнь (в летописи научных открытий). Прим. перев.
354
Глава 8
в том, что данные от предсказания вторичной структуры используют для последующего приближения к разгадке трехмерного строения РНК и узлы могут быть введены в структуру на этой стадии моделирования.
Итак, задаем необходимый риторический вопрос: Какой алгоритм мог бы быть предложен для предсказания вторичной структуры молекулы РНК? Прежде чем ответить на него, окинем нашу задачу более пристальным взглядом. Как было упомянуто выше, мы будем определять структуры с минимальной свободной энергией. Для этого необходимо некоторым образом вычислять значения энергии генерируемых конформаций. Мы просто допустим, что существует одна или несколько эмпирически полученных функций, которые выполняют эту задачу. Таким образом, простейший из всех возможных алгоритмов был бы следующий: Генерировать все возможные структуры и выбрать одну с минимальной свободной энергией. К сожалению, число возможных структур находится в экспоненциальной зависимости от числа оснований в последовательности и такой алгоритм не был бы практически применим для больших молекул (но все же стоит сказать, что некоторые исследователи разрабатывают и используют такие алгоритмы, основанные на методе перебора). Поэтому мы должны искать другие, более эффективные пути определения структуры с минимальной свободной (нергией. В этом разделе мы представляем две формулировки задачи, которые дают простые алгоритмы метода динамического программирования для достижения поставленной перед нами цели.
Независимые пары оснований
Первая формулировка задачи поиска структуры с минимальной свободной энергией основана на допущении о том, что в любой структуре РНК энергия пары оснований не зависит от состава и расположения всех остальных пар. Это грубое приближение, но оно полезно и поможет нам понять основы более сложных алгоритмов. Сделав такое допущение, выразим полную свободную энергию Е структуры S формулой
Д5) = $2 Q(rbrj), (n,rj)es
(8.1)
где a(ri.rj) — свободная энергия пары оснований (г\,гу). Мы принимаем а(г"г, г,) < 0 при i j и а(г,, rj) = 0 при г = j.
Допущение о независимости энергии пар оснований дает ключ к построению эффективного алгоритма, так как для расчета энергии больших строк мы можем использовать решения, полученные для строк меньшей длины. Например, предположим, что мы хотим определить вторичную
8.1. ПРЕДСКАЗАНИЕ ВТОРИЧНОЙ СТРУКТУРЫ РНК
355
структуру Sij с минимальной энергией для строки Ri.3 = г,гг+1... г}. Рассмотрим возможное поведение основания Tj. Либо оно образует пару с основанием, стоящим в некоторой позиции между г и j, либо нс образует. Если не образует, то = E'(SI j-i). Если основание гу стоит в паре с основанием гг, то мы можем сказать, что E'(Sjj) = а(гг, ту) + E(Sl+\Ly-i). Наконец, может оказаться и так, что основание ту образовало пару с некоторым основанием rjt, где г < k < j. В этом случае мы можем расщепить строку на две: Ri,k-i и Rk,j и сказать, что для некоторого к энергия	= E(St'k-i) + E'(Sjtj). (Это возможно благодаря допущению
об отсутствии узлов в структуре.) Проблема здесь состоит в том что мы не знаем, какое значение k дает минимальную полную энергию, так что функцию энергии мы должны записать в виде E(Sij) = min{	) +
+ E’(Sfcj)}, где параметр к должен изменяться между г и j. Это значит, что мы можем вычислить величину E(Stj) на основании значений, найденных для более коротких строк. Эта ситуация нам знакома: для решения этой задачи мы можем использовать метод динамического программирования. В частности, мы можем преобразовать вышеупомянутые уравнения к следующим выражениям, весьма подобным рекурсивным соотношениям, приведенным в главе 3:
р/С. л _ m:n	+ a(ri>rj)	(8 2)
Случай, когда основание Vj не образует пару, рассмотрен выше (при к — j энергия E(Sj,j) = 0.) Алгоритм вычисления энергии E(Si,n) во многом подобен описанным в разделе 3.2 (необходимо заполнить матрицу размером пхп соответствующими значениями), так что не будем повторяться. Но обратите внимание, что, как и в разделе 3.2, решение рекурсивных соотношений дает нам значение минимальной свободной энергии; реальная структура должна быть найдена на этапе некоторой заключительной обработки данных из матрицы динамического программирования, — так же, как мы получали выравнивание из матрицы сравнения последовательностей.
Вычислим время счета данного алгоритма. В основном алгоритме сравнения последовательностей, приведенном в разделе 3.2, на каждый элемент матрицы мы затрачиваем постоянное время; следовательно, для матрицы размером п х п время счета должно быть равно О(п2). Здесь несколько иная ситуация, поскольку мы должны вычислять суммы, используя переменное число предыдущих элементов матрицы для каждой пары i,j, как
356
Глава 8
показано в выражении (8 2). Точное общее число сумм определяется как
п 3 1
EEu-i-D.	(83)
j=l £=1
то есть равно О(п3) и определяет полное время счета алгоритма3
Структуры с петлями
Теперь ослабим допущение о независимости энергий, чтобы можно было учесть тот факт, что свободная энергия пары оснований зависит от смежных с ней пар. Это ослабление ведет к рассмотрению структур РНК, называемых петлями. Предположим, что (гг, г3) — пара оснований структуры S и рассмотрим позиции и, v и ш, где i<u<v<w<j. Мы говорим, что основание rv достижимо из пары (г,, г,), если пара оснований (ru,rw) не принадлежит структуре S для любых позиций и и w. Петля — множество всех неспаренных оснований, достижимых от пары оснований (г,,г7). Па рис. 8.1 изображены различные виды петель. Допущение об отсутствии узлов подразумевает, что любая структура S расчленяет строку В на непе-рссскающисся петли.
Размер петли — число неспаренных оснований, которое она содер жит. Здесь мы обобщаем понятие петли и рассматриваем пары оснований как петли нулевого размера. Когда несколько пар оснований примыкают дру| к другу, мы получаем так называемые «шпильки»4 или «спиральные области». Таким образом, число петель в структуре определяется числом содержащихся в ней пар оснований.
Пример зависимости свободной энергии от присутствия или отсутствия определенных структур связан с тем фактом, что спиральные области обладают отрицательной (стабилизирующей) свободной энергией, тогда как пегли размером больше нулевого имеют положительную (дестабилизирующую) энергию. Из этого факта следует, что если некоторая пара оснований (л, г^) закрывает петлю, то структура St+ij-i может нс быть структурой с минимальной свободной энергией для подстроки	Другими
словами, может оказаться, что существует структура S'41 j i с более низкой
3 Алгоритм (8.2) определяет только энергию, но при этом структура не восстанавливается’ Советую читателю придумать модификацию этого алгоритма и процедуру обратного прохода для восстановления оптимальной структуры (см. упр. 4). Прим. ред.
4Строго говоря, шпильки это петли особого типа, которые замкнуты одной парой спаренных оснований (см. рис. 8 I, а), а спираль это непрерывная последовательность спаренных оснований (см. рис. 8.1, г). Прим. ред.
8.1 ПРЕДСКАЗАНИЕ ВТОРИЧНОЙ СТРУКТУРЫ РНК
357
Рис. 8.1. Вторичные структуры РНК, не содержащие узлов. Черными кружками обозначены рибонуклеотиды, двойными линиями - пары оснований а - петля так называемой шпильки; б — боковая петля; в — внутренняя петля; г — спиральная область. (Взято из [105].)
358
Глава 8
энергией, чем Sj+ij_i, но когда к энергии структуры S,+ij_ 1 мы добавляем энергию пары (rt,rj), стабилизирующая энергия этой пары становится более чем достаточной для покрытия разницы энергий. Это означает, что в дополнение к соотношениям (8.2) мы должны сформулировать новые рекурсивные соотношения.
Новые рекурсивные соотношения все еще содержат некоторые упрощения по сравнению с полной общей моделью петли. Эти упрощения необходимы для того, чтобы алгоритм динамического программирования был более эффективным. Можно показать, что общая модель ведет к алгоритму с экспоненциальным временем счета.
Первое упрощение заключается в том, что мы пренебрегаем свободными энергиями оснований, которые не принадлежат никаким петлям. Согласно второму упрощению, для того чтобы вычислить полную свободную энергию структуры, мы можем попросту суммировать энергии ее компонентов. Наконец, мы допускаем петли только тех видов, что изображены на рис. 8.1. Рассмотрим эти упрощения подробнее.
Мы хотим определить структуру Зг,3 строки R1}. Сначала предположим, что основание гг не образует пару. Тогда £’(5'г^) = E(Si+i j). Предположим теперь, что неспаренным является основание rj. Аналогично, энергия E(Sij) = E(Si'j-i). Теперь предположим, что основания и г3 образуют пару, но не друг с другом. Тогда мы можем сказать (как мы делали выше для ситуации без петель), что при i < к < j энергия £(S] j)
min{E'(SIjx:) + E(Sk+i.j)}, где z/c — любое основание между парами, стоящими в позициях i и j. Наконец, допустим, что (?у,гу) — пара оснований. Эго означает, что между позициями г и j может находиться одна или более петель. Тогда обозначим структуру с минимальной свободной энергией через Ll} и запишем полное рекурсивное соотношение:
E’(SIJ) = min <
min{E(Sitk) +
для г < к < j
(8.4)
Теперь рассмотрим подробнее случай со структурой Мы должны рассчитывать различные виды петель, показанных на рис. 8.1, а для этого необходимо записать выражения для значений свободной энергии. Как и прежде, мы допустим, что эти значения были определены экспериментально и выражены в виде функций. Свободная энергия пары оснований (ту, гу) определяется функцией а(гу,гу). Кроме этой, мы имеем следующие функции свободной энергии:
8.1. ПРЕДСКАЗАНИЕ ВТОРИЧНОЙ СТРУКТУРЫ РНК 359
£(fc) — дестабилизирующая свободная энергия петли шпильки размером к;
г) - стабилизирующая свободная энергия смежных пар оснований;
fi(k) — дестабилизирующая свободная энергия боковой петли размером к;
Т(А’) дестабилизирующая свободная энергия внутренней петли размером к.
С помощью этих функций мы можем записать следующие рекурсивные соотношения для минимальной свободной энергии Е(Ьг<})'.
если Ьг ] — петля шпильки, то
а(п, г,) + (.(j - г - 1);	(8.5)
если Ll3 — спиральная область, то
о(г,, fj) + т? +	(8.6)
если - боковая петля в позиции i, то
min{a(r„r,) + (3(к) + E(S,+fc+ij-i)};	(8.7)
fc^l
если Lt j	боковая петля в позиции j, то
пйп{а(гг,гу) +/?(fc) +	л)},	(8.8)
если j — внутренняя петля, то
min {о(гг,г^ + 7(/с1+fc2)+£(5г+1+*1,з-1-к2)}-	(89)
Значение энергии E(Ltj) определяют путем выбора минимального среди всех значений, вычисленных по приведенным выше рекурсивным соотношениям. Эти уравнения, вместе с уравнением (8.4), дают нам всю информацию, необходимую для преобразования уже знакомого нам алгоритма динамического программирования для того, чтобы было возможно предсказывать вторичную структуру РНК с петлями. Схематическая компоновка матрицы, представленная на рис. 8.2, показывает се области, в которых значения энергии должны быть известны прежде, чем мы сможем вычислить величину E(Ltj) по рекурсивным соотношениям (8.6)-(8.9).
360
Глава 8
Рис. 8.2. Компоновка матрицы, построенная для вычисления рекурсивных соотношений (8.6)-(8.9). Номера уравнений помечают области матрицы, в которых значения эперпш L(L1>3) должны бьпь известны заранее
Поскольку самая сложная часть алгоритма — это вычисление рекурсивных соотношений для энергии Е(Ьг]), рассмотрим эти соотношения подробнее. Два простейших случая — когда структура Ljj представлена спиральной областью или петлей шпильки. В этих случаях на каждую пару (j,j) мы затрачиваем постоянное время и, следовательно, время счета равно О(п2). В случае боковых петель параметр к варьирует между 1 и разницей j — i. Поэтому этот случай подобен вычислению минимальных энергий в структурах без петель и время счета равно О(п3) (см. уравнение 8.3). И, наконец, вычисление энергии внутренних петель. Поскольку в данном случае мы имеем дело с двумя параметрами, к\ и fco, мы должны оценивать ранее вычисленные значения энергии Е, которые находятся в подматрице, ограниченной элементами i и j. Это означает, что для каждой пары i,j мы должны анализировать подматрицу из О(п2) элементов; таким образом,
8 1. ПРЕДСКАЗАНИЕ ВТОРИЧНОЙ СТРУКТУРЫ РНК
361
полное время счета алгоритма равно О(п4). В более формальной записи мы имеем.
где с — некоторая константа. Величину этой константы определяет время, необходимое для вычисления выражения ст(гг,ту) +	+ А‘г) +
+ E(St+i+k!,3-1-кг) а'чя частных значений переменных г, j, ку и Аг.
Повышение эффективности вычисления энергии внутренних петель
Итак, нам ясно, что в представленной методике вычисление внутренних петель является наиболее затратным. Покажем, как время счета может быть снижено до О(п3). Это возможно, так как по диагоналям матрицы размер петли постоянный. Поясним вышесказанное примером.
Как и раньше, аргументом функции 7 является размер внутренней петли, то есть сумма ку 4- Аг На параметры к] и Аг мы налагаем ограничения 2 ку + Аг j г 2 /mim где Zmjn минимальный размер петли Предположим, что мы хотим вычислить энергию £(£4 is) и что Lmin = 1 Тогда 2 Ai + Аг 11. Пусть в некоторой точке ку = 2 и Аг = б и тогда мы вычисляем значения функций 7(8) и E(Sio 14), а в некоторой другой точке А] = 5 и А2 = 3 и мы вычисляем опять же 7(8) и E(S7tyy). Оказывается, что пары (10,14) и (7,11) лежат на одной и той же диагонали магрицы и размеры петель постоянны.
На этом свойстве основана следующая уловка. Для каждой пары (г,у) мы сохраняем вектор V 7, индексированный значениями всех возможных размеров петель. Существует самое большее 2тг 1 диагоналей, так что этот вектор содержит самое большее 2п — 1 элементов. В каждом элементе мы храним минимальное значение, найденное для каждой диагонали. Та ким образом, когда мы должны вычислить энергию Е(Ьг ]) для внутренней петли и данной пары (г, у), мы должны всего лишь вычислить минимум функции {а(г,,Гу) +7(Z) + Цу[/]} для всех возможных значений I (размера петли). Тогда на каждую пару (г.у) потребуется время О(п) и полное время счета будет равно О(п3) Чтобы наша уловка работала, мы должны организовать вспомогательную матрицу для хранения всех векторов и обновлять эти векторы по мерс обращения к исходной матрице Л£ К счастью, мы можем осуществлять эти операции методом приращений. Например, когда мы переходим от строки г к строке г + 1, каждому элементу строки г + 1 соответствует элемент (диагональ в матрице Л/) вектора Ц 3.
362
Глава 8
Элементы вектора I'i+lj могут быть вычислены путем сравнения элементов строки г + 1 матрицы М с элементами вектора Vltj, что также требует время 0(71). Таким образом, на полное обновление векторов мы тратим то же время О(п3). Из этого следует, что из формулы времени счета алгоритма вычисления внутренних петель мы можем устранить множитель п, но при этом пространство памяти возрастет вдвое.
Данное время счета может быль еще улучшено (подобно усовершенствованиям, полученным в главе 3 для функций штрафов за пропуски), если мы тщательно проанализируем используемые функции свободной энергии Учитывая, что конечные алгоритмы намного сложнее представленных в этой книге, мы не будем описывать эти усовершенствования, ссылки на некоторые источники даны в библиографических примечаниях И все же мы отметим, что с линеиными дестабилизирующими функциями время счета может быть улучшено до О(?12) (для внутренних и боковых петель). Однако эксперименты показали, что дестабилизирующие функции растут по логарифмическому закону.
Описанные нами алгоритмы предсказания структуры РИК имеют серьезный недостаток: они предсказывают только одну структуру. На практике мы хотели бы получить множество возможных решений, и, возможно, некоторые из них будут условно оптимальны в отношении свободной энергии. Причина та же, что и в других задачах, рассматриваемых в этой книге: вследствие упрощения алгоритма за счет различных допущений в модели, найденное оптимальное решение (или вообще любое оптимальное решение) не обязательно будет тождественно истинной структуре. По этой причине было бы весьма полезно расширить вышеупомянутые алгоритмы, чтобы они находили не только оптимальные, но также и условно оптимальные решения в пределах некоторого порога энергии Ссылка на материалы по такому расширению алгоритмов дана в библиографических примечаниях.
8.2.	СВЕРТЫВАНИЕ БЕЛКОВЫХ МОЛЕКУЛ
Вспомним, что главная цель задачи свертывания белка состоит в определении трехмерной структуры белка по последовательности аминокислот. Эту задачу интенсивно исследовали с начала 1950-х гг., но пока что никакое полностью удовлет ворительное решение не было найдено Известно множество интересных работ по этой теме, но настоящий раздел претендует лишь на роль очень краткого введения. В следующем разделе мы представляем один из многих известных подходов к решению этой задачи. Мы верим, что эти два раздела содержат достаточно материала, чтобы дать читателю хо
8.2. СВЕРТЫВАНИЕ БЕЛКОВЫХ МОЛЕКУЛ
363
рошее начало в освоении предмета. Ссылки для более глубокою изучения даны в конце главы.
Важное допущение, принятое во всех методах предсказания сложных структур белка, — гипотеза о том, что последовательность аминокислот полностью и однозначно определяет свертывание молекулы. Обоснованность 1того допущения подтверждается следующим экспериментальным свидетельством. Если мы денатурируем белок in vitro (и при этом никакие другие вещества нс присутствуют в среде), а затем прекратим внешнее воздействие, то белок немедленно свертывается обратно в ту же трехмерную структуру, которую он имел прежде. Процесс свертывания занимает менее одной секунды. Таким образом, вполне очевидно, что вся информация, необходимая белку для восстановления своей «нативной» конформации, содержится в его аминокислотной последовательности. (Этот вывод верен нс для всех белков, потому что существуют белки, которым для правильного свертывания необходимы специфические «вспомогательные молекулы»5.)
Перед обсуждением трудностей предсказания свертывания белка, мы вкрат цс опишем основные сведения о трехмерной структуре белковых молекул. Вспомним из главы I, что белки имеют несколько уровней трехмерной структуры. Выше первичной линейной структуры стоит уровень вторичных структур, которые в свою очередь классифицируются на три основных вида: а-спирали, [3-листы и петли6 — особые структуры, которые нельзя отнести ни к спиралям, ни к листам.
о-Спираль простая спираль, сосгояшая в среднем из 10 остатков, образующих три витка; некоторые спирали могут содержать до 40 остатков Исследования показали, что некоторые аминокислоты появляются в спиралях чаще других, этот факт помогает в предсказании вторичной структуры, но не достаточно силен, чтобы дать точные результаты.
/J-Лист состоит из нескольких связанных между собой сегментов аминокислотной последовательности. Каждый такой сегмент представляет собой /3-нить и обычно содержит от 5 до 10 остатков. Нити продольно при мыкают друг к другу, формируя своего рода складчатый лист. Некоторые аминокислоты выказывают заметное предпочтение /3-нитям, но опять же, их поведение не столь однозначно.
Петли — это участки последовательности, соединяющие вторичные структуры двух других видов. В отличие от спиралей и листов, петли — нерегулярные структуры, как в форме, так и в размере. Вообще, петли находятся вне свернутого белка, тогда как остальные структуры белковой
5Так называемые белки-шапероны, или наставники. Прим, перев.
6На самом деле есть еще целый рад элементов вторичной структуры, однако они не столь распространены — Прим. ред.
364
Глава 8
молекулы формируют ее ядро. Эволюционно родственные белки обычно состоят из одинаковых спиралей и листов, но могут иметь весьма различные нерегулярные структуры. В связи с этим мы говорим, что формирующие ядро сегменты консервативны. Понятие ядра очень важно для следующего раздела.
Известны белковые структуры и более высокого уровня. Их называют мотивами и доменами. Мотив7 — простая комбинация нескольких вто ричных структур, встречающаяся в различных белках. Пример мотива — цепочка типа спираль петля спираль. Исследования показали, что такой мотив является участком связывания атомов кальция, так что функция этой структуры ясна. Другие мотивы, кажется, вообще нс играют никакой роли в функции белка. Домен представляет собой более сложную комбинацию вторичных структур, по своему определению имеет строго специфическую функцию и поэтому содержит активный участок Активный участок сегмент белка, предназначенный для связывания его е определенными молекулами. Белковая молекула может состоять из одного или нескольких доменов. Группа доменов формирует третичную структуру белка.
Сформулируем задачу свертывания белка подробнее. Имея аминокислотную последовательность белка, мы хотели бы алгоритмически обрабо тать ее и определить точное положение всех а-спиралей, /2-листов и петель в структуре, а также их пространственное расположение в мотивах и доменах. Располагая достаточной и надежной химической и физической информацией о каждой входящей в состав белка аминокислоте, в принципе должно быть возможно вычислить свободную энергию конформаций молекулы. Алгоритм предсказания мог бы просто генерировать все возможные конформации, вычислить свободную энергию каждой и выбрать конформацию с минимальной свободной энергией (если допустить, что она представляет модель нативной структуры белка, что не являегся установленным фактом). Теперь обсудим вопрос относительно числа возможных конформаций типичной молекулы белка. Вспомним из раздела 1.2, что белки могут свертываться в основном за счет углов вращения ф и v между атомом о-углерода и соседними атомами. Эксперименты показали, что эти углы могут независимо друг от друга принимать только несколько дис кретных значений; для каждой пары значений в каждом остатке мы имели бы одну возможную конформацию. Предположим, что каждый угол может принять только три значения. Поэтому каждый остаток всякий раз будет
7Это мотив пространственной (а точнее, сверхвторичной) структуры. Не следует путать с мотивами в последовательности Прим, ред
яЭто неверно. В пространстве ф и ф (карта Рамачандраки) есть несколько разрешенных областей. Прим. ред.
8.3. ПРОТЯГИВАНИЕ БЕЛКОВ
365
находиться в одной из девяти возможных конформаций. Таким образом, для белка, состоящего из сотни остатков (который можно счссгь небольшим), существует 9100 возможных конформаций - астрономическое число, которое совершенно исключает алгоритмы, основанные на поиске решения методом перебора.
Но ситуация оказывается еще хуже; даже если ученые признают, что нативная структура — это структура с минимальной свободной энергией, то все равно они никак не могут договориться о том, как именно следует вычислять энергию конформаций. Необходимо учитывать слишком много факторов типа формы и размера макромолекулы, полярности различных входящих в се состав компонентов, относительной силы взаимодействий на молекулярном уровне и т. д Опираясь на современные знания, возмож но лишь сформулировать некоторые общие правила например требования, чтобы в растворе гидрофобные аминокислоты оставались «внутри» белка, а гидрофильные располагались «снаружи» молекулы (вода универсальный растворитель, содержащийся как во внутренней среде клеток, так и в межклеточном пространстве).
Столь плачевное состояние дел вынуждает исследователей довольствоваться лишь методами предсказания вторичной структуры белка. Замечание о трудностях в определении значений свободной энергии третичных структур относится также и ко вторичным структурам. Поэтому для предсказания вторичной структуры белка не известен никакой общий и надежный алгоритм метода динамического программирования. Отсюда широкий ассортимент практических методов: от программ для нейронных сетей до распознавания структур на основании оценки статистических свойств распределения остатков в белках с известной структурой. Однако эти методы все еще не столь надежны, как хотелось бы. По этой причине были развиты другие методы, призванные помочь ученому справиться с непосильной задачей, и именно один из таких методов является темой следующего раздела.
8.3.	ПРОТЯГИВАНИЕ БЕЛКОВ
Старый метод, используемый для предсказания вторичной структуры, был основан на представлении о том, что подобные последовательности должны иметь подобные структуры. Если мы знаем структуру белка А (например, по данным рентгеноструктурного анализа), а белок В сильно подобен ему на уровне последовательности аминокислотных остатков, то кажется разумным предположить, что структуры белка В будут полностью или почти полностью соответствовать структурам белка А. К сожалению,
366
ГЛАВА 8
обычно это не верно. Белки, подобные на уровне последовательности, могут иметь сильно отличающиеся вторичные структуры. С другой стороны, было замечено, что некоторые белки, весьма различные на уровне последовательности, структурно родственны в следующем смысле: Хотя они имеют различные виды петель, их ядра очень подобны. Эти наблюдения привели исследователей к тому, чтобы предложить обратную задачу свертывания белка. Вместо того, чтобы пытаться предсказать структуру белка по его последовательности, мы пытаемся сопоставить его последовательность с известными структурами из базы данных.
Прежде чем сопоставлять структуру с последовательностью, мы должны точнее определить, что именно мы подразумеваем под «структурой». В этом разделе слово «структура» фактически означает структурную модель, и такая модель может быть получена следующим образом. Имея белок, структура которого известна, мы получаем структурную модель, заменяя аминокислоты метками-заполнителями и приписывая к каждой метке-заполнителю несколько основных свойств исходной аминокислоты. Эти свойства могут меняться в зависимости от принятой модели, но они должны нести информацию о том, находилась ли исходная аминокислота в п-спирали, в /3-листе или в петле, а также отражать пространственные ограничения структуры например расстояний до других аминокислот, данных о количестве меток-заполнителей внутри или снаружи целой структуры и т. д. Здесь мы не будем рассматривать такие модели подробно, однако примем допущение о том, что подобное описание локальной структуры возможно.
Построив структурную модель, мы можем выбрать белок с неизвестной структурой и пытаться «выровнять» его с моделью, учитывая при этом свойства, занесенные в данную модель. Этот специальный вид выравнивания известен как протягивание белка9. Как мы увидим, протягивание приводит к точной комбинаторной задаче оптимизации, поскольку может быть много способов протянуть одну последовательность через модель белка. Как и многие другие задачи в этой книге, эта также оказывается НП-трудной. Однако задача может быть подана таким образом, что с помощью известной методики обращения с НП-трудными задачами справиться с ней будет HF -трудно. Успех, достигнутый в применении этого подхода, явился стимулом для написания настоящего раздела. Рассмотрим задачу подробнее.
9В общем метод протягивания напоминает поиск гомологии, только на этот раз последовательность белка с неизвестной структурой выравнивается не с последовательностями белков из БД (структура которых известна), а со структурными моделями этих белков. Название метода связано с тем, что мы «протягиваем» последовательность сквозь ядерные сегменты, пытаясь найти ее наиболее вероятное положение в них. При этом некоторые части последовательности будут «входить» в эти сегменты, а некоторые — выдаваться из них в визе петель. — Прим, перев.
8.3. ПРОТЯГИВАНИЕ БЕЛКОВ 367
Мы допускаем, что вход задачи выглядит следующим образом:
1.	Последовательность белка А, состоящая из п аминокислот аг.
2.	Ядерная структурная модель С, с т ядерными сегментами Сг. Для этой модели мы имеем следующую информацию:
а)	длина сг каждого сегмента ядра;
б)	ядерные сегменты Сг и Сгц связаны петельной областью At, и для каждой области Аг мы знаем се максимальную (ZJnax) и минимальную (Z™,n) длины;
в)	локальная структурная среда для позиции каждой аминокислоты в модели (химические свойства, пространственные ограничения и т.д.).
3.	Функция счета, применяемая для оценки протягивании
Желательный выход множество Т = {tj, t-2, • - , Gn} целых чисел, где значение t, указывает, какая аминокислота из белка Д занимает первую позицию в ядерном сегменте г. Таким образом, прогягивание представляет собой выравнивание между последовательностью и ядерной структурной моделью.
Ясно, что в этой формулировке функция счета играет ключевую роль. При известном протягивании и известных локальных структурных средах, функция счета должна быть способна вычислять аминокислоты последовательности индивидуально в их распределенных позициях в модели, так же, как конечные взаимодействия между различными аминокислотами. Предположительно, взаимодействия могут происходить между парами аминокислот, а также группами из трех, четырех и т.д. оснований.
Если мы пренебрегаем взаимодействиями между отдельными аминокислотами и при этом допускаем петельные области переменной длины, то задача может быть решена стандартными методами динамического программирования. Если мы учитываем взаимодействия пар аминокислотных остатков, то задача становится НП-трудной (см. библиографические примечания). Вместо того, чтобы чрезмерно упрощать модель и таким образом обеспечить себе возможность обращаться к (теперь уже) знакомым алгоритмам динамического программирования, мы постараемся учитывать взаимодействия между парами остатков и покажем, как с помощью стандартного метода решения НП-трудных задач можно найти точное решение и этой задачи. Данный метод известен как метод ветвей и границ. В следующем разделе мы слегка отклонимся от темы, чтобы объяснить этот метод, после чего мы увидим, как он может быть применен для решения задачи проляги-вания с учетом взаимодействий между парами аминокислотных остатков.
368
Глава 8
Метол ветвей и границ
В комбинаторной задаче оптимизации мы ищем оптимальное решение среди многих возможных, составляющих пространство решений. Оптимум относится к максимальному (или минимальному) значению некоторой функции /, которая может быть вычислена для каждого варианта решения. Для большинства задач пространство решений является экспоненциально большим, хотя для задач класса П оптимум может быть найден за полиномиальное время. Однако в случае НП-трудных задач нс известен никакой алгоритм, способный за полиномиальное время найти оптимум в пространстве решений. Поэтому единственная альтернатива, позволяющая получить гарантированно оптимальное решение, - последовательный перебор, оценка всех возможных решений и последующий выбор лучшего. И все же, мы можем постараться немного ускорить этот процесс, применяя следующий метод.
Во первых, ясно, что согласно некоторым ограничениям пространство решений возможно разбить на подпространства. 11апример, имея пространство решений S, мы могли бы разбить его на два подмножества Si и S2-Подмножество Si состояло бы из всех решений, обладающих некоторым свойством, a S2 — из всех тех, которые им не обладают. Это процедура ветвления метода ветвей и границ.
Во вторых, очевидно, возможно получить границу (предел значений) функции оптимизации f для всех вариантов во множестве решений. Этот предел может быть использован для устранения многих решений из области рассмотрения следующим способом. Предположим, что мы решаем задачу минимизации и что мы уже знаем значение f(s) некоторого варианта решения .я. Теперь рассмотрим подмножество X пространства решений и предположим, что мы можем получить нижний предел I для значения любого решения из подмножества X Наконец, предположим, что I > f (s). Эго означает, что ни одно решение из подмножества X нс может улучшить найденное решение и поэтому все они должны быть отброшены. Если, напротив, I < /(•>), то мы должны исследовать подмножество X, потому что оптимум может в нем находиться.
Таким образом, мы видим, что ключевые компоненты алгоритма минимизации, основанного на методе ветвей и границ, правило разбиения пространства решений некоторым эффективным способом и нижний предел значений функции оптимизации для вариантов решения. Нижний предел должен быть как можно ближе к действительному значению функции, с тем чтобы мы могли найти оптимум быстрее, чем с более слабым нижним пределом; помимо этого, он должен быть вычислим эффективно. Однако
8.3. ПРОТЯГИВАНИЕ БЕЛКОВ
369
мы должны иметь в виду, что в наихудшем случае время счета алгоритмов метода ветвей и границ, примененных к НП-трудным задачам, всегда экспоненциально
Приложим эти понятия к задаче протягивания белка. Сначала мы должны определить возможные решения, для чего необходимо перечислить ограничения, с которыми сталкивается каждое возможное протягивание. Пространственные ограничения могут быть описаны следующими неравенствами:
1 + £(с, +	< tt < п + 1 -	+ /™п).
Э<«
Еще одно ограничение связано с тем, что любое протягивание должно подчиняться порядку ядерных сегментов в модели (в более общем подходе оно может быть ослаблено):
+ Cj + /J""1 ^г+1 tj + Q - /уаХ-
Эти ограничения подразумевают, что все первые позиции t, должны лежать в интервалах, определяемых величинами Ьг и ег. Таким образом, множество возможных протягиваний может быть выражено множеством интервалов: один интервал для каждой первой позиции t, в т ядерных сегментах (см. рис. 8.3).
Теперь можно объяснить ветвящуюся часть алгоритма. Выбираем один ядерный сегмент, например ?, и позицию щ из интервала [Ьг, е,]. Разобьем пространство решений на три подмножества: то, в котором новый интервал для будет Ьг, щ — 1), второе, в котором новый интервал для С будет [г/, 4-+ l.ej], и третье, в котором позиция вынуждена быть равной позиции и,. Мы ничего не сказали ни о выборе ядерного сегмента, ни о выборе позиции в интервале сегмента. Например, этот выбор может быть сделан на основании оценки размера интервала
Обратимся теперь к нижнему пределу. Функция счета может быть выражена уравнением
/СЛ =	+ 1252й2(г,7,^,^),
(8.10)
где Т — некоторое протягивание.
Обратите внимание, что функция счета оценивает ядерные сегменты, а не отдельные аминокислоты. Это связано с тем, что значение переменной t, определяет позицию всех аминокислот из последовательности белка А в ядерном сегменте г, и, следовательно, пара аргументов (г, ti) полностью
370
Глава 8
определяет сегмент г. Первый член в правой части уравнения (8.10) вносит вклад каждого отдельного ядерного сегмента в общее значение функции, тогда как второй член вносит вклад пар ядерных сегментов. Функции д\ и Р2 — часть входа задачи.
Рис. 8.3. Множества протягиваний. Ядерные сегменты изображены в виде многоугольников с обозначенными стартовыми позициями г — 1, г и i + 1. Между ними расположены петельные области. Горизонтальная линия внизу — протягиваемая последовательность; штриховые стрелки показывают интервалы позиций в последовательности, которым может соответствовать первая позиция каждого ядерного сегмента, то есть изображают множества возможных протягиваний
Простой нижний предел для известного множества протягиваний Т определяется следующим образом:
min /(Г) = min £ Si М + 52 ®2('’ 3, h,
rnin/(T)>^2 тй» + V min </2(i,j,y,z) t |_	J>i
(8-П)
(8-12)
8.3. ПРОТЯГИВАНИЕ БЕЛКОВ
371
Algorithm Protein Threading10
input: последовательность белка, ядерная структурная модель функции счета и функция нижнего предела /ц,
output: протягивание Т
Т «— все возможные протягивания
lb fib(T)
И Используем приоритетную очередь Q для хранения протягиваний
И В Q каждый элемент — множество протягиваний
И и его нижний предел
Jnsert(Q, Т, lb) while истина do
И Удаляем множество вариантов протягивания из Q
Тс *— RemoveMin(Q)
if I Тс I = 1 then
return Tc
// Единственное оставшееся протягивание — искомое решение else
Split(Tc)
for каждого нового подмножества Tt множества Тс do
1Ьг 4 flblTi)
Insert(Q, Ti, lb,)
Рис. 8.4. Основанный на методе ветвей и границ алгоритм протягивания белка
Этот нижннй предел вычисляется путем суммирования нижннх пределов каждого члена в отдельности. Может быть найден и более строгий нижний предел (см. упражнение 7). Желательно получить нижний предел для отдельного протягивания, потому что соответствующее ему протягивание может быть использовано в процессе разбиения пространства решений. Предположим, что протягивание Т в настоящее время имеет минимальное значение нижнего предела. Из этого протягивания мы выбираем один ядср-ный сегмент С, и разбиваем его в точке гг„ определяемой данным протягиванием. Выбранный ядерный сегмент может быть сегментом с максимальным размером интервала. Описание алгоритма приведено на рис. 8.4.
На этом мы завершаем описание применения алгоритма метода ветвей и границ к задаче протягивания белка. Мы заканчиваем настоящий раздел несколькими комментариями относительно использования этой методики. Во-первых, эта методика совсем новая и поэтому должна быть подвергнута различным испытаниям. Эти испытания могут быть грубо разделены на три категории. В первом испытании, после того, как получена структурная
|0Протягивание белка. — Прим, перев.
372
Глава 8
модель некоторой структуры, мы выполняем самопротягивание; то есть мы протягиваем ту самую последовательность белка, на основе которой была построена данная структурная модель. Второе испытание вовлекает белки, которые являются генетически близкими (и, следовательно, содержат подобные последовательности) и имеют подобные структуры (гомологичные белки). Заключительное испытание вовлекает структурные ана юги структурно подобные белки, но состоящие из различных последовательностей. В этих испытаниях все структуры известны заранее, так что мы точно знаем, каким должен быть ответ, и можем обнаружить аномалии. Ободрительные результаты получаются, если найденная структура в целом хорошо приближена к образцовой. В случае присутствия ошибок относительно легко задать дополнизельные ограничения и избавиться от них. Это еще одно преимущество данной методики, и, следовательно, она позволяет использовать большой объем информации о характерных особенностях структуры белка, которая накапливалась в течение многих лет.
Каргина практической реализации этой методики должна выглядеть примерно так: Поддерживается база данных структурных моделей. Исследователь расшифровывает новую последовательность белка и представляет ее серверу базы данных. Программа поочередно выравнивает последовательность со всеми моделями из базы данных и возвращает одну или несколько моделей, с которыми было найдено хорошее соответствие. Обратите внимание, что это означало бы решение одной задачи протягивания белка для каждой структурной модели в базе данных, — проблема, которая требует быстрого поиска решения каждой такой задачи.
РЕЗЮМЕ
В этой главе мы представили краткую выборку алгоритмов предсказания молекулярной структуры. Мы изучили два алгоритма метода динамического программирования для предсказания вторичной структуры РНК, а также показали, как можно улучшить время счета самого сложного алгоритма от О(п4) до О(п3). Затем мы кратко объяснили задачу свертывания белка, указав, что многочисленные исследования способствовали разработке многих подходов к ее решению, из которых мы представили один, называемый протягиванием белка. Этот подход опирается на алгоритмическую обработку, основанную на все той же методике решения НП-трудных задач.
УПРАЖНЕНИЯ
1.	Определите вторичную структуру следующей последовательности РНК: AUGGCAUCCGUA. Постарайтесь получить структуру с максимальным числом пар оснований.
БИБЛИОГРАФИЧЕСКИЕ ПРИМЕЧАНИЯ
373
2.	Приведите пример последовательности РНК, в которой может появиться узел
3.	Напишите подробную программу алгоритма метода динамического программирования для предсказания структуры РНК. Примите допущение о независимости энергии пар оснований.
4.	Постройте алгоритм восстановления вторичной структуры РНК, вычисленной по рекурсивному соотношению (8.2).
5.	Мы упомянули, что вид дестабилизирующей функции, используемой в предсказании вторичной структуры РНК, может влиять на время счета алгоритма метода динамического программирования. Объясните, почему это так, используя в качестве примеров линейную, логарифмическую и квадратическую дестабилизирующие функции или простую таблицу соответствия.
6.	Докажите, что задача протягивания белка является НП-полной.
7.	Предложите более строгий нижний предел функции счета протягивания.
8.	Отыщите все НП-трудныс задачи в этой книге и попытайтесь построить алгоритмы метода ветвей и границ для их решения.
* 9. Вычисление нижнего предела (8.10) требует вычисления всех точек, попадающих в некоторый интервал (в случае gi), или всех точек, попадающих в некоторую область (в случае <?2)- Каким образом мы можем предварительно обработать все точки, чтобы решение этих задач было эффективным?
БИБЛИОГРАФИЧЕСКИЕ ПРИМЕЧАНИЯ
Общая opi анизация раздела 8.1 основана прежде всего на статье Цук-кера [207], которая содержит много дополнительного материала. Принцип улучшения времени счета вычисления внутренних петель взят из статьи Уо-термена и Смита [201]. Дальнейшие улучшения времени счета специальных классов функций были достигнуты Эшицтейном, Галилом и Жанкарло [55], а также Лармором и Шибером [121]. Работа над вычислением оптимальных и условно оптимальных структур в пределах некоторого порога энергии была проведена Цукксром [206] Неплохой общий обзор методов предсказания структуры РНК даст статья 1 срнсра и Сугимото [ 186].
Задаче свертывания белка посвящена колоссальная масса литературы. Здесь мы указываем несколько недавних важных обзоров. Ричардс [161]
374
Глава 8
представил краткий обзор, рассчитанный на широкую аудиторию. Крейтон [38] приводит технический обзор. Различные молекулярные взаимодействия, играющие роль в свертывании белка рассмотрены Диллом [48]. Наше обсуждение задачи свертывания белка частично опирается на статью Канехиса и Дслиш [105]. Два рисунка перерисованы из этой статьи. Вычислительная трудность предсказания свертывания белка была изучена Унгером и Моултом [189], а также Френкелем [65], которые доказали, что получение белковых конформаций с минимальной энергией с помощью простых решетчатых моделей является НП-трудной задачей. Бергер [21], а также Бергер и Вильсон [22] представляют успешный подход для распознавания мотивов белка.
Раздел, посвященный задаче протягивания белка, основан на работе Лэтропа и Смита [123]. Рисунок 8.3 перерисован с подобного же рисунка из их статьи. Эта статья содержит много дополнительного материала по проведенным испытаниям, а также детальное описание различных методов ускорения вычислительного процесса. Лэтроп [122] доказал НП-полноту задачи протягивания белка с петельными областями переменной длины и учтенными взаимодействиями пар аминокислот.
Глава 9
ЭПИЛОГ: ВЫЧИСЛЕНИЯ С ПОМОЩЬЮ ДНК
В этой книге мы познакомили читателя с интересными алгоритмами, призванными помочь ему в решении задач молекулярной биологии. В этой главе мы представляем удивительные результаты, отвечающие противоположной цели: использовать методы молекулярной биологии для решения трудных алгоритмических задач. Эти результаты явились толчком для захватывающей экспедиции к новому полю научной деятельности, названному вычислением с помощью ДНК, конечная цель которой - создание высокоэффективных биомолекулярных компьютеров. До практического освоения целины еще очень и очень далеко, но настойчивые усилия ученых, постоянно направленные на ее возделывание, очевидно, дадут первые всходы уже в недалеком будущем.
9.1.	ЗАДАЧА О ГАМИЛЬТОНОВОМ ПУТИ
В этом разделе мы описываем метод решения задачи о Гамильтоновом пути в ориентированных графах с помощью молекул ДНК. Число лабораторных процедур этого метода линейно возрастает с увеличением числа вершин графа. Вспомним из раздела 2.3, что задача о Гамильтоновом пути НП-полная. Этот метод отнюдь не доказательство того, что П = НП, потому что в основу его заложен алгоритм метода решения задачи «в лоб», выполняющий экспоненциальное число операций. Но почему число лабораторных процедур линейно? Это достижение возможно благодаря тому, что в первой такой процедуре экспоненциальное число операций проводят параллельно.
Формальное описание задачи выглядит следующим образом. Имея ориентированный граф G = (V, Е), где |V| = п и |£| = т, и две выдающиеся (в геометрическом смысле) вершины s и t, требуется проверить, содержит ли этот граф путь (s, щ, г>2 - -., t), длина которого (выраженная в числе
376
ГЛАВА 9
ребер) равна п — I и вес вершины которого различны. Такую задачу мы называем задачей об ориентированном Гамильтоновом пути (ОГП). Пример задачи показан на рис. 9.1. Алгоритм решения в лоб очень прост: генерируем вес возможные пути, содержащие точно п — 1 ребро, и затем проверяем, подчиняется ли один из этих путей ограничениям задачи. Существует самое большее (п — 2)! таких путей, потому что для первой вершины пути мы можем выбрать (п — 2) вершины, для второй вершины пути мы имеем (п — 3) возможности выбора и т. д.
Представленный ниже алгоритм генерирует пути иным способом. На первом шаге алгоритм генерирует огромное число случайных путей. Тот факт, что генерируются именно случайные пути, позволяет генерировать их независимо друг от друга, и, следовательно, получать вес пути одновременно. С другой стороны, алгоритм становится вероятностным. Полный алгоритм включает в себя следующие этапы решения:
1.	Генерируем случайные пути.
2.	Пт всех путей, генерированных на предыдущем этапе, оставляем только те, что начинаются вершиной s и оканчиваются вершиной t.
3.	Из всех оставшихся путей оставляем только те, что содержат точно п вершин.
4.	Из всех оставшихся путей оставляем только тс, которые посещаю г каждую вершину по крайней мере один раз.
5.	Если остался хотя бы один путь, то возвращаем ответ «да»; в противном случае возвещаем: «нет».
Опишем принципы практической реализации этих этапов в лабораторных условиях.
9.1. ЗАДАЧА О ГАМИЛЬТОНОВОМ ПУТИ
377
Генерация случайных путей
Мы допускаем, что случайные однонитевые последовательности ДНК с 20 нуклеотидами имеются в наличии и что генерация астрономических количеств (более 1О10) копий коротких нитей ДНК нс представляет никакой сложности. Вспомним, что S обозначает обратный комплемент строки S.
•	Представление вершин'. Выбираем наугад п различных однонитевых последовательностей ДНК длиной 20 знаков и к каждой вершине v приписываем последовательность Sl;. Для каждой такой последовательности получаем ес обратный комплемент Sv. Генерируем много копий каждой последовательности 5’„ в пробирке Т).
•	Представление ребер: Если ребро (г/, v) G Е, то строим последовательность Suv, сцепляя суффикс (10 оснований) последовательности Su с префиксом (10 оснований) последовательности Sv. Суффиксы и префиксы отличаются направлением нитей ДНК 5' —» 3'. При и = s используется целая последовательность Ss, и, следовательно, сцепление Ssv состоит из 30 оснований. Гак же поступаем при v = t. Обратите внимание, что при таком построении Suv Svu. Генерируем много копий каждой последовательности Suv в пробирке 7г-
•	Построение путей: Вливаем содержимое пробирок Т\ и 7г в пробирку 7з- Мы допускаем, что в пробирке 7з происходит любое произвольное связывание последовательностей (то есть в пробирке 7з находится много различных лигаз).
Выполнив эти три шага, мы получаем множество случайных путей. Почему случайных? 11оясним этот вопрос на примере. Рассмотрим последовательности Su, Sv, Sw, Suv и Svw, где и, v и w — различные вершины графа. Поскольку множество копий этих последовательностей свободно плавает в пробирке 7з, есть высокая вероятность того, что суффикс (10 оснований) последовательности Su свяжется с префиксом (10 оснований) некоторой последовательности Suv (вследствие комплементарности); в то же самое время суффикс (10 оснований) той же последовательности S,^увязывается с префиксом (10 оснований) случайной последовательности Sv, чей суффикс (10 оснований) связывается с префиксом (10 оснований) некоторой последовательности Svw. И в то же самое время суффикс (10 оснований) этой же последовательности Svu, связывается с префиксом (10 оснований) произвольной последовательности Sw. Полученная таким образом конечная двойная нить кодирует путь (и, v, w) в графе G. Иллюстрируем этот механизм наглядным примером иа рис. 9.1. Пусть граф G построен на п = 7
378
Глава 9
вершинах. Предположим, что для представления вершин 2, 4 и 5 выбраны следующие последовательности:
S2 = GTCACACTTCGGACTGACCT
S4 - TGTGCTATGGGAACTCAGCG
S5 = CACGTAAGACGGAGGAAAAA
Обратные комплементы этих последовательностей следующие:
S2 ~AGGTCAGTCCGAAGTGTGAC
Si = CGCTGAGTTCCCATAGCACA
S5 = TTTTTCCTCCGTCTTACGTG
Мы строим ребра (2,4) и (4,5) и получаем следующие последовательности:
(2,4) = GGACTGACCTTGTGCTATGG
(4, 5) = GAACTCAGCGCACGTAAGAC
Наконец, путь (2,4,5) будет закодирован следующей двойной последовательностью оснований:
(2.4) а	,,
GTCACACTTC GGACTGACCTTGTGCTATGG...
CAGTGTGAAGCCTGACTGGAACACGATACCCTTGAGTCGC...
«— S2	Si
,(Vj)	3,
... GAACTCAGCGCACGTAAGAC GGAGGAAAAA
..GTGCATTCTGCCTCCTTTTT
Дальнейшие этапы вычислений алгоритма зависят от допущения о том, что с высокой вероятностью все возможные пути в графе на п вершинах могут быть представлены по крайней мере одной двойной нитью. Кроме того, обратите внимание, что число 20 было выбрано для уменьшения вероятности того, что две последовательности, приписанные к двум различным вершинам, будут иметь обшие длинные подпоследовательности. Если это происходит, то мы получаем двунитевые последовательности, не кодирующие никаких путей в графе.
9.2. ЗАДАЧА ВЫПОЛНИМОСТИ
379
Последующие шаги алгоритма
После генерации множества случайных путей мы пропускаем содержимое пробирки Тз через последовательные биохимические сита, которые вы бирают пути с необходимыми свойствами. Шаг 2 выполняют посредством ПЦР (см. раздел I 5 2), используя праймеры Ss и St. Шаг 3 осуществляют отделением двунитевых ДНК, имеющих точно 20п оснований и поэтому представляющих пути, содержащие точно п вершин. Шаг 4 осуществляют, выбирая нити, где для каждой вершины и 6 V, отличной от s и t, присутствует последовательность Su. В заключительном шаге мы оцениваем то, что у нас осталось, применяя обычный гель-электрофорез.
Дадим оценку этому алгоритму. Для построения графа необходимо выполнить число операций, пропорциональное его размеру. После этого мы должны выполнить серию операций, число которых пропорционально числу вершин в графе, главным образом из-за шага 4. На этом шаге мы должны последовательно проверять присутствие в пробирке каждой представляющей вершину последовательности.
9.2.	ЗАДАЧА ВЫПОЛНИМОСТИ
В этом разделе мы опишем методику применения подхода, подобного представленному в предыдущем разделе, для решения задачи выполнимости. Это очень важная задача в теории вычислений, так как она была первой, причисленной к классу НП-полных задач. Кроме того, обобщение описанного здесь алгоритма дает общий подход к непосредственному решению любых НП-полных задач (см. упражнение 4).
Следующие несколько определений помогут объяснить задачу выполнимости. Бучева переменная — это переменная, которая может принимать шачения 0 либо 1. Из Булевых переменных можно составлять формулы, используя операторы V (логическое или), А (логическое и) и круглые скобки. Кроме того, переменную х мы можем использовать также в инвертированном виде, х. Это означает, что если значение х равно 1, то значение х равно 0; и наоборот. Форму, в которой мы используем переменные, называю! буквенной. Можно показать, что любая Булева формула может быть выражена набором предложений, где каждое предложение - набор букв, связанных только оператором V, каждое предложение ограничено круглыми скобками, и предложения связаны друг с другом оператором А (мы говорим, что такие формулы записаны в нормальной конъюнктивной форме) Пример такой формулы — F = (ад V тг) А (тг V Х3) А (х3). Мы будем рассматривать формулы, состоящие из п переменных, т предложений и фиксированно
380
Глава 9
го числа букв в предложении. Задача выполнимости заключается в поиске такого присвоения значений переменным, которое удовлетворяет данной формуле, то есть присвоения, при котором решение формулы имеет значение 1. В нашем примере присвоение Xi = 1, Хг = 0 и а.'з = 0 удовлетворяет формуле F, тогда как любое другое присвоение не удовлетворяет. Вообще, для формулы может может быть найдено как более одного, так и ни одного удовлетворяющего присвоения.
Алгоритм проверки выполнимости формул заключается в проверке всех возможных значений переменных. Очевидно, что для п переменных существует 2" таких присвоений. Более систематический способ проверки возможных вариантов присвоения и притом фактически применяемый для решения задачи выполнимости с помощью ДНК, состоит из следующих шагов:
1.	Генерируем все возможные 2П присвоений и помещаем их во множество So-
2.	Из всех присвоений во множестве So оставляем только тс, которые удовлетворяют предложению I, и помещаем их во множество Si.
3.	Из всех присвоений во множестве Si оставляем только те, которые удовлетворяют предложению 2, и помещаем их во множество S-_>.
тп Из всех присвоений во множестве Sm > оставляем только те, которые удовлетворяют предложению т, и помещаем их во множество Sm.
После шага т выполняем еще одну операцию: Если множество Sm непустое, то возвращаем ответ «да»; иначе выдаем: «нет».
Чтобы осуществить эти операции на молекулах ДНК, мы должны знать некоторый код присвоений Булевых переменных. Будем осуществлять кодирование на графе. Для каждого отдельного числа переменных необходимо построить один граф; таким образом, Gn - зраф для задачи с п переменными. На рис. 9.2 показан граф Gn при п = 3. Заметим, что граф G„ ориентированный и что он имеет вершины трех типов: вершины типа пг, где	а также вершины типа Xj и типа Xj, где 1 j п.
Каждое возможное присвоение будет соответствовать одному частному пути (г?1 — оп+1) в этом графе следующим образом. Начав обход с вершины щ, мы можем идти либо в вершину а?], либо в вершину xj. Выбор вершины xt означает присвоение переменной xi значения 1; выбор вершины Xi означает присвоение переменной Xj значения 0. Затем путь должен идти через вершину vq, и снова мы должны сделать выбор, который будет соответствовать значению, присвоенному переменной хг, и так далее. Таким образом.
9.2. ЗАДАЧА ВЫПОЛНИМОСТИ
381
Рис. 9.2. Пример графа, в котором пути вида (n — iy>+i) кодируют присвоения значений Булевым переменным
путь (dj — v„+i) в графе Gn кодирует n-битовое число, соответствующее одному частному присвоению Булевых значений п. переменным.
Следующий шаг после такого кодирования — построение всех путей в графе Gn, что мы делаем точно так же, как в задаче об ориентированном Гамильтоновом пути (см. предыдущий раздел). Таким образом, отправная точка в нашем ДНК-алгоритме задачи выполнимости — пробирка То. содержащая огромное число последовательностей, представляющих пути в графе Gn; с высокой вероятностью в пробирке То будут присутствовать последовательности, представляющие все пути (гч — tM+i) в графе.
Для выполнения следующих шагов нам необходимы следующие (двух видов) операции с пробирками: Обнаружить и Извлечь. Обнаружить — операция, уже применявшаяся в задаче об ориентированном Гамильтоновом пути (шаг 5); она просто сообщает, содержит ли пробирка определенную последовательность ДНК. Операция Извлечь подобна операциям, использованным в алгоритме для задачи об ориентированном Гамильтоновом пути, — в том смысле, что мы применяем ее для извлечения последовательностей, обладающих заданным свойством. Здесь мы интересуемся только одним специфическим свойством: Мы применяем операцию Извлечь к пробирке Т, чтобы выбрать из нее последовательности ДНК, содержащие заданную точную подстроку ДНК фиксированной длины. Вовсе нс требуется, чтобы из пробирки Т были извлечены все такие последовательности; таким образом, не страшно, если в пробирке Т среди оставшихся последовательностей есть все еще некоторые, которые содержат данную подстроку. Проблема возникает тогда, когда мы извлекаем последовательности, которые не обладают требуемым свойством, или когда мы не в состоянии извлечь необходимые последовательности, содержащиеся в пробирке Т. Несмотря на то, что на практике такие неудачи весьма вероятны, в этом разделе мы допускаем, что операция Извлечь работает идеально.
Опишем процесс обработки первого предложения формулы F. Допустим, что это предложение записано в виде (a:j V Жг)- Рассмотрим первую
382
Глава 9
букву этого предложения, Xi. Поскольку она не инвертирована, вариантом искомого решения будет присвоение = 1. Таким образом, в первой позиции (при чтении слева направо) соответствующего п-битового числа стоит 1. Точно так же, присвоение зу = 0 — другой возможный вариант. Объединяя эти варианты, мы можем сказать, что формуле F, возможно, удовлетворяют только n-битовые числа с 1 в первой позиции или с 0 во второй позиции; все остальные не годятся. Это означает, что мы должны извлечь из пробирки То все последовательности, кодирующие n-битовые числа, которые удовлетворяют этому требованию. Тогда эти последовательности будут входом для процедуры обработки следующего предложения формулы.
Algorithm DNA Satisfiability'
input: пробирка То с последовательностями, кодирующими все n-битовые числа.
Булева формула F в нормальной конъюнктивной форме
(п переменных и т предложений)
output: ДА, если F выполнима, иначе — НЕТ
// Используем фиксированное число вспомогательных пробирок At for i *— 1 to m do
Ao ♦— Tj_i
for j «— 1 to Ц do // Ц — число букв в предложении i
if Vj = Xj then
A} «— Извлечь^A'j	1)
else Aj +— ff3&3e4b(Aj_j, j, 0)
Aj*—A’ j // остаток
Тг ♦— Ai + Ao + • • • + Ац
if Обнаружить(Тт) then return ДА else return IIFT
Рис. 9.3. Д11К-алгоритм решения задачи выполнимости
Из вышеприведенного Описания становится ясно, что операция Извлечь должна быть представлена в формате Извлечь(Т, г, Ь), где Г пробирка, г — индекс переменной, а Ь значение Булевой переменной. Теперь мы можем более формально описать шаги обработки первого предложения, при допущении о том, что оно состоит из двух букв:
// То, Ti, Aj, Aj, Аг — пробирки
II Vi — первая буква
if vj = Xi then
4i <— Извлечь (То, 1,1)
1 ДНК-выгюлнимость. Прим, персе.
9.3 ПРОБЛЕМЫ И ПЕРСПЕКТИВЫ
383
else // vi = ал
Л1 «— Извлечь(То, 1,1)
«— То // остаток
// 1>2 - вторая буква
if V2 = Х2 then
А? «— Изе /ечь(Л'1.1,1)
else Лг	Извлечь(А\, 1 0)
Т\ ♦— А] + Лг // Смешиваем содержимое пробирок
Заметим, что при обработке второй буквы мы извлекаем последовательности из остатка от первого извлечения. Это замечание существенно для правильной работы алгоритма. Должно быть ясно, что если бы предложение имело вид (тт V х), то в пробирке 7) мы получили бы все последовательности кодирующие n-битовые числа с 1 в первой позиции (которые были в пробирке Л]), и все последовательности, кодирующие п-битовые числа с 0 во второй позиции (которые были в пробирке Лг). Используя пробирку Г], мы готовы перейти к следующему предложению, где шаги обработки подобны уже описанным Полный алгоритм приведен на рис. 9.3.
Вполне очевидно, что этот алгоритм выполняет О(т) операций Извлечь и только одну операцию Обнаружить.
93.	ПРОБЛЕМЫ И ПЕРСПЕКТИВЫ
Когда алгоритм из раздела 9.1 был впервые использован (на графе с семью вершинами), он показал неплохие результаты и подтвердил осуществимость ДНК-подхода. Но есть несколько проблем, которые должны быть разрешены прежде, чем перспектива вычислений с помощью ДНК может быть реализована на практике. Некоторые из трудностей перечислены ниже.
Может ли подход ДНК конкурировать с современными алгоритмами на электронных вычислительных машинах при решении задачи об ориентированном Глмильтоновом пути? Не в настоящее время, очень не скоро и по двум причинам. Во-первых, в настоящее время с помощью этого подхода могут быть решены только маленькие варианты задачи об ориентированном Гамильтоновом пути. Для представления графа на п вершинах (допустим с запасом) нам понадобится по крайней мере 2" молекул, кодирующих отдельные пути. Так, для представления графа на 100 вершинах нам потребовалось бы приблизительно 1О30 молекул. Известно, что в одном грамме воды находится не более 1023 молекул. Таким образом, для решения
384
Глава 9
задачи на 100 вершинах нам понадобилось бы, по самым скромным оценкам, 107 грамм, или... 10 тонн воды! Вторая причина состоит в том, что хотя в этом методе решения используется небольшое число лабораторных процедур, на их выполнение уходит много времени. Однако можно ожидать, что большая часть операций вскоре будет автоматизирована. С другой стороны, к настоящему времени разработаны компьютерные программы, способные решить варианты задачи коммивояжера (которая, несомненно, по крайней мере столь же трудна, как задача об ориентированном Гамильтоновом пути) на 100 вершинах в течение нескольких минут; кроме того, были решены намното большие варианты (с тысячами вершин), хотя из этого вовсе не следует, что эти программы могут быстро решить новой большой вариант задачи.
Какие ошибки могут возникнуть? Как мы неоднократно показывали в этой книге, биохимические эксперименты всегда содержат ошибки; и это, конечно, относи гея и к процедурам, описанным в настоящем разделе. Более того, в таком подходе компонент случайности присутствует уже в самом начале процесса; но биохимические ошибки вызывают намного большее беспокойство. Онн могут появиться при разделении нитей операцией Извлечь.
Мы можем пропустить «хорошую» нить или извлечь «плохую». Существуют различные методы, призванные уменьшить возможность наступления таких событий, и этот вопрос активно исследуется. Другой источник ошибок - процесс постепенного распада ДНК в пробирке с течением времени, так что лабораторные процедуры не должны превышать допустимый временной предел.
Можно ли применять зтот подход для решения других задач? Здесь мы привели только алгоритмы решения задачи об ориентированном Гамильтоновом пути и задачи выполнимости. Даже при том, что любая НП-полная задача может быть преобразована в любую другую за полиномиальное время, было бы хорошо, если бы мы могли использовать этот подход для непосредственного решения задач класса НП. Алгоритм решения задачи выполнимости - фактически, шаг в этом направлении (см. упражнение 4). Однако наша конечная цель — создание универсального ДНК-компьютера. Материал этой главы показывает, что в принципе такие компьютеры возможны и что они могут работать намного быстрее и потреблять намного меньше энергии по сравнению с обычными компьютерами. Если когда-нибудь эта мечта осуществится, то, вероятно, мы сможем сесть за такую машину и раскрыть многие еще не разгаданные тайны молекулярной био
логии.
УПРАЖНЕНИЯ
385
УПРАЖНЕНИЯ
1.	Предположим, что входной граф ДНК-алгоритма решения задачи об ориентированном Гамильтоновом пути содержит I 000 вершин, и допустим, что искомый путь был найден. Как мы можем определить сам путь?
2.	Покажите, каким образом мы можем использовать ДНК для анализа орграфов на содержание Гамильтоновых циклов.
3.	Определите вероятность появления неправильного пути в алгоритме решения задачи об ориентированном Гамильтоновом пути в графе на семи вершинах. Иными словами, определите вероятность того, что суффикс (10 оснований) случайной последовательности из 20 оснований является обратным комплементом суффикса (10 оснований) другой случайной последовательности из 20 оснований. Как эта вероятность изменяется в зависимости оз числа оснований в последовательностях? Как эта вероятность зависит от числа вершин графа?
* 4. Обобщите ДНК-алгоритм для задачи выполнимости так, чтобы с его помощью могла быть решена любая Булева формула. Определение общей Булевой формулы дано в следующей рекурсивной форме: а) любая переменная .т — формула; б) если F есть формула, то и F - также формула; в) если F, и F2 — формулы, то предложения Г V F2 и Е, Л F2 также являются формулами.
БИБЛИОГРАФИЧЕСКИЕ ПРИМЕЧАНИЯ И ДРУГИЕ ИСТОЧНИКИ
Крупное достижение, приведшее к созданию области вычислений с помощью ДНК, стало возможным благодаря Эйдлмену [2], открывшему способ решения задачи об ориентированном Гамильтоновом пути посредством манипуляций с молекулами ДНК. Затем Липтон [ 128] расширил этот результат на задачу выполнимости и с его помощью доказал, что любая НП-полная задача поиска может быть непосредственно решена ДНК-подходом. Карп, Кеньон и Ваартс [112] изучали способы учета ошибок, свойственных основанным на ДНК методам, и указали на многие другие статьи, посвященные этой теме. Хотя область вычисления посредством ДНК зародилась лишь в конце 1994 года, объем соот ветствующей литературы растет удивительно быстро.
В этой заключительной главе мы пользуемся возможностью дать ссылки на дополнительные источники информации по вычислительной молекулярной биологии. Весьма интересная книга Уотермсна [199] содержит
386
Глава 9
дополнительные темы и, в частности, описание некоторых статистических вопросов. «Журнал вычислительной биологии», посвященный этой области, начал публикацию в 1994 году и может быть посещен по адресу:
http://brut.gdb.org/compbio/j cb/
Отдельные статьи по вычислительной биологии иногда можно встретить в журналах по теоретической информатике и математике, например: «Журнал алгоритмов», «Журнал вычислений СИАМ», «Журнал по дискретной математике СИАМ» и «Достижения прикладной математики». Другие тематические журналы — «Бюллетень математической биологии» и «Компьютеры в биологических науках».
Результаты более поздних исследований могут быть найдены в тезисах исследовательских конференций. «Международная конференция по вычислительной молекулярной биологии» (RECOMB) — ежегодная конференция, посвященная молекулярной биологии; первое заседание прошло в январе 1997 года. Другая важная встреча - ежегодная конференция «Интеллектуальные системы для молекулярной биологии», где для поиска нужных статей предусмотрены методы искусственного интеллекта. Ежегодная конференция «Комбинаторное сопоставление структур» — также важный форум для результатов разработки алгоритмических методов для вычислительной биологии.
Кроме перечисленных журналов, статьи по вычислительной биологии публикуются также в виде сборников конференций по теории вычислений. Среди них: «Симпозиум АСМ СИАМ по дискретным алгоритмам», «Симпозиум АСМ по теории вычислений», «Симпозиум IEEE по основам информатики» и «Международный коллоквиум по автоматам, языкам и программированию»2.
И последний источник, естественно, «Всемирная паутина». Адреса некоторых страниц уже были даны в тексте (см. статью «Адрес www» в предметном указателе). Здесь мы упомянем адреса виртуальных курсов, доступных в 1996 году. Через «Интернет» может быть найден материал по крайней мере трех курсов по вычислительной биологии. Один из них поддерживается Далитом Наором и Роном Шамиром на сервере «Тель-Авивского университета». Дополнительная информация относительно этого курса находится по адресу:
http://www.math.tau.ас.il/shamir/algmb.html
2Центральным журналом no биоинформатике является журнал «Баиоинформатикс» (Bioinformatics). — Прим. ред.
БИБЛИО1 РАФИЧЕСКИЕ ПРИМЕЧАНИЯ И ДРУГИЕ ИСТОЧНИКИ 387
Другой лекционный курс, составленный Ричардом Карпом, Ларри Руз-зо и Мартином Томпой из «Вашингтонского университета», выложен на странице:
http://www.cs.washington.edu/education/courses/590bi/
Наконец, «Секция биоинформатики виртуальной школы естествознания», поддерживаемая группой специалистов и студентов исследовательского факультета под руководством Роберта Гигерика и Георга Фусллена из «Билефсльдского университета», находится по адресу:
http://www.techfak.uni-bielefeld.de/bcd/Curric/welcome.html
ОТВЕТЫ К ИЗБРАННЫМ УПРАЖНЕНИЯМ
Глава 1
1.	Последовательное!ь TAATCGAATGGGC:
РС1:	ТАА stop	TCG Ser	ААТ Asn	GGG Gly
РС2:	ААТ	CGA	ATG	GGC
	Asn	Arg	Met	Gly
РСЗ:	АТС	GAA	TGG	
	Пс	Glu	Trp	
Образный комплемент GCCCATTCGATTA:
PCI:	GCC Ala	CAT His	TCG Ser	ATT lie
PC2:	CCC	ATT	CGA	TTA
	Pro	He	Arg	Leu
PC3:	CCA	TTC	GAT	
	Pro	Phc	Asp	
2.	Нить ДНК, начинающаяся триплетом ATG, — кодирующая. Верхняя нить идет в направлении 5' —» 3', а нижняя — в направлении 3' —» 5'.
a.	AUG AUA CCG ACG UAC GGC AUU UAA
б.	М I Р Т Y G I (X)
3.	Есть двенадцать возможных последовательностей: восемь из них могут быть представлены строкой вида CTNATGAAR, где N обозначает любое основание, a R — основание А или G. Оставшиеся четыре последовательности определяются строкой вида TTRATGAAR.
ОТВЕТЫ К ИЗБРАННЫМ УПРАЖНЕНИЯМ
389
5. 4-Рестриктаза один раз отрезает каждые 44 = 256 оснований. Следовательно, мы ожидаем 40000/256 = 156,25 сечений, то есть приблизительно 157 фрагментов.
6. Нсповирус хромистой мозаики лозы венгерского винограда.
Глава 2
1. Эта строка содержит три различные подстроки с одним знаком, три с двумя, три с тремя, две с четырьмя и одну с пятью, то есть всего 12 различных подстрок.
4.	Полный орграф содержит п(п — 1) ребер; если он неориентирован, то это число в два раза меньше. Дерево с п узлами состоит из п — 1 ребра.
7.	Если, например, время счета одного алгоритма равно п2/2, а другого — 10п, то при п = 4 квадратичный алгоритм затрачивает 8 единиц времени против 40 у линейного.
8.	Быстрее работает алгоритм со временем счета О(у/п).
12.	В разделе 4.3.5 представлен метод, который может быть обобщен для любого ациклического графа следующим образом. Необходимо повторять операцию поиска и удаления источника в графе. Последовательность удаленных источников дает топологический порядок. Источники — вершины со степенью захода, равной единице.
13.	Начните с одного множества для каждого узла. Для каждого ребра выполните условие: если его вершины находятся в разных множествах, то объедините соответствующие этим вершинам множества. После того, как будут обработаны все ребра, конечные множества дадут связные компоненты графа.
15.	Для заданного графа G и целого числа К требуется ответить на вопрос: Имеется ли в графе G покрытие вершин размером по крайней мере К?
17.	Необходимо показать, что задача о ГЦ может быть сведена к задаче о ГП. На основании процедуры для ГП, проверьте ГЦ следующим образом. Поочередно удаляйте одно из ребер входного графа, после чего вызывайте процедуру для ГП. ГЦ верен тогда и только тогда, когда по крайней мере один из ответов процедуры для ГП верен.
20. Подсказка: Используйте массив п х А’, где элемент (i.j) означает, что существует решение для объектов с весом j вплоть до г-го индекса.
390
ОТВЕТЫ К ИЗБРАННЫМ УПРАЖНЕНИЯМ
Глава 3
1.
Задача 1: k-Band
Задача 2: полуглобальное сравнение
Задача 3: фильтр и татем полуглобальное сравнение
Задача 4: локальное сравнение
Задача 5: поиск в базах данных
2.	Счет равен 8.
AAAG	AAAG	AAAG
AC-G	A-CG	-ACG
4.	Попробуйте построить выравнивание последовательностей CGCG и GCGC.
ACGGAGG
’ ACGTAGG
8.	Мы всегда имеем глобальное Sj полуглобальное Sj -шкальное подобие, потому что каждое глобальное выравнивание включает в себя полуглобальное выравнивание, а каждое полуглобальное выравнивание локальное выравнивание.
11. Выравнивание
GAGTTATCCGCCATC
AAGAGTTATCCGCCA
имеет счет —7. Никакое выравнивание с k Sj 1 самое большее одна пара пропусков — не имеет лучший счет. Но следующее выравнивание, с двумя парами пропусков, имеет счет +9:
—GAGTTATCCGCCATC
AAGAGTTATCCGCCA—
14.	Для хранения массивов полных счетов сху необходимо пространство
ОТВЕТЫ К ИЗБРАННЫМ УПРАЖНЕНИЯМ
391
15.	Пусть D — диагональная матрица, где Daa = У/ра. Счета будут симметричны, если матрица MkD также симметрична, то есть если (МкD)' MkD, где верхний индекс t означает транспонирование. Ранее мы привели доказательство для к = 1, то есть
(Л1£>)‘ = DM* = HD.
Допуская, что оно верно и для к — 1, находим:
(A/fc£>)t=(A/A/fc“1£>)‘= (Л/к-1£>)'Л/‘ =ЛТк“1РЛГ‘=ЛГк-1Л/Р MkD.
16.	Нет. Фактическое число ниже 2 %, потому что есть маленький шанс, что после двух мутаций аминокислота возвратится к дикому состоянию.
17.	Гены а-коиксина Coix lacrima-jobi.
18.	Используйте двойную индукцию. Сначала индукцией на к докажите, что w(k + 1) ги(к) + ш(1), а затем индукцией на т докажите, что и>(к + т) w(k) + гг(т).
20. Функция штрафов за пропуски должна быть аддитивна, то есть w(x + у) = w(x) + w{y).
22. Одной возможной системой очков была бы р(а, Ь) = 2 при а = = b, р(а, b) = 1 при а b и д = 0.
Глава 4
1.	Одна возможная сборка:
CCTCGAGTTAA--------GCCCGCGGCTTCAACGGAT-------------------
--------TTAAGTACTGCCCG---------------ATCTGTGTCGGG--------
----------AAGTACTGCCCGCG-----------------TGTGTCGGGAGTCG
-CTCGAGTTAAGTA-----CCCGCGGCTTCAACGGATCTGTG---------------
CCTCGAGTTAAGTACTGCCCGCGGCTTCAACGGATCTGTGTCGGGAGTCG
2.	Минимальное = 1, максимальное = 3, среднее = 2,22.
3.	Наименьшее значение е = 1/6.
4.	Наименьшие значения: е = 1/6 для рис. 4.3 и е = 1/5 для рис. 4.4.
5.	Такой фрагмент вызвал бы неопределенность, потому что единственная компоновка, совместимая с этим фрагментом - нижняя компоновка на рис. 4.8.
392 О1 ВЕТЫ К ИЗБРАННЫМ УПРАЖНЕНИЯМ
6.	Кратчайшая общая надстрока равна ТТАААТА.
7.	Последовательность в вершине-истоке: АС. Последовательность в вершине-стоке: GT. Последовательности в середине: CG, CAG, CTG.
8.	Подсказка: используйте суффиксные деревья.
10.	Последовательность АААААААААА.
12.	При е = 0.1 мы имеем компоновку
—CGTT
АТС---
-TCG—
ATCGTT,
а при с = 0.25 — компоновку
AACG
АТС-
-TCG ATCG.
13.	Минимальное число контигов равно одному:
ТСССТАСТТ---------
-----AATCCGGTT -----GACATC-GGT-.
14.	Подсказка: не выбирайте свободное от подстрок множество.
15.	Возможное множество с тремя строками: AC*Gfc, CfcT, GfcACfe. Назовем их, соотве 1 ственно, /, д и h. Тогда w(h.f) — к + 1, w(f,h) = к и w(h. д) = к — единственные ненулевые ребра. Самое тяжелое ребро делает недействительными другие два, которые вместе образуют путь с весом 2к против к + 1 — веса отдельного ребра с максимальным весом.
16.	Необходимо заполнить пробелы буквами Y и Y или Z и X в зтом порядке.
17.	Используйте последовательность вектора в качестве последовательности запроса и множество фрагментов — как базу данных.
18.	Во множестве Т7 из задачи поиска КОН замените каждый знак х в каждом фрагменте / Е J7 на ААдгСС. Отдайте полученное множество на обработку алгоритму ВОССТАНОВЛЕНИЕ, установив б = 0. В конечном построении должны будут использоваться все фрагменты в той же самой ориентации, поскольку обратный комплемент ААхСС = GGxTT не будет соответствовать никакому фрагменту в прямой ориентации.
ОТВЕТЫ К ИЗБРАННЫМ УПРАЖНЕНИЯМ
393
Глава 5
1.	Фермент А: 3, 10, 8, 6. Фермент В: 5,7,4, 11.
2.	Фермент А: 4, 7, 5, 12, 8. Фермент В; 6, 4, 9, 3, 10, 4.
3.	3, 7, 2, 9, 8.
9. Перестановка столбцов: 3, 5, 1, 8, 10, 4, 7, 6. 9, 2.
11. См. [67] или [74].
20.	Это алгоритм поиска основания цикла из [79].
21.	Обозначьте крайние зонды номером 2. Задача теперь состоит в получении такой перестановки столбцов, чтобы все 1-цы в каждой строке были последовательными и, возможно, окружены двумя или четырьмя 2-ми. Этот прием несколько упрощает задачу, но не намного. См. [9].
23.	Выбирайте значения к, при которых Л*, было бы мало, а Вк — велико, и выбирайте другой расщепитель i так, чтобы |Xi| ~ |В,|.
Глава 6
3. Используйте для этого круглые скобки. Например, выражение вида (a((b)(c(rf)(e)))) могло бы описывать дерево, где а — корень, b и с — его сыновья, d и е — сыновья узла с.
4. Сортируйте столбцы, интерпретируя каждый столбец как бинарное число, и удаляйте столбцы, которые являются равными. Новая матрица допускает совершенную филогению тогда и только тогда, когда старая также допускает.
6. Простой алгоритм см. в [82].
8. Вход допускает совершенную филогению. Признаки Ci и сг совместимы, если предковое состояние принять за 1.
10. См. [107].
11. См. [106].
13. Попарная совместимое гь признаков (для определения ребер графа) должна быть найдена с помощью алгоритма из раздела 6.3.
15. Запустите алгоритм и затем сравните парные расстояния на дереве с расстояниями на матрице. Если онн равны, то матрица аддитивна; если не равны — нет.
394
ОТВЕТЫ К ИЗБРАННЫМ УПРАЖНЕНИЯМ
Глава 7
—________
1.	d с b а.
J	4___>	—	>	_
2.	La, a b , f е , е R.
4.	а = (7, 7, 7), Р = (7, 7,7).
5.	7,7.7,7,7.
—-> <- 4— - <- ->
6.	4 , 1 , 3 , 5 , 2 .
10. ABC, ABD, AEF, BEF, С BE, CBF, CEF, DBE, DBF, DEF и их инверсии.
11. Пройдите по диаграмме желаемого и действительного и составьте кольцевой список, отмечая компоненты, которым принадлежит каждое ребро действительного. Рассматривайте только плохие компоненты; если ребро действительного принадлежит хорошему компоненту, то просто игнорируйте его. Кроме того, убедитесь, что имя одного и того же компонент не присутствует в списке дважды. Например, для диаграммы на рис. 7.18 мы получили бы кольцевой список —> EFEBDCBA —>. С помощью этого списка легко вычислить искомую информацию: стены соответствуют элементам, которые появляются только однажды; стена X защищает мираж Y, когда в список внесены компоненты YXY и это единственные появления компонента У в списке.
Глава 8
5. См. раздел 3.3.3.
6. Доказательство следует строить на задаче выполнимости (см. раздел 9.2), ограниченной следующим образом: Каждое предложение состоит из трех букв, и мы ищем удовлетворяющее присвоение, при котором истинность каждого предложения определяется только одной буквой. Подробное описание данного построения см. в [122].
9. Воспользуйтесь методами поиска по измерениям. Для одного измерения достаточно использовать простое бинарное дерево поиска. Для двух измерений используйте двумерное дерево. См. [170].
Глава 9
1. Такой путь будет кодироваться последовательностью, состоящей из 20 000 пар нуклеотидов. Для его определения необходимо обратиться к методам главы 4.
4. См. [128].
ЛИТЕРАТУРА
1.	МА Adams, С Fields, and J C Venter, editors Automated DNA Sequencing and Analysis. New York: Academic Press, 1994.
2.	L. M. Adlcman. Molecular computation of solutions to combinatorial problems. Science, 266:1021 1024, 1994.
3.	R Agarwala, V Bafna, M. Farach, В Narayanan, M Paterson, and M Thorup. On the approximability of numerical taxonomy. In Proceedings of the Seventh Annual ACM-SIAM Symposium on Discrete Algorithms, pages 365 372, 1996.
4.	R. Agarwala and D. Fernandez-Baca. A polynomial-time algorithm for the phylogeny problem when the number of character states is fixed. SIAM Journal on Computing, 23(6): 1216 1224, 1994.
5.	R Agarwala, D. Fernandez-Baca, and G. Slutzki Fast algorithms for inferring evolutionary trees. In Proceedings of the 30th Allerton Conference on Communication. Control, and Computation, pages 594-603, 1992.
6.	A. V. Aho. Algorithms for finding patterns in strings. In J. van Leeuwen, editor, Handbook of Theoretical Computer Science, volume A, pages 255-300 Amsterdam/Cambridge, MA: Elsevier/МП Press, 1990.
7.	B. Alberts, D. Bray, J Lewis, M. Raff, K. Roberts, and J. D. Watson. Molecular Biology of the Cell. New York & London: Garland Publishing, 1994.
8.	F Alizadeh, R.M.Karp, L. A. Newberg, and D. K. Wcisser. Physical mapping of chromosomes: A combinatorial problem in molecular biology Algorithniica, 13(l/2):52 76, 1995.
9.	F. Alizadeh, R.M.Karp, D.K. Weisser, and G.Zweig. Physical mapping of chromossomes using unique probes. Journal of Computational Biology, 2(2): 159 184, 1995.
10.	S. F. Altschul. Amino acid substitution matrices from an information theoretical perspective. Journal of Molecular Biology, 219:555 565, 1991
11.	S. F Altschul, M. S Boguski, W. Gish, and J. C. Wootton. Issues in searching molecular sequence databases. Nature Genetics, 6:119-129, Feb. 1994
396
литератора
12.	S. F. Altschul, W. Gish, W. Miller, E. W. Myers, and D. J. Lipman. A basic local alignment search tool. Journal of Molecular Biology, 215:403-410, 1990.
13.	S.F. Altschul and D. J. Lipman. Trees, stars, and multiple biological sequence alignment. SIAM Journal on Applied Mathematics, 49(1): 197 209, 1989.
14.	A. Amir and D Kesclman. Maximum agreement subtrees in multiple evolutionary trees. In Proceedings of the IEEE Thirty-Fifth Annual Symposium on Foundations of Computer Science, pages 758-769, 1994.
15.	C. Armen and C. Stein. Short superstrings and the structure of overlapping strings. Journal of Computational Biology, 2(2):307-332, 1995.
16.	C. Armen and C. Stein. A 2 2/3-approximation algorithm for the shortest superstring problem. In Proceedings of the Seventh Symposium on Combinatorial Pattern Matching, volume 1075 of Lecture Notes in Computer Science pages 87-103. Berlin: Springer-Vcrlag, 1996.
17.	H.Atlan and M. Koppel. The cellular computer DNA: program or data? Bulletin of Mathematical Biology, 52(3):335-348, 1990.
18.	V. Bafna and P. A. Pevzner. Genome rearrangements and sorting by reversals. SIAM Journal on Computing, 25(2):272-289, 1996.
19.	G. 1. Bell. The human genome: an introduction. In Bell and Marr [20J, pages 3-12.
20.	G. LBell and T. M. Marr, editors. Computers and DNA. Reading, MA: Addison-Wesley, 1990.
21.	B. Berger. Algorithms for protein structural motif recognition. Journal of Computational Biology, 2( 1): 125-138, 1995.
22.	B. Berger and D. B. Wilson. Improved algorithms for protein motif recognition. In Proceedings of the Sixth Annual ACM-SIAM Symposium on Discrete Algorithms, pages 58-67, 1995.
23.	P. Berman and S. Hannenhalli. Fast sorting by reversal. In Proceedings of the Seventh Symposium on Combinatorial Pattern Matching, volume 1075 of Lecture Notes in Computer Science, pages 168-185. Berlin: Springer-Verlag, 1996.
24.	A. Blum, T. Jiang, M. Li, J. Tromp, and M. Yannakakis. Linear approximation of shortest superstrings. In Proceedings of the Twenty-Third Annual ACM Svmposium on Theory of Computing, pages 328-336, 1991.
ЛИТЕРАТУРА
397
25.	Н. L. Bodlaender, М. R. Fellows, and T. J. Wamow. Two strikes against perfect phylogeny. In Proceedings of the International Colloquium on Automata, Languages and Programming, volume 623 of Lecture Notes in Computer Science, pages 273-283. Berlin: Springer-Verlag, 1993.
26.	H. L. Bodlaender and T. Kicks. A simple linear time algorithm for triangulating three-colored graphs. Journal of Algorithms, 15:160 172, 1993.
27.	K.S. Booth and G. S. Lueker. Testing of the consecutive ones property interval graphs, and graph planarity using PQ-tree algorithms. Journal of Computer and System Sciences, 13(3):335-379, 1976.
28.	C. Brandon and J. Tooze. Introduction to protein structure. New York & London: Garland Publishing, 1991.
29.	P. Buncman. A characterisation of rigid circuit graphs. Discrete Mathematics, 9:205-212, 1974.
30.	A. Caprara. Sorting by reversals is difficult. In Proceedings of the First Annual International Conference on Computational Molecular Biology, 1997.
31.	A. Caprara, G. Lancia, and S.-K.Ng. A column-generation-based branch-and-bound algorithm for sorting by reversals. Presented at the 4th DIMACS Implementation Challenge Workshop, 1995.
32.	H. Carrillo and D. Lipman. The multiple sequence alignment problem in biology. SIAM Journal on Applied Mathematics, 48(5): J 073 1082, Oct. 1988.
3.	3. S. C. Chan, А. К. C. Wong, and D. K. Y. Chiu. A survey of multiple sequence comparison methods. Bulletin of Mathematical Biology, 54(41:563-598, 1992.
34.	W. I. Chang and E. L. Lawler. Approximate string matching in sublinear expected time. In Proceedings of the IEEE Thirty-First Annual Symposium on Foundations of Computer Science, pages 116-124, 1990.
35.	K.-M.Chao and W. Miller. Linear-space algorithms that build local alignments from fragments. Atgorithmica, 13:106 134, 1995.
36.	K.-M.Chao, J.Zhang, J.Ostell, and W. Miller. A local alignment tool for very long DN A sequences. Computer Applications in the Biosciences, 11(2): 147-153, 1995.
37.	T. H. Cormen, С. E. Leiscrson, and R. L. Rivest. Introduction to Algorithms. Cambridge, МА/New York: MIT Press/McGraw-Hill, 1990.
38.	T. E. Creighton. Protein folding. Biochemistry Journal, 270:1-16, 1990.
398
ЛИТЕРАТУРА
39.	М. Crochcmore and W. Rytter. Text Algorithms. Oxford: Oxford University Press, 1994.
40.	J. C. Culberson and P. Rudnicki. A fast algorithm for constructing trees from distance matrices. Information Processing Letters, 30:215-220, 1989.
41.	A. Czumaj, L.Gasicnec, M. Piotrow, and W. Rytter. Parallel and sequential approximations of shortest superstrings. In Proceedings of the Fourth Scandinavian Workshop on Algorithm Theory, pages 95-106, 1994.
42.	W. E. Day. Computational complexity of inferring phylogenies from dissimilarity matrices. Bulletin of Mathematical Biology, 49(4):461 -467, 1987.
43.	W. F. Day, D. S. Johnson, and D. Sankoff. The computational complexity of inferring rooted phylogenies by parsimony. Mathematical Biosciences, 81:33-42, 1986.
44.	W. E. Day and D. Sankoff. Computational complexity of inferring phylogenies by compatibility. Systematic Zoology, 35(2):224 229, 1986.
45.	M. Dayhoff, R. M. Schwartz, and B.C. Orcutt. A model of evolutionary change in proteins. In M. Dayhoff, editor, Atlas of Protein Sequence and Structure, volume 5, pages 345-352. National Biomedical Research Foundation, Silver Spring, MD, 1978. Supplement 3.
46.	S. Dean and R. Stadcn. A sequence assembly and editing program for efficient management of large projects. Nucleic Acids Research, 19(141:3907-3911,1991.
47.	J. Devereux, P. Haeberli, and D. Smithies. A comprehensive set of sequence analysis programs for the VAX. Nucleic Acids Research, 12:387-395, 1984.
48.	K. A. Dill. Dominant forces in protein folding. Biochemistry, 29(31):7133 7155, 1990.
49.	A. J. Dobson. Unrooted trees for numerical taxonomy. Journal of Applied Probability, 11:32-42, 1974.
50.	R. F. Doolittle. Proteins. Scientific American, 253(4):74-83, Oct. 1985.
51.	R. F. Doolittle, editor. Molecular Evolution: Computer Analysis of Protein and Nucleic Acid Sequences, volume 183 of Methods in Enzvmology. New York: Academic Press, 1990.
52.	A. Dress and M. Steel. Convex tree realizations of partitions. Applied Mathematics Letters, 5(3):3-6, 1992.
53.	M. L. Engle and C. Burks. Artificially generated data sets for testing DNA fragment assembly algorithms. Genomics, 16:286-288, 1993.
ЛИТЕРАТУРА
399
54.	M.L. Engle and C. Burks. Genfrag 2.1: New features for more robust fragment assembly benchmarks. Computer Applications in the Biosciences, 10:567-568, 1994.
55.	D. Eppstein, Z. Galil, and R. Giancarlo. Speeding up dynamic programming. In Proceedings of the IEEE Twenty-Ninth Annual Symposium on Foundations of Computer Science, pages 488-495, 1988.
56.	M. Farach, S. Kannan, and T. Wamow. A robust model for finding optimal evolutionary trees. Algorithmica, 13:155 179, 1995.
57.	M. Farach, T. M. Przytycka, and M. Thorup. On the agreement of many trees. Unpublished manuscript, 1995.
58.	C. Fauron and M. Havlik. The maize mitochondrial genome of the normal type and the cytoplasmic male sterile type have very different organization. Current Genetics, 15:149-154, 1989.
59.	M. R. Fellows, M. T. Hallett, and H. T. Wareham. DNA physical mapping: Three ways difficult. In Proceedings of the First Annual European Symposium on Algorithms, volume 726 of Lecture Notes in Computer Science, pages 157-168. Berlin: Springer-Verlag, 1993.
60.	J. Fclsenstcin. Numerical methods for inferring evolutionary trees. The Quarterly Review of Biology, 57(4):379-404, 1982.
61.	J. Fclsenstcin. PHYL1P Phylogeny Inference Package (Version 3.2). Cladistics, 5:164 166,1989.
62.	V. Ferreti, J. H. Nadeau, and D. Sankoff. Original syntony. In Proceedings of the Seventh Symposium on Combinatorial Pattern Matching, number 1075 in Lecture Notes on Computer Science, pages 159- 167. Berlin: Springcr-Verlag, 1996.
63.	J. Fickett. Fast optimal alignment. Nucleic Acids Research, 12( 1): 175-179, 1984.
64.	L. R. Foulds and R. L. Graham. The Steiner problem in phylogeny is NP-complete. Advances in Applied Mathematics, 3:43-49, 1982.
65.	A. S. Fraenkel. Complexity of protein folding. Bulletin of Mathematical Biology, 55(6): 1199 1210, 1993.
66.	K. A. Frenkel. The human genome project and informatics. Communications of the A CM, 34( 11), Nov. 1991.
67.	D. R. Fulkerson and O. A. Gross. Incidence matrices and interval graphs. Pacific Journal of Mathematics, 15(3):835-855, 1965.
68.	M. R. Garey and D. S. Johnson. Computers and Intractability: A Guide to the Theory of NP-Completeness. New York: Freeman, 1979.
400
ЛИТЕРАТУРА
69.	W. Н. Gates and С. H. Papadimitriou. Bounds for sorting by prefix reversal. Discrete Mathematics, 2TA1-51, 1979.
70.	D.G.George, W.C.Barker, and L.T.Bunt. Mutation data matrix and its uses. In Doolittle [51], pages 333 351.
71.	T. Gingerias, J. Milazzo, D. Sciaky, and R. Roberts. Computer programs for assembly of DNA sequences. Nucleic Acids Research, 7:529 545. 1979.
72.	P. W. Goldberg, M. C. Golumbic, H. Kaplan, and R. Shamir. Three strikes against physical mapping of DNA. Unpublished manuscript, 1993.
73.	L.Goldstein and M.S. Waterman. Mapping DNA by stochastic relaxation. Advances in Applied Mathematics, 8:194-207, 1987.
74.	M. C. Golumbic. Algorithmic Graph Theory and Perfect Graphs. New York: Academic Press, 1980.
75.	M. C. Golumbic, H. Kaplan, and R. Shamir. On the complexity of physical mapping. Advances in Applied Mathematics, 15:251-261, 1994.
76.	G. H.Gonnct and R. Baeza-Yates. Handbook of Algorithms and Data Structures, 2nd ed. Reading, MA: Addison-Wesley, 1991.
77.	O. Gotoh. Optimal alignments between groups of sequences and its application to multiple sequence alignment Computer Applications in the Biosciences, 9(3):361-370, 1993.
78.	D. Greenberg and S. Istrail. The chimeric mapping problem: Algorithmic strategies and performance evaluation on synthetic genomic data. Computers and Chemistry, 18(3):207-220, 1994.
79.	D. Greenberg and S. Istrail. Physical mapping by S TS hybridization: Algorithmic strategies and the challenge of software evaluation. Journal of Computational Biology’, 2(2):219-274, 1995.
80.	A. Grigoriev, R. Mott, and H. I ehrach. An algorithm to detect chimeric clones and random noise in genomic mapping. Genomics, 22:482-486, 1994.
81.	S. K. Gupta, J. Kccccioglu, and A. A. Schaffer. Improving the practical space and time efficiency of the shortest-paths approach to sum-of-pairs multiple sequence alignment. Journal of Computational Biology, 2(3):459 472,1995.
82.	D. Gusficld. Efficient algorithms for inferring evolutionary trees. Networks, 21:19-28, 1991.
83.	D. Gusfield. Efficient methods for multiple sequence alignment with guaranteed error bounds. Bulletin of Mathematical Biology, 55(1): 141-154, 1993.
84.	D. Gusfield. Faster implementation of a shortest superstring approximation. Information Processing Letters, 51:271-274, 1994.
ЛИТЕРАТУРА
401
85.	D. Gusfield. Algorithms on Strings, Trees, and Sequences: Computer Science and Computational Biology. Cambridge, UK: Cambridge University Press, 1997. Forthcoming.
86.	D. Gusfield, G. M. Landau, and B. Schieber. An efficient algorithm for the all pairs suffix-prefix problem. Information Processing Letters, 41:181-185. 1992.
87.	S. Hannenhalli and P. A.Pevzner. Transforming cabbage into turnip (polynomial algorithm for sorting signed permutations by reversals). In Proceedings of the Twenty-Seventh Annual ACM Symposium on Theory of Computing, pages 178-189, 1995.
88.	S. Hannenhalli and P. A. Pevzner. Transforming men into mice (polynomial algorithm for genomic distance problem). In Proceedings of the IEEE Thirty-Sixth Annual Svmposium on Foundations of Computer Science, pages 581 -592, 1995.
89.	J. Hein. A new method that simultaneously aligns and reconstructs ancestral sequences for any number of homologous sequences, when the phylogenj is given. Molecular Biology and Evolution, 6(6):649-668, 1989.
90.	J. Hein. An optimal algorithm to reconstruct trees from additive distance data. Bulletin of Mathematical Biology, 5l(5):597-603, 1989.
91.	J. Hein. A tree reconstruction method that is economical in the number of pairwise comparisons used. Molecular Biology and Evolution. Ь(6у.Ь69 684, 1989.
92.	J. Hein. Unified approach to alignment and phylogenies. In Doolittle [51], pages 626-645.
93.	S. Henikoff and J G. Henikoff. Amino acid substitution matrices from protein blocks. Proceedings of the National Academv of Sciences of the U.S. A., 89:10915 10919,1992.
94.	D. Hirschberg. A linear space algorithm for computing maximal common subsequences. Communications of the ACM, 18:341 343, 1975.
95.	R. J. Hoffmann, J. L. Boore, and W. M. Brown. A novel mitochondrial genome organization for the blue mussel, mytilus edulis. Genetics, 131:397 412, 1992.
96.	D. Hofstadter. Godel, Escher, Bach. New York: Basic Books, 1979.
97.	W.-L. Hsu. A simple test for the consecutive ones property. In Proceedings of the International Svmposium on Algorithms & Computation (ISAAC), 1992.
402
ЛИТЕРАТУРА
98.	X. Huang. A contig assembly program based on sensitive detection of fragment overlaps. Genomics, 14:18-25, 1992.
99.	X. Huang. An improved sequence assembly program. Genomics, 33:21-31, 1996.
100.	X. Huang, R. C. Hardison, and W. Miller. A space-efficient algorithm for local similarities. Computer Applications in the Biosciences, 6(4):373-381, 1990.
101.	R. Idury and A. Schaffer. Triangulating three-colored graphs in linear time and linear space. SIAM Journal on Discrete Mathematics, 6(2), 1993.
102.	T. Jiang, E. Lawler, and L. Wang. Aligning sequences via an evolutionary tree: complexity and approximation. In Proceedings of the Twenty-Sixth Annual ACM Symposium on Theory of Computing, pages 760 769, 1994.
103.	R. Jones, W. Taylor, IV, X. Zhang, J.RMesirov, and E. Lander. Protein sequence comparison on the connection machine CM-2: In Bell and Man [20], pages 99 108.
104.	D. Joseph, J. Meidanis, and P. Tiwari. Determining DNA sequence similarity using maximum independent set algorithms for interval graphs. In Proceedings of the Third Scandinavian Workshop on Algorithm Theory, volume 621 of Lecture Notes in Computer Science, pages 326-337. Berlin: Springer-Vcrlag, 1992.
105.	M. Kanehisa and C. DeLisi. The prediction of a protein and nucleic acid structure: problems and prospects. In G. Koch and M. Hazewinkci, editors. Mathematics of Biology, pages 115-137. Dordrecht: D Reidcl, 1985.
106.	S. K. Kannan and T.J. Wamow. Triangulating 3-colored graphs. SIAM Journal on Discrete Mathematics, 5(2):249 258, 1992.
107.	S.K. Kannan and T.J. Wamow. Inferring evolutionary history from DNA sequences. SIAM Journal on Computing, 23(4):713-737, 1994.
108.	H. Kaplan, R. Shamir, and R. E.Tarjan. Tractability of parameterized completion problems on chordal and interval graphs: Minimum fill-in and physical mapping. In Proceedings of the IEEE Thirty-Fifth Annual Symposium on Foundations of Computer Science, pages 780-791, 1994.
109.	S. Karlin and S. F. Altschul. Methods for assessing the statistical significance of molecular sequence features by using general scoring schemes. Proceedings of the National Academy of Sciences of the U. S. A., 87:2264 2268, 1990.
110.	S. Karlin, A. Dembo, and T. Kawabata. Statistical composition of high-scoring segments from molecular sequences. Annals of Statistics, 18(2):571 581, 1990.
ЛИТЕРАТУРА
403
111.	R. М. Karp. Mapping the genome: some combinatorial problems arising in molecular biology. In Proceedings of the Twenty-Fifth Annual ACM Symposium on Theory of Computing, pages 278-285, 1993.
112.	R. M. Karp, C. Kenyon, and O. Waarts. Error-resilient DNA computation. In Proceedings of the Seventh Annual ACM-SIAM Symposium on Discrete Algorithms, pages 458 467, 1996.
113.	J. D. Kececioglu. The maximum weight trace problem in multiple sequence alignment. In Proceedings of the Fourth Symposium on Combinatorial Pattern Matching, volume 684 of Lecture Notes in Computer Science, pages 106-119. Berlin: Springer-Verlag, 1993.
114.	J. D. Kececioglu. Exact and approximation algorithms for DNA sequence reconstruction. Ph. D. thesis, University of Arizona, 1991.
115.	J. D. Kececioglu and E. W. Myers. Combinatorial algorithms for DNA sequence assembly. Algorithmica, 13:7-51, 1995.
116.	J. D. Kececioglu and D. Sankoff. Exact and approximate algorithms for sorting by reversals, with application to genome rearrangement. Algorithmica, 13:180-210. 1995.
117.	E. V. Koonin and V. V. Dolja. Evolution and taxonomy of positive-strand RNA viruses: implications of comparative analysis of amino acid sequences. Critical Reviews in Biochemistry’ and Molecular Biology, 28(5):375-430, 1993.
118.	R. Kosaraju, J. Park, and C. Stein. Long tours and short superstrings. In Proceedings of the IEEE Thirty-Fifth Annual Svmposium on Foundations of Computer Science, pages 166-177, 1994.
119.	E. S. Lander. Analysis with restriction enzymes. In Waterman [196], pages 35-51.
120.	E.S. Lander and M. S. Waterman. Genomic mapping by fingerprinting random clones: a mathematical analysis. Genomics, 2:231-239, 1988.
121.	L. Larmore and B. Schieber. On-line dynamic programming with applications to the prediction of RNA secondary structure. In Proceedings of the First Annual ACM-SIAM Symposium on Discrete Algorithms, pages 503-512, 1990.
122.	R. И. I athrop. The protein threading problem with sequence amino acid interaction preferences is NP-complete. Protein Engineering, 7(9): 1059 1068, 1994.
123.	R. H. Lathrop and T.F. Smith. Global optimum protein threading with gapped alignment and empirical pair score functions. Journal of Molecular Biology, 255(4):641-665, 1996.
404
ЛИТЕРАТУРА
124.	В. Lewin. Genes V. Oxford: Oxford University Press, 1994.
125.	R. Lewontin. Biology as Ideology. New York: Harper Perennial, 1993.
126.	M. Li. Towards a DNA sequencing theory (learning a string). In Proceedings of the IEEE Thirty-First Annual Symposium on Foundations of Computer Science pages 125 134, 1990.
127.	D. J. Lipman and W. R. Pearson. Rapid and sensitive protein similarity search. Science, 227:1435 1441, 1985.
128.	R. J. Lipton. Using DNA to solve NP-completc problems. Science, 268:542 545, 1995.
129.	U. Manbcr. Introduction to Algorithms. Reading, MA: Addison-Wesley, 1989.
130.	U. Manbcr and E. W. Myers. Suffix arrays: A new method for on-line string searches. In Proceedings of the First Annual ACM-SIAM Svmposium on Discrete Algorithms, pages 319-327, 1990.
131.	С. K. Mathews and К. E. van Holde. Biochemistry. Redwood City, CA: Benjamin/Cummings, 1990.
132.	F. R. McMorris. On the compatibility of binary qualitative taxonomic characters. Bulletin of Mathematical Biology, 39:133-138, 1977.
133.	F. R. McMorris, T. Wamow, and T. Wimer. Triangulating vertex-colored graphs. SIAM Journal on Discrete Mathematics, 7(2), May 1994.
134.	J. Meidanis. Distance and similarity in the presence of nonincreasing gap-weighting functions. In Proceedings of the Second South American Workshop on String Processing, pages 27-37, Valparaiso, Chile, Apr. 1995.
135.	J. Meidanis and E.G. Munucra. A simple linear time algorithm for binary phylogeny. In Proceedings of the Fifteenth Intel national Conference of the Chilean Computing Society, pages 275-283, 1995.
136.	J. Meidanis and E. G. Munuera. A theory for the consecutive ones property. In Proceedings of the Third South American Workshop on String Processing, volume 4 of International Informatics Series, pages 194-202. Carleton University Press, 1996.
137.	J. Meidanis and J. C. SctubaL Multiple alignment of biological sequences with gap flexibility. In Proceedings of Latin American Theoretical Informatics, volume 911 of Lecture Notes in Computer Science, pages 411-426. Berlin: Springer-Verlag, 1995.
138.	J.Messing, R.Crca, and P.H.Seeburg. A system for shotgun DNA sequencing. Nucleic Acids Research, 9:309-321, 1981.
ЛИТЕРАТУРА
405
139.	W. Miller. Building multiple alignments from pairwise alignments. Computer Applications in the Biosciences, 9(2):I69-I76, 1993.
140.	W. Miller and E. W. Myers. Sequence comparison with concave weighting functions. Bulletin of Mathematical Biology, 50(2):97-120. 1988.
141.	К. B. Mullis. The unusual origin of the polymerase chain reaction. Scientific American. 262(4):56 65, Apr. 1990.
142.	E. W. Myers. An O(ND) difference algorithm and its variations. Algorithmica. 1:251-266, 1986.
143.	E.W. Myers. Advances in sequence assembly. In Adams et al. [1], pages 231 238.
144.	E. W. Myers. Toward simplifying and accurately formulating fragment assembly. Journal of Computational Biology, 2(2):275-290, 1995.
145.	E. W. Myers and W. Miller. Optimal alignments in linear space. Computer Applications in the Biosciences, 4(1): 11 17, 1988.
146.	S. B. Needleman and C. D. Wunsch. A general method applicable to the search for similarities in the amino acid sequence of two proteins. Journal of Molecular Biology, 48:443-453, 1970.
147.	M. Nci. Molecular Evolutionary Genetics. New York: Columbia University Press 1987.
148.	J. D. Palmer. Chloroplast DNA evolution and biosystcmatic uses of chloroplast DNA variation. The American Naturalist, 130:S6-S29, 1987. Supplement.
149.	J. D. Palmer and L. A. Herbon. Unicircular structure of the brassica hirta mitochondrial genome. Current Genetics, 11:565-570, 1987.
150.	J. D. Palmer, B. Osorio, and W. F. Thompson. Evolutionary significance of inversions in legume chloroplast DNAs. Current Genetics, 14:65-74, 1988.
15I.	C. H. Papadimitriou. Computational Complexity. Reading, MA: Addison-Wesley, 1994.
152.	С. H. Papadimitriou and K. Steiglitz. Combinatorial Optimisation: Algorithms and Complexity. Englewood Cliffs, NJ: Prentice-Hall, 1982.
153.	W. R. Pearson. Rapid and sensitive sequence comparison with FASTP and FASTA. In Doolittle [51], pages 63 98.
154.	W. R. Pearson. Searching protein sequence libraries: Comparison of the sensitivity and selectivity of the Smith-Waterman and FASTA algorithms. Genomics, 11:635 650, 1991.
406
ЛИТЕРАТУРА
I55.	W.R. Pearson and D. J. Lipman. Improved tools for biological sequence comparison. Proceedings ofthe National Academy of Sciences of the U.S.A., 85:2444-2448, 1988.
156.	W. R. Pearson and W. Miller. Dynamic programming algorithms for biological sequence comparison. In L. Brand and M.L. Johnson, editors, Numerical Computer Methods, volume 210 of Methods in Enzymology, pages 575-601. New York: Academic Press, 1992.
157.	H.Peltola, H. Sodcrlund, J.Tarhio, and E. Ukkonen. Algorithms for some string matching problems arising in molecular genetics. In Information Processing 83: Proceedings of the International Federation for Information Processing (IFIP) Ninth World Computer Congress, pages 53 64. Amsterdam: North Holland, 1983.
158.	H. Pcltola, H. Sodcrlund, and E. Ukkonen. SEQAIDS: A DNA sequence assembling program based on a mathematical model. Nucleic Acids Research, 12:307-321, 1984.
159.	D. Penny, M.D. Hendy, and M. A. Steel. Progress with methods for constructing evolutionary trees Trends in Ecology and Evolution, 7(3):73 79, 1992.
160.	P. A. Pevzner. DNA physical mapping and alternating Eulerian cycles in colored graphs. Algorithmica, 13( 1/2):77—105, 1995.
161.	F. M. Richards. The protein folding problem. Scientific American, 264(1 ):54 63, Jan. 1991.
162.	R. J. Robbins. Challenges in the human genome project. IEEE Engineering in Medicine and Biology, 11(1 ):25-34, Mar. 1992.
163.	К. H. Rosen. Discrete Mathematics and Its Applications, 2nd ed. New York: McGraw-Hill, 1991.
164.	M. Rosenberg and D. Court. Regulatory sequences involved in the promotion and termination of RNA transcription. Annual Review of Genetics, 13:319 353, 1979.
165.	1. Rosenfeld, E. Ziff, and V. van Loon DNA for beginners. Writers and Readers, 1984.
166.	D. Sankoff. Minimal mutation trees of sequences. SIAM Journal on Applied Mathematics, 28:35-42, 1975.
167.	D. Sankoff. Analytical approaches to genomic evolution. Biochimie, 75(409-413), 1993.
ЛИТЕРАТУРА
407
168.	D. Sankoff and J. В. Kruskal. Time Warps, String Edits, and Macromolecules: the Theory and Practice of Sequence Comparison. Reading MA: Addison-Wesley, 1983.
169.	W. Schmitt and M. S. Waterman. Multiple solutions of DNA restriction mapping problems. Advances in Applied Mathematics, 12:412-427, 1991.
170.	R. Sedgcwick. Algorithms, 2nd ed. Reading, MA: Addison-Wesley, 1988.
171.	D. Seto, B. Koop, and L.Hood. An experimentally derived data set constructed for testing large-scale DNA sequence assembly algorithms. Genomics, 15:673-676, 1993.
172.	1. Simon. Sequence comparison: some theory and some practice. In Proceedings of the LITP Spring School on Theoretical Computer Science, volume 377 of Lecture Notes in Computer Science, pages 79-92. Berlin: Springer-Verlag, 1987.
173.	J. Sims, D. Capon, and D. Dressier. dnaG (Primase)-dependent origins of DNA replication. Journal ofBiolical Chemistry, 254:12615-12628, 1979.
174.	S. S. Skiena and G. Sundaram. A partial digest approach to restriction site mapping. Bulletin of Mathematical Biology, 56(2):275-294, 1994.
175.	Т.Е Smith and M. S. Waterman. Identification of common molecular subsequences. Journal of Molecular Biology, 147:195-197, 1981.
176.	T. F. Smith, M. S. Waterman, and W.M. Fitch. Comparative biosequcnce metrics. Journal of Molecular Evolution, 18:38 46, 1981.
177.	C. Soderlund and C. Burks. GRAM and genfragll: solving and testing the single-digest, partially ordered restriction map problem. Computer Applications in the Biosciences, 10(3):349-358, 1994.
178.	R. Stadcn. A strategy of DNA sequencing employing computer programs. Nucleic Acids Research, 6:2601-2610, 1979.
179.	M. A. Steel. The complexity of reconstructing trees from qualitative characters and subtrees. Journal of Classification, 9:91- 116, 1992.
180.	G. A. Stephen. String Searching Algorithms. Singapore: World Scientific, 1994.
181.	D. L. Swofford and W. P. Maddison. Reconstructing ancestral character states under Wagner parsimony. Mathematical Biosciences, 87:199-229, 1987.
182.	D. L. Swofford and G. J. Olsen. Phylogeny reconstruction. In D. M. Hillis and C. Moritz, editors, Molecular Systematics, pages 411-501. Sunderland, MA: Sinauer Associates, 1990.
183.	R. Tamarin. Principles of Genetics. Dubuque, 1A: Wm. C. Brown, 1991.
408
ЛИТЕРАТУРА
184.	R. Е. Tarjan. Data Structures and Network Algorithms. CBMS-NSF Regional conference scries in applied mathematics. Society for Industrial and Applied Mathematics, 1983.
185.	S.-H.Teng and E Yao. Approximating shortest superstrings. In Proceedings of the IEEE Thirty-Fourth Annual Symposium on Foundations of Computer Science, pages 158 165, 1993.
186.	D. H. Turner and N. Sugimoto. RNA structure prediction. Annual Review of Biophysics and Biophysical Chemistry. 17:167-192, 1988.
187.	J. S. Turner. Approximation algorithms for the shortest common superstring problem. Information and Computation, 83:1 20, 1989.
188.	E. Ukkoncn. Algorithms for approximate string matching. Information and Control, 64:100 118, 1985.
189.	R. Unger and J. Moult. Finding the lowest free energy conformation of a protein is an NP-hard problem: proof and implications. Bulletin of Mathematical Biology, 55(6): 1183-1198, 1993.
190.	M. Vingron and A. von Haescler. Towards integration of multiple alignment and phylogenetic tree construction. Unpublished manuscript, 1995.
191.	G. von Hcijnc. Sequence Analysis in Molecular Biology: Treasure Trove or Trivial Pursuit? New York: Academic Press, 1987.
192.	L. Wang and D. Gusficld. Improved approximation algorithms for tree alignment. In Proceedings of the Seventh Symposium on Combinatorial Pattern Matching, volume 1075 of Lecture Notes in Computer Science, pages 220 233. Berlin: Springer-Verlag, 1996.
193.	L. Wang and T. Jiang. On the complexity of multiple sequence alignment. Journal of Computational Biology, 1 (4):337—348, 1994.
194.	T. J. Wamow. Constructing phylogenetic trees efficiently using compatibility criteria. Unpublished manuscript, 1993.
195.	T. J. Wamow. Tree compatibility and inferring evolutionary history. Journal of Algorithms, 16:388^107, 1994.
196.	M. S. Waterman, editor. Mathematical Methods for DNA Sequences. Boca Raton, FL: CRC Press 1989.
197.	M. S. Waterman. Sequence alignments. In Waterman [196], pages 53-92.
198.	M.S.Waterman. Parametric and ensemble sequence alignment algorithms. Bulletin of Mathematical Biology, 56(4):743-767, 1994.
199.	M. S. Waterman. Introduction to Computational Biology. London: Chapman & Hall, 1995.
ЛИТЕРАТУРА
409
200.	М. S. Waterman and J. R. Griggs. Interval graphs and maps of DNA. Bulletin of Mathematical Biology, 48(2): 189 195, 1986.
201.	M. S. Waterman and T.F. Smith. Rapid dynamic programming algorithms for RNA secondary structure. Advances in Applied Mathematics, 7:455-464, 1986.
202.	M.S. Waterman, T.F.Smith, M.Singh, and W. A.Beyer. Additive evolutionary trees. Journal of Theoretical Biology, 64:199-213, 1977.
203.	J. D. Watson et al. Molecular Biology of the Gene, volume 1. Redwood City, CA: Benjamin/Cummings, 1987.
204.	J. D. Watson et al. Molecular Biology of the Gene, volume 2. Redwood City, CA: Benjamin/Cummings, 1987.
205.	G. A. Watterson, W. J. Ewens, and T. E. Hall. The chromosome inversion problem. Journal of Theoretical Biology, 99:1-7, 1982.
206.	M. Zukcr. On finding all suboptimal foldings of an RNA molecule. Science, 244:48 52, 1989.
207.	M. Zukcr. The use of dynamic programming algorithms in RNA secondary structure prediction. In Waterman [196], pages 159-185.
предметный указатель
о-снираль 363
/3-лист 363
/?-нить 363
Аддитивные
— деревья 284
матрицы 283
расстояния 283
функции 101
Адрес www
«Журнал вычислительной биологии» 386
— банки последовательностей 51
— курсы 386
— проект «Геном человека» 265
страница книги 31
Активный участок
— в белках 363
Алгоритм
- СПЕ 230
— анализ 69
время счета 69
жадный 74
--коммивояжер 249
— поиска КОН 191
—	метода ветвей и границ Збб
—	модель МПД 68
—	операторы 69
определение 68
—	система обозначений 68
Алгоритм аппроксимации
выравнивания деревьев 126
— определение 72
— покрытия вершин 77
— сортировки неориентированной перестановки 346
Алгоритмические программы
— /Г-полоса 107
— вычисление весов сечений 292
— жадный, построение Гамильтонова пути 192
— изоморфизм бинарных деревьев 301
— множественное выравнивание 122
— оптимальное выравнивание 88
--- оптимальное выравнивание в линейном пространстве 98
— перестановка зондов 253
— подобие в линейном пространстве 95
построение корневого бинарного дерева R 291
— построение ультрамсгричсского дерева U 292
— размотка белка 370
— расположение строк с СПЕ 236
— решение о совершенной филогении 271
— согласие корневых бинарных деревьев 301
— сортировка 74
--- сортировка неориентированной перестановки 346
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
411
- сортировочная инверсия (для ориентированной перестановки) 338
Аллель 38
Алфавит 61
Аминокислоты
— структура 21
таблица 22
Анализ сложности 71
Антикодирующая иить 32
Антипараллельиые нити 27
Антисмысловая нить 32
БДБ 52
БЛАСТ 133
База данных
—	поиск 127
—	последовательностей 51
Бактерии 42
Бактериофаг 44
Байк данных белка 52
Банки последовательностей 51
Белок
—	активный участок 363
—	вторичная структура 363
ориентация 24
—	размотка 366
—	свертывание 362
—	структура 24
—	функции 24
Блоки
в выравнивании последовательностей 101
— генов 313
Боковая петля
- РНК 356
«Вверх» 34
Вектор
— в клонировании 46
Вирус 42
Вогнутая штрафная функция 160 Возврат
— состояний при шаков 265
Восстановление
-	модель сборки фрагментов 180
Встройка 46
Вторичная структура — белка 24 Выполнимость 379 Выравнивание
-	деревьев 126
—	звезд 122
—	локальное 91
—	множественное 111 127
—	наивысшее 89
—	наипизшес 89
пары последовательностей 82
—	полуглобальное 92
 счет 84
ГПС 276
Гамильтонов
— граф 66
—	ориентированный путь 375
—	путь 66
—	цикл 66
Гаплоидные клетки 38
Гель 46
Гель-электрофорез 46
Ген
—	локус 41
—	определение 31
—	экспрессия 38
Генбанк 51
Генетический код 32
Геном
—	определение 38
—	перестройки 312
—	типичные размеры 38
—	уровни изучения 42
412
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
—	усредненный 49
Гибридизация
в картографировании 218, 221
—	в секвенировании 176
—	граф 246
Гидрофильные аминокислоты 364
Гидрофобные аминокислоты 364
Глобальное сравнение последовательностей 82
Гомологичные
—	блоки генов 313
—	признаки в филогениях 262 хромосомы 38
Граф
—	Гамильтонов 66
—	Эйлеров 66
—	ациклический 65
двудольный 65
интервалов 66
клика 281
насыщенный 66
неориентированный 63
—	определение 63
—	ориентированный 63
—	псрсмсжаюшннся 329
—	пересечений 276
—	полный 65
—	полустспснь захода 63 полустепснь исхода 63
—	разреженный 66
—	связные компоненты 65
степень 63
—	триангулированный 275
Граф пересечений 276
Граф пересечений состояний 276
ДИХ 46
ДНК
—	амплификация 45
—	двойная спираль 27
—	избыточная 37
—	компьютеры 375
—	копирование 45
—	ориентация 27
—	разрезание и расщепление 44
—	строение молекулы 25
—	чтение и измерение 46
Дезоксирибонуклеиновая кислота 25
Дерева выравнивание 126
Дерево
—	определение 65
—	поддерево 265
—	уточнение 299
Дерево вывода 265
Диат рамма желаемого и действительного 321
Динамическое программирование
—	в предсказании структуры РНК 354
—	во множественном выравнивании 114
—	определение 74
—	при сравнении последовательностей 84
Диплоидные клетки 38
Дискретные признаки
—	в филогениях 262
Длиннейшая общая подпоследовательность 152
Домен
— структуры белка 363
Дрожжевая искусственная хромосома 46
Дулиттл, Рассел Ф. 21
ЕМБЛ 52
Европейская лаборатория молекулярной биологии 52
Жадный алгоритм
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
413
определение 74
поиска КОН 191
поиска взвешенного Гамильтонова пути в мультиграфах 191
— решения задачи коммивояжера 249
Задача коммивояжера
в картографировании посредством гибридизации 240, 249
—	определение 66
эвристика 249
Задача о ранне 77
Задача с двойным перевариванием 219, 222
Задача с последовательными единицами 226
Запрос
—	в базу данных 127
Звезда 122
Знак
в строках 61
Зонд
в секвенировании посредством гибридизации 177
в составлении физических карт 221
Избирательность
—	поиска в БД 139
Избыточная ДНК 37
Изоморфизм
деревьев 301
Инверсия
в ориентированных перестройках генома 318
в перестройках генома 313
расстояние (неориентированное) 318
расстояние (ориентированное) 341
Индикаторы
при составлении физических карт 218
Индукция
при построении алгоритмов 74 Индуцированное попарное выравнивание 114
Интервал — строки 62 Интервальный граф в составлении физических карз 225 определение 66
Интроны 34
КОН 177
Карта
сцепления генсгических признаков 41
— физическая 41,217
Карта сцепления генетических признаков 41
Качественные признаки — в филогениях 265 Кладистическис признаки — в филогениях 265 Клика 279, 281
Клон
— в картографировании 221 — химерный 222 Клонирование 45 Клонотека 221
Кнут, Дональд Эрвин 24
Кол
генетический 32
Кодирующая нить 32
Кодон 31
Комплементарные основания 27
414
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Компоновка
— в сборке фрагментов 166 Конечный автомат
— в программе БЛАСТ 136
Крайние пробелы
— в выравнивании последовательностей 92
Кратчайшая общая надстрока 177
Крепость 335
Крик, Френсис X Ч. 27
Лес иепсресекающихся множеств
— в алгоритме построения ультра-метрических деревьев 291
в жадном алгоритме поиска Гамильтонова пути 192
—	определение 75
Лигазы 377
Линейная
—	функция 104
—	функция штрафов за пропуски 104
Ложное перекрытие
при сборке фрагментов 221
Ложное совпадение
— при гибридизации зондов 198,221
Локальное выравнивание 91
Локус 41
МНПО
— модель сборки фрагментов 181
Маркер
в составлении фггзических карт 217-218
Массив суффиксов 155
Матрица ПТМ 127
Матрица состояний признаков 264
Матрицы BLOSUM 161
Матричная нить 32
Машина с произвольным доступом 68
Мера ПС
во множественном выравнивании 113
Метод ветвей и границ 366
Метод дробовика
—	в сборке фрагментов 166
—	определение 45
Метод поиска в глубину
—	в алгоритме поиска изоморфизма 301
—	определение 74
Метод поиска в ширину 74
Метрическое пространство 284
Меченый участок последовательности
в составлении физических карт 222
Минимальное остовное дерево
—	алгоритм 74
—	в алгоритме восстановления филогений 289
—	определение 66
Мираж 333
Митохондрия 28
Множественное выравнивание 111 127
Множественное сравнение последовательностей 111 127
Мотив
—	в структуре белка 363
Муллис, Кэри Б. 46
Мультиграф 186
НП-класс (задач) 71
НП-полная задача
—	с-триангуляции графа 278
МНПО 184
—	восстановление 181
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
415
— выполнимости 379
—	выравнивания дерева 126
—	вычислимая с помощью ДНК 375
— картографирования посредством гибридизации нс уникальными зондами 228
—	клика 281
—	коммивояжера 72
—	коммивояжера на узкие места 243
—	множественного выравнивания 116
—	модели на интервальных графах 225-226
—	на соответствие признаков 281
—	о Гамильтоновом пути 375
—	о Гамильтоновом цикле 72
—	о разбиении множества 223
о совершенной филогении 268
—	определение 71
—	оптимизации СПЕ 228
—	подход к решеннию 72
—	поиска КОН 180
—	размотки белка 366
—	раскрашивания графа 72
—	с двойным перевариванием 223
—	сортировки неориентированной перестановки 339
—	экономичности филогений 281 НП-полнота 223 НП-трудная задача
—	определение 71
—	см. НП-полная задача
НПО
—	в сборке фрагментов 174, 203
—	в физических картах 219
—	кажущаяся 176
Надпоследовательность 61
Над строка
—	кратчайшая общая 177
—	определение 62
Наинизший общий предок 291
Недетерминированное полиномиальное время (НП) 71
Неориентированная перестановка
339
Несовпадение
— в выравнивании последовательностей 84
Неупорядоченные признаки
— в филогениях 265
«Ниже» 34
Номер доступа 51
Нуклеотид
—	в последовательности ДНК 27
Облитератор 62
Обратная задача свертывания белка
364
Обратный комплемент 28
Обход
—	в секвенировании 174
Объект
—	в филогениях 261
Олигонуклеотид 27
Ориентация
—	блоков генов 313
—	в структуре белка 24
—	нитей ДНК 27
—	фрагментов 170
Ориентированная перестановка 317
Ориентированное секвенирование
176
Ориентированные признаки
—	в филогениях 265
Основание
-	ДНК 27
—	комплементарное 27
—	парное 27
416
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Основное программное средство поиска локальных выравниваний 133
Остаток
— аминокислотный 22
Остовный подграф 65
Открытая рамка считывания 37
Отсутствие подстрок 190
Отсутствие подынтервалов 195 Ошибки
при вычислении с помощью ДНК 383
— при картографировании посредством гибридизации 221 при переваривании 219 при сборке фрагментов 167 при чтении гелевых пленок 48
п. н. (пара нуклеотидов) 27
П-класс (задач) 71
11 ГМ (матрица) 127
ПЦР 46
Палиндром 44
Пара сегментов 133
Паросочетанис
—	в графах 66
11сптидная связь 22
Перекрывающийся граф 191
Перекрывающийся мультиграф 184 Перекрытие
—	между фрагментами 16б Перемежающийся граф 329 Перес гановка
—	неориентированная 339
—	ориентированная 317
Петли
—	в структуре РНК 356
—	в структуре белков 363
Петля шпильки
—	в структуре РНК 356
Плазмида 46
Повторение
в сборке фрагментов 171, 196
— в составлении физических карг 222
Подграф 65
Подобие
- в программе БЛАСТ 135
—	в сравнении последовательностей 140
—	глобальное 84
—	локальное 91
—	определение 84
—	полуглобальное 94
11одпослсдовательность
—	длиннейшая общая 152
—	определение 61
Подстрока 61
Покрытие
—	выборки фрагментов 174 компоновки фрагментов 203 сборки фрагментов 171 физической карты 249
Полимеразная цепная реакция 46, 379
Полиномиальное время 71
Полипептидная цепь 22
Полосы 342
Полуглобальное выравнивание
—	определение 92
—	сборки фрагментов 205
Полустспснь захода 63
Полустепень исхода 63
Полярные признаки
—	в филогениях 265
Последовательность 61
Правильный
—	цикл 330
Праймер 46, 155, 176
Предсказание структуры 352-373
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
417
Префикс
—	строки 62
Признак
—	в филогениях 262
Принцип «Разделяй и властвуй» в алгоритме поиска подобия 95
Пробел в выравнивании последовательностей 82
Проект «Геном человека»
-	адрес www 257 — описание 48 Проекция
множественного выравнивания 114
Прокариоты 34
Промотор 32
Пропуск в выравнивании последовательностей 98
Пуассона распределение
—	в модели картографирования 244
в программе БЛАСТ 137
Пути в модели КОН 188
Путь — Гамильтонов 66 Эйлеров 66
—	в графе 65
РИЬ 52
РНК 353, информационная 32 описание 29 предсказание вторичной структуры 353-362
—	рибосомальная 34
—	транспортная 34
иРНК 32
рРНК 34
тРНК 34
Разбиение множества 223
Размотка
 белка 366
Рамка считывания 37
Раскраска
—	графов 66
—	интервальных графов 226
триангулированных графов 278
Расстояние
Левснштейна 145
—	Хсммингово 242
в филогениях 262, 283
инверсионное 318, 341
при сравнении последовательностей 140
редактирующее 145
Расстояние Левснштейна 145
Расхождение
ребер действительного 326 Редактирующее расстояние 145 Рекомбинация 41
Рекурсивное соотношение
в предсказании структуры РНК 354, 356, 359
в сравнении последовательностей 91, 102
Рекурсия
— в алгоритме оптимального выравнивания 88
— в алгоритме сортировки 74
определение 74
Рестриктазы
— в картографировании 218, 219
определение 44
Ресурс идентификации белка 52
Рибонуклеиновая кислота 29
Рибосома 25, 34
СПГ 176
СПЕ 226
418
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Свободная энергия
— молекулы РНК 353
Связные компоненты 65
Секвенирование
—	встречное 176
—	длинных фрагментов 165
—	метод дробовика 166
—	определение 39
—	ориентированное 176
—	посредством гибридизации 176
Секвенирование длинных фрагментов 165
Секвенирование с двух концов 176
Система очков 142, 145, 151
Слабейшая связь
в сборке фрагментов 183
Слово 135
Смежности
—	матрица 66
—	список 66
Смысловая нить 32
Собственный
—	интервальный граф 257
—	подграф 65
Совершенная филогения (задача) 265
Совпадение
—	в выравнивании последовательностей 84
Согласие
—	между филогениями 299
Согласованная последовательность
—	вычисление 209
—	определение 167
Сокращение
—	вычислительной сложности 72
Соответствие
—	бинарных признаков 271,275
—	максимизация в филогениях 281
между деревьями 299
— признаков в филогениях 266 Сопоставление строк 154 Сортировка инверсиями — в перестройках генома 313 Составление физических карт — посредством гибридизации 221 — приближённое 240 — участков рестрикции 219 Состояние — признака 262 Спиральная область — в структуре РНК 356 Сравнение последовательностей — выбор параметров 151 — точное 155 Стена 333 Степень
—	вершины графа 63
Строка
—	облитсратор 61
—	опредспустаялснис 61
—	порождающая путь в графе 184 — префикс 62
—	суффикс 62
Структуры объединения-поиска данных 75
Субаддитивная функция 104 Суффикс — строки 62
Суффиксное дерево
—	в алгоритме поиска КОН 191
—	определение 155
Схождение
—	ребер действительного 326
—	состояний в филогениях 264 Сцепление
—	в сборке фрагментов 183, 203 Счет
—	в программе БЛАСТ 136
в программе ФАСТ 139
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
419
— в сборке фрагментов 202 — выравнивания 84	Функции штрафов за пропуски 98 Хеммингово расстояние 242
Таксономическая категория 261 Таксономия 261 Топологическое упорядочение в алгоритме Cl 1Е 237 — в алгоритме поиска КОН 199 —	в эвристике сборки фрагментов 209 определение 77 Топология —	деревьев 261 Точка разрыва 316, 320 Транскрипция 32 Трансляция 35 Третичная структура  белка 24 Триангулированный граф 275	Химеры — в сборке фрагментов 169 — отсев 250 при составлении физических карт 222 Хлоропласт 28 Хозяин — в клонировании 46 Хромосома —	гомологичность 38 —	набор 38 —	определение 31 —	физическая карта 217 Целевая ДНК —	в сборке фрагментов 165 —	в составлении физических карт
Узлы в структуре РНК 353 Ультрамстрическис деревья 288 Уотсон, Джеймс Д. 27 Уотсона Крика пары оснований 27 Упорядоченные признаки — в филогениях 265 Участки рестрикции — в картографировании 218 определение 44	218 Центральная догма 35 Цикл Гамильтонов 66 — Эйлеров 66 - графа 65 — диаграммы желаемого и действительного 324 Частичное переваривание (задача) 219
ФАСТ 137 Фаг 44, 46 Ферменты —	определение 21 —	рестрикции 44 Физическая карта 41 Филогенетическое дерево 260 Филогения 260 Фра! мент 165	Четвертичная структура 24 Чувствительность — поиска в БД 139 Эвристика — в картографировании посредством гибридизации 250 — в сборке фрагментов 202 — для задачи коммивояжера 249 — определение 72