МГУ-ШКОЛЕ
В. Ф. Бутузов
С. Б. Кадомцев
В. В. Прасолов
Геометрия
Учебник
для общеобразовательных
учреждений
Допущено
Министерством образования и науки
Российской Федерации
Под редакцией В. А. Садовничего
Москва
«Просвещение»
2010
УДК 373.167.1:514
ББК 22.151я72
Б93
Серия «МГУ — школе» основана в 1999 году
На учебник получены положительные заключения
Российской академии наук (№ 10106-5215/78 от 22.10.09)
и Российской академии образования (№ 01~5/7д~71 от 10.07.09)
Бутузов В. Ф.
Б93 Геометрия. 7 класс : учеб, для общеобразоват. учреждений /
В. Ф. Бутузов, С. Б. Кадомцев, В. В. Прасолов; под ред. В. А. Садовни-
чего. — М. : Просвещение, 2010. —127 с. : ил. — (МГУ — школе). —
ISBN 978-5-09-018009-2.
УДК 373.167.1:514
ББК 22.151я72
ISBN 978-5-09-018009-2
© Издательство «Просвещение», 2010
© Художественное оформление.
Издательство «Просвещение», 2010
Все права защищены
введение
Дорогие семиклассники!
Вы начинаете изучать новый предмет —
геометрию. Что это такое — геомет-
рия? Для чего она нужна? Кратко мож-
но сказать так: геометрия нужна для описания формы предметов, опре-
деления их размеров и взаимного расположения. Например, обложка
книги и каждый её лист имеют форму прямоугольника (рис. 1, а). Крыш-
ка письменного стола также имеет форму прямоугольника. Посмотрите
вокруг: перед вами очень много предметов, имеющих форму прямо-
угольника. Итак, для описания формы большого числа предметов ис-
пользуется слово «прямоугольник».
б)
Прямоугольник
составлен из
четырёх отрезков
Рис. 2
Рис 1
Прямоугольник составлен из четырёх отрезков (рис. 1, б). Эти
отрезки называются сторонами прямоугольника. Отрезок тоже геомет-
рическая фигура (рис. 2). Концы отрезка — точки Из точек состоит лю-
бая геометрическая фигура: отрезок, треугольник, окружность (рис. 3),
прямоугольник и т. д.
Мы сказали, что прямоугольник составлен из четырёх отрезков Но
для описания прямоугольника этого мало. На рисунке 4 изображена
Окружность
Рис. з
Четырёхугольник
Рис. 4
Т
Многие предметы вокруг нас име-
ют форму прямоугольника: облож-
ка книги и её страницы; оконная
рама и стёкла; крышка стола и эле-
менты её оформления; полки шка-
фов, паркет и двери; рамка кар-
тины.
геометрическая фигура, также состоящая из четырёх отрезков, которая
называется четырёхугольником. Но эта фигура, конечно же, не является
прямоугольником. Само название «прямоугольник» говорит о том, что
его углы прямые, т. е. каждый из них равен 90е.
Итак, прямоугольник — это четырёхугольник, у которого все углы
прямые.
Два прямоугольника могут отличаться друг от друга размерами —
у одного из них стороны могут быть меньше или больше, чем у друго-
го (например, обложка учебника и крышка стола) Так возникает дру-
гая важная задача геометрии — задача об измерении геометрических
фигур.
Геометрия возникла очень давно, более 4000 лет назад. Само сло-
во «геометрия» в переводе с греческого означает «землемерие» (по-гре-
чески «гео» — земля, а «метрео» — мерить). Это название объясняется
тем, что возникновение геометрии было связано с практической дея-
тельностью — разметкой земельных участков, прокладыванием дорог,
строительством сложных архитектурных сооружений (например, египет-
ских пирамид). С развитием мореплавания появилась потребность ори-
ентироваться по звёздам и составлять географические карты. Так воз-
никла ещё одна из задач геометрии — задача об изучении взаимного
расположения геометрических фигур.
Итак, в геометрии изучаются
форма, размеры и взаимное распо-
ложение геометрических фигур.
На первых порах развития гео-
метрии появлялись и постепенно
накапливались правила, связанные
с геометрическими измерениями
и построениями. Но затем благодаря
древнегреческим учёным (Фалесу,
Пифагору, Евклиду и др.) всё боль-
шую роль в геометрии стали играть
рассуждения, позволяющие выво-
дить новые формулы и неизвестные
ранее факты из уже известных. К на-
чалу нашей эры геометрия сформи-
ровалась как наука, в которой свой-
мид использовались накопленные
с глубокой древности практические
геометрические правила.
ства геометрических фигур изучаются
с помощью рассуждений. Подробнее об истории возникновения гео-
метрии написано в Исторической справке (с. 115).
Для чего нужна геометрия, мы частично ответили: есть много
практических задач, которые решаются с её помощью. (Примеры таких
задач можно найти на с. 112.) Но это не всё. Геометрия развивает наши
пространственные представления. Но и это ещё не всё. Обосновывая
справедливость каких-то утверждений, доказывая их, мы учимся рассу-
ждать, а это важно в любом деле. Геометрия поражает воображение
тем, что путём рассуждений в ней порой устанавливаются совершенно
неожиданные факты. Неудивительно, что на протяжении многих веков
люди самых разнообразных профессий посвящали часы досуга заняти-
ям геометрией.
Школьный курс геометрии состоит из двух частей — планиметрии
и стереометрии. В планиметрии рассматриваются плоские фигуры —
прямоугольники, отрезки, треугольники, окружности, четырёхугольники
(см. рис. 1—4) и т. д., в стереометрии — пространственные фигуры,
например параллелепипеды, шары, цилиндры (рис. 5). Планиметрию
вы будете изучать в 7—9 классах, стереометрию — в 10—11 классах.
Материал учебника разделён на главы, главы — на параграфы, па-
раграфы — на пункты; ориентироваться в этом материале вам поможет
предметный указатель (с. 122). К каждому параграфу даны задачи, яв-
ляющиеся основными. Дополнительные задачи (они немного труднее)
приведены в конце каждой главы. Наиболее трудные из них отмечены
Параллелепипед
Рис. 5
Шар
Цилиндр
звёздочкой. Кроме того, в конце учебника приведены задачи повышен-
ной трудности. Среди них есть очень трудные. Они предназначены для
тех, кому понравится решать задачи и доказывать теоремы. В конце
книги к задачам даны ответы и указания.
Не бойтесь заглядывать вперёд и читать те параграфы, которые
ещё не проходили в классе. Задавайте вопросы учителю, товарищам,
родителям и, конечно же, думайте сами. Мы надеемся, что красота
геометрии не оставит вас равнодушными.
Авторы
Глава 1
Начальные
геометрические
сведения
Точка, прямая, отрезок
§ 1
Простейшие
геометрические
фигуры
Простейшей из геометрических фигур
является точка. Изображение точки
можно получить, прикасаясь к листу
бумаги остро отточенным карандашом.
Обычно точки обозначают большими
латинскими буквами: А, В, С и т. д.
Представление о прямой даёт натянутая нить. Прямую как геомет-
рическую фигуру мыслят себе простирающейся бесконечно в обе сто-
роны. Как правило, прямые обозначаются малыми латинскими буква-
ми: а, Ъ, с и т. д.
Прямая, как и любая геометрическая фигура, состоит из точек.
Для краткости вместо слов «точка А лежит на прямой а» используют
запись А е а, а вместо слов «точка В не лежит на прямой а» — запись
В ё а Если А е а, то говорят также, что
прямая а проходит через точку А.
Чтобы провести прямую на листе бума-	&
ги, пользуются линейкой (рис. 6). При	//
этом, однако, изображается лишь часть	//
прямой, называемая отрезком. Можно ска-
зать, что отрезок — это геометрическая фи-
гура, состоящая из двух точек’ пря-
мой — концов отрезка и всех точек этой Рис 6
прямой, лежащих между концами.
Отметим какие-нибудь две точки и проведём через них прямую
(см. рис. 6). Ясно, что через отмеченные точки нельзя провести другую
’Здесь и далее, говоря «две точки», «три прямые» и т. д , мы будем считать,
что эти точки, прямые и т. д. различны.
Представление
о прямой даёт
натянутая нить.
Разметка на авто-
мобильной доро-
ге даёт представ-
ление о прямой
и отрезках.
a
Прямые а и Ъ имеют одну
р общую точку, а прямые р
и q не имеют общих точек
Ъ
Рис. 7
прямую, не совпадающую с проведённой. Таким образом, через две
точки проходит прямая, и притом только одна.
Из этого следует, что
две прямые либо имеют только одну общую точку, либо не
имеют общих точек (рис. 7).
В самом деле, если бы две прямые имели две общие точки,
то через эти две точки проходили бы две прямые, чего не может
быть, так как через две точки проходит только одна прямая.
Если две прямые имеют общую точку, то говорят, что они пересе-
каются, а общая точка называется точкой пересечения этих прямых.
Прямую, проходящую через две точки, например А и В, иногда
обозначают двумя буквами: АВ или ВА (рис. 8). Отрезок с концами
А и В также обозначают двумя буквами: АВ или ВА (рис. 9).
Луч и полуплоскость
Рассмотрим прямую а и точку О, лежащую на этой прямой (рис. 10).
Точка О разделяет прямую а на две части, каждая из которых называ-
ется лучом, исходящим из точки О (на рисунке 10 один из лучей си-
Рис 9
Точка О разделяет
прямую на два луча
Рис 8
Рис. 10
ний, а другой зелёный), а точка О на-
зывается началом каждого из лучей.
Обычно луч обозначают либо ма-
лой латинской буквой (например, луч h
на рисунке 11, а), либо двумя больши-
ми латинскими буквами, первая из ко-
торых обозначает начало луча, а вто-
рая — какую-нибудь точку на луче
(например, луч ОА на рисунке 11, 6).
Любая прямая разделяет плоскость на две части, каждая из которых
называется полуплоскостью, а сама прямая называется границей каждой
из этих полуплоскостей. На рисунке 12 одна из полуплоскостей с грани-
цей а красная, а другая — синяя.
a)	h
Луч h
б)	О	А
Луч ОА
Рис. 11	Рис. 12
УГОЛ
Угол — это геометрическая фигура, состоящая
из точки и двух лучей, исходящих из этой
точки. Общее начало двух лучей называется
вершиной угла, а сами лучи — сторонами угла.
Угол с вершиной О и сторонами ОА
и ОВ (рис. 13, а) обозначают так: ZAOB
(читается «угол АОВ»), Иногда используют
более краткое обозначение: АО. Если сторо-
нами угла являются лучи h и k, то угол обо-
значают так: Ahk (рис. 13, б). На рисунках
углы иногда обозначают цифрами.
Угол называется развёрнутым, если его
стороны лежат на одной прямой. На рисун-
ке 13 изображены неразвёрнутые углы АОВ
Рис. 13
р а)	у	6)	-А
Е	Внешняя
область	Внутренняя
угла /	область
угла	о	в
Развёрнутый угол DEF
Рис 14	Рис. 15
h
с
А
и hk, а на рисунке 14 — развёрнутый угол DEF. Говорят, что каждая
сторона развёрнутого угла является продолжением другой стороны.
Неразвёрнутый угол разделяет плоскость на две части, одна из кото-
рых называется внутренней, а другая — внешней областью этого угла. На
рисунке 15, а внутренняя область угла закрашена синим. Можно ска-
зать, что внутренняя область неразвёрнутого угла АОВ — это общая
часть двух полуплоскостей: полуплоскости
с границей АО, содержащей луч ОВ,
и полуплоскости с границей ВО, содержа-
щей луч О А. На рисунке 15, б эти полу-
плоскости заштрихованы синими и крас-
ными линиями, в результате чего
внутренняя область угла АОВ оказалась
заштрихованной двумя цветами.
На рисунке 16 точка А лежит внутри
неразвёрнутого угла hk (т. е. во внутрен-
ней области этого угла), точка В лежит на стороне угла hk, а точка С —
вне угла hk (т. е. во внешней области
этого угла). Фигуру, состоящую из не-
развёрнутого угла и его внутренней
области, также называют углом.
Рассмотрим теперь развёрнутый
угол (рис. 14). Прямая, на которой лежат
его стороны, разделяет плоскость на
две полуплоскости. Любую из этих по-
луплоскостей можно выбрать в качестве
внутренней области развёрнутого угла.
Если луч исходит из вершины не-
развёрнутого угла и проходит внутри
угла, то говорят, что он делит этот угол
В k
Рис. 16
на два угла. На рисунке 17, а луч ОМ делит
угол АОВ на два угла: ААОМ и АМОВ.
Если угол АОВ — развёрнутый, то любой луч
ОМ, не совпадающий с лучами О А и ОВ,
делит этот угол на два угла: ААОМ и АМОВ
(рис. 17, 6).
Вопросы и задачи
1.	а) Посмотрите на рисунок 18. Имеют
ли общие точки: отрезки АВ и CD;
прямые АВ и CD?
б)	Перечертите рисунок 18 в тетрадь и от-
метьте точку Р, лежащую на прямой CD, но
не лежащую на отрезке АВ, и точку Q, лежа-
щую как на прямой CD. так и на отрезке АВ.
Как называется точка Q?
в)	Сколько отрезков с концами К, L, М и N
изображено на рисунке 19?
г)	Перечертите рисунок 19 в тетрадь и от-
метьте точку В, лежащую на прямой КМ, так,
чтобы прямая АВ пересекала прямые KL
и LM, но не пересекала отрезок КМ.
д)	Отметьте в тетради точки А, В. С и D так,
чтобы прямые АВ и CD пересекались, а от-
резки АВ и CD не имели общих точек.
е)	Сколько точек нужно отметить на отрезке
PQ, чтобы получилось ровно шесть различ-
ных отрезков с концами в точках Р, Q и отме-
ченных точках?
ж)	Прямые PQ и LM пересекаются в точке М.
Имеет ли прямая LM общие точки с отрез-
ком PQ?
з)	На рисунке 20 изображены три прямые.
Можно ли провести прямую так, чтобы она
проходила через точку С и пересекала пря-
мые АВ и AD?
и)	Даны четыре точки. Через каждую пару
этих точек проведена прямая Сколько всего
Угол ОМ делит угол АОВ
на два угла: Z1 и Z2
Рис. 17
Рис. 18
проведено прямых? Рассмотрите все возможные случаи и для каждого слу-
чая сделайте рисунок.
к) Сколько отрезков с концами в обозначенных буквами точках изображе-
но на рисунке 21?
2.	а) Имеют ли общие точки прямая PQ и отрезок RT на рисунке 22?
б)	Посмотрите на рисунок 22. Существуют ли точки, которые одновременно
лежат на прямой PQ и прямой RT?
в)	Сколько отрезков с концами А, В, С и D изображено на рисунке 23?
г) Перечертите рисунок 23 в тетрадь и отметьте точку N, лежащую на от-
резке BD, так, чтобы прямая MN пересекала прямые АС и ВС, но не пере-
секала отрезок ВС.
д) Отметьте в тетради точки Р, Q, R и Т так, чтобы прямая PQ имела с от-
резком RT общую точку, а прямая RT не имела общих точек с отрезком PQ.
е) На рисунке 24 изображены три отрезка.
Перечертите этот рисунок в тетрадь и прове-	у z
дите прямую так, чтобы образовалось ещё
ровно три отрезка с концами в обозначенных	\
точках и общих точках проведённой прямой	\
и данных отрезков.	х	w
ж)	Отрезок АВ не имеет общих точек с пря-
мой CD. Может ли прямая АВ иметь общую Рис. 24
точку с отрезком CD?
з)	На рисунке 25 изображены четыре прямые. Можно ли провести прямую
так, чтобы она прошла через точку А и пересекла прямые МВ, МС и MD?
и) Даны четыре прямые, каждые две из которых пересекаются. Найдите
число точек, каждая из которых принадлежит по крайней мере двум из дан-
ных прямых. Рассмотрите все возможные случаи и сделайте рисунки.
к)	Сколько отрезков с концами в обозначенных буквами точках изображе-
но на рисунке 26?
3.	а) Перечертите рисунок 27 в тетрадь и проведите через точку О прямую а
так, чтобы лучи ОА, ОВ и ОС лежали в одной полуплоскости с границей а.
Рис. 25
Рис 26
Рис 27
Рис 29
Рис. 30
б)	Перечертите рисунок 28 в тетрадь и проведите два луча с началом А
так, чтобы один из них пересекал луч ВС, а другой не пересекал.
в)	Перечертите рисунок 29 в тетрадь и проведите два луча с началом М
так, чтобы один из них пересекал луч АВ, а другой пересекал луч ВС. Мож-
но ли провести луч с началом М, удовлетворяющий обоим условиям?
4.	а) Перечертите рисунок 30 в тетрадь и проведите через точку М прямую а
так, чтобы лучи МР и MQ лежали в одной полуплоскости с границей а,
а луч МВ — в другой полуплоскости.
б)	Перечертите рисунок 31 в тетрадь и проведите два луча с началом А так,
чтобы один из них пересекал луч ВС, а другой не пересекал.
в)	Перечертите рисунок 32 в тетрадь и проведите два луча с началом М
так, чтобы один из них пересекал луч АВ, а другой не пересекал луч ВС.
Можно ли провести луч с началом М, удовлетворяющий обоим условиям?
5.	а) Сколько углов изображено на рисунке 27? Назовите эти углы.
б)	Начертите неразвёрнутый угол и отметьте точку А, лежащую на его сто-
роне, точку В, лежащую в его внутренней области, и точку С, лежащую
в его внешней области.
в)	Сколько неразвёрнутых углов и сколько развёрнутых углов, вершинами
которых являются обозначенные буквами точки, изображено на рисунке 28?
г) Сколько неразвёрнутых углов и сколько развёрнутых углов с вершиной О
изображено на рисунке 33? Общей частью каких полуплоскостей является
внутренняя область угла DOE?
д) Через вершину неразвёрнутого угла провели прямую. Сколько новых
углов при этом образовалось?
6.	а) Сколько углов изображено на рисунке 30? Назовите эти углы.
б)	Начертите неразвёрнутый угол и изобразите отрезок АВ, все точки кото-
рого лежат во внутренней области угла, отрезок CD, все точки которого ле-
Рис. 31
Рис 32
Рис. 33
жат во внешней области угла, и отрезок PQ,
часть точек которого лежит во внутренней, А
а часть — во внешней области угла.
в)	Сколько неразвёрнутых углов и сколько Е ° в
развёрнутых углов, вершинами которых явля-
ются обозначенные буквами точки, изображе-	D	с
но на рисунке 31?
г)	Сколько неразвёрнутых углов и сколько раз- Рис-34
вёрнутых углов с вершиной О изображено на
рисунке 34? Общей частью каких полуплоскостей является внутренняя
область угла AOD?
д)	Сколько прямых нужно провести через данную точку, чтобы образовалось
ровно шесть углов с вершинами в этой точке?
Равенство
$2
геометрических фигур
Сравнение
отрезков и углов
В повседневной жизни часто встреча-
ются предметы, имеющие одинаковую
форму и одинаковые размеры (две
страницы одной книги, две одинако-
вые вилки, два одинаковых стула и т. д.). В геометрии две фигуры,
имеющие одинаковую форму и одинаковые размеры, называют рав-
ными
Пусть даны две фигуры — Ф-, и Ф2. Чтобы узнать, равны они или
нет, можно скопировать фигуру ф2 на прозрачную бумагу (рис. 35, а)
и попытаться наложить копию на фигуру Фт (рис. 35, б) той или другой
стороной так, чтобы полностью совместить её с фигурой Ф? Если это
Примерами рав-
ных фигур могут
служить многие
предметы: две
одинаковые моне-
ты, два одинако-
вых флюгера.
удастся (рис. 35, в), то фигуры Ф, и Ф2 равны. Мысленно можно предста-
вить себе, что на фигуру Ф, накладывается сама фигура Ф2, а не её копия.
Таким образом, можно сказать: две геометрические фигуры назы-
ваются равными, если их можно совместить наложением.
. а нени отрезков и >гло
Пусть даны два отрезка — АВ и СВ. Наложим отрезок СВ на луч АВ
так, чтобы точка С совместилась с точкой А. Если при этом точка В
совместится с точкой В, то отрезки АВ и СВ совместятся, и, следова-
тельно, они равны (рис. 36, а); если же точки В и В не совместятся, то
с
CD=AB
6)
А
Отрезок CD накладывается
на луч АВ
Угол DEF накладывается на угол АВС
Рис. 36
Рис. 37
Биссектриса —
от латинского bis
(дважды) и sectio
(рассечение), т. е.
рассекаюшая на-
двое.
меньшим из данных отрезков считается тот, который составит часть
другого (рис. 36, б).
Пусть теперь даны два неразвёрнутых угла (углы АВС и DEF на
рисунке 37). Наложим угол DEF на угол АВС так, чтобы вершина Е со-
вместилась с вершиной В, сторона ED совместилась со стороной ВА,
а стороны EF и ВС оказались по одну сторону от прямой ВА. Если при
этом стороны EF и ВС также совместятся, то и углы совместятся, и, сле-
довательно, они равны (на рисунке 37, a Z.DEF = ZABC); если же сто-
роны EF и ВС не совместятся, то меньшим считается тот угол, который
составит часть другого (на рисунке 37, б ZDEF < ZABC).
Неразвёрнутый угол составляет часть развёрнутого угла (рис 38),
поэтому развёрнутый угол больше любого неразвёрнутого угла. Любые
два развёрнутых угла равны.
Точка отрезка, делящая его на два равных отрезка, называется
серединой этого отрезка (рис. 39).
Луч, исходящий из вершины угла и делящий его на два равных
угла, называется биссектрисой этого угла (рис. 40).
Неразвёрнутый угол СОВ
составляет часть
развёрнутого угла АОВ
Точка М — середина Луч I — биссектриса
отрезка АВ	угла hk
Рис. 38
Рис 39
Рис. 40
Вопросы и задачи
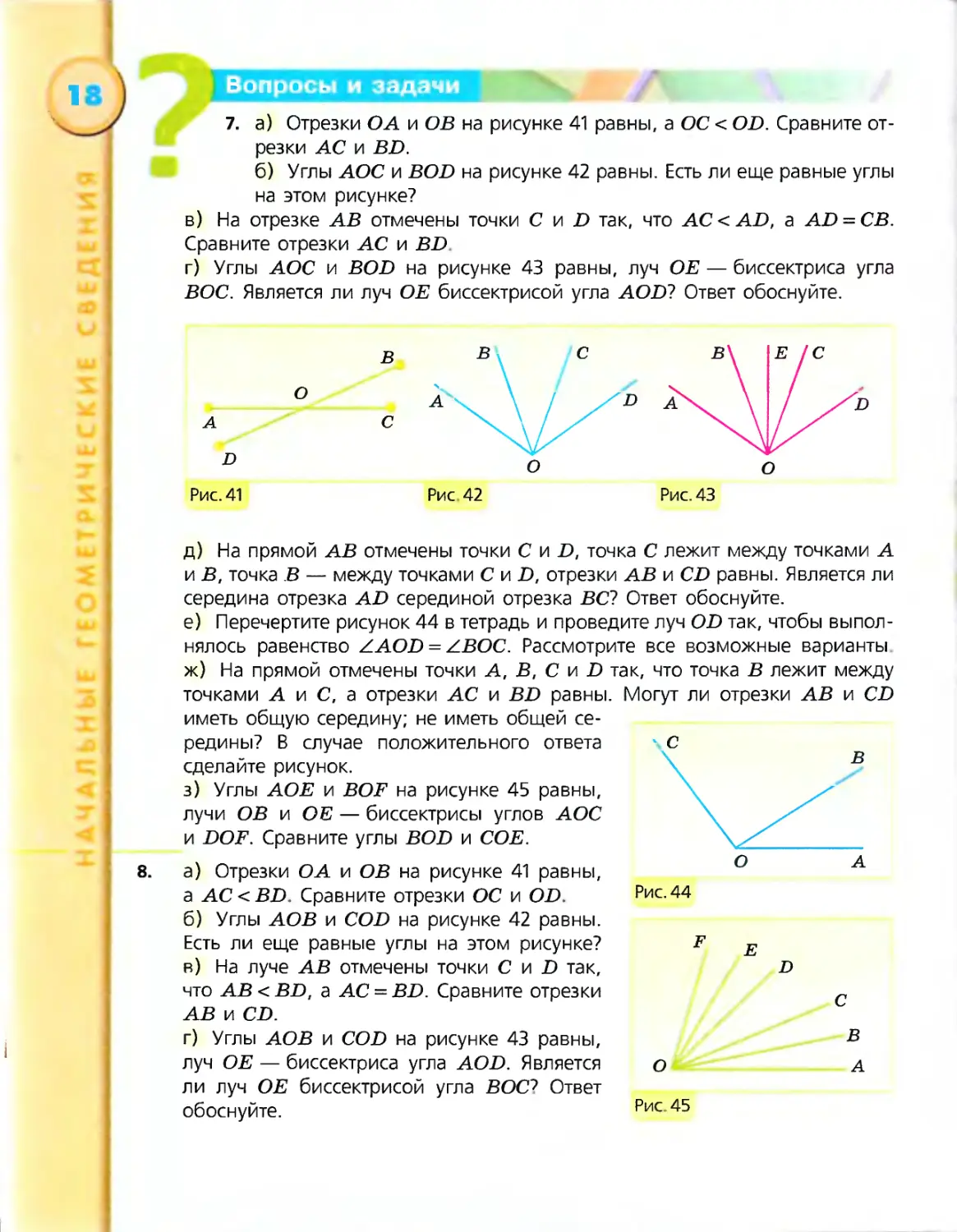
7.	а) Отрезки О А и ОБ на рисунке 41 равны, а ОС < OD. Сравните от-
резки АС и BD.
б)	Углы АОС и BOD на рисунке 42 равны. Есть ли еще равные углы
на этом рисунке?
в)	На отрезке АВ отмечены точки С и D так, что АС< AD, a AD = CB.
Сравните отрезки АС и BD
г)	Углы АОС и BOD на рисунке 43 равны, луч ОЕ — биссектриса угла
ВОС. Является ли луч ОЕ биссектрисой угла AOD? Ответ обоснуйте.
Рис 42
Рис. 43
д)	На прямой АВ отмечены точки С и D, точка С лежит между точками А
и В, точка В — между точками С и D, отрезки АВ и CD равны. Является ли
середина отрезка AD серединой отрезка ВС? Ответ обоснуйте.
е)	Перечертите рисунок 44 в тетрадь и проведите луч OD так, чтобы выпол-
нялось равенство ZAOD = АВОС. Рассмотрите все возможные варианты
ж) На прямой отмечены точки А, В, С \л D так, что точка В лежит между
точками А и С, а отрезки АС и BD равны. Могут ли отрезки АВ и CD
иметь общую середину; не иметь общей се-
редины? В случае положительного ответа С
сделайте рисунок.	в
з)	Углы АОЕ и ВОЕ на рисунке 45 равны,
лучи ОВ и ОЕ — биссектрисы углов АОС
и DOF. Сравните углы BOD и СОЕ. 
8.	а) Отрезки О А и ОВ на рисунке 41 равны,	°	А
a AC<BD. Сравните отрезки ОС и OD. Рис. 44
б)	Углы АОВ и COD на рисунке 42 равны.
Есть ли еще равные углы на этом рисунке?	F Е
в)	На луче АВ отмечены точки С и D так,	D
что АВ < BD, а АС = BD. Сравните отрезки
АВ и CD.
г)	Углы АОВ и COD на рисунке 43 равны,
луч ОЕ — биссектриса угла AOD. Является
ли луч ОЕ биссектрисой угла ВОС1 Ответ
обоснуйте.
Рис 45
д)	На рисунке 46 точка С — сере-
дина отрезка АЕ, точка В — се- А в с D Е
редина отрезка АС, а точка D —	—	~ ... ~
середина отрезка СЕ. Назовите се-
редину отрезка BD. Сравните от- Рис;46
резки AD и BE. Ответы обоснуйте.
е)	Перечертите рисунок 44 в тетрадь и проведите луч ОВ так, чтобы выпол-
нялось равенство Z.BOD = ЛАОС. Рассмотрите все возможные варианты,
ж) Точки К, L, М и N расположены на одной прямой так, что точка L ле-
жит между точками К и М, а два отрезка с концами в данных точках имеют
общую середину. Могут ли отрезки LAI и KN быть равными? неравными?
В случае положительного ответа сделайте рисунок.
з)	Углы BOD и СОЕ на рисунке 45 равны, лучи ОВ и ОЕ — биссектрисы
углов АОС и DOF. Сравните углы АОЕ и BOF.
Измерение
отрезков и углов
Измерение отрезков
Измерение отрезков основано на
сравнении их с отрезком, принятым
за единицу измерения. В странах —
участницах Метрической конвенции
(в частности, в России) в качестве основной единицы измерения отрез-
ков используется метр. Для измерения отрезков, изображённых на ли-
сте бумаги, удобнее использовать сантиметр — одну сотую часть метра
или дециметр — одну десятую часть метра. Если за единицу измерения
принят сантиметр, то для измерения отрезка нужно узнать, сколько раз
в нём укладывается сантиметр. На рисунке 47 сантиметр укладывается
в отрезке АВ ровно три раза. В этом случае говорят, что длина отрез-
ка АВ равна 3 сантиметрам, или
кратко: отрезок АВ равен 3 см
(пишут: АВ = 3 см).
Конечно, отрезок, принятый
за единицу измерения, может не
уложиться целое число раз в из-
меряемом отрезке — получится
остаток. Например, на рисунке 47
в отрезке АС сантиметр уклады-
Рис. 47
вается четыре раза с остатком, но
не укладывается пять раз.
Метр — от греческого pexpov [мет-
ром] — мера.
Сантиметр — от латинского centum
(сто), сотая часть метра.
Дециметр — от латинского decern
(десять), десятая часть метра.
Миллиметр — от латинского mille
(тысяча), тысячная часть метра.
Для измерения остатка пользу-
ются одной десятой частью санти-
метра — миллиметром: он укладывается в остатке ровно четыре раза,
поэтому длина отрезка АС равна 4,4 см. Если же и миллиметр не
укладывается в остатке целое число раз, и получается новый остаток,
то его можно измерить с помощью долей миллиметра
На практике пользуются приближёнными значениями длин отрез-
ков, но мысленно процесс измерения можно продолжать всё дальше
и дальше. Таким образом,
при выбранной единице измерения длина каждого отрезка
выражается положительным числом, показывающим, сколько
раз единица измерения и её части укладываются в измеряе-
мом отрезке.
Если два отрезка равны, то единица измерения и её части уклады-
ваются в них одинаковое число раз, т. е.
равные отрезки имеют равные длины.
Если же один отрезок меньше другого, то единица измерения (или
её часть) укладывается в нём меньшее число раз, чем в другом, т. е.
меньший отрезок имеет меньшую длину.
Ясно также, что
если точка делит отрезок
на два отрезка, то длина
всего отрезка равна сумме
длин этих двух отрезков
(рис. 48).
Длина отрезка называется
также расстоянием между конца-
ми этого отрезка.
а	св
И, 1Г |	I	i(|HU!
СО1 2 3 4 5-
АВ=АС+СВ
Рис. 48
Иэмгос ннр углов
Градус — от латинского gradus (шаг,
ступень, степень). Деление развёр-
нутого угла на 180 частей восходит
к астрономам и математикам Вави-
лонии. Такое деление было удобно
для их вычислений, потому что у них
число 60 играло такую же роль, как
у нас число 10.
Минута — от латинского minutus
(уменьшенный, малый).
Секунда — от латинского secunda di-
visio, второе деление градуса
Транспортир — от латинского trans-
portare (переносить)
Измерение углов основано на сравнении их с углом, принятым за еди-
ницу измерения. Обычно за единицу измерения принимают градус —
угол, равный -Т- части развёрнутого угла. Градусная мера угла показы-
180
вает, сколько раз градус и его части укладываются в данном угле. Гра-
дус обозначается знаком °. Если, например, угол А содержит ровно
60°, то говорят: угол А равен 60° (пишут: ZA = 60c). При измерении
углов используются также — часть градуса (она называется минутой
60
и обозначается знаком ') и — часть минуты (она называется секундой
60
и обозначается знаком "). Например, градусную меру угла, в котором
укладывается 35 градусов, 42 минуты и 27 секунд, можно записать так:
35°42'27". Поскольку 42'= 0,7° и 27"= 0,0075°, то градусную меру этого
угла можно также записать в виде 35,7075°.
Для измерения углов, изображённых на чертеже, используют
транспортир (рис. 49).
Если два угла равны, то градус и его части укладываются в них
одинаковое число раз, т. е.
равные углы имеют равные градусные меры.
Если же один угол меньше другого, то
градусная мера меньшего угла меньше градусной меры боль-
шего угла.
Развёрнутый угол равен 180° (вспомните: градус — это —— часть
развёрнутого угла), неразвёрнутый угол меньше 180'
Рис. 49
ZAOB = ЛАОС + АСОВ
Рис. 50
Ясно также, что
если луч делит угол на два угла, то градусная мера всего
угла равна сумме градусных мер этих углов (рис. 50).
Угол называется прямым, если он равен 90°. Угол, меньший пря-
мого, называется острым, а угол, больший прямого, но меньший раз-
вернутого, — тупым (рис. 51).
□___________
Прямой угол
'Л__________
Тупой угол
Рис. 51
 Вопросы и задачи
9.	а) На прямой отмечены точки А, В и С так, что АВ = 1,22 дм
и АС = 6 мм. Найдите длину отрезка ВС в сантиметрах Не забудьте
рассмотреть все возможные случаи.
б)	От середины М отрезка АВ, равного 2,4 м, отложены на прямой АВ
отрезки МР = 72 см и MQ = 0,25 м. Найдите длины отрезков АР и BQ в де-
циметрах, если PQ = ¥7 см.
в)	На отрезке АВ, равном 24 см, отмечены точки Р и Q. Найдите рас-
стояние между серединами отрезков АВ и PQ, если АР = 2РВ и PQ = 3QB.
г) Точка М лежит на прямой АВ. Найдите длину отрезка AM, если
AM = IBM и АВ = 6 см.
д) Отрезок длиной 32 см разделён на четыре неравные части. Расстояние
между серединами средних частей равно 7 см. Найдите расстояние между
серединами крайних частей.
10.	а) На прямой АВ отмечена точка С. Найдите длину отрезка АС в децимет-
рах, если АВ = 25 см и ВС = 2,5 м.
б)	От середины М отрезка АВ, равного 5,6 см, отложены на прямой АВ
отрезки МР = 18 мм и MQ = 0,32 дм. Найдите длины отрезков АР и BQ
в миллиметрах, если PQ = 1,4 см.
в)	На отрезке АВ, равном 30 м, отмечены точки Р и Q. Найдите расстояние
между серединами отрезков AQ и PQ, если ЗАР = 2РВ и AQ = 2AP.
г)	Точка М лежит на прямой АВ. Найдите длину отрезка AM, если
АВ = 16 см и ВМ = ЗАМ.
д)	Отрезок АВ разделён на четыре неравные части. Расстояние между се-
рединами крайних частей равно 50 см, а между серединами средних час-
тей — 20 см. Найдите длину отрезка АВ.
11.	а) Найдите угол ВОС, если ZAOB = 70° и ААОС = 35е. Каким углом
(острым, прямым, тупым или развёрнутым) является искомый угол?
б)	Луч ОМ — биссектриса угла АОВ, равного 100е. Найдите углы АОР
и BOQ, если APOQ = 50°, АМОР = 30° и AMOQ = 20е.
в)	Луч ОР делит угол АОВ, равный 150е, на два угла так, что 2ААОР =
= ЗАВОР', луч OQ делит угол АОР на два угла так, что 3AAOQ=2APOQ
Найдите угол между биссектоисами углов АОВ и POQ.
г)	Найдите угол АОМ, если А АО В = 90° и ААОМ = 2АВОМ.
д)	Луч ОР — биссектриса угла АОВ, равного 144°, луч OQ — биссектриса
угла ВОР. Найдите угол между биссектрисами углов АОР и BOQ.
12.	а) Найдите угол ВОС, если ZAOB = 140e и ААОС = 70°. Каким углом
(острым, прямым, тупым или развёрнутым) является искомый угол?
б)	Луч ОМ — биссектриса угла АОВ, равного 60°. Найдите углы АОР
и BOQ, если APOQ = 25°, АМОР = 20° и AMOQ = 45°.
в)	Луч ОР делит угол АОВ, равный 100°, на два угла так, что ЗААОР =
= 7АВОР; луч OQ делит угол АОР на два угла так, что 3AAOQ = 4APOQ.
Найдите угол между биссектрисами углов АОР и BOQ.
г)	Найдите угол АОМ, если ААОВ = 120е и ААОМ = 2АВОМ.
д)	Луч ОР — биссектриса угла АОВ. луч OQ — биссектриса угла ВОР.
Найдите угол АОВ, если угол между биссектрисами углов АОР и BOQ ра-
вен 75°.
Смежные
§4	и вертикальные углы
Перпендикулярные Два Угла- у которых одна сторона —
ИПЯЛЛЫе J	общая, а две другие являются про-
ripzilviDlc	должениями одна другой, называют-
ся смежными. На рисунке 52 изо-
бражены смежные углы АОВ и ВОС. Поскольку угол АОС равен 180е,
то ААОВ + АВОС = А АОС = 180° Таким
образом,
сумма смежных углов равна 180е.
Два угла называются вертикальными,
если стороны одного угла являются про-
должениями сторон другого. На рисун-
ке 53 вертикальными являются углы 1 и 3,
а также углы 2 и 4.
Докажем, что
Рис. 52
вертикальные углы равны.
Угол 2 на рисунке 53 является
смежным как с углом 1, так и с углом 3.
Значит, Z1 + Z2 = 180° и Z3 + Z2 = 180°,
' откуда Z1 = 180° - Z2 и Z3 = 180° - Z2,
и, следовательно, Z1 = Z3. Аналогично
доказывается, что Z2 = Z4.
2
1 з
4
Пгоплндикуля; ныо прямы*1
Перпендикуляр к прямой
Две пересекающиеся прямые образуют
четыре неразвёрнутых угла (углы 1, 2, 3
и 4 на рисунке 53). Если один из них
прямой, то и остальные углы прямые.
Доказательство этого утверждения при-
ведено на рисунке 54.
Две пересекающиеся прямые назы-
ваются перпендикулярными (или взаим-
но перпендикулярными), если они обра-
зуют четыре прямых угла.
Z1 =180=-Z2 = Z3
Рис 53
Z1 =90°,
Z2 = Z4 = 90°
(как смежные с углом 1),
Z3 = Z1 = Z90°
(как вертикальные)
Рис. 54
Для краткости вместо слов «прямая АС
перпендикулярна к прямой BD» используют
запись AC LBD.
Рассмотрим прямую а и точку А, не ле-
жащую на этой прямой. Отрезок, соединяю-
щий точку А с точкой Н пря-
мой а, называется перпендику-
ляром, проведённым из точки А
к прямой а, если прямые АН
и а перпендикулярны (рис. 55).
Точка Н называется основани-
Шоссе и ответ-
вляющаяся от
него дорога
образуют два
смежных угла.
ем перпендикуляра АН.
Отрезок АН — перпендикуляр к прямой а
Рис. 55
Мы ввели понятие перпендикуляра, про-
ведённого из данной точки к данной прямой.
А есть ли такой перпендикуляр? Чтобы отве-
тить на этот вопрос, необходимо провести рас-
суждение. В математике утверждение, спра-
ведливость которого устанавливается путем
рассуждения, называется теоремой, а само
рассуждение — доказательством теоремы.
Обычно сначала формулируют теорему
(т. е. то утверждение, которое хотят дока-
зать), а затем её доказывают. Например, ко-
гда мы ввели понятие вертикальных углов,
то сначала сформулировали теорему (хотя
и не называли её теоремой): вертикальные
углы равны, а затем привели доказательство
этой теоремы.
Перпендикуляр —
от латинского
perpendicularis
(отвесный).
Докажем теорему о существовании перпендикуляра к прямой.
Из точки, не лежащей на прямой, можно провести перпен-
дикуляр к этой прямой.
Доказательство Пусть А — точка, не лежащая на данной пря-
мой а (рис. 56, а). Докажем, что из точки А можно провести перпен-
дикуляр к прямой а. Мысленно перегнём плоскость по прямой а
(рис. 56, б) так, чтобы полуплоскость с границей а, содержащая точ-
ку А, наложилась на другую полуплоскость. При этом точка А нало-
жится на некоторую точку. Обозначим её буквой В. Разогнём плос-
кость и проведём через точки А и В прямую.
Пусть Н — точка пересечения прямых АВ и а (рис. 56, в). При
повторном перегибании плоскости по прямой а точка Н останется на
месте. Поэтому луч НА наложится на луч НВ, и, следовательно,
угол 1 совместится с углом 2. Таким образом, Z1 = Z2. Так как углы
1 и 2 — смежные, то их сумма равна 1803, поэтому каждый из них —
прямой. Следовательно, отрезок АН — перпендикуляр к прямой а
Теорема доказана.
Рис. 56
Теорема — греческое
слово бесбртща, озна-
чающее рассматри-
ваю, обдумываю.
Докажем теперь теорему о единственности перпендикуляра к прямой.
|Из точки, не лежащей на прямой, нельзя провести два пер-
пендикуляра к этой прямой.
Доказательств Пусть А — точка, не лежащая на данной пря-
мой а (см. рис. 56, а). Докажем, что из точки А нельзя провести два
перпендикуляра к прямой а. Предположим, что из точки А можно
провести два перпендикуляра АН и АК к прямой а (рис. 57). Мыс-
ленно перегнём плоскость по прямой а так, чтобы полуплоскость с гра-
ницей а, содержащая точку А, наложилась
на другую полуплоскость. При перегибании	в
точки Н и К остаются на месте, точка А на-
кладывается на некоторую точку. Обозна-
чим её буквой В. При этом отрезки АН	а
и АК накладываются на отрезки ВН и ВК. -----------------------
Углы АНВ и АКБ — развёрнутые,
так как каждый из них равен сумме двух
прямых углов. Поэтому точки А, Н и В ле-	А
жат на одной прямой и также точки А, К
и В лежат на одной прямой.	Рис. 57
Таким образом, мы получили, что че-
рез точки А и В проходят две прямые АН и АК. Но этого не может
быть. Следовательно, наше предположение неверно, а значит, из
точки А нельзя провести два перпендикуляра к прямой а. Теорема
доказана.
Замечание Теоремы о существовании и о единственности пер-
пендикуляра к прямой можно объединить в одну теорему:
из точки, не лежащей на прямой, можно провести перпенди-
куляр к этой прямой, и притом только один.
28
Из теоремы о единствен-
ности перпендикуляра к прямой следует, что
НАЧАЛЬНЫЕ ГЕОМЕТРИЧЕСКИЕ СВЕДЕНИЯ
две прямые, перпендикулярные к одной
и той же прямой, не пересекаются.
Предположим, что две прямые, перпен- —-------
дикулярные к прямой а, пересекаются в не-
которой точке М. Точка М не может лежать
на прямой а, так как в этом случае образуется б) м
развёрнутый угол, больший 180° (рис. 58, а).
Если же точка М не лежит на прямой а
(рис. 58, б), то из точки М будут проведены а г
два перпендикуляра к прямой а, что невоз-
можно. Таким образом, две прямые, перпен-
дикулярные к прямой а, не пересекаются. Рис.58
13.	а) Один из смежных углов на 60е меньше другого. Найдите эти углы,
б) Две пересекающиеся прямые образуют четыре неразвёрнутых
угла, один из которых в три раза больше половины другого. Найди-
те эти углы.
в)	Исходя из рисунка 59, докажите, что Z1 + Z2 + Z3 = 180°.
г)	Три прямые пересекаются в одной точке и делят плоскость на шесть
углов, два из которых равны 30° и 50°. Найдите остальные четыре угла.
14.	а) Один из смежных углов в три раза больше другого. Найдите эти углы,
б) Две пересекающиеся прямые образуют четыре неразвёрнутых угла, один
из которых на 30° меньше половины другого. Найдите эти углы.
в) Исходя из рисунка 60, докажите, что Z1 + Z2+Z4-i-Z7=Z3 + Z5 + Z6-i-Z8.
г) Три прямые пересекаются в одной точке и делят плоскость на шесть
углов. Один из этих шести углов в два раза больше другого и в три раза
меньше третьего. Найдите остальные три угла
Рис 59
Рис. 60
Рис. 61
Рис. 62
Рис. 63
Рис. 64
15.	а) На рисунке 61 прямые АЕ и BF взаимно перпендикулярны. Найдите
углы ВОС, EOD и AOD, если ЛАОС = 30°.
б)	Угол, образованный биссектрисами углов АОВ и ВОС. изображённых
на рисунке 62, равен 60°, а АВОС = 30°. Докажите, что О А 1 ОВ.
в)	На рисунке 63 прямые ОА и ОВ взаимно перпендикулярны и
ЛАОС = ABOD. Докажите, что ОС ± OD.
16.	а) На рисунке 61 прямые АЕ и BF взаимно перпендикулярны. Найдите
углы DOF, ВОС и АОС, если ABOD = 140°.
б)	Угол, образованный биссектрисами углов АОВ и АОС, изображённых
на рисунке 64, равен 25°, а ААОВ = 40°. Докажите, что О А ± ОС.
в)	На рисунке 63 прямые О А и ОВ, а также прямые ОС и OD взаимно пер-
пендикулярны. Докажите, что ААОС = ABOD.
Вопросы для повторения
1.	Объясните, что такое отрезок и концы отрезка.
2.	Сколько прямых проходит через две данные точки?
3.	Сколько общих точек могут иметь две прямые? Что означают слова
«две прямые пересекаются»? Как называется общая точка двух прямых?
4.	Объясните, что такое луч и что такое полуплоскость.
5.	Какая фигура называется углом? Что называется вершиной угла и что —
сторонами угла?
6.	Какой угол называется развёрнутым?
7.	Что означают слова: «луч делит угол на два угла»?
8.	Какие фигуры называются равными?
9.	Объясните, как сравнить два отрезка и как сравнить два угла.
10.	Какая точка называется серединой отрезка?
11.	Какой луч называется биссектрисой угла?
12.	Объясните, как производится измерение отрезков.
13.	Как связаны между собой длины отрезков АВ и CD, если: а) отрезки АВ
и CD равны; 6) отрезок АВ меньше отрезка CD?
\ 14. Точка С делит отрезок АВ на два отрезка. Как связаны между собой длины
отрезков АВ, АС и СВ?
15.	Что такое градус? Что показывает градусная мера угла?
16.	Какая часть градуса называется минутой, а какая — секундой?
17.	Как связаны между собой градусные меры двух углов, если: а) эти углы
равны; б) один угол меньше другого?
18.	Луч ОС делит угол АОВ на два угла. Как связаны между собой градусные
меры углов АОВ, АОС и СОВ?
19.	Какой угол называется острым, какой — прямым, а какой — тупым?
20.	Какие углы называются смежными? Чему равна их сумма?
21.	Какие углы называются вертикальными? Каким свойством они обладают?
22.	Какие прямые называются перпендикулярными?
23.	Объясните, какой отрезок называется перпендикуляром, проведённым из
данной точки к данной прямой. Что такое основание перпендикуляра?
24.	Что такое теорема и доказательство теоремы?
25.	Докажите теорему о существовании перпендикуляра к прямой.
26.	Докажите теорему о единственности перпендикуляра к прямой.
Дополнительные задачи |
17. Точка М — середина отрезка АВ, а точка N — середина отрез-
ка МВ. Расстояние между серединами отрезков AM и NB равно d.
шл Найдите АВ и расстояние между серединами отрезков AM и MN.
18. Отрезок разделен на п равных частей. Расстояние между серединами край-
них частей равно d. Найдите длину данного отрезка.
19*. Точка С лежит на прямой АВ, причем ВС = Зсм и АС>ВС. Расстояние
между серединами отрезков АС и ВС равно 7 см. Найдите АС.
20*. Точка С лежит на прямой АВ Расстояние между серединами отрезков АВ
и АС равно d. Найдите ВС.
21. Найдите угол АОС, если: а) ААОВ = 28° и АВОС = 82°; б) ААОВ = 135°
___________и ZBOC = 55°.
22. Какой угол образуют стрелки часов в 3 ч 10 мин?
23. Докажите, что биссектрисы смежных углов взаимно перпендикулярны.
24*. Докажите, что если биссектрисы углов АОВ и ВОС взаимно перпендику-
 _лярны, то АС = АО + ОС.
25*. Известно, что Ahk + ZfcZ = 180°. Могут ли углы hk и hl быть: а) смежными;
____ _ б) несмежными?
26*. Из точки М проведены перпендикуляры МН и МК к двум пересекающим-
ся прямым. Докажите, что точки М, Н и К не лежат на одной прямой
Треугольники
32
Треугольник
ТРЕУГОЛЬНИКИ
§5
РаВНОбедЮвННЫй Выберем какие-нибудь три точки, не
лежащие на одной прямой. Соединив
rripcjfcU/lDHMlx	их Тремя отрезками, получим геомет-
рическую фигуру, называемую тре-
угольником (рис. 65, а). Выбранные точки называются вершинами тре-
угольника, а соединяющие их отрезки — его сторонами. Сумма длин
всех сторон треугольника называется его периметром.
Рис. 65
С
Треугольник
с вершинами А, В, С
и сторонами АВ, ВС, СА
Если вершины треугольника обозначены какими-нибудь буквами,
например А, В \л С (рис. 65, б), то его называют треугольником АВС
(или ВАС, или САВ и т. д.). Иногда вместо слов «треугольник АВС»
используют запись А АВС. Углы CAB, АВС и ВСА (см. рис. 65, б)
называются углами треугольника АВС.
Парус имеет треугольную форму.
Треугольник можно увидеть и на
фасаде здания. Какие ещё пред-
меты имеют форму треугольника7
Для каждой стороны треугольника
можно указать противоположную вер-
шину, а для каждой вершины — про-
тивоположную сторону. На рисунке 65, б
противоположными являются сторона
ВС и вершина А, сторона СА и вер-
шина В, сторона АВ и вершина С.
Теорема об углах
равнобедренного
треугольника
Треугольник называется равнобед-
ренным, если две его стороны равны
Периметр — от греческих тгерг [пе-
ри] — вокруг, около и pETpEtv [мет-
рейн] — измерять.
Равные стороны называются боковыми сторонами, а третья сторона —
основанием равнобедренного треугольника (рис. 66, а). Треугольник,
у которого все стороны равны, называется равносторонним (рис. 66, б).
Равнобедренный
треугольник
б)
Равносторонний
треугольник
Рис. 66
Докажем теорему об углах равнобедренного треугольника
Углы при основании равнобедренного треугольника
равны.
Рассмотрим равнобедренный треугольник АВС
с основанием ВС (рис. 67, а) и докажем, что АВ = АС.
Мысленно скопируем треугольник АВС на лист прозрачной
бумаги, перевернём копию (рис. 67, б) и наложим её на треуголь-
2—Бутузов, 7 кл.
Рис. 67
ник АВС так, чтобы вершина А копии совместилась с вершиной А
треугольника, а отрезок АС копии — с равной ему стороной АВ тре-
угольника (рис. 67, в).
Так как угол А копии равен углу А треугольника, то отрезок АВ
копии наложится на луч АС, а поскольку АВ = АС, то отрезок АВ
копии совместится со стороной АС треугольника. В результате копия
полностью совместится с треугольником АВС (рис. 67, г). При этом
угол В копии совместится с углом С треугольника АВС, а значит, эти
углы равны. Теорема доказана.
Признак равнобедренного треугольника
KZX2XEX1
|Если два угла треугольника равны, то этот треугольник
равнобедренный.
Доказательство. Рассмотрим треугольник АВС, углы В и С
которого равны (рис. 68, а), и докажем, что АВ = АС.
Воспользуемся идеей доказательства теоремы об углах равно-
бедренного треугольника. Мысленно скопируем треугольник АВС на
лист прозрачной бумаги, перевернём копию (рис 68, б) и наложим
её на треугольник АВС так, чтобы вершина В копии совместилась
с вершиной С треугольника, а вершина С копии — с вершиной В
треугольника. Поскольку углы В и С равны, то угол В копии совме-
стится с углом С треугольника, а угол С
копии — с углом В треугольника. Поэтому
точка А копии совместится с вершиной А
треугольника. При этом отрезок АВ копии
совместится со стороной АС треугольни-
ка АВС. Следовательно, АВ = АС. Теоре-
ма доказана
Таким образом, равенство у треуголь-
ника двух углов позволяет сделать вывод
о том, что этот треугольник равнобедрен-
ный, т. е. равенство двух углов является
признаком равнобедренного треугольника.
Теорема о высоте
равнобедренного треугольника
Рис. 68
400
о
Q
09
X
о
ох
ф
J3
Т5
Ф
X
X
JF
х<
На рисунке 69 биссектриса угла А треугольника АВС пересекает
сторону ВС в точке N. Отрезок AN называется биссектрисой тре-
угольника.
Отрезок, соединяющий вершину треугольника с серединой проти-
воположной стороны, называется медианой треугольника (рис. 70).
Перпендикуляр, проведённый из вершины треугольника к прямой,
содержащей противоположную сторону, называется высотой треуголь-
ника (рис. 71).
Докажем теорему о высоте равнобедренного треугольника.
ф
В N	С В М С В Н	С
AN — биссектриса	AM — медиана	АН — высота
треугольника АВС	треугольника АВС треугольника АВС
Рис. 69
Рис 70
Рис. 71
2*
Медиана — от латинского
mediana (средняя).
Высота равнобедренного треуголь-
ника, проведённая к основанию,
является медианой и биссектрисой.
Доказательство Рассмотрим равно-
бедренный треугольник АВС, в котором
отрезок AD — высота, проведённая к
основанию ВС (рис. 72, а). Докажем, что
отрезок AD является также медианой
и биссектрисой треугольника АВС.
Мысленно скопируем треугольник АВС на лист прозрачной бу-
маги, перевернём копию (рис. 72, б) и наложим её на треугольник
АВС так, чтобы совместились вершина А копии с вершиной А тре-
угольника, а отрезок АВ копии с равной ему стороной АС треуголь-
ника. В результате (как мы знаем из п. 11) копия полностью совме-
стится с треугольником АВС.
Так как из точки А можно провести только один перпендикуляр
к прямой ВС, то отрезок AD копии совместится с высотой AD тре-
угольника АВС (рис. 72, в). При этом отрезок BD копии совместится
с отрезком CD треугольника, и поэтому BD = CD, а угол BAD копии
совместится с углом CAD треугольника, и, значит, ABAD = ACAD.
Из этого следует, что отрезок AD является медианой и биссектрисой
треугольника АВС. Теорема доказана.
Утверждение, которое выводится непосредственно из теоремы, на-
зывается следствием. Поскольку мы установили, что биссектриса, ме-
диана и высота равнобедренного треугольника, проведённые к основа-
Рис.72
пересекаются в одной точке
пересекаются в одной точке
Рис 74
Рис 73
нию, совпадают, то в качестве следствий из доказанной теоремы
можно вывести следующие утверждения:
Медиана равнобедренного треугольника, проведённая
к основанию, является высотой и биссектрисой.
Биссектриса равнобедренного треугольника, проведённая
к основанию, является высотой и медианой.
.амечание Любой треугольник имеет три медианы (рис. 73),
три биссектрисы (рис. 74) и три высоты (рис. 75). Посмотрим на рисун-
ки 73—75. Мы видим, что три медианы треугольника на рисунке 73 пе-
ресекаются в одной точке, три биссектрисы треугольника на рисунке 74
пересекаются в одной точке, три высоты треугольника или их продол-
жения на рисунках 75, а, б, в также пересекаются в одной точке. Случай-
но это или так будет в любом треугольнике? Оказывается, что так будет
в любом треугольнике, но доказать это мы сможем только в 8 классе.
Три высоты треугольника или их продолжения пересекаются в одной точке
Рис. 75
Вопросы и задачи
27. а) Периметр треугольника АВС, изображённого на рисунке 76,
отличается от периметра треугольника BCD на 5 см Найдите пери-
метр треугольника ABD, если АВ = BD = DA = DC.
б) Точка М — середина стороны АС треугольника АВС, в котором
АВ = 6 см. Периметры треугольников АВМ и ВСМ отличаются на 10 см.
Найдите сторону ВС.
в) На стороне АС треугольника АВС с пе-
риметром 17 см отмечена точка D. Перимет-	в
ры треугольников ABD и BCD отличаются
на 3 см. Найдите сумму АВ + AD.
28.	а) Периметр треугольника ABD, изобра-
жённого на рисунке 76, равен 27 см. Найди- А  D	с
те разность периметров треугольников АВС
и BCD, если АВ = BD = DA = DC.	рис 75
б)	Точка М — середина стороны АС тре-
угольника АВС, сторона АВ меньше сторо-
ны ВС на 2 мм, периметр треугольника АВМ равен 16 мм. Найдите пери-
метр треугольника ВСМ.
в)	На стороне АС треугольника АВС отмечена такая точка D, что перимет-
ры треугольников ABD и BCD отличаются на 5 см. Найдите периметр тре-
угольника АВС, если АВ + AD = 28 см.
29.	а) Отрезки АВ и АС на рисунке 77 равны. Сравните углы 1 и 2.
б)	Отрезки BD и DC на рисунке 76 равны. Сравните углы АВС и АСВ.
30.	а) Отрезки АВ и АС на рисунке 78 равны Сравните углы 1 и 2.
б)	Отрезки АВ и AD на рисунке 76 равны Сравните углы АВС и ADB.
31.	а) Углы 1 и 2 на рисунке 77 равны Сравните отрезки АВ и АС.
б)	Отрезки АВ и ВС на рисунке 79 равны и Z1 = Z2. Докажите, что тре-
угольник CDE равнобедренный.
Рис. 77
Рис 78
Рис 79
32.
33.
в) На рисунке 76 AABD = ABDA = ADAB,
ААСВ = ACBD, а периметр треугольника
ABD равен 33 см. Найдите разность пери-
метров треугольников АВС и BCD.
г) Отрезки АВ и АС на рисунке 80 равны и
Z1 = Z2. Докажите, что треугольник DBC
равнобедренный.
а)	Углы 1 и 2 на рисунке 78 равны. Сравните
отрезки АВ и АС.
б)	Отрезки CD и DE на рисунке 79 равны
и Z3 = Z4. Докажите, что АВ = ВС.
в)	На рисунке 76 AABD = ABDA = AD АВ
и ААСВ = ACBD, периметр
треугольника АВС отличается от периметра треугольника BCD на 6 см
Найдите периметр треугольника ABD.
г)	Отрезки DB и DC на рисунке 80 равны и Z1 = Z2. Докажите, что тре-
угольник АВС равнобедренный.
а) На продолжении основания АС равнобедренного треугольника АВС за точ-
ку С отмечена точка М. Для каких из треугольников АВС, АВМ и СВМ осно-
вание высоты, проведённой из вершины В, лежит на продолжении стороны?
б) В треугольнике АВС точка М — середина стороны АВ и АА = АВ До-
кажите, что АВ ± СМ.
в)	Из середины М основания ВС равнобедренного треугольника АВС про-
ведены биссектрисы МР и MQ треугольников АВМ и АСМ. Докажите, что
APMB = AQMC.
г)	Сторона АВ равнобедренного треугольника АВС с основанием АС про-
должена за точку В на отрезок BD, равный АВ. Докажите, что высоты ВН
и BE треугольников АВС и BCD взаимно перпендикулярны.
д)	Докажите, что прямая, проходящая через середину основания равно-
бедренного треугольника и перпендикулярная к основанию, проходит через
вершину треугольника.
€00
СЛ
"U
Q
со
X
о
о\
о
Ja
(D
X
X
Г
Х<
"О
(D
О
Гз
сг
X
X
*
34. а) На продолжении основания АС равнобедренного треугольника АВС за
точку С отмечена точка D. Для каких из треугольников ABC, ABD и CBD
основание высоты, проведённой из вершины В, лежит на стороне?
б)	В треугольнике АВС точка М — середина стороны АВ и АА = АВ До-
кажите, что ААСВ - 2ААСМ.
в)	Точка М — середина основания ВС равнобедренного треугольника
АВС, точки D и Е лежат на сторонах АВ и АС так, что ADMB- 45°
и ADME = 90°. Докажите, что отрезок ME — биссектриса угла АМС.
г)	Медиана СМ треугольника АВС в два раза меньше его стороны АВ.
Докажите, что медианы МР и MQ треугольников АМС и ВМС взаимно
перпендикулярны.
д)	Отрезок АВ — общее основание равнобедренных треугольников АВС
и ABD. Докажите, что прямая CD проходит через середину отрезка АВ.
Равные треугольники
Признаки
равенства
треугольников
Напомним, что две фигуры, в частно-
сти два треугольника, называются
равными, если их можно совместить
наложением. Рассмотрим равные тре-
угольники АВС и ApBjCj (рис. 81).
Каждый из них можно наложить на другой так, что они полностью со-
вместятся, т. е. вершины, стороны и углы одного треугольника совме-
стятся с вершинами, сторонами и углами другого
Таким образом, если два тре-
угольника равны, то элементы (т. е.
стороны и углы) одного треуголь-
ника соответственно равны элемен-
там другого треугольника. Отметим,
что в равных треугольниках против
равных сторон лежат равные углы,
а против равных углов — равные
стороны. Так, например, на рисун-
ке 81 против равных сторон АВ
и AjB! лежат равные углы С и Сг
Равенство треугольников АВС и
условимся обозначать так:
ААВС = AA^Cf
Отметим, что при наложении
равных треугольников друг на дру-
га совмещаются не только сторо-
ны и углы этих треугольников, но
и соответствующие медианы, биссектрисы и высоты. Таким образом,
в равных треугольниках соответствующие медианы, биссектрисы и высоты
равны.
Оказывается, что равенство двух треугольников можно установить
путем сравнения некоторых их элементов, т. е. без фактического нало-
жения треугольников друг на друга. Возможность установить равенство
двух фигур, не производя наложения одной на другую, а лишь изме-
ряя и сравнивая некоторые их элементы, важна на практике, например
при сравнении двух земельных участков, которые, конечно же, нельзя
наложить один на другой. В этом параграфе мы докажем три теоремы
о равенстве треугольников.
Первый признак равенства треугольников
 Если две стороны и угол между ними одного треугольника
соответственно равны двум сторонам и углу между ними
другого треугольника, то такие треугольники равны.
Доказательство. Рассмот-
рим треугольники АВС и А^В^С^
у которых АВ = А1В1, АС=АгСг,
АА=АА1 (рис. 82, а), и докажем,
что эти треугольники равны.
Мысленно наложим треуголь-
ник АВС на треугольник А1В1С1
так, чтобы вершина А совмести-
лась с вершиной А1( а стороны
АВ и АС наложились на лучи
AjBx и АгСг. Это можно сделать,
так как углы А и Ах равны
(рис. 82, б).
Поскольку АВ = АгВг
и АС = AiC^ то сторона АВ со-
вместится со стороной А1В1, а сто-
рона АС совместится со стороной
AtCi (рис. 82, в), в частности со-
вместятся точки В и Bv С и Сг.
Следовательно, совместятся сто-
роны ВС и BjCp Итак, треуголь-
ники полностью совместятся, поэто-
му они равны. Теорема доказана.
Доказанная теорема выражает
признак (равенство у треугольни-
ков двух сторон и угла между
ними), по которому можно сде-
лать вывод о равенстве треуголь-
ников. Он называется первым при-
знаком равенства треугольников.
Рис 82
Второй признак равенства треугольников
Если сторона и два прилежащих к ней угла одного тре-
угольника соответственно равны стороне и двум прилежа-
щим к ней углам другого треугольника, то такие треуголь-
ники равны.
Доказательство Рассмотрим треугольники АВС и	у ко-
торых АВ = А1В1, ZA=AA1, AB-Z.B1 (рис. 83, а), и докажем, что
эти треугольники равны.
Рис. 83
Мысленно наложим треугольник АВС на треугольник
так, чтобы вершина А совместилась с вершиной А}, сторона АВ —
с равной ей стороной АрВр а вершины С и Сг оказались по одну
сторону от прямой А1В1 (рис. 83, б).
Так как АА = АА1 и АВ-АВХ, то сторона АС наложится на луч
А1С1, а сторона ВС — на луч Поэтому вершина С — общая
точка сторон АС и ВС — совместится с общей точкой лучей А1С1
и BjCp т. е. с точкой Сг (рис. 83, в). Из этого следует, что стороны
АС и ВС совместятся соответственно со сторонами А±Сг и BjCj.
Итак, треугольники полностью совместятся, и, следовательно, они
равны. Теорема доказана.
Третий признак равенства треугольников
I
43
(Если три стороны одного треугольника соответственно рав-
ны трём сторонам другого треугольника, то такие треуголь-
ники равны.
Доказательство Рассмотрим треуголь-
ники АВС и AuBjCj, у которых АВ=А1В1,
ВС = В1С1, СА = С1А1 (рис. 84), и дока-
жем, что эти треугольники равны.
Приложим треугольник АВС к тре-
угольнику AjBjCj так, чтобы вершины А
и Av В и Вг совместились, а вершины С
и оказались по разные стороны от пря-
мой АгВг (рис. 85, а). Проведем отрезок
ССр Если он пересекает отрезок А1В1, то
получим два равнобедренных треуголь-
ника: АгСгС и В^С (рис. 85, б). Значит,
Z1 = Z2 и Z3 = Z4, и, следовательно,
ZC = ZCV Итак, АС = А1С1, ВС = В1С1
и ZC = ZC1( поэтому треугольники АВС
и AiBiCj равны по первому признаку ра-
венства треугольников.
Рис. 84
Рис. 85
Big Стойки стремянки могут свободно
раздвигаться до тех пор, пока они
не будут зафиксированы перемыч-
*^^8 кой. Жёсткость такой конструкции
I основана на третьем признаке ра-
‘ * *— * *	-	—1 венства треугольников.
Кроме рассмотренного нами случая (рис. 85, б), возможны ещё
два (рис. 86, а, б). Доказательства равенства треугольников АВС и
А1В1С1 в этих случаях приведены на рисунках 86, а, б. Теорема до-
казана.
АС=А1С1, поэтому ZC = ZClf с АС=А1С1 и ВС=В1С1, поэтому Z1 =Z2
следовательно, ДАВС = ДАрВ^	и Z3 =Z4. Следовательно, АС = АС1
и ДАВС = ДА1В1С1
Рис. 86
Вопросы и задачи
35. а) Углы AOQ и BOQ на рисунке 87 равны. Докажите, что если
О А = ОВ, то ДАОС = ДВОС.
б)	Докажите, что если медиана треугольника является его высо-
той. то этот треугольник равнобедренный.
в)	Углы АОС и ВОС на рисунке 87 равны. Докажите, что если О А = ОВ, то
ААВС = ABAC и AQ = BQ.
г)	Углы AQC и ВРС на рисунке 88 равны. Докажите, что если AP = BQ, то
А АВС = ABAC.
Рис 87
С
А Р Q В
Рис 88
36.
37.
38.
Рис. 89
д)	На рисунке 87 ОА = ОВ и AQ = BQ. До-
кажите, что АС АО = АСВО.
е)	На рисунке 87 АС = ВС и AR = ВР. Дока-
жите, что АР = BR.
ж)	На сторонах АВ, ВС и СА равносторон-
него треугольника АВС взяты такие точки М,
Р и К, что AM : МВ = ВР : PC = СК : КА =
= 1:3. Докажите, что треугольник МРК —
равносторонний.
з)	На рисунке 87 АС = ВС и СР = СВ. Дока-
жите, что АР = ВВ.
а)	Отрезки ОР и ОВ на рисунке 87 равны и
APOQ = A.ROQ. Докажите, что АСОР = АСОВ.
б)	На рисунке 87 АР = ВВ и ОА = ОВ. До-
кажите, что АВ = ВР.
в)	Отрезки PQ и BQ на рисунке 89 равны и
APQC = ARQC. Докажите, что ACPR = ACRP
и CQ ± PR.
г)	Углы AQC и ВРС на рисунке 88 равны
и AQ = ВР. Докажите, что ААСР = ABCQ.
д)	Углы СРВ и CRP на рисунке 89 равны
и PQ = RQ. Докажите, что CQ ± PR.
е)	На рисунке 87 О А = ОВ и OP = ОВ. Дока-
жите, что ААВС = ABAC.
ж)	Стороны АВ, ВС и СА равносторонне-
го треугольника АВС продолжены за точки А,
В и С на отрезки AM, ВК и СР так, что
МА : АВ = КВ : ВС = PC : СА = 2 : V Дока-
жите, что треугольник МРК равносторонний.
з)	На рисунке 88 СР = CQ, АР = BQ и AM = BN. Докажите, что MP = NQ.
а)	На рисунке 89 ACQP = ACQR, АС = ВС и AQ = BQ. Докажите, что
A AQR = ABQR.
б)	Докажите, что если биссектриса треугольника является его высотой, то
этот треугольник равнобедренный
в)	На рисунке 88 АСМР = ACNQ, АС = ВС и MC = NC. Докажите, что
MP = NQ.
г)	На рисунке 87 ААВО = АВ АО и АО АС = АОВС. Докажите, что АР = BR.
д) На рисунке 87 ОА = ОВ и AQ = BQ. Докажите, что ОР = ОВ.
а)	На рисунке 89 ACPQ = ACRQ, АС = ВС и AR = BP. Докажите, что
AAQR = ABQP.
б)	На рисунке 87 луч CQ — биссектриса угла АСВ, а луч OQ — биссектри-
са угла АОВ. Докажите, что АС = ВС.
в)	Углы ACQ и ВСР на рисунке 88 равны и АС = ВС. Докажите, что СР = CQ.
г)	На рисунке 89 АС = ВС и О А = ОБ. Докажите, что АР = BR.
д)	Углы АСО и ВСО на рисунке 87 равны и CP = CR. Докажите, что
AR = BP.
39.	а) На рисунке 87 АС = ВС и ОА = ОВ. Докажите, что ZAOQ = ZBOQ.
б)	На рисунке 89 CP = CR и QP = QR. Докажите, что OP = OR
в)	На рисунке 89 СР = RQ и CR = PQ. Докажите, что СО = OQ и РО = OR.
г)	На рисунке 87 AP = BR и AR = BP. Докажите, что Z_PAR = Z.RBP
40.	а) На рисунке 89 CP = RQ и CR = PQ. Докажите, что ACQP = Z.QCR.
б)	На рисунке 87 АС = ВС и О А = ОВ. Докажите, что CQ ± АВ.
в)	Углы AQR и BQP на рисунке 89 равны и СР = PQ = QR = RC. Докажите,
что AR = BP.
г)	На рисунке 87 AR = BP и CR = CP. Докажите, что Z_PAR = ARBP.
§7
Прямоугольник
прямоугольные
треугольники
Рассмотрим фигуру, составленную из
отрезков АВ, ВС, CD и DA, никакие
два из которых не лежат на одной пря-
мой и не имеют общих точек, отличных
от концов. Такая фигура называется четырёхугольником ABCD (рис. 90),
указанные отрезки называются сторонами, а концы сторон (точки А, В,
С, D) — вершинами четырёхугольника.
Две стороны четырёхугольника, имеющие
общую вершину, называются смежными,
а две стороны, не имеющие общей верши-
ны, — противоположными. Смежными сто-
ронами четырёхугольника ABCD (рис. 90)
являются стороны АВ и ВС, ВС и CD, CD
и DA, DA и АВ, а противоположными —
стороны АВ и CD, ВС и DA. Отрезок, со-
единяющий две вершины и отличный от
стороны (отрезки АС и BD на рисунке 90),
называется диагональю четырёхугольника.
Четырёхугольник ABCD называется
прямоугольником, если углы ABC, BCD,
CD А и DAB прямые (рис. 91).
Докажем теорему о противоположных
В ]--------------1 - с
лЛ---------------Dp
Прямоугольник ABCD
сторонах прямоугольника.
Рис. 91
Противоположные стороны
прямоугольника равны.
Доказательство Рассмотрим
прямоугольник ABCD (рис. 92, а)
и докажем, что его противополож-
ные стороны, например АВ и DC,
равны.
Через середину М стороны
AD проведём прямую, перпенди-
' ’«Льяя
3:
о
Если посмотреть на город с боль-
шой высоты, то можно увидеть, что
многие дома выглядят как прямо-
угольники. Это хорошо видно на
плане города.
о
кулярную к AD. Она пересечёт сто-
рону ВС в некоторой точке N (рис. 92, б). Мысленно перегнём плос-
кость по прямой MN так, чтобы одна из полуплоскостей с границей
MN наложилась на другую. При этом точки М \л N останутся на месте.
Углы AMN и DMN прямые, поэтому луч МА наложится на луч MD.
Кроме того, МА = MD. Следовательно, точки А и D совместятся.
Поскольку углы А и D прямые, то сторона АВ наложится на луч
DC. Если при этом точки В и С совместятся, то совместятся стороны
АВ и DC, и, следовательно, они равны (рис. 92, в).
Но не может ли получиться так, что точка В совместится не с точ-
кой С, а с какой-то другой точкой Е луча DC (рис. 92, г)? В этом случае
мы обнаружим, что прямой угол NBA совместился с прямым углом NED
и, следовательно, из точки N к прямой DC проведены два перпенди-
куляра — NC и NE. Но этого не может быть, так как из точки, не ле-
Рис. 92
\ жащей на прямой, можно провести только один перпендикуляр к этой
 ' ) прямой. Следовательно, точка В совместится с точкой С. Таким образом,
стороны АВ и DC совместятся, а значит, АВ = DC. Теорема доказана.
Если две смежные стороны прямоугольника равны, то все его
стороны равны.
Прямоугольник, все стороны которого
равны, называется квадратом.
Если один из углов треугольника пря-
мой, то сумма двух других углов этого
треугольника равна 90°.
В самом деле, пусть угол С треуголь-
ника АВС прямой (рис. 93, а). Докажем,
что АА + Z.B = 90°.
Наряду с треугольником АВС рас-
смотрим прямоугольник1, смежные стороны
которого равны соответственно отрезкам
СВ и СА (рис. 93, б). Диагональ прямо-
угольника разделяет его на два треугольни-
ка, у которых эта диагональ является общей
стороной, а другие стороны попарно равны
как противоположные стороны прямоуголь-
ника (рис. 93, в). Каждый из этих треуголь-
ников равен треугольнику АВС (по двум
сторонам и заключённому между ними пря-
мому углу). Значит, Z1 = Z.A и Z2 = Z.B. Но
Z1 + Z2 = 90°, поэтому Z.A + ZB = 90°, что
и требовалось доказать.
Смежные стороны прямо-
угольника равны соответ-
ственно сторонам СВ и СА
треугольника АВС
Диагональ прямоугольника
разделяет его на два
треугольника, равных
треугольнику АВС
Рис 93
1 Здесь и в дальнейшем мы будем исходить из того, что для любых двух
отрезков существует прямоугольник, две смежные стороны которого равны этим
отрезкам.
Z3 = 90°-Z1, Z4 = 90°-Z2,
Z1 + Z2 = 90°, следовательно,
ZD = Z3+Z4=180°-(Z1 +Z2) =
= 180°-90° = 90°
Квадрат — от латинского quadrates
(четырёхугольный).
Рис 94
45
&
Г
о
Если в четырёхугольнике ABCD углы DAB, АВС и BCD пря-
мые, то этот четырёхугольник — прямоугольник.
Требуется доказать, что угол CDA также является прямым. Доказа-
тельство смотрите на рисунке 94.
Виды треугольников
В пункте 18 мы доказали, что если один из углов треугольника прямой,
то сумма двух других углов равна 90°, поэтому каждый из них острый.
Рассмотрим теперь треугольник АВС, угол А которого тупой
(рис. 95, а). Проведём из точки А во внутренней области угла ВАС луч,
перпендикулярный к прямой АВ, и обозначим буквой D точку его пере-
сечения со стороной ВС (рис. 95, б). Угол В является углом треугольни-
ка ABD с прямым углом BAD. Следовательно, угол В острый. Анало-
гично доказывается, что угол С острый (рис. 95, в).
о
ст
X
О
I ГС
X
I -I
2з
р*
т
я
X
Рис. 95
ЭЛЬНИКИ
Итак, если один из углов треугольника тупой, то два других угла
острые. Таким образом, мы приходим к заключению:
в любом треугольнике либо все три угла острые, либо два
угла острые, а третий прямой или тупой.
Отсюда, в частности, следует, что
углы при основании равнобедренного треугольника острые.
Остроугольный	Тупоугольный
треу гол ь н и к	треу гол ь н и к
в)
Рис. 96
1 Катет
Прямоугольный
треугольник
Если все углы треугольника острые,
то треугольник называют остроугольным
(рис. 96, а).
Если один из углов треугольника ту-
пой, то треугольник называют тупоугольным
(рис. 96, б).
Если один из углов треугольника пря-
мой, то треугольник называют прямоуголь-
ным (рис. 96, в).
Рис. 97
Гипотенуза — от греческих ътго [гипо] —
под и TEivco [тейно] — натягивать. Такое
название связано с тем, что раньше было
принято изображать прямоугольный тре-
угольник стоящим на гипотенузе.
Катет — от греческого кс/.Оето^ [катетос] —
отвес
Сторону прямоугольного треугольника, лежащую против прямого
угла, называют гипотенузой, а две другие стороны — катетами
Докажем, что
гипотенуза прямоугольного треугольника больше катета.
51
COO
Для этого рассмотрим треугольник АВС с прямым углом С и на
луче АВ отложим отрезок AM, равный катету АС (рис. 97).
Треугольник АСМ равнобедренный, поэтому угол АСМ при его
основании острый. Следовательно, луч СМ проходит внутри прямого
угла АСВ, а точка М лежит на гипотенузе АВ (как и показано на
рис. 97). Таким образом, АВ > AM - АС,
т. е. гипотенуза АВ больше катета АС.
Справедливость неравенства АВ>ВС до-
казывается аналогично.
5Q
3
О
о
Рассмотрим произвольную прямую а
и точку А, не лежащую на ней. Пусть точ-
ка Н — основание перпендикуляра, прове-
дённого из точки А к прямой а, а М —
любая другая точка прямой а. Отрезок AM
называется наклонной, проведённой из точ-
ки А к прямой а (рис. 98).
Перпендикуляр АН является катетом,
а наклонная AM — гипотенузой прямо-
угольного треугольника АНМ. Так как ка-
тет меньше гипотенузы, то
перпендикуляр, проведённый из точки к прямой, меньше
любой наклонной, проведённой из той же точки к этой
прямой.
Длина перпендикуляра, проведённого из точки к прямой, называ-
ется расстоянием от этой точки до прямой. На рисунке 98 расстояние
от точки А до прямой а равно длине отрезка АН.
Рис. 98
Отрезок AM —
наклонная к прямой а
о
о
о
Прямоугольный треугольник с углом в 30
Докажем сначала, что
катет прямоугольного треугольника, лежащий против угла
в 30°, равен половине гипотенузы.
Из двух равных прямо-
угольных треугольников
с углами в 30° состав-
лен равносторонний
треугольник
Рис. 99
Рассмотрим прямоугольный треугольник АВС с прямым углом А
и углом В, равным 30° (рис. 99, а), и докажем, что AC --ВС.
Приложим к треугольнику АВС равный ему треугольник ABD
так, как показано на рисунке 99, б. Получится треугольник BCD, в кото-
1
ром AD = АВ - 60°. Следовательно, DC - ВС. Но АС = -DC, поэтому
1
АС = ±ВС.
Докажем теперь, что
если катет прямоугольного треугольника равен половине ги-
потенузы, то угол, лежащий против этого катета, равен 30°.
Рассмотрим прямоугольный треугольник АВС с катетом АС, рав-
ным половине гипотенузы ВС (рис. 100, а), и докажем, что АВ = 30°.
Приложим к треугольнику АВС равный ему треугольник ABD
так, как показано на рисунке 100, б. Получится треугольник BCD, в ко-
тором DB - ВС, а так как ВС = 2АС - DC, то DB = DC. Следовательно,
ADBC = AC, а так как ADBC=2AB и ZC = 90°-ZB, то 2ZB=90°-ZB,
откуда ZB = 30°.
К треугольнику АВС
приложили равный
ему треугольник ABD.
Так как DB = ВС
и BC = 2AC = DC.
то DB = DC
Рис. 100
Признаки равенства прямоугольных треугольников
53
В прямоугольном треугольнике угол между катетами прямой, а любые
два прямых угла равны. Поэтому согласно теоремам о первом и втором
признаках равенства треугольников справедливы следующие утверждения:
если катеты одного пря-
моугольного треугольника
соответственно равны ка-
тетам другого прямоуголь-
ного треугольника, то та-
кие треугольники равны
(рис. 101);
если катет и прилежащий
к нему острый угол одного
прямоугольного треуголь-
ника соответственно рав-
ны катету и прилежащему
к нему острому углу дру-
гого прямоугольного тре-
угольника, то такие тре-
угольники равны (рис. 102).
Учитывая, что сумма двух
острых углов прямоугольного
треугольника равна 90°, полу-
чаем ещё два признака равен-
ства прямоугольных треуголь-
ников:
если гипотенуза и острый
угол одного прямоугольно-
го треугольника соответст-
венно равны гипотенузе и
острому углу другого пря-
моугольного треугольника,
то такие треугольники рав-
ны (рис. 103);
если катет и противолежа-
щий ему угол одного пря-
моугольного треугольника
Рис. 101
Прямоугольные
треугольники
равны по двум
катетам
Прямоугольные
треугольники
равны по катету
и прилежащему
острому углу
Прямоугольные
треугольники
равны по
гипотенузе
и острому углу
Рис. 103
Прямоугольные
треугольники
равны по катету
и противо-
лежащему углу
о
О
о
т
X
Е
Ф
«г
X
X
я
X
ТРЕУГОЛЬНИКИ
соответственно равны катету и противолежащему углу друго-
го прямоугольного треугольника, то такие треугольники рав-
ны (рис. 104).
В самом деле, в таких треугольниках два других острых угла
также равны, поэтому указанные треугольники равны по второму
признаку равенства треугольников
---•
Рассмотрим ещё один признак равенства прямоугольных треуголь-
ников.
|Если гипотенуза и катет одного прямоугольного треугольни-
ка соответственно равны гипотенузе и катету другого пря-
моугольного треугольника, то такие треугольники равны.
Доказательств?. Рассмотрим прямоугольные треугольники
АВС и	у которых углы АиА1 прямые, ВС = В^ и
АВ- А1В1 (рис. 105, а). Докажем, что эти треугольники равны.
Приложим треугольник АВС к треугольнику А1В1С1 так, чтобы
вершина А совместилась с вершиной Alt вершина В — с вершиной
Вг, а вершины С и Сг оказались по разные стороны от прямой А^
(рис. 105, б). Поскольку АСА1С1 = 90° + 90° - 180°, то точки С, Аг
и Сг будут лежать на одной прямой. Треугольник СВ1С1 равнобед-
ренный, поэтому AC-ACV Следовательно, прямоугольные треуголь-
ники АВС и А1В1С1 равны по гипотенузе (ВС - BjCJ и острому
углу (АС-АСг). Теорема доказана.
АА =	= 90°, ВС = B^L АВ = А1В1
Рис. 105
Серединный перпендикуляр к отрезку
Серединным перпендикуляром к отрезку называется прямая, прохо-
дящая через середину отрезка и перпендикулярная к нему. На рисун-
ке 106 прямая а — серединный перпендикуляр к отрезку АВ. Докажем
теорему о серединном перпендикуляре к отрезку.
Каждая точка серединного перпендикуляра к отрезку рав-
ноудалена от концов этого отрезка.
Доказательство. Обозначим буквой М произвольную точку сере-
динного перпендикуляра а к отрезку АВ и докажем, что AM -ВМ.
Если точка М совпадает с середи-
ной О отрезка АВ, то справедливость ра-
венства AM = ВМ очевидна. Если же М	а
и О — различные точки, то прямоугольные
треугольники ОАМ и ОВМ (рис. 107) рав-
ны по двум катетам, поэтому AM = ВМ.
Теорема доказана.	А л ?в
В любой теореме различают две части:
условие и заключение. Условие теоремы —
это то, что дано, заключение — то, что требу-
ется доказать. Рассмотрим, например, тео-
рему об углах равнобедренного треугольника.
Чтобы выделить в ней условие и заключе-
ние, сформулируем её так: «если треуголь-
ник равнобедренный, то углы при его осно-
вании равны». Условием здесь является
первая часть утверждения; «если треуголь-
ник равнобедренный», а заключением —
вторая часть: «то углы при его основании
равны». Можно сказать так: дан равнобед-
ренный треугольник; требуется доказать, что
Прямая а — серединный
перпендикуляр к отрезку АВ
Рис. 106
Треугольники ОАМ и ОВМ
равны по двум катетам
углы при его основании равны.
Теоремой, обратной данной, называет-
ся такая теорема, в которой условием являет-
ся заключение данной теоремы, а заключени-
льники
—------.............“..-1-
пендикуляром к отрезку, соединяю-
щему две деревни, то эти деревни
равноудалены от моста через реку
Докажем теорему, обратную
к отрезку.
ем — её условие. Обратной теореме
об углах равнобедренного треугольника
является теорема о признаке равнобед-
ренного треугольника: если два угла
треугольника равны, то этот треуголь-
ник равнобедренный.
Отметим, что если доказана ка-
кая-нибудь теорема, то из этого ещё
не следует справедливость обратного
утверждения. Более того, обратное
утверждение не всегда оказывается
верным. Например, мы знаем, что
если углы вертикальные, то они равны.
Обратное утверждение: «если углы
равны, то они вертикальные», конеч-
но же, неверно.
теореме о серединном перпендикуляре
 Каждая точка, равноудалённая от концов отрезка, лежит на
серединном перпендикуляре к этому отрезку.
Доказательство. Рассмотрим произвольную точку М, равноуда-
лённую от концов отрезка АВ, и докажем, что точка М лежит на сере-
динном перпендикуляре а к этому отрезку.
Если точка М лежит на прямой АВ,
то она совпадает с серединой О отрезка
АВ, а значит, лежит на прямой а. Если же
точка М не лежит на прямой АВ, то точки
А, В и М — вершины равнобедренного
треугольника (рис. 108), так как AM = ВМ
по условию. Отрезок МО — медиана этого
треугольника, а следовательно, и высота,
поэтому МО А. АВ. Таким образом, прямая
МО — серединный перпендикуляр к отрез-
ку АВ, и точка М лежит на нем. Теорема
доказана.
Медиана МО равнобед-
ренного треугольника AM В
является высотой
Рис. 108
Множество всех точек плоскости, каждая из которых равноуда-
лена от концов отрезка, есть серединный перпендикуляр к этому
отрезку.
Обозначим это множество буквой Ф. По теореме о серединном
перпендикуляре к отрезку каждая точка серединного перпендикуляра
принадлежит множеству Ф. К по обратной теореме каждая точка
множества Ф принадлежит серединному перпендикуляру к отрезку.
Следовательно, множество Ф и есть этот серединный перпендикуляр.
---•
Множество всех точек, удовлетворяющих какому-либо условию,
называют также геометрическим местом точек, удовлетворяющих этому
условию. Можно сказать, что серединный перпендикуляр к отрезку —
это геометрическое место точек, равноудалённых от его концов.
Свойство биссектрисы угла
Докажем сначала теорему о биссектрисе угла, а затем обратную ей теорему.
 Каждая точка биссектрисы неразвёрнутого угла равноуда-
лена от его сторон1.
§7. Прямоугольные треугольники
Доказательство Обозначим бук-
вой М произвольную точку биссектрисы
неразвёрнутого угла А, проведём перпен-
дикуляры МН и МК к сторонам угла и
докажем, что МН=МК (рис. 109).
Прямоугольные треугольники АМН
и АМК равны по гипотенузе и острому
углу (AM — общая гипотенуза, Z1 = Z2
по условию). Следовательно, МН = МК
Теорема доказана.
Треугольники АМН и АМК
равны по гипотенузе
и острому углу
Рис. 109
’То есть равноудалена от прямых, содержа-
щих стороны угла.
ТРЕУГОЛЬНИКИ
(Каждая точка, лежащая внутри неразвёрнутого угла и рав-
ноудалённая от сторон угла, лежит на его биссектрисе.
Доказательство. Рассмотрим точку М,
которая лежит внутри неразвёрнутого угла
А и равноудалена от его сторон, т. е. пер-
пендикуляры МН и МК к сторонам равны
(рис. 110). Докажем, что луч AM — бис-
сектриса угла А.
Прямоугольные треугольники АМН
и АМК равны по гипотенузе и катету (AM—
общая гипотенуза, МН-МК по усло-
вию). Поэтому, Z1 = Z2, т. е. луч AM —
биссектриса угла А. Теорема доказана.
Треугольники АМН и АМК
равны по гипотенузе
и катету
Рис. 110
J Множество всех точек плоскости, каждая из которых лежит внут-
ри неразвёрнутого угла и равноудалена от его сторон, есть бис-
сектриса этого угла.
Проекция отрезка
Проекцией точки М на прямую а называется основание перпендикуля-
ра, проведённого из точки М к прямой а, если точка М не лежит на
прямой а, и сама точка М, если она лежит на прямой а Проекцией
отрезка на прямую а называется множество проекций всех точек этого
отрезка на прямую а.
Рассмотрим острый угол POQ и отрезок АВ, лежащий на стороне
ОР этого угла (рис. 111, а). Пусть Ах и Вг — проекции точек А и В на
прямую OQ. Наглядно видно, что отрезок А1В1 является проекцией от-
резка АВ на прямую OQ. Однако этот факт требует обоснования: нуж-
но доказать, что проекция каждой точки отрезка АВ лежит на отрезке
ArBr и, обратно, каждая точка отрезка ArBt является проекцией неко-
торой точки отрезка АВ.
Начнём с доказательства первого утверждения
Пусть Мг — проекция точки М отрезка АВ на прямую OQ (рис. 111, б).
Докажем, что точка лежит на отрезке АЛВХ. Так как прямые AAt и ММ1
перпендикулярны к прямой OQ, то они не пересекаются (см замечание 2 на
с. 28), поэтому точка А! лежит по ту же сторону от прямой ММУ что и точ-
ка А. По аналогичной причине точка Вт лежит по ту же сторону от прямой
ММУ что и точка В. Но точки А и В лежат по разные стороны от прямой
ММ1г поскольку эта прямая пересекает отрезок АВ. Следовательно, точки
Аг и Вг также лежат по разные стороны от прямой ММУ поэтому точка
лежит между точками Аг и Вг, т. е. лежит на отрезке А^Вр Первая часть
утверждения доказана
59
Точки Аг и Вг — проекции
точек А и В на прямую OQ
MiN±OQ
Рис. 111
точки М на прямую OQ
Прямая M]N пересекает
отрезок АВ в точке М
§7. Прям оугольные тр е у г о л ь н и к и
Пусть теперь — произвольная точка отрезка ArBv Докажем, что
она является проекцией некоторой точки отрезка АВ. Проведём прямую
перпендикулярную прямой OQ (рис. 111, в). Точки А и Аг лежат по
одну сторону от этой прямой (поскольку прямые ААг и MrN не пересека-
ются), точки В и Вг также лежат по одну сторону от прямой MTN, а точки
Аг и Вг лежат по разные стороны от этой прямой. Следовательно, точки А
и В также лежат по разные стороны от прямой MrN, и поэтому прямая
MXN пересекает отрезок АВ в некоторой точке М (рис. 111, г). Проекцией
этой точки на прямую OQ и является точка Мг. Утверждение доказано.
Отметим, что точки Аг и Вг лежат на стороне OQ угла POQ, а не на
её продолжении. В самом деле, если предположить, что точка Аг лежит на
продолжении стороны OQ (рис. 112), то
получается треугольник ААуО с прямым
углом Ау и тупым углом О, чего не может
быть. Итак, мы доказали, что
проекцией отрезка, лежащего на
одной из сторон острого угла, на рис 112
другую сторону является отрезок.
Докажем теперь теорему о проекциях равных отрезков
 Если два отрезка, лежащие на одной стороне острого угла,
равны, то их проекции на другую сторону также равны.
Доказательстве Рассмотрим равные отрезки АВ и CD. лежа-
щие на одной из сторон острого угла О (рис. 113, а). Пусть Ау, Ви Су
и Dy — проекции точек А, В, С и D на другую сторону данного угла.
Требуется доказать, что АуВу = Cj-Dp
Пусть А2 — проекция точки А на а)	D/
прямую ВВу, С2 — проекция точки С на	с .
прямую DDV Прямоугольные треуголь-	гс2
ники АВА2 и CDC2 равны по гипотенузе	।
и острому углу (АВ = CD по условию,	, —^Аг
АОВВу - 90° - АО = AODDy), поэтому
аа2 = сс2.
“I Г__т_Г
Ау ^1 -°1
В четырёхугольнике АА1В1А2 углы
Ау, А2 и By прямые, поэтому этот четы-
рёхугольник — прямоугольник, и его
противоположные стороны АА2 и АуВу
равны. Аналогично СС2 = CyDy. Итак,
АуВу = АА2 = СС2 = CyDy, и, значит,
АуВу = CyDy. Теорема доказана.
Проекции равных
отрезков равны

гчание Если равные отрезки АВ
и CD расположены так, как показано на
рисунке 113, б (т. е. точка А совпадает
с вершиной угла), то их проекции АВу и
CyDy равны. Доказательство этого утверж-
дения приведено на рисунке 113, б.
AABB1 = ACDC2, поэтому
АВу = ССг, а так как
CC2 = CyDy, то ABy — CyDy
Рис 113
Если на одной из сторон острого угла лежат два отрезка, один
из которых в п раз больше второго (л — натуральное число),
то проекция первого отрезка на другую сторону угла в п раз
больше проекции второго отрезка.
Действительно, обратимся к ри-
сунку 114, на котором А0А1 = АГА2 =
= ... - Ап_1Ап и, следовательно, B0Bj =
= BXB2 = ... = Вп_ ^п. Из этих равенств
следует, что A0An = nA0Alt В0Вп =
= пВ0Вг. Мы видим, что отрезок А0Ап
в п раз больше отрезка AqAj и его
проекция В0В„ в п раз больше проек-
ции В0В1 отрезка AqAj.
Рис. 114
Середина гипотенузы прямоугольного треугольника равноудале-
на от всех его вершин.
В самом деле, пусть точка М —
середина гипотенузы АВ прямоугольно-
го треугольника АВС, точка Мг — про-
екция точки М на прямую АС (рис. 115).
Поскольку отрезки МА и МВ равны, то
их проекции М]А и МгС также равны.
Итак, ММг J. АС и MtA = МгС. Это
означает, что прямая ММг — середин-
ный перпендикуляр к отрезку АС. Сле-
довательно, МА = МС. Таким образом,
МА = МВ - МС, что и требовалось до-
казать.
ММг — серединный перпен-
дикуляр к отрезку АС
Рис 115
Следствие 2 можно сформулировать иначе:
медиана прямоугольного треугольника, проведённая из вер-
шины прямого угла, равна половине гипотенузы.
Вопросы и задачи
ТРЕУГОЛЬНИКИ
в котором ZC = 63° и
Рис. 116
41. а) Докажите, что если четырёхугольник ABCD — прямоугольник,
то ACAD = ABDA.
б)	Диагонали прямоугольника ABCD пересекаются в точке О. До-
кажите, что О А = О В = ОС = OD.
в)	Отрезок АН — высота треугольника АВС,
АВАН = 27°. Докажите, что АВ = АС.
г)	На рисунке 116 изображён квадрат ABCD,
в котором AP = BQ = CR=DS. Докажите,
что четырёхугольник PQRS — квадрат.
д)	Докажите, что высота прямоугольного
треугольника, проведённая к гипотенузе,
разделяет его на два треугольника, углы каж-
дого из которых соответственно равны углам
данного треугольника.
е)	Из точки М стороны АВ треугольника
АВС с углом С, равным 72°, проведён пер-
пендикуляр МН к стороне АС. Известно,
что ААМН = 18°. Докажите, что АВ = ВС.
ж)	Основания высот ААг и ВВг треугольника АВС лежат на его сторонах,
АСААг = AABBV Докажите, что треугольник АВС — равнобедренный.
з)	Докажите, что перпендикуляр, проведённый из точки стороны прямо-
угольника к прямой, содержащей противоположную сторону, разделяет
прямоугольник на два прямоугольника.
и)	Диагонали прямоугольника ABCD пересекаются в точке О, точки М
и N — середины сторон АВ и AD. Докажите, что четырёхугольник
AMON — прямоугольник.
к)	В четырёхугольнике ABCD диагонали АС и BD пересекаются в точке О,
причём О А = ОВ = OD. Точки М и N — середины сторон АВ и AD. Дока-
жите, что четырёхугольник AMON — прямоугольник.
л)	Отрезки МВХ и МСГ — перпендикуляры, проведённые из точки М осно-
вания ВС равнобедренного треугольника АВС к прямым АС и АВ, отре-
зок ВН — высота этого треугольника. Дока-
жите, что МВг + МСГ = ВН.
42.	а) Докажите, что диагонали прямоугольни-
ка равны.
б)	Точка Н — основание перпендикуляра,
проведённого из точки пересечения диагона-
лей прямоугольника ABCD к прямой AD.
Докажите, что АН = HD.
в)	На рисунке 116 углы А и D прямые,
ZAPS = 61° и ADRS = 29°. Докажите, что
PSARS.
Рис. 117
г)	На рисунке 117 изображён квадрат ABCD, стороны которого продолжены
так, что АР = BQ = CR = DS. Докажите, что четырёхугольник PQRS—
квадрат.
д)	Из точки М, лежащей во внутренней области острого угла А, проведены
перпендикуляры МН и МК к сторонам угла. Известно, что 2АМН = А АМК.
Докажите, что луч AM — биссектриса угла А.
е)	На сторонах АВ и ВС треугольника АВС отмечены точки М и Д’ соответ-
ственно, отрезки МН и NK — перпендикуляры, проведённые из этих точек
к стороне АС. Известно, что Л АМН = ACNK. Докажите, что АВ = ВС.
ж)	Отрезки AD и АН — биссектриса и высота равнобедренного треуголь-
ника АВС с основанием АС. Найдите углы треугольника ADH, если ZB = 44°.
з)	Докажите, что если АВ ± AC, CD ± АС и BD ± АВ, то АС = BD.
и)	Диагонали прямоугольника ABCD пересекаются в точке О, точка М —
середина стороны AD. Докажите, что АВ = 2ОМ.
к)	В четырёхугольнике ABCD диагонали АС и BD пересекаются в точке О,
причём О А = ОВ = ОС = OD. Докажите, что четырёхугольник ABCD — пря-
моугольник.
л)	Докажите, что сумма длин перпендикуляров, проведённых из точки
внутренней области1 равностороннего треугольника к его сторонам, равна
высоте этого треугольника.
43.	а) Высота АН прямоугольного треугольника АВС, проведённая к гипоте-
нузе, равна 7 см, а угол С равен 60°. Найдите АВ.
б)	Биссектриса CD прямоугольного треугольника АВС с гипотенузой ВС
равна 8 см. Найдите АВ, если Z_BDC = 120е.
в)	Отрезок CD — высота треугольника АВС с прямым углом С. Известно,
что ВС = 2BD. Докажите, что AD = 3BD.
г)	Расстояние от середины стороны ВС равностороннего треугольника АВС
до прямой АВ равно 7 см. Найдите расстояние от точки А до прямой ВС.
д) Угол прямоугольного треугольника равен 30е. Докажите, что расстояние от
середины гипотенузы до вершины прямого угла равно длине одного из катетов.
44.	а) Высота АН прямоугольного треугольника АВС, проведённая из верши-
ны прямого угла, равна 4 см, АВ = 8 см. Найдите угол С.
б)	Биссектриса CD прямоугольного треугольника АВС с гипотенузой ВС
равна отрезку BD. Найдите угол BDC.
в)	Отрезок BD — высота треугольника АВС с прямым углом В. Известно,
что АВ = 2BD. Докажите, что ЗАС = 4 АЛ.
г)	Угол В равнобедренного треугольника АВС равен 120°. Найдите рас-
стояние от вершины С до прямой АВ, если АС = 30 см.
д)	Докажите, что если в прямоугольном треугольнике расстояние от сере-
дины гипотенузы до вершины прямого угла равно длине катета, то один из
его углов равен 30°.
1 Внутренняя область треугольника — это общая часть внутренних областей
трёх его углов.
§7. Прямоугольные треугольники
45.	а) Докажите, что если две высоты треугольника равны, то этот треугольник —
равнобедренный.
б)	Докажите, что если сторона, прилежащий к ней угол и высота, прове-
дённая к этой стороне, одного треугольника соответственно равны стороне,
прилежащему к ней углу и высоте, проведённой к этой стороне, другого
треугольника, то такие треугольники равны.
в)	Докажите, что если острый угол и биссектриса, проведённая из верши-
ны этого угла, одного прямоугольного треугольника соответственно равны
острому углу и биссектрисе, проведённой из вершины этого угла, другого
прямоугольного треугольника, то такие треугольники равны.
г)	Докажите, что если прямая пересекает отрезок в его середине, то концы
отрезка равноудалены от этой прямой.
д)	Докажите, что если в треугольнике биссектриса является медианой, то
этот треугольник — равнобедренный.
46.	а) Высоты ААг и ВВГ треугольника АВС равны, АВг = CAV Найдите угол А.
б) Две стороны и высота, проведённая к одной из них, одного треугольни-
ка соответственно равны двум сторонам и высоте, проведённой к одной из
них, другого треугольника Могут ли такие треугольники быть неравными?
в) Докажите, что если сторона и проведённые к ней высота и медиана од-
ного треугольника соответственно равны стороне и проведённым к ней вы-
соте и медиане другого треугольника, то такие треугольники равны.
г)	Докажите, что если концы отрезка равноудалены от прямой, пересекаю-
щей отрезок, то эта прямая проходит через середину отрезка.
д)	Точки М и N — середины сторон АВ и АС треугольника АВС. Докажи-
те, что эти точки равноудалены от прямой ВС.
М. а) Серединный перпендикуляр к стороне АВ треугольника АВС пересекает
сторону ВС в точке Е. Найдите АС, если ВС = 24 см, а периметр треуголь-
ника АЕС равен 30 см.
б)	Серединные перпендикуляры к сторонам АВ и АС треугольника АВС
пересекаются в точке стороны ВС. Докажите, что Z.A = Z.B + Z.C.
в)	Две биссектрисы треугольника проходят через точку О. Докажите, что
и третья биссектриса проходит через точку О.
г)	Точки Н и К — проекции середин сторон АВ и АС треугольника АВС на
прямую ВС. Докажите, что ВС = 2НК. Рассмотрите все возможные случаи
48. а) Серединные перпендикуляры к двум сторонам треугольника проходят
через точку О. Докажите, что и серединный перпендикуляр к третьей сторо-
не проходит через точку О.
б)	Серединные перпендикуляры к двум сторонам треугольника пересека-
ются в точке, лежащей на третьей стороне. Докажите, что этот треугольник
прямоугольный, а указанная точка — середина гипотенузы.
в)	Биссектрисы внешних углов при вершинах В и С треугольника АВС пе-
ресекаются в точке О. Докажите, что луч АО — биссектриса угла А.
г)	Докажите, что прямая, проходящая через середины двух сторон тре-
угольника, является серединным перпендикуляром к одной из его высот
Соотношения между
сторонами и углами
треугольника
Неравенство
треугольника
Рис. 118
 Каждая сторона треугольника меньше суммы двух других
сторон.
Рассмотрим треугольник АВС и докажем, что
АВ<ВС + СА, СА<АВ + ВС, ВС<СА + АВ.	(1)
Пусть, например, АВ^ВС и СА^ВС. Тогда первые два из
неравенств (1), очевидно, выполняются.
Докажем справедливость третьего неравенства Проведём высо-
ту АН (рис. 118). Так как катеты прямоугольных треугольников АВН
и АСН меньше их гипотенуз, в частности НВ < АВ и СН < СА, и так
как АВВС и СА С ВС, то НВ < ВС и СН < ВС. Из двух последних
неравенств следует, что точка Н лежит между точками В и С. Таким
образом, ВС = СН + НВ < С А + АВ. Теорема доказана.
i—Бутузов, 7 кл.
ТРЕУГОЛЬНИКИ
Доказанную теорему можно сформулировать иначе:
для любых трёх точек А, В и С, не лежащих на одной пря-
мой, справедливы неравенства (1).
Каждое из них называется неравенством треугольника.
Теоремы о соотношениях между
сторонами и углами треугольника
IB треугольнике против большего угла лежит большая сто-
рона.
ZA>ZB
Рис. 119
BD=AD, поэтому BC=AD + DC>AC
Доказательство. Рассмотрим треугольник АВС, угол А кото-
рого больше угла В (рис. 119, а), и докажем, что ВС > АС.
Отложим от луча АВ угол BAD, равный углу В, так, как пока-
зано на рисунке 119, б. Поскольку ABAD < ABAC, то точка D лежит
между точками В и С.
Из равенства ABAD = АВ следует,
что треугольник BAD равнобедренный:	с
BD-AD. Поэтому
ВС - BD + DC = AD + DC.
Но в силу неравенства треугольника
AD + DC > АС.
Следовательно, ВС > АС. Теорема до- А	в
казана	вс>ас
Докажем теперь обратную теорему.
Рис. 120
IB треугольнике против большей стороны лежит больший
угол.
Доказательство. Рассмотрим треугольник АВС, в котором
ВС > АС (рис. 120), и докажем, что АА > АВ.
Допустим, что это не так. Тогда либо АА - АВ, либо АА < АВ.
Если АА = АВ, то ВС = АС, а если АА < АВ, то ВС < АС. И то и дру-
гое противоречит условию: ВС > АС. Поэтому угол А не может быть
равным углу В и не может быть меньше угла В. Следовательно,
АА > АВ. Теорема доказана.
Замечание При доказательстве теоремы мы использовали способ
рассуждений, который называется методом доказательства от против-
ного. Мы предположили, что АА < АВ, т. е. предположили противопо-
ложное (противное) тому, что хотим доказать. Исходя из этого предпо-
ложения, путем рассуждений мы пришли к противоречию с условием
теоремы. Это означает, что наше предположение неверно, и, следова-
тельно, АА > АВ.
Такой способ рассуждений часто используется в математике при
доказательствах утверждений. Мы тоже неоднократно им пользова-
лись. Попробуйте вспомнить, где именно.
соо
со
п
о
О
X
о
Е
CD
X
X
50
3
Ф
X
За
п
О
О
X
Q
5
X
Сумма углов треугольника
*
X
Сумма углов треугольника равна 180°.
Доказательство. Рассмотрим про-
извольный треугольник АВС и дока-
жем, что АА + АВ + АС = 180°.
В любом треугольнике хотя бы
два угла острые.
Пусть, например, в треугольнике
АВС острыми являются углы В и С.
Проведём высоту ААГ (рис. 121).
Рис. 121
о
±1
X
*
о
3*
Точка Ах лежит как на луче ВС, так и на луче СВ (см. п. 24),
т. е. лежит между точками В и С. Следовательно,
ZA = ZBAAi + ZCAAr
Поскольку ZBAAi = 90° - ZB и АСААХ = 90° - ZC, то
А А = 90° - ZB + 90° - АС,
откуда
АА + АВ + АС = 180°.
Теорема доказана.
Внешним углом треугольника называется угол, смежный с каким-
нибудь из углов этого треугольника.
Из теоремы о сумме углов треугольника
внешний угол треугольника равен
сумме двух углов треугольника, не
смежных с этим внешним углом.
В самом деле, обратимся к рисун-
ку 122, на котором угол 4 — внешний угол,
' смежный с углом 3 данного треугольника.
Угол 3 в сумме с углом 4 составляет 180°.
Этот же угол 3 в сумме с углами 1 и 2 так-
же составляет 180°. Поэтому Z4 = Z1 + Z2,
что и требовалось доказать.
следует что:
угол треугольника
Z4 = Z1 + Z2
Рис. 122
Вопросы и задачи
49.	а) На стороне АВ треугольника АВС, в котором АС = 14 см, ВС = 6 см,
отмечена точка М. Может ли отрезок AM быть равным 20 см?
б)	В равнобедренном треугольнике одна сторона равна 25 см,
а другая равна 10 см. Какая из них является основанием?
в)	Точки А и В лежат по разные стороны от прямой CD, причём
Z.ACD = ZBDC и АС = BD. Докажите, что ВС < АС + CD.
г)	Докажите, что медиана AAt треугольника АВС меньше полусуммы сто-
рон АВ и АС.
д)	Докажите, что прямая, проходящая через середину стороны треугольни-
ка перпендикулярно к этой стороне, пересекает большую из двух других
сторон треугольника.
е)	Докажите, что каждая сторона треугольника меньше половины его пери-
метра.
ж)	Докажите, что сумма медиан AAt и ВВг треугольника АВС больше
полусуммы сторон АС и ВС
50.	а) На стороне АВ треугольника АВС, в котором АС = 20 см, отмечена та-
кая точка М, что СМ = 16 см. Может ли сторона АВ быть равной 4 см?
б) Найдите сторону равнобедренного треугольника, если две другие сторо-
ны равны 5 см и 2 см.
в)	Точки А и В лежат по разные стороны от прямой CD, причём
/ACD = /.BCD и АС = ВС. Докажите, что BD < АС + CD.
г)	Докажите, что медиана треугольника АВС больше полуразности
сторон АВ и АС.
д)	На сторонах ВС, СА и АВ треугольника АВС отмечены соответственно
точки А1г Вт и Clf отличные от вершин треугольника. Докажите, что пери-
метр треугольника ApBjCj. меньше периметра треугольника АВС.
е)	Докажите, что сумма медиан треугольника меньше его периметра.
ж)	Точки А и С лежат по разные стороны от прямой BD, а точки В и D —
по разные стороны от прямой АС. Докажите, что 2 {АС + BD) > АВ + ВС +
+ CD + DA.
51.	а) Стороны треугольника АВС связаны неравенствами АВ > ВС > АС.
Сравните углы этого треугольника и выясните, может ли угол А быть тупым,
б) Углы треугольника АВС связаны неравенствами /А> /В> /С. Срав-
ните стороны этого треугольника.
в)	Сравните углы АВС и ACD четырёхугольника ABCD, если /ВАС = /CAD,
АВ = AD = 7 см и АС = 10 см.
г)	Докажите, что отрезок, соединяющий точку основания равнобедренного
треугольника с противоположной вершиной, не больше боковой стороны,
д) Отрезок AM — медиана треугольника АВС, в котором АВ > АС. Дока-
жите, что /ВАМ < /САМ.
52.	а) Стороны треугольника АВС связаны соотношением АВ = АС < ВС.
Сравните углы этого треугольника и выясните, может ли угол А быть тупым,
б) Углы треугольника АВС связаны соотношениями /А> /В = /С. Срав-
ните стороны этого треугольника.
в)	Сравните стороны АВ и CD четырёхугольника ABCD, если /ВАС =
= /CAD = 30° и /АСВ = /ACD = 45°.
г)	Докажите, что отрезок, соединяющий вершину треугольника с точкой
противоположной стороны, не больше большей из двух других сторон.
д)	Отрезок AD — биссектриса треугольника АВС, в котором АВ > АС.
Докажите, что BD > DC.
53.	а) Найдите углы треугольника АВС, если /А : /В : /С = 1:2:3.
б)	Внешний угол треугольника больше углов, не смежных с ним, соответ-
ственно на 30° и 70°. Найдите углы этого треугольника
в)	Биссектрисы углов при основании АС равнобедренного треугольника АВС
пересекаются в точке О, причём /АОС = 150°. Найдите углы этого треугольника,
г) На стороне АВ треугольника АВС, в котором /В = 30°, отмечена точ-
ка D, причем/ACD + /ADC = 120°. Докажите, что треугольник АВС прямо-
угольный.
д)	Докажите, что если один из внешних углов треугольника в два раза
больше угла треугольника, не смежного с ним, то треугольник равнобед-
ренный. Верно ли обратное утверждение?
е)	Во внутренней области угла АВС, равного 60°, отмечена точка D так,
что ZBAD = 100° и ABCD = 80°. Найдите угол ADC.
ж)	Точка, равноудалённая от вершин треугольника, лежит в его внутренней
области. Докажите, что этот треугольник — остроугольный.
з)	Отрезок AD — биссектриса треугольника АВС с прямым углом С. Дока-
жите, что CD < АС < AD < АВ.
54.	а) Один из углов равнобедренного треугольника в два раза больше друго-
го. Найдите эти углы.
б)	Найдите углы равнобедренного треугольника, если один из его внешних
углов равен 100°.
в)	На стороне АВ треугольника АВС отмечена точка D. Известно, что
BD = DC, AADC = 4QQ и ZACP = 30c. Найдите углы треугольника АВС.
г) Биссектрисы ААХ и ВВХ треугольника АВС пересекаются в точке О,
причём ААОВ = 135°. Докажите, что треугольник АВС прямоугольный
д) Прямые, содержащие биссектрисы внешних углов при вершинах В и С
треугольника АВС, пересекаются в точке О. Найдите угол ВОС, если угол А
равен а.
е)	Во внутренней области прямого угла АВС отмечена такая точка D, что
ZBAP = 20° и ABCD = 10°. Найдите угол ADC.
ж)	Точка, равноудалённая от вершин треугольника, лежит во внешней
области одного из его углов. Докажите, что этот треугольник — тупо-
угольный.
з)	Отрезок AD — медиана треугольника АВС с прямым углом С. Докажи-
те, что ABAD < А АВС < AADC < ААСВ.
L Вопросы для повторения
1.	Объясните, какая фигура называется треугольником Что такое сто-
роны, вершины, углы и периметр треугольника?
2.	Какой треугольник называется равнобедренным? равносторонним?
Как называются стороны равнобедренного треугольника?
3.	Сформулируйте и докажите теорему об углах равнобедренного треугольника.
4.	Докажите теорему (признак равнобедренного треугольника): если два угла
треугольника равны, то этот треугольник равнобедренный.
5.	Какой отрезок называется медианой треугольника? Сколько медиан имеет
треугольник?
6.	Какой отрезок называется биссектрисой треугольника? Сколько биссектрис
имеет треугольник?
7.	Какой отрезок называется высотой треугольника? Сколько высот имеет тре-
угольник?
8.	Сформулируйте и докажите теорему о высоте равнобедренного треуголь-
ника.
9.	Какое утверждение называется следствием? Сформулируйте следствия из
теоремы о высоте равнобедренного треугольника
10.	Сформулируйте и докажите теорему, выражающую первый признак равен-
ства треугольников.
11.	Сформулируйте и докажите теорему, выражающую второй признак равен-
ства треугольников.
12.	Сформулируйте и докажите теорему, выражающую третий признак равен-
ства треугольников.
13.	Объясните, какая фигура называется четырёхугольником. Что такое верши-
ны, смежные стороны, противоположные стороны и диагонали четырёх-
угольника?
14.	Какой четырёхугольник называется прямоугольником?
15.	Сформулируйте и докажите теорему о противоположных сторонах прямо-
угольника. Какой четырёхугольник называется квадратом?
16.	Докажите, что если один из углов треугольника прямой, то сумма двух дру-
гих углов этого треугольника равна 90°.
17.	Докажите, что если три угла четырёхугольника прямые, то этот четырёх-
угольник — прямоугольник.
18.	Докажите, что в любом треугольнике либо все три угла острые, либо два
угла острые, а третий прямой или тупой.
19.	Докажите, что углы при основании равнобедренного треугольника —
острые.
20.	Какой треугольник называется остроугольным? прямоугольным? тупоуголь-
ным? Как называются стороны прямоугольного треугольника?
21.	Докажите, что гипотенуза прямоугольного треугольника больше катета.
22.	Объясните, какой отрезок называется наклонной, проведённой из данной
точки к данной прямой. Докажите, что перпендикуляр, проведённый из точ-
ки к прямой, меньше любой наклонной, проведённой из той же точки к этой
прямой Что называется расстоянием от точки до прямой?
23.	Докажите, что катет прямоугольного треугольника, лежащий против угла
в 30°, равен половине гипотенузы.
24.	Докажите, что если катет прямоугольного треугольника равен половине ги-
потенузы, то угол, лежащий против этого катета, равен 30°.
25.	Сформулируйте четыре признака равенства прямоугольных треугольников,
вытекающие из первого и второго признаков равенства треугольников.
26.	Сформулируйте и докажите теорему, выражающую признак равенства пря-
моугольных треугольников по гипотенузе и катету.
27.	Какая прямая называется серединным перпендикуляром к отрезку? Докажи-
те теорему: каждая точка серединного перпендикуляра к отрезку равноуда-
лена от концов этого отрезка.
28.	Что такое условие теоремы и заключение теоремы? Какая теорема называ-
ется обратной данной теореме?
29.	Докажите теорему: каждая точка, равноудалённая от концов отрезка, лежит
на серединном перпендикуляре к этому отрезку По отношению к какой тео-
реме эта теорема является обратной?
30.	Докажите, что множество всех точек плоскости, каждая из которых равно-
удалена от концов отрезка, есть серединный перпендикуляр к этому от-
резку.
31.	Докажите теорему: каждая точка биссектрисы неразвёрнутого угла равно-
удалена от его сторон.
32.	Докажите теорему: каждая точка, лежащая внутри неразвёрнутого угла
и равноудаленная от сторон угла, лежит на его биссектрисе По отношению
к какой теореме эта теорема является обратной?
33.	Докажите, что множество всех точек плоскости, каждая из которых лежит
внутри неразвёрнутого угла и равноудалена от его сторон, есть биссектриса
этого угла.
34*. Докажите, что проекцией отрезка, лежащего на одной из сторон острого
угла, на другую сторону является отрезок.
35.	Сформулируйте и докажите теорему о проекциях равных отрезков.
36.	Докажите, что если на одной из сторон острого угла лежат два отрезка,
один из которых в п раз больше второго (п — натуральное число), то про-
екция первого отрезка на другую сторону угла в п раз больше проекции
второго отрезка.
37.	Докажите, что середина гипотенузы прямоугольного треугольника равно-
удалена от всех его вершин.
38.	Докажите теорему: каждая сторона треугольника меньше суммы двух дру-
гих сторон. Объясните, что такое неравенство треугольника.
39.	Докажите теорему: в треугольнике против большего угла лежит большая
сторона.
40.	Докажите теорему: в треугольнике против большей стороны лежит больший
угол. По отношению к какой теореме эта теорема является обратной?
41.	Объясните, в чем состоит метод доказательства от противного. Приведите
пример доказательства теоремы методом от противного.
42.	Сформулируйте и докажите теорему о сумме углов треугольника.
43.	Какой угол называется внешним углом треугольника? Докажите, что внеш-
ний угол треугольника равен сумме двух углов треугольника, не смежных
с этим внешним углом.
> Дополнительные задачи ]
f §5
55.	Точка С лежит на прямой АВ, а точка D не лежит на этой прямой.
Докажите, что по крайней мере два из трёх отрезков AD, BD и CD
 не равны друг другу.
56.	Биссектрисы углов при основании АС равнобедренного треугольника АВС
пересекаются в точке О. Докажите, что ZABO = ZCBO.
57.	Докажите, что если в треугольнике АВС стороны АВ и АС не равны, то ме-
диана AM треугольника не является высотой.
58*. Докажите, что каждый угол имеет биссектрису.
59*. Докажите, что каждый отрезок имеет середину.
§6
60.	В треугольниках АВС и AjBjCj стороны АВ и А^ равны и ZA=ZAP
ZB = ZBr На сторонах АС и А^ отмечены точки D и D± так, что
CD = ClD1. Докажите, что треугольники BDC и В1Р1С1 равны, и сравните
отрезки BD и B1D1.
61	В треугольниках АВС и АрВ^ углы А и Аг равны и АВ = А1В1,
АС = АгСг. На сторонах АС и А1С1 отмечены точки D и Dx так, что
ZDBC =	Докажите, что треугольники BDC и B^D^C^ равны,
и сравните углы BDC и B^D^.
62.	На боковых сторонах АВ и ВС равнобедренного треугольника АВС отме-
чены точки D \л Е так, что AD = СЕ. Отрезки DC и АЕ пересекаются в точ-
ке О. Докажите, что АО = ОС.
63.	Вершины В и D равнобедренных треугольников АВС и ADC с общим
основанием АС лежат по разные стороны от прямой АС На отрезке BD
отмечена точка Е, не лежащая на прямой АС. Докажите, что ZBAC =
= ZACB.
64.	На сторонах ОК и OL треугольников ОКВ и OLC с прямыми углами
при вершине О отмечены точки А и D. Известно, что OA = OD, AK = DL
и ZKAB = ZCDL. Докажите, что КВ = CL.
65.	Отрезки AD и BE пересекаются в точке С, причём АС = СВ и ZBAC = ZDEC
Докажите, что ДАВВ = ABBA.
74
к 66. Докажите, что в равнобедренном треугольнике равны: медианы, проведён-
) ные к боковым сторонам; биссектрисы, проведённые к боковым сторонам
67.	Докажите, что середины сторон равнобедренного треугольника являются
вершинами другого равнобедренного треугольника
68.	На боковых сторонах АВ и АС равнобед-
ренного треугольника АВС отмечены такие
точки Р и Q, что АРМВ = AQMC, где М —
середина основания ВС. Докажите, что
BQ = СР.
69.	На рисунке 123 отрезки АС и BD равны и
ACAD = ABDA. Докажите, что ABAC = ACDB.
70.	На рисунке 124 AB = CD, AD = BC, BE
и DF — высоты треугольников АВС и ADC.
Докажите, что ДАВВ = ACDF.
71.	В треугольниках АВС и A^Cj равны сторо-
ны АВ и AjBp ВС и В1С1, медианы AM
и AaMv Докажите, что ЛАВС - ЛА1В1С1.
72.	В треугольниках АВС и A^Cj равны углы
А и Ар стороны АВ и AjBp биссектрисы AD
и ArDv Докажите, что &АВС = AAjBjCp
Рис. 123
§7
73.	Докажите, что основание одной из высот тупоугольного треугольника лежит
на стороне треугольника, а основания двух других высот — на продолжени-
ях сторон.
74.	Отрезки АН и AD — высота и биссектриса треугольника АВС. Докажите,
что угол HAD равен модулю полуразности углов В и С.
75.	Продолжения высот ВВг и ССг треугольника АВС с тупым углом А пересе-
каются в точке Н. Докажите, что ААВН = ААСН и АА + АВНС = 180е.
76.	Докажите, что в равнобедренном треугольнике две высоты, проведённые из
вершин основания, равны.
77.	Докажите, что если сторона и высоты, проведённые из концов этой сторо-
ны, одного остроугольного треугольника соответственно равны стороне
и высотам, проведённым из концов этой стороны, другого остроугольного
треугольника, то такие треугольники равны.
78.	Докажите, что середина основания равнобедренного треугольника равно-
удалена от боковых сторон.
79.	Из точки М биссектрисы неразвёрнутого угла О проведены перпендикуляры
МА и МВ к сторонам этого угла. Докажите, что АВ ± ОМ
80.	Что представляет собой множество всех точек плоскости, равноудалённых
 от двух данных пересекающихся прямых?
81	Биссектрисы углов при основании АВ равнобедренного треугольника АВС
пересекаются в точке М. Докажите, что прямая СМ — серединный перпен-
дикуляр к отрезку АВ.
82.	Высоты ААг и ВВг равнобедренного треугольника АВС, проведённые
к боковым сторонам, пересекаются в точке М. Докажите, что прямая МС —
серединный перпендикуляр к отрезку АВ
83*. На диагонали АС квадрата ABCD отмечена такая точка N, что AN = 3NC,
точка М — середина стороны АВ. Докажите, что ADNM = 90е.
§8
84.	Точка М лежит во внутренней области треугольника АВС. Докажите, что
МВ + МС < АВ + АС.
85.	Точка М лежит во внутренней области треугольника АВС. Докажите, что
МА + МВ + МС < АВ + ВС + С А.
86.	Докажите, что для любых точек А. В и С имеет место неравенство
АВ < АС + СВ.
87.	Отрезок AM — медиана треугольника АВС, причём АСАМ < АВ + АС.
Докажите, что АВ < 2AM.
88.	Отрезок AM — медиана треугольника АВС, причём АС > 2АМ. Докажите,
что АС + АВ < AM АВ.
89.	В четырёхугольнике ABCD диагонали АС и BD пересекаются, а сторона
АВ больше диагонали BD. Докажите, что АС > CD
90.	Во внутренней области равностороннего треугольника АВС отмечена точ-
ка D. Докажите, что DA < DB + DC.
91	Треугольники АВС и DEF на рисунке 125 равносторонние Докажите, что
_AD = BE = CF.
92.	На гипотенузе АВ прямоугольного треуголь-	в
ника АВС отмечены такие точки D и Е,
что BD = ВС и АЕ = АС. Найдите угол DCE.	Е
93.	На гипотенузе АС прямоугольного треуголь-	F
ника АВС отмечена такая точка Р, что
АР = АВ. Отрезок BD — высота треуголь- а	С
ника. Докажите, что луч ВР — биссектриса	D
угла CBD.	Рис. 125
§8. Соотношения между сторонами и углами треугольника
\ 94. На рисунке 126 АВ = АС и АР = PQ = QR =
= RB = BC. Найдите угол А и докажите, что
BQ = BR.
95. Биссектрисы углов А и В треугольника АВС
пересекаются в точке М, причём ААМВ = 142°.
Найдите углы АСМ и ВСМ.
"  —
96. Отрезок ААг — биссектриса треугольника АВС.
Докажите, что АВ > АХВ и АС > А1С.
97*. В треугольнике АВС угол С прямой, a ZB = 35°.
На сторонах АВ и ВС отмечены такие точки Р
и Q, что АРСВ = 20° и ZBAQ = 10е. Найдите
угол CPQ.
Рис. 126
98*. Перпендикуляр МН к прямой, содержащей катет АС прямоугольного тре-
угольника АВС, пересекает гипотенузу ВС в точке D. Известно, что
ACDH= 50°, АСМН = 45° и ZABH = 10°. Найдите угол ВМН.
глава 3
Окружность
§9
Отрезки и углы,
связанные
с окружностью
(с. 10), треугольника (с. 32) и
ление.
Определение
окружности
Предложение, в котором разъясняется
смысл какого-либо слова или слово-
сочетания, называется определением.
В нашем учебнике уже были опреде-
ления. например определение угла
т. д. Сформулируем ещё одно опреде-
Определение
Окружностью называется геометрическая фигура, состоящая из всех то-
чек плоскости, расположенных на заданном расстоянии от данной точки
Окружность
радиуса г с центром О
Круг содержит
точку О и все точки М
для которых ОМ г
Отрезок АВ —
диаметр окружности
Рис. 127
Рис. 128
Рис. 129
Данная точка (точка О на рис. 127) называется центром окружно-
сти, а отрезок, соединяющий центр с какой-либо точкой окружно-
сти, радиусом окружности (отрезок ОМ на рис. 127). Из определения
окружности следует, что все радиусы равны друг другу. Часть
Радиус — от латинского radius (спи-
ца в колесе).
Диаметр — от греческого 5шиетрод
[диаметрос] — поперечник
плоскости, ограниченная окружностью, называется кругом (рис. 128).
Отрезок, соединяющий две точки окружности и проходящий через её
центр, называется диаметром (рис. 129).
Поскольку центр окружности является серединой диаметра, то
диаметр окружности в два раза больше её радиуса.
Для построения окружности пользуются циркулем (рис. 130). Для
проведения окружности на местности пользуются веревкой и двумя
колышками (рис. 131).
Докажем, что
никакие три точки окружности не лежат на одной прямой.
Воспользуемся методом доказательства от противного: допу-
стим, что какие-то три точки А, В \л С окружности с центром О лежат
на некоторой прямой а.
Пусть М и N — середины отрезков АВ и ВС (рис. 132). По-
скольку ОА = ОВ, то точка О лежит на серединном перпендикуляре
Построение окружности
с помощью циркуля
Построение окружности с помощью
веревки и двух колышков
□
X
X
г
О
X
X
о
Рис 130
Рис 131
к отрезку АВ, поэтому ОМ ± а. Аналогич-
но (исходя из равенства ОВ = ОС) получа-
ем ON ± а.
Таким образом, из точки О проведе-
ны два перпендикуляра к прямой а — ОМ
и ON. Но этого не может быть Следова-
тельно, точки А, В и С не лежат на одной
прямой, что и требовалось доказать.
—•
Взаимное расположение
прямой и окружности
Рассмотрим окружность с центром О радиу-
са г и прямую а.
Если прямая а проходит через точку О,
то она пересекает окружность в двух точ-
ках — концах диаметра, лежащего на этой
прямой (рис. 133).
Если же прямая а не проходит через
точку О, то проведём перпендикуляр ОН
к прямой а и обозначим его длину, т. е. рас-
стояние от центра данной окружности до
прямой а, буквой d. Выясним, сколько об-
щих точек имеют прямая а и окружность
в зависимости от соотношения между d и г.
Возможны три случая.
Точка М и N — середины
отрезков АВ и ВС
Рис. 132
К и L — концы
диаметра
Рис. 133
Г d < г. Поскольку ОН < г, то точка Н лежит внутри круга, огра-
ниченного данной окружностью (рис. 134, а). На прямой а от точки Н
отложим отрезок HD = r (рис. 134, б). Гипотенуза OD прямоугольного
треугольника OHD больше катета HD, поэтому OD > г. Это означает,
что точка D лежит вне круга, ограниченного данной окружностью. Та-
ким образом, один конец отрезка HD (точка Н) лежит внутри указан-
ного круга, а другой (точка D) — вне этого круга. Следовательно, на
отрезке HD найдется точка А, лежащая на окружности (рис. 134, в),
т. е. О А = г.
Отложим на продолжении луча НА отрезок НВ, равный отрезку
НА (рис. 134, г). Прямоугольные треугольники ОНА и ОНВ равны
по двум катетам. Следовательно, ОВ = ОА = г, поэтому точка В также
является общей точкой прямой и окружности. Поскольку никакие три
о
о
НВ = НА,
ОВ=ОА=г
м н
L-	а
d = r
О
п
i о
р »
ы
I Q
х
X
Е
Ф
л
О
' я
I’D
X
X
X
о
л
сг
5
Рис. 134
точки окружности не лежат на одной прямой, то других общих точек
у прямой а и окружности нет.
Итак,
если расстояние от центра окружности до прямой меньше ра-
диуса окружности (d < г), то прямая и окружность имеют две
общие точки.
В этом случае прямая называется секущей по отношению к окруж-
ности.
2° d = г. Так как ОН = г, то точка Н
лежит на окружности и, следовательно,
является общей точкой прямой а и
окружности (рис. 135). Для любой дру-
гой точки М прямой а наклонная ОМ
больше перпендикуляра ОН, т. е.
ОМ > ОН - г, и поэтому точка М не
лежит на данной окружности.
Таким образом,
если расстояние от центра окруж-
ности до прямой равно радиусу
окружности (d = г), то прямая
и окружность имеют только одну
общую точку.
Наклонная ОМ больше
перпендикуляра ОН,
поэтому точка М не лежит
на окружности
Рис. 135
82
В этом случае прямая называется
касательной по отношению к окруж-
ности, а их общая точка называется точ-
ОКРУЖНОСТЬ
кой касания прямой и окружности.
3° d>r. Так как ОН> г, то для
любой точки М прямой а справедливо
неравенство ОМ^ОН >г (рис. 136).	о
Следовательно, точка М не лежит на
окружности. Итак,
если расстояние от центра
окружности до прямой больше	Точка м лежит вне окружности
радиуса окружности (d > г), то	так как ом>он>г
прямая и окружность не имеют
общих точек.	Рис. 136
Касательная
Докажем теорему о свойстве касательной.
 Касательная к окружности перпендикулярна к радиусу,
проведённому в точку касания.
Доказательство Пусть а — касательная к окружности с цен-
тром О, А — точка касания (рис. 137). Докажем, что а 1 ОА.
Допустим, что это не так. Тогда радиус ОА будет наклонной
к прямой а, поэтому расстояние от точки О до прямой а меньше
радиуса. Из этого следует, что прямая а является секущей, а не
касательной, что противоречит условию. Следовательно, прямая а
перпендикулярна к радиусу ОА. Теорема доказана.
Рассмотрим две касательные к окружности с центром О, проходя-
щие через точку А. Пусть В и С — точки касания (рис. 138). Отрезки
АВ и АС назовем отрезками касательных, проведёнными из точки А.
Они обладают следующим свойством:
отрезки касательных к окружности, проведённые из одной
точки, равны и составляют равные углы с прямой, проходя-
щей через эту точку и центр окружности.
Рис. 137
Прямая а — касательная
к окружности, А — точка касания
Рис. 138
В самом деле, по теореме о свойстве касательной Z.ABO = 90°
и ZACO = 90°, т. е. треугольники АВО и АСО прямоугольные. Эти
треугольники имеют общую гипотенузу О А и равные катеты ОВ и ОС,
поэтому они равны. Следовательно, АВ- АС и АОАВ-АОАС, что
и требовалось доказать.
1—•
Докажем теперь теорему, обратную теореме о свойстве касатель-
ной (признак касательной).
Г Если прямая проходит через конец радиуса, лежащий на
окружности, и перпендикулярна к этому радиусу, то она
является касательной.
Доказательство. По условию данный
радиус (радиус ОА на рис. 139) является
перпендикуляром, проведённым из центра
окружности к данной прямой а, поэтому
расстояние от центра окружности до пря-
мой а равно радиусу. Следовательно, пря-
. мая а и окружность имеют только одну
общую точку, т. е. данная прямая является
касательной к окружности. Теорема до-
казана.
ОА — радиус окружности
ОА ± а
Рис. 139
Хорды и дуги
ОКРУЖНОСТЬ
Отрезок, соединяющий две точки окружно-
сти, называется хордой. На рисунке 140
отрезки АВ, CD и EF — хорды окружности
(CD является и диаметром окружности).
Отметим на окружности какие-нибудь
две точки — А и В. Прямая АВ разделяет
окружность на две части, каждая из которых
называется дугой окружности. На рисунке 141
изображены две дуги с концами А и В:
дуга АРВ (синяя) и дуга AQB (зелёная).
Дуги АРВ и AQB обозначают так: '-'АРВ
и '-'AQB. В тех случаях, когда ясно, о какой
из двух дуг с концами А и В идет речь,
используют краткое обозначение: '-'АВ.
Если отрезок, соединяющий концы
дуги, является диаметром окружности, то
дуга называется полуокружностью. На ри-
сунке 142, а изображены две полуокружно-
сти (синяя и зелёная).
Угол с вершиной в центре окружности
называется её центральным углом (угол
АОВ на рис. 142, б). С помощью централь-
ных углов можно измерять дуги в градусах
АВ, CD и EF — хорды
окружности
Рис 140
'-'АРВ и ^AQB — дуги
окружности, ограниченные
точками А и В
Рис. 141
Если дуга АВ окружности с центром О лежит внутри угла
АОВ или является полуокружностью, то её градусная мера
считается равной градусной мере центрального угла АОВ\
если же дуга АВ не лежит внутри угла АОВ, то её градусная
мера считается равной 360° - Z.AOB (рис. 142).
'-’ALB = AAOB
^ALB = 3bOa-AAOB
Рис. 142
Хорда — от греческого /орбт) (струна, жила).
Градусная мера дуги обозначается так
же, как и сама дуга (см. рис. 142).
Из определения градусной меры дуги
следует, что
сумма градусных мер двух дуг
окружности с общими концами рав-
на 360°.
'-'BCD = 155е
'-'АВ = 25е
^ADB = 335°
Рис. 143
О
о
о
U
X
S
X
На рисунке 143 градусная мера дуги BCD равна 155°, поскольку
^BCD = ^ВС + ^CD = 45° + 110° = 155°.
Обычно говорят кратко: дуга BCD равна 155°, и пишут: ^ВСВ = 155°.
На этом же рисунке
^АВ = 180° - 155° = 25°f ^ADB = 360е - 25° = 335е.
Угол между касательной и хордой
Рассмотрим окружность с центром О и прямую CClf касающуюся
окружности в точке А (рис. 144). Проведём хорду АВ. Каждый из
углов ВАС и ВАС^ будем называть углом
между касательной и хордой.
Докажем теорему об угле между каса-
тельной и хордой.
Л
Ж)
W
О
X
X
сг
0
п
D
Ж
X
х
О
А
<г
5
Угол между касательной и хордой
измеряется половиной заключён-
ной внутри этого угла дуги.
Рис. 144
ОКРУЖНОСТЬ
ZBAC = 90° = ^AMB
'-'AMB='W)°
Рис. 145
Доказательство. Если хорда АВ — диаметр (рис. 145, а), то ду-
ги, заключённые внутри углов ВАС и ВАСГ, являются полуокружно-
стями и, следовательно, равны 180°. Поскольку АВАС-АВАСХ = 90°,
то утверждение теоремы справедливо.
Если же хорда АВ не является диаметром (рис. 145, б), то острый
угол С АВ между касательной ССХ и хордой АВ равен 90° - АО АВ,
а тупой угол С]АВ равен 90° + АО АВ.
Обозначим буквой а величину центрального угла АОВ (рис. 145, в).
Тогда '-'АВ = а и '-'ADB = 360° - а. В равнобедренном треугольнике
АОВ угол О АВ равен
^(180°-а) = 90°-у
поэтому
АС АВ = 90° - АО АВ = 90° - |90° - yj = у,
АС^АВ = 90° + АО АВ = 90° + ^90° “ у) = 180° - | j (360° - а).
Таким образом, каждый из углов между касательной ССг и хордой
АВ измеряется половиной заключённой внутри него дуги. Теорема
доказана.
Вписанный угол
Угол, вершина которого лежит на окруж-
ности, а стороны пересекают окружность,
называется вписанным углом. Говорят,
что вписанный угол опирается на дугу, за-
ключённую внутри этого угла. На рисун-
ке 146 вписанный угол АВС опирается на
дугу АМС.
Докажем теорему о вписанном угле.
в
м
Рис. 146
 Вписанный угол измеряется половиной дуги, на которую
он опирается.
Доказательство Рассмотрим вписанный угол АВС, опирающийся
на дугу АС окружности (рис. 147, а), и докажем, что А АВС = -^АС.
Проведём через точку В касательную PQ к окружности
(рис. 147, б). Лучи ВА и ВС делят развёрнутый угол PBQ на три угла:
; АРВА, ААВС и ACBQ. Поэтому ААВС = 180° - АРВА - ACBQ.
Угол РВА (угол между касательной PQ и хордой АВ) равен ^АВ.
1
Аналогично ACBQ = -'-'СВ. Следовательно,
ААВС = 180° - | ^АВ - j ^СВ = | (360° - ^АВ - ^СВ) = ^АС.
Теорема доказана.
ААВС = 180е - АРВА - ACBQ =
= 180°-	1^СВ =
= -1-(360е - ^АВ - ^СВ) = ^АС
Рис. 147
1. Вписанные углы, опирающиеся на
одну и ту же дугу, равны (рис. 148).
2. Вписанный угол, опирающийся на
полуокружность, прямой (рис. 149).
Отметим также, что
если диаметром окружности являет-
ся гипотенуза прямоугольного тре-
угольника, то вершина прямого угла
треугольника лежит на этой окруж-
ности.
Рис 148
В самом деле, середина гипотену-
зы прямоугольного треугольника равно-
удалена от его вершин (см. п. 24), поэто-
му если диаметром окружности является
гипотенуза (рис. 150), то окружность про-
ходит через все вершины треугольника и,
следовательно, вершина прямого угла ле-
жит на этой окружности.
Рис. 149
Диаметр окружности —
гипотенуза прямоуголь-
ного треугольника
Рис. 150
Вопросы и задачи
99. а) Точки А, В, С и D лежат на окруж-
ности с центром О, причем ААОВ =
= ZCOD. Докажите, что АВ = CD.
б) Точки А, В, С и D лежат на окружности
с центром О, причем АВ = CD. Докажите, что точка О равноудалена от пря-
мых АВ и CD.
в) Отрезок AD — высота треугольника АВС. На прямой ВС отмечена точ-
ка L так, что точка D является серединой отрезка CL', на прямой АВ отме-
чены точки М и N так, что AM = АС и точка А является серединой отрез-
ка MN. Докажите, что точки С, L, М и N лежат на одной окружности.
100. а) Точки М, N, Р и Q лежат на окружности с центром О, причём MN = PQ.
Докажите, что AMON = APOQ.
б) Точки М, N, Е и F лежат на окружности с центром О, причём точка О
равноудалена от прямых MN и EF. Докажите, что MN = EF.
в) Отрезки О А и ОВ — радиусы окружности, причём ZAOB = 120°. Бис- /
сектриса ОР угла АОВ пересекает окружность в точке Q, при этом ( 89
PQ = OQ. Докажите, что точки А, В, О и Р лежат на одной окружности.
101. а) Отрезок АВ — гипотенуза прямоугольного треугольника АВС. Докажи-
те, что прямая ВС является касательной к окружности с центром А радиуса
АС, а прямая АВ не является касательной к окружности с центром С радиу-
са ВС.
б)	В прямоугольном треугольнике АВС гипотенуза АВ равна 20 см и
ZA = 60°. Каким должен быть радиус окружности с центром А, чтобы она:
1) касалась прямой ВС;
2)	не имела с прямой ВС общих точек;
3)	имела с прямой ВС две общие точки?
в)	В прямоугольном треугольнике АВС катеты АС и ВС равны и АВ = 10 см.
Каково взаимное расположение прямой АВ и окружности с центром С ра-
диуса 5 см?
г)	Точки А и В лежат на касательной к окружности с центром О по разные
стороны от точки касания, причем О А = ОВ = 8 см и Z.AOB = 120°. Найдите
радиус окружности.
д)	Прямые МА и МВ — касательные к окружности, А и В — точки каса-
ния, отрезок АВ равен радиусу окружности. Найдите угол АМВ.
е)	Прямые МА и МВ — касательные к окружности радиуса 4 см, А и В —
точки касания,/.АМВ = 60е. Найдите расстояние от точки М до прямой АВ.
ж) Дуга АВ окружности с центром О меньше 180° На этой дуге отмечена
точка М. Прямая, касающаяся окружности в точке М, пересекает касатель-
ные СА и СВ в точках Р и Q. Докажите, что периметр треугольника CPQ
и величина угла POQ не зависят от выбора точки М на дуге АВ.
102. а) Отрезок АН — перпендикуляр, проведённый из точки А к прямой, про-
ходящей через центр О окружности радиуса 5 см. Является ли прямая АН
касательной к окружности, если:
1)	ААОН = 45° и АН =6 см;
2)	ААОН = 60° и О А = 10 см?
б)	Точка М — середина стороны АВ квадрата ABCD со стороной 10 см.
Каким должен быть радиус окружности с центром М, чтобы она:
1)	касалась прямой CD;
2)	не имела с прямой CD общих точек;
3)	имела с прямой CD две общие точки?
в)	В треугольнике АВС угол С — прямой, АВ = 2АС, ВС = 6 см. Каково
взаимное расположение прямой АВ и окружности с центром С радиуса 3 см?
г) Точки Р и Q лежат на касательной к окружности с центром О так, что
OP = OQ, PQ = 20 см и APOQ = 90е. Найдите радиус окружности
д)	Прямые МА и МВ — касательные к окружности с центром О радиуса
3 см, А и В — точки касания, МО = 6 см. Найдите угол АМВ.
О
о
ы
я
X
е)	Перпендикулярные прямые АВ и АС — касательные к окружности с цент-
ром О (В и С — точки касания). Докажите, что четырёхугольник ОВАС —
квадрат.
ж)	Дуга АВ окружности с центром О больше 180°. На этой дуге отмечена
точка М. Прямая, касающаяся окружности в точке М, пересекает касатель-
ные С А и СВ в точках Р и Q. Докажите, что величина СР + CQ - PQ и угол
POQ не зависят от выбора точки М на дуге АВ.
ЮЗ. а) Дуга АВ окружности с центром О и радиуса 8 см равна 30° Найдите
расстояние от точки А до прямой ОВ.
б)	Диаметр ААГ окружности перпендикулярен к хорде ВВГ. Докажите, что
градусные меры дуг АВ и ABlt меньших 180°, равны.
104.	а) Отрезки ОА и ОВ — радиусы окружности, расстояние от точки А до
прямой ОВ в два раза меньше радиуса. Найдите дугу АВ.
б)	Точки А, В, С и D лежат на окружности. Докажите, что если
'-'АВ = '-'CD, то АВ = CD.
105.	а) Через конец хорды, равной радиусу, проведена касательная. Найдите
углы между касательной и хордой.
б)	Через точку А, лежащую на окружности, проведены касательная АВ
и хорда АС. На дуге АС, лежащей внутри угла ВАС, отмечена точка М так,
что ^АМ = '-'МС. Расстояние от точки М до прямой АС равно 10 см Най-
дите расстояние от точки М до прямой АВ.
в)	Отрезки МА и МВ — хорды окружности радиуса 6 см, ZAMB = 30c.
Найдите хорду АВ.
г)	Центральный угол АОВ на 27° больше вписанного угла, опирающегося
на дугу АВ. Найдите каждый из этих углов.
д)	Хорды АС и BD пересекаются, причем АВ = CD. Докажите, что АС = BD.
е) Отрезок ОА является диаметром одной окружности и радиусом другой
окружности с центром О. Хорда АВ второй окружности пересекает первую
окружность в точке С. Докажите, что АС = ВС
ж)	Через точку А, лежащую на окружности с центром О, проведены хор-
да АВ и касательная а. Через точку О проведена прямая, перпендикулярная
к прямой ОВ и пересекающая хорду АВ в точке С, а касательную а в точ-
ке D. Докажите, что AD = CD.
з)	Исходя из рисунка 151, докажите, что ААМС = \^ALC + ^BKD).
106.	а) Радиус О А окружности с центром О проходит через середину хорды ВС.
Через точку В проведена касательная к окружности, пересекающая прямую
ОА в точке М. Докажите, что луч ВА — биссектриса угла СВМ.
б)	Точки А, В и С лежат на окружности, прямая МА — касательная к ней.
Докажите, что если точка С равноудалена от прямых АВ и AM, то она де-
лит дугу АСВ пополам.
в)	Отрезки МА и МВ — хорды окружности с центром О, ААМВ = А5°,
АВ = 7 см. Найдите расстояние от точки О до прямой АВ
Рис. 152
Рис. 151
г)	На окружности отмечены точки А, В, М и N так, что АМ = ВМ
и ^АМВ - ^ANB = 160°. Найдите угол АВМ
д)	Равные хорды АС и BD пересекаются. Докажите, что либо AB = CD,
либо AD = ВС.
е)	На диаметре АВ отмечена точка С. Хорды BD и BE пересекают окруж-
ность с диаметром ВС в точках Р и Q соответственно. Докажите, что
ABED = ABQP и ABDE = ABPQ
ж)	Отрезки АВ и АС — диаметр и хорда окружности. Через точку С прове-
дена касательная, пересекающая прямую АВ в точке D. Докажите, что
AACD = ACBD.
-
з)	Исходя из рисунка 152, докажите, что А.АМВ = - ('-'ALB - ^CKD)
§10
Задачи
на построение
§10. Задачи на построение
Построение циркулем
и линейкой
Для изображения геометрических фи-
гур пользуются различными чертёж-
ными инструментами: линейкой
(в том числе линейкой с делениями),
циркулем, угольником, транспортиром. Оказывается, что многие фи-
гуры можно построить с помощью только циркуля и линейки без де-
лений.
Задачи, в которых требуется построить какую-то фигуру с помощью
только этих двух инструментов, называются задачами на построение.
При этом предполагается, что с помощью линейки можно построить
прямую, проходящую через две данные точки, а с помощью циркуля —
построить окружность с центром в данной точке и радиусом, равным
данному отрезку.
a)
б)
В
В
Откладывание на луче отрезка, равного данному
Рис. 153
Начнём с простейшей задачи на построение.
Задача
На данном луче от его начала отложить отрезок, равный данному
отрезку.
Решение
На рисунке 153, а изображены данный луч ОС и данный отрезок
АВ. С помощью циркуля построим окружность радиуса АВ с цент-
ром О. На рисунке 153, б изображена дуга этой окружности, пересе-
кающая данный луч в точке D. Отрезок OD — искомый, так как
OD = АВ.
В следующих пунктах мы рассмотрим более сложные задачи.
Построение треугольника по трём сторонам
Задача
Построить треугольник по трём сторонам.
Эту задачу нужно понимать так: даны три отрезка — -PiQi, P2Q2
и P3Q3 (рис. 154). Требуется построить треугольник АВС, стороны ко-
торого соответственно равны этим трём отрезкам:	Pi 	 Qj
АВ — P^Qi, ВС = P2Q2 и С-А = Рз^з- Решение Проведем произвольную прямую, отме- тим на ней точку А и отложим отрезок АВ.	рз	Q3
равный PiQx (рис. 155, а). Затем построим две окружности: радиуса P3Q3 с центром	Рис. 154
Рис. 155
Построение треугольника по трем сторонам
§10. Задачи н а постр о е к и е
в точке А и радиуса P2Q2 с центром в точке В. Одну из точек пере-
сечения этих окружностей обозначим буквой С. Проведя отрезки АС
и ВС, получим искомый треугольник АВС (рис. 155, б), поскольку
АВ = ВС = P2Q2 и СА = P3Q3.
Замечание При решении этой задачи мы исходили из того, что
искомый треугольник существует. Если же это заранее неизвестно, то
может оказаться, что задача на построение не имеет решения. Напри-
мер, если в задаче о построении треугольника по трём сторонам зара-
нее неизвестно, что искомый треугольник существует, то данная задача
не всегда имеет решение. Действительно, в треугольнике каждая сто-
рона меньше суммы двух других сторон. Поэтому если какой-нибудь
из данных отрезков больше или равен сумме двух других, например
Р&г >P2Q2 + P3Q3, то нельзя построить треугольник, стороны которого
равны данным отрезкам. Если мы попытаемся это сделать, то обнаружим,
что окружности с центрами А и В не пересекутся (рис. 156). В связи
с этим возникает вопрос: всегда ли можно построить треугольник, сто-
роны которого равны данным отрезкам,
в том случае, когда каждый из данных
отрезков меньше суммы двух других?
К этому вопросу мы вернемся в конце
8 класса, а пока скажем лишь, что ответ
на него оказывается утвердительным.
Отметим, что задача о построении
треугольника по трём сторонам явля-
ется одной из важнейших задач на по-
строение. В частности, на ней основаны
решения задач в пунктах 36—39.
Рис. 156
Построение угла, равного данному
Задача
Отложить от данного луча угол, равный данному.
Решение
Пусть даны неразвёрнутый угол А (для развёрнутого угла решение
очевидно) и луч ОМ (рис. 157, а). Требуется построить угол, равный
углу А, одной из сторон которого будет луч ОМ.
Проведём окружность произвольного радиуса с центром А и
обозначим точки её пересечения со сторонами угла буквами В и С
(рис. 157, б). Затем построим окружность с центром О радиуса АВ
и обозначим точку её пересечения с лучом ОМ буквой Р (рис. 157, а).
Наконец, проведём окружность с центром Р радиуса ВС и обозначим
буквой Q одну из точек её пересечения с окружностью с центром О
(рис. 157, г, д). Угол MOQ — искомый (рис. 157, е).
В самом деле, треугольники АВС и OPQ равны по трём сторонам
(АВ = OP, АС = OQ и ВС = PQ), поэтому Z.MOQ = Z.A.
Построение угла, равного данному
Рис. 157
Замечание. Построение угла, равного
данному, лежит в основе решения ещё двух
задач на построение:
построить треугольник по двум сторо-
нам и углу между ними;
построить треугольник по стороне
и двум прилежащим к ней углам
Решите эти задачи самостоятельно.
Построение биссектрисы угла
Задача
Построить биссектрису данного нераз-
вёрнутого угла.
Решение
Проведём окружность произвольного
радиуса с центром в вершине А данного
угла и обозначим точки её пересечения со
сторонами угла буквами Б и С (рис. 158, а).
Затем построим две окружности радиуса ВС
с центрами В и С (рис. 158, б, в). Они пе-
ресекутся в двух точках (см. задачу 109).
Ту из точек пересечения окружностей, ко-
торая лежит с точкой А по разные сторо-
ны от прямой ВС, обозначим буквой D
(см. рис. 158, в). Наконец, проведём луч AD
(рис. 158, г). Это и есть искомая биссектриса
данного угла А.
В самом деле, треугольники ABD
и ACD равны по трём сторонам (АВ = АС,
BD-CD, AD — общая сторона). Поэтому
ABAD - Z.CAD, т. е. луч AD — биссектриса
данного угла А.
Замечание Проведя биссектрису данно-
го угла А, мы разделили его на два равных
угла. Если каждую половину разделить по-
полам, то угол А окажется разделённым
на четыре равных угла. А можно ли с по-
мощью циркуля и линейки разделить данный
Построение
биссектрисы угла
Рис. 158
§ 10. Задачи на п о с т р о ение
Трисекция — от латинского tri (натрое)
и sectio (рассечение).
угол на три равных угла? Эта зада-
ча называется задачей о трисекции
угла. В течение веков её пытались
решить многие математики. И лишь
в 1837 году французский математик
Пьер Лоран Ванцель (1814—1848)
доказал, что с помощью циркуля
и линейки разделить произвольный угол на три равных угла невоз-
можно. Правда, для некоторых углов эта задача имеет решение, на-
пример для прямого угла (объясните, почему).
Построение серединного перпендикуляра
Задача
Построить серединный перпендикуляр к данному отрезку.
Решение
Пусть АВ — данный отрезок (рис. 159, а). Построим две окружности
радиуса АВ с центрами А и В (рис. 159, б, в). Они пересекутся в двух
точках — Р и Q (см. задачу 109). Проведём прямую PQ (рис. 159, г).
Она и является искомым серединным перпендикуляром к отрезку АВ.
В самом деле, по построению точки Р и Q равноудалены от кон-
цов отрезка АВ, поэтому они лежат на серединном перпендикуляре
к этому отрезку. Таким образом, серединный перпендикуляр к отрезку
АВ проходит через точки Р и Q, т. е. совпадает с прямой PQ.
Замечание Построив серединный перпендикуляр к данному отрез-
ку АВ, мы попутно решили ещё одну задачу
Построение серединного перпендикуляра
Рис. 159
построить середину данного отрезка АВ.
Действительно, точка М, в которой серединный перпендикуляр
пересекается с отрезком АВ (см. рис. 159, г), и есть середина этого
отрезка.
Построение прямой, перпендикулярной к данной
Задача
Построить прямую, проходящую через данную точку и перпендику-
лярную к данной прямой.
Построение прямой, проходящей через точку М и перпендикулярной к прямой а
Рис. 160
Решение
Данная точка М может лежать на данной прямой а, а может и не
лежать на ней. И в том и в другом случае решение задачи сводится
к построению серединного перпендикуляра к отрезку.
В самом деле, построим какую-нибудь окружность с центром М,
пересекающую прямую а в двух точках — А и В (рис. 160, а). Точка М
равноудалена от точек А и В и, следовательно, лежит на серединном
перпендикуляре к отрезку АВ Осталось построить этот серединный пер-
пендикуляр (как его построить, мы знаем) — он и будет искомой пря-
мой, проходящей через точку М перпендикулярно к прямой а (рис. 160, б).
Построение прямоугольного треугольника
по гипотенузе и катету
Опираясь на результаты пп. 34—39, нетрудно построить прямоуголь-
ный треугольник по следующим элементам:
по двум катетам;
по гипотенузе и острому углу;
по катету и любому из острых углов;
4—Бутузов, 7 кл.
(объясните, как выполнить эти построения). Решим ещё одну из важ-
нейших задач на построение.
Задача
Построить прямоугольный треугольник по гипотенузе и катету.
Решение
Пусть MN и PQ — данные отрезки, причём MN> PQ (рис. 161, а).
Требуется построить прямоугольный треугольник, гипотенуза которого
равна MN, а один из катетов равен PQ.
Проведём произвольную прямую, отметим на ней точку А и отло-
жим отрезок АВ, равный PQ. Через точку А проведём прямую а, пер-
пендикулярную к прямой АВ (рис 161, б); как это сделать, мы знаем.
Затем построим окружность радиуса MN с центром В (рис. 161, в). По-
скольку ВА = PQ < MN, то расстояние от точки В до прямой а мень-
ше радиуса этой окружности, поэтому прямая а и построенная окруж-
ность пересекаются в двух точках. Обозначим одну из них буквой С.
Треугольник АВС — искомый
Построение прямоугольного треугольника по гипотенузе и катету
Рис. 161
Из нашего построения следует, что если один из отрезков меньше
другого, то существует прямоугольный треугольник, гипотенуза которо-
го равна большему, а катет — меньшему из этих отрезков.
Замечание Эту задачу можно решить другим способом, основан-
ным на том, что вписанный угол, опирающийся на полуокружность,
прямой (см. следствие 2, п. 33). Действительно, построим середину О
отрезка MN и проведём окружность с центром О радиуса ОМ
(рис. 162, а). Затем построим окружность с центром М радиуса PQ.
Одну из точек пересечения этих окружностей обозначим буквой L
(рис. 162, б). Поскольку вписанный угол L опирается на диаметр MN,
то этот угол — прямой, поэтому MN — гипотенуза прямоугольного
треугольника LMN, a ML — катет, равный PQ. Таким образом, тре-
угольник LMN искомый.
Построение касательной
Задача
Через данную точку А провести каса-
тельную к данной окружности с центром О.
Решение
Если точка А лежит на данной окруж-
ности, то проведём прямую ОА, а за-
тем построим прямую а, проходящую че-
рез точку А перпендикулярно к прямой ОА
(рис. 163). По признаку касательной пря-
мая а является искомой касательной.
Если точка А лежит внутри круга, ограниченного данной окружно-
стью, то задача решения не имеет, поскольку любая прямая, проходя-
щая через точку А, является секущей (докажите это).
Наконец, если точка А лежит вне круга, ограниченного данной
окружностью, то будем рассуждать так. Допустим, что задача реше-
на и АВ — искомая касательная (рис. 164, а). Поскольку прямая АВ
перпендикулярна к радиусу ОВ, то решение задачи сводится к по-
строению прямоугольного треугольника АОВ с гипотенузой ОА и ка-
4*
100
Рис. 164
тетом ОВ, равным радиусу данной окружности. Эту задачу, как вы
знаете, можно решить разными способами В данном случае удобно
воспользоваться идеей, высказанной в замечании п. 40. Проведём от-
резок О А и построим его середину М. Затем проведём окружность
с центром М радиуса МА (рис. 164, б). Одну из точек пересечения
этой окружности с данной окружностью обозначим буквой В. Посколь-
ку ABLOB, то прямая АВ — искомая касательная (рис. 164, в).
Вопросы и задачи
107.	а) Даны равносторонний треугольник АВС и точка на сторо-
не АС. На сторонах ВС и АВ постройте точки Аг и Ci так чтобы
треугольник	был равносторонним.
6)	Постройте окружность данного радиуса, проходящую через две данные
точки.
в)	Даны острые углы АВС и DEF. Отложите от луча ВА во внешнюю об-
ласть угла АВС угол, равный углу DEF.
г)	Дан треугольник АВС. Постройте треугольник DEF, в котором AD = АА,
DE = 2AB и DF = 3AC.
д)	Дан треугольник АВС. Постройте треугольник DEF, в котором AD = АА,
АЕ = АВ и DE = 2AB.
е)	От данного луча отложите угол, равный половине данного угла
ж)	Дан треугольник АВС. На стороне ВС этого треугольника постройте
точку, равноудалённую от прямых АВ и АС.
з)	Постройте угол, равный 60°; 30°.
и)	Начертите неравнобедренный треугольник АВС и постройте точку пере-
сечения его медианы AM и биссектрисы BD.
к)	Даны точки А, В и С. Постройте точку, равноудалённую от точек А и В
и удалённую от точки С на расстояние, равное АВ. Сколько решений может
иметь эта задача?
л)	Даны прямая а и точки А иВ, лежащие по одну сторону от неё. На пря-
мой а постройте точку, равноудалённую от точек А и В. Всегда ли эта зада-
ча имеет решение?
м) Постройте угол, равный 45°.
н) Постройте равнобедренный треугольник по высоте, проведённой к осно-
ванию, и углу при основании.
о)	Постройте прямоугольный треугольник по катету и медиане, проведён-
ной к другому катету.
п) Постройте остроугольный треугольник АВС по стороне АВ, высоте АН
и углу А.
р)	Постройте остроугольный треугольник по углу и двум высотам, одна из
которых проведена из вершины этого угла.
108. а) Постройте равнобедренный треугольник, основание которого равно
данному отрезку, а боковая сторона вдвое больше основания.
б)	Дан равнобедренный треугольник АВС с основанием АС и точка D на
стороне АВ. Постройте на стороне АС точку Е так, чтобы угол AED был
равен углу С.
в)	Даны острый угол АВС и тупой угол DEF. Отложите от луча ЕЕ во внут-
реннюю область угла DEF угол, равный углу АВС.
г)	Даны неразвёрнутый угол и отрезок. Постройте треугольник, в котором
одна сторона в четыре раза меньше другой и равна данному отрезку,
а угол, заключённый между этими сторонами, равен данному углу.
д)	Постройте треугольник, сторона которого равна утроенной стороне АВ
данного треугольника АВС, а прилежащие к ней углы равны углам А и В
этого треугольника.
е)	Дан угол АОВ. Постройте луч ОМ так, чтобы углы МО А и МОВ были
равными тупыми углами.
ж)	Дан треугольник АВС с прямым углом А. На катете АВ постройте точ-
ку М, находящуюся на расстоянии AM от прямой ВС.
з)	Постройте угол, равный 15°; 120°.
и)	Начертите треугольник АВС с тупым углом В и постройте точку пере-
сечения биссектрисы внешнего угла с вершиной А и продолжения медиа-
ны СМ.
к)	Дан неравнобедренный треугольник АВС. На сторонах этого треуголь-
ника постройте точки, равноудалённые от вершин А и В.
л)	Постройте центр данной окружности.
102
ОКРУЖНОСТЬ
м) Постройте угол, равный 150°; 135°.
н) Высоты AD и BE остроугольного треугольника АВС пересекаются
в точке Н. Постройте треугольник АВС по отрезкам АЕ, НЕ и AD.
о) Постройте равнобедренный треугольник по боковой стороне и высоте,
проведённой к основанию.
п) Постройте остроугольный треугольник по двум сторонам и высоте, про-
ведённой к одной из них.
р) Постройте остроугольный треугольник по стороне и двум высотам, про-
ведённым к другим сторонам.
Ь Вопросы для повторения
1.	Что такое определение?
2.	Дайте определение окружности.
3.	Объясните, что такое центр, радиус и диаметр окружности. Что та-
кое круг?
4.	Докажите, что никакие три точки окружности не лежат на одной прямой.
5.	Сколько общих точек имеют прямая и окружность в зависимости от соотно-
шения между радиусом окружности и расстоянием от её центра до прямой?
6.	Какая прямая называется секущей по отношению к окружности?
7.	Какая прямая называется касательной к окружности? Какая точка называет-
ся точкой касания прямой и окружности?
8.	Сформулируйте и докажите теорему о свойстве касательной.
9.	Докажите, что отрезки касательных к окружности, проведённые из одной
точки, равны и составляют равные углы с прямой, проходящей через эту
точку и центр окружности.
10.	Сформулируйте и докажите теорему, обратную теореме о свойстве каса-
тельной.
11.	Объясните, что такое хорда и дуга окружности.
12.	Какой угол называется центральным углом окружности?
13.	Объясните, какая дуга называется полуокружностью.
14.	Как определяется градусная мера дуги? Как она обозначается?
15.	Сформулируйте и докажите теорему об угле между касательной и хордой
16.	Какой угол называется вписанным? Сформулируйте и докажите теорему
о вписанном угле.
17.	Докажите, что вписанные углы, опирающиеся на одну и ту же дугу, равны.
18.	Докажите, что вписанный угол, опирающийся на полуокружность, прямой.
19.	Докажите, что если диаметром окружности является гипотенуза прямо-
угольного треугольника, то вершина прямого угла треугольника лежит на
этой окружности.
20.	Объясните, как построить треугольник по трём сторонам. Всегда ли эта за-
дача имеет решение?
21.	Объясните, как отложить от данного луча угол, равный данному,
22.	Объясните, как построить треугольник по двум сторонам и углу между ними.
23.	Объясните, как построить треугольник по стороне и двум прилежащим
к ней углам.
24.	Объясните, как построить биссектрису данного неразвёрнутого угла.
25.	Объясните, как построить серединный перпендикуляр к данному отрезку.
26.	Объясните, как построить середину данного отрезка.
27.	Объясните, как построить прямую, проходящую через данную точку и пер-
пендикулярную к данной прямой.
28.	Объясните, как построить прямоугольный треугольник по двум катетам; по
гипотенузе и острому углу; по катету и прилежащему острому углу; по катету
и противолежащему острому углу.
29.	Объясните, как построить прямоугольный треугольник по гипотенузе и кате-
ту. Приведите два решения этой задачи. При каком условии задача имеет
решение?
30.	Объясните, как с помощью циркуля и линейки через данную точку провести
касательную к данной окружности.
Дополнительные задачи }
109.	Докажите, что окружности радиуса АВ с центрами А и В пересека-
_____ются в двух точках.
110.	Расстояние от точки до центра данной окружности равно диаметру
этой окружности. Найдите угол меж-
ду отрезками касательных, прове-
дёнными из указанной точки к дан-
_____ной окружности.
111.	На рисунке 165 прямые АВ и АС — каса-
тельные к окружности, В и С — точки каса-
ния. Докажите, что ABAC = 180° - ^BDC.
112.	Докажите, что если точки А, В и С не лежат на
одной прямой, то точка пересечения окруж-
ностей с диаметрами АВ и ВС. отличная от В,
лежит на прямой АС.
X 113. Две окружности имеют общую точку М и об-
104 щую касательную в этой точке. Прямая АВ
касается одной окружности в точке А, а дру-
гой — в точке В. Найдите угол АМВ.
114.	На рисунке 166 прямая АВ — касательная к
окружности, В — точка касания. Докажите,
ЧТО ABAC = -(y-'BLD - ^ВКС}
2
115.	Вершины остроугольного треугольника АВС
лежат на окружности с центром О отрезок
АН — высота этого треугольника. Докажи-
те, что АО АС = АВАН.
116.	Вершины треугольника АВС лежат на окруж-
ности. Хорды АА}, ВВг и ССг содержат его
биссектрисы. Выразите углы треугольника
АВС через углы треугольника
117.	Отрезки ААг и ВВГ — высоты остроуголь-
ного треугольника АВС. Докажите, что
ААА1В1 = AABBV
Рис 167
118.	Высоты АА± и ВВХ остроугольного треугольника АВС пересекаются в точ-
ке Н. Докажите, что АСНВХ = АСА1В1.
119.	Из точки М катета АС прямоугольного треугольника АВС проведён пер-
пендикуляр МН к гипотенузе АВ. Докажите, что АМНС = АМВС.
120.	Исходя из рисунка 167, докажите, что AP=AQ.
121’. Точки А, В, С и D лежат на одной окружности, луч BD содержит биссек-
трису ВМ треугольника АВС. Докажите, что AAMD = ABAD.
122*. Хорды АВ и CD взаимно перпендикулярны, луч АВ — биссектриса
угла DAE. Докажите, что АЕ 1 ВС. Рассмотрите все возможные случаи.
123	На сторонах угла с вершиной О отложены равные отрезки ОА и ОВ, а во
внутренней области этого угла отмечена точка С. Постройте точку М так,
чтобы угол МАО был равен углу МВО, а отрезок МС был равен отрезку
АВ. Сколько решений может иметь эта задача?
124.	Постройте равнобедренный треугольник:
а)	по боковой стороне и углу при основании;
б)	по основанию и медиане, проведённой к основанию;
в)	по основанию и углу между боковыми сторонами.
125.	Постройте прямоугольный треугольник:
а)	по острому углу и высоте, проведённой к гипотенузе;
б)	по острому углу и биссектрисе, проведённой из вершины этого угла.
126 Постройте треугольник:
а)	по двум сторонам и медиане, проведённой к одной из этих сторон;
б)	по двум сторонам и высоте, проведённой к третьей стороне;
в)	по углу, высоте и биссектрисе, проведённым из вершины этого угла;
г)	по двум сторонам и углу, противолежащему одной из них. Сколько ре-
шений может иметь эта задача?
127.	Постройте угол, равный 160е; 75е; 105е.
128.	Постройте остроугольный треугольник АВС по сумме углов А и В, высоте
BD и стороне АС.
129.	Постройте остроугольный треугольник АВС по разности углов А и В, высо-
те CD и стороне ВС.
130.	На стороне АС треугольника АВС отмечена точка М. Постройте треуголь-
ник АВС по отрезкам АВ, ВМ и углам АМВ, ВСМ.
131.	На стороне АС треугольника АВС отмечена точка М. Постройте треуголь-
ник АВС по отрезкам ВС, AM и углам АВМ, АМВ.
132.	Разделите данный угол в 54е на три равные части.
133.	Разделите данный угол в 35° на семь равных частей
повышенном
трудности
ЗАДАЧИ ПОВЫШЕННОЙ ТРУДНОСТИ
Глава 1
134. Даны четыре попарно пересекающиеся прямые. Известно, что через точку
пересечения любых двух из них проходит по крайней мере ещё одна из
данных прямых. С помощью рассуждений
убедитесь в том, что все данные прямые пе-
ресекаются в одной точке.
135.	Даны четыре точки. Известно, что прямая,
проходящая через любые две точки, содер-
жит по крайней мере ещё одну из данных
точек. С помощью рассуждений убедитесь
в том, что все данные точки лежат на одной
прямой.
136.	Решите: а) задачу 134 для случая, когда даны
пять прямых; б) задачу 135 для случая, когда
даны пять точек.
137.	На луче с началом О отмечены точки А. Б
и С так, что ОА = ВС и ОВсОС. Докажи_е,
что ОВ = АС.
Рис 168
138.	На луче с началом О отмечены три точки —
А, В и С так, что О А = ВС и ОВ < ОС. Дока-
жите, что середины отрезков АВ и ОС совпа-
дают.
139.	На рисунке 168 изображены пять прямых, пе-
ресекающихся в одной точке. Найдите сумму
углов 1, 2, 3, 4 и 5.
140.	На рисунке 169 углы 1 и 2 равны. Докажите,
что прямые а и Ъ не пересекаются.
а
1
2	Ъ
	———II |||И
Рис. 169
Глава 2
141. На сторонах угла POQ отмечены точки А,
В, С и D так, что ОА-ОВ и AC = BD
(рис. 170). Прямые AD и ВС пересекаются
в точке Е. Докажите, что луч ОЕ — биссек-
триса угла POQ. Опишите основанный на
этом факте способ построения биссектрисы
угла.
Рис. 170
142.	Отрезки АВ и CD пересекаются в середине М отрезка АВ, причём
АС = BD = AM. Докажите с помощью наложения, что точка М является се-
рединой отрезка CD.
143.	Докажите, что если АВ = А^р АС = А^ и AM = A^I^ где AM и АгМг —
медианы треугольников АВС и А1В1С1, то эти треугольники равны.
144.	Докажите, что если сторона, поилежащий к ней угол и сумма двух других
сторон одного треугольника соответственно равны стороне, прилежащему
к ней углу и сумме двух других стооон другого треугольника, то такие тре-
угольники равны.
145.	Докажите, что если медиана и углы, на которые она разделяет угол, одного
треугольника соответственно равны медиане и углам, на которые она раз-
деляет угол, другого треугольника, то такие треугольники равны.
146.	Сторона и два угла одного треугольника равны какой-то стороне и каким-то
двум углам другого треугольника. Могут ли эти треугольники быть нерав-
ными?
147.	Две стороны и угол одного треугольника равны каким-'1’© двум сторонам
и какому-то углу другого треугольника. Могут ли эти треугольники быть не-
равными?
148.	Точки С и D расположены по разные стороны от прямой АВ, причем
АС = BD и ABAC = AABD. Докажите, что прямая CD пересекает отрезок
АВ и делит его пополам.
Задачи повышенной трудности
149.	Докажите, что четырёхугольник, стороны которого лежат на биссектрисах
углов прямоугольника, является квадратом
150.	Углы А и D четырёхугольника ABCD — прямые и АВ = CD. Докажите, что
этот четырёхугольник — прямоугольник.
151.	На стороне АВ квадрата ABCD отмечена точка Р. Биссектриса угла DCP
пересекает AD в точке Q. Докажите, что СР = DQ -ь ВР.
152.	На рисунке 171 изображены три квад-
рата. Найдите сумму углов 1, 2 и 3.
153.	Биссектрисы равнобедренного тре-
угольника АВС пересекаются в точ-
ке!), точка О равноудалена от всех
вершин треугольника. Середина
отрезка OD лежит на основании АВ.
Найдите углы треугольника АВС.
Рис. 171
154.	В треугольнике АВС высота, проведённая из вершины А, не меньше сторо-
ны ВС, а высота, проведённая из веошины В, не меньше стороны АС До-
кажите, что треугольник АВС — равнобедренный и прямоугольный.
155.	Точки М и Лт — середины сторон АВ и CD четыоёхугольника ABCD с пря-
мыми углами А и В. Докажите, что 2MN = AD - ВС.
156.	Докажите, что в прямоугольном треугольнике с неравными катетами бис-
сектриса прямого угла делит пополам угол между высотой и медианой,
проведёнными из той же вершины.
157.	В треугольнике АВС сторона АВ меньше стороны АС, отрезки AD и АН —
биссектриса и высота треугольника. Докажите, что точка Н лежит на
луче DB.
158.	Отрезок AD — биссектриса треугольника АВС с неравными сторонами АВ
и АС. Докажите, что точка D лежит между серединой стороны ВС и основа-
нием высоты АН.
159.	Вне равностороннего треугольника АВС отмечена точка Е, а внутри него —
точка М. Докажите, что МА < BE -г ЕС.
160.	Исходя из рисунка 172, найдите сумму углов
1,2,	3,4 и 5.	_	1
5	2
161.	Внутри квадрата ABCD взята такая точка М,
что ААВМ = 75е и Z.CDM = 30е. Найдите
угол МАВ.
д .	з
162.	Каждый угол треугольника меньше суммы
двух других его углов. Определите вид этого	«
треугольника.	Рис. 172
163.	Докажите, что отрезок с концами на разных
сторонах треугольника не превосходит наибольшей из сторон треугольника.
164.	Точка М расположена внутри треугольника АВС так, что АМ= АВ Дока-
жите, что АВ < АС.
165.	Точка D расположена на биссектрисе внешнего угла с вершиной А тре-
угольника АВС. Докажите, что периметр треугольника BCD больше пери-
метра треугольника АВС
166.	Внутри треугольника АВС с тупым углом А отмечены точки Р и Q, а на луче
QB вне треугольника отмечена точка М. Может ли выполняться неравен-
ство АС АР > АСВМ?
167.	Можно ли внутри треугольника АВС с тупым углом А отметить точки Р и Q
так, чтобы угол ВАР был не меньше угла BQC?
168.	На биссектрисе угла ВАС отмечена точка О, а на продолжении луча АВ
отмечена точка D Может ли выполняться равенство О А = OD? Рассмотрите
все возможные случаи.
169.	Докажите, что угол треугольника является острым, прямым или тупым, если
медиана, проведённая из вершины этого угла, соответственно больше, рав-
на или меньше половины противоположной стороны.
170.	Докажите, что если угол треугольника является острым, прямым или тупым,
то медиана, проведённая из вершины этого угла, соответственно больше,
равна или меньше половины противоположной стороны.
171.	Высота и медиана треугольника, проведённые из одной вершины, делят
угол треугольника на три равных угла. Докажите, что этот треугольник —
прямоугольный.
172.	Внутри равнобедренного треугольника АВС с основанием ВС и углом А,
равным 80е, отмечена такая точка М, что АМВС = 30е и АМСВ = 10°. Най-
дите угол АМС.
173.	Внутри равнобедренного треугольника АВС с основанием ВС и углом А,
равным 80е, отмечена такая точка М, что АМВС = 30е и АМСА = 10е. Най-
дите угол МАВ.
174.	Дан треугольник АВС, в котором АВ = 70е, АС = 50е. На сторонах АВ и АС
отмечены такие точки М и Л7, что АМСВ = 40е и ANBC = 50е. Найдите
угол NMC.
175.	На боковых сторонах ВА и ВС равнобедренного треугольника АВС с углом В,
равным 20е, отмечены соответственно точки Q и Р так, что AACQ = 60°
и АС АР = 50° Найдите угол APQ.
Глава 3
176.	К двум окружностям с центрами О и проведены две общие касательные,
не пересекающие отрезка OOY, и одна общая касательная, пересекающая их
в точках А, В и касающаяся окружностей в точках Alt Bv Докажите, что
ААг =BBV
177.	Внутри угла АВС равностороннего треугольника АВС взята точка М так,
что ААМВ = 30° и АМВС = 23е. Найдите углы ВАМ и ВСМ.
178.	Гипотенузы ВС и ВГСХ прямоугольных треугольников АВС и	рав-
ны, АВ < AjBp Докажите, что АС > АгСг
179.	Докажите, что основания высот остроугольного треугольника являются вер-
шинами треугольника, в котором эти высоты являются биссектрисами
ЗАДАЧИ ПОВЫШЕННОЙ ТРУДНОСТИ
\ 180. Вершины Р и Е равностсоон-е_о тоеугольн/ка АРЕ лежат на сторонах ВС
] и CD прямоугольника ABCD л>'ки К и — сеоедины сторон АЕ и АР.
/ Докажите, что треугольники ВКС и CMD — оав-осторонние.
181.	Вершины А и В тоеу голь ника АВС с -юямь м утлом С скользят по сторонам
прямого угла с вершиной Р. Докажите, '-то *очка С перемещается при этом
по отрезку.
182.	Через данную точку Л грсведе-ь. всевозможные “сямь.е, на которых дан-
ная окружность с цен-ром О отсекает с^оезки, являющиеся её хордами. Что
представляет собой множество середин таких хосд, если точка М:
а) лежит вне окружности;
б)	лежит внутри окружности и не совпадаем с ^ентоом;
в)	лежит на окружности?
183.	Отрезок АВ является диаметоом скоужности с иечтоом О. На каждом ра-
диусе ОМ окружности отложен стоезск ОХ, равный пеопендикуляру, про-
ведённому из точки М к прямой АВ. Что представляет собой множество то-
чек X?
184.	Постройте треугольник по двум сторонам и медиане, проведённой к треть-
ей стороне.
185.	Даны три попарно пересекающиеся прямые, не проходящие через одну точ-
ку Постройте точку, равноудалённую о’ этих прямых. Сколько решений
имеет задача?
186.	На данной окружности постройте точку, равноудалённую от двух данных пе-
ресекающихся прямых. Сколько решений может иметь задача?
187.	Постройте точку, лежащую на данной окружности и равноудалённую от кон-
цов данного отрезка. Сколько решений может иметь задача?
188.	Точки А и В лежат по одну сторону от прямой а. Постройте точку М пря-
мой а так, чтобы сумма AM-г МВ была меньше суммы АХ + ХВ, где
X — любая точка прямой а, отличная от М.
189.	Даны окружность с центром О и точка А вне неё. Проведите через точку А
прямую, пересекающую окружность в точках В и С, так, что АВ = ВС. При
каком соотношении между отрезком О А и радиусом В окружности задача
имеет решение?
190.	Постройте треугольник по периметру и двум углам.
191.	Постройте треугольник по стороне, разности углов при этой стороне и сум-
ме двух других сторон.
192.	Даны отрезок АВ и прямая а, пересекающая этот отрезок. Постройте на
прямой а точку С так, чтобы эта прямая содержала биссектрису треугольни-
ка АВС. Всегда ли задача имеет оешение?
193.	Постройте общую касательную к двум данным окружностям. Сколько реше-
ний может иметь эта задача?
194.	Даны окружность, точка и два отоезка — АВ и CD. Постройте хорду MN,
равную отрезку АВ, ’ак, чтобы расстояние от дан-.о/. точки до прямой MN
было равно CD.
195.	Даны окружность и точка внутри неё. Постоойте наименьшую хорду, прохо-
дящую через эту точку.
Задачи повышенной труд
ЗАДАЧИ С ПРАКТИЧЕСКИМ СОДЕРЖАНИЕМ
с практическим
содержанием
Глава 1
1.	В парке к цветочной клумбе ведут той до-
рожки (рис. 173). Можно ли проложить поя-
молинейную дорожку, соединяющую: а) пае-
вую и вторую дорожки; б) первую и третью
дорожки; в) все три дооожки?
2.	Как на садовом участке прокопать узкую пря-
молинейную канавку между двумя вбитыми
в землю колышками, если в вашем распооя-
жении есть верёвка, которая короче расстоя-
ния между колышками?
Рис. 173
3.	Как отметить середину прямолинейной дорожки, если у вас есть только ве-
рёвка, которая короче, чем дорожка?
4.	Можно ли ствол дерева длиной 10 м распилить на куски длиной: а) 70 см
и 90 см; б) 70 см и 80 см? Если можно, то сколькими способами?
5.	Электропоезд длиной 100 м проезжает мимо километрового столба за 5 се-
кунд. За какое время он проедет мост длиной 800 м?
6.	Найдите угол между часовой и минутной стрелками часов, если они пока-
зывают: а) 9 ч; б) 14 ч; в) 18 ч; г) 19 ч; д) 19 ч 30 мин.; е) 18 ч 20 мин.
Рис. 174
7.	Сколько раз угол между часовой и минутной стрелками часов оказывается
прямым за время от 15 до 17 часов?
8.	В зубчатой передаче сцеплены два колеса, имеющие 24 и 30 зубьев. На ка-
кой угол повернётся второе колесо, когда первое повернётся: а) на 8 зубь-
ев; б) на 45е?
9.	Как провести перпендикуляр к прямой, на-
черченной на листе бумаги, из отмеченной
точки, если у вас есть только линейка, каран-
даш и прозрачная бумага?
Глава 2
1.	Как, пользуясь только верёвкой и острыми ко-
лышками, начертить на земле прямой угол?
2.	От оконного стекла прямоугольной формы
откололись два куска (рис. 174). Можно ли
Рис. 175
по сохранившейся иаст/ вырезать таксе же прямоугольное стекло? Какие
следует снять размерь ?
3.	Предложите способ измерения расстояния между двумя точками, если
нельзя пройти по прямой от одной точки до другой. (В случае затруднения
обратитесь к рис. 175.)
4.	Предложите способ измерения расстояния между двумя точками, одна из
которых недоступна. (В случае затруднения обратитесь к рис. 176.)
5.	Угол между равными стропилами крыши дома равен 90е. Как узнать высоту
крыши, если известна ширина дома?
6.	Имеется пластина в форме четырёхугольника. Как с помощью только нити
убедиться в том, что это: а) прямоугольник; б) квадрат?
7.	Два населенных пункта А и В расположены по разные стороны от прямоли-
нейной дороги. В каком месте дороги нужно построить автобусную остановку X,
чтобы сумма расстояний от А и В до X была наименьшей? Решите ту же зада-
чу в случае, когда населённые пункты расположены по одну сторону от дороги.
8.	Плотнику нужно заделать квадратное отверстие размером 12 см на 12 см,
а у него есть только кусок доски размером 9 см на 16 см. Как разрезать этот
кусок на две части, чтобы ими можно было точно закрыть отверстие?
Рис. 176
□ д< чи	' >  .1 к < и ч е' к и м соде.’О'И'
ИМ СОДЕРЖАНИЕМ
\ 9. У хозяйки был любимый квадратный плед оазмеоом 3 м на 3 м. О" него от-
) резали два износившихся противоположных уголка — прямоугольные тре-
угольники с катетами 1 м. Хозяйка хоче^ сшить из оставшейся части новый
плед прямоугольной формы, предварительно разрезав её на два куска. Как
ей это сделать?
10. Бедуин прежде чем вернуться в свои шатёр, должен накормить коня на
пастбище и напоить его в реке. Гранина пастбища и берег реки прямоли-
нейные (рис. 177). Как он должен еха~=>, ч~обы суммарный путь был наи-
меньшим? Объясните следующее “’оавило: бедуин прицеливается из ружья
в точку пересечения берега секи и границы "аслб/ща, и если его шатёр бу-
дет справа, то он должен ехать налево, и наоборот. Эта задача взята из за-
мечательной книги Гуго Штейнгауза «Математический калейдоскоп», биб-
лиотечка «Квант», выпуск 8, М.: Наука, 198'J
Глава 3
1.	Градусная мера дуги обода велосипедного колеса, расположенной между
двумя соседними спицами, равна 20-. Сколько сг.ищ в колесе?
2.	Сколько оборотов должна сделать секундная стрелка часов, чтобы часовая
стрелка повернулась на Г?
3.	На листе бумаги нарисована дуга окружности. Как (с помощью циркуля
и линейки) построить всю окружность?
4.	В парке расположена клумба радиуса 3 м. В семи метрах от центра клумбы
проходит дорожка (ОА = 7 м на рис. 178). Строители начали рыть траншею
под углом 60е к дорожке (см. рисунок). Не заденет ли эта траншея клумбу?
5.	В плоскости расположено 5 зубчатых колес так, что первое колесо сцеплено
своими зубьями со вторым, второе — с третьм, третье — с четвёртым, чет-
вёртое — с пятым, а пятое — с первым. Могут ли вращаться колёса такой
системы?
историческая
справка
Геометрия зародилась 4000 лет назад в Древнем Египте и Вавилонии
в связи с потребностями измерения земельных участков, построения
храмов и дворцов. Когда Нил размывал участок обрабатываемой зем-
ли, для взимания налогов было важно знать, сколько именно земли
потеряно. Египетские землемеры использовали для своих измерений
и построений туго натянутые верёвки.
Примерно тогда же геометрия появилась в Древней Индии и Древ-
нем Китае. В Индии геометрические сведения излагались в многочи-
сленных трактатах о построении алтарей. Эти трактаты назывались «Пра-
вила верёвки», поскольку основным инструментом для построений, как
и в Египте, были верёвки. В Китае составлением трактатов по арифмети-
ке и геометрии занимались важные сановники. Математика была одним
из шести искусств, которым обучались дети китайских аристократов.
Важнейшее изменение в понимании того, что такое геометрия,
произошло в Древней Греции До греков геометрия представляла со-
бой собрание полученных из опыта правил и фактов, и только у гре-
ков появились теоремы и доказательства, и именно тогда геометрия
приобрела близкий к современному вид.
Одним из первых древнегреческих геометров был Фалес (около
625—548 гг. до н. э.), который родился в городе Милете в Малой Азии.
Фалес Милетский многое перенял из геометрии Египта и Вавилонии во
время своих путешествий. Известен рассказ о том, что он вычислил вы-
соту египетской пирамиды, измерив её тень в тот момент, когда длина
тени, отбрасываемой предметом, равна длине самого предмета. Однаж-
ды Фалес, предвидя большой урожай оливок, взял в наём все маслода-
вильни и, став фактическим монополистом в изготовлении
масла, нажил целое состояние. Но это он сделал не
из-за стремления к наживе, а чтобы показать, что учё-
ному разбогатеть совсем не трудно.
Считается, что Фалес открыл следующие геомет-
рические факты: 1) диаметр делит круг пополам;
2) углы при основании равнобедренного треугольника
равны; 3) вертикальные углы равны; 4) если сторона
и прилежащие к ней углы одного треугольника равны
стороне и прилегающим к ней углам другого треуголь-
оливкового
Фалес
ИСТОРИЧЕСКАЯ СПРАВКА
Платон
Пифагор
ника, то такие треугольники равны; 5) вписанный
угол, опирающийся на диаметр, прямой.
Фалеса, когда он уже был стариком, посетил
юноша Пифагор (около 580—500 гг. до н. э.). Фалес
поделился с ним тем, что знал, и посоветовал поехать
в Египет для продолжения изучения геометрии. По
возвращении из Египта Пифагор создал философ-
ско-математическое учение и основал школу пифаго-
рейцев, просуществовавшую многие века. Пифагорей-
цем был и Архит Тарентский (428—347 гг. до н. э.), обучивший
математике Евдокса (408—355 гг. до н. э.) и Платона (427—347 гг.
до н. э.). Платон основал философскую школу, получившую название
«Академия» от рощи близ Афин, в которой она находилась. Платон
требовал от всех своих учеников, чтобы они основательно изучили
геометрию, прежде чем он обучит их своей философии.
Последователь платоновской школы Евклид (око-
ло 325—265 гг. до н. э.) подробно и систематически
изложил достижения древнегреческих геометров
в трактате «Начала», состоящем из 13 книг. Евклид
описывал геометрию как систему предложений (тео-
рем), которые последовательно выводятся из несколь-
ких перечисленных им основных понятий и истин. Все
написанные впоследствии учебники геометрии очень
многим обязаны книге Евклида. Его схему изложения
использовали не только в книгах по математике, но
(Ньютон) и даже по философии (Спиноза).
и по механике
О жизни Евклида до нашего времени дошло мало сведений. Изве-
стно, что он преподавал математику в Александрии, и, когда царь Египта
Птолемей I спросил у него, нет ли более короткого пути к геометрии, чем
его «Начала», Евклид смело ответил, что в геометрии нет царских дорог.
В первой книге «Начал» обсуждаются различные геометрические
построения. Начинается она с построения равносто-
роннего треугольника, затем следуют построение бис-
сектрисы угла и построение перпендикуляра к пря-
мой. Далее в первой книге доказываются признаки
равенства треугольников. В третьей книге «Начал»
обсуждаются свойства вписанных углов и касатель-
ных. Помимо этого в «Началах» доказано много дру-
гих важных теорем, с которыми вам ещё предстоит
познакомиться.
Евклид
Ответы
и указания
Глава 1
1. а) Нет; да. б) Точка пересечения прямых АВ и СВ. в) Пя^ь. е) Две. ж) Может
иметь, а может и не иметь, з) Да. и) Шесть, четыре или одна, к) Пятнадцать.
2. а) Нет. б) Да. в) Пять, ж) Да. з) Да. и) Шесть, четыре или одна, к) Пятнад-
цать. 3. в) Да. 4. в) Да. 5. а) Три угла — А АОВ, АВОС, ААОС. в) Двенадцать
неразвёрнутых углов и шесть развёрнутых углов, г) Двенадцать неразвёрнутых
углов и три развёрнутых угла. Полуплоскости с границей OD, содержащей
точку Е, и полуплоскости с границей ОЕ, содержащей точку D. д) Пять или
два. 6. а) Три угла — АРМЕ, APMQ, AEMQ. в) Шестнадцать неразвёрнутых
углов и восемь развёрнутых углов, г) Восемь неоазвёрнутых углов и два раз-
вёрнутых угла. Полуплоскости с границей ОА, содержащей точку D, и полу-
плоскости с границей OD, содержащей точку А. д) Две. 7. а) АС < BD. б) Да.
в) АС = BD. г) Да. д) Да. ж) Да; да. з) ABOD = АСОЕ. 8. а) ОС < OD. б) Да.
в) АВ = CD. г) Да. д) С; AD = BE. ж) Да; да. з) ААОЕ = ABOF. 9. а) 12,8 см
или 11,6 см. б) 4,8 дм и 9,5 дм или 19,2 дм и 14,5 дм. в) 7 см. г) 4 см или 12 см.
д) 23 см. 10. а) 27,5 дм или 22,5 дм. б) 10 мм и 60 мм или 46 мм и 4 мм. в) б м.
г) 4 см или 8 см. д) 60 см. 11. а) острый угол в 35е или тупой угол в 105е. б) 20°
и 30° или 80° и 70°. в) 12е. г) 60е или 180е. д) 90е. 12. а) острый угол в 70е или
тупой угол в 150°. б) 10° и 75е или 50° и 15е. в) 35е. г) 80е или 160°. д) 120е.
13. а) 60° и 120°. б) 108е, 72 е, 108е, 72е. г) 100е, 30е, 50е, 100е. 14. а) 135е и 45е.
б) 40°, 140°, 40е, 140е. г) 40е, 20е, 120е. 15. а) 60е, 30е и 150е. 16. а) 40е, 40°
и 50°. 17. 1,6d и 0,6d. 18.	19. 11 см или 17 см. 20. 2d. У к а з а н и е. Рассмот-
п — 1
реть два возможных случая: точки В и С лежат по разные стороны или по одну
сторону от точки А. 21. а) 110° или 54е. б) 80е или 170е. 22. 35е. 23. Указа-
ние. Воспользоваться определением биссектрисы угла и свойством смежных
углов. 24. Указание. Доказать, что угол АОС развёрнутый. 25. а) Да. б) Да.
26. Указание. Предположить, что прямые МН и МК совпадают, и восполь-
зоваться теоремой п. 9.
Глава 2
27. а) 15 см. б) 16 см. в) 10 см или 7 см. 28. а) 9 см. б) 18 мм. в) 61 см или
51 см. 29. a) Z1 = Z2. б) ААВС > ААСВ. 30. a) Z1 = Z2. б) ААВС > AADB.
31. а) АВ = АС. в) 11 см. 32. а) АВ = АС. в) 18 см. 33. а) АСВМ. 34. а) ААВС
и AABD. 41. л) Указание. Провести перпендикуляр МК к прямой ВН
УКАЗАНИЯ
\ и рассмотреть четырёхугольник МКНВГ 42. ж) АН = 90“, ZA = 12е и AD = 78е.
) л) Указание. Воспользоваться утверждением и идеей решения задачи 41л).
43. а) 14 см. б) 12 см. г) 14 см. 44. а) 60е. б) 120е. г) 15 см. 45. д) Указание.
Воспользоваться утверждением задачи 45 г). 46. а) 60е. б) Могут. 47. а) 6 см.
49. а) Нет. б) Сторона, равная 10 см. г) Указание. Продолжить отрезок ААХ
на отрезок АгМ, равный AAV 50. а) Нет. б) 5 см. г) См. указание к задаче 49 г).
51. а) АС> АА> АВ, нет. б) ВС > АС > АВ. в) ААВС > AACD. д) Указание.
Продолжить отрезок AM на отрезок MD, равный AM. 52. а) АС = АВ< АА,
да. б) ВС > АС = АВ. в) АВ > CD. д) Указание. Восполсзоваться утверж-
дением задачи 51 д). 53. a) AA = 30z, АВ = 60е, АС = 90е. б) 70е, 30е, 80е.
в) 30°, 30е, 120е. д) Да. е) 120е. 54. а) 90е и 45е или 72е и 36е. б) 80е, 80е, 20е
или 50е, 50°, 80е. в) 110е, 20е, 50е. д) 90е - -. е) 120е. 56. Указание. Сна-
2
чала доказать, что высота ОН треугольника АОС являемся его медианой.
57. Указание. Предположить, что медиана AM является высотой, и мыслен-
но перегнуть плоскость по прямой AM. 58. Указание. Отложить на сторонах
угла от вершины равные отрезки и рассмотреть высоту полученного равнобед-
ренного треугольника. 59. Указание. Для данного отрезка АВ провести лучи
АР и AQ так, что АР А АВ, луч AQ проходит внутри угла РАВ и AQAB = АРВА.
Затем провести высоту МН треугольника АМВ, где М — точка пересечения
лучей AQ и ВР. 60. BD = BrDv 61. ABDC = АВ^^С^ 73. Указание. Сначала
доказать, что если основание высоты лежит на продолжении стороны, то один
из углов, прилежащих к этой стороне, — тупой. 75. Указание. Сначала до-
казать, что АВАСг = 90е - ААВН и АВНС = 90е - ААСН. 80. Две прямые,
содержащие биссектрисы углов, образованных при пересечении данных пря-
мых. 83. Указание. Рассмотреть проекции точки X на стороны квадрата.
84. Указание. Продолжить отрезок ВМ до пересечения со стороной АС
в точке D и воспользоваться неравенством треугольника применительно
к треугольникам ABD и MDC. 85. Указание. Воспользоваться задачей 84.
87. Указание. На луче AM отметить точку D так, что DM = AM. 88. Ука-
зание. См. указание к задаче 87. 90. Указание. Продолжить отрезок AD до
пересечения со стороной ВС в точке М и воспользоваться утверждением зада-
чи 51 г). 91. У к а з а н и е. Воспользоваться равенствами AADE + AAED = 120°
и ABEF + AAED = 120°. 92. 45°. 94. 20°. 95. 52е и 52е. 96. Указание. Вос-
пользоваться свойством внешнего угла треугольника. 97. 80е. Указание.
Сначала доказать, что АС = CQ и АС = СР. 98. 85е. Указание. Сначала до-
казать, что СН = МН и СН = ВН.
101. б) 10 см; меньше 10 см; больше 10 см. в) Прямая касается окружности.
г) 4 см. д) 120°. е) 6 см. 102. а) Нет; да. б) 10 см; меньше 10 см; больше 10 см
в) Прямая касается окружности, г) 10 см. д) 60е. 103. а) 4 см. 104. а) 30е.
105. a) 30s и 150s. 6) 10 см. в) 6 см. ri 54- / 27s или 138“ и 11Г. 106. в) 3,5 см.
г) 65s. 107. к) Два, одно или н/ сдно_о. л') Не всегда. 109. Указание.
Рассмотреть течки пеоесече.-гия одно/ из окружностей с серединным перпен-
дикуляром к отрезку АВ <см. задачу 59) и доказать, что вторая окружность
проходит через эти -очки. 110. 60s. 112. Указание. Провести высоту ВН
треугольника АВС. 113. 90s. Указание. Рассмотреть точку пересечения
двух указанных касательно х. 115. Указание. Продолжить отрезок АО до
пересечения с окружностью в -очке D и сассмотоеть угль АВС и ADC.
116. ZA = ZBX - ZC} - ZAP ZB = ZCj - ААг - ABlt AC = AAX + ZBj - ZCV
117. Указание. Рассмотреть окружность с диаметром АВ. 118. Указание.
Рассмотреть окружность с диаметром СН. 119. Указание. Рассмотреть окруж-
ность с диаметром ЛВ. 123. Два, одно /ли ни одного. 126. г) Два, одно или ни
одного. 130. Указание. Воспользоваться задачей 107м). 131. Указание.
Сначала построить треугольник ABAI. 132. Указание. Сначала построить
угол, равный сумме трёх дачнь х углов. 133. Указание. Сначала построить
угол, равный сумме пяти данных углов.
Задачи повышенной трудности
134. Указание. Пусть три из данных прямых проходят через точку А. Пред-
положить, что четвёртая прямая не проходит через точку А, и прийти к про-
тиворечию с условием задачи. 135. Указание. Пусть три из данных точек
лежат на прямой а. Предположить, что четвёртая точка не лежит на прямой а,
и прийти к противоречию с условием задачи. 136. Указание. Воспользо-
ваться указаниями к задачам 134 и 135. 137. Указание. Рассмотреть два
случая. 138. Указание. Рассмотреть два случая. 139. 180s. 140. У к а з а н и е.
Предположить, что прямые а и Ъ пересекаются в некоторой точке, и, исполь-
зуя наложение копии рисунка на сам рисунок, вывести из этого предположе-
ния, что прямые пересекаются ещё в одной точке. 141. Указание. Пользуясь
последовательно первым, вторым и третьим признаками равенства треуголь-
ников, доказать, что AOAD = А.ОВС, АЕАС = AEBD, АОЕС = A.OED.
142. Указание. Наложить треугольник АМС на треугольник BMD так,
чтобы сторона МА совместилась со стороной МВ, а луч МС наложился
на луч MD. 143. Указание. Рассмотреть треугольники ABD и A^B^D^
где точки В и D такие, что М и MY — середины отрезков AD и AXDY.
144. Указание Пусть в треугольниках АВС и AxBxCa АА = AAlt АС = А^,
АВ + ВС = А1В1 + ВхСг. Продолжить стороны АВ и AXBX на отрезки BD = ВС
и BYBX = BYCY и рассмотреть треугольники ADC и	145. Указание.
Задача решается аналогично задаче 143. 146. Могут. Например, равнобедрен-
ный треугольник АВС с основанием АВ и треугольник ABD, где D — точка
на стороне ВС такая, что АВ = AD. 147. Могут. Рассмотрим, например, рав-
нобедренный треугольник АВС с основанием АВ и отметим какую-нибудь
точку D на продолжении стороны АВ Тогда треугольники ACD и BCD
ОТВЕТЫ И УКАЗАНИЯ
\ обладают указанным свойством, но не являются равными. 148. Указание.
) Отметить середину О отрезка АВ и рассмотреть треугольники ОАС
и OBD. 149. Указание. Через середину стоооны данного поямо\тельни-
ка провести прямую, перпендикулярную к зтой сгосоне, а затем мысленно
перегнуть плоскость по проведённой прямой. 150. Указание. Соединить
отрезками середину стороны AD с вершинами В z С. 151. Указание.
На луче РВ отложить отрезок РХ, равный отрезку СР, и доказать, что
АВСХ = ADCQ. 152. 90е. 153. 36е, 36е и 108е. Указание. Доказать, что
3ABAD = AACD = 90е - 2ABAD. 154. Указание. Учесть, ч’О в прямоуголь-
ном треугольнике гипотенуза больше кате_а. 155. Указание. Рассмотреть
проекцию стороны CD на большую из сторон AD и ВС. 156. Указание.
Воспользоваться тем, что середина гипотенузы прямоуголеного треугольника
равноудалена от его вершин. 157. Указание. Сначала доказать, что
Z.ADC > ZADB. 158. Указание. Пусть в треугольнике АВС АВ < АС,
AM— медиана. Сначала доказать, что ZBAM > АСАМ, и далее воспользо-
ваться утверждением задачи 157. 159. Указание. Сначала доказать, что
AM < АВ. 160. 180е. 161. 30е. Указание. На луче DM отложить отрезок
DN = АВ и доказать, что точка Д' совпадает с точкой М. 162. Остроугольный.
163. Указание. Соединить один из концов отрезка с вершиной треугольника
и воспользоваться задачей 52г). 164. Указание. Продолжить отрезок AM
до пересечения с ВС и воспользоваться задачей 52 г). 165. Указание. Про-
должить отрезок ВА на отрезок AM = АС и воспользоваться неравенством
треугольника применительно к треугольнику BDM. 166. Не может. Указа-
ние. Сравнить указанные углы с внешним углом треугольника АВС при вер-
шине В. 167. Нельзя. Указание. Продолжить отрезок BQ до пересечения
со стороной АС в точке М и сравнить указанные углы с углом М треуголь-
ника CQM. 168. Не может. Указание. Доказать, что угол OAD тупой.
169. Указание. Пусть AM — медиана треугольника АВС. В каждом из трёх
случаев сравнить углы ВАМ и В, САМ и С. 170. Указание. Воспользо-
ваться утверждением задачи 169. 171. Указание. Пусть в треугольнике АВС
медиана AM и высота АН делят угол А на три равных угла, АС > АВ. Про-
вести перпендикуляр MD к стороне АС и доказать сначала, что MD = - МС.
172. 70°. Указание. Пусть О — точка пересечения биссектрисы угла А и пря-
мой ВМ. Сначала доказать равенство треугольников АОС и МОС. 173. 60е.
Указание. Пусть О — точка пересечения биссектрисы угла А и прямой ВМ.
Сначала доказать, что лучи СМ и ОМ - биссектрисы углов треугольника АОС.
174. 30°. Указание. Рассмотреть треугольник NBC и воспользоваться ре-
зультатом задачи 173. 175. 80°. Указание. Пусть О — точка пересечения бис-
сектрисы угла В и прямой CQ. Сначала доказать, что ОА = СО = АС = СР,
а затем доказать, что прямая PQ — серединный перпендикуляр к отрезку ОМ,
где М — точка пересечения прямых АО и ВС. 176. Указание. Воспользо-
ваться равенством отрезков касательных, проведённых из одной точки.	/
177. 113е и 134°. Указание. Сначала доказать, что точка М лежит на окруж- (
ности с центром С радиуса АВ. 178. Указание. Воспользоваться тем, что
если диаметром окружности является гипотенуза прямоугольного треугольника,
то вершина прямого угла треугольника лежит на этой окружности. 179. Указа-
ние. Воспользоваться утверждением задачи 117. 180. Указание. Сначала
доказать, что точки С и К лежат на окружности с диаметром РЕ, и, следова-
тельно, ЛРСК = 60е; аналогично доказать, что Z.PBK = 60е. 181. Указание.
Сначала доказать, что точки Р и С лежат на окружности с диаметром АВ, по-
этому величина угла АРС постоянна. 182. а) Дуга окружности с диаметром МО
без своих концов; б) окружность с диаметром МО; в) окружность с диамет-
ром МО без точки М. 183. Пусть CD — диаметр, перпендикулярный к диа-
метру АВ; искомое множество точек состоит из двух окружностей с диамет-
рами ОС и OD. 184. Указание. Пусть ААВС — искомый треугольник,
AM — его данная медиана. Сначала построить треугольник ADC, в котором
точка М — середина стороны AD. 185. Четыре. Указание. Воспользоваться
результатом задачи 80. 186. Четыре, три (это возможно в двух случаях), два
(в трёх случаях), одно или ни одного решения. Указание. Воспользоваться
результатом задачи 80. 187. Два, одно или ни одного решения. Указание.
Воспользоваться свойством серединного перпендикуляра. 188. Указание.
Сначала построить такую точку что прямая а является серединным пер-
пендикуляром к отрезку AAlt а затем провести отрезок А}В. 189. ОА^ЗВ.
Указание. Сначала построить треугольник OAD, в котором AD = R
и OD = 2R. 190. Указание. Сначала построить треугольник, у которого сторо-
на равна данному периметру, а прилежащие к ней углы равны половинам дан-
ных углов. 191. Указание. Пусть ВС, АС + АВ, АВ - АС — данные элементы
искомого треугольника АВС. На продолжении стороны СА за точку А отло-
жить отрезок ААТ, равный отрезку АВ. Построить сначала треугольник CBAV
192. Не всегда. Указание. Сначала построить такую точку D, что прямая а
является серединным перпендикуляром к отрезку BD, а затем построить точку
пересечения прямых а и AD. Задача не имеет решения, если прямые а и AD
не пересекаются. 193. Четыре, три, два, одно или ни одного. Указание.
В случае, когда ни одна из окружностей не содержится внутри другой, при > г2
для построения касательных сначала построить две окружности с центром Ог
радиусов г\ - г2\л + г2, а затем воспользоваться утверждением задачи 150.
194. Указание. Пусть О — центр данной окружности, Р — данная точка,
Q — середина какой-нибудь хорды, равной АВ. Сначала построить две окруж-
ности: радиуса OQ с центром О и радиуса CD с центром Р, а затем построить
общую касательную к этим двум окружностям (задача 193). 195. Указание.
Сначала, пользуясь утверждением задачи 178, доказать, что наименьшей будет
хорда, перпендикулярная к диаметру, проходящему через данную точку.
Ответы и указания
122) Предметный
предметный указатель
Б
Биссектриса треугольника 35
— угла 27
Боковые стороны равнобедренного
треугольника 33
В
Ванцель П. Л. 96
Вершина угла 10
Вершины прямоугольника 46
— треугольника 32
Внешний угол треугольника 68
Внешняя (внутренняя) область угла 11
Второй признак равенства треуголь-
ников 42
Высота треугольника 35
г
Геометрическое место точек 57
Гипотенуза прямоугольного тре-
угольника 51
Градус 21
Градусная мера дуги 84
-----угла 21
Граница полуплоскости 10
д
Дециметр 19
Диагональ четырёхугольника 46
Диаметр окружности 79
Длина отрезка 19
Доказательство теоремы 25
— методом от противного 67
Дуга окружности 84
Е
Единица измерения отрезков 19
-----углов 21
3
Задачи на пос_роение 91
Заключение теоремы 55
к
Касательная к окружности 82
Катет прямоугольного треугольника 51
Квадрат 48
Концы отрезка 8
Круг 79
л
Луч 9
— делит угол на два угла 11
м
Медиана треугольника 35
Метр 19
Миллиметр 20
Минута 21
н
Наклонная, проведённая из точки
к прямой 51
Начало луча 10
Неравенство треугольника 66
о
Окружность 78
Определение 78
Основание перпендикуляра, прове-
дённого из точки к прямой 25
—	равнобедренного треугольника 33
Отрезки касательных, проведённые
из одной точки 82
Отрезок 8
Первый признак равенства треуголь-
ников 41
Периметр треугольника 32
Перпендикуляр, проведённый
из точки к прямой 25
Перпендикулярные прямые 24
Полуокружность 84
Полуплоскость 10
Построение биссектрисы угла 95
—	касательной 99
—	перпендикулярных прямых 97
—	прямоугольного треугольника
по гипотенузе и катету 97
—	серединного перпендикуляра 96
—	середины отрезка 97
—	треугольника по трём сторонам 92
—	угла, равного данному 94
Признак касательной 83
—	равнобедренного треуголь-
ника 35
Проекция отрезка на прямую 58
—	точки на прямую 58
Противоположные стороны четырёх-
угольника 46
Прямая 8
Прямоугольник 46
Прямые пересекаются 9
Равные фигуры 16
Радиус окружности 78
Расстояние между двумя точками 20
—	от точки до прямой 51
Сантиметр 19
Секунда 21
Секущая по отношению к окруж-
ности 81
Середина отрезка 17
Серединный перпендикуляр
к отрезку 55
Следствие 36
Смежные стороны четырёхугольни-
ка 46
Стороны треугольника 32
—	угла 10
—	четырёхугольника 46
Теорема 25
— о биссектрисе угла 57
----вписанном угле 87
----высоте равнобедренного тре-
угольника 35
----перпендикуляре к прямой
26, 27
----проекциях равных отрезков 60
----противоположных сторонах
прямоугольника 46
----свойстве касательной 82
----серединном перпендикуляре
к отрезку 55
----сумме углов треугольника 67
— об углах равнобедренного тре-
угольника 33
----угле между касательной
и хордой 85
—, обратная данной теореме 55
----теореме о биссектрисе угла 58
---------- серединном перпенди-
куляре к отрезку 56
Точка 8
—	касания прямой и окружности 82
—	пересечения прямых 9
Транспортир 21
Третий признак равенства треуголь-
ников 43
Треугольник 32
—	остроугольный 50
—	прямоугольный 50
—	равнобедренный 33
—	равносторонний 33
—	тупоугольный 50
Трисекция угла 96
Предметный указатель
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
у
У	глы вертикальные 24
—	смежные 24
—	треугольника 32
Угол 10
—	вписанный 87
-----опирается на дугу 87
—	между касательной и хордой 85
—	развёрнутый 10
—	острый 22
—	прямой 22
—	тупой 22
—	центральный 84
У	словие теоремы 55
Фигуры равные 16
Хорда окружности 84
ц
Центр окружности 78
ч
Четырёхугольник 46
э
Элементы треугольника 40
Оглавление
( 25
Введение........... ........	.	.	3
Начальные геометрические сведения	7
§ 1.	Простейшие геометрические с/~урь .	8
1.	Точка, прямая, отрезок ...	.	—
2.	Луч и полуплоскос"=> .	9
3.	Угол.......	.	.10
Вопросы и задачи .	  12
§ 2.	Сравнение отрезков и углов .................................. 15
4.	Равенство геометрических фигур. .	—
5.	Сравнение отрезков и углов . .	.	16
Вопросы и задачи ............................................  18
§ 3.	Измерение срезков и углов .	19
6.	Измерение отрезков . .	.	. .	—
7.	Измерение углов. . .	21
Вопросы и задачи ...	22
§ 4, Перпендикулярные прямые ....	24
8.	Смежные и вертикальные углы........................... .	—
9.	Перпендикулярные прямые. Перпендикуляр к прямой .	—
Вопросы и задачи ...	...... .	28
Вопросы для повторения ...	.	29
Дополнительные задачи . .	30
Треугольники	31
§ 5.	Равнобедренный треугольник . .	32
10.	Треугольник ........................ ...	—
11.	Теорема об углах равнобедренного треугольника	33
12.	Признак равнобедренного треугольника..................... .34
13.	Теорема о высоте равнобедренного треугольника . .	.35
Вопросы и задачи ....	38
§6.	Признаки равенства треугольников. .	. 40
14.	Равные треугольники ...................................... —
15.	Первый признак равенства треугольников .	. 41
16.	Второй признак равенства треугольников .	42
17.	Третий признак равенства треугольников .	43
Вопросы и задачи ...	44
§ 7.	Прямоугольные треугольник/ .	46
18.	Прямоугольник ....	—
19.	Виды треугольников...................................... .49
20.	Прямоугольный треугольник с углом в	ЗЭ=	. ............... 51
21.	Признаки равенства прямоугольных ~реугслз-/<о= .	53
22.	Серединный перпендикуляр к стоезкх....................... 55
23.	Свойство биссектрисы угла -	.57
24.	Проекция отрезка ...	58
Воп	росы и задачи ....	.	....	62
§ 8.	Соотношения между сторонам/ и углами -ре/голз-лка .	65
25.	Неравенство треугольника.................................. —
26.	Теоремы о соотношениях между сторонами и углами треугольника 66
27.	Сумма углов треугольника	.	 67
Воп	росы и задачи .....	.	68
Вопросы для повторения .	70
Дополнительные задачи	73
Окружность.............................. .77
§9.	Отрезки и углы, связанные с окружностью .	78
28.	Определение окружности.......................... . —
29.	Взаимное расположение прямой и окружности .	.........80
30.	Касательная ....	82
31.	Хорды и дуги.................. . . 84
32.	Угол между касательной и хордой .	85
33.	Вписанный угол. -	.	.87
Вопросы и задачи . .	88
§ 10.	Задачи на построение......................................   91
34.	Построения циркулем и линейкой................ .	. . —
35.	Построение треугольника по трём сторонам ....	92
36.	Построение угла, равного данному. .	94
37.	Построение биссектрисы угла .	.	95
38.	Построение серединного перпендикуляра.................... 96
39.	Построение прямой, перпендикулярной к данной............. 97
40.	Построение прямоугольного треугольника по гипотенузе и катету —
41.	Построение касательной.	............. 99
Вопросы и задачи . .	...	100
Вопросы для повторения .	. 102
Дополнительные задачи .	.	103
Задачи повышенной трудности . .	....	. . 106 /
Глава 1....................................................... —	(
Глава 2 . .	. —
Глава 3 . .	. .	. 109
Задачи с практическим содержанием....	........ 112
Глава 1..................................................     —
Глава 2........................   .	...... —
Глава 3........................................ .	. .	114
Историческая справка .	115
Ответы и указания...	....	117
Предметный указатель .	. .	......122
Оглавление
Учебное издание
Серия «МГУ — школе»
Бутузов Валентин Фёдорович
Кадомцев Сергей Борисович
Прасолов Виктор Васильевич
ГЕОМЕТРИЯ
7 класс
Учебник для общеобразовательных учреждений
Зав. редакцией Т. А. Бурмистрова
Редактор П. А. Бессарабова
Младший редактор Е. А. Андреенкова
Художественный редактор О. П. Богомолова
Художники О. П. Богомолова, И. А. Андреев
Технический редактор и верстальщик А. Г. Хуторовская
Корректоры М. А. Терентьева, С. В. Николаева
Налоговая льгота — Общероссийский классификатор продукции ОК 005-93 — 953000.
Изд. лиц. Серия ИД № 05824 от 12.09.01. Подписано в печать с оригинал-макета 11.01.10.
Формат 70 х 90 71б. Бумага офсетная. Гарнитура FreeSetC. Печать офсетная.
Уч.-изд. л. 7,47 + форз. 0,5. Тираж 10 000 экз. Заказ № 24226 :n-r3,.
Открытое акционерное общество «Издательство «Просвещение».
127521, Москва, 3-й проезд Марьиной рощи, 41.
Открытое акционерное общество «Смоленский полиграфический комбинат».
214020, г. Смоленск, ул. Смольянинова, 1.
ИЯ
1 шт