Vasili P. Minorski
Aufgabensammlung
der höheren Mathematik
HANSER
Vasili P. Minorski
Aufgabensammlung
der höheren Mathematik
Gute Studienergebnisse setzen in der Mathematik neben Kennt-
nissen auch Fertigkeiten voraus. Die Fertigkeiten kann man sich
nur durch Üben aneignen.
Mehr als 2500 Aufgaben wurden dafür in diesem Buch zusam-
mengestellt. Ihre Lösungen, teils sogar mit Lösungsweg, sind
am Ende der Sammlung zu finden.
Diese moderne Aufgabensammlung, gedacht vor allem für
Studenten ingenieurwissenschaftlicher Studiengänge an
Hochschulen,
	ist auf den Grundkurs Mathematik (Analysis, lineare Algebra)
abgestimmt,
	enthält viele Aufgaben mit technikorientierten Problemstellungen,
	ermöglicht effektive Wiederholung und optimale Prüfungsvor-
bereitung.
Aber auch Studenten der Mathematik und naturwissenschaftlicher
Studiengänge können aus der Aufgabensammlung Nutzen ziehen.
www.hanser.de
HANSER
ISBN 978-3-446-41616-1
Vasili P. Minorski
Aufgabensammlung
der höheren Mathematik
Bearbeitet von Prof. Klaus Dibowski und Dr. Horst Schlegel
15., aktualisierte Auflage
Mit 68 Bildern und 2670 Aufgaben mit Lösungen
Fachbuchverlag Leipzig
I k im Carl Hanser Verlag
Aus dem Russischen übersetzt von Eberhardt Lacher, Schwarzenberg und
Gerhard Liebold, Chemnitz
Bearbeitung der deutschsprachigen Ausgabe von Heinz Birnbaum, Leipzig
Titel der Originalausgabe: CöopHHK 3a#an no Bbicnieii MaTeMaTmce, 7. Auflage,
Staatlicher Verlag für physikalisch-mathematische Literatur, Moskau 1962
Bearbeiter der 15. Auflage
Prof. Dr. Klaus Dibowski
Hochschule für Technik, Wirtschaft und Kultur Leipzig (FH)
FB Informatik, Mathematik und Naturwissenschaften
Dr. rer. nat. Horst Schlegel, Leipzig
Bibliografische Information der Deutschen Nationalbibliothek
Die Deutsche Nationalbibliothek verzeichnet diese Publikation in der Deutschen
Nationalbibliografie; detaillierte bibliografische Daten sind im Internet
über http://dnb.d-nb.de abrufbar.
ISBN 978-3-446-41616-1
Dieses Werk ist urheberrechtlich geschützt.
Alle Rechte, auch die der Übersetzung, des Nachdruckes und der Vervielfältigung des Buches,
oder Teilen daraus, vorbehalten. Kein Teil des Werkes darf ohne schriftliche Genehmigung des
Verlages in irgendeiner Form (Fotokopie, Mikrofilm oder ein anderes Verfahren), auch nicht für
Zwecke der Unterrichtsgestaltung, reproduziert oder unter Verwendung elektronischer Systeme
verarbeitet, vervielfältigt oder verbreitet werden.
Fachbuchverlag Leipzig im Carl Hanser Verlag
© 2008 Carl Hanser Verlag München
www.hanser.de
Lektorat: Christine Fritzsch
Herstellung: Renate Roßbach
Satz: Klaus Dibowski, Leipzig
Druck und Binden: Druckhaus „Thomas Müntzer“ GmbH, Bad Langensalza
Printed in Germany
Vorwort
Gute Studienergebnisse setzen in der Mathematik neben Kenntnissen auch Fer-
tigkeiten voraus. Die Fertigkeiten kann man sich nur durch Üben aneignen. Mit
einer Fülle ausgesuchter Aufgaben möchte die Aufgabensammlung der Höheren
Mathematik dazu animieren.
Die Aufgabensammlung, die auf einer Übersetzung aus dem Russischen fußt,
richtet sich vor allem an Ingenieurstudenten an Hochschulen. Sie lehnt sich eng an
die Lehrpläne für den Grundkurs Mathematik dieser Einrichtungen an. Aufgaben
aus denjenigen Teilgebieten der Mathematik stehen im Vordergrund, die Bestand-
teil einer jeden Ingenieurausbildung aus heutiger Sicht sein sollten. Aber auch
Studenten der Mathematik können aus der Aufgabensammlung Gewinn ziehen.
Prof. Dibowski lehrt an der HTWK Leipzig. Er und der Koautor Dr. Schlegel
verfügen über jahrzehntelange Erfahrung in der Mathematikausbildung von Inge-
nieuren an Hochschulen. Die vorliegende Ausgabe ist eine völlige Neubearbeitung
der Originalausgabe.
Jedem Abschnitt werden die Formeln, Definitionen und andere kurze Erläu-
terungen zur Theorie vorangestellt, die für die Lösung der folgenden Aufgaben
unbedingt erforderlich sind. Außerdem helfen Lösungshinweise im Aufgabenteil,
aber vor allem der umfangreiche Lösungsteil. Zu fast allen Aufgaben sind die Lö-
sungen angegeben. Bei einführenden Aufgaben werden die Lösungsschritte meist
ausführlicher dargestellt. Dadurch eignet sich die Aufgabensammlung hervorra-
gend zur Vorbereitung auf Prüfungen.
Das Kapitel 0 will angehenden Studenten bei ihrer Vorbereitung auf das Stu-
dium Hilfestellung geben, den Übergang von Schule zur Hochschule erleichtern.
Auch die sorgfältigste Arbeit kann Fehler leider nicht vollständig verhindern.
Mit der vorliegenden 15. Auflage hoffen wir, die meisten ausgemerzt zu haben und
bedanken uns für die vielen konstruktiven Hinweise.
Leipzig, im Sommer 2008
Klaus Dibowski
Inhaltsverzeichnis
0	Wiederholung Elementarmathematik	9
0.1	Polynomdivision (Partialdivision)............................... 9
0.2	Potenzen........................................................ 9
0.3	Wurzeln ....................................................... 10
0.4	Logarithmen.................................................... 11
0.5	Quadratische und biquadratische Gleichungen.................... 12
0.6	Wurzelgleichungen.............................................. 13
0.7	Goniometrische Gleichungen..................................... 14
1	Einführende Grundlagen	16
1.1	Notwendige und hinreichende Bedingungen, Beweismethoden . .	16
1.2	Mengen, Abbildungen, Funktionen................................ 18
1.3	Reelle Zahlen.................................................. 20
1.3.1 Darstellung reeller Zahlen.............................. 20
1.3.2 Beträge und Ungleichungen............................... 22
1.3.3 Fakultät, Binomialkoeffizient, binomischer Lehrsatz ....	24
1.4	Kombinatorik................................................... 26
2	Komplexe Zahlen	29
2.1	Darstellungsformen, Rechnen mit komplexen Zahlen............... 29
2.2	Horner-Schema, Vietascher Wurzelsatz........................... 31
3	Vektorrechnung, Analytische Geometrie	34
3.1	Darstellung von und Rechnen mit Vektoren im R3................. 34
3.2	Skalarprodukt, Vektorprodukt, Spatprodukt...................... 37
3.3	Geradengleichung............................................... 40
3.4	Ebenengleichung................................................ 42
4	Lineare Algebra	47
4.1	Determinanten.................................................. 47
4.2	Matrizen....................................................... 49
4.3	n-dimensionaler reeller Vektorraum............................. 52
4.4	Rang von Matrizen, Gaußscher Algorithmus....................... 54
4.5	Lineare Gleichungssysteme...................................... 57
4.5.1 Die Cramer sehe Regel................................... 57
4.5.2 Das (allgemeine) lineare Gleichungssystem (LGS) ........ 58
4.6	Inverse Matrix (Austauschverfahren) ........................... 61
4.7	Lineare Transformationen....................................... 64
4.7.1 Affine und orthogonale Tranformationen ................. 64
INHALTSVERZEICHNIS
7
4.7.2 Eigenwerte, Eigenvektoren.............................. 66
4.7.3 Hauptachsentransformation für Kurven und Flächen 2.Ord-
nung ......................................................... 68
5	Zahlenfolgen und Zahlenreihen	72
6	Differenzialrechnung für reelle Funktionen einer Veränderlichen 78
6.1	Darstellung und Eigenschaften von Funktionen................. 78
6.2	Grenzwert einer Funktion..................................... 81
6.3	Stetigkeit einer Funktion.................................... 83
6.4	Ableitung und Differenzial einer Funktion.................... 84
7	Mitt eiwert sätze der Differenzialrechnung und Taylor-Formel	91
7.1	Mittelwertsätze ............................................. 91
7.2	Grenzwertsätze von Bernoulli-l’Hospital...................... 92
7.3	Taylor-Formel................................................ 93
7.4	Relative Extrema, Kurvendiskussion........................... 95
7.5	Newtonsches Verfahren....................................... 101
8	Integralrechnung für reelle Funktionen einer Veränderlichen	102
8.1	Unbestimmtes Integral....................................... 102
8.1.1 Grundintegrale, Integrationsregeln.................... 102
8.1.2 Integration rationaler Funktionen .................... 107
8.1.3 Integration weiterer Funktionenklassen ............... 110
8.1.4 Vermischte Aufgaben zur Integration .................. 111
8.2	Das Riemannsche Integral ................................... 113
8.3	Uneigentliche Integrale..................................... 116
8.4	Trapezformel, Simpsonsche Regel............................. 118
8.4.1 Trapezformel.......................................... 118
8.4.2 Simpsonsche Regel..................................... 119
9	Elemente der Differenzial- und Integralgeometrie	121
9.1	Kurvendarstellungen ........................................ 121
9.2	Tangente, Krümmung ebener Kurven, Normalebene............... 123
9.3	Inhalt ebener Flächen....................................... 129
9.4	Bogenlänge eines Kurvenstückes, Krümmung von Raumkurven . . 131
9.5	Volumen, Mantelfläche von Rotationskörpern.................. 136
9.6	Aufgaben aus der Physik..................................... 139
10	Funktionenreihen	142
10.1	Grundbegriffe............................................... 142
10.2	Potenzreihen und Taylor-Reihen.............................. 144
10.3	Fourier-Reihen.............................................. 148
8
INHALTSVERZEICHNIS
11	Differenzialrechnung für reelle Funktionen mehrerer
Veränderlicher	151
11.1	Niveaulinien, -flächen, -hyperflächen.......................... 151
11.2	Grenzwert, Stetigkeit.......................................... 152
11.3	Partielle Ableitung, Gradient, Richtungsableitung.............. 154
11.4	Zerlegungssatz, totales Differenzial........................... 157
11.5	Fehlerrechnung................................................. 159
11.6	Tangentialebene, Flächennormale................................ 161
11.7	Kettenregel.................................................... 162
11.8	Taylor-Formel.................................................. 165
11.9	Lokale Extrema................................................. 166
11.10	Extrema bei Nebenbedingungen in Gleichungsform ................ 168
12	Bereichs- und Mehrfachintegrale	171
12.1	Integrale über ebene Bereiche (Flächenintegrale)............... 171
12.2	Integrale über räumliche Bereiche (Raumintegrale).............. 173
12.3	Substitution................................................... 176
13	Gewöhnliche Differenzialgleichungen	181
13.1	Begriff der Differenzialgleichung.............................. 181
13.2	Differenzialgleichungen 1. Ordnung ............................ 182
13.2.1 Differenzialgleichungen mit	getrennten Veränderlichen ... 182
13.2.2 Durch Substitution lösbare Differenzialgleichungen.......185
13.2.3 Lineare Differenzialgleichungen
(Variation der Konstanten)............................... 187
13.2.4 Bernoullische Differenzialgleichungen	................ 188
13.2.5 Exakte Differenzialgleichungen, integrierender	Faktor ... 189
13.3	Differenzialgleichungen höherer Ordnung........................ 191
13.3.1 Lineare Differenzialgleichungen mit konstanten Koeffizienten 191
13.3.2 Eulersche Differenzialgleichungen....................... 196
13.4	Systeme linearer Differenzialgleichungen mit	konstanten	Koeffizi-
enten 	 197
13.5	Näherungsmethoden.............................................. 199
13.5.1 Potenzreihenansatz ..................................... 199
13.5.2 Runge-Kutta-Verfahren................................... 199
14	Vektoranalysis	202
14.1	Felder, Differenzialoperatoren .................................202
14.2	Kurvenintegrale.................................................205
14.3	Oberflächenintegrale............................................211
14.4	Integralsätze...................................................214
Lösungen
219
0 Wiederholung Elementarmathematik
0.1 Polynomdivision (Partialdivision)
Bei der Division P(x) : S(a?) zweier Polynome mit reellen Koeffizienten
P(x) = anxn + an-ixn 1 H---F ag	(0.1)
S(x) = bmxm + b^x™-1 + • • • + b0	(0.2)
(5(x)	0; GradP = n, Grad S = m; n > m) werden zwei Polynome Q(x) und
R(x) eindeutig so bestimmt, dass die Identität
P(x) = S(x) • Q(x) + R(x) mit Gradl? < GradS	(0.3)
erfüllt wird. Dann lautet das Ergebnis der Polynomdivision:
Das Polynom P(x) ist durch das Polynom S(x) teilbar, falls R(x) = 0 ist (bei
m > 1).
1. Führe die Polynomdivision aus:
a)
b)
c)
d)
ll.;;1 — 13.c3 + 26x2 — 15a?
7x2 — 4x + 3
2x3 - 5x2 + 7x - 13
x + 6
—21x2 - 3x4 - 4x3 + 12x - 5
x2 + 2x + 8
5	1\
36	6)
7	2x2 — 0, Ix+ 3
f) [ax4 + (2a — b)x3 — 2bx2 — cx
—2c] : (x + 2)
2. Unter welchen Voraussetzungen ist
die Polynomdivision
(x3 + px + q) : (x2 + ax — 1)
ohne Rest ausführbar?
0.2 Potenzen
Für natürliche Exponenten m, n (ausschließlich 0) und reelle Basen a, b gilt:
am	/ a\rn
am  bm = (a  b)m; — = (-) , (b 0)	(0.5)
am-an = am+n-, (am)n = (an)m = am'n	(0.6)
m
— = am~n, (m>n, a 0)	(0.7)
10
0 Wiederholung Elementarmathematik
Unter der Voraussetzung
a 7^ 0, b 7^ 0
(0-8)
gelten die Potenzgesetze (0.5), (0.6) auch, wenn m, n negative ganze Zahlen oder
null sind, wobei (für a^0) gilt:
a° = 1; — = a
an
(0.9)
(0.7) gilt jetzt ohne die Einschränkung m > n.
1.	Stelle die gegebenen Summen oder
Differenzen als Produkte bzw. Po-
tenzen dar.
a)	x2 + 6x + 9
b)	4x2 - 20x + 25
c)	x4 — 2x2 + 1
d)	1 + a — a2 — a3
e)	(x2 + l)4 — (x2 — l)4
Hinweis: Binomische Formeln.
2.	Vereinfache durch Anwendung der
Potenzgesetze:
4 • (125)4 • 1624
a) 3-2 • (2 • 32)18 • 166
/3a~sxy°\2 (2a3x-2)-3
’ \ 4a7a?-4 ) : (3arc-3)-2
/ 25x2 — 4?/2 \ n
\ a2 — 2562 J
/ a2 — 10a6 + 2562
\5ax — 2ay — 25bx + 106t/
(rs + rt)m+3um+1
(rsu + rut)m~2
0.3 Wurzeln
Ist a > 0 reell und n eine natürliche Zahl (n > 2), dann ist b = y/ä die nichtnega-
tive Zahl 6, für die bn = a gilt. Damit gilt insbesondere
%/ä2 =	= |a| =
für a
für a
> 0
< 0
(0.10)
Mit y/ä = a1/71 gelten die Potenzgesetze für rationale Exponenten, und die Wur-
zelgesetze lassen sich auf die Potenzgesetze zurückführen, z. B.:
\/a - b = (a • b)n = an -bn = y/ä • tfb
(0.11)
Potenzen mit reellen (also auch irrationalen) Exponenten sind definiert, falls die
Basis positiv ist. Dann gelten die Potenzgesetze (0.5), (0.6) und (0.7) (ohne die
Einschränkung m > n).
0.4 Logarithmen
11
1.	Vereinfache durch Anwendung der
Wurzelgesetze.
a)	Va2b3 •	• ^Tä2
b)	(\/4x2 — 20x?/ + 25?/2)
c) Vxn+2 • \/x2n~r • (y/x}n 2
2.	Mache die Nenner folgender Brüche
rational:
3 — 2x72	x/4-V15
3 +	\/4 + x/15
. 2y/5 + 3y/2
c) —-F---~i=
3\/5-x/2
62
Hinweis: Binomische Formeln.
h) \J{x- yf
j) x + \/x2 — 2x + X
3.	Vereinfache
3 — 2\/2 _ 2y/6 + y/3
3 + 2y/2	2\/6-3x/3'
4"
^0,5
0, 750,5 +
4. Stelle den gegebenen Term als Sum-
me von zwei Quadratwurzeln dar.
0.4 Logarithmen
Unter dem Logarithmus logb a versteht man die reelle Zahl, mit der man die Basis
b potenzieren muss, um den Numerus a zu erhalten:
bios»a = a; a > 0, b > 0, b^l	(0-12)
lga = log10a; lna = logea; e = 2,71828...	(0.13)
log/, 1 = 0; logfc 6 = 1	(0-14)
log/, (x-y) = logb x + logfc y; x > 0, y > 0	(0.15)
X logö - = logö X - logö y- X > 0, y > 0 y	(0.16)
logb xy = y • logb x; x > 0	(0-17)
logb tfx = - • logb x; x > 0, y 0	(0.18)
1. Bestimme x durch Anwendung der
Logarithmendefinition oder der Lo-
garithmengesetze.
a) x = log17 17 b) log5 x = 0,4
1	3
c) X = log3 - d) log,, v8 = -
y	o
e) logi x = —4 f) x = log3 17
g) logfc x = log6 w + - log6 u—
12
0 Wiederholung Elementarmathematik
3.
h)	In x = In \/n — b + - In (a + b)
-|ln (a2 -b2)
ö
i)	In \/l + x — - In (1 — x)
= lglOln^
j)	x = log6 16, wenn log12 27 = a
2. Wende die Logarithmengesetze an:
x _ a3b4
a) 1g------
b) 1g	:
%/a2 + 62
a4Vb • (a + ö)2
c) lg---~
Va7b5
0.5 Quadratische und biquadratische Gleichungen
Die quadratische Gleichung (in Normalform)
x2 + px + q = 0; p, q reell
(0.19)
hat für D = —
4
q > 0 die zwei verschiedenen reellen Lösungen
P ,
^2 = -2±
(0.20)
Für D = 0 ist x\ = x^ (Doppelwurzel).
Wurzelsatz von Vietax
Xi+x2 = -p, X1-X2 = Q	(0.21)
Die biquadratische Gleichung
x4 + px2 + q = 0	(0.22)
lässt sich durch die Substitution z = x2 auf eine quadratische Gleichung zurück-
führen:
z2 + pz + q = 0
Zu jeder Lösung zq > 0 von (0.23) erhält man die Lösungen
^oi = vAÜ ^02 = — \Aö
(0.23)
(0.24)
der Ausgangsgleichung (0.22).
0.6 Wurzelgleichungen
13
1.	Berechne alle reellen Lösungen der
gegebenen Gleichungen.
a)	x1 2 * — 2x — 63 = 0
b)	18x2 - 3x = 10
c)	x4 - 34x2 + 225 = 0
d)	13x2 — 9x4 = 4
e)	x2 + 6x + 13 = 0
f)	x4 + 4x2 = 0
. x x — 1	9	3
h)----------------= —------------
x — 2 x + 1 x2 — x — 2
2x + 8	x — 5 3x — 5
x + 3	x — 4	x2 — x — 12
2.	Für welche Werte des reellen Pa-
rameters A besitzt die quadratische
Gleichung
(A - l)x2 - 2(A + l)x + A - 2 = 0
zusammenfallende Lösungen?
3.	Für welche Werte des ganzzahligen
Parameters A besitzt die quadrati-
sche Gleichung
Ax2 - (1 - 2A)x + A - 2 = 0
rationale Wurzeln?
4.	Für welche Werte von a > 0 besitzt
x2 — 4x — log2 a = 0
reelle Lösungen?
0.6 Wurzelgleichungen
Da die Gleichungsvariable wenigstens einmal im Radikanden einer Wurzel auftritt,
lässt sich durch (ggf. wiederholtes) Isolieren einer solchen Wurzel und anschließen-
des Potenzieren der Gleichung die Wurzelgleichung oftmals in eine mit bekannten
Methoden lösbare Gleichung überführen. Dabei können als Folge einer nicht-
äquivalenten Umformung Lösungen auftreten, die die gegebene Gleichung nicht
erfüllen. Solche Scheinlösungen lassen sich manchmal schon mit Hilfe des Defini-
tionsbereiches der gegebenen Wurzelgleichung, stets aber durch die Probe (d. h.
durch Einsetzen der gefundenen Lösungen in die gegebene Gleichung) ausschalten.
1. Bestimme alle reellen x, die die fol-
genden Wurzelgleichungen erfüllen.
a) \/2x + 7 + y/x — b = 7
b) \/5 — 2x — \/x — 7 = 3
c) 2\/2x + 9 + \/5 — x = \/29 + x
d) 3^3x + 1 - 2\/2x - 1 = 4x/x
e) 4x + 3 + \/2x + 11
-3^x -3 = 0
f) 2 y/Hc2 — 5 \/x = 3
. 3/ x + 3	3/5x + 2	13
g) \-----------H \ -------= —
67 V bx + 2 v X + 3	6
/ _|_ 2
Hinweis: Substitution z = \
V bx + 2
/	i~2
h) J12- —+
V x2
2.	Zeige, dass die Wurzelgleichung
V5 - 3a? + V3a? - 5 = 4
keine reelle Lösung haben kann, ohne
diese Gleichung zu lösen.
14
0 Wiederholung Elementarmathematik
0.7 Goniometrische Gleichungen
Bei den hier ausschließlich zu lösenden rein-goniometrischen Gleichungen tritt die
Gleichungsvariable nur im Argument von Winkelfunktionen auf. Außerdem ge-
hören die ausgewählten Aufgaben zu den Sonderfällen, die sich rechnerisch ex-
akt lösen lassen. Da als Lösungsgrundbereich die Menge der reellen Zahlen zu-
gelassen wird, gibt es im allgemeinen keine eindeutigen Lösungen, weil die Win-
kelfunktionen keine eineindeutigen Funktionen sind. Die Lösung der Gleichung
sinx = 0, 5 lautet z. B. (im Bogenmaß) : x\ =	+ k • 27t, x% =	+ k • 27t mit
k = 0, ±1,±2, ±3, ... Manchmal existiert überhaupt keine Lösung wie z.B. für
sinx = 2.
Hilfreich beim Lösen einer rein-goniometrischen Gleichung kann es beispiels-
weise sein
•	unterschiedliche Argumente bei den Winkelfunktionen auf ein einziges Argu-
ment,
•	verschiedene Winkelfunktionen auf eine einzige Winkelfunktion
zurückzuführen. Dies gelingt durch die Anwendung geeigneter trigonometrischer
Formeln, von denen hier nur eine kleine Auswahl angegeben werden kann:
/7t	\	/7t	\
cos x = sin-----x ; cot x = tan-------x j
\2	7’	\2	J
2	. 2	.	sin X
cos x + sm x = 1; tanx-cotx = l; tanx =---------
cosx
sin 2x = 2 sin x cos x; cos 2x = cos1 2 x — sin2 x
r /	7t\	r- / 7t
cos x + sm x = v 2 sm \x 4— ; cos x — sm x = v 2 cos \x 4—
\	47	\	4
sin (x ± y) = sin x cos y ± cos x sin y
(0.25)
(0.26)
(0.27)
(0.28)
(0.29)
Die Probe muss alle gefundenen Lösungen umfassen, weil beim Lösen oft nicht-
äquivalente Gleichungsumformungen vorgenommen werden müssen.
1. Bestimme alle reellen Lösungen der
folgenden Gleichungen:
\	(	7t\	1
a) sm 3x 4— = -
7	\	67	2
b) sin3x = sin2x
Hinweis: Aus sinarr = sin&r folgt
ax = bx 4- k • 27t, ax 4- bx = 7t 4- k • 27t;
k = 0, ±1, ±2, ±3, ...
c) tanx — tan2x = 0
d) tan 3x — cot 5x = 0
e) sin 2x + sinx = 0
f) tan
+ sin 2x = 0
h)	sinx + cosx = 1
i)	3 sinx = 2 cos2 x
j)	sin2 2x + sin2 x = 1
k)	3 cos2 x + sin2 x = 2 — sin x
1)	3 cos x — 8 sin x + 4 = 0
0.7 Goniometrische Gleichungen
15
m)	3 sin2 x + cos 2x + 3 cos x + 8 = 0
n) 8 sin2 x + 6 cos2 x = 13 sin 2x
o) cotx + 3 • tanx = 5 • (sinx)-1
p) 3 + sin2 x — 3 cos2 x
= 3 sinx + cos 2x
2. Durch die Anwendung von trigono-
metrischen Formeln lassen sich die
folgenden Gleichungen auf die Form
/(x) • g(x) = 0 bringen. Die gesuch-
ten Lösungen erhält man dann aus
den beiden Gleichungen
/(x) = 0,	= 0.
a)	sin x + tan x = (cos x)-1 — cos x
b)	4 sin3 x + 4 sin2 x = 3 sin x + 3
c)	tan x + cot x — 2 = 0
d)	cos 2x = 1 — tan2 x
e)	(1 + tanx) sin2 x
= 3 + 3(cos x — sin x) sin x
1 Einführende Grundlagen
1.1 Notwendige und hinreichende Bedingungen, Beweis-
methoden
A, B,... (zweiwertige) Aussagen
Sie sind entweder wahr (w) oder falsch (f).
A
A/\B
A V B
A H
A<H
Negation
Konjunktion
Disjunktion
Implikation
Äquivalenz
(nicht A)
(A und B)
(A oder B)
(wenn A, so B)
(A genau dann, wenn B)
A(x), B(x),... (einstellige) Aussageformen: durch Ersetzen der Variablen
x durch Elemente einer vorgegebenen Menge gehen Aussageformen in Aussagen
über.
Vx A(x) Allquantor (Für jedes x gilt A(x).)
Ax A(x) Existenzquantor (Es existiert wenigstens ein x, für das
A(x) gilt.)
Wenn aus der Aussage A die Aussage B gefolgert werden kann (A	B), so heißt
A hinreichende Bedingung für B und B notwendige Bedingung für A.
Beim direkten Beweis wird die Behauptung B aus einer Aussage A durch ma-
thematisch richtiges Schließen hergeleitet (A B). Ist A wahr, so ist auch B
wahr.
Beim indirekten Beweis einer Behauptung B schließt man aus ihrer Negation
B auf die Richtigkeit einer Aussage A, was jedoch im Widerspruch zu der (bereits
bekannten) Wahrheit von A steht: (A A (B A)) B.
Die vollständige Induktion ist ein Verfahren zum Beweis einer Behauptung
P(n) für alle natürlichen Zahlen n > hq:
A:	Man zeigt: Es gilt P(no). (Induktionsanfang)
B:	Man nimmt an: P(k) ist für ein beliebiges aber festes n = k > /zq eine wahre
Aussage. (Induktions annahme)
C:	Man zeigt: Unter der Voraussetzung B ist auch P(k + 1) eine wahre Aussage.
(Induktionsbeweis)
D:	Bei der Gültigkeit von A, B, C kann man folgern: P(n) gilt für alle n> nQ.
1.1 Notwendige und hinreichende Bedingungen, Beweismethoden
17
1.	Beweise die Behauptung
B : a2 + b2 > 2ab gilt für alle reellen
Zahlen a und b
a) indirekt, b) direkt.
2.	Beweise die Richtigkeit der folgenden
Behauptungen direkt:
a)	Aus a + n-1 = 10 folgt a3 + a~3
= 970.
b)	Aus a — a[ = 5 folgt a3 — a~3
= 140.
c)	Für spitze Winkel a und ß gilt
sin(<a + ß) < sin a + sin ß.
d)	Gilt sin a cos(q + ß) = sin/?, so
ist tan(a + ß) = 2 tan a.
e)	Für jedes beliebige Dreieck mit
den Seiten a, 6, c und deren Ge-
genwinkeln et, /?, 7 gilt:
1 sin(<a — /?)	a2 — b2
sin(<a + /?) c2
tan a a2 + c2 — b2
tan ß b2 + c2 — a2
3.	a sin(/? — 7) + b sin(7 — a)
+ csin(<a — ß) = 0
3.	Beweise die Richtigkeit der folgenden
Behauptungen indirekt:
a)	Für spitze Winkel a und ß gilt:
sin(<a + ß) < sin a + sin ß.
b)	\/7 ist irrational.
c)	lg 5 ist irrational.
d)	----- > — 1 für 0 < x < 00
7 7x + 5
e)	Für beliebige reelle Zahlen
a, 6, c, d gilt:
+ b)2 + (c + d)2 <
\/&2 + c2 + \/b2 d2.
4.	Beweise durch vollständige Indukti-
on:
\ • n(n + 1)
2=1
b)E^ = 2-^
7 / 2z	2n
2=1
72 1	p -1
C) E = ---------z-, q 1 n > 2
17	«-1
72	2
d)	E/3 = y(n + 1)2
2=1
e)	£,(t + 1) ="(" + 1)(" + 2>
i=l	3
n -
f)	y 1	=
i(i + 1) n + 1
2=1 x 7
g)	y’ < E'2 < |(n+1)3
2=1
h)	2n > 2n + 1 fürn > 3
i)	n > ln(2n)
j)	n2 > n
k)	3n > 3n
5. n o/zmsche Widerstände ergeben bei
Reihenschaltung den Gesamtwider-
stand Rr:
Rr = R± + R2 + • • • + Rn
und bei Parallelschaltung den Ge-
samtwiderstand Rp\
1 _ 1	1	1
Rp R±	R2	Rn
Beweise	die	Ungleichung
'n Rp
durch vollständige Induktion.
6. Untersuche in den folgenden Aufga-
ben, ob die Bedingung A nur not-
wendig, nur hinreichend, notwendig
und hinreichend oder weder notwen-
dig noch hinreichend für die Bedin-
gung B ist.
a)	A: Das Parallelogramm ist ein
Quadrat.
B: Alle Winkel des Parallelo-
gramms sind rechte Winkel.
18
1 Einführende Grundlagen
b)	A: Alle Seiten des Parallelo-
gramms sind gleich lang.
B: Das Parallelogramm ist ein
Quadrat.
c)	A: a > b und a, b reell
B: a2 > b2 und a, b reell
d)	A: x2 +px + q = 0 hat zwei reelle
verschiedene Wurzeln.
B: D = (l)2-9>0
e)	A: Für die reellen Koeffizien-
ten a, b, c, d des linearen Glei-
chungssystems
ax + by = 0
ex + dy = 0
gilt: ad — bc 0
B: Das System (*) hat nur die Lö-
sung x = y = 0.
f)	A: a > 0 ist eine gerade Zahl.
B: a2 ist eine gerade Zahl.
1.2 Mengen, Abbildungen, Funktionen
A, B,... Mengen
A := {«i, U2, «3,... } Menge A, bestehend aus den Elementen ai, U2, «3,...
ai e A ai ist Element der Menge A.
b A b ist nicht Element der Menge A
0 leere Menge.
A C B A ist Teilmenge von B
A C B A ist echte Teilmenge von B
B := {x | x e T A H(x)} Menge B, bestehend aus allen Elementen x, die
Elemente der Menge T sind und für die die Aussageform B(x) zu einer wahren
Aussage wird.
V ereinigungsmenge:
Durchschnittsmenge:
Differenzmenge:
Produktmenge:
K omplementär menge:
AuB:={x|xeAVxe B}
A A B := {x | x e A A x e B}
A \ B := {x \ x E A /\ x B}
A x B := {(x, y) | x E A A y E B
A (#,?/) geordnetes Paar}
Ä := M\ A
[M Universalmenge (Grundgesamtheit)]
Zahlenmengen (nach DIN 1302):
N Menge der nichtnegativen ganzen Zahlen
Z Menge der ganzen Zahlen
Q Menge der rationalen Zahlen
R Menge der reellen Zahlen
C Menge der komplexen Zahlen
Eine Abbildung A ordnet gewissen Elementen x E M ein oder mehrere Elemente
y E N zu und ist damit eine Teilmenge von M x N: A C M x N.
1.2 Mengen, Abbildungen, Funktionen
19
A 1 ist die zu A gehörige Umkehrabbildung (inverse Abbildung).
Eine Abbildung A C M x N heißt
•	eindeutig, wenn ((x,?/i) e A A (x,y2) £ A) y± = y%
•	eineindeutig (umkehrbar eindeutig), wenn sowohl A als auch A-1 eindeutig sind.
Jede eindeutige Abbildung F heißt Funktion.
Ist F eineindeutig, so ist F-1 die zu F gehörige Umkehrfunktion.
Zwei Mengen M und N heißen äquivalent (gleichmächtig): M ~ N, wenn
eine eineindeutige Abbildung von M auf N existiert.
Eine unendliche Menge, die der Menge der natürlichen Zahlen N äquivalent ist,
heißt abzahlbar unendlich.
Die Menge {x|xgRA0<x<1} der reellen Zahlen zwischen 0 und 1 ist nicht
abzahlbar.
1.	Stelle die gegebenen Mengen durch
Aufzählung ihrer Elemente dar.
a)	A = {x | x e R
A x3 + x2 — 2x = 0}
b)	B = {x | x e R
4
A xF— < 4 A x > 0}
x
c)	C = {x I X e N
A x2 — 4x — 5 < 0}
d)	D = {x | x e Z A - < 2X < 6}
8
2.	Stelle die gegebenen Mengen im x, y-
Koordinatensystem graphisch dar.
a)	A = {(x,y) | (x,y) e R2
A xiy- 3 = 0}
b)	B = {(x,y) | (x,y) e R2
A 4x2 - y2 < 0}
c)	C = {(x,y) I (x,y) G R2
A (x2 - 4)(y + 1) = 0}
d)	D = {(x,y) | (x, y) G R2
A y > x + 1 A x > — 1}
3.	Gib die Mengen A U B, A A B,
A \ B, B \ A, A x B und B x A
durch die Aufzählung ihrer Elemente
an, wenn
A = {x | x e R A x2 — 2x = 15}
B = {x | x e R A x2 — 4x = 5}.
4.	A, B, C seien gegebene Mengen.
Überprüfe die folgenden Behauptun-
gen unter Verwendung von ebenen
Punktmengen, oder führe einen ma-
thematisch exakten Beweis.
a)	Stets gilt A A B C A und
A AB C B.
b)	Stets gilt A C A U B und
B C AuB.
c)	(I) = A
d)	Aus A C B folgt A D B.
e)	Au B = AC\B
f)	ÄÄTB = Ä U B
g)	(A u B) n C = (A n C) u (B n C)
h) (A n B) U C = (A U C) n (B U C)
i) (A\B) n (Ä U B) = A
5.	Beweise für beliebige Mengen A, B :
a) A n B = B B C A
bjü Jß = B -== .4 C B
6.	Zeige, dass die unendliche Menge
A = {/n |mGNAm = »i2 + l
A n G N}
abzählbar ist.
20
1 Einführende Grundlagen
7.	Sind die beiden unendlichen Mengen
A = {2; 4; 6; 8;... } und
B = {1; 0,1; 0,01; 0,001;...} äqui-
valent?
8.	F = {(a, 6), (c, 6), (d, e)} und
G = {(c, /)> (c, 6)> e)} sind
zwei Abbildungen aus der Menge
M = {a, c, d, d, g} in die Menge
N = {b,e,f,k}.
a)	Welche Abbildung ist eine Funk-
tion?
b)	Sind die Umkehrabbildungen
Funktionen?
9.	Es seien Fi(x), F2(x), F3(x) Poly-
nome höheren Grades. Ferner seien
die folgenden 3 Mengen bekannt:
Li = {x | Pßx) = 0} (i = 1,2,3)
Stelle mit Hilfe der Mengen Li, L2
und L3 die Lösungsmengen dar für
a) die Gleichung
Fi^)-F2^)-F3^)=0
b)	das System
Fi(x) = 0
F2(x)-F3(x) = 0
c)	das System
Fi(x) =0
F2(x) = 0
F3(x) = 0
10.	Skizziere die Produktmenge
A x B in der x, ?/-Ebene, wenn
a)	A = {x | x e R A (1 < x < 2
V x = 3)}
B = {y|yeRA(2<y<3
V y = 4}
b)	A = {x | x = i A i E {1, 2, 3,4}}
s = {y|yeRAi<y<3}.
11.	Gegeben sind die Mengen
M = {a, b, c} und N = {a, ß}. Bilde
alle eindeutigen Abbildungen
a)	von M in bzw. auf N
b)	von bzw. aus N in M.
1.3 Reelle Zahlen
1.3.1 Darstellung reeller Zahlen
Die Menge der rationalen Zahlen Q und die Menge der irrationalen Zahlen zusam-
men bilden die Menge der reellen Zahlen R.
Zwischen den Punkten der Zahlengeraden und der Menge R besteht eine einein-
deutige Zuordnung.
Jede reelle Zahl lässt sich im dekadischen System durch einen unendlichen
Dezimalbruch darstellen: rationale Zahlen durch periodische, irrationale Zahlen
durch (nichtperiodische) unendliche Dezimalbrüche.
Nicht nur jeder abbrechende Dezimalbruch, sondern auch jede ganze Zahl lässt
sich als periodischer Dezimalbruch darstellen:
1 = 0,25 = 0,24999-•• = 0,249	- 2 = -1,999• • • = -1,9
4
Um z.B. die rationale Zahl x = 2,34 als Bruch ganzer Zahlen darzustellen, kann
1.3 Reelle Zahlen
21
man wie folgt verfahren:
100x =	= 234,444...
-(	10a: =	=	23,444... )
90x =	’	90
Intervalle sind spezielle Mengen reeller Zahlen:
[a, b]
[a, b)
[a, oo)
(oo, b]
= {x I
= {x I
= {x I
= {x I
x e R A a < x};
x e R A x < b};
x e R A a < x < 6};
x d /\a < x < b};
(a, b]	:= {>	x e R A a <	C x < b}
(a, b)	:= {>	x E R A a <	Z x < b}
(a, oo)	:= {x	\ x e R A a <	' x}
(oo, b)	:= {x	\ x e R A x <	
Das abgeschlossene Intervall [a, b] wird auf der Zahlengeraden durch eine Strecke
dargestellt.
Im Folgenden sollen Pq und P Punkte der Zahlengeraden (R1), der Ebene (R2)
bzw. des Raumes (R3) bedeuten.
Unter der e-Umgebung (s > 0) eines Punktes Pq versteht man die Menge aller
Punkte P, für die gilt:
1.	| P — Pq | = | x — xq |= ^/(x — xq)2 < £ (offenes Intervall auf der Zahlengeraden)
2.	| P — Pq |= y/(x — xq)2 + (y — yo)2 < £ (offene Kreisfläche)
3.	I P - Po 1= \/(x- Xq)2 + (y - y0)2 + (z ~ zq)2 < £ (offene Kugel)
M sei eine Teilmenge von R2 (-£ = 1,2,3).
Als Häufungspunkt von M bezeichnet man einen Punkt P E R2, wenn in jeder
e-Umgebung von P unendlich viele Punkte aus M liegen.
Für die Räume R2 gilt der
Satz 1.1 (Bolzano-Weierstraß) Jede unendliche beschränkte Teilmenge von R2
besitzt mindestens einen Häufungspunkt.
Es sei H(M) die Menge aller Häufungspunkte der Menge M C R.
Ist H(M)
•	nach oben beschränkt, dann ist das Supremum von H(M) der Limes superior
von M : supF(M) = limsupM = lim M
•	nach unten beschränkt, dann ist das Infimum von H(M) der Limes inferior
von M : inf H(M) = liminf M = lim M
22
1 Einführende Grundlagen
1.	Sind die gegebenen reellen Zahlen x
rational oder irrational?
a)	x =
b)	x =
2 + 5\/2
x/2 - 1
<47-A45
%/5- %/3
c) X = log9 5 • log25 27
2.	Gegeben sind zwei irrationale Zah-
len: a = \/7 + 0,2 und b = \/7 — 0, 2.
Überprüfe, dass a — 6, a2 + b2 und
a3 — b3 rational sind. Kann man all-
gemein die folgende Behauptung be-
weisen: (a — b e QAö2 + 52 e Q)
a3 — b3 E Q?
3.	Stelle die folgenden periodischen De-
zimalbrüche als Bruchzahlen dar:
a) 0,321 b) 0,132	c)2,59
4.	Gegeben sind die Intervalle
a)	A = [-2,3) und I2 = [1,5)
b)	A = (-5,1) und 12 = (-2,0]
c)	li = [—1, 5; 3, 5) und
12 = (0,5; 4, 5).
Bilde jeweils
I1UI2, 11A12, li\12, h\h-
5.	Gib von folgenden Mengen M die
Menge der Häufungspunkte H(M)
und limM oder lim M an, falls sie
existieren:
+ 1
a)	M = {rclrc =----A n G bJ} C R
n
b)	M = {x|x = (-1)"+1^<
An G N} c R
. r ,	3n+ (—l)n
c)	M = {rckc =----------
' L	2n
An G bJ} C R
2 77 -I- 7
d)	M = {x|x = (-l)n •
An e N} C R
2
e)	M = {(x, ?/, z)\x = 2 H—
n
4
A y = 4 H—
n
5
\z = 5 + - A n G bß C R3
n
1.3.2 Beträge und Ungleichungen
Betrag einer reellen Zahl:
für a
für a
> 0
< 0
(1-1)
Auf der Zahlengeraden lässt sich |a| als Abstand der (positiven oder negativen)
reellen Zahl a vom Nullpunkt deuten. |a| ist stets nichtnegativ.
Regeln für das Rechnen mit Beträgen
| -a| = |a|
|x| = a	x = ±a; |x| < a	— a < x < a
|x| > a	((x < — d) V (x > a))
\a’b\ = H • l6l; |^| = -pq- für |b| 7^0
(1-2)
(1-3)
(1-4)
(1-5)
1.3 Reelle Zahlen
23
\a + b\ < |a| + \b\ (Dreiecksungleichung)	(1.6)
Regeln für das Rechnen mit Ungleichungen
a <	b	alc<b±c		(1-7)
a <		a • c < b • c für c >	 0	(1-8)
a <	b^	a • c > b • c für c <	: o	(1-9)
((a	< b) A	(c < d))	a + c <	< b + d	(1-10)
		f - > r für a-b'.	> 0	
a <	b^>	Ja	b | - < r für a-b' \ a	b	< 0	(1-11)
1. Bestimme die Menge aller reellen
Zahlen x, für die gilt:
Zahlen x, für die die folgenden Glei-
chungen bzw. Ungleichungen gelten:
a) 2x + 6 < 18 — 9x
b) -l,5x -3 < 3 — 4, 5x
c) 3x + 6 < 4x + 2
d) (1 — x)(x + 2) > 0
e) x1 2 + 2x — 8 < x — 2
x + 3
2x — 5
> 3
b) |2x-3| < 6
c) |3-2x| > 5
f) x3 — x2 < 4x — 4
5 — x
5+ <
4x + 10
4x — 3
1^ - 2I
k)
3x + 2 <
2x — 3 “ ”
4x + 3
2,5-
2x2 -|- 12x -|- 8
x2 + x — 6
g)	|6x — 5| — |7x + 3| = 3x — 4
h)	|2x — 1| = \x — 1|
i)	|x — 5| < |x + 2|
j)	\x - 5| + |3 - x\ < 2
1) \/4x-8 < 1
m) 1g (2 + x) < 1
2. Beweise: Für beliebige reelle Zahlen
a, b gilt
a) \a + b\ > |a| - \b\
J7mwezs:Dreiecksungleichung.
b) \a + b\ > ||a| - \b\\
3. Bestimme die Menge aller reellen
1) |x-3| < 10 A |x + 2| > 3
4. Für welche reellen Wertepaare (x,?/)
gelten die folgenden Beziehungen?
Stelle die Lösungsmengen zeichne-
risch als Punktmengen dar.
a)	(x - 3y + l)(2x + y - 1) < 0
b)	x2 — 3xy + 2y2 > 0
c)	x + \y — 2| < 5
24
1 Einführende Grundlagen
1.3.3 Fakultät, Binomialkoeffizient, binomischer Lehrsatz
Für n E N \ {0} definiert man
n\ := 1 • 2 • 3 • ... • n (n Fakultät)
(1-12)
und setzt 0! := 1. Es ist n\ = n • (n — 1)!
a
k
Eine mit
(a über k) bezeichnete reelle Zahl heißt Binomialkoeffizient.
Sie ist für beliebiges reelles a und natürliches k nach
a(a — 1)(q — 2)... (q — k + 1)
kl
(1-13)
definiert, und es gilt
Binomischer Lehrsatz:
(1-14)
(1-15)
(1-16)
(1-17)
(1-18)
(1-19)
n / \
(a + b)n =
fc=0 ' '
(1-20)
1.	Gib die in den folgenden Termen auf-
tretenden Fakultäten als Produkte
an. (n sei jeweils eine geeignete na-
türliche Zahl.)
a) (n + 3)!
c) 3n + n\
e) (2n —3)!
b) n + 3!
d) 3nl - 5
f) nl/3
2.	Vereinfache folgende Terme, (n, k
seien jeweils geeignete natürliche
Zahlen.)
a)	(n + 1) • (n + 2) • nl
b)	n • (n — 1) • (n — 2)!
(n + 1)!	(n + 1)!
; n • (n - 1)	; n • (n - 1)!
1.3 Reelle Zahlen
25
(n + 3)!
n + 3
(n-fc)!
(n — 2 — k)l
(2n + l)!
(2n — 1)!
(2n- 2)!
(2n)!
3.	Addiere die folgenden Brüche, (n
sei jeweils eine geeignete natürliche
Zahl.)
£ 1
n! (n + 1)!
1 1
) (2n — 1)! + (2n + 1)!
1
(n — 1)! n!
1 1
(2n —2)! + (2n)!
4.	Berechne die folgenden Binomialko-
effizienten:
5.	Beweise die Formel (1.16).
6.	Beweise die Formeln (1.17) und
(1.18)	durch vollständige Induktion.
7.	Entwickle die folgenden Terme nach
dem binomischen Lehrsatz:
a)	(3xy~2 — 7z)2
b)	(a + 2b)3
c)	(2x-1 — 3x2)5
d)	1, l3 = (1 + 0,l)3
8.	Beweise mit Hilfe des binomischen
Lehrsatzes:
n	/ \
b> D-1>’(") = °
2 = 0
9.	Gib das 5. Glied der Entwicklung
/	/—\ n
i CL	\/X \
von —= H--------nach dem bino-
\\Jx a )
mischen Lehrsatz an, wenn sich der
Koeffizient des 3. zum Koeffizienten
des 2. Gliedes wie 11:2 verhält.
10.	Bestimme nach dem binomischen
Lehrsatz das Glied der Entwicklung
von (a/3 + V2^ , das ganzzahlig ist.
11.	Bestimme x so, dass das 4. Glied der
Entwicklung von (xlg x — x) nach
dem binomischen Lehrsatz gleich
(-106) ist.
12.	Eine Folge Fibonaccischer Zahlen ist
gegeben durch Fn+2 = Fn+i +Fn für
n > 0 mit Fq = Fi = 1.
a)	Gib die ersten 20 Zahlen dieser
Folge an.
b)	Beweise durch vollständige In-
duktion:
n r- i
1=0 tur k >
\k )
ist.
wobei
m zu beachten
13.	Entwickle die folgenden Terme nach
dem binomischen Lehrsatz und
schreibe das Ergebnis mit dem Sum-
menzeichen:
a) (x — l)25 b) (a2 + b)n
c) \an -a~n)n
14.	Das wievielte Glied in der Ent-
wicklung von (\/a2x + a-1x~2^
nach dem binomischen Lehrsatz ent-
hält keinen Faktor x?
26
1 Einführende Grundlagen
1.4 Kombinatorik
Berechnet wird die Anzahl der möglichen verschiedenen Zusammenstellungen von
vorgegebenen endlich vielen Elementen bei Beachtung bestimmter Bedingungen:
o.W.: ohne Wiederholung gleicher Elemente; m.W.: mit Wiederholung gleicher Elemente
Permutationen o.W. (n verschiedene Elemente, die sich in ihrer Anordnung
unterscheiden):
Pn = n! = 1 • 2 • 3 • ... • n	(1.21)
Permutationen m.W. (n Elemente, die sich in ihrer Anordnung unterscheiden,
wobei das i-te Element n^-mal auftritt; i = 1, 2,..., s) :
p(n1,n2,...,ns) = n!--------	+	+ .. . +	= n
Wn	ni!n2!...ns!
Variationen o.W. (Aus n verschiedenen Elementen werden k verschiedene Ele-
mente bei Berücksichtigung der Anordnung ausgewählt):
= ri • (n — 1) • ... • (n — k + 1); 1 < k < n	(1.23)
Variationen m.W. (Aus n verschiedenen Elementen werden k Elemente bei Be-
rücksichtigung der Anordnung ausgewählt, wobei sich die Elemente bis zu Zc-mal
wiederholen):
= nk	(1.24)
Kombinationen o.W. (Aus n verschiedenen Elementen werden k verschiedene
Elemente ohne Berücksichtigung der Anordnung ausgewählt):
= (A ; 1 < k < n	(1.25)
1.4 Kombinatorik
27
Kombinationen m.W. (Aus n verschiedenen Elementen werden k Elemente ohne
Berücksichtigung der Anordnung ausgewählt, wobei sich die Elemente bis zu Zc-mal
wiederholen):
(fc) _
wn ~
k > 1
C
(1-26)
1.	Wie viele verschiedene fünfziffrige
natürliche Zahlen kann man unter
Verwendung der Ziffern 3,4, 5, 7, 9
bilden, wenn ein und dieselbe Zif-
fer mehrmals in der Zahl auftreten
darf?
2.	Wie viele verschiedene vierziffrige
natürliche Zahlen kann man aus den
folgenden 4 Ziffern bilden, wenn in
jeder Zahl sämtliche 4 Ziffern vertre-
ten sein sollen?
a)	2,3, 5, 7
b)	2, 5, 7,0
3.	Wie viele verschiedene sechsziffrige
natürliche Zahlen lassen sich mit den
Ziffern
a)	2, 2,3,3,3,4
b)	0,0,3,4,4, 5
bilden, wenn in jeder Zahl jede dieser
Ziffern vertreten sein soll?
4.	Wie viele verschiedene Tips gibt es
beim Zahlenlotto „6 aus 49“?
5.	Wie viele verschiedene Würfe sind
mit 3 Würfeln möglich, wenn man
die Würfel
a)	nicht unterscheidet
b)	unterscheidet?
6.	Zehn Personen verschiedenen Na-
mens tragen sich in eine Liste ein.
Wie viele verschiedene Reihenfolgen
sind möglich?
7.	Wie viele verschiedene Tips gibt es
beim Pferderennen mit 10 Pferden,
wenn man auf die 5 Erstplazierten
in der richtigen Reihenfolge wetten
soll?
8.	In wie vielen Permutationen der sie-
ben Elemente a, 6, c, d, e, /, g ste-
hen die Elemente a, c, e nebeneinan-
der, und zwar
a) in der angegebenen Reihenfolge
b) in beliebiger Reihenfolge?
9.	Bei einem Versuch seien vier ver-
schiedene Ergebnisse möglich. Die-
ser Versuch wird fünfzehnmal wie-
derholt. Wie viele verschiedene
Versuchsprotokolle sind insgesamt
möglich? (Ein Versuchsprotokoll ent-
hält die Angabe der möglichen Er-
gebnisse in der Reihenfolge ihres be-
obachteten Auftretens.)
10.	Wie lautet die 30. Permutation der
fünf Elemente a, 6, c, d, e bei lexiko-
graphischer Anordnung, und die wie-
vielte Permutation ist „caebd“?
11.	Wie viele Variationen zur 3. Klasse
der 6 Elemente a, 6, c, d, e, f begin-
nen mit
a) d, b) ca. c) dab?
12.	Die wievielte Kombination zur 3.
Klasse ohne Wiederholung der Ele-
mente a, 6, c, d, e, /, p, h lautet
„öd/“ bei lexikographischer Anord-
nung?
13.	Es stehen fünf einzelne Normalwi-
28
1 Einführende Grundlagen
derstände von 1, 2, 5,10 und 20 Ohm
zur Verfügung. Wie viele verschie-
dene Widerstände können gemessen
werden, wenn die Normalwiderstän-
de in Reihe geschaltet werden?
14.	Die Morsezeichen bestehen aus den
beiden Elementen Punkt und Strich.
Wie viele verschiedene Zeichen las-
sen sich insgesamt bilden, wenn
höchstens fünf Elemente pro Zeichen
verwendet werden sollen?
15.	Aus einer Lieferung von 25 Erzeug-
nissen werden k Stück zur Überprü-
fung ausgewählt (1 < k < 25).
a)	Wie viele Möglichkeiten der Aus-
wahl von k Stück gibt es?
b)	Wie viele Möglichkeiten der Aus-
wahl gibt es insgesamt, wenn k die
Werte 1, 2,..., 25 annimmt?
16.	Für einen Sprachkurs im Ausland
bewerben sich 20 Damen und 25 Her-
ren. Es können aber nur 15 Damen
und 20 Herren teilnehmen. Wie viele
verschiedene Möglichkeiten der Aus-
wahl unter den Bewerbern gibt es?
17.	An 10 Erzeugnissen wird eine Gut-
schlecht-Prüfung vorgenommen.
a)	Wie viele verschiedene Prüfungs-
protokolle sind insgesamt mög-
lich?
b)	Wie viele Prüfungsprotokolle ent-
halten genau siebenmal „gut“?
c)	Wie viele Prüfungsprotokolle ent-
halten mindestens siebenmal
„gut“?
d)	Wie viele Prüfungsprotokolle ent-
halten höchstens siebenmal
„gut“?
18.	Ein Los von 100 Teilen enthält genau
3 Ausschussstücke. Dem Los wird ei-
ne Stichprobe vom Umfang 5 ohne
Zurücklegen entnommen. Zwei Stich-
proben gelten als gleich, wenn sie aus
denselben Teilen bestehen.
a)	Wie groß ist die Anzahl ver-
schiedener Stichproben, die genau
2 Ausschussstücke enthalten?
b)	Wie groß ist die Gesamtzahl S der
verschiedenen Stichproben?
c)	Wie groß ist die Anzahl S\ der
Stichproben, die mindestens ein
Ausschussteil enthalten?
2 Komplexe Zahlen
2.1 Darstellungsformen, Rechnen mit komplexen Zahlen
i2 = — 1; i (oft auch j) heißt imaginäre Einheit.
•	Arithmetische Darstellung:
z = a + bi mit a, b reell
a = Rc z Realteil von z, b = Im 2 Imaginärteil von z
z = a — bi die zu z konjugiert komplexe Zahl
•	Trigonometrische Darstellung:
z = r(cos p> + i sin p>)
r = \z\ (Betrag von z); p> = Ktcz (Arcus von z)
r > 0; 0 < p> < 27t
\z\ = r = \/ a2 + 62; tanc/? = - zur Berechnung von ip = arctan - bei Beachtung
des Quadranten für z in der Gänschen Zahlenebene.
•	Exponentielle Darstellung:
z = re1(p
e1<y? = cosc/2 + isinc/p (Eulersche Formel)
ei(^+/v27t) =	ganze Zahl)
Rechnen mit komplexen Zahlen in arithmetischer Darstellung
Mit z\ = ui + fei und z2 = «2 + fei ist:
z\ ± z2 = (ui + 6ii) ± («2 + fei) = (ui ± u2) + (fe ± fe)i
Z\ • z2 = (ui + fei) • («2 + fei) = (ui«2 - fefe) + (uife + U2fe )i
_	Ul + fei	«2	- fei	_	U1U2 + fefe	«2fe	- Ulfe	.
^1 • ^2	7 7 "	7 7	9 7 O	~I-	9	7 o	" 1
a2 + fei	U2	- fei	«2 + fe	a2	+ fe
(2.1)
(2.2)
(2.3)
Rechnen mit komplexen Zahlen in trigonometrischer bzw.
exponentieller Darstellung
Mit z\ = ri e1<y?1 = ri(cos(/?i + isin^i) und z2 = r2 e1<y?2 = 7*2(cos (^2 + isin^) ist:
Z\ • z2 = nr2 e1^1“^2) = rir2 [cos (^1 + (^2) + i sin (^1 + (^2)]	(2.4)
^i :	= — e1^1-^2) = — [cos ((£1 - p)2} + i sin (^1 - (^2)]	(2.5)
30
2 Komplexe Zahlen
Mit z = re1^ = r(cos</? + isint/?) folgt nach dem Satz von Moixrez
zn = (r • e1<y7)n = rn elw = rn (cos ncp + isinn^); neZ	(2.6)
Zk+\ = \[z= y/r e^ =
. / cp 2kn\
r~ 1 \ n" ~vT ) r~ F (2k7t\	. . ( X) 2Ä:7r\”1	, _
y/r e	n J = cos----------------1-----+ isin----------1-----	(2.7)
|_ \n n J \n n J\
(k = 0,1, 2,..., n — 1; n G N; n > 1)
1. Berechne z\ + ^2, ^1 — ^2, ^1 • ^2,
zi • ^2, ^T-^2 und ^2 • ^1 (Ergeb-
nisse in arithmetischer Darstellung),
wenn
a) zi = 9 — 7 i, z^ = 3 + 2 i
1X	4	1.	4	1.
bni = 3 + 2k i2 = 3 - 2‘
c)	z\ = 2(cos 15° + isin 15°),
z2 = 3ei7t/6
d)	zi = (1 + 2 i)2, z2 = (1 — i)3
e)	z\ = 2e1571/12, z2 = 4e17t,/6
2.	Berechne die reellen Variablen x,y
bzw. u, x, y, z aus
a) (1 + 2 i)x + (3 — 5 i)?/= 1 — 3 i
(1 + i)u + (1 + 2i)x
b) <
+(1 + 3i)y + (1 + 4i)z =
1 + 5i
(3 — i)u + (4 — 2 i)x
+(1 + i)y + 4 i z = 2 - i
3.	Berechne (Ergebnisse in arithmeti-
scher Darstellung):
a)	i • \fx* • i • y/y2 mit x, y G R
b)	(—i)18 c) —i17
d) 1 + 1 e) (2^3 - 31 vG2
f) i123 g) i-99 h) i1
4.	Berechne die folgenden Quotienten,
indem der Nenner reell gemacht
wird:
7 1 — 2 i	7 3i
73 + i72 d) —
’ 73-i72	2 + 5i\/2
5.	Von den gegebenen komplexen Zah-
len sind die arithmetische, die tri-
gonometrische und die exponentielle
Darstellung anzugeben.
a) z = — 5 i b) z = 9
C) r = 3 , v? = -
d)	r = 8 , p = — Ti
\	71
e)	r	= 2	,	p =	-
n	t	5n
f)	r	= 7	,	p =	—
\	27t
g)	r = 1 , p = —-
ö
h)	r = 5 , p) = -127°
i)	Re z = 4 , Im z = —6
j)	Re z = 0 , Im z = 2
k)	z = cos 60° + i sin 30°
1)	Re 7 = —0,5 , Inu = 8
m)	Re z = \/3 , Im z = — 1
n) Re z = — Im z = —2
o) Rc2 = — \/3 , Im 7 = —3
p) z = cos 30° — i sin 30°
q) z = 9(- cos 270° + i sin 270°)
r)	z = e-3171
s)	z = e2+317r
t)	z = e4-11’5171
2.2 Horner-Schema, Vietascher Wurzelsatz
31
6.	Berechne Ilez und Im 2 von
d)	z = (1 + i)7 + (1 - i)7
e)	= (1 - ix/3)10 - (1 + i\/3)10
(-1 + iV3)15
(1 - i)20
(1 + i)20
7.	Beweise
a)	cos =------------
- e"^
b)	sin^ =-----—-----
8.	Berechne mit Hilfe des Satzes von
Moivre
a)	alle komplexen zweiten Wurzeln
von z = — 1 + i%/3
b)	alle komplexen dritten Wurzeln
von z = 3 + 4 i
c)	alle komplexen vierten Wurzeln
vonz = 2\/3 + 2 i
d)	alle komplexen vierten Wurzeln
von z = —16
e)	alle komplexen fünften Wurzeln
von z = cos 225° — isin225°
(Ergebnisse in arithmetischer
Darstellung)
9.	Löse die folgenden Gleichungen in
der Menge der komplexen Zahlen
(Ergebnisse in arithmetischer Dar-
stellung):
a) x6	=	1	b)	x5	= — 1
c) x2	=	— 3 + i	d)	x3	= — 2 — 3 i
e) x4	=	1 — i	f)	x4	= —i
2.2 Horner-Schema, Vietascher Wurzelsatz
Mit dem Horn er-Schema lässt sich der Wert /(xq) einer reellen Polynomfunk-
tion
/(x) = Pn(x) = anxn + an_^xn -----+ an 0	(2.8)
berechnen und die Division Fn(x) : (x — xq) ausführen :
	c	In	®n-1	an-2	«2	ai	«o
		xobn_i	xobn_2	x0b2	zobi	xobo
x0	l	hi— 1	bn—2	bn—3	 b\	bo	f{x0)
Pn(x) : (x - x0) = bn-rx71 1 + bn_2xn 2 H----H b^x +	(2.9)
X — Xq
Ist /(xq) = 0, d.h., ist xq Nullstelle des Polynoms, so lässt sich ein Linearfaktor
von Pn(x) abspalten:
Pn(x) = (x - x0)(bn_1xn~1 + bn_2xn~2 H-------Hix + M	(2.10)
32
2 Komplexe Zahlen
Aus dem Fundamentalsatz der Algebra folgt:
Jede algebraische Gleichung n-ten Grades Pn(x) = 0 mit reellen oder komplexen
Koeffizienten an, an-i,..., «i, «o hat im Körper der komplexen Zahlen C genau n
Lösungen (Wurzeln), wenn man jede Lösung entsprechend ihrer Vielfachheit zählt.
Sind xi, X2,..., xk die verschiedenen Wurzeln mit den entsprechenden Vielfach-
heiten Qi, «2, • • •, (*k und Qi + Q2 + • • • + (*k = u. so gilt die Produktdarstellung
Fn(x) = an(x - xi)ai (x - x2)a2 ... (x - xk)ak	(2.11)
Hat die algebraische Gleichung Fn(x) = 0 nur reelle Koeffizienten, so gilt:
•	Mit x± = q + iß ist auch x2 = xÄ = Q — iß Wurzel (ß 0).
•	Ist n ungerade, so existiert mindestens eine reelle Lösung.
Indem man die algebraische Gleichung Fn(x) = 0 durch an 0 dividiert, erhält
man ihre Normalform:
pn(x) = xn + 6n-ixn-1 H------F b^x + &o = o
mit an 2 = bn_i (i = 1, 2,..., n).
dn
Sind xi, X2,..., xn die n Wurzeln von pn(x) = 0 (Q^-fache Wurzeln sind Q^-mal
aufgeführt), so gilt der folgende Zusammenhang zwischen den Wurzeln x^ und den
Koeffizienten bi~i (i = 1, 2,..., n):
Wurzelsatz von Vieta:
n
Xi -F x2 ~F    ~F xn — Xi — bn—i
2=1
n
X1X2 + X1X3 H-----F Xn-l%n = XiX3 = ^n-2
i, j=l
n
XjX2X3 + X^X2X4 H-----b Xn^Xn-iXn =	XiXjXk = ~bn-3
i,j,k=l
(i<j<k)
xix2 .. .xn = (-l)n60
Sind die Koeffizienten ^2, • • •, frn-i sämtlich ganzzahlig und hat pn(x) = 0
ganzzahlige Wurzeln, so sind diese Wurzeln Teiler des absoluten Gliedes bo.
Soll das Polynom Fn(x) als Polynom in (x — xq) dargestellt werden, also
y (^r)	-Pn(^) UQn(^ *^o) T ^Q,n—1(*£	^o) “F * * * “F UQ1(^ X(ß ~F &OCb
so wendet man das vollständige Horner-Schema zur Berechnung von
&och aon • • •, uon an:
2.2 Horner-Schema, Vietascher Wurzelsatz
33
1.	Bestimme alle vier Wurzeln der Glei-
chung
2x4 + x3 + 2x2 + x = 0
und mache die Probe durch Einset-
zen der gefundenen Lösungen in die
gegebene Gleichung.
2.	Löse folgende Gleichungen und ma-
che die Probe nach Vieta:
a)	x2 + (5 — 2i)x + 5(1 — i) = 0
b)	x2 + (1 — 2i)x — 2i = 0
c)	x3 + 5x2 — 16x — 80 = 0
d)	x4 - llx3 + 49x2 - lOLr + 78 = 0
e)	x3 — 3x2 + 3x — 1 = 0
f)	x4 — 2x3 — 3x2 + 4x + 4 = 0
3.	Löse die gegebenen Gleichungen.
a)	x4 + 2x3 + 2x2 + lOx + 25 = 0,
wenn xi = 1 + 2i
b)	x3 + 2x4 — 3x3 — 4x2 + 4x = 0
c)	0, 5x3 — 2x2 — 1, 5.r + 9 = 0
d)	x4 - 3x3 - 27x2 - 13x + 42 = 0
e)	x4 — 2x3 + 2x2 + 4x — 8 = 0,
wenn x± = 1 — i\/3
f)	x4 — (ix3 + 10x2 — 2x — 3 = 0
g)	x4 — 2x3 + 4x2 + 2x — 5 = 0
h)	x4 + 2x3 — 2x — 1 = 0
i)	16x4 — 64x3 + 56x2 + 16x — 15 = 0
j)	12x6 + 16x5 + 7x4 - 17x3 + 2x = 0
k)	2X - ^22x+6 + 5\/2* - 2 = 0
1)	Ogx 5)3 - 44(logx \/5)2
+17, 51ogx 25 - 25 = 0
4.	Zerlege die gegebenen Polynome wei-
testgehend in ein Produkt von reel-
len Polynomen.
a)	Pg(x) = x6 — 2x5 — 2x4 + 8x2
b)	P5(^) = 2x5 + 2x4 - 12x3 - 2x2
-2x+ 12
c)	P$(x) = x3 + 3x4 + 4x3 — 18x2
— 104x — 120
d)	Py(x) = (x3 — 17x2 + 63x
+81)(x4 + 16)
5.	Entwickle mit Hilfe des vollständigen
Horner-Schemas die Polynome
a)	Fß(x) = 2x3 — 9x2 + llx + 3
nach Potenzen von (x — 3)
b)	P$(x) = —x3 + x3 — x2 + 1
nach Potenzen von (x + 2)
c)	Fß(x) = 2(x — l)3 — 4(x — 1) + 6
nach Potenzen von x
3 Vektorrechnung, Analytische Geometrie
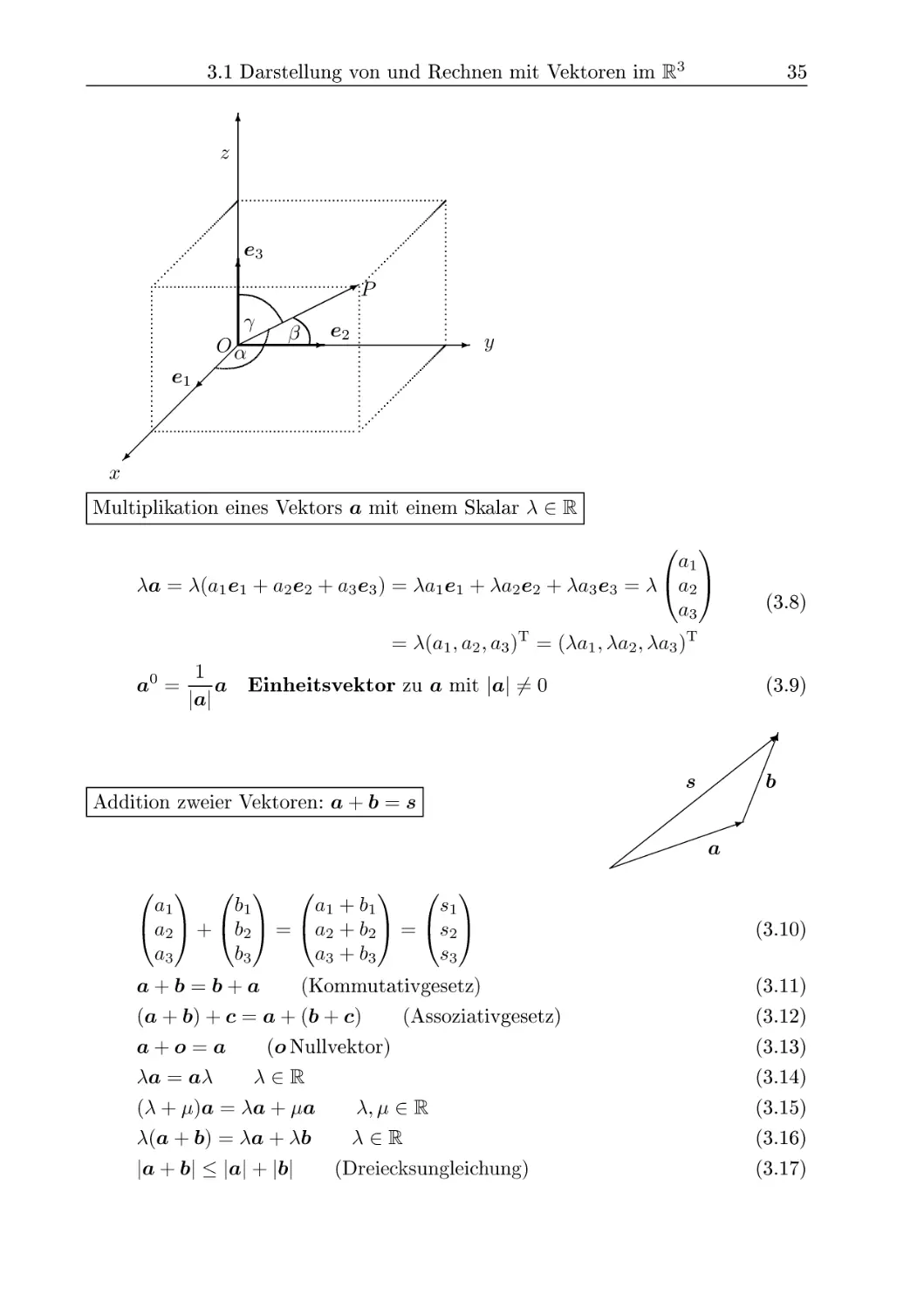
3.1 Darstellung von und Rechnen mit Vektoren im R3
Im räumlichen kartesischen Koordinatensystem (rechtwinkliges x, ?/, ^-System)
wird ein Vektor a mit Hilfe der Einheitsvektoren ei, 62, 63 in der Form
a = ciiei + 6X262 + 6X363
(3-1)
dargestellt. Dabei sind
•	6X1, 6X2, 6X3 die skalaren Komponenten (oder Koordinaten) des Vektors a,
•	6X161, 6X262, 6X363 die vektoriellen Komponenten des Vektors a.
Üblich ist auch die Darstellung eines Vektors durch Angabe seiner skalaren Kom-
ponenten in Spaltenform oder auch in Zeilenform mit dem Transpositionszeichen
T:
(6X1 \
«2	= («1, «2, «3)
&3 /
o = (0, 0, 0)T ist der Nullvektor
(3-2)
(3-3)
Die Vektoren ei, 62, 63 von der Länge 1 weisen in die positive Richtung der x-
bzw. y- bzw. z-Achse.
| a| = y 6X^ + 6X2 + 6X3 Betrag (Länge) des Vektors a
r = OP = (x, y, z)T Ortsvektor zum Punkt F(x; y, z) mit dem
Angriffspunkt im Koordinatenursprung
(3-4)
(3-5)
Sind 6r, /?, 7 die Winkel zwischen dem Ortsvektor r = (x, y, z)1- und der positiven
x- bzw. y- bzw. z-Achse, so erhält man ihre Riehtungsko sinus zu
x n	y	z	(<>a\
cosa = —, cosp = —, cos 7 = —	(3.6)
|r|	\r\	\r\
Daraus folgt:
cos2 a + cos2 ß + cos2 7 = 1	(3.7)
3.1 Darstellung von und Rechnen mit Vektoren im R3
35
Multiplikation eines Vektors a mit einem Skalar A E 1
(di
d2
a3
(3.8)
= X^cl±^3)^ = (Adi, Ad2, Ad3)T
aQ = -—-a Einheitsvektor zu a mit \a\	0
|a|
Addition zweier Vektoren: a + b = s
(dA
d2 I + I 52
«3 /	yfrß /
a + b = b + a
di + 5i
d2 + 52
«3 + 53
(Kommutativgesetz)
(a + b) + c = a + (b + c) (Assoziativgesetz)
a + o = a (p Nullvektor)
Xcl — aX A E R
(A +	= Xa + ßa
X(cl V b) = Xcl V Ab
\a + b| < \a\ + |b|
A,/i E R
A E R
(Dreiecksungleichung)
(3-12)
(3.13)
(3-14)
(3.15)
(3.16)
(3-17)
36
3 Vektorrechnung, Analytische Geometrie
Subtraktion zweier Vektoren: a — b = d
(3.18)
(3.19)
Den Verbindungsvektor a, der vom Punkt Pi(#i, ?/i, zi) zum Punkt ^2(^2, Z/2, ^2)
zeigt, erhält man in der Form
(X2 — Xl
V2 - y\
Z2 ~
(3.20)
Dieser Verbindungsvektor wird auch mit P1P2 bezeichnet: a = P1P2 •
1.	Berechne a°, b°, a + b,
b — a. a — b, —2a + 3b für
a = (—3, 2, —1)T und
b = 5ei — 3e2 + 2e3. Bestätige für
a + b und für — 2a + 3b die Dreiecks-
ungleichung.
2.	Berechne die skalaren Kom-
ponenten des Vektors a,
------------------> ---->
wenn a = AB + CD ist und
A(0; 0; 1), B(3; 2; 1), C(4; 6; 5) und
79(1; 6; 3).
3.	Berechne den Betrag des Vektors
a = Aei + (A + 1)^2 V A(A + 1)63.
4.	Berechne die Länge des Vektors
a =	(20,30, —60)t und seine
Richtungskosinus. Kontrolliere:
cos2 a + cos2 ß + cos2 7 = 1
5.	Gegeben ist ein Dreieck ABC mit
>1(1; 2; 3), B(3; 2; 1) und C(l;4;l).
Zeige, dass dieses Dreieck gleichsei-
tig ist.
6.	Der Ortsvektor des Punktes P bildet
mit der ?/-Achse einen Winkel von
60° und mit der z-Achse einen Win-
kel von 45°; sein Betrag ist gleich 8.
Berechne die Koordinaten des Punk-
tes P, wenn seine x-Koordinate ne-
gativ ist.
7.	Von	einem	Parallelogramm
ABCD	sind	drei Eckpunk-
te A(3; —4; 7), B(—5; 3; —2) und
C(l; 2; —3) gegeben.
a)	Bestimme den vierten Eckpunkt
D, der dem Punkt B gegenüber
liegt.
b)	Gib die beiden Diagonalvektoren
an und berechne ihre Länge.
8.	Der Vektor x hat den Betrag
|a?| = 5\/6 und die Richtung der
3.2 Skalarprodukt, Vektorprodukt, Spatprodukt
37
Halbierenden des Winkels zwischen
den Vektoren a = (7, —4, —4)T und
b = (—2, —1, 2)t. Bestimme x.
Hinweis’. Die Rhombuswinkel werden von
ihren Diagonalen halbiert.
9.	rc seien die den Eckpunk-
ten entsprechenden Ortsvektoren des
Dreiecks ABC. Bestimme damit den
Ortsvektor rs des Dreiecksschwer-
punktes S.
Berechne den Dreiecksschwerpunkt,
wenn A(2; 3; 4), B(3; 1; 2) und
C7(4; — 1; 3) gegeben sind.
10.	Gegeben sind die Punkte A(3; 3; 3)
und B(—1; 5; 7). Bestimme die Punk-
te C und D. die die Strecke AB in
drei gleiche Teile teilen.
11.	Im Dreieck ABC liegt ein Punkt
P auf der Seite BC so, dass
\BP\ : \PC\ = A : 1 gilt. Gib den
Verbindungsvektor v von A nach P
an, wenn AC = b und AB = c ist.
12.	Bestimme den Punkt P der x-Achse,
der von den Punkten A(2; —4; 5) und
B(—3; 2; 7) den gleichen Abstand be-
sitzt.
13.	Gegeben ist das Dreieck ABC mit
A(l; 1; 1), B(2,l;0) und 0(1; 2; 3).
Berechne
a)	die Längen der Seiten a, c, b des
Dreiecks.
b)	die Mittelpunkte Ma, AA, Mc der
Dreieckseiten.
c)	den Vektor m von A nach Ma so-
wie \m\.
14.	Welcher Punkt der x, ?/-Ebene
hat von den Punkten A(l; —1;5),
B(3; 4; 4) und C(4; 6; 1) gleichen Ab-
stand?
3.2 Skalarprodukt, Vektorprodukt, Spatprodukt
Skalarprodukt
a • b = |a| • \b\ • cosc/?, 0 < <p < 7t
(3-21)
cp ist der von a und b eingeschlossene Winkel, p> = Z(a, b)
(aA	Ai\
«2	^2	= «lbi + «2^2 + «3^3
«3 /	\^3/
_ ab _	+ «2^2 + a^bs
\a\ l&l + «2 + a3\Al + ^2 + ^3
a • b = b • a (Kommutativgesetz)
a(b + c)=ab + ac (Distributivgesetz)
o  a = 0
A(a • b) = (Aa) b = a- (Ab), A 6 R
a • a = a2 = |a|2
(3.22)
(3.23)
(3.24)
(3.25)
(3.26)
(3.27)
(3.28)
38
3 Vektorrechnung, Analytische Geometrie
Für a o, b o gilt: a • b = 0 a. b orthogonal (a ± 6)	(3.29)
ei = 62 = 63 = 1, ei • e2 = ei • e3 = e2 • e3 = 0	(3.30)
Vektorprodukt
a x b = p mit den Eigenschaften:
p = a x b
1.	\p\ = |a| • \b\ -sin^ mit 0 < cp < 7t (Maßzahl der Flä-
che des von a und b aufgespannten Parallelogramms)
2.	p ± a und p ± b
3.	a, b, p bilden in dieser Reihenfolge ein Rechtssystem
Es gilt:
a x b = —(6 x a)
ax(b + c) = axb + axc
A(a x b) = (Aa) x b = a x (Ah), A el
o x a = o
(aA	Ai
a2 x b2
&3 /	V3
ei	e2	e3
eil	u2	u3
bi	b2	b3
— (^2^3 — <^3^2)61 — (dlb3 — d3^1)62 + (&lb2 — U2bi)e3
Für a^o,b^o gilt: a x b = o a, b kollinear <^> b = Xa
Spatprodukt
(a x b) • c = [a, b, c]
Es gilt:
(3.31)
(3.32)
(3.33)
(3.34)
(3.35)
[a, b, c] = [b, c, a] = [c, a, b] = — [a, c, b] = — [c, b, a] = — [b, a, c] (3.36)
CZ3
[a, b, c] =
63 = ^i(52c3 — b3c2) — a2(bic3 — b3ci) + «3(^162 — b2ci)
(3.37)
Ul
bi
Cl
CL2
^2
C2
Der Betrag von [a, b, c] ist gleich der Maßzahl
V des Volumens des von den drei Ortsvektoren
a, b, c aufgespannten Spats.
Für a 7^ o, b 7^ o, c 7^ o, gilt: [a, b, c] > 0 O
a, b, c bilden ein Rechtssystem.
[a, b, c] < 0 O a, b, c bilden ein Linkssystem.
[a, b, c] = 0 O a, b, c komplanar o c = Xa + pb.
3.2 Skalarprodukt, Vektorprodukt, Spatprodukt
39
1.	Gegeben sind zwei Vektoren a =
ei + 2e2 T 3^3, b = 6ei + 4e2 — 2e3
Berechne
a)	a • b
b)	a x b
c)	den Winkel cp zwischen a und b.
2.	Zeige, dass die beiden Vektoren a =
3ei + 4e2 + 7es und b = (2, —5, 2)T
aufeinander senkrecht stehen.
3.	Für welchen Wert von A sind a und b
orthogonal, wenn a = Aei+3e2+4e3
und b = 4ei + Ae2 — 7es?
4.	Berechne (5a + 3b) • (2a — b), wenn
|a| = 3, |b| = 5 und a und b ortho-
gonal sind.
5.	Wie groß ist der Flächeninhalt des
Parallelogramms aus
a)	a = (—6, —3, 2)T und
b= (—3,2,—6)t
b)	a + 5b und 5a + b, wenn |a| =
|b| =3 und Z(a,b) = 30°?
6.	Berechne den Flächeninhalt
des Dreiecks ABC, wenn
A(4; 3; 2), B(2; 3; 4) und 0(1; 1; 1)
gegeben sind.
7.	Berechne den Winkel zwischen den
Vektoren a = (3,4, 5)T und
b = (—4, —5,3)T.
8.	Berechne das Spatprodukt der Vek-
toren a = (2, —1, — 1)T,
b = (-1, -3,1)T, c = ei + e2 + 4e3.
9.	Zeige, dass die drei Vektoren a =
(2,5,7)T, b = (1,1,—1)T und c =
(1,2,2)t komplanar sind. Stelle den
Vektor a mit Hilfe der Vektoren b
und c dar.
(Ansatz: a = Ab + /zc)
10.	Berechne das Volumen	einer
dreiseitigen Pyramide mit den
Eckpunkten >1(2; 2; 2), 7E>(4;3;3),
0(4; 5; 4) und O>(5; 5; 6).
11.	Berechne das Spatprodukt
[(a-b),(b-c),(c-a)].
12.	Gegeben sind die Vektoren
a = (2,2,1)t und b = (6,3,2)T.
Berechne die Projektionen von a auf
b und von b auf a.
13.	Berechne das Skalarprodukt von
4a + 3b + 2c und 7a + 6b + 5c,
wenn |a| = 3, |b| = 2, |c| = 1,
Z(a, b) = Z(a, c) = Z(b, c) = —.
ö
14.	Bestimme den Einheitsvektor s°, der
senkrecht auf den Vektoren a =
(1,1, 2)t und b = (2,1,1)T steht.
15.	Zeige, dass es keinen Wert für A
gibt, so dass die drei Vektoren a =
(1,1, A)t, b = (1,1, A + 1)T und c =
(1,-1, A)t komplanar sind.
16.	Die drei Vektoren a, b, c sind von
gleicher Länge und bilden paarwei-
se gleiche Winkel. Bestimme c, wenn
a = ei + e2 und b = e2 + 63.
17.	Berechne das Volumen des Te-
traeders mit den Eckpunkten
A(l; 1; -1), B(l; -1; 1), C(-l; 1; 1),
n(l;l;l).
18.	Berechne den Vektor a x (a x b) +
(b x a) x a für a = (2,1, —3)T und
b= (1,-1,1)T.
19.	Gegeben sind die vier Punkte
A(l; 2; -1), B(-l; 3; -4), C(0; 5; -7)
und 79(2; 4; — 4). Zeige, dass diese
vier Punkte
a)	in einer Ebene liegen
b)	Eckpunkte eines Parallelogramms
sind
40
3 Vektorrechnung, Analytische Geometrie
c)	einen Rhombus aufspannen, und
bestätige die Orthogonalität der
Diagonalen.
20.	Beweise vektoriell:
a)	Der Umfangswinkel über dem
Kreisdurchmesser ist ein rechter
Winkel. (Satz des Thales)
b)	Halbieren in einem Viereck die
Diagonalen einander, so ist das
Viereck ein Parallelogramm.
c)	den Kosinussatz der ebenen Tri-
gonometrie (c2 = a2 + b2
—2a6cos7) und den Satz des Py-
thagoras (c2 = a2 + b2).
3.3 Ger adengleichung
Parameterdarstellung einer Geraden g:
g : r = tq + Xv
(3.38)
ro Ortsvektor zu festem Punkt Pq auf g
v Richtungsvektor von g
X Parameter (—oo < A < +oo)
Gleichung der Geraden durch die Punkte Pi(xi; t/i ; ^i) und ^2(^2; 2/2^2)
r = ri + A(r2 — ri)	(3.39)
mit n = (xi, yi, zi)T und r2 = (x2, y2, z2)T
Fußpunkt F(xF-,yF] zf) eines Lotes l von einem Punkt Pi(xi; 2/1; ^1)
auf eine Gerade g
g : r = tq + Xv
rF = (xF, yF, zf)t =r0 + —-------- v	(3.40)
vz
Schnittpunkt S^xs^ys', zs) zweier Geraden pi und p2
pi : r = ri + Xv gz : r =	+ yw
Im R3 sind dann
ri + Xv = r2 + yw	(3.41)
drei Gleichungen für A und /z. Besitzt das Gleichungssystem (3.41)
1. keine Lösung Es existiert kein Schnittpunkt S.
3.3 Geradengleichung
41
2. genau eine Lösung Es existiert genau ein Schnittpunkt S mit
rs = (xs, ys, zs^ = ri + Xv = r2 + pw.
3. unendlich viele Lösungen Die beiden Geraden sind identisch gleich
(öl = Ö2)-
Abstand \l\ zweier windschiefer Geraden pi und p2
pi : r = ri + Xv : r =	+ gw
Der Ansatz l : l =	+ gw — Xv für das gemeinsame Lot l von pi und
führt auf zwei Gleichungen für A und g:
l v = 0
l • w = 0
(3.42)
Sind pi und g^ windschief, so hat das System (3.42) genau eine Lösung.
1.	Gib eine Parameterdarstellung der
Geraden an, die durch die Punkte Fi
und P2 geht, wenn
a)	Fi(-2; 3; -5) und F2(l; -4; -1)
b)	Fi(3; —2; 1) und F2(l; -2; 2)
gegeben sind.
2.	Prüfe, ob die Punkte A(—5; 1; 2)
und B(3; — 3; 1) auf der Geraden
r = (1, —2, 5)t + A(2, —1,1)T liegen.
3.	Wo schneiden sich die folgenden Ge-
radenpaare bzw. wie liegen sie zuein-
ander?
a) r = 5ei + e2 - 2e3 + A(4ei - e2
-3e3)
r = (7 - 3/i)ei + (2/z - 2)e2
+ (11 - 5/z)e3
r = (—4,3, —1)T
+/z(\/3,--+,3)t
c)	r = (2 + 4A, -1 + 2A, 3 - A)T
r = (1 + 2/z,2 - /z,2 + 3/z)t
d)	r = (2 + 2\/3,-3, 7)t
+A(\/12, -2, 4)t
r = (2 - VÜ,0,1)T
+/z(-A1, —2)T
e)	r = (3,-1,2)t + A(2,4,10)t
r = (—1,5,3)T +/i(—4,4,6)T
f)	r = (3, —1,2)t + A(2,4, 3)t
r = (—1,5,10)T + /i(—4,4, 6)t
(von a)...f) gilt: —00 < X < 00,
—00 < g < oc)
4.	Wo und unter welchem Winkel
schneiden sich die beiden Geraden
r = (—2,5,1)T + A(—1,2,3)t und
r = (3, —1, 2)T +/z(l, —1,1)T?
(—oc < A, g < 00)
5.	Gegeben sind die beiden Punkte
Fi(3;-1;2) und F2(l; 2; — 1).
a)	Gib eine Parameterdarstellung
der Geraden g an, die durch Fi
und F2 geht.
b)	Bestimme den Fußpunkt F des
Lotes vom Nullpunkt auf g.
c)	Berechne den Abstand des Null-
punktes von g.
6.	Berechne den Abstand der beiden
42
3 Vektorrechnung, Analytische Geometrie
windschiefen Geraden pi und g2:
gi: r = (-1,0,1)T + A(l, 1, 2)T
92 : r = /zei + (3/z-l)e2 + (4/z + 2)e3
(—oc < A, g < +oo)
7.	Die Gerade pi geht durch die Punk-
te Pi(l;-2;1) und P2(-2; 3; 5); die
Gerade p2 geht durch die Punkte
Qi(l; —5; —2) und Q2(10;-11;-5).
Wo und unter welchem spitzen Win-
kel schneiden sich pi und p2?
8.	Gib eine Parameterdarstellung der
Geraden an, die durch den Punkt
P(2; — 3; 4) geht und senkrecht auf
der y-Achse steht.
9.	Gegeben ist die Gerade
g : r = (1 + A, -2 + 2A, 5 - 2A)T
(—00 < A < +oo).
Der Punkt P0(l; — 2; 5) liegt auf g
(für A = 0). Für welche Werte von
A erhält man diejenigen Punkte von
p, die von Pq
a)	den Abstand 3,
b)	den Abstand 18
haben, und welche Punkte sind dies?
10.	Berechne den Fußpunkt F des Lo-
tes l von Pi(—2;1;1) auf die durch
P2(0;0; 1) und P3(l;— 1; 0) gehende
Gerade, den Lotvektor l sowie seine
Länge \l\.
11.	Die Ecken eines Dreiecks sind
>1(1; 2; 3), B(-2; 3; 1) und
C(2; -3;-1).
a)	Berechne den Flächeninhalt, die
Längen der Seiten und die Innen-
winkel des AABC.
b)	Gib Parameterdarstellungen für
die Geraden an, auf denen die
Höhen, die Mittelsenkrechten und
die Winkelhalbierenden des Drei-
ecks liegen.
c)	Ermittle den Schwerpunkt und
die Mittelpunkte von In- und Um-
kreis sowie die zugehörigen Radi-
en für dieses Dreieck.
d)	Gib eine Parameterdarstellung
für die Gerade an, die senkrecht
auf dem Dreieck steht und durch
den Punkt A geht.
3.4 Ebenengleichung
Parameterdarstellung einer Ebene E:
E : r = ro + Xv + yw
(3.43)
ro Ortsvektor zu einem festem Punkt Po(xo;Z/o; ^o) der Ebene E
v.w zwei (nicht parallele) Vektoren in E
A, y Parameter (—oo < A < oo, — oo < y < oo)
Skalarform der Gleichung einer Ebene E:
E : n • r = d
(3.44)
n Normalenvektor von E
d = n • ro, wobei tq = (xq, y<g zq)1- bzw. Pq(xo; 2/o5 ^o) ein fester Punkt von E ist.
3.4 Ebenengleichung
43
Ist n = (a,6, c)T, so erhält man eine
Darstellung von E in Normalform:
ax Eby + cx = d	(3.45)
Abstand A eines Punktes (a?i; 3/1; zi) von einer Ebene E
E : n • r = d bzw. ax + by + cz = d
Darstellung von E in der ETesseschen Normalform:
_ n  r — d ,	ax Eby E cz — d
E : —— = 0 bzw.	—/	= 0
\n\	\/a2 Eb2 E c2
Dann gilt:
\n-r1-d\	\ax± E by± E cz± — d\
A = ------:-:- bZW. A = -------,	---
\n\	Va2 Eb2 E c2
(3.46)
(3.47)
Umwandlung einer Parameter dar Stellung von E in eine Skalarform
Aus r = rQ E Xv E yw erh„lt man mit n = v x w und d = n • tq die gesuchte
Gleichung n • r = d.
Umwandlung einer Skalarform von E in eine Parameter dar Stellung
Ist E : n • r = d mit n = (ni,n2,ns)T gegeben, so erhält man v und w aus den
beiden Gleichungen n • v = 0 und n • w = 0, denen z.B. v = (0,ns, — nzf und
w = (n2, —ni, 0)T genügen. Außerdem muss vq die Bedingung n • tq = d erfüllen,
/ d	\T
die z.B. von tq = ( —,0,0 ) befriedigt wird, falls ni 0 gilt. Mit ro, v, w
\ni	J
erhält man E : r = E Xv E yw.
Durchstoßpunkt S^xs^ys') zs) einer Geraden g durch eine Ebene E
g : r = tq E Xv und E : n • r = d
44
3 Vektorrechnung, Analytische Geometrie
Dann ist
/	d — n • ro	/o
rs = (xs,yS)Zs) =r0H---------------v	(3.48)
n • v
Fußpunkt F{xp\yF\ zf) des Lotes von einem Punkt Pi(xi; 2/1; ^i)T
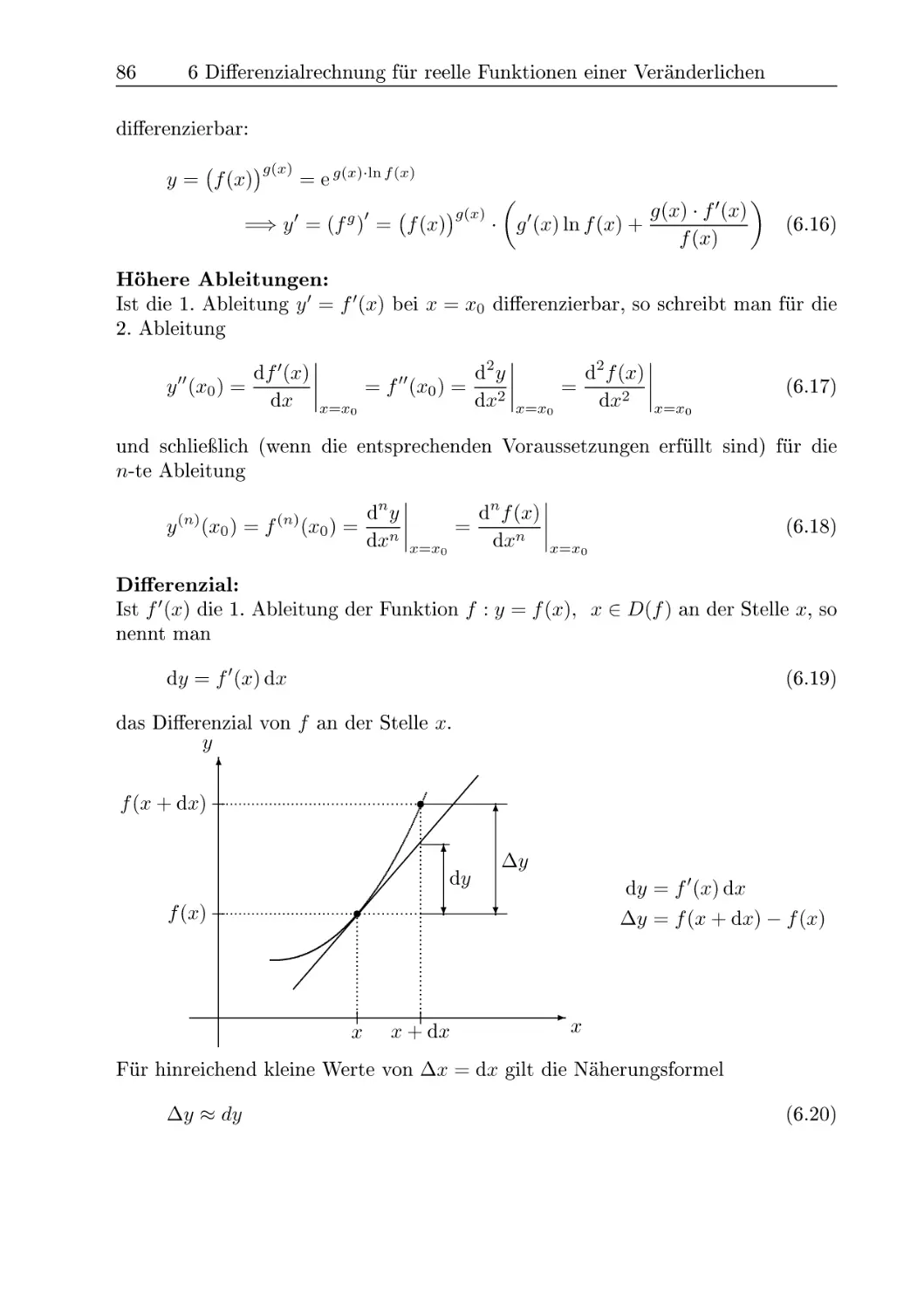
auf eine Ebene E
E : n • r = d
Dann ist mit ri = (a?i, 3/1, ^i)T
rF = (%f, yF, zf)1 2 = ri H---x----n	(3.49)
n~
Schnittgerade g zweier Ebenen Ei und E2
Ei : m - r = di und E2 : ri2 • r = cfe
Ansatz für g : r = tq + A • v
Dabei ist v = ni x 77,2; und tq = (xcnZ/Ch^o)T muss den zwei Gleichungen
ni • ro = di und 712 •	= cfo für die drei Unbekannten xq, t/o, zq genügen. Dazu
gibt man einer der Unbekannten einen solchen Zahlenwert (z.B. null), dass man
die restlichen zwei Unbekannten bequem berechnen kann.
Spiegelpunkt F2 (^2; 2/25 ^2) eines Punktes Pi(xi; 2/1; ^1) bezüglich einer Ebene E
Bei gegebenen n = (a?i, 3/1, zi)T und E : n • r = d ist
d — n • ri
r2 = ri +2 ------------- n
n~
(3.50)
1. Weise nach, dass die beiden ge-
gebenen Parameterdarstellungen
die gleiche Ebene darstellen (also
Ei = E2), indem z.B. bei Ei und
E2 zur Normalform übergegangen
wird.
Ei : r = (4, —2, —11)T
+A(—2,5,15)T + ^(2,10,21)T
E2 : r = (2,3, 4)t + A(4,5, 6)t
+//(0,5, 12)t
(—00 < A, g < oc)
2. Berechne den Abstand des Punktes
Pi von der Ebene E, wenn
a) E : x + y — z = —1; Pi(2; 1; 1)
b) E : 6x - 3y + 2z = 28;
Fi(3;5;-8)
3.	Wie lautet die Gleichung der Ebene
E in Skalarform, wenn E durch den
Punkt P(2; 3; 5) geht und der Vektor
a = (4, 3, 2)t auf E senkrecht steht?
4.	Gegeben ist die Ebene
E : 2x + 3y + z = 6.
Skizziere den Teil von E, der im
1. Oktanten des Koordinatensystems
(x > 0, y > 0, z > 0) liegt.
5.	Für die gegebene Ebenengleichung
ist eine Parameterdarstellung anzu-
geben.
a)	E : (3, —2,5) - r = 8
3.4 Ebenengleichung
45
b)	E : -y + 7z = 13
6.	Unter welchem Winkel schneiden
sich die Ebenen Ei und E2?
Ei : 2x + y — 2z — 4 = 0
E2 : 3x + 6y - 2z - 12 = 0
7.	Zeige, dass die	Ebenen	Ei
und E2	parallel sind	und
berechne ihren Abstand.
Ei : x — 2y + z = 1
E2 : (—2,4, —2)-r = -1
8.	In welchem Punkt durchstößt die
Gerade g die Ebene E?
a)	g : x — l = 2?/ + 2 = z + 3 = A
—00 < A < +00
E: x + y- z + 1 = 0
b)	g : r = (1,2,1)T + A(2, -1,2)T
—oo < A < +oo
E: 2x + y — z — 4 = 0
9.	Bestimme die Schnittgerade g der
Ebenen Ei und E2. Wie groß ist der
Schnittwinkel?
a)	Ei : 2x — y + 3z = 1
E2 : (1,1,—l)-r = 2
b)	Ei : 2x — 2y + 2z = 3
E2 : — 2x — 3y + 6z = 7
c)	Ei : —x + 3y — 3z = 2
E2 : 3x + 2y + z = 5
10.	Gegeben sind drei Punkte
A(2; 1; -2), B(0; 2; 1), C(l; 2; 0). Be-
stimme
a)	die Gleichung der Ebene E durch
A, B, C in Skalarform
b)	die Gleichung der Geraden g
durch A, die senkrecht auf E
steht.
11.	Eine Ebene E enthält den Punkt
B(3;2;—1) und die Gerade
r = (—2,0,1)T + A(—1,3, — 2)T
(—oc < A < +oo).
Gib die Gleichung von E in Skalar-
form an.
12.	Vom Punkt Pi(l; 2; 1) wird auf die
Ebene
E: x — 2y + z = 7
das Lot gefällt. Welche Koordinaten
hat sein Fußpunkt?
13.	Bestimme den zum Punkt Bi (2; 3; 4)
spiegelbildlichen Punkt B2 in bezug
auf die Ebene E.
E : x - 3y + 5z + 22 = 0
14.	Gegeben sind die drei Punkte
A(—3; 2; 5), B(—2; 1; 6), 0(1; 3; 2)
und die Gerade
g : r = (5 + 9A)ei - (5 + 6A)e2
- (4 + 3A)e3
(—oc < A < +oo).
Bestimme
a)	die Gleichung der Ebene E, die
durch diese drei Punkte festgelegt
ist.
b)	den Durchstoßpunkt S der Gera-
den g durch die Ebene E.
15.	Gesucht ist die zur Ebene
E : x — 2y — 3z = 0
parallele Ebene E2 durch den Punkt
Bi(2;2;-2).
16.	Stelle die Gleichung der Ebe-
ne E auf, die durch den Punkt
Bi(—1;—1;2) geht und senkrecht
auf den Ebenen Ei und E2 steht.
Ei : (1,—2,l)-r = 4
E2 : (1,2,-2) r = -4
17.	Bestimme den Schnittpunkt S der
Ebenen Ei, E2, E3.
Ei : (2, —1, 3) • r — 9 = 0
E2 : (1,2,2) r- 3 = 0
E3 : (3,1, —4) • r + 6 = 0
18.	Wie lautet die Gleichung der Ebene
46
3 Vektorrechnung, Analytische Geometrie
E, die durch den Punkt Pi(l; 2; 4)
sowie durch die Schnittgerade der
Ebenen Ei und geht?
Ei : 2x — y + 3z — 6 = 0
E2 : x + 2y — z + 3 = 0
19.	Bestimme die Gleichungen der Ebe-
nen Ei und E2, die parallel zur Ebe-
ne E : 2x + 2y + z — 8 = 0 liegen und
von ihr einen Abstand A = 4 haben.
20.	Wie lautet die Gleichung der Ebe-
ne E, die durch die Schnittgerade
der Ebenen Ei und E2 geht und
senkrecht auf der Ebene Es steht?
Ei : 4x — y + 3z — 6 = 0
E2 : x + by — z + 10 = 0
E3 : 2x — y + bz — 5 = 0
21.	Gegeben sind die beiden parallelen
Geraden
51 : r = (—2,5,2)T + A(l, 0, —1)T
52 : r = (2, -4,2)T + M(l, 0, - 1)T
(—oc < A,/z < +oc)
Bestimme
a)	die Ebene E, die gi und p2 enthält
b)	den Abstand des Punktes
Fi(4;-2;5) von E
c)	die Gerade p3, die in E liegt und
die Gerade gi im Punkt P2 mit
x = X2 = — 1 orthogonal schnei-
det
d)	den Schnittpunkt S von p2 und
P3-
22.	Ein in Richtung a = — e3 durch den
Punkt Fi (1; 2; 4) im Medium Mi ver-
laufender Lichtstrahl wird an der
Ebene
E: x + y — z = 2
gebrochen und verläuft im Medium
M2 durch den Punkt F2(2; 3; —3).
a)	In welchem Punkt A trifft der
Lichtstrahl die Ebene E?
b)	Auf welchem Strahl verläuft das
Licht im Medium M2?
c)	Wie groß ist das Brechungsver-
u-u • sin Qi
haltms n =---------f
siuq2
4 Lineare Algebra
4.1 Determinanten
Eine n-reihige quadratische Matrix
/an a12	... ai„\
«21	«22	 • 	«2n
\«nl «n2	• • • ^nn /
ist ein System von n2 Größen (Elemente der Matrix), die in n (waagerechten)
Zeilen und n (senkrechten) Spalten angeordnet sind. Die Elemente (i ist der
Zeilen-, k ist der Spaltenindex) sind im Folgenden reelle Zahlen. Die Determinante
n-ter Ordnung Dn einer solchen n-reihigen quadratischen Matrix
Dn = det A =
«11	U12
«21	«22
«In
«2n
(4-2)
«nl «n2	• • • «nn
ist eine reelle Zahl.
Den Wert einer Determinante 2. Ordnung erhält man nach der Formel
n2 =
«ii
«21
«12
«22
= du • U22 — «12 • «21
(4-3)
Streicht man in Dn die Ute Zeile und die Zc-te Spalte, entsteht die Unterdetermi-
nante Aik der Ordnung (n — 1).
Entwicklung von Dn nach der Uten Zeile:
Dn = (—1)?'+1uh • Ai\ + (—l)z+2a£2 • Ai + • • • + (—l)z+n«m  An (4.4)
Entwicklung von Dn nach der Zoten Spalte:
Dn = ( — 1)1+A1, • A\k + ( — l)2+/c«2/v • ^2k + • • • + ( — l)n+/c«n/v • Ank	(4.5)
Hilfreich bei Ermittlung des Vorzeichens (—l)z+/c ist die „Schachbrettregel“:
48
4 Lineare Algebra
Eigenschaften von Determinanten:
1.	Der Wert einer Determinante ändert sich nicht, wenn man ihre Elemente an
der Hauptdiagonale spiegelt (d.h. die Zeilen mit den Spalten vertauscht). (Die
Elemente an, a22, • • •, Unn bilden die Haupt diagonale.)
2.	Der Wert einer Determinante ändert sein Vorzeichen, wenn man zwei Zeilen
oder zwei Spalten miteinander vertauscht.
3.	Wird eine Zeile oder eine Spalte mit einer reellen Zahl A multipliziert, so wird
auch die Determinante mit A multipliziert.
4.	Addiert man zu einer Zeile (Spalte) das A-fache einer anderen Zeile (Spalte),
so ändert sich der Wert der Determinante nicht.
5.	Ist eine Zeile (Spalte) von Dn das A-fache einer anderen Zeile (Spalte), so ist
Dn = 0.
Eine Dreiecksdeterminante hat unterhalb oder oberhalb der Hauptdiagonalen
nur Nullen als Elemente; für ihren Zahlenwert gilt: Dn = an • (122 • • • • • ann
1. Berechne die Determinante
d3 =	-3	10	9 1	—4	—2 5	-16	12
determinante
2	3	4
5-21.
1	2	3
a)	durch Entwicklung nach der 1.
und nach der 2. Zeile
b)	durch Entwicklung nach der 2.
und nach der 3. Spalte
c)	nachdem zuvor unter Anwendung
der Determinanten-Eigenschaften
vereinfacht wurde
d)	nachdem eine Dreiecksdetermi-
nante hergestellt wurde.
2. Berechne die gegebenen Determinan-
ten.
4.
Berechne die folgenden Determinan-
ten, indem zunächst geschickt ver-
einfacht wird:
3. Berechne die
M 2	3
b) 6 -10
1X sina cos q
d)
— cos a sm a
gegebene Determinante
a)	durch Entwicklung nach allen drei
Zeilen und allen drei Spalten
b)	durch Erzeugung einer Dreiecks-
	a	—a	a	
a)	a	a	-a	
	a	—a -	-a	
	1	2		5
b)	3	—4		7
	-3	12	—	15
	x2	x 1		
c)	y2	y i		
	z2	z 1		
	1 + cos a		1 + sin a	
d)	1 -	sina	1 + cos a	
		1		1
	1	—2	—	6 4
	-3	1		5 -5
e)	4	0	—	4 3
	6	0	1	8
1
1
1
4.2 Matrizen
49
	-1	0	2	-3	Einsetzen der Lösungen in die betret-							
	2	1	-3	2			fenden Determinanten.					
	-3	2	1	-1				x2	4 9			
	1	3	2	1			a)	X	2 3		= 0	
	2	6	0	1		2		1	1 1			
	-3	5	-1	2		-1		x2	3	2		
g)	7	-1	3		2	3	b)	X	-1	1	= 0	
	-9	2	2	3		5		0	1	4		
	1	1	1		1	—2		2 -	X	1	-1	
5. Bestimme x aus den gegebenen Glei-
chungen und mache die Probe durch
4.2 Matrizen
Eine Matrix A vom Format oder Typ (m, n) ist ein System von m • n (reellen)
Zahlen <2^, Elemente genannt, die in m Zeilen und n Spalten angeordnet sind:
	( du	(212	• • (Lin	
-4 A(m^ ((Lik) (jn,n)	&21	(222	(L2n	(4-6)
	y(2mi	Um2 • 	• • (Lmn J	
Das Element <2^ steht in der z-ten Zeile und A:-ten Spalte.
Zwei Matrizen A = (a^) und B = (6^) sind genau dann gleich, wenn A und
B gleiches Format haben und <2^ = bik für alle i und k gilt.
Zwei Matrizen A = (a^) und B = (6^) vom gleichen Format werden addiert
(subtrahiert), indem man entsprechende Elemente addiert (subtrahiert):
-4(m,n)	(m,n)
dik±bik = sik (i = 1,2,... ,m; k = 1, 2,..., ri)	(4.7)
Dann gilt:
A + B = B + A; A + (B + C) = (A + B) + C	(4.8)
Eine Matrix A = (a^) wird mit einer reellen Zahl A multipliziert, indem
man jedes Element <2^ von A mit A multipliziert:
XA = AX = (Xaik)	(4.9)
(-1) A = -A- A(A + B) = XA + AB	(4.10)
(A + /i) A = XA + /iB	(4.11)
Das Produkt A • B zweier Matrizen A und B, die verkettet sein müssen
(d.h. der 1. Faktor A ist vom Typ (m, ri) und der 2. Faktor B ist vom Typ (n, r)),
50
4 Lineare Algebra
ist eine Matrix P (vom Typ (m,r)), deren Elemente pik das skalare Produkt der
z-ten Zeile des 1. Faktors A mit der A;-ten Spalte des 2. Faktors B sind:
‘	(n,r) P(m,r)
ail ‘	‘ &2k T • • • T din ’ bnk = Pik
(i = 1, 2,..., m; k = 1, 2,..., r)
(4-12)
Es gilt:
(A + B) • C = AC + BC- (AB)C = A(BC)	(4.13)
AB 7^ BA (im allgemeinen); (AA)B = A(AB)
(4.14)
Zur Berechnung des Matrizenproduktes eignet sich folgendes Schema (von Falk):
AB		&n ... ...		bik • bnk	b±r .. bnr
Uli Clßl	• •	d\n . .	U277		—>	Pik	
0-777,1					
Alle Elemente der Nullmatrix 0 sind vom Wert 0. Es gibt Nullmatrizen jeden
Formats (m,n). Es gilt (Verknüpfbarkeit vorausgesetzt):
A+0 = A; A-A=0- Ü-A=O	(4.15)
Eine Matrix vom Format (n, n) heißt quadratisch. Ihre Elemente
011,022, • • •, dnn bilden die Hauptdiagonale.
Eine quadratische Matrix heißt
•	obere Dreiecksmatrix, wenn = 0 für alle i > k.
•	untere Dreiecksmatrix, wenn = 0 für alle i < k.
•	Diagonalmatrix, wenn = 0 für alle i k.
Eine Diagonalmatrix mit an = 1 für alle i heißt Einheitsmatrix E und hat
die folgenden Eigenschaften:
-^(n,n) ‘ A(n,n)	‘ -^(n,n)	(4.16)
(4-17)
Für schreibt man kürzer En.
4.2 Matrizen
51
Vertauscht man in einer Matrix A = (dik\m,n) die Zeilen mit den Spalten, so
erhält man die transponierte Matrix
A (^ki) (n,m)
(4-18)
Es gilt (Verknüpfbarkeit vorausgesetzt):
(ÄT)T = A- (A + B)t = At + Bt; (ABf = B1A1
(4-19)
Eine quadratische Matrix A heißt symmetrische
A = At gilt, d.h., aik = aki = 1,2,..., n).
Matrix, wenn für sie
1.	Gegeben sind die Matrizen
/ 4	3 -1\	/ 2 \
C = | 2	1 -2 , d= -1 .
\-l 3 4/	\ 3 /
Berechne folgende Ausdrücke, sofern
sie definiert sind:
a)	5A - 3B, 2B + 7C
(A + B)C, 2AB, BA
2A^B, 3B^A, —BC, CB
b)	Ad, Bd, Cd, dA, dTC
d? A?
c)	AA, AtA, AAt, CC, CCt
CTCT, dd, cfdk dd\ dTd.
2.	Berechne für die Matrizen
/ 1	-2\
A = -2	3
\ 4 ~5/
1
2
2 3
4 6
0-2	1 \
2	3-4
5	1	3
1	0	2
2	2	1	/
-i\
i
i 
2/
5. Berechne det A, wenn
/1	0	0\	/0	0
A =	0	1	0	0	b	0
\0	0	1/	\c	0	0/
/0 0 1\
x 0 1 0 .
0 0/
6. Berechne alle (reellen) symmetri-
schen (2,2)-Matrizen X, die Lösun-
gen der Gleichung
v vT — f4
A A - ^0 9/
sind.
a) AB	b) BA.
3. Berechne det (44T), wenn
/3 2 1 2\
y4 1 1 3/
4. Berechne ABC,
(2
A = 1—2	0
\ 1	2
wenn
3 1	2 \
4 1-3
3 1	0 /
7. Beweise: Ist A eine beliebige quadra-
tische Matrix vom Format (n,n), so
güt
det (AA) = Xn • det A
für A e R.
8. Es sei A vom Format (3,2) und D
vom Format (3,4). Von welchem For-
mat müssen dann die Matrizen B
52
4 Lineare Algebra
und C sein, damit AB — 2(C + D)
definiert ist?
9. Aus vier Einzelteilen Ti,T2,T3,T4
werden drei Baugruppen B^B2,B3
hergestellt, die in zwei Enderzeugnis-
se Ei und E2 eingehen. Die Tabelle
enthält die benötigten Stückzahlen:
ET
Ti T2 T3 T4
Bi	4	2	0	5
B2	1	2	1	3
B3	0	3	4	1
BG
Ei E2
2	1
3	2
1 1
ET: Anzahl der T\ pro Stück von Bi
BG: Anzahl der Bi pro Stück von Ej
Berechne die bereitzustellenden
Stückzahlen von (k = 1,2,3,4)
mit Hilfe der Matrizenrechnung,
wenn 150 Stück von Ei und 250
Stück von E2 zu produzieren sind.
10. Beweise: Ist A eine beliebige quadra-
tische Matrix, dann ist die Matrix
Matrix S = A + AT symmetrisch.
4.3 n-dimensionaler reeller Vektorraum
Ein geordnetes n-Tupel reeller Zahlen nennt man auch n-dimensionalen Vektor
alle ai e R
(4.20)
Die di heißen Komponenten des Vektors a. Man kann a als (n, 1)- Matrix auf-
fassen (Spaltenvektor) und ihn durch Transponieren als (l,n)- Matrix schreiben
(Zeilenvektor):
aT = (ai,a2,... ,an)
(4.21)
Für solche n-dimensionalen Vektoren werden Addition und Multiplikation mit
einer reellen Zahl A erklärt:
Ist a1 = («i, a2,..., dn) und bT = (bi,b2,..., bn), so definiert man:
-h bT = (di + bi, a2 + b2,..., dn + bn)	(4.22)
AaT = (Aai, Aa2,..., Aan)	(4.23)
Rn bezeichnet den Raum dieser n-dimensionalen Vektoren mit reellen Komponen-
ten.
Für a,b,c E Rn und A,/i E 1 gilt:
a + b = b + a; (a + b) + c = a + (b + c); (A + /i)a = Xa + fia (4.24)
A(a + b) = Xa + Ab; A(/ia) = (A/i)a	(4.25)
Mit a — b = a + (—1) • b ist die Subtraktion auf die Addition zurückgeführt.
4.3 n-dimensionaler reeller Vektorraum
53
Gegeben sei eine Menge S = {ai, 02,..., von m Vektoren a>i E Rn und m
reellen Zahlen A*, i = 1, 2,..., m. Dann heißt der Ausdruck
Aidi + A2GL2 + • • • + Amam — y XiCLi
(4.26)
eine Linearkombination von S.
Ein Vektor x E Rn heißt linear abhängig von S genau dann, wenn er eine Li-
nearkombination von S ist. Anderenfalls heißt x linear unabhängig von S.
Die Menge S heißt linear abhängig genau dann, wenn es (mindestens) einen
Vektor ak E S gibt, der linear abhängig von S\{ak} ist. Anderenfalls heißt S
linear unabhängig.
S ist linear abhängig genau dann, wenn m reelle Zahlen Xi (z = 1, 2,..., m) exis-
m	m
tieren, für die sowohl A^ > 0 als auch ^A^a* = o gilt, (o ist der Nullvektor
2=1	2=1
0= (0,0,..., 0)T.)
Es sei T eine beliebige Menge von Vektoren x E Rn. Eine Menge
B = {bi, &2, • • •, bm} ist eine Basis in T, wenn gilt:
•	bi E T, i = 1, 2,..., m
•	B ist linear unabhängig.
•	Für jeden Vektor x E T existieren reelle Zahlen an,..., am, so dass
m
x = y^akbk.
k=i
Die reellen Zahlen an, an, • • •, ow heißen dann Koordinaten des Vektors x be-
züglich B.
Eine besonders einfache Basis im Rn ist die kanonische oder Standardbasis
{ei,e2,... ,en} mit
ei = (0 , ... , 0 , 1, 0 , ... , 0)T
T	(4.27)
z-te Position
1.	Zeige, dass die Vektoren
ai = (2,4,4)T, a2 = (—3, 2, —2)t,
<2.3 = (2, — 1,4)T linear unabhän-
gig sind, und stelle den Vektor b =
(2,2,8)t als Linearkombination der
drei Vektoren ai, 02, 03 dar.
2.	Die Menge
5i = {a, b, c|a, b, c E R3}
sei linear unabhängig. Zeige, dass
dann auch
S2 = {a, a + b, a + b + c}
linear unabhängig ist.
3.	Zeige, dass die Menge
S = {(3,-1,1)T, (-1,3,1)T,
linear abhängig ist.
54
4 Lineare Algebra
4.	Gegeben sind die Vektoren
ai = (4,1,3, — 2)t
a2 = (1,2, -3, 2)t
a3 = (16,9,1, — 3)t
a4 = (0,1,2, 3)t
a5 = (1,—l,15,0)T
a)	Berechne
3o.| + 50.2 — O.3, 2o,| +I0.3 — 2o,r,
1 1
— ai + 3ö3 — —a.i + äs
b)	Berechene x aus
1.	2x + ai — 2a2 — «5 = o
2.	2(ai — x) + 5(ö4 + x) = o
3.	3(ö3 + 2x) — 2(ö5 — x) = o
5.	Zeige, dass der Vektor
x = (19, l,10)T linear abhängig ist
von der Menge
S = {(1,1,-1)T, (0,-1,1)T,
(5,0, 3)t, (—2,1 — 3)t}.
6.	Zeige, dass der Vektor
x = (1, — 3, 5)t nicht linear abhängig
ist von der Menge
S = {(1, —1,0)T, (3,5,0)T}.
7.	Gegeben sind die Vektoren
&i = (1,1,1,1,1)T
b2 = (0, 1, 1, 1, 1)T
b3 = (0,0,1,1,1)T
&4 = (0,0,0,l,l)T
b5 = (0,0,0,0,l)T
a)	Zeige, dass
B = {^1, ^2- &3, &4, b$}
eine Basis in R5 ist.
b)	Berechne die Koordinaten der fol-
genden Vektoren x bezüglich B:
x = (1,1,0,1,0)T
x = (3,5,4, —1, —2)T
x = (—5,4, —3, 2, —1)T
4.4 Rang von Matrizen, Gaußscher Algorithmus
Aus einer (m,n)-Matrix A streicht man Zeilen oder/und Spalten so heraus, dass
eine (r, r)-Matrix übrig bleibt. Die Determinante dieser (r, r)-Matrix nennt man
eine Unterdeterminante r-ter Ordnung von A.
Besitzt A eine Unterdeterminante r-ter Ordnung mit einem Wert verschieden von
null, während der Wert aller Unterdeterminanten (r-Fl)-ter Ordnung von A gleich
null ist, dann nennt man r den Rang von A:
Rang(A) = r(A) = r; r < min (m, n)
(4.28)
Der Rang einer Matrix bleibt ungeändert, wenn man
•	beliebige Zeilen (Spalten) mit von null verschiedenen Konstanten multipliziert
•	beliebige Zeilen (Spalten) miteinander vertauscht
•	zu einer Zeile (Spalte) das Vielfache einer anderen Zeile (Spalte) addiert
Auf diesen Aussagen beruht der Gaußsche Algorithmus zur Rangbestimmung.
Mit diesem Verfahren wird eine Matrix A =	mit r(A) = r systematisch
4.4 Rang von Matrizen, Gaußscher Algorithmus
55
in eine Matrix
du	di2 ..	dir	^l,r+l • • •	d]_n
0	d22 • •	. d2r	d2,r+l • • •	d2n
0	0	..	. dr r	dr?r+l • • •	drn
0			0	
(4.29)
vom gleichen Rang r umgewandelt.
Der Algorithmus besteht aus folgenden Schritten:
1.	Man ordnet, falls nötig, Zeilen oder Spalten von A so um, dass das (evtl, neue)
Element an 0 ist.
2.	Die erste Zeile (Eliminationszeile) wird jeweils mit ( —	) multipliziert und
\ «11 J
zur z-ten Zeile addiert (z = 2, 3,..., m). Es entsteht eine Matrix der Gestalt
«11
o
«12
«In
(4.30)
3.	Die Matrix B wird ebenso behandelt wie die Matrix A (Schritte 1 und 2).
4.	Das Verfahren wird solange fortgesetzt, bis die Gestalt (4.29) erreicht ist.
Der Rang r(A) ist gleich der Anzahl r der Diagonalelemente der Dreiecksma-
trix = (dik)
Es seien m n-dimensionale Vektoren af = («n, «^ • • •, «in), = 1, 2,..., m gege-
ben. Wendet man auf die daraus gebildete (m, n)-Matrix
/an	ai2	ain\
«21	«22	• • •	«2n
«m2	• • • «mn
(4-31)
den Gaußschen Algorithmus zur Bestimmung von r(A) = r an, so gilt:
•	Ist r = m, so sind die m Vektoren ai linear unabhängig.
•	Ist r < m, so sind die m Vektoren ai linear abhängig. Unter den m Vektoren
ai sind diejenigen r Vektoren linear unabhängig, die an der Bildung der Matrix
(d^)(rr) beteiligt sind.
56
4 Lineare Algebra
1.	Bestimme den Rang der Matrix
/ 2	1	—4	1	3	\
-4	7	5	—2	0
A “	5	6	9	-3	-3
\ 0	3	-1	0	2	/
2.	Bestimme den Rang der gegebenen
Matrizen mit Hilfe des Gänschen
Algorithmus.
	/2	-1	3	—2	4\
a) A = I	4	—2	5	1	7
	^2	-1	1	8	2/
	/I	3	5	—	e
b) B =	2	-1	-3	4	
	5	1	-1	7	
	V	7	9	1	/
		3 -	-5	2	3 \
	8	6 -	-7	4	2
c) C =	4	3 -	-8	2	7
	4	3	1	2	-5
		6 -	-1	4	-6/
	/ 0	2		-4\	
	3	1		7	
d) D =	0	5		-10	
	-1	. -4	1	5	
	V	3		0 )	
	<2	2 -	-1	1	2\
OA JA 		4	3 -	-1	2	1
	8	5 -	-3	4 -	-1
	<3	3 -	-2	2	1/
	/25	31	17	43 \	
f) G =	75	94	53	132	
	75	94	54	134	
	\25	32	20	48 /	
3.	Welchen Rang besitzen die gegebe-
nen Matrizen in Abhängigkeit von
Ael?
/3	1	1	4\
A4 A 4 10 1
a)	A -	x	7	17	3
\2	2	4	3/
/I	A	-1	2\
b)	B =	| 2	-1	A	5
\1	10	-6	A/
4.	Mit Hilfe des GW/? sehen Algorith-
mus ist zu untersuchen, ob die gege-
benen Vektoren linear abhängig oder
linear unabhängig sind.
a)	ai = (1,1,1,1)T
a2 = (1,1,-1,-1)T
a3 = (1,-1,-1,1)T
a4 = (1, —1,1, — 1)T
b)	ai = (4, —1,5, 6)t
a2 = (4, -5,2, 6)t
a3 = (2, —2,1,3)T
a4 = (6, - 3,3, 9)t
5.	Gegeben ist eine Menge von Vekto-
ren T = {01,02,03,04}. Bestimme
ihren Rang sowie eine Basis B in T,
und stelle die nicht zu B gehörenden
Vektoren von T als Linearkombina-
tion von B dar, wenn
a)	ai = (—3, —6,0,0)t
a2 = (1,2,3,4)T
a3 = (1, 2,0,0)T
b)	a4 = (3,4, — 1, 2)t
a2 = (1,1,-1,-2)t
a3 = (4,1,-2,3)T
a4 = (5,2, — 3,1)T
4.5 Lineare Gleichungssysteme
57
4.5 Lineare Gleichungssysteme
4.5.1 Die Cramersche Regel
Ein System von n linearen Gleichungen mit n Variablen hat die Form:
U11X1 + U12X2 + ... + alnxn = Ul
0'21^1 “F 0-22^2 + • • • + CL2nxn = tt2
(4.32)
Unl^l V Un2^2 “F • • • “F &nnxn — xn
Die Koeffizienten und die Absolutglieder (Störglieder) ai sind reelle Zahlen
(i,k = 1, 2,... , n). Das System (4.32) ist genau dann eindeutig lösbar, wenn die
Koeffizientendeterminante
	un	U12		
D =	&21	«22	•	• •	^2n	7^0
	Uni	Un2 • 	> • ^nn	
(4.33)
ist. Sind die Determinanten Dk (k = 1,2,..., n) durch
	an	• ai,k-i ui ai^+1	. . Uin	
Dk =	«21	•	U2,fc-1 U2 U2,fc+1	• • U2n	(4.34)
	Uni • • 	Un,A;—1 Un Un,A;+l	• • Unn	
erklärt, dann ist				
Bi		D-2	Dn		
X1 = ~j^X2 =		— ,...,xn = —		(4.35)
die Lösung des Gleichungssystems (4.35).
1.	Löse die folgenden linearen Glei-
chungssysteme mit Hilfe der Regel
von Cramer’.
a)	2axi — 36^2 = 0
3axi — 66x2 = ab (ab 0)
b)	3xi — X2 + 2x3 = 3
-xi + 3x2 - 2x3 = -1
2xi + 2x2 + 3x3 = 14
c)	Xi —	X2 +	X3	—	X4 =	—2
Xi +	X2 +	X3	+	X4 =	0
Xi +	2X2	=	5
3X3	+	4X4 = —10
d)	3xi + 4x2 + X3 + 2x4 = —3
3xi + 5x2 + 3x3 + 5x4 = —6
6xi + 8x2 + X3 + 5X4 = —8
3xi + 5x2 + 3x3 + 7x4 = —8
58
4 Lineare Algebra
2.	Bestimme mit Hilfe der Regel von
Cramer das Polynom
a)	P2 (x) = ax2 + bx + c mit
P2(l) = -1, F2(-1) = 9 und
F2(2) = -3
b)	P3(x) = ax3 + bx2 + cx + d mit
F3(l) = 2, F3(—1) = 8
F3(2) = —10, P3(—2) = 26
3.	Bei Anwendung der Kirchhoff sehen
Regeln auf ein elektrisches Netzwerk
ergab sich das Gleichungssystem
R • i = u mit
i = (h,h,I3,h,I5,I6)T
u = (0,0,0,0,0,E)t
R =					
/ o	-1	0	-1	1	0\
0	0	-1	1	0	1
-1	1	0	0	0	-1
0	-f2	0	F4	0	—Fß
-Fi	0	f3	0	0	Fß
\ Fi	f2	0	0	0	0?
und					
E = 10V, Rr = R-i = R3 = 2Q
/? i = /?5 = /?6 = 4<L Berechne die
Stromstärke Iq mit Hilfe der Cra-
mersch en Regel.
4.5.2 Das (allgemeine) lineare Gleichungssystem (LGS)
Gegeben ist ein System von m linearen Gleichungen mit n Variablen:
U11X1	+	CZ12X2	+	...	+	alnxn	=
ß2l^l	+	CL22%2	4“	• • •	4“	CL2nxn	=	^2
«ml^l +	Öm2^2	+
oder in Matrizendarstellung:
&11	^12	• • • Clin
U2i	«22	• • • Cl2n
( Xl\
J'-i
44
&2
(4.37)
\Clml CLm2	C^mn
kurz: A • x = b
mit der reellen Koeffizientenmatrix A = («ifc)(m,n)? dem Lösungsvektor
x = (xi, X2,..., xn)T und dem Vektor der absoluten Glieder (Störvektor)
& = (W2,...,Mt er.
Die um den Störvektor erweiterte Koeffizientenmatrix heißt erweiterte Koeffi-
zientenmatrix B = (A|b).
Das System (4.36) heißt homogen genau dann, wenn b = o ist, anderenfalls
heißt es inhomogen.
Das homogene System besitzt stets wenigstens eine Lösung, nämlich die so ge-
nannte triviale Lösung x = o E Rn.
Während sich die Anwendung der Cramerschen Regel auf den Sonderfall m = n
und det A 0 beschränkt, gestattet der GW/?sche Algorithmus die Lösung des all-
gemeinen Falles m = n. Indem man den GW/? sehen Algorithmus auf A an wendet
4.5 Lineare Gleichungssysteme
59
und dabei die Zeilenoperationen auf ganz B = (A|ö) erstreckt, erhält man eine
Matrix der Form
X\ X2 ... xr	Xr_|-1	... xn	1
du di2 ... dir	dl^r+l • • • din	bl
0	c/21	• • • d2r	^2,r+l	• • • d2n	b2
0	0	... drr	dr,r-\-^	• • • drn	bp
		br-\-i
0	0	
		br-\~s
		0
(4.38)
mit det(difc)(r,r) 7^ 0- (Mit Xi^bk wird angedeutet, dass der Spaltenaustausch
bei A eine Umbenennung der Variablen zur Folge hat, der Zeilenaustausch bei
B = (A|ö) eine Umbenennung der absoluten Glieder.)
Das System (4.36) ist genau dann lösbar, wenn gilt:
r(A) = r(B) = r	(4.39)
d.h., wenn in (4.38)
6r+i = 6r+2 = ... = br+s = 0
ist. Anderenfalls ist das System (4.36) unlösbar.
Im Falle der Lösbarkeit findet man die Lösung nach (4.38) schrittweise aus dem
gestaffelten LGS:
dn^i	• • • H- d±pXr — bi	...	dinxn
d22%2	• • • H- d2rXp — 1)2	d2.T-j-l^r-l-l • • •	d2nXn
(4-40)
drprpXp — bp	d'p p_|_ixp_|_... d'p^x
mit (n — r) freien Variablen (Parametern):
4^+1 — G i ^r+2 — ^21 i — tn—r	( x
/	x	(4.41)
— oo < ti < +oo (i = 1, 2,..., n — r)
60
4 Lineare Algebra
1.	Löse die gegebenen linearen Glei-
chungssysteme mit dem Gänschen
Algorithmus.
a)	4xi + 6x2 + 17x3 + 8x4 = —20
— x3 + 2x4 =	4
2xi + 3x2 + 7x3 + 7x4 = —4
2xi + 3x2 + 8x3 + 5x4 = —8
b)	4xi + 6x2 + 17x3 + 8x4 = —20
— x3 + 2x4 =	5
2xi + 3x2 + 7x3 + 7x4 = —4
2xi + 3x2 + 8x3 + 5x4 = —8
(Beachte: lb entsteht aus la durch ge-
ringfügige Änderung der rechten Seite.)
2.	Löse die gegebenen linearen Glei-
chungssysteme mit dem Gänschen
Algorithmus.
a)	xi — X2 + x3 = 2
2xi + x2 - x3 = 1
5xi + x2 - x3 = 4
b)	xi - x2 + x3 = 2
2xi + x2 - x3 = 1
5xi + x2 - x3 = 0
c)	Xi — X2 + X3 = 2
2xi + X2 — X3 = 1
-xi + 2x2 - x3 = 0
d)	xi + x2 + x3 = 3
xi — 2x2 — %3 = — 2
2xi + X2 — 3x3 = 0
e)	xi + x2 + x3 = 3
xi — 2x2 — %3 = — 2
-xi + 5x2 + 3x3 = 7
f)	xi + x2 + x3 + x4 = 4
Xi + X2 — X3 — X4 = 0
3xi -|- 3x2 H- x3 -|- X4 = 8
g)	—3xi + 3x2 — 2x3 = 0
2xi — 2x2 + 5x3 = 0
xi + 3x2 + 2x3 = 0
h)	xi — X2 + 5x3 + 8x4 = 0
4xi + X2 — 3x3 + X4 = 0
2xi — 4x2 + 3x3 — 4x4 = 0
3xi + X2 — 2x3 + 2X4 = 0
/ 2 11 6 -4 -2\
6 -9-2 4 2
-10 6 —2 -3 -1
\ 1 -5-2 2 1 /
<xA
x2
x3
X4
w
/I 2 3 4
2 4 3 2
0 0 3 5
3 6 9 11
\1 2 2 2
2 3\
2 1
1 1
4 1
V -1 2/
/6\
6
3
7
W
/I 2 3 2 1\
3 2 12 3
11111
\1 2 3 4 5/
/xA
x2
x3
X4
\XJ
6
3
\6/
m) 2xi + 3x2 + 4x3 + 3x4 = —4
xi — 2x2 — 3x3 — 4x4 = 6
3xi + X2 + 2x3 + 4x4 = 7
4xi — 3x2 — 5x3 — 8x4 = 13
n) 2xi — 2x2 + 3x3 + 5x4 = 7
3xi + 3x2 + 2x3 — 4x4 = 6
o) 3xi — 2x2 + 5x3 = 5
—2xi + 3x2 — 6x3 = —7
5xi — 7x2 + 4x3 = —4
4.6 Inverse Matrix (Austauschverfahren)
61
q)
/ 2 3
-3 2
5 —4
\ 3 3
—2 -11\
3 10
2 —2
-5 — 19/
^2
^3
\XJ
= (-9,7,10,-18)
T
3.	Für welche reellen Werte von A
ist das folgende System lösbar? Be-
rechne die zugehörigen Lösungen.
x + y +	z =	3
3x + by +	z =	9
2x + 3y +	z = A2	— 4A + 6
bx + 6y + Az =	15
4.	Die folgenden linearen Gleichungs-
systeme sind durch Bestimmung des
Ranges der Koeffizientenmatrix und
des Ranges der erweiterten Koeffizi-
entenmatrix auf ihre Lösbarkeit zu
untersuchen:
b) Xi — 2x2 — 3x3 = —3
Xi + 3X2 — 5X3 = 0
-xi + 4x2 + x3 = 3
3xi + X2 — 13x3 = —6
c) 2xi +	X2	— X3 — X4 + X5	=	1
Xi —	X2	+ X3 + X4 — 2X5	=	0
3xi +	3x2	— 3x3 — 3x4 + 4x5	=	2
4xi +	5x2	— 5x3 — 5x4 + 7x5	=	3
5.	a) Bestimme alle Lösungen des li-
nearen Gleichungssystems:
/—2 1 -3 3\
1-3-14 X2
12-132/ X3
= (5,9,10)T.
b) Welche Lösungen genügen der Zu-
satzbedingung
a) xi + X2 + x3 = 3
X1 + X2 — 3^3 = — 1
2xi + X2 — 2X3 = 1
Xi + 2X2 — 3X3 = 1
|xi — X2 + 3X3 — 3X4 | = 4?
4.6 Inverse Matrix (Austauschverfahren)
Jeder quadratischen Matrix A^n^ = (azA;)(n?n) kann man ihre Determinante
det zuordnen.
Ist det A 7^ 0, so heißt die quadratische Matrix A regulär, anderenfalls heißt sie
singulär.
Zu jeder regulären Matrix A = (azA;)(n?n) existiert genau eine Matrix
A“1 = (M(n,™)	(4.42)
sodass gilt:
AA'1 = A~tA = En	(4.43)
(En Einheitsmatrix).
Die Matrix A-1 heißt die zu A inverse Matrix. In (4.42) ist
bik = (-l)i+fc
Aki
det A
(4.44)
62
4 Lineare Algebra
wobei die Unterdeterminanten der Matrix A sind:
A	(pik) (n,n)
1
det A
( An — A2i A3i .. A
— Ä12	A22	— A32 . . .
A13	—A23	A33
\....................../
Für reguläre Matrizen gilt:
(A-lp'=A: (A-1)t = (AT)"1
(AB)-1 = B1 • A“1; (AA)“1 = A“1 (A 0)
A
det A-1 = (det A)-1
(4.45)
(4.46)
(4.47)
(4.48)
Man kann die inverse Matrix A-1 zu einer regulären Matrix A auch aus der
Lösung x = A~ry eines linearen Gleichungssystems (LGS) y = Ax erhalten.
Die Lösung eines solchen LGS gelingt mit dem Gänschen Algorithmus, aber ef-
fektiver mit dem Austauschverfahren. Beim Austauschverfahren werden Schritt
für Schritt in einem System von (in diesem Falle) n homogenen linearen Funktio-
nen in n Variablen
n
yi = '^2 aikXk = auxi + ai2x2 + . •. + ainxn (i = 1,2,..., n) (4.49)
k=l
eine Variable Xk gegen eine Variable yi ausgetauscht. Dazu wird das System (4.49)
schematisch dargestellt:
5i	Xi	Xs	xn	
yi	an		... d\n	Es können xs und yz ausgetauscht wer- den, falls das Pivotelement dzs 0 ist.
yz		fdZs j	... dzn	(Die z-te Zeile heißt Pivotzeile, die s-te Spalte heißt Pivotspalte.)
yn	cini ...	dns	• • • dnn	
Bei dem Austausch xs			gegen yz geht	das Schema Si in das Schema S2 über:
s2	Xi	yz •	• • xn	Dafür gelten die Austauschregeln:
yi	bn	b\s	• • b\n	1
				1. bzs =	 dzs
xs	bzi	bzs	bzn	2. bis =	für alle i z dzs
yn	bnl	bns	• • bnn	3. bzk = — für alle k z dzs
4. bik — dik		dis ‘ dzk dzs	für alle i z	und alle k s
4.6 Inverse Matrix (Austauschverfahren)
63
In Worten:
1.	Das Pivotelement wird durch seinen reziproken Wert ersetzt.
2.	Die übrigen Elemente der Pivotspalte werden durch das Pivotelement dividiert.
3.	Die übrigen Elemente der Pivotzeile werden durch das Pivotelement dividiert
und mit dem entgegengesetzten Vorzeichen versehen.
4.	Die restlichen Elemente werden nach der so genannten „Rechteckregel“ trans-
formiert. Das Rechteck ist festgelegt durch das zu transformierende Element t
und das Pivotelement p:
0	...	b	b	...	0	a	...	UJ	UJ	...	a
•	y	;	oder	'•	:	oder	:	:	oder	:	y	:
a	 • 	@	0)	•  •	a	0	...	b	b	...	0
Die Transformation des Elementes t nach der Rechteckregel ergibt: t —
P
1. Unter welchen Voraussetzungen		X1	Xz	x3	X4
lässt sich die Matrix X aus der	yi	4	1	-1	-1
Matrizengleichung	V2	-9	-3	3	2
X(A + B) + C= 0		1	-1	0	-1
berechnen?	Z/4	9	4	—2	—2
2.	Berechne die Matrix X aus
den folgenden Matrizengleichun-
gen, wenn alle hierzu erforderli-
chen Voraussetzungen als erfüllt
angesehen werden können:
a)	AXB + 2XB - 3D = 5C
b)	AXB + 4AX = 8C-3AXB.
3.	Wende das Austausch verfahren
an, um
a)	im gegebenen Schema Si die
Variablen X3 und yz auszutau-
schen (sie erhalten das Schema
S2)
b)	im Schema Sz die Varia-
blen X4 und 2/4 auszut-
auschen (sie erhalten S3).
4.	Berechne die inverse Matrix A 1
zu
/ 2	2	3\
A =	1	-10
\-l	2	1/
a)	durch Anwendung der Formel
(4.45)
b)	nach dem Austausch verfahren.
5.	a) Berechne die inverse Matrix zu
der Matrix
/ 3	-1	0\
A = 1—2	1	1
\2 -1 4/
und bestätige
AA-1 = A-1A = E.
b) Berechne die Matrix X aus der
Gleichung
ATXA~T + A = (A-1)T
64
4 Lineare Algebra
	wenn A die Matrix von a ist.	d) D = |	/2 3	1 2	1\ 1
6.	Berechne die Matrix X aus der			2	0/
	Gleichung		<1	2	-1 -2\
	2(B+X)+XA = X(B-A)+3X		3	8	0 —4
		e} F =			
	wenn		2	2	—4 -3
	/2 1	1 \ A = 0 1 —2 1		<3	8	-1 —6/
	\2 2	2 /		<-2		2 -7\
	?4 3	1 \	f) G =	1		2	5
	B = 3 2 -1 .		^—3		1	— 12/
	\8 5	3 /		/2	5	4 3\
			0	3	4 2
7.	Berechne die inverse Matrix zu	g) H =	0	0	3 1
	den gegebenen Matrizen.			0	0 4/
	a) A = (2 5)		/3 0	—2 2	0 2	1
	b)B=(l2 3)	h) K =	1	—2 1	-3 -2 2	1/
	/1 0 o\		^8	0	0\
	c) C = 3	1	0	i)L =	0	-3	0
	\4 -5 1/		k°	0	2/
4.7 Lineare Transformationen
4.7.1 Affine und orthogonale Tranformationen
Die lineare Transformation
Z/i	=	CZ11X1	+	U12^2	+ ..	.. +	^In^n	+	Cl
V2	=	«21^1	+	<222^2	+ ..	.. +	^2n^n	+	C2
Vn	=	^nl^l	+	«n2^2	+ ..	.. +	^nn^n	+	
(4.50)
oder mit
kurz
y = Ax + c
(4-51)
bildet den Raum Rn in sich selbst ab und heißt affine Abbildung.
Man nennt sie
4.7 Lineare Transformationen
65
•	inhomogen, falls c o.
•	homogen, falls c = o.
•	regulär, falls det A 0.
•	singulär, falls det A = 0.
Bei der Anwendung der homogenen affinen Abbildung
y = Ax
(4-52)
zur Koordinatentransformation in Rn gilt:
•	Das Bild des z-ten Einheitsvektors e* des x-Systems ist im ^/-System der i-te
Spaltenvektor a7 = ((/zi. 0^2,..., nm)T von A.
•	Sind ai = (a*i, a*2, • • •, a*n)T, i — l,2,...,n, Vektoren im x-System und
bi = (bä, bi<2,..., bin)1.	= 1,2,... ,n, ihre Bilder im ^/-System, so gilt für
das Spatprodukt
an a2i	ai2 . a22	•	• • ain • • a2n	= det A •	6n 621	612 • 622 •	• • 6in 6277,
ani	an2	• • ann		bnl	6n2 •	• • bnn
(4.53)
Die homogene affine Transformation y = Ax bewirkt eine Drehung und Ver-
zerrung des Koordinatensystems, wenn det A > 0 ist. Für det A < 0 kommt noch
eine Umklappung hinzu.
Der Vektor c o. der in der inhomogenen affinen Tranformation auftritt, bedeutet
nur eine Verschiebung des Koordinatensystems.
Eine Matrix A = A(n>n) heißt genau dann orthogonal, wenn
AtA = En	(4.54)
Ist A orthogonal, so ist det A = ±1; dies gilt aber nicht umgekehrt. Eine qua-
dratische Matrix ist dann und nur dann orthogonal, wenn gilt:
a) A-1 = A1
b) Die Zeilenvektoren (Spaltenvektoren) von A sind paarweise orthogonale Ein-
heitsvektoren, d.h.
f 0 für i k
dil^kl T	T • • • T O'inO'kn = S «.. .	7
II tur i = k
f 0 für i 7^ k
O’liO’lk T &2iCl2k T • • • T dniC^nk = S «...	7
1 tur z = k
Eine affine Transformation heißt orthogonale Transformation, wenn die Ma-
trix A orthogonal ist. Im homogenen Fall mit det A = 1 bewirkt sie eine reine
Drehung des Koordinatensystems.
66
4 Lineare Algebra
1.	Diskutiere die gegebenen affinen
Transformationen.
a)	Z/i = xi +1,5
Z/2= x2 — 2,5
, x	4	3
b)	yi = -xi + -x2
5	5
3	4
1/2 = --^1 + ~X2
5	5
x	4	3
c)	yi = -~xi + -x2 + 1,5
5	5
3	4
1/2 = -xi + -x2-2,5
5	5
2.	Gegeben ist die Matrix
a 1 <5 4\
- 3 \4 5)
/1 3	5	\
A = 2 4 -1
V 7	3	/
ordnet jedem Vektor ai einen
Vektor bi zu. Berechne das Spat-
produkt [&i,b2,&3] und kontrol-
liere die Formel [&i,b2,&3] =
det A • [ai, a2. 03].
Zeige: det A = 1, aber A ist keine
Orthogonalmatrix.
3.	Im Raum R3 mit der Standardbasis
{ei, e2, 63} wird jedem Vektor x als
Bild seine Projektion auf die Ebene
E : xi + x2 + X3 = 0 zugeordnet.
Wie lautet die Matrix P dieser Ab-
bildung?
4.	Im Raum R3 mit der Standardbasis
{ei,e2,es} sind drei Vektoren
aj = (2, 3, -1), aj = (1, -1, -3),
aj = (1,9,—11) gegeben.
a)	Berechne das Spatprodukt
[ai, a2, a3].
b)	Die homogene affine Transforma-
tion bi = Aa, mit
5.	a) Zeige, dass
Z1 2	-2\
A = - 2	1	2
3 \2 —2 -1/
eine Orthogonalmatrix ist und gib
A-1 an.
b) Zeige, dass das System paarweise
orthogonaler Vektoren
X1 = (4,5,—2)T
= (1, —2, —3)t
x3 = (19, —10, 13)t
durch die orthogonale Transfor-
mation y = Ax mit obiger
Matrix A wieder in ein System
l/i, 1/2, 1/3 paarweise orthogona-
ler Vektoren übergeführt wird.
6. Zeige, dass die folgenden Matrizen
Orthogonalmatrizen sind:
/1 1 1 -1\
-1111
-1 -1 1 -1
V -1 1 1/
4.7.2 Eigenwerte, Eigenvektoren
Ist A = A(n>n) eine quadratische Matrix, so ist
det (A — XEn) = 0
(4.55)
eine algebraische Gleichung n-ten Grades in A. Sie heißt charakteristische Glei-
chung der Matrix A.
4.7 Lineare Transformationen
67
Ihre n Lösungen Ai, A2,..., Xn heißen Eigenwerte der Matrix A, und die dazu-
gehörigen nichttrivialen Lösungen Xi des homogenen linearen Gleichungssystems
(A — XiE)x = o
(4.56)
heißen Eigenvektoren.
Mit Xi ist auch jedes Vielfache ßXi (ji 0) Eigenvektor, insbesondere heißt
(4-57)
normierter Eigenvektor.
Für jede reelle symmetrische Matrix (ÄT = A) gilt:
a)	Ihre Eigenwerte sind reell.
b)	Die zu verschiedenen Eigenwerten gehörenden Eigenvektoren sind orthogonal.
c)	Zu einem ^-fachen Eigenwert existieren k paarweise orthogonale Eigenvektoren.
d)	Die n normierten Eigenvektoren ri können so gewählt werden, dass sie ein
orthonormiertes Rechtssystem bilden, d.h., es gilt:
{1 TI 1T* 7 — jG
0 f” ‘ k
2.	die aus ihnen gebildete Matrix
R = (n,r2,... ,rn)	(4.58)
ist orthogonal und det R = 1.
3.	mit R lässt sich A auf Diagonalgestalt transformieren:
1.	Gegeben ist die reelle symmetrische
Matrix
/6	2	2 \
A =	2	3	—4	.
\2	—4	3 /
Ermittle
a)	die Eigenwerte von A
b)	die zugehörigen Eigenvektoren
so, dass sie ein orthonormiertes
Rechtssystem bilden.
c)	Kontrolliere
RtAR = D.
2.	Bestimme die Eigenvektoren der ge-
gebenen symmetrischen Matrix A
so, dass sie ein orthonormiertes
Rechtssystem bilden und kontrollie-
re
68
4 Lineare Algebra
/Ai 0	0 \
RTAR =	0 Ä2 0
\ 0 0 a3/
wobei Ai, A2, A3 die Eigenwerte der
Matrix A sind.
x /15	6	0\
a)	A =	— 6	22	6 |
11 \0	6	29/
/—2	2	-4\
b)	A =	- 2	-5	-2
3 \-4	—2	-2/
/ 4	-5	7\
d) D =	1	-4	9
\-4	0	5/
3.	Berechne die Eigenwerte der gegebe-
nen Matrizen.
/	° t	0\
a)	A	=	0	0	1
\-6 -1 4/
/	2	-1	2	\
b)	B	=	5	-3	3
\-l	0	—2/
/4 -5 2\
c)	C = 5 —7 3 |
\6 -9 4/
/5 1 3 2\
2 3 13
4 2 4 6
\3 1 3 4/
/ 0	1	0	0\
0	0	10
0	0	0	1
\48 -28 -8 7/
4.	Bestimme die Eigenvektoren der ge-
gebenen Matrizen so, dass sie ein or-
thonormiertes Rechtssystem bilden.
/1	2
b) B = 2	1
\2 —2
4.7.3 Hauptachsentransformation für Kurven und Flächen
2. Ordnung
Die Menge aller Punkte P mit dem zugehörigen Ortsvektor cc. die die quadratische
Gleichung
xv Ax + aTx + «o = 0
(4.60)
mit reeller symmetrischer Matrix A (ÄT = A) erfüllen, heißen
•	Kurven 2.Ordnung (Kegelschnitte), falls
4_/«n «12A	_ (ai\ _
\«21 «22/ a	\«2/ ’ X V?2/
•	Flächen 2.Ordnung, falls
(«11
«21
«31
«12
«22
«32
«13 \	/ «1 \	/ X±
«23	, a = I «2	, x = \X2
«33 /	\«3 /	V3
(Man beachte: CZ12 = «21, «13 = «31, «23 = «32)
4.7 Lineare Transformationen
69
Hauptachsentransformation |
1. Fall: A ist regulär (det A ± 0)
Bei einer Verschiebung
x = y — v mit v = ^A-1a	(4.61)
verschwinden die linearen Glieder und (4.60) geht über in
yTAy + bo = 0 mit bo = ao — -aTA~ra	(4.62)
Durch die Drehung
y = Rz	(4.63)
wird (4.62) auf die Form
ztDz + bo = 0	(4.64)
gebracht. Dabei ist D die Diagonalmatrix der Eigenwerte von A, und R ist die
Matrix der zugehörigen orthonormierten Eigenvektoren mit det R = 1.
(4.64) heißt auch Normalform der Kurve (Fläche) 2. Ordnung. Sie gestattet eine
Klassifizierung, wie die folgenden (nicht vollständigen) Tabellen zeigen. (Ai > 0
ist ggf. durch Vertauschen von Variablen oder durch Multiplikation der Gleichung
mit (-1) zu erreichen.)
Kurven 2. Ordnung: Aizf + A2Z2 + ^0 = 0
Ai	A2	bo	
> 0	> 0	< 0	Ellipse
> 0	< 0	7^0	Hyperbel
> 0	< 0	= 0	zwei sich schneidende Geraden
Flächen 2. Ordnung: Aizf + A2Z2 + X3Z3 + bo = 0
Ai	A2	A3	bo	
> 0	> 0	> 0	< 0	Ellipsoid
> 0	> 0	< 0	7^0	Hyperboloid
> 0	> 0	< 0	= 0	Doppelkegel
> 0	7^0	= 0	7^0	Zylinder
2. Fall: A ist singulär (det A = 0)
Mindestens ein Eigenwert ist gleich null. Analog zum 1. Fall wird hier zunächst
die Drehung
x = Ry
(4.65)
70
4 Lineare Algebra
ausgeführt, und (4.60) geht über in
yT Dy + Ry + a0 = 0
(4.66)
Dabei ist zu beachten: Ist A = 0 zweifacher Eigenwert, dann ist einer der zu-
gehörigen Eigenvektoren so zu wählen, dass er sowohl orthogonal zu a als auch
orthogonal zum anderen Eigenvektor ist.
In (4.66) ist gegebenenfalls noch eine Verschiebung
y = z — v
(4.67)
so durchzuführen, dass höchstens ein lineares Glied übrigbleibt:
Ist Xi 7^ 0, so fasst man quadratisches und zugehöriges lineares Glied zu einem
vollständigen Quadrat zusammen (quadratische Ergänzung!):
Az^/z A hihi —
r+
kL
4V
also
(4.68)
Zum Schluss könnten das noch vorhandene lineare und das absolute Glied zusam-
mengefasst werden:
(4.69)
Kurven 2. Ordnung: Aizf + c±Z2 + C2 = 0
Ai	ci	C2	
> 0	7^0	beliebig	Parabel
> 0	= 0	< 0	parall. Geraden
= 0	7^0	beliebig	Gerade
Flächen 2. Ordnung: Aizf + A2Z2 + C1Z3 = 0
Ai	A2	ci	
> 0	> 0	< 0	elliptisches Paraboloid
> 0	< 0	< 0	Sattelfläche
> 0	= 0	7^0	parabolischer Zylinder
1.	Führe die Hauptachsentransformati-
on durch und fertige für das Ergebnis
eine Skizze an.
a) 3x^ + 10x1^2 + 3^2 — 2xi — 14x2
-13 = 0
b) 4xi + x2 + 4xß — 4xiX2 — 8x1X3
+4x2X3 — 28xi + 2x2 + 16x3 + 45
= 0
4.7 Lineare Transformationen
71
2.	Klassifiziere die folgenden Kegel-
schnitte, und gib jeweils Lage und
Parameter an.
a)	x2 — y2 + 2(x — y) = 1
b)	6xi — ^2 — 4x2 — 16 = 0
c)	x2 + y2 — 8x + 2y + 13 = 0
d)	16x2 + Hy2 + 64x - 18?/ = 71
Hinweis: Quadratische Ergänzung.
3.	Bestimme den Mittelpunkt und den
Radius der gegebenen Kugel.
a)	x2 + X2 + x2 — 3xi + 5x2 — 4x3 = 0
b)	x2 + y2 + z2 = 2az (a 0)
Hinweis: Quadratische Ergänzung.
4.	Führe für
a)	41x2 + 41x2 — 18x1X2 + 46xi
+146x2 - 631 = 0
b)	5x2 + 5x2 — 26x1X2 — 36xi
+36x2 - 36 = 0
die Hauptachsentransformation
durch und stelle die Ergebnisse zeich-
nerisch dar.
5.	Gegeben sind die Kurven 2. Ord-
nung:
a)	13x2 — 12xiX2+ 4x2+ 88x1— 48x2
+144 = 0
b)	3x2 — 4xiX2 — 2xi + 4x2 — 5 = 0
C) X2 — 2X1X2 + X2 — 10xi — 6x2
+25 = 0
d) 4x2—4X1X2+X2 —6xi+3x2—4 = 0
Gib die Kurvengleichung in Normal-
form an. Um welche Kurve handelt
es sich?
6.	Gegeben sind die Flächen 2. Ord-
nung:
a)	7x2— 4xiX2— 8x1X3+4x2+4x2X3
+7x2 + 2xi — 4x2 + 16x3 + 18 = 0
b)	—2x2 — 4xiX2 — 4xiX3 + X2
+8x2X3 + x2 + 16xi — 14x2
—8x3 + 6 = 0
c)	x2 — 4X1X2 + 4X1X3 — 2X2 +
—2x2 + 4xi — 12x2 + 4x3 + 7 = 0
d)	2x2 + 4xiX2 — 4xiX3 + 5x2
—8x2X3 + 5x2 + 16xi + 32x2
-30x3 + 54 = 0
e)	2x2 — 7x2 — 4x2 + 4xiX2 — I6X1X3
+20x2X3 + 60xi — 12x2
+12x3 - 90 = 0
f)	2x2 + 5x2 + 2x2 — 2xiX2 — 4xiX3
+2x2X3 + 2xi — 10x2 — 2x3 — 1 = 0
Gib die Flächengleichung in der Nor-
malform und den Namen der Fläche
an.
7.	Gegeben sind die Flächen 2. Ord-
nung:
a)	5x2 + 6x2 + 7x2
-4xix2 + 4x2x3
— lOxi + 8x2 + 14x3 — 6 = 0
b)	2x2 + 5x2 + llx2
— 20X1X2 + 4X1X3 + I6X2X3
—24xi — 6x2 — 6x3 — 18 = 0
\ 2 । 2 । 2
C/ X± + X2 + X3
—6x1 + 8x2 + IOX3 + 1 = 0
Gib die Flächengleichung in der Nor-
malform sowie die Formeln für die
Koordinatentransformation an.
Wie lauten die Ursprungskoordina-
ten des verschobenen Systems im
Ausgangssystem?
5 Zahlenfolgen und Zahlenreihen
Folgen
Eine (reelle) Zahlenfolge ai,«2,«3,... oder kurz {an} nennt man
•	beschränkt genau dann, wenn es eine Zahl K > 0 gibt, sodass für alle n E
N \ {0} gilt: \an\<K
•	monoton wachsend (bzw.monoton fallend) genau dann, wenn für alle
n G N \ {0} gilt: an+1 > an (bzw. an+1 < an)
•	konvergent mit dem Grenzwert a genau dann, wenn für jedes e > 0 ein
no = n0(s) derart existiert, dass gilt:

für alle n > tiq.
(5-1)
Man schreibt : lim an = a , lim an = a , an a
n^oo
•	divergent, wenn sie nicht konvergent ist
•	bestimmt divergent mit liman = 00 (bzw. mit liman = —00) genau dann,
wenn für jedes K > 0 ein no = no(K) derart existiert, dass gilt:
an > K (bzw. an < —K) für alle n > no
(5-2)
•	unbestimmt divergent, wenn sie divergent, aber nicht bestimmt divergent ist
Grenzwerte spezieller Zahlenfolgen:
1. lim — = 0
n
2. lim
= e
3. lim =1 (c > 0)
4. lim y/n = 1
5. lim — =0	6- bm f 1 +
n	\ nJ
0	für \q\ < 1
_ r n 1	für q = 1
7. hm q = <
+00 (bestimmt divergent) für q > 1
= e,
d E R
k unbestimmt divergent
für q < — 1
Grenzwertsätze:
Wenn liman = a und limön = b existieren, so existieren auch die folgenden Grenz-
werte :
1. lim(can) = c • liman = c • a (c Konstante)
5 Zahlenfolgen und Zahlenreihen
73
2. lim(an ± bn) = lim an ± lim bn = a ± b
3. lim(an • bn) = lim an • lim bn = a • b
dn	lim dn	d
4-lmX = i^ = s
5. liman^ = (liman)lim61
(bn + 0 A 0)
6. lim log an = log lim an = loga (a.
Reihen
Ist {an} eine Zahlenfolge, so nennt man die Folge {sn} ihrer Teilsummen
sn — di T d2 T 
(5-3)
eine (unendliche) Zahlenreihe und schreibt
s = d± d2 = y di mit s = lim sn
n^-oo
2=1
(5-4)
falls die Reihe konvergiert, d.h., der Grenzwert limsn = s existiert; s heißt dann
auch der Wert oder die Summe der Reihe.
Eine Reihe nenn^ m^n
2=1
• alternierend, falls die Glieder dn abwechselnd verschiedene Vorzeichen haben
absolut konvergent, falls | di | konvergent ist
Wichtige Reihen:
n
1. Sn = ^2(ai + (z - l)d)
2=1
^(2ai + (n - l)d)
o	2-1 Q — -L
2. S„ = > CliQ = «1-----------—
L'	<7—1
für q 1
3. s = diq1 1
2=1
für | q |< 1 absolut konvergent
4. 5^ - divergent
z
2=1
6.	— konvergent für d
5. 5^---------- konvergent
'	7,
1 und divergent für d < 1
74
5 Zahlenfolgen und Zahlenreihen
Konvergenzkriterien für Reihen:
Notwendige Konvergenzbedingung
konvergent
lim an = 0
n—^oo
Wurzelkriterium bzw. Quotientenkriterium
lim \/\an\ lim n+1
n^oo	n^oo dn
< 1
> 1
= 1
IN
____________2=1_____________
absolut konvergent
divergent
Entscheidung so nicht möglich
Leibnizsches Konvergenzkriterium für alternierende Reihen
l)z+1ai mit di > 0 für alle i ist konvergent, wenn{aj eine monotone Null-
2=1
folge ist, d. h., lim an = 0 und an+i < an für alle n > n0-
n—»oo
Maj orantenkriterium
üi ist absolut konvergent, wenn es eine konvergente Majorante bi mit
2=1	2=1
nichtnegativen Gliedern gibt, so dass gilt: | an |< bn für alle n > n0-
Minorantenkriterium
üi ist bestimmt divergent, wenn es eine divergente Minorante bi mit
2=1	2=1
nichtnegativen Gliedern gibt, so dass gilt: an > bn für alle n0 > tiq.
Rechenregeln:
1.	Konvergente Reihen dürfen gliedweise addiert und subtrahiert werden.
2.	Absolut konvergente Reihen dürfen wie Polynome miteinander multipliziert
werden.
3.	Ist üi konvergent (bzw. divergent) und c 0, so ist auch cdi konvergent
2=1	2=1
(bzw. divergent).
Im Falle der Konvergenz gilt:	c • di = Uj.
2=1	2=1
4.	Entfernt man aus einer Reihe endlich viele Glieder oder fügt man endlich viele
Glieder hinzu, so hat das keinen Einfluss auf ihr Konvergenz verhalt en.
5 Zahlenfolgen und Zahlenreihen
75
1. Bestimme den Grenzwert der gege-
benen Zahlenfolge.
( 2n3 — 5n2 + 81
[	7n3 + 2 J
{/	9	\ n+71
(1-------J	1
\	n — 6 J	I
c) {\/4n2 + 3n — 2n}
2. Bestimme den Grenzwert a der
durch das allgemeine Glied
>.	_ 3n + 4	1 -p y/n
a)an~2n + l ^an = —^~
gegebenen Zahlenfolge.
Gib ein no = no(s) derart an, dass
| an — a | < e ist für n > no und kon-
trolliere die Lösung für e = 0, 001 so-
wie für weitere selbst gewählte Werte
von s.
3. Untersuche das Monotonie verhalt en
der gegebenen Folgen und gib den
Grenzwert a an.
, f 2n 1	( n2 1
C)tn2 + lJ d)\n2 + i|
4. Zeige:
Wenn
lim
n—^oo
dann ist
^n+1
CZn
q < 1 gilt,
lim an = 0.
n—?DG
Bestätige damit die folgenden Grenz-
werte:
n
a) lim — =0
2n
n!
c) lim —- = 0
n—»oo fln
b) lim —- = 0
n^oo n!
d) li.» = 0
J (2n)!
b) Cln —	2n(n — l)2 (n + 2)3
	(2n - l)3
c) dn =	(4n — 1)2(1 — 5n)
d) an =	i-ir —-— k J n2 +1
e) &n —	(-ir- fi++
	\ n J
	3 21
f) dn =	
	n y/n
	/5n-2\3
g) CLn =	\3n— 1J
	n — 10
h) dn =	3
	3/ n — 1
i) dn =	A /		
	V 8n + 10
	n
J) an —	\/8n3 — n — n
k) dn =	\/n2 + n — n
dn =	(-0,3)" 3n - 2
	/	1 V
m) an =	: I 1 + —— )
	\ 2n J
	/ 5V+3
n) dn =	1	
	\ n /
o) dn =	
	27loSsn
p) dn =	lßlog2 n
	/	। 0 \ n 1 n + 3 \
q) dn =	\ n — 5 7
6. Gib Beispiele für Zahlenfolgen an,
die
5. Berechne die Grenzwerte der Zah-
lenfolgen, deren allgemeine Glieder
durch die folgenden Terme gegeben
sind:
6n — 3
+ dn —
6 — 5n
a)	monoton wachsen und den Grenz-
wert a = 7 haben
b)	monoton fallen und den Grenz-
wert a = 3 haben
c)	die „oszillierend“ ihrem Grenzwert
a = — 6 zustreben und für die
76
5 Zahlenfolgen und Zahlenreihen
Ko = — 3 eine obere und Ku =
— 12 eine untere Schranke ist
7.	Bestimme die Summe s folgender un-
endlicher Reihen als Grenzwert der
Folge {sn} ihrer Teilsummen:
x 1	1	1
a)	r2 + r3 + F4 + ---
TT . . 1 11
Hinweis:——-----— = ----------
/c(/c + l) k k + 1
. x 1	1	1
b)	"rä	+ Fs +	5~7 +'"
	1
Hinweis:-------—-------	=
(2/c- l)(2/c + l)
1	(	i	1	\
2 \2k- 1 “ 2k+ 1)
8.	Verwandle den gegebenen periodi-
schen Dezimalbruch mit Hilfe der
unendlichen geometrischen Reihe in
einen gemeinen Bruch:
a) 0,25 b) 0,49 c) 0,562
9.	Das 6. Glied einer arithmetischen
Reihe hat den Wert 17, das 26. Glied
den Wert 71.
a)	Welchen Wert hat das 1. Glied?
b)	Welchen Wert hat die Summe der
ersten 40 Glieder dieser Reihe?
10.	In eine Kugel vom Radius r wird ein
Zylinder mit quadratischem Achsen-
schnitt, in diesen die berührende Ku-
gel, in diese wieder ein Zylinder von
quadratischem Achsenschnitt hinein-
gestellt, u.s.w. ad infinit um.
Wie groß ist
a)	die Summe aller Kugelflächen
b)	die Summe der Mantelflächen al-
ler Zylinder
c)	die Summe der Oberflächen aller
Zylinder
d)	die Summe der Rauminhalte aller
Kugeln
e)	die Summe der Rauminhalte aller
Zylinder?
11.	In wie viel Jahren verdoppelt sich
ein Kapital, das zu 5% auf Zinseszins
ausgeliehen worden ist?
12.	Untersuche das Konvergenz verhal-
ten der gegebenen Reihen.
x 10	102	103	104
c)Tr + ir + ^r + vr + -- -
1	2	3	4
^ 2 22 + 1 + 32 + 1 42 + 1
111 1
e)^ + ^ + ^ + lp+'-'
13.	Ist für die folgenden Reihen die not-
wendige Konvergenzbedingung er-
füllt?
14.	Untersuche mit Hilfe des Wurzel-
kriteriums die Konvergenz folgender
Reihen:
5 Zahlenfolgen und Zahlenreihen
77
15.	Untersuche mit Hilfe des Quotien-
tenkriteriums die Konvergenz folgen-
der Reihen:
2^	23	24
a) 2 + 215 + 315 + 415 +   
.24	6	8
b)3 + 9 + 27 + 81+-"
, ,	2	4	8	16
C) 1+2! + 3! + 4!+¥ + "'
£1 (^ + 1)' 3fc
12	23	34	45
e) 2! + 3! + 4! + 5! +
16.	Untersuche mit Hilfe desLeibnizschen
Kriteriums die Konvergenz der gege-
benen alternierenden Reihen.
a) 1,1 - 1,01 + 1,001 - 1,0001 ±
b)l--b + -b--b±...
y/2	y/3	y/4
, 1	22	33	44 ,
c) — — —~ ~b —~ — —- dz . . .
’ 2	32	43	54
„ 1 1 1 1
d) 	 — 	 d- 	 — 	 d~ . . .
J ln2 ln3 ln4 ln5
x 111 11
e) 1 o + o	zb-• •+ 0	zb
2 8 3	n3 n -b 1
schen Reihe die folgenden Reihen auf
Konvergenz:
x	111
a) 1 —I—2= d—7= d—7= d- ...
\/2	y/3 V±
. . sina	sin 2a	sin 3a
b) 1	+	22	+		32 + ’' ’
x 1	1	1
C) 1 + 22	+ 1 + 24 1 1 + 26 + l + 28 +	
„ 1	1 1	1
d) 		F	i	 “b —7	d- 		 d- • • •
7 In 2	In 3 In 4	In 5
18. Untersuche folgende Reihen auf
Konvergenz:
x ,	1	1	1
a) 1 d--= d---7= d---7= + ...
3\/3 5V$ T\H
1	2	3
b 1 + l4 + 1 + 24 + 1 + 34 + ' ’'
. Zv!	.	sin2fc
C) U 4Q5fc	d) gfc
fe=l	fe=l
WV vvvv
k=l	k=l
19.	Für welche (reellen) Werte von x
sind nachfolgende Reihen konver-
gent?
17.	Untersuche durch Vergleich mit der
harmonischen Reihe bzw. mit ei-
ner geeignet gewählten geometri-
g) ^2 & •
k=l
6 Differenzialrechnung für reelle Funktionen
einer Veränderlichen
6.1 Darstellung und Eigenschaften von Funktionen
Zur eindeutigen Bestimmung einer (reellwertigen) Funktion einer (reellen) Verän-
derlichen x gehört die Angabe
•	der Zuordnungsvorschrift (z.B. y = /(x))
•	des Definitionsbereiches D(f) C R
Jedem x e D(f) wird genau ein y aus dem Wertebereich IV(f) zugeordnet,
y E W(/) C R. Bei der Zuordnungsvorschrift unterscheidet man insbesondere
•	die explizite Darstellung: y = /(x), x E D(f)
•	die implizite Darstellung: F(x,y) = 0, x E D(f)
•	die Parameterdarstellung: x = (^(t), y = i/ftt), t E D(p) = D(^)
Zu f : y = /(x), x E D(f) existiert genau dann eine Umkehrfunktion /-1,
wenn f eineindeutig ist:
r1: y = r1(^), x 6 d (r1) = w)	(e-i)
Die Grafen von y = /(x) und y = /-1(x) liegen spiegelsymmetrisch zur Geraden
y = x.
y = /(x), x E D(f) heißt monoton im Intervall I C D(f), wenn für alle
xi, X2 E I mit xi < X2 eine der folgenden Ungleichungen gilt:
1-	/(a;i) < f (^2) (monoton wachsend)
2.	/(xi) < f (X2) (streng monoton wachsend)
3.	f(xi) > f(x2) (monoton fallend)
4.	f(xft) > f(x2) (streng monoton fallend)
y = /(x), x E D(f) heißt
• beschränkt auf E C D(f) genau dann, wenn ein K > 0 derart existiert, dass
gilt:
| f(x) |< K für alle x E E	(6.2)
• gerade (bzw. ungerade), wenn für alle x E D(f) gilt:
/(-z) = (bzw. /(-x) = -/(x))	(6.3)
6.1 Darstellung und Eigenschaften von Funktionen
79
• periodisch mit der Periode p (p > 0), wenn gilt
f(x + p) = /(x) für alle x e D(f)
(6-4)
Durch Verkettung zweier Funktionen y = f(u), u E D(f) und u = p(x), x e D(g)
unter der Voraussetzung W(p) C D(f) erhält man eine mittelbare Funktion von
x:
y = f(glx)), x e D(g)
(6.5)
1. Gib den größtmöglichen Definitions-
bereich D(f) C R für /(x) an.
a) flx) = y/x + 1	
b) fix)	_ 1
	4 — x2
c) fix)	= V'x4 — 2x2
d) fix)	= \/x — X3
e) fix)	.	 1 = yx + 	 y/2 + x
f) flx)	, x2 — 3x + 2 = lg	, 1 X + 1
g) fix)	2x = arccos	 1 + X
h) fix)	= arcsin ( 1g — ) V6 10/
i) fix)	-y/x+J	9 lg(2x 3) V x — 2
j) flx)	= 21/(1-x)
k) fix)	= x — arctanx
1) fix)		2 = arcsin —		lg(4 — x)
.) fix) =	,	1	=
^/| x2 — 2x — 3 |
Hinweis: Intervallschreibweise.
2. Gib den größtmöglichen Definitions-
bereich D(f) C R und den zugehöri-
gen Wertebereich W(f) in Mengen-
schreibweise an.
x ,/ x 3
a) V =	= ------
V X	o
b) y =	fix) =	x — 3
		
		x1 — x — 6
		1 1
c) y = fix) = d) y = fix) = < 3. Skizziere: _ 10		x + 2 x — 2 3 — x2 für x | < 1 2 			 für Lr > 1 l 1 x | _ 2x - 3
y — c) y =	X2 + 1 sinx	V ~ 3x + 2
d) y =	-|x/2f 5	) — X2 7I\
e) y =	5 sm [2x	 \	2/	
f) y =	|x| x2 — 1	g) y = •> • 1
h) y =	x2 — 4	i) y = arcsm — X
4.	Sind die folgenden Funktionen gera-
de, ungerade bzw. weder gerade noch
ungerade? Begründung!
a)	/(x) = — 7 sinx cos x
b)	/(x) = | sinx|
c)	/(x) = 6 e-2x
d)	/(x) = 3x + 7
e)	/(x) = 5x4 — 2x2 + 3
f)	/(x) = lgl±^
1 — X
80
6 Differenzialrechnung für reelle Funktionen einer Veränderlichen
1 4- x2
g)	=ln
5.	Zeige, dass die Funktion
1 - VI + 4a:
V = KX> = i , /V~T:
1 + V1 + 4x
a) f(x + 1) = x2 — 3x + 2
0
streng monoton fallend ist!
Wie lautet ihre Umkehrfunktion ein-
schließlich Definitions- und Wertebe-
reich?
10. Zeige, dass jede auf dem Intervall
[—a,a] definierte Funktion f(x) als
Summe einer geraden und einer un-
geraden Funktion dargestellt werden
kann.
6.	Zeige, dass die Funktion / in ihrem
Definitionsbereich D(f) streng mo-
noton ist.
Gib die inverse Funktion /-1 sowie
ihren Definitionsbereich an.
a)	y = f(x) = y/(x~ 5)3;
D(f) = [5,+oo)
b)	y = f(x) = \/x2 + 1;
Z>(/) = (—oo, 0]
c)	y = f(x) = (x- 3)2;
Z)(/) = (—oo , 3]
d)y = /(x) = ^;
Z>(/) = (-oo, -1) U (-1, +oo)
7.	Löse nach x auf.
A . 3-2x
a) y = y In arcsm —-—
b) y =	--
7 v^TT-3
_ r3x-l । 7
d) y = In
8.	Bestimme /(/(/(z))) , wenn /(x) =
1
9.	Gib /(x) an, wenn gilt:
11.	Von der gegebenen rationalen Funk-
tion mit größtmöglichem Definitions-
bereich D(f) C R sind Nullstellen,
Pole, Lücken und Asymptoten, der
Schnittpunkt mit der Ordinatenach-
se zu bestimmen, die Zerlegung in
eine ganze und eine echtgebrochene
rationale Funktion anzugeben sowie
eine Skizze anzufertigen.
x x x3 — 2x2 — 9x + 18
x2 - 7x + 12
x2 — 4
•2 - 2x + 1
12.	Bestimme die kleinste (primitive)
Periode po der gegebenen periodi-
schen Funktionen.
b) y = f(x) =
a)	/(x) = sin 2x + 3 sin (3x — 2)
—0, 5 cos (0, 8x + 1) + 2
b)	/(x) = sin — + 2 cos —---3 sinl.r
c)	j (x) = tan — — 2 tan —
d)	/(x) = cos2 2x
13.	Zeige, dass die gegebenen Funktio-
nen nichtperiodisch sind.
a)	y = /(x) = cos
D(f) = [0,+oo)
b)	y = /(x) = cosx2; D(f) = R
6.2 Grenzwert einer Funktion
81
6.2 Grenzwert einer Funktion
(Im Folgenden wird stets vorausgesetzt: f ist in einer Umgebung U(xq) der Stelle
xq definiert, eventuell mit Ausnahme der Stelle xq selbst.)
Eine Funktion f hat für x gegen xq den Grenzwert g:
lim /(x) = g oder /(x) —> g für x xq	(6.6)
X^Xq
wenn gilt:
lim f(xn) = g für jede Folge {xn} mit xn e U(xq') \ {xq} und lim xn = xq
n—»oo	ti—?dg
\;
Wählt man hierbei nur Folgen mit xn > xq (bzw. xn < xq), so erhält man den
rechtsseitigen Grenzwert lim /(x) = gr (bzw. den linksseitigen Grenz-
x^x'o+O
wert lim /(x) = gi).
x^xo-0
Es gilt: lim f(x) = g <=^ gr = gi = g.
X^Xq
Eine Funktion heißt bei der Bildung des Grenzwertes, d.h. für x xq,
x xq + 0, x xq — 0, x +oo bzw. x — oo:
•	konvergent, wenn sie einen (endlichen) Grenzwert besitzt
•	bestimmt divergent, wenn sie einen uneigentlichen Grenzwert +oo oder — oo
besitzt
•	unbestimmt divergent, wenn sie weder konvergent noch bestimmt divergent
ist
Grenzwertsätze:
Existieren die Grenzwerte lim /i(x) = pi und lim /2W = P2, so existieren auch
X^X()	X^X()
die folgenden Grenzwerte:
lim (c/i(z)) = c • 51 ( ^Xq	c Konstante)	(6-7)
lim (/i(x) ±fa(x)) = ^Xo	91 ±52 5	Um (/i(x) •/2(a:)) = 51'52 X^Xo	(6-8)
/i(^)	51 (f( hm f , x =	W /2W	52	’) + 0, 52 + 0)	(6-9)
lim (/i(x))/2(a:) = 5?2 Z^Xq	(/i(x) > 0, 51 > 0)	(6.10)
Wichtige Grenzwerte
1.	2- J“. 0 + i)’' = e
82	6 Differenzialrechnung für reelle Funktionen einer Veränderlichen
3. lim (1 + x} x = e
5. lim xx = 1
x^+O
7. lim — = +oo
x^+O X
4.	lim ex x^+0	= oo;	lim ex = 0 x^—0
6.	lim xx x^+0	= 0	
8.	lim — x^-Q X	= —oo	
9. lim arctan —	—
x^+o x	2
10. lim arctan — =---
x^-o x 2
1. Berechne folgende Grenzwerte ohne
Verwendung der Regeln von
Bernoulli-lHospital.
a)
lim
x2 — 2x — 15
x2 - 25
	sin 3x
b)	lim	
	x^Q X
	/ x + 1 \ x2
c)	
	.t^+oc\3.t + 2/
	2x — 2
d)	lim 		r x^l-0 \x — 1
x arcsm7x
e) hm---------
X
,x arcsmx
i) hm---------
x—>0 X
,x _ arctan 2x
1) hm-----------
sin3x
1 — x2
k) lim-------
sin7ur
2x2 — :i
1) lim
7 x^+oo X2 + 10
m) lim (\/x2 + 1 — \Är2 — 1)
x^ + oo
n) lim (1 + tanx)cot
x—X)
\ ,.	f x + 1 \ x
o) hm -----------
— 1 /
2. Bestimme die folgenden Grenzwer-
te ohne Verwendung der Regeln von
Bernoulli-rHospital.
d)
lim
x—>7
2 - Vx^3
x2 — 49
3. Bestimme linksseitige und rechtssei-
tige Grenzwerte der folgenden Funk-
tionen an den angegebenen Stellen.
\	\ sinx c- n
a)	f[x) = -j—p- tur x = 0
b)	fix) = x für x = 2
7 v 7	4 - x2
1
c)	f(x} = e1-^3 für x = 1
d)	f(x} = x für x = — 2
lim
x—^0
sin 7x
2x
.. sinöx
hm------
f)
x—^o sin2x
	1 — COS X
g)	llmn	2
	x^Q	X2 sinx — cosx
h)	hm 	
	1 — tanx
f)	f(x) =  ---——	für x = 1
7 J v 7	| tan (x - 1)|
g)	f(%) = arctan------ für x = 1
1 — x
+ 12 — 3
h)	fix} =-------—-— für x = -3
xz — 9
6.3 Stetigkeit einer Funktion
83
6.3	Stetigkeit einer Funktion
y = /(x) sei in einer Umgebung U(xq) der Stelle x = definiert.
Dann heißt f
•	stetig in xQ	lim /(x) = /(x0)
X^Xq
•	linksseitig stetig in xq	lim /(x) = /(xq)
x^xo-0
•	rechtsseitig stetig in xq < > Um f(x) = f(xo)
x^xo-\-0
•	stetig auf dem Intervall I f ist stetig in jedem x E I
•	unstetig in x$ f ist nicht stetig in xq
f ist genau dann stetig in xq, wenn f links- und rechtsseitig stetig in xq ist.
Die Unstetigkeit in x = x$ ist
•	hebbar durch die Neufestlegung /(xq) = p, falls lim /(x) = g und bisher
X^X()
/(®o) g Oder x0 £ D(f)
•	eine Sprungstelle mit endlichem Sprung, falls lim f(x) = gi,
X—>Xq— 0
lim f(x) = gr und gi gr
x^xo+0
•	eine Unendlichkeitsstelle, falls lim /(x) = lim /(x) = +oo (oder —oo)
x^xo-0	x^xo+0
•	eine Sprungstelle mit unendlichem Sprung, falls lim /(x) = +oo (oder —oo)
x—^xq—O
und lim /(x) = — oo (oder +oo) oder genau einer dieser beiden einseitigen
Grenzwerte endlich ist
Alle elementaren Funktionen sind auf ihren Definitionsintervallen stetig.
Summe, Produkt und Verkettung zweier stetiger Funktionen sind ebenfalls stetig.
Die Kehrfunktion 4 sowie die Umkehrfunktion /-1 einer stetigen Funktion / sind
ebenfalls stetig, sofern diese existieren.
1. Für welche Werte von x besitzen die		e) f(x)	X
folgenden Funktionen Unstetigkeits- stellen und von welcher Art sind die-		f) g) fix')	sinx l^~2|
se? a) /(a?)	= e1^		x — 2 sinx X
b) /(a?)	_ 1		1
	“ l + 2W-i) X	h) f(x)	
c) f(x) d) /(a?)			(x — l)2
	CM 1 1 s 1	1	2. Welcher Wert ist den folgenden Funktionen an der angegebenen Un-	
	x2 — 3x + 2	stetigkeitsstelle zuzuordnen, um die	
84	6 Differenzialrechnung für reelle Funktionen einer Veränderlichen
Unstetigkeit zu beheben?
a)	f(x) = X---------- bei x
b)	/(x) = x sin — bei x = 0
c) f(x) =	sm x	. 	 bei x = 0 X
	x2 + 3x — 10 ,
d) f(x) =	—	-	 bei x = 2 x2 + 4x — 12
e) f(x) =	(1 + xf-l 	 bei x = 0;
n e N \ {0}
ln(l + x) - ln(l - x)
T T) = ---------------------
bei x = 0
g) f(x) = x2 sin — bei x = 0
3.	Warum ist es nicht möglich, die
Funktion
y = /(x) = arctan ——-
für x = 2 so zu definieren, dass /(x)
in x = 2 stetig ist?
4.	Ist die Funktion
_z . f 2x für x e [0,1)
y = f (x) = <
|^3 — x für x e [1,2]
auf dem Intervall [0,2] stetig?
5.	Für welchen Wert von a ist die Funk-
tion
{x In (.r2) für x 7^ 0
r- n
a	tur x = 0
auf dem Intervall (—oo, +oo) stetig?
6.	Wie ist /(0) zu definieren, damit
/(x) = 1 — x sin — auf dem Intervall
I = (—oo , +oo) stetig ist?
6.4	Ableitung und Differenzial einer Funktion
Eine Funktion f : y = /(x), x E D(f) nennt man differenzierbar an der Stelle
xq E U(xq) C wenn der Grenzwert (Differenzialquotient, 1. Ableitung)
..	f(x0 + h) - f(x0)	,	.
hm -------------- = hm------------------- (0.11)
x—^xq X — Xq	h^Q	h
existiert. Dieser Differenzialquotient wird auch wie folgt bezeichnet:
dy = d/Q)
dx x=Xq dx
(6.12)
Bei der linksseitigen (bzw. rechtsseitigen) Ableitung ist in (6.11) x x$
oder h 0 durch x x$ — 0 oder h —0 (bzw. x x$ + 0 oder h +0) zu
ersetzen.
Eine Funktion f ist differenzierbar auf einem Intervall /, wenn f in jedem
inneren Punkt von I differenzierbar und in den zu I gehörigen Randpunkten ent-
sprechend einseitig differenzierbar ist.
Geometrisch bedeutet die 1. Ableitung den Anstieg der Tangente im Punkt
Pq (x0;/(x0)):
6.4 Ableitung und Differenzial einer Funktion
85
Allgemeine Differenziationsregeln:
Sind /i und auf dem Intervall I differenzierbar, so gilt auf I:
•	(c • /i(x))z = c • /i(x) (c Konstante)
•	± AC^))' = fi(x) ± /2W
•	(/iW • h(x))' = f[(x)  f2(x) + /i(x) • f2(x) (Produktregel)
. ((M,;)
\h(x)J	(h(x))
Kettenregel zur Ableitung einer mittelbaren Funktion
Ist g an der Stelle xq und f an der Stelle zq = g(#o) differenzierbar, dann ist die
Verkettung y = /(#(#)) an der Stelle differenzierbar, und es gilt
d/(g(a;))
dx
= f'(z0) -g'lxo) mit z0 = g(x0)
x=x0
(6-14)
. 1 äy
oder kurz: —
dx
dy dz
dz dx
Ableitung der Umkehrfunktion
Ist y = /(x) in einer Umgebung U von x$ differenzierbar und ist f'(x) 7^ 0 für
alle x E U, so ist f dort auch umkehrbar, d.h. es existiert x = f~r(y) und für
yo = f(x0) gilt
4-/ 1(yo) = (f 1(yo')Y = x
dy	f(x0)
(6.15)
_	_ d.r l
oder kurz:	.
dy dy
y dx
Ableitung von y = (/(^))^^^
Sind /(x) und p(x) differenzierbar mit /(x) > 0, dann ist auch y =
86
6 Differenzialrechnung für reelle Funktionen einer Veränderlichen
differenzierbar:
y =	=e9(.^nf(.X)
=^y' = (f9)' =	 (g'W in f(x) + gW/Z(a:)) (6.16)
Höhere Ableitungen:
Ist die 1. Ableitung y' = f(x) bei x = differenzierbar, so schreibt man für die
2. Ableitung
y"(xo) =

X = Xq
Xy
d.r2
x=x0
d2/(z)
dx2
x=x0
(6.17)
= f"(x0) =
und schließlich (wenn die entsprechenden Voraussetzungen erfüllt sind) für die
n-te Ableitung

dxn
(6.18)
X=Xq
Differenzial:
Ist /'(x) die 1. Ableitung der Funktion f : y = /(x), x e D(f) an der Stelle x, so
nennt man
dy=f'(x)dz
(6.19)
das Differenzial von f an der Stelle x.
dy = f'(x) dx
Ay = f(x + dz) - /(z)
Für hinreichend kleine Werte von Ax = dx gilt die Näherungsformel
Ay « dy
(6.20)
6.4 Ableitung und Differenzial einer Funktion
87
1.	Bilde von folgenden Funktionen die
1. Ableitung:
r3
a) y = —— 2x2 + 4x — 5 7
O
b) y =	— övCr2 + 4 vC? X6 5x2 — 3y/x + 3x3 y/x
c>y -	„ 31-^2 2vr

d) y - .	2 1 - XZ
e) y = \Jx\J3x^2x
3x2 + 6x — 1
fh/= 3 0 l7 xö — 2x + 7
g) y = In 01
n x	9 sinx	7 h) y = 3x2			H 27 tan x
..	cosx tanx
b y =	2	/-
Xz	y/X
cosx
j) y = ,
1 — sm x
k) y =	1
xJX + 1
1) y = x In x — 1g (5x3)
x	1 + In x
m) y =
X
n) y = 2x3 ex — 3X + e5
x	7x2 — 6x
°)y = ex
2. Wie lautet die Formel für die 1. Ab-
leitung eines Produktes
a)	mit drei Faktoren:
y = u(x) • v(x) • w(x) = uvw
b)	mit vier Faktoren:
y = u(x) • v(x) • w(x) • z(x) =
uvwzl
Hinweis: Produktformel.
3.	Die Funktion
y = /OO = -x +	2)2
ist definiert für x e (—oo , +oo).
In welchem Bereich ist sie stetig, in
welchem differenzierbar?
Gib die Ableitung f'(x) an.
Skizziere den Graphen von y = /(x).
4.	In welchem Bereich sind die folgen-
den Funktionen stetig, in welchem
differenzierbar? Gib die 1. Ableitung
an.
a)	y = fix') = Oh
Df = (—oo , +oo)
b)	y = /(x) = | sinx|, Df = [0,2tt]
5.	Bilde von folgenden Funktionen die
1.	Ableitung:
a)	y =----------.
(1 + x2)\/l + x2
b)	y = \Jx + 2^x-, /'(l) =?
c)	y = In tan (3x + 2)
d)	y = In (x + \A‘2 + a2)5 & 7^ 0
f)	y = a • ebx coscx
g)	y = In | lnx|
x
h)	y = In tan —
1 — sinx	
y —	V 1 + sin x (X 7I\
j) y =	In tan —|- — \2	4/
k) y =	x4 /	2	1\ — (Inx) — In x/x H— 4 V	8/
1) y =	^\/ x2 — 25
	25	z		> — — In	+ \/x2 — 25
1 + \Ah2 + 1	/ 2 I 1
m) y = In---------------y x 1
x
n) y = 2 (ex/2 — e-x/2)
88
6 Differenzialrechnung für reelle Funktionen einer Veränderlichen
x 1+e~3x
°) ^ = ! _ e-3a;
Hinweis: Kettenregel beachten!
6.	Bilde von folgenden Funktionen die
1.	und die 2. Ableitung:
a)	y = y(t) = sint • cost
b)	x = x(t) = cos2 t
c)	v = v(s} = —-—
s — 1
d)	w = w(s) = s4 In s
x3
e)	y =	= —y
7.	Bilde von folgenden Funktionen die
ersten vier Ableitungen:
a) y = sin x b) y = In x
c) y = vx + 1 d) y = cos3x
8.	Zeige, dass die angegebene Funktion
/(x) Lösung der betreffenden Diffe-
renzialgleichung ist.
ln(l+x)
a)	y = —-------—, a reell,
7 y (1 + x)<* ’
ist eine Lösung von
(1 + x)^ + ay = (1 + x)~a
dx
b)	y = Ci e~x +C2 e~2x ist eine Lö-
sung von y" + 3y' + 2y = 0
9.	Bilde von folgenden Funktionen die
1.	Ableitung:
a)	y = 10x-3x; x > 0
b)	y = xx/lnx; x > 0
c)	y = (tan:i‘)1//cos'T; 0 < x <
i\	x ~ 1
d)	y = exp ——-
x + 1
e)	y = xx- x > 0
f)	y = x1^; x > 0
Hinweis: Formel (6.16).
10.	Beweise:
a)	Die 1. Ableitung einer geraden
Funktion ist eine ungerade Funk-
tion.
b)	Die 1. Ableitung einer ungeraden
Funktion ist eine gerade Funkti-
on.
c)	Die 1. Ableitung einer periodi-
schen Funktion ist wieder eine pe-
riodische Funktion.
11.	Bilde von folgenden Funktionen die
1.	Ableitung:
a)	y = x • arctanx — In
q x 1
b)	y = arccos —
c)	y = arcsin \ 2x y 1 — x2 j
d)	y = cosh3 x2
e)	y = In cosh (ax + 6), a 0
f)	y = - (x2 + sinh2 x)
y = x arsinh x — \/^2 + 1
y = (arctanx)'1', x > 0
g)
h)
1—	2x -|- 1
+v 3 arctan-----
Vs
j)
y = In
+ 2 arctanx
k)
y =
1) y = Inarctanx
m) y = cosh (sinx)
n) y = tanh3 x2
o)	y = arcsin (tanhx)
p)	y = ä/1 + sinh2 4x
q)	y = \/4x — 1 + arccot \/4x — 1
Hinweis: Ableitung der Arkus-, Hyperbel-
und Areafunktionen.
12.	Bestimme den allgemeinen Ausdruck
für y(n\ wenn gegeben ist:
6.4 Ableitung und Differenzial einer Funktion
89
a) y =	b) y = eax
1 — X
c) y = \fx d) y = sin2 x
13.	Gegeben ist f (x) =	2 •
Zeige:
n\ für n = 2m
0 für n = 2m — 1
Hinweis: Beachte die Identität
1 _ 1 / 1 1 \
1 — x2 2	+ 1 - x J
ftn\0) =
14.	Durch dreimalige Differenziation der
Identität
(x — l)(x2+x3H----\-xn) = xn+1 — x2
nach x und anschließende Substituti-
on x = 1 ist die Summe
y>:-i)= (" + 1”‘("-1)
k=l
und schließlich die Summe der Quad-
rate der ersten n natürlichen Zahlen
(ausschließlich 0)
n
£ fc2 = p + 22 + ... + n2 =
fc=i
n(n + l)(2n + 1)
6
zu bestimmen.
15.	Berechne f (2), /'(2) und //z(2) für
a • 1
j(x) = arcsm —.
16.	Zeige, dass für /(x) = xn gilt:
, Hi) , r(i),
1!	2!
, /H(!) =9n
+ n\
17.	Ein Punkt bewege sich auf der
x-Achse und habe zum Zeitpunkt t
die Koordinate x = f(t). Dann sind
in diesem Zeitpunkt seine
dx
Geschwindigkeit v = —
dx d2x
Beschleunigung a =
dt dt2
a)	Ein Körper bewegt sich auf der
x-Achse nach dem Gesetz
t3 2
x =-----2t2 + 3t.
o
Bestimme Geschwindigkeit und
Beschleunigung der Bewegung.
Zu welchen Zeitpunkten ändert
der Körper die Richtung der Be-
wegung?
b)	Die Schwingung eines Masse-
punktes um seine Ruhelage wird
durch das Gesetz x = A cos axt be-
schrieben. Bestimme Geschwin-
digkeit und Beschleunigung der
Bewegung für x = und
x = 0. Zeige, dass die Beschleu-
d2x
nigung —- und die Auslenkung
dt2
x durch die Differenzialgleichung
x = —cx2x Zusammenhängen.
c) Ein Gefäß von der Form einer
Halbkugel vom Radius r wird mit
einem konstanten Wasservolumen
je Zeiteinheit v gefüllt. Bestim-
me die Steiggeschwindigkeit des
Wasserspiegels, wenn dieser be-
reits die Höhe h aufweist.
Zeige, dass diese Steiggeschwin-
digkeit umgekehrt proportional
dem Flächeninhalt der freien
Oberfläche der Flüssigkeit ist.
Hinweis: Das Volumen eines Kugelseg-
mentes beträgt
V = V(h)=7th2 (r-
Beide Seiten dieser Gleichung differen-
ziere man nach t, dabei ist in unserem
Fall = v,
dt
d)	Die Abhängigkeit der Menge x ei-
nes Stoffes, der bei einer gewis-
sen chemischen Reaktion gewon-
nen wird, von der Zeit t wird
90
6 Differenzialrechnung für reelle Funktionen einer Veränderlichen
durch die Gleichung x = A(1 —
e~kt) ausgedrückt. Bestimme die
Reaktionsgeschwindigkeit.
e)	Ein Körper wird aus einer Höhe
von 10 m über dem Boden vertikal
nach oben geschleudert. Dabei er-
hält er eine Anfangsgeschwindig-
keit von 20 m • s-1.
Welche Höhe x über dem Boden
hat er nach der Zeit t erreicht? Be-
stimme Geschwindigkeit und Be-
schleunigung der Bewegung. Nach
wie viel Sekunden hat der Kör-
per seinen höchsten Punkt er-
reicht und in welcher Höhe über
dem Boden befindet er sich dann?
18.	Bestimme die Differenziale der gege-
benen Funktionen.
a)	y = xn
b) y = \/l +
c)	r =	= 2<p — sin2(/?
d)	h = h(t) = sin2 t
e)	z = z(tp) = cos
19.	a) y = x2; bestimme den Nähe-
rungswert dy der Änderung Ay
von y, wenn x von 2 nach 2,01
geht.
b) y = \/x; bestimme den Nähe-
rungswert der Änderung von y,
wenn x von 100 nach 101 geht.
Vergleiche jeweils die Näherungs-
werte mit den exakten Werten.
20.	a) Die Kantenlänge eines Würfels ist
x = 5 m ± 0, 01 m. Bestimme den
absoluten und den relativen Feh-
ler bei der Berechnung des Wür-
felvolumens.
b) Die Länge eines Telegrafendrah-
/	2/2\
tes ist s = 2b 1 H--— , wobei
\ 3bz)
2b der Abstand zwischen den Auf-
hängepunkten und f die Pfeilhö-
he der Durchhängung ist. Um wie
viel vergrößert sich diese Durch-
hängung /, wenn sich der Draht
durch Wärmewirkung um ds aus-
dehnt?
21.	a) Mit welcher Genauigkeit muss
man die Abszisse der Kurve y =
x2\fx im Bereich x < 4 messen,
damit der Fehler bei der Berech-
nung ihrer Ordinate den Wert 0,1
nicht übersteigt?
b) Mit welcher relativen Genauigkeit
muss man den Radius einer Kugel
messen, damit der relative Fehler
bei der Berechnung des Kugelvo-
lumens 1% nicht übersteigt?
7 Mittelwertsätze der Differenzialrechnung und
Taylor-Formel
7.1 Mittelwertsätze
Satz 7.1 (Satz von Rolle) /(x) sei stetig auf [a^b], differenzierbar auf (a,b) und
f(a) = f(b). Dann existiert mindestens eine Stelle £ e (a, 6), an der gilt:
m = o
(7.1)
Satz 7.2 (Mittelwertsatz) /(x) sei stetig auf [a, b] und differenzierbar auf
Dann existiert mindestens eine Stelle £ e (a, 6), an der gilt:
f(b) - f(a)
b — a
=/'(£)
(7-2)
Oder: Unter den gemachten Voraussetzungen existiert zu je zwei (voneinander
verschiedenen) Werten x E (a, b) und xq E (a, b) mindestens eine Stelle £ zwischen
xq und x, an der gilt:
f(x) - /(a?o) =
X — Xq
bzw.
(7-3)
f(x) = /(a?0) + (a? - z0) • /'(£)	(7.4)
bzw. (mit h = x — xq):
f{xQ + hf) = /(x0) + h • f\xQ + t%), (0 < t? < 1)	(7.5)
Satz 7.3 (erweiterter Mittelwertsatz) f(x) und g(x) seien stetig auf [a, b]
und differenzierbar auf (c^b) mit g'(x)	0 für alle x E (a,b). Dann existiert
mindestens eine Stelle £ E (a^b), an der gilt:
fX) - f(a) /'(£)
p(&) - g(a) p'(£)
(7-6)
1. Kontrolliere, ob sich tatsächlich zwi-
schen den Nullstellen der Funktion
/(x) = x1 2 — l.r + 3 eine Nullstelle
ihrer Ableitung befindet. Deute den
Sach verhalt geometrisch.
2.	Ist der Satz von Rolle für die Funk-
tion /(x) = 1 — im abgeschlos-
senen Intervall [—1,1] anwendbar?
Deute den Sach verhalt geometrisch.
92	7 Mittelwertsätze der Differenzialrechnung und Taylor-Formel
3.	In welchem Punkt ist die Tangen-
te an die Parabel y = x2 parallel
zu der Sehne, die die Parabelpunk-
te A(—1; 1) und B(3;9) verbindet?
4.	Stelle für die gegebenen Funktionen
auf dem angegebenen abgeschlosse-
nen Intervall die Formel des Mittel-
wertsatzes der Differenzialrechnung
auf und bestimme £.
a)	/(x) = x — x3; x e [—2,1]
b)	f(x) = arctanx; x E [0,1]
c)	/(x) = arcsinx; x E [—1,0]
d)	/(x) = Inx; x E [1,2]
5.	Sei /(x) = x(x + l)(x + 2)(x + 3).
Zeige, dass die Gleichung /'(x) = 0
drei reelle Wurzeln besitzt.
6.	Gehe vom Mittelwertsatz der Diffe-
renzialrechnung in der Form f(x +
Ax) — /(x) = Ax • /'(x +1? • Ax) aus,
0 < i? < 1. Stelle diese Formel für die
Funktionen
a) f(X) =X2 , b) /(x) = x3
auf. Zeige, dass $ im Falle a nicht von
x abhängt, bei der Funktion b von x
und Ax abhängig ist.
7.	Beweise mit dem Mittelwertsatz der
Differenzialrechnung die Richtigkeit
der folgenden Ungleichungen:
a)	ex > 1 + x für x > 0
b)	V1 + x < 1 +	für x > 0
c)	1	> 1 —	für x > 0
7 yr+^ 2
8. Zeige, dass gilt:
x/TÖT =10 +
1
2yT00 + tf
für 0 < 1? < 1 und bestätige damit
die Abschätzung
io + l<yiol<1o+l
9. Stelle für die folgenden Funktionen
die Formel des erweiterten Mittel-
wertsatzes der Differenzialrechnung
auf und bestimme £.
a)	/(x) = sinx; p(x) = cosx;
x £ [0, 2 ]
b)	= X2', g(x) = y/x',
x E [1,4]
c)	/(x) = x2 + 2; p(x) = x3 — 1;
x E [1,2]
7.2 Grenzwertsätze von Bernoulli-l’Hospital
/(x) und p(x) seien in einer Umgebung U von xq (aber nicht notwendig in xq
selbst) differenzierbar, ferner sei pz(x) 0 in jedem inneren Punkt von U.
Ist dann
lim /(x) = lim p(x) = 0,
X^Xo	X^X0
SO gilt
hm —— = hm —-
^XO p(x) X^xo g\x)
(7-7)
(7-8)
ist
lim /(x) = lim p(x) = +oo (oder -oo),
X^Xq
(7-9)
7.3 Taylor-Formel
93
so gilt
r /(n r Hn
hm —- = hm ——,
g(x) x^x0 g (x)
(7-10)
falls in (7.8) bzw. (7.10) der jeweils letzte Grenzwert existiert oder ein uneigent-
licher Grenzwert ist (d.h. +oo oder —oo).
Dieser Satz gilt auch für einseitige Grenzwerte, für x +oo und für x — oo.
Grenzwerte vom Typ „0 • (±oo)“, „l±o°“, ,,(+oo)°“, „0°“, „(+oo) — (+oo)“ werden
durch Umformungen auf die oben besprochenen Typen oder gebracht.
1. Bestimme die folgenden Grenz-
werte mit der Regel von
Bernoulli-l ’Hospital.
.. sinöx
hm--------
x—^o 3x
n ex -1
hm--------
x—^o sin 2x
a)
b)
c)
lim
d)
f)
g)
h)
lim —---
x^i Imr
1 — cosnx ,	,	1 , .
hm -------—, (a ^0, ö^O)
x—^Q 1 — cos bx
_	1 — COS X
hm---------
x—^Q X2
.. x — sinx
hm---------
x^O Xö
_ tanx — sinx
hm-------------
x—^o x — sinx
lim
lim
k)
_ In.r
hin ------
.. In.r
hin -------
cot X
.	tanx
m) hm ---------
-o tan 3x
n) lim (71 — x) tan —
X—>7T —0	2
o)	lim x In x
x^+0
p)	lim xn • e (n > 1)
x^ + oo
q)	lim xx
x^+0
r)	lim (sinx)tan
.T^ + 0	7
f 3 \
s)	lim ( 1 H— )
x^+oo y x J
In (1 + x2)
x.li+oc	\
In-----arctan x
\2	J
u) lim x1^
x^ + oo
lim (
2
x2 — 1
w) lim (1 + sin2 x)x/tan
x) lim
x^Q
y) lim
7.3 Taylor-Formel
Satz 7.4 (Taylorsche Formel für Polynome)
/(x) = Pn(x) = a0 + a±x + a2x2 H--F anxn, (an 0),
(7.11)
94
7 Mittelwertsätze der Differenzialrechnung und Taylor-Formel
dann gilt für die Entwicklung an der Stelle x = xq:
/(a?) = f(x0) H-— (x - x0) H---—(a? - z0) + ...
+ ^f^x-xor (7.12)
n\
(Das absolute Glied /(xq) sowie die Koeffizienten	,...,	kann
man mit dem vollständigen Horner-Schema berechnen, vgl. Abschnitt 2.2.)
Satz 7.5 (Taylor-Formel) /(x) sei auf [a, b] n-mal stetig differenzierbar und
auf (a, b) (n + l)-m,al differenzierbar. Dann gilt für zwei Werte xq,xE (a, b):
/(x) = /(x0)H-----— (x-xq)H----------—(x-xq) +...
+ ^f^^x - x0)n + Rn (7.13)
n\
mit dem Lagrangeschen Restglied:
Rn = /(W+1)(^° + xo)) (X - x0)n+1-, 0<tf<l.	(7.14)
(n + 1)!
Für xq = 0 erhält man aus (7.13) als Spezialfall die MacLaurinsche Formel:
/w./(0)+ffll+m?+...+^..+fl„	(7,5)
_.n+l
Rn = r—v..f{n+1\'&x), 0 < $ < 1.	(7.16)
(n + 1)!
Taylor-Entwicklung von f an der Stelle xq :
Ist /(x) bei x = xq beliebig oft differenzierbar und gilt
lim Rn = 0	(7.17)
n^oo
für alle x aus einer Umgebung von xq, so gilt dort
=	(7.18)
i=0 l-
7.4 Relative Extrema, Kurvendiskussion
95
1.	Entwickle
a)	f (x) = 3 + llx — 9x2 + 2x3 nach
Potenzen von (x — 2),
b)	f(x) = —1000 + 300(x + 5)
—30(a? + 5)2 + (x + 5)3
nach Potenzen von x,
c)	/(x) = x4 — x2 nach Potenzen von
(x + 3)
unter Verwendung
1.	der Formel (7.12)
2.	des vollständigen Horner-
Schemas.
2.	Entwickle	f (x)	nach der
7ß?/Zor-Formel an der angegebenen
Stelle x = xq bis zum Glied n = 3
einschließlich. Das Restglied Rq ist
nicht explizit anzugeben.
a)	/(x) = e2x-a+ Xq = 0
b)	/(x) = xx — 1; Xq = 1
c)	f (x) = sin (sinx); xq = 0
3.	Entwickle	f (x)	nach der
7h?/Zor-Formel an der angegebenen
Stelle x = xq bis zum Glied n = 4.
Das Restglied R\ ist nicht explizit
anzugeben.
a)	y = /(x) = +; xq = 2
yx
X 1 + x + x2
b)	JW = ;------;—2? x° = 0
1 - x + xz
4. Entwickle mit Hilfe der 7h?/Zor-Formel
a)	/(x) = ex nach Potenzen von
(x + 1) bis zum Glied mit (x + l)3
b)	/(x) = Inx nach Potenzen von
(x — 1) bis zum Glied mit (x — l)2
und gib das Lagrangesche Restglied
an.
um nicht mehr als -h2 ab-
2
5. Zeige, dass sin(xo + h) von sinxo +
h COS Xq
weicht.
6. Schätze
den Fehler der Formel e
1 1 n
3! + 4! !,b'
7.	Zeige, dass die Kettenlinie
y = a • cosh — für |x| < a näherungs-
a	x2
weise durch die Parabel y = a 4----
2a
ersetzt werden kann (a > 0). Schätze
den Fehler ab.
8.	Berechne In 1, 5 nach der Näherungs-
formel
9	9	4
,	k	«Ay	«Ay	«Ay	_
ln(l + x)	x-----— + —------- und
v 7	2	3	4
schätze den Fehler ab.
9.	Berechne mit Hilfe der Taylor-Formel
sinh 0,75 auf sechs Stellen hinter
dem Komma genau.
10.	Entwickle /(x) = sin2 x an der Stel-
le x = 0 nach der Taylor-Formel und
zeige, dass lim Rn = 0 für |x| < oo
n—^oo
gilt.
7.4 Relative Extrema, Kurvendiskussion
/(x) sei auf [a, b] stetig und auf (a, b) differenzierbar; dann ist /(x) auf [a, b]
•	monoton wachsend, falls /z(x) > 0 für alle x G (a, 6);
•	streng monoton wachsend, falls /z(x) > 0 für alle x G (a,6);
•	monoton fallend, falls /z(x) < 0 für alle x G (a, b);
•	streng monoton fallend, falls /z(x) < 0 für alle x G (a, 6).
96
7 Mittelwertsätze der Differenzialrechnung und Taylor-Formel
/(x) hat an der Stelle xq ein relatives (oder lokales) Extremum, wenn eine
Umgebung U(xq) C D(f) derart existiert, dass
•	/(x) < /(xq) für alle x E U(xq) \ {xq} (d. i. relatives Maximum bei xq)
•	/(x) > /(xq) für alle x E U(xq') \ {xq} (d. i. relatives Minimum bei xq)
Gilt /(x) < /(xq) (bzw. /(x) > /(xq)) für alle x E D(f) \ {xq}, so liegt bei xq ein
absolutes Maximum (bzw. ein absolutes Minimum) vor.
Um die folgende Darstellung straffen zu können, wird vorausgesetzt, dass /(x) an
der Stelle xq hinreichend oft differenzierbar ist.
Für ein relatives Extremum oder einen Wendepunkt mit waagerechter Tangente an
der Stelle xq ist
/'(^o) = 0	(7.19)
notwendig und
/'(z0) =/"(z0) = • • • == 0	An >2	(7.20)
hinreichend.
Ist n gerade, so liegt bei xq ein relatives Extremum vor und zwar
•	ein relatives Minimum, falls /(n\xo) > 0;
•	ein relatives Maximum, falls f(n\xo) < 0.
Ist n ungerade, so liegt bei x$ ein Wendepunkt mit waagerechter Tangente vor.
Für einen Wendepunkt an der Stelle x$ ist
/"(xo) = 0	(7.21)
notwendig und
/"(xo) =/"'(xo) = ••• == 0
A /^n\xo) 7^ 0 A n > 3 A n ungerade (7.22)
hinreichend.
f(x) ist auf dem Intervall I
•	von unten konvex genau dann, wenn f”(x) > 0 für alle x E I,
•	von unten konkav genau dann, wenn f"(x) < 0 für alle x E I.
Streng konvexes bzw. streng konkaves Verhalten auf I liegt vor für f"(x) > 0 bzw.
f"(x) < 0 für alle x E I.
Die Kurvendiskussion dient der Untersuchung von Funktionsgraphen, wobei
insbesondere die Möglichkeiten der Differenzialrechnung angewendet werden.
Dabei ist es zweckmäßig, u. a. auf folgende Eigenschaften zu achten:
7.4 Relative Extrema, Kurvendiskussion
97
1.	Symmetrie-Eigenschaften
2.	Schnittpunkte mit den Koordinatenachsen
3.	Unstetigkeitsstellen
4.	Extremalpunkte
5.	Wendepunkte und Tangenten in den Wendepunkten
6.	Konvexität und Konkavität
7.	Verhalten für x +oo bzw. für x — oo, asymptotisches Verhalten
8.	Periodizität.
Sind /(x) und g(x) z.B. auf [a, oo) definiert und gilt lim (/(x) — p(x)) = 0,
dann ist der Graph von g eine asymptotische Linie des Graphen von f und
umgekehrt, d.h., die eine Kurve nähert sich der anderen um so mehr, je weiter
man sie durchläuft. (Entsprechendes gilt für ein Intervall (—oo,a] und x — oo.)
1. Bestimme für die gegebenen (reel-
len) Funktionen den größtmöglichen
Definitionsbereich, die lokalen Extre-
malpunkte sowie die Intervalle, auf
denen sie streng monoton wachsen
oder streng monoton fallen.
a) /(x) = cosh2 x + 1
b) f(x)
2;j:~ — 1
X4
c) /(a?)
d)
= xy/1 — X2
X
Inx
e) /(x) = x — 2 sinx
2.	Auf welchen Intervallen sind die
gegebenen Funktionen von unten
streng konvex oder von unten streng
konkav?
a)/(x)=x3; D(f) = (-00, +00)
b)/(x) = ea:; £>(/) = (-00,+00)
c)
£>(/) = (-00,-1) U (-1,1)
u(l, +00)
3.	Bestimme die Extremalpunkte der
folgenden Funktionen:
a)	/(x) = 2x + 3 vCr2:
D(/) = (-00,+00)
b)	/(x) = In \/l +	+ arctanx;
D(/) = (-00,+00)
c)	/(x) = 2x ex~2 +4 ex~2 —x2 — 6x;
D(/) = (-00,+00)
d)	/(x) = sin3 x + cos3 x;
D(/) = [0,27t)
e)	/(x) = |(x — 4) • cosh (2x + 3)
— - sinh (2x + 3);
D(/) = (—oo, Too)
f)	/(x) = - (x2 — 6x + 5) • In (x — 1)
D(/) = (l,+oo)
g)	/(x) = x(ln x)2 — x In x + x;
D(/) = (0,+oo)
4.	Bestimme den größten und den
kleinsten Wert der gegebenen Funk-
tionen in ihrem Definitionsbereich:
a) /(x) = y/x(10 - x);
B(/) = [0,10]
98
7 Mittelwertsätze der Differenzialrechnung und Taylor-Formel
b) f(x) = x3 — 3x ± 3;
W) =
3 5
2’2
5.	Bestimme die lokalen Extrema sowie
die Wendepunkte der GW/?-Kurve
y = /(x) = e~x ; —oo < x < ±oo.
Untersuche das Verhalten von y für
x ±oo.
Stelle die Kurve graphisch dar.
6.	Führe für die gegebenen (reellen)
Funktionen eine Kurvendiskussion
durch. Ermittle zunächst den größt-
möglichen Definitionsbereich, auch
den Wertebereich, und skizziere ab-
schließend den Graphen der Funkti-
on.
a) y = f{x)
b) y = f(x)
c)y = f(x)
d) y = f(x)
e) y = f[x)
f) y = f(x)
g) y = f(x)
h) y = f(x)
i) y = fix)
j) y = fix)
k) y = fix)
1) y = fix)
= 2x3 - 6.c2
= x2(9 — x2)
= -x3 — x2 — 3x
ö
_ 2x2 ± 1
x2 — 9
x2 ± x ± 14
x ± 2
x ± 3
x — 3
- 6
3 ± x2
x ± 2
yTr
= y/x{x2 ~ 9)
= x2 In x
= xex
3x2 — 9x ± 6
x2 ± 2x ± 1
Extremwertaufgaben
7.	Eine an ein Haus angrenzende recht-
eckige Fläche von möglichst großem
Inhalt soll durch einen Zaun mit ei-
ner Länge von 120 m eingezäunt wer-
den. Bestimme die Abmessungen der
rechteckigen Fläche.
8.	Zerlege die Zahl 10 so in zwei Sum-
manden, dass deren Produkt mög-
lichst groß wird.
9.	In ein Dreieck mit der Grundlinie a
und der Höhe h ist ein Rechteck mit
möglichst großem Flächeninhalt ein-
zubeschreiben. Bestimme den Flä-
cheninhalt des Rechtecks.
10.	Aus einem quadratischen Stück Pap-
pe mit der Seite a werden an den
Ecken gleich große Quadrate heraus-
geschnitten; aus dem übriggebliebe-
nen Teil wird ein rechteckiger Karton
zusammengeklebt. Wie lang muss ei-
ne Seite des auszuschneidenden Qua-
drates sein, damit der Rauminhalt
des oben offenen Kartons möglichst
groß wird?
11.	Bestimme die Abmessungen eines
(oben offenen) Bassins mit quadrati-
scher Bodenfläche, das ein Volumen
von 32 m3 hat, wenn für den Anstrich
seiner Wände und seines Bodens ei-
ne möglichst geringe Materialmenge
verbraucht werden soll.
12.	Die Schenkel und die kleinere
Grundlinie eines Trapezes sind je
10 cm lang. Bestimme seine größe-
re Grundlinie so, dass der Flächen-
inhalt des Trapezes möglichst groß
wird.
13.	Einem Halbkreis wird ein Trapez
einbeschrieben, dessen eine Grundli-
nie der Halbkreisdurchmesser ist. Be-
stimme die Basiswinkel des Trapezes
so, dass der Flächeninhalt des Tra-
pezes möglichst groß wird.
7.4 Relative Extrema, Kurvendiskussion
99
14.	Der Querschnitt eines Tunnels ha-
be die Form eines Rechtecks mit
aufgesetztem Halbkreis. Der Umfang
des Querschnitts beträgt 18 m. Für
welchen Halbkreisradius wird der
Flächeninhalt des Querschnitts am
größten?
15.	Zwei Lichtquellen befinden sich 30 m
voneinander entfernt. Ermittle auf
der die Lichtquellen verbindenden
Geraden den am schwächsten be-
leuchteten Punkt, wenn sich die Stär-
ken der Lichtquellen wie 27 : 8 ver-
halten.
16.	Zwei Flugzeuge fliegen in einer Ebe-
ne und geradlinig unter einem Win-
kel von 120° mit gleichförmiger Ge-
schwindigkeit v. Zu einem gewissen
Zeitpunkt erreicht das eine Flugzeug
den Schnittpunkt der beiden Bahn-
kurven, während das zweite Flug-
zeug noch um die Strecke s von die-
sem Punkt entfernt ist. Nach wel-
cher Zeit t wird die Entfernung bei-
der Flugzeuge voneinander möglichst
gering, und wie groß ist diese mini-
male Entfernung?
17.	Ein Balken rechteckigen Quer-
schnitts, der an den Enden frei auf-
liegt, wird in seiner gesamten Länge
gleichmäßig belastet. Die Pfeilhöhe
seiner Durchbiegung ist umgekehrt
proportional dem Trägheitsmoment
Q
n	n	n • t XV
des Balkenquerschnitts J =
wobei x und y die Abmessungen des
Balkens sind. Bestimme die Abmes-
sungen eines Balkens mit möglichst
kleiner Pfeilhöhe der Durchbiegung,
wenn der Balken aus einem kreis-
runden Stamm des Durchmessers d
herausgeschnitten werden soll.
18.	Wie groß ist das Volumen einer Ku-
gel in Bezug auf das Volumen des
größten Zylinders, der in diese Ku-
gel einbeschrieben werden kann?
19.	Zwei Korridore der Breite 2,4 m und
1,6 m schneiden einander unter ei-
nem rechtem Winkel. Bestimme die
größte Länge einer Leiter, die man
(horizontal) aus dem einen Korridor
in den anderen tragen kann.
20.	Einem geraden Kreiskegel mit dem
Radius 4 dm und der Höhe 6 dm wird
ein Zylinder maximalen Volumens
einbeschrieben. Bestimme dieses ma-
ximale Volumen.
21.	Einem Halbkreis mit dem Radius r
wird ein Rechteck maximalen Flä-
cheninhalts einbeschrieben. Bestim-
me die Abmessungen dieses Recht-
ecks sowie seinen Inhalt.
22.	Ein Bild wird an die Wand gehängt.
Sein unterer Rand ist um die Län-
ge 6, sein oberer um a höher als
das Auge eines Betrachters über dem
Boden, a > b. In welcher Entfer-
nung von der Wand muss der Be-
trachter stehen, um das Bild unter ei-
nem möglichst großen Winkel sehen
zu können?
23.	Einem rechtwinkligen Dreieck mit
der Hypotenuse 8 cm und einem
Winkel von 60° wird ein Rechteck
einbeschrieben, dessen eine Seite in
die Hypotenuse fällt. Welche Abmes-
sungen erhält das Rechteck, wenn
sein Flächeninhalt möglichst groß
sein soll?
24.	Die Festigkeit eines Balkens gegen-
über Längsdruck ist proportional
dem Flächeninhalt des Querschnitts.
Bestimme die Abmessungen des Bal-
kens, der aus einem kreisrunden
Stamm vom Durchmesser d geschnit-
100
7 Mittelwertsätze der Differenzialrechnung und Taylor-Formel
ten wird, wenn dessen Druckfestig-
keit so groß wie möglich werden soll.
25.	Aus einem Kreis wird ein Sektor mit
dem Zentriwinkel a herausgeschnit-
ten. Der Sektor wird zu einem kegel-
förmigen Trichter zusammengerollt.
Bei welcher Größe des Winkels a
wird das Volumen des Kegels am
größten?
26.	Eine Last mit dem Gewicht G, die
auf einer horizontalen Ebene liegt,
soll durch eine im Schwerpunkt an-
greifende Kraft F weggerückt wer-
den.
Unter welchem Winkel a zur Hori-
zontalen muss man die Kraft F wir-
ken lassen, damit sie so klein wie
möglich sein kann? Der Reibungsko-
effizient sei y = 0, 25.
27.	Wie muss man n = 48 gleicharti-
ge Elemente, jedes mit einem inne-
ren Widerstand von Ri = 0,25 Q,
zu einer Batterie vereinigen, damit
der Außenwiderstand von Ra = 3 Q
eine maximale Leistung aufnehmen
kann? (Hinweis für den Ansatz: Die
Batterie bestehe aus y parallelge-
schalteten Gruppen von je x hinter-
einandergeschalteten Elementen.)
28.	Ein homogener Stab AB, der im
Punkt A drehbar gelagert ist, trägt
in einer Entfernung a (in m) von
A eine Last von Q (in N), wäh-
rend er von einer am freien Ende
B angreifenden senkrechten Kraft F
im Gleichgewicht gehalten wird. Das
Metergewicht des Stabes beträgt q
N
(in —). Bestimme die Stablänge x
m
so, dass die Kraft F ihren kleinsten
Wert annimmt. Wie groß ist Fm^
29.	Der Wirkungsgrad einer Schrauben-
spindel mit Flachgewinde und dem
Steigungswinkel a ist durch die Glei-
_	tana
chung r] = -—-——- gegeben,
tan (q + q)
worin q den konstanten Reibungs-
winkel bedeutet (/z = tan£>). Für
welchen Steigungswinkel a wird y ein
Maximum?
30.	Für einen oben offenen Kanal ist die
m3
Durchflussmenge Q (in —) bei ei-
s
ner konstanten Strömungsgeschwin-
digkeit v (in —) vorgesehen. Der Ka-
s
nalquerschnitt soll ein rechtwinkliges
Trapez sein und die Tiefe soll h (in
m) betragen.
7.5 Newtonsches Verfahren
101
Wie groß ist die Kanalsohle x zu
wählen, damit der benetzte Umfang
U und damit die Reibungsverluste
möglichst klein werden?
7.5 Newtonsches Verfahren
Es handelt sich um ein Näherungsverfahren zur Nullstellenbestimmung einer Funk-
tion, d.h. um die Lösung einer Gleichung der Form /(x) = 0. Ist x\ eine erste
Näherung der gesuchten Lösung xq von /(x) =0, so bildet man die Folge
^n+l — %n
(7.23)
Ist /(x) in einem Intervall I mit xq G I und Xi G I für alle i zweimal stetig diffe-
renzierbar, ist f'(x)	0 für alle x G I und gilt dort
f<X) 
dann gilt auch
lim xn = Xq.
n—»oo
(7.24)
(7-25)
1. Bestimme alle reellen Lösungen der
gegebenen Gleichungen, indem die
auf graphischem Wege ermittelten
Näherungswerte durch Anwendung
des Newtonschen Näherungsverfah-
rens verbessert werden, und zwar auf
möglichst fünf Stellen genau.
a) 2x — In x — 4 = 0
b) 1g x---= 0
x
c) 2X — 4, 2x = 0
d) xx + 2x — 6 = 0
e) x1 2 +	— lOx = 0
x/
f) x Inx — 14 = 0
g) ex + e"3x -4 = 0
h) sinx + 3x — 3 = 0
i) xarctanx — 1 = 0
j) Inx — arctanx = 0
2.	Die Kurve y = sinx, 0 < x < 7i, und
die x-Achse begrenzen ein Flächen-
stück, dem
a)	ein Rechteck von größtmöglichem
Flächeninhalt
b)	ein gleichschenkliges Trapez von
größtmöglichem Flächeninhalt
einzubeschreiben ist. Eine Rechteck-
seite bzw. eine Trapezseite soll auf
der x-Achse liegen. Berechne den
maximalen Flächeninhalt für a und
b.
3.	Ein liegender zylindrischer Kessel
mit gegebenem Grundkreisradius R
hat ein Fassungsvermögen von 1500
Liter. Er ist mit 900 Liter Flüssigkeit
gefüllt. Wie hoch steht der Flüssig-
keitsspiegel?
8 Integralrechnung für reelle Funktionen einer
Veränderlichen
8.1 Unbestimmtes Integral
8.1.1 Grundintegrale, Integrationsregeln
Ist F(x) auf dem Intervall I differenzierbar mit
F'(x) = /(x) für x E I,	(8.1)
so nennt man F(x) eine Stammfunktion von /(x) auf diesem Intervall.
Die Menge aller Stammfunktionen einer Funktion /(x) heißt unbestimmtes In-
tegral /(x) dx der Funktion /(x) und es gilt:
y /(x) dx = F(x) + const = F(x) + C,	(8.2)
falls F(x) irgendeine Stammfunktion von /(x) ist, d.h., F(x) muss die Bedingung
(8.1) erfüllen.
Zu jeder auf einem Intervall stetigen Funktion existiert eine Stammfunktion auf
diesem Intervall.
Formelsammlungen enthalten eine Tabelle der Grundintegrale, auf die man
ein gegebenes unbestimmtes Integral durch Anwendung von Integrationsregeln
zurückzuführen versucht. In vielen Fällen ist es jedoch nicht möglich, das unbe-
stimmte Integral einer gegebenen Funktion „geschlossen“ darzustellen, d.h. durch
elementare Funktionen auszudrücken. Schon bei relativ einfachen Funktionen
gelingt dies nicht, wie z.B. bei e~x ,
Eigenschaften unbestimmter Integrale:
A(/ /(z)da:) = /(a?)	(8.3)
da: \J J
y f'(x)dx = /(a?) + C	(8.4)
y kf(x) da? = k j f(x) dx, (k Konstante, k 7^ 0)	(8-5)
y(/i(a;) ±/2(a?)) da: = y/i(a?)da?± f f2(x)dx	(8.6)
dx = x + C
(8-7)
8.1 Unbestimmtes Integral
103
Partielle Integration:
Sind u = u(x) und v = v(x) auf einem Intervall I stetig differenzierbar und u'v
auf I integrierbar, so gilt auf 1:
Substitutionsmethode:
Ist u = g(x) auf [«i,6i] stetig differenzierbar, f(u) auf [02,62] stetig und
^2 <	< 62, so gilt auf [ui, 61]:
j"  g\x) da? = y f(u) du|M=s(;E)	(8.9)
In dem rechts stehenden unbestimmten Integral ist nach Auflinden einer Stamm-
funktion F(u) die Variable u durch p(x) zu ersetzen.
Ist g'(x)	0 auf [«i, &i], so erhält man
y/(a?)da? = y  g'(z) dz\z=g-i(x)	(8.10)
Sonderfalle:
/ da? = In |/(a?)| + C; (f(x)	0)	(8.11)
y f(ax + b)dx = ^F(ax + b) + C; (a o), falls F'(z) = f(z) (8.12)
1. Berechne die folgenden Integrale
durch Zurückführen auf Grundinte-
grale:
m
2(1 + .i;2)
104	8 Integralrechnung für reelle Funktionen einer Veränderlichen
r / e-x\
n) J e V1 “ dx
o)	[ax(l + P=\dx
f x2 + 5x + 6
p)	/ ------T---dx
J x + 3
. f / .	2
q)	/ sm x — cos x 4------—
J \	cos2x
7 V
----2— )dx
sin x)
r) / .	2
J sm x cos2 x
2x -|- 3
-------dx
2x + 1
k) / ^7 d',;
m) / sin2 tp d(/?
4. Berechne die folgenden Integrale mit
Hilfe der Substitutionsmethode:
2. Berechne die folgenden Integrale
durch Anwendung der partiellen In-
tegration:
a) / sin3 * * x cos x dx
a) / x In x dx
Inx dx
xcos x dx
x2 cos x dx
sinx _
---— dx
cosö x
c) / ecosx sinxdx
e) / x2 ex dx
ex sin x dx
ex x2 dx
Lnx dx
e / e
cos x dx
3. Berechne die folgenden Integrale,
wobei die Formeln (8.11) und (8.12)
sich fest eingeprägen werden sollten:
ev^
—— dx
x f 2x	r	x2
a) / I—rdx b) /
J X2 - 5	’ J 7x3 + 8
c) /(5x + 6)7dx d) y \/2.z- — Ttd.c
. f + ,	n f x+2
e) / cotxdx	t) / ------- dx
’ J	’ J 2 + 3x2
x2 + 1 dx
( 2x2 dx
J W7S
! sinxdx
J %/l + 2 cosx
8.1 Unbestimmtes Integral
105
j) j
1)
arcsin —
—.	dx
V^x
x cos x dx
ö
sm x
— 1 dx
eat coscjt dt
/v/arctanx
—r-—— dx
1 + x/
/cos (Ins) n
---------- ds
( sin3 p
P) / ---g— X
J cosö p>
/ex \/arctanex 1
---:---ö-----dx
1 + e2x
r dx
J sin (4x — 2)
r dx
1 + COS2 X
5. Berechne die folgenden Integrale
durch Anwendung der partiellen In-
tegration bzw. der Substitutionsregel:
eat sincjt dt
m
— dx
O
6. Leite folgende Rekursionsformeln
durch partielle Integration her:
a) [ sinnxdx =------cosxsinn-1x
J	n
n - 1 f .	2
H-------- / sm xdx
n J
cosn x dx = — sin x cosn-1 x
n
n - 1	7
-I------ / cos x dx
n J
und berechne nach diesen Formeln:
sin6 x dx
cos6 x dx
arctanx dx
5 i
sm xdx
cos5 x dx
7. Berechne
x f dx
a) / ~~3
J sm x
die Formeln von Aufgabe
und
dx
cos3 x
(2x — 3) cos (5x + 1) dx
indem
/dx
—
sinx
/' dx	,	,
/ --- angewendet werden.
J cosx
8.	Berechne die folgenden Integrale, in-
dem die Formel
sin 2x
sin x cos x = —-—
und die Rekursionsformeln von Auf-
gabe 6 beachtet werden:
106
8 Integralrechnung für reelle Funktionen einer Veränderlichen
a)	/* sin2 x cos2 x dx
a) i bin .< cos .< ii.(
b)	sin3 x cos3 x dx
9.	Berechne die folgenden Integrale
durch Anwendung der Formeln
sin a cos ß = - (sin (a + ß)
+ sin (a — /?))
cos a cos ß = - (cos (a + ß)
+ cos (q — /?))
sin a sin ß = - (cos (a — ß)
— cos (q + /?)) :
a)	y sin 3x cos x dx
b)	y cos mx cos nx dx
c)	y sin 3x sin bx dx
d)	y sinmxsinnxdx
e)	y sin mx cos nx dx
10.	Integriere nach geeignet gewählter
Substitution'.
a)	y \/a2 — x2 dx
(z. B. x = a sinu, a > 0)
b)	[ . dx
J \/ß ~ X2
c)	f , ,tr
f X3 dx
d)	J
e)	[ dx
J x2\/d — x2
f CI2 — 2x2
f)	/ .	= dx, a > 0
7 J Va2 - x2
g)	y tan3xdx (z.B. x = arctanu)
h) y cot3 x dx
i) ysin5xdx (z.B. u = cosx)
j) y cos7xdx
(z. B. x = a sinh u, a > 0)
r x2 dx
7 J 7^=2
(z.B. x = 2 coshu)
m) / 4 /—-— dx (x = 2 sin2 u)
J V
x f dx
o) / —y
J (\/9 + x2)3
\ [ x3 d
p) / t dx
P7 J
11. Folgende Integrale lassen sich durch
Umformungen (quadratische Ergän-
zung!), Zerlegungen und geeignete
Substitutionen auf Integrale zurück-
führen, die in Formelsammlungen zu
finden sind.
a)	[ , dC
b)	f dx
J y/2-3x- 4x2
x f dx
c)	/	.	=
J vl+x + x2
d)	/ /5 idX 1
/* dx
e)	/ ,
J \/9x2 + 6x + 5
f)	/ \/^2 + 4x + 29 dx
8.1 Unbestimmtes Integral
107
3x + 5
y/x(2x — 1)
dx
7 (x + 3) dx
J J V4x2 + 4x + 3
f	x2 — x + 1	,
/ ---------- ------- (IX
J (x2 + l)\Ar2 + 1
8.1.2 Integration rationaler Funktionen
Rationale Funktionen
g(x) =
Cs(x)
Dn(x)
CSXS + Cs-iXs 1 + ... + C]X + Co
dnxn + dn-ixn-1 + ... + dix + do
(8.13)
(cs 7^ 0, dn 7^ 0) lassen sich stets geschlossen integrieren. Ist s > n, so führt man
zunächst die Polynomdivision Cs(x) 4- Dn(x) durch und erhält die Summe aus
einem Polynom, das sich sofort integrieren lässt, und einer rationalen Funktion
Pm(x) _ bmxm^bm_1xm 1 + ... + 6ix + 6q
Qn(x) xn + an-ixn-1 + ... + a±x + a0
(8.14)
mit | m < n |. (Indem man die Koeffizienten des Zähler- und des Nennerpolynoms
durch den Koeffizienten von xn dividiert, kann man stets erreichen, dass der Ko-
effizient von xn in Qn(x) gleich 1 ist.)
Für /(x) mit m < n führt man eine Partialbruchzerlegung durch, d.h., /(x) wird
in eine Summe von Brüchen zerlegt, die sich unmittelbar oder unter Zuhilfenahme
einer Formelsammlung leicht integrieren lassen. Bei Verzicht auf die Angabe der
Integrationskonstanten seien einige wenige von diesen Formeln angegeben:
7 dx	1	x
/ —------- = - arctan —
J x2 + a2	a	a
/' dx	x
(x2 + a2)2	2a2 (x2 + ö2)
4----7 arctan —
2aö a
(8.15)
(8.16)
108
8 Integralrechnung für reelle Funktionen einer Veränderlichen
Die folgenden Formeln gelten unter der Voraussetzung 4ac — b2 > 0 .
f dx	2	2ax + b
J ax2 + bx + c yjdac - b2 arctan yfdac - b2
f mx + n _ m 1 , 2	x
/ —-----------dx =— In (ax + bx + c)
J axz + bx + c 2a
2an — bm	2ax + b
H-----	: • arctan	=
a V dac — b2	\/ dac — b2
t' dx	1 2ax + b
J (ax2 + bx + c)2 dac — b2 ax2 + bx + c
da	2ax + b
4--,	= • arctan .	=
y/ (dac — b2)3	\/ dac — b2
r x dx	1 bx + 2c
(ax2 + bx + c)2 dac — b2 ax2 + bx + c
2b	2ax + b
---.	= • arctan .	=
(dac — b2)3	dac — b2
(8.17)
(8.18)
(8.19)
(8.20)
Am Anfang der Partialbruchzerlegung steht die Bestimmung der Nullstellen des
Nennerpolynoms Qn(x) von (8.14) und seine Zerlegung in ein Produkt reeller Fak-
toren (Fundamentalsatz der Algebra!):
Ist z.B. x = xi eine fe-fache reelle Nullstelle, so ergibt dies den Faktor (x — xi)k;
ist ferner x = a ± ßi ein Paar konjugiert komplexer Nullstellen der Vielfachheit /,
so erhält man den Faktor (x2 + px + q)1 mit p = — 2a und q = a2 + ß2.
Der Ansatz für die Partialbruchzerlegung lautet dann für die betrachteten Null-
stellen:
fm(^)	__ ^1	। A2 ।	। Aj~
(x — xß)k(x2 + px + q)1... x — Xi (x — Xi)2	(x — x\)k
Mix + TVi M2X + N2 ,	, Mix + Ni	/qo-ia
h 0—--------:—h / 2 ।-----;—Ä2 + ••• + ( 2 ।------;—v + •••
x1 P px P q (xz + px + q)z (xz + px + q)L
übliche Methoden zur Berechnung der Koeffizienten dieses Ansatzes sind der
Koeffizientenvergleich, die Einsetzmethode, die Grenzwertmethode.
1. Berechne die folgenden Integrale ein-
facher rationaler Funktionen, wie sie
nach Ausführung der Partialbruch-
zerlegung auftreten können:
f dx
a) / -----
J x - 7
[ dx
C) J x2 + 16
A\ ( bX A
d) / —s-----dx
7 J x2 + 8
e)	t___________dx
’ J (x2 + 15)3
f)	/ (x2 + 9)2 d:E
g)	[______________
87 J 2x2 - 5x + 7
8.1 Unbestimmtes Integral
109
---------------d t
(x2 + 2x + 3)2
3x + 5
---------------d t
(x2 + 2x + 2)2
3 dx r 9 dx
(x + 17)2 J (x — 6)3
/* 19 dx
x3 — 2x + 2
dx
x4 — 2x3 + 2x2 — 2x + 1
3x3 — x2 — 4x + 13 .
----------------------n t
a?4 - 4a?3 + 13a?2
da;
ry»5 _ ry»2
dx
x dx
(x — l)2(x2 + 2x + 2)
2. Leite eine Rekursionsformel her für
und berechne I2 und I3.
dx
dx
m
3.	Gib für die folgenden (echtgebro-
chenen) rationalen Funktionen den
Ansatz für die Partialbruchzerlegung
an:
a)	Qm(xy((x + l)(x - l)3(x2 + 1)
x (x2 + 2x + 3)2); m < 10
b)	Qm(x)/((3x — 15)2(x + 2)
x(1 + x2)2(x2 — 2x + 5)); m<9
\ Qm(x)
C) (x2 — 4)3(x2 + 4)2(x — l)4 ’
m < 14
4.	Integriere durch Anwenden der Par-
tialbruchzerlegung.
. f 5x3 + 9x2 — 22x — 8 1
a) / ---------—--------dx
J xö — 4x
f x2 + x-l
J 2a?3 + 2a?2 - 12a? X
, [	2a?2 + 41a;-91
C) ./ r>-2l»-ll, + 12dl
.2 f 3a;+ 2
d) / —;-----3----Ö-----dx
J x4 + 3x3 + 3x2 + x
f	x2 dx
J x4 + 12x3 + 52x2 + 96x + 64
fj 3x + 2
i) /	------t-t dx
J x(x + l)3
f x4 + 5x3 — 7x2 + 5 1
------2“^-----rdX
J xö — x2 + 5x — 5
x f dx
5. Hinweis: Bei den folgenden Aufga-
ben lässt sich die Methode der un-
bestimmten Koeffizienten (Ansatz für
die Partialbruchzerlegung) vermeiden,
wenn man z.B. in den Zähler des zu in-
tegrierenden Bruches die Differenz der
Faktoren des Nenners schreibt und das
Integral durch die im Zähler entstehen-
de Zahl dividiert.
x /* dx
dx
1
dx
dx
A — x2 — 2
dx
7 7 (x2 - 3)(x2+ 2)
e)/^ (>.l
dx
.4 _ <r.2
110
8 Integralrechnung für reelle Funktionen einer Veränderlichen
dx	f dx
x3 + 4x J x2 + 5x
dx	f dx
x4 + 3x2 J J x4 — 1
8.1.3 Integration weiterer Funktionenklassen
Durch die im Folgenden angegebenen Substitutionen wird die Berechnung des
gegebenen Integrals stets auf die Integration einer rationalen Funktion zurückge-
führt. Die Bezeichnung 7?(x, /(x), p(x)) bedeutet hier einen rationalen Ausdruck
in x, /(x), p(x).
1.
ax
dx
~(tn-b\ dx=-tn~1dt
Substitution: t = vox + 6
2.
d • tn - b
a — c-tn'
tn~L
dx = n(ad — bc) • -------— dt
v 7 (a - ctn)2
3.
Substitution: t = e:
, dt
dx = —
t
4.
~	dt
Substitution: t = tanx x = arctan t, dx =------------------
’	1 + t2
5.
sinx, cosx) dx
~ .	x	, 2dt	2t
Substitution: t = tan— => x = 2 arctan t, dx =---------sinx =----------z-,
2	’	1 + t2’	1 + t2’
1 — t2
cosx =---------
1 +12
Hinweis: Manchmal kommt man schon mit einer einfacheren Substitution zum Ziel:
t = sinx oder t = cosx.
8.1 Unbestimmtes Integral
111
6. 7?(sinhx, coshx) dx
qX __ Q X
Wegen sinhx = -----------, coshx =
damit die Substitution: t = ex.
ex + e x
2
liegt der 3.Fall vor (s.o.) und
Integriere mit Hilfe der oben angegebe-	m)	fex+l, / 	dx
nen Substitutionen.		/ e*-l
f	x dx	x	f dx
	n)	
a J V2x + 1 + 1	’ J	' e2x+ex-2
M f dx	o)	f	dx
b) /	' J	sin x + cos x
fe3x-2ex ’J e2*+l	’b	r x3 dx ' 1 + v'x4 + 1
/* e3x dx		/• x + 1 /	.	: dX
	q) j	' w + 1
r		f e3x dx
e) / tan4 x dx	r)J	‘ ex+2
r	cd	r e2x dx
f) / tarn x dx	S)J	' e^-l
		f	dx
f dx	t) i	
J 5 + 3 cos x	' J	' V2x - 1 - $2x - 1
f _	dx	 J 3sinx + 4cosx		x^a — x dx; a > 0
f	dx		f 1	l1 + xJ /	ä /	dx
J sinh x + 2 cosh x	v) J	(1 — x)(l + x)2 V 1 — X
,x f dx	wd	r	dx
j) /	. J cosh x	vv7	/ yjx + 1 + y/(x + l)3
, x f x3 dx k) J vCT	X)J	[	1	/^^d ' (1 - x)2 V 1 + X
f	dx		fJl-x	1
1 / 	—		y) j	1 \ 	7--.	?7da;
J 1 + sin x + cos x		V 1 + x (1 + x)2
8.1.4 Vermischte Aufgaben zur Integration
_ x f arctan x
dx
1 + sinx
112
8 Integralrechnung für reelle Funktionen einer Veränderlichen
e
dx
1 dx
cot4 x dx
dx
• 2	9
sm x cosz x
g) J	a2	b2 x cos2 x da:	2. a) j	r V4 — x2 ' x2 dx
	r dx	b) j	r cos x dx cos 3x
	( e2x ex		/ sin x
			
‘9	f l1~x^ dx ' V 1 + x	CV) d9 e9	dx sm 3x f	dx
'9	r cos2 x . 4 da: ' sm x		y/x + a + yfx r	dx
k) J	x tan2 x dx		\Ar2 + 1 — x
	f cos2 x / —	dx sin x	f9	
“'9	f sin x ' b2 + cos2 x X f	dx	s9	/ \Ar2 + 2x 1 '	x3 dx f dx
"9	ä/x2 + 2^/x r ai- — A	h) j 9; j) J	x\/x3 — 1 f dx
°9 p9 q9	f	Lz	_ / 7	7TT dx ' (ax + ö)4 f dx		1 + tanx f arcsin y/x 1 	—	dx
	' x4 + X2 f	dx		/ sin2x / A dx
	' (sinx + cosx)2	k) J	COS4 X
'9	/*	dx	i) J	C cos2x , . 4 daJ sm x
	xy/a-\-blnx		
	f x2 dx	m)	J	f In (cosx) , / ——- dx sin x r dx
	' (a — bx3)n	\	
’9	\/l — 2x — x2 dx	“9	' g3x 	qX
	f dx		f sin3 x dx
“9	' (1 + v^)3		COS5 X
v9	r arctanx '	X2	dx f^dx 1 e2'+l	”9	f In (x + 1) dx X2
w9		q9	[ V1 — sinxdx
8.2 Das Riemannsche Integral
113
xarcsinx ,
—. dx
\/l — a?2
dx
X2\/x2 — 1
%/tanx dx
sin 2x
In (x2 + 1) dx
x3
ax dx
a2x + 1
1 — sin a/x
-----=----dx
yx
r x2 dx
d)./ wn
cos3 X + 1
sin2 x
8.2 Das Riemannsche Integral
Die Funktion /(x) sei auf dem Intervall [a, b] definiert und beschränkt. Das Intervall
[a, b] wird durch die Punkte xi, X2,xn~i mit a = xq < Xi < X2 < ... < xn~i <
xn = b in n Teilintervalle li = [xi-i,Xi] (z = 1,2, ...,n) zerlegt. Man setzt Ax* =
Xi — Xi-i, wählt ein beliebiges G [x*_i,Xi] und bildet die Summe
n
sn = ^f(tx/\Xl
2=1
Hat Sn stets den Grenzwert 5, also:
Sn S für n oo und max A* —> 0
(8.22)
(8.23)
wie auch immer [a, b] aufgeteilt und G li gewählt wird, so ist /(x) auf [a, b]
Äzemcmn-integrierbar (kurz: integrierbar) und man schreibt für das Riemann-
Integral:
und nennt es auch bestimmtes Integral.
(8.24)
114
8 Integralrechnung für reelle Funktionen einer Veränderlichen
Geometrische Bedeutung des bestimmten Integrals:
b
Ist f(x) > 0 für x e [a, b], so ist J* f(x)dx die Maßzahl des Inhaltes der Fläche,
a
die von y = /(x), der ./-Achse und den Geraden x = a und x = b begrenzt wird.
Falls /(x) < 0 für x e [a, b], so ist die Maßzahl des entsprechenden Flächeninhaltes
b
gleich — f(x) dx.
a
Eigenschaften des bestimmten Integrals:
Ist f(x) auf [a, b] stetig und F(x) eine Stammfunktion von f(x) auf [a, b], so gilt
b
Sind /(x),	/2W auf [a, b] integrierbar und c e (a, bß so gilt
b
= 0
(8.25)
(8.26)
(8.27)
(8.28)
(8.29)
(ki,k2 Konstanten)
Bestimmtes Integral mit variabler oberer Grenze:
f(t) sei stetig auf I = [a, ß] , a ein fester und x ein variabler Wert aus I, dann gilt
a
1. Berechne durch Aufstellen der Sum-
me Sn (Formel (8.22)) und Grenz-
übergang die gegebenen bestimmten
Integrale.
a
0
x2 dx
8.2 Das Riemannsche Integral
115
*3	Q
/I + tan x q
—---------— dx
(1 + tanx)2
T
«) I —
J 1 T x/2x + 1
o
2
r dx	r
j),/TO k) siMx
0	0
9
/dx
—=---mit Hilfe der Substitu-
Vx -1
4
tion t = \/x. Dabei ändern sich
die Grenzen, wie folgende Tabelle
zeigt:
X	4	9
t	2	3
1	5
/dx	T x dx
ex+1 j
o	1
4
1
dx
cos2 2x
dx
(1 + y/x)2
3. Berechne die folgenden bestimmten
Integrale:
—	3
c	f dx
a) / tan3zdz b) J x + x?
X/2
2	V 4
c) xcosxdx d) y \/2 — x2 dx
0	1
Vs
o) [ , <1J;
J V(l + x2)3
4. Aus den Formeln von Aufgabe 6 des
Abschn. 8.1 erhält man die beiden
Beziehungen:
"2	"2
f . ri i	1 I . ri— 2 i
/ sm x dx =-------- / sm x dx
J	n J
0	0
und
116
8 Integralrechnung für reelle Funktionen einer Veränderlichen
2	2
f n i	1 /	n—2 i
/ cos x dx =------- / cos x dx
J	n J
0	0
Berechne danach:
2
c) / sin6 x dx
o
2
/ cos2 x dx
o
a) Lin^d.,:
2
\	/ 4i
e) / cos xdx
2
/ cos6 x dx
sin4 x dx
o
0
0
0
8.3	Uneigentliche Integrale
Unendliche Integrationsintervalle:
Die folgenden uneigentlichen Integrale sind konvergent, wenn die angegebenen
Grenzwerte existieren und endlich sind:
b
J fbo	dx = lim / f (x) dx;	(8.30)
a	b^+oo J a	
b	b	
/ f(x	) dx = lim / /(x) dx;	(8.31)
	a	
+oo	b	
/	) dx = lim / /(x) dx.	(8.32)
	a^ — oo J b^Xoü a	
Bei (8.32) streben a und b unabhängig voneinander nach —oo bzw. +oo. Wählt
man in (8.32) a = — b = z, so heißt
lim
(8.33)
— z
der Cauchy sehe Hauptwert des uneigentlichen Integrals (8.32).
Unbeschränkter Integrand:
Ist /(x) auf [a, b] an der Stelle x = c nicht beschränkt, so können trotzdem die
folgenden Grenzwerte existieren und endlich sein; dann sind die entsprechenden
8.3 Uneigentliche Integrale
117
uneigentlichen Integrale konvergent:
b
b
b
dx = lim / s^+0 J CL~|- s b-l	/(x) dx, falls c = a;	(8.34)
dx = lim / s^+0 J a	/(x) dx, falls c = b\	(8.35)
	-ei	b
dx = lim i £1^+o /	f /(x)dx+ lim [ /(x)dx, falls c e (a, 6). (8.36) £2^+0	/
c+s2
Bei (8.36) streben si und £2 unabhängig voneinander nach +0. Wird si = £2 = £
gesetzt, so erhält man den Cauchysehen Hauptwert dieses uneigentlichen Integrals:
lim
s —>+0
(8.37)
Konvergenzkriterien werden meist für uneigentliche Integrale der Form
formuliert, für die anderen Typen gelten analoge Sätze.
Beispielsweise gilt:
Sind /(x) und p(x) nichtnegativ und gilt für x > xq > a stets /(x) < p(x), so
folgt aus der Konvergenz von J* g(x) dx die Konvergenz von
aus
der Divergenz von J* f(x) dx die Divergenz von
4
Als Vergleichsfunktion eignet sich z.B. p(x) = —, (A > 0,a
1).
1. Berechne die gegebenen uneigentli-
chen Integrale:
118
8 Integralrechnung für reelle Funktionen einer Veränderlichen
2.	Zeige: Wenn m ganzzahlig und posi-
tiv ist, so gilt:
a)	e~x xm dx = ml
o
b)	y e~x2 x2m+1 dx =
o
3.	Berechne	die folgenden	unei-
gentlichen Integrale bzw. ihren
Cauchysehen Hauptwert:
cot x dx
dx
xlnx
4. Untersuche die gegebenen uneigent-
lichen Integrale auf Konvergenz bzw.
Divergenz.
dx
\Ar4 — 1
e
dx
3x +	+ 7
8.4	Trapezformel, Simpsonsche Regel
8.4.1 Trapezformel
Das Integrationsintervall [a, b] wird in n gleiche Teile der Länge h = -—- zerlegt.
n
Dann gilt:
]X>
a	'
mit yi = f(a + hi), i = 0,1,2,n.
(8.38)
8.4 Trapezformel, Simpsonsche Regel
119
Der sich durch Anwendung der Näherungsformel (8.38) ergebende Fehler wird
nach der Formel
e(/i) < (l|)Lr|
(8.39)
abgeschätzt. \y"\max ist das Maximum von |//z(x)| auf dem Intervall [a, b\.
8.4.2 Simpsonsche Regel
Das Integrationsintervall [a, b] wird in eine gerade Anzahl 2n von Teilintervallen
der gleichen Länge h = ----- zerlegt.
2n
b
j" ,f(x) da?
a
n
yo + y2n +4 ^2^21-1
1=1
(8.40)
mit yi = /(a + hi), i = 0,1, 2,..., 2n
Abschätzung des Fehlers bei Anwendung der Szmpsonschen Regel (8.40):
AL|y(4)|max mit |y(4)\max = max |/3 (4)(a?)|
loU	a<x<b
(8-41)
3
r dx
1. Berechne In 3 = / — nach der
J x
1
a) Trapezformel (mit n = 10)
b) Szmpsonschen Regel
(mit 2n = 10)
und schätze den Fehler nach den For-
meln (8.39) bzw. (8.41) ab.
1
2. Berechne J* e~x dx nach der
o
Trapezformel (n = 10) und
schätze den Fehler nach der
Formel (8.39) ab.
1
3. Berechne ex dx nach der Simp-
o
sonschen Regel und schätze den Feh-
ler nach der Formel (8.41) ab (2n =
10).
4.	Berechne nach der Szmpsonschen
Regel die Integrale
1	o
schätze nach der Formel (8.41) den
jeweiligen Fehler ab und vergleiche
die Ergebnisse mit den exakten Wer-
ten der Integrale.
5.	Berechne angenähert den Wert von
7i aus
1
dx
\/4 — x2
o
durch Anwendung der Szmpsonschen
Regel.
120	8 Integralrechnung für reelle Funktionen einer Veränderlichen
6.	Berechne nach der Simpsonschen
Regel die Integrale
2
a)	\/l + -^3	(2n = 4)
o
"2
b)	y \/3 cos 2x dx (2n = 6)
o
4
/dx
—(2"=4)
0
und schätze den Fehler ab. Setze da-
bei in Formel (8.41) angenähert
~ IA4y|maa.
9 Elemente der Differenzial- und
Integralgeometrie
9.1 Kurvendarstellungen
In diesem wie auch in den folgenden Abschnitten wird weitestgehend auf die An-
gabe des Intervalls für die unabhängige Variable verzichtet ebenso wie auf die
Angabe der notwendigen Voraussetzungen über Stetigkeit oder Differenzierbarkeit
der betrachteten Funktionen.
_Eben^J^rver^
In der x, ?/-Ebene lässt sich eine Kurve u.a. wie folgt definieren:
y = /(x) oder y = y(x) (explizite Darstellung)	(9.1)
F(x,y)=0 (implizite Darstellung)	(9.2)
x = x(t), y = y(t) (Parameterdarstellung) bzw.
r =	+ y(f)e2 = (a?(i), y(i))T
r = r(p>) (Darstellung in Polarkoordinaten)	(9.4)
Zwischen den kartesischen Koordinaten und den Polarkoordinaten bestehen die
folgenden Beziehungen, wenn man den Koordinatenurprung als Pol und die posi-
tive x-Achse als Polarachse wählt:
x = r cos	y = r sin <p	(9-5)
r = \/ x1 2 + y2.	i_	y cp = arctan — X	(9-6)
		
x = x(t), y = y(t), z = z(t) (Parameterdarstellung) bzw.
r = x(t)ei + y(t)e2 + z{t)e3 =	y(t), ZX))T
F(x,y,z) = 0, G(x,y,z) = 0 (Schnitt zweier Flächen)	(9.8)
1. Die in Parameterdarstellung gegebe-
nen ebenen Kurven sind in der Form
F(x, y) = 0 anzugeben. Um welche
Kurve handelt es sich jeweils?
a)	x = x(t) = 8t2 — 7
y = y(t) = ißi2 + 4
b)	x = x(t) = 5t2
y = y(t) = 3t
122
9 Elemente der Differenzial- und Integralgeometrie
c)	x = x(t) = r cos t
y = y(t) = r sin t
d)	x = x(t) = a cost
y = y(t) = 6sint
e)	x = x(t) = 3cost
y = y(t) = 4 — 3 sin t
f)	x = x(t) = 2 + 3 cos t
y = y(t) = — 3 + 4 sin t
2.	Die in Polarkoordinaten dargestell-
ten Kurven sind in der Form
F(x, y) = 0 anzugeben. Um welche
Kurve handelt es sich jeweils?
a)	r =	= 4(2 cos + — sin^)
b)	r = r(+) =
x/cos 2<p
3.	Gib von folgenden Kurven eine Pa-
rameterdarstellung an:
a)	x2 + y2 — 25 = 0
b)	9x2 - 2by2 = 225
c)	y — 4x2 = 0
d)	y = \/^2 +	+ 105
e)	y = f(x)
4.	Auf dem Kreis x2 + y2 = 36 be-
wegt sich ein Punkt P(x,y) mit der
konstanten Winkelgeschwindigkeit w
im mathematisch positiven Sinn. Gib
die Parameterdarstellung für die Be-
wegungsbahn mit der Zeit t als Pa-
rameter an, wenn
a)	x(0) = 6; 7/(0) = 0
b)	x(0) = 0; 7/(0) = —6.
5.	Die Gleichung der Archimedisehen
Spirale lautet in Polarkoordinaten
/X	7	5
r = r(+) = acp + 6: cp >----
(a, b reell und konstant, a 0).
Gib für diese Kurve eine Parameter-
darstellung an. Wie lautet die Kur-
vengleichung in der impliziten Form
F(x, t/) = 0?
6.	Zeige, dass die gewöhnliche Zykloide
x = x(t) = a(t — sint)
y = y(t) = a(l — cost)
(a > 0; a konstant) auch durch die
Gleichung
/ x	a-y
x = x(y) = a • arccos-----
-\/y{2a - y)
dar gestellt werden kann.
7.	Gegeben ist die Kardioide (Herz-
linie) r = r(+) = 1 + cost/z
a) Skizziere diese Kurve.
Hinweis: Polarkoordinatenpapier.
b) Gib eine Parameterdarstellung
dieser Kurve an.
8.	Stelle in Polarkoordinaten die Glei-
chung einer Geraden auf, die
a)	auf der Polarachse den Abschnitt
a erzeugt und senkrecht auf ihr
steht
b)	durch den Punkt A(cp = a; r =
d) geht und parallel zur Polarach-
se verläuft
c)	durch den Punkt A(cp = a; r =
d) geht und mit der Polarachse
den Winkel ß bildet
9.	Stelle in Polarkoordinaten die Glei-
chung eines Kreises mit dem Mittel-
punkt in M(+ = 0; r = d) und dem
Radius a auf.
10.	Skizziere die Kurven, die durch fol-
gende Parameterdarstellungen gege-
ben sind:
a)	x = x(t) = 1 + 2cost
y = 7/(t) = — 1 + 3 sint
(0 < t < 27t)
b)	x = x(t) = t — sin t
y = yX = 1 -cosi
( — 271 < t < 27t)
11.	Skizziere die Kurven, die durch fol-
9.2 Tangente, Krümmung ebener Kurven, Normalebene
123
gende Darstellungen in Polarkoordi-
naten gegeben sind:
a)	r = r(+) =	(0 < p> < 37t)
b)	r = r(+) = e0,2<^
( — 71 < ip < 27t)
c)	r = r(p) = 2 + cos 3p>
Hinweis zu c: Bestimme zunächst die
Winkel, für die sich ein rmax bzw. rmin
ergibt.
12.	Gib für die folgenden Kurvenglei-
chungen die Darstellung in Polarko-
ordinaten an:
\	2	2	2 u\ 2 ।	2	2
a)	x — y = a b) x + y = a
c)	x cos a + y sin a — p = 0
d)	y = x
e)	x2 + y2 = ax
f)	(x2 + y2)2 = a2 (x2 — y2)
13.	Gib für die folgenden Kurven die
Darstellung in kartesischen x,y-Ko-
ordinaten an:
a)	r cos p> = a b) r = 2a sin p>
c)	r2 sin2(/? = 2a2
7t
d)	r sin (++—) = ay 2
e)	r = a(l + cos^)
14.	Im Raum ist die Parameterdarstel-
lung eines Kreises gegeben:
x = x(t) = 4 + cos t + 2 sin t
y = y(t) = — 4 + 2 cos t + sin t
z = z(t) = 2 + 2 cos t — 2 sin t
a)	Berechne die Koordinaten des
Mittelpunktes M(x,y,z) sowie
den Radius r dieses Kreises.
b)	Projiziert man diesen Kreis in
die x,?/-Ebene (Projektionsstrah-
len parallel zur z-Achse), so er-
hält man eine Ellipse. Wie lautet
die Gleichung dieser Ellipse in der
Form F(x, y) = 0?
9.2 Tangente, Krümmung ebener Kurven, Normalebene
_Eben^J^rver^
1.	Die Kurve ist gegeben durch y = /(x) :
Im Kurvenpunkt F(xq,2/o) erhält man für
•	die Tangentengleichung: y — yQ = /'(xq) • (x — xq)
•	die Normalengleichung: y — y$ = — (x — xq)
•	die Krümmung: x = ---------7-
(i + cmw
•	den Krümmungsmittelpunkt:
,	1 + cn«»2 ,,, ,	, , 1 + / J
2. Die Kurve ist gegeben durch x = x(t^y = y(t) :
Im Kurvenpunkt F(x(to), Z/(M) erhält man für
124
9 Elemente der Differenzial- und Integralgeometrie
•	die Tangentengleichung: ±(t0) • (y ~ y(to)) = 2/(^0) •	- ^o))
•	die Normalengleichung: yffy) • (y — 2/(^o)) =	• (x — x(to))
..	..	xy — yx
•	die Krümmung: x = —---;—- mit t = to
den Krümmungsmittelpunkt:
7.2	"2 _|_
y2 .
—x mit t = to
xy — yx
xy — yx
3.	Die Kurve ist gegeben durch r = r(</?) :
Mit x =	= r(^) cos y = y(jp) = r(^) sin tp wird dieser Fall auf den
zweiten Fall zurückgeführt (siehe Aufgabe 3).
Im Kurvenpunkt (<Ah ^(<A))) erhält man für
• die Krümmung:
r2 + 2(F)2
f dr	n d2r
mit <p = (/?o, r = —, r =
d(/? dpr
4.	Die Kurve ist gegeben durch F(x,y) = 0 :
Im Kurvenpunkt F(xq,2/o) erhält man für
•	die Tangentengleichung: F^xq, 2/0) • (2/ - 2/o) + Fx(x0, yo) • (x - x0) = 0
•	die Normalengleichung: Fx(xo,2/o) • (y ~ 2/o) - Fy(xQ,yQ) • (x - x0) = 0
•	die Krümmung:
_ F . c \^FFF — f2f
Fy Fxx F X1 y1 xy 1 x 1 yy
X = ---------------Ö-------- mit X = Xq , y = 2/0
(F2+F2)i
• den Krümmungsmittelpunkt:
Fx(F2 + F%)
X° F^Fxx-2FxFyFxy + F^Fyy
= yo -	2	_2F-	-	2 mit x = X0,y = y0
ryrxx	xryrXy	rxryy
Jedem Punkt (xq, yo) einer ebenen Kurve kann zugeordnet werden:
•	Krümmungsradius: q = -—-
•	Krümmungskreis: (x — ^)2 + (y — y)2 = q2
Ist 5(xq,//o) der Schnittpunkt der Kurven y = y\(x) und y = 2/2(^), so erhält man
ihren Schnittwinkel 1? aus
tand =
^2(^0) - 3/1 (gp)
1 + y'i(®o) • y^o)
(9-9)
9.2 Tangente, Krümmung ebener Kurven, Normalebene
125
y
Für x = x(t),y = y(t) ist yr = —.
F * X
Für F(x,y) = 0 ist yf = — —
Die Evolute einer Kurve ist die Menge ihrer Krümmungsmittelpunkte. Deshalb
ist
C = £(®) = x -
1 + CfW
/"(*)
/'(*)
(9.10)
1 + CfW
»7 = ^(x) = /(x) +
eine Parameterdarstellung der Evolute der Kurve y = /(x).
Bemerkung 9.1 Ist die Kurve durch F(x,y) = 0 gegeben, so kann man zur
Bestimmung von y' beide Seiten der Gleichung F(x, y) = 0 nach x differenzieren
und dabei y als Funktion von x ansehen (meistens erfordert dies die Anwendung
der Kettenregel). Aus der entstandenen Gleichung lässt sich die gesuchte Ableitung
y' finden. Zur Bestimmung von y" differenziert man die Gleichung F(x,y) = 0
zweimal nach x usw.
Punkte einer Kurve, in denen die Krümmung ein Maximum oder Minimum besitzt,
heißen Scheitelpunkte.
_^uumkurveij
Ist eine Raumkurve in Parameterdarstellung
x = x(t), y = y(t\ z = z(t) bzw.
r = x(t)ei + y(t)e2 + z(t)e3 =	*/(*), z(i))T
gegeben, dann ist
är = r = ±(i)ei + y(t)e2 + z(i)e3 =	y(t), z(i))T	(9.12)
der Tangentenvektor der Kurve an der Stelle t. Seine Richtung entspricht der
positiven Richtung der Kurve (im Sinne wachsender Werte des Parameters t).
Die Raumkurve (9.11) hat im Punkt F(x(to), y(to), z(toY) eine Tangente mit der
Parameterdarstellung
X = z(A) = x(to) + Ai(to), y = y(A) = y(t0) + Ay(t0),
z = z(X) = z(to) + Az(to); —oo < A < oo
bzw.
(x, y, zf = (x(to), y(t0), z(t0))T + A(i(t0), y(t0), z(M)T	(9-14)
9.11
126
9 Elemente der Differenzial- und Integralgeometrie
Die Normalebene enthält den Tangentenberührungspunkt und steht auf der Tan-
gente senkrecht. Jede Gerade, die durch den Tangentenberührungspunkt geht und
in der Normalebene liegt, heißt Normale.
Gleichung der Normalebene im Punkt F(x(to), Z/(£o)^(^o)) der Raumkurve
(9.11):
x(to)(x - x(t0)) + y(tQXy - ?/(M) + ^o)(^ - 4M) = o
(9.15)
Bemerkung 9.2 Ist t die Zeit und r = (x(t), ?/(t), z(t))T die Bahnkurve einer
dr	d2r
Bewegung, dann ist — = r = v der Geschwindigkeitsvektor und —T = r = v = a
dt	dtz
der Beschleunigungsvektor.
1.	Bestimme für die gegebenen Kurven
die Tangentengleichungen an den an-
gegebenen Stellen:
a)	y = bei x = — 1
O
b)	y2 = x3 bei x± = 0, x% = 1
g
c)	y = ------~ (Lockenkurve) bei
4 + xz
x = 2
d)	y = sinx bei x = 7t
e)	y = sinhx bei x = — 2
f)	x = x(t) = a(t — sint)
y = y(t) = a(l — cost)
, i i i \ i •	7r	37t
(Zykloide) bei G = -,t2 = —
g)	x = x(t) = a cos3 t
y = y(t) = a sin3 t
7t
(Astroide) bei t = —
h)	x = x(t) = a(cos t -\~t sin t)
y = y(t) = a(sint — tcost)
7t
(Kreisevolvente) bei t = —
2.	Bestimme für die gegebenen Kurven
die Gleichungen der Tangente und
der Normalen an den angegebenen
Stellen:
x — 1
a)	y = arcsin —-— im Schnittpunkt
mit der x-Achse
b)	y = arccos 3x im Schnittpunkt
mit der y- Achse
c)	y = e1-x in den Schnittpunkten
mit der Geraden y = 1
d)	y2 = 4 — x in den Schnittpunkten
mit der y- Achse
e)	x = x(f) = E2
. ,	3	1
“ = ’(t) = 2? + ~f
im Punkt mit x = 2
f)	x = x(t) = t3 — 2t
y = y(t) = t2 +1
im Punkt mit t = 1
g)	x3 + y2 + 2x — 6 = 0 im Punkt mit
Z/ = 3
h)	y = -x3 — 2x2 + 3x — 1 im Wen-
ö
depunkt
3.	Der Pol eines Polarkoordinatensys-
tems sei Ursprung eines kartesi-
schen x, ^/-Systems, dessen positive
x-Achse mit der Polarachse zusam-
menfällt. Eine ebene Kurve sei in
Polarkoordinaten dargestellt:
r = r((/?)
Zeige durch Zurückführen auf eine
Parameterdarstellung, dass die Stei-
gung m = m((/?) dieser Kurve nach
9.2 Tangente, Krümmung ebener Kurven, Normalebene
127
der Formel
rf(p>) sin p> + r(p>) cos p>
m = m(pp) = ——--------------——------
r'lpp) cos cp — r{<p) sm p>
berechnet werden kann.
Bestimme für die gegebenen Kurven
die Gleichungen der Tangente und
der Normalen an den angegebenen
Stellen im oben beschriebenen x, y-
System.
a)	r =	= 2acos(/? (a > 0)
u •	71
bei p> = —
4
7t
b)	r = r((p) = 5p> bei p> = —
O
4.	Berechne für die folgenden ebe-
nen Kurven den Steigungswinkel der
Tangente an der angegebenen Stelle:
a) x = x(t) = 2 cos t — cos 2t,
y = y(t) = —2 sin t + sin 2t
_ . 71
bei t = —
6
b)	x = x(t) = sin 2t,
y = yX = sin2t
, . 7T
bei t = —
8
c)	x = x(t) = arcsin .	,
7	v 7	VTTt2
/ x	1
y = y(t) = arccos .
y	yy J	VT+t2
bei t = a/ö
5.	Vom Punkt Pi(l; 0) ist an die Kurve
y = ex die Tangente zu legen. Be-
rechne die Koordinaten des Tangen-
tenberührungspunktes .
6.	Die Koordinatenachsen begrenzen
auf den Tangenten an die Hyperbel
xy = a2 eine Strecke. Zeige, dass
der Tangentenberührungspunkt die-
se Strecke halbiert.
7.	Unter welchem Winkel schneiden
sich die gegebenen Kurvenpaare?
a)	y = x2 und y = x-1
b)	y = sinx und y = 0
c)	2y = x2 und 2y = 8 — x2
d)	x2 + y2 = 5 und y2 = 4x
8.	Bestimme die gemeinsame Tangente
an die Kurven y = x2 und x = y2.
9.	Berechne die Schnittpunkte der Nor-
malen zur Hyperbel x2 — y2 = 9
im Punkt (5; 4) mit den Asymptoten
dieser Hyperbel.
10.	Stelle die Gleichung der Tangente im
Punkt (a?0; Z/o) an die gegebenen Kur-
ven auf:
b) y2 = 2px
11.	Berechne die Krümmung der gege-
benen Kurven in den angegebenen
Punkten:
a)	y = x4 — 4x3 — 18x2 für x = y = 0
b)	x2 + xy + y2 = 3 für x = y = 1
2	2
x^1 y
c)	—r + — = 1 den Scheiteln
az bz
A(a\ 0) und B(0; b)
d)	x = t2 , y = t3 für x = y = 1
e)	r2 = 2a2 cos 2p> für ip = 0
(a > 0)
12.	Berechne den Krümmungsradius
und zeichne die Kurve und deren
Krümmungskreis im Scheitelpunkt:
x 1
a)	y = z——
1 + xz
b)	x2 — y2 = 4
c)	y = sinx
d)	2y = x2 + 4x
e)	y = ex
i)y = e~x2
g) x = a(t — sint), y = a(l — cost)
h) y = xe~x
128
9 Elemente der Differenzial- und Integralgeometrie
13.	Bestimme den Krümmungsradius in
einem beliebigen Punkt der gegebe-
nen Kurven:
a)	r = r(cp) = a(l — cos</?), a > 0
b)	r2 = a2 cos 2(/?, a > 0
14.	In welchen Punkten der Parabel
y2 = 8x ist die Krümmung gleich
0,128?
15.	Berechne die Koordinaten des
Krümmungsmittelpunktes für die
folgenden Kurven an den angege-
benen Stellen:
a)	xy = 4 bei x = 2
b)	y = In.r im Schnittpunkt mit der
?/-Achse
c)
X3 + 1
y =
mit der x-Achse
im Schnittpunkt
d)	y = ex im Schnittpunkt mit der
?/-Achse
x^
e)	y = -— bei x = — 1
O
f)	y2 = x3 im Punkt (1; 1)
g)	y = cos x bei x = —
16.	Wie lautet die Gleichung des Krüm-
mungskreises der Parabel
y = x2 — 6x + 10 im Punkt Pq(3; 1)?
17.	Beweise, dass der Krümmungsradi-
us der Kettenlinie y = a cosh - in
einem beliebigen Punkt gleich y2/a
und gleich dem Normalenabschnitt
zwischen Kurve und x-Achse ist (a >
o).
18.	Stelle für die gegebenen Kurven die
Gleichung der Evolute auf:
a) y = x2
c) x = 2cost, y = sint
d)x = acosht, ?/ = asinht
e)	x = a(cos t + t sin t)
y = a(sin t — t cost)
f)	y2 = 2x + 2
t3
g)	x = t , y= —
ö
h)	x = a cos3 t, y = a sin3 t
i) r = e^
19.	Wie heißen die Bahnkurven, die
durch die folgenden Parameterdar-
stellungen r = r(t) gegeben sind?
a)	r = aei cos t + ae^ sin t + ctes
b)	r = ei cos t + 62 + 63 sin t
c)	r = t(l, 1,1)T
d)	r = (1,1, t)T
e)	r = (cosh t, 0, sinh t)T
20.	Gegeben sind die Bewegungsglei-
chungen eines Punktes. Berechne die
Geschwindigkeit und die Beschleu-
nigung für den angegebenen Zeit-
punkt:
a)	r = (3 cos t, 3 sint, 4t)T, t= —
b)	r = tei + t2e2 + t3es, t = 1
21.	Zeige, dass die Vektoren r und r auf-
einander senkrecht stehen, wenn
r = (cos t, sint, 1)T.
22.	Stelle für die gegebenen Kurven im
angegebenen Punkt die Gleichungen
der Tangente und der Normalebene
auf:
a)	r = (cos t, sin t, t\/3)T, t = —
b)	r = (a sin2 t, b sin t cos t, c cos2 t)T,
9.3 Inhalt ebener Flächen
129
c)
, V2 , v2 , xT
r = (— e sin t, 1, — e cos t) ,
v 2	’ ’ 2	7 ’
t = 0
d)	r = (i,f2,f3), F(2;4;8)
\	2 sin 2t x 7i
e)	r = 7?(cos t,—-—, sint), t= —
f)	r = t(cos t, sin t, 6)T, F(0; 0; 0)
g) x2 + y2 = 10, y2 + z2 = 25,
F(l;3;4)
Hinweis: Man bildet das Differenzial
der linken und der rechten Seite jeder
Gleichung und findet daraus das Ver-
hältnis dx : dy : dz.
23.	Wie lauten die Gleichungen der Tan-
genten an die Raumkurve
t4 t3 t2
r = —G! + —e2 + —e3,
die parallel zur Ebene
xi + 3^2 + 2x3 = 0 verlaufen?
24.	In welchem Punkt P(x, y, z) der
Raumkurve
r = r(t) = (t + l,t2 - l,i3)T
ist die Tangente parallel zur Ebene
x + 2y + z — 1 = 0?
25.	Welchen Winkel bildet die Tangente
an die Schraubenlinie
r = (cos t, sin t, 2t\/2)T
71
mit der x,?/-Ebene, wenn t = — ?
26.	Zeige, dass sich die Kurven
r = r(u) = (u + l)ei + u2e2
+ (2u — l)e3 und
r = r(x) = 2x2ei + (3x — 2)e2 + v2e3
in einem Punkt schneiden und be-
rechne den Schnittwinkel.
9.3 Inhalt ebener Flächen
Mit Inhalt ist hier wie auch im Folgenden stets die Maßzahl des Inhaltes gemeint.
Die zu integrierenden Funktionen sollen stets über alle hierzu vorauszusetzenden
Eigenschaften verfügen.
Berechnung des Flächeninhaltes
• ebener Normalbereiche:
A =
falls f2(x) > /i(x) für jedes x e [a, b\.
(9.16)
t2
A = J y(t)x(t) dt,
ti
falls a = x(ti), b = x(t2)
und y(t) > 0 für alle t e [ti,t2]-
(9.17)
130
9 Elemente der Differenzial- und Integralgeometrie
J (fl2(y) -yi(y))dy,
d
A =
falls y2(y) > gi (y) für alle y & [c,d].
^2
A = J x(t\y(t) dt,
ti	(9.19)
falls c = p(ti), d = y(t2)
und x(t) > 0 für alle t e
• ebener Sektorflächen:
^2
A= ||/(a?y — yi) di|
ii	(9.20)
falls k : x = x(t), y = y(t) für t G [ti, t2]
und Fi(x(ti),y(ti)), P2(x(t2'),yXX-
</?2
A = J dp, falls k : r = r(p),
^1
V [^1,^2]
(9-21)
und OP± = r(pi), OP2 =
1.	Berechne den Inhalt der Flächen, die
von den gegebenen Kurven begrenzt
werden:
a)	p = 4 — x2, y = 0
b)	y = 6.1; — x2, y = 0
d)	y2 = 2px, x = h (p > 0, h > 0)
e)	y = 3 — 2x — x2, y = 0
f)	y = x3, y = 8, x = 0
g)	xy = 4, x = 1, x = 4, y = 0
h)	y2 = 1 — x, x = — 3
i)p = lnx, x = e, p = 0
j)	y2 = 2x + 4, x = 0
k)	y2 = x3, y = 8, x = 0
1)	y2 = (4 — x)3, x = 0
9.4 Bogenlänge eines Kurvenstückes, Krümmung von Raumkurven 131
m)	Schlinge der Kurve:
4(?/2 — x2) + x3 = 0
n) y2 + x4 = x2
o)	y = x2 + 4x + 5, x = 0, y = 0
und die kleinste Ordinate
p)	Halbperiode von y = sinx und
y = 0
q)	y = x2, y = 2 — x2
r)	4y = x2, y2 = 4x
s)	y = x2 + 4x, y = x + 4
t)	xy = 6, x + y — 7 = 0
u)	a2y2 = x3(2a — x)
v)	(y — x)2 = x3, x = 1
w)	Schlinge der Kurve:
x3 + x2 — y2 = 0
x)	Schlinge der Strophoide:
y2(2a — x) = x(x — a)2
x
y) Kettenlinie y = a cosh —
a
und x = ±a, y = 0
2. Berechne den Inhalt der Flächen, die
von den gegebenen Kurven begrenzt
werden:
a)	y = 0 und ein Bogen der Zykloide
x = a(t — sint), y = a(l — cost)
b)	x = a cos3 t, y = a sin3 t (Astro-
ide)
c)	r2 = a2 cos 2cp (Lemniskate)
d)	r = a(l — cos</?) (Kardioide)
e)	1.) r = 3 + sin 2cp
2.) r = 2 — cos 3cp
und jeweils benachbarte größte
und kleinste Radiusvektoren
f)r = ne^, ip = — 7t, cp = 7t
g)	r = |acos2^|
h)	r = \a sin 3^|
i)	r = a(sin ip + cos ip)
an
j)	r = -, -<(/?< 27t
ip 4
k)	r = a(l + sin2 2^), r = a
1)	durch den Teil der Kurve
• 3 T5
r = asm —,
o
der unter der Polarachse verläuft
m)	Schlinge des kartesischen Blattes
x3 + y3 — 3axy = 0
Hinweis: Gehe zu Polar koordinaten
über.
9.4 Bogenlänge eines Kurvenstückes, Krümmung von
Raumkurven
Bogenlänge oder Länge eines Bogenstückes bedeutet genauer die Maßzahl der
Länge. Die zu integrierenden und zu differenzierenden Funktionen sollen stets die
hierzu vorauszusetzenden Eigenschaften besitzen.
Länge s des Bogenstückes AB einer ebenen Kurve:
y = f (x), Xi < x < x2
x2
s =	y/1 + (y'}2 dx mit dem Bogendifferenzial
Xi
ds = y/1 + (y'y&x = y/dx2 + d?/2
(9.22)
132
9 Elemente der Differenzial- und Integralgeometrie
x = x(t), y = y(t), h <t<t2
t2
“=I /^d,	d.,=/^d,
tl
(9.23)
r = r(cp'), </?i < </? < </?2
ds = \/r2 + (r')2d</?
(9.24)
Länge s des Bogenstückes AB einer Raumkurve:
r = r(t) =	y(t), z(t))T, ti < t < t2
tl	tl
ds = \/^2 + Z/2 + dt = \/dx2 + d?/2 + dz2
(9.25)
Zwischen zwei Punkten Fq und P der Raumkurve r = r(t), die den Parame-
terwerten t0 bzw. t entsprechen, ist die Bogenlänge
t
S = / V(i(i))2 + (y(t))2 + (i(t))2 dt.
to
(9.26)
Bei festgehaltenem Pq kann man dann die Bogenlänge s als neuen Kurvenparame-
ter einführen und erhält für die Raumkurve die Darstellung
Der Tangentenvektor t
(9.27)
t = — = (a/(s),y'(s),z'(s))T
(9.28)
besitzt die Länge \t\ = 1.
Senkrecht auf dem Tangentenvektor steht der Hauptnormalenvektor n:
dt
ds
d2r
ds2
d2r
ds2
mit \n\ = 1.
(9.29)
9.4 Bogenlänge eines Kurvenstückes, Krümmung von Raumkurven 133
Senkrecht auf t und n steht der Binormalenvektor b:
b = t x n mit \b\ = 1	(9.30)
6, n. b bilden das begleitende Dreibein der Kurve.
Die Normalebene wird aufgespannt von n und b, die Schmiegebene von t und
n und die rektifizierende Ebene von t und b.
Die Krümmung x > 0 der Raumkurve r = r(s) an der Stelle s ist gleich dem
d2r
Betrag des Vektors —
ds2
d2r
ds2
(q ist der Krümmungsradius).
Für die Torsion oder Windung w gilt:
dr d2r d3r
ds ’ ds2 ’ ds3
ds2
Damit ist dann
dt	1	db
-— = k  n = - • n. = —w • n
ds	q	ds
(9.31)
(9.32)
(9.33)
Wird die Raumkurve durch [r = r(t) j mit einem beliebigen Parameter t dar-
gestellt, so ist
dr
T = — = r ein Vektor in Tangentenrichtung,
dt
(9.34)
Q
134
9 Elemente der Differenzial- und Integralgeometrie
B = — x = r x r ein Vektor in Binormalenrichtung, (9.35)
TV = B x T ein Vektor in Hauptnormalenrichtung,	(9.36)
und es gilt für die Einheitsvektoren t, 6, n:
T B N
t=m' b = W\’ n = W\'	(9’37)
Krümmung und Windung erhält man wie folgt:
dr d1 2r
dt dt2
\r x r|
H3
(9.38)
dt
dr d2r d3r
di ’ dt2 ’ dt3
dr d2r 2
dt dt2
(9.39)
1. Berechne die Bogenlänge der gegebe-
nen ebenen Kurvenstücke.
y2 = x3, der Bogen wird durch die
4
Gerade x = - abgeschnitten
O
y2 = ^(2 — x)3, abgeschnitten
durch x = — 1
2	2	2
x + y = a , insgesamt
2	2	2	.
x3 + y3 = a3, insgesamt
1 / . x ti 271
y = In(smx), ~ X~
Z/ = ln(l-x2),	<x< |
y2 = (x+1)3, abgeschnitten durch
b)
d)
f)
g)
h)
x2
y =------1, abgeschnitten durch
y = o2
y = a cosh —,
k)	y2 = 2px, abgeschnitten durch
_ P
X 2
1)	y = In (2 cos x) zwischen den be-
nachbarten Schnittpunkten mit
der y- und der x-Achse
m)	tyy2 = x(x — 3)2 zwischen den
Schnittpunkten mit der x-Achse
n) e2?/tanhx = 1, 1 < x < 2
o)	ein Bogen der Zykloide
x = a(t — sint), y = a(l — cost)
t6	t4
p)	x = —, y = 2---zwischen den
7	6	4
Schnittpunkten mit den Koordi-
natenachsen
q)	x = t2, y = -t(t2 — 3) zwi-
o
sehen den Schnittpunkten mit der
x-Achse
r)	Kardioide r = a(l — cos</?)
9.4 Bogenlänge eines Kurvenstückes, Krümmung von Raumkurven 135
s)	erste Windung der Spirale
r = acp
t)	r = asm —, insgesamt
O
2.	Ein biegsamer Faden ist in zwei
Punkten A und B aufgehängt. Die
Punkte A und B befinden sich in
gleicher Höhe und haben einen Ab-
stand AB = 2b voneinander. Die
Pfeilhöhe des Bogens sei /. Nimmt
man als Form des Fadens eine Pa-
rabel an, dann lässt sich für hinrei-
f
chend kleines — die Fadenlänge mit
b
2 f2
bestimmen. Zeige dies unter Verwen-
dung der Näherungsformel
V7! + a « 1 + -a für kleines a.
3.	Berechne die Bogenlänge der gegebe-
nen Raumkurvenstücke.
x	9	2 O
a) x = t, y = t, z = -t ,
0 < t < 3	3
b)x = 3cost, /a = 3sint, z = 4t,
0 < t < t0
x2	x3
c)	y = —, z = —, 0 < x < 3
7 y 2	6
d)	x = t — sint, y = 1 — cost,
z = 4 sin 0 < t < 7i
2’	“ “
e)	x = e*, y = e-t, z = t\/2,
0 < t < 1
1	x2
f)	y = - Inx, z = —, 1 < x < 2
7 y 2	’	2
g)	x = t — sint, y = 1 — cost,
.	t	.
z = 4 cos - zwischen zwei
2
Schnittpunkten der Kurve mit der
x, z-Ebene
4.	Bestimme den Tangentialvektor T,
den Binormalenvektor B und den
Hauptnormalenvektor TV sowie die
zugehörigen Einheitsvektoren t, b
und n im Punkt t = 0 der Kurve
x = l —sint, y = cost, z = t.
5.	Stelle die Gleichungen der Haupt-
normalen, der Binormalen und der
Schmiegebene zur Kurve x = t, y =
T2, z = t3 im Punkt t = 1 auf.
6.	Stelle die Gleichungen der Hauptnor-
malen und der Binormalen der Kur-
ve x = e*, y = e-t, z = t im Punkt
t = 0 auf.
7.	Gegeben ist die Kurve
r = (t cos t, t sint, t)T. Zeige, dass
diese Kurve eine konische Schrau-
benlinie darstellt und stelle die Glei-
chungen der Hauptnormalen, der Bi-
normalen und der Tangente an die
Kurve im Koordinatenursprung auf.
8.	Gehe bei den gegebenen Raumkur-
ven r = r(t) vom Parameter t zum
Parameter s (Bogenlänge) mit dem
Anfangspunkt in t = 0 über. Berech-
ne für r = r(s) die Einheitsvektoren
t, b, n sowie die Krümmung x und
die Windung w in dem angegebenen
Kurvenpunkt. Kontrolliere die For-
meln (9.33) für die Kurve der Auf-
gabe a:
a)	r = r(t) = (2 cost, 2 sint, tx/5)T
in einem beliebigen Kurvenpunkt
b)	r = r(t) =
(t — sint, 1 — cos T, 4 sin -)T
im Punkt F(x = 7t, y = 2, z = 4)
9.	Berechne für die Raumkurve r =
r(t) = (e^, e-t, tx/2)T
die Winkel des Binormalenvektors b
im Punkt t = 0 mit den Koordina-
tenachsen.
10.	Stelle die Gleichungen der Haupt-
136
9 Elemente der Differenzial- und Integralgeometrie
normalen und der Binormalen der
Kurve y = x , z = y im Punkt
x = 1 auf.
11.	Zeige, dass man durch Differenziati-
on der Gleichung v = vt nach der
Zeit t mit Hilfe von Formel (9.33)
die Zerlegung der Beschleunigung a
in eine tangentiale und eine normale
v
Komponente erhält: a = vt H------n.
Q
12.	Ein Punkt bewegt sich auf der Pa-
rabel x = t, y = t — t , wobei t die
Zeit der Bewegung bedeutet. Berech-
ne die Krümmung der Bahnkurve
und die tangentiale und die normale
Komponente der Beschleunigung im
Zeitpunkt t = 0 und in einem belie-
bigen Zeitpunkt.
13.	Ein Punkt bewegt sich auf der Ellip-
se x = 4 cos t, y = 3 sin t, wobei t die
Zeit der Bewegung bedeutet. Berech-
ne die Krümmung der Bahnkur-
ve und die tangentiale und normale
Komponente der Beschleunigung im
nr	i	71
Zeitpunkt t = —.
14.	Berechne die Krümmung der
Bahnkurve und die tangentiale und
die radiale Beschleunigung in einem
beliebigen Zeitpunkt t und für t = 1,
wenn die Bewegung durch
2
r = r(t) = (t,t , -t )T gegeben ist.
15.	Berechne die Krümmung und die
Windung w der gegebenen Kurven:
a)	r = r(t) = (t,t )T in einem
beliebigen Punkt und für t = 0
b)	r = r(t) = (e*, e-t, tV2)T in ei-
nem beliebigen Punkt und für
t = 0
x	x
c)	y = —, z = — in einem belie-
’ y 2	3
bigen Punkt und für x = 1
d)	r = r(t) = (2t,lnt,t )T in einem
beliebigen Punkt und für t = 1
e)	x = —, z = x in einem beliebi-
gen Punkt und für y = 1
f)	r = r(t) = (e^ sin t, e^ cos t, et)T
im Punkt t = 0
16.	Zeige, dass die Windung einer
Rechtsschraube
(r = r(t) = (a cos t, a sint, 6t)T) po-
sitiv, die einer Linksschraube
(r = r(t) = (a cos t, —a sint, 6t)T)
negativ ist (a > 0, b > 0).
Inhaltsberechnung bedeutet auch hier die Berechnung der Maßzahl des Inhaltes.
Die auftretenden Funktionen sollen alle notwendigen Voraussetzungen erfüllen, so
dass die Integranden im Integrationsintervall stetig sind.
In Bezug auf ein (rechtwinkliges) kartesisches x, y, ^-Koordinatensystem sei x
die untere und x die obere Grenze eines räumlichen Bereiches B. Für jedes
x E [x , x ] sei Ex diejenige Ebene, die den Punkt (x; 0; 0) enthält und parallel
zur ?/, z-Ebene liegt. Q(x) sei der Inhalt der durch Ex aus B ausgeschnittenen
9.5 Volumen, Mantelfläche von Rotationskörpern
137
Fläche. Für das Volumen Vb von B gilt dann
VB
(9.40)
Berechnung der Mantelfläche A und des Volumens V von Rotations-
körpern:
y = /(x) >0, xi < x < X2 bei Rotation um die x-Achse:
x2
Ax = 27t [
x2
(9-41)
X!
X!
x — p(z/) > 0, Z/i < Z/ < Z/2 bei Rotation um die ?/-Achse:

y2
Vy = n^\
yi
(9.42)
x = x(t), y = y(t\ A < t < tz bei Rotation um die x-Achse:
t2
A’ = P
tl
^2
(9.43)
ti
falls die Kurve bez. der x-Achse der
Graph einer Funktion ist.
(9.44)
r = r(</?), epi < cp < bei Rotation um die Polarachse p:
^2
Ap = 2n j* ri
^2
2 r
Vp = -7i / r (^)sin^d(/?, falls der Körper durch die Rotation des
von r((/?i), r(</?2) und r = r(cp) gebilde-
ten Sektors um p entsteht.
dr \
—	sm(/2d(/2
d(/? /
(9.45)
(9.46)
138
9 Elemente der Differenzial- und Integralgeometrie
1.	Berechne die Volumina der im Fol-
genden beschriebenen Körper durch
Anwendung der Formel (9.40):
a)	Gerade Pyramide mit rechtecki-
ger Grundfläche (Seitenlängen a
und b) und Höhe h
b)	Kugel (Radius R)
c)	Körper, begrenzt von den Ebenen
x = 1 und x = 3, Inhalt Q(x)
der Querschnittsfläche ist umge-
kehrt proportional dem Quadrat
ihres Abstandes vom Ursprung
und Q(2) = 27
d)	Obelisk, dessen parallele Grund-
und Deckfläche Rechtecke mit den
Seitenlängen A und B bzw. a und
b sind, während die Höhe gleich h
ist
e)	gerader elliptischer Kegel von der
Höhe h, dessen Grundfläche eine
Ellipse mit den Halbachsen a und
b ist
f)	Zylinderhuf, den eine Ebene von
einem geraden Kreiszylinder (Ra-
dius R) abschneidet, wobei die
Schnittebene durch einen Durch-
messer des Zylindergrundkreises
geht und mit dieser Fläche den
Winkel a bildet
2.	Berechne das Volumen des Rotati-
onskörpers, der durch Rotation der
angegebenen Kurvenstücke um die
x-Achse erzeugt wird.
a)	y2 = 2px, x = h
b)	xy = 4, x = 1, x = 4
\	u x	।
c)	y = a cosh —, x = ±a
d)	y = cos (x - -
571
x = 0, x = —
6
f)	y = i 2 2’ x = ±]-
1 + X21
g)	xi + yi = ai
h)	x2 — y2 = ö2, x = ±2a
i)	(y — 3)2 + 3x = 0, x = —3
j)	ein Bogen der Zykloide
x = a(t — sint), y = a(l — cost)
k)	x = a cos3 t, y = a sin3 t,
t = 0, t = 71
1)	x = a cos t, y = a sin 2t,
71
t = 0, t = -
3.	Berechne das Volumen des Rotati-
onskörpers, der durch Rotation der
angegebenen Kurven- bzw. Flächen-
stücke um die y-Achse entsteht.
x2 v2
a)	— -	= 1, y = ±b
a2 b2
b)	y2 = (x + 4)3, x = 0
c)	y2 = 4 — x, y = ±2
d)	y = x^, x = —4, y = 0
x2
e)	y = a----und x + y = a
a
f)	x2 — y2 = 4, y = ±2
X2 7/2
g)	~ + 72 = 1
a2 b2
h)	y = x3, x = 0, y = 8
4.	Berechne das Volumen des angegebe-
nen Rotationskörpers.
a)	Die Kurven 2y = x2 und 2x + 2y
— 3 = 0 begrenzen eine Fläche, die
um die x-Achse rotiert.
b)	Die Kurven y = e~2x —1,
y = e~x +1 und x = 0 begrenzen
eine Fläche, die um die x-Achse
rotiert.
c)	Die durch x2 + y2 = o2 begrenz-
te Fläche rotiert um die Gerade
x = b (6 > a > 0).
9.6 Aufgaben aus der Physik
139
Hinweis: dV = 7t(ö + rr)2d7/
—7t(ö — rr)2d7/ = 47tÖ£üd7/
d)	Die durch y = x2 und y = 4 be-
grenzte Fläche rotiert um die Ge-
rade x = 2.
e)	Die durch y = cosx, y = — l,x =
±7i begrenzte Fläche rotiert um
die Gerade y = — 1.
5.	Berechne das Volumen der Körper,
die durch Rotation der gegebenen
Kurven um die Polarachse entstehen.
a)	r = a(l ± cos <p)
Ti
b)	r = asin2(/?, 0 < p> < —
c)	r = a cos2 <p
6.	Berechne den Inhalt der Flächen, die
durch die Rotation der gegebenen
Kurven um die x-Achse erzeugt wer-
den.
a)	x ± y = r
x
b)	y = a cosh —, x = ±a
a
c)?/ = sinx, x = 0, x = 7i
d)	y = |x3, x = ±2
e)	y2 = 4 + x, x = 2
f)	x = a(t — sint),
y = a(l — cost), 0 < t < 2ti
g)	x = a cos3 t, y = a sin3 t
t3	t2
h)	x = —, y = i-----zwischen den
Ö	Zi
Schnittpunkten mit den Koordi-
natenachsen
i)	die von x = t2, y = ^-(t2 — 3)
o
gebildete Schlinge
7. Berechne den Inhalt der angegebe-
nen Rotationsflächen.
a) x2 ± y2 = a2 rotiert um die Gera-
de x = b (b > a > 0)
Hinweis:
b) der durch
dA = 2ti(ö + rr)ds + 2ti(ö — rr)ds
x2
y = 1,5 von y = —
abgeschnittene Bogen rotiert um
die y- Achse
c)	y = e-x, 0 < x < ±oo, rotiert
um die x-Achse
d)	x3 ± y3 = a3 rotiert um die y-
Achse
e)	r2 = a2 cos 2ip rotiert um die Po-
larachse
f)	r = 2a(l ± cos</?) rotiert um die
Polarachse
9.6 Aufgaben aus der Physik
1.	Berechne die Druckkraft des Was-
sers auf ein vertikales rechteckiges
Schleusentor mit einer Breite von
8 m und einer Höhe von 6 m. Berech-
ne weiterhin die Druckkraft auf die
untere Hälfte des Schleusentores.
2.	Berechne die Kraft, mit der Wasser
auf eine vertikale dreieckige Fläche
drückt, deren Basis a gerade an der
Wasseroberfläche liegt und deren Hö-
he gleich h ist.
3.	Berechne die Kraft, mit der Was-
ser auf einen vertikalen Halbkreis
drückt, dessen Durchmesser 2r gera-
de an der Wasseroberfläche liegt.
4.	Die Mauer einer Talsperre habe die
Form eines Trapezes mit der obe-
ren Grundlinie von 20 m, der unte-
ren Grundlinie von 10 m und der Hö-
he von 6 m. Berechne die Druckkraft
des Wassers auf die Mauer.
140
9 Elemente der Differenzial- und Integralgeometrie
5.	Berechne die Druckkraft des Wassers
auf eine vertikale dreieckige Fläche
der Höhe h, deren Basis a parallel
zur Wasseroberfläche liegt. Der ent-
gegengesetzte Eckpunkt liegt gerade
an der Wasseroberfläche.
6.	Berechne die Druckkraft des Was-
sers auf ein vertikales Parabelseg-
ment, dessen Grundlinie die Länge
4 m hat und gerade an der Wassero-
berfläche liegt. Der Scheitelpunkt be-
findet sich in einer Tiefe von 4 m.
7.	Ermittle die Wassertiefe x, in der
man sich ein rechteckiges Schleusen-
tor der Höhe h horizontal so in zwei
Teile geteilt denken kann, dass das
Wasser auf beide Teile mit gleicher
Kraft drückt.
8.	Ein zylindrischer Behälter mit ho-
rizontaler Achse ist zur Hälfte mit
Öl gefüllt (Dichte 0,9kg/dm3). Be-
rechne die Druckkraft des Öls auf je-
de der beiden ebenen Stirnseiten des
Behälters. Der Radius sei R = 2 m.
9.	Berechne die Trägheitsmomente be-
züglich der ./ -und der y- Achse für die
Fläche des Rechtecks, das durch die
Kurven x = 0, x = a, y = 0 und
y = h begrenzt wird.
Hinweis: Wird die Fläche begrenzt von y =
/(x), y = 0, x = xi, x = X2, so gilt:
X2	X2
Ix = | y f/3 Iy = J x2ydx.
10.	Berechne das Trägheitsmoment in
Bezug auf die x- bzw. die y-Achse für
die Fläche des Dreiecks, das durch
x y
die Kurven x = 0, y = 0 und — fff- =
a b
1 begrenzt wird.
11.	Berechne das Trägheitsmoment der
durch die Kurven x = 2, y = x2 und
y = 0 begrenzten Fläche in Bezug
auf die y-Achse.
12.	Berechne das Trägheitsmoment der
Viertelkreisfläche
x = acost, y = asint in Bezug auf
die x-Achse.
13.	Berechne die statischen Momente
bezüglich der x- bzw. der ?/-Achse
und die Koordinaten des Schwer-
punktes eines Dreiecks, das durch die
Kurven x = 0, y = 0 und x + y = a
gebildet wird.
Hinweis: Wird die Fläche begrenzt von y =
/(x), y = 0, x = xi, x = X2, so gilt:
Statische Momente:
X2	x2
Mx = j y2 dx, My = J xydx.
X1 X1
Koordinaten des Schwerpunktes:
M/	Mx .... .
xs = —A ys = —dabei bedeutet A
xi.	xi.
den Flächeninhalt der Figur.
14.	Bestimme den Schwerpunkt des
Halbkreises x2 + y2 = a2 oberhalb
der x-Achse.
15.	Bestimme den Schwerpunkt der Flä-
che, die durch die Kurven a2y =
bx2, x = a und y = 0 begrenzt wird.
16.	Berechne die Koordinaten des
Schwerpunktes der Fläche, die von
den Kurven y = 4 — x2 und y = 0
begrenzt wird.
17.	Berechne die Arbeit, die man auf-
wenden muss, um das Wasser aus
einem zylindrischen Bassin vom
Grundkreisradius 0,5 m auszupum-
pen, wenn im Augenblick des Be-
ginns der Wasserstand im Bassin
2,8 m beträgt und um 0,2 m niedri-
ger liegt als die Austrittsöffnung für
das Wasser im Zylinder.
18.	In einem Zylinder befindet sich unter
9.6 Aufgaben aus der Physik
141
dem Kolben Luft mit einem Volumen
Vo = 0,2 m3 und einem Druck po =
10330 Pa. Berechne die Arbeit für ei-
ne isotherme Verdichtung der Luft
auf ein Volumen Li = 0, Im3.(Nach
dem Gesetz von Boyle-Mariotte ist
PiVi = PoVq.)
19.	Berechne die Arbeit für die adiabati-
sche Verdichtung von Luft des Volu-
mens Vq = 0,1 m3 und des Drucks
Po = 101337 Pa auf ein Volumen
Vi = 0,03m3. (Nach dem Gesetz
von Poisson ist p\V™ = PoKf mit
x ~1.4.)
20.	In einem Stromkreis nimmt die
Spannung im Verlaufe von einer Mi-
nute gleichmäßig von 0 V auf 120 V
zu. Der Widerstand im Stromkreis
ist gleich 100 Q. Berechne die Strom-
arbeit für die betrachtete Minute.
(Induktivität und Kapazität werden
vernachlässigt.)
21.	Der Widerstand eines metallischen
Leiters möge sich bei Temperaturän-
derungen nach folgendem Gesetz än-
dern:
R = 7?o(l + 0, 0041?), mit
Ro - Widerstand bei 0°C
i? - Temperatur in °C.
Ein Leiter, dessen Widerstand bei
0°C gleich 10 Q ist, erwärmt sich
gleichmäßig von i?i = 20 °C auf i?2 =
200 °C im Verlaufe von 10 Minuten.
Während dieser Zeit liegt an ihm
eine Spannung von 120 V an. Wel-
che Elektrizitätsmenge fließt in die-
ser Zeit durch den Leiter?
10 Funktionenreihen
10.1 Grundbegriffe
Ist	(z = 1, 2,...) eine Folge von (reellen) Funktionen einer reellen Variablen
x, die alle auf einer gewissen Menge D C R definiert sind, so wird
f>(x)	(10.1)
2=1
eine Funktionenreihe genannt. Die Menge M aller x E D. für die die Reihe
(10.1) konvergiert, ist ihr Konvergenzbereich. Für die Funktionenfolge {sn(x)}
der Partialsummen
n
Sn(x) =	(10.2)
2=1
der Reihe (10.1) gilt im Falle der Konvergenz: Für jedes feste x E M existiert eine
Zahl s(x) mit
lim sn(x) = s(x), x E M.	(10.3)
n^oo
Die Funktion s(x) nennt man Summenfunktion (kurz: Summe) der Funktionen-
reihe (10.1). Die Differenz
rn(x) = s(x) - sn(x)	(10-4)
wird Rest genannt.
Die Funktionenreihe fi(x) ist au^ einem Intervall I = [a, b] gleichmäßig
2=1
konvergent gegen s(x) genau dann, wenn zu jedem beliebigen c > 0 ein von x
unabhängiges no(e) derart existiert, dass
|rn(x) | < s für alle n > no(e) und alle x E I	(10.5)
gilt.
Satz 10.1 (Kriterium von Weierstraß) Die Reihe (10.1) konvergiert gleich-
mäßig auf dem Intervall I = [a, b], wenn eine konvergente Zahlenreihe ci
2=1
nur positiven Gliedern Ci existiert, so dass
|/i(x)| < Ci für alle x E I und alle i	(10.6)
erfüllt ist.
10.1 Grundbegriffe
143
Eigenschaften gleichmäßig konvergenter Reihen:
1. Reihen von auf I = [a, b] stetigen Funktionen fi(x) (i = 1,2,3,...) die auf I
gleichmäßig konvergent sind, darf man gliedweise integrieren’.
b
(10-7)
2. Besitzen die Glieder der Funktionenreihe fi(x) aRf dem Intervall I = [a, b]
2=1
stetige Ableitungen /'(x) und sind fi(x) URd 12 fi(x) au^ gleichmäßig
2=1	2=1
konvergent, darf man gliedweise differenzieren:
5? A(a^) ) = 52= s'(x) für alle x G 1
.2=1
(10.8)
1. Bestimme für |x| < 1 die Summe und
den Rest der Reihe
1 + x + x2 + x3 + . . .
und zeige, dass sie auf dem Intervall
[0,1/2] gleichmäßig konvergiert.
Für welches n gilt für den Rest
|rn(x)| < 0,001 bei beliebiger Wahl
von x aus dem gegebenen Intervall?
2. Zeige, dass die Reihe
1 1 1
x2 + 1 x2 + 4 + x2 + 9
1
x2 + 16
auf der gesamten Zahlengeraden
gleichmäßig konvergiert. Für welches
n (bei beliebigem x) ist der Rest der
Reihe |rn(x)| < 0,0001?
3. Zeige, dass die Reihe
x + x(l — x) + x(l — x)2
+x(l — x)3 + ...
auf dem Intervall [0,1] nicht gleich-
mäßig, jedoch auf dem Intervall
[1/2,1] gleichmäßig konvergiert.
Für welches n gilt für den Rest
M^)| < o, 01 bei beliebiger Wahl
von x aus dem Intervall [1/2,1]?
4.	Zeige, dass die Reihe
9	9	4
ry*
auf dem Intervall [0,1] gleichmäßig
konvergiert.
Für welche n und beliebiges x gilt auf
diesem Intervall |rn(x)| < 0,1?
5.	Zeige, dass die Reihe
o	vC	vC
X + T~;	3 +	;	312 + • • •
i + xö (i + x6y
für x > 0 nicht gleichmäßig,
für x > 1 jedoch gleichmäßig konver-
giert.
Für welches n ist der Rest \rn\ <
0, 001 für beliebiges x > 1?
6.	Zeige, dass die Reihe
1 1
x(x + 1) + (x + l)(x + 2)
1
+ (x + 2)(x + 3) + ” ’
auf (0,+oo) gleichmäßig gegen 1/x
konvergiert.
144
10 Funktionenreihen
Für welches n (bei beliebigem x > 0)
gilt für den Rest |rn(x)| < 0,1?
7.	Zeige durch Anwendung des Krite-
riums von Weierstraß, dass die ge-
gebenen Reihen auf dem Intervall
[0 , +oo) gleichmäßig konvergieren.
Für welches n gilt
|rn(x)| < 0,01?
x 1	1
a) —	-|----	:
\/l A 3\/l 3.r
1 1
+ 3Vl + 5rc + 33V1 + 7rc + ’' ’
1 1 1
x/l+V \/22 + 2.c	y/21 + 3.c
1
H—,	- + • • •
\/26 + 4x
8.	Zeige durch Anwendung des Kriteri-
ums von Weierstraß, dass die gege-
benen Funktionenreihen auf dem In-
tervall (—oo,+oo) gleichmäßig kon-
vergent sind.
a)	cos x H— cos 2x H—- cos 3x
2	2~
+ — cos4x + ...
_ x .	1.x	1.x
b)	smx + — sm - + — sm -
1 x
+ — sm - + ...
42	4
9.	Für welche Werte von x konvergieren
die folgenden Funktionenreihen?
a)	1 + e~x + e~2x + e-3® + ...
111
b)	1 + + + +
2^	4,L
1 1 1
1 + X2 + 1 + X4 + 1 + X6 +
10.2 Potenzreihen und Taylor-Reihen
Potenzreihen sind spezielle Funktionenreihen:
anxn = ao + aix + a2x2 + CZ3X3 + ...
n=0
CLn(x - X0)n = «0 +	- Xq) + ü2(x - Xq)2 + . . .
n=0
(10.9)
(10.10)
Die Potenzreihe (10.9) besitzt den Mittelpunkt xq = 0; sie hat den Konver-
genzradius r, wenn die Reihe (10.9) für |x| < r konvergiert, für |x| > r jedoch
divergiert. Darum heißt das Intervall (—r ,r) auch Konvergenzintervall der Po-
tenzreihe (10.9).
Die Potenzreihe (10.10) hat den Mittelpunkt xq 0. Ist r ihr Konvergenzra-
dius, so besitzt sie das Konvergenzintervall (xq — r , xq + r).
Falls die folgenden Grenzwerte existieren, gilt für den Konvergenzradius r
(r > 0):
(10.11)
bzw.
(10.12)
10.2 Potenzreihen und Taylor-Reihen
145
Für | r = 01 ist die Potenzreihe nirgends konvergent.
Für [r = oo) ist die Potenzreihe beständig konvergent (d.h. für alle x E R).
Für 10 < r < oo ] ist die Potenzreihe für alle x mit \x — xq| < r absolut konver-
gent und für alle x mit |x — xq| > r divergent. Für x = x$ ± r kann Konvergenz,
aber auch Divergenz vorliegen. Deshalb müssen die Randpunkte des Konvergenz-
intervalls gesondert untersucht werden.
Eigenschaften konvergenter Potenzreihen:
1. Konvergente Potenzreihen lassen sich multiplizieren:
ist E aiXz = si(x) für |x| < r± und bkXk = <§2(x) für |x| < ^2, so gilt für
z=0	k=Q
|x| < r = min(ri,r2):
(10.13)
mit
Cn — y @4 ‘ bn—l — kl^bn T kL\bn—\ T • • • T CLnl)Q
(10.14)
z=o
2. Eine konvergente Potenzreihe darf man in ihrem Konvergenzintervall gliedweise
differenzieren und integrieren:
Entwicklung von Funktionen in Potenzreihen
(10.15)
(10.16)
(10.17)
Ist /(x) auf einem Intervall 7, das die Entwicklungsstelle x$ im Inneren enthält,
beliebig oft differenzierbar, so heißt die formal gebildete Reihe

E
fc=0
(10.18)
146
10 Funktionenreihen
Taylor-Reihe der Funktion /(x) mit dem Mittelpunkt xq.
/(x) = 53 ~— x^k für alle x e I	(10.19)
fc=0
gilt genau dann, wenn
lim Rn(x) = 0 für alle x e 1,	(10.20)
wobei Rn(x) das Restglied der Taylor-Formel ist (siehe Abschnitt 7.3).
Die MacLaurin-Fteihe zu /(x) ist ein Sonderfall der Taylor-Reihe (für xq = 0):
(W.2I)
k=0
Formelsammlungen enthalten Potenzreihenentwicklungen der wichtigsten elemen-
taren Funktionen nebst zugehörigem Konvergenzintervall.
1. Bestimme das Konvergenzintervall
der gegebenen Reihe. Untersuche die
Reihe auch auf Konvergenz für |x| =
r.
n=l
D
ry*	ry*
eXy	eXy	eXy
+ 3^2 + 32 • 3 + 33 • 3 + ’' ’
3nxn
y/(3n - 2)2"
j) E(-d
n=l
ry»	ry*Kj
।
5?2 + 52^3	53y/4
c) 1 +	+ 32y/3	4x2 52^32 8a;3 +72^/33 +
2x d) 1 + —f= 4 \/5Ü5	4x2 x/9-52 8a;3 V13 • 53
2	x4
e) 1-^^= 3-2^2	+ 32 • 3a/3
	X^ 	F ± 33 -4\/4
k) 52xn 1?2'
n=l
m) (x + 1) +
x2n~1
2n — 1
(x + l)2
2-4
+
, (a^ + 1)3
3 • 42
(* + l)4 ,
4.43
2x - 3
1
(2x - 3)2
3
+ (2a? - 3)3
10.2 Potenzreihen und Taylor-Reihen
147
2. Bestimme das Konvergenzintervall
und die Summe s(x) der gegebenen
Reihen.
a)	1 T 2x T 3x2 -|- 4x^ T ...
b)	1 — 3x2 + 5x4 5 — 7x6 ± ...
d)	a? + — + — + .
£ ö
e)	1 + 3x + 5x2 + 7x3 + ...
f)	1 — 4x + 7x2 — 10x3 ± ...
Hinweis: Zur Bestimmung von s(x) ermitt-
le man bei a) und b) zunächst: j* s(t) dt;
o
bei c) und d):	. pej e). s _ s . x unj
dx
bei f): s + s • x.
3. Stelle für die gegebenen Funktionen
die MacLaurin-Reihe auf, bestimme
das Konvergenzintervall und gib das
Restglied an (vgl. Abschnitt 7.3).
Untersuche das Restglied für n
oo.
a) f(x) = coshx
b) /(x) = sin2 x
4. Stelle für die Funktion /(x) = ex^a
die Taylor-Reihe mit dem Mittel-
punkt xq = a auf, bestimme das
Konvergenzintervall und untersuche
das Restglied.
5. Gib für die folgenden Funktionen
die ersten drei nichtverschwindenden
Glieder ihrer Taylor-Reihe mit dem
angegebenen Mittelpunkt xq an:
a)	fix') = ecosx, x0 = 0
b)	f(x) = Vx3, Xq = 1
c)	f(x) = 1, x0 = 2
X
d)	y(x) = In COS X, Xq = 0
6. Gib für die folgenden Funktionen die
Potenzreihenentwicklungen mit dem
Mittelpunkt xq = 0 und die zuge-
hörigen Konvergenzintervalle unter
Verwendung bekannter Potenzreihen
an:
a)	= (1 + x)3
b)	f(x) =	1
c)	f{x) = In
1 — X
d)	/(x) = In (2 — 3x + x2)
e)	/(x) = In (1 — x + x2)
v 1 —
g) f(x) = e~x2
h) f(x) = xe~2x
j)	~
9 + x2
k)	/(x) = sin 3x + x cos 3x
1)	/(x) = cos2 x
m)	/(x) =
7 V 7	x/3T2^
7. Gib für die folgenden Funktionen die
Taylor-Reihen mit dem geforderten
Mittelpunkt xq sowie das zugehö-
rige Konvergenzintervall unter Ver-
wendung bekannter Potenzreihen an:
a) /(x) = Inx, xq = 1
148
10 Funktionenreihen
b)	f(.x) =	*	, z0 = -4
Xz + 6X + 2
c)	f(X) = xo = —2
X
d)	f(x) = cos|, x0 =
7t
e)	f(x) = sin 3z, x0 = --
O
f)	f(x) = Ex, xo = -1
g)	f(x) = x4 — 4z2, xq = —2
Hinweis: vollständiges Horner-Schema.
h) /(z) = sin^, x0 = 1
i) /(z) = x/z, x0 = 4
j) f(x) = e*, xo = —2
k) f(x) = xo = -1
X1
8. a) Berechne mit Hilfe der geometri-
schen Reihe die MacLaurin-Reihe
der Funktion fix) = ----------------
v 7	1 + x2
und gib das Konvergenzintervall
an. Ermittle aus dem Ergebnis
durch Integration die Reihenent-
wicklung für arctan x.
b) Setze x = —= in der Reihen-
V3
entwicklung für arctan x. Gewin-
ne daraus eine Reihe zur Berech-
nung von 7t und berechne 7t nähe-
rungsweise unter Verwendung der
ersten fünf Glieder dieser Reihe.
9.	Berechne die folgenden unbestimm-
ten Integrale unter Verwendung
der entsprechenden Reihenentwick-
lungen:
a f smx	f £ dx
J x	J x
10.	Stelle die Funktion
4>(x) = e-t dt durch ihre Potenz-
o
reihe (xq = 0) dar. Berechne $(|),
indem so viele Reihenglieder verwen-
det werden wie nötig sind, um den
Fehler kleiner als 0, 000001 zu halten.
11.	Stelle die Funktion
4>(x) = y \/l +12 dt in Gestalt ei-
o
ner Reihe dar und berechne <h(|).
Verwende dazu so viele Glieder wie
nötig sind, um den Fehler kleiner als
0, 00001 zu halten.
12.	Entwickle die Funktion
r t2
<h(x) = / cos — dt in eine Reihe und
o
berechne 4>(|) mit einer Genauigkeit
von 0,000001.
13.	Berechne den Umfang der Ellipse
x = acost, ?/ = &sint, a > b > 0.
10.3 Fourier-Reihen
Auf dem Intervall I = [—l, /] sei /(x) beschränkt, stückweise stetig, stückweise
monoton, und es gelte für alle x E I:
/(z) = i(/(z-0) + /(z + 0)).	(10.22)
Dann lässt sich /(x) durch eine Fourier-Reihe darstellen:
nnx 7 nnx
an cos —--H bn sm —-—
(10.23)
10.3 Fourier-Reihen
149
wobei
WIX 1
cos —— dx ;
. WIX 1
sm —-— dx
(10.24)
n = 0,1,2,...
n = 1,2,3,...
Wegen der Periodizität der trigonometrischen Funktionen lassen sich auch Funk-
tionen auf (—00, +00) durch eine Fourier-Reihe darstellen, falls sie periodisch mit
der Periode 21 sind und die oben auf I gemachten Voraussetzungen erfüllen.
Spezielle Fälle:
1. /(x) ist eine gerade periodische Funktion ^/(—x) =
/(z)
WIX
an cos —-—
(10.25)
nnx
cos—-—dx, n = 0,1,2,...
(10.26)
0
2. /(x) ist eine ungerade periodische Funktion /(—x) = —/(x)J:
K \	' n7lX
/w = 2^™ sm —~
(10.27)
b-,
727TX
sm—-—dx, n = 1,2,3,...
(10.28)
0
1. Entwickle die folgenden periodischen
Funktionen mit der Periode 21 = 2ti
in eine Fourier-Reihe und bestätige
mit Hilfe der erhaltenen Reihen die
Richtigkeit der jeweils angegebenen
Formeln für die Summen von Zah-
lenreihen:
a)	/(x) = 1 für x e (0,7t) und
/(-x) = -/(x);
1 1 1
1-3 + 5“7
4
.2
b)	/(x) = x für x e [0,7r] und
f(~x) =
111	_ 71
1+32 + 52 + 72+'"__8
c)	f(x) = x2 für x G [—7t,7t];
111 -2
1 - 22 + 32 “42
1 1 1
+ 22 + 32 + 42
12
^2
6
d) =
für x e (—71,0)
für x E [0,7i]
150
10 Funktionenreihen
g) f(X) =
7T — X
e) /(x) = —-— für x E (0,7t] und
f(-x) = f(x)
f) f(X) = I sinx|;
1 1 1 _ 1
T~3 + 3J5 + 5~7 +"' ” 2
x für x e [0,7i/2]
71 — x für x E [n/2,7i]
und /(-x) = -/(x)
2.	Entwickle die folgenden periodischen
Funktionen mit der Periode 21 in eine
Fourier-Reihe:
a)	/(x) = 1 für x E (0, Z) und
/(-x) = -y(x)
b)	/(x) = 1 — x für x E [0,1],
/(—x) = f(x) und l = 1
[o für x E (-/,0]
c /(x) = <	r
für x E [0, /)
d)	f(x) = x für x E [0, /) und
f(~x) = /(x)
e) /(®) = S
und l = 1
für x E [—1,0)
für x E (0,1]
f) /(x) = ex für x E (—l /)
3.	/(x) ist auf dem Intervall [0,2] durch
seinen Grafen gegeben
1---------------\
und wird auf folgende Weise fortge-
setzt:
a)	als gerade Funktioon
b)	als ungerade Funktion
mit der Periode 21 = 4.
Entwickle beide Funktionen in eine
Fourier-Reihe.
11 Differenzialrechnung für reelle Funktionen
mehrerer Veränderlicher
Eine reellwertige Funktion f von n reellen Variablen xi, ... , ordnet jedem
geordneten n-Tupel (xi, . , xn) e D(f) C Rn genau eine reelle Zahl
y e W(f) C R zu:
y =	 •  ,xn) = f(x) = f(P), x e D(f)	(11.1)
wobei
x = xiei + x2e2 H------F xnen = (xi, x2,... , xn)T	(11.2)
der Ortsvektor des Punktes P(#i,	. , xn) ist.
Statt (11.1) schreibt man z.B. auch
bei n = 2:	z = /(x,?/),
bei n = 3:	w = /(x, y, z); u = /(x, y, z).
Unter dem Abstand d(P,Q) zweier Punkte P(pi,P2, • • • ,Pn) und
Q(qi, Q2, • • •, Qn) versteht man die (reelle) Zahl
d(P, Q) = \/(pi - Qi)1 2 + (P2 - ®>)2 H-F (p„ - g„)2 = \p - q\ (11.3)
11.1 Niveaulinien, -flächen, -hyperflächen
Das geometrische Bild einer Funktion mit zwei Veränderlichen
z = .f(x,y), (z, y) G £>(/)	(11-4)
ist eine Fläche im R3.
Die Menge aller Punkte P(#i,	. , xn) e Rn, die der Gleichung
/(xi, X2,..., xn) = c = const.	(11-5)
genügen, heißt Niveauhyperfläche von /(xi, X2,... , xn) mit dem Niveau c.
Die Niveauhyperflächen von (11.4) sind Kurven (Niveaulinien, Höhenlinien) im
R2, die Niveauhyperflächen von w = f(x, y, z) sind Flächen (Niveauflächen) im R3.
1. Gib von den folgenden Funktionen
z = f(x,y) den größtmöglichen De-
finitionsbereich an, zeichne wenigs-
tens vier Niveaulinien, indem das Ni-
veau selbst gewählt wird und be-
schreibe das geometrische Bild, wo-
bei ggf. weitere Schnittkurven zu
nutzen sind:
152 11 Differenzialrechnung für reelle Funktionen mehrerer Veränderlicher
a)	z = /(x, y) = -3x + 4y + 8
b)	z = /(x, y) = \/25 - x2 - y2
c)	z = f(x,y) = xy
d)	z = f(x,y) = x2 + y2
4
e)	z = /(az,y) =
x2 + y2
f)	z = f(x,y) = y/xy
2.	Stelle den größtmöglichen Definiti-
onsbereich der gegebenen Funktio-
nen in der x, ?/-Ebene dar.
a)	f(x, y) =	1	=
y 4 — x2 — y2
b)	/(x, y) = arcsin — + y/xy
c)	f(x,y) = In (rc + y)
d)	f{x, y) =	1
vy - \/x
e)	f(x, y) = \/l - .z-2 + \/l - y2
f)	f(x, y) = x/^2 + y2 -1
+ In (x2 + y)
g) f(x,y) = ln(l - e'z'+!/)
3.	Stelle die Niveaulinien der gegebe-
nen Funktionen in der x, ?/-Ebene dar
(c = —4, —1,0, +1, +4).
a)	z = f(x,y) =x + y
b)	z = f(x,y) =x2 — y2
4.	Bestimme die Niveauflächen von
W = f(x,y,z).
a)w = x + y + z
b)	w = x2 + y2 + z2
c)	w = x2 + y2 — z2
5.	Zeige für f(x,y) = \A;4 + ?/4
— 2xy, dass f(tx, ty) = t2 • f(x,y).
x
6.	Zeige für f(x,y) =--------, dass
+ f(b,a) = 1.
7.	Bestimme den größtmöglichen Defi-
nitionsbereich der gegebenen Funk-
tionen w = /(x, y, z).
a)	w = y/x + y/y + \fz
b)	w = In (xyz)
c)	w = arcsin x + arcsin y + arcsin z
d)	w = \/l — a?2 — ?/2 —
11.2 Grenzwert, Stetigkeit
Eine Folge {a?m} von Punkten Pm(xim,	= 1, 2,..., konver-
giert genau dann gegen den Punkt A(ai, ö2,..., an\ wenn
lim x^ = ai für i = 1, 2,..., n
m—^OG
gilt. Man schreibt dann auch (mit a = (ai, U2,..., nn)T):
lim xm = a = lim Pm = A
rn—^DG	rn—^DG
(11-6)
(11-7)
Die Funktion y = /(a?) = /(xi,	• • -^n) sei in einer Umgebung U von defi-
niert, eventuell mit Ausnahme von x$.
Eine (reelle) Zahl a heißt Grenzwert von f(x) für x gegen xq, wenn für alle
Folgen {xm} mit xm e xm a?0 und lim xm = xG gilt:
m^oG
lim = a	(11-8)
m^-OG
11.2 Grenzwert, Stetigkeit
153
Dafür schreibt man
lim /(a?) = a	(11.9)
CC—>£Cq
Die Beziehung (11.9) gilt genau dann, wenn zu jedem e > 0 ein ö = ö(s) >0 derart
existiert, dass für alle x mit
0 < \x — a?o| < S folgt |/(a?) — q| < e.	(11.10)
Eine Funktion /(a?) heißt stetig an der Stelle xq, wenn f in einer Umgebung U
von xq definiert ist, und wenn gilt
lim f(x) = /(a?0)	(U-ll)
CC—>CCq
1.	Für z = f(x,y) lassen sich folgende
Differenzen definieren:
Az = f(x + Ax, y + Ay) - /(x, y)
A.rz = /(x + Ax, y) - /(x, y)
AyZ = /(x, y + Ay) - /(x, y)
Gegeben ist z = x~ — xy + y1.
Berechne Az, Axz, Ayz.
Berechne Az, Axz, Ayz für den Fall,
dass sich x von 2 auf 2,1 und y von
2 auf 1, 9 ändert.
2.	Zeige, dass der Grenzwert
r y
hm ---------------
(x;2/)^(0;0) X - y
nicht existiert, indem die Annähe-
rung des Punktes (x; y) an den
Punkt (0; 0) längs der Geraden y =
mx betrachtet wird. Wähle Beispie-
le aus, die bei dieser Annäherung die
Zahlenwerte 3 bzw. 2 bzw. —2 erge-
ben.
3.	Gegeben sind:
x^1 — vp1
a)	f(x,y) = y
x2 + y2
b)	f(x,y) =	-----
x2y2 + \x — y)2
Berechne die Grenzwerte
lim (lim/(x, ?/)) und
y—X) yx—X)	7
lim (lim /(x, y)).
x—X)yy—X)	7
Zeige, dass lim
(x;?/)^(0;0)
existiert.
/(x,y) nicht
4.	Berechne die folgenden Grenzwerte,
falls sie existieren:
2 - y/xy + 4
a) hm -------------------
O;y)^(0;0) Xy
b)
sin(xy)
hm -----------—-
(x;2/)^(0;0) xy
lim
sin (xy)
(x;2/)^(0;0) X
, sin (xy)
lim ---------
(x;i/)^(0;2) X
lim (x2 + y2) sin —
(x;2/)^(0;0)	xy
f) lim --------------
(x;2/)^(0;0) x + y
h) hm ----------------
(x;i/)^(4;4) y - X
lim exp
x^-0,5
2(2x + y) In (x2y3)
y2 _ 4^2
5.	Untersuche die folgenden Funktionen
154 11 Differenzialrechnung für reelle Funktionen mehrerer Veränderlicher
z = f(x,y) an der Stelle (0; 0) auf
Stetigkeit:
a)
?Xy 2 fürs?2 + y2 > 0
= < xz +
0	für x = y = 0
b)
(x - l)2 + fy + l)2
sin x sin y
c)	z = In (1 — x2 — y2)
d)z =______x2 + v2____
(x + y){y2 - x)
0	für x = y = 0
c) f(x,y)
/ Q
x y	n o o
4 , 2	für x2 + y2 > 0
= x4 + yz
k 0	für x = y = 0
6. Finde die Unstetigkeitsstellen der ge-
gebenen Funktionen z = f(x,y).
7. Wo sind die gegebenen Funktionen
w = /(x, y, z) unstetig?
x 1
a) w =-----
xyz
b)w - • -	—
xS + yz — zz
x2 + y2 — z2 + 1
11.3 Partielle Ableitung, Gradient, Richtungsableitung
Die Ableitung einer Funktion mehrerer Variabler nach einer ihrer Variablen, wobei
die anderen Variablen als konstant angesehen werden, heißt partielle Ableitung
(1.Ordnung) der Funktion nach dieser Variablen. So ist
lim f (*^10 ’ * * * ’ %i—1,01 XiQ “h h, Xi~\_ 1 i i ^no) f (^101 • • • •> ^no)
h^0	h
df
(11-12)
die partielle Ableitung von f nach Xi an der Stelle xq (z = 1, 2,..., n) sofern dieser
Grenzwert existiert.
Für die gemischten höheren partiellen Ableitungen gilt nach dem Satz von
Schwarz:
Sind die gemischten partiellen Ableitungen stetig, so ist die Reihenfolge ihrer Dif-
ferenziation beliebig, z.B. fX1X2 = fX2X1, fX1X1X4 = fX1X4X1 = fX4X1X1 usw.
Ist y = f(x) an der Stelle xq nach allen Xi stetig differenzierbar, so nennt man
den Vektor
df df
dx±' dx2'
= grad/(o:)|aj=aJo
(11.13)
Gradient von f an der Stelle x$.
11.3 Partielle Ableitung, Gradient, Richtungsableitung
Mit Hilfe des Nabla-Operators
____L 9 A
\öxi ’ dx2 '	’ dxnJ
kann man auch schreiben
(11-14)
grad/(a?) = V/(a?)
155
(11.15)
Für die Ableitung von f(x) an der Stelle xq in Richtung des Vektors
S = (si, 82,  • , Sn)T gilt:
df(x)
ds
= fs(xo) = (gradf(x)f
X = Xq
X = Xq
S
H
i n
= 7-| 52/^(^o) • Sk (11-16)
|s| fc=i
1.	Bilde von den gegebenen Funktionen
die partiellen Ableitungen 1. Ord-
nung.
a)	f(x,y) = x3 + 3x1 2y - y3
b)	f(x,y) = In (x2 +y2)
c)	f(x,y) = arctan —
d)	g(x,t) = In ( A“ A)
\ v	vx /
e)	c(a, 6,7) = \A2 +	— cos 7
n p/	x	y	.	z	x
f)	f(x,y,z)	=	-	+----
x	y	z
g)	f(x,y)	=	xe~yx
o) f(x,y) = xy
y
p) /(x, y) = exp sin —
q) /(x, y) = arcsin
r) f(x,y,z) = (xy)z
s) f(x,y,z) = zxy
t) f(x,y,z) = exyz
\ tt \ 1 cosy
u) f(x,y) = In----
cosx
2.	Berechne für die angegebenen Funk-
tionen die geforderten partiellen Ab-
leitungen.
a)	z = In (y — x2); gesucht:
i)	<a(x, t) = arcsin (t^/x)
j)	f&y) = cos(ax - by)
k)	/(x, y) = arcsin —
x
1) f(x,y) = -——
J J v 3y — 2x
m) h(x, t) = In sin (x — 2t)
n) p(x, y) = sin2 (x + y) — sin2 x
— sin2 y
Zxx') ^xyi Zyy
T \	U + V	1
b)	w = arctan--------; gesucht:
1 — uv
^UUl ^UV) ^vv
c)	z = x3 + x2y + y3\ gesucht:
Zxxxi ^xxyi Zxyyi %yyy
3.	Zeige, dass für die gegebenen Funk-
tionen die angegebenen Gleichungen
erfüllt sind.
a) z = In (V-r + Vy)
156 11 Differenzialrechnung für reelle Funktionen mehrerer Veränderlicher
b)
c)
dz dz 1
= 5
r • y
z = y x sm —
x
dz dz z
r^+,)äi=2
X
u = exp —
tz
du du
2^+*^7 =°
dx dt
x — y
d2z	d2z	d2z	2
------L- 2----1____= ------
dx2	dxdy	dy2 x — y
f) z = ex^y
d2z	dz	dz
dxdy	dy	dx
4. Zeige, dass die Funktion
für beliebige zweimal differenzierba-
re Funktionen f und cp der partiellen
Differenzialgleichung
xyuxy + y~'uyy + xux + 2yuy = 0
genügt.
5.	Verifiziere die Gleichung
d2 z	d2z
=	für die folgenden
dxdy	dydx
Funktionen:
a) z = sin {ax — by)
^2
b)z=-
y2
c) z = In {x — 2y)
6.	Gegeben ist die Funktion
z = f(x,y) = x2 + y2.
a)	Berechne grad z allgemein und im
Punkt (3; 4).
b)	Zeichne die durch den Punkt
(3; 4) verlaufende Niveaulinie und
den Gradienten.
c)	Berechne die Ableitung der
Funktion f in der Richtung
a = 30° gegenüber der positiven
x-Achse allgemein und im Punkt
(3; 4).
7.	Berechne für
z = f{x,y) =x2 -y2
den Gradienten allgemein und im
Punkt P(2; 1). Zeichne die durch den
Punkt P verlaufende Niveaulinie und
den Gradienten.
8.	Berechne die Ableitung der Funktion
/(x, y) = x3 — 2x2y + xy2 + 1
im Punkt M(l;2) in der Richtung,
die von M nach TV (4; 6) weist.
9.	Berechne grad // im Punkt P(l; 2; 3)
für u = /(x, ?/, z) = xyz.
10.	Berechne den Winkel zwischen den
Gradienten der Funktion
z = f(x,y) = ln^
in den Punkten A ( - : - ) und
\2 4J
11.	Berechne die Ableitung der Funkti-
on
Z = f(x,y) = x2 - xy- 2y2
im Punkt P(l;2) in der Richtung,
die mit der x-Achse einen Winkel von
60° bildet.
12.	Berechne die Ableitung der Funkti-
on
z = f{x,y) = In y/x2 + ?/2
im Punkt P(l; 1) in Richtung der
Winkelhalbierenden des 1. Quadran-
ten (der x,?/-Ebene).
13.	Berechne die Ableitung der Funkti-
on
w = /(x, y, z) = x2 — 3yz + 5
im Punkt M(l;2;—1) in der Rich-
11.4 Zerlegungssatz, totales Differenzial
157
tung, die mit allen (positiven) Ko-
ordinatenachsen gleiche Winkel ein-
schließt.
14.	Berechne die Ableitung der Funkti-
on
w = /(x, ?/, z) = xy + yz + zx
im Punkt M(2; 1; 3) in der Richtung,
die von M nach 7V(5; 5; 15) führt.
15.	Berechne grad/(a?) für
/(xi, X2, X3, X4) = 6x1X2 + 3X1
— cos X3 + X4 eX2.
16.	Berechne den größten Anstieg der
Fläche z2 = xy (z > 0) im Punkt
(4; 2).
11.4 Zerlegungssatz, totales Differenzial
Die totale Änderung einer Funktion y = /(a?) an der Stelle xq entsprechend den
Änderungen hi = Axi, h2 = Ax2,...,hn = Axn ist die Differenz
At/ = A/
= /(^10 + ^1, X20 +	• • • , Xno + hn) - /(Xio, X20, • • • , XnQ)
= /(^10 + Axi, X20 + Ax2, ... ,xn0 + Axn) - /(xio, X20, . . . ,^no) (11-17)
wobei vorauszusetzen ist:
®oeP(/), x^hED(f)	(11.18)
mit
h = (Zii, h2,..., hn)T = (Axi, Ax2, ..., Axn)T.	(11.19)
f(x) heißt an der Stelle xq total (vollständig) differenzierbar, wenn an allen
Stellen xq + h E D(f) die folgende Zerlegungsformel gilt:
Ay = A/ = fX1 (a?0)^i + fX2 (a?o)fr2 H-F fXn (xQ)hn + y • p
n
= ZZx^xor Axk+r]- p (11.20)
k=l
mit
p = \/(Axi)2 + (Ax2)2 + • • • + (Axn)2	(11.21)
V = rj(x10,xn0; Axi,..., Aa?„)	(11.22)
und
lim 77 = 0.	(11.23)
p^O
Der lineare Anteil der totalen Änderung in der Zerlegung (11.20) heißt totales
(vollständiges) Differenzial dy der Funktion y = /(#) an der Stelle xq:
n
dy = 'Zfxk(.x0) • ^xk	(11.24)
fc=l
158 11 Differenzialrechnung für reelle Funktionen mehrerer Veränderlicher
Ay = dy + y • p	(11.25)
Aus der Definition des totalen Differenzials (11.24) folgt für die speziellen Funk-
tionen y = XP
dxi = Axi, do*2 = Ax2,..., dxn = Axn	(11.26)
Damit gilt für das totale Differenzial einer Funktion y = /(xi, X2,... ^xn\.
d„-AirI + Arlrs+...+Arlr„	(11.27)
UX\ (JX2	dxn
Für hinreichend kleines p folgt aus (11.25) die Näherungsbeziehung (11.28) für
eine differenzierbare Funktion y = /(xi, X2,..., xn):
Ay dy	(11.28)
oder
/(a?! + Arci,..., xn + Axn) « /(a?1;..., xn) + d/(rci,..., a?n) (11.29)
Das vollständige Differenzial 2. Ordnung einer Funktion z = f(x,y) wird
folgendermaßen definiert:
d1 2z = da;2 + 2^“7Tda:dy + f“ld2/2	(11-30)
dx2 dxdy	dyz
Die Gleichung (11.30) gestattet die symbolische Schreibweise:
f d	d	\ 2
d2z = ( —— dx + ——dy ) z	(11.31)
\dx	dy J
Besitzt /(xi, X2,...,xn) stetige partielle Ableitungen A:-ter Ordnung, so gilt für
das vollständige Differenzial fc-ter Ordnung:
/ d	d	\k
dfe/(xi,...,x„) = (-—da?i H----F ——d.z-„) /(a?i,..., xn) (11.32)
yuxi	dxn	j
1. Berechne für die gegebenen Funktio-
nen z = f(x,y) die vollständige Än-
derung Az allgemein und an der an-
gegebenen Stelle (x; y) bei vorgege-
benen Änderungen Ax und A?/. Lies
aus beiden Darstellungen von Az das
totale Differenzial dz ab.
a)	z = xy an der Stelle (5; 4) und
Ax = 0,1; Ay = -0,2
b)	z = x2y an der Stelle (—3; 2) und
Ax = 0,01; Ay = -0,02
c)	z = x2 — 3xy + y2 an der Stelle
(2; 1) und Ax = -0,1; Ay = 0, 2
11.5 Fehlerrechnung
159
2.	Bilde das totale Differenzial von den
gegebenen Funktionen.
a)	f(x,y) = ^-
x-y
b)	y{s,t) = es/t
c)	f(x,y) = y/x2 + y2
d)	u(x, y, z) = \/x2 + y2 + z2
y
e)	/(x, y) = In tan —
g)	</?(x, y) = ex cos y + y sin 3x
%
h)	y, z) =
Vx+y
i) /(xi, X2, X3, X4) = 0*12-'r'3 ln^4
3.	Gib den Wert des totalen Differenzi-
als an.
a)	f(x,y) = - an der Stelle (2; 1)
x
und Ax = 0,1; Ay = 0, 2
b)	g(x,y) = exy an der Stelle (1; 2)
und Ax = —0,1; Ay = 0,1
y
c)	</?(x, y) = arctan — an der Stelle
(2; 3) und Ax = 0,1; Ay = —0, 5
4.	Berechne die Werte Az und dz für
die Funktion z = In (x2 +y2), wenn
sich x von 2 auf 2,1 und y von 1 auf
0, 9 ändert.
5.	Berechne von den gegebenen Funk-
x-	j2
tionen d u.
y^
a)	u(x,y) =
xz
b)	u(x, y) = x In —
c)	u(x, y, z) = xy + yz + xz
d)	u(x, y) = cos (mx + ny)
11.5 Fehlerrechnung
Ist /(xi, X2,..., xn) eine von den Variablen xi, X2,..., xn abhängige Größe, de-
ren partielle Ableitungen fx. stetig sind, und hat man Xi mit einem Fehler Axi
gemessen (z = 1, 2,..., n), so gilt für den absoluten Fehler Af der Größe f die
Abschätzung
IA/I « |d/| < £
df(xr, ...,xn)
dxi
(11.33)
 | |
Für die Abschätzung des relativen Fehlers gilt damit:
A/
f
a/
f
(11.34)
Die Anwendung der Abschätzungen (11.33) und (11.34) setzt voraus, dass alle
|Aa?j| hinreichend klein sind, denn nur dann lässt sich die Ersetzung von |A/|
durch |d/| rechtfertigen.
Oft lassen sich für |J^-| bei Beachtung von Xi — |Aa^| < Xi < Xi + |Aa^|
(i = l,2,...,n) obere Schranken angeben. Setzt man diese in (11.33) ein, so
erhält man eine obere Schranke für |A/|.
160 11 Differenzialrechnung für reelle Funktionen mehrerer Veränderlicher
1.	Es ist der Wert der Funktion
x
z = /(x, y) = — für x = 2 ± 0,1 und
y = 4±0, 3 zu berechnen und der da-
bei auftretende Fehler zu ermitteln.
a)	Berechne /(l, 9; 3,7),
/(1,9; 4,3), /(2,1; 3, 7),
/(2,1; 4,3), weil 1,9 < x < 2,1
und 3, 7 < y < 4, 3 gilt. Welche
größte Abweichung |Az|max von
/(2; 4) ergibt sich dabei?
b)	Berechne eine Abschätzung von
Az mit Hilfe der Formel

(2;4)
dz
• IM + V
dy
und vergleiche das Ergebnis
|Az|
max •
c)	Berechne obere Schranken
dz
dx
(2;4)
mit
für
dz
und — bei Beachtung
dy
von 1,9 < x < 2,1; 3, 7 < y <
4, 3 und berechne damit eine obe-
re Schranke für | Az|. Vergleiche
auch dieses Ergebnis mit | Az\rnax-
2.	Für den Ersatzwiderstand R von
zwei parallelgeschalteten Widerstän-
den R1 und 7?2 güt
_ R\R2
R\ “h 7?2
Es wurde gemessen R^ = (550 ± 3)Q
und R2 = (150 ± 1)Q.
a)	Berechne eine Abschätzung für
den absoluten und den relativen
Fehler von R nach Formel (11.33).
b)	Berechne eine obere Schranke für
den absoluten und den relativen
Fehler.
3.	Von einem geraden Kreiskegel wur-
den der Radius r = (5±0,01)cm und
die Höhe h = (12 ± 0, 04)cm gemes-
sen. Zu berechnen ist die Kegelober-
fläche Aq.
a)	Berechne eine Abschätzung für
den absoluten und den relativen
Fehler von Aq.
b)	Berechne eine obere Schranke für
den absoluten und den relativen
Fehler.
4.	Von einem geraden Kegelstumpf
wurden gemessen die beiden Radien
R = (400 ± 5)mm, r = (300 ± 6)mm
und die Höhe h = (500 ± 8)mm. Be-
rechne eine Abschätzung für den re-
lativen Fehler des Volumens.
5.	Bei einem Dreieck schließen die Sei-
ten a und b den Winkel 7 ein. Ge-
messen wurde a = (92, 5 ± 0, 2)m,
b = (65, 6 ± 0, l)m und
7 = (57,8° ±0,3°).
Berechne eine Abschätzung für den
relativen Fehler, der bei der Berech-
nung der Länge der dritten Dreieck-
seite c auftritt.
6.	Schätze den relativen Fehler bei
der Volumenberechnung einer ge-
raden quadratischen Pyramide ab,
wenn die Messungen der Quadratsei-
te einen relativen Fehler von 3 % und
der Höhe einen relativen Fehler von
4% aufweisen.
7.	Bei adiabatischer Zustandsänderung
von Gasen gilt piVf = P2IA
Berechne eine Abschätzung des rela-
tiven Fehlers bei der Berechnung von
Vi, wenn V2, Pi, P2 mit den relati-
ven Fehlern 0,05 % bzw. 0,04 % bzw.
0,1 % gemessen wurden (^ = 1,4).
8.	Die Leistung P am Außenwiderstand
Ra sei
Berechne eine Abschätzung des rela-
tiven Fehlers bei der Berechnung von
11.6 Tangentialebene, Flächennormale
161
Pa, wenn
= =10%und
Ra Ri
Ra = 1007?i bekannt sind (E =
const.).
11.6 Tangentialebene, Flächennormale
Im Punkt Fo(^o; 3/o; ^o) der Fläche F(x, y,z) = 0 lautet die Gleichung der Tan-
gentialebene:
{x - x0)Fx(x0,y0,z0) + (y - y0)Fy (x0, yo, ?o)
+ (z - z0)Fz(x0,y0,z0) = 0 (11.35)
Ihr Normalenvektor ist
n= (Fx(x0,y0,z0), Fy(x0,y0, z0), Fz(x0,y0, z0))T
und damit ist
r = (xq, ^o)T +	— oo < A < oo
(11.36)
(11.37)
die Gleichung der Flächennormalen im Punkt F(xq;//o;^o) der Fläche
F(x, y, z) = 0.
Ist die Fläche in der expliziten Form z = f(x,y) gegeben, wird sie durch Umfor-
mung (z.B. f(x,y) — z = 0) auf die implizite Form F(x,y, z) = 0 gebracht.
Gilt für einen Punkt der Fläche Fx = Fy = Fz = 0, so heißt dieser Punkt
singulär. In einem singulären Punkt existieren weder eine Tangentialebene noch
eine Flächennormale.
1. Stelle die Gleichung der Tangential-
ebene und der Flächennormalen der
gegebenen Flächen auf.
a) z = 1 + x2 + y2 an der Stelle
x = y = 1
b) x2 + 2y2 + 3z2 — 21 = 0 im Punkt
Fo(1;2;2)
c) z = In (x2 + y2) an der Stelle
x = 1, y = 0
d) z = sin x cos y an der Stelle
71
x = y = —
y 4
2. Stelle die Gleichung der Tangential-
ebene der gegebenen Flächen auf.
a) xy = z2 im Punkt Fq(xo; Z/o5 ^o)
b)	xyz = a3 im Punkt Pq^xq; yo', zq)
9	9	9
X V
c)	^7 + TV----y = 1 im Punkt
cP b1 2 c2
Fi(xi; ?/i; zi) und im Punkt
P2(a; b; c)
3.	Bestimme die Gleichung der Ebene,
die die Fläche x2 + 4?/2 + z2 = 36 be-
rührt und parallel zur Ebene x + y —
z = 0 liegt.
4.	Stelle die Gleichungen der Norma-
len im Punkt (3; 4; 5) zur Kegelfläche
x2 + y2 = z2 auf. In welchem Kegel-
punkt existiert keine Normale?
5.	Berechne die Winkel, die die Norma-
162 11 Differenzialrechnung für reelle Funktionen mehrerer Veränderlicher
le an der Stelle x = 0, y = 2 der
Fläche x2 + y2 — xz — yz = 0 mit den
Koordinatenachsen bildet.
6.	Zeige, dass die Tangentialebenen der
Fläche xyz = a3 mit den Koordi-
natenebenen Pyramiden konstanten
Volumens bilden.
7.	Zeige, dass die Summe der Qua-
drate der Abschnitte, die von
der Tangentialebene der Fläche
2	2	2	2
x3 + y3 + z3 = a3 auf den Koordi-
natenachsen erzeugt werden, gleich
der konstanten Größe a2 ist.
8.	Stelle die Gleichung der Normalen
der Fläche x2 + y2 — (z — 5)2 = 0
im Punkt xq = 4, zq = 0 und yo > 0
auf.
9.	Berechne den Abstand des Ko-
ordinatenursprungs von der Tan-
gentialebene des Konoids (Keils)
(2a2 — z2)x2 — a2y2 = 0 im Punkt
(a; a; a).
10.	In welchem Punkt ist die Tangential-
ebene der Fläche z = 4 — x2 — y2
parallel
a)	zur x, ?/-Ebene,
b)	zur Ebene 2x + 2y + z = 0?
Stelle die Gleichungen dieser Tan-
gentialebenen auf.
11.7 Kettenregel
1.	Ist y = /(xi, X2,..., xn) eine stetig partiell differenzierbare Funktion der Va-
riablen xi, X2,..., xn, die wiederum differenzierbare Funktionen der einen un-
abhängigen Variablen t sind:
x1 = cp1(t), X2=V2(t),...,Xn = lf>n(t)	(11.38)
so erhält man die Ableitung der Funktion
y = /(V’lW- ^2(t), •  • ,	(11.39)
nach der Variablen t mit Hilfe der erweiterten Kettenregel (einfache Form):
dy _	dy_	dxi	+ dy_	d.r2 dy_	d.r„	_
dt	dx\	dt dx-2 dt	dxn	dt
dy . . dy . . dy .
7;—zi + 7;—H----------F —xn (11.40)
UX\ 0X2	uXn
2.	Ist y = /(xi, X2,..., xn) eine stetig partiell differenzierbare Funktion der Va-
riablen xi,X2,... ,xn und diese wiederum partiell differenzierbare Funktionen
der m unabhängigen Variablen G, ^2,...,
^1 = ^1(G, ^2, • • • , tm), X2 = ^(G, ^2, • • • , tm), • • •
Xn = ^n(G,^2, • • • ,^m)	(H-41)
so erhält man die m partiellen Ableitungen der Funktion
y = f (^i(G,^2, • • •,^m), (/Mg,£2 1 • • • 1 tm ),	^„(tl,t2,...,tm)) (H-42)
11.7 Kettenregel
163
nach den m Variablen G,t2, • • • mit Hilfe der erweiterten Kettenregel
(allgemeine Form):
dy	= ^y.	dxr dy	dx-2	dy	dxn	
dti	dxi	dti 3x2	1 dtw"	dxn	dt±	
dy	= dy	dx± dy	9x2	_ _	dy	dxn	
dt-2	dx±	dtz + dx^	dt2	dxn	dt2	(11.43)
dy	= dy	dx± dy	. 9x2 _ .		dxn	
dtm	dx±	dtm dx2	dtm	.. + 9xn	dtm	
3.	Wird durch die Gleichung |^F(xi, X2,...,xn, y) = Oj eine Funktion
\y = y^x^xz,...,xn) j implizit definiert, wobei F stetig differenzierbar nach
allen Variablen ist, so erhält man die partiellen Ableitungen der implizit
gegebenen Funktion y an der Stelle xq = (xio, X20, • • •, ^no)T mit Hilfe der
Formeln
dy = FXk(x1o,...,xno,yo) = T 2
dxk Xo Fy(xw,...,xnO,yo)
wobei vorausgesetzt werden muss:
^(rcio,..., xn0, y0) ± 0; y0 = y(xw,a?n0)
F(xw,.. .,xn0,y0) = 0
(11.44)
(11.45)
1.	Berechne — nach der Formel
dt
(11.40),	wenn gegeben sind:
db) z = x + xy + y , x = t , y = t
b) z = \/x2 iy1, x = sint,
y = cos t
Mache die Probe durch Einsetzen
von x(t) und y(t) in z.
. dz
2.	Berechne —.
dt
a)	z =—, x = e^, y = 1 — e2t
x
b)	z = Ax2 + 2Bxy + Cy2,
x = sin t, y = cos t
c)	z = arctan —, x = e2t +1,
x
y = e2t-l
1X vw t 1
d)	z = —, u = e , v = mt
u
w = t2 — 1
e)	z = uvw, u = t2 + 1,
v = In t, w = tan t
_	. dz	1.1
3.	Berechne —, wenn gegeben sind:
dx
a)	z = uv, u = u(x), v = vfir)
b)	z = xey, y = y(x)
4.	Eine Funktion /(^i, ^2, • • •, xn)
heißt homogen vom Grad k, wenn
f(txi, t^2,..., tXn) = tk
x/(xi,x2, . . . ,Xn).
Differenziere beide Seiten dieser
164 11 Differenzialrechnung für reelle Funktionen mehrerer Veränderlicher
Gleichung nach t, setze im Ergeb-
nis t = 1 und beweise so den Satz
von Euler über homogene Funktio-
nen:
dxi
2=1
(stetige Differenzierbarkeit voraus-
gesetzt).
dz	d.z
5.	Berechne —— und —, wenn gegeben
dx	ctx
sind:
a) z = In (ex + e27),
1 3
y = — x'
y 3
b) z = x27, y = p{x)
dz
— und
du
6.	Berechne
x2
z = —, X = u — 217,
y
dz
—, wenn
dv
y = v + 2u.
7.	Es sei z = f{x,y). Drücke — und
dx
dz	dz	dz
—- durch ——	und —-	aus,	wenn
dy	du	dv
a)	u	= rnx +	ny,	v =	px	+	qy
ua	y
b)	u = xy, v = —
c)	u = y/xy, v = x + y
8.	Gegeben ist u = f{x,y),
•• i du
x = rcos</2, y = rsint/?. Drucke ——
dr
. du .	. du	du
und —— durch —— und —— aus und
dp dx	dy
zeige:
(du\2	71
\dr / \r
du^2
J
I du \ i du \
\ dx J + \dy J
9.	Gegeben ist z = y + f{u), wobei
9	9
u = x — y .
Zeige, dass yzx + xzy = x für je-
de beliebige differenzierbare Funkti-
on f(u) gilt.
d?/
10.	Berechne — aus folgenden Glei-
d.r
chungen:
a)	x2 + y2 — 4x + 6y = 0
b)	^2/3 + y2/3 = a2/3
c)	xe2y —ye2x = 0
d)	xy + In y + In x = 0
e)	y + x = e27^
f)	2 cos (x — 2y) = 2y — x
dz	dz
11.	Berechne —— und —— aus folgenden
dx	dy
Gleichungen:
a)	x2 + y2 + z2 — 6x = 0
b)	z2 = xy
c)	cos {ax + by — cz)
= k • {ax + by — cz)
d) x2 + y2 + z2 — 2zx = a2
12.	Berechne die Tangentensteigung der
folgenden Kurven in den angegebe-
nen Punkten:
a)	x2 + y2 = 10t/ in ihrem Schnitt-
punkt mit der Geraden x = 3
b)	x3 + y3 — 2axy = 0 im Punkt
x = y = a
c)	y2 — xy = 4 in ihren Schnittpunk-
ten mit der Geraden x = 3
13.	Ermittle die Punkte, in denen
die Tangente an die Kurve
x2 + y2 + 2x — 2y = 2
a)	parallel zur x-Achse
b)	parallel zur y-Achse
verläuft.
14.	Zeige, dass für xyz = a3 gilt:
xzx + yzy = -2z.
15.	Zeige, dass der Differenzialgleichung
xzx+yzy = z eine Funktion z genügt,
die durch die Gleichung (für konische
f y \
Flächen) — = p ( — ) definiert ist.
x \xJ
11.8 Taylor-Formel
165
11.8	Taylor-Formel
Ist y = /(a?) an der Stelle a?o = (#io, #20, • • • ,#no)T und in einer Umgebung U
von xq (m + l)-mal stetig differenzierbar, so gilt für xq + h e U:

+ Rm mit
X = Xq
(11.46)
«... _
x=XQ-\-,0h
und h = (ft-i, , /in)T, 0 < 1? < 1, wobei V den Nablaoperator bedeutet.
Daraus folgt speziell für n = 2 und m = 3:
f(x0 + h, y0 + k) = f(x0, y0) + fx(x0, y0)h + fy(x0, y0)k
^fxx(x0, yo)h2 + 2fxy(x0, y0)hk + fyy(x0, y0)fc2)
d" \^fxxx(^XQ^ yo)h -(- xxy(xQ, yo)h k -(- xyy^XQ, y3^hk
+ fyyy(xo, yo~)k3j + R3 mit
o 1A d , d\
— — I h——F k— j
4! \ dx dy J
f(xo + d/i, y0 + ilfc)
4! \ ox[ oxöoy	oxzoyz
+ 4Mc3
d4f
dxdy3
(11.47)
+ k4
xo+'Oh
yo+ßk
1.	Gib die Entwicklung der Funkti-
on /(xq + h, yo + k) mit Hil-
fe der 7ß?/Zor-Formel an, wenn
/(x, y) = x2 + xy + y2 ist.
2.	Entwickle f(x,y) = x3 + 2xy2 nach
Potenzen von (# — 1) und (y — 2).
Hinweis: Taylor-Formel mit xq = 1, yo = 2
und h = x — 1, k = y — 2.
3. Entwickle f(x,y) = x2y nach Poten-
zen von (x — 1) und (y + 1)
a) mit Hilfe der Taylor-Formel
b) mathematisch elementar.
4.	Entwickle f(x,y) = In (x — y) nach
Potenzen von x und (y + 1) bis zu
Gliedern 2. Grades einschließlich und
gib das Restglied an.
5.	Entwickle
/(x, y) = sin (mx + ny)
nach Potenzen von x und y bis zu
Gliedern 3. Grades einschließlich und
gib das Restglied an.
6.	Entwickle f(x,y,z) = x2 + y2
+ z2 + 2xy — yz — 4x — 3y — z — 4
an der Stelle x = y = z = 1 mit
Hilfe der Taylor-Formel.
166 11 Differenzialrechnung für reelle Funktionen mehrerer Veränderlicher
7.	Entwickle die gegebenen Funktionen
an der angegebenen Stelle mit Hilfe
der 7h?/Zor-Formel bis zu Gliedern 2.
Grades einschließlich ohne explizite
Angabe des Restgliedes.
a)	/(x, y) = arctan —, x = 1,
x
y =
b)	f(x,y) = yx, x = 2, y = 1
und berechne damit näherungs-
weise 1, l2,1
c)	/(x, ?/, z) = In (xy + z2),
x = y = z = 0
8.	z(x,y) ist durch die Gleichung z3
-2xz-\-y = 0 implizit definiert. Dar-
aus folgt: z = 1 für x = y = 1. Ent-
wickle z nach Potenzen von (x — 1)
und (y — 1) bis zu Gliedern 2. Grades
einschließlich ohne explizite Angabe
des Restgliedes.
11.9	Lokale Extrema
Eine Funktion /(a?) = /(xi, a?2,..., xn) sei in einer Umgebung der Stelle xq =
xio, ^20, • • •, ^no)T partiell differenzierbar. Besitzt f in xq einen lokalen (relativen)
Extremwert, so gilt:
/x1(^o) = O, /X2(a?0) = 0, ...,/^(a?0) = 0	(11.48)
oder kurz:
grad/(a?)|£C=£Co = o	(11.49)
(notwendige Bedingung für ein lokales Extremum).
Ist f zweimal stetig partiell differenzierbar in einer Umgebung der Stelle xq,
so heißt die symmetrische Matrix
(«Tq) ••• fxixn(&o)\
.................................................. (11.50)
fxnX1(xo)  fx„x„(Xo)/
Hessesche Matrix von f an der Stelle xq. Ihre Hauptabschnittsdeterminan-
ten sind
Di = fX1X1(xo), D2 =
fxiXi (a>o) fx±X2 (^o)
/x2xi (®o) fx2X2 (^o)
D3 =
/xixi («Tf))
fx2X! (^o)
fX3X]_ (®o)
fx±X2 (^o) fX±X3 (®o) I
fx2X2 (®o) fx2x3 (®o) ,...,Dn = detH(x0)
fx3x2(xo) fx3x3(xo)
(11.51)
Für ein lokales Extremum an der Stelle xq ist hinreichend, dass gilt:
1-	[grad/(a;)|a;=g!o = o]
2.	für die Hauptabschnittsdeterminanten der Kesseschen Matrix von f an der
Stelle xq gilt:
11.9 Lokale Extrema
167
a)	im Falle eines Minimums:
[z?! >0, n2>0, n3>o,...,z?w>o^
b)	im Falle eines Maximums:
(z?i<o, n2>o, n3 <o,...,z?w(-i)w >o)
Daraus folgt speziell für n = 2:
Ist z = f(x,y) an der Stelle (xq,?/o) zweimal stetig partiell differenzierbar, so ist
hinreichend dafür, dass f(x,y) bei (xq,?/o) einen Extremwert besitzt, dass an der
Stelle (xo,?/o) güt:
1.	/X(xo,?/o) = 0, fy(xo,yo) = 0
2.	D(x0,7/0) = fxx^XQ, 7/0) • fyy(xQ, 7/0) - /^(x0,7/0) > 0
3.	/xx(^o,t/o) > 0 bzw. fyy(xo, ?/o) > 0 im Falle eines Minimums
fxx(xo,yo) < 0 bzw. fyy(xo, ?/o) < 0 im Falle eines Maximums.
Gilt jedoch statt 2.: D(xq,?/o) < 0, so liegt kein Extremum vor;
oder D(xq,t/o) = 0, so muss durch andere Untersuchungen geklärt werden, ob ein
Extremum vorliegt oder nicht.
1.	Bestimme Lage und Art der Extre-
ma für die folgenden Funktionen z =
a)	z = x2 — xy + y2 + 9x — 6y + 20
b)	z = yy/x -y2 - x + 6y
c)	z = x3 + 8y3 — 6xy + 1
d)	z = 2xy — 4x — 2y
e)	z = 2x3 — xy2 + 5x2 + y2
f)	z = ex/2(x + y2)
g)	z = x(x2 — 3) cos?/, 0 < y < 7t
h)	z = x4 + ?/4 — 2x2 + 4x?/ — 2y2
i)	z = x2 — 6x + (3 — x)(?/3 — 3y)
2.	Bestimme Lage und Art der Extre-
ma für die folgenden Funktionen u =
f&y,zy.
a)	u = x2 + y2 + z2 — 4x + 6y — 2z
b)	u = £üt/2^3(1 — x — 2y — 3z)
(x > 0, y > 0, z > 0)
\ y z 2
c)	u = x + - H----F -
x y z
(x > 0, y > 0, z > 0)
e)	u = x2 + 2y3 + 4z2 + 2yz + 6x
—2y — 6z-h 13
f)	u = x2 + y2 + z2 — xy + x — 2z
3.	Berechne den größten und den
kleinsten Wert der Funktion z =
f(x,y) im Bereich B.
a)	z = x3 + y3 — 3xy,
B : 0 < x < 2, -1 < y < 2
b)	z = x2 — y2, B : x2 + y2 < 1
c)	z = sinx + sin?/ + sin (x + ?/),
_	71	71
B : 0 < x < —, 0 < y < —
~ - 2’	~ y ~ 2
4.	Bestimme die Abmessungen eines
rechtwinkligen offenen Bassins von
minimaler Fläche unter der Bedin-
gung, dass sein Rauminhalt gleich V
ist.
5.	Ermittle das Maximalvolumen ei-
nes Quaders, dessen Raumdiagonale
gleich 2\/3 ist.
168 11 Differenzialrechnung für reelle Funktionen mehrerer Veränderlicher
6.	Bestimme mit Hilfe der Methode der
kleinsten Quadrate für N gegebene
Wertepaare (^, yi) eines Mess Vor-
ganges die Ausgleichskurve y = /(x)
der vorgegebenen Art.
a)	(0; — 1), (1; 2), (2; 4), (3; 6), (4; 9);
y = ax + b
b)	(1;5), (2; 3), (4; 1), (5;-1);
b
y = a+-
x
c)	(1;5), (2; 18), (4; 129), (5; 250),
(8; 1025); y = ax3 + -
x
d)	(1; 7,1), (2; 27, 8), (3; 62,1),
(4; 110), (5; 161); y = axb
Hinweis: Beachte zur Vereinfachung der
Rechnung: 1g y = 1g a + b 1g x.
Hinweis: Die angegebene Ausgleichskurve
enthält noch unbekannte Parameter, z.B. a
und 5, die aus der Forderung
N
Q(a,b) =	- /(®i))2 —> Min
7=1
zu berechnen sind.
7.	Gegeben ist die reelle symmetrische
Matrix /1	2	2
4=2	1	—2
\2	—2	1
a)	Berechne die Eigenwerte von A.
b)	Berechne die Extremwerte
Rayleigh-Quotienten R:
XL X
xT = (xi,x2,x3)
c)	Welchen mathematischen
sammenhang vermutet man
Grund der Ergebnisse?
des
Zu-
auf
11.10 Extrema bei Nebenbedingungen in Gleichungsform
Es seien /, </?i,..., cpm Funktionen von n (reellen) Variablen xi, x2,... ,
(m < n). Gesucht sind lokale Extrema von f(x) = /(xi, x2,..., xn) unter den
Nebenbedingungen
^i(^) = (^i(xi,x2,... ,xn) = 0
^2(jt) = ^2(^1,^2,... ,xn) = 0
(11.52)
</?m(a?) = 9^771(^1, ^2, • • • > ^77) = 0
Die Funktionen /, </?i,..., seien in einem Gebiet G C Rn stetig partiell diffe-
renzierbar. Mit beliebigen reellen Zahlen Ai, A2,...,Am (Lagrangesche Multipli-
katoren) wird die Zagrange-Funktion
777
L = f(x)+ ^Xi 	(11.53)
7=1
gebildet.
Notwendig dafür, dass f an der Stelle xq = (xio, x2o, • • • ,^77o)T £ G unter
den Nebenbedingungen (11.52) einen lokalen Extremwert besitzt, ist das Bestehen
11.10 Extrema bei Nebenbedingungen in Gleichungsform
169
der folgenden Gleichungen:
771 /O
LXk = fXk{Xo) + E A, •	= 0 (fc = 1, 2,..., n)	(n_54)
LXl = (pi(xo) =0 (/ = l,2,...,m)
Damit erhält man als notwendige Bedingung ein System von (n + m) Gleichungen
für die (n + m) Unbekannten xio, X20, • • •, Ai, A2,..., Am.
Ob an einer auf diese Weise gefundenen Stelle x$ tatsächlich ein Extremum
vorliegt, bedarf weiterer Überlegungen.
a)
1
2
b)
1. Berechne die Extrema der gegebenen
Funktionen unter den angegebenen
Nebenbedingungen.
z = f(x,y) = - + x + y = 2
x y
. 11
z = j(x,y)=x+y, — + — =
xz yz
Z = f(x, y) = xy, x1 + y2 3 4 5 = 2
u = /(x, ?/, z) = x — 2y + 2z,
x + y + z =9
u = /(x, y, z) = xyz.
c)
d)
2. Bestimme den Punkt auf der Hyper-
bel x2 — y2 = 4, der vom Punkt (0; 2)
den geringsten Abstand hat.
3. Bestimme die Abmessungen eines
Zylinders von größtem Volumen un-
ter der Bedingung, dass dessen Ge-
samtoberfläche A = 671 dm2 beträgt.
4. Der Ellipse x2 + 3y2 = 12 ist ein
gleichschenkliges Dreieck einzube-
schreiben, dessen Basis der großen
Achse der Ellipse parallel ist. Be-
rechne den Inhalt der Dreiecksfläche,
wenn diese so groß wie möglich sein
soll.
5. Die x-Achse stelle die Grenze zwei-
er optischer Medien dar. Welchen
Weg muss ein Lichtstrahl vom Punkt
(0; a) zum Punkt (c; —6) nehmen, um
zum Durchlaufen dieser Entfernung
eine möglichst kurze Zeit zu benöti-
gen (a > 0, b > 0, c > 0)?
Hinweis: Man hat das Minimum der Funk-
cv	h
tion T = T(a,ß) = ---------- + --------
vi cos a V2 cos ß
unter der Bedingung a tan a + b tan ß = c
zu ermitteln, wobei und V2 die Lichtge-
schwindigkeiten in den beiden Medien und
a bzw. ß der Einfalls- bzw. der Brechungs-
winkel sind.
x2	v2
6.	Der Ellipse — +	= 1 ist ein
aß	bz
Rechteck größten Flächeninhalts ein-
zubeschreiben. Berechne diesen Flä-
cheninhalt.
7.	Berechne den Radius r und die Hö-
he h eines geraden Kreiskegels von
größtem Volumen unter der Bedin-
gung, dass seine Mantelfläche gleich
A ist.
8.	Berechne die Seitenlängen a, 6, c des
Dreiecks von größtem Flächeninhalt,
das man einem gegebenen Kreis (Ra-
dius r) einbeschreiben kann.
9.	Berechne die n Teile
xi, X2,..., xn, in die eine positi-
ve Zahl c zerlegt werden muss
/ n	\
( 52 Xi = c I ’ damit das Produkt
v=i	/
170 11 Differenzialrechnung für reelle Funktionen mehrerer Veränderlicher
der n Teile xi • x% • ... • xn ein Maxi-
mum wird (xi > 0; i = 1, 2,..., n).
10.	Bestimme die Abmessungen a, b und
c eines Quaders, der bei gegebener
Gesamtoberfläche A das größte Vo-
lumen besitzt.
12 Bereichs- und Mehrfachintegrale
12.1 Integrale über ebene Bereiche (Flächenintegrale)
ist das Volumen von Z.
B
v =
• f(x,y) = 1 :
db ist der Flächeninhalt von B.
B
Eigenschaften:
1.
db
2. B = Bi U B2 ; Bi und B2 haben höchstens Randpunkte
gemeinsam.
B	Br	B2
Berechnen über Doppelintegrale:
1. B ist Normalbereich bez. x-Achse
B :
b
Dann kann das Bereichsintegral über
folgendes Doppelintegral berechnet
werden:
b BO)
b
BO)
172
12 Bereichs- und Mehrfachintegrale
2.	B ist Normalbereich bez. y-Achse
B :	c < y < d
^i(y) < X < ip2(y)
Dann kann das Bereichsintegral über folgen-
des Doppelintegral berechnet werden:
d
/ f(x,y)db= /	/ f(x,y)dxdy (12.2)
B	y=cx=ip1(y}
Anwendungen:
Die Fläche B der x,?/-Ebene sei mit einer Masse der Massendichte q = Q(x,y)
belegt. Masse, Schwerpunktskoordinaten und Trägheitsmomente werden nach Ta-
belle 12.1 berechnet. Dabei ist zu beachten, dass die Integranden nur Funktionen
der zwei Veränderlichen x und y sind (q = q(x, y), rA = va(x, ?/)).
Trägheitsmomente
Bezugsachse A liegt in x, ?/-Ebene: äquatoriales Flächenträgheitsmoment
Bezugsachse A ± x, ?/-Ebene:	polares Flächenträgheitsmoment
1. Berechne das Bereichsintegral
x&b für den Bereich B. der von
B
den Kurven mit den Gleichungen
y = x1 2 und y = x + 2 begrenzt
wird, durch Zurückführung auf ein
Doppelintegral. Berechne das Dop-
pelintegral, indem
a) über x b) über y
zwischen konstanten Grenzen inte-
griert wird.
2. Berechne mit Hilfe des Doppelinte-
grals den Flächeninhalt der ebenen
Bereiche, die von den folgenden Kur-
ven begrenzt werden. Fertige zu jeder
Aufgabe eine Skizze an.
a) y = x , xy = 4 , x = 4
b) y2 = 4 + x , x + 3y = 0
c) (x-2)Q/-2)=4
(x + 3)Q/ + 3)=4
d)?/ = lnx, x — y = l, y = — 1
3.	Skizziere die Bereiche, deren Flä-
cheninhalte durch folgende Integrale
dargestellt werden. Berechne den In-
halt dieser Flächen. Ändere die Rei-
henfolge der Integration.
2	x+2
X = -ly = X2
1 2—x2
x=0 y=x
12.2 Integrale über räumliche Bereiche (Raumintegrale)
173
a y/2a2-y2
d) I = j* dxdy
y=Q x=y/äy
4.	Berechne xy2 dx dy, wenn B von
B
der Parabel y2 = 2px und der Gera-
den x = p begrenzt wird (p > 0).
5.	Berechne die folgenden Bereichsinte-
grale, wenn B von den angegebenen
Kurven begrenzt wird:
a)	j*xydb, B : (x — 2)2 + y2 = 1
B
b)	y (x2 + y2) db
B
B : y = x2, y = 1
6.	Berechne das Bereichsintegral
a)	yy xy — y2 dx dy, wenn B ein
B
Dreieck mit den Eckpunkten
0(0; 0), A(10; 1) und B(l; 1) ist
b)	yy ex^y dxdy, wenn B von der
B
Parabel y2 = x (p > 0) und den
Geraden y = 1 und x = 0 be-
grenzt wird
c)	y^ xy dx dy, wenn B von der
B
x-Achse und dem oberen Halb-
kreis (x — 2)2 + y2 =	1
begrenzt wird.
7.	Berechne das Trägheitsmoment der
Fläche, die von der Hyperbel xy = 4
und der Geraden x + y = 5 begrenzt
wird, bezüglich der Geraden y = x
8. Berechne
B
wenn B das
Parabelsegment ist, das von der
Parabel y = -x2 und der Geraden
y 2
y = x begrenzt wird.
9.	Berechne von dem Dreieck mit
den Eckpunkten (0; 0), (0; 1), (1; 0)
das polare Trägheitsmoment be-
züglich des Nullpunktes, wenn
q = 1 ist.
10.	Bestimme die äquatorialen Träg-
heitsmomente Jx, Jy und das po-
lare Trägheitsmoment Jp (bez.
des Nullpunktes) der Fläche eines
Rechtecks, das durch die Kurven
x = 0, x = a, y = 0 und y = b
begrenzt wird (q = 1).
11.	Bestimme den Schwerpunkt der Flä-
che, die durch folgende Kurven be-
grenzt wird (q = 1):
a)	y = 0 und eine Halbperiode der
Sinuskurve y = sin x
b)	y = x2, x = 4, y = 0
12.	Berechne xydb, wenn B von den
B
Koordinatenachsen und dem Aste-
roidenbogen x = a cos3 t,
y = asin3t, 0 < t < 7r/2 (a > 0)
begrenzt wird.
12.	2 Integrale über räumliche Bereiche (Raumintegrale)
yyy f^y^^x dydz
174
12 Bereichs- und Mehrfachintegrale
Der Bereich B ist ein Körper im Raum R3.
Sonderfall /(x, ?/, z) = 1
V = db ist das Volumen von B.
Raumintegrale weisen die gleichen Eigenschaften auf wie Flächenintegrale (siehe
Abschn. 12.1).
Berechnen über Dreifachintegrale:
1. B ist Normalbereich bez. x^y-Ebene
B : (x, y) e Br
gi(x,y) <z< g2(x,y)
Dabei ist Bf ein Normalbereich in der x, ?/-Ebene.
Dann gilt:
/(z,y,z)dz
Ist B' beispielsweise ein Normalbereich bez. der x-Achse, d. h.
B = {(x,y,z)\a < x < b, /i(x) < y <	gi(x,y) < z < g2(x,y)}
dann kann das Bereichsintegral mit Hilfe des folgenden Dreifachintegrals be-
rechnet werden:
b	fz(x)	g2(x,y)
y* f(x,y,z)db = y	y	y	f(x,y, z)dzdydx
B	x=ay=f1(x) z=g1(x,y)
2. B ist Normalbereich bez. X, z-Ebene
B = {(x, y, z) e R3| (x, z) e B\ gi(x, z) <y < gz(x, z)}
Dabei ist Bf ein Normalbereich in der x, z-Ebene. Dann gilt:
(12.39
y f(x,y,z) dö =
B
f(x,y,z)dy
dx dz
(12-4)
3. B ist Normalbereich bez. y, z-Ebene
B = {(x,y,z) G R3| (y,z) e B', gi(y,z) <x< g2(y,z)}
12.2 Integrale über räumliche Bereiche (Raumintegrale)
175
Dabei ist Bf ein Normalbereich in der y, z-Ebene. Dann gilt:
(12.5)
Anwendungen:
q = q(x, y, z) sei die Massendichte im Punkt F(x; y, z) des Körpers B.
Bei q = const. spricht man von einem homogenen Körper.
Tabelle 12.1: Masse, Schwerpunkt, Trägheitsmomente des Körpers B
Masse	m = y ydb B		
Schwerpunkts- koordinaten	1 f xs = — / xydb m J B	ys = — [ yydb m J B	1 f zs = — / zydb m J B
Trägheitsmoment bez. beliebiger Achse A	Ja = J" r2AQdb B	va =	y,z)... Abstand von F(x;y;z)eB zur Achse A	
1. Berechne mit Hilfe von Dreifachinte-
gralen die Volumina der Körper, die
von folgenden Flächen begrenzt wer-
den:
a)	y = x2, x + ?/ + z = 2,
y = 1, z = 0
b)	z = xy, x + y = l, x = 0,
y = 0, z = 0
2. Berechne / (x + y + z) db, wenn B
jb
von den Ebenen x = 0, x = l,?/ = 0,
y = 1, z = 0 und z = 1 begrenzt
wird.
3. Berechne
fff dxdy dz
JJJ (x + y + z + l)3’
B
wobei B von den Koordinatenebenen
und der Ebene x + y + z = 1 begrenzt
wird.
4.	Berechne das Volumen des Körpers,
der begrenzt wird von den Flächen
z = x2 + y2, x + y = 4, x = 0, y = 0,
z = 0.
5.	Berechne das Bereichsintegral
x3?/2zd6, wenn B durch die Un-
B
gleichungen 0 < x < 1, 0 < y < x ,
0 < z < xy definiert ist.
6.	Bestimme die Masse einer Py-
ramide, die durch die Ebenen
x + y + z = a, x = 0, y = 0, z = 0
begrenzt wird, wenn die Dichte in
jedem Punkt gleich dem z-Wert (Hö-
he) dieses Punktes ist.
7.	Bestimme die Masse des Körpers, der
durch die Flächen x = a, 2x+z = 2a,
x + z = a, y2 = ax, y = 0 begrenzt
wird (für y > 0), wenn die Dichte in
176
12 Bereichs- und Mehrfachintegrale
jedem Punkt gleich der Ordinate y
dieses Punktes ist.
8.	Bestimme den Schwerpunkt eines
homogenen Körpers (q = 1), der
durch folgende Flächen begrenzt
wird:
a)x + i/ + z = a, x = 0, i/ = 0, z = 0
(a > 0)
b) az = a2 — x2 — y2. z = 0 (a > 0)
9.	Bestimme das Trägheitsmoment be-
züglich der z-Achse für einen Körper,
der durch folgende Flächen begrenzt
wird (Dichte q = 1):
a)	x = 0, y = 0, y = a, z = 0 und
x + z = a (a > 0)
b)	x + y + z = a%/2, x2 + y2 = a2,
z = 0 (a > 0)
c)	z2 = 2ax, z = 0,
x2 + y2 = ax (a > 0)
12.3 Substitution
Raumintegrale
Ausgeführt werde die Koordinatentransformation
T : x = x(iz, 1?, w)
y = i/(iz, 1?, w)
Z = z(ll, 17, 117)
(12.6)
Dabei bezeichnen u, 17, w die neuen Koordinaten. B sei das Bild von B* vermittels
T: B = T(B*). Erfüllt T gewisse Eigenschaften, auf die hier nicht eingegangen
werden soll, so gilt die Substitutionsregel
j f(x,y,z) d6 B	= f (x(u,v,w),y(u,v,w), z(u^v^w)^) B*	d(x, y, z) d(u, 17, w)	<16* (12.7a)
mit Ö(x, 1/, z)	dx	dx	dx du	dv	dw dy	dy	dy —	—	-z- ... Funktional det er minante		(12.7b)
Ö(1Z, 17, w)	du dv dw dz dz dz du dv dw		
Aus (12.7a) liest man ab (Transformation des Raumelementes db):
db =
d(x,y,z)
d(u, v, w)
d6*
oder
dx dy dz =
d(x,y,z)
d(u, v, w)
du di7 dw
(12-8)
12.3 Substitution
177
Flächenintegrale
Die Substitution erfolgt analog zu den Raumintegralen. Es sind lediglich die Ko-
ordinaten z und w wegzulassen. So erhält man z.B. als Funktionaldeterminante
dx dx
d(x,y) = du dv
d(u, v) dy dy
du dv
Anstelle von einem Raumelement spricht man von einem Flächenelement db.
Flächen- bzw. Raume le mente für wichtige Koordinatensysteme
Polarkoordinaten
XX)
r ... Abstand vom Koordinatenursprung
(/?... Winkel von der positiven x-Achse zum Orts-
vektor im mathematisch positiven Drehsinn
0 < r <
oo, 0 < cp < 27t
Transformation in kartesische Koordinaten
T : x = r cos cp
y = r sin cp
(12-9)
{(r, </?)| r = const., p> e [0, 27t)} ... ^-Linien (Kreise um Nullpunkt)
Verallgemeinerte Polarkoordinaten
(r, (/?), 0 < r < oo , 0 < <p < 27t
Die Transformationsgleichungen lauten:
T : x = a r cos p>
y = 6 r sin (/?, a,b positive Konstanten
(12.10)
Die ^-Linien sind Ellipsen mit den Halbachsen r • a und r • b. Man spricht auch
von elliptischen Koordinaten.
178
12 Bereichs- und Mehrfachintegrale
Zylinderkoordinaten
(r, (/?, z)
P' ... orthogonale Projektion von P in x, ?/-Ebene
r, p ... Polarkoordinaten von P'
z... „Abstand“ von x, ?/-Ebene
z
oo
Transformation in kartesische Koordinaten
T : x = r cos p
y = r sin p
z = z
Die Koordinatenflächen {(r, p^z)\r = const., p e [0,2%), z e (—00,00)} sind
Kreiszylindermäntel.
Kugelkoordinaten
(r, 1?, p)
r ... Abstand vom Koordinatenursprung
1?... Winkel von positiver z-Achse zum Ortsvektor
p... wie bei Zylinderkoordinaten
0 < r < 00 , 0 < 1? < %, 0 < </? < 2%
Transformation in kartesische Koordinaten
T : x = r sin 1? cos p
y = r sin 1? sin p
z = r cos 1?
Die Koordinatenflächen {(r, 1?, </?)| r = const. , 1? e [0, %] , p E [0, 2%)} sind Kugel-
oberflächen.
Flächen- bzw. Raumelemente
Polarkoordinaten (r, p)
db = rdrd^
elliptische Koordinaten (r, p)
Zylinderkoordinaten (r, p, z)
Kugelkoordinaten (r, 'd, p)
db = rabdrdp
db = rdr d^ dz
db = r2 sin 1? dr dd d^
12.3 Substitution
179
1. Berechne
— x2 — y2 Ax Ay
B
durch Übergang zu Polarkoordina-
ten. B ist der Kreis mit dem Mittel-
punkt (0,0) und dem Radius r = 1.
2. Berechne JJ (x2 + y2)AxAy, wenn
B
B von der Kurve x2 + y2 = ‘lax
(a > 0) begrenzt wird (Übergang zu
Polarkoordinaten).
3. Gehe im Integral
Ay Ax
x=0 y=Q
zu Polarkoordinaten über.
4.	Berechne das Bereichsintegral
a)	[[	wenn B der
JJ -X2-y2
B
Teil des Kreises vom Radius a und
dem Mittelpunkt (0; 0) ist, der im
I. Quadranten liegt
b)	// xy Ax Ay, wenn B von der
B
x-Achse und dem oberen Halb-
kreis (x — 2)2 + y2 = 1 begrenzt
wird.
5.	Gehe im Integral
1 1
/ y y) dy da?
x=0 y=Q
zu den neuen Variablen u und v über:
u = x + y, v = x — y.
6.	Berechne die Flächen, die durch fol-
gende Kurven begrenzt werden:
a2	2
a)	xy = —, xy = la ,
x
y= 2 > y = 2x
Hinweis: Führe die neuen Koordinaten
xy = u und y = vx ein.
b)	y2 = ax, y2 = 16ax,
ay2 = x3, 16a?/2 = x3 (a > 0)
Hinweis: Koordinatentransformation
2	2	3
y =ux. vy =x .
c)	X2/3 + y2/3 = a2/3 (a > 0)
Hinweis: Koordinatentransformation
x = r cos3 99, y = r sin3 99.
7.	Berechne mit Hilfe eines Doppelinte-
grals die Fläche, die von den Kur-
ven mit den Gleichungen Z/2 = x>
y2 = 16x, y2 = x3, 16x/2 = x3 be-
grenzt wird. Führe dabei die Varia-
bientransformation aus: x = y/uv,
y = yuöv.
8.	Berechne das Trägheitsmoment der
Fläche, die von den Kurven
x2 + y2 = 1, x = 0, y = 0 be-
grenzt wird, bezüglich der //-Achse,
wenn die Flächendichte q = 1 ist.
9.	Berechne mit Hilfe eines Dreifachin-
tegrals unter Anwendung der Varia-
bientransformation x = rcos(/?, y =
2r sin cp, z = z das Volumen des Kör-
pers, der von den Flächen mit den
Gleichungen x2 + —— z2 = 1 und
z = ±\/3 begrenzt wird.
10.	Ein Körper wird von dem Zylinder
x2 + z2 = a2 und den Ebenen y = 0,
z = 0, y = x begrenzt. Berechne das
Volumen dieses Körpers.
11.	Berechne j'j'j' zAxAyAz, wenn B
B
h2
von dem Kegel z2 = —— (x2 + y2)
und der Ebene z = h (h > 0) be-
grenzt wird.
180
12 Bereichs- und Mehrfachintegrale
12.	Berechne
y/a?2 + Z/2 + z2 dx dydz,
B
wenn B der von der Kugel x2 + y2
+ z2 = z eingeschlossene Bereich ist,
durch Übergang zu Kugelkoordina-
ten.
13.	Berechne
.z
durch Übergang zu Zylinderkoordi-
naten, wenn B von den Flächen
y = 0, z = 0, z = a > 0, x2 + y2 = 2x
begrenzt wird.
14.	Berechne das Bereichsintegral
a) /// x2dxdydz, wenn
B von
z2
2	2
dem Ellipsoid	= 1
begrenzt wird
b) zdxdydz, wenn B von der
B
Ebene z = 0 und der oberen Hälf-
te des Ellipsoides
x2 y2	z2
— + fr- +	—	=	1	begrenzt	wird.
ax bz	c2
15.	Berechne die	Volumina	der	Körper,
die durch folgende Flächen begrenzt
werden:
9	9
x	z	x	y
a)	- = 1-----j ” T2 ’ z = 0
c	a/	b2
Hinweis: Gehe zu verallgemeinerten (el-
liptischen) Zylinderkoordinaten über:
x = ar cos 99, y = br sin 99, z — z.
b)	aV3 + y2/3 + z2'3 = a > 0
(Substitution x = r cos3 cp, y =
r sin3 </9, z = z)
c)	dz = 16 — x2 — y2, z = 0, x2 + y2
= 4 (außerhalb des Zylinders)
d) z2 = (x + a)2, x2 + y2 = a2
4
e)	z = —-----z = 0, x2 + y2 = 1,
x2 + y2
x2 + y2 = 4
f)	az = x2 + y2, z = 0, x2 + y2 ± ax
= 0 (a > 0)
g)	az = a2 — x2 — y2, z = 0, x2 +
y2 ± ax = 0, a > 0 (innerhalb
der Zylinder)
Hinweis: Gehe in den Aufgaben c) bis g) zu
Zylinderkoordinaten über.
16.	Bestimme die Masse der Hohl-
kugel, die durch die Gleichungen
x2 + y2 + z2 = a2 und x2 + y2 + z2 =
4a2 bestimmt wird, wenn die Dich-
te in jedem Punkt umgekehrt pro-
portional dem Abstand des Punktes
vom Koordinatenursprung ist. Ver-
wende Kugelkoordinaten.
17.	Bestimme das Volumen des Körpers,
der durch die geschlossene Fläche
a) (x2 + y2 + z2)2 = a3x
b) (x2 + y2 + z2)2 = az(x2 + y2)
(a > 0) begrenzt wird.
Hinweis: Gehe zu Kugelkoordinaten über.
18.	Zeige, dass der einbeschriebene Ke-
gel x2 + y2 — z2 = 0 das Volumen der
Kugel x2 + y2 + z2 = 2az im Verhält-
nis 3:1 teilt (a > 0).
19.	Bestimme die Gesamtladung Q des
durch die Flächen x2 + y2 — z2 = 0
und z = h > 0 begrenzten Kör-
pers, wenn die Ladungsdichte durch
q(x, y,z) = z gegeben ist.
13 Gewöhnliche Differenzialgleichungen
13.1 Begriff der Differenzialgleichung
Allgemeine Form einer gewöhnlichen Differenzialgleichung n-ter Ordnung:
F (x,	y^) = 0 implizite Form
y(n) _ y	explizite Form
Jede n-mal differenzierbare Funktion y(x), die die Differenzialgleichung für alle
x e [a,b\ erfüllt, heißt Lösung der Differenzialgleichung im Intervall [a, b\.
•	allgemeine Lösung ... Gesamtheit aller Lösungen einer Differenzialgleichung
•	Sind an nur einer Stelle x = a zusätzliche Bedingungen (Anfangsbedingungen)
an die Lösung gestellt, spricht man von einer Anfangswertaufgabe.
•	Sind an mindestens zwei Stellen a, 6,... Zusatzbedingungen (Randbedingungen)
an die Lösung gestellt, liegt eine Randwertaufgabe vor.
Richtungsfeld
y' =
Durch f(x,y) ist die Tangentenrichtung der Lösungskurve im Punkt P(x\y)
gegeben. Ordnet man jedem Punkt der x, ?/-Ebene die Tangentenrichtung zu,
erhält man das Richtungsfeld.
Isokline ... Kurve gleicher Richtungen des Richtungsfeldes (f(x,y) = d = const.)
In vielen Anwendungen ist die Zeit t die unabhängige Veränderliche. Für die
d?/
Ableitungen wird dann die Newtonsche Notation verwendet: — = y.
1. Bilde die Differenzialgleichungen fol-
gender Kurvenscharen:
a) y = ex b) y = et2
c) y2 = 2cx	d) x2 + y2 = c2
e) y = cd	f) t3 = c(t2 — y2)
g) y2 + - = 2 + ce-I/2/2
x
X
h) In — = 1 + ay
i)	(y - yo)2 = 2/w
j)	y = c1e2t+c2e~t
k)	y = ci cos 2t + C2 sin 2t
1)	y = (ci + c2t) el +c3
2.	Zeichne das Bild der Schar
a)	aller Kreise x2 + y2 = 2cx
b)	aller Parabeln y = x2 + 2cx
182
13 Gewöhnliche Differenzialgleichungen
und stelle deren Differenzialgleichun-
gen auf.
3.	Untersuche, ob die angegebenen
Funktionen Lösungen der gegebenen
Differenzialgleichungen sind.
a)	xy' = 2t/, y = 5x2
b)	(y)2 = t2 + y2, y = |
c2 - x2
c)	(x+y) dx+xdy = 0, y = ———
d)	y + y = 0, y = 3 sin t — 4 cos t
d2T
x UL Jy	o
e)	a?+"-'; = °
x = Ci cos art + C2 sin a)t
f)	y - 2y + y = 0
1.	y = t e1 2. y = t2 e*
g)	y" — (Ai + ^y' + A1A22/ = 0
y = ci eA1X +C2 eÄ2X
4.	Zeige, dass die Funktionenschar y =
cx3 (c E R) Lösung der Differenzial-
gleichung 3y — xy' = 0 ist. Zeichne
die Integralkurven, die durch folgen-
de Punkte gehen:
a) (1;U b)(l;l) c)(l;-U
\ ö J	\ ö J
5.	Skizziere die Richtungsfelder folgen-
der Differenzialgleichungen:
a)t/=j b) y = y - t
c) y = y +12
6.	Gegeben ist die Differenzialgleichung
y = f(t, y) = y/t2 + y2-
Skizziere mit Hilfe der Isoklinen
/(t, y) = d = const. für
d =	1; 2; 3 das Richtungsfeld der
Differenzialgleichung.
Wie verläuft die durch den Koordi-
natenursprung gehende Integralkur-
ve in etwa?
13.2 Differenzialgleichungen 1. Ordnung
13.2.1 Differenzialgleichungen mit getrennten Veränderlichen
u(t) , x
y = yy , v(y) 0
v(.y)
Durch Trennen der Veränderlichen erhält man unter Beachtung von y =
dt
«(y) dy = dt
Formales Integrieren führt auf die allgemeine Lösung:
v(y) dy = [ u(t) dt V(y) = U(t) + C
V{y) bzw. U(t) .. .eine Stammfunktion von bzw. u(t)
C	... Integrationskonstante
13.2 Differenzialgleichungen 1. Ordnung
183
1.	Bestimme die allgemeine Lösung
von:
a)	x2y' + y = 0
b)	x + xy + y\y + xy) = 0
c)	<^)2dr + (r — a)d(f> = 0
d)	2st2ds = (1 + t2)dt
e)	t\/l + ?/2 + ?/\/l + t2 y = 0
f)	tyy = 1 - t2
g)	y-ty = a + at2y
h)	yf tanx = y
i)	yrx3 = 2y
j)	(x2 + x)y' = 2y + 1
k)	y'y/a2 + x2 = y
1)	(1 + x2)yf + 1 + y2 = 0
2.	Löse folgende Anfangs wert aufgaben:
a)	2yry/x = y, 7/(4) = 1
b)	y1 = (2?/ + l)cotx, y
c)	x2yr + y2 = 0, y(-l) = 1
t dt ydy
1 + y 1 +
. y(l) = 1	2. y(0) = 1
e)	(1 + X)yy = ef, y(l) = 1
f)	dr + r tan d(j) = 0, r(7t) = 2
g)	y' = 2^/ylnx, y(e) = 1
h)	(1 + x2)y' + y\/l + x2 = xy
y(0) = 1
3.	In welcher Zeit kühlt sich ein Kör-
per, der auf 100 °C erhitzt wurde, in
einem Zimmer mit einer Temperatur
von 20 °C bis auf 25 °C ab, wenn er
sich in 10 Minuten bis auf 60 °C ab-
kühlt? (Nach dem Newtonschen Ge-
setz ist die Geschwindigkeit der Ab-
kühlung proportional der Tempera-
turdifferenz.)
4.	Ein Kondensator mit der Kapazität
C wird mit einem Ohmschen Wider-
stand R in Reihe geschaltet und die
Schaltung an eine Gleichspannungs-
quelle der Spannung U = const.
angeschlossen. Ermittle die Ladung
q = q(t) des Kondensators, wenn
q(0) = 0 gilt.
5.	Welche Stromstärke I stellt sich in
einem Gleichstromkreis mit U = 3 V,
R = 6Q, L = 0,06H zur Zeit
t = 0,01s ein, wenn der Strom zur
Zeit t = 0 eingeschaltet wird? Nach
welcher Zeit ist die Stromstärke auf
I
- angewachsen r
R L
6.	Die Belastung des Seils (ohne Biege-
steifigkeit) einer Hängebrücke ist in
jeder Längeneinheit des horizontalen
Trägers gleich q. Bestimme - ohne
Berücksichtigung des Seilgewichts -
die Kurve des Seils, wenn die Hori-
zontalkraft des Seiles in seinem tiefs-
ten Punkt den Betrag H hat.
Hinweis: In einem beliebigen Punkt P des
Seiles wirken die Tangentialkraft Fr, die
konstante Horizontalkraft Fh und die Last-
kraft Fl.
7.	Die Geschwindigkeitsverteilung eines
Flusses der Breite 2a und der Ge-
184
13 Gewöhnliche Differenzialgleichungen
schwindigkeit \vp\ = vo in der Mit-
te sei als Funktion des Abstandes x
von der Mittellinie als parabolisch
/	x2\
angenommen: \vf\ = xo I 1------ö )•
\ a /
Ein Schwimmer mit der Eigenge-
schwindigkeit |vs| = vs = const.
schwimmt, um den Fluss möglichst
schnell zu überqueren, dauernd senk-
recht zur Strömungsrichtung. Wie
groß ist seine Abdrift?
8.	Seien p(x) der Druck und q(x) die
Dichte der Atmosphäre in der Hö-
he x über der Erdoberfläche. Eine
Atmosphärensäule der Grundfläche
1 und der Höhe Ax hat in etwa
das Gewicht gg(x)/\x. Somit beträgt
die Druckänderung näherungsweise
Ap := p(x+Ax)- p(x) « —pp(x)Ax.
Nach dem Boyle-Mariotteschen Ge-
setz ist in einem idealen Gas (bei
konstanter Temperatur T)
- = — = const. Seien po •= p(0)
Q Qq
bzw. £>o •= £>(0) der Druck bzw.
die Dichte unmittelbar über der Erd-
oberfläche.
Leite die barometrische Höhenformel
durch Lösen einer Anfangswertauf-
gabe her.
9.	p(x) bezeichne den wöchentlichen
Verkauf eines bestimmten Produktes
zum Stückpreis von x€. Mit steigen-
dem Preis geht der Verkauf zurück.
Deshalb scheint es plausibel, die Ab-
nahmerate des Verkaufes — umge-
y
kehrt proportional zum Preis anzu-
setzen:
— = — — (A > 0, konstant).
p x
Ermittle die allgemeine Lösung der
Differenzialgleichung. Weshalb ist
der Ansatz
y' =
x + p
realistischer?
10.	Ein Gerücht verbreite sich in einer
menschlichen Population der Größe
p ausschließlich durch Erzählen. Die
Anzahl der zur Zeit t schon über
das Gerücht Informierten sei y(t). Je-
der Informierte habe pro Zeiteinheit
k > 0 Kontakte mit Mitgliedern der
Population. Bei jedem Kontakt wer-
de das Gerücht weitererzählt.
Stelle die Differenzialgleichung für
y(t) auf und ermittle die Lösung,
wenn das Gerücht von genau einem
Mitglied der Population in Umlauf
gebracht wurde.
11.	Bestimme und zeichne die Kurve,
die durch den Punkt P(—a; d) geht,
wenn der durch die Schnittpunkte A
und B mit den Koordinatenachsen
begrenzte Abschnitt einer beliebigen
Kurventangente vom jeweiligen Be-
rührungspunkt M halbiert wird.
12.	Gesucht sind die orthogonalen Tra-
jekt orien folgender Kurvenscharen:
a) cy = x2 (Parabeln)
b)	xy = c (Hyperbeln)
c)	x2 + 4p2 = c2 (Ellipsen)
d)	x2 — 2y2 = c2 (Hyperbeln)
13.	Bestimme die Kurve, für die der
Ortsvektor eines Punktes die Län-
ge des Normalenabschnitts zwischen
Kurve und x-Achse besitzt.
14.	Bestimme und zeichne die Kurve,
die durch den Punkt P(—1; — 1) geht
und für die die Strecke OT, die auf
der x-Achse durch die Kurventan-
gente in einem beliebigen Punkt er-
zeugt wird, gleich dem Quadrat der
Abszisse des Berührungspunktes ist.
13.2 Differenzialgleichungen 1. Ordnung
185
15.	Eine eiserne Hohlkugel mit dem in-
neren Radius r und dem äußeren Ra-
dius 2r hat an der Innenfläche ei-
ne konstante Temperatur von 100 °C
und an der Außenfläche von 20 °C.
Bestimme die Temperatur innerhalb
der Wandung in einem beliebigen
Abstand e vom Mittelpunkt (r <
e < 2r) und für e = 1, 6 r.
Hinweis: Die Geschwindigkeit des Absin-
kens der Temperatur dT/de in einem wär-
meleitenden Medium mit stationärer Tem-
peraturverteilung ist umgekehrt proportio-
nal der Fläche des Querschnitts.
16.	Ermittle die Kurve eines an bei-
den Enden befestigten homoge-
nen Seiles unter dem Einfluss sei-
nes Eigengewichtes. Wählt man
das Koordinatensystem wie in der
Abbildung, dann erfüllt die Seil-
kurve das Anfangswertproblem
y" = a\/l + (y')2 , y(0) = b,
y'(0) = 0.
(Fh Horizontalkraft, H := \Fh|,
a := ^7, q Seilgewicht pro Längen-
H
einheit)
Hinweis: Setze zunächst v(x) := y (x).
13.2.2 Durch Substitution lösbare Differenzialgleichungen
y = f(at + by + c)
Die Substitution \z = at + by + c führt auf eine Differenzialgleichung mit getrenn-
ten Veränderlichen:
z = a + by z = a + bf(z)

Diese Differenzialgleichung nennt man auch Ähnlichkeitsdifferenzialgleichung. Die
Substitution
liehen:
z = - führt auf eine
t J
Differenzialgleichung mit getrennten Veränder-
yt-y = y~t
t2 t
=^> z =
/(^) -
t
186
13 Gewöhnliche Differenzialgleichungen
at + by
y=	। j
ct + dy
Durch eine kleine Umformung erhält man eine Ahnlichkeitsdifferenzialgleichung:
at + by + e
ct + dy + h
c d
(13-1)
•	Für 7^ 0~j wird die Koordinatentransformation [t = ts + r , y = ys d~ aus-
geführt. Dabei ist S(ts,ys) der Schnittpunkt der Geraden
pi : at + by + e = 0 und gz : ct + dy + h = 0
Man erhält die Differenzialgleichung
dvy ar + brj
dr ct + dy
•	Im Fall [ D = o] führt die Substitution [z = at + by + e für 6 7^ 0~j oder
[z = ct + dy + h für d 7^ 0 J auf eine Differenzialgleichung mit getrennten Ver-
änderlichen.
1. Bestimme die allgemeine Lösung
von:
a) ty = y (1 + In
b) 2t2d?/ = (t2 + ?/2)dt
x
c) x In — dy — y dx = 0
y
d) yy' = 2y - x
e) x2 + y2 — 2xyyf = 0
ds _ s t
dt t s
. , y	y
g) xy cos — = y cos-----x
x	x
h) x2yf = y2 + xy
i)ty-y = 2t
2.	Löse folgende Anfangs wert aufgaben:
x / y2 y / ..x t
a)	y y(-1) = 1
b)	xy' = y (1 + In , y(l) = 2=
3.	Gesucht ist die Form eines Spiegels,
der alle Strahlen, die von einem ge-
gebenen Punkt ausgehen, parallel zu
einer gegebenen Richtung reflektiert.
13.2 Differenzialgleichungen 1. Ordnung
187
Hinweis: Wir betrachten einen ebenen
Schnitt des Spiegels, wählen den gegebenen
Punkt als Koordinatenursprung und die ge-
gebene Richtung als y-Achse. Die Tangente
an die gesuchte Kurve im Punkt M bildet
mit OM und der 7/-Achse gleiche Winkel,
das heißt, sie schneidet auf der y-Achse ei-
ne Strecke ON = OM ab.
4.	Ein Hund schwimmt von einem Ufer
eines Flusses der Breite a zu sei-
nem Herrn, der senkrecht gegenüber
am anderen Ufer steht. Er schwimmt
so, dass er immer auf seinen Herrn
blickt. Die Geschwindigkeit des Flus-
ses sei an jedem Ort gleich und ha-
be den Betrag vf = const. Der
Hund schwimme stets gleich schnell
(|v#| = vh = const.). Diskutiere
den Verlauf der Bahn des Hundes in
Abhängigkeit von der Relation zwi-
schen vf und vh-
5.	Ermittle die allgemeine Lösung von:
a) y = (8t + 2y + l)2
b)	y' = (a? + y)2
c)	(2x + 3y — l)dx
+ (4x + 6y — 5)d?/ = 0
d)	(2t — y)dt + (4t — 2y + 3)d?/ = 0
e)	y' = (x - y)2 + 1
f)	(i + y)2y = 4
13.2.3 Lineare Differenzialgleichungen
(Variation der Konstanten)
y+ a(i)y = r(t) |
Die Differenzialgleichung heißt
homogen
inhomogen
Ihre allgemeine Lösung hat die Form
f r(t) = 0 1
wenn <	> ist.
I r(t) 0 J
y(i) = z(t) + y(t)
(13-2)
mit
z(t) ... allgemeine Lösung der zugehörigen homogenen Differenzialgleichung
z + a(t)z = 0
y(t) ... spezielle Lösung der (inhomogenen) Ausgangsdifferenzialgleichung
Ermitteln von z(t)
Die zugehörige homogene Differenzialgleichung z + a(t)z = 0 lässt sich durch Tren-
nen der Veränderlichen lösen. Man erhält
z(t) = Ce~A^	(13.3)
wobei A(t) eine Stammfunktion von a(t) ist.
188
13 Gewöhnliche Differenzialgleichungen
Ermitteln von y(t)
Man geht von dem Ansatz
y(t) = C(t) eA(t)
(13-4)
aus (Variation der Konstanten). Nach Einsetzen in die Ausgangsdifferenzial-
gleichung erhält man C(t).
1.	Bestimme die allgemeine Lösung
bzw. löse die angegebene Anfangs-
wert aufgabe.
a)	y - +y-ty = ty
b)	y - 4y = e2f
c)	y - ytanht = |
d)	y sin t cos t + y cos21 = sin21
e)	y' + X 2y = 1, \y\ < 1
1 — X1
y(0) = 1
d(/?
f)	— = a sin t + bcp
g)	y cos t = y sin t + cos2 t
h)	ty - (t + l)y - t2 +t3 4 = 0
dz 2s 3s2
ds + 1 + s2 1 + s2
•x . y t - 1
k) /	' ; y '' 3/(0) = 1
r । T
i)	y + | + e‘ = y(i) =0
2.	Gegeben: RC-Glied nach Schaltbild
mit ue = uo sin cjt, üj 0 ;
MO) =0.
Gesucht: ua = ua(t) im eingeschwun-
genen Zustand.
R = const.
ue C = const. —]—	ua
Hinweis: Setze r = RC (Zeitkonstante).
3. Integriere die Differenzialgleichung
xyf + y = Inx + 1.
4. Die Rotwildpopulation p(t) in einem
ausgedehnten Waldstück nimmt mit
der Wachstumsrate r(t) = 1/(1 +1)
zu. Diese Wachstumsrate entspricht
der Selbstreproduktion ohne äußere
Einflüsse. Pro Zeiteinheit werden a
Stück Rotwild (a = const.) abge-
schossen. Wann ist die Population
ausgestorben?
13.2.4 Bernoullische Differenzialgleichungen
y + 9X)y = h(t)yr , reR\{0;l}i
Mit Hilfe der Substitution v = y1 r erhält man die lineare Differenzialgleichung
v + (1 — r)y(t)v = (1 — r)h(t)
(13.5)
13.2 Differenzialgleichungen 1. Ordnung
189
Löse folgende Differenzialgleichungen c) y + ty = ty3
bzw. Anfangs wert aufgaben:	-2
d) y = 72 _	=1
a)yi + y- ty	e) 3y2y + y3 = t + l- y(l) =-1
b) y - ty = -y3e~t2	f) (1 - t2)y - ty = ty2; y(0) = 0,5
13.2.5 Exakte Differenzialgleichungen, integrierender Faktor
Diese Differenzialgleichung heißt exakt, wenn eine Funktion &(t,y) existiert mit
t	[P(t,y)\	/1O
grad^> = v	V y \	(13.6)
\^y(t,y)J	\Q(t,y))
Man nennt auch eine Stammfunktion der exakten Differenzialgleichung.
P(t,y) und Q(t,y) seien in einem offenen Rechteck R = {(t,7/)| a < t < b,
c < y < d} stetig differenzierbar. Die Differenzialgleichung ist genau dann in R
exakt, wenn
Py(t,y) = Qt(t,y) (Integrabilitätsbedingung)	(13.7)
Ist eine Stammfunktion der exakten Differenzialgleichung bekannt, lautet die
allgemeine Lösung
^(t,Z/) = C	(13.8)
Ermitteln einer Stammfunktion
•	Aus <I>t = P (s. (13.6)) erhält man
y) = y P(t, y) di = ^(t, y) + g(y)
Integrationskonstante
Wegen &y = Q folgt hieraus
tyy + d' — Q • • • Differenzialgleichung für g(y)
Mit einer speziellen Lösung g(y) ergibt sich
= ^(i,y) +g(y)
•	Anstelle von = P kann man auch von $>y = Q ausgehen. Die auszuführenden
Schritte lauten dann:
190
13 Gewöhnliche Differenzialgleichungen
1-	y) = f Q(t, y) dy = ^(t, y) + g(t)
2.	^t + g = P
3-	#(£,y) = W(t,y) + g(t)
Integrierender Faktor |
Ist die Differenzialgleichung F(t,?/)dt + Q(t,y)dy = 0 nicht exakt, dann lässt
sich in den folgenden Fällen (darüber hinaus existieren weitere) ein Faktor m(t,y)
so bestimmen, dass |^m(t, y)P(t, y) dt + m(t, y)Q(t, y) dy = oj exakt ist und beide
Differenzialgleichungen die gleiche allgemeine Lösung besitzen.
Zunächst bildet man die Differenz [5 := Qt — Py
1.	5 a''~~Q	a = a(t)	m = m(t)		II •£l £
2.		b = b(y)	m = fn(y)		— = b(y) m
3.	5 C'~ P-Q	c = c(t + y)	m = m(t + y)	x = t + y	— = c(x) m
4.	"- P + Q	d = d(t — y)	m = m(t — y)	x = t — y	m' \ — = d(x) m
5.	5 e :=	 tP -yQ	e = e(t  y)	m = m(t • y)	x = t-y	— = ex) m
An der dritten Zeile soll demonstriert werden, wie die Tabelle zu lesen ist:
Man bildet c nach Spalte 2. Ist c eine Funktion von t + y, dann ist auch der
integrierende Faktor m eine Funktion von t + y. Nach Ausführen der Substitution
x = t + y erhält man m als eine spezielle Lösung der Differenzialgleichung =
c(x).
1. Bestimme die allgemeine Lösung von
a) (d -	dt + — dy = 0
7 \ t2 / t
e~y
c)	y =---------
te-y-1
d)	3x2 ey dx + (x3 ey — l)d?/ = 0
e)	e~y dx + (1 — xe~y)dy = 0
f)	2x cos2 ydx
+(2y — x2 sin2?/)d?/ = 0
2. Ermittle den integrierenden Faktor
und löse die Differenzialgleichungen.
a)	(e2t -y2)dt + y dy = 0
b)	2t tan y dt + (t2 — 2 sin y)dy = 0
c)	(1 + 3t2 sin y)dt — t cot y dy = 0
d)	(tsin?/ + y)dt
-\-(t2 cos y + t In t)dy = 0
e)	(3ty2 + y)dt + (2t2y — t)dy = 0
f)	(cost + y2 — sint) dx
+ (cos t + y2 + 2y) dy = 0
13.3 Differenzialgleichungen höherer Ordnung
191
g) (x2 — y)dx + x dy = 0
h) ?/2dx + (yx — l)d?/ = 0
i) (x2 — 3y2)dx + 2xy dy = 0
j) (sin x + ey)dx + cos x dy = 0
13.3 Differenzialgleichungen höherer Ordnung
13.3.1 Lineare Differenzialgleichungen mit konstanten
Koeffizienten
dny^ + • • • + apy + cioy = r(t), uq,..., an e R ... Konstanten I
Ist y eine spezielle Lösung der inhomogenen Differenzialgleichung (r(t)	0) und
z die allgemeine Lösung der zugehörigen homogenen Differenzialgleichung
dnz^ T • • • T d±z T = 0	(13.9)
lautet die allgemeine Lösung der Differenzialgleichung
y = + y
(13.10)
Ermitteln von z
Die allgemeine Lösung der zugehörigen homogenen Differenzialgleichung ist die
Linearkombination der n Elemente eines Systems {zi(t),..., zn(t)} linear unab-
hängiger Lösungen von (13.9) (Fundamentalsystem):
Z — C±Z±(t) + C2Zz(t) + • • • + Cnzn(t)
(13.11)
Über den Ansatz \y = eA j lassen sich die Elemente des Fundamentalsystems er-
mitteln. Der Ansatz führt auf die charakteristische Gleichung
dnXn T • • • T diA T czq — 0
(13.12)
Zu den n Nullstellen Xj~ 6 C der charakteristischen Gleichung erhält man die
Funktionen des Fundamentalsystems mit Hilfe der Tabelle 13.1.
Ermitteln von y
Ansatzmethode
Gehört die Inhomogenität r(t) zu einer speziellen Klasse von Funktionen, führt
ein Ansatz für y nach der Tabelle 13.2 zum Ziel.
• p und q stehen auch für Polynome. Sei m ihr Höchstgrad.
P=Pmtm H----Vppt +po
oder
A — Amtm T • • • T Apt T Aq
und
<7 —	+ • • • + Qlt + Qo	B — Bmtm + • • • + Bpt + Bq
Dies gilt auch, wenn eines der Polynome das Nullpolynom ist.
192
13 Gewöhnliche Differenzialgleichungen
Tabelle 13.1: Fundamentalsystem von (13.9)
Nullstelle	Ordnung der Nullstelle	Elemente des Fundamentalsystems
Xk = a ± i b	einfach	eat cos bt, eat sin bt
	z/-fach	eatcosbt, teatcosbt, • ••, ^-1 eat cos bt eat sin bt, teatsinbt, ..., ty~1 eat sin bt
Sonderfall b = 0		
^k — &	1 z/-fach	eat, teat,	t1'-1 eat
Tabelle 13.2: Ansatz für y
r(t)	Ansatz für y	Ansatz bei Resonanz	
eat (p cos uat + q sin uat)	eat (A cos A + B sin ivt)	N := a + icj	Ist N z/-fache Nullstelle
Sonderfall a = 0			der charak-
p cos cvt + q sincjt	A cos cot + B sin art	N := icj	teristischen Gleichung, so
Sonderfall uj = 0			ist der Ansatz
peat	Aeat	N := a	mit ty zu mul- tiplizieren.
•	Nach Einsetzen des Ansatzes für y in die Differenzialgleichung erhält man die
unbekannten Koeffizienten Aj~ und B^ über Koeffizientenvergleich.
•	Ist r(t) eine Summe der angegebenen Funktionen, dann setzt sich y entsprechend
zusammen.
Variation der Konstanten
Ausgehend von der allgemeinen Lösung z = C\Z\(t) + • • • + Cnzn(t) der zugehö-
rigen homogenen Differenzialgleichung macht man für eine Partikulärlösung der
inhomogenen Differenzialgleichung den Ansatz
y =	H------F Cn(t)zn(t)
(13.13)
und erhält für die unbekannten Ansatzfunktionen Cfc(t) das lineare Differenzial-
13.3 Differenzialgleichungen höherer Ordnung
193
gleichungssystem 1. Ordnung
< 0
0
\ dn /
(13.14)
Das Differenzialgleichungssystem lässt sich eindeutig nach Ci,...,Cn auflösen.
Gliedweise Integration der Ck = fk(t) liefert die gesuchte Partikulärlösung y.
1.	Bestimme die allgemeine Lösung
bzw. löse die angegebene Anfangs-
wert aufgabe.
a)	y(4) - 2y" = 0
b)	+ 8y" + 16y = 0
c)	y" - 4y' + 3y = 0
d)	y" - 4y' + 4y = 0
e)	y" ~ dy' + 13y = 0
f)	y" - 4y = 0
g)	y" + 4y = 0
h)	y" + 4y' = 0
.. d2x da?
’^ + 3d7-4l = (l
d2p
j)	+ Q = 0
n x d2s (Ls
k)	äe +2äF+ s =
wenn to = 0, <sq = 1, Sq = 1
1)	y"f - 5y" + 8y'-4y = 0
m)	~ = o
n) y'" -Sy = 0
o) y"' + 3ay" + 3a2y' + a3y = 0
P) y(4) + 4y = 0
q) 4y(4) - 3y" - y = 0
2.	Bestimme die Gleichung für die
Schwingung eines Pendels. Das Pen-
del bestehe aus der Masse m, die an
einem Faden der Länge l aufgehängt
ist. Wie groß ist die Schwingungspe-
riode?
Hinweis: Der Luftwiderstand bleibe unbe-
rücksichtigt. Der Ausschlagswinkel 99 sei
klein, so dass wir sin 99 « 99 setzen können.
3.	Zwei gleiche Massen sind am En-
de einer vertikalen Feder angehängt.
Durch die Wirkung der einen Mas-
se verlängert sich die Feder um b.
Bestimme die Bewegung der ersten
Masse, wenn die zweite Masse herun-
terfällt (Luftwiderstand bleibt unbe-
rücksichtigt). Bestimme die Schwin-
gungsperiode.
Hinweis: Eine Masse betrage m. y-Achse
zeige senkrecht nach unten. Ruhelage der
mit m belasteten Feder befinde sich im
Nullpunkt.
4.	Löse die Aufgabe 3 mit Berücksichti-
gung des Widerstandes, der propor-
tional der Geschwindigkeit der Bewe-
gung ist. Für die Proportionalitäts-
konstante a gelte a2b — 4m2p < 0.
5.	Bestimme die allgemeine Lösung
der homogenen Differenzialgleichung
und gib den Ansatz für eine spezielle
Lösung der inhomogenen Differenzi-
algleichung an.
194
13 Gewöhnliche Differenzialgleichungen
a)	-y-y^y = t2Ptet
+(t3 - 1) e~2t sint
b)	y^ + y — y + y - 2?/= 2 + 4 cos t
+ (t2 -t + l)e°’5t
c)	y + 3y + 2y = (2t — 4) e-t sin 3t
— e~2t +5
6.	Bestimme die allgemeine Lösung fol-
gender Differenzialgleichungen:
a)	y + 9y = e5f
b)	y - y = e*(t2 - 1)
c)	y + 4// = cos 2t
d)	y — dy + 8y = e1 + e2t
e)	y" -2y' + y = e2®
f)	y" - 4y = 8x3
g)	y" + 3y' + 2y = sin 2x + 2 cos 2x
h)	y" + y — x + 2 ex
i)	y,r + 3yr = 9x
j)	y" + dyf + 3y = 5x2 — 32x + 5
k)	y" - 3y' d~2y = ex
d2r
1)	-—7- + k2x = 2k sm kt
dt~
m)	y" — 2y = xe~x
n)	yff — 2yf = x2 — x
o)	yff + dy' + 6// = e~x + e~2x
p)	x + 2kx + 2k2x = 3k2 sin kt
q)	/' + / = 6x + e-'
r)	y^ - 81?/ = 27e-3x
s)	x + x = 3t2
t)	y'" + 8y = e“2x
u)	x + 4± + dx = e~2t
v)	a3x + ax = 1
7.	Löse folgende Anfangs wert aufgaben:
a)	y + 2y + 2y + y = t
?/(0) = y(0) = y(0) = 0
b)	y + 2y + dy = 3t2
7/(0) =0, 7/(0) = 3
c)	y + dy = sin t
?/(0) = ?/(0) = 1
d)	y - 2y = e2t +t2 - 1
y(o) = y(o) = i
o
8.	Gib die allgemeine Lösung an.
a)	y" + 4y = +—
sm 2x
2x
b)	y" ~ ky' + 5y = ——
cosx
d)	y” + y' = J x
1 + ex
— 2x
e)	y” + 4y' + 4y =
f)	y" + 4?/ + 4y = e~2x In x
a //	1
g)	y + y = —
COSÖ X
h)	y" + ly =
sm x
i)	y"-2y' + y=^=£=
V 4 — xz
•2
9.	Ein Zylinder vom Grundkreisradius
r und der Masse m schwimmt mit
vertikaler Achsenlage im Wasser. Sei-
ne Eintauchtiefe ist l. Gesucht ist die
Periode der Schwingung, die sich er-
gibt, wenn man den Zylinder ein we-
nig in das Wasser eintaucht und da-
nach loslässt. Der Bewegungswider-
stand ist angenähert gleich null an-
zunehmen.
Hinweis: Beachte das Archimedische Prin-
zip (Auftrieb = Gewicht des verdrängten
Wassers). Die //-Achse weise vertikal nach
unten. Der Nullpunkt sei auf der Wassero-
berfläche.
10.	Bestimme die Kurve der Durch-
biegung eines horizontalen Balkens
der Länge /, dessen eines Ende
fest eingespannt ist und an des-
sen anderem Ende eine Gesamtkraft
13.3 Differenzialgleichungen höherer Ordnung
195
vom Betrag F angreift, bei kon-
stanter Biegesteifigkeit a (Gewicht
des Balkens bleibe unberücksichtigt;
die Durchbiegung sei so klein, dass
l + y'2«l).
11.	Bestimme im Intervall [0,1] die
Kurve, die die x-Achse im Koordi-
natenursprung berührt, wenn ihre
Krümmung x = x ist, das heißt
entlang der x-Achse gleichförmig an-
wächst (Übergangskurve).
Rechne näherungsweise mit
12.	Eine Masseeinheit bewegt sich unter
dem Einfluss einer längs der x-Achse
wirkenden konstanten Kraft F auf
der x-Achse. Der Bewegung wirkt ein
Widerstand entgegen, der zahlenmä-
ßig gleich der Geschwindigkeit der
Bewegung ist. Gesucht ist das Bewe-
gungsgesetz, wenn zur Zeit t = 0 so-
wohl x = 0 als auch die Geschwin-
digkeit v = 0 ist.
13.	Ein Körper fällt aus der Höhe h un-
ter dem Einfluss der Schwerkraft und
einer Reibungskraft herab, die pro-
portional der Geschwindigkeit ist.
Die Anfangsgeschwindigkeit ist null.
Ermittle die Formel für die Höhe y,
in der sich der Körper t Sekunden
nach dem Beginn der Bewegung be-
findet.
14.	Ein Teilchen der Masse m, das an
einer horizontalen Feder (Federkon-
stante k > 0) befestigt ist, sei längs
der x-Achse widerstandsfrei beweg-
lich. Bei ungespannter Feder befin-
de sich das Teilchen im Nullpunkt
(Gleichgewichtslage). Wird das Teil-
chen aus der Gleichgewichtslage ge-
bracht und losgelassen, beginnt es
zu schwingen. Ermittle die allgemei-
ne Lösung x(t) der Schwingungsglei-
chung.
15.	Betrachtet wird der Federschwinger
aus Aufgabe 14. Auf die Masse wir-
ke noch zusätzlich die zeitabhängi-
ge Zwangskraft F = 2uxm cos uxt ex
(w > 0).
Wähle den Parameter w so, dass
Resonanz im Sinne der Theorie der
linearen Differenzialgleichungen mit
konstanten Koeffizienten auftritt.
Wie lautet dann die allgemeine Lö-
sung der Schwingungsgleichung?
Was gilt für t —> oo?
16.	Ein Träger der Länge l wird
durch eine Streckenlast vom Be-
trag q(x) = kx belastet. Für
konstante Biegesteifigkeit a er-
hält man die Biegelinie w(x) als
Lösung der Randwertaufgabe
w(4) = !lx , w(o) = w(/) = 0,
w"(0) =w'(Z) = 0.
Gib die Biegelinie an.
17.	Ein Träger der Länge l wird durch
eine Axiallast F mit \F\ = F belas-
tet:
Bei konstanter Biegesteifigkeit a ge-
nügt die Biegelinie w(x) der Diffe-
renzialgleichung + X2w" = 0
196
13 Gewöhnliche Differenzialgleichungen
( A2 := — ) und den Randbedingun-
\ a J
gen w(0) = w(/) = 0, w"(0) = 0,
w'(/) = 0. Die Axiallast werde bis zu
einem Wert Fr gesteigert, bei dem
plötzlich eine seitliche Auslenkung
des Trägers erfolgt (Knicklast). Er-
mittle die Knicklast F&.
Hinweis: Die obige Differenzialgleichung
hängt vom Parameter A ab. Die Werte von
A, für die die Randwertaufgabe nichttrivia-
le Lösungen w(x) 0 besitzt, heißen Ei-
genwerte. Der kleinste Eigenwert liefert die
gesuchte Knicklast.
13.3.2 Eulersche Differenzialgleichungen
+ an_itn 1y<^n H-----F a^ty + aoy = r(t)
ao,... ,an 61 ... Konstanten
•	Für [ t > o] führt die Substitution [ t = ex ] auf eine lineare Differenzialgleichung
mit konstanten Koeffizienten für die Funktionen v(x) := y (ex).
Deren charakteristische Gleichung lautet
anA(A — 1)... (A — n T 1) T • • • T U2A(A — 1) T cqA T czq — 0
Nach Lösen der Differenzialgleichung erhält man durch Rücksubstitution
y(t) = iz(lnt).
•	Für [ t < o] ersetzt man in der Differenzialgleichung und dann bei der Rücksub-
stitution t durch — t.
Ermittle die allgemeine Lösung
von:
a)	t2y — ty + 2y = t In t
b)	t3 y — t2y + 2ty — 2y = t3 + 3t
c)	t2y - 2y = t2 + |
d)	t2y + ty - y = t
e)	t2y + ty - y = i-1
f)	t2y + ty + y = cos In\t\
g)	x3yfff — 3xy' + 3y = 0
h)	x2y" — 2y = 0
i)	x2yff + 2xyf — n(n + l)y = 0
j)	x2y" + bxyf + 4?/ = 0
k)	x2y" F xy' Fy = 0
1)	xy" + 2yf = lOx
m)	x2y" — 6y = 12 Inx
n) x2y" — 2xy' + 2y = 4x
o)	x3y" + 3x2y' + xy = 6 In x
p)	x2yff — 4xyf + 6y = x5
q)	x2y" + xy' + y = x
13.4 Systeme linearer Differenzialgleichungen mit konstanten Koeffizienten 197
13.4 Systeme linearer Differenzialgleichungen mit konstan-
ten Koeffizienten
yi = anyi +•	• + alnyn + ri(t)		,. reelle Konstanten
i)n = anlyx + • 	' H" Clnnyn H“	Vi =	 	.. gesuchte Funktionen
Mat rixschreibweise:
y = Ay + r	(13.15)
Ist y eine spezielle Lösung des inhomogenen Differenzialgleichungssystems
(r(t) o) und z die allgemeine Lösung des zugehörigen homogenen Systems
z = Az, dann ist y = z + y die allgemeine Lösung von (13.15).
Für die Lösung von
z = Az	(13.16)
macht man den Ansatz z = xext. Einsetzen in (13.16) führt auf das Eigenwert-
problem (A — XE)x = o.
• Fall 1: A& sei ein ^/-facher reeller Eigenwert von A. Einsetzen von
zk := eXkt (c0 + c±t H-----F c^-iP7-1)
in (13.16) liefert über Koeffizientenvergleich die unbekannten Vektoren
cq, ..., Cp-i. Diese Vektoren hängen von genau v freien Konstanten ab.
• Fall 2: Bilden Xk = a ± ib ein Paar konjugiert komplexer, ^/-facher Eigenwerte
von A, so setzt man
zk := eat [(co + crt H----F c^-iP7-1) cos bt
+ (do + d]t + • • • + dzy-it* *7-1) sinbt^
(13.16) liefert über Koeffizientenvergleich die gesuchten Vektoren a, di
(i = 0,..., v — 1), die von 2z/ freien Konstanten abhängen.
Die allgemeine Lösung z von (13.16) erhält man als Summe aller ermittelten zk :
z = ^zk . z kann auf die Form
k
z = CiZi + --- + Cnzn	(13.17)
198
13 Gewöhnliche Differenzialgleichungen
mit den freien Konstanten Ci gebracht werden. Dabei sind die Vektoren Zi linear
unabhängige Lösungen von (13.16).
Ermitteln von y
Analog zu linearen Differenzialgleichungen mit konstanten Koeffizienten lässt sich
die spezielle Lösung y des inhomogenen Systems durch Variation der Konstanten
oder durch Ansatz ermitteln.
• Variation der Konstanten: Ausgehend von (13.17) macht man den Ansatz
y = Ci(t)zi(t)H-------VCn(t)zn(t). Einsetzen in die Ausgangsdifferenzialgleichung
(13.15) liefert ein Differenzialgleichungssystem 1. Ordnung für die unbekannten
Funktionen Cfc(t), das sich eindeutig nach Ci,..., Cn auflösen lässt. Durch glied-
weise Integration der Ck = fk(t) erhält man y.
• Ansatzmethode: Entsprechend der Tabelle 13.2 erhält man für zu einer spezi-
ellen Funktionenklasse gehörende r(t) einen Ansatz für y. Dabei ist zu beachten,
dass in allen Komponenten alle Anteile des Vektors r(t) zu berücksichtigen sind.
1. Bestimme die allgemeine Lösung von	h) ii = -z\ + z-i
a) z\ = —z\ — z^	Z2=	- Z2 + 4z3 Z3 = Z1	- 4z3
b) ±1 = X2 X2 = xi + e1 + e-t	i) yi = yi + 4y2 y-2 = 2yi + 3y2 + ef x dx
c) ii = -5^i - Z2 22 = 2^1 - 3z2	j) + X - y = ef dy	,	t — - x + y = e dt , x dx	dy ,	,
d) 2x = -2x + 22 + 23 22 =	2^ - 22 + 23 23=	2^ + 22 - 23	k) 5— - 2-y + l.r - y = e dt	dt dx + 8x — 3y = 5e-t dt
e) z\ = -5^i - Z2 22 =	^1 - 3Z2	1) x = y y = x + 2 sinh t m) x — dx + dx — y = 0
f) Zx= 2x - 2Z2 - 23 22 = ~2\ + ^2+^3 23 =	2^	~ Z3	y + dy — 25x + dy = 16 2. Löse folgende Anfangs wert aufgaben: a) ±1 = 3xi — x2 + 8
g) ±1 = -Xi - X2	+ t2 X2 =	- X2 - X3 + 2t X3 =	- X3 + t	x2 = —xi + 3x2 + 8e3t xi(0) = 4, x2(0) = —6 b) x + 3x + y = 0	x(0) = 1 y - x + y = 0	?/(0) = 1
13.5 Näherungsmethoden
199
13.5 Näher ungsmet ho den
y = f(t, y(t)), y(t0) = yo	(13.18)
13.5.1 Potenzreihenansatz
Gesucht: Näherungsfunktion y für die Lösungsfunktion y(t) der Anfangs wert auf-
gabe (13.18).
Die abgebrochene 7ß?/Zor-Reihe von y(t) liefert (bei entsprechender Differenzier-
barkeit von /) die gesuchte Näherung:
= yo +	M + • • • +
mit
y(M = /(<o,yo)
y(to) = yo) + fy(t0, yo)y(io)
y(to) = /t«(io,yo) + 2/tIZ(io,yo)y(io) + /TO(^o,yo)[y(io)]2
+ /j/(io,yo)y(io)
(13.19a)
(13.19b)
(13.19c)
(13.19d)
Das beschriebene Verfahren lässt sich analog auch auf Anfangswertaufgaben
bei Differenzialgleichungen n-ter Ordnung
y(n) = f	, y(t0) = y0, y(t0') = y0,... ,y(n-1)(t0) = yo”-1)
an wenden.
Approximiere die Lösung y(t) der jewei-
ligen Anfangswertaufgabe durch die ers-
ten fünf von null verschiedenen Glieder
ihrer Taylorreihe.
a) y~ (t2 + l)y = t
y(i) = i, y(i) = |
b)y-y + efy = 0
y(0) = 0, y(0) =-1
c) y + ty + e* y = t2
y(0) = l, y(0) = 0
d) y = t2 + y2 , y(0) = 1
13.5.2 Runge-Kutta-Verfahren
Gesucht: Näherungswerte yn für die Funktionswerte der gesuchten Lösungsfunk-
tion der Anfangswertaufgabe (13.18) an den Stellen tn.
200
13 Gewöhnliche Differenzialgleichungen
Dabei gilt mit der vorgegebenen Schrittweite h > 0:
tn = to + nh , n = 0,1,..., N
Für dieses Problem existiert eine Reihe von numerischen Verfahren. Eines
der gebräuchlichsten ist das (klassische) Runge-Kutta-Verfahren. Beim
Runge-Kutta-Verfahren handelt es sich um ein explizites Einschrittverfahren
4. (Genauigkeits-)Ordnung. Die Rechenvorschrift lautet:
Z/n+i = Vn + ~ (&i + 2ä:2 + 2ä:3 + ZC4)	(13.20a)
o
mit
k\=f(tn,yn)	k2 = f (^tn +^,yn +(13.20b)
k3 = f (tn + yn + fc4 = f (tn + h,yn + hk3)	(13.20c)
In jedem Schritt wird nur das Ergebnis des vorangegangenen Schrittes benötigt
(Einschrittverfahren), und die Rechenvorschrift ist nach yn+i aufgelöst (explizit).
Es existiert eine Konstante M > 0, sodass bei genügend kleinem h für alle n
die Fehlerabschätzung
\yn-y(tn)\ <Mh4	(13.21)
gilt (4. Ordnung).
Eine Halbierung der Schrittweite bewirkt somit, dass die Fehlerschranke auf ein
16tel reduziert wird.
Das Runge-Kutta-Verfahren lässt sich auch auf Anfangswertaufgaben von Dif-
ferenzialgleichungssystemen anwenden:
Anfangswertaufgabe: y = f(t,y(t)), y(t0) = y0
Runge-Kutta-Verfahren:
y„+i = yn + (fci + 2fc-_> + 2fc3 + k4)
mit
ki = f(tn, yn)	k2 = f (tn + yn + ^fci
k3 = f (in + yn + |fca) k4 = f (tn + h,yn + hk3)
13.5 Näherungsmethoden
201
Ermittle zu den folgenden Anfangswert-
aufgaben Näherungswerte der Lösung
an der Stelle t = t nach dem Runge-
Kutta-Verfahren mit der angegebenen
Schrittweite h. Wiederhole die Berech-
nung mit der Schrittweite h/2.
a) y-y = t, y(0) = 0
r = 0,4; ft = 0, 2
^ = 1
t = 1,2; h = 0,1
c) yi = -yi - y-2	yi(o) = o
y2 =	- yi	3/2(0) = 1
r = 0,4; h = 0,2
d) y + y = t - 2
2/(0) = 0, y(0) =-3
t = 0,2; h = 0,1
Hinweis: Überführe die Differenzialglei-
chung zweiter Ordnung in ein äquivalentes
System von Differenzialgleichungen erster
Ordnung.
e)y = -l + 2i+-^L-2, y(0) = 2
t = 1; ft = 0,2
14 Vektoranalysis
14.1 Felder, Differenzialoperatoren
Felder
Eine Funktion
v : D C Rn —> Rn
(14-1)
heißt n-dimensionales Vektorfeld.
Eine Funktion
y : D C r —> R
(14-2)
heißt Skalarfeld.
Wir behandeln nur n = 2 oder n = 3. Im Falle n = 3 schreiben wir
und v(x)
Für n = 2 sind in (14.3) jeweils die letzten Komponenten zu streichen.
Veranschaulichung von Vektorfeldern: Jedem Punkt aus D wird ein Ortsvektor
v(x) zugeordnet. Einige der Vektoren zeichnet man ein.
Stromlinie (oder Feldlinie): Kurve, für die v(a?) in jedem Punkt ein Richtungs-
vektor der Tangente an die Kurve ist.
Anwendung: Flussmodelle (Flüssigkeiten, Gase, Elektrizität,...)
Die Stromlinien stellen dann die Bahnen der bewegten Teilchen dar.
Differenzialoperatoren |
Nabla-Operator: V = ( —— , — , —
dx i dy i dz
Gradient eines Skalarfeldes f: gradf = Vf = —— , —— , ——
\ dx dy dz
•	gradf zeigt in Richtung des größten Wachstums der Funktion f.
dP dQ dR
Divergenz eines Vektorfeldes v = (P , Q , R)T : div v = V • v = ——H ——I-
dx dy dz
•	divv(a?o) ist die Quellergiebigkeit (oder Quelldichte) des Feldes v(x) in xq.
•	Gilt überall divv(ic) = 0, heißt das Vektorfeld v quellenfrei.
14.1 Felder, Differenzialoperatoren
203
Rotation eines Vektorfeldes v = (P , Q , P)T
Cy ez
d d d
dx dy dz
P Q R
(Ry — Qz , Pz — Rx , Qx —
pvr
• rotv(ico) zeigt in Richtung Rotationsachse lokaler Wirbel um xq; | rot v(a?o)|
misst die Wirbelstärke.
• Gilt überall rotv(a?) = o, heißt das Vektorfeld v wirbelfrei.
d2	d2	d2
Laplace-Operator: A = V • V =	+ —w + —w ,
dxz	dyz	dzz
&f = fxx+fyyPfZZ
Rechenregeln
V(q/i+/?/2)=qV/i+/?V/2
V • (a vi + ß V2) = q V • vi + /? V • v2
> q, ß e R
V x (a vi + ß V2) = <a V x vi + ß V x u2
A-u = (AF,AQ,A/?)T
Klassifikation von Vektorfeldern
	quellenfrei (div v = 0)	Quellenfeld
wirbelfrei (rot v = 0)	Laplace-Feld	Poisson-Feld
Wirbelfeld	solenoidales Feld	allgemeines Feld
Man nennt v ein Potenzialfeld (oder konservatives Feld), wenn ein Skalarfeld
f mit V/(a?) = v(x) existiert.
pßx) := — f(x) ... Potenzial von v
Bei einem Kraftfeld hat cp die Bedeutung der potentiellen Energie.
Satz 14.1 v sei ein stetig differenzierbares Vektorfeld (P(x,y,zß Q(x,y,zß
R(x,y,z) sind stetig differenzierbar). Ist v ein Potenzialfeld, so gilt rotv = o.
Ein Potenzial von v lässt sich wie folgt ermitteln:
f(x,y,z)= P(x,y,z)dx = SP(x,y,z) + g(y,z)
Integrationskonstante
204
14 Vektoranalysis
+ 9y(y, z) = Q(x, y, z) =^> gy(y, z)
9(y, z) = y gy(y, z) dy = S9y (y, z) + h(z)
Integrationskonstante
f(x,y,z) = SP(x,y,z) + S9v(y,z') + h(z)
[SP(x, y, z) + S9y (y, z)] + ti(z) = R(x, y, z) => h(z)
v(x,y,z) = -f(x,y,z)
Hierbei bezeichnet Sp(x,y,z) eine Stammfunktion aus f P(x,y, z) dx (analog
$gy (?/, V>)-
Bei einem zweidimensionalen Vektorfeld ist rot v = o durch Qx = Py zu ersetzen,
sonst geht man analog vor (vgl. auch 13.2.5).
•	Die Niveauflächen eines Potenzials nennt man Äquipotenzialflächen.
•	Die Feldlinien stehen stets senkrecht auf den Äquipotenzialflächen.
1.	Veranschauliche folgende Vektorfel-
der:
a)	v(x,y) = (a?,y)T
b)	v(x,y) = (—y,a:)T
c)	v(x,y) = (—x, —y)T
d)	v(x,y) = (x,—y)1:
2. Skizziere die Stromlinien der Vektor-
felder.
a) v(x,y) = (a?,y)T
b) v(x,y) = (—y,a:)T
c) v(x,y) = (x,-y)T
3. Beweise
a) div rot v = 0
b) rot grad f = o
c) div grad f = A f
d) grad div v = A v + rot rot v
wenn f und v zweimal stetig diffe-
renzierbare Felder sind.
4.	Zeige, dass
a)	grad(/ • g) = f grad g + g grad /
b)	div(/v) = f div v + v • grad f
c)	rot(/v) = f rot v + grad f x v
d)	div(v x w) = w • rot v — v • rot w
wenn /, g und v, w differenzierbare
Felder sind.
5.	Zeige, dass
x
grad \x\n = n -—-— , n e Z,
6	1 1	\x\2 3~n '
x o.
6.	Gegeben sei das räumliche Skalarfeld
f(x) = dx + 9y  z~r.
Berechne
a)	den Funktionswert im Punkt
P(l; 2; 3) und die Gleichung sei-
ner Niveaufläche
b)	das Gradientenfeld
c)	den Gradienten im Punkt P und
seinen Betrag
7.	Berechne den Funktionswert, den
Gradienten und seinen Betrag für
folgende Skalarfelder:
14.2 Kurvenintegrale
205
a)	f(x) = xz + yz + zx + 10
im Punkt (—1; 2; —3)
b)	f(x) = xy im Punkt (2; 0)
8.	Gegeben ist das Vektorfeld
v(x) = (x2 , — x~1yz2 , xz^T
und das Skalarfeld
/(a?) = 4x2 + 6y2 + z3.
Berechne für den Punkt F(l; — 2; 4)
die Komponente von rotv in Rich-
tung des größten Anstieges der Orts-
funktion f.
9.	Klassifiziere die Vektorfelder.
a)v = (?/ + z,x + z,x + y)T
b) v = (2xyz + y2z + yz2 , x2z
-\-2xyz + xz2 , x2y + xy2 + 2xyz
c) v = (yz , xz , xy}1
10.	Ermittle alle Funktionen
/ = /(|a?|), für die das Vektorfeld
v = xf (|a?|), x 7^ o
a) quellenfrei b) wirbelfrei
ist.
11.	Gib zu den Feldern aus der Aufgabe
9 je eine Potenzialfunktion tp an. Sei
f(x) := — p(x). Was gilt dann für
A/ in den einzelnen Fällen?
12.	Untersucht werden soll das Gravi-
tationsfeld der Erde. Der Bezugs-
punkt befinde sich auf der Erdober-
fläche. Die betrachtete Umgebung
sei so klein, dass die Erdoberflä-
che als eben angenommen werden
kann. Es wird ein kartesisches x, ?/, z-
Koordinatensystem eingeführt. Der
Koordinatenursprung befinde sich im
Bezugspunkt, die x,?/-Ebene liege
auf der Erdoberfläche und die z-
Achse messe die Höhe über der Erd-
oberfläche. Auf eine Masse m, die
sich im Punkt P(x^y^z} befindet,
wirkt dann die Gewichtskraft F =
(0,0, —mg^-
Zeige rot F = o und ermittle die po-
tentielle Energie von m. Im Koordi-
natenursprung betrage die potentiel-
le Energie null.
14.2 Kurvenintegrale
Raumkurven
x = (x, ?/, z)T e R3
Parameterdarstellung eines Kurvenstückes:
k : x = x(t), t e [q, ß] (a < ß)
(14-4)
x(a) ... Anfangspunkt von k 1	7 . ,	.	,
v	k ist orientiert.
x(ß) ... Endpunkt von k J
Soll k entgegengesetzt durchlaufen werden, schreiben wir
— k : x = x(—t), t e [—/?, — q]	(14.5)
Gilt für zwei Kurvenstücke
fei : a?i = ici(t), t e [oq,/?i] ; k2 : x2 = x2(t), t e [«2,^2]
206
14 Vektoranalysis
#	i(/?i) = ^2(02). sind sie aneinandergekettet und bilden die Kurve \k = k^ ßß &2 j •
Für k lässt sich stets eine Parameterdarstellung finden, sodass t ein Intervall [a, ß]
durchläuft.
Unter einer Kurve k verstehen wir die Aneninanderkettung einer endlichen Anzahl
von Kurvenstücken &i,..., kn, also k = k\ © k-i ®	® kn.
•	einfache Kurve k: x(tß y(tß z(t) sind stetig in [«,/?] und k ist doppelpunktfrei
(ti,t2 G [a,ß],	=^> x(ti) x(t2~)).
Gilt x(a) = x(ßß ist k sonst aber doppelpunktfrei, spricht man von einer ein-
fachen geschlossenen Kurve.
•	(stetig) differenzierbares Kurvenstück: x(tß y(tß z(t) sind (stetig) diffe-
renzierbar in [q,ß].
•	glattes Kurvenstück k: k ist stetig differenzierbar und besitzt in jedem Punkt
eine Tangente (x(t) 7^ o).
•	stückweise < • • • > Kurve: Kurvenstücke sind < • • • >.
•	glatte Kurve: Kurvenstücke sind glatt und gehen an den Verkettungspunkten
glatt ineinander über.
Ist k eine stückweise stetig differenzierbare Kurve, so kann man die Bogenlänge s
als „natürlichen“ Parameter benutzen:
k : x = x(s), s e [0 , L]	(14.6)
(14.6) heißt natürliche Parameterdarstellung von k. Dabei bezeichnet L die Länge
von k.
Es seien
•	PCI3
•	k : x = x(t), t E [a,/?] eine stückweise stetig differenzierbare Kurve
•	k c D
•	f : D —> R ein stetiges Skalarfeld
•	v : D —> R3 ein stetiges Vektorfeld (F(a?), Q(xß R(x) sind stetige Funktionen)
Kurvenintegral 1. Art:
ß
y /(®) ds = y /(®(i)) |x(t)| di	(14.7)
k	a
Kurvenintegral 2. Art:
ß
v(x) - dx = y v(a?(t)) • x(t) dt	(14.8)
k	a
14.2 Kurvenintegrale
207
Es ist da? = (dx, d?/, dz)T und damit |^r(a?) • da? = F(a?) dx + Q(a?) dy + R(x) dzj.
In (14.7) bzw. (14.8) steht links die Schreibweise des Kurvenintegrals und rechts,
wie man es unter den obigen Voraussetzungen leicht berechnen kann.
Die entsprechenden /?/omm-Summc'n. die man aus der natürlichen Parame-
terdarstellung von k erhält, geben Auskunft zur Anwendung der Kurvenintegrale.
natürliche Parameterdarstellung von k: x = a?(s), s E [0 , L]
Zerlegung von [0, L] : 0 = so < si < • • • < sn = L
Xj^x^sV (j = Q,...,n)
.— S{	Si — 1 , Axt .— Xi	Xi — 1	(i — 1, . . . , n)
Bei hinreichend feiner Zerlegung gilt:
n
^ftXi-VASi
1=1
Charakteristische Anwendungsfälle:
•	Kurvenintegral 1. Art'. Ist k mit einer Masse der Dichte £>(a?) belegt, so gibt
£>(a?) ds die Gesamtmasse von k an.
•	Kurvenintegral 2. Art: Ist F(a?) ein Kraftfeld, so gibt fk F(x) - da? die Arbeit an,
die bei Bewegung eines Massepunktes entlang k durch das Kraftfeld geleistet
wird.
Eigenschaften:
2. a,ß e R
a)	+ ß f2(x)] ds = a f /i(a?)ds + /l f fz^ds
k	k	k
• da?
208
14 Vektoranalysis
3. k = k\ ® k? ®	® kn
ds
Kurvenhauptsatz, Potenzialkriterium
• Eine Menge M C Rn heißt offen, wenn mit x E M auch eine volle Kugel um x
zu M gehört.
• Eine offene Menge M E Rn ist genau dann zusammenhängend, wenn man je
zwei Punkte aus M durch eine einfache Kurve in M verbinden kann.
• Eine offene und zusammenhängende Menge G E Rn wird als Gebiet bezeichnet.
• Hängt das Kurvenintegral fkv(x) • da? nur vom Anfangs- und Endpunkt, nicht
aber von der verbindenden Kurve k ab, nennt man das Kurvenintegral wegun-
abhängig.
Satz 14.2 (Kurvenhauptsatz) Sei v : G —> Rn ein stetiges Vektorfeld auf
dem Gebiet G C Rn (n = 2,3). Genau dann ist v ein Potenzialfeld, wenn alle
Km„te3„le . * * über	d^erenaerbm und Snn. ,n G
k
verlaufende Kurven k wegunabhängig sind.
Ist v ein Potenzialfeld und cp ein Potenzial von v, dann gilt für das Kurvenintegral
über eine von A nach B verlaufende Kurve:
v(a?) • da? =	— <p(B)
AB
(14.9)
Ein Gebiet G C Rn heißt einfach zusammenhängend, wenn es - grob ge-
sprochen - keine „Durchbohrungen“hat.
Beispiele nicht einfach zusammenhängender Gebiete im R2 bzw. R3:
R2
G
14.2 Kurvenintegrale
209
Satz 14.3 (Potenzialkriterium) Ein stetig differenzierbares Vektorfeld
v : G —> Rn auf einem einfach zusammenhängenden Gebiet G C Rn ist ge-
nau dann ein Potenzialfeld, wenn <	> für < n % >.
I rot v = o I I n = 3 I
1.	Gegeben sind die Punkte
A(4;2) und B(2;0). Berechne
[(x F y)dx — x dy]
k
a)	längs der Geraden OA
b)	längs des Streckenzuges OBA.
2.	Löse Aufgabe 1 für das Integral
y\ydx + xdy). Warum hängt der
k
Wert des Integrals hier nicht vom ge-
wählten Integrationsweg ab?
3.	Gegeben seien die Punkte A(a;0;0),
B(a;a;0) und C(a;a;a). Berechne
das Integral j\ydx F zdy F xdz)
k
längs der Geraden OC und längs des
Streckenzuges OABC.
4.	Ein Kraftfeld sei bestimmt durch
F = (x — y,x)T. Konstruiere den
Kraftvektor F in jedem Eckpunkt
des Quadrates mit den Seiten x =
Fa und y = Fa. Berechne die Ar-
beit, die notwendig ist für eine Ver-
schiebung der Masseeinheit auf dem
vollen Umfang des Quadrates.
5.	Ein Kraftfeld wird bestimmt durch
F = (P , Q)t = (x + y , 2x)t. Kon-
struiere den Kraftvektor F im An-
fangspunkt jedes Viertelbogens des
Kreises x = a cost, y = a sint. Be-
rechne die Arbeit, die notwendig ist
für eine Verschiebung der Masseein-
heit auf dem Kreisumfang. Löse die
gleiche Aufgabe unter der Bedingung
P = x + y, Q = x. Warum ist hier
die Arbeit gleich null?
6.	Ein Kraftfeld wird durch die Kraft
F = (y,a)T bestimmt. Ermittle
die Arbeit, die notwendig ist für ei-
ne Verschiebung der Punktmasse m
längs der Kurve, die durch die Ko-
ordinatenhalbachsen und das erste
Viertel des Ellipsenumfanges x =
a cost, y = b sint gebildet wird.
7.	Ein Feld wird durch die Kraft
F =	. z)1 bestimmt. Berech-
ne die Arbeit, die notwendig ist für
die Verschiebung der Masseeinheit
längs des Streckenzuges OABCO,
der die Punkte 0(0; 0;0), A(0;a;0),
B(a;a;0) und C(a;a;a) verbindet.
8.	Berechne folgende Kurvenintegrale:
a) y (2xy dx + x2 dy)
AB
b)	y (cos2?/dx — 2x sin2?/d?/)
AB
x /' f _ x \
c)	/ ItanT/d.rH-------—d?/
J \	cos2 y J
AB
längs einer beliebigen Kurve vom
Punkt A (1: —} nach B f2; — Y
\ ’ 6/ V 4/
9.	Gegeben sind die Punkte A(0; 1),
B(2;5) und 0(0; 5). Berechne
/ [Gr + y) dz - 2y dy]
fc
a)	längs der Geraden AB
210
14 Vektoranalysis
b)	längs des Bogens AB der Parabel
y = x2 + 1
c)	längs des Streckenzuges ACB.
10.	Gegeben sind die Punkte A(—a; 0)
und B(0; a). Berechne die Arbeit, die
eine Kraft F = (y ,y — a?)T leistet bei
Verschiebung der Masseeinheit
a)	längs der Strecke AB
b)	längs des Streckenzuges AOB
c)	längs des Bogens AB der Parabel
x2
y = a-----.
a
11.	Zeige, dass j) [ydx + (x + y) dy], ge-
k
nommen über eine beliebige ge-
schlossene Kurve, gleich null ist.
Überprüfe das Ergebnis, indem das
Integral längs der Kurve berechnet
wird, die das durch y = x2 und y = 4
begrenzte Gebiet umschließt.
12.	Gegeben	ist	das	Vektorfeld
v = v(x) = (y , z , x)T.	Berechne
das Kurvenintegral J* v(x) • dx,
k
wenn die Kurve k gegeben ist
durch die Parameterdarstellung
k : x = a cos t
y = a sin t
z = bt,	0 < t < 2 7i
(Schraubenlinie) und k in Richtung
wachsender Parameterwerte durch-
laufen wird.
13.	Gegeben ist das Vektorfeld v(x) =
(y2 — z3,2yz , — .r2)'. Berechne das
Kurvenintegral v(x) • dx, wenn
k
die Kurve k gegeben ist durch die Pa-
rameterdarstellung
k : x = t
y = t2
z = t3 ,	0 < t < 1
und k in Richtung wachsender Para-
meter durchlaufen wird.
14.	Berechne das Kurvenintegral
/c x
v(x)-dx für das Feld v(x) = -——,
\x\
k
c > 0. Die Kurve k ist dabei gegeben
durch
\ f oT
a)	x = cos t, sm t, —	,
J \	' 2nJ '
0 < t < 27t
b)	x = (1,0, t)T, 0 < t < 1
und soll in beiden Fällen in Richtung
wachsender Parameterwerte t durch-
laufen werden.
15.	Zeige, dass das Kurvenintegral
• da? über einem einfach zu-
|a?|3
k
sammenhängenden Gebiet wegunab-
hängig ist.
16.	Untersuche die Kurvenintegrale
v(a?) • da? über einem einfach zu-
k
sammenhängenden Gebiet auf Weg-
unabhängigkeit, wenn
a)	v(a?) = (—y,x,z)T
b)	v(a?) = (x , y , z)T
c)	v(a?) = (y ,x, 0)T
d)	v(a?) = (z , x , y)1
ist.
17.	Berechne das Integral
y \(z—y) dx+(x—z) dy+(y—x) dz],
k
das über die Berandung des Dreiecks
ABC mit den Eckpunkten A(a; 0; 0),
B(0;a;0) und C(0;0;a) erstreckt
wird (a > 0).
14.3 Oberflächenintegrale
211
14.3 Oberflächenintegrale
|_Fläche^^
x = (x, y, z)T E R3
Parameterdarstellung eines Flächenstückes:
F : x = x(u, v) = (x(u, v), y(u, v), z(u, v))T , (u,i?) e B CR2 (14.10)
B sei ein messbarer Bereich, dessen Rand eine stückweise glatte Kurve ist.
o
B ... Inneres von B
o
•	doppelpunktfreies Flächenstück: ic(u,i?) ist eineindeutig auf B.
•	glattes Flächenstück: x(u,v) ist stetig differenzierbar und
( dx(u,v) dy(u,v) dz(u,v)\T	(dx(u,v) dy(u,v) dz(u,v)\T
Xu \ du 1 du 1 du J 7 Xv \ dv dv dv J
o
sind für alle (u,i?) e B linear unabhängig (xu x xv o).
•	reguläres Flächenstück F: F ist doppelpunktfrei und glatt.
Unter einer regulären Fläche verstehen wir die Aneinanderkettung endlich vie-
ler regulärer Flächenstücke (je zwei solcher Flächenstücke haben höchstens Rand-
punkte gemeinsam).
Bemerkung 14.1 Die Oberflächen physikalischer Körper sind reguläre Flächen.
_^tormalenvektor^Orientieru]^^
Es seien
•	F : x = a?(u, v), (u,i?) e B ein reguläres Flächenstück
o
•	xq = x(uo,vo), (uq^o) £ B ein Punkt auf F
Normalenvektor von F in xq:
n(a?0) = xu{uq,vq)xxv{uq,vq) oder n(a?0) = ^(w, 'M x xu(u0, v0) (14.11)
Orientierte Fläche:
Es werden ausschließlich zweiseitige Flächen betrachtet. (Beispiel einer einseitigen
Fläche: MöVm/xsches Band.) Durch Markieren wird eine Seite hervorgehoben
(„Außenseite“). Die Normalenvektoren (14.11) sind dann so zu wählen, dass sie
stets nach „außen“ zeigen.
212
14 Vektoranalysis
Oberflächenintegrale 1. und 2. Art |
Es seien
•	G C R3 ein Gebiet
•	F : x = a?(u, v) , (u,v) e B ein reguläres Flächenstück
•	F c G
•	f : G —> R ein stetiges Skalarfeld
•	v : G —> R3 ein stetiges Vektorfeld
Oberflächenintegral 1. Art:
/(a?)da = y/(a?(u,i?)) |n(a?(u, i?)) | db	(14.12)
F	B
Oberflächenintegral 2. Art:
y v(x) • der = y v(x(u, i?)) • n(x(u, v)) db	(14.13)
F	B
Es ist da = (dai, da2, das)T und damit
[r (a?) • da = P(x) dai + Q(x) da2 + R(x) da^.
In (14.12) bzw. (14.13) steht links die Schreibweise des Oberflächenintegrals
und rechts, wie man es unter den obigen Voraussetzungen leicht berechnen kann.
a deutet auf surface (Oberfläche) hin.
Zwischen der und da besteht die Beziehung der = da = nQ da .
H
Charakteristische Anwendungsfälle:
•	Oberflächenintegral 1. Art'. Ist F mit der Ladungsdichte q(x) geladen, so gibt
Q = fF q(x) da die Gesamtladung Q von F an.
•	Oberflächenintegral 2. Art: Ist v(x) das (stationäre) Geschwindigkeitsfeld ei-
ner strömenden Flüssigkeit, so ist [u = fF v(x) • da^ der Fluss von v durch F
(Flüssigkeitsmenge, die F pro Zeiteinheit durchströmt.
Gilt U > 0, so strömt mehr Flüssigkeit in Richtung der Normalenvektoren (nach
auäen) als entgegengesetzt.
Aus (14.12) erhält man mit /(a?) = 1 den Flächeninhalt A von F:
A =
da
(14.14)
F
14.3 Oberflächenintegrale
213
Ist [F : z = z(x,y), (x,y) 6 BJ die explizite Darstellung der (gekrümmten) Flä-
che F, so gilt
h = i(-zx, - Zy, i)t । = y^+^+1
Für die implizite Darstellung [$(#, y, z) = Oj der Fläche F : z = z(x, yß (x, y) e B
erhält man
11- iV _ VEHEH
’ j	|$2 |
1.	Berechne den Flächeninhalt
a)	der Fläche des Zylinders 2z = .r2.
x
die von den Ebenen y = —, y =
2x, x = 2\/2 ausgeschnitten wird
b)	der Fläche des Kegels z2 = 2xy,
die von den Ebenen x = a und
y = a für x > 0 und y > 0 abge-
schnitten wird
c)	der Kegelfläche y2 + z2 = x2. die
innerhalb des Zylinders x2 + y2 =
a2 liegt
d)	der Fläche az = xy, die innerhalb
des Zylinders x2 + y2 = a2 liegt
e)	der Kegelfläche x2 + y2 = z2, die
innerhalb des Zylinders z2 = 2px
liegt
f)	der Fläche des Zylinders x2Fy2 =
a2, die innerhalb des Zylinders
x2 + y2 = a2 liegt
g)	der Fläche der Kugel x2 + y2 +
z2 = a2, die innerhalb der Zylin-
der x2 + y2 ± ax = 0 liegt
h)	der Fläche des Paraboloids x2 +
y2 = 2az, die innerhalb des Zy-
linders x2 + y2 = 3a2 liegt.
2.	Bestimme mit Hilfe eines Doppelin-
tegrals den Flächeninhalt des Teils
der Erdoberfläche, der durch die Me-
ridiane 0° und ß, durch den Äqua-
tor und den Parallelkreis a begrenzt
wird. Betrachte den Spezialfall a =
30°, ß = 60°.
3.	Berechne das Oberflächenintegral
v(x) • der mit
F
v = (.r3.y3.23) , wenn F die Au-
ßenfläche der Pyramide ist, die durch
die Ebenen x + y + z = a, x = 0,
y = 0, z = 0 (a > 0) gebildet wird.
4.	Berechne das Oberflächenintegral
y v(x) • da. wenn
F
v = (3x, 3y, 3z)T und F die Ober-
fläche der Kugel ist, deren Mittel-
punkt im Koordinatenursprung liegt
und deren Radius 2 beträgt.
5.	Berechne das Oberflächeninte-
gral y v(x) • da für das Vek-
F
C X
torfeld v(x) = -—75-, c > 0, wobei
l®l3
F .	(z + 3)2 =
’ 16	16	25
Die Normalenvektoren n(a?) sind so
zu wählen, dass sie nach außen weisen.
214
14 Vektoranalysis
Hinweis: Verwende die verallgemeinerten
Kugelkoordinaten x = 4r sin $ cos 92, y =
4r sin cos 99, z — —3 + 5r cos
6.	Berechne für das Vektorfeld
v(x) = -—— (c > 0) das Oberflä-
M
chenintegral J* v(x) • da. wobei F
F
derjenige Teil des Rotationsellipsoids
1/9	2\	(z ~ 3)2	.
— (x2 + y2) + V—— = 1 ist, für
16 v 7	25
den — 2 < z < 3 gilt. Die Norma-
lenvektoren n(a?) sind so zu wählen,
dass sie nach außen weisen. (Das
Integral stellt den Fluss des New-
tonschen Gravitationsfeldes oder des
Coulumbschen (elektrischen) Feldes
durch F dar.)
Hinweis: Führe verallgemeinerte Kugelko-
ordinaten ein.
7.	Berechne das Integral
v(x) • da mit v = (x, y, z)T,
F
erstreckt über die obere Seite (Au-
ßenseite) der Ebene x + y + z = a
(a > 0) im ersten Oktanten.
8.	Berechne das Integral
y v(x) • da mit v = (x2, ?/2, z2)T,
F
erstreckt über die Oberseite (Außen-
seite) der Paraboloidfläche x2 + y2
+ 2az = a2 (a > 0) im zweiten Ok-
tanten (dort ist x < 0, y > 0, z > 0).
14.4 Integralsätze
^raußschei^bitegralsa^^
Es seien
•	G C R3 ein Gebiet
•	v : G —> R3 ein stetig differenzierbares Vektorfeld
•	B C G ein Bereich mit regulärer, orientierter (n(a?) stets nach außen gerichtet)
Oberfläche F
Dann gilt
y v(x) • da = y divv(a?)d6	(14.15)
F	B
Im Falle, dass v(x) das (stationäre) Geschwindigkeitsfeld einer strömenden Flüs-
sigkeit darstellt, lautet die Aussage von (14.15): Die Flüssigkeitsmenge, die durch
die Oberfläche F des Körpers B herausströmt, ist gleich der Flüssigkeitsmenge,
die die Quellen in B hervorbringen.
Gaußscher Integralsatz in der Ebene
In den obigen Voraussetzungen ist R3 durch R2 zu ersetzen.
B C G ist ein ebener Bereich, der von einer stückweise glatten Kurve k umrandet
14.4 Integralsätze
215
wird, k sei so orientiert, dass B im mathematisch positiven Sinn umlaufen wird.
Dann gilt
Py) db , wobei v =
(14.16)
j) v(x) • da? heißt Zirkulation von v bez. k. Die Zirkulation gibt an, wie
z-n
stark B umströmt wird.
Koordinatenfreie Darstellung der Divergenz
Für einen Punkt xq e G wird die Folge {Bn} von Kugeln Bn C G mit dem Ra-
dius — und dem Mittelpunkt xq betrachtet. Fn sei die Oberfläche von Bn und
n
4 71
Vn =----t das Volumen. Dann folgt aus (14.15)
3 nö
div v(x) I
\	/ I £C = CC0
lim
Stokesscher Integralsatz |
Es seien
•	G C R3 ein Gebiet
•	v : G —> R3 ein stetig differenzierbares Vektorfeld
•	F C G eine reguläre, orientierte (n(a?) stets nach außen gerichtet) Fläche, die
von einer stückweise glatten Kurve k umrandet wird
•	k so orientiert, dass F bei Blick auf die Außenseite im mathematisch positiven
Sinn umlaufen wird
Dann gilt
j) v(x)  dx = (rotv(a?)) • da	(14.17)
k	F
(14.17) beinhaltet die Aussage:
„Zirkulation von v bez. ka = „Fluß von rotv durch F“
= „Gesamtwirbelstärke auf F“
Koordinatenfreie Darstellung der Rotation
Für eien festen Punkt xq e G und eine feste Richtung n° (|n°| = 1) wird eine
216
14 Vektoranalysis
Folge {Fn} von Kreisen Fn C G mit dem Radius — und dem Mittelpunkt
n
Ti
betrachtet, die senkrecht auf n° stehen. kn sei die Peripherie von Fn und An = —
der Flächeninhalt. Die Kurven kn werden so durchlaufen, dass sie mit n° ein
Rechtssystem bilden. Dann folgt aus (14.17)
( rot v I )
y I 33 = 330 /
kn
1.	Berechne j v(x) • da nach dem
F
Gaußschen Integralsatz, wenn v =
(x2,?/2,z2) ist und F die Oberflä-
che des Würfels mit der Kantenlän-
ge a, der eine Ecke im Ursprung hat
und im 1. Oktanten liegt.
2.	Berechne das Oberflächenintegral
in Aufgabe 3(14.3) nach dem
Gaußschen Integralsatz.
3.	Berechne das Kurvenintegral in Auf-
gabe 17(14.2) nach dem SW;cs sehen
Integralsatz.
Hinweis: Berechne das Oberflächenintegral
über die Ebene x + y + z — a.
4.	Aus dem einschaligen Hyperboloid
x2 + 2y2 — z2 = 1 wird durch die
Ebenen z = 0 und z = 3 eine ringför-
mige Fläche herausgeschnitten, de-
ren im 1. Oktanten liegendes Stück
mit F bezeichnet werde. Berechne
rotv(a?)) • da für das Vektorfeld
F
T
mit
Hilfe des Satzes von Stokes.
5.	Wende den Gaußschen Satz auf
den Vektor v = uigradu2 an
(ui und U2 seien zweimal ste-
tig differenzierbare Skalarfelder) und
v(a?) = [	9,0 , In (1 + z)
\l + y2
leite den 1. Greenschen Satz
B
+ grad ui • grad U2) dx dy dz
= (uigradu2) • da
her.
Wie ergibt sich hieraus der 2.
Green sehe Satz
/// ^U1 ^u<2 ~ u<2^u^
B
— (uigradu2 —U2 gradui) • da?
F
6.	Berechne die Zirkulation von v =
(l,x)T entlang der ebenen Kur-
ve k = ki ® k2 ® ks mit
ki : y = x2 , x E [0,1]
/	1 \2	1
-fc2 :	“ 2) + (y ~ 1')2 = 4 ’
x e [0,1], y > 1
—ks : x = (0 , t)T , t E [0,1].
7.	Im Raum sei elektrische Ladung
2 e
mit der Dichte verteilt q = -—r
l®l
(s ... Dielektrizitätskonstante). Die-
se Ladung erzeugt ein Feld E =
x
।—r. Zwischen Ladung und Feld be-
M
steht die Beziehung q = edivE.
14.4 Integralsätze
217
Berechne die im Innern der Kugel
B mit dem Radius a um den Ko-
ordinatenursprung liegende Ladung
Q = gdb mit Hilfe des Gänschen
B
Integralsatzes.
8.	Verifiziere den Integralsatz von Sto-
kes für das Vektorfeld
v = (2x — y, —yz2, —y2z)1-, wenn F
die obere Hälfte der Kugel x2 + y2 +
z2 = 1 ist.
9.	Verifiziere den Integralsatz von Gauß
für das Vektorfeld v =	(4x,
—2y2,z2)T, wenn der Bereich B
durch die Flächen x2 + y2 = 4, z = 0
und z = 3 begrenzt wird.
10.	a) Zeige, dass der Fluss
U = v(x) • der von v = -^7
J	R3
F
durch jede geschlossene Fläche,
die den Nullpunkt umfasst, gleich
ist.
Hinweis: Gaußscher Integralsatz
b) Berechne U, wenn speziell die Ku-
gelflächen x2+y2-\-z2 = r2 gwählt
werden.
11.	a) Zeige, dass die Zirkulation Z =
(p v(x) • da? von v = —----------
J	x2 + y2
k
x(—y,x,(ß)T entlang jeder ge-
schlossenen Kurve, die die z-
Achse umläuft, gleich ist.
Hinweis: Stokesscher Integralsatz
b) Berechne Z, wenn speziell die
Kreise x2 + y2 = r2 als Kurven
gewählt werden.
12.	Verifiziere den Gaußschen Integral-
satz in der Ebene für das Vektorfeld
v = (a? + ?/, — 2x)T, wenn k die Kurve
ist, die das von den Geraden x = 0,
y = d, xFy = a gebildete Dreieck
umschließt.
13.	Berechne unter Verwendung des
Gaußschen Integralsatzes in der
Ebene das Integral
^[y2dx + (x + y)2dy] längs des
k
Umfangs des Dreiecks ABC mit
den Eckpunkten A(a; 0), B(a; a) und
C(0;a).
14.	Verifiziere den Gaußschen Integral-
satz in der Ebene für das Vektorfeld
/I 1\T
v =	-,---- über den Umfang
\y xj
des Dreiecks ABC mit den Eckpunk-
ten A(l; 1), B(2; 1) und C(2; 2).
15.	Berechne das Integral
y v(x) • der , wobei v = (x,y,z)T,
F
das über die Oberfläche der Kugel
x2 + y2 + z2 = a2 erstreckt wird.
a2 + b2 + c2
18. Zeige mit
von Stokes,
16.	Berechne das Integral
y v(x) -der , wobei v = (x2, y2, z2)T,
F
das über die äußere Fläche innerhalb
des ersten Oktanten eines Körpers
erstreckt wird, der durch die Flächen
x2 + y2 + 2az = a2, x = 0, y = 0,
z = 0 begrenzt wird.
17.	Für v = (x, y, z)T liefert der
Gaußsche Integralsatz eine Formel
für das Volumen:
V = t y (a; d<Ti + y d<T2 + Z dcr3)
F
Berechne nach dieser Formel das Vo-
lumen des Ellipsoids
= 1.
Hilfe des Satzes
dass das Integral
218
14 Vektoranalysis
j (yz dx + xz dy + xy dz),
k
erstreckt über eine beliebige ge-
schlossene Kurve, gleich null ist.
Überprüfe diesen Sachverhalt durch
Berechnen des Integrals längs des
Umfangs des Dreiecks OAB mit den
Eckpunkten 0(0; 0; 0), A(l; 1; 0) und
B(l;l;l).
19.	Wende den GW/? sehen Integralsatz
auf das Integral
y (x3 dcri+^3 dcr2 + ^3 da3)
F
an, das über die Oberfläche der Ku-
gel x2 + y2 + z2 = a2 erstreckt wird.
Überprüfe das Ergebnis durch direk-
te Berechnung des Oberflächeninte-
grals.
20.	Wende den S£oA;esschen Integralsatz
auf das Integral
j) \x(z — y) dx + y(x — z) dy
k	Fz(y — x) dz]
an, wobei über den Umfang des Drei-
ecks mit den Eckpunkten A(a;0;0),
B(0;a;0) und C(0; 0; a) zu inte-
grieren ist. Überprüfe das Ergebnis
durch direkte Berechnung des Kur-
venintegrals.
21.	Zeige, dass sich für das Vektorfeld
v = gradu aus dem Gaußschen In-
tegralsatz
fff A AAA f du
/au dxdy dz = / — da
B	F
ergibt (u sei ein zweimal stetig diffe-
renzierbares Skalarfeld).
22.	Überprüfe die Richtigkeit der in der
Aufgabe 21 gewonnenen Formel für
das Skalarfeld u = x2 + y2 + z2 und
die Oberfläche F : x2 + y2 + z2
= a2.
Lösungen
Aufgaben aus Abschnitt 0.1
1. a) 2a?2 — 5a?
b) 2a?2 - 17a; + 109
667
x + 6
Aufgaben aus Abschnitt 0.2
1.	a) (x + 3)2
b)	(2x — 5)2
c)	(x — l)2(x + l)2
d)	(1 + a)2(l — d)
e)	8x2(x4 + 1)
c) — 3x2 + 2x — 1
2x - 3
x2 + 2x + 8
2.	a) 144
<r.io
b) 2^3’
ax 7^ 0
c) (
5x + 2y
a + 5b

e)	0,25
0,375a? + 0,45
~ 2a;2 - 0, la; + 3
f)	ax3 — bx2 — c
2. a = q-, p = —q2 — 1
|a|	5|&|
5|a?| t2 2|y|
d) r5u3(s + t)5
ru 7^ 0, s 7^ — t
Aufgaben aus Abschnitt 0.3
1. a) |a| • b3 • Va8^9
b > 0
b)	|2x — 5t/|
c)	xn • tfx2 , x > 0
d)	a > 0
e)	+ 1 für x > 0
—\/^3 + 1
für x < 0
f)	x — y, x > y
g)	|a?|3
h)	|a? - y\
i)	^Tö - 2
j)	2a; — 1 für x > 1
1 für x < 1
2.	a) 17-1272
, x 36 + 11710
b)—«—
c) 4-715
3.	28 - 472
4.	72 + 76
Aufgaben aus Abschnitt 0.4
1. a) 1
b)	725
c)	—2
d)	16
e)	16
kl 7
f) 7— = 2,57890...
Ig3
h) \Ja1 — 62
i) 0,8
4(3 - a)
3 + a
2. a) 3Iga + 41g \b\ — Igc
a>0, 67^0, c>0
220
Lösungen
b)	-|lg(a2 + ö2)
a2 + b2 0
c)	41ga+ |lgb
+21g (a + b)
7,	5, ,
-xlga- x!g^
a > 0, b > 0
Aufgaben aus Abschnitt 0.5
M 2 5
b) ~3; 6
c) -3; 3; -5; 5
7X 2 2
d -1; 1
J 3’ 3’
e)	keine reelle Lösung
f)	.Tl = X? = 0
X3;4 nichtreell
g)	-7; -3
h)	7; (2 entfällt)
i)	nicht lösbar
2-Ä=I
3. A = n2 + n mit
n = 1,2,3,4,...
4. a > —
“ 16
Aufgaben aus Abschnitt 0.6
1. a) 9
b) keine reelle Lösung
c) —4
d) 1
e) 7
f) 27
a ,	30
g) 5;-----
67 ,	127
h) —2; 2
Aufgaben aus Abschnitt 0.7
Beachte: Alle angegebenen Lösungen goniometrischer Gleichungen sind durch den
Zusatz k = 0, ±1, ±2, ... zu ergänzen.
. 7	271 271	7	271	Ö7t 7 — + k • 27t		193, 22135°+A;-360o
7	3	9	3	6		346, 77865°+Ä;-360o
b) k • 27t, (2k + 1) • - 6	7 k) —7t + k • 27t 6	2. a)	k • 7t
c) k • 71	117t	7		37t	7t
7t		H k • 27t	b)		I-A:-27t, —+ Ä>7t
d) (2fc + l)-- 2 7t	6 Tl —H k • 27t		2	3 27t — + k • 7t
e) (2k + l)7t, k  —	2		3
3	1) 48,47127°+	360°		7t
4 f) —7t+ k  7t	172, 64082°+A;-360o	c)	- + k • 7t 4
15 x 7t 7 7t 7t , 7t g) —Vk -	—Vk- —	m) keine Lösung	d)	7	71 A; • 7t,	—H k • Ti 4
67 6	5 9	3	n) 1, 24905 +/c • 7t		37t 7
h) k • 27t, — + k • 27t	0, 24498 + k • 7t		T+fc-n
2 .x 7t 7	Ö7t _ 1) — +Ä?27t,	|-Ä?27t	x 7t 7	57t	7 O) — +Ä?27t, — + Ä?27t O	O	e)	37t	7	7t — + k • 7t, — + 7t 4	3
6	6 ,x	7t	7t j)	-	+ fc-7t,	- +	fc-27t	p) 46,77865° +fc-360° 133,22135°+fc-360°		27t — + k • 7t ö
Aufgaben aus Abschnitt 1.1
221
Aufgaben aus Abschnitt 1.1
1. a) Indirekter Beweis:
B : a2 + b2 < 2ab
gilt für alle reellen
a, b.
a2 — 2ab + b2 < 0
A : (a — b)2 < 0
gilt für alle reellen
a, b.
A ist offensichtlich
falsch (das Qua-
drat einer reellen
Zahl ist nichtnega-
tiv). Somit ist B
wahr.
b)	Direkter Beweis:
A : (a — b)2 > 0
gilt für alle reellen
a, b.
a2 — 2ab + b2 > 0
B : a2 + b2 > 2ab
gilt für alle reellen
a, b.
Zur Beweisdurchführung
werden Hinweise gegeben.
2. a), b) mit 3 potenzie-
ren
c)	Ist a spitz, so gilt
0 < cos o: < 1.
d)	Trigonometrische
Formeln an wenden.
e)	Sinussatz und Kosi-
nussatz
3.	b), c) Jede rationale
Zahl ist als Quo-
tient zweier tei-
lerfremder ganzer
Zahlen darstellbar.
4.	a) P(ri) :
m 2
P{n^ = F(l) :
1 • 2
1 =--- ist wahr.
2
F(fc):
. k(k + 1)
=	2
sei wahr für ein
k > 1.
(Tc) + (fc+1)
fc+l
(fe + 1)
2
x (/c + 2)
k+l
F(fc + 1):
2=1
_ (& + l)(/c + 2)
2
Also gilt F(n) für
alle n > 1
5.	Man beweise indirekt
a > 0 und b > 0
und wende diese For-
mel wiederholt beim
Induktionsbeweis an!
6.	a) hinreichend, nicht
notwendig
b)	notwendig, nicht
hinreichend
c)	weder notwendig
noch hinreichend
d)	notwendig und hin-
reichend
e)	notwendig und hin-
reichend
f)	hinreichend, nicht
notwendig
Aufgaben aus Abschnitt 1.2
1. a) A = {-2,0,1}
b)	B = {2}
c)	C = {1,2, 3,4, 5}
d)	D = {-3,-2,-1,
0,1,2}
2. z. b. b) (2x — y)(2x
+y) < 0 ^ (?/ > 2x
A y > — 2x) V (y < 2x
/\ y < —2x)
(Die gesuchte Punkt-
menge wurde schraf-
fiert; die Punkte der
gestrichelten Geraden
gehören nicht dazu.)
y
222
Lösungen
3. ÄUB = {-3, -1, 5}
Ar\B = {5}
A\B = {-3}
B\A = {-\}
AxB = {(-3,-1),
(-3,5),(5,-1),(5,5)}
B x A = {(-1,-3),
(-1,5),(5,-3),(5,5)}
4. Die Veranschauli-
chung mit Hilfe ebener
Punktmengen macht
kaum Schwierigkeiten.
Um die Gleichheit
zweier Mengen X und
Y mathematisch ex-
akt zu beweisen, zeigt
man oft (1) X C Y
und (2) Y C X und
schließt aus (1), (2) auf
X = Y. Zum Beweis
von (1) zeigt man: Ist
x ein beliebiges Ele-
ment von X, so ist es
auf Grund der Vor-
aussetzungen auch ein
Element von Y. Ana-
log zeigt man (2). Für
4e) sei (1) gezeigt:
x e A U B
=^> x AU B
=> (x A /\x B)
=> (x e Ä A x e B)
> ./ c ÄnB =>
(1) AuB c ÄnB
Nun ist noch
(2) Än ß C AuB
zu zeigen.
5. a) x G B =>
x G A n B =>
x e A => B C A;
xeB^>xeA =
(xe AaxeB)
x e A n B =>
(1)	BcAnß
Stets:
(2)	A n B C B (s.
4a)).
Aus (1) und (2)
folgt
AnB = B
6.	Die Bildungsvorschrift
m n2 + 1
An G {1,2,...}
stellt eine eineindeuti-
ge Abbildung dar.
7.	A ~ B, denn
(n = 1,2,3,...)
ist eineindeutig.
8.	a) F ist Funktion,
G nicht.
b) G 1 ist Funktion,
F-1 nicht.
9.	a) L± U L2 U L3
b)	L\ n (L2 U L3)
c)	Li n £2 A L3
11. a) Fi =
{(a, <a), (b, a), (c, <a)}
F2 =
{(a,a),(ö,a),(c, ß)}
F3 =
{(a, <a), (b, ß), (c, <a)}
F4 =
{(a,ß),(ö,a),(c, a)}
F5 =
{(a,a),(b,ß'),(G /?)}
F6 =
{(«,/?), (b,a),(c, /?)}
F7 =
{(a,ß),(ö,/3),(c, a)}
Fs =
{(a,/3),(M),(cX)}
b) Gi =
{(a,a),(/?,a)}
£^2 __
Gz =
G4 =
G5 =
Gq =
G7 =
G^ =
G9 =
G10 = {(a, a)}
G11 = {(q, b)}
G12 = {(ct, c)}
G13 = {(/?, n)}
G14 = {(/?, b)}
G15 = {(/?, c)}
Aufgaben aus Abschnitt 1.3.1
223
Aufgaben aus Abschnitt 1.3.1
1.	a) irrational
b) x = —0, 7; rational
c) x = 0, 75; rational
Hinweis: x = log9 5
^log2B3 = ^
2.	Hinweis:
a3 — b3 = (a — 6)(n2
-1-ab -|- 62)
3.	a)
107
333
b) ---
J 990
13
C)T
4.	a) [-2,5), [1,3)
[-2,1), [3,5)
b) (-5,1), (-2,0]
(-5,2] U (0,1), 0
c) [-1,5; 3,5), (0,5; 3,5)
[—1,5;0,5], [3,5;4,5)
5.	a) {1}
b){-l,l}
lim M = 1
lim M = —1
c) {3}
---	z
lim M = -
3
2
lim M = —
---	3
e) {(2,4,5)}
Aufgaben aus Abschnitt 1.3.2
1. L in Intervallschreib-
weise
b)	(—oo, 2)
c)	[4,+oo)
d)	(-2,1)
e)	(-3,2)
f)	(-oo,-2] U [1,2]
g)	(-oo,-5)
( „3
U -3-,+o
j) (-oo; 1,2]
U (2,5; +oo)
k) (-oo,-3) U [-2,2)
m) (-2,8]
3. L in Intervall- bzw.
Mengendarstellung
a) Lösung durch Fall-
unterscheidung:
Skizze
ff+ 3 >
2x — 5 “
|a? + 3|
|2x-5| “
(*) |x + 3| > 3|2x
5
-5| \x -
Fall 1:	x < — 3
(*)	-(x + 3)
> —3(2a? — 5)
5
Fall 2:	-3 < x < -
2
(*) o x + 3
> —3(2x — 5)
12
" '- T
Mtl)
5
Fall 3:	- < x
2
(*) o x + 3
> 3(2x - 5)
18
Gesamtlösungs-
menge:
L — L\ U Z/2 U Z/3
c) (—oo, — 1)U(4, +oo)
d) b“' d
e)
j) [3,5]
224
Lösungen
k) (-00, —2)	y
4. z.B. b)
Aufgaben aus Abschnitt 1.3.3
1.	a) 1 • 2 •... • n • (n + 1)
x(n + 2) • (n + 3)
b)	n + 1 • 2 • 3
c)	3n + 1 • 2 • 3 •... • n
d)3-l-2-...-n — 5
e) 1 • 2 •... • (2n — 4)
x (2n — 3)
f)	. .-(n—l)-n
O
2.	a) (n + 2)!
b)	n\
c)	(n — 2)!(n + 1)
d)	n + 1
e)	(n + 2)!
f)	2n • (2n + 1)
g)	(n — k — 1) • (n — k)
h)	-----------
(2n — 1) • 2n
4n2 + 2n + 1
b) (2n+l)!
f)
g)
h)
4n2 — 2n + 1
J) (2,.)!
4. a) 21
b)	3921225
c)	0
d)	-36
e)	0
1
” 8
1155
2048
14
— 81
(-l)n • (2n- 1)!
n!(n — 1)!
7.	a) 9X2?/-4 — 42x?/_2z
+49^2
b) ci2 + 6cz26 + 12a62
+863
c) 32x"5 - 240x-2
+720x - 1080x4
+810x7 - 243x10
d) 1 + 0,3 + 0,03
+0,001 = 1,331
8.	a) Hinweis:
2n = (l + l)n
b) Hinweis:
0n = (1 - l)n
9.	495a4x-2
10.	60
11.	xi = 10“2’5; x2 = 10
12.	a) 1,1,2,3,5,8,13,21,
34,55,89,144,233,
377,610,987,1597,
2584,4181,6765
k=0 V 7
OEf-D*©
fc=0 x 7
xan2~2kn
14. 6. Glied
Aufgaben aus Abschnitt 1.4
225
Aufgaben aus Abschnitt 1.4
1.	V$ = 3125 2.	a) P4 = 24 b) P4 - P3 = 18 3.	a) Pg34) = 60 b) F^1’2’1’ - 5 x4;2’x) = 120 oder 10 • P$ = 120 W4 4.	C$ = 13 983 816	b) P3 • P5 = 720 9.	+45) = 1073 741824 10.	a) baedc b) 54. Permut. 11.	a) V5(2) = 20 b)	V4(1) = 4 c)	1 12.	28. Komb.	25 '+ + = 225 — i k=l = 33 554431 16. G^5) • C§>0) = 823 727 520 17. a) l+” = 1024 b) P™ = 120 10 c) VF^’10-i) = 176 / /	W1O 2 = 7
5.	a) cg = 56 b) V™ = 216 6.	F10 = 3 628 800 7.	= 30 240 8.	a) P5 = 120	5 13. ^2 C5} = 31 2=1 5 14. V V$ = 62 /	VV2 2=1 13. a) C“« = P) \ r\j J	d) 968 18. a) N2 = C$  C'X = 442 320 b) S = <+> = 75 287520 c) Si = S - C$ = 10 841496
Aufgaben aus Abschnitt 2.1		
1. a) 12 - 5i; 6 - 9i 41 - 3i; 1 - 3i 41	3 13 + 39i;	1	i ’	130	130 8 . 73	55	48. 3’ 11 36’	73 + 731 55	4.	, M " 7'5	1 36	3 c) 4, 52993 + 2,01764i - 0,66622 —0,98236i 4, 24264 + 4, 24264i 0, 64395- 0,17255i 5,79555 + l,55291i 1,06066- l,06066i d) -5 + 2i; -1 + 6i 4	4	14	2 - 2 + 14i; 25 + + e) 3,98174 + 3,93185i - 2,94646 —0,06815i - 2,07055 +7, 72741i 0, 35355+ 0,35355i -0,51764 -1,93185i 4	5 2. a x =	; y = — 7 11’ y 11 3 b) u = —2; x = - y = 2; z =	 ’	2 3. a) — \xy\	b)	-1 c)	—i d)	1 + i e)	-6- 12v/6i f)	-i g)	i h)	e"71/2 4. a) 1 + 2i M 1	17‘ b) ~3 - T‘ . 1 , 2V&. c 7 + -7-1 5	5 d)7T + 6 5. a) 0 - 5i = 5 ei(-7t/2)
226
Lösungen
= 5 (cos (-90°)
+i sin (—90))
b) 9 + 0i = 9ei>0
= 9(cos0°+isin0°)
c) 0 + 3i = 3ei7t/2 =
3(cos 90° + i sin 90°)
d) —8 + 0 • i = 8e17T
= 8(cos 180°
+i sin 180°)
e) 1 + x/3i = 2 ei7t/3 =
2(cos 60° + i sin 60°)
7 r- 7
f)“2^+2i
= 7 ei57i/6
= 7(cosl50°
+isin 150°)
g) “2 “ V
= ei(-27t/3)
= cos (-120°)
+i sin (-120°)
h) -3,00908
—3,99318i
= 5ei(-2,21657)
= 5 (cos (-127°)
+i sin (-127°))
i)	4 — 6i
= v^e^“0’98279)
= 7ö2(
cos (-56,30993°)+
isin (-56,30993°))
j)	0 + 2i = 2ei7t/2 =
2(cos 90° +isin 90°)
k)	0,5 + i  0,5
__ 71! iyr/4
“ 2
a/2
= —(cos 45°
+i sin 45°)
1)	—0, 5 + 8 i
= 7^4,25 eb 1,63322
= 764,25(
cos 93,57633°
+i sin 93,57633°)
m) y/3 — i = 2 e't-71/6)
= 2 (cos (-30°)
+i sin (—30°))
n) —2 + 2i
= 2\/2ei37t/4
= 272(008 135°
+i sin 135°)
o) -73-3i
= 2T3ei(-27t/3)
= 273(cos(-120°)
+i sin (—120°))
P) |i
= ei(-7t/6)
= cos (—30°)
+i sin (-30°)
q) 0 — 9i = 9e1(-71/2)
= 9 (cos (-90°)
+i sin (-90°))
r)	-1 + Oi = e171 =
cos 180° + isin 180°
s)	- e2 +0 i = e2 e171
= e2(cos 180°
+i sin 180°)
t) 0 + e4 -i = e4 • e12"
= e4 (cos 90°
+isin90°)
6.	a) Re z = 2
Im z = 1
3
b)	Rez = --
T 3
Im z = -
2
c)	Re z = 0
Im z = — 2
d)	Re z = 16
Im z = 0
e)	Re z = 0
Imz = 102473
f)	Rez = -64
Im z = 0
7.	Hinweis:
Eulersche Formel
8.	a) zi = | (\/2 + i\/6)
Z2 = -
+i\/6)
b)	zr = 1,62894
+0,52017i
z<2 = -1,26495
+1,15061 i
23 = —0, 36398
-1, 67079 i
c)	= 1,40211
+0,18459 i
z2 = -0,18459
+1,40211 i
z3 = -1,40211
-0,18459 i
24 = 0,18459
— 1,40211 i
d)	+ i\/2
z2 = —ä/2 -|- i\/2
z3 = -V2-1V2
z4 = V2-1V2
e)	zr = 0,89101
+0,45399 i
z2 = -0,15643
+0, 98769 i
z3 = -0,98769
+0,15643 i
= -0,45399
-0,89101 i
z3 = 0,70711
-0, 70711 i
9.	a) 1; - + -V3
Aufgaben aus Abschnitt 2.2
227
b)	0,80902 + 0, 58779 i
- 0, 30902
+0,95106 i
- 1; -0,30902
-0,95106 i
0,80902-0, 58779 i
c)	0,28485+ 1, 75532 i
- 0,28485
-1, 75532 i
d)	0,29863+ 1, 50405 i
- 1,45186
-049340i
1,15323- 1,01065 i
e)	0,21275+ 1,06955 i
- 1,06955
+0, 21275 i
-0,21275
-1,06955 i
1,06955-0, 21275 i
f)	0,38268 + 0,92388 i
- 0,92388
+0, 38268 i
- 0,38268
-0,92388 i
0,92388-0, 38268 i
Aufgaben aus Abschnitt 2.2
1.	Wegen
x(2x3 +x2+2x+l) = 0
ist xi = 0. Es verbleibt
2x3 + x2 + 2x + 1 = 0.
Der Grad ist ungera-
de, die Koeffizienten
alle positiv, deshalb
muss wenigstens eine
Wurzel negativ sein.
Die Normalform hat
jedoch nicht nur ganz-
zahlige Koeffizienten.
Deshalb:
Multiplikation mit
a™-1 = a2 = 22 :
23x3 + 22x2 + 22 • 2x
+22 = 0
und Substitution
y = anx = a3x = 2x :
y3 + y2 + 4t/ + 4 = 0.
D.i. Normalform ei-
ner Gleichung 3. Gra-
des mit nur ganzzah-
ligen Koeffizienten.
Wegen b3 = 4 = 22
müssen etwaige ganz-
zahlige Wurzeln un-
ter ±1, ±2, ±4 zu fin-
den sein. Man findet
yi = -i:
	114	4 -1 0 —4
-1	10 4	0
Aus y2 + 4 = 0 folgen
V2 = 2i; y3 = -2i.
Aus Xk =
k = 2,3,4 erhält man
x2, x3, x4 :
xi =0; x2 =
x3 = i; x \ = —i.
Anmerkung: Aus
y3 + y2 + 4y + 4 = 0
folgt
+ + 4)(y + 1) = 0
also
yi = -1; z/2,3 = ±2i.
2.	a) xi = —3 + i
x2 = -2 + i
xi + x2 = — 5 + 2i
= -br
x±x2 = 5 — 5i = b3
b)	xi = 2i; x2 = —1
c)	X1?2 = ±4
x3 = -5
Xi + x2 + x3 = -5
= — b2
XiX2 + X1X3
+x2x3 = -16 = 61
X1X2X3 = 80 = —b3
d)	xi = 2; x2 = 3
x3,4 = 3 ± 2i
Xi + x2 + x3 + X4
= 11 = -b3
X±X2 + X1X3 + X1X4
+X2X3 + X2X4
+X3X4 = 49 = b2
X^X2X3 + X1X2X4
+X1X3X4 + X2X3X4
= 101 = -61
X1X2X3X4 = 78
= b3
e)	xi = x2 = x3 = 1
f)	xi = x2 = -1
x3 = x4 = 2
3.	a) xi?2 = 1 ± 2i
^3,4 = ~2 ± i
b)	xi = 0; x2,3 = 1;
3^4,5	2
c)	xi = -2; x2,3 = 3
d)	xi = 1; x2 = —2
x3 = —3; x4 = 7
e)	£1,2 = 1 ± i\/3
^3,4 = ix/2
228
Lösungen
f)	xi = 1; X2 = 3
£3,4 = 1 ± V2
g)	£1,2 = ±1
£3,4 = 1 i 2i
h)	xi = 1;
£2 = £3 = £4 = -1
i)	Substitution:
2x = y
1 1
X1 = ~2’ X2=2
3	5
X3 = 25 X4 = 2
j)	Subst.: 12.;; = y
=0; x2 = --
ö
1
£3 = £4 = -
£5,6 = -1 ± i
k)	Subst.: y = 2X^3
x± = 0; .7'2 = 3
1)	Subst.: y = log,. 5
xi =5; X2 = Vb
4.	a) x2(x — 2)2(x2 + 2x
+2)
b)	2(x — l)(x — 2)(x
+3)(x2 + x + 1)
c)	(x — 3)(x + 2)2(x2
+2x + 10)
d)	(x + l)(x — 9)2(.t2
-2V2 + 4) • (x2
-\-2y/2x + 4)
5. a)
2-9 11 3
6-9 6
32-3	29
3	2—329 6 9
3	2	3 11 	6_
3	2	9
3	2
F3(£) = 2(x — 3)3
+9(x-3)2
+ll(x-3) + 9
b) — (x + 2)5 + 10(x
+2)4 - 39(x + 2)3
+73(x + 2)2 — 64(x
+2)+ 21
c) 2.t3 — 6x2 + 2x + 8
(für x = — 1)
Aufgaben aus Abschnitt 3.1
1. a° = (
'M
3	2	1 \T
x/14’ x/14’ vW
5	3	2 \T
?38’ ?38’ ?38/
a + b = (2, -1, 1)T
b — a = (8, -5, 3)t
— 2a + 3b = (21, -13, 8)T
2.	cii = 0, ci2 = 2, <23 = —2
3.	A2 + A + 1
2
4.	|a| = 70, cos q = -
n 3	f 6
cos/1 = -, COS7 = --
5.	\ÄB\ = |ÄC | = \BC\ = 2V2
6.	F(-4; 4; 4\/2)
7.	a) Z>(9; -5; 6)
b) ÄC = (—2, 6, -10)T
BD = (14, -8, 8)t
|ÄC| = 2\/35, \BD \ = 18
35 10\T
T’ T)
r A + rB + rc
'• a) rs =----------------
ö
b) 5(3; 1; 3)
10.
L 11. Uh pfl. 11. ll^i
3’ T’ Tr \3' T’ 's)
11. V =
c + Ab
1 + A
12.	P(~ —; 0; 0
k 10’ M
13.	a) a = x/TT, b = \/T).c = \/2
b)M(|;	|),M&(1;	2)
\ Zj Zj Zj /	x Zj /
14.	F(16; -5; 0)
Aufgaben aus Abschnitt 3.2
229
Aufgaben aus Abschnitt 3.2
1. a) 8 b) (-16, 20, —8)t c) 7 « 73,39845°	9. [a, b, c] = 0	16. (1,0,1)T oder a = — b + 3c	/ 1 4	1\T 10.C 3' 6	4
2. a • b = 0	17. - 11.0, denn die 3 Vektoren	3
3. A = 4	sind komplanar.	18 (_36j 24, -16)T
4. 15	19 20 20 i2’ 7 ’ 3	19. a) [AB, AC, AD]
5. a) 49 b) 108	13. 547		> = ° i	b) AB = -CD
6. 2^6 7. « 109,87687° 8. -33	14’ ,s°= ±7TT -3,1')T	BC=-DA 15. Die Annahme	c)	। ~ [a, b, c] = 0 führt auf		= [DA | = a/14 einen Widerspruch.	AC • BD = 0
Aufgaben aus Abschnitt 3.3
1. a) r = (—2,3, —5)t +A(3, —7, 4)t b) r = (3, —2,1)T +A(—2,0,1)T — oo < A < +oo	bi f( — • — • -—	b=V42, c=014 1	Vll’	22’ 22/	a = 90° 01826	ß = 60° C)	22	7 = 30° ß AL 3	b) Höhen:
2. A liegt auf der Gera- den (A = — 3), B nicht.	7. S(4; —7; —3)	r = (l,2,3)T 7 « 29.62018°	_|_Af—2, — —-V
3. a) 5(1; 2; 1) b) parallel c) windschief d) fallen zusammen e) windschief f> s(r l: 3)	8. r = (2, -3,4)T	r = (-2,3,2l)T2? +A(1’0’2)	+/z(3, —1,2)t — oo < A < oo	r = (2, —3, —1)T 9. a) A = ±1, Fi(2;0;3)	+7(-l,5,4)T F2(0;-4;7)	-oo<A,/z,7 b) A = ±6, F3(7; 10; -7)	<+°° ’	, _	, .Mittelsenkrechten: P4(-5;-14;17) 1 An 1 5 V
4. S(—1; 3; —2),	10. F(-l;l;2)	r = A ( 2’ 2’ 2 ) Z = (1, 0, 1)T	/3V i /t
5. a) r = (3, — 1, 2)t +A(—2,3, —3)t — oo < A < +oo	|Z| = ^	r=l2’-2’0 11. a) Aa = 703	+^-1’2)T a = 2\/14	r=\2,2,2)
230
Lösungen
+7(1,—5,—4)t
— 00 < A, /z, 7
< +00
Winkelhalbieren-
den:
r = (1,2,3)T
+A(—303 + 1,
03 — 5, -2V3-4)t
r = (—2,3,1)T
Mff(0;0;0)
p=y7(2-^)
r = a/14
+/z(5, -4,1)T
r = (2, —3, —1)T
+7(—203 — 1,
303 + 5, v/3 + 4)t
— 00 < X, n, 7
d) r = (1, 2, 3)t
+A(1,1,-1)T
— 00 < A < +00
Aufgaben aus Abschnitt 3.4
l.Ei: 15x — 24?/+ 10z
= —2
E2 : 15x — 24?/ + 10z
= —2
2. a) 03	b) y
3. (4,3, 2)t r = 27
/8	\T
5. a) r = (	0,0 j
\ ö	J
+A(0,5, 2)t
+m(-2, -3,0)t
b) r = (0, —13,0)t
+A(0,7,1)T
+Ai(-l,0,0)T
— 00 < A, y. < +00
6. 7 « 40,36759°
8.	a) S(-7; -5; -11)
b) S(3;l;3)
9.	a) r = (1,1,0)T
+A(-2,5, 3)t
7 « 72,02472°
b)	r =	2,0J
+A(3,8, 5)t
V? « 54,73561°
c)	r = (1,1,0)T
+A(9, -8, - 11)T
7 = 90°
— oo < A < +oo
10.	a) (-1,1,-1)T r = 1
b) r = (2,1, —2)t
+A(-1,1,-1)T
— oo < A < +oo
11.	(2,12, 17)t r = 13
5
12.	xF = zf =
Vf = -1
13.	F2(0; 9; -6)
14.	a) (2,7,5)T • r = 33
b) £(—13; 7; 2)
15.	x - 2y - 3z = 4
16.	2x + 3y + 4z = 3
17.	S(l;-1;2)
18.	x — Sy + 9z = 21
19.	2x + 2?/ + z = 20
2x + 2y + z = — 4
20.	7x + 14?/ + 24 = 0
21.	a) 9x + 4?/ + 9z = 20
, . 53^178
b
c)	r = (—1, 5,1)T
+v(2, -9, 2)T
— OO < V < +oo
d)	S(l; —4; 3)
22.	a) A(l; 2; 1)
b)	r = (1,2,1)T
+Az(l,l,-4)T
0 < y < +oo
c)	n = 02/2
Aufgaben aus Abschnitt 4.1
231
Aufgaben aus Abschnitt 4.1
-(+1)
10
-16
9
12
+(-4)
9
12
10
-16
= 56
c) Z.B.: Durch Addi-
tion des 3-fachen
der 2. Zeile zur
1. Zeile und des
(—5)-fachen der 2.
Zeile zur 3. Zei-
le und Entwicklung
nach der 1. Spalte
erhält man
0-2 3
1 -4 -2 =
0 4 22
d) Austausch der 1.
und der 2. Zeile:
1	—4	—2
- -3 10	9
5 -16 12
Addition des 3-fa-
chen der 1. Zeile
zur 2. Zeile und des
(—5)-fachen der 1.
Zeile zur 3. Zeile:
1 —4 —2
-0-23
0 4 22
Addition des 2-fa-
chen der 2. Zeile
zur 3. Zeile:
1 —4 —2
-0-23=
0 0 28
-1-(-2)-28 = 56
2.	a) 26
b)	-38
c)	2a
d)l
3.	-10
4.	a) —4a3
b) 144
c) (x-y)(x-z)(y-z')
d)l
e)	35
f)	86
g)	470
5.	a) a?i = 2, x% = 3
b) a?i =0, X2 = —2
c) xi = 1, a?2 = 2
X3 = 3
Aufgaben aus Abschnitt 4.2
1. a) Nicht definiert:
2A + 7C, 2AB
BA, CB
5A — 3B =
8 3	0
1 25 -11
(A + B)C =
14 7 —14
29 23 -11
2ATB =
/10 8 8 '
24 24 20
\-6 0 -4,
3BtA =
232
Lösungen
/15 36 -9
12 36 0
\12 30 -6
— BC =
-4 -1 7
-10 -15 -5
/ 5 13 -2\
13 34 -5
\—2 —5 1/
C C =
dTd = 14
/ -6 -9 -3\
2. a) 8	12	4
\—12 -18 —6/
b) Nicht definiert: dA
Ad = ( -1 |
\-4/
( 2
Cd= -3
\ 7 .
dTC = (3, 14, 12)
dTÄT = (Äd)T
= (-1, -4)
c) Nicht definiert:
AA, dd, dTdT
AtA =
/ 23 12 -14'
12 1 -12
\-2 12 11 ,
C-C,T =
/26 13 1 \
13 9 —7
\ 1 —7 26/
CTCT =
(CC)T =
/ 23	12	-2
12	1	12
14 -12 11,
d • dT =
/4 —2 6
—2 1 -3
\6 -3 9 ,
3.	45
/—83 66\
4.	-46 31
\—34 19/
5.	abc
8. B vom Format (2, 4)
C vom Format (3, 4)
9. 3150 Stck. Ti
4200 Stck. T<2
2550 Stck. T3
6000 Stck. T4
Aufgaben aus Abschnitt 4.3
1. Die Annahme der li-
nearen Abhängigkeit
führt zu einem Wider-
spruch.
b = A 0-2 A 2(13
3.	Es ist z.B.
(3,-1,1)T
+(-1,3,1)T
- 2(1,1,1)T = o
4.	a) (1,4, — 7, 7)t
(70,40, —20, —16)t
(51,26,18^,
-llfi’
2
, 1, 3, 3
X =
X =
8	7
3’ 3’
16	11\T
23	29
T’ “T’
27 9\T
T’ 8/
5.	Es ist z.B.
2(1,1, - 1)T
+3(5,0,3)T
— (—2,1, —3)t = x
6.	Jede	Linear kombi-
nation von S liefert
einen Vektor, dessen
3. Komponente null
ist.
7.	b) Qi = 1, «2 = 0
Q3 = — 1, q4 = 1
q5 = -1
Ql = 3, Q2 = 2
Q3 = —1, q4 = —5
Q5 = —1
Ql = —5, Q2 = 9
Q3 = —7, q4 = 5
Q5 —	3
Aufgaben aus Abschnitt 4.4
233
Aufgaben aus Abschnitt 4.4
1. In A z.B. 1.			und	Spaltentausch in		der
4. Spalte austauschen:	neuen Matrix B:						
/1	1	—4	2	3	( 1 1 —4	2 3	
r	7	5	—4 0	0 3-1	0 2	
	e	9	5 -3	0 0 11	0 0	
\0		-1	0	2 )	\0 0	0	0 0 )	
(4—	Kennzeichnet die	somit r(A)				= 3.	
Eliminationszeile.)				Oder kürzer: Die		Eli-
Addition des 2-fachen	minationszeilen						wer-
(bzw.		3-fachen) der	den nicht immer				wie-
Eliminationszeile zur	derholt notiert,						auch
2. (b	zw. 3.)		Zeile:	die bewusst erzeugten		
			\	Nullen nicht. Ebenso		
	1	—4	2 3 \	wenig ist es erforder-		
0	9	-3	0 6	lieh, einen Zeilen-		oder
0	9	-3	11 6	Spaltenaustausch		auf-
V	3	-1	0 2/	zuschreiben: A :		
Vereinfachung der 1				21 —4 m		3
Zeile von B						
	1	—4	2 3 \	-47	5-2		0
		—		5 6	9 -3		-3
0	3	-1	0 2^-			
				0 3-1	0		2
0	9	-3	11 6	—		
				0 9-3		6
\0	3	-1	0 2/			
X /			/ \	11 9 -3		6
1 1	1	—4	2 3 \	0 3 Q		2
0	3	-1	0 2			
				0 0		0
0	0	0	11 0	hü o		0
\0	0	0	0 0/			
r(A) = 3
2.	a) 2
b)	3
c)	2
d)	2
e)	4
f)	3
3.	a) r(A) =
2 für A = 0
<
3 für A 7^ 0
b) r(B) = 3 für alle
A G R
4. a) linear unabhängig
(r = m = 4)
b) linear abhängig
(r = 3 < m = 4)
5. a)r = 2<m = 3
z.B. B = {a2, a3}
Ql = —3q3
b) r = 3 < m = 4
z.B.
B = {ai, a2, Q3}
(I4 = a2 + a3
Aufgaben aus Abschnitt 4.5.1
1. a) = —b
2
= -~CL
ö
b) = —1; X2 = 2
x3 = 4
c) xi = 1; X2 = 2
x% = —2; X4 = —1
d) xi = 2; X2 = —2
X3 = 1; X4 = — 1
2. a) x2 — bx + 3
b) — 2x3 + x2 — x + 4
3. I6 = — A
19
234
Lösungen
Aufgaben aus Abschnitt 4.5.2
1.	a) Das jeweilige Ele-
ment, in dessen
Spalte durch Addi-
tion von Vielfachen
der ausgewählten
Zeile zu allen an-
deren Zeilen Nul-
len erzeugt werden,
wird eingerahmt
(Pivot).
Durch dieses Mar-
kieren werden
Zeilen- bzw. Spal-
tenvertauschungen
überflüssig.
Das gestaffelte
Gleichungssystem
für die Rückrech-
nung besteht aus
allen so markierten
Gleichungen.
Die Variablen, nach
denen das gestaffel-
te System aufgelsst
werden muss, ste-
hen in den markier-
ten Spalten.
Xi x2	x3	X4		1_
4 6	17	8	-20
0 0	-1	2	4
@ 3	7	7	—4
2 3	8	5	-8
0	3	-6	-12
0	0	2	4
0	1	—2	—4
0		0	0
0		0	0
Um in der 1. Spalte			
Nullen	zu	erzeugen	
wurden das (-2)-fa-
che der 3. zur 1.
Zeile, das 0-fache
der 3. zur 2. Zeile
und das (-1)-fache
der 3. zur 4. Zeile
addiert.
r(A) = r(B)
= 2 = r
Das System ist lös-
bar. In der Lösung
treten (n — r) =
2-2 = 2 freie Va-
riable auf, nämlich
x2 und X4, da sie
nicht in den mar-
kierten Spalten ste-
hen. Gestaffeltes
System:
2xi + 7x3 =
—4 — 3x2 — 7x4
— X3 = 4 — 2X4
Man erhält daraus:
3
xi = 12 - -x2
21
V4
X3 = — 4 -F 2X4
Für die freien Va-
riablen setzt man
hier zweckmäßig
x2 = 2G, x4 = 2t2
und erhält die Lö-
sung:
xi = 12-3G-21t2
x2 = 2G
x3 = —4 + 4t2
x4 = 2t2
— oo < G, t2 < +oo
oder:
x =
(12, 0, —4, 0)T +
+ ti(-3, 2, 0, 0)T
+i2(—21, 0, 4, 2)t
X1 x2 x3 x4		1_
4 6 17 8	-20
0 0-12	5
@377	—4
2 3 8 5	-8
0 3-6	-12
00 2	5
0	1 —2	—4
0	0	3
0	0	1
r(A) = 2, r(B) = 3
r(A) r(B)
Das System ist un-
lösbar.
2.	a) x = (1, -1, 0)T
+t(0, 1, 1)T
b) nicht lösbar
c) x = (1, 2, 3)t
d) xi = a?2 = a?3 = 1
f)	Xi = 2 — ti
x2 = ti
£3 = 2 — t2
Xi = t2
g)	Xi = X-2 = X3 = 0
(triviale Lösung)
h)	x = t(l,3,2, —1)T
i)	x =
ti(l, -4,0, -13, 5)t
+t2(0, —2,1, —6, 4)t
j) Xi = 21 - 2h - Qt2
Aufgaben aus Abschnitt 4.6
235
-12t3
x2 = ti
x3 = —20 + 7t2
+14t3
.ri = 15 — 5t2 — 9t3
X5 = ^2, Xq = t3
k)	X = (1, 1, 1)T
1)	Xi = ti - t2
9
x2 = — — 2ti 4- 2t2
x3 = ti
3 o
X4 = -- - 2t2
Xq = t2
m)	x =
(l -2 -S fV
\3’	’ 3’ 3/
n) xi = — — 13ti —7t2
3 r
x2 = -- + 5ti
+23t2
x3 = 12ti
.1:4 = 12t2
o)	x = (-1, 1, 2)t
p)	xi = 3 + ti
x2 = —2 + t2
X3 = ti, -7'1 = t2
q)	xi = 2t
x2 = -1 + t
x3 = 3 — 2t, .1:4 = t
3.	Ai = 0 :
x = 3, y = z = 0
A2 = 0 : x = 3 - 2t
y = t. z = t
4.	a) r(A) = 3, r(B) = 4
unlösbar
b) r(A) = r(B)
= r = n = 3
eindeutige Lösung
c) r(A) = r(B)
= r = 2
n — r = 4 — 2 = 2
2 Parameter
5.	a) x = (3, 2, 0, 3)t
+t(-2, -1, 1, 0)T
b) ti = 2 :
x = (-1, 0, 2, 3)t
t2 = 6 :
x = (-9, -4, 6, 3)t
Aufgaben aus Abschnitt 4.6
1. X = -C (A + B)“1	b) S3	Xl x2	Z/2	Z/4
A, B vom Format	Z/i	-i -1	0	1 2
(n, n)				
C vom Format (m, n)	x3	0 -1	1	1
det(A + B) 0	V3	-1 -4 2	1	3 2
	X4	9	9 2	ö	-1	3 2
2. a) X = (A + 2B)“1
x(5C + 3Z>) • B1
b) X = 2A-1C(B
+ E)~X
3. a) S2	X1 x2	7/2 X4
yi	1 0	1	1 3	3
x3	3 1	1	2 3	3
yz	1 -1	0 -1
Z/4	3 2	2	2 3	3
4. a) det A =
2 2 3
1 -1 0
-1 2 1
= -1^0
(A ist regulär)
An =	-1 0 2 1		= -1
A12 =	1 0 -1 1		= 1
Ai3 =	1 -1 -1 2		= 1
A-21 = 	-4, A22		= 5
A2.3 = 6, A3i = 3
A32 = —3
A33 = —4
A^ =
i A1 4 3)
—j-- -1 5	3
\ 1 -6 —4/
/ 1 —4 -3\
=	1-5-3
\-l 6 4/
b) Si	Xi	x2	x3
yi	2	2	3
y2	1	-1	0
yz	-1	2	1
s2	x\ y2 x3
Z/i x2 yz	4-2 3 1 -1 0 1 —2 1
236
Lösungen
S3
yi
xz
x3
xx yz y3
1 4 3
1 -1 0
-1	2	1
Xi 1 —4 -3
x2 1 —5 —3
x3 — 1	6	4
Aus wird A-1
abgelesen.
5. a) Anmerkung: A 1
x / 5 4 -1\
= 7 • 10 12 —3 I
5	I
\0 1 1 /
b) X =
Z-4 3,8 -0,6\
-3 3,84 -4,88
b) B1
c) C“1
\—3 0,64 —2,48/
d) D1 =
/—2 2 -1
1 -1 1
\ 4 -3 1
f) G“1 =
/ 3 -15 -8\
ö- -1 1	1
\-l 4	2 /
h) K' =
/ 1 1 -2 -4Ä
0 10-1
-1-13	6
\ 2 1-6-10/
Aufgaben aus Abschnitt 4.7.1
1 0
0 1
1,5
-2,5
A = E2 ist Ortho-
gonalmatrix
(£Jt • E = E)
mit det A = 1.
Es liegt eine rei-
ne Parallelverschie-
bung des Koordina-
tensystems vor.
4	1 ( 4 3
A = - I
5 y-3 4
ät=1 A -3
5 \3 4
det A = 1
AtA = E2
A ist Orthogonal-
matrix. Es liegt ei-
ne reine Drehung
des Koordinaten-
systems vor. Wegen
A-1 = At lautet
die inverse Trans-
formation:
4	3
%x = -yx - -yz
5	5
3	4
xz = -yx + -yz
5	5
Für die reine Dre-
hung des kartesi-
schen Koordinaten-
systems um den
c)
Winkel im ma-
thematisch positi-
ven Sinne sind aus
der analytischen
Geometrie der Ebe-
ne die folgenden
Formeln bekannt:
yx = xx cos <p
+x2 sincp
yz = —xx sin^
+.1*2 COS
4	1 /-4 3\
4 — — I I
5 y 3 4/
det A = — 1
A1 = 1 (-4 3
5 \ 3 4
Aufgaben aus Abschnitt 4.7.2
237
ata = e2
Zunächst ergibt
z = Ax eine rei-
ne Drehung mit
Umklappung. An-
schließend erfolgt
eine Verschiebung
y = z + c mit
c= (1,5; -2, 5)t.
Hinweis: Zu allen drei Lö-
sungen der 1. Aufgabe soll-
ten die zugehörigen Skizzen
angefertigt werden.
2. ATA 7^ -E/(2,2)
3P=I
( 2
-1
-1 -1
2 -1
-1 2
4.	a) 90
b) 48 • 90 = 4320
5.	a) Hinweis:
A-1 = At
6.	Zu zeigen:
det A = ±1 und
AtA = E
Aufgaben aus Abschnitt 4.7.2
1. a) Charakteristische
Gleichung
6-A 2	2
2	3-A	—4
2	-4	3-A
= 0
oder
A3 - 12A2 + 21A
+98 = 0
liefert als Lösungen
die Eigenwerte
Ai = A2 = 7
A3 = —2
b) Berechnung der zu-
gehörigen Eigen-
vektoren:
Ai = A2 = 7 :
X1 X2 X3 1
-12	2 0
2-4-40
2-4-40
Lösung:
xi = 2ti -|- 2t2
X2 = tl, X3 = ^2
— OO < tl, t2 < + OO
Das ist eine zweipa-
rametrische Schar
von Eigenvektoren:
xi = (2ti + 2t2)ei
+tiC2 + t2^3
So erhält man z.B.
für ti = 0 und
t2 = 1 den Eigen-
vektor
xi = 2ei + e3.
Nun werden ti und
t2 so gewählt, dass
xi und
a?2 = (2ti + 2t2)ei
+tiC2 + t2C3
orthogonal sind,
also
2(2ti + 2t2) 4“ 0 • ti
+1 -12 = 0
gilt, so z. B.:
ti = 5, t2 = —4 :
x2 = 2ei + 5e2
-4e3
A3 = -2 :
X1 X2 X3	1
8	2	2 2	5-4 2-4	5	0 0 0
Lösung:
xi = t, x^ = —2t
x3 = —2t
— oo < t < +oo
Das ist eine einpa-
rametrische Schar
von Eigenvektoren:
a?3 = tei — 2te2
-2te3
So erhält man z.B.
für t = 1 den Ei-
genvektor
x3 = ei — 2e2 —2e3
Somit:
(z = 1,2,3)
also:
ri = 4=(2, °’ 1)T
v 5
r2 =
5 -4>
Ts = |(1.-2. -2)T
ö
und
Wegen det R = — 1
tauscht man 2. und
1. Spalte aus:
238
Lösungen
R =
/ -2-
V5
3
\ 3?5
gibt
R AR = D
/7 0
= 07
\0 0
0
0
—2
mit det R = 1.
Zu Ai = A2 = 7
gehören die Eigen-
vektoren
fi =
^f'2-5' ~4)T
r2 = ~z=(2, 0, 1)T
v 5
und zu A3 = —2
r3 = |(1, —2, —2)t
ö
2. a) Zur Kontrolle:
Ai = 1, A2 = 2
A3 = 3
R =
/ 9 6 2\
ü “6 7 6
\ 2 —6 9/
b) Zur Kontrolle:
Aj = —2, A2 = -2
A3 = 1
c) Die Rechnung er- 3. a) —1; 2; 3
b)	-1; -1; -1
c)	0; 0; 1
d)	1; 2 ± 3i
e)	0; 2; 2; 12
f)	—2; 2; 3; 4
4. a) r/ = |(1, 2, 2)
d = |(2, 1, —2)
rj = |(-2, 2, -1)
b) d =
d = -L(l, 1, 0)
d = -4(1, -1, 2)
Aufgaben aus Abschnitt 4.7.3
a = (-2, —14)t
uo = —13
det A 7^ 0
1. Fall:
Verschiebung:
x = y — v
Die Lösung des
LGS 2Av = a oder
die Berechnung von
-A~ra ergibt
v = (—2, 1)T und
7	1 T
ö0 = u0 - -a V
= -13 + 5 = -8
Nach (4.62):
3yi + 10yiy2 + 3j/2
-8 = 0
Drehung: y = Rz
Eigenwerte von
A :
Ai =8, A2 = —2
mit den zugehöri-
gen Eigenvektoren
= (1,1)T
X-2 = (-1, 1)T
Nach (4.64):
8zl - 2zl - 8 = 0
oder Zi —	= 1
(Hyperbel)
Die Formeln für die
Koordinatentrans-
formation sind:
x = Rz — v
/ 4 —2 -4’
b) A = —2 1 2
\-4 2 4 ,
det A = 0
Aufgaben aus Abschnitt 4.7.3
239
a = (-28, 2, 16)t
uq = 45
2. Fall:
Drehung: x = Ry
A hat die Eigen-
werte Ai = 9,
A2 = A3 = 0 mit
den zugehörigen Ei-
genvektoren
Zi = (-2, 1, 2)t
^2;3 = (<1 + ^2,
2ti, i2)T-
Die Forderung
a ± I3 führt auf
2ti -|- ^2 = 0
und damit
Z3 = (—G, 2ti,
- 2ti)T.
Die weitere Forde-
rung I2 ± I3 ergibt
ti(ti —	= 0.
Die Lösung G = 0
entfällt, da sie
I3 = o ergibt.
Es verbleibt
ti = ^2 = t und
l2 = (2t, 2t, f)T
l3 = [-t, 2t, —2i)T.
Wählt man z.B.
t = 1:
1-2 = (2, 2, 1)T und
l3 = (-1, 2, —2)t.
Somit
/-2 2 -1\
R=0 122
\ 2 1 -2/
mit det	R	=	1.
/	9	0	0 \
D=	0	0	0
\	0	0	0/
a'R
= (30, —12, 0)
Nach (4.66):
9yl + 30yi - 12y2
+45 = 0
Verschiebung:
y = z — v
Die Anwendung der
quadratischen Er-
gänzung und die
Zusammenfassung
des weiteren linea-
ren und des absolu-
ten Gliedes ergibt:
n ( 5V
9 bi + 0
(	5\
-12 h/2-- =0.
Mit der Verschie-
bung
5
= 2/1 + ö
ö
5
^2 = Z/2 - "
ö
erhält man:
9zl - 12z2 = 0
(parabolischer Zy-
linder)
2. a) gleichseitige Hyper-
bel: M(-l; -1),
a = b = 1
b) Parabel: 5(2; —2),
p = 3
c) Kreis: M(4; —1),
r = 2
3. a) M
d) Ellipse: M(-2; 1),
a = 3, 6 = 4
1^
b) M(0; 0; a), r = |a|
4.	a) 32zx -|- 50^
-800 = 0
z2 z2
“leK 2S + 11 = 1
Ellipse
b) 18z? - 8z? - 72 = 0
z2 z2
oder: —-------- = 1
4	9
Hyperbel
5.	a) 16z? + z? - 16 = 0
Ellipse
b)	4zx —^—4=0
Hyperbel
c)	= 4x/2z2
Parabel
d)	4 - | = 0
paralleles Geraden-
paar
6.	a) 12^x -|- 3^2 4“ 3^
-1 = 0
Ellipsoid
b)	6zx — 3^ — 3^
-1 = 0
(zweischaliges) Hy-
perboloid
c)	2^x + 2^ — 7^3
-1 = 0
(einschaliges) Hy-
perboloid
d)	10zx +^ + ^3
-1 = 0
Ellipsoid
240
Lösungen
e)	9z% — 18^
+36^3 = 0
bzw.
18zl - 9zf
—36^3 = 0
Sattelfläche (hyper-
bolisches Parabolo-
id)
f)	3^1 + 6zf = 6
elliptischer Zylin-
der
7.	a) 3z? + 62^2 + 9^3
-18 = 0
Ellipsoid
2	2
O	O
“ÖZ3 + 1
O
2	1
3'2 =	+ V2
ö	ö
2
+ ö^3
%3 = -~Zi - ~Z2
ö ö
O(xi = 1;
x2 = 0; x3 = -1)
b)	18^1 + 9^ — 9^
-18 = 0
Hyperboloid
1	2
%1 = “ö+l + ö^2
ö	ö
2
+ +
2	1
X2 = “+1 - -Z2
ö	ö
2
+ ö^3 - 1
2	2
X3 = ÖZ1 + öz2
O	O
~3Z3 + 1
O(a?i = 0;
x2 = -1; x3 = 1)
c)	yl+y^+yl-49 = 0
Kugel
xi = ?/i + 3
X2 = y2 - 4
x3 = V3 - 5
O(xi = 3;
x2 = -4; x3 = -5)
Aufgaben aus Abschnitt 5
1. a)
2n3 — 5n2 + 8
hm -------------
7n3 + 2
2-0+0	2
7 + 0	7
b) lim (1
n—»oo \
2 \n+7
~ n — 3/
Substitution: m = n
— 3. Aus n oo folgt
m oo.
= e"2-(1 - O)10
1
e2
c) lim (v 4n2 + 3n
n—^oo v
—2n) = lim
7 n^oG
(4n2 + 3n) — 4n2
\/4n2 + 3n + 2n
r 3
= hm —----------
V4+^+2
- 3 _3
_ x/4 + 2 ~ 4
o X	3
2- a) a = -
"»(=) = I -1
b) a = 0
= 1/7
o x 3
3.	a) a = -
5
monoton wachsend
b)	a = 0
für n = 1, 2,..., 5
monoton wachsend,
für n > 5 monoton
fallend
c)	a = 0
monoton fallend
d)	a = 1
monoton wachsend
4.	üi konvergiert
2=1
nach Quotientenkri-
terium. Damit ist die
notwendige Konver-
genzbedingung erfüllt:
lim an = 0
A 1
a)<7=2
Aufgaben aus Abschnitt 5
241
b)
c)
d)
5. a)
b)
Q = 0
1
Q = ~
e
1
9=4
_6
~5
2
1
" IÖ
c)
d)	0
e)	unbest. divergent
f)	0
x 125
g)
h) +oo best. divergent
.]) 1
1
2
1)0
m) y/e
x 1
k)
o)
P)
q)
6. a)
b)
c)
7. a)
e </e
1
0
e8
12.
z.B.
z.B.
z.B.
_ 7n-2
n
3n2 + n
n2
= -6
5
v nö
1
— 1	: T
n + 1
s = 1
b)
$n —
8. a)
b)
c)
1 \
2n -|- 1 /
1
S ~ 2
25	25
TÖÖ + 10000
- _?£
- Töö
1
1____L_
100
-
“ 99
1
2
557
990
9. a) m = 3, 5
b) S40 = 2246
10. a) 87ir2		d) konvergent nach
b) 47ir2 c) 67ir2		dem Leibnizschen Kriterium: lim an
87ir3 d)^r	(4 + ^/2)	n—»00 = hm
		n^oo H2 + 1
x 2	3 e) -7ir 7 7	(2V2 +1)	= lim 	y n + - n
11. in 14, 2067 ... Jahren
ist nicht
a) divergent; notwen-
dige Konvergenzbe-
dingung
erfüllt:
lim an
lim
lim
n
3n-l
1 _
F —
1
3
^0
b) a.
n
2n + 3 J
Wurzelkriterium:
lim VTöj
lim
lim ----
1
_ 2 < * 1
Konvergenz
x 10n
C) ün ~ (2n-l)!
10n+1
ön+1 “ (2n+l)!
Quotientenkrit.:
lim
^n+1
i-	10
= hm —---------
2n(2n + 1)
= 0 < 1
Konvergenz
= 0
Es gilt < an
für n > 1, denn die
Annahme:
^n+l > also
führt auf einen Wi-
derspruch:
1 > n2 + n
für n > 1.
Die Reihe ist nicht
absolut konvergent,
denn es gilt
n 1
n n2 + 1 — 2n
für n > 1. Damit
ist die harmonische
242
Lösungen
Reihe eine diver-
gente Minor ante:
“2^2
2=1
(Dies kann weder
mit dem Wurzel-
noch mit dem Quo-
tientenkriterium
entschieden wer-
den, z. B. ist
y/n
(\/n)2(l +
=> lim
1
- phö -
e) konvergent, denn
1
ttn ~ (3n - 1)2
1 ...
< — tur n > 1.
Damit ist die ver-
allgemeinerte har-
monische Reihe
(für a = 2) eine
konvergente Majo-
rante. (Weder mit
dem Wurzel- noch
mit dem Quotien-
tenkriterium kann
hier entschieden
werden.)
13.	a) nein
b)	ja
c)	nein
d)	nein
14.	a) konvergent
b) konvergent
c) konvergent
d) konvergent
e) divergent
15.	a) divergent
b) konvergent
c) konvergent
d) konvergent
e) divergent
16.	a) divergent
b)	konvergent
c)	divergent
d)	konvergent
e)	divergent
17.	a) divergent
b) absolut konvergent
c) absolut konvergent
d) divergent
18.	a) konvergent
b)	konvergent
c)	divergent
d)	absolut konvergent
e)	konvergent
f)	konvergent
19.	a) -1 < x < 1
b)	—oo < x < +oo
c)	0 < x < +oo
d)	|x| < 1
e)	|x| < 2
f)	— 1 < x < 1
g)	— 1 < x < 1
Aufgaben aus Abschnitt 6.1
243
Abbildung L.l: 3b links, 3e Mitte, 3f rechts
Abbildung L.2: 3h links, 3i rechts
Aufgaben aus Abschnitt 6.1
1.	a) [—1; +oo)
b)	(—oo; — 2)U
(—2; 2) U (2; +oo)
c)	(—oo; —a/2] U {0}
U[a/2; +00)
d)	(—00; —1] U [0; 1]
e)	(-2; 0]
f)	(-1; 1) U (2; +00)
g)	1
ö
h)	[1; 100]
i)	(2; +00)
j)	(-00; 1) U (1; +00)
k)	(—00; +00)
1)	[i; 4)
m)	(—00; —1)U
(-1; 3) U (3; +oo)
2.	a) D(f) =
{x | x 6 R A x > 5}
W) =
{y \y e RAy > 0}
b) Z>(/) = {x | x G R
/\x	— 2 A x 3}
IV(/) = {y|yGR
Ay ^OAy A
5 J
c)	= {x | x e R
Ax 7^ —2 A x 7^ 2}
W) = {z/|z/eR
/\y E (—oo; 0)
U[l; +oo)}
d)	D(f) = {x | x e R}
W) = {z/|z/eR
At/ e (0; 3]}
3.	b) Siehe Abb. L.l.
e)	Siehe Abb. L.l.
f)	Siehe Abb. L.l.
h)	Siehe Abb. L.2.
i)	Siehe Abb. L.2.
4.	a) ungerade, denn
= 7 sin x cos x
= -f(x)
b)	gerade
c)	weder gerade noch
ungerade
d)	weder gerade noch
ungerade
e)	gerade
f)	ungerade
244
Lösungen
Abbildung L.3: 11a links, 11b rechts
g)	weder gerade noch
ungerade
5.y = f 1(x')
_ 1 ’/1-aA2
4 \ 1 + x )
DU-1) = (-1; 1]
W1)
8. x
6- a) y = f 1(x') = 5
+X\/x
mr1) = [0; +oo)
b)	y = —	—1
[1; +oo)
c)	y = 3 — y/x
[0; +oo)
d)	y = —: (-oo; -
U(—1; +oo)
7. a) x = - ^3 — 5sine27
9.	a) x2 — bx + 6
10-	^{f(x)+f(-x^
+|(/(X) -
11.	a) xn± = 2; xn2 = —3
xp = 4; xl = 3
3
für x = 0 ist y = -
Asymptoten:
x = 4; y = x + b
f(x) = x + 5
26x - 42
+ x2 - 7a? + 12
Siehe Abb. L.3.
b) xN1 = —2; xN2 = 2
xp = 1 (zweifach)
y\x=o ~ —
Asymptoten :
x = 1; y = 1
f 0) = 1
2x - 5
+ x2 — 2x + 1
Siehe Abb. L.3.
12.	a) po = lOn
b)	po = 4n
c)	po = Qn
d)	Po =
13.	Der Nachweis lässt
sich indirekt erbrin-
gen.
Aufgaben aus Abschnitt 6.2
245
Aufgaben aus Abschnitt 6.2
(x-5)(x + 3)
1. a) hm 7----77----7-
7 (x — 5)(x + 5)
x +
= hm-----
10	5
! \ o ( n sm ax
b) 3: hm ------
x
d)
r 2(z-l)
hm —---------
£—>1—0 — (x — 1)
= —2
e) Substitution:
z = arcsin 7x
x 0 => z 0
1
x = - sm z\ somit
7
lim
z^O ± sjn z
= 7 x lim ——
2^0 Sm^
m) 0
n) e
o) e1 2
3. a) —1 für x	—0;
+ 1 für x	+0
b)	—00 für x 2 — 0
+ 00 für x 2 + 0
c)	+00 für x 1 — 0
0 für x 1 + 0
d)	2 für x —2 — 0
— 2 für x — 2 + 0
e)	+00 für x —1 — 0
— 00 für x —1 + 0
f)	— 1 für x 1 — 0
+ 1 für x 1 + 0
7t
g)	— für x 1 — 0
7t
— — für x 1 + 0
h)	—— für x —3+0
7 Qß
Aufgaben aus Abschnitt 6.3
1. a) Bei xq = 0 Sprung-
stelle mit unendli-
chem Sprung.
b) Bei xq = 1 Sprung-
stelle mit endli-
chem Sprung.
c) Bei xqi = —2
und X02 = 2 je-
weils Sprungstelle
mit unendlichem
Sprung.
d) Bei xqi = 1
Sprungstelle mit
unendlichem
Sprung; bei X02 = 2
Lücke, d.h. heb-
bare Unstetig-
keit (hebbar durch
/(2) = 1).
e)	Bei xqi = 0 heb-
bare Unstetig-
keit (hebbar durch
/(0) = 1). Bei
Xq = kn
(k = ±1, ±2,...)
Sprungstellen mit
unendlichen Sprün-
gen.
f)	Bei xq = 2 Sprung-
stelle mit endli-
chem Sprung.
g)	Bei xq = 0 Sprung-
stelle mit endli-
chem Sprung.
h)	Bei xq = 1 Unend-
lichkeitsstelle.
2- a) /(0) = 2
b)	/(0) = 0
c)	/(0) = 1
7
d)	f(2) = -
o
[ ri\
e)	/(0) = (1) = n
f)	/(0) = 2
246
Lösungen
g) /(0) = 0
3- Äo/(a;)
7^ lim /(x)
x—»2+0 v 7
4. Ja, denn es ist
Jimo/(a?)
= =2-
5. a = 0
6. /(0) = 1
Aufgaben aus Abschnitt 6.4
1(1 — x2) — x(—2x)
(1-x2)2
zuletzt:
1 _L
1. a) x2 — 4x + 4
= (x-2)2
b) Zunächst: y =
10x-3 — 6x1 +4x4
dann:
y' = —30x
12 _i
—x 3 +
ö
zuletzt:
,	30
y =~^ä 
2 cos x
x3
tan./'
sinx
x2
1
-4_
4-3
y (1-x2)'
e) Zunächst (z.B.):
y =
4
\/x
3
>6 .
= V3^2x7/8
dann:	___
j)
k) 27^(7^+ i)2
1) Zunächst:
y = x In x — 1g 5
—3 Igx
c) Zunächst: y =
5x2 — 3x2 -p 3x~
2x1
5 4
= -x3
2
3 31
dann:
,	5 4i
• -a?3
y =8‘
zuletzt:
3a/2 x 8
y=2
2
3
3
’ 2
y
f) - (3a?4 + 12a;3 + 3a?2
-42a?-40)/(a?3
dann:
yr = In x + x • —
x
1 n
-3-lge
x
zuletzt:
X
Inx
g) Zunächst:
y = In |x|
Inx
3 31 19
- • —x12
2 12
zuletzt:
,	10 3r
y = y v4?+
1 +1
---= H----x- vx‘
4x^/x	8
d) Zunächst:
In (—x)
dann:
y' =
f 1
(-1) i
zuletzt:
y‘
1 r-
— tur x

dann:
y' = 7TX
h) 6x —
27
2	1 cos2 x
cos x
n) 6x2 ex +2x3 ex
—3X In 3
x —7x2 + 20x — 6
">—?—
2. a) u'vwuv'wuvw'
b) u'vwz + uv'wz
+uvw' z + uvwz'
3.
y
—2x + 2
—2
—2
für
für
2
0
stetig für x
e (—co, +oo)
Aufgaben aus Abschnitt 6.4
247
differenzierbar für x
e (—00, 2) u (2, +00)
Knick an der x = 2, y = — 2		Stelle
4- a) y = < y' = ‘ stetig x e (-	—x , a? < 0 x , a? > 0 — 1 , x < 0 1	,	x	>	0 für -00, +00)	
differenzierbar für
x e (—00, 0)
U(0, +00)
b) y =
sinx , x e [0,7i]
\ — sin.r ,
x e (71, 2tt]
y' =
COS .T , X E [0, 7t)
\ — COS X ,
x e (71, 2tt]
stetig für
x e [0, 2tt]
differenzierbar für
x e [0, 7t)
U(7T, +2ti]
5. a) Zunächst:
y = 5 (1 + a?2) 2
dann:
+a?2) 2 • 2x
zuletzt:
yr =
15./'
(1 + .T2)2 \/l + x2
b) Zunächst:
y = (x + 2a?2) 2
dann:
y' = 2	+ 2X^)
x (1 + x~^
zuletzt:
y' =
y[x + 1
2^/a? + 2y/x • y/x
9
l>m = 57W?
\/3
) sin (6.7; + 4)
e) Zunächst:
y = - In (1 - ,/ j
-|ln(l + x)
dann:
2 ’ 1 + x
1	1 + a? + 1 — X
2	(1 — a?)(l + x)
zuletzt:
y'= 21 1
X2 — 1
f) ae6x (6 cos ca?
—csin cx)
g) Z/ =
ln(— In.r) ,
<	0 < x < 1
In (Ina?) , x > 1
y' = —
xlnx
h) -A-
smr
i) j) k)	1 cosx 1 cosa? x3(lnx)2	
1) VX2		-25
m) n) 0) 6. a) b) c)	II II II II	< l 1 1 1 0	T II	1 O	1	ü M tr x	’z 1 cd	l	1 5’	CD 1	“l“ O 7B	1	W	1—L H KD	bC	W to	
	ds d%	1 TA bO 1 Al
d) e)	< ,r 11	%i «	H	11	। Hz?“	'z^~ “	To	r -x "7 1	।	| cc	1	bo ET H w	<*> +	_L Cd	+ Ä	Ai	
7. a) b) c)	(x - l)3 cos.,/'. — sin./'. — cos./'. sina? 112	6 ry»	ry»2 ry»3	ry»4 1	
^7	2y/x + 1 ’ 1	
4x/(^ + l)3’
3
8^/(0: + l)5’
15
16t|/(x +1)7
248
Lösungen
d) —3sin3x,
— 9 cos3x,
27 sin3x, 81 cos3x
8. Nachweis
9. a) Zunächst:
In?/ = In 10—3x Inx
dann:
y' n 9 1
— = 0 — 3 In x
y
—3x • —
x
= — 3(lnx + 1)
zuletzt:
yf = —30x-3x(lnx
+1)
b)	In?/ = 1, — = 0
y
yf = 0, denn:
x1^ = e = const.
c)	(tanx)cosx
x(—
sinx	\
H------— In tan x
cos2 x	/
2
d)	(7We"‘
e)	xx(l + Inx)
10- a) f(-x) = f{x)
gerade =>
- /'(-*) = ra)
= -/'(*)
ungerade
b) f(~x) = -f(x)
ungeradem
-f'(-x)=-f'(x)
f'(-x) = /'(x)
gerade
c) f(x+p) = f(x)
periodisch mit Peri-
ode p =>
/'(a?+p) = f(x)
periodisch mit Peri-
ode p
11. a) arctanx
1
b) 	;	 \x\y/x2 — 1
c) y' =
✓

<	2_

< M < 1
d) 6x cosh2 x2 sinh x2
e) a • tanh (ax + b)
f) x + - sinh 2x
g) arsinhx
h) (arctan x)x
x (inarctanx
x	\
(1 + x2') arctanx)
x + 2
X2 + X + 1
4x2
J x4 - 1
3^
} 2(1+ x3)
x 1
1) 	 (1 + x2) arctanx
m) cosxsinh (sinx)
x 6x tanh2 x2
n) 	5	
cosh x2
°) -4-
p) 4sinh4x
%/4x — 1
12.	a) ,/”> =	2'"!
b)	= an  eax
c)	yW = (-1)”-1
(2n — 3)!
X22"-2(n-2)!
xx^-n
d)	= 2”-1
• n — 1
x sm \ 2x H----—7i
13.	Anmerkung:
f(n\x) =
1	4 (-1)71
— • T) ’ I   ---
2	'^(l+.z-)''+l
1 \
+ (l-;r)»+1 J
14.	Durch dreimalige Dif-
ferenziation erhält
man:
n
3 i(i — l)x2-2
2 = 2
n
+a -1) •	-1)
2 = 3
x (? — 2)x2-3
= (n + V)n(n — l)xn~2
Für x = 1 folgt:
n
i)
2 = 2
= (n + l)n(n — 1)
oder, da k — 1 = 0 für
k = l:
n
^k(k- 1)
k=l
(n + V)n(n — 1)
=	3
Für das Weitere der
Hinweis:
n
^k(k- 1)
k=l
Aufgaben aus Abschnitt 7.1
249
^2 & arithmetische
fc=i
Reihe, deren Summen-
formel bekannt ist.
1K 7r	x/3 7\/3
6’	6 ’ 36
16.	Anmerkung:
/W(x) = fAfc!a;n-fe
VA:/
und
17.	a) v = t2 - 4t + 3
a = 2t — 4
für Umkehrpunkte
ist v = 0 :
U = 1, t2 = 3
b) x = AcoscjA
x = — Ax sincjt
x = — Ax2 cosxt
= — x2A cosxt
= — x2x
x = 0
71
=^> xt = — + kn
(Ti \
+ kn) =
/7t	7 \
x — + kn ) = 0
x = A
=> xt = 2kn
x(2kn) = 0
7(2/c7t) = — Ax2
x = —A
=> xt = (2k + 1)ti
x((2k + l)7t) = 0
x((2k + l)7t)
= Ax2
(feeZ)
dt n(2r — h)h
v
ng2
d) v = x = Ak e kt =
k-Ae~kt = k(A—x)
x	1	9
e) x = 10+20A---gt2
v = 20 — gt
m
a = — g = —9, 81 —
s2
18.	a) dy = rixn xdx
b)	dy = . X dx
7 y tüü?
c)	dr = 4 sin2 cp d^
d)	d(sin2t) = sin2tdt
/ x\
e)	d (^cos - J
1 •
=-----sm — da
2	2
19.	a) dy = 0,04
Ay = 0,0401
b) d?/ = 0,05
Ay 0,049876
KX	36ds
b) df =
21. a) dx = -^A=	2-0,1
	
	
dx < 0,005 , x dV 3dr b) V = — a = r dr 1 — = r 3	5 -4V^
Der Radius	ist zu
messen mit	einem
Fehler von	nicht
mehr als |%.
Aufgaben aus Abschnitt 7.1
1. Nullstellen der Funkti-
on:
xi = 1; x2 = 3
Nullstellen der Ablei-
tung:
x = 2 e (1,3)
2. Nein; für x = 0 exis-
tiert keine Ableitung.
Auf [—1,1] existiert
keine waagerechte
Tangente.
3. Anstieg der Sehne AB:
f(x) = 2x = 2
x = 1
An der Stelle x = 1
ist die Tangente paral-
lel zur Sehne.
4. a) - «-2>
l-(-2)
f'(x) = 1 - 3x2
1 - 3£2 = —2
250
Lösungen
-IG (-2,1)

b)e =
4
----1
/Xx \ /Xx
c) e =
G (0,1)
-
7T2
7. a) ex = e° +x • e°x
denn e$x > 1 für
x > 0
1
In2
= 1,4426...
ee(l,2)
5. Anwendung des Sat-
zes von Rolle auf die
Intervalle [-3,-2],
d)e =
2 VI +
für x > 0
x 1	1
c) h—— = ~~r-
1
2
y/xn + h = y/x^
h
+ $h
mit xq = 100, h = 1.
Ferner ist
10 < V100 + i?
< x/TÖT
für 0 < i? < 1.
x sin — sin 0
a) ------------
cos — cos 0
cos£
— sin£
6. a) (x + Ax)2 — x2 =
Ax • 2 • (x +$ • Ax)
-I
b) $ genügt der Glei-
chung:
für x > 0
2^/(1+I?x)3
-4
8. Mittelwertsatz für
Aufgaben aus Abschnitt 7.2
.. sm5x
hm------
x—^o 3x
.. 5cos5x
= hm
h) 3
b)
c)
1
2
1
d)
f)
g)
3
5-1
T
5
3
j)0
k) 0
1)0
m) 3
> tan£ = 1
G(l,4)
14
C)e = - 6(1,2)
y
nan~L
1
a sin ax
hm .	=
ösmox
9
.. a cosax
hm —-------—
x—^q b2 cos bx
1
2
1
6
lim
tan |
= 2
a2
&
o) 0
aq ry» • -L
p) lim ™---------= ...
x^+oo ex
n\
= hin — = 0
q) „0°“
= lim e*111*
x^+0
lim xlnx
= ex^+0
= e° = l
(vgl. o))
r)	1
s)	„1°°“
Hm IntB+^-ln»
= x
= ... = e3
t)	-2
u)	„oo°“
lim
_ e„ + oo
lim
_ eX_ + oo X
= e° = l
v)	„oo — oo“
Aufgaben aus Abschnitt 7.3
251
w) e
1
2
>4
Aufgaben aus Abschnitt 7.3
1. a) /(2) = 5
/'(2) = -1
/"(2) = 6
/"'(2) = 12
f(x) = 5-(z-2) +
3(z —2)2 + 2(z —3)3
	2-9 11 3 4 -10 2
2	2-5	1 5=/(2) 4 —2
2	2-1 	4
2	2 3=^21
2	|ND | to II ICC ”7? II 4=
b) f(x) = -125 + 75z
— 15z2 + z3
	1-30 300-1000 5-125	875
5	1 -25 175 -125 5-100
5	1 -20	75 	5
5	£-15
	1
c) /(x) = 72 - 102(z
+3) + 53(z + 3)2—
12(z + 3)3 + (z + 3)4
2. a) /(z) = e2a; '
/(O) = 1
/'(z) = e2x-
x(2 - 2z)
/'(O) = 2
/"(O) = 2
/"'(O) = —4
/(z) = 1 + 2z + z2
2 q „
— “Z + i?3
O
b) /(x) = (x—l) + (x—
1)2 + |(z-1)3 + 7?3
c) /(z) = z-|z3 + l?3
ö
3- a) /(z) = 2_
z —2
4^2
+ 32^(a: “ 2)2
“12872(X “ 2)3
+ Ä^“2)4
+-R4
b) /(x) = 1 + 2x
+2x2 — 2x4 + 7?4
A \ X 1	, X + 1
4. a) e = - H----
e e
, (z + l)2 1
2!	' e
5.
(z+14 1
3! e
(z + l)4
4!
0 < t? < 1
b) Inx = (x — 1)
1)2
!	~ i)3
3(1 + il(z — l))3
0 < 1? < 1
| sin (xq + h) — sinxo
— h cosxol
h2
= —\sin(z0 + i?h)|
< —
“ 2
9	3
2!	3!
ry»4 ^5
X
+ 4! + 5!
0 < 1? < 1
el = 1 + 1 + lf + l!
1 e0
+ 4!+ 5!
Der Fehler ist:
5!
e1 3_ _ 1
5? < 5! “ 4Ö
x2
7. a cosh — = a H---
a 2a
x4	$x
cosh---
4!a3	a
Für |x| < a ist der
252
Lösungen
Fehler
x4
——r cosh —
24a3 a
< Of(oshl
< M L6<O5o7N
x2
8. In (1 + x) = x ——
x3 x4
+T“T
x5 1
+ 5 (1 + da*)5
Fehler:
0,55	1
~5~” ' (1 + 1? • 0, 5)5
= ö
0,0008 < ö < 0,0063
In 1,5 « 0,401
0,4018 < In 1,5
< 0,4073
9. 0,822317
10. sin2 x =
R^n —
22n+l
(2n + 2)!
, 2n-1- 2
sin (o/dx + (2n + 1)—)
_ 1 (2n)2n+2
” 2 ’ (2n + 2)!X
sin (^dx + (2n + 1)—)
0	\
sin ^2i?x + (2n + 1)—)
1
- 2
(2x)2n+2 M
hm --------— = 0
n^oo (2n + 2)!
für alle |x| < oo;
somit lim R^n = 0.
Aufgaben aus Abschnitt 7.4
1.	a) D(f) = (—oo,+oo)
^Min = 0, yMin = 2
Auf (0, +oo) streng monoton
wachsend.
Auf (—oo,0) streng monoton fal-
lend.
b)	D(f) = (—oo, 0) U (0, +oo)
%Maxl =	1, yMaxl = 1
*' Max2 = yMax2 = 1
Auf (—oo, —1) U (0,1) streng mo-
noton wachsend.
Auf (—1, 0) U (1, +oo) streng mo-
noton fallend.
c)	n(/) = [-i,+i]
02	1
%Min —	5 yMin —
V2 1
^Max —	2 ’ iJMax —
Auf (^—1, —Ll streng
monoton fallend.
/ \/2 y/2\
Auf	streng monoton
wachsend.
d)	/?(/) = (0,l)U(l,+oo)
%Min — yMin —
Auf (0,1) U (1, e) streng monoton
fallend.
Auf (e, +00) streng monoton
wachsend.
e)	D(f) = (-00,+00)
71
%Min — “T 4“ k 2?T
ö
71 r-
yMin = “T V 3 4“ k 27T
O
571	7
%Max — “Z“ 4“ k • 271
ö
571 r~ _
yMax —	—F V 3 + k • 271
Auf f(6A: —1) —, (6A: + 1)—streng
monoton fallend.
Auf ((6A; + 1) —, (6A; + 5)—) streng
monoton wachsend, k E Z.
2.	a) Auf (0, +00) von unten streng
konvex.
Auf (—oo,0) von unten streng
konkav.
b)	Auf (—00,+00) von unten streng
konvex.
Aufgaben aus Abschnitt 7.4
253
c)	Auf (—00, —1) U (0,1) von unten
streng konvex.
Auf (—1,0) U (l,±oo) von unten
streng konkav.
3.	a) XMax — 1, ÜMax — 1
XMin — VMin — 0
(An der Stelle x = 0 nicht diffe-
renzierbar.)
b)	XMin = 1, yMin = In v 2 —
c)	— 3, UMax — 9 2 e
XMin — 2, yMin — 8
d)	Maxima: x\ = 0, y\ = 1
71	i
?/2 = l
5
±3 = ^71, Z/3 = “
71
Minima: x^ = —,

y4 = 1^2
n =n, y5 = -1
3
^6 — 2	— i
e)	XMax — 4, yMax ~ 7484,2677
XMin — 1> 5, yMin — 2, 75
f)	XMax — 2, yMax — 4
XMin = 3, yMin = 5, 25 - In 4
« 3,86371
g)	XMax =	, yMax = 3 ('
XMin = yMin = 1
4.	a) /(5) = 5, /(0) = f (10) = 0
Mi)=4 ,f(l)=l
5.	XMax — 0, yMax — 1
,72
xw = ± —
yw = e-0,5 ^ 0,60653
lim /(x) = 0
6.	a) D(/) = W(/) = (-oo, ±oo)
xn± = 0, xn2 = 3 (Nullstellen)
XMax = yMax = 0
XMin = 2, yMin = 8
xw = 1, yw = — 4 (Wendepunkt)
Wendetangente: y = — 6x ± 2
lim = +oo; lim y = —oo
b)	-C*(/) = (-0O, +oo)
W(f) = (-00; 20,25]
/(—x) = /(x) (gerade Funktion)
^TVi = 0, Xyv2 = — 3, Xyy3 = 3
XMin = yMin = 0
3 r
XMax± =	2^^’ IjMaxi = 20,25
3 r
XMax2 — ~ * 2, yMax2 — 20, 25
Wi,2 =	Wi,2 = 11,25
lim y = — oo
x^±oo
Wi,2 : ^ = ±127175^-6,75
c)	D(/) = W(/) = (-00, ±00)
xn± = 0, xtv23 = 1,5±1, 5\/5
2
XMax — 1, yMax — 1X
ö
XMin = 3, yMin = 9
2
xw = 1, yw = 3-
C)
W : y = —4x + -
lim y = ±00, lim y = —00
x^+00	x^-00
d)	D(/) = (—00, —3) U (—3, 3)
U(3, ±00)
IV(/) = (-00,-|] u (2,+00)
/(—x) = /(x) gerade Funktion
keine Nullstellen
Polstellen: xp± = — 3, xp2 = 3
lim y = 2
keine Wendepunkte
XMax — 0, yMax — g
e)	D(f) = (—00, —2) U (—2, ±00)
W(/) = (—00, —11] U [5, ±00)
/(0) = 7; keine Nullstellen
Asymptote: y = x — 1
xp = —2
XMax = 0, yMax = H
XMin = 2, yMin = 3
254
Lösungen
keine Wendepunkte
f)	D(/) = (—oo, 3) U (3,+oo)
VK(/) = (—00,1) U (1, +00)
/(O) = —1, xn = —3, xp = 3
lim f(x) = 1
keine Extrema
keine Wendepunkte
g)	D(f) = (-00,+00)
W(/) = (0,2]; gerade Funktion
keine Nullstellen; keine Polstellen
XMax — 0, yMax — 2
lim y = 0
XVK1,2 = Wl,2 =1,5
3
m,2 : z/ = ±-x + 2,25
h)	D(/) = (0,+oo)
iy(/) = [2O2, +00)
lim y = +00, lim y = +oo
x^+00	x^+0
XMin = 2, yMin = 2\/2
A	/Ä
xw = 6, yw = -v6
O
/g
W :y = —x + VQ
io
i)	D(J) = [-3,0] U [3,+00)
W(f) = [0;+00)
lim y = +00
X^ + 00
XNr = 3. xn2 — 0, xn3 — 3
XMax — a/3, VMax —	6\/3
xw ~ 4,40367, yw ~ 6, 76493
W : y 3, 63x - 9, 24
j)	DX) = (0,+oo)
W(f) = [-^’+0O); XN = 1
lim.Q?/ = — 0, lim y = +oo
—0 5	I
%Min = e ’ , yMin = X
2 e
-15	1,5
xw = e ’ , yw =------ö-
e’
W: y«-0,446®+ 0,025
k)	D(f) = (-oo,+oo)
!+(/)= [--,+oot ®w=0
L e /
lim y = +oo, lim y = —0
x^ + oo	X—^ — OG
XMin =	1, VMin =
xw — ~2, yw — —2e 2
W: y = — e-2® — 4e-2
1)	-0(7) = (-00, -1) U (-1, +oo)
!+(/) = f-k+oo); xP = -1
L o /
xn± = 1, xn2 = 2
lim y = 3
x—>ioo
_ 7	1
%Min — T ’ yMin —	77
5	8
2
xw = 2, 6; yw = -
y
W: ?/^0,39x-0,78
7.	30 m x 60 m
8.	5 und 5
9.	ÄMax =
11.	4m x 4m x 2m
12.	20 cm
13.	60°
18
14.	---m ~ 2. 52 m
4 + 71
15.	In 18 m Entfernung von der stärke-
ren Lichtquelle.
ß
16.	Nach der Zeit t = — beträgt die
kleinste Entfernung
s
2’
_ d d r~
17.	x = -, y = -V3
2’ y 2
18.	VK + Vz = \/3 + 1
19.	I ~ 5,619 m; wird bestimmt als Ma-
ximum der Funktion
l = l(a) =
2,4	1,6
—:------1-----
sm a cos a
Aufgaben aus Abschnitt 7.5
255
1ZÖ7L o
20.	VMax = —-— dm bei einer Höhe
von 2 dm.
21.	AMax = bei einer Höhe von
26. F = F(a) =------—------
cos a + [i sin a
tana = // = 0, 25
a « 14,036°
22.	Väb
23.	4 cm und Fßcm
24.	Die Schnittfläche ist ein Quadrat mit
der Seitenlänge - \J~2.
25.	Für a = 27ty | = 120°\/6
« 293,94°.
27.	Zwei parallelgeschaltete Gruppen
von je 24 hintereinandergeschalteten
Elementen.
28.	Q - a + q- x- ^ = F - x
F^Min = 2Q(ZQ
7t p
29.	OtMax =
Aufgaben aus Abschnitt 7.5
1. a) xi = 0,01903; x2 = 2,44754
b) x = 2,50618
c)	X! = 0,29138; x2 = 4,10927
d)	x = 1,72310
e)	Xi = 0,47170; x2 = 9,99900
f)	x = 7,12813
g)	X1 = -0,40103; x2 = 1,38233
h)	x = 0,76835
i)	Xi = 1,16234; x2 = -1,16234
j)	x = 3,69259
2. a) ÄMax = 1,12219
b) 4^ = 1,81971
3. h = 1,157692?
Aufgaben aus Abschnitt 8.1.1
X3
1. a) —- + x2 + In |x| + C
O
b) 2x5 - 2- + G
xö
x 1 — X
c) —----F C
xz
x^	1
d)T + 21n|x|-2^ + c
2	>	—	~
e)	-xy/x + —xy/x + C
3	4
f)	2Vx-4^x + G
2
g)	-x\fx — 3x + 6\/x — In |x| + C
ö
3
h)	-x^x — 3\/x + C
j)	arcsin x — arsinhx + C =
arcsin x — In ( x + \/l + «
k)	2 arctan x — 3 arcsin x + C
2
1)	-x^/x + x + C
ö
x 3	1	. 1
m)	- arctan x — - arsmhx + C
. x 1
n) e H------1- C
x
256
Lösungen
2
2
p)	y+2z + G
q)	— cosx—sinx+2 tanx+7cot x+C
r)	tan x — cot x + C
s)	x + cosx + C
t)	-x3 — x + arctanx + C
o
u)	tanx — x + C
v)	— cothx + x + C
w)	—2 cosx + C
x)	|(x — sinx) + C
y) |(x + sinx) + C
2. a) —- Inx---- + C
2	4
b)	x In.r — x + C
c)	x sin x + cos x 4- C
d)	x2 sin x + 2x cos x — 2 sin x + C
e)	x2 ex — 2x ex +2 ex +C
qX
f)	— (sinx — cosx) + C
g) x + In |2z + 1| + C
h)
k)
-	e~x +C
o2x —1
äkä + c
-	In (8 - 3z)2 + C
1) ln|l+lnz| +C
£ _ sm2£
7 2	4
n) In | tan t\ + C
o)	2 sin — 3^ + C
p)	- tan (9x + 8) + C
ö
q)	-1 In | cos (2x + 1) | + C
x 3, r 1
r)	- in cosh
2
x	T	f
s)	cos
7	271	\
/2
-z - v6I +
\ ö	/
271t	\
+ ^0 ) + C
1
3(2u + 3)V2u + 3
2
3
b)	-Lln|7x3 + 8|+G
c)	^O + 6)8 + C
d)	|(2x — 7r)\/2x — 7i + C
e)	In | sinx| + C
f)	j In (2 +3z2)
+Vlarctan (v^Ix)
b) -------H
2 cos2 x
c) - ecosx+c
d) |e*3+C
e) -e-sina:+C
g)	|v/(*2 + i)3 + c'
ö
h)	Y(i + z3)2 + c'
i)	— -\/l + 2 cos z + C
9
j)	-Y(l + lnz)3 + C
ö
Aufgaben aus Abschnitt 8.1.1
257
k)	y/(1 + 4 sinh x)3 + C
o
2
1)	- y/(arcsin t)3 + C
ö
1 Q
m)	- In3 x + C
ö
3	__________
n) - (arctan x)4 -F C
o)	sin In s + C
p)	| tan4 92 + C
2
q)	- y/ (arctan eT)3 + C
O
r)	- In | tan (2x — 1)| + C
. \/2	(tanx\
s)	— arctan —=r-	+ i
2	\ a/2 7
j)	x arctan \/2x — 1 — | \/2x — 1 + C
k)	—-(u coscj+cj sincjt) e°4+C
az + xx
1)	-----(—(x cos c++ sincjt) eat +C
a/1 + xx
m)	(x — x + 9) arctan-----3x
3
+1 In (a;2 + 9) + C
6. a)
b)
5	( sin5 x
—x - cosrr ——
16	\	5
5 sinx
16
5	. I cos5 x
—x + sm x ------
16	\	5
5 sin3 x
24
5 cos3
24
5. a) x arctan x — - In (1 + a;2
, . 2a? — 3 . lr
b) -------sm (5a; + 1)
0
5 cosx
16
2
+ — cos (5x + 1) + C
2 ,______
c) — V7x - 5 • (7x + 24) + C
Z/'2	61 \ n f 1\
' - sö /1,1 r+s)
1 2 61
-r +6oi+c
tan (5x + 6)
3
+ — In | cos (bx -F 6)| -F C
2u
9 \
-a?) e4-3® +C
3x — 1
x x — 5	.
g)	—tan (3a? + 1)
ö
+ - In | cos (3x + 1)|+O
h)	4\/2 + x — 2\/2 — x • arcsin — + C
2
1 / x	\
i)	- - —----F cot x + C
2 ksimx	)
c)
d)
b)
COSX / . 4	4	2	8\
-----sm x H— sm x H—
5 \	3	3 J
+C
sinx/ 4	4	2	8\
— cos x H— cos x H— +G
5 \	3	3 /
cos x	1	i	x\
~ ~  2 +xln pan- +C
2 sm x	2	I	2 1
1 sinx	1	|	fx	7i\
----ö--F z hi tan —F —
2 cos2 x	2	I	\ 2	4 7
x sin 4x
—+c
8
1	3
— cos 2x — — cos 2x + C
— - (cos 4x + 2 cos 2x) + C
8
b) für m 7^ n :
1	Fsin (m + n)x
2	m + n
b)
,3
9. a)
sin (m — 7
m — n
+C
für m = n :
x 1 .
— + -— sm 2mx + G
2 4m
5
1
258
Lösungen
c)	- sin 2x---sin 8x 4 C
4	16
d)	für m 7^ n :
sin (m — ri)x sin (m 4 n)
2(m — ri) 2(m4n)
für m = n :
x sin2mx
2 4m
e)	für m n :
cos (m 4 n)x
2(m 4 n)
cos (m — ri)x
2(m — n)
4G
für m = n :
cos 2mx
4m
sin2 mx
2m
2
a	xx /—z-----------
10. a) — arcsm —|- — v a2 — x2 4
b) - arcsin x — y/1 — x2 4 C
c)
\/l — a?2
-|(7 +4
ö
\/4 — x2
4x
d)
f)
g)
h)
-	tan2 x 4 In | cos x\ 4 C
—	- cot2 x — In | sinx| 4 C
2	3	1	5
—	cos x H— cos x-cos x 4 G
3	5
•	-3	3 . 5
jjsmx —sm m—sm x
5
1 • 7
--sm x + G
7
>2
2 v
a2
4— In
2
m) 2 arcsin
+^4-?+C
o)	7 x +c
	9 \/9 4 x2
p)	| y/1 4 x2 • (x2 — 2) 4 C ö
	2x 4 3
11. a)	arcsm —-=^ 4 G
	717
	1	. 8x + 3
b)	- arcsm —-=^ 4 G
	2	741
c) In 4 - 4 \Jx2 4 x 4 1J 4 C	
d)	\/5	/ — In (lOx — 1 5	\
	+ 720(5x2 -x-1)) +G
e)	1 f	/	\ - In +1 + 7Qz2 + 6a? + 5J
	+C ™ | O 		
	
f)	—-— v x2 4 4x 4 29
	25	/		\ + — In 4 + 2 + 7^2 + 4x + 29J
	+C
g)	| \/2x2 — x
	93	/		\ + ^^_ In 4^ — 1 + 7^(2a:2 — a:)j
	+C
h) In (x + 7ä7+7) H— 1	+ C
\/x2 4 1
i) | \/(x2 4 x 4 l)3
1 (	r~o------7	3
-- ( x 4 - I v^ +^ + l- j^
x In (x 4 | 4 \/x2 4 x 4 1) 4 C
j) | V4x2 4 4x 4 3
4^ In ^2x 4 14 \/4x2 4 4x 4 3^
4G
Aufgaben aus Abschnitt 8.1.2
259
Aufgaben aus Abschnitt 8.1.2
1. a) In |x — 7| + C
b)	-i • -—3—- + c
1	4 (x + 2)4
x 1	x
c)	- arctan — + G
4	4
5
d)	- In (x2 + 8) + C
3
e)	2(x2 + 15)2 +
4x 4 x
f)5ü^) + 5f“ct“5 + c
x 2	4x - 5
g) -=- arctan —=----1- G
x/31	\/31
3
h) - In (x2 — x + 1)
1 2x - 1
4—= arctan----=----1- G
V3 V3
x + 2
~2(x2 + 2x + 3)
a/2 x -|- 1
--— arctan —=—p G
4	x/2
2x - 1
2(x2 + 2x + 2)
+ arctan (x + 1) + C
3	9
x + 17 + 2(x — 6)2
+191n|x + 6| +C
D Ex A F
+ (x — l)3 + x2 + 1
Gx A H Ix AK
+ x2 + 2x + 3 + (x2 A2x + 3)2
A	B
3(x — 5) + 9(x — 5)2
C Dx A E
+ x + 2 + x2 + l
FxAG Hx Al
+ (x2 + l)2 + x2 — 2x + 5
A B C
C) x - 2 + (x - 2)2 + (x - 2)3
D E	F
+ x + 2 + (x + 2)2 + (x + 2)3
GxAH IxAK L
+ x2 + 4 + (x2 + 4)2 + x — 1
M N P
+ (x — l)2 + (x — l)3 + (x — l)4
4. a) 5x + 2 In |x| + 3 In |x — 2|
+41n|x + 2| AC
b) In \x\ + |ln|x-2|
—|— — In | □? —|— 31 A C
c) 4 In |x — 1| — 7 In |x + 3|
+5 In |x — 4| + C
4x + 3
2(x + l)2
+ 2 In
AC
x + 1
2(n — l)a2 (x2 + a2)n-1
4
x + 4
+ 21n
x + 4
x + 2
AC
+ (2n — 3)7n-i	für n > 2
I2 = tW 2^ 2+~ arctan -W
2az \xz A ax a a/
1 r x(3x2 + 5a2)
3	4a2 l.2a2(x2 + a2)2
3	xi
+	7 arctan — + G
2a z	a J
3. a)
A B C
X + 1 + X — 1 + (x — l)2
f) 2 In Ixl — 2 In Ix + 11 4-
x + 1
1	। (j
2(x + l)2
s)-5(JLI) + 51,,('‘'2 + 1)
3
A~ arctan x + C
1	3
h)-----1— In (x2 — 4x A 13)
x 2
260
Lösungen
j)
k)
m)
4	x-2
+ - arctan —-----1- G
ö	ö
— + - In Ix — 11 — - In (x2 + x + 1)
x 3	6
\/3 2x + 1
H----arctan------=--1- G
3	x/3
x + 2	1
2(rr2 + 1) + 2 ln +
— - In (x2 + 1) + 2 arctan x + C
1	1 , (x - l)2
-----------1---In —--------—
5(x — 1)	50 x2 + 2x + 2
7
— — arctan (x + 1) + C
Zu
x2 _ Ix — 11
----H x+In ,	— arctan x + G
2
I1”
1 / 2x + l
H----= arctan-----
2\/3 \ V3
2x- 1
+ arctan---
V3
x2	2
n) — + 6x + - In |x — 1|
10. / 2	95 x
----In (x + 5)-----= arctan —=
3	3 Xi	\/5
+C
1	(a? + 2)2
24 x2 — 2x + 4
Aufgaben aus Abschnitt 8.1.3
a)	^|-(2^27+T-3) + C
b)	2\/x — 3^0 + Q^x
-61n(l + ^) + C
c)	| In (e2® +1) - 2 arctan (e®) + C
d)	ex +| In
\ 1	3
e)	- tan x — tan x + x + G
ö
ex -1
ex +1
5
f)
g)
h)
b)
d)
f)
g)
h)
j)
2	2C__
H----arctan ——
12	x/3
lln
1
a — b
In
x + b
— In
12
-—In
30
I1'1
x + %/2
X + y/3
1-*
1
—I"	lrl
2
1
----arctan x + G
ö
v2	x
-----arctan —= + C
10	x/2
Ln _LL=
4 \Ar2 + 4
I1”
x + 5
1
3x
I1'1
V3	x
-----arctan —= + C
9	x/3
x — 1	1
----------arctanx + C
x -|- 1	2
1
- tan4 x — - tan2 x — In | cos x| + C
2
1
- arctan
2
1
5
In tan - + -
2	2
I x
— In tan----------2
I 2
Aufgaben aus Abschnitt 8.1.4
261
• \ 2\/3	/ /z- <
i)	arctan (^v3e
j)	2 arctan (ex) + C
 (SV -- 1
k) 2y/ X — 1
7
! 3(a? — l)* 2
1) In 11 + tan | + C
m) 2 In | ex —1| — x + C
x 1	I
n) -2X+ 3 n'e
+ tln(e* +2) + C
a/2
°) — In
P)
o
\/2 + 1 — tan 2-
+ l)2 - |
+ | In ( \/x4 + 1 + 1) + C
q)	(3z+ 1)2 + 0
0
2x
r)----------2 ex +4 In (ex +2) + C
s)	ex +ln | ex -1| + C
t)	\/2x- 1 + 2v/2x — 1
_______________________ 2
+ ln(^2z-l-l) +C
2
u)	— (3x2 — clx — 2a2)^a — x + C
w) 2 arctan \/x + 1 + C
Aufgaben aus Abschnitt 8.1.4
+ In
2 + x - 2x/TTx
cot3 x
3
+ C
b) -(arctanx)2 + C
c) 4ln
1
ax
k) xtanx — -x2 + In | cosx| + C
1) In |tan | + cos x + C
.	1	/cosx\
m) — - arctan —-— + C
b	\ b /
d)		+ C
cosx
e)	2 arcsin y/x + C
(Substitution: x = sin2 t)
f)	ab • arctan ( - tanx | + C
\a )
g)	t I x2 + x sin 2x H— cos 2x | + C
4 \	2	J
h)	—x — e~x + In (ex +1) + C
i)	arcsinx + yl — x2 + C
n) 3^/x-12^ + 241n(^ + 2) + C
b — 3ax
6a(ax + b)3
(Substitution: t = ax + b)
x 1
p)------arctanx + C
x
q)“tanz + l+C
2 ---------
r) -y/a blnx C
s) für n 1 :
262
Lösungen
t)
y)
1
3b(n - 1) ‘
für n = 1 :
1
— 6x3)n-1
i
arcsm —=-
V2
+ X^\/l~2x — x2 + C
arctan x 1 x2 „
------+ -In—-^C
x 2	1 + xz
}-x + In (e2x +4)
2	4 v 7
1 ex
+ - arctan — + G
\/2x + l
k) tan2 x + C =-5---H Ci
cos2 x
1) cot x — - cot3 x + C
ö
m) — cot x In (cos x) — x + C
. _x 1, e^-l
")e +2ln ?Ti+c
o) - tan4 x + C
4
P) In M -
ln|x + l| +C
1	3
— cot x + cot x + x + C
ö
\/4 — x2	x
------------arcsm —|- C
x	2
q) 2\/l + sina* + C
r) arctan (\/2t<
1	|x2 - 2|
s ä ln 2 II + C
6 xz + 1
u) 2x/ä? arctanx — In |1 + a?| + C
v) x/tanx + C
x/3 + cot x
b)
x/3 + tan x
d)
f)
g)
/3
V1"
b)
2
\/a:2 — 1
c)
3.z'2 + 3a? + 1
d)
(Substitution: x = t x)
n) In |x|----ln(a;2
x) -— arctan (ax) + C
Ina
+2^21„
\/ x 1 + \pl
h)
3
(2a: — l)2
e) ln 1^2 ,
Aufgaben aus Abschnitt 8.2
263
1 + cos x + sin2 x	1 + C	+ ö	[arctan (x + 1)
sinx x 1 x2 + 2x + 2	o	+ arctan (x — 1)] + C
g) — In —			
7 16 xz — 2x + 2		
Aufgaben aus Abschnitt 8.2		
a2 /	1\ 1. a) Sn = - 1 + -	h) 1	w) 2 — In 2
2 \ nJ 2	i) 3(e—1)	x) 1
s = lim Sn =	j) In (1 + V2)	’ 3 2 . 7TOT
a3 ( 1 \ b) Sn =	( 1 + - ) 6 \ n J	k)l	v) I? x \/3 - \/2
(	1) 2(1 +In 2)	3. a)
x 2 + - \ n J	X . 2e m) In		z b) In 1, 5
Q3 5 = t	7	e+1 n —	. 7t- 2 C) 4
, „	a(e°—l)n	7 6	x 71
c Sn = -r	~i~ 7	]_ _ e—a/n S = e° —1	1	x l-ln2 e	o
2. a) 20	p) 2In 1,5 - - O	2 x 1	71
h'i “3 b)~y	71 q) arctan e	 7	4	4. a - • - 7 2 2 t x 1 -3	71
c) 2-	x 71	\/3	)	' 2
7 8	J 3	2	1-3-5 7T
	7t- 2 s)a- 4	C) 2 • 4 • 6 ’ 2 1 7t
\ 71 e) 		. a/2 + In (1 + a/2)	d) 2 ' 2
7 12a	2	, 1-3 7t
f) i	u) 21n2 - 1	e) 		 — 7 2 -4 2
g) i 67 6	2-V3 V) 2	n 1-3-5 7T ±7 2-4-6 ’ 2
Aufgaben aus Abschnitt 8.3
1. a) 1	e) 1
b)	+oo; divergent	1
c)	+oo; divergent	2
1 f- i	g) -
d)	------tur n > 1,	07 4
n — 1
divergent für n < 1 h) 1
i) In 2
16
k)
1)
6
71 In 2
4 + ~
264
Lösungen
x 7t — 2
m) -----
7	8
n) 6^2
o) divergent
P) 6
r)	1
s)	divergent
t)	In (1 + ^2)
u)	1
\ 71
V) 4
2.	a) / e~x xmdx
=
-hm f e~x xm~1dx
7°
= rn /' e~x xm'~1dx
Jo
—> ml
b) Hinweis: Substitu-
tion x2 = z
3. a) -^=
\/5
4 7t
b)
3/1
c) 0 als Cauchyscher
Hauptwert
d) 7t als Cauchyscher
Hauptwert
e) divergent
g) 0 als Cauchyscher
Hauptwert
4. a) konvergent; Hin-
weis:
| e~x2 | < e~x für
x > 1 und
e~x dx ist kon-
vergent
b) konvergent; Hin-
weis:
Aufgaben aus Abschnitt 8.4
1.	a) In 3 « 1,1016
e ( | ) < 0,014
\5 /
b) In 3 « 1,0987
eQ) < 0,00043
2.	« 0,746
-'□<°.002
3.	« 1,4627
< 0,00012
4. a) 156; e(Ji) = 0; der
exakte Wert 156
stellt sich bereits
bei 2n = 2 ein.
4
b) |e(^)| < — < 0,3
5. 7t 3,141593
für 2n = 20
6. a) « 3,239
Differenzenschema:
s. Tabelle L.l
0 < 1
vH?
—2für x 1
r00 dx
A ^72 lst
vergent
kon-
c) konvergent
d) konvergent; Hin-
weis:
1
\Ar4 — 1
1
\Jx — 1
für x > 1
e) divergent, denn
1
dx + 7
1
3x + ^/x + 7
für n > 2 und
/,oc dx
'2 4x + 7
vergent
ist di-
h4  |y(4)|MO:!; «
|A4y|Maa; = 0,1244
/l\
£ V2J -
2 • 0,1244
—^7— < 0,002
180
b) « 2,701
£O < 0)0002
c) « 1,06
e(1) < 0,02
Aufgaben aus Abschnitt 9.1
265
Tabelle L.l: Differenzenschema
y	A1	A2	A3	A4
1,0000	0,0607			
1,0607	0,3535	0,2928	0,0312	
1,4142	0,6775	0, 3240	-0,0932	-0,1244
2,0917	0,9083	0,2308		
3,0000				
Aufgaben aus Abschnitt 9.1
1.	a) 2x — y + 18 = 0; Gerade
b)	9x — 5y2 = 0; Parabel
c)	x2 + y2 — r2 = 0; Kreis
2	2
d)	^- + ^--1=0; Ellipse
e)	x2 + (y — 4)2 — 32 = 0; Kreis
lipse
2.	a) (x - 4)2 + (y + 2)2 - 20 = 0; Kreis
b) x2 — y2 — a2 = 0; Hyperbel
3.	a) z.B. x = x(t) = 5cost,
y = y(t) = 5sint;
r = 5 cos t • ei + 5 sin t • 62
b)	z.B. x = x(t) = 5cosht
y = y(t) = 3 sinht
r = (5cosht, 3sinht)T
c)	z.B. x = x(t) = t
y = y(t) = 4t2
r = t • ei + 4t262
d)	z.B. x = x(t) = t
y = y(t) = \A2 + 9t + 105
r = (t, \/t2 + 9i + 10ö)T
e)	z.B. x = x(t) = t
y = y(f) = fX)
r = t • ei + /(t)e2
4.	a) x = 6coscjt, y = 6shwt
/	7T\
b) x = 6cos \uxt — —j
y = 6 sm \wt — —j
5.	x =	+ b) cos <p
y = y^) = (a^ + &)sinv?
r = (aip + b) cos <p e±
+{a(p + 6) sin p> 62
a/x2 + ?/2 = a arctan — + b
x
6.	Hinweis: x = at — asint
a — y	a — y
cos t =-----, t = arccos-------
a	a
7.	a) Hinweis: Aufstellen einer Werte-
tabelle:
266
Lösungen
	0°	15°		360°
r	2	1,97		2
b)	x =	=	(1 + cos (/?)	cos	(/?
y =	y(pp)	=	(1 + cos (/?)	sin p>
r =	r (</?)	=	(1 + cos (/?)	cos p> e±
+(1 + cos p>) sin p> 62
b) Logarithmische Spirale
r = aekcp (k > 0) mit a = 1,
k = 0,2
c)	Hinweis: rMax = 3 bei
p> = 0°, 120°, 240°; rMin = 1 bei
p> = 60°, 180°, 300°
8. a) r = r(p7) = b) r = r(pp) =	a
	COS p) a sina sin p) a sin (ß — a)
c) r = r(p7) =	sin (ß - tp)
9. r = 2acos(/?
10.	a) Ellipse mit M(l; — 1) und a = 3
(in y-Richtung), b = 2 (in x-
Richtung)
b) Zykloide (mit a = 1); Skizze er-
hält man mit Hilfe einer Werteta-
belle.
11.	a) Archimedische Spirale r = ap> mit
b) r = a (a > 0)
c) r =----7-----Ä
cos ((/? — a)
71
d)^=4
e)	r = a cos p>
f)	r2 = a2 cos 2p)
13.	a) x = a
b)	x2 + y2 = 2ay
c)	xy = a2
d)	x + y = 2a
e)	(x2 + y2 — ax)2 = a2(x2 + y2)
14.	a) M(4;-4;2); r = 3
b) 5x2 + by2 — 8xy — 72x + 72y
+279 = 0
Aufgaben aus Abschnitt 9.2
2
1.	a) y = x + -
ö
b)7i: y = 0
T2: y = ±|(3a?-l)
c)	y = - ja; + 2
d)	y = —x + 7t
e)	y « 3,76220a? + 3,897531
n	, (4 “ n)a
f)	71 : y = x H-------
T2-. y = -x + a(^— + 2J
x	aß2
g) y = -x + ~y~
2.	a) T : y = -x-
2	2
N : y = — 2x + 2
b)	T : y = -3x + |
AT	1	7t
N: y= -xH—
^32
c)	S1>2(±1; 1)
Ti : y = —2a; + 3
M? y=|^ + |
Aufgaben aus Abschnitt 9.2
267
T2 : y = 2x + 3
N2'- y = ~lx+l
d)	Ti : y = - ja: + 2
TVi : y = 4x + 2
T2 : V =	- 2
: y = — 4,i; — 2
x	7	3
e)T: »=w’'+5
Ä7 10	34
N : y = ~—x+ —
f)	T : y = 2x + 4
»r	13
N : y = x H—
y 2	2
x	5	13
g)	T : y= -~x+ —
6	6
Ar	6	21
A : y =	—
5	5
5
h)	T : y = -x + -
ö
Ä7	7
N : y = x - -
3.	Hinweis: m(y>) = ^14
x(sp)
a)	T : y = a; N : x = a
b)	T : (3t/3 + 7t)r - (3 - 7n/3)y
10 2
3 n
N : (3 — nVtyx + (3\/3 + n)y
= 107t
4. a) <p = 135°
b) p « 26,565°
c) = 45°
5. a?0 = 2; y0 = e2
6. Hinweis: Tangentengleichung:
y — a x0 = —a x0 [x — xq)
Schnittpunkte der Tangente mit den
Koordinatenachsen:
A(2xo; 0) und B(0; 2t/q)
Damit ist der Tangentenberührungs-
punkt P(xq; yo) der Halbierungs-
punkt der Strecke AB.
7.	a) 1? « 71,565° (108,435°)
b)	45° und 135°
c)	di 53,130°; ^2- 126,870°
d)	« 71,565°; d2^ 108,435°
8.	T : 4x + 4?/ + 1 = 0
/40 40\
9-51(t;v); 4 5 62(-40;40)
10. a)
b)
11. a)
112 yy° _-\
a? &
yy0 = p(x + reo)
b)
c)
d)
12. a)
b)
c)
d)
V2
X“ 6~
a	b
^A = —Tp HB =----
a21
_ 6/13
X“ 169
_ 3y/2
2a
Q = | in (0; 1)
q = 2 in (±2;0)
Q = 1
q= 1 in (-2;-2)
3 A
2=-V3
f)2=|
g) Q = 4a
h) q = e in (1; e-1)
2 >--------
a)	q = -v 2ar
hi °2
b’ e = 37
r3
c>e=^
268
Lösungen
15.	a) (4; 4)
b)	(3;-2)
c)	(0;l)
d)	(-2; 3)
/	4\
e)	(0;-d
*) (ü
7\ 2	3/
x / 7t	3	/—\
g)
/	2	/1\2
16,(a;_3)2+(2/--) =(-)
3
fl + sinh2 j 2
17' ß = cosli^
a
2
i 2 ^0	Z/0
= a cosh — = —
a a
Ist Pq(xq; yo) ein beliebiger Punkt
der Kettenlinie und n(xyv; 0) der
Normalenschnitt punkt mit der
x-Achse, so wird
P0N = (xN - x0)2 + yl
I-------------- 9
/ 2 • 1. 2 ^0	2	^0
= y Vo sinh —+y2 = —
1	/ / A \ 2
18.	a)7? = - + 3^|j
b)	27£2 + 8y2 = 0
c)	(2£)% + yi = 3g
d)	^i — yi = (2a)i
\ z-2 1	2	2
e)	£ + y = a
f)	8£3 - 27y2 = 0
/	t2\
g)e = e(i) = -i2(i + v)
y = y(t) = 4t fl + b2)
h)	(£ +	+ (£ -	= 2a^
Bei einer Drehung der Achsen
um 45° erhält diese Gleichung die
2	2	2
Form xf + y^ = (2a)3, d.h., die
Evolute der Astroide ist wieder-
um eine Astroide: von doppelter
Größe und um 45° gedreht.
i)	n = n(^) = e^
19.	a) Schraubenlinie:
x2 + y2 = a2, z = ct
b)	Kreis: x2 + z2 = 1, y = 1
c)	Gerade durch Ursprung, die mit
den Koordinatenachsen gleiche
Winkel bildet.
d)	Gerade durch (1; 1; 0), parallel zur
z-Achse.
e)	x2 — z2 = 1, y = 0; d. i. gleichsei-
tige Hyperbel in der x, z-Ebene.
20.	a) v = (—3sint, 3cost, 4)T
a = (—3cost, —3sint, 0)T
b) |v(l)| = aZT4; |a(l)| = x/4Ö
21.	Hinweis: r • r = 0
22.	a) T : r = (o,l,^\/3)T
+A(-l,0, V^)T ; —00 < A < 00
En : 2x - 2z\/3 + 37t = 0
b)	T : r = b, c)T + A(a, 0, — c)T
En : 2ax — 2cz — a2 + c2 = 0
/	T
/	a/2 \
c)	T : r = 0,1,—
\	2 7
+A(1,0,1)t
En : 2x + 2z — V2 = 0
d)T: r = (2,4,8)T + A(l, 4,12)T
En : x + 4y + 12z = 114
e)T: r=|(l,l^)T
/	V%\T
+A7?(^-l,0,^-J
En : xa/2 — z = 0
Aufgaben aus Abschnitt 9.3
269
f)	T : r = A(l, 0, &)T	T . r = M
En : x + bz = 0	V4’ 3’ 2/
T	>T	+A(1, —1
g)T: r = (1,3,4)T + A(12, -4,3)T
En : 12a? - 4y + 3z = 12	24. Fx(0; 0;-1); P2 (;------)
\3	9	27/
t	25.^^ 70,53°
23.	Ti: r=(4,-|,2) + A(4,-2,1)T 26. S(2;l;l); <p« 29,94°
\ Ö /
Aufgaben aus Abschnitt 9.3
..	.	32	4	3na2 1- a) A = y	n) A = -	d) A = -y
b> A = 36	0) A =	e) .4, ,
CM = ^	p) A = 2	Ä2=3n ,l)A=|(2^)/,.	q) .4 = |	’	4
d.h. 2/3 des Pro-	f) A =—sinh27i
duktes aus der	r) A = —	1 oo 07 2 Grundlinie 2 y/2ph	2
und der Höhe h.	s) A = 20-	g) A = 71(2
e)4 = io|	t) A = 17,5-61n6	y
f) A = 12	u) A = na2	h) A = ~
v) A = 0,8	7ia2
g)A = 81n2	i)A=— (Kreis)
32	w) A = — hM = “	>4 i)A = 1	' 2	,, a _n 2
16	y) A = 2a2 sinh 1	k) 4 — na J)	3	« 2.3504a2	1) A = (10n
k) A = 19,2	2. a) A = 3na2	+27\/3) —
1)'4 = 25'6	l>)A=|™,’	3a2	M
\ A q 8	9	m) A = 	 m) A = 8—	c A = a2	J	2 15	7
Aufgaben aus Abschnitt 9.4
x	112 1. a) s = —— J	27	. x	28 b) s = — o	,	670 6).’ = ^-
c) s = 27ia	d) s = 6a	h) a +111 (,/2+
e) s = In 3	f) s = 21n3-l	i) s = 2a sinh 1
270
Lösungen
j)	s = 1, 35 + In 2
k)	s = p (V2 + In (1 + a/2^ )
1)	s = In (2 + x/3)
m)	s = 4\/3
n) s = - In (2 cosh 2)
1
o) s = 8a	p) s = 4-
q) s = 4a/3	r) s = 8a
s) s = 7ta\/l + 47t2
+ | In (27t + \/l + 47t2)
x 3
t) s = -7ta
man die Gleichung einer Kegelfläche:
2 ।	2	2
x +y = z .
HN : r = A(0,1,0)T (y-Achse)
BN : r = A(—1,0,1)T
Tangente: r = A(l, 0,1)T
8. a) s = f \/ x2 + y2 + z2dt = 3t
Jo
r = r(s)
/ s . s \/5 ’
= 2cos-, 2sm-, --------s
\	3’	3 3 >
2 . s 2 s v'
- sm -, - cos -, —
3	3’3	3’ 3
rb
2. s = 2 / V1 + Q/)2dx
Jo
(‘+
mit y = Z-Z als Parabelgleichung
(s s \ ±
— cos -, — sin -, 0 )
3’	3’ J
b = - ( Vb sin -, — Vb cos -, 2 )
3\	3	3 J
3. a) s = 21	b) s = 5to
c) s = 7,5	d) s = 27t
e) s = 2 sinh 1	3 + ln2 f) " =	2
g) s = 8 \/2
4.	T = (—1,0,1)T; B = (1,0,1)t
N = (0, —2,0)T
t = -L(-l,0,1)T;
y/2
b= -)=(l,0,l)T; n = (0, —1,0)t
5.	Hauptnormale HN :
r = (1,1,1)T + A(ll,8, —9)t, AeR
Binormale BN :
r = (1,1,1)T + A(3, —3,1)T, AeR
Schmiegebene Es : 3x — 3y + z = 1
6.	HN : r = (1,1,0)T + A(1,1,0)t
BN : r = (1,1,0)T + A(-l, 1,2)T
7.	Durch Elimination von t aus
x = tcost, y = tsint, z = t erhält
— w • n
1 ( [b	s V5 . s \
3 yv 3	3’3	3’ J
ds
ß
b) f = 2; r =
(G	G	G	G \ T
---sin-, 1 —cos-, 4sin-^
2--2	2	4/
/II	s 1 . s	S\T
t =------cos -, - sm -, cos -
\2 2	2’ 2	2	4/
für s = 27t:
t = (1,0,0)T
9.	ai = 120°; a2 = 60°; a3 = 45°
10.	HN: r = (l,l,l)T
Aufgaben aus Abschnitt 9.4
271
+A(26,31, —22)T
BN : r = (1,1,1)T + A(8, —6,1)T
11 d	dt	dt
11.	a = — (vt) = vt + v— = vt + v •
dr J dt	ds
ds	1	v1 2
x = vt + v • -nv = vt H------n
dt	Q	Q
12.	v = r = (1,1 - 2t, 0)T
a = r = (0, —2,0)t
\r x r\ 2
v = |r| = \/2 — 4t + 4t2
4t - 2	2
a+ = v = ,	; ari = —
V2-4t + 4t2	v
für t = 0 :
v = a/2; at = — x/2; an = a/2
_ 12	_ 7 sin 2t _ 12
13.	x — t , df —	~	. dn —
4 ’
24\/2	r
X“^2T;
an = 2,4\/2
2
14.	x = —: dt = 4t; dn = 2
vz
2
für t = 1 : x = dt = 4; dn = 2
15.	a) Zunächst stellt man die Matrix
der Vektorkoordinaten auf:
r
r
r
r
r x r
t
1
0
0
6t2
t2 t3
2t 3t2
2 6t
0	6
-6t 2
Dann findet man
\r x r|
4.	x =	—--
M3 ___________________
2\/9t4 + 9t2 + 1
” v/(l + 4t2 + 9t^
[r, r, ’r]
5.	w = —----—
\r x r|2
12
“ 4(9t4 + 9t2 + 1)
für t = 0 : x = 2; w = 3
V2
(e* + e-t)2
\/2
W (e^ + e-^)2
\/2	\/2
für t = 0 : x = -----; w =------
4	4
\/t4 + 4t2 + 1
V(i + t2 + t4)3Z
2
W “ t4 + 4t2 + 1
C- .	4	1
tur t = 1 : x = -----; w = -
3 ’	3
2t
X “ (2t2 + l)2
2t
W~ “(2t2 + l)2
2	2
für t = 1 : x=-; w =--------
__________9	9
\/9t4 + 4t6 + 1
V(t2 + i + t6)3
-6t
w = ---------------
9t4 + 4t6 + 1
+ i	V42	3
tur t = 1 : x = -----; w =------
9 ’	7
1. |r| = \/l + 4t2 + 9t4
2. |r x r| = 2x/9t4 + 9t2 + 1
3. [r, r, ’r] = (r x r) • r = 12
16. Rechtsschraube: w = —-----— > 0
dz +
Linksschraube: w =---------— < 0
dz + oz
272
Lösungen
Aufgaben aus Abschnitt 9.5
1. a) Q(a?) = ^x2 VB ab	2. = T>	x dx h2 Jo = -abh	e) Vx f) vx g) K	7T2 T (7t + 2)71 4 _ 327ta3 105	e) V = 37t2 87ta3 5- a) Vp = ö ») V, = x	47ta3
b) VB = ^R3 ö	h) Vx i) Vx	87ta3 3 = 727t	0VP= 21 6. a) Ax = 47tr2
c) Q(x) =	j) K	= 57t2a3	b) Ax =
VB =72 d) Q(x) =	k) Vx	32	3 = 	Kd 105 o 3	7ta2(sinh 2 + 2) c) Ax = 27t [^2
/ A — a\ 1 a H  —x 1	1)K	871GT 15	+ ln(l + V/2)]
\	/2	/ /,	B-b \ x { b H		—x \	n	/	3. a) Vy	8 2r = -red b ö	A 34^17-2 d) Ax =	7t
\ / VB = \(äB	b) Vy	2048 “ Ü5-71	x .	62 e) Ax = —n
O \ Ab + aß	\ +	9	+ ab)	c) V,	_ 5127t 15	rx 4	64	2 f) Ax = —na2 ö
2	/ e) Q(x) = db ,	. 2 7t—(/z- 4?)	d) Vy e) Vy	_ 5127t 7 7ta3	g) Ax = 2,47ta2 h) Ax = 29, 67t i) ^-x = 37t
•£ Vb = -Ttdbh ö	f)Vy	647t	7. a) A = 47t2a6 t X 4	147t b) ^-y = ö c) Ax = 7t [x/2
x	2 o f) Vb = -R3 tana ö 2. a) Vx = nph2	g) Vy h) Vy	o 4	2t. = —rurb ö = 19,27t	
b) Vx = 127t c) Vx =	4. a) Vx	272 = 	7t 15 11	+ ln (1 + V^)] d) Ay = ^-na2
o / sinh 2	\	b) Vx	= T71	y 5
™( 2	+1)	c) V -	4 = 27i2d2b	e) Ap = ‘Ina2 (2 - ^2)
1X Tr 71/571	V3\ d>K=4(T + -)	d) V -	_ 1287t 3	rx 4	128	2 f) Ap = —na2 0
Aufgaben aus Abschnitt 9.6
273
Aufgaben aus Abschnitt 9.6
1.	1,413 MN bzw.
1,059 MN
1	9
2.	F = -ggwah1 2
6
2 o
3.	F = -ggwr3
ö
4.	F = 2, 3544 MN
1	2
5.	F = -ggwah
ö
6.	167,424 kN
h
7.	x =
8.	47,088 kN je Stirnseite
9.	Ix = ^ah3
ö
1 q
ly = 3^
10.	Ix = — ab3
12
1 q
Iv = —aöb
y 12
11.	Iy = 6,4
12.	Ix = —
16
d3	d3
13.	Mx = —; Mv= —
6 ’	y 6
a	a
xs = ^; ys = ö
ö	ö
14.	xs = 0; ys = —
071
3
15.	xs = -a; ys = 0,35
„„ n 8
16.	xs = 0; ys = -
5
17.	« 34,517 kJ
18.	aufzuwendende Ar-
beit: « 1,432 kJ
19.	« 15,6729 kJ
20.	2880 Ws
21.	« 5108,3 As
Aufgaben aus Abschnitt 10.1
1. Summe der Reihe s(x) =-------(geo-
1 — x
metrische Reihe)
Rest rn(x) =-------
1 — x
Auf dem Intervall 0; - ist
L ’ 2J
KOOI <	< 0,001, sobald
1g 1000
n — 1 > —------, also n > 11.
Ig2
beliebiges x.
3. s(x) = <
r(x) = <
0
für 0 < x < 1
für x = 0
(1 -x)n
0
für 0 < x < 1
für x = 0
2. Für konvergente alternierende Rei-
hen ^(—l)z+1Ui mit di > 0 für alle
2=1
i gilt
Bei beliebigem, aber festem n wird
rn größer, z.B. größer als 0,9, so-
bald x < 1 — 4J/0,9, d. h. auf dem
Intervall [0,1] konvergiert die Rei-
he nicht gleichmäßig. Auf dem Inter-
vall I =
aber konvergiert sie
gleichmäßig, denn dann gilt für jedes
Ö-n+l
x e. I :
und damit:
, Z x,	1
|rn(x) | < e sobald n >
-Igg.
Ig2 ’
spezi-
ell ist |rn(x)| < 0,01 für n > 7.
1
1
~ (n + l)2 "" n2
für alle x E (—oo, +oo).
Es gilt:	< 10-4 für n > 100 und
4. Für den Rest dieser alternierenden
Reihe gilt
1
für x e [0, 1]. Es ist |rn(x)| < 0,1,
274
Lösungen
sobald n > 9.
5. s(x) = < r(x) = < Bei beli<	✓ 1 + x3 für x > 0 0	für x = 0 r 1	,.. n
	-1	1 Lil vL	x-z (1+ 0	für x = 0 obigem, aber festem n wird
rn(x) größer, z. B. größer als 0,1, so-
bald x3 < ^“a/TÖ — 1, d. h. für x > 0
konvergiert die Reihe nicht gleich-
mäßig. Für x > 1 konvergiert sie
gleichmäßig, denn dann gilt für jedes
x > 1 :
Mz)| < und M®)l < E
1g 6
sobald n > 1 — -—;
lg2’
speziell für e = 0,001 : n > 11.
6- fi(X) = J . ~ -L:
x + z — 1 x + z
1 . / \ 1 1
damit: sn(x) =-------------
x x + n
s(x) = lim sn(x) = —
n—i X
lrn(x)l =------ < — für x > 0
x + n n
=>	< 0,1 für n > 10
7. a) Für jedes x > 0 sind die Glieder
der gegebenen Reihe kleiner (oder
gleich) den Gliedern der konver-
genten Zahlenreihe
1 1 1
1 + 3 + 3^ +	+ '
Nach dem Satz von Weierstrass
konvergiert die Reihe gleichmä-
ßig für x > 0. rn(x) ist höchstens
gleich dem Rest der Zahlenreihe,
d. h.	i
Mz)| < 2.3„_i, und es gilt:
|rn(x)| < 0,01 für n > 5 und alle
x > 0.
b) Für x > 0 sind die Glieder der
gegebenen Reihe höchstens gleich
den Gliedern der konvergenten
Zahlenreihe
1 1 1
1 + 2 + 4 + 8 + '
Deshalb konvergiert die Reihe
gleichmäßig für alle x > 0;
Mz)| <
|rn(x)| < 0,01, sobald n > 8.
x | cos nx\ 1	,	1
8. a) ----— < --------- und > -------
7 | 2n-1 I — 2n-1	'	2n~
n=l
ist konvergent.
b)
1 X
— sm -
nx n
vergiert.
1
— und
kon-
9. a) konvergent für x > 0
b) konvergent für x > 1
c) konvergent für |x| > 1
Aufgaben aus Abschnitt 10.2
1. a) [-3,3)
g) (-1,1]
e) [-V3, a/3]
f) (—00,00); beständig konvergent
1 1
iö’ 107
j) [-1,1]
k) nirgends konvergent
1) r = e
n) (1,2]
m) [—5, 3)
o) [-1,3)
Aufgaben aus Abschnitt 10.2
275
p) [-1,0)
2. a) s(x) =
1
00	p2n—1
sin2a? = ^(-l)n+1—-a?2n
n=l	'
für |x| < 00
.2
c) s(x) = arctanx, |x| < 1
d) s(x) = — In (1 — x), x e [—1,1)
|x| < 00

7 v 7	(1-x)2
rx / x 1 - 2X
f) S(X) = /I , ^2
00x2n
3. a) > -—— für Ixl < 00 ist die
7	(2n)!	1 1
n=0 '	'
MacLaurinsche Reihe der gegebe-
nen Funktion.
x2n+1
R2n^ = (2n+l)!Sinhl?a:
^&x _^—'Ox
2
e
| sinhi?x| =
für 0 < $ < 1;
I rß 12n+l
somit |i?2n(a;)| < (2n+ 1)! eN
°°	|r|2n+l
Da die Reihe V X-l-------
A; 2n + l !
beständig konvergiert, ist die not-
wendige Konvergenzbedingung
erfüllt:
lxl2n+1
lim --------— = 0 für Ixl < oo
n-oo(2n + l)!	1 1
folglich: lim |7?2n(^)| =0
n—»oo
für | x| < oo, und damit
x2n
coshx = > -—— für Ixl < oo
. (2n)!
n=0 '	'
b) Mit 0 < d < 1 ist R2n(a?) = (-1)”
T2n+1
x --------- • 22n sin (2i9a?).
(2n+l)!	v ’
, ..	|2a?|2n+1
|i?2n(x)l < (2n+l)!
lim |7?2n(^)| = 0 (vgl. Lösung
n^oo
von Aufgabe 3a), also
/	9	4	\
X (. x x	\
5. a) e ( 1 - — + y - ...]
3,	3 (a? — l)2
i»i + 5x-i> + ISr2-
1 x - 2	(» - 2)7
c>5- — + hrA~-
ry»2	™6
_ k	«A> «Ay
)	~ 12 - 45 -
6.
n=0
2
,2n
n=0
<2»)! 2n
22n(n<)2
00 9k — 1
c)	/(-) = 2E f^T; N<
k=l
d)	/(x) = In 2 + In (1 — x)
+ In (1 — — = In 2
e)	/(x) = In (1 + x3) — In (1 + x)
cos
276
Lösungen
f)	f(*) = E 22S)2^2ra; M<i
n=0 k
__	7V>2n
g)	f(x) = EX1)”^-; M <00
n=0
00	an
h)	/W = £(-i)n^n+1;
n=0
|x| < OO
0 /w=-1  i“hi
00 z	2 \
n=0
JE	r2n+l
j)/W = E(-i)"-ö^r; W < 3
n=0
k) /Cr)=2£(-ir-32n
n=0
(n + 2)x2n+1
x------rrr—rr; x < 00
(2n + l)!x2n+1 1 1
>)/w=1+|£(-i) »<g;;
n=l	x '
|x| < OO
n=0	x 7
7. a) /(x) = In [1 + (x — 1)] =
^(-1)I,+1(J ~1)''; 0<x<2
n=l
b) /(z) = -| •
1	1	y—\ /	1
^2	1	— x+4	— A—/\2n+1
2	n=0
-^r)(^ + 4)n;	-ß<x<-2
\ p/ \	(x + 2)n
c) /(*) = - E 2w+1 ;
n=0
— 4 < x < 0
/	\ n— 1
d) f(x) = E (n_
n=l v 7
(2n - l)n
x cos--------- tur \x < 00
4
00	o2n+l
n=0	x	7
/	7£\ 2n+l
x ( x + — ) für |x| < 00
\ O /
r) /w = -1 +	+
£2-5-8--/(3'‘-4)(J+ir
n\3n
n=2
für —2 < x < 0
g)	f(x) = —16(x + 2) + 20(rc + 2)2
-8(x + 2)3 + (x + 2)4
bW/ x V2' nn(x- l)n
h)	f(x) = X 3ran,
n=0
x sin (— + n— 1 für |x| < 00
\ ö .Z /
x — 4
i)	f(x)=2 + ^ +
V, _n„-i	(2n)!Cr-4)"
}	24"-1(n!)2(2n-l)
für 0 < x < 8
•\ es \	—2	2)n
j) f(x)=e
n=0
für |x| < 00
k) /Cr) = f> + l)(x + ir
n=0
für —2 < x < 0
8. a) /(x) = E(-l)"+1x2n-2
n=l
für |x| < 1
= arctan x
= £(-ir+i
^»2n—1
2n- 1’
Aufgaben aus Abschnitt 10.3
277
,„1 <2" “ ')' '
n^2V3(l----— + —-----—
\	3-35-9 7-27
+Xl+3'112
°°	T2n— 1
OO 4
b) C + ln.r + y 4-
nln
n=l
„.2n+l
io. $(x) = y (-i)n+2-4—TV
V 7	’	n!(2n + l)
<4iK--- + —
\3/	3	34	35 • 10
--J-— « 0,321388
1 x’>
U.*(x)=X +
ö ö
2-5 x7
+ 33 • 3! ’ T ”
2 x5
~ 322!' T
2-5-8 x9
34 -4! ’ ~9
44«- + —
\5/	5	9-53
Fehler < tY? ' 76 < °’00001
32 • 2! 5°
= 0,2008
5	9
ry*''-'	ry*'-'
’	=X-2!-42-5 + 4!-44-9=F'"
= 0,499805
13. U = ia I (1 — e2 cos2 t) 2 dt
Jo
\/ a2 — b2
e = -------- (numerische Exzentn-
a
zität)
r e2 /I • 3\ 2 e4
t/ = 2«,[l-- + ( —) -
/l-3-5\2 e6
\2-4-6/ ’ 5
/l-3-5-7\2 e8 1
\2-4-6-8z
Aufgaben aus Abschnitt 10.3
1. a) l = 7t; ungerade Funktion
2 rn
bn = —	1 • sin nx dx
7t Jo
_ 2 1 - (-l)n
2	00
\ „z \ 7t	z x cosnx
C f = v + 4E -1
3	nz
n=l
7t n
4
7t(2n — 1)
p/ x 37t	2 vY cos (2n — l)x
>) .«’) = T + n £ (2,. - 1)»
XI— 1 v	'
^2n = 0; ^2n-
n = 1,2,3,...
4 sin (2n — l)x
sm nx
2n- 1
sin (2n — 1)^
2n — 1
also: ^2
n=l
(-l)n+1
2n- 1
7t
4
b) /Y) = |
4 cos (2n — l)x
7t (2n — l)2
n=l x	7
e) /(a?)
f) f{x~)
g) fOO
Ti 2 cos (2n — l)x
4 + 7tE (2n — l)2
2
7t
4	cos2nx
~^41(2n-l)(2n+l)
4 4 (~l)ra+1
74 xi o-1-)2
x sin (2n — l)x
278
Lösungen
2. a) f(x) = - V —
’ J v ’ 7T 2n - 1
n=l
. (2n - l)nx
x sm -----—
b) =
n=l
cos (2n — 1)ttx
(2n — l)1 2
c) f<X) = |-
21	1	(2n — l)nx
A (2n—l)2 C°S * l
n=l v	7
1	sinn7tx
7i	n
n=l
f) /(x) =sinh/[ |+2^(-l)n
\	n=l
l • cos — nn sin
l2 + n27t2
3
3. a) /(x) = -
( —l)n+1	WIX
--------sin ——
n-------l
WIX
COS----
2
t \ p/ \	2	1	• nTCX .
b) f^ = ^-sln—+
1	4/
d) /(*) = ? - -2
2 7TZ
X (2n- l)2
n=l v	7
(2n - 1)to
cos----------
x pz x 3	2 cos (2n — l)7ur
n=l v	7
4	(—l)n+1 . (2n — l)7tx
7t2 2^ (2n- 1)2 sm 2
n=l v	7
Aufgaben aus Abschnitt 11.1
1. a) D(f) = {(x, y) \ x E R A y E R}
= R2
— 3x + 4?/ + 8 = c; die Niveaulini-
en sind parallele Geraden mit der
o .	3 *
Steigung m = -.
z = f(x,y) ist eine Ebene in R3.
b) D(f) = {(£>y)k2 + y2 < 52}
Die Niveaulinien sind konzen-
trische Kreise um M(0;0) mit
r < 5.
z = /(x, y) ist eine Halbkugel mit
M(0;0;0), r = 5 und 0 < z < 5.
c) D(f) = R2; die Niveaulinien sind
gleichseitige Hyperbeln:
für c > 0 im I. und HL,
für c < 0 im II. und IV. Quadran-
ten.
z = f(x,y) ist ein hyperbolisches
Paraboloid (Sattelfläche).
d)	D(f) = R2; die Niveaulinien
sind konzentrische Kreise um
M(0;0), c > 0.
z = f(x,y) ist ein Rotationspara-
boloid.
e)	D(f) = R2\{(0; 0)}; die Niveauli-
nien sind konzentrische Kreise um
M(0;0) bei c > 0.
z = f(x,y) ist eine Rotationsflä-
che, die die Kurve
4
z = —, y = 0 bei Rotation um
x21
die z-Achse erzeugt (z > 0).
f)	D(f) = {(.x, y)| (x > 0 A y > 0)
V(x < 0 A y < 0)}
Die Niveaulinien sind gleichseiti-
ge Hyperbeln im I. und III. Qua-
dranten (c > 0). Für c = 0 erge-
Aufgaben aus Abschnitt 11.1
279
Abbildung L.4: lf links, 3a Mitte, 3b rechts
ben sich die Koordinatenachsen.
z = f(x,y) ist eine Kegelfläche,
zu deren Darstellung die Schnitte
x = a, z2 = ay und
y = 6, z2 = bx verwendet werden
können (siehe Abbildung L.4).
2. a) £>(/) = {(x,y)|x2 + y2 < 4}
b) Z)(/) = {(x, y)| (—2 < x < 0
Ay < 0) V (0 < x < 2 A t/ > 0)}
c) £>(/) = {(x,y)\y > -x}
d) D(f) = {Cay)l y > Vx A;r > 0}
e) £>(/) = {(®,y)l - 1 < x < 1
A -1 < y < 1}
f)	D(f) = {V,y)\x2 +y2 > 1
Ay > -x2}
g)	D(J) = {(x,y)\y < —x}
3.	a) Siehe Abb. L.4.
b) Siehe Abb. L.4.
4.	a) alle Ebenen mit dem Normalen-
vektor n = (1,1,1)T
b)	alle konzentrischen Kugeln mit
dem Mittelpunkt im Ursprung
c)	c > 0: einschalige Rotationshy-
perboloide um die z-Achse;
c < 0: zweischalige Rotationshy-
perboloide um die z-Achse;
c = 0: Kegel
5.	f(tx, ty) = V(to)4 + (iy)4 -	• ty
= t2 (\/a;2 + y2 - 2xy) = t2 • /(x, y)
a — b b — a
7. a) 1. Oktant einschließlich Begren-
zungen (r>0Ay>0Az>0)
b)	l.,3.,6. und 8. Oktant ohne Be-
grenzungen (xyz > 0)
c)	Würfel mit den begrenzenden
Ebenen x = ±1, y = ±1 und
z = ±1, die Würfeloberfläche ein-
geschlossen
d)	Kugel mit dem Radius r = 1
um 0(0; 0; 0), die Kugeloberfläche
eingeschlossen.
280
Lösungen
Aufgaben aus Abschnitt 11.2
1.	A.,.z = (2a? — y + Ax)Ax
Ayz = (2y - x + Ay)Ay
Az = Axz + Ayz — AxAy
Für x = 2, Ax = 0,1, y = 2,
Ay = -0,1 :
Axz = 0,21; Ayz = -0,19
Az = 0,03
TTL
2.	lim /(x, y) =---- auf y = mx.
x—^o	1 — rn
3	2
Auf y = -x bzw. y = -x bzw.
y = 2x gegen (0;0) erhält man die
Werte 3 bzw. 2 bzw. (—2).
3.	a) lim ( lim /(x, y)) = — 1
y—X) \x—X)	/
lim ( lim f(a?,y)) = 1
x^O \y^0	/
limif(x,y) = 1 m2 auf
x—^q	1 + rn2
y = mx.
Der Grenzwert existiert nicht.
b) lim ( lim /(x, y) ) = 0
y^O \x^0	/
lim ( lim= 0
x^O \y^0	/
lim /(.,,)	=	*	"*»-«•
0 auf y = 2x
4.	a)	-i	b)	1
4
c) 0	d) 2
e) 0	f) existiert nicht
g) 1	h) existiert nicht
1	
1 4	
5. a) unstetig	b) stetig
c) unstetig	
6.	a) x = 1, y = — 1
b)	unstetig an allen Stellen, die auf
den Geraden x = rrm und y = nn
liegen (m, n e Z)
c)	unstetig an allen Stellen, die auf
dem Kreis x2 + y2 = 1 liegen
d)	unstetig an allen Stellen, die auf
der Geraden x + y = 0 oder auf
der Parabel y2 = x liegen
7.	a) unstetig an allen Stellen, die auf
den Koordinatenebenen liegen:
x = 0, y = 0, z = 0
b) unstetig an allen Stellen, die auf
dem Kegel z2 = x2 + y2 liegen
c) unstetig an allen Stellen, die auf
dem zweischaligen Hyperboloid
z2 — x2 — y2 = 1 liegen
Aufgaben aus Abschnitt 11.3
1. a) fx = 3x(x + 2y\, fy = 3(x2 - y2)
uw - 2x f - 2y
x x2 + y2 1 y x2 + y2
f =______y— f = x
x x2 + y2' y x2 + y2
3x{y/x —
\/x
9v =
.	a — b cos 7
e) ca = ----------
c
b — a cos 7	a&sin7
Cb —	, Cy —
c	c
y1
g) fx = e xy(l - xy)
fy = -x2 e~xy
Aufgaben aus Abschnitt 11.3
281
UA n	5t	5
9x —	(a? + 2i)2’ 9t~ (x + 2t)2
	t
LXx —	2^x — x2t2
	/ X
(Xt —	\ 1 — xt2
j) X =	—a sin (ax — by)
fy = b sin (ax — by)
	x2\/x2 — y2
fy l)/x fy	= M
	x\/ x2 — y2 3y
	(3y - 2a?)2 3a?
	(3y - 2a?)2
m) hx	= cot (x — 2t)
ht	= —2 cot (x — 2t)
n) gx	= 2 sin y cos (2x + y)
9y	= 2 sin x cos (x + 2y)
o) fx	= yxy~1; fy = xy Inx
P) fx	— _ _L esin S cos — Q	vVU
fy q) fx fy	1 ein	V = — e x cos — X	X xy2y/2x2 — 2y2
	|y|(a?4 - y4) x2yy/2x2 — 2y2
	|y|(a?4 - y4)
r) fx	= yz(xy)z~r
fy	= xz{xy)z~1
fz	= (xyY In (a?y)
S) fx	= yzxy In z\ fy = xzxy In z
fz	= xyzxy~x
t) fx	= yz exyz; fy = xz exyz
fz	= xy exyz
U) fx	= tanx; fy = — tan?/
_	2(y + a?2) ' a) Zxx ~ (y — x2)2	
2x
Zxy= (y-x2)2
1
Zyy ~
- 2u .	- r
b)	wuu —	+	, wuv — (
2v
Wvv ~ “(1 W)2
c)	zxxx = 6; zXXy = 2; zXyy —
zyyy = 6
3. Es werden nur Hinweise gegeben:
2(x + y/xy)
1
y 2(ß+y)
i \	i . y vVx	y.
b) zx = zy =	—= sm	— cos 2yjx x x1 yß y 	cos —	X
c) Ux —	1 x/t2	2x a ^e / 5 ut = -^3e	:/t2
d) ux =	x	y	z 5	Uy =	—;	uz =	— u	u	u n,2	
e) zxx — Zxy ~ zyy ~	= 2^	 (a? - y)3 - o xy (x - y)3 2	-	 (x - y)3	
f) Zx =	Ix	X X -e^; zy =	-ey y	y2 1 X	X X	
4. Hinweis:
2x/	1 „
'yy~ y3 + x2^
282
Lösungen
5.	a) zXy — Zyx — cbbz
M -	- - —
^7 Zxy — Zyx —
xy
\	2
c; Zxy - zvx -	_ 2y)2
6.	a) grad z = (2x, 2?/)T
grad £|(3.4) = (6, 8)t
b) Hinweis: Niveaulinie ist Kreis um
(0; 0) mit r = 5
\ 9z
c)-=^ + #
^1 =3^+4
Oa I (3;4)
2	2 o
X - y = 3
8. a = MN = (3,4)t
n=(_i.2)n 4=1
9. (6,3,2)T
|=; d w 18,43'
12. A
10. cosi? =
n.->
15. ^6x1 + 6x2, 6x1 + x4
14. —
13
eX2
7. grad z = (2x, — 2t/)t
grad z|(2;1) = (4, -2)T
Hinweis für Niveaulinie:
v2
16. grad z|(4;2) = —(1,2)T
Aufgaben aus Abschnitt 11.4
1. a) Az = yAx + xAy + Ax • Ay
dz = ydx + xdy
Az = —0, 62; dz = —0, 6
b) Az = 2xyAx + x2Ay + y(Ax)2
+2xAxAy + (Ax)2Ay
dz = 2x?/dx + x2d?/
Az = -0,298602; dz = -0, 30
f) dh =
(,l,+|)y[(9+i)2d.l.
+(* - p)1«1»
(X \ /	X \
xy -|— ) In (xy 4— ) dz
yJ \	yJ .
c) Az = (2x — 3y)Ax + (2y — 3x)Ay
+(Ax)2 — 3AxAy + (Ay)2
dz = (2x — 3y)dx + (2y — 3x)dy
Az = -0,79; dz = -0,9
g) d(/? = (ex cos y + 3y cos 3x)dx
+ (sin3x — ex siny)dy
, x , ,	(x2 + ?/2)dz — z(xdx + ydy)
h dw =-----------7	=-------
2. a) df
—y2dx + x2d?/
(x - y)2
b) dg = | es9 (ds — |dt)
xdx+ydy
c) dj = —.
\A2 + ?/2
xdx + ydy + zdz
d) du = —.
y/x2 y2 z2
i) df = (x2 — xs)xX2~X3~r lnx4 dxi
+.i;p_'r'3 In xi In x4 d^2
—2-'r'3 In xi In x4 dx3
1	X4
3. a) 0,075 b) « -0,738906
c) -0,1
e) df =
2(xdy — ydx)
x2 sin
4. A^ = In 1,044 « 0,04306
dz = 0,04
2
5. a) d2u = — (3?/2dx2 — dxydxdy
+x2dy2
Aufgaben aus Abschnitt 11.5
283
2 (ydx - xdy)2
b) d u =----------5----
xyz
c) d2u = 2(cLrd?/ + dxdz + dydz)
d) d2// = — u(rndx + ndy)2
Aufgaben aus Abschnitt 11.5
1. a) |Az|jyaa,	2. a)	Aß| < 0,755Q		4.	AV	< 4. 71 %		
= /(2,l;3,7)		AR	< 0,64%		V	—		
—/(2; 4) = 0,06757		R			AC			
b) Az < 0,0625	b)	AR\ < 0,773Q		5.	c	< 0, 63 %		
< Az Ma®		p	< 0,66 %	6.	AV		Aa	
c) \fx\ < 2^	3. a)	_n AAo|	< 1,363 cm2		V		a Ah	< 10%
। f । < 2> 1 IJi/l — 3 72		AAp ^0	< 0,48%		AU Vi	+	h	
- 3J2 =	b)	AAo| AAp	< 1,373 cm2	7.		< 0,15 %		
0,07305 > \Az\Max		Aq	< 0,49%	8. |	APa\	< 10%		
Aufgaben aus Abschnitt 11.6
1. a) 2x + 2y — z = 1
r = (1,1,3)T + A(2, 2, — 1)T
b) x + dy + 6z — 21 = 0
r = (1, 2, 2)t + A(1,4,6)T
c) 2x — z — 2 = 0
r = (1,0,0)T + A(2,0, —1)T
d) x — y — 2z + 1 = 0;
2. a) a?yo + yxü = 2zzü
b) xy^ZQ + yxQZQ + zxoyo = 3a3
xxx , yyx	zzx
C> a2 b2	c2
x y z
a b c
Im Punkt (0; 0; 0) existiert keine
Normale.
5.	cos a = — cosß = cos7 = — ~^=
9 o
6.	V = -a = const
2
7.	Hinweis: Sx (a2/3 4 •	0; 0^
Sv = (O; a2/3 • o)
Sz = (0; 0; a2/3 •
8.	r = (4,3,0)T + A(4,3,5)T
3. x + y — z = ±9
4. r = (3,4,5)T + A(3,4, —5)T
10. a) Fi(0; 0; 4); z-4 = 0
b) P2(l; 1;2); 2x + 2y + z = 6
284
Lösungen
Aufgaben aus Abschnitt 11.7
1. a) — = 4t3 + 3t2 + 2t
, . dz
b) — = 0
7 dt
2.	a) —2 cosht
b) (A — C) sin 2t + 2B cos 2t
x 2e2t
C) e1' +1
u(w + 2vt2) — vwd
e) 2t • In t • tan t 3--—- tan t
cos2 t
o . dz	du n di?
3.	a) -— = vu -------H u In u
dx	dx	dx
< x dz	?.	?. dy
b) — = ey +x ey
dx	dx
4.	Hinweis:
ydf	k.tk-lf
h Ö(ta2)
5. a)
ex + ey -x
ex + ey
b)
c)	dz	dz 1 Fy dz dx du 2 V x + dv dz dz 1 Fy dz dy du 2 \ x + dv
8. Hinweis:	
Ux	= ux cos + Uy sin (/?
U(_p	= —uxr sin (p + uyr cos p
9. Hinweis:	
	= f-2x-, zy = l-2f'y
10. a)	,	2 — x y = o . 3 + y
b)	= - p
c)	, 2ye2x — e2y 2x e2y — e2x
d)	/ y y = — X
e)	, x2 + xy + y2 y = xy
f)	
11. a)	S 1 II o 1 CO II o
b)	y	x zx = —; zv = — 2z v 2z
a b
c) zx = z^ = -
c y c
dz
du
dz
dv
7. a)	dz dx	dz dz = m—~ + p— du dv
	dz dy	dz dz = "ei + ’S
b)	dz dx	dz	y dz du	x2 dv
	dz dy	dz 1 dz du x dv
d) zx = 1; zy =-
x - z
12.aW = Z; y' = -4
b) y' = -1
.,1,4
c) y = y = -
5	5
13. a) (-1; -1) und (-1; 3)
b) (—3; 1) und (1; 1)
14. Hinweis:
Aufgaben aus Abschnitt 11.8
285
15.	Hinweis:
y /	/
zx =	---p ; zy = p
Aufgaben aus Abschnitt 11.8
1.	Xq + xoyo + yl + (2rc0 + y0)h
+(rco + 2yo)/c + h? + hk +
2.	/(a?, y) = 9 + ll(a? — 1) + 8(y — 2)
+3(x - l)2 + 8(z - l)(y - 1)+
2(y - 2)2 + (x -1)3 + 2(x - l)(y - 2)2
3-	a) f(x, y) = -1 - 2(x - 1) + (y + 1)
-(x - l)2 + 2(x - l)(y + 1)
+ (a? — l)2(y + 1)
b) Hinweis:
x2y = [1 + (a: — l)]2 • [—1 + (y + 1)]
a?2
4-	/(a:,y) = x - (y + 1) - —
+x(y + 1) - i(y + l)2 + R2
z? = 1.	(x~y~ !)3
2	3 [19a: + 1 — i9(y + l)]3
0 < i? < 1
_ ,z x	,	(mx + ny)3
5-	J (x, y) = mx + ny------------
+R3
R3 = ^mx + ny^ sin (mtfx + ni9y)
6-	f(x, y, z) = (a? - l)2 + (y - l)2
+ (z — l)2 + 2(a? — l)(y — 1)
-(x- l)(z- 1)
7-	a) f(x, y) = y - (x - l)y + R2
b) f(x,y) = 1 + 2(y - 1)
+(z - 2)(y - 1) + (y - l)2 + R2
1, l2’1 « 1,22
c) f(x, y) = (x - 1) + (y - 1)-
|(y-l)2 + z2+l?2
8. z(x, y) = 1 + 2(x - 1) - (y - 1)
- 8(z-l)2+10(a:-l)(y-1)-3(y-1)2
+^2
Aufgaben aus Abschnitt 11.9
1. a) XMin —	4; yMin — 1
%Min =	1
b) XMax = IjMax = 4i %Max = 12
1
Cj XMin — 1, yMin — %Min — 0
d)	kein Extremum
e)	XMin = yMin = %Min = 0
f)	XMin = 2; yMin = 0
2
%Min —
e
g) XMin = 1? yMin = 0
%Min =	2
%Max —	1, yMax — 0
%Max — 2
h) XMin = a/2; yMin = V^2
%Min = 8
XMin = ä/2^ yMin = V^2
%Min — 8
286
Lösungen
i) stationärer Punkt zxx	A	z
xi = 3; 7/i = 0	2 > 0	< 0	Sattelpunkt z\ = — 9
x<i = 3; 7/2 = a/3	2 > 0	< 0	Sattelpunkt zd = — 9
a?3 = 3; y3 = -\/3 2>0	< 0	Sattelpunkt z3 = — 9
a?4 = 2; 7/4 = 1	2 > 0	> 0	Minimum ZMin = —10
a?5 = 4; i/5 = -1 2 > 0 2. a) XMin = 2; yMin = 3 %Min = 1; UMin = 14 x	> 0	Minimum ZMin = —10 4. XMin = yMin =	2V ZMin —	^/2V
b) XMax = yMax = %Max = y 1 UMax — c) XMin —	yMin — %Min = ä/8; UMin = 4 • ä/2 . 1 *		5. ^Max = 8 6. a) y = 2,4x — 0,8 b) y = -1,21 + X
d) XMin —	yMin — %Min — UMin = 4 1 e) XMin — 3; yMin — ~z _ 2.	_ 44 %Min — q , UMin — ö	Z ( 2	1 l) XMin — X- yMin — ~Z ö	ö 4 %Min — 1; UMin — X O 3. a) ZMin = -1 bei x = y = 1	1	c) 7/ = 2, 00x3 + X d) y = 7,164 • x1’953 7. a) Ai = A2 = 3: A3 = —3 b) R = (Xi + X2 + X3 +4xix2 + 4xix3 - 4x2x3) +x2 +x3) Extrema von R sind: R = -3; R = 3
ZMax = 13 bei x = 2, y = - b) %Max = 1? %Min =	1 3 r CJ %Max — 2 V 3’ %Min — 0	-1	c) Bei einer reellen symmetrischen Matrix sind die Eigenwerte die Extremwerte des Rayleigh-Q\io>- tienten.
Aufgaben aus Abschnitt 11.10
1. a) XMin — yMin — 1} %Min — 2
b) XMax = yMax = 2
zMax = —4
XMin = yMin = 2; %Min = 4
c) XMax — yMax — 4zl, ZMax — 1
XMin = —yMin = ±1
%Min =	1
d) XMax — 1? yMax — 2
%Max — 2, UMax — 9
XMin = L yMin = 2
%Min =	2: UMin =	9
.	11	5
e) XMax —	• yMax —
11	_ 605
X'Max —	UMax —
2.	(±a/5; 1)
Aufgaben aus Abschnitt 12.1
287
3.	r = 1 dm; h = 2 dm
4.	A\yu = 9
5.	Der Strahl muss so verlaufen, dass
sin a 4- sin ß =	4-•
6-	Amclx — 2ab
A _ / 2A
8. a = b = c = r\/3
9. Xi = — (i = 1, 2,..., n)
n
Aufgaben aus Abschnitt 12.1
4
4
3
3. a) 6 + 41n0,5
b)2°-
c) 15-8 In 4
. 8^2 5
3-
6. a) 0
b)^
’ 105
7. a) 6
4
8. 161n2 —9-
8
7i\
8/
b) (3; 4,8)
80
Aufgaben aus Abschnitt 12.2
1. a)	28 15	4.42|	7.34 12
b)	1 24		x f a a a 8- “> 4 r i
4	5	1	pa pa—x pa—x—y 6. / /	/ z&zAy&x Jo Jo Jo - jL	b) (0; 0; aß
3. --	— + - ln2 16	2	~ 24	!>. 4) T
288
Lösungen
b)
7ta5
\/2
x 32v/2a5
,;)^r
Aufgaben aus Abschnitt 12.3
1. \
3
2. |™4
/>7t/4	/»2/ COS (p
3. /	/ f(r)rdrdtp
J cp=O J r=0
x CLTi
“>T
'4
5.
x - di? du
2—u
x - di? du ,
wobei x = -(u + v)
und y = |(u - v).
6. a) L- In 2
868 2
b’ 7?"
\ 3	2
c) -TO
o
1736
7-^r
8.	—
16
9.	8715/3
10.	L3
ö
nh2R2
4
12. —
10
8 o
!3. -a2
14.	a) 0
b) -7t • abc2
4
x nabe
15.	a) —
n x 47ta3
c)	1871
d)	27ta3
e)	8tt In 2
f)	TT™3
16
. 57ta3
e) —
16.	dkrta2, wobei k ein
Proportionalitätsfaktor
ist.
7103
17.	a) —
b)4
7 60
4	3
=
O
1
Kegel: Vc = -7ta
ö
VB - Vc
damit ——------= 3
Vc
18.	Kugel : Vb
19.	Q = / @(x,y, z) db =
JB
p2tc ph pz
/	/	/ zrdrdzdtp
Jo Jo Jo
71 h4
= ~T~
Aufgaben aus Abschnitt 13.1
1.	a) y — xy' = 0
b)	ty - 2y = 0
c)	y — 2xy' = 0
d)	x + yy' = 0
e)	y = y
f)	3y2 - t2 = 2tyy
g)	xyy' (xy2 + 1) = 1
h)	y = xy' In —
y
i)	2xy" + y' = 0
j)	y - y - 2y = 0
k)	y + 4y = 0
1)	V - 2y + y = 0
2.	a) y2 — x2 = 2xyy'
b) x2 + y = xy'
3.	a) ja
b)	nein
c)	ja
d)	ja
e)	ja
f)	1. ja; 2. nein
Aufgaben aus Abschnitt 13.2.1
289
g)	ja
5. a) Isoklinen: Geraden
durch O
b) Isoklinen: Geraden,
parallel zu y = t
c) Isoklinen: auf t-
Achse verschobene,
nach unten geöffne-
te Normalparabeln
6. Isoklinen: Kreise um
O;
Integralkurve durch O
ähnelt y = t3.
Aufgaben aus Abschnitt 13.2.1
1. a)
b)
c)
d)
g)
h)
y = C e1/®
x + y = In C(x
+i)(y +1)
r = Ce1/4’ +a
2 t2 - 1 + Ct
8 = -------------
t
e) v7! + y2
+^l + i2 = C
f) t2 + y2 = InCt2
Ct
y 1 +at
y = C sin x
y = C e-1/^2
_ Cx2 _
V (1 + x)2
k)
y =
2. a)
b)
V = 1 + Cx
y = Ce^,
y = e'/'7~2
C sin2 x — 1
y = —2—’
y = 2 sin2 x-
y	2
11^
- + - = C; y = —x
x y
d)	1. y = t
2.	2 (t3 - y3)
+3 (t2 — y2) + 5
= 0
e)	y2 — 1
= 2 In (e4+l)
-21n(e+l)
f)	r = C cos<^,
r = — 2 cos^
g)	y/y = xlnx — x+C,
y/y = x In x — x + 1
n. cvmc
h)	y =	, /t—
X -F V 1 +
\/l + a?2
x + \/l + a?2
3.	In 40 Minuten.
Lösungsweg: Nach der
Zeit t sei die Tempe-
ratur des Körpers T;
dT
= —A:(T —20°C),
wobei k der noch un-
bekannte Proportiona-
litätsfaktor ist;
ln(T- 20 °C) = -kt
bei t = 0 ist T =
100 °C, daher ist
C = In 80, kt =
In 80 °C
T- 20 °C’
nachdem wir Ti =
25 °C und T2 = 60 °C
eingesetzt haben, eli-
minieren wir die Un-
bekannte k\
kt In 16
A: • 10 “ ln2 ’
t = 40 min.
4-	q = qX)
= CU ( 1 - e~RC
5.	I = 0,316 A; t « 7 ms
6.	Fh =
Ft = fr (cos a, sino)T
Fl = (0, -qx)T
Gleichgewicht:
-Fh + Ft + Fl = o
H = Ft cosq,
qx = Ft sin a
Eliminieren von Ft :
qx	,
= tan a = y
XL
Anfangs wert aufgabe:
y' = f, y(o) = «
qx2
Lösung: y = — + a
Ztl
7.	vs = (us,0)T
vf =
res. Geschwindigkeit:
v = vf + vs
v greift tangential an
Bahnkurve y = y(x)
des Schwimmers an.
> y = tan a = —
Anfangs wert aufgabe:
290
Lösungen
/	9 \
/ V0 (	xz\
y = — 1 —2 b
Vs \ a )
y{-a) = o
Lösung:
vq ( x3 2 \
y = ““
vs \	3 /
Abdrift: y(a) = - — a
3 vs
8.	Anfangs wert aufgabe:
p' = -gp—, .p(o) = o
Po
Lösung:
P = Po e~9Qox/po
9.	erster Fall:
y = Cx~x mit C > 0;
y(x) —> oo für
x —> 0 (unrealistisch)
zeiter Fall:
y(x) —> Cp~x für
x —> 0
10.	y(t + At) « y(t)
p
Anfangs wert aufgabe:
/ iP-y
y = k------y,
P
y(0) = 1
Lösung:
= p
1 + (p — 1) e~kt
11.	Die Gleichung der
Tangente lautet
Y - y = y'(X - x).
Setzen wir Y = 0, fin-
den wir die Abszisse
des Schnittpunktes A
der Tangente mit der
y
x-Achse: Xa = x-----
y
Nach der Bedingung
Xa = 2x ist x = — — -
y
die Lösung dieser Dif-
ferenzialgleichung lie-
fert die gesuchte Kur-
9
ve xy = — a , eine
Hyperbel.
12.	a) x2 + 2y2 = c2 (El-
lipsen)
b)	y2 — x2 = c (Hyper-
beln)
c)	y = ex4
d)	yx2 = c
13.	Radiusvektor:
OP = y/x2
N ormalabschnitt:
~PN =
cosa
= y\/1+tan2 a
= yy/^ + y'2-
Die gesuchte Kurve
ist entweder ein Kreis
x2 + y2 = c2 oder eine
Hyperbel x2 — y2 = c2.
15. 4£ = _2l_
de 47ie2 ’
_ k
T = ~Ä---G
47ie
k und c finden wir
aus den Bedingungen
20 °C = —---F c und
47i2r
100 °C = X +c;
4nx
T=i«rcr_60-c.
e
Füre = 1, 6 r wird T =
40 °C.
16. y = - (cosh ax — 1) + b
Aufgaben aus Abschnitt 13.2.2
1. a) y = tect
2t
b)	Ct = e y~t
c)	x = yeCy+1
d)	y — x = Cey~x
e)	x2 — y2 = Cx
f)	s2 = 2t2 In y
y
g)	sin — + In x = C
x
h’" = öttt;
i) y = t In t2 + Ct
\ 2x
2-a)y= i _ Gx2 ’
2x
y ~ 1 - 3x2
b) y = xeCx,
y = xe-x/2
3. Wenn wir in der Tan-
gentengleichung
Y - y = y\x - x)
X = 0 setzen, finden
wir
Vq = -ON = y - xyf,
ON = xyf — y
= OM = y/x2 Y y2.
x2 — c2
Daher ist y =--------.
y 2c
Der Spiegel muss ein
Rotationsparaboloid
sein.
4. x, ^-Koordinatensystem:
?/-Achse in Flussrich-
tung,
x = 0 linkes Flussufer,
Aufgaben aus Abschnitt 13.2.3
291
x = a rechtes Ufer.
Herr in O.
vf = (0 , w)T
VH =
^/x* 2 + ?/2
> v = vf + vh
— Vh (
y/x2 +y2\
\ T
VF / 2 i 2	I
— y/x1 + yz - y ]
vh	J
v greift tangenti-
al an „Hundekurve“
y = y(x) an.
x /	v<2
y = —
vi
Anfangs wert aufgabe:
y' = -
_^/1 + m2,
vh V V x /
y(a) = 0
Lösung:
. k ( vf i
y = x sinh — In —
\vh xJ
— x(vH-vF)/vH
a2vF/vH _ x2vf IVh
X 2aVF/VH
vF = VH
o
a x
2 - 2Ü’
• y =
Abdrift: -
2
vf < vh : Hund er-
reicht Herrn.
vF > vH  y = y(x)
hat bei x = 0 Pol.
Hund wird von Strö-
mung fortgerissen.
5. a) 8t + 2y + 1
= 2 tan(4t -P C)
b)	arctan(x -P y)
= x + C
c)	x + 2p
+3 In |2x + 3p — 7|
= C
d)	5t + 10p + C
= 3 In 110t — by + 6|
'>" = x- Xc
f)t = -y
“F2 tun (c -|-
g) (y—2)2—2(y—2)(i—
l)-(i-l)2 + C = 0
t \	y — i
h) arctan-----
7	t+ 2
-|ln[(i + 2)2
+(y -1)2] + C = o
Aufgaben aus Abschnitt 13.2.3
1. a) y = C e t — e t
b)	y = -ie2f +Ce4i
c)	y = (arctan el +C)
x cosht
d)	y = -1
+ In
tan-----
\ 4
t
+ 2
e)	y = (arcsin x -P 1)
x \/l — a?2
f)	p = Cebt
-TFtba'mt
+ cost)
x 1 t -P C
g)y = ^smt + 5—;
2	2 cos t
-P C / sint
h) y = t2 + Ct
j) y = tln |t| + 1 + Ct
k) y
1) y
.4	,3
1   t _______ t
1	4	3
l + t
Uo
2. ua(t) =
x reue r -psincjt
—rcjcoscjt ;
im eingeschwungenen
Zustand ist somit
= 1 ! Z^O2
x (sin wt — tüj cos cjt)
C
3. y = Inx 4--
x
P
4. - = r(t) oder
P
dp = pr(t) dt
Reduzierung durch
Abschuss:
dp = pr(t) dt — a dt
Differenzialgleichung:
allg. Lösung:
p = [C — a ln(l -P t)]
x (1 -p t) mit C = p(0)
pX = 0 =>
C — a ln(l -P t) = 0
= eJ’(°)/o-l
292
Lösungen
Aufgaben aus Abschnitt 13.2.4
. _ 1	7/2 _	1	e) y3 = t + C e \
t In Ct	c) y -	 1 + Ce*2	y3 = t — 2 e1-t
	d) y =	2t	n 7/ 			
2	e^2		1 - Ct2 ’ 2t	y 3V1 - t2 - 1
b) 9 = 2t + C	y =	1 - 3t2	
Aufgaben aus Abschnitt 13.2.5
1.	a) 4£2 + y2 = Ct
b)	t3 ey —y = C
c)	t e~y +y = C
d)	x3 ey —y = C
e)	y + xe~y = C
f)	x2 cos2 y + y2 = C
2.	m = e~2ip
y2 = 2(C - f) e2t
b)	m = cos?/;
2t2 sin?/ + cos 2y
= C
c)	m = 1/sin?/;
—+f- = C
sm?/
d)	m = 1/t;
t sin y + y In t = C
e)	m = (t2y2-\-2ty)~1;
t(2 + ty)5 _
---------- — c
y
f)	m = et+y;
et+y (y2 + cos/;)
= C
1 v
g)	m =	x+- = C
h)	m =
y
xy — In y = 0
.X -	1
m =
y2 = Cx3 + x2
j) m = e~y;
e~y cosx = C + x
Aufgaben aus Abschnitt 13.3.1
1. a) y = Ci+C2x+C3 exV2 +C4 e~xV2
b) y = (Ci + C2x) cos 2x
+(63 + C4X) sin 2x
c) y = Ci ex +C2 e3x
d) y = (Ci + C2x) e2x
e) y = e2x (A cos 3x + B sin 3x)
i)y = C1 e2x +C2 e~2x
= A cosh 2x + B sinh 2x
g) y = A cos 2x + B sin 2x
= a sin(2x + <^)
h) y = Ci + C2 e~4x
i) x = Ci C +C2 e"4t
j) q = Acos-+Bsm-
k) s = e-t (A cos t + B sin t);
s = e-t (cos t + 2 sin t)
l)?/ = Ci ex+(C2 + C3x)e2x
m) y = Ci cosh 2x + C2 sin 2x
+C3 cos 2x + C4 sin 2x
n) y = Ci e2x + e-x
x (c2 cos xV3 + C3 sin xV3^
o)?/ = (Ci+C2x + C3x2)e-^
p) y = A sin x sinh x
-\-B sin x cosh x + C cos x sinh x
+D cosx coshx
q) y = A cosh x + B sinh x
AC cos | + D sin |
2.	Schwingungsgleichung: (p +	= 0
allg. Lösung:
=
Aufgaben aus Abschnitt 13.3.1
293
Periode: T = 2tu / -
3.	zum Nullpunkt zurücktreibende Fe-
derkraft: F = —kyey
Anfangs wert aufgabe:
my + kx = 0; y(0) = —6, y(0) = 0
my
Federkonstante k = ——
b
Lösung: y = -bcost\^-
V b
Periode: T = 2tta / —
Vp
4.	Schwingungsgleichung:
my + ay + ky = 0
__
y = —be coscG,
, . [g
wobei x = \ -----------
V b
_ . , _	271
Periode: T = —
X
5.	a) = Ci + (G2 + G3t) e£ +G4 e"£
Ansatz:
y = t(Ao 4- A±t + A2t2) + t2(Bo
-\-Bit) e£ —H(_Dq -|- D^t
-\-D2t2 + D3t3) e~2t cost
-\-(EQ-\-Eit-\-E2t2-\-E3t3) e 2^ sin t
b)	z = Ci e2t +G2 e-£ +G3 cos t
+G4 sin t
Ansatz:
y = A + (B0 + Bit + B2t2)e°’5t
-\-tDo cos t + tEo sin t
c)	z = C1^C2et +G3e2£
Ansatz: y = tA + B e~2t
+ (D0 + D^t) e~t sin 3t
-\-(Eq -|- E^t) e t cos 3t
6. a) y = Gi cos 3t + G2 sin 3t +	e5£
, x t /I 3	1 9	1 \
b)	y = et ( -t3--12---1 )
7 y \6	4	4 )
+Gi e £ +G2 e£
c)	y = Gi cos 2t + ( C2 + j j sin 2t
d)	y = I(J + Gi - id e2* +G2 e1'
Ö	\	zL J
e)y = (C1+C2x)ex + e2x
f)y = C1 e2x +C2 e~2x -2x3 - 3x
g)	y = Ci e~x +C2 e~2x
+0,25cos f v — 2d
\4	/
h)	y = Ci cos x + C*2 sin x + x + ex
i)	y = Ci + C2 e~3x +|a;2 _ x
j)	y = e~2x(C\ cosx + C2 sina?)
+x2 — 8x + 7
k)	y = Gi e2x +(G2 - x) ex
1)	x = A sin k(t — to) — t cos kt
m)	y = Gi e'z'v/2 +G2
— {x — 2) e~x
n)y = C1^C2e2x-^-
6
o) y = | e~x -\-x e~2x +Ci e~2x
AC2e~3x
p) x = e~kt (Ci cos kt + G2 sin kt)
+ sin kt — 2 cos kt
q)7/ = Gi+G2x + (G3+x)e-'
+x3 — 3x2
r)y = Ci e3x + (g2 - |) e~3x
+G3 cos 3x + G4 sin 3x
s) x = Gi + G2 cost+G3 sint+t3 — 6t
^y = (C1 + 5) e~^
+ (g2 cos xV3 + G3 sin xV3^ ex
k	t2\
u) x = ( Gi + G2t + — \ e 2t
X 4 t T. . t 1
v) x = A cos —H B sm —|—
a	a a
_+	—i.
7. a) y = e £ + e 2
(	\/3	\/3	\/3 \
x cos —t H----sin —t
y	2	3	2 J
-\~t — 2
294
Lösungen
b)
_ t2 t 1
“ 7 “ 3 “ 18
e / r— 61 . r—
+ —— costvo H—— smtv5
18 \	v5
10. Differenzialgleichung der Biegelinie:
„	F/7 x
Anfangswerte: ?/(0) = y'(fi) = 0
Z? /	\
c)
d)
y = cos 2t + - sin 2t + - sin t
ö	ö
(1 t \ t t2 t3
y=e (8+2 +4-4-6
y =	— — J cos2x
+ f C2 + - In sin 2xj sin 2x
b) y = [(Ci + In cos x) cos x
+ (C2 + x) sinx] e2x
y
= Ci cos x + C2 sin x
— cosx In tan
Lösung: y = — ( Ix2
2a \
x3
n'y=T
o
12. x = a (e-t — 1)
13. my = —mg — ay
(a > 0, Proportionalitätskonstante)
Anfangswerte: ?/(0) =	?/(0) = 0
Lösung: y = ft.-^+-^(l- e~ßt)
P P
mit ß = a/rn
3
14. Anfangs wert aufgabe:
d)7/ = Ci+C2e-x-(l + e-x)
mx + kx = 0; x(0) = xq, x(0) = 0
x ln(l + ex) + x
Lösung: x = xq cos
y = e~2x (c1+C2x+2.
\	2x
v'+‘
f)y =
/ x2 In x	3x2	~	~
( —-------+Gi +C2xj e2x
g)
h)
y = Ci sin x + C2 cos x H-------
2 cosx
y = (Ci — In | sinx|) cos 2x
+ f C2 — x — - cot x \ sin 2x
i) y = (Ci + \/4 - x2
• x ~ \ T
+x arcsin — + C2xJ e
15. Schwingungsgleichung:
mx + kx = 2cjmcoscjt
Resonanz bei uj = \ —
m
allg. Lösung: x = Ci coscjt
+C2 sin cut 1 sin cvt = x sin (art + cp)
mit x = y/Cf + (C2 +1)2
lim x = 00 (Amplitude der
Schwingung strebt gegen 00)
kl4x — 2kl2x3 + kx5
12Öä
16. w(x)
9. Drückt man den Zylinder y Längen-
einheiten in das Wasser, hat man die
Kraft F = ynr2 gg ey aufzubringen.
Schwingungsgleichung:
my + ynr2 og = 0, m = 7ir2lg
17. allg. Lösung.:
w(x) = Ci + C2x
+C3 cos Ax + C4 sin Ax
w(0) = w'(0) = 0 Ci = C3 = 0
w(Z) = IC2 + C4sinA/ = 0
w'(Z) = C2 + C4AcosA/ = 0
Koeffizient endet erminante:
allg. Lösung:
XI cos XI — sin XI = 0
y =
t + C2 sin
Periode: T = 27t


tan XI = XI
kleinste positive Wurzel:
XI = 4,4934
Knicklast:	=
20,1907q
P
Aufgaben aus Abschnitt 13.3.2
295
Aufgaben aus Abschnitt 13.3.2
a)	y = t(Ci cos In t + C2 sin In t) + t In t
Q	1
b)	V = -^tln2 \t\ + -i3+
(Ci + (72 In |i|) • |t| + C^i2
c)	y = -7- + Czt2 + | G - 7) In |«|
b	O \	b J
d)	y = | In |t| + Cii-1 + (72t
e)	y = -|i-1 In N + fi^-1 + C*2i
f)	y = - In \t\ sin In \t\
+Gi cos In \t\ + C2 sin In \t\
g)	2/ =	+ C2.1;-1 + C3x3
h)	y = — + C2x2
X
i)	y = C\xn + G2x"(n+1)
j)	y = ^-2(Gi + G2lnx)
k)	y = Gi cos In x + G2 sin In x
HC ry>2
y — ~z i" C\x 1 + g2
ö
m) y = Ciz3 +	_ 2 In x + |
xz	3
n) y = C\x + G2x2 — 4x In x
, Gi + G2 In x + In3 x
o)y=--------------------
X
p) y = (	+ cix + g2 ) x2
\ o	/
X
q) y = — + Gi cos In x + G2 sin In x
Aufgaben aus Abschnitt 13.4
1.	a) Zi = (Ci -C2i)e-f
z2 = C2 e *
b) Xr =
J'2 =
f+ |+^)ef
c)	z\ = e-4t (A cos t + B sin t)
Z2 = e-4t[(Ä — B) sint
— (A + B) cos t]
d)	Z\ = Gi e* +G2 e 2^
Z2 = Ci et +G3 e 2t
^3 = Gi —G2 e-2t —G3 e-2t
e)	Z\ = (Git + G2) e 4^
^2 = (-Git-G2-Gi)e-4t
f)	^1 =G2 + 3G3e2t
Z2 — Gi e * —2G3 e2t
^3 — ~2Gi e * +G2 + G3 e2t
g)	Xi = (Git2 + G2t + G3) e t
+t2 - 3t + 3
x^ =	— C2) e t -\-t
a?3 = 2C*i e * +t — 1
h)	zi = 4Ci + C2 e~3t +C3te~3t
=4Ci -2C2e-3*
+C3(-2t+l)e-3f
z3 = Ci + C*2 e 3t -\~C3(t — 1) e 3t
i)	yi = Ci e5t +C2 e-t -1 et
y2 = Gie5t-te-t
j)	x = e4+Gi + G2e-2t
y = ef +Gi -G2e-2f
k)	x = 2e-t+Ci ef+G2 e-2f
y = 3e"* +3Cief +2G2e“2t
1)	x = Ci e* +C2 e-t +t cosh t
m)	x = e* +Ci e3t +C2 e-3t
+C3 cos(t + (/>)
2.	a) X! = -3 - 3 e2f +8 e3t +2 e4f
x2 = -1 - 3e2* —2e4f
b) x = e-2t(l - 2t)
296
Lösungen
Aufgaben aus Abschnitt 13.5.1
a)	2/« 1 + |(>-1) + |(®-l)2	c)
+ >-1)3 + ^-1)4 d)
p2 ~»4	™5	„.6
L	vL	vL	vL
T + 12 + 15 + 60
y
y
r2	x3 .z'1	x5
T	TT	' TT	' 2ü
9	4rc3	5a?4
t? + x2 +	+ ——
3	6
b) y
Aufgaben aus Abschnitt 13.5.2
ä) h — 0, 2 . tn yn
0	0
0,2 0,0214
0,4 0,091818
h = 0,1 : *4 = 0,4,2/4 = 0, 0918242
b)	h = 0,1 : t2 = 1, 2 , y2 = 0, 941176
fr = 0,05 :
t4 = 1,2, 2/4 = 0,941176
c)	fr = 0,2 :
tn yin	y2n
0	0	1
0,2 -0,163733 0,818733
0,4 -0,268108 0,670324
fr = 0,1 :
*n	frln	y2n
0	0	1
0,1	-0,0904833	0,904838
0,2	-0,163745	0,818731
0,3	-0,222245	0,740818
0,4	-0,268127	0,67032
d)	2/1 := y, y2 := y
fr = 0,1: ^2 = 0,2,
2/12 = -0,58, 2/22 = -2,8
fr = 0,05: *4 = 0,2,
2/14 = -0,58, 2/24 = -2,8
e)	fr = 0,2: *5 = 1, 2/5 = 2,99997
fr = 0,1 : *io = 1, 2/io = 3
Aufgaben aus Abschnitt 14.1
1. a) v(xo,2/o) greift an
Kreis x2 + y2 =
Xq +2/0 an URd weist
radial nach außen.
Alle an den Kreis
x2 + y2 = r2 angrei-
fenden v haben die
Länge r.
b) v(xo,2/o) greift an
Kreis x2 + y2 =
Xq +2/0 an un(l weist
tangential in Rich-
tung mathematisch
positiven Umlauf-
sinnes. Alle an den
Kreis x2 + y2 = r2
angreifenden v ha-
ben die Länge r.
c) Wie Lösung zu la,
nur weist v(xo,2/o)
in Kreisinneres.
d) v(x0,2/0) greift an
Hyperbel x2 — y2 =
a2 mit a2 = Xq — 2/§
bzw. y2 — x2 = a2
mit a2 = 2/0 — xo
oder Gerade y = x
bzw. y = —x an,
steht senkrecht auf
ihr und endet auf x-
Achse.
2. a) von O ausgehende
Strahlen
b) Kreise um O, ma-
thematisch positiv
orientiert
c) Hyperbeln y • x = c
oder (für c = 0) x-
Achse bzw. y-Achse
3. (Beweis)
Aufgaben aus Abschnitt 14.2
297
4. (Beweis)
5. (Beweis)
6. a) 10; z =
( 9
b) (4,-,
$y
10-4x
_MT
z J
c) (4, 3, —2)T ; \/29
7. a) 5; (-1, -4,1)T ;
3V2
b) 0; (0,2)T ; 2
36
x/n
9.	a) Laplace-Feld
b) Poisson-Feld
c) Laplace-Feld
10.	a) div v = 3f (\x|)
+l*l/>l) = o
(CeR)
b) rotv = 0 v ist
für alle differenzier-
baren f wirbelfrei.
11.	a) 92 = —xy — xz — yz
A/ = 0
b)	92 = —x2yz — xy2z
—xyz2
A f = div v
= 2yz + 2xz + 2xy
c)	92 = —xyz
A/ = 0
12.	Ep = 92(0?) = rngz
Aufgaben aus Abschnitt 14.2
1. a) 8	b)	12. —7ia2
b) 4		1	13. —
	c) 2 - -	—	35 /3
2. y(xdy + ydx) = 8	9. a) -16	14. a) 4= f\/2- 11
in beiden Fällen wegen	, 52	V2
dQ _ dP_ dx dy	b)’T c) -12	
	9	(das Integral ist we-
3. a) 1, 5a2	-i rx \ 3d2 10- a) —	gunabhängig)
b) a2	2 „2	r	X
4. 8a2	b)y	15. rot -—— = o \x\3
	11a2	
5. 7ia2	c “V“ n	16. a) wegabhängig
rcrriab 6. —\—	dy	d<^x +	b) wegunabhängig
4	ii.	= ^y	dx	~	c) wegunabhangig
7. 0	1, also	die Integrabi-	d) wegabhängig
x 571	litätsbedingung Py =	
s- a) -	Qx erfüllt.	17. 3a2	
Aufgaben aus Abschnitt 14.3
1. a) 13
. x 8x/2 2
b) ~^~a
ö
c) 27ia2
d>
e) 27tp2v/2
f) 8a2
g) 4a2 (n - 2)
14	2
h) —na2
298
Lösungen
2.	A = J da =
p/3	p90°
/	/ R2 sin 'O di?
7^=0 711=90°— a
= R2ß cos(90° — a)
(R... Erdradius)
7lR2
A= —
3.	-u5
20
4.	967t (Einführung von
Kugelkoordinaten)
5.	4tic
. iß
6.	-7tC
5
4
a4 / 4 7i
 T ( 5 + 16
Aufgaben aus Abschnitt 14.4
1. 3a4
9
4. -- +21n2
5. Hinweis:
Zur Herleitung des
zweiten Greenschen
Satzes wendet man
den Gaußschen Satz
auf den Vektor v =
ui grad 1/2 — 112 grad ui
an.
7. Q = / Qdb
JB
= s div E db
JB
=	[ E  da = a2
(14-15) JF
pTi
x / sini?di?d(/p
7 F=o 7 ii=o
= 4a27ie
x = cos (/?,!/ = sin (/?,
z = 0; p E [0,2tt]
F :
x = cos p sini?,
y = sin p sini?,
z = cosi?; (</?, i?) e B
B :
0 < p < 27t
9.	/ divr db = 84 7t
JB
= / v(x) • der
JF
F = F± U F2 U F3
Fi :
x = 2 cos (/?,
y = 2 sin p, z = z\
(<p, z) e B\
Bi :
0 < </? < 2 71
0 < z < 3
B2 :
x = r cos ip,
y = r sin p, z = 0;
(r ,	6 B2
b2 
0 < r < 2
0 < p < 27t
F3 : wie F2, nur z = 3
f ••• =47t
JF1
jf2
= 36 7t
10.	a) Nach Aufgabe 10
(14.1) gilt divr = 0
für x 7^ o
(14.15)
fF v(x) • der = 0,
wenn F den Null-
punkt nicht um-
fasst.
b) G = 47t
11.	a) Man zeigt leicht:
rot v = o für x mit
x2 + y2 7^ 0.
(14.17)
fkv(x) - da? = 0,
wenn k die z-Achse
nicht umläuft. Au-
ßerdem hängt v
nicht von z ab.
b) Z = 27t
12.	/ [(x + y)dx — 2xdy\
Jk
Za pa—x
/ 3 dy dx
=0 7 i/=o
	Aufgaben aus Abschnitt 14.4	299
_ 1 “ 2	a4 / 4 7t \	, Q 12 5 16. — - H		19- Ta 71 3 \5	16/	5 20. a3 47t 7
15. 47ta3	17. — abc	22. 8na3 ö
HANSER
»Absolut Spitze das Buch!«
Ein begeisterter Leser
Bartsch
Taschenbuch mathematischer Formeln
21.	Auflage
832 Seiten. 510 Abbildungen.
ISBN 978-3-446-40895-1
Das umfassende Taschenbuch zur Mathematik ist ein kompaktes und kompetentes
Nachschlagewerk für Studenten technischer Fachrichtungen an Fachhochschulen
und Hochschulen, für Lehrer und für den Praktiker zum Auffrischen der Kenntnisse.
Bisher weit über eine Million verkaufter Exemplare bestätigen den Erfolg dieser
praktischen Formelsammlung.
•	Zahlreiche Beispiele veranschaulichen die abstrakten mathematischen Formeln
•	Unentbehrlich zur Prüfungsvorbereitung
•	Integraltabellen mit fast 600 unbestimmten und bestimmten Integralen
•	Ein zusätzliches Plus - in vielen Fällen zur Klausur zugelassen
Mehr Informationen unter www.hanser.de/taschenbuecher