Автор: Маланюк М.П. Лукавецький В.І
Теги: завдання з математики олімпіади посібник для вчителів
Год: 1985
Текст
МЛМаланюк,
ВІЛукавецькии
ОЛІМПІАДИ
юних .
математиків
Посібник для вчителів
Видання друге
КИЇВ «РАДЯНСЬКА ШКОЛА» 1985
74.262
хМ18
Рекомендовано управлінням шкіл Міністерства ос-
віти УРСР
МАЛАНЮКМ. П., ЛУКАВЕЦКИЙ В. И. Олимпиадьі
юньїх математикові Пособие для учителей. — 2-е изд.,
перераб. и доп. — К.: Рад. шк., 1985.—88 с. 15 к.
40 000 зкз.
В пособии представлено около 200 олимпиадньїх за-
дач с подробньїми решениями. Задачі! сгруппированьї
по методам их решения: логические, комбинаторньїе, на
отьіскание закономерностей, на построение графиков
функций и геометрических мест, на составление и ре-
шение уравнений. Приводятся условия задач, предла-
гавшихся на XXIV республйканской олимпиаде юньїх
математиков (1984 г.) с указаниями к решениям.
Предназначается учителям математики общербразова-
тельной школьї.
Рукопис рецензували: завідуюча кафедрою методи-
ки викладання математики Київського педагогічного
інституту, кандидат педагогічних наук 3. І. Слєпкань,
вчитель математики С. Б. Маргуліс (м. Тульчин) та
В. А. Я мінський (м. Вінниця).
М
4306010000 —281 _пп о„
М210 (04) —85 2°9 85
Видавництво «Радянська школа».
ПЕРЕДМОВА
Здійснювана в нашій країні реформа загальноосвітньої
та професійної школи має насамперед такий стратегічний
орієнтир: виховати всебічно й гармонійно розвинену особис-
тість, здатну до творчої продуктивної праці. А працювати по-
справжньому творчо може лише та людина, яка в проце-
сі оволодіння основами наук ’ навчилася самостійно поповню-
вати свої знання, пристосовуючи їх до стрімкої динаміки
сучасного виробництва й вимог науково-технічного прогресу.
Отже, формування в учнів навичок самостійної пізнавальної
діяльності і невіддільного від них стійкого інтересу до на-
вчання є одним з найважливіших завдань сучасної школи.
Значна роль в успішному його розв’язанні належить
не тільки урокам, а й різним видам позакласних занять.
Ефективною формою позакласних занять з математики
є математичний гурток, своєрідний підсумок роботи якого
являють собою математичні олімпіади різного рівня: шкіль-
ні, районні, міські, обласні, республіканські, загальносо-
юзні та міжнародні. Олімпіада — змагання, яке стимулює
потяг учнів до самоосвіти, викликає поглиблений інтерес
до математики, настирливість, вміння долати труднощі, ви-
робляє навички роботи 3' довідковою та науково-популярною
літературою.
На математичних олімпіадах пропонуються задачі, які
мають виявити рівень математичної підготовленості учнів,
їхнє вміння логічно мислити, аналізувати, порівнювати, зістав-
ляти. виконувати узагальнення.
До участі в олімпіадах (районних та вищих рівнів)
залучають учнів, починаючи лише з VI чи навіть VII кла-
сів. Проте, як свідчить досвід, шкільні математичні олім-
піади доцільно проводити й серед учнів IV—V і навіть
початкових класів, оскільки вони успішно й зацікавлено
розв’язують досить складні задачі.
Зважаючи на це, а також тому, що бібліотека вчите-
ля математики поповнилася останнім часом цілим рядом
збірників олімпіадних задач, розрахованих на учнів старших
класів, переважна більшість вміщених у цій книжці задач
доступна учням IV — V класів.
З
ОЛІМПІ А ДНІ ЗАДАЧІ
1. Логічні задачі на принцип Діріхле*
1.1. У школі 740 учнів. Довести, що принаймні троє
з них народилися в один і той самий день.
Розв’язання. Якби щодня двоє учнів святкували
свій день народження, то в школі було б 732 учні.
1.2. Довести, що серед 101 цілого числа можна ви-
брати два, різниця яких ділиться на 100.
Розв’язання. При діленні числа на 100 може бути
100 остач: 0, 1,2, ..., 99. Серед 101 остачі, які ми дістає-
мо від Ділення 101 числа на 100, принаймні дві одинакові..
Різниця цих двох чисел і ділиться на 100.
1.3. Довести, що із п 4-1 різних натуральних чисел,
менших від 2п, можна вибрати три таких, сума двох з яких
дорівнює* третьому числу.
Розв’язання. Наприклад, серед чотирьох чисел' 1, 2,
4, 5, кожне з яких менше 6, є три таких, що задовольня-
ють потрібну умову: 1 4-4 = 5. Розмістимо дані числа в по-
рядку зростання і позначимо їх так: аг, а2, а3,..., а^. Утво-
римо числа а2—аг', а3— ау\ а4— а-^ ...; де аг —
найменше з даних чисел. Тоді серед чисел а1$ а2, ..., ал,
ап+1, а2 — а1У ..., ап+і—принаймні два однакових. Справді,
усього чисел 2п 4- 1, і кожне з них — додатне число, менше
від 2л, тому принаймні два з них однакові. Серед даних чи-
сел немає однакових, немає їх і серед утворених різниць, то-
му можлива лише така рівність: а* = а, — а1г звідки а/ = а* 4-
4~ ах.
1.4. У місті налічується 10 000 телефонів, їх номери по-
значаються чотирма цифрами. У центральному районі встанов-
лено більш як половину всіх телефонів. Довести, що хоча б
один з номерів телефонів центрального району дорівнює су-
мі номерів двох інших телефонів цього ж району.
* Твердження, яке називають принципом Діріхле, формулюється так:
„Якщо п 4- 1 об’єктів розмістити на п, місцях, то знайдеться принаймні
два об’єкти, які розмістяться на одному і тому самому місці". У жартівли-
вій формі цей принцип іноді формулюють так: „П’ять кроликів не мож-
на побадити у чотири клітки так, щоб кожний з них сидів в окремій
клітці”.
4
Розв’язання. Позначимо найменший номер телефону
центрального району через а1 і розглянемо номери телефонів
цього району, розміщені в порядку зростання а1г а2, а3, а4,
..., Л500Г Вважатимемо їх чотирицифровими, позначаючи число
1 як 0001, 12 — як 0012, 173 — як 0173 тощо. Утворимо різ-
ниці а2 — а3 — аг, .... а5ооі — Чотирицифрові числа, які
ми дістали, додатні, і їх кількість більша від 10 000. Тому
принаймні два з них рівні, звідки а/ = а* 4- а4.
1.5. У квадраті із стороною 1 довільно розміщені 126
точок. Довести, що деякі шість із них обов’язково лежать
1
усередині круга, радіус якого дорівнює у.
Розв’язання. Якщо поділити квадрат на 25 рівних
квадратиків, то принаймні в одному з них буде 6 точок. Як-
.1
що з центра цього квадрата описати коло радіусом -=7 то всі
точки квадрата лежатимуть усередині круга. Справді, -=
> -уф-, тому цей круг і буде шуканим.
1.6. Щодня протягом року учень розв’язував не менше
однієї задачі, причому щотижня він розв’язував не більше 12
задач. Довести, що знайдеться кілька послідовних днів, за
які він розв’язав рівно 20 задач.
Розв’язання. Вважатимемо, що рік має 52 тижні. За
цей час учень розв’язав не більше як 624 задачі. Позначимо
через ал кількість задач, розв’язаних за перший день; через
а2 — кількість задач, розв’язаних протягом двох днів; через
а3 — кількість задач, розв’язаних протягом трьох днів, і т. д.,
через а364—кількість задач, розв’язаних за 52 тижні. Кожне
з чисел а1г а2, а3, ..., азв4 не перевищує 52- 12 = 624. Усі ці
числа різні. Розглянемо також 364 таких числа: а4 4- 20,
а2 4- 20, а3 4- 20, ..., агв4 4- 20. Серед цих чисел немає жод-
ної пари однакових і кожне з них менше 644.-
Отже, серед 728 цілих додатних чисел, кожне з яких
менше 644, знайдеться -більш як одна пара рівних. Нехай
0* = 0і 20, тоді аи— аі — 20. А це й означає, що за час
між „&-тим“ та „ї-тим“ днями учень розв’язав рівно 20 задач;
До речі, протягом 52 тижнів було 84 таких проміжки часу,
коли учень розв’язував по 20 задач.
У даній задачі достатньо обмежитись часом, значно мен-
шим від року. Аналогічними міркуваннями можна показати,
наприклад, що протягом 77 днів теж знайдеться кілька по-
слідовних днів, протягом яких учень розв’яже рівно 20 задач.
5
1.7. На площині задано 17 точок, з яких жодні три не
лежать на одній прямій. Кожні дві точки сполучено відрізком
одного з трьох кольорів. Довести, що існує трикутник з вершина’
ми в даних точках, сторони якого зафарбовано в один і той
самий колір.
Розв’язання. Припустимо, що не існує такого трикут-
ника. Доведемо, що таке припущення неправильне. Нехай з
деякої точки виходить 16 відрізків, які сполучають її з інши-
ми точками. Серед цих відрізків принаймні 6 зафарбовано
однаково, наприклад, червоним кольором. Очевидно, що жод-
ну пару з цих 6 кінців відрізків вже не можна сполучити червоним
кольором, бо тоді утвориться трикутник, усі сторони якого
зафарбовані в червоний колір. Сполучимо деяку з цих точок
з іншими точками. Серед п’яти утворених відрізків при-
наймні три зафарбовані одним кольором, наприклад, зеленим.
Якщо кінці цих трьох відрізків сполучимо червоним або зеленим
кольором, то дістанемо шуканий трикутник. Такий самий три-
кутник утвориться, якщо сполучити ці кінці відрізками тре-
тього кольору.
1.8. У залі р > 2 людей. Довести, що серед них знайдеть-
ся принаймні дві людини, які мають серед присутніх однако-
ву кількість знайомих.
Розв’язання. Вважаємо, що коли А знайомий з В, то
В знайомий з А. Зрозуміло, не можна вважати, що хтось
знайомий сам собі. Якщо в залі буде принаймні дві людини,
які не мають жодного знайомого серед присутніх, то твер-
дження доведене. Нехай залишилось к осіб, кожна з яких мо-
же мати 1, 2, ..., к — 1 знайомих. На основі принципу Діріх-
ле принаймні дві з к осіб мають однакову кількість знайомих.
2. Інші типи логічних задач
2.1. Довести, що до ощадної каси можна внести без здачі
довільне ціле число карбованців, більше від 7 крб., маючи
купюри лише по 3 і 5 крб.
Розв’язання. Очевидно, що 8, 9, 10 крб. можна внес-
ти зазначеними купюрами. Будь-яке інше ціле число, більше
від.ДО, можна дістати, якщо до одного з цих трьох чисел
додати відповідно число 3/г (к — ціле додатне число). Цю за-
дачу можна розв’язати, використовуючи спосіб математичної
індукції. Число к — 8 задовольняє умову задачі. Припусти-
мо, що, маючи купюри по 3 і 5 крб., до ощадкаси можна
внести к крб. Тоді, забравши одну купюру вартістю 5 крб.
і замінивши її двома купюрами по 3 крб., дістанемо к-\- 1 крб.
Якщо ж число к утворене без купюр по 5 крб., то в
6 •
ньому не менше ніж три купюри по 3 крб. Забравши 9 крб.
купюрами по 3 крб., внесемо замість них дві купюри по 5крб.
і знову дістанемо /^4- 1 крб.
Можливий такий варіант цієї задачі: „Які цілі додатні числа
можна і які не можна записати у вигляді Зх 5//, де х і
у — невід’ємні числа ?“.
2.2. Довести, що дво- і п’ятикопійковими монетами мож-
на розміняти 1 крб. більшою кількістю способів, ніж три- і
п ’ ятикопійковпми.
Розв’язання. Розглянемо числа 100, 95, 90, ..., 10,
5, 0, які можна дістати, віднявши 5 від 100. Серед них біль-
ше тих, що діляться на 2, ніж тих, що діляться на 3. Цю
задачу можна розв’язати ще й так. Невизначене рівняння
2х + % = 100 має більше цілих невід’ємних розв’язків, ніж
невизначене рівняння Зх -{- 5у = 100.
2.3. В автобусі їхали 20 учнів. Маючи монети лише по
10, 15 і 20 к., кожний з них розрахувався за проїзд і одер-
жав відповідну здачу. Довести, що в учнів було не менше
25 монет.
Розв’язання. Оскільки кожний учень одержав не мен-
ше однієї монети, а в касу опустили не менше 5 монет, то,
очевидно, в учнів було не менше 25 монет.
Легко показати, що 5 монет — мінімальна кількість для
оплати проїзду 4 чоловік. Це монети 15, 15, 10, 10 і 20 к.
Тому можна довести, що в учнів разом має бути не менше
З крб. 50 к., бо (15 Ч- 20 4- 15 + 10 + 10) • 5 = 350.
2.4. В одному місяці три середи випали на парні числа.
Якого числа в цьому місяці була друга неділя?
Розв’язання. Це можливо лише тоді, коли місяць
розпочинається з вівторка. Друга неділя припадає на 13-й день
місяця.
2.5. Було 6 аркушів паперу. Деякі з них розрізали на
6 частин, потім деякі знову розрізали на 6 частин. Коли
підрахували загальну кількість аркушів, то виявилося, що
їх було.1984. Довести, що підрахунок виконано неправильно.
Р о з в ’ язання. Внаслідок кожного розрізування кіль-
кість аркушів збільшується на 5, тому загальне число арку-
шів, зменшене на 6, повинно ділитись на 5. Цієї властивос-
ті число 1984 не має.
Запропонуємо ще кілька задач такого типу, які можна роз-
в’язувати „з кінця“, тобто з аналізу передбачуваної відповід1’.
2.6. Маємо аркуш паперу. Розріжемо його на 8 або 12
частин. Далі кожну з них знову розріжемо на 8 або 12 час-
тин, або ж залишимо без змін. Чи можна, продовжуючи та-
ким чином розрізування, дістати 60 частин з цього аркуша?
7
Розв’язання. Після кількох розрізувані дістанемо
14-7/г + 11п частин аркуша, де к— кількість розрізувань
на 8 частин, п — кількість розрізувань на 12 частин. Рів-
няння 1 + 7к 4- 1 \п = 60 не має розв’язків у цілих числах,
к 59 — 7к
бо п = —— при жодному цілому 0 с к < 8 не буде ці-
лим числом.
2.7. У туриста був рюкзак, чемодан, саквояж і кошик.
Маса чемодана більша від маси рюкзака; маса саквояжа і рюк-
зака разом більша від маси кошика і чемодана, але маса ко-
шика і саквояжа разом така сама, як і маса чемодана і рюк-
зака. Маса якого з цих вантажів найбільша, а якого най-
менша?
Розв’язання. Позначимо масу предметів їх першими
буквами: Дістанемо співвідношення ч> р; с 4- Р > я 4- 4 і
к с = ч р. Додавши почленно два останні співвідношення,
дістанемо, що с > ч. З різниці цих співвідношень випливає,
що р > к. Тому, с > ч > р > к.
2.8. Дано набір 2/г різних чисел. Як розбити цей набір
на пари* так, щоб сума добутків усіх цих пар була найбіль-
шою? В якому випадку сума добутків буде-найменшою?
Розв’язання.. Розмістимо дані числа у порядку зростан-
ня. Доведемо, що сума ага.2 4- а3а4 4- ... 4- а2л-іЯ2п = $ буде
найбільшою. Покажемо, що а2„_1а2л є доданком 5. Припус-
тимо супротивне. Нехай два найбільші числа а2л-і і є спів-
множниками інших доданків: а.2Пак 4- я2л-іСр- Покажемо, що
незалежно від значень індексів к і р а2Па2П-і 4- аьаР > а2п X
X йк 4~ а2п-іО,р. Справді, цю нерівність можна подати так:
{а2П — вр) • (а2п-і — ак)>0. Аналогічно покажемо, що й ін-
ші попарні добутки є доданками 5. Неважко довести, що
сума 4-02а2л-і + ••• + буде найменшою.
2.9. За квадратним столом університетської їдальні під
час обіду зустрілись чотири колишні однокласники, які на-
вчаються на різних факультетах. Математик сидів проти Ва-
силя поруч з майбутнім істориком. Біолог сидів біля Андрія.
Сусіди Григорія — Борис та філолог. Чи можна дізнатись,
на якому факультеті навчається кожний юнак і як вони роз-
містились за столом?
Розв’язання. Якби Василь був філологом, то Андрій
мусить бути біологом. Але це суперечить умові задачі, тому
Василь — біолог, тоді Григорій — математик, Андрій — філо-
лог і Борис — історик. Проти Василя сидів Григорій, а про-
ти Андрія — Борис.
2.10. У ящику лежить 100 кульок: ЗО червоних, ЗО си-
ніх, ЗО зелених, решта — білі та чорні. Яку найменшу кіль-
8
кість кульок треба вийняти, щоб. напевно дістати 20 кульок
якого-небудь одного кольору?
Розв’язання. Розв’ язуючи такі задачі, корисно пере-
фразувати запитання задачі так: Яку найбільшу кількість
кульок можна вийняти так, щоб при цьому не можна було б
дістати 20 кульок одного кольору? Зрозуміло, що серед
19 + 19 + 19 + 10 = 67 кульок може не бути 20 кульок
одного кольору, зате серед 68 кульок 20 кульок одного ко-
льору будуть обов’язково.
2.11. Трьом учням у темній кімнаті наділи на голови
чорні шапки. Перед ними поставили завдання: відгадати, хто
в якій шапці, якщо всіх шапок було п’ять, причому дві з них
сірі і три чорні. Сірі шапки заховали перед тим, як у кім-
наті увімкнули світло. Через деякий час один учень відгадав,
що він у чорній шапці. Як він це зробив?
Розв’язання. Цей учень міркував так: „Припустимо,
що я в сірій шапці, тоді мій сусід зліва буде бачити мене
в сірій, а третього учня в чорній шапці. Оскільки сірих шапок
дві, то один з моїх товаришів повинен відразу здогадатись,
що він у чорній шапці. Але він мовчить, а тому я не можу
бути в сірій шапці. Отже, на мені чорна шапка".
2.12. Дано півсклянки води і півсклянки молока. Три
ложки води долили до молока, а потім три ложки суміші
знову перелили в склянку з водою. Чого виявилось біль-
ше внаслідок цих переливань: води в молоці чи молока
У воді?
Розв’язання. Порівну, бо скільки відлили молока,
стільки ж долили води.
2.13. Три подруги одягли плаття різних кольорів. Одна —
блакитне, друга — біле і третя — зелене. їхнє взуття було
не таких самих кольорів, як плаття; лише в Олі колір взут-
тя і плаття був однаковий. Наталка була в зелених босоніж-
ках. Плаття і взуття Валі не були білими. Хто і як був
одягнений?
Розв’язання. Зрозуміло, що колір Валиного взуття
блакитний. Отже, Оля була у білому платті і білих босоніж-
ках. Наталка одягла блакитне плаття, а Валя — зелене.
2.14. Один з трьох братів забруднив чорнилом скатерку.
На запитання, хто це зробив, Олекса відповів: «Віктор не за-
бруднював скатерку, це зробив Борис». Віктор заперечив, що
Борис цього не міг зробити, а сам він ще не сідав до столу.
Борис твердив, що не Олекса забруднив .скатерку, бо це зро-
бив Віктор. З'ясувалося,"що два брати обидва рази сказали
правду, а один брат дав дві неправдиві відповіді. Хто забруд-
нив скатерку?
9
Розв’язання. Відповіді Олекси і Бориса суперечать
□дна одній і не можуть бути одночасно правдивими. Це саме
можна сказати про відповіді Віктора та Олекси. Тому неправ-
ду сказав Олекса, отже, скатерку забруднив Віктор.
2.15. Один із п’яти братів розбив вікно. На запитання
батька вони відповіли:
Андрій. Це зробив або Віктор, або Борис.
Віктор. Це зробив не я і не Юрко.
Борис. Ви обидва говорите неправду.
Дмитро. Тільки один з братів сказав правду.
Юрко. Ні, Дмитре, ти сам говориш неправду.
Батько переконаний, що принаймні три брати сказали прав-
ду. Хто розбив вікно?
Розв’язання. З Борисової відповіді, яка суперечить
сказаному раніше Віктором та Андрієм, випливає, що він
говорить неправду. Тому твердження Андрія і Віктора прав-
диві. Отже, вікно розбив Борис.
2.16. Кожний з трьох друзів зіграв однакову кількість
шахових партій з іншими. Перший з них виграв найбільшу
кількість партій, другий програв найменшу кількість партій,
а третій дістав найбільшу кількість очок. Чи могло так бути?
Обгрунтуйте свої міркування.
Розв’язання. Таке могло трапитися. Нехай кожні два
друга зіграли між собою по 10 партій. При цьому перший ви-
грав у другого 3 партії, а другий виграв у нього стільки ж.
У третього перший виграв 4 партії, але програв йому п’ять
партій. Усі інші партії закінчилися внічию. Тоді перший, який
виграв 7 партій, програв 8 і 5 закінчив внічию, матиме 9,5 оч-
ка, другий, який виграв 3 партії і програв 3 партії, а в чо-
тирнадцяти партіях набрав по 0,5 очка, матиме 10 очок. Тре-
тій набере 11,5 очка, бо в нього 5 виграшів, 4 програші і
11 нічиїх.
2.17. Два учні на змаганнях із стрільби зробили по 5 по-
стрілів. При цьому були такі попадання: 10, 9, 9, 8, 8, 5, 4,
4, 3 і 2. Відомо, що за перші три постріли вони набрали од-
накову кількість очок. А за три останні перший учень набрав
у три рази більше очок, ніж другий. Визначити, скільки очок
кожний з них набрав під час третього пострілу.
Розв’язання. Найменша кількість очок, яку зарахову-
ють за три постріли, дорівнює 9, а найбільша 28. Очевидно,
що перший учень за три останні постріли дістав 27 очок, а
другий — лише 9. Це стає можливим, коли перший набере від-
повідно 10, 9, 8 очок, а другий —2, 3, 4 очки. Під час пер-
ших двох пострілів було вибито 9, 8, 4, 5 очок. Сума очок
за перші два постріли першого учня принаймні на 4 менша
10
від суми очок за перші два постріли другого. Тому перший
набрав за два постріли лише 9 очок, а другий 17. Щоб ці
суми були рівні між собою від додавання по одному додан-
ку, потрібно, щоб перший учень під час третього пострілу
набрав 10 очок, а другий — лише 2.
2.18. Серед шести офіцерів, прізвища яких починаються
буквами А, Б, В, Г, Д, К, три полковники, два майори
і один капітан. Відомо, що А першим вітає Б\ що Г і Д ма-
ють однакові звання; що В і К служать в одному полку.
Полковник, майор і Г — танкісти, Б і капітан—артилеристи.
Один із офіцерів — зв’язківець. Яке він має звання? Яка пер-
ша буква його прізвища?
Розв’язання. В умові підкреслено, що Б і капітан —
артилеристи, тому В і К мають бути танкістами. Один із
них — полковник, а другий — майор. Оскільки Г і Д мають
однакові звання, то капітаном може бути лише А. Тоді Д —
зв’язківець. Він має з Г однакові звання. Майорами вони не
можуть бути, бо тоді майорами були б Д, Г і ще один тан-
кіст. Отже, Д — полковник.
2.19. Плитка шоколаду складається з 35 квадратиків (7 х
X 5 мм). Її ламають по прямих, що розділяють квадратики,
доти, поки не буде 35 окремих квадратиків. Скільки разів
доведеться ділити плитку шоколаду?
Розв’язання. При будь-якому розламуванні кількість
квадратиків збільшується на 1. Щоб вийшло 35 квадратиків
з однієї плитки, треба розламати її 34 рази.
2.20. Яку найбільшу кількість слонів можна розставити
на шахівниці, щоб жодні два з них не були під взаємною за-
грозою?
Розв’язання. Слон, який стоїть на внутрішній клітці
шахівниці, тримає під загрозою більшу частину кліток, ніж
слон, який стоїть на клітці будь-якого крайнього ряду (го-
ризонтального чи вертикального). Треба розставити слонів
так, щоб вони загрожували найменшій кількості кліток, отже,
їх слід поставити на клітки одного з крайніх рядів. Ці вісім
слонів не загрожуватимуть шести кліткам протилежного край-
нього ряду (в цьому ряді під загрозою поставлених восьми
слонів лише дві крайні клітки) — на ці шість кліток і поста-
вимо ще по слону на кожну. Отже, 8 + 6= 14 слонів, це
найбільша кількість слонів, яку можна розставити на шахів-
ниці, щоб жодні два з них не були під взаємною загрозою.
2.21. Вантаж 270 ц упаковано в певну кількість ящиків,
масою яких можна нехтувати. Маса кожного ящика з ванта-
жем не перевищує 700 кг. Довести, що цей вантаж можна
перевезти на 11 тритонних автомашинах.
11
Розв’язання. Завантажимо першу машину так, щоб увесь
вантаж не перевищував 3000 кг. Останній ящик знімемо і по-
кладемо поряд з машиною. Завантажимо таким способом 8 ма-
шин. Маса вантажу на машинах і поряд з ними не перевищує
8 • 3000 кг = 24 000 кг. Тому вантаж, який залишився, забере
дев’ята машина, 8 ящиків, що лежать поряд з автомашинами,
можна розкласти по 4 на кожну з двох останніх автомашин.
3. Задачі на зважування
Серед логічних задач певне місце займають задачі на зва-
жування: за допомогою терезів без пір пропонується за пев-
ну кількість зважувань, виявити один з предметів, що відріз-
няється від інших лише масою. Найпростіші з таких задач ті,
в яких відомо, чи більша маса шуканого предмета від маси ін-
ших чи ні^Крім того, цей предмет — один серед інших (тоб-
то всі інші мають однакову масу). Загальний спосіб розв’язу-
вання таких задач полягає в тому, що задану сукупність пред-
метів ділять на три рівні частини. Коли її не можна поділи-
ти без остачі, то дві частини роблять рівними, а третю —
близькою до кожної з них (трохи меншою). При такому по-
ділі за одне зважування виділяється частина, що містить шу-
каний предмет. Далі процес повторюється, аж поки виділена
третина складатиметься з одного предмета. Якщо ми маємо
а предметів, то легший (важчий) з них виділиться за п зва-
жувань, де З"-1 < а < З". Починати розв’язування таких за-
дач треба з найпростішого випадку (три предмети). .
3.1. Серед трьох монет одна фальшива (легша від двох ін-
ших, однакових за імасою). За допомогою одного зважування
на терезах без гир виділити фальшиву монету.
Р о з в’я з а н н я. Покладемо на кожну шальку терезів по
одній монеті, а третю відкладемо. Якщо шальки перебувають
у рівновазі, то відкладена монета і є фальшивою; у протилеж-
ному випадку терези покажуть легшу, тобто фальшиву, монету.
3.2. З 61 монети за 4 зважування виділити фальшиву (важ-
чу за справжні).
Розв’язання. Розділимо монети на три групи: 21,
21 та. 19. На терези покладемо перші дві групи по 21 монеті.
При цьому можуть бути два випадки: 1) шальки терезів зрів-
новажені; 2) не зрівноважені. Розглянемо кожний з цих ви-
падків. .
1) Шальки зрівноважені, отже, важча монета серед 19 від-
кладених. Розділимо ці 19 монет на три групи (7, 7 і 5) та
порівняємо на терезах масу перших двох груп (це буде друге
зважування). Знову може трапитись, що терези:
12
а) зрівноважені;
б) не зрівноважені.
У випадку а) фальшива монета серед п’яти відкладених.
З них за наступні два зважування спочатку порівняємо 2 та 2
монетп, відклавши п’яту; якщо п’ята не фальшива, то зважу-
ємо дві монети з тієї шальки, що переважила.
У випадку б) фальшива монета серед 7 монет. Розділимо
цю групу на З, 3 і 1 монету та покладемо на шальки тере-
зів по три монети і т. д. І в цьому випадку для розв’язуван-
ня потрібно не більш як чотири зважування.
2) Шальки з монетами (на кожній по 21) не зрівноважені.
Відклавши 7 монету покладемо на кожну шальку по 7 мо-
нет. Це буде друге зважування. Отже, і в цьому випадку
потрібно чотири зважування.
У тому разі, коли з умови задачі невідомо, яка маса «особ-
ливого» предмета (легший він чи важчий від інших), для
його виділення необхідно, як правило, виконати додаткове зва-
жування. Так, у задачі про виділення з 9 монет однієї фаль-
шивої (невідомо, легша вона від справжніх чи важча) двома
зважуваннями вже не обійтись, доведеться переважувати мо-
нети тричі.
Іноді такі задачі дещо видозмінюють, вводячи, наприклад,
обмежену кількість гир певної маси.
3.3. Є 5 монет, серед яких одна фальшива (невідомо, лег-
ша вона чи важча від справжньої). Маса справжньої монети
5 г. Як за допомогою двох зважувань на 'терезах можна ви-
явити фальшиву монету, маючи одну гирю масою 5 г?
Розв’язання. Позначимо могіети А, В, С, О, Е. По-
кладемо монети А і В на одну шальку терезів та монету С
з гирею — на другу. Якщо терези зрівноважені, тоді фаль-
шива монета серед відкладених Р та £. Наступним зважу-
ванням, поклавши на терези гирю та монету Р, виявляємо
фальшиву (при рівновазі терезів—Е', при нерівновазі — Р).
В одному з- цих випадків не можна встановити, легша чи важча
фальшива монета, але цього й не вимагається в умові задачі.
Коли ж терези не зрівноважені, слід розглянути два ви-
падки. Якщо переважує шалька з монетами А і В, то фаль-
шива монета серед трьох: А, В (тоді вона важча) або С (то-
ді С легша). Відкладені ж монети Р та Е — справжні.
Для другого зважування покладемо на одну шальку те-
резів монети А та С, а на другу — обидві справжні (або од-
ну справжню і гирю, що одне й те саме), а монету В від-
кладемо'. Якщо зважувані монети зрівноважаться, то- монета
В — фальшива (важча від справжньої). Якщо ж терези не зрів-
новажені і переважує шалька з монетами А та С, то фаль-
13
шпва А (важча), коли ж ця шалька легша, то і фальшива мо-
нета (С) легша.
3.4. З 12 монет одна фальшива, причому невідомо, важ-
ча вона чи легша від справжніх.' За три зважування на тере-
зах без гир треба виділити фальшиву і визначити, легша во-
на чи важча від справжньої.
Розв’язання. Схема розв’язання показана на мал. 1.
Монети на ній пронумеровані від 1 до 12, значком А позна-
чено шальку, яка при зважуванні йде вгору, значком V —
шальку, що йде вниз; знак = означає рівновагу шальок; дво-
стороння стрілка позначає дію, яка випливає із знайденого
Мал. 1.
результату; одностороння стрілка вказує на фальшиву моне-
ту; якщо монета, можливо, фальшива і легша від справжніх,
її позначено рискою над номером монети (наприклад, 4); як-
що ж монета, можливо, фальшива і важча від справжніх, то
риска ставиться під номером монети (4); якщо ж точно вста-
новлено, що монета фальшива, то на це вказує літера Ф,
наприклад: П (Ф)— легша від справжньої; 11 (Ф) — важча
від справжньої.
Під час першого зважування покладемо на кожну шальку
по 4 монети. При цьому може трапитись два випадки.
1) Якщо шальки терезів зрівноважені, то Ф (фальшива
монета) має один з номерів 9, 10, 11, 12. Візьмемо три та-
ких монети (на схемі 9, 10, 11) і порівняємо їх масу з масою
трьох монет з номерами 1, 2 і 3. Якщо при цьому терези
залишаться зрівноваженими, то 12-та монета фальшива. По-
рівнявши її імасу з масою однієї з монет 1,2, 3, 4, з’ясуємо,
важча чи легша вона від справжньої: 12 (Ф) чи 12 (Ф). У ви-
падку нерівноваги Ф має один з номерів 9, 10, 11, при цьо-
14
му видно: Ф чи Ф. Третім зважуванням порівняємо 9 і 10;
терези покажуть, яка з монет фальшива, якщо ж маси цих
монет однакові, то відповідь буде: 11 (Ф).
2) Якщо після першого зважування шальки не зрівнова-
жились, тоді одне з двох 2, 3, 4 або 5, 6, 7^ 8? і в обох
випадках кожна з монет 9, 10, 11—справжня.
Для другого зважування на одну шальку терезів покла-
демо монети 9, 10, 11, 5, а на другу — 3, 4, 6, 7. Тоді мож-
ливі такі випадки:
а) Шальки зрівноважені, звідки 8 (Ф) або Ф задовольняє
умову: 1, 2. В останньому випадку третім зважуванням по-
рівняєм масу монет і 2.
б) Переважить шалька з монетами 3, 4, 6, 7. Тоді Ф за-
довольняє умову 3, _4 або 5 (Ф). Третім зважуванням монет
З і 4 виявимо серед них легшу. Вона і буде фальшивою.
Якщо ж маса монет однакова, то фальшивою є монета 5:
вона легша. _
в) Переважить шалька з монетами 9, 10, П, 5. У цьому
випадку фальшива монета — серед монет іншої шальки, на
яку покладено 3, 4, 6, 7, причому Ф задовольняє умову: 6, 7.
Третім зважуванням порівняємо 6 та 7 і виявляємо серед них
фальшиву.
3.5. Маємо 9 монет. З них 8 однакової маси, а дев’ята —
фальшива (легша від інших). Маємо також двоє терезів; од-
ні з них точні, другі неточні. Якщо на шальки неточних те-
резів покласти однакову кількість монет, то вони показують
рівновагу, навіть якщо одна з монет фальшива. Якщо ж на
одній з шальок монет більше, то вона перетягує так само,
як і на точних терезах. За зовнішнім виглядом терези одна-
кові. Яку найменшу кількість зважувань треба зробити, щоб
виявити фальшиву монету?
Р о з в’я з а н н я. Фальшиву монету можна знайти за допо-
могою трьох зважувань. Позначимо монети цифрами від 1 до 9.
Позначимо одні терези буквою А, другі — буквою В. Покла-
демо на кожну шальку терезів по 4 монети. Якщо одна шаль-
ка переважує другу, то це означає, що терези А точні і що
фальшива монета серед монет шальки, яка показала меншу
масу. Два додаткові зважування на цих терезах дозволяють
знайти фальшиву монету.
Якщо шальки терезів показали рівновагу, то це означає,
що або фальшива монета дев’ята, а терези А точні, або
15
терези А неточні (і через це терези В точні), або дев’ята монета
фальшива і терези А неточні. Перекладемо по 3 монети на шаль-
ки терезів В. Якщо терези зрівноважені, то третім зважу-
ванням порівняємо на терезах В дві монети, що їх ми
зважували першого разу на терезах А і не зважували на
терезах В. Якщо і на цей раз монети зрівноважаться, то
фальшивою буде дев’ята монета. Якщо під час другого або
третього зважування не буде рівноваги на точних терезах В, то.
наступним зважуванням обов’язково визначимо фальшиву
монету.
1234 А 5 6 76
Мал. 2.
На мал. 2 схематично зображено варіанти зважуван-
ня. Умовні позначення на цій схемі ті ж самі, що й на
мал. 1.
Оскільки ми не знаємо, на яких терезах розпочали зва-
жування, двома зважуваннями обійтись неможливо, тому в
усіх випадках треба робити три зважування.
3.6. За допомогою терезів і гирки масою в 1 г відважити
1 кг цукру за найменшу кількість зважувань.
Р о з в’я з.а н н я. Позначимо: Л та П — відповідно ліва та
права шалька терезів, Г — гирка масою в 1 г.
Відваживши за допомогою гирки масу цукру в 1 г (на Л)
покладемо туди ж і гирку, що дасть змогу на другий раз
відважити 2 г цукру. Всиплемо його на Л — там буде вже
З г цукру, покладемо туди ж гирку і відважимо ще 4 г. Хід
відважування зрозумілий з такої схеми:
16
№ 1 2 3 4 5 6 7 8 9 10
П 1 2 4 8 16 31 63 125 250 500
Л Г 1 + Г 3 + Г 7 + Г 15+ Г 31 62 4-Г 125 250 500
Отже, щоб відважити 1 кг цукру гиркою в 1 г, потрібно
10 зважувань. Доведемо, що меншою кількістю зважувань
обійтись не можна. Дійсно, за одне зважування маса щойно
відваженого цукру не може перевищувати масу перед цим
відваженого цукру більш ніж на 1 г, тобто за 9 разів не-
можливо зважити більше 511
3.7^ У кожному з 10 гаманців міститься по 10 монет,
причому в одному з них усі монети фальшиві; маса кожної
з них на 1 г більша від маси справжньої монети. Враховуючи, що
маса справжньої монети невідома, за одне зважування ви-
явити, в якому з гаманців містяться фальшиві монети. Для
зважування можна користуватись набором потрібних гир.
Задача розв’язується аналогічно до попередньої.
4. Комбінаторні задачі
Під час математичних змагань часто пропонуються різно-
манітні задачі, які вимагають уміння підраховувати кількість
елементів заданої сукупності.
Наводимо окремі задачі цього типу.
4.1. Скільки існує цілих додатних чисел, менших від 100, які:
діляться на 2 і 3;
діляться на 2, але не діляться на 3;
діляться на 3, але не діляться на 2;
діляться на 3 або на 2;
не діляться ні на 2, ні на З?
Розв’язання. Числа, які одночасно діляться на 2 і
на 3, діляться на 6. Серед перших 99 додатних чисел є ли-
ше 16, кратних 6, або 6 • 16 + 3 = 99. Отже,.чисел, які одно-
часно діляться на 2 і на 3, буде 16.
Щоб знайти числа, які діляться на 2, визначимо кількість
парних чисел, більших від 1 і менших від 99. Таких чисел
буде 49, бо 49 • 2 + 1 = 99. Але серед цих парних чисел є
і такі, які діляться на 3. Вище ми підрахували, що їх 16.
Тому чисел, які діляться на 2, але не діляться на 3, буде
49—16 = 33.
Чисел, які діляться на 3, буде 33. Оскільки 33— 16 = 17,
то цілих додатних чисел, менших від 100, які діляться на З,
але не діляться на 2, буде 17.
17
Чисел, що діляться на 3 або на 2, буде 49 4- 33— 16 =
= 66. Якщо від 99 відняти попередній результат: 99 — 66 =
= 33, то дістанемо ті числа першої сотні, які не діляться
ні на 2, ні на 3.
4.2; Скільки існує цілих додатних чисел, менших від 100,
цифри яких ідуть: а) у зростаючому порядку; б) у спадно-
му порядку; в) у незростаючому порядку?
Розв’язання. 1-й спосіб. Цифри додатного двоциф-
рового числа ідуть у зростаючому порядку тоді, коли пер-
ша цифра менша за другу. Однак незрозуміло, як бути з чис-
лами 1, 2, 3, 4, 5, 6, 7, 8, 9. Перетворимо ці числа в дво-
цифрові, ставлячи перед кожним з них нуль: 1 = 01; 2 = 02;
...,9 = 09.
Випишемо підряд усі такі числа: 01, 02, 03, ..., 09, 12, 13,
...» 19, 23, ..., 29, 34, ..., 89 і перелічимо їх. Помічаємо, що
в першому десятку їх 9, у другому — 8, у третьому — 7 і т. д.
У дев’ятому десятку — 1, а в десятому їх взагалі не буде.
Тому треба додати числа 94-84-74-64-54-44-34-24-
4- 1 = 45.
У випадку б) можна зробити такий самий підрахунок, як
і у випадку а). Тоді відразу стане відомо, що відповідь така
сама, як і у випадку а), бо якщо в кожному числі, цифри
якого ідуть у зростаючому порядку, поміняти ці цифри міс-
цями, дістанемо число, цифри якого йдуть у спадному по-
рядку.
До таких чисел, цифри яких ідуть у незростаючому по-
рядку, відносяться числа, цифри яких ідуть у спадному
порядку, і числа, обидві цифри яких однакові. Кількість
чисел із зростаючим порядком цифр ми вже знаємо. Чисел
в однаковими цифрами — 9: 11, 22, 33, 44, 55, ..., 99.
(Відповідь: 54 числа.)
2-й спосіб. Двоцифрових чисел, обидві цифри яких
різні, 90, а чисел, менших від 100, цифри яких однакові —
9. Двоцифрові числа з двома різними цифрами діляться
на два класи, що складаються з чисел із зростаючим по-
рядком і чисел із спадним порядком цифр, причому кількість
перших і других однакова. Отже, чисел із зростаючим по-
, . 90 .с
рядком цифр буде — = 45.
4.3. Скільки існує цілих додатних восьмицифрових чисел,
цифри яких ідуть у спадному порядку?
Розв’язання. Випишемо усі 10 цифр у спадному по-
рядку. Якщо в цьому ряді викреслити дві які-небудь цифри,
то дістанемо восьмицифрове число, цифри якого йдуть у спад-
ному порядку. Йому відповідатиме двоцифрове число, утво-
18
реве викресленими цифрами. Отже, між двоцифровими числами,
цифри яких ідуть у спадному порядку, і восьмицифровими
числами, цифри яких теж ідуть у спадному порядку, можна
встановити взаємно однозначну відповідність. Тому і тих
і других буде 45.
4.4. Скільки існує цілих додатних чисел, менших від
1000, що складаються з різних цифр?
Розв’язання. У попередній задачі ми встановили, що
існує 90 двоцифрових чисел, які складаються з різних цифр.
Якщо до кожного з них дописати третю цифру, яку не ви-
користовували у запису цього числа, то дістанемо трицифрове
число з різних цифр. З кожного такого двоцифрового числа мож-
на утворити 8 трпцифрових чисел з різними цифрами. Буде 720
трицифрових цілих чисел, що складаються з різних цифр.
4.5. Скільки існує додатних трицифрових чисел, цифри
яких записані в зростаючому порядку?
Розв’язання. З трьох різних цифр можна утворити
шість різних трицифрових чисел, серед яких лише в одному
цифри йтимуть у зростаючому порядку. Тому шукані числа
становитимуть шосту частину всіх трицифрових чисел з різ-
ними цифрами, тобто 120.
4.6. Скільки існує трицифрових чисел, перша цифра яких
більша від двох інших, а друга — менша від третьої?
Розв’язання. Таке число дістаємо з кожного трициф-
рового числа, цифри якого йдуть у спадному порядку, якщо
в ньому переставити місцями другу і третю цифри. Таких
чисел буде 120.
4.7. Скільки існує чотирицифрових чисел, які діляться
на 4 і в запису яких немає цифр 3, 0, 8? (Таку умову за-
довольняє, наприклад, число 4564 і не задовольняє число 3548).
Розв’язання. Знайдемо спочатку кількість, чисел, що
діляться на 4. Для цього необхідно, щоб двг останні цифри
цих чисел утворювали число, кратне 4. Можна назвати лише
одинадцять двоцифрових чисел, що діляться на 4 і в запису
яких немає цифр 3, 0 і 8 (наприклад, 12, 52, 72 і т. д.). До
кожного з них допишемо спереду будь-які з цифр 1,2, 4, 5,
6, 7, 9. Тоді з кожного числа ми дістанемо 49 чотирицифро-
вих чисел, що задовольняють умову задачі. Тому всіх шука-
них чисел буде 539.
4.8. Чи 'існує дев’яті і цифрове число, записане цифрами
1, 2, 3, 4, 5, 6, 7, 8, 9, з якого не можна викреслити жодних
п’яти цифр так, щоб чотири цифри, які залишаться, були
записані у зростаючому чи в спадному порядку?
Розв’язання. Існують такі числа. Одним з них буде
число 321 654 987. Якщо будь-які з цифр записані в спадно-
19
му порядку, то вони обов’язково містяться в першій, або в
другій, або в третій трійці. Тому в цьому числі неможливо
вибрати більш як три цифри, записані у спадному порядку.
Аналогічно доводиться, що неможливо вибрати більш як
три цифри, записані у зростаючому порядку.
4.9. Скільки різних добутків, кратних 10, можна утвори-
ти з чисел 2, 3, 5, 7, 9?
Розв’язання. Щоб добуток вибраних чисел ділився на
10, серед співмножників мають бути числа 2 і 5. З трьох чи-
сел, що лишились, можна скласти 8 труп. Одна з них міс-
тить три числа, три містять по два числа і три — по одному
числу. Восьма група не містить жодного з цих чисел. Отже,
з цих п’яти чисел можна скласти 8 шуканих добутків.
4.10. Знайти суму цифр усіх шестицифрових чисел, які
можна утворити за допомогою цифр 2, 3, 4, 5, 6, 7 (цифри
в числах не повторюються).
Розв’язання. Знайдемо всі шестицифрові числа, які
можна записати за допомогою зазначених цифр. На перше
місце можна поставити будь-яку з шести цифр, на друге —
будь-яку з п’яти, що залишились після того, як вибрали
першу цифру. Міркуючи так, визначимо, що всіх чисел буде
720. Сума цифр кожного з них одна і та сама — 27. Отже,
сума цифр усіх чисел буде 19440.
4.11. Яких чисел більше серед перших 10 000 000 цілих
додатних чисел: тих, у запису яких є -1, чи тих, у запису
яких її немає?
Розв’язання. Семицифрових чисел, у запису яких
немає цифри 1, усього 97 — 1. Усіх семицифрових чисел 108,
тому чисел з цифрою 1 буде 108 — (97— 1). Встановимо, яке
з чисел 108 — (97— 1) чи 97—1 більше.
97 = 729 • 729 • 9 = 4 782 969
. . 10 000 000 — 4782 969 = 5 217 032.
Отже, семицифрових чисел, у запису яких є цифра 1, біль-
ше, ніж чисел без цієї цифри. Зауважимо, що для шести-
цифрових чисел таке твердження буде неправильним.
4.12. На площині 10 точок. Скільки існує відрізків, що
сполучають ці точки?
Розв’язання. Відповідь у цій задачі така сама, як
і в задачі 4.3, тобто 45 відрізків. Щоб переконатись в цьо-
му, позначимо 10 точок цифрами 0, 1,2, 3, 4, 5, 6, 7, 8, 9.
Розглянемо тепер будь-який відрізок, що сполучає ці точки.
На кінцях відрізка стоять дві різні цифри. Поставивши їх
у порядку зростання, дістанемо двоцифрове число із зрос-
таючим порядком цифр.
20
Отже, двом різним відрізкам відповідають два різних
числа і двом різним числам—два різних відрізки.
4.13. Чи можна організувати такий турнір, щоб у ньому
брало участь 40 команд і кожна команда зіграла рівно 3 матчі?
Розв’язання. Позначимо кожну команду точкою, а кож-
ний матч, зіграний двома командами,—дугою, яка сполучає
ці точки. Тоді з кожної точки має виходити три дуги. Всіх
40 • З с
матчів буде —х— = 60.
£•4
4.14. Чи можна організувати такий турнір, щоб у ньому
брали участь 13 команд і кожна команда зіграла рівно 5 матчів?
Розв’язання. Як і в попередній задачі, підрахуємо
кількість дуг, які відповідають зіграним матчам: —^—= 32,5.
£*
Кількість дуг не виражається цілим числом, тому такий тур-
нір не можна провести.
4.15. Серед студентів, присутйіх у' кімнаті, 6 знають
англійську мову, стільки ж — німецьку і 7 студентів — фран-
цузьку. Один студент знає всі ці три мови, чотири студен-
ти знають німецьку й англійську, два — французьку і ан-
глійську і 3 студенти знають німецьку і французьку мови.
Скільки присутніх у цій кімнаті, якщо кожний з них знає
хоча б одну мову?
Розв’язання. Для відшукання відповіді скористаємось
табличним записом умови задачі:
а н ф ан аф нф анф
6 6 7 4 2 3 1
Якби з кімнати вийшов той студент, який знає всі три мови,
то таблиця набрала б вигляду:
а н Ф ан аф нф анф
5 5 6 3 1 2 0
Якщо ж вийдуть студенти, які знають по дві мови, таблиця
матиме такий вигляд:
21
а н ф ан аф нф анф
1 0 3 0 0 0 0
У кімнаті залишилося б 4 студенти.* 3 них лише один знає
тільки англійську мову. Оскільки могло вийти 7 студентів,
то шукана відповідь 11.
5. Відшукання закономірностей
5.1. Довести, що к'ожне з чисел виду 16, 1156, 111 556
і т. д., яке дістають вписуванням числа 15 у середину по-
переднього числа, є квадратом натурального числа.
Розв’язання. Неважко побачити, що 16 = 42, 1156 =
= 342, 111556 = 3342 і т. д. Виникає гіпотеза: 2п-цифровим
числом виду 111 ... 1555 ... 56 буде число (33 ... 34)2.
« цифр _ ]) цифра (л — 1) цифра
Доведемо ЇЇ.
Загальний вигляд розглядуваних чисел
111 ... 110000 .... 0 + 555 ... 50 + 6 = 10"(10«—1 +
п цифр /і цифр (л—1) цифра
+ 10"-’ + ... + 10 + 1) + 50(10"-’ + 10"-3 +...+
+ 1) + 6 = 10'1—+5-10 І0П~І~І + 6 =
У У
_ 1()2п 4 . ]0л 4 /]0п + 2\2
“ 9 “ \ 3 ) *
Оскільки число 10"+2 ділиться на 3, то __—ціле
о
число. Отже, дані числа є квадратами натуральних чисел.
5.2. Довести, що числа виду 49, 4489, 444889 і т. д.,
кожне з яких дістають, вписуванням 48 у середину поперед-
нього числа, є квадратами чисел виду 666 ... 67.
(л — 1) цифра
5.3. Якщо між кожними двома цифрами числа 1331 впи-
сати к нулів, то дістанемо куби цілих чисел. Довести це.
Розв’язання. Легко побачити, що 1331 = II3 = (10 +
+ І)3, 1 030301 = 1013 = (100 + І)3 = (102 + І)3. Вписавши
к нулів, дістанемо (ІО*-*-1^ І)3.
22
5.4. Довести, що при натуральному п число 111 ... 1 —
2п цифр
Л . /„ /10" —1\2\
— 222 ... 2 є квадратом цілого числа, і Це число І ——1 ).
п цифр
5.5. Довести, що при натуральному п число 11 ... їх
Зп цифр
X -----11 ... 1-10" є кубом цілого числа. (Це число
п. цифр
/ 10л — 1 \з\
( — г
5.6. Довести, що натуральне число, сума цифр якого до-
рівнює 15, не може бути квадратом цілого числа. Чи може
число, записане у будь-якому порядку за допомогою довіль-
ної кількості нулів і ЗО одиниць, бути' квадратом цілого
числа?
Розв’язання. Дані числа діляться на 3, але не ді-
ляться на 9. Тому вони не можуть бути квадратами цілих
чисел.
5.7. У квадратну таблицю записано підряд числа від 1
до 64. Довести, що, як би з цієї таблиці не вибирали вісім
чисел по одному з кожного рядка і кожного стовпчика, їх су-
ма буде одна і та сама. Знайти цю суму.
Розв’язання. Числа, які містяться в одному стовп-
чику, можна подати як х-{-8(&—1), де х— число з пер-
шого рядка, а к— номер рядка. Оскільки ми будемо брати
по одному числу з кожного рядка і кожного стовпчика, то
в суму вибраних чисел увійдуть як доданки числа 1, 2, 3, 4,
5, 6, 7, 8, а також усі цілі невід’ємні числа, кратні 8, від
0 до 56. Сума їх буде 260.
5.8. У рядок виписано підряд 1976 цифр так, що кожне
двоцифрове число, записане двома сусідніми цифрами, ді-
литься на 17 або на 23. Яка перша цифра, якщо остання 1?
Якою була б остання цифра, якби число починалося з • циф-
ри 4?
Розв’язання. Існує лише 5 двоцифрових чисел, що
діляться на 17, і 4 двоцифрових, що діляться на 23. Якщо
першою записати цифру 2, то дістанемо одну з двох послі-
довностей цифр: 234 692 або 23 468 517. Перша послідовність
циклічно повторюється через кожних 5 цифр, друга — закін-
чується цифрою 7. Останньою цифрою могла б бути 1, якщо
1970-та цифра була 6 2, а це можливо лише тоді, коли
23
запис розпочинається цифрою 3. Якщо запис розпочинається
цифрою 4, то остання цифра буде 4 або 7.
5.9. Тарасик та 'Оленка по черзі набирають воду у по-
ливальниці, -кожна з яких наповнюється через 10 с. Відразу
після їх наповнення Тарасик та Оленка поливають квіти,
спорожнюючи поливальниці відповідно за 60 та 45 с. Потім
знову наповнюють їх водою. Якщо поливальниці не підстав-
лені під кран, вода наповнює бочку, яка стоїть під краном.
Порожня бочка може наповнитись за 15 хв. Хто з дітей пер-
ший підійде набирати воду після того, як бочка наповниться?
Розв’язання. Графічно можна встановити, що через
кожні 230 с процес повторюється. З цих 230 с бочка напов-
нюється протягом 145 с. Вона наповниться за 900 с. Для
цього повинно пройти 6 повних періодів і ще 55 с. Тому
бочка наповнюється через 23 хв 55 с. Першою до бочки,
після того як вона наповниться, підійде Оленка.
5.10. Є дві посудини, в одну з яких налито 1 л води,
а друга порожня. З першої переливають половину води у другу
посудину, а потім з другої переливають третину наявної
там води у першу і т. д. Далі з першої посудини відливають
у другу четверту частину наявної води, з другої переливають
у першу п’яту частину тієї води, яка в ній є в даний мо-
мент і т. д. Скільки води виявиться у кожній посудині після
25-го переливання? Яка кількість води буде в посудинах
після п-го переливання?
Розв’язання. Зауважимо, що з першої посудини від-
1
ливають завжди п _р_— частину води, де п — непарне число, яке
визначає черговий номер переливання, з другої посудини завжди
відливають непарну частину наявної води. Після першого, тре-
тього, п’ятого переливання води в обох посудинах буде порівну,
тому напрошується думка, що після 25-го переливання в обох
посудинах теж буде по л води. Доведемо, що це так. Нехай
п— 1—непарне число. Тоді з першої посудини, в якій ма-
ло б бути -й- л води, відливаємо — частину води. Матимемо
£ ҐІ
І 1 1 п — 1 . „ . п -4- 1- т,
у — • — = ~2п~ у пеРш,и 1 У Другій. Наступне пе-
реливання приведе до рівної кількості води в обох посуди*
. п. 4- 1 п 4- 1 1 п 1
нах. Справді, --------—-------—г = — = —.
г ’ 2л 2л Л 4- 1 2л 2
5.11. Діти стоять колом і вибирають ведучого гри таким
чином: кожна дитина, на яку випадає парний номер, відразу
24
виходить з кола. Підрахунок ведуть у певному напрямку
з місця, яке хтось назве першим. Коло постійно звужується,
поки не залишиться одна дитина. Визначити, хто залишиться,
якщо в колі було 32 дитини. Хто стане ведучим гри у випад-
ку, коли дітей 70?
Розв’язання. Якщо‘дітей було 2, 4,8, . . 2п, то
ведучим стане той,, кого названо першим при підрахунку.
Якщо дітей 70, то залишиться той, на кого випаде номер
в момент, коли дітей залишиться 64. А це буде номер (70 —
— 64) • 2 + 1, тобто залишиться дитина, яка стояла під но-
мером 13 від початку підрахунку.
5.12. Натуральне число п називають зрівноваженим, якщо
в його десятковому запису деякий початок числа збігається
з деяким його кінцем. Наприклад, 1981, 230723 тощо. До-
слідити, чи можуть існувати числа, які стануть зрівноваже-
ними після приписування до них праворуч будь-якої .з деся-
ти цифр.
Розв’язання. Якщо ми користувались лише однією
цифрою, то кожне число у цьому випадку було б зрівноваже-
"ним. Якщо для запису чисел використовують тільки дві цифри:
1 і 2, то записати таке число можна було б, наприклад, так:
121. Яку б цифру не приписати: 1 чи 2, число, яке дістанемо, буде
зрівноваженим. Міркуючи таким чином, бачимо, що число
1 213 121 буде зрівноваженим, якщо у запису беруть участь
лише перші три цифри. Шукане число, очевидно, матиме
вигляд аО#, де а — число, яке зрівноважується приписуванням
будь-якої з дев’яти значущих цифр. Останнє число містить
2к—1, де к— кількість цифр у числі а. Посередині запису
стоїть цифра 0. Чисел, які мають цю властивість, існує без-
ліч, ал$ найменша кількість цифр у шуканому числі буде
210— 1.
5.13. З пункту А в заданому напрямі з сталою швидкістю
і через однакові проміжки часу ходять автобуси, які .йдуть
до наступного міста без зупинок. Дорожній майстер пройшов
4 км, і за цей час його обігнали 6 автобусів. Другого разу
він пройшов 7 км, і його-обігнали 8 автобусів. Третього ра-
зу він пройшов 17 км. Скільки автобусів обігнало майстра
цього разу, якщо всі автобуси кожного разу йшли з одна-
ковою швидкістю?
Розв’язання: За чає, який проходить між моментами
зустрічі з першим і другим автобусами, майстер пройшов х км.
Такі самі відстані він пройде за час між кожними двома по-
слідовними зустрічами. Відстань 4 км не менша, ніж 5 таких
відстаней, але менша, ніж 7. Тому маємо співвідношення
5х < 4 < їх. Аналогічно їх с 7 < 9х. Зіставляючи ці співвід-
25
ношення, знаходимо. > що Проходячи відстань 17 км,
дорожній майстер зустріне 21 або 22 автобуси.
5.14. Відстань між пунктами А і В кратна 5. Автобус
проходить її із сталою швидкістю 60 км/год. Кожні 5 км він
зупиняється на 5 хв. Велосипедист проїжджає цю відстань із
сталою швидкістю за 1 год. Спочатку автобус обігнав вело-
сипедиста, а на зупинці автобуса велосипедист проїхав повз
нього. Потім автобус знову обігнав велосипедиста і більше з
ним не зустрічався. Встановити, чи витратив автобус на про-
їзд від А до В більш як 45 хв чи ні.
Розв’язання. Швидкість велосипедиста має 'бути мен-
шою від ЗО км/год. Тому відстань між пунктами А і В не
перевищує 25 км, і час, протягом якого автобус проходить її,
не перевищує 45 хв.
5.15. За 9 однакових книжок заплатили більше ніж 11 крб.,
але менше ніж 12 крб. За 13 таких книжок заплатили 15 крб.
і кілька копійок, але не більше ніж 16 крб. Яка. вартість
однієї книжки?
Розв’язання. Очевидно, що одна книжка коштує 1 крб.
і х копійок. Враховуючи те, що 200 < 9х < 300, матимемо
23 < х < 33. Але, крім того, х задовольняє умови 200 < ІЗх <
< 300, тому 16 < х < 23. Отже, вартість книжки 1 крб. 23 к.
5.16. Усі цифри деякого чотирицифрового числа, яке є
точним квадратом, можна зменшити на одне і те саме число
так, що нове чотирицифрове число теж буде точним квадра-
том. Знайти всі такі числа.
Розв’язання. Нехай дане число дорівнює а2. Тоді п<
< 100. Позначимо через х число, на яке зменшується кож-
на цифра даного числа. Матимемо а2—1111х = Ь2. Звідки
а2 — Ь2 — 111 їх або {а ~гЬ) • (а — Ь) = 101 • 1 їх. Значення для
а і Ь мають задовольняти рівності а -{- Ь = 101 і а — Ь = 1 їх.
Числа а і Ь різної парності, тому х непарне число. Якщо
х = 1, то а = 56 і Ь = 45, якщо х = 3, то а = 67 і Ь = 34.
Коли х > 3, то число ІЇ2 не буде чотирицифровим. Отже, шу-
кані числа 3136 і 4489.
5.17. У вершинах декількох рівних правильних трикутни-
ків у довільному порядку записано числа 1, 2, 3. Ці трикут-
ники наклали один на одний. Чи може сума чисел у всіх
вершинах, що сумістились, дорівнювати 25?
Розв’язання. Не може, бо тоді сума всіх чисел дорів-
нювала б 75. Проте число 75 не можна дістати описаним
способом, бо воно не ділиться на 6.
5.18. В одному з під’їздів восьмиповерхового будинку на
першому поверсі розміщені квартири від № 97 до 102. На
26
якому поверсі і в якому під’їзді розміщена квартира № 222,
якщо всі під’їзди побудовано однаково і на кожному поверсі
однакова кількість квартир?
Розв’язання. Очевидно, що на кожному поверсі є по
6 квартир, а в одному під’їзді 48 квартир. Оскільки 222 =
= 4 • 48 4- ЗО, то квартира № 222 розміщена у п’ятому під'ї-
зді на п’ятому поверсі.
5.19. Визначити всі цілі додатні п, при яких число 2,:— 1
ділиться на 7. Чи знайдуться цілі додатні значення /г, при
яких число 2Я + 1 ділиться на 7?
Р о з в’я з а н н я. Якщо п = Зк, то вираз 2п — 1 = 23* 1 =
= Зк — 1 ділитиметься на 7. При п = Зк 4- 1 матимемо
23*4-і — 1 = 2-8* — 1 = (8* — 1)4-8* — вираз, який не ділить-
ся на 7. Оскільки 2ЗА можна подати як 7 т 4- 1, то при п =
= 36 4-2 вираз 2з*+2—1 = 4-23* — 1 = 4(7/ті 4-1)-* 1 =
= 28/714~ 3. Отже, якщо п = Зк 4- 2, вираз 2П — 1 при ділен-
ні на 7 дає в остачі 3.
Відповідь на друге запитання задачі заперечна. Якщо п =
= Зк, вираз 2п 4-1 = 23* 4- 1 = 7т 4- 2 в результаті ділення
на 7 дає в остачі 2. Якщо п = 36 4” 1, то вираз 2п 4- 1 при
діленні на 7 дає в остачі 3. Якщо ж п = Зк 4- 2, то 2п 4-
4- 1 = 23*+24- 1 = 4 • 234 4- 1 = 4(7/п 4- 1) 4-1 = 28т 4- 5. Це
число внаслідок ділення на 7 дає в остачі 5.
6. Властивості цілих чисел
6.1. Усі цілі числа, починаючи з 1, виписані підряд. Яка
цифра стоїть на 1975-му місці?
Розв’язання. Одноцифрові числа займають 9 місць,
90 двоцифрових чисел—180 місць. Залишається 1975 —
—Д89 = 1786 місць. 1785 місць займуть 595 трицифрових чи-
сел, останнім з яких буде число 694. Отже, на 1975-му міс-
ці стоятиме цифра 6.
6.2. Знайти найменше трицифрове число, кратне 3, одна
з цифр якого 8.
Відповідь. Шукане число 108.
6.3. Дано п’ятицифрове число 25 762. Яку цифру і на
якому місці слід записати, щоб дістати число, яке ділиться
на 36?
Розв’язання. Число ділиться на 36 тоді, коли воно ді-
литься на 4 і 9. Шукане шестицифрове число поділиться на 4,
якщо друга від кінця цифра в нього буде непарною або ос-
тання цифра кратна 4. Щоб це число поділилось на 9, слід
дописати цифру 5. Її можна дописати лише ца місце десят-
ків. Отже, шукане число 257 652.
27
6.4. Усі цілі числа від 1 до 100 написані підряд. Викрес-
лити з утвореного числа 100 цифр так, щоб утворене число
було найбільшим.
Р о з в’я з а н н я. Треба, щоб в результаті викреслювання
спереду - залишилось якомога більше дев’яток. Перша цифра 9
буде після викреслювання 8 цифр, 4 інші дев’ятки дістанемо,
викресливши 19 • 4 = 76 цифр. З 16 цифр, які ще можна викрес-
лити, 15 витратимо на викреслювання цифр 505152535455565,
щоб залишити найбільшу можливу цифру 7. Після цього ви-
креслимо ще одну цифру 5 і дістанемо число 9999978596061...
99100. ____
6.5. Число ааЬЬ є повним квадратом. При яких а і Ь це
можливо?
Розв’язання.-Відповідь можна знайти в чотиризначних
таблицях квадратів: 882 = 7744. А можна — і на основі влас-
тивостей чисел виду ааЬЬ. Вони, безумовно, діляться на II,
тому число Юх + у, таке, що (Юх + у)2 = ааЬЬ, теж має діли-
тись на 11, причому 10х+г/>31.
Оскільки добуток двох останніх цифр квадрата ц ілого чис-
ла є парне число, то умову задачі можуть задовольнити ли-
ше парні числа 44, 66 і 88. Безпосередньою перевіркою вста-
новимо, що шукане число 88, отже, а = 7, Ь = 4.
Властивість цілих чисел, використану для розв’язання по-
передньої задачі, сформулюємо як окрему задачу.
6.6. Довести, що добуток двох останніх цифр квадрата
цілого числа — парне число.
Справді, (Юх + у)2= 100х2+ 20ху + у2. Сума 100х2-|- 20ху
має парне число десятків. Перевіримо, чи не дає у2 числа,
яке закінчується двома непарними цифрами. Це неможливо,
бо І2 = 1, З2 = 9, 52 = 25, 72 = 49, 92 = 81.
Цю задачу можна сформулювати ще й так: Довести, що
коли дві останні цифри цілого числа непарні, то це число
не може бути точним квадратом.
6.7. Знайти найменше натуральне число, яке закінчується
цифрою 6 і збільшується в 4 рази, якщо його останню цифру
поставити'на перше місце.
Розв’язання. Оскільки остання цифра даного числа 6,
то останньою цифрою числа, більшого в 4 рази від даного,
буде 4. Цифра, яка стоїть перед нею, буде останньою циф-
рою числа 4 • 4 + 2, тобто 8. Перед цифрою 8 стоїть 3, то
8.4 + 1 = 33. Наступна цифра 5, перед нею 1 і остання циф-
ра 6. Отже, шукане число 153846.
Цю задачу можна розв’язати ще й так. Позначимо шука-
не число через ІОх + 6. Записавши цифру 6 на першому міс-
28
ці, дістанемо число 6-10*4-*- Складемо рівняння4(10л*4-
_!_ 6) = 6 • 10* 4~ х. Звідси 39л: = 6(10* — 4). Оскільки число
10* —4 без остачі ділиться на 13, то найменше ціле додат-
не число к, яке задовольняє умову, дорівнює 5, а отже, най-
менше ціле додатне значення х буде 15 384. Отже, шукане
число 153 846.
6.8. Знайти, найменше п’ятиЦифрове число, кратне 360,
всі цифри якого різні.
Розв’язання. Остання цифра шуканого числа 0. По-
трібно підібрати такі чотири різні цифри, сума яких дорівнює
18, щоб скласти з них мінімальне число, кратне 36. Шукане
число 12 960.
6.9. Довести, що не існує відмінних від нуля цілих чисел,
які б подвоювались від перенесення першої цифри в кінець
числа.
Розв’язання. Якщо таке число існує, то має бути пар-
ною цифра одиниць числа, в два рази більшого за дане. До
речі, ця цифра не може бути більшою 5, тому перша цифра
у шуканому числі або 2, або 4. Нехай- розглядуване число
має п цифр, перша цифра з них х. Це число можна подати
так: 10а-1 х 4-У, де у — (п—1)-цифрове число. Після пере-
становки цифри х у кінець числа дістанемо 10г/4-х = 2 х
X (10п~гх 4- у), звідки 8у = х(2 • 10п-1 — 1). Права частина
рівності при жодному цілому п і х не ділиться на 8, тому
числа, про яке йдеться в умові задачі, не існує.
6.10. Три простих числа, більших від 10, утворюють ариф-
метичну прогресію. Довести, що різниця прогресії ділиться на 6.
Розв’язання. Усі дані прості числа непарні, тому їх
різниця ділиться на 2. Покажемо, що вона ділиться й на 3.
Нехай дані числа будуть а 4- 4\ а+ 24. Жодне з них не ді-
литься на 3, тому кожне при діленні на 3 дає остачу 1 або 2.
Звідси випливає, що принаймні два з чисел при діленні на З
мають однакові остачі. Різниця цих чисел, що дорівнює 4
або 24, ділиться на 3. Отже, різниця прогресії, яка ділиться
і на 2, і на 3, ділиться на 6.
6.11. Розв’язати в цілих числах рівняння ху = х + у..
Р б з в’я з а н н я. 1-й спосіб, х = ; * буде цілим
числом, якщо у— 1 = 1 або у — \ =—1. Тому розв’язками
рівняння будуть пари чисел (0; 0) і (2; 2).
2-й спосіб. З умови ху = х4-у дістаємо:
(х— 1) +у— 1) = 1, звідки
х— 1 = 1, [х — 1 = — 1,
і і або ' , ,
(у —1 = 1, (у —1 = — 1.
29
6.12. Знайти трицифрове число, квадрат якого дорівнює
п’ятому степеню числа, утвореного сумою його цифр.
Розв’язання, (х + у + 2)5 = (1 ООх + 1 Оу + г)2. Встано-
вимо, скільки трицифрових чисел є п’ятим степенем цілого
числа: 25 = 32, З5 — 243, 45 = 1024.
Отже, існує лише одне трицифрове число, яке може 31-
довольняти умову задачі. Справді, 2 4-3 + 4 = 9, а 95 = 2432.
6.13. Не існують такі числа, що
аЬссІ — а = 111 ... 11
1981 раз
аЬсі — 6=111...11
1982 рази
аЬссІ — с = 111 ... 11
1983 рази
аЬсЛ — а = 111 . . . 11
1984 рази
Довести це.
Р о з в’я з а н н я. Як бачимо, праві частини даних різнос-
тей, у запису яких є лише одиниці, непарні числа. Жодне з
чисел а, Ь, с, (і не може бути парним, бо тоді одна з різниць
у лівій частині була б парною. Справді, добуток чотирьох
чисел, з яких одне парне, парний. Різниця двох парних чисел
парна.
Ці числа не можуть бути і непарними, бо тоді всі різни-
ці були б парними. Тому таких чисел не існує.
6.14. Поставити замість зірочок цифри так, щоб вийшла
тотожність: (**)3 = (***9)-
Розв’язання. Шукане число двоцифрове, яке не пере-
вищує 22. Крім того, воно закінчується цифрою 9. Тому
задане число 19 (193 = 6859).
6.15. Вік студента у 1977 році дорівнював сумі цифр
його року народження. Скільки років студентові?
Розв’язання. Нехай студент народився у 19хі/ році.
Його вік буде 10 + х + у. Тоді 1900 + Юх + у + 10 + х +
+ у= 1977. 11х + 2(/ = 67. Звідси х = 67-=,гі'.
Оскільки х, у < 9, то х = 5, у = 6. Студент народився
у 1956 році і в 1977 році йому сповнився 21 рік.
6.16. До якого трицифрового числа можна дописати зліва
деякі три цифри, щоб дістати квадрат цього числа?
Розв’язання. Нехай шукане число аЬс. Відомо, що
хугаЬс = аЬс~. Якщо шукане число позначити через /г, то
ЗО
справджується рівність к2— к = 1000/г, де п— ціле число.
Тоді к(к— 1)= 1000/г. Безпосередньою перевіркою легко
переконатися, що ні к ні к—1 не можуть ділитись на 1000.
Оскільки числа к і к—1 взаємно прості, то можливі два
випадки: к ділиться на 8, а к — 1 на 125 або, навпаки,
к—1 ділиться на 8, а к — на 125. Розглянемо кожний ви-
падок окремо. Нехай: к = 8рі к—1 = 125*7. Оскільки к —
трицифрове число, то *7 < 8, Зр = 125*7 4' Число 125*7 4-
4- 1 = 120*7 4- 5*7 + 1 ділиться на .8, тому ділиться на 8
і 5*7 -І- 1, що можливо лише при у = 3. Отже к = 376. Якщо
к = 125р, к—1=8*7, то 125р—1 = 8у; 120р 4-5р—1 =
= 8*7. Число 5р — 1 ділиться на 8, коли р = 5. Звідси к =
= 625. Задача має два розв’язки: 376 і 625.
6.17. Довести, що коли до 1 додати добуток чотирьох
послідовних чисел, то дістанемо повний квадрат.
Розв’язання. 14-п(и—1)(п 4- 1)(л 4- 2) = 1 (п2—1)
(/г2 4- 2/г) = 1 + п4 4- 2п3 — п2 — 2п = п4 4- л2 4“ 1 ~Ь 2/г3 —
— 2/г2 — 2п = (/г2 4- п — І)2.
6.18. Якщо число є точним квадратом, то сума його ци(| р
або ділиться на 3, або в результаті ділення на 3 дає в ос-
тачі 1. Довести це.
Розв’язання. Будь-яке число можна подати у вигля-
ді одного з виразів: Зк, Зк—1, 3& 4- 1. Квадрат першого
виразу ділиться на 3, квадрати двох останніх виразів при
діленні на три дають в остачі 1.
6.19. Довести, що ціле число М5 закінчується тією са-
мою цифрою, що й число N.
Вказівка. Нехай число М = . .. 4- Юа 4- Остання цифра чис-
ла № збігається з останньою цифрою числа Лідставивши послідев-
но замість Ь числа 0, 1, . . ., 9, побачимо, що (№— Ь) ділиться на 10.
6.20. Довести, що не існує цілих чисел х і у, які задоволь-^
няли б рівняння 'х2 4- 1978 = у2.
Розв’язання, у2 — х2 = 1978, (у — х) • (у + х) =1978.
Числа х і у однакової парності, тому. (х + #) і (у — х)—
парні числа. їх добуток повинен ділитись на 4, а число 1978
цієї властивості не має.
6.21. Знайти всі пари цілих чисел х і у, які задовольня-
ють рівняння х2 4- х = у4 4- у3 4- у2 4- у.
Розв’язання. Розклавши на множники обидві частини
даного рівняння, дістанемо: х(х 4- 1) = у(у 4- 1) (у2 4- 1 ), або
х(х 4-1) = (у2 4- 1) (у2 4- у). Така рівність можлива, якщо
ліва і права частини дорівнюють 0 або являють собою добуток
двох послідовних цілих чисел. Тому, прирівнюючи до 0
31
можливі множники, дістанемо 4 пари шуканих значень
змінних:
хг = 0; х2 = 0; х3 = — 1; х4 = —1;
//1 = 0; г/2= —1; у3 = 0; */4 = — 1.
Добуток (//2 + 1)(ї/2 + у) можна розглядати як добуток
двох послідовних цілих чисел, відмінних від нуля, лише
при у = 2. Тому х(х + 1) = ЗО, звідки хь = 5, х6 = —6.
Отже, існує ще дві пари цілих чисел, які задовольняють
дане рівняння:
л'5 = 5; у-о = 2; хв = —6; у3 = 2.
6.22. Слюсар та його учень, працюючи разом, виконали
певну роботу за 12 год. За скільки днів кожний з них
зміг би виконати цю роботу, працюючи окремо, якщо робо-
чий день кожного складається з цілого числа годин, причо-
му у слюсаря він на годину довший, ніж у його учня?
Розв’язання. Нехай робітник та його учень викона-
ють цю роботу відповідно за х та у годин. Тоді —+ — =
І х у
= -|у. Оскільки х#=0, #У=0, то 12х 4- 12г/ = ху\ ху'—
—12х—12ї/+144=144; (х — 12) • (у — 12) = 144. Згідно з
умовою, множники х—12 та у—12 — цілі додатні числа.
Розкладемо 144 на множники: 144 = 1 • 144 = 2 • 72 = 3 х
X 48 = 4 • 36 = 6 • 24 = 8 • 18 = 9 • 16 = 12 • 12.
Знайдемо, яких значень набуватимуть х та у залежно
від можливих значень множників х—12 та у.— 12.
х—12 і/-12 X У
1 144 13 156
2 72 14 84
3 48 15 60
4 36 16 48
6 24 18 36
8 18 20 зо
9 16 21 28
У слюсаря може бути семи- або восьмигодинний робочий
день (залежно від кількості робочих днів тижня). Отже,
значення х має бути кратним 7 або 8. Цю умову задоволь-
няють другий, четвертий• та сьомий рядки таблиці. Але в цих
же рядках значення у має бути кратним 6 або відповідно 7.
Обидві ці вимоги задовольняє лише другий рядок.
Отже, робітник зміг би виконати роботу за 14:7 = 2 дні,
а його учень за 84 • 6 = 14 днів.
32
6.23. Довести, що п3 — п ділиться на 6, якщо п — ціле
число.
Розв’язання. Вираз п3 — п розкладається на добуток
п(п 1) (п + 1). Добуток трьох послідовних цілих чисел
ділиться і на 2, і на 3, тому він ділиться і на 6.
6.24. Сума трьох цілих чисел ділиться на 6. Довести,
що й сума кубів цих чисел ділиться на 6.
Розв’язання. Досить показати, що різниця х3 4-
4- р3 4- з3 — (х у 4- г) ділиться на 6. Це справді так, бо
кожний з доданків х3 — х, у3 — у, г3 — г ділиться на 6,
оскільки а3 — а можна подати як добуток трьох цілих по-
слідовних чисел.
6.25. Довести, що р2— д2 ділиться на 24, якщо р і д—
прості числа, більші від 3.
Розв’язання. Кожне з простих -чисел р та д можна по-
дати як 3/? — 1 або 3/г 4- 1 • Але р2 = (Зк + І)2 = 9/?2 ± 6к 4-
4- 1. д- = (3/і -ь 1 )2 = 9п2 + 6п 4- 1 • Отже, їх різниця ділить-
ся на 3. р2 — д2 = (р + д)(р — ?)•
Оскільки р та д непарні числа, то вираз в одних дуж-
ках ділиться на 4, а в других — на 2, отже, їх добуток
ділиться на 8.
6.26. Знайти всі прості р, для яких число р2 4- 14 також
буде простим числом.
Розв’язання. Як і в попередніх задачах, маємо: р2 4-
4-14= (3/г ± І)2 414= 9'£2 ± Зк 4- 15 = 3 (3&2 + 2к 4- 5).
Отже, для будь-якого к вираз ((Зк ± І)2 4- 14) ділиться на 3.
Тому прості числа, які можна подати як Зк + 1, не задо-
вольняють умови задачі. Отже, р = 3, звідки З2 4- 14 = 23 —
— просте число.
6.27. Якщо 1 2 3 .... (п — 2)(п — 1)4-1 ділиться на и,
то п — просте число. Довести це.
Розв’язання. Нехай п— складене число. Тоді воно
має дільник р, причому 1 < р < п.. Але це неможливо, бо
перший доданок, який містить п — 1 множників, ділиться на
р. а 1 не ділиться на р, тому і дана сума не ділиться на р.
Отже, п— просте число.-
6.28. Чи ділиться на 81 число 1111...111?
81 одиниця
Розв'язання. Випишемо дане число так:
11111111110000...000 4- 1111111110000...0004-...4-1111111Н
72 63
Якщо винести за дужки число 11П11111, то в дужках
залишиться число, сума цифр якого' 9. Отже, дане число
ділиться на 92, тобто на 81.
2 4-846
33
6.29. Розв’язати рівняння х3 + [х] = 3, де [х] — найбільше
ціле число, не більше від х.
Розв’язання. Зрозуміло, що число х додатне, причо-
му 1 < х < 2, бо інакше сума не може дорівнювати 3.
[х] = 1; х3 — 2; х = у^2 .
Мал. 3.
X_ І
Розв’язання. За умовою задачі —~---ціле число,
тому х—ціле непарне число.
Отже, Хі = 1, х2 = 3, х3 = 5. Такі задачі зручніше розв’я-
зувати графічно (мал. 3).
6.31. Довести, що вираз п2 + Зп + 5 не ділиться на 121 при
жодному цілому п.
Розв’язання. 1 - й с п о с і б. ;г2 + 3/? +5 = /г2 + 3/г —
— 28 + 33 =(п + 7) • (п — 4) + 33. Числа п + 7 і п — 4 дають
однакові остачі при діленні на 11. Тому/г2 + 3/г + 5 не ді-
литься на 121.
2-й спосіб.
+ З/?. + 5 =
4п= + 12п + 20 _ (2н + З)2 + 11
4 ~ 4
34
Перевіримо, чи може вираз (2а 4- З)3 4- 11 ділитись на 121.
Якщо вираз 2/і 4- 3 ділиться на 11, то (2/г 4- З)2 ділиться.на
121, але другий доданок 11 на 121 не ділиться. Якщо (2/і 4-
4- З)2 не ділиться на 11, то вся сума не поділиться ні на 11 т
ні на 121.
6.32. Знайти всі прості числа виду 1 -\-пп, менші від 1019
(/і — натуральне число).
Розв’язання. Якщо п = 1, то 1 4- пп = 2 — просте
число; якщо п = 2, то 14- пп = 5 — просте число; якщо п =
= 4, то 1 4- пп = 257 — просте число.
Оскільки 1616 > 1019, то потрібно розглядати лише п < 16.
Якщо п— непарне число, відмінне, від 1, то сума 1 4- пп—
парне число, яке не може бути простим. При п = 6 маємо
суму б6 4- 1, яку можна розкласти на множники, як суму тре-
тіх степенів б6 4- 1 = Зб3 4~ 1 • Так само суми 88 4- 1 = 224 4-
4-1 = 25634- 1; Ю10 4- 1 = 1005 4- 1; 1212 4- 1 = (124)3 + 1;
1414 4- 1 = 1977 4- 1- теж розкладаються на множники. Отже,
лише при п = 1, /і = 2, п = 4 дістаємо прості числа.
п оо г> 10а 4- 8 . *
6.33. Вираз —д2— є цілим числом при будь-якому нату-
ральному а. Довести.
Розв’язання. Оскільки сума цифр числа 10а дорівнює
І, то сума чисельника — 9, а таке число ділиться на 9.
6.34. Довести, що нескінченний неперіодичний десятковий
дріб 0,123456789101112 .. ., який дістаємо дописуванням
послідовних натуральних чисел, — ірраціональне число.
Розв’язання. Припустимо, що це не так і в цьому
числі знайдеться період, що містить к цифр. Згідно з законом
утворення нескінченного дробу, ці цифри різні. У результаті
послідовного виписування ми випишемо число, в якому к ну-
лів чи к інших однакових цифр. Зрозуміло, що послідовність
однакових цифр, яку ми дістали-, буде відрізнятись від пері-
оду. а це суперечить нашому припущенню. Отже, дане чис-
ло — ірраціональне.
6.35. При яких значеннях а дріб |~Нг| можна скоротити?
Розв’язання. Нехай й 1 —найбільший спільний діль-
ник чисельника і знаменника при деякому а. Тоді
10а 4- 15 = 5хй\
10а 4- 14 = 2//с?;
1 = (5л— 2//)б/.
•- *
Але 5л*—2у— ціле число, тому 5л—2у = 1 і сі = 1. Отже,
.. 2а 4-З
дріо £—т~7 нескоротний.
2*
35
_ 2а 4-3 <. о . 5а 4-7
Якщо дріб скоротним, то скоротний 1 дріб 2а'^1з ~
__ і 1 । п
~ 2Т+3 £’ ’ .
^О- 4~ 3 л .
В СВОЮ чергу ПОВИННІ скорочуватись 1 дроои -р-т =Г 24-
а ( 1
4- р Але дріб нескоротний, отже, і даний дріб не-
скоротний.
7. Побудова графіків функцій*
7.1. Побудувати графік функції у = 1о£2зіп |х|.
Розв’язання. Функція парна, її графік симетричний від-
носно осі Оу, тому розглянемо поведінку функції при х > 0.
Спочатку побудуємо графік допоміжної функції V = зіп |х |;
для додатних значень, х значення функції будуть періодич-
но повторюватись, тому досить розглянути особливості функ-
ції у ~ 1о§2 зіп | х | на проміжку [0; 2л]. Для х=0 тах£[л;
2л] ЗІП | х | < 0, тому у = 1о§2 ЗІП | х | не існує. На проміжку
функції у = ІО£2 V І V = ЗІП | X | МОНОТОННО ЗроСТЗ-
хЄ]0;
ють, тому зростатиме і функція у = 1о§2 зіп |х|. На проміж-
ку х с ; *
функція, яку ми досліджуємо, спадає. Найбіль-
шим значенням функції у =• 1о§2 зіп | х |, яке відповідає зна-
ченню зіп | х' = 1, буде число нуль. Ці міркування дають
можливість побудувати графік складної функції у = 1о§2
зіп | х | нл проміжку [0; 2л]. Користуючись властивостями
функціїх | та періодичністю функції зіпх, побудуємо шука-
ний графік на всій області визначення (мал. 4).
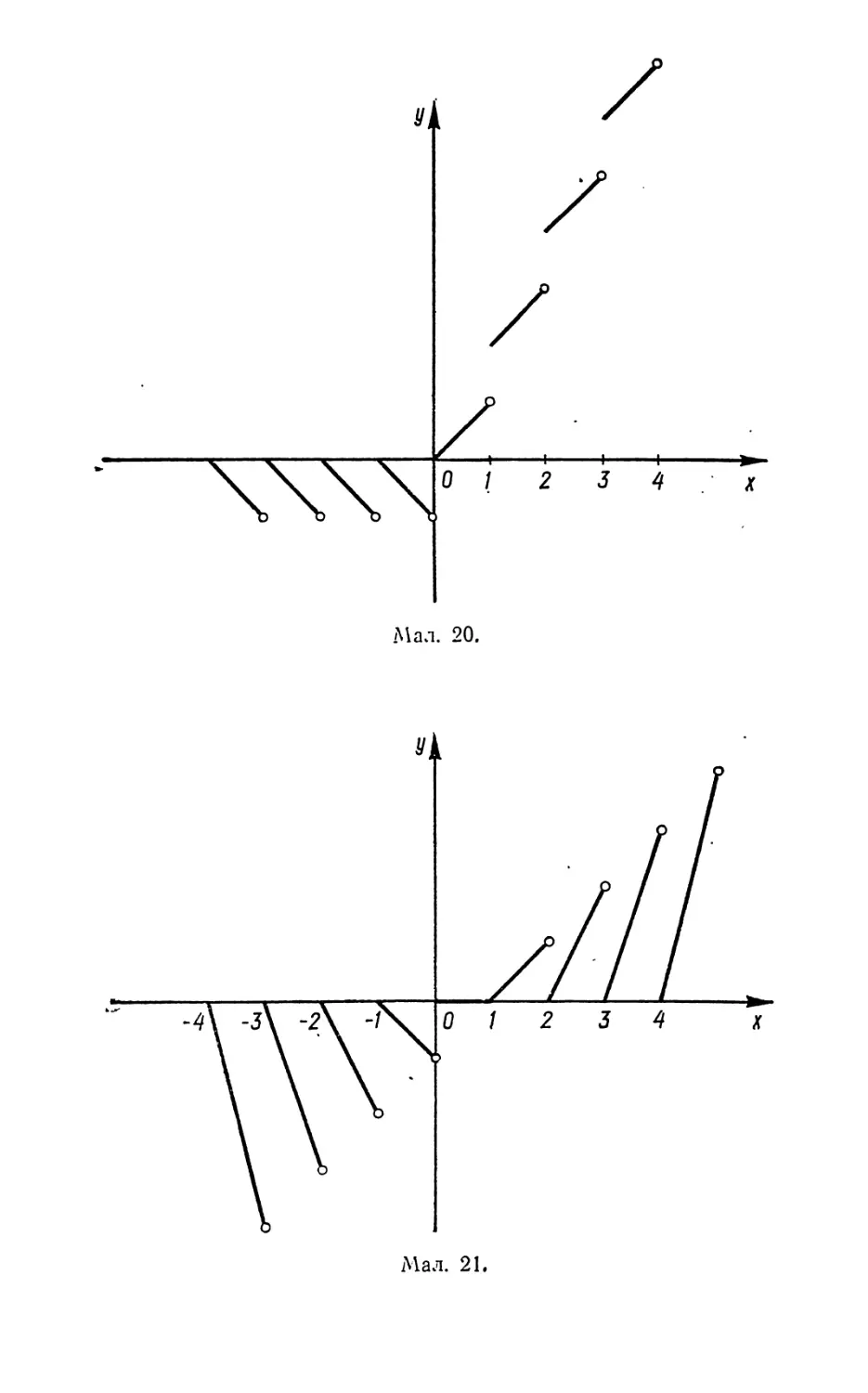
7.2. Побудувати графік функції у = /(х), де /(х) — від-
стані від числа х до найближчого цілого від'ємного числа.
Розв’язання. Дана функція втрачає зміст при значен-
ня.х X =----, де й — оудь-яке ціле додатне число, ос-
кільки -для всіх цих значень х не існує найближчого цілого
(З \
— н-; 01 од-
паково віддалена як від —2, так і від —1. Неважко побачи-
ти, що для будь-яких цілих від’ємних чисел у = 0. Для до-
: Докладніше з побудовою графіків можна ознайомитися за книж-
кою Н. М. Шундн «Функції та їх графіки» (К., Рад. шк., 1983. — 192 с.).
36
датних значень х, як і для чисел з інтервалу ]—1; 0], най-
ближчим ЦІЛИ1М від’ємним ЧИСЛОМ'буде число —1. Тому для
всіх х > —1 у = х — (—1) = х -г 1. Для лівих частин інтер-
валів ]—1£|; — графіком даної функції буде у =
— х — (—| к |) = х + | к |, де |£|#= 1. Для правих частин ін-
тервалів: ]— | к |; | к | 4-1 [ у = / (х) = — \к | 4- 1 — х, де | к |
1 (мал. 5)..
Примітка. Аналізуючи умову задачі, ми вважали, що найближче
ціле від’ємне число—це таке єдине число, яке віддалене від х менше,
. ............, — (2/г 4-1)
ніл< усі інші цілі від ємні числа, тому для випадку х=------4 та-
ких чисел не існувало, і функція втрачала зміст. Якщо ж під терміном
снайближче ціле від’ємне число» розуміти не одне таке число, то най-
37
ближчими цілими від’ємними числами будуть числа —3 і —2. У точках
х =-------— функція існуватиме і дорівнюватиме — . 1 рафік такої
£ і/
7.3. Побудувати графік функції у = | х | + зіп | х [.
На проміжку х £ [0; оо[ побудуємо графік суми двох функ-
цій. тобто побудуємо графіки допоміжних функцій ц = |х| та
ш = зіп|х| (мал. 7, тонка лінія), і знайдемо суму ординат
цих функцій у кожній точці. Оскільки дана функція парна,
відобразимо симетрично відносно осі Оу графік, який ми ді-
стали для л'£!0; оо[ (жирна лінія).
38
7.4. Побудувати графік функції # = 25іп|хі.
Р о з в’я з а н н я. Дана функція парна і періодична на про-
міжках ]—оо; 0[ і ]0; +оо[. Період Т=2л. Побудувавши
графік допоміжної функції ер (х) = зіп х на проміжку [0; 2л]
та врахувавши періодичність даної функції на проміжку [0;
оо] і її парність, дістанемо графік функції у = 25іп| *і (мал. 8).
Застосування графіків іноді дає можливість спростити роз-
в’язання задачі. Так, ми вже бачили, що задачу 6.30 значно
простіше розв’язувати графічно (мал. 8).
7.5. Дана функція = +
Побудувати її графік для х£[—2; 2].
Розв’язання. Для х£ [—2;' 2]у > 0 — графік функції,
розміщений у верхній півплощині. Оскільки функція парна,
то досить побудувати її графік для х > 0
1 4- р4 — х2 > 0, тому 11 4- ]/4 — х21 — 1 4- ]/ 4 — х2.
Розкриємо знак другого модуля: 1) 1—]/ 4 — х2 > 0**
<=*]/ 4 — х2 < 1. Оскільки ]/4 — х2 > 0, то, піднісши до квад-
рата, матимемо:
х2^3 >0=>хЄ]—оо; —]/3]иП/3; 4-°°[.
Тоді у = |(1 + 1<4 + х2 + 1 -У 4-х2) = 1.
Враховуючи область визначення даної функції та викону-
ючи побудову поки що для х > 0, бачимо, що для х £ []/3; 2]
графіком функції є відрізок прямої у =1.
39
о
2) Знайдемо множину значень х, для яких 1—У4— х- <
< 0. Розв’язавши цю нерівність, дістанемо: х£]—] 3;
Для цих х 11—У 4 — х21 = —1-}-]/4—х2, " звідки у =
= У 4 — х2 => х2 Н- у2 = 4, тобто графіком функції на проміж-
ку [0; ]/3] є коло, радіус
якого 2 одиниці, з центром
в (0; 0). Відобразивши цю ча-
стину графіка симетрично
осі Оу, матимемо шуканий
графік (мал. 9).
7.6. Побудувати графік
функції у = 1о§х 10.
Розв’язання. £> (1о§х 10) =
=]0; 1 (О ]1; -гоо[. Аналітич-
ний вираз даної функції замі-
нимо більш зручним: у =
.Побудуємо графік допоміжної функції V—\§>x і, враху-
вавши, що допоміжна функція зростаюча (отже, функція у =
= — спадна), побудуємо шуканий графік. Для контролю
знайдемо точки (10; 1), (0,1; —1), врахувавши, що прих-^-О
«/-> 0, а при х -> 1 (х < 1) //-> —оо, при х —> 1 (х > 1) у-+ -ф
-г оо (мал. 10).
Зауважимо насамперед, що для побудови графіка функ-
ції у = [/ (х)] будують спочатку графік допоміжної функ-
ції V = / (х), а потім прямими у = п (п £ 2) розбивають
40
координатну площину на смуги, що містяться між кожною
парою цих прямих (тобто між у = п та у = п + 1). Ординати
точок перетину графіка у — / (х) з прямими у = її є цілими
числами, тому ці точки пере-
тину належать графіку у =
= [/(х)]. Щоб знайти інші
точки графіка, проектують
частини графіка у = / (х), що
лежать між у = її та у = її -г
+ 1, на пряму у = п. Мно-
жина збудованих у такий
спосіб напіввідкритих (в ок-
ремих випадках — відкритих)
відрізків і утворить шука-
ний графік.
7.7. Побудувати графік
функції ї/[(|х—1) (х — 3)].
Розв’язання. Побуду-
вавши графік допоміжної
функції V = (|х| — 1) (х — 3)
та виконавши вказані вище
допоміжні побудови, матиме-
мо потрібний графік (мал. 11).
7.8. Побудувати графік
функції у = х 4- [х].
Розв’язання. Складе-
мо таблицю.
X И У
[0; і[ • 0 X
[і; 2[ 1 х 1
[2; 3[ 2 х + 2
[д; р -Ь П • • • р х-Ьр
(РЕ2)
Графік зображено на мал. 12.
Зауважимо, що графік можна побудувати також • за
гою додавання графіків функцій V— х та [х].
допомо-
7.9. Побудувати графік функції у =
Розв’язання. Складемо таблицю.
X
41
X [V] У
[0; 1[ [і; 2[ [2; 3[ [3; 4[ • • • ір; р + Н 0 і 2 3 • • • р не існує X X 2 X 3 • • • X р
(р Є 2)
Графік функції зображено на мал. 13.
7.10. Побудувати графік функції #=[|л|].
Р о з в’я з а н н я. Для х > 0 V = [х]. Врахувавши парність
даної функції, відобразимо графік функції V = [х] симетрич-
но відносно осі Оу. Дістанемо шуканий графік (мал. 14).
7.11. Побудувати графік функції г/=|[х]|.
Розв’язання. Будуємо вже знайомий нам графік допо-
міжної функції V = [х]. Скориставшись означенняіМ абсолют-
ної величини, будуємо ту частину шуканого графіка, що від-
повідає значенням аргументу х£]—оо; 0[. Дістанемо шука-
ний графік (мал. 15).
Для побудови графіків функцій виду у = {/ (х)], як і в
попередньому випадку, розбивають координатну площину з
42
побудованим на ній допоміжним графіком а =/(х) на гори-
зонтальні смуги прямими у = п(п£2,). Через точки перетину
проведених прямих з графіком функції у — ї (х) проводять
ще одну серію прямих, паралельних осі Оу. Ті частини гра-
фіка, що попали в утворені прямокутники, будуть відповіда-
ти шуканому графіку, якщо змістити їх в напрямі осі абсцис
4 4
Мал. 16. Мал. 17.
на п одиниць з верхньої півплощини та на п 4- 1 — з нижньої.
7.12. Побудувати графік функції у = {х2 — 4х-{-3).
Розв’язання. Побудуємо графік допоміжної функції
V = х2—4х-|-3. Перетнувши цей графік прямими
43
у = р (р £ 2) та врахувавши означення функції у = {х}, діста-
немо шуканий графік (мал. 16).
7.13. Побудувати графік функції р = {2|х|].
Розв’язання. Дана функція парна, тому спочатку по-
будуємо її графік для всіх л*£[0; оо[. Врахувавши власти-
вість парної функції, дістанемо шуканий графік (мал. 17).
7.14. Побудувати графік функції у = х 4- {х} -4 [х] 4- | х|.
Розв’язання. Враховуючи, що [л] 4- {х} = х, маємо
у = 2х 4- | х |, тобто
_ І Зх при х > 0,
~ ( х при х < 0.
Графік даної функції зображено на мал. 18.
7.15. Побудувати графік функції у = [х] — {х}.
Розв’язання. Побудувавши графік суми двох функцій,
дістанемо шуканий графік (мал. 19).
7.16. Побудувати графік функції у = [х] 4- |х|.
Розв’язання. Міркуємо так само, як і при побудові
попереднього графіка (мал. 20).
7.17. Побудувати графік функції р=[х]-(х).
Розв’язання. Тут краще скористатись означенням ці-
лої та дробової частини числа:
[х] = к при к < х < к 4- 1»
{х} = х — к при /г с х < к 4- 1 (£ С 2).
44
Тоді у = [х] (х) = к (х— к) = кх—к~. Побудову викону-
ємо для кожного інтервалу к с х < к 1 (де к — ціле чис-
ло) окремо (мал. 21).
7.18. Побудувати графік функції //І—;.
Розв’язання. Міркуємо так само, як і при побудові
попереднього графіка (мал. 22).
8. Побудова геометричних місць точок
У задачах на побудову геометричних місць точок (ГМТ)
здебільшого ставиться завдання відшукати всі точки площи-
ни (або простору), кожна з яких має певну властивість. У цьо-
му випадку шукане ГМТ задається, як правило, рівняннями
з двома або трьома змінними, які описують координати точок,
що належать до нього.
8.1. Дано квадрат із стороною 1. Визначити ГМТ, сума
відстаней від яких до всіх сторін квадрата (або їх продов-
жень) дорівнює 3.
Розв’язання. Жодна точка квадрата не належить до
шуканого ГМТ, бо відстань від неї до інших сторін дорів-
нює 2. Це саме можна сказати і про точки, які лежать усе-
редині квадрата.
Нехай точка шуканого ГМТ лежить зовні квадрата, але
так, що основа перпендикуляра, опущеного з цієї точки хоч на
одну сторону, міститься на ній, а не на її продовженні. По-
значаємо відстань до найближчої сторони, на яку проекту-
ється точка, через х. Складемо рівняння: х 4- (х -Ь 1) + 1 =
= 3. Розв’язком цього рівняння буде х — 0,5.
На відстані 0,5 від кожної сторони квадрата проведемо
відрізок довжиною 1, який проектується на цю ж сторону.
46
Матимемо чотири таких відрізки. Якщо кінці їх сполучити,
то вийде восьмикутник, точки якого становлять шукане ГМТ
(мал. 23).
8.2. Знайти ГМТ, з яких протилежні сторони квадрата
видно під однаковими кутами.
Розв’язання. До шуканого ГМТ належать усі точки
осей симетрії квадрата, за винятком його вершин та точок
кола, описаного навколо цього квадрата, за виняткоїМ назва-
них вище вершин (мал. 24).
8.3. Усередині кола.дано дві точки Р і <2. Вписати у ко-
ло прямокутний трикутник, катети якого проходять через
Розв’язання. Припустимо, що шуканий трикутник
побудовано. Якщо точки Р і <2 е кінцями катетів, то відрізок
Рф буде гіпотенузою цього трикутника. Вершина його лежа-
тиме на перетині даного кола і кола, діаметром якого є відрі-
зок Рф. Задача може мати один чи два розв’язки або не ма-
ти жодного розв’язку. Це ж розв’язання дає ті самі вершини
прямокутного трикутника у випадку, коли точки Р і 0, не є
кінцями катетів.
8.4. Дано квадрат АВСО. Знайти ГМТ площини, якщо
сума відстаней від кожної з них до двох протилежних сторін
даного квадрата дорівнює сумі відстаней до двох інших його
протилежних сторін.
Розв’язання. Умові задачі відповідає кожна точка
площини, яка лежить усередині квадрата, і всі точки, які ле-
жать на його сторонах, а також точки, які лежать на про-
довженнях діагоналей квадрата.
8.5. Знайти ГМТ площини, сума відстаней від кожної з
яких до двох протилежних сторін даного прямокутника до-
рівнює сумі відстаней до двох інших його протилежних сторін.
47
Розв’язання. Жодна внутрішня точка прямокутника
не належить до шуканого ГМТ. Не буде до нього належати
і жодна точка, яка лежить між продовженнями більших сто-
рін цього прямокутника. Нехай точка А лежить між продов-
женнями менших сторін прямокутника. Позначимо через х
відстань від неї до ближчої з більших сторін, а через а і
Ь довжини відповідно меншої і більшої сторін прямокутника.
Складемо рівняння: х + а + х = Ь, звідки х = -~~а.
Розглянемо точки, які лежать усередині кутів, утворених
продовженнями двох сусідніх сторін прямокутника. Нехай
деяка точка В віддалена на відстань х та у відповідно від
продовжень більшої та меншої сторін прямокутника. Тоді
х -- х ~ а = у -г У ~г Ь, звідки у = х — —. Шукане ГМТ
зображено на малюнку у вигляді двох ламаних ліній (мал. 25).
8.6. Точка /VI належить відрізкові АВ. На відрізках АМ
та ДІВ як на сторонах побудовані квадрати АМСО та МВЕР,
розміщені по рдин бік від прямої АВ. Кола, описані навколо
квадраив з центрами Р і 0, перетинаються у точках М та N.
Знайти ГМТ середин відрізка коли /И переміщається по
відрізку АВ.
Розв’язання. Нехай Р — середина відрізка РС{, тоді
відрізок РР дорівнює відрізку. РО (мал. 26). Побудуємо
відрізок РРг, перпендикулярний до прямої АВ, РРг АВ
та ± АВ. Чотирикутник РР-&& — трапеція, у якій від-
РР - 00
різок РРг — середня лінія, тому РР± = —1 Оскільки
по АЛІ . МВ гуп АЛІ -Д- ЛІ В АВ
РР1 = 1 <№1 = —, ТО РРі =------Отже, точ-
48
ка шуканої множини належить прямій, паралельній до пря-
АВ
мої АВ, що проходить від неї на відстані 7?^ = —.
8.7. Побудувати на координатній площині ГМТ, коорди-
нати яких задовольняють рівняння | у | = соз х.
Розв’язання. На допоміжному графіку у = соз х (мал.
27, тонка лінія) залишаємо лише ті його частини, де созх >
> 0 (бо |г/1 > 0). Кожній точці залишеної частини графіка
у = соз х (а вони залишені для х £
к £ X) відповідатиме ще одна точка, симетрична їй відносно
осі Ох. Ця точка теж належить графіку рівняння |#| = созх
У
о ІҐ'Ч / X
у = $іпх^
Мал. 28.
(адже |—у\ = |#|). Зрозуміло, що періодичність функції у ==
= соз х враховується під час побудови шуканого ГМТ.
8.8. Побудувати ГМТ, координати яких задовольняють
рівняння | у | = |созес х|.
Розв’язання. Знову побудуємо допоміжний графі-к у =
= Ісозесл'І (мал. 28). На відміну від попередньої, у цій зада-
чі у > 0 для всіх я -|- я&[ з області визначення, то-
му для побудови шуканого ГМТ усі точки допоміжного гра-
фіка дзеркально відобразимо симетрично осі Ох (мал. 29).
З" -1-846
49
8.9. Знайти ГМТ, координати яких задовольняють рівність
[{/] = [х].
Розв’язання. За означенням цілої частини числа
х£[/г; п + 1[ у^[п\ п 4- 1(, де Складемо таблицю зна-
чень [х] та [#]. *
X І И 1 У [//1
[0; 1[ 0 //€[0; 1[ 0
[і; 2[ 1 уї [і; 2[ 1
х С [2; 3[ 2 УЇ[2; 3[ 2
а- € [я; «4-Н • • • п //С [я; л4-1[ • • • п
Таблиця допомагає краще уявити шукане ГМТ. Це буде
сукупність внутрішніх точок квадратів, сторона кожного з
яких дорівнює 1, а діагональ розміщена на прямій у = х. Крім
І 1 1 1 І
------------------1---------------------------------------------------1--------------------------------------------------1-1 г
-уГі 8-і _ 1 _ _
1 ! ! І 1
і х
Мал. 29.
того, до шуканого ГМТ належать точки нижньої та лівої сто-
рін кожного квадрата (мал. ЗО).
8.10. Знайти ГМТ, координати яких задовольняють рівність
|х-1| + |//-1|= 1.
Розв’язання. Прямими у = 1 та х = 1 розіб’ємо коор-
динатну площину на чотири частини і залежно від того, який
знак мають вирази х — 1 та у — 1 у кожній з цих частин, послі-
довно побудуємо шукане ГМТ (мал. 31).
Зауваження. Побудову виду (|х 4- а| 4- \у 4- 6| = 1) можна та-
кож виконати, побудувавши спочатку ГМТ |х| 4- |!/| = 1 та перенісши
координатні осі на відповідне число одиниць.
8.11. Знайти ГМТ, координати яких задовольняють рівність
я 4~ ІЛ"І 4" У 4~ І*/І = 2.
50
Розв’язання. Побудову виконаємо по чвертях коорди -
натної площини.
• Дана рівність після розкриття знака модуля
І X 5 >0, У^ >0 У = 1
II X < ^0, У< »0 У = 1
III X < со, У < с 0 не має смислу
IV х 5 >0, У < С0 = 1
Мал. 33.
Шукане ГМТ подано на мал. 32.
8.12. Знайти множину точок, координати яких задоволь-
няють рівність у + |ї/| = х + |х|.
Розв’язання виконується так само, як і в попередній за-
дачі (мал. 33).
*/23*
51
9. Тотожні перетворення
9.1. Якщо — 4- * = 4, то х = у=£0. Довес-
ху ~г У~
= 1, то (х — у)2 = 0, звід-
ти це.
Розв’язання. Поділивши обидві частини даної рівності на
2, дістанемо + х?+у2 = 2- Якщо сума двох взаємно обер-
нених чисел дорівнює 2, то ці числа рівні між собою і кож-
Х“ ~~~
не з них дорівнює 1. Якщо - -
КИ X = у.
а 9 Якіпп х2-У2 = у2 — хг
9.2. Якщох(1_уг) у{ї_хг} >
х * У 1 2
Довести це.
7
Розв’язання. З умови випливає, що (х2 — уг) (у —
— хуг) = (у2 — хг) (х — хуг), звідси ху (х — у) — хуг (х2 — у2)—
— хуг2 (х — у) + г(х2—у2) = 0 або (х — у) (ху 4- хг 4- уг) =
= хуг (х — у) (х 4- у + г).
Враховуючи згадані обмеження, дістаємо ху + хг 4- уг =
= хуг(х + у + г) або 1+ 4- ^- = х + г/ + г.
9.3. Довести тотожність а3 4- Ь3 4- с3 = ЗаЬс, якщо а 4-
4- Ь 4- с = 0.
Розв’язання. З умови випливає, що а 4- Ь = —с.
Піднесемо обидві частини цієї рівності до куба. Дістанемо:
а3 4- Ь3 4- ЗаЬ (а 4- Ь) = — с3. Підставивши замість а 4- Ь =
= — с, матимемо а3 4- Ь3 — ЗаЬс = — с3, звідки а3 4- Ь3 4- с3 =
= ЗаЬс.
9.4. Довести, що вираз За2 — ЗаЬ 4- ЗЬ2 додатний, якщо
а і Ь одночасно не дорівнюють нулю.
Розв’язання. 1-й спосіб. Якщо числа а і Ь різних
знаків, то висновок очевидний, бо всі три доданки невід’-
ємні.
Якщо аЬ > 0, матимемо За2 — 5аЬ 4- Зд2 = За2 —ЗаЬ 4-
4- ЗЬ2 4-Ьа = 3(а — Ь)2 + аЬ>$. <
2-й спосіб. Відомо, що одночасно не можуть мати місця
рівності- а =0 і Ь = 0. Нехай Ь =£ 0, тоді Ь2 > 0 і За2 — 5аЬ 4-
4-ЗЬ- = Ьп- — 5 -2- + 3) = (Зі2 — 51 + 3) Ь2, де / = у. Вираз
З/2—5/4-3 завжди додатний, тому додатний і вираз За2 —
— 5аЬ 4- ЗЬ2.
9.5. Довести, що сума квадратів . п’яти послідовних на-
туральних чисел не може бути повним квадратом.
52
Розв’язання. Доводимо методом від супротивного.
Позначивши ці п’ять чисел п—1; п— 2; п; п 4- 1; п 4- 2,
дістанемо: (п — 2)2 + (п — 1 )2 п2 + (и + 1 )* 4- (я 4- 2)2 =
= 5/г2 4- 10 = 5 (п2 4- 2). Вираз 5 (п2 4- 2) може бути повним
квадратом лише при умові, що п2 4- 2 ділиться на 5, що
неможливо, бо тоді б п2 закінчувалося цифрою 8 або циф-
рою 3. Отже, дане твердження доведено.
9.6. Довести, що величина добутку Іо^Л^Іо^ЛГа ...
... 1оос,Мп не зміниться, якщо довільним способом переставити
основи логарифмів.
Розв’язання. Для доведення візьмемо довільну пару
множників заданого в умові добутку 1о§а Л^1о§арМр і дове-
демо, ЩО ЇХ добуток дорівнює добутку МНОЖНИКІВ \о£арМі X
X \о£аіМр- Скористаємося тотожністю 1о£аМ = .
У першому множнику перейдемо ДО ОСНОВИ ас, у друго-
му — до основи ар. Дістанемо: 1о&а • 1ода = =—-— X
і Р І0^аіар
р і \т і АГ " £. еі
X [ 0- 1°£0Др, що й треба було довести.
9.7. Обчислити 1о?243288, якщо 1о§52 = т, 1о§53 = п.
Розв’язання. Оскільки 288 = 25 • З2, то 1о£243288 =
Сі О , О 1.- о _ 5 ІО£5 2 ! 2 ІО£5 3 _ 5/п 4- 2л
— 5 ІОГ;243- ! 2 1оь2433 1О£_ 243- 4- 1о& 243 — 5п •
1о& Ь ІО£ а
9.8. Спростити вираз: а с —о с ’
Розв’язання. Запишемо даний вираз так: а1ог^6 —
1О£еа
— (о °е° ’) . Перейдемо у показнику степеня від’ємника
до основи с. Дістанемо: — (й1ОЄсЬ ) 1ое*а = а°*сЬ—
=0.
9.9. Довести нерівність: ^ + ^>2.
1 2
Розв’язання. —_=10§я2, = 1о£я5, 1о£я2 4-
4- 1о§л5 = 1о£л 10 > 2 (бо 1о£я я2 = 2). Що й треба було
довести.
9.10. Довести, що г—т/4-і—Ц? + ••• 4-і—-—иг 4*
. ІО&2 N 1 1О£з 1 1 І0ЙІЙ8Й N ~
1 _ 1
1°І1983 N 1°о1983! А7
63
Розв’язання. г-1 1 д7 + ••• + 1-----Г/ =
1о§2 N ' 1о§з # ІО£1983 N
= 1о&у2 + 1о£?уЗ + . . . + 1о£л, 1983 = 1о&# 1983! Але
1983! = . Що й треба довести.
9.11. Довести, що 1§5 — ірраціональне число.
Розв’язання. Доводимо від супротивного. Припус-
р
тимо, що 1^5 раціональне число, тоді 5= 10 я або 5Р =
= 10р, що неможливо при жодній парі цілих чисел р і д.
Тому наше припущення неправильне і 1^5 — число ірраці-
ональне.
9.12. Довести, що/20+ 14/2 + У 20—14/2 = 4.
Розв’язання. В області дійсних чисел з рівності п3 =
= Ь3 випливає рівність а = Ь. Оскільки (2 + /2)3 = 20 +
__ 3 г--------— 3 і------------2 З Г------
+ 14/2, то у 20 + 14/2 + У 20—14/2 = У (2'+
------— з /--------—
+ /2)3 + у (2 — /2)3 = 4. Що й треба було довести.
9.13. Відомо, що ~г°6^ = гЄ°л/ • Довести, що а,
Ь, с—послідовні члени геометричної прогресії з додатни-
ми членами.
Розв’язання. За умовою задачі 1о£^—1о£сМ=/=0,
тому числа а, Ь і с — різні. Звівши до спільного знамен-
ника, дістанемо: (1о£вМ — Іо&Д) 1о£сМ = 1о£аМ (1о§6М—
— ІО&Л0-
Ця рівність спрощується, якщо перейти до основи Ь:
, аЛіо^ = іойь# Лпа хг _ 1о&Л\
Скоротивши обидві частини рівності на 1о£^У=#0, ма-
тимемо ~ 1(?бьа = -І08ьС ~~ 1 звідки 1о£ьа + 1о£6с = 2, тоб-
1о&,а Іо^с Іо&а • 1о&>с ’ 1 ьо
то 1о£6ас = 2. Що й треба було довести.
Можна показати, що є правильним і обернене твер-
дження: якщо а, Ь, с—послідовні члени геометричної про-
І0§ауУ — 1о§/У ІО£иЛ;
гресц, то справджується рівність: .
9.14. Довести тотожність 1о§25 = 1о§23 • 1о§34 • 1о£45.
Розв’язання: 1о§23 • 1о§34 • 1о§45 = 1о§23 =
= 1ой25.
Наведемо приклади інших завдань з логарифмами.
9.15. Обчислити добуток: 1§і§30° • І£І^31° • 1§і^32° х ...
... X І£І§60в.
54
Розв’язання. Шуканий добуток дорівнює нулю, бо
серед його множників є і£І&45° = 0.
9.16. Знайти область визначення функції г/ = І£І£І§|26 —
—X2 І.
Розв’язання. З умови 1&1&[26 — х2.| >0 дістанемо
І£,26—х21 > 1 і !26—х2| > 10. З цієї нерівності маємо
26—х2 > 10, або х2 — 26 > 10. Шукана відповідь:
хС]-оо;-6[ и ]-4;4[ 0 ]6;4-ооЬ
9.17. Відомо, що числа а, Ь, Уа — Уб— раціональні.
Довести, що -/а і — теж раціональні числа.
Розв’язання. Розглянемо добуток (І^а — ]/Ь) (уга +
+ ]'Ь) = (а — Ь). ЧислоУа + У 6, що дорівнює
а — Ь
У~а-Уь'
раціональне, бо частка від ділення двох раціональних
чисел — число раціональне. Сума двох раціональних чисел
— УЬ),+ у (Уа + У?) = V сі— число раціональне,
їх різниця ]/д— теж раціональне число.
9.18. Довести, що при будь-якому дійсному а справ-
джується нерівність а8 + а8 — 4а4 4- а2 + 1 0.
Розв’язання. Дану нерівність можна записати так:
(а4 — І)2 + а2 (а2 — І)2 0, що очевидно. Рівність можлива
лише при а = ± 1.
9.19. Довести, що при будь-якому справджується
нерівність 2а3 2а2 + 1 > а.
Розв’язання. 2а3 + 2а2 -І- 1 = а / 2а2 -{- 2а + —= а X
X ( (2а2 + сі) + (а + > 2а > а, бо а 4- у 2.
9.20. Довести нерівність і + 4т + -к + ••• + -= >
У 2 Уз УЇ978
> У 1978.
1 1 11
Розв’язання.1+^+-+... + — = ^х
X ( /1978 4- 1-^ + + ... + 1 У
І /2 /3 )
Другий співмножник у даній рівності—це сума 1978-ми
доданків, кожний з яких більший від 1. Отже, добуток бу-
де більшим від —-— • 1978 = ]/ 1978. Що й треба було
У1978
довести.
55
а і Ь сі Ь
9.21. Довести нерівність г-'. 1 . г < Т“і---------Ь гт-г (я > 0,
Ь>0).
Розв’язання: т-?. = т-, ° , 4- г , д . Але
і 0
+ г+з *
9.22. Довести нерівність (х 4- у)2^ 4ху.
Розв’язання, (х — у)2^®, що очевидно, тобто х2—
— 2ху 4- у2 0. Додавши до обох частин даної рівності ви-
раз 4ху, дістанемо те, що й треба було довести.
9.23. Довести нерівність: т • Т • у ’ Т • • • їоо < То ’
Розв’язання. Очевидно, що дт<-д-; 4- < 4-; ~ <
2 о 4 Об
_6 . 99 100
< 7 ’ ’ ’ ’ ’ 100 < 10Г
Якщо почленно перемножити ці нерівності, дістанемо
1 З 5 99 2_ _4 _6 100
2 ’ Т ’ б- ’ ‘ 100 < з- ’ б- ’ 7 ’ ’ Тої ’
Помножимо обидві частини цієї нерівності на добуток
1 3 99 п. / 1 3 5 99 12 ‘1
2 ’ 4 ' ' ‘ ’ 100 • Д1станемо: (2 ’ 4 ’ 6 ’ ’ ’ ’ ’ Юо) < 101<
< ТЗо’ звідки т • т "І • • ’ їбб< та Щ° й треба бУл0 до’
вести.
Віднесемо до цього ж типу кілька завдань, для розв’я-
зання яких використовуються властивості прогресій.
' 9.24. При яких .х числа 1^2, І£(2Х—1), (2 х'4- 3) є
трьома послідовними членами арифметичної прогресії?
Розв’язання. На основі означення арифметичної про-
гресії: 2 (2 х—1) = 1^2 + І£ (2 х 4- 3), звідки (2х—1)2 =
= 2(2Х 4- 3); 22х — 4 • 2х — 5 = 0. Розв’язком останнього
рівняння буде х = 1о£25. Отже, при х = 1о§25 числа 1^2,
І£ (2х—1), І£ (2х 4-3) будуть послідовними членами ариф-
метичної прогресії.
9.25. Знайти арифметичну прогресію, сума членів якої
для будь-якого натурального п дорівнює її1.
Розв’язання. За умовою 8п=ії1. Для її = 1 =
= аг = 1, для п = 2 £2 = а* 4- а2 = 4. Звідси = 1, а2 = 3;
ії = 2, і шукана прогресія буде 1, 3, 5, 7, ... , 2п— 1.
9.26. Довести, що числа V 2, /З, У 5 не можуть бути
членами арифметичної прогресії.
56
Розв’язання. Порівнянням величини даних чисел
можна встановити, що ці числа не є послідовними членами
арифметичної прогресії. Тоді припустимо, що вони несусідні
члени прогресії, тобто що
= (1)
4-(т—1)4/=/З, _ (2)
4- (п — 1) сі = ) 5. (3)
Віднімемо від першої і третьої рівностей другу. Діс'та-
нехмо: (т—к) й = У 3 — У 2 і (п — т) сі = 1^5— УЗ:
о . т — к У З—У2 п .< • •• . . ..
овідки ----= —2—-— . Як бачимо, в лівій частині цієї
п ~т У 5 — /з
рівності стоїть ірраціональне число, а у правій — раціональ-
не. Справді, нехай = Р- Тоді У 3 — У 2 = р (У 5 —
— Уз). Перевіримо, чи можлива така рівність. Піднесемо
обидві частини її до квадрата: 5 — 2 • ] 6 = р- (8 — 2]/15),
звідки /15 - /б = , або 15 + 6 - 6 /10 =
____/Оп2____ СІ\2
Дістали: —буїО—т—- — 21, що неможливо. Отже,
числа У 2, У З, ]/5 не можуть бути членами однієї ариф-
метичної прогресії.
9.27. Довести, що три числа , сова, І£а, взяті
в даному порядку, є членами геометричної прогресії лише
ТС
при а = ± -X- + 2кл, де к £ 2.
Розв’язання. Якщо дані числа будуть членами гео-
метричної прогресії, то справджуватиметься рівність сов2 а —
=-----т——, аоо бсовчх — віп-а, звідки 6соз3а 4~ сов“а — 1 =
О
— 0. Це рівняння має один дійсний корінь сов а = 4-, звід-
ки а = ± у + 2^я, де к£%, що й треба було довести.
9.28. Знайти суму:
1 4- 2 • 2 4- 3 • 22 4- ... -у 99 - 298 Ч- 100 - 2".
Розв’язання. Позначимо шукану суму через 5, тобто
8 = 1 4- 2 • 2 + 3 • 22 + ... 4- 99 • 298 4- ЮО • 2". (1)
Тоді
28 = 1 • 2 4- 2 • 22 4- 3 • 23 4- ... 4- 100 • 2100. (2)
57
Віднімемо від рівності (2) рівність (1). Дістанемо!
5 = 100 • 2100 — (1 + 2 + 22 + ... + 2м) = 100 2100 —
9100 _ 1
г = 99-2100 + 1.
9.29. Знайти добуток
Розв’язання.
1 _ 22 — 1 __ 1 3 .
4 ~ 4 ~ 2 * 2 ’
_1_ 32 — 1 _ 2 4 .
У ~ 9 — 3 3 ’
1 (п— 1)2— 1 _ п — 2 л
1 (л— 1)2 " (л— 1)2 ~ п— Гл- !’
. І л2 — 1 п — 1 л 4~ 1
Л3 «2 п п •
Перемноживши ліві і праві частини цих
132435 л—2
станемо: р = - . - . у у . ...
л+1 л л 4-1
х __ . Отже, р = —.
рівностей, ді-
л л — 1
~----ї х
Л — 1 л
10. Розв’язування рівнянь
10.1. Розв’язати рівняння (х— 4)(х— 5)(х— 6)(х— 7) =
= 24.
Розв’язання. . Перемноживши перший і четвертий,
другий і третій співмножники, дістанемо (х2 — 11x4- 28) х
X (х2 — 11x4- ЗО) = 24. Позначивши х2 — 1 їх 4- 28 = г ма-
тимемо 2 (г 4-, 2) = 24, звідки 2Х = 4; 22 = — 6. Розв’язавши
рівняння х2 1 їх 4- 28 = 4, дістанемо: хх = 3, х2 = 8. Дру-
ге рівняння дійсних розв’язків немає.
10.2. Розв’язати рівняння (х2 — 9х4~20)(х2—ІЗх —
— 42) = 24.
Вказівка. Розклавши дані квадратні тричлени на множники,
дістанемо рівняння попередньої задачі.
10.3. Розв’язати рівняння 3х 4- 4х = 5х.
Розв’язання. Поділимо обидві частини даного рівняння
_ ТІГ / З \Х , / 4 V 1 П З
на 5х. Матимемо + т-| = Ь Позначимо-?- = $іпа,
І о / І о / о
58
4
тоді -е- = соза, дістаємо (зіп а)х 4- (соза)* = 1. Оскільки
О
0 < ос < "н*, то рівність можлива лише при х = 2.
10.4. Розв’язати рівняння х3 — Юх5 4“ 28х4 — 15х2 — 4 =
= 0.
Розв’язання: х8 — Юх5 4- 28х1 — 15х2 — 4 = (х8 -Ь
4- 25Х4 4- 1 — 10х6 4- 2х4 — Юх2) 4- (х4 — 5х2 4- 1) — 6 = 0,
(Xі — 5х2 4- 1)2 4-(х4 — 5х24- 1) —6 = 0.
Позначивши Xі — 5х2 4-1=2, матимемо г2 + г — 6 = 0,
звідки 2Ь = — 3, г.2 — 2. Розв’язавши біквадратні рівняння
х4 — 5х2 4-1 = — 3 та х4— 5х2 4-1 = 2, дістаємо: хі;г =
10.5. Довести, що рівняння х! 4-= Ю* 4-9 не має
розв’язків у цілих числах.
Розв’язання. Вираз х! 4-у\ має бути непарним чис-
лом, тому х < 2 або у < 2.
Нехай х = 1, тоді у\ = 10г 4- 8. Оскільки 10г 4- 8 не ді-
литься на 5, у < 4. Легко перевірити, що жодне з чисел
у = 1, у =2, у = 3, у = 4 не задовольняє умови.
10.6. Розв’язати рівняння 2 зіп х = 5х2 4- 2х 4- 3.
Розв’язання. 1-й спосіб. 5х24-2х4-3=5/х + уі +
14 14
£->-е->2. Але 2зіпх<2. Отже, ліва частина рівнян-
ня менша від правої, і рівняння розв’язків не має.
Цей результат можна виразно проілюструвати, зіставивши
ірафіки функцій уг = 2 зіп х та у2 = 5х2 4- 2х 4- 3, які не
мають спільних точок.
10.7. Розв’язати рівняння зіп х 4- зіп 5х = 2.
Розв’язання. Якщо дане рівняння має розв’язки, то
вони будуть також і розв’язками системи:
зіп х = 1,
зіп5х = 1,
звідки
. х = 5- 4- 2/гл,
х—— уд 4 > де & £ 2, ґі £2
Отже, розв’язком рівняння буде: х = у4-2£л, де к£2.
10.8. Розв’язати рівняння зіп2х- зіп9х= 1.
Розв’язання: 4-(соз7х— соз11х)=1.
соз7х — соз 11х = 2.
4*
59
Якщо дане рівняння має розв’язки, то вони будуть також
і розв’язками системи:
звідки
соз7х = 1,.
соз 1 їх = —4,
2Лл
X ,
х = ± -ц +-Ц-, де
Оетання система розв’язків не має, отже, і дане рівнян-
ня не має розв’язків.
10.9. Розв’язати рівняння зіп4 х — соз7 х = 1.
Розв’язання. Оскільки зменшуване 0 < зіп4х < 1,
то еоз7 х < 0.
Отже, дане рівняння матиме вигляд зіп4 х 4- | соз7 х І = 1.
Але зіп4 х < зіп2 х; і соз7 х | < соз2 х, тому зіп4 х 4-1 соз7 х | =
= 1 лише тоді, коли
ЗІП4 X = ЗІП2 X,
І СОЗ7 XІ = СОЗ2 X,
тобто можливі два випадки: зіп2 х = 1 і соз7 х = 0, або
соз7 х = — 1 і зіп х = 0. Звідси х = ~ 4~ Лл, або х = (2л ±
± 1)л, де п£2. Обидва знайдені розв’язки задоволь-
няють умову.
Но цього ж типу віднесемо рівняння з параметрами і рів-
няння, розв’язки яких повинні задовольняти певні умови.
Ці задачі складніші, бо, розв’язуючи їх, слід врахувати всі
допустимі значення параметрів.
10.10. Знайти розв’язки рівняння х| х 4-11 4- а = 0, де
Розв’язання. Розглянемо два випадки: х < — 1 і х^
— 1. У першому випадку рівняння набирає вигляду х2 +
4- х — а = 0. Це рівняння матиме дійсні розв’язки при 1 4-
4-4л^0, звідки Крім того, значення параметра
а мав задовольняти нерівності:
2
~~ 1 чц- < — 1. Перша з цих нерівностей, яку можна
звести до виду 1 < 1^1 + 4а, справджується при будь-якому
а > 0, друга з нерівностей не має розв’язків. Отже, при
— -4 < а с 0 дане рівняння не має жодного розв язку,
який би задовольняв умову х< — 1; при а>0 рівняння
має єдиний розв’язок: "X =
2
60
Якщо х^— 1, х2 4- х 4- а = 0. Це рівняння матиме
дійсні розв’язки за умови: 1—4а 2^0, тобто при а^у’
Крім того, значення параметра а має задовольняти нерів-
. — 1 + У1 —4а . . — 1 — У1 — 4а '
ності -----у------с —її—-—п------------— 1. Перша з
нерівностей, яку можно звести до виду 1 + V1 — 4а ^0,
справджується при всіх допустимих значеннях параметра а,
друга—при а > 0.
Отже, при а < 0 дане рівняння має розв’язок х =
__ ] _!_ 1 І _4^ І
=-----1—; при 0 < а < воно матиме три розв’язки:
_ — 1 — /1 —,4а . _ — 1 4- У ї — 4а . , — 1 — У Г + 4а
Л і — 2 ’ 2
Л 1 ч
(якщо а = 0, то хг=х3, якщо а = у, то хх = х2); при
1 . , — 1 •— /Г4-4а
а > у рівняння має один розв язок х =-------.
10.11 . При яких значеннях параметра а рівняння (2а 4-
4- 1)х2 — ах 4-а — 2=^0 має два дійсні корені, з яких один
більший від одиниці, а другий менший від одиниці?
Розв.’язання. Нехай /(х) = (2а 4-1) х2— ах 4- а—2.
Задача матиме розв’язок при /(1) > 0 і 2а4-1<0 або при
/(1) < 0 і 2а 4- 1 > 0- Тому 2а — 1 та 2а 4- 1 повинні мати
різні знаки. З двох систем [2а — 1 < 0,
2а 4- 1 >0
2а — 1 > 0,
2а 4- 1 < 0
, 1 1
друга суперечлива, а перша має розв язок —-2<а< — -
10.12 . При яких дійсних значеннях параметра а рівняння
ах4 — (а — 3) х2 4- За = 0 має один корінь, менший Від — 2,
і три корені, більші від — 1?
Р о з в’я з а н н я. Біквадратне рівняння матиме чотири дій-
* / ох9 ю 9 а (л—'З) і У (а—~3)2—12а2-^^
сних розв язки при (а — З)2 — 12а2 0; і---' г. *— --------
0. Друга з нерівностей задовольняється при а < 0,
або а >3. Перша — при ---------—— < а < ур , тому
розв’язки рівняння доцільно шукати лише для значень а
з проміжку ----------< а < 0. Оскільки рівняння має
4 дійсні розв’язки, ліву частину його можна розкласти на
61
множники: }(х) = а(х—х^)(х — х2)(х—х3)(х— х4). Відо-
мо, що а<0, тому /(— 2)>0, бо хх<—2; —1<х2<
< х3 < х4. Одночасно /(— 1) > 0.
Дістали дві додаткові умови: /(— 2) = 16а — 4(а — 3) +
4
4-За = 15а 4-12 > 0, звідки а>—і /( — 1) = а — а-Р
О
4
4-За 4-3 >0, звідки а> — 1. Тому —=-<а<0.
10.13 . Розв’язати рівняння 21о£Л а 4- 1о§аха 4- 31о§а2Ха ==
= 0.
Розв’язання. З умови випливає, що
х=#1, х>0 і а > 0. Якщо а=/=1, то дане рівняння наби-
2 1 З
рає вигляду: ;---Ь п— 4-тг-гп-----= 0- Позначивши і =
1 7 1о§ах 14-Іобах 2-ріо§ах
= Іо§ох, дістанемо рівняння б/2 4- 11/4-4 = 0, звідки =
= —-п-;/2 =—-н- і відповідно --------= і х2 =— . Якщо
6 2 а Уа ,
а— 1, то розв’язком даного рівняння буде: х£ ] 0; 1 [ 0 ] 1; <х> [.
10.14 . Знайти всі розв’язки рівняння соз4^х— т) = а X
л
~2 *
х(14-8Іп2л:), які лежать у проміжку 0
я
Р о з в’я з а.н н я. Відомо, що соз2^х——-2-
= 4а(1 4- зіп2х). Напроміж-
“ 2
п. я
ку 0; т
14"5Іп2хУ=0, тому після спрощення рівняння
маємо зіп2х=4а—1. -Якщо 0 < 4а— 1 < 1, тобто при
с а < у, рівняння має два корені, якщо 4а — 1 = 1, тобто
при а = -д-, рівняння має один корінь 8іп2х=1; х = —.
Отже, при а < дане рівняння не має розв язків на
11
< а < воно має два розв яз-
л — агс$іп(4а—1) п 1
- ------ Якщо а = у,
л 1
-у І рівняння не має
І
проміжку
2 —
0; ~ ,
агсзіп (4а — 1)
ки: хх=----------------
то х = у; при а > 4- на проміжку 0;
* м
розв’язків.
10.15 . При яких значеннях параметра а рівняння 1 4-
зіп2 ах = соз х має єдиний розв’язок?
€2
Розв’язання. Нерівності созхсі і 1-|-8Іп2ах^1
очевидні. Отже, шукане рівняння може мати розв’язки ли-
ше тоді, коли:
1 4- зіп2 ах = 1,
СО5 х = 1,
звідки
зіп ах = 0,
<
. СОЗ X = 1.
Маємо:
ах — кл,
х = 2лп,
де к£2,
(кл
X = —
а ’ де к£%, Остання система оівнянь
х = 2лл,
має безліч розв’язків х = -у» де к£2 при раціональному а,
і єдиний розв’язок х=0, якщо а — ірраціональне число.
10.16 . Знайти всі значення параметрів а і Ь, при яких
[ хуг 4-2 = а,
система І хуг2 4- 2 = Ь,
І х2 4- у2 4- 22 = 4
має лише один дійсний розв’язок.
Р о з в’я з а н н я. Нехай (х0; у0\ г0) — розв’язок даної си-
стеми рівнянь. Кожне рівняння системи не зміниться, якщо
одночасно замінити х на —х і у на —у. Тому три чис-
ла (— х0; — г/0; 20) теж будуть розв’язком цієї системи рів-
нянь. Цей розв’язок буде єдиним тоді, коли х = у — §.
Отже, шуканий розв’язок — (О;О;зо).
Підставивши ці' значення, дістаємо:
2ф — Л,
20 = Ь,
. 2? = 4,
звідки 20 = + 2 і а = Ь = ± 2.
Якщо а = Ь = 2, то система
( хуг 4- 2 = 2,
І хуг2 4-2 = 2,
( х2 4- у2 4- г2 = 4,
одним з розв’язків якої є (0; 0; 2), має ще інші дійсні роз-
в’язки. Віднявши друге рівняння системи від першого, ді-
станемо хуг(г—1) = 0. Якщо х = 0 (або у = 0), то мати-
мемо вже відому нам трійку чисел. Якщо 2 = 0, система
суперечлива, якщо 2=1, то х2 4- уг = 3 і ху = 1, звідки
63
дістанемо ще 4 дійсні розв’язки. Тому значення а = Ь=2
не задовольняє умови. Якщо а = Ь = — 2, матимемо: .
хуг 4- г = —2,
• хуг2 4- г = — 2,
. х2 4- У2 + 22 = 4.
Ця система, як видно, має розв’язок {0,0,^2}. Отже, ли-
ше при а = Ь = — 2 дана система рівнянь має єдиний дій-
сний розв’язок х = 0, у = 0 і г = —2.
11. Задачі на екстремуми
11.1. Огорожею, довжина якої 200 м, відгородити прямокутну
ділянку суші найбільшої площі, що прилягає, до прямоліній-
ного берега моря. .
Розв’язання. Нехай х — ширина ділянки, тоді її дов-
жина 200 — 2х. Площа 5 = х (200 — 2х) == — 2х2 4- 200х.
Цей вираз набуватиме найбільшого значення при х = — »
В
тобто при х = 50 м.
11.2. Серед усіх Прямо-
кутників, вписаних у дане
півколо так, що одна сто-
рона лежить на діаметрі,
знайти прямокутник най-
більшої площі.
Розв’язання. Не-
хай радіус півкола г, сто-
рона прямокутника, що ле-
Мал. 34. жить на діаметрі, має дов-
жину 2х, а висота пря-
мокутника Н. Тоді 5 = 2хк = 2г соз ер • г $іп<р = г2 зіп2 <р, де
<р — гострий кут між радіусом, проведеним у одну з вер-
шин прямокутника, що лежить на півколі, і діаметром пів-
кола. 5тах = т2 При 8ІП 2ф = 1, звідки х — к = . Отже,
£
найбільшу площу матиме прямокутник, відношення сторін
якого дорівнює 1:2.
11.3. На гіпотенузі даного прямокутног-о трикутника знай-
ти точку, для якої відстань між її проекціями на катети най-
менша (мал. 34).
Розв’язання. -Нехай а і Ь—катети даного прямокутно-
го трикутника, х і у— відстані від точки М до катетів, 3 подібно-
64
сті трикутників АВС і ВМ7 маємо: ^ = ь — х' зв’дкн У~
= ь ~ = = ^2 + (о — Т) =—3“X
X х2 — — а2. Останній вираз набуває свого найменшого
2и2 2 (а2 + Ь2) а2Ь
значення при х = -г-; '—- = -о--,-
о Ь2 и2 4“ Ь2
Такий же результат дістанемо і з геометричних міркувань,
врахувавши, що N7 = МС; МС набуває свого найменшого
значення тоді, коли точка -М є основою перпендикуляра, опу-
щеного з вершини С на гіпотенузу АВ,
Н.4. При якому а сума квадратів коренів рівняння х2—
— ах 4- а — 2 = 0 мінімальна?
Розв’язання. За теоремою Вієта: + х2 = а\ хух2 =
= а — 2. Тоді х2і + хі = а2 — 2 (а — 2) = а2 — 2а + 4 = (а —
— І)2 + 3. Останній вираз буде мінімальний при а = 1.
11.5. На основі АВ даного рівнобедреного трикутника
АМВ (мал. 35) Побудувати такий''прямокутник АВСЕ, сто-
рона С£> якого перетинала б бічні сторони даного трикутни-
ка ВМ і АМ відповідно у точках К і Е так, щоб сума
площ трикутників АЕЕ, ЕМК і ВСК була найменшою.
Розв’язання. Висота ЛІ N ділить трикутник ЕМК
на два рівні трикутники ЕММ і ММК, тому 5 = 8аое +
+ + $ксв — 2 (8аое + 8емі\)-
Позначимо МО = її, АВ = 2а, АЕ = .г, ЕЕ = у, тоді
ЕХ: = а — у, ЛІЛ' = Л — х. А АОЕ ~ Д ГМ#; - = —-,звід-
у а — у
65
ки ах— ху — уН — ху? У = -£• Маємо 8аое = тр $емн =
= <й-*Иа~у>,5 = ху + (й — х) (а — у).
Дослідимо на екстремум вираз + — х)(а — у). Під-
сіх х2а . , г ч ( ах\
ставивши замість у , матимемо -у 4-(а — х) І я — Ті / ~
= (Х2 + х2 _ 2}ІХ Д2) = £ (2х2 — 2Нх + А2). Квадратний
тричлен, що стоїть у дужках (старший коефіцієнт його додат-
ний), набуває найменшого значення при х = ^=^. Отже,
5 буде мінімальною при х = х.
11.6. Знайти довжину найкоротшого відрізка, який ділив
би рівносторонній трикутник з стороною а на дві рівновели-
кі частини.
Розв’язання. Припустимо, що шуканим відрізком є
/відрізок ЕЕ (мал. 36).Нехай АЕ = у; АО =чх; ОЕ = сі. Тоді
Іл.Л « 1 о . Л
^ЛВС = 2 а 5ІП з » = 4 51пз •
Але 8аео = $хУ 5‘п з• Отже, ху зіп а2 зіп , звідки
2ху = а*> У = ?& За теоремою косинусів: (і2 = х2 4- у2 —
— 2ху соз у Тому сі2 — х2 + — -?> і Л буде найменшим тоді,
коли буде найменшим й2. Сума х2 4- набуває найменшого
2 а« л .
значення при х2 = т-у, тобто при х = у- = —.
11.7. Села А і В розміщені на різних берегах річки. В
якому місці доцільно було б побудувати дерев’яний міст
через річку, щоб відстань між селами була найменшою? (Вва-
жаємо, що річка тече між селами прямолінійно і має одна-
кову ширину).
Розв’язання. Відомо, що міст будується перпенди-
кулярно до берегів річки.
Припустимо, що АКЬВ — шуканий шлях. Ламана АКЬВ
має таку ж довжину, що і ламана АКВіВ, де ВВ± = А (ши-
рина річки), причому ВВі X Ламана АКВ1 матиме най-
меншу довжину, якщо вона перейде у відрізок прямої АВ±.
66
Тому найкоротшою буде відстань — АСйВ, де С — точка пе-
ретину прямої АВг з найближчим до села берегом (мал. 37).
11.8. Дано кут АВС і дві точки Р і (}. Знайти такі точ-
ки С і І) на прямих АВ і ВС, щоб ламана РС'ВО мала
найменшу довжину.
Р'
Мал. 37. Мал. 38.
Розв’язання. Побудуємо точки Р' і ф' симетричні
відповідно точкам Р і (? відносно сторін АВ і ВС кута АВС.
Точки перетину прямої Р'<2' з сторонами кута будуть шука-
ними точками С' і бо тоді дов-
жина ламаної РСБ0_ дорівнюватиме І*
довжині відрізка Р'С}' (мал. 38).
11.9. На даній прямій І знайти \ /
таку точку, різниця відстаней до N. \ /
якої від двох даних точок А і В буде N. \ /
найменшою. N.\ І
Розв’язання. Нехай точки А_________________________/
і В містяться в одній півплощині /
(мал. 39). Тоді величина АХ— ВХ . 39
набуватиме свого найменшого значен- а*' ’
ня при АХ = ВХ. Отже, побудував-
ши множину точок, рівневіддалеких від даних точок А і
В, і знайшовши перетин і! з прямою, визначимо шукану точ-
ку X. Задача не матиме розв’язку, якщо АВ і І. Якщо то-
чки А і В лежатимуть по різні боки від прямої /, побудову
виконуємо так само.
67
11.10. У даний кут вписати трикутник найменшого пери-
метра так, щоб одна з його вершин містилась у даній точці
всередині кута.
Розв ’лзання. Відобразимо точку /И симетрично віднос-
но обох сторін даного кута (мал. 40). Відрізок перети-
нає сторони кута в шуканих точках N і К. Трикутник МКУ
має найменший периметр, що дорівнює
11.11. Яку найбільшу площу може мати трикутник, сто-
рони якого л, Ь, с містяться в таких межах 0< а < 1; 1 <
< 6 < 2; 2 < с < З?
Розв’язання." Будемо
вважати, що довжина третьої сто-
рони не підпорядкована обмежен-
ням. Площа трикутника із сторо-
нами «, Ь дорівнює ^аЬ х зіп С
і буде максимальною, якЩо
кожний із співмножників макси-
мальний, а це можливо лише при
л=1, Ь = 2, зіп С ==.1... Отже,
шуканий трикутник повинен бу-
ти прямокутним із сторонами 1,
2, ] 5 (мал. 40).
11.12. З’ цифр 0, 1,2, ... 9
скласти п’ять двоцифрових чи-
сел, добуток яких був би най-
більшим (кожна цифра повинна
використовуватись лише один
раз).
Розв’язання. В утворених числах цифра десятків по-
винна бути більшою від цифри одиниць, бо, переставивши
їх, ми збільшили б число і весь добуток. Тому цифра 9 стоїть у
своєму числі на першому місці. Доведемо, що після цифри
9 стоїть цифра 0. Припустимо, що числа утворені іншим спо-
собом і після цифри 9 стоїть не 0, а цифра «л»; цифра ж «0»
стоїть у другому числі після цифри Ь. Покажемо, що від
переставляння, цифр «0» і «я» добуток вказаних двох чисел
збільшиться. Справді,
(90 + а) • (106 + 0) = 9006 + ІОаб.
(90 + 0) (106+ а) = 9006 + 90л.
Але 90л > ІОлб, бо 6 < 9. Тому другий добуток більший.
Міркуючи аналогічно, покажемо, що після цифри 8 повинна
стояти цифра 1, після 7 — цифра 2, після 6 — цифра 3 і пі-
сля 5 — цифра 4. Шуканими числа будуть: 90, 81, 72, 63, 54.
11.13. Знайти десять чисел: аг, а2, а3, ... > а10 так, щоб
виконувались умови:
«і < а2 < а3 с а4 < а3 < аб < ... с а10, а? 4- °2 4- °з 4~ • • • 4-
4-оіо = 1
і щоб при цьому а7 було найбільшим.
Розв’язання. Число а7 буде найбільшим тоді, коли
а7 = а3 = а9 = а10. Крім того, з суми «і 4- ^2 4" оз 4- • • • 4-
4- о?о випливає, що а7 буде найбільшим тоді, коли сума пер-
ших шести доданків а? 4- °2 4- °з 4- 4- аь 4- а& набуватиме
найменшого значення, тобто 0. Отже, а4 — а2 — а3 = а4 =
= аь - а9 = 0, а7 = ай = а9 = ам = о|-|- о| 4- & 4- «іо = 1;
4о? = 1; — і 2 •
З двох чисел ± ^вибираємо більше. Тому а7 —
Покажемо застосування так званої нерівності Коші — Буня-
ковського
(х?4-^-Ь?34-...4-^)(а?4-сІ4-
4~ °з 4~ • • • 4~ #л) (аіхі 4-
4“ @2Х2 4“ * • • 4- О.пхп}^
.для знаходження екстремальних зна-
чень функцій.
11.14. У трикутнику АВС знайти
точку О, сума квадратів відстаней
якої від сторін трикутника буде най-
меншою.
Розв’язання. Позначимосторо-
ни»трикутника буквами а, Ь, с, а відста- Мал. 41.
ні шуканої точки від цих сторін 02 = х,
N0 = у, ОК = г (мал. 41).- Тоді матимемо: ах 4- Ьу 4- сг = 25,
де 5 — площа даного трикутника. За нерівністю Коші — Буня-
ковського (х2 4- у2 4- г2) • (а2 4- &24-с2) > (ах 4- Ьу 4- сг)2, звід-
ки х2 4- у2 4- 22 У правій частині нерівності —
стала. Тому ліва частина досягає найменшого значення, коли
нерівність перетвориться у рівність, тобто коли ^ = -| = З*
Позначаючи х = о/; у=Ьі\ г^сі, матимемо: а2і2 ~^Ь2і2 4- сН2
69
452
452
ЗВІДКИ а2/2 >
4а252
2а5 л • м 2^5 2с5
-яг-;—- Аналогічно оі —5; сг = . ,
Мінімальними значення будуть: х = ттїгі—-і
7 а2 о2 + с-
265 2сЗ
г/ = о . 2 = о , ,о ,—о- Учням можна повідомити та-
а- + Ь~ + с- ’ п2 + б2 4- с2
кож, що коли сума двох додатних величин стала, то їх до-
буток буде найбільшим тоді, коли значення цих величин збі-
гаються. Якщо ж добуток двох додатних величин сталий, то
їх сума буде найменшою тоді і тільки тоді, коли значення цих
величин збігаються.
Сформульовані властивості можна узагальнити.
ДобуТОК Х\х • х?2 • ... • Хнп (змінних хп х2, . .. , хп > 0,
сума яких дорівнює даному числу 5) набуває найбільшого
• Х\ Ха Хп
значення тоді, коли— = — = • • • = —, де ті, т2,.... тп —
! /Лх ГП2 Піп
довільні додатні раціональні числа. Аналогічно 5 = Хі4-
+ х2 4- • • • + хп набуває найменшого значення, коли добуток
степенів хГ1 • Х2г • ... • Хп'1 сталий і виконується співвідно-
шення: — = — = •••= —. Застосовуючи ці теореми, можна
/Их т, піп і г
розв’язати багато цікавих задач на знаходження найбільших
і найменших значень.
11.15. Серед усіх прямокутників, що мають даний пери-
метр 2р, знайти той, площа якого найбільша.
Розв’язання. Нехай х і у довжини двох суміжних
сторін прямокутника. 'Тоді х + У = Р, а шукана площа 5 =
= ху. Якщо сума х-\-у = р стала, то добуток чисел ху на-
буватиме найбільшого значення тоді, коли х = у = А, це
можливо, коли прямокутник — квадрат.
11.16. Міцність балки з прямокутним перерізом прямо про-
порційна її ширині та квадрату висоти. При яких розмірах
перерізу балка, вирізана з круглої колоди діаметром є/, мати-
ме найбільшу міцність?
Розв’язання. Міцність балки обчислюється за форму-
лою Р = кх2у, де к — сталий коефіцієнт, х — висота і у —
ширина перерізу балки. За умовою х2 + у2 = сі2. Добуток кх2
^2 п2
набуває свого найбільшого значення при у х~ = 2р2, зві-
70
дки х2 4- у2 = Зу2, Зу2 = Л2, у = X = У2у =
“З *
11.17. У дану кулю вписати циліндр найбільшого об’єму.
Розв’язання. Розглянемо осьовий переріз кулі і ци-
ліндра (мал. 42). Шуканий об’єм У = АО2 ОС. Але АР2 4-
і
4- ОС2 = 4Я2, тому V = ? АО2 (ОС2)'2. Отже,' найбільший
об’єм буде при умові, що ЛВ2 = ; Ай2 = 2ВС2, тому
~2
ЗВС2 = 4/?2, отже, ВС =
АО = 2*Д ’ ,
О
11.18. Зробити розрахунок попе-
речного перерізу каналу, що має
форму рівнобедреної трапеції, так,
щоб на бетонування внутрішньої по-
верхні каналу пішло мінімум матеріа-
лу (при цьому, щоб канал був зада-
ної пропускної спроможності).
Розв’язання. Нехай АВСО —
переріз каналу (мал. 43). Бетонувати
треба стінки АВ, ВС, СО. Позначи-
мо АВ = СО = х, ВС = у, АК = 2,
тоді АО = 2г + у. Висота трапеції КВ
матиме величину У х2 — г2. Площа
трапеції 5 = у • (2г 4- 2у) ]^х2 — г2—
величина стала. Визначимо, коли функ-
ція І = 2х 4- у набуває мінімального
значення. Якщо 5 стала, то сталою
буде і 352. 3$2 = 3(2 + у)2(х2 — г
Вираз 21 = (г 4- у) 4- (2 4- у) 4- (2 4- х) 4- (Зх — Зг) = 4х 4-
4~ 2у набуватиме мінімального значення тоді, коли 2 4- у =
= г 4- х = Зх — Зг, звідки х = у, 2 = -^-. Тому £ АВС = 30°.
Отже, трапеція, яку ми дістанемо у перерізі, повинна
мати розміри АВ = ВС =^О і /. АВС = 120°.
71
Аналогічно розв’язується й така задача.
З прямокутного листа заліза зробити жолоб з перерізом
у формі рівнобедреної трапеції, щоб місткість його була най-
більшою. У цій задачі за умови сталої суми 2х + у потріб-
но знайти найбільше значення виразу 52 = 3 (г + у)- (х- — г2).
11.19. Виготовляють бак у формі прямокутного паралеле-
піпеда з площею основи, рівною їм2. Сума довжин усіх ребер
паралелепіпеда повинна дорівнювати 20 м. При яких розмірах
площа поверхні бака буде найбільшою?
Розв’язання. Для розв’язування задачі .не має значення,
який це бак: відкритий чи закритий. Якщо бак відкритий, поз-
начимо довжини ребер паралелепіпеда через х, у і 2. За умовою
4х -4- 4у + 4г = 20, тому х + у + з = 5 і ху = 1. Треба знайти
значення х та у, при яких вираз 5 = ху + хг + уг = 1 + г х
X (х + у) набуває найбільшого значення. Оскільки сума чи-
сел 2 і (х + у) стала, то добуток г (х + у) набуває найбіль-
шого значення, коли 2 = х + У-
Отже, 2 = 2,5 м. З системи
їх+// = 2,5, .
\ху = 1
визначаємо х і у.
11.20. У квадратному фанерному листі, сторона якого до-
рівнює 10 одиницям, вирізано прямокутний отвір з діагонал-
лю, що дорівнює 5 одиницям. Отвір охоплено тонкою заліз-
ною рамкою. Маса одиниці площі фанери 2 г, а маса .одиниці
довжини рамки 7 г. Які розміри повинні мати сторони отво-
ру, щоб маса листа була найбільшою?
Розв’язання. Маса листа Р — 200 — 2ху + 14 (х + у).
Відомо, що х2 4- у1 = 25, де х та у відповідно довжина і
ширина отвору. Тоді Р = 200 — ((х 4 у)2, — (х2 + Уг)) +14 (х+
+ у) = 225 — (х + у)1 + 14 (х + у). Квадратний тричлен відно-
сно (х + #) набуватиме найбільшого значення тоді, коли х +
+ у = тг = 7. З системи
2
(х±у = 7,
. [х* + у- = 25
визначаємо довжину і ширину отвору — 3 і 4 одиниці довжини.
У всіх задачах, які ми розглянули, екстремальні значення
функцій ми визначали на основі їх певних властивостей або
використовували для цього тотожні перетворення.
72
12. Геометричні задачі
12.1. У колі проведено два радіуси. Побудувати хорду,
яка ділиться цими радіусами на три рівні відрізки.
Розв’язання. Нехай ОС і ОО — радіуси даного кола
з центром О (мал. 44). Проведемо бісектрису ОК гострого кута
СОО і через довільну її точку К побудуємо пряму РР _1_ ОК.
Від точок А і В відкладемо на прямій РР відрізки АЛ^ та
ВІЇ!, що дорівнюють відрізку АВ. Провівши коло радіусом
ОМ± із центра О, визначимо,’ що хорда ділиться ра-
діусами 05 та ОТ на три рівні відрізки (за побудовою). Кін-
Мал. 44.
Мал. 45.
ці шуканої хорди — точки ЛІ та N — дістанемо, провівши від-
різки 0М.г та ОЛ/і (бо відрізок М1Лі1 гомотетичний відрізку
М№ відносно центра О).
12.2. У прямокутних трикутниках АВС і Лі#/?! кути С
і Сі прямі. Довжина відрізка АС дорівнює довжині відрізка
ДСі і дорівнює 1. Довжина відрізка ВХСХ дорівнює 2, а від-
різка ВС — 3. Обчислити суму кутів В і Вг.
Розв’язання. З чотирьох трикутників, які дорівнюють
трикутнику-АВС, утворимо фігуру, зображену на малюнку
45. 0РМ.Т — квадрат. Кут між діагоналлю цього квадрата
РТ та відрізком РК (РК = ВС) дорівнює куту Вх. Тоді 2.В +
+ гВі= 2:1 + /2 = 45°.
12.3. Які кути може мати рівнобедрена трапеція, коли ві-
домо, що вона розбивається діагоналлю на два рівнобедрені
трикутники?
Розв’язання. Умову задачі задовольняє лише така тра-
пеція, у якої А В = ВС і АС = АО (мал. 46). Тоді /_ВАО 4=
73
= ^АОС. Згідно з позначеннями на малюнку 46: 2а = 90° —
—5а = 180°; а = 36°. Отже, кути шуканої трапеції до-
рівнюють 72° і 108°.
12.4. У колі проведені хорди АВ і АС. Через точку А
проведена дотична до кола, а через точку В — пряма, пара-
лельна дотичній і така, ща перетинає пряму АС у точці Р.
Довести, що АВ2 = АС • АО (мал. 47).
Розв’язання. А АВС—ДАВО, бо XА — спільний,
X 1 = ХС — ХАВО, тому 4^ = тн > звідки АВ2 = АО • АС.
ЛС /1.0
12.5. Довести, що коли середини сторін опуклих чотири-
кутників збігаються, то їх площі рівні між собою.
Р о зв’я з а н н я. Довжини діагоналей таких чотирикутни-
ків рівні між собою і паралельні, бо кожна з них дорівнює
подвоєній довжині відповідних відрізків, що сполучають се-
редини сторін. Врахувавши, що площа опуклого чотирикут-
ника дорівнює півдобутку діагоналей на синус кута між ними,
доводимо дане твердження.
12.6. Дано опуклий чотирикутник, що має три тупі кути.
Довести, що довжина діагоналі, яка виходить з вершини чет-
вертого кута, більша від довжини другої діагоналі цього чо-
тирикутника.
Розв’язання. Якщо діагональ, яка виходить з вершини
гострого кута, взяти за діаметр кола, то інші дві вершини
будуть лежати в його середині. Довжина другої діагоналі
менша, ніж діаметр кола.
12.7. Довжини двох висот трикутника відповідно дорів-
нюють 40 см і 60 см. Довести, що довжина Третьої висоти
більша ніж 24 см.
74
Р о з в’я з а н н я. Нехай 5 — площа трикутника. Тоді аг =
25 25 95
— а і д3 = Скориставшись умовою, що ах 4-
/Ц л п2 П3
4- а2 > а3, матимемо:
25 , 25 25
Лі "г Л2 /із ’
Звідси
/із > 24.
12.8. Яку найбільшу кількість гострих кутів може мати
опуклий чотирикутник?
Розв’язання. Сума зовнішніх кутів опуклого чотири-
кутника дорівнює 360°, отже, він не може мати більше трьох
гострих кутів. Чотирикутник з трьома гострими кутами мож-
н§ побудувати.
12.9. Тисяча точок є вершинами опуклого тисячокутника,
всередині якого так розташовано 500 точок, що жодні три з
них не лежать на одній прямій. Многокутник розрізують на
трикутники, вершинами яких є дані- 1500 точок. Скільки три-
кутників ми дістанемо?
Р о з в’я з а н н я. Сума внутрішніх кутів усіх трикутників
дорівнює сумі кутів тисячокутника та ще 360° • 500. Тому
. 180° . (1000—2) 4-360° • 500 1ППО
всіх трикутників буде: ---------18~---------= 1998.
12.10. Через точку Л4, яка лежить поза трикутником АВС,
треба провести пряму так, щоб відрізок цієї прямої між сто-
ронами трикутника дорівнював сумі відрізків, які відтинає
ця пряма від сторін трикутника (якщо лічити від основи).
Р о з в’я з а н н я. Сформулюємо умову інакше: через дану
точку провести пряму так, щоб вона від одного кута трикут-
ника відтинала трикутник даного периметра, довжина якого
дорівнює АВА-ВС. На сторонах кута треба відкласти від-
АВ + ВС :
різки ---— і провести коло, що дотикається до сторін цьо-
го кута у точках, які є кінцями відкладених відрізків. Тоді
дотична до цього кола, проведена з точки М так, щоб вер-
шина кута і центр кола лежали по різні боки від неї, і бу-
де шуканою прямою.
, 12.11. Довести, що сума добутків протилежних сторін
вписаного чотирикутника дорівнює добутку його діагоналей
(теорема Птолемея).
Розв’язання. У чотирикутнику- АВСй, вписаному в ко-
ло (мал. 48), будуємо /АВМ. = /СВй. Оскільки /ВАС =
=/ВИС, то ДДЯМ—ДЯСР. Тому АВ:АМ = ВО:СО.
Звідки
АВ-Сй = АМ-ВО (1)
75
Оскільки АМВС = /.АВВ (бо /.МВС = /.СВВ + /.ВВМ,
^АВВ = /.АВМ + ВВМ) та ^АСВ = АВВ, то ДВСЛ4 —
— ДЛВВ. Отже, ВС: МС = ВВ: ЛР. Звідки:
ВС • ЛР = МС • ВВ. (2)
Додамо почленно рівності (1) і (2):
АВ • СВ + ВС • ЛР = (АМ + МС) ВВ,
АВ • СВ-}-АВ - ВС = АС-ВВ.
12.12. Довести, що в результаті перетину діагоналей н-
кутника можна дістати опуклий многокутник з не більш як
п сторонами.
Мал. 48. Мал. 49.
Розв’язання. Сторони такого многокутника можуть
бути утворені не більше як двома діагоналями даного п-кут-
ника, проведеними з однієї вершини. В добутку 2п кожну з
таких діагоналей беруть двічі, тому не більш як у = п діа-
гоналей можуть утворити сторони внутрішнього многокутника.
12.13. Довести, що на папері у клітку довжина будь-яко-
го замкненого шляху, що складається з кількох відрізків,
є парне число (сторона клітки вважається рівною 1).
Розв’язання. У фігурі, усі кути якої 90° або 270°, сто-
рони або паралельні, або взаємно перпендикулярні. Тому, як-
що п відрізків шляху напрямлені вгору, то стільки ж відріз-
ків напрямлені вниз, якщо п відрізків — вліво, то стільки ж
відрізків — вправо. Отже, довжина шляху: 2к 4- 2п = 2 (п -|- к).
12.14. На продовженнях сторін опуклого чотирикутника
АВСВ відкладаються відрізки ВВ' = АВ, СС' = ВС, ВВ' —
= СВ і АА' = В А. Довести, що площа чотирикутника А'В'С'В'
у 5 разів більша від площі чотирикутника АВСВ (мал. 49).
Розв’язання. Медіана поділяє площу трикутника попо-
лам, тому площі трикутників АВС, ВВ'С і СС'В' рівні між
собою. Площа .трикутника АСВ дорівнює площі трикутника
7$
АОО', а площа- трикутника 4 £>£)'. дорівнює площі трикутни-
ка АА'О' і т. д. Тоді
Свв'с = 25двс,
Зсс'Р’ = 28всв,
8А А'В' ~ 28 О А В,
_________$РР'А' = ~$СРА,______
*$.4.4'ф' “І" В В' С “Г $&Р'. 4' = 48двСР
Якщо площу чотирикутника АВСО позначити через (?. то
сума площ чотирьох прибудованих трикутників дорівнює
Площа всього чотирикутника
А'В'С'О' дорівнює 5^. В п
12.15. На карті Європи
сполучаємо кожне місто з / \
найближчим до нього, при- /
пускаючи при цьому, що від-
стані між будь-якими парами -----------------------
міст не рівні між собою. До- В
вести, ЩО жодне МІСТО не буде- ц 50
з’єднане більше ніж з п’ять-
ма сусідніми. • •
Розв’язання. Припустимо, що місто /< сполучене з міс-
тами .4, В, С, О, ..., Е. У Д.4В/( АК < АВ, ВК < АВ.
бо інакше було б сполучення АВ. Тому ДДЛ'В>60о, бо
ХА< ЛК, ЛВ < /'4 4- /В 4- //(< ЗЛАКВ. 'У вер-
шин і 1\ не може сходитись більше ніж 5 кутів.
12.16. У трапеції АВСО (мал. 50) з діагоналями АС та
ВО площі трикутників АОО та ВОС відповідно дорівнюють
5Х та В2. Обчислити площу трапеції.
Розв’язання. Для зручності записів позначимо площі
трикутників АОВ та ООС відповідно через ’53 і. В4. Нехай
/.СОО = а, тоді В4 = -і- ОС • ОО • зіп а, АО • ОО х
X зіп а.
Поділивши почленно ці рівності, дістанемо:
54 ОС
“ АО •
гр • 0’0 $9
Те саме для трикутників з площами о2 і 53: >
звідки: = у , або 54 • 53 = 52 • 5Х. Оскільки 53 = 54, то,
позначивши площу трапеції через 5, дістанемо:
77
12,17. Усі протилежні сторони шестикутника попарно па-
ралельні і всі три діагоналі, що з’єднують протилежні вер-
шини,, рівні. Довести, що навколо цього шестикутника мож-
на описати коло.
Р о з в’я з а н н я. Навколо шестикутника можна описати ко-
ло тоді, коли серединні перпендикуляри до всіх його сторін
перетинаються в одній точці. Покажемо, що цю властивість
має даний шестикутник (мал. 51). Побудуємо відрізок ВЕ
паралельно до Л7). У рівнобедреному трикутнику АВК
А А = /_К (бо кожен з них дорівнює куту В). Тому ДЛО3В
і А03ЕВ— подібні і .рівнобедрені. Медіана, проведена до
сторони АВ, буде одночасно бісектрисою і висотою. Тому се-
рединний перпендикуляр до.ЛВ і ЕВ буде бісектрисою ку-
та 03 в ДО1О2О3. Серединні перпендикуляри до двох пар ін-
ших сторін будуть бісектрисами кутів О± і О2 цього трикут-
ника, тому вони перетинаються в одній точці.
12.18. Точка А лежить усередині шести кіл. Довести, що
центр одного з кіл лежить усередині будь-якого іншого з них.
Розв’язання. Якщо один з центрів кіл збігається з точ-
кою А, то твердження задачі очевидне. Розглянемо той ви-
падок, коли точка А не збігається з жодним центром. Спо-
лучимо її з центрами кіл. Сума шести кутів, які ми при цьо-
му дістали, дорівнює 360°, тому принаймні один з кутів не
більше від 60°. Нехай цим кутом буде /_ ОгАО2. Якщо
£ ОхАОг = 0°, то один з відрізків ОХЛ або О.,Л є частиною
іншого. Тому точка А лежить усередині кола більшого ра-
діуса. Всередині цього ж кола лежатиме центр другого кола.
78
Якщо 0° < 2Г0М0., < 60°, ТО г/ОА ч- гЛО.Ої = 180° —
— /0^40, > 120°. ‘
Отже, один із двох розглянутих кутів має не менше
ніж 60°. Нехай /_ А.0^0^ 60°. У трикутнику АОГО2 проти
більшого кута лежить більша сторона, тому А02 > С^О.,. Ко-
ло з центром О2 містить точку А і його радіус г > АО„ >
> тому центр Ог лежить усередині кола з центром в О2.
12.19. Чи існує рівносторонній трикутник з вершинами у
вузлах паперу в клітку (у вершинах квадратів)?
Розв’язання. Припустимо, що такий трикутник існує
х2 /З
(мал. 52). Виразимо його площу через сторону х: 5 = —.
Оскільки х2 = АМ2 + МС2, то х2 — ціле число, а площа —
ірраціональне число. Розглядаючи цю площу як різницю площ
прямокутника МКЬС і трикутників ЛКВ, ВЬС і СМА, виз-
начимо, що площа має бути раціональним числом. Супереч-
ність, яку ми дістали, доводить, що такого трикутника не
існує.
12.20. Обчислити площу трикутника, довжини сторін яко-
го чисельно дорівнюють кореням рівняння х*— тх2 А-пх —
— 10 = 0.
Р о з в’я з а н н я. Нехай сторони трикутника дорівнюють
а, Ь, с.
За теоремою Вієта ма'ємо:
а 4- Ь 4- с = т, аЬ 4- ас 4- Ьс = п, аЬс = 10.
Визначимо площу трикутника через його сторони:
$ =Ур(р — а)(р — Ь)(р — с)=_________
= — р3 (а 4- Ь 4- с) 4- р2 (аЬ 4- ас 4- Ьс) — р-аЬс =
= V - —5п-
12.21. Довести, що в перерізі куба площиною не можна
дістати правильний п’ятикутник.
Розв’язання. Якщо перетнути протилежні грані куба
площиною, то лінії перетину будуть паралельні між собою.
А в правильному п’ятикутнику кожна пара сторін не пара-
лельна.
12.22. В усякому правильному многограннику сума від-
станей внутрішньої точки М від його граней є величина ста-
ла для даного правильного многогранника і не залежить від
положення точки М.
Розв’язання. Сполучимо точку М з кожною вершиною
правильного многогранника. Тоді многогранник можна роз-
глядати як сукупність пірамід із спільною вершиною М, бічні
79
ребра яких—відрізки, проведені від точки М до вершин
многогранника, основи пірамід — грані многогранника, а ви-
соти— відстані від точки Л4 до граней.
Позначивши через V об’єм даного правильного многогран-
ника, через 5 — площу кожної з його бічних граней, тобто
площі основ пірамід через Л2, . .. , Лп — відстані від точ-
ки М до граней многогранника, тобто висоти пірамід, діста-
немо V = 4- 5АХ 4- 8Н2 4-... 4- 4- 5Лл, звідки: V = 4 5 х
О о о о
X (А* 4- А2 4-... 4- /і»), або 4~ А2 4~ • • • 4~ Ал = -о- •
12.23. За допомогою циркуля і лінійки поділити на 19
рівних частин кут 19°.
Р о з. в’я за н н я. З будь-якої точки кола відкласти 19 дуг,
що відповідають кутові 19°. Оскільки 19°-19 = 361°, то
361° —360°= 1°.
12.24. На бісектрисі прямого кута взято точку К. Через
неї проведено довільну пряму, що відтинає на сторонах кута
відрізки довжиною а і Ь. Довести, що величина ~ 4- у не
залежить від положення прямої, що проходить через точку /С.
Р о з в’я з а н н я. Нехай АВ — довільна пряма, що прохо-
дить через точку Л і ОА = а, ОВ = Ь. Проведемо
КР ± ОВ і позначимо КР = с. Тоді ОР = РК = с. А АОВ оо
а ігпв ОА К? о • с Ь—С 1.1
~ а ЛРВ, тому ов = рд • Звідси: - = — або - + - =
= 4 . Оскільки с — ордината точки К, то у 4- у не залежить
від положення АВ.
12.25. З якої точки земної кулі треба вилетіти, щоб, про-
летівши 100 км на південь, потім 100 км по паралелі на схід
і 100 км по меридіану на північ, повернутись у початкову
точку?
Розв’язання. Зрозуміло, що однією з таких точок є
Північний полюс. Для визначення інших точок міркуємо так.
У південній кулі візьмемо паралель, довжина якої 100 км.
З довільної точки А цієї паралелі відлічимо в північному на-
прямку АВ — 100 км. Зрозуміло, що такий відрахунок вико-
нується по меридіану, що проходить через точку А.
Розглянемо нову паралель, що проходить через точку А.
Кожна точка цієї паралелі задовольняє умову задачі. Дійсно,
нехай з довільної точки М цієї паралелі літак вилітає на
південь, тоді через 100 км він буде в точці /VIі, що належить
100-кілометровій паралелі. Повернувши у цій точці на схід
і пролетівши у східному напрямку 100 км, літак потрапляє
80
у ту саму точку Мт. Повернувши з неї на північ, літак по-
трапляє у початкову точку М.
12.26. Яку найбільшу кількість ребер правильної /г-кут-
ної піраміди можна перетнути площиною?
Р о з в’я з а н н я. Многокутник, який дістанемо у перерізі,
не може мати більше сторін, ніж граней у піраміді. Площи-
на, яка проходить через середину висоти піраміди і середини
двох суміжних ребер її основи, перетинає всі грані. Много-
кутник, який ми дістали, матиме (л + 1) сторін.
12.27. За допомогою циркуля і лінійки розділити на 3 рів-
ні частини кут 54°.
Р о з в’я з а н н я. 90° — 54° 36°; 54°: 3 = 36° : 2.
Додаток
XXIV РЕСПУБЛІКАНСЬКА ОЛІМПІАДА ЮНИХ МАТЕМАТИКІВ (1984 р.)
VII КЛАС
Завдання 1.
1. У якому відношенні потрібно змішати щестипроцент-
ний і тридцятипроцентний розчини кухонної солі, щоб одер-
жати дванадцятипроцентний розчин?
2. Центри вписаного й описаного навколо трикутника
АВС кіл збігаються. Довести, що цей трикутник правильний.
3. Чи можна на координатній площині розмістити без
перекриття чотири однакових квадрати так, щоб кожна з
двох координатних осей перетинала кожний квадрат по дея-
кому відрізку?
Завдання 2.
1. Знайти квадратний тричлен ах2 + Ьх + с, який у точ-
ках 1983, 1984, 1985 набуває відповідно значень 2, 0, 2.
- 2. Знайти точку М всередині трикутника АВС, сума від-
станей від якої до вершини трикутника і середини його сто-
рін набуває найменшого значення.
3. У чемпіонаті країни з футболу беруть участь 18 ко-
манд, кожна з яких має свій стадіон. Усі команди повинні
зіграти між собою; у кожному турі чемпіонату беруть участь
усі 18 команд (тобто проводиться 9 ігор). Чи можна скласти
розклад турів чемпіонату так, щоб в довільних двох послі-
довних турах кожна команда проводила одну гру на своєму
полі, а іншу — на полі суперника?
VIII КЛАС
Завдання 1.
1. У якому відношенні слід змішати шестипроцентний
і тридцятипроцентний розчини кухонної солі, щоб одержати
дванадцятипроцентний розчин?
2. У клітках 'шахової дошки розміром п х п розміщені
лампочки. Відомо, що в будь-яких чотирьох клітках зі спіль-
ною вершиною горить парне число лампочок (тобто 0, 2, 4).
Довести, що таку саму властивість мають чотири кутові
клітки дошки.
3. Усередині трикутника АВС взято точку О і через
неї проведено прямі О А, ОВ, ОС, які перетинають сторони
ВС, АС, АВ у точках Вг, Ск відповідно. Довести, що
82
ОАі 4- ОВі + ОСТ < АС, де АС — найдогша сторона трикут-
ника АВС.
4. На крузі за годинниковою стрілкою через 120° запи-
сано числа 1, 2, 3. Центр круга прикріплений до дошки
так, що круг може повертатися на кути, кратні 120°. Спо-
чатку поруч з кожним числом 1, 2, 3 на дошці написано
нуль. Дозволяється повертати круг кілька разів і після
кожного повороту до кожного з написаних на дошці чисел
додати те число, яке виявилося поруч з ним на крузі. Чи
можна в результаті дістати на дошці записані-за годинни-
ковою стрілкою числа 11, 11, 14?
Завдання 2.
1. Дано шестикутник АВСВЕР. Довести, що його пери-
метр Р більший, ніж'у (42) + ВЕ 4- СР).
2. Уздовж прямої дороги розставлено світлофори на від-
стані 1 км один від одного. На початку кожної години на
них спалахує червоне світло, яке горить протягом 1 хв (у
цей час проїзд заборонено), а решту часу горить зелене
світло. Мотоцикліст почав рух із сталою швидкістю біля
світлофора, на якому щойно спалахнуло зелене світло, і за
10 год, протягом яких він був у дорозі і жодного разу не
зустрів червоного світла (ні разу не загальмував). Яку най-
більшу кількість світлофорів він міг зустріти за цей час?
3. Якого найбільшого значення набуває різниця аЬс —
— (а3 + Ь3 + с3) (трицифрового числа аЬс і суми кубів його
цифр)?
4. Усі грані куба розбили на 4 однакових квадрати і
кожний з них пофарбували однією з трьох наявних фарб.
Доведіть, що коли квадрати із спільним ребром пофарбова-
ні в різні кольори, то всього маємо по 8 квадратів кожно-
го кольору. Наведіть приклад такого розфарбування.
IX КЛАС
Завдання 1.
1. Знайти суму всіх натуральних чисел від 1 до 1000,
що не діляться на 7.
2. Два рівних кола дотикаються в точці А. Коло под-
війного радіуса містить всередині одне з них, дотикаючись
до нього в точці В, а друге перетинає в точках Р і (^. До-
вести, що пряма АВ проходить через точку Р або через
точку <2.
83.
3. Довести, що існують три дотичні до графіка функ-„
ції у = х3, які перетинаються в одній точці.
4. На площині дано 2п точок , Л2л і точку В.
Точка симетрична В відносно Ах\ точка В2 симетрична
Вх відносно Л2; В3 симетрична В2 відносно Л3 і т. д. Ві-
домо, що В2п = В. Довести, що коли довільну точку М
послідовно відобразити симетрично відносно точок Л2, Л3,
Л4, ... , А2п, Ль то дістанемо точку М2л = М.
Завдання 2.
1. Довести, що коли « > Із Ь >1, с > 1, (1 > 1 і ас —
— а — с = Ь~ — 2Ь, Ь(1 — Ь — сі = с2— 2с, то асі Ь'А-с—
= Ьс -{- а Л- 1
2. Дано шестикутник АВСОЕР. Довести, що його пери-
2
метр Р більший ніж у (АО ВЕ + СЕ).
3. ' Відомо, що набір попарно різних п чисел а1г . .. , ап
має таку властивість: кожне з чисел а, дорівнює добутку1
якихось двох інших чисел з цього набору: аі^о^ь. . ' »
а) Для якого найменшого п такий набір існує? б) Для
якого найменшого п такий набір існує, якщо кожне з чисел
ах, ...» ап є сумою двох інших? •
4. На площині взяли 1984 точки, кожні 3 з яких не
лежать на одній прямій. Кожні 2 точки сполучили: відріз-
ком і зафіксували на ньому один з двох напрямків. Довес-
ти, що існує точка, з якої в довільну іншу точку можна
потрапити, пройшовши не більш як 2 відрізки.
X КЛАС ’
Завдання 1.
1. Знайти границю ііш —4'ЇИ— ’
2. Знайти кути між векторами а, Ь, с в просторі, коли
відомо, що ці кути попарно рівні, а | а і = | Ь | = | с і = | а +
+ Ь + с|,
3. Довести, що існують три дотичні до графіка функції
у = х3, які перетинаються в одній точці.
4. На крузі за годинниковою стрілкою через 120° запи-
сано числа 1, 2, 3. Центр круга прикріплений до дошки
так, що круг може повертатися на кути, кратні 120°. На
початку поруч з кожним числом 1, 2, 3 на дошці написано
нуль. Дозволяється повертати круг кілька разів і після
кожного повороту до кожного з написаних на дошці чисел
84
додавати те число, яке виявилося поруч з ним на крузі.
Чи можна в результаті одержати записані за годинниковою
стрілкою числа 15, 14, 13?
Завдання 2.
1. Довести, що число 101 не можна зобразити у вигля-
ді суми 9 попарно взаємно простих натуральних чисел, від-
мінних від 1.
2. На прямій дано 9 точок Лх, Л2, ... » Лв. Знайти на
цій прямій точку А, сума відстаней від якої до даних-то-
чок найменша.
3. Скільки розв'язків має рівняння
- х = 6 зіп (6 зіп х) ?
4. У центральносиметричному опуклому *многокутнику
..... 1
одиничної площі можна розмістити трикутник, площа якого-н-.
Скільки сторін може мати такий многокутник?
ВІДПОВІДІ ТА ВКАЗІВКИ
VII КЛАС
Завдання 1.
1. Позначимо шукану кількість першого розчину через а*, а дру-
гого через Ь. Тоді: 6а + 306 = 12 (а -|- &); а : Ь = 3.
2. Відомо, що коли з центра вписаного кола (точки перетину бісект-
рис) опустити перпендикуляри до сторін трикутника, то вони будуть рів-
ними між собою. Крім того, основи перпендикулярів поділять кожну
сторону пополам, оскільки центр описаного кола збігається з точкою
перетину бісектрис. Тому цей трикутник рівностороннін.
~3. Побудуємо квадрати, сторонами яких будуть відрізки з кінця-
ми в точках Аг (0;5), (12;0), Л2 (5;0), В2(0; — 12), Л3 (0; — 5),
В3 (—12;0).і А4 (— 5:0), В4 (0;12). Довжини сторін цих квадратів
становлять по 13 одиниць. Продовжимо, кожний із згаданих відрізків
по обидва боки на відрізок завдовжки а (наприклад, на 1) і побуду-
ємо нові квадрати із сторонами 13 +2а. Ці квадрати матимуть пот-
рібні властивості (Зауважимо, що відрізок а не повинен перевищувати
половину відстані між паралельними найближчими сторонами будь-
яких двох сусідніх квадратів.)
Завдання 2.
1. /(х) = 2(х— 1984)2.
2. Шукана точка — центр перетину медіан.
3. Такого розкладу не існує. Нехай команди занумеровані й до-
держують такого правила: непарні тури грають на полях команд з
непарними номерами. Тоді,' очевидно, неможливою є зустріч команд,
номери яких однакової парності.
85
VIII КЛАС
Завдання 1.
1. 3: 1.
2. Поставимо у відповідність кожній засвіченій лампочці число 1,
а кожній лампочці, що не горить, число — 1. Тоді добуток чисел у будь-
якому квадраті, що містить 4 лампочки, дорівнюватиме 1. Добуток
чисел з усіх можливих квадратів, які складаються з чотирьох кліток,
теж дорівнює 1. У цей добуток у парних степенях увійдуть усі числа,
що відповідають лампочкам не з кутової клітки. Лише чотири числа,
які належать до кутових кліток, входять у добуток по одному разу.
Добуток цих чотирьох чисел дорівнює 1, тому серед них парне число
мінус одиниць.
3. Якщо через точку О провести відрізки, паралельні сторонам три-
кутника, то вони поділять його на 6 частин. Серед них будуть три па-
ралелограми і три трикутники, кожний з яких подібний даному трикут-
нику. У кожному з цих трикутників відрізки ОАі, ОВі і ОС± менші
від найдовшої сторони, паралельної АС, тому їх сума менша від АС.
4. Нехай х разів круг займав вихідне положенця, у разів повертався
на 120° і г разів на 240°. Тоді справджуватиметься система рівнянь
(х 4- Зу+2г= 11,
’ 2х + у 4- Зг = 11,
Зх 4- 2у 4- г = 14.
П розвозками будуть х= 3, у = 2, г = 1.
Завдання 2.
1. Очевидно, що периметр Р шестикутника задовольняє нерівності
о
Р>2АР, Р>2ВР, Р>2СГ, звідки Р > т (АР 4- ВЕ 4- СР).
О
2. Мотоцикліст має їхати з швидкістю 60 км/год. Тому він зустріне
600 світлофорів.
3. Найбільша різниця 396. Трицифрове число може бути 620 або 621.
4. Побудувати розгортку куба і на ній схематично показати, що
грані куба можна розфарбувати потрібним чином.
IX КЛАС
Завдання 1.
1. Шукана сума 429 429.
2. Рівні кола гомотетнчні. Показати, що пряма АВ є діагоналлю
паралелограма В^^М, де В^ — діаметр одного з рівних кіл, а С}М—
діаметр другого кола; ММ точкою А ділиться пополам і /ВАМ =
= / МАЦ.
3. Координати точки (х; у), через яку проходять три дотичних, задо-
У — а3
вольняють рівняння ——— = За2, де а — абсциса однієї з точок дотику.
Візьмемо за а будь-яке число, наприклад 1. Тоді записане рівняння
одним з коренів матиме 1. Крім того, воно має ще два інші корені.
66 • ’’
Рівняння 2а3 — Зл2х 4- у = 0 можна подати у вигляді 2 (а — ад) (а —
— а2) (а — а3) = 0, звідки
, . 3
а і + а2 -г а3 = ~2 х,
а1а2 4“ а1а3 4“ °2а3 =
у
аіа2а3 = — ^.
о 2 п 14 . В
а2 = 2, то а3 = у. При цьому х = у і у = у -
/14 8\ о о
Іо’» Т/ проходять три дотичних у = Зх— 2, # =
\ У о /
= \2х — 16, у = у х — .
Якщо а і = 1,
Отже, через точку
4
:----------' а ~~ З
4. З умови випливає: ВВ2= 2А1А2, ВіВ3 = 2Л2Л3, ..., ВаП_2В=
" >
= 2Л2д_іЛ2д,
Оскільки
В^и-іві — 2Л2Л_1Л2н.
^1^2 4“ Л3Л4 4“ ’* * 4“ ^2П-1^2П = 0 І
-> ------» * ----------> —-----------» ------>
ЛдЛ2 4~ Л2Л3 4~ * • • 4“ Л2ПЛ і = 0, то Л2Л3 4~ Л4Л6 4~ * * * 4~ ~
Завдання 2.
1. Оскільки ас — а — с-]-\=Ь-—264" 1 і М — Ь — ^4~ 1 = с2 — 2с4~
4-1, то (а — 1) (е — 1) = (6 — І)2 і (6—1) (гі—1) = (с—І)2; (а-1)Х
X (с — 1) (6 — 1) (4 - 1) = (Ь - І)2 (с - 1 )2; (а — 1) (сі — 1) = (Ь — 1) X
Х(с—1),
звідки
асі 4- Ь 4- с = Ьс 4- а 4~ (і-
3. Таких чисел існує 5. Ними можуть бути —1, а, —а, —,-------—.
а а
Існують шість чисел з одним знаком, які задовольняють умову: а, Ь,
. 1 1 1
а Ь аЬ
а) Якщо ці числа додатні, то їх логарифми задовольняють умову б).
4. Шуканою точкою буде та, з якої виходить найбільше стрілок.
Справді, нехай з точки А виходить найбільше стрілок. Якщо їх бу-
де к, то точка А безпосередньо пов’язана з іншими, к точками, а через
них і з рештою точок. Припустимо, що існує точка Л5, до якої не
можна дістатися з точки Л/, пройшовши не більш як два відрізки.
Тоді точка А5 така, з якої виходить 44~і стрілка. Ця суперечність
і доводить твердження.
X КЛАС
Завдання 1.
2. (а 4- Ь 4- с)2 = (а)2, звідки соз ер = —- •
О
87
3. Див. задачу 3 із завдання І, IX клас.
4. Якщо скласти систему рівнянь, як у задачі 4, із завдання 1, IX
клас
’ х + Зг/ + 2з = 15,
< 2х + // + 3г= 14,
Зх 4* 2у + 2 = 13,
то вона не матиме цілих розв’язків. Тому такі числа дістати не можна.
Завдання 2.
1. Доведемо методом ВІД супротивного, ЩО Рі 4- р2 4- 4" Рз 4"
4-р9= 101.
Серед, доданків лише одне число парне. Нехай ним буде р1 = 2д.
При д — 1 матимемо такі можливі доданки: 2, За, 5Ь, Тс. Очевидно, що
а, Ь, с мають дорівнювати 1, бо сума чисел 24-34-54-74- 11 4~ 134-
4- 17 4- 19 4- 23= ЮО. Жодний з доданків не можна збільшити на Г або
на деяке інше число.
2. Шуканою буде точка Д5.
3. Розв’язати систему рівнянь
у = 6 зіп х,
х = 6 зіп у.
Графічно можна показати, що вона має 15 розв’язків.
4. Многокутник може мати 4 сторони.
СПИСОК ВИКОРИСТАНОЇ ТА РЕКОМЕНДОВАНОЇ ЛІТЕРАТУРИ
1. Васильєв Н. Б., Гутенмахер В. Л. Прямьіе и кривьіе.
М., 1978. 160 с.
2. Гельфанд И. М., Г л а г о л ь е в а Е. Г., К н р и л л о в А. А.
Метод коордийат. М., 1973. 88 с.
3. Заочньїе математические о.іимпиадьі /Н. Б. Васильєв, В. Л. Гу-
тенмахер, Ж- М. Раббот и др. М., 1981. 128 с.
4. Збірник задач республіканських математичних олімпіад /За ред.
В. І. Михайловського. К., 1979. 264 с.
5. Лоповок Л. М. Збірник математичних задач логічного харак-
теру. К., 1972. 152 с.
6. Колягин Ю. В., О. ганесян В. А. Учись решать задачи.
М., 1980. 96 с.
. '7. Конфоровнч А. Г. Визначні математичні задачі. К., 1981.
192 с.
8. Пойа Д. Как решать задачу. М., 1961. 208 с.
9. Пойа Д. Математнческое открьітие. М., 1972. 452 с.
ЗМІСТ
Передмова З
Олімп іадні задачі
1. Логічні задачі на принцип Діріхле 4
2. Інші типи логічних задач 6
3. Задачі на зважування 12
4. Комбінаторні задачі 17
5. Відшукання закономірностей 22
6. Властивості цілих чисел 27
7. Побудова графіків функцій 36
8. Побудова геометричних місць точок 46
9. Тотожні перетворення 52
10. Розв’язування рівнянь 58
11. Задачі на екстремуми 64
12. Геометричні задачі 73
Додаток
XXIV республіканська олімпіада юних математи-
ків (1984 р.) 82
Список використаної та рекомендованої літератури 88
Мирон Петрович Маланюк{ Ваеалий Иванович Лукавецкий
Олимпнадьі юньїх математико»
Пособие для учителей
Издание второе
(на украннском язяке)
Киев, «Радянська школа»
Зав. редакцією математики О. П. Бондаренко. Редактор Л. П. Сла-
бошпицька. Літредактор Л. О. Поповченко. Художній редактор
П. В. Кузь. Обкладинка художника О. В. Пермякова. Технічний
редактор А. Г. Фрідман. Коректори: І.М. Ситниченко, Р. А. За-
церковна.
Гнформ. бланк № 4222
Здано до набору 17.07.81. Підписано до друку 24.12.81. Формат
34х108/а,. Папір № 3 друкарський. Гарнітура літературна. Спосіб
друку високий. Умови, арк. 4,62. Умови, фарбо-відб. 4,92. Обл-
видавн. арк.4,79. Тираж 40 000. Видави. № 27994. Зам. № 4-846.
Ціна 15 к.
Видавництво «Радянська школа»,- 252053, Київ, Ю. Коцюбинського, 5
Книжкова фабрика ім. М. В. Фрунзе, 310057, Харків-57, Донець-
Захаржевського. 6/8.
15 к.
<