Текст
EUCLID'S BOOK
ON DIVISIONS OF FIGURES
(irepl Biaipe&ewp /3i(3\iov)
WITH A RESTORATION BASED ON
WOEPCKE'S TEXT
AND ON THE
PRACTICA GEOMETRIAE
OF LEONARDO PISANO
BY
RAYMOND CLARE ARCHIBALD, Ph.D.
ASSISTANT PROFESSOR OF MATHEMATICS IN BROWN
UNIVERSITY, PROVIDENCE, RHODE ISLAND
Cambridge:
at the University Press
1915-
Cambtitige:
PRINTED BY JOHN CLAY, M.A.
AT THE UNIVERSITY PRESS
TO
MY OLD TEACHER AND FRIEND
ALFRED DEANE SMITH
PROFESSOR OF GREEK AND LATIN
AT MOUNT ALLISON UNIVERSITY
FOR FORTY-FOUR YEARS
SCHOLAR OF GREAT ATTAINMENTS
THE WONDER OF ALL WHO KNOW HIM
THESE PAGES ARE AFFECTIONATELY DEDICATED
INTRODUCTORY
T^UCLID, famed founder of the Alexandrian School of
^-^ Mathematics, was the author of not less than nine
works. Approximately complete texts, all carefully edited,
of four of these, (i) the Elements, (2) the Data, (3) the Optics,
(4) the Phenomena, are now our possession. In the case of
(5) the Pseudaria, (6) the Surface-Loci, (7) the Conies, our
fragmentary knowledge, derived wholly from Greek sources,
makes conjecture as to their content of the vaguest nature.
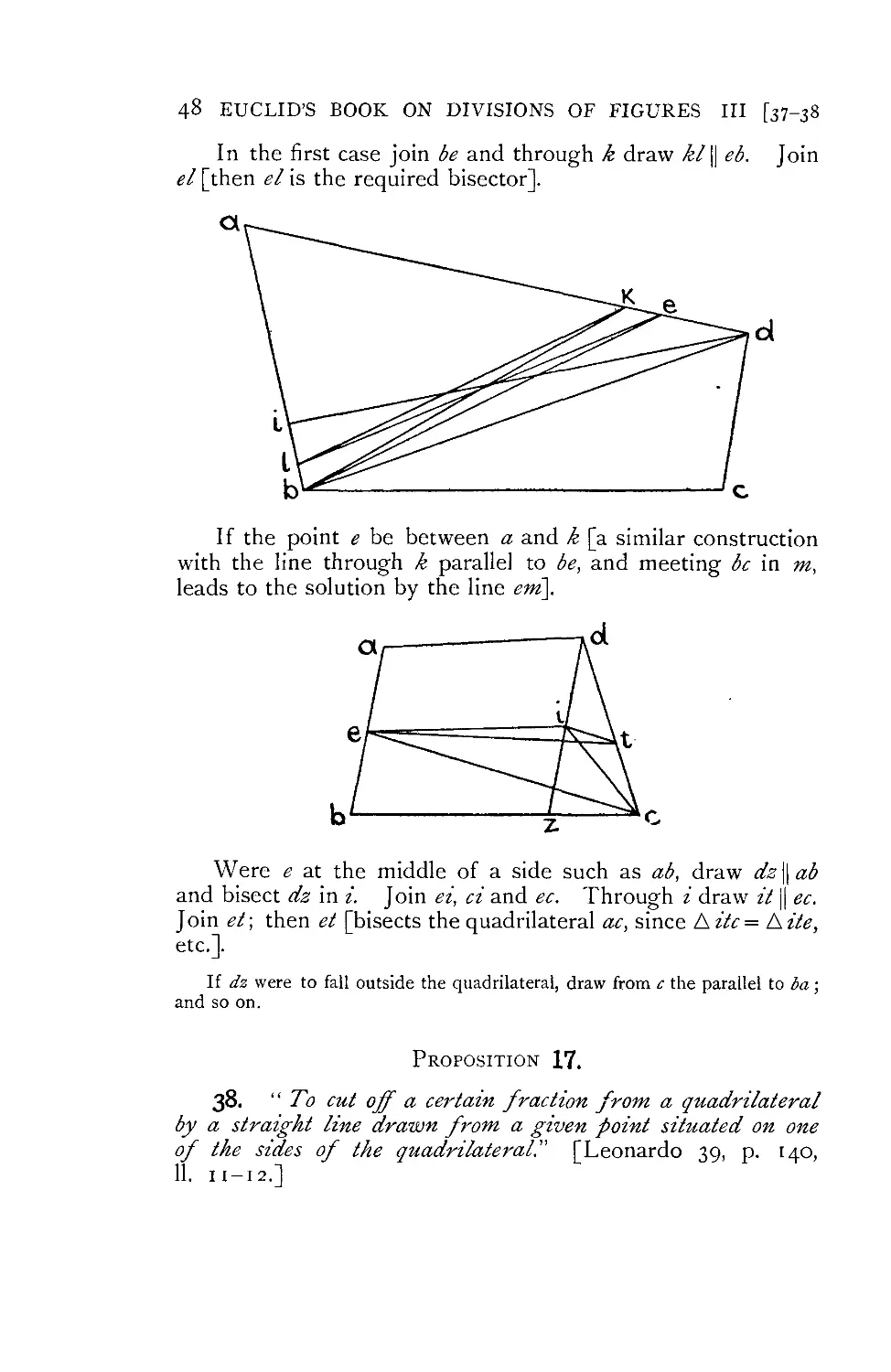
On (8) the Porisms, Pappus gives extended comment. As
to (9), the book On Divisions {of figures), Proclus alone among
Greeks makes explanatory reference. But in an Arabian
MS., translated by Woepcke into French over sixty years ago,
we have not only the enunciations of all of the propositions
but also the proofs of four of them.
Whilst elaborate restorations of the Porisms by Simson
and Chasles have been published, no previous attempt has
been made (the pamphlet of Ofterdinger is not forgotten) to
restore the proofs of the book On Divisions (of figures). And,
except for a short sketch in Heath's monumental edition of
Euclid's Elements, nothing but passing mention of Euclid's
book On Divisions has appeared in English.
In this little volume I have attempted :
(1) to give, with necessary commentary, a restoration
of Euclid's work based on the Woepcke text and on a
thirteenth century geometry of Leonardo Pisano.
(2) to take due account of the various questions which
arise in connection with (a) certain MSS. of " Muhammed
Bagdedinus," (d) the Dee-Commandinus book on divisions
of figures.
(3) to indicate the writers prior to 1500 who have dealt
with propositions of Euclid's work.
INTRODUCTORY
VII
(4) to make a selection from the very extensive
bibliography of the subject during the past 400 years.
In the historical survey the MSS. of "Muhammed Bagde-
dinus " play an important role, and many recent historians,
for example Heiberg, Cantor, Hankel, Loria, Suter, and
Steinschneider, have contributed to the discussion. As it is
necessary for me to correct errors, major and minor, of all of
these writers, considerable detail has to be given in the first
part of the volume ; the brief second part treats of writers on
divisions before 1500; the third part contains the restoration
proper, with its thirty-six propositions. The Appendix deals
with literature since 1500.
A score of the propositions are more or less familiar as
isolated problems of modern English texts, and are also to be
found in many recent English, German and French books
and periodicals. But any approximately accurate restoration
of the work as a whole, in Euclidean manner, can hardly fail
of appeal to anyone interested in elementary geometry or in
Greek mathematics of twenty-two centuries ago.
In the spelling of Arabian names, I have followed Suter.
It is a pleasure to have to acknowledge indebtedness to
the two foremost living authorities on Greek Mathematics.
I refer to Professor J. L. Heiberg of the University of
Copenhagen and to Sir Thomas L. Heath of London.
Professor Heiberg most kindly sent me the proof pages of
the forthcoming concluding volume of Euclid's Opera Omnia,
which contained the references to Euclid's book On Divisions
of Figures. To Sir Thomas my debt is great. On nearly
every page that follows there is evidence of the influence of
his publications; moreover, he has read this little book in
proof and set me right at several points, more especially in
connection with discussions in Note 113 and Paragraph 50.
R. C. A.
Brown University,
June, 1915.
CONTENTS
PAGE
Introductory ......... vi
PARAGRAPH I
NUMBERS
i Proclus, and Euclid's Book On Divisions of Figures . i
2-6 De Divisionibus by "Muhammed BaGdedinus" and the
Dee MS i
7-9 The Woepcke-Euclid MS. 9
10-13 Practica Geometriae of Leonardo Pisano (Fibonaci) . 10
14-17 Summary:
14 Synopsis of Muhammed's Treatise .... 13
15 Commandinus's Treatise . . . . . . 14
16 Synopsis of Euclid's Treatise ..... 15
17 Analysis of Leonardo's Work . . . . . 16
II
18 Abraham Savasorda, Jordanus Nemorarius, Luca Paciuolo 19
19 "Muhammed BaGdedinus" and other Arabian writers
on Divisions of Figures ...... 24
20 Practical Applications of the problems on Divisions of
Figures ; the ixerpiKa. of Heron of Alexandria . 26
21 Connection between Euclid's book On Divisions, Apol-
lonius's treatise On Cutting off a Space and a
Pappus-lemma to Euclid's book of Porisms . . 27
III
22-57 Restoration of Euclid's irepl Siaipe'o-ew /3i/3aw . . 30
IV
Appendix .......... 78
Index of Names 86
I.
Proclus, and Euclid's book On Divisions.
I. Last in a list of Euclid's works "full of admirable
diligence and skilful consideration," Proclus mentions, without
comment, nepl Ziaipecrecav /3t/3X.iov'. But a little later2 in
speaking of the conception or definition of figure and of the
divisibility of a figure into others differing from it in kind,
Proclus adds : " For the circle is divisible into parts unlike
in definition or notion, and so is each of the rectilineal figures;
this is in fact the business of the writer of the Elements in
his Divisions, where he divides given figures, in one case into
like figures, and in another into unlike3."
De Divisionibus by Muhammed Bagdedinus and
the Dee MS.
2. This is all we have from Greek sources, but the
discovery of an Arabian translation of the treatise supplies
the deficiency. In histories of Euclid's works (for example
1 Prodi Diadochi in firimum Euclidis elementorum librum commentarii ex rec.
G. Friedlein, Leipzig, 1873, P- 69. Reference to this work will be made by
" Proclus."
2 Proclus1, p. 144.
3 In this translation I have followed T. L. Heath, The Thirteen Books of
Euclid's Elements, I, Cambridge, 1908, p. 8. To Heath's account (pp. 8-10) of
Euclid's book On Divisions I shall refer by " Heath."
"Like" and "unlike" in the above quotation mean, not "similar" and
"dissimilar" in the technical sense, but "like" or "unlike in definition or notion":
thus to divide a triangle into triangles would be to divide it into "like" figures, to
divide a triangle into a triangle and a quadrilateral would be to divide it into
"unlike" figures. (Heath.)
A.
I
2 EUCLID'S BOOK ON DIVISIONS OF FIGURES I [2
those by Hankel4, Heiberg5, Favaro0, Loria7, Cantor8, Hultsch9,
Heath3) prominence is given to a treatise De Divisionibus, by
one "Muhammed Bagdedinus." Of this in 156310 a copy (in
Latin) was given by John Dee to Commandinus who published
it in Dee's name and his own in 1570". Recent writers whose
publications appeared before 1905 have generally supposed
that Dee had somewhere discovered an Arabian original of
Muhammed's work and had given a Latin translation to
Commandinus. Nothing contrary to this is indeed explicitly
4 H. Hankel, Zicr Geschichte der Mathematik, Leipzig, 1874, p. 234.
5 J. L. Heiberg, Litterargeschichtliche Studien iiber Euklid, Leipzig, 1882,
pp. 13-16, 36-38. Reference to this work will be made by " Heiberg."
0 E. A. Favaro. " Preliminari ad una Restituzione del libro di Euclide sulla
divisione delle figure piane," Atti del reale Istituto Veneto di Scienze, Lettere ed
Arti, l6, 1883, pp. 393-6. " Notizie storico-critiche sulla Divisione delle Aree"
(Presentata li 28 gennaio, 1883), Memorie del reale Istiticto Veneto di Scienze, Lettere
ed Arti, XX11, 129-154. This is by far the most elaborate consideration of the
subject up to the present. Reference to it will be made by " Favaro."
7 G. Loria, " Le Scienze esatte nell: antica Grecia. Libro 11, II periodo aureo
della geometria Greca." Memorie delta regia Accademia di Scienze, Lettre ed Arti
in Modena, XI2, 1895, PP- 68-70, 220-221. Le Scienze esatte nelP antica Grecia,
Seconda edizione. Milano, 1914, pp. 250-252, 426-427.
8 M. CANTOR, Vorlesungen iiber Geschichte der Mathematik, I3, 1907, pp. 287-8 ;
II2, 1900, p. 555.
9 F. Hultsch, Article "Eukleides" in Pauly-Wissowa's Real-Encyclopddie dei
Class. Altertumsivissenschaften, vi, Stuttgart, 1909, especially Cols. 1040-41.
10 When Dee was in Italy visiting Commandinus at Urbino.
11 De superficierum divisionibus liber Machometo Bagdedino ascriptus nunc
primum Joannis Dee Londinensis 6° Federici Commandini Urbinatis opera in
lucem editus. Federici Commandini de eadem re libellus. Pisauri, mdlxx. In
the same year appeared an Italian translation : Libro del tnodo di dividere le
superficie attribuito a Machometo Bagdedino. Mandato in luce la prima volta da
M. G. Dee...e da M. F...Commandino... Tradotti dal Latino in volgare da F. Viani
de* Malatesti,.... In Pesaro, del MDLXX... 4 unnumbered leaves and 44 numbered
on one side.
An English translation from the Latin, with the following title-page, was
published in the next century : A Book of the Divisions of Superficies : ascribed
to Machomet Bagdedine. Now put forth, by the pains of John Dee of London, and
Frederic Commandine of Urbin. As also a little Book of Frederic Co?nmandine,
concerning the same matter. London Printed by R. <&•» W. Ley bourn, 1660.
Although this work has a separate title page and the above date, it occupies the
last fifty pages (601-650) of a work dated a year later : Euclid's Elements of
Geometry in XV Books..-to which is added a Treatise of Regular Solids by
Campane and Flussas likewise Euclid's Data and Marinus Preface thereunto
annexed. Also a Treatise of the Divisions of Superficies ascribed to Machomet
Bagdadine, but published by Commandine, at the request of John Dee of London j
whose Preface to the said Treatise declares it to be the Worke of Euclide, the
Author of the Elements. Published by the care and Industry of John Leeke and
George Serle, Students in the Mathematics. London...MDCLXI.
A reprint of simply that portion of the Latin edition which is the text of
Muhammed's work appeared in : EYKAEIAOY TA 2QZOMENA. Euclidis quae
supersunt omnia. Ex rescensione Davidis L7r^tfra...Oxoniae...MDCCIII. Pp. 665-
684 : "EYKAEIAOY Q2 OIONTAI TINES, IIEPI AIAIPE2E0N BIBAOS. Euclidis, Ut
quidam arbitrantur, de divisionibus liber—vel ut alii volunt, Machometi Bagdedini
liber de divisionibus superficierum."
2] MSS. OF MUHAMMED BAGDEDINUS AND DEE 3
stated by Steinschneider when he writes in 190512, "Machomet
Bagdadinus ( = aus Bagdad) heisst in einem alten MS. Cotton
(jetzt im Brit. Mus.) der Verfasser von: de Superficierum
divisione (22 Lehrsatze) ; Jo. Dee aus London entdeckte es
und iibergab es T. Commandino...." For this suggestion as
to the place where Dee found the MS. Steinschneider gives
no authority. He does, however, give a reference to
Wenrich13, who in turn refers to a list of the printed books
(" Impress!") of John Dee, in a life of Dee by Thomas
Smith" (1638-1710). We here find as the third in the
list, " Epistola ad eximium Ducis Urbini Mathematicurn,
Fredericum Commandinum, praefixa libello Machometi Bag-
dedini de superficierum div'isiombus...Pisauri, 1570. Exstat
MS. in Bibliotheca Cottoniana sub Tiberio B ix."
Then come the following somewhat mysterious sentences
which I give in translation15: "After the preface Lord Ussher
[1581-1656], Archbishop of Armagh, has these lines: It is to
be noted that the author uses Euclid's Elements translated
into the Arabic tongue, which Campanus afterwards turned
into Latin. Euclid therefore seems to have been the author
of the Propositions [of De Divisionibus] though not of the
demonstrations, which contain references to an Arabic edition
of the Elements, and which are due to Machometus of Bagded
or Babylon." This quotation from Smith is reproduced, with
various changes in punctuation and typography, by Kastner10.
Consideration of the latter part of it I shall postpone to a later
article (5).
12 M. Steinschneider, "Die Europaischen Ubersetzungen aus dem Arabischen
bis Mitte des 17. Jahrhunderts." Sitzungsberichte der Akademie der Wissenschaften
in Wien (Philog.-histor. Klasse) CL1, Jan. 1905, Wien, 1906. Concerning "171.
Muhammed" cf. pp. 41-2. Reference to this paper will be made by "Steinschneider."
13 J. G. Wenrich, De auctorum Graecorum versionibus. Lipsiae, mdcccxlii,
p. 184.
14 T. SMITH, Vitae quorundam eruditissimorum et illustrium virorum...
Londini...MDCCVII, p. 56. It was only the first 55 pages of this "Vita Joannis
Dee, Mathematici Angli," which were translated into English by W. A. Ayton,
London, 1908.
15 " Post praefationem haec habet D. Usscrius Archiepiscopus Armachanus.
Notandum est antem, Auctorem hunc Euclide usum in Arabicam linguam con-
verso, qtiempostea Campanus Latinum fecit. Auctor igitur propositionum videtur
fuisse Euclides : demonstrationum, in quibus Euclides in Arabico codice citatar,
Machometus Bagded sive Babylonius."
It has been stated that Campanus (13. cent.) did not translate Euclid's
Elements into Latin, but that the work published as his (Venice, 1482—the first printed
edition of the Elements) was the translation made about 1120 by the English monk
Athelhard of Bath. Cf. Heath, Thirteen Books of Euclid's Elements, I, 78, 93-96.
10 A. G. Kastner, Geschichte der Mathematik...TLrster Band...G6ttingen, 1796,
pp. 272-3. See also "Zweyter" Band, 1797, pp. 46-47.
t—2
4 EUCLID'S BOOK ON DIVISIONS OF FIGURES I [3-4
3. Following up the suggestion of Steinschneider, Suter
pointed out", without reference to Smith14 or Kastner10, that in
Smith's catalogue of the Cottonian Library there was an
entry18 under "Tiberius19 B ix, 6": "Liber Divisionum
Mahumeti Bag-dadini." As this MS. was undoubtedly in
Latin and as Cottonian MSS. are now in the British Museum,
Suter inferred that Dee simply made a copy of the above
mentioned MS. and that this MS. was now in the British
Museum. With his wonted carefulness of statement, Heath
does not commit himself to these views although he admits
their probable accuracy.
4. As a final settlement of the question, I propose to
show that Steinschneider and Suter, and hence also many
earlier writers, have not considered all facts available. Some
of their conclusions are therefore untenable. In particular :
(1) In or before 1563 Dee did not make a copy of any
Cottonian MS. ;
(2) The above mentioned MS. (Tiberius, B. ix, 6) was
never, in its entirety, in the British Museum ;
(3) The inference by Suter that this MS. was probably
the Latin translation of the tract from the Arabic, made by
Gherard of Cremona (n 14-1187)—among the lists of whose
numerous translations a " liber divisionum " occurs—should
be accepted with great reserve ;
(4) The MS. which Dee used can be stated with absolute
certainty and this MS. did not, in all probability, afterwards
become a Cottonian MS.
(1) Sir Robert Bruce Cotton, the founder of the Cottonian
Library, was born in 1571. The Cottonian Library was not,
therefore, in existence in 1563 and Dee could not then have
copied a Cottonian MS.
(2) The Cottonian Library passed into the care of the
nation shortly after 1700. In 1731 about 200 of the MSS.
17 H. Suter, "Zu dem Buche 'De Superficierum divisionibus' des Muhammed
Bagdedinus." Bibliotheca Mathematical vi3, 321-2, 1905.
18 T. SMITH, Catalogns Librorum Manuscriptorum Bibliothecae Cottonianae...
Oxonii,...MDCXCVl, p. 24.
19 The original Cottonian library was contained in 14 presses, above each of
which was a bust ; 12 of these busts were of Roman Emperors. Hence the
classification of the MSS. in the catalogue.
4] MSS. OF MUHAMMED BAGDEDINUS AND DEE 5
were damaged or destroyed by fire. As a result of the
parliamentary inquiry Casley reported20 on the MSS. destroyed
or injured. Concerning Tiberius ix, he wrote, " This volume
burnt to a crust." He gives the title of each tract and the
folios occupied by each in the volume. " Liber Divisionum
Mahumeti Bag-dadini" occupied folios 254-258. When the
British Museum was opened in IJ53, what was left of the
Cottonian Library was immediately placed there. Although
portions of all of the leaves of our tract are now to be seen
in the British Museum, practically none of the writing is
decipherable.
(3) Planta's catalogue21 has the following note concerning
Tiberius ix : "A volume on parchment, which once consisted
of 272 leaves, written about the XIV. century [not the
XII. century, when Gherard of Cremona flourished],
containing eight tracts, the principal of which was a ' Register
of William Cratfield, abbot of St Edmund'" [d. 1415].
Tracts 3, 4, 5 were on music.
(4) On "A0 1583, 6 Sept." Dee made a catalogue of the
MSS. which he owned. This catalogue, which is in the
Library of Trinity College, Cambridge22, has been published23
20 D. CASLEV, p. I5ff. of A Report from the Committee appointed to view the
Cottonian Library ...Published by order of the House of Commons. London,
MDCCXXXII (British Museum MSS. 24932). Cf also the page opposite that
numbered 120 in A Catalogue of the Manuscripts in the Cottonian Library ...with
an Appendix containing an account of the damage sustaitied by the Fire in 1731 ;
by S. Hooper... London : ...mdcclxxvii.
21 J. Plant A, A Catalogue of the Manuscripts in the Cottonian Library deposited
in the British Museum- Printed by command of his Majesty King George III... 1802.
In the British Museum there are three MS. catalogues of the Cottonian
Library :
(1) Harleian MS. 6018, a catalogue made in 1621. At the end are memoranda
of loaned books. On a sheet of paper bearing date Novem. 23, 1638, Tiberius
B IX is listed (folio 187) with its art. 4: "liber divisione Machumeti Bagdedini."
The paper is torn so that the name of the person to whom the work was loaned is
missing. The volume is not mentioned in the main catalogue.
(2) MS. No. 36789, made after Sir Robert Cotton's death in 1631 and before
1638 (cf. Catalogue of Additions to the MSS. in Ihitish Museum, 1900-1905...
London, 1907, pp. 226-227), contains, apparently, no reference to " Muhammed."
(3) MS. No. 36682 A, of uncertain date but earlier than 1654 (Catalogue of
Additions...I.e. pp. 188-189). On folio 78 verso we find Tiberius B ix, Art.
4 : " Liber divisione Machumeti Bagdedini."
A "Muhammed" MS. was therefore in the Cottonian Library in 1638.
The anonymously printed (1840?) " Index to articles printed from the Cotton
MSS., & where they may be found" which may be seen in the British Museum,
only gives references to the MSS. in "Julius."
22 A transcription of the Trinity College copy, by Ashmole, is in MS. Ashm.
1142. Another autograph copy is in the British Museum : Harleian MS. 1879.
23 Camden Society Publications, XIX, London, m.dccc.xlii.
6 EUCLID'S BOOK ON DIVISIONS OF FIGURES I [4-5
under the editorship of J. O. Halliwell. The 95th item
described is a folio parchment volume containing 24 tracts
on mathematics and astronomy. The 17th tract is entitled
" Machumeti Bagdedini liber divisionum." As the contents
of this volume are entirely different from those of Tiberius ix
described above, in (3), it seems probable that there were two
copies of "Muhammed's" tract, while the MS. which Dee
used for the 1570 publication was undoubtedly his own, as we
shall presently see. If the two copies be granted, there is no
evidence against the Dee copy having been that made by
Gherard of Cremona.
5. There is the not remote possibility that the Dee MS.
was destroyed soon after it was catalogued. For in the same
month that the above catalogue was prepared, Dee left his
home at Mortlake, Surrey, for a lengthy trip in Europe.
Immediately after his departure "the mob, who execrated
him as a magician, broke into his house and destroyed a great
part of his furniture and books24..." many of which " were the
written bookes25." Now the Dee catalogue of his MSS.
(MS. O. iv. 20), in Trinity College Library, has numerous
annotations26 in Dee's handwriting. They indicate just what
works were (1) destroyed or stolen ("Fr.")27 and (2) left (" T.")28
after the raid. Opposite the titles of the tracts in the volume
including the tract "liber divisionum," " Fr." is written, and
opposite the title " Machumeti Bagdedini liber divisionum "
is the following note: "Curavi imprimi Urbini in Italia per
Federicum Commandinum exemplari descripto ex vetusto isto
monumento (?) per me ipsum." Hence, as stated above, it is
now definitely known (1) that the MS. which Dee used was
his own, and (2) that some 20 years after he made a copy, the
MS. was stolen and probably destroyed29.
On the other hand we have the apparently contradictory
24 Dictionary of National Biography, Article, " Dee, John."
25 "The compendious rehearsall of John Dee his dutifull declaration A. 1592"
printed in Chetham Miscellanies, vol. 1, Manchester, 1851, p. 27.
26 Although Halliwell professed to publish the Trinity MS., he makes not the
slightest reference to these annotations.
27 " pr." js no doubt an abbreviation for Furatum.
28 "T.", according to Ainsworth {Latin Dictionary), was put after the name of a
soldier to indicate that he had survived (superstes). Whence this abbreviation ?
29 The view concerning the theft or destruction of the MS. is borne out by the
fact that in a catalogue of Dee's Library (British Museum MS. 35213) made early
in the seventeenth century (Catalogue of Additions and Manuscripts...1901,
p. 211), Machumeti Bagdedini is not mentioned.
5-6] MSS. OF MUHAMMED BAGDEDINUS AND DEE 7
evidence in the passage quoted above (Art. 2) from the life
of Dee by Smith14 who was also the compiler of the Catalogue
of the Cottonian Library. Smith was librarian when he
wrote both of these works, so that any definite statement
which he makes concerning the library long in his charge is
not likely to be successfully challenged. Smith does not
however say that Dee's "Muhammed" MS. was in the
Cottonian Library, and if he knew that such was the case
we should certainly expect some note to that effect in the
catalogue18; for in three other places in his catalogue
(Vespasian B x, A ii]3) Galba E vm), Dee's original
ownership of MSS. which finally came to the Cottonian
Library is carefully remarked. Smith does declare, however,
that the Cottonian MS. bore, "after the preface," certain
notes (which I have quoted above) by Archbishop Ussher
(1581-1656). Now it is not a little curious that these notes
by Ussher, who was not born till after the Dee book was
printed, should be practically identical with notes in the
printed work, just after Dee's letter to Commandinus (Art. 3).
For the sake of comparison I quote the notes in question30;
" To the Reader.—I am here to advertise thee (kinde Reader)
that this author which we present to thee, made ufe of Euclid
tranflatedintotheArabick Tongue, whom afterwards Campanus
made to fpeake Latine. This I thought fit to tell thee, that
fo in fearching or examining the Propofitions which are cited
by him, thou mighteft not fometime or other trouble thy felfe
in vain, Farewell."
The Dee MS. as published did not have any preface.
We can therefore only assume that Ussher wrote in a MS.
which did have a preface the few lines which he may have
seen in Dee's printed book.
6. Other suggestions which have been made concerning
" Muhammed's " tract should be considered. Steinschneider
asks, " Ob identisch de Curvis superficiebus, von einem
Muhammed, MS. Brit. Mus. Harl. 623s (1, 191 )31?" I have
examined this MS. and found that it has nothing to do with
the subject matter of the Dee tract.
But again, Favaro states3'2: " Probabilmente il manoscritto
30 This quotation from the Leeke-Serle Euclid11 is an exact translation of the
original.
31 This should be 625 s (I, 391).
32 Favaro, p. 140. Cf. Heiberg, p. 14. This suggestion doubtless originated
with Ofterdinger38, p. [1].
8 EUCLID'S BOOK ON DIVISIONS OF FIGURES I [6
del quale si servi il Dee e lo stesso indicato dall' Heilbronner33
comme esistente nella Biblioteca Bodleiana di Oxford." Under
date "6. 3. 1912" Dr A. Cowley, assistant librarian in the
Bodleian, wrote me as follows: "We do not possess a copy
of Heilbronner's Hist. Math. Univ. In the old catalogue of
MSS. which he would have used, the work you mention is
included—but is really a printed book and is only included in the
catalogue of MSS. because it contains some manuscript notes—
" Its shelf-mark is Savile T 20.
" It has 76 pages in excellent condition. The title page
has : De Superficierum | divisionibus liber j Machometo Bag-
dedino j ascriptus | nunc primum Joannis Dee | ... | opera in
lucem editus | ...Pisauri mdlxx.
"The MS. notes are by Savile, from whom we got the
collection to which this volume belongs."
The notes were incorporated into the Gregory edition11
of the Dee tract. Here and elsewhere34 Savile objected to
attributing the tract to Euclid as author35. His arguments
33 J. C. Heilbronner, Historia niatheseos Universae...Lipsiae, mdccxlii,
p. 620: (" Manuscripta mathematica in Bibliotheca Bodlejana") "34 Mohammedis
Bagdadeni liber de superficierum divisionibus, cum Notis H. S."
34 H. Savile, Praelectiones trcsdccim in principhcm elementorum Evclidis,
Oxonii liabitae M.DC.XX. Oxonii..., 1621, pp. 17-18.
35 Dee's statement of the case in his letter to Commandinus (Leeke-Serle
Euclid", cf. note 30) is as follows : "As for the authors name, I would have you
understand, that to the very old Copy from whence I writ it, the name of
MACHOMET BAGDEDINE was put in ziphers or Characters, (as they call them)
who whether he were that Albategnas whom Copernicus often cites as a very
considerable Author in Astronomie ; or that Machomet who is said to have been
Al/a'ndus's scholar, and is reported to have written somewhat of the art of
Demonstration, 1 am not yet certain of: or rather that this may be deemed a Book
of our Euclide, all whose Books were long since turned out of the Greeke into the
Syriack and Arabick Tongues. Whereupon, It being found some time or other to
want its Title with the Arabians or Syrians, was easily attributed by the transcribers
to that most famous Mathematician among them, Machomet : which I am able to
prove by many testimonies, to be often done in many Moniments of the Ancients ;
...yea further, we could not yet perceive so great acuteness of any Machomet in the
Mathematicks, from their moniments which we enjoy, as everywhere appears in
these Problems. Moreover, that Euclide also himself wrote one Book -rrtpi
hiaLpecraov, that is to say, of Divisions, as may be evidenced from Proclus's
Commentaries upon his first of Elements : and we know none other extant under
this title, nor can we find any, which for excellencie of its treatment, may more
rightfully or worthily be ascribed to Euclid. Finally, I remember that in a certain
very ancient piece of Geometry, I have read a place cited out of this little Book in
expresse words, even as from amost (sic) certain work of Euclid. Therefore we
have thus briefly declared our opinions for the present, which we desire may carry
with them so much weight, as they have truth in them....But whatsoever that Book
of Euclid was concerning Divisions, certainly this is such an one as may be .both
very profitable for the studies of many, and also bring much honour and renown to
every most noble ancient Mathematician ; for the most excellent acutenesse of the
invention, and the most accurate discussing of all the Cases in each Probleme...."
6-7]
THE WOEPCKE-EUCLID MS.
9
are summed up, for the most part, in the conclusions of
Heiberg followed by Heath : "the Arabic original could not
have been a direct translation from Euclid, and probably was
not even a direct adaptation of it; it contains mistakes and
unmathematical expressions, and moreover does not contain
the propositions about the division of a circle alluded to by
Proclus. Hence it can scarcely have contained more than
a fragment of Euclid's work."
The Woepcke-Euclid MS.
7. On the other hand Woepcke found in a MS. (No. 952. 2
Arab. Suppl.) of the Bibliotheque nationale, Paris, a treatise
in Arabic on the division of plane figures, which he translated,
and published in 1851s6. "It is expressly attributed to Euclid
in the MS. and corresponds to the description of it by Proclus.
Generally speaking, the divisions are divisions into figures of
the same kind as the original figures, e.g. of triangles into
triangles ; but there are also divisions into ' unlike' figures,
e.g. that of a triangle by a straight line parallel to the base.
The missing propositions about the division of a circle are
also here: ' to divide into two equal parts a given figure
bounded by an arc of a circle and two straight lines including
a given angle' and ' to draw in a given circle two parallel
straight lines cutting off a certain part of a circle.' Unfortunately
the proofs are given of only four propositions (including the
two last mentioned) out of 36, because the Arabian translator
found them too easy and omitted them." That the omission
is due to the translator and did not occur in the original is
indicated in two ways, as Heiberg points out. Five auxiliary
propositions (Woepcke 21, 22, 23, 24, 25) of which no use is
made are introduced. Also Woepcke 5 is : " ...and we divide
the triangle by a construction analogous to the preceding
construction "; but no such construction is given.
The four proofs that are given are elegant and depend
36 F. Woepcke, " Notice sur des traductions Arabes de deux ouverages perdus
&'E.\ic\ide" Journal Asiatique, Septembre-Octobre, 1851, xvtu4, 217-247. Euclid's
work On the division (of'planefigures) : pp. 233-244. Reference to this paper will
be made by "Woepcke." In Euclidis opera omnia, vol. 8, now in the press, there
are "Fragmenta collegit et disposuit J. L. Heiberg," through whose great courtesy
I have been enabled to see the proof-sheets. First among the fragments, on pages
227-235, are (1) the Proclus references to rrep\ Simpea-ewv, and (2) the Woepcke
translation mentioned above. In the article on Euclid in the last edition of the
Encyclopaedia Britannica no reference is made to this work or to the writings
of Heiberg, Hultsch, Steinschneider and Suter.
lO EUCLID'S BOOK ON DIVISIONS OF FIGURES I [7-10
only on the propositions (or easy deductions from them) of
the Elements, while Woepcke 18 has the true Greek ring:
"to apply to a straight line a rectangle equal to the rectangle
contained by AB, AC and deficient by a square!'
8. To no proposition in the Dee MS. is there word for
word correspondence with the propositions of Woepcke but
in content there are several cases of likeness. Thus, Heiberg
continues,
Dee 3 = Woepcke 30 (a special case is Woepcke 1);
Dee 7 = Woepcke 34 (a special case is Woepcke 14);
Dee 9 = Woepcke 36 (a special case is Woepcke 16);
Dee 12 = Woepcke 32 (a special case is Woepcke 4).
Woepcke 3 is only a special case of Dee 2 ; Woepcke 6,
7, 8, 9 are easily solved by Dee 8. And it can hardly be
chance that the proofs of exactly these propositions in Dee
should be without fault. That the treatise published by
Woepcke is no fragment but the complete work which was
before the translator is expressly stated37, "fin du traite." It
is moreover a well ordered and compact whole. Hence we
may safely conclude that Woepcke's is not only Euclid's own
work but the whole of it, except for proofs of some propositions.
9. For the reason just stated the so-called Wieder-
herstellung of Euclid's work by Ofterdinger38, based mainly on
Dee, is decidedly misnamed. A more accurate description of
this pamphlet would be, " A translation of the Dee tract with
indications in notes of a certain correspondence with 15 of
Woepcke's propositions, the whole concluding with a
translation of the enunciations of 16 of the remaining 21 propositions
of Woepcke not previously mentioned." Woepcke 30, 31, 34,
35, 36 are not even noticed by Ofterdinger. Hence the claim
I made above (" Introductory") that the first real restoration
of Euclid's work is now presented. Having introduced
Woepcke's text as one part of the basis of this restoration,
the other part demands the consideration of the
Practica Geometriae of Leonardo Pisano (Pzbonaci).
10. It was in the year 1220 that Leonardo Pisano, who
occupies such an important place in the history of mathematics
37 Woepcke, p. 244.
38 L. F. Ofterdinger, Beitrdge zur Wiederherstellungder Schrift des Euklides
iiber der Theilung der Figuren, Ulm, 1853.
io-ii] PRACTICA GEOMETRIAE OF LEONARDO PISANO II
of the thirteenth century39, wrote his Practica Geometriae, and
the MS. is now in the Vatican Library. Although it was
known and used by other writers, nearly six and one half
centuries elapsed before it was finally published by Prince
Boncompagni40. Favaro was the first6 to call attention to
the importance of Section IIII41 of the Practica Geometriae in
connection with the history of Euclid's work. This section
is wholly devoted to the enunciation and proof and numerical
exemplification of propositions concerning the divisions of
figures. Favaro reproduces the enunciations of the
propositions and numbers them i to 5742. He points out that in both
enunciation and proof Leonardo 3, 10, 51, 57 are identical
with Woepcke 19, 20, 29, 28 respectively. But considerably
more remains to be remarked.
II. No less than twenty-two of Woepcke's propositions
are practically identical in statement with propositions in
Leonardo ; the solutions of eight more of Woepcke are either
given or clearly indicated by Leonardo's methods, and all six
of the remaining Woepcke propositions (which are auxiliary)
are assumed as known in the proofs which Leonardo gives of
propositions in Woepcke. Indeed, these two works have
a remarkable similarity. Not only are practically all of the
Woepcke propositions in Leonardo, but the proofs called
for by the order of the propositions and by the auxiliary
propositions in Woepcke are, with a possible single exception91,
invariably the kind of proofs which Euclid might have given—■
no other propositions but those which had gone before or
which were to be found in the Elements being required in
the successive constructions.
Leonardo had a wide range of knowledge concerning
Arabian mathematics and the mathematics of antiquity. His
Practica Geometriae contains many references to Euclid's
Elements and many uncredited extracts from this work43.
39 M. Cantor, Vorlesungen iiber Geschichte der Mathematik, n2, 1900, pp. 3-53 ;
"Practica Geometriae," pp. 35-40.
40 Scritti di Leonardo Pisano matematico del secolo decimoterzo publicati da
Baldasarre Boncompagni. Volume 11 (Leonardi Pisani Practica Geometriae
ed opuscoli). Roma... 1862. Practica Geometriae, pp. 1-224.
41 Scritti di Leonardo Pisano...II, pp. 110-148.
42 These numbers I shall use in what follows. Favaro omits some auxiliary
propositions and makes slips in connection with 28 and 40. Either 28 should
have been more general in statement or another number should have been
introduced. Similarly for 40. Compare Articles 33-34, 35.
43 For example, on pages 15-16, 38, 95, 100-1, 154.
12 EUCLID'S BOOK ON DIVISIONS OF FIGURES I [11-12
Similar treatment is accorded works of other writers. But
in the great elegance, finish and rigour of the whole,
originality of treatment is not infrequently evident. If
Gherard of Cremona made a translation of Euclid's book
On Divisions, it is not at all impossible that this may have
been used by Leonardo. At any rate the conclusion seems
inevitable that he must have had access to some such MS. of
Greek or Arabian origin.
Further evidence that Leonardo's work was of Greek-
Arabic extraction can be found in the fact that, in connection
with the 113 figures, of the section On Divisions, of Leonardo's
work, the lettering in only 58 contains the letters c or f\ that
is, the Greek-Arabic succession a, b, g, d, e, z ... is used almost
as frequently as the Latin a, b, c, d, e,f,g,... ; elimination of
Latin letters added to a Greek succession in a figure, for the
purpose of numerical examples (in which the work abounds),
makes the balance equal.
12. My method of restoration of Euclid's work has been
as follows. Everything in Woepcke's text (together with
his notes) has been translated literally, reproduced without
change and enclosed by quotation marks. To all of Euclid's
enunciations (unaccompanied by constructions) which
corresponded to enunciations by Leonardo, I have reproduced
Leonardo's constructions and proofs, with the same lettering
of the figures4,1, but occasional abbreviation in the form of
statement; that is, the extended form of Euclid in Woepcke's
text, which is also employed by Leonardo, has been sometimes
abridged by modern notation or briefer statement. Occasionally
some very obvious steps taken by Leonardo have been left
out but all such places are clearly indicated by explanation
in square brackets, [ ]. Unless stated to the contrary, and
indicated by different type, no step is given in a construction
or proof which is not contained in Leonardo. When there
is no correspondence between Woepcke and Leonardo I have
exercised care to reproduce Leonardo's methods in other
propositions, as closely as possible. If, in a given proposition,
the method is extremely obvious on account of what has gone
before, I have sometimes given little more than an indication
of the propositions containing the essence of the required
44 This is done in order to give indication of the possible origin of the construction
in question (Art. 11).
12-14] SYNOPSIS OF MUHAMMED'S TREATISE 13
construction and proof. In the case of the six auxiliary-
propositions, the proofs supplied seemed to be readily
suggested by propositions in Euclid's Elements.
13. Immediately after the enunciations of Euclid's
problems follow the statements of the correspondence with
Leonardo; if exact, a bracket encloses the number of the
Leonardo proposition, according to Favaro's numbering, and
the page and lines of Boncompagni's edition where Leonardo
enunciates the same proposition.
The following is a comparative table of the Euclid and, in
brackets, of the corresponding Leonardo problems: 1 (5);
2 (14); 3 (2, 1); 4 (23); 5 (33); 6 (16); 7(20)-; 8(27)*;
9 (30, 3i)4?; 10(18); n (o); 12(28)*; 13 (32)47; 14(36);
15 (40); 16 (^7); 17 (39); 18 (o); 19 (3); 20 (10); 21 (o);
22 (o); 23 (o); 24 (o); 25 (o) ; 26 (4); 27 (11); 28 (57);
29 (SO45; 3o(o); 31 (o); 32(29); 33(35); 34 (4o)42; 35 (o);
36 (o).
Summary.
It will be instructive, as a means of comparison, to set
forth in synoptic fashion: (1) the Muhammed-Commandinus
treatise; (2) the Euclid treatise; (3) Leonardo's work. In
(1) and (2) I follow Woepcke closely48.
14. Synopsis of Muhammed's Treatise—
I. In all the problems it is required to divide the proposed
figure into two parts having a given ratio.
II. The figures divided are: the triangle (props. 1-6);
the parallelogram (11); the trapezium89 (8, 12, 13); the
quadrilateral (7, 9, 14-16); the pentagon (17, 18, 22); a pentagon
with two parallel sides (19), a pentagon of which a side is
parallel to a diagonal (20).
45 Leonardo considers the case of "one third" instead of Euclid's "a certain
fraction," but in the case of 20 he concludes that in the same way the figure may
be divided "into four or many equal parts." Cf. Article 28.
46 Woepcke 8 may be considered as a part of Leonardo 27 or better as an
unnumbered proposition following Leonardo 25.
47 Leonardo's propositions 30-32 consider somewhat more general problems
than Euclid's 9 and 13. Cf. Articles 30 and 34.
48 Woepcke, pp. 245-246.
14 EUCLID'S BOOK ON DIVISIONS OF FIGURES I [14-15
III. The transversal required to be drawn :
A. passes through a given point and is situated :
1. at a vertex of the proposed figure (1, 7, 17);
2. on any side (2, 9, 18);
3. on one of the two parallel sides (8).
B. is parallel:
1. to a side (not parallel) (3, 13, 14, 22) ;
2. to the parallel sides (11, 12, 19);
3. to a diagonal (15, 20);
4. to a perpendicular drawn from a vertex of the
figure to the opposite side (4);
5. to a transversal which passes through a vertex
of the figure (5) ;
6. to any transversal (6, 16).
IV. Prop. 10 : Being given the segment AB and two
lines which pass through the extremities of this segment and
form with the line AB any angles, draw a line parallel to AB
from one or the other side of AB and such as to produce
a trapezium of given size.
Prop. 21. Auxiliary theorem regarding the pentagon.
15. Commandinus s Treatise—Appended to the first
published edition oi Muhammed's work was a short treatise49
by Commandinus who said80 of Muhammed: "for what things
the author of the book hath at large comprehended in many
problems, I have compendiously comprised and dispatched in
two only." This statement repeated by Ofterdinger51 and
Favaro52 is somewhat misleading.
The " two problems" of Commandinus are as follows :
" Problem I. To divide a right lined figure according to
a proportion given, from a point given in any part of the
ambitus or circuit thereof, whether the said point be taken in
any angle or side of the figure."
"Problem II. To divide a right lined figure GABC,
49 Commandinus11, pp. 54-76.
50 Commandinus11, p. [ii] ; Leeke-Serle Euclid, p. 603.
51 Ofterdinger38, p. 11, note. 52 Favaro6, p. 139.
i5-i6] SYNOPSIS OF EUCLID'S TREATISE 15
according to a proportion given, E to F, by a right line
parallel to another given line D"
But the first problem is divided into 18 cases : 4 for the
triangle, 6 for the quadrilateral, 4 for the pentagon, 2 for the
hexagon and 2 for the heptagon ; and the second problem, as
Commandinus treats it, has 20 cases : 3 for the triangle, 7 for
the quadrilateral, 4 for the pentagon, 4 for the hexagon, 2 for
the heptagon.
16. Synopsis of Euclid's Treatise—
I. The proposed figure is divided :
1. into two equal parts (1, 3, 4, 6, 8, 10, 12, 14, 16,
19, 26, 28);
2. into several equal parts (2, 5, 7, 9, 11, 13, 15, 17, 29);
3. into two parts, in a given ratio (20, 27, 30, 32, 34,36);
4. into several parts, in a given ratio (31, 33, 35, 36).
The construction 1 or 3 is always followed by the
construction of 2 or 4, except in the propositions 3, 28, 29.
II. The figures divided are :
the triangle (1, 2, 3, 19, 20, 26, 27, 30, 31) ;
the parallelogram (6, 7, 10, 11);
the trapezium (4, 5, 8, 9, 12, 13, 32, 33);
the quadrilateral (14, 15, 16, 17, 34, 35, 36) ;
a figure bounded by an arc of a circle and two lines
(28);
the circle (29).
III. It is required to draw a transversal:
A. passing through a point situated :
1. at a vertex of the figure (14, 15, 34, 35);
2. on any side (3, 6, 7, 16, 17, 36) ;
3. on one of two parallel sides (8, 9) ;
4. at the middle of the arc of the circle (28);
5. in the interior of the figure (19, 20) ;
6. outside the figure (10, 11, 26, 27) ;
7. in a certain part of the plane of the figure (12,
13).
16 EUCLID'S BOOK ON DIVISIONS OF FIGURES I [16-17
B. parallel to the base of the proposed figure (1, 2,
4, 5. 3o-33)-
C. parallel to one another, the problem is
indeterminate (29).
IV. Auxiliary propositions :
18. To apply to a given line a rectangle of given size
and deficient by a square.
21, 22, when a . d< b. c, it follows that a\b%c:d\
23, 24, when a\b>c:d, it follows that
(a + b): b > (c + d) : d;
25, when a :b<c : d, it follows that (a — b) : b < (c — d): d.
In the synopsis of the last five propositions I have
changed the original notation slightly.
17. Analysis of Leonardo s Work. I have not thought
it necessary to introduce into this analysis the unnumbered
propositions referred to above42.
I. The proposed figure is divided :
1. into two equal parts (1-5, 15-18, 23-28, 36-38,
42-46, 53-55. 57);
2. into several equal parts (6, 7, 9, 13, 14, 19, 21,
33, 47-50. 56);
3. into two parts in a given ratio (8, 10-12, 20, 29-
32- 34. 39. 40, 51' 52);
4. into several parts in a given ratio (22, 35, 41).
The construction 1 or 3 is always followed by the
construction of 2 or 4 except in the propositions 42-46,
5i. 54- 57-
II. The figures divided are :
the triangle (1-14) ;
the parallelogram (15-22);
the trapezium (23-35) >
the quadrilateral (36-41) ;
the pentagon (42-43);
the hexagon (44);
the circle and semicircle (45-56) ;
a figure bounded by an arc of a circle and two lines (57).
17] ANALYSIS OF LEONARDO'S WORK i7
III.
(i) It is required to draw a transversal:
A. passing through a point situated :
i. at a vertex of the figure (i, 6, 26, 31, 34, 36,
41-44);
2. on a side not produced (2, 7, 8, 16, 20, 37, 39);
3. at a vertex or a point in a side (40);
4. on one of two parallel sides (24, 25, 27, 30);
5. on the middle of the arc of the circle (53, 55,
57);
6. on the circumference or outside of the circle
(45);
7. inside of the figure (3, 10, 15, 17, 46);
8. outside of the figure (4, 11, 12, 18);
9. either inside or outside of the figure (38) ;
10. either inside or outside or on a side of the
figure (32) ;
11. in a certain part of the plane of the figure (28).
B. parallel to the base of the proposed figure (5, 14,
19, 21-23, 29, 33, 35, 54);
C. parallel to a diameter of the circle (49, 50).
(ii) It is required to draw more than one transversal
(a) through one point (9, 47, 48, 56); (b) through
two points (13); (c) parallel to one another, the
problem is indeterminate (51).
(iii) It is required to draw a circle (52).
18 EUCLID'S BOOK ON DIVISIONS OF FIGURES I [17
IV. Auxiliary Propositions :
Although not explicitly stated or proved, Leonardo makes
use of four out of six of Euclid's auxiliary propositions113. On
the other hand he proves two other propositions which Favaro
does not number: (1) Triangles with one angle of the one
equal to one angle of the other, are to one another as the
rectangle formed by the sides about the one angle is to that
formed by the sides about the equal angle in the other;
(2) the medians of a triangle meet in a point and trisect one
another.
II.
l8. Abraham Savasorda, Jordanus Nemorarius, Luca
Paciuolo.—In earlier articles (10, 11) incidental reference was
made to Leonardo's general indebtedness to previous writers
in preparing his Practica Geometriae, and also to the debt
which later writers owe to Leonardo. Among the former,
perhaps mention should be made of Abraham bar Chijja ha
Nasi53 of Savasorda and his Liber embadorum known through
the Latin translation of Plato of Tivoli. Abraham was a
learned Jew of Barcelona who probably employed Plato of
Tivoli to make the translation of his work from the Hebrew.
This translation, completed in 1116, was published by Curtze,
from fifteenth century MSS., in 190254. Pages 130-159 of this
edition contain " capitulum tertium in arearum divisionum
explanatione" with Latin and German text, and among the
many other propositions given by Savasorda is that of
Proclus-Euclid ( = Woepcke 28 = Leonardo 57). Compared
with Leonardo's treatment of divisions Savasorda's seems
rather trivial. But however great Leonardo's obligations to
other writers, his originality and power sufficed to make
a comprehensive and unified treatise.
Almost contemporary with Leonardo was Jordanus
Nemorarius (d. 1237) who was the author of several works, all
probably written before 1222. Among these is Geometria vel
53 That is, Abraham son of Chijja the prince. Cf- Steinschneider, Bibliotheca
Mathematica, 1896, (2), x, 34-38, and Cantor, Vorlesungen iiber Geschichte d.
Math. 13, 797-800, 907.
54 M. CURTZE, " Urkunden zur Geschichte der Mathematik im Mittelalter und
der Renaissance..." Erster Teil {Abhandlung zur Geschichte der Mathematischen
Wissenschaften...yii\. Heft), Leipzig, 1902, pp. 3-183.
2—2
20 EUCLID'S BOOK ON DIVISIONS OF FIGURES II [18
De Triangulis™ in four books. The second book is principally
devoted to problems on divisions : Propositions 1-7 to the
division of lines and Propositions 8, 13, 17, 18, 19 to the
division of rectilineal figures. The enunciations of Propositions
8, 13, 17, 19 correspond, respectively, to Euclid 3, 26, 19, 14
and to Leonardo 2, 4, 3, 36. But Jordanus's proofs are quite
differently stated from those of Euclid or Leonardo. Both
for themselves and for comparison with the Euclidean proofs
which have come down to us, it will be interesting to reproduce
propositions 13 and 17 of Jordanus.
"13. Triangulo dato et puncto extra ipsum signato
lineam per punctum transeuntem designare, que triangulum
per equalia parciatur" [pp. 15-16].
m n
" Let abc be the triangle and d the point outside but
contained within the lines aef, hbl, which are lines dividing
the triangle equally and produced. For if d be taken in any
such place, draw dg parallel to ca meeting cb produced in g.
Join cd and find run such that
A cdg : A aec (= \ A abc) = eg : mn.
55 Edited with Introduction by Max Curtze, Mitteilungen des Copernicus-
Vereins fiir Wissenschaften midKunst zu Thorji. VI. Heft, 1887. In his discussion
of the second book, Cantor (Vorlesungen ii. Gesck. d. Math. 11,, 75) is misleading
and inaccurate. One phase of his inaccuracy has been referred" to by Enestrom
{Bibliotheca Matheniatica, Januar, 1912, (3), xn, 62).
18] JORDANUS NEMORARIUS 21
Then divide eg in k such that
gk : kc = kc : mn.
Produce dk to meet ca in /. Then I say that dp divides the
triangle abc into equal parts.
For, since the triangle ckp is similar to the triangle kdg,
by 4 of sixth56 and parallel lines and 15 of first and definitions
of similar areas,
A ckp : A kdg = mn : kg
by corollary to 17 of sixth87. But
A kdg : A edg = kg : eg.
Therefore, by equal proportions,
A ckp : A edg = mn : eg.
.\ Ackp : Acdg= Aaec : Acdg.
And A ekp = A aec ( = ^-A abc)
by 9 of fifth, and this is the proposition.
And by the same process of deduction we may be led to
an absurdity, namely, that all may equal a part if the point k
be otherwise than between e and b or the point/ be otherwise
than between h and a; the part cut off must always be either
all or part of the triangle aec."
"17. Puncto infra propositum trigonum dato tineam per
ipsum deducere, que triangulum secetper equalia" [pp. 17-18].
" Let abc be the triangle and d the point inside and
contained within the part between ag and be which divide
two sides and triangle into equal parts. Through d draw fdh
parallel to ac and draw db. Then by 12 of this book58 draw
mn such that
bf: mn = Abdf: Abee ( = ^Aabc).
56 That is, Euclid's Elements, vi. 4.
57 I do not know the MS. of Euclid here referred to ; but manifestly it is the
Porism of Elements VI. 19 which is quoted: "If three straight lines be
proportional, then as the first is to the third, so is the figure described on the first to that
which is similar and similarly described on the second."
58 That is, De Triangulis, Book 2, Prop. 12 : "Data recta linea aliam rectam
inuenire, ad quam se habeat prior sicut quilibet datus triangulus ad quemlibet
datum triangulum" [p. 15].
2 2 EUCLID'S BOOK ON DIVISIONS OF FIGURES II [18
Also find ty such that
bf: ty = Abfh : Abee.
And since Abfh> Abdf, mn>ty
by 8 and 10 of fifth.
Now bf:bc = bc:ty
by corollary to 17 of sixth58a, and Abfh< A bee since fh, ce
are parallel lines.
t >y
But be : ty > be : mn
by second part of 8 of fifth.
. •. bf:bc> be: mn ;
.*. fe<\mn
by 6 of this book59.
58a Rather is it the converse of this corollary, which is quoted in note 57. It
follows at once, however :
bf: ty = AifA : Abec=bfi : bc\ .: bf. ty = bci or bf: bc=bc : ty.
59 "Cum sit linee breuiori adiecte major proporcio ad compositam, quam
:omposite ad longiorem, breuiorem quarta longioris minorem esse necesse est
'P- 13]-
i8]
LUCA PACIUOLO
23
Add then to the line cf from f a line fz, by 5 of this book00,
such that
fz : zc = zc : mn ;
and fz will be less than fb by the first part of the premise.
[Supposition with regard to d ?]
Join zd and produce it to. meet ac in k; then I say that
the line zdk divides the triangle abc into equal parts. For
Abdf:Azdf=bf:zf
by 1 of sixth.
But A zdf': A zkc = zf': mn
by corollary to 17 of sixth57 and similar triangles.
Therefore by 1 and by equal proportions
A bdf: A zkc = bf: mn.
But A bdf': A bee = bf: mn.
Therefore by the second part of 9 of fifth
Azkc = A bee = ^Aabc." q. e.f.
Proposition 18 of Jordanus is devoted to finding the centre
of gravity of a triangle6011 and it is stated in the form of a
problem on divisions. In Leonardo this problem is treated109 by
showing that the medians of a triangle are concurrent; but
in Jordanus (as in Heron83) the question discussed is, " to find a
point in a triangle such that when it is joined to the angular
points, the triangle will be divided into three equal parts "(p. 18).
A much later work, Summa de Arithmetica Geometria
Proportioni et Proportionalita... by Luca Paciuolo (b. about
1445) was published at Venice in 149461. In the geometrical
section (the second, and separately paged) of the work,
pages 35 verso-43 verso, problems on divisions of figures are
solved, and in this connection the author acknowledges great
debt to Leonardo's work. Although the treatment is not as
60 " Duabus lineis propositis, quarum una sit minor quarta alterius uel equalis,
minori talem lineam adiungere, ut, que adiecte ad compositam, eadem sit
composite ad reliquam propositarum proporcio " [p. 12J.
60,1 Archimedes proved (Works of Archimedes, Heath ed., 1897, p. 201 ; Opera
omnia iterum edidit J. L. Heiberg, 11, 150-159, 1913) in Propositions 13-14, Book I
of "On the Equilibrium of Planes" that the centre of gravity of any triangle is at
the intersection of the lines drawn from any two angles to the middle points of the
opposite sides respectively.
01 A new edition appeared at Toscolano in 1523, and in the section which we are
discussing there does not appear to be any material change.
24 EUCLID'S BOOK ON DIVISIONS OF FIGURES II [18-19
full as Leonardo's, yet practically the same figures are
employed. The Proclus-Euclid propositions which have to do
with the division of a circle are to be found here.
19. " Muhanimed Bagdedinus "and other A rabian writers
on Divisions of Figures.—We have not considered so far
who " Muhammed Bagdedinus" was, other than to quote the
statement of Dee35 that he may have been "that Albategnus
whom Copernicus often cites as a very considerable author, or
that Machomet who is said to have been Alkindus's scholar."
Albategnius or Muhammed b. Gabir b. Sinan, Abu 'Abdallah,
el Battani who received his name from Battan, in Syria,
where he was born, lived in the latter part of the ninth and in
the early part of the tenth century62. El-Kindi (d. about 873)
the philosopher of the Arabians was in his prime about 85063.
"Alkindus's scholar" would therefore possibly be a
contemporary of Albategnius. It is probably because of these
suggestions of Dee64 that Chasles speaks65 of " Mahomet
Bagdadin, geometre du xe siecle."
It would be scarcely profitable to do more than give
references to the recorded opinions of other writers such
as Smith66, Kastner67, Fabricius68, Heilbronner69, Montucla70,
Hankel71, Grunert72—whose results Favaro summarizes73.
The latest and most trustworthy research in this connection
seems to be due to Suter who first surmised74 that the author
02 M. Cantor, Vorlesungen it. Gesch. d. Math. I3, 736.
03 M. Cantor, Vorlesungen ii. Gesch. d. Math. i3, 718.
04 Cf. Steinschneider'12.
05 Chasles, Apercu historique... 3e ed., Paris, 1889, p. 497.
06 T. Smith, Vitae quoriimdam...viroritm, 1707, p. 56. Cf. notes 14, 15.
67 A. G. Kastner, Geschichte der Mat/iematik..., Bandi, Gottingen, 1796, p. 273.
See also his preface to N. Morville, Lehre von der geomettischen und bkono-
mischen Vertheilung der Felder, nach der ddnischen Schrift bearbeitet von J. W.
Christiani, begleitet mit einer Vorrede...von A. G. Kastner, Gottingen, 1793.
08 J. A. Fabricius, Bibliotheca Graeca...Edttio nova. Volumen quartum,
Hamburgi, mdcclxxxv, p. 81.
fi9 J. C. Heilbronner, Histoiia Matheseos universae...Lipsiae, mdccxlii,
p. 438, 163-4.
70 J. F. MONTUCLA, Histoire des mathe'matiques...£&. nouv. Tome I, An vn,
p. 216.
71 H. Hankel, Zur Geschichte der Math, in Alterthum u. Mittelalter, Leipzig,
1874, p. 234.
72 J. A. GRUNERT, Math. W6rterbuch...von G. S. Khigel, fortgesetzt von C. B.
Mollweide und beendigt von J. A. Grunert...Erste Abteilung, die reine Math.,
fiinfter Theil, erster Band, Leipzig, 1831, p. 76.
73 Favaro, pp. 141-144.
74 H. Suter, "Die Mathematiker und Astronomen der Araber und ihre Werke"
(Abh. z. Gesch. d. Math. Wiss. X. Heft, Leipzig, 1900), p. 202, No. 517.
ig] ARABIAN WRITERS ON DIVISIONS OF FIGURES 25
of the Dee book On Divisions was Muh. b. Muh. el-Bagdadi
who wrote at Cairo a table of sines for every minute. A little
later", however, Suter discovered facts which led him to
believe that the true author was Abu Muhammed b. 'Abdel-
baqi el-Bagdadi (d. 1141 at the age of over 70 years) to whom
an excellent commentary on Book x of the Elements has been
ascribed. Of a MS. by this author Gherard of Cremona
(1114-1187) may well have been a translator.
Euclid's book On Divisions was undoubtedly the ultimate
basis of all Arabian works on the same subject. We have
record of two or three other treatises.
1. Tabitb. Qorra (826-901) translated parts of the works
of Archimedes and Apollonius, revised Ishaq's translation of
Euclid's Elements and Data and also revised the work
On Divisions of Figures translated by an anonymous
writer76.
2. Abu Muh. el-Hasan b. 'Obeidallah b. Soleiman b.
Wahb (d. 901) was a distinguished geometer who wrote
"A Commentary on the difficult parts of the work of Euclid''
and "The Book on Proportion." Suter thinks77 that another
reading is possible in connection with the second title, and
that it may refer to Euclid's work On Divisions.
3. Abu'l Wefa el-Buzgani (940-997) one of the greatest
of Arabian mathematicians and astronomers spent his later
life in Bagdad, and is the author of a course of Lectures on
geometrical constructions. Chapters vii-ix of the Persian
form of this treatise which has come down to us in roundabout
fashion were entitled: "On the division of triangles," "On
the division of quadrilaterals," " On the division of circles "
respectively. Chapter vn and the beginning of Chapter vm
are, however, missing from the Bibliotheque nationale Persian
MS. which has been described by Woepcke78. This MS.,
which gives constructions without demonstrations, was made
from an Arabian text, by one Abu Ishaq b. 'Abdallah with
73 H. SUTER, idem, "Nachtrage und Berichtigung" {Abh. z. Gcsch. d. Math.
Wiss. XIV. Heft, 1902), p. 181 ; alio llibliotheca Mathematical, iv3, 1903, pp. 22-27.
70 H. SUTER, "Die Mathematiker...," pp. 34-38.
77 H. Suter, "Die Mathematiker...,'' pp. 48 and 211, note 23.
78 F. Woepcke, " Recherches sur l'histoire des Sciences mathematiques c'.iez
lea orientaux, d'apres des traites inedits Arabes et Persans. Deuxieme ?.' icle.
Analyse et extrait d'un recueil de constructions geometriques par Aboul '\\'afa,:'
Journal asiatique, Fevrier—Avril, 1855, (5), V, 218-256, 309-359 ; reprint, Paris,
1855, pp. 89.
26 EUCLID'S BOOK ON DIVISIONS OF FIGURES II [19-20
the assistance of four pupils and the aid of another translation.
The Arabian text was an abridgment of Abu'l Wefa's lectures
prepared by a gifted disciple.
The three propositions of Chapter ixV9 are practically
identical with Euclid (Woepcke) 28, 29. In Chapter vin80
there are 24 propositions. About a score are given, in
substance, by both Leonardo and Euclid.
In conclusion, it may be remarked that in Chapter xn
of Abu'l Wefa's work are 9 propositions, with various
solutions, for dividing the surface of a sphere into equiangular and
equilateral triangles, quadrilaterals, pentagons and hexagons.
20. Practical applications of the problems On Divisions of
Figures ; the \ierpiKa. of Heron of Alexandria.—The popularity
of the problems of Euclid's book On Divisions among Arabians,
as well as later in Europe, was no doubt largely due to the
possible practical application of the problems in the division
of parcels of land of various shapes, the areas of which,
according to the Rhind papyrus, were already discussed in
empirical fashion about 1800 b.c. In the first century before
Christ81 we find that Heron of Alexandria dealt with the
division of surfaces and solids in the third book of his
Surveying (/ier/aiKa)82. Although the enunciations of the
propositions in this book are, as a whole, similar63 to those
70 F. Woepcke, idem, pp 340-341 ; reprint, pp. 70-71.
80 F. Woepcke, idem, pp. 338-340 ; reprint, pp. 68-70.
81 This date is uncertain, but recent research appears to place it not earlier
than 50 B.C. nor later than 150 A.D. Cf. HEATH, Thirteen Books of Euclid's
Elements, I, 20-21; or perhaps better still, Article "Heron 5" by K. Tittel in
Pauly-Wissowa's Real-Encyclopadie der class. Altertu/nswissenschaften, will,
Stuttgart, 1913, especially columns 996-1000.
82 Heronis Alexandrini opera quae supersu?it omnia, Vol. Ill, Rationes Dimetiendi
et commentatio Dioptrica recensuit Hermannus Schoene, Lipsiae, MCMIII. Third
book, pp. 140-185. Cf. CANTOR, Vorlesungen..., i3, 380-382.
83 Only two are exactly the same: Il-ni ( = Euclid 30), vn ( = Euclid 32),
the problem considered in X is practically Euclid 27 (Art. 48), while XVIII is closely
related to Euclid 29 (Art. 50). In XIX Heron finds in a triangle a point such that
when it is joined to the angular points, the triangle will be divided into three equal
parts. The divisions of solids of which Heron treats are of a sphere (xxin) and
the division in a given ratio, by a plane parallel to the base, of a Pyramid (XX) and
of a Cone (xxi). For proof of Proposition XXHI : To cut a sphere by a plane so
that the volumes of the segments are to one another in a given ratio, Heron refers
to Proposition 4, Book II of "On the Sphere and Cylinder:' of Archimedes ; the
third proposition in the same book of the Archimedean work is (Heron XVII) : To
cut a given sphere by a plane so that the surfaces of the segments may have to one
another .1 given ratio. {Works of Archimedes, Heath ed., 1897, pp. 61-65 I Opera
omnia iterum edidit J. L. Heiberg, 1, 184-195, 1910.)
Propositions II and VII are also given in Heron's ire pi Sio-n-rpas (Schoene's
2o-2i] HERON OF ALEXANDRIA, APOLLONIUS OF PERGA 27
in Euclid's book On Divisions, Heron's discussion consists
almost entirely of " analyses" and approximations. For
example, 11: " To divide a triangle in a given ratio by a
line drawn parallel to the base"—while Euclid gives the
general construction, Heron considers that the sides of the
given triangle have certain known numerical lengths and
thence finds the approximate distance of the angular points of
the triangle to the points in the sides where the required line
parallel to the base intersects them, because, as he expressly
states, in a field with uneven surface it is difficult to draw a
line parallel to another. Most of the problems are discussed
with a variety of numbers although theoretical analysis
sometimes enters. Take as an example Proposition x84: "To divide
a triangle in a given ratio by a line drawn from a point in a
side produced."
" Suppose the construction made. Then the ratio of triangle
AEZ to quadrilateral ZEBY is known;
also the ratio of the triangle A BY to A
the triangle AZE. But the triangle
ABY is known, therefore so is the
triangle AZE. Now A is given.
Through a known point A there is
therefore drawn a line which, with two
lines AB and AY intersecting in A,
encloses a known area.
Therefore the points E and Z are
given. This is shown in the second
book of On Cutting off a Space. Hence the required proof.
If the point A be not on BY but anywhere this will make
no difference."
21. Connection between Euclid's book On Divisions,
Apollonius s treatise On Cutting off a Space and a Pappus-
lemma to Euclid's book of Porisms.—Although the name of
the author of the above-mentioned work is not given by
Heron, the reference is clearly to Apollonius's lost work.
According to Pappus it consisted of two books which
contained 124 propositions treating of the various cases of the
edition, pp. 278-281). Cf. "Extraits des Manuscrits relatifs a la geometrie grecs'
par A. J. C. Vincent, Notices et extraits des Manuscrits de la bibliotheque impe'riale,
Paris, 1858, XIX, pp. 157, 283, 285.
84 Heron, idem, p. i6of.
28 EUCLID'S BOOK ON DIVISIONS OF FIGURES II [21
following problem : Given two coplanar straight lines A1P1,
B2P2, on which AY and B2 are fixed points; it is required to
draw through a fixed point A of the plane, a transversal AZE
forming on A1P1, B2P2 the two segments AXZ, B2E such that
AYZ. B2E is equal to a given rectangle.
Given a construction for the particular case when AXPX,
B,P„ meet in A, and when A1 and B2 coincide with A—
Heron's reasoning becomes clear. The solution of this
particular case is practically equivalent to the solution of Euclid's
Proposition 19 or 20 or 26 or 27. References to restorations
of Apollonius's work are given in note 111.
To complete the list of references to writers before 1500,
who have treated of Euclid's
problems here under discussion, ^- £ -,
I should not fail to mention the ^v / /
last of the 38 lemmas which \. / /
Pappus gives as useful in con- ^/ /
nection with the 171 theorems / x. /
of Euclid's lost book of Porisms: / ^"n/h
Through a given point E in BD I /\.
produced to draw a line cutting ~Q * -* -^ E
the parallelogram AD such that
the triangle ZYH is equal to the parallelogram AD.
After "Analysis" Pappus has the following
" Synthesis. Given the parallelogram AD and the
point E. Through E draw the line EZ such that the
rectangle YZ. YH equals twice the rectangle AY. YD. Then
according to the above analysis [which contains a reference
to an earlier lemma discussed a little later8" in this book] the
triangle ZYH equals the parallelogram AD. Hence EZ
satisfies the problem and is the only line to do so85."
The tacit assumption here made, that the equivalent of
a proposition of Euclid's book On Divisions {of Figures') was
well known, is noteworthy.
85 Pappus ed. by Hultsch, Vol. 2, Berlin, 1877, pp. 917-919. In Chasles's
restoration of Euclid's Porisms, this lemma is used in connection with " Porism CLXXX :
Given two lines SA, SA', a point P and a space v : points / and/7 can be found in
a line with P and such that if one take on SA, SA' two points m, m', bound by the
equation Im.J'm'= v, the line mm' will pass through a given point." Les trots
livres de Porismes d'Euclide, Paris, i860, p. 284. See also the restoration by
R. Simson, pp. 527-530 of "De porismatibus tractatus," Opera quaedam reliqua...
Glasguae, m.dcclxxvi.
III.
" The Treatise of Euclid on the Division (of plane Figures)."
Proposition 1.
22- " To dividem a given triangle into equal parts by
a line parallel to its base!' [Leonardo 5, p. 119, 11. 7-9.]
Let abg be the given triangle which it is required to bisect
by a line parallel to bg. Produce ba to
d till ba = 2ad. Then in ba find a point
e such that
ba : ae = ae : ad.
Through e draw ez parallel to bg; then
the triangle abg is divided by the line
ez into two equal parts, of which one
is the triangle aez, and the other the
quadrilateral ebgz.
Leonardo then gives three proofs, but as the
first and second are practically equivalent, I shall Jj.
only indicate the second and third. ^
I. When three lines are proportional, as the first is to the
third so is a figure on the first to the similar and similarly
situated figure described on the second [vi. 19, " Porism "J87.
ba: ad= figure on ba : similar and similarly situated
figure on ae.
Hence ba : ad= Aabg: Aaez
= 2:1.
Aabg= 2Aaez.
II. ba : ae = ae : ad.
ba . ad=ae2,
86 Literally, the original runs, according to Woepcke, " We propose to
ourselves to demonstrate how to divide, etc." I have added all footnotes except those
attributed to Woepcke.
87 Throughout the restoration I have added occasional references of this kind
to Heath's edition of Euclid's Elements ; VI. 19 refers to Proposition 19 of
Book vi. Cf. note 57.
22]
PROPOSITION i
31
and since ad is one-half of ba,
ba2 = 2ae"-.
And since bg is parallel to ez,
ba : ae =ga : az.
ba2: ae2=ga2 : az2. [vi. 22]
But ba2 = 2ae2.
.". ga2=2az1.
Then ba . ag= 2ae . az, [vi. 22]
.-. Aabg= 2Aaezm.
Then follows a numerical example.
88 The theorem here assumed is enunciated by Leonardo (p. Ill, 11. 24-27)
as follows : Et si d trigono recta protracta fuerit
secans duo latera trigonj, que cu/n ipsis duobus
lateribus faciant trigonum habentem angulum unum
comunem cum ipso trigono, erit proportio unius
trigoni ad alium, sicut facta ex lateribus conti-
nentibus ipsum angulum. This is followed by the
sentence " Ad cuius rei euidentiam.'' Then come
the construction and proof:
Let abc be the given triangle and de the line
across it, meeting the sides ca and cb in the points
d, e, respectively. I say that
A abc : A dec=ac. cb : dc. ce.
Proof: To a<r apply the triangle afc = A dec. [i. 44]
Since the triangles abc, afc are of the same
altitude,
But
and since A dec=A acf
be : fc = A abc :
be : fc=ac. be :
A afc.
ac .fc,
[vi. 1]
[V- 15]
A abc : A afc= ac .be : ac .fc,
A act : A dee — ac. be : ac. cf
Again, since the triangles acf, dee are equal and have a common angle, as in
the fifteenth theorem of the sixth book of Euclid, the sides are mutually
proportional.
.". ac : dc=ce : cf, .-. ac.cf—dc. ce,
.'. A acb : A dce = ac. cb : dc. ce.
" quod oportebat ostendere."
It is to be observed that the Latin letters are used with the above figure. This
suggests the possibility of the proof being due to Leonardo.
The theorem is assumed in Euclid's proof of proposition 19 (Art. 40) and it
occurs, directly or indirectly, in more than one of his works. A proof, depending
on the proposition that the area of a triangle is equal to one-half the product of its
base and altitude, is given by Pappus (pp. 894-897) in connection with one of his
lemmas for Euclid's book of Porisins: Triangles which have one angle of the one
equal or supplementary to one angle of the other are in the ratio compounded of the
32 EUCLID'S BOOK ON DIVISIONS OF FIGURES III [23
Proposition 2.
23. " To divide a given triangle into three equal parts
by tivo lines parallel to its base." [Leonardo 14, p. 122, 1. 8.]
Let abg be the given triangle with base bg. Produce ba
to d till ba = 2,ad, and produce ad to
e till ad=de; then ae = \ba. Find
as, a mean proportional between ba
and ad, and ia a mean proportional
between ba and #£. Then through
z and z draw 2/, ik parallel to bg
and I say that the triangle abg is
divided into three equal parts of
which one is the triangle azt,
another the quadrilateral zikt, the third
the quadrilateral ibgk.
Proof: Since
ba : az = az : ad,
ba: ad= Aabg : Aazt, [vi. 19, Porism]
for these triangles are similar.
ratios of t/ie sides about the equal or supplementary angles. {Cf R. SlMSON, " Ue
Porismatibus Tractatus" in Opera quaedam reliqua...1776, p. 515 ff.—P. BRETON
(de Champ), " Recherches nouvelles sur les porismes d'Euclide," Journal de mathe-
matiques pures et appliquees, XX, 1855, p. 233 ff. Reprint, p. 25 ff.—M. Chasles,
Les trots livres de Porismes d'Euclide...Paris, i860, pp. 247, 295, 307.)
The first part of this lemma is practically equivalent to either (1) [vi. 23] :
Equiangular parallelograms have to one another the ratio compounded of the ratio
of their sides ; or (2) the first part of Prop. 70 of the Data (Euclidis ZWa...edidit
H. Menge, Lipsiae, 1896, p. i3of.): If in two equiangular parallelograms the sides
containing the equal angles have a given ratio to one another [i.e. one side in one to
one side in the other], the parallelograms themselves will also have a given ratio to
one another. Cf Heath, Thirteen Books of Euclid's Elements, II, 250.
The proposition is stated in another way by Pappus85 (p. 928) who proves that
a parallelogram is to an equiangular parallelogram as the rectangle contained by
the adjacent sides of the first is to the rectangle contained by the adjace/it sides of the
second.
The above theorem of Leonardo is precisely the first of those theorems which
Commandinus adds to vi. 17 of his edition of Euclid's Elements and concerning
which he writes "a nobis elaborata" ("fatti da noi"): Euclidis Elementorum
LibriXV... A Federico Commandino...Pisauri, mdlxxii, p. 81 recto (Degli Elementi
d' Euclide libri quindici con gli scholii antichi tradotti prima 171 lingua latina da
M. Federico Commandino da Urbino, et con commentarii illustrati, et hora d' ordine
dell' istcsso transportati nella nostra vulgare, et da lui riveduti. In Urbino,
m.d.lxxv, p. 88 recto).
23-24] PROPOSITIONS 2-3 33
Now ba=i)ad; .-. Aabg = ^Aazt.
.". Aazt = \Aabg.
Again, ba : ia = ia : ae ;
ba:ae — A on £« : similar and similarly situated A on ai.
But triangles aik, abg are similar and similarly described
on ai and ab; and
ea : ab= 2 : 3.
Aaik = \Aabg.
And since Aazt = ^Aabg, there remains the quadrilateral
zikt = \t\abg. We see that the quadrilateral ibgk will be the
other third part; hence the triangle abg has been divided into
three equal parts ; "quod oportebat facere."
Leonardo continues: " Et sic per demonstrates modos omnia
genera trigonorum possunt diuidi in quatuor partes uel
plures." Cf. note 45.
Proposition 3.
24. " To divide a given triangle into two equal parts
by a line drawn from a given
point situated on one of the sides V)
of the triangle!' [Leonardo 1, 2, A\
p. 110, 1. 31 ; p. 111, 11. 41-43-] /] \
Given the triangle bgd; if a / I \
be the middle point of gd the line / I \
ba will divide the triangle as re- / I \
quired; either because the tri- / J \
angles are on equal bases and of / I \
the same altitude [1. 38; Leonardo g^- ^ ^d
1], or because
A bgd: Abad= bd. dg : bd. dam.
Whence Abgd= 2Abad.
A.
3
34 EUCLID'S BOOK ON DIVISIONS OF FIGURES III [24-25
But if the given point be not the middle point of any
side, let abg be the triangle and
d the given point nearer to b
than to g. Bisect bg at e and
draw ad, ae. Through e draw
ez parallel to da ; join dz. Then
the triangle abg is bisected by
dz.
Proof: Since
ad || ez, A adz = Aade.
To each add A add. Then
quadl. abdz = Aabd+ Aade,
= Aabe.
But Aabe = \Aabg;
quadl. abdz = \Aabg\
and the triangle zdg is the other half of the triangle abg.
Therefore the triangle abg is divided into two equal parts by
the line dz drawn from the point d;
" ut oportebat facere."
Then follows a numerical example.
Proposition 4.
25- " To 'divide a given trapezium™ into two equal
parts by a line parallel to its base." [Leonardo 23, p. 125,
11. 37-38.]
Let abgd be the given trapezium with parallel sides ad,
bg, ad being the lesser. It is required to bisect the trapezium
by a line parallel to the base bg. Let gd, ba, produced, meet
in a point e. Determine z such that
ze* = ±(eb2 + eaya
Through z draw zi parallel to gb. I say that the trapezium
abgd is divided into two equal parts by the line zi parallel to
the base bg.
89 Here, and in what follows, this word is used to refer to a quadrilateral two of
whose sides are parallel.
90 The point z is easily found by constructions which twice make use of I. 47.
A
25-26]
PROPOSITIONS 3-5
35
Proof: For since
ize~ = eb2 + ed-,
and all the triangles are
similar,
2Aezi= Aebg+ Aead.
[vi. 19]
From the triangle ebg take
away the triangle ezi. Then
A££rz'=quadl. zbgi+Aeda.
And taking away from the
equals the triangle eda, we
get
quadl. ai = quadl. zg.
Therefore the trapezium
abgd is divided into two equal
parts by the line zi parallel to its base. q. o. f.
A numerical example then follows.
Proposition 5.
26. "And we divide the given trapezium into three equal
parts as we divide the triangle, by a construction analogous to
the preceding construction^" [Leonardo 33, p. 134, 11. 14-15.]
Let abgd be the trapezium with parallel sides ad, bg and
other sides ba, gd produced to meet in e. Let zti be a line
such that
zi: it = eb": ea'.S2
91 It is to be noticed that Leonardo's discussion of this proposition is hardly
"analogous to the preceding construction" which is certainly simpler than if it had
been similar to that of Prop. 5. A construction for Prop. 4 along the same lines,
which may well have been Euclid's method, would obviously be as follows :
Let zti be a line such that
zi : it=eb2 : ea2.
Divide tz into two equal parts, tk, kz. Find m such that
em2 : eb"- = ki : zi.
Then m leads to the same solution as before. [For, in brief,
--eb2
ki
Izt ;.
'■ ( zi + it
eb2 /ed2 + eb2'
'ir{ eb2
= \{ea2 + eb2).]
92 From VI. 19, Porism, it is clear that the construction here is to find a line .
which is a third proportional to eb and ea. Then zi : it=eb : x.
3—2
36 EUCLID'S BOOK ON DIVISIONS OF FIGURES III [26
Divide tz into three equal parts tk, kl, Iz.
Find m and n in be such that
eitf : eb~ = ik : zi,
and en*: eff = il: zi.
Through m and n draw mo, np parallel to the base bg.
Then I say that the quadrilateral ag is divided into three
equal parts : ao, mp, ng.
Proof: For eh1 :ea2 = A ebg : A ead. [vi. 19]
.'. zi :it—Isebg : l\ead. [1]
But
So also
Whence
and therefore
zi : ik = eft : em?,
zi : ik = A £$£": A emo [2]
zi :i/= A ebg : A enp [3]
it: tk = Isead: quadl. ao,^
tk : kl= quadl. ao : quadl. mp.^
93 This may be obtained by combining [1] and [2], and applying v. 11, 16, 17.
94 Relations [1], [2] and [3] may be employed, as in the preceding, to give,
it: kl=t\ ead: quadl. mp ;
combining this with it: tk = A ead: quadl. ao, we get the required result,
tk : kl= quadl. ao : quadl. mp.
26-27] PROPOSITIONS 5-6 Z7
But tk = kl. r. quadl. ao = quadl. mp.
So also kl': lz — quadl. mp : quadl. ng;
and kl=lz. .'. quadl. mp = quadl. ng.
Therefore the quadrilateral is divided into equal
quadrilaterals ao, mp, ng; " ut prediximus."
Then follows a numerical example.
Proposition 6.
27. " To divide a parallelogram into two equal parts by a
straight line drawn from a given point situated on one of the
sides of the parallelogram." [Leonardo 16, p. 123, 11. 30-31.]
Let abed be the parallelogram and i any point in the side
ad. Bisect ad in f and be in e.
Join fe. Then the
parallelogram ac is divided into equal
parallelograms ae, fc on equal
bases.
Cut off eh=fi. Join hi.
Then this is the line required.
Leonardo gives two proofs:
I. Let hi meet fe in k. b1 ^
Then [As fki, kke are equal;
add to each the pentagon kfabh, etc.]
II. Since ae, fc are 1 !s, af=be and fd=ec. But
fd=\ad.
.'. fd= af= ec.
And since fi=he, ai = ch.
So also di=bh, and hi is common.
.-. quadl. iabh = quadl. ihed^
95 The first rather than the second proof is Euclidean. There is no proposition
of the Elements with regard to the equality of quadrilaterals whose sides and
angles, taken in the same order, are equal. Of course the result is readily
deduced from I. 4, if we make certain suppositions with regard to order. Cf.
the proof of Prop. 10.
38 EUCLID'S BOOK ON DIVISIONS OF FIGURES III [27-28
Similarly if the given point were between a and f [etc.;
or on any other side]. And thus a parallelogram can be
divided into two equal parts by a straight line drawn from a
given point situated on any one of its sides.
Proposition 7.
28. '' To cut off a certain fraction from a given
parallelogram by a straight line drawn from a given point situated
on one of the sides of the parallelogram." [Leonardo 20 (the
case where the fraction is one-third), p. 124, 11. 24-26.]
Let abed be the given parallelogram. Suppose it be
required to cut off a third of this parallelogram, by a straight
line drawn from i, in the side ad.
m
b g K K c
(The figure here is a combination of two in the original.)
Trisect ad in e and f and through e,f draw eg, fh parallel
to dc; [then these lines trisect the 1 I. If the point i be in
the line ad, at either e or f then the problem is solved. But
if it be between a and e, draw ik to bisect the I 1 ah
(Prop. 6), etc. Similarly if i were between e and f, or
between f and d~\.
After finishing these cases Leonardo concludes :
"eodem modo potest omnem paralilogramum diuidi in
quatuor uel plures partes equales45."
The construction in this proposition is limited to the case where "a certain
fraction " is the reciprocal of an integer. But more generally, if the fraction
were m : n (the ratio of the lengths of two given lines), we could proceed in a
very similar way : Divide ad in e, internally, so that ae :ed=m:n — m (n> m).
In ad cut off ef= ae and through / draw fh parallel to ab. Then, as before,
the problem is reduced to Proposition 6.
If the point e should fall at i or in the interval ai the part cut off from the
parallelogram by the required line would be in the form of a triangle which
might be determined by 1. 44.
29]
PROPOSITIONS 6-8
39
Proposition 8.
29. " To divide a given trapezium into two equal parts by
a straight line drawn from a given point situated on the
longer of the sides of the trapezium." [Part of Leonardo 27 s6,
p. 127, 11. 2-3.]
This enunciation means, apparently, " from a given point situated on the
longer of the [parallel] sides." At any rate Leonardo gives constructions for
the cases when the given point is on any side. These I shall take up
successively. The figure is made from more than one of Leonardo's, and
there is a slight change in the lettering.
Let ad be the shorter of the parallel sides ad, bg, which
are bisected in / and k respectively. Join tk. Then if bt, gt
be joined, [it is clear, from triangles on equal bases and
between the same parallels, that tk bisects the trapezium].
[This is Leonardo 24, p. 126, 1. 31.]
Next consider the given point as any point on the shorter side
[Leonardo 25, p. 127, 11. 2-3].
First let the point be at the angle a. Cut off kl in kg,
equal to at. Join al, meeting tk in m ; then the quadrilateral
is divided as required by al. For [the triangles atm, mkl are
equal in all respects, etc.].
Similarly if d were the given point ; in kb cut off kn equal
to td, and dn divides the quadrilateral into two equal parts
which is proved as in the preceding case.
96 Leonardo 27 : " Quomodo quadrilatera duorum laterum equidistantium
diuidantur i. puncto dato super quodlibet latus ipsius" [p. 129, 11. 2-3].
Cf. note 46.
40 EUCLID'S BOOK ON DIVISIONS OF FIGURES III [29
[Were the given point anywhere between a and / the
other end of the bisecting line would be between k and /.
Similarly if the given point were between / and d, the
corresponding point would be between k and n.~\
Although not observed by Favaro, Leonardo now considers :
If the given point be in the side bg; either /, or n, or a
point between / and n, then the above construction is at once
applicable.
Suppose, however, that the given point were at b or in
the segment bn, at g or in the segment Ig. First consider
the given point at b. Join bd and through n draw nc parallel
to bd to meet gd in c. Join be. Then be bisects the trapezium.
For [abnd is half of the trapezium ag, and the triangle bnd
equals the triangle bde etc.].
Similarly from a given point between b and n, a line could
be drawn meeting gd between c and d, and dividing the
quadrilateral into two equal parts.
So also from g a line gf could be drawn [etc.] ; and
similarly for a given point between g and /.
Leonardo then concludes (p. 127, 11. 37-40):
"Jam ostensum est quomodo in duo equa quadrilatera
duorum equidistantium laterum diuidi debeant a linea pro-
tracta ab omni dato puncto super lineas equidistantes ipsius ;
nunc uero ostendamus quomodo diuidantur a linea egrediente
a dato puncto super reliqua latera."
This is overlooked by Favaro, though implied in his 27 [Leonardo, p. 129,
1. 4]. I may add Leonardo's discussion of the above proposition although it
does not seem to be called for by Euclid.
Let the point be in the side gd. For g or c or d or any
point between c and d the above
constructions clearly suffice. Let
us, then, now consider the given
point h as between c and g.
Draw the line iz parallel to gb
to bisect the trapezium (Prop. 4).
Suppose h were between g and i.
Join zh. Through i draw ik
parallel to hz, and meeting ab
in k.
(The lettering of the original figure is somewhat changed.)
29-30] PROPOSITIONS 8-9 41
Join hk, then [this is the line required; since
A izh = A kzh, etc.].
[Similarly if h were between i and d.~]
[So also for points on the line ab.~]
Proposition 9.
30. " To cut off a certain fraction from a given trapezium
by a straight line drawn from a given point situated on the
longer side of the trapezium." [Leonardo 30, 3197, p. 133,
11. 17-19, 31.]
I shall interpret "longer side" as in Proposition 8, and lead up to the
consideration of any given point on bg after discussing the cases of points on
the shorter side ad.
(This figure is made from three of Leonardo's.)
Suppose it be required to divide the trapezium in the ratio
ez: ziw.
Divide ad, bg in the points t, k, respectively, such that
at: td~ez : zi = bk : kg.
97 As 30, Favaro quotes, " Per rectam protractam super duo latera equi-
distantia quadrilaterum abscisum in data aliqua proportione dividere " ; as 31 :
" Divisionem in eadem proportione ab angulis habere."
98 Here, as well as in 15 and 36, Leonardo introduces the representation of
numbers by straight lines, and in considering these lines he invariably writes the
word number in connection with them ; e.g. 'number ez : number zi,' not ez : zi.
Euclidean MSS. of the Elements, Books vil to ix, adopt this same method. In
what follows, I shall use the abbreviated form.
42 EUCLID'S BOOK ON DIVISIONS OF FIGURES III [30-31
Join tk. Then by joining bt and gt [it is easily seen by vi. 1
and v. 12, that the trapezium ag is divided by tk in the ratio
ez: zf\.
If the given point be at a or d, make kl=at and gn = bl.
Join al, dn. [Adding the quadrilateral ak to the congruent
triangles with equal sides at, kl, we find al divides the
trapezium in the required ratio. Then from vi. 1, dn does
the same.]
As in Proposition 8, for any point / between a and /, or / and d, we have
a corresponding point k' between / and k or n and k, such that the line t'k'
divides the trapezium in the given ratio.
If the given point be in bg at / or ?i or between / and n, the above
reasoning suffices.
Suppose however that the given point were at b. Join bd.
Through n draw nc parallel to bd. Join be. Then be divides
the trapezium in the required ratio. Similarly for the pointy
and for any point between b and n, or between g and /.
Some of the parts which I have filled in above are covered by the general
final statement: " nee non et diuidemus ipsum quadrilaterum ab
omni puncto dato super aliquod laterum ipsius " (Page 134,
11. 10-11. Compare Proposition 13.)
Proposition 10.
31. "To divide a parallelogram into two equal parts by a
straight line drawn from a given point outside the
parallelogram." [Leonardo 18, p. 124, 11. 5-7.]
Let abed be the given parallelogram and e the point
outside. Join bd and bisect it in g. Join eg meeting be in k
31-34]
PROPOSITIONS 9-13
43
and produce it to meet ad in f. Then the parallelogram has
been divided into two equal parts by the line drawn through e,
as may be proved by superposition; and one half is the
quadrilateral fabk, the other, the quadrilateral fkcd®.
Proposition 11.
32. " To cut off a certain fraction from a parallelogram
by a straight line drawn from a given point outside of the
parallelogram.
This proposition is not explicitly formulated by Leonardo ; but the general
method he would have employed seems obvious from what has gone before.
Suppose it were required to cut off one-third of the given parallelogram ac
by a line drawn through a point e outside of the parallelogram. Then by the
method of Proposition 7, form a parallelogram two-thirds of ac. There are four
such parallelograms with centres gu g2, g3, gt. Lines lu L2, /s, /4 through
each one of these points and e will bisect a parallelogram (Proposition 10).
There are several cases to consider with regard to the position of e but it
may be readily shown that, in one case at least, there is a line lt(i= 1, 2, 3, 4),
which will cut off a third of the parallelogram ac.
Similarly for one-fourth, one-fifth, or any other fraction such as m: n which
represents the ratio of lengths of given lines.
Proposition 12.
33. '' To divide a given trapezium into two equal parts by
a straight line drawn from a point which is not situated on the
longer side of the trapezium. It is necessary that the point be
situated beyond the points of concourse of the two sides of the
trapezium." [Leonardo 28, p. 129, 11. 2-4, and another,
unnumbered100.]
Proposition 13.
34. " To cut off a certain fraction from a [parallel-)
trapezium by a straight line which passes through a given
point lying inside or outside the trapezium but so that a
straight line can be drawn through it cutting both the parallel
99 The proof also follows from the equality of the triangles fgd, bgk, by I. 26 and
of the triangles abd, bdc by I. 4. This problem is possible for all positions of the
point e.
100 As Leonardo 28 Favaro gives, " Qualiter quadrilatera duorum laterum
equidistantium dividi debeant a dato puncto extra figuram " and entirely ignores
the paragraph headed, " De diuisione eiusdem generis, qua quadrilaterorum
per rectam transeuntem per punctum datum infra ipsum " [p. 131, 11. 13-14].
44 EUCLID'S BOOK ON DIVISIONS OF FIGURES III [34
sides of the trapezium™!' [Part of Leonardo 32102, p. 134,
11. 11-12.]
We first take up Leonardo's discussion of Proposition 12.
In the figure of Proposition 8, suppose al to be produced
in the directions of the points e and r; tk in the directions of
q and v, dn of z and h, cb of i and 0, gf of s and p. Then for
[any such exterior points e, q, z, i, s, r, v, h, 0, p, lines are
drawn bisecting the trapezium].
If the given point, x, were anywhere in the section of the
plane above ad and between ea and dz, the line joining x to
m would [by the same reasoning as in Proposition 8] bisect
the trapezium. Similarly for all points below nl and between
101 The final clauses of Propositions 12 and 13, in Woepcke's rendering, are the
same. I have given a literal translation in Proposition 12. Heath's translation
and interpretation (after Woepcke) are given in 13. Concerning 12 and 13
Woepcke adds the following note : " Suppose it were required to cut off the «th
part of the trapezium ABDC ; make Aa and Cy respectively equal to the rath parts
of AB and of CD ; then AayC will be the «th part of the trapezium, for ya
produced will pass through the intersection of CA, DB produced. Now to draw
through a given point E the transversal which cuts off a certain fraction of tbe
trapezium, join the middle point ju. of the segment ay, and the point E, by a line ;
this line EFG will be the transversal required to be drawn, since the triangle aFy.
equals the triangle yGji.
"But when the given point is situated as E' or E" such that the transversal
drawn through ju. no longer meets the two parallel sides but one of the parallel sides
and one of the two other sides, or the other two sides ; then the construction
indicated is not valid since CG'py is not equal to BF'pa. It appears that this is
the idea which the text is intended to express. The 'points of concourse' are the
vertices where a parallel side and one of the two other sides intersect ; and the
expression ' beyond' refers to the movement of the transversal represented as
turning about the point p,"
102 " Quadrilaterum [trapezium] ab omni puncto dato super aliquod laterum
ipsius, et etiam ab omni puncto dato infra, uel extra diuidere in aliqua data
proportion!."
34-35]
PROPOSITIONS 13-14
45
hn and Ir [ so also for all points within the triangles
amd, nml~\.
This seems to be all that Euclid's Proposition 12 calls for. But just as
Leonardo considers Proposition 8 for the general case with the given point
anywhere on the perimeter of the trapezium, so here, he discusses the
constructions for drawing a line from any point inside or outside of a trapezium
to divide it into two equal parts.
Leonardo does not give any details of the discussion of Euclid's
Proposition 13, but after presentation of the cases given in Proposition 9
concludes: " et diuidemus ipsum quadrilaterum ab omni puncto
dato super aliquod laterum ipsius, et etiam ab omni puncto
dato infra uel extra" [Leonardo 32, p. 134, 11. 10-12].
From Leonardo's discussion in Propositions 8, 9, 12, not only are the
necessary steps for the construction of 13 (indicated in the Woepcke note
above101) evident, but also those for the more general cases, not considered
by Euclid, where restrictions are not imposed on the position of the given
point.
Proposition 14.
35. " To divide a given quadrilateral into two equal parts
by a straight line drawn from a given vertex of the
quadrilateral" [Leonardo 36, p. 138, 11. 10-11.]
Let abed be the quadrilateral and a the given vertex.
Draw the diagonal bd, meeting the diagonal ac me. If be, ed
are equal, [ac divides the quadrilateral as required].
I f be be not equal to ed, make bz = zd.
Draw zi\\ac to meet dc in i. Join ai. Then the
quadrilateral abed is divided as required by the line ai.
Proof: Join az and zc. Then the triangles adz, azd are
respectively equal to the triangles cbz, cdz.
46 EUCLID'S BOOK ON DIVISIONS OF FIGURES III [35-36
Therefore the quadrilateral abcz is one-half the
quadrilateral abed.
And since the triangles azc, aic are on the same base and
between the same parallels ac, zi, they are equal.
To each add the triangle abc.
Then the quadrilateral abcz is equal to the quadrilateral
abet. But the quadrilateral abcz is one-half of the
quadrilateral abed. Therefore abcz is one-half of the quadrilateral
abed; "utoportet."
Proposition 15.
36. '' To cut off a certain fraction from a given
quadrilateral by a line drawn from a given vertex of the
quadrilateral" [Leonardo 40, p. 140, 11. 36-37.]
Let the given fraction be as ez : zi, and let the
quadrilateral be abed and the given
vertex d. Divide ac in t such , , .
that
at: tc = ez : zi.
If bd pass through t [then bd is
the line required].
But if bd&o not pass through
/ it will intersect either ct or ta ;
let it intersect ct. Join bt, id.
Then
quadl. tbed: quadl. tbad= ct: ta = ez : zi.
Draw //parallel to the diagonal bd, and join dl. Then the
quadrilaterals /bed, tbed are equal and the construction has
been made as required ; for
ct: ta = ez : zi = quadl. /bed: A dal.
And if bd intersect ta [a similar construction may be given
to divide the given quadrilateral, by a line through d, into a
quadrilateral and triangle in the required ratio].
Leonardo then gives the construction for dividing a quadrilateral in
a given ratio by a line drawn through a point which divides a side of the
quadrilateral in the given ratio.
37]
PROPOSITIONS 14-16
47
Proposition 16.
37- " To divide a given quadrilateral into two equal parts
by a straight line drawn from a given point situated on one
of the sides of the quadrilateral." [Leonardo 37, p. 138,
11. 28-29.]
Let abed be the given quadrilateral, e the given point.
Divide ac into two equal parts by the line dt [Prop. 14]. Join
et. The line et either is, or is not, parallel to dc.
(Two of Leonardo's figures are combined in one, here.)
If et be parallel to dc, join ec. Then the quadrilateral ac
[is bisected by the line ec, etc.].
If et be not parallel to dc, draw dz\\et. Join ez. Then
ac [is bisected by the line ez, etc.].
Leonardo does not consider the case of failure of this construction, namely
when dz falls outside the quadrilateral. Suppose in such a case that the
problem were solved by a line joining «toa point z (not shown in the figure)
on dc. Through t, draw tt' || cd. Join ct'. Then i\ct'd = /\ctd = Aedz'.
Whence £\et'c = /\ez'c, or t'z' || ce. Therefore from t', z' may be found and the
solution in this case is also possible, indeed in more than one way, but it is
not in Euclid's manner to consider this question.
Should the diagonal db bisect the quadrilateral ac, the
discussion is similar to the above.
But if the line drawn from d to bisect the quadrilateral
meet the side ab in i, draw bk bisecting the quadrilateral ac.
If k be not the given point, it will be between k and d or
between k and a.
48 EUCLID'S BOOK ON DIVISIONS OF FIGURES III [37-38
In the first case join be and through k draw kl\ eb. Join
el [then el is the required bisector].
If the point e be between a and k [a similar construction
with the line through k parallel to be, and meeting be in m,
leads to the solution by the line em\.
Were e at the middle of a side such as ab, draw dz || ab
and bisect dz in i. Join ei, ci and ec. Through i draw it || *?<:.
Join £/; then et [bisects the quadrilateral ac, since Aitc = Aite,
etc.].
If dz were to fall outside the quadrilateral, draw from c the parallel to ba;
and so on.
Proposition 17.
38. " To cut off a certain fraction from a quadrilateral
by a straight line drawn from a given point situated on one
of the sides of the quadrilateral." [Leonardo 39, p. 140,
11. 11-12.]
38]
PROPOSITIONS 16-17
49
Let abed be the given quadrilateral and suppose it be
required to cut off one-third by a line drawn from the point e
in the side ad.
Draw dz cutting off one-third of ac [Prop. 15].
Join ez, ec.
If ez || dc, then ecd [is the required part cut off, etc.].
But if ez be not parallel to dc, draw di || ez and join ei.
[Then this is the line required, etc.]
The case when ei cuts dc is not taken up but it may be considered as in
the last proposition.
So also to divide ac into any ratio : draw dz dividing it in that ratio
(Prop. 15), and then proceed as above.
A particular case which Leonardo gives may be added.
Let ab be divided into three equal parts ae, ef, fb ; draw
dg || ab and cut off gh = \gd. Join fc and through h draw
hi\fc, meeting dc in i. Join fi\ and the quadrilateral fbci
will be one-third of the quadrilateral ac. [As in latter part of
Prop. 16.]
50 EUCLID'S BOOK ON DIVISIONS OF FIGURES III [38-39
Then ek may be drawn to bisect the quadrilateral a/id
[Prop. 16], and thus the quadrilateral abed will be divided
into three equal portions which are the quadrilaterals ak, ei,fc.
Proposition 18.
39. " To apply to a straight line a rectangle equal to the
rectangle contained by AB, AC and deficient by a square™!'
103 This proposition is interesting as illustrating the method of application of
areas which was " one of the most powerful methods on which Greek Geometry
relied." The method first appears in the Elements in I. 44 : To a given straight
line to apply, in a given rectilineal angle, a parallelogram equal to a given triangle
—a proposition which Heath characterises as "one of the most impressive in all
geometry" while the "marvellous ingenuity of the solution is indeed worthy of the
' godlike men of old ' as Proclus calls the discoverers of the method of ' application
of areas ' ; and there would seem to be no reason to doubt that the particular
solution, like the whole theory, was Pythagorean, and not a new solution due to Euclid
himself."
[I continue to quote mainly from Heath who may be consulted for much greater
detail: Heath, Thirteen Books of Euclid's Elements, 1, 9, 36, 343-7, 383-8 ; II, 187,
257-67—Heath, Apollonius of Perga Treatise on Conic Sections, Cambridge, 1896,
pp. lxxxi-lxxxiv, cii-cxi —Heath, The Works of Archimedes, Cambridge, 1897,
pp. xl-xlii, no and " Equilibrium of Planes," Bk II, Prop. I, and "On conoids and
spheroids," Props. 2, 25, 26, 29. See also: Cantor, Vorlesungen iiber Ge-
schichte der Math. I3, 289-291, etc. (under index heading ' Flachenanlegung') —
H. G. Zeuthen, Geschiclite der Matliematik im Alterthum und Mittelalter, Kopen-
hagen, 1896, pp. 45-52 (French ed. Paris, 1902, pp. 36-44)—C. Taylor, Geometry
of Conies..., Cambridge, 1881, pp. XLIII-xliv.]
The simple applicatioii of a parallelogram of given area to a given straight line
as one of its sides is what we have in the Elements I. 44 and 45 ; the general form
of the problem with regard to exceeding and falling- short may be stated thus :
" To apply to a given straight line a rectangle (or, more generally, a
parallelogram) equal to a given rectilineal figure and (1) exceeding or (2) falling-short by a
square (or, in the more general case, a parallelogram similar to a given
parallelogram)."
What is meant by saying that the applied parallelogram (1) exceeds or {2) falls
short is that, while its base coincides and is coterminous at one end with the
straight line, the said base (1) overlaps or (2) falls short of the straight line at
the other end, and the portion by which the applied parallelogram exceeds a
parallelogram of the same angle and height on the given straight line (exactly) as
base is a parallelogram similar to a given parallelogram (or, in particular cases, a
square). In the case where the parallelogram is to fall short, some such remark
as Woepcke's (note 104) is necessary to express the condition of possibility of
solution. For the other case see note 116.
The solution of the problems here stated is equivalent to the solution of a
quadratic equation. By means of 11. 5 and 6 we can solve the equations
ax + x2=i2,
x2 — ax=b'1,
but in vi. 28, 29 Euclid gives the equivalent of the solution of the general
equations
ax±px'i =A.
vi. 28 is : To a given straight line to apply a parallelogram equal to a given
rectilineal figure and deficient by a parallelogrammic figure sunilar to a given one:
39]
PROPOSITIONS 17-18
51
" After having done what was required, if some one ask,
How is it possible to apply to the line AB a rectangle such
A £ c 5 B
• * 1 1 1
that the rectangle AE. EB is equal to the rectangle AB. AC
and deficient by a square—we say that it is impossible, because
AB is greater than BE and AC greater than AE, and
consequently the rectangle BA.AC greater than the rectangle
AE . EB. Then when one applies to the line AB a
parallelogram equal to the rectangle AB. AC the rectangle AZ.ZB
In this problem it is required to find in the given line AB a point Z such
that
AB.ZB- ZB*[=AZ. ZB by 11. 3; cf. x. 16 lemma] = AB. AC105.
Find, by n. 14, the side, b, of a square equal in area to the rectangle
AB . A C, then the problem is exactly equivalent to that of which a simple
solution was given by Sanson106:
thics the given rectilineal figure must not be greater than the parallelogram
described on the half of the straight line and similar to the defect.
The Proposition 18 of Euclid under consideration is a particular case of this
problem and as the fragment of the text and Woepcke's note (note 104) are
contained in it, doubt may well be entertained as to whether Euclid gave any
construction in his book On Divisions. The problem can be solved without the
aid of Book vi of the Elements and by means of 11. 5 and 11. 14 only, as indicated
in the text above.
The appropriation of the terms parabola {application), hyperbola {exceeding) and
ellipse falling-short) to conic sections was first introduced by Apollonius as
expressing in each case the fundamental properties of curves as stated by him.
This fundamental property is the geometrical equivalent of the Cartesian equation
referred to any diameter of the conic and the tangent at its extremity as (in general,
oblique) axes. More particulars in this connection are given by Heath.
The terms "parabolic," "hyperbolic" and "elliptic," introduced by Klein for
the three main divisions of Geometry, are appropriate to systems in which a
straight angle equals, exceeds and falls short of the angle sum of any triangle.
Cf. W. B. FRANKLAND, The First Book of Euclid's Elements with a Commentary
based principally upon that of Proclus Diadoclius... Cambridge, 1905, p. 122.
im Woepcke here remarks : " Evidently if a denote the length of the line to
which the rectangle is to be applied, Problem 18 is only possible when
AB.AC<{^\
Then if a be taken as AB one of the two sides of the given rectangle, relatively to
AB
the other side, AC< . It is probably the demonstration of this which was
given in the missing portion of the text."
106 If AB = a, ZB = x, AB. AC = b2, the problem is to find a geometric
solution of the equation ax — x1 — b'2. Ofterdinger38 (p. 15) seems to have quite
missed the meaning of this problem. He thought, apparently, that it was
equivalent to X. 16, lemma, of the Elements.
106 R. Simson, Elements of Euclid, ninth ed., Edinburgh, 1793, pp. 335-6.
4—2
52 EUCLID'S BOOK ON DIVISIONS OF FIGURES III [39-40
To apply a rectangle which shall be equal to a given square, to a given
straight line, deficient by a square: but the given square must not be greater
than that upon the half of the given line.
N
(fo^—i
D
0
-~-^z
V
H
B
Bisect AB in D, and if the square on AD be equal to the square on b,
the thing required is done. But if it be not equal to it, AD must be greater
than b according to the determination. Then draw DO perpendicular to AB
and equal to b; produce OD to JV so that ON= DB (or \d); and with O as
centre and radius ON describe a circle cutting DB in Z
Then ZB (or x) is found, and therefore the required rectangle AH.
For the rectangle AZ. ZB together with the square on DZ is equal to the
square on DB, [11. 5]
i.e. to the square on OZ,
i.e. to the squares on OD, DZ. [1. 47]
Whence the rectangle AZ. ZB is equal to the square on OD.
Wherefore the rectangle AH equals the given square upon b (i.e. the
rectangle AB. AC) and has been applied to the given straight line AB,
deficient by the square HBm.
Proposition 19.
40. " To divide a given triangle into two equal parts by a
line which passes through a point situated in the interior of the
triangle" [Leonardo 3, p. 115, 11. 7-10.]
107 It is not in the manner of Euclid to take account of the two solutions found
by considering [F), as well as Z, determined by the circle with centre O.
Although Leonardo's construction for Problem 19 is identical with that of Euclid
who makes use of Problem 18, Leonardo does not seem to have anywhere formulated
Problem 18. He may have considered it sufficiently obvious from VI. 28, or from
11. 5 and II. 6, of which he gives the enunciations in the early pages (15-16) of his
Practica Geometriae ; he also considers (p. 60) the roots of a resulting quadratic
equation, ax -x'1 = b (cf. Cantor, Vorlesungen..., Il2, 39), but does not give II. 14.
Cf. Bibliotheca Mathematical (3), 1907-8, vin, 190 ; and also IX, 245.
4°]
PROPOSITIONS 18-19
53
TB.DE
TB =
" Let the given triangle be ABC, and the given point in
the interior of this triangle, D.
It is required to draw through
D a straight line which divides
the triangle ABC into two equal
parts.
Draw from the point D a line
parallel to the line BC, as DE,
and
Apply to DE a rectangle equal
to half of the rectangle AB. BC,
such as
AB. BC
2DE
Apply to the line TB a
parallelogram equal to the rectangle BT.BE and deficient
by a square 107\ [Prop. 18]
Let the rectangle applied be
BH. HT [(TB - HT). HT= TB. BE].
Draw the line HD and produce it to Z.
Then this is the line required and the triangle ABC is
divided into two equal parts HBZ and HZCA.
Demonstration. The rectangle TB. BE is equal to the
rectangle TH.HB, whence it follows that
BT: TH=HB:BE;
then dividendo™ TB : BH= BH: HE.
But BH :HE = BZ:ED; [vi. 2]
therefore TB : BH= BZ : ED.
Consequently the rectangle TB. ED is equal to the rectangle
BH.BZ. But the rectangle TB .ED is equal to half the
rectangle AB. BC; and
BH. BZ: AB. BC = AHBZ: A ABCm,
107a The corresponding sentence in Leonardo is (p. 115, 11. 15-17): " Deinde
linee gz applicabis paralilogramum deficiens figura tetragona, quod sit equale
superficies ge in gz."
108 "Elements, Book v, definition 16" (Woepcke). This is definition 15 in
Heath, The Thirteen Books of Euclid's Elements, 11, 135.
54 EUCLID'S BOOK ON DIVISIONS OF FIGURES III [40-41
since the angle B is common. The triangle HBZ is, then,
half the triangle ABC.
Therefore the triangle ABC is divided into two equal
parts BHZ and AHZC.
If, in applying to TB a parallelogram equal to the
rectangle TB. BE and of which the complement is a square,
we obtain the rectangle AB. AT™, we may demonstrate in
an analogous manner, by drawing the line AD and prolonging
it to K, that the triangle ABK is one-half of the triangle
ABC. And this is what was required to be demonstrated."
Proposition 20.
41. " To cut off a certain fraction from a given triangle
by a line drawn from- a given point situated in the interior of
the triangle!' [Leonardo 10, p. 121, 11. 1-2.]
" Let ABC be the given triangle and D the given point
in the interior of the triangle.
It is required to pass through
the point D a straight line
which cuts off a certain fraction
of the triangle ABC.
" Let the certain fraction
be one-third. Draw from the
point D a line parallel to the
line BC, as DE, and apply
to DE a rectangle equal to
one-third of the rectangle
AB. BC Let this be
BZ.ED
BZ =
AB .BC
~l^D J
109 " jn other words when H coincides with A. This can only be the case
when D is situated on the line which joins A to the middle of the base BC"
(Woepcke). If D were at the centre of gravity of the triangle, three lines could be
drawn through D dividing the triangle into two equal parts. As introductory to
his Prop. 3, Leonardo proved that the medians of a triangle meet in a point, and
trisect one another—results known to Archimedes™11, but no complete, strictly
geometric proof has come down to us from the Greeks. Leonardo then proves
that if a point be taken on any one of the medians, or on one of the medians
produced, the line through this point and the corresponding angular point of the
triangle will divide the triangle into two equal parts. He next shows that lines
through the vertices of a triangle and any point within not on one of the medians,
41-42]
PROPOSITIONS 19-21
55
Then apply to ZB a rectangle equal to the rectangle ZB. BE
and deficient by a square. [Prop. 18.] Let the rectangle
applied be the rectangle
BH. HZ [(ZB - HZ) HZ = ZB. BE].
Draw the line HD and produce it to T.
" On proceeding as above we may demonstrate that the
triangle HTB is one-third of the triangle ABC; and by
means of an analogous construction to this we may divide
the triangle in any ratio. But this is what it is required
to do110."
Proposition 21.
42. " Given the four lines A, B, C, D and that the
product of A and D is greater than the product of B and C;
I say that the ratio of A to B will be greater than the ratio
of C to Dmr
will divide the given triangle into triangles whose areas are each either greater
than or less than the area of half of the original triangle. This leads Leonardo to
the consideration of the problem, to draw through a point, within a triangle and
not on one of the medians, a line which will bisect the area of the triangle.
(Euclid, Prop. 19.)
The last paragraph of Euclid's proof, as it has come down to us through
Arabian sources, does not ring true, and it was not in the Euclidean manner to
consider special cases.
After Leonardo's proof of Proposition 19, a numerical example is given.
110 Leonardo gives the details of the proof for the case of one-third and does
not refer to any other fraction. If, however, the "certain fraction" were the ratio
of the lengths of two given lines, m : n, we could readily construct a rectangle equal
to — . AB. BC, and then find the rectangle BZ. ED equal to it. The rest of the
construction is the same as given above.
According to the conditions set forth in Proposition 18, there will be two,
one, or no solutions of Propositions 19 and 20. Leonardo considers only the
Euclidean cases. Cf. notes 104 and 107.
The case where there is no solution may be readily indicated. Suppose, in the
above figure, that BE = EJT, then of all triangles formed by lines drawn through
D to meet AB and BC, the triangle HBT\\z& the minimum area. (Easily shown
synthetically as in D. CRESSWELI,, An Elementary Treatise on the Geometrical and
Algebraical Investigations of Maxima and Minima. Second edition, Cambridge,
1817, pp. 15-17.) Similar minimum triangles may be found in connection with the
pairs of sides AB, A C and AC, CB. Suppose that neither of these triangles is less
than the triangle HBT. Then if
LHBT:hABC>m\n,
the solution of the problem is impossible.
111 This and the next four auxiliary propositions for which I supply possible
proofs, seem to be neither formally stated nor proved by Leonardo. At least some
of the results are nevertheless assumed in his discussion of Euclid's later
propositions, as we shall presently see. Although these auxiliary propositions are not
56 EUCLID'S BOOK ON DIVISIONS OF FIGURES III [42
Given A . D > B. C. To prove A : B > C: D.
Let the lines A, D be adjacent sides of a rectangle; and let there be
another rectangle with side B lying along A and side C along D. Then
either A is greater than B, or 1) greater than C, for otherwise the rectangle
A . D would not be greater than the rectangle B . C.
given in the Elements, they are assumed as known by Archimedes, Ptolemy and
Apollonius.
For example, in Archimedes' " On Sphere and Cylinder," 11. 9 (Heiberg, ed. I,
1910, p. 227 ; Heath, ed. 1897, p. 90), Woepcke 21 is used. See also Eutocius'
Commentary (Archimedis Opera omnia ed. Heiberg, in, 1881, p. 257, etc.), and
Heiberg, Quaestiones Archimedeae, Hauniae, 1879, p. 45 *"• For a possible
application by Archimedes (in his Measurement of a circle) of what is practically
equivalent to Woepcke 24, see Heath's Archimedes..., 1897, p. xc.
The equivalent of Woepcke 24 is assumed in the proof of a proposition given
by Ptolemy (87-165 A.D.) in his Syntaxis, vol. 1, Heiberg edition, Leipzig-, 1898,
pp. 43-44. This in turn is tacitly assumed by Aristarchus of Samos {circa
310-230 B.C.) in his work On the Sizes and Distances of the Sun and Moon (see
Heath's edition Aristarchus of Samos the Ancient Copernicus, Oxford, 1913,
pp. 367, 369, 377, 381, 389, 391).
As to the use of the auxiliary propositions in the two works Proportional
Section and On Cutting off a Space, of Apollonius, we must refer to Pappus'
account (Pappi Alexandrini Collectionis...ed. Hultsch, vol. 11, 1877, pp. 684 ff.).
Woepcke 21, 22 occur on pp. 696-697 ; Woepcke 24 enters on pp. 684-687 ;
Woepcke 23, 25 are given on pp. 687, 689. Perhaps this last statement should be
modified ; for whereas Euclid's propositions affirm that if
a :b g c : d, a — b:b<c-d:d,
Pappus shows that if
a : b g c : d, a : a — b $ c : c — d;
but these propositions are immediately followed by others which state that if
a : b < c :d, then b : a > d : c.
Below is given a list of the various restorations of the above-named works of
Apollonius, based on the account of Pappus. By reference to these restorations
the way in which the auxiliary propositions are used or avoided may be observed.
We have already (Art. 21) noticed a connection of Apollonius'work On Cutting off
a Space with our subject under discussion. Some of these titles will therefore
supplement the list given in the Appendix.
Wilebrordi Snellii R. F. irepl \uyov anorofirjs hi! nfp\ ^rnpiou aTroTOfirjs (Apol-
lonii) resi/scitata geometria. Lugodini, ex ojficina Platiniana Raphelengii, MD.CV11
pp. 23.
More or less extensive abridgment of Snellius's work is given in :
(a) Universae geometriae mixtaeque mathematicae synopsis et bini refrac-
tionum demonstratarum tractatus. Studio et opera F. M. Mersenni.
Parisiis, M.DC.xi.iv, p. 382.
(b) Cursus mathematicus, P. Herigone. Paris, 1634, tome I, pp. 899-904 ;
also Paris, 1644.
Apollonii Pergaei de sectione rationis libri duo ex Arabico MS10 Latine versi
accedunt ejusdem de sectione s-patii libri duo restituti...opera &° studio Edmundi
H'alley...Oxonii,...MDCCvl, pp. 8 -t- 1 iii + 168.
(a) Die Biicher des Apollonius von Perga De sectione rationis nach dem
Lateinischen des Edm. Halley frey bearbeitet, und mit einem Anhange
verseheii von IV. A. Diesterweg, Berlin, 1824, pp. xvi + 218 + 9 pi.
(b) Des Apollonius von Perga zwei Biicher vom Verhaltnissschnitt (de
sectione rationis) aus dem Lateinischen des Halley iibersetzt und mit
Anmerkungen begleitet und einem Anhang versehen von August Richter
...Elbing, 1836, pp. xxii + 143 + 4 P1-
42-43] PROPOSITIONS 21-22 57
Let then A > B. To D apply the rectangle B. C and we get a rectangle
A'.D = B.C; [1-44-45]
then A' : B = C : D. [vn. 19]
But since A > A',
A:B>A':B; [v. 8]
.-. A : B> C: D. [v. 13]
Q. E. D.
Pappus remarks : Conversely if A : B > C : D, A . D> B . C. The proof
follows at once.
For, find A' such that A' : B = C': D;
then A :B> A' : B,
and A > A'. But A'. D = B. C. .-. A.D>B.C. q. e. d.
Proposition 22.
43- "And when the product of A and D is less than the
product of B and C, then the ratio of A to B is less than the
ratio of C to D."
Die Bticker des Apollonius von Perga de sections spatii wiederhergestellt von
Dr IV. A. Diesterweg...Elberfeld, 1827...pp. vi + 154 + 5 pi.
Des Apollonius von Perga zwei Biicher %>om Raumschnitt. Ein Versuch in der
alten Geometrie von A. Richter. Halberstadt, 1828, pp. xvi + 105 + 9 pi.
Die Biicher des Apollonius von Perga de sectione spatii, analytisch bearbeitet
nnd mit eine/n Anhange von mehreren Aufgaben iihnlicher Art verse hen
von M. G. Grabow...Frankfurt a. M., 1834, pp. 80 + 3 pi.
Geometrische Analysis enthaltend des Apollonius von Perga sectio rationis,
spatii tiud detenninata, nebst einem Anhange zu der letzten, neu bearbeitet vow
Prof. Dr Georg Paucker, Leipzig, 1837, pp. xii + 167 + 9 pi.
M. Chasles discovered that by means of the theory of involution a single
method of solution could be applied to the main problem of the three books of
Apollonius above mentioned. This solution was first published in The
Mathematician, vol. in, Nov. 1848, pp. 201-202. This is reproduced by A. Wiegand in
his Die schwierigeren geometrischen Aufgaben aus des Herrn Prof. C. A. facobi
Anhdngen zu Van Swinden's Elementen der Geometrie. Mit Erganzungen
englischer Matheniatiker...Halle, 1849, pp. 148-149, and it appears at greater
length in Chasles' Traite de Gdowetrie supMeure, Paris, 1852, pp. 216-218 ; 2e ed.
1880, pp. 202-204. It was no doubt Chasles who inspired Die Elemente der
projectivischen Geometrie in synthetischer Beliandlung. Vorlesungen von H. Hankel,
(Leipzig, 1875), "Vierter Abschnitt, Aufgaben des Apollonius," pp. 128-145;
"sectio rationis," pp. 128-138; "sectio spatii," pp. 138-140.
The " Three Sections" the " Tangencies " and a " Loci Problem " of Apollonius
...by M. Gardiner, Melbourne, i860. Reprinted from the Transactions of the Royal
Society of Victoria, 1860-1861, v, 19-91 4- 10 pi.
Die sectio rationis, sectio spatii und sectio detenninata des Apollonius nebst
einigen verwandten geometrischen Aufgaben von Fr. von Liihmann. Progr.
Konigsberg in d. N. 1882, pp. 16+ 1 pi.
" Ueberdie funf Aufgaben des Apollonius," von L. F. Ofterdinger. fahreshefte
des Vereines fiir Math. u. Naturwiss. in Ulm a. D. 1888, I, 21-38; " Verhaltniss-
schnitt," pp. 23-25 ; "Flachenschnitt," pp. 26-27.
58 EUCLID'S BOOK ON DIVISIONS OF FIGURES III [43-44
From the above proof we evidently have
C : D > A : B,
that is,
A : B < C : D.
Conversely, as above, if A : B < C : D, A . B < C. D.
It is really this converse, and not the proposition, which Euclid uses in
Proposition 26. Proclus remarks (page 407) that the converses of Euclid's
Elements, 1. 35, 36, about parallelograms, are unnecessary "because it is easy
to see that the method would be the same, and therefore the reader may
properly be left to prove them for himself." No doubt similar comment is
justifiable here.
Proposition 23.
44- " Given any two straight lines and on these lines the
points A, B, and D, E; and let the ratio of AB to BC be
BC A
1 1 1
E [W] Z. D
1 , h ,
greater than the ratio of DE : EZ; I say that dividendo the
ratio of AC to CB will be greater than the ratio of DZ to
ZE."
Given AB : BC>DE: EZ.
To prove AC: CB>DZ: ZE.
To AB, BC, DE find a fourth proportional EW. [vi. 12]
Then AB : BC' = DE : EW. (1)
But AB :BC>DE : EZ;
:. DE : EW>DE : EZ. [v. 13]
.'. E W< EZ. [v. 8]
From(i) AC: CB^DW: WE; (2) [v. 17]
since DW>DZ, DW : WE > DZ : WE. [v. 8]
.'. AC : CB>DZ: WE. [v. 13]
But WE<ZE; .: DZ: WE> DZ : ZE. [v. 8]
.'. AC: CB>DZ : ZE. From (2) and [v. 17]
Q. E. D.
45-46]
PROPOSITIONS 22-25
59
Proposition 24.
45. "And in an exactly analogous manner I say that
when the ratio of AC to CB is greater than the ratio of DZ
to ZE, we shall have componendo112 the ratio of AB to BC is
greater than the ratio of DE to EZ."
Given AC : CB>DZ: ZE.
To prove AB : BC> DE : EZ.
Determine W, as before, such that
AB : BC=DE: EW.
Then AC: CB = DW: WE.
:. DW: WE>DZ:ZE.
Now either E W> EZ or E W< EZ.
If E W> EZ, D W< DZ, and
DW:EW<DZ: EW.
So much the more is
DW:EW<DZ:EZ
which contradicts (1).
.-. EW<EZ.
But AB :BC = DE :EW,
and DE : EW> DE : EZ;
:. AB :BC>DE : EZ.
....(1)
[v. 17]
[>■ r3]
[v. 8]
[v.8]
[v. 8]
[>• 13]
Q. E. D.
Proposition 25.
46. " Suppose again that the ratio of AB to BC were
B c
1 1—
D
-+
less than the ratio of DE to EZ; dividendo the ratio of
AC to CB will be less than the ratio of DE to ZE113."
112 "Elements, Book V, definition 15" (Woepcke). This is definition 14 in
HEATH, The Thirteen Books of Euclid's Elements, II, 135.
113 The auxiliary propositions are introduced, apparently, to assist in rendering,
with faultless logic, the remarkable proof of Proposition 26. In this proof it will be
observed that we are referred back to Proposition 21, to the converse of Proposition
22 and to Proposition 25 only, although 23 is really the same as 25. But no step
in the reasoning has led to Proposition 24. If this is unnecessary, why has it been
introduced ? [continued overleaf.
60 EUCLID'S BOOK ON DIVISIONS OF FIGURES III [46-47
Just as the proof of Proposition 22 was contained in that for
Proposition 2i, so here, the proof required is contained in the proof of Proposition 23.
Similarly the converse of Proposition 25 flows out of 24.
Proposition 26.
47- "To divide a given triangle into two equal parts by
a line draivn from a given point situated outside the triangle."
[Leonardo 4, p. 116, 11. 35-36.]
Let the triangle be abg and d the point outside.
Join ad and let ad meet bg in e. If be = eg, what was
required is done. For the triangles abe, aeg being on equal
bases and of the same altitude are equal in area.
But if be be not equal to eg, let it be greater, and draw
through d, parallel to bg, a line meeting ab produced in z.
Since be > -gbg,
area ab. be > ijarea ab . bg ; [_Cf. vn. 17]
much more then is
area ab. zd> ^area ab . bg, since zd> be.
Now take
area ib. zd— \ area ab.bg; [1. 44]
then area ab . be> area ib . zd,
and zd: be < ba : bim. [Prop. 21 or 22]
To answer this question, let us inspect the auxiliary propositions more closely.
In a sense Propositions 21 and 22 go together: If «(/< fc, then a : b g c : d.
So also for Propositions 23 and 25: If a ; b ^ c : d, then a — b:b%c-d:d.
Proposition 24 is really the converse of 23 : If a : b > c : d, then a + b :b> c + d: d.
Had Euclid given another proposition : If a : b < c : d then a + b : b < c + d : d,
we should have had two groups of propositions 21, 22, and 23, 25 with their
converses. Now the converses of 21 and 22 are exceedingly evident in both
statement and proof. But this can hardly be said of the proof of 24, the
converse of 23. The converse of 23 having been given the formulation of the
statement and proof of the converse of 25 is obvious and unnecessary to state,
according to Euclid's ideals (cf. Art. 43). It might therefore seem that Proposition 24
is merely given to complete what is not altogether obvious, in connection with the
statement of the four propositions 21 and 22, 23 and 25, and their converses. In
Pappus' discussion some support is given to this view, since Propositions 21 and 22
and converses are treated as a single proposition ; Propositions 23, 25 as another
proposition, while the converses of 23 and 25 are dealt with separately.
The more probable explanation is, however, that Propositions 23 and 24 were
given by Euclid because they were necessary for the discussion of other cases of
Proposition 26 (assuming that the first case of Leonardo was that given by Euclid),
for it was not his manner to consider different cases. Indeed if we take be less than
ge in the first part of Leonardo's discussion exactly Propositions 23 and 24 are
necessary.
1H Therefore bi<ba, and if bi be measured along ba, i will fall between b and a.
47]
PROPOSITIONS 25-26
61
But
or
zd\be — za : ab, [vi. 4]
.'. zb:ba<ai:ib; [v. 13 and Prop. 25]
area zb . bi< area ba . at.
[Converse of Prop. 22]
Apply a rectangle equal to the rectangle zb. bi to the line
bi, but exceeding by a square115; that is to bi apply a line such
that when multiplied by itself and by bi the sum will be equal
to the product of zb and Si; let ti be the side of the square116.
Draw the straight line tkd. Since
area zb . bi = bi. ti + tP = area bt. ti,
115 Here again we have an expression with the true Greek ring : "adiungatur
quidem recte .bi. paralilogramum superhabundans figura tetragona equale super-
ficiei . zb. in . bi."
116 \ye have seen that i lies between b and a. And since it has been shown that
zb.bi<ba.ai, we now have ba. ai>bt. ti. If bt>ba, ti is also greater than at,
and bt. ti<K.ba. ai. Therefore bl-cba and t falls between b and a. But it also falls
between a and i by reason of the construction (always possible) which is called for.
In his book on Divisions (offigures) Euclid does not formulate the proposition
here quoted, possibly because of its similarity to Proposition 18 (see note 103).
A C
/ B
n
If we let the rectangle zb ■ 1
the quadratic equation :
i=c2, ti—x, and bi=a, we have to solve geometrically
ax + x1 — (T2. [continued overleaf.
62 EUCLID'S BOOK ON DIVISIONS OF FIGURES III [47
or
But
and
But
zb :bt = ti : ib, [vil. 19]
zt: bt = bt: bi. [v. 18]
zt: bt = zd: bk, [vi. 4]
. •. zd: bk = bt: bi,
area kb . bt = area zd. bi.
area zd. bi = ^-area ab . bg,
.-. l\tbk = \L\abg™.
Therefore the triangle abg is
divided by a line drawn from the
point d, that is, by the line tkd, into ;
two equal parts one of which is
the triangle tbk, and the other the quadrilateral tkga.
Q. E. F.
Leonardo now gives a numerical example. He then continues :
Heath points out (Elements, vol. 1, pp. 386-387) that the solution of a problem
theoretically equivalent to the solution of a quadratic equation of this kind is
presupposed in the fragment of Hippocrates' Quadrature ofdunes (5th century B.C.)
preserved in a quotation by Simplicius (fl. 500 A.D.) from Eudemus' History oj
Geometry (4th century B.C.). See Simplicius' Comment, in Aristot. Phys. ed.
H. Diels, Berlin, 1882, pp. 61-68 ; see also F. Rtjdio, Der Bericht des Simplicius
iiber die Quadratur des Antiphon und Hippokrates, Leipzig, 1907.
Moreover as Proposition 18 is suggested by the Elements, n. 5, so here this
problem is suggested by 11. 6 : If a straight line be bisected and a straight line be
added to it in a straight line, the rectangle contained by the whole with the added
straight line and the added straight line together with the square on the half
is equal to the square on the straight line made up of the half and the added
straight line.
If AB is the straight line bisected at C and BD is the straight line added, then
by II. 6,
AD.DB+CBi = CDi.
In his solution of our problem, Robert Simson proceeds, in effect, as follows
(Elements of Euclid, ninth ed., Edinburgh, 1793, p. 336): Draw BQ at right angles
to AB and equal to c. Join CQ and describe a circle with centre C and radius
CQ cutting AB produced in D. Then BD or x is found. For, by II. 6,
AE>.E>B + CB2=CE>%
= CQ\
= CB* + BQ\
:. AD.DB = BQ2,
whence (a + x)x = c2
or ax-\-x2=ci.
It was not Euclid's manner to consider more than one solution in this case.
47] PROPOSITION 26 63
[If the point d were on one
side, ab, produced at say, 2],
through z draw ze parallel to
bg and meeting ag produced
in e.
Make
area ze . gi = ^area ag. gb,
and apply a rectangle, equal to
the rectangle eg.gi, to the line z
gi, but exceeded by a square;
then eg .gi=gt. ti.
Join tz, then [this is the required line. The proof is step
for step as in the first case].
Leonardo then remarks: "Que etiam demonstrentur in numeris," and
proceeds to a numerical example. Thereafter he continues :
But let the sides ab, gb of the triangle be produced to d
and e respectively ; and let i
be the given point in the angle
ebd from which a line is to be
drawn dividing the triangle
abg into two equal parts. Join
ib and produce it to meet ag in
z. If az = zg, the triangle abg
is divided into two equal parts
by the line iz. But [if az>zg,~]
let za produced meet, in the
point t, the line drawn through
i parallel to ab.
Since
za>\ag, area ab .az>\area ba. ag.
Make area it .ak = \area ba. ag;
then make area al. /£/=area ta . ak.
Join il. Then as above the triangle abg is divided into
two equal parts by the line il, one part the triangle lac, the
other the quadrilateral lebg.
To this statement Leonardo adds nothing further. The proof that k lies
between a and z, and / between k and z, follows as in the first part.
64 EUCLID'S BOOK ON DIVISIONS OF FIGURES III [48
Proposition 27.
48. " To cut off a certain fraction of a triangle by a
straight line drawn from a given point situated outside of the
triangle™." [Leonardo 11, p. 121, 11. 22-23.]
Let abg be. the given triangle and dthe. given point outside.
It is required to cut off from the triangle a certain fraction, say
one-third, by a line drawn through d. Join ad, cutting bg in c.
If either be or eg be one-third of bg,
then the line ad through the point d a
cuts off one-third of the triangle abg.
But if this be not the case produce ab,
ag to meet in z and e respectively
the line drawn through d parallel
to bg.
Make
area de -gi = \ area ag. gb,
and apply to the line gi a rectangle
equal to the rectangle eg .gi, but exceeded by a square ; then
eg . gi—ik . kg.
Draw the line kmd. I say that the triangle kmg is one-third
of the triangle abg.
Proof: For since
area eg. gi = area gk . ki,
eg:gk = ki : ig.
Hence ek : gk=gk:gi. [v. 17]
117 Some generalizations of the triangle problems in Propositions 19, 20, 26 and
27 may be remarked. Steiner, in 1827, solved the problem : through a give71 point
071 a sphere to draw an arc of a gr eat circle cutting two give7i great circles such that
the intercepted area is equal to a given area. (J. STEINER, " Vervvandlung und
Theilung spharischen Figuren durch Construction," Crelle jl, 11 (1827), pp. 56 f.
Cf. Syllabus of Townsend's course at Dublin Univ., 1846, in Nouvelles Annates
de Mathematiques, Sept. 1850, IX, 364; also Question 427(7) proposed by Vannson
in Nouvelles An/iales...]a.r\. 1858, XVII, 45 ; answered Aug. 1859, XVIII, 335-6.)
See also GUDERMANN, "Uber die niedere Spharik," Crelle J I, 1832, vin, 368.
In the next year Bobillier solved, by means of planes and spheres only, the
problem, to draw through a given line a plane which shall cut off front a given
cone of revolution a required volume. [Correspondance Math, et Physique
(Quetelet), vie livraison, IV, 2-3, Bruxelles, 1828.)
48-49] PROPOSITIONS 27-28 65
But ek : kg = de :gm ; [vi. 2]
.*. ed:gm=gk :gi.
.: area gk . gm = area de . gi.
But area de . gi — \ area ag .gb;
.: area gk. gm = | area ag. gb.
And since
area gk . gm : area ag. gb — Akgm : A agb™,
A kgm = ^A agb.
In a similar manner any part of a triangle may be cut off
by a straight line drawn from a given point, on a side of the
triangle produced, or within two produced sides.
Proposition 28.
49- " To divide into two equal parts a given figure bounded
by an arc of a circle and by two straight lines which form a
given angle" [Leonardo 57, p. 148, 11. 13-14.]
" Let ABC be the given figure bounded by the arc BC
and by the two lines AB, AC
which form the angle BAC
It is required to draw a straight
line which will divide the figure
ABC into two equal parts.
" Draw the line BC and
bisect it at E. Through the
point E draw a line
perpendicular to BC, as EZ} and
draw the line AE. Then
because BE is equal to EC, the
area BZE is equal to the area
EZC, and the triangle ABE
is equal to the triangle AEC Then the figure ABZE will
equal the figure ZCAE. If the line AE lie in EZ produced,
the figure will be divided into two equal parts ABZE and
CAEZ. But if the line AE be not in the line ZE produced,
join A to Z by a straight line and through the point E draw
a line, as ET, parallel to the line AZ. Finally draw the line
5
66 EUCLID'S BOOK ON DIVISIONS OF FIGURES III [49-50
TZ. I say, that the line TZ is that which it is required to
find, and that the figure ABC is divided into two equal parts
ABZT and ZCT.
"For since the two triangles TZA and EZA are
constructed on the same base AZ and contained between the
same parallels AZ, TE: the triangle ZTA is equal to the
triangle AEZ. Then, adding to each the common part
AZB, we have TZBA equal to ABZE. But this latter figure
was half of the figure ABC; consequently the line ZT is
the line sought and BZCA is divided into two equal parts
ABZT, TZC, which was to be demonstrated."
Leonardo's proof is practically word for word as the above. He gives two
figures and in each he uses the Greek succession of letters.
It is doubtless to this Proposition and the next that reference is made in
the account of Proclus [Art. 1].
Proposition 29.
50. "To draw in a given circle two parallel lines cutting
off a certain fraction from the circle." [Leonardo 5 1 (the case
where the fraction is one-third), p. 146, 11. 37-38.]
" Let the certain fraction be one-third, and the circle be
ABC. It is required to do that which is about to be
explained.
" Construct the side of the triangle (regular) inscribed in
this circle. Let this be AC. Draw the two lines AD, DC
and draw through the point D a line parallel to the line AC,
such as DB. Draw the line CB. Divide the arc AC into
5°]
PROPOSITIONS 28-29
67
two equal parts at the point E, and draw from the point E
the chord EZ parallel to the line BC. Finally draw the line
AB. I say that we have two parallel lines EZ, CB cutting
off a third of the circle ABC, viz. the figure ZBCE.
"Demonstration. The line AC being parallel to the line
DB, the triangle DAC will be equal to the triangle BAC;
add to each the segment of the circle A EC'; the whole figure
DAEC will be equal to the whole figure BAEC But the
figure DAEC is one-third of the circle. Consequently the
figure BAEC is also one-third of the circle. Since EZ is
parallel to CB, the arc EC will be equal to the arc BZ; but
EC is equal to EA, hence EA equals ZB. Add to these
equal parts the arc ECB; the whole arc AB will equal the
whole arc EZ. Consequently the line AB will be equal to
the line EZ, and the segment of the circle AECB will be
equal to the segment of the circle ECBZ. Taking away the
common segment BC, there remains the figure EZBC equal
to the figure BAEC. But the figure BAEC was one-third
of the circle ABC. Then the figure EZBC is one-third of
the circle ABC; which was to be demonstrated.
" When it is required to cut off a quarter of a circle, or a
fifth or any other definite fraction, by means of two parallel
lines, we construct in this circle the side of a square or of the
pentagon (regular) inscribed in the circle and we draw from
the centre to the extremities of this side the two straight lines
as above. (The remainder of) the construction will be
analogous to that which has gone before"8."
The statement and form of discussion of this proposition are not wholly
satisfactory. For " a certain fraction " in the enunciation we should rather
expect "one-third,"as in Leonardo; while at the conclusion of the proof might
possibly occur a remark to the effect that a similar construction would apply
when the certain fraction was one-quarter [by means of iv. 6], one-fifth [iv. 11],
one-sixth [iv. 15], or one-fifteenth [iv. 16], but is it conceivable that Euclid
added "or any other definite fraction"? Moreover the lack of definition of
D and certain matters of form seem to further indicate that modification of
the original has taken place in its passage through Arabian channels.
118 This problem is clearly not susceptible of solution with ruler and compasses,
in such a case as when the "certain fraction," -, is one-seventh. In fact the only
n
cases in which the problem is possible, for a fraction of this kind, is when n is of
the form 2" (2^+ 1) (22*2 + 1) ... {2*'m+ 1),
where/, and .r's (all different), are positive integers or zero, anda2 m+ 1 (m = 1,2, ...m)
is a prime number. (Cf. C. F. Gauss, Disquisiliones Arithmeticae, Lipsiae, 1801,
French ed., Paris, 1807, p. 489.)
5—2
68 EUCLID'S BOOK ON DIVISIONS OF FIGURES III [50
On the other hand Leonardo presents the proposition as if drawn from
the pure well of Euclid undented. Here is his discussion. (I have
substituted C for his b, and B for his g.)
" And if, by means of two parallel lines, we wish to cut off from a circle
ACB, whose centre is D, a given part which is one-third, draw the line AC,
the side of an equilateral triangle inscribed in the circle abg. Through the
centre D draw DB parallel to this line and join CB. Bisect the arc AC at
E and draw EZ parallel to bg. I say that the figure contained between the
lines CB and EZ and the arcs EC and BZ is one-third part of the circle
ACB.
" Proof: Draw the lines DA and DB and AB.
"The triangles BACand DACare equal. To each add the portion ABE.
Then the figure bounded by the lines BA and BC and the arc AEC is
equal to the sector DAEC which is a third part of the circle ABC.
" Therefore the figure bounded by the lines BA and BC and the arc AEC
is a third part of the circle.
"And since the lines CB and EZ are parallel, the arcs EC and BZ are
equal. But arc EC is equal to arc AE. Therefore arc AE is equal to the
arc BZ. To each add the arc EB, and then the arc AECB will be equal to
the arc ECBZ.
"Hence the portion EZBC of the circle is equal to the portion ABCE.
Take away the common part between the line CB and the arc BC and there
remains the figure, bounded by the lines BC and EZ and the arcs CE and
BZ, which is the third part of the circle since it is equal to the figure bounded
by the lines BA and BC and the arc AEC; quod oportebat ostendere."
In his fniTpLKa (in. 18) Heron of Alexandria considers the problem : To
divide the area of a circle into three equal parts by two straight lines. He
remarks that "it is clear that the problem is not rational"; nevertheless "on
account of its practical use " he proceeds to give an approximate solution.
By discussion similar to that above he finds the figure BCEA, formed by
the triangle BCA and the segment CEA, to be one-third of the circle.
Neglecting the smaller segment with chord BC, we have, that BA cuts off
"approximately" one-third of the circle. Similarly a second chord from B
might be drawn to cut off another third of the circle, and the approximate
solution be completed.
5i-S2]
PROPOSITIONS 29-31
69
Proposition 30.
51. " To divide a given triangle into two parts by a line
parallel to its base, such that the ratio of one of the two parts
to the other is equal to a given ratio."
Although Leonardo does not explicitly formulate this problem or the
next, the method to be employed is clearly
indicated in the discussion of Proposition 5
(Art. 26).
Let abg be the triangle which is to be
divided in the given ratio ez : zi, by a line
parallel to bg. Divide ab in h such that
ah2 : aW = ez : eiS2.
Draw hk |] bg and meeting ag in k. Then
the triangles ahk and abg are similar and
A ahk : A abg=ah% : ab\ [vi. 19]
But ah2 : ab2 = ez : ei,
.'. Aahk : Aabg=ez : ei;
whence A ahk : quadl. hbgk=ez : zi;
and the triangle abg has been divided as required.
te
■z
U
[v. 16, 17]
Proposition 31.
52. "To divide a given triangle by lines parallel to its
base into parts which have given ratios to one another!'
Again in the manner of Proposition 5, suppose it be required to divide
the triangle abg into three parts in the ratio
ez : zi : ti. Then determine the points h, I
in ab such that
ah? : ab2 -
aP : ab* =
ah? : at2 = ez : et. [v. 16, 20]
and
Then
-ez : et"'
- et : ei.
- ez : et.
.'. Aahk : Aa/m = ez : et,
and .'. Aahk : quadl. hlmk = ez : zt.
Similarly
A aim : quadl. lbgm = et : ti.
But A ahk : A aim = ez : et.
A ahk : quadl. Ibgm = ez : ti.
Hence,
[v. 20]
Aahk : quadl. hlmk : quadl. Ibgm =ez : zt : ti,
and the triangle abg has been divided into three parts in a given ratio to one
another. So also for any number of parts which have given ratios to one
another.
70 EUCLID'S BOOK ON DIVISIONS OF FIGURES III [53
Proposition 32.
53. " To divide a given trapezium by a line parallel to its
base, into two parts such that the ratio of one of these parts to
the other is equal to a given ratio." [Leonardo 29, p. 131,
11. 41-42.]
Let abgd be the trapezium which is to be divided in the
ratio ez : zi by a line parallel to
the base. Produce the sides ba,
gd through a and d to meet in /.
Make tl2 : af = zi : ez*2,
and ht2 : (bf + tl2) = ez : ei.
Through /, h, draw Im, hk
parallel to bg and ad. Then I say
that the quadrilateral ag is divided
in the given ratio, ez : zi, by the
line hk.
Proof: For since the triangles
tlm, tad are similar
ll2 : af=Atlm : Atad:
but
Whence
or
tl2 : af — zi : ez ;
. •. zi : ez = A tint : A tad.
ei : ez = (Atlm + Atad) : Atad,
ez : ei= Atad : (Atlm + Atad).
But by construction
ez : ei^hf : (bt' + tl2),
and he : (bf + tl2) = Athk : (Atbg+ Atlm).
.-. ez : ei— Athk : (Atbg+ Atlm).
But Athk = Atad+quad\. ak.
Similarly
Atbg+ Atlm = quad]. ag+ Atad+ Atlm.
.-. ez : £z'=(quadl. ak + Atad) : (quadl. ag+ Atad+ Atlm)
[v. 18]
[v. 16]
[vi. 19]
S3l
PROPOSITION 32
71
But ez : et = Atad : (Atad+ Atlm);
.*. ez : ez'=quadl. ak : quadl. ag; [v. 11, 19]
whence ez : zi= quadl. ak : quadl. kg.
And the trapezium has been divided in the given ratio.
Then follows a numerical example and this alternative construction and
proof:
Draw mis such that,
ms : ls = t62 : td1,92
and divide ml in n, such that In is to nm in the given
proportion.
t-m
In tb determine h such that
th'1 : tb* — ns : sm.
Draw hk\\bg. Then,
quadl. ak : quadl. hg=ln : nm.
Proof: For, tb"1 : ta2=Atbg : A tad; [vi. 19]
and ms : ls = tb* : ta2.
.'. ms : Is = Atbg : Atad. [1]
Again, since tb* : th* = ms : sn,
and Atbg : Atkk = tb* : th*,
.'. ms : ns = Atbg : Athk; [2]
.". sm : nm = Atbg : quadl. kg. [v. 16, 21]
[3]
72 EUCLID'S BOOK ON DIVISIONS OF FIGURES III [53-54
But sm : ls= t\tbg : A*W118a,
or ms : t\tbg — ls : A tad,
while ms : l\tbg=ns : t\thk; [from [2]]
.'. Is : ns = Atad : Athk [4]
From [3] ms : Atbg=nm : quadl. kg.
But from [4] si : In = Atad : quadl. ak, [v. 16, 21]
.". si: £\tad=ln : quadl. ak.
But from [1] ms : &tbg = sl: £\tad,
.'. ms : A tbg = In : quadl. ak;
.'. mn : quadl. hg=ln : quadl. ak;
.'. In: nm = quadl. ak : quadl. kg.
Hence the quadrilateral ag is divided by the line kk,
parallel to the base bg, in the given proportion as the
number In is to the number nm.
Then follows a numerical example.
Which was to be done.
Proposition 33.
54. " To divide a given trapezium, by lines parallel to its
base, into parts which have given ratios to one another."
[Leonardo 35, p. 137, 11. 6-7.]
Let abgd be the given trapezium and [let ez : zi : it denote
the ratios of the three parts
into which the trapezium is to
be divided by lines parallel to
the base bg]. Let ba, gd
produced meet in k and find / such
that
b&* : afc = tl: el.
Then determine m and n such
that
bk1 : km? = tl: Is,
and bk2 : kn2 = // : il.
ll8a Such mixed ratios as these (ratios of lines to areas), and others of like kind
which follow in this proof, are very un-Greek in their formation. This is sufficient
to stamp the second proof as of origin other than Greek. The first proof, on the
other hand, is distinctly Euclidean in character.
e
z
L
54] PROPOSITIONS 32-33 73
Through m, n draw lines mo, np parallel to bg. In the
same manner as above
quadl. ao : quadl. mp = ez : zi;
and quadl. mp : quadl. ng=zi : it.
Then follows a numerical example in which the line kfhrs, perpendicular
to bg, is introduced into the figure.
Here is a proof of the Proposition :
By construction, v. 16 and vi. 19,
Akbg: Akad = tl:el. [1]
So also A kbg: A kmo = tl: Iz, [2]
and Akbg: Aknp=tl:il. [3]
From [1] A kad: A kbg = el: tl.
But from [2] Akbg : Akmo = tl: lz;
hence, by [v. 20], A kad: A kmo -el:lz, [4]
or alternately A kmo : A kad = lz : el.
Hence, separando, quadl. ao : A kad = ez : el. [5]
So also from [2] and [3]
A kmo : A knp = lz : tl;
and A kmo : quadl. mp = lz : iz.
But from [4] A kad: A kmo = el: lz;
therefore, by [v. 20], A kad: quadl. mp=el:iz [6]
Hence from [5], by [v. 20],
quadl. ao : quadl. mp = ez : zi.
Again, from [3], quadl. ng : Akbg= ti : tl;
and since from [1], Akbg : Akad= tl: el,
we have quadl. ng: A kad = it: el.
Hence from [6], by [v. 20], we get
quadl. ng: quadl. mp = it: zi,
or alternately quadl. mp : quadl. ng = zi: it.
And since quadl. ao : quadl. mp = ez : zi, the trapezium ag has been divided
by lines parallel to the base ag, into three parts which are in the required
ratios to one another. Q. e. f.
74 EUCLID'S BOOK ON DIVISIONS OF FIGURES III [55
Proposition 34.
55« " To divide a given quadrilateral, by a line drawn
front a given vertex of the quadrilateral, into two parts such
that the ratio of one of these parts to the other is equal to a
given ratio." [Leonardo 40, p. 140, 11. 36-37.]
Let abcdbe the given quadrilateral, and ez : zi the given ratio.
It is required to draw from the
angle d a line to divide the ~ z. L
quadrilateral in the ratio ez : zi. ' '
Draw the diagonal ac and
on it find / such that
ct : at = ez : zi.
Draw the diagonal bd. Then
if bd pass through t the
quadrilateral is divided as required,
in the ratio ez : zi.
'or,
But
Add : Adta — ct : ta,
= Acbt: Atba.
.'. ct : ta = Adcb : Aabd.
ct : ta~ ez : zi;
.*. ez : zi= Abdc : Abda :
[v. 18]
and the quadrilateral ac is divided, by a line drawn from a
given angle, in a given ratio.
But if bd do not pass through /, it will cut ca either
between c and / or between t and a. Consider first when
bd cuts ct. Join bt and td. Then,
quadl. tbcd : quadl. tbad— ct : ta = ez : zi.
Draw tk\\bd and join dk. Then
quadl. kbcd= quadl. tbcd;
.". quadl. kbcd: Adak — ez : zi,
and the line dk has been drawn as required.
55-57]
PROPOSITIONS 34-35
75
If the diagonal bd cut at, through t draw ^/parallel to the
diagonal bd. Join dl. Then as before,
ct : ta = ez : zi — Add: quadl. abld.
Hence in every case the quadrilateral has been divided as required by a
line drawn from d. Similarly for any other vertex of the quadrilateral.
Proposition 35.
56. " To divide a given quadrilateral by lines drawn
from a given vertex of the quadrilateral into parts which
are in given ratios to one another"
Although Leonardo does not explicitly formulate this problem, the
method he would have followed is clear from his discussion of the last
Proposition. Let abed be the quadrilateral to be divided, by lines drawn
from d, into three parts in the ratios to one another of ez ; zi : it.
, 1 1 ——. 1
e z L t
Divide ca at points r, t so that
cr : rt : ta = ez : zi : it.
Through r, t draw lines parallel to bd, and meeting be (or ab) in / and
ab (or be) in m.
Then as above dl, dm divide the quadrilateral as required.
We may proceed in a similar manner to divide the quadrilateral abed, by
lines drawn from the angular point d, into any number of parts in given ratios
to one another.
76 EUCLID'S BOOK ON DIVISIONS OF FIGURES III [57
Proposition 36.
57- "Having resolved those problems which have gone
before, we are in a position to divide a given quadrilateral in
a given ratio or in given ratios by a line or by lines drawn
from a given point situated on one of the sides of the
quadrilateral, due regard being paid to the conditions mentioned above."
This problem, also, is not formulated by Leonardo ; but from his discussion
of Euclid's Propositions 16, 17 and of his own 41, the methods of construction
which Euclid might have employed are clearly somewhat as follows.
Let abed be the given quadrilateral and g the given point.
(1) Let it be required to divide abed into two parts in the ratio ez : zi by
a line drawn through a point g in the side ad.
Draw dl such that A eld : quadl. Ibad = ez : zi. [Prop. 34]
Join gl. If gl\\de, join ge, then this line divides the quadrilateral as required.
If gl be not parallel to dc draw dh \\gl, and meeting be in h. Join gh.
Then gh divides the quadrilateral as required.
If dh fell outside the quadrilateral draw //' || cd (not indicated in the figure)
to meet ad in /'. Draw I'z \\gc to meet dc in z'. Then gz' is the line required.
The above reasoning is on the assumption that dl meets be in /. Suppose
now it meet ab in /. Join bd and
draw bk such that
quadl. bedk : A kab = ez : zi.
If k do not coincide with g there
are two cases to consider according
as k is between g and d or between
g and a. Consider the former case.
Through k draw km parallel to gb
and meeting be in m. ]oin gm. Then
this is the required line dividing the
quadrilateral ac in such a way that
quadl. abmg : quadl. gmed = ez : zi.
57] PROPOSITION 36 77
Similarly if k were between g and a.
(2) Let it be required to divide abed into, say, three parts in the ratios
ez : zi : it, by lines through any point g in the side ad (first figure).
Draw dl, dm dividing the quadrilateral ac into three parts such that
t^amd : quadl. dmbl: Adle = ez : zi : it.
There are various cases to consider according as /and m are both on be, both
on ab, or one on ab and one on be. The method will be obvious from working
out one case, say the last.
Join ge, gl. If gl be parallel to ed, ge cuts off the triangle gdc such that
&gde : quadl. abeg = it: ei(-ez + zi). [v. 24]
If gl be not parallel to dc, draw dh parallel to gl and meeting be in h;
then gh divides the quadrilateral in such a way that
quadl. gdeh : quadl. ghba = it : ei.
Then apply Proposition 34 to draw from g a line to divide the
quadrilateral abhg in the ratio of ez : zi.
Hence from g are drawn two lines which divide the quadrilateral abed
into three parts whose areas are in the ratios of ez : zi : it.
The case when dh meets be produced may be considered as above.
We could proceed in a similar manner if the quadrilateral abed were to be
divided by lines drawn from g, into a greater number of parts in given ratios.
The enunciation of this proposition is a manifest corruption of what Euclid
may have given. Such clauses as those at the beginning and end he would
only have included in the discussion of the construction and proof.
After the enunciation of Proposition 36, Woepcke's
translation of the Arabian MS. concludes as follows :
" End of the treatise. We have confined ourselves to
giving the enunciations without the demonstrations, because
the demonstrations are easy."
IV.
APPENDIX
In the earlier pages I have referred to works on Divisions of Figures
written before 1500. Several of these were not published till later; for
example, that of Muhammed Bagdedinus in 1570, of Leonardo Pisano in
1862 and the second edition of Luca Paciuolo's "Summa" in 1523119.
It has been remarked that Fra Luca's treatment of the subject was based
entirely upon that of Leonardo. But, on account of priority in publication,
to Paciuolo undoubtedly belongs the credit of popularizing the problems on
Divisions of Figures.
While few publications treat of the subject in the early part, their number
increases in the latter part, of the sixteenth century. In succeeding centuries
the tale of titles is enormous and no useful purpose would be served by the
publication here of an even approximately complete list. It would seem,
however, as if the subject matter were of sufficient interest to warrant, as
completion of the history of the problems, a selection of such references in
this period, (1) to standard or popular works, (2) to the writings of eminent
scientists like Tartaglia, Huygens, Newton, Kepler and Euler; (3) to special
articles, pamphlets or books which treat parts of the subject; (4) to
discussions of division problems requiring other than Euclidean methods for
their solution.
No account is taken of the extensive literature on the division of the
circumference of a circle, from which corresponding divisions of its area
readily flow. Considerations along this line may be found in : P. Bachmann,
Die Lehre von der Kreisteilung unci ihre Beziehungen zur Zahlentheorie, Leipzig,
1872, 12 + 300 pp.; and in A. Mitzscherling, Das Problem der Kreisteilung,
Leipzig und Berlin, 1913, 6 + 214 pp.
Except for about a dozen titles, all the books or papers mentioned have
been personally examined. In many cases it will be found that only a single
problem (often Euclid's Propositions 19, 20, 26 or 27) is treated in the place
referred to.
Some titles in note in may also be regarded as forming a supplement to
this list.
1539—W. Schmid. Das Erst [Zweit, Dritt und Viert] Buck der Geometria.
Niirnberg.
"Dritter Theil, von mancherley Art der Flachen, wie dieselben gemacht und
ausgetheilt werden, auch wie eine Flache in die andern fiir sich selbst, oder gegen
einer andern in vorgenommener Proporz, geschatzt, verandert mag werden. Theilungen
und Zeichnungen von Winkeln, Figuren, ordentlichen Vielecken, die letzten, wie man
leicht denken kann, nicht alle geometrisch richtig. Verwandlung von Figuren."
1547—L. Ferrari. A "Cartello'' which begins: " Messer N. Tartaglia, gia
otto giorni, cioe alii 16 di Maggio, in risposta della mia replica io riceuetti
la uostra tartagliata, etc." [Milan.]
Dated June 1, 1547; a challenge to a mathematical disputation from L. F. to
N. Tartaglia.
119 A synopsis of the portion of the work on divisions of figures is given on pages 106 and
275-284 of Scritti inediti del P. D. Pietro C<«ttz/«... pubblicati da Baldassarre Boncompagni,
Roma, 1857. Cf. note 61.
APPENDIX 1539-1609
79
1547—N. Tartaglia. Terza Risposta data da N. Tartalea.. .al eccellente
M. H. Cardano...et al eccellente Messer L. Ferraro...con la resolutione,
ouer risposta de 31 quesiti, ouer quistioni da quelli a lui proposti.
[Venice, 1547.]
Dated July 9, 1547. For the discussion between Ferrari (1522-1565) and Tartaglia
(1500-1557) 6 "cartelli" by Ferrari and 6 "Risposte" by Tartaglia were published at
Milan, Venice and Brescia in 1547-48'20. They contained the problems and their
solutions. These publications are of excessive rarity. Only about a dozen copies
(which are in the British Museum and Italian Libraries) are known to exist. But they
have been reprinted in: / sei cartelli di matematica disfida prii}iamente intorno alia
generate risohtzione delle equazioni cubiche, di Ludovico Ferrari, coi sei contro-cartelli in
risposta di Nicolo Tartaglia...comprendenti le soluzioni de1 quesiti dalV una e dalP altra
parte proposti. ..Raccolti, autografati e pubblicaii da Enrico Giordani.. .Milano 1876.
On pages 6-7 of the ill0 cartello (Giordani's edition pp. 94-95), Questions 5 and
14, proposed by Ferrari, are :—
"5. To bisect, by a straight line, an equilateral, but not equiangular, heptagon."
" 14. Through a point without a triangle to draw a line which will cut off a third."
On pages 12 and 20 of the ill0 Risposta Tartaglia gives the solutions and assigns
due credit to the treatment of problems on the Division of Figures by Luca Paciuolo.
The general subject was treated much more at length by Tartaglia in a part of his
"General trattato" published in 1560.
1560—N. Tartaglia. La quinta parte del general trattato de' numeri et
misure. Venetia.
On folio 6 recto we have a section entitled "Del modo di saper dividere una figure
cioe pigliar, over formar una parte di quella in forma propria." The division of figures
is treated on folios 23 verso-i,\ recto (23-32, triangles; 32-34, parallelograms; 34-44,
quadrilateral, pentagon, hexagon, heptagon, circle without the Euclid-Proclus case).
Cf. the synopsis in Scritti inediti del P. D. Pietro Cossali chierko regolare teatino
pubblicati da Baldassarre Boncompagni, Roma, 1857, pp. 299-300.
1574—J. Gutman. Feldmessunggewiss, richtig und kurzgestellt. Heidelberg.
1574—E. Rein hold. Griindlicher und wahrer Bericht vom Feldmessen,
samt allem, was dem anhiingig, darinn alle die Irrthum, so bis daher im
Messen fiirgeloffen, entdeckt werden. Dessgleichen vom Afarkscheiden,
kurzer und griindlicher Unterricht. Erffurdt.
"Der dritte Theil von Theilung der Aecker. Theilungen aller Figuren, auch des
Kreises mit Exemplen und Tafeln erlautert."
1585—G. B. Benedetti. Diversarum speculationum mathematicarutn et
physicarum liber. Taurini.
Pages 304-307.
1604—C. Clavius. Geometria Practica. Romae.
Pages 276-297.
1609—J. Kepler. Astronomia nova ... commentariis de motibus stella
Mart is... [Pragae].
"Kepler's Problem" occurs on p. 300 of this work (Opera Kepleri ed. Frisch,
III, 401). It is : "To divide the area of a semicircle in a certain ratio by a straight
line drawn through a given point on the diameter or on the diameter produced." (Cf.
A. G. Kastner, Ceschichte der Math, lv, 256, Gottingen, 1800; M. Cantor, Vor-
lesungen etc., II, 708, Leipzig, 1900). Kepler was led to this problem in his
theory of the path of the planets- It has been attacked by many mathematicians,
notably by Wallis, Hermann, Cassini, D. Gregory, T. Simpson, Clairaut, Lagrange,
120 Cf. Cantor, Vorlesungen iiber Gesch. d. Math. Bd 11, 2te Aufl., 1900, pp. 490-491,
where the exact dates are given.
80 EUCLID'S BOOK ON DIVISIONS OF FIGURES IV
Bossut, and Laplace. {Cf. G. S. Klugel, Mathematisches IVorterduch...¥.rste Ab-
theilung, Dritter Theil, Leipzig, 1808; Article, "Kepler's Aufgabe." See also
C. Hutton, Philosophical and Alathematical Dictionary. New edition, London,
1815, 1, 703.)
1612—Sybrandt Cardinael. Hondert geometrische questien met hare
solutien. Amsterdam.
This work is also to be found at the end of Johan Sems ende Ian Dou
Practijck des land/Helens. Amsterdam, 1616. Another edition: Tractatus geo-
metricus. Darinnen hundert schone...Questien [libersetzt] durch Sebastianum Curtium.
Amsterdam, 1617; Questions 78, 90-93.
With these problems Huygens (1629-1695) busied himself when about 17 or 18
years of age. Cf Oeuvres completes de Chr. Huygens, Amsterdam, xi, 24 and 29, 1908.
I have elsewhere (Nieuw ArcAief, 1914) shown that Sybrandt Cardinael s work
was translated into English, rearranged and published as an original work by
Thomas Rudd (1584?-!656): A hundred geometrical Questions with their solutions
and demonstrations. London, M.DC.L.
1615—Ludolph van Ceulen. Fundamenta arithmetica et geometrica cum
eorundem usu...e vernaculo in Latinum translata a W. S\nellio\ R. F.
Lugduni Batavorum.
Contains several problems on Change, and Division, of Figures.
1616—J. Speidell. A geometrical! Extraction or a compendiovs collection of
the chiefe and choyse Froblemes, collected out of the best, and latest writers.
Wherevnto is added about 30 Froblemes of the Authors Invention, being for
the most part, performed by a better and briefer way, than by any former
writer. London.
Another edition, 1617; second edition "corrected and enlarged," London, 1657;
"Now followeth [pp. 84-125] a compleat Instruction of the diuision of all right lined
figures Very pleasant and full of delight in practise: Also, most profitable to all
surveighers, or others that are desirous to make any Inclosure."
1619—A. Anderson. Exercitationum mathematicarum Decas prima. Con-
tinens, Questionum aliquot, quae nobilissimorum turn hujus turn veteris
aevi, Mathematicorum ingenia exercuere, Enodationem. Parisiis.
Problems in division of a triangle, with reference to Clavius (1604). Cf. The Ladies^
Diary, London, 1840, pp. 55—56.
1645—C. Huygens. Oeuvres Completes, xi, 1908, pp. 26-27; 219-225.
Solution of "Datum triangulum, ex puncto in latere dato, bifariam secare" (1645);
two solutions of "Triang. ABC, sectus utcumque linea DE, dividendus est alia linea,
FG, ita ut utraque pars DBE et ADEC bifariam dividatur" (1650-1668). See also
note under 1687—J. Bernoulli.
1657—F. van Schooten. Exercitationvm mathematicarum liber primus
continens propositionum arithmelicarvm et geometricarvm centuriam.
Lugd. Batav.
Prop. L, pp. 107-110. Dutch edition, Amsterdam, [659. pp. 107-110. Concerning
a Schooten MS. of 1645-6, used by Huygens and of interest in this connection, cf.
C. Huygens, Oeuvres Completes, tome xi, 1908, p. 13 ff.
1667 — D. Schwenter. Geometriae Practicae novae et auciae Libri IV...
tnit vielen nutzlichen Additionen und neuen Figuren vermehret durch
G. A. Bbcklern. Niirnberg.
"Von Austheilung der Figuren in gleiche und ungleiche Theil," pp. 269-279;
p. 350; the problem on this last page is taken from B. Bramer, Trigonometria
planarum mechanica, Marpurg, 1617, p. 99. "Von Austheilungen der Aecker
Wiesen,..." pp. 567-583.
APPENDIX 1609-1747
81
1674—C. F. M. Deschales. Cursus seu mundus mathematicus. Ltigduni.
"De figurarum planarum divisione," 1, 371-381 ; second edition, 1690.
1676—I. Newton. Arithmetica Universalis. Cantabrigiae, mdccvii.
Prob. x, p. 126 (Prob. XX, pp. 254-255 of the 1769 edition). This problem was
discussed in a lecture delivered October, 1676 (see Correspondence of Sir Isaac Newton
and Professor Cotes...by J. Edleston, London, 1850, p. xciii).
1684—T. Strode. A Discourse of Combinations, Alternations and Aliquod
Parts by John Wallis. London, 1685.
On pages 163-164 is printed a letter, dated Nov. 1684, from Strode to Wallis. It
discusses two problems on divisions of a triangle.
1687—J. Bernoulli. " Solutio algebraica problematis de quadrisectione
trianguli scaleni, per duas normales rectas." Acta Eruditorum, 1687,
pp. 617-623.
Also in Opera, Genevae, 1744, I, 328-335 ; see further 11, 671. In the solution of this
question Bernoulli is led to the intersection of a conic and a curve of the fourth degree,
that is, to an equation of the eighth degree. And yet, in the seventh edition of
R.OUCHE et CoMBEROUSSE, Train de Geometric, Paris, 1900, we find Problem 453 is:
" Partager un triangle quelconque en quatre parties equivalentes par deux droites
perpendiculaires entre elles!" The problem was solved by L' Hospital before 1704,
the year of his death, in a posthumous work. Traite' analytique des Sections coniques,
Paris, 1707, pp. 400-407. As the result of correspondence in Vlntermidiaire des
Math.., tomes i-vil, 1894-1900, Questions 3 and 587, Loria wrote the history of the
problem: " Osservazioni sopra la storia di un problema pseudoelementare." Bibl.
Math., 1903 (3), IV, 48-51. Leibnitz's name appears in this connection. See note on
1645—C. Huygens.
1688—J. Ozanam. D usage du compas de proportion explique et demontre d'une
maniere court et facile, et augmente d'un Traite de la division des champs.
Paris.
"Division des champs," pp. 89-138. Edition revu, corrige et entierement refondu
par J. G. Gamier. Paris, 1794, pp. 165—257.
1694—S. le Clerc. Traite de Geometrie sur le terrain at end of Geometric
pratique, ou pratique de la geometrie sur le papier et sur le terrain.
Amsterdam.
1699—J. Ozanam. Cours de mathemalique, nouv. ed. tome 3. Paris.
Pages 23-64. German translation: Anweisung, die geradlinickten Figuren nach
einen gegebenen Verhaltniss ohne Rechnung zu theilen. Frankfurt u. Leipzig, 1776.
1704—Guisnee. Application de Palgebre a la geometrie. Paris.
Although the "approbation" signed by Fontenelle is dated "15 Juillet 1704" the
work was first published in 1710; second edition "revue, corrigee et considerablement
augmentee par l'auteur," Paris, 1733, pp. 42-47; analytic discussion only.
1739—I'abbe Deidier. La science des geometres (sic) ou la theorie et la
pratique de la geometrie. Paris.
"De la geodesie ou division des champs," pp. 279-320; divisions of triangles,
rectangles, trapeziums, polygons.
1740—N. Saunderson. Elements of Algebra in ten books, vol. 2. Cambridge.
Pages 546-554-
1747—T.Simpson. Elements of Plane Geometry. London.
Pages 151-152; new ed., London, 1821, pp. 207-208; taken from Newton (1676).
A. 6
82 EUCLID'S BOOK ON DIVISIONS OF FIGURES IV
1748—L. Euler. Introductio in analysin infinitorum. Tomus secundus.
Lausanne.
Chapter 22: " Solutio nonnullorum problematum ad circulum pertinentium."
Three of the eight problems which Euler here discusses by the method of trial and
error, and tables of circular arcs and logarithmic sines and tangents, are of interest to
us. These are: Problem 2, "To find the sector of the circle ACB which is divided
by the chord AB into two equal parts, so that the triangle ACB shall be equal to the
segment AEB." Problem 4, " Given the semi-circle AEDB, to draw from the point
A a chord AD which will divide the semi-circle into two equal parts." Problem 5,
" From a point A of the circumference of a circle, to draw two chords AB, ^Cwhich
shall divide the area of the circle into three equal parts." (Heron, cf. Art. 50.)
Gregory (1840) considers these problems at the close (pp. 186-188) of his Appendix.
For other editions of Euler's " Introductio," tomus 2, see Verzeichnis der Schriflen
Leonhard Eiders. Bearbeitet von G. Enestroin. Erste Lieferung. Leipzig, 1910.
1752—T. Simpson. Select Exercises for young proficients in the mathematics.
London.
Problem xlii, pp. 145-6; new ed. by J. H. Hearding. London, 1810, pp. 148-9.
1754—J. le R. d'x\lembert. Encyclopedie ou Dictionnaire raisonne des
sciences...mis en ordre et publie par M. Diderot...; et quant a la partie
mathematique par M. d'Alembert. Paris.
Article "Geodesie"; mostly descriptive of methods of Guisnee (1704) and Clerc
(1694).
1768—J. A. Euler. "Aufiosung einiger geometrischen Aufgaben," Ab-
handlungen der Churfiirstlich-baierischen Akademie der Wissenschaften, v,
165-196.
Erste Aufgabe, pp. 167-182: "Man soil zeigen, wie eine jede geradlinichte Figur
durch Parallellinien in eine gegebene Anzahl gleicher Theile zerschnitten werden
kann." Zweite Aufgabe, pp. 182-187: "Eine Zirkel-flache durch parallellinien in
eine gegebene Anzahl gleicher Theile zu zerschneiden." Dritte Aufgabe, pp. 187-196 :
"Die Hohe und Grundlinie einer aufrecht-stehenden geschlossenen Parabelflache ist
gegeben, man soil dieselbe durch Parallellinien in n gleiche Theile zerschneiden."
Discussion mostly analytic.
x772 (?)—J- H- Lamberts deutscher gek.hrter Briefwechsel. Herausgegeben
von Joh. Bernoulli. Band 2, Berlin, 1782.
Pages 412-13, undated fragment of a letter from Lambert to J. E. Silberschlag.
Analytic solution by quadratic equation of the problem: " Ein Feld ABCD welches
in ABFE Wiesen, in EECD Ackerfeld ist, soil durch eine gerade Linie KM so
getheilt werden, dass so wohl die Wiesen als das Ackerfeld in beliebiger Verhaltniss
getheilt werde." [ABCD is a quadrilateral and EF is a straight line segment joining
points on the opposite sides AD, BC respectively.]
In the Journal of the Indian Mathematical Society, 1914, VI, 159, N. P. Pandya
proposed as Question 563 : "Given two quadrilaterals in the plane of the paper show
how to draw a straight line bisecting them both." A solution by means of common
tangents to hyperbolas was offered in 1915, vn, 176.
1783—J. T. Mayer. Grilndlicher und ausfiihrlicher Unierricht zur praktischen
Geometrie, 3. Teil. Gottingen.
Pages 215-303 : "Theilung der Felder durch Rechnung, Theilung der Felder durch
blose Zeichnung, Anwendung der Theilungsmethoden auf mancherley, in gemeinen
Leben vorkommende Falle"; dritte Auflage, 1804, PP- 232—337-
1793—J. W. Christiani. Die Lehre von der geometrischen und okonomischen
Vertheilung der Felder, nach der Diinischen Sckrift des N. Morville
bearbeitet von J. IV. Christiani Preface by A. G. Kastner. Gottingen.
1795—Gentleman's Diary, London.
No. 54, 1794, p. 47, Question 691 by J- Rodham: "Within a given triangle to find
APPENDIX 1748-1831 83
a point thus, that if lines be drawn from it to cut each side at right angles, the three
parts into which the triangle thus becomes divided, shall obtain a given ratio." Solution
by hyperbolas in No. 55, 1795, pp. 37-38. See also Davis's edition of the Gentleman's
Diary, vol. 3, London, 1814, pp. 233-4.
1801—L. Puissant. Recueil de divers propositions de geomStrie resolues ou
d&montrees par ['analyse alge'brique suivant les principes de Monge et de
Lacroix. Paris.
Pages 33-36; German ed., Berlin, 1806; second French ed., Paris, 1809, pp. 107-
111 ; third ed., Paris, 1824, pp. 139-142.
1805—M. HlRSCH. Sammlunggeometrischer Aufgaben, Erster Theil. Berlin.
"Theilung der Figuien durch Zeichnung," pp. 14-25; "Theilung der Figuren
durch Rechnung," pp. 42-53 ; Reprint, 1855; English edition translated by J. A. Ross
and edited by J. M. F. Wright. London, 1827.
1807—A. Bratt. Problema geometricum triangulum datum a dato puncto in
2 partes aequales secandi. Greifswald.
This title is taken from C. G. Kavser, Backer-Lexicon, Erster Teil, Leipzig, 1834.
1807—J. P. Carlmark. Triangulus datus a dato puncto in 2 partes aequales
secandus. Greifswald.
This title and the next two are taken from E. Wolffing, Math. Bilcherschatz, 1903.
1809—J. Kullberg. Problema geometricum triangulum datum e quovis dato
puncto in 2 partes aequales secandi. Diss. Lund.
1810—J. Kullberg. Problema geometricum triangulum quodcunque datum in
2 aequales divisum ittrum in partes aequales ita secandi, ut rectae secantes
angulum constituant rectum. Diss. Upsala.
1811—J. P. Gruson. Geoddsie oder vollstdndige Anleitung zur geometrischen
und bkonomischen Feldertheilung. Halle.
1819—L. Bleibtreu. Theilungslehre oder ausfuhrliche Anleitung, jede
Grundfldche auf die zii'eckmdssigste Art ... geometrisck zu theilen.
Frankfurt am Main.
1821—J. Leslie. Geometrical Analysis and Geometry of Curve Lines
Edinburgh.
Pages 64-66.
1823—A- K. P- von Forstner. Sammlung systematisch geordneter und
synthetisch aufgeloseter geometrischer Aufgaben. Berlin.
"Theilung der Flachen, mittelst der Proportion und der Aehnlichkeit," pp. 310-371.
1827—Correspondance mathbnatique et physique publie par A. Quetelet,
tome 111.
Page 180: "On donne dans un plan un angle et un point, et Ton demande de faire
passer par le point une droite qui coupe les cotes de l'angle, de maniere que l'aire
intercepted soit de grandeur donnee." Solution by Verhulst, pp. 269-270. Answer
by Bobillier, tome IV, pp. 2-3. Generalizing his solution, he gets the result: "tous
les plans tangens d'un hyperboloide a deux nappes, interceptent sur le cone asymptotique
des volumes equivalens." Compare note 117.
1831—P. L. M. Bourdon. Application de I'algebre a la geometrie comprenant
la geometrie analytique a deux et a trois dimensions, troisieme edition.
Paris.
Pages 46-54; 5e ed., Paris, 1854, pp. 33-41; 8e ed. rev. par Darboux, Paris, 1875,
pp. 30-38. Analytic discussion only.
84 EUCLID'S BOOK ON DIVISIONS OF FIGURES IV
1831—H. v. Holi.eben, und P. Gerwten. Geometrische Analysis. Berlin,
2 Bde, 1831-1832.
" Theilungen," j, 184-191; 11, 144^51.
1837—G. Ritt. Problemes d''applications de I'algebre a la geometric avec les
solutions developpees, 2e partie. Paris.
Pages 108-109.
1840—O. Gregory. Hints theoretical, elucidatory and practical, for the use
of Teachers of elementary Mathematics and of self-taught students; with
especial reference to the first volume of Iliitton's course and Simson's Euclid,
as Text-Books. Also a selection of miscellaneous tables, and an Appendix
on the geometrical division of plane surfaces. London.
"Appendix: Problems relative to the division of Fields and other surfaces,"
pp. 158-188; partly taken from Hirsch (1805). See also Euler (1748).
1844—Dreser. Die Teilung der Figuren. Darmstadt.
This title is taken from E. Wolffing, Math. Bucherschatz, 1903.
1847—R. Potts. An appendix to the larger edition of Euclid's Elements of
Geometry; containing...Hints for the solution of the Problems.. .Cambridge
and London.
Ex. 91, pp. 72-73.
1852—H. Ch. de La Fremoire. Theoremes et Problemes de Geometric
elementaire, second ed. revue et corrigee par E. Catalan. Paris.
Pages 107-108; 6e ed. par Catalan, Paris, 1879, pp. 190-191.
1852—F. Rummer. Die Verwandlung und Theilung der Fldchen in einer
Reihe von Constructions- u. Berechnungs-Aufgaben. Mit 3 Steintafeln.
Heidelberg. 6 + 90 pp.
1855—P. Kelland. "On Superposition." Transactions of the Royal Society
of Edinburgh, 1885, xxi, 271-273 + 1 pi.
This paper deals, for the most part, with solutions of the following problem proposed
to Professor Kelland by Sir John Robison: " From a given square one quarter is cut
off, to divide the remaining gnomon into four such parts that they shall be capable of
forming a square." In the Transactions, 1891, xxxvi, 91-95,+ 2 pis., Robert Brodie
has a paper entitled " Professor Kelland's Problem on Superposition."
1857—E. Catalan. Manuel des Candidats a I'ccole poly technique. Paris,
Tome 1.
Pages 233-4 : " To divide a circle into two equal parts by means of an arc with its
centre, A, on the circumference of the given circles." This is stated by A. REBifeRE
{Maihimatique et Mathemaliciens, 2e ed., Paris, 1893, p. 519) under the form : "Quelle
doit etre la longueur de la longe d'un cheval pour qu'en la fixant au contour d'un pre
circnlaire l'animal ne puisse tondre que la moitie du pre?"
The solution of this problem leads to a transcendental equation
7T
sin x — x cos x = —,
2
where x is the angle under which the points of section of the circumferences are seen
from A. Catalan finds x= 1090 n' 18", correct to within a second of arc.
Cf. VIntermidiaire des Mathimaticiens, 1914, Question 4327, xxi, 5, 69, 90, 115,
180.
1863—J. McDowell. Exercises on Euclid and in Modern Geometry.
Cambridge.
No. 157, pp. 145-6; 3rd ed. 1881, p. 118.
APPENDIX 1831-1911
85
1864—Educational Times Reprint, Vols. 1, 40, 44, 66, 68, 69; new series,
Vol. 1; 1864-1910.
The problems here solved are Euclid's 19, 10, 16, 27: No. 1457 (1, 49. old edition,
1864) proposed by R. Palmer; solution by Rutherford who slates that it was also
published in Thomas Bradley's Elements of Geometrical Drawing, 1861—Nos. 7336 and
7369 (xl, 39, 1884) proposed by W. H. Blythe and A. H. Curtis; solutions by
G. Heppel and Matz—No. 8271 (xi.iv, 92, 1886) proposed by E. Perrin; solution by
D. Biddle—No. 12973 (lxvi, 29, 1897) proposed by Radhakrishnan; solution by
I. Arnold—No. 13460 (lxviii, 35, 1898) proposed by I. Arnold; solution by
W. S. Cooney, etc.—No. 13647 (LXIX, 42, 1898) proposed by I. Arnold; solution by
W. C. Stanham—No. 16747 (new series xvin, 46, 1910) proposed by I. Arnold;
solution by proposer, by Euclid's Elements Bk I.
1864—H. Holscher. Anleitung zur Berechnung und Teilung der Polygone
bei rechtwinkligen Koordinaten. Berlin and Charlottenburg.
This work and the two following are representative of those which treat of
Divisions of Figures by computation, rather than by graphical methods: (1) F. G. Gauss,
Die Teilung der Grundstiicke, insbesondere unter Zugrundelegung Koordinaten,
1 Auflage, Berlin, 1890; (2) L. Zimmerman, Tafeln fir die Teilung der Dreiecke,
Vierecke, und Polygone, Zweite vermehrte und verbesserte Auflage, Liebenwerda,
1896; 118 + 64 PP-
1870—F. Lindman. "Problema geometricum." Archiv der Math. u. Phys.
(Grunert), Bd 51, 1870, pp. 247-252.
1879—P. M. Ff. Laurent. Traite d'algebre a Vusage des candidats....
Troisieme edition. Paris.
Tome 1, p. 191: "To divide a triangle into two equal parts by the shortest possible
line." Solutions in VIntermediaire des Mathimaticiens, 1902, IX, 194-5. See also
F. G. M., Exercices de Ge'ome'trie, Cinquieme edition. Tours et Paris, 1912, p. 802.
1892—H. S. Hall and F. H. Stevens. Key to the Exercises and Examples
contained in a Text-Book of Euclid''s Elements. London.
Ex. 7, 8, 10, n, pp. 163-164.
1894—G. E. Crawford. "Geometrical Problem." Proc. Edinb. Math.
Soc, Vol. 13, 1895, p. 36.
Paper read Dec. 14, 1894.
1899—W. J. Dilworth. A New Sequel to Euclid. London.
Ex. xxxv, p. 190.
1901—A. Larmor. Geometrical Exercises from Nixon's 'Euclid Revised.'
Oxford.
Ex. 15, p. 122.
1902—C. Smith. Solution of the Problems and Theorems in Smith and
Bryant's Elements of Geometry. London.
Ex. 121, pp. 177-178; T. Simpson's solution and another.
1910—H. Flukiger. Die Flache7iteilung des Dreiecks mit Hilfe der Hyperbel.
Diss. Bern. 50 pp. + 3 plates.
1910—R. Zdenek. " Halbiernng der Dreiecksflache." Wien, Zeitschrift fur
das Realwesen, Jahrgang xxxv, Heft 10, 8 pp.
Discussion by projective geometry leading to hyperbolic arcs.
1911—D. Biddle. Problem 17197, Educational Times, London, November,
lxiv, 475.
" Divide a square into five right-angled triangles, the areas of which shall be in
arithmetic progression." Solutions in the Educational Times Reprint, new series,
xxvi, in, 1914.
INDEX OF NAMES
In the following list, references are given to paragraph and footnote (= n.)
numbers, except in the case of the Appendix (= App.) where the numbers
are the years in the chronological list. App., without a number, refers to
the introductory paragraphs on page 78.
Abraham bar Chijja ha Nasi or
Abraham Savasorda 18, n. 53
Abu Ishaq b. 'Abdallah 19
Abu Jusuf Ja'qub b. Ishaq b. el-Sabbah
el-Kindi, see el-Kindt
Abu'l Wefa 19, n. 78
Abu Muh. b. Abdalbaqi el Bagdad!
el-Faradi, see el-Bagdadi
Abu Muh. el-Hasan b. 'Obeidallah b.
Soleiman, see el-Hasan
Ainsworth, R. n. 28
Albategnius = Al-Battani = el-Battani,
see there
Al-Kindi = el-Kindi
Anderson, A. App. 1616
Antiphon n. 116
ApoUonius of Perga 19, 21, n. 103, n. in
Archimedes 19, n. 60a, n. 83, n. 101,
n. 103, n. 109, n. 111
Aristarchus of Samos n. in
Aristotle n. 116
Armagh, Archbishop of, see Ussher, J.
Arnold, I. App. 1864
Ashmole n. 22
Athelhard of Bath n. 15
Ayton, W. A. n. 14
Bachmann, P. App.
Benedetti, G. B. App. 1585
Bernoulli, J. App. 1645, App. 1687,
App. 1772 (?)
Biddle, D. App. 1864, App. 1911
Bleibtreu, L. App. 1819
Blythe, W. H. App. 1864
Bobillier, E. E. n. 117, App. 1827
Bocklern, G. A. App. 1667
Boncompagni, B. 10, 13, n. 40, n. 119,
App., App. 1560
Bossut, C. App. 1609
Bourdon, P. L. M. App. 1831
Bradley, T. App. 1864
Bramer, B. App. 1667
Bratt, A. App. 1807
Breton (de Champ), P. n. 88
Brodie, R. App. 1855
Bryant, S. App. 1902
Cainpanus, J. 2, 5, n. 11, n. 15
Candale, see Flussates
Cantor, M. 2, n. 8, n. 39, n. 53, n. 55,
n. 62, n. 63, n. 82, n. 103, n. 107, n. 120,
App. 1547, App. 1609
Cardan, G. App. 1547
Cardinael, S. App. 1612
Carlmark, J. P. App. 1807
Casley, D. 4, n. 20
Cassini, J. App. 1609
Catalan, E. App. 1852, App. 1857
Chasles, M. 19, n. 65, n. 85, n. 88,
n. in
Christiani, J. W. n. 67, App. 1793
Clairaut, A. C. App. 1609
Clavius, C. App. 1604
Clerc, S. le App. 1694, App. 1754
Comberousse, C. de App. 1687
Commandinus, F. 2, 5, 15, n. 10, n. 11,
n. 35, n. 49, n. 50, n. 88
Copernicus 19, n. 35, n. ill
Cossali, P. n. 119, App., App. 1560
Cotes, R. App. 1676
Cotton, R. B. 4, n. 21
Cottonian MSS. 2-5, n. 18, n. 19,
n. 20, n. 21
Cowley, A. 6
Cratfield, W. 4
Crawford, G. E. App. 1894
Crelle n. 117
Cresswell, D. n. no
Curtis, A. H. App. 1864
Curtius, S. App. 1612
Curtze, M. 18, n. 54, n. 55
D'Alembert, J. le R. App. 1754
Darboux, G. App. 1831
Davis, A. App. 1795
Dee, J. 2-6, 8, 9, 18, 19, n. 10, n. n,
n. 14, n. 24, n. 25, n. 29, n. 35
Deidier, rabbe" App. 1739
Deschales, C. F. M. App. 1674
Diderot, D. App. 1754
Diels, H. n. 116
Diesterweg, W. A. n. in
Dilworth, W. J. App. 1899
Dou, I. App. 1612
Dreser App. 1844
Edelston, J. App. 1676
el-Bagdadi* 2-6, 13-15, 19, n. 11,
* All the " Muhammeds" of Bagdad referred to in this volume are here supposed to be
indicated by this single name.
INDEX OF NAMES
87
n. 12, n. 15, n. 17, n. 21, n. 29, n. 33,
n. 35, App.
el-Battani 19, n. 35
el-Btizgani, .sw Abu'l Wefa
el-Hasan 19
el-Kindi 19, n. 35
Enestrom, G. n. 55, App. 1748
Euclid 1, 2, 5, 6, 7-13, 16-21, 34, 50,
57, «. 1, n. 3, ». 5, n. 6, «. 9, «. 11,
n. 15, «. 30, n. 34, «. 35, «. 36, n. 38,
«. 45, n. 47, «. 50, «. 56, n. 57, «. 81,
n. 83, «. 85, «. 87, n. 88, «. 91, n. 94,
«. 95, «. 98, it. 103, «. 105, n. 106,
«. 108, «. 109, n. in, «. 113, n. 116,
>2. 118 a, App., App. 1560, App. 1840,
App. 1864
Eudemus n. 116
Euler, J. A. App. 1768
Euler, L. App., App. 1748, App. 1840
Eutocius n. 111
Fabricius, J. A. 19, n. 68
Favaro, E. A. 2, 6, 10,13, 15 19, 29, n. 6,
n. 32, n. 42, n. 52, n. 73, u. 97, n. 100
Ferrari App. 1547
F. G. M. App. 1879
Fibonaci, see Pisano Leonardo
Fliikiger, H. App. 1910
Flussates or Foix, i.e. Francois de
Foix-Candalle n. 11
Fontenelle App. 1704
Forstner, A. K. P. von App. 1823
Frankland, W. B. n. 103
Friedlein, G. n. 1
Frisch, C. App. 1609
Gardiner, M. n. 111
Gamier, J. G. App. 1688
Gauss, C. F. n. 118
Gauss, F. G. App. 1864
Gerwien, P. App. 1831
Gherard of Cremona 4, 11, 19
Giordani, E. App. 1547
Grabow, M. G. n. 111
Gregory, D. 6, n. 11, App. 1609
Gregory, O. App. 1748, App. 1840
Griison, J. P. App. 1811
Grunert, J. A. 19, n. 72, App. 1870
Gudermann, C. n. 117
Guisnee App. 1704, App. 1754
Gutman, J. App. 1574
Hall, H. S. App. 1892
Halley, E. n. in
Halliwell, J. O. 4, n. 26
Hankel, H. 2, 19, n. 4, n. 71, n. in
Harleian MSS. 6, n. 21, n. 22, 11. 31
Hearding, J. H. App. 1752
Heath, T. L. 2, 3,6, n. 3, «. 15, n. 60a,
n. 81, n. 83, «. 87, 11. 88, «. 99, n. 101,
«. 103, «. 108, n. in, «. 112, n.
116
Heiberg, J. L. 2, 6-8, ». 5, «. 32, n. 36,
«. 60a, n. 83, «. in
Heilbronner, J. C. 6, 19, n. 33, n. 69
Heppel, G. App. 1864
Herigone, P. n. 111
Hermann, J. App. 1609
Heron of Alexandria 18, 20, 21, n. 81,
n. 82, «. 83, «. 84
Hippocrates n. 116
Hirsch, M. App. 1805
Holscher, H. App. 1864
Holleben, H. von App. 1831
Hooper, S. n. 20
Hultsch, F. 2, n. 9, n. 36, n. 85, n. 109
Hutton, C. App., App. 1840
Huygens, C. App., App. 1612, App.
1645, APP- l657> APP- l687
Ishaq b. Hunein b. Ishaq el-'Ibadi,
Abu Ja'qub 19
Jacobi, C. J. A. n. in
Jordanus Nemorarius 18, n. 58
Kastner, A. G. 2, 3, 19, n. 16, n. 19,
n. 67, App. 1609, App. 1793
Kayser, C. G. App. 1807
Kelland, P. App. 1855
Kepler, J. App., App. 1609
Klein, F. n. 103
Kliigel, G. S. n. 72, App. 1609
Kullberg, J. App. 1809, App. 1810
La Fre"moire, H. C. de App. 1852
Lagrange, J. L. App. 1609
Lambert, J. H. App. 1772(F)
Laplace, P. S. App. 1609
Larmor, A. App. 1901
Laurent, P. M. H. App. 1879
Leeke, J. n. n, n. 30, n. 35, n. 50
Leibnitz, G. W. App. 1687
Leonardo Pisano, see Pisano
Leslie, J. App. 1821
Leybourn, R. and W. n. 11
L'Hospital, G. F. de App. 1687
Lindman, C. F. App. 1870
Loria, G. 2, n. 7, App. 1687
Ludolph van Ceulen App. 1615
Luhmann, F. von n. 111
McDowell, J. App. 1863
Marinus n. 11
Matz, F. P. App. 1864
Mayer, J. T. App. 1783
Menge, H. n. 88
Mersenne, M. n. 111
Mitzscherling, A. App.
Mollweide, C. B. n. 72
88
INDEX OF NAMES
Montucla, J. F. 19, n. 70
Morville, N. n. 67, App. 1793
Muhammed Bagdedinus, see
el-Bagdadi
Muhammed b. 'Abdelbaqi el-Bagdadi
el-Fardi, see el-Bagdadi
Muhammed b. Gabir b. Sinan, Abu
'Abdallah el-Battani, see ei-Battani
Muhammed b. Muhammed el-Bagdadi,
see el-Bagdadi
Muhammed b. Muhammed el-Hasib
Abu'l Wef&, see Abu'l Wefa
Nemorarius, see Jordanus
Newton, I. App., App. 1676, App. 1747
Nixon, R. C. J. App. 1901
Ofterdinger, L. F. 9, 15, n. 32, n. 38,
n. 51, n- 105, n. in
Ozanam, J. App. 1688, App. 1699
Pacioli, see Paciuolo, L.
Paciuolo, L. 18, App.
Palmer, R. App. 1864
Pandya, N. P. App. 1772 (?)
Pappus of Alexandria 21, n. 85, n. 88,
n. in, n. 113
Paucker, G. 11. 111
Pauly-Wissovva it. 9, n. 81
Perrin, E. App. 1864
Pisano, Leonardo ro-13,17, 18, 19,22-38,
40-41, 47-57, "■ 40, «■ 41, «■ 45, «■ 46,
n. 47, n. 88, n. 96, «. 98, n. 100, «. 107,
«. 109, n. no, #. in, n. 113, App.
Planta, J. 4, n. 21
Plalo of Tivoli 18
Potts, R. App. 1847
Proclus Diadochus 1, 6, 7, 18, 49, n. 1,
«. 2, «. 35, «. 36, 11. 103, App. 1560
Ptolemy n. 111
Puissant, L. App. 1801
Quetelet, A. n. 117, App. 1827
Radhakrishnan App. 1864
Rebiere, A. App. 1857
Reinhold, E. App. 1574
Rhind Papyrus 20
Richter, A. n. in
Ritt, G. App. 1837
Robison, J. App. 1855
Rodham, J. App. 1795
Ross, J. A. App. 1805
Rouche, E. App. 1687
Rudd, T. App. 1612
Rudio, F. 11. 116
Rummer, F. App. 1852
Rutherford, W. App. 1864
Saunderson, N. App. 1740
Savile, H. 6, 11. 34
Schmid, W. App. 1539
Schoene, H. n. 82, n. 83
Schooten, F. van App. 1657
Schwenter, D. App. 1667
Sems, J. App. 1612
Serle, G. n. 11, n. 30, n. 50
Silberschlag, J. App. 1772 (?)
Simplicius n. 116
Simpson, T. App. 1609, App. 1747,
App. 1752, App. 1902
Simson, R. 39, n. 85, n. 88, n. 106,
n. 116, App. 1840
Smith, C. App. 1902
Smith, T. 2, 3, 5, 19, n. 14, n. 18,
n. 66
Snellius, W. n. in, App. 1615
Speidell, J. App. 1616
Stanham, W. C. App. 1864
Steiner, J. n. ny
Steinschneider, M. 2, 3, 4, 6, n. 12,
«■ 36, «• 53, »■ 64
Stevens, F. H. App. 1892
Strode, T. App. 1684
Suter, H. 3, 4, 19, n. 17, n. 36, n. 74,
n. 75, n. 76, n. yy
Swinden, G. H. van n. 111
Tabit b. Qorra 19
Tartaglia, N. App., App. 1547, App.
1560
Taylor, C. ». 103
Tittel, K. n. 81
Townsend, R. n. 117
Urbin, Duke of 2
Ussher, J. 2, 5, 11. 15
Vannson n. 111
Verhulst, P. F. App. 1827
Viani de' Malatesti, F. 11. 11
Vincent, A. J. C. n. 83
Wallis, J. App. 1609, App. 1684
Wenrich, J. G. 2, n. 13
Wiegand, A. n. in
Wissowa n. 9, n. 81
Wolfnng, E. App. 1807, App. 1844
Woepcke, F. 7-13, 18, 19, 57, n. 36,
n. 37, 72. 46, n. 48, «. 78, n. 79, «. 80,
«. 86, n. 101, «. 103, n. 104, «. 108,
«. 109, 11. in, 72. 112
Wright, J. M. F. App. 1805
Zdenek, R. App. 1910
Zeuthen, H. G. n. 103
Zimmerman, L. App. 1864
CAMBRIDGE: PRINTED BY JOHN CLAY, M.A. AT THE UNI VERSITY PRESS